Difference between revisions of "Search Page"
From mispar
| Line 1: | Line 1: | ||
{{#annotask: | {{#annotask: | ||
[[category: practical arithmetic]] | [[category: practical arithmetic]] | ||
| + | }} | ||
| + | |||
| + | {{#annotask: | ||
| + | [[category: Elements]] | ||
}} | }} | ||
Revision as of 13:38, 12 June 2018
| Category | Category | Category | Comment | Link | Annotated text |
|---|---|---|---|---|---|
| calculation/accurately | ד.ק.ד.ק./בדקדוק | term | אגרת_המספר#db7b | בדקדוק | |
| calculation/accurately | ד.ק.ד.ק./בדקדוק | term | עיר_סיחון#d2tL | בדקדוק | |
| addition/addend | ח.ב.ר./מחובר | term | ספר_דיני_ממונות#eqSv | המספרים המחוברים | |
| addition/addend | ק.ב.צ./נקבץ | term | ספר_המספר_/_אליהו_מזרחי#hzuu | הנקבצים | |
| addition/addend | י.ס.פ./מוסף | term | ספר_מעשה_חושב#QY1Z | המוסף | |
| addition/addend | ח.ב.ר./מחובר | term | אגרת_המספר#BCCl | מחובר | |
| addition/addend | י.ס.פ./נוסף | term | ספר_עיון_העקרים_לחשבון_ההנדיים#qRIy | המספר הנוסף | |
| addition/addend | ח.ב.ר./מחובר | term | ספר_ציפרא#daNJ | מחובר | |
| addition/addend | ק.ב.צ./נקבץ | term | מלאכת_המספר#NcT4 | נקבץ | |
| addition/addend | ח.ב.ר./מחובר | term | עיר_סיחון#hrzp | מחוברים | |
| addition/addend | ק.ב.צ./נקבץ | term | קצור_המספר#MDHK | הנקבצים | |
| addition/addend | ח.ב.ר./מחובר | term | עיר_סיחון#my36 | המספרים המחוברים | |
| addition/addend | ק.ב.צ./מקובץ | term | ספר_החשבון_לאל_חצאר#YlNp | המקובץ אליו | |
| addition/addend | ק.ב.צ./נקבץ | term | קצור_המספר#nc21 | המספרים הנקבצים | |
| addition/addend | י.ס.פ./נוסף | term | ספר_ג'יבלי_אלמוקבאלא#rt6p | המספר הנוסף | |
| addition/addend | י.ס.פ./מוסף | term | Anonymous#4xfy | המוספים | |
| basic operations/addition | ח.ב.ר./חבור | term | מלאכת_המספר#Efmr | חבור | |
| basic operations/addition | 4373+2389 | Takmila_fi_al-Hisāb_-_Arabic_in_Hebrew_Characters#R29K | Example: we wish to add 23[89 to 4373].
: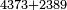 מתאלה ארדנא זיאדה אלפין ותלת מאיה ותלתה '''וסבעין'''
מתאלה ארדנא זיאדה אלפין ותלת מאיה ותלתה '''וסבעין''' | ||
| basic operations/addition | 3465+5643 | Takmila_fi_al-Hisāb_-_Arabic_in_Hebrew_Characters#CrX7 | Example: we wish to add 5643 to 3465.
: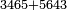 מתאלה ארדנא אן נזיד כמסה אלאף וסתמאיה ותלתה וארבעין עלי תלתה אלאף וארבעמאיה וכמסה וסתין
מתאלה ארדנא אן נזיד כמסה אלאף וסתמאיה ותלתה וארבעין עלי תלתה אלאף וארבעמאיה וכמסה וסתין | ||
| basic operations/addition | ח.ב.ר./חבור | term | Anonymous_text_from_Latin#cq4h | חבור | |
| basic operations/addition | ק.ב.צ./קבוץ | term | ספר_החשבון_לאל_חצאר#JPfd | קבוץ | |
| basic operations/addition | ק.ב.צ./קבוץ | term | עיר_סיחון#AtJO | קבוץ | |
| basic operations/addition | ח.ב.ר./מחברת | term | Anonymous#WXEA | מחברת זה עם זה | |
| basic operations/addition | ח.ב.ר./מחברת | term | Anonymous#cjIw | מחברת | |
| basic operations/addition | ח.ב.ר./חבור | term | Anonymous#fHVb | חבור | |
| basic operations/addition | ח.ב.ר./חבור | term | Anonymous#Tp2r | חבור | |
| basic operations/addition | ח.ב.ר./חבור | term | קצור_המספר#I3rL | חבור | |
| basic operations/addition | term | Arithmetic_Textbook_by_Meir_Shapira#hayQ | חבור | ||
| basic operations/addition | 205003+390005+625002 | בר_נותן_טעם#XaDs | You wish to sum up two hundred and five thousand and five with three hundred ninety thousand and five and with six hundred twenty five thousand and two.
: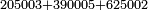 רצית לחבר מאתים וחמשת אלפים ושלשה עם שלש מאות ותשעים אלף וחמשה ועם שש מאות ועשרים וחמשת אלפים ושנים
רצית לחבר מאתים וחמשת אלפים ושלשה עם שלש מאות ותשעים אלף וחמשה ועם שש מאות ועשרים וחמשת אלפים ושנים | ||
| basic operations/addition | 1215+2322 | ספר_החשבון_והמדות#dkkp | We wish to sum one thousand two hundred and fifteen with two thousand three hundred and twenty-two.
: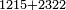 רצינו לקבץ אלף ומאתים וחמש עשרה ואלפים ושלש מאות ועשרים ושנים
רצינו לקבץ אלף ומאתים וחמש עשרה ואלפים ושלש מאות ועשרים ושנים | ||
| basic operations/addition | ח.ב.ר./חבור | term | עיר_סיחון#W34i | חבור | |
| basic operations/addition | ק.ב.צ./קבוץ | definition | קצור_המספר#7Hdc | The essential act of summing the separates is the first arithmetical [operations] called '''addition''' ואמנם [מפעל]P1005 om. הנפש בהחבר הנפרדים היה מין אחד מהמספר שנקרא הקיבוץ | |
| basic operations/addition | 223+342+422 | ספר_דיני_ממונות#1c0M | If a person says: sum three numbers, the first is 223, the second 342 and the third 422.
: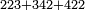 אם יאמר לך אדם קבץ לי שלשה מספרים אשר הא' הוא רכ"ג והשני שמ"ב והשלישי תכ"ב
אם יאמר לך אדם קבץ לי שלשה מספרים אשר הא' הוא רכ"ג והשני שמ"ב והשלישי תכ"ב | ||
| basic operations/addition | 1215+2322+9657+8563 | ספר_החשבון_והמדות#GVc4 | We draw another diagram, in which the ranks are summed up to tens, by adding two other lines beneath these two lines: one is nine thousand, six hundred, and fifty-seven; the other is eight thousand, five hundred, and sixty-three.
: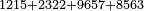 ונצייר עוד צורה אחרת המגעת במדרגותיה לכלל העשרות והיא שנחבר עוד תחת אלה השני טורים שני טורים אחרים האחד תשעת אלפי' ושש מאות וחמשים ושבעה והשנית שמנת אלפים וחמש מאות וששים ושלש
ונצייר עוד צורה אחרת המגעת במדרגותיה לכלל העשרות והיא שנחבר עוד תחת אלה השני טורים שני טורים אחרים האחד תשעת אלפי' ושש מאות וחמשים ושבעה והשנית שמנת אלפים וחמש מאות וששים ושלש | ||
| basic operations/addition | ח.ב.ר./חבור | term | עיר_סיחון#xIzg | חבור | |
| basic operations/addition | 203+402+809 | ספר_דיני_ממונות#LN0V | As if you say: sum 203 with 402 and with 809.
: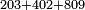 כאלו תאמר קבץ לי ר"ג עם ת"ב ועם תת"ט
כאלו תאמר קבץ לי ר"ג עם ת"ב ועם תת"ט | ||
| basic operations/addition | 200+240+403 | ספר_דיני_ממונות#Kmhn | If you wish to add up numbers: the first of which has zeros in the units and the tens and 2 in the hundreds; the second has a zero in the units, 4 in the tens and 2 in the hundreds; the third has 3 in the units, zero in the tens and 4 in the hundreds.
: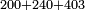 ואם תרצה לחבר שום מספר אשר בראשון יהיה ציפרא באחדים ובעשרות וב' במאיות ובמספר השני יהיה ציפרא באחדים ובעשרות ד' ובמאיות ב' ובמספר השני יהיה ג' באחדים וציפרא בעשרות וד' במאיות
ואם תרצה לחבר שום מספר אשר בראשון יהיה ציפרא באחדים ובעשרות וב' במאיות ובמספר השני יהיה ציפרא באחדים ובעשרות ד' ובמאיות ב' ובמספר השני יהיה ג' באחדים וציפרא בעשרות וד' במאיות | ||
| basic operations/addition | ח.ב.ר./מחברת | term | עיר_סיחון#ZM9D | מחברת | |
| basic operations/addition | WP | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#SgWd | Example: Reuven owes Yehuda 484 dinar and 389 more.
: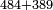 המשל ראובן חייב ליהודה תפ"ד די' ועוד שפ"ט
המשל ראובן חייב ליהודה תפ"ד די' ועוד שפ"ט | ||
| basic operations/addition | 4204+212+12+30 | ספר_דיני_ממונות#06Fy | If you wish to add up four numbers: the first of which has 4 thousands, 2 hundreds and 4; the second has 2 hundreds and 12; the third has 12; and the fourth has 30.
: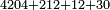 ואם תרצה לחבר ד' מספרים אשר בראשון יש בו ד' אלפים וב' מאות וד' ובשני יש ב' מאות וי"ב ובשלישי יש י"ב וברביעי ל'
ואם תרצה לחבר ד' מספרים אשר בראשון יש בו ד' אלפים וב' מאות וד' ובשני יש ב' מאות וי"ב ובשלישי יש י"ב וברביעי ל' | ||
| basic operations/addition | WP | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#hI3B | Example: Reuven, Shimon and Levy borrowed money from Yehuda: Reuven borrowed two thousand and eighty dinar; Shimon [borrowed] three thousand and sixty; and Levy [borrowed] four thousand and sixty.
:We wish to know the total amount [they borrowed].
המשל בזה ראובן שמעון לוי השאילו ממון מיהודה הנה ראובן שאל ב' אלפים ושמונים די' ושמעון ג' אלפים ושישים ולוי ד' אלפים ושישים ורצינו לדעת סך כולם | ||
| basic operations/addition | WP | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#gJmS | Another example: we sum 248 kors of wheat with 773; the result is one thousand and 21 kors of wheat.
: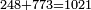 משל אחר חיברנו רמ"ח כורי חיטה עם תשע"ג יעלו אלף וכ"א כורי חיטה
משל אחר חיברנו רמ"ח כורי חיטה עם תשע"ג יעלו אלף וכ"א כורי חיטה | ||
| basic operations/addition | ק.ב.צ./קבוץ | term | ספר_החשבון_והמדות#wpkG | קבוץ | |
| basic operations/addition | ק.ב.צ./קבוץ | term | מלאכת_המספר#Ka8Q | קבוץ | |
| basic operations/addition | 9208+3801 | עיר_סיחון#Hq9T | We wish to know how much is the sum of nine thousand, two hundred and eight, with three thousand, eight hundred and one.
: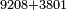 בקשנו לידע כמה מחובר תשע אלפים ומאתים ושמונה עם שלשת אלפים ושמונה מאות ואחד
בקשנו לידע כמה מחובר תשע אלפים ומאתים ושמונה עם שלשת אלפים ושמונה מאות ואחד | ||
| basic operations/addition | 335+453 | אגרת_המספר#1UCT | Example: three hundred and thirty-five with four hundred and fifty-three.
: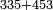 והמשל שלש מאות ושלשים וחמשה עם ארבע מאות וחמשים ושלשה
והמשל שלש מאות ושלשים וחמשה עם ארבע מאות וחמשים ושלשה | ||
| basic operations/addition | ח.ב.ר./חבור | term | אגרת_המספר#NImF | חבור | |
| basic operations/addition | ק.ב.צ./קבוץ | term | ספר_המספר_/_אליהו_מזרחי#V5Jg | קבוץ | |
| basic operations/addition | י.ס.פ./תוספת | term | עיר_סיחון#83ML | תוספת | |
| basic operations/addition | 5243+8962 | מלאכת_המספר#xuJe | As can be seen in this diagram:
: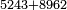 כפי הנראה {{#annot:term|1631,1510|URI5}}בצורה הזאת{{#annotend:URI5}}
כפי הנראה {{#annot:term|1631,1510|URI5}}בצורה הזאת{{#annotend:URI5}} | ||
| basic operations/addition | 875+798 | ספר_החשבון_לאל_חצאר#kEdB | Example: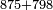 והדמיון קבוץוהדמיון קבוץ: MS V ודמיון זה קבץ חמשה ושבעים ושמונה מאות אל שמנה ותשעים ושבע מאות
והדמיון קבוץוהדמיון קבוץ: MS V ודמיון זה קבץ חמשה ושבעים ושמונה מאות אל שמנה ותשעים ושבע מאות | ||
| basic operations/addition | 432+354 | ספר_החשבון_לאל_חצאר#dic6 | Example: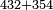 דמיון זה קבץ שנים ושלשים וארבעהוארבעה: MS V וארבע מאות אל ארבעה וחמשים ושלש מאות
דמיון זה קבץ שנים ושלשים וארבעהוארבעה: MS V וארבע מאות אל ארבעה וחמשים ושלש מאות | ||
| basic operations/addition | term | ספר_ג'יבלי_אלמוקבאלא#Jt7q | דיציאוני | ||
| basic operations/addition | 432+245+321 | ספר_החשבון_לאל_חצאר#Bugy | Example: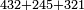 דמיון זה קבץ שנים ושלשים וארבע מאות אל חמשה וארבעים ומאתים אל אחד ועשרים ושלש מאות
דמיון זה קבץ שנים ושלשים וארבע מאות אל חמשה וארבעים ומאתים אל אחד ועשרים ושלש מאות | ||
| basic operations/addition | 6503+7020 | ספר_החשבון_לאל_חצאר#d7iF | Example: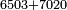 כמו שתקבץ שלשה וחמש מאות וששת אלפים
כמו שתקבץ שלשה וחמש מאות וששת אלפים | ||
| basic operations/addition | 699+7156+867 | ספר_החשבון_לאל_חצאר#t50Z | Example: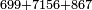 ואם יאמר לך קבץ תשעה ותשעים ושש מאות אל ששה וחמשים ומאה ושבעת אלפים אל שבעה וששים ושמנה מאות
ואם יאמר לך קבץ תשעה ותשעים ושש מאות אל ששה וחמשים ומאה ושבעת אלפים אל שבעה וששים ושמנה מאות | ||
| basic operations/addition | ח.ב.ר./חבור | term | תחבולות_המספר#LMS9 | חבור | |
| basic operations/addition | ח.ב.ר./חבור | term | ספר_דיני_ממונות#PQOr | חבור | |
| basic operations/addition | ח.ב.ר./חבור | term | ספר_אגריס#JhNc | חיבור | |
| basic operations/addition | ח.ב.ר./מחברת | term | עיר_סיחון#gszd | מחברת | |
| basic operations/addition | 1+999 | ספר_החשבון_לאל_חצאר#LV4P | Example: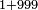 ואם יאמריאמר: MS O אמר לךלך: MS O om. קבץ אחד אל תשעה ותשעים ותשע מאות
ואם יאמריאמר: MS O אמר לךלך: MS O om. קבץ אחד אל תשעה ותשעים ותשע מאות | ||
| basic operations/addition | ק.ב.צ./קבוץ | term | מלאכת_המספר#ThwY | קבוץ | |
| basic operations/addition | ח.ב.ר./חבור | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#FlfS | חיבור | |
| basic operations/addition | 3372+3392 | ספר_ציפרא#5lLo | If you wish to sum three thousand three hundred and seventy-two with three thousand three hundred ninety-two.
: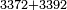 אם תרצה לחבר שנים ושבעים וג' מאות וג' אלפים עם שנים ותשעים וג' מאות וג' אלפי'
אם תרצה לחבר שנים ושבעים וג' מאות וג' אלפים עם שנים ותשעים וג' מאות וג' אלפי' | ||
| basic operations/addition | 3372+9892 | ספר_ציפרא#ZOaG | Example: we want to sum 3372 with 9892.
: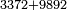 דומיון בקשנו לחבר ע"ב וג' מאות וג' אלפי' עם צ"ב וח' מאות וט' אלפים
דומיון בקשנו לחבר ע"ב וג' מאות וג' אלפי' עם צ"ב וח' מאות וט' אלפים | ||
| basic operations/addition | 209+3089+7639 | ספר_מעשה_חושב#Ai3K | Example: We wish to sum 209 with 3089 and with 7639.
: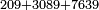 דמיון נרצה לחבר מאתים ותשע עם שלשת אלפים ושמנים ותשע ועם ז' אלפים ושש מאות ושלשים ותשע
דמיון נרצה לחבר מאתים ותשע עם שלשת אלפים ושמנים ותשע ועם ז' אלפים ושש מאות ושלשים ותשע | ||
| basic operations/addition | 56ⁱⁱ+(20ⁱ+40ⁱⁱ+30ⁱⁱⁱ)+(46ⁱ+27ⁱⁱ+55ⁱⁱⁱ) | ספר_מעשה_חושב#hd8e | Example: if you want to sum 56 seconds with 20 primes, 40 seconds, and 30 thirds, and with 46 primes, 27 seconds, and 55 thirds.
: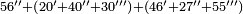 דמיון נרצה לחבר נ"ו שנים ול' שלישים עם כ' ראשונים ומ' שניים ול' שלישיים ועם מ"ו ראשונים כ"ז שניים כ"ה שלישיים
דמיון נרצה לחבר נ"ו שנים ול' שלישים עם כ' ראשונים ומ' שניים ול' שלישיים ועם מ"ו ראשונים כ"ז שניים כ"ה שלישיים | ||
| basic operations/addition | 44+55 | ספר_אגריס#HyDz | Example: you wish to add 44 to 55.
: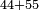 דומיון רצונך לחבר ד' וארבעים לה' וחמשים
דומיון רצונך לחבר ד' וארבעים לה' וחמשים | ||
| basic operations/addition | 99+11 | ספר_אגריס#my7M | Another example:
: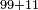 דומיון אחר
דומיון אחר | ||
| basic operations/addition | 142+968 | ספר_אגריס#EWxV | Another example:
: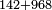 דומיון אחר
דומיון אחר | ||
| basic operations/addition | 1101+3931+9755+57052+28067 | ספר_המספר_/_אליהו_מזרחי#Xque | Example: we wish to sum 1101, 3931, 9755, 57052 and 28067.
: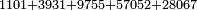 המשל בזה רצינו לקבץ אלף ומאה ואחד וג' אלפים תשע מאות ל"א וט' אלפים תשנ"ה ונ"ז אלפים ונ"ב וכ"ח אלפי' וס"ז
המשל בזה רצינו לקבץ אלף ומאה ואחד וג' אלפים תשע מאות ל"א וט' אלפים תשנ"ה ונ"ז אלפים ונ"ב וכ"ח אלפי' וס"ז | ||
| basic operations/addition | 723+865+957 | ספר_המספר_/_אליהו_מזרחי#AhVn | Example: we wish to sum 723, 865 and 957.
: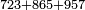 המשל בזה אם רצינו לקבץ תשכ"ג ותתס"ה ותתקנ"ז
המשל בזה אם רצינו לקבץ תשכ"ג ותתס"ה ותתקנ"ז | ||
| basic operations/addition | ח.ב.ר./חבור | term | ספר_ג'יבלי_אלמוקבאלא#ZO9e | חבור | |
| basic operations/addition | ח.ב.ר./חבור | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#hnw4 | חבור | |
| basic operations/addition | א.ס.פ./אסיפה | term | ספר_הכללים_במספר#Jbg2 | אסיפת | |
| basic operations/addition | ק.ב.צ./קבוץ | definition | ספר_המספר_/_אליהו_מזרחי#kGrD | I say that the addition is restoring many numbers, whatever given numbers they may be, whether equal or different, into one number. ואומר שהקבוץ הוא השבת מספרים רבים איזה מספרים מונחים שיהיו שוים או מתחלפים למספר אחד | |
| basic operations/addition | ח.ב.ר./חבור | definition | אגרת_המספר#rzsJ | addition is summing numbers one to another, so they are expressed in one expression. אמר החבור הוא קבוץ מספרי' קצתם לקצת אל שידובר בהם בדבור אחד | |
| basic operations/addition | ק.ב.צ./קבוץ | term | מלאכת_המספר#FS0Q | קבוץ | |
| basic operations/addition | ח.ב.ר./חבור | term | ספר_ציפרא#yGi5 | חיבור | |
| basic operations/addition | ק.ב.צ./קבוץ | definition | מלאכת_המספר#qlUB | Addition is summing two numbers or more to one inclusive number. קבוץ הוא חבור שני מספרים או יותר במספר אחד כולל לכולם | |
| basic operations/addition | י.ס.פ./הוספה | term | בר_נותן_טעם#b7h5 | הוספת ה | |
| basic operations/addition | ח.ב.ר./חבור | term | ספר_מעשה_חושב#sAIn | חבור | |
| basic operations/addition | י.ס.פ./תוספת | term | תחבולות_המספר#BWZo | תוספת | |
| basic operations/addition | ח.ב.ר./חבור | term | תחבולות_המספר#b105 | חבורם | |
| basic operations/addition | ק.ב.צ./קבוץ | term | קצור_המספר#1bs0 | קבוץ | |
| basic operations/addition | ק.ב.צ./קבוץ | term | קצור_המספר#bGdx | קיבוץ | |
| basic operations/addition | ח.ב.ר./חבור | term | בר_נותן_טעם#BNXU | חיבור | |
| basic operations/addition | י.ס.פ./הוספה | term | האריתמטיקה_של_ניקומכוס#Mdou | הוספת | |
| basic operations/addition | י.ס.פ./הוספה | term | האריתמטיקה_של_ניקומכוס#SHEd | הוספת | |
| basic operations/addition | ק.ב.צ./קבוץ | term | אגרת_המספר#XmwZ | קבוץ | |
| basic operations/addition | ח.ב.ר./חבור | term | ספר_ג'יבלי_אלמוקבאלא#4FgY | חבורי' | |
| basic operations/addition | י.ס.פ./תוספת | term | ספר_האלזיברא#srDw | תוספת | |
| basic operations/addition | ח.ב.ר./חבור | term | ספר_ג'יבלי_אלמוקבאלא#6RzR | חבורו עם ה | |
| basic operations/addition | ח.ב.ר./חבור | definition | Anonymous_text_from_Latin#zq5n | The addition indicates how much are separate numbers summed to one number. חבור הוא המורה כמה מספרי' פרטיי' להביא ולכולל למספר אחד | |
| basic operations/addition | ח.ב.ר./חבור | term | חשבון_השטחים#UARr | חבור | |
| basic operations/addition | י.ס.פ./תוספת | term | חשבון_השטחים#bk9p | תוספת | |
| basic operations/addition | term | ספר_ציפרא#89Mu | אדירין | ||
| basic operations/addition | י.ס.פ./תוספת | term | ספר_עיון_העקרים_לחשבון_ההנדיים#7kwN | תוספת | |
| basic operations/addition | 1098+9067 | קצור_המספר#ixn8 | Example: we wish to sum up one thousand ninety-nine with nine thousand sixty-seven.
: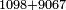 ויהיה המשל בזה רצינו לקבץ אלף ותשעים ושמונה עם תשע אלפים ושישים ושבעה
ויהיה המשל בזה רצינו לקבץ אלף ותשעים ושמונה עם תשע אלפים ושישים ושבעה | ||
| simple fraction/addition of fractions | (¾+⅘)+(⅚+⁶/₇) | Al-HAṢṢĀR_-_Arabic_in_Hebrew_Characters#FBQz | When you are told: add three-quarters and four-fifths to five-sixths and six-sevenths.
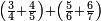 אדא קיל לך אגמע תלאתת ארבאע וארבעת אכמאס אלי כמסת אסדאס וסתת אסבאע
אדא קיל לך אגמע תלאתת ארבאע וארבעת אכמאס אלי כמסת אסדאס וסתת אסבאע | ||
| simple fraction/addition of fractions | (2+½)+(3+⅖) | ספר_החשבון_לאל_חצאר#wr3v | When you are told: add two and a half to three and two-fifths.
: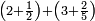 כשיאמ' לך קבץ שנים וחצי אל שלשה ושני חומשים
כשיאמ' לך קבץ שנים וחצי אל שלשה ושני חומשים | ||
| simple fraction/addition of fractions | (¾·5½)+(⅚·6⅓) | ספר_החשבון_לאל_חצאר#S0T2 | When you are told: add three-quarters of five and a half to five-sixths of six and a third.
:![\scriptstyle\left[\frac{3}{4}\sdot\left(5+\frac{1}{2}\right)\right]+\left[\frac{5}{6}\sdot\left(6+\frac{1}{3}\right)\right]](/mediawiki/images/math/3/8/c/38c6011f1c3aa05525cc220db0b08a58.png) כשיאמר לך קבץ שלשה רביעי חמשה וחצי אל חמשה שתותי ששה ושליש
כשיאמר לך קבץ שלשה רביעי חמשה וחצי אל חמשה שתותי ששה ושליש | ||
| simple fraction/addition of fractions | (⅚+½·⅙)+(⁷/₈+⁸/₉) | Al-HAṢṢĀR_-_Arabic_in_Hebrew_Characters#kF6m | When you are told: add five-sixths and half a sixth to seven-eighths and eight-ninths.
:![\scriptstyle\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]+\left(\frac{7}{8}+\frac{8}{9}\right)](/mediawiki/images/math/4/c/4/4c4b65fa69c305cfcc4cb5e5a2e49e9e.png) אדא קיל לך אגמע כמסת אסדאס ונצף סדס אלי סבעת אתמאן ותמאנית אתסאע
אדא קיל לך אגמע כמסת אסדאס ונצף סדס אלי סבעת אתמאן ותמאנית אתסאע | ||
| simple fraction/addition of fractions | (2+½)+(3+⅖) | Al-HAṢṢĀR_-_Arabic_in_Hebrew_Characters#tX9U | When you are told: add two and a half to three and two-fifths.
: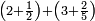 אדא קיל לך אגמע אתנין ונצף אלי תלאתה וכמסין
אדא קיל לך אגמע אתנין ונצף אלי תלאתה וכמסין | ||
| simple fraction/addition of fractions | ⅓+½ | ספר_דיני_ממונות#HbM4 | 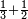 דמיון זה נרצה לחבר שליש אחד עם חצי אחד
דמיון זה נרצה לחבר שליש אחד עם חצי אחד | ||
| simple fraction/addition of fractions | (¾+⅘)+(⅚+⁶/₇) | ספר_החשבון_לאל_חצאר#ig9f | When you are told: add three-quarters and four-fifths to five-sixths and six-sevenths.
: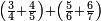 כשיאמ' לך קבץ שלשה רביעים וארבעה חומשים אל חמשה שתותים והשש שביעיות
כשיאמ' לך קבץ שלשה רביעים וארבעה חומשים אל חמשה שתותים והשש שביעיות | ||
| simple fraction/addition of fractions | ⅔+⅘+⅚+(¾·⅙) | ספר_מעשה_חושב#PAjd | Example: if we wish to sum 2 thirds with 4 fifths and with 5 sixths and with 3 quarters of a sixth.
::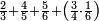 דמיון זה אם רצינו לחבר ב' שלישיות עם ד' חמשיות ועם ה' ששיות ועם ג' רביעיות ששית
דמיון זה אם רצינו לחבר ב' שלישיות עם ד' חמשיות ועם ה' ששיות ועם ג' רביעיות ששית | ||
| simple fraction/addition of fractions | ⅔+¾ | קצור_המספר#dzyZ | We give an example: we wish to sum two thirds with 3 quarters.
: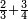 ונשים משל לזה רצינו לקבץ ב' שלישיות בג' רביעיות
ונשים משל לזה רצינו לקבץ ב' שלישיות בג' רביעיות | ||
| simple fraction/addition of fractions | ⅜+⁷/₁₀ | ספר_יסודי_התבונה_ומגדל_האמונה#IYtH | As the one who says: add 3 eighths to 7 tenths
: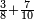 כגון האומר הוסף ג' שמיניות על ז' עשיריות
כגון האומר הוסף ג' שמיניות על ז' עשיריות | ||
| simple fraction/addition of fractions | ³/₉+¼ | Kaufmann_A_519_-_Collection_of_Word_Problems#fyjX | How much is  and and  ?
|22Quanto sono ?
|22Quanto sono  et et  | ||
| simple fraction/addition of fractions | ³/₇+⁴/₉ | Kaufmann_A_519_-_Collection_of_Word_Problems#VqIh | How much is 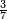 and and  ?
|24Quanto sono ?
|24Quanto sono 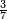 et et  | ||
| simple fraction/addition of fractions | (8+⅚+½·⅙)+(6+⁵/₇+¹⁰/₁₁) | ספר_החשבון_לאל_חצאר#4RTQ | When you are told: add eight, five-sixths and half a sixth to six, five-sevenths and ten parts of eleven.
:![\scriptstyle\left[8+\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]+\left(6+\frac{5}{7}+\frac{10}{11}\right)](/mediawiki/images/math/5/5/2/5526b3773d4250a1b558ca73bb605f6c.png) כשיאמר לך קבץ שמונה וחמשה שתותים וחצי שתות אל ששה וחמשה שביעיות ועשרה חלקים מאחד עשר
כשיאמר לך קבץ שמונה וחמשה שתותים וחצי שתות אל ששה וחמשה שביעיות ועשרה חלקים מאחד עשר | ||
| simple fraction/addition of fractions | ⅖+⅔ | Kaufmann_A_519_-_Collection_of_Word_Problems#JvIj | How much is  and and 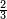 ?
|26Quanto sono ?
|26Quanto sono  et et 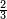 | ||
| simple fraction/addition of fractions | ¾+⅘ | ספר_החשבון_לאל_חצאר#uU8q | When you are told: add three-quarters to four-fifths.
: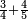 כשיאמר לך קבץ שלשה רביעים אל ארבעה חומשים
כשיאמר לך קבץ שלשה רביעים אל ארבעה חומשים | ||
| simple fraction/addition of fractions | ⅔+²/₆ | Kaufmann_A_519_-_Collection_of_Word_Problems#T0eI | How much is 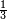 and and  ?
|28Quanto sono ?
|28Quanto sono 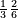 | ||
| simple fraction/addition of fractions | (⁵/₁₁+¾·¹/₁₁)+(¹⁰/₁₃+⁸/₉·¹/₁₃) | Al-HAṢṢĀR_-_Arabic_in_Hebrew_Characters#YivK | When you are told: add five parts of eleven and three-quarters of one parts of eleven to ten parts of thirteen and eight-ninths of one parts of thirteen.
:![\scriptstyle\left[\frac{5}{11}+\left(\frac{3}{4}\sdot\frac{1}{11}\right)\right]+\left[\frac{10}{13}+\left(\frac{8}{9}\sdot\frac{1}{13}\right)\right]](/mediawiki/images/math/1/1/1/111cfe95df77cdc573d3d8c3a15e0491.png) אדא קיל לך אגמע כמסת אגזא מן אחדי עשר ותלאתת ארבאע אלגז מן אחדי עשר אלי עשרת אגזא מן תלת עשר ותמאנית אתסאע אלגז מן תלת עשר
אדא קיל לך אגמע כמסת אגזא מן אחדי עשר ותלאתת ארבאע אלגז מן אחדי עשר אלי עשרת אגזא מן תלת עשר ותמאנית אתסאע אלגז מן תלת עשר | ||
| simple fraction/addition of fractions | ⅓+¼ | ספר_דיני_ממונות#8So2 | 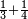 דמיון אחר נרצה לחבר שלישית אחד ורביעית אחד
דמיון אחר נרצה לחבר שלישית אחד ורביעית אחד | ||
| simple fraction/addition of fractions | ¼+²/₈ | Kaufmann_A_519_-_Collection_of_Word_Problems#OE3r | How much is  and and  ?
|30Quanto sono ?
|30Quanto sono  et et  | ||
| simple fraction/addition of fractions | (3+½)+⅖ | ספר_דיני_ממונות#nfiA | 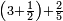 דמיון זה נרצה לחבר ג' וחצי עם ב' חמישיות
דמיון זה נרצה לחבר ג' וחצי עם ב' חמישיות | ||
| simple fraction/addition of fractions | (⅔·7)+(⁷/₈·9) | ספר_החשבון_לאל_חצאר#mtkR | When you are told: add two-thirds of seven to seven-eighths of nine.
: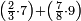 כשיאמר לך קבץ שני שלישי שבעה אל שבע שמיניות תשעה
כשיאמר לך קבץ שני שלישי שבעה אל שבע שמיניות תשעה | ||
| simple fraction/addition of fractions | ½+⅓+¼ | מלאכת_המספר#M63c | As the one who wants to add or to know the sum of a half, a third, and a quarter.
: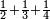 כמו שרוצה לחבר או לדעת [קבוץ]marg. חצי ושליש ורביע
כמו שרוצה לחבר או לדעת [קבוץ]marg. חצי ושליש ורביע | ||
| simple fraction/addition of fractions | ⅔+¾+⅘+⅚ | מלאכת_המספר#oskZ | Suppose we wish to sum up 2-thirds, 3-quarters, 4-fifths, and 5-sixths.
: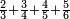 ונניח שנרצה לקבץ ב' שלישיות וג' רביעיות וד' חמישיות וה' ששיות
ונניח שנרצה לקבץ ב' שלישיות וג' רביעיות וד' חמישיות וה' ששיות | ||
| simple fraction/addition of fractions | (2+½)+(3+¼) | ספר_דיני_ממונות#maWV | 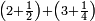 דמיון זה נרצה לחבר ב' וחצי עם ג' ורביע
דמיון זה נרצה לחבר ב' וחצי עם ג' ורביע | ||
| simple fraction/addition of fractions | ⅜+⁷/₁₀ | ספר_חשבון#tIym | If one says: add 3-eighths to 7-tenths, how much are they?
: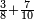 ואם יאמר הוסף ג' שמיניות על ז' עשיריות כמה יהיו
ואם יאמר הוסף ג' שמיניות על ז' עשיריות כמה יהיו | ||
| simple fraction/addition of fractions | (2+⅜+²/₄·⅛)+⅘+(⁶/₇+⅜·⅐) | בר_נותן_טעם#O6E2 | For instance, if in the example for the expansion to a common denominator that we have presented at the beginning of the third chapter, you are asked to sum up them and say how much they are:
:![\scriptstyle\left[2+\frac{3}{8}+\left(\frac{2}{4}\sdot\frac{1}{8}\right)\right]+\frac{4}{5}+\left[\frac{6}{7}+\left(\frac{3}{8}\sdot\frac{1}{7}\right)\right]](/mediawiki/images/math/1/0/f/10fe63879aceb251d84882daff3b8503.png) כי ע'ד'מ' אם במשלנו אשר עשינו בהשואה בתחלת השער הג' שאלו לך שתחברם ותאמ' כמה הם
כי ע'ד'מ' אם במשלנו אשר עשינו בהשואה בתחלת השער הג' שאלו לך שתחברם ותאמ' כמה הם | ||
| simple fraction/addition of fractions | (¾·5)+6 | ספר_החשבון_לאל_חצאר#61Wa | When you are told: add three-quarters of five [to six].
: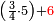 כשיאמר לך קבץ שלשה רביעי חמשה אל דומה לו
כשיאמר לך קבץ שלשה רביעי חמשה אל דומה לו | ||
| simple fraction/addition of fractions | ¾+⅘+⅚ | ספר_דיני_ממונות#InZ8 | 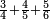 דמיון זה נרצה לחבר ג' רביעיות וד' חמישיות וה' שישיות
דמיון זה נרצה לחבר ג' רביעיות וד' חמישיות וה' שישיות | ||
| simple fraction/addition of fractions | ½+⅓+¼ | ספר_דיני_ממונות#StZc | 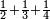 דמיון נרצה לחבר חצי עם שליש ועם רביעית
דמיון נרצה לחבר חצי עם שליש ועם רביעית | ||
| simple fraction/addition of fractions | ⅓+¼+⅕+⅙+⅐ | ספר_הכללים_במספר#753y | 2) How much are a third, a quarter, a fifth, a sixth, and a seventh of one pašuṭ?
: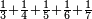 ב אם ישאלך אדם כמה הוא שליש פשוט ורביע וחומש ושתות ושביעית
ב אם ישאלך אדם כמה הוא שליש פשוט ורביע וחומש ושתות ושביעית | ||
| simple fraction/addition of fractions | ¾+⅘ | Al-HAṢṢĀR_-_Arabic_in_Hebrew_Characters#6MOy | When you are told: add three-quarters to four-fifths.
: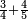 אדא קיל לך אגמע תלאתת ארבאע אלי ארבעת אכמאס
אדא קיל לך אגמע תלאתת ארבאע אלי ארבעת אכמאס | ||
| simple fraction/addition of fractions | (¾·5½)+(⅚·6⅓) | Al-HAṢṢĀR_-_Arabic_in_Hebrew_Characters#LMik | When you are told: add three-quarters of five and a half to five-sixths of six and a third.
:![\scriptstyle\left[\frac{3}{4}\sdot\left(5+\frac{1}{2}\right)\right]+\left[\frac{5}{6}\sdot\left(6+\frac{1}{3}\right)\right]](/mediawiki/images/math/3/8/c/38c6011f1c3aa05525cc220db0b08a58.png) אגמע תלאתת ארבאע כמסה ונצף אלי כמסת אסדאס סתה ותלת
אגמע תלאתת ארבאע כמסה ונצף אלי כמסת אסדאס סתה ותלת | ||
| simple fraction/addition of fractions | (8+⅚+½·⅙)+(6+⁵/₇+¹⁰/₁₁) | Al-HAṢṢĀR_-_Arabic_in_Hebrew_Characters#N6Q0 | When you are told: add eight, five-sixths and half a sixth to six, five-sevenths and ten parts of eleven.
:![\scriptstyle\left[8+\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]+\left(6+\frac{5}{7}+\frac{10}{11}\right)](/mediawiki/images/math/5/5/2/5526b3773d4250a1b558ca73bb605f6c.png) אדא קיל לך אגמע תמאניה וכמסה אסדאס ונצף סדס אלי סתה וכמסת אסבאע ועשר[ה] אגזא מן אחדי עשר
אדא קיל לך אגמע תמאניה וכמסה אסדאס ונצף סדס אלי סתה וכמסת אסבאע ועשר[ה] אגזא מן אחדי עשר | ||
| simple fraction/addition of fractions | ⅓+¼+⅕+⅙ | ספר_חשבון#pvs7 | Whoever has a third, a quarter, a fifth, and a sixth of the thing.
: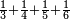 וכן מי שיש לו שליש ורביע וחומש ושתות מן הדבר
וכן מי שיש לו שליש ורביע וחומש ושתות מן הדבר | ||
| simple fraction/addition of fractions | (¾·5)+6 | Al-HAṢṢĀR_-_Arabic_in_Hebrew_Characters#Sozl | When you are told: add three-quarters of five to six.
: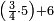 אגמע תלאתת ארבאע כמסה אלי סתה
אגמע תלאתת ארבאע כמסה אלי סתה | ||
| simple fraction/addition of fractions | ⁵/₉+(⅘·⅐) | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#M4kF | Example: we wish to sum 5-ninths with 4-fifths of a seventh
: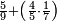 וזה כמו שרצינו לחבר ה' תשיעיות עם ד' חמשיות שביעית
וזה כמו שרצינו לחבר ה' תשיעיות עם ד' חמשיות שביעית | ||
| simple fraction/addition of fractions | ⅓+⅐ | ספר_חשבון#c6OW | Whoever has a third and a seventh of the thing.
: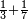 וכן מי שיש לו שליש ושביע מן הדבר
וכן מי שיש לו שליש ושביע מן הדבר | ||
| simple fraction/addition of fractions | ¼+⅕ | ספר_חשבון#nQTO | Whoever has a quarter and a fifth of the thing.
: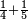 וכן מי שיש לו הרביע והחומש מן הדבר
וכן מי שיש לו הרביע והחומש מן הדבר | ||
| simple fraction/addition of fractions | (⅔·7)+(⁷/₈·9) | Al-HAṢṢĀR_-_Arabic_in_Hebrew_Characters#T4oj | When you are told: add two-thirds of seven to seven-eighths of nine.
: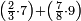 אגמע תלתיי סבעה אלי סבעת אתמאן תסעה
אגמע תלתיי סבעה אלי סבעת אתמאן תסעה | ||
| simple fraction/addition of fractions | ⅓+⅕ | ספר_חשבון#Asm1 | Whoever has a third and a fifth of the thing.
: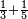 וכן מי שיש לו השליש והחומש מן הדבר
וכן מי שיש לו השליש והחומש מן הדבר | ||
| simple fraction/addition of fractions | ¾+⅚ | עיר_סיחון#Sh9x | As we say for example: we sum three quarters with five sixths. How much is the result?
: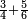 כאשר נאמר על דרך משל חברנו שלש רביעיות עם חמש ששיות
כאשר נאמר על דרך משל חברנו שלש רביעיות עם חמש ששיותכמה העולה | ||
| simple fraction/addition of fractions | ⅗+⁴/₇ | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#l8qf | Example: we wish to sum 3-fifths with 4-sevenths
: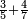 המשל בזה רצינו לחבר ג' חמשיות עם ד' שביעיות
המשל בזה רצינו לחבר ג' חמשיות עם ד' שביעיות | ||
| simple fraction/addition of fractions | ³/₇+⅔ | בר_נותן_טעם#Gi6C | Example: if it is said: add 3-sevenths to 2-thirds.
: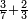 המשל אם אמרו חבר ג' שביעיות עם ב' שלישיות
המשל אם אמרו חבר ג' שביעיות עם ב' שלישיות | ||
| simple fraction/addition of fractions | (⁵/₁₁+¾·¹/₁₁)+(¹⁰/₁₃+⁸/₉·¹/₁₃) | ספר_החשבון_לאל_חצאר#GENu | When you are told: add five parts of eleven and three-quarters of one parts of eleven to ten parts of thirteen and eight-ninths of one parts of thirteen.
:![\scriptstyle\left[\frac{5}{11}+\left(\frac{3}{4}\sdot\frac{1}{11}\right)\right]+\left[\frac{10}{13}+\left(\frac{8}{9}\sdot\frac{1}{13}\right)\right]](/mediawiki/images/math/1/1/1/111cfe95df77cdc573d3d8c3a15e0491.png) כשיאמר לך קבץ חמשה חלקים מאחד עשר ושלשה רביעי החלק מאחד עשר על עשרה חלקים משלשה עשר ושמונה תשיעיות החלק משלשה עשר
כשיאמר לך קבץ חמשה חלקים מאחד עשר ושלשה רביעי החלק מאחד עשר על עשרה חלקים משלשה עשר ושמונה תשיעיות החלק משלשה עשר | ||
| simple fraction/addition of fractions | ⅓+¼ | ספר_חשבון#595p | Whoever has a third and a quarter of the thing, how much does he have of that thing?
: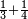 ואם מי שיש לו השליש והרביעי מן הדבר כמה חלק יש לו ממנו
ואם מי שיש לו השליש והרביעי מן הדבר כמה חלק יש לו ממנו | ||
| simple fraction/addition of fractions | ½+⅓ | ספר_חשבון#Prkw | If it is said: whoever has a half and a third of one thing, how much does he have of that thing?
: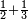 ואם יאמ' מי שיש לו החצי והשליש מדבר אחד כמה חלק יש לו מן הדבר ההוא
ואם יאמ' מי שיש לו החצי והשליש מדבר אחד כמה חלק יש לו מן הדבר ההוא | ||
| simple fraction/addition of fractions | (⅚+½·⅙)+(⁷/₈+⁸/₉) | ספר_החשבון_לאל_חצאר#cKDq | When you are told: add five-sixths and half a sixth to seven-eighths and eight-ninths.
:![\scriptstyle\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]+\left(\frac{7}{8}+\frac{8}{9}\right)](/mediawiki/images/math/4/c/4/4c4b65fa69c305cfcc4cb5e5a2e49e9e.png) כשיאמר לך קבץ חמש' שתותים וחצי שתות אל שבע שמיניות שמנה תשיעיות
כשיאמר לך קבץ חמש' שתותים וחצי שתות אל שבע שמיניות שמנה תשיעיות | ||
| simple fraction/addition of fractions | (⅖·²/₉·2)+(⅛+²/₉·⅐·⅛)·(¼+²/₆·¼) | בר_נותן_טעם#GkGP | Example: two-fifths of 2-ninths of 2 integers, and one-eighth, and two-ninths of one-seventh of one-eighth of one-quarter and two-sixths of one-quarter.
:![\scriptstyle\left(\frac{2}{5}\sdot\frac{2}{9}\sdot2\right)+\left[\left[\frac{1}{8}+\left(\frac{2}{9}\sdot\frac{1}{7}\sdot\frac{1}{8}\right)\right]\sdot\left[\frac{1}{4}+\left(\frac{2}{6}\sdot\frac{1}{4}\right)\right]\right]](/mediawiki/images/math/e/2/5/e2537ec7557a116d21369f6f61831a30.png) המשל שני חמישיות מב' תשיעיות מב' שלמים ועוד שמינית אחת ושני תשיעיות שביעית שמינית מרביעית ושתי ששיות רביעית
המשל שני חמישיות מב' תשיעיות מב' שלמים ועוד שמינית אחת ושני תשיעיות שביעית שמינית מרביעית ושתי ששיות רביעית | ||
| simple fraction/addition of fractions | ⅔+¾+⅘ | קצור_המספר#tZFO | As if you say: 2-thirds, 3-quarters and 4-fifths.
: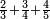 כאלו תאמר שני שלישיות וג' רביעיות וד' חמישיות
כאלו תאמר שני שלישיות וג' רביעיות וד' חמישיות | ||
| simple fraction/addition of fractions | ⅔+⁴/₉ | קצור_המספר#hh0G | As if you say: we wish to sum up two-thirds with 4-ninths.
: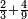 כאלו תאמר רצינו לקבץ שני שלישיות בד' תשיעיות
כאלו תאמר רצינו לקבץ שני שלישיות בד' תשיעיות | ||
| simple fraction/addition of fractions | ¾+⁴/₆ | קצור_המספר#km8a | As if you say: we wish to sum up 3-quarters with 4-sixths.
: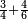 כאלו תאמר רצינו לקבץ ג' רביעיות בד' שישיות
כאלו תאמר רצינו לקבץ ג' רביעיות בד' שישיות | ||
| extraction of root/addition of roots | √18+√8 | חשבון_השטחים#Pk5I | 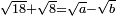 וכאשר תרצה לחבר שרש שמנה עשר ושרש שמנה עד שיהיו שורש המספר האחד פחות שורש המספר האחר
וכאשר תרצה לחבר שרש שמנה עשר ושרש שמנה עד שיהיו שורש המספר האחד פחות שורש המספר האחר | ||
| extraction of root/addition of roots | √9+√4 | תחבולות_המספר#1OzL | As if you say: nine and four - we wish to sum their roots so that they become a root of a single number.
: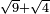 כאלו תאמ' תשעה וארבעה ורצינו לחבר שרשיהם עד שיהיו שרש למספר אחד
כאלו תאמ' תשעה וארבעה ורצינו לחבר שרשיהם עד שיהיו שרש למספר אחד | ||
| extraction of root/addition of roots | √18+√8 | תחבולות_המספר#H0sg | He said: if we wish to sum up the root of eighteen with the root of eight, so they become a root of a single number.
: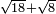 306vאמר ואם רצינו לחבר שרש שמנה עשר עם שרש שמנה עד שיהיו שרש למספר אחד
306vאמר ואם רצינו לחבר שרש שמנה עשר עם שרש שמנה עד שיהיו שרש למספר אחד | ||
| extraction of root/addition of roots | √10+√2 | תחבולות_המספר#MvKX | He said: if we wish to sum up the root of ten with the root of two.
: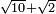 אמ' ואם רצינו לחבר שרש עשרה עם שרש שנים
אמ' ואם רצינו לחבר שרש עשרה עם שרש שנים | ||
| extraction of root/addition of roots | √16+√36 | ספר_המספר_/_אליהו_מזרחי#BeUd | The example: if you want to know the root of which square is the result of addition of the root of 16 to the root of 36. המשל בזה אם רצית לדעת העולה מקבוץ שרש הי"ו עם שרש הל"ו לאיזו מרובע הוא שרש | ||
| extraction of root/addition of roots | 2√9+3√16 | ספר_המספר_/_אליהו_מזרחי#Qk3E | The example: if you want to know the root of which square is the sum of two times the root of 9 with 3 times the root of 16? המשל בזה אם רצית לדעת העולה משני כפלי שרש הט' עם ג' כפלי שרש הי"ו לאיזו מרובע הוא שרש | ||
| extraction of root/addition of roots | ⅔√9+¾√16 | ספר_המספר_/_אליהו_מזרחי#0OPo | The example: if you want to know the root of which square is the sum of two-thirds the root of 9 with 3-quarters the root of 16? המשל בזה אם רצית לדעת העולה מקבוץ שני שלישי שרש הט' עם ג' רביעיות שרש הי"ו לאיזו מרובע הם שרש | ||
| extraction of root/addition of roots | √3+√12 | ספר_ג'יבלי_אלמוקבאלא#c9le | 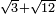 נניח שרצית לחבר שרש ג' עם שרש י"ב
נניח שרצית לחבר שרש ג' עם שרש י"ב | ||
| extraction of root/addition of roots | √6+√7 | ספר_ג'יבלי_אלמוקבאלא#A3AW | 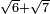 ונניח שרצית לחבר שרש ו' עם שרש ז'
ונניח שרצית לחבר שרש ו' עם שרש ז' | ||
| extraction of root/addition of roots | (4+√12)+(5+√3) | ספר_ג'יבלי_אלמוקבאלא#Jwfs | 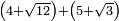 ונניח שבקשת לחבר ד' ושרש י"ב עם ה' ושרש ג'
ונניח שבקשת לחבר ד' ושרש י"ב עם ה' ושרש ג' | ||
| extraction of root/addition of roots | (4+√3)+(√12-3) | ספר_ג'יבלי_אלמוקבאלא#MsOS | 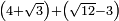 ואם רצית לחבר ד' ושרש ג' עם שרש י"ב פחות ג'
ואם רצית לחבר ד' ושרש ג' עם שרש י"ב פחות ג' | ||
| extraction of root/addition of roots | (4+√3)+(√12-3) | ספר_ג'יבלי_אלמוקבאלא#YJQX | 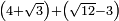 הדמיון לזה לחבר ד' ושרש ג' עם שרש י"ב פחות ג'
הדמיון לזה לחבר ד' ושרש ג' עם שרש י"ב פחות ג' | ||
| extraction of root/addition of roots | (4+√3)+(√12-2) | ספר_ג'יבלי_אלמוקבאלא#mDrF | 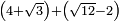 עוד אם יאמר לך אדם חבר ד' עם שרש ג' עם שרש י"ב פחות ב'
עוד אם יאמר לך אדם חבר ד' עם שרש ג' עם שרש י"ב פחות ב' | ||
| extraction of root/addition of roots | (4-√3)+(√12-2) | ספר_ג'יבלי_אלמוקבאלא#N7Qh | 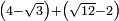 ומזה תקח המשל שיהיה ד' פחות שרש ג' עם שרש י"ב פחות ב'
ומזה תקח המשל שיהיה ד' פחות שרש ג' עם שרש י"ב פחות ב' | ||
| extraction of root/addition of roots | √3+√6+√12+√24 | ספר_ג'יבלי_אלמוקבאלא#Nydh | 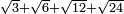 נניח שרצונך לחבר שרש ג' עם שרש ו' ועם שרש י"ב ועם שרש כ"ד
נניח שרצונך לחבר שרש ג' עם שרש ו' ועם שרש י"ב ועם שרש כ"ד | ||
| extraction of root/addition of roots | √9+√4 | חשבון_השטחים#qIr6 | 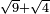 ויהיו שני המספרים המרובעים תשעה וארבעה וכאשר תרצה לחבר שורש תשעה ושורש ארבעה עד שיהיו שורש למספר אחד
ויהיו שני המספרים המרובעים תשעה וארבעה וכאשר תרצה לחבר שורש תשעה ושורש ארבעה עד שיהיו שורש למספר אחד | ||
| extraction of root/addition of roots | √9+√4 | ספר_דיני_ממונות#CvCx | 145) Question: if you want to add a root of 9 to [a root] of 4.
: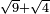 קמה)MS L: קמב שאלה אם תרצה להוסיף שרש מט' עם מד'
קמה)MS L: קמב שאלה אם תרצה להוסיף שרש מט' עם מד' | ||
| extraction of root/addition of roots | ³√96+³√324 | ספר_האלזיברא#nF3r | 14) If you wish to add a cube root of 96 to a cube root of 324.
:![\scriptstyle\sqrt[3]{96}+\sqrt[3]{324}](/mediawiki/images/math/8/f/5/8f58716ec5d5049f48b1b6af09db62e2.png) יד ואם רצית לחבר שרש מעקב צ"ו עם שרש מעקב שכ"ד
יד ואם רצית לחבר שרש מעקב צ"ו עם שרש מעקב שכ"ד | ||
| extraction of root/addition of roots | √10+√2 | חשבון_השטחים#zdrv | 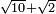 ואם באת לחבר שורש עשרה עם שורש שנים
ואם באת לחבר שורש עשרה עם שורש שנים | ||
| extraction of root/addition of roots | √8+√19 | ספר_האלזיברא#mDwl | 13) If you wish to add a root of 8 to a root of 19.
: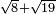 יג ואם רצית לחבר שרש ח' בשרש י"ט
יג ואם רצית לחבר שרש ח' בשרש י"ט | ||
| extraction of root/addition of roots | √12+√48 | ספר_האלזיברא#PyOq | 12) If you wish to add a root of 12 to a root of 48, for example.
: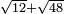 יב ואם רצית לחבר שורש י"ב בשרש מ"ח דרך משל
יב ואם רצית לחבר שורש י"ב בשרש מ"ח דרך משל | ||
| addition/additive | ר.ב.ה./מרבה | term | ספר_ג'יבלי_אלמוקבאלא#AGuK | מרבה | |
| addition/additive | י.ס.פ./נוסף | term | חשבון_השטחים#MIgg | נוסף | |
| addition/additive | י.ס.פ./נוסף | term | תחבולות_המספר#jc0t | נוסף | |
| addition/additive | י.ס.פ./תוספת | term | ספר_האלזיברא#ef0g | תוספת | |
| addition/additive | term | ספר_האלזיברא#D1CZ | יותר | ||
| addition/additive | י.ת.ר./יתרון | term | ספר_האלזיברא#Rvmb | יתרון | |
| addition/additive | י.ס.פ./נוסף | term | חשבון_השטחים#ivcP | הנוספים | |
| addition/additive | י.ס.פ./נוסף | term | ספר_ג'יבלי_אלמוקבאלא#Clw0 | נוסף | |
| addition/additive | י.ס.פ./נוסף | term | ספר_ג'יבלי_אלמוקבאלא#PUZW | המספר הנוסף | |
| addition/additive | י.ס.פ./נוסף | term | ספר_החשבון_לאל_חצאר#Uff5 | נוספים | |
| addition/additive | י.ס.פ./נוסף | term | תחבולות_המספר#nzAv | הנוספים | |
| addition/additive | י.ת.ר./יותר | term | ספר_ג'יבלי_אלמוקבאלא#SWhc | יותר | |
| addition/additive supplementation | ש.ל.מ./השלמה | term | Anonymous#hmsG | השלמת | |
| addition/additive supplementation | ש.ל.מ./השלמה | term | בר_נותן_טעם#bcFr | השלמתם לשלם | |
| addition/additive supplementation | ש.ל.מ./השלים | term | חשבון_השטחים#L7uX | השלימך אותו הוא ש | |
| addition/additive supplementation | ש.ל.מ./תשלום | term | מלאכת_המספר#fwOp | תשלום | |
| addition/additive supplementation | ש.ל.מ./השלמה | term | בר_נותן_טעם#xbp0 | השלמה | |
| addition/and (plus) | term | חשבון_השטחים#SdE4 | עם | ||
| addition/and (plus) | י.ס.פ./תוספת | term | Anonymous#POyO | בתוספת | |
| addition/and (plus) | term | ספר_האלזיברא#s4BT | יותר | ||
| addition/and (plus) | term | תחבולות_המספר#fL8e | עם | ||
| calculation/approximate | ק.ר.ב./קרוב | term | קצור_המספר#ZAMn | קרוב | |
| calculation/approximate | ד.ק.ד.ק./מדוקדק | term | עיר_סיחון#Grmt | המדוקדקת | |
| calculation/approximate | ק.ר.ב./קרוב | term | עיר_סיחון#mIl2 | הקרוב | |
| calculation/approximate | ק.ר.ב./קרוב | term | עיר_סיחון#V5kt | קרוב | |
| calculation/approximate | ד.ק.ד.ק./מדוקדק | term | Anonymous#LPQR | מדוקדקים היטב | |
| calculation/approximate | ת.ק.נ./מתוקן | term | Anonymous#pRz4 | השרש המתוקן | |
| calculation/approximate | ד.ק.ד.ק./מדוקדק | term | Anonymous#iu8f | מדוקדק | |
| calculation/approximate | ד.ק.ד.ק./מדוקדק | term | עיר_סיחון#WRW2 | מדוקדקת | |
| calculation/approximate | ד.ק.ד.ק./מדוקדק | term | Anonymous#qx2G | השרש המדוקדק | |
| calculation/approximate | ק.ר.ב./קרוב אל האמת | term | Anonymous#K8ML | קרוב אל האמת | |
| approximate/approximately | ק.ר.ב./בדרך קרובה | term | Anonymous#NJvW | בדרך קרובה | |
| approximate/approximately | ק.ר.ב./בקרוב | term | קצור_המספר#P7vg | בקרוב | |
| approximate/approximately | ק.ר.ב./בקרוב | term | עיר_סיחון#9E0B | בקירוב | |
| approximate/approximately | ק.ר.ב./בקרוב | term | משנת_המדות#7j2y | בקרוב לו | |
| approximate/approximately | ק.ר.ב./על דרך הקרוב | term | עיר_סיחון#4eYJ | על דרך קרוב | |
| approximate/approximately | ק.ר.ב./בדרך קרובה | term | Anonymous#bDAb | בדרך קרובה אל האמת | |
| approximate/approximately | ק.ר.ב./על דרך הקרוב | term | קצת_מענייני_חכמת_המספר#lC3Q | על דרך קרוב | |
| approximate/approximate root | י.ש.ר./מיושר | term | Anonymous#2oyj | המיושר | |
| approximate/approximate root | י.ש.ר./מיושר | term | Anonymous#k2cu | מיושר | |
| approximate/approximate root | י.ח.ד./מיוחד | term | Anonymous#FBUc | השורש המיוחד | |
| approximate/approximate root | י.ש.ר./מיושר | term | Anonymous#nXz7 | השרש המיושר | |
| approximate/approximate root | י.ש.ר./מיושר | term | Anonymous#Ofvh | השורש המיושר | |
| extraction of root/binomial | בעל שני שמות | term | אגרת_המספר#E0zj | בעל השני שמות | |
| extraction of root/binomial | בעל שני שמות | term | אגרת_המספר#1jkB | בעלי השני שמות | |
| practical arithmetic/calculation | ח.ש.ב./חשבון | term | ספר_ציפרא#SSQq | החשבונו' | |
| practical arithmetic/calculation | ח.ש.ב./חשבון | term | מלאכת_המספר#YR77 | חשבונינו | |
| practical arithmetic/calculation | ח.ש.ב./חשבון | term | ספר_החשבון_לאל_חצאר#YtnR | חשבונך | |
| practical arithmetic/calculation | ח.ש.ב./חשבון | term | ספר_ג'יבלי_אלמוקבאלא#E0MU | חשבון | |
| practical arithmetic/calculation | ח.ש.ב./חשבון | term | חשבון_השטחים#h88L | חשבון | |
| practical arithmetic/calculation | ח.ש.ב./חשבון | term | ספר_האלזיברא#TLWR | החשבון | |
| practical arithmetic/calculation | term | ספר_המספר_/_אברהם_אבן_עזרא#m9oU | החשבון | ||
| practical arithmetic/calculation | ח.ש.ב./חשבון | term | קצור_המספר#fx9A | חשבון | |
| practical arithmetic/calculation | ח.ש.ב./חשבון | term | ספר_ג'יבלי_אלמוקבאלא#09KJ | חשבונות | |
| practical arithmetic/calculation | ח.ש.ב./חשבון | term | קצור_המספר#CiMN | חשבונות | |
| calculation/calculation diagram | צ.ו.ר./צורה | term | קצור_המספר#VhSS | צורה | |
| calculation/calculation diagram | צ.ו.ר./צורה | term | מלאכת_המספר#URI5 | בצורה הזאת | |
| calculation/calculation diagram | תמונה | term | ספר_האלזיברא#HN3t | תמונת הכפל | |
| calculation/calculation diagram | צ.ו.ר./צורה | term | קצור_המספר#7lQN | צורה | |
| subtraction/carrying over from a higher rank | ספר_החשבון_לאל_חצאר#1eJ2 | התיר | |||
| check/casting out | י.צ.א./הוצאה | term | ספר_דיני_ממונות#nLMb | הוצאת התשיעיות | |
| casting out/cast out nines | ש.ל.כ./השליך | term | מלאכת_המספר#KrpK | נשליך [{{#annot:term|388,1217|y8PZ}}המקובץ{{#annotend:y8PZ}}]P1095 om. ט' ט' | |
| casting out/cast out nines | י.צ.א./הוציא ט"ט | term | Anonymous#DoBZ | הוציאם ט'ט' | |
| denominator/change of denominator | ח.ז.ר./חזרה | term | ספר_יסודי_התבונה_ומגדל_האמונה#W5Gm | חזרת החלקים אחד אל אחד | |
| denominator/change of denominator | ש.ו.ב./השבה | term | ספר_המספר_/_אליהו_מזרחי#slH4 | השבת המין הא' אל האחר | |
| denominator/change of denominator | ח.ז.ר./החזרה | term | בר_נותן_טעם#4KPL | החזרת | |
| denominator/change of denominator | ח.ז.ר./חזרה | term | בר_נותן_טעם#6pAM | חזרת השלימים לחלקים | |
| denominator/change of denominator | פ.ר.ט./פריטה | term | ספר_החשבון_לאל_חצאר#iJi8 | פריטה | |
| denominator/change of denominator | פ.ר.ט./פריטה | term | ספר_החשבון_לאל_חצאר#9zhU | פריטת השברים | |
| denominator/change of denominator | מ.ו.ר./המרה | term | קצור_המספר#gTzU | המרת | |
| denominator/change of denominator | נ.ת.כ./התכה | term | אגרת_המספר#bPva | התכה | |
| practical arithmetic/check | א.ז.נ./מאזנים | term | עיר_סיחון#pDG1 | מאזני | |
| practical arithmetic/check | א.ז.נ./מאזנים | term | Anonymous#CacN | מאזנים | |
| practical arithmetic/check | א.ז.נ./מאזנים | term | עיר_סיחון#ZHa7 | מאזנים | |
| progression/chess | נרדשיר | term | אגרת_המספר#QCjE | נרדשיר | |
| progression/chess | אשקקור | term | ספר_החשבון_לאל_חצאר#xbBW | אשקקור | |
| progression/chess | נרדשיר | term | ספר_החשבון_לאל_חצאר#1ZlF | נרדשיר | |
| progression/chessboard square | בית | term | ספר_החשבון_לאל_חצאר#ZKnj | בתי הנדרשיר | |
| progression/chessboard square | בית | term | ספר_החשבון_לאל_חצאר#bUtW | בית | |
| progression/chessboard square | בית | term | אגרת_המספר#jRXc | בית | |
| progression/chessboard square | בית | term | אגרת_המספר#w4bF | בתי הנרדשיר | |
| denominator/common denominator | י.ר.ה./מורה | term | בר_נותן_טעם#A7R5 | אם המורים | |
| denominator/common denominator | ש.ת.פ./משותף | term | מלאכת_המספר#KA82 | המספר המשותף | |
| denominator/common denominator | א.ב.י./אב | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#iDcz | אב המורים | |
| denominator/common denominator | י.ר.ה./מורה | term | מלאכת_המספר#fWu1 | מורה | |
| denominator/common denominator | כ.ל.ל./כולל | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#cjk4 | מורה כולל לכולם | |
| denominator/common denominator | ש.ל.מ./שלם | term | מלאכת_המספר#rBif | מקום השלם | |
| denominator/common denominator | י.ר.ה./מורה | term | ספר_מעשה_חושב#scqk | המורה הראשון | |
| denominator/common denominator | ד.מ.י./מדומה | term | עיר_סיחון#sJ8p | החשבון המדומה | |
| denominator/common denominator | ד.מ.י./מדומה | term | עיר_סיחון#wryg | מדומה | |
| denominator/common denominator | כ.ל.ל./כולל | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#AUNc | האב הכולל | |
| denominator/common denominator | כ.ל.ל./כללי | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#Ka1M | מורה כללי | |
| denominator/common denominator | ש.ת.פ./משותף | term | מלאכת_המספר#Mi00 | משותף | |
| denominator/common denominator | ש.ל.מ./שלם | term | מלאכת_המספר#QjPs | מקום שלם | |
| denominator/common denominator | definition | בר_נותן_טעם#V17G | first we examine which number has all these denominators alone, i.e. that consists of them and we call this number "the common denominator" [lit. the mother of the denominators], for it gave tham birth and they came out from it. |style="width:45%; text-align:right;"|נעיין תחלה איזהו המספר שהוא בעל אלו המורים כלם לבדם ר"ל שהוא מורכב מהם ונקרא למספר הזה אם המורים כי היא ילדתם וממנה יצאו | ||
| denominator/common denominator | ח.ל.ק./מחלק | term | מלאכת_המספר#Z1nS | מחלק | |
| factor/common factor | ש.ת.פ./שתוף | term | אגרת_המספר#hqzG | שתוף | |
| factor/common factor | ש.ת.פ./משותף | term | חשבון_השטחים#2ykN | משותף בהכאה | |
| composing denominators/composed | ר.כ.ב./הורכב | term | בר_נותן_טעם#4sLD | מורכב מהם | |
| composing denominators/composed | ר.כ.ב./הורכב | term | בר_נותן_טעם#8YuF | הורכב | |
| composing denominators/composed | ר.כ.ב./הורכב | term | בר_נותן_טעם#b4YC | הורכבה מהם | |
| composing denominators/composed | ר.כ.ב./הורכב | term | בר_נותן_טעם#Dhiz | מורכב מ | |
| fraction/composing denominators | ר.כ.ב./הרכבה | term | בר_נותן_טעם#vWrI | הרכבתן | |
| quantity/continuous quantity | ד.ב.ק./מתדבק | term | מלאכת_המספר#Iw5Y | הכמה המתדבק | |
| quantity/continuous quantity | ד.ב.ק./מתדבק | term | אגרת_המספר#qTpv | כמה מתדבק | |
| quantity/continuous quantity | ד.ב.ק./מתדבק | term | מלאכת_המספר#GbuM | כמות מתדבק | |
| basic operations/conversion | ש.ו.ב./השבה | term | Anonymous#fagX | השבת זה לזה | |
| calculation/corresponding | ק.ב.ל./נקבל | term | ספר_עיון_העקרים_לחשבון_ההנדיים#a3xB | נקבלת ל | |
| calculation/corresponding | גילי | term | ספר_מעשה_חושב#wqLW | המספרים הגיליים | |
| calculation/corresponding | ק.ב.ל./הקביל | term | ספר_עיון_העקרים_לחשבון_ההנדיים#LM34 | יקביל לה | |
| calculation/corresponding | גילי | term | ספר_מעשה_חושב#kEgw | גיליים | |
| calculation/corresponding | גיל | term | ספר_מעשה_חושב#7VzV | גילו | |
| counting/counted | ס.פ.ר./ספור | term | קצור_המספר#tW7C | ספור | |
| calculation/counting | ס.פ.ר./ספירה | term | קצור_המספר#YZCy | ספירות | |
| methods of multiplication/cross-multiplication | בשתי וערב | term | ספר_ג'יבלי_אלמוקבאלא#Msif | תכה בשתי וערב | |
| methods of multiplication/cross-multiplication | נ.כ.י./הכאת אלכסון | term | קצת_מענייני_חכמת_המספר#eZiE | הכאת אלכסון | |
| methods of multiplication/cross-multiplication | בשתי וערב | term | ספר_ג'יבלי_אלמוקבאלא#EqX1 | תכה בשתי וערב | |
| methods of multiplication/cross-multiplication | בשתי וערב | term | ספר_ג'יבלי_אלמוקבאלא#vvgf | תכפול בשתי וערב | |
| methods of multiplication/cross-multiplication | בשתי וערב | term | ספר_ג'יבלי_אלמוקבאלא#tlny | תכפול המספרי' בשתי וערב | |
| exponentiation/cubed number | 3³ | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#syCx | Example: we wish [to know] the cube of 3.
: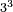 המשל בזה רצינו מעוקב ג'
המשל בזה רצינו מעוקב ג' | ||
| exponentiation/cubed number | ע.ק.ב./מעוקב | term | ספר_האלזיברא#600F | מעקב | |
| exponentiation/cubed number | 4³ | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#inPD | Another example: we wish [to know] the cube of 4.
: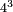 משל אחר רצינו מעוקב ד'
משל אחר רצינו מעוקב ד' | ||
| exponentiation/cubed number | ע.ק.ב./מעוקב | term | ספר_האלזיברא#OJjV | מעקב | |
| root/cube root | ק.ו.י./קו | term | Anonymous#fqgq | הקו | |
| root/cube root | ע.ק.ב./עקובי | term | ספר_מעשה_חושב#4ErI | שרשו העקוביי | |
| root/cube root | י.ס.ד./יסוד | term | ספר_מעשה_חושב#Wn8n | יסודו | |
| root/cube root | ע.ק.ב./מעוקב | term | ספר_האלזיברא#xMv2 | שורש מעקב | |
| root/cube root | ע.ק.ב./מעוקב | term | מלאכת_המספר#oTWr | שורש מעוקב | |
| root/cube root | ע.ק.ב./עקובי | term | ספר_מעשה_חושב#iJYF | השרש העקוביי | |
| root/cube root | ע.ק.ב./עקובי | term | ספר_מעשה_חושב#TrxL | השרש העקובי | |
| root/cube root | ע.ק.ב./מעוקב | term | מלאכת_המספר#AKK7 | השרש המעוקב | |
| root/cube root | ע.ק.ב./עקובי | term | ספר_מעשה_חושב#6NFF | יסודו העקוביי | |
| root/cube root | ע.ק.ב./עקובי | term | ספר_מעשה_חושב#Jish | יסוד מספרי עקוביי | |
| root/cube root | ע.ק.ב./עקובי | term | ספר_מעשה_חושב#C8w1 | השרשים העקוביים | |
| root/cube root | ע.ק.ב./עקובי | term | ספר_מעשה_חושב#wv0m | יסודו העקובי | |
| root/cube root | ע.ק.ב./מעוקב | term | ספר_ג'יבלי_אלמוקבאלא#7PFn | שרש מעוקב | |
| root/cube root | ק.ו.י./קו | term | Anonymous#HT70 | קו הגוף | |
| exponentiation/cubing | ע.ק.ב./הכאה מעוקבת | term | מלאכת_המספר#CoWD | הכאה מעוקבת | |
| exponentiation/cubing | ע.ק.ב./הכאה מעוקבת | term | מלאכת_המספר#t6HT | הכאה המעוקבת | |
| decimal rank/decade | כ.ל.ל./כלל | term | ספר_המספר_/_אליהו_מזרחי#kH1m | כללים | |
| decimal rank/decade | ק.ש.ר./קשר | term | אגרת_המספר#68sc | קשרים | |
| decimal rank/decade | כ.ל.ל./כולל | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#i5tK | כוללים | |
| decimal rank/decade | ק.ש.ר./קשר | definition | אגרת_המספר#59O6 | The decade ["kesher"] is ten, and a thousand and ten thousand. והקשר הוא עשרה ואלף ועשרת אלפים | |
| decimal rank/decade | כ.ל.ל./כלל | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#2vY6 | כללים | |
| decimal rank/decade | כ.ל.ל./כלל | definition | ספר_המספר_/_אליהו_מזרחי#4uwA | The non-units ranks are the numbers that are analogous to the units, which are the tens, hundreds, thousands, tens of thousands, and their similar. והכללים לבד הם המספרים הנמשלים לאחדים והם העשרות והמאות והאלפים והרבבות ודומיהם | |
| decimal rank/decade | כ.ל.ל./כלל | term | ספר_החשבון_והמדות#fR77 | כלל | |
| decimal rank/decade | כ.ל.ל./כלל | term | ספר_מעשה_חושב#3woq | כלל | |
| decimal rank/decade | ק.ש.ר./קשר | term | אגרת_המספר#qZKw | קשר | |
| decimal rank/decade | term | ספר_המספר_/_אברהם_אבן_עזרא#cKsd | כללים | ||
| decimal rank/decade | כ.ל.ל./כלל | term | ספר_החשבון_והמדות#dgr6 | כללים | |
| decimal positional system/decimal place | ק.ו.מ./מקום | term | ספר_החשבון_לאל_חצאר#pKHY | מקום | |
| decimal positional system/decimal place | אבן | term | ספר_מעשה_חושב#7ciS | אבנים | |
| decimal positional system/decimal place | ק.ו.מ./מקום | term | ספר_החשבון_לאל_חצאר#9EEZ | מקום | |
| decimal positional system/decimal place | ע.ר.כ./מערכה | term | Arithmetic_Textbook_by_Meir_Shapira#C7oL | מערכה | |
| decimal positional system/decimal place | ק.ו.מ./מקום | term | ספר_מעשה_חושב#0DaF | מקומות | |
| decimal positional system/decimal place | ק.ו.מ./מקום | term | ספר_החשבון_והמדות#UPoy | מקום | |
| decimal positional system/decimal place | ק.ו.מ./מקום | term | מלאכת_המספר#wgo4 | מקומם | |
| decimal positional system/decimal place | אבן | term | ספר_מעשה_חושב#Q2kZ | אבן | |
| decimal positional system/decimal place | ק.ו.מ./מקום | term | ספר_המספר_/_אליהו_מזרחי#IzZR | מקום | |
| decimal positional system/decimal place | אבן | term | ספר_מעשה_חושב#sO79 | האבן הראשה | |
| decimal positional system/decimal place | ק.ו.מ./מקום | term | מלאכת_המספר#J3XJ | מקום | |
| practical arithmetic/decimal positional system | י.ס.ד./יסוד | term | ספר_החשבון_לאל_חצאר#uf0x | יסוד | |
| practical arithmetic/decimal positional system | ד.ר.כ./דרך המספר | term | מלאכת_המספר#Sbjs | בדרך המספר | |
| decimal positional system/decimal rank | ב.ד.ל./הבדל | term | מלאכת_המספר#JMIK | הבדלי' | |
| decimal positional system/decimal rank | ב.ד.ל./הבדל | term | מלאכת_המספר#uKQ3 | הבדלותיו | |
| decimal positional system/decimal rank | ק.ו.מ./מקום | term | מלאכת_המספר#TJaw | מקומותיו | |
| decimal positional system/decimal rank | ק.ו.מ./מקום | term | מלאכת_המספר#8neY | מקומות | |
| decimal positional system/decimal rank | ע.ל.ה./מעלה | term | ספר_יסודי_התבונה_ומגדל_האמונה#r36A | מעלות המנין | |
| decimal positional system/decimal rank | ע.ל.ה./מעלה | term | ספר_יסודי_התבונה_ומגדל_האמונה#Z3kN | מעלה | |
| decimal positional system/decimal rank | ד.ר.ג./מדרגה | term | מלאכת_המספר#THnl | מדרגות | |
| decimal positional system/decimal rank | ע.ל.ה./מעלה | term | אגרת_המספר#cEXF | מעלה | |
| decimal positional system/decimal rank | ח.נ.י./מחנה | term | אגרת_המספר#wXIJ | מחנות | |
| decimal positional system/decimal rank | ד.ר.ג./מדרגה | term | ספר_החשבון_לאל_חצאר#lh0T | מדרגות | |
| decimal positional system/decimal rank | ע.ל.ה./מעלה | term | אגרת_המספר#BLwf | מעלות | |
| decimal positional system/decimal rank | ד.ר.ג./מדרגה | term | אגרת_המספר#eHky | מדרגות | |
| decimal positional system/decimal rank | term | ספר_המספר_/_אברהם_אבן_עזרא#dJ7O | מעלה | ||
| decimal positional system/decimal rank | ע.ל.ה./מעלה | term | ספר_ציפרא#wDMc | מעלה | |
| decimal positional system/decimal rank | ע.ל.ה./מעלה | term | מלאכת_המספר#e6Wj | מעלה | |
| decimal positional system/decimal rank | ע.ל.ה./מעלה | term | Anonymous_text_from_Latin#wamR | מעלה | |
| decimal positional system/decimal rank | term | Al-HAṢṢĀR_-_Arabic_in_Hebrew_Characters#R2QU | מרתבה | ||
| decimal positional system/decimal rank | term | Al-HAṢṢĀR_-_Arabic_in_Hebrew_Characters#gEOX | מנזלה | ||
| decimal positional system/decimal rank | כ.ל.ל./כלל | term | קצור_המספר#nibh | כלל | |
| decimal positional system/decimal rank | ד.ר.ג./מדרגה | term | קצור_המספר#hVYc | מדרגה | |
| decimal positional system/decimal rank | ד.ר.ג./מדרגה | term | עיר_סיחון#OdWT | מדרגה | |
| decimal positional system/decimal rank | ד.ר.ג./מדרגה | term | אגרת_המספר#CUtk | מדרגה | |
| decimal positional system/decimal rank | ע.ל.ה./מעלה | term | ספר_החשבון_לאל_חצאר#YPrt | מעלה | |
| decimal positional system/decimal rank | ח.נ.י./מחנה | term | אגרת_המספר#SaW4 | מחנה | |
| decimal positional system/decimal rank | ע.ל.ה./מעלה | term | ספר_החשבון_לאל_חצאר#7tye | מעלות | |
| decimal positional system/decimal rank | ד.ר.ג./מדרגה | term | ספר_עיון_העקרים_לחשבון_ההנדיים#UU7O | מדרגה | |
| decimal positional system/decimal rank | ד.ר.ג./מדרגה | term | ספר_מעשה_חושב#LUmp | מדרגה | |
| decimal positional system/decimal rank | ע.ל.ה./מעלה | term | ספר_החשבון_לאל_חצאר#ME7g | מעלה | |
| decimal positional system/decimal rank | ע.ל.ה./מעלה | term | ספר_מעשה_חושב#EvUQ | מעלה | |
| decimal positional system/decimal rank | ד.ר.ג./מדרגה | term | ספר_המספר_/_אליהו_מזרחי#51hZ | מדרגה | |
| decimal positional system/decimal rank | ד.ר.ג./מדרגה | term | ספר_החשבון_והמדות#YA7u | מדרגה | |
| decimal positional system/decimal rank | ע.ל.ה./מעלה | term | ספר_החשבון_והמדות#Q4tG | מעלה | |
| decimal positional system/decimal rank | ד.ר.ג./מדרגה | term | ספר_דיני_ממונות#L5l8 | מדרגה | |
| decimal positional system/decimal rank | ד.ר.ג./מדרגה | term | מלאכת_המספר#ayGQ | מדרגה | |
| decimal positional system/decimal rank | ע.ל.ה./מעלה | term | בר_נותן_טעם#Yypw | מעלה | |
| decimal positional system/decimal rank | ד.ר.ג./מדרגה | term | בר_נותן_טעם#ahn0 | מדרגה | |
| decimal positional system/decimal rank | term | Takmila_fi_al-Hisāb_-_Arabic_in_Hebrew_Characters#9KnA | מנזלה | ||
| decimal positional system/decimal rank | term | Takmila_fi_al-Hisāb_-_Arabic_in_Hebrew_Characters#1As6 | מרתבה | ||
| decimal positional system/decimal rank | term | Kitāb_al-Kāfī_fī_Mukhtaṣar_al-Hind_-_Arabic_in_Hebrew_Characters#Q9iK | מנזלה | ||
| decimal positional system/decimal rank | ע.ל.ה./מעלה | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#0wNB | מעלה | |
| decimal positional system/decimal rank | term | Arithmetic_Textbook_by_Meir_Shapira#7DlJ | מעלה | ||
| decimal positional system/decimal rank | term | Arithmetic_Textbook_by_Meir_Shapira#Thbp | מערכה | ||
| decimal positional system/decimal rank | ד.ר.ג./מדרגה | term | Anonymous#WfnU | מדרגות | |
| decimal positional system/decimal rank | ד.ר.ג./מדרגה | term | Anonymous#CscP | מדרגה | |
| decimal positional system/decimal rank | ע.ל.ה./מעלה | term | Anonymous#hUiz | מעלותיו | |
| decimal positional system/decimal rank | ע.ל.ה./מעלה | term | Anonymous#bf5A | מעלה | |
| decimal positional system/decimal rank | ע.ל.ה./מעלה | term | בר_נותן_טעם#Ze8E | מעלות | |
| decimal positional system/decimal rank | ד.ר.ג./מדרגה | term | בר_נותן_טעם#LiSQ | מדרגות | |
| decimal positional system/decimal rank | ע.ר.כ./מערכת | term | Anonymous#L9Qk | מערכות | |
| decimal positional system/decimal rank | ע.ר.כ./מערכת | term | Anonymous#PXCn | מערכת | |
| decimal positional system/decimal rank | כ.ל.ל./כלל | term | קצור_המספר#t5Mc | כללים | |
| decimal positional system/decimal rank | ד.ר.ג./מדרגה | term | קצור_המספר#nJhi | מדרגות | |
| decimal positional system/decimal rank | ד.ר.ג./מדרגה | term | עיר_סיחון#f28e | מדרגות | |
| decimal positional system/decimal rank | ע.ל.ה./מעלה | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#sQKr | מעלות | |
| decimal positional system/decimal rank | ד.ר.ג./מדרגה | term | ספר_החשבון_לאל_חצאר#z1pv | מדרגה | |
| decimal positional system/decimal rank | ע.ל.ה./מעלה | term | ספר_אגריס#38lN | מעלה | |
| decimal positional system/decimal rank | ק.ו.מ./מקום | term | מלאכת_המספר#PagF | מקום | |
| decimal positional system/decimal rank | ב.ד.ל./הבדל | term | מלאכת_המספר#ZZlm | הבדל | |
| decimal positional system/decimal rank | ד.ר.ג./מדרגה | term | ספר_עיון_העקרים_לחשבון_ההנדיים#9Eju | מדרגות | |
| basic operations/decomposing to a fraction | פ.ר.ט./פריטה | term | בר_נותן_טעם#YyGS | פריטה | |
| basic operations/decomposing to a fraction | נ.ת.כ./התכה | term | ספר_החשבון_לאל_חצאר#3mIa | התכה | |
| basic operations/decomposing to a fraction | פ.ר.ט./פריטה | definition | בר_נותן_טעם#EbbI | To the conversion of fractions that are related together into the lowest type of fractions I called '''Periṭah''' [decomposing to a fraction]. ולהשבת השברים הנקשרים כלם יחד למין השברים הגרועים מהם קראתי פריטה | |
| basic operations/decomposing to a fraction | פ.ר.ט./פריטה | definition | בר_נותן_טעם#xxm5 | Decomposing to a fraction is converting the integers to fractions of whichever type you wish. הפריטה היא {{#annot:term|2612,2489|6pAM}}חזרת השלימים לחלקים{{#annotend:6pAM}} מהמין אשר תרצה | |
| basic operations/decomposing to a fraction | נ.ת.כ./התכה | term | ספר_החשבון_לאל_חצאר#wNtw | התכת המדרגות | |
| basic operations/decomposing to a fraction | נ.ת.כ./התכה | term | עיר_סיחון#7pST | התכה | |
| calculation/decreasing | ג.ר.ע./גרע | term | קצור_המספר#TP9F | גורע | |
| calculation/decreasing | ג.ר.ע./גרע | term | קצור_המספר#2obI | גורע ופוחת | |
| calculation/decreasing | ח.ס.ר./חסרון | term | קצור_המספר#7gWT | חסרון | |
| sexagesimal fraction/degree | ע.ל.ה./מעלה | term | עיר_סיחון#DYe8 | מעלה | |
| sexagesimal fraction/degree | ע.ל.ה./מעלה | term | עיר_סיחון#lmGW | מעלות | |
| sexagesimal fraction/degree | ע.ל.ה./מעלה | term | ספר_המספר_/_אליהו_מזרחי#MZ5T | מעלות | |
| sexagesimal fraction/degree | ע.ל.ה./מעלה | term | ספר_המספר_/_אליהו_מזרחי#zoiW | מעלה | |
| sexagesimal fraction/degree | ע.ל.ה./מעלה | term | ספר_עיון_העקרים_לחשבון_ההנדיים#tNzV | מעלות | |
| sexagesimal fraction/degree | ע.ל.ה./מעלה | term | ספר_החשבון_לאל_חצאר#rRSt | מעלות | |
| denominator/denomination | ק.ר.א./קריאת שם | definition | אגרת_המספר#zP3w | He said that the name of the division of the greater by the smaller is known as denomination, i.e. that you call the smaller by the name of the greater. ואמ' כי חלוק הרב על המעט נודע שמו כקריאת שם ר"ל שתקרא שם לקטן מהגדול | |
| denominator/denomination | ק.ר.א./קריאת שם | term | ספר_החשבון_לאל_חצאר#rpoj | קריאת השם | |
| denominator/denomination | ק.ר.א./קריאת שם | definition | אגרת_המספר#AlWr | the general known procedure of the denomination is that you dissolve that by which it is denominated into the numbers of which it is composed; you take them as denominators, and divide by them what you wish to denominate, so the result is the required, and its measure is known from the ratio of its divisors to the denominators by which it is divided. אמר ואמנם קריאת שם המעשה המפורסם הכולל בה שתתיך הנקרא ממנו אל מספריו אשר הורכב מהם ותקח אותם למורים תחלק עליהם מה שתרצה קריאת שמו יצא המבוקש ויודע שעורו ביחס חלקיו אל אותם המורים המחולק עליהם | |
| denominator/denomination | ק.ר.א./קריאת שם | term | ספר_החשבון_לאל_חצאר#MPKo | קריאת שם | |
| fraction/denominator | י.ר.ה./מורה | term | אגרת_המספר#H9Pl | מורה | |
| fraction/denominator | ש.ב.ר./שם השבר | term | קצור_המספר#RYbq | שם השבר | |
| fraction/denominator | ש.ב.ר./שם השבר | term | קצור_המספר#HGbK | שם השבר | |
| fraction/denominator | י.כ.ח./מוכיח | term | ספר_יסודי_התבונה_ומגדל_האמונה#olDk | המוכיח | |
| fraction/denominator | ס.ו.כ./סך | term | ספר_החשבון_לאל_חצאר#oLEl | סך | |
| fraction/denominator | א.ב.י./אב | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#t613 | אבות | |
| fraction/denominator | א.ב.י./אב | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#7Ljs | אב | |
| fraction/denominator | י.ר.ה./מורה | term | בר_נותן_טעם#TAZT | המורה החלק | |
| fraction/denominator | י.ר.ה./מורה | term | בר_נותן_טעם#BOwU | מורה החלק | |
| fraction/denominator | ע.מ.ד./מעמד | term | ספר_החשבון_לאל_חצאר#hVQb | מעמדים | |
| fraction/denominator | ק.ו.מ./מקום | term | ספר_החשבון_לאל_חצאר#kJI0 | מקומות | |
| fraction/denominator | י.ר.ה./מורה | term | ספר_החשבון_לאל_חצאר#ZDhv | מורה | |
| fraction/denominator | ע.מ.ד./מעמד | term | ספר_החשבון_לאל_חצאר#Eaco | מעמד | |
| fraction/denominator | ק.ו.מ./מקום | term | ספר_החשבון_לאל_חצאר#vPpW | מקום | |
| fraction/denominator | י.כ.ח./מוכיח | term | Anonymous#YnO1 | מוכיח | |
| fraction/denominator | ק.ר.א./קורא | term | ספר_מעשה_חושב#tg1Q | המספר הקורא | |
| fraction/denominator | א.י.כ./איכות | term | קצת_מענייני_חכמת_המספר#A7GN | איכות | |
| fraction/denominator | ק.ר.א./קורא | term | ספר_מעשה_חושב#TIK2 | המספרים הקוראים | |
| fraction/denominator | ע.מ.ד./עמוד | term | אגרת_המספר#sYPB | עמודי השברים | |
| fraction/denominator | י.כ.ח./מוכיח | term | Anonymous#C79S | המספר המוכיח | |
| fraction/denominator | י.ר.ה./מורה | term | Anonymous#zHyZ | מורה | |
| fraction/denominator | י.ר.ה./מורה | term | אגרת_המספר#ORAD | מורי השברים | |
| fraction/denominator | י.ר.ה./מורה | term | אגרת_המספר#ymcA | מורים | |
| fraction/denominator | term | ספר_מעשה_חושב#jbtF | המספר אשר נקרא בו | ||
| fraction/denominator | י.ר.ה./מורה | term | ספר_מעשה_חושב#KrLh | מורה | |
| fraction/denominator | א.י.כ./איכות | term | ספר_המספר_/_אליהו_מזרחי#rT91 | איכות | |
| fraction/denominator | י.ר.ה./מורה | term | ספר_מעשה_חושב#N4Hm | מורים | |
| fraction/denominator | ס.כ.מ./סכום | term | ספר_החשבון_לאל_חצאר#W4g6 | סכום | |
| fraction/denominator | ע.מ.ד./מעמד | term | ספר_החשבון_לאל_חצאר#XS6s | מעמדות השברים | |
| fraction/denominator | א.י.כ./איכות | definition | ספר_המספר_/_אליהו_מזרחי#TPFh | Its name that is derived from the quality is the name of the number that indicates the total parts of the whole - אולם השם אשר לו מהאיכות הוא שם המספר המורה על חלקי השלם | |
| fraction/denominator | י.כ.ח./מוכיח | term | ספר_יסודי_התבונה_ומגדל_האמונה#gv1J | המספר המוכיח | |
| fraction/denominator | י.ר.ה./מורה | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#ltLi | מורים | |
| fraction/denominator | י.ר.ה./מורה | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#Ng5A | מורה | |
| fraction/denominator | א.י.כ./איכות | term | ספר_ג'יבלי_אלמוקבאלא#SjG1 | איכות | |
| fraction/denominator | ס.כ.מ./סכום | term | ספר_החשבון_לאל_חצאר#IrJf | סכומים | |
| fraction/denominator | ח.ל.ק./מחלק | term | מלאכת_המספר#p3yB | מחלק | |
| fraction/denominator | י.ר.ה./מורה | term | Anonymous#7NHw | מורה | |
| fraction/denominator | term | ספר_מעשה_חושב#MvBy | המספר הקורא לחלק | ||
| denominator/determining the common denominator | י.צ.ע./הצעה | term | אגרת_המספר#JdQ2 | הצעה | |
| denominator/determining the common denominator | י.צ.ע./הצעה | definition | אגרת_המספר#adHL | determining the common denominator is that we convert all that was given in the question itself to the smaller fraction in it. אמ' וההצעה הוא שנשיב כל מה שהונח בשאלה בעינה אל פחות שבר שבה | |
| calculation/difference | ג.ר.ע./גרעון | term | חשבון_השטחים#Mp0Z | הגרעון | |
| calculation/difference | פ.ח.ת./פחת | term | חשבון_השטחים#O9PD | פחת | |
| calculation/difference | ב.ד.ל./הבדל | term | ספר_ג'יבלי_אלמוקבאלא#Vd6Q | ההבדל שהוא בין זה לזה | |
| calculation/difference | ב.ד.ל./הבדל | term | ספר_ג'יבלי_אלמוקבאלא#1e2w | ההבדל | |
| calculation/difference | פ.ר.ש./הפרש | term | קצור_המספר#0diP | הפרש בין | |
| calculation/difference | ח.ס.ר./חסר | term | קצור_המספר#1XQd | חסר עד | |
| calculation/difference | ח.ס.ר./חסרון | term | קצור_המספר#lsbC | חסרונם | |
| calculation/difference | ב.ד.ל./הבדל | term | חשבון_השטחים#Jjoi | ההבדל | |
| quantity/discrete quantity | ח.ל.ק./מתחלק | term | אגרת_המספר#67Az | כמה מתחלק | |
| quantity/discrete quantity | ח.ל.ק./מתחלק | term | מלאכת_המספר#LP0f | כמות מתחלק | |
| quantity/discrete quantity | ח.ל.ק./מתחלק | term | מלאכת_המספר#GME2 | כמות מתחלק | |
| quantity/discrete quantity | ח.ל.ק./מתחלק | term | מלאכת_המספר#TNrb | כמה המתחלק | |
| division/dividend | ח.ל.ק./נחלק | term | קצור_המספר#SrcA | המספר הנחלק | |
| division/dividend | ח.ל.ק./מתחלק | term | ספר_האלזיברא#cnxx | המתחלק | |
| division/dividend | ח.ל.ק./נחלק | term | Anonymous#nmhU | הנחלקים | |
| division/dividend | ח.ל.ק./מחולק | term | Anonymous#SyYf | המחולק | |
| division/dividend | ח.ל.ק./נחלק | term | Anonymous#bSCg | הנחלק | |
| division/dividend | ח.ל.ק./מחולק | term | Anonymous#vZNL | החשבון המחולק | |
| division/dividend | ח.ל.ק./נחלק | term | תחבולות_המספר#nQFD | המספר שנחלק | |
| division/dividend | ח.ל.ק./מחולק | term | תחבולות_המספר#E3Gq | המספר המחולק | |
| division/dividend | ח.ל.ק./מחולק | term | קצור_המספר#f2cL | המחולק | |
| division/dividend | ח.ל.ק./מתחלק | term | קצור_המספר#Yzdu | מתחלק | |
| division/dividend | ח.ל.ק./מתחלק | term | קצור_המספר#CZzd | המספר המתחלק | |
| division/dividend | ח.ל.ק./נחלק | term | חשבון_השטחים#Hlhj | המספר הנחלק | |
| division/dividend | ח.ל.ק./נחלק | term | קצור_המספר#I8wS | המספר הנחלק | |
| division/dividend | ח.ל.ק./נחלק | term | ספר_ג'יבלי_אלמוקבאלא#9YPR | המספר הנחלק | |
| division/dividend | ח.ל.ק./מתחלק | term | בר_נותן_טעם#dYoj | המתחלק | |
| division/dividend | ח.ל.ק./מחולק | term | אגרת_המספר#kvMY | המספר המחולק | |
| division/dividend | ח.ל.ק./מחולק | term | קצת_מענייני_חכמת_המספר#NPOJ | מחולק | |
| division/dividend | ח.ל.ק./מחולק | term | מלאכת_המספר#FEEo | מחולק | |
| division/dividend | ח.ל.ק./מחולק | term | חשבון_השטחים#EPMe | המספר המחולק | |
| division/dividend | ח.ל.ק./נחלק | term | חשבון_השטחים#Kh5g | השעור הנחלק | |
| division/dividend | ח.ל.ק./נחלק | term | Anonymous_text_from_Latin#rMzk | הנחלק | |
| division/dividend | ח.ל.ק./נחלק | term | תחבולות_המספר#XrCl | המספר הנחלק | |
| division/dividend | ח.ל.ק./מחולק | term | ספר_מעשה_חושב#Ib08 | המחולקת | |
| division/dividend | ח.ל.ק./מחולק | term | ספר_מעשה_חושב#psuo | המחולקים | |
| division/dividend | ח.ל.ק./מחולק | term | ספר_מעשה_חושב#8hGd | המספר המחולק | |
| division/dividend | ח.ל.ק./מתחלק | term | ספר_האלזיברא#wHYI | המספר המתחלק | |
| division/dividend | ח.ל.ק./מחולק | term | מלאכת_המספר#GwzK | מחולק | |
| division/dividing (adjective) | ח.ל.ק./חולק | term | חשבון_השטחים#AAZ6 | החולקת | |
| division/divisible | ח.ל.ק./התחלק | term | בר_נותן_טעם#Ze9g | יתחלק כלו לשלימים | |
| division/divisible | ח.ל.ק./התחלק | term | בר_נותן_טעם#OK90 | יתחלק כלו לשלמים | |
| division/divisible | ח.ל.ק./נחלק | term | בר_נותן_טעם#sEuM | נחלק לשלמים | |
| division/divisible | ח.ל.ק./התחלק | term | Anonymous#LyjR | יתחלק | |
| division/divisible | ח.ל.ק./התחלק | term | Anonymous#W47r | יתחלק | |
| division/divisible | ח.ל.ק./התחלק | term | בר_נותן_טעם#SD1U | יתחלק אליו לשלימים מבלי שארית | |
| division/divisible | ח.ל.ק./התחלק | term | בר_נותן_טעם#sJQw | יתחלק ל | |
| basic operations/division | ח.ל.ק./חלוק | definition | אגרת_המספר#DmqB | Division is the dissolving of the dividend into equal parts whose number is as the units that are in the divisor. אמר החילוק הוא התכת המחולק אל חלקים שוים יהיה מספרם כדמות מה שבמחולק עליו מן האחדים | |
| basic operations/division | definition | ספר_המספר_/_אליהו_מזרחי#w0a6 | division is the announcing of the number of parts of a given number that are equal to a given number that is smaller than it. החלוק הוא המודיע מספר חלקי מספר מה מונח השוים למספר מה מונח קטן ממנו | ||
| basic operations/division | 38÷101 | בר_נותן_טעם#h3tR | Example: to divide 38 by 101, because this number, i.e. 101 [is prime].
: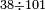 המשל לחלק ל"ח לק"א כי זה המספר ר"ל ק"א
המשל לחלק ל"ח לק"א כי זה המספר ר"ל ק"א | ||
| basic operations/division | ח.ל.ק./חלוקה | term | עיר_סיחון#h7Iv | חלוקת | |
| basic operations/division | ח.ל.ק./החלק | term | מלאכת_המספר#pHYk | החלק | |
| basic operations/division | ח.ל.ק./החלק | term | מלאכת_המספר#rOge | החלק | |
| basic operations/division | 100÷12 | עיר_סיחון#E8oD | We wish to divide one hundred by twelve.
: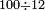 64vעוד בקשנו לחלק מאה על שנים עשר
64vעוד בקשנו לחלק מאה על שנים עשר | ||
| basic operations/division | 901÷32 | עיר_סיחון#qhod | We wish to divide nine hundred and one by thirty-two.
: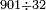 ועוד בקשנו לחלק אחד ותשע מאות על שלשים ושתים
ועוד בקשנו לחלק אחד ותשע מאות על שלשים ושתים | ||
| basic operations/division | 891÷40 | עיר_סיחון#chBm | We wish to divide eight hundred and ninety-one by forty.
: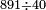 ועוד בקשנו לחלק שמונה מאות ותשעים ואחד על ארבעים
ועוד בקשנו לחלק שמונה מאות ותשעים ואחד על ארבעים | ||
| basic operations/division | ח.ל.ק./חלוקה | term | תחבולות_המספר#Hf8m | חלוקת | |
| basic operations/division | 321÷9 | עיר_סיחון#ERZO | We wish to divide three hundred and twenty-one by nine.
: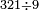 ועוד בקשנו לחלק שלש מאות ועשרים ואחד על תשעה
ועוד בקשנו לחלק שלש מאות ועשרים ואחד על תשעה | ||
| basic operations/division | 583696÷764 | עיר_סיחון#2mgj | We wish to divide five hundred and eighty-three thousand, six hundred and ninety-six by seven hundred and sixty-four.
: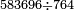 ועוד בקשנו לחלק חמש מאות אלף ושמונים ושלשת אלפים ושש מאות ותשעים וששה על שבע מאות וששים וארבעה
ועוד בקשנו לחלק חמש מאות אלף ושמונים ושלשת אלפים ושש מאות ותשעים וששה על שבע מאות וששים וארבעה | ||
| basic operations/division | ח.ל.ק./חלוקה | term | ספר_עיון_העקרים_לחשבון_ההנדיים#uDSp | חלוקה | |
| basic operations/division | ח.ל.ק./חלוק | definition | מלאכת_המספר#azQi | division is dividing any number into equal parts as the number of units in the divisor. חלוק הוא חלוקת איזה מספר שיהיה בכך חלקים שוים כמספר האחדים שבמחלק | |
| basic operations/division | 5086÷19 | ספר_אגריס#o1gb | Another example: we want to know: how many times 19 there are in 5086?
: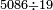 דומיון אחר בקשנו לידע כמה פעמים י"ט בתוך שמנים ושש וחמש אלפים
דומיון אחר בקשנו לידע כמה פעמים י"ט בתוך שמנים ושש וחמש אלפים | ||
| basic operations/division | 654÷70 | ספר_אגריס#074J | Here is an example: we want to know how many times 70 there are in 654?
: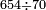 והא לך דומיון ביקשנו לדע כמה פעמים ע' בתוך תרנ"ד
והא לך דומיון ביקשנו לדע כמה פעמים ע' בתוך תרנ"ד | ||
| basic operations/division | ח.ל.ק./חלוק | definition | ספר_יסודי_התבונה_ומגדל_האמונה#YHCS | division of a number by a number is that you divide a greater number by a smaller number. חלוק מנין על מנין הוא שתחלק מנין רב על מעט | |
| basic operations/division | 987654321÷9437 | ספר_מעשה_חושב#vmqK | Example: we wish to divide line 987654321 by line 9437
: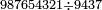 דמיון זה רצינו לחלק טור א'ב'ג'ד'ה'ו'ז'ח'ט' על טור ז'ג'ד'ט'
דמיון זה רצינו לחלק טור א'ב'ג'ד'ה'ו'ז'ח'ט' על טור ז'ג'ד'ט' | ||
| basic operations/division | 100÷9 | עיר_סיחון#u08O | We wish to divide one hundred by nine.
: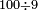 ועוד בקשנו לחלק מאה על ט'
ועוד בקשנו לחלק מאה על ט' | ||
| basic operations/division | ח.ל.ק./חלוק | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#PtHW | חילוק | |
| basic operations/division | 125÷11 | עיר_סיחון#PuIG | We wish to divide one hundred and twenty-five by eleven.
: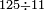 בקשנו לחלק חמשה ועשרים ומאה על אחד עשר
בקשנו לחלק חמשה ועשרים ומאה על אחד עשר | ||
| basic operations/division | 200÷50 | ספר_דיני_ממונות#kQox | Example: we wish to divide two hundred by 50.
: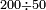 דמיון זה נרצה לחלק מאתים על נ'
דמיון זה נרצה לחלק מאתים על נ' | ||
| basic operations/division | ח.ל.ק./חלוקה | term | ספר_ג'יבלי_אלמוקבאלא#iGwr | חלוקת | |
| basic operations/division | ח.ל.ק./חלוק | definition | אגרת_המספר#wTUv | The meaning of division is the ratio of one of the numbers from the other וירצה בחלוק יחס אחד המספרים מן האחר | |
| basic operations/division | ח.ל.ק./חלוק | term | אגרת_המספר#8HTN | חלוק | |
| basic operations/division | 70213÷136 | ספר_דיני_ממונות#K0QH | Another example: we wish to divide 70213 by 136.
: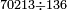 דמיון אחר נרצה לחלק שבעים אלף ורי"ג על קל"ו
דמיון אחר נרצה לחלק שבעים אלף ורי"ג על קל"ו | ||
| basic operations/division | ח.ל.ק./חלוקה | term | מלאכת_המספר#T0Pj | חלוקה | |
| basic operations/division | ח.ל.ק./חלוק | term | ספר_אגריס#Vnia | חלוק | |
| basic operations/division | ח.ל.ק./חלוק | term | מלאכת_המספר#W8wP | חלוק | |
| basic operations/division | 4321÷23 | ספר_דיני_ממונות#VgnQ | Example: we wish to divide 4321 by 23.
: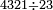 דמיון זה נרצה לחלק ד' אלפים שכ"א על כ"ג
דמיון זה נרצה לחלק ד' אלפים שכ"א על כ"ג | ||
| basic operations/division | 20503÷304 | ספר_דיני_ממונות#G2dY | Example: we wish to divide 20503 by 304.
: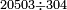 דמיון זה נרצה לחלק עשרים אלף תק"ג על מספר ש"ד
דמיון זה נרצה לחלק עשרים אלף תק"ג על מספר ש"ד | ||
| basic operations/division | 12345÷234 | ספר_דיני_ממונות#omXn | Example: we wish to divide 12345 by 234.
: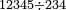 דמיון זה נרצה לחלק י"ב אלפים ושמ"ה על רל"ד
דמיון זה נרצה לחלק י"ב אלפים ושמ"ה על רל"ד | ||
| basic operations/division | 245÷34 | ספר_דיני_ממונות#iYfX | Example: we wish to divide 245 by 34.
: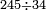 דמיון זה נרצה לחלק רמ"ה על ל"ד
דמיון זה נרצה לחלק רמ"ה על ל"ד | ||
| basic operations/division | ח.ל.ק./חלוק | term | תחבולות_המספר#Mj3r | חלוק | |
| basic operations/division | 5÷17 | ספר_דיני_ממונות#TGzh | Example: we wish to divide 5 into 17 parts.
: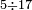 דמיון אחר נרצה לחלק ה' לי"ז חלקים
דמיון אחר נרצה לחלק ה' לי"ז חלקים | ||
| basic operations/division | 11÷19 | ספר_דיני_ממונות#B3RV | Example: we wish to divide 11 by 19.
: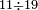 דמיון זה נרצה לחלק י"א על י"ט
דמיון זה נרצה לחלק י"א על י"ט | ||
| basic operations/division | 37÷48 | ספר_דיני_ממונות#aycb | Example: we wish to divide 37 by 48.
: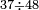 דמיון זה נרצה לחלק ל"ז על מ"ח
דמיון זה נרצה לחלק ל"ז על מ"ח | ||
| basic operations/division | 23÷36 | ספר_דיני_ממונות#AkSQ | Another example: we wish to divide 23 by 36.
: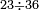 דמיון אחר נרצה לחלק כ"ג על ל"ו
דמיון אחר נרצה לחלק כ"ג על ל"ו | ||
| basic operations/division | 11÷18 | ספר_דיני_ממונות#XYtI | Example: we wish to divide 11 by 18.
: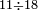 דמיון זה נרצה לחלק י"א על י"ח
דמיון זה נרצה לחלק י"א על י"ח | ||
| basic operations/division | 36÷48 | ספר_דיני_ממונות#ZGyk | Example: we wish to divide 36 by 48.
: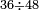 דמיון זה נרצה לחלק ל"ו על מ"ח
דמיון זה נרצה לחלק ל"ו על מ"ח | ||
| basic operations/division | 144÷8 | מלאכת_המספר#a1bh | Example: we wish to divide 144 by 8.
: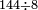 המשל נרצה לחלק קמ"ד על ח'
המשל נרצה לחלק קמ"ד על ח' | ||
| basic operations/division | ח.ל.ק./חלוק | definition | אגרת_המספר#3eZ3 | The crowd means by division generally to the knowledge of what comes to a whole unit of the units of the divisor from the whole dividend. וההמון ירצו בחלוק בסתם ידיעת מה שראוי לאחד השלם מאחדי המחולק עליו מן כלל המחולק | |
| basic operations/division | 583696÷1080 | עיר_סיחון#BBPT | We wish to divide five hundred and eighty-three thousand, six hundred and ninety-six by one thousand and eighty.
: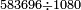 ועוד בקשנו לחלק חמש מאות אלף ושמנים ושלשת אלפים [ושש מאות ותשעים ושש]marg. על אלף ושמונים
ועוד בקשנו לחלק חמש מאות אלף ושמנים ושלשת אלפים [ושש מאות ותשעים ושש]marg. על אלף ושמונים | ||
| basic operations/division | 218÷7 | ספר_ציפרא#vVRf | If one asks: how many times 7 is in two hundred and 18?
: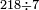 אם ישאל השואל כמה פעמי' ז' יש במאתים וי"ח
אם ישאל השואל כמה פעמי' ז' יש במאתים וי"ח | ||
| basic operations/division | 100÷15 | Anonymous#SXQ5 | Such as when you wish to divide one-hundred by 15.
::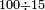 כגון שתרצה לחלק מאה על ט"ו
כגון שתרצה לחלק מאה על ט"ו | ||
| basic operations/division | 9876÷12 | מלאכת_המספר#stc2 | Suppose we wish to divide 9876 into 12 parts. ונניח שנרצה לחלק ט' אלפי' ותתע"ו בי"ב חלקים | ||
| basic operations/division | 1000÷72 | Anonymous#WAFS | If you divide one-thousand by seventy-two.
::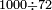 ואם תחלק אלף על שנים ושבעים
ואם תחלק אלף על שנים ושבעים | ||
| basic operations/division | 11350÷110 | ספר_המספר_/_אברהם_אבן_עזרא#SdNR | Another example: we wish to divide 11350 by 110.
: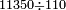 דמיון אחר רצינו לחלק י"א אלף וש"נ על ק"י
דמיון אחר רצינו לחלק י"א אלף וש"נ על ק"י | ||
| basic operations/division | ח.ל.ק./חלוקה | term | ספר_ג'יבלי_אלמוקבאלא#fhJq | חלוקה | |
| basic operations/division | ח.ל.ק./חלוק | term | ספר_ג'יבלי_אלמוקבאלא#MLlZ | חלוק | |
| basic operations/division | WP | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#rzDk | The first example: we wish to divide [...]
: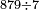 משל ראשון [...] רצינו לחלק [...] הצורה
משל ראשון [...] רצינו לחלק [...] הצורה | ||
| basic operations/division | WP | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#S8zi | The second example: we wish to divide 246 pešiṭim by 12.
: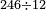 משל שני רצינו לחלק רמ"ו פשיטין לי"ב
משל שני רצינו לחלק רמ"ו פשיטין לי"ב | ||
| basic operations/division | WP | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#g5Nb | The third example: we wish to divide 497 liters of money by 34.
: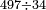 משל שלשי רצינו לחלק תצ"ז לטרי ממון על ל"ד
משל שלשי רצינו לחלק תצ"ז לטרי ממון על ל"ד | ||
| basic operations/division | WP | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#3wFN | The fourth example: we wish to divide 2 thousand 987 liters by 39.
: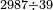 המשל רביעי רצינו לחלק ב' אלפים תתקפ"ז [ליט'] על ל"ט
המשל רביעי רצינו לחלק ב' אלפים תתקפ"ז [ליט'] על ל"ט | ||
| basic operations/division | ח.ל.ק./חלוק | term | ספר_ג'יבלי_אלמוקבאלא#LTmk | חלוקי' | |
| basic operations/division | 40÷7 | Anonymous#LN7a | Such as when you wish to divide 40 by 7.
::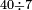 כגון שתרצה לחלק מ' על ז'
כגון שתרצה לחלק מ' על ז' | ||
| basic operations/division | WP | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#hspE | The fifth example: we wish to divide 5 thousand 852 peraḥim by 56.
: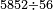 משל חמשי רצינו לחלק ה' אלפים תתנ"ב פרחים לנ"ו
משל חמשי רצינו לחלק ה' אלפים תתנ"ב פרחים לנ"ו | ||
| basic operations/division | WP | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#3h3o | The sixth example: we wish to divide 156 liters of pepper by 14.
: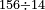 משל ששי רצינו לחלק קנ"ו לטרי פלפל לי"ד
משל ששי רצינו לחלק קנ"ו לטרי פלפל לי"ד | ||
| basic operations/division | WP | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#9mgM | The seventh example: we wish to divide two hundred and 85 thousands and 976 kikkar of wool by 372.
: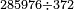 משל שביעי רצינו לחלק מאתים ופ"ה אלפים ותתקע"ו כיכרי צמר על שע"ב
משל שביעי רצינו לחלק מאתים ופ"ה אלפים ותתקע"ו כיכרי צמר על שע"ב | ||
| basic operations/division | 104034÷114 | ספר_החשבון_והמדות#WKuz | Another example: we wish to divide 104034 by 114.
: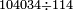 דמיון אחר רצינו לחלק מאת אלף וסיפרא וארבעת אלפים וסיפרא ושלשים וארבעה על קי"ד
דמיון אחר רצינו לחלק מאת אלף וסיפרא וארבעת אלפים וסיפרא ושלשים וארבעה על קי"ד | ||
| basic operations/division | 4215÷14 | ספר_החשבון_והמדות#dIVO | Example: we wish to divide 4 thousand, two hundred and 15 by 14.
: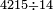 דמיון רצינו לחלק ד' אלפים ומאתים וט"ו על י"ד
דמיון רצינו לחלק ד' אלפים ומאתים וט"ו על י"ד | ||
| basic operations/division | 5214÷108 | ספר_החשבון_והמדות#BDX8 | Another example: we wish to divide five thousand, two hundred, and fourteen by one hundred and eight.
: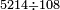 דמיון אחר רצינו לחלק חמשת אלפים ומאתים וארבעה עשר על מאה וסיפרא ושמנה
דמיון אחר רצינו לחלק חמשת אלפים ומאתים וארבעה עשר על מאה וסיפרא ושמנה | ||
| basic operations/division | 104034÷114 | ספר_החשבון_והמדות#XR8w | Another example: we wish to divide one hundred thousand, four thousand, a zero and thirty-four by 114.
: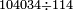 דמיון אחר רצינו לחלק מאת אלף וארבעת אלפים וספרא ושלשים וארבעה על קי"ד
דמיון אחר רצינו לחלק מאת אלף וארבעת אלפים וספרא ושלשים וארבעה על קי"ד | ||
| basic operations/division | 4215÷14 | ספר_החשבון_והמדות#kF9U | Example: we wish to divide four thousand, two hundred and fifteen by fourteen.
: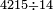 דמיון רצינו לחלק ארבעת אלפים ומאתים 33vוחמשה עשר על ארבעה עשר
דמיון רצינו לחלק ארבעת אלפים ומאתים 33vוחמשה עשר על ארבעה עשר | ||
| basic operations/division | 204612÷289 | קצור_המספר#7SX6 | Let the dividend be two hundred and four thousand six hundred and twelve, and the divisor be two hundred and eighty-nine.
::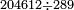 ויהיה {{#annot:term|1563,605|CZzd}}המספר המתחלק{{#annotend:CZzd}} מאתים וארבעת אלפים ושש מאות ושתים עשרה ו{{#annot:term|1226,604|2rny}}הנחלק עליו{{#annotend:2rny}} מאתים ושמונים ותשעה
ויהיה {{#annot:term|1563,605|CZzd}}המספר המתחלק{{#annotend:CZzd}} מאתים וארבעת אלפים ושש מאות ושתים עשרה ו{{#annot:term|1226,604|2rny}}הנחלק עליו{{#annotend:2rny}} מאתים ושמונים ותשעה | ||
| basic operations/division | 823÷278 | קצור_המספר#x8uJ | Example: we wish to divide eight hundred and twenty-two by two hundred and seventy-eight.
::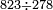 והנה המשל בזה רצינו לחלק שמונה מאות ועשרים ושלשה למאתים ושבעי' ושמונה
והנה המשל בזה רצינו לחלק שמונה מאות ועשרים ושלשה למאתים ושבעי' ושמונה | ||
| basic operations/division | 54093÷2945 | ספר_המספר_/_אברהם_אבן_עזרא#UHr3 | Another example.
: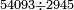 דמיון אחר
דמיון אחר | ||
| basic operations/division | 15÷100 | Anonymous#S5mt | Such as 15 by 100.
::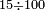 כמו ט"ו על ק'
כמו ט"ו על ק' | ||
| basic operations/division | 4÷50 | קצור_המספר#pJiZ | The first example: we wish to divide 4 by fifty.
: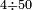 ומשל לאחד רצינו לחלק ד' על חמישים
ומשל לאחד רצינו לחלק ד' על חמישים | ||
| basic operations/division | 6÷50 | קצור_המספר#XvMs | The second example: we wish to divide six by fifty.
: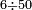 ומשל לשני רצינו לחלק ששה על חמישים
ומשל לשני רצינו לחלק ששה על חמישים | ||
| basic operations/division | 4÷12 | קצור_המספר#Kc3e | Example: we wish to divide 4 by 12.
: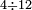 המשל בזה נרצה לחלק ד' על י"ב
המשל בזה נרצה לחלק ד' על י"ב | ||
| basic operations/division | ח.ל.ק./חלוק | term | ספר_ג'יבלי_אלמוקבאלא#CtRD | בחלוק על | |
| basic operations/division | 9381÷296 | ספר_המספר_/_אברהם_אבן_עזרא#05kI | Another example.
: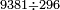 דמיון אחר
דמיון אחר | ||
| basic operations/division | 8213÷353 | ספר_המספר_/_אברהם_אבן_עזרא#ZaHA | Example: we wish to divide 8213 by 353.
: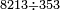 דמיון זה
דמיון זה | ||
| basic operations/division | 777777777÷9999 | ספר_המספר_/_אברהם_אבן_עזרא#qk7v | Example: we wish to divide 9 sevens by 4 nines.
: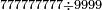 דמיון בקשנו לחלק חשבון ט' שביעיות על ד' תשיעיות
דמיון בקשנו לחלק חשבון ט' שביעיות על ד' תשיעיות | ||
| basic operations/division | 83521÷903 | ספר_המספר_/_אברהם_אבן_עזרא#PTa2 | Example: we wish to divide 83521 by 903.
: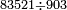 דמיון רצינו לחלק פ"ג אלפים ותקכ"א על תתק"ג
דמיון רצינו לחלק פ"ג אלפים ותקכ"א על תתק"ג | ||
| basic operations/division | 680402÷2009 | ספר_המספר_/_אברהם_אבן_עזרא#q1Q1 | Another example: we wish to divide 680402 by 2009.
: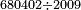 דמיון אחר נרצה לחלק תר"פ אלפים ות"ב על אלפים וט'
דמיון אחר נרצה לחלק תר"פ אלפים ות"ב על אלפים וט' | ||
| basic operations/division | 68921÷7053 | ספר_המספר_/_אברהם_אבן_עזרא#eXVh | Another example: we wish to divide 68 thousands, 9 hundred and 21 by 7 thousands and 53.
: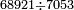 דמיון אחר בקשנו לחלק ס"ח אלפים וט' מאות וכ"א על ז' אלפים ונ"ג
דמיון אחר בקשנו לחלק ס"ח אלפים וט' מאות וכ"א על ז' אלפים ונ"ג | ||
| basic operations/division | 4032÷30 | ספר_המספר_/_אברהם_אבן_עזרא#wcHu | Example: we wish to divide 4 thousands and 32 by 30.
: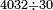 דמיון בקשנו לחלק ד' אלפים ול"ב על שלשים
דמיון בקשנו לחלק ד' אלפים ול"ב על שלשים | ||
| basic operations/division | 20000÷90 | ספר_המספר_/_אברהם_אבן_עזרא#dbse | Example: we wish to divide 20 thousands by 90.
: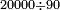 דמיון בקשנו לחלק כ' אלף על צ'
דמיון בקשנו לחלק כ' אלף על צ' | ||
| basic operations/division | ח.ל.ק./חלוקה | term | ספר_מעשה_חושב#HT8N | חלוקה | |
| basic operations/division | 7÷40 | Anonymous#zZxW | Such as 7 by 40.
::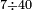 כגון ז' על מ'
כגון ז' על מ' | ||
| basic operations/division | ח.ל.ק./חלוק | term | ספר_ג'יבלי_אלמוקבאלא#K0ln | בחלוק ב | |
| basic operations/division | ח.ל.ק./חלוקה | definition | קצור_המספר#q2Wu | The essential act of separating the multiples is the fourth of the arithmetical [operations] called '''division''' ומפועל הנפש בהפריש הכפלים נמצא מין ד' והוא החלוקה | |
| basic operations/division | ח.ל.ק./חלוקה | term | קצור_המספר#59Qd | חלוקה | |
| basic operations/division | ח.ל.ק./חלוקה | term | קצור_המספר#EHvm | חלוקה | |
| basic operations/division | ח.ל.ק./חלק | term | ספר_מעשה_חושב#jalT | חלק מספר על מספר | |
| basic operations/division | ח.ל.ק./חלוקה | term | Anonymous#kTLd | חלוקת | |
| basic operations/division | 9000÷70 | ספר_המספר_/_אברהם_אבן_עזרא#ZS2i | Example: we wish to divide 9 thousands by 70.
: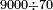 דמיון בקשנו לחלק ט' אלפים על ע'
דמיון בקשנו לחלק ט' אלפים על ע' | ||
| basic operations/division | ח.ל.ק./חלוק | term | Anonymous#09hR | חלוק | |
| basic operations/division | ח.ל.ק./חלק | term | ספר_מעשה_חושב#Omu6 | חלק | |
| basic operations/division | ח.ל.ק./החלק | term | חשבון_השטחים#jp7b | בהחלק | |
| basic operations/division | ח.ל.ק./חלוקה | term | חשבון_השטחים#RUlr | החלוקה | |
| basic operations/division | term | Arithmetic_Textbook_by_Meir_Shapira#M2Fj | חלוק | ||
| basic operations/division | ח.ל.ק./חלוק | term | קצור_המספר#07Sc | חלוק | |
| basic operations/division | ח.ל.ק./חלוק | term | Anonymous_text_from_Latin#IqRw | חילוק | |
| basic operations/division | term | Anonymous_text_from_Latin#evwb | דיוידירו | ||
| basic operations/division | ח.ל.ק./חלוק | term | קצור_המספר#5ty3 | חלוק | |
| basic operations/division | ח.ל.ק./מחלוקת | term | Anonymous#RJWg | מחלוקת זה על זה | |
| basic operations/division | ח.ל.ק./חלוק | term | עיר_סיחון#hOsK | חלוק | |
| basic operations/division | 2447235÷50335084800 | בר_נותן_טעם#khi4 | Example: we wish to divide 2447235 by 50335084800.
: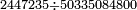 המשל רצינו לחלק 2447235 על 50335084800
המשל רצינו לחלק 2447235 על 50335084800 | ||
| basic operations/division | 70÷100 | בר_נותן_טעם#rm2i | If we wish to divide 70 by 100.
: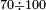 ולזה אם רצינו לחלק ע' על ק'
ולזה אם רצינו לחלק ע' על ק' | ||
| basic operations/division | 3123740520÷216 | בר_נותן_טעם#Z5A9 | We wish to divide 3123740520 by 216.
: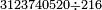 המשל רצינו לחלק 3123740520 על 216
המשל רצינו לחלק 3123740520 על 216 | ||
| basic operations/division | 4380408998÷46079 | בר_נותן_טעם#5u2A | We wish to divide 4380408998 by a smaller number, which is 46079.
: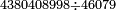 רצינו לחלק 4380408998 על מספר קטן ממנו והוא 46079
רצינו לחלק 4380408998 על מספר קטן ממנו והוא 46079 | ||
| basic operations/division | 140÷100 | בר_נותן_טעם#ftSN | We wish to divide 140 by 100.
: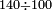 המשל רצינו לחלק ק"מ על ק'
המשל רצינו לחלק ק"מ על ק' | ||
| basic operations/division | 73÷240 | בר_נותן_טעם#Fs1g | Example: we wish to divide 73 by 240.
: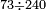 המשל רצינו לחלק 73 על 240
המשל רצינו לחלק 73 על 240 | ||
| basic operations/division | ח.ל.ק./מחלוקת | term | Anonymous#J9rH | מחלוקת | |
| basic operations/division | ח.ל.ק./חלוקה | term | Anonymous#PV7k | חלוקת | |
| basic operations/division | ח.ל.ק./חלוקה | term | חשבון_השטחים#HMM9 | חלוקת | |
| basic operations/division | ח.ל.ק./חלוקה | term | עיר_סיחון#gTvm | חלוקה | |
| basic operations/division | ח.ל.ק./חלוקה | term | עיר_סיחון#zfrI | חלקות | |
| simple fraction/division of fractions | (⅔·⅕)÷7 | ספר_החשבון_לאל_חצאר#3Kr3 | 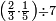 חלק שני שלישי חומש על שבעה
חלק שני שלישי חומש על שבעה | ||
| simple fraction/division of fractions | (⁷/₈·⅑)÷(3+½) | ספר_החשבון_לאל_חצאר#1AHL | 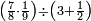 כשיאמר לך חלק שבעה שמיניות תשיעית על שלשה וחצי
כשיאמר לך חלק שבעה שמיניות תשיעית על שלשה וחצי | ||
| simple fraction/division of fractions | (⁹/₁₀·¹/₁₃)÷(6+⅜+⅓·⅛) | ספר_החשבון_לאל_חצאר#XwlM | ![\scriptstyle\left(\frac{9}{10}\sdot\frac{1}{13}\right)\div\left[6+\frac{3}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)\right]](/mediawiki/images/math/4/5/1/451bee3fb541e81d2eb989739ad43640.png) כשיאמר לך חלק תשע עשיריות חלק משלשה עשר על ששה ושלש שמיניות ושליש שמינית
כשיאמר לך חלק תשע עשיריות חלק משלשה עשר על ששה ושלש שמיניות ושליש שמינית | ||
| simple fraction/division of fractions | (⅗·⅐)÷(1+⅚+⅔) | ספר_החשבון_לאל_חצאר#dbH6 | 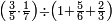 כשיאמר לך חלק שלשה חומשי השביעית על אחד וחמשה שתותים ושני שלישים
כשיאמר לך חלק שלשה חומשי השביעית על אחד וחמשה שתותים ושני שלישים | ||
| simple fraction/division of fractions | (⁵/₉·⅒)÷⅗ | ספר_החשבון_לאל_חצאר#xSYZ | 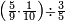 חלק חמש תשיעיות העשירית על שלשה חומשים
חלק חמש תשיעיות העשירית על שלשה חומשים | ||
| simple fraction/division of fractions | (¾·⅕)÷(³/₆+½·⅙) | ספר_החשבון_לאל_חצאר#2EzV | ![\scriptstyle\left(\frac{3}{4}\sdot\frac{1}{5}\right)\div\left[\frac{3}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]](/mediawiki/images/math/e/2/6/e2635a129664cacdecfb3781e889b1cc.png) כשיאמר לך חלק שלש רביעיות חמישית על שלשה שתותים וחצי שתות
כשיאמר לך חלק שלש רביעיות חמישית על שלשה שתותים וחצי שתות | ||
| simple fraction/division of fractions | (½·⅐)÷(¾+⅗) | ספר_החשבון_לאל_חצאר#y2Bj | 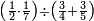 חלק חצי שביעית על שלש רביעיות ושלשה חומשים
חלק חצי שביעית על שלש רביעיות ושלשה חומשים | ||
| simple fraction/division of fractions | ⅗÷⅔ | מלאכת_המספר#Gm9m | Example: we wish to divide:
: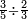 המשל נרצה לחלק
המשל נרצה לחלק | ||
| simple fraction/division of fractions | 50÷2½ | מלאכת_המספר#qEdH | Example: we wish to divide 50 by two and a half, like this:
: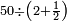 המשל שנרצה לחלק נ' בשניים וחצי כזה
המשל שנרצה לחלק נ' בשניים וחצי כזה | ||
| simple fraction/division of fractions | 3⅓÷4 | מלאכת_המספר#8ozH | We wish to divide 3 and one-third by 4, like this:
: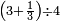 המשל רצינו לחלק ג' ושלישית בד' כזה
המשל רצינו לחלק ג' ושלישית בד' כזה | ||
| simple fraction/division of fractions | 4⅓÷⅚ | מלאכת_המספר#dTkL | Example: we wish to divide 4 and one-third by 5-sixths, like this:
: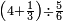 המשל נרצה לחלק ד' ושליש אחד בה' ששיות כזה
המשל נרצה לחלק ד' ושליש אחד בה' ששיות כזה | ||
| simple fraction/division of fractions | 12÷⁴/₉ | מלאכת_המספר#274g | As the one who wants to divide 12 by 4-ninths, like this:
: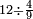 כמי שרוצה לחלק י"ב בד' תשיעיות כזה
כמי שרוצה לחלק י"ב בד' תשיעיות כזה | ||
| simple fraction/division of fractions | 9½÷3⅘ | מלאכת_המספר#JaOc | As the one who wants to divide 9 and a half by 3 and 4-fifths. Like this:
: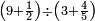 כמי שרוצה לחלק ט' וחצי בג' וד' חמישיות כזה
כמי שרוצה לחלק ט' וחצי בג' וד' חמישיות כזה | ||
| simple fraction/division of fractions | ⅔÷4½ | מלאכת_המספר#6eRM | As the one who wants to divide 2-thirds by 4 integers and a half.
: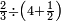 23vכמי שרוצה לחלק ב' שלישיות בד' שלמי' וחצי
23vכמי שרוצה לחלק ב' שלישיות בד' שלמי' וחצי | ||
| simple fraction/division of fractions | ⅜÷2 | מלאכת_המספר#dQmz | Suppose we wish to divide 3-eighths by 2 integers.
: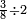 נניח שרצינו לחלק ג' שמיניות בב' שלמי'
נניח שרצינו לחלק ג' שמיניות בב' שלמי' | ||
| simple fraction/division of fractions | ¾÷⅔ | מלאכת_המספר#F0gV | As the one who wants to divide 3-quarters by 2-thirds.
: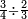 כמי שרוצה לחלק ג' רביעיות בב' שלישיות
כמי שרוצה לחלק ג' רביעיות בב' שלישיות | ||
| simple fraction/division of fractions | ¼÷2 | מלאכת_המספר#6C9g | As the one who wants to halve one-quarter, whose form is this:
: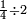 כמי שרוצה לחלק רביע אחד באמצע [שצורתו זאת]P1095 om.
כמי שרוצה לחלק רביע אחד באמצע [שצורתו זאת]P1095 om. | ||
| simple fraction/division of fractions | ⁶/₇÷⅖ | בר_נותן_טעם#KqBF | Example: if you are told in our first example: we wish to divide 6-sevenths by 2-fifths.
: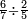 המשל אם אמרו לך במשלינו הראשון רצינו לחלק
המשל אם אמרו לך במשלינו הראשון רצינו לחלק | ||
| simple fraction/division of fractions | ⁶/₇÷⅖ | בר_נותן_טעם#WIah | Example: we wish to divide 6-sevenths by 2-fifths.
: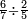 המשל רצינו לחלק ו' שביעיות על ב' חמישיות
המשל רצינו לחלק ו' שביעיות על ב' חמישיות | ||
| simple fraction/division of fractions | (¾+⅔·¼)÷(⁴/₉+⅚·⅑)·⅔ | בר_נותן_טעם#t3ba | We wish to divide three-quarters and 2-thirds of a quarter by 4-ninths and 5-sixths of a ninth of 2-thirds.
:![\scriptstyle\left[\frac{3}{4}+\left(\frac{2}{3}\sdot\frac{1}{4}\right)\right]\div\left[\left[\frac{4}{9}+\left(\frac{5}{6}\sdot\frac{1}{9}\right)\right]\sdot\frac{2}{3}\right]](/mediawiki/images/math/a/0/b/a0bf54c86fb59c4b365c62aeb651544d.png) רצינו לחלק שלש רביעיות וב' שלשיות רביעית על ד' תשיעיות וה' ששיות תשיעית מב' שלישיות
רצינו לחלק שלש רביעיות וב' שלשיות רביעית על ד' תשיעיות וה' ששיות תשיעית מב' שלישיות | ||
| simple fraction/division of fractions | (²/₇÷⅙)-(¾÷⅔) | ספר_המספר_/_אליהו_מזרחי#xuFi | If you wish to subtract the result of division of 3-quarters by 2-thirds from the result of division of 2-sevenths by one-sixth, without having to divide first, then subtract, but you get the right result all at once.
::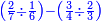 ואולם אם רצית לחסר היוצא מחלוק הג' רביעיות על הב' שלישיות מהיוצא מחלוק הב' שביעיות על הששית מבלתי שתצטרך לחלק ראשונה ואח"כ לחסרם אבל יצא לך הכל מתוקן בדרך א'
ואולם אם רצית לחסר היוצא מחלוק הג' רביעיות על הב' שלישיות מהיוצא מחלוק הב' שביעיות על הששית מבלתי שתצטרך לחלק ראשונה ואח"כ לחסרם אבל יצא לך הכל מתוקן בדרך א' | ||
| simple fraction/division of fractions | (¾-⅔)÷(²/₇-⅙) | ספר_המספר_/_אליהו_מזרחי#rxLg | If you wish to divide the remainder from subtraction of 2-thirds from 3-quarters by the remainder from subtraction of one-sixth from 2-sevenths, without having to subtract first then divide, but you get the right result all at once.
*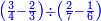 ואולם אם רצית לחלק הנשאר מחסור הב' שלישיות מהג' רביעיות על הנשאר מחסור הששית מהב' שביעיות מבלתי שתצטרך לחסר ראשונה ואח"כ לחלק אבל יצא לך הכל מתוקן בדרך אחת
ואולם אם רצית לחלק הנשאר מחסור הב' שלישיות מהג' רביעיות על הנשאר מחסור הששית מהב' שביעיות מבלתי שתצטרך לחסר ראשונה ואח"כ לחלק אבל יצא לך הכל מתוקן בדרך אחת | ||
| simple fraction/division of fractions | (¾÷⅔)×(²/₇÷⅙) | ספר_המספר_/_אליהו_מזרחי#S6kH | If you wish to multiply the result of division of 3-quarters by 2-thirds by the result of division of 2-sevenths by one-sixth, without having to divide first, then multiply, but you get the right result all at once.
*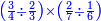 ואולם אם רצית להכות היוצא מחלוק הג' רביעיות על הב' שלישיות עם היוצא מחלוק הב' שביעיות על הששית מבלתי שתצטרך לחלק תחלה ואח"כ להכות אבל יצא לך הכל מתוקן בדרך אחת
ואולם אם רצית להכות היוצא מחלוק הג' רביעיות על הב' שלישיות עם היוצא מחלוק הב' שביעיות על הששית מבלתי שתצטרך לחלק תחלה ואח"כ להכות אבל יצא לך הכל מתוקן בדרך אחת | ||
| simple fraction/division of fractions | (⅔×¾)÷(²/₇×⅙) | ספר_המספר_/_אליהו_מזרחי#SxBq | If you wish to divide the product of 2-thirds by 3-quarters by the product of 2-sevenths by one-sixth, without having to multiply first, then divide, but you get the right result all at once.
::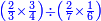 ואולם אם רצית לחלק העולה מהכאת הב' שלישיות עם הג' רביעיות על העולה מהכאת הב' שביעיות עם הששית מבלתי שתצטרך להכות תחלה ואח"כ לחלק אבל יצא לך הכל מתוקן בדרך אחת
ואולם אם רצית לחלק העולה מהכאת הב' שלישיות עם הג' רביעיות על העולה מהכאת הב' שביעיות עם הששית מבלתי שתצטרך להכות תחלה ואח"כ לחלק אבל יצא לך הכל מתוקן בדרך אחת | ||
| simple fraction/division of fractions | (¾÷⅔)+(²/₇÷⅙) | ספר_המספר_/_אליהו_מזרחי#69mH | If you wish to sum up the result of division of 3-quarters by 2-thirds with the result of division of 2-sevenths by one-sixth, without having to divide first, then sum up, but you get the right result all at once.
::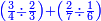 ואולם אם רצית לקבץ היוצא מחלוק הג' רביעיות על הב' שלישיות עם היוצא מחלוק הב' שביעיות על הששית מבלתי שתצטרך לחלק תחלה ואח"כ לקבץ אבל יצא לך הכל מתוקן בדרך אחת
ואולם אם רצית לקבץ היוצא מחלוק הג' רביעיות על הב' שלישיות עם היוצא מחלוק הב' שביעיות על הששית מבלתי שתצטרך לחלק תחלה ואח"כ לקבץ אבל יצא לך הכל מתוקן בדרך אחת | ||
| simple fraction/division of fractions | (⅔+¾)÷(²/₇+⅙) | ספר_המספר_/_אליהו_מזרחי#Yb86 | If you wish to divide, for instance, [the sum of] 2-thirds and 3-quarters by [the sum of] 2-sevenths and one-sixth, without having to sum up first, then to divide, but you get the right result all at once.
::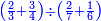 הנה אם רצית לחלק עד"מ הב' שלישיות והג' רביעיות יחד על הב' שביעיות וששית מבלתי שתצטרך לקבץ תחלה ואח"כ לחלק אבל הכל יצא לך מתוקן בדרך א'
הנה אם רצית לחלק עד"מ הב' שלישיות והג' רביעיות יחד על הב' שביעיות וששית מבלתי שתצטרך לקבץ תחלה ואח"כ לחלק אבל הכל יצא לך מתוקן בדרך א' | ||
| simple fraction/division of fractions | (²/₇÷⅙)-(¾÷⅔) | קצת_מענייני_חכמת_המספר#8JsO | If you wish to subtract the result of division of 3-quarters by 2-thirds from the result of division of 2-sevenths by [one-sixth], without having to divide first, then subtract.
::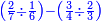 ואולם אם רצית לחסר היוצא מחלוק הג' רביעיו' על הב' שלישיו' מהיוצא מחילוק הב' שביעיו' על הו' מבלתי שתצטרך לחלק ראשונה ואח"כ לחסרם
ואולם אם רצית לחסר היוצא מחלוק הג' רביעיו' על הב' שלישיו' מהיוצא מחילוק הב' שביעיו' על הו' מבלתי שתצטרך לחלק ראשונה ואח"כ לחסרם | ||
| simple fraction/division of fractions | (¾-⅔)÷(²/₇-⅙) | קצת_מענייני_חכמת_המספר#C9my | If you wish to divide the remainder from subtraction of 2-thirds from 3-quarters by the remainder from subtraction of one-sixth from 2-sevenths, without having to subtract first then divide.
::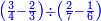 ואולם אם רצית לחלק הנשאר מחצור הב' שלישיות מג' רביעיות על הנשאר מחסור הששית מהב' שביעיות מבלתי שתצטרך לחסר ראשונה ואח"כ לחלק
ואולם אם רצית לחלק הנשאר מחצור הב' שלישיות מג' רביעיות על הנשאר מחסור הששית מהב' שביעיות מבלתי שתצטרך לחסר ראשונה ואח"כ לחלק | ||
| simple fraction/division of fractions | (¾÷⅔)×(²/₇÷⅙) | קצת_מענייני_חכמת_המספר#Rr95 | If you wish to multiply the result of division of 3-quarters by 2-thirds by the result of division of 2-sevenths by [one-sixth], without having to divide first, then multiply.
::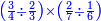 ואולם אם רצית להכות היוצא מחלוק הג' רביעיות על הב' שלישיות עם היוצא מחלוק הב' שביעית על הו' מבלתי שתצטרך לחלק תחלה ואח"כ להכות
ואולם אם רצית להכות היוצא מחלוק הג' רביעיות על הב' שלישיות עם היוצא מחלוק הב' שביעית על הו' מבלתי שתצטרך לחלק תחלה ואח"כ להכות | ||
| simple fraction/division of fractions | (⅔×¾)÷(²/₇×⅙) | קצת_מענייני_חכמת_המספר#TQ16 | If you wish to divide the product of 2-thirds by 3-quarters by the product of 2-sevenths by one-sixth, without having to multiply first, then divide.
::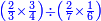 ואולם אם רצית לחלק העולה מהכאת הב' שלישיו' עם הג' רביעי' על העולה מהכאת הב' שביעיו' עם הששי' מבלתי שתצטר' להכות תחלה ואח"כ לחלק
ואולם אם רצית לחלק העולה מהכאת הב' שלישיו' עם הג' רביעי' על העולה מהכאת הב' שביעיו' עם הששי' מבלתי שתצטר' להכות תחלה ואח"כ לחלק | ||
| simple fraction/division of fractions | (¾÷⅔)+(²/₇÷⅙) | קצת_מענייני_חכמת_המספר#Vj8S | If you wish to sum up the result of division of 3-quarters by 2-thirds with the result of division of 2-sevenths by [one-sixth], without having to divide first, then sum up.
::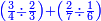 ואולם אם רצית לקבץ היוצא מחלוק הג' רביעיות על הב' שלישיות עם היוצא מחלוק הב' שביעיו' על הו' מבלתי שתצטרך לחלק תחלה ואח"כ לקבץ
ואולם אם רצית לקבץ היוצא מחלוק הג' רביעיות על הב' שלישיות עם היוצא מחלוק הב' שביעיו' על הו' מבלתי שתצטרך לחלק תחלה ואח"כ לקבץ | ||
| simple fraction/division of fractions | (⅔+¾)÷(²/₇+⅙) | קצת_מענייני_חכמת_המספר#8XVT | If you wish to divide the sum of 2-thirds and 3-quarters by the sum of two-sevenths and one-sixth, without having to sum up first, then to divide.
::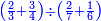 ואולם אם רצית לחלק קבוץ הב' שלישיות וג' רביעיו' על קבוץ שני שביעיות וששית מבלתי שתצטרך לקבץ תחלה ואח"כ לחל'
ואולם אם רצית לחלק קבוץ הב' שלישיות וג' רביעיו' על קבוץ שני שביעיות וששית מבלתי שתצטרך לקבץ תחלה ואח"כ לחל' | ||
| simple fraction/division of fractions | ¾÷⅖ | ספר_המספר_/_אליהו_מזרחי#B4Qv | Example: if you wish to divide 3-quarters by 2-fifths. המשל בזה אם רצית לחלק הג' רביעיות על הב' חמישיות | ||
| simple fraction/division of fractions | ¾÷⅖ | ספר_המספר_/_אליהו_מזרחי#n2Fz | Example: if you wish to divide 3-quarters by 2-fifths. המשל אם רצית לחלק ג' רביעיות על ב' חמשיות | ||
| simple fraction/division of fractions | ¾÷⅖ | קצת_מענייני_חכמת_המספר#GaRS | When you wish to divide 3-quarters by two-fifths.
::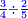 רצית לחלק ג' רביעיות על שני חמישיות
רצית לחלק ג' רביעיות על שני חמישיות | ||
| simple fraction/division of fractions | ⅜÷⅖ | ספר_חשבון#gX0D | If one says: divide 3-eighths by 2-fifths
: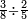 ואם יאמ' חלק ג' שמיניות על ב' חמשיות
ואם יאמ' חלק ג' שמיניות על ב' חמשיות | ||
| simple fraction/division of fractions | ⁶/₈÷²/₄ | קצור_המספר#7oEL | We wish to divide six-eighths by two-quarters.
: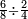 כיצד רצינו לחלק ששה שמיניות בשני רביעיות
כיצד רצינו לחלק ששה שמיניות בשני רביעיות | ||
| simple fraction/division of fractions | 4÷¾ | ספר_דיני_ממונות#p5E8 | 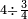 כאלו תאמר ד' על ג' רביעיות
כאלו תאמר ד' על ג' רביעיות | ||
| simple fraction/division of fractions | (4+½)÷(2+¼) | ספר_דיני_ממונות#3ekG | 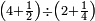 דמיון זה נרצה לחלק ד' וחצי על ב' ורביע
דמיון זה נרצה לחלק ד' וחצי על ב' ורביע | ||
| simple fraction/division of fractions | ⅝÷¼ | ספר_דיני_ממונות#urwn | 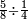 דמיון זה נרצה לחלק ה' שמיניות על רביעית א'
דמיון זה נרצה לחלק ה' שמיניות על רביעית א' | ||
| simple fraction/division of fractions | ⅜÷⅖ | ספר_יסודי_התבונה_ומגדל_האמונה#rzHD | As the one who says to you: divide 3 eighths by 2 fifths
: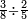 כגון האומר לך חלק ג' שמיניות על ב' חמישיות
כגון האומר לך חלק ג' שמיניות על ב' חמישיות | ||
| simple fraction/division of fractions | ⁷/₉÷²/₇ | ספר_המספר_/_אברהם_אבן_עזרא#wf6O | Example of fractions alone: divide 7 ninths by 2 sevenths.
: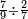 דמיון לנשברים לבדם חלק ז' תשיעיות על ב' שביעיות
דמיון לנשברים לבדם חלק ז' תשיעיות על ב' שביעיות | ||
| simple fraction/division of fractions | (4+⅔)÷(2+⅖) | עיר_סיחון#eAW6 | Example for dividing integers and fractions by integers and fractions: we wish to divide four integers and two thirds by two integers and two fifths.
: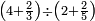 דמיון לחלק שלמים ושברים על שלמים ושברי'
דמיון לחלק שלמים ושברים על שלמים ושברי'רצינו לחלק ארבעה שלמים ושתי שלישיות על [שני]Vatican om. שלימים ושתי חמשיות | ||
| simple fraction/division of fractions | ⅔÷²/₇ | עיר_סיחון#VpDd | Example for dividing fractions by fractions: we wish to divide two thirds by two sevenths.
: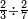 91vדמיון בחלוקת שברים על שברים
91vדמיון בחלוקת שברים על שבריםרצינו לחלק שני שלישיות על שני שביעיות | ||
| simple fraction/division of fractions | ⅓÷4 | ספר_החשבון_לאל_חצאר#y9to | Example: divide a third dirham between four people.
: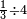 המשל בו חלק שליש דרהם על ארבעה אנשים
המשל בו חלק שליש דרהם על ארבעה אנשים | ||
| simple fraction/division of fractions | ⅚÷8 | ספר_החשבון_לאל_חצאר#tDid | 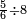 כשיאמר לך חלק חמשה שתותים על שמנה
כשיאמר לך חלק חמשה שתותים על שמנה | ||
| simple fraction/division of fractions | ⁵/₁₁÷7 | ספר_החשבון_לאל_חצאר#YwG4 | 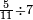 ואם יאמר לך חלק חמשה חלקים מאחד עשר על שבעה
ואם יאמר לך חלק חמשה חלקים מאחד עשר על שבעה | ||
| simple fraction/division of fractions | ⁷/₉÷17 | ספר_החשבון_לאל_חצאר#5uEQ | 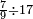 המשל בו חלק שבע תשיעייות על שבעה עשר
המשל בו חלק שבע תשיעייות על שבעה עשר | ||
| simple fraction/division of fractions | (⅚+½·⅙)÷5 | ספר_החשבון_לאל_חצאר#oUQe | ![\scriptstyle\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\div5](/mediawiki/images/math/f/3/5/f35247a33fdf18d5e069da1dd98835fe.png) המשל בו חלק חמשה שתותים וחצי שתות על חמשה
המשל בו חלק חמשה שתותים וחצי שתות על חמשה | ||
| simple fraction/division of fractions | (¹⁰/₁₁+⅗·¹/₁₁)÷63 | ספר_החשבון_לאל_חצאר#xGql | ![\scriptstyle\left[\frac{10}{11}+\left(\frac{3}{5}\sdot\frac{1}{11}\right)\right]\div63](/mediawiki/images/math/9/b/0/9b0959a66fde808099c9dfefd633a000.png) ואם אמר חלק עשרה חלקים מאחד עשר ושלש' חומשי החלק מאחד עשר על שלשה ושישים
ואם אמר חלק עשרה חלקים מאחד עשר ושלש' חומשי החלק מאחד עשר על שלשה ושישים | ||
| simple fraction/division of fractions | (⅗+⁷/₈)÷6 | ספר_החשבון_לאל_חצאר#E5mo | 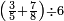 כשיאמר לך חלק שלשה חומשים ושבע שמינייות על ששה
כשיאמר לך חלק שלשה חומשים ושבע שמינייות על ששה | ||
| simple fraction/division of fractions | ⁶/₇÷(5+½) | ספר_החשבון_לאל_חצאר#Uvo0 | 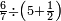 חלק ששה שביעייות על חמשה וחצי
חלק ששה שביעייות על חמשה וחצי | ||
| simple fraction/division of fractions | 1÷(3+⅓) | ספר_החשבון_לאל_חצאר#RYfW | 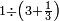 דמיון זה חלק אחד על שלשה ושליש
דמיון זה חלק אחד על שלשה ושליש | ||
| simple fraction/division of fractions | 1÷(6+¼) | ספר_החשבון_לאל_חצאר#Tklv | 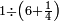 ודמיון זה חלק אחד על ששה ורביע
ודמיון זה חלק אחד על ששה ורביע | ||
| simple fraction/division of fractions | ¹⁰/₁₁÷(6+⅔) | ספר_החשבון_לאל_חצאר#FN6q | 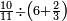 חלק עשרה חלקים מאחד עשר על ששה ושני שלישים
חלק עשרה חלקים מאחד עשר על ששה ושני שלישים | ||
| simple fraction/division of fractions | ⅘÷(3+⁶/₇+½·⅐) | ספר_החשבון_לאל_חצאר#px9K | ![\scriptstyle\frac{4}{5}\div\left[3+\frac{6}{7}+\left(\frac{1}{2}\sdot\frac{1}{7}\right)\right]](/mediawiki/images/math/5/7/b/57b7577cb03e6f202ca23aa4cd5ee3c2.png) כשיאמר לך חלק ארבעה חומשים על שלשה ושש שביעיות וחצי שביעית
כשיאמר לך חלק ארבעה חומשים על שלשה ושש שביעיות וחצי שביעית | ||
| simple fraction/division of fractions | ⁶/₁₃÷(4+⅓+⁶/₁₁) | ספר_החשבון_לאל_חצאר#dj09 | 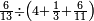 כשיאמר לך חלק ששה חלקים משלשה עשר על ארבעה ושליש וששה חלקים מאחד עשר
כשיאמר לך חלק ששה חלקים משלשה עשר על ארבעה ושליש וששה חלקים מאחד עשר | ||
| simple fraction/division of fractions | (⁷/₈+⅓·⅛)÷(3+½) | ספר_החשבון_לאל_חצאר#lSPB | ![\scriptstyle\left[\frac{7}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)\right]\div\left(3+\frac{1}{2}\right)](/mediawiki/images/math/a/3/1/a31d77578b5729c94a448c48170007e1.png) כשיאמר לך חלק שבע שמיניות ושליש שמינית על שלשה וחצי
כשיאמר לך חלק שבע שמיניות ושליש שמינית על שלשה וחצי | ||
| simple fraction/division of fractions | 2÷(5+½) | ספר_החשבון_לאל_חצאר#5qLA | 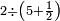 כשיאמר לך חלק שנים על חמשה וחצי
כשיאמר לך חלק שנים על חמשה וחצי | ||
| simple fraction/division of fractions | (6+¼)÷(8+⅓) | ספר_החשבון_לאל_חצאר#TrmN | 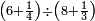 כשיאמר לך חלק ששה ורביעית על שמונה ושליש
כשיאמר לך חלק ששה ורביעית על שמונה ושליש | ||
| simple fraction/division of fractions | ⅓÷¾ | ספר_החשבון_לאל_חצאר#SWXt | 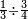 כשיאמר לך חלק שליש על שלשה רביעים
כשיאמר לך חלק שליש על שלשה רביעים | ||
| simple fraction/division of fractions | ⅔÷¾ | ספר_החשבון_לאל_חצאר#QsiS | 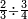 וכן אילו אמר שני שליש משלשה רביעים
וכן אילו אמר שני שליש משלשה רביעים | ||
| simple fraction/division of fractions | ⅗÷⁷/₉ | ספר_החשבון_לאל_חצאר#oavz | 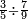 ואם אמר חלק שלשה חומשים על שבע תשיעיות
ואם אמר חלק שלשה חומשים על שבע תשיעיות | ||
| simple fraction/division of fractions | ²/₁₃÷⁹/₁₀ | ספר_החשבון_לאל_חצאר#d7JZ | 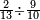 ואלו אמר לך חלק שני חלקים משלשה עשר על תשע עשיריות
ואלו אמר לך חלק שני חלקים משלשה עשר על תשע עשיריות | ||
| simple fraction/division of fractions | ⁵/₁₁÷⁹/₁₇ | ספר_החשבון_לאל_חצאר#KnrU | 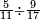 ואם אמר חלק חמשה חלקים מאחד עשר על תשעה חלקים משבעה עשר
ואם אמר חלק חמשה חלקים מאחד עשר על תשעה חלקים משבעה עשר | ||
| simple fraction/division of fractions | (²/₈+½·⅛)÷⁹/₁₀ | ספר_החשבון_לאל_חצאר#QbO0 | ![\scriptstyle\left[\frac{2}{8}+\left(\frac{1}{2}\sdot\frac{1}{8}\right)\right]\div\frac{9}{10}](/mediawiki/images/math/3/b/0/3b05212d5998323229d3e3d7d2023235.png) כשיאמר לך חלק שתי שמיניות וחצי שמינית על תשע עשרות
כשיאמר לך חלק שתי שמיניות וחצי שמינית על תשע עשרות | ||
| simple fraction/division of fractions | (⅓+⅐)÷¹⁰/₁₁ | ספר_החשבון_לאל_חצאר#wObx | 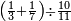 חלק שליש ושביעית על עשרה חלקים מאחד עשר
חלק שליש ושביעית על עשרה חלקים מאחד עשר | ||
| simple fraction/division of fractions | ⅔÷(⁹/₁₀+⅝·⅒) | ספר_החשבון_לאל_חצאר#Z46I | ![\scriptstyle\frac{2}{3}\div\left[\frac{9}{10}+\left(\frac{5}{8}\sdot\frac{1}{10}\right)\right]](/mediawiki/images/math/d/d/2/dd244e384f4422a279cba9537b8b864b.png) חלק שני שלישים על תשע עשרות וחמש שמיניות העשירית
חלק שני שלישים על תשע עשרות וחמש שמיניות העשירית | ||
| simple fraction/division of fractions | ⁷/₉÷(¾+⁷/₈) | ספר_החשבון_לאל_חצאר#Cq7e | 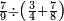 חלק שבע תשיעיות על שלשה רביעיות ושבע שמיניות
חלק שבע תשיעיות על שלשה רביעיות ושבע שמיניות | ||
| simple fraction/division of fractions | (⁴/₉+½·⅑)÷(⁷/₈+⅓·⅛) | ספר_החשבון_לאל_חצאר#CV2f | ![\scriptstyle\left[\frac{4}{9}+\left(\frac{1}{2}\sdot\frac{1}{9}\right)\right]\div\left[\frac{7}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)\right]](/mediawiki/images/math/8/a/1/8a111107fc608a5ae9f5d99f4f2ec182.png) חלק ארבע תשיעיות וחצי תשיעית על שבע שמיניות ושליש שמינית
חלק ארבע תשיעיות וחצי תשיעית על שבע שמיניות ושליש שמינית | ||
| simple fraction/division of fractions | (⅔+⅗)÷(⁹/₁₀+¹⁰/₁₁) | ספר_החשבון_לאל_חצאר#jJLl | 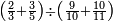 חלק שני שלישים ושלשה חומשים על תשע עשיריות ועשרה חלקים מאחד עשר
חלק שני שלישים ושלשה חומשים על תשע עשיריות ועשרה חלקים מאחד עשר | ||
| extraction of root/division of roots | 12÷√4 | ספר_דיני_ממונות#RTqg | I.e. if you divide 12 by a root of 4.
::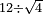 ר"ל אם תחלק י"ב עם שרש ד'
ר"ל אם תחלק י"ב עם שרש ד' | ||
| extraction of root/division of roots | 19÷(2+√16) | ספר_ג'יבלי_אלמוקבאלא#6lxt | Example: suppose you wish to divide 19 by 2 plus a root of 16.
: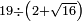 והמשל בזה נניח שרצית לחלק י"ט בב' ושרש י"ו
והמשל בזה נניח שרצית לחלק י"ט בב' ושרש י"ו | ||
| extraction of root/division of roots | √36÷√9 | ספר_המספר_/_אליהו_מזרחי#D7ep | The example: if you want to know the result of division of a root of 36 by a root of 9, without knowing their roots. המשל בזה אם רצית לדעת היוצא מחלוק שרש הל"ו על שרש הט' מבלתי שנדע שרשם | ||
| extraction of root/division of roots | 4÷√9 | ספר_ג'יבלי_אלמוקבאלא#o4Lu | Suppose you wish to divide 4 by a root of 9.
: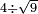 ונניח שרצית לחלק ד' בשרש ט'
ונניח שרצית לחלק ד' בשרש ט' | ||
| extraction of root/division of roots | √6÷³√10 | ספר_האלזיברא#x86i | 22) If you wish to divide the square root of 6 by the cube root of 10.
:![\scriptstyle\sqrt{6}\div\sqrt[3]{10}](/mediawiki/images/math/9/a/0/9a0da3d2826409356d860ea699ebe6c3.png) כב ואם רצית לחלק שרש מרבע ו' בשרש מעקב י'
כב ואם רצית לחלק שרש מרבע ו' בשרש מעקב י' | ||
| extraction of root/division of roots | √30÷√6 | ספר_האלזיברא#4Ayu | 15) If you wish to divide a root of 30 by a root of 6.
: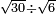 טו ואם רצית לחלק שרש ל' על שרש ו'
טו ואם רצית לחלק שרש ל' על שרש ו' | ||
| extraction of root/division of roots | 70÷(√4+√9+√16+√25) | ספר_ג'יבלי_אלמוקבאלא#W9ga | Suppose you wish to divide 70 by the sum of a root of 4, a root of 9, a root of 16, and a root of 25, as if the roots were inexpressible.
: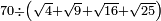 נניח שרצית לחלק ע' בשרש ד' ובשרש ט' ובשרש י"ו ובשרש כ"ה מחוברי' באופן כאלו היו שרשי' בלתי מדברי'
נניח שרצית לחלק ע' בשרש ד' ובשרש ט' ובשרש י"ו ובשרש כ"ה מחוברי' באופן כאלו היו שרשי' בלתי מדברי' | ||
| extraction of root/division of roots | 70÷(√4+√9+√16+√25) | ספר_ג'יבלי_אלמוקבאלא#cUYO | Suppose you wish to divide 70 by the sum of a root of 4, a root of 9, a root of 16, and a root of 25, as if these roots were inexpressible.
: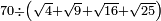 ונניח שרצית לחלק ע' בשרש ד' ובשרש ט' ובשרש י"ו ובשרש כ"ה מחוברי' כלם יחד באופן כאלו היו השרשי' האלו בלתי מדוברי'
ונניח שרצית לחלק ע' בשרש ד' ובשרש ט' ובשרש י"ו ובשרש כ"ה מחוברי' כלם יחד באופן כאלו היו השרשי' האלו בלתי מדוברי' | ||
| extraction of root/division of roots | 20÷(4-√9) | ספר_ג'יבלי_אלמוקבאלא#dg3U | Suppose you wish to divide 20 by 4 minus a root of 9.
: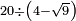 נניח שבקשת לחלק כ' בד' פחות שרש ט'
נניח שבקשת לחלק כ' בד' פחות שרש ט' | ||
| extraction of root/division of roots | 8÷(3+√4) | ספר_ג'יבלי_אלמוקבאלא#qqDu | Suppose you wish to divide 8 by 3 plus a root of 4.
: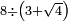 נניח שרצית לחלוק ח' בג' ושרש ד'
נניח שרצית לחלוק ח' בג' ושרש ד' | ||
| extraction of root/division of roots | (5+√16)÷3 | ספר_ג'יבלי_אלמוקבאלא#snlR | Suppose you wish to divide 5 plus a root of 16 by 3.
: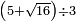 נניח שרצית לחלק ה' ושרש י"ו בג'
נניח שרצית לחלק ה' ושרש י"ו בג' | ||
| extraction of root/division of roots | 5√9÷2√36 | ספר_המספר_/_אליהו_מזרחי#DGAY | The example: if you want to know the result of division of 5 times the root of 9 by 2 times the root of 36. המשל בזה אם רצית לדעת היוצא מחלוק העולה מה' כפלי שרש הט' על העולה מב' כפלי שרש הל"ו | ||
| extraction of root/division of roots | √64÷(√8-√4) | ספר_האלזיברא#pY8l | 19) If you wish to divide a root of 64 by a root of 8 minus a root of 4.
: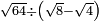 יט ואם רצית לחלק שרש ס"ד על שרש ח' פחות שרש ד'
יט ואם רצית לחלק שרש ס"ד על שרש ח' פחות שרש ד' | ||
| extraction of root/division of roots | √10÷√2 | תחבולות_המספר#pYYI | If it is said: divide ten by a root of two.
: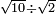 ואם אמרו תחלק שרש עשרה על שרש שנים
ואם אמרו תחלק שרש עשרה על שרש שנים | ||
| extraction of root/division of roots | 36÷(√4+√9+√16) | ספר_ג'יבלי_אלמוקבאלא#UR1i | Suppose you wish to divide 36 by a root of 4, a root of 9, and a root of 16.
: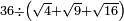 ונניח שרצית לחלק ל"ו בשרש ד' ובשרש ט' ובשרש י"ו בדבר
ונניח שרצית לחלק ל"ו בשרש ד' ובשרש ט' ובשרש י"ו בדבר | ||
| extraction of root/division of roots | √64÷(√8+√4) | ספר_האלזיברא#fOaX | 20) If you wish to divide the root of 64 by the root of 8 plus the root of 4.
: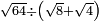 כ וכן אם רצית לחלק שרש ס"ד על שרש ח' ושרש ד' יותר
כ וכן אם רצית לחלק שרש ס"ד על שרש ח' ושרש ד' יותר | ||
| extraction of root/division of roots | ⅔√36÷⅔√9 | ספר_המספר_/_אליהו_מזרחי#sMby | The example: if you want to know the result of division of 2-thirds of the root of 36 by 2-thirds of the root of 9, without knowing their root. המשל בזה אם רצית לדעת היוצא מחלוק ב' שלישיות שרש הל"ו על ב' שלישיות שרש הט' מבלתי שנדע שרשם | ||
| extraction of root/division of roots | (2×√20)÷(3×√6) | תחבולות_המספר#sCCw | If you are told: divide two roots of twenty by three roots of six.
: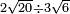 ואם אמר לך תחלק שנים שרשים מעשרים על שרשים שלשה מששה
ואם אמר לך תחלק שנים שרשים מעשרים על שרשים שלשה מששה | ||
| extraction of root/division of roots | (19+√25)÷(5+√9) | ספר_ג'יבלי_אלמוקבאלא#B0XU | Suppose you wish to divide 19 and a root of 25 by 5 and a root of 9.
: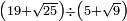
| ||
| extraction of root/division of roots | √9÷√4 | תחבולות_המספר#1Gu9 | He said: if you are told: divide the root of nine by the root of four.
: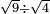 305vאמ' ואם יאמרו לך תחלק שרש תשעה על שרש ארבעה
305vאמ' ואם יאמרו לך תחלק שרש תשעה על שרש ארבעה | ||
| extraction of root/division of roots | ³√18÷⁴√10 | ספר_האלזיברא#gW75 | 23) If you wish to divide the cube root of 5 by the square root of 8.
:![\scriptstyle\sqrt[3]{5}\div\sqrt{\sqrt{8}}](/mediawiki/images/math/7/c/c/7ccb0df6503c7cea5808fd6aeaf22fe9.png) כג ואם רצית לחלק שרש מעקב ה' בשרש שרש מרבע ח'
כג ואם רצית לחלק שרש מעקב ה' בשרש שרש מרבע ח' | ||
| extraction of root/division of roots | √9÷√4 | חשבון_השטחים#AVTk | 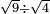 ואם יאמרו תחלק שורש תשעה על שורש ארבעה
ואם יאמרו תחלק שורש תשעה על שורש ארבעה | ||
| extraction of root/division of roots | 20÷√10 | ספר_האלזיברא#QIDd | 16) If you wish to divide 20 by a root of 10.
: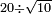 יו ואם רצית לחלק מספר כ' על שרש י'
יו ואם רצית לחלק מספר כ' על שרש י' | ||
| extraction of root/division of roots | (2×√20)÷(3×√6) | חשבון_השטחים#cvXn | 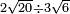 ואם יאמרו לך תחלק שנים שרשים מעשרים על שלשה שרשים מששה
ואם יאמרו לך תחלק שנים שרשים מעשרים על שלשה שרשים מששה | ||
| extraction of root/division of roots | √10÷√2 | חשבון_השטחים#qjLW | 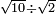 ואם יאמרו תחלק שורש עשרה על שורש שנים
ואם יאמרו תחלק שורש עשרה על שורש שנים | ||
| extraction of root/division of roots | √4÷√9 | ספר_ג'יבלי_אלמוקבאלא#i3Y0 | Suppose you wish to divide a root of 4 by a root of 9.
: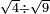 נניח שרצית לחלק שרש ד' בשרש ט'
נניח שרצית לחלק שרש ד' בשרש ט' | ||
| division/divisor | ח.ל.ק./מחלק | term | תחבולות_המספר#yKxa | מחלק | |
| division/divisor | ח.ל.ק./מחולק עליו | term | אגרת_המספר#Lesu | המספר המחולק עליו | |
| division/divisor | ח.ל.ק./חלק | term | Anonymous#Go1q | חלק | |
| division/divisor | י.ר.ה./מורה | term | בר_נותן_טעם#P3U8 | מורה | |
| division/divisor | ח.ל.ק./מחולק עליו | term | Anonymous#JrfP | המחולק עליו | |
| division/divisor | י.ר.ה./מורה | term | בר_נותן_טעם#gIva | מורים | |
| division/divisor | ח.ל.ק./נחלק | term | ספר_יסודי_התבונה_ומגדל_האמונה#XbXc | נחלק עליו | |
| division/divisor | ח.ל.ק./מחלק | term | חשבון_השטחים#mAIU | המספר המחלק | |
| division/divisor | מ.נ.י./מונה | term | קצור_המספר#KxS2 | המונה ל | |
| division/divisor | מ.נ.י./מונה | term | קצור_המספר#wCQT | מונה | |
| division/divisor | ח.ל.ק./נחלק | term | קצור_המספר#2rny | הנחלק עליו | |
| division/divisor | ח.ל.ק./מחולק עליו | term | ספר_יסודי_התבונה_ומגדל_האמונה#cqC1 | המחולק עליו | |
| division/divisor | ח.ל.ק./מחלק | term | ספר_ג'יבלי_אלמוקבאלא#PG8h | המחלק | |
| division/divisor | ח.ל.ק./התחלק | term | ספר_האלזיברא#1fXl | החלק אשר אליו יתחלק | |
| division/divisor | ח.ל.ק./מחלק | term | ספר_ג'יבלי_אלמוקבאלא#lfgo | מחלק | |
| division/divisor | term | ספר_האלזיברא#qwTn | מספר אשר אליו יתחלק | ||
| division/divisor | ח.ל.ק./מחלק | term | תחבולות_המספר#S2en | המספר המחלק | |
| division/divisor | ח.ל.ק./נחלק | term | Anonymous#pHVT | הנחלק עליו | |
| division/divisor | ח.ל.ק./חולק | term | Anonymous_text_from_Latin#ERvy | החולק | |
| division/divisor | ח.ל.ק./מחלק | term | חשבון_השטחים#ai4t | המחלק | |
| division/divisor | י.ר.ה./מורה | term | בר_נותן_טעם#TmQF | מורה | |
| division/divisor | term | בר_נותן_טעם#FDOf | אשר נחלק עליו | ||
| division/divisor | י.ר.ה./מורה | term | בר_נותן_טעם#Qr95 | מורים | |
| division/divisor | ח.ל.ק./חלוקה | term | ספר_ג'יבלי_אלמוקבאלא#eN1F | חלוקות | |
| division/divisor | ח.ל.ק./מחלק | term | קצת_מענייני_חכמת_המספר#XDL2 | מחלק | |
| division/divisor | ח.ל.ק./מחלק | term | מלאכת_המספר#pwCG | מחלק | |
| division/divisor | ח.ל.ק./מחלק | term | מלאכת_המספר#WxiF | מחלק | |
| division/divisor | ח.ל.ק./מחלק | term | תחבולות_המספר#qzrP | המחלק | |
| doubling/double | כ.פ.ל./כפל | term | עיר_סיחון#UCaJ | כפל | |
| doubling/double | כ.פ.ל./כפל | term | עיר_סיחון#5j57 | כפל | |
| doubling/double | כ.פ.ל./נכפל | term | מלאכת_המספר#TqFZ | נכפלים | |
| doubling/double | כ.פ.ל./כפל | term | מלאכת_המספר#5IOg | כפל | |
| doubling/double | כ.פ.ל./כפל | term | קצור_המספר#7ThA | כפלו | |
| doubling/double | כ.פ.ל./כפל | term | ספר_מעשה_חושב#DZhd | כפל | |
| doubling/double | term | ספר_ג'יבלי_אלמוקבאלא#QOoq | פי שנים מ | ||
| doubling/double | כ.פ.ל./כפל | term | קצור_המספר#tJQe | כפל | |
| doubling/double | כ.פ.ל./כפל | term | ספר_ג'יבלי_אלמוקבאלא#HqHc | כפל ה | |
| doubling/double | כ.פ.ל./נכפל | term | מלאכת_המספר#Sg4E | נכפלי' | |
| doubling/double | term | ספר_האלזיברא#VVnt | פעמים | ||
| doubling/double | כ.פ.ל./כפל | term | תחבולות_המספר#J8oI | כפל | |
| doubling/double | כ.פ.ל./כפל | term | חשבון_השטחים#RBru | כפל | |
| doubling/double | term | ספר_האלזיברא#hCqO | שני דמיוני | ||
| doubling/double | כ.פ.ל./כפל | term | ספר_ג'יבלי_אלמוקבאלא#vbVH | כפלו | |
| doubling/double | כ.פ.ל./כפל | term | ספר_האלזיברא#eXTO | הכפל מ | |
| doubling/double | term | חשבון_השטחים#piMO | שני דמיוניו | ||
| false position/double false position | א.ז.נ./מאזנים | term | אגרת_המספר#0ZtD | מאזנים | |
| false position/double false position | נ.ו.ח./מונח כוזב | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#bDQQ | ב' מונחים כוזבים | |
| false position/double false position | נ.ו.ח./מונח כוזב | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#WMXD | ב' מונחי כוזבים | |
| false position/double false position | נ.ג.ד./דרך המתנגדים | term | מלאכת_המספר#txU9 | בדרך המתנגדים | |
| false position/double false position | ח.פ.נ./חפנים | term | ספר_החשבון_לאל_חצאר#RaNA | חפנים | |
| false position/double false position | נ.ג.ד./דרכי המתנגדות | term | מלאכת_המספר#W87t | דרכי המתנגדות | |
| basic operations/doubling | 2·974537 | Takmila_fi_al-Hisāb_-_Arabic_in_Hebrew_Characters#v5GK | Example: we wish to double 974537.
: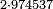 מת'אלה ארדנא תצ'עיף תסעמאיה וארבעה וסבעין אלפא וכמס מאיה וסבעה ותלתין
מת'אלה ארדנא תצ'עיף תסעמאיה וארבעה וסבעין אלפא וכמס מאיה וסבעה ותלתין | ||
| basic operations/doubling | כ.פ.ל./הכפלה | term | תחבולות_המספר#FDYc | הכפלה | |
| basic operations/doubling | 2·5372 | מלאכת_המספר#yLqy | As can be seen in this diagram:
::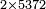 כפי הנראה בצורה הזאת
כפי הנראה בצורה הזאת | ||
| basic operations/doubling | כ.פ.ל./הכפלה | term | חשבון_השטחים#B5ey | הכפלה | |
| basic operations/doubling | כ.פ.ל./כפול | term | מלאכת_המספר#XTTg | כפול | |
| basic operations/doubling | כ.פ.ל./הכפלה | term | תחבולות_המספר#h7Ad | הכפלת | |
| basic operations/doubling | כ.פ.ל./כפול | definition | מלאכת_המספר#jEGw | Doubling is summing any two numbers that are equal. כפול הוא קבוץ איזה ב' מספרים שיהיו שוים | |
| basic operations/doubling | term | ספר_עיון_העקרים_לחשבון_ההנדיים#F9NX | תצעיף | ||
| basic operations/doubling | ד.מ.י./דומה | term | ספר_עיון_העקרים_לחשבון_ההנדיים#dpia | דומה | |
| basic operations/doubling | כ.פ.ל./כפל | term | תחבולות_המספר#j4A9 | כפל | |
| basic operations/doubling | כ.פ.ל./כפול | term | מלאכת_המספר#64kf | כפול | |
| basic operations/doubling | 2·95386349 | Takmila_fi_al-Hisāb_-_Arabic_in_Hebrew_Characters#1JUd | Example: if we wish to double 95386349. מת'אלה אן כאן ארדנא תצ'עיף כמסה ותסעין אלף אלף ותלת מאיה וסתה ותמנין אלפא ותלאתמ מאיה ותסעה וארבעין | ||
| basic operations/doubling | 2·795347 | Takmila_fi_al-Hisāb_-_Arabic_in_Hebrew_Characters#lrw1 | Example: we wish to double 795347.
: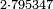 מתאלה ארדנא תצ'עיף סבע מאיה כמסה ותסעין אלף ותלת מאיה וסבעה וארבעין
מתאלה ארדנא תצ'עיף סבע מאיה כמסה ותסעין אלף ותלת מאיה וסבעה וארבעין | ||
| numeral/dust letters | א.ב.ק./אבק | term | ספר_החשבון_לאל_חצאר#Iz4E | אותיות האבק | |
| numeral/dust letters | א.ב.ק./אבק | term | ספר_החשבון_לאל_חצאר#zkhe | באבק | |
| numeral/dust letters | א.ב.ק./אבק | term | ספר_החשבון_לאל_חצאר#dc62 | צורות האבק | |
| numeral/dust letters | א.ב.ק./אבק | term | ספר_החשבון_לאל_חצאר#8Uzb | תמונות האבק | |
| decimal rank/empty rank | ע.ל.ה./מעלה חלקה | term | בר_נותן_טעם#6jNM | מעלות חלקות מהמספר | |
| decimal rank/empty rank | ע.ל.ה./מעלה חלקה | term | בר_נותן_טעם#STuT | מעלה חלקה ממספר | |
| calculation/equal | ש.ו.ה./שוה | term | תחבולות_המספר#QJYS | שוה ל | |
| calculation/equal | ש.ו.ה./שוה | term | מלאכת_המספר#xvUp | שוה | |
| calculation/equal | ש.ו.ה./שוה | term | חשבון_השטחים#KCUM | השוה | |
| calculation/equal | ש.ו.ה./שוה | term | ספר_ג'יבלי_אלמוקבאלא#oP1J | שוים זה לזה | |
| calculation/equal | ש.ו.ה./שוה | term | ספר_ג'יבלי_אלמוקבאלא#pUat | שוות זו לזו | |
| calculation/equal | ש.ו.ה./שוה | term | ספר_ג'יבלי_אלמוקבאלא#3Nbo | השוה לו | |
| calculation/equal | ש.ו.ה./שוה | term | חשבון_השטחים#IV26 | שוים | |
| calculation/equal | ש.ו.ה./שוה | term | תחבולות_המספר#Shsn | שוים ל | |
| calculation/equal | ש.ו.ה./שוה | term | קצור_המספר#epow | שוה | |
| calculation/equal | ש.ו.ה./שוה | term | קצור_המספר#FsNi | שוה ל | |
| false position/error of a false position | ח.ט.א./חטא | term | אגרת_המספר#WpQI | החטא | |
| false position/error of a false position | ט.ע.י./טעות | term | ספר_החשבון_לאל_חצאר#dRbe | טעות | |
| false position/error of a false position | ט.ע.י./טעות | term | ספר_החשבון_לאל_חצאר#RhBw | טעיות | |
| false position/error of a false position | ח.ט.א./חטא | term | אגרת_המספר#F2fj | החטאים | |
| calculation/exact | ת.ק.נ./מתוקן | term | ספר_המספר_/_אליהו_מזרחי#mdOc | מתוקן | |
| calculation/exact | ת.ק.נ./מתוקן | term | קצת_מענייני_חכמת_המספר#i968 | מתוקן | |
| calculation/exact | ת.ק.נ./מתוקן | term | Anonymous#i0rV | השרש שאיננו מתוקן | |
| excess/exceeding | ע.ד.פ./עודף | term | Anonymous#7f8a | עודפים על | |
| excess/exceeding | ע.ד.פ./עודף | term | Anonymous#YLfG | עודף | |
| excess/exceeding | י.ס.פ./מוסיף | term | ספר_מעשה_חושב#R3mj | המוסיף עליו | |
| excess/exceeding | ע.ד.פ./עודף | term | ספר_ציפרא#VP6t | עודף על | |
| excess/exceeding | ע.ד.פ./מעדיף | term | חשבון_השטחים#YtIi | המעדיף | |
| calculation/excess | י.ת.ר./מותר | term | האנציקלופדיה_של_אבו_אלצלת#TRPO | מותרות | |
| calculation/excess | ע.ד.פ./עודף | term | קצור_המספר#AcJ8 | עודף על | |
| calculation/excess | ע.ד.פ./עודף | term | קצור_המספר#yiRK | עודף מ | |
| calculation/excess | י.ס.פ./תוספת | term | ספר_הכללים_במספר#Vj4x | תוספת | |
| calculation/excess | י.ת.ר./מותר | term | ספר_האלזיברא#NrRw | מותר | |
| calculation/excess | ע.ד.פ./עודף | term | חשבון_השטחים#Tr1I | העודף | |
| calculation/excess | ש.ל.מ./תשלום | term | חשבון_השטחים#Eme3 | תשלום | |
| calculation/excess | י.ת.ר./יתרון | term | חשבון_השטחים#kjZl | היתרון | |
| calculation/excess | י.ס.פ./תוספת | term | Anonymous#Ku0r | תוספת | |
| calculation/excess | י.ת.ר./מותר | term | האנציקלופדיה_של_אבו_אלצלת#s6XK | מותר | |
| calculation/excess | י.ת.ר./נותר | term | קצור_המספר#9tfv | הנותר | |
| calculation/excess | ע.ד.פ./העדף | term | חשבון_השטחים#fgly | ההעדף | |
| calculation/excess | ע.ד.פ./העדף | term | חשבון_השטחים#wfey | ההעדף | |
| calculation/excess | י.ס.פ./תוספת | term | עיר_סיחון#15Co | תוספת | |
| calculation/excess | י.ת.ר./יתרון | term | ספר_מעשה_חושב#2YIG | יתרון | |
| calculation/excess | י.ס.פ./תוספת | term | עיר_סיחון#updy | תוספת | |
| calculation/excess | י.ס.פ./תוספת | term | Anonymous#uuzM | תוספת שיש בין | |
| denominator/expansion to a common denominator | ש.ו.ה./השואה | definition | בר_נותן_טעם#FYfS | The expansion to a common denominator is when you have fractions of various types that are not related to each other at all, i.e. the type of these fractions is not the type of fractions of the others. ההשואה היא כאשר יהיו לך שברים ממינים שונים בלתי נקשרים זה בזה כלל ר"ל שאין אלו שברי שברים אלו | |
| denominator/expansion to a common denominator | ש.ו.ה./השואה | definition | בר_נותן_טעם#7E8S | For, to the conversion of the fractions that are not related together into one type of fractions by multiplying each of these fractions by the denominators of the others, I called '''Hašavah''' [expansion to a common denominator], yet our intention is not at all to sum the fractions together, but only to equalize [their denominators]. כי ל{{#annot:term|2612,1428|4KPL}}החזרת{{#annotend:4KPL}} השברים הבלתי נקשרות למין אחד בהכאת כל אחד מהם במורי חברותיה קראתי השואה שאין כונתינו חבור כלל כי אם ההשואה לבד | |
| root/expressible | ד.ב.ר./מדובר | term | אגרת_המספר#0T9g | שרשו ידוע ומדובר | |
| root/expressible | term | ספר_עיון_העקרים_לחשבון_ההנדיים#uigP | מנטק | ||
| root/expressible | ד.ב.ר./דובר | term | האריתמטיקה_של_ניקומכוס#aqYC | ידובר בגדרם | |
| root/expressible | ד.ב.ר./מדובר | term | אגרת_המספר#N395 | מדובר | |
| root/expressible | ד.ב.ר./מדובר | term | אגרת_המספר#AsEh | מדוברים | |
| root/expressible | ד.ב.ר./דובר | term | האריתמטיקה_של_ניקומכוס#VuXT | ידובר בו | |
| root/expressible | ד.ב.ר./מדבר | term | ספר_עיון_העקרים_לחשבון_ההנדיים#edFi | מדבר | |
| root/expressible | ד.ב.ר./דובר | term | אגרת_המספר#tGJ9 | ידובר בלשון | |
| root/expressible | ד.ב.ר./מדובר | term | ספר_ג'יבלי_אלמוקבאלא#4Qky | שרש מדובר | |
| root/expressible | ד.ב.ר./מדובר | term | ספר_ג'יבלי_אלמוקבאלא#tf2L | המדוברים | |
| root/expressible | ד.ב.ר./מדבר | term | ספר_עיון_העקרים_לחשבון_ההנדיים#S3iN | מדברות | |
| root/expressible | ד.ב.ר./מדובר | term | אגרת_המספר#Wvby | שרש מדובר | |
| root/expressible | ד.ב.ר./מדובר | term | ספר_ג'יבלי_אלמוקבאלא#orLt | מספרי' מדוברי' | |
| root/expressible | ד.ב.ר./דובר | term | האריתמטיקה_של_ניקומכוס#7pvI | גדר מספר ידובר בו | |
| root/expressible | ד.ב.ר./מדובר | term | ספר_ג'יבלי_אלמוקבאלא#npuB | מספר מדובר | |
| root/expressible | ד.ב.ר./מדבר | term | ספר_עיון_העקרים_לחשבון_ההנדיים#q7Zb | מדברת | |
| basic operations/extraction of root | ש.ר.ש./הוצאת שרש | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#A6aI | הוצאת השרשים | |
| multiplication/factor | ס.כ.מ./הסכמה | term | אגרת_המספר#tksU | הסכמות | |
| multiplication/factor | צלע | term | קצור_המספר#J6tD | צלע | |
| multiplication/factor | ס.כ.מ./הסכמה | term | אגרת_המספר#uFMj | הסכמת | |
| multiplication/factor | צלע | definition | ספר_היסודות_לאקלידס#9saF | The two numbers that are multiplied one by the other, so that the plane number is produced, are called the two sides of the plane. ויקראו שני המספרים אשר הוכה אחד משניהם באחר והתקבץ משניהם המשוטח ההוא שני צלעי השטח | |
| multiplication/factor | ס.כ.מ./הסכמה | term | אגרת_המספר#EKAg | הסכמה | |
| multiplication/factor | ס.כ.מ./הסכמה | term | אגרת_המספר#s3b0 | הסכימות | |
| basic operations/factorization | נ.ת.כ./התכה | term | בר_נותן_טעם#rzvM | התכת | |
| basic operations/factorization | נ.ת.כ./התכה | term | בר_נותן_טעם#CHAD | התכת | |
| fraction/forming a fracion | ש.ב.ר./שבירה | term | אגרת_המספר#vU9u | שבירה | |
| fraction/forming a fracion | ש.ב.ר./שבירה | definition | אגרת_המספר#CxKi | fractionalizing is the ratio between two numbers, be it a part or parts, so that the ratio between the part and its denominations is called fractionalizing. אמר השבירה היא היחס אשר בין שני מספרים כשיהיה חלק או חלקים הנה היחס אשר בין החלק וכנויו יקרא שבירה | |
| fraction/forming a fracion | ש.ב.ר./שבירה | term | קצור_המספר#RSkL | שבירת | |
| practical arithmetic/fraction | ש.ב.ר./שבור | term | ספר_החשבון_לאל_חצאר#hDNe | שבור | |
| practical arithmetic/fraction | ח.ל.ק./חלק | term | ספר_יסודי_התבונה_ומגדל_האמונה#hSko | חלק | |
| practical arithmetic/fraction | ח.ל.ק./חלק | term | ספר_יסודי_התבונה_ומגדל_האמונה#CwpQ | חלקים | |
| practical arithmetic/fraction | ש.ב.ר./נשבר | term | ספר_מעשה_חושב#iQVf | מספר נשבר | |
| practical arithmetic/fraction | ש.ב.ר./שבר | term | ספר_אגריס#yiqq | שברים | |
| practical arithmetic/fraction | פ.ח.ת./פחות | term | משנת_המדות#dK8m | פחותים | |
| practical arithmetic/fraction | ש.ב.ר./שבר | term | ספר_החשבון_לאל_חצאר#IMxp | שברים | |
| practical arithmetic/fraction | ש.ב.ר./שבור | term | משנת_המדות#Yg7D | שבורים | |
| practical arithmetic/fraction | ש.ב.ר./שבר | term | ספר_החשבון_לאל_חצאר#4prq | שבר | |
| practical arithmetic/fraction | ח.ל.ק./חלק | term | ספר_מעשה_חושב#vliz | חלקים | |
| practical arithmetic/fraction | ש.ב.ר./נשבר | term | תחבולות_המספר#jSnE | נשבר | |
| practical arithmetic/fraction | ח.ל.ק./חלק | term | ספר_מעשה_חושב#QZWm | חלק | |
| practical arithmetic/fraction | ש.ב.ר./נשבר | term | חשבון_השטחים#Xlsp | נשבר | |
| practical arithmetic/fraction | ש.ב.ר./נשבר | term | עיר_סיחון#2zQm | נשבריהם | |
| practical arithmetic/fraction | ש.ב.ר./שבר | term | חשבון_השטחים#YxC9 | שבריו | |
| practical arithmetic/fraction | ש.ב.ר./שבר | term | עיר_סיחון#8HjB | שברים | |
| practical arithmetic/fraction | ש.ב.ר./שבר | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#XroP | שבר | |
| practical arithmetic/fraction | ש.ב.ר./שבר | definition | מלאכת_המספר#f0zh | A fraction is any part that is taken from the integer. השבר הוא אי זה חלק שילקח מהשלם | |
| practical arithmetic/fraction | ש.ב.ר./שבר | term | עיר_סיחון#Rn7j | שבר | |
| practical arithmetic/fraction | ש.ב.ר./שבר | term | ספר_מעשה_חושב#ZWys | שברים | |
| practical arithmetic/fraction | ש.ב.ר./שבר | term | קצור_המספר#iq94 | שברים | |
| practical arithmetic/fraction | ש.ב.ר./שבר | term | קצור_המספר#4t9b | שבר | |
| fraction/fraction of fraction | ⅓·¼ | ספר_חשבון#KdCj | If it is said: whoever has a third of a quarter of the thing, how much does he have of [that thing]?
: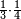 אמנם אם יאמר מי שיש לו השליש מן הרביע מן הדבר כמה חלק יש לו ממנו
אמנם אם יאמר מי שיש לו השליש מן הרביע מן הדבר כמה חלק יש לו ממנו | ||
| fraction/fraction of fraction | ⅓·¼·⅕·⅙·⅐·⅛·⅑ | ספר_חשבון#XLXN | Who has the third of the quarter of the fifth of the sixth of the seventh of the eighth of the ninth
: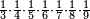 ומי שיש לו השליש מן הרביע מן החומש מן השתות מן השביע מן השמין מן התשיע
ומי שיש לו השליש מן הרביע מן החומש מן השתות מן השביע מן השמין מן התשיע | ||
| fraction/fraction of fraction | term | חשבון_השטחים#fKqo | שברי שבריו | ||
| fraction/fraction of fraction | ⅓·¼·⅕·⅙·⅐·⅛·⅑·⅒ | ספר_חשבון#8EWq | Who has the third of the quarter of the fifth of the sixth of the seventh of the eighth of the ninth of the tenth
: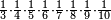 ומי שיש לו השליש מן הרביע מן החומש מן השתות מן השביע מן השמין מן התשיע מן העשור
ומי שיש לו השליש מן הרביע מן החומש מן השתות מן השביע מן השמין מן התשיע מן העשור | ||
| fraction/fraction of fraction | ⅜·⅖ | ספר_יסודי_התבונה_ומגדל_האמונה#Vq4n | As the one who says: how much are 3 eighths of 2 fifths
: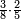 כגון האומר כמה הם ג' שמיניות מב' חמישיות
כגון האומר כמה הם ג' שמיניות מב' חמישיות | ||
| fraction/fraction of fraction | ⅓·¼·⅕·⅙ | ספר_חשבון#B38F | Who has the third of the quarter of the fifth of the sixth
: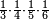 ומי שיש לו השליש מן הרביע מן החומש מן השתות
ומי שיש לו השליש מן הרביע מן החומש מן השתות | ||
| fraction/fraction of fraction | ⅕·⅑ | ספר_חשבון#3ST2 | Whoever has a fifth of a ninth.
: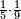 37rוכן מי שיש לו החומש מן התשיעית
37rוכן מי שיש לו החומש מן התשיעית | ||
| fraction/fraction of fraction | ⅓·⅕ | ספר_חשבון#dqBo | If it is said: whoever has a third of a fifth [of the thing], how much does he have of [that thing]?
: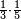 ואם יאמר מי שיש לו השליש מן החומש כמה חלק יש לו
ואם יאמר מי שיש לו השליש מן החומש כמה חלק יש לו | ||
| fraction/fraction of fraction | ⅜·⅖ | ספר_חשבון#8Loc | If one says: how much are 3-eighths of 2-fifths?
: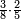 ואם יאמ' כמה הם ג' שמיניות מב' חמישיות
ואם יאמ' כמה הם ג' שמיניות מב' חמישיות | ||
| fraction/fraction of fraction | ⅓·¼·⅕·⅙·⅐·⅛ | ספר_חשבון#Xp93 | Who has the third of the quarter of the fifth of the sixth of the seventh of the eighth
: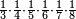 ומי שיש לו השליש מן הרביע מן החומש מן השתות מן השביע מן השמין
ומי שיש לו השליש מן הרביע מן החומש מן השתות מן השביע מן השמין | ||
| fraction/fraction of fraction | ⅓·¼·⅕ | ספר_חשבון#SN3Z | Who has the third of the quarter of the fifth
: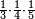 MS Ithaca om.מי שיש לו השליש מן הרביע מן החומש
MS Ithaca om.מי שיש לו השליש מן הרביע מן החומש | ||
| fraction/fraction of fraction | ⅓·¼·⅕·⅙·⅐ | ספר_חשבון#ysjE | Who has the third of the quarter of the fifth of the sixth of the seventh
: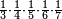 ומי שיש לו השליש מן הרביע מן החומש מן השתות מן השביע
ומי שיש לו השליש מן הרביע מן החומש מן השתות מן השביע | ||
| fraction/fraction of fraction | ש.ב.ר./שבר השבר | term | קצור_המספר#hZwf | שברי שברים | |
| fraction/fraction of fraction | ש.ב.ר./שבר השבר | term | קצור_המספר#fE38 | שבר השבר | |
| methods of multiplication/gelosia | לוח | term | אגרת_המספר#aqgh | הכאה בלוח | |
| methods of multiplication/gelosia | לוח | term | אגרת_המספר#PWj0 | לוח | |
| calculation/given number | נ.ו.ח./מונח | term | ספר_החשבון_לאל_חצאר#QULF | מונח | |
| calculation/given number | term | ספר_עיון_העקרים_לחשבון_ההנדיים#IKu7 | המספר הנרצה | ||
| calculation/given number | נ.ו.ח./מונח | term | ספר_החשבון_לאל_חצאר#fDnM | מונחים | |
| calculation/given number | נ.ו.ח./מונח | term | ספר_החשבון_לאל_חצאר#VWHt | המספר המונח | |
| divisor/greatest common divisor | term | ספר_האלזיברא#kT67 | המספר היותר גדול שימנה | ||
| false position/guess in false position | ח.פ.נ./חופן | term | ספר_החשבון_לאל_חצאר#wLNH | חופן | |
| halving/half of | term | ספר_ג'יבלי_אלמוקבאלא#5itx | מחצית מ | ||
| halving/half of | term | חשבון_השטחים#mhD7 | מחצית ה | ||
| halving/half of | term | ספר_ג'יבלי_אלמוקבאלא#sDfL | מחציתו | ||
| halving/half of | term | ספר_האלזיברא#Q7KZ | מחצית ה | ||
| halving/half of | term | ספר_האלזיברא#C8F3 | חצי ה | ||
| basic operations/halving | ח.צ.י./חציה | term | חשבון_השטחים#MeX1 | בחצאת | |
| basic operations/halving | ח.צ.י./חציה | term | חשבון_השטחים#OSXA | בחצות | |
| basic operations/halving | ח.צ.י./חציה | term | ספר_עיון_העקרים_לחשבון_ההנדיים#BWk6 | חציה | |
| basic operations/halving | ח.צ.י./חציה | term | ספר_עיון_העקרים_לחשבון_ההנדיים#zYkJ | חצייה | |
| basic operations/halving | 262144÷2 | מלאכת_המספר#igUm | As this diagram:
: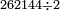 כצורה הזאת
כצורה הזאת | ||
| basic operations/halving | ח.צ.י./חציה | term | ספר_עיון_העקרים_לחשבון_ההנדיים#gg3T | חסייה | |
| basic operations/halving | ח.ל.ק./חלוק באמצע | definition | מלאכת_המספר#MyS6 | Halving is dividing any number into two equal parts. [חלוק באמצע]P1095 om. והוא חלוק איזה מספר שיהיה בשני חלקים שוים | |
| basic operations/halving | term | ספר_עיון_העקרים_לחשבון_ההנדיים#Qv5Z | תנציף | ||
| basic operations/halving | ח.ל.ק./חלוק באמצע | term | מלאכת_המספר#dC7k | חלוק באמצע | |
| basic operations/halving | ח.צ.י./חציה | term | ספר_עיון_העקרים_לחשבון_ההנדיים#nCqW | חסייא | |
| basic operations/halving | 54376÷2 | Takmila_fi_al-Hisāb_-_Arabic_in_Hebrew_Characters#4pF4 | Example: we wish to halve 54376.
: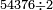 מתאלה ארדנא תנציף ארבעה וכמסין ותלת מאיה וסתה וסבעין
מתאלה ארדנא תנציף ארבעה וכמסין ותלת מאיה וסתה וסבעין | ||
| basic operations/halving | 9876374÷2 | Takmila_fi_al-Hisāb_-_Arabic_in_Hebrew_Characters#GFQB | Example: we wish to halve 98[7]6374.
: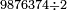 מתאלה ארדנא תנציף תסעה אלאף אלף ותמאן מאיה וסתה וסתין אלפא ותלאת מאיה וארבעה וסבעין
מתאלה ארדנא תנציף תסעה אלאף אלף ותמאן מאיה וסתה וסתין אלפא ותלאת מאיה וארבעה וסבעין | ||
| basic operations/halving | 698536÷2 | Takmila_fi_al-Hisāb_-_Arabic_in_Hebrew_Characters#SLMu | Example: we wish to halve 698536.
: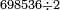 מתאלה ארדנא תנציף סת מאיה ותמניה ותסעין אלפא וכמס מאיה וסתה ותלתין
מתאלה ארדנא תנציף סת מאיה ותמניה ותסעין אלפא וכמס מאיה וסתה ותלתין | ||
| basic operations/halving | 9835834÷2 | Takmila_fi_al-Hisāb_-_Arabic_in_Hebrew_Characters#vEjn | We wish to halve 9835834.
: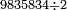 3vארדנא תנציף תסעה אלאף [ותמאן] מאיה וכמסה ותלתין אלף ותמאן מאיה ארבעה ותלתין
3vארדנא תנציף תסעה אלאף [ותמאן] מאיה וכמסה ותלתין אלף ותמאן מאיה ארבעה ותלתין | ||
| basic operations/halving | 1048876÷2 | מלאכת_המספר#gTqP | Another diagram:
: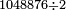 צורה אחרת
צורה אחרת | ||
| exponentiation/higher power | term | ספר_האלזיברא#LGS1 | מרבע מרובע | ||
| root/higher root | term | ספר_ג'יבלי_אלמוקבאלא#tWs7 | שרש מעו' משרש מעו' | ||
| root/higher root | term | ספר_ג'יבלי_אלמוקבאלא#v7op | שרש משרשו המעו' | ||
| root/higher root | term | ספר_ג'יבלי_אלמוקבאלא#ZtBh | שרש מרובע מהשרש מעוקב | ||
| root/higher root | term | חשבון_השטחים#dE2e | שרש שרשו | ||
| root/higher root | term | ספר_ג'יבלי_אלמוקבאלא#UL3S | שרשו המעוקב משרשו המרובע | ||
| root/higher root | term | ספר_האלזיברא#BfAK | שורש מרבע מן שרש מעקב | ||
| root/higher root | term | ספר_האלזיברא#8ZRS | שורש מרובע מן שרש מעקב | ||
| root/higher root | term | ספר_ג'יבלי_אלמוקבאלא#PC05 | שרש מרובע משרש מעוק' מ | ||
| root/higher root | term | ספר_האלזיברא#8ztM | שרש שרש מרבע מן שרש מעקב | ||
| root/higher root | term | ספר_ג'יבלי_אלמוקבאלא#Cbs1 | שרש משרש מעוקב מ | ||
| root/higher root | term | ספר_ג'יבלי_אלמוקבאלא#Ihbw | שרש משרש מעו' מ | ||
| root/higher root | term | ספר_ג'יבלי_אלמוקבאלא#2lKu | שרש מעו' משרש מעו' מ | ||
| root/higher root | term | ספר_ג'יבלי_אלמוקבאלא#r7zL | שרש מעוקב משרש מרובע מ | ||
| root/higher root | term | ספר_האלזיברא#Pr6D | שורש שורש מרובע | ||
| root/higher root | term | ספר_ג'יבלי_אלמוקבאלא#oDfj | שרש שרש מהשרש המעוקב מ | ||
| root/higher root | term | ספר_ג'יבלי_אלמוקבאלא#K6Hj | השרש מעוקב משרש השרש מ | ||
| root/higher root | term | ספר_ג'יבלי_אלמוקבאלא#mNas | השרש המעוקב משרש המרובע מ | ||
| methods of multiplication/horizontal multiplication | ש.כ.ב./שוכב | term | אגרת_המספר#gJup | שוכב | |
| decimal rank/hundreds | term | מלאכת_המספר#Outu | מאות | ||
| calculation/increasing | י.ס.פ./הוסיף | term | קצור_המספר#8pQt | מוסיף | |
| calculation/increasing | י.ס.פ./הוסיף | term | קצור_המספר#PlWp | מוסיף | |
| calculation/increasing | ר.ב.ה./רבה | term | קצור_המספר#AJWg | מרבה | |
| progression/increment | מ.ש.כ./המשך | term | ספר_מעשה_חושב#w1IT | מספר ההמשך | |
| progression/increment | מ.ש.כ./המשך | term | ספר_מעשה_חושב#zELC | המשך | |
| progression/increment | י.ס.פ./תוספת | term | Anonymous#ZsOM | תוספת | |
| progression/increment | י.ס.פ./תוספת | term | Anonymous#75Lg | תוספות | |
| numeral/Indo-Arabic numerals | א.ו.ת./אותיות הודו | term | Anonymous#J6jU | אותיות הודו | |
| root/inexpressible | ח.ר.ש./חרש | term | עיר_סיחון#Efkq | מספרים חרשים | |
| root/inexpressible | ד.ב.ר./מדובר | term | אגרת_המספר#LW8Y | בלתי מדובר | |
| root/inexpressible | ד.ב.ר./מדבר | term | ספר_מעשה_חושב#CdFT | מדבר בכח לבד | |
| root/inexpressible | ד.ב.ר./מדובר | term | אגרת_המספר#BDP9 | שרש בלתי מדובר | |
| root/inexpressible | ד.ב.ר./מדובר | term | אגרת_המספר#2p0x | בלתי מדוברים | |
| root/inexpressible | ד.ב.ר./מדובר | term | ספר_ג'יבלי_אלמוקבאלא#IRIo | השרש אינו מדובר | |
| root/inexpressible | ד.ב.ר./דובר | term | ספר_ג'יבלי_אלמוקבאלא#TruA | לא ידובר בו | |
| root/inexpressible | א.ל.מ./אלם | term | ספר_עיון_העקרים_לחשבון_ההנדיים#bjWZ | אלמות | |
| root/inexpressible | term | ספר_עיון_העקרים_לחשבון_ההנדיים#UhdQ | אסם | ||
| root/inexpressible | א.ל.מ./אלם | term | ספר_עיון_העקרים_לחשבון_ההנדיים#YiQ0 | אלם | |
| root/inexpressible | ד.ב.ר./דובר | term | האריתמטיקה_של_ניקומכוס#X6wY | לא ידובר בשרש | |
| root/inexpressible | ח.ר.ש./חרש | term | עיר_סיחון#cS1r | חרש | |
| root/inexpressible | א.ל.מ./אלם | term | עיר_סיחון#Kk7l | אלם | |
| root/inexpressible | א.ל.מ./אלם | term | עיר_סיחון#jG3R | אלמים | |
| root/inexpressible | ס.ת.מ./סתום | term | Anonymous#u59W | הסתומים והנעלמים | |
| root/inexpressible | ס.ת.מ./סתום | term | Anonymous#WCCW | הסתומים | |
| practical arithmetic/integer | ש.ל.מ./שלם | term | ספר_ג'יבלי_אלמוקבאלא#xzGs | מספר שלם | |
| practical arithmetic/integer | ש.ל.מ./שלם | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#lNzX | שלם | |
| practical arithmetic/integer | ש.ל.מ./שלם | term | ספר_מעשה_חושב#pknd | שלמים | |
| practical arithmetic/integer | ש.ל.מ./שלם | term | קצור_המספר#TzQK | שלמים | |
| practical arithmetic/integer | ש.ל.מ./שלם | term | ספר_מעשה_חושב#o7Wq | המספר השלם | |
| practical arithmetic/integer | ש.ל.מ./שלם | term | עיר_סיחון#c745 | שלם | |
| practical arithmetic/integer | ש.ל.מ./שלם | term | ספר_דיני_ממונות#9JzT | מספר שלם | |
| practical arithmetic/integer | ש.ל.מ./שלם | term | ספר_ג'יבלי_אלמוקבאלא#Cn6i | מספרי' שלמים | |
| practical arithmetic/integer | ש.ל.מ./שלם | term | תחבולות_המספר#Kd1b | שלם | |
| practical arithmetic/integer | ש.ל.מ./שלם | term | ספר_ג'יבלי_אלמוקבאלא#HWds | שלם | |
| practical arithmetic/integer | ש.ל.מ./שלם | term | ספר_ג'יבלי_אלמוקבאלא#A11m | שלמי' | |
| practical arithmetic/integer | ש.ל.מ./שלם | term | ספר_החשבון_לאל_חצאר#XuUw | שלמים | |
| practical arithmetic/integer | ש.ל.מ./שלם | term | קצור_המספר#9F3Z | שלם | |
| practical arithmetic/integer | ש.ל.מ./שלם | term | ספר_אגריס#68kh | שלמין | |
| practical arithmetic/integer | ש.ל.מ./שלם | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#9bab | שלמים | |
| practical arithmetic/integer | ש.ל.מ./שלם | term | עיר_סיחון#X06q | שלמים | |
| practical arithmetic/integer | ת.מ.מ./תמים | term | Anonymous#q4zm | התמימים | |
| practical arithmetic/integer | ש.ל.מ./שלם | term | ספר_החשבון_לאל_חצאר#gEjo | שלם | |
| practical arithmetic/integer | א.ח.ד./אחד | term | משנת_המדות#R50g | אחדים | |
| practical arithmetic/integer | ש.ל.מ./שלם | term | ספר_החשבון_לאל_חצאר#UMqY | מספר שלם | |
| practical arithmetic/integer | ש.ל.מ./שלם | term | ספר_החשבון_לאל_חצאר#Fqya | מספר השלם | |
| practical arithmetic/integer | ש.ל.מ./שלם | term | חשבון_השטחים#DXqj | שלם | |
| practical arithmetic/integer | ש.ל.מ./שלם | term | עיר_סיחון#xrE0 | המספר השלם | |
| practical arithmetic/integer | term | ספר_עיון_העקרים_לחשבון_ההנדיים#hxBM | סיחח | ||
| practical arithmetic/integer | ש.ל.מ./שלם | term | ספר_אגריס#zWcd | שלימים | |
| calculation/large | term | מלאכת_המספר#U5st | הגדול | ||
| calculation/large | term | ספר_ציפרא#k2sM | גדול מן | ||
| calculation/large | י.ס.פ./מוסיף | term | ספר_מעשה_חושב#flAW | המוסיף | |
| calculation/large | term | תחבולות_המספר#OVQO | יותר מ | ||
| calculation/large | י.ס.פ./מוסיף | term | ספר_מעשה_חושב#DcyS | המוסיפים | |
| common multiple/least common multiple | ק.ט.נ./קטן יחס | term | קצת_מענייני_חכמת_המספר#BsIH | קטן היחס | |
| common multiple/least common multiple | ק.ט.נ./קטן יחס | term | קצת_מענייני_חכמת_המספר#Gu26 | קטן יחסם | |
| common multiple/least common multiple | ק.ט.נ./קטן יחס | term | קצת_מענייני_חכמת_המספר#qAyd | המספר הקטון יחסם | |
| subtraction/less (minus) | פ.ח.ת./פחות | term | ספר_האלזיברא#oaTM | פחות | |
| subtraction/less (minus) | אלא | term | ספר_החשבון_לאל_חצאר#0ZkW | אלא | |
| subtraction/less (minus) | ז.ו.ר./נזורות | term | אגרת_המספר#AwtB | אות הנזורות | |
| subtraction/less (minus) | פ.ח.ת./פחות | term | אגרת_המספר#BTxR | תבת פחות | |
| subtraction/less (minus) | ז.ו.ר./נזורות | term | אגרת_המספר#K7Jw | מלת הנזורות | |
| subtraction/less (minus) | אלא | term | אגרת_המספר#aUcw | מלת אלא | |
| subtraction/less (minus) | פ.ח.ת./פחות | term | Anonymous#DRZq | פחות | |
| subtraction/less (minus) | ח.ס.ר./חסר | term | ספר_החשבון_לאל_חצאר#d5zW | חסר | |
| subtraction/less (minus) | פ.ח.ת./פחות | term | תחבולות_המספר#9fZc | פחות | |
| subtraction/less (minus) | פ.ח.ת./פחות | term | ספר_ג'יבלי_אלמוקבאלא#wS2q | פחות | |
| subtraction/less (minus) | פ.ח.ת./פחות | term | חשבון_השטחים#SAJY | פחות | |
| decimal positional system/lowering the rank | י.ר.ד./הורדה | term | ספר_מעשה_חושב#WUdK | הורדות | |
| decimal positional system/lowering the rank | י.ר.ד./הורדה | term | ספר_מעשה_חושב#kLNH | הורדה | |
| calculation/measure | ש.ע.ר./שעור | term | ספר_האלזיברא#uRLs | שיעור | |
| calculation/measure | ס.כ.מ./סכום | term | חשבון_השטחים#citm | סכום | |
| calculation/measure | מ.ד.ד./מדה | term | קצור_המספר#o8Pr | מדה | |
| calculation/measure | ש.ע.ר./שעור | term | תחבולות_המספר#aHEz | שיעור | |
| calculation/measure | ש.ע.ר./שעור | term | חשבון_השטחים#7xKY | שִעור | |
| calculation/measure | ש.ע.ר./שעור | term | תחבולות_המספר#zIfA | שעורו | |
| calculation/measure | מ.ד.ד./מדה | term | ספר_האלזיברא#kzJH | מדה | |
| calculation/measure | ג.ד.ל./גודל | definition | ספר_יסודי_התבונה_ומגדל_האמונה#X25y | the measures are the values, in one expression it is every thing that has a dimension. והגודלים הם הערכים בלשון אחת הוא כל דבר שיש לו מרחק | |
| calculation/measure | מ.ד.ד./ממד | term | קצור_המספר#VoKc | ממד | |
| calculation/measure | מ.ד.ד./מדה | term | ספר_האלזיברא#teeF | מדות | |
| measure/measured | ש.ע.ר./שוער | term | מלאכת_המספר#Nm1C | ישוער | |
| measure/measured | מ.ד.ד./מדוד | term | קצור_המספר#e3Gw | מדוד | |
| decimal rank/millions | ח.ש.ב./חשבון | term | בר_נותן_טעם#PJuV | חשבונות | |
| decimal rank/millions | ס.פ.ר./מספר | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#QtdT | מספרים | |
| decimal rank/millions | term | ספר_ציפרא#U78S | אלף אלפים | ||
| decimal rank/millions | ס.פ.ר./מספר | definition | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#87nA | Know that the name "million" [lit. number] is a thousand times thousand ודע כי שם מספר הוא אלף פעמים אלף | |
| subtraction/minuend | ג.ר.ע./גרוע | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#buW7 | הגרוע | |
| subtraction/minuend | ג.ר.ע./נגרע | term | חשבון_השטחים#fP1q | הנגרע ממנו | |
| subtraction/minuend | ש.ל.כ./מושלך ממנו | term | ספר_החשבון_לאל_חצאר#WoHw | המושלך ממנו | |
| subtraction/minuend | ג.ר.ע./נגרע ממנו | term | אגרת_המספר#HOGC | הנגרע ממנו | |
| subtraction/minuend | term | אגרת_המספר#eEkB | אשר ממנו תגרע | ||
| sexagesimal fraction/minute | term | ספר_מעשה_חושב#VJCT | שברים ראשונים | ||
| sexagesimal fraction/minute | term | ספר_עיון_העקרים_לחשבון_ההנדיים#BuzL | דקים | ||
| sexagesimal fraction/minute | ר.א.ש./ראשון | term | ספר_עיון_העקרים_לחשבון_ההנדיים#XbmH | ראשונים | |
| sexagesimal fraction/minute | ר.א.ש./ראשון | term | ספר_המספר_/_אליהו_מזרחי#tmPL | ראשונים | |
| multiplication/multiple | כ.פ.ל./כפל | term | קצור_המספר#xmjo | כפלים | |
| multiplication/multiple | ר.כ.ב./הרכבה | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#IfKO | הרכבה | |
| multiplication/multiple | ר.כ.ב./הרכבה | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#sl7b | הרכבות | |
| multiplication/multiple | ר.כ.ב./הרכבה | term | אגרת_המספר#pS1V | הרכבה | |
| multiplication/multiple | definition | ספר_היסודות_לאקלידס#gPT0 | The greater number is a multiple of the smaller number, when the smaller counts it. המספר הרב יהיה כפלים למספר הקטן כאשר היה הקטן מונה אותו | ||
| multiplication/multiple | ר.כ.ב./הרכבה | term | אגרת_המספר#Sq2m | הרכבת | |
| multiplication/multiple | כ.פ.ל./כפל | term | ספר_מעשה_חושב#KKBZ | כפלי | |
| multiplication/multiple | כ.פ.ל./כפל | term | ספר_מעשה_חושב#vonH | כפלים | |
| multiplication/multiple | ר.כ.ב./הרכבה | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#BjO7 | הרכבת | |
| multiplication/multiple | כ.פ.ל./כפל | term | קצור_המספר#ZZMW | כפל | |
| multiplication/multiplicand | נ.כ.ה./מוכה | term | ספר_המספר_/_אליהו_מזרחי#WVMb | המוכים | |
| multiplication/multiplicand | פ.ע.ל./פעול | term | מלאכת_המספר#vkxf | פעול | |
| multiplication/multiplicand | נ.כ.ה./מוכה | term | אגרת_המספר#8tYZ | המספר המוכה | |
| multiplication/multiplicand | כ.פ.ל./נכפל | term | קצור_המספר#Qa9l | הנכפלים | |
| multiplication/multiplicand | נ.כ.ה./מוכה | term | ספר_מעשה_חושב#0s9o | המוכה | |
| multiplication/multiplicand | כ.פ.ל./נכפל | term | עיר_סיחון#u4Sk | החשבונות הנכפלים | |
| multiplication/multiplicand | פ.ע.ל./פעול | term | מלאכת_המספר#Ul6I | פעול | |
| multiplication/multiplicand | נ.כ.ה./מוכה | term | ספר_המספר_/_אליהו_מזרחי#RCOv | המספר המוכה | |
| multiplication/multiplicand | נ.כ.ה./מוכה | term | ספר_עיון_העקרים_לחשבון_ההנדיים#EFwP | המספר המוכה | |
| multiplication/multiplicand | נ.כ.ה./מוכה | term | אגרת_המספר#cf9r | המוכה | |
| multiplication/multiplicand | נ.כ.ה./מוכה | term | ספר_עיון_העקרים_לחשבון_ההנדיים#pH9K | המוכים | |
| multiplication/multiplicand | נ.כ.ה./מוכה | term | ספר_המספר_/_אליהו_מזרחי#IWnc | המוכה | |
| multiplication/multiplicand | כ.פ.ל./נכפל | term | קצור_המספר#1sz7 | המספרים הנכפלים | |
| basic operations/multiplication | 20×35 | ספר_המספר_/_אליהו_מזרחי#hfWP | Example for tens by tens and units: multiplication 20 by 35.
: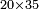 ומשל הכלל עם הכלל והפרט הוא כמו הכאת הכ' עם הל"ה
ומשל הכלל עם הכלל והפרט הוא כמו הכאת הכ' עם הל"ה | ||
| basic operations/multiplication | נ.כ.ה./הכאה | definition | אגרת_המספר#klBL | the multiplication is an allusion of the duplication of one of the numbers by the measure of the units that are in the other. ההכאה רמז על כפל אחד המספרים בשעור מה שבשני מן האחדים | |
| basic operations/multiplication | 352×343 | Takmila_fi_al-Hisāb_-_Arabic_in_Hebrew_Characters#d9wr | Example: we wish to multiply 352 by 343.
: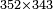 מתאלה ארדנא צ'רב תלתמאיה ואת'[נין] וכמסין פי תלאת מאיה ותלתה ומ'
מתאלה ארדנא צ'רב תלתמאיה ואת'[נין] וכמסין פי תלאת מאיה ותלתה ומ' | ||
| basic operations/multiplication | 5432×5323 | Takmila_fi_al-Hisāb_-_Arabic_in_Hebrew_Characters#tvuc | Example: we wish to multiply 5432 by 5323.
: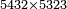 מת'אלה ארדנא צ'רב כמס אלאף וארבע מאיה ואתנין ותלתין פי כמסה 17rאלאף תלת מאיה ותלתה ועשרין
מת'אלה ארדנא צ'רב כמס אלאף וארבע מאיה ואתנין ותלתין פי כמסה 17rאלאף תלת מאיה ותלתה ועשרין | ||
| basic operations/multiplication | כ.פ.ל./כפל | term | עיר_סיחון#90GV | כפל | |
| basic operations/multiplication | 462×323 | Takmila_fi_al-Hisāb_-_Arabic_in_Hebrew_Characters#bqji | Example: we wish to multiply 462 by 323.
: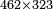 מת'אלה ארדנא צ'רב ארבע מאיה ואתנין וסתין פי תלת מאיה ותלתה ועשרין
מת'אלה ארדנא צ'רב ארבע מאיה ואתנין וסתין פי תלת מאיה ותלתה ועשרין | ||
| basic operations/multiplication | 54321×54321 | Kitāb_al-Kāfī_fī_Mukhtaṣar_al-Hind_-_Arabic_in_Hebrew_Characters#Fi30 | This is as when you multiply 54321 by its same.
: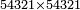 וד'אלך מת'ל אן תצ'רב ארבעה וכ'מסין אלף ות'לאת' מאיה וואחד ועשרון פי מת'להא
וד'אלך מת'ל אן תצ'רב ארבעה וכ'מסין אלף ות'לאת' מאיה וואחד ועשרון פי מת'להא | ||
| basic operations/multiplication | כ.פ.ל./כפילה | term | עיר_סיחון#0iJL | כפילתם | |
| basic operations/multiplication | ח.ש.ב./חשבון | term | ספר_יסודי_התבונה_ומגדל_האמונה#lGtp | חשבון | |
| basic operations/multiplication | נ.כ.ה./הכאה | term | ספר_מעשה_חושב#yxBo | הכאה | |
| basic operations/multiplication | נ.כ.ה./הכאה | term | ספר_עיון_העקרים_לחשבון_ההנדיים#e4rM | הכאה | |
| basic operations/multiplication | נ.כ.ה./הכאה | term | חשבון_השטחים#Pmwb | הכאת ה | |
| basic operations/multiplication | ח.ש.ב./חשבון | definition | ספר_יסודי_התבונה_ומגדל_האמונה#VSR7 | the operation of multiplying a number by a number is that a person duplicates one number as many times as the number of units that are in the second number. דרך חשבון מנין במנין הוא שיהיה האדם שונה מספר אחד פעמים שיהיה מנינם כמנין האחדים אשר במספר השני | |
| basic operations/multiplication | נ.כ.ה./הכאה | term | ספר_מעשה_חושב#SASc | הכאת | |
| basic operations/multiplication | ר.ב.ע./רבוע | term | מלאכת_המספר#AgYC | רבוע | |
| basic operations/multiplication | כ.פ.ל./כפל | term | ספר_מעשה_חושב#H5pU | כפל | |
| basic operations/multiplication | כ.פ.ל./הכפלה | term | ספר_מעשה_חושב#JopB | הכפלת | |
| basic operations/multiplication | נ.כ.ה./הכאה | term | ספר_המספר_/_אליהו_מזרחי#BroT | הכאה | |
| basic operations/multiplication | נ.כ.ה./הכאה | term | ספר_דיני_ממונות#HLMy | הכאות | |
| basic operations/multiplication | נ.כ.ה./הכאה | term | ספר_דיני_ממונות#L9nW | הכאה | |
| basic operations/multiplication | כ.פ.ל./הכפלה | term | ספר_דיני_ממונות#9MRl | הכפלה | |
| basic operations/multiplication | כ.פ.ל./כפל | term | ספר_דיני_ממונות#ykbd | כפל | |
| basic operations/multiplication | נ.כ.ה./הכאה | term | מלאכת_המספר#Ig5e | הכאת | |
| basic operations/multiplication | נ.כ.ה./הכאה | term | מלאכת_המספר#MFpo | הכאה | |
| basic operations/multiplication | כ.פ.ל./כפל | term | ספר_אגריס#aYSZ | כפל | |
| basic operations/multiplication | כ.פ.ל./כפל | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#ZtiH | כפל | |
| basic operations/multiplication | term | ספר_המספר_/_אברהם_אבן_עזרא#gpNl | לכפול חשבון על עצמו | ||
| basic operations/multiplication | כ.פ.ל./הכפל | term | בר_נותן_טעם#AiFV | הכפלם | |
| basic operations/multiplication | כ.פ.ל./הכפל | term | בר_נותן_טעם#LxoE | בהכפל | |
| basic operations/multiplication | ש.נ.י./שנוי | term | בר_נותן_טעם#KoBz | השינוי | |
| basic operations/multiplication | WP | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#tv8T | It is also as saying two hundred kikkar of copper at two hundred dinar for one kikkar. והוא גם כן כאומר מאתים ככרי נחושת לסך מאתים די' כל כיכר | ||
| basic operations/multiplication | WP | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#Qt03 | Or, as saying: 26 weights of a thing for 26 dinar, or peraḥim, or liter; how much will it cost? או כמו האומר כ"ו משקלי דבר מה לסך כ"ו די' או פרחים או לטרין כמה יעלה | ||
| basic operations/multiplication | WP | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#u3Eg | As saying: 26 cubits of cloth at 26 dinar for one cubit; how much will it cost? והוא כאומר כ"ו אמות בגד לסך כ"ו די' האמה כמה יעלה | ||
| basic operations/multiplication | ר.ב.ה./התרבות | term | חשבון_השטחים#LBvR | התרבות | |
| basic operations/multiplication | ⁵/₇×40 | ספר_מעשה_חושב#2aj0 | Example: we wish to multiply 5 sevenths by 40 integers.
: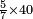 והמשל שנרצה להכות ה' שביעיות על מ' שלמים
והמשל שנרצה להכות ה' שביעיות על מ' שלמים | ||
| basic operations/multiplication | נ.כ.ה./הכאה | term | עיר_סיחון#8IVB | הכאה | |
| basic operations/multiplication | נ.כ.ה./הכאה | term | ספר_האלזיברא#poG8 | הכאת ה | |
| basic operations/multiplication | כ.פ.ל./כפל | term | ספר_האלזיברא#xLvl | כפל | |
| basic operations/multiplication | 902×246 | עיר_סיחון#JEg5 | We wish to multiply nine hundred and two by two hundred and forty-six.
: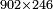 בקשנו לכפול ולהכות שנים ותשע מאות על ששה וארבעים [ומאתים]Vatican marg.
בקשנו לכפול ולהכות שנים ותשע מאות על ששה וארבעים [ומאתים]Vatican marg. | ||
| basic operations/multiplication | נ.כ.ה./הכאה | term | עיר_סיחון#v6iU | הכאות | |
| basic operations/multiplication | כ.פ.ל./כפילה | term | עיר_סיחון#7voJ | כפילת | |
| basic operations/multiplication | 30×200 | ספר_המספר_/_אברהם_אבן_עזרא#8PCw | Example: we wish to multiply thirty by two hundred.
::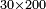 דמיון רצינו לכפול שלשים על מאתים
דמיון רצינו לכפול שלשים על מאתים | ||
| basic operations/multiplication | 200×700 | ספר_המספר_/_אברהם_אבן_עזרא#gpzH | Another example: we wish to multiply two hundred by seven hundred.
::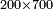 דמיון אחר בקשנו לכפול מאתים על שבע מאות
דמיון אחר בקשנו לכפול מאתים על שבע מאות | ||
| basic operations/multiplication | 29×31 | ספר_המספר_/_אברהם_אבן_עזרא#jFgw | Example: we wish to multiply 29 by 31.
::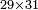 דמיון רצינו לכפול כ"ט על ל"א
דמיון רצינו לכפול כ"ט על ל"א | ||
| basic operations/multiplication | 66×54 | ספר_המספר_/_אברהם_אבן_עזרא#mnFQ | Another example: we wish to multiply 66 by 54.
::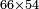 דמיון אחר רצינו לכפול ס"ו על נ"ד
דמיון אחר רצינו לכפול ס"ו על נ"ד | ||
| basic operations/multiplication | 250×350 | ספר_המספר_/_אברהם_אבן_עזרא#jWUi | Another example: one number is 250 and the other number 350.
::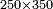 דמיון אחר {{#annot:term|35|PgHE}}המספר{{#annotend:PgHE}} האחד ר"נ והמספר האחר ש"נ
דמיון אחר {{#annot:term|35|PgHE}}המספר{{#annotend:PgHE}} האחד ר"נ והמספר האחר ש"נ | ||
| basic operations/multiplication | 13×28 | ספר_המספר_/_אברהם_אבן_עזרא#1CfA | Example: we wish to multiply 13 by 28.
::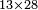 דמיון רצינו לכפול י"ג על כ"ח
דמיון רצינו לכפול י"ג על כ"ח | ||
| basic operations/multiplication | 13×16 | ספר_המספר_/_אברהם_אבן_עזרא#2VDH | Example: we wish to multiply 13 by 16.
::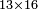 דמיון בקשנו לכפול י"ג על י"ו
דמיון בקשנו לכפול י"ג על י"ו | ||
| basic operations/multiplication | כ.פ.ל./כפילה | term | קצור_המספר#j0gQ | כפילת | |
| basic operations/multiplication | 24×26 | ספר_המספר_/_אברהם_אבן_עזרא#HqY7 | Example: we wish to multiply 24 by 26.
::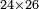 דמיון בקשנו לכפול כ"ד על כ"ו
דמיון בקשנו לכפול כ"ד על כ"ו | ||
| basic operations/multiplication | כ.פ.ל./הכפלה | term | ספר_ג'יבלי_אלמוקבאלא#URB9 | הכפלתו | |
| basic operations/multiplication | כ.פ.ל./כפל | term | ספר_ג'יבלי_אלמוקבאלא#a8tg | כפל | |
| basic operations/multiplication | 127×355 | ספר_המספר_/_אברהם_אבן_עזרא#cmWh | Example: we wish to multiply 127 by 355.
: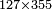 דמיון זה רצינו לכפול קכ"ז על שנ"ה
דמיון זה רצינו לכפול קכ"ז על שנ"ה | ||
| basic operations/multiplication | כ.פ.ל./הכפלה | term | ספר_ג'יבלי_אלמוקבאלא#qtuD | הכפלה | |
| basic operations/multiplication | 869×6 | קצור_המספר#mrSa | Example: we wish to multiply eight hundred sixty-nine by the six units of another number.
::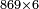 והנה המשל בזה רצינו לכפול שמונה מאות וששים ותשעה במספר אחדי ששה שיש במספר אחר
והנה המשל בזה רצינו לכפול שמונה מאות וששים ותשעה במספר אחדי ששה שיש במספר אחר | ||
| basic operations/multiplication | 869×46 | קצור_המספר#ytmk | As if you say: we multiply these eight hundred sixty-nine by the units and the tens of forty-six.
::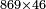 כאלו תאמ' שרצינו לכפול הח' מאות וששים ותשעה במספר אחדים ועשרות של ארבעים וששה
כאלו תאמ' שרצינו לכפול הח' מאות וששים ותשעה במספר אחדים ועשרות של ארבעים וששה | ||
| basic operations/multiplication | כ.פ.ל./כפל | term | ספר_ג'יבלי_אלמוקבאלא#0vQW | כפלים | |
| basic operations/multiplication | כ.פ.ל./כפילה | term | ספר_ג'יבלי_אלמוקבאלא#G42r | כפילת ה | |
| basic operations/multiplication | 80×500 | ספר_החשבון_והמדות#x20n | Example: we wish to multiply eighty by five hundred.
: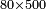 דמיון בזה רצינו לכפול שמנים על חמש מאות
דמיון בזה רצינו לכפול שמנים על חמש מאות | ||
| basic operations/multiplication | נ.כ.ה./הכאה | term | קצור_המספר#xcIV | הכאתם | |
| basic operations/multiplication | כ.פ.ל./הכפלה | term | ספר_ג'יבלי_אלמוקבאלא#w4ij | הכפלות | |
| basic operations/multiplication | נ.כ.ה./הכאה | term | ספר_ג'יבלי_אלמוקבאלא#UTLc | הכאה | |
| basic operations/multiplication | 25×43 | ספר_החשבון_והמדות#vPL0 | Example: we wish to multiply twenty-five by forty-three.
: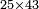 דמיון רצינו לכפול עשרים וחמשה על ארבעים ושלשה
דמיון רצינו לכפול עשרים וחמשה על ארבעים ושלשה | ||
| basic operations/multiplication | נ.כ.ה./הכאה | term | ספר_ג'יבלי_אלמוקבאלא#23wI | הכאת | |
| basic operations/multiplication | נ.כ.ה./הכאה | term | ספר_ג'יבלי_אלמוקבאלא#DpJh | הכאות | |
| basic operations/multiplication | כ.פ.ל./כפילה | term | קצור_המספר#7rW8 | כפילה ב | |
| basic operations/multiplication | 348×235 | ספר_החשבון_והמדות#a8Vc | Example: we wish to multiply three hundred forty-eight by two hundred thirty-five.
: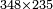 דמיון רצינו לכפול שלש מאות וארבעים ושמנה על מאתים ושלשים וחמשה
דמיון רצינו לכפול שלש מאות וארבעים ושמנה על מאתים ושלשים וחמשה | ||
| basic operations/multiplication | 105×224 | ספר_החשבון_והמדות#SSgu | We wish to multiply a hundred and five by two hundred and twenty-four.
: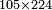 רצינו לכפול מאה וחמשה על מאתים ועשרים וארבעה
רצינו לכפול מאה וחמשה על מאתים ועשרים וארבעה | ||
| basic operations/multiplication | 348×235 | ספר_החשבון_והמדות#VJUW | Example: we wish to multiply three hundred and forty-eight by two hundred and thirty-five.
: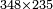 דמיון רצינו לכפול שלש מאות וארבעים ושמנה על מאתים ושלשים וחמשה
דמיון רצינו לכפול שלש מאות וארבעים ושמנה על מאתים ושלשים וחמשה | ||
| basic operations/multiplication | 25×35 | ספר_החשבון_והמדות#n8hI | Example: we wish to multiply twenty-five by thirty-five.
: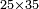 דמיון רצינו לכפול כ"ה על ל"ה
דמיון רצינו לכפול כ"ה על ל"ה | ||
| basic operations/multiplication | 23×24 | ספר_דיני_ממונות#w4Hh | Example: we wish to multiply 23 by 2[4].
: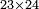 דמיון זה נרצה לכפול כ"ג על כ"ג
דמיון זה נרצה לכפול כ"ג על כ"ג | ||
| basic operations/multiplication | 234×24 | ספר_דיני_ממונות#rKP4 | Example: we wish to multiply 234 by 24.
: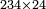 דמיון נרצה לכפול רל"ד על כ"ד
דמיון נרצה לכפול רל"ד על כ"ד | ||
| basic operations/multiplication | 222×333 | ספר_דיני_ממונות#79NX | Example: we wish to multiply 222 by 333.
: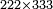 דמיון זה נרצה לכפול 202rרכ"ב על של"ג
דמיון זה נרצה לכפול 202rרכ"ב על של"ג | ||
| basic operations/multiplication | 6845×327 | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#UId5 | [...] 6 thousand 845 by 327
: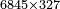 31r / [י"ג][...] ו' אלפים תתמ"ה על שכ"ז
31r / [י"ג][...] ו' אלפים תתמ"ה על שכ"ז | ||
| basic operations/multiplication | 230×324 | ספר_דיני_ממונות#HEIx | Example: we wish to multiply 230 by 324.
: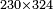 דמיון זה נרצה לכפול מספר ר"ל על מספר שכ"ד
דמיון זה נרצה לכפול מספר ר"ל על מספר שכ"ד | ||
| basic operations/multiplication | 240×368 | ספר_דיני_ממונות#V6r3 | Example: we wish to multiply 240 by 368.
: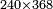 דמיון נרצה לכפול ר"ם על שס"ח
דמיון נרצה לכפול ר"ם על שס"ח | ||
| basic operations/multiplication | 403×230 | ספר_דיני_ממונות#AjXB | Example: we wish to multiply 403 by 230.
: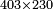 דמיון נרצה לכפול מספר ת"ג על מספר ר"ל
דמיון נרצה לכפול מספר ת"ג על מספר ר"ל | ||
| basic operations/multiplication | 24×25 | ספר_דיני_ממונות#wgpZ | Example: we wish to multiply 24 by 25.
: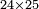 דמיון זה נרצה לכפול כ"ד על כ"ה
דמיון זה נרצה לכפול כ"ד על כ"ה | ||
| basic operations/multiplication | 123×456 | ספר_דיני_ממונות#4PSP | Example: we wish to multiply 123 by 456.
: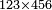 דמיון זה נרצה לכפול קכ"ג על תנ"ו
דמיון זה נרצה לכפול קכ"ג על תנ"ו | ||
| basic operations/multiplication | 246×140 | ספר_דיני_ממונות#KISe | Example: we wish to multiply 246 by 140.
: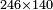 דמיון זה נרצה לכפול רמ"ו על ק"מ
דמיון זה נרצה לכפול רמ"ו על ק"מ | ||
| basic operations/multiplication | נ.כ.ה./הכאה | term | תחבולות_המספר#KmBA | ההכאה | |
| basic operations/multiplication | 23×17 | ספר_דיני_ממונות#niLJ | Example: we wish to multiply 23 by 17.
: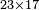 דמיון זה נרצה לכפול כ"ג על י"ז
דמיון זה נרצה לכפול כ"ג על י"ז | ||
| basic operations/multiplication | ח.ש.ב./חשבון | term | Anonymous#YSqP | חשבון | |
| basic operations/multiplication | 242×144 | ספר_דיני_ממונות#RZyL | Example: we wish to multiply 242 by 144.
: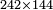 דמיון זה נרצה לכפול רמ"ב על קמ"ד
דמיון זה נרצה לכפול רמ"ב על קמ"ד | ||
| basic operations/multiplication | 13×14 | ספר_החשבון_והמדות#9FsV | As the one who wants to multiply 13 by 14.
: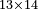 כגון הרוצה לכפול י"ג על י"ד
כגון הרוצה לכפול י"ג על י"ד | ||
| basic operations/multiplication | ע.ר.כ./מערכת | term | Anonymous#CHKw | מערכת | |
| basic operations/multiplication | 240×170 | ספר_דיני_ממונות#szcC | Example: we wish to multiply 240 by 170.
: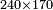 דמיון זה נרצה לכפול ר"ם על ק"ע
דמיון זה נרצה לכפול ר"ם על ק"ע | ||
| basic operations/multiplication | ע.ר.כ./מערכת | term | Anonymous#GOSD | מערכת זה על זה | |
| basic operations/multiplication | 122×232 | ספר_דיני_ממונות#XFc5 | Example: we wish to multiply 122 by 232.
: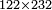 206vדמיון זה נרצה לכפול קכ"ב על רל"ב
206vדמיון זה נרצה לכפול קכ"ב על רל"ב | ||
| basic operations/multiplication | 470×580 | ספר_דיני_ממונות#6FQI | Example: we wish to multiply 470 by 580.
: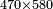 דמיון זה נרצה לכפול ת"ע על תק"פ
דמיון זה נרצה לכפול ת"ע על תק"פ | ||
| basic operations/multiplication | 27×32 | ספר_דיני_ממונות#gchY | Example: we wish to multiply 27 by 32.
: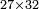 דמיון זה נרצה לכפול כ"ז על ל"ב
דמיון זה נרצה לכפול כ"ז על ל"ב | ||
| basic operations/multiplication | 231×342 | ספר_דיני_ממונות#5Cep | Another example: we wish to multiply 231 by 342.
: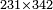 דמיון אחר נרצה לכפול רל"א על שמ"ב
דמיון אחר נרצה לכפול רל"א על שמ"ב | ||
| basic operations/multiplication | WP | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#poq3 | It is the same as saying 245 liṭra of pepper at 75; the total price is the mentioned amount. והוא הדין כאומר רמ"ה לטרין פלפל לסך ע"ה שיעלה הסך הנז' מערוך | ||
| basic operations/multiplication | WP | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#8edj | Another example: If one asks for 245 kor of wheat at 19 dinar.
: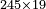 משל אחר אם שאל רמ"ה כורי חיטה לסך י"ט די'
משל אחר אם שאל רמ"ה כורי חיטה לסך י"ט די' | ||
| basic operations/multiplication | 321×654 | ספר_ציפרא#lJrF | Example: if you wish to know how much is 3 hundred and 21 times 654, written 321 by 654.
::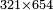 דמיון אם תרצה לידע כמה כ"א וג' מאות פעמי' נ"ד ות"ר שרשימתו אב"ג דה"ו
דמיון אם תרצה לידע כמה כ"א וג' מאות פעמי' נ"ד ות"ר שרשימתו אב"ג דה"ו | ||
| basic operations/multiplication | 464×464 | ספר_ציפרא#bkz3 | 464 times 464: the result is 215296.
::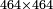 דו"ד פעמי' דו"ד יעלה חשבונו וט"בהא"ב ודו"ק
דו"ד פעמי' דו"ד יעלה חשבונו וט"בהא"ב ודו"ק | ||
| basic operations/multiplication | 25×25 | ספר_דיני_ממונות#daU2 | Example: we wish to multiply 25 by 25.
: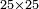 דמיון זה נרצה לכפול כ"ה על כ"ה
דמיון זה נרצה לכפול כ"ה על כ"ה | ||
| basic operations/multiplication | 212×132 | ספר_דיני_ממונות#fM0G | Example: we wish to multiply 212 by 132.
: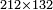 דמיון זה נרצה לכפול רי"ב על קל"ב
דמיון זה נרצה לכפול רי"ב על קל"ב | ||
| basic operations/multiplication | 33×10 | ספר_דיני_ממונות#pgpm | Example: we wish to multiply 33 by 10.
: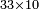 דמיון זה נרצה לכפול ל"ג על י'
דמיון זה נרצה לכפול ל"ג על י' | ||
| basic operations/multiplication | 45×20 | ספר_דיני_ממונות#vUC8 | Example: we wish to multiply 45 by 20.
: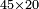 דמיון זה נרצה לכפול מ"ה על עשרים
דמיון זה נרצה לכפול מ"ה על עשרים | ||
| basic operations/multiplication | term | Anonymous_text_from_Latin#4Ict | מולטי פליציטיאן | ||
| basic operations/multiplication | term | Arithmetic_Textbook_by_Meir_Shapira#GjWo | כפל | ||
| basic operations/multiplication | 15×40 | ספר_דיני_ממונות#46Gd | Example: we wish to multiply 15 by 40.
: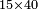 דמיון זה נרצה לדעת כפל ט"ו על מ'
דמיון זה נרצה לדעת כפל ט"ו על מ' | ||
| basic operations/multiplication | (4-2)×(8-3) | ספר_דיני_ממונות#MzgG | Example: we wish to multiply 4 minus 2 by 8 minus 3.
: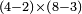 דמיון זה נרצה לכפול ד' פחות שנים עם ח' פחות ג'
דמיון זה נרצה לכפול ד' פחות שנים עם ח' פחות ג' | ||
| basic operations/multiplication | (7-2)×(8-4) | ספר_דיני_ממונות#VBTJ | Another example: we wish to multiply 7 minus 2 by 8 minus 4.
: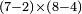 דמיון אחר נרצה לכפול ז' פחות ב' על ח' פחות ד' הורידם בזאת הצורה
דמיון אחר נרצה לכפול ז' פחות ב' על ח' פחות ד' הורידם בזאת הצורה | ||
| basic operations/multiplication | 30×20 | מלאכת_המספר#KE0A | Example: 30 times 20. We triple 20; it is 60. We add zero; it is 600 and this is its shape by the positional system: 600.
::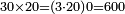 המשל ל' פעמים כ' נשלש הכ' ויהיו ס' ונוסיף ספרא ויהיו ת"ר וזו היא צורתו בדרך המספר 00וP1095: 600
המשל ל' פעמים כ' נשלש הכ' ויהיו ס' ונוסיף ספרא ויהיו ת"ר וזו היא צורתו בדרך המספר 00וP1095: 600 | ||
| basic operations/multiplication | 20×5 | מלאכת_המספר#dsqN | Example: 20 times 5. We double the 5; it is 10. We add zero; it is 100.
::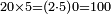 המשל כ' פעמי' ה' {{#annot:term|785,1230|TSoW}}נכפול{{#annotend:TSoW}} הה' ויהיו י' ונוסיף 0' ויהיו ק'
המשל כ' פעמי' ה' {{#annot:term|785,1230|TSoW}}נכפול{{#annotend:TSoW}} הה' ויהיו י' ונוסיף 0' ויהיו ק' | ||
| basic operations/multiplication | 10×12 | מלאכת_המספר#GKtA | Example: if we want to know how much is 10 times 12, we add 0 to 12; it is 120, and in the positional system they are written as 120.
::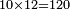 המשל אם נרצה לדעת י' פעמים י"ב כמה הם נוסיף 0' על י"ב ויהיו ק"כ ו{{#annot:term|202,1355|Sbjs}}בדרך המספר{{#annotend:Sbjs}} יסודרו כן 0באP1095: 120
המשל אם נרצה לדעת י' פעמים י"ב כמה הם נוסיף 0' על י"ב ויהיו ק"כ ו{{#annot:term|202,1355|Sbjs}}בדרך המספר{{#annotend:Sbjs}} יסודרו כן 0באP1095: 120 | ||
| basic operations/multiplication | 8×9 | מלאכת_המספר#kHdF | Example: we wish to know the product of 8 by 9.
::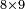 המשל שנרצה לדעת קבוץ הכאת ח' בט'
המשל שנרצה לדעת קבוץ הכאת ח' בט' | ||
| basic operations/multiplication | כ.פ.ל./כפל | term | חשבון_השטחים#w6Sg | כפל | |
| basic operations/multiplication | נ.כ.ה./הכאה | term | חשבון_השטחים#F8E5 | ההכאה | |
| basic operations/multiplication | 1234×4321 | ספר_ציפרא#ZdlX | If you wish to multiply 1234 by 4321.
: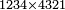 אם בקשנו לכפול רל"ד ואלף על ד' אלפי' ושכ"א
אם בקשנו לכפול רל"ד ואלף על ד' אלפי' ושכ"א | ||
| basic operations/multiplication | 209×3030 | ספר_ציפרא#Lq1V | Another example: we wish to multiply 209 by 3030.
: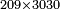 112rדומיון אחר הנה בקשנו לכפול ט' ומאתים על ג' אלפי' ול'
112rדומיון אחר הנה בקשנו לכפול ט' ומאתים על ג' אלפי' ול' | ||
| basic operations/multiplication | 15×1080 | ספר_ציפרא#5pXt | If you wish to know how much are 15 times 1080.
: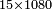 אם תרצה [לידע]M om. כמה ט"ו פעמי' תתר"ף
אם תרצה [לידע]M om. כמה ט"ו פעמי' תתר"ף | ||
| basic operations/multiplication | 7000030×180640 | ספר_מעשה_חושב#yltH | Example: we wish, in this diagram, to multiply 7 thousand of thousand and thirty by one hundred and eighty thousand, six hundred and forty.
: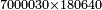 {{#annot:term|197,1712|YSWE}}דמיון{{#annotend:YSWE}} נרצה בזאת הצורה להכות ז' אלפי אלפים ושלשים על מאה ושמנים אלף ושש מאות וארבעים
{{#annot:term|197,1712|YSWE}}דמיון{{#annotend:YSWE}} נרצה בזאת הצורה להכות ז' אלפי אלפים ושלשים על מאה ושמנים אלף ושש מאות וארבעים | ||
| basic operations/multiplication | 34×57 | ספר_מעשה_חושב#Jdhf | Example: we wish to multiply 34 by 57.
: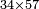 נרצה להכות ל"ד על נ"ז
נרצה להכות ל"ד על נ"ז | ||
| basic operations/multiplication | 43×57 | ספר_מעשה_חושב#T3Oo | Example: you have to multiply 43 by 57.
: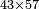 משל זה שיהיה לך להכות מ"ג על נ"ז
משל זה שיהיה לך להכות מ"ג על נ"ז | ||
| basic operations/multiplication | 23×23 | ספר_אגריס#FKmC | Example: multiply 23 by 23.
: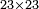 דומיון על כפול כ"ג על כ"ג
דומיון על כפול כ"ג על כ"ג | ||
| basic operations/multiplication | 5×320 | ספר_המספר_/_אליהו_מזרחי#lqtO | The example of the first method is:
: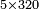 משל הדרך הראשון הנה הוא כזה
משל הדרך הראשון הנה הוא כזה | ||
| basic operations/multiplication | 236×135 | ספר_המספר_/_אליהו_מזרחי#9PF9 | The example of the second method, which is multiplication of tens, or tens and units together, by tens, or tens and units together, is as follows:
: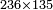 ומשל הדרך השני והוא הכאת הכללים או הכללים והפרטים יחד עם הכללים או עם הכללים ופרטים יחד הנה הוא כזה
ומשל הדרך השני והוא הכאת הכללים או הכללים והפרטים יחד עם הכללים או עם הכללים ופרטים יחד הנה הוא כזה | ||
| basic operations/multiplication | (355×296)+(447×178)+(396×539) | ספר_המספר_/_אליהו_מזרחי#zrCv | Such as, for example: the multiplication of 355 by 296 and the multiplication of 447 by 178 and the multiplication of 396 by 539.
: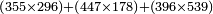 כמו על דרך משל הכאת מספר שנ"ה עם מספר רצ"ו והכאת מספר תמ"ז עם מספר קע"ח והכאת מספר שצ"ו עם מספר תקל"ט
כמו על דרך משל הכאת מספר שנ"ה עם מספר רצ"ו והכאת מספר תמ"ז עם מספר קע"ח והכאת מספר שצ"ו עם מספר תקל"ט | ||
| basic operations/multiplication | 755×653 | ספר_המספר_/_אליהו_מזרחי#OB4i | Example: if you wish to multiply 755 by 653.
: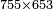 המשל בזה אם רצית להכות מספר תשנ"ה עם מספר תרנ"ג
המשל בזה אם רצית להכות מספר תשנ"ה עם מספר תרנ"ג | ||
| basic operations/multiplication | 20×200 | ספר_המספר_/_אליהו_מזרחי#4Ol5 | Example of the multiplication of tens by tens: multiplication of twenty by two hundred.
: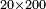 והמשל בהכאת כלל עם כלל הוא הכאת עשרים במאתים עד"מ
והמשל בהכאת כלל עם כלל הוא הכאת עשרים במאתים עד"מ | ||
| basic operations/multiplication | 9×200 | ספר_המספר_/_אליהו_מזרחי#M5z8 | Example of the multiplication of units by tens: multiplication of 9 by two hundred.
: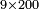 ומשל הכאת הפרט עם הכלל הוא כמו הכאת הט' במאתים עד"מ
ומשל הכאת הפרט עם הכלל הוא כמו הכאת הט' במאתים עד"מ | ||
| basic operations/multiplication | כ.פ.ל./כפל | term | תחבולות_המספר#Q6eQ | כפל ה | |
| basic operations/multiplication | ר.ב.ע./רבוע | definition | מלאכת_המספר#M4Ct | The product is a third number that is necessarily obtained from multiplying any two numbers one by the other so that each of them is found in [the third number] as many times as the units are in the other. רבוע הוא מספר שלישי מתחייב מהכאת איזה שני מספרי' שיהיו האחד באחר שכל כך פעמים ימצא כל אחד מהם בו כאחדים שבאחרP1095: שבאחד | |
| basic operations/multiplication | 5×220 | ספר_המספר_/_אליהו_מזרחי#CZjH | Example: multiplication 5 by 220.
: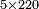 משל זה הכאת הה' בר"כ
משל זה הכאת הה' בר"כ | ||
| basic operations/multiplication | 5×27 | ספר_המספר_/_אליהו_מזרחי#Uvhu | Example for units by tens and units together: multiplication 5 by 27.
: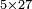 ומשל הפרטים לבד עם הכללים והפרטים יחד הוא כמו הכאת הה' בכ"ז
ומשל הפרטים לבד עם הכללים והפרטים יחד הוא כמו הכאת הה' בכ"ז | ||
| basic operations/multiplication | כ.פ.ל./כפילה | definition | קצור_המספר#HuF6 | The essential act of multiplying is the third of the arithmetical [operations] called '''multiplication''' ומפועל הנפש בהכפיל הדברים היה מין שלישי מהמספר שיקרא הכפילה | |
| basic operations/multiplication | 20×230 | ספר_המספר_/_אליהו_מזרחי#ws8l | Example for tens by tens: multiplication 20 by 230.
: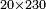 ומשל הכלל עם הכלל הוא הכאת הכ' עם הר"ל
ומשל הכלל עם הכלל הוא הכאת הכ' עם הר"ל | ||
| basic operations/multiplication | 9007500×5400920 | בר_נותן_טעם#Anhy | Example: we wish to multiply the number 9007500 by another number 5400920.
: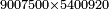 המשל רצינו לכפול מספר 9007500 במספר אחר שהוא 5400920
המשל רצינו לכפול מספר 9007500 במספר אחר שהוא 5400920 | ||
| basic operations/multiplication | 29×31 | ספר_המספר_/_אליהו_מזרחי#2iNx | Example: we wish to multiply 29 by 31.
: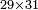 המשל בזה רצינו להכות כ"ט עם ל"א
המשל בזה רצינו להכות כ"ט עם ל"א | ||
| basic operations/multiplication | 1¼×1⅕ | ספר_הכללים_במספר#uW3p | 81) If a man asks you: How much are one integer and a quarter by one integer and a fifth?
: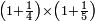 פא אם ישאלך אדם א' ורביע על א' וחמישית כמה הוא
פא אם ישאלך אדם א' ורביע על א' וחמישית כמה הוא | ||
| basic operations/multiplication | 1⁵/₇×1⅘ | ספר_הכללים_במספר#Iwhd | 75) If a man asks you: How much are one integer and five sevenths by one integer and four fifths?
: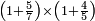 עה אי"א א' וה' שבעיות על א' וד' חמשיות כמה הוא
עה אי"א א' וה' שבעיות על א' וד' חמשיות כמה הוא | ||
| basic operations/multiplication | 3⅖×2⁴/₇ | ספר_הכללים_במספר#9pSN | If a man asks you: How much are three integers and two fifths by two integers and four sevenths?
: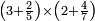 אי"א ג' שלמים וב' חמשיות על ב' שלמים וד' שבעיות כמה הוא
אי"א ג' שלמים וב' חמשיות על ב' שלמים וד' שבעיות כמה הוא | ||
| basic operations/multiplication | 250×350 | ספר_המספר_/_אליהו_מזרחי#8ywW | Also if we wish to multiply 250 by 350.
: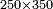 וכן אם רצינו להכות ר"נ עם ש"נ
וכן אם רצינו להכות ר"נ עם ש"נ | ||
| basic operations/multiplication | 50×7000 | Anonymous#DsCO | Such as 50 by 7 thousand.
::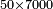 כמו נ' בז' אלפים
כמו נ' בז' אלפים | ||
| basic operations/multiplication | 40×600 | Anonymous#X9sf | Such as 40 by six hundred.
::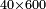 כמו מ' בשש מאות
כמו מ' בשש מאות | ||
| basic operations/multiplication | 20×30 | Anonymous#CSsq | Such as 20 by 30.
::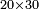 כמו כ' על ל'
כמו כ' על ל' | ||
| basic operations/multiplication | ע.ר.כ./מערכת | definition | Anonymous#BNPE | the multiplication of a number by a number is that you count the first number by the multitude of the second number. ומערכת מספר על מספר הוא שתהיה מונה המספר האחד במנין המספר השני | |
| basic operations/multiplication | 5×300 | Anonymous#dnZv | Such as five by three hundred.
::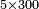 כמו חמשה על שלש מאות
כמו חמשה על שלש מאות | ||
| basic operations/multiplication | 5×70 | Anonymous#kmOR | If you multiply five by seventy.
::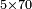 כמו חמשה על שבעים
כמו חמשה על שבעים | ||
| basic operations/multiplication | 125×125 | Anonymous#GRmk | If you multiply 125 by itself.
::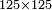 ואם תערוך קכ"ה על עצמו
ואם תערוך קכ"ה על עצמו | ||
| basic operations/multiplication | 54×66 | Anonymous#KaQ7 | If you multiply 54 by 64.
::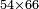 ואם תערוך נ"ד בס"ו
ואם תערוך נ"ד בס"ו | ||
| basic operations/multiplication | 25×28 | Anonymous#BQkO | Such as 25 by 28.
::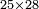 כמו כ"ה על כ"ח
כמו כ"ה על כ"ח | ||
| basic operations/multiplication | 600×4000 | ספר_יסודי_התבונה_ומגדל_האמונה#nEsS | As if you wish to multiply six hundred by four thousand.
::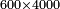 וכאלו היית רוצה לחשוב שש מאות בד' אלפים
וכאלו היית רוצה לחשוב שש מאות בד' אלפים | ||
| basic operations/multiplication | 600×4000 | Anonymous#ZjcQ | As if you want to [multiply] six hundred by four thousand.
::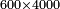 כמו שתרצה שש מאות על ארבעת אלפים
כמו שתרצה שש מאות על ארבעת אלפים | ||
| basic operations/multiplication | 5×6 | ספר_ציפרא#XdEP | Another example: if you want to know 5 times 6.
::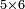 MS Oxford 440, 115r: supplementדמיון אחר אם תרצה לידע הפ"ו
MS Oxford 440, 115r: supplementדמיון אחר אם תרצה לידע הפ"ו | ||
| basic operations/multiplication | 6×8 | ספר_ציפרא#s2II | Another example: you wish to multiply 6 times 8.
::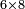 דמיון אחר הנה רצונך לכפול ו’ פעמים ח’
דמיון אחר הנה רצונך לכפול ו’ פעמים ח’ | ||
| basic operations/multiplication | 7×9 | ספר_ציפרא#lzGK | Example: you wish to multiply 7 times 9.
::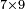 דמיון הנה רצונך לכפול ז’ פעמים ט’
דמיון הנה רצונך לכפול ז’ פעמים ט’ | ||
| basic operations/multiplication | 4×3 | ספר_ציפרא#wODz | Example: if you want to multiply 4 by 3.
::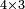 דימיון אם בקשת לכפול ד' על ג'
דימיון אם בקשת לכפול ד' על ג' | ||
| basic operations/multiplication | 4×4 | ספר_ציפרא#yXdJ | I will teach you an example: if you want to multiply 4 times 4.
::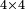 דומיון אם תרצה לחשוב ד'פ'ד’
דומיון אם תרצה לחשוב ד'פ'ד’ | ||
| basic operations/multiplication | 4×4 | ספר_ציפרא#ynhp | Example: 4 times 4.
::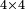 דמיון ד'פ'ד'
דמיון ד'פ'ד' | ||
| basic operations/multiplication | 7×8 | ספר_ציפרא#B4fP | Example: if you wish to know [how much is] 7 times 8.
::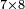 כגון את"ל ז'פ'ח'
כגון את"ל ז'פ'ח' | ||
| basic operations/multiplication | 6×6 | ספר_ציפרא#sgDh | Example: if you wish to know how much is 6 times 6
::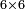 MS Paris 1088, 4v: supplementדומיון אם תחפוץ לידע כמה ו' פעם ו'
MS Paris 1088, 4v: supplementדומיון אם תחפוץ לידע כמה ו' פעם ו' | ||
| basic operations/multiplication | 9×8 | ספר_ציפרא#FWoZ | Also if you want to know how much is 9 times 8
::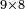 וכן אם תרצה לידע כמה ט' פעמים ח'
וכן אם תרצה לידע כמה ט' פעמים ח' | ||
| basic operations/multiplication | 9×9 | ספר_ציפרא#OZ9T | If you wish to know how much is 9 times 9
::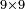 אם תחפוץ לידע כמה ט’ פעמי' ט’
אם תחפוץ לידע כמה ט’ פעמי' ט’ | ||
| basic operations/multiplication | כ.פ.ל./כפילה | term | עיר_סיחון#TXfT | כפילה | |
| basic operations/multiplication | כ.פ.ל./כפילה | term | עיר_סיחון#QXoD | כפילת | |
| basic operations/multiplication | 253×1335 | אגרת_המספר#tCQB | If you wish to multiply 253 by 1335 for example.
: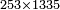 ואם רצית להכות רנ"ג באלף של"ה ד"מ
ואם רצית להכות רנ"ג באלף של"ה ד"מ | ||
| basic operations/multiplication | 54×45 | אגרת_המספר#gYvC | Example: we wish to multiply 54 by 45.
: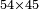 המשל רצינו להכות מספר נ"ד במספר מ"ה
המשל רצינו להכות מספר נ"ד במספר מ"ה | ||
| basic operations/multiplication | 18×15 | אגרת_המספר#mYxE | Example: multiplication of 18 by 15.
: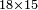 והמשל הכאת י"ח בט"ו
והמשל הכאת י"ח בט"ו | ||
| basic operations/multiplication | נ.כ.ה./הכאה | definition | אגרת_המספר#ofqi | the meaning of the multiplication in the Holy tongue is known and here it is translated and refers to the duplication of a number as many times as the number of the units that are in another number. פירוש ההכאה הנחתה בלשון הקדש ידועה וכאן היא מועתקת ורומזת על כפילת מספר פעמים רבות כמספר האחדים אשר במספר אחר | |
| basic operations/multiplication | נ.כ.ה./הכאה | term | אגרת_המספר#G79Y | הכאה | |
| basic operations/multiplication | 56023×70235 | Takmila_fi_al-Hisāb_-_Arabic_in_Hebrew_Characters#AAvF | Example: we wish to multiply 56023 by 70235.
: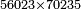 מתאלה ארדנא צ'רב סתה וכמסין אלפא ותלתה ועשרין פי סבעין אלף ומאיתין כמסה ותלתין
מתאלה ארדנא צ'רב סתה וכמסין אלפא ותלתה ועשרין פי סבעין אלף ומאיתין כמסה ותלתין | ||
| basic operations/multiplication | נ.כ.ה./הכאה | definition | ספר_המספר_/_אליהו_מזרחי#ZprF | multiplication is summing identical numbers, as many as they may be, so that not all of them are given but one alone. ההכאה הוא קבוץ מספרים שוים כמה שיהיו בלתי מונחים מכללם רק האחד לבד | |
| methods of multiplication/multiplication by shifting | ע.ת.ק./בהעתק | term | אגרת_המספר#2u5E | הכאה בהעתק | |
| methods of multiplication/multiplication by shifting | ע.ת.ק./בהעתק | definition | אגרת_המספר#4Na3 | the first part is called multiplication by shifting, i.e. that he writes first the ranks of the first number and the second [number] in a known order. He starts to multiply one rank of the first number by all the ranks of the second number, then shifts the order of the ranks beneath another rank. This is called shifting. החלק הא' יקרא הכאה בהעתק ר"ל שיכתוב תחלה מדרגות המספר האחד והשני לו בסדר ידוע ויתחיל להכות מדרגה אחת מן המספר האחד בכל מדרגו' המספר השני אח"כ יעתיק סדר המדרגות לתחת מדרגה אחרת זהו הנקרא העתק | |
| simple fraction/multiplication of fractions | (5+⅔)×(2+³/₆) | עיר_סיחון#NcZF | Example of multiplying integers and fractions by integers and fractions that are not of the same type: we wish to multiply five integers and two thirds by two integers and three sixths.
: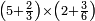 דמיון לכפול שלמים ושברים על שלמים ושברים שאינם השברים ממין אחד
דמיון לכפול שלמים ושברים על שלמים ושברים שאינם השברים ממין אחדרצינו לכפול חמשה שלמים ושתי שלישיות 90vעל שני שלמיות ושלש ששיות | ||
| simple fraction/multiplication of fractions | (2+¾)×(3+²/₄) | עיר_סיחון#lTDC | Example of multiplying integers and fractions by integers and fractions of the same type: we wish to multiply two integers and three quarters by three integers and two quarters.
: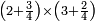 דמיון לכפול שלמים ושברים על שלמים [ושברים]Vatican om. ששבריהם ממין אחד
דמיון לכפול שלמים ושברים על שלמים [ושברים]Vatican om. ששבריהם ממין אחדרצינו לכפול שני שלמים ושלש רביעיות על שלשה שלמים ושתי רביעיות | ||
| simple fraction/multiplication of fractions | (⅔+⁵/₇+⅙·⅐)×(⅘+⁹/₁₀+⁸/₉·⅒) | ספר_החשבון_לאל_חצאר#fJdW | Example: multiply two-thirds, five-sevenths and a sixth of a seventh by four-fifths, nine-tenths and [eight-ninths] of a tenth.
:![\scriptstyle\left[\frac{2}{3}+\frac{5}{7}+\left(\frac{1}{6}\sdot\frac{1}{7}\right)\right]\times\left[\frac{4}{5}+\frac{9}{10}+\left({\color{red}{\frac{8}{9}}}\sdot\frac{1}{10}\right)\right]](/mediawiki/images/math/0/4/1/041283e02911225ffbfa4564ed3aefef.png) הנה דמיון זה הכה שני שלישים וחמש שביעיות ושתות שביעית בארבעה חומשים ותשע עש[י]ר[י]ות ושמינית תשיעית העשירי'
הנה דמיון זה הכה שני שלישים וחמש שביעיות ושתות שביעית בארבעה חומשים ותשע עש[י]ר[י]ות ושמינית תשיעית העשירי' | ||
| simple fraction/multiplication of fractions | (4+⅖)×¾ | עיר_סיחון#IoIr | Example of multiplying integers and fractions by fractions that are not of one type: we wish to multiply four integers and two fifths by three quarters.
: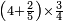 דמיוןVatican: דמין לכפול שלמים ושברים על שברים לבדם שאינם ממין אחד
דמיוןVatican: דמין לכפול שלמים ושברים על שברים לבדם שאינם ממין אחדרצינו לכפול ארבעה שלמים ושתי חמשיות על שלש רביעיות | ||
| simple fraction/multiplication of fractions | (3+⅘)×⅗ | עיר_סיחון#TGUm | Example of multiplying integers and fractions by fractions of one type alone: we wish to multiply three integers and four-fifths by three-fifths.
: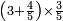 דמיון לכפלת שלמים ושברים על שברים לבדם שהם ממין אחד
דמיון לכפלת שלמים ושברים על שברים לבדם שהם ממין אחדרצינו לכפול שלשה שלמים וארבע חמישיות על שלש חמישיות | ||
| simple fraction/multiplication of fractions | 5×⁴/₆ | עיר_סיחון#chfZ | Example of multiplying integers by fractions: we wish to multiply five integers by four sixths.
: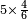 דמיון ל{{#annot:term|156,1253|QXoD}}כפילת{{#annotend:QXoD}} שלמים על שברים
דמיון ל{{#annot:term|156,1253|QXoD}}כפילת{{#annotend:QXoD}} שלמים על שבריםרצינו לכפול חמשה שלמים בארבע שישיות | ||
| simple fraction/multiplication of fractions | ⅓×⅓ | ספר_חשבון#p54W | When we multiply a third by a third, it is a third of a third.
: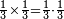 וכשנרבה שליש בשליש הוא שליש בשליש
וכשנרבה שליש בשליש הוא שליש בשליש | ||
| simple fraction/multiplication of fractions | ⅓×2 | ספר_חשבון#CmHn | When we multiply the third by two it is 2-thirds.
: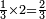 וכשנרבה השליש בשנים הוא ב' שלישי האחד
וכשנרבה השליש בשנים הוא ב' שלישי האחד | ||
| simple fraction/multiplication of fractions | ⅓×1 | ספר_חשבון#dp1H | When we multiply the third by one, it is a third.
: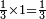 כשנרבה השליש באחד הוא שליש
כשנרבה השליש באחד הוא שליש | ||
| simple fraction/multiplication of fractions | 2×(3+¼) | Anonymous#rNFH | Such as two by three and a quarter.
: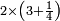 כגון שנים על שלשה ורביע
כגון שנים על שלשה ורביע | ||
| simple fraction/multiplication of fractions | (¾+⅘+½·⅐)×(⅞+⁸/₉+⅓·⅒) | ספר_החשבון_לאל_חצאר#xekW | Example: when you are told: multiply three-quarters, four-fifths and half a seventh by seven-eighths, eight-ninths and [a third of a tenth].
:![\scriptstyle\left[\frac{3}{4}+\frac{4}{5}+\left(\frac{1}{2}\sdot\frac{1}{7}\right)\right]\times\left[\frac{7}{8}+\frac{8}{9}+\left({\color{red}{\frac{1}{3}}}\sdot\frac{1}{10}\right)\right]](/mediawiki/images/math/6/6/a/66a68e771cb067c2d84865ea8830d7ae.png) דמיון זה כשיאמר לך הכה שלשה רביעים וארבעה חומשים וחצי שביעית בשבע שמיניות ושמונה תשיעיות ושלש עשיריות
דמיון זה כשיאמר לך הכה שלשה רביעים וארבעה חומשים וחצי שביעית בשבע שמיניות ושמונה תשיעיות ושלש עשיריות | ||
| simple fraction/multiplication of fractions | (⅔+⅗+⁴/₆)×(⁵/₇+⅞+⁹/₁₁) | ספר_החשבון_לאל_חצאר#5uwE | When you are told: multiply two-thirds, three-fifths and four-sixths by five-sevenths, seven-eighths and nine parts of eleven.
: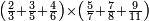 כשיאמר לך הכה שני שלישים ושלשה חומשים וארבעה שתותים בחמש שביעיות ושבע שמיניות ותשעה חלקים מאחד עשר
כשיאמר לך הכה שני שלישים ושלשה חומשים וארבעה שתותים בחמש שביעיות ושבע שמיניות ותשעה חלקים מאחד עשר | ||
| simple fraction/multiplication of fractions | (¾·5)×(⅚·7) | ספר_החשבון_לאל_חצאר#651M | When you are told: multiply three-quarters of a five by five-sixths of a seven.
: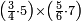 כאשר יאמר לך הכה שלשה רביעי חמשה בחמשה שתותי שבעה
כאשר יאמר לך הכה שלשה רביעי חמשה בחמשה שתותי שבעה | ||
| simple fraction/multiplication of fractions | (⅚+½·⅙)·8×(⁸/₉+⅕·⅑)·12 | ספר_החשבון_לאל_חצאר#eyub | ![\scriptstyle\left[\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\sdot8\right]\times\left[\left[\frac{8}{9}+\left(\frac{1}{5}\sdot\frac{1}{9}\right)\right]\sdot12\right]](/mediawiki/images/math/1/6/0/1600fa727c35dec4f3c4ad5a9afdabb3.png) כאשר יאמר לך הכה חמשה שתותים וחצי שתות שמונה בשמונה תשיעיות וחומש תשיעית שנים עשר
כאשר יאמר לך הכה חמשה שתותים וחצי שתות שמונה בשמונה תשיעיות וחומש תשיעית שנים עשר | ||
| simple fraction/multiplication of fractions | (⅔+⅗)·8×(⁶/₇+⁵/₉)·4 | ספר_החשבון_לאל_חצאר#U7GU | ![\scriptstyle\left[\left(\frac{2}{3}+\frac{3}{5}\right)\sdot8\right]\times\left[\left(\frac{6}{7}+\frac{5}{9}\right)\sdot4\right]](/mediawiki/images/math/5/1/a/51a5f2c5f34e3fd50333a6ab3d89872a.png) כאשר יאמר לך הכה שני שלישים ושלשה חומשי שמונה בששה שביעיות וחמש תשיעיות ארבעה
כאשר יאמר לך הכה שני שלישים ושלשה חומשי שמונה בששה שביעיות וחמש תשיעיות ארבעה | ||
| simple fraction/multiplication of fractions | (¾·⅕)·8×(⅚·⅐)·15 | ספר_החשבון_לאל_חצאר#8z4Z | ![\scriptstyle\left[\left(\frac{3}{4}\sdot\frac{1}{5}\right)\sdot8\right]\times\left[\left(\frac{5}{6}\sdot\frac{1}{7}\right)\sdot15\right]](/mediawiki/images/math/0/5/f/05f9355bfe0fc140027cb8b0dd02c1ec.png) כאשר יאמר לך הכה שלשה רביעי חמישית השמונה בחמשה שתותי שביעית חמשה עשר
כאשר יאמר לך הכה שלשה רביעי חמישית השמונה בחמשה שתותי שביעית חמשה עשר | ||
| simple fraction/multiplication of fractions | ⅔×⅘ | מלאכת_המספר#5jnJ | As the one who wants to multiply 2-thirds by 4-fifths.
: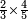 כמי שרוצה לרבע [ב' שלישיו' וד' חמישיו']marg.
כמי שרוצה לרבע [ב' שלישיו' וד' חמישיו']marg. | ||
| simple fraction/multiplication of fractions | (²/₄ײ/₆)+(⅘×⅚) | קצת_מענייני_חכמת_המספר#shmO | For instance: you wish to know the sum of the product of two quarters by 2-sixths with the product of 4-fifths by 5-sixths, without having to multiply first then to sum, and still the total result is exact.
: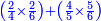 כגון שרצית לידע קבוץ הכאת שני רביעיות עם ב' ששיות עם קבוץ הכאת ד' חומשיות עם ה' ששיות מבלתי שתצטרך תחלה להכות ואח"כ לקבץ אבל יצא הכל {{#annot:term|2447,1386|i968}}מתוקן{{#annotend:i968}} ביחד
כגון שרצית לידע קבוץ הכאת שני רביעיות עם ב' ששיות עם קבוץ הכאת ד' חומשיות עם ה' ששיות מבלתי שתצטרך תחלה להכות ואח"כ לקבץ אבל יצא הכל {{#annot:term|2447,1386|i968}}מתוקן{{#annotend:i968}} ביחד | ||
| simple fraction/multiplication of fractions | ⅔·(5+⅚)×⁵/₇·(8+⁴/₉) | ספר_החשבון_לאל_חצאר#aMXd | ![\scriptstyle\left[\frac{2}{3}\sdot\left(5+\frac{5}{6}\right)\right]\times\left[\frac{5}{7}\sdot\left(8+\frac{4}{9}\right)\right]](/mediawiki/images/math/0/b/f/0bf7045fc49295b61cbc8cb9708697cd.png) כאשר יאמר לך הכה שני שלישי חמשה וחמשה שתותים בחמש שביעיות שמונה וארבע תשיעיות
כאשר יאמר לך הכה שני שלישי חמשה וחמשה שתותים בחמש שביעיות שמונה וארבע תשיעיות | ||
| simple fraction/multiplication of fractions | ¾·(5+⁶/₇+⅙·⅐)×⅞·(3+³/₁₀+⅑·⅒) | ספר_החשבון_לאל_חצאר#kJTB | ![\scriptstyle\left[\frac{3}{4}\sdot\left[5+\frac{6}{7}+\left(\frac{1}{6}\sdot\frac{1}{7}\right)\right]\right]\times\left[\frac{7}{8}\sdot\left[3+\frac{3}{10}+\left(\frac{1}{9}\sdot\frac{1}{10}\right)\right]\right]](/mediawiki/images/math/e/d/2/ed219e497be7d0951c74faa4e0f2f7d7.png) דמיון זה הכה שלשה רביעי חמשה וששה שביעיות ושתות שביעית בשבע שמיניות שלשה ושלש עשיריות ותשיעית העשירית
דמיון זה הכה שלשה רביעי חמשה וששה שביעיות ושתות שביעית בשבע שמיניות שלשה ושלש עשיריות ותשיעית העשירית | ||
| simple fraction/multiplication of fractions | 2½×4¾ | מלאכת_המספר#I0sb | As the one who wants to multiply this number:
: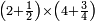 כמי שרוצה לרבע זה המספר
כמי שרוצה לרבע זה המספר | ||
| simple fraction/multiplication of fractions | ½·(2+⅕+⅙)×⅐·(3+⅛+⅑) | ספר_החשבון_לאל_חצאר#Fxsj | ![\scriptstyle\left[\frac{1}{2}\sdot\left(2+\frac{1}{5}+\frac{1}{6}\right)\right]\times\left[\frac{1}{7}\sdot\left(3+\frac{1}{8}+\frac{1}{9}\right)\right]](/mediawiki/images/math/0/0/4/004e700b6414538394bc342a34fa598e.png) כשיאמר לך הכה חצי שנים וחומש ושתות בשביעית שלשה ושמינית ותשיעית
כשיאמר לך הכה חצי שנים וחומש ושתות בשביעית שלשה ושמינית ותשיעית | ||
| simple fraction/multiplication of fractions | ((¾·5½)+(⅚·3⅖))×((⅔·4⅐)+(⅜·2³/₁₁)) | ספר_החשבון_לאל_חצאר#z3zR | כאשר יאמר לך הכה שלשה רביעי חמשה וחצי וחמשה שתותי שלשה ושני חומשים בשני שלישי ארבעה ושביעית ושלש שמיניות שנים ושלשה חלקים מאחד עשר | ||
| simple fraction/multiplication of fractions | (3+⅓)×(4+¼) | ספר_חשבון#PNQv | How much are 3 and a third times 4 and a quarter?
: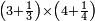 אם תרצה לדעת ג' ושליש פעמים ד' ורביע כמה עולי'
אם תרצה לדעת ג' ושליש פעמים ד' ורביע כמה עולי' | ||
| simple fraction/multiplication of fractions | ⁹/₁₃×¹⁷/₁₉ | ספר_החשבון_והמדות#v4BY | 1) How much are 9 parts of 13 multiplied by 17 parts of 19?
: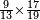 א כמה ט' חלקים מי"ג הכפולים על י"ז חלקים מי"ט
א כמה ט' חלקים מי"ג הכפולים על י"ז חלקים מי"ט | ||
| simple fraction/multiplication of fractions | (⅔·¾·⅘·⅚·⁶/₇·⅞·⁸/₉·⁹/₁₀·¹⁰/₁₁)×(⅔·¾·⅘·⅚·⁶/₇·⅞·⁸/₉·⁹/₁₀·¹⁰/₁₁) | ספר_החשבון_לאל_חצאר#UDjw | והמשל בו כשיאמר לך הכה שני שלישי שלשה רביעי ארבעה חומשי חמשה שתותי שש שביעיות שבעה שמיניות שמונה תשיעיות תשע עשיריות עשרה חלקים מאחד עשר בדומה לו | ||
| simple fraction/multiplication of fractions | ((⅖·⅚)+½)·3×((⅔·⁶/₇)+⅗)·10 | ספר_החשבון_לאל_חצאר#2suQ | ![\scriptstyle\left[\left[\left(\frac{2}{5}\sdot\frac{5}{6}\right)+\frac{1}{2}\right]\sdot3\right]\times\left[\left[\left(\frac{2}{3}\sdot\frac{6}{7}\right)+\frac{3}{5}\right]\sdot10\right]](/mediawiki/images/math/f/5/6/f563fe0da1c5a32c4b4bb95452e54bc5.png) כשיאמר לך הכה שני חומשי חמשה שתותים וחצי שלשה בשני שלישי שש שביעיות ושלשה חומשי עשרה
כשיאמר לך הכה שני חומשי חמשה שתותים וחצי שלשה בשני שלישי שש שביעיות ושלשה חומשי עשרה | ||
| simple fraction/multiplication of fractions | 4⅓×6 | מלאכת_המספר#r9pQ | As the one who wants to multiply 4 and a third by 6.
: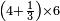 כמי שרוצה לרבע ד' ושליש עם ו'
כמי שרוצה לרבע ד' ושליש עם ו' | ||
| simple fraction/multiplication of fractions | ((⅔·⁶/₉)·(6+¾))×((¾·⁸/₉)(2+⅖)) | ספר_החשבון_לאל_חצאר#gWo2 | ![\scriptstyle\left[\left(\frac{2}{3}\sdot\frac{6}{9}\right)\sdot\left(6+\frac{3}{4}\right)\right]\times\left[\left(\frac{3}{4}\sdot\frac{8}{9}\right)\sdot\left(2+\frac{2}{5}\right)\right]](/mediawiki/images/math/f/a/4/fa4daab5fb3c530e96d4f4be1abe9aec.png) כשיאמר לך הכה שני שלישי ששה תשיעיות של ששה ושלשה רביעים בשלשה רביעי שמונה תשיעיות שנים ושני חומשים
כשיאמר לך הכה שני שלישי ששה תשיעיות של ששה ושלשה רביעים בשלשה רביעי שמונה תשיעיות שנים ושני חומשים | ||
| simple fraction/multiplication of fractions | ((⅗·⁴/₇)·(3+⅚+½·⅙))×((⅔·⅚)·(6+⅞+⅔·⅛)) | ספר_החשבון_לאל_חצאר#sIo1 | ![\scriptstyle\left[\left(\frac{3}{5}\sdot\frac{4}{7}\right)\sdot\left[3+\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\right]\times\left[\left(\frac{2}{3}\sdot\frac{5}{6}\right)\sdot\left[6+\frac{7}{8}+\left(\frac{2}{3}\sdot\frac{1}{8}\right)\right]\right]](/mediawiki/images/math/2/5/5/2550673eb8dc78a12727d2d5dc0b5427.png) כשיאמר לך הכה שלשה חומשי ארבעה שביעי שלשה וחמשה שתותי וחצי שתות בשני שלישי חמשה שתותי ששה ושבע שמיניות ושני שלישי שמינית
כשיאמר לך הכה שלשה חומשי ארבעה שביעי שלשה וחמשה שתותי וחצי שתות בשני שלישי חמשה שתותי ששה ושבע שמיניות ושני שלישי שמינית | ||
| simple fraction/multiplication of fractions | 4×⅔ | ספר_דיני_ממונות#at7F | 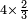 דמיון זה נרצה לכפול ד' שלמים על ב' שלישיות
דמיון זה נרצה לכפול ד' שלמים על ב' שלישיות | ||
| simple fraction/multiplication of fractions | 4½×⅔ | ספר_דיני_ממונות#zVQ8 | 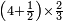 דמיון זה נרצה לכפול ד' וחצי על ב' שלישיות
דמיון זה נרצה לכפול ד' וחצי על ב' שלישיות | ||
| simple fraction/multiplication of fractions | ⅖×⅒ײ/₈×⅓ | ספר_יסודי_התבונה_ומגדל_האמונה#gymG | If you are told: multiply two parts of 5 by one tenth by two parts of eighth by one third?
: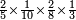 וכן אם יאמר חשוב בב' חלקים מחמשה בעשירית האחד בב' חלקים משמנה בשלישית האחד
וכן אם יאמר חשוב בב' חלקים מחמשה בעשירית האחד בב' חלקים משמנה בשלישית האחד | ||
| simple fraction/multiplication of fractions | (⅗·³/₇·²/₉·⅒)×(⅔·⁶/₇·⅘·⁷/₉) | ספר_החשבון_לאל_חצאר#kkRY | ודמיון זה כשיאמר לך הכה שלשה חומשי שלש שביעיות שתי תשיעיות עשרה בשני שלישי שש שביעיות ארבעה חומשי שבע תשיעיות | ||
| simple fraction/multiplication of fractions | ((¾·⅘)+(⅚·⁶/₇)+(⅞·⁸/₉))×((⅔·¾)+((⅘·⅚)+(⁶/₇·⅞)) | ספר_החשבון_לאל_חצאר#LTY9 | כשיאמר לך הכה שלשה רביעי ארבעה חומשים וחמשה שתותי שש שביעיות ושבע שמיניות שמונה תשיעיות בשני שלישי שלשה רביעי ארבעה חומשי חמשה שתותים ושש שביעיות שבע שמיניות | ||
| simple fraction/multiplication of fractions | ⁶/₇·(5+½·⅙)×⅞·(3+⅗·⅑) | ספר_החשבון_לאל_חצאר#KGXW | ![\scriptstyle\left[\frac{6}{7}\sdot\left[5+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\right]\times\left[\frac{7}{8}\sdot\left[3+\left(\frac{3}{5}\sdot\frac{1}{9}\right)\right]\right]](/mediawiki/images/math/5/f/5/5f53be0be7aff5af1d6d8efd389472f7.png) כשיאמר לך הכה שש שביעיות חמשה וחצי שתות בשבעה שמיניות ושלשה חומשי התשיעית
כשיאמר לך הכה שש שביעיות חמשה וחצי שתות בשבעה שמיניות ושלשה חומשי התשיעית | ||
| simple fraction/multiplication of fractions | (3+⅘)×(2+⅗) | ספר_המספר_/_אברהם_אבן_עזרא#UZBp | Another example: we wish to multiply 3 integers and 4 fifths by 2 integers and 3 fifths.
: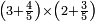 דמיון אחר רצינו לכפול ג' שלמים וד' חומשין על ב' שלמים וג' חומשין
דמיון אחר רצינו לכפול ג' שלמים וד' חומשין על ב' שלמים וג' חומשין | ||
| simple fraction/multiplication of fractions | ⅖×⅒×⅔ | ספר_יסודי_התבונה_ומגדל_האמונה#yQcZ | If you are told: multiply two parts of 5 by one tenth by two thirds?
: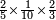 ואם יאמר לך חשוב ב' חלקים מה' בעשירית האחד בב' שלישי האחד
ואם יאמר לך חשוב ב' חלקים מה' בעשירית האחד בב' שלישי האחד | ||
| simple fraction/multiplication of fractions | (⅔·⅕)·(8+⅙)×(⁵/₇·⅛)·(6+⅑) | ספר_החשבון_לאל_חצאר#LYqM | ![\scriptstyle\left[\left(\frac{2}{3}\sdot\frac{1}{5}\right)\sdot\left(8+\frac{1}{6}\right)\right]\times\left[\left(\frac{5}{7}\sdot\frac{1}{8}\right)\sdot\left(6+\frac{1}{9}\right)\right]](/mediawiki/images/math/9/a/0/9a08cbb7c870dbf982d1d194761990fe.png) כשיאמר לך הכה שני שלישי חומש שמונה ושתות בחמש שביעיות שמינית ששה ותשיעית
כשיאמר לך הכה שני שלישי חומש שמונה ושתות בחמש שביעיות שמינית ששה ותשיעית | ||
| simple fraction/multiplication of fractions | ²/₁₁ײ/₁₃ | ספר_יסודי_התבונה_ומגדל_האמונה#BW7X | If you are told: multiply two parts of 11 by two parts of 13?
: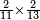 ואלו היו אומרים לך חשוב שני חלקים מי"א באחד בב' חלקים מי"ג באחד
ואלו היו אומרים לך חשוב שני חלקים מי"א באחד בב' חלקים מי"ג באחד | ||
| simple fraction/multiplication of fractions | 4½×⅔ | מלאכת_המספר#V2wD | As the one who wants to multiply 4 and a half by two-thirds.
: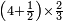 כמי שרוצה לרבע ד' וחצי עם שני שלישיות
כמי שרוצה לרבע ד' וחצי עם שני שלישיות | ||
| simple fraction/multiplication of fractions | 4×⅔ | מלאכת_המספר#qjqo | Example: we wish to multiply 4 integers by 2-thirds.
: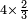 המשל נרצה לרבע ד' שלמים בב' שלישיות
המשל נרצה לרבע ד' שלמים בב' שלישיות | ||
| simple fraction/multiplication of fractions | ⅔×⅖ | ספר_יסודי_התבונה_ומגדל_האמונה#SOeb | The multiplication of two thirds by two fifths
: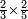 חשבון ב' שלישיים על ב' חמישיים
חשבון ב' שלישיים על ב' חמישיים | ||
| simple fraction/multiplication of fractions | ⅔×⅔ | ספר_יסודי_התבונה_ומגדל_האמונה#2Gb7 | If you are told: multiply two thirds by two thirds, how much are they?
: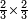 אם יאמר לך חשבו שני שלישים בשני שלישים כמה הם
אם יאמר לך חשבו שני שלישים בשני שלישים כמה הם | ||
| simple fraction/multiplication of fractions | ¾×¾ | ספר_המספר_/_אברהם_אבן_עזרא#UP2Z | Example: we wish to multiply 3 quarters by 3 quarters.
: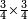 דמיון רצינו לכפול ג' רביעיות על ג' רביעיות
דמיון רצינו לכפול ג' רביעיות על ג' רביעיות | ||
| simple fraction/multiplication of fractions | (¾·⅕)·(6+³/₁₁+⅚·¹/₁₁)×(⁵/₇·⅑)·(12+⁶/₁₃+⅜·¹/₁₃) | ספר_החשבון_לאל_חצאר#6CY2 | כשיאמר לך הכה שלשה רביעי חומש בששה ושלשה חלקים מאחד עשר וחמש שתותי החלק מאחד עשר בחמש שביעיות תשיעית שנים עשר וששה חלקים משלשה עשר ושלש שמיניות החלק משלשה עשר | ||
| simple fraction/multiplication of fractions | ⅗×⅘ | ספר_המספר_/_אברהם_אבן_עזרא#Audh | Example: we want to multiply 3 fifths by 4 fifths.
: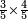 דמיון בקשנו לכפול ג' חמישיות על ד' חמישיות
דמיון בקשנו לכפול ג' חמישיות על ד' חמישיות | ||
| simple fraction/multiplication of fractions | ⅖×⅒ײ/₈×⅓ | ספר_חשבון#aUsg | If one says: 2 parts of five by one-tenth by two parts of eight by one-third.
: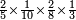 ואם יאמ' ב' חלקים מחמשה בעשירית האחד בשני חלקים משמנה בשלישית האחד
ואם יאמ' ב' חלקים מחמשה בעשירית האחד בשני חלקים משמנה בשלישית האחד | ||
| simple fraction/multiplication of fractions | 2×¾ | מלאכת_המספר#uzlZ | As the one who wants to double this number, which is 3-quarters.
: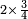 כמי שירצה לכפול זה המספר שהוא ג' רביעיות
כמי שירצה לכפול זה המספר שהוא ג' רביעיות | ||
| simple fraction/multiplication of fractions | ⅔×¾ | ספר_המספר_/_אברהם_אבן_עזרא#0gKn | One says: multiply 2 thirds by 3 quarters.
: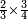 שיאמר כפול לי ב' שלישיות אחד על ג' רביעיותיו
שיאמר כפול לי ב' שלישיות אחד על ג' רביעיותיו | ||
| simple fraction/multiplication of fractions | (⅔·⅕)·(8+³/₆+⁴/₇)×(⁴/₉·⅒)·(18+⁶/₁₁+⅝) | ספר_החשבון_לאל_חצאר#4NIN | ![\scriptstyle\left[\left(\frac{2}{3}\sdot\frac{1}{5}\right)\sdot\left(8+\frac{3}{6}+\frac{4}{7}\right)\right]\times\left[\left(\frac{4}{9}\sdot\frac{1}{10}\right)\sdot\left(18+\frac{6}{11}+\frac{5}{8}\right)\right]](/mediawiki/images/math/9/7/d/97d9dfda0018e2b0241f56adec4bb691.png) כשיאמר לך הכה שני שלישי חומש שמונה ושלשה שתותים וארבעה שביעיות בארבע תשיעיות עשירית שמונה עשר וששה חלקים מאחד עשר וחמש שמיניות
כשיאמר לך הכה שני שלישי חומש שמונה ושלשה שתותים וארבעה שביעיות בארבע תשיעיות עשירית שמונה עשר וששה חלקים מאחד עשר וחמש שמיניות | ||
| simple fraction/multiplication of fractions | (⅔+⅗)·(9+⅚)×(³/₇+⁷/₈)·(12+⁷/₉) | ספר_החשבון_לאל_חצאר#6akx | ![\scriptstyle\left[\left(\frac{2}{3}+\frac{3}{5}\right)\sdot\left(9+\frac{5}{6}\right)\right]\times\left[\left(\frac{3}{7}+\frac{7}{8}\right)\sdot\left(12+\frac{7}{9}\right)\right]](/mediawiki/images/math/b/b/8/bb89089481d6771d64a646f1b2604e99.png) כשיאמר לך הכה שני שלישים ושלשה חומשי תשעה וחמשה שתותים בשלשה שביעיות ושבע שמיניות שנים עשר ושבע תשיעיות
כשיאמר לך הכה שני שלישים ושלשה חומשי תשעה וחמשה שתותים בשלשה שביעיות ושבע שמיניות שנים עשר ושבע תשיעיות | ||
| simple fraction/multiplication of fractions | ⁴/₇×⁷/₉ | ספר_המספר_/_אברהם_אבן_עזרא#m7n3 | Question: how much are 4 sevenths multiplied by 7 ninths?
: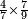 שאלה כמה ד' שביעיות כפולים על ז' תשיעיות
שאלה כמה ד' שביעיות כפולים על ז' תשיעיות | ||
| simple fraction/multiplication of fractions | (⅔+⅗)·(7+¾+⅗)×(⅚+⅝)·(4+⅚+⁹/₁₀) | ספר_החשבון_לאל_חצאר#aFMz | ![\scriptstyle\left[\left(\frac{2}{3}+\frac{3}{5}\right)\sdot\left(7+\frac{3}{4}+\frac{3}{5}\right)\right]\times\left[\left(\frac{5}{6}+\frac{5}{8}\right)\sdot\left(4+\frac{5}{6}+\frac{9}{10}\right)\right]](/mediawiki/images/math/b/4/9/b497ed9da24bcbdf311fe9fdd582187b.png) כשיאמר לך הכה שני שלישים ושלשה חומשי שבעה ושלשה רביעים ושלשה חומשים בחמשה שתותים וחמש שמיניות ארבעה וחמש שתותים ותשע עשיריות
כשיאמר לך הכה שני שלישים ושלשה חומשי שבעה ושלשה רביעים ושלשה חומשים בחמשה שתותים וחמש שמיניות ארבעה וחמש שתותים ותשע עשיריות | ||
| simple fraction/multiplication of fractions | (⅔·¼·⅕)×(⁶/₇·⅛) | עיר_סיחון#6SFy | We wish to multiply two thirds of one quarter of a fifth by six sevenths of an eighth.
: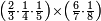 בקשנו לכפול שתי שלישיות מרביעית חמישית על שש 87vשביעיות שמינית
בקשנו לכפול שתי שלישיות מרביעית חמישית על שש 87vשביעיות שמינית | ||
| simple fraction/multiplication of fractions | (3+⅗·⅚)×(4+²/₇·⅜) | ספר_החשבון_לאל_חצאר#9253 | ![\scriptstyle\left[3+\left(\frac{3}{5}\sdot\frac{5}{6}\right)\right]\times\left[4+\left(\frac{2}{7}\sdot\frac{3}{8}\right)\right]](/mediawiki/images/math/c/c/6/cc62007c7e8709f4fde684e0c6ff424c.png) כשיאמר לך הכה שלשה ושלשה חומשי חמשה שתותים בארבעה ושתי שביעיות שלש שמיניות
כשיאמר לך הכה שלשה ושלשה חומשי חמשה שתותים בארבעה ושתי שביעיות שלש שמיניות | ||
| simple fraction/multiplication of fractions | (2+½)×(3+⅓) | ספר_דיני_ממונות#v1HK | 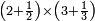 דמיון זה נרצה לכפול ב' וחצי על ג' ושליש
דמיון זה נרצה לכפול ב' וחצי על ג' ושליש | ||
| simple fraction/multiplication of fractions | (4+⅖)×(5+⅗) | ספר_המספר_/_אברהם_אבן_עזרא#izuY | Example: we wish to multiply 4 integers and 2 fifths by 5 integers and 3 fifths.
: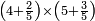 דמיון רצינו לכפול ד' שלמים וב' חמישיות על ה' שלמים וג' חמישיות
דמיון רצינו לכפול ד' שלמים וב' חמישיות על ה' שלמים וג' חמישיות | ||
| simple fraction/multiplication of fractions | (⅗+½·⅕)·(4+⅙+½·⅙)×(⁶/₇+⅖·⅐)·(3+⁵/₁₁+⅝·¹/₁₁) | ספר_החשבון_לאל_חצאר#UfbP | כאשר יאמר לך הכה שלשה חומשים וחצי חומש ארבעה ושתות וחצי שתות בששה שביעיות ושני חומשי שביעית שלשה וחמשה חלקים מאחד עשר וחמש שמיניות החלק מאחד עשר | ||
| simple fraction/multiplication of fractions | ⅔×⅚×⁴/₇ | ספר_המספר_/_אברהם_אבן_עזרא#ix44 | Such as 2 thirds and 5 sixths and 4 sevenths.
: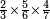 כמו ב' שלישיות וה' ששיות וד' שביעיות
כמו ב' שלישיות וה' ששיות וד' שביעיות | ||
| simple fraction/multiplication of fractions | ⁹/₁₅×¹¹/₁₇ | עיר_סיחון#YOwx | We wish to multiply nine parts of fifteen by eleven parts of seventeen.
: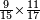 בקשנו לכפול תשע חלקים מחמשה עשר בשלם על אחד עשר עשר חלקים משבעה עשר בשלם
בקשנו לכפול תשע חלקים מחמשה עשר בשלם על אחד עשר עשר חלקים משבעה עשר בשלם | ||
| simple fraction/multiplication of fractions | 4×⅗ | ספר_המספר_/_אברהם_אבן_עזרא#uLMJ | Example: we wish to multiply 4 integers by 3 fifths.
: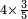
דמיון רצינו לכפול ד' שלמים על ג' חמישיות אחד | ||
| simple fraction/multiplication of fractions | ⅔×¾ | ספר_דיני_ממונות#ilbx | 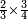 דמיון זה נרצה לכפול ב' שלישיות על ג' רביעיות
דמיון זה נרצה לכפול ב' שלישיות על ג' רביעיות | ||
| simple fraction/multiplication of fractions | ⅘׳/₁₃ | עיר_סיחון#Wi3Z | We wish to multiply four fifths by three parts of thirteen.
: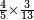 בקשנו לכפול ארבע חמישיות על שלשה חלקים משלשה עשר בשלם
בקשנו לכפול ארבע חמישיות על שלשה חלקים משלשה עשר בשלם | ||
| simple fraction/multiplication of fractions | (⅔·⅕)·(8+¼·⅙)×(³/₇·⅛)·(12+½·¹/₁₃) | ספר_החשבון_לאל_חצאר#Cjr7 | ![\scriptstyle\left[\left(\frac{2}{3}\sdot\frac{1}{5}\right)\sdot\left[8+\left(\frac{1}{4}\sdot\frac{1}{6}\right)\right]\right]\times\left[\left(\frac{3}{7}\sdot\frac{1}{8}\right)\sdot\left[12+\left(\frac{1}{2}\sdot\frac{1}{13}\right)\right]\right]](/mediawiki/images/math/b/d/3/bd39d71c41ffa67e9904a9b88747ee73.png) כשיאמר לך הכה שני שלישי חמישית שמנה הרביע שתות בשלש שביעיות שמינית שנים עשר וחצי חלק משלשה עשר
כשיאמר לך הכה שני שלישי חמישית שמנה הרביע שתות בשלש שביעיות שמינית שנים עשר וחצי חלק משלשה עשר | ||
| simple fraction/multiplication of fractions | ⁵/₇×⁷/₈ | עיר_סיחון#NoxQ | We wish to multiply five sevenths by seven eighths.
: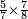 בקשנו לכפול חמש שביעיות בשבע שמינית
בקשנו לכפול חמש שביעיות בשבע שמינית | ||
| simple fraction/multiplication of fractions | ⅔×⅖ | Anonymous#Tlt0 | Such as two thirds by two fifths.
: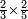 כגון שני שלישיים על שני חמישיים
כגון שני שלישיים על שני חמישיים | ||
| simple fraction/multiplication of fractions | ⅖×⅒×⅔ | Anonymous#j0VS | If you multiply 2 parts of five by a tenth by 2 thirds.
: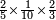 |style="width: 50%; text-align:right;"|ואם תערוך ב' חלקים מחמשה בעשירית האחד בב' שלישי אחד
|style="width: 50%; text-align:right;"|ואם תערוך ב' חלקים מחמשה בעשירית האחד בב' שלישי אחד | ||
| simple fraction/multiplication of fractions | (¾·⅗)×(⅚·³/₇) | Anonymous#ySC3 | If you multiply 3 quarters of 3 fifths by 5 sixths of 3 sevenths.
: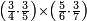 |style="width: 50%; text-align:right;"|ואם תערוך ג' רביעיות של ג' חומשין בה' שתותין של ג' רביעיות
|style="width: 50%; text-align:right;"|ואם תערוך ג' רביעיות של ג' חומשין בה' שתותין של ג' רביעיות | ||
| simple fraction/multiplication of fractions | (⅖·⅒)×(²/₈·⅓) | Anonymous#bfok | If you multiply two parts of a five by one-tenth by two parts of an eight by one-third.
: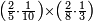 ואם תערוך שני חלקים מחמשה בעשירית האחד בשני חלקים משמונה בשלישית האחד
ואם תערוך שני חלקים מחמשה בעשירית האחד בשני חלקים משמונה בשלישית האחד | ||
| simple fraction/multiplication of fractions | ⁴/₇×⁵/₉ | ספר_מעשה_חושב#jfRX | Example: we wish to multiply 4 sevenths by 5 ninths.
: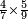 והמשל שנרצה להכות ד' שביעיות על ה' תשיעיות
והמשל שנרצה להכות ד' שביעיות על ה' תשיעיות | ||
| simple fraction/multiplication of fractions | ¾×⅘ | עיר_סיחון#EMJE | We wish to multiply three quarters by four fifths.
: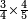 בקשנו לכפול שלש רביעיות בארבע חמישיות
בקשנו לכפול שלש רביעיות בארבע חמישיות | ||
| simple fraction/multiplication of fractions | (⁵/₇·⅓)×⅞ | ספר_מעשה_חושב#t63W | Example: if we wish to multiply 5 sevenths of thirds by 7 eighths.
::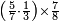 דמיון זה אם רצינו להכות ה' שביעיות שלישיות על ז' שמיניות
דמיון זה אם רצינו להכות ה' שביעיות שלישיות על ז' שמיניות | ||
| simple fraction/multiplication of fractions | ⅚×10 | ספר_החשבון_לאל_חצאר#yH5g | When you are told: multiply five-sixths by ten.
: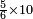 כאשר יאמר לך הכה חמשה שתותים בעשרה
כאשר יאמר לך הכה חמשה שתותים בעשרה | ||
| simple fraction/multiplication of fractions | (⅕+½·⅕)×12 | ספר_החשבון_לאל_חצאר#NiJT | When you are told: multiply a fifth and half a fifth by twelve.
:![\scriptstyle\left[\frac{1}{5}+\left(\frac{1}{2}\sdot\frac{1}{5}\right)\right]\times12](/mediawiki/images/math/3/8/d/38d26a85ea2cfc361c9a8a6775ab9e5b.png) כאשר יאמר לך הכה חומש וחצי חומש בשנים עשר
כאשר יאמר לך הכה חומש וחצי חומש בשנים עשר | ||
| simple fraction/multiplication of fractions | (⅓·⅐)×25 | ספר_החשבון_לאל_חצאר#STpd | When you are told: multiply a third of a seventh by twenty-five.
: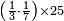 כאשר יאמר לך הכה שליש השביעית בחמשה ועשרים
כאשר יאמר לך הכה שליש השביעית בחמשה ועשרים | ||
| simple fraction/multiplication of fractions | ⅖×⅒×⅔ | ספר_חשבון#q3mD | If one says: how much are 2 parts of 5 by one-tenth by 2-thirds?
: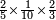 ואם יאמ' ב' חלקים מה' בעשירית האחד בב' שלישי האחר כמה הם
ואם יאמ' ב' חלקים מה' בעשירית האחד בב' שלישי האחר כמה הם | ||
| simple fraction/multiplication of fractions | (¾+⅘)×15 | ספר_החשבון_לאל_חצאר#5CHI | When you are told: multiply three-quarters and four-fifths by fifteen.
: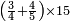 כשיאמר לך הכה שלשה רביעים וארבעה חומשים בחמשה עשר
כשיאמר לך הכה שלשה רביעים וארבעה חומשים בחמשה עשר | ||
| simple fraction/multiplication of fractions | ⅗×(9+⅓) | ספר_החשבון_לאל_חצאר#BOiT | When you are told: multiply three-fifths by nine and a third.
: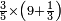 כאשר יאמר לך הכה שלשה חומשים בתשעה ושליש
כאשר יאמר לך הכה שלשה חומשים בתשעה ושליש | ||
| simple fraction/multiplication of fractions | (⅚+½·⅙)×(6+⅗) | ספר_החשבון_לאל_חצאר#Af60 | When you are told: multiply five-sixths and half a sixth by six and three-fifths.
:![\scriptstyle\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\times\left(6+\frac{3}{5}\right)](/mediawiki/images/math/7/3/9/739d727bdcdfb4c09f59bba584125807.png) כשיאמר לך הכה חמשה שתותים וחצי שתות בששה ושלשה חומשים
כשיאמר לך הכה חמשה שתותים וחצי שתות בששה ושלשה חומשים | ||
| simple fraction/multiplication of fractions | (½·⅐)×(10+⅗) | ספר_החשבון_לאל_חצאר#2tjq | When you are told: multiply half a seventh by ten and three-fifths.
: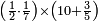 כאשר יאמר לך הכה חצי שביעית בעשרה ושלשה חומשים
כאשר יאמר לך הכה חצי שביעית בעשרה ושלשה חומשים | ||
| simple fraction/multiplication of fractions | (¾+⅘)×(5+⅚) | ספר_החשבון_לאל_חצאר#LV1r | When you are told: multiply three-quarters and four-fifths by five and five-sixths.
: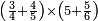 כשיאמר לך הכה שלשה רביעים וארבעה חומשים בחמשה וחמשה שתותים
כשיאמר לך הכה שלשה רביעים וארבעה חומשים בחמשה וחמשה שתותים | ||
| simple fraction/multiplication of fractions | ²/₄×¾ | עיר_סיחון#vUPh | We wish to multiply two quarters by three quarters
: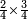 בקשנו לכפול ולהכות שתי רביעיות על שלש רביעיות
בקשנו לכפול ולהכות שתי רביעיות על שלש רביעיות | ||
| simple fraction/multiplication of fractions | ¾×(5+⅞+⅙·⅛) | ספר_החשבון_לאל_חצאר#8Jha | When you are told: multiply three-quarters by five, seven-eighths, and a sixth of an eighth.
:![\scriptstyle\frac{3}{4}\times\left[5+\frac{7}{8}+\left(\frac{1}{6}\sdot\frac{1}{8}\right)\right]](/mediawiki/images/math/f/f/e/ffe897c7d6abf4185f4ffb7c669d3ce1.png) כאשר יאמר לך הכה שלשה רביעיות בחמשה ושבעה שמיניות ושתות שמינית
כאשר יאמר לך הכה שלשה רביעיות בחמשה ושבעה שמיניות ושתות שמינית | ||
| simple fraction/multiplication of fractions | ⅘×⅘ | עיר_סיחון#yepM | We wish to multiply four fifths by four fifths
: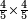 בקשנו לכפול ארבע חמישיות בארבע חמישיות
בקשנו לכפול ארבע חמישיות בארבע חמישיות | ||
| simple fraction/multiplication of fractions | ⅔×⅖ | Kaufmann_A_519_-_Collection_of_Word_Problems#AcY7 | How much is the multiplication of 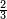 by by  ?
|10Quanto fa a moltiplicare ?
|10Quanto fa a moltiplicare 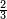 con con  | ||
| simple fraction/multiplication of fractions | ¾×1⅔ | Kaufmann_A_519_-_Collection_of_Word_Problems#Pm1D | How much is the multiplication of  by 1 and by 1 and 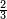 ?
|Quanto fa a moltiplicare ?
|Quanto fa a moltiplicare  con 1 et con 1 et 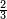 | ||
| simple fraction/multiplication of fractions | ⅚×(8+⁵/₇·⅑) | ספר_החשבון_לאל_חצאר#wQkm | When you are told: multiply five-sixths by eight and five-sevenths of a ninth.
:![\scriptstyle\frac{5}{6}\times\left[8+\left(\frac{5}{7}\sdot\frac{1}{9}\right)\right]](/mediawiki/images/math/e/5/f/e5f35b79321220d2b908e6078c54c785.png) כשיאמר לך הכה חמשה שתותים בשמונה וחמש שביעיות התשיעית
כשיאמר לך הכה חמשה שתותים בשמונה וחמש שביעיות התשיעית | ||
| simple fraction/multiplication of fractions | ⅔×(9+³/₇·⅘) | ספר_החשבון_לאל_חצאר#Hxq9 | When you are told: multiply two-thirds by nine, three-sevenths and four-fifths.
: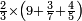 כאשר יאמר לך הכה שני שלישים בתשעה ושלשה שביעיות וארבעה חומשים
כאשר יאמר לך הכה שני שלישים בתשעה ושלשה שביעיות וארבעה חומשים | ||
| simple fraction/multiplication of fractions | 1½×1⅓×1¼×1⅕×1⅙×1⅐×1⅛×1⅑×1⅒ | ספר_החשבון_לאל_חצאר#kOwq | Example: multiply one and a half by one and a third by one and a quarter by one and a fifth by one and a sixth by one and a seventh by one and one-eighth by one and a ninth by one and a tenth. המשל בו הכה אחד וחצי באחד ושליש באחד ורביע באחד וחומש באחד ושתות באחד ושביעית באחד ושמינית באחד ותשיעית באחד ועשירית | ||
| simple fraction/multiplication of fractions | ²/₁₁ײ/₁₃ | ספר_חשבון#md7k | If one says: multiply 2 parts of 11 by 2 parts of 13.
: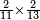 ואם יאמר חשוב ב' חלקים מי"א באחד על ב' חלקים מי"ג מן האחד
ואם יאמר חשוב ב' חלקים מי"א באחד על ב' חלקים מי"ג מן האחד | ||
| simple fraction/multiplication of fractions | ⅔×⅖ | ספר_חשבון#BRVP | If one says: multiply 2-thirds by 2-fifths.
: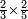 ואם יאמר חשוב ב' שלישים עם ב' חמישיות
ואם יאמר חשוב ב' שלישים עם ב' חמישיות | ||
| simple fraction/multiplication of fractions | (⅚+½·⅙)×(8+⁵/₇+⅕·⅐) | ספר_החשבון_לאל_חצאר#AAEA | Example: when you are told: multiply five-sixths and half a sixth by eight, five-sevenths and one-fifth of a seventh.
:![\scriptstyle\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\times\left[8+\frac{5}{7}+\left(\frac{1}{5}\sdot\frac{1}{7}\right)\right]](/mediawiki/images/math/b/7/f/b7f33a721f2cc7aa748520999089bce0.png) דמיון זה כאשר יאמר לך הכה חמשה שתותים וחצי שתות בשמונה וחמש שביעיות וחומש שביעית
דמיון זה כאשר יאמר לך הכה חמשה שתותים וחצי שתות בשמונה וחמש שביעיות וחומש שביעית | ||
| simple fraction/multiplication of fractions | ¼×¼ | קצור_המספר#dX0i | As if you say: we multiply once a quarter of 1 by a quarter.
: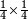 כאלו תאמ' נכפול רביע א' ברביע פעם
כאלו תאמ' נכפול רביע א' ברביע פעם | ||
| simple fraction/multiplication of fractions | ¼×⅓ | קצור_המספר#5veT | You say the same about the product of a quarter by a third, which is quarter of a third.
: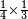 וכן תאמר בכפילת רביע בשליש שהעולה הוא רביע משליש
וכן תאמר בכפילת רביע בשליש שהעולה הוא רביע משליש | ||
| simple fraction/multiplication of fractions | ⅔×⅘ | קצור_המספר#cuXj | If you wish to multiply two-thirds by 4-fifths.
: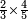 כיצד אם רצית לכפול שני שלישיות בד' חמישיות
כיצד אם רצית לכפול שני שלישיות בד' חמישיות | ||
| simple fraction/multiplication of fractions | (⅚+½·⅙)×(9+⅙·⅐) | ספר_החשבון_לאל_חצאר#LWbK | ![\scriptstyle\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\times\left[9+\left(\frac{1}{6}\sdot\frac{1}{7}\right)\right]](/mediawiki/images/math/9/6/a/96a8fdd4fab69e58c8a676b813acc28d.png) דמיון זה הכה חמשה שתותים וחצי שתות בתשעה ושתות שביעית
דמיון זה הכה חמשה שתותים וחצי שתות בתשעה ושתות שביעית | ||
| simple fraction/multiplication of fractions | (⅗·5+⅚·7)×(⅔·4+½·5) | ספר_החשבון_לאל_חצאר#Ln6q | ![\scriptstyle\left[\left(\frac{3}{5}\sdot5\right)+\left(\frac{5}{6}\sdot7\right)\right]\times\left[\left(\frac{2}{3}\sdot4\right)+\left(\frac{1}{2}\sdot5\right)\right]](/mediawiki/images/math/9/e/f/9efa063bb7945eb7d7c881b90eeae9c3.png) כשיאמר לך הכה שלשה חומשי חמשה וחמשה שתותי שבעה בשני שלישי ארבעה וחצי חמשה
כשיאמר לך הכה שלשה חומשי חמשה וחמשה שתותי שבעה בשני שלישי ארבעה וחצי חמשה | ||
| simple fraction/multiplication of fractions | ⁴/₇×⅚ | בר_נותן_טעם#sNi1 | Example: we wish to multiply 4-sevenths from 5-sixths.
: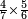 המשל רצינו לכפול ד' שביעיות בה' שישיות
המשל רצינו לכפול ד' שביעיות בה' שישיות | ||
| simple fraction/multiplication of fractions | (⅗·3+¾·2⅔)×(⅘·2+⁵/₇·3½) | ספר_החשבון_לאל_חצאר#lKub | ![\scriptstyle\left[\left(\frac{3}{5}\sdot3\right)+\left[\frac{3}{4}\sdot\left(2+\frac{2}{3}\right)\right]\right]\times\left[\left(\frac{4}{5}\sdot2\right)+\left[\frac{5}{7}\sdot\left(3+\frac{1}{2}\right)\right]\right]](/mediawiki/images/math/a/c/9/ac90cb543446e9ef209b88692cd48240.png) כשיאמר לך הכה שלשה חומשי שלשה ושלשה רביעי שנים ושני שלישים בארבעה חומשי שנים וחמשת שביעיות שלשה וחצי האחד
כשיאמר לך הכה שלשה חומשי שלשה ושלשה רביעי שנים ושני שלישים בארבעה חומשי שנים וחמשת שביעיות שלשה וחצי האחד | ||
| simple fraction/multiplication of fractions | (⅚+½·⅙)×(8+⁹/₁₀·¹⁰/₁₁) | ספר_החשבון_לאל_חצאר#Hazk | ![\scriptstyle\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\times\left(8+\frac{9}{10}+\frac{10}{11}\right)](/mediawiki/images/math/8/c/a/8ca9548a897d46b48ef337cafe7ed47c.png) דמיון זה כשיאמר לך הכה חמשה שתותים וחצי שתות בשמונה ותשע עשיריות ועשרה חלקים מאחד עשר
דמיון זה כשיאמר לך הכה חמשה שתותים וחצי שתות בשמונה ותשע עשיריות ועשרה חלקים מאחד עשר | ||
| simple fraction/multiplication of fractions | (3½+5⅓)×(4¾+6⅘) | ספר_החשבון_לאל_חצאר#5zBH | ![\scriptstyle\left[\left(3+\frac{1}{2}\right)+\left(5+\frac{1}{3}\right)\right]\times\left[\left(4+\frac{3}{4}\right)+\left(6+\frac{4}{5}\right)\right]](/mediawiki/images/math/d/c/e/dce671800feba457094cdfcc90b5a6f2.png) כאשר יאמר לך שלשה וחצי וחמשה ושני שלישים בארבעה ושלשה רביעים וששה וארבעה חומשים
כאשר יאמר לך שלשה וחצי וחמשה ושני שלישים בארבעה ושלשה רביעים וששה וארבעה חומשים | ||
| simple fraction/multiplication of fractions | ⅔×4 | קצור_המספר#tfPH | We wish to multiply 2-thirds by 4 integers.
: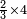 כיצד רצינו לכפול ב' שלישיות בד' שלמים
כיצד רצינו לכפול ב' שלישיות בד' שלמים | ||
| simple fraction/multiplication of fractions | ⅔×(¾·⅓) | קצור_המספר#ZHnp | We wish to multiply 2-thirds by 3-quarters of one-third.
: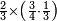 כיצד רצינו לכפול ב' שלישיות בג' רביעיות שליש אחד
כיצד רצינו לכפול ב' שלישיות בג' רביעיות שליש אחד | ||
| simple fraction/multiplication of fractions | (⅔·⅐)×(6+⁹/₁₀+⅘·⅒) | ספר_החשבון_לאל_חצאר#YN6C | ![\scriptstyle\left(\frac{2}{3}\sdot\frac{1}{7}\right)\times\left[6+\frac{9}{10}+\left(\frac{4}{5}\sdot\frac{1}{10}\right)\right]](/mediawiki/images/math/4/c/0/4c07b959f75b107b9a85f4431149a854.png) דמיון זה הכה שני שלישי שביעית בששה ותשעה עשיריות וארבעה חומשי העשור
דמיון זה הכה שני שלישי שביעית בששה ותשעה עשיריות וארבעה חומשי העשור | ||
| simple fraction/multiplication of fractions | (⅞·(5+⅓))×(⅗·(6+¼)) | Anonymous#tInL | If you multiply seven eighths of 5 and a third by 3 fifths of 6 and a quarter.
:![\scriptstyle\left[\frac{7}{8}\sdot\left(5+\frac{1}{3}\right)\right]\times\left[\frac{3}{5}\sdot\left(6+\frac{1}{4}\right)\right]](/mediawiki/images/math/3/c/4/3c44a996a735d16f077b6f5636f1fd0a.png) |style="width: 50%; text-align:right;"|ואם תערוך שבעה שמיניות של ה' ושליש בג' חמישיות של ו' ורובע
|style="width: 50%; text-align:right;"|ואם תערוך שבעה שמיניות של ה' ושליש בג' חמישיות של ו' ורובע | ||
| simple fraction/multiplication of fractions | (¾·⅑)×(8+⅚·⅐) | ספר_החשבון_לאל_חצאר#57dS | ![\scriptstyle\left(\frac{3}{4}\sdot\frac{1}{9}\right)\times\left[8+\left(\frac{5}{6}\sdot\frac{1}{7}\right)\right]](/mediawiki/images/math/d/f/e/dfe926298d98140474daec8e3ef52953.png) דמיון זה כשיאמר לך הכה שלשה רביעי התשיעית בשמונה וחמשה שתותי השביעית
דמיון זה כשיאמר לך הכה שלשה רביעי התשיעית בשמונה וחמשה שתותי השביעית | ||
| simple fraction/multiplication of fractions | ⁴/₇·(⁵/₉·⅛)×(⅗·⅑)·(⅔·5) | בר_נותן_טעם#WIlB | Example: we wish to multiply 4-sevenths of 5-ninths of an eighth by 3-fifths of a ninth of 2-thirds of 5 integers.
:![\scriptstyle\left[\left[\frac{4}{7}\sdot\left(\frac{5}{9}\sdot\frac{1}{8}\right)\right]\right]\times\left[\left(\frac{3}{5}\sdot\frac{1}{9}\right)\sdot\left(\frac{2}{3}\sdot5\right)\right]](/mediawiki/images/math/8/e/1/8e1455aa8265c18c2b288e543c19aede.png) המשל רצינו לכפול ד' שביעיות מה' תשיעיות שמינית על ג' חמשיות תשיעית מב' שלישיות מה' שלמים
המשל רצינו לכפול ד' שביעיות מה' תשיעיות שמינית על ג' חמשיות תשיעית מב' שלישיות מה' שלמים | ||
| simple fraction/multiplication of fractions | (2+(⅔+¾)·3+(⅘+⅚)·4)×(1+(⅗+½)·2+(³/₁₁+⁹/₁₀)·3) | ספר_החשבון_לאל_חצאר#mbJg | When you are told: multiply two, two-thirds plus three-quarters of three, and four-fifths plus five-sixths of four by one, [three-fifths plus a half of two], and three parts of eleven plus [nine]-tenths of three. כשיאמר לך הכה שנים ושני שלישים ושלשה רביעי שלשה וארבעה חומשים וחמשה שתותי ארבעה באחד ושלשה חלקים מאחד עשר ושבע עשיריות שלשה | ||
| simple fraction/multiplication of fractions | (⅚·⅛)×(6+¾+⅘) | ספר_החשבון_לאל_חצאר#Qxpv | 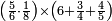 כשיאמר לך הכה חמשה שתותי השמינית בששה ושלשה רביעים וארבעה חומשים
כשיאמר לך הכה חמשה שתותי השמינית בששה ושלשה רביעים וארבעה חומשים | ||
| simple fraction/multiplication of fractions | (¾+⅘)×(6+⅞+⅙·⅛) | ספר_החשבון_לאל_חצאר#D3h3 | ![\scriptstyle\left(\frac{3}{4}+\frac{4}{5}\right)\times\left[6+\frac{7}{8}+\left(\frac{1}{6}\sdot\frac{1}{8}\right)\right]](/mediawiki/images/math/1/d/e/1de58acd88921baf39cf31c2001274d7.png) כאשר יאמר לך הכה שלשה רביעים וארבעה חומשים בששה ושבע שמיניות ושתות השמינית
כאשר יאמר לך הכה שלשה רביעים וארבעה חומשים בששה ושבע שמיניות ושתות השמינית | ||
| simple fraction/multiplication of fractions | (¾+⅘)×(6+⅐·⅛) | ספר_החשבון_לאל_חצאר#lctD | When you are told: multiply three-quarters and four-fifths by six and a seventh of an eighth.
:![\scriptstyle\left(\frac{3}{4}+\frac{4}{5}\right)\times\left[6+\left(\frac{1}{7}\sdot\frac{1}{8}\right)\right]](/mediawiki/images/math/a/0/8/a08d4959f373c7157cdca395fae419df.png) כאשר יאמר לך הכה שלשה רביעים וארבעה חומשים בששה ושביעית השמינית
כאשר יאמר לך הכה שלשה רביעים וארבעה חומשים בששה ושביעית השמינית | ||
| simple fraction/multiplication of fractions | (½+⅔)×(5+⁶/₇+⁸/₉) | ספר_החשבון_לאל_חצאר#KjF8 | Example: multiply half and two-thirds by five, six-sevenths and eight-ninths.
: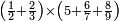 המשל בו הכה חצי ושני שלישים בחמשה ושש שביעיות ושמונה תשיעיות
המשל בו הכה חצי ושני שלישים בחמשה ושש שביעיות ושמונה תשיעיות | ||
| simple fraction/multiplication of fractions | (3+⅕)×(7+⅜) | ספר_החשבון_לאל_חצאר#QD1A | When you are told: multiply three and a fifth by seven and three-eighths.
: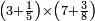 כאשר יאמר לך הכה שלשה וחומש בשבעה ושלש שמיניות
כאשר יאמר לך הכה שלשה וחומש בשבעה ושלש שמיניות | ||
| simple fraction/multiplication of fractions | (2+⅗+½·⅕)×(4+⁷/₉+⁶/₈·⅑) | ספר_החשבון_לאל_חצאר#0JUU | The example: when you are told: multiply two plus three-fifths and half a fifth by four plus seven-ninths and six-eighths of a ninth.
:![\scriptstyle\left[2+\frac{3}{5}+\left(\frac{1}{2}\sdot\frac{1}{5}\right)\right]\times\left[4+\frac{7}{9}+\left(\frac{6}{8}\sdot\frac{1}{9}\right)\right]](/mediawiki/images/math/1/9/4/194f683354067debfa65dc8b696fb706.png) המשל כשיאמר לך הכה שנים ושלשה חומשים וחצי חומש בארבעה ושבעה תשיעיות ושש שמיניות התשיעית
המשל כשיאמר לך הכה שנים ושלשה חומשים וחצי חומש בארבעה ושבעה תשיעיות ושש שמיניות התשיעית | ||
| simple fraction/multiplication of fractions | (¾·(3+⅓))×(⁶/₇·5) | Anonymous#Na7V | If you multiply three-quarters of three and one-third by six-sevenths of five.
:![\scriptstyle\left[\frac{3}{4}\sdot\left(3+\frac{1}{3}\right)\right]\times\left(\frac{6}{7}\sdot5\right)](/mediawiki/images/math/1/a/c/1ac4f88a6d78fe1ca6efd685e4d7383f.png) |style="width: 50%; text-align:right;"|ואם תערוך שלשה רביעיות [ש]ל שלשה ושליש על ששה שביעיות חמשה
|style="width: 50%; text-align:right;"|ואם תערוך שלשה רביעיות [ש]ל שלשה ושליש על ששה שביעיות חמשה | ||
| simple fraction/multiplication of fractions | (3+¼)×(5+⅙·⅐) | Anonymous#ubkD | Such as three and a quarter by five and one-sixth of one-seventh.
:![\scriptstyle\left(3+\frac{1}{4}\right)\times\left[5+\left(\frac{1}{6}\sdot\frac{1}{7}\right)\right]](/mediawiki/images/math/a/e/2/ae2eb1d97e60b3daefe628a8a4333262.png) כמו שלשה ורביעית על חמשה וששית שביעית
כמו שלשה ורביעית על חמשה וששית שביעית | ||
| simple fraction/multiplication of fractions | (6+⅔+⅗)×(9+⅚+⅞) | ספר_החשבון_לאל_חצאר#iJeR | When you are told: multiply six, two-thirds and three-fifths by nine, five-sixths and seven-eighths.
: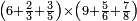 כאשר יאמר לך הכה ששה ושתי שלישיות ושלשה חומשים בתשעה וחמשה שתותים ושבע שמיניות
כאשר יאמר לך הכה ששה ושתי שלישיות ושלשה חומשים בתשעה וחמשה שתותים ושבע שמיניות | ||
| simple fraction/multiplication of fractions | (3+⅐)×(5+⅛) | Anonymous#t8Al | Such as three and a seventh by five and an eighth.
: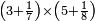 כגון שלשה ושביעית על חמשה ושמינית
כגון שלשה ושביעית על חמשה ושמינית | ||
| simple fraction/multiplication of fractions | (2+³/₇·⅗+⅔)×(3+¾·⅚+½) | ספר_החשבון_לאל_חצאר#q8JN | When you are told: multiply two, plus three-sevenths of three-fifths, and two-thirds by three plus three-quarters of five-sixths and a half.
:![\scriptstyle\left[2+\left(\frac{3}{7}\sdot\frac{3}{5}\right)+\frac{2}{3}\right]\times\left[3+\left(\frac{3}{4}\sdot\frac{5}{6}\right)+\frac{1}{2}\right]](/mediawiki/images/math/b/a/0/ba08b2bb8f498724f17c160ad860406d.png) כשיאמר לך הכה שנים ושלש שביעיות שלשה חומשים ושני שלישים בשלשה ושלש רביעיות חמשה שתותים וחצי
כשיאמר לך הכה שנים ושלש שביעיות שלשה חומשים ושני שלישים בשלשה ושלש רביעיות חמשה שתותים וחצי | ||
| simple fraction/multiplication of fractions | (2+¾+⅘+½·⅕)×(6+⁶/₇+⁹/₁₀+⅜·⅒) | ספר_החשבון_לאל_חצאר#5qBm | For example: multiply two, three-quarters, four-fifths and half a fifth by six, six-sevenths, nine-tenths and three-eighths of a tenth.
:![\scriptstyle\left[2+\frac{3}{4}+\frac{4}{5}+\left(\frac{1}{2}\sdot\frac{1}{5}\right)\right]\times\left[6+\frac{6}{7}+\frac{9}{10}+\left(\frac{3}{8}\sdot\frac{1}{10}\right)\right]](/mediawiki/images/math/c/a/5/ca56729c1329c7234d2a3479bc3a4064.png) הנה דמיון זה שתכה שנים ושלשה רביעים וארבעה חומשים וחצי חומש בששה ושש שביעיות ותשע עשריות ושלש שמיניות העשור
הנה דמיון זה שתכה שנים ושלשה רביעים וארבעה חומשים וחצי חומש בששה ושש שביעיות ותשע עשריות ושלש שמיניות העשור | ||
| simple fraction/multiplication of fractions | ((⅔·¾)·6)×((¾·⁴/₇)·8) | ספר_החשבון_לאל_חצאר#BTOS | ![\scriptstyle\left[\left(\frac{2}{3}\sdot\frac{3}{4}\right)\sdot6\right]\times\left[\left(\frac{3}{4}\sdot\frac{4}{7}\right)\sdot8\right]](/mediawiki/images/math/b/b/5/bb5eed5e9b25166de1f36bb9904c0f62.png) כשיאמר לך הכה שני שלישים שלשה רביעי ששה בשלשה רביעי ארבעה שביעיות שמונה
כשיאמר לך הכה שני שלישים שלשה רביעי ששה בשלשה רביעי ארבעה שביעיות שמונה | ||
| simple fraction/multiplication of fractions | (2+⅓+⅕+⅐·⅛)×(3+⅑+⅒+⅙·¹/₁₁) | ספר_החשבון_לאל_חצאר#XcJg | Example: multiply two, a third, a fifth and a seventh of an eighth by three, a ninth, a tenth and a sixth of one part of eleven.
:![\scriptstyle\left[2+\frac{1}{3}+\frac{1}{5}+\left(\frac{1}{7}\sdot\frac{1}{8}\right)\right]\times\left[3+\frac{1}{9}+\frac{1}{10}+\left(\frac{1}{6}\sdot\frac{1}{11}\right)\right]](/mediawiki/images/math/2/6/7/2674bbca8a320135a18e2259c80cbc80.png) דמיון זה הכה שנים ושליש וחומש ושביעית שמינית בשלשה ותשיעית ועשירית ושתות חלק מאחד עשר
דמיון זה הכה שנים ושליש וחומש ושביעית שמינית בשלשה ותשיעית ועשירית ושתות חלק מאחד עשר | ||
| simple fraction/multiplication of fractions | ⅑×⅐ | ספר_הכללים_במספר#P04R | If he had asked for one ninth by one seventh.
: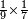 תאמ' אם היה שואל א' תשיעית על א' שבעית
תאמ' אם היה שואל א' תשיעית על א' שבעית | ||
| simple fraction/multiplication of fractions | ⁷/₉×⁴/₇ | ספר_הכללים_במספר#S123 | 74) If a man asks you: How much are seven ninths by four sevenths?
: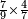 עד אי"א כמה הוא ז' תשיעיות על ד' שבעיות
עד אי"א כמה הוא ז' תשיעיות על ד' שבעיות | ||
| simple fraction/multiplication of fractions | ⅕×⅕ | ספר_הכללים_במספר#ubzN | Say: if he had asked for one fifth by one fifth.
: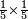 תאמר אם היה שואל א' חמישית על א' חמישית
תאמר אם היה שואל א' חמישית על א' חמישית | ||
| simple fraction/multiplication of fractions | ⅘×⅘ | ספר_הכללים_במספר#kvFj | 73) If a man asks you: How much are four fifths by four fifths?
: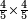 עג אם ישאלך אדם כמה הוא ד' חמשיות על ד' חמשיות
עג אם ישאלך אדם כמה הוא ד' חמשיות על ד' חמשיות | ||
| simple fraction/multiplication of fractions | ((¾·⅗)·(2+³/₇·⅚))×((½·¾)·(3+⅖·⁴/₉)) | ספר_החשבון_לאל_חצאר#kCKV | ![\scriptstyle\left[\left(\frac{3}{4}\sdot\frac{3}{5}\right)\sdot\left[2+\left(\frac{3}{{\color{red}{7}}}\sdot\frac{5}{6}\right)\right]\right]\times\left[\left(\frac{1}{2}\sdot\frac{3}{4}\right)\sdot\left[3+\left(\frac{2}{5}\sdot\frac{4}{9}\right)\right]\right]](/mediawiki/images/math/1/5/2/152a8c6ac1567adaf8da7c7a05dcaa70.png) כשיאמר לך הכה שלשה רביעי שלשה חומשי שנים ושלש תשיעיות חמשה שתותים בחצי שלשה רביעי שלשה ושני חומשי ארבע תשיעיות
כשיאמר לך הכה שלשה רביעי שלשה חומשי שנים ושלש תשיעיות חמשה שתותים בחצי שלשה רביעי שלשה ושני חומשי ארבע תשיעיות | ||
| simple fraction/multiplication of fractions | ⅔×⅔ | ספר_חשבון#Nlzy | If we multiply 2-thirds by 2-thirds.
: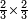 ואם נרבה ב' שלישי בב' שלישי
ואם נרבה ב' שלישי בב' שלישי | ||
| simple fraction/multiplication of fractions | ¾×9 | Anonymous#lhz8 | Such as three quarters by nine.
: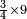 כגון שלשה רביעיות בתשעה
כגון שלשה רביעיות בתשעה | ||
| simple fraction/multiplication of fractions | (2+⅓+⅕+⅙)×(4+⅐+⅛+⅑) | ספר_החשבון_לאל_חצאר#yOZQ | Example: multiply two, a third, a fifth, and a sixth by four, a seventh, an eighth and a ninth.
: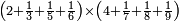 דמיון זה הכה שנים ושליש וחומש ושתות בארבעה ושביעית ושמינית ותשיעית
דמיון זה הכה שנים ושליש וחומש ושתות בארבעה ושביעית ושמינית ותשיעית | ||
| simple fraction/multiplication of fractions | ⅔×¾ | Kaufmann_A_519_-_Collection_of_Word_Problems#DhIn | How much is the multiplication of 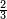 by by  ?
|12Quanto fa a moltiplicare ?
|12Quanto fa a moltiplicare 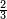 con con  | ||
| simple fraction/multiplication of fractions | 2¼×1⅓ | Kaufmann_A_519_-_Collection_of_Word_Problems#J6Ie | How much is the multiplication of 2 and  by 1 and by 1 and 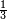 ?
|14Quanto fa a moltiplicare 2 et ?
|14Quanto fa a moltiplicare 2 et  con 1 et con 1 et 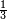 fa fa | ||
| simple fraction/multiplication of fractions | ⅞×⁹/₁₀ | ספר_החשבון_לאל_חצאר#gRBn | When you are told: multiply seven-eighths by nine-tenths.
: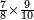 כאשר יאמר לך הכה שבעה שמיניות בתשעה עשיריות
כאשר יאמר לך הכה שבעה שמיניות בתשעה עשיריות | ||
| simple fraction/multiplication of fractions | ⅕×⅕ | ספר_חשבון#GtWm | The fifth by a fifth is a fifth of a fifth.
: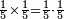 וחומש בחומש הוא חומ' החומש
וחומש בחומש הוא חומ' החומש | ||
| simple fraction/multiplication of fractions | (2+(½·⅕)·3+(⅔·⅙)·5)×(3+(¼·⅐)·4+(⅚·⅛)·2) | ספר_החשבון_לאל_חצאר#gG0q | When you are told: multiply two , half a fifth of three, and two-thirds of a sixth of five by three, a quarter of a seventh of four, and five-sixths of an eighth of two. כשיאמר לך הכה שנים וחצי חמישית שלשה ושני שלישי שתות חמשה בשלשה רביעי שביעית ארבעה וחמשה שתותים משמינית שנים | ||
| simple fraction/multiplication of fractions | ¹⁰/₁₁×¹²/₁₃ | ספר_החשבון_לאל_חצאר#qdg2 | If you are told: multiply ten parts of eleven by twelve parts of thirteen.
: ואם יאמר הכה עשרה חלקים מאחד עשר בשנים עשר חלקים משלשה עשר
ואם יאמר הכה עשרה חלקים מאחד עשר בשנים עשר חלקים משלשה עשר | ||
| simple fraction/multiplication of fractions | (⁶/₇+⅓·⅐)×⁸/₉ | ספר_החשבון_לאל_חצאר#eHK7 | When you are told: multiply six-sevenths and a third of a seventh by eight-ninths.
:![\scriptstyle\left[\frac{6}{7}+\left(\frac{1}{3}\sdot\frac{1}{7}\right)\right]\times\frac{8}{9}](/mediawiki/images/math/f/9/7/f97a19d668836f661a08889fa51e299c.png) כשיאמר לך הכה שש שביעיות ושליש שביעית בשמונה תשיעיות
כשיאמר לך הכה שש שביעיות ושליש שביעית בשמונה תשיעיות | ||
| simple fraction/multiplication of fractions | (¹/₁₁+½·¹/₁₁)×¹²/₁₃ | ספר_החשבון_לאל_חצאר#kLzs | If you are told: multiply one part of eleven and half a part of eleven by twelve parts of thirteen.
:![\scriptstyle\left[\frac{1}{11}+\left(\frac{1}{2}\sdot\frac{1}{11}\right)\right]\times\frac{12}{13}](/mediawiki/images/math/b/3/1/b3108e0fc4b9e093af19900912f9dbb5.png) ואם יאמר לך הכה חלק מאחד עשר וחצי חלק מאחד עשר בשנים עשר חלק משלשה עשר
ואם יאמר לך הכה חלק מאחד עשר וחצי חלק מאחד עשר בשנים עשר חלק משלשה עשר | ||
| simple fraction/multiplication of fractions | (⅔+⁴/₇)×¹⁰/₁₁ | ספר_החשבון_לאל_חצאר#pU7o | When you are told: multiply two-thirds and four-sevenths by ten parts of eleven.
: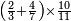 כשיאמר לך הכה שני שלישים וארבע שביעיות בעשרה חלקים מאחד עשר
כשיאמר לך הכה שני שלישים וארבע שביעיות בעשרה חלקים מאחד עשר | ||
| simple fraction/multiplication of fractions | (⅚+½·⅙)×(⁹/₁₀+⅞·⅒) | ספר_החשבון_לאל_חצאר#q1f8 | When you are told: multiply five-sixths and half a sixth by nine-tenths and seven-eighths of a tenth.
:![\scriptstyle\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\times\left[\frac{9}{10}+\left(\frac{7}{8}\sdot\frac{1}{10}\right)\right]](/mediawiki/images/math/5/7/8/5781c5536b7840a71d28f8ec3a3dcbdc.png) כשיאמר לך הכה חמשה שתותים וחצי שתות בתשע עשיריות ושבע שמיניות העשירית
כשיאמר לך הכה חמשה שתותים וחצי שתות בתשע עשיריות ושבע שמיניות העשירית | ||
| simple fraction/multiplication of fractions | ¼×¼ | ספר_חשבון#q5Pm | The quarter by a quarter is a quarter of a quarter.
: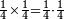 והרביע ברביע הוא רביע הרביע
והרביע ברביע הוא רביע הרביע | ||
| simple fraction/multiplication of fractions | (¾+⅘)×(¹⁰/₁₁+⁸/₉·¹/₁₁) | ספר_החשבון_לאל_חצאר#oNjy | When you are told: multiply three-quarters and four-fifths by ten parts of eleven and eight-ninths of one parts of eleven.
:![\scriptstyle\left(\frac{3}{4}+\frac{4}{5}\right)\times\left[\frac{10}{11}+\left(\frac{8}{9}\sdot\frac{1}{11}\right)\right]](/mediawiki/images/math/d/d/e/dde0eb7bd402c0e93bfdac59da3033c0.png) כשיאמר לך הכה שלש רביעיות וארבעה חומשים בעשרה חלקים מאחד עשר ושמונה תשיעיות החלק מאחד עשר
כשיאמר לך הכה שלש רביעיות וארבעה חומשים בעשרה חלקים מאחד עשר ושמונה תשיעיות החלק מאחד עשר | ||
| simple fraction/multiplication of fractions | ⅔×(⅘·⅑) | ספר_החשבון_לאל_חצאר#3T6D | When you are told: multiply two-thirds by four-fifths of a ninth.
: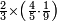 כאשר יאמר לך הכה שני שלישים בארבעה חומשי התשיעית
כאשר יאמר לך הכה שני שלישים בארבעה חומשי התשיעית | ||
| simple fraction/multiplication of fractions | (⅓+⅗)×(⅐+²/₉) | ספר_החשבון_לאל_חצאר#icTs | When you are told: multiply [a third] and three-fifths by a seventh and two-ninths.
: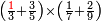 כשיאמר לך הכה שני שלישי' ושלשה חומשים בשביעית ושתי תשיעיות
כשיאמר לך הכה שני שלישי' ושלשה חומשים בשביעית ושתי תשיעיות | ||
| simple fraction/multiplication of fractions | ²⁰/₃×¹⁹/₃ | מלאכת_המספר#8ihF | Example: we wish to multiply:
: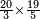 המשל נרצה להכות
המשל נרצה להכות | ||
| extraction of root/multiplication of roots | (√8+√4)×(√8-√4) | ספר_האלזיברא#Gjqg | 17) If you wish to multiply a root of 8 minus a root of 4 by a root of 8 plus a root of 4, for example.
: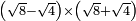 יז אם רצית לכפול שורש ח' פחות שרש ד' בשרש ח' ושרש ד' {{#annot: term | #plus | s4BT}}יותר{{#annotend:s4BT}} דרך משל
יז אם רצית לכפול שורש ח' פחות שרש ד' בשרש ח' ושרש ד' {{#annot: term | #plus | s4BT}}יותר{{#annotend:s4BT}} דרך משל | ||
| extraction of root/multiplication of roots | ³√3×⁴√4 | ספר_האלזיברא#NYWq | Example: you wish to multiply the cube root of 3 by the square root of the square root of 4.
:![\scriptstyle{\color{blue}{\sqrt[3]{3}\sdot\sqrt{\sqrt{4}}}}](/mediawiki/images/math/6/a/2/6a2e44e521ace253aeea448334c43738.png) המשל רצית לכפל שרש מעקב ג' בשרש שרש מרבע ד'
המשל רצית לכפל שרש מעקב ג' בשרש שרש מרבע ד' | ||
| extraction of root/multiplication of roots | (5+√6)×(5+√6) | ספר_האלזיברא#JXeS | 9) If you wish to multiply 5 plus the root of 6 by itself.
: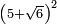 ט ואם רצית לכפול מספר ה' ושרש מספר ו' בעצמו
ט ואם רצית לכפול מספר ה' ושרש מספר ו' בעצמו | ||
| extraction of root/multiplication of roots | (√32-3)×(√32-3) | ספר_האלזיברא#vr1a | 10) If you wish to multiply a root of 32 minus 3 by itself.
: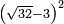 י ואם רצית לכפול שרש ל"ב {{#annot: term | #minus, #פחות | oaTM}}פחות{{#annotend:oaTM}} מספר ג' בעצמו
י ואם רצית לכפול שרש ל"ב {{#annot: term | #minus, #פחות | oaTM}}פחות{{#annotend:oaTM}} מספר ג' בעצמו | ||
| extraction of root/multiplication of roots | 2×⁴√5 | ספר_האלזיברא#BT9a | Example: you wish to multiply the square root of the root of 5 by 2.
: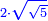 המשל רצית לכפול שרש שרש מרבע ה' במספר ב'
המשל רצית לכפול שרש שרש מרבע ה' במספר ב' | ||
| extraction of root/multiplication of roots | √9×√36 | ספר_המספר_/_אליהו_מזרחי#gnkn | The example: if you want to know the root of which square is the result of multiplication of the root of 9 by the root of 36, without knowing their roots? המשל בזה אם רצית לדעת העולה מהכאת שרש הט' עם שרש הל"ו מבלתי שנדע שרשם לאיזה מרובע הוא שרש | ||
| extraction of root/multiplication of roots | ⅔×√9 | ספר_המספר_/_אליהו_מזרחי#8wZL | Question: if one asks: what is the square, whose root is 2-thirds of the root of 9, without knowing the root of 9 nor its two-thirds? שאלה אם שאל שואל איזהו המרובע אשר העולה מב' שלישיות שרש הט' הוא שרשו מבלתי שנדע שרש הט' ולא שתי שלישיותיו | ||
| extraction of root/multiplication of roots | ⅓×√9 | ספר_המספר_/_אליהו_מזרחי#DBO5 | The example: if one asks: how much is a third of the root of nine? המשל בזה אם שאל שואל כמה הוא שלישית שרש התשעה | ||
| extraction of root/multiplication of roots | 4√9×3√36 | ספר_המספר_/_אליהו_מזרחי#eUGp | The example: if you want to know the root of which square is the result of multiplication of 4 times the root of 9 by 3 times the root of 36? המשל בזה אם רצית לדעת העולה מהכאת ד' כפלי שרש הט' עם ג' כפלי שרש הל"ו לאיזה מרובע הוא שרש | ||
| extraction of root/multiplication of roots | ⅔√9×½√36 | ספר_המספר_/_אליהו_מזרחי#wUFC | The example: if you want to know the root of which square is the result of multiplication of two-thirds of the root of 9 by half the root of thirty-six. המשל בזה אם רצית לדעת העולה מהכאת שתי שלישיות שרש הט' עם חצי שרש הששה ושלשים לאיזה מרובע הוא שרש | ||
| extraction of root/multiplication of roots | 4×√9 | ספר_המספר_/_אליהו_מזרחי#cO5T | The example: if one asks: the root of which square results from four times the root of nine, without knowing the root of 9? המשל בזה אם שאל שואל לאיזה מרובע יהיה שרש העולה מארבעה כפלי שרש התשעה מבלתי שנדע שרש הט' | ||
| extraction of root/multiplication of roots | 4×√9 | ספר_המספר_/_אליהו_מזרחי#r2q9 | The example: if one asks: how much is the result of 4 times the square root of 9? המשל בזה אם שאל שואל כמה הוא העולה מד' כפלי שרש מרובע הט' | ||
| extraction of root/multiplication of roots | ⁴√4×⁴√7 | ספר_האלזיברא#XzLn | Example: you wish to multiply the square root of the root of 4 by the square root of the root of 7.
: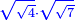 המשל רצית לכפול שרש שרש מרובע ד' בשרש שרש מרובע ז'
המשל רצית לכפול שרש שרש מרובע ד' בשרש שרש מרובע ז' | ||
| extraction of root/multiplication of roots | √9׳√8 | ספר_האלזיברא#z96Z | In order to teach you, I will give you an example of numbers that have roots and say: you wish to multiply the square root of 9, which is 3, by the cube root of 8, which is 2.
:![\scriptstyle{\color{blue}{\sqrt[3]{8}\sdot\sqrt{9}=2\sdot3}}](/mediawiki/images/math/f/7/8/f78292cfdbe9c405071e1cd7a1fa2151.png) ולמען תשכיל אמשול לך משל ב{{#annot: term | #to have a root | v3W5}}מספרים בעלי שורש{{#annotend:v3W5}} ואומר רצית לכפול שורש מרובע ט' שהוא ג' בשורש מעקב ח' שהוא ב'
ולמען תשכיל אמשול לך משל ב{{#annot: term | #to have a root | v3W5}}מספרים בעלי שורש{{#annotend:v3W5}} ואומר רצית לכפול שורש מרובע ט' שהוא ג' בשורש מעקב ח' שהוא ב' | ||
| extraction of root/multiplication of roots | 3׳√5 | ספר_האלזיברא#fsBI | Example: you wish to multiply the cube root of 5 by 3.
:![\scriptstyle{\color{blue}{3\sdot\sqrt[3]{5}}}](/mediawiki/images/math/a/9/9/a99dd5644ea050837fd5c7b6558148b1.png) המשל רצית לכפול שורש מעקב ה' במספר ג'
המשל רצית לכפול שורש מעקב ה' במספר ג' | ||
| extraction of root/multiplication of roots | √7×√8 | ספר_דיני_ממונות#LgsC | 153) Question: multiplication of roots - if you want to [multiply] the root of 7 by the root of 8.
: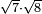 קנג)MS L: קנ שאלה לכפול בשרשים אם תרצה למצא שרש ז' על שרש מח'
קנג)MS L: קנ שאלה לכפול בשרשים אם תרצה למצא שרש ז' על שרש מח' | ||
| extraction of root/multiplication of roots | √7×8 | ספר_דיני_ממונות#m2AG | 154) Question: if you want to multiply the root of 7 by 8.
: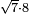 קנד)MS L: קנא שאלה אם תרצה לכפול השרש מכפילת ז' עם ח'
קנד)MS L: קנא שאלה אם תרצה לכפול השרש מכפילת ז' עם ח' | ||
| extraction of root/multiplication of roots | ³√5׳√6 | ספר_האלזיברא#VoGt | Example: you wish to multiply the cube root of 5 by the cube root of 6.
:![\scriptstyle{\color{blue}{\sqrt[3]{5}\sdot\sqrt[3]{6}}}](/mediawiki/images/math/6/b/c/6bcd61acffa1345e487600bdb7ef40ff.png) המשל רצית לכפול שורש מעקב ה' בשורש מעקב ו'
המשל רצית לכפול שורש מעקב ה' בשורש מעקב ו' | ||
| extraction of root/multiplication of roots | 3׳√8 | ספר_ג'יבלי_אלמוקבאלא#O0bJ | If you multiply 3 by a cube root of 8.
:![\scriptstyle3\times\sqrt[3]{8}](/mediawiki/images/math/1/3/2/1328cc433a8d6f068d82010e6cd86a87.png) ואם תכפול ג' בשרש מעוקב מח'
ואם תכפול ג' בשרש מעוקב מח' | ||
| extraction of root/multiplication of roots | (√48+√10)×(√48-√10) | ספר_האלזיברא#V3f6 | 11) If you wish to multiply a root of 48 plus a root of 10 by a root of 48 minus a root of 10.
: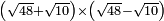 יא ואם רצית לכפול שרש מ"ח ושרש י' בשרש מ"ח פחות שרש י'
יא ואם רצית לכפול שרש מ"ח ושרש י' בשרש מ"ח פחות שרש י' | ||
| extraction of root/multiplication of roots | 3×√4 | ספר_ג'יבלי_אלמוקבאלא#eTRG | Suppose you want to multiply 3 by a square root of 4.
: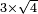 ונניח שבאת 7rלכפול ג' בשרש מרובע מד'
ונניח שבאת 7rלכפול ג' בשרש מרובע מד' | ||
| extraction of root/multiplication of roots | √6×3 | ספר_ג'יבלי_אלמוקבאלא#aKDT | Suppose you wish to multiply a root of six by three.
: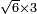 נניח שרצית לכפול
נניח שרצית לכפול | ||
| extraction of root/multiplication of roots | √4×√9 | ספר_ג'יבלי_אלמוקבאלא#NYp7 | Suppose you wish to multiply a root of four by a root of nine.
: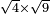 נניח שרצית לכפול שרש ארבעה בשרש תשעה
נניח שרצית לכפול שרש ארבעה בשרש תשעה | ||
| extraction of root/multiplication of roots | √5×(√7+4) | ספר_ג'יבלי_אלמוקבאלא#ek9n | Suppose you wish to multiply a root of 5 by a root of 7 plus 4.
: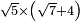 נניח שרצית לכפול שרש ה' בשרש ז' וד'
נניח שרצית לכפול שרש ה' בשרש ז' וד' | ||
| extraction of root/multiplication of roots | √3×(6-√8) | ספר_ג'יבלי_אלמוקבאלא#tW5A | Suppose you wish to multiply a root of 3 by six minus a root of 8.
: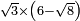 נניח שרצית לכפול שרש ג' בששה פחות שרש ח'
נניח שרצית לכפול שרש ג' בששה פחות שרש ח' | ||
| extraction of root/multiplication of roots | (3+√5)×(3+√5) | ספר_ג'יבלי_אלמוקבאלא#gk0X | Suppose you wish to multiply 3 plus a root of 5 by 3 plus a root of 5.
: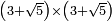 נניח שרצית לכפול ג' ושרש ה' בג' ושרש ה'
נניח שרצית לכפול ג' ושרש ה' בג' ושרש ה' | ||
| extraction of root/multiplication of roots | (3+√4)×(4+√9) | ספר_ג'יבלי_אלמוקבאלא#QhWc | Suppose you wish to multiply 3 plus a root of 4 by 5 plus a root of 9.
: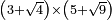 ונניח כי בקשת לכפול ג' ושרש ד' בה' ושרש ט'
ונניח כי בקשת לכפול ג' ושרש ד' בה' ושרש ט' | ||
| extraction of root/multiplication of roots | (3-√5)×(4-√7) | ספר_ג'יבלי_אלמוקבאלא#0gkX | Example: if you wish to multiply 3 minus a root of 5 by 4 minus a root of 7.
: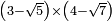 {{#annot:term|197,1712|bB8m}}נעשה הדמיון ש{{#annotend:bB8m}}רצית לכפול ג' פחות שרש ה' בד' פחות שרש ז'
{{#annot:term|197,1712|bB8m}}נעשה הדמיון ש{{#annotend:bB8m}}רצית לכפול ג' פחות שרש ה' בד' פחות שרש ז' | ||
| extraction of root/multiplication of roots | (3+√5)×(4+√7) | ספר_ג'יבלי_אלמוקבאלא#SjVv | Suppose you wish to multiply 3 plus a root of 5 by 4 plus a root of 7.
: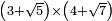 נניח שרצונך לכפול ג' ושרש ה' בד' ושרש ז'
נניח שרצונך לכפול ג' ושרש ה' בד' ושרש ז' | ||
| extraction of root/multiplication of roots | (3-√5)×(4-√7) | ספר_ג'יבלי_אלמוקבאלא#X7yi | Suppose you wish to multiply 3 minus a root of 5 by 4 minus a root of 7.
: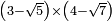 נניח שרצית לכפול ג' פחות שרש ה' בד' פחות שרש ז'
נניח שרצית לכפול ג' פחות שרש ה' בד' פחות שרש ז' | ||
| extraction of root/multiplication of roots | (3-√5)×(3-√5) | ספר_ג'יבלי_אלמוקבאלא#H3RC | Suppose you wish to multiply 3 minus a root of 5 by 3 minus a root of 5.
: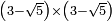 ונניח שרצית לכפול ג' פחות שרש ה' בג' פחות שרש ה'
ונניח שרצית לכפול ג' פחות שרש ה' בג' פחות שרש ה' | ||
| extraction of root/multiplication of roots | (5+√3)×(5-√3) | ספר_ג'יבלי_אלמוקבאלא#YkgW | Suppose you wish to multiply 5 plus a root of 3 by 5 minus a root of 3.
: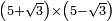 נניח שרצית לכפול ה' ושרש ג' בה' פחות שרש ג'
נניח שרצית לכפול ה' ושרש ג' בה' פחות שרש ג' | ||
| extraction of root/multiplication of roots | (3+√4)×(5-√9) | ספר_ג'יבלי_אלמוקבאלא#zo1g | Suppose you wish to multiply 3 plus a root of 4 by 5 minus a root of 9.
: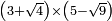 נניח שרצית לכפול ג' ושרש ד' בה' פחות שרש ט'
נניח שרצית לכפול ג' ושרש ד' בה' פחות שרש ט' | ||
| extraction of root/multiplication of roots | √8×(√8-2) | ספר_ג'יבלי_אלמוקבאלא#p4H3 | Suppose you wish to multiply a root of 8 by a root of 8 minus 2.
: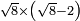 נניח שרצית לכפול שרש ח' בשרש ח' פחות ב'
נניח שרצית לכפול שרש ח' בשרש ח' פחות ב' | ||
| extraction of root/multiplication of roots | (√8-2)×(√10-3) | ספר_ג'יבלי_אלמוקבאלא#hEei | Suppose you wish to multiply a root of 8 minus 2 by a root of ten minus 3.
: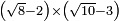 ונניח שרצית לכפול שרש ח' פחות ב' בשרש עשרה פחות ג'
ונניח שרצית לכפול שרש ח' פחות ב' בשרש עשרה פחות ג' | ||
| extraction of root/multiplication of roots | (√12-2)×(√12-2) | ספר_ג'יבלי_אלמוקבאלא#zWp7 | Suppose you wish to multiply a root of 12 minus 2 by a root of 12 minus 2.
: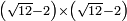 ונניח שרצית לכפול שרש י"ב פחות ב' בשרש י"ב פחות ב'
ונניח שרצית לכפול שרש י"ב פחות ב' בשרש י"ב פחות ב' | ||
| extraction of root/multiplication of roots | (√15-3)×(√12+2) | ספר_ג'יבלי_אלמוקבאלא#ITr2 | Suppose you wish to multiply a root of 15 minus 3 by a root of 12 plus 2.
: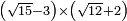 נניח שרצית לכפול שרש ט"ו פחות ג' בשרש י"ב וב'
נניח שרצית לכפול שרש ט"ו פחות ג' בשרש י"ב וב' | ||
| extraction of root/multiplication of roots | (√8+2)×(√8-2) | ספר_ג'יבלי_אלמוקבאלא#E8mu | Suppose you wish to multiply a root of 8 plus 2 by a root of 8 minus 2.
: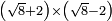 ונניח
ונניח | ||
| extraction of root/multiplication of roots | √7×3 | ספר_האלזיברא#raEn | Example: you wish to multiply the root of 7 by 3.
: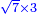 {{#annot: term | #example, #משל | 8k7T}}המשל{{#annotend:8k7T}} רצית לכפול שורש מספר ז' במספר ג'
{{#annot: term | #example, #משל | 8k7T}}המשל{{#annotend:8k7T}} רצית לכפול שורש מספר ז' במספר ג' | ||
| extraction of root/multiplication of roots | √5×(√7+√10) | ספר_ג'יבלי_אלמוקבאלא#DUGD | Suppose you wish to multiply a root of 5 by a root of 7 plus a root of ten.
: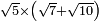 ונניח שרצית לכפול שרש ה' בשרש ז' ושרש עשרה
ונניח שרצית לכפול שרש ה' בשרש ז' ושרש עשרה | ||
| extraction of root/multiplication of roots | √5×(√12-√8) | ספר_ג'יבלי_אלמוקבאלא#PUFC | Suppose you wish to multiply a root of 5 by a root of 12 minus a root of 8.
: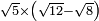 ונניח שבקשת לכפול שרש ה' בשרש י"ב פחות שרש ח'
ונניח שבקשת לכפול שרש ה' בשרש י"ב פחות שרש ח' | ||
| extraction of root/multiplication of roots | (√5+√7)×(√10+√15) | ספר_ג'יבלי_אלמוקבאלא#r71h | Suppose you wish to multiply a root of 5 plus a root of 7 by a root of ten plus a root of 15.
: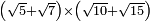 ונניח שבקשת לכפול שרש ה' ושרש ז' בשרש עשרה ושרש ט"ו
ונניח שבקשת לכפול שרש ה' ושרש ז' בשרש עשרה ושרש ט"ו | ||
| extraction of root/multiplication of roots | (√5+√7)×(√5+√7) | ספר_ג'יבלי_אלמוקבאלא#QSUQ | Suppose you wish to multiply a root of 5 plus a root of 7 by a root of 5 plus a root of 7.
: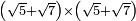 ונניח שרצית לכפול שרש ה' ושרש ז' בשרש ה' ושרש ז'
ונניח שרצית לכפול שרש ה' ושרש ז' בשרש ה' ושרש ז' | ||
| extraction of root/multiplication of roots | (√5+√7)×(√10-√6) | ספר_ג'יבלי_אלמוקבאלא#fJYv | Suppose you wish to multiply a root of 5 plus a root of 7 by a root of ten minus a root of 6.
: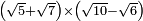 ונניח שרצית לכפול שרש ה' ושרש ז' בשרש עשרה פחות שרש ו'
ונניח שרצית לכפול שרש ה' ושרש ז' בשרש עשרה פחות שרש ו' | ||
| extraction of root/multiplication of roots | (√10+√7)×(√10-√7) | ספר_ג'יבלי_אלמוקבאלא#cbco | Suppose you wish to multiply a root of ten plus a root of 7 by a root of ten minus a root of 7.
: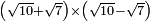 ונניח שרצית לכפול שרש עשרה ושרש ז' בשרש עשרה פחות שרש ז'
ונניח שרצית לכפול שרש עשרה ושרש ז' בשרש עשרה פחות שרש ז' | ||
| extraction of root/multiplication of roots | (√12-√7)×(√15-√10) | ספר_ג'יבלי_אלמוקבאלא#IWqT | Suppose you wish to multiply a root of 12 minus a root of 7 by a root of 15 minus a root of ten.
: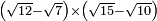 נניח שרצית לכפול שרש י"ב פחות שרש ז' בשרש ט"ו פחות שרש עשרה
נניח שרצית לכפול שרש י"ב פחות שרש ז' בשרש ט"ו פחות שרש עשרה | ||
| extraction of root/multiplication of roots | (√12-√7)×(√12-√7) | ספר_ג'יבלי_אלמוקבאלא#ISCj | Suppose you wish to multiply a root of 12 minus a root of 7 by a root of 12 minus a root of 7.
: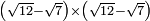 ונניח שרצית לכפול שרש י"ב פחות שרש ז' בשרש י"ב פחות שרש ז'
ונניח שרצית לכפול שרש י"ב פחות שרש ז' בשרש י"ב פחות שרש ז' | ||
| extraction of root/multiplication of roots | √4׳√8 | ספר_ג'יבלי_אלמוקבאלא#J15w | Suppose you wish to multiply a square root of 4 by a cube root of 8.
:![\scriptstyle\sqrt{4}\times\sqrt[3]{8}](/mediawiki/images/math/6/4/6/646c5ba2e5f167061f7a7ccea09fdf58.png) נניח שרצית לכפול שרש מרובע מד' בשרש מעוקב מח'
נניח שרצית לכפול שרש מרובע מד' בשרש מעוקב מח' | ||
| extraction of root/multiplication of roots | ³√8×⁴√16 | ספר_ג'יבלי_אלמוקבאלא#ek3B | If you are told: multiply a cube root of 8 by a root of a root of 16.
:![\scriptstyle\sqrt[3]{8}\times\sqrt[4]{16}](/mediawiki/images/math/b/e/2/be2421d68cb602563f762c6471b4910a.png) עוד אם יאמרו לך תכפול שרש מעוקב מח' בשרש שרש י"ו
עוד אם יאמרו לך תכפול שרש מעוקב מח' בשרש שרש י"ו | ||
| extraction of root/multiplication of roots | 2×√16 | חשבון_השטחים#USTm | 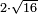 ו{{#annot:term|197,1712|suQU}}דמיון זה{{#annotend:suQU}} כאשר רצינו לכפול שורש ששה עשר
ו{{#annot:term|197,1712|suQU}}דמיון זה{{#annotend:suQU}} כאשר רצינו לכפול שורש ששה עשר | ||
| extraction of root/multiplication of roots | ½×√9 | חשבון_השטחים#FlzO | 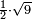 וכאשר תרצה לקחת חצי שורש תשעה
וכאשר תרצה לקחת חצי שורש תשעה | ||
| extraction of root/multiplication of roots | ⅔×√9 | חשבון_השטחים#4FLj | 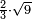 וכאשר תרצה לקחת שני שלישי שורש תשעה
וכאשר תרצה לקחת שני שלישי שורש תשעה | ||
| extraction of root/multiplication of roots | √9×√4 | חשבון_השטחים#WruF | 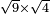 ואם תרצה להכות שורש תשעה על שורש ארבעה
ואם תרצה להכות שורש תשעה על שורש ארבעה | ||
| extraction of root/multiplication of roots | 2×√16 | תחבולות_המספר#tRoE | He said: we give an example for this: when we wish to know the double root of sixteen.
: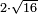 אמ' ונניח {{#annot:term|197,1712|Ahnf}}דמיון לזה{{#annotend:Ahnf}} כאשר
אמ' ונניח {{#annot:term|197,1712|Ahnf}}דמיון לזה{{#annotend:Ahnf}} כאשר | ||
| extraction of root/multiplication of roots | ½×√9 | תחבולות_המספר#UOpW | He said: when we wish to take half a root of nine.
: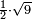 אמ' וכאשר נרצה לקחת חצי שרש תשעה
אמ' וכאשר נרצה לקחת חצי שרש תשעה | ||
| extraction of root/multiplication of roots | ⅔×√9 | תחבולות_המספר#MSsU | If we wish to take two-thirds of a root of nine.
: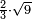 ואם נרצה לקחת שני שלישי שרש תשעה
ואם נרצה לקחת שני שלישי שרש תשעה | ||
| extraction of root/multiplication of roots | √9×√4 | תחבולות_המספר#nTrH | He said: if you wish to know how much is the product of a root of nine by a root of four.
: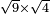 אמ' ואם תרצה לדעת כמה העולה מהכאת שרש תשעה בשרש ארבעה
אמ' ואם תרצה לדעת כמה העולה מהכאת שרש תשעה בשרש ארבעה | ||
| extraction of root/multiplication of roots | (2×√10)×(½×√5) | תחבולות_המספר#FwAB | He said: if you are told: how much is the product of two roots of ten by half a root of five?
: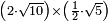 אמ' ואם יאמרו לך כמה יהיה מהכאת שני שרשי עשרה בחצי שרש חמשה
אמ' ואם יאמרו לך כמה יהיה מהכאת שני שרשי עשרה בחצי שרש חמשה | ||
| extraction of root/multiplication of roots | √5×√12 | ספר_האלזיברא#pCiL | When you wish to multiply the root of 5 by the root of 12.
: כאשר רצית לכפול שורש מספר ה' בשורש מספר [י"ב]Mantova: ב'
כאשר רצית לכפול שורש מספר ה' בשורש מספר [י"ב]Mantova: ב' | ||
| extraction of root/multiplication of roots | (2×√10)×(½×√5) | חשבון_השטחים#fTi5 | 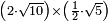 ואם יאמרו לך כמה יהיו הכאת שני שרשי עשרה על חצי שורש חמשה
ואם יאמרו לך כמה יהיו הכאת שני שרשי עשרה על חצי שורש חמשה | ||
| sexagesimal fraction/multiplication of sexagesimal fractions | (2+24'+43)×(3+3'+8) | מלאכת_המספר#vIL0 | Here you have an example of some of them: suppose we want to multiply 2 degrees, 24 minutes, and 43 seconds by 3 degrees, 3 minutes, and 8 seconds. והנה לך צורה אחת בקצת זה נניח שרצינו להכות ב' מעלות וכ"ד ראשוניים ומ"ג שניים על ג' מעלות וג' ראשוניים וח' שניים | ||
| sexagesimal fraction/multiplication of sexagesimal fractions | (4+6'+8+12)×(5+15'+10+13) | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#qQv2 | Example: we wish to multiply 4 degrees, 6 minutes, 8 seconds, and 12 thirds by 5 degrees, 15 minutes, ten seconds, and 13 thirds.
: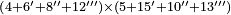 והמשל בזה רצינו לכפול ד' מעלות ו' דקים ח' שניים י"ב שלישיים על ה' מעלות ט"ו דקים עשרה שניים י"ג שלישים
והמשל בזה רצינו לכפול ד' מעלות ו' דקים ח' שניים י"ב שלישיים על ה' מעלות ט"ו דקים עשרה שניים י"ג שלישים | ||
| multiplication/multiplication table | לוח הרבוע | term | מלאכת_המספר#SJrR | לוח הרבוע | |
| multiplication/multiplication table | לוח ההכאות | term | מלאכת_המספר#DKnV | לוח ההכאות | |
| methods of multiplication/multiplication tower | ג.ד.ל./מגדל | term | אגרת_המספר#m22P | מגדל | |
| methods of multiplication/multiplication wings | כנף | term | אגרת_המספר#y5jw | כנף | |
| methods of multiplication/multiplication wings | כנף | term | אגרת_המספר#Y3IF | בעל הכנפים | |
| multiplicative supplementation/multiplicative inverse | ש.ל.מ./תשלום | term | ספר_יסודי_התבונה_ומגדל_האמונה#Qujf | תשלומי | |
| multiplicative supplementation/multiplicative inverse | ש.ל.מ./תשלום | term | Anonymous#bgPF | תשלומי | |
| multiplicative supplementation/multiplicative inverse | ש.ל.מ./תשלום | term | ספר_יסודי_התבונה_ומגדל_האמונה#krFT | תשלומי | |
| multiplicative supplementation/multiplicative inverse | ש.ל.מ./תשלום | term | Anonymous#dz28 | תשלומי | |
| multiplicative supplementation/multiplicatively supplemented | י.ר.ד./מורד | term | אגרת_המספר#E1R8 | המורד אליו | |
| multiplicative supplementation/multiplicatively supplemented | ש.ל.מ./מושלם | term | אגרת_המספר#BD2Z | המושלם | |
| multiplicative supplementation/multiplicatively supplemented | ש.ל.מ./מושלם | term | אגרת_המספר#5seF | המושלם אליו | |
| multiplicative supplementation/multiplicatively supplemented | י.ר.ד./יורד | term | אגרת_המספר#7y64 | היורד | |
| multiplicative supplementation/multiplicatively supplemented | י.ר.ד./מורד | term | אגרת_המספר#hS3l | המורד | |
| multiplication/multiplicative supplementation | ש.ל.מ./השלמה | term | חשבון_השטחים#mh4y | השלמתך | |
| multiplication/multiplicative supplementation | י.ר.ד./הורדה | term | אגרת_המספר#a3kE | הורדה | |
| multiplication/multiplicative supplementation | י.ר.ד./ירידה | term | ספר_החשבון_לאל_חצאר#1Kef | ירידה | |
| multiplication/multiplicative supplementation | ח.ת.מ./חתום | term | ספר_החשבון_לאל_חצאר#4srA | חתום | |
| multiplication/multiplicative supplementation | ש.ל.מ./השלמה | term | אגרת_המספר#e48U | השלמה | |
| multiplication/multiplicative supplementation | י.ר.ד./הורדה | ש.ל.מ./השלמה | definition | אגרת_המספר#6zM1 | completion is repairing and degrading is its opposite. The intention in completion and degrading is knowing what should be multiplied by a certain number, so that the result is the required. The completion is from the smaller to the greater and the degreding is vice versa. אמר והשלמה היא התיקון וההורדה היא הפכו והרצון בהשלמה וההורדה ידיעת מה שיוכה במספר מה ויבא ממנו המבוקש ולא תהיה ההשלמה אלא מן המעט אל הרב וההורדה בהפך |
| multiplication/multiplicative supplementation | ח.ת.מ./חתום | term | ספר_החשבון_לאל_חצאר#Zf9D | חיתום | |
| multiplication/multiplied | נ.כ.ה./הוכה | term | תחבולות_המספר#slFD | יוכה ב | |
| multiplication/multiplied | כ.פ.ל./כפול | term | ספר_האלזיברא#G4iq | כפול | |
| multiplication/multiplied | נ.כ.ה./הוכה | term | חשבון_השטחים#nopa | יוכו | |
| multiplication/multiplied | נ.כ.ה./הוכה | term | ספר_ג'יבלי_אלמוקבאלא#vDc8 | מוכים ב | |
| multiplication/multiplied | נ.כ.ה./מוכה | definition | ספר_היסודות_לאקלידס#KOz0 | The number that is multiplied by a number is that which is duplicated as many times as there are units in the multiplicand and the product is some number. המספר המוכה במספר הוא אשר יכפל פעמים כמנין מה שבמוכה בו מן האחדים ויהיה מה שיתקבץ מספר אחד | |
| multiplication/multiplied | נ.כ.ה./הוכה | term | ספר_ג'יבלי_אלמוקבאלא#l2on | יוכה | |
| multiplication/multiplied | כ.פ.ל./נכפל | term | ספר_מעשה_חושב#E5wW | נכפל | |
| multiplication/multiplied | כ.פ.ל./נכפל | term | ספר_מעשה_חושב#zpm1 | נכפלים על | |
| multiplication/multiplied | נ.כ.ה./הוכה | term | תחבולות_המספר#IkGn | הוכה ב | |
| multiplication/multiplied | ח.ש.ב./נחשב | term | ספר_יסודי_התבונה_ומגדל_האמונה#n4Tu | נחשב על | |
| multiplication/multiplied | ר.ב.ה./מרובה | term | חשבון_השטחים#AuYy | מורבה | |
| multiplication/multiplied | ר.ב.ה./מורבה | term | חשבון_השטחים#TG7z | מורבה | |
| multiplication/multiplied | ר.ב.ה./התרבה | term | חשבון_השטחים#UT0F | יתרבו | |
| multiplication/multiplied | נ.כ.ה./הוכה | term | חשבון_השטחים#CDTl | הוכה | |
| multiplication/multiplied | כ.פ.ל./נכפל | term | עיר_סיחון#Smu2 | יכפלו | |
| multiplication/multiplied | ש.נ.י./נשנה | term | בר_נותן_טעם#6UQE | ישנו | |
| multiplication/multiplied | כ.פ.ל./נכפל | term | עיר_סיחון#GoLz | נכפלות | |
| multiplication/multiplied | ש.נ.י./נשנה | term | בר_נותן_טעם#p9UV | נשנים | |
| multiplication/multiplied | ר.ב.ה./התרבה | term | חשבון_השטחים#On98 | יתרבה | |
| multiplication/multiplied | כ.פ.ל./הכפל | term | ספר_ג'יבלי_אלמוקבאלא#fHCE | בהכפלם | |
| multiplication/multiplied | term | ספר_המספר_/_אברהם_אבן_עזרא#oO4Y | כפול על עצמו | ||
| multiplication/multiplied | כ.פ.ל./הכפל | term | ספר_ג'יבלי_אלמוקבאלא#rxHJ | בהכפל | |
| multiplication/multiplied | נ.כ.ה./הוכה | term | ספר_ג'יבלי_אלמוקבאלא#QSst | הוכה ב | |
| multiplication/multiplier | נ.כ.ה./מכה | term | ספר_המספר_/_אליהו_מזרחי#YwOJ | המכים | |
| multiplication/multiplier | נ.כ.ה./מכה | term | ספר_המספר_/_אליהו_מזרחי#phwF | המכה | |
| multiplication/multiplier | פ.ע.ל./פועל | term | מלאכת_המספר#h4pD | פועל | |
| multiplication/multiplier | פ.ע.ל./פועל | term | מלאכת_המספר#uhV0 | פועל | |
| multiplication/multiplier | נ.כ.ה./מוכה בו | term | אגרת_המספר#AzG1 | המוכה בו | |
| multiplication/multiplier | נ.כ.ה./מוכה בו | term | אגרת_המספר#v8Q1 | המספר המוכה בו | |
| multiplication/multiplier | נ.כ.ה./מכה | term | ספר_מעשה_חושב#ufRv | המספר המכה | |
| multiplication/multiplier | נ.כ.ה./מכה | term | ספר_מעשה_חושב#1ZdD | המכה | |
| progression/natural succession | מ.ש.כ./על המשך | term | ספר_החשבון_לאל_חצאר#VQPq | על המשך המספר | |
| progression/natural succession | ס.ד.ר./סדור | term | האנציקלופדיה_של_אבו_אלצלת#fbLn | סדור המספרים הנמשכים | |
| progression/natural succession | ט.ב.ע./טבעי | term | האריתמטיקה_של_ניקומכוס#5ppE | על סדר משך המספרים הטבעיים | |
| progression/natural succession | מ.ש.כ./המשכות | term | האנציקלופדיה_של_אבו_אלצלת#Kg5J | ההמשכות הטבעי | |
| progression/natural succession | ט.ב.ע./טבעי | term | האריתמטיקה_של_ניקומכוס#jubr | משך המספרים הטבעיים | |
| progression/natural succession | ט.ב.ע./טבעי | term | האריתמטיקה_של_ניקומכוס#L8bg | סדר המספרים הטבעיים | |
| progression/natural succession | ט.ב.ע./טבעי | term | האריתמטיקה_של_ניקומכוס#pHYO | על סדר המספרים הטבעיים ימשכו קצתם לקצת | |
| progression/natural succession | ט.ב.ע./טבעי | term | האריתמטיקה_של_ניקומכוס#mtpu | על סדר המספרים הטבעיים | |
| progression/natural succession | ס.ד.ר./סדור | term | האנציקלופדיה_של_אבו_אלצלת#TmGX | בסדור הטבעי למספר | |
| progression/natural succession | ד.ר.כ./דרך המספר | term | Anonymous#KBdx | על דרך המספר | |
| progression/natural succession | ר.צ.פ./רצוף | term | עיר_סיחון#ETrE | המספרים הרצופים | |
| progression/natural succession | מ.ש.כ./המשכות | term | האריתמטיקה_של_ניקומכוס#KEpZ | המשכות טבעי | |
| progression/natural succession | מ.ש.כ./המשכות | term | האנציקלופדיה_של_אבו_אלצלת#F8FS | המשכות טבעי | |
| progression/natural succession | ד.ר.כ./דרך המספר | term | Anonymous#ZAwr | על דרך המספר | |
| progression/natural succession | ר.צ.פ./רצוף | term | עיר_סיחון#h4eV | רצופים | |
| progression/natural succession | י.ל.ד./תולדת | term | Anonymous#NFbm | בתולדת זה אחר זה | |
| progression/natural succession | ד.ר.כ./דרך החשבון | term | Anonymous#IXVK | על דרך החשבון | |
| decimal positional system/numeral | תמונה | term | מלאכת_המספר#OAzt | תמונה | |
| decimal positional system/numeral | א.ו.ת./אות | term | ספר_עיון_העקרים_לחשבון_ההנדיים#9bnm | אות | |
| decimal positional system/numeral | א.ו.ת./אות | term | ספר_החשבון_לאל_חצאר#yuS2 | אותיות | |
| decimal positional system/numeral | תמונה | term | מלאכת_המספר#AygT | תמונות המספר | |
| decimal positional system/numeral | א.ו.ת./אות | term | מלאכת_המספר#Duvu | אות | |
| decimal positional system/numeral | צפרא | term | ספר_ציפרא#YFdI | ציפרא | |
| decimal positional system/numeral | א.ו.ת./אות | term | ספר_החשבון_לאל_חצאר#6oja | אות | |
| decimal positional system/numeral | א.ו.ת./אות | term | בר_נותן_טעם#PBaR | אותיות | |
| decimal positional system/numeral | א.ו.ת./אות | term | בר_נותן_טעם#EozN | אות | |
| decimal positional system/numeral | ס.פ.ר./מספר | term | בר_נותן_טעם#hWEo | מספר | |
| decimal positional system/numeral | ס.פ.ר./מספר | term | בר_נותן_טעם#xdbP | מספרים | |
| decimal positional system/numeral | ר.ש.מ./רושם | term | בר_נותן_טעם#RSnD | רשמי המספרים | |
| decimal positional system/numeral | א.ו.ת./אות | term | אגרת_המספר#nckU | אות | |
| decimal positional system/numeral | א.ו.ת./אות | term | אגרת_המספר#BaEX | אותיות | |
| decimal positional system/numeral | א.ו.ת./אות | term | קצור_המספר#Rmee | אותיות | |
| decimal positional system/numeral | א.ו.ת./אות | term | קצור_המספר#mTHy | אות | |
| decimal positional system/numeral | א.ו.ת./אות | term | ספר_ציפרא#b7Xx | אותיו' | |
| decimal positional system/numeral | ח.ש.ב./חשבון | term | ספר_ציפרא#Zu7z | חשבון | |
| decimal positional system/numeral | א.ו.ת./אות | term | ספר_המספר_/_אליהו_מזרחי#EYyI | אות | |
| decimal positional system/numeral | ס.מ.נ./סימן | term | ספר_המספר_/_אליהו_מזרחי#oizn | סימנים | |
| decimal positional system/numeral | א.ו.ת./אות | term | ספר_אגריס#vv7v | אות | |
| decimal positional system/numeral | א.ו.ת./אות | term | ספר_אגריס#CMl9 | אותיות | |
| decimal positional system/numeral | term | ספר_המספר_/_אברהם_אבן_עזרא#caYJ | אותיות | ||
| decimal positional system/numeral | term | ספר_המספר_/_אברהם_אבן_עזרא#1E4G | מספרים | ||
| decimal positional system/numeral | term | ספר_המספר_/_אברהם_אבן_עזרא#z6R9 | חשבון | ||
| decimal positional system/numeral | א.ו.ת./אות | term | ספר_עיון_העקרים_לחשבון_ההנדיים#mq5P | אותיות | |
| decimal positional system/numeral | ר.ש.מ./רושם | term | בר_נותן_טעם#RC87 | רשמים | |
| decimal positional system/numeral | ר.ש.מ./רושם | term | בר_נותן_טעם#O5d7 | רושם | |
| decimal positional system/numeral | ס.מ.נ./סימן | term | מלאכת_המספר#KHDy | סימן | |
| decimal positional system/numeral | א.ו.ת./אות | term | ספר_החשבון_לאל_חצאר#voac | אותיות | |
| decimal positional system/numeral | א.ו.ת./אות | term | עיר_סיחון#phuN | אותיות | |
| decimal positional system/numeral | א.ו.ת./אות | term | עיר_סיחון#OGlo | אות | |
| fraction/numerator | ש.ב.ר./שבר | term | בר_נותן_טעם#iMq3 | שברים | |
| fraction/numerator | ב.נ.י./בן | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#OSYp | בן | |
| fraction/numerator | ש.ב.ר./שבר | term | בר_נותן_טעם#fPu0 | שברים | |
| fraction/numerator | ס.פ.ר./מספר | term | קצור_המספר#hYaF | מספרים | |
| fraction/numerator | כמות | term | ספר_המספר_/_אליהו_מזרחי#WEM7 | כמות | |
| fraction/numerator | כמות | definition | ספר_המספר_/_אליהו_מזרחי#YtQi | Its name that is derived from the quantity is the name of the number that indicates the parts that are taken from the whole. ואולם השם אשר לו מהכמות הוא שם המספר המורה על החלקים הלקוחים מהשלם | |
| fraction/numerator | כמות | term | קצת_מענייני_חכמת_המספר#p9Nv | כמות | |
| fraction/numerator | י.צ.ע./הצעה | term | אגרת_המספר#pR6Z | הצעתם | |
| fraction/numerator | ח.ל.ק./מחולק | term | מלאכת_המספר#sKbK | מחולק | |
| fraction/numerator | י.צ.ע./הצעה | term | אגרת_המספר#ZoZR | הצעה | |
| fraction/numerator | ב.נ.י./בן | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#VW8P | בנים | |
| decimal positional system/numerical value | שם | term | אגרת_המספר#SKHx | שם | |
| decimal positional system/numerical value | נ.ג.ע./הגעה | term | האריתמטיקה_של_ניקומכוס#CcHP | הגעות מספריהם | |
| decimal positional system/numerical value | שם | definition | אגרת_המספר#z2Ks | The knowledge of the second is called naming, that is, to know the name of the numerals. וידיעת השני יקרא שם כלומ' לדעת שם המספרים | |
| decimal positional system/numerical value | כמות | term | מלאכת_המספר#Gqn8 | כמות מספר | |
| decimal positional system/numerical value | ע.ר.כ./ערך | term | ספר_עיון_העקרים_לחשבון_ההנדיים#RTN0 | ערכו | |
| decimal positional system/numerical value | כמות | term | ספר_המספר_/_אליהו_מזרחי#yBsP | כמות | |
| decimal positional system/numerical value | שם | term | מלאכת_המספר#XPnB | בשם | |
| decimal positional system/numerical value | שם | term | מלאכת_המספר#RDxn | בשם | |
| decimal positional system/numerical value | ס.כ.מ./סכום | term | עיר_סיחון#Ydqn | סכום האותיות | |
| decimal positional system/numerical value | נ.ג.ע./הגעה | term | האריתמטיקה_של_ניקומכוס#6yiz | בהגעה | |
| decimal positional system/numerical value | כמות | term | מלאכת_המספר#Cm8o | כמות | |
| calculation/one who calculates | term | ספר_ציפרא#Wgio | המחשב | ||
| calculation/one who calculates | term | ספר_ציפרא#7Y4T | המפתח | ||
| calculation/order | ס.ד.ר./סדור | term | ספר_מעשה_חושב#qswI | סדור | |
| calculation/order | ס.ד.ר./סדור | term | האנציקלופדיה_של_אבו_אלצלת#frV5 | סדור | |
| division/part | term | ספר_האלזיברא#f0RR | חלקים מ | ||
| division/part | ח.ל.ק./חלק | term | חשבון_השטחים#fHwt | חלקים מ | |
| division/part | ח.ל.ק./חלק | term | חשבון_השטחים#yMIi | החלק | |
| division/part | term | ספר_האלזיברא#MlY8 | חלק אחד מ | ||
| division/part | ח.ל.ק./חלק | term | תחבולות_המספר#Vr9G | חלקים | |
| division/part | ח.ל.ק./חלק | definition | ספר_היסודות_לאקלידס#3rk2 | The smaller number is a part of the greater number, when it counts it. המספר הקטן יהיה חלק מן המספר הרב כאשר היה שימנה אותו | |
| division/part | ח.ל.ק./חלק | term | קצור_המספר#FVly | חלק מ | |
| division/part | ח.ל.ק./חלק | term | תחבולות_המספר#85Ut | החלק | |
| division/part | ח.ל.ק./חלק | term | חשבון_השטחים#Tptl | חלקים | |
| division/part | ח.ל.ק./חלק | term | קצור_המספר#weNL | חלקים מ | |
| division/part | term | חשבון_השטחים#Xx6b | חלק אחד מ | ||
| zero/place holder | ש.מ.ר./שומר המעלות | ספר_ציפרא#pxwf | שומר המעלה | ||
| zero/place holder | ש.מ.ר./שומר המעלות | term | ספר_ציפרא#4yzF | שומר המעלות | |
| zero/place-holding | ש.מ.ר./שמירת המדרגות | term | בר_נותן_טעם#UO8O | שמירת המדרגות | |
| decimal positional system/positional value | ע.ר.כ./ערך | term | ספר_עיון_העקרים_לחשבון_ההנדיים#7twl | ערך | |
| decimal positional system/positional value | י.ס.ד./מוסד | term | אגרת_המספר#CjSQ | מוסד | |
| decimal positional system/positional value | א.י.כ./איכות | term | ספר_המספר_/_אליהו_מזרחי#TZ6W | איכות | |
| decimal positional system/positional value | ע.ר.כ./ערך | term | ספר_עיון_העקרים_לחשבון_ההנדיים#lBDf | ערך מדרגיי | |
| decimal positional system/positional value | י.ס.ד./יסוד | term | ספר_יסודי_התבונה_ומגדל_האמונה#XIfl | יסוד | |
| decimal positional system/positional value | אוש | term | ספר_יסודי_התבונה_ומגדל_האמונה#teOX | אוש | |
| decimal positional system/positional value | ג.ב.ה./גובה | term | ספר_מעשה_חושב#cFqk | גובה המעלה | |
| decimal positional system/positional value | י.ס.ד./מוסד | term | אגרת_המספר#op8W | מוסדים | |
| decimal positional system/positional value | י.ס.ד./מוסד | definition | אגרת_המספר#rrql | The knowledge of the first is called position, that is, the knowledge of the positioning of the numerical ranks and their writing. וידיעת הראשון יקרא מוסד כלומ' ידיעה ליסד מדרגות המספר ולכתבם | |
| calculation/procedure | ד.ר.כ./דרך | term | מלאכת_המספר#RaxY | דרך | |
| calculation/procedure | ע.ש.ה./מעשה | term | חשבון_השטחים#E6aP | המעשה | |
| calculation/procedure | ד.ר.כ./דרך | term | עיר_סיחון#uQiQ | דרך | |
| calculation/procedure | ע.ש.ה./מעשה | term | תחבולות_המספר#ZaEb | מעשה ה | |
| calculation/procedure | term | ספר_ג'יבלי_אלמוקבאלא#GL9Q | פעלת | ||
| calculation/procedure | term | ספר_ג'יבלי_אלמוקבאלא#S30z | פעולתו | ||
| calculation/procedure | ע.ש.ה./מעשה | term | ספר_ג'יבלי_אלמוקבאלא#TvqK | מעשהו | |
| calculation/procedure | term | ספר_ג'יבלי_אלמוקבאלא#0aqc | אופני' | ||
| calculation/procedure | term | ספר_ג'יבלי_אלמוקבאלא#LfEg | אופן | ||
| calculation/procedure | ע.ש.ה./מעשה | term | ספר_ג'יבלי_אלמוקבאלא#Vs9i | מעשה | |
| calculation/procedure | ח.ב.ל./תחבולה | term | תחבולות_המספר#Tgbh | תחבולה | |
| calculation/procedure | ע.ש.ה./מעשה | term | ספר_האלזיברא#UEyC | המעשה | |
| calculation/procedure | ח.ב.ל./תחבולה | term | תחבולות_המספר#bFjo | תחבולות | |
| calculation/procedure | ע.ש.ה./מעשה | term | חשבון_השטחים#zeFW | המעשה בזה ש | |
| calculation/procedure | מלאכה | term | חשבון_השטחים#iF6H | מלאכתו ש | |
| calculation/procedure | term | חשבון_השטחים#vkSa | פעולתו ש | ||
| calculation/procedure | ע.ש.ה./מעשה | term | חשבון_השטחים#JwIy | מעשהו ש | |
| calculation/procedure | ע.ש.ה./מעשה | term | קצור_המספר#U3qx | מעשה | |
| calculation/procedure | פ.ע.ל./פועל | term | ספר_ג'יבלי_אלמוקבאלא#qnF0 | הפעל | |
| calculation/procedure | ע.ש.ה./מעשה | term | קצור_המספר#QNsz | המעשה | |
| calculation/procedure | ע.ש.ה./מעשה | term | חשבון_השטחים#QQDX | אופן מעשהו ש | |
| calculation/procedure | מלאכה | term | חשבון_השטחים#KJqC | מלאכתם | |
| calculation/procedure | פ.ע.ל./פועל | term | מלאכת_המספר#JClZ | הפעל | |
| multiplication/product | ר.ב.ע./רבוע | term | מלאכת_המספר#biGu | רבוע | |
| multiplication/product | ח.ב.ר./מחובר | term | ספר_עיון_העקרים_לחשבון_ההנדיים#mujB | המחובר מההכאה | |
| multiplication/product | כ.פ.ל./הכפלה | term | ספר_ג'יבלי_אלמוקבאלא#vPsa | הכפלת ה | |
| multiplication/product | ש.ט.ח./שטח | term | ספר_מעשה_חושב#31TM | שטח | |
| multiplication/product | כ.פ.ל./הכפלה | term | ספר_ג'יבלי_אלמוקבאלא#lSOt | הכפלות | |
| multiplication/product | כ.פ.ל./כפילה | term | ספר_ג'יבלי_אלמוקבאלא#gaGU | כפילות | |
| multiplication/product | ק.ב.צ./מקובץ | term | תחבולות_המספר#QOm4 | המקובץ | |
| multiplication/product | ע.ל.ה./עולה | term | ספר_ג'יבלי_אלמוקבאלא#dSq6 | העולה מהכאתו | |
| multiplication/product | ע.ל.ה./עולה | term | ספר_ג'יבלי_אלמוקבאלא#jjjX | העולה מן ההכאה | |
| multiplication/product | ק.ב.צ./מקובץ | term | בר_נותן_טעם#F3u6 | המקובץ | |
| multiplication/product | ק.ב.צ./מתקבץ | term | תחבולות_המספר#icEh | המתקבץ מהכאת | |
| multiplication/product | ח.ב.ר./מחובר | term | בר_נותן_טעם#1nHC | המחובר | |
| multiplication/product | נ.כ.ה./הכאה | term | ספר_דיני_ממונות#FRJf | הכאות | |
| multiplication/product | ח.ב.ר./מחובר | term | Anonymous#1RGU | המחובר | |
| multiplication/product | term | ספר_האלזיברא#L8fd | העולה מכפל | ||
| multiplication/product | term | ספר_האלזיברא#7pPN | מספר העולה מכפל | ||
| multiplication/product | ש.ט.ח./משוטח | term | קצור_המספר#f6QT | משוטח | |
| multiplication/product | ק.ב.צ./מקובץ | term | תחבולות_המספר#sb1O | המקובץ מההכאה | |
| multiplication/product | ש.ט.ח./מושטח | term | קצור_המספר#oO0u | מושטח | |
| multiplication/product | כ.פ.ל./כפולה | term | עיר_סיחון#SA5F | כפילות | |
| multiplication/product | ע.ל.ה./עולה | term | ספר_האלזיברא#Tf0w | העולה | |
| multiplication/product | נ.כ.ה./הכאה | term | עיר_סיחון#8xHy | הכאת | |
| multiplication/product | ק.ב.צ./מתקבץ | term | חשבון_השטחים#p4nS | המתקבץ | |
| multiplication/product | נ.כ.ה./הכאה | term | עיר_סיחון#Ey7X | מספר ההכאה | |
| multiplication/product | כ.פ.ל./כפילה | term | עיר_סיחון#ARoF | כפילה | |
| multiplication/product | נ.כ.ה./הכאה | term | עיר_סיחון#OjLW | מספר הכאת | |
| multiplication/product | ק.ב.צ./מקובץ | term | חשבון_השטחים#aphl | המקובץ | |
| multiplication/product | כ.פ.ל./כפילה | term | עיר_סיחון#i2pU | כפילה | |
| multiplication/product | כ.פ.ל./כפל | term | חשבון_השטחים#TgEv | כפל | |
| multiplication/product | כ.פ.ל./כפל | term | ספר_ג'יבלי_אלמוקבאלא#bonD | כפל ה | |
| multiplication/product | כ.פ.ל./נכפל | term | עיר_סיחון#yEhP | נכפלים | |
| multiplication/product | כ.פ.ל./נכפל | term | עיר_סיחון#Oq7Z | נכפל | |
| multiplication/product | כ.פ.ל./כפל | term | עיר_סיחון#1IMe | כפל | |
| multiplication/product | כ.פ.ל./נכפל | term | עיר_סיחון#m9hV | נכפל | |
| multiplication/product | ע.ל.ה./עולה | term | ספר_ג'יבלי_אלמוקבאלא#UxpB | העולה מכפל | |
| multiplication/product | כ.פ.ל./הכפלה | term | ספר_ג'יבלי_אלמוקבאלא#AM16 | הכפלה | |
| multiplication/product | ש.ט.ח./שטח | term | ספר_המספר_/_אליהו_מזרחי#Xw68 | שטח | |
| multiplication/product | ח.ב.ר./מחובר | term | ספר_דיני_ממונות#LUum | המחובר | |
| multiplication/product | ש.ט.ח./שטח | term | ספר_המספר_/_אליהו_מזרחי#jOCp | שטחים | |
| multiplication/product | ק.ב.צ./מתקבץ | term | תחבולות_המספר#OF0L | המתקבץ | |
| multiplication/product | ק.ב.צ./מקובץ | term | מלאכת_המספר#bLMx | מקובץ מההכאה | |
| multiplication/product | נ.כ.ה./הכאה | term | מלאכת_המספר#tMkM | הכאה | |
| multiplication/product | ע.ר.כ./נערך | term | Anonymous#ijKL | הנערך | |
| multiplication/product | ח.ב.ר./נחבר | term | Anonymous#PvrY | הנחבר | |
| multiplication/product | ח.ב.ר./נחבר | term | Anonymous#WdtT | הנחבר | |
| multiplication/product | ק.ב.צ./נקבץ | term | Anonymous#2rFl | הנקבץ | |
| multiplication/product | term | ספר_המספר_/_אברהם_אבן_עזרא#LewN | מחובר | ||
| multiplication/product | ע.ר.כ./נערך | term | ספר_מעשה_חושב#XXYN | הנערך | |
| calculation/product by a power of ten | ד.מ.י./דומה | term | Anonymous#mDS8 | הדומה ל | |
| calculation/product by a power of ten | ד.מ.י./דומה | term | Anonymous#0Car | השרש הדומה | |
| calculation/product by a power of ten | term | ספר_המספר_/_אברהם_אבן_עזרא#z6f9 | דומה ל | ||
| calculation/product by a power of ten | ד.מ.י./דומה | term | Anonymous#tNf9 | הדומה הקרוב | |
| practical arithmetic/progression | מ.ש.כ./המשך | term | ספר_מעשה_חושב#a1RK | המשך | |
| practical arithmetic/progression | מ.ש.כ./המשך | term | ספר_מעשה_חושב#jUpK | המשך | |
| division/proportional share | מ.כ.ס./מכס | term | אגרת_המספר#hnEp | מכס | |
| division/proportional share | ח.ל.ק./חלק | term | אגרת_המספר#6e1F | חלקי המכס | |
| division/proportional share | ח.ל.ק./חלק | term | אגרת_המספר#F322 | חלקי המכסי' | |
| division/proportional share | מ.כ.ס./מכס | term | אגרת_המספר#23bp | מכסים | |
| calculation/quantity | כמות | term | מלאכת_המספר#4Iqq | כמות | |
| calculation/quantity | כמה | term | מלאכת_המספר#TuTA | כמה | |
| calculation/quantity | כמות | term | חשבון_השטחים#Dt1C | כמות | |
| calculation/quantity | כמות | term | מלאכת_המספר#Cw2f | כמות | |
| division/quotient | ח.ל.ק./עלה לחלק | term | תחבולות_המספר#G4yP | מה שעלה לחלק | |
| division/quotient | ע.ל.ה./עלה | term | ספר_ג'יבלי_אלמוקבאלא#rNkJ | עולה בחלוק | |
| division/quotient | ח.ל.ק./חלוק | term | ספר_ג'יבלי_אלמוקבאלא#C2SF | החלוק הבא לך בחלוק | |
| division/quotient | ב.ו.א./בא | term | ספר_ג'יבלי_אלמוקבאלא#o62i | יבא בחלוק | |
| division/quotient | ב.ו.א./בא | term | ספר_ג'יבלי_אלמוקבאלא#wZdW | המספר הבא בחלוק | |
| division/quotient | ח.ל.ק./הגיע לחלק | term | תחבולות_המספר#WDb6 | הגיע לחלק | |
| division/quotient | נ.ג.ע./מגיע | term | ספר_ג'יבלי_אלמוקבאלא#b3N0 | המספר המגיע מן החלוקה | |
| division/quotient | term | ספר_האלזיברא#hpOU | יגיע בחלוק | ||
| division/quotient | ח.ל.ק./הגיע לחלק | term | חשבון_השטחים#xL9B | יגיע לחלק | |
| division/quotient | ע.ל.ה./עלה | term | ספר_ג'יבלי_אלמוקבאלא#avzC | יעלה לחלוק | |
| division/quotient | term | ספר_האלזיברא#98lo | יגיע | ||
| division/quotient | term | ספר_האלזיברא#43x0 | מספר אשר | ||
| division/quotient | ח.ל.ק./חלק | term | מלאכת_המספר#K4OR | חלק | |
| division/quotient | term | ספר_האלזיברא#hrnK | המספר המגיע בחלוק | ||
| division/quotient | ח.ל.ק./הגיע לחלק | term | חשבון_השטחים#ClCY | המגיע לחלק | |
| division/quotient | ח.ל.ק./הגיע לחלק | term | חשבון_השטחים#E8nF | המגיע אל החלק | |
| division/quotient | term | ספר_האלזיברא#6PKQ | המגיע בחלוק | ||
| division/quotient | ח.ל.ק./חלק | term | תחבולות_המספר#yDPN | חלק | |
| division/quotient | ח.ל.ק./חלק | term | תחבולות_המספר#U8c0 | חלק | |
| division/quotient | ח.ל.ק./עלה לחלק | term | חשבון_השטחים#PRFr | העולה אל החלק | |
| division/quotient | term | ספר_האלזיברא#CaNZ | היוצא בחלוק | ||
| division/quotient | ח.ל.ק./עלה לחלק | term | חשבון_השטחים#QtBr | עלה אל החלק | |
| division/quotient | term | בר_נותן_טעם#TwBn | היוצא בחילוק | ||
| division/quotient | ח.ל.ק./חלוק | term | ספר_ג'יבלי_אלמוקבאלא#TQpW | מספר החלוק העולה | |
| division/quotient | ח.ל.ק./חלוק | term | ספר_ג'יבלי_אלמוקבאלא#lP6v | החלוק | |
| division/quotient | ח.ל.ק./חלוק | term | ספר_ג'יבלי_אלמוקבאלא#gR5o | החלוק הבא בַחלוק | |
| division/quotient | ח.ל.ק./הגיע לחלק | term | תחבולות_המספר#tdF2 | המגיע לחלק | |
| division/quotient | ח.ל.ק./חלק | term | מלאכת_המספר#YlhE | חלק | |
| division/quotient | נ.ג.ע./מגיע | term | ספר_ג'יבלי_אלמוקבאלא#zngW | המספרי' המגיעי' לך בחלוק | |
| division/quotient | ח.ל.ק./חלק | term | קצת_מענייני_חכמת_המספר#Ej2y | חלק | |
| division/quotient | ב.ו.א./בא | term | ספר_ג'יבלי_אלמוקבאלא#D7Be | יבא לחלק | |
| division/quotient | ח.ל.ק./עלה לחלק | term | תחבולות_המספר#uIRR | העולה לחלק | |
| division/quotient | ח.ל.ק./עלה לחלק | term | חשבון_השטחים#lJql | העולה לחֶלק | |
| division/quotient | ח.ל.ק./חלק | term | ספר_יסודי_התבונה_ומגדל_האמונה#ebS6 | חלק | |
| extraction of root/radicand | נ.ק.ב./נקוב | term | ספר_ג'יבלי_אלמוקבאלא#AA9e | הנקובים היות להם שרשים | |
| extraction of root/radicand | נ.ק.ב./נקוב | term | ספר_ג'יבלי_אלמוקבאלא#89gu | הנקובים שהם להם שרש | |
| extraction of root/radicand | נ.ק.ב./נקב | term | ספר_ג'יבלי_אלמוקבאלא#DLNs | אשר נקבו להיות להם שרש | |
| extraction of root/radicand | נ.ק.ב./נקב | term | ספר_ג'יבלי_אלמוקבאלא#NJIn | אשר נקבו היות להם שרשים | |
| extraction of root/radicand | נ.ק.ב./נקב | term | ספר_ג'יבלי_אלמוקבאלא#yY63 | אשר נקבו שרש | |
| extraction of root/radicand | נ.ק.ב./נקוב | term | ספר_ג'יבלי_אלמוקבאלא#jxnc | הנקוב בשם שיש לו שרש | |
| extraction of root/radicand | נ.ק.ב./נקוב | term | ספר_ג'יבלי_אלמוקבאלא#asPd | הנקוב שהוא לו שרש | |
| extraction of root/radicand | נ.ק.ב./נקוב | term | ספר_ג'יבלי_אלמוקבאלא#BaGE | הנקובים להם שרשים' | |
| extraction of root/radicand | נ.ק.ב./נקוב | term | ספר_ג'יבלי_אלמוקבאלא#RNkz | הנקוב אשר לו השרש | |
| extraction of root/radicand | נ.ק.ב./נקב | term | ספר_ג'יבלי_אלמוקבאלא#Wjor | שנקבו להיות להם שרש | |
| extraction of root/radicand | י.ס.ד./יסוד | term | משנת_המדות#baMV | יסוד | |
| extraction of root/radicand | נ.ק.ב./נקוב | term | ספר_ג'יבלי_אלמוקבאלא#5VRC | הנקובים להיות להם שרש | |
| extraction of root/radicand | נ.ק.ב./נקוב | term | ספר_ג'יבלי_אלמוקבאלא#JxaB | הנקובים שרש | |
| raising the rank/raised to a higher rank | ר.ו.מ./מורם | term | ספר_עיון_העקרים_לחשבון_ההנדיים#rKyb | מורם | |
| raising the rank/raised to a higher rank | term | ספר_עיון_העקרים_לחשבון_ההנדיים#BeYs | מרפוע | ||
| reduction/reduced | ק.צ.ר./מקוצר | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#MBO7 | מקוצרים | |
| reduction/reduced | צ.מ.צ.מ./מצומצם | term | אגרת_המספר#MDt8 | שרש ממספר שלם מצומצם | |
| reduction/reduced | ק.ט.נ./קטן יחס | term | קצת_מענייני_חכמת_המספר#bkdb | קטן היחס | |
| reduction/reduced | ק.צ.ר./מקוצר | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#5n4Z | מקוצר | |
| reduction/reduced | צ.מ.צ.מ./מצומצם | term | אגרת_המספר#U22y | שרש מצומצם | |
| reduction/reduced | ק.צ.ר./מקוצר | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#Lrzr | המורה המקוצר | |
| reduction/reduced | ק.ט.נ./קטן יחס | term | קצת_מענייני_חכמת_המספר#Cyg5 | קטני היחס | |
| simple fraction/reduction | צ.מ.צ.מ./צמצום | term | בר_נותן_טעם#suVP | בצמצום | |
| simple fraction/reduction | צ.מ.צ.מ./צמצום | term | בר_נותן_טעם#86e8 | בצמצום | |
| simple fraction/reduction | כלילת יופי | term | בר_נותן_טעם#ea69 | כלילת יופי | |
| simple fraction/reduction | ק.צ.ר./קצור | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#jwbs | קיצור | |
| simple fraction/reduction | ק.צ.ר./קצור | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#z8Jb | קיצור המורים | |
| simple fraction/reduction | ס.ו.ר./הסרה | term | אגרת_המספר#k2xs | הסרת השתוף | |
| simple fraction/reduction | כלילת יופי | term | בר_נותן_טעם#Mkxu | כלילת יופי | |
| division/remainder of division | ש.א.ר./שיור | term | אגרת_המספר#BVNx | שיור | |
| division/remainder of division | ש.א.ר./שיור | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#Asag | שיור | |
| division/remainder of division | ש.א.ר./שיור | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#70Yo | שיור | |
| division/remainder of division | ש.א.ר./שארית | term | בר_נותן_טעם#Jb3s | השארית הנשארה | |
| division/remainder of division | ש.א.ר./שארית | term | בר_נותן_טעם#S7vn | שארית | |
| division/remainder of division | ש.א.ר./שיור | term | אגרת_המספר#bI5B | שיורים | |
| calculation/result | ע.ל.ה./עולה | term | חשבון_השטחים#PjY5 | העולה | |
| calculation/result | י.צ.א./יוצא | term | ספר_ג'יבלי_אלמוקבאלא#QU3I | היוצא | |
| calculation/result | ע.ל.ה./עולה | term | ספר_ג'יבלי_אלמוקבאלא#0sNH | העולה מ | |
| calculation/result | י.צ.א./יוצא | term | תחבולות_המספר#fGOj | היוצא בהכאת | |
| calculation/result | י.צ.א./יוצא | term | ספר_ג'יבלי_אלמוקבאלא#2AKq | המספר היוצא מ | |
| calculation/result | ע.ל.ה./עולה | term | תחבולות_המספר#C1zj | העולה מהם | |
| calculation/result | ע.ל.ה./עולה | term | ספר_ג'יבלי_אלמוקבאלא#JBFu | העולה | |
| calculation/result | ע.ל.ה./עולה | term | תחבולות_המספר#i6yt | העולה מ | |
| calculation/result | ע.ל.ה./עולה | term | קצור_המספר#ec7l | העולה | |
| calculation/result | ע.ל.ה./עולה | term | קצור_המספר#iSMo | העולה | |
| calculation/result | י.צ.א./יוצא | term | קצור_המספר#YZcb | היוצא ב | |
| calculation/result | י.צ.א./יוצא | term | קצור_המספר#UEpW | היוצא | |
| calculation/result | נ.ג.ע./מגיע | term | חשבון_השטחים#a3tR | המגיע | |
| calculation/result | נ.ג.ע./מגיע | term | ספר_ג'יבלי_אלמוקבאלא#Wi1E | המגיע | |
| calculation/result | ע.ל.ה./עולה | term | ספר_האלזיברא#iVbQ | העולה | |
| calculation/result | י.ל.ד./נולד | term | ספר_עיון_העקרים_לחשבון_ההנדיים#lrIS | נולד | |
| casting out/result of casting out | ש.ק.ל./משקל | term | Anonymous#SqpY | משקל | |
| subtraction/result of subtraction | ש.א.ר./שארית | term | ספר_ג'יבלי_אלמוקבאלא#hLvJ | השארית עד | |
| subtraction/result of subtraction | י.ת.ר./מותר | term | מלאכת_המספר#xh8h | המותר | |
| subtraction/result of subtraction | ש.א.ר./נשאר | term | ספר_ג'יבלי_אלמוקבאלא#wr1s | הנשאר | |
| subtraction/result of subtraction | ש.א.ר./נשאר | term | ספר_ג'יבלי_אלמוקבאלא#dhSG | הנשאר מגרעון | |
| subtraction/result of subtraction | ש.א.ר./שארית | term | ספר_ג'יבלי_אלמוקבאלא#Lxgt | השארית בגרעון | |
| subtraction/result of subtraction | ש.א.ר./שארית | term | ספר_ג'יבלי_אלמוקבאלא#DqCw | השארית | |
| subtraction/result of subtraction | ש.א.ר./נשאר | term | ספר_ג'יבלי_אלמוקבאלא#nYQ2 | הנשאר מהוצאת | |
| subtraction/result of subtraction | ש.א.ר./נשאר | term | תחבולות_המספר#SFsp | מה שנשאר מה | |
| subtraction/result of subtraction | ש.א.ר./נשאר | term | תחבולות_המספר#yZVt | הנשאר מ | |
| subtraction/result of subtraction | ש.א.ר./נשאר | term | קצור_המספר#CjpB | המספר הנשאר | |
| subtraction/result of subtraction | ש.א.ר./נשאר | term | קצור_המספר#xvYY | הנשאר | |
| subtraction/result of subtraction | ש.א.ר./שארית | term | בר_נותן_טעם#fYDP | שארית | |
| subtraction/result of subtraction | ש.א.ר./נשאר | term | חשבון_השטחים#NZKg | הנשאר | |
| subtraction/result of subtraction | ש.א.ר./נשאר | term | מלאכת_המספר#FQ1g | הנשאר | |
| subtraction/result of subtraction | י.ת.ר./נותר | term | מלאכת_המספר#e481 | הנותר מ | |
| subtraction/result of subtraction | ש.א.ר./נשאר | term | ספר_דיני_ממונות#9ifm | הנשאר | |
| subtraction/result of subtraction | ש.א.ר./נשאר | term | ספר_האלזיברא#MC5r | הנשאר | |
| subtraction/result of subtraction | ש.א.ר./נשאר | term | ספר_האלזיברא#Xt9P | הנשאר מן | |
| extraction of root/root | √5 | עיר_סיחון#CVSH | Example of a number, whose excess over the preceding square is less than the root of the square: We wish to know the measure of each side of the square that is five.
::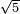 דמיון במספר שהעודף על המרובע שעבר פחות מגדר המרובע 95vההוא
דמיון במספר שהעודף על המרובע שעבר פחות מגדר המרובע 95vההוארצינו לדעת מדת כל {{#annot:term|439,1464|45q9}}צלע{{#annotend:45q9}} וצלע ממרובע שהוא חמשה | ||
| extraction of root/root | √7 | עיר_סיחון#313V | Example of a number, whose excess over the preceding square is greater than its root: We wish to know the measure of the sides of the square that is seven.
::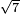 דמיון במספר שהעודף על המרובע שעבר יתר מגדרו
דמיון במספר שהעודף על המרובע שעבר יתר מגדרורצינו לדעת מדת הצלעות ממרובע שהוא שבעה | ||
| extraction of root/root | √6 | עיר_סיחון#nS0s | Example of a number, whose excess over the preceding square is the same as the root of the preceding square: We wish to know the measure of the square that is six.
::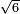 דמיון במספר שהעודף על המרובע שעבר הוא כגדר המרובע ההוא שעבר
דמיון במספר שהעודף על המרובע שעבר הוא כגדר המרובע ההוא שעבררצינו לדעת מדת צלעות מרובע שהוא ששה | ||
| extraction of root/root | ³√(3+¼) | ספר_דיני_ממונות#n2ZL | As the one who says: extract for me the [cube] root of 3 and a quarter.
::![\scriptstyle\sqrt[3]{3+\frac{1}{4}}](/mediawiki/images/math/3/5/9/359c46cf0f610e5d6b77ea058a73a35f.png) כמו האומר קח לי שרש ג' ורביע א'
כמו האומר קח לי שרש ג' ורביע א' | ||
| extraction of root/root | ³√15 | ספר_דיני_ממונות#9HTO | Example: we wish to know the cube [root] of 15.
::![\scriptstyle\sqrt[3]{15}](/mediawiki/images/math/0/c/8/0c82b7d8e6efa71d3ec9075bc747ff5f.png) דמיון זה נרצה לדעת מעוקב ט"ו
דמיון זה נרצה לדעת מעוקב ט"ו | ||
| extraction of root/root | צלע | term | עיר_סיחון#AnW4 | צלעות | |
| extraction of root/root | ג.ד.ר./גדר | term | עיר_סיחון#aqMn | גדרים | |
| extraction of root/root | √100 | עיר_סיחון#qY9w | We also want the root of a hundred.
: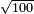 ועוד בקשנו שורש וגדר מאה
ועוד בקשנו שורש וגדר מאה | ||
| extraction of root/root | √400 | עיר_סיחון#2Rcj | We wish to know the root of four hundred.
: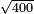 וכן רצינו לדעת שרש ארבע מאות
וכן רצינו לדעת שרש ארבע מאות | ||
| extraction of root/root | √4000 | עיר_סיחון#ZH6A | If we wish to know the approximate root of four thousand.
: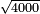 ואם רצינו לדעת הגדר הקרוב אל ארבעת אלפים
ואם רצינו לדעת הגדר הקרוב אל ארבעת אלפים | ||
| extraction of root/root | ³√10 | ספר_דיני_ממונות#WS2D | 107) Question: if you want to extract the cubic root of ten.
:![\scriptstyle\sqrt[3]{10}](/mediawiki/images/math/9/d/f/9df29fc2932ecfc10526c2086beee64c.png) קז) שאלה אם תרצה להוציא שרש מעוקב עשרה
קז) שאלה אם תרצה להוציא שרש מעוקב עשרה | ||
| extraction of root/root | ש.ר.ש./שרש | term | ספר_האלזיברא#SuJC | שורש מספר | |
| extraction of root/root | ש.ר.ש./שרש | term | ספר_האלזיברא#dALe | שורש ה | |
| extraction of root/root | ³√(1+½) | ספר_דיני_ממונות#Mbz5 | Example: we wish to know the root of 1 and a half.
::![\scriptstyle\sqrt[3]{1+\frac{1}{2}}](/mediawiki/images/math/a/a/4/aa43fab9d4b2b4090452203972ea8cf1.png) דמיון זה נרצה לדעת שרש א' וחצי
דמיון זה נרצה לדעת שרש א' וחצי | ||
| extraction of root/root | √973182 | קצור_המספר#dYxZ | One example for this: we wish to know the root of nine hundred and seventy-three thousand, one hundred and eighty-two.
::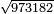 ויהיה משל אחד לזה רצינו לדעת שורש תשע מאות ושבעים ושלשה אלפים ומאה ושמונים ושנים
ויהיה משל אחד לזה רצינו לדעת שורש תשע מאות ושבעים ושלשה אלפים ומאה ושמונים ושנים | ||
| extraction of root/root | ³√15 | ספר_דיני_ממונות#ZCaV | Example: we wish to know the cube root of 15.
::![\scriptstyle\sqrt[3]{15}](/mediawiki/images/math/0/c/8/0c82b7d8e6efa71d3ec9075bc747ff5f.png) דמיון זה נרצה לדעת שרש מעוקב ט"ו
דמיון זה נרצה לדעת שרש מעוקב ט"ו | ||
| extraction of root/root | ³√1072000 | ספר_דיני_ממונות#fVf2 | ![\scriptstyle\sqrt[3]{1072000}](/mediawiki/images/math/2/b/0/2b069db83734f1b9f13fe1d933e0f309.png) דמיון זה נרצה לדעת שרש מעוקב מאלף אלפים וע"ב אלפים 293vאלפים
דמיון זה נרצה לדעת שרש מעוקב מאלף אלפים וע"ב אלפים 293vאלפים | ||
| extraction of root/root | √2000 | ספר_המספר_/_אליהו_מזרחי#XKsB | Example: if you wish to know the root of 2000.
: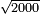 המשל בזה אם רצית לדעת שרש הב' אלפים
המשל בזה אם רצית לדעת שרש הב' אלפים | ||
| extraction of root/root | √5499025 | ספר_המספר_/_אליהו_מזרחי#Qmnu | Example: if you wish to know the root of 5499025.
: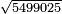 המשל בזה אם רצית לדעת שרש ה' פעמים אלף אלפים ותצ"ט אלף וכ"ה
המשל בזה אם רצית לדעת שרש ה' פעמים אלף אלפים ותצ"ט אלף וכ"ה | ||
| extraction of root/root | √6169004404 | ספר_המספר_/_אליהו_מזרחי#QPxe | Example of a number that does not have a root, whose approximate root is required.
: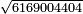 ומשל המספר הבלתי נגדר המבוקש שרשו היותר קרוב הוא זה
ומשל המספר הבלתי נגדר המבוקש שרשו היותר קרוב הוא זה | ||
| extraction of root/root | ³√(½) | ספר_דיני_ממונות#RFa1 | Example: we wish to know the cube root of a half.
::![\scriptstyle\sqrt[3]{\frac{1}{2}}](/mediawiki/images/math/3/7/d/37d8077abb00a82f2b7844e523ea4470.png) דמיון זה נרצה לדעת שרש מעוקב חצי
דמיון זה נרצה לדעת שרש מעוקב חצי | ||
| extraction of root/root | ³√(⅕) | ספר_דיני_ממונות#eKzs | Another example: we wish to know the cube [root] of a fifth.
::![\scriptstyle\sqrt[3]{\frac{1}{5}}](/mediawiki/images/math/f/b/2/fb26d52f658e67321b9383ce42dd7084.png) דמיון אחר נרצה לדעת מעוקב חומש
דמיון אחר נרצה לדעת מעוקב חומש | ||
| extraction of root/root | √6169002849 | ספר_המספר_/_אליהו_מזרחי#XNue | Example of a number that has a root, whose root is required
: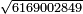 משל המספר הנגדר אשר יבוקש שרשו הוא זה
משל המספר הנגדר אשר יבוקש שרשו הוא זה | ||
| extraction of root/root | ³√(1+½) | ספר_דיני_ממונות#6gdU | Example: we wish to know [the cube] root of 1 and a half.
::![\scriptstyle\sqrt[3]{1+\frac{1}{2}}](/mediawiki/images/math/a/a/4/aa43fab9d4b2b4090452203972ea8cf1.png) דמיון זה רצינו לדעת שרש א"נ א' וחצי
דמיון זה רצינו לדעת שרש א"נ א' וחצי | ||
| extraction of root/root | ³√(½) | ספר_דיני_ממונות#IldO | Example: we wish to know the cube root of a half.
::![\scriptstyle\sqrt[3]{\frac{1}{2}}](/mediawiki/images/math/3/7/d/37d8077abb00a82f2b7844e523ea4470.png) דמיון זה נרצה לדעת שרש מעוקב חצי
דמיון זה נרצה לדעת שרש מעוקב חצי | ||
| extraction of root/root | term | ספר_עיון_העקרים_לחשבון_ההנדיים#QMYr | גדר | ||
| extraction of root/root | ג.ד.ר./גדר | term | עיר_סיחון#WdP4 | גדר | |
| extraction of root/root | ע.ק.ר./עיקר | term | משנת_המדות#vJmG | עיקר | |
| extraction of root/root | ע.ק.ר./עיקר | term | משנת_המדות#hixV | עקר | |
| extraction of root/root | ש.ר.ש./שרשי | term | קצור_המספר#jxvb | מספר שרשי | |
| extraction of root/root | ש.ר.ש./שרשי | term | קצור_המספר#sq9F | מספר שרשי | |
| extraction of root/root | ש.ר.ש./שרש | term | קצור_המספר#DDAg | שרשים | |
| extraction of root/root | ש.ר.ש./שרש | term | קצור_המספר#DXBk | שורש | |
| extraction of root/root | √225 | עיר_סיחון#Y95w | We wish to know the root of two hundred and twenty-five.
: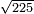 הנה בקשנו לדעת גדר מאתים ועשרים וחמשה
הנה בקשנו לדעת גדר מאתים ועשרים וחמשה | ||
| extraction of root/root | √925 | עיר_סיחון#k6sa | We wish to know the approximate root of nine hundred and twenty-five.
: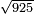 ועוד בקשנו לדעת הגדר קרוב יותר אל תשע מאות ועשרים וחמשה
ועוד בקשנו לדעת הגדר קרוב יותר אל תשע מאות ועשרים וחמשה | ||
| extraction of root/root | √7056 | עיר_סיחון#WCca | We wish to know the root of seven thousand and fifty-six.
: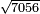 ועוד בקשנו לדעת גדר שבעת אלפים וחמשים וששה
ועוד בקשנו לדעת גדר שבעת אלפים וחמשים וששה | ||
| extraction of root/root | ש.ר.ש./שרש | term | חשבון_השטחים#CVyr | שורש מספר | |
| extraction of root/root | צלע | term | עיר_סיחון#45q9 | צלע | |
| extraction of root/root | ³√10 | ספר_דיני_ממונות#Clg9 | Example: to know the root of ten.
::![\scriptstyle\sqrt[3]{10}](/mediawiki/images/math/9/d/f/9df29fc2932ecfc10526c2086beee64c.png) דמיון זה לדעת שרש עשרה
דמיון זה לדעת שרש עשרה | ||
| extraction of root/root | term | חשבון_השטחים#Oiea | שורש ה | ||
| extraction of root/root | ש.ר.ש./שרש | term | תחבולות_המספר#N0WY | שרש מספר | |
| extraction of root/root | ש.ר.ש./שרש | term | תחבולות_המספר#lhFz | שרש ה | |
| extraction of root/root | √456789 | ספר_דיני_ממונות#Wuta | Example: we wish to know the root of 456789
::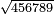 דמיון זה נרצה לדעת שרש ד' מאות וחמישים אלף וו' אלפים ותשפ"ט
דמיון זה נרצה לדעת שרש ד' מאות וחמישים אלף וו' אלפים ותשפ"ט | ||
| extraction of root/root | √164960 | ספר_דיני_ממונות#l3L6 | Example: we wish to know the root of 164960.
::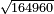 דמיון נרצה לדעת שרש קס"ד אלפים ותתק"ס
דמיון נרצה לדעת שרש קס"ד אלפים ותתק"ס | ||
| extraction of root/root | ש.ר.ש./שרש | term | ספר_מעשה_חושב#DP7k | שרשי | |
| extraction of root/root | ³√12812904 | מלאכת_המספר#kjtd | In order to expand the explanation, we give another example and here is its diagram:
:![\scriptstyle\sqrt[3]{12812904}](/mediawiki/images/math/0/7/a/07aafd0c5fd061d54bb34d4011050183.png) |style="width:45%; text-align:right;"|וכדי להוסיף ביאור נעשה משל אחר והנה לך צורתו
|style="width:45%; text-align:right;"|וכדי להוסיף ביאור נעשה משל אחר והנה לך צורתו | ||
| extraction of root/root | י.ס.ד./יסוד | term | ספר_מעשה_חושב#PWkS | יסוד | |
| extraction of root/root | ש.ר.ש./שרש | term | חשבון_השטחים#mhPt | שרש מ | |
| extraction of root/root | term | חשבון_השטחים#gcfE | שורש מ | ||
| extraction of root/root | term | חשבון_השטחים#B9ne | שרשים מ | ||
| extraction of root/root | ש.ר.ש./שרש | term | חשבון_השטחים#urwH | שרשים | |
| extraction of root/root | י.ס.ד./יסוד | term | ספר_מעשה_חושב#ny0B | יסוד מספרי | |
| extraction of root/root | ³√571787 | מלאכת_המספר#UntD | Another example that occurs in a different way: assuming that we wish to know the cube root of 571787.
:![\scriptstyle\sqrt[3]{571787}](/mediawiki/images/math/3/e/8/3e8cc95dfa131c676806e901de31e5fc.png) |style="width:45%; text-align:right;"|ומשל אחר אם יקרה באופן אחר נניח שנרצה לדעת השרש המעוקב מת"ק ע"א אלף ותשפ"ז
|style="width:45%; text-align:right;"|ומשל אחר אם יקרה באופן אחר נניח שנרצה לדעת השרש המעוקב מת"ק ע"א אלף ותשפ"ז | ||
| extraction of root/root | ³√12167 | מלאכת_המספר#DZbA | Example: we wish to know the cube root of 12162.
:![\scriptstyle\sqrt[3]{12167}](/mediawiki/images/math/a/b/c/abc38f531fb13e4a1ec9492e6194fa3a.png) המשל נרצה לדעת השורש המעוקב של י"ב אלף וקס"ז
המשל נרצה לדעת השורש המעוקב של י"ב אלף וקס"ז | ||
| extraction of root/root | √5625 | מלאכת_המספר#NwlA | Example: suppose we want to look for the root of a number, which is 5625.
המשל שנניח מספר אחד שנרצה לבקש שורשו והוא | ||
| extraction of root/root | √76543 | עיר_סיחון#p0o5 | We wish to know the the approximate root of seventy-six thousand, five hundred and forty-three.
: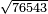 ועוד בקשנו לדעת הגדר הקרוב שבעים וששה אלף וחמש מאות וארבעים 75vושלשה
ועוד בקשנו לדעת הגדר הקרוב שבעים וששה אלף וחמש מאות וארבעים 75vושלשה | ||
| extraction of root/root | ³√10000 | ספר_דיני_ממונות#JRw7 | We wish to know the root of ten thousand.
::![\scriptstyle\sqrt[3]{10000}](/mediawiki/images/math/6/c/4/6c42e6b302b8432f7020b406fee3ccf7.png) נרצה לדעת שרש עשרת אלפים
נרצה לדעת שרש עשרת אלפים | ||
| extraction of root/root | ³√(2+½) | ספר_דיני_ממונות#OMsl | Example: we wish to know the [cube] root of 2 and a half.
::![\scriptstyle\sqrt[3]{2+\frac{1}{2}}](/mediawiki/images/math/2/1/b/21bb73f8e7e91638887f37289a16fa16.png) דמיון נרצה לדעת שרש ב' וחצי
דמיון נרצה לדעת שרש ב' וחצי | ||
| extraction of root/root | √²/₈ | בר_נותן_טעם#5dVA | Example: we wish to know the root of 2-eighths.
: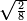 המשל רצינו לדעת שרש ב' שמיניות
המשל רצינו לדעת שרש ב' שמיניות | ||
| extraction of root/root | √583696 | עיר_סיחון#gS7X | We wish to know the root of five hundred and eighty-three thousand, six hundred and ninety-six.
: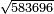 ועוד בקשנו לדעת גדר חמש מאות ושמונים ושלשת אלפים ושש מאות ותשעים וששה
ועוד בקשנו לדעת גדר חמש מאות ושמונים ושלשת אלפים ושש מאות ותשעים וששה | ||
| extraction of root/root | √(⁴/₆·(4+⁵/₉)) | בר_נותן_טעם#FQUg | Example: we wish to know the root of 4-sixths of 4 integers and 5-ninths.
: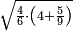 המשל רצינו לדעת שרש ד' שישיות מד' 60rשלמים וה' תשיעיות
המשל רצינו לדעת שרש ד' שישיות מד' 60rשלמים וה' תשיעיות | ||
| extraction of root/root | √824464 | עיר_סיחון#nzC6 | We wish to know the root of this number, which is eight hundred and twenty-four thousand, four hundred and sixty-four.
: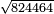 ועוד בקשנו לדעת גדר 79rהמספר הזה שהוא שמונה מאות אלף ועשרים וארבעת אלף וארבע מאות וששים וארבעה
ועוד בקשנו לדעת גדר 79rהמספר הזה שהוא שמונה מאות אלף ועשרים וארבעת אלף וארבע מאות וששים וארבעה | ||
| extraction of root/root | ³√(⁸/₂₇) | ספר_דיני_ממונות#41Kp | Example: we wish to know the [cube] root of 8 parts of 27.
::![\scriptstyle\sqrt[3]{\frac{8}{27}}](/mediawiki/images/math/4/b/8/4b82e09026615fc0ec7aa9b037739f7c.png) דמיון נרצה לדעת שרש מח' חלקים מכ"ז
דמיון נרצה לדעת שרש מח' חלקים מכ"ז | ||
| extraction of root/root | √144 | קצור_המספר#SblR | The way to extract the root of 144:
: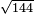 והנה דרך בקשת שורש קמ"ד
והנה דרך בקשת שורש קמ"ד | ||
| extraction of root/root | √29 | בר_נותן_טעם#rK5S | Example: if we wish the root of 29.
: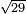 40rהמשל אם בקשנו שרש כ"ט
40rהמשל אם בקשנו שרש כ"ט | ||
| extraction of root/root | √7 | בר_נותן_טעם#ROfW | When we seek the root of 7.
::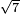 המשל כאשר בקשנו שרש ז'
המשל כאשר בקשנו שרש ז' | ||
| extraction of root/root | √6 | בר_נותן_טעם#cUME | Example: we wish to know the root of 6.
::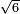 והמשל בקשנו לידע שרש ו'
והמשל בקשנו לידע שרש ו' | ||
| extraction of root/root | √7 | בר_נותן_טעם#TblT | Example: we seek the root of 7.
::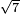 המשל בקשנו שרש ז'
המשל בקשנו שרש ז' | ||
| extraction of root/root | √10375 | בר_נותן_טעם#WnAI | Another example: we wish to know the root of the number 10375.
: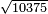 משל אחר רצינו לדעת שרש מספר זה 10375
משל אחר רצינו לדעת שרש מספר זה 10375 | ||
| extraction of root/root | √344680129066 | בר_נותן_טעם#lfu5 | We wish to seek the root of 344680129066.
: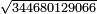 המשל רצינו לבקש שרש 344680129066
המשל רצינו לבקש שרש 344680129066 | ||
| extraction of root/root | ³√(2+¹⁰/₂₇) | ספר_דיני_ממונות#X3JD | Another example of fractions with integers: we wish to know the [cube] root of 2 and 10 parts of 27.
::![\scriptstyle\sqrt[3]{2+\frac{10}{27}}](/mediawiki/images/math/2/5/0/2502ba1789941bb08207b874b20e4ff6.png) דמיון אחר בשברים עם שלמים נבקש לדעת שרש ב' וי' חלקים מכ"ז
דמיון אחר בשברים עם שלמים נבקש לדעת שרש ב' וי' חלקים מכ"ז | ||
| extraction of root/root | ³√(3+³/₂₇) | ספר_דיני_ממונות#DY5m | Example: extract for me the [cube] root of 3 and 3 parts of 27.
::![\scriptstyle\sqrt[3]{3+\frac{3}{27}}](/mediawiki/images/math/c/b/e/cbe8600fe75f050c69dd902d601dd58c.png) דמיון תוציא לי שרש ג' וג' חלקים מכ"ז
דמיון תוציא לי שרש ג' וג' חלקים מכ"ז | ||
| extraction of root/root | √2 | מלאכת_המספר#DS3Y | Example: we wish to know the approximate root of two
: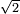 המשל נרצה לדעת השרש היותר קרוב שאיפשר לשנים
המשל נרצה לדעת השרש היותר קרוב שאיפשר לשנים | ||
| extraction of root/root | √20 | ספר_המספר_/_אברהם_אבן_עזרא#Q6nf | Example: the number twenty.
: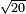 דמיון המספר עשרים
דמיון המספר עשרים | ||
| extraction of root/root | √200 | ספר_המספר_/_אברהם_אבן_עזרא#Eak5 | We wish to know the root of two hundred.
: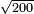 בקשנו לדעת שרש מאתים
בקשנו לדעת שרש מאתים | ||
| extraction of root/root | √20000 | ספר_המספר_/_אברהם_אבן_עזרא#RyVX | If you wish to know the root of twenty thousand.
: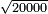 ואם רצית לדעת שרש עשרים אלף
ואם רצית לדעת שרש עשרים אלף | ||
| extraction of root/root | √18 | ספר_המספר_/_אברהם_אבן_עזרא#aS7F | Example: we wish to know how much is the root of 18.
: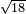 דמיון רצינו לדעת כמה שרש י"ח
דמיון רצינו לדעת כמה שרש י"ח | ||
| extraction of root/root | √10 | ספר_המספר_/_אברהם_אבן_עזרא#7Wyo | We want to extract the root of 10.
: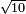 בקשנו להוציא שרש י'
בקשנו להוציא שרש י' | ||
| extraction of root/root | √5 | ספר_החשבון_לאל_חצאר#BKbE | When you are told: how much is the root of five?
: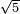 כשיאמר לך כמה שורש חמשה
כשיאמר לך כמה שורש חמשה | ||
| extraction of root/root | √10 | ספר_החשבון_לאל_חצאר#NpFP | How much is the root of ten?
: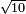 כמה שורש עשרה
כמה שורש עשרה | ||
| extraction of root/root | √15 | ספר_החשבון_לאל_חצאר#nd9x | If one says: how much is the root of fifteen?
: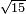 ואם אמר כמה שורש חמשה עשר
ואם אמר כמה שורש חמשה עשר | ||
| extraction of root/root | √20 | ספר_החשבון_לאל_חצאר#UEVk | If one says: how much is the root of twenty?
: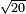 ואם אמר כמה שרש עשרים
ואם אמר כמה שרש עשרים | ||
| rounding/rounded number | ש.ל.מ./השלמה | term | ספר_מעשה_חושב#5lgS | שעור ההשלמה | |
| rounding/rounded number | ש.ל.מ./מושלם | term | ספר_מעשה_חושב#8Ptd | המספר המושלם | |
| rounding/rounded number | ש.ל.מ./השלמה | term | ספר_מעשה_חושב#cN0Y | מספר ההשלמה | |
| basic operations/rounding | ש.ל.מ./השלמה | term | ספר_מעשה_חושב#8ukR | השלמה | |
| basic operations/rounding | ש.ל.מ./השלמה | term | ספר_מעשה_חושב#3U9F | השלמה למגרעת | |
| basic operations/rounding | ש.ל.מ./השלמה | term | ספר_מעשה_חושב#4q0N | השלמה לתוספת | |
| check/scales | א.ז.נ./מאזנים | term | Anonymous#kRMI | מאזני | |
| check/scales | term | ספר_המספר_/_אברהם_אבן_עזרא#DwmZ | מאזני מספר | ||
| check/scales | א.ז.נ./מאזנים | term | ספר_עיון_העקרים_לחשבון_ההנדיים#MoOc | מאזנים | |
| check/scales | ש.ק.ל./משקל | term | ספר_ציפרא#mImR | משקל | |
| check/scales | ש.ק.ל./משקל | term | ספר_ציפרא#LdXM | משקלים | |
| sexagesimal fraction/second | term | ספר_מעשה_חושב#NyKd | שניים | ||
| sexagesimal fraction/second | ש.נ.י./שני | term | ספר_המספר_/_אליהו_מזרחי#zSTg | שני | |
| sexagesimal fraction/second | ש.נ.י./שני | term | ספר_המספר_/_אליהו_מזרחי#hf7M | שניים | |
| progression/sequential number | פאה | term | האנציקלופדיה_של_אבו_אלצלת#wYlv | פאה | |
| progression/sequential number | term | ספר_המספר_/_אברהם_אבן_עזרא#gUdN | פאה | ||
| progression/sequential number | פאה | term | האנציקלופדיה_של_אבו_אלצלת#uyxT | פאותיו | |
| calculation/set aside | ש.מ.ר./שמור | term | ספר_ג'יבלי_אלמוקבאלא#K3AP | המספר השמור | |
| calculation/set aside | ש.מ.ר./שמור | term | תחבולות_המספר#VFtS | השמור | |
| calculation/set aside | ש.מ.ר./שמור | term | ספר_ג'יבלי_אלמוקבאלא#IWQm | השמור | |
| calculation/set aside | ש.מ.ר./שמור | term | ספר_האלזיברא#0xSg | השמור | |
| fraction/sexagesimal fraction | ש.ב.ר./שברי חכמי המזלות | term | Anonymous#Iq0j | שברי חכמי המזלות | |
| fraction/sexagesimal fraction | ח.ל.ק./חלקי חכמי המזלות | term | Anonymous#XVRP | חלקי חכמי המזלות | |
| fraction/sexagesimal fraction | ש.ב.ר./שברי תכונה | term | מלאכת_המספר#MObd | שברי התכונה | |
| fraction/sexagesimal fraction | ס.פ.ר./מספרי תכונה | term | מלאכת_המספר#cx9l | מספרי התכונה | |
| fraction/sexagesimal fraction | ש.ב.ר./שבר תכני | term | מלאכת_המספר#lunR | השברים התכונים | |
| false position/single false position | נ.ו.ח./מונח כוזב | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#myNd | מונח כוזיב | |
| false position/single false position | נ.ו.ח./מונח כוזב | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#1VMV | מונח כוזב | |
| false position/single false position | term | ספר_דיני_ממונות#uMkU | פלצא פוסיסיאוני | ||
| calculation/small | term | ספר_ציפרא#ILMp | קטן מן | ||
| calculation/small | ח.ס.ר./מחסיר | term | ספר_מעשה_חושב#4wuS | המחסירים | |
| calculation/small | term | מלאכת_המספר#NWE0 | הקטן | ||
| calculation/small | ח.ס.ר./מחסיר | term | ספר_מעשה_חושב#eXuI | המחסיר | |
| calculation/small | term | תחבולות_המספר#qbXp | פחות מה | ||
| calculation/small | פ.ח.ת./פחות | term | מלאכת_המספר#KbEe | פחות ממנו | |
| exponentiation/squared number | 22² | ספר_המספר_/_אברהם_אבן_עזרא#tUlx | Another example: we wish to know how much is the square of 22.
::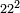 דמיון אחר רצינו לדעת כמה מרובע כ"ב
דמיון אחר רצינו לדעת כמה מרובע כ"ב | ||
| exponentiation/squared number | 60² | ספר_החשבון_והמדות#KA59 | Example: we wish to multiply sixty by sixty.
: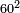 דמיון רצינו לכפול ששים על ששים
דמיון רצינו לכפול ששים על ששים | ||
| exponentiation/squared number | 50² | ספר_החשבון_והמדות#l9hv | Example: we wish to multiply fifty by fifty.
: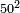 דמיון רצינו לכפול חמשים על חמשים
דמיון רצינו לכפול חמשים על חמשים | ||
| exponentiation/squared number | 11² | ספר_החשבון_והמדות#CGBe | Example: we wish to multiply 11 by 11.
: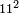 דמיון רצינו לכפול י"א על י"א
דמיון רצינו לכפול י"א על י"א | ||
| exponentiation/squared number | 12² | ספר_החשבון_והמדות#MxZM | We wish to multiply 12 by 12.
: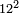 רצינו לכפול י"ב על י"ב
רצינו לכפול י"ב על י"ב | ||
| exponentiation/squared number | 14² | ספר_החשבון_והמדות#mw4t | We wish to multiply 14 by 14.
: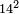 רצינו לכפול י"ד על י"ד
רצינו לכפול י"ד על י"ד | ||
| exponentiation/squared number | 13² | ספר_החשבון_והמדות#PUDk | We wish to multiply 13 by 13.
: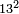 רצינו לכפול י"ג על י"ג
רצינו לכפול י"ג על י"ג | ||
| exponentiation/squared number | ר.ב.ע./מרובע | term | ספר_האלזיברא#QIyI | מרובע | |
| exponentiation/squared number | 12² | קצור_המספר#aLsp | For example: we wish to multiply twelve by twelve: they are 144: ומשל לזה רצינו לכפול שנים עשר על שנים עשר והוא קמ"ד | ||
| exponentiation/squared number | 7² | קצת_מענייני_חכמת_המספר#kNhC | Such as: you wish to know the square of 7. כגון רצית לידע מרובע ז' | ||
| exponentiation/squared number | 23² | ספר_המספר_/_אברהם_אבן_עזרא#eFIa | Example: we wish to know how much is the square of 23.
::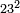 דמיון בקשנו לדעת כמה מרובע כ"ג
דמיון בקשנו לדעת כמה מרובע כ"ג | ||
| exponentiation/squared number | 47² | ספר_מעשה_חושב#y1NY | Example: if you wish to know the square of 47.
: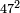 משל זה אם רצית לדעת מרובע מ"ז
משל זה אם רצית לדעת מרובע מ"ז | ||
| exponentiation/squared number | ר.ב.ע./מרובע | term | חשבון_השטחים#z2Fu | מספרים מרובעים | |
| exponentiation/squared number | ר.ב.ע./מרובע | term | תחבולות_המספר#iEXI | מספרי' מרובעי' | |
| exponentiation/squared number | 9² | ספר_החשבון_והמדות#b4f5 | Example: we wish to know the square of 9.
: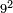 דמיון רצינו לדעת מרובע ט'
דמיון רצינו לדעת מרובע ט' | ||
| exponentiation/squared number | 24² | ספר_המספר_/_אליהו_מזרחי#Divz | Example: we wish to multiply 24 by itself.
::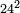 המשל בזה רצינו להכות כ"ד עם עצמו
המשל בזה רצינו להכות כ"ד עם עצמו | ||
| exponentiation/squared number | 25² | ספר_המספר_/_אליהו_מזרחי#kQVs | Example of a number [that exceeds the number that has a third]: 25.
::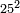 המשל במספר הפחות הוא כ"ה
המשל במספר הפחות הוא כ"ה | ||
| exponentiation/squared number | 30² | ספר_מעשה_חושב#kLiX | Example: we wish to know how much is the square of thirty.
: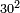 דמיון רצינו לדעת כמה מרובע שלשים
דמיון רצינו לדעת כמה מרובע שלשים | ||
| exponentiation/squared number | 33² | ספר_מעשה_חושב#hibu | Example: you wish to know the square of thirty-three.
: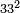 דמיון זה אם רצית לדעת מרובע שלשים ושלשה
דמיון זה אם רצית לדעת מרובע שלשים ושלשה | ||
| exponentiation/squared number | ר.ב.ע./מרובע | term | ספר_האלזיברא#tDCK | מרבע המספר | |
| exponentiation/squared number | 33² | ספר_מעשה_חושב#dhRJ | Example: you wish to know the square of 33.
: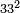 דמיון רצית לדעת מרובע ל"ג
דמיון רצית לדעת מרובע ל"ג | ||
| exponentiation/squared number | 23² | ספר_המספר_/_אליהו_מזרחי#4gKU | Example of a number [that is less than the number that has a third]: 23.
::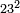 ומשל המספר היתר הוא כ"ג
ומשל המספר היתר הוא כ"ג | ||
| exponentiation/squared number | 25² | ספר_המספר_/_אליהו_מזרחי#yJQV | Example: 25.
::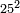 המשל בזה מספר כ"ה
המשל בזה מספר כ"ה | ||
| exponentiation/squared number | 26² | ספר_המספר_/_אליהו_מזרחי#tGyp | Example when the required number exceeds the number that has a fifth by one: 26.
::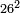 המשל כשהדרוש נוסף מהמספר שיש לו חומש אחד הוא מספר כ"ו
המשל כשהדרוש נוסף מהמספר שיש לו חומש אחד הוא מספר כ"ו | ||
| exponentiation/squared number | 27² | ספר_המספר_/_אליהו_מזרחי#bbq3 | Example [when the required number] exceeds [the number that has a fifth] by 2: 27.
::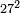 ומשל הנוסף ב' הוא מספר כ"ז
ומשל הנוסף ב' הוא מספר כ"ז | ||
| exponentiation/squared number | 24² | ספר_המספר_/_אליהו_מזרחי#kgbD | Example [when the required number] is smaller [than the number that has a fifth] by one: 24.
::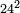 ומשל הפחות אחד הוא מספר כ"ד
ומשל הפחות אחד הוא מספר כ"ד | ||
| exponentiation/squared number | 23² | ספר_המספר_/_אליהו_מזרחי#EzUv | Example [when the required number] is smaller [than the number that has a fifth] by 2: 23.
::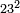 ומשל הפחות מספר ב' הכ"ג
ומשל הפחות מספר ב' הכ"ג | ||
| exponentiation/squared number | 10² | ספר_החשבון_והמדות#BrJN | Example: we wish to know the square of ten.
: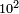 דמיון רצינו לדעת מרובע עשרה
דמיון רצינו לדעת מרובע עשרה | ||
| exponentiation/squared number | 11² | ספר_החשבון_והמדות#YlLr | Example: we wish to know the square of 11.
: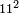 דמיון רצינו לדעת מרובע י"א
דמיון רצינו לדעת מרובע י"א | ||
| exponentiation/squared number | ר.ב.ע./מרובע | term | חשבון_השטחים#wbKW | מרובע | |
| exponentiation/squared number | 8² | קצת_מענייני_חכמת_המספר#IvM9 | Example: if you wish to know the square of 8. המשל אם תרצה לידע מרובע הח' | ||
| exponentiation/squared number | 3² | ספר_המספר_/_אברהם_אבן_עזרא#GMCO | Example: we wish to know how much is the square number of 3.
::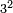 דמיון בקשנו לדעת כמה מספר מרובע ג'
דמיון בקשנו לדעת כמה מספר מרובע ג' | ||
| exponentiation/squared number | 15² | ספר_המספר_/_אברהם_אבן_עזרא#FZlV | Another example: we wish to know the square of 15.
::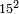 דמיון אחר בקשנו לדעת מרובע ט"ו
דמיון אחר בקשנו לדעת מרובע ט"ו | ||
| exponentiation/squared number | 24² | ספר_המספר_/_אברהם_אבן_עזרא#Ny3j | Another example: we wish to know how much is the square of 24.
::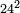 דמיון אחר בקשנו לדעת כמה מרובע כ"ד
דמיון אחר בקשנו לדעת כמה מרובע כ"ד | ||
| exponentiation/squared number | 7² | ספר_המספר_/_אברהם_אבן_עזרא#FUPY | Example: we wish to know the square of 7.
::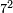 דמיון בקשנו לדעת מרובע ז'
דמיון בקשנו לדעת מרובע ז' | ||
| exponentiation/squared number | 9² | קצת_מענייני_חכמת_המספר#2n2J | Example: if you wish to know how much is the square of 9. המשל אם תרצה לידע כמה הוא מרובע הט' | ||
| root/square root | term | ספר_דיני_ממונות#M1Ii | ראדיצי קואדרא | ||
| root/square root | ש.ר.ש./שרש | term | ספר_עיון_העקרים_לחשבון_ההנדיים#EsV8 | שרש | |
| root/square root | ר.ב.ע./מרובע | term | ספר_ג'יבלי_אלמוקבאלא#JaBu | שרש מרובע | |
| root/square root | ש.ר.ש./שרש | term | ספר_מעשה_חושב#9a8g | שרשו | |
| root/square root | ש.ר.ש./שרש | term | ספר_מעשה_חושב#25L8 | שרש | |
| root/square root | ר.ב.ע./רבועי | term | ספר_מעשה_חושב#L93J | יסודו הרבועי | |
| root/square root | ר.ב.ע./מרובע | term | ספר_האלזיברא#pwvB | שורש מרובע | |
| root/square root | ש.ר.ש./שרש | definition | מלאכת_המספר#vgE3 | The definition of the root of the square is another number that generates it when it is multiplied by itself. וא"כ גדר שרש המרובע הוא מספר אחר כשיוכה בעצמו מוליד אותו | |
| root/square root | ר.ב.ע./רבועי | term | ספר_מעשה_חושב#g92p | השרשים הרבועיים | |
| root/square root | ר.ב.ע./רבועי | term | ספר_מעשה_חושב#RFWp | שרשו הרבועיי | |
| root/square root | ש.ר.ש./שרש | definition | ספר_המספר_/_אליהו_מזרחי#ratf | The numbers that are multiplied by themselves, such as 3 and 4, from which the "same" numbers are created, are called roots, because they are similar to the roots of the plants. ואולם המספרים המוכים בעצמם כמו הג' והד' במשלנו אשר מהם יצמחו המספרים ההוהויים נקראים שרשים כי הם כדמות השרשים לצמחים | |
| root/square root | ר.ב.ע./רבועי | term | ספר_מעשה_חושב#uUd4 | השרש הרבועיי | |
| root/square root | term | ספר_דיני_ממונות#JY2L | שרשם המרובע | ||
| root/square root | definition | מלאכת_המספר#VZQ2 | Another definition: or it is a number, such that when it is multiplied by itself it generates a square number.
גדר אחר או הוא מספר אחד כשיוכה בעצמו יוליד מספר | ||
| basic operations/subtraction | 2000-1999 | ספר_אגריס#IREb | Example:
: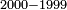 דומיון
דומיון | ||
| basic operations/subtraction | י.צ.א./הוצאה | term | ספר_החשבון_לאל_חצאר#MxmB | הוצאת | |
| basic operations/subtraction | 76540304-40438 | בר_נותן_טעם#EpGw | We wish to subtract 40438 the smaller from the greater number that is 76540304.
: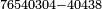 רצינו לחסר 40438 הקטן ממספר הגדול והוא 76540304
רצינו לחסר 40438 הקטן ממספר הגדול והוא 76540304 | ||
| basic operations/subtraction | י.צ.א./הוצאה | term | ספר_החשבון_לאל_חצאר#PDJH | הוצאה | |
| basic operations/subtraction | ג.ר.ע./מגרעת | term | עיר_סיחון#Chcd | מגרעת | |
| basic operations/subtraction | (31080+46ⁱⁱ+35ⁱⁱⁱ+47ⁱᵛ+53ᵛⁱ)-(206+50ⁱ+37ⁱⁱⁱ) | ספר_מעשה_חושב#qt9K | Example: if we want to subtract two hundred and six and fifty primes, and 37 thirds from 31 thousands and eighty and 46 seconds, 35 thirds, 47 fourths, and 53 sixths. דמיון נרצה לגרוע מאתים ושש ונ' ראשונים ל"ז שלישים מל"א אלפים ושמנים ומ"ו שניים ל"ה שלישיים מ"ז רביעים כ"ג ששיים | ||
| basic operations/subtraction | ג.ר.ע./גרוע | term | ספר_מעשה_חושב#z62j | גרוע | |
| basic operations/subtraction | 90020235-63295223 | Takmila_fi_al-Hisāb_-_Arabic_in_Hebrew_Characters#01eR | Example: we wish to subtract 63295223 dirham from 90020235.
: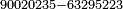 מתאלה ארדנא אן ננקץ תלתה וסתין אלף אלף ומאיתין וכמסה ותסעין אלפא ומאיתי' ותלתה ועשרין דרהמא מן תסעין אלף אלף ועשרין אלפא ומאיתי' וכמסה ותלתין
מתאלה ארדנא אן ננקץ תלתה וסתין אלף אלף ומאיתין וכמסה ותסעין אלפא ומאיתי' ותלתה ועשרין דרהמא מן תסעין אלף אלף ועשרין אלפא ומאיתי' וכמסה ותלתין | ||
| basic operations/subtraction | ג.ר.ע./מגרעת | term | ספר_ג'יבלי_אלמוקבאלא#kkyF | מגרעת | |
| basic operations/subtraction | ח.ס.ר./חסור | term | ספר_אגריס#qLXy | חסור | |
| basic operations/subtraction | 107-59 | קצור_המספר#58yM | Example: we wish to subtract fifty-nine from one hundred and seven.
: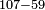 ויהיה המשל בזה רצינו לגרוע ממאה ושבעה חמישים ותשעה
ויהיה המשל בזה רצינו לגרוע ממאה ושבעה חמישים ותשעה | ||
| basic operations/subtraction | 1000-999 | ספר_ציפרא#F3VH | We wish to subtract 9 hundred and ninety-nine from one thousand
: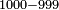 הנה בקשנו לחסיר ט' מאות ותשעים ותשע מאלף
הנה בקשנו לחסיר ט' מאות ותשעים ותשע מאלף | ||
| basic operations/subtraction | ג.ר.ע./מגרעת | term | בר_נותן_טעם#9ZbD | מגרעת | |
| basic operations/subtraction | י.צ.א./הוצאה | term | ספר_ג'יבלי_אלמוקבאלא#IGX3 | הוצאות | |
| basic operations/subtraction | י.צ.א./הוצאה | term | ספר_ג'יבלי_אלמוקבאלא#pBiX | הוצאה | |
| basic operations/subtraction | 5114-4225 | ספר_החשבון_והמדות#9uj3 | We wish to subtract four thousand two hundred and twenty-five from five thousands one hundred and fourteen.
: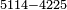 נרצה לחסר ד' אלפים ומאתים ועשרים וחמשה מה' אלפים ומאה וארבעה עשר
נרצה לחסר ד' אלפים ומאתים ועשרים וחמשה מה' אלפים ומאה וארבעה עשר | ||
| basic operations/subtraction | ג.ר.ע./מגרעת | term | ספר_מעשה_חושב#Hgy0 | מגרעת | |
| basic operations/subtraction | י.צ.א./הוצאה | term | ספר_ג'יבלי_אלמוקבאלא#rrCQ | הוצאת | |
| basic operations/subtraction | ג.ר.ע./גרעון | term | ספר_ג'יבלי_אלמוקבאלא#P7E1 | גרעון | |
| basic operations/subtraction | WP | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#jQ7J | I say that Reuven owed Shimon 573 dinars and he paid him 352. We want to subtract what he paid from the debt.
: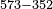 ואומר כי ראובן חייב לשמעון תקע"ג די' ופרע לו שנ"ב והנה רצינו לגרע מה שפרע מן החיוב
ואומר כי ראובן חייב לשמעון תקע"ג די' ופרע לו שנ"ב והנה רצינו לגרע מה שפרע מן החיוב | ||
| basic operations/subtraction | ח.ס.ר./חסרון | term | בר_נותן_טעם#ljpi | חסרון | |
| basic operations/subtraction | WP | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#RwHV | Another example: Reuven owed Shimon 5047 liter and he paid him 958 liter.
: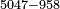 משל אחר ראובן חיב לשמעון ה' אלפים ומ"ז לטרי ופרע לו תתקנ"ח לטרין
משל אחר ראובן חיב לשמעון ה' אלפים ומ"ז לטרי ופרע לו תתקנ"ח לטרין | ||
| basic operations/subtraction | WP | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#pBrg | [Illegible].
: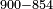 30r / י"ד[...] החיוב [...]עון והשיור [...]עון תת"ק כורי חיטה [...] רצינו לדעת הנשאר
30r / י"ד[...] החיוב [...]עון והשיור [...]עון תת"ק כורי חיטה [...] רצינו לדעת הנשאר | ||
| basic operations/subtraction | 956-867 | ספר_ציפרא#GybI | As if you wish to subtract 867 from 956, like this:
::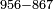 כגון אם תרצ' לחסר זוח מן והט כזה
כגון אם תרצ' לחסר זוח מן והט כזה | ||
| basic operations/subtraction | WP | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#U9zP | Another example with zeros: the amount of the debt is two hundred thousand weights of wool and he paid 123 thousand and 345.
: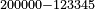 משל אחר כולו ספרות הנה מספר החיוב הוא מאתים אלפים משקלי צמר ופרע קכ"ג אלפים שמ"ה
משל אחר כולו ספרות הנה מספר החיוב הוא מאתים אלפים משקלי צמר ופרע קכ"ג אלפים שמ"ה | ||
| basic operations/subtraction | י.צ.א./הוצאה | term | בר_נותן_טעם#Ktg3 | הוצאת | |
| basic operations/subtraction | 5083-92 | עיר_סיחון#ZVaI | Example: we wish to subtract ninety-two from five thousand eighty-three.
: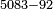 המשל בזה בקשנו לגרוע מחמשת אלפים ושמונים ושלש תשעים ושנים
המשל בזה בקשנו לגרוע מחמשת אלפים ושמונים ושלש תשעים ושנים | ||
| basic operations/subtraction | 3735-425 | Takmila_fi_al-Hisāb_-_Arabic_in_Hebrew_Characters#MP98 | Example: if we wish to subtract 425 from 3735.
: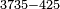 מתאלה אדא ארדנא אן ננקץ אן ארבע מאיה וכמסה ועשרין מן תלת אלאף וסבע מאיה וכמסה ותלתין
מתאלה אדא ארדנא אן ננקץ אן ארבע מאיה וכמסה ועשרין מן תלת אלאף וסבע מאיה וכמסה ותלתין | ||
| basic operations/subtraction | ח.ס.ר./חסור | definition | מלאכת_המספר#J7kh | Subtraction is knowing the remainder of any number after a number that is smaller than it was subtracted from it. חסור הוא ידיעת הנישאר מאיזה מספר שיהיה כש{{#annot:term|181,1842|g9jn}}יוסר ממנו{{#annotend:g9jn}} מספר א' {{#annot:term|341,1366|KbEe}}פחות ממנו{{#annotend:KbEe}} | |
| basic operations/subtraction | ג.ר.ע./גרעון | term | תחבולות_המספר#lyQn | גרעון | |
| basic operations/subtraction | ג.ר.ע./גרעון | term | תחבולות_המספר#bJ2u | גרעונם | |
| basic operations/subtraction | ג.ר.ע./גרעון | term | קצור_המספר#2P8a | גרעון | |
| basic operations/subtraction | 245-123 | ספר_דיני_ממונות#8i9G | Example: we wish to subtract 123 from 245.
: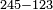 דמיון זה נרצה לגרוע מן רמה קכ"ג
דמיון זה נרצה לגרוע מן רמה קכ"ג | ||
| basic operations/subtraction | 349-207 | ספר_דיני_ממונות#Re2v | Another example: we wish to subtract 207 from 349.
: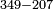 דמיון אחר נרצה להוציא ממספר שמ"ט מספר ר"ז
דמיון אחר נרצה להוציא ממספר שמ"ט מספר ר"ז | ||
| basic operations/subtraction | 304-253 | ספר_דיני_ממונות#3Vjd | Another example: we wish to subtract 253 from 304.
: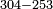 דמיון אחר נרצה לגרוע מג' מאות וד' רנ"ג
דמיון אחר נרצה לגרוע מג' מאות וד' רנ"ג | ||
| basic operations/subtraction | 2040-1403 | ספר_דיני_ממונות#olKE | Another example: we wish to subtract 1403 from 2040.
: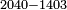 דמיון אחר נרצה לגרוע ממספר ב אלפים ומ' מספר אלף ות"ג
דמיון אחר נרצה לגרוע ממספר ב אלפים ומ' מספר אלף ות"ג | ||
| basic operations/subtraction | 246-135 | ספר_דיני_ממונות#Ih2Z | Example: we wish to subtract 135 from 246.
: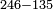 דמיון נרצה לגרוע מן רמ"ו מספר קל"ה
דמיון נרצה לגרוע מן רמ"ו מספר קל"ה | ||
| basic operations/subtraction | 468-382 | ספר_דיני_ממונות#7rnd | Example: we wish to subtract 382 from 468.
: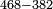 דמיון נרצה לגרוע מתס"ח מספר שפ"ב
דמיון נרצה לגרוע מתס"ח מספר שפ"ב | ||
| basic operations/subtraction | 4321-3456 | ספר_דיני_ממונות#MMZ6 | Example: we wish to subtract 3456 from 4321.
: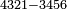 דמיון נרצה לגרוע מן ד' אלפים ושכ"א ג' אלפי' ותנ"ו
דמיון נרצה לגרוע מן ד' אלפים ושכ"א ג' אלפי' ותנ"ו | ||
| basic operations/subtraction | 5060-2304 | ספר_דיני_ממונות#vy0Q | Example: we wish to subtract 2304 from 5060.
: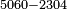 דמיון זה נרצה לגרוע מן ה' אלפים וס' ב' אלפים וש"ד
דמיון זה נרצה לגרוע מן ה' אלפים וס' ב' אלפים וש"ד | ||
| basic operations/subtraction | ש.ל.כ./השלכה | term | אגרת_המספר#aJcu | השלכת | |
| basic operations/subtraction | ס.ו.ר./הסרה | term | עיר_סיחון#E95p | הסרת | |
| basic operations/subtraction | ג.ר.ע./גריעה | term | אגרת_המספר#wS50 | גריעתם | |
| basic operations/subtraction | ח.ס.ר./חסר | term | חשבון_השטחים#L9iY | בחסרך | |
| basic operations/subtraction | 21333-221 | אגרת_המספר#wpfH | As when the upper ranks are 21333 and the bottom [ranks are] 221.
::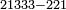 כמו שהיו מדרגות העליונה כ"א אלף של"ג והתחתונה רכ"א
כמו שהיו מדרגות העליונה כ"א אלף של"ג והתחתונה רכ"א | ||
| basic operations/subtraction | ג.ר.ע./גרעון | term | ספר_דיני_ממונות#5cEI | גרעון | |
| basic operations/subtraction | ג.ר.ע./מגרעת | term | קצור_המספר#PIoJ | מגרעת | |
| basic operations/subtraction | ג.ר.ע./מגרעת | term | ספר_דיני_ממונות#CJai | מגרעת | |
| basic operations/subtraction | 654-321 | ספר_ציפרא#j8ha | Another example: if we wish to subtract 321 from 654.
: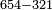 דומיון [אחר אם]M om. בקשנו לחסיר אב"ג מדה"ו
דומיון [אחר אם]M om. בקשנו לחסיר אב"ג מדה"ו | ||
| basic operations/subtraction | ג.ר.ע./מגרעת | term | חשבון_השטחים#w4ku | מגרעת | |
| basic operations/subtraction | ג.ר.ע./גרעון | term | קצור_המספר#xU5c | גרעון | |
| basic operations/subtraction | 4282-2432 | מלאכת_המספר#z4AR | As can be seen in this diagram:
: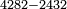 כפי הנראה בצורה הזאת
כפי הנראה בצורה הזאת | ||
| basic operations/subtraction | 4288-3268 | אגרת_המספר#EQw8 | Subtract 3268 from 4288.
::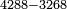 תגרע ג' אלפים רס"ח מד' אלפי' רפ"ח
תגרע ג' אלפים רס"ח מד' אלפי' רפ"ח | ||
| basic operations/subtraction | 39-20 | אגרת_המספר#3gFA | Example: subtract 20 from 39.
::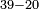 והמשל תגרע כ' מל"ט
והמשל תגרע כ' מל"ט | ||
| basic operations/subtraction | 3333-2445 | אגרת_המספר#tybi | Example: we wish to subtract 2445 from 3333.
::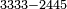 והמשל רצינו לגרוע ב' אלפים תמ"ה מג' אלפים של"ג
והמשל רצינו לגרוע ב' אלפים תמ"ה מג' אלפים של"ג | ||
| basic operations/subtraction | 5787-3456 | אגרת_המספר#OoZU | We wish to subtract three thousand and four hundred and fifty-six from five thousand seven hundred and eighty-seven.
::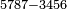 רצינו לגרוע ג' אלפי' וארבע מאות וחמשים ושש מחמשה אלפים ושבע מאות ושמנים ושבעה
רצינו לגרוע ג' אלפי' וארבע מאות וחמשים ושש מחמשה אלפים ושבע מאות ושמנים ושבעה | ||
| basic operations/subtraction | ח.ס.ר./חסרון | term | ספר_מעשה_חושב#s92g | חסרון | |
| basic operations/subtraction | ג.ר.ע./מגרעת | term | ספר_החשבון_לאל_חצאר#baSK | מגרעות | |
| basic operations/subtraction | ח.ס.ר./חסרון | term | ספר_עיון_העקרים_לחשבון_ההנדיים#XmAc | חסרון | |
| basic operations/subtraction | ג.ר.ע./גרעון | definition | אגרת_המספר#xhQw | subtraction is the inquiry of the remainder after subtracting one of the numbers from the other. אמר הגרעון הוא שאלת הנשאר אחר השלכת אחד המספרים מן האחר | |
| basic operations/subtraction | ח.ס.ר./חסרון | term | ספר_יסודי_התבונה_ומגדל_האמונה#EXzI | חסרון | |
| basic operations/subtraction | ג.ר.ע./מגרעת | term | תחבולות_המספר#qHq1 | מגרעת | |
| basic operations/subtraction | ג.ר.ע./גרעון | term | חשבון_השטחים#PuOw | גרעונם | |
| basic operations/subtraction | definition | ספר_המספר_/_אליהו_מזרחי#6GMW | subtraction is the subtraction of a number from another number that is greater than it. החסור הוא מגרעת מספר מה ממספר אחר גדול ממנו | ||
| basic operations/subtraction | ג.ר.ע./גרעון | term | אגרת_המספר#v5pN | גרעון | |
| basic operations/subtraction | 5432-2379 | ספר_המספר_/_אברהם_אבן_עזרא#lNHB | Example: The top row is 5432 and the bottom row is 2379.
: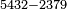 דמיון הטור העליון ב'ג'ד'ה' והטור השפל ט'ז'ג'ב'
דמיון הטור העליון ב'ג'ד'ה' והטור השפל ט'ז'ג'ב' | ||
| basic operations/subtraction | ג.ר.ע./מגרעת | term | קצור_המספר#Hnho | מגרעת | |
| basic operations/subtraction | ס.ו.ר./הסרה | term | עיר_סיחון#You5 | הסרה | |
| basic operations/subtraction | ח.ס.ר./חסור | term | ספר_ציפרא#Otja | חיסור | |
| basic operations/subtraction | ס.ל.ק./סלוק | term | ספר_אגריס#VrLL | סלוק | |
| basic operations/subtraction | 6475-2343 | ספר_החשבון_לאל_חצאר#ONSp | Example: 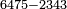 דמיון זה הוצא שלשה וארבעים ושלש מאות ואלפים מחמשה ושבעים וארבע מאות וששת אלפים
דמיון זה הוצא שלשה וארבעים ושלש מאות ואלפים מחמשה ושבעים וארבע מאות וששת אלפים | ||
| basic operations/subtraction | term | Anonymous_text_from_Latin#xiXX | זוכט רַצטיאן | ||
| basic operations/subtraction | נ.כ.י./נכוי | term | Anonymous_text_from_Latin#EKVU | נכוי | |
| basic operations/subtraction | ח.ס.ר./חסור | term | Anonymous_text_from_Latin#lthR | חיסור | |
| basic operations/subtraction | ג.ר.ע./גרעון | term | Anonymous#uQGa | גרעון | |
| basic operations/subtraction | term | Arithmetic_Textbook_by_Meir_Shapira#LCca | חסור | ||
| basic operations/subtraction | 234-122 | ספר_דיני_ממונות#L1oj | Example: we wish to subtract 122 from 234. דמיון זה נרצה לגרוע מן רל"ד קכ"ב | ||
| basic operations/subtraction | ג.ר.ע./מגרעת | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#nMPF | מגרעת | |
| basic operations/subtraction | ג.ר.ע./גרעון | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#UqB3 | גרעון | |
| basic operations/subtraction | ג.ר.ע./מגרעת | definition | קצור_המספר#6dts | The essential act of separating is the second of the arithmetical [operations] called '''subtraction''' ומפועל הנפש בהפרדה היה מין שני מהמספר שיקרא המגרעת | |
| basic operations/subtraction | 100000-1 | ספר_החשבון_לאל_חצאר#jhPB | Example: 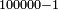 ואם יאמר לך השלך אחד ממאה אלף
ואם יאמר לך השלך אחד ממאה אלף | ||
| basic operations/subtraction | 9385-5496 | ספר_החשבון_לאל_חצאר#0FuM | Example: 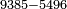 ואם יאמר השלך ששה ותשעים וארבע מאות וחמשת אלפים מחמשה ושמנים ושלש מאות ותשעה אלפים
ואם יאמר השלך ששה ותשעים וארבע מאות וחמשת אלפים מחמשה ושמנים ושלש מאות ותשעה אלפים | ||
| basic operations/subtraction | ח.ס.ר./חסור | term | מלאכת_המספר#vx53 | חסור | |
| basic operations/subtraction | ג.ר.ע./גרוע | term | חשבון_השטחים#nkuv | בגרוע | |
| basic operations/subtraction | ג.ר.ע./מגרעת | term | Anonymous#L8O7 | מגרעת זה מזה | |
| basic operations/subtraction | ג.ר.ע./גרעון | term | ספר_מעשה_חושב#WTlI | גרעון | |
| basic operations/subtraction | ג.ר.ע./מגרעת | term | Anonymous#pUkT | מגרעת | |
| basic operations/subtraction | ג.ר.ע./גרעון | term | חשבון_השטחים#NiwT | גרעון | |
| basic operations/subtraction | ג.ר.ע./גרוע | term | ספר_ג'יבלי_אלמוקבאלא#vyPV | בגרוע ממנו | |
| basic operations/subtraction | 46-24 | ספר_אגריס#KF3P | Example: to subtract 24 from 46.
: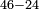 דומיון להסיר כ"ד מן מ"ו
דומיון להסיר כ"ד מן מ"ו | ||
| simple fraction/subtraction of fractions | (⁸/₉+³/₇·⅕·⅑)·(⅚·3)-(¾+⅖·¼)·²/₉ | בר_נותן_טעם#0SK8 | Example: if you are told: three-quarters and two-fifths of a quarter of two-ninths, subtract them from eight-ninths and three-sevenths of a fifth of a ninth of five-sixths of 3 integers
:![\scriptstyle\left[\left[\frac{8}{9}+\left(\frac{3}{7}\sdot\frac{1}{5}\sdot\frac{1}{9}\right)\right]\sdot\left(\frac{5}{6}\sdot3\right)\right]-\left[\left[\frac{3}{4}+\left(\frac{2}{5}\sdot\frac{1}{4}\right)\right]\sdot\frac{2}{9}\right]](/mediawiki/images/math/d/6/d/d6d3383d94cc0c6f1b9eabdd1be5711c.png) המשל אם אמרו לך שלש רביעיות ושתי חמישיות רביעית משתי תשיעיות חסרם משמונה תשיעיות ושלש שביעיות חמשית תשיעית מחמש ששיות מג' שלמים
המשל אם אמרו לך שלש רביעיות ושתי חמישיות רביעית משתי תשיעיות חסרם משמונה תשיעיות ושלש שביעיות חמשית תשיעית מחמש ששיות מג' שלמים | ||
| simple fraction/subtraction of fractions | ⅖-⅜ | ספר_חשבון#fRT6 | If one says: how much greater are 3-eighths than 2-fifths?
: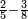 ואם יאמר כמה הם יותר ג' שמניות מב' חמשיות
ואם יאמר כמה הם יותר ג' שמניות מב' חמשיות | ||
| simple fraction/subtraction of fractions | ²/₄-⅕ | עיר_סיחון#tqJF | As we say for example: we subtract one fifth from two quarters. How much is the remainder?
: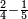 כאשר נאמר על דרך משל גרענו משני 92vרביעיות חמישית אחד כמה הנשאר
כאשר נאמר על דרך משל גרענו משני 92vרביעיות חמישית אחד כמה הנשאר | ||
| simple fraction/subtraction of fractions | ¾-½ | ספר_דיני_ממונות#aoCt | 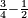 דמיון זה נרצה לחסר מג' רביעיות חצי א'
דמיון זה נרצה לחסר מג' רביעיות חצי א' | ||
| simple fraction/subtraction of fractions | (3+¾)-(2+½) | ספר_דיני_ממונות#a71P | 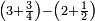 דמיון זה נרצה לחסר מג' שלמים וג' רביעיות ב' שלמים וחצי
דמיון זה נרצה לחסר מג' שלמים וג' רביעיות ב' שלמים וחצי | ||
| simple fraction/subtraction of fractions | (2+½)-¾ | ספר_דיני_ממונות#aBIR | 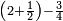 דמיון זה נרצה לגרוע ג' רביעיות מב' שלמי' וחצי
דמיון זה נרצה לגרוע ג' רביעיות מב' שלמי' וחצי | ||
| simple fraction/subtraction of fractions | ⁵/₇-⁴/₉ | ספר_המספר_/_אברהם_אבן_עזרא#YZWt | Example: we wish to subtract 4 ninths from 5 sevenths.
: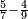 דמיון רצינו לגרוע ד' תשיעיות מה' שביעיות
דמיון רצינו לגרוע ד' תשיעיות מה' שביעיות | ||
| simple fraction/subtraction of fractions | ⅔-³/₇ | ספר_יסודי_התבונה_ומגדל_האמונה#jZco | As the one who says: subtract 3 sevenths from 2 thirds.
: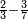 כגון האומר השלך ג' שביעיות מב' שלישיות
כגון האומר השלך ג' שביעיות מב' שלישיות | ||
| simple fraction/subtraction of fractions | ¹⁴/₁₆-⁸/₁₂ | קצור_המספר#pRUj | As if you say: we wish to subtract 4-twelfths from 14-sixteenths.
: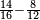 כאלו תאמר רצינו לגרוע ח' שנים עשיריות מי"ד שש עשיריות
כאלו תאמר רצינו לגרוע ח' שנים עשיריות מי"ד שש עשיריות | ||
| simple fraction/subtraction of fractions | ¹²/₁₆-⁴/₈ | קצור_המספר#l5nz | As if you say: we wish [to subtract] 4-eighths from 12-sixteenths.
: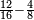 כאלו תאמר רצינו
כאלו תאמר רצינו | ||
| simple fraction/subtraction of fractions | ⁶/₈-²/₄ | קצור_המספר#9I3R | We wish to subtract two-quarters from 6-eighths.
: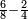 כיצד רצינו
כיצד רצינו | ||
| simple fraction/subtraction of fractions | ⅝-⅜ | קצור_המספר#Lbi7 | For, if we wish to subtract 3-eighths from 5-eighths:
: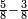 כי אם נרצה לגרוע ג' שמיניות מה' שמיניות
כי אם נרצה לגרוע ג' שמיניות מה' שמיניות | ||
| simple fraction/subtraction of fractions | 1-⅝ | קצור_המספר#kerj | The first example: we subtract five-eighths from one integer.
: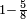 ויהיה 107vהמשל תחלה נגרע חמש שמיניות מאחד שלם
ויהיה 107vהמשל תחלה נגרע חמש שמיניות מאחד שלם | ||
| simple fraction/subtraction of fractions | ¾-⅔ | מלאכת_המספר#PCmR | As seen in this diagram: suppose we want to subtract from three-quarters of the whole two-thirds of the whole and we wish to know how much remains.
: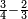 כנראה בזה הצורה 20rשנעשה ונניח שמהשלשה רביעי שלם נרצה לחסר שני שלישי שלם ונרצה לדעת כמה ישארו
כנראה בזה הצורה 20rשנעשה ונניח שמהשלשה רביעי שלם נרצה לחסר שני שלישי שלם ונרצה לדעת כמה ישארו | ||
| simple fraction/subtraction of fractions | (3+⁵/₉+³/₇·⅑+²/₄·⅐·⅑)-(⁷/₉+⁵/₇·⅑+¾·⅐·⅑) | בר_נותן_טעם#eMzX | Example: we wish to subtract 7-ninths, 5-sevenths of a ninth, and 3-quarters of a seventh of a ninths, from 3 integers, 5-ninths, and three-sevenths of a ninth.
:![\scriptstyle\left[3+\frac{5}{9}+\left(\frac{3}{7}\sdot\frac{1}{9}\right)+\left(\frac{2}{4}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\right]-\left[\frac{7}{9}+\left(\frac{5}{7}\sdot\frac{1}{9}\right)+\left(\frac{3}{4}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\right]](/mediawiki/images/math/c/9/c/c9c6d9287898412880ce3955aec5dcbf.png) המשל רצינו לגרוע ז' תשיעיות וה' שביעיות תשיעית וג' רביעיות שביעית תשיעית מג' שלמים וה' תשיעיות ושלש שביעיות תשיעית
המשל רצינו לגרוע ז' תשיעיות וה' שביעיות תשיעית וג' רביעיות שביעית תשיעית מג' שלמים וה' תשיעיות ושלש שביעיות תשיעית | ||
| simple fraction/subtraction of fractions | ⅔-³/₇ | ספר_חשבון#mJ1K | If one says: subtract 3-sevenths from 2-thirds.
: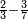 ואם יאמר השלך ג' שביעיות מב' שלישיות
ואם יאמר השלך ג' שביעיות מב' שלישיות | ||
| simple fraction/subtraction of fractions | ¾-²/₈ | בר_נותן_טעם#ZncT | Example: we wish to subtract 2-eighths from 2-quarters.
: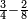 המשל רצינו לחסר ב' שמיניות מג' רביעיות
המשל רצינו לחסר ב' שמיניות מג' רביעיות | ||
| simple fraction/subtraction of fractions | ⅓-¼ | ספר_חשבון#Gem8 | If a man says: by how much is the third greater than the quarter?
: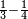 אמנם אם יאמר אדם כמה הוא יותר השליש מן הרביע
אמנם אם יאמר אדם כמה הוא יותר השליש מן הרביע | ||
| simple fraction/subtraction of fractions | ¼-⅕ | ספר_חשבון#wkXD | If a man says: by how much is the quarter greater than the fifth?
: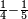 וכן אם יאמר אדם כמה הוא יותר הרביע מן החומש
וכן אם יאמר אדם כמה הוא יותר הרביע מן החומש | ||
| simple fraction/subtraction of fractions | ⅓-⅐ | ספר_חשבון#ebvM | If it is said: by how much is the third greater than the seventh?
: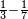 וכן אם יאמר כמה הוא יותר השליש מן השביע
וכן אם יאמר כמה הוא יותר השליש מן השביע | ||
| simple fraction/subtraction of fractions | (⅓+¼)-(⅕+⅙) | ספר_חשבון#e3Ts | If it is said: by how much are the third and the quarter greater than the fifth and the eighth?
: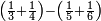 ואם יאמר כמה הם יותר השליש והרביע מן החומש ושתות
ואם יאמר כמה הם יותר השליש והרביע מן החומש ושתות | ||
| simple fraction/subtraction of fractions | ⅓-¼ | ספר_הכללים_במספר#Sdu0 | 1) If a man asks you: how large is the third from the quarter?
: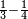 88rא אם ישאלך אדם כמה הוא יותר השליש מן הרביע
88rא אם ישאלך אדם כמה הוא יותר השליש מן הרביע | ||
| simple fraction/subtraction of fractions | ¼-⅕ | ספר_הכללים_במספר#hEgl | If you are asked: how large is the quarter from the fifth?
: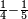 וכן אם ישאלך כמה יותר הרביע מן החומש
וכן אם ישאלך כמה יותר הרביע מן החומש | ||
| simple fraction/subtraction of fractions | ⅓-⅕ | ספר_הכללים_במספר#t2Xm | If you are asked: how large is the third from the fifth?
: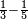 וכן אם ישאלך כמה הוא יותר השליש מן החמישית
וכן אם ישאלך כמה הוא יותר השליש מן החמישית | ||
| extraction of root/subtraction of roots | √9-√4 | תחבולות_המספר#YpmS | He said: when you wish to subtract a root of four from a root of nine, so that what remains is a root of a single number.
: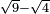 אמ' וכאשר תרצה לגרוע שרש ארבעה משרש
אמ' וכאשר תרצה לגרוע שרש ארבעה משרש | ||
| extraction of root/subtraction of roots | √18-√8 | ספר_האלזיברא#MH27 | 24) If you wish to subtract the root of 8 from the root of 18, for instance.
: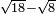 כד ואם רצית לגרוע שרש ח' משרש י"ח דרך משל
כד ואם רצית לגרוע שרש ח' משרש י"ח דרך משל | ||
| extraction of root/subtraction of roots | ⅔√36-½√16 | ספר_המספר_/_אליהו_מזרחי#pNmf | The example: if you want to know the root of which square is the remainder from subtraction of half the root of 16 from two-thirds of the root of 36? המשל בזה אם רצית לדעת הנשאר מחסור חצי שרש הי"ו משתי שלישיות שרש הל"ו לאיזו מרובע הוא שרש | ||
| extraction of root/subtraction of roots | √36-√16 | ספר_המספר_/_אליהו_מזרחי#xDJz | The example: if you want to know the root of which square is the remainder from subtraction of the root of 16 from the root of 36? המשל בזה אם רצית לדעת הנשאר מחסור שרש הי"ו משרש הל"ו לאיזה מרובע הוא שרש | ||
| extraction of root/subtraction of roots | 3√36-2√16 | ספר_המספר_/_אליהו_מזרחי#zlnd | The example: if you want to know the root of which square is the remainder from subtraction of two times the root of 16 from three times the root of 36? המשל בזה אם רצית לדעת הנשאר מחסור שני כפלי שרש הי"ו משלשה כפלי שרש הל"ו לאיזו מרובע הוא שרש | ||
| extraction of root/subtraction of roots | √12-√3 | ספר_ג'יבלי_אלמוקבאלא#1zTf | Suppose you wish to subtract a root of 3 from a root of 12.
: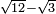 נניח שרצית לגרוע שרש ג' משרש י"ב
נניח שרצית לגרוע שרש ג' משרש י"ב | ||
| extraction of root/subtraction of roots | √7-√6 | ספר_ג'יבלי_אלמוקבאלא#VGtp | 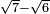 ונניח שרצית להוציא שרש ו' משרש ז'
ונניח שרצית להוציא שרש ו' משרש ז' | ||
| extraction of root/subtraction of roots | 19-(10-√12) | ספר_ג'יבלי_אלמוקבאלא#UiBt | 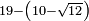 ואם רצית להוציא עשרה פחות שרש י"ב מי"ט
ואם רצית להוציא עשרה פחות שרש י"ב מי"ט | ||
| extraction of root/subtraction of roots | 16-(8+√50) | ספר_ג'יבלי_אלמוקבאלא#ouRF | 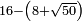 ואם רצית להוציא ח' ושרש נ' מי"ו
ואם רצית להוציא ח' ושרש נ' מי"ו | ||
| extraction of root/subtraction of roots | 10-(24-√250) | ספר_ג'יבלי_אלמוקבאלא#K9xs | 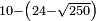 עוד אם בקשת להוציא כ"ד פחות שרש מר"נ מעשרה
עוד אם בקשת להוציא כ"ד פחות שרש מר"נ מעשרה | ||
| extraction of root/subtraction of roots | (13-√20)-(6-√5) | ספר_ג'יבלי_אלמוקבאלא#0TcW | 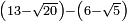 עוד אם יאמר לך תוציא ו' פחות שרש ה' מי"ג פחות שרש כ'
עוד אם יאמר לך תוציא ו' פחות שרש ה' מי"ג פחות שרש כ' | ||
| extraction of root/subtraction of roots | √16-√9 | ספר_דיני_ממונות#Otry | 147) Question: if you want to subtract a root of 9 from a root of 16.
: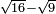 קמז)MS L: קמד שאלה אם תרצה להוציא שרש ט' משרש י"ו
קמז)MS L: קמד שאלה אם תרצה להוציא שרש ט' משרש י"ו | ||
| extraction of root/subtraction of roots | √9-√4 | חשבון_השטחים#e8VS | 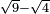 וכאשר תרצה לגרוע שרש ארבעה משורש תשעה עד שיהיה מה שישאר משורש תשעה שורש מספר אחד פחות שורש מהמספר האחר
וכאשר תרצה לגרוע שרש ארבעה משורש תשעה עד שיהיה מה שישאר משורש תשעה שורש מספר אחד פחות שורש מהמספר האחר | ||
| extraction of root/subtraction of roots | √18-√8 | חשבון_השטחים#HW4Q | 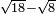 ואם רצונך לגרוע שורש ח' משורש י"ח
ואם רצונך לגרוע שורש ח' משורש י"ח | ||
| extraction of root/subtraction of roots | √18-√8 | תחבולות_המספר#uKgY | If we want to subtract the root of eight from the root of eighteen.
: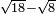 ואם באנו לגרוע שרש שמנה משרש שמנה עשר
ואם באנו לגרוע שרש שמנה משרש שמנה עשר | ||
| subtraction/subtractive | ג.ר.ע./נגרע | term | Anonymous#jTt2 | החשבון הנגרע | |
| subtraction/subtractive | ג.ר.ע./נגרע | term | תחבולות_המספר#n1Lf | הנגרעים | |
| subtraction/subtractive | ג.ר.ע./גורע | term | תחבולות_המספר#XaSa | גורעי' | |
| subtraction/subtractive | פ.ח.ת./פוחת | term | תחבולות_המספר#Slaq | הפוחתים | |
| subtraction/subtractive | פ.ח.ת./פוחת | term | תחבולות_המספר#tzGj | הפוחת | |
| subtraction/subtractive | ח.ס.ר./נחסר | term | תחבולות_המספר#8MgA | הנחסר | |
| subtraction/subtractive | ג.ר.ע./גורע | term | תחבולות_המספר#sJWW | הגורע | |
| subtraction/subtractive | ח.ס.ר./חסר | term | ספר_החשבון_לאל_חצאר#auFp | חסרים | |
| subtraction/subtractive | ג.ר.ע./נגרע | term | Anonymous#qM5I | חשבון הנגרעים | |
| subtraction/subtractive | ח.ס.ר./מחוסר | term | בר_נותן_טעם#MPXZ | המחוסר | |
| subtraction/subtractive | ג.ר.ע./מגרעת | term | ספר_החשבון_לאל_חצאר#twdU | מגרעת | |
| subtraction/subtractive | ז.ו.ר./נזור | term | אגרת_המספר#yV1u | נזור | |
| subtraction/subtractive | ז.ו.ר./נזור | term | אגרת_המספר#cU17 | נזוריי | |
| subtraction/subtractive | ז.ו.ר./נזור | term | אגרת_המספר#0puL | הנזור | |
| subtraction/subtractive | ג.ר.ע./נגרע | term | חשבון_השטחים#A0yd | נגרע | |
| subtraction/subtractive | ח.ס.ר./חסר | term | אגרת_המספר#fclT | חסר | |
| subtraction/subtractive | ג.ר.ע./מגרעת | term | ספר_החשבון_לאל_חצאר#4euO | מגרעות | |
| subtraction/subtractive | ז.ו.ר./נזור | term | אגרת_המספר#52Fw | נזור | |
| subtraction/subtractive | ח.ס.ר./חסרון | term | ספר_ג'יבלי_אלמוקבאלא#7vBD | חסרון | |
| subtraction/subtractive | ש.נ.י./נשנה | term | חשבון_השטחים#yDPc | הנשנים | |
| subtraction/subtractive | ש.נ.י./נשנה | term | חשבון_השטחים#wDgr | הנשנה | |
| subtraction/subtractive | ג.ר.ע./נגרע | term | חשבון_השטחים#gbxy | נגרעים | |
| subtraction/subtractive | פ.ח.ת./פוחת | term | ספר_ג'יבלי_אלמוקבאלא#wD9K | פוחתי' | |
| subtraction/subtractive | פ.ח.ת./פחות | term | ספר_ג'יבלי_אלמוקבאלא#5kZw | פחות | |
| subtraction/subtractive | ג.ר.ע./גורע | term | חשבון_השטחים#QB6c | הגורע | |
| subtraction/subtractive | פ.ח.ת./פוחת | term | ספר_ג'יבלי_אלמוקבאלא#i18t | פוחת | |
| subtraction/subtractive | פ.ח.ת./פוחת | term | ספר_ג'יבלי_אלמוקבאלא#trCC | הפוחתים | |
| subtraction/subtractive | פ.ח.ת./פוחת | term | ספר_ג'יבלי_אלמוקבאלא#65AD | הפוחתות | |
| subtraction/subtractive | ז.ו.ר./נזור | term | אגרת_המספר#FMif | נזורים | |
| subtraction/subtractive | פ.ח.ת./פחות | term | ספר_האלזיברא#owsm | פחות | |
| subtraction/subtractive | פ.ח.ת./נפחת | term | ספר_ג'יבלי_אלמוקבאלא#Xmmo | הנפחת | |
| subtraction/subtractive | ג.ר.ע./גורע | term | ספר_ג'יבלי_אלמוקבאלא#CZ3Y | הגורעי' | |
| subtraction/subtractive | ג.ר.ע./גורע | term | ספר_ג'יבלי_אלמוקבאלא#vkgW | הגורע | |
| subtraction/subtractive | פ.ח.ת./פחת | term | ספר_ג'יבלי_אלמוקבאלא#0Fi8 | הפחת | |
| subtraction/subtractive | ח.ס.ר./חסרון | term | ספר_האלזיברא#RmOb | חסרון | |
| subtraction/subtractive | פ.ח.ת./פחת | term | ספר_ג'יבלי_אלמוקבאלא#fBvk | מפחת | |
| subtraction/subtractive | ג.ר.ע./נגרע | term | תחבולות_המספר#sdZM | מספר הנגרע | |
| subtraction/subtractive | ש.נ.י./נשנה | term | תחבולות_המספר#DTnp | הנשנה | |
| subtraction/subtractive | ש.נ.י./נשנה | term | תחבולות_המספר#qchh | הנשנים | |
| subtraction/subtractive | ג.ר.ע./נגרע | term | תחבולות_המספר#zWaV | נגרע | |
| subtraction/subtrahend | ג.ר.ע./מוגרע | term | אגרת_המספר#FkOz | מוגרע | |
| subtraction/subtrahend | ג.ר.ע./נגרע | term | בר_נותן_טעם#DOGq | הנגרעי' | |
| subtraction/subtrahend | ג.ר.ע./גורע | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#tDIi | המספר הגורע | |
| subtraction/subtrahend | ז.ו.ר./נזור | term | אגרת_המספר#mUoh | הנזור | |
| subtraction/subtrahend | ג.ר.ע./נגרע | term | אגרת_המספר#lq5S | הנגרע | |
| subtraction/subtrahend | term | מלאכת_המספר#AM8k | המספר שחסרנו | ||
| subtraction/subtrahend | ג.ר.ע./גורע | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#QV00 | הגורע | |
| subtraction/subtrahend | ש.ל.כ./מושלך | term | ספר_החשבון_לאל_חצאר#rusQ | המספר המושלך | |
| subtraction/subtrahend | ס.ו.ר./מוסר | term | ספר_החשבון_לאל_חצאר#Ih7g | מוסרים | |
| subtraction/subtrahend | ג.ר.ע./נגרע | term | קצור_המספר#aW8D | המספר הנגרע | |
| subtraction/subtrahend | ג.ר.ע./נגרע | term | קצור_המספר#Zlhm | המספר הנגרע | |
| subtraction/subtrahend | ג.ר.ע./נגרע | term | אגרת_המספר#HoQQ | המספר הנגרע | |
| subtraction/subtrahend | ג.ר.ע./נגרע | term | בר_נותן_טעם#siXg | הנגרעים | |
| progression/successive | מ.ש.כ./נמשך | definition | ספר_מעשה_חושב#RBpf | The number succeeding the number is the number that exceeds over that number by one. המספר הנמשך למספר מה לאחריו הוא מה שיוסיף על המספר ההוא אחד | |
| progression/successive | מ.ש.כ./נמשך | definition | ספר_מעשה_חושב#mh8n | The number preceding the number is the number that is smaller than that number by one. המספר הנמשך למספר מה לפניו הוא מה שיחסר מהמספר ההוא אחד | |
| progression/successive | term | מלאכת_המספר#ujuo | הנמשכת אחריה | ||
| progression/successive | מ.ש.כ./נמשך | term | קצת_מענייני_חכמת_המספר#JKKR | המספרים הנמשכים אחריו | |
| progression/successive | term | ספר_המספר_/_אברהם_אבן_עזרא#hWcF | הבאים אחריו | ||
| progression/successive | מ.ש.כ./נמשך | term | קצת_מענייני_חכמת_המספר#lqnv | המספרים הנמשכים אחריו | |
| progression/successively | ס.ד.ר./סדר | term | Anonymous#1GdV | על סדר חשבון | |
| progression/successively | מ.ש.כ./על המשך | term | ספר_דיני_ממונות#hVPL | על המשך | |
| progression/successively | ס.ד.ר./סדר | term | Anonymous#laQt | על הסדר | |
| progression/successively | מ.ש.כ./על המשך | term | ספר_החשבון_לאל_חצאר#QlNi | על המשך | |
| addition/sum | ח.ב.ר./חבור | term | ספר_ציפרא#fuG0 | חבורו | |
| addition/sum | ח.ב.ר./חבור | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#3cef | חיבור כולם | |
| addition/sum | ק.ב.צ./נקבץ | term | חשבון_השטחים#nj2G | נקבץ | |
| addition/sum | א.ס.פ./נאסף | term | Anonymous#kKah | נאסף | |
| addition/sum | ק.ב.צ./מתקבץ | term | חשבון_השטחים#tVwp | המתקבץ | |
| addition/sum | ק.ב.צ./מקובץ | term | ספר_החשבון_והמדות#B2GO | המקובץ | |
| addition/sum | ח.ב.ר./מחובר | term | חשבון_השטחים#tWcg | המחובר | |
| addition/sum | ח.ב.ר./נחבר | term | Anonymous#Cezq | הנחבר | |
| addition/sum | ק.ב.צ./נקבץ | term | ספר_מעשה_חושב#M3JO | נקבצי | |
| addition/sum | ח.ב.ר./מחובר | term | Anonymous#DrP0 | המחובר | |
| addition/sum | ח.ב.ר./מחובר | term | Anonymous#GP8R | המחובר | |
| addition/sum | ח.ב.ר./מחובר | term | ספר_דיני_ממונות#Y7WR | המחובר | |
| addition/sum | ס.כ.מ./סכום | term | ספר_החשבון_והמדות#Jik0 | סכום | |
| addition/sum | ק.ב.צ./מקובץ | term | תחבולות_המספר#M6zW | מקובץ ה | |
| addition/sum | 7i,1-9 | ספר_מעשה_חושב#sEo5 | Example: the first is seven, the second fourteen, the third 21, the fourth 28, and so on in this way up to nine numbers.
::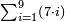 דמיון זה שיהיה הראשון שבעה והשני ארבעה עשר והשלישי כ"א והרביעי כ"ח וימשכו בזה הדרך עד תשעה מספרים
דמיון זה שיהיה הראשון שבעה והשני ארבעה עשר והשלישי כ"א והרביעי כ"ח וימשכו בזה הדרך עד תשעה מספרים | ||
| addition/sum | ק.ב.צ./קבוץ | term | עיר_סיחון#EMLg | קבוץ | |
| addition/sum | ק.ב.צ./נקבץ | term | ספר_מעשה_חושב#CFq5 | נקבץ | |
| addition/sum | צ.ר.פ./צרוף | term | ספר_אגריס#oJpi | צירופם | |
| addition/sum | ק.ב.צ./נקבץ | term | אגרת_המספר#o8fj | נקבץ | |
| addition/sum | ח.ב.ר./מחובר | term | עיר_סיחון#ba1O | מחובר | |
| addition/sum | ק.ב.צ./קבוץ | term | תחבולות_המספר#gdu7 | קבוץ ה | |
| addition/sum | ק.ב.צ./מתקבץ | term | אגרת_המספר#XQ69 | מתקבץ | |
| addition/sum | ח.ב.ר./מחובר | term | תחבולות_המספר#NOya | המחובר מ | |
| addition/sum | ק.ב.צ./מקובץ | term | חשבון_השטחים#vQSL | המקובץ | |
| addition/sum | ק.ב.צ./מקובץ | term | ספר_המספר_/_אליהו_מזרחי#ylP6 | המקובץ | |
| addition/sum | ח.ב.ר./מחובר | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#YLpV | המחובר | |
| addition/sum | ח.ב.ר./מחובר | term | ספר_עיון_העקרים_לחשבון_ההנדיים#zFwh | המחובר | |
| addition/sum | ק.ב.צ./מקובץ | term | אגרת_המספר#X9St | מקובץ | |
| addition/sum | ק.ב.צ./מקובץ | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#0UG8 | המקובץ | |
| addition/sum | ח.ב.ר./חבור | term | ספר_ג'יבלי_אלמוקבאלא#lRWw | חבורם יחד | |
| addition/sum | ק.ב.צ./מקובץ | term | עיר_סיחון#qKhT | מקובץ | |
| addition/sum | ס.כ.מ./סכום | term | קצור_המספר#34wB | סכום | |
| addition/sum | ח.ב.ר./מחובר | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#9eSr | המספר המחובר | |
| addition/sum | ק.ב.צ./מקובץ | term | ספר_ג'יבלי_אלמוקבאלא#lWWr | מקובץ | |
| addition/sum | ק.ב.צ./מקובץ | term | ספר_מעשה_חושב#QVVL | המקובץ | |
| addition/sum | ק.ב.צ./מקובץ | term | קצור_המספר#6azS | המקובץ | |
| addition/sum | ק.ב.צ./נקבץ | term | ספר_ג'יבלי_אלמוקבאלא#9yER | נקבץ | |
| addition/sum | ח.ב.ר./מחברת | term | עיר_סיחון#V2sT | מחברת | |
| addition/sum | term | ספר_ג'יבלי_אלמוקבאלא#az6A | זינטו | ||
| addition/sum | 3i, 1-7 | ספר_דיני_ממונות#7Gpu | Question: sum for me seven numbers successively, such that each exceeds over the one that precedes it by 3. שאלה תחבר לי ז' מספרים על דרך ההמשך שכל אחד יוסיף על חבירו ג' | ||
| addition/sum | י.ס.פ./נוסף | term | ספר_ג'יבלי_אלמוקבאלא#tBcJ | נוסף | |
| addition/sum | ק.ב.צ./קבוץ | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#KPG4 | קיבוץ | |
| addition/sum | ח.ב.ר./חבור | term | חשבון_השטחים#q5we | חיבורם | |
| addition/sum | ק.ב.צ./מקובץ | term | חשבון_השטחים#3Vqd | מקובצם | |
| addition/sum | ק.ב.צ./מקובץ | term | מלאכת_המספר#y8PZ | המקובץ | |
| addition/sum | ק.ב.צ./מקובץ | term | מלאכת_המספר#NXBw | מקובץ | |
| addition/sum | י.ס.פ./הוספה | term | האריתמטיקה_של_ניקומכוס#0Mtq | הוספות | |
| addition/sum | ק.ב.צ./נקבץ | term | ספר_מעשה_חושב#2u17 | הנקבצים | |
| addition/sum | ק.ב.צ./קבוץ | term | מלאכת_המספר#nKTt | קבוץ | |
| addition/sum | ח.ב.ר./חבור | term | ספר_החשבון_והמדות#TgJj | חבורם | |
| addition/sum | ק.ב.צ./מקובץ | term | תחבולות_המספר#ju7P | מקובצם | |
| addition/sum | ח.ב.ר./מחובר | term | ספר_ציפרא#sXvR | מחובר | |
| addition/sum | ח.ב.ר./מחובר | term | עיר_סיחון#szGK | מחובר | |
| addition/sum | צ.ר.פ./צרוף | term | ספר_ציפרא#fjvy | צירופו | |
| addition/sum | ח.ב.ר./מחובר | term | בר_נותן_טעם#76oh | המחובר | |
| addition/sum | ק.ב.צ./קבוץ | term | בר_נותן_טעם#I2Z0 | קיבוץ | |
| addition/sum | ח.ב.ר./חבור | term | בר_נותן_טעם#mibG | חיבורם | |
| addition/sum | term | ספר_האלזיברא#hPZo | העולה מחבור | ||
| addition/sum | ק.ב.צ./קבוץ | term | מלאכת_המספר#c4M5 | קבוץ | |
| addition/sum | ק.ב.צ./קבוץ | term | Anonymous#gZOi | קבוץ | |
| addition/sum | ס.ו.כ./סך | term | ספר_החשבון_והמדות#8jqg | סך | |
| addition/sum | ח.ב.ר./חבור | term | Anonymous#w79b | חבור | |
| addition/sum | ק.ב.צ./מקובץ | term | עיר_סיחון#AFvL | מקובץ | |
| sum/sum of cubic numbers | aₙ, 1, 225 | ספר_דיני_ממונות#mrIH | 33) Question: we summed up all the cubes from 1 to an unknown number and the sum is 225.
:How much is the unknown number?
: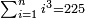 לג) שאלה אם אמר קבצנו כל המעוקבים מא' עד מספר נעלם ועלה המחובר רכ"ה
לג) שאלה אם אמר קבצנו כל המעוקבים מא' עד מספר נעלם ועלה המחובר רכ"הכמה הוא המספר הנעלם | ||
| sum/sum of cubic numbers | aₙ, 1, 3025 | ספר_החשבון_לאל_חצאר#Sivd | If he said: sum from the cube of one to the cube of an unknown number and the result is 3025, how much is the unknown number?
: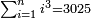 ואם אמר קבץ ממעוקב אחד עד מעוקב מספר מושכל והגיע חמשה ועשרים ושלשת אלפים כמה {{#annot:term|941,1806|Ye6i}}המספר המוסכל{{#annotend:Ye6i}}
ואם אמר קבץ ממעוקב אחד עד מעוקב מספר מושכל והגיע חמשה ועשרים ושלשת אלפים כמה {{#annot:term|941,1806|Ye6i}}המספר המוסכל{{#annotend:Ye6i}} | ||
| sum/sum of cubic numbers | 4-10 | ספר_החשבון_לאל_חצאר#KOJ6 | If he said: sum from the cube of four to the cube of ten.
: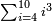 ואם אמר קבץ ממעוקב ארבעה עד מעוקב עשרה
ואם אמר קבץ ממעוקב ארבעה עד מעוקב עשרה | ||
| sum/sum of cubic numbers | 1-10 | ספר_החשבון_לאל_חצאר#Nfkl | Sum from the cube of one to the cube of ten by the succession of the numbers.
: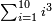 קבץ מן מעוקב אחד עד מעוקב עשרה על המשך המספר
קבץ מן מעוקב אחד עד מעוקב עשרה על המשך המספר | ||
| sum/sum of cubic numbers | 1-5 | ספר_המספר_/_אברהם_אבן_עזרא#mhj4 | Example: we wish to know how much is the sum of the cubes up to 5?
: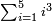 דמיון רצינו לידע כמה מספר המעוקבים המחוברים עד ה'
דמיון רצינו לידע כמה מספר המעוקבים המחוברים עד ה' | ||
| sum/sum of cubic numbers | 5-10 | קצת_מענייני_חכמת_המספר#JGRe | As if you wish to know [the sum of] the cube numbers from 5 to 10. כגון שרצית לידע מעוקבי מספרים מה' עד הי' | ||
| sum/sum of cubic numbers | 4i,1-5 | ספר_מעשה_חושב#P0Rk | Example: Let the first number be four, the second eight, and so on according to this way up to five numbers.
::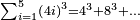 דמיון זה שיהיה הראשוןהראשון: MS P2271 ראשון ארבעה והשני שמנה ונמשכו בזה הדרך עד חמשה
דמיון זה שיהיה הראשוןהראשון: MS P2271 ראשון ארבעה והשני שמנה ונמשכו בזה הדרך עד חמשה | ||
| sum/sum of cubic numbers | 1-6 | ספר_מעשה_חושב#T9BI | Example: We want to know [the sum of] the cubes of the successive numbers from one up to six.
::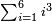 דמיון זה רצינו לדעת מעוקבימעוקבי: MS P2271 מעוקב המספרים הנמשכים מן האחד עד ששה
דמיון זה רצינו לדעת מעוקבימעוקבי: MS P2271 מעוקב המספרים הנמשכים מן האחד עד ששה | ||
| sum/sum of cubic numbers | 1-7 | ספר_דיני_ממונות#nV2h | 31) Question: sum up from the cube of 1 to the cube of 7
: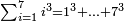 לא) שאלה קבץ לי ממעוקב א' עד מעוקב ז'
לא) שאלה קבץ לי ממעוקב א' עד מעוקב ז' | ||
| sum/sum of cubic numbers | 5-12 | ספר_דיני_ממונות#SUpM | 32) Question: sum up from the cube of 5 to the cube of 12.
: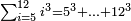 לב) שאלה קבץ לי ממעוקב ה' עד מעוקב י"ב
לב) שאלה קבץ לי ממעוקב ה' עד מעוקב י"ב | ||
| sum/sum of even cubes | 8-16 | ספר_החשבון_לאל_חצאר#cBXr | If he said: sum from the cube of eight to the cube of sixteen.
: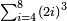 ואם אמר קבץ ממעוקב שמנה עד מעוקב ששה עשר
ואם אמר קבץ ממעוקב שמנה עד מעוקב ששה עשר | ||
| sum/sum of even cubes | aₙ, 2, 400 | ספר_דיני_ממונות#aCf5 | 39) Question: we sum up all the cubes of the evens from 2 until an unknown number and the sum is 400.
: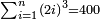 לט) שאלה אם יאמר לך קבצנו כל המעוקבים מב' עד מספר נעלם על דרך הזוגות ועלה המחובר ד' מאות
לט) שאלה אם יאמר לך קבצנו כל המעוקבים מב' עד מספר נעלם על דרך הזוגות ועלה המחובר ד' מאות | ||
| sum/sum of even cubes | 4-12 | ספר_דיני_ממונות#mv1u | 38) Question: sum up the cubes of the even numbers from 4 to 12.
: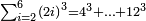 לח) שאלה קבץ ממעוקב ד' עד מעוקב י"ב על המשך הזוגות
לח) שאלה קבץ ממעוקב ד' עד מעוקב י"ב על המשך הזוגות | ||
| sum/sum of even cubes | 2-10 | ספר_החשבון_לאל_חצאר#V9ri | Sum from the cube of two to the cube of ten by the sequence of the evens.
: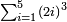 קבץ ממעוקב שנים עד מעוקב עשר' על המשך הזוגות
קבץ ממעוקב שנים עד מעוקב עשר' על המשך הזוגות | ||
| sum/sum of even cubes | 2-6 | ספר_מעשה_חושב#ve6G | Example: If you want to know [the sum of] the cubes of the successive even numbers up to six.
::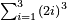 דמיון זהזה: MS P2271 om. אם 39rרצית לדעת מעוקבי הזוגות הנמשכים עד ששה
דמיון זהזה: MS P2271 om. אם 39rרצית לדעת מעוקבי הזוגות הנמשכים עד ששה | ||
| sum/sum of even cubes | 2-12 | ספר_דיני_ממונות#jOk3 | 37) Question: sum up the cubes of the even numbers from 2 to 12.
: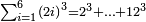 לז) שאלה קבץ ממעוקב ב' עד מעוקב י"ב על המשך הזוגות
לז) שאלה קבץ ממעוקב ב' עד מעוקב י"ב על המשך הזוגות | ||
| sum/sum of even cubes | aₙ, 2, 1800 | ספר_החשבון_לאל_חצאר#6aQ3 | If he said: sum from the cube of two to the cube of an unknown number by the sequence of the evens and the result is [1]800, how much is the unknown number?
: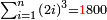 ואם אמר קבץ ממעוקב שנים עד מעוקב {{#annot:term|941,1806|LGBq}}מספר מוסכל{{#annotend:LGBq}} על המשך הזוגות והגיע שני אלפים ושמנה מאות כמה המספר המוסכל
ואם אמר קבץ ממעוקב שנים עד מעוקב {{#annot:term|941,1806|LGBq}}מספר מוסכל{{#annotend:LGBq}} על המשך הזוגות והגיע שני אלפים ושמנה מאות כמה המספר המוסכל | ||
| sum/sum of even numbers | 2-12 | ספר_דיני_ממונות#WfgD | 23) Question: if you want to know the sum of all the evens from 2 to 12.
: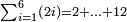 כג) שאלה אם תרצה לדעת חבור כל הזוגות אשר הם מב' עד י"ב
כג) שאלה אם תרצה לדעת חבור כל הזוגות אשר הם מב' עד י"ב | ||
| sum/sum of even numbers | 2-20 | ספר_חשבון#qYPE | If he says: I continued until twenty.
: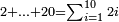 ואם אומר הלכתי עד עשרי'
ואם אומר הלכתי עד עשרי' | ||
| sum/sum of even numbers | 2-10 | ספר_החשבון_לאל_חצאר#6jsl | When you are told: sum from two to ten by the sequence of the evens.
: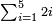 כשיאמר לך קבץ משנים עד עשרה על המשך הזוגות
כשיאמר לך קבץ משנים עד עשרה על המשך הזוגות | ||
| sum/sum of even numbers | 2-10 | ספר_מעשה_חושב#Cm3W | Example: if you want to sum the evens up to ten.
::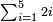 דמיון זה אם רצית לחבר הזוגות עד עשרה
דמיון זה אם רצית לחבר הזוגות עד עשרה | ||
| sum/sum of even numbers | 2-12 | מלאכת_המספר#voap | Example of this: if the last even number is 12.
::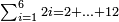 המשל בזה שאם הזוג האחרון יהיה י"ב
המשל בזה שאם הזוג האחרון יהיה י"ב | ||
| sum/sum of even numbers | 2-12 | ספר_חשבון#Gsfn | As 2, 4, 6, 8, 10, 12 - how much is the total?
: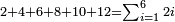 כמו ב' וד' וו' וח' וי' וי"ב כמה יהיה בין כלם
כמו ב' וד' וו' וח' וי' וי"ב כמה יהיה בין כלם | ||
| sum/sum of even numbers | aₙ, 2, 30 | ספר_החשבון_לאל_חצאר#F8bu | If he said: sum from two up to an even number by the succession of the evens and the sum is thirty, how much is the unknown number up to which it is summed?
: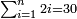 ואם אמר קבץ משנים אל מספר זוג על המשך הזוגות והתקבץ שלשים כמה המספר הבלתי ידוע אשר התקבץ אליו
ואם אמר קבץ משנים אל מספר זוג על המשך הזוגות והתקבץ שלשים כמה המספר הבלתי ידוע אשר התקבץ אליו | ||
| sum/sum of even numbers | aₙ, 2, 42 | ספר_דיני_ממונות#U8Ey | 25) Question: we summed up all the evens from 1 to an unknown number and the sum is 42.
: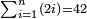 כה) שאלה חברנו כל הזוגות מא' עד מספר בלתי ידוע ועלה המחובר מ"ב
כה) שאלה חברנו כל הזוגות מא' עד מספר בלתי ידוע ועלה המחובר מ"ב | ||
| sum/sum of even numbers | 6-12 | ספר_החשבון_לאל_חצאר#tzpR | If he said: sum from six to twelve by the sequence of the evens.
: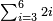 ואם אמר קבץ מששה עד שנים עשר על המשך הזוגות
ואם אמר קבץ מששה עד שנים עשר על המשך הזוגות | ||
| sum/sum of even numbers | 2-8 | ספר_הכללים_במספר#zzdV | 80) 2, 4, 6, 8 - that are evens.
: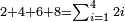 פ ב ד' ו' ח' שהם כלם זוגות
פ ב ד' ו' ח' שהם כלם זוגות | ||
| sum/sum of even numbers | definition | ספר_מעשה_חושב#jHt7 | The sum of the successive even numbers is [formed] when two, which is the first even, is summed with four and with six and so on successively. נקבץ הזוגות הנמשכים בדרך המספר הוא כשחובר שנים שהוא הזוג הראשון עם ארבעה ועם ששה וכן מה שהגיע | ||
| sum/sum of even squares | 2-8 | ספר_דיני_ממונות#FdKc | 29) Question: if you want to sum up all the squares of the even numbers from 2 to 8.
: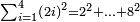 כט) שאלה אם תרצה לקבץ כל המרובעים אשר הם מב' עד ח' {{#annot:term|2494,1976|hVPL}}על המשך{{#annotend:hVPL}} הזוגות
כט) שאלה אם תרצה לקבץ כל המרובעים אשר הם מב' עד ח' {{#annot:term|2494,1976|hVPL}}על המשך{{#annotend:hVPL}} הזוגות | ||
| sum/sum of even squares | 6-16 | ספר_החשבון_לאל_חצאר#UbTz | If he said: sum from the square of six to the square of sixteen.
: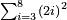 ואם אמר קבץ ממרובע ששה עד מרובע ששה עשר
ואם אמר קבץ ממרובע ששה עד מרובע ששה עשר | ||
| sum/sum of even squares | 2-10 | ספר_החשבון_לאל_חצאר#2Xeo | Sum from the square of two to the square of ten by the sequence of the evens.
: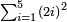 קבץ ממרובע שנים עד מרובע עשרה על המשך הזוגות
קבץ ממרובע שנים עד מרובע עשרה על המשך הזוגות | ||
| sum/sum of natural numbers | 1-10 | ספר_החשבון_והמדות#4op2 | Example: we wish to add the numbers that are from 1 up to 10 one by the one.
: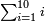 דמיון רצינו להוסיף המספרים שהם מא' עד י' [זה על זה]P1031 om.
דמיון רצינו להוסיף המספרים שהם מא' עד י' [זה על זה]P1031 om. | ||
| sum/sum of natural numbers | 1-10 | ספר_החשבון_לאל_חצאר#4THN | When you are told: sum from one to ten in arithmetic succession.
: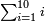 כשיאמר לך קבץ מאחד עד עשרה על המשך המספר
כשיאמר לך קבץ מאחד עד עשרה על המשך המספר | ||
| sum/sum of natural numbers | a₁, 10, 45 | קצת_מענייני_חכמת_המספר#Sm0l | We know the 10, which is [the last] summed number, and that the sum is 45, but the 5 is unknown.
::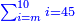 ידענו הי' שהוא המספר שהנקבץ עד מ"ה ונעלם הה'
ידענו הי' שהוא המספר שהנקבץ עד מ"ה ונעלם הה' | ||
| sum/sum of natural numbers | 1-13 | מלאכת_המספר#3sxY | Example: we wish to know the sum from one to 13.
::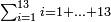 המשל נרצה לדעת ה{{#annot:term|388,1217|NXBw}}מקובץ{{#annotend:NXBw}} מאחד עד י"ג
המשל נרצה לדעת ה{{#annot:term|388,1217|NXBw}}מקובץ{{#annotend:NXBw}} מאחד עד י"ג | ||
| sum/sum of natural numbers | 1-12 | מלאכת_המספר#V836 | Example: we wish to know the sum from one to 12.
::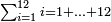 המשל שנרצה לדעת קבוץ אחד מאחד עד י"ב
המשל שנרצה לדעת קבוץ אחד מאחד עד י"ב | ||
| sum/sum of natural numbers | 1-11 | עיר_סיחון#pHD6 | If we want to know how much are the numbers summed up up to eleven.
: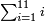 ואם נרצה לדעת כמה עולים {{#annot:term|787,1220|my36}}המספרים המחוברים{{#annotend:my36}} על אחד עשר
ואם נרצה לדעת כמה עולים {{#annot:term|787,1220|my36}}המספרים המחוברים{{#annotend:my36}} על אחד עשר | ||
| sum/sum of natural numbers | aₙ, 1, 210 | עיר_סיחון#Xl23 | Reverse question: the sum of the successive numbers starting from one is 210. What is the last number of the summed [numbers]?
: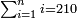 נהפוך השאלה ונאמר עלה המחובר ממספרים {{#annot:term|2576,1835|h4eV}}רצופים{{#annotend:h4eV}} המתחילים מאחד מאתים ועשרה
נהפוך השאלה ונאמר עלה המחובר ממספרים {{#annot:term|2576,1835|h4eV}}רצופים{{#annotend:h4eV}} המתחילים מאחד מאתים ועשרהאיזה הוא המספר האחרון מהמחוברים | ||
| sum/sum of natural numbers | 1-18 | ספר_המספר_/_אברהם_אבן_עזרא#IeC7 | Another example for an even number [of terms]: how much is the sum up to 18?
: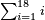 דמיון אחר בזוגות כמה המחובר עד סוף י"ח
דמיון אחר בזוגות כמה המחובר עד סוף י"ח | ||
| sum/sum of natural numbers | 1-11 | ספר_המספר_/_אברהם_אבן_עזרא#OprP | Example: we wish to know how much are the numbers that are summed from 1 to 11?
: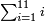 דמיון רצינו לדעת כמה הם המספרים המחוברים מא' עד סוף י"א
דמיון רצינו לדעת כמה הם המספרים המחוברים מא' עד סוף י"א | ||
| sum/sum of natural numbers | 1-10 | קצת_מענייני_חכמת_המספר#mfsN | To know the numbers that are set in succession.
: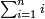 לידע מספרים מונחים על סדר המספר
|-
|
::Such as: 1; 2; 3; 4; 5; 6; 7; 8; 9; 10
::
לידע מספרים מונחים על סדר המספר
|-
|
::Such as: 1; 2; 3; 4; 5; 6; 7; 8; 9; 10
::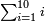 כגון אבג"ד ה"ו זחט"י
כגון אבג"ד ה"ו זחט"י | ||
| sum/sum of natural numbers | definition | ספר_מעשה_חושב#iKHo | The sum of the successive natural numbers starting from one is [formed] when one is summed with two and with three and so on successively. נקבץ הנמשכים בדרך המספר מתחילים מן האחד הוא כשחובר אחד עם שנים ועם שלשה וכן מה שהגיע | ||
| sum/sum of natural numbers | 1-19 | ספר_חשבון#CIoT | If he continues until 19.
: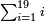 ואם הלך עד י"ט
ואם הלך עד י"ט | ||
| sum/sum of natural numbers | 1-10 | ספר_מעשה_חושב#oa4i | Example: if you want to sum one, two, three, four, and so on up to ten, including ten.
::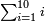 דמיון אם רצית לחבר אחד ושנים ושלשה וארבעה וכן עד עשרה ועשרה עמהם
דמיון אם רצית לחבר אחד ושנים ושלשה וארבעה וכן עד עשרה ועשרה עמהם | ||
| sum/sum of natural numbers | 1-6 | לקוטים_מספר_פראלוקא#hPlC | Example: we wish to sum from 1 to 6.
::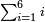 משל נרצה לחבר מא' עד ו'
משל נרצה לחבר מא' עד ו' | ||
| sum/sum of natural numbers | 1-7 | לקוטים_מספר_פראלוקא#xJHj | If you want to sum from 1 to 7.
::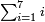 ואם תרצה לחבר מא' עד ז'
ואם תרצה לחבר מא' עד ז' | ||
| sum/sum of natural numbers | 1-7 | ספר_הכללים_במספר#bsMG | 78) 1, 2, 3, 4, 5, 6, 7.
: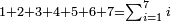 עח א ב' ג' ד' ה' ו' ז'
עח א ב' ג' ד' ה' ו' ז' | ||
| sum/sum of natural numbers | aₙ, 1, 120 | ספר_דיני_ממונות#ZASk | 21) Question: we sum up all the numbers until an unknown number and the sum is 120.
: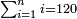 כא) שאלה חברנו כל המספרים עד מספר נעלם ועלה המחובר ק"כ
כא) שאלה חברנו כל המספרים עד מספר נעלם ועלה המחובר ק"כ | ||
| sum/sum of natural numbers | 4-10 | ספר_דיני_ממונות#mA7A | 20) Question: sum from 1 to 10 without the [first] three.
: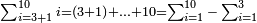 כ) שאלה קבץ מא' עד י' ולא יהיו הג' בכלל
כ) שאלה קבץ מא' עד י' ולא יהיו הג' בכלל | ||
| sum/sum of natural numbers | aₙ, 1, 55 | ספר_החשבון_לאל_חצאר#Q7I1 | Sum from one up to an unknown number by the succession of the numbers and the result is fifty five, how much is the unknown number?
: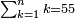 קבץ מאחד עד {{#annot:term|941,2010|HeCs}}מספר בלתי ידוע{{#annotend:HeCs}} על המשך המספר והגיע חמשה וחמישים כמה המספר הבלתי ידוע
קבץ מאחד עד {{#annot:term|941,2010|HeCs}}מספר בלתי ידוע{{#annotend:HeCs}} על המשך המספר והגיע חמשה וחמישים כמה המספר הבלתי ידוע | ||
| sum/sum of natural numbers | 1-8 | ספר_הכללים_במספר#zy8k | 77) 1, 2, 3, 4, 5, 6, 7, 8.
: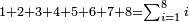 עז א ב' ג' ד' ה' ו' ז' ח'
עז א ב' ג' ד' ה' ו' ז' ח' | ||
| sum/sum of natural numbers | 6-11 | ספר_מעשה_חושב#uFgw | Example: The first number is six, and we want to sum the successive numbers that follow it up to eleven.
::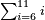 דמיון זה שיהיה המספר הראשון ששה ורצינו לחבר הנמשכים לו לאחריו עד מספר אחד עשר
דמיון זה שיהיה המספר הראשון ששה ורצינו לחבר הנמשכים לו לאחריו עד מספר אחד עשר | ||
| sum/sum of natural numbers | 1-16 | ספר_דיני_ממונות#afC8 | Example: we want to know [the sum] from 1 to 16.
: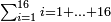 דמיון 230vזה נרצה לדעת מא' עד י"ו
דמיון 230vזה נרצה לדעת מא' עד י"ו | ||
| sum/sum of natural numbers | 1-12 | לקוטים_מספר_פראלוקא#GKFV | Example: we wish to know the sum of all the numbers from 1 to 12.
::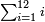 דמיון נרצה לדעת חבור כל המספרי' מא' עד י"ב
דמיון נרצה לדעת חבור כל המספרי' מא' עד י"ב | ||
| sum/sum of natural numbers | 1-25 | ספר_דיני_ממונות#uz7F | Example: we want to know the sum from 1 to 25.
: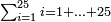 דמיון זה נרצה לדעת המחובר מא' עד כ"ה
דמיון זה נרצה לדעת המחובר מא' עד כ"ה | ||
| sum/sum of natural numbers | aₙ, 1, 465 | ספר_המספר_/_אברהם_אבן_עזרא#GXqn | Example: one asks: I sum all the numbers until they reach a known number and the sum is 465. How much is the last number?
: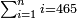 דמיון שאל שואל חברתי מספרים עד שהגיעו למספר ידוע ועלה המחובר תס"ה כמה הוא סוף החשבון
דמיון שאל שואל חברתי מספרים עד שהגיעו למספר ידוע ועלה המחובר תס"ה כמה הוא סוף החשבון | ||
| sum/sum of natural numbers | 1-9 | ספר_חשבון#2b1t | If he continues his question until 9.
: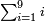 וכן אם הלך בשאלתו עד ט'
וכן אם הלך בשאלתו עד ט' | ||
| sum/sum of natural numbers | 1-7 | ספר_חשבון#Hvdz | As the one who says: I continue my calculation until 7. How much is the total?
: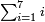 כגון האומר הלכתי בחשבוני עד ז' כמה יהיו כלם
כגון האומר הלכתי בחשבוני עד ז' כמה יהיו כלם | ||
| sum/sum of natural numbers | 1-100 | ספר_חשבון#YfUq | If he continues his question until one hundred.
: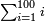 ואם הלך עד מאה
ואם הלך עד מאה | ||
| sum/sum of natural numbers | 1-20 | ספר_חשבון#u3dY | If he continues his question until 20.
: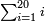 ואם הלך בשאלתו עד כ'
ואם הלך בשאלתו עד כ' | ||
| sum/sum of natural numbers | 1-17 | ספר_חשבון#T2rf | If he continues until 17.
: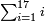 ואם הלך עד י"ז
ואם הלך עד י"ז | ||
| sum/sum of natural numbers | 1-12 | ספר_חשבון#kTQb | If he continues his question until 12.
: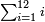 ואם הלך בשאלתו עד י"ב
ואם הלך בשאלתו עד י"ב | ||
| sum/sum of natural numbers | 1-10 | ספר_חשבון#QIjG | If a person says: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 - how much is the total?
: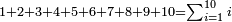 אם יאמר אדם א' וב' וג' וד' וה' וו' וז' וח' וטי' וי' כמה שוי בין כלם
אם יאמר אדם א' וב' וג' וד' וה' וו' וז' וח' וטי' וי' כמה שוי בין כלם | ||
| sum/sum of natural numbers | 1-12 | ספר_המספר_/_אברהם_אבן_עזרא#xE2F | Example: we wish to know how much is the sum up to 12?
: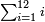 דמיון רצינו לדעת כמה המחברים עד י"ב
דמיון רצינו לדעת כמה המחברים עד י"ב | ||
| sum/sum of natural numbers | 4-10 | ספר_החשבון_והמדות#A9Sh | Question: I summed from 4 up to 10. How much are they?
: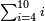 שאלה חברתי מד' עד י' כמה יהיו
שאלה חברתי מד' עד י' כמה יהיו | ||
| sum/sum of natural numbers | 1-14 | ספר_דיני_ממונות#EW6C | 17) Question: if you want to sum from 1 to 14, i.e. 1 with 2, with 3, and so on until 14.
: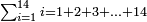 יז) שאלה אם תרצה לקבץ מא' עד י"ד ר"ל א' עם ב' ועם ג' וכן עד י"ד
יז) שאלה אם תרצה לקבץ מא' עד י"ד ר"ל א' עם ב' ועם ג' וכן עד י"ד | ||
| sum/sum of natural numbers | 1-20 | עיר_סיחון#2heg | Question: we summed all the successive numbers from one to twenty and it is the sum. How much is the sum?
: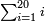 שאלה חברנו כל {{#annot:term|2576,1835|ETrE}}המספרים הרצופים{{#annotend:ETrE}} מאחד עד עשרים והם הכלל כמה המחובר
שאלה חברנו כל {{#annot:term|2576,1835|ETrE}}המספרים הרצופים{{#annotend:ETrE}} מאחד עד עשרים והם הכלל כמה המחובר | ||
| sum/sum of natural numbers | aₙ, 1, 55 | ספר_החשבון_והמדות#GzAy | Question: if a person asks you: I summed numbers and they are 55, how much are the numbers?
: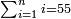 36rשאלה אם ישאלך אדם חברתי מספרים והיו נ"ה כמה יהיו המספרים
36rשאלה אם ישאלך אדם חברתי מספרים והיו נ"ה כמה יהיו המספרים | ||
| sum/sum of natural numbers | 1-10 | ספר_החשבון_והמדות#QkuV | Example: we wish to know how much is the sum of the numbers that are from 1 up to 10.
: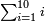 דמיון רצינו לדעת כמה תוספת המספרים שהם מא' עד י'
דמיון רצינו לדעת כמה תוספת המספרים שהם מא' עד י' | ||
| sum/sum of natural numbers | aₙ, 1, 55 | קצת_מענייני_חכמת_המספר#2wMi | Numbers that are summed successively and the result is a known number.
: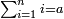 חשבון שחובר על הסדר ועלה מספר ידוע
|-
|
::Such as the number 55, how much is the last number?
::
חשבון שחובר על הסדר ועלה מספר ידוע
|-
|
::Such as the number 55, how much is the last number?
::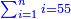 כגון מספר נ"ה כמה הוא מספר האחרון
כגון מספר נ"ה כמה הוא מספר האחרון | ||
| sum/sum of natural numbers | 5-10 | קצת_מענייני_חכמת_המספר#6eLr | If the numbers that are given in succession do not start from 1.
ואם המספרים המונחים על סדר המספר לא יתחילו מהא'
|-
|
: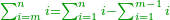 |
|-
|
::As saying: from 5 to 10.
::
|
|-
|
::As saying: from 5 to 10.
::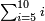 כאמרך מה' עד י'
כאמרך מה' עד י' | ||
| sum/sum of natural numbers | aₙ, 5, 45 | קצת_מענייני_חכמת_המספר#xRiD | Numbers that are summed from a known number.
: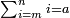 חשבון שחובר מתחלת מספר ידוע
|-
|
::As saying: from 5 and the sum is 45, how much is the last number?
::
חשבון שחובר מתחלת מספר ידוע
|-
|
::As saying: from 5 and the sum is 45, how much is the last number?
::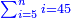 כאמרך מה' ועלה מ"ה כמה הוא סוף המספר
כאמרך מה' ועלה מ"ה כמה הוא סוף המספר | ||
| sum/sum of natural numbers | 1-9 | ספר_החשבון_והמדות#vKJf | Another example for an odd [number of terms]: we wish to know how much is the sum of the numbers from 1 up to 9.
: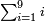 דמיון אחר לנפרדים רצינו לדעת כמה תוספת המספרים זה על זה מא' עד ט'
דמיון אחר לנפרדים רצינו לדעת כמה תוספת המספרים זה על זה מא' עד ט' | ||
| sum/sum of natural numbers | 5-10 | ספר_החשבון_לאל_חצאר#hJtL | If you are told: sum from five to ten.
: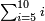 ואם אמר לך קבץ מחמשה עד עשרה
ואם אמר לך קבץ מחמשה עד עשרה | ||
| sum/sum of odd cubes | 5-9 | ספר_דיני_ממונות#79pn | 35) Question: sum up the cubes of the odd numbers from 5 to 9.
: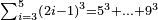 לה) שאלה אם ישאל לך אדם קבץ לי ממעוקב ה' עד מעוקב ט' על המשך הנפרדים
לה) שאלה אם ישאל לך אדם קבץ לי ממעוקב ה' עד מעוקב ט' על המשך הנפרדים | ||
| sum/sum of odd cubes | 1-13 | ספר_דיני_ממונות#kjWM | 34) Question: sum up the cubes of the odd numbers from 1 to 13.
: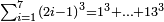 לד) שאלה אם נשאל לך קבץ לי ממעוקב א' עד מעוקב י"ג כדרך הנפרדים
לד) שאלה אם נשאל לך קבץ לי ממעוקב א' עד מעוקב י"ג כדרך הנפרדים | ||
| sum/sum of odd cubes | aₙ, 1, 1225 | ספר_החשבון_לאל_חצאר#Hsvy | If he said: sum from the cube of one to the cube of an unknown number by the sequence of the odds and the result is 1225, how much is the unknown number?
: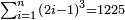 קבץ ממעוקב אחד עד מעוקב {{#annot:term|941,1804|pNEK}}מושכל{{#annotend:pNEK}} על המשך הנפרדים והתקבץ חמשה ועשרים ומאתים ואלף כמה המספר המושכל
קבץ ממעוקב אחד עד מעוקב {{#annot:term|941,1804|pNEK}}מושכל{{#annotend:pNEK}} על המשך הנפרדים והתקבץ חמשה ועשרים ומאתים ואלף כמה המספר המושכל | ||
| sum/sum of odd cubes | aₙ, 1, 256 | ספר_דיני_ממונות#3zw4 | 36) Question: we sum up all the cubes of the odds from 1 until an unknown number and the result is 256.
: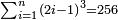 לו) שאלה קבצנו כל המעוקבים מא' עד מספר נעלם על דרך הנפרדים ועלה רנ"ו
לו) שאלה קבצנו כל המעוקבים מא' עד מספר נעלם על דרך הנפרדים ועלה רנ"ו | ||
| sum/sum of odd cubes | 1-9 | ספר_החשבון_לאל_חצאר#ZShx | Sum from the cube of one to the cube of nine by the succession of the odds.
: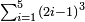 קבץ ממעוקב אחד עד מעוקב תשעה על המשך הנפרד
קבץ ממעוקב אחד עד מעוקב תשעה על המשך הנפרד | ||
| sum/sum of odd cubes | 7-11 | ספר_החשבון_לאל_חצאר#OrOM | If he said: sum from the cube of seven to the cube of eleven.
: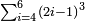 ואם אמר קבץ ממעוקב שבעה עד מעוקב אחד עשר
ואם אמר קבץ ממעוקב שבעה עד מעוקב אחד עשר | ||
| sum/sum of odd numbers | aₙ, 1, 36 | ספר_החשבון_לאל_חצאר#Yciw | If he said: sum from one up to an unknown number by the succession [of the odds] and the sum is 36, how much is the [unknown] number?
: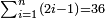 ואם אמר קבץ מאחד עד מספר בלתי ידוע על המשך והתקבץ ששה ושלשים כמה המספר הנפרד
ואם אמר קבץ מאחד עד מספר בלתי ידוע על המשך והתקבץ ששה ושלשים כמה המספר הנפרד | ||
| sum/sum of odd numbers | 1-9 | ספר_דיני_ממונות#2PiX | 22) Question: sum all the odds from 1 to 9.
: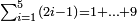 כב) שאלה קבץ מא' עד ט' כל הנפרדים
כב) שאלה קבץ מא' עד ט' כל הנפרדים | ||
| sum/sum of odd numbers | 1-11 | ספר_חשבון#NxSy | If he continues his question until 11.
: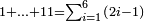 ואם הלך בשאלתו עד י"א
ואם הלך בשאלתו עד י"א | ||
| sum/sum of odd numbers | 1-15 | מלאכת_המספר#FKII | Example of this: we wish to know the sum of all the odd numbers from one to 15.
::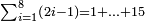 המשל בזה נרצה לדעת המקובץ מכל הנפרדים מהאחד עד ט"ו
המשל בזה נרצה לדעת המקובץ מכל הנפרדים מהאחד עד ט"ו | ||
| sum/sum of odd numbers | 1-9 | ספר_חשבון#rGAn | As 1, 3, 5, 7, 9 - how much is the total?
: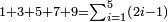 כגון א' וג' וה' וז' וט' כמה הם בין כלם
כגון א' וג' וה' וז' וט' כמה הם בין כלם | ||
| sum/sum of odd numbers | definition | ספר_מעשה_חושב#zAgk | The sum of the successive odd numbers starting from one is [formed] when one is summed with three and with five and so on successively. נקבץ הנפרדים הנמשכים בדרך המספר מתחילין מן האחד הוא כשחובר אחד עם שלשה ועם חמשה וכן מה שהגיע | ||
| sum/sum of odd numbers | 1-19 | ספר_החשבון_לאל_חצאר#RTIO | Sum from one to nineteen by the sequence of the odds.
: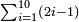 קבץ מאחד עד תשעה עשר על המשך הנפרדים
קבץ מאחד עד תשעה עשר על המשך הנפרדים | ||
| sum/sum of odd numbers | 7-13 | ספר_החשבון_לאל_חצאר#TVil | If he said: sum from seven to thirteen by the sequence of the odds.
: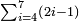 ואם אמר קבץ משבעה עד שלשה עשר על המשך הנפרדים
ואם אמר קבץ משבעה עד שלשה עשר על המשך הנפרדים | ||
| sum/sum of odd numbers | 1-13 | ספר_חשבון#2g6v | If he continues until 13.
: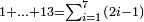 ואם הלך עד י"ג
ואם הלך עד י"ג | ||
| sum/sum of odd numbers | 1-9 | ספר_הכללים_במספר#djRx | 79) 1, 3, 5, 7, 9 - that are odds.
: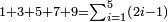 עט א ג' ה' ז' ט' שהם פרדים
עט א ג' ה' ז' ט' שהם פרדים | ||
| sum/sum of odd numbers | 1-9 | ספר_מעשה_חושב#Mp2k | Example: If you want to sum the successive odds up to nine including one.
::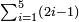 דמיון זה אם רצית לחבר הנפרדים הנמשכים עד תשעה והאחד עמהם
דמיון זה אם רצית לחבר הנפרדים הנמשכים עד תשעה והאחד עמהם | ||
| sum/sum of odd numbers | aₙ, 1, 25 | ספר_דיני_ממונות#nd14 | 24) Question: we sum up all the odds until an unknown numbers and the sum is 25.
: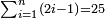 כד) שאלה חברנו כל הנפרדים עד מספר נעלם ועלה כ"ה
כד) שאלה חברנו כל הנפרדים עד מספר נעלם ועלה כ"ה | ||
| sum/sum of odd squares | 1-9 | ספר_מעשה_חושב#24Cc | Example: We want to know [the sum of] the squares of the successive odd numbers up to nine.
::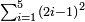 דמיון זה רצינו לדעת מרובעי הנפרדים הנמשכים עד תשעה
דמיון זה רצינו לדעת מרובעי הנפרדים הנמשכים עד תשעה | ||
| sum/sum of odd squares | 1-9 | קצת_מענייני_חכמת_המספר#l12R | To know [the sum of] the squares of the odd numbers [that are set] in succession.
: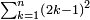 לידע מרובעי הנפרדים על הסדר
|-
|
::As if you say: 1; 3; 5; 7; 9.
::
לידע מרובעי הנפרדים על הסדר
|-
|
::As if you say: 1; 3; 5; 7; 9.
::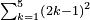 כאלו תאמר א' ג' ה' ז' ט'
כאלו תאמר א' ג' ה' ז' ט' | ||
| sum/sum of odd squares | 1-9 | ספר_החשבון_לאל_חצאר#gBq8 | If he said: sum from the square of one to the square of nine by the sequence of the odds.
: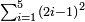 ואם אמר קבץ ממרובע אחד עד מרובע תשעה על המשך הנפרד
ואם אמר קבץ ממרובע אחד עד מרובע תשעה על המשך הנפרד | ||
| sum/sum of odd squares | 1-7 | ספר_דיני_ממונות#sUpB | 30) Question: sum up the squares of the odd numbers from 1 to 7
: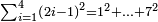 ל) שאלה קבץ ממרובע א' עד מרובע ז' על המשך הנפרדים
ל) שאלה קבץ ממרובע א' עד מרובע ז' על המשך הנפרדים | ||
| sum/sum of powers of four | 1-16 | ספר_חשבון#aAn8 | As 1, 4, 16.
: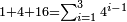 כגון א' ד' י"ו
כגון א' ד' י"ו | ||
| sum/sum of powers of three | 1-27 | ספר_חשבון#mIQm | As 1, 3, 9, 27.
: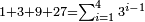 כגון א' ג' ט' כ"ז
כגון א' ג' ט' כ"ז | ||
| sum/sum of powers of two | 1-32 | ספר_חשבון#6kg5 | Example: one says: I summed the doubles from 1 to 32. How much is their sum?
: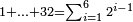 דמיון זה האומר קבצתי מספרים כפולי' מא' ועד ל"ב כמה הם
דמיון זה האומר קבצתי מספרים כפולי' מא' ועד ל"ב כמה הם | ||
| sum/sum of powers of two | 1-64 | ספר_חשבון#WJGn | If he says: I started from 1 and doubled until 64. How much is [their sum]?
: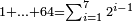 ואם יאמ' התחלתי מא' וכפלתי עד ס"דס"ד: MS Ithaca קכ"ח כמה יהיו
ואם יאמ' התחלתי מא' וכפלתי עד ס"דס"ד: MS Ithaca קכ"ח כמה יהיו | ||
| sum/sum of powers of two | 4-32 | ספר_חשבון#ghpP | If he says: I started from 4 and doubled until 32. How much is their sum?
: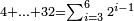 ואם יאמר התחלתי מד' וכפלתי עד ל"ב כמה יהיו
ואם יאמר התחלתי מד' וכפלתי עד ל"ב כמה יהיו | ||
| sum/sum of powers of two | 1-4095 | ספר_דיני_ממונות#GokE | [41)] If you want to sum 1 with 2, 4, 8, 16, and so on double 12 times.
::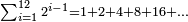 MS L: מ"אואם תרצה לחבר א' עם ב' ועם ד' ועם ח' ועם י"ו וכן תמיד תכפול עד י"ב פעמים
MS L: מ"אואם תרצה לחבר א' עם ב' ועם ד' ועם ח' ועם י"ו וכן תמיד תכפול עד י"ב פעמים | ||
| sum/sum of powers of two | 1-128 | ספר_דיני_ממונות#29bw | 40) Question: if you want to know the sum of 1, 2, 4, 8, 16, and so on, each consecutive number is double the preceding number, and the last number is 128.
: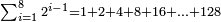 מ) שאלה אם תרצה לדעת המחובר מא' עם ב' עם ד' עם ח' ועם י"ו וכן לעולם 232rמוסיף המספר הבא על המספר העבר ב' פעמים כמוהו והמספר האחרון עולה קכ"ח
מ) שאלה אם תרצה לדעת המחובר מא' עם ב' עם ד' עם ח' ועם י"ו וכן לעולם 232rמוסיף המספר הבא על המספר העבר ב' פעמים כמוהו והמספר האחרון עולה קכ"ח | ||
| sum/sum of powers of two | 1-32 | ספר_חשבון#y2at | As 1, 2, 4, 8, 16, 32.
: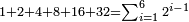 כגון א' וב' וד' וח' וי"ו ול"ב
כגון א' וב' וד' וח' וי"ו ול"ב | ||
| sum/sum of powers of two | 1-128 | ספר_חשבון#IUR1 | If he says: I started from one and doubled until 128. How much is [their sum]?
: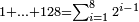 ואם יאמר התחלתי מאחד וכפלתי עד
ואם יאמר התחלתי מאחד וכפלתי עד | ||
| sum/sum of square numbers | 1-10 | ספר_החשבון_לאל_חצאר#6e94 | Sum from the square of one to the square of ten by the succession of the numbers.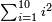 קבץ ממרובע אחד עד מרובע עשרה על המשך המספר
קבץ ממרובע אחד עד מרובע עשרה על המשך המספר | ||
| sum/sum of square numbers | 1-4 | ספר_דיני_ממונות#JRLl | 26) Question: if you want to sum up all the squares [of the numbers] from 1 to 4.
: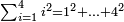 כו) שאלה אם תרצה לחבר כל המרובעים אשר הם מא' ועד ד'
כו) שאלה אם תרצה לחבר כל המרובעים אשר הם מא' ועד ד' | ||
| sum/sum of square numbers | 4i,1-7 | ספר_מעשה_חושב#Ujwo | Example: If you want to sum the squares of the successive numbers, the first number of which is four, the second is eight, the third is twelve, and so on they follow each other this way up to seven numbers.
::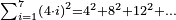 דמיון זה אם רצית לחבר מרובעי מספרים נמשכיםמרובעי מספרים נמשכים: MS P2271 מספרי 38vשהראשון ארבעה והשני שמנה והשלישי שנים עשר וימשכו בזה הדרך עד שבעה מספרים
דמיון זה אם רצית לחבר מרובעי מספרים נמשכיםמרובעי מספרים נמשכים: MS P2271 מספרי 38vשהראשון ארבעה והשני שמנה והשלישי שנים עשר וימשכו בזה הדרך עד שבעה מספרים | ||
| sum/sum of square numbers | 1-10 | קצת_מענייני_חכמת_המספר#EiRm | To know the squares of the natural numbers [that are set] in succession until whichever number you wish.
: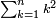 לידע מרובעי המספרים הטבעיי' על הסדר עד איזה מספר שתרצה
|-
|
::Such as from 1 to 10.
::
לידע מרובעי המספרים הטבעיי' על הסדר עד איזה מספר שתרצה
|-
|
::Such as from 1 to 10.
::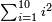 כגון מהא' עד י'
כגון מהא' עד י' | ||
| sum/sum of square numbers | 1-12 | ספר_המספר_/_אברהם_אבן_עזרא#nrny | Another example: how much is the sum of the squares up to 12?
: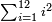 דמיון אחר כמה המחובר מהמרובעים שהם עד סוף י"ב
דמיון אחר כמה המחובר מהמרובעים שהם עד סוף י"ב | ||
| sum/sum of square numbers | 1-7 | ספר_המספר_/_אברהם_אבן_עזרא#ad1Q | Example: we wish to know how much are the squares up to seven?
: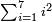 דמיון רצינו לדעת כמה המרובעים שהם עד סוף שבעה
דמיון רצינו לדעת כמה המרובעים שהם עד סוף שבעה | ||
| sum/sum of square numbers | 4-8 | ספר_דיני_ממונות#VWnE | 28) Question: sum up [the squares] from the square of [4] to the square of 8.
: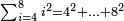 כח) שאלה ואלו אמר קבץ ממרובע ג' עד מרובע ח'
כח) שאלה ואלו אמר קבץ ממרובע ג' עד מרובע ח' | ||
| sum/sum of square numbers | 5-12 | ספר_החשבון_לאל_חצאר#YeOS | If he said: sum from the square of five to the square of twelve.
: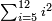 ואם אמר קבץ ממרובע חמשה עד מרובע שנים עשר
ואם אמר קבץ ממרובע חמשה עד מרובע שנים עשר | ||
| sum/sum of square numbers | 1-4 | ספר_החשבון_והמדות#pOla | Example: how much are the squares that are summed from 1 up to 4?
: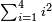 דמיון כמה הם המרובעים המחוברים מא' עד ד'
דמיון כמה הם המרובעים המחוברים מא' עד ד' | ||
| sum/sum of square numbers | 1-5 | ספר_מעשה_חושב#Wmsv | Example: If you want to know [the sum of] the squares of the successive numbers up to five.
::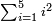 דמיון זה אם רצית לדעת מרובעי המספריםהמספרים: MS P2271 המספר הנמשכים עד חמשה
דמיון זה אם רצית לדעת מרובעי המספריםהמספרים: MS P2271 המספר הנמשכים עד חמשה | ||
| sum/sum of square numbers | 1-5 | ספר_דיני_ממונות#HKRB | 27) Question: if you want to sum up all the squares [of the numbers] from 1 to 25
: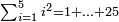 כז) שאלה אם תרצה לחבר כל המרובעים אשר הם מא' עד כ"ה
כז) שאלה אם תרצה לחבר כל המרובעים אשר הם מא' עד כ"ה | ||
| decimal rank/tens | term | מלאכת_המספר#MCe0 | מדרגת העשרות | ||
| decimal rank/tens | term | מלאכת_המספר#Gjcy | עשרות | ||
| decimal rank/tens | term | ספר_המספר_/_אברהם_אבן_עזרא#vPba | העשרות | ||
| decimal rank/tens of thousands | term | ספר_ציפרא#I84k | מעלת הרבבות | ||
| multiplication/times | ד.מ.י./דמיוני | term | ספר_מעשה_חושב#7UWx | דמיוני | |
| multiplication/times | term | תחבולות_המספר#7Pir | פעם | ||
| multiplication/times | term | חשבון_השטחים#A11e | פעמים | ||
| multiplication/times | term | ספר_ציפרא#W5M9 | פעמים | ||
| multiplication/times | כ.פ.ל./כפל | term | חשבון_השטחים#LiAR | כפלי | |
| multiplication/times | term | תחבולות_המספר#KqmN | פעמים | ||
| multiplication/times | ד.מ.י./דמיוני | term | תחבולות_המספר#boLf | דמיוני | |
| multiplication/times | ד.מ.י./דמיוני | term | חשבון_השטחים#WJAs | דמיוני ה | |
| multiplication/times | ד.מ.י./דמיוני | term | ספר_מעשה_חושב#bPoB | דמיוני | |
| multiplication/times | term | תחבולות_המספר#122q | פעמים ה | ||
| multiplication/times | term | תחבולות_המספר#8T1l | דמיוני מה | ||
| multiplication/times | term | תחבולות_המספר#kMd8 | פעמי ה | ||
| multiplication/times | term | תחבולות_המספר#e2Si | דמיוני ה | ||
| multiplication/times | ד.מ.י./דמיוני | term | ספר_האלזיברא#kSY6 | דמיוני ה | |
| addition/to add | ח.ב.ר./חבר | term | תחבולות_המספר#5oer | נחבר אליו | |
| addition/to add | י.ס.פ./הוסיף | term | מלאכת_המספר#0QE7 | נוסיף | |
| addition/to add | ק.ב.צ./קובץ | term | ספר_ג'יבלי_אלמוקבאלא#9zb6 | קובץ עם | |
| addition/to add | ח.ב.ר./חבר | term | תחבולות_המספר#iC9I | תחברם עם | |
| addition/to add | ח.ב.ר./חובר | term | ספר_ג'יבלי_אלמוקבאלא#5gSG | מחובר עם | |
| addition/to add | ק.ב.צ./קובץ | term | ספר_ג'יבלי_אלמוקבאלא#FwN9 | קובצו ל | |
| addition/to add | ק.ב.צ./קובץ | term | ספר_ג'יבלי_אלמוקבאלא#Nbrj | קובצו יחד | |
| addition/to add | י.ס.פ./הוסיף | term | ספר_החשבון_לאל_חצאר#SzjN | הוסף | |
| addition/to add | ח.ב.ר./חבר | term | ספר_המספר_/_אליהו_מזרחי#1ztg | תחבר | |
| addition/to add | ח.ב.ר./חובר | term | ספר_האלזיברא#ulEY | חוברו | |
| addition/to add | ח.ב.ר./חובר | term | ספר_האלזיברא#6rFP | מחברים | |
| addition/to add | ח.ב.ר./נחבר | term | ספר_האלזיברא#NbAk | יחברו | |
| addition/to add | term | ספר_המספר_/_אברהם_אבן_עזרא#vIio | תחבר מספר אל מספר | ||
| addition/to add | י.ס.פ./נוסף | term | ספר_האלזיברא#9qBx | נוסף עליו | |
| addition/to add | ח.ב.ר./חבר | term | חשבון_השטחים#bNiF | תחברם | |
| addition/to add | ח.ב.ר./חבר | term | חשבון_השטחים#qgPe | חברנו | |
| addition/to add | ח.ב.ר./נחבר | term | ספר_מעשה_חושב#QiAO | נחבר עם | |
| addition/to add | ק.ב.צ./התקבץ | term | חשבון_השטחים#p91B | יתקבץ | |
| addition/to add | ח.ב.ר./חבר | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#CYLW | חבר | |
| addition/to add | ק.ב.צ./קובץ | term | חשבון_השטחים#3XM6 | יקובץ | |
| addition/to add | ק.ב.צ./קובץ | term | תחבולות_המספר#IXND | יקובץ | |
| addition/to add | ק.ב.צ./קובץ | term | חשבון_השטחים#bS37 | מקובצים על | |
| addition/to add | ס.פ.י./ספה | term | ספר_יסודי_התבונה_ומגדל_האמונה#REti | לספות מנין אל מנין | |
| addition/to add | ח.ב.ר./חבר | term | עיר_סיחון#vicf | נחבר | |
| addition/to add | ק.ב.צ./קובץ | term | תחבולות_המספר#WYz5 | מקובצים עם | |
| addition/to add | י.ס.פ./הוסיף | term | ספר_הכללים_במספר#xJzM | תוסיף עליו | |
| addition/to add | ח.ב.ר./מחובר | term | חשבון_השטחים#TLFY | מחוברים עם | |
| addition/to add | י.ס.פ./הוסיף | term | ספר_מעשה_חושב#sRFw | הוסיף | |
| addition/to add | ז.ר.ק./זרק | term | ספר_ציפרא#zhZv | זרקתי | |
| addition/to add | ח.ב.ר./חובר | term | חשבון_השטחים#ycQq | יחובר | |
| addition/to add | term | Arithmetic_Textbook_by_Meir_Shapira#gFRx | לחבר | ||
| addition/to add | צ.ר.פ./צרף | term | ספר_הכללים_במספר#LVqT | צרף | |
| addition/to add | א.ס.פ./אסף | term | ספר_הכללים_במספר#0AVj | אסוף עם | |
| addition/to add | ח.ב.ר./חבר | term | עיר_סיחון#m6K8 | נחברם | |
| addition/to add | י.ס.פ./התוסף | term | חשבון_השטחים#4ANA | יתוסף על | |
| addition/to add | י.ס.פ./הוסיף | term | עיר_סיחון#uiMr | נוסיף | |
| addition/to add | צ.ר.פ./צרף | term | ספר_הכללים_במספר#5dOg | צרף כולם | |
| addition/to add | כ.ל.ל./כלל | term | ספר_ציפרא#DAsZ | כללם יחד | |
| addition/to add | א.ס.פ./אסף | term | ספר_הכללים_במספר#7LIm | אסוף | |
| addition/to add | צ.ר.פ./צרף | term | ספר_ציפרא#GrJ7 | צרוף | |
| addition/to add | ק.ב.צ./קבץ | term | Anonymous#Mgyh | מקבץ | |
| addition/to add | ק.ב.צ./קבץ | term | חשבון_השטחים#Jc8x | קבצנוהו | |
| addition/to add | י.ס.פ./הוסיף | term | ספר_ציפרא#PctD | נוסיף | |
| addition/to add | ק.ב.צ./קבץ | term | חשבון_השטחים#tf9m | תקבצם | |
| addition/to add | ק.ב.צ./קבץ | term | מלאכת_המספר#Ff8O | נקבץ | |
| addition/to add | ק.ב.צ./קבץ | term | מלאכת_המספר#ZluY | נקבץ | |
| addition/to add | ק.ב.צ./קבץ | term | תחבולות_המספר#E3eY | תקבץ עם ה | |
| addition/to add | ק.ב.צ./קבץ | term | עיר_סיחון#feiE | יקבץ | |
| addition/to add | י.ס.פ./הוסיף | term | Anonymous#ghsv | הוסף עליו | |
| addition/to add | י.ס.פ./הוסיף | term | Anonymous#3Bta | הוסף עליהם | |
| addition/to add | ק.ב.צ./קבץ | term | ספר_ג'יבלי_אלמוקבאלא#6iBe | קבצהו עם | |
| addition/to add | י.ס.פ./הוסיף | term | ספר_הכללים_במספר#NQJm | נוסיף על | |
| addition/to add | ח.ב.ר./חבר | term | ספר_ציפרא#W4ax | תחבר | |
| addition/to add | י.ס.פ./הוסיף | term | תחבולות_המספר#rbV4 | יוסיף | |
| addition/to add | צ.ר.פ./צרף | term | ספר_עיון_העקרים_לחשבון_ההנדיים#qdsw | נצרפם ל | |
| addition/to add | ק.ב.צ./קבץ | term | ספר_ג'יבלי_אלמוקבאלא#YVkR | קבץ יחד | |
| addition/to add | שם | term | ספר_הכללים_במספר#pmlr | נשים עמהם | |
| addition/to add | ק.ב.צ./קבץ | term | ספר_מעשה_חושב#kxdw | קבצנו זה כלו | |
| addition/to add | ח.ב.ר./חבר | term | ספר_הכללים_במספר#47QY | חבר עליהם | |
| addition/to add | ק.ב.צ./קבץ | term | ספר_מעשה_חושב#RmxC | קבצנו | |
| addition/to add | ח.ב.ר./חבר | term | ספר_הכללים_במספר#fIwp | חברם יחד | |
| addition/to add | ק.ב.צ./קבץ | term | ספר_החשבון_והמדות#kqZX | קבצנו אותם | |
| addition/to add | ק.ב.צ./קבץ | term | קצור_המספר#YXyp | לקבץ | |
| addition/to add | י.ס.פ./הוסיף | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#PPaM | נוסיף עליהם | |
| addition/to add | ח.ב.ר./חבר | term | ספר_מעשה_חושב#G6Oa | חברנו | |
| addition/to add | ח.ב.ר./חבר | term | ספר_מעשה_חושב#3R8x | חבר | |
| addition/to add | י.ס.פ./הוסיף | term | עיר_סיחון#uPja | נוסיף | |
| addition/to add | י.ס.פ./הוסיף | term | חשבון_השטחים#Yepk | יוסיפו | |
| addition/to add | ק.ב.צ./קבץ | term | קצור_המספר#AfJh | תקבצם עם ה | |
| addition/to add | ק.ב.צ./התקבץ | term | תחבולות_המספר#b8IK | יתקבצו אלו עם אלו | |
| addition/to add | ק.ב.צ./קבץ | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#B7vU | תקבץ מהם | |
| addition/to add | ק.ב.צ./התקבץ | term | תחבולות_המספר#jloK | התקבץ מהכל | |
| addition/to add | ק.ב.צ./התקבץ | term | תחבולות_המספר#JEm6 | יתקבץ | |
| addition/to add | ד.ב.ק./דובק | term | תחבולות_המספר#i0Dg | מדובקים | |
| addition/to add | ק.ב.צ./קבץ | term | תחבולות_המספר#ADZM | קבצנום עם ה | |
| addition/to add | א.ס.פ./נאסף | term | תחבולות_המספר#bAsG | להאסף יחד | |
| addition/to add | ח.ב.ר./חובר | term | בר_נותן_טעם#Fg9j | מחובר עם | |
| addition/to add | ק.ב.צ./קבץ | term | עיר_סיחון#gkYV | נקבץ | |
| addition/to add | ק.ב.צ./קבץ | term | ספר_החשבון_לאל_חצאר#CPUU | קבץ | |
| addition/to add | י.ס.פ./נוסף | term | תחבולות_המספר#qo0g | נוספים על | |
| addition/to add | ק.ב.צ./קבץ | term | ספר_דיני_ממונות#ZDXA | נקבץ | |
| addition/to add | ק.ב.צ./קבץ | term | ספר_המספר_/_אליהו_מזרחי#LgEl | נקבץ | |
| addition/to add | ח.ב.ר./חבר | term | ספר_ג'יבלי_אלמוקבאלא#tJmU | חבר | |
| addition/to add | י.ס.פ./נוסף | term | תחבולות_המספר#TGnE | נוסף ב | |
| addition/to add | ק.ב.צ./קובץ | term | בר_נותן_טעם#6Saf | המקובץ מ | |
| addition/to add | ח.ב.ר./חבר | term | ספר_ג'יבלי_אלמוקבאלא#2ZJa | בחבר יחד | |
| addition/to add | ח.ב.ר./חבר | term | קצור_המספר#QRmZ | נחבר אליהם ה | |
| addition/to add | ח.ב.ר./חבר | term | ספר_ג'יבלי_אלמוקבאלא#3DfE | חברם יחד | |
| addition/to add | ח.ב.ר./חבר | term | ספר_אגריס#4Gks | חבר | |
| addition/to add | term | ספר_ציפרא#RBW2 | מצורף ל | ||
| addition/to add | ח.ב.ר./חבר | term | קצור_המספר#j352 | תחבר אל ה | |
| addition/to add | י.ס.פ./מוסף | term | חשבון_השטחים#jBWq | מוסף עליו | |
| addition/to add | צ.ר.פ./צרף | term | ספר_אגריס#UT9N | צרוף | |
| addition/to add | י.ס.פ./נוסף | term | חשבון_השטחים#ATZ7 | נוספים על | |
| addition/to add | ח.ב.ר./חבר | term | ספר_ג'יבלי_אלמוקבאלא#1jU5 | תחבר אל | |
| addition/to add | י.ס.פ./נוסף | term | חשבון_השטחים#Yhf0 | נוסף ב | |
| addition/to add | ח.ב.ר./חבר | term | ספר_ג'יבלי_אלמוקבאלא#nw9m | בחבר אליו | |
| addition/to add | ח.ב.ר./חבר | term | ספר_ג'יבלי_אלמוקבאלא#tvJI | חברם על | |
| addition/to add | ח.ב.ר./חבר | term | ספר_עיון_העקרים_לחשבון_ההנדיים#InHw | נחבר | |
| addition/to add | י.ס.פ./הוסיף | term | ספר_עיון_העקרים_לחשבון_ההנדיים#iDI8 | נוסיף | |
| addition/to add | י.ס.פ./הוסיף | term | קצור_המספר#fNu8 | בהוסיפנו | |
| addition/to add | י.ס.פ./הוסיף | term | קצור_המספר#74BW | נוסיף | |
| addition/to add | ק.ב.צ./נקבץ | term | ספר_המספר_/_אליהו_מזרחי#73tH | נקבצו | |
| addition/to add | י.ס.פ./נתוסף | term | בר_נותן_טעם#mjLV | נתוספו | |
| addition/to add | י.ס.פ./התוסף | term | בר_נותן_טעם#g91P | יתוסף | |
| addition/to add | י.ס.פ./נתוסף | term | בר_נותן_טעם#ELza | ניתוסף | |
| addition/to add | י.ס.פ./נתוסף | term | בר_נותן_טעם#cJCp | נתוסף | |
| addition/to add | ח.ב.ר./התחבר | term | בר_נותן_טעם#PVjr | המתחבר | |
| addition/to add | ח.ב.ר./חובר | term | בר_נותן_טעם#2zri | מחוברות יחד | |
| addition/to add | ק.ב.צ./קובץ | term | ספר_מעשה_חושב#3Lvs | מקובצים | |
| addition/to add | ח.ב.ר./חבר | term | ספר_דיני_ממונות#aITu | נחבר | |
| addition/to add | א.ס.פ./אסף | term | תחבולות_המספר#fDEF | אספנו יחד | |
| addition/to add | ח.ב.ר./התחבר | term | חשבון_השטחים#ZNEK | יתחברו אלו עם אלו | |
| addition/to add | ח.ב.ר./נתחבר | term | Anonymous#VXAj | נתחבר | |
| addition/to add | ח.ב.ר./נחבר | term | Anonymous#PfY5 | הנחברים | |
| addition/to add | ק.ב.צ./התקבץ | term | Anonymous#exwB | בהתקבצם | |
| addition/to add | ח.ב.ר./התחבר | term | Anonymous#bTMn | יתחבר | |
| addition/to add | ח.ב.ר./חובר | term | Anonymous#EL9d | יחובר | |
| addition/to add | ח.ב.ר./התחבר | term | Anonymous#FtVj | יתחברו עם | |
| addition/to add | י.ס.פ./הוסיף | term | ספר_החשבון_והמדות#GTDu | הוספנו | |
| addition/to add | י.ס.פ./הוסיף | term | ספר_החשבון_והמדות#kYgo | הוספנום על | |
| addition/to add | ח.ב.ר./חבר | term | ספר_החשבון_והמדות#mWwI | חברהו עם | |
| addition/to add | ח.ב.ר./חבר | term | ספר_החשבון_לאל_חצאר#yB8A | חבר | |
| addition/to add | ח.ב.ר./התחבר | term | ספר_ג'יבלי_אלמוקבאלא#wORm | יתחבר עם | |
| addition/to add | ח.ב.ר./חבר | term | ספר_החשבון_והמדות#I96y | חברנו אותם | |
| addition/to add | י.ס.פ./הוסיף | term | מלאכת_המספר#dLb7 | הוספנום | |
| addition/to add | ח.ב.ר./התחבר | term | ספר_ג'יבלי_אלמוקבאלא#C3R4 | בהתחברו עם | |
| addition/to add | י.ס.פ./נוסף | term | ספר_ג'יבלי_אלמוקבאלא#joz1 | נוספו ה | |
| addition/to add | י.ס.פ./נוסף | term | ספר_ג'יבלי_אלמוקבאלא#Or7I | נוסף על | |
| addition/to add | Takmila_fi_al-Hisāb_-_Arabic_in_Hebrew_Characters#0V7x | תזיד | |||
| addition/to add | ח.ב.ר./חובר | term | ספר_ג'יבלי_אלמוקבאלא#P8Kr | יחובר ל | |
| addition/to add | ח.ב.ר./חובר | term | ספר_ג'יבלי_אלמוקבאלא#Zy0c | חוברו יחד | |
| addition/to add | ח.ב.ר./חובר | term | ספר_ג'יבלי_אלמוקבאלא#nEt8 | מחוברי' יחד | |
| addition/to add | ק.ב.צ./נקבץ | term | ספר_ג'יבלי_אלמוקבאלא#l0Bm | נקבצים | |
| addition/to add | י.ס.פ./נוסף | term | ספר_ג'יבלי_אלמוקבאלא#Pza2 | נוסף עם | |
| addition/to add | י.ס.פ./נוסף | term | ספר_ג'יבלי_אלמוקבאלא#SkZ4 | הנוספים יחד | |
| addition/to add | ח.ב.ר./חבר | term | מלאכת_המספר#x2wE | נחבר | |
| addition/to add | ק.ב.צ./קובץ | term | ספר_ג'יבלי_אלמוקבאלא#wUQf | מקובץ עם | |
| addition/to add | ח.ב.ר./חובר | term | ספר_מעשה_חושב#jbbo | חובר עמו | |
| addition/to add | י.ס.פ./נוסף | term | ספר_מעשה_חושב#6di8 | נוסף עליו | |
| addition/to add | ק.ב.צ./התקבץ | term | עיר_סיחון#WrFA | יתקבצו | |
| addition/to add | ק.ב.צ./קובץ | term | ספר_ג'יבלי_אלמוקבאלא#7s8E | מקובצי' יחד | |
| addition/to add | י.ס.פ./הוסיף | term | חשבון_השטחים#ufnE | הוסיף | |
| addition/to add | י.ס.פ./הוסיף | term | חשבון_השטחים#PIWL | נוסיף | |
| addition/to add | ח.ב.ר./נתחבר | term | ספר_מעשה_חושב#dV6d | נתחבר עם | |
| addition/to add | צ.ר.פ./צרף | term | ספר_החשבון_לאל_חצאר#9E5f | תצרפם | |
| addition/to add | ח.ב.ר./התחבר | term | ספר_מעשה_חושב#7xxY | התחבר זה כלו | |
| addition/to add | י.ס.פ./הוסיף | term | ספר_המספר_/_אליהו_מזרחי#w4kH | הוסף עליו | |
| addition/to add | ק.ב.צ./התקבץ | term | ספר_מעשה_חושב#sBDk | התקבץ זה כלו | |
| addition/to add | י.ס.פ./הוסיף | term | ספר_ג'יבלי_אלמוקבאלא#zdWP | הוסיפם על | |
| addition/to add | ח.ב.ר./נחבר | term | ספר_מעשה_חושב#MD4Z | נחברים | |
| addition/to add | י.ס.פ./הוסיף | term | בר_נותן_טעם#fbiZ | נוסיף עליהם | |
| addition/to add | י.ס.פ./הוסיף | term | בר_נותן_טעם#2EI3 | הוסיף | |
| addition/to add | י.ס.פ./הוסיף | term | ספר_ג'יבלי_אלמוקבאלא#TtZP | בהוסיפו על | |
| addition/to add | י.ס.פ./הוסיף | term | ספר_ג'יבלי_אלמוקבאלא#2UjC | תוסיף על | |
| addition/to add | ק.ב.צ./קובץ | term | מלאכת_המספר#9dRP | יקובצו | |
| addition/to add | ח.ב.ר./חובר | term | מלאכת_המספר#5BYq | מחובר | |
| addition/to add | ק.ב.צ./קובץ | term | מלאכת_המספר#vpyY | מקובץ | |
| addition/to add | ק.ב.צ./קובץ | term | ספר_מעשה_חושב#c0wk | מקובץ עם | |
| addition/to add | ק.ב.צ./נקבץ | term | ספר_מעשה_חושב#aLRk | הנקבץ | |
| addition/to add | ק.ב.צ./נקבץ | term | אגרת_המספר#g9L0 | הקבצן | |
| addition/to add | ח.ב.ר./התחבר | term | אגרת_המספר#qc6v | יתחבר | |
| addition/to add | ח.ב.ר./התחבר | term | אגרת_המספר#laVE | התחברם | |
| addition/to add | ח.ב.ר./חובר | term | ספר_מעשה_חושב#BfTD | מחובר עם | |
| addition/to add | ח.ב.ר./חבר | term | מלאכת_המספר#MKG7 | נחברם | |
| addition/to add | ק.ב.צ./התקבץ | term | אגרת_המספר#4f0z | התקבצם | |
| addition/to add | י.ס.פ./נוסף | term | ספר_עיון_העקרים_לחשבון_ההנדיים#Kp3e | נוספה | |
| addition/to add | ח.ב.ר./חבר | term | בר_נותן_טעם#sFLm | חברת אותם | |
| addition/to add | ח.ב.ר./חבר | term | בר_נותן_טעם#8h5b | תחבר | |
| addition/to add | ח.ב.ר./חבר | term | Anonymous#aTlG | חבר | |
| addition/to add | ק.ב.צ./התקבץ | term | ספר_החשבון_והמדות#tLsc | התקבצו | |
| addition/to add | ח.ב.ר./חובר | term | ספר_החשבון_והמדות#Ycx9 | יחוברו | |
| addition/to add | ח.ב.ר./חבר | term | ספר_האלזיברא#bKYA | חבר אליו | |
| addition/to add | י.ס.פ./הוסיף | term | ספר_האלזיברא#V5jy | הוסיפהו על | |
| addition/to add | ק.ב.צ./קובץ | term | ספר_החשבון_והמדות#Fg96 | מקובצים | |
| addition/to add | ק.ב.צ./קובץ | term | ספר_החשבון_והמדות#GFVv | והכל מקובצים | |
| addition/to add | י.ס.פ./הוסיף | term | תחבולות_המספר#OfGE | תוסיף ה | |
| addition/to add | י.ס.פ./הוסיף | term | תחבולות_המספר#nC0o | הוסיף ה | |
| addition/to add | צ.ר.פ./הצטרף | term | ספר_ציפרא#8C34 | תצטרף | |
| addition/to add | ח.ב.ר./חבר | term | Anonymous#cO31 | תחבר | |
| approximate/to approximate | ק.ר.ב./התקרב | term | בר_נותן_טעם#MDGB | יתקרב אל האמת | |
| approximate/to approximate | ד.ק.ד.ק./דקדק | term | עיר_סיחון#kaxo | לדקדקה | |
| approximate/to approximate | ק.ר.ב./התקרב | term | בר_נותן_טעם#Kx0D | יתקרב מאד מאד | |
| approximate/to approximate | ק.ר.ב./קרב | term | קצור_המספר#bqXY | נקרב | |
| approximate/to approximate | ת.ק.נ./תקן | term | Anonymous#mYU2 | תקנהו | |
| approximate/to approximate | ת.ק.נ./תקן | term | Anonymous#o2Bz | תקן אותו | |
| approximate/to approximate | ק.ר.ב./התקרב | term | בר_נותן_טעם#Y7il | יתקרב לנשאל | |
| approximate/to approximate | ד.ק.ד.ק./דקדק | term | עיר_סיחון#XsfT | לדקדק | |
| approximate/to approximate | ק.ר.ב./התקרב | term | בר_נותן_טעם#05Nl | מתקרב יותר | |
| approximate/to approximate | ק.ר.ב./התקרב | term | בר_נותן_טעם#blCK | להתקרב עוד אל השרש | |
| approximate/to approximate | ק.ר.ב./התקרב | term | בר_נותן_טעם#Odqz | נתקרב יותר אל האמת | |
| integer/to be an integer | נ.ק.פ./מקיף | term | ספר_מעשה_חושב#GS9z | מקיף בשלמים | |
| integer/to be an integer | נ.ק.פ./מקיף | term | ספר_מעשה_חושב#j2AE | המקיפים בשלמים | |
| equal/to be equal to | ש.ו.ה./שוה | term | חשבון_השטחים#YPlM | ישוו | |
| equal/to be equal to | ש.ו.ה./שוה | term | ספר_האלזיברא#rAGC | ישוה ל | |
| equal/to be equal to | ש.ו.ה./שוה | term | ספר_ג'יבלי_אלמוקבאלא#1WQx | שוים ל | |
| equal/to be equal to | ש.ו.ה./שוה | term | ספר_האלזיברא#oCp6 | שוה ל | |
| equal/to be equal to | ש.ו.ה./השתוה | term | חשבון_השטחים#PacO | ישתוו | |
| equal/to be equal to | ש.ו.ה./השתוה | term | קצור_המספר#koK9 | ישתוה | |
| equal/to be equal to | ש.ו.ה./שוה | term | תחבולות_המספר#pKg9 | ישוו ל | |
| equal/to be equal to | ש.ו.ה./שוה | term | תחבולות_המספר#baOU | ישוה ל | |
| equal/to be equal to | ש.ו.ה./שוה | term | ספר_האלזיברא#X8k9 | יהיו שוים ל | |
| equal/to be equal to | ש.ו.ה./השתוה | term | תחבולות_המספר#qEnf | השתוו | |
| equal/to be equal to | ש.ו.ה./השתוה | term | קצור_המספר#Twb9 | ישתוו ל | |
| equal/to be equal to | ש.ו.ה./שוה | term | ספר_ג'יבלי_אלמוקבאלא#a8Fj | ישוו אל | |
| equal/to be equal to | ש.ו.ה./שוה | term | חשבון_השטחים#qoFg | ישוה | |
| equal/to be equal to | ש.ו.ה./שוה | term | מלאכת_המספר#1ULy | תהיה שוה ל | |
| equal/to be equal to | ש.ו.ה./שוה | term | ספר_ג'יבלי_אלמוקבאלא#2p0q | שוה | |
| equal/to be equal to | ש.ו.ה./שוה | term | ספר_האלזיברא#hkKx | יהיה שוה ל | |
| equal/to be equal to | ש.ו.ה./שוה | term | ספר_ג'יבלי_אלמוקבאלא#V3XA | יבא לשוות ה | |
| equal/to be equal to | ש.ו.ה./השתוה | term | חשבון_השטחים#sGN6 | השתוו | |
| calculation/to be worth | ש.ו.ה./שוה | term | קצור_המספר#7U2Y | ישוה | |
| calculation/to be worth | ש.ו.ה./שוה | term | קצור_המספר#zbKO | שוה | |
| calculation/to calculate | ח.ש.ב./חשב | term | קצור_המספר#Ysl7 | נחשב | |
| calculation/to calculate | ח.ש.ב./חשב | term | חשבון_השטחים#jk4s | תחשבה | |
| calculation/to calculate | י.צ.א./הוציא | term | חשבון_השטחים#xhpA | נוציאהו | |
| calculation/to calculate | ח.ש.ב./חשב | term | ספר_האלזיברא#NOzT | לחשוב | |
| calculation/to calculate | ח.ש.ב./חשב | term | עיר_סיחון#0uI3 | נחשוב | |
| calculation/to calculate | ח.ש.ב./חשב | term | עיר_סיחון#c5VF | נחשבם | |
| calculation/to calculate | ח.ש.ב./התחשב | term | Anonymous#b1kl | מתחשב | |
| calculation/to calculate | ח.ש.ב./חשב | term | ספר_ג'יבלי_אלמוקבאלא#fUWL | יחשבו | |
| casting out/to cast out | י.צ.א./יצא | term | בר_נותן_טעם#jc6j | יצא הכל לשביעיות | |
| casting out/to cast out | ש.ל.כ./השליך | term | ספר_החשבון_לאל_חצאר#3i8Q | השליכהו שבעה שבעה | |
| casting out/to cast out | ה.ל.כ./הלך | term | קצור_המספר#oFgG | הלכו להם | |
| casting out/to cast out | ש.ל.כ./מושלך | term | ספר_החשבון_לאל_חצאר#Smf0 | מושלך | |
| casting out/to cast out | י.צ.א./יצא | term | בר_נותן_טעם#sB7E | יצא הכל לט' ט | |
| casting out/to cast out | י.צ.א./יצא | term | בר_נותן_טעם#D5Ek | יצא החשבון לט' ט' | |
| casting out/to cast out | ש.ל.כ./השליך | term | ספר_ציפרא#9i9c | השלך ט"ט | |
| casting out/to cast out | ה.ל.כ./הלך | term | קצור_המספר#JW01 | הלכו להם | |
| casting out/to cast out | ש.ל.כ./השליך | term | ספר_החשבון_לאל_חצאר#IrwN | השליכהו שמנה שמנה | |
| casting out/to cast out | ס.ו.ר./הסיר | term | אגרת_המספר#hnL3 | תסיר ממנו כל תשעה | |
| casting out/to cast out | ש.ל.כ./השליך | term | ספר_דיני_ממונות#KfA4 | השלך כל התשיעיות | |
| casting out/to cast out | ג.ר.ע./הוגרע | term | אגרת_המספר#H5UM | מוגרעים שמנה שמנה | |
| casting out/to cast out | ש.ל.כ./נשלך | term | ספר_החשבון_לאל_חצאר#7sWe | נשלכים | |
| casting out/to cast out | ג.ר.ע./הוגרע | term | אגרת_המספר#9HDn | מוגרעים | |
| casting out/to cast out | ש.ל.כ./השליך | term | ספר_החשבון_לאל_חצאר#nNPq | השלך | |
| casting out/to cast out | ח.ס.ר./חסר | term | בר_נותן_טעם#LIme | חסר כל ט' ט' | |
| casting out/to cast out | ש.ל.כ./השליך | term | ספר_החשבון_והמדות#QkW0 | תשליכם תשעה תשעה | |
| casting out/to cast out | י.צ.א./הוציא | term | בר_נותן_טעם#tDVX | הוצא הי"ג י"ג | |
| casting out/to cast out | ס.ו.ר./הסיר | term | אגרת_המספר#jSL4 | תסיר כל ז' | |
| casting out/to cast out | ש.ל.כ./נשלך | term | ספר_החשבון_לאל_חצאר#JbiL | נשלכת | |
| casting out/to cast out | י.צ.א./יצא | term | בר_נותן_טעם#293n | יצא הכל | |
| casting out/to cast out | י.צ.א./יצא ט"ט | term | Anonymous#CsCl | יצא כלו ט'ט' | |
| casting out/to cast out | ש.ק.ל./שקל במאזני תשעה | term | Anonymous#uKUT | שקלנוהו במאזני ט' | |
| casting out/to cast out | ש.ל.כ./הושלך | term | ספר_החשבון_לאל_חצאר#Gqbg | יושלך | |
| casting out/to cast out | ש.ל.כ./הושלך | term | ספר_החשבון_לאל_חצאר#6Cbc | הושלך | |
| casting out/to cast out | נ.פ.ל./הפלה | term | קצור_המספר#rbnf | הפלת | |
| casting out/to cast out | ש.ל.כ./השליך | term | קצור_המספר#N0jH | השליך | |
| casting out/to cast out | נ.פ.ל./הפלה | term | קצור_המספר#2BcF | הפלת | |
| casting out/to cast out | ש.ל.כ./השליך | term | בר_נותן_טעם#yHcy | השלך לעולם הז' ז' | |
| casting out/to cast out | ש.ל.כ./השליך | term | בר_נותן_טעם#07O7 | השלך אותו ח' ח' | |
| casting out/to cast out | ש.ל.כ./השליך | term | קצור_המספר#Ij5z | השליך | |
| casting out/to cast out | ש.ק.ל./שקל במאזני תשעה | term | Anonymous#XFyB | שקלו במאזני תשעה | |
| casting out/to cast out | ש.ל.כ./הושלך | term | בר_נותן_טעם#DNT7 | יושלך לי"א י"א | |
| casting out/to cast out | ש.ל.כ./הושלך | term | בר_נותן_טעם#Cxib | יושלך כלו י"א י"א | |
| casting out/to cast out | ש.ל.כ./מושלך | term | ספר_החשבון_לאל_חצאר#N2cf | מושלכים | |
| casting out/to cast out | ש.ל.כ./נשלך | term | ספר_החשבון_לאל_חצאר#O5pZ | נשלך | |
| change of denominator/to change denominator | מ.ו.ר./המיר | term | קצור_המספר#VL41 | נמיר | |
| change of denominator/to change denominator | פ.ר.ט./פרט | term | ספר_החשבון_לאל_חצאר#mqJ3 | נפרוט | |
| change of denominator/to change denominator | פ.ר.ט./פרט | term | ספר_החשבון_לאל_חצאר#1o0K | תפרטם | |
| change of denominator/to change denominator | פ.ר.ט./מפורט | term | ספר_החשבון_לאל_חצאר#kPHm | מפורט | |
| change of denominator/to change denominator | ח.ז.ר./החזיר | term | בר_נותן_טעם#4lUo | להחזירם | |
| change of denominator/to change denominator | נ.ת.כ./התיך | term | אגרת_המספר#fUXi | תתיך | |
| change of denominator/to change denominator | מ.ו.ר./המיר | term | קצור_המספר#tCoy | נמיר | |
| check/to check | ש.ק.ל./שקל | term | ספר_ציפרא#QPGO | נשקול | |
| check/to check | ש.ק.ל./שקל | term | ספר_ציפרא#YQDx | תשקול | |
| conversion/to convert | ש.ו.ב./שב | term | מלאכת_המספר#toWc | ישובו | |
| conversion/to convert | ש.ו.ב./השיב | term | ספר_עיון_העקרים_לחשבון_ההנדיים#T1ts | להשיבם ל | |
| conversion/to convert | ש.ו.ב./השיב | term | עיר_סיחון#NmWX | נשיב | |
| conversion/to convert | ש.ו.ב./השיב | term | עיר_סיחון#HTld | נשיב | |
| counting/to count | מ.נ.י./מנה | term | קצור_המספר#w006 | נמנה | |
| counting/to count | מ.נ.י./מנה | term | קצור_המספר#tcEX | למנות | |
| counting/to count | מ.נ.י./מנה | term | חשבון_השטחים#gUTt | ימנהו ה | |
| counting/to count | מ.נ.י./מנה | term | תחבולות_המספר#eFA0 | ימנהו ה | |
| counting/to count | מ.נ.י./מנה | term | תחבולות_המספר#zsPl | ימנה ל | |
| counting/to count | מ.נ.י./מנה | term | חשבון_השטחים#KaXj | ימנה | |
| cross-multiplication/to cross-multiply | נ.כ.י./הכה אלכסונות | term | קצת_מענייני_חכמת_המספר#9prx | תכה האלכסון | |
| cross-multiplication/to cross-multiply | נ.כ.י./הכה אלכסונות | term | קצת_מענייני_חכמת_המספר#PyIk | נכה האלכסונות | |
| cross-multiplication/to cross-multiply | נ.כ.י./הכה אלכסונות | term | קצת_מענייני_חכמת_המספר#Cj00 | תכה אלכסונות | |
| exponentiation/to cube | ע.ק.ב./באופן מעוקב | term | מלאכת_המספר#D8vH | נכה הב' באופן מעוקב | |
| exponentiation/to cube | ע.ק.ב./באופן מעוקב | term | מלאכת_המספר#m7gc | מוכה בעצמו באופן מעוקב | |
| decomposing to a fraction/to decompose to a fraction | פ.ז.ר./פזר | term | ספר_עיון_העקרים_לחשבון_ההנדיים#2ml9 | נפזרנו ל | |
| decomposing to a fraction/to decompose to a fraction | ע.ש.ה./עשה | term | קצור_המספר#yJDs | עשינו אותם | |
| decomposing to a fraction/to decompose to a fraction | ש.ו.ב./השיב | term | ספר_החשבון_לאל_חצאר#n6Wi | השיב | |
| decomposing to a fraction/to decompose to a fraction | ש.ו.ב./השיב | term | עיר_סיחון#QhxO | נשיב | |
| decomposing to a fraction/to decompose to a fraction | נ.ת.כ./התיך | term | ספר_החשבון_לאל_חצאר#iTfx | תתיך | |
| decomposing to a fraction/to decompose to a fraction | ש.ו.ב./השיב | term | עיר_סיחון#N2KM | נשיבם | |
| decomposing to a fraction/to decompose to a fraction | נ.ת.כ./התיך | term | עיר_סיחון#6FfN | נתיך | |
| decomposing to a fraction/to decompose to a fraction | נ.ת.כ./התיך | term | קצור_המספר#4PHG | נתיכהו ל | |
| decomposing to a fraction/to decompose to a fraction | נ.ת.כ./התיך | term | קצור_המספר#TzKD | נתיך אותו ל | |
| decomposing to a fraction/to decompose to a fraction | ש.ו.ב./השיב | term | ספר_יסודי_התבונה_ומגדל_האמונה#t6ao | להשיב מנין אל מנין | |
| decomposing to a fraction/to decompose to a fraction | ש.ו.ב./שב | term | ספר_עיון_העקרים_לחשבון_ההנדיים#XGfg | שבו | |
| decomposing to a fraction/to decompose to a fraction | ע.ש.ה./עשה | term | קצור_המספר#lnq2 | נעשה ה | |
| decreasing/to decrease | פ.ח.ת./פחת | term | Anonymous#vany | פחות פוחת והולך | |
| decreasing/to decrease | ח.ס.ר./חסר | term | קצור_המספר#q1nO | חסרים ה | |
| decreasing/to decrease | ח.ס.ר./חסר | term | קצור_המספר#0436 | יחסרו | |
| decreasing/to decrease | פ.ח.ת./פחת | term | Anonymous#kxA9 | פוחת | |
| denomination/to denominate | ק.ר.א./קרא שם | term | ספר_החשבון_לאל_חצאר#oYqA | תקרא שם | |
| denomination/to denominate | ק.ר.א./קרא שם | term | ספר_החשבון_לאל_חצאר#77NB | קרא שם | |
| division/to divide | ח.ל.ק./חלק | term | ספר_ג'יבלי_אלמוקבאלא#Nfe3 | חלקהו ב | |
| division/to divide | ח.ל.ק./התחלק | term | ספר_מעשה_חושב#XETc | התחלקו | |
| division/to divide | ח.ל.ק./נחלק | term | ספר_ג'יבלי_אלמוקבאלא#Orfk | נחלק ב | |
| division/to divide | מ.נ.י./מנה | term | ספר_יסודי_התבונה_ומגדל_האמונה#s1jI | מונה את | |
| division/to divide | ח.ל.ק./חלק | term | ספר_יסודי_התבונה_ומגדל_האמונה#K1Vd | מחלק | |
| division/to divide | ב.ק.ע./הבקיע | term | ספר_ג'יבלי_אלמוקבאלא#1It4 | להבקיע | |
| division/to divide | ב.ק.ע./בקע | term | ספר_ג'יבלי_אלמוקבאלא#mVRl | בבקעו | |
| division/to divide | ב.ק.ע./בקע | term | ספר_ג'יבלי_אלמוקבאלא#Kn1N | לבקע | |
| division/to divide | ח.ל.ק./נחלק | term | חשבון_השטחים#zejH | נחלק | |
| division/to divide | ח.ל.ק./חלק | term | ספר_ג'יבלי_אלמוקבאלא#5Goa | חלקנו על | |
| division/to divide | ח.ל.ק./חלק | term | מלאכת_המספר#lqJn | נחלק | |
| division/to divide | ח.ל.ק./חלק | term | קצור_המספר#w7dv | לחלק | |
| division/to divide | ח.ל.ק./חלק | term | ספר_אגריס#k7XL | חלקם ב | |
| division/to divide | ח.ל.ק./חלק | term | מלאכת_המספר#ECP2 | נחלקם | |
| division/to divide | ח.ל.ק./חלק | term | ספר_מעשה_חושב#7JWG | חלקנו | |
| division/to divide | ח.ל.ק./חלק | term | ספר_האלזיברא#wzno | תחלק ה | |
| division/to divide | ח.ל.ק./חלק | term | ספר_מעשה_חושב#OlUF | תחלוק | |
| division/to divide | ח.ל.ק./נחלק | term | תחבולות_המספר#YCAx | יחלק אחד מהם על האחר | |
| division/to divide | ח.ל.ק./חלק | term | ספר_האלזיברא#gsye | תחלק אליו | |
| division/to divide | ח.ל.ק./חולק | term | תחבולות_המספר#PxDD | מחולק על | |
| division/to divide | ח.ל.ק./חלק | term | ספר_ג'יבלי_אלמוקבאלא#nCpc | בחלקך | |
| division/to divide | ח.ל.ק./נחלק | term | תחבולות_המספר#iB1v | נחלק על | |
| division/to divide | ח.ל.ק./חלק | term | חשבון_השטחים#DIrO | חלקנוהו | |
| division/to divide | ח.ל.ק./התחלק | term | Anonymous#p8BY | יתחלקו עליו | |
| division/to divide | ח.ל.ק./חלק | term | תחבולות_המספר#XtqU | תחלק | |
| division/to divide | ח.ל.ק./חלק | term | קצור_המספר#z4QZ | נחלוק | |
| division/to divide | ח.ל.ק./חולק | term | ספר_האלזיברא#p2Os | חלק | |
| division/to divide | ח.ל.ק./חלק | term | תחבולות_המספר#Ssec | חלקנו | |
| division/to divide | ב.צ.ע./בצע | term | ספר_ג'יבלי_אלמוקבאלא#OTlz | לבצע | |
| division/to divide | ח.ל.ק./נחלק | term | חשבון_השטחים#jYsx | יחלק | |
| division/to divide | ח.ל.ק./חלק | term | ספר_ג'יבלי_אלמוקבאלא#FUXT | בחלקו ב | |
| division/to divide | ח.ל.ק./חלק | term | חשבון_השטחים#JKjD | תחלק | |
| division/to divide | ח.ל.ק./חלק | term | חשבון_השטחים#VS8F | בחלקך | |
| division/to divide | ח.ל.ק./חולק | term | ספר_ג'יבלי_אלמוקבאלא#F78a | תחולק ב | |
| division/to divide | ח.ל.ק./נחלק | term | ספר_ג'יבלי_אלמוקבאלא#rNoY | להחלק על | |
| division/to divide | ח.ל.ק./חולק | term | חשבון_השטחים#l1Xz | מחולק | |
| division/to divide | ח.ל.ק./התחלק | term | חשבון_השטחים#rMai | יתחלקו | |
| division/to divide | term | Arithmetic_Textbook_by_Meir_Shapira#kjW7 | לחלק | ||
| division/to divide | ח.ל.ק./חולק | term | חשבון_השטחים#LBME | חולק | |
| division/to divide | ח.ל.ק./נחלק | term | ספר_ג'יבלי_אלמוקבאלא#ci6L | נחלק על | |
| division/to divide | ח.ל.ק./התחלק | term | Anonymous#FWr3 | יתחלק על | |
| division/to divide | ח.ל.ק./חלק | term | עיר_סיחון#Mgse | חלק | |
| division/to divide | ח.ל.ק./חולק | term | ספר_מעשה_חושב#4uAl | חולק על | |
| division/to divide | ח.ל.ק./התחלק | term | ספר_מעשה_חושב#NDfS | יתחלק | |
| doubling/to double | כ.פ.ל./כפל | term | ספר_האלזיברא#W3QG | כפלת | |
| doubling/to double | כ.פ.ל./כפל | term | תחבולות_המספר#qQ43 | תכפלהו | |
| doubling/to double | כ.פ.ל./כפל | term | ספר_ג'יבלי_אלמוקבאלא#Ln1v | תכפלהו | |
| doubling/to double | כ.פ.ל./כפל | term | ספר_ג'יבלי_אלמוקבאלא#zfVw | כפלהו | |
| doubling/to double | כ.פ.ל./כפל | term | מלאכת_המספר#TSoW | נכפול | |
| doubling/to double | term | ספר_האלזיברא#6Ual | קח שני דמיוניו | ||
| doubling/to double | כ.פ.ל./כפל | term | ספר_מעשה_חושב#vspJ | כפלהו | |
| doubling/to double | כ.פ.ל./כפל | term | מלאכת_המספר#DHAI | נכפלם | |
| doubling/to double | כ.פ.ל./כפל | term | תחבולות_המספר#BSiQ | תכפול | |
| doubling/to double | כ.פ.ל./נכפל | term | מלאכת_המספר#tZOv | נכפל | |
| doubling/to double | כ.פ.ל./כפל | term | ספר_יסודי_התבונה_ומגדל_האמונה#wLYa | כופל אותו | |
| doubling/to double | כ.פ.ל./כפל | term | חשבון_השטחים#R0ee | כפלהו | |
| doubling/to double | כ.פ.ל./כפל | term | חשבון_השטחים#FGpT | תכפול | |
| error of a false position/to err | ט.ע.י./טעה | term | ספר_החשבון_לאל_חצאר#nJub | טעית | |
| calculation/to estimate | ש.ע.ר./שער | term | מלאכת_המספר#cYZh | תשער | |
| excess/to exceed | ע.ד.פ./העדיף | term | תחבולות_המספר#z69a | יעדיפו ה | |
| excess/to exceed | י.ס.פ./הוסיף | term | עיר_סיחון#mYzg | יוסיף ב | |
| excess/to exceed | י.ס.פ./הוסיף | term | Anonymous#j9Nz | יוסיפו | |
| excess/to exceed | ע.ד.פ./העדיף | term | תחבולות_המספר#DjtG | יעדיף על ה | |
| excess/to exceed | term | ספר_ציפרא#3fXQ | יותר על | ||
| excess/to exceed | י.ס.פ./הוסיף | term | Anonymous#8f0E | מוסיף על | |
| excess/to exceed | term | ספר_ציפרא#Qkw0 | למעלה מ | ||
| excess/to exceed | ע.ד.פ./העדיף | term | חשבון_השטחים#03rs | יעדיף | |
| excess/to exceed | י.ס.פ./הוסיף | term | קצור_המספר#e7jH | הוסיף ממנו | |
| excess/to exceed | י.ת.ר./יתר | term | Anonymous#UrqP | יתר עליו | |
| excess/to exceed | י.ס.פ./נוסף | term | Anonymous#gUhh | נוסף | |
| excess/to exceed | ע.ד.פ./העדיף | term | חשבון_השטחים#mKdq | העדיף | |
| excess/to exceed | י.ס.פ./הוסיף | term | ספר_מעשה_חושב#Kj4g | מוסיף על | |
| excess/to exceed | ע.ד.פ./העדיף | term | ספר_ג'יבלי_אלמוקבאלא#x2qf | יעדיף | |
| excess/to exceed | י.ס.פ./הוסיף | term | קצור_המספר#kf30 | יוסיף | |
| excess/to exceed | י.ס.פ./הוסיף | term | בר_נותן_טעם#DvAU | יוסיף | |
| excess/to exceed | נ.ת.ר./התיר | term | ספר_ציפרא#do7f | יתיר על | |
| excess/to exceed | ע.ד.פ./העדיף | term | חשבון_השטחים#bV78 | יעדיף | |
| to extract a root/to extract a cube root | term | ספר_האלזיברא#0RDt | קח שרשו המעקבי' | ||
| to extract a root/to extract a cube root | ש.ר.ש./לקח שרש | term | ספר_ג'יבלי_אלמוקבאלא#Ys8Q | תקח שרשו המעו' | |
| to extract a root/to extract a cube root | ש.ר.ש./לקח שרש | term | ספר_האלזיברא#Yevf | קח שרש מעקב | |
| to extract a root/to extract a cube root | ע.ק.ב./עקב | term | מלאכת_המספר#ov1e | לעקב | |
| extraction of root/to extract a root | term | ספר_ג'יבלי_אלמוקבאלא#Shkx | תקח השרש מרובע משרשו המעוקב | ||
| extraction of root/to extract a root | ש.ר.ש./הוציא שרש | term | תחבולות_המספר#EXDI | הוצאנו שרשו | |
| extraction of root/to extract a root | ש.ר.ש./לקח שרש | term | תחבולות_המספר#LS8c | קח שרש ה | |
| extraction of root/to extract a root | ש.ר.ש./נלקח שרש | term | חשבון_השטחים#OCAo | הנלקח ממנו שרשו | |
| extraction of root/to extract a root | ש.ר.ש./לקוח שרש | term | חשבון_השטחים#IH6t | לקוח שורשו | |
| extraction of root/to extract a root | ש.ר.ש./לקח שרש | term | ספר_ג'יבלי_אלמוקבאלא#92E1 | תקח שרש | |
| extraction of root/to extract a root | ש.ר.ש./נלקח שרש | term | חשבון_השטחים#lSQn | הנלקח שרשו | |
| extraction of root/to extract a root | ש.ר.ש./לקח שרש | term | ספר_ג'יבלי_אלמוקבאלא#zzEO | תקח שרשם | |
| extraction of root/to extract a root | term | ספר_ג'יבלי_אלמוקבאלא#Kjmi | לוקח שרש השרש | ||
| extraction of root/to extract a root | term | ספר_ג'יבלי_אלמוקבאלא#QuYq | תקח מהעולה שרש השרש מהשרש | ||
| extraction of root/to extract a root | ג.ד.ר./לקח גדר | term | עיר_סיחון#FMAT | נקח גדר | |
| extraction of root/to extract a root | term | ספר_ג'יבלי_אלמוקבאלא#Cvo2 | תקח שרש השרש מ | ||
| extraction of root/to extract a root | ש.ר.ש./שרש | term | קצור_המספר#fB23 | שרשנו | |
| extraction of root/to extract a root | ש.ר.ש./לקח שרש | term | קצור_המספר#GYKU | נקח שרשם | |
| extraction of root/to extract a root | ש.ר.ש./שרש | term | קצור_המספר#Msmr | לשרש | |
| extraction of root/to extract a root | ש.ר.ש./לקח שרש | term | חשבון_השטחים#ZKv6 | קח שרשו | |
| extraction of root/to extract a root | term | ספר_האלזיברא#sauN | קח שרש שרשו | ||
| extraction of root/to extract a root | ש.ר.ש./לקח שרש | term | חשבון_השטחים#rLQ7 | לקחנו שרשו | |
| extraction of root/to extract a root | ש.ר.ש./הוציא שרש | term | תחבולות_המספר#zwGy | תוציא שרש | |
| extraction of root/to extract a root | ש.ר.ש./לקח שרש | term | תחבולות_המספר#JNXl | תקח שרש | |
| extraction of root/to extract a root | ש.ר.ש./הוציא שרש | term | ספר_האלזיברא#ByvD | הוצא שרשו | |
| extraction of root/to extract a root | ש.ר.ש./לקח שרש | term | ספר_האלזיברא#D8hY | קח שרשו | |
| extraction of root/to extract a root | term | ספר_ג'יבלי_אלמוקבאלא#rOMz | תקח שרש שרשו | ||
| to extract a root/to extract a square root | term | ספר_האלזיברא#kvxi | קח שרשו המרבעי' | ||
| factorization/to factorize | נ.ת.כ./התיך | term | בר_נותן_טעם#4u2l | התיכנו אותו | |
| factorization/to factorize | נ.ת.כ./התיך | term | בר_נותן_טעם#WuM8 | נתיך | |
| factorization/to factorize | נ.ת.כ./הותך | term | בר_נותן_טעם#t3lA | יותך | |
| common factor/to find a common factor | ס.כ.מ./הסכים | term | אגרת_המספר#HnrP | תסכים ביניהם | |
| common factor/to find a common factor | ס.כ.מ./הסכים | term | אגרת_המספר#Q2Xb | הסכים | |
| forming a fracion/to form a fracion | ש.ב.ר./שבר | term | קצור_המספר#e7Da | נשבור | |
| halving/to halve | term | ספר_האלזיברא#TWsM | קח מחצית | ||
| halving/to halve | ח.צ.י./חצה | term | ספר_האלזיברא#Gtn0 | תחצה | |
| halving/to halve | ח.צ.י./חצה | term | תחבולות_המספר#pjRW | תחצה ה | |
| halving/to halve | ח.ל.ק./נחלק לחצאים | term | תחבולות_המספר#Ug7u | נחלק לחצאין | |
| halving/to halve | term | תחבולות_המספר#dCUR | תקח מחצית | ||
| halving/to halve | ח.צ.י./נחצה | term | תחבולות_המספר#syRB | יחצה | |
| halving/to halve | ח.צ.י./חצה | term | ספר_ג'יבלי_אלמוקבאלא#wzLZ | תחצה ה | |
| halving/to halve | ח.צ.י./חצה | term | תחבולות_המספר#FAc4 | לחצות ה | |
| halving/to halve | ח.ל.ק./חולק באמצע | term | מלאכת_המספר#UBCg | מחולק באמצע | |
| halving/to halve | ח.צ.י./חצה | term | ספר_ג'יבלי_אלמוקבאלא#KdWB | נחצה ה | |
| halving/to halve | ח.צ.י./חצה | term | חשבון_השטחים#MXfL | לחצות ה | |
| halving/to halve | term | ספר_ג'יבלי_אלמוקבאלא#S7Kl | תחלק לחצי | ||
| extraction of root/to have a root | ש.ר.ש./החזיק שרש | term | חשבון_השטחים#CmsP | יחזיקו שורש | |
| extraction of root/to have a root | term | ספר_האלזיברא#MNsQ | בעלי שרש | ||
| extraction of root/to have a root | term | ספר_האלזיברא#v3W5 | מספרים בעלי שורש | ||
| extraction of root/to have a root | ש.ר.ש./החזיק שרש | term | חשבון_השטחים#xyU6 | מחזיק שורש | |
| extraction of root/to have a root | ש.ר.ש./החזיק שרש | term | תחבולות_המספר#jeLt | יחזיקו שרש | |
| extraction of root/to have a root | ש.ר.ש./החזיק שרש | term | תחבולות_המספר#6J6W | מחזיקים שרש | |
| increasing/to increase | צ.מ.ח./צמח | term | חשבון_השטחים#HEX5 | הצומח | |
| increasing/to increase | ר.ב.ה./התרבה | term | קצור_המספר#q3Bs | יתרבה | |
| increasing/to increase | ר.ב.ה./התרבה | term | קצור_המספר#i0V2 | להתרבות | |
| increasing/to increase | י.ס.פ./התוסף | term | ספר_מעשה_חושב#NOrW | יתוסף | |
| increasing/to increase | צ.מ.ח./צמח | term | תחבולות_המספר#Zu8A | יצמח | |
| increasing/to increase | ר.ב.ה./התרבה | term | תחבולות_המספר#QBGR | יתרבו ה | |
| to remain/to leave a remainder | ש.א.ר./השאיר | term | אגרת_המספר#vrGm | ישאיר | |
| lowering the rank/to lower the rank | י.ר.ד./הוריד | term | ספר_מעשה_חושב#br4o | הורד | |
| lowering the rank/to lower the rank | י.ר.ד./הוריד | term | ספר_מעשה_חושב#MJYV | הורדנום | |
| lowering the rank/to lower the rank | י.ר.ד./הורד | term | ספר_מעשה_חושב#6kBQ | הורד אל | |
| measure/to measure | מ.ד.ד./מדד | term | משנת_המדות#VnJh | מודדין | |
| multiplication/to multiply | נ.כ.ה./הכה | term | ספר_המספר_/_אליהו_מזרחי#BbPB | נכה | |
| multiplication/to multiply | ח.ש.ב./חשב | term | ספר_ציפרא#5Lxo | תחשוב | |
| multiplication/to multiply | כ.פ.ל./כפל | term | קצור_המספר#imW6 | לכפול | |
| multiplication/to multiply | כ.פ.ל./כפל | term | ספר_האלזיברא#r4DP | כפול | |
| multiplication/to multiply | ר.ב.ה./הרבה | term | חשבון_השטחים#YyK7 | תרבה | |
| multiplication/to multiply | כ.פ.ל./כפל | term | עיר_סיחון#57b8 | כפלת | |
| multiplication/to multiply | נ.כ.ה./הכה | term | עיר_סיחון#2Esg | נכה | |
| multiplication/to multiply | מ.נ.י./מנה | term | ספר_יסודי_התבונה_ומגדל_האמונה#QCdf | מונה אותו | |
| multiplication/to multiply | צ.ר.פ./צרף | term | משנת_המדות#7dnt | מצרף | |
| multiplication/to multiply | ח.ש.ב./חשב | term | משנת_המדות#fzOU | מחשב | |
| multiplication/to multiply | נ.כ.ה./הכה | term | ספר_עיון_העקרים_לחשבון_ההנדיים#iUHv | נכה | |
| multiplication/to multiply | כ.פ.ל./הכפיל | term | קצור_המספר#c1eL | להכפל | |
| multiplication/to multiply | ר.ב.ע./רבע | term | מלאכת_המספר#l346 | לרבע | |
| multiplication/to multiply | term | ספר_האלזיברא#VQU3 | לכפלו בהם | ||
| multiplication/to multiply | ש.נ.י./שנה | term | ספר_יסודי_התבונה_ומגדל_האמונה#9JoI | שונה | |
| multiplication/to multiply | כ.פ.ל./כפל | term | עיר_סיחון#Dkeb | כפלנום | |
| multiplication/to multiply | כ.פ.ל./כפל | term | ספר_אגריס#OCbf | תכפול | |
| multiplication/to multiply | נ.כ.ה./הכה | term | עיר_סיחון#TnDR | הכית | |
| multiplication/to multiply | כ.פ.ל./כפל | term | ספר_ג'יבלי_אלמוקבאלא#PDGQ | כפלנו בדרך הקסילי | |
| multiplication/to multiply | כ.פ.ל./כפל | term | ספר_ג'יבלי_אלמוקבאלא#f2dm | כפלת | |
| multiplication/to multiply | ע.ר.כ./ערך | term | Anonymous#zAiS | לערוך | |
| multiplication/to multiply | כ.פ.ל./הכפיל | term | קצור_המספר#DrxX | הכפל | |
| multiplication/to multiply | נ.כ.ה./הכה | term | ספר_מעשה_חושב#Dxtq | הכינו | |
| multiplication/to multiply | נ.כ.ה./הכה | term | תחבולות_המספר#KfKq | הכינום על | |
| multiplication/to multiply | נ.כ.ה./הכה | term | תחבולות_המספר#Ties | תכה על | |
| multiplication/to multiply | נ.כ.ה./הכה | term | חשבון_השטחים#L5RH | נכהו | |
| multiplication/to multiply | כ.פ.ל./כפל | term | תחבולות_המספר#O1PQ | כפול ה | |
| multiplication/to multiply | ספר_ציפרא#WCLM | תצרף | |||
| multiplication/to multiply | נ.כ.ה./הכה | term | חשבון_השטחים#Atu2 | הכינו | |
| multiplication/to multiply | term | ספר_המספר_/_אברהם_אבן_עזרא#acHE | תכפול | ||
| multiplication/to multiply | נ.כ.ה./הכה | term | עיר_סיחון#iesE | תכה | |
| multiplication/to multiply | כ.פ.ל./כפל | term | עיר_סיחון#RIxQ | כפול | |
| multiplication/to multiply | ח.ש.ב./חשב | term | Anonymous#bBid | חושב את | |
| multiplication/to multiply | כ.פ.ל./כפל | term | ספר_ג'יבלי_אלמוקבאלא#7joL | בכפלנו | |
| multiplication/to multiply | נ.כ.ה./הכה | term | ספר_ג'יבלי_אלמוקבאלא#5mJU | בהכות ה | |
| multiplication/to multiply | כ.פ.ל./כפל | term | קצור_המספר#9B2r | לכפול אותם ב | |
| multiplication/to multiply | ע.ש.ה./עשה | term | ספר_ג'יבלי_אלמוקבאלא#KZ2l | לעשות | |
| multiplication/to multiply | ע.ש.ה./עשה | term | ספר_ג'יבלי_אלמוקבאלא#yJC5 | לעשות כפל | |
| multiplication/to multiply | כ.פ.ל./הכפיל | term | ספר_מעשה_חושב#lvfo | תכפיל | |
| multiplication/to multiply | כ.פ.ל./כפל | term | ספר_מעשה_חושב#Sl4N | תכפלהו על | |
| multiplication/to multiply | כ.פ.ל./כפל | term | ספר_מעשה_חושב#VQqD | כפול אותו על | |
| multiplication/to multiply | ע.ר.כ./ערך | term | ספר_מעשה_חושב#DU0z | ערכנו | |
| multiplication/to multiply | ע.ר.כ./ערך | term | ספר_מעשה_חושב#k45K | נערך | |
| multiplication/to multiply | כ.פ.ל./כפל | term | ספר_ג'יבלי_אלמוקבאלא#eY2X | בכפול | |
| multiplication/to multiply | כ.פ.ל./כפל | term | ספר_ג'יבלי_אלמוקבאלא#AGhb | כפול | |
| multiplication/to multiply | נ.כ.ה./הכה | term | מלאכת_המספר#8G0z | הכהו | |
| multiplication/to multiply | term | Arithmetic_Textbook_by_Meir_Shapira#VH0l | לכפול | ||
| multiplication/to multiply | כ.פ.ל./כפל | term | ספר_ציפרא#TNoO | תכפול | |
| multiplication/to multiply | ר.ב.ע./רבע | term | מלאכת_המספר#4rnB | נרבע | |
| multiplication/to multiply | כ.פ.ל./כפל | term | עיר_סיחון#qOaQ | נכפיל | |
| multiplication/to multiply | כ.פ.ל./הכפיל | term | ספר_ג'יבלי_אלמוקבאלא#nXdE | בהכפילם ב | |
| multiplication/to multiply | נ.כ.ה./הכה | term | מלאכת_המספר#I01K | נכה | |
| multiplication/to multiply | ח.ש.ב./חשב | term | ספר_יסודי_התבונה_ומגדל_האמונה#EOYd | תחשוב | |
| multiplication/to multiply | נ.כ.ה./הכה | term | ספר_ג'יבלי_אלמוקבאלא#Ppcv | נכהו נגד | |
| multiplication/to multiply | נ.כ.ה./הכה | term | ספר_ג'יבלי_אלמוקבאלא#IS0U | הכות | |
| multiplication/to multiply | נ.כ.ה./הכה | term | ספר_ג'יבלי_אלמוקבאלא#QPTS | תכה ב | |
| multiplication/to multiply | ח.ש.ב./חשב | term | Anonymous#KApw | חשוב | |
| raising the rank/to raise the rank | ע.ל.ה./העלה | term | ספר_עיון_העקרים_לחשבון_ההנדיים#uRUO | העלהו אל המדרגה | |
| reduction/to reduce | ק.ט.נ./הקטין | term | קצור_המספר#HCE6 | להקטין | |
| reduction/to reduce | ק.צ.ר./קצר | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#4Qdw | לקצר המורה הכללי | |
| reduction/to reduce | ק.צ.ר./קצר | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#F2sR | נקצרם | |
| reduction/to reduce | ק.צ.ר./קצר | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#hiD0 | נקצר המורה | |
| reduction/to reduce | ס.ו.ר./הסיר | term | אגרת_המספר#bYXf | תסיר השתוף בין החלקים | |
| reduction/to reduce | ס.ו.ר./הוסר | term | אגרת_המספר#Woe9 | יוסר השתוף בין ההצעה והמורים | |
| reduction/to reduce | ב.ד.ל./הבדיל | term | ספר_מעשה_חושב#EQSo | הבדלנו | |
| subtraction/to remain | ש.א.ר./נשאר | term | ספר_ג'יבלי_אלמוקבאלא#tWMC | ישאר | |
| subtraction/to remain | ש.א.ר./נשאר | term | ספר_האלזיברא#04z1 | נשאר | |
| subtraction/to remain | ש.א.ר./נשאר | term | ספר_החשבון_והמדות#mfAW | ישארו בידך | |
| subtraction/to remain | ש.א.ר./נשאר | term | תחבולות_המספר#xbF2 | ישארו | |
| subtraction/to remain | ש.א.ר./נשאר | term | קצור_המספר#PS0z | ישארו | |
| subtraction/to remain | ש.א.ר./נשאר | term | חשבון_השטחים#yzCK | נשאר | |
| subtraction/to remain | ש.א.ר./נשאר | term | ספר_האלזיברא#YNKM | ישאר | |
| subtraction/to remain | ש.א.ר./נשאר | term | ספר_החשבון_והמדות#bl2G | נשארו | |
| subtraction/to remain | ש.א.ר./נשאר | term | ספר_ג'יבלי_אלמוקבאלא#a2Jj | ישאר לך | |
| subtraction/to remain | ש.א.ר./נשאר | term | קצור_המספר#4Vx6 | ישאר | |
| subtraction/to remain | ש.א.ר./נשאר | term | תחבולות_המספר#My33 | נשאר | |
| subtraction/to remain | ש.א.ר./נשאר | term | ספר_האלזיברא#tAEN | ישאר בידך | |
| subtraction/to remain | ש.א.ר./נשאר | term | חשבון_השטחים#YkLt | ישאר | |
| result/to result | ב.ו.א./בא | term | ספר_ג'יבלי_אלמוקבאלא#wv2i | יבאו אל | |
| result/to result | ע.ל.ה./עלה | term | ספר_האלזיברא#lULj | עלה בידינו | |
| result/to result | ע.ל.ה./עלה | term | ספר_האלזיברא#pihJ | יעלה | |
| result/to result | ב.ו.א./בא | term | ספר_ג'יבלי_אלמוקבאלא#A46L | יבא מזה | |
| result/to result | ב.ו.א./בא | term | ספר_ג'יבלי_אלמוקבאלא#nGmC | יבאו לך ה | |
| result/to result | ב.ו.א./בא | term | ספר_ג'יבלי_אלמוקבאלא#aTvl | יבא מזה | |
| result/to result | ב.ו.א./בא | term | ספר_ג'יבלי_אלמוקבאלא#c7MZ | יבא | |
| result/to result | י.צ.א./יצא | term | ספר_ג'יבלי_אלמוקבאלא#EMxT | יצא ממנו | |
| result/to result | נ.ג.ע./הגיע | term | ספר_ג'יבלי_אלמוקבאלא#aPlU | יגיע מ | |
| result/to result | נ.ג.ע./הגיע | term | ספר_ג'יבלי_אלמוקבאלא#eaEl | יגיע לך | |
| result/to result | נ.ג.ע./הגיע | term | ספר_ג'יבלי_אלמוקבאלא#aTkY | יגיע | |
| result/to result | י.צ.א./יצא | term | ספר_ג'יבלי_אלמוקבאלא#0Vbm | יצא לך כי | |
| result/to result | נ.ג.ע./הגיע | term | ספר_ג'יבלי_אלמוקבאלא#y4WU | יגיע לידך כי | |
| result/to result | ע.ל.ה./עלה | term | חשבון_השטחים#IZr3 | עלה | |
| result/to result | נ.ג.ע./הגיע | term | קצור_המספר#gfwC | יגיע | |
| result/to result | ע.ל.ה./עלה | term | קצור_המספר#sHaI | יעלה | |
| result/to result | ע.ל.ה./עלה | term | קצור_המספר#KLdO | עלה | |
| result/to result | י.צ.א./יצא | term | קצור_המספר#Kief | יצאו | |
| result/to result | נ.ג.ע./הגיע | term | קצור_המספר#J0PL | יגיע | |
| result/to result | י.צ.א./יצא | term | קצור_המספר#A08v | יצא | |
| result/to result | נ.ג.ע./הגיע | term | חשבון_השטחים#1cnD | הגיע | |
| result/to result | נ.ג.ע./הגיע | term | חשבון_השטחים#Ekhi | יגיע | |
| result/to result | ק.ב.צ./התקבץ | term | חשבון_השטחים#AQjO | מה שהתקבץ | |
| result/to result | ק.ב.צ./התקבץ | term | חשבון_השטחים#C114 | מה שיתקבץ | |
| result/to result | ק.ב.צ./התקבץ | term | תחבולות_המספר#uAfn | התקבץ | |
| result/to result | ע.ל.ה./עלה | term | תחבולות_המספר#Cb29 | עלה | |
| result/to result | י.צ.א./יצא | term | תחבולות_המספר#cUNj | יצא | |
| result/to result | ק.ב.צ./התקבץ | term | תחבולות_המספר#A8hb | מה שיתקבץ | |
| result/to result | נ.ג.ע./הגיע | term | תחבולות_המספר#ELrL | הגיע | |
| result/to result | נ.ג.ע./הגיע | term | תחבולות_המספר#iEjB | יגיע | |
| result/to result | ע.ל.ה./עלה | term | תחבולות_המספר#pBmN | יעלה ל | |
| result/to result | ע.ל.ה./עלה | term | ספר_ג'יבלי_אלמוקבאלא#pv3B | יעלה ה | |
| result/to result | ב.ו.א./בא | term | קצור_המספר#V981 | הבא מ | |
| result/to result | ב.ו.א./בא | term | קצור_המספר#yIbU | הבא מן | |
| result/to result | ע.ל.ה./עלה | term | ספר_ג'יבלי_אלמוקבאלא#AULn | עולות | |
| result/to result | ע.ל.ה./עלה | term | ספר_ג'יבלי_אלמוקבאלא#2G63 | יעלו | |
| result/to result | ע.ל.ה./עלה | term | ספר_ג'יבלי_אלמוקבאלא#Aiix | עולה | |
| result/to result | ע.ל.ה./עלה | term | חשבון_השטחים#qdtE | יעלה | |
| result/to result | י.צ.א./יצא | term | חשבון_השטחים#aljc | יצא | |
| result/to result | י.צ.א./יצא | term | חשבון_השטחים#ruSO | יצאו | |
| result/to result | ב.ו.א./בא | term | תחבולות_המספר#ksmA | יבאו | |
| result/to result | ק.ב.צ./התקבץ | term | תחבולות_המספר#hbgc | יתקבץ | |
| result/to result | ב.ו.א./בא | term | ספר_ג'יבלי_אלמוקבאלא#E07H | יבא אל | |
| result/to result | ב.ו.א./בא | term | ספר_ג'יבלי_אלמוקבאלא#lGob | יבאו להיות | |
| result/to result | ש.ו.ב./שב | term | תחבולות_המספר#OIkJ | ישוב | |
| rounding/to round | ש.ל.מ./השלים | term | ספר_מעשה_חושב#Yv34 | תשלים | |
| rounding/to round | ש.ל.מ./השלים | term | ספר_מעשה_חושב#Td2W | להשלימו אל הכלל הקרוב | |
| set aside/to set aside | ש.מ.ר./שמר | term | ספר_ג'יבלי_אלמוקבאלא#xPel | שמרם בעבור | |
| set aside/to set aside | ש.מ.ר./שמר | term | קצור_המספר#85VU | נשמור ה | |
| set aside/to set aside | ש.מ.ר./שמר | term | קצור_המספר#HEuJ | נשמור אותו | |
| set aside/to set aside | ש.מ.ר./שמר | term | תחבולות_המספר#OqHn | שמור | |
| set aside/to set aside | ש.מ.ר./שמר | term | ספר_ג'יבלי_אלמוקבאלא#mGTf | תשמור ל | |
| set aside/to set aside | ש.מ.ר./שמר | term | מלאכת_המספר#ln2L | שמור אותו | |
| set aside/to set aside | ש.מ.ר./שמר | term | ספר_האלזיברא#bPVc | שמרם | |
| set aside/to set aside | ש.מ.ר./שמר | term | חשבון_השטחים#QzMa | שמרת | |
| set aside/to set aside | ח.ז.ק./החזיק | term | ספר_ג'יבלי_אלמוקבאלא#osZk | תחזיק ל | |
| set aside/to set aside | ח.ז.ק./החזיק | term | חשבון_השטחים#gptO | תחזיק | |
| set aside/to set aside | ש.מ.ר./שמר | term | תחבולות_המספר#hP4L | שמרנום | |
| set aside/to set aside | ש.מ.ר./שמר | term | חשבון_השטחים#ycfQ | תשמרם | |
| set aside/to set aside | ש.מ.ר./שמר | term | ספר_ג'יבלי_אלמוקבאלא#Tim1 | תשמרם | |
| set aside/to set aside | ש.מ.ר./שמר | term | חשבון_השטחים#nRcT | שמרם | |
| common factor/to share a common factor | ס.כ.מ./מסכים | term | אגרת_המספר#znBk | מסכים עם | |
| common factor/to share a common factor | ש.ת.פ./משתתפים | term | קצור_המספר#0Yun | משתתפים ב | |
| common factor/to share a common factor | ס.כ.מ./מסכים | term | אגרת_המספר#LoM5 | מסכימים | |
| common factor/to share a common factor | ש.ת.פ./משתתפים | term | קצור_המספר#7UbV | משתתפים ל | |
| common factor/to share a common factor | ס.כ.מ./מסכים | term | אגרת_המספר#PTSC | מסכימים בה | |
| common multiple/to share a common multiple | ש.ת.פ./השתתף | term | קצור_המספר#32CU | ישתתפו בו | |
| common multiple/to share a common multiple | ש.ת.פ./השתתף | term | קצור_המספר#0XHv | ישתתפו בו | |
| subtraction/to subtract | ג.ר.ע./גרע | term | קצור_המספר#Kiuc | נגרע אותם מ | |
| subtraction/to subtract | פ.ח.ת./פחת | term | Anonymous#fNvT | תפחות מ | |
| subtraction/to subtract | פ.ח.ת./פחת | term | Anonymous#BhEN | פוחת | |
| subtraction/to subtract | term | Arithmetic_Textbook_by_Meir_Shapira#x9f0 | לגרוע | ||
| subtraction/to subtract | ס.ו.ר./הסיר | term | Anonymous#eJZh | נסיר | |
| subtraction/to subtract | ס.ו.ר./הסיר | term | Anonymous#BfTN | תסיר | |
| subtraction/to subtract | ס.ו.ר./הוסר | term | ספר_החשבון_לאל_חצאר#bMqC | הוסרו | |
| subtraction/to subtract | ח.ס.ר./חוסר | term | ספר_החשבון_לאל_חצאר#1PXj | חוסר | |
| subtraction/to subtract | ח.ס.ר./נחסר | term | בר_נותן_טעם#RhZG | החסרו מ | |
| subtraction/to subtract | ג.ר.ע./גרע | term | קצור_המספר#oV5C | לגרוע | |
| subtraction/to subtract | י.צ.א./יצא | term | ספר_החשבון_לאל_חצאר#zkNo | יוצא | |
| subtraction/to subtract | ח.ס.ר./חסר | term | ספר_האלזיברא#rg2F | חסר ממנו | |
| subtraction/to subtract | ש.ל.כ./השליך | term | קצור_המספר#TOAm | נשליך מ | |
| subtraction/to subtract | ש.ל.כ./השליך | term | קצור_המספר#U8cN | נשליך מ | |
| subtraction/to subtract | י.צ.א./הוציא | term | ספר_החשבון_לאל_חצאר#7sS5 | הוצא | |
| subtraction/to subtract | ג.ר.ע./נגרע | term | בר_נותן_טעם#QX0c | יגרע מהם | |
| subtraction/to subtract | י.צ.א./הוציא | term | בר_נותן_טעם#J2LS | נוציא מהם | |
| subtraction/to subtract | י.צ.א./הוציא | term | בר_נותן_טעם#F2P9 | נוציאם מ | |
| subtraction/to subtract | ס.ו.ר./הסיר | term | בר_נותן_טעם#nAHE | תסיר | |
| subtraction/to subtract | ח.ס.ר./חוסר | term | ספר_מעשה_חושב#vFce | יחוסרו | |
| subtraction/to subtract | ג.ר.ע./גרע | term | בר_נותן_טעם#CoHV | גרע ממנו | |
| subtraction/to subtract | ס.ו.ר./הוסר | term | מלאכת_המספר#g9jn | יוסר ממנו | |
| subtraction/to subtract | ג.ר.ע./גרע | term | ספר_מעשה_חושב#AUHG | נגרע מהם | |
| subtraction/to subtract | term | Arithmetic_Textbook_by_Meir_Shapira#ydpy | לחסר | ||
| subtraction/to subtract | ח.ס.ר./חסר | term | מלאכת_המספר#sqqk | מחסר | |
| subtraction/to subtract | ג.ר.ע./נגרע | term | תחבולות_המספר#hqB8 | יגרע | |
| subtraction/to subtract | ש.ל.כ./השליך | term | ספר_החשבון_לאל_חצאר#6OJ5 | השליך | |
| subtraction/to subtract | פ.ח.ת./פחת | term | ספר_ציפרא#dEcZ | תפחת | |
| subtraction/to subtract | ס.ו.ר./הסיר | term | ספר_ציפרא#0AVC | הסיר | |
| subtraction/to subtract | ג.ר.ע./גרוע | term | חשבון_השטחים#xSLK | גרוע מ | |
| subtraction/to subtract | ס.ו.ר./סר | term | ספר_ציפרא#jTqA | נסיר | |
| subtraction/to subtract | ש.ל.כ./השליך | term | ספר_ציפרא#839i | השלך | |
| subtraction/to subtract | י.צ.א./הוצא | term | ספר_ג'יבלי_אלמוקבאלא#sbL4 | הוצא מהם | |
| subtraction/to subtract | ח.ס.ר./חסר | term | ספר_ציפרא#Dk5a | נחסיר | |
| subtraction/to subtract | פ.ח.ת./פחת | term | ספר_יסודי_התבונה_ומגדל_האמונה#E8q1 | תפחות | |
| subtraction/to subtract | י.צ.א./הוציא | term | קצור_המספר#IUir | הוצאנו | |
| subtraction/to subtract | פ.ח.ת./פחת | term | תחבולות_המספר#47pj | נפחות ממנו | |
| subtraction/to subtract | term | ספר_המספר_/_אברהם_אבן_עזרא#lNwV | לגרוע חשבון מחשבון | ||
| subtraction/to subtract | ג.ר.ע./גרע | term | תחבולות_המספר#lyZc | תגרע ממנו | |
| subtraction/to subtract | term | ספר_המספר_/_אברהם_אבן_עזרא#o7zA | לחסר מספר ממספר | ||
| subtraction/to subtract | ג.ר.ע./גרע | term | ספר_החשבון_לאל_חצאר#4FPV | גרענום | |
| subtraction/to subtract | ש.ל.כ./השליך | term | משנת_המדות#6oQ4 | משליך ממנו | |
| subtraction/to subtract | ג.ר.ע./גרע | term | ספר_האלזיברא#HMbj | תגרע ממנו ה | |
| subtraction/to subtract | נ.כ.י./נכה | term | ספר_ציפרא#poHT | תנכה מן | |
| subtraction/to subtract | term | Anonymous_text_from_Latin#bUjh | לנכות | ||
| subtraction/to subtract | נ.כ.י./נכה | term | ספר_ציפרא#zXtY | נכיהו מן | |
| subtraction/to subtract | פ.ח.ת./פחת | term | ספר_האלזיברא#OG9A | נפחות מ | |
| subtraction/to subtract | ג.ר.ע./גרע | term | ספר_ג'יבלי_אלמוקבאלא#V6IU | תגרע ה | |
| subtraction/to subtract | י.צ.א./הוציא | term | ספר_החשבון_לאל_חצאר#UROp | הוציא | |
| subtraction/to subtract | ג.ר.ע./גרע | term | ספר_ג'יבלי_אלמוקבאלא#VsLC | תגרע ממנו | |
| subtraction/to subtract | י.צ.א./הוצא | term | ספר_ג'יבלי_אלמוקבאלא#zCID | מוצא מ | |
| subtraction/to subtract | נ.פ.ל./הפיל | term | ספר_ג'יבלי_אלמוקבאלא#2fXN | תפיל מהם | |
| subtraction/to subtract | נ.פ.ל./הפיל | term | ספר_ג'יבלי_אלמוקבאלא#1Vvm | נפיל ממנו | |
| subtraction/to subtract | ס.ו.ר./הסיר | term | בר_נותן_טעם#SGlf | נסירם ממנה | |
| subtraction/to subtract | נ.פ.ל./הפיל | term | תחבולות_המספר#h4dm | נפיל | |
| subtraction/to subtract | י.צ.א./הוציא | term | ספר_ג'יבלי_אלמוקבאלא#o28u | תוציא מ | |
| subtraction/to subtract | ח.ס.ר./חסר | term | בר_נותן_טעם#CfXy | חסרנו ממנו | |
| subtraction/to subtract | י.צ.א./הוציא | term | ספר_ג'יבלי_אלמוקבאלא#vluk | בהוציאנו מ | |
| subtraction/to subtract | ח.ס.ר./חסר | term | בר_נותן_טעם#q7lM | חסר | |
| subtraction/to subtract | י.צ.א./הוציא | term | ספר_ג'יבלי_אלמוקבאלא#ls9T | תוציא חוצה מ | |
| subtraction/to subtract | ס.ו.ר./הסיר | term | ספר_דיני_ממונות#dA53 | נסיר | |
| subtraction/to subtract | י.צ.א./הוציא | term | ספר_דיני_ממונות#PpWo | תוציא | |
| subtraction/to subtract | ש.ל.כ./השליך | term | חשבון_השטחים#IIW3 | תשליך | |
| subtraction/to subtract | ש.ל.כ./השליך | term | ספר_עיון_העקרים_לחשבון_ההנדיים#TZdW | השליכהו מה | |
| subtraction/to subtract | ג.ר.ע./גרע | term | ספר_עיון_העקרים_לחשבון_ההנדיים#XgIk | נגרע | |
| subtraction/to subtract | ס.ו.ר./הסיר | term | ספר_החשבון_לאל_חצאר#HnQ8 | תסיר | |
| subtraction/to subtract | ג.ר.ע./גרע | term | חשבון_השטחים#DBQy | גרע | |
| subtraction/to subtract | ס.ו.ר./הסיר | term | ספר_אגריס#0CKI | הסר | |
| subtraction/to subtract | ח.ס.ר./חסר | term | מלאכת_המספר#H3G5 | נחסר | |
| subtraction/to subtract | י.צ.א./הוציא | term | Anonymous#ULKJ | הוצאת ממנו | |
| subtraction/to subtract | י.צ.א./הוציא | term | Anonymous#UdlW | הוצא מהם | |
| subtraction/to subtract | י.צ.א./הוציא | term | ספר_אגריס#59y7 | והוציא | |
| subtraction/to subtract | ח.ס.ר./חסר | term | Anonymous#TmDO | חסר ממנו | |
| subtraction/to subtract | ח.ס.ר./חסר | term | ספר_מעשה_חושב#CGgF | חסרנו ממנו | |
| subtraction/to subtract | ג.ר.ע./גרע | term | Anonymous#fMF7 | תגרעם מ | |
| subtraction/to subtract | ח.ס.ר./חסר | term | ספר_אגריס#Veye | לחסר | |
| subtraction/to subtract | ח.ס.ר./חסר | term | ספר_דיני_ממונות#RD85 | תחסר מהם | |
| subtraction/to subtract | ח.ס.ר./חסר | term | Anonymous#imnV | תחסרם מן | |
| subtraction/to subtract | ח.ס.ר./חסר | term | ספר_עיון_העקרים_לחשבון_ההנדיים#b7xn | חסר | |
| subtraction/to subtract | ג.ר.ע./גרע | term | Anonymous#prjt | גרע מהם | |
| subtraction/to subtract | ש.ל.כ./השליך | term | ספר_החשבון_לאל_חצאר#D9WY | השליך | |
| subtraction/to subtract | י.צ.א./הוציא | term | ספר_ג'יבלי_אלמוקבאלא#WwoT | הוצא ה | |
| subtraction/to subtract | נ.פ.ל./הפיל | term | ספר_דיני_ממונות#EYy0 | תפיל מן ה | |
| subtraction/to subtract | ח.ס.ר./חסר | term | חשבון_השטחים#fpQd | תחסרם | |
| subtraction/to subtract | ג.ר.ע./גרע | term | ספר_דיני_ממונות#W1y1 | תגרע | |
| subtraction/to subtract | ג.ר.ע./נגרע | term | ספר_ג'יבלי_אלמוקבאלא#E6D3 | יגרע ה | |
| subtraction/to subtract | ח.ס.ר./חסר | term | ספר_החשבון_לאל_חצאר#YiBj | חסרם | |
| subtraction/to subtract | ח.ס.ר./חוסר | term | ספר_מעשה_חושב#V0Lu | חוסר מהם | |
| subtraction/to subtract | ח.ס.ר./חסר | term | ספר_האלזיברא#09gZ | חסרם מ | |
| subtraction/to subtract | י.צ.א./הוציא | term | ספר_עיון_העקרים_לחשבון_ההנדיים#Zs5x | נוציא | |
| subtraction/to subtract | ג.ר.ע./נגרע | term | תחבולות_המספר#ufK4 | נגרע מ | |
| subtraction/to subtract | ח.ס.ר./חסר | term | חשבון_השטחים#HfJe | נחסרם | |
| subtraction/to subtract | ח.ס.ר./חסר | term | ספר_החשבון_לאל_חצאר#PkHK | חסר | |
| subtraction/to subtract | ג.ר.ע./גרע | term | תחבולות_המספר#RYq4 | גרענו | |
| subtraction/to subtract | ג.ר.ע./גרע | term | חשבון_השטחים#l46g | תגרעם | |
| subtraction/to subtract | נ.פ.ל./הפיל | term | ספר_החשבון_לאל_חצאר#f805 | הפיל | |
| subtraction/to subtract | ח.ס.ר./נחסר | term | בר_נותן_טעם#t72G | יחסר | |
| subtraction/to subtract | ח.ס.ר./נחסר | term | בר_נותן_טעם#oVAO | החסרו | |
| subtraction/to subtract | ח.ס.ר./חסר | term | Anonymous#qrBI | חשבון הולך הלוך וחסור | |
| subtraction/to subtract | ח.ס.ר./נחסר | term | בר_נותן_טעם#zdQE | יחסר | |
| subtraction/to subtract | ג.ר.ע./נגרע | term | חשבון_השטחים#bLLT | נגרע | |
| subtraction/to subtract | ג.ר.ע./נגרע | term | חשבון_השטחים#yZxg | יגרע | |
| subtraction/to subtract | י.צ.א./הוצא | term | ספר_ג'יבלי_אלמוקבאלא#55eP | הוצאו | |
| subtraction/to subtract | ס.ו.ר./הסיר | term | קצור_המספר#bdwV | הסר מהם | |
| subtraction/to subtract | י.צ.א./הוציא | term | קצור_המספר#JJQt | הוצאנו | |
| subtraction/to subtract | ס.ו.ר./הסיר | term | קצור_המספר#qcZk | הסר | |
| subtraction/to subtract | ג.ר.ע./גרע | term | ספר_החשבון_לאל_חצאר#Usbo | נגרע | |
| subtraction/to subtract | ש.ל.כ./השליך | term | תחבולות_המספר#Ygi3 | תשליך | |
| subtraction/to subtract | נ.פ.ל./הפיל | term | קצור_המספר#fqIy | נפיל | |
| subtraction/to subtract | נ.פ.ל./הפיל | term | קצור_המספר#ynmt | הפלנו מ | |
| calculation/to suffice | ס.פ.ק./הספיק | term | ספר_מעשה_חושב#xzyI | מספיק | |
| calculation/to suffice | ס.פ.ק./הספיק | term | ספר_מעשה_חושב#Yw04 | יספיק | |
| additive supplementation/to supplement additively | ש.ל.מ./השלים | term | חשבון_השטחים#SNAR | תשלים ה | |
| additive supplementation/to supplement additively | ש.ל.מ./השלים | term | קצור_המספר#D0xO | להשלים | |
| multiplicative supplementation/to supplement multiplicatively | ש.ל.מ./השלים | term | Anonymous#OrbI | ישלים | |
| multiplicative supplementation/to supplement multiplicatively | ש.ל.מ./שלם | term | Anonymous#jhIl | ישלמו | |
| multiplicative supplementation/to supplement multiplicatively | ש.ל.מ./שלם | term | Anonymous#u2bz | ישלמו | |
| multiplicative supplementation/to supplement multiplicatively | י.ר.ד./ירד | term | ספר_החשבון_לאל_חצאר#DnRu | ירד | |
| multiplicative supplementation/to supplement multiplicatively | ח.ת.מ./החתים | term | ספר_החשבון_לאל_חצאר#N6sa | תחתים | |
| multiplicative supplementation/to supplement multiplicatively | ש.ל.מ./השלים | term | ספר_יסודי_התבונה_ומגדל_האמונה#h2Bf | תשלים | |
| multiplicative supplementation/to supplement multiplicatively | י.ר.ד./הוריד | term | ספר_החשבון_לאל_חצאר#mMKS | תוריד | |
| calculation/total | כ.ל.ל./כלל | term | קצור_המספר#5rcg | הכלל העולה | |
| calculation/total | כ.ל.ל./כלל | term | ספר_מעשה_חושב#7u0p | בכללם | |
| calculation/total | כ.ל.ל./כלל | term | קצור_המספר#zY5k | הכלל העולה | |
| multiplication/to triple | ש.ל.ש./שלש | term | מלאכת_המספר#f4EQ | נשלש | |
| multiplication/to triple | ש.ל.ש./שלש | term | מלאכת_המספר#GBfe | נשלש | |
| division/true divisor | י.ר.ה./מורה צדק | term | בר_נותן_טעם#uyDf | מורה צדק | |
| calculation/unequal | term | ספר_ג'יבלי_אלמוקבאלא#mEAx | בלתי שוים | ||
| calculation/unequal | term | חשבון_השטחים#uDWm | הבלתי שוים | ||
| calculation/unequal | term | ספר_האלזיברא#YR2q | הבלתי שוים | ||
| calculation/unequal | ש.ו.ה./שוה | term | ספר_ג'יבלי_אלמוקבאלא#fpHc | הבלתי שוים | |
| decimal rank/units | term | תחבולות_המספר#CRDI | אחדי ה | ||
| decimal rank/units | definition | ספר_המספר_/_אברהם_אבן_עזרא#tNZb | והנה הַסְּפָר תשעה {{#annot:term|204|1E4G}}מספרים{{#annotend:1E4G}}ובעל ספר: O187 וספר ספר יצירה: V171 ס"י אמר: O187 אומר החכמה: O187; P1029; P1051; V171; V397 חכמה וספר: P1051 om. בִּסְפָר וְסֵפֶר וְסִפּוּר: Lo10785; Mo30 בסֶפֵר וסְפַר וְסיפור הַסְּפָר: Mu43 הַסְפַר; N2627; P1050 המספר; P1052 הספור; V171 הסופר תשעה: V171; V397 הם ט' |- | *The resemblance of the ranks to the rank of units :*units – as foundations of all numbers | |- | ::For nine is the end of every number and these are called units that are the first rank. כי תשעה סוף כל {{#annot:term|204|z6R9}}חשבון{{#annotend:z6R9}} ואלה יקראו {{#annot:term|287|f4NJ}}האחדים{{#annotend:f4NJ}} שהם ב{{#annot:term|203|dJ7O}}מעלה{{#annotend:dJ7O}} הראשונה | ||
| decimal rank/units | פ.ר.ד./נפרד | term | ספר_עיון_העקרים_לחשבון_ההנדיים#WdMe | נפרדים | |
| decimal rank/units | term | ספר_המספר_/_אברהם_אבן_עזרא#f4NJ | האחדים | ||
| decimal rank/units | פ.ר.ט./פרט | term | ספר_המספר_/_אליהו_מזרחי#yXEq | פרטים | |
| decimal rank/units | פ.ר.ט./פרט | definition | ספר_המספר_/_אליהו_מזרחי#8AAe | The units alone are the numbers from 1 to 9. והפרטים לבד הם המספרים אשר מא' ועד ט' | |
| decimal rank/units | א.ח.ד./אחד | term | חשבון_השטחים#gEdV | אחדי | |
| decimal rank/units | פ.ר.ט./פרט | term | ספר_החשבון_והמדות#jltG | פרטים | |
| decimal rank/units | א.ח.ד./אחד | term | חשבון_השטחים#7FQL | האחדים | |
| decimal rank/units | term | תחבולות_המספר#tOUJ | האחדים | ||
| decimal rank/units | א.ח.ד./אחד | term | ספר_האלזיברא#3eXG | האחדים | |
| decimal rank/units | term | ספר_ציפרא#vrY4 | מעלת היחידים | ||
| calculation/unknown | ש.כ.ל./מושכל | term | ספר_החשבון_לאל_חצאר#pNEK | מושכל | |
| calculation/unknown | ב.ק.ש./מבוקש | term | קצור_המספר#tuhe | המבוקש | |
| calculation/unknown | ש.כ.ל./מושכל | term | ספר_החשבון_לאל_חצאר#6X1n | מספר מושכל | |
| calculation/unknown | term | ספר_האלזיברא#fglu | אשר רציתי למצא | ||
| calculation/unknown | term | ספר_האלזיברא#BKZw | המספר אשר רציתי למצא | ||
| calculation/unknown | ב.ק.ש./מבוקש | term | תחבולות_המספר#UPUi | המבוקש | |
| calculation/unknown | ב.ק.ש./מבוקש | term | ספר_האלזיברא#wTdp | המבקש | |
| calculation/unknown | ע.ל.מ./נעלם | term | קצור_המספר#cdfg | הנעלם | |
| calculation/unknown | ע.ל.מ./נעלם | term | קצור_המספר#MyRc | הנעלם | |
| calculation/unknown | ב.ק.ש./מבוקש | term | ספר_האלזיברא#GFkd | המבוקש | |
| calculation/unknown | ב.ק.ש./מבוקש | term | קצור_המספר#lL4h | המספר המבוקש | |
| calculation/unknown | ב.ק.ש./מבוקש | term | ספר_האלזיברא#fd1E | הוא המבוקש | |
| calculation/unknown | term | חשבון_השטחים#C3xB | הנשאל | ||
| calculation/unknown | ב.ק.ש./מבוקש | term | חשבון_השטחים#nfZc | המבוקש | |
| calculation/unknown | ש.כ.ל./מושכל | term | ספר_החשבון_לאל_חצאר#SY5E | המספר המושכל | |
| calculation/unknown | ס.כ.ל./מוסכל | term | ספר_החשבון_לאל_חצאר#LGBq | מספר מוסכל | |
| calculation/unknown | י.ד.ע./בלתי ידוע | term | ספר_החשבון_לאל_חצאר#HOoK | המספר הבלתי ידוע | |
| calculation/unknown | י.ד.ע./בלתי ידוע | term | ספר_החשבון_לאל_חצאר#HeCs | מספר בלתי ידוע | |
| calculation/unknown | ע.ל.מ./נעלם | term | ספר_החשבון_לאל_חצאר#mqJN | נעלם | |
| calculation/unknown | ס.כ.ל./מוסכל | term | ספר_החשבון_לאל_חצאר#Ye6i | המספר המוסכל | |
| calculation/verified | כ.ו.נ./נכון | term | תחבולות_המספר#2DB8 | נכון | |
| calculation/verified | כ.ו.נ./מכוון | term | ספר_ציפרא#HkVh | מכוון | |
| calculation/verified | כ.ו.נ./מכוון | term | חשבון_הנקרא_ציפור#cxRK | מכוון | |
| methods of multiplication/vertical multiplication | ע.מ.ד./עומד | term | אגרת_המספר#mItq | עומד | |
| decimal positional system/zero | term | לקוטים_מספר_פראלוקא#sSXU | זירי | ||
| decimal positional system/zero | ס.פ.ר./ספרא | term | קצור_המספר#3EKZ | סיפרא | |
| decimal positional system/zero | ס.פ.ר./ספרא | term | עיר_סיחון#OR0i | סיפרא | |
| decimal positional system/zero | ס.פ.ר./ספרא | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#FGyu | ספרה | |
| decimal positional system/zero | צפרא | term | אגרת_המספר#1Efh | צפרות | |
| decimal positional system/zero | ס.פ.ר./ספרא | term | בר_נותן_טעם#E3nK | סיפרא | |
| decimal positional system/zero | term | ספר_החשבון_והמדות#zXTj | נולא | ||
| decimal positional system/zero | ס.פ.ר./ספרא | term | בר_נותן_טעם#p3vj | ספרות | |
| decimal positional system/zero | ס.פ.ר./ספרא | term | בר_נותן_טעם#ab8C | סיפרות | |
| decimal positional system/zero | ס.פ.ר./ספרא | term | קצור_המספר#8fKK | סיפרא | |
| decimal positional system/zero | ס.פ.ר./ספר | term | אגרת_המספר#GWeK | ספר | |
| decimal positional system/zero | ע.ג.ל./עגולה | term | אגרת_המספר#E72I | עגולות | |
| decimal positional system/zero | ע.ג.ל./עגולה | term | אגרת_המספר#HULO | עגולה | |
| decimal positional system/zero | ס.פ.ר./ספרא | term | ספר_עיון_העקרים_לחשבון_ההנדיים#vK1V | סיפרא | |
| decimal positional system/zero | צפרא | term | ספר_החשבון_לאל_חצאר#1htX | צפרי | |
| decimal positional system/zero | ס.פ.ר./ספרא | term | ספר_המספר_/_אליהו_מזרחי#VobJ | סיפרש | |
| decimal positional system/zero | ס.פ.ר./ספרא | term | ספר_עיון_העקרים_לחשבון_ההנדיים#6i88 | סיפרין | |
| decimal positional system/zero | ס.פ.ר./ספרא | term | אגרת_המספר#Othg | סיפרא | |
| decimal positional system/zero | ס.פ.ר./ספר | term | אגרת_המספר#frSn | ספרי' | |
| decimal positional system/zero | ס.פ.ר./ספרא | definition | מלאכת_המספר#X7Io | The tenth is called sifra [= zero] and it is not worth anything in itself, but indicates a rank that designate a greater numerical value to the next digit. והעשירית תקרא ספרא ואינו שוה דבר בעצמו אבל להורות מקום מקנה יותר {{#annot:term|217,1857|Cm8o}}כמות{{#annotend:Cm8o}} לאות הנמשכת אליה | |
| decimal positional system/zero | term | ספר_המספר_/_אברהם_אבן_עזרא#Ul6o | גלגל | ||
| decimal positional system/zero | צפרא | term | ספר_החשבון_לאל_חצאר#oT1F | צפר | |
| decimal positional system/zero | צפרא | term | ספר_דיני_ממונות#bGEQ | ציפרא | |
| decimal positional system/zero | ס.פ.ר./ספרא | term | האנציקלופדיה_של_אבו_אלצלת#ONwA | ספרא | |
| decimal positional system/zero | צפרא | term | האנציקלופדיה_של_אבו_אלצלת#TfGB | ציפרי | |
| decimal positional system/zero | צפרא | term | אגרת_המספר#RyC4 | צפר | |
| decimal positional system/zero | צפרא | term | ספר_החשבון_לאל_חצאר#oOqX | צפרים | |
| decimal positional system/zero | צפרא | term | ספר_החשבון_לאל_חצאר#bAnH | ציפרא | |
| decimal positional system/zero | צפרא | term | ספר_החשבון_לאל_חצאר#eHM0 | ציפראות | |
| decimal positional system/zero | ג.ל.ג.ל./גלגל | term | ספר_החשבון_והמדות#ISDZ | גלגל | |
| decimal positional system/zero | ג.ל.ג.ל./גלגל | term | ספר_דיני_ממונות#jTVW | גלגל | |
| decimal positional system/zero | ס.פ.ר./ספרא | term | עיר_סיחון#iNJi | סיפראש | |
| decimal positional system/zero | ס.פ.ר./ספרא | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#TmrI | ספרא | |
| decimal positional system/zero | ס.פ.ר./ספרא | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#Mxik | ספראש | |
| decimal positional system/zero | term | ספר_החשבון_והמדות#m3tb | אודין | ||
| decimal positional system/zero | צפרא | term | ספר_החשבון_לאל_חצאר#wjfq | ציפראש | |
| decimal positional system/zero | term | ספר_המספר_/_אליהו_מזרחי#nyHG | אודן | ||
| decimal positional system/zero | צפרא | term | אגרת_המספר#D6PF | צפרא | |
| decimal positional system/zero | ס.פ.ר./ספרא | term | ספר_החשבון_והמדות#41uG | סיפרא | |
| decimal positional system/zero | ג.ל.ג.ל./גלגל | term | ספר_אגריס#8fnF | גלגל | |
| decimal positional system/zero | ג.ל.ג.ל./גלגל | term | ספר_מעשה_חושב#j6Iv | גלגל | |
| decimal positional system/zero | ס.פ.ר./ספרא | term | ספר_המספר_/_אליהו_מזרחי#NSB9 | סיפרא | |
| decimal positional system/zero | ג.ל.ג.ל./גלגל | term | ספר_ציפרא#tNw7 | גלגל | |
| decimal positional system/zero | צפרא | definition | ספר_ציפרא#FxB3 | and before it a numeral, which is a zero [lit. wheel], like this 0, that has no substance but is a place holder and a remnant of a thing ''like a wheel, [like stubble] before the wind'' [Psalms 83, 14]. ולפניו ציפרא שהוא גלגל כזה 0 שאין בו ממש אלא שומר המעלות וזכר לדב' ''{{#annot:Ps83-14|494|JOTU}}כגלגל לפני רוח{{#annotend:JOTU}}'' תהלים פג, יד | |
| decimal positional system/zero | ג.ל.ג.ל./גלגל | term | Anonymous_text_from_Latin#fYsr | גלגל | |
| decimal positional system/zero | term | ספר_המספר_/_אליהו_מזרחי#8tTn | נולא | ||
| sexagesimal fraction/zodiac sign | מ.ז.ל./מזל | term | ספר_המספר_/_אליהו_מזרחי#t7YM | מזל |
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| Elements/Elements II-1 | a·∑bᵢ=∑(a·bᵢ) | ספר_המלכים#Sjh3 | For every two numbers, such that one of them is divided into as many parts as there are, [the product of] the number that is not divided by the divided number is equal to the sum of its products by each part of the divided number.
: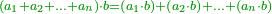 כל שני מספרים יחלק אחד מהם בחלקים כמו שיהיו הנה המספר שלא חולק במספר שחולק כמו הכאתו בכל חלקי המספר הנחלק כאשר יקובצו
כל שני מספרים יחלק אחד מהם בחלקים כמו שיהיו הנה המספר שלא חולק במספר שחולק כמו הכאתו בכל חלקי המספר הנחלק כאשר יקובצו |
| Elements/Elements II-1 | definition | ספר_המספר_/_אליהו_מזרחי#8mWV | It was already clarified in Euclid's Book of Elements, in the [second] section, in the first proposition that for any two straight lines, one of which is cut into segments as many as they may be, the sum of the surfaces generated from the whole straight line and each of the segments of the other straight line equals the surface generated from the whole straight line and the whole divided line.
: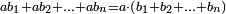 וזה שכבר התבאר בספר היסודות לאקלידס במאמר השלישי ממנו בתמונה הראשונה שכל שני קוים שנחלק אחד מהם לחלקים כמה שיהיו הנה השטח ההוא מהקו האחד כלו עם כל אחד מחלקי הקו האחר יחד הוא שוה לשטח ההווה מהקו האחד עם כל הקו הנחלק
וזה שכבר התבאר בספר היסודות לאקלידס במאמר השלישי ממנו בתמונה הראשונה שכל שני קוים שנחלק אחד מהם לחלקים כמה שיהיו הנה השטח ההוא מהקו האחד כלו עם כל אחד מחלקי הקו האחר יחד הוא שוה לשטח ההווה מהקו האחד עם כל הקו הנחלק |
| Elements/Elements II-1 | a·∑bᵢ=∑(a·bᵢ) | ספר_מעשה_חושב#4J1r | When there are two given numbers and one of them is divided into parts, as many as they may be, the product of the first number by the second is equal to the [sum of] the products of each of the parts of the first number by the second.
: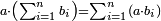 ב כאשר היו שני מספרים מונחים וחולק המספר האחד לחלקים כמה שיהיו הנה שטח המספר האחד בשני שוה לשטחי כל אחד מחלקי המספר האחד בשני מקובצים
ב כאשר היו שני מספרים מונחים וחולק המספר האחד לחלקים כמה שיהיו הנה שטח המספר האחד בשני שוה לשטחי כל אחד מחלקי המספר האחד בשני מקובצים |
| Elements/Elements II-1 | a·∑bᵢ=∑(a·bᵢ) | לקוטים_מספר_פראלוקא#t9Uk | If you have two numbers and you divide one of the two numbers, then you multiply each part by the second number, the total sum is the same as the product of the first number by the second.
: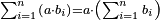 156 אם יש לך ב' מספרים ותחלק א' מהב' מספרים ותכפול כל חלק על המספר השני הנה הסך העולה הוא כמו מה שיעלה מכפל המספר הראשון על השני
156 אם יש לך ב' מספרים ותחלק א' מהב' מספרים ותכפול כל חלק על המספר השני הנה הסך העולה הוא כמו מה שיעלה מכפל המספר הראשון על השני |
| Elements/Elements II-1 | 10,2+3+5+2 | לקוטים_מספר_פראלוקא#1Q9z | Example: the two numbers are 10 and 12 and we divide 12 to 2, 3, 5, 2, so their sum is 12. המשל הנה ב' מספרים והם י' וי"ב ונחלק י"ב על ב' ועל ג' ועל ה' ועל ב' והנה כלם י"ב |
| Elements/Elements II-1 | ספר_החשבון_והמדות#fGS3 | I say: if you divide any number into parts as you wish, [the sum of] the products of each of the parts by the whole number is equal to the square of the whole number.
:![\scriptstyle{\color{OliveGreen}{\sum_{k=1}^n \left[\left(\sum_{i=1}^n a_i\right)\sdot a_k\right]=\left(\sum_{i=1}^n a_i\right)^2}}](/mediawiki/images/math/9/9/f/99fd3737e42a1acf970a92fb7a977c13.png) ואומר כל מספר שחלקת אותו לחלקים איך שרצית הנה כפל כל אחד מהחלקים על כל המספר מקובץ שוה למרובע כל המספר
ואומר כל מספר שחלקת אותו לחלקים איך שרצית הנה כפל כל אחד מהחלקים על כל המספר מקובץ שוה למרובע כל המספר | |
| Elements/Elements II-1 | 4,2+3+5 | ספר_המספר_/_אליהו_מזרחי#1rE2 | Example: if we divide the 10 into three parts randomly, one part of them is 2, the second is 3 and the third is 5. משל זה אם נחלק הי' לג' חלקים איך מה שקרה והיה החלק האחד מהם מספר ב' והשני מספר ג' והשלישי מספר ה' |
| Elements/Elements II-1 | a·∑bᵢ=∑(a·bᵢ) | ספר_המספר_/_אליהו_מזרחי#me96 | For every number divided into many parts randomly, the number that is generated from the product of a number by the whole given divided number is equal to the number generated from the sum of the products of that number by each part of the divided number.
: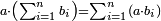 השנית שכל מספר נחלק לחלקים רבים איך מה שקרה הנה המספר ההווה מהכאת מספר מה עם המספר המונח הנחלק בכללו הוא שוה למספר ההווה מהכאת המספר ההוא עם כל אחד מחלקי המספר הנחלק כאשר יקובצו
השנית שכל מספר נחלק לחלקים רבים איך מה שקרה הנה המספר ההווה מהכאת מספר מה עם המספר המונח הנחלק בכללו הוא שוה למספר ההווה מהכאת המספר ההוא עם כל אחד מחלקי המספר הנחלק כאשר יקובצו |
| Elements/Elements II-10 | 10,2 | ספר_החשבון_והמדות#zIUc | Example: we have the number ten, we divide it into two halves, which are 5, and add to it another number 2, so it bacomes 12. דמיון יש לנו מספר מניינו עשרה וחלקנוהו לשני חצאים על ה' והוספנו עליו 33rמספר אחר ב' ונהיה י"ב |
| Elements/Elements II-10 | (a+b)²+b²=2·((½a)²+((½a)+b)²) | לקוטים_מספר_פראלוקא#ijBn | If you divide any number into two equal parts, then add another number to the divided number, square it and add to it the square of the [number] you added, it is twice [the sum of] the square of the additional [number] plus half [the number] with the square of half [the number].
:![\scriptstyle\left(a+b\right)^2+b^2=2\sdot\left[\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2+\left(\frac{1}{2}\sdot a\right)^2\right]](/mediawiki/images/math/5/e/9/5e9b4c74db157126a2fd01aad4693992.png) 165 אם תחלק איזה מספר על ב' חלקים שוים ואחר תוסיף מספר אחר על המספר המחולק ותרבענו ותוסיף על זה מרובע שהוספת יהיה ב' פעמים כמו כפל ממה שיעלה התוספת הנוסף על החצי עם מרובע החצי נוספים
165 אם תחלק איזה מספר על ב' חלקים שוים ואחר תוסיף מספר אחר על המספר המחולק ותרבענו ותוסיף על זה מרובע שהוספת יהיה ב' פעמים כמו כפל ממה שיעלה התוספת הנוסף על החצי עם מרובע החצי נוספים |
| Elements/Elements II-10 | (a+b)²+b²=2·((½a)²+((½a)+b)²) | ספר_המלכים#CVU6 | For any even number divided into half and another number is added to it, [the sum of] twice the product of half the number by itself and twice the product of half the number plus the additional [number] by itself is equal to [the sum of] the product of the [whole] number plus the additional [number] by itself and [the product] of the additional [number] by itself.
:![\scriptstyle{\color{OliveGreen}{\left[2\sdot\left(\frac{1}{2}\sdot a\right)^2\right]+\left[2\sdot\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2\right]=\left(a+b\right)^2+b^2}}](/mediawiki/images/math/b/6/e/b6e91cc251302ce6002e5d5c009f9286.png) כל מספר זוג יחלק לחציים ונוסף בו מספר אחר הנה ההווה מהכאת חצי המספר בכמהו שני פעמים והכאת חצי המספר עם התוספת בכמהו שני פעמים
כל מספר זוג יחלק לחציים ונוסף בו מספר אחר הנה ההווה מהכאת חצי המספר בכמהו שני פעמים והכאת חצי המספר עם התוספת בכמהו שני פעמים |
| Elements/Elements II-10 | 12,8 | לקוטים_מספר_פראלוקא#wuja | Example: we have 12, you divide it to 6 and 6, then add to 12 another number. Suppose that we add 8 to it. המשל יש לנו מספר י"ב ותחלקהו על ו'ו' ותוסיף על י"ב 148vמספר אחר ונניח כי נוסיף בם ח' |
| Elements/Elements II-10 | 10,2 | ספר_המספר_/_אליהו_מזרחי#0WFg | Example: we have the number ten, we divide it into two halves and add to it the number 2, so it bacomes 12. דמיון יש לנו מספר עשרה וחלקנוהו לשני חציים והוספנו עליו מספר ב' ונהיה י"ב |
| Elements/Elements II-10 | (a+b)²+b²=2·((½a)²+((½a)+b)²) | ספר_החשבון_והמדות#w9pW | If you divide any number into half and add to it another number, [the sum of] the square of the whole number plus the additional [number] and the square of the additional [number] is equal to twice [the sum of] the square of half the number and the square of half the number plus the additional [number] together.
:![\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2+b^2=2\sdot\left[\left(\frac{1}{2}\sdot a\right)^2+\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2\right]}}](/mediawiki/images/math/0/1/f/01f5c12dc0db0f20f362991f00bed1d8.png) עוד כל מספר שחלקת אותו לשני חציים והוספת עליו מספר אחר הנה מרובע המספר עם התוספת יחד ומרובע התוספת בעצמו הם כפל שני המרובעים שהם מרובע חצי המספר ומרובע חצי המספר עם התוספת יחד כאשר {{#annot:term|178,2083|Ycx9}}יחוברו{{#annotend:Ycx9}}
עוד כל מספר שחלקת אותו לשני חציים והוספת עליו מספר אחר הנה מרובע המספר עם התוספת יחד ומרובע התוספת בעצמו הם כפל שני המרובעים שהם מרובע חצי המספר ומרובע חצי המספר עם התוספת יחד כאשר {{#annot:term|178,2083|Ycx9}}יחוברו{{#annotend:Ycx9}} |
| Elements/Elements II-10 | (a+b)²+b²=2·((½a)²+((½a)+b)²) | ספר_המספר_/_אליהו_מזרחי#FJSe | Any number that you divide into half and add to it another number, [the sum of] the square of the [whole] number plus the additional [number] and the square of the additional [number] is equal to twice [the sum of] the square of half the number and the square of half the number plus the additional [number] when they are summed together.
:![\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2+b^2=2\sdot\left[\left(\frac{1}{2}\sdot a\right)^2+\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2\right]}}](/mediawiki/images/math/0/1/f/01f5c12dc0db0f20f362991f00bed1d8.png) עוד כל מספר שחלקת אותו לשני חצאים והוספת עליו מספר אחר הנה מרובע המספר עם התוספת יחד ומרובע התוספת בעצמו הם כפל שני המרובעים שהם מרובע חצי המספר ומרובע חצי המספר עם התוספת יחד כאשר יחוברו
עוד כל מספר שחלקת אותו לשני חצאים והוספת עליו מספר אחר הנה מרובע המספר עם התוספת יחד ומרובע התוספת בעצמו הם כפל שני המרובעים שהם מרובע חצי המספר ומרובע חצי המספר עם התוספת יחד כאשר יחוברו |
| Elements/Elements II-2 | 10,7+3 | ספר_החשבון_והמדות#KF6o | Example: the number ten; we divide it into 7 and 3. דמיון המספר עשרה וחלקנוהו על ז' וג' |
| Elements/Elements II-2 | ∑ₖ((∑ᵢaᵢ)·aₖ)=(∑ᵢaᵢ)² | קצת_מענייני_חכמת_המספר#4EHv | If you divide any number into parts as you wish, [the sum of] the products of each of the parts by the whole number is equal to the square of the whole number.
:![\scriptstyle{\color{OliveGreen}{\sum_{k=1}^n \left[\left(\sum_{i=1}^n a_i\right)\sdot a_k\right]=\left(\sum_{i=1}^n a_i\right)^2}}](/mediawiki/images/math/9/9/f/99fd3737e42a1acf970a92fb7a977c13.png) אחת כל מספר שחלקת אותו לחלקים איך שרצית הנה הכאת כל אח' מהחלקי' בכל המספר השוה למרובע הכל
אחת כל מספר שחלקת אותו לחלקים איך שרצית הנה הכאת כל אח' מהחלקי' בכל המספר השוה למרובע הכל |
| Elements/Elements II-2 | 12,3+4+5 | לקוטים_מספר_פראלוקא#Gj4L | Example: we wish to divide 12 into three parts 5, 3, 4. המשל נרצה לעשות מי"ב ג' חלקים ה' ג' ד' |
| Elements/Elements II-2 | 12,3+4+5 | ספר_החשבון_והמדות#pdf0 | Example: the number 12; we divide it into three, four and five. דמיון המספר י"ב וחלקנוהו על שלשה וארבעה וחמשה |
| Elements/Elements II-2 | ∑ₖ((∑ᵢaᵢ)·aₖ)=(∑ᵢaᵢ)² | לקוטים_מספר_פראלוקא#nMHc | If you have a number and you divide iy into parts as you wish, if you multiply each part by the divided number, then sum all the [products] they are equal to the divided number multiplied by itself.
:![\scriptstyle\sum_{k=1}^n \left[\left(\sum_{i=1}^n a_i\right)\sdot a_k\right]=\left(\sum_{i=1}^n a_i\right)^2](/mediawiki/images/math/2/a/1/2a190390030d9c138d548197fab10837.png) 157 אם יש לך מספר אחד ותחלק אותו לכ"כ חלקים שתרצה אם תכפול כל חלק על המספר המחולק ותקבץ כל החלקים יהיו שוים אל המספר המחולק כפול על עצמו
157 אם יש לך מספר אחד ותחלק אותו לכ"כ חלקים שתרצה אם תכפול כל חלק על המספר המחולק ותקבץ כל החלקים יהיו שוים אל המספר המחולק כפול על עצמו |
| Elements/Elements II-2 | 12,3+4+5 | ספר_המספר_/_אליהו_מזרחי#Nxlm | Example: the number 12, we divide it to three, four and five. דמיון זה המספר י"ב וחלקנוהו על שלשה וארבעה וחמשה |
| Elements/Elements II-2 | ∑ₖ((∑ᵢaᵢ)·aₖ)=(∑ᵢaᵢ)² | ספר_החשבון_והמדות#DxvK | For every number that you divide randomly into two parts, the sum of the products of each of the two parts by the whole number is equal to the square of the whole number.
:![\scriptstyle{\color{OliveGreen}{\left[\left(a+b\right)\sdot a\right]+\left[\left(a+b\right)\sdot b\right]=\left(a+b\right)^2}}](/mediawiki/images/math/8/a/a/8aae9db1c4694d4c859578e458487970.png) עוד כל מספר שחלקת אותו לשני חלקים איך שקרה הנה כפל כל אחד משני החלקים על כל המספר מקובץ שוה למרובע כל המספר
עוד כל מספר שחלקת אותו לשני חלקים איך שקרה הנה כפל כל אחד משני החלקים על כל המספר מקובץ שוה למרובע כל המספר |
| Elements/Elements II-2 | ∑ₖ((∑ᵢaᵢ)·aₖ)=(∑ᵢaᵢ)² | ספר_המספר_/_אליהו_מזרחי#mQeQ | Any number that you divide into parts as you wish, [the sum of] the products of each of the parts by the whole number is equal to the square of the whole number.
:![\scriptstyle{\color{OliveGreen}{\sum_{k=1}^n \left[\left(\sum_{i=1}^n a_i\right)\sdot a_k\right]=\left(\sum_{i=1}^n a_i\right)^2}}](/mediawiki/images/math/9/9/f/99fd3737e42a1acf970a92fb7a977c13.png) והוא שכל מספר שחלקת אותו לחלקים איך שרצית הנה הכאת כל אחד מהחלקים עם כל המספר שוה למרובע כל המספר
והוא שכל מספר שחלקת אותו לחלקים איך שרצית הנה הכאת כל אחד מהחלקים עם כל המספר שוה למרובע כל המספר |
| Elements/Elements II-3 | (a+b)·b=(a·b)+b² | קצת_מענייני_חכמת_המספר#PVyt | For any number divided into two parts as you wish, the product of the whole number by any of its two parts is equal to the product of the one part by the other plus the square of the part by which you multiplied the whole number.
: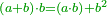 ב כל מספר שחלקת אותו לב' חלקים איך שקרה הנה הכאת המספר כלו עם כל אחד מב' חלקיו איזה שיהיה שוה להכאת החלק האחד עם האחר ולמרובע החלק אשר בו הכית כל המספר
ב כל מספר שחלקת אותו לב' חלקים איך שקרה הנה הכאת המספר כלו עם כל אחד מב' חלקיו איזה שיהיה שוה להכאת החלק האחד עם האחר ולמרובע החלק אשר בו הכית כל המספר |
| Elements/Elements II-3 | (a+b)·b=(a·b)+b² | לקוטים_מספר_פראלוקא#fYtF | If you divide any number into two parts, then multiply any of the two parts by the divided number and keep the product, so will be the result if you multiply the same part by itself, then add to it the product of the one part by the other.
: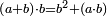 158 אם תחלק איזה מספר על ב' חלקים ותכפול החלק שיהיה מב' החלקים על המספר המחולק ושמור העולה כך יעלה אם תכפול אותו חלק על עצמו ותוסיף בו העולה מהכפל מהחלק האחד על השני
158 אם תחלק איזה מספר על ב' חלקים ותכפול החלק שיהיה מב' החלקים על המספר המחולק ושמור העולה כך יעלה אם תכפול אותו חלק על עצמו ותוסיף בו העולה מהכפל מהחלק האחד על השני |
| Elements/Elements II-3 | (a+b)·b=(a·b)+b² | ספר_מעשה_חושב#BvNU | When a number is divided into two parts, the product of the whole number by one of its parts is equal to the product of the one part by the other plus the square of the mentioned part.
: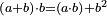 ד כאשר חולק מספר מה בשני חלקים הנה שטח כל המספר באחד מחלקיו שוה לשטח החלק האחד באחר ולמרובע החלק אשר זכרנו
ד כאשר חולק מספר מה בשני חלקים הנה שטח כל המספר באחד מחלקיו שוה לשטח החלק האחד באחר ולמרובע החלק אשר זכרנו |
| Elements/Elements II-3 | (a+b)·b=(a·b)+b² | ספר_המספר_/_אליהו_מזרחי#oIDS | For any number that you divide into two parts randomly, the product of the whole number by any of its two parts is equal to the product of the one part by the other plus the square of the part by which you have multiplied the whole number.
: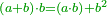 עוד כל מספר שחלקת אותו לשני חלקים איך שקרה הנה הכאת המספר כלו עם כל אחד משני חלקיו איזה שיהיה שוה להכאת החלק האחד עם השני ולמרובע החלק אשר הכית עם כל המספר
עוד כל מספר שחלקת אותו לשני חלקים איך שקרה הנה הכאת המספר כלו עם כל אחד משני חלקיו איזה שיהיה שוה להכאת החלק האחד עם השני ולמרובע החלק אשר הכית עם כל המספר |
| Elements/Elements II-3 | 10,3+7 | ספר_החשבון_והמדות#zmnp | Example: the number ten, we divide it into two parts - three and seven. דמיון המספר עשרה חלקנוהו לשני חלקים על שלשה ושבעה |
| Elements/Elements II-3 | (a+b)·b=(a·b)+b² | ספר_החשבון_והמדות#Eu5r | For any number divided into two parts as you wish, the product of the whole number by any of its two parts is equal to the product of the one part by the other plus the square of the part by which you multiplied the whole number.
: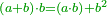 עוד כל מספר שחלקת אותו בשני חלקים איך שקרה הנה כפל המספר כולו על אחד משני חלקיו איזה שיהיה שוה לכפול החלק האחד על השני ולמרובע החלק משניהם אשר כפלת על כל המספר
עוד כל מספר שחלקת אותו בשני חלקים איך שקרה הנה כפל המספר כולו על אחד משני חלקיו איזה שיהיה שוה לכפול החלק האחד על השני ולמרובע החלק משניהם אשר כפלת על כל המספר |
| Elements/Elements II-3 | 10,3+7 | ספר_המספר_/_אליהו_מזרחי#CANO | Example: the number ten, we divide into two parts - three and seven. דמיון המספר עשרה חלקנוהו לשני חלקים על שלשה ושבעה |
| Elements/Elements II-3 | 12,4+8 | לקוטים_מספר_פראלוקא#XIpE | Example: we have 12 and you divide it to 8 and 4. המשל אם יש לנו י"ב ותחלק אותו ח' ד' |
| Elements/Elements II-3 | 10,3+7 | קצת_מענייני_חכמת_המספר#MLKI | Example: the number 10 is divided into two parts - 7 and 3. כמשל מספר הי' נחלק לב' חלקים לז' ולג' |
| Elements/Elements II-4 | 12,4+8 | לקוטים_מספר_פראלוקא#HYCk | Example: we divide 12 to 4 and 8. המשל הנה נחלק 147vמספר י"ב על ד' ועל ח' |
| Elements/Elements II-4 | 10,3+7 | ספר_החשבון_והמדות#hh0J | Example: the number ten; we divide it into three and seven. דמיון המספר עשרה חלקנוה על שלשה ושבעה |
| Elements/Elements II-4 | (a+b)²=a²+b²+2(a·b) | ספר_המספר_/_אליהו_מזרחי#oC2j | For any number that you divide into two parts randomly, the square of the whole number is equal to [the sum of] the squares of the two parts and twice the product of the one part by the other.
:![\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2=a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]}}](/mediawiki/images/math/d/f/2/df26d1cdaf50844081193e48666b1eeb.png) עוד כל מספר שחלקת אותו לשני חלקים איך שקרה הנה מרובע כל המספר שוה לשני המרובעי' ההווים משני החלקים ולהכאת החלק האחד עם חברו פעמים
עוד כל מספר שחלקת אותו לשני חלקים איך שקרה הנה מרובע כל המספר שוה לשני המרובעי' ההווים משני החלקים ולהכאת החלק האחד עם חברו פעמים |
| Elements/Elements II-4 | (a+b)²=a²+b²+2(a·b) | ספר_המלכים#wUeW | For any number divided into [two] parts, whichever they may be, the product of the whole number by itself is equal to the sum of the products of each of the two parts by itself and double the product of one of the two parts by the other.
:![\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2=a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]}}](/mediawiki/images/math/d/f/2/df26d1cdaf50844081193e48666b1eeb.png) |style="width:45%; text-align:right;"|כל מספר יחלק בחלקים כמו שיהיו הנה הכאת המספר כלו בעצמו כמו הכאת כל אחד משני החלקים בעצמו וכפל הכאת אחד משני החלקים באחר כאשר יקובצו
|style="width:45%; text-align:right;"|כל מספר יחלק בחלקים כמו שיהיו הנה הכאת המספר כלו בעצמו כמו הכאת כל אחד משני החלקים בעצמו וכפל הכאת אחד משני החלקים באחר כאשר יקובצו |
| Elements/Elements II-4 | (a+b)²=a²+b²+2(a·b) | ספר_המספר_/_אליהו_מזרחי#TApz | For any number divided into two parts randomly, the square of the whole number is equal to [the sum of] the squares of the two parts and twice the product of the one part by the other.
:![\scriptstyle\left(a+b\right)^2=a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]](/mediawiki/images/math/7/2/7/727b0c35fd93a7a347bed8413905049f.png) האחת שכל מספר נחלק לשנים חלקים איך מה שקרה הנה המרובע ההווה מן המספר כלו הוא שוה לשני המרובעים ההווים משני חלקיו עם כפל המספר ההווה מהכאת החלק האחד עם האחר
האחת שכל מספר נחלק לשנים חלקים איך מה שקרה הנה המרובע ההווה מן המספר כלו הוא שוה לשני המרובעים ההווים משני חלקיו עם כפל המספר ההווה מהכאת החלק האחד עם האחר |
| Elements/Elements II-4 | (a+b)²=a²+b²+2(a·b) | קצת_מענייני_חכמת_המספר#v7Dx | For any number divided into two parts as you wish, the square of the whole number is equal to [the sum of] the squares of the two parts and twice the product of the one part by the other.
:![\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2=a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]}}](/mediawiki/images/math/d/f/2/df26d1cdaf50844081193e48666b1eeb.png) ג כל מספר שחלקת אותו לשני חלקים איך שקרה הנה מרובע כל המספר שוה לב' המרובעים ההווים מב' החלקים ולהכאת החלק האחד עם חבירו ב' פעמים
ג כל מספר שחלקת אותו לשני חלקים איך שקרה הנה מרובע כל המספר שוה לב' המרובעים ההווים מב' החלקים ולהכאת החלק האחד עם חבירו ב' פעמים |
| Elements/Elements II-4 | 10,3+7 | ספר_המספר_/_אליהו_מזרחי#Ca24 | Example: the number ten, we divide it to three and seven. דמיון המספר עשרה חלקנוהו על שלשה ושבעה |
| Elements/Elements II-4 | (a+b)²=a²+b²+2(a·b) | ספר_החשבון_והמדות#q5ib | For any number divided into two parts as you wish, the square of the whole number is equal to [the sum of] the squares of the two parts and twice the product of the one part by the other.
:![\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2=a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]}}](/mediawiki/images/math/d/f/2/df26d1cdaf50844081193e48666b1eeb.png) עוד כל מספר שחלקת אותו לשני חלקים איך שקרה הנה מרובע כל המספר שוה לשני המרובעים ההוים משני החלקים ולכפל החלק האחד על חברו פעמים
עוד כל מספר שחלקת אותו לשני חלקים איך שקרה הנה מרובע כל המספר שוה לשני המרובעים ההוים משני החלקים ולכפל החלק האחד על חברו פעמים |
| Elements/Elements II-4 | definition | ספר_האלזיברא#JPnC | When a straight line is cut randomly into two segments, the square on the whole line equals the sum of the two squares that are generated from the two segments plus twice the rectangle encompassed by the two segments.
: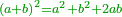 כי כאשר נחלק קו ישר לב' חלקים איך שקרה הנה מרבע הקו כלו שוה לשני המרבעים ההווים משני החלקים ולכפל השטח הנצב הזויות אשר יקיפו בו שני החלקים
כי כאשר נחלק קו ישר לב' חלקים איך שקרה הנה מרבע הקו כלו שוה לשני המרבעים ההווים משני החלקים ולכפל השטח הנצב הזויות אשר יקיפו בו שני החלקים |
| Elements/Elements II-4 | reference | ספר_האלזיברא#Eeue | It was already clarified in [[ספר_היסודות_לאקלידס#Elements_II_4|'''Euclid, Elements, Book II, proposition 4''']] that: וכבר נתבאר ב'''תמונת הרביעית מן המאמר השני לאקלידס''' |
| Elements/Elements II-4 | (a+b)²=a²+b²+2(a·b) | לקוטים_מספר_פראלוקא#lAxq | If you have a number and you divide it into two unequal parts, I say that if you sum the [parts] that are multiplied by themselves, then you multiply the smaller [part] by the greater, multiply the product by 2 and sum it with the reserved, the result is equal to the [original] number multiplied by itself.
:![\scriptstyle\left(a+b\right)^2=a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]](/mediawiki/images/math/7/2/7/727b0c35fd93a7a347bed8413905049f.png) 169 אם יש לך מספר ותחלקהו על ב' חלקים בלתי שוים אומר כי אם תקבץ המספרי' המוכפלים על עצמם ואח"כ תכפול המספר הקטון על הגדול והעולה כפול על ב' ותקבץ זה עם השמור יעלה הכל כמו המספר כפול על עצמו
169 אם יש לך מספר ותחלקהו על ב' חלקים בלתי שוים אומר כי אם תקבץ המספרי' המוכפלים על עצמם ואח"כ תכפול המספר הקטון על הגדול והעולה כפול על ב' ותקבץ זה עם השמור יעלה הכל כמו המספר כפול על עצמו |
| Elements/Elements II-4 | 10,3+7 | קצת_מענייני_חכמת_המספר#OusC | Example: the number 10 is divided into 7 and 3. כמשל הי' נחלק לז' ולג' |
| Elements/Elements II-4 | 10,3+7 | ספר_המספר_/_אליהו_מזרחי#6oZu | Example: if we divide the 10 into two parts randomly, one part of them is 3 and the other 7. משל זה אם נחלק הי' לשנים חלקים איך מה שקרה והיה החלק האחד מהם ג' והאחר ז' |
| Elements/Elements II-4 | (a+b)²=a²+b²+2(a·b) | לקוטים_מספר_פראלוקא#lb40 | If you divide any number into two and multiply each part by itself, you multiply also one [part] by the other and multiply [the product] by 2, then you sum all, the result is equal to the divided number multiplied by itself.
:![\scriptstyle a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]=\left(a+b\right)^2](/mediawiki/images/math/8/2/e/82e411d047c5fc9961bdf7306ae1b255.png) 159 אם תחלק איזה מספר שיהיה על ב' ותכפול כל חלק על עצמו וג"כ כפול הא' על הב' וכפלם על ב' ותקבץ הכל הנה העולה יהיה שוה אל המספר המחולק כפול על עצמו
159 אם תחלק איזה מספר שיהיה על ב' ותכפול כל חלק על עצמו וג"כ כפול הא' על הב' וכפלם על ב' ותקבץ הכל הנה העולה יהיה שוה אל המספר המחולק כפול על עצמו |
| Elements/Elements II-4 | (a+b)²=a²+b²+2(a·b) | ספר_מעשה_חושב#lUMx | When a number is added to a number, the square of the two numbers that are summed together is equal to [the sum of] the squares of these numbers and twice the product of the one by the other.
:![\scriptstyle\left(a+b\right)^2=a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]](/mediawiki/images/math/7/2/7/727b0c35fd93a7a347bed8413905049f.png) ו כאשר נוסף על מספר מונח מספר מה הנה מרובע שני המספרים מחוברים שוה למרובעי המספרים ההם ולכפל שטח זה בזה
ו כאשר נוסף על מספר מונח מספר מה הנה מרובע שני המספרים מחוברים שוה למרובעי המספרים ההם ולכפל שטח זה בזה |
| Elements/Elements II-5 | 10,3+7 | ספר_החשבון_והמדות#zKhJ | Example: the number ten, we divide it to five and five, which are equal parts, then we divide it also to 7 and 3, which are unequal parts. דמיון המספר עשרה חלקנו לחמשה וחמשה שהם חלקים שוים גם חלקנוהו לז' וג' שהם חלקים בלתי שוים |
| Elements/Elements II-5 | 12,4+8 | לקוטים_מספר_פראלוקא#pZPT | Example: we divide 12 into two equal parts 6 and 6, and into two unequal parts 4 and 8. המשל נחלק מספר י"ב לב' חלקים שוים ו'ו' ולב' חלקים בלתי שוים ד' וח' |
| Elements/Elements II-5 | 10,3+7 | ספר_המספר_/_אליהו_מזרחי#zYJb | Example: the number ten, we divide it to five and five, which are equal parts, then we divide it also to seven and three, which are unequal parts. דמיון המספר עשרה חלקנוהו לחמשה וחמשה שהם חלקים שוים גם חלקנוהו לשבעה ושלשה שהם חלקים בלתי שוים |
| Elements/Elements II-5 | (½(a+b))²=(a·b)+(b-½(a+b))²=(a·b)+(½(a+b)-a)² | קצת_מענייני_חכמת_המספר#9QNa | For any number divided into two equal parts and into two unequal parts, [the sum of] the product of one of the unequal parts by the other and the square of the difference between the two parts, i.e. between the equal part [= the half of the whole number] and the unequal [part] is equal to the square of half the [whole] number.
:![\scriptstyle{\color{OliveGreen}{\left(a\sdot b\right)+\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]^2=\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2}}](/mediawiki/images/math/9/3/3/9338487b12c6a0e6ee74fab15e061cb9.png) ד כל מספר כאשר תחלקהו לב' חלקים שוים ולב' חלקים בלתי שוים הנה הכאת החלק הא' עם חבירו מהחלקים הבלתי שוים ומרוב' מה שבין ב' חלקים ר"ל בין החלק השוה ובלתי שוה שוה למרובע חצי המספר
ד כל מספר כאשר תחלקהו לב' חלקים שוים ולב' חלקים בלתי שוים הנה הכאת החלק הא' עם חבירו מהחלקים הבלתי שוים ומרוב' מה שבין ב' חלקים ר"ל בין החלק השוה ובלתי שוה שוה למרובע חצי המספר |
| Elements/Elements II-5 | (½(a+b))²=(a·b)+(b-½(a+b))²=(a·b)+(½(a+b)-a)² | ספר_החשבון_והמדות#43lj | For any number divided into two equal parts and into two unequal parts, [the sum of] the product of one of the unequal parts by the other and the square of the difference between the two parts, i.e. between the equal part [= the half of the whole number] and the unequal [part] is equal to the square of half the [whole] number.
:![\scriptstyle{\color{OliveGreen}{\left(a\sdot b\right)+\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]^2=\left(a\sdot b\right)+\left[b-\left[\frac{1}{2}\sdot\left(a+b\right)\right]\right]^2=\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2}}](/mediawiki/images/math/7/0/c/70cf1effca1e2303b584ecf2bb737846.png) עוד כל מספר כאשר תחלקהו לשני חלקים שוים ולשני חלקים בלתי שוים הנה כפל החלק האחד אל חברו מהחלקים הבלתי שוים ומרובע מה שבין שני 32vהחלקים ר"ל בין החלק השוה ובלתי שוה שוה למרובע חצי המספר
עוד כל מספר כאשר תחלקהו לשני חלקים שוים ולשני חלקים בלתי שוים הנה כפל החלק האחד אל חברו מהחלקים הבלתי שוים ומרובע מה שבין שני 32vהחלקים ר"ל בין החלק השוה ובלתי שוה שוה למרובע חצי המספר |
| Elements/Elements II-5 | (½(a+b))²=(a·b)+(b-½(a+b))²=(a·b)+(½(a+b)-a)² | ספר_המלכים#4PpZ | For any even number divided into halves and into [two] unequal parts, the product of half the [whole] number by itself is equal to [the sum of] the product of the greater part by the smaller [part] and the product of the excess of the half of the [whole] number over the smaller part by itself.
:![\scriptstyle{\color{OliveGreen}{\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2=\left(a\sdot b\right)+\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]^2}}](/mediawiki/images/math/d/b/e/dbe95ea8054f7a459368b72c0c2ba9fb.png) כל מספר זוג יחלק לחצאים ולחלקים מתחלפים הנה אשר יהיה מהכאת [חצי]M om. המספר בעצמו כמו ההווה מהכאת החלק הגדול בקטן עם הכאת מותר חצי המספר על החלק
כל מספר זוג יחלק לחצאים ולחלקים מתחלפים הנה אשר יהיה מהכאת [חצי]M om. המספר בעצמו כמו ההווה מהכאת החלק הגדול בקטן עם הכאת מותר חצי המספר על החלק |
| Elements/Elements II-5 | 10,3+7 | קצת_מענייני_חכמת_המספר#41Hj | Example: the number 10 that is divided into 7 and 3. במש' הי' שנחלק לז' ולג' |
| Elements/Elements II-5 | (½(a+b))²=(a·b)+(b-½(a+b))²=(a·b)+(½(a+b)-a)² | לקוטים_מספר_פראלוקא#24rA | If you divide any number into two equal parts and into two unequal parts, the product of the equal parts one by the other is as the product of the unequal parts one by the other, when you add to it the [square] of the difference between the [equal] part and the [unequal part]. 160 אם תחלק מספר אחד לב' חלקים שוים ולב' חלקים בלתי שוים הנה כל כך יעלה כפל החלקים השוים זה על זה כמו כפל החלקים הבלתי שוים זה על זה ותוסיף בם כפל היתרון שיש מהחלק האחד על האחר |
| Elements/Elements II-5 | reference | ספר_האלזיברא#7B0h | [[ספר_היסודות_לאקלידס#Elements_II_5|'''Euclid, Elements, Book II, proposition 5''']]: the square formed by AZ, which is four measures, and is as the square of half [the number of] the things that is known to be 16, is equal to surface BH, which is equal to the right-angled surface encompassed by the two unequal segments, whose area is known to be 12, plus the square formed by ZB that is the difference between the two parts.
:![\scriptstyle{\color{OliveGreen}{\left(a\sdot b\right)+\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-b\right]^2=\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2}}](/mediawiki/images/math/8/0/9/8094ef8a2f57faab6825944b3c1aef85.png) :
: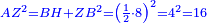 והנה כפי מה שנתבאר ב'''תמו' החמישית מן המאמר השני לאקלידס'''
והנה כפי מה שנתבאר ב'''תמו' החמישית מן המאמר השני לאקלידס''' |
| Elements/Elements II-5 | (½(a+b))²=(a·b)+(b-½(a+b))²=(a·b)+(½(a+b)-a)² | ספר_המספר_/_אליהו_מזרחי#yKYx | For any number, when you divide it into two equal parts and into two unequal parts, [the sum of] the product of one of the unequal parts by the other and the square of the difference between the two parts, i.e. between the equal part [= the half of the whole number] and the unequal [part] is equal to the square of half the [whole] number.
:![\scriptstyle{\color{OliveGreen}{\left(a\sdot b\right)+\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]^2=\left(a\sdot b\right)+\left[b-\left[\frac{1}{2}\sdot\left(a+b\right)\right]\right]^2=\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2}}](/mediawiki/images/math/7/0/c/70cf1effca1e2303b584ecf2bb737846.png) עוד כל מספר כאשר תחלקהו לשני חלקים שוים ולשני חלקים בלתי שוים הנה הכאת החלק האחד עם חברו מהחלקים הבלתי שוים ומרובע מה שבין שני החלקים ר"ל בין החלק השוה ובלתי שוה שוה למרובע חצי המספר
עוד כל מספר כאשר תחלקהו לשני חלקים שוים ולשני חלקים בלתי שוים הנה הכאת החלק האחד עם חברו מהחלקים הבלתי שוים ומרובע מה שבין שני החלקים ר"ל בין החלק השוה ובלתי שוה שוה למרובע חצי המספר |
| Elements/Elements II-5 | (½(a+b))²=(a·b)+(b-½(a+b))²=(a·b)+(½(a+b)-a)² | ספר_מעשה_חושב#AHZr | The product of half the given number by itself is equal to [the sum of] the product of a part of that number by the other part and the square of the difference between one of the [unequal] parts and half of the [whole] given number. ח השטח ההוה מחצי המספר המונח בעצמו שוה לשטח ההוה מחלק מה מהמספר ההוא בחלק השני ולמרובע יתרון אחד מן החלקים על חצי המספר המונח |
| Elements/Elements II-6 | 10,2 | ספר_המספר_/_אליהו_מזרחי#bDvj | Example: the number ten, we divide it into two halves, which are five each, then we add two to the ten, they are 12. דמיון המספר עשרה וחלקנוהו לשני חצאים שהם כל חצי חמשה הוספנו על העשרה שנים והיו י"ב |
| Elements/Elements II-6 | reference | ספר_האלזיברא#XaGL | [[ספר_היסודות_לאקלידס#Elements_II_6|'''Euclid, Elements, Book II, proposition 6''']] that the right-angled surface encompassed by the whole line with the addition and the addition, which is equal to surface ZD, whose area is 2 in our example, with the square formed by half the line, which is 16 in our example, both together are 36, equals the square of the line formed by half the line with the addition, which is line TB in our illustration.
:![\scriptstyle{\color{OliveGreen}{\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2}}](/mediawiki/images/math/a/9/2/a92046fe5abf282c91d09104586c53a7.png) וכבר נתבאר ב'''תמונה הששית מן המאמר השני לאקלידס'''
וכבר נתבאר ב'''תמונה הששית מן המאמר השני לאקלידס''' |
| Elements/Elements II-6 | 12,4 | לקוטים_מספר_פראלוקא#qQuN | Example: we have 12, you divide it to 6 and 6, then add to 6 whichever number you wish. Suppose that we wish to add 4 to 6. המשל יש לנו מספר י"ב ותחלק אותו על ו"ו ותוסיף על ו' מספר איזה שתרצה ונניח כי נרצה להוסיף על ו' ד' |
| Elements/Elements II-6 | 10,2 | ספר_החשבון_והמדות#yd9c | Example: the number ten, we divide it into two halves, which are five each, then we add two to the ten, they are 12. דמיון המספר עשרה וחלקנוהו לשני חצאים שהם כל חצי חמשה {{#annot:term|178,1206|GTDu}}הוספנו{{#annotend:GTDu}} על העשרה שנים והיו י"ב |
| Elements/Elements II-6 | (a+b)·b+(½a)²=(½a+b)² | ספר_מעשה_חושב#vsiV | When a number is divided into two halves and a number is added to it, [the sum of] the product of the additional [number] by the whole number plus the additional [number] and the square of half the number is equal to the square of half the number and the additional [number] summed together.
:![\scriptstyle\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2](/mediawiki/images/math/a/0/b/a0b403dd8b7c15a5cb1dc47a5f8ca5bb.png) ה כאשר חולק מספר מה לחציין והוסף עליו מספר מה הנה שטח התוספת במספר כלו עם התוספת עם מרובע חצי המספר שוה למרובע חצי המספר והתוספת מקובצים
ה כאשר חולק מספר מה לחציין והוסף עליו מספר מה הנה שטח התוספת במספר כלו עם התוספת עם מרובע חצי המספר שוה למרובע חצי המספר והתוספת מקובצים |
| Elements/Elements II-6 | reference | ספר_האלזיברא#BJrm | [[ספר_היסודות_לאקלידס#Elements_II_6|'''Euclid, Elements, Book II, proposition 6''']] that the right-angled surface encompassed by the whole line with the addition and the addition, which is equal to surface AW, whose area is known as 48, plus the square of half the line, whose area is known, which is 1, both together are 49, equals the square of the line formed by half the line with the addition, which is line AZ.
:![\scriptstyle{\color{OliveGreen}{\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2}}](/mediawiki/images/math/a/9/2/a92046fe5abf282c91d09104586c53a7.png) וכבר נתבאר ב'''תמונה הששית 131vמן המאמר השני לאקלידס'''
וכבר נתבאר ב'''תמונה הששית 131vמן המאמר השני לאקלידס''' |
| Elements/Elements II-6 | (a+b)·b+(½a)²=(½a+b)² | לקוטים_מספר_פראלוקא#77le | If you divide any number into two equal parts, then add an additional [number] to the divided number, multiply [the sum] by the additional [number] and add [the product] to the square of one of the parts, I say that it is equal to the square of half [the number] with the additional [number].
:![\scriptstyle\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2](/mediawiki/images/math/a/0/b/a0b403dd8b7c15a5cb1dc47a5f8ca5bb.png) 161 אם תחלק איזה מספר לב' חלקים שוים ותוסיף בם א' מהחלקי' כפול על עצמו ותוסיף בם התוספת על כל המספר המחולק ותכפול אותו המספר אשר הוספת ותחברם עם כפל אחד מהחלקים אומר כי הוא שוה אל כפל המחצית עם התוספת
161 אם תחלק איזה מספר לב' חלקים שוים ותוסיף בם א' מהחלקי' כפול על עצמו ותוסיף בם התוספת על כל המספר המחולק ותכפול אותו המספר אשר הוספת ותחברם עם כפל אחד מהחלקים אומר כי הוא שוה אל כפל המחצית עם התוספת |
| Elements/Elements II-6 | (a+b)·b+(½a)²=(½a+b)² | קצת_מענייני_חכמת_המספר#nmaV | If we divide any number into half and add to it another number, [the sum of] the product of the whole number plus the additional [number] by the additional [number] and the square of half the number is equal to the square of half the number and the additional [number] together.
:![\scriptstyle{\color{OliveGreen}{\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2}}](/mediawiki/images/math/a/9/2/a92046fe5abf282c91d09104586c53a7.png) ה כל מספר כאשר חלקנו אותו לחצי והוספת עליו מספר אחר הנה הכאת המספר כלו מחובר עם התוספ' בתוספת ומרובע חצי המספר שוה למרובע חצי המספר והתוספת ביחד
ה כל מספר כאשר חלקנו אותו לחצי והוספת עליו מספר אחר הנה הכאת המספר כלו מחובר עם התוספ' בתוספת ומרובע חצי המספר שוה למרובע חצי המספר והתוספת ביחד |
| Elements/Elements II-6 | (a+b)·b+(½a)²=(½a+b)² | ספר_החשבון_והמדות#A9xw | If you divide any number into half and add to it another number, [the sum of] the product of the whole number plus the additional [number] by the additional [number] and the square of half the number is equal to the square of half the number and the additional [number] together.
:![\scriptstyle{\color{OliveGreen}{\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2}}](/mediawiki/images/math/a/9/2/a92046fe5abf282c91d09104586c53a7.png) עוד כל מספר כאשר חלקת אותו לחצאים והוספת עליו מספר אחר הנה כפל המספר כלו מקובץ עם התוספת בתוספת והמרובע ההוה מחצי המספר שוה למרובע חצי המספר והתוספת ביחד
עוד כל מספר כאשר חלקת אותו לחצאים והוספת עליו מספר אחר הנה כפל המספר כלו מקובץ עם התוספת בתוספת והמרובע ההוה מחצי המספר שוה למרובע חצי המספר והתוספת ביחד |
| Elements/Elements II-6 | (a+b)·b+(½a)²=(½a+b)² | ספר_המספר_/_אליהו_מזרחי#tcs6 | For any number, when you divide it into half and add to it another number, [the sum of] the product of the whole number plus the additional [number] by the additional [number] and the square of half the number is equal to the square of half the number and the additional [number] together.
:![\scriptstyle{\color{OliveGreen}{\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2}}](/mediawiki/images/math/a/9/2/a92046fe5abf282c91d09104586c53a7.png) עוד כל מספר כאשר חלקת אותו לחצי והוספת עליו מספר אחר הנה הכאת המספר כלו מקובץ עם התוספת בתוספת והמרובע ההווה מחצי המספר שוה למרובע חצי המספר והתוספת ביחד
עוד כל מספר כאשר חלקת אותו לחצי והוספת עליו מספר אחר הנה הכאת המספר כלו מקובץ עם התוספת בתוספת והמרובע ההווה מחצי המספר שוה למרובע חצי המספר והתוספת ביחד |
| Elements/Elements II-6 | (a+b)·b+(½a)²=(½a+b)² | ספר_המלכים#c7yY | For any number divided into two halves and another number is added to it, the product of half the number and the additional [number] together by itself is equal to [the sum of] the product of the [whole] number plus the additional [number] by the additional [number] and the product of half the original number by itself.
:![\scriptstyle{\color{OliveGreen}{\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2=\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2}}](/mediawiki/images/math/8/5/e/85ec1e0db93c2d4e5ffad82b081e922d.png) כל מספר זוג יחלק לשני חצאים ויתוסף בו מספר אחר הנה הכאת חצי המספר עם התוספת בכמהו כהכאת המספר עם התוספת בתוספת והכאת חצי המספר הראשון בעצמו
כל מספר זוג יחלק לשני חצאים ויתוסף בו מספר אחר הנה הכאת חצי המספר עם התוספת בכמהו כהכאת המספר עם התוספת בתוספת והכאת חצי המספר הראשון בעצמו |
| Elements/Elements II-7 | 10,3+7 | ספר_החשבון_והמדות#L1Xh | Example: the number ten, we divide it randomly to seven and three. דמיון המספר עשרה וחלקנוהו איך שקרה על שבעה ועל שלשה |
| Elements/Elements II-7 | (a+b)²+a²=(2·(a+b)·a)+b² | ספר_החשבון_והמדות#hdYZ | For any number divided into two parts, the sum of the square of the whole number and the square of one of the parts is equal to twice the product of this part by the whole number plus the product of the other part by itself.
:![\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2+a^2=2\sdot\left[\left(a+b\right)\sdot a\right]+b^2}}](/mediawiki/images/math/0/3/a/03a8d96192812ea7db90d5166ad5177a.png) עוד כל מספר כשתחלקהו בשני חלקים איך שיקרה הנה המרובע ההוה מן המספר כלו והמרובע ההוה מאחד משני חלקים כאשר {{#annot:term|178,1216|tLsc}}התקבצו{{#annotend:tLsc}} שוים לכפל המספר כלו עם החלק הנזכר פעמים והמרובע ההוה מן החלק השני
עוד כל מספר כשתחלקהו בשני חלקים איך שיקרה הנה המרובע ההוה מן המספר כלו והמרובע ההוה מאחד משני חלקים כאשר {{#annot:term|178,1216|tLsc}}התקבצו{{#annotend:tLsc}} שוים לכפל המספר כלו עם החלק הנזכר פעמים והמרובע ההוה מן החלק השני |
| Elements/Elements II-7 | (a+b)²+a²=(2·(a+b)·a)+b² | לקוטים_מספר_פראלוקא#lBZs | If you have a number and you divide it into two unequal parts, you multiply the greater part by itself and multiply also the divided number by itself, then sum both products, the result is equal to the product of the greater number by the divided number multiplied by two, then you add to it the square of smaller part.
:![\scriptstyle\left(a+b\right)^2+a^2=2\sdot\left[\left(a+b\right)\sdot a\right]+b^2](/mediawiki/images/math/5/e/f/5ef738b800e1b84fc257df70a83fb86b.png) 162 אם יש לך מספר ותחלקהו לב' חלקים בלתי שוים ותכפול החלק הגדול על עצמו גם תכפול המספר המחולק על עצמו ותחבר הב' הכפלות הנה העולה יהיה שוה אל כפל המספר הגדול על המספר המחולק ותכפלהו אח"כ על ב' גם תוסיף על זה כפל החלק הקטן ותחבר הכל יהיה שוה
162 אם יש לך מספר ותחלקהו לב' חלקים בלתי שוים ותכפול החלק הגדול על עצמו גם תכפול המספר המחולק על עצמו ותחבר הב' הכפלות הנה העולה יהיה שוה אל כפל המספר הגדול על המספר המחולק ותכפלהו אח"כ על ב' גם תוסיף על זה כפל החלק הקטן ותחבר הכל יהיה שוה |
| Elements/Elements II-7 | 10,3+7 | קצת_מענייני_חכמת_המספר#nE0O | Example: the number 10 is divided into 7 and 3. במשל הרי הי' נחלק לז' ולג' |
| Elements/Elements II-7 | 10,3+7 | ספר_המספר_/_אליהו_מזרחי#VZVn | Example: the number ten, we divide it randomly to 7 and 3. דמיון המספר עשרה וחלקנוהו איך שקרה על ז' ועל ג' |
| Elements/Elements II-7 | (a+b)²+a²=(2·(a+b)·a)+b² | ספר_המלכים#isjp | For any number divided into two parts, [the sum of] the product of the [whole] number by itself and [the product of] one of the two parts by itself is equal to twice the product of the [whole] number by the part that is multiplied by itself plus the [product of the] other part by itself.
:![\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2+a^2=\left[2\sdot\left(a+b\right)\sdot a\right]+b^2}}](/mediawiki/images/math/5/0/0/5002e3f78e2c682da17cd0da9b8a0cf2.png) כל מספר יחלק לשני חלקים
כל מספר יחלק לשני חלקים |
| Elements/Elements II-7 | (a+b)²+a²=(2·(a+b)·a)+b² | ספר_המספר_/_אליהו_מזרחי#WZG6 | For any number, when you divide it into two parts randomly, [the sum of] the square of the whole number and the square of one of the two parts is equal to twice the product of the whole number by the mentioned part plus the square of the second part.
:![\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2+a^2=2\sdot\left[\left(a+b\right)\sdot a\right]+b^2}}](/mediawiki/images/math/0/3/a/03a8d96192812ea7db90d5166ad5177a.png) עוד כל מספר כאשר תחלקהו בשני חלקים איך שיקרה המרובע ההווה מן המספר כלו והמרובה ההווה מאחד משנים החלקים כאשר התקבצו שוים להכאת המספר כלו עם החלק הנזכר פעמים והמרובע ההווה מן החלק השני
עוד כל מספר כאשר תחלקהו בשני חלקים איך שיקרה המרובע ההווה מן המספר כלו והמרובה ההווה מאחד משנים החלקים כאשר התקבצו שוים להכאת המספר כלו עם החלק הנזכר פעמים והמרובע ההווה מן החלק השני |
| Elements/Elements II-7 | (a+b)²+a²=(2·(a+b)·a)+b² | קצת_מענייני_חכמת_המספר#DEFA | For any number divided into two parts, the sum of the square of the whole number and the square of one of the parts is equal to twice the product of this part by the whole number plus the product of the other part by itself : ![\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2+a^2=2\sdot\left[\left(a+b\right)\sdot a\right]+b^2}}](/mediawiki/images/math/0/3/a/03a8d96192812ea7db90d5166ad5177a.png) ו כל מספר שתחלקהו בב' חלקים איך שקרה המרובע ההווה מהמספר כלו והמרובע ההווה מא' מב' אלו החלקים כאשר התקבצו שוה להכאת החלק הנזכ' עם המספר כלו ולהכאת החלק הב' הנשאר בעצמו
ו כל מספר שתחלקהו בב' חלקים איך שקרה המרובע ההווה מהמספר כלו והמרובע ההווה מא' מב' אלו החלקים כאשר התקבצו שוה להכאת החלק הנזכ' עם המספר כלו ולהכאת החלק הב' הנשאר בעצמו |
| Elements/Elements II-7 | 12,4+8 | לקוטים_מספר_פראלוקא#R7rS | Example: we wish to divide 12 to 4 and 8. המשל נרצה לחלק י"ב על ח' וד' |
| Elements/Elements II-7 | definition | ספר_האלזיברא#cvaS | When a straight line is cut randomly into two segments, the sum of the squares on both segments equals twice the rectangle encompassed by both segments plus the square that is generated from the excess of the larger segment over the smaller segment. [ [[ספר_היסודות_לאקלידס#Elements_II_7|'''Euclid, Elements, Book II, proposition 7''']] ]
: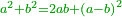 כי כאשר נחלק קו ישר 128rלשני חלקים איך שקרה הנה מרבעי שני החלקים שוים לכפל השטח הנצב הזויות אשר יקיפו בו שני החלקים ולמרבע ההוה ממותר החלק הגדול על הקטן
כי כאשר נחלק קו ישר 128rלשני חלקים איך שקרה הנה מרבעי שני החלקים שוים לכפל השטח הנצב הזויות אשר יקיפו בו שני החלקים ולמרבע ההוה ממותר החלק הגדול על הקטן |
| Elements/Elements II-8 | (4·(a+b)·a)+b²=((a+b)+a)² | לקוטים_מספר_פראלוקא#TRuX | If you have a number and you divide it into unequal two parts, if you add one of the parts to the whole number, i.e. the divided number, [its square] is equal to the same part that you added multiplied by the whole number, then multiplied by four, when you add to it the square of the second part.
:![\scriptstyle\left[\left(a+b\right)+a\right]^2=4\sdot\left[\left(a+b\right)\sdot a\right]+b^2](/mediawiki/images/math/b/3/2/b32320b109ede228563dccc608b448d3.png) 163 אם יש לך מספר ותחלקהו לב' חלקים בלתי שוים אם תוסיף א' מהחלקים על כל המספר ר"ל על המספר המחולק יהיה שוה אל אותו החלק אשר הוספת כפול על כל המספר אח"כ העולה תכפול על ד' ותוסיף על זה מרובע החלק השני
163 אם יש לך מספר ותחלקהו לב' חלקים בלתי שוים אם תוסיף א' מהחלקים על כל המספר ר"ל על המספר המחולק יהיה שוה אל אותו החלק אשר הוספת כפול על כל המספר אח"כ העולה תכפול על ד' ותוסיף על זה מרובע החלק השני |
| Elements/Elements II-8 | 10,3+7 | קצת_מענייני_חכמת_המספר#9UoH | Example: the number 10 is divided into 7 and 3. במשל הי' נחלק לז' ולג' |
| Elements/Elements II-8 | 10,3+7 | ספר_המספר_/_אליהו_מזרחי#pqrO | Example: we have the number ten, we divide it randomly to 3 and 7. דמיון יש לנו מספר עשרה וחלקנוהו איך שהזדמן על ג' ועל ז' |
| Elements/Elements II-8 | 12,4+8 | לקוטים_מספר_פראלוקא#NtVp | Example: we wish to divide 12 to 4 and 8. המשל נרצה לחלק י"ב על ד' וח' |
| Elements/Elements II-8 | (4·(a+b)·a)+b²=((a+b)+a)² | קצת_מענייני_חכמת_המספר#R68t | For any number divided into two parts as you wish, if you multiply the whole number by one of the parts four times, the sum of the product with the square of the other part is equal to the [square] of the whole number plus the one part
:![\scriptstyle{\color{OliveGreen}{4\sdot\left[\left(a+b\right)\sdot a\right]+b^2=\left[\left(a+b\right)+a\right]^2}}](/mediawiki/images/math/c/a/f/caf2f89aa2a00ea5e45e6eed3d4bc694.png) ז כל מספר שחלקת אותו לב' חלקים איך שקרה אם הכית המספר כלו עם חלק אח' מהם ד' פעמים וקבצת הכל עם מרובע החלק הב' הנשאר היה שוה להכאת מספרו החלק הנזכר כאשר תחברם יחד
ז כל מספר שחלקת אותו לב' חלקים איך שקרה אם הכית המספר כלו עם חלק אח' מהם ד' פעמים וקבצת הכל עם מרובע החלק הב' הנשאר היה שוה להכאת מספרו החלק הנזכר כאשר תחברם יחד |
| Elements/Elements II-8 | 10,3+7 | ספר_החשבון_והמדות#AJOP | Example: we have the number ten, we divide it randomly to 3 and 7. דמיון יש לנו מספר מנינו העשרה וחלקנוהו איך שהזדמן על ג' ועל ז' |
| Elements/Elements II-8 | (4·(a+b)·a)+b²=((a+b)+a)² | ספר_המלכים#Ocvs | For any number divided into two parts and one of the two parts is added to it, the product of the [whole] number plus the additional [part] by itself is equal to [the sum of] the product of the [whole] number by the additional [part] four times and the product of the other part by itself.
:![\scriptstyle{\color{OliveGreen}{\left[\left(a+b\right)+a\right]^2=\left[4\sdot\left(a+b\right)\sdot a\right]+b^2}}](/mediawiki/images/math/3/4/8/348f212d9f2bb23aebbed2132e172f55.png) כל מספר יחלק בשני חלקים ונוסף עליו כמו אחד משני החלקים הנה הכאת המספר עם התוספת בכמהו כהכאת המספר בתוספת ד' פעמים והכאת החלק האחר בכמהו
כל מספר יחלק בשני חלקים ונוסף עליו כמו אחד משני החלקים הנה הכאת המספר עם התוספת בכמהו כהכאת המספר בתוספת ד' פעמים והכאת החלק האחר בכמהו |
| Elements/Elements II-8 | (4·(a+b)·a)+b²=((a+b)+a)² | ספר_המספר_/_אליהו_מזרחי#LHo4 | For any number, when you divide it into two parts randomly and you multiply the whole number by one of the two parts four times, then sum [the product] with the square of the other part [it] is equal to the [square] of the whole number plus the mentioned part when you sum them together.
:![\scriptstyle{\color{OliveGreen}{4\sdot\left[\left(a+b\right)\sdot a\right]+b^2=\left[\left(a+b\right)+a\right]^2}}](/mediawiki/images/math/c/a/f/caf2f89aa2a00ea5e45e6eed3d4bc694.png) עוד כל מספר כאשר חלקת אותו בשני חלקים איך שיקרה והכית המספר כלו עם אחד משני חלקיו ארבעה פעמים וחברת אותו עם מרובע החלק הנשאר שוה למרובע ההווה מן המספר כלו והחלק הנזכר כאשר תחברם ביחד
עוד כל מספר כאשר חלקת אותו בשני חלקים איך שיקרה והכית המספר כלו עם אחד משני חלקיו ארבעה פעמים וחברת אותו עם מרובע החלק הנשאר שוה למרובע ההווה מן המספר כלו והחלק הנזכר כאשר תחברם ביחד |
| Elements/Elements II-8 | (4·(a+b)·a)+b²=((a+b)+a)² | ספר_החשבון_והמדות#EAD6 | For any number divided into two parts as you wish, if you multiply the whole number by one of the parts four times, the sum of the product with the square of the other part is equal to the [square] of the whole number plus the one part.
:![\scriptstyle{\color{OliveGreen}{4\sdot\left[\left(a+b\right)\sdot a\right]+b^2=\left[\left(a+b\right)+a\right]^2}}](/mediawiki/images/math/c/a/f/caf2f89aa2a00ea5e45e6eed3d4bc694.png) עוד כל מספר כאשר חלקת אותו בשני חלקים איך שיקרה וכפלת המספר כלו עם אחד משני חלקיו ארבעה פעמים ועם מרובע החלק הנשאר שוה למרובע ההוה מן המספר כלו והחלק הנזכר כאשר תחברם ביחד ותקח מרובעם
עוד כל מספר כאשר חלקת אותו בשני חלקים איך שיקרה וכפלת המספר כלו עם אחד משני חלקיו ארבעה פעמים ועם מרובע החלק הנשאר שוה למרובע ההוה מן המספר כלו והחלק הנזכר כאשר תחברם ביחד ותקח מרובעם |
| Elements/Elements II-9 | a²+b²=2·((½·(a+b))²+(a-(½·(a+b)))²) | לקוטים_מספר_פראלוקא#E95L | If you divide any line into two equal parts and into two unequal parts, then you multiply each of the unequal parts [by itself] and sum them, they are twice [the sum of] the product of the equal parts plus the [square of] excess of the greater [part] over [half the number].
:![\scriptstyle a^2+b^2=2\sdot\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2+\left[a-\left[\frac{1}{2}\sdot\left(a+b\right)\right]\right]^2\right]](/mediawiki/images/math/5/e/8/5e87deb6f6b5cec598e43b4b3374a25c.png) 164 אם תחלק איזה קו לב' חלקים שוים ולב' חלקים בלתי שוים וכפול כל אחד מהחלקים בלתי שוים ותחברם הם כפל מהחלקים השוים נוסף בם יתרון החלק הגדול על הקטן
164 אם תחלק איזה קו לב' חלקים שוים ולב' חלקים בלתי שוים וכפול כל אחד מהחלקים בלתי שוים ותחברם הם כפל מהחלקים השוים נוסף בם יתרון החלק הגדול על הקטן |
| Elements/Elements II-9 | a²+b²=2·((½·(a+b))²+(a-(½·(a+b)))²) | ספר_המספר_/_אליהו_מזרחי#ClRv | For any number that you divide into two equal parts and into two unequal parts, [the sum of] the two squares of the unequal parts is equal to twice [the sum of] the square of half the [whole] number and [the square] of the excess of the large part over the half [of the whole number].
:![\scriptstyle{\color{OliveGreen}{a^2+b^2=2\sdot\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2+\left[a-\left[\frac{1}{2}\sdot\left(a+b\right)\right]\right]^2\right]}}](/mediawiki/images/math/3/7/c/37cd2d64c6505f872e3604129685d3bc.png) עוד כל מספר שחלקת אותו לשני חלקים שוים ושני חלקים בלתי שוים הנה שני המרובעים אשר יהיו מהחלקים הבלתי שוים הם כפל שני המרובעים אשר יהיו מחצי המספר ומהתוספת אשר לחלק הגדול על הה' שהוא המחצית
עוד כל מספר שחלקת אותו לשני חלקים שוים ושני חלקים בלתי שוים הנה שני המרובעים אשר יהיו מהחלקים הבלתי שוים הם כפל שני המרובעים אשר יהיו מחצי המספר ומהתוספת אשר לחלק הגדול על הה' שהוא המחצית |
| Elements/Elements II-9 | 10,3+7 | ספר_המספר_/_אליהו_מזרחי#LnLo | Example: the number 10, we divide it into two equal parts, which are 5, and into two unequal parts, which are 7 and 3. דמיון המספר י' וחלקנוהו לשני חלקים שוים והם ה' ולשני חלקים בלתי שוים והם ז' ג' |
| Elements/Elements II-9 | a²+b²=2·((½·(a+b))²+(a-(½·(a+b)))²) | ספר_החשבון_והמדות#CM8j | For any number divided into two equal parts and into two unequal parts, [the sum of] the squares of the unequal parts is equal to twice [the sum of] the square of half the [whole] number and the square of the difference between the large part and the half [of the whole number].
:![\scriptstyle{\color{OliveGreen}{a^2+b^2=2\sdot\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2+\left[a-\left[\frac{1}{2}\sdot\left(a+b\right)\right]\right]^2\right]}}](/mediawiki/images/math/3/7/c/37cd2d64c6505f872e3604129685d3bc.png) עוד כל מספר שחלקת אותו לשני חלקים שוים ושני חלקים בלתי שוים הנה שני המרובעים אשר יהיו מהחלקים הבלתי שוים הם כפל שני המרובעים אשר יהיו מחצי המספר ומהתוספת אשר לחלק הגדול על המחצית
עוד כל מספר שחלקת אותו לשני חלקים שוים ושני חלקים בלתי שוים הנה שני המרובעים אשר יהיו מהחלקים הבלתי שוים הם כפל שני המרובעים אשר יהיו מחצי המספר ומהתוספת אשר לחלק הגדול על המחצית |
| Elements/Elements II-9 | 12,4+8 | לקוטים_מספר_פראלוקא#QBwh | Example: we wish to divide 12 into two equal parts 6 and 6 and into two unequal parts 8 and 4. המשל נרצה לחלק מספר י"ב לב' חלקי' שוים ו'ו' ולב' חלקים בלתי שוים ח' ד' |
| Elements/Elements II-9 | a²+b²=2·((½·(a+b))²+(a-(½·(a+b)))²) | ספר_המלכים#g6A2 | For any even number divided into two halves and into two unequal parts, [the sum of the products of] each of the two unequal parts by themselves is equal to [the sum of] twice the product of half the [whole] number by itself and twice the product of the excess of half the [whole] number over the smaller part by itself.
:![\scriptstyle{\color{OliveGreen}{a^2+b^2=\left[2\sdot\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2\right]+\left[2\sdot\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]^2\right]}}](/mediawiki/images/math/2/a/b/2abb4b772df68504faed6649a992d8d3.png) כל מספר זוג יחלק בשני חצאים ובשני חלקים מתחלפים הנה כל אחד משני החלקים המתחלפים בכמהו כהכאת חצי המספר בכמהו שני פעמים והכאת מותר חצי המספר על החלק הקטן בכמהו שני פעמים
כל מספר זוג יחלק בשני חצאים ובשני חלקים מתחלפים הנה כל אחד משני החלקים המתחלפים בכמהו כהכאת חצי המספר בכמהו שני פעמים והכאת מותר חצי המספר על החלק הקטן בכמהו שני פעמים |
| Elements/Elements II-9 | 10,3+7 | ספר_החשבון_והמדות#O8o8 | Example: we have the number ten, we divide it into two equal parts, which are 5, and into two unequal parts, which are 3 and 7. דמיון יש לנו מספר מנינו עשרה וחלקנוהו לשני חלקים שוים על ה' ושני חלקים בלתי שוים על ג' וז' |
| Elements/Elements-Introduction | a=b,a-c=b-c | ספר_המספר_/_אליהו_מזרחי#tNTC | For, when equal is subtracted from equals, then the remainders are necessarily equal, according to what is clarified in the introduction of the first section of Euclid's [book].
: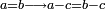 כי כאשר יחוסר מהשוים שוה יהיו הנשארים שוים בהכרח לפי מה שהתבאר בפתיחת המאמר הראשון מאקלידס
כי כאשר יחוסר מהשוים שוה יהיו הנשארים שוים בהכרח לפי מה שהתבאר בפתיחת המאמר הראשון מאקלידס |
| Elements/Elements-Introduction | a=b,a-c=b-c | ספר_המספר_/_אליהו_מזרחי#gaDw | This is because it was already clarified in the introduction of Euclid's book that when equal is subtracted from equals, then the remainders are equal
: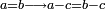 וזה שכבר התבאר בפתיחת ספר אקלידס כאשר חוסר מהשוים שוה יהיה הנשאר שוה
וזה שכבר התבאר בפתיחת ספר אקלידס כאשר חוסר מהשוים שוה יהיה הנשאר שוה |
| Elements/Elements IX-21 | definition | ספר_המספר_/_אליהו_מזרחי#qiN5 | When even numbers are summed, as many as they may be, their sum is an even number. הוא כאשר נקבצו מספרי זוגות כמה שיהיו הנה קבוצם מספר זוג |
| Elements/Elements IX-22 | definition | ספר_המספר_/_אליהו_מזרחי#yrIb | When odd numbers are summed, as many as they may be, and their multitude is even, their sum is an even number. וכאשר נקבצו מספרים נפרדים כמה שיהיו והיה מספרם זוג הנה קבוצם מספר זוג |
| Elements/Elements IX-23 | definition | ספר_המספר_/_אליהו_מזרחי#1A6m | When odd numbers are summed, as many as they may be, and their multitude is odd, their sum is an odd number. וכאשר נקבצו מספרים נפרדים כמה שיהיו והיה מספרם מפרד הנה קבוצם נפרד |
| Elements/Elements IX-28 | definition | ספר_המספר_/_אליהו_מזרחי#RVMm | When an even number is multiplied by an odd number, or by an even number, then the product is even.
: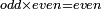 ; ; 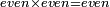 הוא שכאשר הוכה מספר זוג במספר נפרד או במספר זוג הנה המקובץ זוג
הוא שכאשר הוכה מספר זוג במספר נפרד או במספר זוג הנה המקובץ זוג |
| Elements/Elements IX-29 | definition | ספר_המספר_/_אליהו_מזרחי#DYPK | When an odd number is multiplied by an odd number, then the product is odd.
: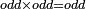 וכאשר הוכה מספר נפרד במספר נפרד הנה המקובץ נפרד
וכאשר הוכה מספר נפרד במספר נפרד הנה המקובץ נפרד |
| Elements/Elements V-15 | (n·a)÷(n·b)=a÷b | ספר_המספר_/_אליהו_מזרחי#PIBA | For, it was already clarified in Euclid's Book of Elements, according to what was preceded in this section, that the given numbers have the same ratio as the ratio of their equimultiples.
: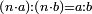 וזה שכבר התבאר בספר היסודות לאקלידס לפי מה שקדם מן המאמר שמהמספרים המונחים הם יחס קצתם אל קצת הוא כיחס כפליהם קצתם אל קצת
וזה שכבר התבאר בספר היסודות לאקלידס לפי מה שקדם מן המאמר שמהמספרים המונחים הם יחס קצתם אל קצת הוא כיחס כפליהם קצתם אל קצת |
| Elements/Elements V-15 | (n·a)÷(n·b)=a÷b | ספר_המספר_/_אליהו_מזרחי#wUJB | For, it was already clarified in Euclid's Book of Elements, in the fifth section, that any numbers, whose multiples are equal, have the same ratio as the ratio of their equimultiples.
: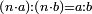 וזה שכבר התבאר בספר היסודות לאקלידס במאמר החמישי ממנו שהמספרים אשר כפליהם שוים הנה יחס קצתם אל קצת כיחס כפליהם קצתם אל קצת
וזה שכבר התבאר בספר היסודות לאקלידס במאמר החמישי ממנו שהמספרים אשר כפליהם שוים הנה יחס קצתם אל קצת כיחס כפליהם קצתם אל קצת |
| Elements/Elements V-9 | definition | ספר_המספר_/_אליהו_מזרחי#2X92 | For, any two magnitudes, which have the same ratio to the same magnitude, necessarily equal one another, according to what is clarified in Euclid's Book of Elements.
: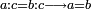 כי כל שני שעורים שיחסם אל שעור אחר בעצמו יחס אחד הנה הם שוים בהכרח לפי מה שהתבאר בספר היסודות לאקלידס
כי כל שני שעורים שיחסם אל שעור אחר בעצמו יחס אחד הנה הם שוים בהכרח לפי מה שהתבאר בספר היסודות לאקלידס |
| Elements/Elements VI-17 | definition | ספר_האלזיברא#KlWg | It is already explained in {{#annot: reference | #Elements VI-17 | cH1a}}[[ספר_היסודות_לאקלידס#Elements_VI_17|'''Euclid, Elements, Book VI, proposition 17''']] that the product of the first by the last is as the product of the mean by its similar.
: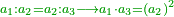 וכבר נתבאר מ'''תמונת י"ז מן המאמר הששי לאקלידס'''{{#annotend:cH1a}} כי {{#annot: term | #multiplication, #הכאה | poG8}}הכאת ה{{#annotend:poG8}}ראשו' באחרון כמו הכאת האמצעי בדומה לו
וכבר נתבאר מ'''תמונת י"ז מן המאמר הששי לאקלידס'''{{#annotend:cH1a}} כי {{#annot: term | #multiplication, #הכאה | poG8}}הכאת ה{{#annotend:poG8}}ראשו' באחרון כמו הכאת האמצעי בדומה לו |
| Elements/Elements VI-17 | reference | ספר_האלזיברא#cH1a | [[ספר_היסודות_לאקלידס#Elements_VI_17|'''Euclid, Elements, Book VI, proposition 17''']] that the product of the first by the last is as the product of the mean by its similar.
: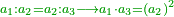 וכבר נתבאר מ'''תמונת י"ז מן המאמר הששי לאקלידס'''
וכבר נתבאר מ'''תמונת י"ז מן המאמר הששי לאקלידס''' |
| Elements/Elements VII-11 | a÷b=c÷d→(c-a)÷(d-b) | ספר_המספר_/_אליהו_מזרחי#Iu2h | when two numbers are subtracted from two numbers and the ratio of the subtrahend to the subtrahend is the same as the ratio of the minuend to the minuend, then the [ratio of] the remainder to the remainder is the same as the ratio of the minuend to the minuend.
::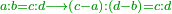 וזה שכבר התבאר בספר היסודות לאקלידס במאמר השביעי ממנו בתמונת י"א שכאשר חוסרו משני מספרים ב' מספרים והיה יחס המחוסר אל המחוסר כיחס הכל אל הכל הנה יהיה הנשאר אל הנשאר כיחס הכל אל הכל
וזה שכבר התבאר בספר היסודות לאקלידס במאמר השביעי ממנו בתמונת י"א שכאשר חוסרו משני מספרים ב' מספרים והיה יחס המחוסר אל המחוסר כיחס הכל אל הכל הנה יהיה הנשאר אל הנשאר כיחס הכל אל הכל |
| Elements/Elements VIII-11 | definition | ספר_המספר_/_אליהו_מזרחי#sPcq | Its reason is also known from what was clarified in Euclid's Book of Elements, in the eighth section that for every two squares numbers the ratio of one of them to the other is as the duplicate ratio of that which the side has to the side.
: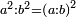 הנה סבתו ג"כ ידועה ממה שהתבאר בספר היסודו' לאקלידס במאמר הח' ממנו שכל שני מספרים מרובעים הנה יחס הא' מהם אל חברו הוא כיחס צלעו אל צלעו שנוי בכפל
הנה סבתו ג"כ ידועה ממה שהתבאר בספר היסודו' לאקלידס במאמר הח' ממנו שכל שני מספרים מרובעים הנה יחס הא' מהם אל חברו הוא כיחס צלעו אל צלעו שנוי בכפל |
| Elements/Elements VIII-11 | reference | ספר_האלזיברא#D3f5 | [[ספר_היסודות_לאקלידס#Elements_VIII_11|'''Euclid, Elements, Book VIII, proposition 11''']] מתמונת י"א מן המאמר השמיני לאקלידס |
| Elements/Elements VIII-11 | definition | ספר_האלזיברא#Nl0O | This is because the ratio of a square to a square is the same as the ratio of its side to its side duplicate.
: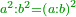 וזה מפני כי {{#annot: term | #ratio, #יחס | Eve2}}יחס{{#annotend:Eve2}} מרובע אל מרובע כיחס צלעו אל צלעו {{#annot: term | #duplicate, #שנוי | Q7dD}}שנוי{{#annotend:Q7dD}} ר"ל {{#annot: term | #multiplied, #כפול | G4iq}}כפול{{#annotend:G4iq}}
וזה מפני כי {{#annot: term | #ratio, #יחס | Eve2}}יחס{{#annotend:Eve2}} מרובע אל מרובע כיחס צלעו אל צלעו {{#annot: term | #duplicate, #שנוי | Q7dD}}שנוי{{#annotend:Q7dD}} ר"ל {{#annot: term | #multiplied, #כפול | G4iq}}כפול{{#annotend:G4iq}} |
| Elements/Elements VIII-11 | definition | ספר_האלזיברא#QcHW | the ratio of a square to a square is as the ratio of its side to its side duplicated. [ [[ספר_היסודות_לאקלידס#Elements_VIII_11|'''Euclid, Elements, Book VIII, proposition 11''']] ]
: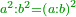 וזה כי מפני כי יחס מרבע אל מרבע כיחס צלעו אל צלעו שנוי
וזה כי מפני כי יחס מרבע אל מרבע כיחס צלעו אל צלעו שנוי |
| Elements/Elements VIII-12 | reference | ספר_האלזיברא#jD6N | According to [[ספר_היסודות_לאקלידס#Elements_VIII_12|'''Euclid, Elements, Book VIII, proposition 12''']] מתמונת י"ב מן המאמר השמיני לאקלידס |
| Elements/Elements VIII-12 | definition | ספר_האלזיברא#eDWE | This is because the ratio of a cube to a cube is the same as the ratio of its side to its side triplicate
: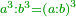 וזה מפני כי יחס מעקב אל מעקב כיחס צלעו אל צלעו {{#annot: term | #triplicate, #משולש | A27z}}משלש{{#annotend:A27z}}
וזה מפני כי יחס מעקב אל מעקב כיחס צלעו אל צלעו {{#annot: term | #triplicate, #משולש | A27z}}משלש{{#annotend:A27z}} |
| Elements/Elements XIII-1 | definition | המחומשים_והמעושרים#1Da2 | Euclid proved that when a line is divided according to the ratio of a mean and two extremes, so that half the whole line is added to the larger segment, and all this is multiplied by itself, then the resulting square is equal to five times the square of half the line [Elements XIII.1]. ובאר אקלידס כי כאשר נחלק קו על יחס אמצעי ושתי קצוות שהחלק הגדול כאשר נוסף בארכו כמו חצי הקו כלו והוכה כל זה בעצמו המרובע ההוה מזה יהיה חמשה דמיוני המרובע ההוה מחצי הדבר |
| Elements/Elements XIII-10 | definition | המחומשים_והמעושרים#w084 | We do this since Euclid has explained that the line that cuts the fifth is on the line that cuts the sixth and the tithe, when they are set on one circle [Elements XIII,10]. ועשינו זה בעבור כי באר אוקלידס כי קו החותך החמישית על הקו החותך הששית והעשירית כאשר הונחו בעגולה אחת |
| Elements/Elements XIII-3 | definition | המחומשים_והמעושרים#mhLN | Euclid has already explained [Elements XIII.3] that when line BH is divided by the ratio of a mean and two extremes, so that the greater part is equal to line DH, it is known that when a line is divided by the ratio of a mean and two extremes and we add half the greater part to the smaller part, then multiply the whole sum by itself, the square formed by the sum of the two is five times the product of [half] the greater part by itself.
: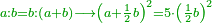 ובאר אוקלידס שקו ב"ה כאשר חולק על יחס אמצעי ושני קצוות שהחלק הגדול הוא שוה אל קו ד"ה והוא ידוע כי כאשר נחלק קו אחד על יחס בעל אמצעי ושני קצוות ונוסיף על החלק הקטן חצי החלק הגדול ונכה הכל בעצמו שהמרובע ההוה משני אלו מקובצים יהיה חמשה דמיוני הכאת החלק הגדול בעצמו
ובאר אוקלידס שקו ב"ה כאשר חולק על יחס אמצעי ושני קצוות שהחלק הגדול הוא שוה אל קו ד"ה והוא ידוע כי כאשר נחלק קו אחד על יחס בעל אמצעי ושני קצוות ונוסיף על החלק הקטן חצי החלק הגדול ונכה הכל בעצמו שהמרובע ההוה משני אלו מקובצים יהיה חמשה דמיוני הכאת החלק הגדול בעצמו |
| Elements/Elements XIII-5 | definition | המחומשים_והמעושרים#3lPz | It is known from what we have said, as Euclid said, that for every line divisible according to the ratio of a mean and two extremes, when another part equal to the larger portion is added to the line, then whole [line] is divisible according to the ratio of a mean and two extremes, and the larger portion of which is the original line [Elements XIII.5]. והוא ידוע מאשר אמרנו שאמרו אקלידס ואמר שכל קו שהוא על יחס אמצעי ושני קצוות ונוסף באורך הקו כמו החלק 60rהגדול וכל זה יחלק על יחס אמצעי ושני קצוות שהחלק הגדול הוא הקו הראשון |
| Elements/Elements XIII-9 | definition | המחומשים_והמעושרים#ScqD | It he said in another place that when the side of a hexagon and the side of a decagon inscribed in the same circle are united in one line, then this whole line is divisible according to the ratio of a mean and two extremes, and the side of the hexagon is the larger portion [Elements XIII.9]. ואמר במקום אחר שכאשר קובצו צלע המשושה עם צלע המעושר אשר בעגולה אחת בקו אחד ישר יהיה כל הקו נחלק על יחס אמצעי ושני קצוות וצלע המשושה הוא החלק הגדול |