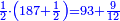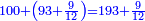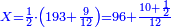Chapter Ten – Knowing the Square Roots of "Deaf" and "Mute" Numbers by Approximation
|
השער העשירי [בידיעת][169] צלעות המרובעים מחשבון החרש והאלם על דרך קרוב
|
Introduction: square numbers and non-square numbers
|
|
| Definition of a square number: Know that every number that has a root is called a square number and it is a "wise number".
|
תדע כי כל מספר נגדר הוא נקרא מרובע והנה הוא מספר פקח
|
| The reason that it is called a "wise number" is that its root, which is the measure of each of the four sides of the square, can be truly found.
|
וטעם היותו נקרא [מספר פקח][170] באשר גדרו שהוא מדת כל אחת ואחת מארבע צלעות המרובע יכול להמצא [באמתות][171]
|
| Therefore, the numbers that do not have a real root are called deaf and mute, because their root cannot be found accurately only approximately
|
ולזאת יקראו המספרים אשר אין להם גדר אמתי מספרים חרשים ואלמים באשר לא יוכל כל נברא למצוא [גדרם][172] בדקדוק כי אם בקירוב
|
| In every scientific discipline there are many secrets hidden and concealed from the hearts of men to be found.
|
ובכל חכמה הרבה דברים נעלמים ונסתרים מלבות בני האדם למצאן
|
| We also see this in the science of medicine, when physicians instruct to take a well-known herb root or stone to heal the sick person who carries them by their virtue, but no wise man can know the reason of the [healing] virtue of the stone, or the herb root, why it is so.
|
והנה נראה זה גם כן בחכמת הרפואה שיצוו הרופאים לקחת שורש עשב ידוע או אבן ידועה להיותם מרפא בסגולה לחולה [הנושאם][173] ואין [174]כח בשום חכם לדעת טעם סגולת האבן או שרש העשב למה הוא ככה
|
| Many things like these are known only to the Knower of all concealed things alone, blessed be He and blessed be His name.
|
ודברים רבים כמו אלו אשר לא יודעו רק ליודע כל [נסתרות][175] לבדו ברוך הוא וברוך שמו
|
Sexagesimal fractions
|
|
| Now, we return to the premises and say: since most ancients extracted the approximate roots of "deaf" or "mute" numbers by using the method of the astronomers, some of their methods should be introduced and explained first, before I discuss the extraction of roots [of non-square numbers].
|
ועתה נשוב אל הראשונות ונאמר כי לבעבור אשר רוב החכמים הקדומים הוציאו קרוב מדת צלעות המרובעים החרשים והאלמים על דרך חכמי המזלות [צריך][176] להקדים ולבאר קצת דרכיהם [בתחלה][177] בטרם שאדבר בדרך הוצאת מדת הצלעות
|
| The astronomers divided the zodiac into twelve shapes that are called zodiacal signs.
|
והנה חלקו חכמי המזלות הגלגל לשנים עשר צורות והמה נקראות מזלות
|
| The reason for this division is that there is no number smaller than twelve that has as many whole parts [= divisors, in modern terminology] like it, for it has a half, a third, a quarter, a sixth, and half a sixth.
|
וטעם החלוקה הזאת היא באשר אין מספר קטן פחות משנים עשר שיהיו לו חלקים רבים שלמים מבלי שבר כמוהו כי ימצא בו [חצי][178] ושלישית ורביעית ושישית וחצי שישית
|
| They divided each zodiacal sign into thirty parts and called them degrees.
|
וחלקו כל מזל לשלשים חלקים קראו אותם מעלות
|
| They divided it into this number, since there is no number smaller than it that has as many parts [= divisors] as it has, for it has a half, a third, a fifth, a sixth, and a tenth.
|
ויחלקוהו למספר זה לפי שאין מספר פחות ממנו אשר ימצא בו חלקים רבים בלתי שבר כמוהו כי ימצא בו חצי ושלישית וחמשית וששית ועשירית
|
| They divided each degree into sixty parts and called them primes.
|
וחלקו כל מעלה לששים [179]חלקים וקראו אותם ראשונים
|
| This number has a half, a third, a quarter, a fifth, a sixth, and a tenth.
|
ובמספר הזה ימצא בו חצי ושלישית ורביעית וחמשית וששית ועשירית[180]
|
| They divided each prime into sixty seconds; each second into sixty thirds; and each third into sixty fourths.
|
וחלקו כל ראשון לששים שניים וכל שני לששים שלישים וכל שלישי לששים רביעיים
|
| And so on, they divided their fractions as needed, endlessly, each one is equal to sixty of the rank that follows it and sixty of each one are a unit of the preceding rank.
|
וכן יחלקו חלקיהם כפי הצורך עד אין תכלית וכל אחד ואחד יהיה שוה ששים מהמדרגה השנייה לו וששים מכל אחד ואחד יעלו אחד מהמדרגה הקודמת לו
|
Multiplication of Sexagesimal Fractions
|
|
| I tell you that the degrees [act] as the integers:
|
והנני מודיע לך [כי המעלות][181] הן הנה כמו השלמים
|
When we multiply degrees by degrees, the result of multiplication are always degrees.
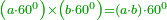
|
ולעולם כשנכפול מעלות על מעלות יהיה העולה מהכפלה מעלות
|
If we multiply them by other fractions, such as primes, seconds, or others, the type of these fractions always remains the same, their type does not change because of this multiplication.
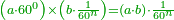
|
ואם נכפול אותם בחלקים אחרים כמו ראשונים או שניים או יותר לעולם יעמוד המין מהחלקים ההם בעצמו לא ישתנו ממינם בעבור הכפלה הזאת
|
| The primes, the seconds, and all other types, follow the rule of the [simple] fractions.
|
ואולם הראשונים או השניים או כל שאר המינין שאחריהן הנה משפטן כמשפט השברים
|
- As when we multiply a half by a half, the result is a quarter.
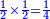
|
כי כמו שאם נכפול חצי על חצי יהיה העולה רביע
|
So, if we multiply seconds by seconds, the product is fourths.
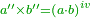
|
ככה אם נכפול חלקים שניים על חלקים שניים יהיה העולה מהכפלה רביעים
|
The product of seconds by primes is thirds.

|
וכפלת שניים על הראשונים יהיה העולה שלישיים
|
The product of primes by primes is seconds.

|
וכפלת הראשונים על ראשונים [182]יהיה העולה שניים
|
The product of seconds by thirds is fifths.
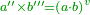
|
ומכפלת שניים בשלישיים יהיה העולה חמשיים
|
The product of sixths by seconds, or fourths by fourths, is eighths.
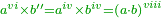
|
וששים בשניים או רביעיים ברביעיים יהיה העולה שמניים
|
The product of seconds by fifths is sevenths.
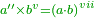
|
ושניים בחמשיים יהיה העולה שביעיים
|
| And so on for all according to the aforementioned method.
|
וככה כלם על דרך זה האמור
|
Written procedure
|
|
| I will give you a method for multiplying these mentioned fractions:
|
ואכין לך דרך לכפילת החלקים החלקים הנזכרים האלה
|
| When you wish to multiply a line of known fractions by a line of known fractions; in each line there are many higher and lower types, do as follows: take one of the two lines and convert all the higher types into the lowest type of that line. Add what you receive from the decomposing to the lowest type, because now they are all the same type. Apply the same procedure with the second line as well.
|
כשתבקש לכפול טור אחד מחשבונות חלקים ידועים על טור אחד מחשבונות חלקים ידועים ויהיה בכל אחת מהטורים חלקים מהרבה מינים גדולים וקטנים תעשה ככה קח הטור האחד משתיהן ויצקת כל המינים הגדולים אל המין היותר קטן שבטור ההיא [וחבר אל שתיהם][183] המין הקטן אל מה שיעלה לך מההתכה כי אז הם כלם ממין אחד כ"ד וכמעשה [הטור][184] הזאת תעשה הטור השנית גם כן מהטור השנית גם כן
|
| We multiply one [line] by the other and see what type the result of multiplication should be, according to what was explained before.
|
נכפול אלו על אלו ותראה כי איזה מין ראוי שיהיה היוצא מהכפלה על פי מה שיתבאר לפנים
|
| Then, divide them by sixty many times, until you reach a type which you cannot divide by sixty.
|
ואחר חלק אותם על ששים הרבה פעמים עד שתבא אל תכלית המין אשר לא תוכל לחלק אותם על ששים
|
| Know that if there is any number left that cannot be divided in each division, the remainder is of the type of the divided number.
|
ותדע אם ישאר שום מספר שלא נתחלק בכל חלוקה וחלוקה יהיה הנשאר ממין המספר המחלק
|
| This multiplication technique is long as well as short, but it is well-guided.
|
[185]ודרך הכפילה הזאת היא ארוכה [ו]קצרה והיא סלולה ומיושבת בטוב
|
|
|
|
| After clarifying and introducing what is appropriate for the art of this chapter, I will return to discuss the method of extracting the root a deaf square:
|
ואחרי אשר בארתי והקדמתי מה שראוי למלאכת השער הזה אשוב לדבר בדרך הוצאת מדת הצלעות ממרובע שמספרו חרש
|
When we want to reach the required purpose, we look at the square that precedes the number we are examining, we find it as explained in chapter seven. We see how much is the excess over the preceding square.
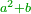
|
והנה כאשר נרצה לבא אל תכלית המבוקש הזה נעיין המרובע שעבר מהמספר אשר אנחנו חוקרים עליו ונגיע לדעת זה על פי מה שהתבאר בשער השביעי ונראה כמה העודף על המרובע שעבר
|
- If it is less than its root, we do as follows:
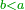
|
ואם היה פחות מגדרו נעשה זאת
|
- First approximation: we convert the excess into primes by multiplying it by sixty, then dividing them by double the root of the preceding square. We add the quotient to the root and this is the approximate root.

|
נשיב העודף ראשונים והוא שנכפל שנכפול אותם בששים ואחר נחלקם על כפל הגדר מהמרובע שעבר ומה שיצא בחלוק נוסיף אותו על הגדר [וככה יהיה מדת הצלעות בקרוב][186]
|
- Second approximation: if we want to correct it further, we multiply this [approximate] root by itself and see by how much the product exceeds over the number we are examining.
![\scriptstyle{\color{OliveGreen}{\left[a+\left(\frac{60\sdot b}{2a}\right)^\prime\right]^2-\left(a^2+b\right)}}](/mediawiki/images/math/d/1/8/d1884d02d5c52436853b8fa19a7b0990.png)
|
ואם נרצה לדקדק אותה עוד נכפול ונכה המדה הזאת על עצמה ונראה מה יוסיף בהכאה על החשבון אשר אנחנו חוקרים עליו
|
- We examine the ratio of [the square of] the excess to double the [approximate] root we found: subtract this ratio from the [approximate] root and the remainder is a more accurate root than it was at first.
![\scriptstyle{\color{OliveGreen}{\sqrt{a^2+b}\approx a+\left(\frac{60\sdot b}{2a}\right)^\prime-\left[\frac{\left(\left(\frac{60\sdot b}{2a}\right)^\prime\right)^2}{2\sdot\left(a+\left(\frac{60\sdot b}{2a}\right)^\prime\right)}\right]}}](/mediawiki/images/math/3/0/e/30e5279dac9bf13aa0f31cfae39a398b.png)
|
ונעיין מה ערך התוספת אל כפל [המדה][187] שמצאנו פעמים וכערך [ההוא][188] תסיר מהמדה והנותר יהיה יותר מדה מדוקדקת מאשר לא היתה בתחלה
|
- Third approximation: to correct it further, we do with the second [approximate] root as we did with the first [approximate] root, and what remains after subtracting the ratio of the excess to double the second [approximate] root from [the second approximate root] is the most accurate approximation.
|
ולדקדקה יותר נעשה מהמדה הזאת השנית כאשר עשינו מהמדה הראשונה [189]ומה שישאר אחרי הסרת ערך התוספת ההכאה אל כפל המדה השנית פעמים ממנה יהיה מדה מדוקדקת מכלנה
|
- From here on, do not trouble yourself to correct it even further, lest you dive into deep water and draw nothing in your hand.
|
ומכאן ואילך אל תיגע עצמך לדקדק כי אולי תצלול במים אדירים וחרס יעלה בידך
|
- If we find that the excess of the number over the preceding square is greater than the root of the preceding square, we proceed in another way:
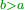
|
ואם מצאנו שהעודף מהמספר על המרובע שעבר הוא יותר מגדר המרובע שעבר נעשה בדרך אחרת
|
- We examine how much is the difference between our number and the next square.
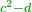
|
נעיין כמה המרחק ממספרנו ועד המרובע העתיד
|
- First approximation: we convert the difference into primes, then divide them by double the root of the next square. We subtract the quotient from the root of the next square and the remainder is the approximate root.

|
ונשיב המרחק ראשונים ונחלקם על כפל [גדר][190] המרובע העתיד פעמים ומה שיצא בחלוק נגרע אותו מגדר המרובע העתיד והנשאר היא מדת הצלעות בקרוב
|
- When we wish to correct it further, we do it in the previously explained way.
|
וכשנבקש לדקדק אותה נעשה בדרך המבואר [בדקדוקיו][191] שלפנינו
|
- If We find that the excess of our number over the preceding square is the same as its root, no less and no more, we call our number a "mean number" [
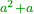 ]. ].
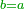
|
והנה אם מצאנו העודף ממספרנו על המרובע שעבר שהוא בכגדרו לא פחות ולא יתר נקרא מספרינו ממוצע
|
- If we want to extract the [approximate] root using the preceding square or the next square, it is the same [procedure], only that one procedure is by addition and the other procedure is by subtraction.
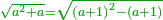
|
ואם נרצה נוציא מדת הצלעות מהמרובע שעבר או מהמרובע שעתיד והכל יהיה שוה רק שמעשה האחד בתוספת ומעשה האחר במגרעת
|
|
|
|
- Example of a number, whose excess over the preceding square is less than the root of the square: We wish to know the measure of each side of the square that is five.
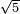
|
דמיון במספר שהעודף על המרובע שעבר פחות מגדר המרובע [192]ההוא
רצינו לדעת מדת כל צלע וצלע ממרובע שהוא חמשה
|
- The excess of the preceding square is one.
|
והנה העודף על המרובע שעבר הוא אחד
|
- We convert it into primes; they are sixty.
|
נשיב אותו ראשונים ויהיו ששים
|
- We divide them by 4, which is double the root of the preceding square; the result of division is fifteen primes.
|
נחלק אותם על הד' שהם כפל מהגדר מהמרובע שעבר פעמים ויהיה היוצא מהחלוקה חמשה עשר ראשונים
|
- We add them to the root of the preceding square; we find that the measure of each side [of the square] is approximately two integers and fifteen primes.
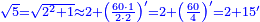
|
נוסיפם על הגדר מהמרובע שעבר ונמצא שיהיה מדה אחת לכל הצלעות שנים שלמים וחמשה עשר ראשונים בקרוב
|
- If we want to correct this root, we multiply the two integers and fifteen primes by themselves; they are five integers plus two hundred and twenty-five seconds, because it has already been explained that the product of primes by primes is seconds.
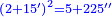
|
ואם נרצה לדקדק המדה הזאת נכה ונכפול השנים שלימים וחמשה עשר ראשונים על עצמם ויהיו חמשה שלמים ומאתים ועשרים וחמש שניים כי מכפלת הראשונים על ראשונים כבר התבאר שיהיה העולה שניים
|
- Now, we should see what is the ratio of the excess over the five integers, which is two hundred and twenty-five seconds, to double the [approximate] root we have found; its ratio to it is as the ratio of one to seventy-two.
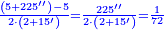
|
ועתה יש לנו לראות הנוסף על החמשה שלמים שהוא מאתים ועשרים וחמש שניים איזה ערך הוא מכפלת המדה שמצאנו פעמים והנה ערכם אליה הוא כערך אחד משבעים ושנים
|
- Therefore, we convert all the fifteen primes we have into seconds; they are nine hundred seconds.
|
ועל כן נשיב החמשה עשר ראשונים שיש לנו כלם שניים ויהיו תשע מאות שניים
|
- We divide them by seventy-two; we receive twelve from the division, and there are thirty-six seconds left that cannot be divided by seventy-two.
|
ונחלק אותם על שבעים ושנים ותצא לנו החלוקה שנים עשר וישארו שלשים וששה שניים [193]שלא נתחלקו על השבעים ושנים
|
- We consider them as a half, which is their part of seventy-two, and this half is thirty thirds. We find that everything is divided by seventy-two; the result is twelve seconds and thirty thirds.
|
ולכן נקח חצי האחד מהם שהיה חלק אחד מהשבעים ושנים ותהיה החצי שלשים שלישיים ונמצא שנחלק הכל על שבעים ושנים והיוצא הוא שנים עשר שניים ושלשים שלישיים
|
- We subtract them from the nine hundred seconds; eight hundred and eighty-seven seconds remain, plus thirty thirds, which is fourteen primes, forty-seven seconds, and thirty thirds; this root is more accurate than the first and its sign is 2, 14′, 47′′, 30′′′ and they are integers, primes, seconds and thirds.
|
נסיר אותם מהתשע מאות שניים ישארו שמנה מאות ושמנים ושבעה שניים ושלשים [שלישיים שהם ארבעה עשר ראשונים וארבעי' ושבעה שניים ושלשים][194] שלישיים וזאת היא המדה המדוקדקת יותר מבראשונה וסימן שלה ב' י"ד מ"ז ל' והנה הם שלמים ראשונים שניים שלישיים
|
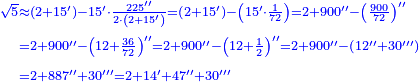
|
- If we want to correct this [approximate] root further, multiply it by itself; you find that the excess over the examined number is 2 primes, [4]8 seconds, 44 thirds, 16 fourths, and 15 fifths.
|
ואם נרצה לדקדק עוד זאת המדה תכה ותכפול אותה בעצמה ותמצא שיהיה העודף על החשבון הנחקר ב' ראשונים ע"ח שניים מ"ד שלישיים י"ו רביעיים ט"ו חמישיים
|
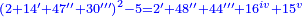
|
- See the ratio of [the square of] this excess to double the [approximate] root and subtract its ratio from the [approximate] root you have, as explained above. The remainder is a more accurate root than the previous roots.
|
ותראה מה ערך הנוסף הזה אל כפל המדה פעמים וכערכו אליה תסיר מהמדה שיש לך כאשר התבאר למעלה ותהיה הנשאר מדה מדוקדקת מהאחרות הקודמות
|
|
|
|
- Example of a number, whose excess over the preceding square is greater than its root: We wish to know the measure of the sides of the square that is seven.
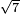
|
דמיון במספר שהעודף על המרובע שעבר יתר מגדרו
רצינו לדעת מדת הצלעות ממרובע שהוא שבעה
|
- Since the excess over the preceding square is greater than its root, we see how much is the difference between our number and the next square: the difference is two, because this is the difference between seven and nine, which is the next square.
|
ובאשר העודף על המרובע שעבר יותר מגדרו נראה כמה מרחק יש ממספרינו [195]ועד המרובע העתיד והנה המרחק הוא שנים כי ככה ירחוק שבעה מתשעה שהוא המרובע העתיד
|
- We convert it into primes; they are a hundred and twenty.
|
נשיבם ראשונים יהיו מאה ועשרים
|
- We divide them by double the next square, which is six; we find it twenty times there and they are primes.
|
נחלקם על כפל גדר המרובע העתיד פעמים העולה ששה נמצאם שם עשרים פעמים והם ראשונים
|
- We subtract them from the root of the next square, which is three; two integers and forty primes remain and this is the root of the examined square approximately
|
נסיר אותם מגדר המרובע העתיד שהוא שלשה וישאר שנים שלמים וארבעים ראשונים וזאת היא מדת צלעות המרובע הנחקר בקרוב
|
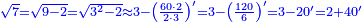
|
- When you want to correct this root, multiply it by itself. You find that the excess over the examined number is only six primes and forty seconds.
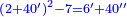
|
וכאשר תרצה לדקדק המדה הזאת ותכנה בכפלה על עצמה תמצא שלא יהיה הנוסף על מספר המרובע הנחקר כי אם ששה ראשונים וארבעים שניים
|
- Finish the procedure as mentioned above.
|
וגמור את המלאכה האמור למעלה
|
|
|
|
- Example of a number, whose excess over the preceding square is the same as the root of the preceding square: We wish to know the measure of the square that is six.
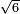
|
דמיון במספר שהעודף על המרובע שעבר הוא כגדר המרובע ההוא שעבר
רצינו לדעת מדת צלעות מרובע שהוא ששה
|
- This square number is mean, so, we can extract the root using the preceding square, if we want, or using the next square; the result is the same, as one procedure is by addition and the other procedure is by subtraction.
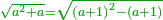
|
והנה מספר המרובע הזה הוא ממוצע ואם נרצה נוכל להוציא המדה מהמרובע העבר או מהמרובע העתיד והכל יבוא אל כוון אחד כאשר יהיה מעשה האחד בתוספת ומעשה האחד במגרעת
|
- We extract it first using the preceding square, which is four: the excess is two, which is a hundred and twenty primes.
|
ונוציאנה [196]בתחלה מהמרובע שעבר [שהוא ארבעה][197] והנה העודף שנים שהם מאה ועשרים ראשונים
|
- We divide them by double the root, which is four, we find it thirty times there and they are thirty primes.
|
נחלקם על כפל הגדר שהוא [ארבעה נמצאם שם שלשים פעמים והם שלשים ראשוני
|
- We add them to the root, which is two and this is the first approximate root.
|
נוסיפם על הגדר שהוא][198] שנים ותהיה זאת המדה הראשונה בקרוב
|
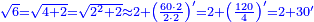
|
- If we extract the root using the next square, which is nine, we do it this way: the difference is three, which is a hundred and eighty primes.
|
ואם נוציא המדה מהמרובע העתיד שהוא תשעה נעשה בדרך זה הנה המרחק שלשה שהם מאה ושמנים ראשונים
|
- We divide them by six, which is double the root of the next square, we find it thirty times there, and they are primes.
|
נחלקם על ששה שהוא כפל הגדר המרובע העתיד נמצאנו שם שלשים פעם והם ראשונים
|
- We subtract them from three, which is the root of the next square; two integers and thirty primes remain, as we found first, when we extracted the root using the preceding square.
|
נסיר אותם משלשה שהם גדר המרובע העתיד וישארו שנים שלמים ושלשים ראשונים כאשר מצאנו כאשר מצאנו בתחלה כאשר היינו מוצאים המדה מהמרובע [שעבר][199]
|
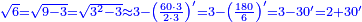
|
- The result is the same, therefore a number like this is called "mean".
|
[והכל אחד ועל כן יקרא כל חשבון כזה ממוצע][200]
|
- If you want to correct the root, do as explained previously.
|
ואם תרצה לדקדק המדות תעשה כאשר התבאר לפנים
|
Chapter Eleven – Here I will Write Nice Rules of Arithmetic Methods for You
|
השער האחד עשר הנה אכתוב לך בזה כללים נחמדים בדרכי החשבון
|
| Multiplication of a number by itself
|
|
- Know that when you wish to multiply a number by itself, whether that number is units alone, or there are tens with them, or tens alone:
|
ותדע כי כאשר תרצה לכפול חשבון אחד על עצמו בין שיהיה החשבון ההוא אחדים בלבד או שיש עמהם עשרות או עשרות לבדן
|
- If it is a number that has a third [= divisible by 3], take its third, multiply it by itself, multiply its square by ten, and subtract its square from [the product]; the remainder is the required.
![\scriptstyle{\color{OliveGreen}{\left(3n\right)^2=\left[10\sdot\left[\frac{1}{3}\sdot\left(3n\right)\right]^2\right]-\left[\frac{1}{3}\sdot\left(3n\right)\right]^2}}](/mediawiki/images/math/8/7/b/87bdc32051b224513066e28e719f373b.png)
|
אם הוא מספר שיש לו שלישית קח שלישיתו והכה אותה על עצמה וכפול מרובעה עשרה פעמים והסר מהם מרובעה והנשאר הוא [201]המבוקש
|
- Example: we wish to multiply six by six.
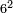
|
דמיון בקשנו לכפול שש על שש
|
- The third is two and its square is four.
|
הנה השלישית שנים ומרובעו ארבעה
|
- We multiply is ten times; it is forty.
|
נכפול אותה עשרה פעמים יהיו ארבעים
|
- We subtract four from it, which is a square of the third; thirty-six remains and this is the product.
|
נסיר מהם ארבעה שהוא מרובע השלישית ישארו ששה ושלשים והוא הנכפל
|
![\scriptstyle{\color{blue}{6^2=\left(3\sdot2\right)^2=\left[10\sdot\left(\frac{1}{3}\sdot6\right)^2\right]-\left(\frac{1}{3}\sdot6\right)^2=\left(10\sdot2^2\right)-2^2=\left(10\sdot4\right)-4=40-4=36}}](/mediawiki/images/math/3/8/d/38d1d5ec3932f81319dd5cf689ea938d.png)
|
- If the number does not have a third but it exceeds by one over a multiple of three, we subtract [the one] and calculate [the square of] the multiple of three in the method explained, then we add the multiple of three and the number that follows it to our number and the sum is the required.
|
ואם לא היה למספר שלישית אך עודף ממנו שלישיות אחד נסירנו משם ונחשוב המשולש בדרך המבואר ואחר נוסיף על חשבוננו המספר האחרון מהמשולש והמספר שאחריו אשר הסירונו והמחובר הוא המבוקש
|
![\scriptstyle{\color{OliveGreen}{\left(3n+1\right)^2=\left[\left[10\sdot\left[\frac{1}{3}\sdot\left(3n\right)\right]^2\right]-\left[\frac{1}{3}\sdot\left(3n\right)\right]^2\right]+3n+\left[\left(3n+1\right)\right]}}](/mediawiki/images/math/b/f/3/bf33f7d7d256c9cce1765e3f38e307be.png)
|
- Example: we wish to multiply ten by itself.
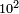
|
דמיון בקשנו לכפול עשרה על עצמם
|
- We subtract one from it; nine remains and it is a product of three.
|
נסיר מהם אחד וישארו תשעה והם משלשים
|
- We take three, which is its third; its square is nine.
|
נקח שלשה שהוא שלישיתם והנה מרובעם תשעה
|
- It product by ten is ninety.
|
וכפלתם עשרה פעמים הם תשעים
|
- We subtract the square of the third from it; eighty-one remains.
|
ונסיר מהם מרובע השלישית וישארו שמונים ואחד
|
- We add nine and ten to it; the result is one hundred and this is the product.
|
נוסיף עליהם תשע ועשרה יעלו מאה והוא הנכפל
|
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle10^2&\scriptstyle=\left(9+1\right)^2=\left[\left(3\sdot3\right)+1\right]^2=\left[\left[10\sdot\left(\frac{1}{3}\sdot9\right)^2\right]-\left(\frac{1}{3}\sdot9\right)^2\right]+9+10=\left[\left(10\sdot3^2\right)-3^2\right]+9+10\\&\scriptstyle=\left[\left(10\sdot9\right)-9\right]+9+10=\left(90-9\right)+9+10=81+9+10=100\\\end{align}}}](/mediawiki/images/math/b/6/4/b644d352f59bcab6ac290785552438e0.png)
|
- If the number is one less than a multiple of three, we add [the one] and calculate [the square of the multiple of three] according to the rule, then we subtract [the multiple of three and] the number that precedes it from [the result] and the remainder is the required.
|
ואם היה המספר פחות משלישיות אחד הוסיפנו עליו ונחשוב אותו כמשפט ואחר נסיר ממנו החשבון שהוספנו עליו החשבון האחרון שלו והנשאר הוא המבוקש
|
![\scriptstyle{\color{OliveGreen}{\left(3n-1\right)^2=\left[\left[10\sdot\left[\frac{1}{3}\sdot\left(3n\right)\right]^2\right]-\left[\frac{1}{3}\sdot\left(3n\right)\right]^2\right]-\left(3n\right)-\left[\left(3n-1\right)\right]}}](/mediawiki/images/math/4/2/4/424921fda72004011eee2ecd49af0392.png)
|
- We wish to multiply eleven by itself.
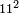
|
דמיון בקשנו [לכפול][202] אחד עשר על עצמם
|
- We add one to it; it is twelve.
|
[203]נוסיף עליהם אחד ויהיו שנים עשר
|
- We calculate it by taking the third; its square is sixteen.
|
נחשבם בדרך לקיחת השלישית והנה מרובעה ששה עשר
|
- Its product by ten is one hundred and sixty.
|
וכפלתם בעשרה מאה וששים
|
- We subtract sixteen from it, which is the square of the third; one hundred and forty-four remains.
|
נסיר מהם ששה עשר שהם מרובע השלישית ישארו מאה וארבעים וארבעה
|
- We subtract from it eleven and twelve, which are twenty-three; one hundred and twenty-one remains and this is the product.
|
נסיר מהם אחד עשר ושנים עשר העולים עשרים ושלשה ישארו מאה ועשרים ואחד והוא הנכפל
|
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle11^2&\scriptstyle=\left(12-1\right)^2=\left[\left(3\sdot4\right)-1\right]^2=\left[\left[10\sdot\left(\frac{1}{3}\sdot12\right)^2\right]-\left(\frac{1}{3}\sdot12\right)^2\right]-11-12\\&\scriptstyle=\left[\left(10\sdot4^2\right)-4^2\right]-11-12=\left[\left(10\sdot16\right)-16\right]-11-12\\&\scriptstyle=\left(160-16\right)-11-12=144-12-11=144-23=121\\\end{align}}}](/mediawiki/images/math/b/0/1/b0167e9801aca57699585726cc550144.png)
|
Multiplication of units and tens by units and tens
![\scriptstyle{\color{OliveGreen}{\left(10+a\right)\times\left(10+b\right)=\left[10\sdot\left[\left(10+a\right)+b\right]\right]+\left(a\sdot b\right)}}](/mediawiki/images/math/6/c/a/6ca9d98590fd0390228cb3a1b7607d13.png)
|
|
- Another example: to know the product of eleven by eleven.
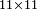
|
דמיון אחרת לדעת כפלת האחד עשר על אחד עשר
|
- We consider this number as if it were written in two lines.
|
הנה נחשוב שהמספר הזה נכתב בשני טורים
|
- We take the one of one line and add it to the other line; it is twelve.
|
ונקח האחד מן הטור האחת ונחברם אל הטור האחרת ויהיו שנים עשר
|
- We multiply it by the remaining ten; it is a hundred and twenty.
|
נכפלם על העשרה הנשארים יהיו מאה ועשרים
|
- We add to it the product of the units by themselves; it is a hundred and twenty-one and this is the product.
|
נוסיף עליהם הכאת האחדים על עצמם ויהיו מאה ועשרים ואחד והוא הנכפל
|
![\scriptstyle{\color{blue}{11\times11=\left[\left(11-1\right)\sdot\left(11+1\right)\right]+\left(1\sdot1\right)=\left(10\sdot12\right)+1=120+1=121}}](/mediawiki/images/math/e/a/1/ea13d6aefaefa54cb18f4c31e4c21646.png)
|
- Likewise if we wish to multiply fifteen by twelve.
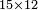
|
וככה אם נבקש לכפול חמשה עשר בשנים עשר
|
- We take the two and add it to fifteen; it is seventeen.
|
נקח השנים ונשים אותם על החמשה עשר ויהיו שבעה עשר
|
- We multiply it by the remaining ten; it is a hundred and seventy.
|
נכפלם על העשרה הנשארים יהיו מאה ושבעים
|
- We multiply the other two by five; it is ten.
|
ונכה השנים האחרים על החמשה ויהיו עשרה
|
- We add it to a hundred and seventy; the product is a hundred and eighty.
|
נחברם עם המאה ושבעים יהיה הנכפל מאה ושמנים
|
![\scriptstyle{\color{blue}{15\times12=\left[\left(12-2\right)\sdot\left(15+2\right)\right]+\left(2\sdot5\right)=\left(10\sdot17\right)+10=170+10=180}}](/mediawiki/images/math/2/e/0/2e0464051c8b288d93d7c642b5cb03ff.png)
|
Word Problems
|
|
| Now, I shall start discussing and mentioning some of the difficult problems, extracting their solutions, and explaining each one of them at length.
|
ועתה אתחיל לדבר ואזכיר קצת מהשאלות הקשות [204]ולהוציא תשובתן אאריך [הביאור][205] כל אחת מהם
|
| Find a Number Problem - Sums
|
|
- Question: we summed all the successive numbers from one to twenty and it is the sum. How much is the sum?
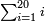
|
שאלה חברנו כל המספרים הרצופים מאחד עד עשרים והם הכלל כמה המחובר
|
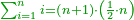
|
|
- We add one to the twenty and multiply [the result] by ten, which is half twenty; the product is two hundred and ten, and this is the required.
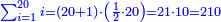
|
הנה נוסיף על העשרים אחד ונכפלם [על][206] עשרה שהוא חצי עשרים ויהיה הנכפל מאתים ועשרה וככה המבוקש
|
- If we want to know how much are the numbers summed up up to eleven.
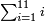
|
ואם נרצה לדעת כמה עולים המספרים המחוברים על אחד עשר
|
- We add one to [the eleven] and multiply [the result] by half the eleven, which is five and a half; the product is sixty-six, and this is the sum.
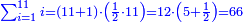
|
נוסיף עליו אחד יהיו שנים עשר נכפלם על חצי האחד עשר שהם חמשה וחצי ויהיה הנכפל ששים וששה וככה המחובר
|
- There are other ways, but what I have wrote is the easiest and the most correct [way].
|
ויש [דרכים][207] אחרים ומה שכתבתי הוא היותר קל ונכון
|
- Reverse question: the sum of the successive numbers starting from one is 210. What is the last number of the summed [numbers]?
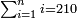
|
נהפוך השאלה ונאמר עלה המחובר ממספרים רצופים המתחילים מאחד מאתים ועשרה
איזה הוא המספר האחרון מהמחוברים
|
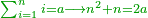
|
|
- We do as follows: we double two hundred and ten; it is four hundred and twenty.
|
נעשה בדרך זה נכפול מאתים ועשרה פעמים ויהיו ארבע מאות ועשרים
|
- We take the closest root, whose extraction method was explained in chapter seven; we find that it is twenty and this is the last number of the summed numbers.
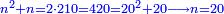
|
נקח מהם הגדר היותר קרוב כאשר התבאר דרך לקיחתו בשער השביעי והנה נמצא שהוא עשרים והוא המספר האחרון מהמחוברים
|
- Thus, what remains from the number that has no root is twenty, as the number of the root.
|
והנה נשאר מהמספר שהוא בלתי נגדר עשרים [208]כמספר הגדר
|
- So should be in all the calculations that are similar to it and if not, then the one who asked has mistaken in his question, when he summed the numbers he made a mistake without a doubt.
|
וכן ראוי שיהיה בכל החשבונות הדומים לזה ואם אין טעה השואל בשאלתו וכאשר חבר המספרים עשה בטעות בלי ספק
|
| Triangulation Problem - Cane
|
|
- Question: a cane 5 cubits tall, is standing next to a wall of the same height.
- If we lower its [top] two cubits down from the top of the wall, so that it will stand on a slope, how far will be the bottom end of the cane from the foot of the wall?
|
שאלה [קנה][209] המדה ארוכה חמש אמות ועומדת זקופה בכותל אחת גבוה כמדתה
אם [נשפיל][210] אותה מראש הכותל אמתיים כדי שתעמוד בשפוע כמה הרחיק ראש הקנה התחתון מיסוד הכותל
|
- We do like this: we take the square of the five cubits; it is twenty-five.
|
נעשה זאת נקח מרובע החמש אמות והם עשרים וחמש
|
- We take also the square of the three cubits that are left from there to the foot of the wall; it is nine.
|
ונקח גם כן מרובע הג' אמות הנשארות משם ועד יסוד הכותל והנה הוא ט'
|
- Its difference from twenty-five is sixteen.
|
ומרחקו מעשרים וחמש ששה עשר
|
- The root of sixteen is four and so is the distance of the bottom end of the cane from the foot of the wall no more and no less.
|
וגדר ששה עשר הוא ארבעה וככה מרחק ראש הקנה התחתון מיסוד הכותל בלתי תוספת ומגרעת
|
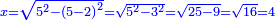
|
- If the difference between a square and a square is an inexpressible number, take its root approximately, as was explained in the preceding chapter, and this will be the measure of the distance from the bottom end of the cane to the foot of the wall.
|
ואם היה החסרון ממרובע אל מרובע מספר חרש ואלם תקח גדרו בקרוב כאשר התבאר בשער הקדום לזה וככה יהיה מדת מרחק מראש הקנה התחתון אל היסוד הכותל
|
| Divide a Quantity Problem - Simple division
|
|
- Question: I gave a messenger 30 dinar and one pašuṭ and ordered him to hire workers as much as his money allows, so that the payment of the one equals the payment of his friend, there will be no worker whose payment is one pašuṭ, and there will be no fractions in one's payment.
- We want to know how many workers he could hire.
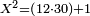
|
שאלה נתתי לשלוחי שלשים דנרים ופשוט וצותי אותו שישכור פועלים כאשר יספיקו לו מעותיו ויהיה שכר האחד כשכר חברו ולא יהיה בהם [211]פועל ששכרו פשוט וגם לא יהיה בשכרו שום שברי שלם
נרצה לדעת כמה פועלים יוכל לשכור
|
- We convert all the dinar into pešuṭim and add the additional pašuṭ to them; they are three hundred and sixty-one pešuṭim.
|
הנה נשיב הדינרים כלם פשוטים ונחבר אליהם הפשוט הנוסף עליהם ויהיו שלש מאות וששים ואחד פשוטים
|
- We extract their root as the method of chapter seven; we find that it is nineteen.
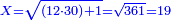
|
נקח גדרם בדרך השער השביעי ונמצא שהוא תשעה עשר
|
- We can answer that the messenger can hire nineteen workers at nineteen pešuṭim each no more and no less.
|
ונוכל להשיב שיוכל לשכור השליח תשעה עשר פועלים ושכר כל אחד ואחד תשעה עשר פשוטים לא פחות ולא יתר
|
| How much Problem - Wall
|
|
- Question: a wall collapsed. It is rebuild with an extension, so that it will be higher than what it was by half the size it had at the beginning, and its sixth, and ninth. With the whole extension, its height was 50 cubits. How much was its original height?
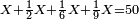
|
שאלה חומה שנפלה והוספו עליה בבנין כדי שתהיה גבוה הרבה חצי מדתה מאשר היתה בתחלה וששיתה ותשיעתה עם כל זה והיתה מדת גבהה חמשים אמה כמה היתה מדתה בראשונה
|
- False Position: We take a denominator that has a half, a sixth, and a ninth. That is, we take two, since the half is derived from it, multiply it by six, for the sixth that is derived from it; the result is twelve. We multiply it also by nine for the ninth; the denominator is one hundred and eight.

|
נקח מדומה שיהיה לו חצי וששית ותשיעית והוא שנקח שנים בעבור אשר יצאה מהם החצי ונכפול אותם בששה בעבור הששית אשר תצא מהם ויהיו שנים עשר ונכפול גם הם בתשעה בעבור התשיעית ויהיה המדומה מאה ושמנה
|
- Its half is fifty-four.
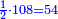
|
ומחציתו חמשים וארבעה
|
- Its sixth is eighteen.
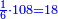
|
וששיתו שמנה עשר
|
- Its ninth is twelve.
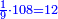
|
ותשיעתו שנים [212]עשר
|
- The sum of all these parts is eighty-four.

|
והמחובר מכל החלקים האלה עולה שמונים וארבעה
|
- We add it to the denominator; it is one hundred and ninety-two.
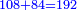
|
נוסיפם אל המדומה ויהיו מאה ותשעים ושנים
|
- Rule of Three: So we take the ratio and say: as the ratio of a hundred and eight, which is the denominator, to a hundred and ninety-two, which results from adding all the mentioned parts to it, so is the ratio of the unknown original measure of the wall to fifty, which is the height now, after the extension of the construction.
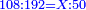
|
והנה נעשה בדרך הערכין ונעריך ונאמר כערך מאה ושמנה שהוא המדומה אל מאה ותשעים ושנים שהוא העולה מתוספת החלקים הנזכרים עליו כן ערך מדת החומה אשר היתה בראשונה הנעלמת ממנו אל חמשים שהיא גבוהה עתה אחר התוספת בבנין
|
- When we multiply the first number by the fourth, it is five thousand and four hundred.
|
וכאשר נכפול המספר הראשון על הרביעי יהיו חמשת אלפים וארבע מאות
|
- We divide it by the known mean, which is one hundred and ninety-two; we find it twenty-eight times in it and four parts remain that cannot be divided, which are parts of the one hundred and ninety-two by which we divided.
|
נחלקם על האמצע הנודע שהוא מאה ותשעים ושנים נמצאנו שם שמנה ועשרים פעמים וישארו מהם עשרים וארבעה חלקים שלא נתחלקו והמה חלקים ממאה ותשעים ושנים בשלם אשר חלקנו עליו
|
- Therefore, we can answer that the measure of the height of the wall originally was twenty-eight cubits and four parts of one hundred and ninety-two in a cubit.
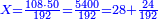
|
ועל כן נוכל להשיב כי מדת גבהות החומה בראשונה היתה שמונה ועשרים אמות ועשרים וארבעה חלקים ממאה ותשעים ושנים באמה
|
- Check: We examine if it is true in this way:
|
ונבחן זה אם הוא אמת בדרך זאת
|
- We decompose all the cubits and convert each into the mentioned parts, then add the result to the twenty-four parts added to the cubits; the sum is five thousand and four hundred.
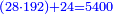
|
נתיך כל האמות ונעשה מכל האחת ואחת החלקים הנזכרים ונחבר העולה אל עשרים וארבע החלקים העודפים על [213]האמות ויהיה המחובר חמשת אלפים וארבע מאות
|
- Its half is two thousand and seven hundred.
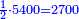
|
מחציתם אלפים ושבע מאות
|
- Its sixth is nine hundred.
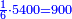
|
ששיתם תשע מאות
|
- Its ninth is six hundred.
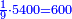
|
תשיעיתם שש מאות
|
- The sum is four thousand and two hundred.

|
המחובר ארבעת אלפים ומאתים
|
- We add it to the five thousand and four hundred; it is nine thousand and six hundred.

|
נוסיף זה על החמשת אלפים וארבע המאות ויהיו כתשע אלפים ושש מאות
|
- If you divide it by the number of parts of the whole cubit, you find it is fifty times there, as the number of cubits of the height of the wall now, after the extension of the construction.
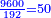
|
ואם תחלקם על מספר חלקי האמה גובה השלמה תמצאנו שם חמשים פעמים כמכסת אמות גובה החומה עתה אחרי תוספת הבנין
|
- Question: the town wall was 100 cubits high. Its third and its quarter had collapsed.
- How high is what remains?
![\scriptstyle X=100-\left[\left(\frac{1}{3}\sdot100\right)+\left(\frac{1}{4}\sdot100\right)\right]](/mediawiki/images/math/0/6/4/064f6c9817381f7419d53dd1707a018a.png)
|
שאלה חומת העיר גבוה מאה אמה ונפרצו ממנה שלישיתה ורביעיתה
כמה גובה הנשאר
|
- False Position: The denominator that has a third and a quarter is twelve.
|
הנה המדומה שיש לו שלישית ורביעית הוא שנים עשר
|
- We take the mentioned parts from it and sum them up; it is seven. We subtract it from the denominator; five remain.
![\scriptstyle{\color{blue}{12-\left[\left(\frac{1}{3}\sdot12\right)+\left(\frac{1}{4}\sdot12\right)\right]=12-7=5}}](/mediawiki/images/math/9/9/4/994410b776b40d19b554ba92d759d4ae.png)
|
נקח ממנו החלקים הנזכרים ונחברם יהיו שבעה נסירם מהמדומה ישארו חמשה
|
- Rule of Three: Now, we take the ratio and say: as the ratio of five to twelve so is the ratio of the unknown to one hundred.

|
ועתה נעריך ונאמר כערך חמשה אל שנים עשר כך ערך הנעלם אל מאה
|
- We multiply the first number by the fourth; it is five hundred.
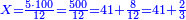
|
כפלנו החשבון הראשון על הרביעי ויהיו חמש מאות
|
- We divide it by the known mean; we find it forty-one times there and eight remain that cannot be divided, which are parts of twelve. So, the height of what remains is forty-one cubits and eight parts of twelve in a cubit, which are two-thirds.
|
נחלקם על האמצעי הנודע נמצאנו שם ארבעים ואחד פעמים ונשארו מהם שמונה שלא נחלקו שהם חלקים משנים עשר וככה הוא גובה הנשאר ארבעים ואחת אמה ושמנה [214]חלקים משנים עשר באמה שהם שני שלישיות
|
- Check: When we examine it:
|
וכאשר נבחן זה
|
- We convert the cubits into parts of twelve each; they are one thousand and two hundred.
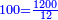
|
ונעשה מהאמה אמות אשר היו שם בראשונה חלקים משנים עשר מכל אחת ואחת יהיו אלף ומאתים
|
- We take their third; it is four hundred.
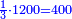
|
נקח שלישיתם שהם ארבע מאות
|
- And their quarter, which is three hundred.
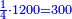
|
ורביעיתם שהם שלש מאות
|
- The resulting sum is seven hundred.

|
והמחובר עולה שבע מאות
|
- We subtract it from one thousand and two hundred; five hundred remain, which are forty-one cubits and eight parts of twelve, as we stated.
 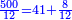
|
נסיר אותם מהאלף ומאתים ישארו חמש מאות שהם ארבעים ואחת אמה ושמנה חלקים משנים עשר כאשר זכרנו
|
| First from last Problem - Amount of grain
|
|
- Question: the landlord harvested his grain and gave a great heave offering by law from [what he collected] at first.
- Afterwards he gave the first tithe from what remained and from what remained then, he gave a second tithe, and he was left with 40 measures of grain.
- How much was the grain at first?
|
שאלה בעל הבית שאסף תבואתו ותרם ממנו בתחלה תרומה גדולה כמשפט ואחרי כן הפריש מהנשאר מעשר ראשון ומהנשאר אחרי זאת הפריש מעשר שני ונשארו לו חמישים מדות חטה
כמה היה הכרי בתחלה
|
![\scriptstyle\left(X-\frac{2}{100}X\right)-\left[\frac{1}{10}\sdot\left(X-\frac{2}{100} X\right)\right]-\left[\frac{1}{10}\sdot\left[\left(X-\frac{2}{100}X\right)-\left[\frac{1}{10}\sdot\left(X-\frac{2}{100} X\right)\right]\right]\right]=50](/mediawiki/images/math/4/a/2/4a2924027b379bac5d8c351156314329.png)
|
- It is known that our late rabbis said that the offering is half a hundred, which is one part of fifty.

|
ידוע כי התרומה אמרו רבותינו ז"ל שהיא תרי ממאה שהיא חלק אחד מהחמשים
|
- Therefore, we take the fifty and multiply it by ten for the first tithe that is subtracted from it; it is five hundred.
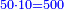
|
על כן נקח חמשים ונכפלם בעשר בעבור המעשר ראשון היוצא ממנו ויהיו חמש מאות
|
- False Position: We multiply it also by ten, for the second tithe; it is five thousand and it is the denominator.
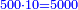
|
ונכפול גם הם בעשר בעבור המעשר שני ויהיה חמשת אלפים והוא המדומה
|
- Hence, his offering is one hundred.
|
והנה תרומתו מאה
|
- We subtract it; four thousand and nine hundred remain.

|
נסירנה ממנו ישארו ארבעת אלפים [215]ותשע מאות
|
- Its tithe is four hundred and ninety.
|
מעשר שלהם ארבע מאות ותשעים
|
- We subtract it; four thousand four hundred and ten remain.
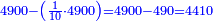
|
נסיר אותו מהם ישארו ארבעת אלפים וארבע מאות ועשרה
|
- Its tithe is four hundred and forty-one
|
מעשר שלהם ארבע מאות וארבעים ואחד
|
- We subtract it; three thousand nine hundred and sixty-nine remain.
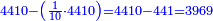
|
נסיר אותו מהם ישארו שלשת אלפים ותשע מאות [וששים ותשעה][216]
|
- Rule of Three: Now, we take the ratio and say: as the ratio of three thousand, nine hundred, and sixty-nine to five thousand so is the ratio of fifty to the unknown.

|
ועתה נעריך ונאמר כערך שלשת אלפים ותשע מאות וששים ותשעה אל חמשת אלפים כן ערך חמשים אל הנעלם
|
- We multiply the means; the result is two hundred and fifty thousand.
|
כפלנו האמצעיים עלו מאתים וחמשים אלף
|
- We divide it by the first known number; we find it sixty-two times there, and three thousand nine hundred and twenty-two remained that cannot be divided, which are parts of three thousand nine hundred and sixty-nine by which we divided; and this was the amount of measures of grain that was at first, when the landlord began to give offering.

|
נחלקם על החשבון הראשון הנודע נמצאנו שם ששים ושתים פעמים ונשארו שלא נתחלקו שלשת [אלפים ותשע מאות ועשרים ושנים והם חלקים משלשת][217] אלפים ותשע מאות וששים ותשעה אשר חלקנו עליו וכזה היה סכום המדות אשר היו בכרי כשהתחיל בעל הבית לתרום
|
| How much Problem - Amount of money
|
|
- Question: Reuven demands from Shimon a hundred measures, which he says he owes him according to an oral [agreement].
- Shimon says: I do not owe you a hundred measures, but as much as I owe you, with the same amount, and one-half of it, and a quarter of it, plus one will make a hundred.
- How much did he admit he owes him?
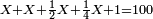
|
שאלה ראובן תובע לשמעון מאה מנה שאומר שהוא חייב לו על פה
ויאמר שמעון אליו אין אני חייב לך מאה מנה אבל כאותם שאני חייב לך ואחרים כמותם ומחציתם ורביעיתם ועם אחד יהיו מאה
נרצה לדעת כמה הודה לו מתביעתו
|
- False Position: We do as follows: we take a denominator that has a half and a quarter; we find it is eight.
|
ונעשה על דרך זה נקח מדומה שיש לו חצי ורביעית [218]והנה נמצא שמונה
|
- We add the same; it is sixteen. We add also half the denominator, which is four; it is twenty; and its quarter, which is two; it is twenty-two.
![\scriptstyle{\color{blue}{8+8+\left[\left(\frac{1}{2}\sdot8\right)+\left(\frac{1}{4}\sdot8\right)\right]=16+4+2=20+2=22}}](/mediawiki/images/math/5/a/3/5a39486b875ef2fbc83b16aa4a933d0a.png)
|
נוסיף כמוהו יהיו ששה עשר וגם הוסיף מחצית המדומה שהיא ארבעה יהיו עשרים ורביעיתו שהוא שנים יהיו עשרים ושנים
|
- Rule of Three: Necessarily as the ratio of eight to twenty-two so is the ratio of the unknown to ninety-nine.
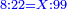
|
ובהכרח כערך שמנה אל עשרים ושנים כן ערך הנעלם אל תשעים ותשע
|
- For it is known that the sum of the parts of the admission is only ninety-nine; and with one it is one hundred.
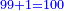
|
כי בידוע כי המחובר מחלקי ההודאה עמה לא יעלה כי אם תשעה ותשעים ועם אחד הם מאה
|
- When we multiply the first number by the fourth, the result is seven hundred and ninety-two.
|
וכאשר נכפול החשבון הראשון על הרביעי יעלו שבע מאות ותשעים ושנים
|
- We divide it by the known mean, which is twenty-two; the result of division is thirty-six and this is the number of measures he admitted that he owes him.
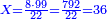
|
חלקנוהו על האמצעי הנודע שהוא עשרים ושנים יצא בחלוק ששה ושלשים וככה הוא מספר המנים שהודה שהוא חייב לו
|
- Examine it and you will find that it is true.
|
ובחון זה ותמצאהו באמת
|
| Purchase Problem - Moneychanger
|
|
- Question: a silversmith has sold to a moneychanger a silver chain that is worth three dinar of one coin or five dinar of another coin or seven dinar of yet another [coin].
- The silversmith asked the moneychanger to pay him its price with these three coins an equal amount of each.
- How much is this amount?
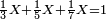
|
שאלה צורף כסף שמכר לשולחני רתוקות כסף ערכה ממטבע אחד שלשה דינרים וממטבע אחר חמשה דינרים ומאחר חמשה דינרים
ושאל הצורף לשולחני שיכוין לו בדמיו משלש המטבעות האלה מכל אחד חלק שוה
ונבקש לדעת מספר החלק ההוא
|
- Common Denominator: We investigate this way: we look for a denominator that has a third, a fifth, and a seventh; we find it is a hundred and five.
|
ונחקור על דרך זה נבקש מדומה שיש לו שלישית וחמישית ושביעית והנה נמצא [219]מאה וחמש
|
- Its third is thirty-five; its fifth is twenty-one; and its seventh is fifteen.
|
שלישיתו שלשים וחמשה וחמישיתו עשרים ואחד שביעיתו חמשה עשר
|
- The sum of all these parts is seventy-one and these are the fractions by which we have to divide each dinar.
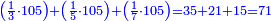
|
והמחובר מכל החלקים האלה שבעים ואחד והמה החלקים אשר נצטרך לחלק [כל][220] דינר אליהם
|
- We divide the denominator by seventy-one; we find it there once and thirty-four parts remain that cannot be divided, which are parts of the seventy-one by which we divide the denominator.
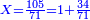
|
והנה נחלק המדומה על שבעים ואחד נמצאנו שם פעם אחת וישארו שלא נתחלקו ארבעה ושלשים והמה חלקים מהשבעים ואחד אשר חלקנו עליהם המדומה
|
- So, the silversmith will take one dinar and thirty-four parts of seventy-one of a dinar from each coin.
|
וככה יקח הצורף מכל מטבע דינר אחד ושלשים וארבעה חלקים משבעים ואחד בדינר
|
- Check: I shall give you a route how to check it:
|
ואתן לך מסלול ודרך איך תבחון זה
|
- Take the denominator, which is one hundred and five, and in order to convert all the coins to the coin of 3, we multiply it by them; they are three hundred and fifteen.
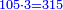
|
תקח המדומה שהוא מאה וחמש וכדי שנשיב כל המטבעות ממטבע שלשה נכפלנו עליהם ויהיו שלש מאות וחמשה עשר
|
- We divide them by five, in order to know how many parts of the coin of 5 are they; the result of division is sixty-three parts.
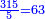
|
נחלקם על [חמשה][221] כדי שנדע כמה חלקים הם ממטבע חמשה יצא בחלוק ששים ושלשה חלקים
|
- We divide the three hundred and fifteen by seven also, in order to know how many parts of the coin of 7 are they; the result of division is forty-five.
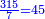
|
גם נחלק שלש מאות וחמשה עשר על שבעה למען נדע כמה חלקים הם ממטבע שבעה יצא בחלוק ארבעים וחמשה
|
- When we sum all the parts of the three coins, which are 105, 63, 45, the result is two hundred and thirteen.
|
וכאשר נחבר כל החלקים משלשת המטבעות שהם מאה וחמש וששים ושלשה וארבעים וחמשה [222]יעלו מאתים ושלשה עשר
|
- We divide them by seventy-one, which are the parts of the whole dinar; we find them there three times, which are three whole dinar.
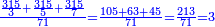
|
נחלקם על שבעים ואחד שהם [חלקי][223] הדינר השלם ונמצאם שם שלשה פעמים והנם שלשה דינרים שלימים
|
- Do likewise if you want to convert the whole amount to the coin of five or the coin of seven; and you will find the truth of this matter.
|
ועל הדרך הזה תעשה אם תרצה להשיב כל חשבון ממטבע חמשה או ממטבע שבעה ותמצא אמתת הדבר
|
| Find a Number Problem
|
|
- Question: a third, a fifth, and a seventh are summed together, how much is [their sum] in relation to the whole?
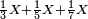
|
שאלה שלישית וחמישית ושביעית מחוברים איזה ערך הם מהשלם
|
- Common Denominator: We take one hundred and five as their denominator.
|
לקחנו להם מאה וחמש למדומה
|
- Its third is thirty-five; its fifth is twenty-one; its seventh is fifteen.
|
שלישיתו חמשה ושלשים וחמישיתו עשרים ואחד ושביעיתו חמשה עשר
|
- We sum up all; it is seventy-one.
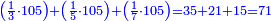
|
נחבר את כלם ויהיו שבעים ואחד
|
- Its ratio to the denominator is four-sevenths, two-sevenths of a third, and one-third of one-fifth of a seventh.
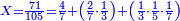
|
והנה ערכם אל המדומה ארבע שביעיותיו ושתי שביעיות שלישיתו ושלישית ושלישית חמישית שביעיתו
|
| Purchase Problem - Buy and Sell
|
|
- Question: a buyer [bought] four fifths of a liṭra for one pašuṭ, and sold his possession at one pašuṭ for five ninths of a liṭra.
- He earned 11 pešuṭim.
- How much was [his] money?
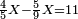
|
שאלה הקונה ארבע חמישיות ליטרא בפשוט ומכר קנייתו בערך חמש תשיעיות ליטרא בפשוט והרויח אחד עשר פשוטים
כמה היה הממון
|
- Common Denominator: The denominator that has a fifth and a ninth is forty-five.
|
הנה המדומה שיש לו חמישית ותשיעית הוא ארבעים וחמשה
|
- Its four-fifths are thirty-six.
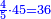
|
וארבע חמישיותיו ששה ושלשים
|
- Its five-ninths are twenty-five.
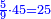
|
וחמש תשיעיותיו עשרים וחמש
|
- So is the amount of money.
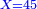
|
וככה הוא הממון
|
- If he says that he earned 22 pešuṭim.
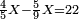
|
ואם אמר שהרויח עשרים ושנים פשוטים
|
- we multiply twenty-five times twenty-two.

|
[224]נכפול חמשה ועשרים שנים ועשרים פעמים
|
- If he says that he earned 33 pešuṭim
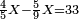
|
ואם אמר שהרויח שלשים ושלשה פשוטים
|
- We multiply them thirty-three times.

|
נכפלם שלשים ושלש פעמים
|
- And so on endlessly.
|
וככה עד אין קץ
|
| Purchase Problem - Buy and Sell - Peanuts
|
|
- Question: a seller bought 20 liṭra of peanut for 20 dinar.
- Then he went and sold 10 liṭra of them at one dinar for five quarters of a liṭra. It turned out that he lost in doing so.
- Afterwards many buyers came and overcharged and he sold the remaining 10 liṭra at one dinar for three quarters of a liṭra.
- Now he comes to us and asks: did he gain or lose?
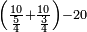
|
שאלה סוחר קנה עשרים ליטראות בטנים בעשרים דינרים
והלך ומכר מהן עשרה ליטרין לערך חמש רביעיות ליטרא בדינר ונמצא שהוא מפסיד בזה
ואחרי כן באו הרבה קונים והפקיעו השערים ומכר העשרה ליטריין הנשארות לערך שלש רביעיות ליטרא בדינר
ועתה בא אלינו לשאול אם הרויח או הפסיד או אם יצא הפסדו בשכרו
|
- We investigate this way: we convert the first 10 liṭra that he sold into quarters; they are forty.
|
והנה נחקור על דרך זה ונשיב העשר ליטראות הראשונות שמכר כלם רביעיות ויהיו ארבעים
|
- We divide them by the 5-quarters that he sold for a dinar; we find them there eight times. We find that he sold the five for eight dinar.
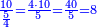
|
נחלקם על החמש רביעיות שמכר בדינר נמצאם שם שמונה פעמים נמצא שה' מכרם בשמונה דינרים
|
- We convert also the other 10 liṭra into quarters, then divide them by the 3-quarters that he sold for a dinar; we find them there thirteen times, which are 13 dinar, and one-quarter remains that cannot be divided, which is a third of a dinar.
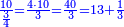
|
נעשה כן [רביעיות][225] מהעשר ליטראות האחרונות ונחלקם על שלש רביעיות שמכר בדינר נמצא שם שלשה עשר פעמים שהם י"ג דינרים ועוד נשאר מהם שלא נתחלק רביעית אחת שהיא שלישית דינר
|
- We add all this to the eight dinar; the sum is twenty-one dinar and four pešuṭim.
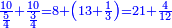
|
נחבר כל זה אל [226]השמונה דינרים יהיו עשרים ואחד דינרים וארבעה פשוטים
|
- We find that he earned sixteen pešuṭim.
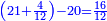
|
נמצא שהרויח ששה עשר פשוטים
|
| Partnership Problem - For the Same Time
|
|
- Question: three invested forty-six dinar - one contributed twelve dinar, the second contributed fifteen dinar, the third contributed nineteen dinar, and they earned together 20 dinar. How much should each one take [from the profit]?
|
שאלה שלשה שותפין בארבעים וששה דינרים חלק האחד שנים עשר דינרים וחלק השני חמשה עשר דינרים וחלק השלישי תשעה עשר דינרים והרויחו בין כלם עשרים דינרים כמה יקח כל אחד ואחד מהם
|
- Rule of Three: It is known that there is no doubt that each and every one will take the ratio to twenty as the ratio of his share to forty-six.

|
ידוע כי אין ספק שכל אחד ואחד מהם יקח ערך מעשרים כערך חלקו אל הארבעים וששה
|
- You will find out this easily by the rule of four [lit. the rules of proportions].
|
ותברר זה במשפטי הערכין בנקלה
|
| Payment Problem - two workers, two different daily wages, the same actual payment
|
|
- Question: one hired Reuven and Shimon for 10 days to do a work for him any one of them in turns so that the work will not cease.
- He agreed with Reuven that if he will do the work alone the whole 10 days he would pay him 2 dinar and to Shimon he said that if he will do the work alone the whole days he would pay him 5 dinar.
- What they did? They did the work together so that when one was tired his friend replaced him and did the work while the other was resting and if the second was tired, the first returned to his work and the second was resting.
- Each one wrote how many days, or parts of days, he worked.
- They did so the whole ten days, and then when they came to the employer he paid both of them and gave each of them money equally.
- How much money did they receive and how many days did each of them work?
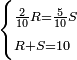
|
שאלה השוכר ראובן ושמעון שיעשו לו בין שניהם מלאכה עשרה ימים ולא תשבות המלאכה
והתנה עם ראובן שאם יעסוק הוא [במלאכה לבדו כל העשרה ימים שיתן לו ב' דינרים
ולשמעון אמר שאם יעסוק הוא][227] לבד במלאכה כל מספר הימים ההם שיתן לו חמשה דינרים
מה עשו החזיקו שניהם במלאכה בדרך זה כשהאחד היה יגיע עומד חבירו תחתיו ועוסק במלאכה והוא שובת היה עיף השני הראשון חוזר למלאכתו והשני שובת וכל אחד ואחד כתב כמה ימים או חלקי ימים עבד
ועשו זה כל העשרה ימים
וכשבאו אל השוכר פרע את שניהם ונתן להם [228]מעות לכל אחד ואחד בשוה
נרצה לדעת כמה מעות נטלו וכמה ימי עבודת כל אחד ואחד
|
- We investigate this way: know that Reuven works five days for one dinar and Shimon is paid one dinar for two days only. The sum of the days of both is seven.
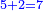
|
והנה נחקור על דרך זה תדע כי ראובן יעבוד חמשה ימים בדינר ושמעון לא ישמש בדינר כי אם שני ימים והמחובר מימי שניהם הוא שבעה
|
- We divide the ten days by them; the result is one integer and three remain that cannot be divided. So the amount of money that each takes is one dinar and three-sevenths of a dinar.
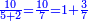
|
נחלקו העשרה ימים עליהם ויהיה היוצא אחד שלם ישארו שלשה שלא נתחלקו וככה הוא סכום המעות אשר יקח כל אחד מהם דינר ושלשה שביעיות דינר
|
- Now we shall investigate how many are the working days of each by his payment according to the conditional ratio, so that they are summed up to ten days:
|
ועתה נחקור כמה משפט ימי כל עבודת כל אחד ואחד בשכרו אשר לקח לפי ערך התנאי וצריך שיספיק בין שניהם לעשרה ימים
|
- We do as follows: it is known that Reuven must work five days for one dinar, we ask to know how many days will he work for the three-sevenths of a dinar; we reach this knowledge by applying the rule of four [lit. the rules of the ratios].
|
ונעשה ככה בידוע כי ראובן חייב לעבוד בדינר אשר לקח חמשה ימים ונרצה לדעת כמה [ימים][229] יעבוד בעבור השלשה שביעיות מהדינר ונגיע לידיעת זה כאשר נעשה במשפטי הערכין
|
- We convert the five days into sevenths; they are thirty-five.
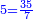
|
ונשיב החמשה ימים חלקי שביעיות ויהיו חמשה ושלשים
|
- Rule of Three: We take the ratio and say: as the ratio of three to seven, so is the ratio of the unknown to thirty-five.
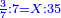
|
ונעריך ונאמר כערך שלשה אל שבעה כן ערך הנעלם אל חמשה ושלשים
|
- We multiply the first number by the fourth; it is a hundred and five.
|
נכפול החשבון הראשון על הרביעי יהיו מאה וחמש
|
- We divide it by the known mean, which is seven; we find it there fifteen times that are parts of a seventh of a day; the result is two days and one-seventh of a day.
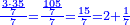
|
נחלקם על [230]האמצעי הנודע שהוא שבעה נמצאם שם חמשה עשר פעמים והנה הם חלקי שביעית יום העולים שני ימים ושביעית יום אחד
|
- We find that Reuven's working days are seven days and one-seventh of a day.
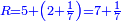
|
ונמצא כל ימי עבודת ראובן שבעה ימים ושביעית יום אחד
|
- It is known that Shimon must work two days for the dinar that he received.
|
וידוע כי שמעון חייב לעבוד שני ימים בעבור הדינר שלקח
|
- When we convert the two days into sevenths, they are fourteen.
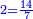
|
וכשנשיב [השני ימים][231] חלקי שביעיות יהיו ארבעה עשר
|
- Rule of Three: As the ratio of the three-sevenths he took to seven, so is the ratio of the unknown to fourteen.
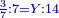
|
והנה כערך השלשה שביעיות שלקח אל שבעה כן ערך הנעלם [אל][232] ארבעה עשר
|
- We multiply the first [number] by the last; it is forty-two.
|
כפלנו החשבון הראשון על האחרון היו ארבעים ושנים
|
- We divide it by the known mean, which is seven; we find it there six times that are parts of sevenths of a day.
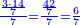
|
חלקנום על האמצעי הנודע שהוא שבעה נמצאם שם ששה פעמים והם חלקי שביעיות יום
|
- We find that Shimon's working days are two days and six-sevenths.
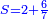
|
ונמצא כל ימי עבודת שמעון שני ימים ושש שביעיות יום
|
- Check: When you sum up the number and the parts of the working days of both and make one day out of every seven parts, you find that they are exactly ten days.
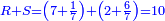
|
וכאשר תחבר מספר הימים והחלקים מעבודת שניהם ותעשה משבעה חלקים יום אחד תמצא שהם עשרה ימים בכיוון
|
| Payment Problem - Messenger
|
|
- Question: I hired a messenger for 13 dinar and we agreed that he will walk for me from now on for 20 days 11 parsa [1 parsa = ca. 4 kilometers] a day, but the messenger embezzled or got injured and walked only 5 parsa a day for 7 days.
- How much should his payment be according to the terms?
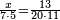
|
שאלה שכרתי שליח אחד בשלשה עשר דינרים [והתנאתי][233] עמו שילך לי מכאן ועד עשרים יום אחד עשר פרסאות בכל יום
והשליח מעל או שנאנס ולא הלך כי אם חמש פרסאות בכל יום עד [234]שבעה ימים
נרצה לידע כמה משפט דמי שכרותו לפי התנאי
|
- We do it in this way: first we think as if the messenger would have walked five parsot the whole 20 days and we look how much should be his hiring payment.
|
נעשה בדרך זאת בתחלה נחשוב כאלו הלך השליח החמש פרסאות כל העשרים יום ונראה מה יגיע אליו מהשכרות
|
- Rule of Three: We take the ratio and say: as the ratio of five to eleven, so is the ratio of the unknown to thirteen, which is the hiring payment.

|
והנה נעריך ונאמר כערך חמשה אל אחד עשר כן ערך הנעלם אל שלשה עשר שהוא ערך השכירות
|
- When we multiply the first number by the fourth, then divide by the known mean, we find that his hiring payment should be 5 dinar and 10 parts of 11 of a dinar.
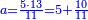
|
כאשר נכפול החשבון הראשון על הרביעי ונחלק על האמצעי הנודע נמצא שיגיע אליו מהשכרות ה' דינרים וי' חלקים מי"א בדינר
|
- Since he walked five parsot for seven days only:
|
ובעבור שלא הלך החמש פרסאות כי אם שבעה ימים
|
- Rule of Three: We take the ratio again and say: as the ratio of seven to twenty, so is the ratio of the unknown to 5 dinar and 10 parts of 11 of a dinar.
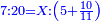
|
נחזור ונעריך ונאמר כערך שבעה אל עשרים כן ערך הנעלם אל ה' דינרים [וי'][235] חלקים מי"א בדינר
|
- We multiply the first number, which is seven, by the fourth number, which is 5 dinar; it is 35.
|
נכפול החשבון הראשון שהוא שבעה על החשבון הרביעי שהוא ה' דינרים ובו' יהיה ל"ה
|
- We multiply it also by the 10 parts; they are seventy parts.
|
גם נכפול אותו על הי' חלקים יהיו שבעים חלקים
|
- When we have to divide the resulting product by the known mean, we return all to the same measure and convert the 35 into parts of 11; they are 385.
|
וכאשר אנחנו צריכים לחלק העולה מהכפילה הזאת על האמצעי הנודע נשיב הכל ממתכונת אחת ונעשה מהל"ה חלקים מי"א ויהיו שפ"ה
|
- We add to them the 70 parts, which are also parts of 11; they are 455.
|
נחבר אליהם הע' חלקים שגם [236]הם המה חלקים מי"א ויהיו תנ"ה
|
- Then we convert the known mean, which is twenty, into parts of 11; they are 220.
|
ואחרי זאת נשיב גם כן האמצעי הנודע שהוא עשרים חלקים מי"א יהיו ר"ך
|
- We divide 455 by them; we find them twice in them and 15 remain that cannot be divided, which are three-quarters of a part of eleven.
|
נחלק תנ"ה עליהם נמצאם שם פעמים וישארו ט"ו שלא נתחלקו והם שלש רביעיות חלק אחד מהאחד עשר חלקים מר"ך שהוא השלם אשר חלקנו עליו
|
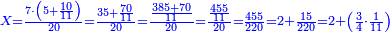
|
- Hence, the salary that the messenger will receive is two dinar and three-quarters of one part of eleven of a dinar.
|
וככה יקח השליח בשכרותו שני דינרים ושלש רביעיות חלק אחד מאחד עשר חלקים בדינר שלם
|
| Divide a Quantity Problem - Proportional Division - Inheritance
|
|
- Question: Jacob's four wives married him on the same day. On that day, he prepared for each of them a ketuba [= Jewish marriage contract] according the Jewish law.
- The name of the one is Leah and her ketuba amount is 4000 zehuvim [= golden coins];
- the name of the second is Zilpah and he ketuba amount is 3000 [zehuvim];
- the name of the third is Rachel and her ketuba amount is 2000 [zehuvim];
- and the name of the fourth is Bilhah and her ketuba amount is 1000 zehuvim.
- Later Jacob died and nothing was left of his property but 4000 zehuvim.
- The widows came to the court in order to divide the money that remained between them
|
שאלה ארבעה נשי יעקב שנשאו לו ביום אחד ועשה לכל אחת ואחת כתובה בו ביום כתקון חכמים
שם האחת לאה וכתובתה [ארבעת][237] אלפים זהובים
ושם השנית זלפה וכתובתה שלשת אלפים
ושם השלישית רחל וכתובתה אלפים
ושם הרביעית בלהה וכתובתה אלף זהובים
לימים מת יעקב ולא נשאר מנכסיו כי אם ארבעת אלפים זהובים
באו האלמנות לבית דין לחלוק להן הממון הנשאר
|
- The division according the sages of Israel: The late sages said that the court law is to divide the money between them in this way:
|
ואמרו חכמים ז"ל שמשפט הבית דין לחלק להן הממון על דרך זה
|
- Bilhah: They shall tell Bilhah whose ketuba has the smallest [amount] of all of them: You have no claim from the others except for a thousand gold coins and they too have a legal right on them, so take the fourth of the thousand, which is two hundred and fifty and go in peace and so each of them will take from it.
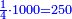
|
יאמרו אל בלהה שכתובתה קטנה מכלנה אין לך ערעור בחברותיך כי אם באלף [238]זהובים וגם הנה יש להן משפט בהן על כן תקח רביעית האלף שהוא ממאתים וחמשים ולכי לשלום וככה תקחן ממנו כל אחת מהן
|
- Rachel: Then, the court shall tell Rachel: You have no claim except for the two thousand that your two friends have a legal right on them too, and you have already taken your share from the one-thousand divided, so take the third of the other thousand required as a payment of your claim, which is three-hundred and thirty-three gold coins and one-third, and return to your home. We find that her total share is 583 gold coins and one-third. Likewise each of the two others will take three hundred and thirty-three gold coins and one-third from the second divided one thousand.
|
אחרי כן יאמרו גם כן ב"ד אל רחל אין לך ערעור רק על אלפים שיש לשתי חברותיך גם כן משפט בהן וכבר לקחת חלקך מהאלף המחולק על כן תקחי מהאלף אחר שצריך לתשלום תביעתך השלש שהוא שלש מאות ושלשים ושלשה זהובים ושליש זהוב ושובי לביתך ונמצא חלוקה בין הכל תקפ"ג זהובים ושליש זהוב וגם כן יקחו כל אחת משתיהן מאותו האלף השני הנחלק שלש מאות ושלשים ושלשה זהובים ושליש זהו'
|

|
- Zilpah: Then, they shall tell Zilpah: You have no claim except for the three-thousand that your friend Leah [too] has a legal right on them, and you have already taken your share from the two thousand divided, so we shall divide the one thousand required as a payment of your claim between the two [of you]. We find that the total share of Zilpah is one thousand eighty-three gold coins and one-third.
|
ואחרי כן אמרו לזלפה אין לך תביעה רק בשלשת אלפים שיש ללאה חברתיך בהן משפט וכבר לקחת חלקך מהשני האלפים המחולקים [על כן][239] נחלק בין שתיהן האלף הצריך לתשלום תביעתך ונמצא שתהיה חלק זלפה בין הכל אלף [ושמנים][240] ושלשה זהובים ושליש זהוב
|

|
- Leah: Leah is left with two thousand and eighty-three gold coins and a third.
|
ונשארו ללאה אלפים ושמנים ושלשה זהובים ושלישית זהוב
|
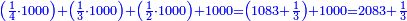
|
- Check: If you sum up [all] these parts according to the rule, you will find the result is four thousand.
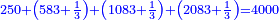
|
ואם תחבר החלקים האלה [241]תמצא העולה ארבעת אלפים
|
- The division according to the arithmeticians: The arithmeticians divide this amount in a different way:
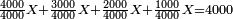
|
והנה חכמי החשבון חולקים הממון הזה בדרך אחרת
|
- False Position: They say that since Bilhah asks for a quarter of the amount, Rachel its half, Zilpah its three-quarters, and Leah its whole, we take a denominator that has a half and a quarter. We find it is eight.
|
ויאמרו כי בעבור שבלהה שואלת רביעית הממון ורחל חציו וזלפה שלש רביעיותיו [ולאה][242] כלו נקח מדומה שיהיה לו חצי ורביעית והנה נמצא שמנה
|
- Its quarter is two; its half is four; its three-quarters are six; the sum of all these parts with [the denominator] is twenty.
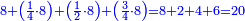
|
ורביעיתם שניים וחציים ארבעה ושלש רביעיותיהם ששה והמחובר מכל החלקים האלה עמו עולה עשרים
|
- Rule of Three: As the ratio of twenty to four thousand, which is the amount that Jacob has left, so is the ratio of eight to the unknown share of Leah.

|
והנה כערך עשרים אל ארבעת אלפים שהוא הממון הנשאר ליעקב ככה יהיה ערך שמנה אל חלק כתובת לאה הנעלם
|
- When we apply the rule of four [lit. the rule of proportions], we find that her share is one thousand and six hundred gold coins.
|
וכאשר נעשה כמשפט הערכין נמצא שתהיה חלקה אלף ושש מאות זהובים
|
- Rule of Three: As the ratio of twenty to four thousand, so is the ratio of six, which is three-quarters of the denominator, to the share of Zilpah.

|
וכערך עשרים אל ארבעת אלפים ככה יהיה ערך ששה שהוא שלש רביעיות [המדומה][243] אל החלק שתקח זלפה בכתובתה
|
- When we examine by the rule of four, we find that her share is one thousand and two hundred gold coins.
|
וכאשר נחקור במשפט הערכין נמצא שתהיה חלקה אלף ומאתים זהובים
|
- Rule of Three: We take the ratio and say: as the ratio of twenty to four thousand, so is the ratio of four, which is half the denominator, to the share of Rachel.

|
ועם נעיין ונאמר כערך עשרים [אל][244] ארבעת אלפים כן ערך ארבעה שהוא חצי המדומה אל החלק שתקח רחל בכתובתה
|
- We find that her share is eight hundred gold coins.
|
[245]ונמצא שיבואו לחלקה שמונה מאות זהובים
|
- Rule of Three: We take the ratio and say: as the ratio of twenty to four thousand, so is the ratio of two to the share of Bilhah.

|
והנה גם כן נעריך ונאמר כערך עשרים אל ארבעת אלפים כן יהיה ערך שניים אל החלק אשר תקח בלהה בכתובתה
|
- We find that her share is four hundred gold coins.
|
ונמצא שתקח לחלקה ארבע מאות זהובים
|
- Check: When you sum up all these four shares, you find that the result is four thousand precisely.

|
וכאשר תחבר כל החלקים האלה ארבעתם תמצא שיהיו עולים ארבעת אלפים מכוונים
|
| Motion Problem - Pursuit
|
|
- Question: a messenger was sent to walk a certain distance on land and he walks 12 parsa a day. After 10 days the sender changed his mind [and decided] to return the walking messenger. He sent another messenger after him to return him, walking 15 parsa a day. In how many days will he catch up with him?
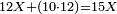
|
שאלה השולח ציר נאמן ללכת בארץ מרחק והוא הולך בכל יום ויום שנים עשר פרסאות אחר עשרה ימים נמלך המשלח להשיב השליח המהלך וישלח אחריו שליח אחר להשיבו שהוא הולך בכל יום חמשה עשר פרסאות [נרצה לידע בכמה ימים ישיגנו
|
- We examine in this way: we think how many parsot the first walked, before the second started to walk; they are a hundred and twenty.

|
ונחקור בדרך זה נחשוב כמה פרסאות][246] הולך הראשון בטרם שנסע השני והנה הם מאה ועשרים
|
- We divide them by the excess of the parsot that the second walks in one day over the first, which is three; we find it forty times there, so he will catch up with him in forty [days].
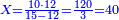
|
נחלקם על יתרון הפרסאות שהולך השני מן הראשון ביום אחד שהם שלשה נמצאם שם ארבעים פעמים והנה ישיגנו בארבעים
|
- Check: You can check it when you calculate how many parsot the first had walked in fifty [days], because the second had walked in [forty] [days] as many as that.

|
ותוכל לבחון זה כשתחשוב כמה פרסאות הלך השליח הראשון בחמשים יום כי ככה הלך השני בארבעה
|
| Motion Problem- Encounter
|
|
- Question: Reuven established his home in a certain town at the eastern border and his brother Shimon established his home in another town at the western border. Through letters they sent to each other they agreed on a time in which each one will leave his town to walk towards his brother, on the first day of Nisan [the 7th month of the Hebrew year]. The walking distance between the two towns is 50 parsa. Reuven is walking 7 parsa a day and his brother Shimon is walking 9 parsa a day. In how many days will they meet?
|
שאלה ראובן קובע את דירתו [247]בעיר אחת בקצה המזרח ושמעון אחיו קובע דירתו באחת הערים בקצה המערב על ידי אגרות ששלחו זה לזה יעדו להם זמן שיצאו כל אחד מעירו ללכת לקראת אחיו ביום ראשון של חדש ניסן והמהלך אשר בין שתי העיירות חמשים פרסאות והנה ראובן הולך בכל יום שבע פרסאות ושמעון אחיו הולך בכל יום תשע פרסאות ונבקש לדעת בכמה ימים יתחברו זה עם זה
|
- We do as follows: we sum up the parsot that they both walk in one day; they are sixteen.
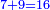
|
ונעשה ככה נחבר פרסאות מהלך שניהם ביום אחד ויהיו ששה עשר
|
- We divide fifty, which is the distance, by them; we find them three times in it and two remain that cannot be divided. We consider them as one-eighth of sixteen. So, they will meet in three days and one-eighth of a day.
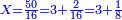 days days
|
נחלק חמשים שהוא המרחק עליהם נמצאם שם שלשה פעמים וישארו שנים שלא נתחלקו ונחשוב אותם שמינית ששה עשר והנה יתחבר זה עם זה בשלשה ימים ושמינית יום
|
| Find a Quantity Problem - Whole from Parts - Cane
|
|
- Question: a third and a quarter of the cane are ingrained in the mud, its height is revealed two zeratot [spans] up [above the mud], what is the height of the tree?
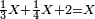
|
שאלה קנה הנעוצה בטיט היון שלישיתה ורביעיתה ונראית קומתה למעלה שני זרתות כמה אורך הקנה
|
- False Position: We do it like this: we take twelve as a denominator, because there is a third and a quarter in it.
|
נעשה כזאת נקח לנו שנים עשר למדומה יען ימצא השלישית ורביעית
|
- The sum of these parts of it is seven.
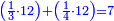
|
ומחברת חלקים אלו ממנו יהיו שבעה
|
- We subtract it from the denominator; five remain.
![\scriptstyle{\color{blue}{12-\left[\left(\frac{1}{3}\sdot12\right)+\left(\frac{1}{4}\sdot12\right)\right]=12-7=5}}](/mediawiki/images/math/9/9/4/994410b776b40d19b554ba92d759d4ae.png)
|
נסיר אותם מהמדומה [248]ישארו חמשה
|
- Rule of Three: Now, we take the ratio and say: as the ratio of five to twelve so is the ratio of the two zeratot to the unknown.
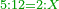
|
ועתה נעריך ונאמר כערך חמשה אל שנים עשר כן ערך השני זרתות אל הנעלם
|
- We multiply the means [by each other]; the product is twenty-four. We divide it by the first known number, which is five; we find four there and four remained from it that cannot be divided, which are fifths. So, the length of the whole cane is four zeratot and four-fifths of a zeret.
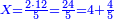 zeratot zeratot
|
כפלנו האמצעיים עלו עשרים וארבעה חלקנום על החשבון הראשון הנודע שהוא חמשה מצאנוהו שם ארבעה פעמים ונשארו מהם שלא נתחלק ארבעה והמה חמישיות וככה הוא אורך כל הקנה ארבעה זרתות וארבעה חמשיות זרת
|
- Check: You can check if this is true when you subtract a third and a quarter from twenty-four and you are left with ten, as the measure of the parts of the two whole zeratot that are seen above the mud.
![\scriptstyle{\color{blue}{\frac{24-\left[\left(\frac{1}{3}\sdot24\right)+\left(\frac{1}{4}\sdot24\right)\right]}{5}=\frac{10}{5}=2}}](/mediawiki/images/math/4/2/6/426ac9e6b1a5cfc0284b012d7d85c37b.png)
|
ותוכל לבחון זה אם הוא אמת כשתסיר מעשרים וארבעה שלישיתו ורביעיתו וישארו לך עשרה כשעור חלקי השני זרתות שלמות הנראות מעל הטיט
|
| Give and Take Problem - Earning and Spending
|
|
- Question: the money changer brought some money to a known town.
- Each day he earned so as doubling his money, but he had to pay a tax of 100 dinar every day.
- He stayed there five days.
- On the fifth day he rose up early at dawn, doubled his money, as in the previous days, then he had to pay his daily tax and he had nothing left.
- We want to know what the amount of money he brought to this town was
![\scriptstyle2\sdot\left[2\sdot\left[2\sdot\left[2\sdot\left(2X-100\right)-100\right]-100\right]-100\right]=100](/mediawiki/images/math/0/2/f/02f6b36951cd14a8b19a17e49a64a0b3.png)
|
שאלה שולחני שהביא ממון לעיר ידועה ובכל יום ויום הוא מרויח עד שכופל ממונו רק שצריך שיפרע למכס בכל יום מאה דינרין
ונתעכב שם חמשה ימים
ויהי ביום החמשי השכים בשחר וכפל ממונו כשאר הימים וכלם נצטרכו לו לפרוע חוק מכס יומו ולא נשאר לו מאומה
נרצה לדעת מכסת הממון שהביא לעיר
|
- We do it this way: it is known that on the fifth day when the amount he had was only fifty dinar, he doubled it; was one hundred, then he paid it as the tax, and he had nothing left.
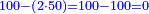
|
ונעשה על זה הדרך בידוע כי ביום החמישי כשהשכים שלא היו לו רק חמישים דינרים וכפלם [249]והיו מאה ופרעם למכס ולא נשאר לו מאומה
|
- The fifty dinar necessarily remained for him from the evening of the fourth day, after he paid the tax of that day.
|
ובהכרח החמשים דינרים נשארו לו מערב היום הרביעי אחרי אשר פרע מכס אותו היום
|
- We find that on the morning of that day he had a half of one-hundred and fifty dinar, which are seventy-five dinar that remained for him from the evening of the third day.
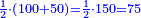
|
ונמצא שהיו לו בשחרית אותו יום מחצית מאה וחמשים דינרים שהם שבעים וחמשה דינרים שנשארו לו מערב היום השלישי
|
- Before he paid the tax of that day, he had one-hundred and seventy-five dinar.
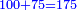
|
וקודם שפרע מכס היום ההוא היו לו מאה ושבעים וחמשה דינרים
|
- We take their half; they are eighty-seven dinar and a half, which he had on the morning that remained for him from the evening of yesterday, which is the second day.
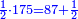
|
נקח מחציתם יהיו שמנים ושבעה דינרים וחצי שהיו לו בשחר שנשארו לו מאמש יום תמולו שהוא היום השני
|
- We find that before paying the tax he had one-hundred eighty-seven dinar and a half.
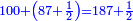 dinar dinar
|
ונמצא שאז יהיו לו קודם פריעת המכס מאה ושמונים ושבעה דינרים וחצי
|
- We take their half; they are ninety-three dinar and nine pešuṭim, which he had on the morning that remained for him from the evening of the first day.
- in the evening he had:
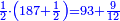
|
נקח חצים יהיו תשעה ושלשים דינרים ותשעה פשיטים משנים עשר בדינר שהיו לו בשחר הנשארים לו מערב יום ראשון
|
- We find that on that first day, before paying the tax he had one-hundred ninety-three dinar and nine pešuṭim.
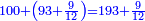
|
ונמצא שביום ההוא הראשון היו לו קודם פריעת המכס מאה ותשעים ושלשה דינרין ותשעה פשיטים
|
- We take their half; they are ninety-six dinar and ten pešuṭim and a half; and so [is the amount of money] he brought.
|
נקח חציים והם תשעים וששה דינרים ועשרה פשיטים וחצי פשוט וככה הביא
|
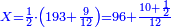
|
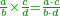
![\scriptstyle{\color{OliveGreen}{\left(n+\frac{a}{b}\right)\times\frac{c}{b}=\frac{\left[\left(n\sdot b\right)+a\right]\sdot c}{b^2}}}](/mediawiki/images/math/e/2/a/e2a27afe2a16c3b3df373989cb100803.png)
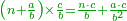
![\scriptstyle{\color{OliveGreen}{\left(n+\frac{a}{b}\right)\times\frac{c}{d}=\frac{\left[\left(n\sdot b\right)+a\right]\sdot c}{b\sdot d}}}](/mediawiki/images/math/6/f/c/6fc4ddbcb93e9730ff64938575eebd7b.png)
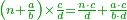
![\scriptstyle{\color{OliveGreen}{\left(n+\frac{a}{b}\right)\times\left(m+\frac{c}{b}\right)=\frac{\left[\left(n\sdot b\right)+a\right]\sdot\left[\left(m\sdot b\right)+c\right]}{b^2}}}](/mediawiki/images/math/3/6/7/367d6ad38e7b5ffc9b90ef64917c17d2.png)
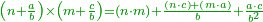
![\scriptstyle{\color{OliveGreen}{\left(n+\frac{a}{b}\right)\times\left(m+\frac{c}{d}\right)=\frac{\left[\left(n\sdot b\right)+a\right]\sdot\left[\left(m\sdot d\right)+c\right]}{b\sdot d}}}](/mediawiki/images/math/6/c/0/6c0d626e6d84cbcd8358a58a669d70e7.png)
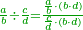
![\scriptstyle{\color{OliveGreen}{\left(n+\frac{a}{b}\right)\div\left(m+\frac{c}{d}\right)=\frac{\left[n\sdot\left(b\sdot d\right)\right]+\left[\frac{a}{b}\sdot\left(b\sdot d\right)\right]}{\left[m\sdot\left(b\sdot d\right)\right]+\left[\frac{c}{d}\sdot\left(b\sdot d\right)\right]}}}](/mediawiki/images/math/9/3/6/9368a096c2c1e1efcbf939db69b4dcda.png)
![\scriptstyle{\color{OliveGreen}{\frac{a}{b}+\frac{c}{d}=\frac{\left[\frac{a}{b}\sdot\left(b\sdot d\right)\right]+\left[\frac{c}{d}\sdot\left(b\sdot d\right)\right]}{b\sdot d}}}](/mediawiki/images/math/d/c/a/dca3987ef7aba952f8772ebaef57fc89.png)
![\scriptstyle{\color{OliveGreen}{\frac{a}{b}-\frac{c}{d}=\frac{\left[\frac{a}{b}\sdot\left(b\sdot d\right)\right]-\left[\frac{c}{d}\sdot\left(b\sdot d\right)\right]}{b\sdot d}}}](/mediawiki/images/math/5/1/3/5137933b83402870b3ff90ea3ed3d4c8.png)
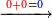
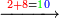
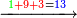
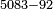
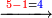
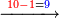
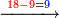
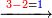
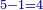
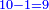
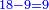



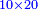
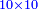
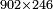
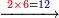
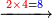
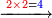
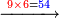
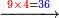
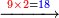
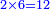
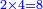


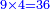

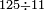
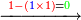
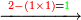
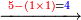

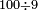


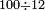

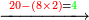

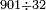
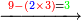
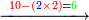

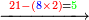

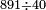
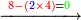
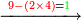

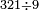



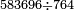

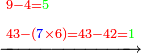
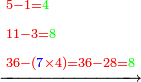
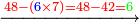
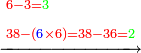
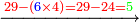
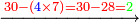
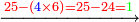
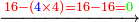

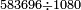
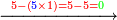
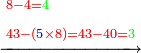
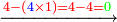
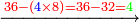
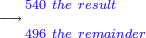
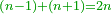

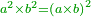
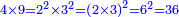
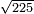
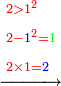
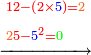
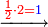
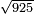
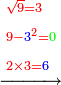



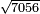
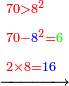
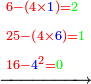


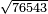
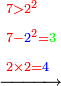
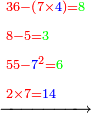
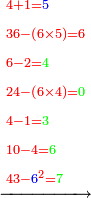
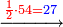

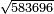
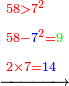
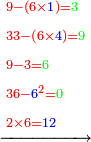
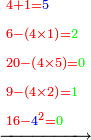

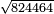
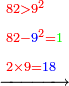
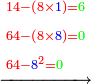

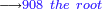
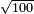
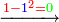
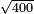


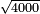
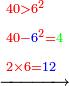
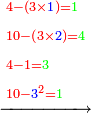

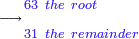
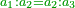
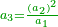
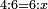
![\scriptstyle{\color{blue}{6:4=\left[\left(1+\frac{1}{2}\right)\sdot4\right]:4}}](/mediawiki/images/math/9/3/1/931ce1931ee11772930a388a4a1cd5e0.png)
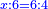
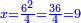
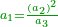
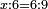
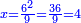
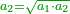
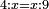
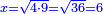
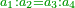
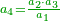
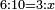
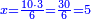
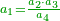
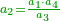
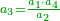
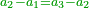

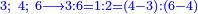
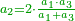
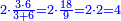
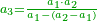
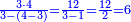
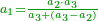
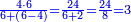

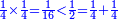


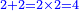
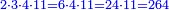
![\scriptstyle{\color{OliveGreen}{\frac{a}{b}\times\frac{c}{d}=\frac{\left[\frac{a}{b}\sdot\left(b\sdot d\right)\right]\sdot\left[\frac{c}{d}\sdot\left(b\sdot d\right)\right]}{\left(b\sdot d\right)^2}}}](/mediawiki/images/math/3/c/1/3c10d1507cb6b8db643f7eafc16665fc.png)
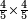
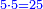
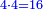
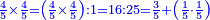
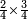

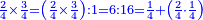
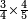
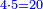
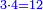
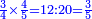


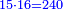
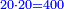
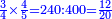
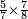
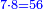
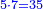
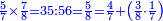
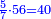
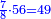
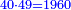
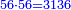
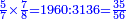
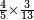
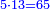

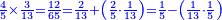
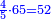

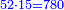
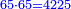

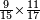
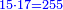
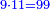
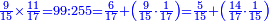

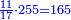
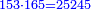
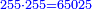
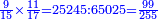
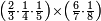
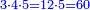
![\scriptstyle{\color{blue}{\frac{2}{3}\sdot\frac{1}{4}\sdot\frac{1}{5}=\frac{\frac{2}{3}\sdot\left[\frac{1}{4}\sdot\left(\frac{1}{5}\sdot60\right)\right]}{60}=\frac{\frac{2}{3}\sdot\left(\frac{1}{4}\sdot12\right)}{60}=\frac{\frac{2}{3}\sdot3}{60}=\frac{2}{60}}}](/mediawiki/images/math/8/f/1/8f11186204ccc044ba6fbebf2d4fc01c.png)
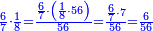
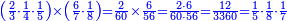
![\scriptstyle{\color{blue}{\frac{1}{5}\sdot\left[\frac{1}{8}\sdot\left(\frac{1}{7}\sdot3360\right)\right]=\frac{1}{5}\sdot\left(\frac{1}{8}\sdot480\right)=\frac{1}{5}\sdot60=12}}](/mediawiki/images/math/f/e/e/feebaeba6f09cbb35ca00b067dbe39c3.png)
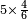
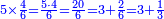
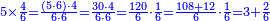
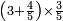
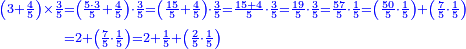
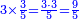
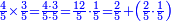
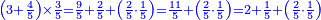
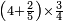
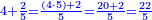
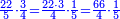
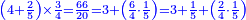
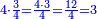
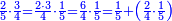
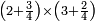

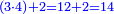
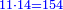
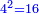
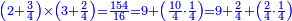
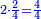

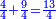
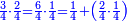
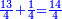
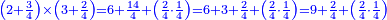
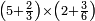
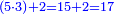
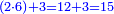
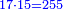
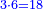
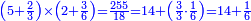
![\scriptstyle{\color{OliveGreen}{\left(n+\frac{a}{b}\right)\times\left(m+\frac{c}{d}\right)=\frac{\left[\left[n\sdot\left(b\sdot d\right)\right]+\left[\frac{a}{b}\sdot\left(b\sdot d\right)\right]\right]\sdot\left[\left[m\sdot\left(b\sdot d\right)\right]+\left[\frac{c}{d}\sdot\left(b\sdot d\right)\right]\right]}{\left(b\sdot d\right)^2}}}](/mediawiki/images/math/6/b/c/6bcbef6f88fa2678c13853f712cdc424.png)
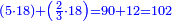
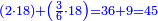
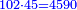
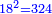

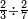
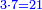
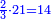
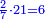
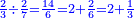
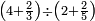
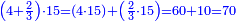
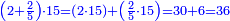
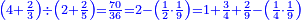
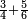
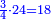
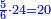

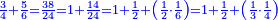
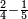


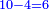
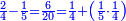
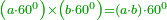
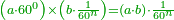
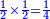
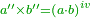


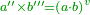
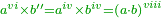
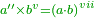
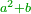
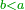

![\scriptstyle{\color{OliveGreen}{\left[a+\left(\frac{60\sdot b}{2a}\right)^\prime\right]^2-\left(a^2+b\right)}}](/mediawiki/images/math/d/1/8/d1884d02d5c52436853b8fa19a7b0990.png)
![\scriptstyle{\color{OliveGreen}{\sqrt{a^2+b}\approx a+\left(\frac{60\sdot b}{2a}\right)^\prime-\left[\frac{\left(\left(\frac{60\sdot b}{2a}\right)^\prime\right)^2}{2\sdot\left(a+\left(\frac{60\sdot b}{2a}\right)^\prime\right)}\right]}}](/mediawiki/images/math/3/0/e/30e5279dac9bf13aa0f31cfae39a398b.png)
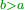
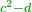

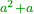 ].
].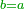
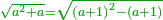
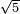
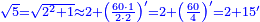
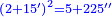
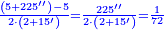
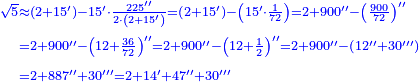
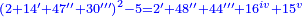
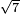
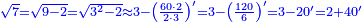
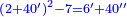
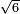
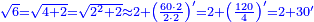
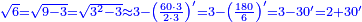
![\scriptstyle{\color{OliveGreen}{\left(3n\right)^2=\left[10\sdot\left[\frac{1}{3}\sdot\left(3n\right)\right]^2\right]-\left[\frac{1}{3}\sdot\left(3n\right)\right]^2}}](/mediawiki/images/math/8/7/b/87bdc32051b224513066e28e719f373b.png)
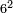
![\scriptstyle{\color{blue}{6^2=\left(3\sdot2\right)^2=\left[10\sdot\left(\frac{1}{3}\sdot6\right)^2\right]-\left(\frac{1}{3}\sdot6\right)^2=\left(10\sdot2^2\right)-2^2=\left(10\sdot4\right)-4=40-4=36}}](/mediawiki/images/math/3/8/d/38d1d5ec3932f81319dd5cf689ea938d.png)
![\scriptstyle{\color{OliveGreen}{\left(3n+1\right)^2=\left[\left[10\sdot\left[\frac{1}{3}\sdot\left(3n\right)\right]^2\right]-\left[\frac{1}{3}\sdot\left(3n\right)\right]^2\right]+3n+\left[\left(3n+1\right)\right]}}](/mediawiki/images/math/b/f/3/bf33f7d7d256c9cce1765e3f38e307be.png)
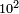
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle10^2&\scriptstyle=\left(9+1\right)^2=\left[\left(3\sdot3\right)+1\right]^2=\left[\left[10\sdot\left(\frac{1}{3}\sdot9\right)^2\right]-\left(\frac{1}{3}\sdot9\right)^2\right]+9+10=\left[\left(10\sdot3^2\right)-3^2\right]+9+10\\&\scriptstyle=\left[\left(10\sdot9\right)-9\right]+9+10=\left(90-9\right)+9+10=81+9+10=100\\\end{align}}}](/mediawiki/images/math/b/6/4/b644d352f59bcab6ac290785552438e0.png)
![\scriptstyle{\color{OliveGreen}{\left(3n-1\right)^2=\left[\left[10\sdot\left[\frac{1}{3}\sdot\left(3n\right)\right]^2\right]-\left[\frac{1}{3}\sdot\left(3n\right)\right]^2\right]-\left(3n\right)-\left[\left(3n-1\right)\right]}}](/mediawiki/images/math/4/2/4/424921fda72004011eee2ecd49af0392.png)
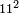
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle11^2&\scriptstyle=\left(12-1\right)^2=\left[\left(3\sdot4\right)-1\right]^2=\left[\left[10\sdot\left(\frac{1}{3}\sdot12\right)^2\right]-\left(\frac{1}{3}\sdot12\right)^2\right]-11-12\\&\scriptstyle=\left[\left(10\sdot4^2\right)-4^2\right]-11-12=\left[\left(10\sdot16\right)-16\right]-11-12\\&\scriptstyle=\left(160-16\right)-11-12=144-12-11=144-23=121\\\end{align}}}](/mediawiki/images/math/b/0/1/b0167e9801aca57699585726cc550144.png)
![\scriptstyle{\color{OliveGreen}{\left(10+a\right)\times\left(10+b\right)=\left[10\sdot\left[\left(10+a\right)+b\right]\right]+\left(a\sdot b\right)}}](/mediawiki/images/math/6/c/a/6ca9d98590fd0390228cb3a1b7607d13.png)
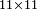
![\scriptstyle{\color{blue}{11\times11=\left[\left(11-1\right)\sdot\left(11+1\right)\right]+\left(1\sdot1\right)=\left(10\sdot12\right)+1=120+1=121}}](/mediawiki/images/math/e/a/1/ea13d6aefaefa54cb18f4c31e4c21646.png)
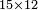
![\scriptstyle{\color{blue}{15\times12=\left[\left(12-2\right)\sdot\left(15+2\right)\right]+\left(2\sdot5\right)=\left(10\sdot17\right)+10=170+10=180}}](/mediawiki/images/math/2/e/0/2e0464051c8b288d93d7c642b5cb03ff.png)
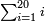
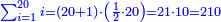
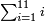
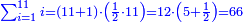
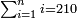
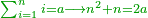
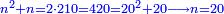
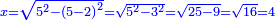
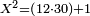
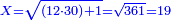
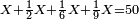

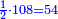
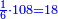
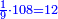

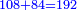
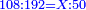
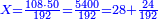
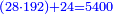
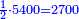
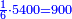
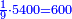


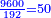
![\scriptstyle X=100-\left[\left(\frac{1}{3}\sdot100\right)+\left(\frac{1}{4}\sdot100\right)\right]](/mediawiki/images/math/0/6/4/064f6c9817381f7419d53dd1707a018a.png)
![\scriptstyle{\color{blue}{12-\left[\left(\frac{1}{3}\sdot12\right)+\left(\frac{1}{4}\sdot12\right)\right]=12-7=5}}](/mediawiki/images/math/9/9/4/994410b776b40d19b554ba92d759d4ae.png)

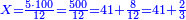
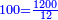
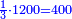
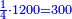


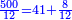
![\scriptstyle\left(X-\frac{2}{100}X\right)-\left[\frac{1}{10}\sdot\left(X-\frac{2}{100} X\right)\right]-\left[\frac{1}{10}\sdot\left[\left(X-\frac{2}{100}X\right)-\left[\frac{1}{10}\sdot\left(X-\frac{2}{100} X\right)\right]\right]\right]=50](/mediawiki/images/math/4/a/2/4a2924027b379bac5d8c351156314329.png)

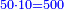
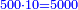

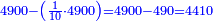
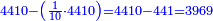


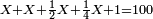
![\scriptstyle{\color{blue}{8+8+\left[\left(\frac{1}{2}\sdot8\right)+\left(\frac{1}{4}\sdot8\right)\right]=16+4+2=20+2=22}}](/mediawiki/images/math/5/a/3/5a39486b875ef2fbc83b16aa4a933d0a.png)
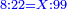
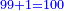
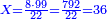
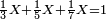
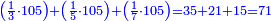
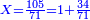
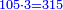
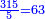
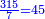
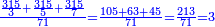
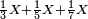
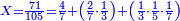
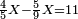
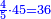
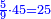
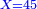
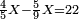

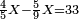

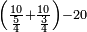
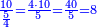
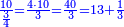
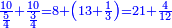
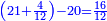
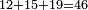

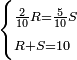
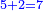
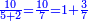
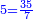
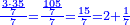
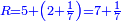
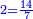
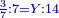
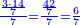
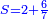
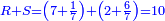
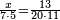

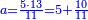
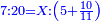
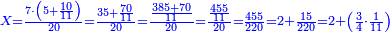
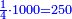


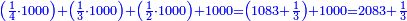
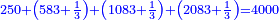
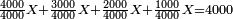
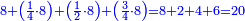





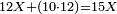

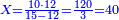

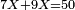
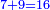
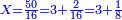 days
days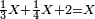
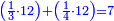
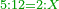
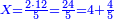 zeratot
zeratot![\scriptstyle{\color{blue}{\frac{24-\left[\left(\frac{1}{3}\sdot24\right)+\left(\frac{1}{4}\sdot24\right)\right]}{5}=\frac{10}{5}=2}}](/mediawiki/images/math/4/2/6/426ac9e6b1a5cfc0284b012d7d85c37b.png)
![\scriptstyle2\sdot\left[2\sdot\left[2\sdot\left[2\sdot\left(2X-100\right)-100\right]-100\right]-100\right]=100](/mediawiki/images/math/0/2/f/02f6b36951cd14a8b19a17e49a64a0b3.png)
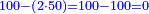
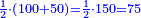
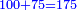
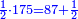
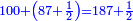 dinar
dinar