Royslist
From mispar
| Category | Category | Comment | Link | Annotated text |
|---|---|---|---|---|
| theoretical arithmetic/absolute quantity | פ.ר.ד./נפרד | term | האריתמטיקה_של_ניקומכוס#GIll | הכמה הנפרד |
| theoretical arithmetic/absolute quantity | פ.ר.ד./נפרד | term | האריתמטיקה_של_ניקומכוס#jC7h | הכמה הניפרד |
| proportion/alternation | מ.ו.ר./תמורה | term | ספר_מעשה_חושב#MixE | על התמורה |
| types of number/amicable numbers | א.ה.ב./נאהב | term | ספר_המלכים#FZKl | נאהבים |
| types of number/amicable numbers | א.ה.ב./נאהב | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#BF4q | נאהב |
| types of number/amicable numbers | א.ה.ב./נאהב | definition | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#7dUG | The first postulate is to extract the amicable numbers and I say that [they are] every two numbers, such that [the sum of] the proper divisors of each is as the other number. הדרוש הראשון הוא להוציא המספרים הנאהבים המסוגלים לאהבה ואומר כי כל שני מספרים אשר החלקים השלמים מכל אחד יהיו כמספר חברו |
| types of number/amicable numbers | א.ה.ב./נאהב | term | ספר_המלכים#q4cm | מספרים נאהבים |
| mean/arithmetic mean | מ.צ.ע./אמצעי | definition | ספר_מעשה_חושב#63cl | The number is mean between a given number and one, if the given number exceeds over it by as much as it exceeds over one. המספר יהיה אמצעי בין מספר מונח ובין האחד אם היה המספר המונח מוסיף עליו בשעור מה שהוא מוסיף על האחד |
| mean/arithmetic mean | מ.צ.ע./אמצעי | term | ספר_מעשה_חושב#zbZC | אמצעי בין |
| mean/arithmetic mean | ס.פ.ר./מספרי | term | האנציקלופדיה_של_אבו_אלצלת#KYdI | אמצעי מספריי |
| proportion/arithmetic proportion | ס.פ.ר./מספרי | term | האנציקלופדיה_של_אבו_אלצלת#zjqy | המתיחסים המספריים הם המתיחסים |
| proportion/arithmetic proportion | ס.פ.ר./מספרי | term | האנציקלופדיה_של_אבו_אלצלת#v8ed | ההתיחסויות המספריים |
| proportion/arithmetic proportion | ס.פ.ר./מספרי | definition | ספר_המספר_/_אליהו_מזרחי#sb9n | The differences are relative by equality ratio, not the measures, so that the ratio of the excess of the first measure over the second to the excess of the second over the third is as the ratio of the excess of the second over the third to the excess of the third over the fourth. These are called arithmetic. ואם שיהיו המותרים מתיחסים ביחס השווי עד שיהיה יחס מותר השעור הראשון על השני אל מותר השני על השלישי כיחס מותר השני על השלישי אל מותר השלישי על הרביעי לא השעורים והם הנקראים מספריים |
| proportion/arithmetic proportion | ס.פ.ר./מספרי | term | האנציקלופדיה_של_אבו_אלצלת#4kcu | יחס מספריי |
| proportion/arithmetic proportion | ס.פ.ר./מספר | term | האריתמטיקה_של_ניקומכוס#Hioi | אמצעי המספר |
| proportion/arithmetic proportion | ס.פ.ר./מספרי | term | האנציקלופדיה_של_אבו_אלצלת#SoRu | התיחסות המספריי |
| proportion/arithmetic proportion | ס.פ.ר./מספרי | term | האנציקלופדיה_של_אבו_אלצלת#kiqz | המתיחסים המספריי' |
| proportion/arithmetic proportion | ח.ש.ב./חשבון | term | האריתמטיקה_של_ניקומכוס#2N34 | אמצעי החשבון |
| proportion/arithmetic proportion | ח.ש.ב./חשבוני | term | האריתמטיקה_של_ניקומכוס#qHu7 | האמצעי החשבוני |
| proportion/arithmetic proportion | ס.פ.ר./מספרי | definition | האריתמטיקה_של_ניקומכוס#3uUu | The arithmetic mean is when three numbers or more are given, set according to the natural addition successively. הנה האמצעי המספריי יהיה כאשר תניח שלשה מספרים או יותר מזה והונחו כפי חבור הטבע ימשכו קצתם לקצת |
| proportion/arithmetic proportion | ס.פ.ר./מספרי | term | האריתמטיקה_של_ניקומכוס#pyLZ | מצוע המספריי |
| proportion/arithmetic proportion | ס.פ.ר./מספרי | term | האריתמטיקה_של_ניקומכוס#hwlm | האמצעי המספרי |
| solid number/beam number | אריחי | term | האריתמטיקה_של_ניקומכוס#Lxft | אריחיים |
| solid number/beam number | ע.מ.ד./עמודי | term | האנציקלופדיה_של_אבו_אלצלת#h7OA | עמודיי |
| parallelepipedon number/brick number | ל.ב.נ./לבני | term | האריתמטיקה_של_ניקומכוס#TRZT | המספרים הלבניים |
| parallelepipedon number/brick number | ל.ב.נ./לבני | term | האריתמטיקה_של_ניקומכוס#en4P | המספרים הדומים ללבנים |
| parallelepipedon number/brick number | ל.ב.נ./לבני | term | האנציקלופדיה_של_אבו_אלצלת#Ium0 | לבניי |
| parallelepipedon number/brick number | ל.ב.נ./לבני | term | האריתמטיקה_של_ניקומכוס#IcRl | לבנים |
| square number/circular number | ס.ב.ב./סבובי | term | האריתמטיקה_של_ניקומכוס#UYp2 | סבוביים |
| square number/circular number | ע.ג.ל./עגול | term | Anonymous#vcGf | חשבון עגול |
| square number/circular number | ק.ש.ת./קשתי | term | האריתמטיקה_של_ניקומכוס#SN4f | קשתיים |
| square number/circular number | ס.ב.ב./סבובי | term | האריתמטיקה_של_ניקומכוס#qSba | המספר הסבוביי |
| types of number/composite number | ר.כ.ב./מורכב | term | ספר_החשבון_לאל_חצאר#ZTsI | מורכב |
| types of number/composite number | ר.כ.ב./מורכב | term | ספר_החשבון_לאל_חצאר#f6Fi | מספר מורכב |
| types of number/composite number | ר.כ.ב./מורכב | term | אגרת_המספר#y4Pq | מורכב |
| types of number/composite number | ר.כ.ב./מורכב | definition | ספר_היסודות_לאקלידס#OCw3 | The number that is called a composite number is that which is counted by a number other than the unit. המספר אשר יאמר לו המספר המורכב הוא אשר ישיגהו המנין במספר זולת אחד |
| types of number/composite number | ר.כ.ב./מורכב | term | אגרת_המספר#kmbh | מורכבים |
| types of number/composite number | ר.כ.ב./מורכב | term | ספר_החשבון_לאל_חצאר#gVQ2 | |
| odd number/composite odd number | term | האריתמטיקה_של_ניקומכוס#rJHn | השני המורכב | |
| odd number/composite odd number | פ.ר.ד./נפרד שני | definition | ספר_יסודי_התבונה_ומגדל_האמונה#lXQg | the second odd [= composite odd number 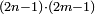 ] is every number that a number is found that counts it and this number is an odd number only.
וההשני הוא כל מספר שאתה מוצא מספר שיהיה מונה אותו ולא יהיה המספר הזה כי אם בנפרדות ] is every number that a number is found that counts it and this number is an odd number only.
וההשני הוא כל מספר שאתה מוצא מספר שיהיה מונה אותו ולא יהיה המספר הזה כי אם בנפרדות |
| odd number/composite odd number | פ.ר.ד./נפרד שני | term | ספר_יסודי_התבונה_ומגדל_האמונה#srLI | נפרד שני |
| odd number/composite odd number | ר.כ.ב./מורכב | term | ספר_המספר_/_אליהו_מזרחי#q7Za | מורכב |
| odd number/composite odd number | פ.ר.ד./נפרד שני | term | האריתמטיקה_של_ניקומכוס#f33t | המספר הנפרד השני המורכב |
| odd number/composite odd number | פ.ר.ד./נפרד שני | definition | האריתמטיקה_של_ניקומכוס#Txwl | The composite odd number has a divisor beside one, and that number is a fractional part of it. המספר הנפרד המורכב הוא אשר לו עם האחד מספר ימנהו וזה המספר הוא חלק לו |
| odd number/composite odd number | פ.ר.ד./נפרד שני | term | האריתמטיקה_של_ניקומכוס#sCb3 | הנפרד השני המורכב |
| solid number/cubic number | definition | ספר_המספר_/_אליהו_מזרחי#BY60 | a cubic [number] is the number resulting from the multiplication of the number by its square. והמעוקב הוא המספר היוצא מהכאת המספר הא' עם מרובעו | |
| solid number/cubic number | ע.ק.ב./מעוקב | term | ספר_ג'יבלי_אלמוקבאלא#4G8I | המספרי' המעוקבי' |
| solid number/cubic number | ע.ק.ב./מעוקב | definition | האריתמטיקה_של_ניקומכוס#YZXv | Hence, the solid number whose dimensions are equal, i.e. the length, breadth and depth, is necessarily the cube number. הנה אם כן המספר הגרמי השוה המרחקים ר"ל האורך והרחב והעומק הוא המעוקב בהכרח |
| solid number/cubic number | ע.ק.ב./מעוקב | term | ספר_מעשה_חושב#QiEv | מעוקב |
| solid number/cubic number | ע.ק.ב./מעוקב | term | ספר_החשבון_לאל_חצאר#uJdg | מעוקבים |
| solid number/cubic number | ע.ק.ב./מעוקב | term | ספר_מעשה_חושב#cdhC | מעוקבות |
| solid number/cubic number | ע.ק.ב./מעוקב | definition | ספר_היסודות_לאקלידס#3TfL | The cube number is the product of a number that is multiplied by its product by its similar, or that which is contained by three equal numbers. המספר המעוקב הוא המקובץ מהכאת מספר במה שיתקבץ מהכאתו בדומה לו או הוא אשר יקיפו בו שלשה מספרים שוים |
| solid number/cubic number | ע.ק.ב./מעוקב | term | ספר_החשבון_לאל_חצאר#91r6 | מעוקב |
| solid number/cubic number | גוף/גוף שוה | term | Anonymous#VNkE | גוף שוה |
| solid number/cubic number | ע.ק.ב./מעוקב | term | ספר_מעשה_חושב#F7ai | מעוקבי המספרים |
| solid number/cubic number | גוף | term | Anonymous#qHD4 | הגופות |
| solid number/cubic number | ע.ק.ב./מעוקב | definition | ספר_המספר_/_אליהו_מזרחי#UkwN | By cubic numbers I mean the numbers whose length, width, and depth are equal. וארצה במעוקבים המספרים אשר ארכם ורחבם ועמקם שוים |
| solid number/cubic number | ע.ק.ב./מעוקב | term | ספר_מעשה_חושב#Pgnj | מספר מעוקב |
| types of number/cyclic number | term | ספר_המספר_/_אברהם_אבן_עזרא#1acb | חשבון עגול | |
| types of number/cyclic number | term | ספר_המספר_/_אברהם_אבן_עזרא#ED58 | מתגלגל על עצמו | |
| polygonal number/decagonal number | ע.ש.ר./מעושר | term | האנציקלופדיה_של_אבו_אלצלת#QsIS | מעשרים |
| perfect number/deficient number | ח.ס.ר./חסר | term | ספר_יסודי_התבונה_ומגדל_האמונה#kLLi | חסר |
| perfect number/deficient number | ח.ס.ר./חסר | definition | ספר_יסודי_התבונה_ומגדל_האמונה#k2pP | the deficient number is that whose parts do not complete its number. והמספר החסר הוא אשר אין חלקיו ממלאים את מספריו |
| perfect number/deficient number | ח.ס.ר./חסר | term | ספר_יסודי_התבונה_ומגדל_האמונה#wZD0 | המספר החסר |
| perfect number/deficient number | definition | לקוטים_מספר_פראלוקא#fHkd | The discussion on the number, which the sum of its parts is less than the number [itself]; as eight, for the sum of its parts, which are the half, quarter and eighth, is only 7; and this number is called in their language "numero povero". 4 המאמר במספר אשר חלקיו מקובצים מחסירים מהמספר כאלו תאמר מספר שמונה כי חלקיו מקובצים אינם כי אם ז' והוא החצי והרובע והשמינית וזה המספר נקרא בלשונם נומירו פווירו | |
| ratio/duplicate | ש.נ.י./שנוי | term | ספר_מעשה_חושב#bplJ | שנוי ביחס |
| ratio/duplicate | ש.נ.י./שנוי | term | ספר_האלזיברא#Q7dD | שנוי |
| ratio/duplicate | ש.נ.י./שנוי | term | תחבולות_המספר#fnbu | שנוי בכפל |
| ratio/duplicate | ש.נ.י./שנוי | term | חשבון_השטחים#TIvo | שינוי |
| ratio/duplicate | ש.נ.י./שנוי | term | תחבולות_המספר#xHbv | שנוי |
| theoretical arithmetic/endlessly | כ.ל.י./אל לא תכלית | term | מלאכת_המספר#uQQd | אל לא תכלית |
| theoretical arithmetic/endlessly | כ.ל.י./עד בלתי תכלית | term | מלאכת_המספר#Usvg | עד בלתי תכלית |
| theoretical arithmetic/endlessly | כ.ל.י./אין תכלית | term | ספר_מעשה_חושב#KcC1 | אין תכלית לו |
| simple ratio/equality ratio | ש.ו.ה./שוה | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#Isne | השוה |
| simple ratio/equality ratio | ש.ו.ה./שווי | term | ספר_מעשה_חושב#hoQQ | יחס השווי |
| simple ratio/equality ratio | ש.ו.ה./שווי | term | ספר_מעשה_חושב#qi9U | יחס השווי |
| simple ratio/equality ratio | י.ש.ר./ישר | term | ספר_יסודי_התבונה_ומגדל_האמונה#iHEw | הקשה הישרה |
| simple ratio/equality ratio | י.ש.ר./ישר | term | ספר_יסודי_התבונה_ומגדל_האמונה#sSUF | הקשת הישר |
| simple ratio/equality ratio | ש.ו.ה./שוה | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#dKea | הערך השוה |
| simple ratio/equality ratio | ש.ו.ה./שוה | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#41HW | ערך שוה |
| types of number/even number | ז.ו.ג./זוג | term | האנציקלופדיה_של_אבו_אלצלת#AGaI | מספר זוג |
| types of number/even number | ז.ו.ג./זוג | term | אגרת_המספר#6a4B | זוגות |
| types of number/even number | ז.ו.ג./זוג | term | ספר_עיון_העקרים_לחשבון_ההנדיים#ofaL | זוגות |
| types of number/even number | ז.ו.ג./זוג | term | Anonymous#j0hi | זוג |
| types of number/even number | ז.ו.ג./זוג | term | מלאכת_המספר#WWds | זוג |
| types of number/even number | ז.ו.ג./זוג | term | אגרת_המספר#arQB | זוג |
| types of number/even number | ז.ו.ג./זוג | term | מלאכת_המספר#Tlb4 | זוגות |
| types of number/even number | definition | האנציקלופדיה_של_אבו_אלצלת#4hko | The even number is any number that is divisible into two equal parts, such as 2 and 4. והזוג הוא כל מספר שיתחלק לשני חלקים שוים כשנים וארבע | |
| types of number/even number | ז.ו.ג./זוג | term | Anonymous#bXwy | זוגות |
| types of number/even number | definition | האריתמטיקה_של_ניקומכוס#N8GS | *The '''even number''' is divisible into two equal parts with no mediator unit between them by which one exceeds the other. וה{{#annot:term|63|vAh2}}זוג{{#annotend:vAh2}} יחלק לשני חלקים שוים אין ביניהם אחדות אמצעי יעדיף בו אחד מהם על האחר | |
| types of number/even number | ז.ו.ג./זוג | term | ספר_מעשה_חושב#VeHw | זוג |
| types of number/even number | ז.ו.ג./זוג | term | ספר_מעשה_חושב#oTp7 | מספר זוג |
| types of number/even number | ז.ו.ג./זוג | term | ספר_החשבון_לאל_חצאר#P8es | זוג |
| types of number/even number | ז.ו.ג./זוג | term | ספר_מעשה_חושב#Ug7V | זוגות |
| types of number/even number | ז.ו.ג./זוג | term | קצור_המספר#fyZ1 | זוגות |
| types of number/even number | term | האריתמטיקה_של_ניקומכוס#vAh2 | זוג | |
| types of number/even number | ז.ו.ג./זוג | term | קצור_המספר#uWQn | זוג |
| types of number/even number | ז.ו.ג./זוג | definition | ספר_יסודי_התבונה_ומגדל_האמונה#pruy | the even number is the number that is divisible [by two] והזוג הוא המספר הנחלק בנתים |
| types of number/even number | ז.ו.ג./זוג | definition | ספר_היסודות_לאקלידס#ei5Y | The even number is that which is divisible into two equal parts. המספר הזוג הוא אשר יחלק בשני חלקים שוים |
| types of number/even number | ז.ו.ג./זוג | term | ספר_החשבון_לאל_חצאר#fv2Q | המספר הזוג |
| types of number/even number | ז.ו.ג./זוג | term | האנציקלופדיה_של_אבו_אלצלת#6NUn | זוגות |
| types of number/even number | ז.ו.ג./זוג | term | ספר_החשבון_לאל_חצאר#Rd9G | זוגות |
| types of number/even number | ז.ו.ג./זוג | term | ספר_החשבון_לאל_חצאר#8a4J | מספר זוג |
| types of number/even number | ז.ו.ג./זוג | term | ספר_יסודי_התבונה_ומגדל_האמונה#wa0f | הזוג |
| types of number/even number | ז.ו.ג./זוג | term | האנציקלופדיה_של_אבו_אלצלת#wfI7 | זוג |
| types of number/even number | ז.ו.ג./זוג | term | ספר_המספר_/_אליהו_מזרחי#ynkB | זוג |
| even number/even-times-even number | ז.ו.ג./זוג הזוג | definition | ספר_יסודי_התבונה_ומגדל_האמונה#neZT | the even-times-even number [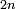 ] is the number that is resulted from doubling the first even number once or more than once.
וזוג הזוג הוא המספר הבא מכפילת הזוג הראשון פעם אחת או יותר מפעם אחת ] is the number that is resulted from doubling the first even number once or more than once.
וזוג הזוג הוא המספר הבא מכפילת הזוג הראשון פעם אחת או יותר מפעם אחת |
| even number/even-times-even number | ז.ו.ג./זוג הזוג | term | ספר_יסודי_התבונה_ומגדל_האמונה#i5Hh | זוג הזוג |
| even number/even-times-even number | ז.ו.ג./זוג הזוג | term | ספר_המספר_/_אליהו_מזרחי#rMLT | זוג הזוג |
| even number/even-times-even number | ז.ו.ג./זוג הזוג | definition | אגרת_המספר#oKPC | if its half is also divisible into halves and the half of the half [is divisible] into halves, until reaching the one, it is called an even-times-even number, such as 8, 16, 32, for it is always divisible into halves as even number until reaching the one. ואם יחלק החצי ג"כ לחצאין וחצי החצי לחצאין עד שיגיע אל האחד יקרא זוג הזוג כמו ח' י"ו ול"ב כי הוא יחלק תמיד לחצאין כזוג עד שיגיע אל האחד |
| even number/even-times-even number | ז.ו.ג./זוג הזוג | term | האנציקלופדיה_של_אבו_אלצלת#PhIH | זוגי הזוגות |
| even number/even-times-even number | ז.ו.ג./זוג הזוג | term | האנציקלופדיה_של_אבו_אלצלת#a7rS | זוג הזוג |
| even number/even-times-even number | ז.ו.ג./זוג הזוג | term | אגרת_המספר#K5hY | זוג הזוג |
| even number/even-times-even number | כ.פ.ל./כפל הכפל | term | Anonymous#bvwq | חשבון כפל הכפל |
| even number/even-times-even number | ז.ו.ג./זוג הזוג | definition | ספר_היסודות_לאקלידס#FVG6 | The number that is called an even-times-even number is that which is counted an even number of times by an even number. המספר אשר יאמר לו זוג הזוג הוא אשר ימנה אותו מספר זוג פעמים מספרם זוג |
| even number/even-times-even number | ז.ו.ג./זוג הזוג | term | האנציקלופדיה_של_אבו_אלצלת#wsFA | מספר זוג הזוג |
| even number/even-times-even number | כ.פ.ל./כפל הכפל | term | Anonymous#AxYM | כפל הכפל |
| even number/even-times-even number | ז.ו.ג./זוג הזוג | term | האנציקלופדיה_של_אבו_אלצלת#kOjL | מספרי זוג הזוג |
| even number/even-times-even number | ז.ו.ג./זוג הזוג | term | האנציקלופדיה_של_אבו_אלצלת#fHMZ | זוגי הזוג |
| even number/even-times-even-times-odd number | ז.ו.ג./זוג הזוג והנפרד | term | ספר_יסודי_התבונה_ומגדל_האמונה#mkhr | זוג הזוג והנפרד |
| even number/even-times-even-times-odd number | ז.ו.ג./זוג הזוג והנפרד | term | אגרת_המספר#CY3L | זוג הזוג והנפרד |
| even number/even-times-even-times-odd number | ז.ו.ג./זוג הזוג והנפרד | definition | ספר_יסודי_התבונה_ומגדל_האמונה#E5GZ | the even-times-even-times-odd number [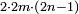 ] is the number that is resulted from doubling the odd number an even number of times.
וזוג הזוג והנפרד הוא המספר הבא מכפילת הנפרד פעמים שיהיה מספרם זוג ] is the number that is resulted from doubling the odd number an even number of times.
וזוג הזוג והנפרד הוא המספר הבא מכפילת הנפרד פעמים שיהיה מספרם זוג |
| even number/even-times-even-times-odd number | ז.ו.ג./זוג הזוג והנפרד | definition | אגרת_המספר#tbJq | if it is first divisible into even numbers then into odd numbers, such as 12, for 12 is divided into six and six, then into 3, all that is similar is called even-times-even-times-odd number, because it consists of two even numbers that consist of odd numbers. ואם יחלק תחלה לזוגות ואח"כ לנפרדים כי"ב כי יחלק לששה ששה א"כ לג' וכל הדומה לזה יקרא זוג הזוג והנפרד כי הורכב מב' זוגות המורכבים מנפרדים |
| even number/even-times-even-times-odd number | ז.ו.ג./זוג הזוג והנפרד | term | האנציקלופדיה_של_אבו_אלצלת#QJO8 | זוג הזוג והנפרד |
| even number/even-times-even-times-odd number | ז.ו.ג./זוג הזוג והנפרד | term | ספר_המספר_/_אליהו_מזרחי#mbnI | זוג הזוג והנפרד |
| even number/even-times-odd number | ז.ו.ג./זוג הנפרד | definition | אגרת_המספר#ikHZ | if it is divisible into halves and each of the halves is odd number, such as six, whose half is 3, or ten, whose half is 5, it is called an even-times-odd number, for it consists of two odd numbers. ואם יחלק לחצאין וכל אחד מהחצאין נפרד כששה שחציו ג' או עשרה שחציו ה' יקרא זוג הנפרד כי הוא מורכב מב' נפרדים |
| even number/even-times-odd number | ז.ו.ג./זוג הנפרד | term | האנציקלופדיה_של_אבו_אלצלת#6Juj | זוג הנפרד |
| even number/even-times-odd number | ז.ו.ג./זוג הנפרד | term | האנציקלופדיה_של_אבו_אלצלת#17FM | מספר זוג הנפרד |
| even number/even-times-odd number | ז.ו.ג./זוג הנפרד | term | אגרת_המספר#ZNs5 | זוג הנפרד |
| even number/even-times-odd number | ז.ו.ג./זוג הנפרד | definition | ספר_היסודות_לאקלידס#lLa0 | The number that is called an even-times-odd number is that which is counted an even number of times by an odd number. המספר אשר יאמר לו זוג הנפרד הוא אשר ימנהו מספר נפרד פעמים מספרם זוג |
| even number/even-times-odd number | ז.ו.ג./זוג הנפרד | term | ספר_המספר_/_אליהו_מזרחי#TwLU | זוג הנפרד |
| even number/even-times-odd number | ז.ו.ג./זוג הנפרד | definition | ספר_יסודי_התבונה_ומגדל_האמונה#gRQC | the even-times-odd number [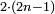 ] is the number that is resulted from doubling the odd number once.
וזוג הנפרד הוא המספר הבא מכפילת הנפרד פעם אחת ] is the number that is resulted from doubling the odd number once.
וזוג הנפרד הוא המספר הבא מכפילת הנפרד פעם אחת |
| even number/even-times-odd number | ז.ו.ג./זוג הנפרד | term | ספר_יסודי_התבונה_ומגדל_האמונה#hK4n | זוג הנפרד |
| relative quantity/extreme | ח.ו.צ./חיצונית | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#bipj | חיצוניות |
| relative quantity/extreme | קצה | term | האנציקלופדיה_של_אבו_אלצלת#xhee | קצוות |
| relative quantity/extreme | קצה | term | האנציקלופדיה_של_אבו_אלצלת#K7OM | קצה |
| relative quantity/extreme | ג.ב.ל./גבול | term | האנציקלופדיה_של_אבו_אלצלת#tvnY | גבולים |
| relative quantity/extreme | ח.ו.צ./חיצונית | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#uOmy | חיצוניות |
| mean/geometric mean | מ.צ.ע./אמצעי | term | ספר_מעשה_חושב#lSuc | אמצעי ביחס בין |
| mean/geometric mean | ש.ב.ר./תשברתי | term | האנציקלופדיה_של_אבו_אלצלת#a53U | אמצעי תשברתיי |
| proportion/geometric proportion | מ.ד.ד./מדותי | definition | ספר_המספר_/_אליהו_מזרחי#km5I | The measures are relative to themselves, not their differences, so that the ratio of the first measure to the second measure is as the ratio of the second measure to the third measure. These are called geometric. והם אם שיהיו השעורים מתיחסים בעצמם עד שיהיה יחס השעור הראשון אל השעור השני כיחס השעור השני אל השעור השלישי לא המותרים והם הנקראים מדותיים |
| proportion/geometric proportion | ש.ב.ר./תשברתי | term | האנציקלופדיה_של_אבו_אלצלת#6SJH | ההתיחסות התשברתיי |
| proportion/geometric proportion | ש.ב.ר./תשברתי | term | האנציקלופדיה_של_אבו_אלצלת#CuIW | יחס תשברתיי |
| proportion/geometric proportion | מ.ד.ד./מדותי | definition | האריתמטיקה_של_ניקומכוס#o5gn | The geometic proportion is when there are three numbers or more, such that the measure of the first of them to the second is as the measure of the second to the third and vice versa.
: ואמנם האמצעי המדותיי הוא כאשר יהיו שלשה מספרים או יותר מזה והיה שעור הראשון מהם אצל השני כשעור השני אצל השלישי וכן בהפך
ואמנם האמצעי המדותיי הוא כאשר יהיו שלשה מספרים או יותר מזה והיה שעור הראשון מהם אצל השני כשעור השני אצל השלישי וכן בהפך |
| proportion/geometric proportion | מ.ד.ד./מדותי | term | האריתמטיקה_של_ניקומכוס#2w0R | אמצעי המדותיי |
| proportion/geometric proportion | הנדסה | term | האריתמטיקה_של_ניקומכוס#9OI3 | אמצעי ההנדסה |
| proportion/geometric proportion | ש.ב.ר./תשברתי | term | האנציקלופדיה_של_אבו_אלצלת#SC4F | ההתיחסויות התשברתיות |
| proportion/geometric proportion | ש.ב.ר./תשברתי | term | האנציקלופדיה_של_אבו_אלצלת#ix2l | התשברתיים |
| proportion/geometric proportion | ש.ב.ר./תשברתי | term | האנציקלופדיה_של_אבו_אלצלת#Fvij | המתיחסי' התשברתיים |
| proportion/geometric proportion | מ.ד.ד./מדותי | term | האריתמטיקה_של_ניקומכוס#ppSt | התיחסות המדותיי |
| proportion/geometric proportion | מ.ד.ד./מדות | term | האריתמטיקה_של_ניקומכוס#YtZ7 | אמצעי המדות |
| mean/harmonic mean | ח.ב.ר./חבורי | term | האנציקלופדיה_של_אבו_אלצלת#2PVB | אמצעי חבוריי |
| proportion/harmonic proportion | מוסיקי | definition | ספר_המספר_/_אליהו_מזרחי#6ZJd | The differences and the measures are relative, meaning that the one of the two given ratios is of the differences and the other is of the measures, so that the ratio of the first measure to the last measure is as the ratio of the excess of the first over the mean to the excess of the mean over the last. These are called harmonic. ואם שיהיו המותרים והשעורים יחד מתייחסים רוצה לומר שהיחס האחד משני היחסים המונחים הוא מהמותרים והאחר הוא מהשעורים עד שיהיה יחס השעור הראשון אל השעור האחרון כיחס מותר הראשון על האמצעי אל מותר האמצעי על האחרון והם הנקראים מוסקיים |
| proportion/harmonic proportion | ח.ב.ר./חבורי | term | האריתמטיקה_של_ניקומכוס#ZR1k | האמצעי החבוריי |
| proportion/harmonic proportion | ח.ב.ר./חבור | term | האריתמטיקה_של_ניקומכוס#UZha | אמצעי החבור |
| proportion/harmonic proportion | נ.ג.נ./נגון | term | האריתמטיקה_של_ניקומכוס#A06f | אמצעי הנגון |
| proportion/harmonic proportion | ח.ב.ר./חבורי | term | האריתמטיקה_של_ניקומכוס#VOB6 | יחס חבוריי |
| proportion/harmonic proportion | ח.ב.ר./חבורי | definition | האריתמטיקה_של_ניקומכוס#XLBu | The harmonic proportion is when there are three given numbers, which are not in one ratio to each other, as the terms in the geometric proportion, and the excesses of each over the other are not equal, as [those of] the terms in the arithmetic proportion, but the measure of the greater term to the measure of the smaller term is as the measure of the excess of the greater term over the mean term to the excess of the mean over the smaller.
: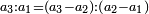 ואמנם האמצעי החבוריי הנה הוא כאשר היו שלשה מספרים מונחים ולא יהיה לקצתם אל קצת יחס אחד כמו הגבולים המדותיים לא יתרוני קצתם על קצת שוים כמו הגבולים המספרים אבל יהיה השעור הגבול הגדול אצל שעור הגבול הקטן כשעור מותר הגבול הגדול על הגבול האמצעי אל מותר האמצעי על הקטן
ואמנם האמצעי החבוריי הנה הוא כאשר היו שלשה מספרים מונחים ולא יהיה לקצתם אל קצת יחס אחד כמו הגבולים המדותיים לא יתרוני קצתם על קצת שוים כמו הגבולים המספרים אבל יהיה השעור הגבול הגדול אצל שעור הגבול הקטן כשעור מותר הגבול הגדול על הגבול האמצעי אל מותר האמצעי על הקטן |
| proportion/harmonic proportion | ח.ב.ר./חבורי | term | האנציקלופדיה_של_אבו_אלצלת#T8Wb | ההתיחסות החבוריי |
| polygonal number/heptagonal number | ש.ב.ע./משובע | term | האנציקלופדיה_של_אבו_אלצלת#cpzV | משבע |
| polygonal number/heptagonal number | ש.ב.ע./משובע | term | האנציקלופדיה_של_אבו_אלצלת#hSin | משבעים |
| plane number/heteromecic number | זולת/זולתי האורך | term | האריתמטיקה_של_ניקומכוס#Rs4e | המספר הזולתי האורך |
| plane number/heteromecic number | זולת/זולתי | definition | ספר_המספר_/_אליהו_מזרחי#R9lF | It has already been clarified in the second section of the Book on Arithmetic by Nicomachus of Gerasa that the heteromecic numbers, which are those whose one side exceeds over the other by one, such as 1 and 2; 2 and 3; 3 and 4; 4 and 5; and so on; are generated by the increment of the natural even numbers.
: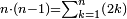 והוא שכבר התבאר בספר הארתמטיקא לניקומכוש הגהרשיני במאמר השני שהמספרים הזולתיים שהם אשר יהיו צלעותיו נוסף אחד מהם על האחר בתוספת האחד כמו א"ב וב"ג וג"ד וד"ה וכן תמיד הנה צמיחתם תהיה בתוספת הזוגות הטבעיים קצתם על קצת
והוא שכבר התבאר בספר הארתמטיקא לניקומכוש הגהרשיני במאמר השני שהמספרים הזולתיים שהם אשר יהיו צלעותיו נוסף אחד מהם על האחר בתוספת האחד כמו א"ב וב"ג וג"ד וד"ה וכן תמיד הנה צמיחתם תהיה בתוספת הזוגות הטבעיים קצתם על קצת |
| plane number/heteromecic number | זולת/זולתי | term | ספר_המספר_/_אליהו_מזרחי#QNd6 | זולתיי |
| plane number/heteromecic number | זולת/זולתי | term | ספר_המספר_/_אליהו_מזרחי#v4QK | המספר הזולתיי |
| plane number/heteromecic number | זולת | term | האריתמטיקה_של_ניקומכוס#kdOx | זולתיי |
| plane number/heteromecic number | זולת | term | האנציקלופדיה_של_אבו_אלצלת#jTnG | זולתיות |
| plane number/heteromecic number | זולת/זולתי האורך | term | האנציקלופדיה_של_אבו_אלצלת#XsrB | זולתיי הארך |
| plane number/heteromecic number | זולת/זולתי האורך | term | האנציקלופדיה_של_אבו_אלצלת#HRNQ | המספרים הזולתיים הארך |
| plane number/heteromecic number | זולת/זולתי | term | האריתמטיקה_של_ניקומכוס#kY9X | המספרים הזולתיים |
| plane number/heteromecic number | זולת/זולתי האורך | term | האנציקלופדיה_של_אבו_אלצלת#DBjI | הזולתיים |
| plane number/heteromecic number | זולת/זולתי האורך | term | האריתמטיקה_של_ניקומכוס#l7zm | זולתיות האורך |
| plane number/heteromecic number | זולת | term | האריתמטיקה_של_ניקומכוס#Gk5s | זולתיות |
| plane number/heteromecic number | זולת | term | האריתמטיקה_של_ניקומכוס#qOjh | הזולת |
| plane number/heteromecic number | זולת | term | האריתמטיקה_של_ניקומכוס#xyKW | זולתיים |
| polygonal number/hexagonal number | ש.ש.י./משושה | term | האנציקלופדיה_של_אבו_אלצלת#2GIl | משושה |
| polygonal number/hexagonal number | ש.ש.י./משושה | term | האנציקלופדיה_של_אבו_אלצלת#edA4 | משששת |
| polygonal number/hexagonal number | ש.ש.י./משושה | term | האנציקלופדיה_של_אבו_אלצלת#EUUb | מששים |
| polygonal number/hexagonal number | ש.ש.י./משושה | term | האנציקלופדיה_של_אבו_אלצלת#7rJH | מששה |
| ratio/inequality | ח.ל.פ./נחלף | term | ספר_יסודי_התבונה_ומגדל_האמונה#Zvfe | הקשה נחלפת |
| ratio/inequality | ח.ל.פ./נחלף | term | ספר_יסודי_התבונה_ומגדל_האמונה#ZzvF | נחלפות |
| types of number/linear number | ק.ו.י./קוי | term | האנציקלופדיה_של_אבו_אלצלת#iEhP | קויי |
| types of number/linear number | ק.ו.י./קוי | term | האנציקלופדיה_של_אבו_אלצלת#C4jI | המספר הקוי |
| types of number/linear number | ס.פ.ר./מספרי | term | האנציקלופדיה_של_אבו_אלצלת#4qvk | קו מספריי |
| types of number/linear number | ק.ו.י./קוי | term | האנציקלופדיה_של_אבו_אלצלת#yUB9 | מספרים קוויים |
| types of number/linear number | ס.פ.ר./מספרי | term | האנציקלופדיה_של_אבו_אלצלת#ZSDE | קוים מספריים |
| types of number/linear number | ק.ו.י./קוי | term | האריתמטיקה_של_ניקומכוס#F5O7 | המספרים הקויים |
| types of number/linear number | ק.ו.י./קוי | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#GXoT | מספר קויי |
| types of number/linear number | ק.ו.י./קוי | definition | האריתמטיקה_של_ניקומכוס#OyFF | Indeed, the linear numbers are all those that are set to begin with two and increase by one according to the order of the natural succession. וזה שהמספרים הקויים הם כל מה שתניח התחלתו מהשנים עוד יתרבו באחד על סדר משך הטבע |
| types of number/linear number | ק.ו.י./קוי | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#Xwoi | המספר הקויי |
| relative quantity/mean | מ.צ.ע./אמצעי | term | האריתמטיקה_של_ניקומכוס#pd2u | אמצעי |
| relative quantity/mean | מ.צ.ע./אמצעי | term | האריתמטיקה_של_ניקומכוס#anLc | אמצעיים |
| relative quantity/mean | מ.צ.ע./אמצעי | term | האריתמטיקה_של_ניקומכוס#POeO | אמצעי |
| simple ratio/multiple ratio | septuple | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#GycF | מולטיפלקש שיטטופלה | |
| simple ratio/multiple ratio | double ratio | האריתמטיקה_של_ניקומכוס#VNE8 | יחס הכפל השניי | |
| simple ratio/multiple ratio | octuple | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#xC7s | מולטיפלקש גוייטופלה | |
| simple ratio/multiple ratio | quintuple | לקוטים_מספר_פראלוקא#TjSu | קואיאינקופלא | |
| simple ratio/multiple ratio | double ratio | לקוטים_מספר_פראלוקא#OcyH | דופלא | |
| simple ratio/multiple ratio | quintuple | לקוטים_מספר_פראלוקא#Y9bZ | קואינקופלא | |
| simple ratio/multiple ratio | quintuple | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#A6C2 | מולטיפלק קינקופלה | |
| simple ratio/multiple ratio | quadruple | האריתמטיקה_של_ניקומכוס#If0k | הכפל הרביעיי | |
| simple ratio/multiple ratio | quadruple | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#hM6e | מולטיפלקש קאטרופלה | |
| simple ratio/multiple ratio | triple ratio | האריתמטיקה_של_ניקומכוס#35hm | יחס הכפל השלישיי | |
| simple ratio/multiple ratio | triple ratio | האריתמטיקה_של_ניקומכוס#YI1E | יחס הכפל השלישי | |
| simple ratio/multiple ratio | triple ratio | לקוטים_מספר_פראלוקא#z4kz | יחס הטריפלא | |
| simple ratio/multiple ratio | double ratio | האריתמטיקה_של_ניקומכוס#m3z8 | יחס הכפל השני | |
| simple ratio/multiple ratio | quadruple | האריתמטיקה_של_ניקומכוס#364l | הכפל הרביעי | |
| simple ratio/multiple ratio | triple ratio | האריתמטיקה_של_ניקומכוס#IG0u | כפל השלישיי | |
| simple ratio/multiple ratio | triple ratio | האריתמטיקה_של_ניקומכוס#jNnr | הכפל השלישי | |
| simple ratio/multiple ratio | double ratio | האריתמטיקה_של_ניקומכוס#EgW9 | הכפל השניי | |
| simple ratio/multiple ratio | double ratio | לקוטים_מספר_פראלוקא#2dKw | יחס הדופלא | |
| simple ratio/multiple ratio | double ratio | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#1rAu | מולטיפלקש דובלה | |
| simple ratio/multiple ratio | quadruple | לקוטים_מספר_פראלוקא#hvVS | קואטרופלא | |
| simple ratio/multiple ratio | triple ratio | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#eGvr | מולטיפלקש טריפלה | |
| simple ratio/multiple ratio | כ.פ.ל./כפל | term | ספר_יסודי_התבונה_ומגדל_האמונה#IiYm | הקשת כפל |
| simple ratio/multiple ratio | sextuple | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#cR7M | מולטיפלקש שישטופלה | |
| simple ratio/multiple ratio | triple ratio | לקוטים_מספר_פראלוקא#dyoh | טריפלא | |
| simple ratio/multiple ratio | quadruple-definition | לקוטים_מספר_פראלוקא#mMjA | If it is generated from the ratio of 1 to 4, it is called quadruple ratio.
: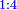 ואם הוא מיחס א' אל ד' נקרא קואטרופלא
ואם הוא מיחס א' אל ד' נקרא קואטרופלא | |
| simple ratio/multiple ratio | triple ratio-definition | לקוטים_מספר_פראלוקא#omoS | If it is generated from the ratio of 1 to 3, it is called triple ratio.
: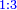 ואם הוא מיחס א' אל ג' נקרא טריפלא
ואם הוא מיחס א' אל ג' נקרא טריפלא | |
| simple ratio/multiple ratio | double ratio-definition | לקוטים_מספר_פראלוקא#3psH | If the ratio is generated from the ratio of 1 to 2, it is called double ratio.
: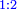 והנה אם היחס הוא מיחס א' אל ב' נקרא דופלא
והנה אם היחס הוא מיחס א' אל ב' נקרא דופלא | |
| simple ratio/multiple ratio | כ.פ.ל./בעל הכפלים | term | האריתמטיקה_של_ניקומכוס#KPTs | בעל הכפלים |
| simple ratio/multiple ratio | כ.פ.ל./בעל הכפלים | term | האריתמטיקה_של_ניקומכוס#3b4R | יחס בעל הכפלים |
| compound ratio/multiple superparticular ratio | double sesquialter | האריתמטיקה_של_ניקומכוס#0eOa | הכפל השניי המוסיף חצי | |
| compound ratio/multiple superparticular ratio | double sesquitertian | האריתמטיקה_של_ניקומכוס#eo7V | הכפל השניי המוסיף שליש | |
| compound ratio/multiple superparticular ratio | double sesquiquintan | האריתמטיקה_של_ניקומכוס#KnWp | הכפל השניי המוסיף חומש | |
| compound ratio/multiple superparticular ratio | כ.פ.ל./כפל וחלק | term | Anonymous#eaey | כפל וחלק |
| compound ratio/multiple superparticular ratio | double sesquiquartan | האריתמטיקה_של_ניקומכוס#aP3C | הכפל השניי המוסיף רביע | |
| compound ratio/multiple superparticular ratio | triple sesquitertian | האריתמטיקה_של_ניקומכוס#fzWx | הכפל השלישי המוסיף שליש | |
| compound ratio/multiple superparticular ratio | triple sesquialter | האריתמטיקה_של_ניקומכוס#QhGF | הכפל השלישיי המוסיף חצי | |
| compound ratio/multiple superparticular ratio | כ.פ.ל./כפל וחלק | term | ספר_יסודי_התבונה_ומגדל_האמונה#MqIb | הקשת כפל וחלק |
| compound ratio/multiple superparticular ratio | כ.פ.ל./כפל וחלק | term | Anonymous#gdw0 | כפלו וחלק ממנו |
| compound ratio/multiple superpartient ratio | כ.פ.ל./כפל וחלקים | term | Anonymous#xtWA | הכפל וחלקים ממנו |
| compound ratio/multiple superpartient ratio | כ.פ.ל./כפל וחלקים | term | ספר_יסודי_התבונה_ומגדל_האמונה#nrOt | הקשת כפל וחלקים |
| compound ratio/multiple superpartient ratio | כ.פ.ל./כפל וחלקים | term | Anonymous#3YUC | כפל וחלקים |
| compound ratio/multiple superpartient ratio | כ.פ.ל./כפל וחלקים | term | Anonymous#VTES | כפלו וחלקים ממנו |
| types of number/natural number | ט.ב.ע./טבעי | term | האריתמטיקה_של_ניקומכוס#8Qcb | המספר הטבעיי |
| types of number/natural number | ט.ב.ע./טבעי | term | האריתמטיקה_של_ניקומכוס#pnyj | המספר הטבעי |
| types of number/natural number | ט.ב.ע./טבעי | term | האריתמטיקה_של_ניקומכוס#j2Pu | המספרים הטבעיים |
| polygonal number/nonagonal number | ת.ש.ע./מתושע | term | האנציקלופדיה_של_אבו_אלצלת#liM4 | מתשעים |
| absolute quantity/number | ס.פ.ר./מספר | term | קצור_המספר#A6qN | מספר |
| absolute quantity/number | ס.פ.ר./מספר | term | מלאכת_המספר#eDTT | מספר |
| absolute quantity/number | מ.נ.י./מנין | term | מלאכת_המספר#co5q | מניין |
| absolute quantity/number | ע.ר.כ./ערך | term | ספר_עיון_העקרים_לחשבון_ההנדיים#2gQE | ערך |
| absolute quantity/number | ח.ש.ב./חשבון | term | מלאכת_המספר#W3aF | חשבונות |
| absolute quantity/number | term | ספר_המספר_/_אברהם_אבן_עזרא#PgHE | המספר | |
| absolute quantity/number | ח.ש.ב./חשבון | term | מלאכת_המספר#9tL0 | חשבון |
| absolute quantity/number | מ.נ.י./מנין | term | תחבולות_המספר#n8lE | המנין |
| absolute quantity/number | ס.פ.ר./מספר | term | תחבולות_המספר#nex3 | מספר ה |
| absolute quantity/number | מ.נ.י./מנין | term | מלאכת_המספר#pn9C | מניין |
| absolute quantity/number | מ.נ.י./מנין | term | תחבולות_המספר#JuGc | מנין ה |
| absolute quantity/number | ח.ש.ב./חשבון | term | עיר_סיחון#pm5x | חשבונות |
| absolute quantity/number | ס.פ.ר./מספר | definition | ספר_היסודות_לאקלידס#MNqP | The number is a multitude composed of units. המספר הוא הקבוץ המורכב מן האחדים |
| absolute quantity/number | ס.פ.ר./מספר | definition | קצור_המספר#mTAa | Hence, the number is a sum of undetermined units; והנה המספר הוא קבוץ אחדים בלתי רמוזים |
| absolute quantity/number | ס.פ.ר./מספר | definition | ספר_המספר_/_אליהו_מזרחי#AiWg | The definition of the number that announces its essence is discontinuous quantity, whose total is measured by the unit. אולם גדר המספר המודיע מהותו הוא כמה מתפרדת אשר החלק אשר בו ישוער כללותו הוא האחד |
| absolute quantity/number | ס.פ.ר./מספר | term | חשבון_השטחים#UWNd | מספר ה |
| absolute quantity/number | definition | ספר_יסודי_התבונה_ומגדל_האמונה#nda9 | know that the number or the counting is the multitude that is summed from units. הוי יודע כי המספר או המנין הוא הרבוי הנקבץ מהאחדות | |
| absolute quantity/number | ס.פ.ר./מספר | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#3cyn | מספר |
| absolute quantity/number | מ.נ.י./מנין | term | קצור_המספר#DjOl | מניינם |
| absolute quantity/number | ס.פ.ר./מספר | term | ספר_דיני_ממונות#5p60 | מספרים |
| absolute quantity/number | definition | ספר_המספר_/_אברהם_אבן_עזרא#E7cZ | Know that that every number is a sum of units. דע כי כל חשבון הוא חברת האחדים | |
| absolute quantity/number | ס.פ.ר./מספר | term | מלאכת_המספר#57Z0 | מספרים |
| absolute quantity/number | ס.פ.ר./מספר | definition | אגרת_המספר#jmz7 | the number is what is summed from the units. אמר המחבר המספר מה שיתחבר מן האחדים |
| absolute quantity/number | ח.ש.ב./חשבון | term | קצור_המספר#c8cY | חשבון |
| absolute quantity/number | מ.נ.י./מנין | term | חשבון_השטחים#uzyY | המנין |
| absolute quantity/number | ס.כ.מ./סכום | term | חשבון_השטחים#KdL1 | סכום |
| absolute quantity/number | ח.ש.ב./חשבון | term | עיר_סיחון#cDwJ | חשבון |
| absolute quantity/number | ס.פ.ר./מספר | definition | מלאכת_המספר#I7x1 | the number is defined as a sum of units. ולכן יגדר המספר בשהוא קבוץ אחדים |
| absolute quantity/number | ס.פ.ר./מספר | term | קצור_המספר#jh2w | מספרים |
| theoretical arithmetic/numerical quantity | ס.פ.ר./מספרי | term | האריתמטיקה_של_ניקומכוס#6gVR | הכמה המספרי |
| polygonal number/octagonal number | ש.מ.נ.י./משומן | term | האנציקלופדיה_של_אבו_אלצלת#uuX7 | משמן |
| polygonal number/octagonal number | ש.מ.נ.י./משומן | term | האנציקלופדיה_של_אבו_אלצלת#TqtO | משמנים |
| types of number/odd number | פ.ר.ד./נפרד | term | קצור_המספר#ddG4 | נפרד |
| types of number/odd number | definition | האנציקלופדיה_של_אבו_אלצלת#mnXP | The odd number is any number that is indivisible into two equal parts. והנפרד הוא כל מספר שא"א שיחלק לשני חלקים שוים | |
| types of number/odd number | פ.ר.ד./נפרד | term | אגרת_המספר#8Vi3 | נפרד |
| types of number/odd number | פ.ר.ד./נפרד | term | Anonymous#vJmF | נפרד |
| types of number/odd number | פ.ר.ד./נפרד | term | Anonymous#1B3Z | הנפרדים |
| types of number/odd number | פ.ר.ד./נפרד | term | Anonymous#S0a2 | המספרים הנפרדים |
| types of number/odd number | פ.ר.ד./נפרד | term | Anonymous#anpd | המספר הנפרד |
| types of number/odd number | פ.ר.ד./נפרד | term | ספר_החשבון_לאל_חצאר#biWu | נפרד |
| types of number/odd number | פ.ר.ד./נפרד | term | ספר_החשבון_לאל_חצאר#p73f | המספר הנפרד |
| types of number/odd number | פ.ר.ד./נפרד | term | מלאכת_המספר#JBYc | נפרד |
| types of number/odd number | פ.ר.ד./נפרד | term | מלאכת_המספר#2aaj | נפרדים |
| types of number/odd number | פ.ר.ד./נפרד | term | ספר_החשבון_לאל_חצאר#PqGa | נפרדים |
| types of number/odd number | פ.ר.ד./נפרד | term | ספר_מעשה_חושב#3kgF | נפרד |
| types of number/odd number | פ.ר.ד./נפרד | term | אגרת_המספר#Yi1w | המספרים הנפרדים |
| types of number/odd number | פ.ר.ד./נפרד | term | ספר_מעשה_חושב#BKlp | מספר נפרד |
| types of number/odd number | פ.ר.ד./נפרד | term | ספר_מעשה_חושב#mj8C | נפרדים |
| types of number/odd number | פ.ר.ד./נפרד | term | האנציקלופדיה_של_אבו_אלצלת#8fTS | מספר נפרד |
| types of number/odd number | פ.ר.ד./נפרד | term | קצור_המספר#Vi4w | נפרדים |
| types of number/odd number | פ.ר.ד./נפרד | term | האנציקלופדיה_של_אבו_אלצלת#R19n | נפרדים |
| types of number/odd number | פ.ר.ד./נפרד | term | ספר_המספר_/_אליהו_מזרחי#1xQM | נפרד |
| types of number/odd number | פ.ר.ד./נפרד | term | ספר_יסודי_התבונה_ומגדל_האמונה#T8BY | הנפרד |
| types of number/odd number | פ.ר.ד./נפרד | definition | ספר_יסודי_התבונה_ומגדל_האמונה#TLt2 | the odd number is the number that is indivisible [by two]. והנפרד הוא המספר שאינו יכול להחלק בנתים |
| types of number/odd number | פ.ר.ד./נפרד | term | האנציקלופדיה_של_אבו_אלצלת#pq13 | נפרד |
| types of number/odd number | פ.ר.ד./נפרד | definition | ספר_היסודות_לאקלידס#XFQh | The odd number is that which is not divisible into two equal parts, and that which differs by a unit from an even number. המספר הנפרד הוא אשר אי אפשר שיחולק לשני חלקים שוים ואשר יתחלף הזוג באחד |
| odd number/odd-times-odd number | פ.ר.ד./נפרד הנפרד | term | אגרת_המספר#bAXG | נפרד הנפרד |
| odd number/odd-times-odd number | פ.ר.ד./נפרד הנפרד | definition | ספר_היסודות_לאקלידס#Fgjc | The number that is called an odd-times-odd number is that which is counted an odd number of times by an odd number. המספר אשר יאמר לו נפרד הנפרד הוא אשר ימנהו מספר נפרד פעמים מספרם נפרד |
| solid number/parallelepipedon number | זולת/זולתי האורך | term | האריתמטיקה_של_ניקומכוס#YQPN | המספרים הגרמים הזולתיים |
| solid number/parallelepipedon number | זולת/זולתי האורך | term | האריתמטיקה_של_ניקומכוס#Flvx | המספרים הגרמיים הזולתיים |
| solid number/parallelepipedon number | זולת/זולתי האורך | term | האריתמטיקה_של_ניקומכוס#NGVt | הזולתיים האורך |
| solid number/parallelepipedon number | זולת/זולתי האורך | term | האריתמטיקה_של_ניקומכוס#jVUX | הזולתיים באורך |
| polygonal number/pentagonal number | ח.מ.ש./מחומש | term | האנציקלופדיה_של_אבו_אלצלת#pedg | המחמשים המספריים |
| polygonal number/pentagonal number | ח.מ.ש./מחומש | term | האנציקלופדיה_של_אבו_אלצלת#HHGc | המספרים המחמשים |
| polygonal number/pentagonal number | ח.מ.ש./מחומש | term | האנציקלופדיה_של_אבו_אלצלת#M8lz | מחמשת |
| polygonal number/pentagonal number | ח.מ.ש./מחומש | term | האנציקלופדיה_של_אבו_אלצלת#r6tO | מחמש |
| polygonal number/pentagonal number | ח.מ.ש./מחומש | term | האנציקלופדיה_של_אבו_אלצלת#FMzG | מחמשים |
| polygonal number/pentagonal number | ח.מ.ש./מחומש | term | האנציקלופדיה_של_אבו_אלצלת#qbh8 | מספר מחמש |
| even number/perfect number | כ.ו.נ./מכוון | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#f3MQ | המספר המכוון |
| even number/perfect number | כ.ו.נ./מכוון | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#dhQJ | המספרים המכוונים |
| even number/perfect number | ש.ל.מ./שלם | term | מלאכת_המספר#K1qA | מספר שלם |
| even number/perfect number | ש.ל.מ./שלם | term | מלאכת_המספר#cqAo | המספרים השלמים |
| even number/perfect number | כ.ו.נ./מכוון | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#vA0c | מספר מכוון |
| even number/perfect number | כ.ו.נ./מכוון | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#kFMH | המכוון |
| even number/perfect number | ש.ל.מ./שלם | definition | ספר_דיני_ממונות#ZJl7 | Know that a [number] is called a perfect number when you sum up all the parts and they are equal to the given number. דע כי מספר שלם נקרא כי כשתקבץ כל החלקים ויהיו שוים אל המספר המונח |
| even number/perfect number | term | ספר_דיני_ממונות#xt6c | מספר שלם | |
| even number/perfect number | term | ספר_דיני_ממונות#aiWm | נומירו פירפיטו | |
| even number/perfect number | ש.ל.מ./שלם | definition | מלאכת_המספר#1ldm | The definition of a perfect number is any number that is generated from the sum of all its divisors, so that when all its divisors are summed they produce it exactly. וגדר המספר השלם הוא כל מספר שיבנה מקבוץ כל חלקיו שבשילקח כל אחד מחלקיו ויקובצו יבנו אותו לא פחות ולא יתר |
| even number/perfect number | מ.ל.א./מלא | definition | ספר_יסודי_התבונה_ומגדל_האמונה#ur7n | the perfect number is that whose parts that count it are completing it, not exceeding over it and not less than it. והמספר המלא הוא אשר חלקיו המוני' אותו ממלאי' אותו ואין עודפין עליו ולא פוחתין ממנו |
| even number/perfect number | מ.ל.א./מלא | term | ספר_יסודי_התבונה_ומגדל_האמונה#Kys0 | מלא |
| even number/perfect number | ש.ל.מ./שלם | definition | לקוטים_מספר_פראלוקא#Ur35 | The discussion on the perfect number, which is the number, which the sum of its parts is the same as the given number no more and no less; as 6, for when you sum all its parts they are the same as it, since its half is 2, its third is 2, its sixth is 1 and the total is 6, as it is; and this number is called "numero perfetto". 5 המאמר במספר שלם והוא המספר אשר חלקיו מקובצים הם כמו המספר המונח לא יוסיף ולא יגרע והוא כמו מספר ו' כי כשתקבץ כל חלקיו יעלו כמוהו כי חציו הוא ג' ושלישיתו הוא ב' ושישיתו א' ובין כלם ו' כמו שהיה וזה המספר נקרא נומירו פירפיטו |
| even number/perfect number | ש.ל.מ./שלם | definition | ספר_היסודות_לאקלידס#ongl | The perfect number is that which is equal to [the sum] of all its parts. המספר השלם הוא השוה לכל חלקיו |
| types of number/plane number | ש.ט.ח./שטוח | term | Anonymous#AcuH | מספרו השטוח |
| types of number/plane number | ש.ט.ח./שטוח | definition | ספר_יסודי_התבונה_ומגדל_האמונה#qPy4 | that whose part counts it as the multitude of another of its parts is called a plane number and it has two sides [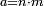 ].
ואשר חלקו מונה אותו כמנין חלק אחר מחלקיו יקרא מספר שטוח ויש לו שני צלעים ].
ואשר חלקו מונה אותו כמנין חלק אחר מחלקיו יקרא מספר שטוח ויש לו שני צלעים |
| types of number/plane number | ש.ט.ח./משוטח | term | ספר_היסודות_לאקלידס#tUaX | משוטח |
| types of number/plane number | ש.ט.ח./שטוח | term | ספר_יסודי_התבונה_ומגדל_האמונה#jFAH | מספרו השטוח |
| types of number/plane number | ש.ט.ח./משוטח | definition | ספר_היסודות_לאקלידס#ZQ6h | The plane number is the product of a number that is multiplied by another, or that which is contained by two numbers. המספר המשוטח הוא המקובץ מהכאת מספר מה שהיה באחר או אשר יקיפו בו שני מספרים |
| types of number/plane number | ש.ט.ח./שטוח | definition | Anonymous#coqV | that whose part counts it as the multitude of one of its parts is called a plane number and it has two sides [ ].
ואשר חלקו מונה אותו כמנין אחד מחלקיו נקרא מספר שטוח ויש לו שתי צלעות ].
ואשר חלקו מונה אותו כמנין אחד מחלקיו נקרא מספר שטוח ויש לו שתי צלעות |
| types of number/plane number | ש.ט.ח./מושטח | term | האנציקלופדיה_של_אבו_אלצלת#3wnz | מספר מושטח |
| types of number/plane number | ש.ט.ח./שטחי | term | האנציקלופדיה_של_אבו_אלצלת#VOd2 | שטחיי |
| types of number/plane number | ש.ט.ח./מושטח | term | האנציקלופדיה_של_אבו_אלצלת#OOPk | מושטח |
| types of number/plane number | ש.ט.ח./שטוח | term | ספר_יסודי_התבונה_ומגדל_האמונה#wLRK | המספר השטוח |
| types of number/plane number | ש.ט.ח./משוטח | term | האריתמטיקה_של_ניקומכוס#xboU | המשוטחים המספריים |
| types of number/plane number | ש.ט.ח./מושטח | term | האנציקלופדיה_של_אבו_אלצלת#ni0k | מושטחים |
| types of number/plane number | ש.ט.ח./שטחי | term | האנציקלופדיה_של_אבו_אלצלת#xBlW | מספרים שטחיים |
| plane number/polygonal number | י.ש.ר./ישר קוים | term | האריתמטיקה_של_ניקומכוס#LmEf | בעלי המספרים הישרי הקוים השוי הזויות |
| odd number/prime incomposite number | ח.ר.ש./חרש | term | אגרת_המספר#7Wz8 | '''חרשים''' |
| odd number/prime incomposite number | פ.ר.ד./נפרד ראשון | term | האריתמטיקה_של_ניקומכוס#rgv9 | הנפרדים הראשונים הבלתי מורכבים |
| odd number/prime incomposite number | ר.כ.ב./בלתי מורכב | term | ספר_החשבון_לאל_חצאר#D1DR | מספר בלתי מורכב |
| odd number/prime incomposite number | פ.ר.ד./נפרד ראשון | term | האריתמטיקה_של_ניקומכוס#ZBCw | מספר ראשון הבלתי מורכב |
| odd number/prime incomposite number | ר.א.ש./ראשון | term | מלאכת_המספר#atVy | מספר ראשון |
| odd number/prime incomposite number | ר.כ.ב./בלתי מורכב | term | ספר_החשבון_לאל_חצאר#S3UA | בלתי מורכב |
| odd number/prime incomposite number | ח.ר.ש./חרש | term | אגרת_המספר#gQUo | המספרים החרשים |
| odd number/prime incomposite number | ר.א.ש./ראשון | definition | מלאכת_המספר#cpKh | The definition of a prime number is every number that is not a result of a product of any number.
וגדר המספר |
| odd number/prime incomposite number | ח.ר.ש./חרש | term | אגרת_המספר#1NVL | חרש |
| odd number/prime incomposite number | פ.ר.ד./נפרד ראשון | term | האריתמטיקה_של_ניקומכוס#Kz95 | המספר הנפרד הראשון הבלתי מורכב |
| odd number/prime incomposite number | ב.ד.ד./בודד | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#oDJq | בודידי |
| odd number/prime incomposite number | ר.א.ש./ראשון | term | אגרת_המספר#PonV | ראשון |
| odd number/prime incomposite number | ב.ד.ד./בודד | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#dABm | בודידים |
| odd number/prime incomposite number | פ.ר.ד./נפרד ראשון | term | האריתמטיקה_של_ניקומכוס#Wnyo | הנפרד הראשון הבלתי מורכב |
| odd number/prime incomposite number | ב.ד.ד./בודד | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#VJry | מספרים בודדים |
| odd number/prime incomposite number | ב.ד.ד./בודד | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#jpir | בודד |
| odd number/prime incomposite number | ר.א.ש./ראשון | definition | אגרת_המספר#nfhL | there are odd numbers that are divisible only by one, such as 5, 7, 11, 13, they are numerous and they are called prime numbers, for they are divisible only by one, which is first of all the numbers. ויש נפרדים שלא יתחלקו כלל כי אם לאחד כמו ה' וז' וי"א וי"ג והם רבים ואלה יקראו מספרים ראשו' בעבור כי לא יחלקו כי אם על האחד שהוא ראשון לכל המספרים |
| odd number/prime incomposite number | פ.ר.ד./נפרד ראשון | definition | האריתמטיקה_של_ניקומכוס#1noC | The first type of odd numbers is incomposite, that has no divisor but the one, such as: 3; 5; 7; 11; 13; 17. These numbers and others like them have no divisors and no fractional parts but the one which [are a part whose name] is derived from the whole number itself. המספר הנפרד הראשון שהוא בלתי מורכב אשר אין לו חלק ימנהו בלתי האחד כמו ג' ה' ז' י"א י"ג י"ז אלו המספרים ומה שימצא כמותם לא ימצא להם מספר ימנם ואין להם חלק כלל ימנם בלתי האחדים שנגזר להם חלק מכלל המספר |
| odd number/prime incomposite number | ב.ד.ד./בודד | definition | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#334C | The meaning of a prime number is that it has no divisors other than one. וטעם בודד שאין לו חלקים [אלא] אחד |
| odd number/prime incomposite number | ר.א.ש./ראשון | term | ספר_החשבון_לאל_חצאר#HpeJ | ראשון |
| odd number/prime incomposite number | א.ר.כ./ארוך | term | ספר_יסודי_התבונה_ומגדל_האמונה#7iYT | המספר הארוך |
| odd number/prime incomposite number | פ.ש.ט./פשוט | term | בר_נותן_טעם#LVhT | מספר פשוט |
| odd number/prime incomposite number | פ.ש.ט./פשוט | term | בר_נותן_טעם#2DxW | פשוט |
| odd number/prime incomposite number | ב.ד.ד./בודד | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#zRu5 | הבודדים |
| odd number/prime incomposite number | פ.ש.ט./פשוט | term | בר_נותן_טעם#O61W | פשוטים |
| odd number/prime incomposite number | א.ר.כ./ארוך | definition | Anonymous#cltb | every number that you count by one alone is called a prime number [lit. lengthy number  ], since it has no other side but one, which is not a number.
וכל מספר שאתה מונה אותו באחד לבדו נקרא מספר ארוך מפני שאין לו צלע שני כי אם האחד שאינו מספר ], since it has no other side but one, which is not a number.
וכל מספר שאתה מונה אותו באחד לבדו נקרא מספר ארוך מפני שאין לו צלע שני כי אם האחד שאינו מספר |
| odd number/prime incomposite number | א.ר.כ./ארוך | definition | ספר_יסודי_התבונה_ומגדל_האמונה#KaDz | every number that you count by one alone is called a prime number [lit. lengthy number 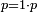 ], since it is the side of itself, and it has no other side but one, which is not a number.
וכל מספר שאתה מונה אותו באחד לבדו נקרא מספר ארוך מפני שהוא צלע עצמו ואין לו צלע שני כי אם האחד שאינו מספר ], since it is the side of itself, and it has no other side but one, which is not a number.
וכל מספר שאתה מונה אותו באחד לבדו נקרא מספר ארוך מפני שהוא צלע עצמו ואין לו צלע שני כי אם האחד שאינו מספר |
| odd number/prime incomposite number | פ.ר.ד./נפרד ראשון | term | האריתמטיקה_של_ניקומכוס#V8xR | הנפרד הראשון |
| odd number/prime incomposite number | פ.ר.ד./נפרד ראשון | definition | ספר_יסודי_התבונה_ומגדל_האמונה#nwIA | the first odd [= prime] is every odd number that only one counts it, no number is found that completes its number other than one alone. הנפרד הראשון הוא כל נפרד שהאחד לבדו מונה אותו ואין אתה מוצא מספר שיהיה משלים את מנינו בלתי האחד לבדו |
| odd number/prime incomposite number | פ.ר.ד./נפרד ראשון | term | ספר_יסודי_התבונה_ומגדל_האמונה#KEfj | נפרד ראשון |
| odd number/prime incomposite number | ר.א.ש./ראשון | term | ספר_המספר_/_אליהו_מזרחי#FGBj | ראשון |
| odd number/prime incomposite number | ר.א.ש./ראשון | definition | ספר_היסודות_לאקלידס#5Z33 | The number that is called a prime number is that which is counted by a unit alone. המספר אשר יקרא ראשון הוא אשר ישיגהו המנין באחד לבד |
| odd number/prime incomposite number | פ.ר.ד./נפרד ראשון | term | האריתמטיקה_של_ניקומכוס#mL7w | המספר הנפרד הראשון |
| ratio/proportion | ע.ר.כ./ערוך | term | ספר_אגריס#I9RW | ערוך |
| ratio/proportion | ע.ר.כ./ערך | term | קצור_המספר#zDSj | ערכין |
| ratio/proportion | ע.ר.כ./ערך | term | קצור_המספר#t7Oi | ערכים |
| ratio/proportion | מ.צ.ע./אמצעי | term | האריתמטיקה_של_ניקומכוס#Dn8O | אמצעיים |
| ratio/proportion | מ.צ.ע./אמצעי | term | האריתמטיקה_של_ניקומכוס#Tfg6 | האמצעי |
| ratio/proportion | י.ח.ס./התיחסות | term | האנציקלופדיה_של_אבו_אלצלת#DoDM | התיחסות |
| proportion/proportional | ס.פ.ק./מספיק | term | ספר_מעשה_חושב#LZET | מספיקות |
| proportion/proportional | י.ח.ס./מתיחס | term | ספר_מעשה_חושב#HBg7 | מתיחסות |
| proportion/proportional | י.ח.ס./מתיחס | term | קצור_המספר#OPt6 | מספרים מתייחסים |
| proportion/proportional | proportional hexad | מלאכת_המספר#AsGv | ו' מספרי' מתייחסים | |
| proportion/proportional | proportional hexad | מלאכת_המספר#hpBk | ששה המספרי' המתייחסי' | |
| proportion/proportional | ע.ר.כ./נערך | term | קצור_המספר#x9VZ | מספרים נערכים |
| proportion/proportional | ע.ר.כ./נערך | term | קצור_המספר#uBgv | הנערכים |
| proportion/proportional | י.ח.ס./יחסי | term | ספר_דיני_ממונות#UDM7 | מספר יחסיי |
| proportion/proportional | י.ח.ס./מתיחס | term | ספר_מעשה_חושב#1BuF | מספרים מתיחסים |
| proportion/proportional | י.ח.ס./מתיחס | term | ספר_דיני_ממונות#VUeX | מספרים מתיחסים |
| proportion/proportional | י.ח.ס./מתיחס | term | ספר_ג'יבלי_אלמוקבאלא#lK1I | מספרים מתיחסים |
| proportion/proportional | י.ח.ס./מתיחס | term | ספר_דיני_ממונות#Qn93 | מתיחסים |
| proportion/proportional | י.ח.ס./יחסי | term | ספר_דיני_ממונות#jjwV | מספרים יחסיים |
| proportion/proportional | term | ספר_דיני_ממונות#DhLM | נומירו פרופורציאונלי | |
| proportion/proportional | י.ח.ס./יחסי | term | ספר_דיני_ממונות#2xtB | מספר יחסיי |
| proportion/proportional | נ.ק.ש./נקוש | term | ספר_יסודי_התבונה_ומגדל_האמונה#iOWD | נקוש אל |
| proportion/proportional | ע.ר.כ./מוערך | term | Anonymous#8IsM | מוערכים |
| proportion/proportional | ח.ב.ר./חבר | definition | ספר_יסודי_התבונה_ומגדל_האמונה#69le | The proportional numbers are called “companions”. והמספרים הנקושים זה לזה נקראים חברים |
| proportion/proportional | י.ח.ס./מתיחס | term | ספר_מעשה_חושב#ZWw5 | מתיחסים |
| proportion/proportional | י.ח.ס./מתיחס | term | חשבון_השטחים#IXmL | מתיחסי' |
| proportion/proportional | י.ח.ס./מתיחס | definition | ספר_היסודות_לאקלידס#ekBL | The proportional numbers are those of which the first is the same part, or the same parts, of the second, as the third is of the fourth. והמספרים המתיחסים הם אשר יהיה הראשון מן השני והשלישי מן הרביעי חלק אחד בעצמו או חלקים אחדים בעינם |
| proportion/proportional | י.ח.ס./מתיחס | term | ספר_האלזיברא#N4p8 | שעורים מתיחסים |
| proportion/proportional | proportional hexad | מלאכת_המספר#HGsA | יחס הו' מספרים המתייחסים | |
| proportion/proportional | proportional hexad | מלאכת_המספר#NwyY | יחס הששה מספרי' המתייחסים | |
| rule of three/proportional triad | term | תחבולות_המספר#Q1PW | שלשה מספרים מתיחסים | |
| rule of three/proportional triad | term | חשבון_השטחים#bD7u | שלשה מספרים מתייחסים | |
| rule of three/proportional triad | term | מלאכת_המספר#NDBY | ג' מספרי' מתייחסים | |
| solid number/pyramidal number | ז.נ.ב./מזדנב | triangular | האריתמטיקה_של_ניקומכוס#OD7J | הגרמיים המזדנבי' המשולשים |
| solid number/pyramidal number | ח.ד.ד./מחודד | pentagonal | האריתמטיקה_של_ניקומכוס#eLrX | המחומש המחודד |
| solid number/pyramidal number | ח.ד.ד./מחודד | term | האנציקלופדיה_של_אבו_אלצלת#CdXq | מחדדים |
| solid number/pyramidal number | ז.נ.ב./מזדנב | term | האריתמטיקה_של_ניקומכוס#lpSn | מזדנבים |
| solid number/pyramidal number | ח.ד.ד./מחודד | square | האריתמטיקה_של_ניקומכוס#4Db7 | הגרמים המרובעים המחודדים |
| solid number/pyramidal number | ז.נ.ב./מזדנב | square | האריתמטיקה_של_ניקומכוס#weJa | מרובע מזדנב |
| solid number/pyramidal number | ז.נ.ב./מזדנב | square | האריתמטיקה_של_ניקומכוס#umoL | המרובעים המזדנבים |
| solid number/pyramidal number | ח.ד.ד./מחודד | triangular | האריתמטיקה_של_ניקומכוס#gfTU | גרם המחודד המשולש |
| solid number/pyramidal number | ז.נ.ב./מזדנב | triangular | האריתמטיקה_של_ניקומכוס#nwxw | המשלש המזדנב |
| solid number/pyramidal number | ח.ד.ד./מחודד | triangular | האריתמטיקה_של_ניקומכוס#XEke | גוף מחודד משולש |
| relative quantity/ratio | י.ח.ס./יחס | term | קצור_המספר#GKJV | יחס |
| relative quantity/ratio | י.ח.ס./יחס | term | חשבון_השטחים#oiQL | יחס |
| relative quantity/ratio | י.ח.ס./יחס | term | תחבולות_המספר#Fyp1 | יחס |
| relative quantity/ratio | י.ח.ס./יחס | term | ספר_האלזיברא#Eve2 | יחס |
| relative quantity/ratio | ע.ר.כ./ערך | term | ספר_האלזיברא#q4jn | הערך |
| relative quantity/ratio | ע.ר.כ./ערך | term | קצור_המספר#Uux7 | ערך |
| relative quantity/ratio | ע.ר.כ./ערך | term | קצור_המספר#T6wQ | ערך |
| relative quantity/ratio | י.ח.ס./יחס | term | קצור_המספר#PVzl | יחס |
| relative quantity/ratio | נ.ק.ש./הקשה | term | ספר_יסודי_התבונה_ומגדל_האמונה#WIT9 | הקשה |
| relative quantity/ratio | נ.ק.ש./הקשה | term | ספר_יסודי_התבונה_ומגדל_האמונה#0s9E | הקשות |
| relative quantity/ratio | נ.ק.ש./הקשה | term | Anonymous#6igK | הקשה |
| relative quantity/ratio | מ.ד.ד./מדה | term | משנת_המדות#qHby | מדת |
| relative quantity/ratio | ע.ר.כ./ערך | term | ספר_אגריס#TXuZ | ערך |
| relative quantity/ratio | י.ח.ס./יחס | term | ספר_מעשה_חושב#hqJA | יחס |
| relative quantity/ratio | ק.צ.ב./קצב | definition | ספר_יסודי_התבונה_ומגדל_האמונה#QvlB | extracting a ratio of a number to a number is that you divide a smaller number by a greater number. והוצאת קצב מנין מן מנין כשאתה מחלק מנין מעט אל רב |
| relative quantity/ratio | ק.צ.ב./קצב | term | ספר_יסודי_התבונה_ומגדל_האמונה#b4Ag | קצב |
| composite number/relatively composite | ש.ת.פ./משותף | definition | ספר_היסודות_לאקלידס#XAQP | The numbers that are relatively composite are those which are counted by a number. המספרים המשותפים הם אשר ימנה אותם מספר אחד |
| types of number/relatively prime | נ.כ.ר./נכרי | definition | ספר_יסודי_התבונה_ומגדל_האמונה#L9Id | Every two numbers that have no number that counts them except one, which is not a number, are called co-prime [lit. strangers] numbers. וכל שני מספרים שאין להם מספר שיהיה מונה אותם זולתי האחד שאינו מספר נקראים מספרים נכריים זה מזה |
| types of number/relatively prime | term | ספר_המספר_/_אליהו_מזרחי#QJHO | ראשון בערך | |
| types of number/relatively prime | ב.ד.ל./מובדל | definition | ספר_היסודות_לאקלידס#QkYH | The numbers that are relatively prime are those which are counted by a unit alone as a common measure. המספרים המובדלים הם אשר אמנם לא ימנם מספר משותף כי אם אחד לבדו |
| types of number/relatively prime | ר.א.ש./ראשון | term | האנציקלופדיה_של_אבו_אלצלת#Ie1G | ראשון בהקש אל |
| types of number/relatively prime | ר.א.ש./ראשון | term | האנציקלופדיה_של_אבו_אלצלת#a04n | ראשון אצל זולתו |
| types of number/relatively prime | ר.א.ש./ראשון | term | האנציקלופדיה_של_אבו_אלצלת#fysN | ראשון בהקש אל זולתו |
| types of number/relatively prime | פ.ר.ד./מתפרד | term | אגרת_המספר#e4Hi | מתפרדים |
| types of number/relatively prime | פ.ר.ד./מתפרד | term | אגרת_המספר#jqRk | מתפרד |
| theoretical arithmetic/relative quantity | צ.ר.פ./מצטרף | term | האריתמטיקה_של_ניקומכוס#mNP3 | הכמה המצטרף |
| theoretical arithmetic/relative quantity | צ.ר.פ./מצטרף | term | האריתמטיקה_של_ניקומכוס#HKl1 | כמות המצטרף |
| theoretical arithmetic/relative quantity | צ.ר.פ./צרופי | term | האריתמטיקה_של_ניקומכוס#k4hQ | הכמה הצירופיי |
| theoretical arithmetic/relative quantity | צ.ר.פ./צרופי | definition | ספר_המספר_/_אליהו_מזרחי#q4kw | The relative quantity is a quantity created from two measures, which is the number of times that the one counts the other. והכמות הצרופיי הוא הכמות המתחדשת מהשני שעורים שהוא שעור הפעמים אשר ימנה אחד את האחר |
| proportion/rule of three | ⅔÷⅗=¼÷X | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#dPRr | Question: if 2-thirds equals 3-fifths, I ask: how much is a quarter equal to?
: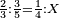 שאלה אם ב' שלישיות שוה ג' חמשיו[ת] שאלתי רביעית מה יהיה שוה
שאלה אם ב' שלישיות שוה ג' חמשיו[ת] שאלתי רביעית מה יהיה שוה | |
| proportion/rule of three | 3⅓÷4¼=5⅕÷X | ספר_חשבון#JsBk | If one says: if 3 and a third equals 4 and a quarter, how much is 5 and a fifth equal to?
: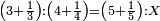 אם יאמר אדם אם ג' ושליש שוים ד' ורביע ה' [ו]חומש כמה שוים
אם יאמר אדם אם ג' ושליש שוים ד' ורביע ה' [ו]חומש כמה שוים | |
| proportion/rule of three | term | ספר_דיני_ממונות#A8te | ריגולא דיטרי דנפיצה | |
| proportion/rule of three | ד.ר.כ./דרך השלשה | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#P157 | דרך השלשה |
| proportion/rule of three | 3⅓÷4¼=5⅕÷X | ספר_הכללים_במספר#Epgk | If three and one third equal four and a quarter, how much are five and one fifth equal?
: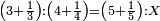 נז אם ג' ושליש שוים ד' ורביע ה' וחומש כמה שוים
נז אם ג' ושליש שוים ד' ורביע ה' וחומש כמה שוים | |
| proportion/rule of three | ד.ר.כ./דרך השלשה | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#YDuj | דרך השלושה |
| proportion/rule of three | ⅓÷¼=⅕÷X | ספר_הכללים_במספר#UdQe | 49) If one third equals a quarter, how much is one fifth equal?
: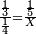 מט אם שליש שוה רביע חומש כמה שוה
מט אם שליש שוה רביע חומש כמה שוה | |
| proportion/rule of three | י.ח.ס./דרך היחס | term | מלאכת_המספר#TciG | דרכי היחסים |
| proportion/rule of three | י.ח.ס./דרך היחס | term | מלאכת_המספר#W6ts | דרך היחסים |
| proportion/rule of three | י.ח.ס./התיחסות ג' מספרים | term | מלאכת_המספר#7OG3 | התיחסות הג' מספרי' |
| proportion/rule of three | (⅖·¾)÷(³/₇·⅚)=(⅘·⅝)÷X | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#PLEV | Question: if 2-fifths of 3-quarters equals 3-sevenths of 5-sixths, I ask: how much is a 4-fifths of 5-eighths equal to?
: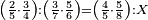 שאלה אחרת אם ב' חמשיות מג' רביעיות שוה ג' שביעיות מה' שישיות שאלתי ד' חמשיות מה' שמיניות מה יהיה שוה
שאלה אחרת אם ב' חמשיות מג' רביעיות שוה ג' שביעיות מה' שישיות שאלתי ד' חמשיות מה' שמיניות מה יהיה שוה | |
| proportion/rule of three | 9÷⅔=8÷X | מלאכת_המספר#9OVO | Another example for further explanation: if 9 are equal 2-thirds, how much are 8 equal to?
: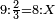 ומשל אחר להוסיף ביאור אם ט' שוים ב' שלישיות כמה שוים ח'
ומשל אחר להוסיף ביאור אם ט' שוים ב' שלישיות כמה שוים ח' | |
| proportion/rule of three | 6÷40½=⅔÷X | מלאכת_המספר#quct | We say: if 6 are equal 40 and a half, how much are 2-thirds equal to?
: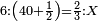 ונאמ' אם ו' שוים מ' וחצי כמה שוים ב' שלישיות
ונאמ' אם ו' שוים מ' וחצי כמה שוים ב' שלישיות | |
| proportion/rule of three | ³/₇÷⁸/₉=⅘÷X | בר_נותן_טעם#FSi7 | I.e. in our example, when we say: if 3-sevenths equal 8-ninths, how much are 4-fifths equal?
: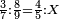 פי' במשלנו כאשר אמרנו אם ג' שביעיות שוים ח' תשיעיות ד' חמישיות כמה הם שוים
פי' במשלנו כאשר אמרנו אם ג' שביעיות שוים ח' תשיעיות ד' חמישיות כמה הם שוים | |
| proportion/rule of three | 2÷3=5÷X | מלאכת_המספר#qiNw | Example: if 2 is equal to 3, how much is 5 equal?
: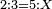 המשל אם ב' שוים ג' כמה ישוו ה'
המשל אם ב' שוים ג' כמה ישוו ה' | |
| proportion/rule of three | 5÷7½=2÷X | מלאכת_המספר#oHFK | Example: if 5 is equal to 7 and a half, how much is 2 equal?
: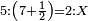 המשל אם [הה' ז' וחצי הב' כמה ישוו]marg.
המשל אם [הה' ז' וחצי הב' כמה ישוו]marg. | |
| proportion/rule of three | ⅔÷7⁴/₉=⁴/₁₃÷X | מלאכת_המספר#YdUe | Example: if we wish to know if 2-thirds are equal to 7 integers and 4-ninths, how much are 4 and 4-thirteenths equal to?
: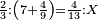 המשל אם נרצה לדעת אם ב' שלישיות שוים ז' שלימי' וד' תשיעיות כמה שוים ד' וד' שלשה עשיריות
המשל אם נרצה לדעת אם ב' שלישיות שוים ז' שלימי' וד' תשיעיות כמה שוים ד' וד' שלשה עשיריות | |
| proportion/rule of three | ⅔÷4½=6÷X | מלאכת_המספר#tHLR | Another example of this category: if two-thirds are equal to 4 and a half, how much is 6 equal to?
: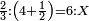 ומשל אחר לזה המין אם שני שלישיות שוות ד' וחצי כמה שוים ו'
ומשל אחר לזה המין אם שני שלישיות שוות ד' וחצי כמה שוים ו' | |
| proportion/rule of three | ⅔÷4½=6÷X | מלאכת_המספר#jTaL | If 2-thirds are equal 4 and a half, how much are six equal to?
: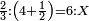 והוא זה אם ב' שלישיות שוים ד' וחצי כמה שוים ששה
והוא זה אם ב' שלישיות שוים ד' וחצי כמה שוים ששה | |
| proportion/rule of three | 9÷⅔=8÷X | מלאכת_המספר#H80d | Example: if 9 are equal 2-thirds, to how much are 8 equal?
::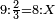 המשל אם ט' שוות ב' שלישיות כמה שוים ח'
המשל אם ט' שוות ב' שלישיות כמה שוים ח' | |
| proportion/rule of three | ⅔÷4½=6÷X | מלאכת_המספר#gfiJ | Example: if 2-thirds are equal 4 and a half, to how much are six equal?
::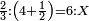 המשל אם ב' שלישיות שוות ד' וחצי מה שוים ששה
המשל אם ב' שלישיות שוות ד' וחצי מה שוים ששה | |
| proportion/rule of three | 1÷⅘=2½÷X | מלאכת_המספר#cjqZ | Example: if one is equal 4-fifths, to how much are two and a half equal?
::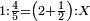 המשל אם אחד שוה ד' חמישיות כמה שוים שנים וחצי
המשל אם אחד שוה ד' חמישיות כמה שוים שנים וחצי | |
| proportion/rule of three | term | מלאכת_המספר#pb1F | יחס הד' מספרים המתייחסים | |
| proportion/rule of three | ⅔÷8=9÷X | מלאכת_המספר#mSGd | Example: if 2-thirds are equal to 8, how much is 9 equal to?
: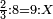 המשל אם ב' שלישיות שוות ח' כמה שווים ט'
המשל אם ב' שלישיות שוות ח' כמה שווים ט' | |
| proportion/rule of three | י.ח.ס./דרך היחס | term | מלאכת_המספר#uRJ7 | דרכי היחסים |
| proportion/rule of three | term | מלאכת_המספר#c9ev | דרך הרביעי הד' מספרי' המתיחסים | |
| proportion/rule of three | ⅔÷8=9÷X | מלאכת_המספר#bXQ4 | Example: if 2-thirds are equal 8, to how much are nine equal?
::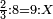 המשל אם ב' שלישיות שוות ח' כמה שוים תשעה
המשל אם ב' שלישיות שוות ח' כמה שוים תשעה | |
| proportion/rule of three | 5⅔÷6¾=8⁵/₁₂÷X | מלאכת_המספר#dWcW | Example: if 5 and 2-thirds are equal to 6 and 3-quarters, how much are 8 and 5-twelfths equal to?
: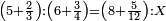 המשל אם
המשל אם | |
| proportion/rule of three | 5²/₇÷4=20÷X | מלאכת_המספר#r5xI | Example: if 5 and 2-sevenths are equal to 4, how much are twenty equal to?
: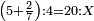 המשל אם ה' וב' שביעיות שוות ד' כמה שוים עשרי'
המשל אם ה' וב' שביעיות שוות ד' כמה שוים עשרי' | |
| proportion/rule of three | 5⅔÷6¾=8⁵/₁₂÷X | מלאכת_המספר#rzvu | Example: if 5 and 2-thirds are equal 6 and 3-quarters, to how much are 8 and 5 parts of 12 equal?
::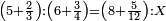 המשל אם ה' וב' שלישיות שוות ו' וג' רביעיות כמה שוים ח' וה' חלקי' מי"ב
המשל אם ה' וב' שלישיות שוות ו' וג' רביעיות כמה שוים ח' וה' חלקי' מי"ב | |
| proportion/rule of three | ⅔÷⁴/₉=⁴/₁₃÷X | מלאכת_המספר#fShM | Example: if 2-thirds are equal 4-ninths, to how much are 4 parts of 13 equal?
: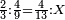 המשל אם ב' שלישיות שוות ד' תשיעיות כמה שוים ד' חלקי' מי"ג
המשל אם ב' שלישיות שוות ד' תשיעיות כמה שוים ד' חלקי' מי"ג | |
| proportion/rule of three | 20÷15⁵/₃₇=5²/₇÷X | מלאכת_המספר#GdAo | Example: if 20 is equal to 15 and 5 parts of 37, how much are 5 and 2-sevenths equal to?
: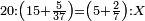 המשל אם כ' שוים ט"ו וה' חלקים מל"ז כמה שוים ה' וב' שביעיות
המשל אם כ' שוים ט"ו וה' חלקים מל"ז כמה שוים ה' וב' שביעיות | |
| proportion/rule of three | ³/₇÷⁸/₉=⅘÷X | בר_נותן_טעם#VvVa | Example: we wish to know, if 3-sevenths are equal to 8-ninths, how much are 4-fifths equal to?
: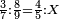 המשל רצינו לידע אם ג' שביעיות שוים ח' תשיעיות ד' חמישיות כמה הם שוות
המשל רצינו לידע אם ג' שביעיות שוים ח' תשיעיות ד' חמישיות כמה הם שוות | |
| proportion/rule of three | ¾·(3-¼)÷⅘·(5-⅕)=⅚·(6-⅙)÷X | בר_נותן_טעם#ELCt | Example: if 3-quarters of 3 integers minus one-quarter are equal to 4-fifths of 5 integers minus one-fifth, how much five-sixths of 6 integers minus one-sixth are equal?
:![\scriptstyle\left[\frac{3}{4}\sdot\left(3-\frac{1}{4}\right)\right]:\left[\frac{4}{5}\sdot\left(5-\frac{1}{5}\right)\right]=\left[\frac{5}{6}\sdot\left(6-\frac{1}{6}\right)\right]:X](/mediawiki/images/math/0/6/b/06b938d3936d7baec8744616f4c89a6b.png) המשל אם ג' רביעיות מג' שלמים פחות רביע שלם שוים ד' חמישיות מה' שלימים פחות חומש שלם חמש שישיות מו' שלימים פחות שישית שלם כמה שוים
המשל אם ג' רביעיות מג' שלמים פחות רביע שלם שוים ד' חמישיות מה' שלימים פחות חומש שלם חמש שישיות מו' שלימים פחות שישית שלם כמה שוים | |
| proportion/rule of three | 3÷7=5÷X | בר_נותן_טעם#Mvdt | Example: if we say: the ratio that 3 is to 7 - to whom does 5 have this ratio?
::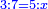 המשל אם אמרנו הערך שיש לג' אצל הז' לה' אצל מי יש לו זה הערך בעצמו
המשל אם אמרנו הערך שיש לג' אצל הז' לה' אצל מי יש לו זה הערך בעצמו | |
| proportion/rule of three | 2÷4=4÷8 | בר_נותן_טעם#wusI | As we say: the ratio of 2 to 4 is as the ratio of 4 to 8
: הוא כאומרנו הערך אשר לב' אצל הד' כערך ד' אצל ח'
הוא כאומרנו הערך אשר לב' אצל הד' כערך ד' אצל ח' | |
| proportion/rule of three | 3÷7=X÷11⅔ | בר_נותן_טעם#SYHL | If it is said: the ratio that 3 is to 7 - to 11 and 2-thirds who has this ratio?
::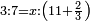 ואם אמרו הערך אשר לג' אצל ז' אצל י"א וב' שלישיות למי יש לו זה הערך
ואם אמרו הערך אשר לג' אצל ז' אצל י"א וב' שלישיות למי יש לו זה הערך | |
| proportion/rule of three | 4÷6=8÷12 | קצור_המספר#N6PS | As if you say that the ratio of 4 to 6 is as the ratio of 8 to 12.
::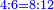 כאלו תאמר {{#annot:term|1280,482|T6wQ}}ערך{{#annotend:T6wQ}} הד' אל הו' הוא כערך הח' אל הי"ב
כאלו תאמר {{#annot:term|1280,482|T6wQ}}ערך{{#annotend:T6wQ}} הד' אל הו' הוא כערך הח' אל הי"ב | |
| proportion/rule of three | 5÷7=10÷X | בר_נותן_טעם#rfV6 | Example: For the ratio that 5 is to 7, 10 has the same ratio to which number?
::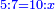 המשל הערך שיש לה' אצל ז' אצל מי יש לי' זה הערך
המשל הערך שיש לה' אצל ז' אצל מי יש לי' זה הערך | |
| proportion/rule of three | ⅓÷¼=⅕÷X | ספר_חשבון#D0xp | When a man says: if a third is worth a quarter, how much is a fifth worth according to this calculation?
: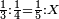 אם יאמר אדם אם שליש שוה רביע החומש כפי זה החשבון כמה שוה
אם יאמר אדם אם שליש שוה רביע החומש כפי זה החשבון כמה שוה | |
| proportion/rule of three | 4÷6=6÷9 | קצור_המספר#Zvs9 | As if you say that the ratio of 4 to 6 is as the ratio of 6 to 9.
:: כאלו תאמר כי ערך הד' אל הו' הוא כערך הו' אל הט'
כאלו תאמר כי ערך הד' אל הו' הוא כערך הו' אל הט' | |
| proportion/rule of three | term | ספר_דיני_ממונות#fJ3e | ריגולא דיטרי | |
| proportion/rule of three | 20÷15⁵/₃₇=5²/₇÷X | מלאכת_המספר#iLX1 | Example: if 20 are equal to 15 and 5 parts of 37, how much are 5 and 2-sevenths equal to?
: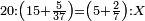 המשל אם כ' שוים ט"ו וה' חלקי' מל"ז כמה שוים ה' וב' שביעיות
המשל אם כ' שוים ט"ו וה' חלקי' מל"ז כמה שוים ה' וב' שביעיות | |
| solid number/scalene number | סולמי | term | האריתמטיקה_של_ניקומכוס#m7iX | סולמיי |
| solid number/scalene number | סולמי | term | האריתמטיקה_של_ניקומכוס#4Hc8 | המספרים הגרמיים הסולמיים |
| solid number/scalene number | סולמי | term | האריתמטיקה_של_ניקומכוס#wKV4 | מספרי הגרמים הסולמיים |
| solid number/scalene number | ח.ל.פ./מתחלף צלעות | term | האריתמטיקה_של_ניקומכוס#NLH5 | המתחלפי הצלעות |
| odd number/sieve | נ.פ.י./נפה | term | אגרת_המספר#YNqm | נפה |
| odd number/sieve | כ.ב.ר./מכבר | term | האריתמטיקה_של_ניקומכוס#TOZ3 | מכבר |
| odd number/sieve | כ.ב.ר./מכבר | term | האריתמטיקה_של_ניקומכוס#xTKM | מכבר |
| odd number/sieve | נ.פ.י./נפה | definition | אגרת_המספר#OERC | the matter of this procedure is called sieve, since the composite and prime odd numbers are written mixed together and through this method they are sieved and the prime and composite numbers are known, as the semolina is sorted from the chaff. פי' קריאת ענין זה המעשה נפה בעבור שיכתבו המספרים הנפרדים מורכבים וחרשים יחד מעורבים ובזה הדרך ינופה ויודעו החרשי' והמורכבים כמו שבנפה יודע הסולת הפסולת |
| types of number/solid number | ג.ש.מ./מוגשם | term | האריתמטיקה_של_ניקומכוס#wtsx | המוגשמים |
| types of number/solid number | ג.ר.מ./גרמי | term | האריתמטיקה_של_ניקומכוס#VXpF | מספר גרמיי |
| types of number/solid number | ג.ש.מ./גשמי | term | האנציקלופדיה_של_אבו_אלצלת#R25D | מספרים גשמיים |
| types of number/solid number | ג.ש.מ./מוגשם | definition | ספר_המספר_/_אליהו_מזרחי#tGWU | Solid numbers are the numbers whose length, width, and depth are unequal, either all of them or some of them. ובמוגשמים המספרים שארכם ורחבם ועמקם בלתי שוים אם כלם ואם קצתם |
| types of number/solid number | ג.ר.מ./גרמי | term | האריתמטיקה_של_ניקומכוס#mazQ | מספרים הגרמיים |
| types of number/solid number | ג.ש.מ./מוגשם | term | האנציקלופדיה_של_אבו_אלצלת#0lbJ | מגשם |
| types of number/solid number | ג.ש.מ./מוגשם | definition | ספר_היסודות_לאקלידס#Q65J | The solid number is the product of a number that is multiplied by the product of two numbers that are multiplied one by the other. והמספר המוגשם הוא המקובץ מהכאת מספר במה שיתקבץ מהכאת שני מספרים אחד באחר |
| types of number/solid number | ג.ר.מ./גרמי | term | האריתמטיקה_של_ניקומכוס#Oja6 | המספרים הגרמיים |
| types of number/solid number | ג.ש.מ./מוגשם | term | האנציקלופדיה_של_אבו_אלצלת#e9bf | מספרים המוגשמים |
| types of number/solid number | ג.ש.מ./מוגשם | term | האנציקלופדיה_של_אבו_אלצלת#lTlq | מוגשמים |
| cubic number/spherical number | כ.ד.ר./כדורי | term | האריתמטיקה_של_ניקומכוס#hHXI | המספרים הכדוריים |
| cubic number/spherical number | כ.ד.ר./כדורי | term | האריתמטיקה_של_ניקומכוס#5Dmo | מספר כדורי |
| cubic number/spherical number | כ.ד.ר./כדורי | term | האריתמטיקה_של_ניקומכוס#gdXU | |
| plane number/square number | הוא הוא | term | האריתמטיקה_של_ניקומכוס#Vzbi | ההוא הוא |
| plane number/square number | ג.ד.ר./נגדר | term | עיר_סיחון#5yXg | נגדרת |
| plane number/square number | הוי | term | ספר_המספר_/_אליהו_מזרחי#bYM1 | ההוהויים |
| plane number/square number | הוי | term | ספר_המספר_/_אליהו_מזרחי#wSYa | ההויים |
| plane number/square number | ג.ד.ר./נגדר | definition | ספר_המספר_/_אליהו_מזרחי#LOOe | The number that has a root is the number that is formed from a product of a number by itself, these are called "same" numbers, because their length equals their width. והנגדר הוא המספר ההווה מהכאת מספר אחד בעצמו והם הנקראים המספרים ההוהויים לפי שארכם שוה לרחבם |
| plane number/square number | פ.ק.ח./פקח | term | עיר_סיחון#3xCB | מספר פקח |
| plane number/square number | הוי | definition | ספר_המספר_/_אליהו_מזרחי#25sh | It has already been clarified in the second section of the Book on Arithmetic by Nicomachus of Gerasa that the same numbers, which are the square numbers, are generated by the increment of the natural odd numbers.
: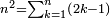 והוא שכבר התבאר בספר הארתימטיקא לניקומכוש הגהרשיני במאמר השני שהמספרים ההויים והם המספרים המרובעים הנה צמיחתם תהיה בתוספת הנפרדים הטבעיים קצתם על קצת
והוא שכבר התבאר בספר הארתימטיקא לניקומכוש הגהרשיני במאמר השני שהמספרים ההויים והם המספרים המרובעים הנה צמיחתם תהיה בתוספת הנפרדים הטבעיים קצתם על קצת |
| plane number/square number | ר.ב.ע./מרובע | definition | ספר_היסודות_לאקלידס#Os89 | The square number is the product of a number that is multiplied by its similar, or that which is contained by two equal numbers. המספר המרובע הוא המקובץ מהכאת מספר בדומה לו או הוא אשר יקיפו בו שני מספרים שוים |
| plane number/square number | definition | ספר_המספר_/_אליהו_מזרחי#ergx | a square is the number resulting from the multiplication of the number by itself, whatever number it may be. והמרובע הוא המספר היוצא מהכאת המספר הא' בעצמו איזה מספר היה | |
| plane number/square number | definition | ספר_המספר_/_אברהם_אבן_עזרא#2NJw | the square [number] is the product of the multiplication of a root by itself והנה המרובע הוא המחובר מכפל שורש על עצמו | |
| plane number/square number | ר.ב.ע./מרובע | definition | Anonymous#7eUa | the number whose part counts it by its number is called a square number [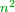 ], since its one side is equal to its other side, and when you count its side by its multitude the product is the square number.
והמספר אשר חלקו מונה אותו כמספרו נקרא מספר מרובע מפני שצלעו האחד שוה לצלעו השני וכשאתה מונה את צלעו כמנינה תקבץ המספר הרבוע ], since its one side is equal to its other side, and when you count its side by its multitude the product is the square number.
והמספר אשר חלקו מונה אותו כמספרו נקרא מספר מרובע מפני שצלעו האחד שוה לצלעו השני וכשאתה מונה את צלעו כמנינה תקבץ המספר הרבוע |
| plane number/square number | ר.ב.ע./רבוע | definition | ספר_יסודי_התבונה_ומגדל_האמונה#5tIu | the number whose part counts it by its number is called a square number [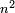 ], since its one side is equal to its other side, and when you duplicate its side by its multitude the product is the square number.
והמספר אשר חלקו מונה אותו במספרו נקרא מספר רבוע מפני שצלעו האחת שוה לצלעו השנית וכשאתה שונה את צלעו כמנינה יתקבץ המספר הרבוע ], since its one side is equal to its other side, and when you duplicate its side by its multitude the product is the square number.
והמספר אשר חלקו מונה אותו במספרו נקרא מספר רבוע מפני שצלעו האחת שוה לצלעו השנית וכשאתה שונה את צלעו כמנינה יתקבץ המספר הרבוע |
| plane number/square number | definition | עיר_סיחון#ifI6 | Know that every number that has a root is called a square number and it is a "wise number". תדע כי כל מספר נגדר הוא נקרא מרובע והנה הוא מספר פקח | |
| plane number/square number | ר.ב.ע./מרובע | term | קצור_המספר#DyDC | מספר מרובע |
| plane number/square number | ר.ב.ע./מרובע | term | Anonymous#GLSP | המרובעים |
| plane number/square number | definition | עיר_סיחון#YpcZ | Know that the product of every number by itself is called a number that has a root, whereas its root is the number that is multiplied by itself. תדע כי כל כפל הכאת חשבון על עצמו הוא הנקרא מספר נגדר או [{{#annot:term|86,1837|6sNp}}נשרש{{#annotend:6sNp}}]Vatican: תשרש כאשר גדרו או שורשו הוא נכפל על עצמו | |
| plane number/square number | ר.ב.ע./מרובע | term | Anonymous#r3kW | חשבון מרובע |
| plane number/square number | ר.ב.ע./מרובע | term | האריתמטיקה_של_ניקומכוס#jK4s | המרובעים המספריים |
| plane number/square number | ר.ב.ע./רבוע | term | Anonymous#JaRl | הרבוע |
| plane number/square number | ר.ב.ע./מרובע | term | Anonymous#jKkY | המרובע |
| plane number/square number | הוא הוא | term | האריתמטיקה_של_ניקומכוס#Bb1J | הוא הוא |
| plane number/square number | ר.ב.ע./מרובע | term | Anonymous#TMvg | המספרים המרובעים |
| plane number/square number | ש.ר.ש./נשרש | term | עיר_סיחון#6sNp | נשרש |
| plane number/square number | ר.ב.ע./מרובע | term | ספר_מעשה_חושב#UkDX | מרובע |
| plane number/square number | ג.ד.ר./נגדר | term | עיר_סיחון#rpzi | נגדר |
| plane number/square number | ר.ב.ע./מרובע | term | ספר_מעשה_חושב#UQ6q | מספר מרובע |
| plane number/square number | ר.ב.ע./מרובע | term | ספר_מעשה_חושב#HT6Z | מרובעי המספרים |
| plane number/square number | ג.ד.ר./נגדר | term | ספר_החשבון_לאל_חצאר#ZHWg | מספר נגדר |
| plane number/square number | ר.ב.ע./מרובע | term | ספר_ג'יבלי_אלמוקבאלא#o04g | המספרי' המרובעי' |
| plane number/square number | ג.ד.ר./נגדר | term | ספר_החשבון_לאל_חצאר#uG3E | נגדרת |
| plane number/square number | ר.ב.ע./מרובע | term | ספר_החשבון_לאל_חצאר#e9Jp | המספרים המרובעים |
| plane number/square number | ג.ד.ר./נגדר | term | ספר_החשבון_לאל_חצאר#MDjx | המספרים הנגדרים |
| plane number/square number | ג.ד.ר./נגדר | term | עיר_סיחון#xWd5 | מספר נגדר |
| plane number/square number | ר.ב.ע./מרובע | term | ספר_מעשה_חושב#KK9n | מרובעות |
| plane number/square number | הוא הוא | term | האריתמטיקה_של_ניקומכוס#t76o | הוא הויים |
| plane number/square number | הוא הוא | term | האנציקלופדיה_של_אבו_אלצלת#eAaB | הוא הוא |
| plane number/square number | ר.ב.ע./מרובע | term | קצור_המספר#8qDF | מספר מרובע |
| plane number/square number | ר.ב.ע./רבוע | term | ספר_יסודי_התבונה_ומגדל_האמונה#J1h0 | המספר הרבוע |
| plane number/square number | ר.ב.ע./מרובע | term | האריתמטיקה_של_ניקומכוס#hsY3 | השטחים המרובעים המספריים |
| plane number/square number | ר.ב.ע./מרובע | term | קצור_המספר#mqV2 | מרובע |
| plane number/square number | ר.ב.ע./מרובע | term | ספר_החשבון_לאל_חצאר#L05d | מרובע |
| plane number/square number | ר.ב.ע./מרובע | term | קצור_המספר#SxrI | מרובע |
| plane number/square number | הוא הוא | term | האריתמטיקה_של_ניקומכוס#Zt3n | ההוא הויית |
| proportion/subcontrary proportion | ק.ב.ל./מקביל | term | האריתמטיקה_של_ניקומכוס#POnR | מקביל |
| proportion/subcontrary proportion | ק.ב.ל./מקביל | term | האריתמטיקה_של_ניקומכוס#UErt | מקבילים |
| perfect number/superabundant number | ע.ד.פ./עודף | term | ספר_יסודי_התבונה_ומגדל_האמונה#0zDU | המספר העודף |
| perfect number/superabundant number | ע.ד.פ./עודף | definition | ספר_יסודי_התבונה_ומגדל_האמונה#gbZ6 | the superabundant number is that whose parts exceed over its number. והמספר העודף הוא אשר חלקיו עודפים על מספריו |
| perfect number/superabundant number | ע.ד.פ./עודף | term | ספר_יסודי_התבונה_ומגדל_האמונה#sFdO | עודף |
| perfect number/superabundant number | י.ס.פ./מוסיף חלק | definition | לקוטים_מספר_פראלוקא#si94 | The discussion on the superabundant number, such as 12 or 24, for the sum of its parts exceeds over it, i.e. when you sum all the parts generated from 12, the result is 16, so its parts are more than its whole, and this number is called in their language "numero abbondante". 3 המאמר במספר המוסיף חלק כמו מספר י"ב או כ"ד כי חלקיו מקובצים יעדיפו עליו ר"ל כי כשתקבץ כל החלקים הנעשים מי"ב יעלו י"ו א"כ חלקיו יותר מכלו וזה המספר נקרא בלשונם נומירו אבונדאנטי |
| simple ratio/superparticular ratio | sesquitertian | האנציקלופדיה_של_אבו_אלצלת#R0iD | יחס המוסיף שליש | |
| simple ratio/superparticular ratio | י.ס.פ./מוסיף חלק | term | האנציקלופדיה_של_אבו_אלצלת#6mUG | מוסיף חלק |
| simple ratio/superparticular ratio | י.ס.פ./מוסיף חלק | term | האנציקלופדיה_של_אבו_אלצלת#xYrQ | יחס המוסיף חלק |
| simple ratio/superparticular ratio | י.ס.פ./מוסיף חלק | term | האנציקלופדיה_של_אבו_אלצלת#GNgl | יחסי הדמיון המוסיף חלק |
| simple ratio/superparticular ratio | י.ס.פ./מוסיף חלק | term | האנציקלופדיה_של_אבו_אלצלת#ssLz | יחס הדמיון המוסיף חלק |
| simple ratio/superparticular ratio | י.ס.פ./מוסיף חלק | term | האנציקלופדיה_של_אבו_אלצלת#7uLZ | הדמיון המוסיף חלק |
| simple ratio/superparticular ratio | ח.ל.ק./חלק | term | ספר_יסודי_התבונה_ומגדל_האמונה#jiSJ | הקשת החלק |
| simple ratio/superparticular ratio | sesquialter | לקוטים_מספר_פראלוקא#fpCH | שקאלטירא | |
| simple ratio/superparticular ratio | כמהו/כמוהו וחלק ממנו | term | Anonymous#Qnb8 | כמוהו וחלק ממנו |
| simple ratio/superparticular ratio | sesquitertian | האנציקלופדיה_של_אבו_אלצלת#qENZ | יחס הדמיון המוסיף שליש | |
| simple ratio/superparticular ratio | sesquialter | האנציקלופדיה_של_אבו_אלצלת#f61F | יחס הדמיון המוסיף חצי | |
| simple ratio/superparticular ratio | sesquitertian | האנציקלופדיה_של_אבו_אלצלת#OyXe | המוסיף שליש | |
| simple ratio/superparticular ratio | sesquialter | האנציקלופדיה_של_אבו_אלצלת#29QX | המוסיף חצי | |
| simple ratio/superparticular ratio | sesquioctavian | האריתמטיקה_של_ניקומכוס#sVbr | יחס דמיון ושמינית | |
| simple ratio/superparticular ratio | sesquialter | האריתמטיקה_של_ניקומכוס#NHoQ | יחס דמיון וחצי | |
| simple ratio/superparticular ratio | sesquitertian | האריתמטיקה_של_ניקומכוס#ctVx | יחס דמיון ושליש | |
| simple ratio/superparticular ratio | sesquiquartan | האנציקלופדיה_של_אבו_אלצלת#zpWW | יחס המוסי' רביע | |
| simple ratio/superparticular ratio | sesquialter | האנציקלופדיה_של_אבו_אלצלת#y0yz | יחס המוסיף חצי | |
| simple ratio/superparticular ratio | sesquiquintan | האריתמטיקה_של_ניקומכוס#KZkH | המוסיף חלק החמשיי | |
| simple ratio/superparticular ratio | sesquiquartan | האריתמטיקה_של_ניקומכוס#oTdk | המוסיף חלק הרביעי | |
| simple ratio/superparticular ratio | sesquitertian | האריתמטיקה_של_ניקומכוס#nS12 | יחס המוסיף חלק השלישי | |
| simple ratio/superparticular ratio | sesquialter | האריתמטיקה_של_ניקומכוס#Dc37 | יחס המוסיף חלק החציי | |
| simple ratio/superparticular ratio | sesquialter | האריתמטיקה_של_ניקומכוס#Gy0u | המוסיף חלק חצי | |
| simple ratio/superparticular ratio | sesquiquintan | האריתמטיקה_של_ניקומכוס#KpVu | המוסיף חומש | |
| simple ratio/superparticular ratio | sesquiquartan | האריתמטיקה_של_ניקומכוס#2VLx | המוסיף רביע | |
| simple ratio/superparticular ratio | sesquitertian | האריתמטיקה_של_ניקומכוס#40Fb | המוסיף שליש | |
| simple ratio/superparticular ratio | sesquialter | האריתמטיקה_של_ניקומכוס#LmLw | המוסיף חצי | |
| simple ratio/superparticular ratio | sesquitertian | האנציקלופדיה_של_אבו_אלצלת#o1rS | דמיון ושליש | |
| simple ratio/superparticular ratio | sesquiquartan | האנציקלופדיה_של_אבו_אלצלת#AkWv | דמיון ורביעיתו | |
| simple ratio/superparticular ratio | sesquitertian | האנציקלופדיה_של_אבו_אלצלת#6trp | דמיון ושלישיתו | |
| simple ratio/superparticular ratio | sesquialter | האנציקלופדיה_של_אבו_אלצלת#JGKv | דמיון וחצי | |
| simple ratio/superparticular ratio | sesquiquartan | האריתמטיקה_של_ניקומכוס#WiHa | יחס המוסיף רביע | |
| simple ratio/superparticular ratio | sesquiquintan-definition | לקוטים_מספר_פראלוקא#yurq | The sesquiquintan ratio is [generated] from the ratio of 6 to 5, for 6 is as 5 plus its fifth added to it.
: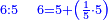 ושישקואיקיאינטא הוא מיחס ו' אל ה' כי ו' כמו ה' וכמו חמישיתו יוסף עליו
ושישקואיקיאינטא הוא מיחס ו' אל ה' כי ו' כמו ה' וכמו חמישיתו יוסף עליו | |
| simple ratio/superparticular ratio | sesquiquartan-definition | לקוטים_מספר_פראלוקא#nIXX | The sesquiquartan ratio is [generated] from the ratio of 5 to 4, for 5 exceeds over 4 by its quarter.
: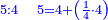 ושישקאיקוארטא נקרא מיחס ה' אל ד' כי ה' הוא מוסיף על ד' רביעיתו
ושישקאיקוארטא נקרא מיחס ה' אל ד' כי ה' הוא מוסיף על ד' רביעיתו | |
| simple ratio/superparticular ratio | sesquitertian-definition | לקוטים_מספר_פראלוקא#uS9A | The sesquitertian ratio is [generated] from the ratio of 4 to 3, for 4 is as 3 plus its third.
: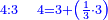 ושישקאיטירציאה נקרא מיחס ד' אל ג' כי ד' כמו ג' וכמו שלישיתו
ושישקאיטירציאה נקרא מיחס ד' אל ג' כי ד' כמו ג' וכמו שלישיתו | |
| simple ratio/superparticular ratio | sesquialter-definition | לקוטים_מספר_פראלוקא#5ncv | The sesquialter ratio is called the ratio of 3 to 2, for 3 is as 2 plus its half.
: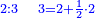 שקיאלטירא נקרא יחס ג' אל ב' כי ג' כמו ב' וכמו חציו
שקיאלטירא נקרא יחס ג' אל ב' כי ג' כמו ב' וכמו חציו | |
| simple ratio/superparticular ratio | sesquitertian | לקוטים_מספר_פראלוקא#zW7N | ששקאיטירציאה | |
| simple ratio/superparticular ratio | sesquitertian-definition | לקוטים_מספר_פראלוקא#2zGt | The sesquitertian ratio is [generated] from the ratio of 4 to 3, for 4 is as 3 plus its third.
: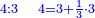 אמנם הששקואיטירציאה הוא מיחס ד' אל ג' כי ד' הוא כמו ג' וכמו שלישיתו
אמנם הששקואיטירציאה הוא מיחס ד' אל ג' כי ד' הוא כמו ג' וכמו שלישיתו | |
| simple ratio/superparticular ratio | sesquialter-definition | לקוטים_מספר_פראלוקא#a275 | The reason is that the sesquialter ratio is [generated] from the ratio of 3 to 2, for 3 is as 2 plus its half.
: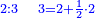 והטעם כי השישקואלטירא הוא מיחס ג' אל ב' כי ג' הוא כמו ב' וכמו חציו
והטעם כי השישקואלטירא הוא מיחס ג' אל ב' כי ג' הוא כמו ב' וכמו חציו | |
| simple ratio/superparticular ratio | sesquitertian | לקוטים_מספר_פראלוקא#lsAf | שישקואיטירציאה | |
| simple ratio/superparticular ratio | sesquialter | לקוטים_מספר_פראלוקא#ZELH | שישקואלטירא | |
| simple ratio/superparticular ratio | sesquialter | האריתמטיקה_של_ניקומכוס#izhT | המוסיף חלק השניי | |
| simple ratio/superparticular ratio | sesquiquartan | האריתמטיקה_של_ניקומכוס#Yooq | יחס המוסיף חלק הרביעיי | |
| simple ratio/superparticular ratio | sesquitertian | האריתמטיקה_של_ניקומכוס#lfra | יחס המוסיף שליש | |
| simple ratio/superparticular ratio | sesquialter | האריתמטיקה_של_ניקומכוס#ihTJ | יחס הדמיון וחצי | |
| simple ratio/superparticular ratio | sesquialter | האריתמטיקה_של_ניקומכוס#kQ7e | יחס המוסיף חצי | |
| simple ratio/superparticular ratio | sesquinona | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#qG0a | שופיר פארסיאין שיקיש קי נונה | |
| simple ratio/superparticular ratio | sesquioctavian | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#egqG | שופיר פארסיאין שיקיש קי גוייטמה | |
| simple ratio/superparticular ratio | sesquiseptan | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#MQ0q | שופיר פארסיאין שיקיש קי שיטימה | |
| simple ratio/superparticular ratio | sesquisextan | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#O6fa | שופיר פארסיאין שיקיש קי שישטה | |
| simple ratio/superparticular ratio | sesquiquintan | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#VbAv | שופיר פרסיאין שיקיש קי קינטה | |
| simple ratio/superparticular ratio | sesquiquartan | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#VduC | שופיר פארסיאין שיקש קי קארטה | |
| simple ratio/superparticular ratio | sesquitertian | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#yuwo | שופיר פארסיאן שיקש קי טירסיאה | |
| simple ratio/superparticular ratio | י.ס.פ./מוסיף חלק | term | האריתמטיקה_של_ניקומכוס#tdFq | יחסי המוסיף חלק |
| simple ratio/superparticular ratio | י.ס.פ./מוסיף חלק | term | האריתמטיקה_של_ניקומכוס#1VcM | מוסיף חלק |
| simple ratio/superparticular ratio | י.ס.פ./מוסיף חלק | term | האריתמטיקה_של_ניקומכוס#I8nQ | יחס המוסיף חלק |
| simple ratio/superparticular ratio | sesquiquartan | האנציקלופדיה_של_אבו_אלצלת#ffTa | יחס המוסיף רביעית | |
| simple ratio/superparticular ratio | sesquiseptan | האנציקלופדיה_של_אבו_אלצלת#zrEv | יחס דמיון ושביעית | |
| simple ratio/superparticular ratio | sesquidecima | האנציקלופדיה_של_אבו_אלצלת#QjiD | דמיון ועשירית | |
| simple ratio/superparticular ratio | sesquinona | האנציקלופדיה_של_אבו_אלצלת#iH9T | יחס דמיון ותשיעית | |
| simple ratio/superparticular ratio | sesquiquartan | האנציקלופדיה_של_אבו_אלצלת#EjrN | יחס דמיון ורביעית | |
| simple ratio/superparticular ratio | sesquinona | האנציקלופדיה_של_אבו_אלצלת#krIu | דמיון ותשיעית | |
| simple ratio/superparticular ratio | sesquioctavian | האנציקלופדיה_של_אבו_אלצלת#jIRf | דמיון ושמינית | |
| simple ratio/superparticular ratio | sesquitertian | האנציקלופדיה_של_אבו_אלצלת#h60a | יחס דמיון ושליש | |
| simple ratio/superparticular ratio | sesquiseptan | האנציקלופדיה_של_אבו_אלצלת#imC5 | דמיון ושביעית | |
| simple ratio/superparticular ratio | sesquisextan | האנציקלופדיה_של_אבו_אלצלת#y0WL | דמיון וששית | |
| simple ratio/superparticular ratio | sesquisextan | האנציקלופדיה_של_אבו_אלצלת#H6fD | יחס דמיון וששית | |
| simple ratio/superparticular ratio | sesquiquintan | האנציקלופדיה_של_אבו_אלצלת#Emnk | יחס דמיון וחומש | |
| simple ratio/superparticular ratio | sesquiquintan | האנציקלופדיה_של_אבו_אלצלת#68dt | דמיון וחומש | |
| simple ratio/superparticular ratio | sesquiquartan | האנציקלופדיה_של_אבו_אלצלת#l13b | יחס דמיון ורביע | |
| simple ratio/superparticular ratio | sesquialter | האנציקלופדיה_של_אבו_אלצלת#g2HQ | יחס דמיון וחצי | |
| simple ratio/superpartient ratio | superbiquintan | האנציקלופדיה_של_אבו_אלצלת#w5sR | המוסיף בשתי חמישיות | |
| simple ratio/superpartient ratio | supertriquintan | האריתמטיקה_של_ניקומכוס#E9gM | המוסיף שלשה חומשים | |
| simple ratio/superpartient ratio | supertripartient | האריתמטיקה_של_ניקומכוס#RzOH | המוסיפים שלשה חלקים | |
| simple ratio/superpartient ratio | superquadripartient | האריתמטיקה_של_ניקומכוס#KN6P | המוסיף ארבעה | |
| simple ratio/superpartient ratio | supertriquartan | האריתמטיקה_של_ניקומכוס#E9k3 | המוסיף שלשה רביעיות | |
| simple ratio/superpartient ratio | superbitertian | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#1M0I | שופיר בי פרסיאין טירטאש | |
| simple ratio/superpartient ratio | supertriquartan | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#BNkU | שופיר טרי פרסיאיני קארטאש | |
| simple ratio/superpartient ratio | superquadriquintan | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#OIWQ | שופר קאטרי פארסי' קינטאש | |
| simple ratio/superpartient ratio | ח.ל.ק./חלקים | term | ספר_יסודי_התבונה_ומגדל_האמונה#yj4Q | הקשת חלקים |
| simple ratio/superpartient ratio | superbitertian | האנציקלופדיה_של_אבו_אלצלת#zbbR | המוסיף שתי שלישיות | |
| simple ratio/superpartient ratio | superbipartient | האנציקלופדיה_של_אבו_אלצלת#bySx | מוסיף בשני חלקים | |
| simple ratio/superpartient ratio | superbipartient-definition | לקוטים_מספר_פראלוקא#76kq | If the ratio is of 5 to 3 it is called superbipartient ratio, for 5 is as 3 plus 2.
: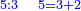 ואם היחס הוא מה' אל ג' נקרא שופירפאריטינש כי ה' כמו ג' ומוסיף עליו ב'
ואם היחס הוא מה' אל ג' נקרא שופירפאריטינש כי ה' כמו ג' ומוסיף עליו ב' | |
| simple ratio/superpartient ratio | supertripartient-definition | לקוטים_מספר_פראלוקא#Kn4X | If the number adds 3 over the other, it is called supertripartient, such as 8 to 5, for 8 is as 5 plus 3.
: ואם המספר מוסיף ג' על האחר נקרא שופירטיפארטיאינש כמו ח' וה' כי ח' כמו ה' ומוסיף עליו ג'
ואם המספר מוסיף ג' על האחר נקרא שופירטיפארטיאינש כמו ח' וה' כי ח' כמו ה' ומוסיף עליו ג' | |
| simple ratio/superpartient ratio | superquadripartient-definition | לקוטים_מספר_פראלוקא#GNot | If it adds 4 [over the other], such as the ratio of 9 to 5, it is called superquadripartient.
: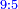 ואם מוסיף ד' כמו יחס ט' אל ה' נקרא שופירקואינדרופארטיאינש
ואם מוסיף ד' כמו יחס ט' אל ה' נקרא שופירקואינדרופארטיאינש | |
| simple ratio/superpartient ratio | superquadripartient | האריתמטיקה_של_ניקומכוס#GDCW | המוסיף ארבעה חלקים | |
| simple ratio/superpartient ratio | י.ס.פ./מוסיף חלקים | term | האריתמטיקה_של_ניקומכוס#ZX2O | היחס המוסיף חלקים |
| simple ratio/superpartient ratio | superquadriquintan | האריתמטיקה_של_ניקומכוס#u8ry | המוסיף ארבעה חומשים | |
| simple ratio/superpartient ratio | י.ס.פ./מוסיף חלקים | term | האריתמטיקה_של_ניקומכוס#DE29 | המוסיף חלקים |
| simple ratio/superpartient ratio | י.ס.פ./מוסיף חלקים | term | האריתמטיקה_של_ניקומכוס#29Ia | יחס המוסיף חלקים |
| simple ratio/superpartient ratio | superbipartient | האריתמטיקה_של_ניקומכוס#DyCx | המוסיף שני חלקים | |
| simple ratio/superpartient ratio | י.ס.פ./מוסיף חלקים | term | האנציקלופדיה_של_אבו_אלצלת#G6ks | המוסיף בחלקים |
| simple ratio/superpartient ratio | י.ס.פ./מוסיף חלקים | term | האנציקלופדיה_של_אבו_אלצלת#VYdM | יחס הדמיון המוסיף חלקים |
| simple ratio/superpartient ratio | כמהו/כמוהו וחלקים ממנו | term | Anonymous#eYgJ | כמוהו וחלקים ממנו |
| simple ratio/superpartient ratio | superbipartient | האנציקלופדיה_של_אבו_אלצלת#ppa4 | יחס המוסיף בשני חלקים | |
| simple ratio/superpartient ratio | supertriquartan | האנציקלופדיה_של_אבו_אלצלת#IWG3 | המוסיף בשלש רביעיות | |
| simple ratio/superpartient ratio | superbitertian | האנציקלופדיה_של_אבו_אלצלת#fH6C | המוסיף בשתי שלישיות | |
| simple ratio/superpartient ratio | supertripartient | האריתמטיקה_של_ניקומכוס#EHqW | המוסיף שלשה חלקים | |
| simple ratio/superpartient ratio | superbiquintan | האנציקלופדיה_של_אבו_אלצלת#9hYQ | המוסיף בשני חמישיות | |
| simple ratio/superpartient ratio | superbiquintan | האנציקלופדיה_של_אבו_אלצלת#Exgb | המוסיף שתי חמישיות | |
| simple ratio/superpartient ratio | superpartient | האריתמטיקה_של_ניקומכוס#6vkL | מוסיף שני שלישים | |
| simple ratio/superpartient ratio | superbitertian | האנציקלופדיה_של_אבו_אלצלת#A9nH | יחס המוסיף שני שלישים | |
| simple ratio/superpartient ratio | superbiquintan | האריתמטיקה_של_ניקומכוס#pCVd | המוסיף שני חומשים | |
| relative quantity/term | ד.ר.ג./מדרגה | term | האנציקלופדיה_של_אבו_אלצלת#6pVQ | מדרגה |
| relative quantity/term | ג.ב.ל./גבול | term | קצור_המספר#ZS9i | גבול |
| relative quantity/term | ג.ב.ל./גבול | term | האנציקלופדיה_של_אבו_אלצלת#rQ2L | גבולים |
| relative quantity/term | ק.ש.ר./קשר | term | ספר_ג'יבלי_אלמוקבאלא#EM5u | קשרים |
| relative quantity/term | ג.ב.ל./גבול | term | האנציקלופדיה_של_אבו_אלצלת#dFs4 | גבול |
| relative quantity/term | ג.ב.ל./גבול | term | קצור_המספר#76Dr | גבולים |
| relative quantity/term | ק.ר.א./קריאת שם | definition | אגרת_המספר#nN9J | קריאת שם |
| relative quantity/term | נושא | term | ספר_מעשה_חושב#Y6eb | נושא |
| relative quantity/term | term | ספר_ג'יבלי_אלמוקבאלא#g8EG | קלאפי | |
| relative quantity/term | נושא | term | ספר_מעשה_חושב#fLgi | נושאים |
| relative quantity/term | ד.ר.ג./מדרגה | term | האנציקלופדיה_של_אבו_אלצלת#6UFr | מדרגה |
| relative quantity/term | ד.ר.ג./מדרגה | term | האנציקלופדיה_של_אבו_אלצלת#NEbn | מדרגות |
| relative quantity/term | ק.ש.ר./קשר | term | ספר_ג'יבלי_אלמוקבאלא#bBb3 | קשרים |
| relative quantity/term | ד.ר.ג./מדרגה | term | האנציקלופדיה_של_אבו_אלצלת#TrIG | מדרגות |
| alternation/to alternate | מ.ו.ר./המיר | term | ספר_מעשה_חושב#SWPT | להמיר |
| alternation/to alternate | ה.פ.כ./הפך | term | ספר_מעשה_חושב#fIbg | הפכנו |
| alternation/to alternate | מ.ו.ר./המיר | term | ספר_מעשה_חושב#YBDC | המירונו |
| relative quantity/to relate | ע.ר.כ./העריך | term | קצור_המספר#G2kb | נעריך |
| relative quantity/to relate | י.ח.ס./התיחס | term | חשבון_השטחים#pz9P | המתיחס אל |
| relative quantity/to relate | ק.ש.ר./נקשר | term | בר_נותן_טעם#KtgV | נקשרים |
| relative quantity/to relate | נ.ק.ש./הוקש | term | ספר_יסודי_התבונה_ומגדל_האמונה#yXrH | מוקש אל |
| relative quantity/to relate | נ.ק.ש./הוקש | term | ספר_יסודי_התבונה_ומגדל_האמונה#A9pr | המספר המוקש אליו |
| relative quantity/to relate | ע.ר.כ./נערך | term | תחבולות_המספר#qQmi | נערך לעצמו |
| relative quantity/to relate | ק.ש.ר./נקשר | term | בר_נותן_טעם#dGUb | נקשרות |
| relative quantity/to relate | י.ח.ס./יוחס | term | קצור_המספר#JYac | מיוחס ל |
| relative quantity/to relate | ק.ש.ר./קשר | term | בר_נותן_טעם#9XkM | לקשרם יחד |
| relative quantity/to relate | נ.ק.ש./הקיש | term | ספר_יסודי_התבונה_ומגדל_האמונה#Uoz4 | מקיש אותו אל |
| relative quantity/to relate | ק.ש.ר./נקשר | term | בר_נותן_טעם#S0DR | נקשרים זו בזו |
| relative quantity/to relate | ק.ש.ר./נקשר | term | בר_נותן_טעם#G7Ca | נקשר |
| plane number/triangular number | ש.ל.ש./משולש | term | האריתמטיקה_של_ניקומכוס#aQyD | המשולשים המספריים |
| plane number/triangular number | ש.ל.ש./משולש | term | האנציקלופדיה_של_אבו_אלצלת#SDvA | משלשת |
| ratio/triplicate | ש.ל.ש./משולש | term | ספר_מעשה_חושב#qzMf | משולש |
| ratio/triplicate | ש.ל.ש./משולש | term | ספר_האלזיברא#A27z | משלש |
| absolute quantity/unit | פ.ר.ט./פרט | term | Arithmetic_Textbook_by_R._Aharon_ben_Isaac#rOsE | פרטים |
| absolute quantity/unit | א.ח.ד./אחדות | definition | ספר_היסודות_לאקלידס#KTZd | The unit is that by which each of the beings is called one. האחדות הוא הדבר אשר יאמר בו לכל דבר אחד מן הנמצאות אחד |
| absolute quantity/unit | א.ח.ד./אחדות | definition | מלאכת_המספר#dYUi | unit is a foundation and the first part of the number, every number consists of it, but it is apart from every number. אחדות הוא יסוד וחלק ראשון מהמספר וכל מספר יורכב ממנו אבל הוא חוץ לכל מספר |
| absolute quantity/unit | א.ח.ד./אחדות | term | האריתמטיקה_של_ניקומכוס#Erja | אחדות |
| absolute quantity/unit | א.ח.ד./אחדות | term | האריתמטיקה_של_ניקומכוס#AZ1I | אחדות |
| absolute quantity/unity | definition | ספר_יסודי_התבונה_ומגדל_האמונה#fjxB | the meaning of unity here is the property that is found in the one, by which it is called one. ומשמע האחדות בכאן הוא ענין הנמצא באחד אשר הוא נק' אחד |