Difference between revisions of "Royslist"

From mispar
Jump to: navigation, search
Line 1: Line 1:
 
{{#annotask:
 
{{#annotask:
−
[[category: #geometry ]]
+
[[category: geometry ]]
 
}}
 
}}

Revision as of 10:48, 30 November 2021

Category Category Comment Link Annotated text
angle/acute angleח.ד.ד./חדtermמשנת_המדות#Fhurחדות
angle/acute angleח.ד.ד./חדtermספר_יסודי_התבונה_ומגדל_האמונה#ohTcזוית חדה
angle/acute angleח.ד.ד./חדdefinitionספר_יסודי_התבונה_ומגדל_האמונה#7qMIthe acute angle is less than the right [angle] in its value והזוית החדה היא המחסרת בערכה מן הנצבת
angle/acute angleצ.ר.ר./צרtermמשנת_המדות#327Hזויות צרים
angle/acute angleח.ד.ד./חדdefinitionספר_היסודות_לאקלידס#V5dbThe smaller than a right angle is called an '''acute angle'''. ואשר היא קטנה מנצבת תקרא חדה
acute angle/acute-angledח.ד.ד./חדtriangleמשנת_המדות#Kt5xחדה
acute angle/acute-angledח.ד.ד./מחודדtriangleספר_יסודי_התבונה_ומגדל_האמונה#JbzHהמשלש מחדד הזויות
acute angle/acute-angledח.ד.ד./מחודדtriangle-definitionספר_יסודי_התבונה_ומגדל_האמונה#lhjkthe first is that whose each angle is acute angle - this is called an acute-angled [triangle]. האחד הוא אשר כל זוית מזויותיו זוית חדה והוא הנקרא מחודד הזוית
acute angle/acute-angledח.ד.ד./חדtriangle-definitionספר_היסודות_לאקלידס#pQ2MThe '''acute-angled triangle''' is that whose three angles are acute. ומשולש חד הזויות והוא אשר כל אחת מזויותיו השלש חדה
geometrical shape/angleזויתtermמלאכת_המספר#2ohUזוית
geometrical shape/angleזויתtermמלאכת_המספר#fvYcזויות
angle/angle between straight linesי.ש.ר./ישרהtermספר_יסודי_התבונה_ומגדל_האמונה#IAoPהזויות הישרות
angle/angle between straight linesי.ש.ר./ישרהtermספר_יסודי_התבונה_ומגדל_האמונה#q7XHהזוית הישרה
point/apexר.א.ש./ראשtermמשנת_המדות#jOb1ראש
line/apotomeב.ד.ל./נבדלdefinitionספר_היסודות_לאקלידס#9THRWhen a segment measurable in a square is subtracted from a straight line and the two lines are commensurable in square only, then the remaining straight line is unmeasurable; let it be called an apotome. ע כאשר הובדל מקו ישר מדבר בכח והיו השני קוים בכח לבד משותפים הנה הקו הנשאר בלתי מדבר ויקרא הנבדל
circle/arcק.ש.ת./קשתtermמשנת_המדות#dLJuקשת
circle/arctermספר_המספר_/_אברהם_אבן_עזרא#Gr5jקשתות
circle/arcק.ש.ת./קשתdefinitionמשנת_המדות#t84rWhat is the arc? it is the part of the circle, as it is said: ''like the appearance of the rainbow that is in the cloud'' [Ezekiel 1, 28]. איזו היא קשת החלק מן העגול שנ' ''כמראה הקשת אשר יהיה בענן''‫יחזקאל א, כח
magnitude/areaש.ב.ר./תשבורתtermקצור_המספר#6eNbתשבורת
magnitude/areatermספר_המספר_/_אברהם_אבן_עזרא#nSsYתשבורת
magnitude/areaמ.ש.ח./משיחהtermמשנת_המדות#hZNEמשיחה
magnitude/areaר.ח.ב./רוחבtermספר_ג'יבלי_אלמוקבאלא#n6dRרחב השטח
magnitude/areaר.ב.ע./רבועtermספר_הכללים_במספר#9C3mרבוע
magnitude/areaש.ב.ר./תשבורתtermספר_הכללים_במספר#pgiuתשבורת
magnitude/areaר.ב.ע./רבועtermספר_הכללים_במספר#ez7pרבוע
magnitude/areaש.ב.ר./תשבורתtermקצור_המספר#ZrPNתשבורת
magnitude/areaש.ט.ח./שטחtermספר_ג'יבלי_אלמוקבאלא#Q9z1שטחו
magnitude/areaש.ט.ח./שטחtermחשבון_השטחים#Fzc9שטח
magnitude/areaש.ט.ח./שטחtermתחבולות_המספר#F1Tdשטח
magnitude/areaמ.ש.ח./משיחהtermספר_הכללים_במספר#DJo0משיחת ה
magnitude/areaמ.ש.ח./משיחהtermספר_הכללים_במספר#INwYמשיחת ה
magnitude/areaש.ב.ר./שברtermספר_הכללים_במספר#1sqcמידת שבריו
magnitude/areaש.ב.ר./שברtermספר_הכללים_במספר#lZxhשבר
magnitude/areaש.ב.ר./תשבורתtermספר_הכללים_במספר#a5B3תשברתו
magnitude/areaש.ב.ר./תשבורתtermספר_האלזיברא#QTLlתשבורתו
magnitude/areaש.ב.ר./שבריםtermספר_האלזיברא#Empfשבריו
magnitude/areaש.ב.ר./שבריםtermספר_האלזיברא#XLwtמספר שברי
magnitude/areaש.ט.ח./שטחtermספר_ג'יבלי_אלמוקבאלא#s6dlשטח
magnitude/areatermספר_המספר_/_אברהם_אבן_עזרא#bkNTשברים
sphere/axisב.ר.ח./בריחdefinitionספר_יסודי_התבונה_ומגדל_האמונה#d6V1if the sphere revolves around this diameter, we call it then the axis of the sphere. ואם יהיה הכדור סובב על האלכסון הזה אנו קורין לו בעת ההיא בריח הכדור
geometrical shape/baseי.ש.ב./תושבתtermספר_המספר_/_אליהו_מזרחי#FVdwתושבתה
geometrical shape/baseק.ב.ע./קבעtermמשנת_המדות#zDsvקבע
geometrical shape/baseק.ב.ע./קבעdefinitionמשנת_המדות#axVOThe base is that upon which two sides are fixed, ''upon which the house rests'' [Judges 16, 26; 29]. והקבע זה ששני צלעים קבועים עליו שני ''אשר הבית נכון עליהם''‫שופטים טז, כ"ו; כ"ט
geometrical shape/baseי.ש.ב./תושבתtermמלאכת_המספר#ojMzתושבת
geometrical shape/baseסוףtermמשנת_המדות#WWjaסוף
solid/beamאריחיtermהאריתמטיקה_של_ניקומכוס#fZcRמוגשמים אריחיים
point/centerצ.י.ר./צירcenter of a circleספר_יסודי_התבונה_ומגדל_האמונה#Xrf7ציר העגול
point/centerר.כ.ז./מרכזcenter of a circleספר_היסודות_לאקלידס#C6nyמרכז העגולה
point/centerר.כ.ז./מרכזcenter of a circleקצת_מענייני_חכמת_המספר#gyB1מרכז העגולה
point/centerצ.י.ר./צירtermספר_הכללים_במספר#0qCrציר העגולה
point/centerצ.י.ר./צירtermספר_הכללים_במספר#a6OGציר העגול
point/centerצ.י.ר./צירcenter of a sphereספר_יסודי_התבונה_ומגדל_האמונה#uFQIציר הכדור
point/centerר.כ.ז./מרכזtermArithmetic_Textbook_by_R._Aharon_ben_Isaac#rFFwמרכז
circle/chordtermספר_המספר_/_אברהם_אבן_עזרא#nGjlיתר
circle/chordי.ת.ר./יתרdefinitionמשנת_המדות#ChKsThe chord is the holder of the arc, as it is said: ''bent bow'' [Isaiah 21, 15]. והיתר זה המחזיק בפי הקשת שנ' ''קשת דרוכה''‫ישעיה כא, טו
circle/chordtermספר_המספר_/_אברהם_אבן_עזרא#BVOwיתרים
circle/chordי.ת.ר./יתרtermמשנת_המדות#ZqPDיתר
circle/chordי.ת.ר./מיתרtermספר_היסודות_לאקלידס#iAOKמיתר
circle/chordי.ת.ר./מיתרtermספר_היסודות_לאקלידס#NCXoמיתר
surface/circleע.ג.ל./עגולהtermאגרת_המספר#CEILעגולה
surface/circledefinition, #עגולהספר_יסודי_התבונה_ומגדל_האמונה#Tyz7we call the surface that the one line that surrounds it is circular, a circle if it is on a plane surface. והשטח אשר קו האחד המקיפו הוא עגול אנו קורין לשטח עגולה ישרה אם הוא בשטח ישר
surface/circleע.ג.ל./עגולהdefinitionספר_היסודות_לאקלידס#uqaXThe '''circle''' is a plane figure contained by one line, within which there is one point such that all the straight lines drawn from it and terminated in the circumference are equal to one another. והעגולה היא תמונה פשוטה שוה יקיף אותה קו אחד בתוכה נקודה כל הקוים הישרים היוצאים ממנה ויכלו אל הקו ההוא שוים קצתם אל קצתם
surface/circleע.ג.ל./עגולdefinitionספר_יסודי_התבונה_ומגדל_האמונה#x37uthe circle is that which at its center there is one point such that all the lines that are drawn from it to the circumference are equal to each other in their value. השטח העגול הוא הנמצא באמצעיתו נקודה אחת אשר כל קו שתוציא ממנה אל הקו המקיף יהיו שוים בערכם זה לזה
surface/circleע.ג.ל./עגולהtermמלאכת_המספר#yHjGעגולה
surface/circletermספר_המספר_/_אברהם_אבן_עזרא#oaVKעגול
surface/circletermספר_המספר_/_אברהם_אבן_עזרא#Twc4עגולה
surface/circleע.ג.ל./עגולtermמשנת_המדות#D5gUעגול
surface/circletermספר_המספר_/_אברהם_אבן_עזרא#PTuVעגול
surface/circleש.פ.ל./שפלtermמשנת_המדות#FIGDשפלה
surface/circleע.ג.ל./עגולהtermמשנת_המדות#43ngעגלה
line/circular lineע.ג.ל./עגולdefinitionספר_יסודי_התבונה_ומגדל_האמונה#NCuEThe circular line is the one on which you cannot find three points that are in the same direction, and inside of it there is a point that is equidistant from all the points of the circle. והקו העגול הוא כל אשר אי אתה יכול למצוא ג' נקדות על נכח וימצא בתוכו נקדה שיהיה מרחקה מכל נקדות העגול מרחק אחד
line/circular lineע.ג.ל./עגולtermספר_יסודי_התבונה_ומגדל_האמונה#bObtקו עגול
geometric relations/commensurableש.ת.פ./משותףdefinitionספר_היסודות_לאקלידס#qiVvThose that have magnitudes, as lines, surfaces, and solids, that are said to be '''commensurable''', are those that are measured by the same measure. בעלי השעורים מן הקוים והשטחים והמוגשמים אשר יאמר להם המשותפים המשותפים הם אשר ישער אותם כלם יחד שעור אחד
geometric relations/commensurableש.ת.פ./בלתי משותפיםdefinition-incommensurableספר_היסודות_לאקלידס#lGqtThose that are said to be '''incommensurable''' are those that cannot be measured the same measure. ואשר יאמר להם בלתי משותפים הם אשר לא ישער אותם כלם שעור אחד
geometric relations/commensurable in squareש.ת.פ./בלתי משותפים בכחdefinition-incommensurable in squareספר_היסודות_לאקלידס#zQYuThey are said to be '''incommensurable in square''', when the squares [that are generated] from them cannot be measured by the same area. ויאמר להם בלתי משותפים בכח כאשר לא יהיה למרובעים הנה נבאר [ההווים] מהם שטח ישער אותם
geometric relations/commensurable in squareש.ת.פ./משותפים בכחdefinitionספר_היסודות_לאקלידס#shEkStraight lines are said to be '''commensurable in square''', when the squares that are generated from them are measured by the same area. והקוים הישרים אשר יאמר להם המשותפים בכח כאשר היה למרובעים ההוים מהם שטח ישער אותם
surface/concave surfaceע.ק.מ./עקמומיdefinitionספר_יסודי_התבונה_ומגדל_האמונה#Rmiathe concave surface is the plane that encompasses the dome from beneath; it is also either circular or curved. והפרוש העקמומי הוא הרקיע המקיף את גב הקובה מלמטה ויהיה כמו כן עגול או עקום
surface/concave surfaceע.ק.מ./עקמומיtermספר_יסודי_התבונה_ומגדל_האמונה#Ue2Nעקמומי
solid/coneאלוןtermספר_יסודי_התבונה_ומגדל_האמונה#7Wx1אלון
solid/coneאתרוגtermמשנת_המדות#8LjVאתרוג
solid/coneמ.ש.כ./משוךdefinitionמשנת_המדות#6tE5The conical, whose apex is sharp and base is planar, whether quadrilateral, or circular, or triangular: ז' והמשוך ראשו חד וסופו {{#annot:term|588,2554|epCp}}ממוצע{{#annotend:epCp}} ואפי' מרובע או שיהיה עגול או משולש
solid/coneאלוניtermספר_יסודי_התבונה_ומגדל_האמונה#w4jzהגולם האלוני
solid/coneח.ר.ט./חרוטtermספר_יסודי_התבונה_ומגדל_האמונה#eKVdחרוטות
solid/coneח.ר.ט./חרוטtermספר_יסודי_התבונה_ומגדל_האמונה#PHTKהגולם החרוט
solid/coneאלוניtermספר_יסודי_התבונה_ומגדל_האמונה#NCUzהאלוני
geometric relations/congruent figuresש.ו.ה./שוהsolids-definitionספר_היסודות_לאקלידס#68bDThe equal similar solid shapes are those that each solid of which is contained by the same number of surfaces as the number of the surfaces containing the other, and each surface is similar and equal in measure to its corresponding surface in the other solid. התמונות המוגשמות השוות הדומות הם אשר יקיפו בכל מוגשם מהם ממנין השטחים כמו מנין מה שיקיפו באחר ויהיה כל שטח מאחד מהם דומה ושוה השיעור לשטח אשר הוא גילו מן המוגשם האחר ועל בריאתו
surface/convex surfaceק.ב.ב./מקובהtermמשנת_המדות#nssaמקובה
surface/convex surfaceק.ב.ב./קבובdefinitionספר_יסודי_התבונה_ומגדל_האמונה#Q7bhthe convex surface is the plane that encompasses the dome from above; this surface is either circular or curved. והפרוש הקבוב הוא הרקיע המקיף את קו הקובה מלמעלה והרקיע הזה יהיה עגול ויהיה עקום
surface/convex surfaceק.ב.ב./קובהtermמשנת_המדות#8Lrzקובה
surface/convex surfaceק.ב.ב./קבובtermספר_יסודי_התבונה_ומגדל_האמונה#txDcקבוב
solid/cubeע.ק.ב./מעוקבtermבר_נותן_טעם#n3HEגשם מעוקב
solid/cubeע.ק.ב./מעוקבtermArithmetic_Textbook_by_R._Aharon_ben_Isaac#gzFsמעוקב
line/curveע.ק.מ./עקוםtermספר_יסודי_התבונה_ומגדל_האמונה#MU5oקו עקום
line/curveע.ק.מ./עקוםdefinitionספר_יסודי_התבונה_ומגדל_האמונה#q5CbThe curve is any line on which you cannot find three points that are in the same direction and you cannot find also any point in it that is equidistant from all the points of the curve. והקו העקום כל קו שאי אתה מוצא ג' נקדות על נכח אחד ואף נקדה שיהיה מרחקה מנקדות העקום מרחק אחד אי אתה מוצא בו
solid/cylinderע.ג.ל./עגולהtermספר_הכללים_במספר#Mt2gמצבה עגולה
solid/cylinderאצטוונאtermספר_המספר_/_אליהו_מזרחי#Enszהאצטוונא העגולה
solid/cylinderע.ג.ל./עגולהtermספר_הכללים_במספר#zGspמצבה עגולה
solid/cylinderאצטוונאtermספר_המספר_/_אליהו_מזרחי#gbMUאיצטיונא עגולה
solid/cylinderאצטוונאtermספר_המספר_/_אליהו_מזרחי#rax7אצטוונא
linear dimension/depthע.מ.ק./עומקtermמלאכת_המספר#i136עומק
linear dimension/depthע.מ.ק./עומקtermמלאכת_המספר#SFscעומק
line/diagonalאלכסוןtermספר_יסודי_התבונה_ומגדל_האמונה#mxolקו האלכסון
line/diagonalאלכסוןtermספר_הכללים_במספר#HaZiאלכסון
line/diagonalאלכסוןtermספר_הכללים_במספר#VGc4אלכסון
line/diagonalחוטdefinitionמשנת_המדות#1yocThe diagonal is the cutting from an angle to an angle, end to end, and it is the greater length of the surface. והחוט זה המפסיק מזוית לזוית מן הקצה אל הקצה והוא היותר בארכו של גג
line/diagonalחוטtermמשנת_המדות#gn1Hחוט
line/diameterק.ט.ר./קוטרtermספר_המספר_/_אליהו_מזרחי#wKt6קוטר
line/diameterאלכסוןdiameter of a sphere-definitionספר_יסודי_התבונה_ומגדל_האמונה#ZeeFevery line passing through the center of the sphere and reaching at its both sides to the surface is called the diameter of the sphere. וכל קו העובר על ציר הכדור והוא מגיע בשני צדיו אל הפרוש נקרא אלכסון הכדור
line/diameterאלכסוןtermספר_הכללים_במספר#vRfGאלכסונו
line/diameterאלכסוןdiameter of a circle-definitionספר_יסודי_התבונה_ומגדל_האמונה#WT1pevery line passing through the center of the circle and reaching at its both sides to the circumference is called the diameter of the circle. וכל קו אשר הוא עובר על ציר העגול ומגיע מב' פנותיו אל הקו המקיף הוא נקרא אלכסון העגול
line/diameterאלכסוןtermמלאכת_המספר#kR8yאלכסון
line/diameterחוטtermמשנת_המדות#6q7Oחוט
line/diametertermספר_המספר_/_אברהם_אבן_עזרא#Ez31אלכסון
line/diameterק.ט.ר./קוטרdefinitionספר_היסודות_לאקלידס#v3BaThe '''diameter''' of the circle is any straight line, drawn through the center of the circle and terminated in both directions by its circumference, that bisects [the circle]. וקוטר העגולה הוא קו ישר ילך במרכז העגולה ויכלה בשני הצדדי' אל הקו המקיף אותה והוא יחתכנה בשני חצאים
magnitude/distanceר.ח.ק./רוחקtermמלאכת_המספר#BkNIרוחק
Elements/Elements II-1a·∑bᵢ=∑(a·bᵢ)ספר_המספר_/_אליהו_מזרחי#me96For every number divided into many parts randomly, the number that is generated from the product of a number by the whole given divided number is equal to the number generated from the sum of the products of that number by each part of the divided number. :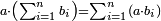\scriptstyle a\sdot\left(\sum_{i=1}^n b_i\right)=\sum_{i=1}^n \left(a\sdot b_i\right) השנית שכל מספר נחלק לחלקים רבים איך מה שקרה הנה המספר ההווה מהכאת מספר מה עם המספר המונח הנחלק בכללו הוא שוה למספר ההווה מהכאת המספר ההוא עם כל אחד מחלקי המספר הנחלק כאשר יקובצו
Elements/Elements II-1a·∑bᵢ=∑(a·bᵢ)ספר_מעשה_חושב#4J1rWhen there are two given numbers and one of them is divided into parts, as many as they may be, the product of the first number by the second is equal to the [sum of] the products of each of the parts of the first number by the second. :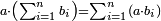\scriptstyle a\sdot\left(\sum_{i=1}^n b_i\right)=\sum_{i=1}^n \left(a\sdot b_i\right) ב כאשר היו שני מספרים מונחים וחולק המספר האחד לחלקים כמה שיהיו הנה שטח המספר האחד בשני שוה לשטחי כל אחד מחלקי המספר האחד בשני מקובצים
Elements/Elements II-1a·∑bᵢ=∑(a·bᵢ)לקוטים_מספר_פראלוקא#t9UkIf you have two numbers and you divide one of the two numbers, then you multiply each part by the second number, the total sum is the same as the product of the first number by the second. :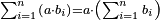\scriptstyle\sum_{i=1}^n \left(a\sdot b_i\right)=a\sdot\left(\sum_{i=1}^n b_i\right) ‫156 אם יש לך ב' מספרים ותחלק א' מהב' מספרים ותכפול כל חלק על המספר השני הנה הסך העולה הוא כמו מה שיעלה מכפל המספר הראשון על השני
Elements/Elements II-1ספר_החשבון_והמדות#fGS3I say: if you divide any number into parts as you wish, [the sum of] the products of each of the parts by the whole number is equal to the square of the whole number. :\scriptstyle{\color{OliveGreen}{\sum_{k=1}^n \left[\left(\sum_{i=1}^n a_i\right)\sdot a_k\right]=\left(\sum_{i=1}^n a_i\right)^2}} ואומר כל מספר שחלקת אותו לחלקים איך שרצית הנה כפל כל אחד מהחלקים על כל המספר מקובץ שוה למרובע כל המספר
Elements/Elements II-1a·∑bᵢ=∑(a·bᵢ)ספר_המלכים#Sjh3For every two numbers, such that one of them is divided into as many parts as there are, [the product of] the number that is not divided by the divided number is equal to the sum of its products by each part of the divided number. :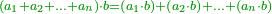\scriptstyle{\color{OliveGreen}{\left(a_1+a_2+\ldots+a_n\right)\sdot b=\left(a_1\sdot b\right)+\left(a_2\sdot b\right)+\ldots+\left(a_n\sdot b\right)}} כל שני מספרים יחלק אחד מהם בחלקים כמו שיהיו הנה המספר שלא חולק במספר שחולק כמו הכאתו בכל חלקי המספר הנחלק כאשר יקובצו
Elements/Elements II-1definitionספר_המספר_/_אליהו_מזרחי#8mWVIt was already clarified in Euclid's Book of Elements, in the [second] section, in the first proposition that for any two straight lines, one of which is cut into segments as many as they may be, the sum of the surfaces generated from the whole straight line and each of the segments of the other straight line equals the surface generated from the whole straight line and the whole divided line. :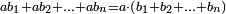\scriptstyle ab_1+ab_2+\ldots+ab_n=a\sdot\left(b_1+b_2+\ldots+b_n\right) וזה שכבר התבאר בספר היסודות לאקלידס במאמר השלישי ממנו בתמונה הראשונה שכל שני קוים שנחלק אחד מהם לחלקים כמה שיהיו הנה השטח ההוא מהקו האחד כלו עם כל אחד מחלקי הקו האחר יחד הוא שוה לשטח ההווה מהקו האחד עם כל הקו הנחלק
Elements/Elements II-110,2+3+5+2לקוטים_מספר_פראלוקא#1Q9zExample: the two numbers are 10 and 12 and we divide 12 to 2, 3, 5, 2, so their sum is 12. המשל הנה ב' מספרים והם י' וי"ב ונחלק י"ב על ב' ועל ג' ועל ה' ועל ב' והנה כלם י"ב
Elements/Elements II-14,2+3+5ספר_המספר_/_אליהו_מזרחי#1rE2Example: if we divide the 10 into three parts randomly, one part of them is 2, the second is 3 and the third is 5. משל זה אם נחלק הי' לג' חלקים איך מה שקרה והיה החלק האחד מהם מספר ב' והשני מספר ג' והשלישי מספר ה'
Elements/Elements II-1012,8לקוטים_מספר_פראלוקא#wujaExample: we have 12, you divide it to 6 and 6, then add to 12 another number. Suppose that we add 8 to it. המשל יש לנו מספר י"ב ותחלקהו על ו'ו' ותוסיף על י"ב ‫148vמספר אחר ונניח כי נוסיף בם ח‫'
Elements/Elements II-10(a+b)²+b²=2·((½a)²+((½a)+b)²)ספר_המלכים#CVU6For any even number divided into half and another number is added to it, [the sum of] twice the product of half the number by itself and twice the product of half the number plus the additional [number] by itself is equal to [the sum of] the product of the [whole] number plus the additional [number] by itself and [the product] of the additional [number] by itself. :\scriptstyle{\color{OliveGreen}{\left[2\sdot\left(\frac{1}{2}\sdot a\right)^2\right]+\left[2\sdot\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2\right]=\left(a+b\right)^2+b^2}} כל מספר זוג יחלק לחציים ונוסף בו מספר אחר הנה ההווה מהכאת חצי המספר בכמהו שני פעמים והכאת חצי המספר עם התוספת בכמהו שני פעמים הכהכאת המספר עם התוספת בכמהו והתוספת בכמהו
Elements/Elements II-10(a+b)²+b²=2·((½a)²+((½a)+b)²)ספר_החשבון_והמדות#w9pWIf you divide any number into half and add to it another number, [the sum of] the square of the whole number plus the additional [number] and the square of the additional [number] is equal to twice [the sum of] the square of half the number and the square of half the number plus the additional [number] together. :\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2+b^2=2\sdot\left[\left(\frac{1}{2}\sdot a\right)^2+\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2\right]}} עוד כל מספר שחלקת אותו לשני חציים והוספת עליו מספר אחר הנה מרובע המספר עם התוספת יחד ומרובע התוספת בעצמו הם כפל שני המרובעים שהם מרובע חצי המספר ומרובע חצי המספר עם התוספת יחד כאשר {{#annot:term|178,2083|Ycx9}}יחוברו{{#annotend:Ycx9}}
Elements/Elements II-1010,2ספר_המספר_/_אליהו_מזרחי#0WFgExample: we have the number ten, we divide it into two halves and add to it the number 2, so it bacomes 12. דמיון יש לנו מספר עשרה וחלקנוהו לשני חציים והוספנו עליו מספר ב' ונהיה י"ב
Elements/Elements II-10(a+b)²+b²=2·((½a)²+((½a)+b)²)ספר_המספר_/_אליהו_מזרחי#FJSeAny number that you divide into half and add to it another number, [the sum of] the square of the [whole] number plus the additional [number] and the square of the additional [number] is equal to twice [the sum of] the square of half the number and the square of half the number plus the additional [number] when they are summed together. :\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2+b^2=2\sdot\left[\left(\frac{1}{2}\sdot a\right)^2+\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2\right]}} עוד כל מספר שחלקת אותו לשני חצאים והוספת עליו מספר אחר הנה מרובע המספר עם התוספת יחד ומרובע התוספת בעצמו הם כפל שני המרובעים שהם מרובע חצי המספר ומרובע חצי המספר עם התוספת יחד כאשר יחוברו
Elements/Elements II-10(a+b)²+b²=2·((½a)²+((½a)+b)²)לקוטים_מספר_פראלוקא#ijBnIf you divide any number into two equal parts, then add another number to the divided number, square it and add to it the square of the [number] you added, it is twice [the sum of] the square of the additional [number] plus half [the number] with the square of half [the number]. :\scriptstyle\left(a+b\right)^2+b^2=2\sdot\left[\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2+\left(\frac{1}{2}\sdot a\right)^2\right] ‫165 אם תחלק איזה מספר על ב' חלקים שוים ואחר תוסיף מספר אחר על המספר המחולק ותרבענו ותוסיף על זה מרובע שהוספת יהיה ב' פעמים כמו כפל ממה שיעלה התוספת הנוסף על החצי עם מרובע החצי נוספים
Elements/Elements II-1010,2ספר_החשבון_והמדות#zIUcExample: we have the number ten, we divide it into two halves, which are 5, and add to it another number 2, so it bacomes 12. דמיון יש לנו מספר מניינו עשרה וחלקנוהו לשני חצאים על ה' והוספנו עליו ‫33rמספר אחר ב' ונהיה י"ב
Elements/Elements II-212,3+4+5לקוטים_מספר_פראלוקא#Gj4LExample: we wish to divide 12 into three parts 5, 3, 4. המשל נרצה לעשות מי"ב ג' חלקים ה' ג' ד‫'
Elements/Elements II-2∑ₖ((∑ᵢaᵢ)·aₖ)=(∑ᵢaᵢ)²ספר_החשבון_והמדות#DxvKFor every number that you divide randomly into two parts, the sum of the products of each of the two parts by the whole number is equal to the square of the whole number. :\scriptstyle{\color{OliveGreen}{\left[\left(a+b\right)\sdot a\right]+\left[\left(a+b\right)\sdot b\right]=\left(a+b\right)^2}} עוד כל מספר שחלקת אותו לשני חלקים איך שקרה הנה כפל כל אחד משני החלקים על כל המספר מקובץ שוה למרובע כל המספר
Elements/Elements II-210,7+3ספר_החשבון_והמדות#KF6oExample: the number ten; we divide it into 7 and 3. דמיון המספר עשרה וחלקנוהו על ז' וג‫'
Elements/Elements II-2∑ₖ((∑ᵢaᵢ)·aₖ)=(∑ᵢaᵢ)²קצת_מענייני_חכמת_המספר#4EHvIf you divide any number into parts as you wish, [the sum of] the products of each of the parts by the whole number is equal to the square of the whole number. :\scriptstyle{\color{OliveGreen}{\sum_{k=1}^n \left[\left(\sum_{i=1}^n a_i\right)\sdot a_k\right]=\left(\sum_{i=1}^n a_i\right)^2}} אחת כל מספר שחלקת אותו לחלקים איך שרצית הנה הכאת כל אח' מהחלקי' בכל המספר השוה למרובע הכל
Elements/Elements II-2∑ₖ((∑ᵢaᵢ)·aₖ)=(∑ᵢaᵢ)²לקוטים_מספר_פראלוקא#nMHcIf you have a number and you divide iy into parts as you wish, if you multiply each part by the divided number, then sum all the [products] they are equal to the divided number multiplied by itself. :\scriptstyle\sum_{k=1}^n \left[\left(\sum_{i=1}^n a_i\right)\sdot a_k\right]=\left(\sum_{i=1}^n a_i\right)^2 ‫157 אם יש לך מספר אחד ותחלק אותו לכ"כ חלקים שתרצה אם תכפול כל חלק על המספר המחולק ותקבץ כל החלקים יהיו שוים אל המספר המחולק כפול על עצמו
Elements/Elements II-212,3+4+5ספר_החשבון_והמדות#pdf0Example: the number 12; we divide it into three, four and five. דמיון המספר י"ב וחלקנוהו על שלשה וארבעה וחמשה
Elements/Elements II-2∑ₖ((∑ᵢaᵢ)·aₖ)=(∑ᵢaᵢ)²ספר_המספר_/_אליהו_מזרחי#mQeQAny number that you divide into parts as you wish, [the sum of] the products of each of the parts by the whole number is equal to the square of the whole number. :\scriptstyle{\color{OliveGreen}{\sum_{k=1}^n \left[\left(\sum_{i=1}^n a_i\right)\sdot a_k\right]=\left(\sum_{i=1}^n a_i\right)^2}} והוא שכל מספר שחלקת אותו לחלקים איך שרצית הנה הכאת כל אחד מהחלקים עם כל המספר שוה למרובע כל המספר
Elements/Elements II-212,3+4+5ספר_המספר_/_אליהו_מזרחי#NxlmExample: the number 12, we divide it to three, four and five. דמיון זה המספר י"ב וחלקנוהו על שלשה וארבעה וחמשה
Elements/Elements II-3(a+b)·b=(a·b)+b²לקוטים_מספר_פראלוקא#fYtFIf you divide any number into two parts, then multiply any of the two parts by the divided number and keep the product, so will be the result if you multiply the same part by itself, then add to it the product of the one part by the other. :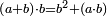\scriptstyle\left(a+b\right)\sdot b=b^2+\left(a\sdot b\right) ‫158 אם תחלק איזה מספר על ב' חלקים ותכפול החלק שיהיה מב' החלקים על המספר המחולק ושמור העולה כך יעלה אם תכפול אותו חלק על עצמו ותוסיף בו העולה מהכפל מהחלק האחד על השני
Elements/Elements II-3(a+b)·b=(a·b)+b²קצת_מענייני_חכמת_המספר#PVytFor any number divided into two parts as you wish, the product of the whole number by any of its two parts is equal to the product of the one part by the other plus the square of the part by which you multiplied the whole number. :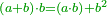\scriptstyle{\color{OliveGreen}{\left(a+b\right)\sdot b=\left(a\sdot b\right)+b^2}} ב כל מספר שחלקת אותו לב' חלקים איך שקרה הנה הכאת המספר כלו עם כל אחד מב' חלקיו איזה שיהיה שוה להכאת החלק האחד עם האחר ולמרובע החלק אשר בו הכית כל המספר
Elements/Elements II-310,3+7קצת_מענייני_חכמת_המספר#MLKIExample: the number 10 is divided into two parts - 7 and 3. כמשל מספר הי' נחלק לב' חלקים לז' ולג‫'
Elements/Elements II-3(a+b)·b=(a·b)+b²ספר_החשבון_והמדות#Eu5rFor any number divided into two parts as you wish, the product of the whole number by any of its two parts is equal to the product of the one part by the other plus the square of the part by which you multiplied the whole number. :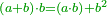\scriptstyle{\color{OliveGreen}{\left(a+b\right)\sdot b= \left(a\sdot b\right)+b^2}} עוד כל מספר שחלקת אותו בשני חלקים איך שקרה הנה כפל המספר כולו על אחד משני חלקיו איזה שיהיה שוה לכפול החלק האחד על השני ולמרובע החלק משניהם אשר כפלת על כל המספר
Elements/Elements II-312,4+8לקוטים_מספר_פראלוקא#XIpEExample: we have 12 and you divide it to 8 and 4. המשל אם יש לנו י"ב ותחלק אותו ח' ד‫'
Elements/Elements II-310,3+7ספר_החשבון_והמדות#zmnpExample: the number ten, we divide it into two parts - three and seven. דמיון המספר עשרה חלקנוהו לשני חלקים על שלשה ושבעה
Elements/Elements II-3(a+b)·b=(a·b)+b²ספר_מעשה_חושב#BvNUWhen a number is divided into two parts, the product of the whole number by one of its parts is equal to the product of the one part by the other plus the square of the mentioned part. :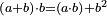\scriptstyle \left(a+b\right)\sdot b=\left(a\sdot b\right)+b^2 ד כאשר חולק מספר מה בשני חלקים הנה שטח כל המספר באחד מחלקיו שוה לשטח החלק האחד באחר ולמרובע החלק אשר זכרנו
Elements/Elements II-3(a+b)·b=(a·b)+b²ספר_המספר_/_אליהו_מזרחי#oIDSFor any number that you divide into two parts randomly, the product of the whole number by any of its two parts is equal to the product of the one part by the other plus the square of the part by which you have multiplied the whole number. :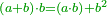\scriptstyle{\color{OliveGreen}{\left(a+b\right)\sdot b=\left(a\sdot b\right)+b^2}} עוד כל מספר שחלקת אותו לשני חלקים איך שקרה הנה הכאת המספר כלו עם כל אחד משני חלקיו איזה שיהיה שוה להכאת החלק האחד עם השני ולמרובע החלק אשר הכית עם כל המספר
Elements/Elements II-310,3+7ספר_המספר_/_אליהו_מזרחי#CANOExample: the number ten, we divide into two parts - three and seven. דמיון המספר עשרה חלקנוהו לשני חלקים על שלשה ושבעה
Elements/Elements II-410,3+7ספר_החשבון_והמדות#hh0JExample: the number ten; we divide it into three and seven. דמיון המספר עשרה חלקנוה על שלשה ושבעה
Elements/Elements II-4(a+b)²=a²+b²+2(a·b)ספר_מעשה_חושב#lUMxWhen a number is added to a number, the square of the two numbers that are summed together is equal to [the sum of] the squares of these numbers and twice the product of the one by the other. :\scriptstyle\left(a+b\right)^2=a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right] ו כאשר נוסף על מספר מונח מספר מה הנה מרובע שני המספרים מחוברים שוה למרובעי המספרים ההם ולכפל שטח זה בזה
Elements/Elements II-4(a+b)²=a²+b²+2(a·b)קצת_מענייני_חכמת_המספר#v7DxFor any number divided into two parts as you wish, the square of the whole number is equal to [the sum of] the squares of the two parts and twice the product of the one part by the other. :\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2=a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]}} ג כל מספר שחלקת אותו לשני חלקים איך שקרה הנה מרובע כל המספר שוה לב' המרובעים ההווים מב' החלקים ולהכאת החלק האחד עם חבירו ב' פעמים
Elements/Elements II-4(a+b)²=a²+b²+2(a·b)ספר_המספר_/_אליהו_מזרחי#TApzFor any number divided into two parts randomly, the square of the whole number is equal to [the sum of] the squares of the two parts and twice the product of the one part by the other. :\scriptstyle\left(a+b\right)^2=a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right] האחת שכל מספר נחלק לשנים חלקים איך מה שקרה הנה המרובע ההווה מן המספר כלו הוא שוה לשני המרובעים ההווים משני חלקיו עם כפל המספר ההווה מהכאת החלק האחד עם האחר
Elements/Elements II-410,3+7קצת_מענייני_חכמת_המספר#OusCExample: the number 10 is divided into 7 and 3. כמשל הי' נחלק לז' ולג‫'
Elements/Elements II-4(a+b)²=a²+b²+2(a·b)ספר_המספר_/_אליהו_מזרחי#oC2jFor any number that you divide into two parts randomly, the square of the whole number is equal to [the sum of] the squares of the two parts and twice the product of the one part by the other. :\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2=a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]}} עוד כל מספר שחלקת אותו לשני חלקים איך שקרה הנה מרובע כל המספר שוה לשני המרובעי' ההווים משני החלקים ולהכאת החלק האחד עם חברו פעמים
Elements/Elements II-410,3+7ספר_המספר_/_אליהו_מזרחי#6oZuExample: if we divide the 10 into two parts randomly, one part of them is 3 and the other 7. משל זה אם נחלק הי' לשנים חלקים איך מה שקרה והיה החלק האחד מהם ג' והאחר ז'
Elements/Elements II-4(a+b)²=a²+b²+2(a·b)ספר_החשבון_והמדות#q5ibFor any number divided into two parts as you wish, the square of the whole number is equal to [the sum of] the squares of the two parts and twice the product of the one part by the other. :\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2=a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]}} עוד כל מספר שחלקת אותו לשני חלקים איך שקרה הנה מרובע כל המספר שוה לשני המרובעים ההוים משני החלקים ולכפל החלק האחד על חברו פעמים
Elements/Elements II-4(a+b)²=a²+b²+2(a·b)לקוטים_מספר_פראלוקא#lb40If you divide any number into two and multiply each part by itself, you multiply also one [part] by the other and multiply [the product] by 2, then you sum all, the result is equal to the divided number multiplied by itself. :\scriptstyle a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]=\left(a+b\right)^2 ‫159 אם תחלק איזה מספר שיהיה על ב' ותכפול כל חלק על עצמו וג"כ כפול הא' על הב' וכפלם על ב' ותקבץ הכל הנה העולה יהיה שוה אל המספר המחולק כפול על עצמו
Elements/Elements II-4referenceספר_האלזיברא#EeueIt was already clarified in [[ספר_היסודות_לאקלידס#Elements_II_4|'''Euclid, Elements, Book II, proposition 4''']] that: וכבר נתבאר ב'''תמונת הרביעית מן המאמר השני לאקלידס'''
Elements/Elements II-4definitionספר_האלזיברא#JPnCWhen a straight line is cut randomly into two segments, the square on the whole line equals the sum of the two squares that are generated from the two segments plus twice the rectangle encompassed by the two segments. :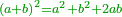\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2=a^2+b^2+2ab}} כי כאשר נחלק קו ישר לב' חלקים איך שקרה הנה מרבע הקו כלו שוה לשני המרבעים ההווים משני החלקים ולכפל השטח הנצב הזויות אשר יקיפו בו שני החלקים
Elements/Elements II-4(a+b)²=a²+b²+2(a·b)לקוטים_מספר_פראלוקא#lAxqIf you have a number and you divide it into two unequal parts, I say that if you sum the [parts] that are multiplied by themselves, then you multiply the smaller [part] by the greater, multiply the product by 2 and sum it with the reserved, the result is equal to the [original] number multiplied by itself. :\scriptstyle\left(a+b\right)^2=a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right] ‫169 אם יש לך מספר ותחלקהו על ב' חלקים בלתי שוים אומר כי אם תקבץ המספרי' המוכפלים על עצמם ואח"כ תכפול המספר הקטון על הגדול והעולה כפול על ב' ותקבץ זה עם השמור יעלה הכל כמו המספר כפול על עצמו
Elements/Elements II-4(a+b)²=a²+b²+2(a·b)ספר_המלכים#wUeWFor any number divided into [two] parts, whichever they may be, the product of the whole number by itself is equal to the sum of the products of each of the two parts by itself and double the product of one of the two parts by the other. :\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2=a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]}} |style="width:45%; text-align:right;"|כל מספר יחלק בחלקים כמו שיהיו הנה הכאת המספר כלו בעצמו כמו הכאת כל אחד משני החלקים בעצמו וכפל הכאת אחד משני החלקים באחר כאשר יקובצו
Elements/Elements II-410,3+7ספר_המספר_/_אליהו_מזרחי#Ca24Example: the number ten, we divide it to three and seven. דמיון המספר עשרה חלקנוהו על שלשה ושבעה
Elements/Elements II-412,4+8לקוטים_מספר_פראלוקא#HYCkExample: we divide 12 to 4 and 8. המשל הנה נחלק ‫147vמספר י"ב על ד' ועל ח‫'
Elements/Elements II-510,3+7ספר_החשבון_והמדות#zKhJExample: the number ten, we divide it to five and five, which are equal parts, then we divide it also to 7 and 3, which are unequal parts. דמיון המספר עשרה חלקנו לחמשה וחמשה שהם חלקים שוים גם חלקנוהו לז' וג' שהם חלקים בלתי שוים
Elements/Elements II-5(½(a+b))²=(a·b)+(b-½(a+b))²=(a·b)+(½(a+b)-a)²ספר_החשבון_והמדות#43ljFor any number divided into two equal parts and into two unequal parts, [the sum of] the product of one of the unequal parts by the other and the square of the difference between the two parts, i.e. between the equal part [= the half of the whole number] and the unequal [part] is equal to the square of half the [whole] number. :\scriptstyle{\color{OliveGreen}{\left(a\sdot b\right)+\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]^2=\left(a\sdot b\right)+\left[b-\left[\frac{1}{2}\sdot\left(a+b\right)\right]\right]^2=\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2}} עוד כל מספר כאשר תחלקהו לשני חלקים שוים ולשני חלקים בלתי שוים הנה כפל החלק האחד אל חברו מהחלקים הבלתי שוים ומרובע מה שבין שני ‫32vהחלקים ר"ל בין החלק השוה ובלתי שוה שוה למרובע חצי המספר
Elements/Elements II-5(½(a+b))²=(a·b)+(b-½(a+b))²=(a·b)+(½(a+b)-a)²ספר_מעשה_חושב#AHZrThe product of half the given number by itself is equal to [the sum of] the product of a part of that number by the other part and the square of the difference between one of the [unequal] parts and half of the [whole] given number. ח השטח ההוה מחצי המספר המונח בעצמו שוה לשטח ההוה מחלק מה מהמספר ההוא בחלק השני ולמרובע יתרון אחד מן החלקים על חצי המספר המונח
Elements/Elements II-5(½(a+b))²=(a·b)+(b-½(a+b))²=(a·b)+(½(a+b)-a)²ספר_המלכים#4PpZFor any even number divided into halves and into [two] unequal parts, the product of half the [whole] number by itself is equal to [the sum of] the product of the greater part by the smaller [part] and the product of the excess of the half of the [whole] number over the smaller part by itself. :\scriptstyle{\color{OliveGreen}{\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2=\left(a\sdot b\right)+\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]^2}} כל מספר זוג יחלק לחצאים ולחלקים מתחלפים הנה אשר יהיה מהכאת [חצי]‫M om. המספר בעצמו כמו ההווה מהכאת החלק הגדול בקטן עם הכאת מותר חצי המספר על החלק ההקטן [בכמהו]‫M וכמוהו
Elements/Elements II-5(½(a+b))²=(a·b)+(b-½(a+b))²=(a·b)+(½(a+b)-a)²לקוטים_מספר_פראלוקא#24rAIf you divide any number into two equal parts and into two unequal parts, the product of the equal parts one by the other is as the product of the unequal parts one by the other, when you add to it the [square] of the difference between the [equal] part and the [unequal part]. ‫160 אם תחלק מספר אחד לב' חלקים שוים ולב' חלקים בלתי שוים הנה כל כך יעלה כפל החלקים השוים זה על זה כמו כפל החלקים הבלתי שוים זה על זה ותוסיף בם כפל היתרון שיש מהחלק האחד על האחר
Elements/Elements II-510,3+7ספר_המספר_/_אליהו_מזרחי#zYJbExample: the number ten, we divide it to five and five, which are equal parts, then we divide it also to seven and three, which are unequal parts. דמיון המספר עשרה חלקנוהו לחמשה וחמשה שהם חלקים שוים גם חלקנוהו לשבעה ושלשה שהם חלקים בלתי שוים
Elements/Elements II-510,3+7קצת_מענייני_חכמת_המספר#41HjExample: the number 10 that is divided into 7 and 3. במש' הי' שנחלק לז' ולג‫'
Elements/Elements II-5referenceספר_האלזיברא#7B0h[[ספר_היסודות_לאקלידס#Elements_II_5|'''Euclid, Elements, Book II, proposition 5''']]: the square formed by AZ, which is four measures, and is as the square of half [the number of] the things that is known to be 16, is equal to surface BH, which is equal to the right-angled surface encompassed by the two unequal segments, whose area is known to be 12, plus the square formed by ZB that is the difference between the two parts. :\scriptstyle{\color{OliveGreen}{\left(a\sdot b\right)+\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-b\right]^2=\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2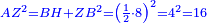}} :\scriptstyle{\color{blue}{AZ^2=BH+ZB^2=\left(\frac{1}{2}\sdot8\right)^2=4^2=16}} והנה כפי מה שנתבאר ב'''תמו' החמישית מן המאמר השני לאקלידס'''
Elements/Elements II-5(½(a+b))²=(a·b)+(b-½(a+b))²=(a·b)+(½(a+b)-a)²קצת_מענייני_חכמת_המספר#9QNaFor any number divided into two equal parts and into two unequal parts, [the sum of] the product of one of the unequal parts by the other and the square of the difference between the two parts, i.e. between the equal part [= the half of the whole number] and the unequal [part] is equal to the square of half the [whole] number. :\scriptstyle{\color{OliveGreen}{\left(a\sdot b\right)+\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]^2=\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2}} ד כל מספר כאשר תחלקהו לב' חלקים שוים ולב' חלקים בלתי שוים הנה הכאת החלק הא' עם חבירו מהחלקים הבלתי שוים ומרוב' מה שבין ב' חלקים ר"ל בין החלק השוה ובלתי שוה שוה למרובע חצי המספר
Elements/Elements II-512,4+8לקוטים_מספר_פראלוקא#pZPTExample: we divide 12 into two equal parts 6 and 6, and into two unequal parts 4 and 8. המשל נחלק מספר י"ב לב' חלקים שוים ו'ו' ולב' חלקים בלתי שוים ד' וח‫'
Elements/Elements II-5(½(a+b))²=(a·b)+(b-½(a+b))²=(a·b)+(½(a+b)-a)²ספר_המספר_/_אליהו_מזרחי#yKYxFor any number, when you divide it into two equal parts and into two unequal parts, [the sum of] the product of one of the unequal parts by the other and the square of the difference between the two parts, i.e. between the equal part [= the half of the whole number] and the unequal [part] is equal to the square of half the [whole] number. :\scriptstyle{\color{OliveGreen}{\left(a\sdot b\right)+\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]^2=\left(a\sdot b\right)+\left[b-\left[\frac{1}{2}\sdot\left(a+b\right)\right]\right]^2=\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2}} עוד כל מספר כאשר תחלקהו לשני חלקים שוים ולשני חלקים בלתי שוים הנה הכאת החלק האחד עם חברו מהחלקים הבלתי שוים ומרובע מה שבין שני החלקים ר"ל בין החלק השוה ובלתי שוה שוה למרובע חצי המספר
Elements/Elements II-612,4לקוטים_מספר_פראלוקא#qQuNExample: we have 12, you divide it to 6 and 6, then add to 6 whichever number you wish. Suppose that we wish to add 4 to 6. המשל יש לנו מספר י"ב ותחלק אותו על ו"ו ותוסיף על ו' מספר איזה שתרצה ונניח כי נרצה להוסיף על ו' ד‫'
Elements/Elements II-6referenceספר_האלזיברא#BJrm[[ספר_היסודות_לאקלידס#Elements_II_6|'''Euclid, Elements, Book II, proposition 6''']] that the right-angled surface encompassed by the whole line with the addition and the addition, which is equal to surface AW, whose area is known as 48, plus the square of half the line, whose area is known, which is 1, both together are 49, equals the square of the line formed by half the line with the addition, which is line AZ. :\scriptstyle{\color{OliveGreen}{\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2}} וכבר נתבאר ב'''תמונה הששית ‫131vמן המאמר השני לאקלידס'''
Elements/Elements II-6referenceספר_האלזיברא#XaGL[[ספר_היסודות_לאקלידס#Elements_II_6|'''Euclid, Elements, Book II, proposition 6''']] that the right-angled surface encompassed by the whole line with the addition and the addition, which is equal to surface ZD, whose area is 2 in our example, with the square formed by half the line, which is 16 in our example, both together are 36, equals the square of the line formed by half the line with the addition, which is line TB in our illustration. :\scriptstyle{\color{OliveGreen}{\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2}} וכבר נתבאר ב'''תמונה הששית מן המאמר השני לאקלידס'''
Elements/Elements II-610,2ספר_החשבון_והמדות#yd9cExample: the number ten, we divide it into two halves, which are five each, then we add two to the ten, they are 12. דמיון המספר עשרה וחלקנוהו לשני חצאים שהם כל חצי חמשה {{#annot:term|178,1206|GTDu}}הוספנו{{#annotend:GTDu}} על העשרה שנים והיו י"ב
Elements/Elements II-6(a+b)·b+(½a)²=(½a+b)²ספר_המלכים#c7yYFor any number divided into two halves and another number is added to it, the product of half the number and the additional [number] together by itself is equal to [the sum of] the product of the [whole] number plus the additional [number] by the additional [number] and the product of half the original number by itself. :\scriptstyle{\color{OliveGreen}{\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2=\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2}} כל מספר זוג יחלק לשני חצאים ויתוסף בו מספר אחר הנה הכאת חצי המספר עם התוספת בכמהו כהכאת המספר עם התוספת בתוספת והכאת חצי המספר הראשון בעצמו
Elements/Elements II-610,2ספר_המספר_/_אליהו_מזרחי#bDvjExample: the number ten, we divide it into two halves, which are five each, then we add two to the ten, they are 12. דמיון המספר עשרה וחלקנוהו לשני חצאים שהם כל חצי חמשה הוספנו על העשרה שנים והיו י"ב
Elements/Elements II-6(a+b)·b+(½a)²=(½a+b)²לקוטים_מספר_פראלוקא#77leIf you divide any number into two equal parts, then add an additional [number] to the divided number, multiply [the sum] by the additional [number] and add [the product] to the square of one of the parts, I say that it is equal to the square of half [the number] with the additional [number]. :\scriptstyle\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2 ‫161 אם תחלק איזה מספר לב' חלקים שוים ותוסיף בם א' מהחלקי' כפול על עצמו ותוסיף בם התוספת על כל המספר המחולק ותכפול אותו המספר אשר הוספת ותחברם עם כפל אחד מהחלקים אומר כי הוא שוה אל כפל המחצית עם התוספת
Elements/Elements II-6(a+b)·b+(½a)²=(½a+b)²קצת_מענייני_חכמת_המספר#nmaVIf we divide any number into half and add to it another number, [the sum of] the product of the whole number plus the additional [number] by the additional [number] and the square of half the number is equal to the square of half the number and the additional [number] together. :\scriptstyle{\color{OliveGreen}{\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2}} ה כל מספר כאשר חלקנו אותו לחצי והוספת עליו מספר אחר הנה הכאת המספר כלו מחובר עם התוספ' בתוספת ומרובע חצי המספר שוה למרובע חצי המספר והתוספת ביחד
Elements/Elements II-6(a+b)·b+(½a)²=(½a+b)²ספר_החשבון_והמדות#A9xwIf you divide any number into half and add to it another number, [the sum of] the product of the whole number plus the additional [number] by the additional [number] and the square of half the number is equal to the square of half the number and the additional [number] together. :\scriptstyle{\color{OliveGreen}{\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2}} עוד כל מספר כאשר חלקת אותו לחצאים והוספת עליו מספר אחר הנה כפל המספר כלו מקובץ עם התוספת בתוספת והמרובע ההוה מחצי המספר שוה למרובע חצי המספר והתוספת ביחד
Elements/Elements II-6(a+b)·b+(½a)²=(½a+b)²ספר_מעשה_חושב#vsiVWhen a number is divided into two halves and a number is added to it, [the sum of] the product of the additional [number] by the whole number plus the additional [number] and the square of half the number is equal to the square of half the number and the additional [number] summed together. :\scriptstyle\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2 ה כאשר חולק מספר מה לחציין והוסף עליו מספר מה הנה שטח התוספת במספר כלו עם התוספת עם מרובע חצי המספר שוה למרובע חצי המספר והתוספת מקובצים
Elements/Elements II-6(a+b)·b+(½a)²=(½a+b)²ספר_המספר_/_אליהו_מזרחי#tcs6For any number, when you divide it into half and add to it another number, [the sum of] the product of the whole number plus the additional [number] by the additional [number] and the square of half the number is equal to the square of half the number and the additional [number] together. :\scriptstyle{\color{OliveGreen}{\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2}} עוד כל מספר כאשר חלקת אותו לחצי והוספת עליו מספר אחר הנה הכאת המספר כלו מקובץ עם התוספת בתוספת והמרובע ההווה מחצי המספר שוה למרובע חצי המספר והתוספת ביחד
Elements/Elements II-7(a+b)²+a²=(2·(a+b)·a)+b²ספר_החשבון_והמדות#hdYZFor any number divided into two parts, the sum of the square of the whole number and the square of one of the parts is equal to twice the product of this part by the whole number plus the product of the other part by itself. :\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2+a^2=2\sdot\left[\left(a+b\right)\sdot a\right]+b^2}} עוד כל מספר כשתחלקהו בשני חלקים איך שיקרה הנה המרובע ההוה מן המספר כלו והמרובע ההוה מאחד משני חלקים כאשר {{#annot:term|178,1216|tLsc}}התקבצו{{#annotend:tLsc}} שוים לכפל המספר כלו עם החלק הנזכר פעמים והמרובע ההוה מן החלק השני
Elements/Elements II-710,3+7ספר_החשבון_והמדות#L1XhExample: the number ten, we divide it randomly to seven and three. דמיון המספר עשרה וחלקנוהו איך שקרה על שבעה ועל שלשה
Elements/Elements II-7(a+b)²+a²=(2·(a+b)·a)+b²לקוטים_מספר_פראלוקא#lBZsIf you have a number and you divide it into two unequal parts, you multiply the greater part by itself and multiply also the divided number by itself, then sum both products, the result is equal to the product of the greater number by the divided number multiplied by two, then you add to it the square of smaller part. :\scriptstyle\left(a+b\right)^2+a^2=2\sdot\left[\left(a+b\right)\sdot a\right]+b^2 ‫162 אם יש לך מספר ותחלקהו לב' חלקים בלתי שוים ותכפול החלק הגדול על עצמו גם תכפול המספר המחולק על עצמו ותחבר הב' הכפלות הנה העולה יהיה שוה אל כפל המספר הגדול על המספר המחולק ותכפלהו אח"כ על ב' גם תוסיף על זה כפל החלק הקטן ותחבר הכל יהיה שוה
Elements/Elements II-7(a+b)²+a²=(2·(a+b)·a)+b²ספר_המספר_/_אליהו_מזרחי#WZG6For any number, when you divide it into two parts randomly, [the sum of] the square of the whole number and the square of one of the two parts is equal to twice the product of the whole number by the mentioned part plus the square of the second part. :\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2+a^2=2\sdot\left[\left(a+b\right)\sdot a\right]+b^2}} עוד כל מספר כאשר תחלקהו בשני חלקים איך שיקרה המרובע ההווה מן המספר כלו והמרובה ההווה מאחד משנים החלקים כאשר התקבצו שוים להכאת המספר כלו עם החלק הנזכר פעמים והמרובע ההווה מן החלק השני
Elements/Elements II-710,3+7קצת_מענייני_חכמת_המספר#nE0OExample: the number 10 is divided into 7 and 3. במשל הרי הי' נחלק לז' ולג‫'
Elements/Elements II-710,3+7ספר_המספר_/_אליהו_מזרחי#VZVnExample: the number ten, we divide it randomly to 7 and 3. דמיון המספר עשרה וחלקנוהו איך שקרה על ז' ועל ג‫'
Elements/Elements II-712,4+8לקוטים_מספר_פראלוקא#R7rSExample: we wish to divide 12 to 4 and 8. המשל נרצה לחלק י"ב על ח' וד‫'
Elements/Elements II-7(a+b)²+a²=(2·(a+b)·a)+b²קצת_מענייני_חכמת_המספר#DEFAFor any number divided into two parts, the sum of the square of the whole number and the square of one of the parts is equal to twice the product of this part by the whole number plus the product of the other part by itself
:\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2+a^2=2\sdot\left[\left(a+b\right)\sdot a\right]+b^2}} ו כל מספר שתחלקהו בב' חלקים איך שקרה המרובע ההווה מהמספר כלו והמרובע ההווה מא' מב' אלו החלקים כאשר התקבצו שוה להכאת החלק הנזכ' עם המספר כלו ולהכאת החלק הב' הנשאר בעצמו
Elements/Elements II-7definitionספר_האלזיברא#cvaSWhen a straight line is cut randomly into two segments, the sum of the squares on both segments equals twice the rectangle encompassed by both segments plus the square that is generated from the excess of the larger segment over the smaller segment. [ [[ספר_היסודות_לאקלידס#Elements_II_7|'''Euclid, Elements, Book II, proposition 7''']] ] :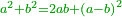\scriptstyle{\color{OliveGreen}{a^2+b^2=2ab+\left(a-b\right)^2}} כי כאשר נחלק קו ישר ‫128rלשני חלקים איך שקרה הנה מרבעי שני החלקים שוים לכפל השטח הנצב הזויות אשר יקיפו בו שני החלקים ולמרבע ההוה ממותר החלק הגדול על הקטן
Elements/Elements II-7(a+b)²+a²=(2·(a+b)·a)+b²ספר_המלכים#isjpFor any number divided into two parts, [the sum of] the product of the [whole] number by itself and [the product of] one of the two parts by itself is equal to twice the product of the [whole] number by the part that is multiplied by itself plus the [product of the] other part by itself. :\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2+a^2=\left[2\sdot\left(a+b\right)\sdot a\right]+b^2}} כל מספר יחלק לשני חלקים [..] הנה הכאת המספר בכמוהו ואחד ‫59vמשני החלקים בכמוהו כמו ההווה מהכאת המספר בחלק המוכה בכמוהו שני פעמים והחלק השני בכמוהו
Elements/Elements II-810,3+7קצת_מענייני_חכמת_המספר#9UoHExample: the number 10 is divided into 7 and 3. במשל הי' נחלק לז' ולג‫'
Elements/Elements II-812,4+8לקוטים_מספר_פראלוקא#NtVpExample: we wish to divide 12 to 4 and 8. המשל נרצה לחלק י"ב על ד' וח‫'
Elements/Elements II-810,3+7ספר_המספר_/_אליהו_מזרחי#pqrOExample: we have the number ten, we divide it randomly to 3 and 7. דמיון יש לנו מספר עשרה וחלקנוהו איך שהזדמן על ג' ועל ז‫'
Elements/Elements II-8(4·(a+b)·a)+b²=((a+b)+a)²ספר_המספר_/_אליהו_מזרחי#LHo4For any number, when you divide it into two parts randomly and you multiply the whole number by one of the two parts four times, then sum [the product] with the square of the other part [it] is equal to the [square] of the whole number plus the mentioned part when you sum them together. :\scriptstyle{\color{OliveGreen}{4\sdot\left[\left(a+b\right)\sdot a\right]+b^2=\left[\left(a+b\right)+a\right]^2}} עוד כל מספר כאשר חלקת אותו בשני חלקים איך שיקרה והכית המספר כלו עם אחד משני חלקיו ארבעה פעמים וחברת אותו עם מרובע החלק הנשאר שוה למרובע ההווה מן המספר כלו והחלק הנזכר כאשר תחברם ביחד
Elements/Elements II-810,3+7ספר_החשבון_והמדות#AJOPExample: we have the number ten, we divide it randomly to 3 and 7. דמיון יש לנו מספר מנינו העשרה וחלקנוהו איך שהזדמן על ג' ועל ז‫'
Elements/Elements II-8(4·(a+b)·a)+b²=((a+b)+a)²ספר_המלכים#OcvsFor any number divided into two parts and one of the two parts is added to it, the product of the [whole] number plus the additional [part] by itself is equal to [the sum of] the product of the [whole] number by the additional [part] four times and the product of the other part by itself. :\scriptstyle{\color{OliveGreen}{\left[\left(a+b\right)+a\right]^2=\left[4\sdot\left(a+b\right)\sdot a\right]+b^2}} כל מספר יחלק בשני חלקים ונוסף עליו כמו אחד משני החלקים הנה הכאת המספר עם התוספת בכמהו כהכאת המספר בתוספת ד' פעמים והכאת החלק האחר בכמהו
Elements/Elements II-8(4·(a+b)·a)+b²=((a+b)+a)²לקוטים_מספר_פראלוקא#TRuXIf you have a number and you divide it into unequal two parts, if you add one of the parts to the whole number, i.e. the divided number, [its square] is equal to the same part that you added multiplied by the whole number, then multiplied by four, when you add to it the square of the second part. :\scriptstyle\left[\left(a+b\right)+a\right]^2=4\sdot\left[\left(a+b\right)\sdot a\right]+b^2 ‫163 אם יש לך מספר ותחלקהו לב' חלקים בלתי שוים אם תוסיף א' מהחלקים על כל המספר ר"ל על המספר המחולק יהיה שוה אל אותו החלק אשר הוספת כפול על כל המספר אח"כ העולה תכפול על ד' ותוסיף על זה מרובע החלק השני
Elements/Elements II-8(4·(a+b)·a)+b²=((a+b)+a)²קצת_מענייני_חכמת_המספר#R68tFor any number divided into two parts as you wish, if you multiply the whole number by one of the parts four times, the sum of the product with the square of the other part is equal to the [square] of the whole number plus the one part :\scriptstyle{\color{OliveGreen}{4\sdot\left[\left(a+b\right)\sdot a\right]+b^2=\left[\left(a+b\right)+a\right]^2}} ז כל מספר שחלקת אותו לב' חלקים איך שקרה אם הכית המספר כלו עם חלק אח' מהם ד' פעמים וקבצת הכל עם מרובע החלק הב' הנשאר היה שוה להכאת מספרו החלק הנזכר כאשר תחברם יחד
Elements/Elements II-8(4·(a+b)·a)+b²=((a+b)+a)²ספר_החשבון_והמדות#EAD6For any number divided into two parts as you wish, if you multiply the whole number by one of the parts four times, the sum of the product with the square of the other part is equal to the [square] of the whole number plus the one part. :\scriptstyle{\color{OliveGreen}{4\sdot\left[\left(a+b\right)\sdot a\right]+b^2=\left[\left(a+b\right)+a\right]^2}} עוד כל מספר כאשר חלקת אותו בשני חלקים איך שיקרה וכפלת המספר כלו עם אחד משני חלקיו ארבעה פעמים ועם מרובע החלק הנשאר שוה למרובע ההוה מן המספר כלו והחלק הנזכר כאשר תחברם ביחד ותקח מרובעם
Elements/Elements II-910,3+7ספר_המספר_/_אליהו_מזרחי#LnLoExample: the number 10, we divide it into two equal parts, which are 5, and into two unequal parts, which are 7 and 3. דמיון המספר י' וחלקנוהו לשני חלקים שוים והם ה' ולשני חלקים בלתי שוים והם ז' ג‫'
Elements/Elements II-912,4+8לקוטים_מספר_פראלוקא#QBwhExample: we wish to divide 12 into two equal parts 6 and 6 and into two unequal parts 8 and 4. המשל נרצה לחלק מספר י"ב לב' חלקי' שוים ו'ו' ולב' חלקים בלתי שוים ח' ד‫'
Elements/Elements II-9a²+b²=2·((½·(a+b))²+(a-(½·(a+b)))²)לקוטים_מספר_פראלוקא#E95LIf you divide any line into two equal parts and into two unequal parts, then you multiply each of the unequal parts [by itself] and sum them, they are twice [the sum of] the product of the equal parts plus the [square of] excess of the greater [part] over [half the number]. :\scriptstyle a^2+b^2=2\sdot\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2+\left[a-\left[\frac{1}{2}\sdot\left(a+b\right)\right]\right]^2\right] ‫164 אם תחלק איזה קו לב' חלקים שוים ולב' חלקים בלתי שוים וכפול כל אחד מהחלקים בלתי שוים ותחברם הם כפל מהחלקים השוים נוסף בם יתרון החלק הגדול על הקטן
Elements/Elements II-9a²+b²=2·((½·(a+b))²+(a-(½·(a+b)))²)ספר_המספר_/_אליהו_מזרחי#ClRvFor any number that you divide into two equal parts and into two unequal parts, [the sum of] the two squares of the unequal parts is equal to twice [the sum of] the square of half the [whole] number and [the square] of the excess of the large part over the half [of the whole number]. :\scriptstyle{\color{OliveGreen}{a^2+b^2=2\sdot\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2+\left[a-\left[\frac{1}{2}\sdot\left(a+b\right)\right]\right]^2\right]}} עוד כל מספר שחלקת אותו לשני חלקים שוים ושני חלקים בלתי שוים הנה שני המרובעים אשר יהיו מהחלקים הבלתי שוים הם כפל שני המרובעים אשר יהיו מחצי המספר ומהתוספת אשר לחלק הגדול על הה' שהוא המחצית
Elements/Elements II-9a²+b²=2·((½·(a+b))²+(a-(½·(a+b)))²)ספר_החשבון_והמדות#CM8jFor any number divided into two equal parts and into two unequal parts, [the sum of] the squares of the unequal parts is equal to twice [the sum of] the square of half the [whole] number and the square of the difference between the large part and the half [of the whole number]. :\scriptstyle{\color{OliveGreen}{a^2+b^2=2\sdot\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2+\left[a-\left[\frac{1}{2}\sdot\left(a+b\right)\right]\right]^2\right]}} עוד כל מספר שחלקת אותו לשני חלקים שוים ושני חלקים בלתי שוים הנה שני המרובעים אשר יהיו מהחלקים הבלתי שוים הם כפל שני המרובעים אשר יהיו מחצי המספר ומהתוספת אשר לחלק הגדול על המחצית
Elements/Elements II-910,3+7ספר_החשבון_והמדות#O8o8Example: we have the number ten, we divide it into two equal parts, which are 5, and into two unequal parts, which are 3 and 7. דמיון יש לנו מספר מנינו עשרה וחלקנוהו לשני חלקים שוים על ה' ושני חלקים בלתי שוים על ג' וז‫'
Elements/Elements II-9a²+b²=2·((½·(a+b))²+(a-(½·(a+b)))²)ספר_המלכים#g6A2For any even number divided into two halves and into two unequal parts, [the sum of the products of] each of the two unequal parts by themselves is equal to [the sum of] twice the product of half the [whole] number by itself and twice the product of the excess of half the [whole] number over the smaller part by itself. :\scriptstyle{\color{OliveGreen}{a^2+b^2=\left[2\sdot\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2\right]+\left[2\sdot\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]^2\right]}} כל מספר זוג יחלק בשני חצאים ובשני חלקים מתחלפים הנה כל אחד משני החלקים המתחלפים בכמהו כהכאת חצי המספר בכמהו שני פעמים והכאת מותר חצי המספר על החלק הקטן בכמהו שני פעמים
Elements/Elements-Introductiona=b,a-c=b-cספר_המספר_/_אליהו_מזרחי#tNTCFor, when equal is subtracted from equals, then the remainders are necessarily equal, according to what is clarified in the introduction of the first section of Euclid's [book]. :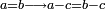\scriptstyle a=b\longrightarrow a-c=b-c כי כאשר יחוסר מהשוים שוה יהיו הנשארים שוים בהכרח לפי מה שהתבאר בפתיחת המאמר הראשון מאקלידס
Elements/Elements-Introductiona=b,a-c=b-cספר_המספר_/_אליהו_מזרחי#gaDwThis is because it was already clarified in the introduction of Euclid's book that when equal is subtracted from equals, then the remainders are equal :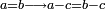\scriptstyle a=b\longrightarrow a-c=b-c וזה שכבר התבאר בפתיחת ספר אקלידס כאשר חוסר מהשוים שוה יהיה הנשאר שוה
Elements/Elements IX-21definitionספר_המספר_/_אליהו_מזרחי#qiN5When even numbers are summed, as many as they may be, their sum is an even number. הוא כאשר נקבצו מספרי זוגות כמה שיהיו הנה קבוצם מספר זוג
Elements/Elements IX-22definitionספר_המספר_/_אליהו_מזרחי#yrIbWhen odd numbers are summed, as many as they may be, and their multitude is even, their sum is an even number. וכאשר נקבצו מספרים נפרדים כמה שיהיו והיה מספרם זוג הנה קבוצם מספר זוג
Elements/Elements IX-23definitionספר_המספר_/_אליהו_מזרחי#1A6mWhen odd numbers are summed, as many as they may be, and their multitude is odd, their sum is an odd number. וכאשר נקבצו מספרים נפרדים כמה שיהיו והיה מספרם מפרד הנה קבוצם נפרד
Elements/Elements IX-28definitionספר_המספר_/_אליהו_מזרחי#RVMmWhen an even number is multiplied by an odd number, or by an even number, then the product is even. :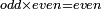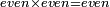\scriptstyle odd\times even=even; \scriptstyle even\times even=even הוא שכאשר הוכה מספר זוג במספר נפרד או במספר זוג הנה המקובץ זוג
Elements/Elements IX-29definitionספר_המספר_/_אליהו_מזרחי#DYPKWhen an odd number is multiplied by an odd number, then the product is odd. :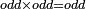\scriptstyle odd\times odd=odd וכאשר הוכה מספר נפרד במספר נפרד הנה המקובץ נפרד
Elements/Elements V-15(n·a)÷(n·b)=a÷bספר_המספר_/_אליהו_מזרחי#PIBAFor, it was already clarified in Euclid's Book of Elements, according to what was preceded in this section, that the given numbers have the same ratio as the ratio of their equimultiples. :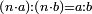\scriptstyle\left(n\sdot a\right):\left(n\sdot b\right)=a:b וזה שכבר התבאר בספר היסודות לאקלידס לפי מה שקדם מן המאמר שמהמספרים המונחים הם יחס קצתם אל קצת הוא כיחס כפליהם קצתם אל קצת
Elements/Elements V-15(n·a)÷(n·b)=a÷bספר_המספר_/_אליהו_מזרחי#wUJBFor, it was already clarified in Euclid's Book of Elements, in the fifth section, that any numbers, whose multiples are equal, have the same ratio as the ratio of their equimultiples. :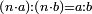\scriptstyle\left(n\sdot a\right):\left(n\sdot b\right)=a:b וזה שכבר התבאר בספר היסודות לאקלידס במאמר החמישי ממנו שהמספרים אשר כפליהם שוים הנה יחס קצתם אל קצת כיחס כפליהם קצתם אל קצת
Elements/Elements V-9definitionספר_המספר_/_אליהו_מזרחי#2X92For, any two magnitudes, which have the same ratio to the same magnitude, necessarily equal one another, according to what is clarified in Euclid's Book of Elements. :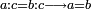\scriptstyle a:c=b:c\longrightarrow a=b כי כל שני שעורים שיחסם אל שעור אחר בעצמו יחס אחד הנה הם שוים בהכרח לפי מה שהתבאר בספר היסודות לאקלידס
Elements/Elements VI-17referenceספר_האלזיברא#cH1a[[ספר_היסודות_לאקלידס#Elements_VI_17|'''Euclid, Elements, Book VI, proposition 17''']] that the product of the first by the last is as the product of the mean by its similar. :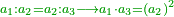\scriptstyle{\color{OliveGreen}{a_1:a_2=a_2:a_3\longrightarrow a_1\sdot a_3=\left(a_2\right)^2}} וכבר נתבאר מ'''תמונת י"ז מן המאמר הששי לאקלידס'''
Elements/Elements VI-17definitionספר_האלזיברא#KlWgIt is already explained in {{#annot: reference | #Elements VI-17 | cH1a}}[[ספר_היסודות_לאקלידס#Elements_VI_17|'''Euclid, Elements, Book VI, proposition 17''']] that the product of the first by the last is as the product of the mean by its similar. :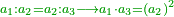\scriptstyle{\color{OliveGreen}{a_1:a_2=a_2:a_3\longrightarrow a_1\sdot a_3=\left(a_2\right)^2}} וכבר נתבאר מ'''תמונת י"ז מן המאמר הששי לאקלידס'''{{#annotend:cH1a}} כי {{#annot: term | #multiplication, #הכאה | poG8}}הכאת ה{{#annotend:poG8}}ראשו' באחרון כמו הכאת האמצעי בדומה לו
Elements/Elements VII-11a÷b=c÷d→(c-a)÷(d-b)ספר_המספר_/_אליהו_מזרחי#Iu2hwhen two numbers are subtracted from two numbers and the ratio of the subtrahend to the subtrahend is the same as the ratio of the minuend to the minuend, then the [ratio of] the remainder to the remainder is the same as the ratio of the minuend to the minuend. ::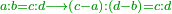\scriptstyle{\color{OliveGreen}{a:b=c:d\longrightarrow\left(c-a\right):\left(d-b\right)=c:d}} וזה שכבר התבאר בספר היסודות לאקלידס במאמר השביעי ממנו בתמונת י"א שכאשר חוסרו משני מספרים ב' מספרים והיה יחס המחוסר אל המחוסר כיחס הכל אל הכל הנה יהיה הנשאר אל הנשאר כיחס הכל אל הכל
Elements/Elements VIII-11definitionספר_האלזיברא#QcHWthe ratio of a square to a square is as the ratio of its side to its side duplicated. [ [[ספר_היסודות_לאקלידס#Elements_VIII_11|'''Euclid, Elements, Book VIII, proposition 11''']] ] :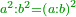\scriptstyle{\color{OliveGreen}{a^2:b^2=\left(a:b\right)^2}} וזה כי מפני כי יחס מרבע אל מרבע כיחס צלעו אל צלעו שנוי
Elements/Elements VIII-11definitionספר_האלזיברא#Nl0OThis is because the ratio of a square to a square is the same as the ratio of its side to its side duplicate. :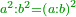\scriptstyle{\color{OliveGreen}{a^2:b^2=\left(a:b\right)^2}} וזה מפני כי {{#annot: term | #ratio, #יחס | Eve2}}יחס{{#annotend:Eve2}} מרובע אל מרובע כיחס צלעו אל צלעו {{#annot: term | #duplicate, #שנוי | Q7dD}}שנוי{{#annotend:Q7dD}} ר"ל {{#annot: term | #multiplied, #כפול | G4iq}}כפול{{#annotend:G4iq}}
Elements/Elements VIII-11referenceספר_האלזיברא#D3f5[[ספר_היסודות_לאקלידס#Elements_VIII_11|'''Euclid, Elements, Book VIII, proposition 11''']] מתמונת י"א מן המאמר השמיני לאקלידס
Elements/Elements VIII-11definitionספר_המספר_/_אליהו_מזרחי#sPcq Its reason is also known from what was clarified in Euclid's Book of Elements, in the eighth section that for every two squares numbers the ratio of one of them to the other is as the duplicate ratio of that which the side has to the side. :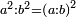\scriptstyle a^2:b^2=\left(a:b\right)^2 הנה סבתו ג"כ ידועה ממה שהתבאר בספר היסודו' לאקלידס במאמר הח' ממנו שכל שני מספרים מרובעים הנה יחס הא' מהם אל חברו הוא כיחס צלעו אל צלעו שנוי בכפל
Elements/Elements VIII-12referenceספר_האלזיברא#jD6NAccording to [[ספר_היסודות_לאקלידס#Elements_VIII_12|'''Euclid, Elements, Book VIII, proposition 12''']] מתמונת י"ב מן המאמר השמיני לאקלידס
Elements/Elements VIII-12definitionספר_האלזיברא#eDWEThis is because the ratio of a cube to a cube is the same as the ratio of its side to its side triplicate :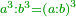\scriptstyle{\color{OliveGreen}{a^3:b^3=\left(a:b\right)^3}} וזה מפני כי יחס מעקב אל מעקב כיחס צלעו אל צלעו {{#annot: term | #triplicate, #משולש | A27z}}משלש{{#annotend:A27z}}
Elements/Elements XIII-1definitionהמחומשים_והמעושרים#1Da2Euclid proved that when a line is divided according to the ratio of a mean and two extremes, so that half the whole line is added to the larger segment, and all this is multiplied by itself, then the resulting square is equal to five times the square of half the line [Elements XIII.1]. ובאר אקלידס כי כאשר נחלק קו על יחס אמצעי ושתי קצוות שהחלק הגדול כאשר נוסף בארכו כמו חצי הקו כלו והוכה כל זה בעצמו המרובע ההוה מזה יהיה חמשה דמיוני המרובע ההוה מחצי הדבר
Elements/Elements XIII-10definitionהמחומשים_והמעושרים#w084We do this since Euclid has explained that the line that cuts the fifth is on the line that cuts the sixth and the tithe, when they are set on one circle [Elements XIII,10]. ועשינו זה בעבור כי באר אוקלידס כי קו החותך החמישית על הקו החותך הששית והעשירית כאשר הונחו בעגולה אחת
Elements/Elements XIII-3definitionהמחומשים_והמעושרים#mhLNEuclid has already explained [Elements XIII.3] that when line BH is divided by the ratio of a mean and two extremes, so that the greater part is equal to line DH, it is known that when a line is divided by the ratio of a mean and two extremes and we add half the greater part to the smaller part, then multiply the whole sum by itself, the square formed by the sum of the two is five times the product of [half] the greater part by itself. :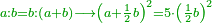\scriptstyle{\color{OliveGreen}{a:b=b:\left(a+b\right)\longrightarrow\left(a+\frac{1}{2}b\right)^2=5\sdot\left(\frac{1}{2}b\right)^2}} ובאר אוקלידס שקו ב"ה כאשר חולק על יחס אמצעי ושני קצוות שהחלק הגדול הוא שוה אל קו ד"ה והוא ידוע כי כאשר נחלק קו אחד על יחס בעל אמצעי ושני קצוות ונוסיף על החלק הקטן חצי החלק הגדול ונכה הכל בעצמו שהמרובע ההוה משני אלו מקובצים יהיה חמשה דמיוני הכאת החלק הגדול בעצמו
Elements/Elements XIII-5definitionהמחומשים_והמעושרים#3lPzIt is known from what we have said, as Euclid said, that for every line divisible according to the ratio of a mean and two extremes, when another part equal to the larger portion is added to the line, then whole [line] is divisible according to the ratio of a mean and two extremes, and the larger portion of which is the original line [Elements XIII.5]. והוא ידוע מאשר אמרנו שאמרו אקלידס ואמר שכל קו שהוא על יחס אמצעי ושני קצוות ונוסף באורך הקו כמו החלק ‫60rהגדול וכל זה יחלק על יחס אמצעי ושני קצוות שהחלק הגדול הוא הקו הראשון
Elements/Elements XIII-9definitionהמחומשים_והמעושרים#ScqDIt he said in another place that when the side of a hexagon and the side of a decagon inscribed in the same circle are united in one line, then this whole line is divisible according to the ratio of a mean and two extremes, and the side of the hexagon is the larger portion [Elements XIII.9]. ואמר במקום אחר שכאשר קובצו צלע המשושה עם צלע המעושר אשר בעגולה אחת בקו אחד ישר יהיה כל הקו נחלק על יחס אמצעי ושני קצוות וצלע המשושה הוא החלק הגדול
solid/ellipsoidב.י.צ./ביצניdefinitionספר_יסודי_התבונה_ומגדל_האמונה#eg9dthat which is surrounded by a curved surface is called ellipsoid [lit. elliptic solid] or a solid that is similar to an ellipse [lit. egg-like solid]. ואשר יקיף אותו פרוש אחד עקום נקרא גולם ביצני או גולם דומה לביצה
solid/ellipsoidב.י.צ./ביצניtermספר_יסודי_התבונה_ומגדל_האמונה#gicsהגולם הביצני
solid/ellipsoidב.י.צ./דומה לביצהtermספר_יסודי_התבונה_ומגדל_האמונה#Rccpהגולם הדומה לביצה
to encompass/encompassedנ.ק.פ./הקיףtermספר_האלזיברא#noZKאשר יקיפו בו קוי
to encompass/encompassedנ.ק.פ./הקיףtermספר_האלזיברא#hrMOאשר יקיפו בו שני החלקים
to encompass/encompassedר.ש.מ./נרשםdefinitionספר_היסודות_לאקלידס#9RjXThe figure is said to be circumscribed about a figure when each of its sides touches each of the respective angles of the figure about which it is circumscribed. ויאמר כי התמונה נרשמת סביב התמונה כשתהיה כל אחת מצלעותיה ממששת לכל אחת מזויות התמונה אשר היא נרשמת סביבה
geometry/endכ.ל.י./תכליתtermמלאכת_המספר#tYDoתכליותיו
geometry/endקצהtermמלאכת_המספר#Idv3קצה
geometry/endקצהtermמלאכת_המספר#Ltilקצה
geometry/endש.פ.י./שפהtermמלאכת_המספר#pd7Lשפת
triangle/equilateral triangleש.ו.ה./שוה זויותtermמלאכת_המספר#dBGuמשולש השוה הזויות
triangle/equilateral triangleש.ו.ה./שוה זויותtermמלאכת_המספר#0szpהמשולש השוה הזויות
triangle/equilateral triangleש.ו.ה./שוה צלעותtermספר_הכללים_במספר#sp6oמשולש שוה הצלעות
triangle/equilateral triangleש.ו.ה./שוה צלעותtermספר_הכללים_במספר#Okmuהמשולש השוה הצלעות
line/extensionמ.ש.כ./המשכותtermהאריתמטיקה_של_ניקומכוס#I0sKהמשכותו
solid/faceצ.ד.ד./צדtermספר_יסודי_התבונה_ומגדל_האמונה#S4QNצדים
solid/faceצ.ד.ד./צדtermספר_יסודי_התבונה_ומגדל_האמונה#TPlFצדדין
solid/faceי.ש.ב./מושבtermספר_יסודי_התבונה_ומגדל_האמונה#H8Afמושבותיהן
solid/faceי.ש.ב./מושבtermספר_יסודי_התבונה_ומגדל_האמונה#FTa7מושבות
solid/faceצ.ד.ד./צדtermספר_יסודי_התבונה_ומגדל_האמונה#OEA8צדין
surface/flat surfaceי.ש.ר./ישרdefinitionספר_יסודי_התבונה_ומגדל_האמונה#WnsWthe plane surface is the drawn on the straightness of the lines that surround it and in parallel to them והשטח הישר הוא הנמשך על יושר הקוים המקיפים אותו ועל נכחם
surface/flat surfaceי.ש.ר./משורtermמלאכת_המספר#wOY6מישור
surface/flat surfaceש.ו.ה./שוהdefinitionספר_היסודות_לאקלידס#kmWDThe '''plane surface''' is that which lies straightly by the arrangement of straight lines on it one by one. והפשוט השוה הוא המוצב על נכוחות אי זה קוים ישרים יהיו עליו קצתם אל קצתם
geometry/geometrical shapeצ.ו.ר./צורהtermקצור_המספר#Tj2aצורתו
geometry/geometrical shapeתמונהtermספר_האלזיברא#sSIxתמונה
geometry/geometrical shapetermספר_המספר_/_אברהם_אבן_עזרא#kCK2דמות
geometry/geometrical shapeתמונהtermחשבון_השטחים#DM4qתמונת גימטריאות
geometry/geometrical shapeתמונהtermתחבולות_המספר#QKAsתמונה
geometry/geometrical shapeצ.ו.ר./צורהtermספר_ג'יבלי_אלמוקבאלא#NU0pצורת ה
geometry/geometrical shapeתמונהtermחשבון_השטחים#ld89תמונות גימאטריות
geometry/geometrical shapeצ.ו.ר./צורהtermקצור_המספר#uLTaצורת ה
geometry/geometrical shapeש.ע.ר./שעוריtermהאנציקלופדיה_של_אבו_אלצלת#1yExהתמונות השעוריות
geometry/geometrical shapeתמונהdefinitionספר_היסודות_לאקלידס#zvgXThe '''figure''' is that which is contained by a boundary or boundaries. והתמונה היא אשר יקיף אותה גבול או גבולים
geometry/geometrical shapeתמונהtermתחבולות_המספר#nDezתמונ' גימטרית
geometry/geometrical shapeתמונהtermחשבון_השטחים#S3ATתמונה
geometry/geometrical shapeתמונהtermתחבולות_המספר#zsC7תמונות גימטריות
geometry/geometrical shapeתמונהtermספר_המספר_/_אליהו_מזרחי#A0eJתמונות
geometry/geometrical shapeתמונהtermתחבולות_המספר#cUJQתמונות גימטריאות
geometry/geometrical shapetermספר_המספר_/_אברהם_אבן_עזרא#6zsxצורות
geometry/geometrical shapeצ.ו.ר./צורהtermספר_ג'יבלי_אלמוקבאלא#aHl6בצורה
geometry/geometrical shapeצ.ו.ר./צורהtermספר_ג'יבלי_אלמוקבאלא#FkFLזאת הצורה
geometry/geometricianח.כ.מ./חכמי השעורtermספר_יסודי_התבונה_ומגדל_האמונה#Rqdkחכמי השעור
geometry/geometricianח.כ.מ./חכמי המדותtermAnonymous#3f0Hחכמי המדות
geometry/geometricianח.כ.מ./חכמי הגימטריאtermתחבולות_המספר#zYpSחכמי הגימטריאה
geometry/geometricianח.כ.מ./חכמי הגימטריאtermחשבון_השטחים#HDsYחכמי הגימאטריאה
geometryהנדסהtermקצור_המספר#oKmZחכמת ההנדסה
geometryגיאומטריהtermספר_יסודי_התבונה_ומגדל_האמונה#WvOrגיאומטריא
geometryגימטריאtermספר_ג'יבלי_אלמוקבאלא#zdcIגימטריא
geometryש.ע.ר./שעורdefinitionספר_יסודי_התבונה_ומגדל_האמונה#QN53 geometry is a science that explains the measures and announces their value, their creation, their types, and their signs. חכמת השיעור היא חכמת מפרשת את הגדלים ומודיעה ערכם ויצירתם ומיניהן וסימניהן
geometryנ.פ.ל./נפלto be situatedחשבון_השטחים#JY7Pנפלה
geometryנ.פ.ל./נפלto be situatedחשבון_השטחים#lEvAתפול
geometryגימטריאtermחשבון_השטחים#Grroגימטריא
geometryש.ע.ר./שעורtermספר_יסודי_התבונה_ומגדל_האמונה#7kbkחכמת השיעור
geometrytermספר_יסודי_התבונה_ומגדל_האמונה#tPavאלהנדסה
geometryנ.פ.ל./נפלto be situatedתחבולות_המספר#azrNנופלת
geometryנ.פ.ל./נפלto be situatedתחבולות_המספר#RPnhתפול
geometryהנדסהtermמלאכת_המספר#PJSBהנדסה
geometryש.ע.ר./שעורtermספר_יסודי_התבונה_ומגדל_האמונה#yCv9חכמת השעור
geometryגיאומטריהtermספר_יסודי_התבונה_ומגדל_האמונה#Sgh4יומטריא
geometryמ.ד.ד./מדותtermספר_המספר_/_אליהו_מזרחי#cAbDמדות
geometryמ.ד.ד./מדידהtermמשנת_המדות#LghNמדידה
geometryמ.ד.ד./מדותtermספר_המספר_/_אליהו_מזרחי#NXxmמלאכת המדות
geometryמ.ד.ד./מדידהtermספר_המספר_/_אליהו_מזרחי#JOJzמדידה
geometryהנדסהtermספר_המספר_/_אליהו_מזרחי#JyR3הנדסה
geometryהנדסהtermספר_המספר_/_אליהו_מזרחי#WrQeחכמת ההנדסה
geometryהנדסהtermספר_המספר_/_אליהו_מזרחי#TWz4הנדסא
geometryהנדסהtermמלאכת_המספר#1nMwמלאכת ההנדסא
geometryהנדסהtermספר_יסודי_התבונה_ומגדל_האמונה#vDEWהנדסה
surface/gnomonר.ש.מ./רושםtermספר_האלזיברא#9D4Qרושם התמונה
semicircle/greater than a semicircleי.ת.ר./יתרtermמשנת_המדות#QxiLיתרה
semicircle/greater than a semicircleי.ת.ר./יתרdefinitionמשנת_המדות#MepoThe surplus segment is any segment that is greater than a semicircle. והיתרה כל שהיא עודפת על חצי העגולה
line/heightג.ב.ה./גובהtermקצור_המספר#2ZCtגובהו
line/heightק.ו.מ./קומהtermמשנת_המדות#bcMzקומה
line/heightג.ב.ה./גובהtermמלאכת_המספר#68a5גובה
line/heightע.מ.ד./עמודtermספר_הכללים_במספר#N2oIעמודה
line/heightע.מ.ד./עמודdefinitionמשנת_המדות#ZKdDThe height is a perpendicular line descending from between the two sides to the base, and it is angled to the walls of the temple. והעמוד זה {{#annot:term|592,2289|H0NU}}חוט{{#annotend:H0NU}} הכולל היורד מבין שני הצלעים לקבע והוא בזוית למקצעות המשכן
line/heightג.ב.ה./גובהtermמלאכת_המספר#w6qQגובה
line/heightג.ב.ה./גובהtermקצור_המספר#Z57hגובה
line/heightג.ב.ה./גובהtermבר_נותן_טעם#B53nגובה
line/heightע.מ.ד./עמודtermספר_הכללים_במספר#iYwSעמוד
line/heightע.מ.ד./עמודtermמשנת_המדות#1RG2עמוד
sphere/hemisheperת.ל.ל./תלולtermמשנת_המדות#zJmFתלולה
polygon/hexagonש.ש.י./משושהtermספר_יסודי_התבונה_ומגדל_האמונה#19s3משושש
line/hypotenuseק.ב.ע./קבעtermמשנת_המדות#AnyJקבע
line/hypotenuseי.ת.ר./יתרtermקצור_המספר#MTF2יתר
line/hypotenuseאלכסוןtermספר_הכללים_במספר#QiEwאלכסון
straight line/in a straight mannerי.ש.ר./על יושרtermתחבולות_המספר#PN28על יושר
straight line/in a straight mannerי.ש.ר./ביושרtermתחבולות_המספר#cDgmביושר
straight line/in a straight mannerי.ש.ר./ביושרtermתחבולות_המספר#hJu6ביושר
straight line/in a straight mannerי.ש.ר./ביושרtermחשבון_השטחים#VB0Uביושר
straight line/in a straight mannerי.ש.ר./על יושרtermספר_האלזיברא#6UEDעל יושר
straight line/in a straight mannerי.ש.ר./על יושרtermחשבון_השטחים#mR21על יושר
geometric relations/inscribedר.ש.מ./מורשםdefinitionספר_היסודות_לאקלידס#A5VwThe figure is said to be inscribed in a figure when each of its angles touches each of the respective sides of the figure in which it is inscribed. יאמר כי התמונה מורשמת בתמונה כאשר תהיה כל אחת מזויותיה ממששת לכל אחת מצלעות התמונה אשר נרשמת בה
surface/isoscelesש.ו.ה./שוה צלעותtriangleמלאכת_המספר#3Lkyמשולש שוה הצלעות
surface/isoscelesש.ו.ה./שוהtrapezoidספר_הכללים_במספר#s0uEקטומת הראש שוה
surface/isoscelesש.ו.ה./שוה שוקיםtriangleספר_הכללים_במספר#SINiמשולש שוה השוקים
to join/joinedד.ב.ק./דובקtermספר_ג'יבלי_אלמוקבאלא#lkPUמדובקים ל
to join/joinedד.ב.ק./דבקtermתחבולות_המספר#FCgjדבק
to join/joinedד.ב.ק./דובקtermתחבולות_המספר#pXGNמדובקים
linear dimension/lengthא.ר.כ./אורךtermמשנת_המדות#SQtoארך
linear dimension/lengthא.ר.כ./אורךtermתחבולות_המספר#dIuFארכו
linear dimension/lengthא.ר.כ./אורךtermחשבון_השטחים#opY6אורכו
linear dimension/lengthא.ר.כ./אורךtermמלאכת_המספר#WuCfאורך
linear dimension/lengthא.ר.כ./אורךtermחשבון_השטחים#CNQzאורך
linear dimension/lengthtermספר_המספר_/_אברהם_אבן_עזרא#tTbnארכו
linear dimension/lengthא.ר.כ./אורךtermספר_האלזיברא#xJSRארכו
linear dimension/lengthא.ר.כ./אורךtermבר_נותן_טעם#wbTkאורך
linear dimension/lengthא.ר.כ./אורךtermבר_נותן_טעם#x8jjארך
linear dimension/lengthא.ר.כ./אורךtermמלאכת_המספר#h6f3אורך
linear dimension/lengthא.ר.כ./אורךtermתחבולות_המספר#vaVjאורך
semicircle/less than a semicircleח.ס.ר./חסרdefinitionמשנת_המדות#qLjqThe deficient segment is any segment that is smaller than a semicircle. החסרה כל שהיא פחותה מחצי העגולה
semicircle/less than a semicircleח.ס.ר./חסרtermמשנת_המדות#ZNjfחסרה
geometrical shape/lineמ.ש.כ./משוךtermמשנת_המדות#aohwמשוכים
geometrical shape/lineק.ו.י./קוdefinitionספר_היסודות_לאקלידס#wN6JThe '''line''' is a length that has no breadth. והקו הוא אורך אין רוחב לו
geometrical shape/lineק.ו.י./קוtermקצור_המספר#NdeCקו
geometrical shape/lineחוטtermמשנת_המדות#H0NUחוט
geometrical shape/lineק.ו.י./קוtermתחבולות_המספר#XNSAקו
geometrical shape/lineק.ו.י./קוtermספר_המספר_/_אליהו_מזרחי#zEkbקוים
geometrical shape/lineק.ו.י./קוtermהאריתמטיקה_של_ניקומכוס#RC38קו
geometrical shape/lineק.ו.י./קוtermספר_המספר_/_אליהו_מזרחי#2j7Uקו
geometrical shape/lineק.ו.י./קוtermספר_האלזיברא#n2q8קו
geometrical shape/lineק.ו.י./קוdefinitionהאריתמטיקה_של_ניקומכוס#3xJtThe line is that which has only length, and that which has only length is a line. והקו מה שהיה לו אורך לבד ומה שהיה לו אורך לבד הוא קו
geometrical shape/lineק.ו.י./קוtermחשבון_השטחים#ZCVZקו
geometrical shape/lineק.ו.י./קוtermחשבון_השטחים#gKGjקוים
geometrical shape/lineק.ו.י./קוtermספר_מעשה_חושב#9DYpקוים
geometrical shape/lineק.ו.י./קוdefinitionמלאכת_המספר#wrX5 the line is a quantity of length without breadth and depth, whose ends are two points. והקו הוא כמות אורך בלתי רוחב ועומק וקצותיו הם ב' נקודות
geometrical shape/lineק.ו.י./קוtermספר_מעשה_חושב#jwYtקו
geometrical shape/lineק.ו.י./קוtermתחבולות_המספר#1nUpקוים
geometrical shape/lineק.ו.י./קוdefinitionהאריתמטיקה_של_ניקומכוס#mITPThe line has one dimension. והקו בעל משך אחד
geometrical shape/lineמ.ש.כ./משוךtermמשנת_המדות#3VKIהמשוך
geometry/linear dimensionר.ח.ק./מרחקdefinitionספר_יסודי_התבונה_ומגדל_האמונה#ehyjthe dimensions are three: length, breadth and depth, or height. והמרחקים הם ג' אורך ורחב ועומק או רום
geometry/linear dimensionר.ח.ק./מרחקtermמלאכת_המספר#0yxeמרחקיו
geometry/linear dimensionר.ח.ק./מרחקtermמלאכת_המספר#sNrAמרחקי'
angle/obtuse angleר.ו.ח./נרוחtermספר_יסודי_התבונה_ומגדל_האמונה#LHoWזוית נרוחת
angle/obtuse angleר.ו.ח./נרוחdefinitionספר_יסודי_התבונה_ומגדל_האמונה#XQbWthe obtuse angle exceeds over the right [angle] in its value. והזוית הנרוחת היא המוסיפה בערכה על הנצבת
angle/obtuse angleר.ו.ח./נרוחdefinitionספר_היסודות_לאקלידס#szjVThe greater than a right angle is called an '''obtuse angle'''. ואשר היא גדולה מנצבת תקרא נרוחת
angle/obtuse angleכ.ס.ח./כסוחהtermמשנת_המדות#hYTAכסוחה
angle/obtuse angleר.ח.ב./רחבtermמשנת_המדות#z0OWזויות רחבים
angle/obtuse angleר.ח.ב./רחבtermמשנת_המדות#lTJwרחבה
obtuse angle/obtuse-angledר.ו.ח./מרוחtriangle-definitionספר_יסודי_התבונה_ומגדל_האמונה#7MuRthe third species is that which has one obtuse angle, which is called an obtuse-angled [triangle]. והמין השלישי הוא אשר יש לו זוית אחת נרוחת והוא נקרא מרווח הזוית
obtuse angle/obtuse-angledר.ו.ח./מרוחtriangleספר_הכללים_במספר#iUfNמשולש מרויח הזויות
obtuse angle/obtuse-angledר.ו.ח./מרוחtriangleספר_יסודי_התבונה_ומגדל_האמונה#dxctהמשלש מרווח הזוית
obtuse angle/obtuse-angledמ.ו.ט./מתמוטטתtrapezoidספר_הכללים_במספר#Bzovמתמוטטת
obtuse angle/obtuse-angledר.ו.ח./נרוחtriangle-definitionספר_היסודות_לאקלידס#g9wmThe '''obtuse-angled triangle''' is that which has an obtuse angle. והמשולש הנרוח הזוית והוא אשר לו זוית נרוחת
obtuse angle/obtuse-angledמ.ו.ט./מתמוטטתtrapezoidספר_הכללים_במספר#xzTsקטומה מתמוטטת
obtuse angle/obtuse-angledפ.ס.ח./פסוחהtriangleמשנת_המדות#uuSeפסוחה
line/parallelנ.כ.ח./נכחיtermחשבון_השטחים#HjSCנכחי ל
line/parallelנ.כ.ח./נכחיtermספר_הכללים_במספר#uvqNנכוחיים
line/parallelנ.כ.ח./נכחיtermספר_הכללים_במספר#E7Zkנכוחית
line/parallelנ.כ.ח./נכחיtermתחבולות_המספר#LCaEנכחי ל
line/parallelנ.כ.ח./נכחיtermחשבון_השטחים#cvrFנכחיים ל
line/parallelנ.כ.ח./נכחיtermתחבולות_המספר#Ycx6נכחיים ל
line/parallelנ.כ.ח./על נכוחותtermתחבולות_המספר#zRs4על נכוחות
line/parallelנ.כ.ח./נכחיdefinitionספר_היסודות_לאקלידס#Zac6The '''parallel straight lines''' are those that are in the same plane such that if they are drawn endlessly in both directions, they do not meet one another in either direction. והקוים הישרים הנכחיים הם אשר יהיו על שטח אחד שוה ואם הוצאו בשני הצדדים אל לא תכלית לא יפגשו באחד מהם
line/parallelנ.כ.ח./נכחיtermספר_הכללים_במספר#Jegsנכוחי
line/parallelנ.כ.ח./על נכוחותtermחשבון_השטחים#w6CYעל נכחות
line/parallelנ.כ.ח./על נכוחותtermתחבולות_המספר#a4Jrעל נכוחות
line/parallelנ.כ.ח./נכחיtermספר_ג'יבלי_אלמוקבאלא#lKmsנכחיים
line/parallelנ.כ.ח./על נכוחותtermחשבון_השטחים#5Sdcעל נכחות
line/parallelנ.כ.ח./נכחיtermספר_האלזיברא#cNKOנכוחי ל
line/parallelנ.כ.ח./נכחיtermספר_ג'יבלי_אלמוקבאלא#dReTנכחי ל
line/parallelנ.כ.ח./נכחיtermספר_האלזיברא#W8aPנכחי לקו
solid/parallelepipedנ.כ.ח./נכחי השטחיםtermספר_היסודות_לאקלידס#w1JCמוגשם נכחיי השטחים
solid/parallelepipedנ.כ.ח./נכחי השטחיםtermספר_היסודות_לאקלידס#5wo6מוגשמי כ"ב וז"ל נכחי השטחים
quadrilateral/parallelogramע.י.נ./דומה למעויןdefinitionספר_יסודי_התבונה_ומגדל_האמונה#Di4Qthe fourth [category] is similar to the second whose two of its sides that are parallel to each other, only that its angles are not right [angles] - this is called a parallelogram. והרביעי דומה לשני שכל שני מצלעותיו העומדות זו כנגד זו נכחיות ושוות אלא שזויותיו אינן נצבות וזה נקרא דומה למעויין
quadrilateral/parallelogramע.י.נ./דומה למעויןdefinitionספר_היסודות_לאקלידס#Wn4uThe '''rhomboid''' is that whose opposite sides are equal to one another but is neither equilateral nor right-angled. ומהם הדומה למעויין והוא אשר כל שתי צלעות ממנו שזו כנגד זו שוות ואינו שוה הצלעות ואינו נצב הזויות
quadrilateral/parallelogramנ.כ.ח./נכחי הצלעותtermספר_היסודות_לאקלידס#9qdLהשטחים נכחיי הצלעות
quadrilateral/parallelogramנ.כ.ח./נכחי הצלעותtermספר_היסודות_לאקלידס#ERBzנכחי הצלעות
polygon/pentagonח.מ.ש./מחומשtermספר_יסודי_התבונה_ומגדל_האמונה#rQuHמחומשות
polygon/pentagonח.מ.ש./מחומשtermספר_יסודי_התבונה_ומגדל_האמונה#w5N9המחומש
polygon/pentagonח.מ.ש./מחומשtermהאריתמטיקה_של_ניקומכוס#m2Dhמחומש
line/perimeterס.ב.ב./סביבהdefinitionמשנת_המדות#AFu9What is the perimeter? it is the line that circumscribes the circle, as it is said: ''and a line of thirty cubits did compass it round about'' [Chronicles 2, 4, 2]. איזו היא סביבה הוא הקו המקיף את העגול שנ' ''וקו שלשים באמה יסב אותו סביב'' ‫דברי הימים ב, ד, ב
line/perimeterנ.ק.פ./הקףtermמלאכת_המספר#ngFUהקף העגולה
line/perimetertermספר_המספר_/_אברהם_אבן_עזרא#Qhljהקו הסובב
line/perimeterכמותtermמלאכת_המספר#RwcDכמות העגולה
line/perimetertermספר_המספר_/_אברהם_אבן_עזרא#kQKOקו העגול
line/perimeterס.ב.ב./סביבהtermמשנת_המדות#ktSBסביבה
line/perpendicularע.מ.ד./מעומדtermמלאכת_המספר#aMf5מעומד
line/perpendicularק.צ.ר./קצורtermמשנת_המדות#3vSqקצורים
line/perpendicularע.מ.ד./מעומדtermמלאכת_המספר#GhS0מעומד
surface/planarי.ש.ר./ישרtermספר_יסודי_התבונה_ומגדל_האמונה#JAjCישר
surface/planarש.ט.ח./שטוחtermספר_המספר_/_אליהו_מזרחי#5c6Jשטוחות
surface/planarמ.צ.ע./ממוצעtermמשנת_המדות#epCpממוצע
angle/plane angleפ.ש.ט./פשוטdefinitionספר_היסודות_לאקלידס#YkbQThe '''plane angle''' is the inclination of two given lines to one another in a plane, so that they meet one another not in a straight line. והזוית הפשוטה היא נטיית כל אחד משני קוים מונחים בשטח שוה מדובקים על בלתי יושר האחד מן האחר
angle/plane angleש.ט.ח./שטוחהtermספר_יסודי_התבונה_ומגדל_האמונה#5Gguזוית שטוחה
geometrical shape/pointנ.ק.ד./נקודהtermתחבולות_המספר#HGlBנקודות
geometrical shape/pointנ.ק.ד./נקודהtermספר_האלזיברא#oWimנקדת
geometrical shape/pointנ.ק.ד./נקודהdefinitionספר_היסודות_לאקלידס#I0AqThe '''point''' is a thing that has no part. |style="width:45%;text-align:right;"|הנקודה היא דבר אין לה חלק ולא הנחה
geometrical shape/pointנ.ק.ד./נקודהtermספר_יסודי_התבונה_ומגדל_האמונה#g5iFנקדה
geometrical shape/pointmidpointספר_המספר_/_אברהם_אבן_עזרא#vdqXנקודה
geometrical shape/pointנ.ק.ד./נקודהtermהאריתמטיקה_של_ניקומכוס#Qk2eנקודה
geometrical shape/pointנ.ק.ד./נקודהtermחשבון_השטחים#G3Unנקודת
geometrical shape/pointנ.ק.ד./נקודת חלוקmidpointמלאכת_המספר#3Tlsנקודת החלוק
geometrical shape/pointנ.ק.ד./נקודהtermקצור_המספר#UMxTנקודה
geometrical shape/pointנ.ק.ד./נקודהtermתחבולות_המספר#eSZcנקדת
geometrical shape/pointנ.ק.ד./נקודת חלוקהmidpointמלאכת_המספר#BIOaנקודת החלוקה
geometrical shape/pointנ.ק.ד./נקודהtermהאריתמטיקה_של_ניקומכוס#u4baנקודות
axis/poleק.ט.ב./קוטבdefinitionספר_יסודי_התבונה_ומגדל_האמונה#TU07the two points that are the ends of the axis are called the beginnings of the axis and in Arabic they are called the poles of the axis. וב' הנקודות אשר הם תכליתי הבריח נקראים ראשי הבריח וקוראים להם בלשון ישמעאל קטבי הבריח
surface/polygonי.ש.ר./ישר קויםtermהאריתמטיקה_של_ניקומכוס#SU8cהשטחים ישרי הקוים
surface/polygonי.ש.ר./ישרtermהאריתמטיקה_של_ניקומכוס#9SO5השטחים הישרים
surface/polygondefinitionספר_יסודי_התבונה_ומגדל_האמונה#K7RFthe third is the polygon that the lines surrounding it exceed four. והשלישי הוא המרבה דפנות אשר הקוים המקיפים אותו הן עודפים על ד'
surface/polygonר.ב.ה./מרבה צלעותtermספר_יסודי_התבונה_ומגדל_האמונה#xQVAהשטח המרבה צלעות
solid/prismח.מ.ש./מחומשpentagonalספר_הכללים_במספר#K9aEמצבה מחומשת
solid/prismג.ר.ר./מתגוררtermהאנציקלופדיה_של_אבו_אלצלת#aqI8מתגורר
solid/prismי.צ.ב./מצבהtermספר_הכללים_במספר#NojBמצבה
solid/prismי.צ.ב./מצבהtermספר_יסודי_התבונה_ומגדל_האמונה#nZFZמצבה
solid/prismג.ר.ר./מגוררtermהאנציקלופדיה_של_אבו_אלצלת#9vMoמגורר
solid/prismע.מ.ד./עמודtermמשנת_המדות#kXIUעמוד
solid/prismג.ר.ר./מגוררtriangular-definitionספר_היסודות_לאקלידס#Dfy8A prism is a solid figure contained by three rectangles and two triangles. התמונה המוגשמת המגוררת היא אשר יקיפו בה שלשה שטחים נכחיי הצלעות ושני שטחים משולשים
solid/prismי.צ.ב./מצבהtermספר_יסודי_התבונה_ומגדל_האמונה#6azbמצבות
solid/prismח.צ.י./חצויהtriangularספר_הכללים_במספר#FrRBמצבה חצוית הראש
solid/prismח.צ.י./חצויהtriangularספר_הכללים_במספר#rw6Pמצבה משולשת חצויה
solid/prismח.צ.י./חצויהtriangularספר_הכללים_במספר#OosOמצבה חצויה
solid/prismר.ב.ע./מרובעsquareמשנת_המדות#aQukעמוד מרבע
solid/pyramidז.נ.ב./מזונבtermהאריתמטיקה_של_ניקומכוס#Ofm0מזונב
solid/pyramidח.ד.ד./מחודדtriangularהאריתמטיקה_של_ניקומכוס#xeb3המשולש המוגשם המחודד
solid/pyramidמ.ש.כ./משוךtermמשנת_המדות#JO3Xמשוך
solid/pyramidח.ד.ד./מחודדtermהאנציקלופדיה_של_אבו_אלצלת#Lvtrמחדדים
solid/pyramidח.ד.ד./מחודדtermמלאכת_המספר#NwMWמחודד
solid/pyramidש.ל.ש./משולשtriangularהאריתמטיקה_של_ניקומכוס#Gr1Yהגרם המשולש
solid/pyramidח.ד.ד./מחודדtermהאריתמטיקה_של_ניקומכוס#pjvtהמוגשם המחודד
solid/pyramidז.נ.ב./מזונבtermהאריתמטיקה_של_ניקומכוס#gLyLמזונבים
solid/pyramidח.ד.ד./מחודדtermהאריתמטיקה_של_ניקומכוס#6x7Yמחודדים
solid/pyramidח.ד.ד./מחודדtermהאריתמטיקה_של_ניקומכוס#CG7Sמחודד
solid/pyramidז.נ.ב./מזדנבtermהאריתמטיקה_של_ניקומכוס#o7LKגרם מזדנב
surface/quadrilateraltermתחבולות_המספר#W9nkשטח הכאת
surface/quadrilateralר.ב.ע./מרובעtermקצור_המספר#0nqLמרובע
surface/quadrilateralש.ט.ח./מושטחtermקצור_המספר#i6VSמושטח
surface/quadrilateralר.ב.ע./מרובעtermמשנת_המדות#4N37מרבעת
surface/quadrilateralר.ב.ע./מרובעdefinitionספר_יסודי_התבונה_ומגדל_האמונה#bfgethe second is the quadrilateral which is the surrounded by four straight lines. והשני הוא המרובע והוא אשר יקיף אותו ד' קוים ישרים
surface/quadrilateralר.ב.ע./מרובעtermמלאכת_המספר#Vy5Iמרובע
surface/quadrilateralש.ט.ח./מושטחtermקצור_המספר#3lahמושטח
surface/quadrilateralר.ב.ע./מרובעtermבר_נותן_טעם#LjAqמרובע
quadrilateral/rectangleטבלהtermמשנת_המדות#wrZoטבלא
quadrilateral/rectangleר.ב.ע./מרובע ארוךtermספר_הכללים_במספר#euTKמרובע ארוך
quadrilateral/rectangleח.ל.פ./מתחלף ארכיםdefinitionספר_היסודות_לאקלידס#bvdVThe '''oblong''' is that which is right-angled but not equilateral. ומהם המתחלף הארכים והוא הנצב הזויות לא שוה הצלעות
quadrilateral/rectangleר.ב.ע./מרובע ארוךtermספר_הכללים_במספר#KIEbמרובע ארוך
quadrilateral/rectangleש.ט.ח./שטח נצב הזויותtermספר_היסודות_לאקלידס#UxZCשטח הנצב הזויות
quadrilateral/rectangleש.ט.ח./שטח נצב הזויותtermספר_היסודות_לאקלידס#PIuXשטח נצב הזויות
quadrilateral/rectangleש.ט.ח./שטח נצב הזויותtermתחבולות_המספר#tLXbשטח נצב הזויות
quadrilateral/rectangleש.ט.ח./שטח נצב הזויותtermספר_האלזיברא#vcTzשטח נצב הזויות
quadrilateral/rectangleש.ט.ח./שטח נצב הזויותtermספר_האלזיברא#oh24השטח הנצב הזויות
quadrilateral/rectangleר.ב.ע./מרובע ארוךdefinitionספר_יסודי_התבונה_ומגדל_האמונה#Ig6Xthe second [category] is that whose two of its sides are parallel and equal, its [two] other sides are also equal, and so are all of its four angles - this is called a rectangle. והשני הוא אשר שני מצלעיו הם נכוחיות ושוות וכן צלעותיו אחרות שוות כמו כן וד' זויותיו כלם וזה נקרא מרובע ארוך
quadrilateral/rhombusע.י.נ./מעויןdefinitionספר_יסודי_התבונה_ומגדל_האמונה#ylyuthe third [category] is similar to the first in its sides that are equal, only that its angles are not right [angles] - this is called a rhombus. והשלישי דומה לראשון בצלעיו שהן שוות אלא שזויותיו אינם נצבות וזה נקרא מעויין
quadrilateral/rhombusע.י.נ./מעויןtermספר_הכללים_במספר#gBopמעויין
quadrilateral/rhombusע.י.נ./מעויןtermספר_הכללים_במספר#6VRnמרובע המעויין
quadrilateral/rhombusע.י.נ./מעויןdefinitionספר_היסודות_לאקלידס#us1TThe '''rhombus''' is that which is equilateral but not right-angled. ומהם המעויין והוא השוה הצלעות ואינו נצב הזויות
angle/right angleי.צ.ב./נצבtermספר_המספר_/_אליהו_מזרחי#4KlCזויות נצבות
angle/right angleי.צ.ב./נצבtermספר_יסודי_התבונה_ומגדל_האמונה#g94rזוית נצבת
angle/right angleי.צ.ב./נצבtermתחבולות_המספר#kliQזוית נצבה
angle/right angleי.צ.ב./נצבtermמשנת_המדות#w2f4נצבה
angle/right angleי.צ.ב./נצבtermמלאכת_המספר#u7EEזויות נצבות
angle/right angleי.צ.ב./נצבtermקצור_המספר#dSxJהזוית הנצבה
angle/right angleי.צ.ב./נצבdefinitionספר_יסודי_התבונה_ומגדל_האמונה#9aNzThe right angle is one of two angles which is on the sides of a line that is perpendicular to another line and each is equal to the other in value. והזוית נצבה היא אחת מב' זויות אשר על צדי קו העומד על קו אחר וכל אחת מהן שוה בערך לחברתה
right angle/right-angledי.צ.ב./נצבtriangleספר_יסודי_התבונה_ומגדל_האמונה#syPTנצב הזויות
right angle/right-angledי.צ.ב./נצבtriangle-definitionספר_יסודי_התבונה_ומגדל_האמונה#KjlNthe second species is that which has one angle that is right and two [angles] that are acute - this is called a right-angled triangle. והמין השני הוא אשר יש לו זוית אחת נצבת ושתים חדות והוא נקרא משלש נצב הזוית
right angle/right-angledי.צ.ב./נצבtriangleספר_הכללים_במספר#c8w5משולש נצב הזויות
right angle/right-angledי.צ.ב./נצבtriangleספר_הכללים_במספר#YJQEמשולש נצב הזוית
right angle/right-angledי.צ.ב./נצבtriangleספר_הכללים_במספר#1xD2משולשים מוצבי זוית
right angle/right-angledי.צ.ב./נצבtriangle-definitionספר_היסודות_לאקלידס#BAtHThe '''right-angled triangle''' is that which has a right angle. המשולש נצב הזוית והוא אשר לו זוית נצבת
right angle/right-angledי.צ.ב./נצבtriangleמשנת_המדות#aKHkנצבה
surface/scaleneח.ל.פ./חלוףtriangleמשנת_המדות#ADtVמשלשת חלופים
surface/scaleneח.ל.פ./חלופהtrapezoidספר_הכללים_במספר#oONPקטומת הראש חלופה
surface/scaleneח.ל.פ./חלוףtriangleמשנת_המדות#O4lyחלופים
surface/scaleneפ.ת.ל./נפתלquadrilateralספר_יסודי_התבונה_ומגדל_האמונה#BUOnמרובע נפתל
surface/scaleneש.נ.י./משונהquadrilateralמשנת_המדות#Tcr7המרבעות המשונות
surface/scaleneח.ל.פ./מתחלף צלעותtriangleספר_הכללים_במספר#F605משולש מתחלף
surface/scaleneח.ל.פ./מתחלף צלעותtriangleמלאכת_המספר#sAxBמשולש מתחלף הצלעות
surface/scaleneח.ל.פ./מתחלף צלעותtriangleספר_הכללים_במספר#Hcvcמשולש מתחלף הצלעות
surface/scaleneש.נ.י./משונהquadrilateralמשנת_המדות#rF67משונה
geometry/sectionק.ט.פ./קטופהtermמשנת_המדות#mCQRקטופה
circle/sectorח.ת.כ./חתוךdefinitionספר_היסודות_לאקלידס#s56dA sector of a circle is a shape that is contained by two straight lines containing an angle at the center of the circle, and the arc that is cut off from the circle by these two lines. י וחתוך העגולה היא תמונה אשר יקיפו בה שני קוים ישרים יקיפו בזוית על מרכז העגולה וקשת יקיפוה אותם שני הקוים מן העגולה
line/segmentח.ל.ק./חלקtermחשבון_השטחים#B51mחלקים
line/segmentח.ל.ק./חלקtermחשבון_השטחים#QXNDחלקיו
line/segmentח.ל.ק./חלקtermתחבולות_המספר#8rKfחלקים
line/segmentח.ל.ק./חלקtermספר_האלזיברא#GSR6חלק
line/segmentפ.ס.ק./פסקהtermמשנת_המדות#hGWlפסקאות
circle/segment of a circleח.ת.כ./חתיכהdefinitionספר_היסודות_לאקלידס#XaeSThe '''segment of the circle''' is the figure contained by a straight line and an arc on the circumference that is either smaller or greater than its half. וחתיכת העגול היא תמונה יקיפו בה קו ישר וקשת ממקיף העגולה אם קטנה מחציה או גדולה
circle/segment of a circleק.ש.ת./קשותהtermמשנת_המדות#qGNQקשותה
circle/segment of a circleח.ת.כ./חתיכהdefinitionספר_היסודות_לאקלידס#ISnGA segment of a circle is that which is contained by a straight line that is called a chord and the segment of circumference that is called an arc. ו חתיכת העגולה היא אשר יקיף בה קו ישר יקרא המיתר והחלק מן הקו המקיף יקרא הקשת
circle/semicircleי.ש.ר./ישרהtermמשנת_המדות#aGCkישרה
circle/semicircleי.ש.ר./ישרהdefinitionמשנת_המדות#YhPnWhich is the semicircle? Any segment that is half a circle, no more and no less. איזו היא ישרה כל שהיא עומדת בחצי העגולה לא חסר ולא יתר
solid/sharp solidל.ה.ב./מתלהבtermהאנציקלופדיה_של_אבו_אלצלת#Pmc5מתלהבים
surface/sideצלעdefinitionמשנת_המדות#IL6wWhat is the side? it is the holder of the surface's walls, as it is said: ''the altar shall be square''. אי זו היא הצלע זה המחזיק דופנותיו של גג שנ' ''רבוע יהיה המזבח''‫שמות כז, א
surface/sideצלעtermעיר_סיחון#YlsDצלעות
surface/sideצלעtermמלאכת_המספר#f9Scצלעות
surface/sideצלעtermקצור_המספר#t24Nצלע
surface/sidetermספר_המספר_/_אברהם_אבן_עזרא#ZJhZפאת
surface/sideצלעtermחשבון_השטחים#CK5Qצלעיו
surface/sideי.ש.ב./תושבתtermספר_המספר_/_אליהו_מזרחי#SLbtתושבות
surface/sideצלעtermתחבולות_המספר#DtxVצלע
surface/sideצלעtermספר_האלזיברא#JpoAצלע
surface/sideצלעtermקצור_המספר#z4ecצלעות
surface/sideצלעtermמלאכת_המספר#Rtkhצלע
surface/sideצלעtermמשנת_המדות#bpGSצלע
surface/sideצלעtermספר_האלזיברא#I58Uצלע מרבע
surface/sideצלעtermתחבולות_המספר#lBcXצלעיו
surface/sideצלעtermחשבון_השטחים#P0Ifצלע
geometric relations/similar figuresד.מ.י./דומהsolids-definitionספר_היסודות_לאקלידס#oKi8The similar solid shapes are those that each solid of which is contained by the same number of surfaces as the number of the surfaces containing the other, and each surface is similar to its corresponding surface in the other solid. התמונות המוגשמות הדומות הם אשר יקיף כל מוגשם מהם ממנין השטחים כמו מנין מה שיקיף באחר ויהיה כל שטח מאחד מהם דומה בשטח אשר הוא גילו מן המוגשם האחר ועל בריאתו
geometric relations/similar figuressurfaces-definitionספר_היסודות_לאקלידס#7gj7The similar rectilinear figures are those whose angles are equal and whose sides about the equal angles are proportional. השטחים המתדמים הם אשר זויותיהם שוות וצלעותיהם המקיפות בזויות השוות מתיחסות
geometrical shape/solidג.ר.מ./גרםdefinitionהאריתמטיקה_של_ניקומכוס#kMEJIt was said that the solid adds a dimension of depth to the surface, since the surface has only length and breadth ואמרנו שהגרם הוא אשר יוסיף משך בעומק על השטח אחר שהשטח אורך ורחב לבד
geometrical shape/solidג.ש.מ./גשםtermמלאכת_המספר#x4VOגשם
geometrical shape/solidג.ש.מ./מוגשםtermמלאכת_המספר#NWfqמוגשם
geometrical shape/solidגוףtermמשנת_המדות#lVlqגוף
geometrical shape/solidגוtermמשנת_המדות#livjגוו
geometrical shape/solidגגtermמשנת_המדות#NnXfגג
geometrical shape/solidג.ש.מ./גשםdefinitionמלאכת_המספר#LrBmThe solid is a quantity that has three dimensions, which are length, breadth and depth, whose limits are surfaces. הגשם הוא כמות שיש לו ג' {{#annot:term|315,1891|sNrA}}מרחקי'{{#annotend:sNrA}} שהם אורך ורוחב ועומק שתכליותיו הם ב' שטחי‫'
geometrical shape/solidג.ש.מ./גשםtermמלאכת_המספר#CTjNגשם
geometrical shape/solidג.ש.מ./גשםtermהאריתמטיקה_של_ניקומכוס#Q8TUגשם
geometrical shape/solidג.ש.מ./גשםdefinitionהאריתמטיקה_של_ניקומכוס#nUtWOne may argue by saying in a general statement that any thing that has length, breadth, and depth is a solid, and every solid has length, breadth, and depth. ואולי יהיה לטוען שיאמר הנה במאמר כולל שכל בעל אורך ורוחב ועומק הוא גשם וכל גשם בעל אורך ורחב ועומק
geometrical shape/solidג.ש.מ./גשםtermספר_מעשה_חושב#RgAmגשם
geometrical shape/solidג.ש.מ./גשםdefinitionהאריתמטיקה_של_ניקומכוס#Sy4lThe three-dimensional is the solid. ומה שהיה בעל שלשה המשכים הוא גשם
geometrical shape/solidג.ש.מ./גשםtermבר_נותן_טעם#eHwoגשם
geometrical shape/solidג.ר.מ./גרםtermהאריתמטיקה_של_ניקומכוס#Ff7gגרמים
geometrical shape/solidגוףtermהאריתמטיקה_של_ניקומכוס#3czYגוף
geometrical shape/solidג.ר.מ./גרםtermהאריתמטיקה_של_ניקומכוס#rQJKהגרם
geometrical shape/solidג.ל.מ./גולםdefinitionספר_יסודי_התבונה_ומגדל_האמונה#5tIPThe first is called solid, and it has three dimensions. הראשון נק' גולם ויש לו ג' מרחקים
geometrical shape/solidג.ל.מ./גולםtermספר_יסודי_התבונה_ומגדל_האמונה#xmtoגלם
geometrical shape/solidג.ל.מ./גולםtermספר_יסודי_התבונה_ומגדל_האמונה#jKvxגולמים
geometrical shape/solidג.ש.מ./גשםtermספר_המספר_/_אליהו_מזרחי#4qT1גשמים
geometrical shape/solidג.ש.מ./גשםtermספר_המספר_/_אליהו_מזרחי#ZoVNגשם
geometrical shape/solidג.ש.מ./מוגשםtermספר_המספר_/_אליהו_מזרחי#yKifמוגשמות
geometrical shape/solidג.ל.מ./גולםtermספר_הכללים_במספר#5Z9lגולם
geometrical shape/solidע.ק.ב./מעוקבdefinitionArithmetic_Textbook_by_R._Aharon_ben_Isaac#Z0L5מעוקב שהוא הגשם אשר ימצאו בו השלושה רחקים שהם אורך ורוחב ועומד
geometrical shape/solidגוףtermספר_הכללים_במספר#EyrJגוף
solid/solid angleקרןtermספר_יסודי_התבונה_ומגדל_האמונה#1mxyקרנות
solid/solid angleקרןtermספר_יסודי_התבונה_ומגדל_האמונה#2LQyקרנות השטח
solid/solid angleג.ל.מ./גלומהtermספר_יסודי_התבונה_ומגדל_האמונה#JS01זוית גולמית
solid/solid angleקרןtermספר_יסודי_התבונה_ומגדל_האמונה#SX31קרן
solid/sphereכ.ד.ר./כדורtermספר_הכללים_במספר#MkFQכדור
solid/sphereכ.ד.ר./כדורdefinitionספר_היסודות_לאקלידס#sI0KThe sphere is when the semicircle is drawn round with the diameter fixed in two points, so it does not move, and the arc, which is half the perimeter, revolves until it returns to its position; it is the circular solid. The center of the sphare and the center of the circle are the same.
הכדור הוא מה שיעבור חצי עגולה כאשר יקוים קו הקוטר בין שני כשורים עד שלא יסור וסבבה הקשת אשר היא חצי הקו המקיף עד שתשוב אל מקומה והוא המוגשם העגול ומרכז הכדור ומרכז העגולה אחד
solid/sphereכ.ד.ר./כדורtermמלאכת_המספר#NYptכדור
solid/sphereכ.ד.ר./כדורdefinitionספר_יסודי_התבונה_ומגדל_האמונה#MjPythe solid that is surrounded by a circular surface is called sphere. והגולם אשר יקיף אותו פרוש אחד עגול הוא הנקרא כדור
solid/sphereכ.ד.ר./כדורdefinitionספר_יסודי_התבונה_ומגדל_האמונה#WlA0It is that which is surrounded by one surface all around and at its center there is one point such that all the lines that are drawn from it to the surface of the sphere are equal to each other. הוא אשר יקיפו פרוש אחד מכל סביביו ובאמצעיתו נקודה אחת וכל הקוים היוצאים ממנה אל פרוש הכדור שוים זה לזה
solid/sphereת.ל.י./תלויtermמשנת_המדות#uV4dתלויה
solid/sphereכ.ד.ר./כדורtermספר_יסודי_התבונה_ומגדל_האמונה#hzZCכדור
quadrilateral/squareש.ו.ה./שוה צלעותtermספר_ג'יבלי_אלמוקבאלא#0caFשטח אחד שוה הצלעות
quadrilateral/squareש.ו.ה./שוה צלעותtermספר_ג'יבלי_אלמוקבאלא#94Ydמרובע שוה הצלעות
quadrilateral/squareשוה צלעות נצב זויותtermספר_ג'יבלי_אלמוקבאלא#DrKdהמרובע שוה הצלעות ונצב הזויות
quadrilateral/squareר.ב.ע./מרובעtermספר_ג'יבלי_אלמוקבאלא#j1oWמרובע
quadrilateral/squareשוה צלעות נצב זויותtermספר_ג'יבלי_אלמוקבאלא#Jhqqשטח אחד שוה הצלעות ונצב הזויות
quadrilateral/squareשוה צלעות נצב זויותtermספר_ג'יבלי_אלמוקבאלא#HdgBמרובע אחד שוה הצלעות נצב הזויות
quadrilateral/squareר.ב.ע./מרובעtermספר_האלזיברא#mzGpמרבע
quadrilateral/squareר.ב.ע./מרובעtermספר_ג'יבלי_אלמוקבאלא#bhc1מרובעי'
quadrilateral/squareש.ו.ה./שוה צלעותtermספר_ג'יבלי_אלמוקבאלא#Eq9Qמרובעי' השוי הצלעות
quadrilateral/squareשוה צלעות נצב זויותtermספר_ג'יבלי_אלמוקבאלא#va50שטח שוה הצלעות נצב הזויות
quadrilateral/squareש.ו.ה./שוה צלעותtermספר_ג'יבלי_אלמוקבאלא#tWbuמרובע אחד שוה הצלעות מד' זויות
quadrilateral/squaretermספר_המספר_/_אברהם_אבן_עזרא#IbQnמרובע {{#annot:term|316|tTbn}}ארכו{{#annotend:tTbn}} כ{{#annot:term|317|FXNE}}רחבו{{#annotend:FXNE}}
quadrilateral/squareר.ב.ע./שטח מרובעtermחשבון_השטחים#VRcAשטח מרובע עליו
quadrilateral/squareר.ב.ע./מרובעtermחשבון_השטחים#OcVTמרובע
quadrilateral/squareר.ב.ע./מרובעdefinitionספר_היסודות_לאקלידס#yeYhThe '''square''' is that which is both equilateral and right-angled. הנה מהן המרובע הוא השוה הצלעות נצב הזויות
quadrilateral/squareר.ב.ע./מרובעtermספר_האלזיברא#D62wמרבע
quadrilateral/squareשוה צלעות נצב זויותtermספר_ג'יבלי_אלמוקבאלא#vsuiשטחי' שוי הצלעות והזויות נצבות
quadrilateral/squareשוה צלעות נצב זויותtermספר_ג'יבלי_אלמוקבאלא#wYJEמרובע נצב הזויות שוה הצלעות
quadrilateral/squareשוה צלעות נצב זויותtermספר_ג'יבלי_אלמוקבאלא#d9eXמרובע אחד שוה הצלעות והזיות נצבות
quadrilateral/squareר.ב.ע./שטח מרובעtermתחבולות_המספר#Q5y3שטח מרובע עליו
quadrilateral/squareכ.ו.נ./נכוןtermקצת_מענייני_חכמת_המספר#MiTKמרובע נכון
quadrilateral/squareר.ב.ע./מרובעtermתחבולות_המספר#QPs4מרובע עליו
quadrilateral/squareר.ב.ע./רבועdefinitionספר_יסודי_התבונה_ומגדל_האמונה#YjuRthe first category is that whose four sides are all equal to each other in their value and each of its four angles is a right angle - this is called a square. החלק הראשון הוא אשר ארבע צלעיו כלם שוים בערכם אחת אל אחת וכן זויות ד' כל אחת מהן זוית נצבה וזה נקרא רבוע
quadrilateral/squareר.ב.ע./מרובעtermתחבולות_המספר#PFLTמרובע
quadrilateral/squareר.ב.ע./מרובעtermהאריתמטיקה_של_ניקומכוס#d8geמרובע
line/straight lineי.ש.ר./ישרdefinitionספר_היסודות_לאקלידס#lFcpThe '''straight line''' is that which lies straightly by the arrangement of points on it one by one. והקו הישר הוא המוצב על נכוחות אי זה נקודות יהיו עליו קצתם אל קצתם
line/straight lineי.ש.ר./מיושרdefinitionספר_יסודי_התבונה_ומגדל_האמונה#RN7aThe straight line is the one that passes directly from the two points that are its ends. והקו המיושר הוא ההולך לנכח ב' הנקדות אשר הם תכליתו
line/straight lineי.ש.ר./ישרtermספר_האלזיברא#4AfEקו ישר
line/straight lineי.ש.ר./ישרtermתחבולות_המספר#yJtOקו ישר
line/straight lineי.ש.ר./מיושרtermספר_יסודי_התבונה_ומגדל_האמונה#iRJOקו מיושר
line/straight lineי.ש.ר./ישרtermחשבון_השטחים#FjaRקו ישר
line/straight lineי.ש.ר./ישרtermספר_האלזיברא#wtKLישר
geometrical shape/surfaceגגtermמשנת_המדות#RwBaגג
geometrical shape/surfaceר.ק.ע./רקיעtermספר_יסודי_התבונה_ומגדל_האמונה#cV12הרקיע גלמי
geometrical shape/surfaceש.ט.ח./שטחtermספר_מעשה_חושב#tBy4שטחים
geometrical shape/surfaceפ.ר.ש./פרושdefinitionספר_יסודי_התבונה_ומגדל_האמונה#vPk1The second is called surface [lit. spread], and it is called by this name, since it is spread on the body as if it apart from it, and this body has length and breadth alone. והשני נק' פרוש וקראו לו בשם הזה מפני שהוא פרוש על הגולם כאלו היה חוצה ממנו וזה הפרוש יש לו ארך ורחב בלבד
geometrical shape/surfaceש.ט.ח./שטחdefinitionהאריתמטיקה_של_ניקומכוס#QKfYLikewise, one may say that what has only length and breadth is a surface, and the surface is that which has only length and breadth. וכמו כן יאמר מה שהיה לו אורך ורחב לבד הוא שטח והשטח הוא מה שהיה לו אורך ורחב לבד
geometrical shape/surfaceש.ט.ח./שטחtermהאריתמטיקה_של_ניקומכוס#Lfgrשטח
geometrical shape/surfaceפ.ר.ש./פרושtermספר_יסודי_התבונה_ומגדל_האמונה#Uadsפרושים
geometrical shape/surfaceפ.ר.ש./פרושtermספר_יסודי_התבונה_ומגדל_האמונה#aIkfפרוש
geometrical shape/surfaceש.ט.ח./שטחtermספר_האלזיברא#eJNdשטח
geometrical shape/surfaceש.ט.ח./שטחtermבר_נותן_טעם#5Pkeשטח
geometrical shape/surfaceש.ט.ח./שטחdefinitionהאריתמטיקה_של_ניקומכוס#B67OThe two-dimensional is the surface. ומה שהיה בעל שני המשכים הוא שטח
geometrical shape/surfaceש.ט.ח./שטחtermספר_מעשה_חושב#KV4Rשטח
geometrical shape/surfaceש.ט.ח./שטחtermתחבולות_המספר#JkjGשטח
geometrical shape/surfaceש.ט.ח./שטחtermמלאכת_המספר#T5GNשטח
geometrical shape/surfacesolid/volumetermספר_הכללים_במספר#F8HSמשיחת שטח הבריכה
geometrical shape/surfaceמ.ש.ח./משיחהtermספר_הכללים_במספר#hb4lמשיחת שטח הכדור
geometrical shape/surfaceש.ט.ח./שטחdefinitionמלאכת_המספר#gJ6uthe surface is a quantity that has length and breadth without depth, whose limits are two lines. השטח הוא כמות בעל אורך ו{{#annot:term|317,1488|SLfo}}רוחב {{#annotend:SLfo}}בלתי עומק ש{{#annot:term|279,1887|tYDo}}תכליותיו{{#annotend:tYDo}} ב' קוים
geometrical shape/surfaceש.ט.ח./שטחtermספר_ג'יבלי_אלמוקבאלא#fIHTשטחי'
geometrical shape/surfaceש.ט.ח./שטחtermחשבון_השטחים#fxB7שטח
geometrical shape/surfaceש.ט.ח./שטחtermספר_המספר_/_אליהו_מזרחי#GMrPשטח
geometrical shape/surfaceש.ט.ח./שטחtermספר_המספר_/_אליהו_מזרחי#P6xSשטחים
geometrical shape/surfaceש.ט.ח./שטחdefinitionספר_היסודות_לאקלידס#PhWlThe '''surface''' is that which has length and breadth only. והשטח הוא אשר לו אורך ורוחב לבד
geometrical shape/surfaceש.ט.ח./שטחtermספר_ג'יבלי_אלמוקבאלא#qKhsשטח
geometrical shape/surfaceגגdefinitionמשנת_המדות#KsSGThe surface itself is the area. והגג עצמו היא המשיחה
geometric relations/to be the side of an areaח.ז.ק./הוחזקtermספר_ג'יבלי_אלמוקבאלא#i2iaהמוחזקי' ב
geometric relations/to be the side of an areaח.ז.ק./החזיקtermספר_האלזיברא#3DECמחזקת ב
geometrical shape/to constructע.מ.ד./העמידtermספר_היסודות_לאקלידס#TWKoנעמיד על
geometrical shape/to constructע.ש.ה./עשהtermקצור_המספר#FaQ9נעשה
geometrical shape/to constructtermספר_האלזיברא#Zpzeנעשה מן א"ב מרבע
geometrical shape/to constructtermספר_האלזיברא#Mz5iנעשה מן קו א"ג מרבע
geometrical shape/to constructtermתחבולות_המספר#GRESנעשה על
geometrical shape/to constructtermתחבולות_המספר#48WGעשה על
geometrical shape/to constructtermתחבולות_המספר#8stUתשים על
geometrical shape/to constructtermתחבולות_המספר#yUj4נשים עליו
geometrical shape/to constructtermתחבולות_המספר#nGtXנשים על
geometrical shape/to constructנ.ו.ח./הניחtermחשבון_השטחים#cuCtנניח על
geometrical shape/to constructע.ש.ה./עשהtermחשבון_השטחים#ZiEAנעשה על
geometrical shape/to constructע.ש.ה./עשהtermחשבון_השטחים#6VxTעשה על
geometrical shape/to constructtermחשבון_השטחים#WKQnנשים על
geometrical shape/to constructtermחשבון_השטחים#yth4אשים על
geometrical shape/to constructע.מ.ד./העמידtermספר_היסודות_לאקלידס#yirgנעמיד על
line/to cut a lineח.ל.ק./נחלק לחצאיםto be halved at pointתחבולות_המספר#JUPfנחלק לחצאין על נקודת
line/to cut a lineח.ל.ק./חלק קוtermחשבון_השטחים#vcluנחלק קו
line/to cut a lineח.ל.ק./חלק קוtermתחבולות_המספר#q7GHנחלק קו
line/to cut a lineח.ל.ק./נחלק לחצאיםto be halved at pointחשבון_השטחים#JnrHנחלק לחצאים על נקודת
line/to cut a lineto be cut randomly at pointספר_האלזיברא#S8Q5יחולק איך שקרה על נקדת
line/to cut a lineto be halved at pointספר_האלזיברא#Wk92נחלק לחצאין על נקדת
line/to cut a lineח.ל.ק./חלק לחצאיםto halve a line at pointחשבון_השטחים#g8x0תחלק קו א"ב לשני חצאים על
line/to cut a lineח.ל.ק./חלק לחצאיםto halve a line at pointתחבולות_המספר#uwUlנחלקהו לחציין על נקודת
line/to cut a lineח.ל.ק./חלק לחצאיםto halve a line at pointתחבולות_המספר#vadkנחלק אותו לחצאין על נקודת
line/to cut a lineח.ל.ק./חלק לחצאיםto halve a line at pointחשבון_השטחים#l2uxנחלק אותו לחציים על נקודת
line/to cut a lineto be cut into two unequal segmentsחשבון_השטחים#Cbhdנחלק לשני חלקים בלתי שוים על נקודת
line/to cut a lineto be cut into two unequal segmentsתחבולות_המספר#sLnnנחלק לשני חלקים בלתי שוים על נקודת
line/to cut a lineח.ל.ק./נחלקto be cut into two segmentsתחבולות_המספר#ms8eיחלק לשני חלקים
line/to cut a lineto cut randomly at pointספר_האלזיברא#6A8lחלק איך שקרה על נקדת
line/to cut a lineח.ל.ק./חלק קוtermתחבולות_המספר#QaGpתחלק קו
line/to cut a lineto halve a lineספר_האלזיברא#CWXyנחלקהו ‫130rלחצאין על נקדת
line/to cut a lineח.ל.ק./נחלק לחצאיםto be halved at pointחשבון_השטחים#Em05נחלק לחציים על נקודת
line/to cut a lineח.ל.ק./חלק קוtermחשבון_השטחים#zVhWתחלק קו
line/to cut a lineto halve a lineספר_האלזיברא#PkWcנחלקהו לב' חלקי' שוים על נקדת
line/to cut a lineto cut into two unequal segmentsספר_האלזיברא#fs2Sנחלקה לשני חלקים בלתי שוים על נקדת
line/to cut a lineח.צ.י./חצהto halve a line at pointספר_ג'יבלי_אלמוקבאלא#yo7tנחצה לשני חלקים שוים בנקודת
geometric relations/to cut offב.ד.ל./הבדילtermתחבולות_המספר#ogvRהבדלנו
geometric relations/to cut offב.ד.ל./הבדילtermתחבולות_המספר#Ptjjנבדיל
geometric relations/to cut offב.ד.ל./הבדילtermחשבון_השטחים#ueVdנבדיל
geometric relations/to cut offב.ד.ל./הבדילtermחשבון_השטחים#LmNgתבדיל
geometric relations/to divide a figureפ.ס.ק./פסקtermמשנת_המדות#rWbWפסקה לשנים
geometric relations/to divide a figureפ.ס.ק./פסקtermמשנת_המדות#pgwrפוסקה שנים
geometry/to drawי.צ.א./הוציאto draw a lineתחבולות_המספר#vgQzנוציא קוי
geometry/to drawי.צ.א./הוציאto draw a lineספר_ג'יבלי_אלמוקבאלא#cMHcתוציא קו אחד מ
geometry/to drawי.צ.א./הוציאtermתחבולות_המספר#eY6oנוציא
geometry/to drawי.צ.א./הוציאtermחשבון_השטחים#2Qhsתוציא מ
geometry/to drawי.צ.א./הוציאtermחשבון_השטחים#xLtyתוציא מנקודות
geometry/to drawי.צ.א./הוציאtermחשבון_השטחים#2Ih7תוציא מנקדות
geometry/to drawי.צ.א./הוציאtermחשבון_השטחים#3P9mתוציא מנקודת
geometry/to drawי.צ.א./הוציאto draw a lineתחבולות_המספר#E2dhתוציא קו
geometry/to drawי.צ.א./הוציאto draw a lineספר_ג'יבלי_אלמוקבאלא#Z0HSנוציא קו אחר ישר
geometry/to drawי.צ.א./הוציאto draw a lineחשבון_השטחים#DwRlתוציא קו
geometry/to drawצ.י.ר./צוירtermספר_ג'יבלי_אלמוקבאלא#9Ak5מצוייר
geometry/to drawק.ו.י./קוהtermספר_היסודות_לאקלידס#qfrQנקוה
geometry/to drawק.ו.י./קוהtermספר_היסודות_לאקלידס#kY7lנקוה
geometry/to drawע.ש.ה./עשהto draw a lineחשבון_השטחים#cXQoלעשות קוי
geometry/to drawע.ב.ר./העבירto draw a lineספר_היסודות_לאקלידס#ztOjנעביר קו
geometry/to drawי.צ.א./הוציאtermספר_האלזיברא#DpZVאוציא מ
geometry/to drawע.ב.ר./העבירto draw a lineספר_האלזיברא#Ii1Bנעביר קו
geometry/to drawצ.י.ר./ציירtermחשבון_השטחים#H57uתצייר
geometry/to drawtermספר_האלזיברא#uW6oצירתי
geometry/to drawי.צ.א./הוציאto draw a lineמלאכת_המספר#DyfVנוציא
geometry/to drawצ.י.ר./ציירtermספר_ג'יבלי_אלמוקבאלא#MU8Fנצייר
geometry/to drawי.צ.א./הוציאto draw a lineמלאכת_המספר#utEhנוציא
geometry/to drawנ.ג.ע./הגיעto draw a lineספר_ג'יבלי_אלמוקבאלא#omwBתגיע קו אחד מ
geometry/to drawי.צ.א./הוציאto draw a lineספר_ג'יבלי_אלמוקבאלא#yF7xנוציא קו
circle/to draw a circleנ.ק.פ./הקיףtermספר_היסודות_לאקלידס#Wj8nנקיף על
circle/to draw a circleח.ק.ק./לחוקtermספר_הכללים_במספר#CyVlלחוק בעגול
circle/to draw a circleנ.ק.פ./הקיףtermספר_היסודות_לאקלידס#Bgcxנקיף עגולה
circle/to draw a circleע.ג.ל./עגלtermספר_יסודי_התבונה_ומגדל_האמונה#fYqfלעגל עליו עגולה
circle/to draw a circleק.ו.י./קוהtermספר_היסודות_לאקלידס#Pgvrנקוה עגולה
circle/to draw a circleח.ק.ק./לחוקtermספר_הכללים_במספר#Wktsלחוק בה עגול
circle/to draw a circleע.ג.ל./עגלtermספר_יסודי_התבונה_ומגדל_האמונה#Oergלעגל בתוכו עגולה
circle/to draw a circleק.ו.י./קוהtermספר_היסודות_לאקלידס#MoiNנקוה
geometric relations/to encompassנ.ק.פ./הקיףtermתחבולות_המספר#jij2יקיפו בו
geometric relations/to encompassנ.ק.פ./הקיףtermתחבולות_המספר#fbeHמקיף
geometric relations/to encompassנ.ק.פ./הקיףtermספר_מעשה_חושב#u8IFהמקיפים בו
geometric relations/to encompassנ.ק.פ./הקיףtermמלאכת_המספר#9qMCמקיף אותו
line/to extend a lineמ.ש.כ./המשיך קוtermחשבון_השטחים#Hlm5נמשיך קו
line/to extend a lineמ.ש.כ./המשיך קוtermספר_האלזיברא#67xxנמשיך קו
line/to extend a lineמ.ש.כ./המשיך קוtermתחבולות_המספר#KMfZנמשיך קו
line/to extend a lineמ.ש.כ./המשיך קוtermספר_ג'יבלי_אלמוקבאלא#zKyQתמשיך קו אחד עליו
surface/to form an areatermתחבולות_המספר#RRCVנשלים שטח
surface/to form an areaש.ל.מ./השליםtermחשבון_השטחים#y3cpנשלים שטח
geometric relations/to intersectח.ב.ר./מחוברtermספר_דיני_ממונות#tuwlקוים מחוברים
geometric relations/to intersecttermספר_האלזיברא#UM04יפגוש קו
geometric relations/to intersectפ.ס.ק./הפסיקtermמשנת_המדות#MXl7מפסיקין זה את זה
geometric relations/to intersectח.ת.כ./חתךtermספר_האלזיברא#NwpIיחתכו
geometric relations/to joinש.ת.פ./שתףtermתחבולות_המספר#LFhkנשתף עמו
geometric relations/to joinד.ב.ק./הדביקtermתחבולות_המספר#iJG4נדביק
geometric relations/to joinד.ב.ק./הדביקtermספר_ג'יבלי_אלמוקבאלא#yNEQנדביק
geometric relations/to joinד.ב.ק./הדביקtermספר_ג'יבלי_אלמוקבאלא#8VeDנדביק
geometric relations/to revolve aroundס.ב.ב./סבבtermספר_יסודי_התבונה_ומגדל_האמונה#Py8cסובב עליו
geometric relations/to revolve aroundס.ב.ב./סבבtermספר_המספר_/_אברהם_אבן_עזרא#gOMDסובבות את
geometric relations/to touchמ.ש.ש./מששtermספר_יסודי_התבונה_ומגדל_האמונה#OH1Tמושש ל
geometric relations/to touchמ.ש.ש./מששtermספר_יסודי_התבונה_ומגדל_האמונה#IbMXמושש
quadrilateral/trapezoidנ.ט.י./נוטהdefinitionספר_היסודות_לאקלידס#JU9NThe quadrilaterals that are other than the above-mentioned figures are called '''trapezia'''. ומה שהיה על זולת מה שספרנו מן התמונות בעלות ארבע צלעות תקרא הנוטה
quadrilateral/trapezoidק.ט.מ./קטומהtermספר_הכללים_במספר#4hrzקטומת הראש
quadrilateral/trapezoidק.ט.מ./קטומהtermספר_הכללים_במספר#0OmPקטומה
surface/triangleש.ל.ש./משולשdefinitionספר_יסודי_התבונה_ומגדל_האמונה#Trd6the first of them is the triangle which is the surrounded by three straight lines. הראשון מהם הוא המשלש והוא המקיף אותו ג' קוים ישרים
surface/triangleש.ל.ש./משולשתtermמשנת_המדות#rrKKמשלשת
surface/triangleש.ל.ש./משולשtermמלאכת_המספר#kEE3משולש
surface/triangleש.ל.ש./משולשdefinitionספר_יסודי_התבונה_ומגדל_האמונה#rvtNExplanation of the properties of the surface that has three sides called triangle !style="text-align:right;"|פירוש עניני השטח אשר לו שלשה צלעים ונקרא משלש
surface/triangletermספר_המספר_/_אברהם_אבן_עזרא#VH1bמשולש
surface/triangleש.ל.ש./משולשtermספר_יסודי_התבונה_ומגדל_האמונה#Sluzמשלש
surface/triangleש.ל.ש./משולשtermספר_יסודי_התבונה_ומגדל_האמונה#jMAMמשלשים
solid/truncated solidח.ס.ר./מחוסרtermהאריתמטיקה_של_ניקומכוס#EfLjמחוסר
solid/truncated solidק.ט.ע./קטועtermמשנת_המדות#njDmקטוע
solid/truncated solidח.ס.ר./מחוסרtermהאריתמטיקה_של_ניקומכוס#fXNBהגשם המחוסר
line/uniform lineפ.ר.ד./מתפרדtermספר_יסודי_התבונה_ומגדל_האמונה#Tv8Yמתפרד
line/uniform lineפ.ר.ד./מתפרדtermספר_יסודי_התבונה_ומגדל_האמונה#Pmlsהקו המתפרד
geometry/upper baseפהtermמלאכת_המספר#Nkohפיו
circle/versineח.צ.צ./חץdefinitionמשנת_המדות#UTQnThe sagitta is the drawn from the middle of the arc until the middle of the chord, as it is said: ''they set their arrow on the bowstring'' [Psalms 11, 2]. והחץ הוא המשוך מאמצע הקשת לאמצע היתר שנ' ''כוננו חצם על יתר''‫תהילים יא, ב
circle/versinetermספר_המספר_/_אברהם_אבן_עזרא#WiTPחץ
circle/versineח.צ.צ./חץtermמשנת_המדות#nlBRחץ
solid/volumeמ.ש.ח./משיחהtermמשנת_המדות#g4GGמשיחת הגג
solid/volumeש.ב.ר./תשבורתtermספר_הכללים_במספר#SpiWתשבורת רבוע ה
solid/volumeש.ב.ר./תשבורתtermספר_הכללים_במספר#RKILתשבורת גוף ה
solid/volumeש.ב.ר./תשבורתtermספר_המספר_/_אליהו_מזרחי#0BrLתשבורת
solid/volumeש.ב.ר./תשבורתtermספר_הכללים_במספר#Lrs9תשבורת
solid/volumeמ.ש.ח./משיחהtermמשנת_המדות#z83Jמשיחת הגוף
linear dimension/widthר.ח.ב./רוחבtermמלאכת_המספר#SLfoרוחב
linear dimension/widthר.ח.ב./רוחבtermספר_ג'יבלי_אלמוקבאלא#gKanרוחב ה
linear dimension/widthר.ח.ב./רוחבtermקצור_המספר#Tl4Aרחבה
linear dimension/widthר.ח.ב./רוחבtermספר_ג'יבלי_אלמוקבאלא#ytPjרחב ה
linear dimension/widthר.ח.ב./מרחבtermספר_ג'יבלי_אלמוקבאלא#nsj0מרחבם
linear dimension/widthר.ח.ב./רוחבtermספר_ג'יבלי_אלמוקבאלא#P8YWרחבו
linear dimension/widthר.ח.ב./מרחבtermספר_ג'יבלי_אלמוקבאלא#4CJIמרחב ה
linear dimension/widthר.ח.ב./מרחבtermספר_ג'יבלי_אלמוקבאלא#jOGZמרחב
linear dimension/widthר.ח.ב./רוחבtermמשנת_המדות#PREyרחב
linear dimension/widthר.ח.ב./רוחבtermבר_נותן_טעם#Ykalרוחב
linear dimension/widthר.ח.ב./רוחבtermמלאכת_המספר#DQWqרוחב
linear dimension/widthtermספר_המספר_/_אברהם_אבן_עזרא#FXNEרחבו
Retrieved from "http://mispar.ethz.ch/mediawiki/index.php?title=Royslist&oldid=50827"