Difference between revisions of "Swen Page"

Revision as of 16:41, 30 November 2021

Category	Category	Comment	Link	Annotated text
angle/acute angle	ח.ד.ד./חד	term	משנת_המדות#Fhur	חדות
angle/acute angle	ח.ד.ד./חד	term	ספר_יסודי_התבונה_ומגדל_האמונה#ohTc	זוית חדה
angle/acute angle	ח.ד.ד./חד	definition	ספר_יסודי_התבונה_ומגדל_האמונה#7qMI	the acute angle is less than the right [angle] in its value והזוית החדה היא המחסרת בערכה מן הנצבת
angle/acute angle	צ.ר.ר./צר	term	משנת_המדות#327H	זויות צרים
angle/acute angle	ח.ד.ד./חד	definition	ספר_היסודות_לאקלידס#V5db	The smaller than a right angle is called an '''acute angle'''. ואשר היא קטנה מנצבת תקרא חדה
acute angle/acute-angled	ח.ד.ד./חד	triangle	משנת_המדות#Kt5x	חדה
acute angle/acute-angled	ח.ד.ד./מחודד	triangle	ספר_יסודי_התבונה_ומגדל_האמונה#JbzH	המשלש מחדד הזויות
acute angle/acute-angled	ח.ד.ד./מחודד	triangle-definition	ספר_יסודי_התבונה_ומגדל_האמונה#lhjk	the first is that whose each angle is acute angle - this is called an acute-angled [triangle]. האחד הוא אשר כל זוית מזויותיו זוית חדה והוא הנקרא מחודד הזוית
acute angle/acute-angled	ח.ד.ד./חד	triangle-definition	ספר_היסודות_לאקלידס#pQ2M	The '''acute-angled triangle''' is that whose three angles are acute. ומשולש חד הזויות והוא אשר כל אחת מזויותיו השלש חדה
geometrical shape/angle	זוית	term	מלאכת_המספר#2ohU	זוית
geometrical shape/angle	זוית	term	מלאכת_המספר#fvYc	זויות
angle/angle between straight lines	י.ש.ר./ישרה	term	ספר_יסודי_התבונה_ומגדל_האמונה#IAoP	הזויות הישרות
angle/angle between straight lines	י.ש.ר./ישרה	term	ספר_יסודי_התבונה_ומגדל_האמונה#q7XH	הזוית הישרה
point/apex	ר.א.ש./ראש	term	משנת_המדות#jOb1	ראש
line/apotome	ב.ד.ל./נבדל	definition	ספר_היסודות_לאקלידס#9THR	When a segment measurable in a square is subtracted from a straight line and the two lines are commensurable in square only, then the remaining straight line is unmeasurable; let it be called an apotome. ע כאשר הובדל מקו ישר מדבר בכח והיו השני קוים בכח לבד משותפים הנה הקו הנשאר בלתי מדבר ויקרא הנבדל
circle/arc	ק.ש.ת./קשת	term	משנת_המדות#dLJu	קשת
circle/arc		term	ספר_המספר_/_אברהם_אבן_עזרא#Gr5j	קשתות
circle/arc	ק.ש.ת./קשת	definition	משנת_המדות#t84r	What is the arc? it is the part of the circle, as it is said: ''like the appearance of the rainbow that is in the cloud'' [Ezekiel 1, 28]. איזו היא קשת החלק מן העגול שנ' ''כמראה הקשת אשר יהיה בענן''‫יחזקאל א, כח
magnitude/area	ש.ב.ר./תשבורת	term	קצור_המספר#6eNb	תשבורת
magnitude/area		term	ספר_המספר_/_אברהם_אבן_עזרא#nSsY	תשבורת
magnitude/area	מ.ש.ח./משיחה	term	משנת_המדות#hZNE	משיחה
magnitude/area	ר.ח.ב./רוחב	term	ספר_ג'יבלי_אלמוקבאלא#n6dR	רחב השטח
magnitude/area	ר.ב.ע./רבוע	term	ספר_הכללים_במספר#9C3m	רבוע
magnitude/area	ש.ב.ר./תשבורת	term	ספר_הכללים_במספר#pgiu	תשבורת
magnitude/area	ר.ב.ע./רבוע	term	ספר_הכללים_במספר#ez7p	רבוע
magnitude/area	ש.ב.ר./תשבורת	term	קצור_המספר#ZrPN	תשבורת
magnitude/area	ש.ט.ח./שטח	term	ספר_ג'יבלי_אלמוקבאלא#Q9z1	שטחו
magnitude/area	ש.ט.ח./שטח	term	חשבון_השטחים#Fzc9	שטח
magnitude/area	ש.ט.ח./שטח	term	תחבולות_המספר#F1Td	שטח
magnitude/area	מ.ש.ח./משיחה	term	ספר_הכללים_במספר#DJo0	משיחת ה
magnitude/area	מ.ש.ח./משיחה	term	ספר_הכללים_במספר#INwY	משיחת ה
magnitude/area	ש.ב.ר./שבר	term	ספר_הכללים_במספר#1sqc	מידת שבריו
magnitude/area	ש.ב.ר./שבר	term	ספר_הכללים_במספר#lZxh	שבר
magnitude/area	ש.ב.ר./תשבורת	term	ספר_הכללים_במספר#a5B3	תשברתו
magnitude/area	ש.ב.ר./תשבורת	term	ספר_האלזיברא#QTLl	תשבורתו
magnitude/area	ש.ב.ר./שברים	term	ספר_האלזיברא#Empf	שבריו
magnitude/area	ש.ב.ר./שברים	term	ספר_האלזיברא#XLwt	מספר שברי
magnitude/area	ש.ט.ח./שטח	term	ספר_ג'יבלי_אלמוקבאלא#s6dl	שטח
magnitude/area		term	ספר_המספר_/_אברהם_אבן_עזרא#bkNT	שברים
sphere/axis	ב.ר.ח./בריח	definition	ספר_יסודי_התבונה_ומגדל_האמונה#d6V1	if the sphere revolves around this diameter, we call it then the axis of the sphere. ואם יהיה הכדור סובב על האלכסון הזה אנו קורין לו בעת ההיא בריח הכדור
geometrical shape/base	י.ש.ב./תושבת	term	ספר_המספר_/_אליהו_מזרחי#FVdw	תושבתה
geometrical shape/base	ק.ב.ע./קבע	term	משנת_המדות#zDsv	קבע
geometrical shape/base	ק.ב.ע./קבע	definition	משנת_המדות#axVO	The base is that upon which two sides are fixed, ''upon which the house rests'' [Judges 16, 26; 29]. והקבע זה ששני צלעים קבועים עליו שני ''אשר הבית נכון עליהם''‫שופטים טז, כ"ו; כ"ט
geometrical shape/base	י.ש.ב./תושבת	term	מלאכת_המספר#ojMz	תושבת
geometrical shape/base	סוף	term	משנת_המדות#WWja	סוף
solid/beam	אריחי	term	האריתמטיקה_של_ניקומכוס#fZcR	מוגשמים אריחיים
point/center	צ.י.ר./ציר	center of a circle	ספר_יסודי_התבונה_ומגדל_האמונה#Xrf7	ציר העגול
point/center	ר.כ.ז./מרכז	center of a circle	ספר_היסודות_לאקלידס#C6ny	מרכז העגולה
point/center	ר.כ.ז./מרכז	center of a circle	קצת_מענייני_חכמת_המספר#gyB1	מרכז העגולה
point/center	צ.י.ר./ציר	term	ספר_הכללים_במספר#0qCr	ציר העגולה
point/center	צ.י.ר./ציר	term	ספר_הכללים_במספר#a6OG	ציר העגול
point/center	צ.י.ר./ציר	center of a sphere	ספר_יסודי_התבונה_ומגדל_האמונה#uFQI	ציר הכדור
point/center	ר.כ.ז./מרכז	term	Arithmetic_Textbook_by_R._Aharon_ben_Isaac#rFFw	מרכז
circle/chord		term	ספר_המספר_/_אברהם_אבן_עזרא#nGjl	יתר
circle/chord	י.ת.ר./יתר	definition	משנת_המדות#ChKs	The chord is the holder of the arc, as it is said: ''bent bow'' [Isaiah 21, 15]. והיתר זה המחזיק בפי הקשת שנ' ''קשת דרוכה''‫ישעיה כא, טו
circle/chord		term	ספר_המספר_/_אברהם_אבן_עזרא#BVOw	יתרים
circle/chord	י.ת.ר./יתר	term	משנת_המדות#ZqPD	יתר
circle/chord	י.ת.ר./מיתר	term	ספר_היסודות_לאקלידס#iAOK	מיתר
circle/chord	י.ת.ר./מיתר	term	ספר_היסודות_לאקלידס#NCXo	מיתר
surface/circle	ע.ג.ל./עגולה	term	אגרת_המספר#CEIL	עגולה
surface/circle		definition, #עגולה	ספר_יסודי_התבונה_ומגדל_האמונה#Tyz7	we call the surface that the one line that surrounds it is circular, a circle if it is on a plane surface. והשטח אשר קו האחד המקיפו הוא עגול אנו קורין לשטח עגולה ישרה אם הוא בשטח ישר
surface/circle	ע.ג.ל./עגולה	definition	ספר_היסודות_לאקלידס#uqaX	The '''circle''' is a plane figure contained by one line, within which there is one point such that all the straight lines drawn from it and terminated in the circumference are equal to one another. והעגולה היא תמונה פשוטה שוה יקיף אותה קו אחד בתוכה נקודה כל הקוים הישרים היוצאים ממנה ויכלו אל הקו ההוא שוים קצתם אל קצתם
surface/circle	ע.ג.ל./עגול	definition	ספר_יסודי_התבונה_ומגדל_האמונה#x37u	the circle is that which at its center there is one point such that all the lines that are drawn from it to the circumference are equal to each other in their value. השטח העגול הוא הנמצא באמצעיתו נקודה אחת אשר כל קו שתוציא ממנה אל הקו המקיף יהיו שוים בערכם זה לזה
surface/circle	ע.ג.ל./עגולה	term	מלאכת_המספר#yHjG	עגולה
surface/circle		term	ספר_המספר_/_אברהם_אבן_עזרא#oaVK	עגול
surface/circle		term	ספר_המספר_/_אברהם_אבן_עזרא#Twc4	עגולה
surface/circle	ע.ג.ל./עגול	term	משנת_המדות#D5gU	עגול
surface/circle		term	ספר_המספר_/_אברהם_אבן_עזרא#PTuV	עגול
surface/circle	ש.פ.ל./שפל	term	משנת_המדות#FIGD	שפלה
surface/circle	ע.ג.ל./עגולה	term	משנת_המדות#43ng	עגלה
line/circular line	ע.ג.ל./עגול	definition	ספר_יסודי_התבונה_ומגדל_האמונה#NCuE	The circular line is the one on which you cannot find three points that are in the same direction, and inside of it there is a point that is equidistant from all the points of the circle. והקו העגול הוא כל אשר ^אי אתה יכול למצוא ג' נקדות על נכח וימצא בתוכו נקדה שיהיה מרחקה מכל נקדות העגול מרחק אחד
line/circular line	ע.ג.ל./עגול	term	ספר_יסודי_התבונה_ומגדל_האמונה#bObt	קו עגול
geometric relations/commensurable	ש.ת.פ./משותף	definition	ספר_היסודות_לאקלידס#qiVv	Those that have magnitudes, as lines, surfaces, and solids, that are said to be '''commensurable''', are those that are measured by the same measure. בעלי השעורים מן הקוים והשטחים והמוגשמים אשר יאמר להם ~~המשותפים~~ המשותפים הם אשר ישער אותם ~~כלם~~ ^יחד שעור אחד
geometric relations/commensurable	ש.ת.פ./בלתי משותפים	definition-incommensurable	ספר_היסודות_לאקלידס#lGqt	Those that are said to be '''incommensurable''' are those that cannot be measured the same measure. ואשר יאמר להם בלתי משותפים הם אשר לא ישער אותם כלם שעור אחד
geometric relations/commensurable in square	ש.ת.פ./בלתי משותפים בכח	definition-incommensurable in square	ספר_היסודות_לאקלידס#zQYu	They are said to be '''incommensurable in square''', when the squares [that are generated] from them cannot be measured by the same area. ויאמר להם בלתי משותפים בכח כאשר לא יהיה למרובעים ~~הנה נבאר~~ [ההווים] מהם שטח ישער אותם
geometric relations/commensurable in square	ש.ת.פ./משותפים בכח	definition	ספר_היסודות_לאקלידס#shEk	Straight lines are said to be '''commensurable in square''', when the squares that are generated from them are measured by the same area. והקוים הישרים אשר יאמר להם המשותפים בכח כאשר היה למרובעים ההוים מהם שטח ישער אותם
surface/concave surface	ע.ק.מ./עקמומי	definition	ספר_יסודי_התבונה_ומגדל_האמונה#Rmia	the concave surface is the plane that encompasses the dome from beneath; it is also either circular or curved. והפרוש העקמומי הוא הרקיע המקיף את גב הקובה מלמטה ויהיה כמו כן עגול או עקום
surface/concave surface	ע.ק.מ./עקמומי	term	ספר_יסודי_התבונה_ומגדל_האמונה#Ue2N	עקמומי
solid/cone	אלון	term	ספר_יסודי_התבונה_ומגדל_האמונה#7Wx1	אלון
solid/cone	אתרוג	term	משנת_המדות#8LjV	אתרוג
solid/cone	מ.ש.כ./משוך	definition	משנת_המדות#6tE5	The conical, whose apex is sharp and base is planar, whether quadrilateral, or circular, or triangular: ז' והמשוך ראשו חד וסופו {{#annot:term\|588,2554\|epCp}}ממוצע{{#annotend:epCp}} ואפי' מרובע או שיהיה עגול או משולש
solid/cone	אלוני	term	ספר_יסודי_התבונה_ומגדל_האמונה#w4jz	הגולם האלוני
solid/cone	ח.ר.ט./חרוט	term	ספר_יסודי_התבונה_ומגדל_האמונה#eKVd	חרוטות
solid/cone	ח.ר.ט./חרוט	term	ספר_יסודי_התבונה_ומגדל_האמונה#PHTK	הגולם החרוט
solid/cone	אלוני	term	ספר_יסודי_התבונה_ומגדל_האמונה#NCUz	האלוני
geometric relations/congruent figures	ש.ו.ה./שוה	solids-definition	ספר_היסודות_לאקלידס#68bD	The equal similar solid shapes are those that each solid of which is contained by the same number of surfaces as the number of the surfaces containing the other, and each surface is similar and equal in measure to its corresponding surface in the other solid. התמונות המוגשמות השוות הדומות הם אשר יקיפו בכל מוגשם מהם ממנין השטחים כמו מנין מה שיקיפו באחר ויהיה כל שטח מאחד מהם דומה ושוה השיעור לשטח אשר הוא גילו מן המוגשם האחר ועל בריאתו
surface/convex surface	ק.ב.ב./מקובה	term	משנת_המדות#nssa	מקובה
surface/convex surface	ק.ב.ב./קבוב	definition	ספר_יסודי_התבונה_ומגדל_האמונה#Q7bh	the convex surface is the plane that encompasses the dome from above; this surface is either circular or curved. והפרוש הקבוב הוא הרקיע המקיף את קו הקובה מלמעלה והרקיע הזה יהיה עגול ויהיה עקום
surface/convex surface	ק.ב.ב./קובה	term	משנת_המדות#8Lrz	קובה
surface/convex surface	ק.ב.ב./קבוב	term	ספר_יסודי_התבונה_ומגדל_האמונה#txDc	קבוב
solid/cube	ע.ק.ב./מעוקב	term	בר_נותן_טעם#n3HE	גשם מעוקב
solid/cube	ע.ק.ב./מעוקב	term	Arithmetic_Textbook_by_R._Aharon_ben_Isaac#gzFs	מעוקב
line/curve	ע.ק.מ./עקום	term	ספר_יסודי_התבונה_ומגדל_האמונה#MU5o	קו עקום
line/curve	ע.ק.מ./עקום	definition	ספר_יסודי_התבונה_ומגדל_האמונה#q5Cb	The curve is any line on which you cannot find three points that are in the same direction and you cannot find also any point in it that is equidistant from all the points of the curve. והקו העקום כל קו שאי אתה מוצא ג' נקדות על נכח אחד ואף נקדה שיהיה מרחקה מנקדות העקום מרחק אחד אי אתה מוצא בו
solid/cylinder	ע.ג.ל./עגולה	term	ספר_הכללים_במספר#Mt2g	מצבה עגולה
solid/cylinder	אצטוונא	term	ספר_המספר_/_אליהו_מזרחי#Ensz	האצטוונא העגולה
solid/cylinder	ע.ג.ל./עגולה	term	ספר_הכללים_במספר#zGsp	מצבה עגולה
solid/cylinder	אצטוונא	term	ספר_המספר_/_אליהו_מזרחי#gbMU	איצטיונא עגולה
solid/cylinder	אצטוונא	term	ספר_המספר_/_אליהו_מזרחי#rax7	אצטוונא
linear dimension/depth	ע.מ.ק./עומק	term	מלאכת_המספר#i136	עומק
linear dimension/depth	ע.מ.ק./עומק	term	מלאכת_המספר#SFsc	עומק
line/diagonal	אלכסון	term	ספר_יסודי_התבונה_ומגדל_האמונה#mxol	קו האלכסון
line/diagonal	אלכסון	term	ספר_הכללים_במספר#HaZi	אלכסון
line/diagonal	אלכסון	term	ספר_הכללים_במספר#VGc4	אלכסון
line/diagonal	חוט	definition	משנת_המדות#1yoc	The diagonal is the cutting from an angle to an angle, end to end, and it is the greater length of the surface. והחוט זה המפסיק מזוית לזוית מן הקצה אל הקצה והוא היותר בארכו של גג
line/diagonal	חוט	term	משנת_המדות#gn1H	חוט
line/diameter	ק.ט.ר./קוטר	term	ספר_המספר_/_אליהו_מזרחי#wKt6	קוטר
line/diameter	אלכסון	diameter of a sphere-definition	ספר_יסודי_התבונה_ומגדל_האמונה#ZeeF	every line passing through the center of the sphere and reaching at its both sides to the surface is called the diameter of the sphere. וכל קו העובר על ציר הכדור והוא מגיע בשני צדיו אל הפרוש נקרא אלכסון הכדור
line/diameter	אלכסון	term	ספר_הכללים_במספר#vRfG	אלכסונו
line/diameter	אלכסון	diameter of a circle-definition	ספר_יסודי_התבונה_ומגדל_האמונה#WT1p	every line passing through the center of the circle and reaching at its both sides to the circumference is called the diameter of the circle. וכל קו אשר הוא עובר על ציר העגול ומגיע מב' פנותיו אל הקו המקיף הוא נקרא אלכסון העגול
line/diameter	אלכסון	term	מלאכת_המספר#kR8y	אלכסון
line/diameter	חוט	term	משנת_המדות#6q7O	חוט
line/diameter		term	ספר_המספר_/_אברהם_אבן_עזרא#Ez31	אלכסון
line/diameter	ק.ט.ר./קוטר	definition	ספר_היסודות_לאקלידס#v3Ba	The '''diameter''' of the circle is any straight line, drawn through the center of the circle and terminated in both directions by its circumference, that bisects [the circle]. וקוטר העגולה הוא קו ישר ילך במרכז העגולה ויכלה בשני הצדדי' אל הקו המקיף אותה והוא יחתכנה בשני חצאים
magnitude/distance	ר.ח.ק./רוחק	term	מלאכת_המספר#BkNI	רוחק
Elements/Elements II-1		a·∑bᵢ=∑(a·bᵢ)	ספר_המספר_/_אליהו_מזרחי#me96	For every number divided into many parts randomly, the number that is generated from the product of a number by the whole given divided number is equal to the number generated from the sum of the products of that number by each part of the divided number. :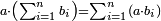 $\scriptstyle a\sdot\left(\sum_{i=1}^n b_i\right)=\sum_{i=1}^n \left(a\sdot b_i\right)$ השנית שכל מספר נחלק לחלקים רבים איך מה שקרה הנה המספר ההווה מהכאת מספר מה עם המספר המונח הנחלק בכללו הוא שוה למספר ההווה מהכאת המספר ההוא עם כל אחד מחלקי המספר הנחלק כאשר יקובצו
Elements/Elements II-1		a·∑bᵢ=∑(a·bᵢ)	ספר_מעשה_חושב#4J1r	When there are two given numbers and one of them is divided into parts, as many as they may be, the product of the first number by the second is equal to the [sum of] the products of each of the parts of the first number by the second. :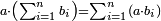 $\scriptstyle a\sdot\left(\sum_{i=1}^n b_i\right)=\sum_{i=1}^n \left(a\sdot b_i\right)$ ב כאשר היו שני מספרים מונחים וחולק המספר האחד לחלקים כמה שיהיו הנה שטח המספר האחד בשני שוה לשטחי כל אחד מחלקי המספר האחד בשני מקובצים
Elements/Elements II-1		a·∑bᵢ=∑(a·bᵢ)	לקוטים_מספר_פראלוקא#t9Uk	If you have two numbers and you divide one of the two numbers, then you multiply each part by the second number, the total sum is the same as the product of the first number by the second. :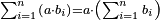 $\scriptstyle\sum_{i=1}^n \left(a\sdot b_i\right)=a\sdot\left(\sum_{i=1}^n b_i\right)$ ‫156 אם יש לך ב' מספרים ותחלק א' מהב' מספרים ותכפול כל חלק על המספר השני הנה הסך העולה הוא כמו מה שיעלה מכפל המספר הראשון על השני
Elements/Elements II-1			ספר_החשבון_והמדות#fGS3	I say: if you divide any number into parts as you wish, [the sum of] the products of each of the parts by the whole number is equal to the square of the whole number. : $\scriptstyle{\color{OliveGreen}{\sum_{k=1}^n \left[\left(\sum_{i=1}^n a_i\right)\sdot a_k\right]=\left(\sum_{i=1}^n a_i\right)^2}}$ ואומר כל מספר שחלקת אותו לחלקים איך שרצית הנה כפל כל אחד מהחלקים על כל המספר מקובץ שוה למרובע כל המספר
Elements/Elements II-1		a·∑bᵢ=∑(a·bᵢ)	ספר_המלכים#Sjh3	For every two numbers, such that one of them is divided into as many parts as there are, [the product of] the number that is not divided by the divided number is equal to the sum of its products by each part of the divided number. :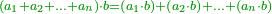 $\scriptstyle{\color{OliveGreen}{\left(a_1+a_2+\ldots+a_n\right)\sdot b=\left(a_1\sdot b\right)+\left(a_2\sdot b\right)+\ldots+\left(a_n\sdot b\right)}}$ כל שני מספרים יחלק אחד מהם בחלקים כמו שיהיו הנה המספר שלא חולק במספר שחולק כמו הכאתו בכל חלקי המספר הנחלק כאשר יקובצו
Elements/Elements II-1		definition	ספר_המספר_/_אליהו_מזרחי#8mWV	It was already clarified in Euclid's Book of Elements, in the [second] section, in the first proposition that for any two straight lines, one of which is cut into segments as many as they may be, the sum of the surfaces generated from the whole straight line and each of the segments of the other straight line equals the surface generated from the whole straight line and the whole divided line. :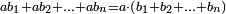 $\scriptstyle ab_1+ab_2+\ldots+ab_n=a\sdot\left(b_1+b_2+\ldots+b_n\right)$ וזה שכבר התבאר בספר היסודות לאקלידס במאמר השלישי ממנו בתמונה הראשונה שכל שני קוים שנחלק אחד מהם לחלקים כמה שיהיו הנה השטח ההוא מהקו האחד כלו עם כל אחד מחלקי הקו האחר יחד הוא שוה לשטח ההווה מהקו האחד עם כל הקו הנחלק
Elements/Elements II-1		10,2+3+5+2	לקוטים_מספר_פראלוקא#1Q9z	Example: the two numbers are 10 and 12 and we divide 12 to 2, 3, 5, 2, so their sum is 12. המשל הנה ב' מספרים והם י' וי"ב ונחלק י"ב על ב' ועל ג' ועל ה' ועל ב' והנה כלם י"ב
Elements/Elements II-1		4,2+3+5	ספר_המספר_/_אליהו_מזרחי#1rE2	Example: if we divide the 10 into three parts randomly, one part of them is 2, the second is 3 and the third is 5. משל זה אם נחלק הי' לג' חלקים איך מה שקרה והיה החלק האחד מהם מספר ב' והשני מספר ג' והשלישי מספר ה'
Elements/Elements II-10		12,8	לקוטים_מספר_פראלוקא#wuja	Example: we have 12, you divide it to 6 and 6, then add to 12 another number. Suppose that we add 8 to it. המשל יש לנו מספר י"ב ותחלקהו על ו'ו' ותוסיף על י"ב ‫148vמספר אחר ונניח כי נוסיף בם ח‫'
Elements/Elements II-10		(a+b)²+b²=2·((½a)²+((½a)+b)²)	ספר_המלכים#CVU6	For any even number divided into half and another number is added to it, [the sum of] twice the product of half the number by itself and twice the product of half the number plus the additional [number] by itself is equal to [the sum of] the product of the [whole] number plus the additional [number] by itself and [the product] of the additional [number] by itself. : $\scriptstyle{\color{OliveGreen}{\left[2\sdot\left(\frac{1}{2}\sdot a\right)^2\right]+\left[2\sdot\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2\right]=\left(a+b\right)^2+b^2}}$ כל מספר זוג יחלק לחציים ונוסף בו מספר אחר הנה ההווה מהכאת חצי המספר בכמהו שני פעמים והכאת חצי המספר עם התוספת בכמהו שני פעמים הכהכאת המספר עם התוספת בכמהו והתוספת בכמהו
Elements/Elements II-10		(a+b)²+b²=2·((½a)²+((½a)+b)²)	ספר_החשבון_והמדות#w9pW	If you divide any number into half and add to it another number, [the sum of] the square of the whole number plus the additional [number] and the square of the additional [number] is equal to twice [the sum of] the square of half the number and the square of half the number plus the additional [number] together. : $\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2+b^2=2\sdot\left[\left(\frac{1}{2}\sdot a\right)^2+\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2\right]}}$ עוד כל מספר שחלקת אותו לשני חציים והוספת עליו מספר אחר הנה מרובע המספר עם התוספת יחד ומרובע התוספת בעצמו הם כפל שני המרובעים שהם מרובע חצי המספר ומרובע חצי המספר עם התוספת יחד כאשר {{#annot:term\|178,2083\|Ycx9}}יחוברו{{#annotend:Ycx9}}
Elements/Elements II-10		10,2	ספר_המספר_/_אליהו_מזרחי#0WFg	Example: we have the number ten, we divide it into two halves and add to it the number 2, so it bacomes 12. דמיון יש לנו מספר עשרה וחלקנוהו לשני חציים והוספנו עליו מספר ב' ונהיה י"ב
Elements/Elements II-10		(a+b)²+b²=2·((½a)²+((½a)+b)²)	ספר_המספר_/_אליהו_מזרחי#FJSe	Any number that you divide into half and add to it another number, [the sum of] the square of the [whole] number plus the additional [number] and the square of the additional [number] is equal to twice [the sum of] the square of half the number and the square of half the number plus the additional [number] when they are summed together. : $\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2+b^2=2\sdot\left[\left(\frac{1}{2}\sdot a\right)^2+\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2\right]}}$ עוד כל מספר שחלקת אותו לשני חצאים והוספת עליו מספר אחר הנה מרובע המספר עם התוספת יחד ומרובע התוספת בעצמו הם כפל שני המרובעים שהם מרובע חצי המספר ומרובע חצי המספר עם התוספת יחד כאשר יחוברו
Elements/Elements II-10		(a+b)²+b²=2·((½a)²+((½a)+b)²)	לקוטים_מספר_פראלוקא#ijBn	If you divide any number into two equal parts, then add another number to the divided number, square it and add to it the square of the [number] you added, it is twice [the sum of] the square of the additional [number] plus half [the number] with the square of half [the number]. : $\scriptstyle\left(a+b\right)^2+b^2=2\sdot\left[\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2+\left(\frac{1}{2}\sdot a\right)^2\right]$ ‫165 אם תחלק איזה מספר על ב' חלקים שוים ואחר תוסיף מספר אחר על המספר המחולק ותרבענו ותוסיף על זה מרובע שהוספת יהיה ב' פעמים כמו כפל ממה שיעלה התוספת הנוסף על החצי עם מרובע החצי נוספים
Elements/Elements II-10		10,2	ספר_החשבון_והמדות#zIUc	Example: we have the number ten, we divide it into two halves, which are 5, and add to it another number 2, so it bacomes 12. דמיון יש לנו מספר מניינו עשרה וחלקנוהו לשני חצאים על ה' והוספנו עליו ‫33rמספר אחר ב' ונהיה י"ב
Elements/Elements II-2		12,3+4+5	לקוטים_מספר_פראלוקא#Gj4L	Example: we wish to divide 12 into three parts 5, 3, 4. המשל נרצה לעשות מי"ב ג' חלקים ה' ג' ד‫'
Elements/Elements II-2		∑ₖ((∑ᵢaᵢ)·aₖ)=(∑ᵢaᵢ)²	ספר_החשבון_והמדות#DxvK	For every number that you divide randomly into two parts, the sum of the products of each of the two parts by the whole number is equal to the square of the whole number. : $\scriptstyle{\color{OliveGreen}{\left[\left(a+b\right)\sdot a\right]+\left[\left(a+b\right)\sdot b\right]=\left(a+b\right)^2}}$ עוד כל מספר שחלקת אותו לשני חלקים איך שקרה הנה כפל כל אחד משני החלקים על כל המספר מקובץ שוה למרובע כל המספר
Elements/Elements II-2		10,7+3	ספר_החשבון_והמדות#KF6o	Example: the number ten; we divide it into 7 and 3. דמיון המספר עשרה וחלקנוהו על ז' וג‫'
Elements/Elements II-2		∑ₖ((∑ᵢaᵢ)·aₖ)=(∑ᵢaᵢ)²	קצת_מענייני_חכמת_המספר#4EHv	If you divide any number into parts as you wish, [the sum of] the products of each of the parts by the whole number is equal to the square of the whole number. : $\scriptstyle{\color{OliveGreen}{\sum_{k=1}^n \left[\left(\sum_{i=1}^n a_i\right)\sdot a_k\right]=\left(\sum_{i=1}^n a_i\right)^2}}$ אחת כל מספר שחלקת אותו לחלקים איך שרצית הנה הכאת כל אח' מהחלקי' בכל המספר השוה למרובע הכל
Elements/Elements II-2		∑ₖ((∑ᵢaᵢ)·aₖ)=(∑ᵢaᵢ)²	לקוטים_מספר_פראלוקא#nMHc	If you have a number and you divide iy into parts as you wish, if you multiply each part by the divided number, then sum all the [products] they are equal to the divided number multiplied by itself. : $\scriptstyle\sum_{k=1}^n \left[\left(\sum_{i=1}^n a_i\right)\sdot a_k\right]=\left(\sum_{i=1}^n a_i\right)^2$ ‫157 אם יש לך מספר אחד ותחלק אותו לכ"כ חלקים שתרצה אם תכפול כל חלק על המספר המחולק ותקבץ כל החלקים יהיו שוים אל המספר המחולק כפול על עצמו
Elements/Elements II-2		12,3+4+5	ספר_החשבון_והמדות#pdf0	Example: the number 12; we divide it into three, four and five. דמיון המספר י"ב וחלקנוהו על שלשה וארבעה וחמשה
Elements/Elements II-2		∑ₖ((∑ᵢaᵢ)·aₖ)=(∑ᵢaᵢ)²	ספר_המספר_/_אליהו_מזרחי#mQeQ	Any number that you divide into parts as you wish, [the sum of] the products of each of the parts by the whole number is equal to the square of the whole number. : $\scriptstyle{\color{OliveGreen}{\sum_{k=1}^n \left[\left(\sum_{i=1}^n a_i\right)\sdot a_k\right]=\left(\sum_{i=1}^n a_i\right)^2}}$ והוא שכל מספר שחלקת אותו לחלקים איך שרצית הנה הכאת כל אחד מהחלקים עם כל המספר שוה למרובע כל המספר
Elements/Elements II-2		12,3+4+5	ספר_המספר_/_אליהו_מזרחי#Nxlm	Example: the number 12, we divide it to three, four and five. דמיון זה המספר י"ב וחלקנוהו על שלשה וארבעה וחמשה
Elements/Elements II-3		(a+b)·b=(a·b)+b²	לקוטים_מספר_פראלוקא#fYtF	If you divide any number into two parts, then multiply any of the two parts by the divided number and keep the product, so will be the result if you multiply the same part by itself, then add to it the product of the one part by the other. :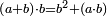 $\scriptstyle\left(a+b\right)\sdot b=b^2+\left(a\sdot b\right)$ ‫158 אם תחלק איזה מספר על ב' חלקים ותכפול החלק שיהיה מב' החלקים על המספר המחולק ושמור העולה כך יעלה אם תכפול אותו חלק על עצמו ותוסיף בו העולה מהכפל מהחלק האחד על השני
Elements/Elements II-3		(a+b)·b=(a·b)+b²	קצת_מענייני_חכמת_המספר#PVyt	For any number divided into two parts as you wish, the product of the whole number by any of its two parts is equal to the product of the one part by the other plus the square of the part by which you multiplied the whole number. :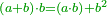 $\scriptstyle{\color{OliveGreen}{\left(a+b\right)\sdot b=\left(a\sdot b\right)+b^2}}$ ב כל מספר שחלקת אותו לב' חלקים איך שקרה הנה הכאת המספר כלו עם כל אחד מב' חלקיו איזה שיהיה שוה להכאת החלק האחד עם האחר ולמרובע החלק אשר בו הכית כל המספר
Elements/Elements II-3		10,3+7	קצת_מענייני_חכמת_המספר#MLKI	Example: the number 10 is divided into two parts - 7 and 3. כמשל מספר הי' נחלק לב' חלקים לז' ולג‫'
Elements/Elements II-3		(a+b)·b=(a·b)+b²	ספר_החשבון_והמדות#Eu5r	For any number divided into two parts as you wish, the product of the whole number by any of its two parts is equal to the product of the one part by the other plus the square of the part by which you multiplied the whole number. :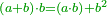 $\scriptstyle{\color{OliveGreen}{\left(a+b\right)\sdot b= \left(a\sdot b\right)+b^2}}$ עוד כל מספר שחלקת אותו בשני חלקים איך שקרה הנה כפל המספר כולו על אחד משני חלקיו איזה שיהיה שוה לכפול החלק האחד על השני ולמרובע החלק משניהם אשר כפלת על כל המספר
Elements/Elements II-3		12,4+8	לקוטים_מספר_פראלוקא#XIpE	Example: we have 12 and you divide it to 8 and 4. המשל אם יש לנו י"ב ותחלק אותו ח' ד‫'
Elements/Elements II-3		10,3+7	ספר_החשבון_והמדות#zmnp	Example: the number ten, we divide it into two parts - three and seven. דמיון המספר עשרה חלקנוהו לשני חלקים על שלשה ושבעה
Elements/Elements II-3		(a+b)·b=(a·b)+b²	ספר_מעשה_חושב#BvNU	When a number is divided into two parts, the product of the whole number by one of its parts is equal to the product of the one part by the other plus the square of the mentioned part. :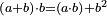 $\scriptstyle \left(a+b\right)\sdot b=\left(a\sdot b\right)+b^2$ ד כאשר חולק מספר מה בשני חלקים הנה שטח כל המספר באחד מחלקיו שוה לשטח החלק האחד באחר ולמרובע החלק אשר זכרנו
Elements/Elements II-3		(a+b)·b=(a·b)+b²	ספר_המספר_/_אליהו_מזרחי#oIDS	For any number that you divide into two parts randomly, the product of the whole number by any of its two parts is equal to the product of the one part by the other plus the square of the part by which you have multiplied the whole number. :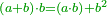 $\scriptstyle{\color{OliveGreen}{\left(a+b\right)\sdot b=\left(a\sdot b\right)+b^2}}$ עוד כל מספר שחלקת אותו לשני חלקים איך שקרה הנה הכאת המספר כלו עם כל אחד משני חלקיו איזה שיהיה שוה להכאת החלק האחד עם השני ולמרובע החלק אשר הכית עם כל המספר
Elements/Elements II-3		10,3+7	ספר_המספר_/_אליהו_מזרחי#CANO	Example: the number ten, we divide into two parts - three and seven. דמיון המספר עשרה חלקנוהו לשני חלקים על שלשה ושבעה
Elements/Elements II-4		10,3+7	ספר_החשבון_והמדות#hh0J	Example: the number ten; we divide it into three and seven. דמיון המספר עשרה חלקנוה על שלשה ושבעה
Elements/Elements II-4		(a+b)²=a²+b²+2(a·b)	ספר_מעשה_חושב#lUMx	When a number is added to a number, the square of the two numbers that are summed together is equal to [the sum of] the squares of these numbers and twice the product of the one by the other. : $\scriptstyle\left(a+b\right)^2=a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]$ ו כאשר נוסף על מספר מונח מספר מה הנה מרובע שני המספרים מחוברים שוה למרובעי המספרים ההם ולכפל שטח זה בזה
Elements/Elements II-4		(a+b)²=a²+b²+2(a·b)	קצת_מענייני_חכמת_המספר#v7Dx	For any number divided into two parts as you wish, the square of the whole number is equal to [the sum of] the squares of the two parts and twice the product of the one part by the other. : $\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2=a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]}}$ ג כל מספר שחלקת אותו לשני חלקים איך שקרה הנה מרובע כל המספר שוה לב' המרובעים ההווים מב' החלקים ולהכאת החלק האחד עם חבירו ב' פעמים
Elements/Elements II-4		(a+b)²=a²+b²+2(a·b)	ספר_המספר_/_אליהו_מזרחי#TApz	For any number divided into two parts randomly, the square of the whole number is equal to [the sum of] the squares of the two parts and twice the product of the one part by the other. : $\scriptstyle\left(a+b\right)^2=a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]$ האחת שכל מספר נחלק לשנים חלקים איך מה שקרה הנה המרובע ההווה מן המספר כלו הוא שוה לשני המרובעים ההווים משני חלקיו עם כפל המספר ההווה מהכאת החלק האחד עם האחר
Elements/Elements II-4		10,3+7	קצת_מענייני_חכמת_המספר#OusC	Example: the number 10 is divided into 7 and 3. כמשל הי' נחלק לז' ולג‫'
Elements/Elements II-4		(a+b)²=a²+b²+2(a·b)	ספר_המספר_/_אליהו_מזרחי#oC2j	For any number that you divide into two parts randomly, the square of the whole number is equal to [the sum of] the squares of the two parts and twice the product of the one part by the other. : $\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2=a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]}}$ עוד כל מספר שחלקת אותו לשני חלקים איך שקרה הנה מרובע כל המספר שוה לשני המרובעי' ההווים משני החלקים ולהכאת החלק האחד עם חברו פעמים
Elements/Elements II-4		10,3+7	ספר_המספר_/_אליהו_מזרחי#6oZu	Example: if we divide the 10 into two parts randomly, one part of them is 3 and the other 7. משל זה אם נחלק הי' לשנים חלקים איך מה שקרה והיה החלק האחד מהם ג' והאחר ז'
Elements/Elements II-4		(a+b)²=a²+b²+2(a·b)	ספר_החשבון_והמדות#q5ib	For any number divided into two parts as you wish, the square of the whole number is equal to [the sum of] the squares of the two parts and twice the product of the one part by the other. : $\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2=a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]}}$ עוד כל מספר שחלקת אותו לשני חלקים איך שקרה הנה מרובע כל המספר שוה לשני המרובעים ההוים משני החלקים ולכפל החלק האחד על חברו פעמים
Elements/Elements II-4		(a+b)²=a²+b²+2(a·b)	לקוטים_מספר_פראלוקא#lb40	If you divide any number into two and multiply each part by itself, you multiply also one [part] by the other and multiply [the product] by 2, then you sum all, the result is equal to the divided number multiplied by itself. : $\scriptstyle a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]=\left(a+b\right)^2$ ‫159 אם תחלק איזה מספר שיהיה על ב' ותכפול כל חלק על עצמו וג"כ כפול הא' על הב' וכפלם על ב' ותקבץ הכל הנה העולה יהיה שוה אל המספר המחולק כפול על עצמו
Elements/Elements II-4		reference	ספר_האלזיברא#Eeue	It was already clarified in [[ספר_היסודות_לאקלידס#Elements_II_4\|'''Euclid, Elements, Book II, proposition 4''']] that: וכבר נתבאר ב'''תמונת הרביעית מן המאמר השני לאקלידס'''
Elements/Elements II-4		definition	ספר_האלזיברא#JPnC	When a straight line is cut randomly into two segments, the square on the whole line equals the sum of the two squares that are generated from the two segments plus twice the rectangle encompassed by the two segments. :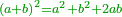 $\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2=a^2+b^2+2ab}}$ כי כאשר נחלק קו ישר לב' חלקים איך שקרה הנה מרבע הקו כלו שוה לשני המרבעים ההווים משני החלקים ולכפל השטח הנצב הזויות אשר יקיפו בו שני החלקים
Elements/Elements II-4		(a+b)²=a²+b²+2(a·b)	לקוטים_מספר_פראלוקא#lAxq	If you have a number and you divide it into two unequal parts, I say that if you sum the [parts] that are multiplied by themselves, then you multiply the smaller [part] by the greater, multiply the product by 2 and sum it with the reserved, the result is equal to the [original] number multiplied by itself. : $\scriptstyle\left(a+b\right)^2=a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]$ ‫169 אם יש לך מספר ותחלקהו על ב' חלקים בלתי שוים אומר כי אם תקבץ המספרי' המוכפלים על עצמם ואח"כ תכפול המספר הקטון על הגדול והעולה כפול על ב' ותקבץ זה עם השמור יעלה הכל כמו המספר כפול על עצמו
Elements/Elements II-4		(a+b)²=a²+b²+2(a·b)	ספר_המלכים#wUeW	For any number divided into [two] parts, whichever they may be, the product of the whole number by itself is equal to the sum of the products of each of the two parts by itself and double the product of one of the two parts by the other. : $\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2=a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]}}$ \|style="width:45%; text-align:right;"\|כל מספר יחלק בחלקים כמו שיהיו הנה הכאת המספר כלו בעצמו כמו הכאת כל אחד משני החלקים בעצמו וכפל הכאת אחד משני החלקים באחר כאשר יקובצו
Elements/Elements II-4		10,3+7	ספר_המספר_/_אליהו_מזרחי#Ca24	Example: the number ten, we divide it to three and seven. דמיון המספר עשרה חלקנוהו על שלשה ושבעה
Elements/Elements II-4		12,4+8	לקוטים_מספר_פראלוקא#HYCk	Example: we divide 12 to 4 and 8. המשל הנה נחלק ‫147vמספר י"ב על ד' ועל ח‫'
Elements/Elements II-5		10,3+7	ספר_החשבון_והמדות#zKhJ	Example: the number ten, we divide it to five and five, which are equal parts, then we divide it also to 7 and 3, which are unequal parts. דמיון המספר עשרה חלקנו לחמשה וחמשה שהם חלקים שוים גם חלקנוהו לז' וג' שהם חלקים בלתי שוים
Elements/Elements II-5		(½(a+b))²=(a·b)+(b-½(a+b))²=(a·b)+(½(a+b)-a)²	ספר_החשבון_והמדות#43lj	For any number divided into two equal parts and into two unequal parts, [the sum of] the product of one of the unequal parts by the other and the square of the difference between the two parts, i.e. between the equal part [= the half of the whole number] and the unequal [part] is equal to the square of half the [whole] number. : $\scriptstyle{\color{OliveGreen}{\left(a\sdot b\right)+\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]^2=\left(a\sdot b\right)+\left[b-\left[\frac{1}{2}\sdot\left(a+b\right)\right]\right]^2=\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2}}$ עוד כל מספר כאשר תחלקהו לשני חלקים שוים ולשני חלקים בלתי שוים הנה כפל החלק האחד אל חברו מהחלקים הבלתי שוים ומרובע מה שבין שני ‫32vהחלקים ר"ל בין החלק השוה ובלתי שוה שוה למרובע חצי המספר
Elements/Elements II-5		(½(a+b))²=(a·b)+(b-½(a+b))²=(a·b)+(½(a+b)-a)²	ספר_מעשה_חושב#AHZr	The product of half the given number by itself is equal to [the sum of] the product of a part of that number by the other part and the square of the difference between one of the [unequal] parts and half of the [whole] given number. ח השטח ההוה מחצי המספר המונח בעצמו שוה לשטח ההוה מחלק מה מהמספר ההוא בחלק השני ולמרובע יתרון אחד מן החלקים על חצי המספר המונח
Elements/Elements II-5		(½(a+b))²=(a·b)+(b-½(a+b))²=(a·b)+(½(a+b)-a)²	ספר_המלכים#4PpZ	For any even number divided into halves and into [two] unequal parts, the product of half the [whole] number by itself is equal to [the sum of] the product of the greater part by the smaller [part] and the product of the excess of the half of the [whole] number over the smaller part by itself. : $\scriptstyle{\color{OliveGreen}{\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2=\left(a\sdot b\right)+\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]^2}}$ כל מספר זוג יחלק לחצאים ולחלקים מתחלפים הנה אשר יהיה מהכאת [חצי]‫M om. המספר בעצמו כמו ההווה מהכאת החלק הגדול בקטן עם הכאת מותר חצי המספר על החלק ה^הקטן [בכמהו]‫M וכמוהו
Elements/Elements II-5		(½(a+b))²=(a·b)+(b-½(a+b))²=(a·b)+(½(a+b)-a)²	לקוטים_מספר_פראלוקא#24rA	If you divide any number into two equal parts and into two unequal parts, the product of the equal parts one by the other is as the product of the unequal parts one by the other, when you add to it the [square] of the difference between the [equal] part and the [unequal part]. ‫160 אם תחלק מספר אחד לב' חלקים שוים ולב' חלקים בלתי שוים הנה כל כך יעלה כפל החלקים השוים זה על זה כמו כפל החלקים הבלתי שוים זה על זה ותוסיף בם כפל היתרון שיש מהחלק האחד על האחר
Elements/Elements II-5		10,3+7	ספר_המספר_/_אליהו_מזרחי#zYJb	Example: the number ten, we divide it to five and five, which are equal parts, then we divide it also to seven and three, which are unequal parts. דמיון המספר עשרה חלקנוהו לחמשה וחמשה שהם חלקים שוים גם חלקנוהו לשבעה ושלשה שהם חלקים בלתי שוים
Elements/Elements II-5		10,3+7	קצת_מענייני_חכמת_המספר#41Hj	Example: the number 10 that is divided into 7 and 3. במש' הי' שנחלק לז' ולג‫'
Elements/Elements II-5		reference	ספר_האלזיברא#7B0h	[[ספר_היסודות_לאקלידס#Elements_II_5\|'''Euclid, Elements, Book II, proposition 5''']]: the square formed by AZ, which is four measures, and is as the square of half [the number of] the things that is known to be 16, is equal to surface BH, which is equal to the right-angled surface encompassed by the two unequal segments, whose area is known to be 12, plus the square formed by ZB that is the difference between the two parts. : $\scriptstyle{\color{OliveGreen}{\left(a\sdot b\right)+\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-b\right]^2=\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2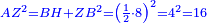}}$ : $\scriptstyle{\color{blue}{AZ^2=BH+ZB^2=\left(\frac{1}{2}\sdot8\right)^2=4^2=16}}$ והנה כפי מה שנתבאר ב'''תמו' החמישית מן המאמר השני לאקלידס'''
Elements/Elements II-5		(½(a+b))²=(a·b)+(b-½(a+b))²=(a·b)+(½(a+b)-a)²	קצת_מענייני_חכמת_המספר#9QNa	For any number divided into two equal parts and into two unequal parts, [the sum of] the product of one of the unequal parts by the other and the square of the difference between the two parts, i.e. between the equal part [= the half of the whole number] and the unequal [part] is equal to the square of half the [whole] number. : $\scriptstyle{\color{OliveGreen}{\left(a\sdot b\right)+\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]^2=\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2}}$ ד כל מספר כאשר תחלקהו לב' חלקים שוים ולב' חלקים בלתי שוים הנה הכאת החלק הא' עם חבירו מהחלקים הבלתי שוים ומרוב' מה שבין ב' חלקים ר"ל בין החלק השוה ובלתי שוה שוה למרובע חצי המספר
Elements/Elements II-5		12,4+8	לקוטים_מספר_פראלוקא#pZPT	Example: we divide 12 into two equal parts 6 and 6, and into two unequal parts 4 and 8. המשל נחלק מספר י"ב לב' חלקים שוים ו'ו' ולב' חלקים בלתי שוים ד' וח‫'
Elements/Elements II-5		(½(a+b))²=(a·b)+(b-½(a+b))²=(a·b)+(½(a+b)-a)²	ספר_המספר_/_אליהו_מזרחי#yKYx	For any number, when you divide it into two equal parts and into two unequal parts, [the sum of] the product of one of the unequal parts by the other and the square of the difference between the two parts, i.e. between the equal part [= the half of the whole number] and the unequal [part] is equal to the square of half the [whole] number. : $\scriptstyle{\color{OliveGreen}{\left(a\sdot b\right)+\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]^2=\left(a\sdot b\right)+\left[b-\left[\frac{1}{2}\sdot\left(a+b\right)\right]\right]^2=\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2}}$ עוד כל מספר כאשר תחלקהו לשני חלקים שוים ולשני חלקים בלתי שוים הנה הכאת החלק האחד עם חברו מהחלקים הבלתי שוים ומרובע מה שבין שני החלקים ר"ל בין החלק השוה ובלתי שוה שוה למרובע חצי המספר
Elements/Elements II-6		12,4	לקוטים_מספר_פראלוקא#qQuN	Example: we have 12, you divide it to 6 and 6, then add to 6 whichever number you wish. Suppose that we wish to add 4 to 6. המשל יש לנו מספר י"ב ותחלק אותו על ו"ו ותוסיף על ו' מספר איזה שתרצה ונניח כי נרצה להוסיף על ו' ד‫'
Elements/Elements II-6		reference	ספר_האלזיברא#BJrm	[[ספר_היסודות_לאקלידס#Elements_II_6\|'''Euclid, Elements, Book II, proposition 6''']] that the right-angled surface encompassed by the whole line with the addition and the addition, which is equal to surface AW, whose area is known as 48, plus the square of half the line, whose area is known, which is 1, both together are 49, equals the square of the line formed by half the line with the addition, which is line AZ. : $\scriptstyle{\color{OliveGreen}{\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2}}$ וכבר נתבאר ב'''תמונה הששית ‫131vמן המאמר השני לאקלידס'''
Elements/Elements II-6		reference	ספר_האלזיברא#XaGL	[[ספר_היסודות_לאקלידס#Elements_II_6\|'''Euclid, Elements, Book II, proposition 6''']] that the right-angled surface encompassed by the whole line with the addition and the addition, which is equal to surface ZD, whose area is 2 in our example, with the square formed by half the line, which is 16 in our example, both together are 36, equals the square of the line formed by half the line with the addition, which is line TB in our illustration. : $\scriptstyle{\color{OliveGreen}{\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2}}$ וכבר נתבאר ב'''תמונה הששית מן המאמר השני לאקלידס'''
Elements/Elements II-6		10,2	ספר_החשבון_והמדות#yd9c	Example: the number ten, we divide it into two halves, which are five each, then we add two to the ten, they are 12. דמיון המספר עשרה וחלקנוהו לשני חצאים שהם כל חצי חמשה {{#annot:term\|178,1206\|GTDu}}הוספנו{{#annotend:GTDu}} על העשרה שנים והיו י"ב
Elements/Elements II-6		(a+b)·b+(½a)²=(½a+b)²	ספר_המלכים#c7yY	For any number divided into two halves and another number is added to it, the product of half the number and the additional [number] together by itself is equal to [the sum of] the product of the [whole] number plus the additional [number] by the additional [number] and the product of half the original number by itself. : $\scriptstyle{\color{OliveGreen}{\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2=\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2}}$ כל מספר זוג יחלק לשני חצאים ויתוסף בו מספר אחר הנה הכאת חצי המספר עם התוספת בכמהו כהכאת המספר עם התוספת בתוספת והכאת חצי המספר הראשון בעצמו
Elements/Elements II-6		10,2	ספר_המספר_/_אליהו_מזרחי#bDvj	Example: the number ten, we divide it into two halves, which are five each, then we add two to the ten, they are 12. דמיון המספר עשרה וחלקנוהו לשני חצאים שהם כל חצי חמשה הוספנו על העשרה שנים והיו י"ב
Elements/Elements II-6		(a+b)·b+(½a)²=(½a+b)²	לקוטים_מספר_פראלוקא#77le	If you divide any number into two equal parts, then add an additional [number] to the divided number, multiply [the sum] by the additional [number] and add [the product] to the square of one of the parts, I say that it is equal to the square of half [the number] with the additional [number]. : $\scriptstyle\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2$ ‫161 אם תחלק איזה מספר לב' חלקים שוים ותוסיף בם א' מהחלקי' כפול על עצמו ותוסיף בם התוספת על כל המספר המחולק ותכפול אותו המספר אשר הוספת ותחברם עם כפל אחד מהחלקים אומר כי הוא שוה אל כפל המחצית עם התוספת
Elements/Elements II-6		(a+b)·b+(½a)²=(½a+b)²	קצת_מענייני_חכמת_המספר#nmaV	If we divide any number into half and add to it another number, [the sum of] the product of the whole number plus the additional [number] by the additional [number] and the square of half the number is equal to the square of half the number and the additional [number] together. : $\scriptstyle{\color{OliveGreen}{\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2}}$ ה כל מספר כאשר חלקנו אותו לחצי והוספת עליו מספר אחר הנה הכאת המספר כלו מחובר עם התוספ' בתוספת ומרובע חצי המספר שוה למרובע חצי המספר והתוספת ביחד
Elements/Elements II-6		(a+b)·b+(½a)²=(½a+b)²	ספר_החשבון_והמדות#A9xw	If you divide any number into half and add to it another number, [the sum of] the product of the whole number plus the additional [number] by the additional [number] and the square of half the number is equal to the square of half the number and the additional [number] together. : $\scriptstyle{\color{OliveGreen}{\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2}}$ עוד כל מספר כאשר חלקת אותו לחצאים והוספת עליו מספר אחר הנה כפל המספר כלו מקובץ עם התוספת בתוספת והמרובע ההוה מחצי המספר שוה למרובע חצי המספר והתוספת ביחד
Elements/Elements II-6		(a+b)·b+(½a)²=(½a+b)²	ספר_מעשה_חושב#vsiV	When a number is divided into two halves and a number is added to it, [the sum of] the product of the additional [number] by the whole number plus the additional [number] and the square of half the number is equal to the square of half the number and the additional [number] summed together. : $\scriptstyle\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2$ ה כאשר חולק מספר מה לחציין והוסף עליו מספר מה הנה שטח התוספת במספר כלו עם התוספת עם מרובע חצי המספר שוה למרובע חצי המספר והתוספת מקובצים
Elements/Elements II-6		(a+b)·b+(½a)²=(½a+b)²	ספר_המספר_/_אליהו_מזרחי#tcs6	For any number, when you divide it into half and add to it another number, [the sum of] the product of the whole number plus the additional [number] by the additional [number] and the square of half the number is equal to the square of half the number and the additional [number] together. : $\scriptstyle{\color{OliveGreen}{\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2}}$ עוד כל מספר כאשר חלקת אותו לחצי והוספת עליו מספר אחר הנה הכאת המספר כלו מקובץ עם התוספת בתוספת והמרובע ההווה מחצי המספר שוה למרובע חצי המספר והתוספת ביחד
Elements/Elements II-7		(a+b)²+a²=(2·(a+b)·a)+b²	ספר_החשבון_והמדות#hdYZ	For any number divided into two parts, the sum of the square of the whole number and the square of one of the parts is equal to twice the product of this part by the whole number plus the product of the other part by itself. : $\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2+a^2=2\sdot\left[\left(a+b\right)\sdot a\right]+b^2}}$ עוד כל מספר כשתחלקהו בשני חלקים איך שיקרה הנה המרובע ההוה מן המספר כלו והמרובע ההוה מאחד משני חלקים כאשר {{#annot:term\|178,1216\|tLsc}}התקבצו{{#annotend:tLsc}} שוים לכפל המספר כלו עם החלק הנזכר פעמים והמרובע ההוה מן החלק השני
Elements/Elements II-7		10,3+7	ספר_החשבון_והמדות#L1Xh	Example: the number ten, we divide it randomly to seven and three. דמיון המספר עשרה וחלקנוהו איך שקרה על שבעה ועל שלשה
Elements/Elements II-7		(a+b)²+a²=(2·(a+b)·a)+b²	לקוטים_מספר_פראלוקא#lBZs	If you have a number and you divide it into two unequal parts, you multiply the greater part by itself and multiply also the divided number by itself, then sum both products, the result is equal to the product of the greater number by the divided number multiplied by two, then you add to it the square of smaller part. : $\scriptstyle\left(a+b\right)^2+a^2=2\sdot\left[\left(a+b\right)\sdot a\right]+b^2$ ‫162 אם יש לך מספר ותחלקהו לב' חלקים בלתי שוים ותכפול החלק הגדול על עצמו גם תכפול המספר המחולק על עצמו ותחבר הב' הכפלות הנה העולה יהיה שוה אל כפל המספר הגדול על המספר המחולק ותכפלהו אח"כ על ב' גם תוסיף על זה כפל החלק הקטן ותחבר הכל יהיה שוה
Elements/Elements II-7		(a+b)²+a²=(2·(a+b)·a)+b²	ספר_המספר_/_אליהו_מזרחי#WZG6	For any number, when you divide it into two parts randomly, [the sum of] the square of the whole number and the square of one of the two parts is equal to twice the product of the whole number by the mentioned part plus the square of the second part. : $\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2+a^2=2\sdot\left[\left(a+b\right)\sdot a\right]+b^2}}$ עוד כל מספר כאשר תחלקהו בשני חלקים איך שיקרה המרובע ההווה מן המספר כלו והמרובה ההווה מאחד משנים החלקים כאשר התקבצו שוים להכאת המספר כלו עם החלק הנזכר פעמים והמרובע ההווה מן החלק השני
Elements/Elements II-7		10,3+7	קצת_מענייני_חכמת_המספר#nE0O	Example: the number 10 is divided into 7 and 3. במשל הרי הי' נחלק לז' ולג‫'
Elements/Elements II-7		10,3+7	ספר_המספר_/_אליהו_מזרחי#VZVn	Example: the number ten, we divide it randomly to 7 and 3. דמיון המספר עשרה וחלקנוהו איך שקרה על ז' ועל ג‫'
Elements/Elements II-7		12,4+8	לקוטים_מספר_פראלוקא#R7rS	Example: we wish to divide 12 to 4 and 8. המשל נרצה לחלק י"ב על ח' וד‫'
Elements/Elements II-7		(a+b)²+a²=(2·(a+b)·a)+b²	קצת_מענייני_חכמת_המספר#DEFA	For any number divided into two parts, the sum of the square of the whole number and the square of one of the parts is equal to twice the product of this part by the whole number plus the product of the other part by itself : $\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2+a^2=2\sdot\left[\left(a+b\right)\sdot a\right]+b^2}}$ ו כל מספר שתחלקהו בב' חלקים איך שקרה המרובע ההווה מהמספר כלו והמרובע ההווה מא' מב' אלו החלקים כאשר התקבצו שוה להכאת החלק הנזכ' עם המספר כלו ולהכאת החלק הב' הנשאר בעצמו
Elements/Elements II-7		definition	ספר_האלזיברא#cvaS	When a straight line is cut randomly into two segments, the sum of the squares on both segments equals twice the rectangle encompassed by both segments plus the square that is generated from the excess of the larger segment over the smaller segment. [ [[ספר_היסודות_לאקלידס#Elements_II_7\|'''Euclid, Elements, Book II, proposition 7''']] ] :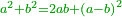 $\scriptstyle{\color{OliveGreen}{a^2+b^2=2ab+\left(a-b\right)^2}}$ כי כאשר נחלק קו ישר ‫128rלשני חלקים איך שקרה הנה מרבעי שני החלקים שוים לכפל השטח הנצב הזויות אשר יקיפו בו שני החלקים ולמרבע ההוה ממותר החלק הגדול על הקטן
Elements/Elements II-7		(a+b)²+a²=(2·(a+b)·a)+b²	ספר_המלכים#isjp	For any number divided into two parts, [the sum of] the product of the [whole] number by itself and [the product of] one of the two parts by itself is equal to twice the product of the [whole] number by the part that is multiplied by itself plus the [product of the] other part by itself. : $\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2+a^2=\left[2\sdot\left(a+b\right)\sdot a\right]+b^2}}$ כל מספר יחלק לשני חלקים ~~[..]~~ הנה הכאת המספר בכמוהו ואחד ‫59vמשני החלקים בכמוהו כמו ההווה מהכאת המספר בחלק המוכה בכמוהו שני פעמים והחלק השני בכמוהו
Elements/Elements II-8		10,3+7	קצת_מענייני_חכמת_המספר#9UoH	Example: the number 10 is divided into 7 and 3. במשל הי' נחלק לז' ולג‫'
Elements/Elements II-8		12,4+8	לקוטים_מספר_פראלוקא#NtVp	Example: we wish to divide 12 to 4 and 8. המשל נרצה לחלק י"ב על ד' וח‫'
Elements/Elements II-8		10,3+7	ספר_המספר_/_אליהו_מזרחי#pqrO	Example: we have the number ten, we divide it randomly to 3 and 7. דמיון יש לנו מספר עשרה וחלקנוהו איך שהזדמן על ג' ועל ז‫'
Elements/Elements II-8		(4·(a+b)·a)+b²=((a+b)+a)²	ספר_המספר_/_אליהו_מזרחי#LHo4	For any number, when you divide it into two parts randomly and you multiply the whole number by one of the two parts four times, then sum [the product] with the square of the other part [it] is equal to the [square] of the whole number plus the mentioned part when you sum them together. : $\scriptstyle{\color{OliveGreen}{4\sdot\left[\left(a+b\right)\sdot a\right]+b^2=\left[\left(a+b\right)+a\right]^2}}$ עוד כל מספר כאשר חלקת אותו בשני חלקים איך שיקרה והכית המספר כלו עם אחד משני חלקיו ארבעה פעמים וחברת אותו עם מרובע החלק הנשאר שוה למרובע ההווה מן המספר כלו והחלק הנזכר כאשר תחברם ביחד
Elements/Elements II-8		10,3+7	ספר_החשבון_והמדות#AJOP	Example: we have the number ten, we divide it randomly to 3 and 7. דמיון יש לנו מספר מנינו העשרה וחלקנוהו איך שהזדמן על ג' ועל ז‫'
Elements/Elements II-8		(4·(a+b)·a)+b²=((a+b)+a)²	ספר_המלכים#Ocvs	For any number divided into two parts and one of the two parts is added to it, the product of the [whole] number plus the additional [part] by itself is equal to [the sum of] the product of the [whole] number by the additional [part] four times and the product of the other part by itself. : $\scriptstyle{\color{OliveGreen}{\left[\left(a+b\right)+a\right]^2=\left[4\sdot\left(a+b\right)\sdot a\right]+b^2}}$ כל מספר יחלק בשני חלקים ונוסף עליו כמו אחד משני החלקים הנה הכאת המספר עם התוספת בכמהו כהכאת המספר בתוספת ד' פעמים והכאת החלק האחר בכמהו
Elements/Elements II-8		(4·(a+b)·a)+b²=((a+b)+a)²	לקוטים_מספר_פראלוקא#TRuX	If you have a number and you divide it into unequal two parts, if you add one of the parts to the whole number, i.e. the divided number, [its square] is equal to the same part that you added multiplied by the whole number, then multiplied by four, when you add to it the square of the second part. : $\scriptstyle\left[\left(a+b\right)+a\right]^2=4\sdot\left[\left(a+b\right)\sdot a\right]+b^2$ ‫163 אם יש לך מספר ותחלקהו לב' חלקים בלתי שוים אם תוסיף א' מהחלקים על כל המספר ר"ל על המספר המחולק יהיה שוה אל אותו החלק אשר הוספת כפול על כל המספר אח"כ העולה תכפול על ד' ותוסיף על זה מרובע החלק השני
Elements/Elements II-8		(4·(a+b)·a)+b²=((a+b)+a)²	קצת_מענייני_חכמת_המספר#R68t	For any number divided into two parts as you wish, if you multiply the whole number by one of the parts four times, the sum of the product with the square of the other part is equal to the [square] of the whole number plus the one part : $\scriptstyle{\color{OliveGreen}{4\sdot\left[\left(a+b\right)\sdot a\right]+b^2=\left[\left(a+b\right)+a\right]^2}}$ ז כל מספר שחלקת אותו לב' חלקים איך שקרה אם הכית המספר כלו עם חלק אח' מהם ד' פעמים וקבצת הכל עם מרובע החלק הב' הנשאר היה שוה להכאת מספרו החלק הנזכר כאשר תחברם יחד
Elements/Elements II-8		(4·(a+b)·a)+b²=((a+b)+a)²	ספר_החשבון_והמדות#EAD6	For any number divided into two parts as you wish, if you multiply the whole number by one of the parts four times, the sum of the product with the square of the other part is equal to the [square] of the whole number plus the one part. : $\scriptstyle{\color{OliveGreen}{4\sdot\left[\left(a+b\right)\sdot a\right]+b^2=\left[\left(a+b\right)+a\right]^2}}$ עוד כל מספר כאשר חלקת אותו בשני חלקים איך שיקרה וכפלת המספר כלו עם אחד משני חלקיו ארבעה פעמים ועם מרובע החלק הנשאר שוה למרובע ההוה מן המספר כלו והחלק הנזכר כאשר תחברם ביחד ותקח מרובעם
Elements/Elements II-9		10,3+7	ספר_המספר_/_אליהו_מזרחי#LnLo	Example: the number 10, we divide it into two equal parts, which are 5, and into two unequal parts, which are 7 and 3. דמיון המספר י' וחלקנוהו לשני חלקים שוים והם ה' ולשני חלקים בלתי שוים והם ז' ג‫'
Elements/Elements II-9		12,4+8	לקוטים_מספר_פראלוקא#QBwh	Example: we wish to divide 12 into two equal parts 6 and 6 and into two unequal parts 8 and 4. המשל נרצה לחלק מספר י"ב לב' חלקי' שוים ו'ו' ולב' חלקים בלתי שוים ח' ד‫'
Elements/Elements II-9		a²+b²=2·((½·(a+b))²+(a-(½·(a+b)))²)	לקוטים_מספר_פראלוקא#E95L	If you divide any line into two equal parts and into two unequal parts, then you multiply each of the unequal parts [by itself] and sum them, they are twice [the sum of] the product of the equal parts plus the [square of] excess of the greater [part] over [half the number]. : $\scriptstyle a^2+b^2=2\sdot\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2+\left[a-\left[\frac{1}{2}\sdot\left(a+b\right)\right]\right]^2\right]$ ‫164 אם תחלק איזה קו לב' חלקים שוים ולב' חלקים בלתי שוים וכפול כל אחד מהחלקים בלתי שוים ותחברם הם כפל מהחלקים השוים נוסף בם יתרון החלק הגדול על הקטן
Elements/Elements II-9		a²+b²=2·((½·(a+b))²+(a-(½·(a+b)))²)	ספר_המספר_/_אליהו_מזרחי#ClRv	For any number that you divide into two equal parts and into two unequal parts, [the sum of] the two squares of the unequal parts is equal to twice [the sum of] the square of half the [whole] number and [the square] of the excess of the large part over the half [of the whole number]. : $\scriptstyle{\color{OliveGreen}{a^2+b^2=2\sdot\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2+\left[a-\left[\frac{1}{2}\sdot\left(a+b\right)\right]\right]^2\right]}}$ עוד כל מספר שחלקת אותו לשני חלקים שוים ושני חלקים בלתי שוים הנה שני המרובעים אשר יהיו מהחלקים הבלתי שוים הם כפל שני המרובעים אשר יהיו מחצי המספר ומהתוספת אשר לחלק הגדול על הה' שהוא המחצית
Elements/Elements II-9		a²+b²=2·((½·(a+b))²+(a-(½·(a+b)))²)	ספר_החשבון_והמדות#CM8j	For any number divided into two equal parts and into two unequal parts, [the sum of] the squares of the unequal parts is equal to twice [the sum of] the square of half the [whole] number and the square of the difference between the large part and the half [of the whole number]. : $\scriptstyle{\color{OliveGreen}{a^2+b^2=2\sdot\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2+\left[a-\left[\frac{1}{2}\sdot\left(a+b\right)\right]\right]^2\right]}}$ עוד כל מספר שחלקת אותו לשני חלקים שוים ושני חלקים בלתי שוים הנה שני המרובעים אשר יהיו מהחלקים הבלתי שוים הם כפל שני המרובעים אשר יהיו מחצי המספר ומהתוספת אשר לחלק הגדול על המחצית
Elements/Elements II-9		10,3+7	ספר_החשבון_והמדות#O8o8	Example: we have the number ten, we divide it into two equal parts, which are 5, and into two unequal parts, which are 3 and 7. דמיון יש לנו מספר מנינו עשרה וחלקנוהו לשני חלקים שוים על ה' ושני חלקים בלתי שוים על ג' וז‫'
Elements/Elements II-9		a²+b²=2·((½·(a+b))²+(a-(½·(a+b)))²)	ספר_המלכים#g6A2	For any even number divided into two halves and into two unequal parts, [the sum of the products of] each of the two unequal parts by themselves is equal to [the sum of] twice the product of half the [whole] number by itself and twice the product of the excess of half the [whole] number over the smaller part by itself. : $\scriptstyle{\color{OliveGreen}{a^2+b^2=\left[2\sdot\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2\right]+\left[2\sdot\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]^2\right]}}$ כל מספר זוג יחלק בשני חצאים ובשני חלקים מתחלפים הנה כל אחד משני החלקים המתחלפים בכמהו כהכאת חצי המספר בכמהו שני פעמים והכאת מותר חצי המספר על החלק הקטן בכמהו שני פעמים
Elements/Elements-Introduction		a=b,a-c=b-c	ספר_המספר_/_אליהו_מזרחי#tNTC	For, when equal is subtracted from equals, then the remainders are necessarily equal, according to what is clarified in the introduction of the first section of Euclid's [book]. :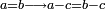 $\scriptstyle a=b\longrightarrow a-c=b-c$ כי כאשר יחוסר מהשוים שוה יהיו הנשארים שוים בהכרח לפי מה שהתבאר בפתיחת המאמר הראשון מאקלידס
Elements/Elements-Introduction		a=b,a-c=b-c	ספר_המספר_/_אליהו_מזרחי#gaDw	This is because it was already clarified in the introduction of Euclid's book that when equal is subtracted from equals, then the remainders are equal :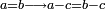 $\scriptstyle a=b\longrightarrow a-c=b-c$ וזה שכבר התבאר בפתיחת ספר אקלידס כאשר חוסר מהשוים שוה יהיה הנשאר שוה
Elements/Elements IX-21		definition	ספר_המספר_/_אליהו_מזרחי#qiN5	When even numbers are summed, as many as they may be, their sum is an even number. הוא כאשר נקבצו מספרי זוגות כמה שיהיו הנה קבוצם מספר זוג
Elements/Elements IX-22		definition	ספר_המספר_/_אליהו_מזרחי#yrIb	When odd numbers are summed, as many as they may be, and their multitude is even, their sum is an even number. וכאשר נקבצו מספרים נפרדים כמה שיהיו והיה מספרם זוג הנה קבוצם מספר זוג
Elements/Elements IX-23		definition	ספר_המספר_/_אליהו_מזרחי#1A6m	When odd numbers are summed, as many as they may be, and their multitude is odd, their sum is an odd number. וכאשר נקבצו מספרים נפרדים כמה שיהיו והיה מספרם מפרד הנה קבוצם נפרד
Elements/Elements IX-28		definition	ספר_המספר_/_אליהו_מזרחי#RVMm	When an even number is multiplied by an odd number, or by an even number, then the product is even. :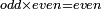 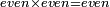$\scriptstyle odd\times even=even$ ; $\scriptstyle even\times even=even$ הוא שכאשר הוכה מספר זוג במספר נפרד או במספר זוג הנה המקובץ זוג
Elements/Elements IX-29		definition	ספר_המספר_/_אליהו_מזרחי#DYPK	When an odd number is multiplied by an odd number, then the product is odd. :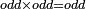 $\scriptstyle odd\times odd=odd$ וכאשר הוכה מספר נפרד במספר נפרד הנה המקובץ נפרד
Elements/Elements V-15		(n·a)÷(n·b)=a÷b	ספר_המספר_/_אליהו_מזרחי#PIBA	For, it was already clarified in Euclid's Book of Elements, according to what was preceded in this section, that the given numbers have the same ratio as the ratio of their equimultiples. :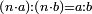 $\scriptstyle\left(n\sdot a\right):\left(n\sdot b\right)=a:b$ וזה שכבר התבאר בספר היסודות לאקלידס לפי מה שקדם מן המאמר שמהמספרים המונחים הם יחס קצתם אל קצת הוא כיחס כפליהם קצתם אל קצת
Elements/Elements V-15		(n·a)÷(n·b)=a÷b	ספר_המספר_/_אליהו_מזרחי#wUJB	For, it was already clarified in Euclid's Book of Elements, in the fifth section, that any numbers, whose multiples are equal, have the same ratio as the ratio of their equimultiples. :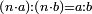 $\scriptstyle\left(n\sdot a\right):\left(n\sdot b\right)=a:b$ וזה שכבר התבאר בספר היסודות לאקלידס במאמר החמישי ממנו שהמספרים אשר כפליהם שוים הנה יחס קצתם אל קצת כיחס כפליהם קצתם אל קצת
Elements/Elements V-9		definition	ספר_המספר_/_אליהו_מזרחי#2X92	For, any two magnitudes, which have the same ratio to the same magnitude, necessarily equal one another, according to what is clarified in Euclid's Book of Elements. :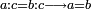 $\scriptstyle a:c=b:c\longrightarrow a=b$ כי כל שני שעורים שיחסם אל שעור אחר בעצמו יחס אחד הנה הם שוים בהכרח לפי מה שהתבאר בספר היסודות לאקלידס
Elements/Elements VI-17		reference	ספר_האלזיברא#cH1a	[[ספר_היסודות_לאקלידס#Elements_VI_17\|'''Euclid, Elements, Book VI, proposition 17''']] that the product of the first by the last is as the product of the mean by its similar. :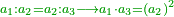 $\scriptstyle{\color{OliveGreen}{a_1:a_2=a_2:a_3\longrightarrow a_1\sdot a_3=\left(a_2\right)^2}}$ וכבר נתבאר מ'''תמונת י"ז מן המאמר הששי לאקלידס'''
Elements/Elements VI-17		definition	ספר_האלזיברא#KlWg	It is already explained in {{#annot: reference \| #Elements VI-17 \| cH1a}}[[ספר_היסודות_לאקלידס#Elements_VI_17\|'''Euclid, Elements, Book VI, proposition 17''']] that the product of the first by the last is as the product of the mean by its similar. :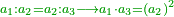 $\scriptstyle{\color{OliveGreen}{a_1:a_2=a_2:a_3\longrightarrow a_1\sdot a_3=\left(a_2\right)^2}}$ וכבר נתבאר מ'''תמונת י"ז מן המאמר הששי לאקלידס'''{{#annotend:cH1a}} כי {{#annot: term \| #multiplication, #הכאה \| poG8}}הכאת ה{{#annotend:poG8}}ראשו' באחרון כמו הכאת האמצעי בדומה לו
Elements/Elements VII-11		a÷b=c÷d→(c-a)÷(d-b)	ספר_המספר_/_אליהו_מזרחי#Iu2h	when two numbers are subtracted from two numbers and the ratio of the subtrahend to the subtrahend is the same as the ratio of the minuend to the minuend, then the [ratio of] the remainder to the remainder is the same as the ratio of the minuend to the minuend. ::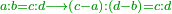 $\scriptstyle{\color{OliveGreen}{a:b=c:d\longrightarrow\left(c-a\right):\left(d-b\right)=c:d}}$ וזה שכבר התבאר בספר היסודות לאקלידס במאמר השביעי ממנו בתמונת י"א שכאשר חוסרו משני מספרים ב' מספרים והיה יחס המחוסר אל המחוסר כיחס הכל אל הכל הנה יהיה הנשאר אל הנשאר כיחס הכל אל הכל
Elements/Elements VIII-11		definition	ספר_האלזיברא#QcHW	the ratio of a square to a square is as the ratio of its side to its side duplicated. [ [[ספר_היסודות_לאקלידס#Elements_VIII_11\|'''Euclid, Elements, Book VIII, proposition 11''']] ] :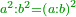 $\scriptstyle{\color{OliveGreen}{a^2:b^2=\left(a:b\right)^2}}$ וזה כי מפני כי יחס מרבע אל מרבע כיחס צלעו אל צלעו שנוי
Elements/Elements VIII-11		definition	ספר_האלזיברא#Nl0O	This is because the ratio of a square to a square is the same as the ratio of its side to its side duplicate. :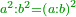 $\scriptstyle{\color{OliveGreen}{a^2:b^2=\left(a:b\right)^2}}$ וזה מפני כי {{#annot: term \| #ratio, #יחס \| Eve2}}יחס{{#annotend:Eve2}} מרובע אל מרובע כיחס צלעו אל צלעו {{#annot: term \| #duplicate, #שנוי \| Q7dD}}שנוי{{#annotend:Q7dD}} ר"ל {{#annot: term \| #multiplied, #כפול \| G4iq}}כפול{{#annotend:G4iq}}
Elements/Elements VIII-11		reference	ספר_האלזיברא#D3f5	[[ספר_היסודות_לאקלידס#Elements_VIII_11\|'''Euclid, Elements, Book VIII, proposition 11''']] מתמונת י"א מן המאמר השמיני לאקלידס
Elements/Elements VIII-11		definition	ספר_המספר_/_אליהו_מזרחי#sPcq	Its reason is also known from what was clarified in Euclid's Book of Elements, in the eighth section that for every two squares numbers the ratio of one of them to the other is as the duplicate ratio of that which the side has to the side. :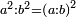 $\scriptstyle a^2:b^2=\left(a:b\right)^2$ הנה סבתו ג"כ ידועה ממה שהתבאר בספר היסודו' לאקלידס במאמר הח' ממנו שכל שני מספרים מרובעים הנה יחס הא' מהם אל חברו הוא כיחס צלעו אל צלעו שנוי בכפל
Elements/Elements VIII-12		reference	ספר_האלזיברא#jD6N	According to [[ספר_היסודות_לאקלידס#Elements_VIII_12\|'''Euclid, Elements, Book VIII, proposition 12''']] מתמונת י"ב מן המאמר השמיני לאקלידס
Elements/Elements VIII-12		definition	ספר_האלזיברא#eDWE	This is because the ratio of a cube to a cube is the same as the ratio of its side to its side triplicate :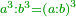 $\scriptstyle{\color{OliveGreen}{a^3:b^3=\left(a:b\right)^3}}$ וזה מפני כי יחס מעקב אל מעקב כיחס צלעו אל צלעו {{#annot: term \| #triplicate, #משולש \| A27z}}משלש{{#annotend:A27z}}
Elements/Elements XIII-1		definition	המחומשים_והמעושרים#1Da2	Euclid proved that when a line is divided according to the ratio of a mean and two extremes, so that half the whole line is added to the larger segment, and all this is multiplied by itself, then the resulting square is equal to five times the square of half the line [Elements XIII.1]. ובאר אקלידס כי כאשר נחלק קו על יחס אמצעי ושתי קצוות שהחלק הגדול כאשר נוסף בארכו כמו חצי הקו כלו והוכה כל זה בעצמו המרובע ההוה מזה יהיה חמשה דמיוני המרובע ההוה מחצי הדבר
Elements/Elements XIII-10		definition	המחומשים_והמעושרים#w084	We do this since Euclid has explained that the line that cuts the fifth is on the line that cuts the sixth and the tithe, when they are set on one circle [Elements XIII,10]. ועשינו זה בעבור כי באר אוקלידס כי קו החותך החמישית על הקו החותך הששית והעשירית כאשר הונחו בעגולה אחת
Elements/Elements XIII-3		definition	המחומשים_והמעושרים#mhLN	Euclid has already explained [Elements XIII.3] that when line BH is divided by the ratio of a mean and two extremes, so that the greater part is equal to line DH, it is known that when a line is divided by the ratio of a mean and two extremes and we add half the greater part to the smaller part, then multiply the whole sum by itself, the square formed by the sum of the two is five times the product of [half] the greater part by itself. :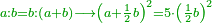 $\scriptstyle{\color{OliveGreen}{a:b=b:\left(a+b\right)\longrightarrow\left(a+\frac{1}{2}b\right)^2=5\sdot\left(\frac{1}{2}b\right)^2}}$ ובאר אוקלידס שקו ב"ה כאשר חולק על יחס אמצעי ושני קצוות שהחלק הגדול הוא שוה אל קו ד"ה והוא ידוע כי כאשר נחלק קו אחד על יחס בעל אמצעי ושני קצוות ונוסיף על החלק הקטן חצי החלק הגדול ונכה הכל בעצמו שהמרובע ההוה משני אלו מקובצים יהיה חמשה דמיוני הכאת החלק הגדול בעצמו
Elements/Elements XIII-5		definition	המחומשים_והמעושרים#3lPz	It is known from what we have said, as Euclid said, that for every line divisible according to the ratio of a mean and two extremes, when another part equal to the larger portion is added to the line, then whole [line] is divisible according to the ratio of a mean and two extremes, and the larger portion of which is the original line [Elements XIII.5]. והוא ידוע מאשר אמרנו שאמרו אקלידס ואמר שכל קו שהוא על יחס אמצעי ושני קצוות ונוסף באורך הקו כמו החלק ‫60rהגדול וכל זה יחלק על יחס אמצעי ושני קצוות שהחלק הגדול הוא הקו הראשון
Elements/Elements XIII-9		definition	המחומשים_והמעושרים#ScqD	It he said in another place that when the side of a hexagon and the side of a decagon inscribed in the same circle are united in one line, then this whole line is divisible according to the ratio of a mean and two extremes, and the side of the hexagon is the larger portion [Elements XIII.9]. ואמר במקום אחר שכאשר קובצו צלע המשושה עם צלע המעושר אשר בעגולה אחת בקו אחד ישר יהיה כל הקו נחלק על יחס אמצעי ושני קצוות וצלע המשושה הוא החלק הגדול
solid/ellipsoid	ב.י.צ./ביצני	definition	ספר_יסודי_התבונה_ומגדל_האמונה#eg9d	that which is surrounded by a curved surface is called ellipsoid [lit. elliptic solid] or a solid that is similar to an ellipse [lit. egg-like solid]. ואשר יקיף אותו פרוש אחד עקום נקרא גולם ביצני או גולם דומה לביצה
solid/ellipsoid	ב.י.צ./ביצני	term	ספר_יסודי_התבונה_ומגדל_האמונה#gics	הגולם הביצני
solid/ellipsoid	ב.י.צ./דומה לביצה	term	ספר_יסודי_התבונה_ומגדל_האמונה#Rccp	הגולם הדומה לביצה
to encompass/encompassed	נ.ק.פ./הקיף	term	ספר_האלזיברא#noZK	אשר יקיפו בו קוי
to encompass/encompassed	נ.ק.פ./הקיף	term	ספר_האלזיברא#hrMO	אשר יקיפו בו שני החלקים
to encompass/encompassed	ר.ש.מ./נרשם	definition	ספר_היסודות_לאקלידס#9RjX	The figure is said to be circumscribed about a figure when each of its sides touches each of the respective angles of the figure about which it is circumscribed. ויאמר כי התמונה נרשמת סביב התמונה כשתהיה כל אחת מצלעותיה ממששת לכל אחת מזויות התמונה אשר היא נרשמת סביבה
geometry/end	כ.ל.י./תכלית	term	מלאכת_המספר#tYDo	תכליותיו
geometry/end	קצה	term	מלאכת_המספר#Idv3	קצה
geometry/end	קצה	term	מלאכת_המספר#Ltil	קצה
geometry/end	ש.פ.י./שפה	term	מלאכת_המספר#pd7L	שפת
triangle/equilateral triangle	ש.ו.ה./שוה זויות	term	מלאכת_המספר#dBGu	משולש השוה הזויות
triangle/equilateral triangle	ש.ו.ה./שוה זויות	term	מלאכת_המספר#0szp	המשולש השוה הזויות
triangle/equilateral triangle	ש.ו.ה./שוה צלעות	term	ספר_הכללים_במספר#sp6o	משולש שוה הצלעות
triangle/equilateral triangle	ש.ו.ה./שוה צלעות	term	ספר_הכללים_במספר#Okmu	המשולש השוה הצלעות
line/extension	מ.ש.כ./המשכות	term	האריתמטיקה_של_ניקומכוס#I0sK	המשכותו
solid/face	צ.ד.ד./צד	term	ספר_יסודי_התבונה_ומגדל_האמונה#S4QN	צדים
solid/face	צ.ד.ד./צד	term	ספר_יסודי_התבונה_ומגדל_האמונה#TPlF	צדדין
solid/face	י.ש.ב./מושב	term	ספר_יסודי_התבונה_ומגדל_האמונה#H8Af	מושבותיהן
solid/face	י.ש.ב./מושב	term	ספר_יסודי_התבונה_ומגדל_האמונה#FTa7	מושבות
solid/face	צ.ד.ד./צד	term	ספר_יסודי_התבונה_ומגדל_האמונה#OEA8	צדין
surface/flat surface	י.ש.ר./ישר	definition	ספר_יסודי_התבונה_ומגדל_האמונה#WnsW	the plane surface is the drawn on the straightness of the lines that surround it and in parallel to them והשטח הישר הוא הנמשך על יושר הקוים המקיפים אותו ועל נכחם
surface/flat surface	י.ש.ר./משור	term	מלאכת_המספר#wOY6	מישור
surface/flat surface	ש.ו.ה./שוה	definition	ספר_היסודות_לאקלידס#kmWD	The '''plane surface''' is that which lies straightly by the arrangement of straight lines on it one by one. והפשוט השוה הוא המוצב על נכוחות אי זה קוים ישרים יהיו עליו קצתם אל קצתם
geometry/geometrical shape	צ.ו.ר./צורה	term	קצור_המספר#Tj2a	צורתו
geometry/geometrical shape	תמונה	term	ספר_האלזיברא#sSIx	תמונה
geometry/geometrical shape		term	ספר_המספר_/_אברהם_אבן_עזרא#kCK2	דמות
geometry/geometrical shape	תמונה	term	חשבון_השטחים#DM4q	תמונת גימטריאות
geometry/geometrical shape	תמונה	term	תחבולות_המספר#QKAs	תמונה
geometry/geometrical shape	צ.ו.ר./צורה	term	ספר_ג'יבלי_אלמוקבאלא#NU0p	צורת ה
geometry/geometrical shape	תמונה	term	חשבון_השטחים#ld89	תמונות גימאטריות
geometry/geometrical shape	צ.ו.ר./צורה	term	קצור_המספר#uLTa	צורת ה
geometry/geometrical shape	ש.ע.ר./שעורי	term	האנציקלופדיה_של_אבו_אלצלת#1yEx	התמונות השעוריות
geometry/geometrical shape	תמונה	definition	ספר_היסודות_לאקלידס#zvgX	The '''figure''' is that which is contained by a boundary or boundaries. והתמונה היא אשר יקיף אותה גבול או גבולים
geometry/geometrical shape	תמונה	term	תחבולות_המספר#nDez	תמונ' גימטרית
geometry/geometrical shape	תמונה	term	חשבון_השטחים#S3AT	תמונה
geometry/geometrical shape	תמונה	term	תחבולות_המספר#zsC7	תמונות גימטריות
geometry/geometrical shape	תמונה	term	ספר_המספר_/_אליהו_מזרחי#A0eJ	תמונות
geometry/geometrical shape	תמונה	term	תחבולות_המספר#cUJQ	תמונות גימטריאות
geometry/geometrical shape		term	ספר_המספר_/_אברהם_אבן_עזרא#6zsx	צורות
geometry/geometrical shape	צ.ו.ר./צורה	term	ספר_ג'יבלי_אלמוקבאלא#aHl6	בצורה
geometry/geometrical shape	צ.ו.ר./צורה	term	ספר_ג'יבלי_אלמוקבאלא#FkFL	זאת הצורה
geometry/geometrician	ח.כ.מ./חכמי השעור	term	ספר_יסודי_התבונה_ומגדל_האמונה#Rqdk	חכמי השעור
geometry/geometrician	ח.כ.מ./חכמי המדות	term	Anonymous#3f0H	חכמי המדות
geometry/geometrician	ח.כ.מ./חכמי הגימטריא	term	תחבולות_המספר#zYpS	חכמי הגימטריאה
geometry/geometrician	ח.כ.מ./חכמי הגימטריא	term	חשבון_השטחים#HDsY	חכמי הגימאטריאה
geometry	הנדסה	term	קצור_המספר#oKmZ	חכמת ההנדסה
geometry	גיאומטריה	term	ספר_יסודי_התבונה_ומגדל_האמונה#WvOr	גיאומטריא
geometry	גימטריא	term	ספר_ג'יבלי_אלמוקבאלא#zdcI	גימטריא
geometry	ש.ע.ר./שעור	definition	ספר_יסודי_התבונה_ומגדל_האמונה#QN53	geometry is a science that explains the measures and announces their value, their creation, their types, and their signs. חכמת השיעור היא חכמת מפרשת את הגדלים ומודיעה ערכם ויצירתם ומיניהן וסימניהן
geometry	נ.פ.ל./נפל	to be situated	חשבון_השטחים#JY7P	נפלה
geometry	נ.פ.ל./נפל	to be situated	חשבון_השטחים#lEvA	תפול
geometry	גימטריא	term	חשבון_השטחים#Grro	גימטריא
geometry	ש.ע.ר./שעור	term	ספר_יסודי_התבונה_ומגדל_האמונה#7kbk	חכמת השיעור
geometry		term	ספר_יסודי_התבונה_ומגדל_האמונה#tPav	אלהנדסה
geometry	נ.פ.ל./נפל	to be situated	תחבולות_המספר#azrN	נופלת
geometry	נ.פ.ל./נפל	to be situated	תחבולות_המספר#RPnh	תפול
geometry	הנדסה	term	מלאכת_המספר#PJSB	הנדסה
geometry	ש.ע.ר./שעור	term	ספר_יסודי_התבונה_ומגדל_האמונה#yCv9	חכמת השעור
geometry	גיאומטריה	term	ספר_יסודי_התבונה_ומגדל_האמונה#Sgh4	יומטריא
geometry	מ.ד.ד./מדות	term	ספר_המספר_/_אליהו_מזרחי#cAbD	מדות
geometry	מ.ד.ד./מדידה	term	משנת_המדות#LghN	מדידה
geometry	מ.ד.ד./מדות	term	ספר_המספר_/_אליהו_מזרחי#NXxm	מלאכת המדות
geometry	מ.ד.ד./מדידה	term	ספר_המספר_/_אליהו_מזרחי#JOJz	מדידה
geometry	הנדסה	term	ספר_המספר_/_אליהו_מזרחי#JyR3	הנדסה
geometry	הנדסה	term	ספר_המספר_/_אליהו_מזרחי#WrQe	חכמת ההנדסה
geometry	הנדסה	term	ספר_המספר_/_אליהו_מזרחי#TWz4	הנדסא
geometry	הנדסה	term	מלאכת_המספר#1nMw	מלאכת ההנדסא
geometry	הנדסה	term	ספר_יסודי_התבונה_ומגדל_האמונה#vDEW	הנדסה
surface/gnomon	ר.ש.מ./רושם	term	ספר_האלזיברא#9D4Q	רושם התמונה
semicircle/greater than a semicircle	י.ת.ר./יתר	term	משנת_המדות#QxiL	יתרה
semicircle/greater than a semicircle	י.ת.ר./יתר	definition	משנת_המדות#Mepo	The surplus segment is any segment that is greater than a semicircle. והיתרה כל שהיא עודפת על חצי העגולה
line/height	ג.ב.ה./גובה	term	קצור_המספר#2ZCt	גובהו
line/height	ק.ו.מ./קומה	term	משנת_המדות#bcMz	קומה
line/height	ג.ב.ה./גובה	term	מלאכת_המספר#68a5	גובה
line/height	ע.מ.ד./עמוד	term	ספר_הכללים_במספר#N2oI	עמודה
line/height	ע.מ.ד./עמוד	definition	משנת_המדות#ZKdD	The height is a perpendicular line descending from between the two sides to the base, and it is angled to the walls of the temple. והעמוד זה {{#annot:term\|592,2289\|H0NU}}חוט{{#annotend:H0NU}} הכולל היורד מבין שני הצלעים לקבע והוא בזוית למקצעות המשכן
line/height	ג.ב.ה./גובה	term	מלאכת_המספר#w6qQ	גובה
line/height	ג.ב.ה./גובה	term	קצור_המספר#Z57h	גובה
line/height	ג.ב.ה./גובה	term	בר_נותן_טעם#B53n	גובה
line/height	ע.מ.ד./עמוד	term	ספר_הכללים_במספר#iYwS	עמוד
line/height	ע.מ.ד./עמוד	term	משנת_המדות#1RG2	עמוד
sphere/hemisheper	ת.ל.ל./תלול	term	משנת_המדות#zJmF	תלולה
polygon/hexagon	ש.ש.י./משושה	term	ספר_יסודי_התבונה_ומגדל_האמונה#19s3	משושש
line/hypotenuse	ק.ב.ע./קבע	term	משנת_המדות#AnyJ	קבע
line/hypotenuse	י.ת.ר./יתר	term	קצור_המספר#MTF2	יתר
line/hypotenuse	אלכסון	term	ספר_הכללים_במספר#QiEw	אלכסון
straight line/in a straight manner	י.ש.ר./על יושר	term	תחבולות_המספר#PN28	על יושר
straight line/in a straight manner	י.ש.ר./ביושר	term	תחבולות_המספר#cDgm	ביושר
straight line/in a straight manner	י.ש.ר./ביושר	term	תחבולות_המספר#hJu6	בי^ושר
straight line/in a straight manner	י.ש.ר./ביושר	term	חשבון_השטחים#VB0U	ביושר
straight line/in a straight manner	י.ש.ר./על יושר	term	ספר_האלזיברא#6UED	על יושר
straight line/in a straight manner	י.ש.ר./על יושר	term	חשבון_השטחים#mR21	על יושר
geometric relations/inscribed	ר.ש.מ./מורשם	definition	ספר_היסודות_לאקלידס#A5Vw	The figure is said to be inscribed in a figure when each of its angles touches each of the respective sides of the figure in which it is inscribed. יאמר כי התמונה מורשמת בתמונה כאשר תהיה כל אחת מזויותיה ממששת לכל אחת מצלעות התמונה אשר נרשמת בה
surface/isosceles	ש.ו.ה./שוה צלעות	triangle	מלאכת_המספר#3Lky	משולש שוה הצלעות
surface/isosceles	ש.ו.ה./שוה	trapezoid	ספר_הכללים_במספר#s0uE	קטומת הראש שוה
surface/isosceles	ש.ו.ה./שוה שוקים	triangle	ספר_הכללים_במספר#SINi	משולש שוה השוקים
to join/joined	ד.ב.ק./דובק	term	ספר_ג'יבלי_אלמוקבאלא#lkPU	מדובקים ל
to join/joined	ד.ב.ק./דבק	term	תחבולות_המספר#FCgj	דבק
to join/joined	ד.ב.ק./דובק	term	תחבולות_המספר#pXGN	מדובקים
linear dimension/length	א.ר.כ./אורך	term	משנת_המדות#SQto	ארך
linear dimension/length	א.ר.כ./אורך	term	תחבולות_המספר#dIuF	ארכו
linear dimension/length	א.ר.כ./אורך	term	חשבון_השטחים#opY6	אורכו
linear dimension/length	א.ר.כ./אורך	term	מלאכת_המספר#WuCf	אורך
linear dimension/length	א.ר.כ./אורך	term	חשבון_השטחים#CNQz	אורך
linear dimension/length		term	ספר_המספר_/_אברהם_אבן_עזרא#tTbn	ארכו
linear dimension/length	א.ר.כ./אורך	term	ספר_האלזיברא#xJSR	ארכו
linear dimension/length	א.ר.כ./אורך	term	בר_נותן_טעם#wbTk	אורך
linear dimension/length	א.ר.כ./אורך	term	בר_נותן_טעם#x8jj	ארך
linear dimension/length	א.ר.כ./אורך	term	מלאכת_המספר#h6f3	אורך
linear dimension/length	א.ר.כ./אורך	term	תחבולות_המספר#vaVj	אורך
semicircle/less than a semicircle	ח.ס.ר./חסר	definition	משנת_המדות#qLjq	The deficient segment is any segment that is smaller than a semicircle. החסרה כל שהיא פחותה מחצי העגולה
semicircle/less than a semicircle	ח.ס.ר./חסר	term	משנת_המדות#ZNjf	חסרה
geometrical shape/line	מ.ש.כ./משוך	term	משנת_המדות#aohw	משוכים
geometrical shape/line	ק.ו.י./קו	definition	ספר_היסודות_לאקלידס#wN6J	The '''line''' is a length that has no breadth. והקו הוא אורך אין רוחב לו
geometrical shape/line	ק.ו.י./קו	term	קצור_המספר#NdeC	קו
geometrical shape/line	חוט	term	משנת_המדות#H0NU	חוט
geometrical shape/line	ק.ו.י./קו	term	תחבולות_המספר#XNSA	קו
geometrical shape/line	ק.ו.י./קו	term	ספר_המספר_/_אליהו_מזרחי#zEkb	קוים
geometrical shape/line	ק.ו.י./קו	term	האריתמטיקה_של_ניקומכוס#RC38	קו
geometrical shape/line	ק.ו.י./קו	term	ספר_המספר_/_אליהו_מזרחי#2j7U	קו
geometrical shape/line	ק.ו.י./קו	term	ספר_האלזיברא#n2q8	קו
geometrical shape/line	ק.ו.י./קו	definition	האריתמטיקה_של_ניקומכוס#3xJt	The line is that which has only length, and that which has only length is a line. והקו מה שהיה לו אורך לבד ומה שהיה לו אורך לבד הוא קו
geometrical shape/line	ק.ו.י./קו	term	חשבון_השטחים#ZCVZ	קו
geometrical shape/line	ק.ו.י./קו	term	חשבון_השטחים#gKGj	קוים
geometrical shape/line	ק.ו.י./קו	term	ספר_מעשה_חושב#9DYp	קוים
geometrical shape/line	ק.ו.י./קו	definition	מלאכת_המספר#wrX5	the line is a quantity of length without breadth and depth, whose ends are two points. והקו הוא כמות אורך בלתי רוחב ועומק וקצותיו הם ב' נקודות
geometrical shape/line	ק.ו.י./קו	term	ספר_מעשה_חושב#jwYt	קו
geometrical shape/line	ק.ו.י./קו	term	תחבולות_המספר#1nUp	קוים
geometrical shape/line	ק.ו.י./קו	definition	האריתמטיקה_של_ניקומכוס#mITP	The line has one dimension. והקו בעל משך אחד
geometrical shape/line	מ.ש.כ./משוך	term	משנת_המדות#3VKI	המשוך
geometry/linear dimension	ר.ח.ק./מרחק	definition	ספר_יסודי_התבונה_ומגדל_האמונה#ehyj	the dimensions are three: length, breadth and depth, or height. והמרחקים הם ג' אורך ורחב ועומק או רום
geometry/linear dimension	ר.ח.ק./מרחק	term	מלאכת_המספר#0yxe	מרחקיו
geometry/linear dimension	ר.ח.ק./מרחק	term	מלאכת_המספר#sNrA	מרחקי'
angle/obtuse angle	ר.ו.ח./נרוח	term	ספר_יסודי_התבונה_ומגדל_האמונה#LHoW	זוית נרוחת
angle/obtuse angle	ר.ו.ח./נרוח	definition	ספר_יסודי_התבונה_ומגדל_האמונה#XQbW	the obtuse angle exceeds over the right [angle] in its value. והזוית הנרוחת היא המוסיפה בערכה על הנצבת
angle/obtuse angle	ר.ו.ח./נרוח	definition	ספר_היסודות_לאקלידס#szjV	The greater than a right angle is called an '''obtuse angle'''. ואשר היא גדולה מנצבת תקרא נרוחת
angle/obtuse angle	כ.ס.ח./כסוחה	term	משנת_המדות#hYTA	כסוחה
angle/obtuse angle	ר.ח.ב./רחב	term	משנת_המדות#z0OW	זויות רחבים
angle/obtuse angle	ר.ח.ב./רחב	term	משנת_המדות#lTJw	רחבה
obtuse angle/obtuse-angled	ר.ו.ח./מרוח	triangle-definition	ספר_יסודי_התבונה_ומגדל_האמונה#7MuR	the third species is that which has one obtuse angle, which is called an obtuse-angled [triangle]. והמין השלישי הוא אשר יש לו זוית אחת נרוחת והוא נקרא מרווח הזוית
obtuse angle/obtuse-angled	ר.ו.ח./מרוח	triangle	ספר_הכללים_במספר#iUfN	משולש מרויח הזויות
obtuse angle/obtuse-angled	ר.ו.ח./מרוח	triangle	ספר_יסודי_התבונה_ומגדל_האמונה#dxct	המשלש מרווח הזוית
obtuse angle/obtuse-angled	מ.ו.ט./מתמוטטת	trapezoid	ספר_הכללים_במספר#Bzov	מתמוטטת
obtuse angle/obtuse-angled	ר.ו.ח./נרוח	triangle-definition	ספר_היסודות_לאקלידס#g9wm	The '''obtuse-angled triangle''' is that which has an obtuse angle. והמשולש הנרוח הזוית והוא אשר לו זוית נרוחת
obtuse angle/obtuse-angled	מ.ו.ט./מתמוטטת	trapezoid	ספר_הכללים_במספר#xzTs	קטומה מתמוטטת
obtuse angle/obtuse-angled	פ.ס.ח./פסוחה	triangle	משנת_המדות#uuSe	פסוחה
line/parallel	נ.כ.ח./נכחי	term	חשבון_השטחים#HjSC	נכחי ל
line/parallel	נ.כ.ח./נכחי	term	ספר_הכללים_במספר#uvqN	נכוחיים
line/parallel	נ.כ.ח./נכחי	term	ספר_הכללים_במספר#E7Zk	נכוחית
line/parallel	נ.כ.ח./נכחי	term	תחבולות_המספר#LCaE	נכחי ל
line/parallel	נ.כ.ח./נכחי	term	חשבון_השטחים#cvrF	נכחיים ל
line/parallel	נ.כ.ח./נכחי	term	תחבולות_המספר#Ycx6	נכחיים ל
line/parallel	נ.כ.ח./על נכוחות	term	תחבולות_המספר#zRs4	על נכוחות
line/parallel	נ.כ.ח./נכחי	definition	ספר_היסודות_לאקלידס#Zac6	The '''parallel straight lines''' are those that are in the same plane such that if they are drawn endlessly in both directions, they do not meet one another in either direction. והקוים הישרים הנכחיים הם אשר יהיו על שטח אחד שוה ואם הוצאו בשני הצדדים אל לא תכלית לא יפגשו באחד מהם
line/parallel	נ.כ.ח./נכחי	term	ספר_הכללים_במספר#Jegs	נכוחי
line/parallel	נ.כ.ח./על נכוחות	term	חשבון_השטחים#w6CY	על נכחות
line/parallel	נ.כ.ח./על נכוחות	term	תחבולות_המספר#a4Jr	על נכוחות
line/parallel	נ.כ.ח./נכחי	term	ספר_ג'יבלי_אלמוקבאלא#lKms	נכחיים
line/parallel	נ.כ.ח./על נכוחות	term	חשבון_השטחים#5Sdc	על נכחות
line/parallel	נ.כ.ח./נכחי	term	ספר_האלזיברא#cNKO	נכוחי ל
line/parallel	נ.כ.ח./נכחי	term	ספר_ג'יבלי_אלמוקבאלא#dReT	נכחי ל
line/parallel	נ.כ.ח./נכחי	term	ספר_האלזיברא#W8aP	נכחי לקו
solid/parallelepiped	נ.כ.ח./נכחי השטחים	term	ספר_היסודות_לאקלידס#w1JC	מוגשם נכחיי השטחים
solid/parallelepiped	נ.כ.ח./נכחי השטחים	term	ספר_היסודות_לאקלידס#5wo6	מוגשמי כ"ב וז"ל נכחי השטחים
quadrilateral/parallelogram	ע.י.נ./דומה למעוין	definition	ספר_יסודי_התבונה_ומגדל_האמונה#Di4Q	the fourth [category] is similar to the second whose two of its sides that are parallel to each other, only that its angles are not right [angles] - this is called a parallelogram. והרביעי דומה לשני שכל שני מצלעותיו העומדות זו כנגד זו נכחיות ושוות אלא שזויותיו אינן נצבות וזה נקרא דומה למעויין
quadrilateral/parallelogram	ע.י.נ./דומה למעוין	definition	ספר_היסודות_לאקלידס#Wn4u	The '''rhomboid''' is that whose opposite sides are equal to one another but is neither equilateral nor right-angled. ומהם הדומה למעויין והוא אשר כל שתי צלעות ממנו שזו כנגד זו שוות ואינו שוה הצלעות ואינו נצב הזויות
quadrilateral/parallelogram	נ.כ.ח./נכחי הצלעות	term	ספר_היסודות_לאקלידס#9qdL	השטחים נכחיי הצלעות
quadrilateral/parallelogram	נ.כ.ח./נכחי הצלעות	term	ספר_היסודות_לאקלידס#ERBz	נכחי הצלעות
polygon/pentagon	ח.מ.ש./מחומש	term	ספר_יסודי_התבונה_ומגדל_האמונה#rQuH	מחומשות
polygon/pentagon	ח.מ.ש./מחומש	term	ספר_יסודי_התבונה_ומגדל_האמונה#w5N9	המחומש
polygon/pentagon	ח.מ.ש./מחומש	term	האריתמטיקה_של_ניקומכוס#m2Dh	מחומש
line/perimeter	ס.ב.ב./סביבה	definition	משנת_המדות#AFu9	What is the perimeter? it is the line that circumscribes the circle, as it is said: ''and a line of thirty cubits did compass it round about'' [Chronicles 2, 4, 2]. איזו היא סביבה הוא הקו המקיף את העגול שנ' ''וקו שלשים באמה יסב אותו סביב'' ‫דברי הימים ב, ד, ב
line/perimeter	נ.ק.פ./הקף	term	מלאכת_המספר#ngFU	הקף העגולה
line/perimeter		term	ספר_המספר_/_אברהם_אבן_עזרא#Qhlj	הקו הסובב
line/perimeter	כמות	term	מלאכת_המספר#RwcD	כמות העגולה
line/perimeter		term	ספר_המספר_/_אברהם_אבן_עזרא#kQKO	קו העגול
line/perimeter	ס.ב.ב./סביבה	term	משנת_המדות#ktSB	סביבה
line/perpendicular	ע.מ.ד./מעומד	term	מלאכת_המספר#aMf5	מעומד
line/perpendicular	ק.צ.ר./קצור	term	משנת_המדות#3vSq	קצורים
line/perpendicular	ע.מ.ד./מעומד	term	מלאכת_המספר#GhS0	מעומד
surface/planar	י.ש.ר./ישר	term	ספר_יסודי_התבונה_ומגדל_האמונה#JAjC	ישר
surface/planar	ש.ט.ח./שטוח	term	ספר_המספר_/_אליהו_מזרחי#5c6J	שטוחות
surface/planar	מ.צ.ע./ממוצע	term	משנת_המדות#epCp	ממוצע
angle/plane angle	פ.ש.ט./פשוט	definition	ספר_היסודות_לאקלידס#YkbQ	The '''plane angle''' is the inclination of two given lines to one another in a plane, so that they meet one another not in a straight line. והזוית הפשוטה היא נטיית כל אחד משני קוים מונחים בשטח שוה מדובקים על בלתי יושר האחד מן האחר
angle/plane angle	ש.ט.ח./שטוחה	term	ספר_יסודי_התבונה_ומגדל_האמונה#5Ggu	זוית שטוחה
geometrical shape/point	נ.ק.ד./נקודה	term	תחבולות_המספר#HGlB	נקודות
geometrical shape/point	נ.ק.ד./נקודה	term	ספר_האלזיברא#oWim	נקדת
geometrical shape/point	נ.ק.ד./נקודה	definition	ספר_היסודות_לאקלידס#I0Aq	The '''point''' is a thing that has no part. \|style="width:45%;text-align:right;"\|הנקודה היא דבר אין לה חלק ולא הנחה
geometrical shape/point	נ.ק.ד./נקודה	term	ספר_יסודי_התבונה_ומגדל_האמונה#g5iF	נקדה
geometrical shape/point		midpoint	ספר_המספר_/_אברהם_אבן_עזרא#vdqX	נקודה
geometrical shape/point	נ.ק.ד./נקודה	term	האריתמטיקה_של_ניקומכוס#Qk2e	נקודה
geometrical shape/point	נ.ק.ד./נקודה	term	חשבון_השטחים#G3Un	נקודת
geometrical shape/point	נ.ק.ד./נקודת חלוק	midpoint	מלאכת_המספר#3Tls	נקודת החלוק
geometrical shape/point	נ.ק.ד./נקודה	term	קצור_המספר#UMxT	נקודה
geometrical shape/point	נ.ק.ד./נקודה	term	תחבולות_המספר#eSZc	נקדת
geometrical shape/point	נ.ק.ד./נקודת חלוקה	midpoint	מלאכת_המספר#BIOa	נקודת החלוקה
geometrical shape/point	נ.ק.ד./נקודה	term	האריתמטיקה_של_ניקומכוס#u4ba	נקודות
axis/pole	ק.ט.ב./קוטב	definition	ספר_יסודי_התבונה_ומגדל_האמונה#TU07	the two points that are the ends of the axis are called the beginnings of the axis and in Arabic they are called the poles of the axis. וב' הנקודות אשר הם תכליתי הבריח נקראים ראשי הבריח וקוראים להם בלשון ישמעאל קטבי הבריח
surface/polygon	י.ש.ר./ישר קוים	term	האריתמטיקה_של_ניקומכוס#SU8c	השטחים ישרי הקוים
surface/polygon	י.ש.ר./ישר	term	האריתמטיקה_של_ניקומכוס#9SO5	השטחים הישרים
surface/polygon		definition	ספר_יסודי_התבונה_ומגדל_האמונה#K7RF	the third is the polygon that the lines surrounding it exceed four. והשלישי הוא המרבה דפנות אשר הקוים המקיפים אותו הן עודפים על ד'
surface/polygon	ר.ב.ה./מרבה צלעות	term	ספר_יסודי_התבונה_ומגדל_האמונה#xQVA	השטח המרבה צלעות
solid/prism	ח.מ.ש./מחומש	pentagonal	ספר_הכללים_במספר#K9aE	מצבה מחומשת
solid/prism	ג.ר.ר./מתגורר	term	האנציקלופדיה_של_אבו_אלצלת#aqI8	מתגורר
solid/prism	י.צ.ב./מצבה	term	ספר_הכללים_במספר#NojB	מצבה
solid/prism	י.צ.ב./מצבה	term	ספר_יסודי_התבונה_ומגדל_האמונה#nZFZ	מצבה
solid/prism	ג.ר.ר./מגורר	term	האנציקלופדיה_של_אבו_אלצלת#9vMo	מגורר
solid/prism	ע.מ.ד./עמוד	term	משנת_המדות#kXIU	עמוד
solid/prism	ג.ר.ר./מגורר	triangular-definition	ספר_היסודות_לאקלידס#Dfy8	A prism is a solid figure contained by three rectangles and two triangles. התמונה המוגשמת המגוררת היא אשר יקיפו בה שלשה שטחים נכחיי הצלעות ושני שטחים משולשים
solid/prism	י.צ.ב./מצבה	term	ספר_יסודי_התבונה_ומגדל_האמונה#6azb	מצבות
solid/prism	ח.צ.י./חצויה	triangular	ספר_הכללים_במספר#FrRB	מצבה חצוית הראש
solid/prism	ח.צ.י./חצויה	triangular	ספר_הכללים_במספר#rw6P	מצבה משולשת חצויה
solid/prism	ח.צ.י./חצויה	triangular	ספר_הכללים_במספר#OosO	מצבה חצויה
solid/prism	ר.ב.ע./מרובע	square	משנת_המדות#aQuk	עמוד מרבע
solid/pyramid	ז.נ.ב./מזונב	term	האריתמטיקה_של_ניקומכוס#Ofm0	מזונב
solid/pyramid	ח.ד.ד./מחודד	triangular	האריתמטיקה_של_ניקומכוס#xeb3	המשולש המוגשם המחודד
solid/pyramid	מ.ש.כ./משוך	term	משנת_המדות#JO3X	משוך
solid/pyramid	ח.ד.ד./מחודד	term	האנציקלופדיה_של_אבו_אלצלת#Lvtr	מחדדים
solid/pyramid	ח.ד.ד./מחודד	term	מלאכת_המספר#NwMW	מחודד
solid/pyramid	ש.ל.ש./משולש	triangular	האריתמטיקה_של_ניקומכוס#Gr1Y	הגרם המשולש
solid/pyramid	ח.ד.ד./מחודד	term	האריתמטיקה_של_ניקומכוס#pjvt	המוגשם המחודד
solid/pyramid	ז.נ.ב./מזונב	term	האריתמטיקה_של_ניקומכוס#gLyL	מזונבים
solid/pyramid	ח.ד.ד./מחודד	term	האריתמטיקה_של_ניקומכוס#6x7Y	מחודדים
solid/pyramid	ח.ד.ד./מחודד	term	האריתמטיקה_של_ניקומכוס#CG7S	מחודד
solid/pyramid	ז.נ.ב./מזדנב	term	האריתמטיקה_של_ניקומכוס#o7LK	גרם מזדנב
surface/quadrilateral		term	תחבולות_המספר#W9nk	שטח הכאת
surface/quadrilateral	ר.ב.ע./מרובע	term	קצור_המספר#0nqL	מרובע
surface/quadrilateral	ש.ט.ח./מושטח	term	קצור_המספר#i6VS	מושטח
surface/quadrilateral	ר.ב.ע./מרובע	term	משנת_המדות#4N37	מרבעת
surface/quadrilateral	ר.ב.ע./מרובע	definition	ספר_יסודי_התבונה_ומגדל_האמונה#bfge	the second is the quadrilateral which is the surrounded by four straight lines. והשני הוא המרובע והוא אשר יקיף אותו ד' קוים ישרים
surface/quadrilateral	ר.ב.ע./מרובע	term	מלאכת_המספר#Vy5I	מרובע
surface/quadrilateral	ש.ט.ח./מושטח	term	קצור_המספר#3lah	מושטח
surface/quadrilateral	ר.ב.ע./מרובע	term	בר_נותן_טעם#LjAq	מרובע
quadrilateral/rectangle	טבלה	term	משנת_המדות#wrZo	טבלא
quadrilateral/rectangle	ר.ב.ע./מרובע ארוך	term	ספר_הכללים_במספר#euTK	מרובע ארוך
quadrilateral/rectangle	ח.ל.פ./מתחלף ארכים	definition	ספר_היסודות_לאקלידס#bvdV	The '''oblong''' is that which is right-angled but not equilateral. ומהם המתחלף הארכים והוא הנצב הזויות לא שוה הצלעות
quadrilateral/rectangle	ר.ב.ע./מרובע ארוך	term	ספר_הכללים_במספר#KIEb	מרובע ארוך
quadrilateral/rectangle	ש.ט.ח./שטח נצב הזויות	term	ספר_היסודות_לאקלידס#UxZC	שטח הנצב הזויות
quadrilateral/rectangle	ש.ט.ח./שטח נצב הזויות	term	ספר_היסודות_לאקלידס#PIuX	שטח נצב הזויות
quadrilateral/rectangle	ש.ט.ח./שטח נצב הזויות	term	תחבולות_המספר#tLXb	שטח נצב הזויות
quadrilateral/rectangle	ש.ט.ח./שטח נצב הזויות	term	ספר_האלזיברא#vcTz	שטח נצב הזויות
quadrilateral/rectangle	ש.ט.ח./שטח נצב הזויות	term	ספר_האלזיברא#oh24	השטח הנצב הזויות
quadrilateral/rectangle	ר.ב.ע./מרובע ארוך	definition	ספר_יסודי_התבונה_ומגדל_האמונה#Ig6X	the second [category] is that whose two of its sides are parallel and equal, its [two] other sides are also equal, and so are all of its four angles - this is called a rectangle. והשני הוא אשר שני מצלעיו הם נכוחיות ושוות וכן צלעותיו אחרות שוות כמו כן וד' זויותיו כלם וזה נקרא מרובע ארוך
quadrilateral/rhombus	ע.י.נ./מעוין	definition	ספר_יסודי_התבונה_ומגדל_האמונה#ylyu	the third [category] is similar to the first in its sides that are equal, only that its angles are not right [angles] - this is called a rhombus. והשלישי דומה לראשון בצלעיו שהן שוות אלא שזויותיו אינם נצבות וזה נקרא מעויין
quadrilateral/rhombus	ע.י.נ./מעוין	term	ספר_הכללים_במספר#gBop	מעויין
quadrilateral/rhombus	ע.י.נ./מעוין	term	ספר_הכללים_במספר#6VRn	מרובע המעויין
quadrilateral/rhombus	ע.י.נ./מעוין	definition	ספר_היסודות_לאקלידס#us1T	The '''rhombus''' is that which is equilateral but not right-angled. ומהם המעויין והוא השוה הצלעות ואינו נצב הזויות
angle/right angle	י.צ.ב./נצב	term	ספר_המספר_/_אליהו_מזרחי#4KlC	זויות נצבות
angle/right angle	י.צ.ב./נצב	term	ספר_יסודי_התבונה_ומגדל_האמונה#g94r	זוית נצבת
angle/right angle	י.צ.ב./נצב	term	תחבולות_המספר#kliQ	זוית נצבה
angle/right angle	י.צ.ב./נצב	term	משנת_המדות#w2f4	נצבה
angle/right angle	י.צ.ב./נצב	term	מלאכת_המספר#u7EE	זויות נצבות
angle/right angle	י.צ.ב./נצב	term	קצור_המספר#dSxJ	הזוית הנצבה
angle/right angle	י.צ.ב./נצב	definition	ספר_יסודי_התבונה_ומגדל_האמונה#9aNz	The right angle is one of two angles which is on the sides of a line that is perpendicular to another line and each is equal to the other in value. והזוית נצבה היא אחת מב' זויות אשר על צדי קו העומד על קו אחר וכל אחת מהן שוה בערך לחברתה
right angle/right-angled	י.צ.ב./נצב	triangle	ספר_יסודי_התבונה_ומגדל_האמונה#syPT	נצב הזויות
right angle/right-angled	י.צ.ב./נצב	triangle-definition	ספר_יסודי_התבונה_ומגדל_האמונה#KjlN	the second species is that which has one angle that is right and two [angles] that are acute - this is called a right-angled triangle. והמין השני הוא אשר יש לו זוית אחת נצבת ושתים חדות והוא נקרא משלש נצב הזוית
right angle/right-angled	י.צ.ב./נצב	triangle	ספר_הכללים_במספר#c8w5	משולש נצב הזויות
right angle/right-angled	י.צ.ב./נצב	triangle	ספר_הכללים_במספר#YJQE	משולש נצב הזוית
right angle/right-angled	י.צ.ב./נצב	triangle	ספר_הכללים_במספר#1xD2	משולשים מוצבי זוית
right angle/right-angled	י.צ.ב./נצב	triangle-definition	ספר_היסודות_לאקלידס#BAtH	The '''right-angled triangle''' is that which has a right angle. המשולש נצב הזוית והוא אשר לו זוית נצבת
right angle/right-angled	י.צ.ב./נצב	triangle	משנת_המדות#aKHk	נצבה
surface/scalene	ח.ל.פ./חלוף	triangle	משנת_המדות#ADtV	משלשת חלופים
surface/scalene	ח.ל.פ./חלופה	trapezoid	ספר_הכללים_במספר#oONP	קטומת הראש חלופה
surface/scalene	ח.ל.פ./חלוף	triangle	משנת_המדות#O4ly	חלופים
surface/scalene	פ.ת.ל./נפתל	quadrilateral	ספר_יסודי_התבונה_ומגדל_האמונה#BUOn	מרובע נפתל
surface/scalene	ש.נ.י./משונה	quadrilateral	משנת_המדות#Tcr7	המרבעות המשונות
surface/scalene	ח.ל.פ./מתחלף צלעות	triangle	ספר_הכללים_במספר#F605	משולש מתחלף
surface/scalene	ח.ל.פ./מתחלף צלעות	triangle	מלאכת_המספר#sAxB	משולש מתחלף הצלעות
surface/scalene	ח.ל.פ./מתחלף צלעות	triangle	ספר_הכללים_במספר#Hcvc	משולש מתחלף הצלעות
surface/scalene	ש.נ.י./משונה	quadrilateral	משנת_המדות#rF67	משונה
geometry/section	ק.ט.פ./קטופה	term	משנת_המדות#mCQR	קטופה
circle/sector	ח.ת.כ./חתוך	definition	ספר_היסודות_לאקלידס#s56d	A sector of a circle is a shape that is contained by two straight lines containing an angle at the center of the circle, and the arc that is cut off from the circle by these two lines. י וחתוך העגולה היא תמונה אשר יקיפו בה שני קוים ישרים יקיפו בזוית על מרכז העגולה וקשת יקיפוה אותם שני הקוים מן העגולה
line/segment	ח.ל.ק./חלק	term	חשבון_השטחים#B51m	חלקים
line/segment	ח.ל.ק./חלק	term	חשבון_השטחים#QXND	חלקיו
line/segment	ח.ל.ק./חלק	term	תחבולות_המספר#8rKf	חלקים
line/segment	ח.ל.ק./חלק	term	ספר_האלזיברא#GSR6	חלק
line/segment	פ.ס.ק./פסקה	term	משנת_המדות#hGWl	פסקאות
circle/segment of a circle	ח.ת.כ./חתיכה	definition	ספר_היסודות_לאקלידס#XaeS	The '''segment of the circle''' is the figure contained by a straight line and an arc on the circumference that is either smaller or greater than its half. וחתיכת העגול היא תמונה יקיפו בה קו ישר וקשת ממקיף העגולה אם קטנה מחציה או גדולה
circle/segment of a circle	ק.ש.ת./קשותה	term	משנת_המדות#qGNQ	קשותה
circle/segment of a circle	ח.ת.כ./חתיכה	definition	ספר_היסודות_לאקלידס#ISnG	A segment of a circle is that which is contained by a straight line that is called a chord and the segment of circumference that is called an arc. ו חתיכת העגולה היא אשר יקיף בה קו ישר יקרא המיתר והחלק מן הקו המקיף יקרא הקשת
circle/semicircle	י.ש.ר./ישרה	term	משנת_המדות#aGCk	ישרה
circle/semicircle	י.ש.ר./ישרה	definition	משנת_המדות#YhPn	Which is the semicircle? Any segment that is half a circle, no more and no less. איזו היא ישרה כל שהיא עומדת בחצי העגולה לא חסר ולא יתר
solid/sharp solid	ל.ה.ב./מתלהב	term	האנציקלופדיה_של_אבו_אלצלת#Pmc5	מתלהבים
surface/side	צלע	definition	משנת_המדות#IL6w	What is the side? it is the holder of the surface's walls, as it is said: ''the altar shall be square''. אי זו היא הצלע זה המחזיק דופנותיו של גג שנ' ''רבוע יהיה המזבח''‫שמות כז, א
surface/side	צלע	term	עיר_סיחון#YlsD	צלעות
surface/side	צלע	term	מלאכת_המספר#f9Sc	צלעות
surface/side	צלע	term	קצור_המספר#t24N	צלע
surface/side		term	ספר_המספר_/_אברהם_אבן_עזרא#ZJhZ	פאת
surface/side	צלע	term	חשבון_השטחים#CK5Q	צלעיו
surface/side	י.ש.ב./תושבת	term	ספר_המספר_/_אליהו_מזרחי#SLbt	תושבות
surface/side	צלע	term	תחבולות_המספר#DtxV	צלע
surface/side	צלע	term	ספר_האלזיברא#JpoA	צלע
surface/side	צלע	term	קצור_המספר#z4ec	צלעות
surface/side	צלע	term	מלאכת_המספר#Rtkh	צלע
surface/side	צלע	term	משנת_המדות#bpGS	צלע
surface/side	צלע	term	ספר_האלזיברא#I58U	צלע מרבע
surface/side	צלע	term	תחבולות_המספר#lBcX	צלעיו
surface/side	צלע	term	חשבון_השטחים#P0If	צלע
geometric relations/similar figures	ד.מ.י./דומה	solids-definition	ספר_היסודות_לאקלידס#oKi8	The similar solid shapes are those that each solid of which is contained by the same number of surfaces as the number of the surfaces containing the other, and each surface is similar to its corresponding surface in the other solid. התמונות המוגשמות הדומות הם אשר יקיף כל מוגשם מהם ממנין השטחים כמו מנין מה שיקיף באחר ויהיה כל שטח מאחד מהם דומה בשטח אשר הוא גילו מן המוגשם האחר ועל בריאתו
geometric relations/similar figures		surfaces-definition	ספר_היסודות_לאקלידס#7gj7	The similar rectilinear figures are those whose angles are equal and whose sides about the equal angles are proportional. השטחים המתדמים הם אשר זויותיהם שוות וצלעותיהם המקיפות בזויות השוות מתיחסות
geometrical shape/solid	ג.ר.מ./גרם	definition	האריתמטיקה_של_ניקומכוס#kMEJ	It was said that the solid adds a dimension of depth to the surface, since the surface has only length and breadth ואמרנו שהגרם הוא אשר יוסיף משך בעומק על השטח אחר שהשטח אורך ורחב לבד
geometrical shape/solid	ג.ש.מ./גשם	term	מלאכת_המספר#x4VO	גשם
geometrical shape/solid	ג.ש.מ./מוגשם	term	מלאכת_המספר#NWfq	מוגשם
geometrical shape/solid	גוף	term	משנת_המדות#lVlq	גוף
geometrical shape/solid	גו	term	משנת_המדות#livj	גוו
geometrical shape/solid	גג	term	משנת_המדות#NnXf	גג
geometrical shape/solid	ג.ש.מ./גשם	definition	מלאכת_המספר#LrBm	The solid is a quantity that has three dimensions, which are length, breadth and depth, whose limits are surfaces. הגשם הוא כמות שיש לו ג' {{#annot:term\|315,1891\|sNrA}}מרחקי'{{#annotend:sNrA}} שהם אורך ורוחב ועומק שתכליותיו הם ב' שטחי‫'
geometrical shape/solid	ג.ש.מ./גשם	term	מלאכת_המספר#CTjN	גשם
geometrical shape/solid	ג.ש.מ./גשם	term	האריתמטיקה_של_ניקומכוס#Q8TU	גשם
geometrical shape/solid	ג.ש.מ./גשם	definition	האריתמטיקה_של_ניקומכוס#nUtW	One may argue by saying in a general statement that any thing that has length, breadth, and depth is a solid, and every solid has length, breadth, and depth. ואולי יהיה לטוען שיאמר הנה במאמר כולל שכל בעל אורך ורוחב ועומק הוא גשם וכל גשם בעל אורך ורחב ועומק
geometrical shape/solid	ג.ש.מ./גשם	term	ספר_מעשה_חושב#RgAm	גשם
geometrical shape/solid	ג.ש.מ./גשם	definition	האריתמטיקה_של_ניקומכוס#Sy4l	The three-dimensional is the solid. ומה שהיה בעל שלשה המשכים הוא גשם
geometrical shape/solid	ג.ש.מ./גשם	term	בר_נותן_טעם#eHwo	גשם
geometrical shape/solid	ג.ר.מ./גרם	term	האריתמטיקה_של_ניקומכוס#Ff7g	גרמים
geometrical shape/solid	גוף	term	האריתמטיקה_של_ניקומכוס#3czY	גוף
geometrical shape/solid	ג.ר.מ./גרם	term	האריתמטיקה_של_ניקומכוס#rQJK	הגרם
geometrical shape/solid	ג.ל.מ./גולם	definition	ספר_יסודי_התבונה_ומגדל_האמונה#5tIP	The first is called solid, and it has three dimensions. הראשון נק' גולם ויש לו ג' מרחקים
geometrical shape/solid	ג.ל.מ./גולם	term	ספר_יסודי_התבונה_ומגדל_האמונה#xmto	גלם
geometrical shape/solid	ג.ל.מ./גולם	term	ספר_יסודי_התבונה_ומגדל_האמונה#jKvx	גולמים
geometrical shape/solid	ג.ש.מ./גשם	term	ספר_המספר_/_אליהו_מזרחי#4qT1	גשמים
geometrical shape/solid	ג.ש.מ./גשם	term	ספר_המספר_/_אליהו_מזרחי#ZoVN	גשם
geometrical shape/solid	ג.ש.מ./מוגשם	term	ספר_המספר_/_אליהו_מזרחי#yKif	מוגשמות
geometrical shape/solid	ג.ל.מ./גולם	term	ספר_הכללים_במספר#5Z9l	גולם
geometrical shape/solid	ע.ק.ב./מעוקב	definition	Arithmetic_Textbook_by_R._Aharon_ben_Isaac#Z0L5	מעוקב שהוא הגשם אשר ימצאו בו השלושה רחקים שהם אורך ורוחב ועומד
geometrical shape/solid	גוף	term	ספר_הכללים_במספר#EyrJ	גוף
solid/solid angle	קרן	term	ספר_יסודי_התבונה_ומגדל_האמונה#1mxy	קרנות
solid/solid angle	קרן	term	ספר_יסודי_התבונה_ומגדל_האמונה#2LQy	קרנות השטח
solid/solid angle	ג.ל.מ./גלומה	term	ספר_יסודי_התבונה_ומגדל_האמונה#JS01	זוית גולמית
solid/solid angle	קרן	term	ספר_יסודי_התבונה_ומגדל_האמונה#SX31	קרן
solid/sphere	כ.ד.ר./כדור	term	ספר_הכללים_במספר#MkFQ	כדור
solid/sphere	כ.ד.ר./כדור	definition	ספר_היסודות_לאקלידס#sI0K	The sphere is when the semicircle is drawn round with the diameter fixed in two points, so it does not move, and the arc, which is half the perimeter, revolves until it returns to its position; it is the circular solid. The center of the sphare and the center of the circle are the same. הכדור הוא מה שיעבור חצי עגולה כאשר יקוים קו הקוטר בין שני כשורים עד שלא יסור וסבבה הקשת אשר היא חצי הקו המקיף עד שתשוב אל מקומה והוא המוגשם העגול ומרכז הכדור ומרכז העגולה אחד
solid/sphere	כ.ד.ר./כדור	term	מלאכת_המספר#NYpt	כדור
solid/sphere	כ.ד.ר./כדור	definition	ספר_יסודי_התבונה_ומגדל_האמונה#MjPy	the solid that is surrounded by a circular surface is called sphere. והגולם אשר יקיף אותו פרוש אחד עגול הוא הנקרא כדור
solid/sphere	כ.ד.ר./כדור	definition	ספר_יסודי_התבונה_ומגדל_האמונה#WlA0	It is that which is surrounded by one surface all around and at its center there is one point such that all the lines that are drawn from it to the surface of the sphere are equal to each other. הוא אשר יקיפו פרוש אחד מכל סביביו ובאמצעיתו נקודה אחת וכל הקוים היוצאים ממנה אל פרוש הכדור שוים זה לזה
solid/sphere	ת.ל.י./תלוי	term	משנת_המדות#uV4d	תלויה
solid/sphere	כ.ד.ר./כדור	term	ספר_יסודי_התבונה_ומגדל_האמונה#hzZC	כדור
quadrilateral/square	ש.ו.ה./שוה צלעות	term	ספר_ג'יבלי_אלמוקבאלא#0caF	שטח אחד שוה הצלעות
quadrilateral/square	ש.ו.ה./שוה צלעות	term	ספר_ג'יבלי_אלמוקבאלא#94Yd	מרובע שוה הצלעות
quadrilateral/square	שוה צלעות נצב זויות	term	ספר_ג'יבלי_אלמוקבאלא#DrKd	המרובע שוה הצלעות ונצב הזויות
quadrilateral/square	ר.ב.ע./מרובע	term	ספר_ג'יבלי_אלמוקבאלא#j1oW	מרובע
quadrilateral/square	שוה צלעות נצב זויות	term	ספר_ג'יבלי_אלמוקבאלא#Jhqq	שטח אחד שוה הצלעות ונצב הזויות
quadrilateral/square	שוה צלעות נצב זויות	term	ספר_ג'יבלי_אלמוקבאלא#HdgB	מרובע אחד שוה הצלעות נצב הזויות
quadrilateral/square	ר.ב.ע./מרובע	term	ספר_האלזיברא#mzGp	מרבע
quadrilateral/square	ר.ב.ע./מרובע	term	ספר_ג'יבלי_אלמוקבאלא#bhc1	מרובעי'
quadrilateral/square	ש.ו.ה./שוה צלעות	term	ספר_ג'יבלי_אלמוקבאלא#Eq9Q	מרובעי' השוי הצלעות
quadrilateral/square	שוה צלעות נצב זויות	term	ספר_ג'יבלי_אלמוקבאלא#va50	שטח שוה הצלעות נצב הזויות
quadrilateral/square	ש.ו.ה./שוה צלעות	term	ספר_ג'יבלי_אלמוקבאלא#tWbu	מרובע אחד שוה הצלעות מד' זויות
quadrilateral/square		term	ספר_המספר_/_אברהם_אבן_עזרא#IbQn	מרובע {{#annot:term\|316\|tTbn}}ארכו{{#annotend:tTbn}} כ{{#annot:term\|317\|FXNE}}רחבו{{#annotend:FXNE}}
quadrilateral/square	ר.ב.ע./שטח מרובע	term	חשבון_השטחים#VRcA	שטח מרובע עליו
quadrilateral/square	ר.ב.ע./מרובע	term	חשבון_השטחים#OcVT	מרובע
quadrilateral/square	ר.ב.ע./מרובע	definition	ספר_היסודות_לאקלידס#yeYh	The '''square''' is that which is both equilateral and right-angled. הנה מהן המרובע הוא השוה הצלעות נצב הזויות
quadrilateral/square	ר.ב.ע./מרובע	term	ספר_האלזיברא#D62w	מרבע
quadrilateral/square	שוה צלעות נצב זויות	term	ספר_ג'יבלי_אלמוקבאלא#vsui	שטחי' שוי הצלעות והזויות נצבות
quadrilateral/square	שוה צלעות נצב זויות	term	ספר_ג'יבלי_אלמוקבאלא#wYJE	מרובע נצב הזויות שוה הצלעות
quadrilateral/square	שוה צלעות נצב זויות	term	ספר_ג'יבלי_אלמוקבאלא#d9eX	מרובע אחד שוה הצלעות והזיות נצבות
quadrilateral/square	ר.ב.ע./שטח מרובע	term	תחבולות_המספר#Q5y3	שטח מרובע עליו
quadrilateral/square	כ.ו.נ./נכון	term	קצת_מענייני_חכמת_המספר#MiTK	מרובע נכון
quadrilateral/square	ר.ב.ע./מרובע	term	תחבולות_המספר#QPs4	מרובע עליו
quadrilateral/square	ר.ב.ע./רבוע	definition	ספר_יסודי_התבונה_ומגדל_האמונה#YjuR	the first category is that whose four sides are all equal to each other in their value and each of its four angles is a right angle - this is called a square. החלק הראשון הוא אשר ארבע צלעיו כלם שוים בערכם אחת אל אחת וכן זויות ד' כל אחת מהן זוית נצבה וזה נקרא רבוע
quadrilateral/square	ר.ב.ע./מרובע	term	תחבולות_המספר#PFLT	מרובע
quadrilateral/square	ר.ב.ע./מרובע	term	האריתמטיקה_של_ניקומכוס#d8ge	מרובע
line/straight line	י.ש.ר./ישר	definition	ספר_היסודות_לאקלידס#lFcp	The '''straight line''' is that which lies straightly by the arrangement of points on it one by one. והקו הישר הוא המוצב על נכוחות אי זה נקודות יהיו עליו קצתם אל קצתם
line/straight line	י.ש.ר./מיושר	definition	ספר_יסודי_התבונה_ומגדל_האמונה#RN7a	The straight line is the one that passes directly from the two points that are its ends. והקו המיושר הוא ההולך לנכח ב' הנקדות אשר הם תכליתו
line/straight line	י.ש.ר./ישר	term	ספר_האלזיברא#4AfE	קו ישר
line/straight line	י.ש.ר./ישר	term	תחבולות_המספר#yJtO	קו ישר
line/straight line	י.ש.ר./מיושר	term	ספר_יסודי_התבונה_ומגדל_האמונה#iRJO	קו מיושר
line/straight line	י.ש.ר./ישר	term	חשבון_השטחים#FjaR	קו ישר
line/straight line	י.ש.ר./ישר	term	ספר_האלזיברא#wtKL	ישר
geometrical shape/surface	גג	term	משנת_המדות#RwBa	גג
geometrical shape/surface	ר.ק.ע./רקיע	term	ספר_יסודי_התבונה_ומגדל_האמונה#cV12	הרקיע גלמי
geometrical shape/surface	ש.ט.ח./שטח	term	ספר_מעשה_חושב#tBy4	שטחים
geometrical shape/surface	פ.ר.ש./פרוש	definition	ספר_יסודי_התבונה_ומגדל_האמונה#vPk1	The second is called surface [lit. spread], and it is called by this name, since it is spread on the body as if it apart from it, and this body has length and breadth alone. והשני נק' פרוש וקראו לו בשם הזה מפני שהוא פרוש על הגולם כאלו היה חוצה ממנו וזה הפרוש יש לו ארך ורחב בלבד
geometrical shape/surface	ש.ט.ח./שטח	definition	האריתמטיקה_של_ניקומכוס#QKfY	Likewise, one may say that what has only length and breadth is a surface, and the surface is that which has only length and breadth. וכמו כן יאמר מה שהיה לו אורך ורחב לבד הוא שטח והשטח הוא מה שהיה לו אורך ורחב לבד
geometrical shape/surface	ש.ט.ח./שטח	term	האריתמטיקה_של_ניקומכוס#Lfgr	שטח
geometrical shape/surface	פ.ר.ש./פרוש	term	ספר_יסודי_התבונה_ומגדל_האמונה#Uads	פרושים
geometrical shape/surface	פ.ר.ש./פרוש	term	ספר_יסודי_התבונה_ומגדל_האמונה#aIkf	פרוש
geometrical shape/surface	ש.ט.ח./שטח	term	ספר_האלזיברא#eJNd	שטח
geometrical shape/surface	ש.ט.ח./שטח	term	בר_נותן_טעם#5Pke	שטח
geometrical shape/surface	ש.ט.ח./שטח	definition	האריתמטיקה_של_ניקומכוס#B67O	The two-dimensional is the surface. ומה שהיה בעל שני המשכים הוא שטח
geometrical shape/surface	ש.ט.ח./שטח	term	ספר_מעשה_חושב#KV4R	שטח
geometrical shape/surface	ש.ט.ח./שטח	term	תחבולות_המספר#JkjG	שטח
geometrical shape/surface	ש.ט.ח./שטח	term	מלאכת_המספר#T5GN	שטח
geometrical shape/surface	solid/volume	term	ספר_הכללים_במספר#F8HS	משיחת שטח הבריכה
geometrical shape/surface	מ.ש.ח./משיחה	term	ספר_הכללים_במספר#hb4l	משיחת שטח הכדור
geometrical shape/surface	ש.ט.ח./שטח	definition	מלאכת_המספר#gJ6u	the surface is a quantity that has length and breadth without depth, whose limits are two lines. השטח הוא כמות בעל אורך ו{{#annot:term\|317,1488\|SLfo}}רוחב {{#annotend:SLfo}}בלתי עומק ש{{#annot:term\|279,1887\|tYDo}}תכליותיו{{#annotend:tYDo}} ב' קוים
geometrical shape/surface	ש.ט.ח./שטח	term	ספר_ג'יבלי_אלמוקבאלא#fIHT	שטחי'
geometrical shape/surface	ש.ט.ח./שטח	term	חשבון_השטחים#fxB7	שטח
geometrical shape/surface	ש.ט.ח./שטח	term	ספר_המספר_/_אליהו_מזרחי#GMrP	שטח
geometrical shape/surface	ש.ט.ח./שטח	term	ספר_המספר_/_אליהו_מזרחי#P6xS	שטחים
geometrical shape/surface	ש.ט.ח./שטח	definition	ספר_היסודות_לאקלידס#PhWl	The '''surface''' is that which has length and breadth only. והשטח הוא אשר לו אורך ורוחב לבד
geometrical shape/surface	ש.ט.ח./שטח	term	ספר_ג'יבלי_אלמוקבאלא#qKhs	שטח
geometrical shape/surface	גג	definition	משנת_המדות#KsSG	The surface itself is the area. והגג עצמו היא המשיחה
geometric relations/to be the side of an area	ח.ז.ק./הוחזק	term	ספר_ג'יבלי_אלמוקבאלא#i2ia	המוחזקי' ב
geometric relations/to be the side of an area	ח.ז.ק./החזיק	term	ספר_האלזיברא#3DEC	מחזקת ב
geometrical shape/to construct	ע.מ.ד./העמיד	term	ספר_היסודות_לאקלידס#TWKo	נעמיד על
geometrical shape/to construct	ע.ש.ה./עשה	term	קצור_המספר#FaQ9	נעשה
geometrical shape/to construct		term	ספר_האלזיברא#Zpze	נעשה מן א"ב מרבע
geometrical shape/to construct		term	ספר_האלזיברא#Mz5i	נעשה מן קו א"ג מרבע
geometrical shape/to construct		term	תחבולות_המספר#GRES	נעשה על
geometrical shape/to construct		term	תחבולות_המספר#48WG	עשה על
geometrical shape/to construct		term	תחבולות_המספר#8stU	תשים על
geometrical shape/to construct		term	תחבולות_המספר#yUj4	נשים עליו
geometrical shape/to construct		term	תחבולות_המספר#nGtX	נשים על
geometrical shape/to construct	נ.ו.ח./הניח	term	חשבון_השטחים#cuCt	נניח על
geometrical shape/to construct	ע.ש.ה./עשה	term	חשבון_השטחים#ZiEA	נעשה על
geometrical shape/to construct	ע.ש.ה./עשה	term	חשבון_השטחים#6VxT	עשה על
geometrical shape/to construct		term	חשבון_השטחים#WKQn	נשים על
geometrical shape/to construct		term	חשבון_השטחים#yth4	אשים על
geometrical shape/to construct	ע.מ.ד./העמיד	term	ספר_היסודות_לאקלידס#yirg	נעמיד על
line/to cut a line	ח.ל.ק./נחלק לחצאים	to be halved at point	תחבולות_המספר#JUPf	נחלק לחצאין על נקודת
line/to cut a line	ח.ל.ק./חלק קו	term	חשבון_השטחים#vclu	נחלק קו
line/to cut a line	ח.ל.ק./חלק קו	term	תחבולות_המספר#q7GH	נחלק קו
line/to cut a line	ח.ל.ק./נחלק לחצאים	to be halved at point	חשבון_השטחים#JnrH	נחלק לחצאים על נקודת
line/to cut a line		to be cut randomly at point	ספר_האלזיברא#S8Q5	יחולק איך שקרה על נקדת
line/to cut a line		to be halved at point	ספר_האלזיברא#Wk92	נחלק לחצאין על נקדת
line/to cut a line	ח.ל.ק./חלק לחצאים	to halve a line at point	חשבון_השטחים#g8x0	תחלק קו א"ב לשני חצאים על
line/to cut a line	ח.ל.ק./חלק לחצאים	to halve a line at point	תחבולות_המספר#uwUl	נחלקהו לחציין על נקודת
line/to cut a line	ח.ל.ק./חלק לחצאים	to halve a line at point	תחבולות_המספר#vadk	נחלק אותו לחצאין על נקודת
line/to cut a line	ח.ל.ק./חלק לחצאים	to halve a line at point	חשבון_השטחים#l2ux	נחלק אותו לחציים על נקודת
line/to cut a line		to be cut into two unequal segments	חשבון_השטחים#Cbhd	נחלק לשני חלקים בלתי שוים על נקודת
line/to cut a line		to be cut into two unequal segments	תחבולות_המספר#sLnn	נחלק לשני חלקים בלתי שוים על נקודת
line/to cut a line	ח.ל.ק./נחלק	to be cut into two segments	תחבולות_המספר#ms8e	יחלק לשני חלקים
line/to cut a line		to cut randomly at point	ספר_האלזיברא#6A8l	חלק איך שקרה על נקדת
line/to cut a line	ח.ל.ק./חלק קו	term	תחבולות_המספר#QaGp	תחלק קו
line/to cut a line		to halve a line	ספר_האלזיברא#CWXy	נחלקהו ‫130rלחצאין על נקדת
line/to cut a line	ח.ל.ק./נחלק לחצאים	to be halved at point	חשבון_השטחים#Em05	נחלק לחציים על נקודת
line/to cut a line	ח.ל.ק./חלק קו	term	חשבון_השטחים#zVhW	תחלק קו
line/to cut a line		to halve a line	ספר_האלזיברא#PkWc	נחלקהו לב' חלקי' שוים על נקדת
line/to cut a line		to cut into two unequal segments	ספר_האלזיברא#fs2S	נחלקה לשני חלקים בלתי שוים על נקדת
line/to cut a line	ח.צ.י./חצה	to halve a line at point	ספר_ג'יבלי_אלמוקבאלא#yo7t	נחצה לשני חלקים שוים בנקודת
geometric relations/to cut off	ב.ד.ל./הבדיל	term	תחבולות_המספר#ogvR	הבדלנו
geometric relations/to cut off	ב.ד.ל./הבדיל	term	תחבולות_המספר#Ptjj	נבדיל
geometric relations/to cut off	ב.ד.ל./הבדיל	term	חשבון_השטחים#ueVd	נבדיל
geometric relations/to cut off	ב.ד.ל./הבדיל	term	חשבון_השטחים#LmNg	תבדיל
geometric relations/to divide a figure	פ.ס.ק./פסק	term	משנת_המדות#rWbW	פסקה לשנים
geometric relations/to divide a figure	פ.ס.ק./פסק	term	משנת_המדות#pgwr	פוסקה שנים
geometry/to draw	י.צ.א./הוציא	to draw a line	תחבולות_המספר#vgQz	נוציא קוי
geometry/to draw	י.צ.א./הוציא	to draw a line	ספר_ג'יבלי_אלמוקבאלא#cMHc	תוציא קו אחד מ
geometry/to draw	י.צ.א./הוציא	term	תחבולות_המספר#eY6o	נוציא
geometry/to draw	י.צ.א./הוציא	term	חשבון_השטחים#2Qhs	תוציא מ
geometry/to draw	י.צ.א./הוציא	term	חשבון_השטחים#xLty	תוציא מנקודות
geometry/to draw	י.צ.א./הוציא	term	חשבון_השטחים#2Ih7	תוציא מנקדות
geometry/to draw	י.צ.א./הוציא	term	חשבון_השטחים#3P9m	תוציא מנקודת
geometry/to draw	י.צ.א./הוציא	to draw a line	תחבולות_המספר#E2dh	תוציא קו
geometry/to draw	י.צ.א./הוציא	to draw a line	ספר_ג'יבלי_אלמוקבאלא#Z0HS	נוציא קו אחר ישר
geometry/to draw	י.צ.א./הוציא	to draw a line	חשבון_השטחים#DwRl	תוציא קו
geometry/to draw	צ.י.ר./צויר	term	ספר_ג'יבלי_אלמוקבאלא#9Ak5	מצוייר
geometry/to draw	ק.ו.י./קוה	term	ספר_היסודות_לאקלידס#qfrQ	נקוה
geometry/to draw	ק.ו.י./קוה	term	ספר_היסודות_לאקלידס#kY7l	נקוה
geometry/to draw	ע.ש.ה./עשה	to draw a line	חשבון_השטחים#cXQo	לעשות קוי
geometry/to draw	ע.ב.ר./העביר	to draw a line	ספר_היסודות_לאקלידס#ztOj	נעביר קו
geometry/to draw	י.צ.א./הוציא	term	ספר_האלזיברא#DpZV	אוציא מ
geometry/to draw	ע.ב.ר./העביר	to draw a line	ספר_האלזיברא#Ii1B	נעביר קו
geometry/to draw	צ.י.ר./צייר	term	חשבון_השטחים#H57u	תצייר
geometry/to draw		term	ספר_האלזיברא#uW6o	צירתי
geometry/to draw	י.צ.א./הוציא	to draw a line	מלאכת_המספר#DyfV	נוציא
geometry/to draw	צ.י.ר./צייר	term	ספר_ג'יבלי_אלמוקבאלא#MU8F	נצייר
geometry/to draw	י.צ.א./הוציא	to draw a line	מלאכת_המספר#utEh	נוציא
geometry/to draw	נ.ג.ע./הגיע	to draw a line	ספר_ג'יבלי_אלמוקבאלא#omwB	תגיע קו אחד מ
geometry/to draw	י.צ.א./הוציא	to draw a line	ספר_ג'יבלי_אלמוקבאלא#yF7x	נוציא קו
circle/to draw a circle	נ.ק.פ./הקיף	term	ספר_היסודות_לאקלידס#Wj8n	נקיף על
circle/to draw a circle	ח.ק.ק./לחוק	term	ספר_הכללים_במספר#CyVl	לחוק בעגול
circle/to draw a circle	נ.ק.פ./הקיף	term	ספר_היסודות_לאקלידס#Bgcx	נקיף עגולה
circle/to draw a circle	ע.ג.ל./עגל	term	ספר_יסודי_התבונה_ומגדל_האמונה#fYqf	לעגל עליו עגולה
circle/to draw a circle	ק.ו.י./קוה	term	ספר_היסודות_לאקלידס#Pgvr	נקוה עגולה
circle/to draw a circle	ח.ק.ק./לחוק	term	ספר_הכללים_במספר#Wkts	לחוק בה עגול
circle/to draw a circle	ע.ג.ל./עגל	term	ספר_יסודי_התבונה_ומגדל_האמונה#Oerg	לעגל בתוכו עגולה
circle/to draw a circle	ק.ו.י./קוה	term	ספר_היסודות_לאקלידס#MoiN	נקוה
geometric relations/to encompass	נ.ק.פ./הקיף	term	תחבולות_המספר#jij2	יקיפו בו
geometric relations/to encompass	נ.ק.פ./הקיף	term	תחבולות_המספר#fbeH	מקיף
geometric relations/to encompass	נ.ק.פ./הקיף	term	ספר_מעשה_חושב#u8IF	המקיפים בו
geometric relations/to encompass	נ.ק.פ./הקיף	term	מלאכת_המספר#9qMC	מקיף אותו
line/to extend a line	מ.ש.כ./המשיך קו	term	חשבון_השטחים#Hlm5	נמשיך קו
line/to extend a line	מ.ש.כ./המשיך קו	term	ספר_האלזיברא#67xx	נמשיך קו
line/to extend a line	מ.ש.כ./המשיך קו	term	תחבולות_המספר#KMfZ	נמשיך קו
line/to extend a line	מ.ש.כ./המשיך קו	term	ספר_ג'יבלי_אלמוקבאלא#zKyQ	תמשיך קו אחד עליו
surface/to form an area		term	תחבולות_המספר#RRCV	נשלים שטח
surface/to form an area	ש.ל.מ./השלים	term	חשבון_השטחים#y3cp	נשלים שטח
geometric relations/to intersect	ח.ב.ר./מחובר	term	ספר_דיני_ממונות#tuwl	קוים מחוברים
geometric relations/to intersect		term	ספר_האלזיברא#UM04	יפגוש קו
geometric relations/to intersect	פ.ס.ק./הפסיק	term	משנת_המדות#MXl7	מפסיקין זה את זה
geometric relations/to intersect	ח.ת.כ./חתך	term	ספר_האלזיברא#NwpI	יחתכו
geometric relations/to join	ש.ת.פ./שתף	term	תחבולות_המספר#LFhk	נשתף עמו
geometric relations/to join	ד.ב.ק./הדביק	term	תחבולות_המספר#iJG4	נדביק
geometric relations/to join	ד.ב.ק./הדביק	term	ספר_ג'יבלי_אלמוקבאלא#yNEQ	נדביק
geometric relations/to join	ד.ב.ק./הדביק	term	ספר_ג'יבלי_אלמוקבאלא#8VeD	נדביק
geometric relations/to revolve around	ס.ב.ב./סבב	term	ספר_יסודי_התבונה_ומגדל_האמונה#Py8c	סובב עליו
geometric relations/to revolve around	ס.ב.ב./סבב	term	ספר_המספר_/_אברהם_אבן_עזרא#gOMD	סובבות את
geometric relations/to touch	מ.ש.ש./משש	term	ספר_יסודי_התבונה_ומגדל_האמונה#OH1T	מושש ל
geometric relations/to touch	מ.ש.ש./משש	term	ספר_יסודי_התבונה_ומגדל_האמונה#IbMX	מושש
quadrilateral/trapezoid	נ.ט.י./נוטה	definition	ספר_היסודות_לאקלידס#JU9N	The quadrilaterals that are other than the above-mentioned figures are called '''trapezia'''. ומה שהיה על זולת מה שספרנו מן התמונות בעלות ארבע צלעות תקרא הנוטה
quadrilateral/trapezoid	ק.ט.מ./קטומה	term	ספר_הכללים_במספר#4hrz	קטומת הראש
quadrilateral/trapezoid	ק.ט.מ./קטומה	term	ספר_הכללים_במספר#0OmP	קטומה
surface/triangle	ש.ל.ש./משולש	definition	ספר_יסודי_התבונה_ומגדל_האמונה#Trd6	the first of them is the triangle which is the surrounded by three straight lines. הראשון מהם הוא המשלש והוא המקיף אותו ג' קוים ישרים
surface/triangle	ש.ל.ש./משולשת	term	משנת_המדות#rrKK	משלשת
surface/triangle	ש.ל.ש./משולש	term	מלאכת_המספר#kEE3	משולש
surface/triangle	ש.ל.ש./משולש	definition	ספר_יסודי_התבונה_ומגדל_האמונה#rvtN	Explanation of the properties of the surface that has three sides called triangle !style="text-align:right;"\|פירוש עניני השטח אשר לו שלשה צלעים ונקרא משלש
surface/triangle		term	ספר_המספר_/_אברהם_אבן_עזרא#VH1b	משולש
surface/triangle	ש.ל.ש./משולש	term	ספר_יסודי_התבונה_ומגדל_האמונה#Sluz	משלש
surface/triangle	ש.ל.ש./משולש	term	ספר_יסודי_התבונה_ומגדל_האמונה#jMAM	משלשים
solid/truncated solid	ח.ס.ר./מחוסר	term	האריתמטיקה_של_ניקומכוס#EfLj	מחוסר
solid/truncated solid	ק.ט.ע./קטוע	term	משנת_המדות#njDm	קטוע
solid/truncated solid	ח.ס.ר./מחוסר	term	האריתמטיקה_של_ניקומכוס#fXNB	הגשם המחוסר
line/uniform line	פ.ר.ד./מתפרד	term	ספר_יסודי_התבונה_ומגדל_האמונה#Tv8Y	מתפרד
line/uniform line	פ.ר.ד./מתפרד	term	ספר_יסודי_התבונה_ומגדל_האמונה#Pmls	הקו המתפרד
geometry/upper base	פה	term	מלאכת_המספר#Nkoh	פיו
circle/versine	ח.צ.צ./חץ	definition	משנת_המדות#UTQn	The sagitta is the drawn from the middle of the arc until the middle of the chord, as it is said: ''they set their arrow on the bowstring'' [Psalms 11, 2]. והחץ הוא המשוך מאמצע הקשת לאמצע היתר שנ' ''כוננו חצם על יתר''‫תהילים יא, ב
circle/versine		term	ספר_המספר_/_אברהם_אבן_עזרא#WiTP	חץ
circle/versine	ח.צ.צ./חץ	term	משנת_המדות#nlBR	חץ
solid/volume	מ.ש.ח./משיחה	term	משנת_המדות#g4GG	משיחת הגג
solid/volume	ש.ב.ר./תשבורת	term	ספר_הכללים_במספר#SpiW	תשבורת רבוע ה
solid/volume	ש.ב.ר./תשבורת	term	ספר_הכללים_במספר#RKIL	תשבורת גוף ה
solid/volume	ש.ב.ר./תשבורת	term	ספר_המספר_/_אליהו_מזרחי#0BrL	תשבורת
solid/volume	ש.ב.ר./תשבורת	term	ספר_הכללים_במספר#Lrs9	תשבורת
solid/volume	מ.ש.ח./משיחה	term	משנת_המדות#z83J	משיחת הגוף
linear dimension/width	ר.ח.ב./רוחב	term	מלאכת_המספר#SLfo	רוחב
linear dimension/width	ר.ח.ב./רוחב	term	ספר_ג'יבלי_אלמוקבאלא#gKan	רוחב ה
linear dimension/width	ר.ח.ב./רוחב	term	קצור_המספר#Tl4A	רחבה
linear dimension/width	ר.ח.ב./רוחב	term	ספר_ג'יבלי_אלמוקבאלא#ytPj	רחב ה
linear dimension/width	ר.ח.ב./מרחב	term	ספר_ג'יבלי_אלמוקבאלא#nsj0	מרחבם
linear dimension/width	ר.ח.ב./רוחב	term	ספר_ג'יבלי_אלמוקבאלא#P8YW	רחבו
linear dimension/width	ר.ח.ב./מרחב	term	ספר_ג'יבלי_אלמוקבאלא#4CJI	מרחב ה
linear dimension/width	ר.ח.ב./מרחב	term	ספר_ג'יבלי_אלמוקבאלא#jOGZ	מרחב
linear dimension/width	ר.ח.ב./רוחב	term	משנת_המדות#PREy	רחב
linear dimension/width	ר.ח.ב./רוחב	term	בר_נותן_טעם#Ykal	רוחב
linear dimension/width	ר.ח.ב./רוחב	term	מלאכת_המספר#DQWq	רוחב
linear dimension/width		term	ספר_המספר_/_אברהם_אבן_עזרא#FXNE	רחבו

Category	Hashtag	Description	id	parent_id
			2639
algebra	#algebra	mathematical science that studies the process of solving equations expressed in words by manipulations that rely on arithmetic operations	132
algebraic operation	#algebraic operation		692	132
normalization	#normalization		694	692
to normalize	#to normalize		970	694
multiplication of algebraic expressions	#multiplication of algebraic expressions		802	692
to equate	#to equate		865	692
confrontation	#confrontation	cancellation of similar terms on opposite sides of the equation	696	692
to confront	#to confront	to cancel similar terms on opposite sides of the equation	972	696
restoration	#restoration	transposition of subtracted terms to the other side of an equation	695	692
to restore	#to restore	to shift a subtracted term to the other side of an equation	866	695
balancing an equation	#balancing an equation	applying to one side of an equation the same addition or subtraction that was applied to the other side when performing algebraic restoration or confrontation	693	692
transformation between kinds	#transformation between kinds	transforming a quantity from one kind (number, root, power) to another	2620	692
to transform between kinds	#to transform between kinds		1071	2620
algebraic expression	#algebraic expression		861	132
algebraic species	#algebraic species		697	861
x	#x	unknown; usually referred to as thing or root	133	697
x²	#x²	square of an algebraic unknown	687	697
x³	#x³	cube of an unknown	688	697
higher power of x	#higher power of x	fourth or higher power of x	689	697
additional unknown	#additional unknown		974	697
number (algebraic context)	#number (algebraic context)	a known independent number in an algebraic equation	242	697
equation	#equation		698	861
unsolvable equation	#unsolvable equation		463	698
quartic equation	#quartic equation	4-degree equation	717	698
biquadratic equation	#biquadratic equation	4-degree equation without the terms of degree 1 and 3	719	717
cubic equation	#cubic equation	3-degree equation	718	698
quadratic equation	#quadratic equation		701	698
canonical equation	#canonical equation		702	701
simple canonical equation	#simple canonical equation		703	702
roots equal numbers	#R equal N		714	703
squares equal numbers	#S equal N		713	703
squares equal roots	#S equal R		715	703
compound canonical equation	#compound canonical equation		704	702
squares and numbers equal roots	#S+N equal R		711	704
roots and numbers equal squares	#R+N equal S		712	704
squares and roots equal numbers	#S+R equal N		710	704
linear equation	#linear equation	first-degree equation	726	698
system of equations	#system of equations		734	698
side of an equation	#side of an equation		859	698
indeterminate equation	#indeterminate equation		1124	698
algebraist	#algebraist	expert in algebra	781	132
arithmetic	#arithmetic	science that consists of the study of numbers, their properties and the the basic operations applied on them - addition, subtraction, multiplication, division, exponentiation, extraction of roots etc.	365
practical arithmetic			14	365
basic operations			153	14
doubling	#doubling	multiplication of a number by 2	159	153
double	#double	twice the number; its product by 2	387	159
to double	#to double	to multiply a number by 2	785	159
halving	#halving		158	153
to halve	#to halve		786	158
half of	#half of		845	158
extraction of root	#extraction of root		436	153
multiplication of roots	#multiplication of roots		737	436
addition of roots	#addition of roots		738	436
subtraction of roots	#subtraction of roots		739	436
division of roots	#division of roots		740	436
to have a root	#to have a root		792	436
to extract a root	#to extract a root		795	436
to extract a square root	#to extract a square root		880	795
to extract a cube root	#to extract a cube root		881	795
radicand	#radicand	denominated within the root, value whose root is taken	1073	436
root	#root	a number that when multiplied by itself a specified number of times yields a specified number	439	436
cube root	#cube root		558	439
square root	#square root	a number that when multiplied by itself yields a specified number	559	439
expressible	#expressible	expressible number or root	1075	439
inexpressible	#inexpressible	inexpressible number or root	2370	439
higher root	#higher root	fourth or higher root	2634	439
binomial	#binomial	a mathematical expression consisting of two terms, at least one of them a root connected by an addition word (plus), or a subtraction word (minus)	2357	436
false position	#false position		583	153
double false position	#double false position	method of solving mathematical problems by using two random guesses	584	583
guess in false position	#guess in false position		1935	583
single false position	#single false position		1914	583
error of a false position	#error of a false position		2348	583
to err	#to err	to form the error in a false position procedure	2012	2348
exponentiation	#exponentiation		849	153
to square	#to square		853	849
to cube	#to cube		854	849
cubed number	#a³		858	849
squared number	#squared number		857	849
higher power	#higher power	fourth or higher power of a number	855	849
cubing	#cubing	multiplying a number by itself twice, raising a number to its cube	1924	849
rounding	#rounding	replacing with the nearest rank	2423	153
rounded number	#rounded number	the closest number that replaces the given number by the rounding operation	2427	2423
to round	#to round	to replace a number with the nearest rank	2424	2423
subtraction	#subtraction	one of the four basic arithmetic operations that determines the difference between two numbers	155	153
carrying over from a higher rank	#carrying over from a higher rank		190	155
result of subtraction	#result of subtraction	remainder in subtraction	184	155
subtrahend	#subtrahend	number to be subtracted from a number	182	155
to remain	#to remain	to be left after a subtraction procedure	936	155
to leave a remainder	#to leave a remainder		2523	936
minuend	#minuend	number from which a number is to be subtracted	991	155
to subtract	#to subtract	to subtract a number from a number	181	155
less (minus)	#minus	particle indicating a subtraction operation	879	155
subtractive	#subtractive	a mathematical expression consisting of subtraction	789	155
addition	#addition	one of the four basic arithmetic operations; combines two or more numbers and determines their sum	154	153
to add	#to add	to sum	178	154
sum	#sum	result of the addition operation	388	154
sum of natural numbers	#sum of natural numbers		669	388
sum of odd numbers	#sum of odds		670	388
sum of even numbers	#sum of evens		671	388
sum of square numbers	#sum of squares		672	388
sum of cubic numbers	#sum of cubes		673	388
sum of powers of two	#sum of powers of two	sum of even-times-evens	674	388
sum of powers of three	#sum of powers of three		675	388
sum of powers of four	#sum of powers of four		676	388
sum of even squares	#squares of evens		1125	388
sum of odd squares	#squares of odds		1126	388
sum of even cubes	#cubes of evens		1127	388
sum of odd cubes	#cubes of odds		1128	388
addend	#addend	a number to be added to a number	787	154
and (plus)	#plus	particle indicating an addition operation	878	154
additive supplementation	#additive supplementation		598	154
additive supplement	#additive supplement		1033	598
to supplement additively	#to supplement additively		929	598
additive	#additive	a mathematical expression consisting of addition	788	154
division	#division	one of the four basic arithmetic operations; calculates the number of times one number is contained within another number and determines their quotient	157	153
divisor	#divisor	a number by which another number is to be divided	604	157
greatest common divisor	#greatest common divisor		839	604
dividend	#dividend	a number divided by another number	605	157
part	#part	part of the whole number	606	157
to divide	#to divide		784	157
dividing (adjective)	#dividing		798	157
true divisor	#true divisor		2135	157
remainder of division	#remainder of division	the number left after a division procedure that is less than the divisor	458	157
divisible	#divisible	a number that can be divided by another number, with no remainder left	2187	157
quotient	#quotient	result of the division operation; number of times that a number is contained in a number	783	157
proportional share	#share	share resulting from the allotment	2363	157
multiplication	#multiplication	one of the four basic arithmetic operations; repeated addition of the same number as many times as a given number; determines the product of two numbers	156	153
multiplier	#multiplier		186	156
to multiply	#to multiply		185	156
multiplied	#multiplied		358	156
product	#product	the result of the multiplication operation	241	156
times	#times	particle indicating a multiplication operation	243	156
multiplicative supplementation	#multiplicative supplementation		1944	156
to supplement multiplicatively	#to supplement multiplicatively		1945	1944
multiplicatively supplemented	#multiplicatively supplemented		1946	1944
multiplicative inverse	#multiplicative inverse	a number which when multiplied by the original number yields 1	1550	1944
multiplication table	#multiplication table		607	156
multiplicand	#multiplicand	a number multiplied by another	608	156
to triple	#to triple	to multiply by three	1919	156
common multiple	#common multiple		1583	156
to share a common multiple	#to share a common multiple		1584	1583
least common multiple	#least common multiple	least common multiple of two or more numbers; the least number that is divisible by all of them	2628	1583
factor	#factor	a number that when multiplied by another produces a given number	1604	156
common factor	#common factor	a factor that is common to two or more products	989	1604
to share a common factor	#to share a common factor		1582	989
to find a common factor	#to find a common factor		2497	989
multiple	#multiple	product of a number by an integer	1630	156
methods of multiplication	#methods of multiplication		2635	156
triplets method	#triplets method		313	2635
multiplication by shifting	#multiplication by shifting		1157	2635
multiplication by partial shifting	#multiplication by partial shifting		1159	2635
gelosia	#gelosia		1162	2635
horizontal multiplication	#horizontal multiplication		1160	2635
multiplication without shifting	#multiplication without shifting		1158	2635
multiplication wings	#multiplication wings		2339	2635
multiplication tower	#multiplication tower	a method for calculating the multiplication of two numbers, in which the digits are written in a tower-like diagram	2338	2635
vertical multiplication	#vertical multiplication		1161	2635
cross-multiplication	#cross-multiplication	multipication of the numerator of one fraction by the denominator of another fraction then the numerator of the other fraction by the denominator of the first fraction	2521	2635
to cross-multiply	#to cross-multiply	to multiply the numerator of one fraction by the denominator of the other fraction then multiply the numerator of the other fraction by the denominator of the first fraction	2627	2521
conversion	#conversion	changing the numerical value of a quantity by using a different unit of measurement	1551	153
to convert	#to convert	to change the numerical value of a quantity by using a different unit of measurement	1553	1551
decomposing to a fraction	#decomposing to a fraction	dividing a fraction or rank into a smaller fraction or rank	1561	153
to decompose to a fraction	#to decompose to a fraction	to divide a fraction or rank into a smaller fraction or rank	1562	1561
factorization	#factorization		2614	153
to factorize	#to factorize		2615	2614
decimal positional system	#decimal positional system		202	14
positional value	#positional value	the value of the rank in the positional decimal system	218	202
numeral	#numeral	digit, numeral; written symbol for any of the numbers 0-9	204	202
Indo-Arabic numerals	#Indo-Arabic numerals		1636	204
dust letters	#dust letters		216	204
numerical value	#numerical value	value of numeral	217	202
zero	#zero	placeholder arithmetical symbol indicating that there is no number in a specific rank	205	202
to hold the decimal place			234	205
place-holding	#place-holding		2453	205
place holder	#place holder	arithmetical symbol indicating that there is no number in a specific rank	233	205
decimal place	#decimal place	the position of a digit in written place value notation indicating its rank	206	202
decimal rank	#rank	a decimal component of a number	203	202
hundreds	#hundreds		289	203
units	#units	the first decimal rank	287	203
tens	#tens		288	203
tens of thousands	#tens of thousands		346	203
hundreds of thousands	#hundreds of thousands		349	203
millions	#millions	thousands of thousands	350	203
thousands	#thousands		290	203
decade	#decade	any rank higher than the units; product of tens	299	203
empty rank	#empty rank		2138	203
raising the rank	#raising the rank		2371	202
to raise the rank	#to raise the rank		2372	2371
raised to a higher rank	#raised to a higher rank		2373	2371
lowering the rank	#lowering the rank		2636	202
to lower the rank	#to lower the rank		2637	2636
integer	#integer	a number that is not a fraction; a whole number	20	14
to be an integer	#to be an integer		2599	20
fraction	#fraction	numerical quantity that is not an integer, describing the ratio of one or more parts to the whole	15	14
simple fraction	#simple fraction		16	15
multiplication of fractions	#multiplication of fractions		17	16
multiplication of fraction by integer			18	17
division of fractions	#division of fractions		552	16
addition of fractions	#addition of fractions		677	16
subtraction of fractions	#subtraction of fractions		678	16
reduction	#reduction	reduction of the numerator and denominator of a fraction by the same factor	1555	16
reduced	#reduced	fraction (or ratio) whose numerator and denominator have no common divisor other than one	2463	1555
to reduce	#to reduce	to reduce the numerator and denominator of a fraction by the same factor	1556	1555
portion	#portion		579	15
fraction of fraction	#fraction of fraction	the product of a fraction multiplied by a fraction	668	15
forming a fracion	#forming a fracion	breaking up into parts or sections	1627	15
to form a fracion	#to form a fracion	to break up into parts or sections	1581	1627
numerator	#numerator	the part of a fraction that is above the line that indicates the number to be divided by the denominator	570	15
sexagesimal fraction	#sexagesimal fraction	a fraction that is based on sixtieths, i.e. whose denominator equals to a power of sixty	19	15
degree	#degree		1970	19
minute	#minute		1971	19
multiplication of sexagesimal fractions	#multiplication of sexagesimal fractions		547	19
addition of sexagesimal fractions	#addition of sexagesimal fractions		1129	19
subtraction of sexagesimal fractions	#subtraction of sexagesimal fractions		1130	19
division of sexagesimal fractions	#division of sexagesimal fractions		1131	19
zodiac sign	#zodiac sign	a sexagesimal unit consisting of 30 degress	2273	19
second	#second	the second degree of the sexagesimal fractions, sixtieth of a minute or a prime	1972	19
denominator	#denominator	the number below the line in a fraction; the divisor of the numerator	571	15
common denominator	#common denominator	multiple of all the denominators of given fractions	1163	571
denomination	#denomination	forming a fraction by setting a divisor or divisors in the denominator	1789	571
to denominate	#to denominate		1968	1789
determining the common denominator	#determining the common denominator		2359	571
expansion to a common denominator	#expansion to a common denominator		2618	571
change of denominator	#change of denominator		2612	571
to change denominator	#to change denominator		2613	2612
composing denominators	#composing denominators	turning a fraction of fraction into a fraction	2490	15
composed	#composed	composed of different factors	2491	2490
check	#check	verification of the calculation procedure	353	14
scales	#scales	checking method of arithmetic operation	354	353
casting out	#casting out	finding the remainder in division by a certain number for the purpose of verification of calculations	456	353
cast out nines	#cast out nines		457	456
to cast out	#to cast out	to subtract repeatedly	1560	456
result of casting out	#result of casting out	the result of casting out	2139	456
to check	#to check	to check the result of the calculation	2449	353
progression	#progression	sequence of numbers such that each differs from the preceding by a constant quantity	326	14
natural succession	#natural succession	natural numbers in their standard sequence	2576	326
sequential number	#sequential number	preceding/succeeding number	327	326
successive	#successive	sequential	404	326
increment	#increment		2412	326
successively	#successively		2494	326
number of terms	#number of terms	number of terms in a sequence	2285	326
aₙ₋₁	#aₙ₋₁	preceding number in the sequence	2286	326
aₙ₊₁	#aₙ₊₁	consecutive number in the sequence	2287	326
chess	#chess	board game mentioned usually as an illustration of the properties of number sequences	1952	326
chessboard square	#chessboard square	usually represents an item in a sequence of numbers	1953	326
calculation	#calculation	mathematical process of determining a size or a number	228	14
small	#small		341	228
large	#large	great	342	228
to calculate	#to calculate	to determine by mathematical processes	229	228
one who calculates	#one who calculates		230	228
to be worth	#to be worth	to be equivalent in value	393	228
corresponding	#corresponding		446	228
equal	#equal	identical in mathematical value	461	228
to be equal to	#to be equal to	to be identical in mathematical value	429	461
procedure	#procedure	particular way of accomplishing something based on a set of instructions	469	228
to estimate	#to estimate		2500	228
result	#result	outcome of a calculation	876	228
to result	#to result	to be derived as a result of a calculation	875	876
excess	#excess	the amount by which one number or quantity exceeds another	877	228
exceeding	#exceeding		996	877
to exceed	#to exceed	to be greater in number than	420	877
unknown	#unknown	unknown number or quantity	941	228
quantity	#quantity		1931	228
discrete quantity	#discrete quantity	discontinuous quantity	1933	1931
continuous quantity	#continuous quantity		1932	1931
unequal	#unequal		962	228
difference	#difference	difference between two numbers or quantities	997	228
product by a power of ten	#product by a power of ten	product of a given number by a power of ten	2506	228
accurately	#accurately		2483	228
exact	#exact	precise	2447	228
to suffice	#to suffice	to be sufficient	2418	228
order	#order	arrangement of numbers or items in a relation to each other according to a specific sequence	2493	228
counting	#counting	enumerating the numbers so as to determine the total number of units involved	1608	228
to count	#to count	to enumerate the numbers so as to determine the total number of units involved	368	1608
counted	#counted	whose total number of units is determined	1609	1608
approximate	#approximate	close in value or number but not precise	1614	228
approximate root	#approximate root		2485	1614
approximately	#approximately	the state in which a value or a number is almost accurate, but not completely precise	1613	1614
to approximate	#to approximate	to come close to the precise value or number	1612	1614
increasing	#increasing	becoming greater in number	1602	228
to increase	#to increase	to become greater in number	1053	1602
decreasing	#decreasing	becoming smaller in number	1601	228
to decrease	#to decrease	to become smaller in number	1585	1601
total	#total		1629	228
given number	#given number		2007	228
verified	#verified		2079	228
measure	#measure	a standard unit that expresses the size, amount, or quantity of something	633	228
to measure	#to measure		1116	633
measured	#measured	having a specified measurement	1621	633
calculation diagram	#calculation diagram	graphic illustration	1631	228
set aside	#set aside	intermediate result kept in mind for a later stage of the calculation process	960	228
to set aside	#to set aside	to keep in mind an intermediate result for a later stage of the calculation process	459	960
theoretical arithmetic			33	365
relative quantity	#relative quantity		107	33
to relate	#to relate	to determine the ratio between numbers or quantities	1567	107
term	#term	each of the elements in a ratio, progression, or mathematical expression	1578	107
extreme	#extreme	first term or the last term of a progression or proportion	2120	107
mean	#mean		2121	107
geometric mean	#geometric mean	mean term among numbers that maintain a geometric ratio, a₂≡√(a₁∙a₃)	2122	2121
harmonic mean	#harmonic mean	mean term among numbers that maintain a harmonic ratio a₂≡[a₁∙(a₃-a₁)]/(a₁+a₃)+a₁	2124	2121
arithmetic mean	#arithmetic mean	mean term among numbers that maintain an arithmetic ratio, a₂≡½∙(a₁+a₃)	2123	2121
ratio	#ratio	relationship between two amounts or quantities, which indicates the number of times that one value contains or is contained within the other	482	107
compound ratio			122	482
multiple superparticular ratio	#multiple superparticular	ratio in which the greater term exceeds the multiple of the less by one ((n·m)+1):n	130	122
multiple superpartient ratio	#multiple superpartient	ratio in which the greater term exceeds the multiple of the less by more than a unit ((n·m)+a):n	131	122
simple ratio			120	482
multiple ratio	#multiple ratio	ratio in which the greater term is a product of the less by an integer (m·n):m	124	120
superparticular ratio	#superparticular	the ratio of two consecutive integer numbers (n+1):n	125	120
superpartient ratio	#superpartient	ratio in which the greater term exceeds the less by more than a unit (n+m):n	128	120
equality ratio	#equality ratio	ratio of equality: ratio in which the antecedent is equal to the consequent	1549	120
duplicate	#duplicate	ratio compounded with itself	968	482
triplicate	#triplicate		969	482
inequality	#inequality		2470	482
proportion	#proportion	equality between two ratios, when the ratio of the first term to the second term is equal to the ratio of the third term to the fourth term	564	482
arithmetic proportion	#arithmetic proportion	proportion in which the difference between any term and its predecessor is a fixed constant, a₃-a₂≡a₂-a₁	1769	564
alternation	#alternation	alternation of the terms in a proportion	2410	564
to alternate	#to alternate	to alternate the terms of a proportion	2408	2410
geometric proportion	#geometric proportion	proportion in which the ratio of one term to the second term is the same as the ratio of the second term to the third term, (a₁:a₂)≡(a₂:a₃)	1770	564
harmonic proportion	#harmonic proportion	proportion in which the ratio of the greater term to the smaller term is the same as the ratio of the excess of the greater term over the mean term to the excess of the mean term over the smaller term, (a₃:a₁)≡(a₃-a₂):(a₂-a₁)	1771	564
rule of three	#rule of three	proportion of four numbers	567	564
proportional triad	#proportional triad	proportion of three numbers	568	567
proportional	#proportional		994	564
subcontrary proportion	#subcontrary proportion		2515	564
absolute quantity	#absolute quantity		34	33
number	#number	arithmetical value that represents a particular quantity; sum of units	35	34
types of number	#types of number		523	35
relatively prime	#relatively prime	numbers that have no common factors other than 1	78	523
plane number	#plane number	product of two integers that represents a two-dimensional shape	83	523
square number	#square number	the product of a number multiplied by itself, a²	86	83
circular number	#circular number	square number that ends with the same digits as its root	95	86
polygonal number	#polygonal number	nth polygonal number is a number that can be represented by distinct dots arranged in the outlines of regular polygons with sides up to n dots that share one vertex	88	83
hexagonal number	#hexagonal number	polygonal number that represents a hexagon, ½∙(4n²-2n)	1777	88
heptagonal number	#heptagonal number	polygonal number that represents a heptagon, ½∙(5n²-3n)	1778	88
octagonal number	#octagonal number	polygonal number that represents an octagon, ½∙(6n²-4n)	1779	88
nonagonal number	#nonagonal number	polygonal number that represents a nonagon, ½∙(7n²-5n)	1780	88
decagonal number	#decagonal number	polygonal number that represents a decagon, ½∙(8n²-6n)	1781	88
pentagonal number	#pentagonal number	polygonal number that represents a pentagon, ½∙(3n²-n)	87	88
oblong number	#oblong number	product of two different number, one of which exceeds the other by more than one, n∙(n+m)	1784	83
heteromecic number	#heteromecic number	product of two consecutive integers, n∙(n+1)	1772	83
triangular number	#triangular number	nth triangular number is a number that can be represented by distinct dots arranged as a full equilateral triangle with n dots on its side, ½∙(n²+n)	85	83
natural number	#natural number		2577	523
cyclic number	#cyclic number		345	523
odd number	#odd number	integer that cannot be divided by two into two equal integers, (2n-1)	65	523
prime incomposite number	#prime incomposite number	a number that cannot be divided by any number other than one	76	65
composite odd number	#composite odd number	an odd number that is a product of any odd numbers other than one	77	65
odd-times-odd number	#odd-times-odd number		2341	65
sieve	#sieve	method for sorting out prime from composite numbers	2365	65
amicable numbers	#amicable numbers	two numbers such that the sum of the divisors of each is equal to the other number	2461	523
linear number	#linear number	a number that represents one side of a plane shape	2462	523
composite number	#composite number		1977	523
relatively composite	#relatively composite	numbers that have a common factor	2546	1977
even number	#even number	a number that is divisible by two with no remainder left, 2n	63	523
even-times-even number	#even-times-even number	a number that is a power of two, 2ⁿ	69	63
even-times-odd number	#even-times-odd number	a number that is a product of two by an odd number, 2∙(2n-1)	70	63
perfect number	#perfect number	a number that is equal to the sum of its proper divisors	75	63
deficient number	#deficient number	a number that is greater than the sum of its proper divisors	1150	75
superabundant number	#superabundant number	a number that is smaller than the sum of its proper divisors	1151	75
even-times-even-times-odd number	#even-times-even-times-odd number	a number that is a product of a power of two by an odd number, 2ⁿ∙(2n-1)	71	63
solid number	#solid number	product of three integers that represents a three-dimensional shape	89	523
scalene number	#scalene number	product of three different integers	92	89
parallelepipedon number	#parallelepipedon number	product of two consecutive numbers multiplied again by one of them, product of a heteromecic number by one of its sides, n²∙(n+1), or n∙(n+1)²	93	89
brick number	#brick number	product of two consecutive numbers multiplied again by the smaller number; product of a heteromecic number by its smaller side; (n-1)²∙n	94	93
pyramidal number	#pyramidal number	the number of stacked spheres in a pyramid with a polygonal base, where each layer of the pyramid is a polygon of spheres	1785	89
cubic number	#cubic number	the product of a number multiplied twice by itself, a³	91	89
spherical number	#spherical number	cubic number that ends with the same digits as its root	96	91
beam number	#beam number	product of a number multiplied by itself then by a greater number	2133	89
unit	#unit		369	34
unity	#unity	the essence of the one; the property of being one	370	34
numerical quantity	#numerical quantity	numerical quantity as a genus	2580	33
endlessly	#endlessly		1918	33
arithmetician	#arithmetician	expert in arithmetic	782	365
authors			509
biblical quotes	#bible		494
combinatorics	#combinatorics		2240
collection	#collection	collection of items	2440	2240
n!	#n!	the number of permutations of n objects without repetition; n factorial	2255	2240
combination	#combination	a selection of objects (order does not matter)	2243	2240
permutation	#permutation	ordered arrangement of a set of objects	2241	2240
variation	#variation	ordered arrangement of a selection of objects	2242	2240
general terminology			192
economic terms	#economic terms		194	192
coins	#coins		2643	194
weights and measures	#weights and measures		1068	194
geographical place	#geographical place		2593
geometry	#geometry	science that is concerned with properties and relations of shapes	302
geometric relations	#geometric relations		2641	302
to revolve around	#to revolve around		274	2641
inscribed	#inscribed	drawn within another shape so that its boundaries touch it but do not cross it	2525	2641
to encompass	#to encompass		1917	2641
encompassed	#encompassed	drawn around another shape so that it touches its boundaries but does not cut it	2526	1917
to intersect	#to intersect		824	2641
to cut off	#to cut off		837	2641
to be the side of an area	#to be the side of an area		964	2641
to divide a figure	#to divide a figure		1114	2641
congruent figures	#congruent figures		2531	2641
to join	#to join		2052	2641
joined	#joined		2053	2052
to touch	#to touch		2230	2641
commensurable	#commensurable	magnitudes that can be measured by the same measure	2539	2641
similar figures	#similar figures		2532	2641
commensurable in square	#commensurable in square	straight lines such that the squares on them are measured by the same area	2541	2641
end	#end	limit	279	302
section	#section		2478	302
geometrical shape	#geometrical shape		303	302
line	#line	breadthless length	592	303
parallel	#parallel		825	592
straight line	#straight line		817	592
in a straight manner	#straight		942	817
to cut a line	#to cut a line		820	592
segment	#segment		821	592
to extend a line	#to extend a line		822	592
perimeter	#perimeter		1110	592
height	#height	the measurement of a thing from base to top or from head to foot	1111	592
diameter	#diameter		1107	592
circular line	#circular line	a line that consists of all the points in a plane that are at a given distance from a fixed point	1152	592
perpendicular	#perpendicular	at an angle of 90° to a given line, plane, or surface	2460	592
hypotenuse	#hypotenuse	the side of a right-angled triangle that is opposite the right angle	1607	592
diagonal	#diagonal	a straight line connecting two opposite vertices of a polygon	1106	592
curve	#curve	a line that is not straight	1153	592
uniform line	#uniform line		2165	592
extension	#extension		2601	592
apotome	#apotome	a segment of a line whose complementary segment is commensurable in power only to the whole line	2358	592
solid	#solid	solid figure, three-dimensional figure	587	303
parallelepiped	#parallelepiped	a three-dimensional shape whose faces are parallelograms	2557	587
cone	#cone	a three-dimensional shape whose base is a circle and whose head is a vertex at a vertical line from the center of the circle	1099	587
truncated solid	#truncated		2481	587
pyramid	#pyramid	a three-dimensional shape whose base is a polygon and its faces are triangles with a common vertex	1097	587
sphere	#sphere	a three-dimensional shape whose all points on its surface are at a given distance from its center	1098	587
axis	#axis	a straight line about which the sphere revolves	1143	1098
pole	#pole	two points that are the ends of the axis of the sphere	1144	1143
hemisheper	#hemisphere	half of a sphere	2321	1098
cylinder	#cylinder	a three-dimensional shape whose two bases are identical parallel circles	1101	587
cube	#cube	three-dimensional regular body	1102	587
ellipsoid	#ellipsoid	a three-dimensional figure whose plane cross sections are either ellipses or circles	1142	587
solid angle	#solid angle	an angle formed by two planes intersecting at a common point	2126	587
sharp solid	#sharp solid	solid with a broad base and a sharp apex	2132	587
volume	#volume	the amount of space occupied by a three-dimensional shape	2219	587
face	#face	surface that forms part of the boundary of a solid	2465	587
beam	#beam	a three-dimensional shape having two equal dimensions and a larger third dimension, bounded by four square faces and two parallel square faces	2434	587
prism	#prism	three-dimensional shape that has two identical parallel polygonal faces and the other faces are parallelograms	1100	587
point	#point	a geometric element that has no dimensions	833	303
apex	#apex		2477	833
center	#center	point inside the circle or sphere, from which all straight lines that are drawn to the the circumference of the circle, or to the surface of the sphere, are equal	1108	833
surface	#surface	a two-dimensional extension	814	303
side	#side	a bounding line joining two adjacent vertice of a geometric figure	325	814
scalene	#scalene		596	814
isosceles	#isosceles		597	814
quadrilateral	#quadrilateral	a four-sided figure	590	814
rectangle	#rectangle	parallelogram with four right angles	591	590
trapezoid	#trapezoid	quadrilateral that have only one pair of parallel sides	1094	590
parallelogram	#parallelogram	a quadrilateral whose opposite sides are parallel and equal	1096	590
rhombus	#rhombus	parallelogram whose all sides are equal, and all angles are not right angles	1095	590
square	#square	quadrilateral with four equal sides and four right angles	305	590
planar	#planar	lying in a plane	588	814
to form an area	#to form an area		838	814
polygon	#polygon	plane closed geometrical shape that comprises three or more connected straight lines	1141	814
pentagon	#pentagon	plane geometrical shape, which has five sides and five angles	2170	1141
hexagon	#hexagon	plane geometrical shape, which has six sides and six angles	2171	1141
flat surface	#flat surface	flat, two-dimensional surface	2167	814
convex surface	#convex surface	surface that curves outward like the exterior of a sphere	2168	814
concave surface	#concave surface	surface that curves inward like the interior of a sphere	2169	814
circle	#circle	a two-dimensional shape whose circumference consists of all the points in a plane that are at a given distance from its center	304	814
to draw a circle	#to circle		2498	304
sector	#sector		2552	304
versine	#versine	sagitta	1117	304
chord	#chord		1118	304
arc	#arc	a part of the circumference of a circle or a curve	1119	304
segment of a circle	#circular segment		2305	304
semicircle	#semicircle		2306	304
less than a semicircle	#less than a semicircle		2307	2306
greater than a semicircle	#greater than a semicircle		2308	2306
gnomon	#gnomon	the part of a parallelogram left when a similar smaller parallelogram has been taken from its corner	815	814
triangle	#triangle	a plane figure having three straight sides and three angles	589	814
equilateral triangle	#equilateral triangle		595	589
angle	#angle	the space between two intersecting lines that meet at one point	1090	303
angle between straight lines	#angle between straight lines		2649	1090
right angle	#right angle	angle created by two lines that are perpendicular to each other, angle of 90º	1091	1090
right-angled	#right-angled		1104	1091
acute angle	#acute angle	angle that is less than 90º	1092	1090
acute-angled	#acute-angled		1103	1092
obtuse angle	#obtuse angle	angle that is greater than 90º	1093	1090
obtuse-angled	#obtuse-angled		1105	1093
plane angle	#plane angle	angle formed by two lines that are contained in the same plane	2127	1090
to construct	#to construct	to construct a geometrical shape	1015	303
base	#base	side or face of a geometric shape from which an altitude can be constructed	1121	303
euclidean propositions			247	302
Elements			248	247
Elements VII-11	#Elements VII-11		2651	248
Elements XIII-1	#Elements XIII-1		2652	248
Elements II-2	#Elements II-2		250	248
Elements XIII-3	#Elements XIII-3		2653	248
Elements XIII-9	#Elements XIII-9		2655	248
Elements XIII-5	#Elements XIII-5		2654	248
Elements XIII-10	#Elements XIII-10		2656	248
Elements II-1	#Elements II-1		249	248
Elements II-3	#Elements II-3		251	248
Elements II-4	#Elements II-4		252	248
Elements II-5	#Elements II-5		253	248
Elements II-6	#Elements II-6		254	248
Elements II-7	#Elements II-7		255	248
Elements II-8	#Elements II-8		256	248
Elements II-9	#Elements II-9		257	248
Elements II-10	#Elements II-10		258	248
Elements VIII-11	#Elements VIII-11		811	248
Elements VIII-12	#Elements VIII-12		812	248
Elements VI-17	#Elements VI-17		813	248
Elements-Introduction	#Elements-Introduction		1132	248
Elements IX-21	#Elements IX-21		1133	248
Elements IX-22	#Elements IX-22		1134	248
Elements IX-23	#Elements IX-23		1135	248
Elements V-8	#Elements V-8		1136	248
Elements V-9	#Elements V-9		1137	248
Elements V-15	#Elements V-15		1138	248
Elements IX-28	#Elements IX-28		1139	248
Elements IX-29	#Elements IX-29		1140	248
magnitude	#magnitude		586	302
area	#area	the measure of the surface of a two-dimensional geometric shape	816	586
distance	#distance		2503	586
to draw	#to draw		819	302
geometrician	#geometrician	expert in geometry	846	302
upper base	#upper base		1122	302
linear dimension	#dimension	measurement in one direction; length, width, height, or depth	315	302
length	#length	the measurement of a thing from end to end	316	315
width	#width	the measurement of a thing from side to side, breadth	317	315
depth	#depth		593	315
science	#science		2642
linguistics	#linguistics		295	2642
grammarian	#grammarian		946	295
philosophy	#philosophy		276	2642
wisdom	#wisdom		277	276
wise	#wise	scholar	355	277
philosopher	#philosopher		1980	276
music	#music		483	2642
harmony	#harmony		1754	483
diatessaron	#diatessaron	interval of a fourth	1755	1754
diapente	#diapente	interval of a fifth	1756	1754
diapason	#diapason	entire range of musical tones	1757	1754
mathematics	#mathematics		534	2642
practical science	#practical science		2469	2642
external science	#external science		2484	2642
physics	#physics		1596	2642
astrology	#astrology		2075	2642
astrologer	#astrologer	expert in astrology	2076	2075
ethics	#ethics		1997	2642
optics	#optics		1998	2642
metaphysics	#metaphysics		2000	2642
politics	#politics		1999	2642
logic	#logic		1996	2642
logical terms			193	1996
example	#example		197	193
to give an example	#to give an example		898	197
proof	#proof		198	193
to prove	#to prove		199	198
rule	#rule		222	193
reason	#reason		311	193
demonstrative	#demonstrative	exemplary	519	193
to assume	#to assume	to suppose	2413	193
quod erat demonstrandum	#QED	what was to be shown, it has been demonstrated	780	193
analogy	#analogy		902	193
to deduce	#to deduce	to conclude	901	193
essence	#essence		1058	193
proposition	#proposition	mathematical statement that is assumed or proved to be true	2633	193
word problem	#word problem		609
magic square	#magic square		2646	609
pricing problem	#pricing problem		610	609
find the price	#find the price		629	610
find the amount	#find the amount		630	610
tare and tret	#tare and tret		631	610
exchange problem	#exchange problem		611	609
currency	#currency		632	611
exchange-measure	#exchange-measure		867	611
payment problem	#payment problem		612	609
barter problem	#barter problem		613	609
cash barter	#cash barter		634	613
compound barter	#compound barter		635	613
simple barter	#simple barter		636	613
interest and discount problem	#interest and discount problem		614	609
simple discount	#simple discount		637	614
compound discount	#compound discount		639	614
compound interest	#compound interest		640	614
find the interest	#find the interest		638	614
find the time	#find the time		660	614
find the interest rate	#find the rate		665	614
find the fund	#find the fund		666	614
rent problem	#rent problem		615	609
partnership problem	#partnership problem		616	609
same time	#same time		661	616
different times	#different times		662	616
mixture and alligation problem	#mixture and alligation problem		617	609
divide a quantity problem	#divide a quantity problem		621	609
simple division	#simple division		644	621
proportional division	#proportional division		645	621
simultaneous division	#simultaneous division		646	621
twins	#twins		647	621
find a quantity	#find a quantity		620	609
how much	#how much		648	620
how many	#how many		649	620
whole from parts	#whole from parts		650	620
first from last	#first from last		651	620
multiple quantities	#multiple quantities		652	620
purchase problem	#purchase problem		622	609
buy and sell	#buy and sell		641	622
equal amount	#equal amount		642	622
unequal amount	#unequal amount		643	622
joint purchase problem	#joint purchase problem		623	609
found purse	#found purse		2644	623
too much and too little	#too much and too little		2645	623
if you give me	#if you give me		664	623
partial payment problem	#partial payment problem		624	609
shared work problem	#shared work problem		625	609
motion problem	#motion problem		626	609
pursuit problem	#pursuit problem		657	626
encounter problem	#encounter problem		658	626
to and from	#to and from		659	626
give and take problem	#give and take problem		627	609
ordering problem	#ordering problem		628	609
geometrical problem	#geometrical problem		653	609
figure problem	#figure problem		654	653
find the point	#find the point		2647	654
find the side	#find the side		679	654
find the area	#find the area		680	654
find the volume	#find the volume		681	654
find the perimeter	#find the perimeter		682	654
find the diagonal	#find the diagonal		683	654
find the height	#find the height		685	654
dividing a figure	#dividing a figure		686	654
triangulation problem	#triangulation problem		655	653
construction problem	#construction problem		656	653
gaging problem	#gaging problem		2582	653
transformation problem	#transformation problem		2583	653
boiling problem	#boiling problem		663	609
find a number	#find a number		618	609
divide a number	#divide a number		619	609
guessing problem	#guessing problem		667	609
works	#works		2650
א.ב.י.	#א.ב.י.		2236
אב	#אב		2239	2236
אבן	#אבן		2404
א.ב.ק.	#א.ב.ק.		1811
אבק	#אבק		1814	1811
א.ה.ב.	#א.ה.ב.		2252
נאהב	#נאהב		2253	2252
אוש	#אוש		2393
א.ו.ת.	#א.ו.ת.		1329
אות	#אות		1332	1329
אותיות הודו	#אותיות הודו		1432	1329
א.ז.נ.	#א.ז.נ.		1449
מאזנים	#מאזנים		1453	1449
א.ח.ד.	#א.ח.ד.		1685
אחדות	#אחדות		1686	1685
אחד	#אחד		2309	1685
א.י.כ.	#א.י.כ.		2267
איכות	#איכות		2269	2267
אלא	#אלא		2015
אלג'בר	#אלג'בר		1307
אלגו	#אלגו		1304
א.ל.ה.	#א.ל.ה.		2274
אלוהית	#אלוהית		1995	2274
אלון	#אלון		2395
אלוני	#אלוני		2396
אלזיברא	#אלזיברא		1825
אלכסון	#אלכסון		1878
א.ל.מ.	#א.ל.מ.		1379
אלם	#אלם		1382	1379
אנושית	#אנושית		1990
א.ס.פ.	#א.ס.פ.		1173
אסף	#אסף		1190	1173
נאסף	#נאסף		1347	1173
אסיפה	#אסיפה		2205	1173
אצטוונא	#אצטוונא		2284
אריחי	#אריחי		2433
אריתמטיקה	#אריתמטיקה		1637
א.ר.כ.	#א.ר.כ.		1482
אורך	#אורך		1489	1482
ארוך	#ארוך		1457	1482
אשקקור	#אשקקור		1949
אתרוג	#אתרוג		2290
ב.ד.ד.	#ב.ד.ד.		2251
בודד	#בודד		2254	2251
ב.ד.ל.	#ב.ד.ל.		1648
מובדל	#מובדל		2547	1648
הבדל	#הבדל		1651	1648
הבדיל	#הבדיל		2040	1648
נבדל	#נבדל		2538	1648
ב.ו.א.	#ב.ו.א.		1565
בא	#בא		1566	1565
ב.י.צ.	#ב.י.צ.		2158
ביצני	#ביצני		2159	2158
דומה לביצה	#דומה לביצה		2160	2158
בית	#בית		1951
ב.נ.י.	#ב.נ.י.		2237
בן	#בן		2238	2237
בניין	#בניין		2246	2237
בעל שני שמות	#בעל שני שמות		2356
ב.צ.ע.	#ב.צ.ע.		2517
בצע	#בצע		2520	2517
ב.ק.ע.	#ב.ק.ע.		2516
בקע	#בקע		2518	2516
הבקיע	#הבקיע		2519	2516
ב.ק.ש.	#ב.ק.ש.		1632
מבוקש	#מבוקש		1633	1632
ב.ר.ח.	#ב.ר.ח.		2176
בריח	#בריח		2179	2176
בשתי וערב	#בשתי וערב		2522
ג.ב.ה.	#ג.ב.ה.		1479
גובה	#גובה		1490	1479
ג.ב.ל.	#ג.ב.ל.		1579
גבול	#גבול		1580	1579
גג	#גג		2288
ג.ד.ל.	#ג.ד.ל.		2196
גודל	#גודל		2197	2196
מגדל	#מגדל		2336	2196
ג.ד.ר.	#ג.ד.ר.		1371
גדר	#גדר		1372	1371
נגדר	#נגדר		1836	1371
לקח גדר	#לקח גדר		2073	1371
גו	#גו		2457
גוף	#גוף		1445
גוף שוה	#גוף שוה		1446	1445
גיאומטריה	#גיאומטריה		2001
גיל	#גיל		2406
גילי	#גילי		2588
גימטריא	#גימטריא		1301
ג.ל.ג.ל.	#ג.ל.ג.ל.		1468
גלגל	#גלגל		1472	1468
ג.ל.מ.	#ג.ל.מ.		2150
גלומה	#גלומה		1339	2150
גולם	#גולם		2151	2150
ג.ר.מ.	#ג.ר.מ.		2569
גרמי	#גרמי		2571	2569
גרם	#גרם		2570	2569
ג.ר.ע.	#ג.ר.ע.		1181
מגרעת	#מגרעת		1193	1181
גרע	#גרע		1192	1181
גרעון	#גרעון		1248	1181
נגרע	#נגרע		1365	1181
גורע	#גורע		2031	1181
גרוע	#גרוע		2070	1181
מוגרע	#מוגרע		2329	1181
נגרע ממנו	#נגרע ממנו		2330	1181
גריעה	#גריעה		2334	1181
הוגרע	#הוגרע		2585	1181
ג.ר.ר.	#ג.ר.ר.		2106
מגורר	#מגורר		2111	2106
מתגורר	#מתגורר		2112	2106
ג.ש.מ.	#ג.ש.מ.		1845
גשם	#גשם		1850	1845
מוגשם	#מוגשם		1851	1845
גשמי	#גשמי		1852	1845
ד.ב.ק.	#ד.ב.ק.		2047
מתדבק	#מתדבק		1859	2047
הדביק	#הדביק		2049	2047
דבק	#דבק		2055	2047
דובק	#דובק		2048	2047
ד.ב.ר.	#ד.ב.ר.		1299
דבר	#דבר		1309	1299
מדובר	#מדובר		2192	1299
דובר	#דובר		2193	1299
מדבר	#מדבר		2369	1299
ד.י.נ.	#ד.י.נ.		2387
מדינית	#מדינית		1991	2387
דינר	#דינר		1302
ד.מ.י.	#ד.מ.י.		1396
דמיון	#דמיון		1712	1396
דומה	#דומה		1397	1396
מדומה	#מדומה		1682	1396
דמיוני	#דמיוני		2026	1396
ד.ק.ד.ק.	#ד.ק.ד.ק.		1384
דקדק	#דקדק		1387	1384
מדוקדק	#מדוקדק		1388	1384
בדקדוק	#בדקדוק		2074	1384
ד.ר.ג.	#ד.ר.ג.		1317
מדרגה	#מדרגה		1344	1317
דרהם	#דרהם		1305
ד.ר.כ.	#ד.ר.כ.		1353
דרך	#דרך		1894	1353
דרך המספר	#דרך המספר		1355	1353
דרך החשבון	#דרך החשבון		1356	1353
דרך השלשה	#דרך השלשה		2258	1353
ה.ג.י.	#ה.ג.י.		2277
הגיון	#הגיון		2278	2277
הוא הוא	#הוא הוא		2514
הוי	#הוי		2270
ה.ל.כ.	#ה.ל.כ.		1593
הלך	#הלך		1594	1593
הנדסה	#הנדסה		1644
ה.פ.כ.	#ה.פ.כ.		2419
הפך	#הפך		2420	2419
השחית חוב	#השחית חוב		2563
ז.ו.ג.	#ז.ו.ג.		1330
זוג	#זוג		1333	1330
זוג הזוג	#זוג הזוג		1334	1330
זוג הזוג והנפרד	#זוג הזוג והנפרד		1335	1330
זוג הנפרד	#זוג הנפרד		2125	1330
זוית	#זוית		1337
זולת	#זולת		2199
זולתי האורך	#זולתי האורך		2115	2199
זולתי	#זולתי		2198	2199
ז.ו.ר.	#ז.ו.ר.		2331
נזור	#נזור		2332	2331
נזורות	#נזורות		2333	2331
ז.נ.ב.	#ז.נ.ב.		1671
מזדנב	#מזדנב		2442	1671
מזונב	#מזונב		1673	1671
ז.ר.ק.	#ז.ר.ק.		2382
זרק	#זרק		2383	2382
ח.ב.ל.	#ח.ב.ל.		2066
תחבולה	#תחבולה		2067	2066
ח.ב.ר.	#ח.ב.ר.		1164
נתחבר	#נתחבר		2436	1164
מחברת	#מחברת		1166	1164
חבר	#חבר		1165	1164
חבור	#חבור		1208	1164
מחובר	#מחובר		1220	1164
התחבר	#התחבר		1215	1164
נחבר	#נחבר		1346	1164
חובר	#חובר		2083	1164
חבורי	#חבורי		2095	1164
ח.ד.ד.	#ח.ד.ד.		1529
חד	#חד		1343	1529
מחודד	#מחודד		1530	1529
חוט	#חוט		2289
ח.ו.צ.	#ח.ו.צ.		2389
חיצונית	#חיצונית		1982	2389
ח.ז.ק.	#ח.ז.ק.		1486
הוחזק	#הוחזק		2564	1486
החזיק	#החזיק		1487	1486
ח.ז.ר.	#ח.ז.ר.		1424
החזרה	#החזרה		1428	1424
החזיר	#החזיר		1429	1424
חזרה	#חזרה		2489	1424
ח.ט.א.	#ח.ט.א.		2346
חטא	#חטא		2347	2346
ח.כ.מ.	#ח.כ.מ.		1298
חכמת המספר והחשבון	#חכמת המספר והחשבון		1807	1298
חכמי האלג'בר	#חכמי האלג'בר		1311	1298
חכמי הגימטריא	#חכמי הגימטריא		1312	1298
חכמי השעור	#חכמי השעור		1323	1298
חכמי המנין	#חכמי המנין		1324	1298
חכמי המספר	#חכמי המספר		1327	1298
חכמי החשבון	#חכמי החשבון		1328	1298
חכמי המזלות	#חכמי המזלות		1439	1298
חכמי המדות	#חכמי המדות		1512	1298
חכמה	#חכמה		1589	1298
חכמי הדקדוק	#חכמי הדקדוק		1829	1298
חכמי האמת	#חכמי האמת		1978	1298
חכמי ערב	#חכמי ערב		1979	1298
ח.ל.פ.	#ח.ל.פ.		1496
מתחלף ארכים	#מתחלף ארכים		2578	1496
מתחלפות בסדר	#מתחלפות בסדר		2429	1496
מתחלפות בנושאים	#מתחלפות בנושאים		2430	1496
מתחלפות אם בסדר אם בנושאים	#מתחלפות אם בסדר אם בנושאים		2431	1496
נחלף	#נחלף		1411	1496
חלוף	#חלוף		1507	1496
מתחלף צלעות	#מתחלף צלעות		1865	1496
חלופה	#חלופה		2207	1496
ח.ל.ק.	#ח.ל.ק.		1172
חולק	#חולק		1966	1172
חלקים	#חלקים		1295	1172
חלוקה	#חלוקה		1221	1172
החלק	#החלק		1222	1172
נחלק	#נחלק		1226	1172
מחולק	#מחולק		1227	1172
מחלק	#מחלק		1228	1172
חלוק	#חלוק		1223	1172
חלק	#חלק		1259	1172
התחלק	#התחלק		1225	1172
מחלוקת	#מחלוקת		1370	1172
חלקי חכמי המזלות	#חלקי חכמי המזלות		1441	1172
מתחלק	#מתחלק		1563	1172
חלוק באמצע	#חלוק באמצע		1866	1172
עלה לחלק	#עלה לחלק		2041	1172
הגיע לחלק	#הגיע לחלק		2042	1172
חלק לחצאים	#חלק לחצאים		2058	1172
נחלק לחצאים	#נחלק לחצאים		2059	1172
חלק קו	#חלק קו		2060	1172
מחולק עליו	#מחולק עליו		2322	1172
חולק באמצע	#חולק באמצע		1867	1172
ח.מ.ש.	#ח.מ.ש.		1670
מחומש	#מחומש		1672	1670
ח.נ.י.	#ח.נ.י.		2020
מחנה	#מחנה		2021	2020
ח.ס.ר.	#ח.ס.ר.		1361
חוסר	#חוסר		1840	1361
חסור	#חסור		1657	1361
מחוסר	#מחוסר		1674	1361
מחסיר	#מחסיר		2438	1361
חסר	#חסר		1362	1361
חסרון	#חסרון		1514	1361
נחסר	#נחסר		2030	1361
ח.פ.נ.	#ח.פ.נ.		1792
חופן	#חופן		1793	1792
חפנים	#חפנים		1794	1792
ח.צ.י.	#ח.צ.י.		1368
חצה	#חצה		1369	1368
נחצה	#נחצה		2057	1368
חצויה	#חצויה		2213	1368
חציה	#חציה		2368	1368
ח.צ.צ.	#ח.צ.צ.		1474
חץ	#חץ		1476	1474
ח.ק.ק.	#ח.ק.ק.		2217
לחוק	#לחוק		2218	2217
ח.ר.ט.	#ח.ר.ט.		2397
חרוט	#חרוט		2398	2397
ח.ר.ש.	#ח.ר.ש.		1378
חרש	#חרש		1381	1378
ח.ש.ב.	#ח.ש.ב.		1183
חשבוני	#חשבוני	אמצעי החשבון	1743	1183
חשבון	#חשבון		1200	1183
חשב	#חשב		1269	1183
התחשב	#התחשב		1460	1183
בעלי החשבון	#בעלי החשבון		1812	1183
חשבן	#חשבן		2087	1183
נחשב	#נחשב		2402	1183
ח.ת.כ.	#ח.ת.כ.		1830
חתיכה	#חתיכה		2551	1830
חתך	#חתך		1831	1830
חתוך	#חתוך		2553	1830
ח.ת.מ.	#ח.ת.מ.		1795
החתים	#החתים		1796	1795
חתום	#חתום		1797	1795
טבלה	#טבלה		2315
ט.ב.ע.	#ט.ב.ע.		2279
טבעי	#טבעי		2575	2279
טבע	#טבע		1994	2279
חכמה טבעית	#חכמה טבעית		1590	2279
טור	#טור		1481
ט.ע.י.	#ט.ע.י.		1962
טעות	#טעות		1963	1962
טעה	#טעה		1964	1962
מוטעה	#מוטעה		2091	1962
י.ד.ע.	#י.ד.ע.		2009
בלתי ידוע	#בלתי ידוע		2010	2009
י.ח.ד.	#י.ח.ד.		2191
מיוחד	#מיוחד		1393	2191
י.ח.ס.	#י.ח.ס.		1275
יוחס	#יוחס		1279	1275
יחס	#יחס		1276	1275
מתיחס	#מתיחס		1277	1275
התיחסות	#התיחסות		1278	1275
התיחסות ג' מספרים	#התיחסות ג' מספרים		1908	1275
דרך היחס	#דרך היחס		1909	1275
יחסי	#יחסי		2263	1275
התיחס	#התיחס		2586	1275
י.כ.ח.	#י.כ.ח.		1442
מוכיח	#מוכיח		1443	1442
י.ל.ד.	#י.ל.ד.		1354
תולדת	#תולדת		1357	1354
נולד	#נולד		2379	1354
י.ס.ד.	#י.ס.ד.		2003
יסוד	#יסוד		2004	2003
מוסד	#מוסד		2005	2003
י.ס.פ.	#י.ס.פ.		1178
מוסיף חלק	#מוסיף חלק	יחס המוסיף חלק	1659	1178
מוסיף חלקים	#מוסיף חלקים		1660	1178
תוספת	#תוספת		1207	1178
מוסיף	#מוסיף		2437	1178
נוסף	#נוסף		1213	1178
מוסף	#מוסף		1214	1178
הוסיף	#הוסיף		1206	1178
התוסף	#התוסף		1212	1178
נתוסף	#נתוסף		2510	1178
הוספה	#הוספה		2511	1178
י.ס.ר.	#י.ס.ר.		2388
המוסר	#המוסר		1993	2388
י.פ.ת.	#י.פ.ת.		1897
מופת	#מופת		1898	1897
י.צ.א.	#י.צ.א.		1186
יוצא	#יוצא		1233	1186
יצא	#יצא		1231	1186
הוציא	#הוציא		1232	1186
הוציא ט"ט	#הוציא ט"ט		1454	1186
יצא ט"ט	#יצא ט"ט		1455	1186
הוצאה	#הוצאה		1462	1186
הוצא	#הוצא		2562	1186
י.צ.ב.	#י.צ.ב.		2185
נצב	#נצב		1341	2185
נצב זוית	#נצב זוית		2186	2185
מצבה	#מצבה		2212	2185
י.צ.ע.	#י.צ.ע.		1973
הצעה	#הצעה		1974	1973
הציע	#הציע		2094	1973
י.צ.ר.	#י.צ.ר.		2385
יצורים	#יצורים		1988	2385
יצורית	#יצורית		1989	2385
י.ר.ד.	#י.ר.ד.		1798
הוריד	#הוריד		1799	1798
ירד	#ירד		1800	1798
ירידה	#ירידה		1801	1798
הורדה	#הורדה		2342	1798
יורד	#יורד		2354	1798
מורד	#מורד		2355	1798
הורד	#הורד		2407	1798
י.ר.ה.	#י.ר.ה.		1188
מורה	#מורה		1239	1188
הורה	#הורה		1444	1188
מורה צדק	#מורה צדק		2134	1188
י.ש.ב.	#י.ש.ב.		1885
תושבת	#תושבת		1893	1885
מושב	#מושב		2401	1885
י.ש.ר.	#י.ש.ר.		1844
משור	#משור		1846	1844
ישר	#ישר		1847	1844
ביושר	#ביושר		1849	1844
ישר קוים	#ישר קוים		2568	1844
ישרה	#ישרה		1340	1844
על יושר	#על יושר		2038	1844
מיושר	#מיושר		2166	1844
י.ת.ר.	#י.ת.ר.		1349
מיתר	#מיתר		2558	1349
יתר	#יתר		1351	1349
נותר	#נותר		1463	1349
מותר	#מותר		1508	1349
יתרון	#יתרון		1513	1349
יותר	#יותר		2536	1349
כ.ב.ר.	#כ.ב.ר.		1484
מכבר	#מכבר		1492	1484
כ.ד.ר.	#כ.ד.ר.		1883
כדורי	#כדורי		2435	1883
כדור	#כדור		1892	1883
כ.ו.נ.	#כ.ו.נ.		2044
כיוון	#כיוון		2045	2044
נכון	#נכון		2062	2044
הכוין	#הכוין		2090	2044
מכוון	#מכוון		2250	2044
כ.ז.ב.	#כ.ז.ב.		2063
כוזב	#כוזב		2064	2063
כ.כ.ב.	#כ.כ.ב.		2381
כוכבים	#כוכבים		1326	2381
כ.ל.י.	#כ.ל.י.		1884
תכלית	#תכלית		1887	1884
עד בלתי תכלית	#עד בלתי תכלית		1920	1884
אל לא תכלית	#אל לא תכלית		1921	1884
אין תכלית	#אין תכלית		2405	1884
כלילת יופי	#כלילת יופי		2488
כ.ל.ל.	#כ.ל.ל.		1318
כלל	#כלל		1552	1318
כללי	#כללי		2244	1318
כולל	#כולל		2245	1318
כמה	#כמה		1928
כמהו	#כמהו		1417
כמוהו וחלק ממנו	#כמוהו וחלק ממנו		1419	1417
כמוהו וחלקים ממנו	#כמוהו וחלקים ממנו		1420	1417
כמות	#כמות		1857
כנף	#כנף		2337
כ.ס.ח.	#כ.ס.ח.		2294
כסוחה	#כסוחה		2295	2294
כ.פ.ל.	#כ.פ.ל.		1184
בעל הכפלים	#בעל הכפלים		1284	1184
הכפלה	#הכפלה		1229	1184
כפל	#כפל		1230	1184
כפילה	#כפילה		1253	1184
כפול	#כפול		1348	1184
כפל הכפל	#כפל הכפל		2508	1184
כפל וחלק	#כפל וחלק	כפל מוסיף חלק	1415	1184
כפל וחלקים	#כפל וחלקים	כפל מוסיף חלקים, כפלים מוסיף חלקים	1416	1184
נכפל	#נכפל		1564	1184
הכפיל	#הכפיל		1622	1184
כפולה	#כפולה		1838	1184
הכפל	#הכפל		2136	1184
ל.ב.נ.	#ל.ב.נ.		2113
לבני	#לבני		2114	2113
ל.ה.ב.	#ל.ה.ב.		2104
מתלהב	#מתלהב		2109	2104
לוח	#לוח		1483
לוח ההכאות	#לוח ההכאות		1922
לוח הרבוע	#לוח הרבוע		1923
ל.מ.ד.	#ל.מ.ד.		2280
למודיות	#למודיות		1643	2280
למודית	#למודית		2281	2280
מ.ד.ד.	#מ.ד.ד.		1615
מדותי	#מדותי	אמצעי המדות	1744	1615
מדה	#מדה		1618	1615
מדוד	#מדוד		1619	1615
ממד	#ממד		1620	1615
מדות	#מדות		2275	1615
מדידה	#מדידה		2276	1615
מדד	#מדד		2310	1615
מ.ו.ט.	#מ.ו.ט.		2208
מתמוטטת	#מתמוטטת		2209	2208
מוסיקה	#מוסיקה		1645
מוסיקי	#מוסיקי		2272
מ.ו.ר.	#מ.ו.ר.		1187
תמורה	#תמורה		2409	1187
המרה	#המרה		1205	1187
המיר	#המיר		1204	1187
מ.ז.ל.	#מ.ז.ל.		1477
מזל	#מזל		1478	1477
מזלות	#מזלות		1511	1477
מ.כ.ס.	#מ.כ.ס.		2361
מכס	#מכס		2362	2361
מ.כ.ר.	#מ.כ.ר.		1499
מכר	#מכר		1502	1499
נמכר	#נמכר		1503	1499
מ.ל.א.	#מ.ל.א.		2145
מלא	#מלא		2146	2145
מלאכה	#מלאכה		1497
מ.מ.נ.	#מ.מ.נ.		1518
ממון	#ממון		1519	1518
מ.נ.י.	#מ.נ.י.		1433
מנין	#מנין		1434	1433
מנה	#מנה		1435	1433
מונה	#מונה		1570	1433
מ.צ.ע.	#מ.צ.ע.		1740
אמצעי	#אמצעי		1741	1740
ממוצע	#ממוצע		2554	1740
מ.ש.ח.	#מ.ש.ח.		2223
משיחה	#משיחה		2224	2223
מ.ש.כ.	#מ.ש.כ.		1975
המשכות	#המשכות		2574	1975
המשך	#המשך		2411	1975
על המשך	#על המשך		1976	1975
המשיך קו	#המשיך קו		2061	1975
משוך	#משוך		2318	1975
נמשך	#נמשך		2630	1975
מ.ש.ל.	#מ.ש.ל.		1895
משל	#משל		1896	1895
מ-ש-ל	#מ-ש-ל		2080	1895
מ.ש.ש.	#מ.ש.ש.		2214
משש	#משש		2215	2214
נ.ג.ד.	#נ.ג.ד.		1882
דרכי המתנגדות	#דרכי המתנגדות		1913	1882
מתנגדים	#מתנגדים		1888	1882
דרך המתנגדים	#דרך המתנגדים		1889	1882
נ.ג.נ.	#נ.ג.נ.		2392
נגון	#נגון		2394	2392
נ.ג.ע.	#נ.ג.ע.		1574
הגעה	#הגעה		1675	1574
הגיע	#הגיע		1575	1574
מגיע	#מגיע		2086	1574
נ.ו.ח.	#נ.ו.ח.		1954
הניח	#הניח		2414	1954
מונח	#מונח		1955	1954
מונח כוזב	#מונח כוזב		2257	1954
נומרי	#נומרי		1315
נושא	#נושא		2432
נ.ט.י.	#נ.ט.י.		2529
נוטה	#נוטה		2530	2529
נ.כ.ה.	#נ.כ.ה.		1254
הכאה	#הכאה		1256	1254
הכה	#הכה		1255	1254
הוכה	#הוכה		2025	1254
מכה	#מכה		2264	1254
מוכה	#מוכה		2265	1254
מוכה בו	#מוכה בו		2325	1254
נ.כ.ח.	#נ.כ.ח.		1820
נכחי	#נכחי		1821	1820
על נכוחות	#על נכוחות		2039	1820
הנכיח	#הנכיח		2089	1820
נכחי הצלעות	#נכחי הצלעות		2555	1820
נכחי השטחים	#נכחי השטחים		2556	1820
נ.כ.י.	#נ.כ.י.		2200
נכה	#נכה		2201	2200
נכוי	#נכוי		2391	2200
הכאת אלכסון	#הכאת אלכסון		2625	2200
הכה אלכסונות	#הכה אלכסונות		2626	2200
נ.כ.ר.	#נ.כ.ר.		1408
נכרי	#נכרי		1409	1408
נ.פ.י.	#נ.פ.י.		2366
נפה	#נפה		2367	2366
נ.פ.ל.	#נ.פ.ל.		1250
הפיל	#הפיל		1251	1250
הפלה	#הפלה		1592	1250
נפל	#נפל		2018	1250
נ.ק.ב.	#נ.ק.ב.		2299
נקב	#נקב		2561	2299
נקוב	#נקוב		2300	2299
נ.ק.ד.	#נ.ק.ד.		1605
נקודת חלוק	#נקודת חלוק		1900	1605
נקודת חלוקה	#נקודת חלוקה		1901	1605
נקודה	#נקודה		1606	1605
נ.ק.פ.	#נ.ק.פ.		1853
הקף	#הקף		1854	1853
הקיף	#הקיף		1855	1853
מקיף	#מקיף		1856	1853
נ.ק.ש.	#נ.ק.ש.		1289
הקשה	#הקשה		1290	1289
היקש	#היקש		2065	1289
הקיש	#הקיש		2071	1289
נקוש	#נקוש		2164	1289
הוקש	#הוקש		2403	1289
נרדשיר	#נרדשיר		1950
נ.ת.כ.	#נ.ת.כ.		1557
התכה	#התכה		1558	1557
התיך	#התיך		1559	1557
הותך	#הותך		2492	1557
נ.ת.ר.	#נ.ת.ר.		1398
התיר	#התיר		1399	1398
ס.ב.ב.	#ס.ב.ב.		2210
סבובי	#סבובי		2444	2210
סביבה	#סביבה		2296	2210
סבב	#סבב		2211	2210
ס.ד.ר.	#ס.ד.ר.		1400
סדר	#סדר		1401	1400
סדור	#סדור		1402	1400
ס.ו.כ.	#ס.ו.כ.		1436
סך	#סך		1437	1436
סולמי	#סולמי		2445
סוף	#סוף		2479
ס.ו.ר.	#ס.ו.ר.		1249
הוסר	#הוסר		1842	1249
הסרה	#הסרה		1679	1249
הסיר	#הסיר		1252	1249
מוסר	#מוסר		2016	1249
סר	#סר		2384	1249
ס.כ.ל.	#ס.כ.ל.		1803
מוסכל	#מוסכל		1806	1803
ס.כ.מ.	#ס.כ.מ.		1599
הסכמה	#הסכמה		1768	1599
סכום	#סכום		1600	1599
הסכים	#הסכים		2464	1599
מסכים	#מסכים		2496	1599
ס.ל.ק.	#ס.ל.ק.		2266
סלוק	#סלוק		2268	2266
ס.מ.נ.	#ס.מ.נ.		1646
סימן	#סימן		1650	1646
סעורה	#סעורה		2482
ס.פ.י.	#ס.פ.י.		2143
ספה	#ספה		2144	2143
ס.פ.ק.	#ס.פ.ק.		2415
מספיק	#מספיק		2416	2415
הספיק	#הספיק		2417	2415
ס.פ.ר.	#ס.פ.ר.		1171
מספרי תכונה	#מספרי תכונה		1877	1171
מספר	#מספר		1174	1171
ספר	#ספר		1461	1171
ספרא	#ספרא		1554	1171
ספירה	#ספירה		1571	1171
ספור	#ספור		1572	1171
בעלי המספר	#בעלי המספר		2033	1171
מספרי	#מספרי		2098	1171
ס.ת.מ.	#ס.ת.מ.		1377
סתום	#סתום		1380	1377
ע.ב.ר.	#ע.ב.ר.		1839
העביר	#העביר		1843	1839
ע.ג.ל.	#ע.ג.ל.		1467
עגול	#עגול		1470	1467
עגולה	#עגולה		1471	1467
עגל	#עגל		2216	1467
ע.ד.פ.	#ע.ד.פ.		1350
עודף	#עודף		1352	1350
העדיף	#העדיף		2035	1350
מעדיף	#מעדיף		2092	1350
העדף	#העדף		2093	1350
ע.י.נ.	#ע.י.נ.		2455
דומה למעוין	#דומה למעוין		2468	2455
מעוין	#מעוין		1526	2455
ע.ל.ה.	#ע.ל.ה.		1185
עלה	#עלה		1240	1185
עולה	#עולה		1241	1185
מעלה	#מעלה		1316	1185
מעלה חלקה	#מעלה חלקה		2137	1185
העלה	#העלה		2378	1185
ע.ל.מ.	#ע.ל.מ.		1634
נעלם	#נעלם		1635	1634
ע.מ.ד.	#ע.מ.ד.		1790
מעומד	#מעומד		1879	1790
מעמד	#מעמד		1791	1790
עמודי	#עמודי		2102	1790
עמוד	#עמוד		2206	1790
עומד	#עומד		2326	1790
העמיד	#העמיד		2550	1790
ע.מ.ל.	#ע.מ.ל.		2390
עמלנית	#עמלנית		1983	2390
ע.מ.ק.	#ע.מ.ק.		1861
עומק	#עומק		1862	1861
ע.ק.ב.	#ע.ק.ב.		1827
עקובי	#עקובי		1965	1827
עקב	#עקב		1875	1827
מעוקב	#מעוקב		1828	1827
הכאה מעוקבת	#הכאה מעוקבת		1925	1827
באופן מעוקב	#באופן מעוקב		1926	1827
ע.ק.מ.	#ע.ק.מ.		2152
עקום	#עקום		2153	2152
עקמומי	#עקמומי		2157	2152
ע.ק.ר.	#ע.ק.ר.		2474
עיקר	#עיקר		2475	2474
ע.ר.כ.	#ע.ר.כ.		1274
העריך	#העריך		1281	1274
מערכה	#מערכה		2446	1274
ערך	#ערך		1280	1274
נערך	#נערך		1282	1274
מערכת	#מערכת		1345	1274
ערוך	#ערוך		1367	1274
מוערך	#מוערך		1405	1274
ע.ש.ה.	#ע.ש.ה.		1423
עשה	#עשה		1426	1423
מעשה	#מעשה		1427	1423
ע.ש.ר.	#ע.ש.ר.		2103
מעושר	#מעושר		2110	2103
ע.ת.ק.	#ע.ת.ק.		2323
בהעתק	#בהעתק		2324	2323
פאה	#פאה		1465
פה	#פה		2235
פ.ז.ר.	#פ.ז.ר.		2376
פזר	#פזר		2377	2376
פ.ח.ת.	#פ.ח.ת.		1363
פחת	#פחת		1364	1363
פחות	#פחות		1366	1363
פוחת	#פוחת		2032	1363
נפחת	#נפחת		2535	1363
פילוסופיה	#פילוסופיה		1591
פלס	#פלס		1303
פ.ס.ח.	#פ.ס.ח.		2292
פסוחה	#פסוחה		2293	2292
פ.ס.ק.	#פ.ס.ק.		2311
הפסיק	#הפסיק		2312	2311
פסקה	#פסקה		2313	2311
פסק	#פסק		2314	2311
פ.ע.ל.	#פ.ע.ל.		1654
פעול	#פעול		1655	1654
פועל	#פועל		1656	1654
פ.ק.ד.	#פ.ק.ד.		2036
הפקדה	#הפקדה		2037	2036
פ.ק.ח.	#פ.ק.ח.		1680
פקח	#פקח		1681	1680
פ.ר.ד.	#פ.ר.ד.		1331
נפרד	#נפרד		1336	1331
נפרד ראשון	#נפרד ראשון		2147	1331
נפרד שני	#נפרד שני		2148	1331
מתפרד	#מתפרד		2154	1331
נפרד הנפרד	#נפרד הנפרד		2340	1331
פ.ר.ט.	#פ.ר.ט.		1936
פריטה	#פריטה		1937	1936
פרט	#פרט		1938	1936
מופרט	#מופרט		1939	1936
מפורט	#מפורט		1948	1936
פ.ר.ש.	#פ.ר.ש.		1625
הפרש	#הפרש		1626	1625
פרוש	#פרוש		2149	1625
פ.ש.ט.	#פ.ש.ט.		2028
פשוט	#פשוט		2029	2028
פשט	#פשט		2399	2028
פ.ת.ל.	#פ.ת.ל.		2161
נפתל	#נפתל		2162	2161
צ.ד.ד.	#צ.ד.ד.		2466
צד	#צד		2467	2466
צ.ו.ר.	#צ.ו.ר.		1509
צורה	#צורה		1510	1509
צינסו	#צינסו		1313
צ.י.ר.	#צ.י.ר.		2175
צייר	#צייר		2567	2175
צויר	#צויר		2566	2175
ציר	#ציר		2178	2175
צ.ל.ל.	#צ.ל.ל.		1473
צל	#צל		1475	1473
צלע	#צלע		1464
צ.מ.ח.	#צ.מ.ח.		2024
צמח	#צמח		2027	2024
צ.מ.צ.מ.	#צ.מ.צ.מ.		2194
צמצום	#צמצום		2509	2194
מצומצם	#מצומצם		2195	2194
צפרא	#צפרא		1813
צ.ר.פ.	#צ.ר.פ.		1676
מצטרף	#מצטרף		2579	1676
צרף	#צרף		1810	1676
הצטרף	#הצטרף		1677	1676
צרוף	#צרוף		1678	1676
צרופי	#צרופי		2271	1676
צ.ר.ר.	#צ.ר.ר.		2458
צר	#צר		2459	2458
ק.ב.ב.	#ק.ב.ב.		2155
קבוב	#קבוב		2156	2155
מקובה	#מקובה		2301	2155
קובה	#קובה		2302	2155
ק.ב.ל.	#ק.ב.ל.		1942
הקביל	#הקביל		1943	1942
הקבלה	#הקבלה		2022	1942
מקביל	#מקביל		2108	1942
נקבל	#נקבל		2380	1942
ק.ב.ע.	#ק.ב.ע.		2303
קבע	#קבע		2304	2303
ק.ב.צ.	#ק.ב.צ.		1209
קובץ	#קובץ		1841	1209
קבוץ	#קבוץ		1211	1209
מקובץ	#מקובץ		1217	1209
מתקבץ	#מתקבץ		1218	1209
נקבץ	#נקבץ		1219	1209
קבץ	#קבץ		1210	1209
התקבץ	#התקבץ		1216	1209
הקבץ	#הקבץ		2335	1209
ק.ד.מ.	#ק.ד.מ.		2631
הקדמה	#הקדמה		2632	2631
קובו	#קובו		1826
קוביקא	#קוביקא		1306
ק.ו.י.	#ק.ו.י.		2548
קו	#קו		1450	2548
קוי	#קוי		2101	2548
קוה	#קוה		2549	2548
ק.ו.מ.	#ק.ו.מ.		1647
קומה	#קומה		2480	1647
מקום	#מקום		1649	1647
קוסא	#קוסא		1314
ק.ט.ב.	#ק.ט.ב.		2177
קוטב	#קוטב		2180	2177
ק.ט.מ.	#ק.ט.מ.		2203
קטומה	#קטומה		2204	2203
ק.ט.נ.	#ק.ט.נ.		1623
הקטין	#הקטין		1624	1623
קטן יחס	#קטן יחס		2624	1623
ק.ט.ע.	#ק.ט.ע.		2319
קטוע	#קטוע		2320	2319
ק.ט.פ.	#ק.ט.פ.		2297
קטופה	#קטופה		2298	2297
ק.ט.ר.	#ק.ט.ר.		2231
קוטר	#קוטר		2232	2231
ק.צ.ב.	#ק.צ.ב.		1818
קצוב	#קצוב		1819	1818
קצב	#קצב		2163	1818
קצה	#קצה		1902
ק.צ.ר.	#ק.צ.ר.		2247
קצר	#קצר		2248	2247
מקוצר	#מקוצר		2249	2247
קצור	#קצור		2259	2247
ק.ר.א.	#ק.ר.א.		1940
קורא	#קורא		2428	1940
קריאת שם	#קריאת שם		1941	1940
קרא שם	#קרא שם		1969	1940
ק.ר.ב.	#ק.ר.ב.		1358
התקרב	#התקרב		1874	1358
בדרך קרובה	#בדרך קרובה		2507	1358
קרוב	#קרוב		1359	1358
קרוב אל האמת	#קרוב אל האמת		1360	1358
קרב	#קרב		1610	1358
בקרוב	#בקרוב		1611	1358
על דרך הקרוב	#על דרך הקרוב		2072	1358
קרן	#קרן		2400
ק.ש.ר.	#ק.ש.ר.		1403
קשר	#קשר		1404	1403
קשור המטבע	#קשור המטבע		1493	1403
נקשר	#נקשר		1494	1403
ק.ש.ת.	#ק.ש.ת.		1466
קשתי	#קשתי		2441	1466
קשת	#קשת		1469	1466
קשותה	#קשותה		2291	1466
ר.א.י.	#ר.א.י.		2386
מראה	#מראה		1325	2386
ר.א.ש.	#ר.א.ש.		1517
ראש	#ראש		1870	1517
ראשון	#ראשון		1520	1517
ר.ב.ה.	#ר.ב.ה.		1586
מרבה	#מרבה		2537	1586
התרבה	#התרבה		1587	1586
רבה	#רבה		1588	1586
התרבות	#התרבות		2068	1586
מרובה	#מרובה		2069	1586
מורבה	#מורבה		2081	1586
הרבה	#הרבה		2082	1586
מרבה צלעות	#מרבה צלעות		2172	1586
ר.ב.ע.	#ר.ב.ע.		1261
רבע	#רבע		1658	1261
מרובע	#מרובע		1263	1261
מרובע ארוך	#מרובע ארוך		1525	1261
רבוע	#רבוע		1531	1261
שטח מרובע	#שטח מרובע		2078	1261
רבועי	#רבועי		2621	1261
ר.ג.ל.	#ר.ג.ל.		2282
הרגלית	#הרגלית		2283	2282
ר.ו.ח.	#ר.ו.ח.		2183
מרוח	#מרוח		2184	2183
נרוח	#נרוח		2524	2183
ר.ו.מ.	#ר.ו.מ.		2374
מורם	#מורם		2375	2374
ר.ח.ב.	#ר.ח.ב.		1480
רחב	#רחב		1912	1480
מרחב	#מרחב		2565	1480
רוחב	#רוחב		1488	1480
ר.ח.ק.	#ר.ח.ק.		1881
רוחק	#רוחק		1890	1881
מרחק	#מרחק		1891	1881
ר.כ.ב.	#ר.כ.ב.		1957
הרכבה	#הרכבה		1958	1957
מורכב	#מורכב		1959	1957
הורכב	#הורכב		1961	1957
בלתי מורכב	#בלתי מורכב		2013	1957
ר.כ.ז.	#ר.כ.ז.		2233
מרכז	#מרכז		2234	2233
ר.צ.פ.	#ר.צ.פ.		1834
רצוף	#רצוף		1835	1834
ר.ק.ע.	#ר.ק.ע.		2173
רקיע	#רקיע		2174	2173
ר.ש.מ.	#ר.ש.מ.		1822
רושם	#רושם		1823	1822
מורשם	#מורשם		2527	1822
נרשם	#נרשם		2528	1822
ש.א.ר.	#ש.א.ר.		1179
שארית	#שארית		2454	1179
נשאר	#נשאר		1236	1179
השאיר	#השאיר		1235	1179
שיור	#שיור		2256	1179
ש.ב.ע.	#ש.ב.ע.		1773
משובע	#משובע		1775	1773
ש.ב.ר.	#ש.ב.ר.		1182
שבור	#שבור		1967	1182
שברי תכונה	#שברי תכונה		1876	1182
שבר	#שבר		1242	1182
שברים	#שברים		1243	1182
תשבורת	#תשבורת		1244	1182
נשבר	#נשבר		1438	1182
שברי חכמי המזלות	#שברי חכמי המזלות		1440	1182
שבר השבר	#שבר השבר		1576	1182
שם השבר	#שם השבר		1577	1182
שבירה	#שבירה		1628	1182
שבר תכני	#שבר תכני		1915	1182
תשברתי	#תשברתי		2097	1182
ש.ב.ש.	#ש.ב.ש.		1394
משובש	#משובש		1395	1394
ש.ו.ב.	#ש.ו.ב.		1425
שב	#שב		1886	1425
הושב	#הושב		2559	1425
השבה	#השבה		1430	1425
השיב	#השיב		1431	1425
ש.ו.ה.	#ש.ו.ה.		1189
שוה זויות	#שוה זויות		1864	1189
שוה צלעות	#שוה צלעות		1863	1189
שוה	#שוה		1247	1189
השווה	#השווה		1246	1189
שווי	#שווי		2439	1189
השתוה	#השתוה		1573	1189
השואה	#השואה		2023	1189
משווה	#משווה		2085	1189
שוה שוקים	#שוה שוקים		2202	1189
שוה צלעות נצב זויות	#שוה צלעות נצב זויות		2560
שטה	#שטה		1485
ש.ט.ח.	#ש.ט.ח.		1300
שטח נצב הזויות	#שטח נצב הזויות		1824	1300
שטחי	#שטחי		1880	1300
שטח	#שטח		1310	1300
שטוחה	#שטוחה		1338	1300
שטוח	#שטוח		1456	1300
משוטח	#משוטח		1568	1300
מושטח	#מושטח		1569	1300
ש.כ.ב.	#ש.כ.ב.		2327
שוכב	#שוכב		2328	2327
ש.כ.ל.	#ש.כ.ל.		1802
מושכל	#מושכל		1804	1802
שכלנית	#שכלנית		1986	1802
שכל	#שכל		1987	1802
ש.כ.ר.	#ש.כ.ר.		1498
שכר	#שכר		1504	1498
שכירות	#שכירות		1505	1498
שכיר	#שכיר		1506	1498
ש.ל.כ.	#ש.ל.כ.		1264
מושלך	#מושלך		1808	1264
מושלך ממנו	#מושלך ממנו		1809	1264
השליך	#השליך		1265	1264
השלכה	#השלכה		2014	1264
הושלך	#הושלך		2017	1264
נשלך	#נשלך		2019	1264
ש.ל.מ.	#ש.ל.מ.		1266
שלם	#שלם		1268	1266
השלים	#השלים		1267	1266
תשלום	#תשלום		1418	1266
נשלם	#נשלם		1421	1266
השלמה	#השלמה		1422	1266
השלם	#השלם		2051	1266
מושלם	#מושלם		2353	1266
ש.ל.ש.	#ש.ל.ש.		1522
שלש	#שלש		1860	1522
שלישי	#שלישי		1524	1522
משולש	#משולש		1527	1522
תחת משולשת	#תחת משולשת		1910	1522
משולשת	#משולשת		1911	1522
שם	#שם		1899
ש.מ.נ.י.	#ש.מ.נ.י.		1774
משומן	#משומן		1776	1774
ש.מ.ר.	#ש.מ.ר.		1180
שומר המעלות	#שומר המעלות		2451	1180
שמירת המדרגות	#שמירת המדרגות		2452	1180
שמור	#שמור		1238	1180
שמר	#שמר		1237	1180
ש.נ.י.	#ש.נ.י.		1521
שני	#שני		1523	1521
נשנה	#נשנה		2034	1521
שנוי	#שנוי		2050	1521
משונה	#משונה		2476	1521
שנה	#שנה		2188	1521
ש.ע.ר.	#ש.ע.ר.		1495
שוער	#שוער		1872	1495
שעורי	#שעורי		2471	1495
שער	#שער		1500	1495
שעור	#שעור		1501	1495
ש.פ.י.	#ש.פ.י.		1868
שפה	#שפה		1871	1868
ש.פ.ל.	#ש.פ.ל.',		2472
שפל	#שפל		2473	2472
ש.ק.ל.	#ש.ק.ל.		1448
משקל	#משקל		1451	1448
שקל במאזני תשעה	#שקל במאזני תשעה		1452	1448
שקל	#שקל		2141	1448
ש.ר.ש.	#ש.ר.ש.		1260
שרש	#שרש		1262	1260
הוצאת שרש	#הוצאת שרש		1373	1260
הוציא שרש	#הוציא שרש		1374	1260
לקח שרש	#לקח שרש		1375	1260
נשרש	#נשרש		1837	1260
שרשי	#שרשי		1598	1260
החזיק שרש	#החזיק שרש		2043	1260
לקוח שרש	#לקוח שרש		2084	1260
נלקח שרש	#נלקח שרש		2088	1260
ש.ש.י.	#ש.ש.י.		1668
משושה	#משושה		1669	1668
ש.ת.פ.	#ש.ת.פ.		1271
בלתי משותפים	#בלתי משותפים		2543	1271
משותפים בכח	#משותפים בכח		2544	1271
בלתי משותפים בכח	#בלתי משותפים בכח		2545	1271
משותף	#משותף		1873	1271
משתתפים	#משתתפים		1273	1271
השתתף	#השתתף		1272	1271
שתוף	#שתוף		1491	1271
נשתתף	#נשתתף		1515	1271
שותף	#שותף		1516	1271
שתף	#שתף		2046	1271
ת.כ.נ.	#ת.כ.נ.		1639
תכונה	#תכונה		1640	1639
ת.ל.י.	#ת.ל.י.		1406
תלוי	#תלוי		1407	1406
ת.ל.ל.	#ת.ל.ל.		2316
תלול	#תלול		2317	2316
תמונה	#תמונה		1308
ת.מ.מ.	#ת.מ.מ.		2501
תמים	#תמים		1376	2501
ת.ק.נ.	#ת.ק.נ.		1383
תקן	#תקן		1385	1383
מתוקן	#מתוקן		1386	1383
ת.ש.ע.	#ת.ש.ע.		2105
מתושע	#מתושע		2107	2105

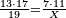
$\scriptstyle\frac{13\sdot17}{19}=\frac{7\sdot11}{X}$

א.ו.ת.

אות: numeral

Category	Category	Comment	Link	Annotated text	author	time
decimal positional system/numeral	א.ו.ת./אות	term	ספר_המספר_/_אליהו_מזרחי#EYyI	אות	Elijah Mizraḥi	1450-1526
decimal positional system/numeral	א.ו.ת./אות	term	ספר_אגריס#CMl9	אותיות		1300-1400
decimal positional system/numeral	א.ו.ת./אות	term	אגרת_המספר#BaEX	אותיות	Ibn al-Bannāʼ al-Marrākushī	1350-1429/1433
decimal positional system/numeral	א.ו.ת./אות	term	ספר_ציפרא#b7Xx	אותיו'		1400-1500
decimal positional system/numeral	א.ו.ת./אות	term	אגרת_המספר#nckU	אות	Ibn al-Bannāʼ al-Marrākushī	1350-1429/1433
decimal positional system/numeral	א.ו.ת./אות	term	ספר_אגריס#vv7v	אות		1300-1400
decimal positional system/numeral	א.ו.ת./אות	term	ספר_החשבון_לאל_חצאר#6oja	אות	Abū Bakr al-Haṣṣār	1271
decimal positional system/numeral	א.ו.ת./אות	term	בר_נותן_טעם#PBaR	אותיות	Jacob Canpanṭon	1430
decimal positional system/numeral	א.ו.ת./אות	term	קצור_המספר#Rmee	אותיות	Judah Ibn Verga	unknown-1450
decimal positional system/numeral	א.ו.ת./אות	term	בר_נותן_טעם#EozN	אות	Jacob Canpanṭon	1430
decimal positional system/numeral	א.ו.ת./אות	term	קצור_המספר#mTHy	אות	Judah Ibn Verga	unknown-1450
decimal positional system/numeral	א.ו.ת./אות	term	ספר_עיון_העקרים_לחשבון_ההנדיים#mq5P	אותיות	Kūšyār Ibn Labbān	1450-1460
decimal positional system/numeral	א.ו.ת./אות	term	עיר_סיחון#phuN	אותיות	Joseph Ben Moses Ṣarfati	unknown-1384
decimal positional system/numeral	א.ו.ת./אות	term	ספר_עיון_העקרים_לחשבון_ההנדיים#9bnm	אות	Kūšyār Ibn Labbān	1450-1460
decimal positional system/numeral	א.ו.ת./אות	term	מלאכת_המספר#Duvu	אות	Isaac Ben Moses ‘Eli	1400-1500
decimal positional system/numeral	א.ו.ת./אות	term	ספר_החשבון_לאל_חצאר#yuS2	אותיות	Abū Bakr al-Haṣṣār	1271
decimal positional system/numeral	א.ו.ת./אות	term	ספר_החשבון_לאל_חצאר#voac	אותיות	Abū Bakr al-Haṣṣār	1271
decimal positional system/numeral	א.ו.ת./אות	term	עיר_סיחון#OGlo	אות	Joseph Ben Moses Ṣarfati	unknown-1384

Category	Comment	Link	Annotated text
word problem/find a number	a/b=¾;(ab)·(a+b)=a²	ספר_ג'יבלי_אלמוקבאלא#bWjS	Find me two numbers such that the one is a part of the other as 3 is of 4; :and when the first is multiplied by the second, and the product is multiplied by the sum of both numbers together, it yields the same as the product of the larger by itself. :I ask: how much will each number be? :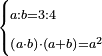 $\scriptstyle\begin{cases}\scriptstyle a:b=3:4\\\scriptstyle\left(a\sdot b\right)\sdot\left(a+b\right)=a^2\end{cases}$ תמצא לי שני מספרים שיהיה חלק האחד מהאחר כמו שהוא ג' מד‫' וכאשר הוכה הראשון בשני ואותה ההכאה תוכה על מקובץ שני המספרי' יחד יעשה כמו הכאת הגדול בעצמו אשאל כמה יבא להיות כל אחד מהמספרי‫'
word problem/find a number	a/b=¾;a√8+b²=48	ספר_ג'יבלי_אלמוקבאלא#aGAJ	Find me two numbers such that the one is a part of the other as 3 is of 4; :and if the first is multiplied by the root of 8, and the second is multiplied by itself, then both products are summed together, it yields 48. :I ask: how much will each number be? :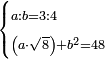 $\scriptstyle\begin{cases}\scriptstyle a:b=3:4\\\scriptstyle\left(a\sdot\sqrt{8}\right)+b^2=48\end{cases}$ תמצא לי שני מספרי' שהאחד יהיה חלק מהאחר כמו שג' הוא מד‫' ומוכה הראשון בשרש ח' והשני בעצמו ואותן שתי הכאות יחוברו יחד יעשו מ"ח אשאל כמה יבא להיות כל האחד מהמספרי‫'
word problem/find a number	2/3=4/a	ספר_דיני_ממונות#PZIU	248) Question: we have four numbers, such that the ratio of the first to the second is the same as the ratio of the third to the fourth, the sum of the four squares is 65, the first is 2, the second is 3, and the third is 4. :I ask: how much is the fourth? רמח) שאלה לנו ד' מספרים שיחס הא' אל הב' כיחס הג' אל הד' והד' מרובעים עולה ס"ה וממון הא' ב' וממון הב' ג' וממון הג' ד‫' אשאל כמה ממון הד‫'
word problem/find a number	a²·a=12a+10a²	ספר_ג'יבלי_אלמוקבאלא#FhTO	Find me a number, such that when it is multiplied by itself, and the product is multiplied by that number, it yields the same as the product of that number by 12, and that number multiplied by itself, then this product is multiplied by ten and this is added to the product by 12. :I ask: how much will the number be? :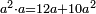 $\scriptstyle a^2\sdot a=12a+10a^2$ עשה לי החשבון תמצא לי מספר אחד שכאשר הוכה בעצמו ואותה ההכאה תוכה במספר ההוא יעשה כמו הכאת המספר האמור בי"ב ואח"כ להכות המספר האמור בעצמו ואותה ההכאה תוכה בעשרה ולחבר עם ההכאה שנעשתה בי"ב אשאל כמה יבא להיות המספר האמור
word problem/find a number	repeated subtraction	מלאכת_המספר#TEa8	Question: if we subtract 12 from the double of any number, then we subtract another 12 from double the remainder also, and double the remainder is 12, how much is the original number? : $\scriptstyle2\sdot\left[\left[2\sdot\left(2X-12\right)\right]-12\right]=12$ שאילה אם מכפלו של אי זה מספר נקח י"ב ומכפל הנשאר נקח ג"כ י"ב אחרי' וכפל הנשאר יהיה י"ב כמה היה המספר הראשון
word problem/find a number	a+½¼a+¾a+¼¼a=2	Arithmetic_Textbook_by_R._Aharon_ben_Isaac#EJ6w	The third question: what is the unknown number that if you add to it one-half of its quarter, its three quarter and one-quarter of its quarter, the total is but two? :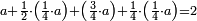 $\scriptstyle a+\frac{1}{2}\sdot\left(\frac{1}{4}\sdot a\right)+\left(\frac{3}{4}\sdot a\right)+\frac{1}{4}\sdot\left(\frac{1}{4}\sdot a\right)=2$ שאלה שלישית מהו המספר הנעלם אשר אם תחבר עליו חצי רביעיתו ושלושת רביעיתו ורביעית רביעיתו ולא יהיה אלא שנים
word problem/find a number	a+b=c;a+c=100b	מלאכת_המספר#Q70A	Question: if there are three numbers, the [sum of the] first and the second is as the third, and the [sum of the] first and the third is as a hundred of the second. How much is each of the three numbers? שאילה אם יהיו ג' מספרי' והראשון והשני יהיו בכמות השלישי והראשון והשלישי כמאה מן השני כמה יהיה כל אחד מהשלשה מספרי‫'
word problem/find a number	¼a=⅓(a-¼a)=½((a-¼a)-⅓(a-¼a))	ספר_דיני_ממונות#irk0	Question: if you take any number, then you take its quarter from it, then a third of the remainder, then half the remainder after taking the third, all parts are the same. שאלה‫MS L שכ אם תחלק איזה מספר שיזדמן ותקח ממנו רביעיתו ומהנשאר שלישיתו ומהנשאר אחר לקיחת השליש מחציתו יש לכלם חלק שוה
word problem/find a number	√a+√(a-√a)=3	ספר_דיני_ממונות#e6ph	156) Question: if you want to find a number such that if you subtract its root and add it to the root of the remainder it makes 3. :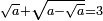 $\scriptstyle\sqrt{a}+\sqrt{a-\sqrt{a}}=3$ קנו)‫MS L: קנג שאלה אם תרצה למצא מספר אשר אם תוציא ממנו השרש ותחבר אותו עם השרש מהנשאר יעשה ג‫'
word problem/find a number	a/b=⅗;(a√a+b√b)√8=100	ספר_ג'יבלי_אלמוקבאלא#dp2A	Find me two numbers such that the one is a part of the other as 3 is of 5; :and when each is multiplied by its root and both products are summed together, then the sum is multiplied by the root of 8, it yields 100. :I ask: how much will each number be? : $\scriptstyle\begin{cases}\scriptstyle a:b=3:5\\\scriptstyle\left[\left(a\sdot\sqrt{a}\right)+\left(b\sdot\sqrt{b}\right)\right]\sdot\sqrt{8}=100\end{cases}$ תמצא לי שני מספרי' שיהיה חלק האחד מהאחר כמו שהוא ג' מה‫' וכשיוכה כל אחד על שרשו ויחוברו שתי אלו ההכאות יחד וזה הסך יוכה בשרש ח' יעשה מאה אשאל כמה יבא להיות כל אחד מהמספרים
word problem/find a number	a/b=⅔;a√a=2b	ספר_ג'יבלי_אלמוקבאלא#Jb23	Find me two numbers such that the first is a part of the second as 2 is of 3; :and when the first is multiplied by its root it yields the same as the product of the second by 2. :I ask: how much will each number be? :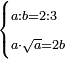 $\scriptstyle\begin{cases}\scriptstyle a:b=2:3\\\scriptstyle a\sdot\sqrt{a}=2b\end{cases}$ תמצא לי שני מספרים שיהיה הראשון חלק מהשני כמו שב' הוא מג‫' וכשיוכה הראשון בשרש עצמו יעשה כמו הכאת השני בשנים אשאל כמה יבא להיות כל אחד מהמספרים
word problem/find a number	a/b=⅔;(ab)²=20+√30	ספר_ג'יבלי_אלמוקבאלא#9iel	[Find me two numbers] such that one is a part of the other as 2 is of 3; :and when the first is multiplied by the second and this product is multiplied by itself, it yields 20 and a root of 20. :I ask: how much will each number be? :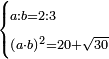 $\scriptstyle\begin{cases}\scriptstyle a:b=2:3\\\scriptstyle\left(a\sdot b\right)^2=20+\sqrt{30}\end{cases}$ עשה לי זה החשבון שיהיה האחד חלק מהאחר כמו שב' הוא חלק מג‫' ובהכות הראשון בשני ואותה ההכאה תוכה בעצמה יעשה כ' ושרש ל‫' אשאל כמה יבא להיות כל אחד מהמספרי‫'
word problem/find a number	a/b=¼;aba=³√216	ספר_ג'יבלי_אלמוקבאלא#nkyB	Find me two numbers such that one is a part of the other as 1 is of 4; :and the one multiplied by the other, and this product is multiplied by the first, yields a cube root of 216. :I ask: how much will each number be? : $\scriptstyle\begin{cases}\scriptstyle a:b=1:4\\\scriptstyle\left(a\sdot b\right)\sdot a=\sqrt[3]{216}\end{cases}$ והנה המשל תמצא לי שני מספרי' שיהיה אחד מהם חלק מהאחר כמו שא' הוא מד‫' ומוכה הראשון בשני וההכאה ההיא תוכה בראשון יעשה שרש מעו' מרי"ו אשאל כמה יבא להיות כל אחד מהמספרי‫'
word problem/find a number	six proportional numbers	ספר_דיני_ממונות#Wrir	For example: we have six proportional numbers, the first is 2 and the sixth is 64. ::We wish to know which is the second. דמיון זה יש לנו ו' {{#annot:term\|994,1277\|VUeX}}מספרים מתיחסים{{#annotend:VUeX}} הראשון ב' והו' ס"ד נרצה לדעת מהו השני
word problem/find a number	a²=2b+8;a²+b²=80	ספר_ג'יבלי_אלמוקבאלא#Ob3R	Find me two numbers such that the one multiplied by itself yields 2 times the second and 8 more; :and when each of them is multiplied by itself, and the two products are summed together, they yield 80. :I ask: how much will each number be? :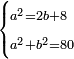 $\scriptstyle\begin{cases}\scriptstyle a^2=2b+8\\\scriptstyle a^2+b^2=80\end{cases}$ והנה המשל עשה לי זה החשבון תמצא לי ב' מספרי' שכאשר יוכה הראשון בעצמו יעשה ב' דמיוני השני וח' יותר ומוכה כל אחד מהם בעצמו ויקובצו ב' ההכאו' יחד יעשו פ‫' אשאל כמה יבא להיות כל אחד מהמספרי‫'
word problem/find a number	(a-⅓a)²=20	ספר_האלזיברא#xJ4O	Question: I want to find a number such that when its third is subtracted from it, the square of the remainder is 20. :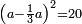 $\scriptstyle\left(a-\frac{1}{3}a\right)^2=20$ שאלה רציתי למצא מספר כאשר חסר ממנו שלישיתו מרבע הנשאר הוא מספר כ‫'
word problem/find a number	(a+b)/(c-a)=4½;(a+c)/(b-a)=5	ספר_מעשה_חושב#UAnP	Example: the ratio of the first and the second summed together to what remains from the third when the first is subtracted from it is 4 integers and a half. ::The ratio of the first and the third summed together to what remains from the second when the first is subtracted from it is 5 integers. ::We wish to know: how much is each of the numbers that meet this condition? ::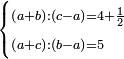 $\scriptstyle\begin{cases}\scriptstyle\left(a+b\right):\left(c-a\right)=4+\frac{1}{2}\\\scriptstyle\left(a+c\right):\left(b-a\right)=5\end{cases}$ והמשל שיהיה יחס הראשון והשני מקובצים אל הנשאר [מהשלישי כשחוסר ממנו הראשון ד' שלמים וחצי ויחס הראשון והשלישי מקובצים אל הנשאר] מהשני כשחוסר ממנו הראשון הוא ה' שלמים ונרצה לדעת כמה כל המספרים שינהגו זה המנהג
word problem/find a number	a/b=⅔;ab=20+√8	ספר_ג'יבלי_אלמוקבאלא#B6TE	Find me two numbers such that the first is a part of the second as 2 is of 3; :and when the first is multiplied by the second it yields 20 and a root of 8. :I ask: how much will each number be? :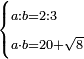 $\scriptstyle\begin{cases}\scriptstyle a:b=2:3\\\scriptstyle a\sdot b=20+\sqrt{8}\end{cases}$ תמצא לי שני מספרים שיהיה הראשון חלק מהשני כמו שב' הוא מג‫' ומוכה הראשון בשני יעשה כ' ושרש ח‫' אשאל כמה יבא להיות כל אחד מהמספרי‫'
word problem/find a number	a+⅓a+⅖a=81	ספר_דיני_ממונות#khzV	136) Question: find me a number such that if you add to it its third and its two fifths it makes [81]. :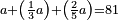 $\scriptstyle a+\left(\frac{1}{3}a\right)+\left(\frac{2}{5}a\right)=81$ קלו)‫MS L: קלג שאלה תמצא לי מספר אשר אם תוסיף עליו שלישיתו ושני חמישיותיו יעשה י"ח
word problem/find a number	b-1=a+1;2(a-1)=b+1	מלאכת_המספר#4BJp	Knowing the relation of two numbers that have the property that if we subtract one from the greater number and add it to the smaller number, the two numbers become equal; and if we subtract one from the smaller number and add it to the greater, the greater becomes double the smaller, or more if we wish ==== \|style="width:45%; text-align:right;"\|הפרק השני בידיעת התייחסות שני מספרי' שיש להם זה הטבע שאם נחסר אחד מהמספר הגדול ונוסיפהו על המספר הקטן יהיו הב' מספרי' שוים ואם נחסר אחד מהמספר הקטן ונוסיפהו בגדול יהיה הגדול כפל הקטן או יותר אם נרצה
word problem/find a number	a-(½a+½)-(½(a-(½a+½))+½)-(½(a-(½a+½)-(½(a-(½a+½))+½))+½)	קצור_המספר#9olE	As when one asks: what is the number such that when we subtract its half and one half more, then [we subtract] from the remainder its half and one half more, then [again we subtract] from the [second] remainder its half and one half more, we are left with one. כמו ששאל אחד איזהו מספר אשר כשנשליך חציו ועוד חצי אחד ומן הנשאר חציו ועוד חצי אחד וישאר אחד ב[ע]ינו
word problem/find a number	repeated subtraction	ספר_חשבון#QPoG	If one asks you: a number, you subtract a tenth from it, then you subtract again a tenth from the remainder, and 100 are left. :How much was the original number before subtracting the two tenths? : $\scriptstyle X-\frac{1}{10}X-\left[\frac{1}{10}\sdot\left(X-\frac{1}{10}X\right)\right]=100$ אם ישאלך אדם חשבון שהסרות ממנו הי' ומן הנשאר הסרות ממנו העשירית פעם שנית ונשארו ק‫' כמה היה כל החשבון בטרם שהסרת ממנו ב' העשיריות
word problem/find a number	a+2⅔a=11	Arithmetic_Textbook_by_R._Aharon_ben_Isaac#ZVW2	First question: What is the number to which you add its two and 2-thirds and it is eleven? :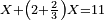 $\scriptstyle X+\left(2+\frac{2}{3}\right)X=11$ שאלה ראשונה מהו המספר ‫119r / [ק"א][אשר תחבר עליו שנים וב' שלישיות ויהיו] אחד עשר
word problem/find a number	a/b=⅘;(ab)²=a²b	ספר_ג'יבלי_אלמוקבאלא#Ukgo	Find me two numbers such that the first is a part of the second as 4 is of 5; :and when the first is multiplied by the second, and this product is multiplied by itself, it yields the same as the product of the first by itself, then that product is multiplied by the second number. :I ask: how much will each number be? :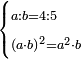 $\scriptstyle\begin{cases}\scriptstyle a:b=4:5\\\scriptstyle\left(a\sdot b\right)^2=a^2\sdot b\end{cases}$ תמצא לי שני {{#annot: term \| #proportional, #מתיחס \| lK1I}}מספרים מתיחסים{{#annotend:lK1I}} שיהיה חלק הראשון מהשני כמו שהוא ד' מה‫' וכשיוכה הראשון בשני ואותה ההכאה תוכה בעצמה ויעשה כמו שעושה הראשון מוכה בעצמו ואותה ההכאה תוכה במספר השני אשאל כמה יבא להיות כל אחד מהמספרים
word problem/find a number	a²=40+41\b	ספר_דיני_ממונות#aiR7	112) Question: find a number such that when you multiply it by itself the result is 40 and 41 parts of a fraction. :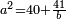 $\scriptstyle a^2=40+\frac{41}{b}$ קיב)‫MS L: קי שאלה תמצא לי מספר אשר כשתכפלהו על עצמו יעלו מ' ומ"א חלקים מאיזה שבר שיזדמן
word problem/find a number	a(mod2)=1,a(mod3)=1,a(mod)4=1,a(mod5)=1,a(mod6)=1,a(mod7)=0	ספר_המספר_/_אליהו_מזרחי#5uWz	Question: if one asks: what is the number that when counted by twos - one remains; by threes - one remains; by fours - one remains; by fives - one remains; by sixes - one remains; and by sevens - nothing remains. שאלה אם שאל שואל איזהו המספר אשר כשימנה מב' ב' ישאר אחד ומג' ג' ישאר אחד ומד' ד' ישאר אחד ומה' ה' ישאר אחד ומו' ו' ישאר אחד ומז' לא ישאר דבר
word problem/find a number	a+¼(b+c)=b+⅙(a+c)=c+⅑(a+b);b=20	ספר_מעשה_חושב#sryH	Example: the first with a quarter of the rest is equal to the second with a sixth of the rest and is also equal to the third with a ninth of the rest. ::The first is added to the greatest part of the rest and the third is added to the smallest part of the rest. ::The second number is 20. ::We wish to know: how much is each of the rest? ::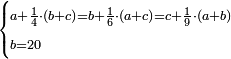 $\scriptstyle\begin{cases}\scriptstyle a+\frac{1}{4}\sdot\left(b+c\right)=b+\frac{1}{6}\sdot\left(a+c\right)=c+\frac{1}{9}\sdot\left(a+b\right)\\\scriptstyle b=20\end{cases}$ והמשל שיהיה הראשון עם רביעית הנשארים שוה אל השני עם ששית הנשארים והוא גם כן שוה אל השלישי עם תשיעית הנשארים וכבר התבאר לך במאמר הראשון מזה הספר שסדר אלו המספרים השלשה הוא על זאת ההדרגה אשר סדרנו רצוני שהראשון הוא אשר יתחבר עמו חלק יותר גדול מהנשארים והשלישי הוא אשר יתחבר עמו חלק יותר קטן מהנשארים והזכרתי לך זה למען לא תתבלבל בסדורם ויהיה המספר השני מהם כ‫' ורצינו לדעת כמה כל אחד מהנשארים
word problem/find a number	six proportional numbers	ספר_דיני_ממונות#FvyI	Example: the first is 2-[eighths] and the sixth is 256 integers. דמיון הראשון ב' שלישיות והו' רנ"ו שלמים
word problem/find a number	(a²·a)+b²=12½c	ספר_ג'יבלי_אלמוקבאלא#iH47	Find me three numbers, such that the first is a part of the second as 2 is of 3, and the second is of the third as 3 is of 4. :If the first is multiplied by itself, then the product is multiplied by the first number, and the second number is multiplied by itself, when both products are summed together, its yields the same as the product of the third number by 12 and a half. :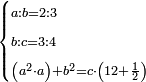 $\scriptstyle\begin{cases}\scriptstyle a:b=2:3\\\scriptstyle b:c=3:4\\\scriptstyle\left(a^2\sdot a\right)+b^2=c\sdot\left(12+\frac{1}{2}\right)\end{cases}$ והנה המשל תמצא לי שלשה מספרים שיהיה חלק הראשון מהשני כמו שהוא ב' מג‫' והשני יהיה מהשלישי כמו שהוא ג' בד‫' ותכה הראשון בעצמו ואח"כ יוכה העולה במספר הראשון בעצמו ואח"כ יוכה המספר השני בעצמו וכשיחוברו יחד שתי אלו ההכאות יעשה כמו הכאת המספר השלישי בי"ב וחצי אשאל כמה יבא להיות כל אחד מהמספרים
word problem/find a number	a+½a+⅕a+⅐a=2	Arithmetic_Textbook_by_R._Aharon_ben_Isaac#hxby	Question one: [What is] the number, such that if you add [to it] its half, its fifth, and its seventh, [the total is 2]. :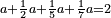 $\scriptstyle a+\frac{1}{2}a+\frac{1}{5}a+\frac{1}{7}a=2$ ‫97r / ע"ט[...] [שאלה ראשונה] [מהו ה]מספר אשר אם תחבר [עליו] חציו חמשיתו ושביעיתו ‫[יהיה עם הכל שנים]
word problem/find a number	3/a=5+7/b	ספר_דיני_ממונות#iyBa	155) Question: if you want to find a number such that if you divide 3 by it, the result is 5 and 7 remain. :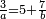 $\scriptstyle\frac{3}{a}=5+\frac{7}{b}$ קנה)MS L: קנב שאלה אם תרצה למצא מספר אשר אם תחלק ג' מאותו המספר יבא ה' וישאר ז‫'
word problem/find a number	a+28=2a²	ספר_האלזיברא#AZ3B	Question: we want to find a number such that when we add to it 28 the sum is twice its square :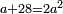 $\scriptstyle a+28=2a^2$ שאלה רצינו למצא מספר כאשר הוספנו עליו כ"ח {{#annot: term \| #to be equal to, #שוה \| hkKx}}יהיה שוה ל{{#annotend:hkKx}}שני דמיוני מרבעו
word problem/find a number	a/b=⅔;a√a=b²	ספר_ג'יבלי_אלמוקבאלא#LtCT	Find me two numbers such that one is a part of the other as 2 is of 3; :and when the first is multiplied by its root it yields the same as the product of the second by itself. :I ask: how much will each number be? :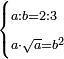 $\scriptstyle\begin{cases}\scriptstyle a:b=2:3\\\scriptstyle a\sdot\sqrt{a}=b^2\end{cases}$ תמצא לי ב' מספרי' שיהיה האחד חלק מהאחר כמו ב' מג‫' ובהכות הראשו' בשרשו יעשה כמו הכאת השני בעצמו אשאל כמה יבא להיות כל אחד מן המספרים
word problem/find a number	b/(c-a)=3⅓;c/(b-a)=6	ספר_מעשה_חושב#353o	Example: the ratio of the second to what remains from the third when the first is subtracted from it is 3 integers and a third. ::The ratio of the third to what remains from the second when the first is subtracted from it is the number 6. ::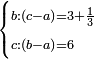 $\scriptstyle\begin{cases}\scriptstyle b:\left(c-a\right)=3+\frac{1}{3}\\\scriptstyle c:\left(b-a\right)=6\end{cases}$ והמשל שיהיה יחס ‫82vהשני אל הנשאר מהשלישי כשחוסר ממנו הראשון ג' שלמים ושליש ויחס השלישי אל הנשאר מהשני כשחוסר ממנו הראשון מספר ו'
word problem/find a number	⅓a+¼a=20	מלאכת_המספר#Auzt	Example: we wish to find a number that the sum of its third and its quarter is 20. :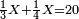 $\scriptstyle\frac{1}{3}X+\frac{1}{4}X=20$ המשל רצינו למצא מספר שקבוץ שלישיתו ורביעיתו יהיה כ‫'
word problem/find a number	b=2a;a²b=9b	ספר_ג'יבלי_אלמוקבאלא#ZaKZ	Find me two numbers such that the one is double the other; :and when the smaller is multiplied by itself, and the product is multiplied by the second number, it yields the same as the second, i.e. the larger, multiplied by 9. :I ask: how much will each number be? :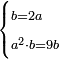 $\scriptstyle\begin{cases}\scriptstyle b=2a\\\scriptstyle a^2\sdot b=9b\end{cases}$ תמצא לי שני מספרים שהאחד יהיה {{#annot: term \| #double, #כפל \| HqHc}}כפל ה{{#annotend:HqHc}}שני וכשהוכה הקטון בעצמו ואותה ההכאה תוכה במספר השני יעשה כמו השני רצו' הגדול מוכה על ט‫' אשאל כמה יבא להיות כל אחד מהמספרים
word problem/find a number	a/b=¾;(ab)²+27=9b²	ספר_ג'יבלי_אלמוקבאלא#gmur	Find me two numbers such that the first is a part of the other as 3 is of 4; :and the first multiplied by the second, and this product is multiplied by itself and 27 is added to it, yield the second number multiplied by itself and this product is multiplied by 9. :I ask: how much will each number be? :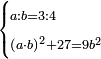 $\scriptstyle\begin{cases}\scriptstyle a:b=3:4\\\scriptstyle\left(a\sdot b\right)^2+27=9b^2\end{cases}$ עשה לי זה החשבון תמצא לי שני מספרי' שיהיה הראשון חלק מהשני כמו שג' הוא מד‫' ומוכה הראשון בשני ואותה ההכאה תוכה בעצמה ויחובר עמה כ"ז יעשה המספר השני בכפלו בעצמו ואותה ההכאה תוכה בט‫' אשאל כמה הוא כל אחד מהמספרים האמורי‫'
word problem/find a number	(a·⅔a)·a=a√8	ספר_ג'יבלי_אלמוקבאלא#iQR6	Find me a number, such that when it is multiplied by its two thirds, and this product is multiplied by that number, it yields the same as the product of that number by the root of 8. :I ask: how much will the number be? :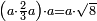 $\scriptstyle\left(a\sdot\frac{2}{3}a\right)\sdot a=a\sdot\sqrt{8}$ תמצא לי מספר אחד שכשיוכה בשני שלישיו ואותה ההכאה תוכה במספר האמור יעשה כמו הכאת המספר ההוא בשרש ח‫' אשאל כמה הוא כל אחד מהמספרי‫'
word problem/find a number	a(mod2)=1,a(mod3)=1,a(mod)4=1,a(mod5)=0	ספר_המספר_/_אליהו_מזרחי#msZ5	Likewise: if one asks: what is the number that when counted by twos - one remains; by threes - one remains; by fours - one remains; and by fives - nothing remains. וכן אם שאל שואל איזהו המספר אשר כשימנה מב' ב' ישאר אחד ומג' ג' ישאר אחד ומד' ד' ישאר אחד ומה' ה' לא ישאר דבר
word problem/find a number	a/b=⅔;ab√8=100	ספר_ג'יבלי_אלמוקבאלא#mV9d	Find me two numbers such that one is a part of the other as 2 is of 3; :and when the one is multiplied by the other, and the product is multiplied by the root of 8, it yields 100. :I ask: how much will each number be? :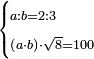 $\scriptstyle\begin{cases}\scriptstyle a:b=2:3\\\scriptstyle\left(a\sdot b\right)\sdot\sqrt{8}=100\end{cases}$ תמצא לי שני מספרי' שיהיה חלק האחד מהאחר כמו שב' הוא מג‫' וכשיוכה האחד באחר ואותה ההכאה תוכה בשרש ח' ועושה ק‫' אשאל כמה יבא להיות כל אחד מהמספרי‫'
word problem/find a number	a/b=⅘;ab=b√8	ספר_ג'יבלי_אלמוקבאלא#roVS	Find me two numbers such that the first is a part of the second as 4 is of 5; :and the one multiplied by the other yields the same as the product of the second by the root of 8. :I ask: how much will each number be? :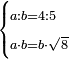 $\scriptstyle\begin{cases}\scriptstyle a:b=4:5\\\scriptstyle a\sdot b=b\sdot\sqrt{8}\end{cases}$ תמצא לי ב' מספרי' שיהיה הראשון חלק מהשני כמו שד' הוא מה‫' ומוכה האחד באחר יעשה כמו הכאת השני בשרש ח‫' אשאל כמה יבא להיות כל אחד מהמספרי‫'
word problem/find a number	a²=4(a+8)	ספר_המספר_/_אליהו_מזרחי#OOxP	The example: if you want to know what is the number whose square equals the product of 4 by the sum of that number with 8. ::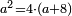 $\scriptstyle a^2=4\sdot\left(a+8\right)$ המשל בזה אם רצית לדעת איזהו המספר אשר יהיה מרובעו שוה לעולה מהכאת הד' עם המספר ההוא מחובר עם ח‫'
word problem/find a number	4a(mod)6=1	ספר_דיני_ממונות#alcr	Find me a number such that when I multiply it by 4, then divide it by 6, the remainder is 1. :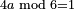 $\scriptstyle4a\bmod6=1$ שאלה תמצא לי מספר שכשאכפלהו בד' ותחלקהו על ו' שישאר א‫'
word problem/find a number	a/b=⅔;a²b+\sqrt{a²b}=342	ספר_ג'יבלי_אלמוקבאלא#oR0N	Find me two numbers such that the first is a part of the second as 2 is of 3; :and if the first is multiplied by itself, then this product is multiplied by the second, and this product is summed with its root, it yields 342. :I ask: how much will each number be? :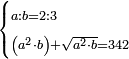 $\scriptstyle\begin{cases}\scriptstyle a:b=2:3\\\scriptstyle\left(a^2\sdot b\right)+\sqrt{a^2\sdot b}=342\end{cases}$ עשה לי זה החשבון תמצא לי שני מספרי' שיהיה הראשון חלק מהשני כמו שב' הוא מג‫' ומוכה הראשון בעצמו ואותה ההכאה תכה בשני ותחובר זאת ההכאה עם שרשה יעשה שמ"ב אשאל כמה יבא להיות כל אחד מהמספרי‫'
word problem/find a number	a/b=⅔;(ab)²+a²√4=4¼	ספר_ג'יבלי_אלמוקבאלא#jPKB	Find me two numbers such that one is a part of the other as 2 is of 3; :and when the first is multiplied by the second and this product is multiplied by itself then summed with the product of the first multiplied by itself then by the root of 4, it yields 4 and a quarter. :I ask: how much will each number be? :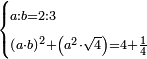 $\scriptstyle\begin{cases}\scriptstyle a:b=2:3\\\scriptstyle\left(a\sdot b\right)^2+\left(a^2\sdot\sqrt{4}\right)=4+\frac{1}{4}\end{cases}$ עשה לי זה החשבון תמצא לי שני מספרי' שיהיה הא' חלק מהאחר כמו שב' הוא מג‫' ומוכה הראשון בשני וזאת ההכאה תוכה בעצמה ותחובר זאת ההכאה עם הכאת הראשון מוכה בעצמו ומה שיבא בשרש ד' יעשה ד' ורביע אשאל כמה יבא להיות כל אחד מהמספרי‫'
word problem/find a number	37a=49	Arithmetic_Textbook_by_R._Aharon_ben_Isaac#b6Ce	The [sixth] question: what is the number, such that when we multiply it by 37, the product is 49. :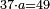 $\scriptstyle37\sdot a=49$ שאלה חמשית מהו המספר אשר כפלנו אותו על ל"ז והיוציא מן הכפל יהיה מ"ט
word problem/find a number	a²+19=b²	ספר_דיני_ממונות#DmeO	149) Question: if you want to find a square number such that if you add to it 19 it will be a square. :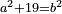 $\scriptstyle a^2+19=b^2$ קמט)‫MS L: קמו שאלה אם תרצה למצא מספר מרובע אשר אם תשים עליו י"ט יהיה מרובע
word problem/find a number	a/b=⅔;3a+4√b=30	ספר_ג'יבלי_אלמוקבאלא#37bI	Find me two numbers such that the one is a part of the other as 2 is of 3; :and when the first is multiplied by 3 and the root of the second by 4, then both the products are summed together, it yields thirty. :I ask: how much will each number be? :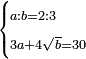 $\scriptstyle\begin{cases}\scriptstyle a:b=2:3\\\scriptstyle3a+4\sqrt{b}=30\end{cases}$ והנה המשל תמצא לי שני מספרי' שיהיה האחד חלק מאחר כמו שב' הוא מג‫' ובהכות הראשון בג' ושרש השני בד' ויחוברו שתי אלו ההכאות יחד יעשה שלשים אשאל כמה יבא להיות כל אחד מהמספרי‫'
word problem/find a number	six proportional numbers	ספר_דיני_ממונות#fNcE	Example: we have six proportional numbers, the first of which is 2 and the sixth is 64. דמיון יש לנו ו' מספרים מתיחסים שהראשון ב' והו' ס"ד
word problem/find a number	six proportional numbers	ספר_דיני_ממונות#Yfpk	111) Question: if you want to find a proportional number: :For example: we have six proportional numbers, i.e. the ratio of the sixth to the fifth is the same as the ratio of the fifth to the fourth, and the same as the ratio of the fourth to the third, and the same as the ratio of the third to the second, and the same as the ratio of the second to the first. :The first number is 2. :The sixth is 2048. :We wish to know how much is the second? קיא)‫MS L: קט שאלה אם תרצה למצא {{#annot:term\|994,2263\|2xtB}}מספר יחסיי{{#annotend:2xtB}} הנקרא בלשונם {{#annot:term\|994\|DhLM}}נומירו פרופורציאונלי{{#annotend:DhLM}} דמיון זה יש לנו ו' {{#annot:term\|994,2263\|jjwV}}מספרים יחסיים{{#annotend:jjwV}} ר"ל שיחס הו' אל הה' כיחס הה' אל הד' וכיחס הד' אל הג' וכיחס הג' אל הב' וכיחס הב' אל הא‫' והמספר הא' ב‫' והו' ב' אלפים ומ"ח ונרצה לדעת מהו השני
word problem/find a number	(a+b)\c=3⅖⅐;(a+c)\b=7⅔¼;b=30	ספר_דיני_ממונות#OJ9R	58) Question: when one number is added to a second number, their ratio to the third is 3 integers, 2-fifths and a seventh. :When the first is added to the third, their ratio to the [second] is 7 integers, 2-thirds and a quarter. :The second number is 30. :We wish to know: how much is each of the rest? נח) שאלה שיהיה מספר ראשון כשחובר אל מספר שני היה יחסו אל הג' ג' שלמים וב' חמישיות ושביעיות וכשחובר הראשון אל הג' היה יחסו הראשון ז' שלמים וב' שלישיות ורביעיות והמספר הב' ל‫' רצינו לדעת כמה כל א' מהנשארים
word problem/find a number	perfect number	ספר_דיני_ממונות#x3Is	109) If you want to find the second [perfect number] קט)‫MS L: om. ואם תרצה למצא השני
word problem/find a number	repeated subtraction	מלאכת_המספר#j27H	Question: if the half of any amount plus one are subtracted, then the half of the remainder plus one, then the half of the remainder plus one, and one remains, how much is the original number? שאילה אם מאי זה כמות ילקח חציו ואחד יותר ומהנשאר חציו ויותר אחד ומהנשאר חציו ויותר אחד ונשאר אחד כמה היה המספר הראשון \|} : $\scriptstyle\left[\left[X-\left(\frac{1}{2}X+1\right)\right]-\left[\left[\frac{1}{2}\sdot\left[X-\left(\frac{1}{2}X+1\right)\right]\right]+1\right]\right]-\left[\left[\frac{1}{2}\sdot\left[\left[X-\left(\frac{1}{2}X+1\right)\right]-\left[\left[\frac{1}{2}\sdot\left[X-\left(\frac{1}{2}X+1\right)\right]\right]+1\right]\right]\right]+1\right]=1$
word problem/find a number	a/b=⅗;(ab)²=a²	ספר_ג'יבלי_אלמוקבאלא#0dhl	Find me two numbers such that the first is a part of the second as 3 is of 5; :and when the smaller is multiplied by the greater and the product is multiplied by itself, it yields the same as the product of the greater by itself. :I ask: how much will each number be? :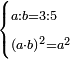 $\scriptstyle\begin{cases}\scriptstyle a:b=3:5\\\scriptstyle\left(a\sdot b\right)^2=a^2\end{cases}$ תמצא לי שני מספרים שיהיה חלק הראשון מהשני כמו שהוא ג' מה‫' וכאשר הוכה הקטון בגדול ומה שיעלה יוכה בעצמו יעשה כמו הכאת הגדול בעצמו אשאל כמה כל אחד מהמספרים
word problem/find a number	(a+b)/(c-a)=4½;(a+c)/(b-a)=5	ספר_דיני_ממונות#UcvZ	61) Question: the ratio of the first and the second summed together to what remains from the third when the first is subtracted from it is 4 integers and a half. :The ratio of the first and the third summed together to what remains from the second when the first is subtracted from it is 5 integers. :We wish to know: how much is each of the numbers that meet this condition? סא) שאלה שיהיה יחס הראשון והשני מקובצים אל הנשאר מהג' כשחוסר ממנו הראשון ד' שלמים וחצי ויחס הראשון והג' מקובצים אל הנשאר מהב' כשחוסר ממנו הראשון הוא ה' שלמים ונרצה לדעת כמה כל המספרים שינהגו זה המנהג
word problem/find a number	seven proportional numbers	ספר_דיני_ממונות#nCKV	258) Question of seven numbers: the first is 1 and the last is 729. רנח) שאלה מז' מספרים הראשון א' והאחרון תשכ"ט
word problem/find a number	13·7·3a=3	Arithmetic_Textbook_by_R._Aharon_ben_Isaac#o8DN	The eighth question: what is the number, such that when we multiply it by 3, then the product by 7, then the product by 13, the result is only 3. :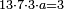 $\scriptstyle13\sdot7\sdot3\sdot a=3$ שאלה שמינית מהוא המספר אשר כפלנו אותו על ג' והיוציא על ז' והיוציא על י"ג ושלא יעלה אלא ג‫'
word problem/find a number	perfect number	ספר_דיני_ממונות#IXt8	108) Question: if you want to find a perfect number קח) שאלה אם תרצה למצא {{#annot:term\|75\|xt6c}}מספר שלם{{#annotend:xt6c}} נקרא בלשונם {{#annot:term\|75\|aiWm}}נומירו פירפיטו{{#annotend:aiWm}}
word problem/find a number	a·b·c=1000;a\b\c	ספר_דיני_ממונות#WgAN	452) Question: we have three proportional numbers such that the ratio of the first to the second is as the ratio of the second to the third. :If we multiply the first by the second, then multiply the result by the third it will be a thousand. :How much are the proportional numbers? ‫116rתנב) שאלה יש לנו ג' מספרים יחסיים אשר יחס הא' אל הב' כיחס הב' אל הג‫' והנה נכפול הא' על הב' והעולה נכפול על ג' הוא אלף כמה הם המספרים היחסיים
word problem/find a number	⅕a/√a=7	ספר_דיני_ממונות#VnZO	Question: find me a number, such that when you divide its fifth by a root of the given number, the result is 7. :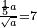 $\scriptstyle\frac{\frac{1}{5}a}{\sqrt{a}}=7$ שאלה‫MS L שיו תמצא לי מספר אשר כשתחלק חמישיתו על שרש המספר המונח שיצא ז‫'
word problem/find a number	a/b=⁵/₇;(ab)²=a²√8	ספר_ג'יבלי_אלמוקבאלא#3fAj	Find me two numbers such that the one is a part of the other as 5 is of 7; :and if the first is multiplied the second, then the product is multiplied by itself, it yields the same as the product of the smaller by itself, then the product multiplied by the root of 8. :I ask: how much will each number be? :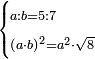 $\scriptstyle\begin{cases}\scriptstyle a:b=5:7\\\scriptstyle\left(a\sdot b\right)^2=a^2\sdot\sqrt{8}\end{cases}$ תמצא לי שני מספרי' שיהיה האחד חלק מהאחר כאשר ה' הוא מז‫' ומוכה הראשון בשני ואותה ההכאה תוכה בעצמה יעשה כמו הכאת המספר הקטן בעצמו וההכאה ההיא תוכה בשרש ח‫' אשאל כמה יבא להיות כל אחד מהמספרי‫'
word problem/find a number	seven proportional numbers	ספר_דיני_ממונות#By9s	259) Question of seven numbers with fractions: the first is an eighth and the seventh is 91 integers and an eighth. רנט) שאלה משברים מז' מספרים הראשון א' שמינית והז' צ"א שלמים ושמינית
word problem/find a number	a²=(3+¹⁰/₁₃)(a+6)	ספר_המספר_/_אליהו_מזרחי#UwCZ	Likewise, if you want to know the number whose square equals the product of three and 10-thirteenths by the sum of that number with 6. ::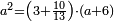 $\scriptstyle a^2=\left(3+\frac{10}{13}\right)\sdot\left(a+6\right)$ וכן אם רצית לדעת המספר אשר יהיה מרובעו שוה לעולה מהכאת השלשה וי' יגיי"ם עם המספר ההוא מחובר עם ו‫'
word problem/find a number	a/b=¾;a²b=√(20¼)	ספר_ג'יבלי_אלמוקבאלא#4NoH	Find me two numbers such that one is a part of the other as 3 is of 4; :and when the one is multiplied by itself, and this product is multiplied by the second, it yields a root of 20 and a quarter. :I ask: how much will each number be? :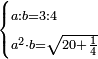 $\scriptstyle\begin{cases}\scriptstyle a:b=3:4\\\scriptstyle a^2\sdot b=\sqrt{20+\frac{1}{4}}\end{cases}$ עשה לי זה החשבון תמצא לי שני מספרים שיהיה חלק האחד מהאחר כמו מה שהוא ג' מד‫' וכשיוכה הראשון בעצמו ואותה ההכאה תכה בשני יעשה שרש כ' ורביע אשאל כמה יבא להיות כל אחד מהמספרים
word problem/find a number	b-1=a+1;20(a-1)=b+1	מלאכת_המספר#osY0	In order to elaborate the explanation, we give another example: we assume two numbers, such that if we subtract one from the greater number and add it to the smaller, both numbers become equal; and if we subtract one from the smaller number and add it to the greater, the greater becomes twenty times the smaller. ‫[ו‫]כדי לה[וסי]ף ביאור נעשה משל אחר בשנניח ב' מספר[ים] שאם נחסר אחד מהמספר הגדול [ו]נוסיפהו לקטן יהיה [ה]שני מספרי' שוים ואם נחסר אחד מהמספר הקטן ונוסיפהו בגדול יהיה הגדול עשרי' פעמי' בקטן
word problem/find a number	a+½½a+⅓⅓a+⅕⅕a=7	Arithmetic_Textbook_by_R._Aharon_ben_Isaac#rLug	Question: What is the unknown number, such that when we add to it half of its half, a third of its third, and a quarter of its quarter, it is exactly 7. :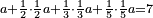 $\scriptstyle a+\frac{1}{2}\sdot\frac{1}{2}a+\frac{1}{3}\sdot\frac{1}{3}a+\frac{1}{5}\sdot\frac{1}{5}a=7$ ‫marg.שאלה מהו המספר הנעלם אשר חיברנו עליו חצי חציו ושלישית שלישיתו ורביעית רביעיתו ולא יהיה אלא ז‫'
word problem/find a number	a(mod)3=2,a(mod5)=4,a(mod7)=6	ספר_דיני_ממונות#hx8d	169) Question: if you are told that the remainder after casting out the threes is 2 etc. :Do it this way: :For instance, if it is said that when we divide it by 3, 2 remains; if its is divided by 5, 4 remains; and if it is divided by 7, 6 remains. קסט) שאלה ואם אמר לך שנשאר בהשליכך ג"ג ב' או ג‫' עשה בדרך הזה עד"מ ואם אמר כשנחלקהו על ג' ישאר ב' ואם יחולק על ה' ישאר ד' ואם יחולק על ז' ישאר ו‫'
word problem/find a number	a(mod2)=1,a(mod3)=2,a(mod)4=3,a(mod5)=1,a(mod6)=5,a(mod7)=1,a(mod8)=7,a(mod9)=8,a(mod10)=1	ספר_המספר_/_אליהו_מזרחי#kMUT	Question: if one asks: what is the number that when counted by twos - one remains; by threes - 2 remains; by fours - 3 remains; by fives - one remains; by sixes - five remains; by sevens - one remains; by eights - 7 remains; by nines - eight remains; and by tens - one remains. שאלה אם שאל שואל איזהו המספר אשר כשימנה מב' ב' ישאר אח' ומג' ג' ישארו ב' ומד' ד' ישארו ג' ומה' ה' ישאר אחד ומו' ו' ישארו חמשה ומז' ז' ישאר אחד ומח' ח' ישארו ז' ומט' ט' ישארו שמנה ומי' י' ישאר אחד
word problem/find a number	four proportional numbers	ספר_דיני_ממונות#Z5m3	Example: the first is 2 and the fourth is 16. דמיון המספר הראשון ב' והד' י"ו
word problem/find a number	a/b=¾;³√(2a+3b)=8	ספר_ג'יבלי_אלמוקבאלא#q0Kk	Find me two numbers such that one is a part of the other as 3 is of 4; :and when the one is multiplied by 2 and the other is multiplied by 3, and the two products are summed together their cube root is 8. :I ask: how much will each number be? : $\scriptstyle\begin{cases}\scriptstyle a:b=3:4\\\scriptstyle\sqrt[3]{2a+3b}=8\end{cases}$ והנה המשל עשה לי זה החשבון תמצא לי ב' מספרי‫' שיהיה הא' חלק מהאחר כמו שג' הוא מד‫' ומוכה הראשון בב' והשני בג' ויקובצו ב' אלו ההכאו' יחד יהיה שרשם המעוקב ח‫' אשאל כמה יבא להיות כל א' מהמספרי‫'
word problem/find a number	four proportional numbers	ספר_דיני_ממונות#VcKa	Example: the first is 3-quarters and the last is 6 integers. דמיון הראשון ג' רביעיות והאחרון ו' שלמים
word problem/find a number	five proportional numbers	ספר_דיני_ממונות#lGXB	257) Example of five numbers: the first is 3 and the last is 48. רנז) דמיון מה' מספרים הראשון ג' והאחרון מ"ח
word problem/find a number	a+b=n², a-b=m²	ספר_דיני_ממונות#U3Ow	332) Question: find me a number such that when you add a certain number to it, it becomes a square, and if you subtract it from it, a square remains. :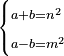 $\scriptstyle\begin{cases}\scriptstyle a+b=n^2\\\scriptstyle a-b=m^2\end{cases}$ שלב) שאלה תמצא לי מספר אשר כשתוסיף עליו מספר מה יהיה מרובע ‫284vואם תגרע ממנו ישאר מרובע
word problem/find a number	a(mod)1=0,a(mod2)=1,a(mod3)=2,a(mod)4=3,a(mod5)=4,a(mod6)=5,a(mod7)=1	ספר_דיני_ממונות#65rT	333) Question: find me a number, such that when you count it by ones it is gone; by twos - 1 remains; by threes - 2; by fours - 3; by fives - 4; by sixes - 5; and by sevens - 1. שלג) שאלה תמצא לי מספר כי כשתמנהו א"א שוה ב"ב ישאר א' ג"ג ב' ד"ד ג' ה"ה ד' ו"ו ה' ז"ז א‫'
word problem/find a number	a/b=¾;a²b=288	ספר_ג'יבלי_אלמוקבאלא#7M0L	Find me two numbers such that the one is a part of the other as 3 is of 4; :and when the smaller is multiplied by itself, and the product is multiplied by the larger, it yields 288. :I ask: how much will each number be? :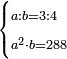 $\scriptstyle\begin{cases}\scriptstyle a:b=3:4\\\scriptstyle a^2\sdot b=288\end{cases}$ תמצא לי שני מספרים שיהיה האחד חלק מהאחר כמו שהוא ג' מד‫' וכשיוכה הקטן בעצמו ו{{#annot: term \| #result, #יוצא \| QU3I}}היוצא{{#annotend:QU3I}} תכה בגדול יעשה רפ"ח אשאל כמה כל אחד מהמספרי‫'
word problem/find a number	(a·⅔a)²=√50	ספר_ג'יבלי_אלמוקבאלא#MvD8	Find me a number, such that when it is multiplied by its two thirds, and that product is multiplied by itself, it yields the root of fifty. :I ask: how much will the number be? :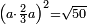 $\scriptstyle\left(a\sdot\frac{2}{3}a\right)^2=\sqrt{50}$ עשה לי זה החשבון תמצא לי מספר אחד שכאשר הוכה בשני שלישיו ואותה ההכאה תוכה בעצמה תעשה שרש חמשים אשאל כמה יבא להיות המספר האמור
word problem/find a number	perfect number	ספר_דיני_ממונות#CaJp	110) If you want to find the third [perfect number] קי)‫MS L: om. ואם ואם תרצה למצא השלישי
word problem/find a number	(a+b)\c=3⅖⅐;(a+c)\b=7⅔¼;b=30	ספר_מעשה_חושב#odgb	Example: when one number is added to a second number, their ratio to the third is 3 integers, 2-fifths and a seventh. ::When the first is added to the third, their ratio to the second is 7 integers, 2-thirds and a quarter. ::The second number is 30. ::We wish to know: how much is each of the rest? ::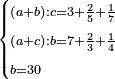 $\scriptstyle\begin{cases}\scriptstyle\left(a+b\right):c=3+\frac{2}{5}+\frac{1}{7}\\\scriptstyle\left(a+c\right):b=7+\frac{2}{3}+\frac{1}{4}\\\scriptstyle b=30\end{cases}$ דמיון שיהיה מספר ראשון כשחובר אל מספר שני היה יחסו אל השלישי ג' שלמים וב' חמשיות ושביעית וכשחובר הראשון אל השלישי יהיה יחסו אל השני‫אל השני: P2271 הראשון ז' שלמים וב' שלישיות ורביעית והמספר השני שלשים ורצינו לדעת כמה כל אחד מהנשארים
word problem/find a number	4a/5=6⅗	ספר_דיני_ממונות#lrPR	Another question: find me a number such that when you multiply it by 4, then divide the product by 5, the result of division is 6 and the remainder is 3. :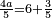 $\scriptstyle\frac{4a}{5}=6+\frac{3}{5}$ שאלה אחרת תמצא לי מספר אשר כשתכפלהו על ד' ותחלקהו על ה' שיצא ו' בחלוק וישאר ג‫'
word problem/find a number	9a=1	Arithmetic_Textbook_by_R._Aharon_ben_Isaac#LF1Q	The seventh question: what is the number, such that when we multiply it by 9, the product is one. :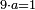 $\scriptstyle9\sdot a=1$ שאלה שביעית מהו המספר שאם כפלנו אותו על ט' והיוציא יהיה אחד
word problem/find a number	8/a/b/27	ספר_דיני_ממונות#cJJC	Question: if you wish to find two numbers standing between 8 and 27, such that the ratio of the second to the first is as the ratio of the third to the second and as the ratio of the fourth to the third. :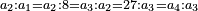 $\scriptstyle a_2:a_1=a_2:8=a_3:a_2=27:a_3=a_4:a_3$ שאלה אם תרצה למצא ב' מספרים יעמדו בין ח' ובין כ"ז שיהיה יחס השני אל הראשון כיחס הג' אל הב' וכיחס הד' אל הג‫'
word problem/find a number	a/b=⅖;ab=8√b	ספר_ג'יבלי_אלמוקבאלא#BstD	Find me two numbers such that the one is a part of the other as 2 is of 5; :and when the first is multiplied by the second, it yields the same as the product of the root of the second by 8. :I ask: how much will each number be? :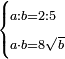 $\scriptstyle\begin{cases}\scriptstyle a:b=2:5\\\scriptstyle a\sdot b=8\sqrt{b}\end{cases}$ תמצא לי שני מספרי' שיהיה האחד חלק מהאחר כמו שב' הוא מה‫' וכשהוכה האחד בשני יעשה כמו הכאת שרש השני בח‫' אשאל כמה יבא להיות כל אחד מהמספרי‫'
word problem/find a number	a/b=⅓;³√a³√b=100	ספר_ג'יבלי_אלמוקבאלא#AP3O	Find me two numbers such that the one is a part of the second as 1 is of 3; :and the cube root of the first multiplied by the cube root of the second yields 100. :I ask: how much will each number be? : $\scriptstyle\begin{cases}\scriptstyle a:b=1:3\\\scriptstyle\sqrt[3]{a}\sdot\sqrt[3]{b}=100\end{cases}$ והנה המשל עשה לי זה החשבון תמצא לי ‫43rשני מספרי' שיהיה הראשון חלק מהשני כמו שא' הוא מג‫' ומוכה שרש מעו' מהראשון בשרש מעו' השני יעשה ק‫' אשאל כמה יבא להיות כל אחד מן המספרי‫'
word problem/find a number	three proportional numbers	ספר_דיני_ממונות#qdnU	Example: we have three proportional numbers, the first is 2, and the third is 18. דמיון יש לנו ג' מספרים מתיחסים הראשון ב' והג' י"ח
word problem/find a number	a(mod)3=a(mod5)=a(mod7)=1	ספר_דיני_ממונות#lQns	168) Question: find me a number, such that if you divide it by 3, by 5, and by 7, 1 remains. קסח) שאלה בקש לי מספר שאם תחלקהו על ג' ועל ה ועל ז' ישאר א‫'
word problem/find a number	4a(mod)5=1	ספר_דיני_ממונות#3egI	Example from which you can understand all that is mentioned concerning the nativities: it is that you find me a number such that when you multiply it by 4, then divide the product by 5, the remainder is 1. :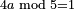 $\scriptstyle4a\bmod5=1$ דמיון אשר ממנו תוכל להבין כל הנזכר במולדות והוא תמצא לי מספר אשר כשתכפלהו על ד' והעולה תחלק על ה' שישאר א‫'
word problem/find a number	a/b=⅔;3a+4b=³√216	ספר_ג'יבלי_אלמוקבאלא#w4Ac	Find me two numbers such that one is a part of the other as 2 is of 3; :and when the first is multiplied by 3 and the second by 4, and both products are summed together, they yield a cube root of 216. :I ask: how much will each number be? : $\scriptstyle\begin{cases}\scriptstyle a:b=2:3\\\scriptstyle3a+4b=\sqrt[3]{216}\end{cases}$ והנה המשל תמצא לי ב' מספרי' שיהיה האחד חלק מהאחר כמו שב' הוא מג‫' ומוכה הראשון בג' והשני בד' ויחוברו ב' אלו ההכאו' יחד יעשה שרש מעוק' מרי"ו אשאל כמה יבא להיות כל א' מהמספרי‫'
word problem/find a number	√(9a)=12	ספר_ג'יבלי_אלמוקבאלא#TeOu	Find me a number, such that when it is multiplied by 9, the root of the product is 12. :I ask: how much will the number be? :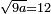 $\scriptstyle\sqrt{9a}=12$ תמצא לי מספר אחד שכאשר יוכה בט' יהיה שרש העולה י"ב אשאל כמה יבא להיות המספר
word problem/find a number	a-⅓a-¼a=29	ספר_דיני_ממונות#3Zd3	135) Question: find me a number such that if you subtract its third and its quarter from it the remainder is 29. :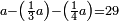 $\scriptstyle a-\left(\frac{1}{3}a\right)-\left(\frac{1}{4}a\right)=29$ קלה)‫MS L: קלב שאלה תמצא לי מספר אשר אם תוציא ממנו שלישיתו ורביעיתו הנשאר כ"ט
word problem/find a number	a²-5a=n², a²+7a=m²	ספר_דיני_ממונות#3YCC	158) Question: if you want to find a square number such that if you subtract its five roots from it the remainder is a square and if you add it to its seven roots it will be a square. :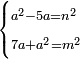 $\scriptstyle\begin{cases}\scriptstyle a^2-5a=n^2\\\scriptstyle7a+a^2=m^2\end{cases}$ קנח)‫MS L: קנה שאלה אם תרצה לדעת מספר אחד מרובע אשר אם תוציא אותו מה' שרשיו וישאר מרובע ואם תוסיף עליו שבעה שורשיו יהיה מרובע
word problem/find a number	³/₇a+⁴/₅a=⅔a+¼a+20	ספר_מעשה_חושב#7YKC	Example: three-sevenths and four-fifths of the unknown number exceed two-thirds and a quarter of the unknown number by twenty and we wish to know how much is the number? ::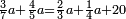 $\scriptstyle\frac{3}{7}a+\frac{4}{5}a=\frac{2}{3}a+\frac{1}{4}a+20$ דמיון זה שיהיו ג' שביעיות וד' חמישיות המספר הנעלם מוסיפים על ב' שלישיות ורביעית המספר הנעלם עשרים ורצינו לדעת כמה המספר
word problem/find a number	a/b=⅔;4a+4b=√100	ספר_ג'יבלי_אלמוקבאלא#FMUp	Find me two numbers such that one is a part of the other as 2 is of 3; :and when each of them is multiplied by 4, and both products are summed together, they yield a root of 100. :I ask: how much will each number be? :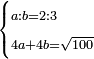 $\scriptstyle\begin{cases}\scriptstyle a:b=2:3\\\scriptstyle4a+4b=\sqrt{100}\end{cases}$ תמצא לי שני מספרים שיהיה חלק האחד מהאחר כמו שהוא ב' מג‫' וכשיוכה כל אחד בארבעה ויקובצו אלו ההכאות יחד יעשו שרש ק‫' אשאל כמה יבא להיות כל מספר מהם
word problem/find a number	a/b=⅔;a²b=b√b	ספר_ג'יבלי_אלמוקבאלא#DcQa	Find me two numbers such that the one is a part of the other as 2 is of 3; :and when the first is multiplied by itself and this product is multiplied by the second, it yields the same as the product of the second by its root. :I ask: how much will each number be? :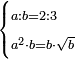 $\scriptstyle\begin{cases}\scriptstyle a:b=2:3\\\scriptstyle a^2\sdot b=b\sdot\sqrt{b}\end{cases}$ תמצא לי שני מספרי' שיהיה האחד חלק מהשני כמו שב' הוא מג‫' ומוכה הראשון בעצמו ואותה ההכאה תוכה במספר השני יעשה ‫34vכמו הכאת השני בשרשו אשאל כמה יבא להיות כל אחד מהמספרי‫'
word problem/find a number	a/b=⅗;ab=³√729	ספר_ג'יבלי_אלמוקבאלא#ai8Z	Find me two numbers such that one is a part of the other as 3 is of 5; :and the one multiplied by the other yields a cube root of 729. :I ask: how much will each number be? : $\scriptstyle\begin{cases}\scriptstyle a:b=3:5\\\scriptstyle a\sdot b=\sqrt[3]{729}\end{cases}$ והנה המשל תמצא לי ב' מספרי' שיהיה האחד חלק מהאחר כמו ג' מה‫' ומוכה הראשון בשני יעשה שרש מעו' מתשכ"ט אשאל כמה יבא להיות כל אחד מהמספרי‫'
word problem/find a number	(a+b)/c=⅗+⅙;(a+c)/b=2⅓;a=20	ספר_דיני_ממונות#gfLj	59) Question: the ratio of the first and the second summed together to the third is 3-fifths plus a sixth. :The ratio of the first and the third summed together to the second is 2 integers and a third. :The first number is 20. :We wish to know: how much is each of the remaining numbers? נט) שאלה יהיה יחס הראשון עם השני מקובצים אל השלישי ג' חמישיות ושישית ויחס הראשון והג' מקובצים אל השני ב' שלמים ושלישית והמספר הראשון עשרים נרצה לדעת כמה כל א' מהמספרים הנשארים
word problem/find a number	a/b=¾;8a=6√b	ספר_ג'יבלי_אלמוקבאלא#8HYy	Find me two numbers such that the one is a part of the second as 3 is of 4; :and the first multiplied by 8, yields the same as the root of the second multiplied by 6. :I ask: how much will each number be? :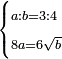 $\scriptstyle\begin{cases}\scriptstyle a:b=3:4\\\scriptstyle8a=6\sqrt{b}\end{cases}$ תמצא לי שני מספרי' שיהיה החלק האחד מהשני כמו שהוא ג' מד‫' וכן יעשה הראשון מוכה בח' כמו השני דהיינו שרשו מוכה בו‫' אשאל כמה יבא להיות כל אחד מהמספרים
word problem/find a number	³/₇a+⁴/₅a=⅔a+¼a+20	ספר_דיני_ממונות#SkQW	46) Question: three sevenths and four fifths of the unknown number exceed two thirds and a quarter of the unknown number by twenty. :We wish to know: how much is the number? :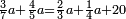 $\scriptstyle\frac{3}{7}a+\frac{4}{5}a=\frac{2}{3}a+\frac{1}{4}a+20$ מו) שאלה ג' שביעיות וד' חמישיות המספר הנעלם מוסיפים על ב' שלישיות ורביעית המספר הנעלם כ‫' רצינו לדעת כמה המספר הנעלם
word problem/find a number	⅓a+⅕a=10	מלאכת_המספר#niUj	Suppose we want to find any whole, such that the sum of its third and its fifth together is ten. :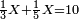 $\scriptstyle\frac{1}{3}X+\frac{1}{5}X=10$ נניח שרצינו למצא אי זה כל שקבוץ שלישיתו וחמישיתו יחד הם עשרה
word problem/find a number	a(mod2)=1,a(mod3)=2,a(mod)4=3,a(mod5)=4,a(mod6)=5,a(mod7)=0	ספר_המספר_/_אליהו_מזרחי#jLBc	Question: if one asks: what is the number that when counted by twos - one remains; by threes - 2 remains; by fours - 3 remains; by fives - 4 remains; by sixes - 5 remains; and by sevens - nothing remains. שאלה אם שאל שואל איזהו המספר אשר כשימנה מב' ב' ישארו א' ומג' ג' ישארו ב' ומד' ד' ישארו ג' ומה' ה' ישארו ד' ומו' ו' ישארו ה' ומז' ז' לא ישארו כלום
word problem/find a number	a+¼(b+c)=b+⅙(a+c)=c+⅑(a+b);b=20	ספר_דיני_ממונות#HxDL	62) Question: the first with a quarter of the rest is equal to the second with a sixth of the rest and is also equal to the third with a ninth of the rest. :It has already been explained to you in the first section of this book that the order of these three numbers is according to this arrangement, meaning that the first is added to the greatest part of the rest and the [third] is added to the smallest part of the rest. I remind you this so that you will not be confused by the explanations. :The second number is 20. :We wish to know: how much is each of the rest? סב) שאלה שיהיה הראשון עם רביעית הנשארים שוה אל השני עם שישית הנשארי' והוא ג"כ שוה אל השלישי עם תשיעית הנשארים כבר התבאר לך במאמ' הראשון מזה הספר שסדור אלו המספרים הג' הוא על זה הסדר אשר סדרוה רצוני שהראשון הוא אשר יתחבר המתחלק יותר גדול מן הנשארים והל' הוא אשר יתחבר עמו יותר קטן והנשארים והזכרתי זה לך למען לא תבלבל בביאורים והנה יהיה המספר השני מהם כ‫' ורצינו לדעת כמה כל א' מהנשארים
word problem/find a number	(½a+⅓a)-(¼a+⅕a)=4	ספר_דיני_ממונות#cQy5	Question: find me a number, such that [the sum of] its half and its third exceeds [the sum of] its quarter and its fifth by 4 integers. :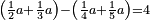 $\scriptstyle\left(\frac{1}{2}a+\frac{1}{3}a\right)-\left(\frac{1}{4}a+\frac{1}{5}a\right)=4$ שאלה‫MS L שו תמצא לי מספר אשר מחציתו ושלישיתו יוסיפו ד' שלמים על רביעיתו וחמישיתו
word problem/find a number	⅓a+¼a=6	מלאכת_המספר#m65t	Example: we wish to find a number, whose quarter and third are 6. :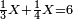 $\scriptstyle\frac{1}{3}X+\frac{1}{4}X=6$ המשל רצינו למצא מספר אחד שרביעיתו ושלישיתו יהיה ו‫'
word problem/find a number	4=⅓·15→a=⅕·25	ספר_דיני_ממונות#RldY	65) Question: if number 4 is a third of number 15 what is the fifth of 25? סה) שאלה אם מספר ד' הוא שליש מספר ט"ו מהו חומש כ"ה
word problem/find a number	⅖a²=a	ספר_דיני_ממונות#LWXU	159) Quaestion: if you want to find a number such that its two fifths are its root. :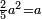 $\scriptstyle\frac{2}{5}a^2=a$ קנט)‫MS L: קנו שאלה אם תרצה למצא מספר אשר ב' חמישיות שלו יהיה שרשו
word problem/find a number	a-⅓a=√a	ספר_האלזיברא#HmbP	Question: I want to find a number such that when its third is subtracted from it the remainder is the root of the original number :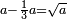 $\scriptstyle a-\frac{1}{3}a=\sqrt{a}$ שאלה רציתי למצא מספר כאשר {{#annot: term \| #to subtract, #חסר \| rg2F}}חסר ממנו{{#annotend:rg2F}} שלישית הנשאר הוא שרש המספר כלו
word problem/find a number	a/b=⅔;(3a+4b)√5=40	ספר_ג'יבלי_אלמוקבאלא#PB7l	Find me two numbers such that one is a part of the other as 2 is of 3; :and when the first is multiplied by 3 and the second by 4, and both products are summed together and multiplied by the root of 5, it yields 40. :I ask: how much will each number be? :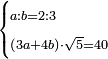 $\scriptstyle\begin{cases}\scriptstyle a:b=2:3\\\scriptstyle\left(3a+4b\right)\sdot\sqrt{5}=40\end{cases}$ והנה המשל תמצא לי שני מספרים שיהיה חלק אחד מהם לאחר כמו שהוא ב' אל ג‫' וכשיוכה הראשון בשלשה והשני בארבעה ואלו שתי ההכאות מחוברים יחד ויוכה בשרש ה' יעשה מ‫' אשאל כמה יבא להיות כל אחד מהמספרי‫'
word problem/find a number	a/b=⅗;a²b=b²√8	ספר_ג'יבלי_אלמוקבאלא#YrhT	Find me two numbers such that the one is a part of the other as 3 is of 5; :and the the first is multiplied by the other, then this product is multiplied by the second number, it yields the same as the product of the second by itself, then the product is multiplied by the root of 8. :I ask: how much will each number be? :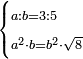 $\scriptstyle\begin{cases}\scriptstyle a:b=3:5\\\scriptstyle a^2\sdot b=b^2\sdot\sqrt{8}\end{cases}$ עשה לי זה החשבון תמצא לי שני מספרי' שיהיה האחד חלק מהאחר כמו שג' הם מה‫' ומוכה הראשון בעצמו ואותה ההכאה תוכה ~~בשני~~ במספר השני יעשה כמו הכאת השני בעצמו ואותה ההכאה תוכה בשרש ח‫' אשאל כמה יבא להיות כל אחד מהמספרי‫'
word problem/find a number	a+⅓a+⅖(a+⅓a)+¾(a+⅓a+⅖(a+⅓a))=13	Arithmetic_Textbook_by_R._Aharon_ben_Isaac#KQWm	Question two: What is the number, such that if you add to it its third, then to the sum 2-fifths of the sum, then to this sum 3-quarters of the sum, [and after all this the result is 13]. שאלה שנית מהו המספר אשר אם תחבר עליו שלישיתו ועל העולה ב' חמשיות מן העולה ועל העולה ג' רביעיות מן ‫[97v]העולה [ ועם כל זה יעלה י"ג]
word problem/find a number	(3a/4)/4=4/6	ספר_דיני_ממונות#mnbD	43) Question: find me a number such that when multiplied by 3 then divided by 4 the ratio of the remainder to 4 is the same as the ratio of 4 to 6. :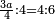 $\scriptstyle\frac{3a}{4}:4=4:6$ מג) שאלה תמצא לי מספר אשר כשתכפול על ג' ותחלק על ד' ומה שישאר יהיה יחסו אל ד' כיחס ד אל ו‫'
word problem/find a number	a/b=⅔;ab=√12	ספר_ג'יבלי_אלמוקבאלא#zNTn	Find me two numbers such that one is a part of the other as 2 is of 3; :and if one is multiplied by the other, it yields a root of 12. :I ask: how much will each number be? :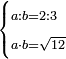 $\scriptstyle\begin{cases}\scriptstyle a:b=2:3\\\scriptstyle a\sdot b=\sqrt{12}\end{cases}$ תמצא לי שני מספרים שיהיה חלק האחד מהאחר כמו שהוא ב' מג‫' ואם יוכה האחד באחר יעשה שרש מי"ב אשאל כמה יבא להיות כל אחד מהמספרים
word problem/find a number	a+4=n², a-4=m²	ספר_דיני_ממונות#bQqS	151) Question: if you want to find a number such that if you add to it 4 it will be a square and if you subtract [from it 4] it will also be a square. :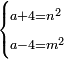 $\scriptstyle\begin{cases}\scriptstyle a+4=n^2\\\scriptstyle a-4=m^2\end{cases}$ קנא)‫MS L: קמח שאלה אם תרצה למצא מספר אשר אם תוסיף עליו ד' יהיה מרובע ואם תחסר ג"כ יהיה מרובע
word problem/find a number	a/b=⅔;5a+7b=16+√8	ספר_ג'יבלי_אלמוקבאלא#qQCL	Find me two numbers such that the one is a part of the other as 2 is of 3; :and when the first is multiplied by 5 and the second by 7, then both the products are summed together, it yields 16 and a root of 8. :I ask: how much will each number be? :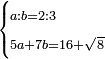 $\scriptstyle\begin{cases}\scriptstyle a:b=2:3\\\scriptstyle5a+7b=16+\sqrt{8}\end{cases}$ תמצא לי שני מספרי' שיהיה האחד מהאחר כמו שב' הוא מג‫' ומוכה הראשון בה' והשני בז' ושתי אלו ההכאות יחוברו יחד יעשו י"ו ושרש ח‫' אשאל כמו' יבא להיות כל אחד מהמספרי‫'
word problem/find a number	a/b=⅔;(ab)²=b√8	ספר_ג'יבלי_אלמוקבאלא#6dSA	Find me two numbers such that the first is a part of the second as 2 is of 3; :and when the smaller is multiplied by the greater, and this product is multiplied by itself, it yields the same as the product of the second by the root of 8. :I ask: how much will each number be? :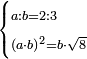 $\scriptstyle\begin{cases}\scriptstyle a:b=2:3\\\scriptstyle\left(a\sdot b\right)^2=b\sdot\sqrt{8}\end{cases}$ תמצא לי שני מספרים שיהיה הראשון חלק מהשני כמו שהוא ב' מג‫' ויוכה הקטון בגדול ואותה ההכאה תוכה בעצמה יעשה כמו הכאת השני בשרש ח‫' אשאל כמה יבא להיות כל אחד מהמספרי‫'
word problem/find a number	a/b=⅔;(ab)b=100+\sqrt{8}	ספר_ג'יבלי_אלמוקבאלא#GBTu	Find me two numbers such that the first is a part of the other as 2 is of 3; :and when the first is multiplied by the second, then this product is multiplied by the second, it yields 100 and a root of 8. :I ask: how much will each number be? :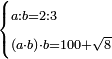 $\scriptstyle\begin{cases}\scriptstyle a:b=2:3\\\scriptstyle\left(a\sdot b\right)\sdot b=100+\sqrt{8}\end{cases}$ עשה לי החשבון תמצא לי שני מספרים שיהיה המספר ראשון חלק מהאחר כמו שב' הוא מג‫' ובהכות הראשון בשני ואותה ההכאה תוכה בשני יעשה מאה ושרש ח‫' אשאל כמה יבא להיות כל אחד מהמספרי‫'
word problem/find a number	2(b-1)=a+1;3(a-1)=b+1	מלאכת_המספר#9M9M	The relation of two numbers such that if the greater gives one to the smaller, the smaller becomes double the greater; and if the smaller gives one to the greater, the greater becomes three times the smaller ==== \|style="width:45%; text-align:right;"\|הפרק הג' ביחס שני מספרי' שאם הגדול יתן אחד לקטן יהיה הקטן כפל הגדול ואם הקטן יתן אחד לגדול יהיה הגדול שלשה פעמי' יותר מהקטן
word problem/find a number	7a/9=45	ספר_דיני_ממונות#d4nh	133) Question: find me a number such that if you multiply it by 7 and divide by 9, your result will be 45. :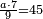 $\scriptstyle \frac{a\sdot7}{9}=45$ קלג)‫MS L: קל שאלה תמצא לי מספר אשר אם תכה אותו בז' ותחלק אותו על ט' שיצא לך מ"ה
word problem/find a number	(5/a)·8=23	ספר_דיני_ממונות#km4W	134) Question: find a number such that if you divide it by 5 and multiply by 8 the result will be 23. :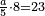 $\scriptstyle \frac{a}{5}\sdot8=23$ קלד)‫MS L: קלא שאלה תמצא מספר אשר אם תחלק אותו עם ה' ותכה אותו עם ח' יעלה כ"ג
word problem/find a number	b/(c-a)=3⅓;c/(b-a)=6	ספר_דיני_ממונות#73tk	60) Question: the ratio of the second to what remains from the third when the first is subtracted from it is 3 integers and a third. :The ratio of the third to what remains from the second when the first is subtracted from it is the number 6. ‫[ס)] שאלה שיהיה יחס הב' אל הנשאר מהג' כשחוסר ממנו הא' ג' שלמים ושליש ויחס הג' אל הנשאר מהב' כשחוסר ממנו הא' מספר ו‫'
word problem/find a number	(a·⅔a)²=36	ספר_ג'יבלי_אלמוקבאלא#IqWv	Find me a number, such that when it is multiplied by its two thirds, and the product is multiplied by itself, it yields 36. :I ask: how much will the number be? : $\scriptstyle\left[a\sdot\left(\frac{2}{3}\sdot a\right)\right]^2=36$ תמצא לי מספר אחד שכשיוכה בשני שלישיו ועולה שני שלישי צינסו והעולה יוכה בעצמו יעשה ל"ו אשאל כמה יבא להיות המספר
word problem/find a number	a²·¾a²=6a	ספר_ג'יבלי_אלמוקבאלא#GJDy	Find me a number, such that when it is multiplied by itself, and the product is multiplied by its three quarters, it yields the same as 6 times the number. :I ask: how much will this number be? :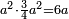 $\scriptstyle a^2\sdot\frac{3}{4}a^2=6a$ תמצא לי מספר אחד שכאשר הוכה בעצמו ומה שיעלה יוכה ב'''שני שלישיו''' יעשה כמו ו' דמיוני המספר האמור אשאל כמה יהיה המספר האמור
word problem/find a number	½a+⅓a+¼a-5=24	Arithmetic_Textbook_by_R._Aharon_ben_Isaac#ywwH	Second question: What is the number whose half, third and quarter, minus five are 24? :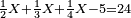 $\scriptstyle\frac{1}{2}X+\frac{1}{3}X+\frac{1}{4}X-5=24$ שאלה שנית מהו המומן הנעלם אשר חציו ושלישיתו ורביעיתו פחות חמשה יהיו כ"ד
word problem/find a number	(a+b)/c=⅗+⅙;(a+c)/b=2⅓;a=20	ספר_מעשה_חושב#0XvG	Another example: the ratio of the first and the second summed together to the third is 3-fifths and a sixth. ::The ratio of the first and the third summed together to the second is 2 integers and a third. ::The first number is 20. ::We wish to know: how much is each of the remaining numbers? ::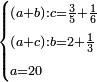 $\scriptstyle\begin{cases}\scriptstyle\left(a+b\right):c=\frac{3}{5}+\frac{1}{6}\\\scriptstyle\left(a+c\right):b=2+\frac{1}{3}\\\scriptstyle a=20\end{cases}$ דמיון אחר יהיה יחס הראשון והשני מקובצים אל השלישי ג' חמשיות וששית ויחס הראשון והשלישי מקובצים אל השני ב' שלמים ושלישית והמספר הראשון עשרים ורצינו לדעת כמה כל אחד מ[ה]מספרים הנשארים
word problem/find a number	a²-15=b²	ספר_דיני_ממונות#eiGo	150) Question: if you want to find a square number such that if you subtract 15 from it, it remains a square. :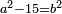 $\scriptstyle a^2-15=b^2$ קנ)‫MS L: קמז שאלה אם תרצה למצא מרובע שאם תוציא ממנו ט"ו ישאר מרובע
word problem/find a number	a²=b-5;a²+b²=100	ספר_ג'יבלי_אלמוקבאלא#a55J	Find me two numbers, such that when the first is multiplied by itself it yields the second minus 5, and when each of them is multiplied by itself, then both products are summed together, it yields 100. :I ask: how much will each of the numbers be? :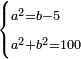 $\scriptstyle\begin{cases}\scriptstyle a^2=b-5\\\scriptstyle a^2+b^2=100\end{cases}$ ואשים לך המשל ואומ' כן עשה לי זה החשבון תמצא לי שני מספרי' שכאשר יוכה הראשון בעצמו יעשה השני פחות ה‫' ויוכו כל אחד מהם בעצמו ויחוברו אותם ההכאות יחד יעשה ק‫' ואשאל יבא כמה להיות כל אחד מהמספרים
word problem/find a number	a/b=⅗;ab√8=b	ספר_ג'יבלי_אלמוקבאלא#nOEQ	Find me two numbers such that the one is a part of the other as 3 is of 5; :and when the one is multiplied by the other, then this product is multiplied by the the root of 8, it yields the same as the second number. :I ask: how much will each number be? :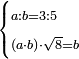 $\scriptstyle\begin{cases}\scriptstyle a:b=3:5\\\scriptstyle\left(a\sdot b\right)\sdot\sqrt{8}=b\end{cases}$ עשה לי זה החשבון תמצא לי ב' מספרי' שיהיה האחד חלק מהאחר כמו שהוא ג' מה‫' וכשיוכה האחד באחר ואותה ההכאה תוכה בשרש ח' יעשה כמו המספר השני אשאל כמה הוא כל אחד מהמספרים
word problem/find a number	five proportional numbers	ספר_דיני_ממונות#BxZ9	[2]52) Question: if you have 5 proportional numbers, the first is 3 and the fifth is 768, what is the second? קנב) שאלה אם יש לך ה' מספרים מתיחסים הא' ג' והה' תשס"ח מהו השני
word problem/find a number	⅓a+¼a=10½	מלאכת_המספר#IQCS	Example for this: suppose the sum of a third and a quarter of the whole is equal to ten and a half and we wish to know the whole. :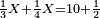 $\scriptstyle\frac{1}{3}X+\frac{1}{4}X=10+\frac{1}{2}$ המשל לזה נניח קבוץ אחד משליש ורביע ששוה עשרה וחצי ורצינו לדעת הכל
word problem/find a number	¼a+⅕a=5	מלאכת_המספר#0Nd6	As the one who asks about the sum of a quarter and a fifth [of a whole], which is 5 integers, and we wish to know how much is the whole. :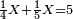 $\scriptstyle\frac{1}{4}X+\frac{1}{5}X=5$ כמי שישאל על קבוץ רביע וחומש שהם ה' שלימי' ונרצה לדעת הכל כמה הוא
word problem/find a number	a(mod2)=1,a(mod3)=2,a(mod)4=3,a(mod5)=0	ספר_המספר_/_אליהו_מזרחי#iIDQ	Likewise: if one asks: what is the number that when counted by twos - one remains; by threes - two remains; by fours - three remains; and by fives - nothing remains. וכן אם שאל שואל איזהו המספר אשר כשימנה מב' ב' ישארו אחד ומג' ג' ישארו שנים ומד' ד' ישארו שלשה ומה' ה' לא ישאר דבר
word problem/find a number	a(mod2)=0,a(mod3)=2,a(mod)4=0,a(mod5)=0,a(mod6)=2,a(mod7)=3,a(mod8)=4,a(mod9)=5,a(mod10)=0	ספר_המספר_/_אליהו_מזרחי#lEfW	Likewise: if one asks: what is the number that when counted by twos - nothing remains; by threes - 2 remains; by fours - nothing remains; by fives - nothing remains; by sixes - two remains; by sevens - three remains; by eights - four remains; by nines - five remains; and by tens - nothing remains. וכן אם שאל שואל איזהו המספר אשר כשימנה מב' ב' לא ישאר דבר ומג' ג' ישארו שנים ומד' ד' לא ישאר דבר וחמשה חמשה לא ישאר דבר ומששה ששה ישארו שנים ומז' ז' ישארו שלשה ומח' ח' ישארו ארבעה ומט' ט' ישארו חמשה ומי' לא ישאר דבר

@@ Line 1: / Line 1: @@
 {{#annotask:
 [[category: geometry ]]
 }}
+{{#annotcat: list}}
 <math>\scriptstyle\frac{13\sdot17}{19}=\frac{7\sdot11}{X}</math>

Difference between revisions of "Swen Page"

Revision as of 16:41, 30 November 2021

א.ו.ת.

Navigation menu

Personal tools

Namespaces

Variants

Views

More

Search

Navigation

Tools