Mathematical formula
From mispar
Contents
Fractions
multiplication of integer and fraction by integer and fraction
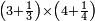
No results found.
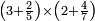
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| basic operations/multiplication | 3⅖×2⁴/₇ | ספר_הכללים_במספר#9pSN | If a man asks you: How much are three integers and two fifths by two integers and four sevenths?
: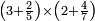 אי"א ג' שלמים וב' חמשיות על ב' שלמים וד' שבעיות כמה הוא
אי"א ג' שלמים וב' חמשיות על ב' שלמים וד' שבעיות כמה הוא |
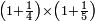
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| basic operations/multiplication | 1¼×1⅕ | ספר_הכללים_במספר#uW3p | 81) If a man asks you: How much are one integer and a quarter by one integer and a fifth?
: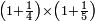 פא אם ישאלך אדם א' ורביע על א' וחמישית כמה הוא
פא אם ישאלך אדם א' ורביע על א' וחמישית כמה הוא |
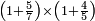
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| basic operations/multiplication | 1⁵/₇×1⅘ | ספר_הכללים_במספר#Iwhd | 75) If a man asks you: How much are one integer and five sevenths by one integer and four fifths?
: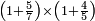 עה אי"א א' וה' שבעיות על א' וד' חמשיות כמה הוא
עה אי"א א' וה' שבעיות על א' וד' חמשיות כמה הוא |
fraction of fraction
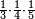
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| fraction/fraction of fraction | ⅓·¼·⅕ | ספר_חשבון#SN3Z | Who has the third of the quarter of the fifth
: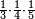 MS Ithaca om.מי שיש לו השליש מן הרביע מן החומש
MS Ithaca om.מי שיש לו השליש מן הרביע מן החומש |
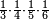
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| fraction/fraction of fraction | ⅓·¼·⅕·⅙ | ספר_חשבון#B38F | Who has the third of the quarter of the fifth of the sixth
: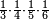 ומי שיש לו השליש מן הרביע מן החומש מן השתות
ומי שיש לו השליש מן הרביע מן החומש מן השתות |
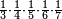
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| fraction/fraction of fraction | ⅓·¼·⅕·⅙·⅐ | ספר_חשבון#ysjE | Who has the third of the quarter of the fifth of the sixth of the seventh
: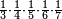 ומי שיש לו השליש מן הרביע מן החומש מן השתות מן השביע
ומי שיש לו השליש מן הרביע מן החומש מן השתות מן השביע |
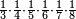
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| fraction/fraction of fraction | ⅓·¼·⅕·⅙·⅐·⅛ | ספר_חשבון#Xp93 | Who has the third of the quarter of the fifth of the sixth of the seventh of the eighth
: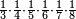 ומי שיש לו השליש מן הרביע מן החומש מן השתות מן השביע מן השמין
ומי שיש לו השליש מן הרביע מן החומש מן השתות מן השביע מן השמין |
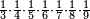
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| fraction/fraction of fraction | ⅓·¼·⅕·⅙·⅐·⅛·⅑ | ספר_חשבון#XLXN | Who has the third of the quarter of the fifth of the sixth of the seventh of the eighth of the ninth
: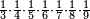 ומי שיש לו השליש מן הרביע מן החומש מן השתות מן השביע מן השמין מן התשיע
ומי שיש לו השליש מן הרביע מן החומש מן השתות מן השביע מן השמין מן התשיע |
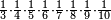
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| fraction/fraction of fraction | ⅓·¼·⅕·⅙·⅐·⅛·⅑·⅒ | ספר_חשבון#8EWq | Who has the third of the quarter of the fifth of the sixth of the seventh of the eighth of the ninth of the tenth
: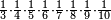 ומי שיש לו השליש מן הרביע מן החומש מן השתות מן השביע מן השמין מן התשיע מן העשור
ומי שיש לו השליש מן הרביע מן החומש מן השתות מן השביע מן השמין מן התשיע מן העשור |
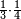
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| fraction/fraction of fraction | ⅓·¼ | ספר_חשבון#KdCj | If it is said: whoever has a third of a quarter of the thing, how much does he have of [that thing]?
: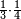 אמנם אם יאמר מי שיש לו השליש מן הרביע מן הדבר כמה חלק יש לו ממנו
אמנם אם יאמר מי שיש לו השליש מן הרביע מן הדבר כמה חלק יש לו ממנו |
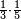
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| fraction/fraction of fraction | ⅓·⅕ | ספר_חשבון#dqBo | If it is said: whoever has a third of a fifth [of the thing], how much does he have of [that thing]?
: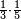 ואם יאמר מי שיש לו השליש מן החומש כמה חלק יש לו
ואם יאמר מי שיש לו השליש מן החומש כמה חלק יש לו |
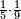
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| fraction/fraction of fraction | ⅕·⅑ | ספר_חשבון#3ST2 | Whoever has a fifth of a ninth.
: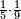 37rוכן מי שיש לו החומש מן התשיעית
37rוכן מי שיש לו החומש מן התשיעית |
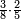
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| fraction/fraction of fraction | ⅜·⅖ | ספר_חשבון#8Loc | If one says: how much are 3-eighths of 2-fifths?
: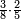 ואם יאמ' כמה הם ג' שמיניות מב' חמישיות
ואם יאמ' כמה הם ג' שמיניות מב' חמישיות |
| fraction/fraction of fraction | ⅜·⅖ | ספר_יסודי_התבונה_ומגדל_האמונה#Vq4n | As the one who says: how much are 3 eighths of 2 fifths
: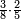 כגון האומר כמה הם ג' שמיניות מב' חמישיות
כגון האומר כמה הם ג' שמיניות מב' חמישיות |
division of fractions
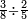
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple fraction/division of fractions | ⅜÷⅖ | ספר_יסודי_התבונה_ומגדל_האמונה#rzHD | As the one who says to you: divide 3 eighths by 2 fifths
: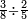 כגון האומר לך חלק ג' שמיניות על ב' חמישיות
כגון האומר לך חלק ג' שמיניות על ב' חמישיות |
| simple fraction/division of fractions | ⅜÷⅖ | ספר_חשבון#gX0D | If one says: divide 3-eighths by 2-fifths
: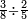 ואם יאמ' חלק ג' שמיניות על ב' חמשיות
ואם יאמ' חלק ג' שמיניות על ב' חמשיות |
multiplication of fractions
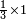
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple fraction/multiplication of fractions | ⅓×1 | ספר_חשבון#dp1H | When we multiply the third by one, it is a third.
: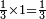 כשנרבה השליש באחד הוא שליש
כשנרבה השליש באחד הוא שליש |
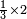
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple fraction/multiplication of fractions | ⅓×2 | ספר_חשבון#CmHn | When we multiply the third by two it is 2-thirds.
: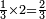 וכשנרבה השליש בשנים הוא ב' שלישי האחד
וכשנרבה השליש בשנים הוא ב' שלישי האחד |
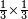
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple fraction/multiplication of fractions | ⅓×⅓ | ספר_חשבון#p54W | When we multiply a third by a third, it is a third of a third.
: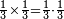 וכשנרבה שליש בשליש הוא שליש בשליש
וכשנרבה שליש בשליש הוא שליש בשליש |
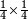
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple fraction/multiplication of fractions | ¼×¼ | ספר_חשבון#q5Pm | The quarter by a quarter is a quarter of a quarter.
: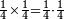 והרביע ברביע הוא רביע הרביע
והרביע ברביע הוא רביע הרביע |
| simple fraction/multiplication of fractions | ¼×¼ | קצור_המספר#dX0i | As if you say: we multiply once a quarter of 1 by a quarter.
: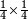 כאלו תאמ' נכפול רביע א' ברביע פעם
כאלו תאמ' נכפול רביע א' ברביע פעם |
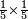
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple fraction/multiplication of fractions | ⅕×⅕ | ספר_הכללים_במספר#ubzN | Say: if he had asked for one fifth by one fifth.
: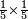 תאמר אם היה שואל א' חמישית על א' חמישית
תאמר אם היה שואל א' חמישית על א' חמישית |
| simple fraction/multiplication of fractions | ⅕×⅕ | ספר_חשבון#GtWm | The fifth by a fifth is a fifth of a fifth.
: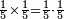 וחומש בחומש הוא חומ' החומש
וחומש בחומש הוא חומ' החומש |
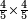
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple fraction/multiplication of fractions | ⅘×⅘ | ספר_הכללים_במספר#kvFj | 73) If a man asks you: How much are four fifths by four fifths?
: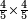 עג אם ישאלך אדם כמה הוא ד' חמשיות על ד' חמשיות
עג אם ישאלך אדם כמה הוא ד' חמשיות על ד' חמשיות |
| simple fraction/multiplication of fractions | ⅘×⅘ | עיר_סיחון#yepM | We wish to multiply four fifths by four fifths
: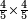 בקשנו לכפול ארבע חמישיות בארבע חמישיות
בקשנו לכפול ארבע חמישיות בארבע חמישיות |
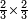
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple fraction/multiplication of fractions | ⅔×⅔ | ספר_יסודי_התבונה_ומגדל_האמונה#2Gb7 | If you are told: multiply two thirds by two thirds, how much are they?
: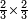 אם יאמר לך חשבו שני שלישים בשני שלישים כמה הם
אם יאמר לך חשבו שני שלישים בשני שלישים כמה הם |
| simple fraction/multiplication of fractions | ⅔×⅔ | ספר_חשבון#Nlzy | If we multiply 2-thirds by 2-thirds.
: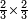 ואם נרבה ב' שלישי בב' שלישי
ואם נרבה ב' שלישי בב' שלישי |
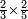
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple fraction/multiplication of fractions | ⅔×⅖ | ספר_חשבון#BRVP | If one says: multiply 2-thirds by 2-fifths.
: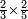 ואם יאמר חשוב ב' שלישים עם ב' חמישיות
ואם יאמר חשוב ב' שלישים עם ב' חמישיות |
| simple fraction/multiplication of fractions | ⅔×⅖ | ספר_יסודי_התבונה_ומגדל_האמונה#SOeb | The multiplication of two thirds by two fifths
: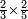 חשבון ב' שלישיים על ב' חמישיים
חשבון ב' שלישיים על ב' חמישיים |
| simple fraction/multiplication of fractions | ⅔×⅖ | Anonymous#Tlt0 | Such as two thirds by two fifths.
: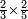 כגון שני שלישיים על שני חמישיים
כגון שני שלישיים על שני חמישיים |
| simple fraction/multiplication of fractions | ⅔×⅖ | Kaufmann_A_519_-_Collection_of_Word_Problems#AcY7 | How much is the multiplication of 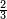 by by  ?
|10Quanto fa a moltiplicare ?
|10Quanto fa a moltiplicare 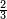 con con  |
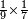
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple fraction/multiplication of fractions | ⅑×⅐ | ספר_הכללים_במספר#P04R | If he had asked for one ninth by one seventh.
: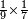 תאמ' אם היה שואל א' תשיעית על א' שבעית
תאמ' אם היה שואל א' תשיעית על א' שבעית |
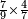
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple fraction/multiplication of fractions | ⁷/₉×⁴/₇ | ספר_הכללים_במספר#S123 | 74) If a man asks you: How much are seven ninths by four sevenths?
: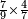 עד אי"א כמה הוא ז' תשיעיות על ד' שבעיות
עד אי"א כמה הוא ז' תשיעיות על ד' שבעיות |
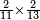
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple fraction/multiplication of fractions | ²/₁₁ײ/₁₃ | ספר_חשבון#md7k | If one says: multiply 2 parts of 11 by 2 parts of 13.
: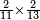 ואם יאמר חשוב ב' חלקים מי"א באחד על ב' חלקים מי"ג מן האחד
ואם יאמר חשוב ב' חלקים מי"א באחד על ב' חלקים מי"ג מן האחד |
| simple fraction/multiplication of fractions | ²/₁₁ײ/₁₃ | ספר_יסודי_התבונה_ומגדל_האמונה#BW7X | If you are told: multiply two parts of 11 by two parts of 13?
: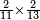 ואלו היו אומרים לך חשוב שני חלקים מי"א באחד בב' חלקים מי"ג באחד
ואלו היו אומרים לך חשוב שני חלקים מי"א באחד בב' חלקים מי"ג באחד |
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple fraction/multiplication of fractions | ⅖×⅒×⅔ | ספר_חשבון#q3mD | If one says: how much are 2 parts of 5 by one-tenth by 2-thirds?
: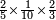 ואם יאמ' ב' חלקים מה' בעשירית האחד בב' שלישי האחר כמה הם
ואם יאמ' ב' חלקים מה' בעשירית האחד בב' שלישי האחר כמה הם |
| simple fraction/multiplication of fractions | ⅖×⅒×⅔ | Anonymous#j0VS | If you multiply 2 parts of five by a tenth by 2 thirds.
: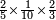 |style="width: 50%; text-align:right;"|ואם תערוך ב' חלקים מחמשה בעשירית האחד בב' שלישי אחד
|style="width: 50%; text-align:right;"|ואם תערוך ב' חלקים מחמשה בעשירית האחד בב' שלישי אחד |
| simple fraction/multiplication of fractions | ⅖×⅒×⅔ | ספר_יסודי_התבונה_ומגדל_האמונה#yQcZ | If you are told: multiply two parts of 5 by one tenth by two thirds?
: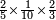 ואם יאמר לך חשוב ב' חלקים מה' בעשירית האחד בב' שלישי האחד
ואם יאמר לך חשוב ב' חלקים מה' בעשירית האחד בב' שלישי האחד |
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple fraction/multiplication of fractions | ⅖×⅒ײ/₈×⅓ | ספר_חשבון#aUsg | If one says: 2 parts of five by one-tenth by two parts of eight by one-third.
: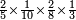 ואם יאמ' ב' חלקים מחמשה בעשירית האחד בשני חלקים משמנה בשלישית האחד
ואם יאמ' ב' חלקים מחמשה בעשירית האחד בשני חלקים משמנה בשלישית האחד |
| simple fraction/multiplication of fractions | ⅖×⅒ײ/₈×⅓ | ספר_יסודי_התבונה_ומגדל_האמונה#gymG | If you are told: multiply two parts of 5 by one tenth by two parts of eighth by one third?
: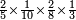 וכן אם יאמר חשוב בב' חלקים מחמשה בעשירית האחד בב' חלקים משמנה בשלישית האחד
וכן אם יאמר חשוב בב' חלקים מחמשה בעשירית האחד בב' חלקים משמנה בשלישית האחד |
addition of fractions
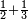
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple fraction/addition of fractions | ½+⅓ | ספר_חשבון#Prkw | If it is said: whoever has a half and a third of one thing, how much does he have of that thing?
: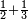 ואם יאמ' מי שיש לו החצי והשליש מדבר אחד כמה חלק יש לו מן הדבר ההוא
ואם יאמ' מי שיש לו החצי והשליש מדבר אחד כמה חלק יש לו מן הדבר ההוא |
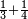
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple fraction/addition of fractions | ⅓+¼ | ספר_דיני_ממונות#8So2 | 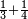 דמיון אחר נרצה לחבר שלישית אחד ורביעית אחד
דמיון אחר נרצה לחבר שלישית אחד ורביעית אחד |
| simple fraction/addition of fractions | ⅓+¼ | ספר_חשבון#595p | Whoever has a third and a quarter of the thing, how much does he have of that thing?
: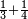 ואם מי שיש לו השליש והרביעי מן הדבר כמה חלק יש לו ממנו
ואם מי שיש לו השליש והרביעי מן הדבר כמה חלק יש לו ממנו |
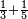
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple fraction/addition of fractions | ⅓+⅕ | ספר_חשבון#Asm1 | Whoever has a third and a fifth of the thing.
: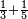 וכן מי שיש לו השליש והחומש מן הדבר
וכן מי שיש לו השליש והחומש מן הדבר |
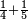
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple fraction/addition of fractions | ¼+⅕ | ספר_חשבון#nQTO | Whoever has a quarter and a fifth of the thing.
: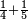 וכן מי שיש לו הרביע והחומש מן הדבר
וכן מי שיש לו הרביע והחומש מן הדבר |
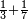
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple fraction/addition of fractions | ⅓+⅐ | ספר_חשבון#c6OW | Whoever has a third and a seventh of the thing.
: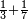 וכן מי שיש לו שליש ושביע מן הדבר
וכן מי שיש לו שליש ושביע מן הדבר |
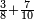
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple fraction/addition of fractions | ⅜+⁷/₁₀ | ספר_חשבון#tIym | If one says: add 3-eighths to 7-tenths, how much are they?
: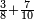 ואם יאמר הוסף ג' שמיניות על ז' עשיריות כמה יהיו
ואם יאמר הוסף ג' שמיניות על ז' עשיריות כמה יהיו |
| simple fraction/addition of fractions | ⅜+⁷/₁₀ | ספר_יסודי_התבונה_ומגדל_האמונה#IYtH | As the one who says: add 3 eighths to 7 tenths
: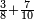 כגון האומר הוסף ג' שמיניות על ז' עשיריות
כגון האומר הוסף ג' שמיניות על ז' עשיריות |
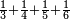
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple fraction/addition of fractions | ⅓+¼+⅕+⅙ | ספר_חשבון#pvs7 | Whoever has a third, a quarter, a fifth, and a sixth of the thing.
: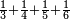 וכן מי שיש לו שליש ורביע וחומש ושתות מן הדבר
וכן מי שיש לו שליש ורביע וחומש ושתות מן הדבר |
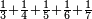
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple fraction/addition of fractions | ⅓+¼+⅕+⅙+⅐ | ספר_הכללים_במספר#753y | 2) How much are a third, a quarter, a fifth, a sixth, and a seventh of one pašuṭ?
: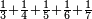 ב אם ישאלך אדם כמה הוא שליש פשוט ורביע וחומש ושתות ושביעית
ב אם ישאלך אדם כמה הוא שליש פשוט ורביע וחומש ושתות ושביעית |
subtraction of fractions
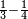
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple fraction/subtraction of fractions | ⅓-¼ | ספר_הכללים_במספר#Sdu0 | 1) If a man asks you: how large is the third from the quarter?
: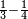 88rא אם ישאלך אדם כמה הוא יותר השליש מן הרביע
88rא אם ישאלך אדם כמה הוא יותר השליש מן הרביע |
| simple fraction/subtraction of fractions | ⅓-¼ | ספר_חשבון#Gem8 | If a man says: by how much is the third greater than the quarter?
: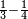 אמנם אם יאמר אדם כמה הוא יותר השליש מן הרביע
אמנם אם יאמר אדם כמה הוא יותר השליש מן הרביע |
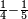
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple fraction/subtraction of fractions | ¼-⅕ | ספר_חשבון#wkXD | If a man says: by how much is the quarter greater than the fifth?
: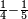 וכן אם יאמר אדם כמה הוא יותר הרביע מן החומש
וכן אם יאמר אדם כמה הוא יותר הרביע מן החומש |
| simple fraction/subtraction of fractions | ¼-⅕ | ספר_הכללים_במספר#hEgl | If you are asked: how large is the quarter from the fifth?
: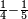 וכן אם ישאלך כמה יותר הרביע מן החומש
וכן אם ישאלך כמה יותר הרביע מן החומש |
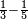
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple fraction/subtraction of fractions | ⅓-⅕ | ספר_הכללים_במספר#t2Xm | If you are asked: how large is the third from the fifth?
: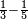 וכן אם ישאלך כמה הוא יותר השליש מן החמישית
וכן אם ישאלך כמה הוא יותר השליש מן החמישית |
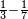
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple fraction/subtraction of fractions | ⅓-⅐ | ספר_חשבון#ebvM | If it is said: by how much is the third greater than the seventh?
: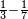 וכן אם יאמר כמה הוא יותר השליש מן השביע
וכן אם יאמר כמה הוא יותר השליש מן השביע |
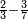
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple fraction/subtraction of fractions | ⅔-³/₇ | ספר_חשבון#mJ1K | If one says: subtract 3-sevenths from 2-thirds.
: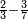 ואם יאמר השלך ג' שביעיות מב' שלישיות
ואם יאמר השלך ג' שביעיות מב' שלישיות |
| simple fraction/subtraction of fractions | ⅔-³/₇ | ספר_יסודי_התבונה_ומגדל_האמונה#jZco | As the one who says: subtract 3 sevenths from 2 thirds.
: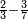 כגון האומר השלך ג' שביעיות מב' שלישיות
כגון האומר השלך ג' שביעיות מב' שלישיות |
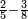
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple fraction/subtraction of fractions | ⅖-⅜ | ספר_חשבון#fRT6 | If one says: how much greater are 3-eighths than 2-fifths?
: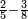 ואם יאמר כמה הם יותר ג' שמניות מב' חמשיות
ואם יאמר כמה הם יותר ג' שמניות מב' חמשיות |
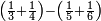
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple fraction/subtraction of fractions | (⅓+¼)-(⅕+⅙) | ספר_חשבון#e3Ts | If it is said: by how much are the third and the quarter greater than the fifth and the eighth?
: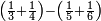 ואם יאמר כמה הם יותר השליש והרביע מן החומש ושתות
ואם יאמר כמה הם יותר השליש והרביע מן החומש ושתות |
rule of four
no such category found: #rule of four
no such category found: #rule of four
Roots
Addition of Roots
no such category found: #R+R
no such category found: #R+R
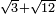
no such category found: #R+R
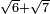
no such category found: #R+R
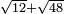
no such category found: #R+R
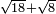
no such category found: #R+R
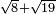
no such category found: #R+R
![\scriptstyle\sqrt[3]{96}+\sqrt[3]{324}](/mediawiki/images/math/8/f/5/8f58716ec5d5049f48b1b6af09db62e2.png)
no such category found: #R₃+R₃
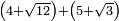
no such category found: #(N+R)+(N+R)
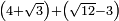
no such category found: #(N+R)+(R-N)
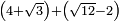
no such category found: #(N+R)+(R-N)
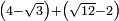
no such category found: #(N-R)+(R-N)
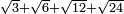
no such category found: #R+R+R+R
Subtraction of Roots
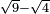
no such category found: #R-R
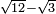
no such category found: #R-R
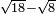
no such category found: #R-R
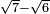
no such category found: #R-R
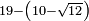
no such category found: #N-(N-R)
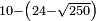
no such category found: #N-(N-R)
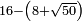
no such category found: #N-(N+R)
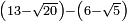
no such category found: #(N-R)-(N-R)
Multiplication of Roots
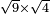
no such category found: #R×R
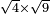
no such category found: #R×R
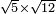
no such category found: #R×R
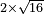
no such category found: #R×N
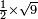
no such category found: #R×N
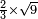
no such category found: #R×N
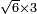
no such category found: #R×N
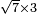
no such category found: #R×N
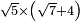
no such category found: #R×(R+N)
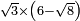
no such category found: #R×(N-R)
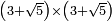
no such category found: #(N+R)×(N+R)
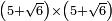
no such category found: #(N+R)×(N+R)
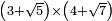
no such category found: #(N+R)×(N+R)
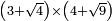
no such category found: #(N+R)×(N+R)
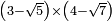
no such category found: #(N-R)×(N-R)
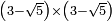
no such category found: #(N-R)×(N-R)
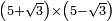
no such category found: #(N+R)×(N-R)
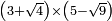
no such category found: #(N+R)×(N-R)
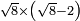
no such category found: #R×(R-N)
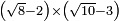
no such category found: #(R-N)×(R-N)
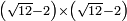
no such category found: #(R-N)×(R-N)
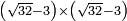
no such category found: #(R-N)×(R-N)
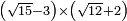
no such category found: #(R-N)×(R+N)
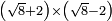
no such category found: #(R+N)×(R-N)
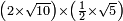
no such category found: #(N×R)×(N×R)
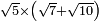
no such category found: #R×(R+R)
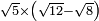
no such category found: #R×(R-R)
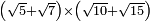
no such category found: #(R+R)×(R+R)
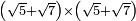
no such category found: #(R+R)×(R+R)
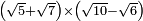
no such category found: #(R+R)×(R-R)
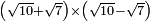
no such category found: #(R+R)×(R-R)
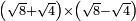
no such category found: #(R+R)×(R-R)
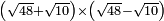
no such category found: #(R+R)×(R-R)
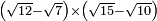
no such category found: #(R-R)×(R-R)
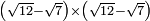
no such category found: #(R-R)×(R-R)
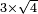
no such category found: #N×R
![\scriptstyle3\times\sqrt[3]{8}](/mediawiki/images/math/1/3/2/1328cc433a8d6f068d82010e6cd86a87.png)
no such category found: #N×R₃
![\scriptstyle3\times\sqrt[3]{5}](/mediawiki/images/math/a/f/6/af6f3ea8e946c33bc42d18277529285f.png)
no such category found: #N×R₃
![\scriptstyle\sqrt{4}\times\sqrt[3]{8}](/mediawiki/images/math/6/4/6/646c5ba2e5f167061f7a7ccea09fdf58.png)
no such category found: #R×R₃
![\scriptstyle\sqrt{9}\times\sqrt[3]{8}](/mediawiki/images/math/4/c/f/4cf0598b07f1500dd82fd96f8e0f7c4b.png)
no such category found: #R×R₃
![\scriptstyle\sqrt[3]{5}\times\sqrt[3]{6}](/mediawiki/images/math/1/8/a/18aa18babb93ca4eb54e701713e95aa6.png)
no such category found: #R₃×R₃
![\scriptstyle2\times\sqrt[4]{5}](/mediawiki/images/math/d/1/f/d1f0006d85c9885ba609dc92ea7557d6.png)
no such category found: #N×R₄
![\scriptstyle\sqrt[3]{8}\times\sqrt[4]{16}](/mediawiki/images/math/b/e/2/be2421d68cb602563f762c6471b4910a.png)
no such category found: #R₃×R₄
![\scriptstyle\sqrt[3]{3}\times\sqrt[4]{4}](/mediawiki/images/math/d/f/a/dfabf0bb07e1856908bb9477f615a484.png)
no such category found: #R₃×R₄
![\scriptstyle\sqrt[4]{4}\times\sqrt[4]{7}](/mediawiki/images/math/2/c/4/2c4052b07cfd24ba0cf8c9519e3dcd0e.png)
no such category found: #R₄×R₄
Division of Roots
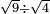
no such category found: #R÷R
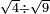
no such category found: #R÷R
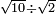
no such category found: #R÷R
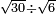
no such category found: #R÷R
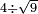
no such category found: #N÷R
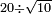
no such category found: #N÷R
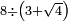
no such category found: #N÷(N+R)
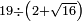
no such category found: #N÷(N+R)
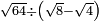
no such category found: #R÷(R-R)
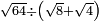
no such category found: #R÷(R+R)
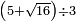
no such category found: #(N+R)÷N
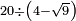
no such category found: #N÷(N-R)
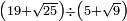
no such category found: #(N+R)÷(N+R)
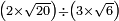
no such category found: #(N×R)÷(N×R)
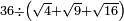
no such category found: #N÷(R+R+R)
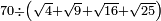
no such category found: #N÷(R+R+R+R)
![\scriptstyle\sqrt{6}\div\sqrt[3]{10}](/mediawiki/images/math/9/a/0/9a0da3d2826409356d860ea699ebe6c3.png)
no such category found: #R÷R₃
![\scriptstyle\sqrt[3]{18}\div\sqrt[4]{10}](/mediawiki/images/math/b/2/c/b2cca0a5467cbf3de7b5c9bf4df59020.png)
no such category found: #R₃÷R₄
Multiplication of Algebraic Species
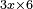
no such category found: #multiplication of algebraic species
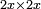
no such category found: #multiplication of algebraic species
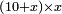
no such category found: #multiplication of algebraic species
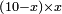
no such category found: #multiplication of algebraic species
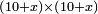
no such category found: #multiplication of algebraic species
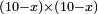
no such category found: #multiplication of algebraic species
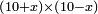
no such category found: #multiplication of algebraic species
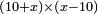
no such category found: #multiplication of algebraic species
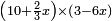
no such category found: #multiplication of algebraic species
Linear Equation
![\scriptstyle bx=\sqrt[3]{c}](/mediawiki/images/math/4/e/c/4eced3ba1c8f51bf47cf911659b6e201.png)
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| equation/linear equation | bx=³√c | ספר_ג'יבלי_אלמוקבאלא#NHZd | When things are equal to a cube root of the numbers:
:![\scriptstyle bx=\sqrt[3]{c}](/mediawiki/images/math/4/e/c/4eced3ba1c8f51bf47cf911659b6e201.png) כאשר הדברי' יהיו שוי' אל שרש מעוק' ממספרי'
כאשר הדברי' יהיו שוי' אל שרש מעוק' ממספרי' |
![\scriptstyle c=\sqrt[3]{bx}](/mediawiki/images/math/5/b/4/5b40a2184fb3c6324ff5fe2eedb9da0b.png)
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| equation/linear equation | c=³√bx | ספר_ג'יבלי_אלמוקבאלא#jGFm | When numbers are equal to a cube root of a thing:
:![\scriptstyle c=\sqrt[3]{bx}](/mediawiki/images/math/5/b/4/5b40a2184fb3c6324ff5fe2eedb9da0b.png) כאשר המספרי' יהיו שוים אל שרש מעו' מדבר
כאשר המספרי' יהיו שוים אל שרש מעו' מדבר |
Quadratic Equation
ax²=bx
squares equal roots 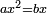
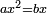
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple canonical equation/squares equal roots | ax²=bx | חשבון_השטחים#bTgP | אלגוש ישוו שרשים |
| simple canonical equation/squares equal roots | ax²=bx | תחבולות_המספר#Udbo | שרשים שיהיו שוי' למרובעים |
| simple canonical equation/squares equal roots | ax²=bx | ספר_האלזיברא#XXXO | המרבעים שוים לדברים |
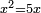
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple canonical equation/squares equal roots | x²=5x | תחבולות_המספר#EqMy | For example: if you are told; five roots are equal to one square. How much is the square?
: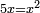 {{#annot:term|197,1712|lPkF}}דמיון זה{{#annotend:lPkF}} אם אמרו לך חמשה שרשי' ישוו למרובע אחד כמה הוא המרובע
{{#annot:term|197,1712|lPkF}}דמיון זה{{#annotend:lPkF}} אם אמרו לך חמשה שרשי' ישוו למרובע אחד כמה הוא המרובע |
| simple canonical equation/squares equal roots | x²=5x | חשבון_השטחים#cbxX | The squares that are equal to roots is as if you say: a square equals five roots.
: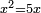 והאלגוש שישוו שרשים הוא כאלו תאמר אלגו ישוה חמשה שרשים
והאלגוש שישוו שרשים הוא כאלו תאמר אלגו ישוה חמשה שרשים |
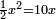
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple canonical equation/squares equal roots | ½x²=10x | תחבולות_המספר#fayj | Also, if he says: half a square is equal to ten roots.
: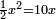 וכן אם יאמ' חצי מרובע ישוה לעשרה שרשים
וכן אם יאמ' חצי מרובע ישוה לעשרה שרשים |
| simple canonical equation/squares equal roots | ½x²=10x | חשבון_השטחים#N1ie | Likewise, if it is said: half a square equals ten roots.
: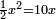 וכמו כן אם יאמר חצי אלגו ישוה עשרה שרשים
וכמו כן אם יאמר חצי אלגו ישוה עשרה שרשים |
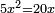
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple canonical equation/squares equal roots | 5x²=20x | תחבולות_המספר#WDhU | Example: if one asks: five squares are equal to twenty roots.
: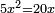 דמיון זה אם ישאל חמשה מרובעי' ישוו לעשרים שרשים
דמיון זה אם ישאל חמשה מרובעי' ישוו לעשרים שרשים |
| simple canonical equation/squares equal roots | 5x²=20x | חשבון_השטחים#sJUh | As if you say: five squares equal twenty roots.
: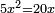 וכמו שתאמר חמשה אלגוש ישוו עשרים שרשים
וכמו שתאמר חמשה אלגוש ישוו עשרים שרשים |
ax²=c
squares equal numbers 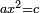
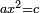
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple canonical equation/squares equal numbers | ax²=c | ספר_האלזיברא#jx5h | המרבעים צינסי שוים לאחדים |
| simple canonical equation/squares equal numbers | ax²=c | חשבון_השטחים#kCXF | ואלאגוש ישוו מספרים |
| simple canonical equation/squares equal numbers | ax²=c | תחבולות_המספר#4O9C | ומרובעי' שישוו למספרים |
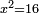
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple canonical equation/squares equal numbers | x²=16 | חשבון_השטחים#lI7w | The squares that are equal to numbers is as a square that equals sixteen.
: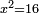 והאלגוש שישוו מספרים כמו אלגו שישוה שש עשרה
והאלגוש שישוו מספרים כמו אלגו שישוה שש עשרה |
| simple canonical equation/squares equal numbers | x²=16 | תחבולות_המספר#fCC4 | As if you are told: the square is equal to sixteen.
: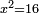 כמו אם יאמרו לך המרובע ישוה לששה עשר
כמו אם יאמרו לך המרובע ישוה לששה עשר |
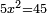
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple canonical equation/squares equal numbers | 5x²=45 | תחבולות_המספר#C4DX | If one says: five squares are equal to forty-five.
: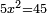 כי אם אמ' חמשה מרובעי' ישוו לחמשה וארבעי'
כי אם אמ' חמשה מרובעי' ישוו לחמשה וארבעי' |
| simple canonical equation/squares equal numbers | 5x²=45 | חשבון_השטחים#yMV8 | Likewise, when five squares are equal to forty-five.
: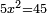 וכן חמשה אלגוש ישוו חמשה וארבעים
וכן חמשה אלגוש ישוו חמשה וארבעים |
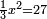
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple canonical equation/squares equal numbers | ⅓x²=27 | חשבון_השטחים#sOLH | Also if you say: a third of the square is equal to twenty-seven.
: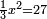 וכן אם תאמר שלישית אלגו שוה 1vשבעה ועשרים
וכן אם תאמר שלישית אלגו שוה 1vשבעה ועשרים |
| simple canonical equation/squares equal numbers | ⅓x²=27 | תחבולות_המספר#Usmi | If one says: a third of the square is equal to twenty-seven.
: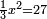 ואם אמ' שלישית המרובע ישוה לשבעה ועשרים
ואם אמ' שלישית המרובע ישוה לשבעה ועשרים |
bx=c
roots equal numbers 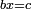
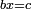
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| simple canonical equation/roots equal numbers | bx=c | חשבון_השטחים#1nZH | ושרשים ישוו מספרים |
| simple canonical equation/roots equal numbers | bx=c | תחבולות_המספר#qsBh | ושרשים שישוו למספרים |
| simple canonical equation/roots equal numbers | bx=c | ספר_האלזיברא#uues | הדברים שוים לאחדים |
ax²+bx=c
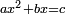
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| compound canonical equation/squares and roots equal numbers | ax²+bx=c | תחבולות_המספר#3sJZ | ושרשים ומרובעי' שישוו למספרים |
| compound canonical equation/squares and roots equal numbers | ax²+bx=c | חשבון_השטחים#XqGp | מרובעי' ושרשי' ישוו למספרים |
| compound canonical equation/squares and roots equal numbers | ax²+bx=c | ספר_האלזיברא#vJ0S | המרבעים והדברי' שוים לאחדים |

| Category | Comment | Link | Annotated text |
|---|---|---|---|
| compound canonical equation/squares and roots equal numbers | x²+10x=39 | תחבולות_המספר#oMPa | He said: when squares and roots are equal to numbers, it is as if you say: the sum of one square and ten of its roots together is equal to thirty-nine dirham.
: אמ' כאשר יהיו המרובעים והשרשים שוים למספרי' כאלו תאמ' המקובץ ממרובע מהאחד ועשרה משרשיו יחד ישוה לשלשים ותשעה דרהמי
אמ' כאשר יהיו המרובעים והשרשים שוים למספרי' כאלו תאמ' המקובץ ממרובע מהאחד ועשרה משרשיו יחד ישוה לשלשים ותשעה דרהמי |
| compound canonical equation/squares and roots equal numbers | x²+10x=39 | ספר_המספר_/_אליהו_מזרחי#efjm | Question: if one asks: what is the square whose sum with ten times its root, for instance, yields thirty-nine.
: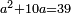 שאלה אם ישאל שואל איזהו המרובע אשר חבורו עם עשר כפלי שרשו על דרך משל יעלו תשעה ושלשים
שאלה אם ישאל שואל איזהו המרובע אשר חבורו עם עשר כפלי שרשו על דרך משל יעלו תשעה ושלשים |
| compound canonical equation/squares and roots equal numbers | x²+10x=39 | חשבון_השטחים#BnUp | Squares and roots are equal to numbers, it is as if you say: a square and ten roots are equal to thirty-nine dirham.
: והאלגוש והשרשים שישוו מספרים הוא כאלו תאמר אלגו ועשרה שרשים ישוו תשעה ושלשים דרהמיש
והאלגוש והשרשים שישוו מספרים הוא כאלו תאמר אלגו ועשרה שרשים ישוו תשעה ושלשים דרהמיש |
| compound canonical equation/squares and roots equal numbers | x²+10x=39 | ספר_ג'יבלי_אלמוקבאלא#jJWT |  ויהיה לך צינסו אחד וי' דברי' שוים לל"ט
ויהיה לך צינסו אחד וי' דברי' שוים לל"ט |
| compound canonical equation/squares and roots equal numbers | x²+10x=39 | ספר_המספר_/_אליהו_מזרחי#5Cr3 | The example in the mentioned question: one square plus ten times its root are thirty-nine.
: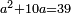 המשל בזה בשאלה הנזכרת והיא שהמרובע הא' עם עשרה כפלי שרשו הם תשעה ושלשים
המשל בזה בשאלה הנזכרת והיא שהמרובע הא' עם עשרה כפלי שרשו הם תשעה ושלשים |
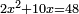
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| compound canonical equation/squares and roots equal numbers | 2x²+10x=48 | חשבון_השטחים#cSpR | 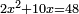 וזה כמו שתאמר שנים אלגוש ועשרה שרשים 2rישוו מ"ח אדרהמיש
וזה כמו שתאמר שנים אלגוש ועשרה שרשים 2rישוו מ"ח אדרהמיש |
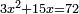
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| compound canonical equation/squares and roots equal numbers | 3x²+15x=72 | תחבולות_המספר#HV5b | Example: if one asks: three squares and 15 roots are equal to 72 dirham.
: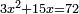 דמיון זה ששאל שלשה מרובעי' וט"ו שרשי' ישוו לע"ב דרהמי
דמיון זה ששאל שלשה מרובעי' וט"ו שרשי' ישוו לע"ב דרהמי |
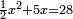
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| compound canonical equation/squares and roots equal numbers | ½x²+5x=28 | חשבון_השטחים#XyaI | 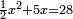 ואם אמרו לך חצי אלגוש וחמשה שרשים ישוו כ"ח אדרהמיש
ואם אמרו לך חצי אלגוש וחמשה שרשים ישוו כ"ח אדרהמישנאמר כי כאשר {{#annot: term | #to add, #חבר | qgPe}}חברנו{{#annotend:qgPe}} על חצי האלגוש חמשה שרשי האלגוש יהיו כ"ח אדרהמיש |
| compound canonical equation/squares and roots equal numbers | ½x²+5x=28 | תחבולות_המספר#FJRf | Likewise, if one asks: half a square plus its five roots are equal to 28 dirham.
: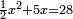 וכמו כן אם שאל השואל חצי מרובע וחמשה משרשיו ישוו לכ"ח דרהמי
וכמו כן אם שאל השואל חצי מרובע וחמשה משרשיו ישוו לכ"ח דרהמי |
ax²+c=bx
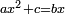
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| compound canonical equation/squares and numbers equal roots | ax²+c=bx | חשבון_השטחים#iECf | ומרובעים ומספרי' ישוו לשרשים |
| compound canonical equation/squares and numbers equal roots | ax²+c=bx | ספר_האלזיברא#oeK8 | המרובעים והאחדים שוים לדברים |
| compound canonical equation/squares and numbers equal roots | ax²+c=bx | תחבולות_המספר#om8w | ומרובעי' ומספרי' שישוו לשרשים |

| Category | Comment | Link | Annotated text |
|---|---|---|---|
| compound canonical equation/squares and numbers equal roots | x²+21=10x | ספר_ג'יבלי_אלמוקבאלא#RpEs | You get one square and 21 numbers equal 10 things.
:: ויהיה לך א' צינסו וכ"א מספרי' שוים לי' דברי'
ויהיה לך א' צינסו וכ"א מספרי' שוים לי' דברי' |
| compound canonical equation/squares and numbers equal roots | x²+21=10x | תחבולות_המספר#u4EA | He said: squares and numbers that are equal to roots is as if you say: when you sum twenty-one dirham with a certain square, they are equal to ten roots of the square.
: אמ' המרובעי' והמספרי' שישוו לשרשים הוא כאלו תאמ' כאשר תקבץ עם מרובע מה עשרים ואחד דרהמי יהיו שוים לעשרה משרשים מהמרובע
אמ' המרובעי' והמספרי' שישוו לשרשים הוא כאלו תאמ' כאשר תקבץ עם מרובע מה עשרים ואחד דרהמי יהיו שוים לעשרה משרשים מהמרובע |
| compound canonical equation/squares and numbers equal roots | x²+21=10x | ספר_המספר_/_אליהו_מזרחי#hfpC | Question: if one asks: what is the square whose sum with twenty-one, for instance, yields the same as ten times its root.
: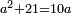 שאלה אם שאל שואל איזהו המרובע אשר חבורו עם עשרים ואחד על דרך משל יעלה כמו עשרה כפלי שרשו
שאלה אם שאל שואל איזהו המרובע אשר חבורו עם עשרים ואחד על דרך משל יעלה כמו עשרה כפלי שרשו |
| compound canonical equation/squares and numbers equal roots | x²+21=10x | חשבון_השטחים#yRRf |  והאלגוש והמספרים שישוו שרשים כאלו תאמר אלגוש ועשרים ואחד אדרהמיש ישוו עשרה שרשים
והאלגוש והמספרים שישוו שרשים כאלו תאמר אלגוש ועשרים ואחד אדרהמיש ישוו עשרה שרשים |
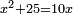
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| compound canonical equation/squares and numbers equal roots | x²+25=10x | תחבולות_המספר#QWm3 | Example: one says: a square plus twenty-five [dirham] are equal to ten roots of the square.
: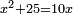 דמיון זה שיאמ' מרובע מה ועשרים וחמשה שרשים ישוו לעשרה שרשים מהמרובע
דמיון זה שיאמ' מרובע מה ועשרים וחמשה שרשים ישוו לעשרה שרשים מהמרובע |
| compound canonical equation/squares and numbers equal roots | x²+25=10x | חשבון_השטחים#5rN4 | 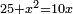 ו{{#annot: term | #to give an example, #משל | ZpYe}}אמשיל זה{{#annotend:ZpYe}} בשאילה אחרת ואניחנה שכ"ה אדרהמיש ואלגוש ישוו עשרה שרשים
ו{{#annot: term | #to give an example, #משל | ZpYe}}אמשיל זה{{#annotend:ZpYe}} בשאילה אחרת ואניחנה שכ"ה אדרהמיש ואלגוש ישוו עשרה שרשים |
bx+c=ax²
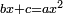
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| compound canonical equation/roots and numbers equal squares | bx+c=ax² | תחבולות_המספר#So10 | ושרשי' ומספרים שישוו למרובעים |
| compound canonical equation/roots and numbers equal squares | bx+c=ax² | ספר_האלזיברא#zm1d | הדברים והאחדים שוים למרובעים |
| compound canonical equation/roots and numbers equal squares | bx+c=ax² | חשבון_השטחים#VBed | ושרשים ומספרי' ישוו למרובעים |
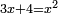
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| compound canonical equation/roots and numbers equal squares | 3x+4=x² | חשבון_השטחים#qrpb | 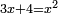 והשרשים ומספרים שישוו אלגוש כמו אם יאמר שלשה שרשים וארבעה מספרים ישוו אלגו
והשרשים ומספרים שישוו אלגוש כמו אם יאמר שלשה שרשים וארבעה מספרים ישוו אלגו |
| compound canonical equation/roots and numbers equal squares | 3x+4=x² | תחבולות_המספר#VKnl | He said: roots and numbers that are equal to a square is as saying three roots and four dirham are equal to a square.
: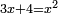 אמ' שרשים ומספרים שישוו למרובע הוא כמו שיאמ' שלשה שרשים וארבעה דרהמי יהיו שוים למרובע
אמ' שרשים ומספרים שישוו למרובע הוא כמו שיאמ' שלשה שרשים וארבעה דרהמי יהיו שוים למרובע |
| compound canonical equation/roots and numbers equal squares | 3x+4=x² | ספר_ג'יבלי_אלמוקבאלא#GUT6 | For example, suppose that 3 things and 4 numbers are equal to 1 square.
::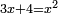 והנה המשל נניח כי שלשה דברי' וד' דרמי רצוני ד' מספרי' יהיו שוים אל א' צינסו
והנה המשל נניח כי שלשה דברי' וד' דרמי רצוני ד' מספרי' יהיו שוים אל א' צינסו |
| compound canonical equation/roots and numbers equal squares | 3x+4=x² | ספר_המספר_/_אליהו_מזרחי#7D6K | Question: if one asks: what is the square such that 3 times its root plus 4 equals 10.
: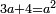 שאלה אם שאל שואל איזהו המרובע אשר ג' כפלי שרשו וד' ישוו לי'
שאלה אם שאל שואל איזהו המרובע אשר ג' כפלי שרשו וד' ישוו לי' |
Compound Quadratic Equations
![\scriptstyle ax^2=\sqrt[3]{c}](/mediawiki/images/math/f/c/0/fc0033e1c190540235d4afbc47b31b11.png)
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| equation/quadratic equation | ax²=³√c | ספר_ג'יבלי_אלמוקבאלא#rGD5 | When squares are equal to a cube root of the numbers:
:![\scriptstyle ax^2=\sqrt[3]{c}](/mediawiki/images/math/f/c/0/fc0033e1c190540235d4afbc47b31b11.png) כאשר הצינסי יהיו שוים אל שרשי' מעו' ממספרי'
כאשר הצינסי יהיו שוים אל שרשי' מעו' ממספרי' |
![\scriptstyle c=\sqrt[3]{ax^2}](/mediawiki/images/math/f/7/6/f7617468fb35452327a7d2d5678e45f0.png)
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| equation/quadratic equation | c=³√ax² | ספר_ג'יבלי_אלמוקבאלא#zK2y | When numbers are equal to a cube root of squares:
:![\scriptstyle c=\sqrt[3]{ax^2}](/mediawiki/images/math/f/7/6/f7617468fb35452327a7d2d5678e45f0.png) כאשר המספרי' יהיו שוים אל שרשי' מעו' מצינסי
כאשר המספרי' יהיו שוים אל שרשי' מעו' מצינסי |
![\scriptstyle\left[x^2-\left(\frac{1}{3}x^2+2\right)\right]^2=x^2+24](/mediawiki/images/math/a/9/5/a957ce494441269eddb2735f8c5cdf54.png)
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| equation/quadratic equation | [x²-(⅓x²+2)]²=x²+24 | חשבון_השטחים#lT08 | [12] If you are told: a square, you subtract its third and two dirham from it, then multiply what remains by itself and the result is the square plus 24 dirham.
:![\scriptstyle\left[x^2-\left(\frac{1}{3}x^2+2\right)\right]^2=x^2+24](/mediawiki/images/math/a/9/5/a957ce494441269eddb2735f8c5cdf54.png) ואם יאמרו לך אלגו גרעת ממנו שלישיתו ושני אדרהמיש ומה שנשאר הכית אותו על עצמו ושב האלגו וכ"ד אדרהמיש יותר
ואם יאמרו לך אלגו גרעת ממנו שלישיתו ושני אדרהמיש ומה שנשאר הכית אותו על עצמו ושב האלגו וכ"ד אדרהמיש יותר |
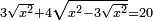
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| equation/quadratic equation | 3√x²+4√(x²-3√x²)=20 | חשבון_השטחים#tZ8i | [13] If you are told: three roots of the square plus four roots of what remains from the square are twenty dirham.
: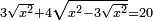 ואם יאמרו לך שלשה שרשים מהאלגו וארבעה שרשים ממה שנשאר מהאלגו יהיה עשרים דרהמי'
ואם יאמרו לך שלשה שרשים מהאלגו וארבעה שרשים ממה שנשאר מהאלגו יהיה עשרים דרהמי' |
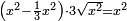
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| equation/quadratic equation | (x²-⅓x²)·3√x²=x² | חשבון_השטחים#ak8r | [14] If you are told: we subtract from a square its third, then multiply what remains by three roots of the original square and the result is the original square.
: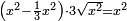 ואם יאמרו לך גרענו מן האלגו שלישיתו והכינו הנשאר על שלשה שרשים מהאלגו הראשון ושב האלגו הראשון
ואם יאמרו לך גרענו מן האלגו שלישיתו והכינו הנשאר על שלשה שרשים מהאלגו הראשון ושב האלגו הראשון |
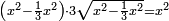
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| equation/quadratic equation | (x²-⅓x²)·3√(x²-⅓x²)=x² | חשבון_השטחים#lFM5 | [15] If you are told: a square, we subtract its third from it, then multiply what remains by three roots of what remains from the square and the result is the square.
: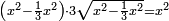 ואם יאמרו לך אלגו גרענו ממנו שלישיתו והכינו הנשאר על שלשה שרשים מהנשאר מהאלגו וישוב האלגו
ואם יאמרו לך אלגו גרענו ממנו שלישיתו והכינו הנשאר על שלשה שרשים מהנשאר מהאלגו וישוב האלגו |
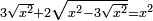
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| equation/quadratic equation | 3√x²+2√(x²-3√x²)=x² | חשבון_השטחים#rq9x | [16] If you are told: a square, its three roots and two roots of what remains are equal to the square.
: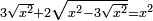 ואם יאמרו לך אלגו שלשת שרשיו ושני שרשי הנשאר ישוו האלגו
ואם יאמרו לך אלגו שלשת שרשיו ושני שרשי הנשאר ישוו האלגו |
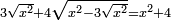
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| equation/quadratic equation | 3√x²+4√(x²-3√x²)=x²+4 | חשבון_השטחים#SNBo | [17] If you are told: a square, its three roots and four roots of what remains from the square are the same as the square plus four dirham.
: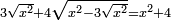 ואם יאמרו לך אלגו שלשת שרשיו וארבעה שרשים ממה שנשאר מהאלגו יהיה כמו האלגו וארבעה דרהמי' יותר
ואם יאמרו לך אלגו שלשת שרשיו וארבעה שרשים ממה שנשאר מהאלגו יהיה כמו האלגו וארבעה דרהמי' יותר |
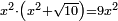
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| equation/quadratic equation | x²·(x²+√10)=9x² | חשבון_השטחים#XpMD | [32] If you are told: a square, multiply it by itself plus a root of ten dirham and it becomes nine times the square.
: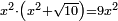 ואם יאמרו לך אלגו תכהו על עצמו ושרש אחד מעשרה דרהמי ויהיה תשעה דמיוני האלגו
ואם יאמרו לך אלגו תכהו על עצמו ושרש אחד מעשרה דרהמי ויהיה תשעה דמיוני האלגו |
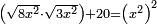
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| equation/quadratic equation | [√(8x²)·√(3x²)]+20=(x²)² | חשבון_השטחים#HcHI | [33] If you are told: a square, multiply a root of eight times the square by a root of three times the square, then add twenty dirham to the result and it is the same as [the product of] the square by itself.
: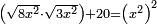 ואם יאמרו לך אלגו תרבה שרש משמנה דמיוני האלגו בשרש משלשה דמיוני האלגו והוספת על העולה עשרים דרהמי ויהיה כמו האלגו על עצמו
ואם יאמרו לך אלגו תרבה שרש משמנה דמיוני האלגו בשרש משלשה דמיוני האלגו והוספת על העולה עשרים דרהמי ויהיה כמו האלגו על עצמו |
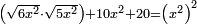
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| equation/quadratic equation | [√(6x²)·√(5x²)]+10x²+20=(x²)² | חשבון_השטחים#stdc | [34] If you are told: a square, multiply a root of its six times by a root of its five times, then add ten times the square plus twenty dirham to the product and it is the same as [the product of] the square by itself.
: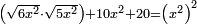 ואם יאמרו לך אלגו תרבה שרש מששה דמיוניו בשרש חמשה דמיוניו והוספת על מה שעלה מההכאה עשרה דמיוני האלגו ועשרים דרהמי יותר ויהיה כמו האלגו על עצמו
ואם יאמרו לך אלגו תרבה שרש מששה דמיוניו בשרש חמשה דמיוניו והוספת על מה שעלה מההכאה עשרה דמיוני האלגו ועשרים דרהמי יותר ויהיה כמו האלגו על עצמו |
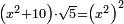
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| equation/quadratic equation | (x²+10)·√5=(x²)² | חשבון_השטחים#hePu | [38] If you are told: a square, you add to it ten dirham, then multiply the sum by a root of five and the result is the same as the product of the square by itself.
: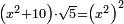 ואם יאמרו לך אלגו הוספת עליו עשרה דרהמי והכית המקובץ בשרש חמשה ויעלה כמו הכאת האלגו על עצמו
ואם יאמרו לך אלגו הוספת עליו עשרה דרהמי והכית המקובץ בשרש חמשה ויעלה כמו הכאת האלגו על עצמו |
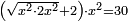
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| equation/quadratic equation | [√(x²·2x²)+2]·x²=30 | חשבון_השטחים#uwLQ | [40] If you are told: a square, you multiply it by its two times, extract the root of the product, add two dirham to it, then multiply the total by that square and the result is thirty dirham.
: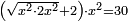 ואם יאמרו לך אלגו תכהו על {{#annot:term|387|piMO}}שני דמיוניו{{#annotend:piMO}} ותקח שרש העולה ותוסיף עליו שני דרהמי ותכה הכל באלגו ההוא ויהיה שלשים דרהמי
ואם יאמרו לך אלגו תכהו על {{#annot:term|387|piMO}}שני דמיוניו{{#annotend:piMO}} ותקח שרש העולה ותוסיף עליו שני דרהמי ותכה הכל באלגו ההוא ויהיה שלשים דרהמי |
![\scriptstyle\left[x^2-\left(2\sqrt{x^2}+10\right)\right]^2=8x^2](/mediawiki/images/math/1/4/5/145c5c99f9bc23a17e6ee34a2c9df452.png)
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| equation/quadratic equation | [x²-(2√x²+10)]²=8x² | חשבון_השטחים#aPQX | If you are told: a square, subtract its two roots and ten dirham from it, then multiply what remains by itself; it becomes eight times the square.
:![\scriptstyle\left[x^2-\left(2\sqrt{x^2}+10\right)\right]^2=8x^2](/mediawiki/images/math/1/4/5/145c5c99f9bc23a17e6ee34a2c9df452.png) ואם יאמרו לך אלגו תגרע ממנו שני שרשיו ועשרה דרהמי ותכה מה שישאר בעצמו ויהיה שמנה דמיוני האלגו
ואם יאמרו לך אלגו תגרע ממנו שני שרשיו ועשרה דרהמי ותכה מה שישאר בעצמו ויהיה שמנה דמיוני האלגו |
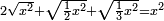
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| equation/quadratic equation | 2√(x²)+√(½x²)+√(⅓x²)=x² | חשבון_השטחים#nPTX | If you are told: a square whose two roots plus a root of half the square and a root of its third are equal to the square - how much is the square?
: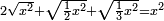 ואם יאמרו לך אלגו אשר שני שרשיו ושרש חצי האלגו ושרש שלישיתו ישוו האלגו כמה הוא האלגו
ואם יאמרו לך אלגו אשר שני שרשיו ושרש חצי האלגו ושרש שלישיתו ישוו האלגו כמה הוא האלגו |
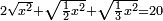
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| equation/quadratic equation | 2√(x²)+√(½x²)+√(⅓x²)=20 | חשבון_השטחים#wOZV | If one says: a square whose two roots plus a root of its half and a root of its third are twenty dirham - how much is the square?
: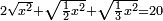 ואם יאמר אלגו אשר שני שרשיו ושרש חציו ושרש שלישיתו עשרים דרהמי כמה הוא האלגו
ואם יאמר אלגו אשר שני שרשיו ושרש חציו ושרש שלישיתו עשרים דרהמי כמה הוא האלגו |
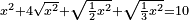
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| equation/quadratic equation | x²+4√(x²)+√(½x²)+√(⅓x²)=10 | חשבון_השטחים#b04G | If you are told: a square, add to it its four roots plus a root of its half and a root of its third; it is ten dirham - how much is the square?
: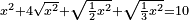 ואם יאמר לך אלגו תוסיף עליו ארבעה שרשיו ושרש חציו ושרש שלישיתו ויהיה עשרה דרהמי כמה הוא האלגו
ואם יאמר לך אלגו תוסיף עליו ארבעה שרשיו ושרש חציו ושרש שלישיתו ויהיה עשרה דרהמי כמה הוא האלגו |
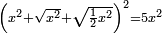
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| equation/quadratic equation | [x²+√(x²)+√(½x²)]²=5x² | חשבון_השטחים#omoo | If you are told: a square, add to it its root and a root of its half, then multiply the result by itself; it is five times the square.
: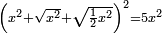 ואם יאמרו לך אלגו תוסיף עליו שרשו ושרש חציו ותכה המקובץ על עצמו ויהיה חמשה דמיוני האלגו
ואם יאמרו לך אלגו תוסיף עליו שרשו ושרש חציו ותכה המקובץ על עצמו ויהיה חמשה דמיוני האלגו |
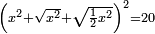
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| equation/quadratic equation | [x²+√(x²)+√(½x²)]²=20 | חשבון_השטחים#OX0E | 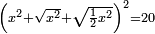 ואם יאמרו לך אלגו הוסף עליו שרשו ושרש חציו ותכה המקובץ בעצמו ויהיה עשרים דרהמי
ואם יאמרו לך אלגו הוסף עליו שרשו ושרש חציו ותכה המקובץ בעצמו ויהיה עשרים דרהמי |
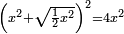
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| equation/quadratic equation | [x²+√(½x²)]²=4x² | חשבון_השטחים#Fvgh | If you are told: a square, you add to it a root of its half, then multiply the result by itself; it becomes four times the square.
: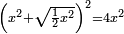 ואם יאמרו לך אלגו הוספת עליו שרש חציו והכית העולה בעצמו ויהיה ארבעה דמיוני האלגו
ואם יאמרו לך אלגו הוספת עליו שרש חציו והכית העולה בעצמו ויהיה ארבעה דמיוני האלגו |
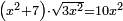
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| equation/quadratic equation | (x²+7)·√(3x²)=10x² | חשבון_השטחים#dAZJ | If you are told: a square, add to it seven dirham, then multiply the sum by a root of three times the square; it becomes ten times the square.
: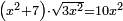 ואם יאמרו לך אלגו תוסיף עליו שבעה דרהמי ותכה המקובץ בשרש שלשה דמיוני האלגו ויהיה עשרה דמיוני האלגו
ואם יאמרו לך אלגו תוסיף עליו שבעה דרהמי ותכה המקובץ בשרש שלשה דמיוני האלגו ויהיה עשרה דמיוני האלגו |
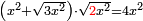
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| equation/quadratic equation | [x²+√(3x²)]·√(2x²)=4x² | חשבון_השטחים#lk6C | If you are told: a square, add to it a root of three times of it, then multiply the sum by a root of [twice] the square; it becomes four times the square.
: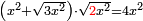 ואם יאמרו לך אלגו תוסיף עליו שרש שלשה דמיוניו ותכה המקובץ בשרש האלגו יהיה ארבעה דמיוני האלגו
ואם יאמרו לך אלגו תוסיף עליו שרש שלשה דמיוניו ותכה המקובץ בשרש האלגו יהיה ארבעה דמיוני האלגו |
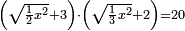
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| equation/quadratic equation | [√(½x²)+3]·[√(⅓x²)+2]=20 | חשבון_השטחים#Y7kO | If you are told: a square, add three dirham to a root of its half, and two dirham to a root of its third, then multiply one [sum] by the other; it is twenty dirham.
: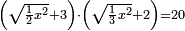 ואם יאמרו לך אלגו תוסיף על שרש חציו שלשה דרהמי ועל שרש שלישיתו שני דרהמי ותכה האחד באחר ויהיה עשרים דרהמי
ואם יאמרו לך אלגו תוסיף על שרש חציו שלשה דרהמי ועל שרש שלישיתו שני דרהמי ותכה האחד באחר ויהיה עשרים דרהמי |
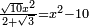
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| equation/quadratic equation | (√10·x²)/(2√3)=x²-10 | חשבון_השטחים#8OnP | If you are told: a square, multiply it by the root of ten, then divide the product by two plus the root of three; the quotient is the same as the square minus ten.
: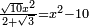 ואם יאמרו לך אלגו תכהו בשרש עשרה ותחלק מה שיעלה על שנים ושרש שלשה ויעלה לאחד כל כך כמו שהוא האלגו פחות עשרה
ואם יאמרו לך אלגו תכהו בשרש עשרה ותחלק מה שיעלה על שנים ושרש שלשה ויעלה לאחד כל כך כמו שהוא האלגו פחות עשרה |
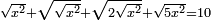
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| equation/quadratic equation | √x²+√(√x²)+√(2√x²)+5√x²=10 | חשבון_השטחים#rWIe | If you are told: a square whose root and the root of its root, plus the root of its two roots, plus the root of five times the square are ten dirham.
: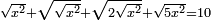 ואם יאמרו לך אלגו אשר שרשו ו{{#annot:term|2634|dE2e}}שרש שרשו{{#annotend:dE2e}} ושרש שני שרשיו ושרש חמשה דמיוני האלגו יהיה עשרה דרהמי
ואם יאמרו לך אלגו אשר שרשו ו{{#annot:term|2634|dE2e}}שרש שרשו{{#annotend:dE2e}} ושרש שני שרשיו ושרש חמשה דמיוני האלגו יהיה עשרה דרהמי |
quadratic equation in two variables
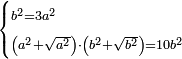
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| equation/quadratic equation | b²=3a², (a²+√a²)·(b²+√b²)=10b² | חשבון_השטחים#nHFm | If you are told: two squares - one is three times the other; you add to each of them its root, then multiply the one by the other; it is ten times the greater square.
: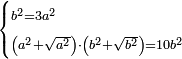 ואם יאמרו שני אלגוש והאחד שלשה דמיוני האחר הוספת על כל אחד מהם שרשו שלו והכית האחד באחר והיה עשרה דמיוני האלגו הגדול
ואם יאמרו שני אלגוש והאחד שלשה דמיוני האחר הוספת על כל אחד מהם שרשו שלו והכית האחד באחר והיה עשרה דמיוני האלגו הגדול |
quadratic equation in three variables
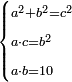
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| equation/quadratic equation | a²+b²=c², ac=b², ab=10 | חשבון_השטחים#gGKe | If you are told: three unequal squares, if you multiply the smaller by itself and the mean by itself; they are as the greater by itself. If you multiply the smaller by the greater it is as the mean by itself. If you multiply the smaller by the mean it is ten dirham.
: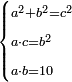 ואם יאמרו לך שלשה אלגוש בלתי שוים
ואם יאמרו לך שלשה אלגוש בלתי שויםאם תכה הקטן בעצמו והאמצעי בעצמו יהיו כמו הגדול בעצמו ואם תכה הקטון בגדול יהיה כמו האמצעי בעצמו ואם תכה הקטן באמצעי יהיה עשרה דרהמי |
Cubic Equation
![\scriptstyle ax^3=\sqrt[3]{c}](/mediawiki/images/math/a/6/4/a64e6eaeaf2d5f64610f741998d43d86.png)
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| equation/cubic equation | ax³=³√c | ספר_ג'יבלי_אלמוקבאלא#eOI5 | It is when cubes are equal to a cube root of the numbers:
:![\scriptstyle ax^3=\sqrt[3]{c}](/mediawiki/images/math/a/6/4/a64e6eaeaf2d5f64610f741998d43d86.png) וזהו כאשר המעוקבי' יהיו שוים אל שרש מעו' ממספרי'
וזהו כאשר המעוקבי' יהיו שוים אל שרש מעו' ממספרי' |
Biquadratic Equation
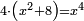
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| quartic equation/biquadratic equation | 4(x²+8)=x⁴ | אגרת_המספר#q2Fw | 6) 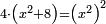 הששית ממון הוספת עליו ח' זוזים והכית המקובץ בארבעה והיה היוצא הכאת הממון בעצמו
הששית ממון הוספת עליו ח' זוזים והכית המקובץ בארבעה והיה היוצא הכאת הממון בעצמו |
| quartic equation/biquadratic equation | 4(x²+8)=x⁴ | תחבולות_המספר#G1Mq | [6] He said: the six problem is as if you are told: we add to a certain square [eight] dirham, then multiply the sum by four dirham and the result is the same as the product of the square [by itself].
: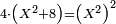 אמ' והשאלה הששית כמו אם יאמרו לך הוספנו על
אמ' והשאלה הששית כמו אם יאמרו לך הוספנו על |
| quartic equation/biquadratic equation | 4(x²+8)=x⁴ | חשבון_השטחים#ZxMx | 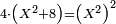 אלגו תוסיף עליו שמנה אדרהם ותכה {{#annot:term|388,1217|vQSL}}המקובץ{{#annotend:vQSL}} על ארבעה אדרהם והיה כמו האלגו על עצמו
אלגו תוסיף עליו שמנה אדרהם ותכה {{#annot:term|388,1217|vQSL}}המקובץ{{#annotend:vQSL}} על ארבעה אדרהם והיה כמו האלגו על עצמו |
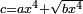
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| quartic equation/biquadratic equation | c=ax⁴+√(bx⁴) | ספר_ג'יבלי_אלמוקבאלא#h9il | When numbers are equal to squares of squares and a root of squares of squares:
: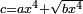 כאשר המספרי' יהיו שוים אל הצינסי מצינסי ואל שרשי צינסי מצינסי
כאשר המספרי' יהיו שוים אל הצינסי מצינסי ואל שרשי צינסי מצינסי |
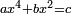
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| quartic equation/biquadratic equation | ax⁴+bx²=c | ספר_ג'יבלי_אלמוקבאלא#Tu7N | When squares of squares plus squares are equal to a number:
: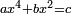 כאשר הצינסי מצינסי וצינסי יהיו שוים אל מספר
כאשר הצינסי מצינסי וצינסי יהיו שוים אל מספר |
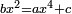
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| quartic equation/biquadratic equation | bx²=ax⁴+c | ספר_ג'יבלי_אלמוקבאלא#tkSO | When squares are equal to squares of squares and a root of a number:
: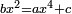 כאשר הצינסי יהיו שוים אל הצינסי מצינסי ואל מספר
כאשר הצינסי יהיו שוים אל הצינסי מצינסי ואל מספר |
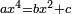
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| quartic equation/biquadratic equation | ax⁴=bx²+c | ספר_ג'יבלי_אלמוקבאלא#CLbn | When squares of squares are equal to a number and squares:
: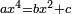 כאשר הצינסי מצינסי יהיו שוים אל המספר והצינסי
כאשר הצינסי מצינסי יהיו שוים אל המספר והצינסי |
indeterminate equation
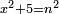
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| equation/indeterminate equation | x²+5=n² | השאלות_החרשות/האלמות#rm8m | 1) When you are told: a square that has a root, if you add five to it, it has a root. How much is the square?
: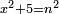 א כאשר יאמרו לך אלגו שמחזיק שרש אם תוסיף עליו חמשה יחזיק שרש כמה הוא האלגו
א כאשר יאמרו לך אלגו שמחזיק שרש אם תוסיף עליו חמשה יחזיק שרש כמה הוא האלגו |
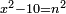
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| equation/indeterminate equation | x²-10=n² | השאלות_החרשות/האלמות#mV1w | 2) When you are told: a square that has a root, if you subtract ten dirham from it, what remains has a root.
: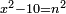 ב וכאשר יאמרו לך אלגו המחזיק שרש אם תגרע ממנו עשרה דרהמי יחזיק מה שישאר שרש
ב וכאשר יאמרו לך אלגו המחזיק שרש אם תגרע ממנו עשרה דרהמי יחזיק מה שישאר שרש |
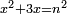
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| equation/indeterminate equation | x²+3x=n² | השאלות_החרשות/האלמות#L1j9 | 3) If you are told: a square that has a root, if you add three times its root to it, it has a root. How much is the square?
: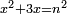 ג ואם יאמרו לך אלגו המחזיק שרש אם תוסיף עליו שרשו שלשה פעמים יחזיק שרש כמה יהיה האלגו
ג ואם יאמרו לך אלגו המחזיק שרש אם תוסיף עליו שרשו שלשה פעמים יחזיק שרש כמה יהיה האלגו |
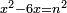
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| equation/indeterminate equation | x²-6x=n² | השאלות_החרשות/האלמות#LfMV | 4) If you are told: a square that has a root, when we subtract six times its root from it, it has a root.
: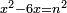 ד ואם יאמרו לך אלגו מחזיק שרש כאשר גרענו ממנו שרשו ששה פעמים יחזיק שרש
ד ואם יאמרו לך אלגו מחזיק שרש כאשר גרענו ממנו שרשו ששה פעמים יחזיק שרש |
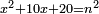
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| equation/indeterminate equation | x²+10x+20=n² | השאלות_החרשות/האלמות#x5bu | 5) If you are told: a square that has a root, if you add to it ten times its root plus ten dirham, it has a root.
: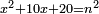 ה ואם יאמרו לך אלגו המחזיק שרש אם תוסיף עליו עשרה פעמים שרשו ועשרה דרהמי יחזיק שרש
ה ואם יאמרו לך אלגו המחזיק שרש אם תוסיף עליו עשרה פעמים שרשו ועשרה דרהמי יחזיק שרש |
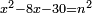
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| equation/indeterminate equation | x²-8x-30=n² | השאלות_החרשות/האלמות#67aP | 6) If you are told: a square that has a root, if you subtract from it eight times its root and thirty dirham, the remainder has a root.
: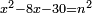 ו ואם יאמרו לך אלגו המחזיק שרש אם תגרע ממנו שרשו שמנה פעמי' ושלשים דרהמי יחזיק מה שישאר שרש
ו ואם יאמרו לך אלגו המחזיק שרש אם תגרע ממנו שרשו שמנה פעמי' ושלשים דרהמי יחזיק מה שישאר שרש |