Difference between revisions of "Sums"
From mispar
| Line 121: | Line 121: | ||
[[category: #sum of powers of two]] | [[category: #sum of powers of two]] | ||
[[comment: 1-128]] | [[comment: 1-128]] | ||
| − | }} | + | }}</div></div><br> |
| + | |||
<div class="mw-collapsible mw-collapsed"><math>\scriptstyle\sum_{i=3}^{6} 2^{i-1}</math><div class="mw-collapsible-content"> | <div class="mw-collapsible mw-collapsed"><math>\scriptstyle\sum_{i=3}^{6} 2^{i-1}</math><div class="mw-collapsible-content"> | ||
{{#annotask: | {{#annotask: | ||
| Line 130: | Line 131: | ||
== Sum of Powers of Three == | == Sum of Powers of Three == | ||
| + | <div class="mw-collapsible mw-collapsed"><math>\scriptstyle\sum_{i=1}^{4} 3^{i-1}</math><div class="mw-collapsible-content"> | ||
{{#annotask: | {{#annotask: | ||
[[category: #sum of powers of three]] | [[category: #sum of powers of three]] | ||
[[comment: 1-27]] | [[comment: 1-27]] | ||
| − | }} | + | }}</div></div><br> |
== Sum of Powers of Four == | == Sum of Powers of Four == | ||
| + | <div class="mw-collapsible mw-collapsed"><math>\scriptstyle\sum_{i=1}^{3} 4^{i-1}</math><div class="mw-collapsible-content"> | ||
{{#annotask: | {{#annotask: | ||
[[category: #sum of powers of four]] | [[category: #sum of powers of four]] | ||
[[comment: 1-16]] | [[comment: 1-16]] | ||
| − | }} | + | }}</div></div><br> |
Revision as of 10:29, 7 January 2020
Contents
[hide]Sum of Natural Numbers
even number of terms = last term is even
[Expand]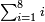
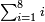
[Expand]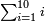
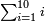
[Expand]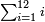
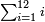
[Expand]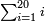
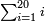
[Expand]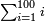
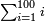
odd number of terms = last term is odd
[Expand]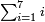
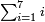
[Expand]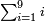
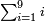
[Expand]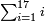
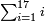
[Expand]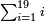
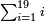
Sum of Evens
[Expand]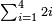
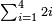
[Expand]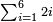
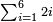
[Expand]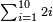
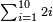
Sum of Odds
[Expand]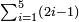
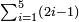
[Expand]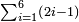
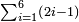
[Expand]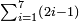
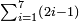
Sum of Powers of Two = Sum of Even-Times-Even Numbers
[Expand]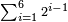
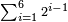
[Expand]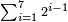
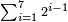
[Expand]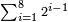
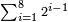
[Expand]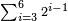
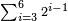
Sum of Powers of Three
[Expand]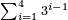
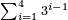
Sum of Powers of Four
[Expand]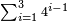
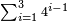
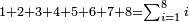 עז א ב' ג' ד' ה' ו' ז' ח'
עז א ב' ג' ד' ה' ו' ז' ח'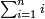 לידע מספרים מונחים על סדר המספר
|-
|
::Such as: 1; 2; 3; 4; 5; 6; 7; 8; 9; 10
::
לידע מספרים מונחים על סדר המספר
|-
|
::Such as: 1; 2; 3; 4; 5; 6; 7; 8; 9; 10
::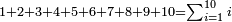 אם יאמר אדם א' וב' וג' וד' וה' וו' וז' וח' וטי' וי' כמה שוי בין כלם
אם יאמר אדם א' וב' וג' וד' וה' וו' וז' וח' וטי' וי' כמה שוי בין כלם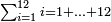 המשל שנרצה לדעת קבוץ אחד מאחד עד י"ב
המשל שנרצה לדעת קבוץ אחד מאחד עד י"ב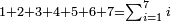 עח א ב' ג' ד' ה' ו' ז'
עח א ב' ג' ד' ה' ו' ז'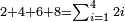 פ ב ד' ו' ח' שהם כלם זוגות
פ ב ד' ו' ח' שהם כלם זוגות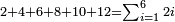 כמו ב' וד' וו' וח' וי' וי"ב כמה יהיה בין כלם
כמו ב' וד' וו' וח' וי' וי"ב כמה יהיה בין כלם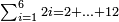 המשל בזה שאם הזוג האחרון יהיה י"ב
המשל בזה שאם הזוג האחרון יהיה י"ב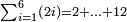 כג) שאלה אם תרצה לדעת חבור כל הזוגות אשר הם מב' עד י"ב
כג) שאלה אם תרצה לדעת חבור כל הזוגות אשר הם מב' עד י"ב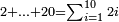 ואם אומר הלכתי עד עשרי'
ואם אומר הלכתי עד עשרי'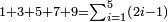 עט א ג' ה' ז' ט' שהם פרדים
עט א ג' ה' ז' ט' שהם פרדים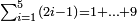 כב) שאלה קבץ מא' עד ט' כל הנפרדים
כב) שאלה קבץ מא' עד ט' כל הנפרדים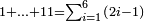 ואם הלך בשאלתו עד י"א
ואם הלך בשאלתו עד י"א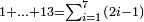 ואם הלך עד י"ג
ואם הלך עד י"ג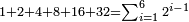 כגון א' וב' וד' וח' וי"ו ול"ב
כגון א' וב' וד' וח' וי"ו ול"ב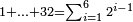 דמיון זה האומר קבצתי מספרים כפולי' מא' ועד ל"ב כמה הם
דמיון זה האומר קבצתי מספרים כפולי' מא' ועד ל"ב כמה הם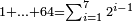 ואם יאמ' התחלתי מא' וכפלתי עד ס"ד
ואם יאמ' התחלתי מא' וכפלתי עד ס"ד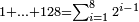 ואם יאמר התחלתי מאחד וכפלתי עד
ואם יאמר התחלתי מאחד וכפלתי עד 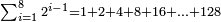 מ) שאלה אם תרצה לדעת המחובר מא' עם ב' עם ד' עם ח' ועם י"ו וכן לעולם
מ) שאלה אם תרצה לדעת המחובר מא' עם ב' עם ד' עם ח' ועם י"ו וכן לעולם 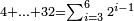 ואם יאמר התחלתי מד' וכפלתי עד ל"ב כמה יהיו
ואם יאמר התחלתי מד' וכפלתי עד ל"ב כמה יהיו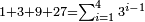 כגון א' ג' ט' כ"ז
כגון א' ג' ט' כ"ז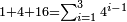 כגון א' ד' י"ו
כגון א' ד' י"ו