Difference between revisions of "Mathematical formula"
From mispar
(→Biquadratic Equation) |
(→Biquadratic Equation) |
||
| Line 52: | Line 52: | ||
[[category: #biquadratic equation]] | [[category: #biquadratic equation]] | ||
[[comment: 4(x²+8)=x⁴]] | [[comment: 4(x²+8)=x⁴]] | ||
| + | }}</div></div> | ||
| + | <br> | ||
| + | <div class="mw-collapsible mw-collapsed"><math>\scriptstyle ax^4+bx^2=c</math><div class="mw-collapsible-content"> | ||
| + | {{#annotask: | ||
| + | [[category: #biquadratic equation]] | ||
| + | [[comment: ax⁴+bx²=c]] | ||
}}</div></div> | }}</div></div> | ||
<br> | <br> | ||
Revision as of 07:11, 9 April 2019
Linear Equation
[Expand]![\scriptstyle bx=\sqrt[3]{c}](/mediawiki/images/math/4/e/c/4eced3ba1c8f51bf47cf911659b6e201.png)
![\scriptstyle bx=\sqrt[3]{c}](/mediawiki/images/math/4/e/c/4eced3ba1c8f51bf47cf911659b6e201.png)
[Expand]![\scriptstyle c=\sqrt[3]{bx}](/mediawiki/images/math/5/b/4/5b40a2184fb3c6324ff5fe2eedb9da0b.png)
![\scriptstyle c=\sqrt[3]{bx}](/mediawiki/images/math/5/b/4/5b40a2184fb3c6324ff5fe2eedb9da0b.png)
Quadratic Equation
[Expand]![\scriptstyle ax^2=\sqrt[3]{c}](/mediawiki/images/math/f/c/0/fc0033e1c190540235d4afbc47b31b11.png)
![\scriptstyle ax^2=\sqrt[3]{c}](/mediawiki/images/math/f/c/0/fc0033e1c190540235d4afbc47b31b11.png)
[Expand]![\scriptstyle c=\sqrt[3]{ax^2}](/mediawiki/images/math/f/7/6/f7617468fb35452327a7d2d5678e45f0.png)
![\scriptstyle c=\sqrt[3]{ax^2}](/mediawiki/images/math/f/7/6/f7617468fb35452327a7d2d5678e45f0.png)
Cubic Equation
[Expand]![\scriptstyle ax^3=\sqrt[3]{c}](/mediawiki/images/math/a/6/4/a64e6eaeaf2d5f64610f741998d43d86.png)
![\scriptstyle ax^3=\sqrt[3]{c}](/mediawiki/images/math/a/6/4/a64e6eaeaf2d5f64610f741998d43d86.png)
Biquadratic Equation
[Expand]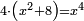
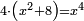
[Expand]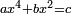
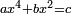
[Expand]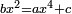
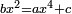
[Expand]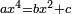
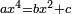
![\scriptstyle\left(3n+1\right)^2=\left[\left[10\sdot\left[\frac{1}{3}\sdot\left(3n\right)\right]^2\right]-\left[\frac{1}{3}\sdot\left(3n\right)\right]^2\right]+3n+\left(3n+1\right)](/mediawiki/images/math/2/a/f/2af90eb131ece9e62879b03d8922a419.png)
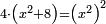 הששית ממון הוספת עליו ח' זוזים והכית המקובץ בארבעה והיה היוצא הכאת הממון בעצמו
הששית ממון הוספת עליו ח' זוזים והכית המקובץ בארבעה והיה היוצא הכאת הממון בעצמו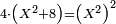 אמ' והשאלה הששית כמו אם יאמרו לך הוספנו על
אמ' והשאלה הששית כמו אם יאמרו לך הוספנו על