Difference between revisions of "Mathematical formula"

Revision as of 07:46, 5 April 2019

Category	Comment	Link	Annotated text
equation/quadratic equation	c=³√ax²	ספר_ג'יבלי_אלמוקבאלא#zK2y	When numbers are equal to a cube root of squares: : $\scriptstyle c=\sqrt[3]{ax^2}$ כאשר המספרי' יהיו שוים אל שרשי' מעו' מצינסי

Category	Comment	Link	Annotated text
equation/cubic equation	ax³=³√c	ספר_ג'יבלי_אלמוקבאלא#eOI5	It is when cubes are equal to a cube root of the numbers: : $\scriptstyle ax^3=\sqrt[3]{c}$ וזהו כאשר המעוקבי' יהיו שוים אל שרש מעו' ממספרי‫'

Category	Comment	Link	Annotated text
quartic equation/biquadratic equation	4(x²+8)=x⁴	אגרת_המספר#q2Fw	6) 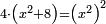$\scriptstyle4\sdot\left(x^2+8\right)=\left(x^2\right)^2$ הששית ממון הוספת עליו ח' זוזים והכית המקובץ בארבעה והיה היוצא הכאת הממון בעצמו
quartic equation/biquadratic equation	4(x²+8)=x⁴	תחבולות_המספר#G1Mq	[6] He said: the six problem is as if you are told: we add to a certain square [eight] dirham, then multiply the sum by four dirham and the result is the same as the product of the square [by itself]. :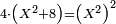 $\scriptstyle4\sdot\left(X^2+8\right)=\left(X^2\right)^2$ אמ' והשאלה הששית כמו אם יאמרו לך הוספנו על ~~התמונ'~~ מרובע מה שלשה דרהמי והכינו המקובץ בארבעה דרהמי והיה העולה כמו הכאת ~~א"ב בעצמו~~ המרובע
quartic equation/biquadratic equation	4(x²+8)=x⁴	חשבון_השטחים#ZxMx	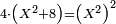$\scriptstyle4\sdot\left(X^2+8\right)=\left(X^2\right)^2$ אלגו תוסיף עליו שמנה אדרהם ותכה {{#annot:term\|388,1217\|vQSL}}המקובץ{{#annotend:vQSL}} על ארבעה אדרהם והיה כמו האלגו על עצמו

@@ Line 4: / Line 4: @@
 <math>\scriptstyle\left(3n+1\right)^2=\left[\left[10\sdot\left[\frac{1}{3}\sdot\left(3n\right)\right]^2\right]-\left[\frac{1}{3}\sdot\left(3n\right)\right]^2\right]+3n+\left(3n+1\right)</math>]]
+{{#annotask:
+	[[category: #quadratic equation]]
+	[[comment: c=³√ax²]]
+}}
 {{#annotask:
 	[[category: #cubic equation]]