ספר מעשה חושב
Contents
ספר מעשה חושב
להחכם הפילוסוף האלקי ר׳
לוי בר גרשום
Prologue |
|
| נאום לוי בן גרשום | |
| The complete perfection in practical crafts is based on knowing the way to perform the craft as well as the reason of doing it in that way | בעבור שההשגה השלמה בעשית המלאכות הוא שנדע במלאכה מלאכה עם ידיעת אופן המעשה למה נעשה אותה בזה האופן |
| The need to investigate the reasons of practical arithmetic: | |
|
והיה החלק המעשיי ממלאכת המספר אחת מהמלאכות המעשיות הוא מבואר שראוי שנחקור בה בסבותיה |
|
ועוד סבה אחרת תחייב לחקור בזאת המלאכה בנתינת הסיבות וזה שהוא מבואר שזאת המלאכה מקפת במינים רבים מאד וכל מין ומין ממנה מקיף בחמרים רבים מתחלפים התחלפות רב יביא לחשב שאינם תחת מין אחד ובהיות הענין כן הוא מבואר שלא תשלם ההשגה בזאת המלאכה בזולת ידיעת הסבות כי אם בקושי גדול |
| Accordingly, the purpose of this book is to teach briefly the arithmetical methods and their reasons | וכאשר היה זה כן ראינו בזה הספור להודיע דרכי המספרים וסבותיהם לפי קצורנו |
| The work is divided into two sections: | וחלקנו זה הספר לפי זאת החקירה לשני מאמרים |
|
המאמר הראשון יקיף על השרשים אשר נתן למה שנרצה לבארו מזאת המלאכה |
|
המאמר השני יקיף על דרכי המלאכה במין מין ממיני המספר ונתינת הסבות |
| The book is called Maʽase Ḥoshev [meaning: the practice of an arithmetician, as a pun on a biblical phrase – "the work of a skilful workman" (Exodus 26, 1; 31; and more)] – because it discusses comprehensively both the practice [= maʽase] and the speculation [= ḥoshev] | ולפי שהיה זה הספר מקיף על המעשה והעיון קראנוהו מעשה חושב |
| Before learning the teaching of the book, it is necessary to study books VII, VIII, IX of the Euclid's Elements, because they will not be quoted here, but are assumed as rules, since they were explained with proofs in Euclid's book | ואולם מדרגות הלמוד הנעשה בזה הספר הנה ראוי שיקדם העיון למעין בו במאמר השביעי והשמיני והתשיעי מאקלידיס כי לא היה רצוננו להשיב בזה הספר דבריו אבל נניחם במדרגת השרשים אחר שהתבארו שם במופת |
Section One |
|
Introduction to Section One – basic definitions |
פתיחת המאמר הראשון |
|---|---|
|
המספר המורכב ממספרים רבים הוא כשהוכה הראשון בשני והעולה על השלישי וכן עד כלותם |
|
מספר המספרים והחלקים המונחים הוא מספר מה שבהם ממספרים או חלקים מונחים |
| היחס המחובר ממספרים מה מונחים אל מספרים מה מונחים הוא היחס המחובר מיחס הראשון מהקודמים אל הראשון מהנמשכים [ומיחס השני מהקודמים אל השני מהנמשכים] וכן עד כלותם | |
|
המספרים הנמשכים מתחילין מן האחד הם אחד ושנים ושלשה וכן מה שהגיע ההמשך |
|
המספר הנמשך למספר מה לפניו הוא מה שיחסר מהמספר ההוא אחד |
|
המספר הנמשך למספר מה לאחריו הוא מה שיוסיף על המספר ההוא אחד |
|
נקבץ הנמשכים בדרך המספר מתחילים מן האחד הוא כשיחובר אחד עם שנים ועם שלשה וכן מה שהגיע |
|
נקבץ הנפרדים הנמשכים בדרך המספר מתחילים מן האחד הוא כשיחובר אחד עם שלשה ועם חמשה וכן מה שהגיע |
|
נקבץ הזוגות הנמשכים בדרך המספר הוא כשיחובר שנים שהוא הזוג הראשון עם ארבעה ועם ששה וכן מה שהגיע |
| המספרים הנמשכים בזולת דרך המספר הוא שיהיה השני מוסיף על הראשון בשיעור מה שיוסיף השלישי על השני וכן מה שהגיע ההמשך | |
| חבור נקבצי הנמשכים בדרך המספר נמשכים בראשיתם ומתחילים מן האחד הם נקבצי הנמשכים אשר תכליתם אחת והראשון מן הנקבצים מתחיל מן האחד והשני משנים וכן לא יסורו נמשכים בראשיתם עד התכלית | |
| חבור נקבצי הנמשכים בדרך המספר נמשכים בתכליתם ומתחילים מן האחד הם נקבצי הנמשכים אשר כל אחד מהם מתחיל מן האחד והאחד מהם הוא אחד לבד והשני נקבץ אחד ושנים והשלישי נקבץ אחד ושנים ושלשה וכן לא יסורו נמשכים באחריתם עד התכלית וכן מה שהגיע | |
| המספר יהיה אמצעי בין מספר מונח ובין האחד אם היה המספר המונח מוסיף עליו בשיעור מה שהוא מוסיף על האחד והמספר המונח קרא הקצווי לזה המספר האמצעי | |
| מיני המספר הם הזוג והנפרד | |
| החלק היותר גדול המספר אשר נקרא בו הוא יותר קטן | |
| והמשל שחצי זוג הוא יותר גדול מחומש | |
| והמספר אשר נקרא בו חצי הוא שנים והוא קטן מחמשה אשר נקרא בו חומש | |
| וכבר אפשר שנבאר זה במופת בשנניח מספר מה והוא א' ויהיו החלקים ממנו מספר ב' ומספר ג' ויהיה מספר ב' יותר גדול ממספר ג' ויהיה מספר ד' המספר הקורא לחלק הנקרא בב' ממספר א' ויהיה מספר ה' המספר הקורא לחלק הנקרא בג' ממספר א' ואומר שמספר ד' יותר קטן ממספר ה' | |
| המופת כי מפני שמספר ד' המספר הקורא לחלק הנקרא בב' ממספר א' הנה ד' יוכה בב' ויהיה א' וכזה יתבאר שמספר ג' יוכה בה' ויהיה א' אם כן ב' בד' כמו ג' בה' הנה אם כן צלעותיהם מספיקות יחס ב' אל ג' כיחס ה' אל ד' אבל מספר ב' יותר גדול ממספר ג' אם כן מספר ה' יותר גדול ממספר ד' והוא מה שרצינו לבאר | |
| החלק או נקבץ החלקים יהיה יותר גדול מחלק או מנקבץ החלקים אם יהיה החלק ההוא או נקבץ החלקים ההם ממספר מה יותר גדול מהחלק האחר או נקבץ החלקים האחרים מהמספר הוא בעינו | |
| יקרה לאחד החלוקה מצד הנושא והוא צד אחד מהעיון באחד המספר המופשט מנושא אבל זה הספר מקיף בשני הענינים יחד ולזה לא נחוש אם יחלק האחד בקצת תמונות המאמר הראשון | |
| המאמר הראשון | |
| והוא מקיף על השרשים אשר נתן בזאת המלאכה | |
Theorems in Euclidean style |
|
| א השטח ההוה מהכאת שני מספרים האחד באחד ימנהו כל מספר מהם במנין אחדי המספר השני | |
|
ב כאשר היו שני מספרים מונחים וחולק המספר האחד לחלקים כמה שיהיו הנה שטח המספר האחד בשני שוה לשטח כל אחד מחלקי המספר האחד בשני מקובצים |
|
ויהיו המספרים המונחים מספר א"ב ג' וחולק המספר א"ב לחלקים א"ה ה"ד ד"ב ואומר ששטח א"ב בג' שוה לשטח א"ה בג' ולשטח ה"ד בג' ולשטח ד"ב בג' מקובצים |
| המופת ששטח א"ה בג' ימנהו ג' במנין מה שבא"ה מן האחדים ושטח ה"ד בג' ימנהו ג' במנין מה שבה"ד מן האחדים ושטח ד"ב בג' ימנהו ג' במנין מה שבד"ב מן האחדים הנה אם כן אלו השטחים מקובצים ימנם ג' במנין מה שבא"ה ה"ד ד"ב מן האחדים אבל מנין מה שבא"ה ה"ד ד"ב מן האחדים הוא מנין מה שבא"ב מן האחדים הנה אם כן אלו השטחים כלם ימנם ג' במנין מה שבא"ב מן האחדים אבל שטח א"ב בג' ימנהו ג' במנין מה שבא"ב מן האחדים א"כ שטח א"ב בג' שוה לאלו השטחים מקובצים | |
|
ג כאשר היו שני מספרים מונחים וחולק כל אחד מהם לחלקים כמה שיהיו הנה שטח המספר האחד באחר שוה לשטח חלקי האחד בכל אחד מחלקי המספר האחר |
|
ויהיו המספרים המונחים מספרי א"ב ג"ד וחולק מספר א"ב לחלקים א"ה ה"ב וחולק מספר ג"ד לחלקים ג"ז ז"ח ח"ד ואומר ששטחי א"ה בכל אחד ממספרי ג"ז ז"ח ח"ד עם שטחי ה"ב בכל אחד ממספרי ג"ז ז"ח ח"ד שוים לשטח א"ב בג"ד |
|
המופת |
|
ששטחי א"ה בחלקי ג"ז ז"ח ח"ד שוים לשטח א"ה בג"ד |
|
וכזה התבאר ששטחי ה"ב בחלקי ג"ז ז"ח ח"ד שוים לשטח ה"ב בג"ד |
|
ואולם שטחי א"ה בג"ד וה"ב בג"ד שוים לשטח א"ב בג"ד |
|
אם כן שטחי חלקי מספר א"ב בכל אחד מחלקי מספר ג"ד שוים לשטח א"ב בג"ד והוא מה שיציגו |
|
ד כאשר חולק מספר מה בשני חלקים הנה שטח כל המספר באחד מחלקיו שוה לשטח האחד באחר ולמרובע חלק אשר זכרנו |
|
ויתחלק מספר א"ב בשני חלקים ויהיו חלקיו א"ג ג"ב ואומר ששטח א"ב בג"ב שוה לשטח א"ג בג"ב ולמרובע ב"ג |
|
המופת |
|
ששטח א"ג בג"ב עם שטח ג"ב בג"ב שהוא מרובע ג"ב שוה לשטח א"ב בג"ב |
|
אם כן שטח א"ב בג"ב שוה לשטח א"ג בג"ב ולמרובע ג"ב והוא מה שרצינו |
|
ה כאשר חולק מספר מה לחצאים והוסף עליו מספר מה הנה שטח התוספת במספר כלו (עם התוספת) עם מרובע חצי המספר שוה למרובע חצי המספר והתוספת מקובצים |
|
ויחולק מספר א"ב לחצאים ויהיו חלקיו א"ג ג"ב והוסף עליו מספר ב"ד ואומר ששטח א"ד בד"ב עם מרובע ג"ב שוה לממרובע ג"ד |
|
המופת |
|
ששטח א"ד בד"ב שוה לשטח ג"ד בד"ב ולשטח א"ג בד"ב שהוא שוה לשטח ב"ג בד"ב |
|
וכאשר חובר עמו מרובע ג"ב היה המקובץ שוה לשטח ג"ד בב"ד ולשטח ב"ג בב"ד ולמרובע ג"ב |
|
וגם כן הנה שטח ג"ד בג"ד שוה לשטח ג"ד בב"ד ולשטח ג"ד בג"ב |
|
אבל שטח ג"ד בג"ב שוה לשטח ג"ב בב"ד ולמרובע ב"ג |
|
אם כן מרובע ג"ד שוה לשטח ג"ד בד"ב ולשטח ג"ב בב"ד ולמרובע ב"ג וזה שוה לפי מה שבארנו לשטח א"ד בד"ב ולמרובע ג"ב ו'מ'ש' |
|
ו כאשר נוסיף על מספר מונח מספר מה הנה מרובע שני המספרים מחוברים שוה למרובע המספרים ההם ולכפל שטח זה בזה |
|
ויהיה המספר א"ב ונוסיף עליו מספר ב"ג הנה אומר שמרובע א"ג שוה למרובעי א"ב וב"ג ולכפל שטח א"ב בב"ג |
|
המופת |
|
ששטח א"ג בא"ג שוה לשטח א"ב בא"ג ולשטח ב"ג בא"ג |
|
ואולם שטח א"ב בא"ג שוה לשטח א"ב בב"ג ולמרובע א"ב |
|
ואולם שטח ב"ג בא"ג שוה לשטח א"ב בב"ג ולמרובע ב"ג |
|
יהיה א"כ מרובע א"ג שוה לשני מרובעי א"ב וב"ג ולכפל א"ב בב"ג והוא מה שרצינו |
|
ז כאשר נוסיף על מספר מה מספר מה הנה מרובע שני המספרים מחוברים שוה לשטח המספרים מחוברים באחד מהם ולשטח זה בזה ולמרובע חלק הנשאר |
|
ויהיה המספר מספר א"ב ונוסף עליו מספר ב"ג ואומר שמרובע א"ג שוה לשטח א"ג בא"ב ולשטח א"ב בב"ג ולמרובע ב"ג |
|
המופת |
|
ששטח א"ג בא"ג שוה לשטח א"ב בא"ג ולשטח ב"ג בא"ג |
|
אבל שטח ב"ג בא"ג שוה לשטח א"ב בב"ג ולמרובע ב"ג |
|
אם כן מרובע א"ג שוה לשטח א"ב בא"ג ולשטח א"ב בב"ג ולמרובע ב"ג והוא מה שרצינו |
|
ח השטח ההוה מחצי המספר המונח בעצמו שוה לשטח ההוה מחלק מה מהמספר ההוא בחלק השני ולמרובע יתרון אחד מן החלקים על חצי המספר המונח |
|
ויהיה המספר המונח מספר א"ב וחולק לחצאים בנקודה ג' וחולק איך שקרה בנקודה ד' ואומר שמרובע מספר א"ג שוה לשטח ההוה מהמספר א"ד במספר ד"ב ולמרובע ההוה ממספר ג"ד |
|
המופת |
|
שמרובע א"ג שוה לשטח א"ג בג"ד ולשטח א"ג בד"ב מקובצים |
|
אבל שטח א"ד בד"ב שוה לשטח א"ג בד"ב ולשטח ג"ד בד"ב |
|
ונחסר שטח א"ג בד"ב המשותף והיה הנשאר למרובע א"ג שוה לשטח א"ג בג"ד שהוא שוה לשטח ג"ב בג"ד |
|
והנשאר לשטח א"ד בד"ב הוא שטח ג"ד בד"ב |
|
והנה יתרון שטח ג"ב בג"ד על שטח ג"ד בד"ב הוא כמו מרובע ג"ד |
|
אם כן מרובע א"ג שוה לשטח א"ד בד"ב ולמרובע ג"ד והוא מה שרצינו |
|
ט כאשר הוכה מספר אחד על מספר מורכב משני מספרים מונחים והיה העולה מה הנה אם הוכה המספר המורכב משני מספרים איזה שיהיו מאלה השלשה על השלישי יהיה המספר ההוא בעינו |
|
ויוכה מספר א' על שטח ב' בג' ויהיה העולה מספר ה"ד ואומר שאם הוכה מספר ב' על שטח א' בג' יהיה העולה גם כן מספר ד"ה |
|
המופת |
| שמספר ד"ה ימנהו שטח ב' בג' כשיעור אחדי א' הנה נחלק ד"ה על דמיוני שטח ב' בג' ויהיו חלקיו השוים לשטח ב' בג' חלקי ד"ז ז"ח ח"ד ויהיה מספר אלו החלקים הוא כמספר מה שבא מן האחדים והוא מבואר שכל אחד מחלקי ד"ז ז"ח ימנהו ב' בשיעור אחד לפי שכל אחד מהם שוה לשטח ב' בג' הנה ד"ה כלו ימנהו מספר ב' כמספר מה שימנה כל חלקיו יחד אבל כל חלקיו יחד ימנם כמספרם מוכה על ג' ומספרם הוא כמספר אחדי א' הנה א"כ ד"ה כלו ימנהו ב' במספר שטח א' בג' הנה א"כ כבר יוכה מספר ב' בשטח א' בג' ויהיה ד"ה והוא מה שרצינו לבאר | |
| ובזה יתבאר שאיזה מספר שיוכה מאלה השלשה על השטח ההוה מאחד המספרים הנשארים בשני יהיה העולה ד"ה ולזה ג"כ ימנהו איזה שיהיה מאלו המספרים כמספר שטח אחד מהנשארים בשני וזה הוא מה שרצינו לבאר | |
|
י כאשר הוכה מספר אחד על מספר מורכב משלשה מספרים מונחים והיה העולה מספר מה הנה אם הוכה איזה מספר שיהיה מאלו על המספר המורכב מהשלשה הנשארים יהיה המספר ההוא בעינו |
|
ויוכה מספר א' על המספר המורכב ממספרי ג'ד'ה' והיה ז"ח הנה אומר שאם הוכה מספר ד' על המספר המורכב ממספרי א'ג'ה' יהיה העולה ז"ח גם כן |
|
המופת |
| שאנחנו נחלק ז"ח בדמיוני המספר המורכב ממספרי ג'ד'ה' ויהיו חלקיו ז"ט ט"ל ל"ח הנה מספר אלו החלקים הוא כמספר אחדי א' מפני שז"ח ימנהו המספר המורכב ממספרי ג'ד'ה' כמספר אחדי א' וכל אחד מחלקי ז"ט ט"ל ל"ה ימנהו ד' כשיעור שטח ג' בה' וזה מבואר ממה שקדם הנה ז"ח ימנהו ד' כמספר מה שימנה כל חלקיו יחד אבל כל חלקיו יחד ימנם ד' כשיעור שטח ג' בה' מוכה על א' אם כן ז"ח כלו ימנהו ד' כשיעור המספר המורכב ממספרי א'ג'ה' א"כ שטח ד' במורכב ממספרי א'ג'ה' הוא ז"ח ג"כ וכזה התבאר שאיזה שיהיה מאלו המספרים שיוכה על המורכב מהמספרים הנשארים יהיה העולה ז"ח | |
| ובזאת ההדרגה יתבאר לבלתי תכלית רצוני שאם הוכה מספר מה על מספר מורכב מארבעה מספרים והוא מספר מה הנה אם הוכה איזה מספר שיהיה מהם על המספר המורכב מהמספרים הנשארים יהיה העולה המספר ההוא בעינו ומפני זה ימנה המספר העולה מהכאת המספר האחד במספר המורכב מהנשארים איזה שיהיה מהמספרים ההם כשיעור המספר המורכב מהמספרים הנשארים | |
|
י"א כאשר הוכה מספר מה על מספר מורכב משלשה מספרים והיה העולה מספר מה הנה אם הוכה המורכב משני מספרים מהם על המספר המורכב מהמספרים הנשארים יהיה העולה המספר ההוא בעינו |
| ויוכה מספר א' על המספר המורכב ממספרי ג'ד'ה' והיה ז'ח' ואומר שאם הוכה שטח א' בד' על שטח ג' בה' יהיה העולה ז'ח' גם כן | |
| המופת שאנחנו נחלק ז'ח' בדמיוני המספר המורכב ממספרי ג'ד'ה' ויהיו חלקיו ז'ט' ט'ל' ל'ח' הנה מספר חלקיו הוא במספר מה שבא' מן האחדים וכל אחד מאלו החלקים ימנהו שטח ג' בה' כשיעור מה שבד' מן האחדים הנה ז'ח' ימנהו שטח ג' בה' כשיעור מה שימנה כל חלקיו יחד אבל כל חלקיו יחד ימנם כמספרם מוכה על ד' והנה מספרם הוא כמספר אחדי א' הנה א"ב ז'ח' ימנהו שטח ג' בה' כשיעור שטח א' בד' אם כן כבר יוכה שטח א' בד' על שטח ג' בה' ויהיה העולה ז'ח' ובזה התבאר שכאשר הוכו המספרים המורכבים משנים מאלו המספרים איזה שיהיו על המספר המורכב מהשנים הנשארים יהיה העולה ז'ח' גם כן | |
| ובזה הביאור בעינו התבאר שאם הוכה מספר מה על המספר המורכב מארבעה מספרים והיה מספר מה הנה אם הוכה המספר המורכב משנים מהם איזה שיהיו על המורכב מהשלשה הנשארים יהיה העולה המספר ההוא בעינו וכזה התבאר לאין תכלית בכמו זה הביאור בעינו ומפני זה ימנה המספר העולה המספר המורכב משני מספרים איזה שיהיו מהמספרים ההם כשיעור מה שבמספר המורכב מן המספרים הנשארים מן האחדים ומש"ל | |
|
י"ב כאשר הוכה מספר מה על המורכב ממספרים כמה שיהיו והיה מספר מה הנה אם הוכה המורכב מאיזה שיהיו מהמספרים ההם על המורכב מהמספרים הנשארים יהיה העולה המספר ההוא בעינו |
| ויוכה מספר א' על המורכב ממספרי ב'ג'ד'ה'ז'ח' ויהיה העולה ט'כ' ואומר שאם הוכה המורכב ממספרי ב'ז'ה'ג' על המורכב ממספרי א'ד'ח' יהיה העולה ט'כ' גם כן | |
| המופת שמספר ט'כ' ימנהו המספר המורכב ממספרי ב'ג' כשיעור אחדי המספר המורכב ממספרי א'ד'ה'ז'ח' הנה נחלק ט'כ' בדמיוני א'ד'ה'ז'ח' ויהיו חלקיו ט'ל' ל'מ' מ'ס' ס'כ' הנה מספר אלו החלקים כשיעור אחדי שטח ב' בג' וג"כ הנה כל אחד מאלו החלקים ימנהו מורכב א'ד'ח' כשיעור אחדי שטח ה' בז' לפי שכל אחד מהם שוה למורכב א'ד'ה'ז'ח' והנה ט'כ' כלו ימנהו מורכב א'ד'ח' כשיעור שטח ה' בז' מוכה על מספרם שהוא כמספר שטח ב' בג' והעולה כבר התבאר שהוא המספר המורכב ממספרי ב'ג'ה'ז' אם כן ט'כ' כלו ימנהו המורכב ממספרי א'ד'ח' כשיעור אחדי המספר המורכב ממספרי ב'ג'ה'ז' א"כ כבר יוכה מורכב א'ד'ח' במורכב ב'ג'ה'ז' ויהיה העולה מספר ט'כ' וכזה התבאר שאם הוכה מורכב איזה שיהיה מאלו המספרים על המורכב מהמספרים הנשארים יהיה העולה ט'כ' גם כן | |
| ובזה התבא[ר] באיזה מספר מורכב מכמה מספרים שיהיו שאם הוכה המספר המורכב ממספרים מה מהם על המספר המורכב מהמספרים הנשארים יהיה העולה המספר ההוא בעינו ולזה ימנה המספר העולה המספר המורכב מאיזה שיהיו מהמספרים ההם כמספר אחדי המורכב מהמספרים הנשארים ומש"ל | |
|
י"ג המספר המורכב ממספרים מה יחסו אל המספר המורכב ממספרים אחרים מספרם כמספר המספרים הקודמים כמו היחס המחובר מהמספרים הקודמים אל המספרים הנמשכים |
| ויהיה מספר א' מורכב ממספרי ב'ג'ד'ה'ז' ומספר ח' מורכב ממספר ט'כ'ל'מ'נ' ואומר שיחס א' אל ח' מחובר מחמשה יחסים מיחס ב' אל ט' ומיחס ג' אל כ' ומיחס ד' אל ל' ומיחס ה' אל מ' ומיחס ז' אל נ' | |
| המופת שאנחנו נכה המורכב ממספר ג'ד'ה'ז' במספר ט' ונשים העולה ס' הנה מורכב ג'ד'ה'ז' הוכה בב' והיה א' והוכה בט' והיה ס' הנה אם כן יחס א' אל ס' כיחס ב' אל ט' וגם כן הנה נכה מורכב ט'ד'ה'ז' בכ' ונשים העולה מספר ע' הנה מורכב ט'ד'ה'ז' הוכה בג' והיה ס' והוכה בכ' והיה ע' הנה יחס ס' אל ע' כיחס נ' אל כ' וגם כן הנה נכה מורכב ט'כ'ה'ז' בל' ונשים העולה מספר פ' ויתבאר כמו הביאור הקודם שיחס ע' אל פ' הוא כיחס ד' אל ל' וגם כן הנה נכה מורכב ט'כ'ל'ז' במספר מ' והיה צ' ויתבאר ג"כ שיחס פ' אל צ' הוא כיחס ה' אל מ' וכזה התבאר שיחס צ' אל ח' כיחס ז' אל נ' ובהיות הענין כן הוא מבואר שיחס א' אל ח' מחובר מחמשה יחסים מיחס א' אל ס' ומיחס ס' אל ע' ומיחס ע' אל פ' ומיחס פ' אל צ' ומיחס צ' אל ח' וכבר התבאר שכל יחס מאלו היחסים הוא כמו גילו מיחסי מספרי ב'ג'ד'ה'ז' אל מספרי ט'כ'ל'מ'נ' א"כ יחס א' אל ח' מחובר מחמשה יחסים מיחס ב' אל ט' ומיחס נ 'אל כ' ומיחס ד' אל ל' ומיחס ה' אל מ' ומיחס ז' אל ג' והוא מש"ל | |
|
י"ד היחס המחובר ממספרים מה קודמים אל מספרים מה נמשכים הנה כאשר הומר סדור המספרים הגיליים ונשארו הקודמים קודמים והנמשכים נמשכים ישאר היחס המחובר כמו היחס המחובר הראשון |
| ויהיו המספרים הקודמים מספרי א'ב'ג'ד' והמספרים הנמשכים מספרי ה'ז'ח'ט' והיה היחס המחובר מיחס א' אל ה' ומיחס ב' אל ז' ומיחס ג' אל ח' ומיחס ד' אל ט' כיחס כ' אל ל' ואומר שאם הומר סדור הגיליים ולוקח היחס המחובר מיחס א' אל ח' ומיחס ב' אל ה' ומיחס ג' אל ט' ומיחס ד' אל ז' יהיה ג"כ כיחס כ' אל ל' | |
| המופת שאנחנו נשים המספר המורכב ממספרי א'ב'ג'ד' מ' והמספר המורכב ממספרי ה'ז'ח'ט' ג' הנה יחס מ' אל נ' הוא כמו היחס המחובר ממספרי א'ב'ג'ד' אל מספרי ה'ז'ח'ט' והמספר המורכב ממספרי ה'ז'ח'ט' הוא כמו המספר המורכב ממספרי ה'ח'ט'ז' אם כן יחס מ' אל נ' הוא כמו היחס המחובר ממספרי א'ב'ג'ד' אל מספרי ה'ח'ט'ז' וכבר היה יחס מ' אל נ' כמו היחס המחובר ממספרי א'ב'ג'ד' אל מספרי ה'ז'ח'ט' א"כ (מפתיחת אקלידיס) היחס המחובר ממספרי א'ב'ג'ד' אל מספרי ה'ז'ח'ט' הוא כמו היחס המחובר ממספרי א'ב'ג'ד' אל מספרי ה'ח'ט'ז' כיחס כ' אל ל' א"כ היחס המחובר ממספרי א'ב'ג'ד' אל מספרי ח'ה'ט'ז' הוא כיחס כ' אל ל' גם כן והוא מה שרצינו לבאר ובזה התבאר שאם הומר סדר הקודמים ונשארו הקודמים קודמים שהיחס המחובר ישאר אחד בעינו והוא מה שרצינו | |
|
ט"ו כל מספר יהיה ראשון ממספר מורכב ממספרים מה מונחים הנה הוא ראשון אצל כל אחד מהם |
| ויהיה מספר א' ראשון אל מספר ה' ויהיה מספר ה' מורכב ממספרי ב'ג'ד' ואומר שמספר א' ראשון אצל כל מספרי ב'ג'ד' | |
| המופת שאי אפשר זולת זה שאם היה אפשר הנה יהיו א'ג' משותפים וימנם מספר מה ונניחהו מספר ז' אבל ג' ימנה ה' וזה שהוא ימנהו כמספר מה שבמורכב ב'ד' מן האחדים הנה ז' ימנה ה' וכבר היה מונה מספר א' א"כ יהיו א'ה' משותפים אבל כבר הונח א' ראשון אל מספר ה' זה שקר אם כן מספר א' ראשון אצל כל אחד ממספרי ב'ג'ד' וזה מה שרצינו | |
|
ט"ז כל מספר שיהיה ראשון אצל כל המספרים הקטנים משרש המרובע המוסיף עליו היותר קרוב לו הנה הוא ראשון |
| ויהיה מספר א' ראשון אצל כל המספרים הקטנים משרש מספר ב' והוא המרובע היותר קרוב למספר א' המוסיף עליו ויהיה יסוד מספר ב' מספר ג' ויהיו המספרים הראשונים הקטנים ממספר ג' מספרי ד'ה'ז' ויהיה א' ראשון אל כל אחד מהם ואומר שמספר א' הוא ראשון | |
| המופת שאם היה אפשר זולת זה ימנהו מספר מה והוא ח' וימנהו כמספר אחדי ט' והוא מבואר שאין כל אחד ממספרי ח'ט' בלתי קטן מג' שאם היה אפשר זה לא יהיה שטח ח' בט' והוא א' קטן משטח ג' בג' והוא ב' וכבר הונח א' קטן מב' זה שקר הנה א"כ אחד ממספרי ח'ט' הוא קטן מג' ויהיה הקטן מג' מספר ח' הנה מספר ח' אם שיהיה ראשון ואם מורכב ואם היה ראשון והוא קטן מג' יהיה א' בלתי ראשון אצל כל הראשונים הקטנים מג' וכבר הונח ראשון אצל כלם זה שקר ואם היה מורכב הנה ימנהו בהכרח מספר ראשון קטן ממספר ח' ולזה יהיה קטן מג' ויתחייב השקר הקודם בעינו אם כן לא ימנה שום מספר מספר א' ולזה יהיה א' מספר ראשון וזה הוא מש"ל | |
|
י״ז כאשר לוקח ממספר מונח חלק מה מונח או חלקים מונחים ולוקח עוד מהנשאר חלק אחר מונח או חלקים אחרים מונחים וכן בזה הדרך מה שהגיע הנה אם הומר הסדור יהיה הנשאר באחרונה אחד בעינו ומקובץ החלקים אחד בעינו |
| ויהיה המספר המונח מספר א' והחלקים הם הנקראים במספרי ב'ג'ד' והם חלק מב' במספר א' וה' חלקים מג' בנשאר וז' חלקים מד' בנשאר ואומר שחלק אחד מב' מא' עם ה' חלקים מג' בנשאר וז' חלקים מד' בנשאר הנה כשהתקבץ זה כלו יהיה שוה לז' חלקים מד' במספר א' וחלק אחד מב' בנשאר וה' חלקים מג' בנשאר | |
| המופת שאנחנו נשים מספר ח' פחות אחד מספר ב' ונשים אחדי מספר ה'ט' שוים לג' ומספרי ז'ב' שוים לד' ויהיה חלק מב' מא' מספר פ' וישאר מספר ל' ויהיו ה' חלקים מג' במספר ל' מספר מ' וישאר מספר ג' ויהיו ז' חלקים מד' במספר ס' מספר נ' וישאר מספר ע' וג"כ הנה ז' חלקים מד' במספר א' מספר צ' ויהיה הנשאר מספר ק' ויהיה חלק מב' במספר ק' מספר ר' ויהיה הנשאר מספר ש' ויהיו חלקים ה' מג' במספר ש' מספר ת' ויהיה הנשאר מספר ץ' ואומר שמספרי ע'ץ' שוים | |
| המופת כי מפני שמספר פ' אחד מב' במספר א' יהיה במספר א' מדמיוני פ' כמו מה שבמספר ב' מן האחדים ולזה יהיה במספר ל' מדמיוני פ' כמו מה שבמספר ב' מן האחדים פחות אחד אבל ח' הוא פחות אחד מב' אם כן במספר ל' מדמיוני פ' כמו מה שבמספר ח' מן האחדים אם כן יחס א' אל ל' כיחס ב' אל ח' לפי שמספרי ב'ח' הוכו במספר פ' ויהיו מספרי א'ל' וג"כ הנה נשים חלק מג' במספר ל' מספר ץ' ולזה יהיה במספר מ' מדמיוני ץ' כמו מה שבמספר ח' מן האחדים ולזה יהיה גם כן במספר ג' מדמיוני ץ' כמו מה שבמספר ט' מן האחדים ויתבאר על האופן הקודם שיחס ל' אל נ' כיחס ג' אל ט' וכזה התבאר שיחס נ' אל ע' הוא כיחס ד' אל כ' אם כן יחס א' אל ע' מחובר ממספרי ב'ג'ד' אל מספרי ח'ט'כ' ובזה יתבאר שיחס א' אל ג' מחובר מיחס מספרי ד'ב'ג' אל מספרי כ'ח'ט' אבל היחס המחובר ממספרי ב'ג'ד' אל מספרי ח'ט'כ' שוה אל היחס המחובר ממספרי ד'ב'ג' אל מספרי כ'ח'ט' א"כ יחס א' אל ע' ואל ץ' אחד ולזה יהיה ע' כמו ץ' ולזה גם כן יחויב שיהיו מספרי פ'מ'ס' מקובצים שוים למספרי צ'ר'ת' מקובצים וזה שיתרון א' על ע' הוא מספרי פ'מ'ס' ויתרון א' על ץ' הם מספרי צ'ר'ת' וכבר התבאר שמספר ע' שוה למספר ץ' א"כ מספרי פ'מ'ס' שוים למספרי צ'ר'ת' והוא מה שרצינו לבאר | |
|
י"ח כאשר הוכה מספר מונח במספר מה מונח ולוקח מהעולה מההכאה חלק מה מונח או חלקים מה מונחים וכן מה שהגיע מלקיחת החלק או החלקים ומההכאות הנה אם הומר הסדור יהיה הנשאר באחרונה אחד בעינו |
| ויהיה המספר המונח מספר א' ויוכה במספר ב' וילקח מהעולה ה' חלקים מג' וילקח מהנשאר ז' חלקים מד' וישאר מספר מה ואומר שאם הומר הסדור שילקח ממספר א' ז' חלקים מד' ויוכה הנשאר במספר ב' וילקח מהנשאר ה' חלקים מג' הנה ישאר המספר ההוא בעינו שנשאר בסדור האחר | |
| וזה שאנחנו נשים על מספר ב' אחד ונשים מספרי ה'ט' שוים לג' ומספרי ז'כ' שוים לד' ויוכה א' על ב' ויהיה העולה ל' ויהיו ה' חלקים מג' במספר ל' מספר מ' וישאר מספר נ' ויהיו ז' חלקים מד' במספר נ' מספר ס' וישאר מספר ע' וגם כן הנה נקח ז' חלקים מד' במספר א' ויהיה מספר פ' וישאר מספר צ' ויוכה צ' בב' ויהיה ק' ויהיו ה' חלקים מג' במספר ק' מספר ר' וישאר מספר ש' ואומר שמספרי ש'ע' שוים | |
| המופת כי א' הוכה בב' והיה ל' הנה יחס א' אל ל' כיחס אחד אל ב' ויתבאר ממה שקדם בתמונה הקודמת שיחס ל' אל נ' הוא כיחס ג' אל ט' ויהס ג' אל ע' הוא כיחס ד' אל כ' א"כ יחס א' אל ע' מחובר ממספרי אחד ג'ד' אל מספרי ב'ט'כ' ובזה התבאר שיחס א' אל ש' מחובר ממספרי ד' אחד ג' אל מספרי כ'ב'ט' אבל היחס המחובר ממספרי אחד ג'ד' אל מספרי ב'ט'כ' הוא כמו היחס המחובר ממספרי ד' אחד ג' אל מספרי ב'כ'ט' א"כ יחס א' אל ע' ואל ש' אחד א"כ ע' כמו ש' והוא מה שרצינו לבאר | |
| והנה קראנו האחד מספר ואם איננו מספר על צד ההעברה כי צד המופת לא יתחלף בזה וזה מבואר מהמופת הנעשה בזה בתמונה י"ג מזה המאמר | |
Arithmetic progressions and sums |
|
|
י"ט כל מספר מונח הנה מספר המספרים הנמשכים מתחילים מן האחד עד שהגיע ההמשך אל המספר המונח הוא כמספר מה שבמספר המונח מן האחדים |
| ויהיה המספר המונח מספר א'ב' ואומר שמספר המספרים הנמשכים המתחילים מן האחד עד שהגיע ההמשך אל מספר א'ב' הוא כמספר מה שבמספר א'ב' מן האחדים | |
|
המופת שאנחנו נחלק א'ב' בדמיוני מה שיש בו מן האחדים והם א'ג' ג'ד' ד'ה' ה'ב' |
| הנה א'ג' הוא אחד | |
| וכאשר חובר עמו ג'ד' שהוא אחד היה א'ד' המספר הנמשך לא'ג' לאחריו | |
| וכזה התבאר שמספר א'ה' הוא הנמשך למספר א'ד' לאחריו | |
| ושמספר א'ב' הוא המספר הנמשך למספר א'ה' לאחריו | |
| הנה אם כן מספרי א'ג' א'ד' א'ה' א'ב' נמשכים ומתחילים מן האחד ומספרם כמספר מה שבא'ב' מן האחדים והוא מש"ל | |
| ובזה התבאר מזאת התמונה בעצמה שמספר אחדי האחרון מהמספרים הנמשכים מתחילים מן האחד הוא כמספר המספרים ההם | |
|
כ כל מספר זוג הנה מספר המספרים הנפרדים הנמשכים מן האחד והאחד עמהם עדיו שוה למספר הזוגות הנמשכים עדיו |
| ויהיה מספר א'ב' מספר זוג ואומר שמספר הזוגות הנמשכים עד א'ב' שוה למספר המספרים הנפרדים הנמשכים עד מספר א'ב' והאחד עמהם | |
|
המופת שנחלק א'ב' במנין מה יש בו מן האחדים והם א'ג' ג'ד' ד'ה' ה'ב' |
|
הנה מפני שא'ב' הוא זוג |
|
יהיה א'ה' נפרד |
|
לפי שא'ב' מוסיף על א'ה' אחד |
|
וכזה התבאר שא'ד' זוג |
|
וא'ג' נפרד והוא אחד |
| הנה אם כן מספר הזוגות הנמשכים עדיו כמו מספר הנפרדים וזהו מש"ל | |
| ומזאת התמונה התבאר שכל מספר נפרד מונח יהיה מספר המספרים הנפרדים מתחילים מן האחד הנמשכים עדיו מוסיף על מספר הזוגות אחד וזה שכאשר נגרע מהם זה המספר הנפרד היה האחרון זוג ויהיה מספר הזוגות שוה למספר הנפרדים יהיה א"כ מספר הנפרדים מוסיף אחד על מספר הזוגות | |
| כ"א כאשר נמשכו אחר מספר מונח מספרים מה הנה מספר עבור סדרת טבעיים האחרון שבמספרים ההם מוסיף על המספר המונח מן האחדים כמו מספר המספרים הנמשכים ההם | |
| וימשכו אחר מספר א'ב' המונח מספרי א'ג' א'ד' א'ה' ויהיה מספר אלו המספרים ז' ואומר שמספר א'ה' מוסיף על מספר א'ב' מספר ז' | |
| המופת שאנחנו נשים מספר המספרים הנמשכים עד א'ב' מספר ח' הנה א"כ מספר אחדי א'ב' הם ח' וג"כ מספר המספרים הנמשכים עד א'ה' מוסיף על מספר המספרים הנמשכים עד א'ב' מספר ז' הנה אם כן מספר מספר המספרים הנמשכים עד א'ה' הם מספרי ח'ז' מקובצים א"כ מספר מה שבא'ה' מן האחדים הוא כמו מספר ח'ז' מקובצים ואולם מספר אחדי א'ב' הוא ח' א"כ מספר א'ה' מוסיף על א'ב' כמו מספר ז' והוא מש״ל | |
| כ"ב כאשר היה מספר הנמשכים לפני מספר מונח כמו מספר עבור סדרת טבעיים הנמשכים לאחריו הנה יתרון המספר המונח על הראשון מהנמשכים לו לפניו הוא כמו יתרון האחרון מהנמשכים לו לאחריו על המספר המונח | |
| ויהיה המספר המונח מספר א'ב' ויהיו המספרים הנמשכים לפניו מספרי א'ג' א'ד' א'ה' והמספרים הנמשכים לו לאחריו מספרי א'ז' א'ח' א'ט' ואומר שיתרון מספר א'ב' על מספר א'ה' שוה ליתרון מספר א'ט' על מספר א'ב' | |
| המופת שמספר מספרי א'ה' א'ד' א'ג' שוה למספר מספרי א'ז' א'ח' א'ט' אבל מספר מספרי א'ד' א'ג' א'ב' שוה למספר מספרי א'ה' א'ד' א'ג' א"כ מספר מספרי א'ד' א'ג' א'ב' שוה למספר מספרי א'ז' א'ח' א'ט' ויתרון א'ב' על א'ה' הוא כמספר מספרי א'ד' א'ג' א'ב' ויתרון א'ט' על א'ב' הוא כמספר מספרי א'ז' א'ה' א'ט' א"כ יתרון א'ב' על א'ה' שוה ליתרון א'ט' על א'ב' ומש"ל | |
| כ"ג כאשר היה מספר הנמשכים לפני מספר מונח כמו מספר הנמשכים לאחריו הנה אם היה הראשון מהנמשכים לפניו זוג הנה האחרון מהנמשכים לאחריו זוג ואם נפרד נפרד | |
| ויהיה המספר המונח מספר ד' והנמשכים לפניו מספרי ג'ב'א' והנמשכים לו לאחריו מספרי ה'ז'ח' ואומר שאם היה מספר א' זוג שמספרם ח' זוג ואם היה מספר א' נפרד הנה מספר ח' נפרד | |
| המופת שאנחנו נשים יתרון מספר ד' על מספר א' ט' ולזה היה יתרון מספר ח' על מספר ד' מספר ט' הנה א"כ יתרון מספר ח' על מספר א' הוא כמו שני דמיוני מספר ט' אבל שני דמיוני ט' הוא זוג הנה א"כ יתרון מספר ח' על מספר א' הוא זוג ולזה אם יהיה א' זוג יהיה ח' זוג ואם יהיה א' נפרד יהיה ח' נפרד והוא מש"ל | |
| כ"ד כאשר חובר מספר והיה יתרון מספר מה מהם על אחד כמו חסרון השני ממספר מה מונח הנח שני המספרים מחוברים שוים אל המספר הנמשך אל המספר המונח לאחריו | |
| ויהיה תוספת א' על אחד כמו חסרון מספר ב' ממספר ג' המונח ויהיה המספר הנמשך אל ג' לאחריו מספר ד'ה' ואומר שמספרי א'ב' מחוברים שוים למספר ד'ה' | |
| המופת שנגרע אחד מד'ה' והוא ה'ז' וישאר ד'ז' שוה לג' ונשים חסרון ב' מג' מספר ז'ח' וישאר ד'ח' שוה לב' אבל ח'ז' הוא ג"כ תוספת א' על אחד וז'ה' הוא אחד א"כ יהיה ה'ח' שוה לא' וכבר היה ד'ח' שוה לב' א"כ ד'ה' שוה לב'א' מחוברים והוא מה שרצינו | |
| כ"ה כאשר חוברו שני מספרים והיה תוספת אחד מהם על מספר מונח שוה לחסרון האחר מהמספר המונח הנה שניהם מחוברים שוים לכפל המספר המונח | |
| ויהיה חסרון מספר א' ממספר ב' המונח שוה לתוספת ג'ה' על מספר ב' המונח ואומר שא' ו'ג'ה' מחוברים שוים לכפל מספר ב' | |
| המופת שנבדיל מג'ה' מה שהוסיף על ב' המונח והוא ה'ז' וישאר ג'ז' שוה לב' וג"כ הנה מפני שה'ז' הוא חסרון מספר א' ממספר ב' כבר יחובר ה'ז' עם א' ויהיה כמו ב' וכבר היה ג'ז' שוה לב' אם כן מספר א' וג'ה' נחברים שוים לשני כפלי מספר ב' והוא מה שרצינו | |
| כ"ו כאשר נקבץ המספרים הנמשכים כדרך המספר מתחילין מן האחד והיה מספר המספרים שחוברו זוג הנה העולה שוה אל שטח חצי מספר המספרים במספר הנמשך אחר המספר האחרון | |
| ויהיו המספרים הנמשכים מספרי א'ב'ג'ד'ה'ו' | |
|
ויהיה המספר הנמשך אחר ו' מספר ז' |
|
וא' הוא אחד ונקראהו מספר בכל זאת החקירה על צד ההעברה |
|
ואומר שא'ב'ג'ד'ה'ו' מקובצים שוה אל הנערך מחצי מספרם על מספר ז' |
|
המופת כי מפני שא' הוא אחד ו' וא' מקובצים שוים לז' |
| אבל תוספת ב' על אחד שוים לחסרון ה' מן ז' מפני שהתוספת הוא אחד אם כן ב'ה' מחוברים שוה לז' וגם יתבאר שיתרון ג' על אחד שוה לחסרון ד' מו' לפי שהתוספת הוא שנים א"כ ג'ד' מחוברים שוים לז' א"כ נקבץ מספרי א'ב'ג'ד'ה'ו' ימנהו ז' כשיעור חצי מספרם לפי שכל שנים מהם ימנהו פעם אחת והוא מה שרצינו | |
| והוא מבואר שבזה הביאור בעינו יתבאר לאין תכלית ואין ספק שהוא מחויב שנגיע בזאת ההדרגה באחרונה אל שני מספרים נמשכים כמו ג'ד' במשלנו זה שאם היה אפשר זולת זה יהיה ביניהם באחרונה מספר אחד אם כן המספר הגדול מהם מוסיף על גילו שנים ונשים חסרון הגדול מהם מהמספר האחרון מספר ט' ולזה יהיה יתרון הקטן מאלו שני המספרים הגיליים על האחד מספר ט' וכבר היה יתרון הגדול על הקטן שנים יהיה א"כ יתרון הגדול על האחד מספר ט' נחבר עם שנים וכבר היה יתרון האחרון על הגדול מספר ט' יהיה אם כן יתרון האחרון על האחד כמו שני דמיוני מספר ט' מקובצים עם שנים אבל שני דמיוני ט' מקובצים עם שנים הוא זוג אם כן יתרון האחרון על האחד מספר זוג אם כן האחרון נפרד וכבר היה זוג זה שקר א"כ הוא מחויב שיגיע באחרונה אל שני מספרים נמשכים וכזה התאמת הספור | |
| כ״ז כאשר חוברו המספרים הנמשכים בדרך המספר והאחד עמהם והיה מספר המספרים שחוברו נפרד הנה העולה שוה אל שטח המספר האמצעי מהם במספר האחרון | |
| ויהיו המספרים הנמשכים א'ב'ג'ד'ה'ו'ז' ואומר שמספרי א'ב'ג'ד'ה'ו'ז' מחוברים שוים אל שטח ד' בז' | |
| המופת שחסרון ג' מד' שוה לתוספת ה' על ד' אם כן ג'ה' מקובצים שוים לשני כפלי ד' וגם כן חסרון ב' מד' שוה לתוספת ו' על ד' א"כ ב'ו' נחברים שוים לשני כפלי ד' וכזה נתבאר שא'ז' מחוברים שוים לשני כפלי ד' א"כ נקבץ מספרי א'ב'ג'ד'ה'ו'ז' ימנהו ד' כמספר המספרים ההם לפי שכל שנים מהם ימנם ד' שני פעמים וד' ימנה עצמו פעם אחת אם כן נקבץ מספרי א'ב'ג'ד'ה'ו'ז' ימנהו כמספר המספרים ההם אבל מספר המספרים ההם הוא ז' א"כ נקבץ מספרי א'ב'ג'ד'ה'ו'ז' ימנהו ד' כמספר אחדי ז' א"כ כבר יוכה ד' בז' ויהיה שוה לנקבץ מספרי א'ב'ג'ד'ה'ו'ז' והוא מה שרצינו ואין ספק שבזה ההדרגה יגיע אל האחרון כהגיענו אל הראשון לפי שמספר ד' הוא האמצעי בין האחרון והראשון ולזה יהיה מספר הנמשכים לפני האמצעי כמו מספר המספרים הנמשכים לאחריו | |
| כ"ח כאשר היו מספרים נמשכים מתחילין מן האחד והיה מספר המספרים נפרד הנה אם הוכה חצי המספר האחרון במספר הנמשך לו לאחריו יהיה העולה שוה אל נקבץ המספרים ההם | |
| ויהיו המספרים מספרי א'ב'ג'ד'ה'ו'ז' וא' הוא אחד ויהיה המספר הנמשך למספר ז' לאחריו מספר ח' ואומר ששטח חצי מספר ז' במספר ח' שוה אל נקבץ מספרי א'ב'ג'דה'ו'ז' | |
| המופת כי מפני שא' עם ז' נחברים שוים לשני כפלי ד' לפי שא' הוא אחד יחיה ח' שוה לכפל ד' וכבר נתבאר שנקבץ מספרי א'ב'ג'ד'ה'ו'ז' שוה לשטח ד' בז' ושטח ד' בז' שוה לשטח כפל ד' בחצי מספר ז' לפי שהצלעות מספיקות רצוני לומר שיחס ד' אל כפל ד' כיחס חצי מספר ז' אל א"כ שטח ד' בז' שוה לשטח ח' בחצי מספר ז' ולזה יהיה שטח ח' בחצי מספר ז' שוה לנקבץ מספרי א'ב'ג'ד'ה'ו'ז' והוא מה שרצינו | |
| כ"ט נקבץ הנפרדים הנמשכים בדרך המספר והאחד עמהם שוה למרובע המספר האמצעי בין הנפרד האחרון והאחד | |
| ויהיו המספרים א'ב'ג'ד'ה'ו'ז'ח'ט' ומספרי א'ג'ה'ז'ט' הם נפרדים ואומר שנקבץ נפרדי א'ג'ה'ז'ט' שוה למרובע האמצעי בין א' ובין ט' | |
| המופת שהמספר האמצעי אם שיהיה זוג ואם שיהיה נפרד ויהיה תחלה נפרד כמו הענין במשלנו זה ואומר שמספרי א'ג'ה'ז'ט' מקובצים שוים למרובע מספר ה' שהוא האמצעי | |
| המופת שא' יחובר עם ט' ויהיה כמו כפל ה' וג' יחובר עם ז' ויהיה כמו כפל ה' אם כן נקבץ מספרי א'ג'ז'ט' ימנהו ה' כשיעור מספר המספרים והוא מבואר שלא ישאר נפרד באחת הפאות שלא יתחבר עם גילו בפאה האחרת לפי שמספר המספרים אשר אחר המספר האמצעי הוא כמו מספר המספרים אשר לפניו והזוגות יתחברו עם הזוגות והנפרדים עם הנפרדים כמו שקדם אם כן מספר הנפרדים אשר לפני האמצעי כמו מספר הנפרדים אשר לאחריו אבל מספר הנפרדים אשר לפני ה' הוא כמו חצי מספר ה' כשנגרע ממנו אחד יהיה אם כן מספר מספרי א'ג'ז'ט' כמו מספר ה' פחות אחד א"כ נקבץ מספרי א'ג'ז'ט' ימנהו ה' כשיעור אחדי ה' פחות אחד וה' ימנה עצמו פעם אחת אם כן נקבץ מספרי א'ג'ה'ז'ט' ימנהו ה' בשיעור אחדי ה' א"כ נקבץ מספרי א'ג'ה'ז'ט' שוה למרובע ה' | |
| ויהיה ג"כ האמצעי זוג כמו הענין במספרי א'ב'ג'ד'ה'ו'ז' ואומר שנקבץ מספרי א'ג'ה'ז' שוה למרובע מספר ד' שהוא האמצעי והנה יתבאר בכמו הביאור הקודם שנקבץ מספרי א'ג'ה'ז' ימנהו ד' כשיעור מספר המספרים ולפי שיהיה מספר ד' זוג יהיו הנפרדים לפניו שוים לחצי מספרם וכבר נתבאר שמספר הנפרדים אשר לאחריו שוה למספר הנפרדים לפניו א"כ מספר הנפרדים לאחריו שוה לחצי מספרם ולזה יהיה מספר הנפרדים אשר לפניו ולאחריו שוה למספר ד' וכבר נתבאר שנקבץ מספרי א'ג'ה'ז' ימנהו ד' במספר הנפרדים ההם אשר הוא שוה למספר ד' א"כ נקבץ מספרי א'ג'ה'ז' שוה למרובע ד' והוא מש"ל | |
| ל כאשר חובר נקבץ הנמשכים בדרך המספר מתחילין מן האחד עד מספר מה מונה עם נקבץ הנמשכים מתחילין מן האחד עד המספר הנמשך אחר המספר המונח הנה העולה שוה למרובע מספר הנמשך אחר המספר המונח | |
| ויחובר נקבץ מספרי א'ב'ג'ד'ה' עם נקבץ מספרי א'ב'ג'ד'ה'ו' ויהיה א' אחד ואומר שהעולה שוה למרובע ו' | |
| המופת שאנחנו נשים מספר הנמשך אחר ו' מספר ז' והוא מבואר שנקבץ מספרי א'ב'ג'ד'ה' שוה לשטח חצי מספר ה' בו' ונקבץ א'ב'ג'ד'ה'ו' שוה לשטח חצי מספר ו' בז' אבל שטח חצי מספר ו' בז' שוה לשטח חצי מספר ז' בו' מפני שהצלעות מספיקות א"כ נקבצי א'ב'ג'ד'ה' א'ב'ג'ד'ה'ו' מחוברים שוים לשטח חצי מספר ה' בו' וחצי מספר ז' בו' והוא כמו שטח חצי מספר ה'ז' בו' ומפני שה' וז' הוא כמו כפל ו' יהיה חצים כמו ו' א"כ נקבצי א'ב'ג'ד'ה' א'ב'ג'ד'ה'ו' מחוברים שוים לשטח ו' בו' והוא כמו מרובע ו' והוא מה שרצינו | |
| ל"א שני דמיוני נקבץ הנמשכים בדרך המספר מן האחד עד מספר מונח שוים אל המספר המונח מחובר עם מרובעו | |
| ויהיו המספרים הנמשכים מספרי א'ב'ג'ד'ה' ויהיה א' אחד ואומר ששני דמיוני נקבץ א'ב'ג'ד'ה' שוה למספר ה' ולמרובע ה' | |
| המופת שכאשר חובר נקבץ א'ב'ג'ד'ה' עם נקבץ א'ב'ג'ד' היה העולה שוה למרובע ה' יהיה אם כן נקבץ א'ב'ג'ד'ה' מחובר עם נקבץ א'ב'ג'ד'ה' מוסיף על מרובע ה' כמו מספר ה' הנוסף והוא מה שרצינו ומזאת התמונה נתבאר שנקבץ הנמשכים מן האחד עד מספר מונח שוה לחצי מרובע המספר המונח ולחציו | |
| ל"ב כאשר חוברו נקבצי המספרים הנמשכים מן האחד נמשכים בתכליתם ומתחילין מן האחד עד מספר מונח הנה העולה שוה למרובע מין המספר המונח הנמשכים בדרך המספר מן האחד עד המספר המונח רצוני שאם היה המספר המונח זוג יהיה העולה שוה למרובעי הנפרדים הנמשכים עד המספר המונח ואם היה המספר המונח נפרד יהיה העולה שוה למרובעי הנפרדים הנמשכים עד המספר המונח והאחד עמהם | |
| ויהיה א' אחד ויחובר עם נקבץ א'ב' ועם נקבץ א'ב'ג' ועם נקבץ א'ב'ג'ד' ועם נקבץ אב'ג'ד'ה' ועם נקבץ א'ב'ג'ד'ה'ו' ויהיה ו' זוג ואומר שהעולה שוה למרובעי ב' ד' ו' שהם הזוגות | |
| המופת שנקבצי א'ב'ג'ד'ה'ו' א'ב'ג'ד'ה' מחוברים שוים למרובע ו' ונקבצי א'ב'ג'ד' א'ב'ג' מחוברים שוים למרובע ד' ונקבצי א'ב' א' מחוברים שוים למרובע ב' אם כן נחבר נקבצי א' א'ב' א'ב'ג' א'ב'ג'ד' א'ב'ג'ד'ה' א'ב'ג'ד'ה'ו' שוים למרובעי ב' ד' ו' ויהיה ג"כ האחרון נפרד ואומר שהעולה שוה למרובעי הנפרדים הנמשכים עד המספר המונח והאחד עמהם המשל שיהיה האחרון א'ב'ג'ד'ה'ו'ז' ויהיה ז' נפרד ואומר שהעולה שוה למרובעי א' ג' ה' ז' הנפרדים | |
| המופת שנקבצי א'ב'ג'ד'ה'ו'ז' א'ב'ג'ד'ה'ו' מחוברים שוה למרובע ז' ונקבצי א'ב'ג'ד'ה' א'ב'ג'ד' מחוברים שוה למרובע ה' ונקבצי א'ב'ג' א'ב' מחוברים שוה למרובע ג' וישאר א' שהוא מבואר שהוא שוה למרובעו מפני שהוא אחד א"כ העולה שוה למרובעי א' ג' ה' ז' והוא מה שרצינו | |
| ל"ג כאשר חוברו נקבצי המספרים הנמשכים מן האחד נמשכים בראשיתם עד שיגיע ההמשך אל האחרון הנה העולה שוה למרובע כל המספרים ההם | |
| ויחובר נקבץ א'ב'ג'ד'ה' עם נקבץ ב'ג'ד'ה' ועם נקבץ ג'ד'ה' ועם נקבץ ד'ה' ועם מספר ה' ואומר שהעולה שוה למרובעי א'ב'ג'ד'ה' | |
| המופת שכל אחד ממספרי א'ב'ג'ד'ה' הוא באלה המספרים כמספר מה שבו מן האחדים וזה שכל מספר יהיה מספר המספרים הנמשכים עדיו כמספרו אבל המספר ימצא בכל אחד מהנקבצים המתחילין מהמספרים הנמשכים עדיו ואיננו בנקבצים המתחילין מהמספרים אשר אחריו כי הוא בלתי אפשר שימשך המספר הקטן אחר הגדול הנה אם כן כל מספר ממספרי א'ב'ג'ד'ה' הוא באלו הנקבצים כמנין מה שבו מן האחדים בשוה וזה שוה למרובעו אם כן אלו הנקבצים מחוברים שוים למרובעי מספרי א'ב'ג'ד'ה' והוא מה שרצינו | |
| ל"ד כאשר חובר נחבר נקבצי הנמשכים מן האחד נמשכים בראשיתם עד שיגיע ההמשך אל האחרון עם נחבר נקבצי הנמשכים מן האחד נמשכים בתכליתם ומתחילים מן האחד עד שיגיע ההמשך אל המספר הנמשך לפני האחרון אשר זכרנו הנה העולה שוה לשטח המספר האחרון בנקבץ הנמשכים מן האחד עדיו | |
| ויחובר נחבר נקבצי א'ב'ג'ד'ה' ב'ג'ד'ה' ג'ד'ה' ד'ה' ה' עם נחבר נקבצי א' א'ב' א'ב'ג' א'ב'ג'ד' ואומר שהעולה שוה לשטח ה' בנקבץ מספרי א'ב'ג'ד'ה' | |
| המופת שהנקבץ הראשון מהנמשכים בראשיתם הוא א'ב'ג'ד'ה' | |
|
וא' יחובר עם ב'ג'ד'ה' ויהיה א'ב'ג'ד'ה' |
|
וא'ב' יחובר עם ג'ד'ה' ויהיה א'ב'ג'ד'ה' |
|
וא'ב'ג' יחובר עם ד'ה' ויהיה א'ב'ג'ד'ה' |
|
וא'ב'ג'ד' יחובר עם ה' ויהיה א'ב'ג'ד'ה' |
| הנה אם כן כאשר יחוברו הנקבצים הנמשכים בראשיתם עם גילים מתקבצים הנמשכים באחריתם היה כל אחד מהם שוה לנקבץ א'ב'ג'ד'ה' אבל מספר נקבצי הנמשכים בראשיתם הוא כמספר אחדי האחרון שהוא ה' מפני שמספר הנמשכים מן האחד עד ה' הם כמספר מה שבה מן האחדים אם כן העולה ימנהו נקבץ א'ב'ג'ד'ה' כמספר אחדי ה' א"כ כבר יוכה נקבץ א'ב'ג'ד'ה' במספר ה' ויהיה שוה אל העולה מזה החבור והוא מה שרצינו | |
| ל"ה כאשר חוסרו שני מספרים נמשכים ממרובעיהם הנה הנשאר שוה לשני כפלי מרובע המספר הקטן | |
| ויהיו שני המספרים ד'ה' נמשכים ויהיה ה' הוא הגדול ואומר כי כשיחוסרו ממרובעיהם מספרי ד'ה' יהיה הנשאר שוה לשני דמיוני מרובע ד' | |
| המופת שמרובע ה' מוסיף על מרובע ד' כפל שטח אחד בד' ומרובע אחד שהוא אחד אם כן מרובע ה' מוסיף על מרובע ד' שני דמיוני ד' ואחד אבל שני דמיוני ד' ואחד שוים לד' וה' מקובצים לפי שה' מוסיף על ד' אחד א"כ מרובע ה' שוה למרובע ד' ולמספרי ד'ה' א"כ מרובעי ד'ה' שוים לשני כפלי מרובע ד' ולמספרי ד'ה' וכאשר נגרע מהם מספרי ד'ה' היה הנשאר שוה לשני דמיוני מרובע ד' והוא מ"ש | |
| ל"ו כאשר חובר נקבץ הנמשכים מן האחד ונמשכים בראשיתם עד שהגיע ההמשך אל האחרון הנה אם חוסרו מהם המספרים ההם הנמשכים יהיה הנשאר שוה לכפל מרובעי המין שלפני האחרון הנמשכים עדיו אם זוג זוג ואם נפרד נפרד והאחד עמהם | |
| ויחוברו נקבצי א'ב'ג'ד'ה' ב'ג'ד'ה' ג'ד'ה' ד'ה' ה' ויחוסרו מהעולה מספרי א'ב'ג'ד'ה' מקובצים ואומר שאם היה המספר שלפני האחרון זוג שהנשאר שוה לכפל מרובעי הזוגות הנמשכים עדיו ואם היה המספר שלפני האחרון נפרד הנה הנשאר שוה לכפל מרובעי הנפרדים הנמשכים עדיו והאחד עמהם ויהיה תחלה זוג כמו הענין במשלנו זה ואומר שהנשאר שוה לכפל מרובעי הזוגות הנמשכים עד ה' והם ב' ד' | |
| המופת שהעולה שוה למרובעי א'ב'ג'ד'ה' פחות מספרי א'ב'ג'ד'ה' אבל הנשאר ממרובעי ד'ה' כשחוסר מהם מספרי ד'ה' שוה לכפל מרובע ד' והנשאר מרובעי ב'ג' כשחוסר מהם מספרי ב'ג' שוה לכפל מרובע ב' ומרובע א' הנשאר לוקח כלו בהלקח א' מפני שא' הוא אחד א"כ הנשאר שוה לכפל מרובעי ד'ב' ויהיה ג"כ המספר שלפני האחרון נפרד ואומר שהנשאר שוה לכפל מרובעי הנפרדים הנמשכים עד האחרון ויהיו המספרים א'ב'ג'ד'ה'ו' והמספר הנמשך לו לפניו הוא נפרד והוא ה' ואומר שהנשאר שוה לכפל מרובעי הנפרדים הנמשכים עד ו' והם א'ב'ג' | |
| המופת שהעולה שוה למרובעי א'ב'ג'ד'ה'ו' פחות מספרי א'ב'ג'ד'ה'ו' אבל הנשאר ממרובעי ה'ו' כשלוקח מהם מספרי ה'ו' שוה לכפל מרובע ה' והנשאר ממרובעי ג'ד' כשלוקח מהם מספרי ג'ד' שוה לכפל מרובע ג' והנשאר ממרובע א'ב' כשלוקח מהם מספרי א'ב' שוה לכפל מרובע א' א"כ הנשאר כלו שוה לכפל מרובעי א'ב'ג' ומ"ש | |
| ל"ז כאשר הוכה מספר מונח על נקבץ הנמשכים מן האחד עד המספר הנמשך לו לאחריו הנה העולה שוה לשלשת מרובעי מין המספר המונח הנמשכים עדיו | |
| ויוכה מספר ה' על נקבץ מספרי א'ב'ג'ד'ה'ו' ואומר שהעולה שוה לשלשת דמיוני מרובע מין ה' הנמשכים עדיו והם מספרי א' ג' ה' | |
|
המופת ששטח ו' בנקבץ א'ב'ג'ד'ה'ו' שוה לנקבץ א' א'ב' א'ב'ג' א'ב'ג'ד' א'ב'ג'ד'ה' מחוברים עם נקבצי א'ב'ג'ד'ה'ו' ב'ג'ד'ה'ו' ג'ד'ה'ו' ד'ה'ו' ה'ו' ו' |
| אבל נקבצי א' א'ב' א'ב'ג' א'ב'ג'ד' א'ב'ג'ד'ה' שוים למרובעי א'ג'ה' ונקבצי א'ב'ג'ד'ה'ו' ב'ג'ד'ה'ו' ג'ד'ה'ו' ד'ה'ו' ה'ו' ו' כשחוסר מהם א'ב'ג'ד'ה'ו' יהיה הנשאר שוה לשני כפלי מרובעי א'ג'ה' אם כי שטח ו' במספרי א'ב'ג'ד'ה'ו' מקובצים שוה לשלשת דמיוני מרובעי א'ג'ה' ולנקבץ א'ב'ג'ד'ה'ו' ושטח ו' בנקבץ א'ב'ג'ד'ה'ו' מוסיף על שטח ה' בנקבץ א'ב'ג'ה'ד'ו' כמו נקבץ א'ב'ג'ד'ה'ו' יהיה אם כן שטח ה' בנקבץ א'ב'ג'ד'ה'ו' שוה לשלשת דמיוני מרובעי א'ג'ה' והוא מ"ש לבאר | |
| ומזאת התמונה יתבאר שאם הוכה שלישית המספר המונח על נקבץ הנמשכים מן האחד עד המספר הנמשך לו לאחריו שהעולה שוה למרובעי מין המספר המונח הנמשכים עדיו וזה שכאשר הוכה המספר ההוא המונח בנקבץ ההוא היה העולה שוה לשלישית מרובעי מין המספר המונח הנמשכים עדיו יהיה א"כ שטח שלישית המספר ההוא המונח במספר ההוא שוה לשלישית שלשת כפלי מרובעי מין המספר המונח הנמשכים עדיו שהוא כמו מרובעי המין ההוא הנמשכים עדיו ומ"ש | |
| ל"ח כאשר הוכה מספר מונח פחות שלישית המספר הנמשך לו לפניו על נקבץ הנמשכים מן האחד עד המספר המונח הנה העולה שוה למרובעי כל המספרים הנמשכים מן האחד עד המספר המונח | |
| ויוכה מספר ו' פחות שלישית מספר ה' על נקבץ א'ב'ג'ד'ה'ו' ואומר שהעולה שוה למרובעי מספרי א'ב'ג'ד'ה'ו' | |
| המופת ששטח ו' במספרי א'ב'ג'ד'ה'ו' מקובצים שוה לנקבצי א'ב'ג'ד'ה'ו' ב'ג'ד'ה'ו' ג'ד'ה'ו' ד'ה'ו' ה'ו' ו' מחוברים עם נקבצי א' א'ב' א'ב'ג' א'ב'ג'ד' א'ב'ג'ד'ה' אבל נקבצי א'ב'ג'ד'ה'ו' ב'ג'ד'ה'ו' ג'ד'ה'ו' ד'ה'ו' ה'ו' ו' שוים למרובעי א'ב'ג'ד'ה'ו' ונקבצי א' א'ב' א'ב'ג' א'ב'ג'ד' א'ב'ג'ד'ה' שוים למרובעי א'ג'ה' א"כ שטח ו' במספרי א'ב'ג'ד'ה'ו' מקובצים שוה למרובעי א'ב'ג'ד'ה'ו' ולמרובעי א'ג'ה' אבל שטח שלישית ה' בנקבץ א'ב'ג'ד'ה'ו' שוה למרובעי א'ג'ה' וישאר שטח ו' פחות שלישית ה' בנקבץ א'ב'ג'ד'ה'ו' שוה למרובעי א'ב'ג'ד'ה'ו' ומש"ל | |
| ל"ט כאשר חוסר מספר מונח ממרובעו הנה חצי הנשאר שוה אל נקבץ הנמשכים מן האחד עד המספר הנמשך לפני המספר המונח | |
| וילקח מספר ו' ממרובעו ויהיה המספר הנמשך לו לפניו מספר ה' ויהיה חצי הנשאר ממרובע ו' מספר ז' ואומר שמספר ז' שוה אל נקבץ הנמשכים מן האחד עד מספר ה' | |
| המופת שמרובע ו' שוה לנקבץ א'ב'ג'ד'ה' מחובר עם נקבץ א'ב'ג'ד'ה'ו' וכאשר הוסר מהמחובר מספר ו' היה הנשאר שוה לנקבץ א'ב'ג'ד'ה' מחובר עם נקבץ א'ב'ג'ד'ה' א"כ חצי הנשאר שוה לנקבץ א'ב'ג'ד'ה' ומש"ל | |
| מ כאשר חובר מספר מה מונח עם חצי הנשאר ממרובעו כשחוסר ממנו המספר המונח הנה העולה שוה אל נקבץ הנמשכים מן האחד עד המספר המונח | |
| ויחובר מספר ו' עם חצי הנשאר ממרובעו כשחוסר ממנו מספר ו' ואומר שהעולה שוה לנקבץ א'ב'ג'ד'ה'ו' | |
| המופת שמרובע ו' שוה לנקבץ א'ב'ג'ד'ה'ו' מחובר עם נקבץ א'ב'ג'ד'ה' וכאשר לוקח מזה ו' וחובר עם חצי הנשאר שהוא נקבץ א'ב'ג'ד'ה' היה העולה א'ב'ג'ד'ה'ו' והם המספרים הנמשכים מן האחד עד ו' ומש"ל | |
| מ"א המרובע ההוה מנקבץ הנמשכים מן האחד עד מספר מונח הוא שוה למעוקב המספר המונח ולמרובע נקבץ הנמשכים מן האחד עד המספר הנמשך לפני המספר המונח | |
| ויהיה נקבץ הנמשכים נקבץ א'ב'ג'ד'ה' ואומר שמרובע נקבץ א'ב'ג'ד'ה' שוה למעוקב ה' ולמרובע נקבץ א'ב'ג'ד' | |
| וזה שמעוקב ה' ימנהו ה' כמספר מה שבמרובעו מן האחדים אבל מרובע ה' שוה לנקבצי א'ב'ג'ד' א'ב'ג'ד'ה' מחוברים א"כ ה' הוכה בנקבצי א'ב'ג'ד'ה' א'ב'ג'ד' והיה כמו מעוקב ה' אבל שטח ה' בנקבצי א'ב'ג'ד' א'ב'ג'ד'ה' שוה לשטח ה' בה' שהוא כמו מרובע ה' ולשטח ה' בנקבצי א'ב'ג'ד' א'ב'ג'ד' שהוא כפל שטח ה' בנקבץ א'ב'ג'ד' אם כן מעוקב ה' שוה למרובע ה' ולכפל שטח ה' בנקבץ א'ב'ג'ד' ואולם מרובע נקבץ א'ב'ג'ד'ה' שוה למרובע ה' ולכפל שטח ה' בנקבץ א'ב'ג'ד' ולמרובע נקבץ א'ב'ג'ד' אם כן מעוקב ה' עם מרובע נקבץ א'ב'ג'ד' שוה למרובע נקבץ א'ב'ג'ד'ה' והוא מה שרצינו ואולם האחד אין מספר לפניו אבל מעוקבו שוה למרובע הנקבץ עדיו כי היה הוא בעינו הנקבץ עדיו ומרובע הנקבץ עדיו והוא בעינו מעוקבו וזה מבואר מאד | |
| מ"ב המרובע ההוה מנקבץ הנמשכים מן האחד עד מספר מונח הנה הוא שוה אל המעוקבים ההוים מהנמשכים מן האחד עד המספר המונח | |
| ויהיה הנקבץ נקבץ א'ב'ג'ד'ה' ואומר שהמרובע ההוה מנקבץ א'ב'ג'ד'ה' שוה למעוקבים ההוים ממספרי א'ב'ג'ד'ה' | |
| המופת שמרובע נקבץ א'ב'ג'ד'ה' שוה למעוקב ה' ולמרובע נקבץ א'ב'ג'ד' אבל מרובע נקבץ א'ב'ג'ד' שוה למעוקב ד' ולמרובע נקבץ א'ב'ג' והנה מרובע נקבץ א'ב'ג' שוה למעוקב ג' ולמרובע נקבץ א'ב' והנה מרובע נקבץ א'ב' שוה למעוקב ב' ולמרובע א' והנה מרובע א' שוה למעוקב א' א"כ מרובע נקבץ א'ב'ג'ד'ה' שוה למעוקבים ההוים ממספרי א'ב'ג'ד'ה' והוא מ"ש | |
| מ"ג כאשר היה מספר מה מונח שוה לנקבץ נמשכים מן האחד מונחים והיה המספר המונח אמצעי בין הנמשכים רצונ' שהוא אמצעי בין האחרון מהם ובין האחד הנה מעוקבי הנמשכים המונחים שוים לנפרדי הנמשכים האחרים והאחד עמהם | |
| ויהיה מספר ו' שוה לנקבץ א'ב'ג' ויהיה ו' אמצעי בין מספרי א'ב'ג'ד'ה'ו'ז'ח'ט'י'כ' הנמשכים מן האחד ואומר שנפרדי מספרי א'ב'ג'ד'ה'ו'ז'ח'ט'י'כ' שוים למעוקבי א'ב'ג' | |
| המופת שמעוקבי א'ב'ג' שוים למרובע ו' ונפרדי א'ב'ג'ד'ה'ו'ז'ח'ט'י'כ' שוים גם כן למרובע שהוא האמצעי א"כ מעוקבי א'ב'ג' שוים לנפרדי א'ב'ג'ד'ה'ו'ז'ח'ט'י'כ' ומש"ל | |
| מ"ד השטח ההוה ממספר מה במספר מה אם חובר אליו מספר אחר מונח מהמספרים ההם הנה העולה ימנהו המספר הנמשך אל המספר הנשאר לאחריו כמנין אחדי המספר המונח | |
| ויוכה א' בב' ויחובר עם העולה א' ויהיה ג' ויהיה מספר הנמשך אחר ב' ד' ואומר שג' ימנהו ד 'במספר אחדי א | |
| המופת ששטח א' בב' ימנהו א' בשיעור אחדי ב' וכאשר יחובר עמו א' הנה העולה ימנהו א' בשיעור אחדי ב' ותוספת אחד והוא מספר אחדי ד' אם כן העולה ימנהו א' כשיעור אחדי ד' ולזה ימנהו ד' כשיעור אחדי א' ומ״ש | |
| מ"ה כאשר היו שלשה מספרים מתחלפים וחובר שטח המספר הגדול ביתרון האמצעי על הקטן עם שטח המספר הקטן ביתרון הגדול על האמצעי הנה העולה ימנהו המספר האמצעי במספר אחדי יתרון הגדול על הקטן | |
| ויהיו שלשה מספרי א'ב'ג' מתחלפים והיה ב' מוסיף על א' בשיעור אחדי ד' ויהיה ג' מוסיף על ב' כשיעור אחדי ה' ואומר ששטח ג' בד' עם שטח א' בה' ימנהו ב' כשיעור אחדי ה'ד' מקובצים שהוא יתרון ג' על א' | |
| המופת ששטח ד' בג' ימנהו ג' כשיעור אחדי ד' הנה נחלק שטח ד' בב' בדמיוני ג' ויהיו חלקיו השוים לג' מספרי ז'ח' ט'כ' ל'מ' הנה מספר אלו החלקים הוא כמספר אחדי ד' וכזה יתחלקו שטחי ה' בא' בדמיוני א' ויהיו חלקיו השוים לא' מספרי נ'ס' ע'פ' הנה מספר אלה החלקים הוא כמספר אחדי ה' ולזה יהיה מספר חלקי ז'ח' ט'כ' ל'מ' נ'ס' ע'פ' כמספר אחדי ד'ה' יחד והוא תוספת ג' על א' הנה נבדיל מזה ז'צ' בשיעור ב' וישאר צ'ח' בשיעור ה' וכזה יהיו ט'ו 'ל'ת' בשיעור ב' וישאר כל אחד מן ו'כ' ת'מ' בשיעור ה' ונחלק צ'ח' בדמיוני מה שבו מן האחדים ויהיו חלקיו השוים לאחד צ'ק' ק'ח' ומספרם כמספר אחדי ה' וכזה יתחלק ו'כ' בדמיוני האחד ויהיו חלקיו ו'ד' ד'כ' ויהיו חלקי ת'מ' השוים לאחד ת'ש' ש'מ' וכבר היה מספר מספרי ז'ח' ט'כ' ל'מ' כמספר מה שבד' מן האחדים אם כן מספר אחדי צ'ק' ו'ד' ת'ש' הוא כמספר מה שבד' מן האחדים הנה יתחבר צ'ק' ו'ד' ש'ת' עם נ'ס' ויהיה שוה לב' לפי שמספר אחדי צ'ק' ו'ר' ש'ת' הוא כמספר מה שבד 'מן האחדים יהיו א"כ אחדי צ'ק' ו'ר' ש'ת' מקובצים שוים לד' ונ'ס' שוה לא' יהיה א"כ נ'ס' מקובץ עם אחדי צ'ק' ו'ר' ש'ת' שוה לא'ד' מקובצים ואולם א'ד' מקובצים שוים לב' יהיה א"כ נ'ס' עם אחדי צ'ק' ו'ר' ש'ת' שוה לב' וכבר התבאר שע'פ' מחובר עם אחדי ק'ח' ר'כ' ש'מ' שוה לב' וכבר התבאר שמספר מספרי נ'ס' ע'פ' שוה למספרי אחדי צ'ק' ק'ה' לפי שכל אחד מהם שוה למספר ה' א"כ סכום מספרי נ'ס' ע'פ' כמו אחדי צ'ק' ק'ח' והנמשך להם הנה כבר התבאר ששטח ד' בג' עם שטח ה' בא' ימנם ב' במספר חלקי ז'ח' ט'כ' ל'מ' נ'ס' ע'פ' והוא כמספר ד'ה' מקובצים שהוא תוספת ג' על א' ומש"ל | |
| מ"ו כאשר היו שלשה מספרים מתחלפים והיה הקטן שנים הנה כשחובר עם כפל השטח ההוה מהמספר הגדול פחות אחד ביתרון האמצעי על הקטן המספר הגדול ויתרון האמצעי על הקטן ויתרון האמצעי על הגדול הנה זה כלו שוה לכפל השטח ההוה מהאמצעי פחות אחד בגדול פחות אחד | |
| ויהיו המספרים המתחלפים שלשה והם מספרי שנים א' ב' ויהיה ב' הגדול ויהיה א' מוסיף על שנים מספר ג' ויהיה א' פחות אחד מספר ז' ויהיה ב' פחות אחד מספר ד' ויהיה יתרון ב' על א' מספר ה' ואומר שכפל שטח ג' בד' מחובר עם מספרי ב' ג' ה' שוה לכפל שטח ז' בד' | |
| המופת ששטח ג' בד' ימנהו ד' כמספר אחדי ג' ושטח ז' בד' ימנהו ד' כמספר אחדי ז' וז' מוסיף על ג' אחד מפני שא' מוסיף על ג' שנים אם כן יתרון שטח ז' בד' על שטח ג' בד' הוא שטח אחד בד' שהוא ד' א"כ יתרון שטח ז' בד' על שטח ג' בד' הוא כמספר ד' ולזה יהיה יתיון כפל שטח ז' בד' על כפל שטח ג' בד' כמו שני כפלי ד' ואומר שמספרי ב'ג'ד' נחברים שוים לשני כפלי ד' | |
| המופת שמספר ב' הוא מוסיף על מספר ד' אחד והנה יתרון מספר ב' על מספר א' הוא ה' א"כ מספרי א'ה' נחברים שוים לב' ולזה יהיו מספרי ב'א'ה' נחברים שוים לכפל ב' אבל יתרון כפל מספר ב' על כפל מספר ד' הוא שנים אם כן מספרי ב'ג'ה' מקובצים שוים לכפל מספר ד' וכבר היה יתרון כפל שטח ז' בד' על כפל שטח ג' בד' כמו כפל מספר ד' א"כ כפל שטח ג' בד' עם מספרי ב'ג'ה' מקובצים שוים לכפל שטח ז' בד' והוא מש"ל | |
| מ"ז כאשר היו שני מספרים מתחלפים הנה שטח הקטן בגדול עם יתרון הגדול על הקטן שוה לשטח ההוה מהקטן פחות אחד בגדול פחות אחד כשחובר עמו המספר הגדול והמספר הנמשך לו לפניו | |
| ויהיו שני המספרים מספרי א'ב' ויהיה מספר ג' נמשך לא' לפניו ומספר ד' נמשך לב' לפניו ויהיה יתרון ב' על א' מספר ה' ואומר שמספר ה' מחובר עם שטח א' בב' שוה למספרי ד'ב' מחוברים עם שטח ג' בד' | |
| המופת ששטח ג' בד' כשחובר עמו ד' ימנהו א' במספר אחדי ד' לפי שא' מוסיף על ג' אחד אם כן שטח ג' בד' כשחובר עם ד' שוה לשטח א' בד' וג"כ הנה מפני שיתרון ב' על א' הוא ה' יהיה ב' שוה לא'ה' נחברים והנה יהיה שטח א' בד' נחבר עם א' שוה לשטח א' בב' הנה מפני זה יהיה שטח א' בד' מחובר עם מספרי א'ה' שוה לשטח א' בב' ולמספר ה' א"כ שטח ג' בד' מחובר עם מספרי ד'ב' שוה לשטח א' בב' ולמספר ה' ומש"ל | |
| מ"ח כאשר היו שלשה מספרים מתחלפים והיה הקטן שנים הנה כפל השטח ההוה מהגדול פחות אחד ביתרון האמצעי על הקטן כשחובר עם הגדול ויתרון האמצעי על הקטן ויתרון הגדול על האמצעי הנה העולה שוה לשטח האמצעי פחות אחד בגדול ולשטח הגדול פחות אחד ביתרון האמצעי על הקטן וליתרון הגדול על האמצעי | |
| ויהיו המספרים המתחלפים מספרי שנים א' ב' ויהיה ב' הגדול והיה א' מוסיף על שנים מספר ג' וד' הוא הנמשך לא' לפניו וה' הוא הנמשך לב' לפניו וז' הוא יתרון ב' על א' ואומר שכפל שטח ה' בג' מחובר עם מספרי ג' ב' ז' שוה לשטח ד' בב' ולשטח ג' בה' ולז' | |
| המופת שאנחנו נבדיל שטח ג' בה' ומספר ז' המשותפים ונאמר ששטח ד' בב' שוה לשטח ג' בה' ולמספרי ג'ב' וזה ששטח ג' בה' מחובר עם ג' שוה לשטח ב' בג' לפי שמספר ב' מוסיף על ה' אחד ולזה יהיה שטח ב' בג' מחובר עם ב' שוה לשטח ד' בב' א"כ שטח ה' בג' מחובר עם מספרי ג'ב' שוה לשטח ד' בב' א"כ כפל שטח ה' בג' מחובר עם מספרי ג' ב' ז' שוה לשטח ד' בב' ולשטח ג' בה' ולז' והוא מה שרצינו לבאר | |
| מ"ט כאשר היו שלשה מספרים מתחלפים והיה יתרון הקטן על שנים מספר מונח הנה כפל השטח ההוה מהגדול פחות אחד ביתרון האמצעי על הקטן כשחובר עם שטח הגדול במספר המונח ועם שטח הגדול פחות אחד במספר המונח והתחבר זה כלו עם המספר הגדול ויתרון האמצעי על הקטן ויתרון הגדול על האמצעי הנה העולה שוה לכפל השטח ההוה מהאמצעי פחות אחד בגדול פחות אחד | |
| ויהיו המספרים המתחלפים מספרי ג' א' ב' ויהיה ג' הוא הקטן וב' הוא הגדול ויהיה יתרון ג' על שנים מספר ד' והיה יתרון א' על ג' מספר ה' והיה מספר ז' נמשך למספר א' לפניו ומספר ה' נמשך למספר ב' לפניו והיה יתרון ב' על א' מספר ט' והיה מספר ב' שוה למספרי ה'ד' מקובצים והוא מבואר שמספר כ הוא פחות שנים מא' לפי שמספרי ג'ה' שוים לא' וד' הוא פחות מג' שנים ולזה ג"כ יהיה מספר ז' נמשך למספר כ' לאחריו לפי שמספר ז' הוא פחות מא' אחד לבד ואומר שכפל שטח ח' בה' כשנחבר עם שטח ד' בב' ועם שטח ד' בח' והתחבר זה כלו עם מספרי ב'ה'ט' הנה העולה שוה לכפל שטח ז' בה' | |
| המופת ששטח ח' בה' כשחובר עמו ה' שוה לשטח ה' בב' וכאשר חובר שטח ה' בב' עם שטח ד' בב' היה העולה שוה לשטח ההוה ממספרי ה'ד' מקובצים בב' והוא כמו שטח כ' בב' וכשנתחבר עם העולה ב' היה העולה שוה לשטח ז' בב' ואולם שטח ח' בה' עם שטח ח' בד' שוה לשטח ה' בד'ה' מקובצים שהוא שטח ח' בב' א"כ כפל שטח ח' בה' עם שטח ד' בב' ועם שטח ח' בד' ועם מספרי ב'ה'ט' שוה לשטח ז' בב' ולשטח כ' בח' ולמספר ט' וא' הוא המספר האמצעי וכ' הוא יתרונו על הקטן שהוא שנים לפי מה שהונח בתמונה הקודמת אבל שטח ז' בב' עם שטח כ' בח' ועם מספר ט' שוה לכפל שטח כ' בה' ולמספרי ב'כ'ט' א"כ כפל שטח ח' בה' עם שטח ד' בב' ועם שטח ח' בד' ועם מספרי ב'ה'ט' שוה לכפל שטח כ' בה' ולמספרי ב'כ'ט' אבל כפל שטח כ' בח' עם מספרי ב'כ'ט' שוה לכפל שטח ז' בח' לפי שמספרי ב'כ'ט' שוים לשני דמיוני ח' וז' הוא הנמשך לכ' לאחריו א"כ כאשר חובר עם שטח כ' בח' מספר ח' יהיה שוה לשטח ז' בח' אם כן כפל שטח כ' בח' עם מספרי ב'כ'ט' שהם שני דמיוני ח' שוים לכפל שטח ז' בח' א"כ כפל שטח ה' בה' עם שטח ד' בב' ועם שטח ח' בד' ועם מספרי ב'ה'ט' שוה לכפל שטח ז' בח' והוא מש"ל | |
| נ כאשר היו שלשה מספרים מתחלפים והיה יתרון הקטן על שנים מספר מונח הנה כפל הגדול פחות אחד ביתרון האמצעי על הקטן עם דמיוני שטחי האמצעי בגדול כמספר מה שבמספר המונח מן האחדים ועם שטח ההוה מיתרון הגדול על האמצעי בקטן פחות אחד ועם המספר הגדול ועם יתרון האמצעי על הקטן הנה כשהתחבר זה כלו יהיה המקובץ ימנהו השטח ההוה מהאמצעי פחות אחד בגדול פחות אחד כמספר מה שבקטן מן האחדים | |
| ויהיו המספרים המתחלפים מספרי ג' א' ב' והיה ג' הוא הקטן והיה יתרון ג' על שנים מספר ד' והיה יתרון א' על ג' מספר ה' והיה מספר ז' נמשך למספר א' לפניו ומספר ח' נמשך למספר ב' לפניו והיה יתרון ב' על א' מספר ט' ויהיה מספר כ' נמשך למספר ג' לפניו ואומר שכפל שטח ח' בה' עם כפלי שטחי א' בב' במנין מה שבד' מן האחדים ועם שטח ט' בב' ועם מספרי ב'ה' ימנהו שטח ז' בח' כמספר אחדי ג' | |
| המופת כי בעבור שהיה שטח א' בב' עם ט' שוה לשטח ז' בה' ולמספרי ב'ח' יהיו כפלי ד' משטחי א' בב' עם כפלי ד' ממספרי ט' שוה לכפלי ד' משטחי ז' בח' ולכפלי ד' ממספרי ב' וכפלי ד' ממספרי ח' יהיה א״כ כפלי ד' משטחי א' בב' מחובר עם שטח ד' בט' שוה לכפלי ד' משטחי ז' בח' ולשטח ד' בב' ולשטח ד' בח' אבל שטח ט' בכ' מוסיף על שטח ט' בד' מספר ט' לפי שמספר כ' מוסיף אחד על מספר ד' א"כ כפלי ד' משטחי א' בב' עם שטח ט' בב' שוה לכפלי ד' משטחי ז' בח' ולשטח ד' בכ' ולשטח ד' בח' ולמספר ט' וכאשר חברנו שטח ד' בכ' ושטח ד' בח' ומספר ט' עם כפל שטח ח' בה' ומספרי ב'ה' שנשארו בידינו היה בידינו כפל שטח ח' בה' ושטח ד' בכ' ושטח ד' בח' ומספרי ב'ה'ט' אבל כאשר התחבר זה כלו הוא שוה לשני שטחי ז' בח' לפי מה שנתבאר במה שקדם א"כ כפל שטח ח' בה' עם דמיוני שטחי א' בב' במה שבמספר ד' מן האחדים ועם שטח ט' בכ' ועם מספרי ב'ה' ימנהו שטח ז' בח' כמספר אחדי ד' נחבר עם שנים אבל מספר ד' נחבר עם שנים הוא ג' א״כ כפל שטח ח' בה' עם דמיוני שטחי א' בב' כמו מה שבמספר ד' מן האחדים ועם שטח ט' בכ' ועם מספרי ב'ה' ימנהו שטח ז' בח' כמספר אחדי ג' ומש"ל ובכזאת יתבאר שהעולה מזה המקובץ ימנהו ג' כמספר אחדי שטח ז' בח' והוא מה שרצינו לבאר | |
| נ"א כאשר היו שלשה מספרים מתחלפים וחובר השטח ההוה מהגדול פחות אחד ביתרון האמצעי על הקטן עם המספר הגדול ועם יתרון האמצעי על הקטן הנה העולה ימנהו המספר הגדול כמספר אחדי המספר הנמשך למספר יתרון האמצעי על הקטן לאחריו | |
| ויהיו השלשה מספרים המתחלפים מספרי א'ב'ג' ויהיה א' הקטן וב' האמצעי וג' הגדול ויהיה יתרון ב' על מספר א' מספר ד' ויהיה המספר הנמשך לג' לפניו מספר ה' והנמשך לד' לאחריו מספר ז' ואומר ששטח ד' בה' עם מספרי ג' ד' ימנהו ג' במספר אחדי ז' | |
| המופת ששטח ד' בה' כשחובר עמו ד' שוה לשטח ד' בג' וכאשר חובר עם שטח ד' בג' מספר ג' היה העולה שוה לשטח ז' בג' אם כן שטח ד' בה' עם מספרי ג' ד' שוה לשטח ז' בג' א"כ שטח ד' בה' עם מספרי ג' ד' ימנהו ג' כמספר אחדי ז' והוא מה שרצינו לבאר | |
| נ"ב כאשר היו שלשה מספרים מתחלפים הנה אם חובר השטח ההוה מהגדול פחות אחד ביתרון האמצעי על הקטן עם השטח ההוה מהקטן פחות אחד ביתרון הגדול על האמצעי ועם המספר הגדול ועם יתרון האמצעי על הקטן הנה העולה כשנתחבר זה כלו ימנהו האמצעי כמספר אחדי המספר הנמשך אחר יתרון הגדול על הקטן | |
| ויהיו המספרים המתחלפים מספרי א' ב' ג' והיה מספר א' הקטן ומספר ג' הוא הגדול והיה יתרון ב' על א' מספר ד' והיה יתרון ג' על ב' מספר ט' והיה המספר הנמשך למספר א' לפניו מספר ה' והנמשך למספר ג' לפניו מספר ל' והיה יתרון ג' על א' מספר ז' והמספר הנמשך למספר ז' לאחריו מספר ח' ואומר ששטח ד' בל' עם שטח ט' בה' ועם מספרי ג' ד' ימנהו מספר ב' כמספר אחדי ח' | |
| המופת ששטח ד' בל' כשחובר עמו ד' הוא שוה לשטח ד' בג' ושטח ט' בה' כשחובר עמו ג' הוא שוה לשטח ט' בא' ולב' מפני שמספר ג' שוה למספר ב' ט' וכאשר חובר ט' עם שטח ט' בה' היה שוה לשטח ט' בא' א״כ כאשר חובר ב'ט' יחד שהוא ג' עם שטח ט' בה' היה העולה שוה לשטח ט' בא' ולב' א"כ שטח ד' בל' עם שטח ט' בה' ועם מספרי ג' ד' שוה לשטח ד' בג' ולשטח ט' בא' ולמספר ב' אבל שטח ד' בג' עם שטח ט בא' שוה לשטח ז' בב' אם כן שטח ד' בל' עם שטח ט' בה' ועם מספרי ג'ד' שוה לשטח ז' בב' ולמספר ב' אבל שטח ז' בב' כשחובר עמו ב' הוא שוה לשטח ח' בב' אם כן שטח ד' בל' עם שטח ט' בה' ועם מספרי ג'ד' ימנהו ג' כמספר אחדי ח' והוא מה שרצינו לבאר | |
|
נ"ג נרצה שנמצא שלשה מספרים יהיה הראשון עם חלק מונח מהמספרים הנשארים כמו השני עם חלק מונח שני מהנשארים יותר קטן מהחלק המונח הראשון וכמו השלישי עם חלק מונח שלישי מהנשארים יותר קטן מהחלק המונח השני |
| ויהיו המספרים אשר אלו החלקים נקראים בהם מספרי א' ב' ג' | |
|
ויהיה החלק היותר גדול החלק הנקרא בא' והחלק היותר קטן החלק הנקרא בג' |
|
ולזה יהיה המספר היותר קטן מספר א' והמספר היותר גדול מספר ג' |
|
ויהיה יתרון ב' על א' מספר ד' |
|
ויתרון ג' על ב' מספר ז' |
|
והמספר הנמשך לג' לפניו מספר ח' |
|
והמספר הנמשך לב' לפניו מספר ל' |
|
הנה בהכרח שיהיה מספר א' אם שנים אם מוסיף על שנים |
|
ויהיה תחלה שנים |
|
הנה נחבר המספר האחרון והוא ג' עם ד' שהוא יתרון ב' על א' ויהיה העולה בידינו מספרי ג'ד' מקובצים ונשים העולה ה' והוא יהיה המספר הראשון |
|
עוד נחבר ה' עם שני שטחי המספר הגדול פחות אחד ביתרון האמצעי על הקטן והם שני שטחי ד' בח' ונשים העולה ט' והוא יהיה המספר השני |
|
עוד נחבר עם ט' כפל שטח הקטן פחות אחד ביתרון הגדול על האמצעי והוא כפל שטח ז' בא' פחות אחד ונשים העולה כ' והוא יהיה המספר השלישי |
|
|
| ונאמר שמספרי ה' ט' כ' הם המספרים המבוקשים | |
| המופת שט' שוה לה' ולשני שטחי ד' בח' וכ' שוה לה' ולשני שטחי ד' בח' ולכפל ז' בא' פחות אחד שהוא שני דמיוני ז' לפי שא' פחות אחד הוא אחד אם כן חצי מספרי ט'כ' שוה לה' ולשני שטחי ד' בח' ולמספר ז' אבל ה' שוה למספרי ג'ד' אם כן חצי מספרי ט'כ' שוה לשני שטחי ד' בח' ולמספרי ג' ד' ז' אבל שני שטחי ד' בח' עם מספרי ג'ד'ז' שוה לכפל שטח ל' בח' אם כן חצי מספרי ט'כ' שוה לכפל שטח ל' בח' א״כ כבר יוכה שנים בשני דמיוני שטח ל' בח' ויהיה העולה שוה למספרי ט'כ' מקובצים הנה א"כ ט'כ' ימנם א' שהוא שנים כמספר שני דמיוני שטח ל' בח' | |
|
ונשים שני דמיוני שטח ל' בח' מספר מ' |
| הנה מספר מ' הוא חלק נקרא בא' ממספרי ט'כ' מקובצים וג״כ ה' כ' שוים לכפל ה' ולשני שטחי ד' בח' ולכפל ז' א"כ חצי מספרי ה'כ' שוה לה' ולשטח ד' בח' ולז' ואולם ה' שוה למספרי ג' ד' אם כן חצי מספרי ה' כ' שוה לשטח ד' בח' ולמספרי ג' ד' ז' אבל מספרי ג' ד' ז' שוים לשטח א' בח' לפי שא' הוא שנים ומספרי ג' ד' ז' שוים לשני דמיוני מספר ח' אם כן חצי מספר ה'כ' שוה לשטח ה' בח' ולשטח א' בח' וזה שוה לשטח ב' בח' לפי שב' שוה לד'א' אם כן חצי מספרי ה'כ' שוה לשטח ב' בח' אם כן חצי מספרי ה'כ' ימנהו ב' כמספר אחדי ח' ולזה ימנה ב' מספרי ה' כ' כמספר אחדי שני דמיוני ח' ונשים שני דמיוני ח' כמו נ' הנה מספר נ' הוא חלק הנקרא בב' ממספרי ה'כ' מקובצים וגם כן הנה יהיו ה'ט' שוים לכפל ה' ולשני שטחי ד' בח' א"כ חצי מספרי ה'ט' שוה לה' ולשטח ד' בה' ואולם ה' שוה למספרי ג' ד' אם כן חצי מספרי ה' ט' שוה לה' ולשטח ד' בח' ולמספרי ג' ד' ואולם שטח ד' בח' עם מספרי ג'ד' ימנהו ג' כמספר אחדי הנמשך אחר ד' והוא ל' אם כן חצי מספר ה'ט' ימנהו ג' כמספר אחדי ל' אם כן מספרי ה'ט' ימנם ג' כמספר אחדי שני כפלי ל' ונשים שני כפלי ל' כמו ס' הנה מספר ס' הוא חלק הנקרא בג' ממספרי ה'ט' מקובצים ונאמר שמספרי ה'מ' מקובצים שוים למספרי ט'נ' מקובצים ולמספרי כ'ס' מקובצים וזה שה'מ' מקובצים שוים לשני דמיוני שטח ל' בח' ולמספר ה' ומספרי ט'נ' מקובצים שוים לפי מה שהתבאר למספר ה' ולשני דמיוני שטח ד' בח' ולשני דמיוני ח' הנה יחובר ח' עם שטח ד' בח' ויהיה שוה לשטח ל' בח' ולזה יהיו שני דמיוני שטח ד' בח' עם שני דמיוני ח' שוים לשני דמיוני ל' בח' א״כ מספרי טנ' מקובצים שוים למספרי ה'מ' מקובצים וג"כ הנה מספרי כ'ס' שוים לפי מה שקדם למספר ה' ולשני דמיוני שטח ד' בח' ולכפל ל' הנה מפני שמספר ז'ב' מקובצים שוים למספר ג' ול' פחות אחד מב' יהיו מספרי ז'ל' מקובצים פחות אחד מג' אם כן מספרי ז'ל' מקובצים שוים לח' אם כן מספרי כ'ס' שוים למספר ה' ולשני שטחי ד' בח' ולכפל ז'ל' מקובצים שהוא כמו כפל ח' אבל שני שטחי ד' בח' עם כפל ח' שוים לשני שטחי ל' בח' אם כן שני מספרי כ'ס' מקובצים שוים ג״כ לשני מספרי ה' מ' הנה כבר מצאנו שלשה מספרים והם מספרי ח' ט' כ' והראשון והוא כ' עם חלק מא' מהנשארים שוה למספר ט' עם חלק מב' מהנשארים והוא ג״כ שוה למספר כ' עם חלק מג' מהנשארים והוא מה שרצינו | |
| ויהיה גם כן מספר א' מוסיף על שנים ויהיה יתרונו על שנים מספר ד' ויהיה יתרון ב' על א' מספר ה' ויתרון ג' על ב' מספר ז' והמספר הנמשך לא לפניו הוא מספר ח' והמספר הנמשך לפני ב' הוא מספר ט' והמספר הנמשך לפני ג' הוא ל' ונשאר הדרוש על ענינו. הנה נקח מדמיוני שטח האמצעי בגדול כשיעור יתרון הקטן על שנים ונחבר עם העולה המספר הגדול ויתרון האמצעי על הקטן רצוני שנקח מדמיוני שטח ב' בג' כמנין מה שבמספר ד' מן האחדים ונחבר עם העולה מספרי ג' ה' ונשים העולה מספר מ' והוא יהיה המספר הראשון. עוד נחבר מספר מ' עם שני שטחי המספר הגדול פחות אחד ביתרון האמצעי על הקטן רצוני שנחבר מ' עם שני שטחי ה' בל' ונשים העולה נ' והוא יהיה המספר השני. עוד נחבר נ' עם שני שטחי הקטן פחות אחד ביתרון הגדול על האמצעי רצוני שנחבר נ' עם שני שטחי ז' בח' ונשים העולה ס' והוא יהיה המספר השלישי ואומר שמספרי מ' נ' ס' הם המספרים המבוקשים | |
| המופת שמספר נ' שוה למספר מ' ולשני שטחי ה' בל' ומספר ס' שוה למספר מ' ולשני שטחי ה' בל' ולשני שטחי ז' בח' א"כ חצי מספרי נ'ס' שוה למספר מ' ולשני שטחי ה' בל' ולשטח ז' בח' אבל מספר מ' שוה לכפל מספר ד' מדמיוני שטח ב' בג' ולמספרי ג'ה' אם כן חצי מספרי נ'ס' שוה לכפל ד' מדמיוני שטח ב' בג' ולשני שטחי ה' בל' ולשטח ז' בח' ולמספרי ג'ה' אבל כפל ד' מדמיוני שטח ב' בג' עם שני שטחי ה' בל' ועם שטח ז' בח' ועם מספרי ג'ה' ימנהו א' כמספר אחדי שטח ט' בל' ולזה ימנה א' מספרי נ'ס' כמספר כפל שטח ט' בל' ונשים כפל שטח ט' בל' מספר ע' הנה מספר ע' הוא חלק הנקרא בא' ממספרי נ'ס' מקובצים וג"כ הנה מ' וס' שוים לכפל מ' ולשני שטחי ה' בל' ולשני שטחי ז' בח' ולזה יהיה חצי מספרי מ'ס' שוה למספר מ' ולשטח ה' בל' ולשטח ז' בח' אבל מספר מ' שוה לכפלי ד' משטחי ב' בג' ולמספרי ג'ה' א"כ חצי מספרי מ'ס' שוה לשטח ה' בל' ולשטח ז' בח' ולמספרי ג'ה' ולכפלי ד' מדמיוני שטח ב' בג' אבל שטח ה' בל' עם שטח ז' בח' ועם מספרי ג'ה' ימנהו ב' כמספר הנמשך אחר יתרון ג' על א' רצוני המספר הנמשך אחר ה' ז' מקובצים ונשימהו מספר ק' והנה כפלי ד' מדמיוני שטח ב' בג' ימנהו ב' כמספר אחדי שטח ד' בג' לפי שכפלי ד' מדמיוני שטח ב' בג' הוא מורכב ממספרי ד' ב' ג' אם כן חצי מספרי מ'ס' ימנהו ב' כמספר שטח ד' בג' וכמספר ק' ולזה התבאר שמספרי מ'ס' מקובצים ימנם ב' כמספר אחדי כפל שטח ד' בג' וכמספר כפל ק' ונשים כפל שטח ד' בג' וכפל מספר ק' מספר פ' הנה מספר פ' הוא חלק נקרא בב' ממספרי מ'ס' מקובצים. וגם כן הנה מ' ונ' שוים לכפל מ' ולשני שטחי ה' בל' א"כ חצי מספרי מ'נ' שוה למ' ולשטח ה' בל' ואולם מספר מ' שוה לכפלי ד' משטח ב' בג' ולמספרי ג'ה' א״כ חצי מספרי מ'נ' שוה לשטח ה' בל' ולמספרי ג'ה' ולכפלי ד' משטח ב' בג' אבל שטח ה' בל' עם מספרי ג'ה' ימנהו ג' כמספר אחדי הנמשך אחר ה' ונשימהו מספר ר' וכפלי ד' משטח ב' בג' ימנהו ג' כמספר אחדי שטח ד' בב' אם כן חצי מספרי מ'נ' ימנהו ג' כמספר אחדי שטח ד' בב' וכמספר ח' א"כ מספרי מ'נ' ימנהו ג' כמספר כפל שטח ד' בב' וככפל מספר ר' ונשים כפל שטח ד' בג' וכפל מספר ר' מספר צ' הנה מספר צ' הוא חלק נקרא בג' ממספרי מ'נ' מקובצים | |
| ונאמר שמספרי מ'ע' מקובצים ומספרי נ'פ' מקובצים ומספרי ס'צ' מקובצים שוים קצתם לקצת | |
| המופת שמ'ע' שוים למספר מ' ולכפל שטח ט' בל' ומספרי נ'פ' שוים למספר מ' ולשני שטחי ה' בל' ולשני שטחי ד' בב' ולכפל מספר ק' ונשליך מספר מ' המשותף ונאמר שכפל שטח ט' בל' שוה לשני שטחי ה' בל' מחוברים עם שני שטחי ד' בג' ועם כפל מספר ק' וזה שיתרון ט' על ה' הוא ח' לפי שא'ה' מקובצים שוים לב' ויהיו א״כ ח'ה' מקובצים שוים לט' א״כ יתרון שטח ט' בל' על שטח ה' בל' הוא שטח ח' בל' ונאמר שק'ד' שוים לל' וזה שמספר ק' שוה לה'ז' ולאחד אבל מספרי ה'ז'א' שוים לג' יהיה אם כן ק'א' מוסיף על ג' אחד אם כן ק'ח' שוה לג' ולזה יהיה ק'ח' מוסיף על ל' אחד אם כן ק'ד' שוה לל' וכאשר התבאר זה הנה התבאר שכפל שטח ט' בל' שוה לכפל שטח ה' בל' ולשני שטחי ד' בג' ולכפל מספר ק' וזה ששטח ד' בל' עם ד' שוה לשטח ד' בג' א"כ שני שטחי ד' בג' שוים לשני שטחי ד' בל' ולכפל ד' א"כ שני שטחי ד' בג' וכפל מספר ק' שוים לשני שטחי ד' בל' ולכפל ד'ק' שהוא כמו כפל ל' אבל שני שטחי ד' בל' כאשר חובר עמהם כפל ל' שוים לכפל שטח ח' בל' אבל כפל שטח ד' בג' עם כפל מספר ק' שוה לכפל שטח ח' בל' וכאשר חובר עם זה כפל שטח ה' בל' היה העולה שוה לכפל שטח ה' בל' ולכפל שטח ח' בל' אבל כפל שטח ה' בל' עם כפל שטח ח' בל' שוה לכפל שטח ט' בל' א״כ מספרי מ'ע' מקובצים שוים למספרי נ'פ' מקובצים וגם כן הנה מספרי ס'צ' שוים למספר מ' ולשני שטחי ה' בל' ולשני שטחי ז' בח' ולשני שטחי ד' בב' ולכפל מספר ר' ומספרי מ'ע' שוים למספר מ' ולכפל שטח ט' בל' ונשליך מספר מ' המשותף ונאמר ששני שטחי ה' בל' ושני שטחי ז' בח' ושני שטחי ד' בב' וכפל מספר ר' שוים לכפל שטח ט' בל' וזה לפי שר' מוסיף על ה' אחד יהיה ז'ר' מוסיף על ז'ה' אחד א"כ ז'ר' שוה לק' וכבר התבאר שיתרון שטח ט' בל' על שטח ה' בל' הוא שטח ח' בל' וכאשר התישב זה כלו הנה נבאר ששני שטחי ז' בח' עם שני שטחי ד' בב' וכפל מספר ר' שוה לכפל שטח ח' בל' וזה ששטח ז' בד' עם ז' שוה לשטח ח' בז' א״כ שני שטחי ז' בח' שוים לשני שטחי ד' בז' ולכפל מספר ז' וג״כ הנה שטח ד' בב' שוה לשטח ד' בט' ולמספר ד' א"כ שני שטחי ד' בב' שוים לשני שטחי ד' בט' ולכפל מספר ד' א״כ שני שטחי ז' בח' עם שני שטחי ד' בב' וכפל מספר ר' שוה לשני שטחי ד' בז'ט' מקובצים ולכפל מספרי ז'ר'ד' ולפי שז'ב' מקובצים שוים לג' יהיו ז'ט' שוים לל' ולפי שמספרי ז'ר' שוים למספר ק' יהיו מספרי ז'ר'ד' שוים לק'ד' אבל ק'ד' שוה לל' א"כ שני שטחי ז' בח' עם שני שטחי ד' בב' וכפל מספר ר' שוה לשני שטחי ד' בל' ולכפל מספר ל' אבל שני שטחי ד' בל' וכפל מספר ל' שוה לשני שטחי ח' בל' וכאשר חובר זה עם כפל שטח ה' בל' יהיה העולה שוה לשני שטחי ח' בל' ולשני שטחי ה' בל' וזה כבר התבאר שהוא שוה לכפל שטח ט' בל' אם כן מספרי ס'צ' מקובצים שוים למספרי נ'פ' מקובצים הנה כבר מצאנו שלשה מספרים והראשון והוא מ' עם חלק מא' מהנשארים הוא כמו השני והוא נ' עם חלק מב' מהנשארים וכמו השלישי והוא ס' עם חלק מג' מהנשארים והוא מש"ל | |
| נ"ד נרצה שנמצא מספר יוסיף חלק מה ממנו או נקבץ חלקים מה ממנו מספר מונח על חלק אחר ממנו או נקבץ חלקים ממנו יותר קטן מן החלק הראשון או מנקבץ החלקים הראשון | |
| ויהיו החלקים אשר מקובצם יותר גדול ב' חלקים מא' במספר הדרוש וג' חלקים מד' בו ואחד מה' בו והחלקים אשר מקובצם יותר קטן ז' חלקים מח' במספר הדרוש וט' חלקים מכ' בו ורצינו שנמצא מספר יהיו החלקים הראשונים ממנו מוסיפים על החלקים השניים אשר מקובצם יותר קטן מספר מ' ויהיה המספר הקטן שימנוהו כל אלו המספרים הקוראים לחלקים האלו בכללם והם א' ד' ה' ח' כ' מספר ל' ויהיו ב' חלקים מא' בו מספר ג' וג' חלקים מד' מספר ס' ואחד מה' בו מספר ע' וכזה יהיה מקובץ החלקים המוסיפים מספרי נ' ס' ע' מקובצים ויהיו ז' חלקים מח' במספר ל' מספר פ' וט' חלקים מכ' בו מספר צ' וכזה יהיה מקובץ החלקים היותר קטן מספרי פ' צ' מקובצים ויהיה יתרון נ' ס' ע' מקובצים על פ' צ' מקובצים מספר ק' ונשים יחס ל' אל ר' כיחס ק' אל מ' ונאמר שמספר ר' הוא המבוקש | |
| המופת שאנחנו נשים ב' חלקים מא' במספר ר' מספר ש' וג' חלקים מד' בו מספר ת' ואחד מה' בו מספר ו' וכזה יהיה מקובץ אלו החלקים מספרי ש'ת'ו' ויהיה גם כן ז' חלקים מח' במספר ר' מספר י' וט' חלקים מכ' בו מספר ך' וכזה יהיה מקובץ אלו החלקים י'ך' והוא מבואר שיחס ב' חלקים מא' במספר ל' אל מספר ל' כיחס ב' חלקים מא' במספר ר' אל מספר ר' לפי שיחס כל אחד מאלו החלקים הוא כיחס ב' חלקים מא' במספר א' אל מספר א' ולזה יתבאר שיחס ב' חלקים מא' במספר ל' אל ב' חלקים מא' במספר ר' הוא כיחס ל' אל ר' על התמורה א״כ יחס נ' אל ש' כיחס ל' אל ר' ובזה יתבאר שיחס ס' אל ת' הוא כיחס ל' אל ר' ושיחס ע' אל ו' הוא כיחס ל' אל ר' וכאשר קבצנו היה יחס מספרי נ'ס'ע' מקובצים אל מספרי ש'ת'ו' מקובצים הוא כיחס ל' אל ר' ובזה התבאר שיחס מספרי פ'ץ' מקובצים אל מספרי י'ך' מקובצים הוא כיחס ל' אל ר' הנה אם כן יחס מספרי נ'ס'ע' אל מספרי ש'ת'ו' כיחס מספרי פ'ץ' אל מספרי י'ך' וכאשר המירונו הנה יחס מספרי נ'ס'ע' אל מספרי פ'ץ' כיחס מספרי ש'ת'ו' אל מספרי י'ך' אבל מספרי נ'ס'ע' מוסיפים על מספרי פ'ץ' א"כ מספרי ש'ת'ו' מוסיפים על מספרי י'ך' ונשים יתרון מספרי ש'ת'ו' על מספרי י'ך' מספר ף' ולפי שיהיה יחס נ'ס'ע' אל ש'ת'ו' כיחס ל' אל ר' ויחס פ'ץ' אל י'ך' הוא ג"כ כיחס ל' אל ר' הנה כאשר הבדלנו יהיה יחס ק' אל ף' כיחס ל' אל ר' א"כ יחס ק' אל מ' ואל ף' אחד א״כ מספרי ף' מ' שוים וכבר היו מספרי ש'ת'ו' מוסיפים על מספרי י'ך' מספר ף' א״כ מספרי ש'ת'ו' מוסיפים על מספרי י'ך' מספר מ' הנה כבר מצאנו מספר והוא ר' וב' חלקים מא' בו עם ג' חלקים מד' בו ואחד מה' בו מוסיפים מספר מ' על ז' חלקים מח' בו וט' חלקים מכ' בו והוא מש"ל | |
| נ"ה כאשר היה מספר מה מונח עם חלק גדול או נקבץ חלקים גדול ממספר מונח שני פחות מספר מה מהמספר השני עם חלק קטן או נקבץ חלקים קטן מהמספר הראשון הנה כבר אפשר שימצא מספר שלישי יהיה המספר הראשון המונח עם החלק הגדול או נקבץ החלקים הגדול משני המספרים הנשארים שוה למספר השני המונח עם החלק הקטן או נקבץ החלקים הקטן משני המספרים הנשארים | |
| ויהיה המספר הראשון המונח מספר א' והמספר השני מספר ב' ויהיה נקבץ החלקים הגדול ג' חלקים מד' ואחד מה' ונקבץ החלקים הקטן ז' חלקים מח' והיה מספר א' עם ג' חלקים מד' במספר ב' ואחד מה' ממנו פחות ממספר ב' עם ז' חלקים מה' במספר א' כמו מספר ט' ונאמר שכבר אפשר שימצא מספר שלישי יהיה מספר א' עם ג' חלקים מד' ואחד מה' בשני הנשארים שוה למספר ב' עם ז' חלקים מח' במספרים הנשארים | |
| המופת כי מפני שנקבץ ג' חלקים מד' ואחד מה' יותר גדול מנקבץ ז' חלקים מה' הנה כבר אפשר שימצא מספר יוסיפו ג' חלקים מד' ואחד מה' בו על ז' חלקים מח' בו כמו מספר ט' ונשים המספר ההוא מספר כ' ונאמר שמספר כ' הוא המבוקש | |
| המופת שאנחנו נשים ז' חלקים מח' במספר כ' מספר ל' יהיה א״כ ג' חלקים מד' במספר כ' ואחד מה' בו שוה למספר לט' מפני שג' חלקים מד' ואחד מה' במספר כ' מוסיפים ט' על ז' חלקים מח' בו ונשים מספר א' עם ג' חלקים מד' ואחד מה' במספר ב' שוה למספר מ' אם כן מספר ב' עם ז' חלקים מח' במספר א' שוה למספרי מ'ט' וכאשר התישב זה כלו הנה נבאר שמספר א' עם ג' חלקים מד' ואחד מה' במספרי כ'ב' שוה למספר ב' עם ז' חלקים מח' במספרי א'ב' וזה שמספר א' עם ג' חלקים מד' ואחד מה' במספר ב' שוה למ' ואולם ג' חלקים מד' ואחד מה' במספר כ' שוה למספרי ל'ט' א״כ מספר א' עם ג' חלקים מד' ואחד מה' במספרי כ'ב' שוים למספרי מ' ל' ט' וג״כ הנה מספר ב' עם ז' חלקים מח' במספר א' שוה למספרי מ'ט' ואולם ז' חלקים מח' במספר כ' שוה למספר ל' הנה אם כן מספר ב' עם ז' חלקים מה' במספרי א'כ' שוה למספרי מ'ל'ט' וכבר היה מספר א' עם ג' חלקים מד' ואחד מה' במספרי כ'ב' שוה למספרי מ'ל'ט' אם כן מספר א' עם ג' חלקים מד' ואחד מה' במספרי ב'כ' שוה למספר ב' עם ז' חלקים מח' במספרי א'ב' ומש"ל | |
| נ"ו נרצה שנמצא מספר מה יהיה חלק מה או נקבץ חלקים מה ממנו שוה לחלק מה או לנקבץ חלקים מה מתחלף לחלק הראשון או לנקבץ החלקים הראשון ויהיה לקוח ממספר מה | |
| המשל שאנחנו נרצה שנמצא מספר יהיה חלק מא' בו' וב' חלקים מג' בו שוה לד' חלקים מה' במספר ז' המונח הנה נשים ד' חלקים מה' במספר ז' מספר ח' ונשים חלק מא' וב' חלקים מג' במספר ז' מספר ט' ונשים יחס ז' אל כ' כיחס ט' אל ח' ואומר שמספר כ' הוא המבוקש | |
| המופת שאנחנו נשים חלק מא' וב' חלקים מג' במספר כ' מספר ל' והוא מבואר שיחס חלק מא' וב' חלקים מג' במספר ז' אל חלק מא' וב' חלקים מג' במספר כ' הוא כיחס מספר ז' אל מספר כ' א"כ יחס ט' אל ל' הוא כיחס ז' אל כ' א״כ יחס ט' אל ח' ואל ל' אחד א״כ ח' שוה לל' הנה אם כן חלק מא' וב' חלקים מג' במספר כ' שוה לד' חלקים מה' במספר המונח והוא מה שרצינו לבאר | |
| נ"ז נרצה שנמצא שני מספרים יהיה האחד עם חלק מה מהשני כמו האחר עם חלק אחר מהמספר הראשון | |
| הנה יהיו המספרים אשר בהם נקראים החלקים האלה מספרי א' ב' ונרצה שנמצא שני מספרים יהיה האחד עם חלק מא' מהאחר כמו המספר השני עם חלק מב' מהמספר הראשון הנה נשים המספר הנמשך למספר א' לפניו מספר ג' והמספר הנמשך למספר ב' לפניו מספר ד' ונקח שטח ג' בב' ונשימהו ה' והוא יהיה המספר הראשון ונקח שטח ד' בה' ונשימהו ז' והוא יהיה המספר השני ונאמר שמספר ה' עם חלק מא' מז' שוה למספר ז' עם חלק מב' במספר ה' | |
| המופת שחלק מא' בז' הוא ד' מפני שא' הוכה בד' והיה ז' וחלק מב' מה' הוא ג' מפני שב' הוכה בג' והיה ה' אם כן מספר ה' עם חלק מא' מז' שוה לשטח ג' בב' ולמספר ד' אבל שטח ג' בב' כשחובר עם ב' שוה לשטח א' בב' א"כ שטח א' בב' מוסיף אחד על שטח ג' בב' עם מספר ד' לפי שב' מוסיף על ד' אחד א״כ שטח א' בב' מוסיף אחד על מספר ה' עם חלק מא' מז' וג״כ הנה מספר ז' עם חלק מב' במספר ה' שוה לשטח ד' בא' ולמספר ג' אבל שטח ד' בא' כשחובר עם א' שוה לשטח א' בב' א״כ שטח א' בב' מוסיף אחד על שטח ד' בא' עם מספר ג' לפי שמספר א' מוסיף על ג' אחד א״כ שטח א' בב' מוסיף אחד על מספר ז' עם חלק מב' במספר ה' וכבר היה ג"כ שטח א' בב' מוסיף אחד על מספר ה' עם חלק מא' במספר ז' א״כ מספר ה' עם חלק מא' במספר ז' שוה למספר ז' עם חלק מב' במספר ה' ומש״ל | |
| נ"ח נרצה שנמצא שלשה מספרים יהיה המספר הראשון כשחובר עם השלישי ימנהו השני כמספר אחדי מספר מונח ויהיה המספר השני כשחובר עם השלישי ימנהו הראשון כשיעור אחדי מספר מונח שני | |
| ויהיו המספרים המונחים מספרי א'ב' הנה נשים המספר הנמשך למספר א' לאחריו מספר ג' ונשימהו המספר הראשון ונשים המספר הנמשך למספר ב' לאחריו מספר ד' ונשימהו המספר השני ונכה א' בב' ונגרע מהעולה אחד ונשים הנשאר ממנו מספר ז' ונשימהו המספר השלישי ונאמר שמספרי ג' ד' ז' הם המבוקשים רצינו שג'ז' מקובצים ימנם ד' כמספר אחדי א' וד'ז' מקובצים ימנם ג' כמספר אחדי ב' | |
| המופת שז' פחות אחד משטח א' בב' וג' שוה לאחד ולא' א"כ מספרי ג'ז' שוים לשטח א' בב' ולא' אבל שטח א' בב' כשחובר עם א' שוה לשטח א' בד' אם כן מספרי ג'ז' שוים לשטח א' בד' ולזה ימנם ד' כמספר אחדי א' וגם כן מפני שז' פחות אחד משטח א' בב' וד' שוה לאחד ולב' יהיו מספרי ד' ז' שוים לשטח א' בב' ולב' אבל שטח א' בב' כשחובר עם ב' הוא שוה לשטח ג' בב' א"כ מספרי ד'ז' שוים לשטח ג' בב' אבל שטח ג' בב' ימנהו ג' כמספר אחדי ב' א״כ מספרי ד'ז' ימנם ג' כמספר אחדי ב' הנה א"כ מספרי ג'ז' ימנם ד' במספר אחדי א' ומספרי ג'ז' ימנם ג' כמספר אחדי ב' ומש"ל | |
| The number that consists of the squares of given numbers is equal to the square of the number that consists of the given numbers. | נ"ט המספר המורכב מהמרובעים ההוים ממספרים מונחים שוה למרובע ההוה מהמספר המורכב מהמספרים המונחים ההם |
| ויהיו המספרים המונחים א'ב'ג' ויהיה המספר המורכב ממרובעי מספרי א' ב' ג' מספר ד' ויהיה המספר המורכב ממספרי א' ב' ג' מספר ה' ואומר שמספר ד' שוה למרובע ההוה ממספר ה' | |
| המופת כי מפני שכל מספר מרובע מורכב משני דמיוני יסודו הנה יהיה מספר ד' מורכב ממספרי א'א' ב'ב' ג'ג' ויתבאר לפי מה שקדם ששטח המספר המורכב ממספרי א' ב' ג' במורכב ממספרי א' ב' ג' הוא מספר ד' א״כ המספר המורכב ממספרי א' ב' ג' והוא ה' הוכה על עצמו והיה ד' א״כ מספר ד' שוה למרובע ההוה ממספר ה' ומש"ל | |
| The number that consists of the cubic powers of given numbers is equal to the cubic power of the number that consists of the given numbers. | ס המספר המורכב ממעוקבי מספרים מונחים שוה למעוקב ההוה מהמספר המורכב מהמספרים המונחים ההם |
| ויהיו המספרים המונחים מספרי א' ב' ג' ויהיה המורכב ממעוקבי מספרי א' ב' ג' מספר ד' ויהיה המספר המורכב ממספרי א'ב'ג' מספר ה' ואומר שמספר ד' שוה למעוקב ההוה ממספר ה' | |
| המופת מפני שכל מעוקב מורכב משלשה דמיוני יסודו יהיה מספר ד' מורכב ממספרי א'א'א' ב'ב'ב' ג'ג'ג' א"כ מספר ד' שוה לשטח ההוה ממורכב מספרי א'ב'ג' על מורכב מספרי א'ב'ג' א'ב'ג' אבל מורכב מספרי א'ב'ג' א'ב'ג' שוה לשטח ההוה ממורכב מספרי א'ב'ג' על מורכב מספרי א'ב'ג' שהוא כמו מרובע המספר המורכב ממספרי א'ב'ג' א״כ מספר ד' שוה לשטח ההוה ממורכב מספרי א'ב'ג' על מרובע מורכב מספרי א'ב'ג' ולזה יהיה מספר ד' שוה לשטח ההוה ממספר ה' על מרובע מספר ה' א״כ מעוקב מספר ה' שוה למספר ד' ומש"ל | |
| ס"א כאשר חובר השטח ההוה ממספר מונח במרובע מספר מונח שני עם השטח ההוה מהמונח השני במרובע המספר המונח הראשון הנה העולה שוה לשטח העולה משטח אחד מהמספרים המונחים באחר על מקובץ המספרים המונחים | |
| ויהיו המספרים המונחים מספרי א'ב' והיה מרובע מספר א' מספר ג' ומרובע מספר ב' מספר ד' וחובר שטח א' בד' עם שטח ב' בג' והיה ה' והיה שטח א' בב' מספר ז' ואומר שמספר ה' שוה לשטח ההוה ממספר ז' במספרי א'ב' מקובצים | |
| המופת ששטח א' בד' מורכב ממספרי א' ב' ב' לפי שמספר ד' הוא מרובע ב' א״כ שטח א' בד' שוה לשטח ההוה ממורכב מספרי א'ב' ב'ב' וכבר היה מורכב א'ב' מספר ז' א״כ שטח א' בד' שוה לשטח ז' בב' ובזה התבאר ששטח ב' בג' שוה לשטח ההוה ממורכב א'ב' במספר א' א״כ שטח ב' בג' שוה לשטח ז' בא' א״כ שטח א' בב' עם שטח ב' בג' שוים לשטח ז' בא' מחובר עם שטח ז' בב' אבל שטח ז' בא' מחובר עם שטח ז' בב' שוה לשטח ההוה ממספר ז' במספרי א'ב' מקובצים אם כן שטח א' בד' עם שטח ב' בג' שוה לשטח ז' בא'ב' מקובצים ומש״ל | |
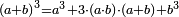
|
ס"ב כאשר היו שני מספרים מונחים הנה המעוקב ההוה ממקובצם מוסיף על המעוקב ההוה מהמספר הראשון מהם כמו שלשה דמיוני השטח ההוה משטח המספר הראשון המונח בשני על מקובצם וכמו מעוקב המספר השני |
| ג = א×ב | ויהיו המספרים המונחים מספרי א' ב' והיה שטח א' בב' מספר ג' |
| ד = 3א | והיה מעוקב א' מספר ד' |
| ה = 3(א+ב) | ומעוקב א'ב' מקובצים מספר ה' |
| ז = 3ב | ומעוקב ב' מספר ז' |
| ז + (א + ב)·ג·3 + ד = ה | ואומר שמספר ה' מוסיף על מספר ד' כמו שלשת דמיוני שטח ג' בא'ב' מקובצים וכמו מספר ז' |
| המופת שא'ב' הוכה על עצמו והיה שוה למרובעי מספרי א'ב' ולכפל שטח א' בב' אם כן מרובע א'ב' מקובצים שוה למרובעי א'ב' ולכפל מספר ג' וכבר הוכה מרובעי א'ב' וכפל מספר ג' על א'ב' מקובצים והיה ה' לפי שמרובע א'ב' מקובצים יוכה על א'ב' מקובצים ויהיה ה' ואומר שמספר ה' מוסיף על מספר ד' כמו שלשה דמיוני שטח ג' בא'ב' מקובצים וכמו מספר ז' וזה שמרובע א' כבר הוכה בא'ב' ויהיה העולה שוה לשטח א' במרובע א' שהוא מספר ד' ולשטח ההוה ממרובע א' במספר ב' וג"כ הנה מרובע ב' כבר הוכה בא'ב' והיה העולה שוה לשטח ההוה ממרובע ב' בב' שהוא מספר ז' ולשטח ההוה ממרובע ב' במספר א' אם כן מרובעי א'ב' כאשר הוכו על א'ב' היה העולה שוה למספר ד' ולמספר ז' ולשטח מרובע א' במספר ב' ולשטח מרובע ב' במספר א' אבל שטח מרובע א' במספר ב' עם שטח מרובע ב' במספר א' שוה לשטח ג' בא'ב' אם כן מרובעי א'ב' כאשר הוכו על א'ב' היה העולה שוה למספר ד' ולמספר ז' ולשטח ג' בא'ב' ואולם מספר ג' כאשר הוכה בא'ב' היה העולה שטח ג' בא'ב' אם כן כפל ג' כאשר הוכה בא'ב' היה העולה שני דמיוני שטח ג' בא'ב' אבל כאשר הוכו מרובעי מספרי א'ב' על א'ב' היה העולה שוה למספר ד' ולמספר ז' ולשטח ג' בא'ב' אם כן כאשר הוכו מרובעי מספרי א'ב' וכפל מספר ג' על א'ב' היה העולה שוה למספר ד' ולמספר ז' ולשלשת דמיוני שטח ג' בא'ב' אבל מרובעי מספרי א'ב' וכפל מספר ג' כאשר הוכו על א'ב' היה העולה ה' א"כ מספר ה' שוה למספר ד' ולמספר ז' ולשלשת דמיוני שטח ג' בא'ב' א"כ מספר ה' מוסיף על מספר ד' כמו שלשת דמיוני שטח ג' בא'ב' מקובצים וכמו מספר ז' ומש"ל | |
| וכבר יתבאר מזאת התמונה בעצמה שמעוקב א'ב' שוה למספר ד' ולמספר ז' ולשלשת דמיוני שטח מרובע א' בב' ולשלשת דמיוני שטח מרובע ב' בא' וזה שמעוקב א'ב' שוה למספר ד' ולמספר ז' ולשלשת דמיוני שטח ג' בא'ב' אבל שטח ג' בא'ב' שוה לשטח מרובע א' בב' ולשטח מרובע ב' בא' א״כ שלשת דמיוני שטח ג' בא'ב' שוים לשלשת דמיוני שטח מרובע א' בב' ולשלשת דמיוני שטח מרובע ב' בא' א"כ מעוקב א'ב' שוה למספר א' ולמספר ד' ולשלשת דמיוני שטח מרובע א' בב' ולשלשת דמיוני שטח מרובע ב' בא' ומש״ל | |
Combinatorics |
|
| Introduction | הקדמה |
| Two possible orders of two things: the one precedes the other or vice versa | שני נושאים יתחלפו בסדר בחבורם בשני דרכים אם שיקדים האחד לאחר או שיקדים האחר לו |
| Two possible differences between combinations of elements: difference of the elements, or difference of the orders of the elements | החלוף בחבורי הנושאים הוא בשני דרכים אם שיתחלפו בנושאיהם וישתתפו בכמות מספרם או שיתחלפו בסדר לבד |
| When an element is added to two combinations of elements that differ from each other, the two consequent combinations differ from each other | חבור הנושאים המתחלף חלוף מה לחבור נושאים אחד כשחובר עוד עם כל אחד מהם נושא אחד בעינו הנה הם מתחלפים ג"כ |
| והמשל שיהיה חבור א'ב'ג' מתחלף לחבור ב'ג'ד' בנושאים וחובר עם כל אחד מהחבורים ה' והיו החבורים ה א'ב'ג' ה' ב'ג'ד' הנה הם מתחלפים בהם גם כן כמו החלוף הקודם | |
| וכן הענין אם היו החבורים מתחלפים רק בסדר לבד וזה שאם חובר ה' עם כל אחד מחבורי א'ב'ג' ב'א'ג' ונשאר סדרם כמו שהיה והיו החבורים ה' א'ב'ג' ה' ב'א'ג' הנה הם מתחלפים ג"כ כמו החלוף הקודם | |
| The number of combinations created from a given number of elements is equal to the number of combinations created from the same given number of other elements, when the combinations are of the same kind - i.e. if the first combinations differ by their element, the other combinations differ also by their elements, and if the first differ by the order of elements, the other differ by the order of their elements as well | מספר החבורים ההוים ממספר מונח מנושאים מה שוה למספר החבורים ההוים מהמספר המונח מנושאים אחרים כשהיו החבורים על דמיון הקודמים רצוני ל׳ שאם היו החבורים הקודמים מתחלפים בנושאיהם יהיו החבורים האחרים מתחלפים בנושאיהם ואם היו החבורים הקודמים מתחלפים בסדר יהיו החבורים האחרים מתחלפים בסדר לבד |
| when different elements are added [each separately] to a given combination of elements, the consequent combinations differ by their elements | כאשר חוברו עם חבור נושאים מונח נושאים מתחלפים הנה החבורים מתחלפים בנושאיהם |
|
משל זה שחבור א'ב'ג' התחבר עם ד' והיה ד' א'ב'ג' ועם ה' והיה ה' א'ב'ג' הנה חבורי ד'א'ב'ג' ה'א'ב'ג' מתחלפים בנושאיהם |
| Combinatorial Identities | |
|
ס"ג כאשר היו מחברות מספר מונח מנושאים מתחלפים המתחלפות בסדר לבד מספר מה הנה מחברות המספר הנמשך אחר המונח מנושאים מתחלפים המתחלפות בסדר לבד הם כמו שטח מספר המחברות הקודמות במספר הנמשך אחר המספר המונח |
| ויהיו הנושאים א'ב'ג'ד'ה' ומספרם ז' ויהיה המספר הנמשך אחר ז' מספר ח' והיה מספר מחברות נושאי א'ב'ג'ד'ה' המתחלפות בסדר לבד מספר ט' ויהיו נושאי א'ב'ג'ד'ה'ו' מוסיפים נושא אחד על מספר נושאי א'ב'ג'ד'ה' ולזה יהיה מספרם מספר ח' ונאמר שמספר מחברות נושאי א'ב'ג'ד'ה'ו' המתחלפות בסדר לבד הוא כמספר שטח ט' בח' | |
| המופת שכבר יחובר ו' ויושת ראשון עם כל אחת ממחברות א'ב'ג'ד'ה' המתחלפות בסדר ותשארנה המחברות מתחלפות בסדר ולזה תהיינה המחברות בהיות ו' ראשון מספר ט' וג"כ הנה מפני שמחברות א'ב'ג'ד'ה' המתחלפות בסדר לבד הם כמספר ט תהיינה מחברות א'ב'ג'ד'ו' ג"כ מספר ט' וכבר יחובר ה' ויושם ראשון עם כל אחת מאלו המחברות ותשארנה המחברות מתחלפות בסדר לבד ולזה תהיינה המחברות בהיות ה' ראשון כמספר ט' וכזה התבאר שכל אחד מאלו הנושאים יושם ראשון ותהיינה המחברות המתחלפות בסדר לבד בהיותו ראשון כמספר ט' תהיינה אם כן אלו המחברות בכללם כמו ט' מוכה על מספרם ואולם מספרם הוא ח' אם כן מספר מחברות א'ב'ג'ד'ה'ו' המתחלפות בסדר לבד הם כמספר שטח ח' בט' והוא מבואר שאין בכל אלו המחברות שמנינו שתים דומות כי בהיות אחד מהנושאים ראשון אין שם שתי מחברות דומות כי המחברות אשר יתחבר עמהם הם מתחלפות וכן תתחלפנה בהתחברו עמהם ואין ספק שכאשר לא היה הנושא הראשון אחד שהמחברות מתחלפות בסדר ובהיות הענין כן הוא מבואר שאין באלו המחברות שמנינו שתי מחברות דומות ונאמר ג"כ שאין שם מחברת זולת אלו שאם היה אפשר תהיה המחברת ההיא ד'ו'ה'ג'א'ב' אבל ד' התחבר עם הנשארים בכל מיני חבור ואחת ממחברות הנשארים ו' ה' ג' א' ב' אם כן ד'ו'ה'ג'א'ב' הוא אחת מהמחברות שמנינו ואחר שכן הוא רצוני שאין באלו המחברות שתים דומות ואין שם מחברת זולת אלו הנה אם כן מספר מחברות א'ב'ג'ד'ה'ו' המתחלפות בסדר לבד הוא כמו שטח ט' בח' ומש"ל | |
|
|
ובכאן התבאר שמספר מחברות נושאים מה המתחלפות בסדר לבד הוא כמספר המורכב ממספרים נמשכים מתחילים מן האחד מספרם כמספר הנושאים ההם וזה שמחברות שנים הם שנים וזה שוה למספר המורכב מאחד ושנים ומחברות השלשה הם כמו השטח ההוה משלשה בשנים וזה שוה למורכב א'ב'ג' ובזה התבאר לאין תכלית |
|
ס"ד מספר מחברות השנים המתחלפות אם כסדר אם בנושאיהם במספר מונח מנושאים מתחלפים הוא שוה לשטח ההוה מהמספר המונח במספר הנמשך לו לפניו |
| ויהיו הנושאים א'ב'ג'ד'ה' ויהיה מספרם מספר ז' והמספר הנמשך לז' לפניו הוא ח' ונאמר שמחברות השנים המתחלפים אם בסדר אם בנושאיהם מנושאי א'ב'ג'ד'ה' הם כמספר שטח ז' בה' | |
| המופת שכבר יושם א' ראשון ויתחבר עם כל אחד מהנשארים אשר מספרם מספר ח' א"ב המחברות המתחלפות בהיות א' ראשון הם כמספר ח' ובזה התבאר שכל אחד מאלו הנושאים יושם ראשון ותהיינה המחברות המתחדשות בהיותו ראשון כמספר ח' יהיה אם כן מספר אלו המתחברות בכללם כמו מספר ח' מוכה על מספר אלו הנושאים ואולם מספר אלו הנושאים הוא מספר ז' תהיינה א"כ אלו המחברות כמספר שטח ז' בח' ונאמר שאין באלו המחברות אשר מנינו שתי מתחברות דומות שלא תתחלפנה אם בסדר אם בנושאיהם וזה כי בהיות האחד מהם ראשון אין שם שתי מחברות דומות לפי שהנושאים אשר התחבר עמהם הם מתחלפים ואין ספק שלא תהיינה דומות אם לא יהיה הנושא הראשון אחד בשניהם כי לכל הפחות יתחלפו בסדר א"כ אין באלו המחברות שתים דומות ונאמר שאין שם מחברת זולת אלו אשר מנינו שאם היה אפשר זה נניח שתהיה המחברת ההוא ג'ה' ואולם ג' התחבר עם כל אחד מהנשארים ואחד מהנשארים הוא ה' אם כן אחת המחברות אשר מנינו היא ג'ה' אם כן אין שם מחברת זולת אלו אשר מנינו וכבר התבאר שאין באלו המחברות שתי מחברות דומות א"כ מספר אלו המחברות הוא כמו מספר שטח ז' בח' ומש"ל | |
|
ס"ה כאשר היה מספר מונח מנושאים מתחלפים והיה מספר מחברות מספר מונח שני מאותם הנושאים מתחלף למספר המונח הראשון וקטן ממנו המתחלפות אם בסדר אם בנושאיהם מספר מונח שלישי הנה מספר מחברות המספר הנמשך אחר המונח השני מאלו הנושאים המתחלפות אם בסדר אם בנושאיהם הם כמספר השטח ההוה מהמספר המונח השלישי ביתרון המספר המונח הראשון על המספר השני |
| ויהיו הנושאים א'ב'ג'ד'ה'ו'ז' ויהיה מספר הנושאים האלה מספר ח' ויהיה מספר ט' מתחלף למספר ח' וקטן ממנו ויהיו מחברות מספר ט' מאלו הנושאים המתחלפות אם בסדר אם בנושאיהם כמספר ל' ויהיה מ' נמשך אחר ט' והיה יתרון ח' על ט' מספר ג' ונאמר שמחברות מספר מ' מאלו הנושאים המתחלפות אם בסדר אם בנושאיהם הם כמספר שטח ל' בג' | |
| המופת שאנחנו נשים אחת ממחברות מספר ט' מאלו הנושאים מחברת א'ב'ג' והנה הנושאים הנשארים הם ד'ה'ו'ז' ומספרם כמספר ג' הנה כבר יושם כל אחד מנושאי ד'ה'ו'ז' הנשארים ראשון עם מחברת א'ב'ג' ותהיינה המחברות מתחלפות ויהיה מספר נושאי המחברת מספר מ' לפי שכבר נוסף על מספר נושאי המחברת הראשונה נושא אחד ולפי שהיה מספר ד'ה'ו'ז' כמו מספר ג' תהיינה המחברות המתחדשות ממחברת א'ב'ג' כמספר ג' ובזה התבאר שמספר המחברות המתחדשות עם כל מחברת ממחברות ט' מאלו הנושאים המתחלפות אם בסדר אם בנושאיהם הם כמספר ג' ולזה יהיה מספר אלו המחברות בכללם רצוני מספר מחברות מ' מאלו הנושאים כמו מספר ג' מוכה על מספר מחברות ט' מאלו הנושאים אבל מספר מחברות ט' מאלו הנושאים הוא ל' א"כ מחברות מ' מאלו הנושאים כמו מספר שטח ג' בל' ונאמר שאין בכל אלו המחברות שמנינו שתי מחברות דומות וזה שהמחברת האחת כבר חוברו עמה נושאים מתחלפים כפעם בפעם ולזה יחויב שתהיינה המחברות ההם מתחלפות ואין ספק שהמחברות המתחלפות לא תהיינה דומות עם איזה נושא שיחוברו הנה אם כן אין באלו המחברות שתי מחברות דומות ונאמר שאין שם מחברת זולת אלו אשר מנינו שאם היה אפשר תהיה המחברת ההיא מחברת ו'ד'ב'ז' אבל מחברת ד'ב'ז' כבר הושם כל אחד מהנושאים הנשארים ראשון עמה ואחד מהנושאים ההם הוא ו' אם כן מחברת ו'ד'ב'ז' היא אחת מהמחברות אשר מנינו ואחר שאין שם שתי מחברות דומות באלו המחברות שמנינו ואין שם מחברת זולת אלו הנה אם כן מחברות מ' מאלו הנושאים המתחלפות אם בסדר אם בנושאיהם הוא כמספר שטח ג' בל' ומש"ל | |
| ובכאן התבאר שמחברות מספר מונח ראשון ממספר מונח שני מנושאים מתחלפים המתחלפות אם בסדר אם בנושאיהם הוא שוה למספר המורכב ממספרים נמשכים מספרם כמו המספר המונח הראשון | |
| ויהיה האחרון המספר השני ויהיה מספר הנושאים מספר ז' ויהיו מספרי א'ב'ג'ד'ה'ו'ז' נמשכים ומתחילין מן האחד והוא מבואר שמחברות השנים מהם הוא כמספר שטח ו' בז' ואולם המספרים מספרם שנים והם נמשכים והאחרון מהם הוא ז' ומחברות השלשה מהם הוא כמו השטח ההוה מה' בשטח ו' בז' לפי שיתרון ז' על שנים הוא ה' וזה שוה למורכב ה'ו'ז' ואלו המספרים מספרם שלשה גם כן והם נמשכים והאחרון מהם הוא ז' ובזה התבאר שמספר מחברות הארבעה מהם הוא שוה למורכב ד'ה'ו'ז' ובזה התבאר באיזה מספר שיהיה | |
|
ס"ו כאשר היה מספר מונח מנושאים מתחלפים והיו מחברות מספר מונח שני מאלו הנושאים המתחלפות בנושאיהם כמו מספר מונח שלישי והיו מחברות המספר המונח השני מנושאים מתחלפים בסדר לבד כמו מספר מונח רביעי הנה מחברות המספר השני מאלו הנושאים המתחלפים אשר מספרם המספר המונח הראשון המתחלפות אם בסדר אם בנושאיהם הם כמספר השטח ההוה מהמספר המונח השלישי במספר המונח הרביעי |
| ויהיו הנושאים ההם נושאי א'ב'ג'ד'ה'ו' והיה מספרם ז' והיו מחברות מספר ח' מהם המתחלפות בנושאיהם כמו מספר ט' והיו מחברות הנושאים המתחלפים אשר מספרם ח' המתחלפות בסדר לבד כמו מספר ל' ואומר שמחברות מספר ח' מנושאי א'ב'ג'ד'ה'ו' המתחלפות אם בסדר אם בנושאיהם הם כמספר שטח ט' בל' | |
| המופת שאנחנו נשים אחת ממחברות ח' מאלו ז' הנושאים המתחלפות בנושאיהם מחברת ב'ג'ד' ויתחדשו ממנה מחברות מתחלפות בסדר לבד כמו מספר ל' ובזה התבאר שמספר המחברות המתחלפות בסדר המתחדשות מכל מחברת ממחברות ח' מאלו הנושאים המתחלפות בנושאיהם הוא כמו מספר ל' א"כ מספר אלו המחברות בכללם הם כמספר מחברות ח' מאלו הנושאים המתחלפות בנושאיהם מוכה על ל' ואולם מספרם הוא ט' אם כן מספר אלו המחברות בכללם הוא כמספר שטח ט' בל' ונאמר שאין באלו המחברות שמנינו שתים דומות לפי שבהיות הנושאים אחרים כבר התחלפו המחברות בסדר והיה מספרם מספר ל' לפי מה שהנחנו ואין ספק שבהיות הנושאים מתחלפים לא תהיינה המחברות דומות ונאמר שאין שם מחברת זולת אלו שמנינו שאם היה אפשר תהיה המחברת ההיא ו'ד'ב' אבל כל נושאי ב'ד'ו' התחברו בכל מיני סדורם ואחד ממיני סדורם הוא ו'ד'ב' א"כ מחברות ו'ד'ב' היא אחת מהמחברות אשר מנינו א"כ אין שם מחברת זולת אלו ובהיות הענין כן רצוני שאין באלו המחברות אשר מנינו שתי מחברות דומות ואין שם מחברת זולת אלו אם כן מספר מחברות ח' המתחלפות אם בסדר אם בנושאיהם מנושאי א'ב'ג'ד'ה'ו' הוא כמו מספר שטח ט' בל' ומש"ל | |
|
ס"ז כאשר היה מספר מונח מנושאים מתחלפים והיה מספר מחברות מספר מונח שני המתחלפות אם בסדר אם בנושאיהם כמו מספר מונח שלישי והיו מחברות המספר המונח השני מנושאים מתחלפים המתחלפות בסדר לבד מספר מונח רביעי הנה מספר מחברות המספר המונח השני ממספר הנושאים המונח המתחלפות בנושאיהם הוא כמספר אחדי מה שימנה המונח הרביעי המונח השלישי |
| ויהיו הנושאים המתחלפים נושאי א' ב' ג' ד' ה' ויהיה מספרם מספר ז' ותהיינה מחברות ה' מאלו הנושאים המתחלפות אם בסדר אם בנושאיהם מספר ט' ותהיינה מחברות הנושאים אשר מספרם ח' המתחלפות בסדר לבד כמו מספר ל' ונאמר שמספר ט' ימנהו ל' במספר אחדי מחברות ח' מנושאי א'ב'ג'ד'ה' המתחלפות בנושאיהם | |
| המופת שאנחנו נשים מחברות ח' מאלו הנושאים המתחלפות בנושאיהם כמו מספר מ' ואולם מחברות הנושאים אשר מספרם ח' המתחלפות בסדר לבד הם כמספר ל' והנה מחברות ח' מאלו הנושאים המתחלפות אם בסדר אם בנושאיהם הם כמו מספר ט' א"כ מספר ט' שוה לשטח ל' במ' ולזה ט' ימנהו ל' כמספר אחדי מ' והוא מספר מחברות ח' מאלו לנושאים המתחלפות בנושאיהם ומש"ל | |
|
ס"ח כאשר היה מספר מונח מנושאים מתחלפים והיה מספר מחברות מספר מונח שני מאלו הנושאים המתחלפים בנושאיהם כמו מספר מונח שלישי והיה יתרון המספר המונח הראשון על המספר המונח השני מספר מונח רביעי הנה מחברות המספר המונח הרביעי המתחלפות בנושאיהם הם כמו המספר המונח השלישי |
| ויהיו הנושאים המתחלפים נושאי א'ב'ג'ד'ה'ו'ז' והיה מספרם מספר ח' והיו מחברות מספר ט' מאלו הנושאים המתחלפות בנושאיהם מספר ל' והיה יתרון ח' על ט' מספר מ' ואומר שמחברות מספר מ' מאלו הנושאים המתחלפות בנושאיהם הם ג"כ כמו מספר ל' | |
| ונבאר תחלה שכאשר היו שני מחברות מתחלפות מאלו הנושאים שמחברות שאריתם מאלו הנושאים מתחלפות בנושאיהן גם כן | |
| וזה שאנחנו נשים מחברות א'ב'ג'ד' א'ג'ד'ה' מאלו הנושאים מתחלפות בנושאיהן ואולם שארית מחברות א'ב'ג'ד' מאלו הנושאים היא מחברת ה'ו'ז' ושארית מחברת א'ג'ד'ה' היא מחברת ב'ו'ז' ונאמר שמחברות ה'ו'ז' ב'ו'ז' מתחלפות בנושאיהן וזה שאם היה אפשר זולת זה יהיה ה' הוא ב' ואם היה הענין כן לא תהיינה מחברות א'ב'ג'ד' א'ג'ד'ה' מתחלפות בנושאיהן וכבר הונחו מתחלפות זה שקר אם כן כבר יחויב שתהיינה מחברות ה'ו'ז' ב'ו'ז' מתחלפות בנושאיהן | |
| ובזה התבאר ששארית כל שתי מחברות מתחלפות מהם הם מתחלפות | |
| וכאשר התישב זה הנה נבאר שמחברות מספר מ' מאלו הנושאים המתחלפות בנושאיהן הם גם כן כמו מספר ל' וזה שאנחנו נקח לכל מחברות מספר ט' מאלו הנושאים מחברת שארית הנושאים שהוא כמו מספר מ' רצוני שארית הנושאים אבל המחברות הראשונות מתחלפות בנושאיהן הנה מחברות שאריתן מתחלפות בנושאיהן ולפי שלקחנו לכל מחברת ט' מאלו הנושאים מחברת שאריתה הנה מספר המחברות המתחדשות מהשאריות הוא כמספר המחברות הראשונות ואולם מחברות ט' מאלו הנושאים המתחלפות בנושאיהן הם כמו מספר ל' אם כן מחברות השאריות שהם מחברות מ' מאלו הנושאים הם כמו מספר ל' גם כן | |
| והוא מבואר שכל מחברת השאריות מתחלפות ונאמר שאין שם מחברת זולת אלו אשר מנינו ממספר מ' מאלו הנושאים שאם היה אפשר תהיה המחברת ההיא ג'ה'ז' ונקח שארית הנושאים והוא א' ב' ד' ו' אבל א' ב' ד' ו' היא אחת ממחברות ט' מאלו הנושאים וכבר לקחנו לכל מחברת מהם את שאריתה ושארית זאת המחברת מחברת נ'ה'ז' אם כן מחברת ג'ה'ז' היא אחת מהמחברות הנמנות וכאשר היה זה כן רצוני שאין שם מחברת זולת אלו אשר מנינו ושכל המחברות אשר מנינו הם מתלפות בנושאיהן א"כ מחברות מ' מאלו הנושאים המתחלפות הוא מספר ל' והוא מה שרצינו לבאר | |
| וכבר התבאר זה במופת אחר וזה שאנחנו נניח שיהיה מספר הנושאים מספר ח' ויהיו המספרים הנמשכים עד ח' מספרי א'ב'ג'ד'ה'ו'ז'ח' ונאמר שמחברות מספר מה מאלו הנושאים המתחלפות בנושאיהן כמספר מחברות שארית המספר הזה ממספר אלו הנושאים ויהיה המספר מספר ג' והיה יתרון ח' על ג' מספר ה' ואומר שמחברות ג' מאלו הנושאים המתחלפות בנושאיהן הם כמספר מחברות ה' מאלו הנושאים המתחלפות בנושאיהן וזה שמחברות מספר ג' מאלו הנושאים כמספר מה שימנה מורכב א'ב'ג' מורכב ו'ז'ח' ומחברות מספר ה' מאלו הנושאים הם כמספר מה שימנה מורכב אב'ג'ד'ה' מורבב ד'ה'ו'ז'ח' ואומר שמורכב א'ב'ג'ד'ה' ימנה מורכב ד'ה'ו'ז'ח' כמספר מה שימנה מורכב א'ב'ג' מורכב ו'ז'ח' וזה שמורכב א'ב'ג'ד'ה' הוא שוה לשטח ההוה ממורכב ד'ה' במורכב א'ב'ג' ומורכב ד'ה'ו'ז'ח' הוא שוה לשטח ההוה ממורכב ד'ה' במורכב ו'ז'ח' הנה ד'ה' הוכו בו שני מורכבי א'ב'ג' ו'ז'ח' והיה מזה מורכב א'ב'ג'ד'ה' ד'ה'ו'ז'ה' אם כן יחס מורכב א'ב'ג'ד'ה' אל מורכב ד'ה'ו'ז'ח' הוא כמו יחס מורכב א'ב'ג' אל מורכב ו'ז'ח' א"כ מורכב א'ב'ג'ד'ה' ימנה מורכב ד'ה'ו'ז'ח' כשיעור מה שימנה מורכב א'ב'ג' מורכב ו'ז'ח' ולזה יהיה מספר מחברות ג' המתחלפות בנושאיהן מאלו הנושאים שוה למספר מחברות ה' המתלפות בנושאיהם מאלו הנושאים | |
| ובזה התבאר שמחברת איזה מספר שיהיה ממספר מונח מנושאים מתחלפים המתחלפות בנושאיהן שוה למספר מחברות שארית המספר המונח מנושאים מהנושאים ההם ומש"ל | |
| ובכאן נשלם המאמר הראשון תהלה ל' יתברך |
Section Two |
המאמר השני | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Introduction to Section Two |
הצעת המאמר | ||||||||||||||||||||||
|
דע כי החכמים המשילו הש׳ יתעלה בעולם השכלים הנפרדים לאחד במספר ואם הוא מקרה | ||||||||||||||||||||||
|
לפי שיסוד כל המספר הוא אחד והוא עלת מציאותם והוא ממציאם והוא עם כלם ואיננו ממנינם | ||||||||||||||||||||||
|
כי הוא בעצמו איננו מספר כי אם בהתחלקו ואז איננו אחד | ||||||||||||||||||||||
|
אם ידומה העדרו יעדרו כלם ואם ידומה העדרם לא יעדר | ||||||||||||||||||||||
|
ואין לו מצד המספר קצה ראשון ולא קצה אחרון עם היות לכל המספרים קצה ראשון וקצה אחרון בפנים מה ואם יתואר לאחד קצה מצד המספר לא יהיה זה כי אם בהחלקו ואז איננו אחד | ||||||||||||||||||||||
|
ואמרנו מצד המספר כי מצד היותו קו או שטח או גשם יש לו קצות והם בקו הנקודות ובשטח הקוים ובגשם השטחים המקיפים בו אמנם אין זה לו מצד המספר כי הקו לא יתחלק לנקודות ולא יורכב מהם והשטח לא יתחלק לקוים ולא יורכב מהם | ||||||||||||||||||||||
|
הנה כל המספרים אב אחד להם ממנו יצאו אליו ישובו | ||||||||||||||||||||||
Numeration |
|||||||||||||||||||||||
| The resemblance of the ranks to the rank of units | |||||||||||||||||||||||
|
כי כאשר יתוספו האחדים עד עשרה ישוב עשרה להיות אחד ויהיו עשרים כשנים ושלשים כשלש וארבעים כארבעה | ||||||||||||||||||||||
|
וכזה ימשך הענין עד שיגיע למאה ויהיה הוא אחד ומאתים כשנים ושלש מאות כשלשה | ||||||||||||||||||||||
|
וכן ימשך עד שיגיע לאלף והוא ישוב להיות אחד וככה עד אין קץ | ||||||||||||||||||||||
| הנה התב׳ בזה שכל המספרים כלו אל תשעה | |||||||||||||||||||||||
| The names of the ranks | |||||||||||||||||||||||
|
והנה האחד ומה שימשך אליו מן האחדים עד תשעה יקרא המעלה הראשונה | ||||||||||||||||||||||
|
והעשרה ומה שימשוך עליו מן העשיריות עד תשעים יקרא המעלה השניה | ||||||||||||||||||||||
|
והמאה ומה שימשך אליו מן המאות עד תשע מאות יקרא המעלה השלישית | ||||||||||||||||||||||
|
והאלף ומה שימשך אליו מן האלפים יקרא המעלה הרביעית | ||||||||||||||||||||||
|
ובזה הדרך ימשכו אחדי המעלות מתיחסים עד אין קץ רצוני שכל אחד מהם יחסו אל אחד מהמעלה שלפניו עשרה | ||||||||||||||||||||||
|
ואמרנו עד אין קץ לפי שהמספר יתוסף אל מה שיתוסף רצוני שכל מה שתוסיף עליו תוכל להוסיף עוד לא שיהיה שם מספר אין תכלית לו כי מן המבואר באיזה מספר שיהיה שיש לו תכלית ותכליתו הוא האחד אשר בו ישלם | ||||||||||||||||||||||
|
סוף דבר אמרנו במספר מה שאין לו תכלית מבואר בנפש המנעו כי אמתת המספר ומהותו היא להודיע תכלית חלקי מה שיקיף בו | ||||||||||||||||||||||
|
ועוד כי כל מספר הוא אם זוג ואם נפרד בהכרח וזה תכליתו | ||||||||||||||||||||||
|
על כן לא יהיה הענין בהפך רצוני שיתחלק אל מה שיתחלק תמיד כמו שיאמר זה בקו כי היה מן המחויב שנגיע לאחד ושם נעמוד | ||||||||||||||||||||||
|
ואולם קרה לאחד המספרי שיתחלק אל מה שיתחלק מצד הנושא | ||||||||||||||||||||||
| the formation of the sexagesimal fractions | כמו שיעשו חכמי התכונה בבואם לדקדק חשבון מה | ||||||||||||||||||||||
|
יחלקו האחד לששים ויקראו שברים ראשונים | ||||||||||||||||||||||
|
וכל אחד מהשברים ההם יחלקו לששים ויקראו שניים | ||||||||||||||||||||||
|
וכל אחד מהשניים יחלקו לששים ויקראו שלישיים | ||||||||||||||||||||||
| ובזה הדרך ימשכו אלו השברים מתיחסים עד אין קץ ויסודם ר"ל התחלתם היא המעלה הראשונה רצוני לו׳ האחד ממנה | |||||||||||||||||||||||
| המספר הדרוש הוא באחד משני דרכים אם במחברת אם במגרעת ומה שיהיה ממנה בזולת אלו הוא הנודע בעצמו | |||||||||||||||||||||||
|
ואשר במחברת הם בשני דרכים | ||||||||||||||||||||||
|
אם שנחבר מספרים דומים | ||||||||||||||||||||||
|
אם בלתי דומים | ||||||||||||||||||||||
|
ואשר בחבור מספרים בלתי דומים הם בשלשה דרכים | ||||||||||||||||||||||
|
אם שיתחלפו בכמותם | ||||||||||||||||||||||
|
אם שיתחלפו בנושאיהם וישתתפו בכמותם | ||||||||||||||||||||||
|
אם שישתתפו בכמותם ובנושאיהם ולא יתחלפו כי אם בסדר לבד | ||||||||||||||||||||||
|
ואשר יתחלפו בכמותם הם בשני דרכים | ||||||||||||||||||||||
|
אם שיהיו המספרים או המספר שנוסיף ידועים | ||||||||||||||||||||||
|
או בלתי ידועים | ||||||||||||||||||||||
|
ואשר הם בלתי ידועים הם בשני דרכים | ||||||||||||||||||||||
|
אם שיתוספו בשיעור שוה רמוז אליו ויהיה זה כשיהיו נמשכים | ||||||||||||||||||||||
|
אם שיתוספו בשיעור בלתי רמוז אליו אבל יהיו מהיחסים רצ׳ שיהיה יחס זה אל זה כיחס זה אל זה | ||||||||||||||||||||||
|
ואשר במגרעת בשני דרכים | ||||||||||||||||||||||
|
אם שיגרע מספר או מספרים ממספר | ||||||||||||||||||||||
|
אם שנחלק מספר על מספר | ||||||||||||||||||||||
| ואשר הוא בחלוק מספר על מספר הוא בשני דרכים אם שיהיה המספר הנחלק עליו ידוע אם בלתי ידוע כהוצאת שרש המרובעים והמעוקבים | |||||||||||||||||||||||
| אלו הם החלקים הפשוטים אשר תפשטם החלקה | |||||||||||||||||||||||
| וכבר תהיה שם מלאכה ישתמשו בה ברוב אלו המינים או בכללם והוא הוצאת המספר אשר ערכו למספר מה כערך מספר מונח על מספר מונח ומה שידמה לזה מהוצאת הנעלם מהידוע בזה האופן | |||||||||||||||||||||||
| ואנחנו בע"ה נבאר ענינינו אלו המלאכות והדרכים אשר בהם יושג הדרוש בזה המאמר וחלקנו זה המאמר לפי זאת החקירה לששה שערים | |||||||||||||||||||||||
| השער הראשון בהוסיף מספר או מספרים ידועים על מספר ובגרוע מספר או מספרים ידועים ממספר | |||||||||||||||||||||||
| השער השני בחבור מספרים דומים | |||||||||||||||||||||||
| השער השלישי בחבור מספרים נמשכים או מתיחסים | |||||||||||||||||||||||
| השער הרביעי בחבור מספר מנושאים מה תתחלפנה המחברות בנושאיהן או בסדריהן לבד או בשניהם יחד | |||||||||||||||||||||||
| השער החמישי בחלק מספר על מספר היה שיהיה המספר שיתחלק עליו ידוע או בלתי ידוע | |||||||||||||||||||||||
| השער הששי בערכין | |||||||||||||||||||||||
Chapter One – Addition and Subtraction |
השער הראשון בחבור המספרים קצתם עם קצת ובמגרעת המספרים קצתם מקצת | ||||||||||||||||||||||
Addition |
|||||||||||||||||||||||
| כבר הת׳ כי כל המספרים יכלו אל תשעה ואחר שכן הוא הנה יהיה המספר אשר בתכלית מעלה אחת מן המעלות הוא תשעה | |||||||||||||||||||||||
| וחבור המספרים שלא יעברו תשעה קצת עם קצת היא הידיעה הראשונה לכל בעלי שכל | |||||||||||||||||||||||
| כאשר תרצה לחבר מספרים כמה שיהיה ראוי שתכתוב כל מספר ומספר מהם בטור אחד ותחלק הטורים לאבנים האבן הראשה תכתוב בה מה שבמספר ההוא מהמעלה הראשונה | |||||||||||||||||||||||
| ואם אין בו מהמעלה הראשונה מאומה תכתוב בה גלגל להורות שאין בזאת המעלה שום מספר והאבן השנית תכתוב בה מה שבמספר ההוא מהמעלה השנית | |||||||||||||||||||||||
| ואם אין בו מהמעלה מאומה תעשה בו גלגל והאבן השלישית תכתוב בה מה שבמספר ההוא מהמעלה השלישית | |||||||||||||||||||||||
| וכזה הדרך עד אין קץ ותעשה הטורים איש תחת אחיו והאבנים תהיינה אשה נגדה מכונות לכל הטורים וכאשר ישלם לך זה כתוב העולה בחברך אלו המספרים תחת הטורים ההם בטור אחד במקומות הראויות לו לפי מעלותיו | |||||||||||||||||||||||
| הדרך תלך בה בחבור אלו המספרים חבר מה שבכל הטורים באבן הראשה ואם עלה יותר מתשעה תעשה מהעשיריות אחדים בשנית כי כל אחד ממנה עשרה מאחדי המעלה הראשונה והנשאר תכתוב בטור אשר תחת כל הטורים באבן הראשה גם כן והוא אשר נקראהו טור העולה אחר כן תשוב לחבר מה שבאבן השנית בכל הטורים ואם עולה יותר מתשעה תעשה מהעשיריות אחדים בשלישית והנשאר תכתוב באבן השנית בטור העולה אחר כך תשוב לחבר מה שבאבן השלישית בכל הטורים ותכתוב העולה בדרך שזכרנו בטור העולה וככה עד כלות כל המספרים שבכל המעלות וכאשר ישלם זה הוא מבואר שהעולה הוא המקובץ מכל המספרים כי כבר חוברו חלקי זה בכללם עם חלקי זה בכללם וכלל הדבר שוה לכל חלקיו | |||||||||||||||||||||||
| דמיון תרצה לחבר ר״ט עם שלשת אלפים שמנים ותשע ועם ז׳ אלפים ושש מאות ושלשים ותשע | |||||||||||||||||||||||
ונכתבם בג' טורים בזו הצורה
| |||||||||||||||||||||||
| הטור הראשון ט׳ בראשונה גלגל בשניה ב׳ בשלישית הטור השני ט׳ בראשונה ח׳ בשניה גלגל בשלישית ג׳ ברביעית הטור השלישי ט׳ בראשונה ג׳ בשניה ו׳ בשלישית ז׳ ברביעית חברנו מה שבראשונה בכל הטורים ועלה כ"ז ותכתוב בטור העולה ז׳ בראשונה והכ' תהיינה ב׳ בשניה חברנו מה שבשניה בכל הטורים ועלה י"א וב׳ שנשארו לנו שם והנה י"ג ותכתוב בטור העולה ג׳ בשניה והעשרה תהיינה א׳ בשלישית חברנו מה שבאבן השלישית בכל הטורים ועלה ח׳ וא׳ שנשאר לנו שם והנה ט׳ ותכתבם בטור העולה באבן השלישית חברנו מה שבמעלה הרביעית בכל הטורים ועלה עשרה על כן תכתוב גלגל בטור העולה והעשרה תכתוב אחד בחמישית בטור העולה ופה נשלם חבור חלקי אלו המספרים קצתם עם קצת והנה העולה בחברך אלו המספרים היא רבוא ותשע מאות ול"ז והקש על זה | |||||||||||||||||||||||
| ואם תרצה לחבר שברים עם שברים ויהיו השברים משברי חכמת התכונה כתוב השברים מהמספר האחד בטור אחד כפי מדרגתם רצוני שאם הראשונים תכתבם באבן האחרונה שבטור הפך מה שעשית בשלמים ואם אין ראשונים תכתוב שם גלגל והשניים תכתוב בשנית לאחרונה לאחור והשלישיים בשלישית לאחור לאחרונה וכן עד השלימך לכתוב כל השברים שבמספר האחד וכן תעשה לשברי כל המספרים תכתבם איש על מקומו בזה הדרך והיה זה כן כי מנהג מדרגת השברים הם בהפך מדרגת השלמים כי מדרגת השלמים ימצא בהם הקצה האחד לבד והיא המדרגה היותר מעטה ובשברים ימצא הענין בהפך כי הקצה הנמצא בהם היא היותר גדולה ולפי שעל הסדר הקודם היתה המדרגה היותר גדולה אחר היותר מעטה והיו הראשונים מהמדרגה היותר גדולה במוחלט ראוי שיהיו הראשונים במדרגה האחרונה מהשברים במוחלט וכאשר ישלם לך זה חבר כל מה שנמצא בכל הטורים במדרגת השברים היותר דקים ואם עולה יותר מששים גרעם מהם ומהששים תעשה אחד במדרגה השניה לה והנשאר כתוב במדרגה ההיא בטור העולה וכן עד חברך כל השברים ובחברך הראשונים עם עלה יותר מששים או ששים תעשה מהששים אחד שלם בטור העולה | |||||||||||||||||||||||
| דמיון נרצה לחבר נ"ו שניים עם כ׳ ראשונים ומ' שניים ול׳ שלישיים ועם מ"ו ראשונים כ"ז שניים נ"ה שלישיים | |||||||||||||||||||||||
ותכתוב בג׳ טורים בזאת הצורה
| |||||||||||||||||||||||
| הטור הראשון גלגל באחרונה נ"ו בשנייה לה לאחור הטור השני כ׳ באחרונה מ׳ בשניה לה לאחור ל׳ בשלישית הטור השלישי מ"ו באחרונה כ״ז בשנית לה נ"ה בשלישית טור העולה | |||||||||||||||||||||||
| והנה המדרגה אשר שבריה יותר דקים באלה הטורים היא השלישית חברנו כל מה שבכל אלו הטורים בשלישית ועלה פ"ה נגרע מהם ס׳ ונשארו כ"ה ותכתבם בטור העולה בשלישית והס׳ שגרענו יהיה א׳ בשנית חברנו מה שבכל אלו הטורים בשנית עם הא׳ שנשאר לנו שם ועלה קכ״ד ונכתוב ד׳ בטור העולה והק"ב תהיינה ב׳ באחרונה חברנו מה שבכל אלו המורים באחרונה עם הב׳ שנשארו לנו שם והנה ס"ח ונכתוב ח׳ בטור העולה באחרונה והס׳ יהיו אחד שלם ונכתוב אחר האחרונה ונעשה שם רושם אחד יבדיל בין השלמים לשברים | |||||||||||||||||||||||
| והנה העולה הוא אחד שלם ה׳ ראשונים ד׳ שניים כ"ה שלישיים והקש על זה | |||||||||||||||||||||||
| ואם היו המספרים שבאת לחברם שלמים ושברים תכתוב תחלה השלמים בדרך שהראיתיך ותעשה רושם בין מעלת האחדים לשברים כדי שלא יתבלבל עליך ותכתוב קודם האחדים השברים הראשונים ולפני הראשונים השניים וכן מה שהגיעו הראשונים כמו שקדם וכאשר ישלם לך זה תחל לחבר מהשברים היותר דקים ותחבר השברים עם השברים והשלמים עם השלמים בדרך שזכרנו ותכתוב העולה בטור אחד תחת אלו הטורים במקומותיו | |||||||||||||||||||||||
| ואתן לך משל איך תכתוב הטור שבו שברים ושלמים | |||||||||||||||||||||||
| אם רצית לכתוב מאתים ושלשים שלמים ל״ז שניים מ"ד רביעיים מ"ה חמישיים | |||||||||||||||||||||||
| הנה השלמים יהיו גלגל בראשונה נ׳ בשניה ב׳ בשלישית ותעשה רושם בין הראשונה והשברים ותכתוב אחר הרושם קודם הראשונה מהשלמים גלגל לפי שאין בזה המספר ראשונים ובשניה לה לאחור תכתוב ל"ז שהם שניים ובשלישית לה לאחור תעשה גלגל לפי שאין בזה המספר שלישיים וברביעית לה לאחור תכתוב מ"ד ובחמישית לה לאחור תכתוב מ"ה כזאת הצורה
מ"ה מ"ד 0 ל"ז 0 | 0 ג ב | |||||||||||||||||||||||
| ואולם החבור בזה ידוע ממה שקדם | |||||||||||||||||||||||
Subtraction |
|||||||||||||||||||||||
| אם רצית לגרוע מספר ממספר כתוב המספר שממנו תגרע בטור אחד כפי מדרגותיו ותחתיו בטור האחר המספר שרצית לגרוע והנה תראה איזה מדרגה היא היותר דקה בכל הטורים ותחל לגרוע במה שמדרגה היותר דקה בטור העליון מה שכנגדה בטור התחתון והנשאר תכתוב בטור העולה במדרגה ההיא ואם לא היה די לגרוע אם היית בשברים הורד אחת מהמדרגה הבאה אחריה אליה יהיו ששים בה ואם היית בשלמים הורד אחת מהמדרגה הבאה אחריה אליה יהיו עשרה בה ואחר תוכל לגרוע מה שתרצה וכן תעשה עד שיגרע כל הטור התחתון מהטור העליון והנשאר תכתוב כפעם בפעם בטור העולה במקומותיו וכאשר ישלם זה הוא מבואר שכבר גרעת המספר התחתון בכללו מהמספר העליון כי חלקי הדבר בכללם שוים לכל הדבר וראוי שיהיה בטור שתגרע ממנו רב הכמות מבטור השני כי אי אפשר לגרוע הרב מהמועט | |||||||||||||||||||||||
| דמיון נרצה לגרוע מאתים ושש וחמשים ראשונים ל״ז שלישיים מל״א אלפים ושמנים ומ"ו שניים ל״ה שלישיים מ"ז רביעיים נ"ג ששיים | |||||||||||||||||||||||
| והנה כתבנו המספר שממנו נגרע בטור העליון והמספר שרצינו לגרוע
בטור התחתון במקומותיהם ועשינו רושם בין השלמים לשברים. והנה המדרגה היותר דקה היו מה ט ז י 0 ששיים ומה שכננדה בטור העליון נג 0 מז לה מו 0 | 0 ח 0 א ג הוא נ״ג ששיים ונגרע מהם מה לז 0 נ | ו 0 ב שכנגדם בטור התחתון ואין שם בטור נג 0 מז נח מה י | ג ז ח 0 ג התחתון דבר על כן תכתוב נ״ג בטור העולה במדרגת הששיים נשוב לגרוע מהגלגל הבא אחר נ"ג מה שכנגדו בטור התחתון ואין שם בטור התחתון דבר על כן תכתוב גלגל בטור העולה במדרגת החמשיים נשיב לגרוע ממ״ז מה שכנגדו בטור התחתון ואין שם דבר ולכן תכתוב מ"ז בטור העולה במדרגת הרביעיים נשוב לגרוע מל״ה שבטור העליון מה שכנגדו בטור התחתון והנה כנגדו ל״ז ולא נוכל לגרוע מל״ה ל״ז על כן נקח אחד ממדרגה הבאה אחר ל"ה ויהיה ששים בה נחברם עם ל"ה ויהיו צ"ח נגרע מהם ל"ז נשארו נ״ח וכתבנום בטור העולה במדרגת השלישיים ולזה נשארו במדרגה הבאה אחריה מ"ה נגרע מהם מה שכנגדם בטור התחתון ואין שם דבר ולזה תכתוב מ"ה בטור העולה במדרגת השניים נשוב לגרע מהגלגל מה שכנגדו בטור התחתון והנה כנגדו ג׳ ולא נוכל לגרוע מגלגל ג׳ וגם במדרגה הסמוכה לה מהשלמים אין מספר מה להוריד אליה ואולם בשלישית לה מספר והוא ח׳ ונוריד מהם אחד אל המעלה שלפניה ונכתוב על הח׳ ז׳ והאחד שנוריד יהיה עשרה בראשונה נוריד מהם א׳ אל מעלת הראשונים וישארו ט׳ בראשונה ונכתבם על הגלגל והאחד שהורדנו יהיה ששים במדרגת הראשונים נגרע מהם ג׳ וישארו י' ונכתבם בטור העולה במדרגת הראשונים נשוב לגרוע מט׳ מה שבעדה בטור התחתון שהוא ו׳ ונשארו ג׳ ונכתבם בטור העולה במדרגת האחדים נשוב לגרוע מז׳ מה שכנגדו בטור התחתון וישארו ז׳ כי אין בו דבר ונכתבם בטור העולה במדרגה השנית נשוב לגרוע מגלגל מה שכנגדו בטור התחתון והיה כנגדו ב׳ ולא נוכל לגרוע ב׳ מגלגל ובמעלה השנית לה א׳ ונורידנו אליו יהיה עשרה בה ונכתוב על הא' גלגל ונגרע מי' ב' ונשארו ח׳ ונכתבם בטור העולה במדרגה השלישית נשוב לגרוע מגלגל מה שכנגדו בטור התחתון ואין שם דבר ונכתוב גלגל בטור העולה במדרגה הרביעית נשוב לגרוע מג' מה שכנגדו בטור התחתון ואין שם בו דבר ולזה נכתוב ג׳ בטור העולה במעלה החמשית והנה העולה הוא שלשים אלף ושמנה מאות ושבעים ושלשה שלמים י׳ ראשונים מ״ה שניים נ"ח שלישיים מ״ז רביעיים נ״ג ששיים והקש על זה ופעמים יבואך החשבון בחכמת התכונה לגרוע מספר רב ממספר מעט וזה במלאכות הככבים ואז תוסיף מעלת הגלגל שהם שלש מאות וששים על המספר המעט שבאת לגרוע ממנו ותוכל לגרוע מה שתרצה לפי שאין להם מספר משלמים במקומות הככבים מוסיף על שלש מאות וששים כי כאשר יהיה להם יותר משלש מאות וששים ישליכו ויקחו הנשאר ובזה יבואך החשבון בחשבון מולד הלבנה המתפשט בהמון לגרוע ממספר מעט מספר רב ואז תוסיף על המספר המעט ז׳ ימים ותוכל לגרוע מה שתרצה וסבת זה כי מחשבי המולדות כאשר יהיה להם מספר מוסיף על ז׳ ימים ישליכו ממנו ז׳ ימים ויקחו הנשאר והקש על זה | |||||||||||||||||||||||
Chapter Two – Multiplication |
השער השני בחבור מספרים דומים והוא הכאת מספר על מספר | ||||||||||||||||||||||
| כבר ידעת
כי כאשר היו ארבעה מספרים מתיחסים רצוני שיחס הראשון אל השני כיחס השלישי אל הרביעי הנה שטח הראשון ברביעי כמו שטח השני בשלישי ולזה יתבאר שהכאת אחד מהשנית באחד מהרביעית הוא אחד מהחמישית וזה שיחס אחד מהראשונה אל אחד מהשנית כיחס אחד מהרביעית אל אחד מהחמישית מעלה חמישית : מעלה רביעית = מעלה שנייה : מעלה ראשונה א״כ שטח אחד מהשנית באחד מהרביעית הוא כמו שטח אחד מהראשונה באחד מעלה חמישית · מעלה ראשונה = מעלה שנייה · מעלה רביעית מהחמשית אבל שטח אחד מהראשונה באחד מהחמשית הוא אחד מהחמשית לפי שהוא אחד מהחמשית פעם אחת אם כן שטח אחד מהשנית באחד מהרביעית הוא אחד מהחמשית ובזה התבאר ששטח אחד מהשלישית באחד מהרביעית הוא אחד מהששית לפי שביחס השוי יהיה יחס אחד מהראשונה אל אחד מהשלישית כיחס אחד מהרביעית אל אחד מהששית וכאשר תנהיג זה יבואר לך שכל אחד ממעלה אי זו שתהיה שיוכה על אחד ממעלה אי זו שתהיה הוא אחד מהמעלה אשר מרחקה מאחד המוכה לאחריה כמרחק מעלת האחד המכה מהראשונה וזה שוה למספר מעלת המכה והמוכה פחות אחד לפי שאחת מהמעלות תמנה שתי פעמים משל זה שיחס הראשונה אל הרביעית כיחס החמשית אל השמינית כי השמינית רביעית לחמשית בהמנות החמשית וכבר נמנית החמשית במספר מעלותיה אם כן החמשית נמנית שתי פעמים ולזה תחסר אחת ממספר מעלות המקובץ ואם הוכה מספר מה מאחדי מעלה מה על אחדי מספר מה מאחדי מעלה מה בזה בעצמו יתבאר שהעולה יושם במעלה אשר מרחקה מהמעלה המוכה לאחריה כמרחק המכה מהראשונה והמשל שיהיה לנו להכות ששה מהשלישית על שבעה מהשנית והוא מבואר שיחס אחד מהראשונה אל אחד מהשלישית כיחס אחד מהשנית אל אחד מהרביעית אבל יחס ששה מהראשונה אל ששה מהשלישית הוא כיחס אחד מהראשונה אל אחד מהשלישית לפי שהכפלים שוים ויחס שבעה מהשנית אל שבעה מהרביעית הוא כיחס אחד מהשנית אל אחד מהרביעית אם כן יחס ששה מהראשונה אל ששה מהשלישית כיחס שבעה מהשנית אל שבעה מהרביעית אם כן שטח ששה מהשלישית בשבעה מהשנית כמו שטח ששה מהראשונה בשבעה מהרביעית ואולם שטח אחד מהראשונה בשבעה מהרביעית הוא מהרביעית אם כן שטח ששה מהראשונה בשבעה מהרביעית הוא מאחדי הרביעית וזה כי הוא ששה דמיוני שבעה מהרביעית ובזה המופת בעינו יתבאר שהכאת שברים משברי חכמי התכונה בשברים הם מהמעלה אשר מרחקה מהמוכה לפניה כמרחק המכה ממעלת השלמים לפי שהמדרגות ההם הם מתיחסות גם כן ולזה יהיה העולה בהכאת מספר ממדרגת שברים על מספר ממדרגת שברים מהמדרגה אשר מספר מעלותיה כמספר המכה והמוכה מקובצים והסבה בזה שלא נמנית בשברים מדרגת האחדים אשר ממנה התחלתם אך התחלת מנין המעלות מהשברים הראשונים וזה מבואר מאד וכזה התבאר מזה שהעולה בהכאת האחדים מהמעלה הראשונה על שברים ממעלה מה הוא ממעלת השברים בעצמם וזה מה שרצינו להציע הנה יתבאר בו מה שרצה לבאר ואולם הכאת שברים בשברים או בשלמים הוא חלוק ע"ד האמת ולזה לא נבאר ענינו בזה השער. הדרך אשר תלך בה בהכאת מספר על מספר ראוי לך שתכתוב המכה בטור אחד כפי מעלותיו והמוכה בטור אחד תחתיו כפי מעלותיו גם כן ולהקל מעליך שים המספר אשר יותר מעט במעלות אחז בטור הראשון ואם הוא רב בכמות כי הכל הולך אל מקום אחד רצוני שהכאת האחד באחר כהכאת האחר בו וזה התבאר באקלידס אחר כן עשה טורים תחת אלו שני הטורים כמספר המעלות אשר יש בהם מספר בטור הראשון והם יהיו הטורים אשר תכתוב בהם העולה בהכאת אלו המספרים איש אל אחיו ואחר עשותך זה הכה המספר הראשון שבטור העליון על המספר הראשון שבטור התחתון והעולה תשים בראשון מטורי העולה במעלה הראויה לפי מה שקדם ולהקל מעליך שלא תצטרך לחשוב אנה תשים העולה כפעם בפעם הכה המספר הראשון שבטור העליון על מה שבמדרגה הראשונה שבטור התחתון וכתוב העולה בטור הראשון מטורי העולה במדרגת המכה תשוב להכותו על מה שבמדרגה במעלה השנית בטור התחתון ותכתוב העולה במעלה הנמשכת למעלה שהחילות לכתוב בה העולה וכזה תכה המספר הראשון שבטור העליון על כל מה שבמדרגות הטור התחתון ותכתוב העולה כפעם בפעם במעלה הנמשכת אחר המעלה אשר כתבת בה קודם זאת ההכאה אחר כן תשוב להכות המספר השני שבטור העליון על כל מה שבמדרגות הטור התחתון על הסדר ותחל לכתוב העולה במעלת המכה בטור השני מטורי העולה ואחר ימשכו מעלות הטור העולה על הסדר אחר כן תשוב להכות המספר השלישי שבטור העליון על כל מה שבמדרגות הטור התחתון על הסדר ותכתוב העולה על הסדר שקדם וכן עד כלות כל מספרי הטור העליון אחר כן תחבר כל מספרי טורי העולה ותכתוב העולה בטור אחד תחת טורי העולה והוא שטח המספר האחר בשני כי כבר הוכו כל חלקי זה בכללם על חלקי זה בכללם. דמיון נרצה בזאת הצורה להכות ז׳ אלפי אלפים ושלשים על מאה ושמנים אלף ושש מאות וארבעים והנה המספר אשר החזוק היותר מעט מהמעלות הוא ז׳ אלפי אלפים ושלשים ונכתבהו בטור העליון במקומותיו והמספר האחר כתבנו בטור אחר תחתיו והנה המספר הראשון שבטור העליון הוא ג׳ בשנית הכינו ג׳ על מה שבמדרגה הראשונה מהטור התחתון שהוא גלגל ועלה גלגל וכתבנוהו במעלה השנית בראשון שבטורי העולה הכינו ג׳ על מה שבמדרגה השנית מהטור התחתון שהוא ד׳ ועלה י"ב ונכתוב ב׳ במדרגה השלישית בטור העולה והעשרה יהיו אחד בשנית לה הכינו ג׳ על מה שבמדרגה השלישית מהטור התחתון שהוא ו׳ ועלה י״ח ואחד שנשאר לנו שם והנה י"ט ונכתוב ט׳ במדרגה הרביעית בטור העולה והעשרה יהיו אחד בשנית לה הכינו ג׳ על מה שבמדרגה הרביעית שהוא גלגל ועלה גלגל ואחד שנשאר לנו שם והנה א׳ וכתבנוהו בטור העולה אחר ט׳ הכינו ג׳ על מה שבמדרגה החמישית שהוא ח׳ ועלה ועלה כ"ד וכתבנו ד׳ אחר הא׳ והכ׳ יהיו שנים בשנית לה הכינו ג׳ על מה שבמדרגה הששית שהוא א׳ ועלה ג׳ וב׳ שנשארו לנו שם והנה ה׳ ונכתוב ה׳ אחר ד׳ בטור העולה ופה נשלמה הכאת ג׳ על כל מה שבמדרגות הטור התחתון. ונכה המספר הבא אחר הג' בטור העליון שהוא ז׳ על כל מה שבטור התחתון הכינו ז׳ על גלגל ועלה גלגל ונשימהו בטורי העולה בטור השני במעלה השביעית כנגד ז׳ במעלה השביעית הכינו ז׳ על ד׳ ועלה כ״ח ונכתוב ח׳ אחר הגלגל והכ' תהיינה ב׳ במעלה השנית לה הכינו ז׳ על ו׳ ועלה מ"ב וב׳ שנשארו לנו 0 ג 0 0 0 0 ז שם והנה מ"ד ונכתוב ד׳ אחר הח' 0 ד ו 0 ח א והמ׳ תהיינה ד׳ בשנית לה הכינו 0 0 ב ט א ד ה ז׳ על גלגל ועלה גלגל וד' שנשארו 0 ח ד ד ו ב א שם והנה ד׳ ונכתבם אחר הד' 0 0 ב ט א ד ה ח ד ד ו ב א הכינו ז׳ על ח' ועלה נ"ו ונכתוב ו׳ אחר הד׳ והג' תהיינה ה׳ בשנית לה הכינו ז' על א' ועלה ז׳ וה' שנשארו לנו שם והנה י"ב ונכתוב ב׳ אחר הו׳ והי' נעשו א׳ במעלה השנית לה ופה נשלמה הכאת כל מספרי הטור התחתון והנה העולה הוא גלגל בראשונה גלגל בשנית ב׳ בשלישית ט׳ ברביעית א׳ בחמשית ד׳ בששית ה׳ בשביעית ה׳ בשמינית ד׳ בתשיעית ד׳ בעשירית ו׳ באחד עשרה ב בשנים עשרה א׳ בשלש עשרה והקש על זה. ואם רצינו לדעת כמה יעלה מספר המרובע ההוה ממספר מונח נכתוב חישוב ריבוע המספר המספר אשר רצינו לדעת מרובעו בטור אחד ותחתיו תשוב ותכתבנו בטור אחר תחת הטור הזה והכה כל מספרי הטור העליון על כל מה שבמדרגות הטור השפל ויצא לך המבוקש ואם רצית לדעת כמה יעלה המספר המעוקב ההוה ממספר מונח חישוב מעוקב המספר תצטרך לעשות שתי תמונות ראשונה תכה המספר ההוא על עצמו ויצא לך מרובע המספר שרצית לדעת מעוקבו עוד תעשה תמונה אחרת ותכה המספר המונח שרצית לדעת מעוקבו על מרובעו שיצא לך והעולה הוא המבוקש. ולהקל מעליך אתן לך דרכים רבים לחשוב בהם הכאת מספר במספר קיצורי דרך בקלות כבר ידעת שהכאת מספר במעלה הראשונה במספר ממעלה הראשונה הוא קל המעשה וכן הכאת מספר נשבר רצוני מספר מה ממעלה ראשונה ושניה על מספר מעלה ראשונה ואם היה לך להכות מספר נשבר על מספר נשבר השלם המספר האחד מהם אל הצד אשר הוא היותר קרוב ואם הוספת על זה המספר להשלימו אל הכלל הקרוב גרע מהמספר האחר כשיעור מה שהוספת על המספר הראשון והנשאר הכה אותו על המספר השלם אשר בידך ושמור העולה ואם גרעת מזה המספר להשלימו הוסף על המספר האחר כשיעור מה שגרעת מזה המספר הראשון והנשאר בידך הכה אותו על המספר השלם אשר בידך ושמור העולה אחר כן ראה המספר הגדול אחר התוספות או אחר הגרעון כמה הוא מוסיף על המספר הקטן טרם התקון והתוספת ההוא ערוך על שיעור המספר שהוספת על אחד מהמספרים והעולה שמור והוא השמור השני וראה אחר כן מאי זה מספר שגרעת ואם גרעת מהמספר הגדול תגרע השמור השני מהשמור הראשון והנשאר בידך הוא המבוקש ואם הוספת על המספר הגדול הוסף השמור השני על השמור הראשון והוא המבוקש. ואתן לך איזה משלים נרצה להכות ל"ד על נ"ז השלמנו מספר נ״ז אל הכלל הקרוב ויהיה ס׳ ולפי שס׳ מוסיף על נ"ז שלשה נגרע מל"ד שלשה ויהיו ל"א ונכה ל"א על ס׳ יהיו אלף ושמנה מאות וששים והוא השמור הראשון ולפי שס׳ מוסיף על ל"ד כ"ו נערוך כ״ו על שלשה והנה ע״ח והוא השמור השני ולפי שהוספנו על המספר הגדול נוסיף השמור השני על השמור הראשון והוא אלף ותשע מאות ול"ח והוא המבוקש ובמשלנו זה אם הורדנו נ"ז אל הכלל שלמטה ממנו יהיה נ׳ הוספנו על ל"ד ז׳ והנה מ"א ערכנו מ"א על נ׳ והנה אלפים וחמשים והוא השמור הראשון ומפני שנ׳ מוסיף על ל"ד י"ו נערוך י"ו על ז׳ והנה קי״ב והוא השמור השני ולפי שגרענו מהמספר הגדול נגרע השמור השני מהשמור הראשון ונשאר אלף וט' מאות ול"ח והוא המבוקש וגם במשלנו זה אם הורדת ל״ד אל הכלל הקרוב אליו יהיה ל׳ הוספת על נ"ז ד׳ והנה ס"א ערכת ל׳ על ס"א והנה אלף ושמנה מאות ושלשים והוא השמור הראשון והנה יתרון ס"א על ל״ד הוא כ"ז ערכנו כ״ז על ד׳ והנה ק"ח והוא השמור השני ולפי שהוספת על המספר הגדול תוסיף השמור השני על השמור הראשון והנה אלף ותתקל"ח והוא המבוקש ואם העלית ל"ד אל מ׳ תגרע מנ״ז ו' והנה נ"א תערכם על מ׳ והנה אלפים וארבעים והוא השמור הראשון והנה יתרון נ"א על ל״ד הוא י"ז תערכם על ו׳ והנה ק״ב והוא השמור השני ולפי שגרעת מהמספר הגדול תגרע השמור השני מהשמור הראשון וישאר אלף ותתקל"ח והוא המבוקש ופעמים יצא לך לפי זה הדרך שיהיה לך להכות מספר על עצמו ואז יקל מאד זה הדרך משל זה שיהיה לך להכות מ"ג על נ"ז ואם תשלים מ"ג על נ׳ תחסר מנ"ז שיעור ההשלמה ויהיה נ׳ ויהיה לך להכות נ׳ על נ׳ ולחסר מהעולה מרובע ז׳ והנשאר הוא המבוקש וזה מבואר מאד ממה שקדם בראש המאמר הראשון מזה הספר והבן ותמצא. דרך אחרת בזה השלם המספר האחד אל הכלל הקרוב ועל העולה ערוך המספר האחר ושמור העולה גם ערוך המספר האחר על שיעור ההשלמה ושמור העולה והוא השמור השני ואם היתה ההשלמה לתוספת נגרע השמור השני מהשמור הראשית והנשאר הוא המבוקש ואם היתה ההשלמה למגרעת תוסיף השמור השני על השמור הראשון והעולה הוא המבוקש דמיון זה במשלנו הקודם השלמנו נ"ז אל הכלל הקרוב והנה ס׳ ערכנו ס׳ על ל"ד והנה אלפים וארבעים והוא השמור הראשון והנה שיעור ההשלמה הוא שלשה ערכנו שלשה על ל"ד והנה ק"ב והוא השמור השני ולפי שהשלמה היתה לתוספת נגרע השמור השני מהשמור הראשון ונשאר אלף ותתקל״ח והוא המבוקש וג"כ במשלנו זה אם השלמנו ל"ד אל הכלל הקרוב יהיו ל׳ ערכנו ל׳ על נ"ז ועולה אלף ת"ש והוא השמור הראשון והנה שיעור ההשלמה הוא ד׳ ערכנו ד׳ על נ״ז ועלה רכ"ח והוא השמור השני ולפי שההשלמה היתה למגרעת נוסיף השמור השני על השמור הראשון ויעלה אלף ותתקל"ח והוא המבוקש ואם תרצה לדעת מרובע מספר נשבר מונח הנה תשלים המספר אל הכלל הקרוב ושיעור ההשלמה תגרע מהמספר המונח והנשאר תכה על המספר המושלם והוסף על העולה מרובע מספר ההשלמה והנה המבוקש משל זה אם רצית לדעת מרובע מ"ז הנה הכלל הקרוב הוא נ׳ ומרחקו ממ"ז הוא שלשה תגרעם ממ״ז והנה מ״ד ערכת מ"ד על נ׳ והנה אלפים ומאתים והנה המרחק הוא שלשה שהוא תשעה והנה אלפים ור"ט והוא המבוקש. דרך לדעת בקלות מרובע מספר ממעלה אחת ראה יחס המספר אל יחס אחד ממעלה הנמשכת וקח כמו היחס ההוא מהמספר שרצית לדעת מרובעו וערכהו על אחת מהמעלה הנמשכת והוא המבוקש דמיון רצית לדעת כמה מרובע שלשים והנה יחס שלשים אל מאה שהוא אחד מהמעלה הנמשכת הוא שלש עשיריות קח שלש עשיריות שלשים והנה ט׳ ערכם על מאה והנה ט׳ מאות והוא המבוקש והיה זה כן לפי ששלשים אמצעי בין ט׳ ובין ק׳ ואם היה המספר שרצית לדעת מרובעו משתי מעלות נמשכות השלם המספר אל הכלל הקרוב ותדע מרובעו ושמור העולה אח"כ חבר המספר השלם אם המספר הנשבר וערכהו על שיעור ההשלמה והוא יהיה השמור השני ואם היתה ההשלמה לתוספת גרע השמור השני מהשמור הראשון ואם היתה ההשלמה לגרעון תוסיף השמור השני על השמור הראשון והעולה הוא המבוקש דמיון זה אם רצית לדעת מרובע שלשים ושלשה הנה תשלים המספר אל הכלל הקרוב והוא ל׳ ומרובע ל׳ הוא ט׳ מאות ושמור אח"ז תחבר שלשים עם שלשים ושלשה והנה ס״ג ערכנום על ג׳ שהוא שיעור ההשלמה והנה קס"ט והוא השמור השני ולפי שההשלמה היתה לגרעון נוסיף קפ"ט על השמור הראשון והנה אלף ופ"ט והוא הדרוש ואם השלמת ל״ג אל מ׳ במשלנו זה הנה היה מרובעו י״ו מאות ושמור ותחבר ל"ג עם מ׳ והנה ע"ג תערכם על ו׳ והנה תקי״א ולפי שההשלמה היתה לתוספת תגרע תקי״א מהשמור הראשון וישאר לך אלף ופ״ט והוא הדרוש והיה זה כן לפי שיתרון מרובע מ׳ על מרובע ל"ג הוא כמו שטח ז׳ במ׳ ושטח ז׳ בל"ג וזה שוה לשטח ז׳ בע"ג והקש. דרך אחרת קח שלישית המספר שרצית לדעת מרובעו קח מרובעו ושמור אח"כ העלהו אל המעלה הנמשכת ותגרע מהעולה השמור והנשאר הוא המבוקש דמיון רצינו לדעת מרובע ל"ג לקחנו שלישיתו והוא י"א ומרובעו קכ"א העלינו קכ״א אל המעלות הנמשכות והנה אלף ומאתים ועשר גרענו מהם קכ"א וישאר אלף ופ״ט והוא המבוקש והיה זה כן לפי שאלף ומאתים ועשר הוא עשרה דמיוני מספר קכ״א והנה יחס מרובע ל״ג אל מרובע י״א הוא יחס צלעו אל צלעו שנוי ביחס אבל יחס צלעו אל צלעו שנוי ביחס הוא יחס תשעה אל אחד א"כ מרובע ל"ג הוא תשעה דמיוני מרובע י"א וכבר היה אלף ור"י עשרה דמיוני מרובע י״א א"כ כאשר גרענו מאלף ור"י מרובע י"א יהיה הנשאר שוה למרובע ל"ג והקש על זה | |||||||||||||||||||||||
Chapter Three – Sums |
השער השלישי בחבור מספרים נמשכים או מתיחסים | ||||||||||||||||||||||
| אם רצית לחבר מספרים
נמשכים מן האחד עד מספר מונח קח חצי מרובע המספר המונח וחברהו עם חצי המספר המונח והוא המבוקש דמיון אם רצית לחבר אחד ושנים ושלשה וארבעה וכן עד עשרה ועשרה עמהם קח חצי מרובע עשרה וחציו והנה נ״ה וככה המבוקש. דרך אחרת ערוך המספר ההוא על חצי המספר הנמשך לו לאחריו או חצי המספר ההוא על המספר הנמשך לו לאחריו והוא המבוקש והנה במשלנו זה ערוך י׳ על חצי י"א או חצי י׳ על י"א והנה נ"ה וככה המבוקש ואם היו המספרים נמשכים בזולת דרך המספר ר"ל שהיה הראשון מספר מונח והשני שני דמיוני המספר המונח והשלישי שלשה דמיוניו וכן בזה הדרך עד מספר מה תחבר הנמשכים עד המספר ההוא בדרך הקודמת והעולה תערוך על המספר הראשון המונח וככה המבוקש. דמיון זה שיהיה הראשון שבעה והשני י"ד והשלישי כ"א והרביעי כ"ח וימשכו בזה הדרך עד תשעה מספרים כבר ידעת כי הנמשכים מן האחד עד תשעה הם מ"ה ערכם על ז׳ שהוא הראשון והנה שט"ו והוא המבוקש ויהיה זה כן לפי שיחס האחד אל הראשון כיחס השנים אל השני וכיחס השלשה אל השלישי וביחס הארבעה אל הרביעי וביחס החמשה אל החמישי וכיחס הששה אל הששי וכיחס השבעה אל השביעי וכיחס השמנה אל השמיני וביחס התשעה אל התשיעי אבל יחס האחד אל קרובו כיחס הכל אל הכל א״כ יחס אחד אל שבעה כיחס הכל אל הכל אבל שבעה ימנהו אחד כמנין אחדי שבעה א"כ כלל אלו המספרים ימנהו מ"ה כמספר אחדי שבעה א״כ כבר יוכה מספר מ"ה בשבעה ויהיה העולה שוה לאלו המספרים המקובצים והקש על זה. אם רצית לחבר נפרדים הנמשכים מתחילים מן האחד עד מספר מונח קח מרובע המספר האמצעי בין האחד והמספר המונח והנה המבוקש דמיון זה אם רצית לחבר הנפרדים הנמשכים עד תשעה והאחד עמהם הנה המספר האמצעי בין אחד ובין תשעה הוא חמשה קח מרובעו והוא כ"ה וככה המבוקש ואם רצית לחבר הזוגות הנמשכים עד מספר מה והנה יהיה המספר הראשון שנים והשני שני דמיוניו והשלישי שלשה דמיוניו וכן ימשכו נמשכים בזולת דרך המספר וכבר קדם דרכו ולזה תקח חצי המספר האחרון לפי שהוא כמספר מספרי הזוגות הנחברים ותדע מה עלו הנמשכים מן האחד עדיו ותערוך העולה על שנים שהוא הראשון והנה המבוקש דמיון זה אם רצית לחבר הזוגות עד עשרה כבר ידעת שהנמשכים עד חמשה הם ט"ו ערכת אותם על שנים שהוא הראשון והנה ל' וככה המבוקש. אם רצית לחבר מרובעי מספרים נמשכים מן האחד עד מספר מונח קח המספר המונח פחות שלישית המספר הנמשך לפניו וערכהו על נקבץ הנמשכים עד המספר המונח דמיון זה אם רצית לדעת מרובעי המספרים הנמשכים עד חמשה הנה המספר הנמשך לחמשה לפניו היא ארבעה גרענו ממנו שלישית ארבעה שהוא ד' שלישית ונשארו ארבעה פחות שלישית ערכנום על ט"ו שהוא נקבץ הנמשכים עד חמשה ועלה נ"ה וככה המבוקש. ואם רצית לחבר מרובעי הנפרדים הנמשכים מן האחד או מרובעי הזוגות הנמשכים עד מספר מונח רצוני שיהיה המספר המונח הוא האחרון קח נקבץ הנמשכים עד המספר הנמשך אחר המספר המונח וערכהו על שלישית המספר המונח דמיון זה רצינו לדעת מרובעי הנפרדים הנמשכים עד תשעה הנה נקבץ הנמשכים מן האחד עד עשרה הוא נ"ה ערכנום על שלישית תשעהו הנה קס"ה וככה המבוקש ואם רצית לחבר מרובעי מספרים נמשכים בזולת דרך המספר עד מספר מונח ערוך מרובעי המספרים הנמשכים מן האחד עד המספר המונח על מרובע המספר הראשון והעולה הוא המבוקש דמיון זה אם רצית לחבר מרובעי מספרים נמשכים שהראשון ארבעה והשני שמנה והשלישי שנים עשר וימשכו בזה הדרך עד שבעה מספרים הנה כבר ידעת שמרובעי כל המספרים עד שבעה הם ק״מ ערכת אותם על י"ו שהוא מרובע המספר הראשון והנה אלפים ר״מ וככה המבוקש והיה זה כן לפי שיחס אחד אל הראשון הוא כיחס שנים אל השני וכיחס כל אחד אל גילו א"כ יהיה יחס מרובע אחד אל מרובע הראשון כיחס מרובע כל אחד מהם אל מרובע גילו ולזה יהיה יחס מרובע האחד אל מרובע גילו כיחס מרובעי הכל אל מרובעי הכל אם רצית לחבר מעוקבי מספרים נמשכים מן האחד עד מספר מונח קח מרובע נקבץ הנמשכים מן האחד עד המספר המונח והעולה הוא המבוקש. דמיון זה אם רצית לדעת מעוקבי המספרים הנמשכים מן האחד עד ששה והנה נקבץ הנמשכים מן האחד עד ששה הוא כ״א לקחנו מרובעו והנה תמ״א והוא המבוקש ואם היו המספרים נמשכים בזולת דרך המספר עד מספר מונח ורצינו לדעת מעוקביהם תוציא מעוקבי המספרים הנמשכים מן האחד עד המספר המונח ותערוך העולה על מעוקב המספר הראשון והוא המבוקש וכבר התבארה סבת זה במה שקדם דמיון זה שיהיה הראשון ארבעה והשני שמנה ונמשך בזה הדרך עד חמשה כבר ידוע שמעוקבי המספרים הנמשכים עד חמשה הם רכ"ה ערכנום על ס״ד שהוא מעוקב המספר הראשון ועלה י"ד אלפים וד' מאות וככה המבוקש. ואם רצינו לדעת מעוקבי הזוגות ממספרים נמשכים מן האחד עד מספר מונח קח מעוקבי הנמשכים עד חצי המספר המונח וערוך העולה על מעוקב המספר הראשון שהוא שנים ומעוקבו שמנה וככה המבוקש וכבר התבארה סבת זה במה שקדם רצו׳ שאלו המספרים שבים אל המספרים הנמשכים בזולת דרך המספר דמיון זה אם רצית לדעת מעוקבי הזוגות הנמשכים עד ששה הנה מעוקבי המספרים הנמשכים עד שלשה הם ל"ו ערכנום על שמנה שהוא מעוקב המספר הראשון ועלה רפ"ח וככה המבוקש ומזה תוכל לדעת מעוקבי הנפרדים הנמשכים מן האחד עד מספר מונח רצוני שתדע תחלה מעוקבי כל המספרים עד המספר המונח ותוצא מן העולה מעוקבי הזוגות והנשאר הוא מעוקבי הנפרדים. אם רצינו לחבר מספרים נמשכים בדרך המספר בלתי מתחילין מן האחד אבל יתחילו ממספר מונח ויכלו במספר מונח שני נקח נקבץ הנמשכים מן האחד עד המספר המונח השני ושמור ונגרע מהשמור נקבץ הנמשכים מן האחד עד המספר הנמשך לפני המספר הראשון דמיון זה שהיה המספר הראשון ששה ורצינו לחבר הנמשכים לו לאחריו עד מספר אחד עשר והנה נקבץ הנמשכים מן האחד עד אחד עשר הוא ס"ו נגרע ממנו מספר הנמשכים מן האחד עד חמשה שהוא ט״ו ונשארו נ"א וככה המבוקש וכן תעשה במרובעי המספרים הנמשכים כאשר לא יתחילו מן האחד או המעוקבים והסבה בזה מבוארת וכן תעשה במרובעי הנפרדים הנמשכים כאשר לא יתחילו מן האחד או במרובעי הזוגות כאשר לא יתחילו משנים לזאת הסבה בעינה. אם רצית לחבר מספר מונח ממספרים נמשכים בזולת דרך המספר והיה הראשון בלתי שוה למספר ההמשך אבל הוא פחות ממנו או יותר עליו מספר מונח שני ערוך המספר המונח השני על המספר המונח הראשון והעולה הוא השמור הראשון גם קח נקבץ הנמשכים מן האחד עד המספר המונח הראשון וערכהו על מספר ההמשך והוא השמור השני ואם היה הראשון פחות ממספר ההמשך תוצא השמור הראשון מהשמור השני והנשאר הוא המבוקש דמיון זה אם רצית לחבר שבעה מספרים שכל אחד מהם מוסיף על המספר שלפניו שלשה והראשון פחות שנים משלשה או מוסיף שנים על שלשה הנה שטח שנים בשבעה הוא י"ד והוא השמור הראשון ונקבץ הנמשכים עד שבעה הוא כ"ח ערכנום על שלשה והנה פ"ד ואם היה הראשון פחות שנים משלשה תגרע י״ד מפ"ד וישאר ע׳ והוא המבוקש והסבה שאם הוספנו חסרון הראשון משלשה על כל אחד מהמספרים היו נמשכים מיחס שלשה ולזה נגרע מהעולה שטח שנים בשבעה ואם היה הראשון מוסיף על שלשה שנים הוסף י"ד על פ"ד והיו צ"ח והוא המבוקש והסבה שאם נגרע תוספת הראשון על שלשה מכל אחד מהמספרים היו נמשכים בזולת דרך המספר והקש על זה... אם רצית לחבר מרובעי מספר מונח ממספרים נמשכים בזולת דרך המספר אלא שהמספר הראשון מתחלף ממספר ההמשך בשיעור מספר מונח שני ערוך המונח השני על כפל נקבץ אלו המספרים והעולה תחבר עם שטח המספר המונח הראשון במרובע המספר המונח השני אם היה הראשון פחות ממספר ההמשך ואם היה הראשון מוסיף על מספר ההמשך תגרע זה השטח שזכרנו מהעולה ומה שישאר בידך אחר התוספת או אחר הגרעון הוא השמור הראשון אח"כ קח מרובעי המספרים הנמשכים מן האחד עד המספר המונח הראשון וערוך העולה על מרובע מספר ההמשך והוא השמור השני ואם היה המספר הראשון פחות ממספר ההמשך גרע השמור הראשון מהשמור השני והנשאר הוא המבוקש ואם היה המספר הראשון מוסיף על המספר המונח השני הוסף השמור הראשון על השמור השני והוא המבוקש. דמיון זה אם רצית לחבר מרובעי ז׳ מספרים שכל אחד מהם מוסיף על המספר שלפניו שלשה והראשון מהם מוסיף שנים על שלשה או פחות ממנו שנים ויהיה תחלה הראשון מוסיף שנים על שלשה הנה ידענו שנקבץ אלו המספרים הוא צ״ח וכפלהו והנה קצ"ו ערכנום על שנים והנה שצ״ב ואולם שטח מרובע שנים שהוא ארבעה בשבעה הוא כ"ח גרענום משצ"ב והנה שס"ד והוא השמור הראשון או אם תערוך שנים על כפל נקבץ שבעה מספרים נמשכים בזולת דרך המספר שכל אחד מהם מוסיף שלשה על שלפניו והראשון שלשה ותחבר עם העולה שטח מרובע שנים בשבעה יעלה שס"ד ג"כ וזה ששטח כפל שנים בפ״ד הוא של"ו חברנו עמו שטח ארבעה בשבעה שהוא כ"ח ועלה שס"ד הנה אלו שני הדרכים יביאוך אל מספר אחד בעינו וזה מבואר מראש המאמר הראשון עם מעט עיון ואולם מרובעי המספרים הנמשכים עד שבעה הם ק״מ ערכנום על תשעה שהוא מרובע מספר ההמשך והנה אלף ור"ס חברנום עם שס"ד והנה אלף ותרכ"ד והוא המבוקש ויהיה גם כן הראשון פחות שנים משלשה במשלנו זה הנה ידענו שנקבץ המספרים האלו הוא ע׳ והנה ק"מ ערכנום על ט׳ שהוא מרובע מספר ההמשך והנה אלף ור"ס גרענו מהם ש"ח והנה תתקנ"ב והוא המבוקש והיה זה כן לפי שאם הוסף שנים על כל אחד מהמספרים היו נמשכים בזולת דרך המספר ואולם יתרון מרובע כל מספר מהם באשר חובר עם שנים על מרובעו הוא כפל שטח שנים במספרו ומרובע שנים וכאשר חובר זה התוספות מכל אלו המספרים היה כמו שטח שנים בכל אלו המספרים נחברים וכמו שטח מרובע שנים במספר המספרים גרענו העולה ממרובעי המספרים הנמשכים בזולת דרך המספר בשיעור זה ההמשך ועד המספר המונח הראשון ונשאר המבוקש ובזה התבאר מקביל זה עם מעט עיון והבן ותמצא. אם רצית לחבר מעוקבי מספר מונח ממספרים נמשכים בזולת דרך המספר אלא שהמספר הראשון מתחלף למספר ההמשך בשיעור מספר מונח שני הנה אם יהיה המספר הראשון פחות ממספר ההמשך תקח מרובעי אלו המספרים ותערוך העולה על שלשה דמיוני המספר המונח השני ותשמור עוד תערוך שלשה מרובעי המספר המונח השני על נקבץ אלו המספרים ושמור עוד תערוך מעוקב המספר המונח השני על המספר המונח הראשון ותחבר העולה עם שני השמורים ויהיה בידך השמור הראשון המתוקן אחר כך קח מעוקבי המספרים הנמשכים מן האחד עד המספר המונח הראשון וערכם על מעוקב מספר ההמשך ומהעולה גרע השמור הראשון המתוקן והנשאר הוא המבוקש דמיון זה אם רצינו לחבר מעוקבי שבעה מספרים שכל אחד מהם מוסיף על שלפניו שלשה והראשון פחות משלשה שנים הנה כבר ידענו שמרובעי אלו המספרים הם תתקנ"ב ערכנו זה על שלשה דמיוני שנים שהוא ו׳ והנה ה׳ אלפים ותשי"ב ונשמרם וגם כן הנה נקבץ אלו המספרים הוא ע׳ ערכנום על שלשה דמיוני מרובע שנים שהוא י"ב והנה תת"מ ונשמרם גם כן ערכנו מעוקב שנים שהוא שמנה על ז׳ והנה נ"ו חברנום עם שני השמורים והנה ו׳ אלפים ותר"ח והוא השמור הראשון המתוקן הוצאנו מעוקב המספרים הנמשכים מן האחד עד ז׳ והנה תשפ״ד ערכנום על כ"ז שהוא מעוקב שלשה והנה כ״א אלפים וקס"ח גרענו מהם השמור הראשון המתוקן ונשאר י"ד אלפים ותק״ס והוא המבוקש. ואם היה המספר הראשון מוסיף על מספר ההמשך מספר מונח שני הוצא נקבץ המספר המונח הראשון ממספרים נמשכים בזולת דרך המספר בשיעור זה ההמשך המונח וכבר ידעת אופן זה המעשה במה שקדם ערוך העולה על שלשה דמיוני מרובע המונח השני והעולה שמור גם קח מרובעי המספר המונח הראשון ממספרים נמשכים בזולת דרך המספר בשיעור זה ההמשך המונח וערוך העולה על שלשה דמיוני המספר המונח השני ושמור העולה עוד תערוך מעוקב המספר המונח השני על המספר המונח הראשון וחבר העולה עם שני השמורים והעולה יהיה השמור הראשון המתוקן אחר כך הוצא מעוקבי המספר הראשון המונח ממספרים נמשכים בזולת דרך המספר בשיעור ההמשך המונח וחבר עם העולה השמור הראשון המתוקן והנה המבוקש דמיון זה במשלנו הקודם רצוני שיהיה המספר הראשון מוסיף שנים על שיעור ההמשך הנה ידענו כי מרובעי שבעה מספרים נמשכים בהמשך שלשה שלשה הם אלף ור"ס ערכנו אלף ור"ס על שלשה דמיוני המספר המונח השני שהוא ו׳ ועלה ז׳ אלפים ותק"ס ונשמור העולה וג"כ הנה נקבץ המספרים הנמשכים בהמשך שלשה עד שבעה הוא פ"ד ערכנום על שלשת דמיוני מרובע המספר המונח השני שהוא י״ב ועלה אלף וח' ונשמרם גם כן וג"כ הנה מעוקב המספר המונח השני הוא ח' ערכנוהו על המספר המונח הראשון שהוא ז׳ ועלה נ"ו חברנום עם שני השמורים ועלה ח׳ אלפים ותרכ"ד והוא השמור הראשון המתוקן וגם כן הנה מעוקבי שבעה מספרים נמשכים בהמשך שלשה הוא כ"א אלפים וקס״ח חברנום עם השמור המתוקן הראשון ועלה כ"ט אלפים ותשצ"ב והוא המבוקש והיה זה כן שאם נגרע מכל אחד מאלו המספרים שנים היו נמשכים בהמשך שלשה ואולם מעוקב כל מספר מהם פחות ממעוקב המספר כשהוסף עליו שנים כמו שלשה דמיוני שטח מרובע המספר ההוא על שנים וכמו שלשה דמיוני שטח המספר ההוא על מרובע מספר שנים וכמו מעוקב שנים וכאשר קבצנו זה בכל המספרים היה מה שזכרנו והבן ותמצא ובזה התבאר הסבה במקביל זה עם מעט עיון. אם רצית לדעת מה יעלה המספר האחרון ממספר מונח ממספרים מתיחסים על יחס מונח מתחילין מן האחד קח מרובע היחס והנה השלישי קח מרובע השלישי והנה החמשי קח מרובע החמשי והנה התשיעי ובזה הדרך תוכל לדעת ממרובע כל מספר מהם מספר קצהו וכאשר תגיע אל מספר קרוב ממספר המונח שמור מספרו אח"כ תדע מרחקו ממספר המונח כמה גם תדע מה יעלה המספר מאלו המתיחסים אשר מרחקו ככה מן האחד ועל מספרו תערוך השמור והנה המבוקש משל זה אם רצית לדעת מה יעלה המספר האחרון מחמשה עשר מספרים מתיחסים על יחס מונח מתחילין מן האחד והיה היחס המונח שלשה ובזה יהיה המספר השני שלשה לקחנו מרובע ג׳ שהוא ט׳ והנה השלישי לקחנו מרובע ט׳ שהוא פ"א והנה החמישי לקחנו מרובע פ״א שהוא ו׳ אלפים ותקס״א והנה התשיעי ואם נקח מרובע התשיעי יהיה לנו השבעה עשר ויעבור המספר המונח ולזה נראה כמה מרחק התשיעי מן החמשה עשר והנה החמשה עשר הוא השביעי לו ולזה ראוי שנדע כמה מספר המספר השביעי לאחד וידענו כי המספר
המונח השני שהוא י״ב ועלה אלף וח' ונשמרם ג״כ וג״כ הנה מעוקבי המספר המונח השני הוא ח' ערכנום על המספר המונח הראשון שהוא ו׳ ועלה נ״ו חברנום עם שני השמורים ועלה ח' אלפים תרכ"ד והוא השמור הראשון המתוקן וג"כ הנה מעקבי שבעה מספרים נמשכים האחד עד ז' הם תשפ״ד ערכנום על כ"ח שהוא מעוקב שלשה עד כ״ז שהוא מעוקב שלשה החמשי לאחד הוא פ״א והשביעי הוא שלישי לחמשי ערכנו פ"א על ט' שהוא השלישי והנה תשכ״ט והוא השביעי ערוך השביעי על התשיעי ויעלה בידך המספר החמשה עשר והוא ד׳ אלפי אלפים וז׳ מאות אלף ושמנים ושמנה אלף ותתקס״ט והוא החמשה עשר והקש על זה והיה זה כן לפי שיחס הראשון אל השני ביחס השני אל השלישי ולזה יהיה שטח הראשון בשלישי כמו שטח השני בעצמו אבל שטח הראשון בשלישי הוא השלישי לפי שהראשון הוא אחד א"כ שטח השני בעצמו הוא שטח השלישי ובזה יתבאר ששטח הראשון בחמשי כמו שטח השלישי בעצמו וכן יתבאר מה שימשוך לזה וגם כן הנה יחס הראשון אל השלישי כמו יחס החמשי אל השביעי א״כ שטח השביעי בתשיעי הוא כמו שטח הראשון בשביעי שהוא כמו השביעי וגם כן הנה יחס הראשון אל השביעי כיחס התשיעי אל החמשה עשר אם כן שטח השביעי בתשיעי הוא כמו שטח הראשון בחמשה עשר שהוא כמו החמשה עשר והקש על זה. ואם רצית לדעת מה יעלה המספר האחרון ממספר מונח ממספרים מתיחסים על יחס מונח בלתי מתחילין מן האחד דע תחלה מה יעלה המספר האחרון ממספר המונח ממספרים מתיחסים על היחס המונח מתחילין מן האחד וערכהו על המספר הראשון וככה המבוקש.. דמיון זה שיהיו המספרים המתיחסים חמשה והיחס שלשה והראשון חמשה ורצית לדעת כמה האחרון הנה כבר ידענו שהחמשי מזה היחס אם היו מתחילין מן האחד הוא פ״א ערכת פ״א על המספר הראשון שהוא חמשה ועלה ת"ה וככה המבוקש והיה זה כן כי ביחס השווי יחס הראשון שהוא אחד אל החמשי לו כיחס החמשי אל החמשי לו מזה היחס וכאשר המירונו הנה יחס הראשון אל הראשון כיחס החמשי אל החמשי ואולם יחס הראשון אל הראשון הוא חמשה הנה יחס החמשי אל החמשי הוא חמשה והקש על זה. אם רצית לחבר מספר מה ממספרים מתיחסים על יחס מונח גרע הראשון מהשני וראה יחס הנשאר מהשני אל הראשון וככה יחס הנשאר מן האחרון כשנגרע ממנו הראשון של כל המספרים שלפניו וזה כבר התבאר בסוף המאמר התשיעי מאקלידס דמיון זה אם רצית לחבר ששה מספרים מתיחסים על יחס ג׳ והראשון ד׳ כבר ידעת שהשני הוא י"ב והאחרון הוא תתקע"ב גרענו מהשני הראשון שהוא ד׳ ונשארו שמנה והנה יחס ד׳ אל ח׳ הוא חצי גרענו מהאחרון ד׳ ונשארו תתקס״ח לקחנו חצים והנה תפ"ד חברנוהו עם תתקע"ב והנה אלף תנ״ו והוא המבוקש | |||||||||||||||||||||||
Chapter Four – Combinatorics |
השער הרביעי בחבור מספר מחברות מנושאים מונחים תתחלפנה המחברות בנושאיהם או בסדרם או בשני הענינים יחד | ||||||||||||||||||||||
| אם רצית לדעת
מספר מחברות מספר מונח מנושאים מתחלפים המתחלפות בסדר לבד קח המספר המורכב מהמספרים הנמשכים מן האחד עד המספר ההוא וככה המבוקש דמיון זה אם רצית לדעת בכמה דרכים יתחברו ה׳ נושאים ותהיינה המחברות מתחלפות בסדר הנה המספרים הנמשכים מן האחד עד ה׳ הם א'ב'ג'ד'ה' והמספר המורכב ממספרי א'ב'ג'ד'ה' הוא ק"ך וככה המבוקש והיה זה כן לפי שמחברות ב׳ הם ב׳ וזה שוה למורכב א׳ב׳ ומחברות שלשה הם כמו שטח ג׳ בב׳ שהוא מורכב א׳ב׳ג׳ וכזה התבאר זה עד אין תכלית. אם רצית לדעת כמה תהיינה מחברות מספר מונח שני ממספר מונח ראשון מנושאים מתחלפים המתחלפות אם בסדר אם בנושאיהן כבר ידעת שמחברות השנים הם כמו שטח המספר המונח הראשון במספר הנמשך לו לפניו ומחברות שלשה ממנו יחסם אל מחברות השנים כמו הנשאר מן המספר המונח הראשון כשנגיע ממנו שנים ומחברות הארבעה ממנו יחסם אל מחברות השלשה כמו הנשאר מן המספר המונח הראשון כשנגרע ממנו שלשה וכזה ימשך הענין לאין תכלית ומפני זה יהיה הדרך בזה שתקח המספר המורכב מהמספר המונח השני ממספרים נמשכים שיהיה האחרון מהס שוה אל המספר המונח הראשון והעולה הוא המבוקש דמיון זה אם רצית לדעת מחברות החמשה מח׳ נושאים המתחלפות אם בסדר אם בנושאיהם הנה מפני שהמספר המונח השני הוא חמשה תקח מורכב חמשה מספרים נמשכים שיהיה האחרון מהם שמנה והם ד'ה'ו'ז'ח' והמספר המורכב מהם הוא ו׳ אלפים תש״כ וככה מחברות החמשה המתחלפות אם בסדר אם בנושאיהם משמנה נושאים מתחלפים והיה זה כן לפי שמחברות השנים ממנו הוא שטח ז' בח׳ ומחברות השלשה ממנו הוא שטח ו׳ בשטח ז׳ בח' לפי מה שהוא במה שקדם ומחברות הארבעה ממנו הוא שטח ה׳ במורכב ממספרי ו'ז'ח' ומחברות החמשה ממנו הוא שטח ד׳ במורכב ממספרי ה׳ו׳ז׳ח׳ וכזה יתבאר לאין קץ וזה כלו מבואר ממה שקדם. אם רצית לדעת כמה תהיינה מחברות מספר מונח שני המתחלפות בנושאיהן ממספר מונח ראשון מנושאים מתחלפים קח מחברות המספר המונח השני המתחלפות אם בסדר אם בנושאיהם מהמספר המונח הראשון מנושאים מתחלפים ושמור העולה קח מחברות המספר המונח השני המתחלפות בסדר לבד וכמו שיעור אחדי המספר שימנה השמור העולה וככה המבוקש דמיון זה אם רצית לדעת מחברות החמשה המתחלפות בנושאיהן משמנה נושאים מתחלפים ראה כמה פעמים ימנה מורכב ד'ה'ו'ז'ח' מורכב א'ב'ג'ד'ה' והנה מורכב ד׳ה׳ו׳ז׳ח׳ הוא ו׳ אלפים תש"כ ומורכב א'ב'ג'ד'ה' הוא ק"ך וו' אלפים תש"כ ימנה ק״ך נ״ו פעמים והנה נ"ו הוא המבוקש וכבר יבוא לך דרך החשבון בזאת החלוקה במה שאחר זה ולהקל מעליך כבר ידעת שמחברות החמשה המתחלפות בנושאיהן משמנה נושאים מתחלפים הם כמספר מחברות השלשה המתחלפות בנושאיהן מאלו הנושאים ולזה תעיין כמה פעמים ימנה מורכב ו׳ז׳ח׳ שהוא של״ו מורכב א'ב'ג' שהוא ו׳ והנה ימנהו נ״ו פעמים וככה מחברות השלשה המתחלפות בנושאיהן משמנה נושאים גם ככה מחברות החמשה שהוא שאריתם וזה כבר התבאר ממה שקדם.
כאלו תומר עמנו עשרה נושאים והוא שקראו מספר ראשון ורצינו חבור שלשה שלשה מהם והוא שקראו מספר שני | |||||||||||||||||||||||
Chapter Five – Division |
השער החמישי בחלק מספר על מספר | ||||||||||||||||||||||
| כבר ידעת שכל שטח ימנהו אחד
מצלעיו כמספר אחדי הצלע השנית על כן אם ידעת מספר השטח וידעת אחת מצלעותיו תוכל להוציא הצלע השנית והנה אופן המעשה בזה שתכתוב מספר השטח בטור אחד ותחתיו תכתוב בטור אחר הצלע הידוע ותחלוק הטור העליון על הטור השפל והעולה בידך הוא הצלע השנית ואולם איך תחלוק הטור העליון על הטור השפל הנה כפי מה שאומ׳ תסתכל תחלה במספר האחרון שבטור התחתון ובמספר שבמעלה הקודמת לו וכל המספרים שלפני המעלה הקודמת לו בטור התחתון תחשוב כאלו הם אחד לבד במעלה הקודמת לו ומה שיעלה בידך מן האחדים במעלה האחרונה שבטור התחתון יהיו לאחדים בידך ומה שיעלה בידך מן האחדים במעלה שלפני האחרונה יהיו לעשיריות אחד שלם ומה שיהיה בידך מן האחדים והעשיריות שמרם אח"כ התבונן במספר התחתון שבטור העליון והיו לאחדים בידך והאחדים שבמעלה שלפניו יהיו עשיריות ולא תחוש לשאר המספרים והעולה בידך מן האחדים והעשיריות אם הם יותר מהשמור או כדי השמור תחשוב כמה פעמים יהיה בו השמור בשלמות והעולה בידך תשימהו בטור אמצעי בין שני הטורים במעלה אשר מרחקה מהמעלה האחרונה שבטור העליון לפניו כמרחק המעלה האחרונה שבטור התחתון ממדרגת האחדים אחר כך ערוך המספר ההוא אשר בטור העולה על הטור התחתון והעולה בידך תגרענו מהטור העליון ותכתוב הנשאר בידך על הטור העליון ותמחוק הטור העליון הקודם ואם לא היה המספר האחרון אשר בטור העליון עם העשיריות אשר שם כמו השמור תוריד המעלה האחרונה אל שלפניה וממנה תחשוב האחדים והעשיריות משלפניה והעולה בידך תראה כמה פעמים ימנהו השמור בשלמות והעולה תכתוב במעלה אשר מרחקה לאחור מהמעלה האחרונה אחר ההורדה שבטור העליון כמרחק המעלה האחרונה שבטור התחתון מהמדרגה הראשונה ותנהג הענין על המנהג הקודם. אח״כ תשוב לעשות מהטור העליון הנשאר בידך כמו מה שעשית מהטור העליון הקודם וכן תעשה עד שלא ישאר לך בטור העליון דבר או שישאר לך פחות מהטור התחתון אם היה שלא ימנה הטור העליון הטור התחתון ועוד נודיעך במה שיבא מה תעשה מהנשאר ההוא ופעמים יקרה שנצטרך לכתוב בטור העולה שתי פעמים במעלה אחת ומעט מה שיקרה זה. דמיון זה רצינו לחלק טור א'ב'ג'ד'ה'ו'ז'ח'ט' על טור ז'ג'ד'ט' והנה המספר האחרון שבטור התחתון והוא ז'ג'ד'ט' הוא ט׳ והם שלמים ובמעלה שלפניו מספר ד׳ וכל מה שלפניו הוא אחד בה על צד האומד והקרוב ויהיו ה׳ והם עשיריות ולזה יהיה השמור ט׳ שלמים וה' עשיריות והנה ט׳ שלמים וח׳ עשיריות ימנם ט׳ שלמים וה׳ עשיריות פעם אחת ולזה נכתוב א׳ בטור האמצעי בין שני אלו הטורים במעלה הרביעית לאחרונה שבטור העליון לפניה לפי שמספר האחרון שבטור התחתון הוא מרביעית ולפי זה יהיה הא׳ שבטור האמצעי מהמעלה הששית הכינו א׳ על הטור התחתון ועלה ז׳ מהששית ג׳ מהשביעית ד׳ מהשמינית ט׳ מהתשיעית גרענו העולה מהטור העליון ונשאר בטור העליון א'ב'ג'ד'ה'ט'ג'ד' ונכתוב זו על הטור העליון ונמחק הטור הקודם והנה במעלה האחרונה שבטור העליון עם מה שלפניו ד׳ שלמים וג׳ עשיריות והוא פחות מהשמור ולזה תוריד ד' אל שלפניו יהיו מ׳ בה וג' שהיו בה והנה מ"ג וט׳ עשיריות במעלה שלפניו חלקנו מ״ג וט' עשיריות על ט׳ וה' עשיריות שהוא השמור ועלה ד׳ בשלמות ונכתוב ד' בטור האמצעי במעלה הרביעית לאחור למעלת המ"ג ולזה יהיו הד׳ מהרביעית הכינו ד׳ על הטור התחתון ועלה ח׳ ברביעית ד׳ בחמשית ז׳ בששית ז׳ בשביעית ג' בשמינית גרענו העולה מהטור העליון השני ונשאר א'ב'ג'ו'0ב'ו' והנה מה שבמעלה האחרונה עם מה שבמעלה שלפניה הוא פחות מהשמור ולזה נוריד הו׳ שבמעלה האחרונה אל שלפניה יהיו ששים בה וב׳ שהיו בה והנה ס"ב ואין במעלה שלפניה דבר נחלק ס"ב על השמור ועלה ו׳ ונשימם בשלישית לפי שהיו ברביעית לאחור ממעלת ס״ב שחלקנו ערכנו ו׳ מהשלישית על הטור התחתון ועלה ב׳ מהשלישית ב' מהרביעית ו׳ בחמשית ו׳ בששית ה׳ בשביעית גרענו העולה מהטור העליון השלישי ונשאר הטור העליון הרביעי א׳ב׳א׳ד׳ד׳ה׳ ונוריד ה׳ אל המעלה שלפניה וד' אשר בה והנה נ"ד וד׳ שבמעלה שלפניה יהיו ד׳ עשיריות חלקנו ג"ד וד׳ עשיריות על השמור ועלה ה׳ ונשימם בטור האמצעי בשנית שהיא הרביעית לאחור מהמעלה שחלקנו ערכנו ה׳ מהשנית על הטור התחתון ועלה ה'ח'א'ז'ד' גרענו העולה מהטור העליון הרביעי ונשאר א'ז'ב'ב'ז' והוא הטור העליון החמשי ונוריד ז' אל המעלה שלפניה וב׳ אשר בה והנה ע"ב חלקנו על השמור ועלה ז׳ ונשימם בטור האמצעי בראשונה שהיא הרביעית לאחור מהעלה אשר חלקנו ערכנו ז' מהראשונה על הטור התחתון ועלה ט'ה'0ו'ו' גרענום מהטור העליון החמשי ונשאר ב'א'ב'ו' והוא פחות מהטור התחתון והוא הנשאר שלא הגיע לחלוק והנה ב א ב ו א ז ב ב ז א ב א ד ד ה א ב ג ו 0 ב ו א ב ג ד ה ט ג ד הטור העליון א ב ג ד ה ו ז ח ט טור העולה ז ה ו ד 0 א הטור שחלקנו עליו ז ג ד ט ז ג ד ט ח ד ז ז ג
ב ב ו ו ה
ה ח א ז ד
ט ה 0 ו ו
העולה בטור האמצעי הוא ז'ה'ו'ד'0א' והנשאר בטור העליון הוא ב׳א׳ב׳ו׳ וכתבנום בטור ששי והקש על זה. וראוי שתדע שאם היו המספרים אשר בטור העליון עד המעלה אשר מרחקה מהמעלה האחרונה ממנו כמרחק המעלה האחרונה שבטור התחתון מן הראשונה כשהורדנום כלם אל המעלה ההיא כמספר הטור התחתון כשהורדנוהו אל המעלה הראשונה או יותר הנה ראוי שתשים אחד בטור העולה במעלה הראויה לפי מה שקדם ואע״פ שלא תשיג בטור העליון על הצד שהיישרנו בשלמות... משל שיהיה לך לחלק טור ג׳ז׳ד׳ט׳ על טור ג'ד'ט' ויהיה השמור לפי מה שהיישרנו אליו ט׳ אחדים וה׳ עשיריות ובטור העליון ט׳ אחדים וד׳ עשיריות ולזה יחשב לפי מה שקדם שיצטרך להוריד ט׳ אל שלפניו ואמנם כשהורדנו ג׳ד׳ט׳ שבטור העליון אל המעלה השלישית לאחור למעלת ט׳ היו תשע מאות ומ״ג וכזה מספר הטור התחתון כשהורד אל הראשונה ולזה תשים בטור העולה אחד במעלה השניה ותערכהו על הטור התחתון ותגרע העולה מהטור העליון ולא ישאר לך בטור העליון כי אם ז׳ מהראשונה והקש על זה ואתה צריך לחוש לזה כשיהיה המספר האחרון שבטור התחתון שוה למספר האחרון שבטור העליון והמספר השני לו לאחור שוה למספר השני אל האחור לאחר. ולפי שראוי שנבאר מה יעשה מהנשאר בטור העליון ואין דרך לזה הביאור אלא אם כן התבאר קודם דרך כפל השברים בשלמים הנה נבאר ראשונה דרך כפל השברים ושברי שברים בכל אופניהם. דע שיחס כל חלק אל אחד כיחס אחד אל המספר המורה אל החלק ההוא והמשל שיהיה יחס שלישית אל אחד כיחס אחד אל שלשה שהוא מורה על שלישית לפי שהאחד הוא שלישית שלשה וכאשר התישב זה הנה יתבאר שיחס שטח שבר מונח באחד אל שטח אחד באחד הוא כיחס אחד אל המורה על השבר המונח והמשל שיחס שטח שלישית באחד אל שטח אחד באחד הוא כיחס אחד אל שלשה וזה שיחס שטח שלישית באחד אל שטח אחד באחד הוא כיחס שלישית אל אחד אבל יחס שלישית אל אחד הוא כיחס אחד אל שלשה ויחס אחד אל שלשה הוא שלישית א״כ שטח שלישית באחד הוא שלישית אחד לפי ששטח אחד באחד הוא אחד וגם כן יתבאר בכמו זה הביאור ששטח מספר מונח משלמים או שלם אחד במספר מונח משברים או בשבר אחד הם חלקים מהמורה באחד כמספר שטח מספר המכה במספר המוכה והמשל שנרצה להכות ה׳ שביעיות על מ׳ שלמים ונאמר שהעולה הוא חלקים משבע באחד כמספר שטח ה׳ במ' שהוא ר׳ והוא שיחס שטח ה׳ שביעיות במ׳ שלמים אל שטח שביעית באחד מחובר משני יחסים מיחס חמשה אל אחד ומיחס מ׳ אל אחד והנה היחס המחובר משני אלו היחסים הוא יחס מאתים אל אחד אבל שטח שביעית באחד הוא שביעית אם כן שטח ה׳ שביעיות במ׳ שלמים הוא ר׳ חלקים משבעה באחד שהם כ"ח שלמים וד׳ שביעיות ואין ספק שבזה הביאור בעצמו התבאר הענין אם לא היה מספר כי אם באחד מהם ר"ל בשברים או בשלמים והקש על זה. ואחר שהתבאר אופן הכאת שברים בשלמים בכל אופניהם הנה נבאר אופן הכאת שברים בשברים ונבאר שיחס שטח שבר בשבר אל אחד כיחס אחד אל השטח ההוה מהמורה האחד במורה האחר והמשל שיחס שטח שלישית בחמשית אל אחד כיחס אחד אל שטח שלשה בחמשה שהוא ט״ו וזה שיחס שטח שלישית בחמשית אל שטח אחד באחד שהוא אחד מחובר משני יחסים מיחס שלישית אל אחד ומיחס חמשית אל אחד וכן יחס שטח אחד באחד שהוא אחד אל שטח שלשה בחמשה מחובר משני יחסים מיחס שלישית אל אחד ומיחס חמשית אל אחד וכבר היה יחס שטח שלישית בחמשית אל שטח אחד באחד מחובר משני אלו היחסים בעצמם א"כ יחס שטח שלישית בחמשית אל אחד כיחס אחד אל שטח שלשה בחמשה אבל יחס אחד אל שטח שלשה בחמשה הוא חלק מט״ו באחד א"כ שטח שלישית בחמשית הוא חלק מט"ו באחד והקש על זה. ובזה התבאר ששטח שלישית בשלישית הוא תשיעית אחד ובזה יתבאר בכמו זה הביאור ששטח מספר מונח משברים מה או שבר מה במספר מונח משברים מה או בשבר מה הוא חלקים משטח המורה האחד באחר כמספר שטח המספר המכה במספר המוכה והמשל שנרצה להכות ד׳ שביעיות על ה׳ תשיעיות ונאמר שהעולה הוא חלקים מס"ג באחד שהוא שטח המורה האחד באחר כמספר שטח ד׳ בה׳ שהוא כ׳ וזה שיחס שטח שביעית בתשיעית אל שטח ד׳ שביעיות בה' תשיעיות מחובר משני יחסים מיחס אחד אל ד׳ ומיחס אחד אל ה׳ אבל זה היחס המחובר הוא יחס אחד אל כ׳ אם כן יחס שטח שביעית בתשיעית אל שטח ד' שביעיות בה׳ תשיעיות הוא יחס אחד אל כ' אבל שטח שביעית בתשיעית הוא חלק מס״ג חלקים באחד א"כ ד׳ שביעיות בה' תשיעיות הוא כ׳ חלקים מס"ג חלקים באחד והקש על זה ואין ספק שבזה הביאור בעצמו יתבאר אם לא היה מספר כי אם באחד מהם. וכאשר התבאר זה כלו נודיעך דרך לקיחת המורה בשבר השבר ונאמר שהמורה על שבר השבר הוא המספר המורכב מהמספרים המורים על השברים ההם והמשל ששלישית חמשית שלישית הוא אחד ממורכב ממספרי שלשה חמשה שלשה באחד ולזה יהיה חלק ממ"ה באחד וזה שיחס שטח חמשית בשלישית אל שטח אחד באחד כיחס שטח אחד באחד אל שטח חמשה בשלשה אם כן חמשית שלישית הוא חלק מט"ו באחד וגם כן הנה יחס שטח שלישית בחלק מט"ו באחד אל שטח אחד באחד כיחס שטח אחד באחד אל שטח שלשה בט"ו א"כ שלישית חמשית שלישית הוא חלק ממ״ה באחד והקש על זה ואחר שידענו המורה תנהיג ההכאה באופן הקודם בין בשברים בין בשלמים דמיון זה אם רצינו להכות ה׳ שביעיות שלישיות על ז׳ שמיניות הנה המורה לשביעית שלישית הוא כ"א והמורה לשמינית הוא שמנה והמורכב משני המורים הוא קס״ח ערכנו ה׳ על ז׳ ועלה ל״ה והם ל"ה חלקים מקס״ח באחד שלם והקש על זה. דרך חבור השברים השונים. קח המספר המעט שימנוהו כל המורים לשברים ההם והוא המורה הנה וממנו תקח השברים ההם בכללם והעולה תחלקהו על המורה והוא המבוקש דמיון זה אם רצינו לחבר ב׳ שלישיות עם ד׳ חמשיות ועם ה׳ ששיות ועם ג׳ רביעיות ששית כבר ידענו שהמספר המעט שימנוהו שלשה וה' וו' וכ"ד הוא ק"כ וכבר התבאר דרך לקיחתו מאקלידס והנה ב׳ שלישיותיו הם פ׳ וזה יתבאר כשנחלק ק״כ על שלשה ונקח ב׳ דמיוני העולה וד׳ חמשיותיו הם צ"ו וה׳ ששיותיו הם ק׳ וג׳ רביעיות ששיותיו הם ט"ו חברנו כל אלו המספרים ועלה רצ״א חלקנו רצ"א על ק״כ ועלה ב׳ שלמים נ״א חלקים מק״כ באחד והיה זה כן לפי שיחס ב׳ שלישיות אחד אל אחד כיחס ב׳ שלישיות ק"כ אל ק"כ וכזה יתבאר בנשאר וכאשר קבצנו הנה יחס כל אלו השברים אל אחד כיחס רצ"א אל ק״כ והקש על זה. דרך לדעת העולה מהכאת השברים בשברים או בשברי השברים. כבר ידעת שהכאת השברים בשברים הם חלקים מהמורה המורכב ממוריהם וכבר התבאר שהמספר המורכב ממספרים מה ימנהו אחד מהמספרים בכמו אחדי המספר המורכב מהמספרים הנשארים וכן ימנהו המספר המורכב ממספרים מה ממנו בכמו אחדי המספר המורכב מהמספרים הנשארים ובהיות הענין כן אם תחלק המספר אשר בידך על אחד מהמספרים יהיה העולה חלקים מהמספר המורכב מהנשארים משל זה אם תכה ו׳ שביעיות על ז׳ שמיניות עלה מ״ב ואם תחלק מ״ב על שבעה יהיה העולה בידך שמיניות לפי שהמספר המורכב מז׳ וח' ימנהו ז׳ כשיעור אחדי ח׳ ולזה יהיה העולה ו׳ שמיניות ואם תחלק על שמנה יעלה בידך שביעיות ולזה יהיה העולה ה׳ שביעיות וב׳ שמיניות שביעית דמיון אחר אם רצית להכות כ"ח חלקים מכ"ט באחד על ו׳ שביעיות שלישית תערוך כ"ח על ו׳ ועלה קס״ח הנה אם תחלק קס״ח על כ"ט יעלו בידך שביעיות שלישית שהם השברים הנשארים ויהיה העולה ה׳ שביעיות שלישית וכ״ג חלקים מכ"ט שביעיות שלישית ואם חלקת על המספר המורכב מז' וג' יעלו בידך חלקים מכ״ט ויהיה העולה ח׳ חלקים מכ"ט באחד ואם תחלוק על ז׳ יעלו בידך שלישיות חלק מכ"ט חלקים באחד ולזה יהיה העולה כ"ד שלישיות חלק מכ"ט באחד ולזה יהיה העולה ח׳ חלקים מכ״ט ואם תחלוק על ג׳ יעלו בידך שביעיות חלק מכ"ט חלקים באחד ולזה יהיה העולה נ"ו שביעיות חלק מכ"ט חלק באחד שהם ח׳ חלקים מכ"ט באחד והקש על זה. דרך להכות שברים על שברים והעולה על שברים וכן מה שיהיה ערוך מספרי השברים הראשונים על מספרי השברים השניים והעולה בידך ערכהו על מספר השברים השלשיים וכן עד כלות כל השברים אחר כך תחלוק העולה על המורה לאחד מהשברים או על המורכב ממספרי מורים מה מהם והעולה בידך יהיו חלקים מה ממורכב מהמורים לשברים הנשארים ואתה תבחר היותר נכון לחלק עליו דמיון זה נרצה להכות ו' שביעיות על ה׳ ששיות והעולה על ג׳ רביעיות והעולה על ז' שמיניות והעולה על ב׳ שלישיות והעולה על ב׳ שביעיות והעולה על שלישיות שלישית הכינו ו׳ על ה׳ ועלה ל׳ הכינו ל׳ על ג׳ ועלה צ׳ הכינו צ׳ על ז׳ ועלה תר"ל הכינו תר״ל על ב׳ ועלה אלף ור״ס הכינו אלף ור״ס על ב׳ ועלה אלפים ותק"כ ערכנו אלפים ותק"כ על אחד ועלה אלפים ותק"כ והנה השברים אשר בידך הם שביעית ששית רביעית שמינית שלישית שביעית שלישית שלישית ואם תחלק אלפים ותק״כ על המורה לאחד מאלו השברים יהיה העולה בידך חלקים מהמספר המורכב ממורי השברים הנשארים והנה מפני שהמספר רב ראוי שתחלקהו על המספר המורכב מקצת המורים אשר יראה בעיניך שהוא יותר נאות לחלק עליו חלקנו אותו על המורכב משבעה וו׳ וג׳ וד׳ שהוא תק"ד ועלה ה׳ והם חלקים ממורכב מורי השברים הנשארים ואולם הנשארים הם שמינית שביעית שלישית שלישית א"כ העולה מזאת ההכאה הם ה׳ שמיניות שביעית שלישית שלישית והקש על זה והיה זה כן לפי שכבר יתבאר ממה שקדם במעט עיון שהעולה שהוא אלפים תק"כ הם חלקים ממורכב מכל מורי השברים באחד והבן ותמצא דרך אחרת קלה לזה דע כי המספר המורכב ממספרים מונחים ומשברים מונחים יחסו אל אחד היחס המחובר מיחסי מספרי השברים ההם כשיושמו קודמים אל מספרי מוריהם כשיושמו נמשכים משל זה שיחס הכאת שלשה שביעיות בד׳ חמשיות והעולה בב׳ חמשיות רביעית להכאת אחד באחד והעולה באחד שהוא אחד לעולם כמה שהגיע הכפל הוא מחובר משלשה יחסים מיחס שלשה שביעיות אל שבעה שביעיות שהוא אחד ומיחס ארבעה חמשיות אל ה׳ חמשיות שהוא אחד ג״כ ומיחס ב' חלקים מי״ב אל י״ב חלקים מי"ב שהוא אחד וכבר ידעת שכאשר הומר סדור הקודמים או הנמשכים או שניהם יחד נשאר היחס המחובר בעינו ובהיות הענין כן אם היה לך להכות מספר שברים על מספר מה משברים וכן מה שהגיע ההרכבה תוכל להמיר מספרי אלה השברים במספר אחר מהשברים האחרים אם היה יותר נאות אל ההכאה משל זה שאם היה לך להכות ג׳ שביעיות על ז׳ שמיניות תוכל להמיר השבעה אל השביעיות ויהיה לך להכות ג׳ שמיניות על ז׳ שביעיות שהוא אחד והעולה הוא ג׳ שמיניות וככה המבוקש . . . . דמיון אחר אם רצית להכות ד׳ שביעיות על ה׳ שמיניות תוכל להמיר הד׳ אל השמיניות ויהיה לך להכות ד׳ שמיניות שהוא חצי אחד על ה׳ שביעיות ויעלה ב׳ שביעיות וחצי וככה המבוקש דמיון אחר אם היה לך להכות ג׳ רביעיות על ד׳ חמשיות והעולה על ו׳ שביעיות והעולה על ז׳ שמיניות תמיר המספרים שהם ג׳ ד׳ ו' ז׳ במקומות היותר נאותים ולזה תשים הז' אצל השביעיות והד׳ אצל הרביעיות והו׳ אצל השמיניות והג׳ אצל החמשיות ולזה תכה ז׳ שביעיות שהוא אחד על ד׳ רביעיות שהוא אחד ויעלה אחד והעולה שהוא אחד תכה על ו׳ שמיניות ויהיו בידך ג׳ רביעיות והעולה תכה על ג׳ חמשיות ויעלה בידך ט׳ רביעיות חמשית ואם תחלקנו על ארבעה יהיה העולה חמשיות ויעלה בידך ב׳ חמשיות ורביעית חמשית ואם תחלקנו על ה׳ יהיה העולה רביעיות ויעלה בידך רביעית וד׳ חמשיות רביעית וככה העולה דמיון אחר אם היה לך להכות ג׳ חמשיות על ששית והעולה על ז' שמיניות והעולה על ד׳ תשיעיות תמיר המספרים שהם ג׳ ד׳ ז׳ במקומות היותר נאותים ולזה תשים הג׳ אצל הששיות וארבעה אצל השמיניות והז' אצל התשיעיות וישאר חמשית בזולת מספר ותכה ג׳ ששיות שהם חצי על ארבעה שמיניות שהם חצי ויעלה בידך רביעית תכהו על חמשית ויהיה רביעית חמשית תכה רביעית חמשית על ז׳ תשיעיות ויעלה בידך ז׳ רביעיות חמשית תשיעית והקש על זה. דרך הכאת שברים מה בשברים שונים אם היה לך להכות שבר מונח או מספר שברים מונחים על שברים מונחים ערוך השבר המונח או השברים המונחים על המין הראשון מהשברים השונים וחלק העולה על המורה על השבר המוכה כדי שיהיה העולה בידך חלקים מהמכה וכן תעשה עד שיוכה הראשון המכה על כל הנמשכים ובזה יהיו כל החלקים אשר בידך בעולה משברי המכה דמיון רצינו להכות ב׳ שלישיות על ו׳ שביעיות ועל ז׳ שמיניות ועל ח׳ תשיעיות נכה ב׳ על ו׳ יהיו י"ב נחלקם על שבעה שהוא מורה לשבר המוכה ועלה אחד וה' שביעיות והוא שלישית וה׳ שביעיות שלישית ערכנו ב׳ על ז׳ ועלה י״ד נחלקם על שמנה שהוא שבר המוכה ועלה א׳ וו׳ שמיניות והוא שלישית וג׳ רביעיות שלישית ערכנו ב׳ על ח׳ ועלה ט״ז נחלקם על תשעה ועלה אחד וז׳ תשיעיות והוא שלישית וז׳ תשיעיות שלישית חברנו כל השברים אשר בעולה שהם ג שלישיות וה' שביעיות שלישית וג׳ רביעיות שלישית וז׳ תשיעיות שלישית ועלה אחד שלם וב׳ שלישיות וס"א חלקים מתשנ״ו באחר והקש על זה ואם היה לך להכות שלמים ושברים כמה שיהיו על שלמים ושברים כמה שיהיו הנה כבר ידעת אופן הכאת שלמים בשלמים ואופן הכאת שלמים בשברים ואופן הכאת שברים בשברים ולזה תכה כל השלמים שבטור המכה על כל השלמים והשברים אשר בטור המוכה עוד תכה כל השברים שבטור המכה על כל השלמים והשברים אשר בטור המוכה דמיון זה אם היה לך להכות י״ב וג' חמשיות וד׳ תשיעיות על כ״א וב׳ שלישיות וג׳ רביעיות הכה י"ב על כ״א ועלה רנ"ב הכה י"ב על ב׳ שלישיות ועלה ח׳ שלמים הכה י"ב על ג׳ רביעיות ועלה ט׳ שלמים הכית ג׳ חמשיות על כ״א שלמים ועלה י״ב שלמים וג׳ חמשיות הכית ג׳ חמשיות על ב׳ שלישיות ועלה ב׳ חמשיות הכית ג׳ חמשיות על ג׳ רביעיות ועלה ב׳ חמשיות הכית ג׳ חמשיות על ג׳ רביעיות ועלה ב׳ חמשיות ורביעית חמשית הכית ד׳ תשיעיות על כ"א ועלה ט׳ שלמים ושלישית הכית ד' תשיעיות על ב׳ שלישיות ועלה ב׳ תשיעיות וב׳ שלישיות תשיעית הכית ד׳ תשיעיות על ג׳ רביעיות ועלה שלישית חברנו כל העולה ועלה רצ"ו שלמים וב׳ חמשיות וז׳ חלקים מתק״ם באחד וזה המבוקש וכן ההקש אם היו שם שברי שברים כי כבר ידעת אופן הכאתם ופעמים תצטרך למלאכות רבות כמו שיהיה לך להכות מספר שלמים ושברים ושטח שברים בשברים או בשלמים גם כן על שלמים ושברים ושטח שברים בשברים והדרך בזה שתוציא ראשונה המספר המכה כשתדע העולה מהשטח ההוא ותחברהו עם השלמים והשברים וסוף דבר תחבר ראשונה כל מה שבמכה עוד תחבר מה שבמוכה ותכה אח"כ הטור האחד על האחר באופן הקודם. ואם היה לך לגרוע שברים כמה שיהיו משברים שונים מהם תקח המספר המעט שימנוהו המורים לכל השברים והוא המורה הנה וממנו תקח השברים שתרצה לגרוע ותשימם בטור אחד עוד תקח ממנו השברים שתרצה לגרוע מהם ומהם תגרע הטור האחר והנשאר בידך הם חלקים מהמורה אשר לקחנו וזה מבואר . . . . דרך אחרת לכפול שלמים ושברים על שלמים ושברים קח המספר המעט שימנוהו המורים לכל השברים והוא המורה הנה ועליו תערוך הטור המכה ותשים העולה בטור אחד ראשון גם על המורה תכה הטור המוכה ותשים העולה בטור אחד שני ותערוך הטור העליון על הטור השפל והעולה בידך הוא המבוקש . . . והמשל אם היה לך להכות י״ב וג׳ חמשיות וד׳ תשיעיות על כ"א וב׳ שלישיות וג׳ רביעיות הנה ידעת שהמספר הראשון שימנה כל אחד מאלו השברים הוא ק"פ לקחת י״ב דמיוני ק"פ וג' חמשיות ק״פ וד׳ תשיעיות ועלה ב׳ אלפים וג׳ מאות וארבעים ושמנה ותשימם בטור אחד לקחת כ"א דמיוני ק"פ וב׳ שלישיותיו וג׳ רביעיותיו ועלה ד׳ אלפים ול"ה ונשימם בטור האחר הכית הטור האחד על הטור האחר ועלה 0 ח׳ א׳ ד׳ ז׳ ד׳ ט׳ חלקת העולה על מרובע ק"פ ועלה רצ"ב שלמים ונשארו 0 ח׳ ג׳ ג׳ א׳ והם חלקים ממרובע ק״פ באחד וכאשר נבחן תמצא הנשאר ב׳ חמשיות ות"ך חלקים ממרובע ק"פ שהם ב׳ חמשיות וז׳ חלקים מתק"ס וזה מסכים לחשבון הראשון והקש על זה. והיה זה כן לפי שנכפל כל אחת מצלעות השטח על ק״פ היה יחס השטח אל השטח יחס צלעו אל צלעו שנוי ביחס לפי שהשטחים מתדמים אבל יחס צלעו אל צלעו הוא ק"פ אם כן יחס השטח אל השטח הוא כמו מרובע ק"פ אם כן השטח אשר צלעיו נכפלים על ק"פ ימנהו מרובע ק"פ במספר אחדי השטח הראשון . . . ואחר שהתבאר אופן כפל השברים בכל מיניהם הנה נבאר לך מה תעשה ממה שלא הגיע לחלוק והדרך בזה שתחלוק כל מה שתוכל לחלקו והנשאר הם חלקים מהמספר הטור שתחלוק עליו באחד . . . דמיון זה אם רצית לחלק נ"ג על י"ד יעלה ג׳ וישארו י"א והם י"א חלקים מי"ד באחד והיה זה כן לפי שהחלק מי״ד כשהוכה על י"ד היה י״ד חלקים מי"ד באחד שהוא אחד שלם אם כן הי״א חלקים כשהוכו על י"ד היו י״א שלמים והוא מה שנשאר לנו והקש על זה. ואם רצית לחלק שלמים ושברים על שלמים ושברים קח המורה הראשון למורה כל השברים ועליו תערוך הטור שרצית לחלק ותשים העולה בטור אחד עוד תערוך על המורה הטור שרצית לחלק עליו ותשים העולה בטור שני תחת הטור האחד בדרך שתוכל לשום טור העולה בין שני הטורים וכאשר ישלם זה חלק הטור העליון על הטור התחתון והעולה הוא המבוקש דמיון זה אם רצית לחלק פ״ד וג׳ חמשיות וג׳ רביעיות על י׳ וב׳ שלישיות וג׳ שמיניות הנה המורה הראשון לכל אלו השברים הוא ק״כ ערכנו פ"ד וג׳ חמשיות וג׳ רביעיות על ק"כ ועלה עשרת אלפים רמ״ב והוא הטור שתחלק ערכנו י׳ וב׳ שלישיות וג׳ שמיניות על ק"כ ועלה אלף שכ"ה והוא הטור שתחלק עליו חלקת הטור העליון על הטור התחתון ועלה ז׳ שלמים ותתקס"ז חלקים מאלף שכ"ה באחד וככה המבוקש והיה זה כן לפי שכבר לוקחו לפ"ד וג׳ חמשיות וג׳ רביעיות והוא הראשון ולמספר י׳ וב׳ שלישיות וג׳ שמיניות והוא השני כפלים שוים והם ק"כ אם כן יחס כפלי הראשון הלקוחים אל כפלי השני כיחס הראשון אל השני אבל יחס כפלי הראשון אל כפלי השני הוא ז׳ שלמים ותתקס"ז חלקים מאלף שכ״ה באחד אם כן יחס הראשון אל השני הוא ז׳ שלמים ותתקס"ז חלקים מאלף שכ"ה באחד והקש על זה ואם תרצה לבחון זה הכה ז׳ שלמים ותתקס"ז חלקים מאלף שכ"ה באחד על י׳ וב׳ שלישיות וג׳ שמיניות ויצא לך פ"ד וג׳ חמשיות וג׳ רביעיות. ואחר שהתבאר זה ראוי שנבאר לך אופן החלוק לפי שברי חכמי התכונה וכבר ידעת שהכאת שברים על שברים הוא מהמעלה אשר מרחקה מהמכה לפניה כמרחק המוכה ממעלת האחדים וכאשר התישב זה אתן לך דרך לכפול שלמים ושברים ומזה תוכל לדעת אופני הכפלת שברים בכל אופניהם . . . כאשר תרצה לכפול שלמים ושברים משברי חכמי התכונה על שלמים ושברים משבריהם ג"כ ראוי שנכתוב המספר אשר אחז יותר מעט מהמדרגות בטור אחד כפי מדרגתו ותעשה רושם בין השלמים והשברים על הדרך אשר זכרנו במה שקדם ואחר תכתוב המספר האחר בטור אחד תחתיו כפי מדרגותיו ותכה הראשון שבטור העליון על הראשון שבטור התחתון ותשים העולה במעלה הראויה ואם עלה יותר מששים תחלוק העולה על ששים והעולה בידך יהיו אחדים במעלה שלאחריו והנשאר תשים במעלה הראויה ואם עלה יותר מששים במעלה שלאחריה תשוב לחלק העולה על ששים וכן עד הגיעך למעלות האחדים ומשם והלאה לא תחלוק כי אם על עשרה והסבה מבוארת וכזה תעשה עד שיוכו כל מספרי הטור העליון על כל מספרי הטור התחתון ויהיו טורי העולה כמספר המדרגות שבטור העליון אשר בהם מספר זולת השלמים שלא יהיה להם כי אם טור אחד כמה שיהיו עוד תחבר כל מה שבטורי העולה בטור שפל תחתיהם והעולה הוא המבוקש וכאשר תגיע להכות השברים על השלמים תכה אותם יחד על כל השלמים שבטור התחתון כדי שלא יתבלבל עליך ותחלק העולה על ששים על הצד הקודם ותשים הנשאר כפעם בפעם במקום הראוי וכן כשתגיע להכות השלמים על השברים תכה גם כן כל השלמים שבטור העליון יחד על השברים שבטור התחתון כפעם בפעם דמיון זה רצינו בזאת הצורה להכות נ״ז שניים וט׳ ראשונים ופ״ג שלמים על שבעת אלפים ותשעים ומ׳ שניים ונ״א שלישיים וג׳ רביעיים הכינו נ״ז שניים על ג׳ רביעיים ועלה ב׳ חמשיים ונ"א ששיים הכינו נ"ז שניים על נ״א שלישיים ועלה מ"ח רביעיים וכ"ז חמשיים הכינו נ״ז שניים על מ׳ שניים ועלה ל"ח שלישיים הכינו נ"ז שניים על ז' אלפים וצ' שלמים ועלה ל׳ שניים ט״ו ראשונים וב' בראשונה א׳ בשנייה א׳ בשלישית וכאשר הנהגו בכמו זאת ההנהגה עד שיוכו כל מספרי הטור העליון על מספרי הטור התחתון תמצא העולה נ"א ששיים נ״ו חמשיים ל"ו רביעיים כ״ג שלישיים ז׳ שניים ל"ב ראשונים ה׳ שלמים ד׳ ו׳ ט׳ ח׳ ה׳ והקש על זה. נז ט ג ח ג נא מ 0 0 ט 0 ז נג ב כז מח 0 לח 0 ל 0 טו ב א א כז לט 0 ז 0 ו ל 0 ג ו 0 א ט ד לג י כ א נה 0 ז ד ח ח ה נא נו לו כג ז לב ה ד ו ט ח ה ואם תרצה לחלק מספר מה על שלמים ושברים מאלה השברים אשר אנחנו בהם תכתוב המספר שרצית לחלק בטור העליון במקומותיו בדרך שתוכל לכתוב העולה בין שני אלו הטורים כמו שעשית במה שקדם אחר כך תראה מה שבמעלה האחרונה שבטור התחתון והיו לאחדים בידך וכל המספרים אשר לפני המעלה הנמשכת לה לפניה תחשוב אחד במעלה הנמשכת לה לפניה ותחברהו עם המספר שבה ואם היתה זאת המעלה שלפני האחרונה שלמים יהיה זה המספר עשיריות ואם היתה זאת המעלה שלפני האחרונה שברים יהיה זה המספר חלקים מששים וחברהו עם האחדים שבמעלה האחרונה והוא השמור ועליו תחלוק המעלה האחרונה שבטור העליון עם מה שבמעלה לפניה אם עשיריות ואם חלקים מששים והעולה תשים במעלה הראויה לפי מה שקדם וערכהו על הטור התחתון והעולה גרע מהטור העליון וכן תעשה עד שישאר לך פחות מהטור שחלקת עליו . . . . דמיון זה רצינו שנחלוק ז׳ מאות ומ׳ ראשונים ונ' שניים על ט׳ שלמים וכ׳ ראשונים ול' שלישיים והנה נחשוב המספרים שלפני המעלה הנמשכת לאחרונה שבטור התחתון אחד בה וכ' שמצאנו בה והנה כ״א והם חלקים מששים ובמעלה האחרונה ט׳ והם אחדים והנה השמור הוא ט׳ אחדים וכ"א חלקים מששים חלקנו על השמור המספר שבמעלה האחרונה שבטור העליון שהוא שבעים אחר שהורדנוהו אל המעלה שלפניה ועלה ז׳ מהמעלה השניה לפי מה שקדם ונכתוב ז׳ בטור האמצעי במעלה השניה ונערכהו על הטור התחתון ובאשר הנהגנו זה על הצד שזכרנו תמצא העולה ז׳ מהמעלה השניה ה׳ מהמעלה הראשונה ונשאר בטור העליון שלא הגיע לחלוק מ׳ ראשונים י"ב שניים ל׳ שלישיים והקש על זה. כח ד כח נב ב ל יב מ 0 0 טו כ ז ד טור הנחלק נ מ 0 0 ד טור העולה יח ד ח ז טור שחלקנו עליו ל 0 כ ט לה כ ג ה ו ל ב 0 מ ו ד ב כ א לו 0 ו מב ב דרך לחלק מה שלא הגיע לחלוק כשהיו בטור התחתון שלמים ונציע לביאור זה שחלוק שברים אי זה שיהיו על שלמים הם שברים מהמעלה ההיא בעינה וזה מבואר מצד הכפל וכאשר התישב לך זה הנה תראה כמה מן הראשונים נשארו לך בטור העליון כשתשיב האחרון שבטור העליון למדרגת הראשונים והמספר ההוא שיהיה לך מן הראשונים יהיו לאחדים בידך ומה שבמדרגה שלפניה יהיו חלקים מששים והעולה תחלוק על השמור והעולה בידך הם ראשונים כתבם במקומותם בטור העולה וערכם על כל הטור התחתון שתחלוק עליו והעולה תגרע מהטור העליון עוד תחלוק האחרון שבטור העליון על השמור ואם לא תוכל לחלק תורידהו אל המדרגה שלפניו ובזה הדרך תוכל לדקדק עד אין קץ ואולם דרך לקיחת השמור הנה יהיה שתוריד כל מה שבטור התחתון מן השלמים אל המעלה הראשונה והעולה יהיה לאחדים בידך ומה שלפני המעלה הראשונה יהיו חלקים מששים על הצד הקודם וזה יהיה לך דרך לקיחת השמור במה שלא הגיע לחלוק כאשר היו בטור התחתון שלמים דמיון זה במה שנשאר במשל הקודם שלא הגיע לחלוק חלקנו מ׳ וי"ב חלקים על השמור שהוא ט׳ וכ"א מששים ועלה ד׳ חלקים והם ראשונים מפני שחלקנו ראשונים על שלמים ערכנו ד׳ ראשונים על הטור התחתון ועלה ל"ז ראשונים כ׳ שניים ב׳ שלישיים וגרענו זה מהטור העליון ונשאר שם ב' ראשונים נ"ב שניים כ"ח שלישיים ולא נוכל לחלק ב׳ ראשונים על השמור הורדנום אל השניים והנה קע״ב וכ"ח חלקים מששים חלקנום על השמור וגרענו העולה מהטור העליון ונשאר שם ד׳ שניים כ"ח שלישיים נ"א רביעיים ובזה הדרך תוכל לדקדק עוד לשלישיים ורביעיים ולזולתם ואין צורך לדקדק אחר שתגיע אל החשבון בקירוב. דרך החלוקה כאשר היתה המדרגה האחרונה שבטור התחתון ממדרגת השברים דע כי חלוק שברים על שברים ממינם הוא שלמים וחלוק שברים יותר גבוהים מהם הוא מהמדרגה אשר מרחקה מהשלמים לפניה כמרחק השברים המחולקים מהשברים אשר חולק עליהם והסבה מבוארת ממה שקדם דמיון זה אם נחלק שניים על שניים יהיה העולה שלמים ואם נחלק שלישיים על ראשונים יהיה העולה שניים והקש על זה. אם רצית לחלק מספר מה על מספר מה והיתה המדרגה האחרונה שבטור שתחלוק עליו ממדרגת השברים הסתכל על המדרגה האחרונה שבטור העליון אם היא יותר גבוהה ממדרגה האחרונה שבטור התחתון אז תורידהו אל המדרגה שבטור התחתון עד שתהיה המדרגה האחרונה שבטור העליון היא בעינה המדרגה האחרונה שבטור התחתון ואז תחלק האחרונה שבטור העליון עם החלקים מששים אשר לפניה על הצד הקודם על השמור והעולה יהיו שלמים ותערכם על הטור התחתון ותגרע העולה מהטור העליון עוד תחלק הנשאר במעלה האחרונה שבטור העליון על השמור והעולה תשים במעלה הראויה ותערכהו על הטור התחתון ותגרע העולה מהטור העליון וכן תעשה עד שתגיע שלא ישאר לך בטור העליון דבר או שיהיה מעט מה שישאר לך שם . . . . דמיון זה רצית לחלק שבעה עשר שלמים ול' ראשונים ומ' שניים על מ"א שניים ונ"ב שלישיים ומ"ה רביעיים ולפי שהמעלה האחרונה שבטור התחתון היא שניים נוריד מה שאחר השניים בטור העליון אל מדרגת השניים ולזה נוריד השבעה עשר אל מדרגת הראשונים ויהיו אלף וכ׳ ול' שהיו שם והנה אלף וג׳ ראשונים הורדנום אל מדרגת השניים ועלה ס"ג אלפים ומ' שניים ואלה יהיו לאחדים בידך והנה מה שבמדרגה האחרונה שבטור התחתון הוא מ"א ונחשבו כמו אחדים ומה שלפניהם הוא לפי מה שקדם נ"ג חלקים מששים ולזה יהיה השמור מ"א ונ״ג חלקים מששים חלקנו ס״ג אלפים ומ׳ על מ״א ונ"ג חלקים מששים ועלה אלף וחמש מאות וחמשה ערכנו אלף ותק״ה על הטור התחתון ועלה י"ז שלמים ל׳ ראשונים כ"ה שניים ח׳ שלישיים מ"ה רביעיים גרענו העולה מהטור העליון ונשאר י״א שניים נ"א שלישיים ט"ו רביעיים ולא נוכל לחלק מה שבמדרגה האחרונה שבטור העליון על השמור ולזה נוריד אל השלישיים ויהיו לנו תשי"א וט"ו חלקים מששים חלקנום על השמור ועלה י"ו והם ראשונים לפי מה שקדם ערכנו י"ו ראשונים על הטור התחתון וגרענו העולה מהטור העליון ונשאר בטור העליון מ״א שלישיים י"א רביעיים ולא נוכל לחלק מ"א וי"א חלקים מששים על השמור ולזה נוריד השלישיים על הרביעיים ויהיו לנו אלפים תע"א ונחלקם על השמור ועלה נ״ח והם שניים לפי מה שקדם ערכנום על הטור התחתון וגרענו העולה מהטור העליון ונשאר בטור העליון ל׳ ששיים מ"ב רביעיים והנה נוכל לחלק האחרון שבטור העליון על השמור ועלה אחד והוא שני לפי מה שקדם ערכנוהו על הטור התחתון וגרענו העולה מהטור העליון ונשארו בטור העליון ז' חמשיים מ"ה ששיים ואם תרצה תוכל לדקדק עוד ולהוריד חמשיים אל הששיים ולחלק על השמור ויהיה העולה רביעיים לפי מה שקדם ואין צורך כי כבר הגענו אל קירוב גדול . . . . ובכאן נשלם הביאור בחלוק מספר על מספר בכל אופני החלוקה. מה ז ל 0 מב יא מא טו נא יא טור הנחלק מ ל ז א טור העולה נח יו ה 0 ה א א טור שחלקנו עליו מה נב מא מה ח כח ל ז א יב נב יב ז ל מג יו נ לח לט מה נד מא | |||||||||||||||||||||||
Dividing a known number by an unknown number |
|||||||||||||||||||||||
| ואחר שהתבאר דרך חלוק מספר ידוע על מספר ידוע ראוי שנבאר דרך חלוק מספר ידוע על מספר בלתי ידוע כמו הוצאת השרשים הרבועיים והמעוקבים ממספרים המונחים | |||||||||||||||||||||||
Extraction of Square Roots |
ונבאר תחלה דרך הוצאת השרשים הרבועיים | ||||||||||||||||||||||
| It is impossible to find the root of an integer whose root is not an integer | ונציע לביאורו הביאור שא׳א׳ שימצא יסוד מספרי למספרים המקיפים בשלמים שאין יסודם אחדים שלמים | ||||||||||||||||||||||
|
וזה שהאחד הוא מרובע | ||||||||||||||||||||||
| Euclid, Elements, Book VIII, proposition 14 | וכבר ידעת מח׳ מאקלידס י״ד שכאשר ימנה מרובע מרובע הנה צלעו ימנה צלעו | ||||||||||||||||||||||
| והאחד ימנה כל מספר ואם היה זה המספר מרובע הנה האחד מונה את יסודו אבל האחד לא ימנהו אם כן אין מספר מרובע | |||||||||||||||||||||||
| ולזה יתבאר שא׳א׳ שיהיה לזה המספר יסוד מספרי | |||||||||||||||||||||||
|
|
משל זה שמספר העשרה אין יסודו מקיף בשלמים | ||||||||||||||||||||||
|
|
לפי שמרובע שלשה הוא תשעה ומפני שהעשרה מוסיף על תשעה יהיה יסודו מוסיף על יסודו ובזה יתבאר שיסוד עשרה הוא פחות מארבעה לפי שמרובע ארבעה הוא ששה עשר א״כ אין יסוד עשרה מקיף בשלמים | ||||||||||||||||||||||
| והנה עשרה ימנהו האחד שהוא מרובע ואם היה עשרה מרובע היה יסוד העשרה ימנהו יסוד האחד שהוא אחד וזה כבר התבאר שהוא שקר | |||||||||||||||||||||||
| אם כן אין למספר עשרה יסוד מספרי לא נשבר ולא בלתי נשבר ולזה יקרא יסודו הוא מדבר בכח לבד והקש על זה | |||||||||||||||||||||||
| The ranks of the square numbers | וכאשר התישב זה נודיעך אי זה מהמדרגות יתכן שילקח השרש מהם ואי זה מהם לא יתכן לו בם | ||||||||||||||||||||||
| The squares of the units: 1; 4; 9; 16; 25; 36; 49; 64; 81 | דע כי מרובעי המספרים הנמשכים מן האחד עד עשרה הם מספר א׳ ד׳ ט׳ ששה עשר כ"ה ל"ו מ"ט ס״ד פ"א | ||||||||||||||||||||||
| ולפי שאחדי המעלות מתיחסים ומתחילין מן האחד והשני שהוא עשרה בלתי מרובע הנה אין שם אחד מרובע אלא הראשון והשלישי והחמשי וכן כל המעלות הנפרדות | |||||||||||||||||||||||
| Squares of integers are in odd ranks | וכאשר התישב זה התבאר שאי זה מספר מרובע שימצא במעלות הנפרדות הוא מרובע לפי שהמספר ההוא ימנה האחד מזאת המעלה שהוא מרובע במספר אחדי מספר מרובע | ||||||||||||||||||||||
| Product of square by square is square | אם כן העולה הוא שטח מספר מרובע במספר מרובע שהוא מרובע לפי מה שקדם | ||||||||||||||||||||||
| Squares of integers cannot be in even ranks | ובכמו זה התבאר שאי זה מספר מרובע שימצא במעלות שהם זוג אי אפשר שיהיה מרובע | ||||||||||||||||||||||
| The ranks of the square sexagesimal fractions | וכזה הת' במעלות השברים משברי חכמי התכונה שכל מעלה שהיא זוג אחדיה מרובעים והמעלות הנפרדות אין אחדיהן מרובעים וזה שמספר הששים איננו מרובע ובהיות הענין כן יתחייב שלא יהיה השבר הראשון מרובע לפי שהוא ימנה האחד והוא מרובע במספר ששים והוא בלתי מרובע אם כן אין השבר הראשון מרובע ואומר שהשבר השני מרובע וזה שיחס האחד אל הראשון כיחס הראשון אל השני א״כ שטח הראשון בעצמו כמו שטח האחד בשני אבל שטח האחד בשני הוא שני אחד אם כן השני מרובע ויסודו הראשון ובזה התבאר שהרביעי מרובע וזה שיחס האחד אל השני כיחס השני אל הרביעי א"כ שטח האחד ברביעי הוא שטח השני בעצמו אם כן הרביעי מרובע ובזה התבאר שכל מעלות הזוגות הם מרובעות | ||||||||||||||||||||||
| ולזה התבאר שאי זה מספר שיהיה במעלות אשר הם זוגות הוא מרובע לפי שאחריה מרובעים | |||||||||||||||||||||||
| ובזה יתבאר זה גם כן בצד הביאור אשר באר אקלידס כי האחד לפי שהוא מרובע השלישי לו מהאחדים המתיחסים הוא מרובע ולזה יהיה השני מרובע והרביעי מרובע ומה שימשך מזה מהמעלות הזוגות | |||||||||||||||||||||||
| Extracting root of a perfect square | דרך הוצאת השרש מהמספר המרובע המקיף בשלמים | ||||||||||||||||||||||
| ראוי שנכתוב המספר שבקשנו לדעת את מרובעו בטור אחד כפי מעלותיו אחר כך חקור על המעלה האחרונה שבטור אם היא מהנפרדות ואם לא היתה מהנפרדות הורידה אל שלפניה כדי שיהיה המספר האחרון שבמעלה נפרד אחר כך ראה המרובע היותר קרוב אל זה המספר ואמנם המעט ויסוד המרובע ההוא תכתוב בטור השרש תחת הטור הקודם במעלה האמצעית בין המעלה הראשונה והמעלה האחרונה והוא אשר נקראה הטור היוצא ומרובע השרש היוצא תגרע מהטור העליון והנשאר תחלוק על כפל השרש היוצא אך השמר שישאר לך אחר החלוקה כמו מרובע השרש היוצא לך מן החלוקה והעולה בחלוק והוא השרש היוצא תכתבהו בטור השרש במעלה אשר מרחקה לאחור מהמעלה שחלקת כמרחק המעלה שחלקת עליה מהראשונה ותערוך זה השרש היוצא לך מן החלוקה והעולה בחלוק תכתבהו בטור השרש במעלה הראויה מצד הקודם והשרש היוצא מן החלוקה תערוך על כפל השרש המוצא ועל עצמו והעולה תגרע מהטור העליון וכן תעשה עד שלא ישאר בטור העליון דבר | |||||||||||||||||||||||
|
|
דמיון זה אם רצית להוציא שרש א׳ח׳ב׳ו׳ד׳ו׳ב׳ח׳ | ||||||||||||||||||||||
| ולפי שהמעלה האחרונה היא שמינית תורידה אל שלפניה והנה פ״ב והנה פ"א הוא המרובע היותר קרוב לזה המספר ושרשו ט׳ תכתוב ט׳ בטור השרש ברביעית שהיא אמצעית בין השביעית והראשונית והנה מרובע ט׳ מהרביעית הוא פ״א מהשביעית גרענום מפ"ב ונשאר אחד בשביעית ולא נוכל לחלק על כפל ט׳ שהוא השרש המוצא הורדנוהו אל שלפניו עם ו׳ שהיו בה והנה י״ו ולא נוכל לחלק על כפל ט׳ הורדנו הי״ו אל שלפניה והנה קס"ד חלקנום על כפל השרש המוצא שהוא י״ח ועלה ט׳ והוא השרש היוצא ונכתבם בטור השרש ברביעית לאחור במדרגת קס"ד ערכנום על כפל השרש המוצא ועל עצמם והעולה גרענו מהטור העליון ונשאר בו א׳ח׳א׳ח׳א׳ חלקנום על כפל השרש המוצא והוא על צד הקודם י״ח אחדים וב' עשיריות ועלה אחד בראשונה בקרוב ונכתבהו בראשונה בטור השרש ערכנוהו על כפל השרש המוצא ועל עצמו וגרענו העולה מהטור העליון ולא נשאר בטור העליון דבר והנה שרש זה המספר הדרוש הוא ט׳ אלפים וצ״א והוא המבוקש | |||||||||||||||||||||||
|
ואם תרצה תוכל לבחון זה בשתכה טור השרש על עצמו ויצא לך הטור העליון והיה זה כן לפי שכבר התבאר שכאשר הוסף מספר על מספר הנה מרובע שני המספרים מקובצים שוים למרובעי שני המספרים ולכפל שטח זה בזה | ||||||||||||||||||||||
| Extracting root of integers and simple fractions | דרך הוצאת השרשים מהמספרים המרובעים אשר הם בלתי מקיפים באחדים שלמים ולא היו השברים בהם משברי חכמי התכונה | ||||||||||||||||||||||
| הוצא המורה הראשון אל השברים ההם ר״ל המספר המעט שימנה מורי השברים ההם בכללם ועליו אם היה מרובע או על מרובעו אם לא היה המורה הראשון מרובע תערוך המספר ההוא ותוצא שרש העולה וחלקהו על שרש המספר אשר כפלת עליו המספר המונח והעולה הוא המבוקש | |||||||||||||||||||||||
|
|
דמיון אם רצית לדעת שרש פ״ב שלמים ורביע וב׳ שביעיות שביעית | ||||||||||||||||||||||
| הנה המורה הראשון לאלו השברים הוא לפי מה שהתבאר מאקלידס קצ"ו והוא המספר המורכב מד׳ ומ״ט שהם מרובעים ולזה יהיה קצ״ו מרובע | |||||||||||||||||||||||
|
|
ערכנו עליו זה המספר ועלה ט׳ב׳א׳ו׳א׳ לקחנו שרשו ועלה קכ"ז חלקנוהו על שרש קצ״ו שהוא י"ד ועלה ט׳ וחצי שביעית וככה המבוקש והקש על זה | ||||||||||||||||||||||
Explanation: 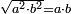
|
והיה זה כן לפי שכבר התבאר שכאשר הוכה מספר מרובע במרובע שיסוד העולה הוא המספר המורכב מיסודי שני המרובעים אם כן העולה ימנה היסוד האחד כמספר אחדי יסוד האחר | ||||||||||||||||||||||
| Approximation method for finding the root of a non-square number when there are integers in the root | דרך להוצאת שרש מספר בלתי מרובע שיהיה בשרשו שלמים בקירוב גדול | ||||||||||||||||||||||
| Description of the procedure – lowering the rank of the remainder | הוצא תחלה השרש הקרוב למספר ההוא בדרך שזכרנו עד שישאר לך בטור העליון פחות מכפל השרש המוצא מקובץ עם אחד שהוא מרובע השרש היוצא והנשאר לך תורידהו אל הראשונים וחלק על כפל כל מה שבטור השרש כשתורידהו למעלת האחדים והזהר שישאר לך בטור העליון כמו מרובע השרש היוצא והעולה יהיו ראשונים לפי מה שקדם ערכם על כפל השרש המוצא ועל עצמם וגרע העולה מהטור העליון והנשאר לך אם הוא פחות מכפל השרש היוצא נחבר עם אחד תורידהו אל המעלה שלפניה ותשוב לחלק על כפל השרש המוצא כשתוריד כל השלמים אל המעלה הראשונה והשברים אשר לפניהם יהיו חלקים מששים והשרש היוצא הוא לפי מה שקדם ממעלת השברים אשר חלקנו ושם תכתבהו בטור העולה ערכהו על כפל השרש המוצא ועל עצמו והעולה גרע מהטור העליון ובזה הדרך תוכל לדקדק כפי מה שתרצה | ||||||||||||||||||||||
|
|
דמיון זה אם רצית למצא שרש מספר א'ב'ג'ד'ה'ו'ז' ומ' ראשונים ול' שניים | ||||||||||||||||||||||
| הנה תוצא השרש הקרוב על הצד הקודם ויעלה ו׳ו׳ז׳ב׳ ונשאר בטור העליון ג׳ אלפים וה' מאות וס״ה שלמים מ׳ ראשונים ל׳ שניים הורדנו השלמים למדרגת הראשונים ויהיו בידינו מאתים אלף וי"ג אלפים וט' מאות ומ׳ ובמדרגה שלפניהם ל׳ והם חלקים מששים חלקנו העולה על כפל הטור התחתון שהוא ה׳ אלפים וה׳ מאות ול"ב בדרך שישאר כמו מרובע השרש היוצא ועלה ל"ח והם ראשונים לפי מה שקדם ושם נכתבם בטור השרש ערכנום על כפל השרש המוצא ועל עצמם וגרענו העולה מהטור העליון ונשאר בטור העליון ס"א שלמים מ׳ ראשונים כ"ו שניים שהם ג׳ אלפים ות״ש ראשונים וכ"ו שניים וזה פחות מכפל השרש המוצא שהוא ה׳ אלפים וה׳ מאות ול"ג שלמים וי"ו חלקים מששים הורדנו הנשאר בטור העליון למדרגת השניים ויהיו בידינו מאתים אלף וכ"ב אלפים וכ״ו חלקנום על כפל השרש המוצא ועלה מ׳ והם שניים לפי מה שקדם ושם נכתבם בטור השרש ערכנום על כפל השרש המוצא ועל עצמם וגרענו העולה מהטור העליון ונשאר בטור העליון י״א ראשונים ל״ד שניים י"ג שלישיים כ׳ רביעיים שהם תרצ"ד שניים י"ג שלישיים כ׳ רביעיים וזה פחות מכפל השרש המוצא ולזה נוריד כל זה למדרגת השלישיים יעלה מ"א אלפים ותרצ"ג וכ׳ חלקים מששים חלקנום על כפל השרש המוצא שהוא ה׳ אלפים ה׳ מאות ול"ג וי"ח חלקים מששים ועלה ז׳ שלישיים ערכנום על כפל השרש המוצא ועל עצמם וגרענו העולה מהטור העליון ומצאנו שהגענו אל השרש הדרוש בקירוב גדול כי הנשאר בטור העליון אינו מגיע לשני אחד והוא מעט כשיוקש אל מה שראוי שיתחלף השרש האמתי בעבורו ואם תרצה תוכל לדקדק עוד ואין צורך | |||||||||||||||||||||||
| Another approximation method | דרך אחרת כשהיה בשרש שלמים | ||||||||||||||||||||||
| The larger the number the more difficult to extract its root | דע כי כל אשר יהיה המספר שתבקש לדעת שרשו יותר גדול תהיה הוצאתו יותר בקושי | ||||||||||||||||||||||
Description of the procedure – lowering the number using division by 100 and multiplication by 36: 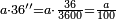
|
ואודיעך איך תעשה ממספר גדול מספר מעט אחר שאבאר לך כי כפל מספר בל"ו שניים הוא שוה לחלוקו אל מאה וזה כי ל"ו שניים הוא חלק אחד ממאה באחד כי השניים אשר באחד הם ל"ו מאות וכאשר התבאר לך זה הנה תחלוק על מאה המספר הגדול וזה החלוק יקל מאד במה שיגיע ממנו לחלוק ומה שלא יגיע ממנו לחלוק תערכהו על ל"ו שניים והעולה בידך מהשלמים והשברים הוא המספר הגדול מורד פעם אחת ואם לא היה זה המספר המורד פחות ממאה תשוב להוריד אותו בזה הדרך עד שיגיע פחות ממאה והמספר האחרון המורד הוא המספר המבקש יסודו והנה תמצאהו בקלות גדול ותדקדק עד חמשיים או עד שלישיים כדי שיהיה החשבון בקירוב מופלג וכאשר תמצאהו תמנה מספר ההורדות וקח המספר המורכב ממספרי עשרה כמספרי ההורדות וזה מסכים למעלה אשר מספרה מוסיף אחד על מספר ההורדות ועל העולה ערוך השרש שיש לך ומה שיגיע מן הכפל הוא המבוקש | ||||||||||||||||||||||
|
|
דמיון רצינו שנוציא שרש א'ב'ג'ד'ה'ו'ז'ח'ט' | ||||||||||||||||||||||
| חלקנו זה המספר על מאה וערכנו הנשאר שלא בא לחלוק על ל״ו שניים ויצא לנו ג׳ד׳ה׳ז׳ח׳ט׳ וי"ב ראשונים ל״ו שניים וזאת היא ההורדה הראשונה ולפי שמה שיצא לנו הוא בלתי קטן ממאה נשוב לחלק זה הטור שיצא לנו על מאה ולערוך מה שלא בא לחלוק על ל"ו שניים ויצא לנו ה׳ז׳ח׳ט׳ וכ"ה ראשונים נ"ה שניים ל״ג ל"ו והיא ההורדה השנית ונשוב עוד לחלק זה הטור שיצא לנו על מאה על הדרך הקודם ויצא לנו ח׳ בראשונה ט׳ בשניה מ״ה ראשונים ט"ו שניים ל"ג שלישיים כ׳ רביעיים ט׳ חמשיים ל״ו ששיים וזה המספר הוא קטן ממאה ולזה לא נשוב להוריד עוד והנה ההורדות שלשה והנה נחקור על שרש זה המספר הקטן ולפי שהמעלה האחרונה שבטור היה מהזוגות נוריד אל שלפניו ויהיו לנו צ"ח בראשונה והנה המרובע הקרוב לזה המספר לפניו הוא פ״א ושרשו ט׳ מהראשונה ונכתוב ט׳ בטור השרש במעלה הראשונה גרענו מרובע ט׳ מצ"ח ונשאר לנו י"ז הורדנום אל מדרגת הראשונים ועלה אלף וס״ה וט"ו חלקים מששים על הצד הקודם חלקנום על כפל השרש המוצא שהוא י"ח בדרך שישאר בטור העליון מרובע השרש היוצא ועלה נ"ו והם ראשונים לפי מה שהתבאר קודם ושם נכתבם בטור השרש ערכנום על כפל השרש המוצא ועל עצמם וגרענו העולה מהטור העליון ונשאר בטור העליון ד׳ ראשונים נ״ט שניים ומה שנמשך להם מן השברים הורדנו הראשונים למדרגת השניים והנה רצ"ט ול"ג חלקים מששים חלקנום על כפל השרש המוצא שהוא י"ט שלמים ונ"ב חלקים מס׳ בדרך שישאר לנו מרובע השרש היוצא מן החלוקה ועלה ט"ו והם שניים ערכנום על כפל השרש המוצא ועל עצמם וגרענו העולה מהטור העליון ונשאר לנו בטור העליון שני אחד כ"ט שלישיים ל״ה רביעיים ט׳ חמשיים ל"ו ששיים וכאשר נהגנו בכמו זה המנהג מצאנו זה השרש בקירוב גדול ט׳ שלמים נ״ו ראשונים ט"ו שניים ד׳ שלישיים ל׳ רביעיים כ״ו חמשיים נ״ב ששיים נ״ב שביעיים והקרוב היה לתוספת אצל המרובע ב׳ שביעיים מ"ב שמיניים ז׳ נ׳ ל׳ ל״ה ל"ח נ״ג ד׳ שמרהו ולפי שההורדות יהיו שלשה נערוך זה השרש על אלף כי המספר המורכב מג׳ דמיוני עשרה הוא אלף והנה העולה הוא ט׳ אלפים ותתקל"ח שלמים ל״ז ראשונים ט"ו שניים ז׳ שלישיים כ"ח רביעיים ג׳ חמשיים ו׳ ששיים מ׳ שביעיים והוא שרש המספר המבוקש בקירוב | |||||||||||||||||||||||
| ולדעת הקירוב ערוך הקירוב הראשון ששמרת על מרובע אלף שערכת עליו השרש והנה הקירוב אל הצד שהיה אליו הקירוב הראשון ולזה יהיה הקירוב הראשון ט׳ רביעיים מ"ד חמשיים י"ח ששיים ל"ב שביעיים 0 ל״ה ל"ד ל"ד ד׳ כ"ו מ׳ וזה קירוב גדול לזה המספר הרב לפי שזה הקירוב איננו מגיע למרובע לרביע אחד מן השברים השלישיים והקש על זה | |||||||||||||||||||||||
| והיה זה כן לפי שמספר הטור הראשון ימנה הטור השני המורד במספר מה שבמאה מן האחדים אם כן הטור השני יוכה במאה ויהיה כמו הטור הראשון וכזה הת׳ שהטור המורד האחרון יוכה במורכב משלשה דמיוני מספר מאה שהוא אלף אלפים ויהיה כמו הטור הראשון א״כ יחס הטור הראשון אל הטור האחרון המורד הוא אלף אלפים | |||||||||||||||||||||||
|
|
וג"כ הנה יחס השרש הגדול אל השרש הקטן הוא אלף | ||||||||||||||||||||||
|
|
ויחס מרובע השרש הגדול אל מרובע השרש הקטן הוא אלף אלפים | ||||||||||||||||||||||
| ולזה יהיה יחס מרובע השרש הגדול אל מרובע השרש הקטן כיחס הטור הראשון אל הטור האחרון וכאשר המירונו הנה יחס מרובע השרש הגדול אל הטור הראשון ביחס מרובע הקטן אל הטור האחרון אבל מרובע השרש הקטן הוא כמו הטור האחרון בקירוב אם כן מרובע השרש הגדול הוא כמו הטור הראשון בקירוב וגם כן הנה מפני שיחס מרובע השרש הגדול אל הטור הראשון ביחס מרובע השרש הקטן אל הטור האחרון והיה מרובע השרש הקטן יותר גדול מהטור האחרון הנה מרובע השרש הגדול יותר גדול מהטור הראשון וכאשר הבדלנו הנה יחס מרובע השרש הגדול אצל יתרונו על הטור הראשון כיחס מרובע השרש הקטן אצל יתרונו על הטור האחרון וכאשר המירונו הנה יחס מרובע השרש הגדול אל מרובע השרש הקטן כיחס יתרון מרובע השרש הגדול על הטור הראשון אל יתרון מרובע השרש הקטן על הטור האחרון אבל יחס מרובע השרש הגדול אל מרובע השרש הקטן הוא אלף אלפים אם כן יחס יתרון מרובע השרש הגדול על הטור הראשון אל יתרון מרובע השרש הקטן על הטור האחרון הוא אלף אלפים והקש על זה | |||||||||||||||||||||||
| Extracting root of sexagesimal fractions | דרך הוצאת השרשים משברים מונחים משברי חכמי התכונה | ||||||||||||||||||||||
| חקור על המדרגה הגבוהה מכלם אם היא מהזוגות ואם היא אינה מהזוגות הורידה אל שלפניה כדי שתהיה מהזוגות ומהעולה הוצא השרש האמתי או הקרוב אמנם המעט ותשימהו בטור השרש במדרגה הממוצעת בין המדרגה ההיא ובין האחד ואם ישאר לך תורידהו אל מדרגה שפלה עד שתוכל לחלקו על כפל השרש המוצא והעולה בחילוק תשים במעלה אשר מרחקה מהמדרגה המחולקת לאחריה כמרחק המדרגה שחלקת עליה מהראשונה וכפי זה הדרך תדקדק כל מה שתרצה | |||||||||||||||||||||||
|
|
דמיון זה אם רצית להוצא שרש נ״ג שלישיים מ״א רביעיים נ׳ חמשיים כ"ה ששיים | ||||||||||||||||||||||
| הנה המדרגה היותר גבוהה היא מדרגת השלישיים ואיננה מהזוגות הורידה ויהיו בידך שלשת אלפים ורכ"א והשרש היותר קרוב לזה המספר הוא נ"ו ונכתבם במדרגת האמצעיים בין מעלת האחדים והרביעיים והם השניים ערכנום על עצמם וגרענו העולה מהטור העליון ונשארו לנו פ"ה רביעיים נורידם אל החמשיים ויהיו בידנו ה׳ אלפים וק"נ חמשיים חלקנום על כפל השרש המוצא שהוא קי"ב בדרך שישאר לנו מרובע השרש היוצא ועלה מ"ה ולפי המעלה שחלקנו עליה היא שלישית למדרגת האחדים נשים המ"ה בטור השרש במעלה השלישית לאחור למעלה המחולקת ולזה יהיו אלו המ"ה שלישיים ערכנום על כפל השרש המוצא ועל עצמם וגרענו העולה מהטור העליון ונשאר בטור העליון ע"ז חמשיים נ׳ ששיים נוריד החמשיים אל הששיים ועלה ארבע אלפים ותר"י חלקנום על כפל השרש המוצא שהוא קי"ג ול"ב חלקים מששים בקירוב ועלה ל"ג והם לפי מה שקדם חמשיים ערכנום על כפל השרש המוצא ועל עצמם וגרענו העולה מהטור העליון ונשאר בטור העליון נ"ד שביעיים ח׳ שמיניים ב׳ תשיעיים נ״א עשיריים וכזה תוכל לדקדק כל מה שתרצה ואין צורך לדקדק עוד הקרוב בלתי מגיע לששי אחד והקש על זה | |||||||||||||||||||||||
Extraction of Cubic Roots |
דרך הוצאת השרשים המעוקבים | ||||||||||||||||||||||
| ואנחנו מציעים לבאורו שקצת המספרים אין להם יסוד מספרי עקוביי וזה שכבר הת׳ שכאשר מעוקב ימנה מעוקב הנה צלעו ימנה צלעו ולזה יחוייב בכל מספר מקיף בשלמים שאין יסודו אחדים שלמים שאי אפשר שימצא לו יסוד מספרי עקוביי וזה שאם היה לו יסוד מספרי היה מספר מעוקב ולפי שזה המספר ימנה האחד שהוא מעוקב הנה צלעו ימנה צלעו ואם היה צלעו מונה צלעו היה יסודו מקיף בשלמים וכבר הונח יסודו בלתי מקיף בשלמים זה ישקר אם כן אין מספר מעוקב ולזה יתבאר שאין מספר העשרה מעוקב ולא מספר הששים ושאי אפשר שימצא להם יסוד מספרי עקוביי וכאשר התבאר זה והיו אחדי המעלות מתיחסים ומתחילים מן האחד והשני שהוא עשרה אינו מעוקב אם כן אין אחד מעוקב זולת הרביעי והשביעי והעשירי והם המדרגות שמספרם מונה שלשה כשחוסר מהם האחד וכזה התבאר שאין במדרגות השברים מעלה מעוקבת זולת השלישיים והששיים והתשיעיים שמספרם מונה שלשה וג"כ הנה מעוקבי המספרים הנמשכים מן האחד עד תשעה הם א׳ ח׳ כ"ז ס"ד קכ"ה רי"ו שמ"ג תקי"ד תשכ"ט וכאשר היה זה כן הוא מבואר שכל מספר מעוקב שימצא במדרגה מעוקבת הוא מעוקב לפי שהוא ימנה האחד המעוקב ההוא במספר מעוקב אם כן המעוקב כבר הוכה במעוקב ולזה יהיה העולה מעוקב בהכרח ובזה הת׳ שהמספר המעוקב במעלה בלתי מעוקבת הוא בלתי מעוקב וכאשר התישב זה כלו הנה נבאר איך ימצא השרש העקובי למספרים המקיפים בשלמים המעוקבים או הקרוב לבלתי מעוקבים ראוי שתכתוב המספר שרצית לדעת יסודו העקובי בטור אחד כפי מדרגותיו אח"כ תראה אם המעלה האחרונה היא מהמעוקבות ואם לא הורד המספר לפניה עד שתהיה במעלה המעוקבת והמספר שיהיה במעלה ההיא המעוקבת תחקור עליה במעוקבים שזכרנו ותקח המעוקב היותר קרוב אליו ואולם המעט ויסודו ידוע לך והיסוד ההוא תשימהו בטור השרש במעלה אשר נבאר לך והוא שתחלוק מספר גובה המעלה ההיא על שלשה וישאר לך אחד בהכרח חברהו עם העולה מן החלוקה ובמעלה אשר מספרה ככה תשים העולה | |||||||||||||||||||||||
| משל זה אם היתה המעלה האחרונה שלש עשרה תחלוק שלש עשרה על שלשה יעלה ארבעה תחברם עם האחד הנשאר מן החלוקה ויהיו חמשה א"כ העולה תשים במעלה החמשית והיה זה כן לפי שהחמשית כאשר הוכתה על עצמה היתה תשיעית עוד הוכתה תשיעית על החמשית והיתה המעלה השלש עשרה והקש על זה | |||||||||||||||||||||||
| גרע מעוקב השרש היוצא מהטור העליון והנשאר שם הוא הנשאר הראשון אח״כ קח השרש המוצא וחברהו עם אחד מהמעלה שלפניו וערוך זה על השרש המוצא והעולה תערוך על שלשה דמיוני האחר המוסף ושמור העולה ואם היה השמור פחות מהנשאר הראשון תחלק הנשאר הראשון על השמור אלא שצריך שתשמור שישאר לך מעוקב השרש היוצא בחלוק ושישאר גם כן בטור העליון מספר יהיה יחסו אל מה שחלקת כיחס השרש היוצא פחות אחד אל השרש המוצא עם העולה מקובצים רצוני שאם היה השרש ו׳ ממעלה מונחת והיה השרש היוצא ה׳ ממעלה שלפניה הנה ראוי שישאר ממה שחלקת מספר יהיה יחסו אל המספר המחולק כיחס ד׳ אל ס"ה בקירוב וזה קשה מאד בנשאר הראשון אמנם ממנו ולהלאה יספיק דבר מועט שישאר על מעוקב השרש היוצא למיעוט יחס שרש היוצא אל שרש המוצא ולהקל מעליך נתתי לך דרך טובה וקרובה תלך בה בנשאר הראשון והיא זאת חקור כמה יוסיף מעוקב המספר הנמשך אל השרש המוצא לאחריו על מעוקב מספר השרש המוצא ועל עשירית היתרון תחלוק הנשאר הראשון והשרש היוצא מן החלוקה הם אחדים מהמעלה אשר לפני מעלת השרש המוצא ואחר שישלם לך זה אם בדרך הראשונה או בשנית תערוך השרש המוצא על השרש המוצא והיוצא והעולה תערוך על שלשת דמיוני השרש היוצא וחבר עם העולה מעוקב השרש היוצא והעולה בידך גרעהו מהנשאר הראשון והנשאר יהיה הנשאר השני ואם לא הגיע הנשאר הראשון לעשירית המספר אשר אמרנו לחלק עליו לא תשפוט מפני זה שלא יהיה אפשר שתשים בשרש המוצא אחד במעלה שלפניו אך תנסה אם תוסיף אחד על השרש המוצא במעלה שלפניה ותכה העולה על השרש המוצא ותערוך העולה מהכפל על שלשה דמיוני התוספת רצוני האחד המוסף על השרש המוצא ותחבר עם העולה מעוקב התוספת אם יהיה בלתי גדול מהנשאר הראשון תגרעהו מהנשאר הראשון ותשים אחד לפני השרש המוצא ואם היה גדול מהנשאר הנה נתבאר לך שאין בזה השרש דבר מהמעלה ההיא ותשוב לנהוג עם אחד מהמעלה האחרת אשר היא שלישית למעלת השרש המוצא רצוני שתחברהו עם השרש המוצא והעולה תערוך על שלשה דמיוני התוספת שהוסף על השרש המוצא ועל העולה תחלוק הנשאר השני בדרך שישאר לך מעוקב העולה ויותר לפי היחס הנזכר אלא שמספר מעט שישאר עתה מספיק והעולה בידך הוא השרש היוצא ותכתבהו בטור השרש במעלה ההיא ותערוך השרש המוצא על השרש המוצא והיוצא מקובצים והעולה תערוך על שלשה דמיוני השרש היוצא וחבר העולה עם מעוקב השרש היוצא והעולה תגרע מהנשאר אשר בידך וכזה תוכל לדקדק עד שתגיע אל שרש המספר המבוקש | |||||||||||||||||||||||
| והנה נתן לך דמיונים לפי הדרכים האלה אחד אחד | |||||||||||||||||||||||
| דמיון זה רצינו בזאת הצורה להוציא שרש א'ב'ג'ד'ה'ו' | |||||||||||||||||||||||
| ולפי שהמעלה האחרונה אינה מעוקבת הורדנוה אל שלפניה והנה המעוקב הקרוב לזה המספר הוא תקי"ב ויסודו ה׳ ולפי שזאת המעלה היא רביעית שמנו השרש שהוא ה׳ בשנית ומעוקבם תקי"ב מהרביעית גרענום מתרנ״ד שיש לנו ברביעית ונשארו לנו קמ"ב ברביעית והוא הנשאר הראשון עם מה שנשאר בשאר המעלות והנה לפי הדרך הראשון נערוך השרש המוצא שהוא ח׳ בשנית על ח׳ מהשנית א׳ מהראשונה ועלה ו׳ אלפים ת״פ ערכנו העולה על נ׳ דמיוני א׳ מהראשונה שהוא התוספת ועלה י"ט אלפים ות"מ חלקנו הנשאר הראשון על זה העולה ויעלה ז׳ אלא שלא ישאר מהנשאר הראשון אחר שגרענו מהנשאר מעוקב מספר ז׳ מהראשונה אלא ה׳ אלפים וח' מאות וצ"ד והנה יחסו אל הנשאר הראשון פחות מיחס ו׳ מהראשונה אל פ״ז מהראשונה שהוא השרש המוצא והיוצא וזה שזה היחס הוא חלק מי"ד בקירוב ואם נשים השרש היוצא מן החלוקה ו׳ יהיה הנשאר מספיק לזה היחס ר״ל ליחס ה׳ אל פ"ד שהוא חלק מי"ז בקירוב לפי שהנשאר הוא כ"ה אלפים תת״ן והוא מוסיף על חלק מי"ז במה שנשאר ולזה יהיה העולה ו׳ מהראשונה והוא השרש היוצא ונערוך ח׳ מהשנית שהוא השרש המוצא על השרש המוצא והיוצא ועלה ו׳ אלפים תת״פ ערכנום על ג׳ דמיוני ו׳ מהראשונה שהוא השרש היוצא ועלה קכ"ג אלפים תת"פ ואולם מעוקב השרש היוצא הוא רי"ו חברנוהו עם העולה ועלה קכ"ד אלפים ונ״ו גרענום מהנשאר הראשון ונשאר י"ח אלפים רס״ה ונתברר לנו שלא נוכל להוסיף אחד על השרש לפי שהאחד המוסף על פ׳ הוסיף על המעוקב י"ט אלפים ותמ"ה והם יותר ממה שישאר לנו עתה ואם רצית להקל מעליך אחר שחלקת על י״ט אלפים ות״מ ושמת העולה ו׳ ונשאר לך כ"ה אלפים תס"ה אחר גרעון מעוקב מהנשאר תערוך השרש המוצא על השטח ההוה מהשרש היוצא פחות אחד על שלשה דמיוני השרש המוצא והעולה תגרע מכ״ה אלפים תס"ה והוא המבוקש | |||||||||||||||||||||||
| משל זה שתערוך פ׳ על שטח ה׳ בי״ח ויעלה ז׳ אלפים ומאתים גרעם מכ"ה אלפים תס"ה וישאר לך י״ח אלפים רס״ה וזה מסכים למה שנשאר קודם ובזה התבאר לך הסבה במה שצויתיך להשמר שיהיה לך היחס הנזכר והיה זה כן לפי שהנערך מפ׳ אל פ"א הוכה בג׳ והעולה בו׳ וזה שוה לשטח פ"א בשטח פ׳ בי"ח וכבר היה ראוי שיוכה לפי מה שקדם שטח פ"ו בשטח פ׳ בי"ח והוא מבואר שאם נחבר עם שטח פ"א בשטח פ׳ בי"ח שטח ה׳ בשטח פ׳ בי״ח יהיה העולה שוה לשטח ההוה ממספר פ"ו בשטח פ׳ בי"ח אשר הוא המבוקש והקש על זה ואם נהגנו בזה הדרך השנית והוא היותר קלה על צד הקירוב נחלק הנשאר שהוא קמ"ב אלפים שכ"א על עשירית יתרון מעוקב ט׳ מהשנית שהוא המספר הנמשך אל השרש המוצא לאחריו על מעוקב ח׳ מהשנית והנה היתרון הוא רי"ז אלף ועשיריתו הוא רי"ז עשיריות והם כמו כ״א אלפים וז׳ מאות חלקנו הנשאר הראשון על כ"א אלפים וז׳ מאות ועלה ו׳ שלמים והוא השרש היוצא ערכנו שרש המוצא שהוא פ׳ על השרש המוצא והיוצא ועלה ו׳ אלפים תת"פ ערכנום על שלשה דמיוני השרש היוצא ועלה קכ"ג אלפים תת״מ חברנו עם זה העולה מעוקב היוצא שהוא רי"ו ועלה קכ"ד אלפים ונ"ו גרענום מן הטור העליון ונשאר י"ח אלפים רס״ה והוא הנשאר השני והקש על זה ואמנם בזה הנשאר השני תנסה אם תוסיף ראשון אחד שהוא המדרגה הנמשכת לפני השרש על השרש המוצא שהוא פ"ו כמה יתוסף המעוקב ושמור העולה וחלק הנשאר השני על העולה והשמר שישאר לך מעוקב השרש היוצא ושטח השרש היוצא פחות אחד בשטח השרש המוצא בשלשה דמיוני העולה ערכנו פ"ו שהוא השרש היוצא על פ"ו וראשון אחד וערכנו העולה על ג׳ ראשונים ועלה שס"ט שלמים נ"ב ראשונים ג׳ שניים חלקנו הנשאר השני על העולה ועלה מ״ט והם ראשונים אלא שלא ישאר מהנשאר השני כמו יחס מ"ח ראשונים אל פ"ו ומ״ט ראשונים שהוא חלק מק"ט בקירוב לפי [ש]הנשאר הוא כמו ק"מ שלמים בקרוב והוא מהנשאר פחות מחלק מק"ט ולזה לא נכתוב בטור השרש כי אם מ"ח ראשונים כי אז יספיק לנו הנשאר אל זה היחס ערכנו פ"ו אל פ"ו מ"ח ראשונים והעולה על שלשת דמיוני מ"ח ראשונים ועלה י״ז אלפים תתקט"ו שלמים ול״א ראשונים וי"ב שניים חברנו עם זה מעוקב מ"ח ראשונים שהוא השרש היוצא והוא ל' ראשונים מ"ג שניים י"ב שלישיים גרענו העולה מהשאר השני ונשאר שנ"ד שלמים נ"ח ראשונים ד׳ שניים מ"ח שלישיים והנה ננסה אם נוסיף שני אחד על השרש המוצא כמה יתוסף המעוקב ערכנו פ"ו שלמים מ"ח ראשונים ושני אחד וערכנו העולה על ג׳ שניים ועלה בקירוב ו׳ שלמים י״ז ראשונים ושמרהו כי לא תצטרך לנסיון אחר מכאן והלאה וזה למיעוט יחס השרש היוצא אצל השרש המוצא חלקנו הנשאר על זה השמור ועלו נ"ה והם שניים והעולה על שלשה דמיוני נ"ה שניים ועם העולה חברנו מעוקב נ"ה שניים שהוא השרש היוצא ועלה שמ"ה שלמים כ"ב ראשונים מ"ח כ״ט י״ו י"ב נ"ה גרענוהו מהנשאר ונשאר נ׳ שלמים ל"ה ראשונים י"ו י״ח מ״ג מ"ז ה׳ חלקנו על חלק מהששים מהשמור שהוא ו׳ ראשונים י"ז שניים והוא השמור השני ועלה ל"ד והם שלישיים כי השלישי הוא החלק מהששים מהם וכבר הוסיף השני המעוקב ו׳ שלמים י"ז ראשונים בקירוב ערכנו השרש המוצא שהוא פ"ו שלמים מ"ה ראשונים נ״ה שניים על פ״ו שלמים מ"ה ראשונים נ״ה שניים ל"ד שלישיים והעולה ערכנו על שלשת דמיוני השרש היוצא שהוא ל"ד שלישיים וחברנו עם העולה מעוקב ל"ד שלישיים ועלה נ׳ שלמים ל"ג ראשונים ל"ב מ״ד כ"ה כ"ז ל״ז מ"ז נ״ה ד׳ גרענום מהנשאר ונשאר ראשון אחד מ"ג ל"ד י"ח כ"ט כ"ח נ"ו ד׳ נ"ו חלקנוהו על חלק מהששים מהשמור השני שהוא ו׳ שניים י״ז שלישיים והוא השמור השלישי ועלה י"ו והם רביעיים ואין צריך לדקדק עוד ואם תרצה תוכל לדקדק בזה הדרך כפי מה שתרצה והנה שרש זה המספר הדרוש העקובי הוא פ"ו שלמים מ"ח ראשונים נ"ה שניים ל"ד שלישיים י״ו רביעיים וראוי שתדע כי בדרך השנית שנתתי לך בנשאר הראשון אם היתה המדרגה שלפני שרש המוצא שברים ראוי שתחלק על ששים יתרון מעוקב המספר הנמשך אל השרש המוצא לאחריו על מעוקב השרש המוצא וזה מבואר בעצמו | |||||||||||||||||||||||
| דרך אחרת להוציא שרש מספר מונח העקוביי אשר יהיו ביסודו שלמים | |||||||||||||||||||||||
| דע כי המספר שלא יגיע לאלף יקל מאד להוציא שרשו העקוביי בערך אל מה שלמעלה ממנו ואודיעך איך תוריד מספר רב אל מספר מעט אחר שאבאר שהכאת מספר מונח על ג׳ שניים ל״ו שלישיים שוה לחלוקו על אלף וזה שאלף פעמים ג׳ שניים ל"ו שלישיים יהיה אחד שלם אם כן ג׳ שניים ל״ו שלישיים הם חלק מאלף באחד שלם וכאשר התישב זה הנה ראוי שתחלוק המספר על אלף והנשאר שלא יבוא לחלוק תכפלהו על נ׳ שניים ל"ו שלישיים והיא ההורדה הראשונה ואם העולה בלתי קטן מאלף תשוב לחלקו על אלף בדרך הקודמת והיא ההורדה השנית וכן לא תסור להוריד עד שיהיה המספר קטן מאלף ותמנה מספר ההורדות ותוציא שרש המספר הקטן ותדקדק עד ששיים או כפי מה שתרצה כי יקל מאד בזה הדרך והעולה בידך תערכהו על המספר המורכב ממספרי עשרה כמספר ההורדות וזה מספרם שוה לאחד מהמעלה אשר מספר גבהם מוסף אחד על מספר ההורדות ויצא לך המבוקש | |||||||||||||||||||||||
|
|
דמיון זה אם רצית להוציא שרש א׳ב׳ג׳ד׳ה׳ו׳ז׳ח׳ט׳ה׳ | ||||||||||||||||||||||
| תורידהו הנה שלשה הורדות כדי שיהיה המספר העולה בידך באחרונה פחות מאלף והנה המספר העולה בידך בהורדה באחרונה ה׳ שלמים נ"ט ראשונים ט"ו ל״ג ז׳ נ"ד ל"ג 0 ל"ד ל"ו תשיעיים והנה המעוקב הקרוב למה שבמדרגה האחרונה שהיא מעוקבת היא אחד ושרשו אחד ותכתוב אחד בטור השרש גרעת מעוקבו מהטור העליון ונשארו ד׳ שלמים נ"ט ראשונים. ומה שנמשך לזה מהשברים והנה ידעת שמעוקב שנים יוסיף על מעוקב אחד ז׳ שלמים והנה המדרגה שלפני השרש המוצא היא ממדרגת השברים וחלקת הנשאר בטור העליון על חלק מששים מז׳ שלמים שהוא ז׳ שברים ראשונים ועלה מ"ב והם חלקים מששים באחד שלם ולזה יהיו שברים ראשונים ערכת השרש המוצא שהוא אחד על אחד ומ״ב ראשונים וערכת העולה על שלשת דמיוני השרש היוצא שהוא מ״ב ראשונים וחברנו עם העולה מעוקב מ"ב ראשונים שהוא השרש היוצא ועלה נ׳ שלמים מ"ב ראשונים ח׳ שלישיים גרענום מהנשאר ונשאר אחד שלם י"ז ראשונים ט״ו כ"ה ז׳ נ"ד ל"ד ל"ג ל"ו והנה ראוי שננסה מה יוסיף ראשון אחד על המעוקב ערכנו השרש המוצא שהוא אחד שלם ומ"ב ראשונים על אחד ומ"ג ראשונים וערכנו העולה על נ׳ דמיוני התוספת שהוא ראשון אחד ועלה בקירוב ה׳ ראשונים מ"ו שניים חלקת עליהם הנשאר ועלה ח׳ והם ראשונים הוספת על השרש המוצא ה׳ ראשונים וערכת א׳ מ"ב ראשונים על ה׳ ונ׳ ראשונים והעולה על כ"ד ראשונים שהוא שלשה דמיוני השרש היוצא שהוא ח׳ ראשונים ועלה אחד שלם י"ד ראשונים נ"ו ל"ב גרענום מהנשאר ונשארו ב׳ ראשונים י״ח שניים נ״ג ז׳ נ"ד ל"ד ל"ג ל״ו והוא הנשאר פחות ממה שיוסיף ראשון אחד על המעוקב והנה ראוי שננסה מה יוסיף שני אחד על המעוקב הזה ערכנו השרש המוצא שהוא א׳ ונ׳ ראשונים על א׳ ונ׳ ראשונים ושני אחד והעולה על שלשה דמיוני התוספת שהוא ג׳ שניים ועלה י׳ שניים מ"ו שלישיים בקרוב והוא השמור הראשון חלקת עליו הנשאר ועלה י״ג ערכת אחד ונ׳ ראשונים על אחד ונ׳ ראשונים י"ג שניים והעולה על שלשה דמיוני השרש היוצא שהוא י״ג שניים וחברת העולה עם מעוקב י״ג שניים ועלה ב׳ ראשונים י"א כ׳ ל"ו ל"ז גרענום מהנשאר ונשאר ז׳ שניים ל"ב ל״ז מ"ח מ"ז כ"ג ל"ד ל״ג ל"ו חלקנו זה הנשאר על חלק מס׳ מזה השמור הראשון שהוא י׳ שלישיים ו׳ רביעיים והוא השמור השני ועלה מ"ד והם שלישיים ערכת אחד ונ׳ ראשונים י"ג שניים על אחד וג' ראשונים י"ג שניים מ"ד שלישיים והעולה על שלשה דמיוני השרש היוצא שהוא מ"ד שלישיים וחברת העולה עם מעוקב מ"ד שלישיים ועלה ז׳ שניים כ"ה שלישיים כ"ו נ״ח א׳ ג׳ נ"ג מ"ד גרענום מהנשאר ונשאר ז׳ שלישיים ט׳ נ״א כ"ב כ"ד נ"ט נ"ב חלקנו הנשאר על חלק מששים מהשמור השני שהוא י׳ רביעיים וו׳ חמשיים בקרוב והוא השמור השלישי ועלה מ"ב והם רביעיים ערכת אחד ונ׳ ראשונים י"ג שניים מ"ד שלישיים על אחד ונ׳ ראשונים י"ג שניים מ"ד שלישיים מ"ב רביעיים והעולה על שלשה דמיוני השרש היוצא שהוא מ"ב רביעיים וחברת העולה עם מעוקב מ"ב רביעיים ועלה ז׳ שלישיים ה׳ ט"ו נ"ד ו' כ"א י"ג כ"ב מ"ח גרענום מהנשאר ונשאר ד׳ רביעיים ל"ה חמשיים כ"ח י"ח כ"ג ל"ד מ"ו ל"ז י"ב ואין צורך לדקדק עוד ואם תרצה עתה תוכל לדקדק לשני מעלות יחד ותהיה קרוב מאד אל המבוקש וזה שאתה אם חלקת הנשאר על חלק מהששי מהשמור השלישי שהוא י׳ חמשיים וו׳ ששיים ועלה כ״ז והם חמשיים וי"ו והם ששיים ולו תחקור תמצא שלא יגיע הקרוב לב׳ שלישיות חמשית אחר ולזה יהיה שרש זה המספר המורד העקוביי אחד ונ׳ ראשונים י״ב שניים מ"ד מ"ב כ"ו י"ו ערכנו זה השרש על אלף לפי שההורדות היו נ׳ ועלה אלף תתל"ז ט׳ ראשונים ה׳ שניים ז׳ שלישיים ל"ד רביעיים מ׳ חמשיים מ׳ ששיים והתבאר בכמו זה הביאור הקודם במספר המורד להוציא שרשו הרבועיי שזהו השרש העקוביי למספר הרב בקרוב ושיחס הקרוב אל הקרוב כיחס המספר אל המספר ר"ל אלף אלפי אלפים וזה שהמספר הגדול ימנה הקטן כמספר אחדי אלף אלפי אלפים לפי שיחס המעוקב אל המעוקב הוא יחס צלעו אל צלעו משולש וכאשר תנהיג זה יתבאר לך בכמו הבאור הקודם שיחס הקירוב אשר ממעוקב השרש הגדול אצל מספר הגדול אל הקרוב אשר ממעוקב השרש הקטן אצל המספר הקטן הוא גם כן אלף אלפי אלפים | |||||||||||||||||||||||
| דרך להוציא שרש מספר מעוקב מונח בלתי מקיף בשלמים העקוביי והשברים אינם משברי חכמי התכונה | |||||||||||||||||||||||
| קח המורה הראשון לכל השברים ואם לא היה המורה מעוקב ערוך המספר על מעוקב המורה או על המורה אם היה מעוקב והעולה חלק על שרש העקוביי שערכת עליו המספר והוא המבוקש | |||||||||||||||||||||||
|
|
דמיון זה אם רצית לדעת שרש מ"ד שלמים וה' שביעיות רביעית וי"ג שביעיות שביעית רביעית רביעית וכ"ז שביעיות שביעית שביעית רביעית רביעית רביעית | ||||||||||||||||||||||
| לקחנו המורה הראשון לאלו השברים ושברי השברים בכלל והיה המספר המורכב ממספרי ז'ז'ז'ד'ד'ד' וזה שוה להכאת מעוקב ז׳ במעוקב ד' אם כן המורה לאלה השברים הוא מעוקב ושרשו העקובי' הוא שטח ז׳ בד' שהוא כ"ח | |||||||||||||||||||||||
|
|
ערכנו מ"ד עם השברים על המורה והוצאנו שרש העולה והנה צ"ט חלקנו צ״ט על כ"ח ועלה ג׳ שלמים וט"ו חלקים מכ"ח באחד וככה המבוקש | ||||||||||||||||||||||
| Extracting cubic root of sexagesimal fractions | דרך הוצאת השרשים העקוביים משברים מונחים משברי התכונה | ||||||||||||||||||||||
| חקור תחלה על המדרגה האחרונה שבטור אם היא מעוקבת ואם אינה מעוקבת הורד המדרגה אל שלפניה עד שתגיע למדרגה מעוקבת והמספר שתמצא במדרגה ההיא תוציא שרשו העקוביי הקרוב ואולם המעט ותשים העולה במעלה אשר אבארה והוא שתחלק שפלות המעלה על ג׳ ושם תשים העולה משל זה אם היתה המדרגה מדרגת הששיים הנה כאשר תחלק שפלות המעלה שהוא ו׳ על ג׳ יעלה ב׳ ולזה תשים העולה במדרגה השנית וזה שהשניים הוכו בעצמם והיו רביעיים והרביעיים הוכו בשניים והיו ששיים ותוציא מעוקב השרש המוצא ותגרעהו מהטור העליון והנשאר לך תנסה אם תוסיף אחד במדרגה שלפני השרש המוצא כמה יתוסף המעוקב ועל העולה חלק הנשאר בדרך שישאר לך מעוקב השרש היוצא ומספר יחסו אל המספר המחולק כיחס השרש היוצא פחות אחד אל השרש המוצא והיוצא וסוף דבר תנהיג בשלמות הוצאתו כמנהג הקודם | |||||||||||||||||||||||
|
|
דמיון זה אם רצית לדעת שרש נ"ט ראשונים כ"ג שניים ז׳ שלישיים מ׳ רביעיים העקוביי | ||||||||||||||||||||||
| הורד הראשונים והשניים אל מדרגת השלישיים ועלה שם ז׳ח׳ז׳ג׳א׳ב׳ הוצאנו השרש הקרוב לזה המספר והוא נ״ט והם ראשונים לפי מה שקדם והנשאר הוא ה׳ אלפים ת"ח שלישיים מ׳ רביעיים והנה ראוי שננסה מה יוסיף שני אחד על המעוקב ערכנו נ״ט ראשונים על נ"ט ראשונים ושני אחד והעולה על ג׳ שניים ועלה ב׳ שניים נ"ה שלישיים בקרוב חלקנו עליו הנשאר והנה השרש היוצא מן החלוקה הוא מ"ז והם שניים ונשאר הראוי לפי יחס מ״ו שניים אל נ"ט ראשונים מ"ז שניים שהוא חלק מע"ח בקרוב ערכנו נ"ט ראשונים על נ"ט ראשונים מ"ז שניים והעולה על ג׳ דמיוני מ"ז שניים וחברנו עם העולה מעוקב מ"ז שניים ועלה ב׳ ראשונים י"ח שניים נ"ו כ״ז כ"ג כ"ג גרענום מהנשאר ונשארו קי״ט שלישיים י״ג רביעיים ל"ו ל"ח וראוי שננסה מה יוסיף שלישי אחד על המעוקב ולא נצטרך עוד לבחינה למיעוט היחס אצל השרש והנה עלה כ׳ שלישיים נ״ט רביעיים בקרוב והוא השמור הראשון והנה השרש היוצא הוא מ׳ והם שלישיים ערכנו נ״ט ראשונים מ"ז שניים על נ"ט ראשונים מ"ז מ׳ והעולה על שלשה דמיוני מ' שלישיים וחברנו עם העולה מעוקב מ׳ שלישיים ועלה קי״ט שלישיים ט׳ רביעיים כ"ה כ׳ נ"ז מ"ו מ׳ גרענוהו מהנשאר ונשאר ד׳ רביעיים י"א כ׳ י"ג כ׳ ואין צריך לדקדק עוד ואם תרצה תוכל לדקדק שתי מעלות יחד וזה שתחלק הנשאר על חלק מששים מהשמור ויעלה בידך רביעי אחד וכ"ה חמשיים והנה השרש אם כן הוא נ"ט ראשונים מ"ז שניים מ׳ שלישיים א׳ רביעי כ"ה חמשיים והקש על זה | |||||||||||||||||||||||
| דרך הוצאת מספר אמצעי ביחס בין שני מספרים מונחים מתחלפים | |||||||||||||||||||||||
| ערוך האחד על האחר והוצא שרש העולה הרבועי והוא המבוקש | |||||||||||||||||||||||
| דמיון זה אם רצית שתמצא המספר האמצעי ביחס בין שני מספרי ד' וי״א ערוך ד׳ על י"א והנה מ"ד הוצא את יסודו הרבועי ועלה ו׳ שלמים ל"ז ראשונים נ"ט שניים מ"ב שלישיים והוא אמצעי ביחס בין מספרי ד׳ וי"א בקירוב גדול | |||||||||||||||||||||||
| דרך הוצאת שני מספרים אמצעים ביחס בין שני מספרים מונחים מתחלפים | |||||||||||||||||||||||
| חלק הגדול על הקטן והעולה בחלוק הוצא את יסודו העקוביי והוא השמור הראשון גם הוצא מרובע יסודו העקוביי והוא השמור השני ערוך השמור הראשון על המספר הקטן משני המספרים המונחים ויצא לך המספר הנמשך ביחס הדרוש למספר הקטן ערוך השמור השני על המספר הקטן ויצא לך המספר השלישי ביחס הדרוש למספר הקטן והנה המבוקש | |||||||||||||||||||||||
| דמיון זה אם רצית שנמצא שני מספרים אמצעים ביחס בין ט"ו וכ"ה | |||||||||||||||||||||||
| חלקנו כ״ה על ט״ו ועלה אחד שלם ומ' ראשונים הוצאנו יסודו העקובי ועלה אחד שלם י״א ראשונים ח׳ שניים ט׳ שלישיים י"ט רביעיים ד׳ חמשיים ל׳ ששיים והוא השמור הראשון והנה מרובע השמור הראשון הוא אחד כ"ד ראשונים כ׳ ל"ה מ"ה ל"ד י׳ כ"ח כ"ז נ״א ב׳ ט"ו והוא השמור השני ערכנו השמור הראשון על המספר הקטן שהוא ט"ו ועלה י״ז שלמים מ"ז ראשונים כ"ד מ"ו ז׳ ל׳ וזה המספר הוא השני למספר ט״ו ערכנו השמור השני על ט״ו ועלה כ"א שלמים ה׳ ח׳ נ"ו כ"ג ל"ב ל"ז ו׳ נ"ז נ"ג מ"ה והוא המספר השלישי למספר ט"ו ואומר שאלו שני המספרים הם אמצעים ביחס הקירוב בין ט"ו ובין כ"ה וזה שכל מעוקב כבר יפול בינו ובין האחד שני מספרים אמצעים והאחד מהם הוא שרש המעוקב והאחר מרובעו וזה שיחס האחד אל שרש המעוקב כיחס השרש אל המרובע וכיחס המרובע אל המעוקב כבר לוקחו לאלו הארבעה כפלים שוים והוא ט"ו וזה שהאחד הוכה בט"ו והיה ט"ו והמעוקב הוכה בט"ו והיה כ"ה והמספרים האמצעים הוכו בט"ו גם כן הנה א"כ אלו הארבעה הכפולים בט"ו הם גם כן מתיחסים בכמו היחס הקודם בעינו והקש על זה |
Chapter Six – Ratios |
השער הששי בערכים |
|---|---|
| והוא הקש המספרים קצתם אל קצת | |
| כבר ידעת שכל ארבעה מספרים מתיחסים הנה שטח הראשון ברביעי כמו שטח השני בשלישי | |
| וכאשר היה זה כן הנה נבאר לך אם היו מספרים מה מונחים והיה לנו מספר אחד מונח שני והוא גיל אחד מונח מהמספרים ההם איך תוציא שאר המספרים הגיליים עד שיהיו המספרים הגיליים בכמו זה היחס הקודם | |
| ראוי שתדע שאם תכה אחד מהמספרים במספר המונח השני ותחלוק על גילו יצא לך המספר הגיליי למספר אשר הוכה על המספר המונח השני | |
| דמיון זה שהמספרים המונחים מספר א'ב'ג'ד'ה' והיה מספר ז' גיליי למספר ד' ונרצה שנמצא המספרים הגיליים למספרי א'ב'ג'ד'ה' | |
| הנה נכה ז' בא' ונחלק על ד' ויצא לנו כ' | |
| הנה מפני ששטח א' בז' כמו שטח כ' בד' הנה יחס א' אל ד' כיחס כ' אל ז' | |
| ועל התמורה הנה יהיה יחס א' אל כ' כיחס ד' אל ז' | |
| ובזה התבאר שאם הוכה ב' בז' וחולק על ד' ויהיה העולה ט' שמספר ט' הוא הגיליי למספר ב' | |
| וגם כן כבר יוכה ג' בז' ויחולק על ד' ויצא ח' הנה ח' גיליי למספר ג' | |
| וג"כ כבר יוכה ה' בז' ויחולק על ד' ויצא ל' הנה ל' גיליי לה' | |
| הנה כבר מצאנו המספרים הגיליים לא'ב'ג'ה' והם כ'ט'ח'ז'ל' והוא מבואר שמספרי כ'ט'ח'ז'ל' על יחס מספרי א'ב'ג'ד'ה' ומש״ל | |
| וגם כן אם לא היה נודע לנו מספר מהמספרים הגיליים ונדע לנו מקובץ שניים מהגיליים או שלשה מהם הנה כבר אפשר שנעמוד מזה על המספרים | |
| והמשל שיהיה נודע לנו במשלנו זה שמקובץ כ'ז'ל' כמו מספר מ' ורצינו לעמוד מזה על המספרים הגיליים למספרי א'ב'ג'ד'ה' המונחים | |
| הנה נשים מקובץ גילי מספרי כ'ז'ל' והם מספרי א'ד'ה' מספר נ' וכמו יחס נ' אל מ' כן נשים יחס כל מספרי א'ב'ג'ד'ה' אל גילו ולזה הנה נכה מ' בא' ונחלק על נ' ויצא מספר כ' ובזה הדרך נוציא מספרי כ'ט'ח'ז'ל' ונאמר שמספרי כ'ט'ח'ז'ל' הם המספרים המבוקשים | |
| המופת שיחס נ' אל מ' כיחס א' אל כ' וכיחס ד' אל ז' וכיחס ה' אל ל' וכאשר קבצנו הנה יחס נ' אל מ' כיחס מספרי א'ד'ה' מקובצים אל מספרי כ'ז'ל' מקובצים וכאשר המירונו הנה יחס נ' אל א'ד'ה' מקובצים כיחס מ' אל כ'ז'ל' מקובצים אבל נ' שוה למספרי א'ד'ה' מקובצים אם כן מ' שוה למספרי כ'ז'ל' מקובצים | |
| אם כן כבר מצאנו המספרים הגיליים למספרי א'ב'ג'ד'ה' ומספרי כ'ז'ל' מהם מקובצים שוים למספר מ' המונח | |
| וג״כ אם לא יודע לנו מהגיליים אלא שיתרון מספר מהם ידוע הגיליות או מקובץ מספרים ידועי הגיליות על מספר מהם ידוע הגיליות או מקובץ מספרים ידועים הוא מספר מונח הנה אפשר לנו שנעמוד מזה על המספרים הגיליים איש על מקומו | |
| והמשל במשלנו זה הקודם שיודע לנו שמקובץ מספרי כ'ח' מוסיף על מספר ל' מספר מ' | |
| ואם רצינו לעמוד מזה על ידיעת המספרים הגיליים למספרי א'ב'ג'ד'ה' הנה נשים מקובץ א'ג' מספר נ' ונבאר שמספר נ' הוא מוסיף על מספר ה' וזה כי לפי שהיה יחס א' הידוע אל כ' הנעלם הוא יחס ג' הידוע אל ח' הנעלם והוא יחס ה' הידוע אל ל' הנעלם | |
| הנה אם כן יחס א'ג' מקובצים אל ה' כיחס כ'ח' מקובצים אל ל' | |
| אבל מקובץ כ'ח' מוסיף על ל' אם כן מקובץ א'ג' מוסיף על ה' ונשים יתרון נ' על מספר ה' מספר ס' הנה נכה א' במ' ונחלק על ס' ויצא לנו מספר כ' והוא גיליי למספר א' וכן לא נסור עד שיצאו לנו מספרי כ'ט'ח'ז'ל' ונבאר שמספרי כ'ט'ח'ז'ל' הם המספרים המבוקשים | |
| המופת שיחס ס' אל מ' הוא יחס כל מספר ממספרי א'ב'ג'ד'ה' אל גילו אם כן יחס ט' אל מ' כיחס מקובץ א'ג' אל מקובץ כ'ח' וכיחס ה' אל ל' וכאשר הבדלנו הנה יחס ס' אל ה' כיחס יתרון כ'ח' מקובצים על ל' אל ל' ובאשר המירונו הנה יחס ס' ליתרון כ'ח' על ל' כיחס ה' אל ל' וכאשר היה גם כן יחס ט' אל מ' כיחס ה' אל ל' א"כ יתרון כ'ח' על ל' הוא מ' א״כ מספרי כ'ט'ח'ז'ל' הם גיליים למספרי א'ב'ג'ד'ה' ויתרון כ'ח' מקובץ על ל' הוא מ' והוא מש"ל | |
| וגם כן אם לא היה גורע מהמספרים הגיליים הנעלמים אלא שמספר מהם ידוע הגיליות או מקובץ מספרים מהם ידועי הגיליות מוסיף על חלק או חלקים ממספרים מהם ידועי הגיליות מספר מונח הנה כבר אפשר לנו שנעמוד מזה על ידיעת המספרים הגיליים למספרים המונחים ויהיה נודע לנו במשלנו זה שמספר ט' מוסיף על חלקים מונחים ממספרי כ'ז' מקובצים מספר מ' הנה נשים החלקים ההם ממספרי א'ד' מקובצים מספר נ' ונבאר שמספר ב' מוסיף על מספר נ' וזה שיחס ב' הידוע אל ט' הנעלם הוא כמו יחס א' הידוע אל כ' הנעלם אם כן יחס ב' אל ט' כיחס מקובץ א'ד' אל מקובץ כ'ז' אבל יחס מקובץ א'ד' אל מקובץ כ'ז' הוא כיחס נ' אל החלקים המונחים ההם ממספרי כ'ז' וזה הוא מבואר שיחס א'ד' אל נ' הוא כיחס כ'ז' אל החלקים ההם המונחים ממספרי כ'ז' וכאשר המירונו התאמת המאמר הנה אם כן יחס ב' אל ט' הוא כמו יחס נ' אל החלקים המונחים ממספרי כ'ז' וכאשר המירונו הנה יחס ב' אל נ' הוא כיחס ט' אל החלקים המונחים ממספרי כ'ז' אבל מספר ט' מוסיף על החלקים הנה אם כן מספר ב' מוסיף על נ' ונשים יתרונו על נ' מספר ע' הנה נכה א' במ' ונחלק על ע' ויצא כ' והוא גיליי למספר א' וכן לא נסור עד שיצאו לנו מספרי כ'ט'ח'ז'ל' ונאמר שמספר כ'ט'ח'ז'ל' הם המספרים המבוקשים | |
| המופת שיחס ע' אל מ' הוא יחס כל מספר ממספרי א'ב'ג'ד'ה' אל גילו אם כן יחס ע' אל מ' כיחס מקובץ א'ד' אל מקובץ כ'ז' וכיחס ב' אל ט' הנה מפני שיחס נ' אל א'ד' כיחס ע' אל כ'ז' יהיה יחס נ' על ע' כיחס א'ד' אל כ'ז' על התמורה אבל יחס א'ד' אל כ'ז' הוא כיחס ב' אל ט' אם כן יחס נ' אל ע' הוא כיחס ב' אל ט' | |
| וכאשר המירונו והפכנו הנה יחס ב' אל נ' כיחס ט' אל ע' אבל ב' מוסיף על נ' מספר ס' | |
| הנה אם כן ט' מוסיף על ע' וכבר היה יחס ב' אל ס' כיחס ט' אל מ' על התמורה אם כן יתרון ט' על ע' הוא מ' אם כן מספרי כ'ט'ח'ז'ל' הם הגיליים למספרי א'ב'ג'ד'ה' ויתרון מספר ט' על החלקים המונחים ממספרי כ'ז' הוא מ' והוא מה ש"ל | |
| זה הוא מה שרצינו להציע והוא מועיל מאד בזה השער כתב המחבר נשלם השער הששי מזה המאמר ובהשלמו נשלם זה הספר והתהלה לאל לבדו והיתה השלמתו בראש ניסן של שנת שמונים ואחת לפרט האלף הששי בהגיעי לשנת שלשים ולשלש משנותי וברוך העוזר |
Word Problems |
|
| והנה נסדר לך שאלות מתחלפות עד שתבין מהם כל מה שידמה להם | |
|
שאל שואל לקחנו חלק מונח או חלקים מונחים ממספר נעלם והיה מספר מונח כמה מספר הנעלם |
|
הדרך בזה שתקח המורה הראשון לכל החלקים ותקח מהמורה החלקים ההם והעולה הוא השמור ערוך המורה על המספר המונח השני וחלק העולה על השמור והנה המספר המבוקש |
|
דמיון זה שיהיו ב' חמישיות וג' רביעיות ושלישית מספר מה עשרים ורצינו לדעת כמה כל המספר |
|
הנה המורה לכל אלו החלקים הוא ס' לקחנו ממנו אלו החלקים ועלה פ"ט והוא השמור |
|
ערכנו המורה על עשרים ועלה י"ב מאות חלקנום על השמור ועלה י"ג שלמים ומ"ג חלקים מפ"ט באחד שלם וככה המבוקש |
| Explanation: | |
|
|
והיה זה כן לפי שיחס ב' חמישיות ס' אל ס' כיחס ב' חמישיות המספר הנעלם אל המספר הנעלם |
|
|
וכן יתבאר שיחס ג' רביעיות ס' אל ס' כיחס ג' רביעיות המספר הנעלם אל המספר הנעלם |
|
|
ושיחס שלישית ס' אל ס' כיחס שלישית המספר הנעלם אל מספר הנעלם |
|
|
וכאשר קבצנו הנה יהיה יחס כל החלקים האלו הלקוחים מס' אל ס' כמו יחס כל החלקים האלו הלקוחים ממספר הנעלם אל המספר הנעלם |
|
|
אם כן יחס פ"ט אל ס' הוא כיחס עשרים אל המספר הנעלם |
|
|
אם כן שטח ס' שהוא השני בעשרים שהוא השלישי כמו שטח פ"ט שהוא הראשון במספר הנעלם והקש על זה |
|
שאלה חלקים ככה מונחים ממספר נעלם מוסיפים על חלקים מונחים שניים מהמספר הנעלם מספר מונח כמה כל המספר |
- Rule of Four:
![\scriptstyle X=\frac{\left(common\ denominator\right)\sdot P}{\left[\sum_{i=1}^n \left[\left(common\ denonminator\right)\sdot\frac{a_i}{b_i}\right]\right]-\left[\sum_{i=1}^m \left[\left(common\ denonminator\right)\sdot\frac{c_i}{d_i}\right]\right]}](/mediawiki/images/math/b/4/3/b43b825ff36278787285157e32ea3157.png)
- Rule of Four:
| קח המורה אל כל החלקים וקח ממנו החלקים המונחים הראשונים ושמור גם קח ממנו החלקים המונחים השניים והוא השמור השני | |
|
דמיון זה שיהיו ג' שביעיות וד' חמישיות המספר הנעלם מוסיפים על ב' שלישיות ורביעית המספר הנעלם עשרים ורצינו לדעת כמה המספר |
|
|
והנה המורה לכל אלו החלקים הוא ת"כ וג' שביעיותיו עם ד' חמישיותיו הוא תקי"ו |
|
|
וב' שלישיות ת"כ ורביעיתו הם שפ"ה |
|
|
והנה החלקים הראשונים מוסיפים על החלקים השניים מספר קל"א |
|
ערכנו המורה על עשרים וחלקנו העולה על קל"א ועלה ס"ד שלמים וי"ו חלקים מקל"א באחד שלם וככה המבוקש |
| Explanation: | ואם תרצה תוכל לבחון זה |
|
|
והיה זה כן לפי שיחס החלקים הראשונים מקובצים הלקוחים מת"כ אל ת"כ כיחס החלקים הראשונים הלקוחים מהמספר הנעלם אל המספר הנעלם |
|
|
וכאשר המירונו הנה יחס החלקים הראשונים הלקוחים מת"כ אל החלקים הראשונים הלקוחים מהמספר הנעלם כיחס ת"כ אל המספר הנעלם |
|
|
וכזה התבאר שיחס החלקים השניים הלקוחים מת"כ אל החלקים השניים הלקוחים מהמספר הנעלם הוא כיחס ת"כ אל המספר הנעלם |
|
|
אם כן יחס החלקים הראשנים הלקוחים מת"כ אל החלקים הראשנים הלקוחים מהמספר הנעלם הוא כמו יחס חלקים השניים הלקוחים מת"כ אל החלקים השניים הלקוחים מהמספר הנעלם |
|
|
וכאשר המירונו הנה יחס החלקים הראשנים הלקוחים מת"כ אל החלקים השניים הלקוחים מת"כ הוא כמו יחס החלקים הראשנים הלקוחים מהמספר הנעלם אל החלקים השניים הלקוחים מהמספר הנעלם |
|
|
וכאשר הבדלנו הנה יחס החלקים הראשנים הלקוחים מת"כ אצל יתרונו על החלקים השניים הלקוחים מת"כ שהוא קל"א הוא כיחס החלקים הראשונים הלקוחים מהמספר הנעלם אצל עשרים שהוא היתרון על החלקים השניים הלקוחים מהמספר הנעלם |
|
|
וכאשר המירונו הנה יחס החלקים הראשונים הלקוחים מת"כ אל החלקים הראשונים הלקוחים מהמספר הנעלם הוא כמו יחס קל"א אל עשרים |
|
|
וכבר היה יחס החלקים הראשונים הלקוחים מת"כ אל החלקים הראשונים הלקוחים מהמספר הנעלם כיחס ת"כ אל המספר הנעלם |
|
|
אם כן יחס ת"כ אל המספר הנעלם כיחס קל"א אל עשרים |
|
|
אם כן שטח ת"כ בעשרים הוא כמו שטח קל"א במספר הנעלם והקש על זה |
|
שאלה ערך מספר מונח ממסחר מה ככה כמה ערך מספר מונח שני מהמסחר ההוא |
|
ערוך הערך המונח על המספר המונח השני וחלק על המספר המונח הראשון וככה המבוקש |
|
דמיון זה שיהיה ערך י"א מדות תבואה ז' די' ותרצה לדעת כמה ערך ט"ו מדות תבואה |
|
ערוך ז' על ט"ו וחלק העולה על י"א ויעלה ט' שלמים וו' חלקים מי"א באחד וככה המבוקש רצוני שערך ט"ו מדות הוא ט' די' וו' חלקים מי"א בדינר |
| Explanation: | |
|
|
והיה זה כן לפי שיחס המסחר הראשון אל המסחר השני כיחס הערך הידוע אל הערך הנעלם וזה מבואר בנפשו |
|
|
ולזה יהיה שטח מספר המסחר השני במספר הערך הידוע כמו שטח מספר המסחר הראשון בערך הנעלם והקש על זה |
| Converting given parts of the day into hours and fractions of hours Converting given parts of the liṭra which is 20 dinar into dinar and pašuṭ and fractions of pašuṭ |
דרך השבת חלקים מונחים מיום אל שעות ושברי שעה והשבת חלקים מונחים מן הליטרא שהוא כ' די' אל הדינרים והפשוטים ושברי הפשו' |
|---|---|
|
והמשל שרצינו לדעת כמה מן השעות ושברי השעה יהיו בפ"ג חלקים מק"ט ביום |
|
והנה ידענו שמספר שעות היום הוא כ"ד |
|
|
והנה כיחס פ"ג אל ק"ט כן יחס מספר השעות הנעלם אל כ"ד |
|
|
הנה נערוך כ"ד על פ"ג ונחלק על ק"ט והנה המבוקש והוא י"ח שעות ונ"א ראשונים וי"ב שניים בקירוב |
|
ואם היה משלינו זה בליט' |
|
הנה ידענו שמספר דינרי הליטרא הם עשרים |
|
|
וכיחס פ"ג אל ק"ט כן יחס הנעלם אל עשרים |
|
|
הנה נכה עשרים בפ"ג ונחלק על ק"ט ויצא ט"ו די' וק"ו חלקים מק"ט בדי' |
|
וכבר תוכל לדעת כמה הם מן הפשוטים |
|
|
בשתערוך י"ב על ק"ו ותחלק על ק"ט ויצא י"א פשו' וע"ג חלקים מק"ט בפשוט שהם ב' שלישיות פשוט אחד בקירוב ובזה תנהיג מה שידמה לזה |
| Converting different fractions into one type of fractions | דרך השבת חלקים מדמיוני שברים מתחלפים חלקים ממין אחד |
|
|
קח המורה הראשון שימנוהו כל המורים על השברים ההם המתחלפים וממנו תקח החלקים ההם והעולה הם חלקים מהמורה |
|
|
דמיון זה אם רצית להשיב ג' שביעיות וד' חלקים מי"ז שברים ממין אחד |
|
|
הנה תקח מהמורה שהוא קי"ט כל אלו החלקים והיה העולה הוא ע"ט חלקים מקי"ט |
| Converting fractions of one type into a unit fraction | דרך השבת החלקים ממין אחד חלק אחד |
|
|
חלק המורה על החלקים ההם על מספר החלקים ההם והעולה הוא המבוקש |
|
|
דמיון זה אם רצית להשיב ג' שביעיות חלק אחד |
|
|
תחלק שבעה על ג' ויהיה העולה ב' ושליש והוא חלק אחד מב' ושליש בדבר ההוא אשר רצית לדעת ג' שביעיותיו והקש על זה |
|
שאלה המתנועע תנועה שוה הולך בזמן מונח שעור מונח מן הדרך כמה ילך מן הדרך בזמן מונח שני |
|
ערוך מספר הזמן המונח השני על שעור המונח מן הדרך והעולה חלק על מספר הזמן המונח ויצא לך המבוקש |
|
ואם היו שעות באחד מהזמנים או בשניהם השב מספר הזמן לשעות והשעות תהיינה לאחדים שלמים |
|
והמשל שיתנועע המתנועע מתנועע בי"ג ימים ז' שעורים מן הדרך ול"ו ראשונים נ"ז שניים ורצינו לדעת כמה מן הדרך ילך בג' ימים וי"ז שעות ונ"ב ראשונים י"ו שניים |
|
הנה נשיב הימים שעות ויהיה הזמן הראשון המונח שי"ב |
|
והזמן השני פ"ט ונ"ב ראשונים י"ו שניים |
|
ערכנו ז' שלמים ל"ו ראשונים נ"ז שניים על פ"ט שלמים ונ"ב ראשונים י"ו שניים וחלקנו העולה על שי"ב ועלה ב' שלמים י' ראשונים נ"ו שניים והוא מספר השעורים שהלך מן הדרך בזמן המונח השני |
| Explanation: | |
|
והיה זה כן לפני שהתנועה השוה תהיה בזמנים שוים שעורים שוים |
|
|
ולזה הוא מבואר שיחס הזמן אל הזמן הוא יחס התנועה אל התנועה |
|
וכבר תפול השאלה בהפך זה ר"ל שישאל השואל במתנועע תנועה שוה ההולך שעור מונח מן הדרך בזמן מונח בכמה מן הזמן ילך שעור מונח שני מן הדרך |
|
ואז תערוך השעור המונח השני מן הדרך על הזמן המונח וזה בשתשיב הימים שעות להקל מעליך והעולה תחלק על השעור המונח הראשון מן הדרך והנה המבוקש |
|
והמשל שילך המתנועע ז' שעורים מן הדרך ול"ו ראשונים נ"ז שניים בי"ג ימים ורצינו לדעת בכמה מן הזמן ילך ג' שעורים מן הדרך |
|
ערכנו ג' שעורים על שי"ב שלמים וחלקנו העולה על ז' שלמים ל"ו ראשונים נ"ז שניים ועלה קכ"ב שעות ונ"ד ראשונים וז' שניים והוא הזמן הנעלם |
| וזה מבואר מהסבה הקודמת בעינה | |
|
שאלה אם היו שני מתנועעים תנועה שוה והיה האחד יותר מהיר במהלכו מן האחר ומרחק המהיר מהמתוני לאחריו מדה מונחת מן הדרך בכמה מן הזמן ישיג המהיר המתוני |
|
|
חלק המדה המונחת על יתרון מהלך המהיר על המתוני לשעה והעולה בידך הם השעות וחלקי השעה אשר ישיג בהם המהיר המתוני |
|
והמשל שיהיה מהלך המהיר לשעה אחת ב' שעורים ול"ז שניים ויהיה מהלך המתוני לשעה אחת ל' ראשונים כ"ד שניים והיה מרחק המתוני מהמהיר לפניו כ"ט שעורים ומ"ה ראשונים |
|
|
והנה יתרון מהלך המהיר על מהלך המתוני לשעה הוא שעור אחד ול' ראשונים וי"ג שניים חלקנו עליו המרחק המונח ועלה י"ט שעות מ"ז ראשונים ט' שניים |
| וזה מבואר הסבה עם מה שקדם מהדברים | |
|
שאלה הכלי המלא המונח יש לו נקבים מתחלפים יצא מאחד מהם כל מה שבכלי בזמן מונח |
|
חקור תחלה על מה שיצא מכל אחד מהנקבים ההם בשעה אחת וקבץ הכל וראה יחסו אל מלא הכלי וכפי יחסו אליו כן יחס השעה אל הזמן שיצא בו מלא הכלי |
|
דמיון זה שהחבית יש בו נקבים מתחלפים בנקב האחד יצא מלא החבית בג' ימים |
|
|
והנה בנקב הראשון יצא מהחבית בשעה אחת חלק אחד מע"ב חלקים במלא החבית |
|
|
ובנקב השני חלק מק"כ |
|
|
ובנקב השלישי חלק מכ' |
|
|
ובנקב הרביעי חלק מי"ב |
|
|
וכאשר קבצנו זה כלו יהיה מה שיצא מכלם יחד בשעה אחת נ"ו חלקים מש"ס חלק במלא החבית |
|
חלקנו ש"ס על נ"ו ועלה ו' שלמים כ"ה ראשונים מ"ג שניים והנה הזמן שיורק בו הכלי הוא ו' שעות כ"ה ראשונים מ"ג שניים בקירוב וסבת זה מבוארת |
|
שאלה ערך המסחר המונח מספר מונח מן הדינרין כמה ערך חלקים מה מונחים ממנו |
|
קח המורה אל כל החלקים וקח ממנו החלקים ההם והעולה הוצא ערכו וכפול אותו על מספר המסחר וחלק העולה על המורה וככה המבוקש |
|
דמיון זה שיהיה ערך דינר זהב כ"ה די' ורצינו לדעת כמה ערך הדינר עם חציו וב' שביעיותיו וג' רביעיותיו |
|
והנה המורה לכל אלו השברים הוא כ"ח לקחת ממנו אלו החלקים ועלה ע"א ערכת ע"א על כ"ה ועלה אלף תשע"ה שהוא ערך החלקים הלקוחים מהמורה |
| Explanation: | ואם תרצה תוכל לבחון זה |
|
|
והיה זה כן לפי שיחס החלקים הלקוחים מהמורה אל החלקים הלקוחים מדינרי הזהב הוא כיחס המורה אל אחד שהוא מספר המסחר |
|
|
ולזה יהיה יחס ערך החלקים הלקוחים מהמורה אל ערך החלקים הלקוחים מדינ' הזהב כיחס המורה אל אחד |
|
|
לפי שהוא מבואר שיחס המסחר אל המסחר הוא יחס הערך אל הערך |
|
|
אם כן שטח מספר ערך החלקים הלקוחים מהמורה באחד שוה לשטח מספר ערך החלקים הלקוחים מן הדינר במורה והקש על זה |
| ואם היה המסחר מספר מה כזה בעינו יתבאר | |
|
והמשל שיהיה ערך ז' מדות תבואה כ"ה די' ורצינו לדעת כמה ערכם עם חציים וב' שביעיותיהם וג' רביעיותיהם |
|
|
לקחנו אלו החלקים מהמורה שהוא כ"ח ועלה ע"א והנה ערכם רנ"ג די' וד' שביעיות הדינר |
|
שאלה הסוחר מוכר מסחרים מתחלפי הערכים כמה שיהיו ורצה הקונה לקנות בסך מה מן הממון מדה שוה מכל אחד מהמסחרים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
הדרך בזה שתקבץ ערכי המדה האחת לכל המסחרים והעולה שמור וכמו יחס הסך שבידו אל השמור יקח מהמדה מכל אחד מהמסחרים והנה המבוקש | ||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון זה שימכור הסוחר מד' סמים ערך הסם הראשון ז' פשו' הליט' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה בג' די' וד' פשו' יקח ליט' מכל אחד | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה יחס ג' די' אל ג' די' וד' פשו' הוא ט' עשיריות וככה יקח מכל סם וסם ר"ל ט' עשיריות ליטרא | ||||||||||||||||||||||||||||||||||||||||||||||||
| ויהיה ערך הכל ג' די' | |||||||||||||||||||||||||||||||||||||||||||||||||
| Explanation: | ותוכל לבחון זה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והיה זה כן לפי שיחס מה שיקח מכל ליטרא מהם אל הליטרא כיחס ערך מה שיקח מכל ליטרא מהם אל ערך הליטרא | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ואולם יחס מה שיקח מליטרא מאחד מהם אל הליטרא הוא כיחס מה שיקח מליטרא מכל אחד מהם אל הליטרא | ||||||||||||||||||||||||||||||||||||||||||||||||
|
יהיה אם כן יחס ערך מה שיקח מאחד מהם אל ערך הליטרא כיחס ערך מה שיקח מכל אחד מהם אל ערך הליטרא | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר קבצנו הנה יחס מה שיקח מכלם יחד אל מספר ליטראות כמספרם כיחס ערך מה שיקח מכלם יחד אל ערך מספר ליטראות כמספרם והקש על זה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ומזאת השאלה יתבאר אם רצה השולחני לקנות בדי' זהב מטבעות מתחלפות הערכים ורצה לקחת מכל מטבע מהם מספר שוה כמה יקח מכל אחד ואחד | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והמשל שיהיה ערך המטבע האחד ג' די' הזהוב וערך השני ה' די' הזהוב | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה בשליש הזהוב יקנה די' מהמטבע האחד | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ובחמישית הזהוב יקנה די' מהמטבע האחר | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ובשביעית הזהוב יקנה די' מהמטבע האחר | ||||||||||||||||||||||||||||||||||||||||||||||||
| אם כן בשלישית הזהוב וחמישיתו ושביעיתו יקח די' מכל אחד מהם | |||||||||||||||||||||||||||||||||||||||||||||||||
|
וכמו יחס הזהוב אל אלו החלקים כן יחס מה שיקח מכל אחד מהם אל הדינר וכזה יקח מכל אחד מהם דינר ול"ד חלקים מע"א בדינר וכפי זה תקיש במה שידמה לזה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
שאלה הסוחר מוכר מסחרים מתחלפי הערכים כמה המספר המעט מן המדות שילקח מאחד אחד מהם ויהיה ערך מה שילקח מזה כערך מה שילקח מזה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הדרך בזה שתכתב ערכי המסחרים זה אחר זה בטור אחד וכנגדם תמיד בטור אחד המספר האחד תחת האחר וכן תעשה לכל המספרים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון זה שימכור הסוחר מארבעה סמים ערך הסם האחד ב' די' הליטרא | ||||||||||||||||||||||||||||||||||||||||||||||||
| הנה תכתב בטור אחד ערכי הליטראות והוא ב' ג' י"ב כ' | |||||||||||||||||||||||||||||||||||||||||||||||||
| ובטור אחר תחתיו תמיד הענין על זה הסדור הנזכר רצוני שתכתוב תחת ב' ג' ותחת ג' ב' | |||||||||||||||||||||||||||||||||||||||||||||||||
| וגם כן הנה תכתוב על זה הדרך תחת ג' י"ב ותחת י"ב ג' | |||||||||||||||||||||||||||||||||||||||||||||||||
| וגם כן הנה תכתוב תחת י"ב כ' ותחת כ' י"ב | |||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||
| ואחר כן תקח קטני המספרים המתיחסים בכמו זה היחס ר"ל מיחס ג' אל ב' ומיחס י"ב אל ג' ומיחס כ' אל י"ב והם לפי מה שהתבאר מאקלידס מספרי ל' כ' ה' ג' | |||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וזה שיחס ל' אל כ' כיחס ג' אל ב' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ויחס כ' אל ה' כיחס י"ב אל ג' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ויחס ה' אל ג' כיחס כ' אל י"ב | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ולזה תקח מן הסם אשר ערכו ב' די' ל' ליט' והוא המספר הנכחי לו | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ומהסם אשר ערכו ג' די' הליט' תקח כ' ליטראות | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ומהסם אשר ערכו י"ב די' תקח ה' ליטראות | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ומהסם אשר ערכו כ' די' תקח ג' ליטראות | ||||||||||||||||||||||||||||||||||||||||||||||||
| ויהיה ערך מה שתקח מכל אחד מהם שוה והקש על זה | |||||||||||||||||||||||||||||||||||||||||||||||||
|
וראוי שתשמר בזה הדרך הנזכר אם היה ערך אחד הסמים מספר הפשוטים שתשיב ערך הסמים הנשארים לפשוטים ומזה תקיש במה שידמה לזה | ||||||||||||||||||||||||||||||||||||||||||||||||
| Explanation: | |||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והיה זה כן לפי שיחס ל' אל כ' הוא כיחס ג' אל ב' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
אם כן שטח ל' בב' הוא כמו שטח כ' בג' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
אבל שטח ל' בב' שוה לערך ל' ליטראות מב' די' הליט' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ושטח כ' בג' שוה לערך כ' ליטראות מג' די' הליטרא | ||||||||||||||||||||||||||||||||||||||||||||||||
|
אם כן ערך ל' ליטראות מב' די' הליטרא שוה לערך כ' ליטר' מג' די' הליטרא | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ובזה התבאר שערך כ' ליטראות מג' די' הליטרא שוה לערך ה' ליטראות מי"ב דינרין הליטרא | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ושערך ה' ליטראות מי"ב די' הליטרא הוא כמו ערך ג' ליטראות מכ' די' הליטרא והקש על זה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
שאלה הסוחר מוכר מסחרים מתחלפי הערכים ובא הקונה לקנות מדה אחת מכלם ויהיה ערך מה שיקח מזה שוה לערך מה שיקח מזה כמה מן המדה יקח מכלם וכמה ערך המדה ההיא | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ראוי שתקח קטני המספרים שילקח מכל אחד מהם מן המדות ויהיה הערך שוה וכאשר ישלם לך זה קבץ מספריהם והוא השמור והשמור הם חלקי המדה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
לקח מכל אחד מהם מאלו החלקים כמו המספר אשר תחתיו והנה המבוקש | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ואולם ערך המדה ההיא תדעהו כשתקבץ ערכי קטני המספרים ההם כל אחד מגילו והוא ערך המקובץ חלקהו על השמור והנה המבוקש | ||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון זה שימכר הסוחר משלשה סמים ערך האחד ז' פשו' הליט' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והנה קטני המספרים שילקחו מאחד אחד מהם ויהיה הערך שוה הם מספרי כ' י"ד ז' והנה מקובצם הוא מ"א והם חלקי הליטרא | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וילקח מאלו החלקים מהסם אשר ערכו ז' פשו' הליטרא כ' חלקים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ומהסם אשר ערך הליטרא ממנו י' פשו' ילקחו י"ד חלקים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ומהסם אשר ערך הליטרא ממנו כ' פשו' ילקחו ז' חלקים | ||||||||||||||||||||||||||||||||||||||||||||||||
| והנה הכל מ"א חלקים שהיא הליטרא | |||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ואולם ערך הליטרא הנה תקח ערך מספרי כ' י"ד ז' כל אחד מהנכחי לו ותקבץ הכל והנה הכל הוא ל"ה די' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
חלקת ל"ה די' על מ"א ועלה י' פשו' וי' חלקים ממ"א בפשו' והוא המבוקש והקש על זה | ||||||||||||||||||||||||||||||||||||||||||||||||
| Explanation: | |||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והיה זה כן כי מפני שערך כ' ליט' מהערך הקטן הוא כערך י"ד ליט' מהערך האמצ[ע]י וכמו ערך ז' ליטרא מהערך הגדול | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והנה יחס כ' חלקים ממ"א בליטרא אל כ' ליט' הוא כמו יחס י"ד חלקים ממ"א בליטרא אל י"ד ליט' וכמו יחס ז' חלקים ממ"א בליטרא אל ז' ליטרין | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ולזה יהיה יחס ערך כ' חלקים ממ"א בליטר' אל ערך כ' ליטראות כמו יחס ערך י"ד חלקים ממ"א בליטר' אל ערך י"ד ליטראות וכמו יחס ערך ז' חלקים ממ"א בליטרא אל ערך ז' ליטראות | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכאשר המירונו הנה יחס ערך כ' חלקים ממ"א בליטרא מהערך הראשון אל י"ד חלקים ממ"א בליטרא מהערך השני הוא כמו יחס ערך כ' ליטר' מהערך הראשון אל ערך י"ד ליטר' מהערך השני | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
אבל ערך כ' ליטראות מהערך הראשון הוא כמו ערך י"ד ליטר' מהערך השני | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
אם כן ערך כ' חלקים ממ"א בליטרא מהערך הראשון הוא כמו ערך י"ד חלקים ממ"א בליטרא מהערך השני | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכזה התבאר שערך י"ד חלקים ממ"א בליטרא מהערך השני הוא כמו ערך ז' חלקים ממ"א בליטרא מהערך השלישי והקש על זה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
שאלה הסוחר מוכר שני מסחרים מתחלפי הערכים ורצה הקונה לקנות מדה אחת משניהם יהיה ערכה מספר מה מוסיף על הערך הקטן ומחסיר מהערך הגדול | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ראוי שתקח מספר יתרון המוסיף על המחסיר והם חלקי המדה ואחר תקח מספר חסרון המחסיר והוא יהיה מספר החלקים שיקח מהמוסיף | ||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון זה שיהיה הסוחר מוכר משני סמים ערך הסם האחד י"ז פשו' הליטרא | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והנה יתרון המוסיף על המחסיר הוא ז' והם חלקי המדה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה חסרון המחסיר מי"ט הוא שנים והם החלקים מחלקי המדה שיקח מהסם אשר ערכו מוסיף | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה יתרון המוסיף הוא חמשה והם חלקים שיקח מהסם אשר ערכו מחסיר | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ויהיה ערך המדה י"ט פשוטי' והקש על זה | ||||||||||||||||||||||||||||||||||||||||||||||||
| Explanation: | |||||||||||||||||||||||||||||||||||||||||||||||||
| והיה זה כן לפי שבכאן שלשה מספרים מתחלפים והם מספרי י"ז י"ט כ"ד | |||||||||||||||||||||||||||||||||||||||||||||||||
|
|
הנה יהיה שטח כ"ד בשנים שהוא יתרון האמצעי על הקטן עם שטח י"ז בחמשה שהוא יתרון הגדול על האמצעי ימנהו י"ט שהוא האמצעי במספר אחדי יתרון הגדול על הקטן שהוא ז' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
אם כן שתי ליטר' מערך כ"ד פשוט' עם חמשה ליטראות מערך י"ז פשוט' יהיה מקובץ הערכים שוה לשטח ז' בי"ט | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ומספר הליטראות ז' אם כן כל אחת תעמד בי"ט פשוטים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וגם כן הנה יחס שתי שביעיות ליטרא אל שתי ליטראות כיחס חמשה שביעיות ליטרא אל חמשה ליטראות | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ולזה יהיה יחס ערך שתי שביעיות ליטרא מהערך הגדול אל ערך שתי ליטראות מהערך הגדול כיחס ערך חמשה שביעיות ליטרא מהערך הקטן אל ערך חמשה ליטראות מהערך הקטן | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ולזה יהיה יחס ערך שתי שביעיות ליטרא מהערך הגדול וחמשה שביעיות ליטרא מהערך הקטן אל ערך שתי ליטראות מהערך הגדול וחמשה ליטראות מהערך הקטן כיחס ערך שתי שביעיות ליטרא מהערך הגדול אל ערך שתי ליטראות מהערך הגדול | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
אבל יחס ערך שתי שביעיות ליטרא מהערך הגדול אל ערך שתי ליטראות מהערך הגדול הוא שביעית הערך | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
אם כן יחס ערך שתי שביעיות ליטרא מהערך הגדול וחמשה שביעיות ליטרא מהערך הקטן אל ערך שתי ליטראות מהערך הגדול וחמשה ליטראות מהערך הקטן הוא שביעית הערך | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכבר התבאר שזה הערך כלו הוא שטח ז' בי"ט | ||||||||||||||||||||||||||||||||||||||||||||||||
|
אם כן ערך זאת הליט' הוא שביעית שטח ז' בי"ט שהוא י"ט פשו' והקש על זה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
שאלה הסוחר מוכר מסחרים מתחלפי הערכים כמה שיהיו ובא הקונה לקנות מדה אחת מכלם יהיה ערכה מוסיף על הערך הקטן ומחסיר מן הערך הגדול כמה מן המדה יקח מאחד אחד מהם | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה ראוי שתזווג עם כל אחד מהמחסירים אחד מהמוסיפים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם לא יספיקו המוסיפים או המחסירים לפי שהיה מספר המוסיפים יותר או פחות הנה תזווג עם כל אחד מהנשארים ממקביליהם המספר אשר ערכו יותר קרוב אל הערך המבוקש כדי שימעט המספר יותר | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר תנהיג מכל זוג וזוג על הצד הקודם והנקבץ מיתרון כל אחד מהמוסיפים על זוגו הם חלקי הליט' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם היה שם מסחר יהיה ערכו כמו הערך המבוקש הנה זה המסחר אין זוג לו ולזה תקח ממנו חלק אחד או חלקים כפי מה שתרצה ותוסיף על מספר החלקים הנקבצים והנקבץ יהיה חלקי הליטרא | ||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון זה שיהיה הסוחר מוכר מז' סמים ערך הסם הראשון ג' פשו' הליטרא | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה המוסיפים הם שנים הסם אשר ערכו י"ט פשו' הליטרא | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והמחסירים הם ארבעה והם הסם אשר ערכו ג' פשו' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה נשים ג' פשו' גיליי לי"ט פשו' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וה' פשו' גיליי לכ"ח פשו' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ומפני שנשארו עוד סמים במחסירים ולא נשאר מהמוסיפים נקח מהמוסיפים היותר קרוב אל ט"ו שהוא הערך המבוקש והוא י"ט ונזווג י"ט עם כל אחד מהנשארים מהמחסירים כמו שתראה בזאת הצורה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||
| וכבר ידענו איך נקח ליטרא מכל זוג וזוג מאלו יהיה ערכה ט"ו פשו' | |||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ולזה נקח מסם ג' ד' חלקים מי"ו בליטרא ומסם י"ט י"ב חלקים מי"ו בליט' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ונקח גם כן מסם ה' י"ג חלקים מכ"ג בליטרא ומסם כ"ח י' חלקים מכ"ג בליטרא | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ונקח גם כן מסם ח' ד' חלקים מי"א בליטרא ומסם י"ט ז' חלקים מי"א בליטרא | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ונקח גם כן מסם י"א ד' חלקים מח' בליטרא ומסם י"ט ד' חלקים מח' בליטרא | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
הנה מספר כל אלו החלקים הוא נ"ח | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ונוסיף שני חלקים בעבור ט"ו שאין לו גיליי והנה ס' והם חלקי הליטרא | ||||||||||||||||||||||||||||||||||||||||||||||||
|
נקח מהם מסם ג' פשו' ד' חלקים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ומסם ה' י"ג חלקים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ומסם ח' ד' חלקים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ומסם יא ד' חלקים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ומסם ט"ו שני חלקים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ומסם י"ט כ"ג חלקים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ומסם כ"ח י' חלקים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ויהיה ערך הליטרא ט"ו פשו' והוא המבוקש | ||||||||||||||||||||||||||||||||||||||||||||||||
| Explanation: | |||||||||||||||||||||||||||||||||||||||||||||||||
|
והיה זה כן לפי שהוא מבואר ממה שקדם שד' ליט' מערך ג' עם י"ב ליטראות מערך י"ט ערכם כמו שטח י"ו בט"ו | ||||||||||||||||||||||||||||||||||||||||||||||||
| ובזה התבאר הענין בכל שני מספרים גיליים מאלו | |||||||||||||||||||||||||||||||||||||||||||||||||
|
והוא מבואר שב' ליטראות מערך ט"ו ערכם גם כן כמו שטח ב' בט"ו | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר קבצנו הכל הנה ערך כל אלו הליטראות במספרם מוכה בט"ו אשר הוא כמו שטח ס' בט"ו | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ואולם יחס חלק מס' בליטרא אל הליטרא כמו יחס ערך חלק מס' בליטרא אל ערך הליטרא | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ויתבאר על צד הבאור הקודם שיחס ערך כל החלקים מקובצים אל ערך מקובץ הליטראות שהוא כמו שטח ס' בט"ו הוא כיחס אחד אל ס' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ולזה יהיה ערך החלקים בכללם ט"ו פשו' שהוא אחד מס' בשטח ס' בט"ו והקש על זה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
שאלה איש אחד שכר איש אחר מספר מונח מהממון שיעשה מלאכתו מספר מונח מן הימים וזאת המלאכה אשר יעשה ישכור לו בכל יום מאלו הימים מספר מונח מן האנשים ינהיג כל אחד מהם מספר מונח מהבהמות תשא כל אחת מהן מספר מונח מן המדות ותלך כל אחת מהן מספר מונח מן הדרך ושנה השכיר בקצת המספרים או בכלם כמה שכירותו | ||||||||||||||||||||||||||||||||||||||||||||||||
|
קח המספר המורכב מכל המספרים שהתנה ושמור גם קח המספר המורכב מכל המספרים שהשלים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון זה ששכר ראובן את שמעון י' ליטר' שיעשה מלאכתו ט' ימים וזאת המלאכה ישכור לו בכל יום י"ג מן האנשים ינהיג כל אחד מהם שבעה מהבהמות תשא כל אחד מהם ט"ו מן המדות ותלך ו' פרסאות והוא שכר לו ח' ימים י"ז מן האנשים ותנהיג כל אחד מהם ששה מהבהמות ונשאה כל אחת מהם י"א מן המדות והלכה ז' פרסאות | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והנה המספר המורכב מהמספרים שהתנה שהם ט' י"ג ז' ט"ו ו' הוא ע"ג אלפים ותש"י והוא השמור | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והמספר המורכב מהמספרים שהשלים שהם ח' י"ז ו' י"א ז' הוא ס"ב אלפים ותתל"ב | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והנה יחס י' ליט' אל מה שהוא חייב לו כיחס השמור אל ס"ב אלפים ותתל"ב | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ואם תערך י' ליט' שהוא הראשון על הרביעי שהוא ס"ב אלפים תתל"ב ותחלק העולה על השמור יצאו לך הליטראות וחלקי הליטרא שהוא חייב לו והם ח' ליט' וחצי ואלף וז' מאות ופ"ה חלקים מס"ב אלפים ותתל"ב בליט' שהם ה' פשו' ונ"ט אלפים תת"נ חלקים מע"ג אלפים תש"י בפשוט | ||||||||||||||||||||||||||||||||||||||||||||||||
| Explanation: | |||||||||||||||||||||||||||||||||||||||||||||||||
|
והיה זה כן לפי שיחס מה שהוא חייב לו אל מה שהתנה הוא כיחס מה שעשה אל מה שהתנה לעשות | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ויחס מה שעשה אל מה שהתנה לעשות הוא מחובר מיחסי המספרים שהתנה אל גיליהם שהשלים וזה היחס המחובר כבר התבאר שהוא כמו יחס המספר המורכב מהמספרים שהתנה אל המספר המורכב מהמספרים שהשלים והקש על זה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ומזה הבאור התבאר אם התנה אדם לאדם למלאת ממסחר מה כלי ארכו מספר מונח ורחבו מספר מונח ועמקו מספר מונח במספר מה מן הממון ומלא לו כלי אחר מתחלף הרחקים לכלי אשר התנה כמה חייב לו | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה שכמו יחס המספר המורכב מהשלשה רחקים אשר התנה אל המספר המורכב מהשלשה רחקים אשר השלים כן יחס הערך שהתנה לו אל מה שהוא חייב לו וכן תשפוט במה שידמה לזה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והמשל שמכר המוכר לקונה מלא כלי משמן בערך כ' די' ארך הכלי עשרה מדות ורחבו תשעה ועמקו י"ב | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והנה המספר המורכב מהרחקים הקודמים הוא אלף ופ' והוא השמור | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והמספר המורכב מהרחקים שהשלים הוא אלף וקכ"ב | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה כיחס השמור אל אלף וקכ"ב כן יחס כ' די' אל מה שהוא חייב לו | ||||||||||||||||||||||||||||||||||||||||||||||||
|
שאלה ראובן קנה חלקים מה מהמדה במספר ככה מהדינרין ומכר ככה מהמדה במספר ככה מהדינרין והיה הממון ככה ורצינו לדעת אם הרויח או הפסיד וכמה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הדרך בזה שתוציא סך דינרי ערך המדה לכל אחד מהערכין | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר כן יתבאר לך אם הפסיד או הרויח במדה וכמה מן הדינר | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ובזה יתבאר לך כמה סך מדות המסחר | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ערוך סך מדות המסחר על מה שהרויח במדה או הפסיד והעולה הוא סך הדינר' שהפסיד או הרויח | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם היתה השאלה בהפך ר"ל שהרויח או הפסיד מספר ככה מהדינרי' ובאת לדעת כמה היה הממון או מדות המסחר | ||||||||||||||||||||||||||||||||||||||||||||||||
|
תחלק המספר מהדינרין שהרויח בכל המסחר או הפסיד על מה שהרויח במדה או הפסיד והעולה הוא סך מדות המסחר | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וערכם לפי מה שקנה הוא הממון | ||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון ראובן קנה ב' חמישיות המדה וג' שביעיותיה ז' דינר וח' חלקים מי"א בדינר ומכר ד' תשיעותיה ח' דינרין וג' שביעיות הדינ' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה ערך המדה לפי מה שקנה ט' דינרין וק"ד חלקים משי"ט בדינר | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וערך המדה לפי מה שמכר י"ח דינר וכ"ז חלקים מכ"ח בדינר | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ולזה היה סך מדות המסחר י' מדות וכ"א מאות ונ' חלקים מכ"ט מאות וע"ה במדה שהם פ"ו חלקים מקי"ט במדה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה הרויח במדה ט' דינר וה' אלפים ותש"א חלקים מח' אלפים תתקל"ב בדינר | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ערכנוהו על מדות המסחר והנה הרויח ק"ג דינר וש"ע אלפים ומ' חלקים מאלף וס"ב אלפים ותתק"ח בדינר והם ג' אלפים וק"צ חלקים מט' אלפים קס"ג בדינר | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם אמר השואל שהרויח ראובן או הפסיד בזה המסחר ק' די' ורצית לדעת כמה הממון | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה תחלק במשלינו זה ק' דינר על מה שהרויח במדה אחת שהוא ט' דינר וה' אלפים תש"א חלקים מח' אלפים תתקל"ב בדינר והעולה תהיינה מדות המסחר והם י' מדות ול"ב אלפים וש"י חלקים מפ"ו אלפים ופ"ט חלקים במדה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תערוך מדות המסחר על סך דינ' ערך המדה לפי מה שקנה יהיה העולה בידך הממון | ||||||||||||||||||||||||||||||||||||||||||||||||
| וזה כלו מבואר הסבה עם מה שקדם מהדברים | |||||||||||||||||||||||||||||||||||||||||||||||||
|
שאלה איש אחד קנה חלק מה או חלקים מה ממדה או ליטרא במספר מונח מהדי' ומכר חלקים אחרים מחסירים מהראשון במספר ההוא בעינו מהדינרין והרויח ככה כמה הממון | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והמשל שקנה ראובן ב' חמישיות המדה וג' שביעיות ב' די' ומכר ד' תשיעיותיה ב' די' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הדרך בזה שתקח המורה לכל אלו החלקים הן מהמדה הן מהדינרין ואם קרה שיהיו בהם חלקים והנה המורה לכל אלו החלקים במשלנו הוא שט"ו והיא המדה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
קח ממנו ב' חמישיותיו וג' שביעיותיו ויעלה רי"ו | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה אם כן בדי' יקנה מאלו החלקים ק"ח | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
גם קח ממנו ד' תשעיותיו ועלה ק"מ | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה אם כן בדי' יתן ע' מאלו החלקים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ולזה ירויח בדי' ל"ח חלקים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכבר היה הריוח ק' די' שהוא ז' אלפים מאלו החלקים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה ראוי שנקח מספר יהיה יחסו אל ק"ח כיחס ז' אלפים אל ל"ח וכבר התבאר דרך לקיחתו | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם חלקת העולה על ע' תמצא מספר הממון עם מה שהרויח יחד | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם חלקת העולה על ק"ח שהוא סך חלקי הדינר לפי מה שקנה תמצא מספר הממון | ||||||||||||||||||||||||||||||||||||||||||||||||
| וזה מבואר הסבה עם מה שקדם מהדברים | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם היתה השאלה בהפך ר"ל שהפסיד ק' די' בשקנה ד' תשיעיות המדה ב' די' ומכר ב' חמישיותיה עם ג' שביעיותיה ב' די' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הדרך אחת אלה שכאשר תחלוק העולה על ע' יהיה לך מספר הממון | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תחלקהו על ק"ח יהיה לך הנשאר לו אחר ההפסד | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם שאל כמה המקח חלק העולה על שפ"ה שהם חלקי המדה והנה מדות המקח והקש על זה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן אם לא היה מספר הדי' שוה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ר"ל שקנה חלקים מה מהמדה בג' די' ומכר חלקים מה ממנה כ"ה די' והרויח או הפסיד ק' די' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
תוציא בדרך הקודם החלקים מהמורה שיקנה די' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
גם החלקים שימכר די' | ||||||||||||||||||||||||||||||||||||||||||||||||
| ותמשיך המעשה על האופן הקודם ויצא לך הדרוש | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם היו החלקים אחדים ומספר הדי' מתחלף | ||||||||||||||||||||||||||||||||||||||||||||||||
|
משל זה שיקנה ד' חלקים מז' בליט' עם ה' חלקים מי"א בה ז' די' וח' חלקים מי"א בדי' וימכר אלו החלקים ט' די' וג' חלקים מי"ג די' והרויח ק' די' ושאל שואל כמה הממון או כמה המקח | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה הדרך שתקח המורה אל כל החלקים הן מהליט' והוא יהיה חלקי הליט' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ותדע סך החלקים שיקנה בדי' וסך החלקים שיתן בדי' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ותמשיך הענין על האופן הקודם הן לדעת מספר הממון הן לדעת מספר המקח | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם ישאל אדם כמה שעור בעל שעור מה שב' שביעיותיו עם ג' חמישיותיו מוסיפים על ד' תשיעיותיו שעור מה או מחסירים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה הדרך בזה מבוארת בתמונת מ"ט | ||||||||||||||||||||||||||||||||||||||||||||||||
|
שאלה: ראובן קנה חלקים ככה מהמדה במספר ככה מהדינרין והיה הממון מספר ככה מהדינר ומכר קצת המסחר חלקים ככה מהמדה במספר ככה מהדי' וקצתו האחר מכר חלקים ככה מהמדה במספר ככה מהדי' | ||||||||||||||||||||||||||||||||||||||||||||||||
| the problem is correct - if he earns at one price and loses at the second price | הנה מן המחוייב אם היתה השאלה צודקת שירויח בערך האחד ויפסיד בערך השני | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה תוציא ערך המדה לכל אחד מהערכים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ותראה כמה הפסיד במדה לערך האחד וכמה הרויח במדה לערך השני | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה כיחס ההפסד אל הריוח כן יחס מה שמכר לערך המותיר אל מה שמכר לערך המחסיר | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה יתבאר במעט עיון מתמונת ל"ט מהמאמר הראשון | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר קבצנו יהיה יחס ההפסד אל הריוח וההפסד מקובצים כיחס מה שמכר לערך המותיר אל כל המסחר | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ולפי ששלשה מאלו ידועים לך תוכל להוציא הרביעי על האופן הקודם בראש זה השער | ||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון זה ראובן קנה ב' שביעיות המדה ג' דינרין ורביע דינר והיה הממון ק' דינ' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה ערך המדה לפי מה שקנה י"א דינר וג' שמיניות הדינר | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וערכה לפי הערך הראשון י"ד דינר ורביע דינר | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ולפי הערך השני יהיה ערכה ט' דינר וו' חלקים מכ"ה בדינר | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ולזה יהיה המסחר ח' מדות וע"ב חלקים מצ"א בדינר | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה מה שהרויח במדה לפי הערך הראשון הם ב' דינר וז' שמיניות הדינר | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ומה שהפסיד במדה לפי הערך השני הם ב' דינר וכ"ז חלקים ממאתים בדינר | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה ההפסד והרויח מקובצים הם ה' דינר וב' חלקים ממאתים בדינר | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ערוך סך דינרי ההפסד ושבריהם על סך מדות המסחר ושבריהן וחלק העולה על סך דינרי ההפסד והריוח מקובצים ושבריהם והעולה הוא סך מדות המסחר שמכר לערך המותיר ושבריהם | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ערכת ב' שלמים וכ"ז חלקים ממאתים באחד על ח' שלמים וע"ב חלקים מצ"א באחד וחלקת העולה על ה' שלמים וב' חלקים ממאתים באחד והעולה מן החלוקה הוא סך המדות שמכר לערך המותיר ושבריהן | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והנשאר מן המסחר מכר לערך המחסיר | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם אמר השואל שהרויח או הפסיד מספר מה מן הדינרין | ||||||||||||||||||||||||||||||||||||||||||||||||
|
תקח מספר המדות אשר ירויח בהם זה הסך אם הרויח או אשר יפסיד בהם זה הסך אם הפסיד ותוציאוהו מן המסחר ושמרהו והנשאר מהמסחר תחלקהו על האופן הקודם ותמצא מה שמכר לערך המותיר ממנו | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והשאר ממנו הוא מה שמכר לערך המחסיר | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם הפסיד תחבר מה שמכר לערך המחסיר עם השמור ואם הרויח תחברהו עם מה שמכר לערך המותיר | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם היתה השאלה שמכר כ' מדות לערך המותיר ורצינו לדעת כמה מן המדות מכר לערך המחסיר בדרך שלא ירויח ולא יפסיד | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה כיחס כ' מדות אל הנעלם כן יחס ב' דינרין וכ"ז חלקים ממאתים בדינר אל ב' דינ' וז' שמיניות הדינר | ||||||||||||||||||||||||||||||||||||||||||||||||
| ולזה תוכל לדעת הנעלם על האופן שקדם | |||||||||||||||||||||||||||||||||||||||||||||||||
|
וממה שקדם יתבאר לך אם החליף אדם מסחר מה במסחר אחר וערך החלקים מן המדה ממה שנתן מספר ככה מן הדינ' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה שתוציא ערך המדה לכל אחד מהערכים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכיחס ערך המדה שנתן אל ערך המדה שקבל כן יחס סך המדות שקבל אל סך המדות שנתן | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ושלשה מאלו המספרים ידועים לך ולזה תוכל להוציא הרביעי | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן אם ידעת סך המדות שנתן ושקבל מקובצות הנה תוכל להוציא כמה מן המדות נתן וכמה קבל | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה שתוציא ערך המדה לכל אחד מהערכים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכיחס ערך המדה ממה שנתן אל מקובץ ערכי המדה ממה שנתן ושקבל כן יחס סך המדות שקבל אל מקובץ סך המדות שנתן ושקבל | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה שלשה מאלו המספרים ידועים לך ומהם תוכל להוציא הרביעי | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן יתבאר לך אם החליף אדם מסחר מה בשני מסחרים וערך חלקים מה מן המדה ממה שנתן מספר ככה מן הדינר' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה תוציא ערך מה שנתן בכללו ותחלקהו על מספר המדות שקבל והוא יהיה ערך המדה המעורבת משני אלו המסחרים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכבר קדמה לך הדרך כמה חלקים מהמדה ילקחו מהמסחר האחד וכמה מהמסחר השני ויהיה ערך המדה ככה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ולזה תכפיל מספר חלקי המדה שיקח מהמספר האחד על מספר מדות השני מסחרים שקבל והחלקים ההם הם חלקי המדה שקבל מזה המסחר | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והשאר קבל מהמסחר השני | ||||||||||||||||||||||||||||||||||||||||||||||||
| וסבת זה מבוארת עם מה שקדם מהדברים | |||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון ראובן נתן לשמעון ז' מדות ממסחר מה ערך המדה ב' דינ' ושביעית וקבל משמעון ט' מדות משני מסחרים ערך המדה מהמסחר האחד דינר וחצי וערך המדה מהמסחר השני ב' דינ' וג' רביעיות | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה ידענו שערך מה שקבל הם ט"ו דינר | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ולזה יהיה ערך המדה ממה שקבל דינר וב' שלישיות | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ולפי שהיה ערך המדה מהמסחר האחד דינר וחצי ומהמסחר השני ב' דינרין וג' רביעיות הנה יקח ב' חלקים מט"ו במדה מהמסחר אשר ערך המדה ממנו ב' דינ' וג' רביעיות | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ויהיה ערך המדה דינר וב' שלישיות הדינר וזה יתבאר כשהשיבונו כל שברי הדינרין אל חלקים ממין אחד רצוני השליש והחצי והרביע וזה שחסרון המחסיר הוא שנים מאלו החלקים ויתרון המוסיף הוא י"ג מאלו החלקים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ובהיות הענין כן הוא מבואר שהוא יקח מהמסחר אשר ערך המדה ממנו דינר וחצי ז' מדות וד' חומשי המדה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והשאר יקח מהמסחר האחר | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכזה התבאר לך אם התנה אדם לתת בשכירות לאיש מה בזמן מה מספר ככה מהדינרין ובכל יום שיבטל הפועל יתן לשוכר מספר ככה מהדינ' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה שתוציא הסך מהדי' שירויח הפועל ביום כשיעשה מלאכתו והסך מהדי' שיפסיד ביום שיבטל | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכיחס סך דינרי ההפסד אל סך דינרי הריוח כן יחס הזמן שבטל אל הזמן שעשה וזה מבואר בנפשו | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והשלשה מאלו המספרים ידועים ומהם תוציא הרביעי | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן אם היה ידוע לך מקובץ שני הזמנים תוכל לדעת באופן הקודם כמה מן הזמן בטל וכמה עשה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
שאלה איש אחד החליף מסחר מה במסחר אחר וערך חלקים מה מן המדה ממה שנתן ככה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והמשל שהמסחר שנתן ישוו ג' חמישיותיו המדה עם ב' תשיעיותיו ב' די' והמסחר שקבל ישוו ג' חלקים מי"א במדה עם ב' שביעיותיה ג' די' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הדרך בזה שתקח המורה אל כל החלקים הן מהמדה הן מהדנרין אם קרה שיהיו שם חלקים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וממנו תקח החלקים שילקחו בדי' לכל אחד מאלו הערכים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכמו חלקי הדי' ממה שנתן אל חלקי הדי' ממה שקבל כן יחס מה שנתן אל מה שקבל | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה המורה לכל אלו החלקים הוא ג' אלפים תס"ה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
לקחנו ג' חמישיותיו וב' תשיעיותיו והנה אלפים תס"ד | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ולזה יהיו החלקים שילקחו בדינר ממה שנתן אלף רל"ב | ||||||||||||||||||||||||||||||||||||||||||||||||
|
לקחנו ב' שביעיותיו וג' חלקים מי"א במדה בו ועלה אלף תתקל"ה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ולזה יהיו החלקים שילקחו בדי' ממה שקבל תרמ"ה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה כיחס אלף רל"ב אל תרמ"ה כן יחס מה שקבל אל כ' מדות | ||||||||||||||||||||||||||||||||||||||||||||||||
| וכבר ידעת דרך לקיחת זה המספר הנעלם וסבת זה מבוארת והקש על זה | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ומזה התבאר לך אם התנה אדם לתת בשכירות לאיש מה בזמן מה מספר ככה מהדינ' ובכל יום שיבטל הפועל יתן לשוכר מספר ככה מהדינ' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
משל זה שראובן שכר שמעון לעשות מלאכתו ויתן לו בשכירותו בז' ימים וחומש יום כ' די' ושמעון יתן לראובן בכל יום שיבטל ד' חלקים מי"א בדי' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
לקחנו המורה לכל החלקים בכללם ועלה שפ"ה והוא חלקי היום | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה נראה בכמה חלקים מאלו ירויח די' ובכמה חלקים מאלו יפסידהו וכיחס מספר חלקי הריוח אל מספר חלקי ההפסד כן יחס ב' ימים וג' שביעיות אל הזמן שבטל | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה בקל"ח חלקים וי"ב חלקים מעשרים בחלק ירויח די' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ובאלף ונ"ח חלקים וג' חלקים מארבעה בחלק יפסיד די' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וככה יחס ב' ימים וג' שביעיות אל הזמן שבטל והקש על זה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם שאל לך אדם כמה המספר שיהיו חלקים מה ממנו כמו חלקים מונחים ממספר מונח | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה הדרך בזה התבארה בתמונת נ"א | ||||||||||||||||||||||||||||||||||||||||||||||||
|
שאלה הכינו מספר במספר מה והיה העולה ככה ומקובץ שני המספרים ככה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
קח מרובע חצי מקובץ שני המספרים וגרע ממנו העולה ומהנשאר הוצא השרש הרבועיי והוסיפהו על החצי ממקובץ שני המספרים והוא המספר האחד ואם גרענו מהחצי יהיה לך המספר השני | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והמשל שיהיו שני המספרים מקובצים י"ג ושטח זה בזה י"ז | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וידענו שמרובע חצי מספר י"ג הוא מ"ב ורביע גרענו ממנו י"ז ונשאר כ"ה ורביע הוצאנו שרשם והנה ה' שלמים וראשון אחד כ"ט שניים מ"ו ל"ד | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
הוספנום על ו' וחצי שהוא חצי י"ג והנה יהיה המספר האחד י"א שלמים ל"א ראשונים כ"ט מ"ו ל"ד | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והמספר השני הוא אחד שלם כ"ח ראשונים ל' י"ג כ"ו | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה שטח זה בזה הוא י"ז בקירוב גדול | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה אי אפשר המצא זה המספר בדיוק מפני שאין לכ"ה ורביע שרש אמתי לפי מה שהתבאר | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וזה שיחס כ"ה ורביע אל כ"ה הוא כיחס מאה ואחד אל מאה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ואין יחס מאה ואחד אל מאה כיחס מספר מרובע אל מספר מרובע | ||||||||||||||||||||||||||||||||||||||||||||||||
|
שאם היה הדבר כן היה מאה ואחד מרובע לפי שמאה הוא מרובע | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם היה מאה ואחד מרובע היה שרשו אחדים שלמים וזה שקר | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם שאל הכינו מספר מונח בחלק מונח ממנו וקבצנו העולה עם שטח החלק המונח בשארית המספר המונח והיה ככה כמה כל אחד מהחלקים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
קח מרובע כל המספר וגרע ממנו זה המספר המקובץ מהכאת המספר בחלק אחד ממנו וחלק אחד ממנו באחר ומהנשאר הוצא השרש והוא החלק האחד והנשאר מהמספר הוא החלק המונח | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והמשל שיהיה שטח עשרה בחלק מונח ממנו עם שטח החלק ההוא בחלק השני שמונים ורצינו לדעת כמה החלק המונח | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והנה מרובע עשרה הוא מאה גרענו מהם שמונים ונשארו עשרים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והנשאר שהוא ה' שלמים ל"א מ' י"ח ל"ט הוא החלק המונח | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תכהו בעשרה ובנשאר יעלה פ' בקירוב גדול | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם שאל הכינו מספר מונח בחלק מונח ממנו וקבצנו העולה עם מרובע החלק הנשאר והיה ככה ורצינו לדעת כמה כל אחד מהחלקים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
גרע הכל ממרובע כל המספר והנשאר בידך גרעהו ממרובע חצי המספר והנשאר בידך הוצא את יסודו והוסיפוהו על חצי המספר והנה החלק האחד והנשאר מהמספר הוא החלק השני | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והמשל שיהיה שטח עשרה בחלק אחד ממנו עם מרובע הנשאר פ' ורצינו לדעת כמה כל אחד מהחלקים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
גרענו פ' ממאה ונשארו עשרים גרענו עשרים מכ"ה ונשארו חמשה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והחלק השני ב' שלמים מ"ה נ' ט' כ' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה שטח י' באי זה חלק שיהיה מאלו עם מרובע החלק הנשאר הוא שמונים בקירוב | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והוא מבואר במעט עיון ממה שקדם שבאי זה מן החלקים שיוכה מספר עשרה ויחובר עם מרובע הנשאר יהיה העולה אחד בעינו | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
לפי שהעולה יהיה שוה לשטח החלק האחד בשני ולמרובעי שניהם | ||||||||||||||||||||||||||||||||||||||||||||||||
|
שאלה חברנו מספר מונח ראשון עם חלקים מונחים ממספר מונח שני והיה העולה שוה למספר המונח השני עם חלקים אחרים מהמספר המונח הראשון והיה העולה מספר ככה כמה כל אחד מהמספרים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הדרך בזה שתשיב החלקים חלק | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר כן תוציא המספרים שינהגו זה המנהג על האופן שהתבאר בתמונת נ"ב וזה יתבאר מהמופת ההוא בעינו | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן ראוי שתדע שכל מה שהתבאר בתמונת מ"ז ומ"ח ונ"ג יצדק בחלקים גם כן כשיושבו חלק וזה יתבאר גם כן מהמופת אשר באלו התמונות | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר שישלם לך המעשה בהוצאת המספרים אשר ינהגו זה המנהג תדע מה יעלה המספר האחד עם החלקים המונחים מהמספר השני | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והוא הגיליי לעולה הידוע ותוכל להוציא הגיליים לשני המספרים על האופן שהתבאר בראש זה השער | ||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון זה שיחובר המספר המונח הראשון עם ב' שביעיות ותשיעית מהמספר המונח השני והיה עשרים ואם יחובר המספר המונח השני עם ב' חמישיות המספר המונח הראשון יהיו עשרים גם כן | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
הנה נשיב ב' שביעיות ותשיעית חלק אחד והנה יהיה חלק אחד משנים וי"ג חלקים מכ"ה באחד | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכן נשיב הב' חמישיות חלק אחד ויהיו חלק אחד משנים וחצי | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר כן נוציא שני מספרים ינהגו זה המנהג על צד שהתבאר בתמונת נ"ב | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ולזה נערוך אחד וי"ג חלקים מכ"ה באחד על ב' שלמים וחצי ועלה ג' וד' חומשים והוא המספר הראשון | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ונערוך אחד וחצי על ב' וי"ג חלקים מכ"ה ויעלה ג' שלמים ול"ט חלקים מנ' והוא המספר השני | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה המספר הראשון עם ב' שביעיות המספר השני ותשיעיתו הוא ה' שלמים וג' עשיריות וככה המספר השני עם ב' חמישיות המספר הראשון | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ולפי שידעת הגיליי לה' שלמים וג' עשיריות והוא עשרים תוציא הגיליים למספר הראשון והשני על זה היחס | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והנה המבוקש ערכת הראשון על עשרים וחלקת על ה' שלמים וג' עשיריות והנה המונח הראשון הוא י"ד שלמים וי"ח חלקים מנ"ג | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ובזה הדרך יהיה המונח השני י"ד שלמים וי"ד חלקים מנ"ג באחד והקש על זה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והיה זה כן לפי שיחס הראשון אל המונח הראשון כיחס העולה אל עשרים וכיחס השני אל המונח השני | ||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכזה הוא מבואר שיחס ב' חומשי הראשון אל ב' חומשי המונח הראשון כיחס הראשון אל המונח הראשון | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכזה יהיה יחס ב' שביעיות השני ותשיעיתו אל ב' שביעיות המונח השני ותשיעיתו כיחס השני אל המונח השני שהוא כיחס הראשון אל המונח הראשון | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכאשר קבצנו שנים גיליים יהיה גם כן יחס מקובצם אל מקובץ גיליהם כיחס העולה אל עשרים ולזה יהיה יחס השני וב' חומשי הראשון מקובצים אל המונח השני וב' חומשי המונח הראשון מקובצים כיחס העולה שהוא ה' שלמים וג' עשיריות אל עשרים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכאשר המירונו יהיה יחס השני וב' חומשי הראשון מקובצים אל העולה כיחס המונח השני וב' חומשי המונח הראשון אל עשרים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
אבל הראשון מאלו הארבעה שוה לשני | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
הנה השלישי שוה לרביעי הנה אם כן המונח השני וב' חומשי המונח הראשון הוא עשרים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ובזה התבאר שהמונח הראשון וב' שביעיות המונח השני ותשיעיתו הוא עשרים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והיתה השאלה לחבר עם הראשון כפלים מה מהשני ועם השני כפלים מה מהראשון ויהיה העולה אחד בעינו | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
תוציא ממספר כפלי הראשון אחד והנשאר הוא השני וכזה תוציא ממספר כפלי השני אחד והנשאר הוא הראשון | ||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון שיהיה הראשון עם שני כפלי השני וחציו כמו השני עם שלשה כפלי הראשון ורביעיתו | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
הנה תשים הראשון אחד וחצי | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והשני ב' שלמים ורביע | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ולזה יהיה הראשון עם שני כפלי השני וחציו הוא הראשון והשני מקובצים ושטח אחד וחצי שהוא הראשון בשני שהוא ב' שלמים ורביע | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכזה יהיה השני עם שלשה כפלי הראשון ורביעיתו שוה לשני ולראשון מקובצים ולשטח השני שהוא שנים ורביע באחד וחצי שהוא הראשון | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ולזה הוא מבואר שהעולה הוא אחד בעצמו והוא ז' שלמים ושמינית | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם אמר השואל שהראשון הוא עשרים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה תוכל להוציא כמה השני וזה שיחס הראשון אל עשרים כיחס השני שהוא ב' ורביע אל הנעלם | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ולזה יהיה השני שלושים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה בתמונת מ"ח ונ"ג הדבר מבואר עם חלקים כמו שהוא עם חלק מהמופת אשר שם בעינו וזה כשיושבו החלקים חלק | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן הענין בתמונת מ"ז כשהיה הראשון שנים אחר שהשיבונו החלקים חלק | ||||||||||||||||||||||||||||||||||||||||||||||||
|
אבל אם היה פחות משנים הנה לא נתבאר שם דרך לקיחת אלו המספרים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ונאמר שהדבר באלו הפך הענין כשהיה הראשון מוסיף על שנים וזה שאז היה הראשון מאלו המספרים השלישי ויתרון השני על הראשון כשחסרנו ממנו השטח ההווה מחסרון הראשון משנים בשטח השני בשלישי והשני והשלישי יוצאו על הצד שהתבאר שם | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והמשל שיהיה המספר אשר ממנו נקח חלק אחד כשהשיבונו החלקים חלק אחד פחות משנים והוא א' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ויהיה חסרונו משנים קצה אחד והוא ד' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ויהיה המספר השני ב' ויהיה יתרונו על א' מספר ה' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ויהיה המספר השלישי ג' ויהיה יתרונו על ב' מספר ז' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ויהיה המספר הנמשך לפני ב' מספר ח' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והנמשך לפני ג' מספר ט' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והנמשך לפני א' מספר ל' והוא יתרון א' על אחד | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ויהיו כ'ל' שוים לא' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ולזה יהיה כ' אחד | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה נגרע ממספרי ג'ה' מורכב ד'ב'ג' ונשים הנשאר מ' והוא יהיה המספר הראשון | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ונחבר עם מ' כפל שטח ה' בט' ויהיה העולה נ' והוא יהיה המספר השני | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ונחבר עם נ' כפל שטח ל' בז' ונשים העולה ס' והוא יהיה המספר השלישי | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ונבאר שאלו המספרים הם המבוקשים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
המופת שהמספר הראשון והוא מ' שוה למספרי ג'ה' פחות מספר ד'ב'ג' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
המספר השני והוא נ' שוה למספרי ג'ה' פחות מורכב ד'ב'ג' ולכפל שטח ה' בט' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והמספר השלישי והוא ס' שוה למספרי ג'ה' פחות מורכב ד'ב'ג' ולכפל שטח ה' בט' ולכפל שטח ל' בז' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ונאמר שהחלק הנקרא בא' ממספרי נ'ס' שוה לכפל שטח ח' בט' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
המופת שחצי מספרי נ'ס' שוים למספרי ג'ה' ולכפל שטח ה' בט' ולשטח ל' בז' כשחוסר מכל זה מורכב ד'ב'ג' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ונשים שטח ל' בח'ג' משותף | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה אם כן חצי מספרי נ'ס' שוים למספרי ג'ה' ולכפלי שטח ה' בט' ולשטח ל' בז' ולשטח ל' בח'ג' כשחוסר מכל זה מורכב ד'ב'ג' ושטח ל' בח'ג' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
אבל שטח ה' בט' עם שטח ל' בז' שוה לשטח ח' במספרי ה'ז' מקובצים | ||||||||||||||||||||||||||||||||||||||||||||||||
| לפי שהיו הנה שלשה מספרים ל'ח'ט' | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ויתרון ח' על ל' ה' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ויתרון ט' על ח' ז' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה מספרי ה'ז'ל' שוים למספר ט' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
אם כן שטח ח' במספרי ה'ז' עם שטח ח' בל' יהיה שוה לשטח ח' בט' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ונגרע משטח ל' בח'ג' שטח ל' בח' וישאר שטח ל' בג' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ומספרי ג'ה' ושטח ה' בט' כשחוסר מכל זה מורכב ד'ב'ג' ושטח ל' בח'ג' ואומר שזה כולו שוה למורכב ל'ח'ט' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
המופת שאנחנו נחבר שטח ה' בט' עם ה' ויהיה שוה לשטח ה' בג' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
עוד נחברוהו עם ג' ויהיה שוה לשטח ה'כ' בג' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
עוד נחברוהו עם שטח ל' בג' ויהיה עולה שוה לשטח ה'כ'ל' בג' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה שוה לשטח ב' בג' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה שוה לשטח ד'ל' שהוא אחד במורכב ב'ג' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ונחסר מזה מורכב ד'ב'ג' וישאר מורכב ל'ב'ג' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה מורכב ל'ח'ט' פחות ממורכב ל'ב'ג' מורכב ל'ח'ג' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה שמורכב ל'ח' בט' עם מורכב ל'ח' שוה למורכב ל'ח'ג' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ומורכב ל'ח'ג' שוה לשטח ח' בל'ג' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר חברנו עם זה מורכב ל'ג' היה העולה שוה לשטח ב' בל'ג' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
אם כן כשחסרהו ממורכב ל'ב'ג' מורכב ל'ח'ג' שיהיה לנו לחסר מהמספר היה הנשאר מורכב ל'ח'ט' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
אם כן חצי מספרי נ'ס' שוה למורכב כ'ח'ט' שהוא שטח ח' בט' ולמורכב ל'ח'ט' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה שוה לשטח כ'ל' במורכב ח'ט' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
אבל כ'ל' הוא א' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
אם כן חצי מספרי נ'ס' שוים למורכב א'ח'ט' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
אם כן שטח ח' בט' הוא חלק נקרא בא' מחצי מספרי נ'ס' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ולזה יהיה כפל שטח ח' בט' חלק נקרא בא' ממספרי נ'ס' מקובצים ונשים העולה מספר ע' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וגם כן הנה חצי מספרי מ'ס' כששמנו שטח ל' בב' משותף שוים למספרי ה'ג' ושטח ה' בט' ושטח ל' בז' ושטח ל' בב' פחות מורכב ד'ב'ג' ושטח ל' בב' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ואומר שזה כלו שוה למורכב ל'ב'ט' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה ששטח ה' בט' עם ה' שוה לשטח ה' בג' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכשחובר עם שטח ה' בג' ג' יהיה שוה לשטח ה'כ' בג' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה שטח ל' בב' עם שטח ל' בז' שוה לשטח ל' בג' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
לפי שה'כ'ל' כמו ב' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
יהיה אם כן זה שוה לשטח ל'ד' במורכב ב'ג' לפי של'ד' הוא אחד | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר חסרנו מזה מורכב ד'ב'ג' ישאר מורכב ל'ב'ג' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר חסרנו מזה מורכב ל'ב' ישאר שטח ט' במורכב ל'ב' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה אם כן חצי מספרי מ'ס' שוים למורכב ב'ל'ט' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
אם כן שטח ל' בט' הוא חלק נקרא בב' מחצי מספרי מ'ס' מקו[בצ]ים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ולזה יהיה כפל שטח ל' בט' חלק נקרא בב' ממספרי מ'ס' מקובצים ונשים העולה מספר פ' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וגם כן הנה חצי מספרי מ'נ' כששמנו שטח ל' בג' משותף שוה למספרי ה'ג' ולשטח ה' בט' פחות מורכב ד'ב'ג' ושטח ל' בג' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ואומר שזה כולו שוה למורכב ל'ח'ג' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה ששטח ה' בט' עם מספרי ה'ג' שוה לשטח ה'כ' בג' כמו שהתבאר קודם | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר חברנו עם זה שטח ל' בג' היה עולה שטח ה'כ'ל' בג' שהוא שוה לשטח ב' בג' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר חסרנו מזה מורכב ד'ב'ג' ישאר מורכב ל'ב'ג' שהוא שטח ב' במורכב ל'ג' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר חסרנו מזה מורכב ל'ג' ישאר שטח ח' במורכב ל'ג' וזה שוה למורכב ל'ח'ג' שהוא שטח ג' במורכב ל'ח' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
אם כן שטח ל' בח' הוא חלק נקרא בג' מחצי מספרי מ'נ' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ולזה יהיה כפל שטח ל' בח' חלק נקרא בג' ממספרי מ'נ' מקובצים ונשים העולה מספר צ' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ואומר שמספרי מ'ע' שוים למספרי נ'פ' או למספרי ס'צ' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה שמספרי מ'ע' שוים למספר מ' ולכפל שטח ח' בט' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ונ'פ' שוים למספר מ' ולכפל שטח ה' בט' ולכפל שטח ל' בט' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
אם כן מספרי נ'פ' שוים גם כן למספר מ' ולכפל שטח ח' בט' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וגם כן הנה מספרי ס'צ' שוים למ' ולכפל שטח ה' בט' ולכפל שטח ז' בל' ולכפל שטח ח' בל' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
אבל כפל שטח ז' בל' עם כפל שטח ח' בל' שוה לכפל שטח ז'ח' בל' וזה שוה לכפל שטח ט' בל' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר חובר עם זה כפל שטח ט' בה' היה העולה כפל שטח ט' בל'ה' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ול'ה' כמו ח' ולזה יהיה העולה שוה לכפל שטח ט' בח' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר חברנו עם זה מספר מ' היה העולה גם כן מספר מ' וכפל שטח ח' בט' והוא מה שרצינו | ||||||||||||||||||||||||||||||||||||||||||||||||
| Examples | ונתן לך דמיונים על זה בכל אחד מהאופנים כשיהיו שם חלקים למען תשכיל ותדע | ||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
נרצה שנמצא שלשה מספרים יהיה האחד עם ב' שביעיות הנשארים כמו האחר עם ב' חמישיות הנשארים וכמו האחר עם ג' חלקים מי"א בנשארים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
השיבונו ב' שביעיות חלק אחד והיה חלק אחד מג' וחצי | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
השיבונו ב' חמישיות חלק אחד והיה חלק אחד מב' וחצי | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
השיבונו ג' חלקים מי"א חלק אחד והיה חלק אחד מג' וב' שלישיים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
חברנו המספר הגדול עם יתרון האמצעי על הקטן וחברנו עם זה השטח ההווה מיתרון הקטן על שנים בשטח האמצעי בגדול ולזה יהיה המספר הראשון י"א שלמים וחלק מי"ב באחד | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
חברנו עם זה כפל שטח יתרון האמצעי על הקטן בגדול פחות אחד ויעלה י"ו שלמים וי"א חלקים מי"ב באחד והוא המספר השלישי | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והיה הראשון עם ב' חמישיות הנשארים שהוא חלק אחד מב' וחצי כמו השני עם ב' שביעיות הנשארים וכמו השלישי עם ג' חלקים מי"א בנשארים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון שני נרצה שנמצא שלשה מספרים יהיה האחד עם חצי הנשארים כמו האחר עם ב' חמישיות הנשארים וכמו האחר עם ג' חלקים מי"א בנשארים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכאשר השיבונו החלקים חלק יהיו המספרים אשר אלו החלקים נקראים בהם שנים ושנים וחצי וג' וב' שלישיות | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ונשים המספר הראשון הגדול ויתרון האמצעי על הקטן מקובצים ולזה יהיה הראשון ד' שלמים וששית אחד | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ויהיה השני על הצד הקודם ו' שלמים וה' ששיות | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ויהיה השלישי ח' שלמים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ויהיה הראשון עם חצי הנשארים כמו השני עם ב' חמישיות הנשארים וכמו השלישי עם ג' חלקים בי"א בנשארים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון שלישי נרצה שנמצא שלשה מספרים יהיה האחד עם ג' חמישיות הנשארים כמו האחר עם ד' חלקים מי"א בנשארים וכמו האחר עם ב' שביעיות הנשארים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכאשר השיבונו אלו החלקים חלק יהיה המספר הקטן מהמספרים אשר אלו החלקים נ[ש]ארים בהם אחד וב' שלישיות והאמצעי ב' וג' רביעיות והגדול ג' וחצי | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והנה יהיה המספר הראשון על האופן שקדם אחד וט' חלקים מכ"ד | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ויהיה המספר השני ח' וב' חלקים מכ"ד | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והמספר השלישי הוא ט' וב' חלקים מכ"ד | ||||||||||||||||||||||||||||||||||||||||||||||||
| Another method | דרך אחרת קלה למצוא מספרים כמה שיהיו יהיה האחד עם חלק או חלקים מהנשארים כמו האחר עם חלק או חלקים מהנשארים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והמשל שנרצה למצוא ארבעה מספרים יהיה האחד עם א' חלקים מד' מהנשארים כמו השני עם ב' חלקים מה' בנשארים וכמו השלישי עם חלק אחד מז' בנשארים וכמו הרביעי עם ג' חלקים מח' בנשארים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה נשים א'ט' שוים למספר ד' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וב'כ' שוים למספר ה' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ול' פחות אחד מז' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וג'מ' שוים לח' | ||||||||||||||||||||||||||||||||||||||||||||||||
| a2+a3+a4 = ד×(כ×ל×מ) = נ | הנה נכה ד' במורכב כ'ל'מ' ונשים העולה נ' והוא יהיה מספר מקובץ שלשה המספרים מלבד הראשון | ||||||||||||||||||||||||||||||||||||||||||||||||
| a1+a3+a4 = ה×(ט×ל×מ) = ס | וגם כן הנה נכה ה' במורכב ט'ל'מ' ונשים העולה ס' והוא יהיה מספר מקובץ שלשה מספרים מלבד השני | ||||||||||||||||||||||||||||||||||||||||||||||||
| a1+a2+a4 = ז×(ט×כ×מ) = ע | וגם כן הנה נכה ז' במורכב ט'כ'מ' ונשים העולה ע' והוא יהיה מספר מקובץ שלשה מספרים מלבד השלישי | ||||||||||||||||||||||||||||||||||||||||||||||||
| a1+a2+a3 = ח×(ט×כ×ל) = פ | וגם כן הנה נכה ח' במורכב ט'כ'ל' ונשים העולה פ' והוא יהיה מספר מקובץ שלשה המספרים מלבד הרביעי | ||||||||||||||||||||||||||||||||||||||||||||||||
| Since the sums of every three numbers of the four are known - the four numbers themselves can be extracted | ואחר שידעת מקובץ כל שלשה מספרים מאלו הארבעה תוכל להוציא כל אחד מהם איש על מקומו | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והדרך היותר נאותה בזה שתקח המספר היותר קטן ממספרי נ'ס'ע'פ' ואחריו הקטן מהנשאר וכן עד שתגיע אל היותר גדול | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ונניח שיהיה היותר קטן מספר ע' [והיותר] קטן אחריו מספר נ' והיותר קטן אחריו מספר פ' ולזה יהיה יותר גדול מספר ס' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ויהיה יתרון ס' על פ' מספר צ' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ויתרון ס' על נ' מספר ק' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ויתרון ס' על ע' מספר ר' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה מפני שס' הוא מקובץ הראשון והשלישי והרביעי | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ופ' הוא מקובץ הראשון והשני והשלישי | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה כאשר חסרנו מהם הראשון והשלישי משותפים נשאר יתרון הרביעי על השני הוא יתרון ס' על פ' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ולזה יהיה יתרון הרביעי על השני מספר צ' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וגם כן הנה מפני שמספר ס' הוא מקובץ הראשון והשלישי והרביעי | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ומספר נ' הוא מקובץ השני והשלישי והרביעי | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה כאשר חסרנו מהם השלישי והרביעי משותפים נשאר יתרון הראשון על השני מספר ק' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכזה יתבאר שיתרון השלישי על השני הוא מספר ר' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
לפי שיתרון ס' על ע' הוא מספר ר' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ובהיות הענין כן הנה המספר השני הוא היותר קטן | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ונקח אחד ממקובץ המספרים אשר המספר השני בכללם והוא ע' במשלינו זה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ולפי שמספר ע' הוא מקובץ הראשון והשני והרביעי | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הוא מבואר שיתרון ע' על שלשה דמיוני השני הוא שוה ליתרון הראשון על השני וליתרון הרביעי על השני מקובצים והם מספרי ק'צ' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ולזה נגרע ממספר ע' מספרי ק'צ' ונחלק הנשאר על מספר המספרים אשר מספר ע' מקובצם ר"ל על שלשה והעולה מן החלוקה הוא המספר השני ונניח שיהיה ש' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ולזה יהיה המספר הראשון ש'ק' מקובצים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והמספר השלישי מספרי ש'ר' מקובצים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והמספר הרביעי מספרי ש'צ' מקובצים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר שמצאנו אלו המספרים הנה נבאר שאלו הם המספרים שינהגו זה המנהג הדרוש | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה שאנחנו נבאר שהנשאר מהמספרים האלו הוא תמיד שוה למורכב ט'כ'ל'מ' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
המופת שהראשון כשחובר עם א' חלקים מד' בנשארים היה הנשאר שטח ט' במורכב כ'ל'מ' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה שהנשארים שוים למספר נ' והוא שטח ד' במורכב כ'ל'מ' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה במספר נ' מדמיוני מורכב כ'ל'מ' כמו מה שבמספר ד' מן האחדים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה מורכב כ'ל'מ' הוא חלק נקרא בד' ממספר נ' ולזה יהיה בא' חלקים מד' במספר נ' מדמיוני מורכב כ'ל'מ' כמו מה שבמספר א' מן האחדים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ולזה יהיה בנשאר מאלו השלשה מספרים מדמיוני מורכב כ'ל'מ' כמו מה שבמספר ט' מן האחדים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
לפי שמספרי ט'א' שוים למספר ד' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה שוה למורכב ט'כ'ל'מ' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכזה התבאר שהשני כשחובר עם ב' חלקים מה' בנשארים היה הנשאר שוה לשטח כ' במורכב ט'ל'מ' וזה שוה למורכב ט'כ'ל'מ' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכזה יתבאר שהשלישי כשחובר עם חלק מז' מהנשארים היה הנשאר שוה לשטח ל' במורכב ט'כ'מ' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה של' פחות אחד מז' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה שוה למורכב ט'כ'ל'מ' | ||||||||||||||||||||||||||||||||||||||||||||||||
| what remains from these four numbers is always equal to the product ט×(כ×ל×מ) →what is subtracted from them is one and the same |
ולפי שהנשאר מארבעה מספרים הוא תמיד כמו מורכב ט'כ'ל'מ' יהיה בהכרח הלקוח מהם אחד בעינו | ||||||||||||||||||||||||||||||||||||||||||||||||
|
כי כשחוסרו מהשוים שוים יהיו הנשארים שוים והוא מה שרצינו לבאר | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ואומר שאם היה מקובץ ק'צ' במשלינו זה יותר ממספר ע' או שוה לו שהשאלה כוזבת בהכרח | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ר"ל שאי אפשר שימצאו מספרים ינהגו זה המנהג | ||||||||||||||||||||||||||||||||||||||||||||||||
|
המופת שאם היה אפשר הנה יהיו המספרים ההם מספרי ת'ך'ץ'ף' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ויהיה ת' עם א' חלקים מד' במספרי ך'ץ'ף' כמו ך' עם ב' חלקים מה' במספרי ת'ץ'ף' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
או כמו ץ' עם חלק אחד מז' במספרי ת'ך'ף' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
או כמו ף' עם ג' חלקים מח' במספרי ת'ך'ץ' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ולזה יהיה הנשאר מארבעה המספרים אחד בעינו והוא מספר ן' על דרך משל | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ויתבאר שיחס ן' אל מספרי ך'ץ'ף' מקובצים הוא כיחס מספרי ט' אל ד' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה שכאשר לקחנו ממספרי ך'ץ'ף' א' חלקים מד' היה הנשאר מהם והוא ן' ט' חלקים מד' במספר ך'ץ'ף' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה שמספרי א'ט' שוים למספר ד' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכזה התבאר שיחס מספרי ת'ץ'ף' אל ן' כיחס ה' אל כ' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכזה התבאר שיחס ת'ך'ף' אל ן' כיחס ז' אל ל' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכזה [התבאר] שיחס ת'ך'ץ' אל ן' הוא כיחס ח' אל מ' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה נחלק מספר ן' בדמיוני מה שבמורכב ט'כ'ל'מ' מן האחדים ויהיה אחד ממורכב ט'כ'ל'מ' במספר ן' מספר ם' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה מפני שיחס ן' אל מספרי ת'ך'ף' הוא כיחס ל' אל ז' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ובמספר ן' מדמיוני ם' כמו מה שבשטח ל' במורכב ט'כ'מ' מן האחדים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה יהיה במספרי ת'ך'ף' מדמיוני ם' כמו מה שבמספר שטח ז' במורכב ט'כ'מ' מן האחדים ולזה יהיה במספרי ת'ך'ף' מדמיוני ם' כמו מה שבמספר ע' מן האחדים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ובזה התבאר שבמספרי ך'ץ'ף' מדמיוני ם' כמו מה שבמספר נ' מן האחדים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ושבמספרי ת'ץ'ף' מדמיוני ם' כמו מה שבמספר ס' מן האחדים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ושבמספרי ת'ך'ץ' מדמיוני ם' כמו מה שבמספר פ' מן האחדים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ולזה יתבאר בכמו הבאור הקודם שיתרון הראשון על השני הוא מדמיוני ם' כמו מה שבמספר ק' מן האחדים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ויתרון הרביעי על השני הוא מדמיוני ם' כמו מה שבמספר צ' מן האחדים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
ולזה יחוייב שיהיה ביתרון ך'ף' על שני דמיוני ת' מדמיוני מספר ם' כמו מה שבמספר ק'צ' מן האחדים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ונניח שיהיה במספר ת' מדמיוני ם' כמו מה שבמספר ו' מן האחדים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכבר היה במספר ת'ך'ף' מדמיוני ם' כמו מה שבמספרי ק'צ' מן האחדים ושלשה דמיוני מה שבת' מדמיוני ם' אם כן במספרי ת'ך'ף' מדמיוני ם' כמו מה שבמספרי ק'צ' ושלשה דמיוני מספר ו' מן האחדים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
אבל במספרי ת'ך'ף' מדמיוני ם' כמו מה שבמספר ע' מן האחדים | ||||||||||||||||||||||||||||||||||||||||||||||||
| → ק + צ + ו·3 = ע | אם כן מספר ע' שוה למספרי ק'צ' ושלשה דמיוני מספר ו' מן האחדים | ||||||||||||||||||||||||||||||||||||||||||||||||
| but ק + צ ≥ ע | וכבר הנחנו שמספרי ק'צ' שוים למספר ע' או מוסיפים על מספר ע' | ||||||||||||||||||||||||||||||||||||||||||||||||
| the part is equal to the whole or greater than the whole → false | זה שקר ר"ל שיהיה החלק שוה לכל או יותר מהכל | ||||||||||||||||||||||||||||||||||||||||||||||||
| → the assumption is false | ובהיות הענין כן הנה השאלה כוזבת והוא מה שרצינו לבאר | ||||||||||||||||||||||||||||||||||||||||||||||||
| והנה נתן לך דמיון על זה | |||||||||||||||||||||||||||||||||||||||||||||||||
|
נרצה שנמצא שבעה מספרים יהיה הראשון עם ב' שביעיות הנשאר כמו השני עם שליש הנשאר וכמו השלישי עם ב' תשיעיות הנשאר וכמו הרביעי עם ג' שמיניות הנשאר וכמו החמישי עם ששית הנשאר וכמו הששי עם רביעית הנשאר וכמו השביעי עם ב' חלקים מי"א חלקים בנשאר | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
הנה לפי הבאור הקודם נכה ז' במורכב ב'ז'ה'ה'ג'ט' כמו שתראה בזאת הצורה והנה העולה ס"ו אלפים וק"נ והם השני והשלישי והרביעי והחמישי והששי והשביעי מקובצים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
הכינו ג' במורכב ה'ז'ה'ה'ג'ט' והנה העולה ע' אלפים ותתע"ה והם ה'א'ג'ד'ה'ו'ז' מקובצים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
הכינו ט' במורכב ה'ב'ה'ה'ג'ט' ועלה ס' אלפים תש"נ והם א'ב'ד'ה'ו'ז' מקובצים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
הכינו ח' במורכב ה'ב'ז'ה'ג'ט' ועלה ע"ה אלפים ות"ר והם א'ב'ג'ה'ו'ז' מקובצים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
הכינו ו' במורכב ה'ב'ז'ה'ג'ט' ועלה נ"ו אלפים וז' מאות והם א'ב'ג'ד'ו'ז' מקובצים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
הכינו ד' במורכב ה'ב'ז'ה'ה'ט' ועלה ס"ג אלפים והם הראשון והשני והשלישי והרביעי והחמישי והשישי והשביעי מקובצים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הכינו י"א במורכב ה'ב'ז'ה'ה'ג' ועלה ע"ז אלפים תש"נ והם הא'ב'ג'ד'ה'ו' מקובצים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והנה היותר קטן מאלו המקובצים הוא נ"ו אלפים וז' מאות ואחריו ס' אלפים תש"נ ואחריו ס"ג אלפים ואחריו ס"ו אלפים וק"נ ואחריו ע' אלפים תתע"ה והאחריו ע"ה אלפים ת"ר ואחריו ע"ז אלפים תש"נ | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והנה יתרון ע"ז אלפים תש"נ על שלפניו הוא ו' אלפים ק"נ וככה יתרון הרביעי על השביעי | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ויתרונו על ע' אלפים ותתע"ה ו' אלפים תתע"ה וככה יתרון השני על השביעי | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ויתרונו על ס"ו אלפים וק"נ י"א אלפים ות"ר וככה יתרון הראשון על השביעי | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ויתרונו על ס"ג אלפים י"ד אלפים תש"נ וככה יתרון הששי על השביעי | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ויתרונו על ס' אלפים תש"נ י"ז אלפים תש"נ וככה יתרון השלישי על השביעי | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ויתרונו על נ"ו אלפים וז' מאות כ"א אלפים ונ' וככה יתרון החמישי על השביעי | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ולזה יהיה החמישי היותר גדול | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והנה מקובץ כל המספרים מלבד החמישי הוא נ"ו אלפים וז' מאות | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ויתרוני הראשון והשני והשלישי והרביעי והששי על חמשה דמיוני השביעי הוא נ"ג אלפים וקכ"ה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
גרענו זה מנ"ו אלפים וז' מאות ונשאר ג' אלפים ותקע"ה חלקנו הנשאר על ששה שהוא מספר אלו המספרים אשר היה נ"ו אלפים וז' מאות מקובצים ועלה תקצ"ה שלמים וה' ששיות אחד וככה המספר השביעי | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
הוספנו על השביעי יתרון הששי עליו שהוא י"ד אלפים תש"נ והנה הששי והוא ט"ו אלפים שמ"ה וה' ששיות אחד | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ולזה יהיה החמישי כ"א אלפים תרמ"ה וה' ששיות | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והרביעי אלפים תשמ"ה וה' ששיות | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והשלישי י"ח אלפים שמ"ה שלמים וה' ששיות אחד | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והשני ז' אלפים ת"ע וה' ששיות אחד | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והראשון י"ב אלפים קצ"ה וה' ששיות אחד | ||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תרצה תוכל לבחון זה | |||||||||||||||||||||||||||||||||||||||||||||||||
| Taking multiples of the rest so that the results are all one and the same | ואם היתה השאלה לקחת הכפלים מה מהנשארים ויהיה העולה אחד בעינו | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והמשל שנרצה למצא ארבעה מספרים יהיה הראשון עם כפלי א' מהנשארים כמו השני עם כפלי ב' מהנשארים וכמו השלישי עם כפלי ג' מהנשארים וכמו הרביעי עם כפלי ד' מהנשארים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה נקח המספרים הנמשכים לפני א'ב'ג'ד' והם ה'ז'ח'ט' רצוני שה' נמשך לפני א' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה נשים מורכב ז'ח'ט' מקובץ כל המספרים מלבד הראשון | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ומורכב ה'ח'ט' מקובץ כל המספרים מלבד השני | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ומורכב ה'ז'ט' מקובץ כל המספרים מלבד השלישי | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ומורכב ה'ז'ח' מקובץ כל המספרים מלבד הרביעי | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר שידעת כל זה הנה תוציא כל המספרים איש על מקומו על האופן שקדם | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ונמצא שאלו המספרים הם המספרים המבוקשים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
המופת שהראשון כאשר חובר עם כפלי א' מהנשארים הנה העולה שוה לראשון ולדמיוני מורכב ז'ח'ט' כמו מה שבמספר א' מן האחדים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה שוה לראשון ולנשארים ולדמיוני מורכב ז'ח'ט' כמו מה שבמספר א' פחות אחד מן האחדים וזה שוה למורכב ה'ז'ח'ט' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
אם כן העולה שוה לארבעה המספרים ולמורכב ה'ז'ח'ט' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכזה התבאר שהשני כאשר חובר עם כפלי ב' מהנשארים היה העולה שוה לארבעה המספרים ולמורכב ה'ז'ח'ט' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והשלישי כאשר חובר עם כפלי ג' מהנשארים היה העולה שוה למקובץ כל המספרים ולמורכב ה'ז'ח'ט' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ושהרביעי כאשר חובר עם כפלי ד' מהנשארים היה העולה שוה למקובץ כל המספרים ולמורכב ה'ז'ח'ט' והוא מה שרצינו לבאר | ||||||||||||||||||||||||||||||||||||||||||||||||
| if the excess of the two numbers over twice the smallest is greater than the sum of the three or equal to it then the question is a false | ונאמר שאם היו יתרוני שני המספרים במשלינו זה על שני דמיוני הקטן יותר ממקובץ שלשתם או שוה לו שהשאלה כוזבת | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והמשל שיהיה הרביעי הוא היותר קטן | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ויהיה מורכב ה'ח'ט' מספר כ' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ויהיו יתרוני הראשון והשלישי על שני דמיוני הרביעי מספר ל' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ויהיה מספר ל' שוה למספר כ' או יותר גדול ממנו ואומר שהשאלה כוזבת | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ושאי אפשר שימצאו מספרים ינהגו זה המנהג | ||||||||||||||||||||||||||||||||||||||||||||||||
|
המופת שאי אפשר שאם היה אפשר יהיו המספרים ההם מספרי מ'נ'ס'ע' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה נחלק מקובץ מ'ס'ע' בדמיון מה שבמורכב ה'ח'ט' מן האחדים ויהיו חלקיו על זה האופן שוים למספר פ' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה במקובץ מ'ס'ע' מדמיוני פ' כמו מה שבמורכב ה'ח'ט' מן האחדים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר חברנו עם ב' מכפלי מ'ס'ע' כמו מה שבמספר ז' מן האחדים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
לפי שמספר ז' הוא פחות אחד מב' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
אבל במ'ס'ע' מדמיוני פ' כמו מה שבמורכב ה'ז'ח'ט' מן האחדים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ולפי שהיה מ' מכפלי א' מהנשארים כמו נ' עם כפלי ב' מהנשארים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והיה מ' עם כפלי א' מן הנשארים שוה למספרי מ'נ'ס'ע' ולדמיוני נ'ס'ע' כמו מה שמספר ה' מן האחדים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
אם כן ה' מוכה על נ'ס'ע' יהיו בו מדמיוני פ' כמו מה שבמורכב ה'ז'ח'ט' מן האחדים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ולזה יהיה במורכב נ'ס'ע' מדמיוני פ' כמו מה שבמורכב ז'ח'ט' מן האחדים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ובזה יתבאר שבמספרי מ'נ'ע' מדמיוני פ' כמו מה שבמורכב ה'ז'ט' מן האחדים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ושבמספרי מ'נ'ס' מדמיוני פ' כמו מה שבמורכב ה'ז'ח' מן האחדים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ולזה יהיו במספרי מ'ס'ע' מדמיוני פ' כמו מה שבמספר כ' מן האחדים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ויתבאר בכמו הביאור הקודם שיתרון מ'ס' על שני דמיוני ע' מדמיוני פ' כמו מה שבמספר ל' מהאחדים | ||||||||||||||||||||||||||||||||||||||||||||||||
| but ל ≥ כ | אבל ל' כמו כ' או יותר | ||||||||||||||||||||||||||||||||||||||||||||||||
| מ + ס + ע ≥ מ + ס → | אם כן מספרי מ'ס' יותר גדולים ממספרי מ'ס'ע' וזה שקר | ||||||||||||||||||||||||||||||||||||||||||||||||
| → the assumption is false | הנה אם כן אי אפשר שימצאו מספרים ינהגו זה המנהג | ||||||||||||||||||||||||||||||||||||||||||||||||
| Example: | והנה נתן לך דמיון על זה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
נרצה שנמצא חמשה מספרים יהיה הראשון עם שלושה דמיוני הנשארים כמו השני עם שלשה דמיוני הנשארים וחצי וכמו השלישי עם שלשה דמיוני הנשארים ושלישיותם וכמו הרביעי עם שלשה דמיוני הנשארים וב' שלישיותיהם וכמו החמישי עם ארבעה דמיוני הנשארים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
הנה יהיה מקובץ הנשארים מלבד הראשון על האופן הקודם מ"ו וב' שלישיות | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ומקובץ הנשארים מלבד השני ל"ז ושליש | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ומקובץ הנשארים מלבד השלישי מ' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ומקובץ הנשארים מלבד הרביעי ל"ה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ומקובץ הנשארים מלבד החמישי ל"א ותשיעית | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והנה יתרון השלישי על הראשון ו' וב' שלישיות | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ויתרון השני על הראשון ט' ושליש | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ויתרון הרביעי על הראשון י"א וב' שלישיות | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ויתרון החמישי על הראשון ט"ו וה' תשיעיות | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
הנה אם כן יתרוני השני והשלישי והרביעי על שלשה דמיוני הראשון הוא כ"ז וב' שלישיות | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
גרענו מזה מקובץ ארבעתם שהוא ל"א ותשיעית ונשאר ג' וד' תשיעיות | ||||||||||||||||||||||||||||||||||||||||||||||||
| חלקנום על מספר אלו המספרים | |||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והנה הראשון ל"א חלקים מל"ו באחד | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והשני י' וז' חלקים מל"ו | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והשלישי ז' וי"ט חלקים מל"ו | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והרביעי י"ב וי"ט חלקים מל"ו | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והחמישי י"ו וט"ו חלקים מל"ו | ||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תרצה תוכל לבחון זה | |||||||||||||||||||||||||||||||||||||||||||||||||
|
שאלה חברנו מספר ראשון עם מספר שני והיה יחס העולה אל מספר שלישי מספר מונח וכשחברנו המספר הראשון אל המספר השלישי היה יחס העולה אל המספר השני מספר מונח שני | ||||||||||||||||||||||||||||||||||||||||||||||||
|
כבר ידעת איך תמצא שלשה מספרים יצדק בהם זה ותוציאם | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ולפי שידעת אחד מן הגיליים לאחד מהם תוכל להוציא הגיליים למספרים הנשארים והנה המבוקש | ||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון שיהיה מספר ראשון כשחובר אל מספר שני היה יחסו אל השלישי ג' שלמים וב' חמישיות ושביעית וכשחובר הראשון אל השלישי יהיה יחסו אל השני ז' שלמים וב' שלישיות ורביעית | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה נוציא תחלה שלשה מספרים יונהגו זה המנהג על הדרך שהתבאר במאמר הראשון מזה הספר | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ולזה תגרע אחד משטח ג' שלמים וב' חמישיות ושביעית בז' שלמים וב' שלישיות ורביעית וישאר כ"ז שלמים ושלישית שביעית והוא המספר הראשון | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ותוסיף אחד על ג' שלמים וב' חמישיות ושביעית ויהיו בידך ד' שלמים וב' חמישיות ושביעית והוא המספר השני | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
גם תוסיף אחד על ז' שלמים וב' שלישיות ורביעית והעולה בידך הוא המספר השלישי והוא ח' שלמים וב' שלישיות ורביעית | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכבר ידעת שהמספר הגיליי לשני הוא שלשים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ולזה יהיה המספר הגיליי לראשון קע"ח שלמים וצ"ח חלקים מקנ"ט באחד | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והמספר השלישי נ"ח שלמים ורפ"א חלקים משי"ח באחד | ||||||||||||||||||||||||||||||||||||||||||||||||
| ואלו השלשה מספרים הם המבוקשים ואלו תחקור ותמצא | |||||||||||||||||||||||||||||||||||||||||||||||||
|
וכבר התבאר לך שאם ידעת מקובץ שנים מאלו הנמשכים איך תוכל לדעת כל המספרים איש על מקומו הגיליים לראשונים הידועים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
או אם ידעת יתרון אחד מהנמשכים ידוע הגיליות או מקובץ שנים מהם ידועי הגיליות על אחד מהם ידוע הגיליות או על מקובץ שנים מהם ידועי הגיליות | ||||||||||||||||||||||||||||||||||||||||||||||||
| ושאר האופנים אשר תוכל לקנות מהם ידיעת המספרים הגיליים איש על מקומו | |||||||||||||||||||||||||||||||||||||||||||||||||
| these proportional numbers are the required numbers - explanation: | ואחר שתדע המספרים הגיליים מאי זה צד שתקנה הידיעה בזה הנה נבאר לך שאלו המספרים הגיליים הם המבוקשים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וזה לפי שיחס הראשון מהקודמים אל השני מהם כיחס הראשון מהנמשכים אל השני מהם | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ויחס השני מהקודמים אל השלישי מהם כיחס השני מהנמשכים אל השלישי מהם | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
הנה כיחס השווי יהיה יחס הראשון מהקודמים אל השלישי כיחס הראשון מהנמשכים אל השלישי | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכאשר קבצנו הנה יחס הראשון והשני מהקודמים מקובצים אל השלישי כיחס הראשון והשני מהנמשכים מקובצים אל השלישי | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
אבל יחס הראשון והשני מהקודמים מקובצים אל השלישי הוא במשלנו זה ג' שלמים וב' חמישיות ושביעית | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
אם כן יחס הראשון והשני מהנמשכים מקובצים אל השלישי הוא ג' שלמים וב' חמישיות ושביעית | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכזה גם כן התבאר שיחס הראשון והשלישי מהנמשכים מקובצים אל השני הוא ז' שלמים וב' שלישיות ורביעית והקש על זה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון אחר יהיה יחס הראשון והשני מקובצים אל השלישי ג' חמישיות ושישית ויחס הראשון והשלישי מקובצים אל השני ב' שלמים ושלישית | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה לפי מה שהתבאר נוציא המספרים אשר מנהגם זה המנהג | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ויהיה המספר הראשון לפי מה שקדם ב' חמישיות ושלישית ושליש שישית | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ויהיה המספר השני אחד שלם וג' חמישיות וששית | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ויהיה מספר השלישי ג' שלמים ושלישית | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ולפי שהיה המספר הגיליי לראשון עשרים יהיה המספר הגיליי לשני מ"ד שלמים ונ"ו חלקים מע"א באחד שלם | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והמספר הגיליי לשלישי פ"ד שלמים ול"ו חלקים מע"א באחד שלם | ||||||||||||||||||||||||||||||||||||||||||||||||
| והם המספרים המבוקשים ואם תרצה תוכל לבחון זה | |||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||
| If the product of the ratio of the first and the second summed together to the third by the ratio of the first and the third summed together to the second is not greater than one whole
|
וראוי שתדע שאם לא עלה יותר מאחד שלם השטח ההווה מיחס הראשון והשני מקובצים אל השלישי ביחס הראשון והשלישי מקובצים אל השני שכבר טעה השואל | ||||||||||||||||||||||||||||||||||||||||||||||||
| Proposition: for any two given numbers, the product of the ratio of the first to the second by the ratio of the second to the first is one whole
|
ונציע לבאור זה הקדמה נבאר בה שכל שני מספרים מונחים הנה שטח יחס הראשון אל השני ביחס השני אל הראשון הוא אחד שלם | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה שאחד מהמספרים המונחים אם שיהיה חלק מהאחר או חלקים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ויהיה תחלה חלק ונאמר שכבר יתאמת מה שאמרנו | ||||||||||||||||||||||||||||||||||||||||||||||||
|
המשל שיהיו המספרים המונחים מספרי א'ב' והיה ב' ימנה א' בשעור אחדי ג' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
אם כן יחס ב' אל א' מספר ג' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ויחס א' אל ב' חלק אחד מג' חלקים באחד | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר הוכה ג' שלמים על חלק אחד מג' חלקים באחד היה העולה אחד לפי מה שהתבאר קודם | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ויהיה גם כן המספר הקטן חלקים מן הגדול | ||||||||||||||||||||||||||||||||||||||||||||||||
| The product of the ratio of one number to the other by the ratio of the other to it is one
|
הנה אומר ששטח יחס המספר האחד אל האחר ביחס המספר האחר אליו הוא אחד | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ויהיה במשלנו זה המספר הקטן ד'ה' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והמספר הגדול ב' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ויהיה ד'ה' ז' חלקים מג' במספר ב' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ויהיה ה'ח' חלק מג' במספר ב' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה ה'ח' הוכה בז' והיה ה'ד' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכה ב' בז' ויהיה ט'כ' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה יחס ח'ה' אל ב' כיחס ד'ה' אל ט'כ' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר המירונו וחלפנו הנה יחס ד'ה' אל ח'ה' כיחס ט'כ' אל ב' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וגם כן הנה יחס ד'ה' אל ב' הוא ז' דמיוני יחס ח'ה' אל ב' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ויחס ב' אל ד'ה' הוא חלק אחד מז' מיחס ט'כ' אל ד'ה' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
אבל יחס ט'כ' אל ד'ה' שהוא ג' כבר יוכה ביחס ח'ה' אל ב' שהוא כיחס ד'ה' אל ט'כ' ויהיה אחד אם כן יחס ד'ה' אל ב' כבר יוכה ביחס ב' אל ד'ה' ויהיה אחד גם כן לפי שהצלעות מספיקות | ||||||||||||||||||||||||||||||||||||||||||||||||
| the product of the ratio of the first and the second summed together to the third by the ratio of the first and the third summed together to the second is greater than one
|
וכאשר התבאר זה הנה יתבאר שהשטח ההווה מיחס הראשון והשני מקובצים אל השלישי ביחס הראשון והשלישי מקובצים אל השני הוא יותר מאחד | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וזה שיחס השלישי והראשון מקובצים אל השני הוא יותר גדול הרבה מיחס השלישי אל הראשון והשני מקובצים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ואולם שטח יחס הראשון והשני מקובצים אל השלישי ביחס השלישי אל הראשון והשני מקובצים הוא אחד שלם | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
אם כן השטח ההווה מיחס הראשון והשני מקובצים אל השלישי ביחס הראשון והשלישי מקובצים אל השני הוא יותר מאחד שלם | ||||||||||||||||||||||||||||||||||||||||||||||||
|
שאלה יחס השני אל הנשאר מהשלישי כשחוסר ממנו הראשון מספר מונח ויחס השלישי אל הנשאר מהשני כשחוסר ממנו הראשון מספר אחר מונח | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ראוי שתוציא שלשת מספרים ינהגו כמו המנהג הנזכר קודם זה באלו היחסים הנזכרים הנה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והנה המספר הראשון הוא יהיה הראשון הנה והראשון והשני מקובצים יהיו המספר השני הנה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והמשל שיהיה יחס השני אל הנשאר מהשלישי כשחוסר ממנו הראשון ג' שלמים ושליש ויחס השלישי אל הנשאר מהשני כשחוסר ממנו הראשון מספר ו' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
הנה תוציא שלשה מספרים על הדרך הקודמת באלו היחסים הנזכרים הנה ר"ל שיהיה יחס מקובץ הראשון והשני אל השלישי ג' שלמים ושליש | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והנה הראשון י"ט | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והשני ד' ושליש | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והשלישי ז' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ולזה יהיה הראשון י"ט | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ותחבר עם השני י"ט ויהיו כ"ג שלמים ושליש והוא המספר השני | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ותחבר עם השלישי י"ט יהיו כ"ו והוא המספר השלישי | ||||||||||||||||||||||||||||||||||||||||||||||||
| והקש על זה וסבת זה מבוארת ממה שקדם | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ומזה גם כן תוכל להוציא כל מה שהוצאת בדרך הקודמת ר"ל שאם נודע לך אחד מהמספרים תוכל לדעת האחרים אחר שהוצאת המספרים שינהגו זה המנהג אשר הם גיליים למספרים הנעלמים ומה שנמשך לזה מהוצאתם מצד הידיעות אשר אפשר לקנות מהם זאת הידיעה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
שאלה חברנו הראשון עם השני והיה יחס המקובץ אל הנשאר מהשלישי כשחוסר ממנו הראשון מספר מונח וכאשר חברנו הראשון עם השלישי היה יחס המקובץ אל הנשאר מהשני כשחוסר ממנו הראשון מספר אחר מונח | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה ראוי שתוציא לפי אלו היחסים שלשה מספרים על הדרך הקודמת | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וחצי המספר הראשון הוא יהיה המספר הראשון הנה והשני מחובר עם הראשון הזה רצוני חצי הראשון הקודם הוא יהיה המספר השני הנה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והמשל שיהיה יחס הראשון והשני מקובצים אל הנשאר מהשלישי כשחוסר ממנו הראשון ד' שלמים וחצי ויחס הראשון והשלישי מקובצים אל הנשאר מהשני כשחוסר ממנו הראשון הוא ה' שלמים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
הנה נוציא המספרים השלשה על הדרך הקודמת לפי אלו היחסים רצוני שיהיה יחס הראשון והשני מקובצים אל השלישי ד' וחצי ויהיה יחס הראשון והשלישי מקובצים אל השני מספר ה' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ולזה יהיה הראשון כ"א וחצי | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והשני ה' וחצי | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והשלישי ו' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והנה חצי הראשון הוא י' וג' רביעיות והוא הראשון | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
הנה חברנו י' וג' רביעיות עם השני ועלה י"ו ורביע והוא השני | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
הנה חברנו י' וג' רביעיות עם השלישי ועלה י"ו וג' רביעיות והוא השלישי הנה | ||||||||||||||||||||||||||||||||||||||||||||||||
| והקש על זה וסבת זה מבוארת ממה שקדם | |||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר שידעת המספרים שינהגו זה המנהג תוכל לקנות מהם הידיעה במספרים הגיליים על הצד הקודם | ||||||||||||||||||||||||||||||||||||||||||||||||
|
רצוני עם קדימת הידיעה באחד מהם ידוע הגיליות או מקובץ שנים מהם או שאר מיני הידיעות הנזכרות קודם אשר נעמוד מהם על ידיעת המספרים הגיליים לשלשה מספרים המונחים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
שאלה המספר הראשון עם חלק מונח מהשני והשלישי מקובצים שוה אל המספר השני עם חלק אחר מונח מהראשון והשלישי מקובצים וכן הוא שוה אל המספר השלישי עם חלק אחר מונח מהראשון והשני מקובצים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה ראוי שתוציא תחלה המספרים שינהגו זה המנהג על הצד שהתבאר במאמר הראשון מזה הספר | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וממה שקדם לך מהידיעה באחד מהמספרים הגיליים תעמד על ידיעת המספרים הגיליים בכללם איש על מקומו והמספרים ההם הם המבוקשים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
והמשל שיהיה הראשון עם רביעית הנשארים שוה אל השני עם ששית [הנשארים] והוא גם כן שוה אל השלישי עם תשיעית הנשארים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכבר ידענו שהמספרים שינהגו כמו זה המנהג הראשון מהם קי"ט והשני קנ"א והשלישי קס"ט מזה הגיליים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והמספר שהוא הגיליי לשני הוא כ' | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ונוציא שאר הגיליים על זה היחס | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ולזה יהיה הגיליי לראשון ט"ו שלמים וקט"ו חלקים מקנ"א באחד שלם והוא הראשון הנה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ויהיה הגיליי לשלישי כ"ב שלמים ונ"ח חלקים מקנ"א באחד והוא השלישי הנה | ||||||||||||||||||||||||||||||||||||||||||||||||
| והם המספרים המבוקשים | |||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תרצה תוכל לבחון זה | |||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והיה זה כן לפי שהנמשכים על יחס הקודמים הנה יהיה יחס הראשון מהקודמים אל השני מהם כיחס הראשון מהנמשכים אל השני מהם | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ולזה יהיה יחס הראשון מהקודמים אל השלישי כיחס הראשון מהנמשכים אל השלישי | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכאשר קבצנו הנה יהיה יחס הראשון מהקודמים אל השני והשלישי מהם מקובצים כמו יחס הראשון מהנמשכים אל השני והשלישי מהם מקובצים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ולזה יהיה יחס הראשון מהקודמים אל רביעית השני והשלישי מהם מקובצים כמו יחס הראשון מהנמשכים אל רביעית השני והשלישי מהם | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכאשר קבצנו הנה יחס הראשון מהקודמים עם רביעית השני והשלישי מהם אל הראשון מהקודמים כיחס הראשון מהנמשכים עם רביעית השני והשלישי אל הראשון מהנמשכים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ובזה התבאר שיחס השני מהקודמים עם ששית השלישי והראשון מהם אל השני מהקודמים הוא כמו יחס השני מהנמשכים עם ששית השלישי והראשון מהם אל השני מהנמשכים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ובזה התבאר שיחס השלישי מהקודמים עם תשיעית הנשארים מהם אל השלישי מהקודמים הוא כמו יחס השלישי מהנמשכים עם תשיעית הנשארים מהם אל השלישי מהנמשכים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכאשר המירונו הנה יחס הראשון מהקודמים עם רביעית הנשארים מהם אל הראשון מהנמשכים עם רביעית הנשארים מהם הוא כיחס הראשון מהקודמים אל הראשון מהנמשכים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ויחס השני מהקודמים עם ששית הנשארים מהם אל השני מהנמשכים עם ששית הנשארים מהם הוא כיחס השני מהקודמים אל השני מהנמשכים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ויחס השלישי מהקודמים עם תשיעית הנשארים מהם אל השלישי מהנמשכים עם תשיעית הנשארים מהם הוא כיחס השלישי מהקודמים אל השלישי מהנמשכים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ואולם יחס הראשון מהקודמים אל הראשון מהנמשכים הוא כיחס השני אל השני וכיחס השלישי אל השלישי | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
אם כן יחס הראשון מהקודמים עם רביעית הנשארים מהם אל הראשון מהנמשכים עם רביעית הנשארים מהם הוא כמו יחס השני מהקודמים עם ששית הנשארים מהם אל השני מהנמשכים עם ששית הנשארים מהם וכמו יחס השלישי מהקודמים עם תשיעית הנשארים מהם אל השלישי מהנמשכים עם תשיעית [הנשארים] מהם | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכאשר המירונו יהיו גם כן מתיחסים אבל הקודמים כלם שוים הנה הנמשכים כלם שוים והקש על זה | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ובזה תוכל להוציא מאי זו ידיעה שתהיה לך באלו המספרים הנעלמים המספרים הגיליים למספרים השלשה הידועים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
רצוני אם ידעת יתרון אחד מהנעלמים ידוע הגיליות על אחד מהם ידוע הגיליות | ||||||||||||||||||||||||||||||||||||||||||||||||
|
או אם ידעת מספר שנים מהנעלמים מקובצים | ||||||||||||||||||||||||||||||||||||||||||||||||
|
ומה שימשך לזה מאפני הידיעה יהיה אפשר לקנות ממנה המספרים האלו הנעלמים על הצד שהתבאר קודם ותבין ותמצא | ||||||||||||||||||||||||||||||||||||||||||||||||
| Colophon | |||||||||||||||||||||||||||||||||||||||||||||||||
| Edition I | |||||||||||||||||||||||||||||||||||||||||||||||||
|
כתב המחבר נשלם השער השישי מזה המאמר ובהשלמו נשלם זה הספר | ||||||||||||||||||||||||||||||||||||||||||||||||
| והתהלה לאל לבדו | |||||||||||||||||||||||||||||||||||||||||||||||||
|
והיתה השלמתו בראש ניסן של שנת שמונים ואחת לפרט האלף הששי | ||||||||||||||||||||||||||||||||||||||||||||||||
|
בהגיעי לשנת שלושים ושלש משנותי | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וברוך העוזר | ||||||||||||||||||||||||||||||||||||||||||||||||
| Edition II | |||||||||||||||||||||||||||||||||||||||||||||||||
|
נשלם השער השישי מזה המאמר ובהשלמו נשלם זה הספר | ||||||||||||||||||||||||||||||||||||||||||||||||
| והתהלה לאל לבדו | |||||||||||||||||||||||||||||||||||||||||||||||||
|
והיתה השלמתו בחודש אלול של שנת שמונים ושתים לפרט האלף השישי | ||||||||||||||||||||||||||||||||||||||||||||||||
|
וברוך העוזר |
Appendix: Bibliography
Levi Ben Gershon (called also: Leo Hebraus, Leo de Balneolis, Maestro Leon; known today as Gersonides)
b. 1288, Bagnols, Provence – d. 1344, Provence
Sefer Ma‛ase Hoshev
1321-2
Manuscripts:
- 1) Jerusalem, The National Library of Israel Ms. Heb. 8°2005 (IMHM: B 400 (8°2005)), (1410)
- [J2005]
- 2) London, British Library Or. 10547 (IMHM: f 7909), ff. 1-118 (14th-15th century)
- [L10547]
- 3) Moscow, Russian State Library, Ms. Guenzburg 30/3 (IMHM: f 6711), ff. 40r-122v (1503)
- [Mo30]
- 4) Moscow, Russian State Library, Ms. Guenzburg 1063 (IMHM: f 48133), ff. 1-84 (15th century)
- 5) München, Bayerische Staatsbibliothek, Cod. hebr. 36/1 (IMHM: f 1166), ff. 1-9 (1485)
- [Mu36]
- 6) München, Bayerische Staatsbibliothek, Cod. hebr. 68/6 (IMHM: f 1131), ff. 376r-432r (Roma, 1552)
- [Mu68]
- 7) New York, Jewish Theological Seminary Ms. 2624/2 (IMHM: f 28877), ff. 11r-59v (16th century)
- [N2624]
- 8) Paris, Bibliothèque Nationale de France heb. 1029/6 (IMHM: f 15721), ff. 236r-295v (15th-16th century)
- 9) Parma, Biblioteca Palatina Parm. 2271 (IMHM: f 13179), (14th century)
- [Parm2271]
- 10) Parma, Biblioteca Palatina Parm. 2462 (IMHM: f 13466), (14th-15th century)
- [Parm2462]
- 11) Vatican, Biblioteca Apostolica ebr. 399/1 (IMHM: f 477), ff. 1r-23v (15th century)
- [V399]
Edition:
- Levi ben Gershon. Sefer Maassei Chosheb: Die Praxis des Rechners, Ein hebräisch-arithmetisches Werk des Levi ben Gerschom aus dem Jahre 1321. Ed. Gerson Lange. Frankfurt am Main: Louis Golde, 1909.
Bibliography:
- Carlebach, Joseph. 1910. Lewi ben Gerson als Mathematiker: ein Beitrag zur Geschichte der Mathematik bei den Juden. Berlin: L. Lamm.
- Chemla, Karine and Serge Pahaut. 1992. Remarques sur les ouvrages mathématiques de Gersonide. In: Freudenthal 1992, pp. 149–191.
- Freudenthal, Gad ed. 1992. Studies on Gersonides: A Fourteenth-Century Jewish Philosopher-Scientist. Leiden: Brill.
- Kellner, Menachem. 1992. An Annotated List of Writings by and about R. Levi ben Gershom, in Freudenthal 1992, pp. 367-414.
- Langermann, Tzvi and Shai Simonson. 2000. The Hebrew Mathematical Tradition. In: Helaine Seline ed. Mathematics Across Cultures. Dordrecht: Kluwer, pp. 167–188.
- Rabinovitch, Nahum. 1970. Rabbi Levi ben Gershon and the Origins of Mathematical Induction, Archive for History of Exact Sciences 6 , pp. 237-248.
- Rashed, Roshdi. 1994. The Development of Arabic Mathematics: Between Arithmetic and Algebra. Translated by A.F.W. Armstrong. Dordrecht, Boston, London: Kluwer Academic Publishers, pp. 65-84.
- Sarfatti, Gad ben ‛Ami. 1968. Mathematical Terminology in Hebrew Scientific Literature of the Middle Ages. Jerusalem: Magnes Press, pp. 220-227.
- Simonson, Shai. 2000a. The Missing Problems of Gersonides. A Critical Edition, Historia Mathematica 27 (3), pp. 243–302 and 27 (4), pp. 384–431.
- ———.2000b. Mathematical Gems of Levi ben Gershon, Mathematics Teacher 93, pp. 659-663.
- ———. 2000c. The Mathematics of Levi ben Gershon, the Ralbag, BDD (Bekhol Derakhekha Daehu= בכל דרכיך דעהו) 10 (2000), pp.5-21.
- Steinschneider, Moritz. 1893-1901. Mathematik bei den Juden. Berlin-Leipzig-Frankfurt: Kaufmann, pp. 129-133 (e103-e107); repr. Hildesheim: G. Olms, 1964 and 2001.
- Weil-Guény, Anne-Marie. 1992. Gersonide en son temps: un tableau chronologique. In: Freudenthal 1992, pp. 355–365.
- Yadegari, Mohammad. 1978. The Use of Mathematical Induction by Abū Kāmil Shujā‛ Ibn Aslam (850-930), Isis 69, 2 (Jun. 1978), pp. 259-262.
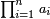
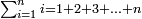
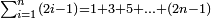
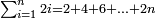
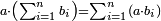
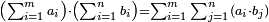
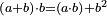
![\scriptstyle\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2](/mediawiki/images/math/a/0/b/a0b403dd8b7c15a5cb1dc47a5f8ca5bb.png)
![\scriptstyle\left(a+b\right)^2=a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]](/mediawiki/images/math/7/2/7/727b0c35fd93a7a347bed8413905049f.png)
![\scriptstyle\left(a+b\right)^2=\left[a\sdot\left(a+b\right)\right]+\left(a\sdot b\right)+b^2](/mediawiki/images/math/6/d/4/6d450eeb47934cad7f1a81a10ccacaf6.png)
![\scriptstyle\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2=\left(a\sdot b\right)+\left[b-\left[\frac{1}{2}\sdot\left(a+b\right)\right]\right]^2](/mediawiki/images/math/0/8/b/08b05b486f02ad6eac6986bfb4a33708.png)
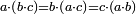
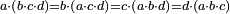
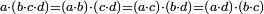
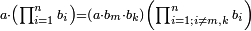
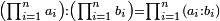
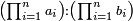 = the product of
= the product of 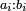 when i=1,2,…,n and j=1,2,…,n each appears exactly once, but are not necessarily equal on the same product.
when i=1,2,…,n and j=1,2,…,n each appears exactly once, but are not necessarily equal on the same product. is relatively prime to
is relatively prime to 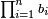 , then
, then 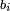 for each i=1,2,…,n
for each i=1,2,…,n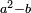 is relatively prime to all integers less than
is relatively prime to all integers less than 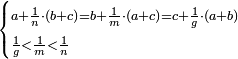
![\scriptstyle{\color{red}{\begin{cases}\scriptstyle a_1=g+\left(m-n\right)+\left[\left(n-2\right)\sdot m\sdot g\right]\\\scriptstyle b_1=a_1+\left[2\sdot\left(m-n\right)\sdot\left(g-1\right)\right]\\\scriptstyle c_1=b_1+\left[2\sdot\left(n-1\right)\sdot\left(g-m\right)\right]\end{cases}}}](/mediawiki/images/math/7/1/f/71f40f40d166d6d1baa46660897a9fe8.png)
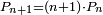
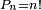
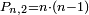
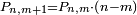
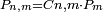
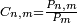
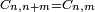
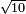
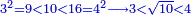
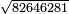
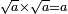
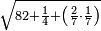
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\sqrt{82+\frac{1}{4}+\left(\frac{2}{7}\sdot\frac{1}{7}\right)}&\scriptstyle=\frac{\sqrt{\left[82+\frac{1}{4}+\left(\frac{2}{7}\sdot\frac{1}{7}\right)\right]\sdot196}}{\sqrt{196}}\\&\scriptstyle=\frac{\sqrt{16129}}{\sqrt{196}}\\&\scriptstyle=\frac{127}{14}=9+\left(\frac{1}{2}\sdot\frac{1}{7}\right)\\\end{align}}}](/mediawiki/images/math/9/4/1/941fe6bf0499c288b907d27928bd0344.png)
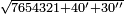
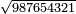
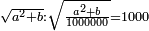
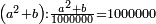
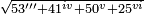
![\scriptstyle\sqrt[3]{5987654321}](/mediawiki/images/math/1/5/4/154d7bdef195b69661f20d89a1a34085.png)
![\scriptstyle\sqrt[3]{44+\left(\frac{5}{7}\sdot\frac{1}{4}\right)+\left(\frac{13}{7}\sdot\frac{1}{7}\sdot\frac{1}{4}\sdot\frac{1}{4}\right)+\left(\frac{27}{7}\sdot\frac{1}{7}\sdot\frac{1}{7}\sdot\frac{1}{4}\sdot\frac{1}{4}\sdot\frac{1}{4}\right)}](/mediawiki/images/math/c/4/c/c4c390f780300248459e24576307674a.png)
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\sqrt[3]{44+\left(\frac{5}{7}\sdot\frac{1}{4}\right)+\left(\frac{13}{7}\sdot\frac{1}{7}\sdot\frac{1}{4}\sdot\frac{1}{4}\right)+\left(\frac{27}{7}\sdot\frac{1}{7}\sdot\frac{1}{7}\sdot\frac{1}{4}\sdot\frac{1}{4}\sdot\frac{1}{4}\right)}\\&\scriptstyle=\frac{\sqrt[3]{\left[44+\left(\frac{5}{7}\sdot\frac{1}{4}\right)+\left(\frac{13}{7}\sdot\frac{1}{7}\sdot\frac{1}{4}\sdot\frac{1}{4}\right)+\left(\frac{27}{7}\sdot\frac{1}{7}\sdot\frac{1}{7}\sdot\frac{1}{4}\sdot\frac{1}{4}\sdot\frac{1}{4}\right)\right]\sdot\left(7^3\sdot4^3\right)}}{\sqrt[3]{7^3\sdot4^3}}\\&\scriptstyle=\frac{99}{28}=3+\frac{15}{28}\\\end{align}}}](/mediawiki/images/math/b/9/6/b96e4c0c4fbf3d23dad729e5ba4f8ade.png)
![\scriptstyle\sqrt[3]{59'+23''+7'''+40^{iv}}](/mediawiki/images/math/c/b/c/cbc677645d952cf081519de2d066fbc0.png)
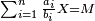
![\scriptstyle X=\frac{\left(common\ denominator\right)\sdot M}{\sum_{i=1}^n \left[\left(common\ denonminator\right)\sdot\frac{a_i}{b_i}\right]}](/mediawiki/images/math/6/2/4/624ee87eb14fc34abd790135e5714849.png)
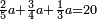
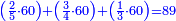
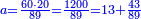



![\scriptstyle{\color{blue}{\left[\left(\frac{2}{5}\sdot60\right)+\left(\frac{3}{4}\sdot60\right)+\left(\frac{1}{3}\sdot60\right)\right]:60=\left(\frac{2}{5}a+\frac{3}{4}a+\frac{1}{3}a\right):a}}](/mediawiki/images/math/0/8/e/08eea7aa880ebf29610ef50897993f71.png)
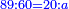
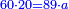
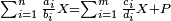
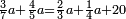
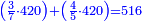
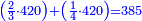

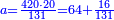
![\scriptstyle{\color{blue}{\left[\left(\frac{3}{7}\sdot420\right)+\left(\frac{4}{5}\sdot420\right)\right]:420=\left(\frac{3}{7}a+\frac{4}{5}a\right):a}}](/mediawiki/images/math/6/a/9/6a9267fa3e8781049316dcfd65d857f2.png)
![\scriptstyle{\color{blue}{\left[\left(\frac{3}{7}\sdot420\right)+\left(\frac{4}{5}\sdot420\right)\right]:\left(\frac{3}{7}a+\frac{4}{5}a\right)=420:a}}](/mediawiki/images/math/a/9/1/a915ae6062576d141b22b0c66f3ffe28.png)
![\scriptstyle{\color{blue}{\left[\left(\frac{2}{3}\sdot420\right)+\left(\frac{1}{4}\sdot420\right)\right]:\left(\frac{2}{3}a+\frac{1}{4}a\right)=420:a}}](/mediawiki/images/math/5/0/0/500b4171ec6647ccf418ed41181d50ef.png)
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\left[\left(\frac{3}{7}\sdot420\right)+\left(\frac{4}{5}\sdot420\right)\right]:\left(\frac{3}{7}a+\frac{4}{5}a\right)\\&\scriptstyle=\left[\left(\frac{2}{3}\sdot420\right)+\left(\frac{1}{4}\sdot420\right)\right]:\left(\frac{2}{3}a+\frac{1}{4}a\right)\\\end{align}}}](/mediawiki/images/math/6/4/d/64dfd64d58543027afc5a7dc15782709.png)
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\left[\left(\frac{3}{7}\sdot420\right)+\left(\frac{4}{5}\sdot420\right)\right]:\left[\left(\frac{2}{3}\sdot420\right)+\left(\frac{1}{4}\sdot420\right)\right]\\&\scriptstyle=\left(\frac{3}{7}a+\frac{4}{5}a\right):\left(\frac{2}{3}a+\frac{1}{4}a\right)\\\end{align}}}](/mediawiki/images/math/2/e/a/2eab5bd868f44e277edec80d2938a54b.png)
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\left[\left(\frac{3}{7}\sdot420\right)+\left(\frac{4}{5}\sdot420\right)\right]:\left[\left[\left(\frac{3}{7}\sdot420\right)+\left(\frac{4}{5}\sdot420\right)\right]-\left[\left(\frac{2}{3}\sdot420\right)+\left(\frac{1}{4}\sdot420\right)\right]\right]\\&\scriptstyle=\left(\frac{3}{7}a+\frac{4}{5}a\right):\left[\left(\frac{3}{7}a+\frac{4}{5}a\right)-\left(\frac{2}{3}a+\frac{1}{4}a\right)\right]\\\end{align}}}](/mediawiki/images/math/1/a/4/1a406abf4ba8bd657b2d862048ea415c.png)
![\scriptstyle{\color{blue}{\left[\left(\frac{3}{7}\sdot420\right)+\left(\frac{4}{5}\sdot420\right)\right]:131=\left(\frac{3}{7}a+\frac{4}{5}a\right):20}}](/mediawiki/images/math/c/a/b/cab06e4b9806531899d40008ed0429a7.png)
![\scriptstyle{\color{blue}{\left[\left(\frac{3}{7}\sdot420\right)+\left(\frac{4}{5}\sdot420\right)\right]:\left(\frac{3}{7}a+\frac{4}{5}a\right)=131:20}}](/mediawiki/images/math/7/8/5/785f7d4e359dca94b959cfe9ad620c75.png)
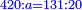
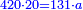
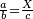
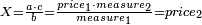
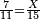
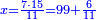
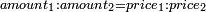
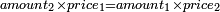

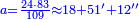
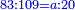
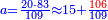
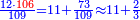
![\scriptstyle\sum_{i=1}^n \frac{a_i}{b_i}=\frac{\sum_{i=1}^n \left[\left(common\ denominator\right)\sdot\frac{a_i}{b_i}\right]}{common\ denominator}](/mediawiki/images/math/a/8/9/a89f55164eff1c64fddf1cf6df9d1875.png)
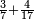
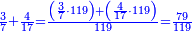
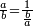
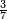
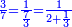
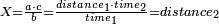
![\scriptstyle\left(13\sdot24\right):\left(7+36'+57''\right)=\left[\left(3\sdot24\right)+17+52'+16''\right]:a](/mediawiki/images/math/7/a/a/7aafb9e9d321ca8d15edcdaa17f0c657.png)
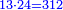
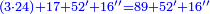
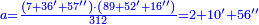
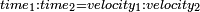
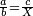
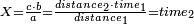
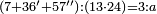
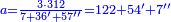
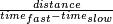
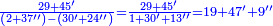
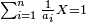
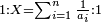
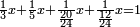
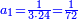
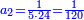
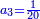
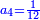
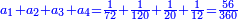
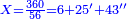
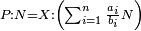
![\scriptstyle X=\frac{\left[\sum_{i=1}^n \left[\left(common\ denonminator\right)\sdot\frac{a_i}{b_i}\right]\right]\sdot\frac{P}{N}\sdot N}{common\ denominator}](/mediawiki/images/math/1/8/0/180b23da1b4bf09eb07f5dd7c63a3063.png)
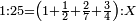
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left(1+\frac{1}{2}+\frac{2}{7}+\frac{3}{4}\right)\sdot25&\scriptstyle=\frac{\left[\left(1\sdot28\right)+\left(\frac{1}{2}\sdot28\right)+\left(\frac{2}{7}\sdot28\right)+\left(\frac{3}{4}\sdot28\right)\right]\sdot25\sdot1}{28}\\&\scriptstyle=\frac{71\sdot25\sdot1}{28}\\&\scriptstyle=\frac{1775\sdot1}{28}\\&\scriptstyle=63+\frac{11}{28}\\\end{align}}}](/mediawiki/images/math/2/6/2/262d6f5bd8af5ff31ba4ab37c0d6a3e4.png)
![\scriptstyle{\color{blue}{\left[\sum_{i=1}^n \left[\left(com\ den\right)\sdot\frac{a_i}{b_i}\right]\right]:\left[\sum_{i=1}^n \left(1\sdot\frac{a_i}{b_i}\right)\right]=\left(com\ den\right):1}}](/mediawiki/images/math/a/b/5/ab5c612f8f7f91d8cd04c93ea5a08225.png)
![\scriptstyle{\color{blue}{price_{\left[\sum_{i=1}^n \left[\left(com\ den\right)\sdot\frac{a_i}{b_i}\right]\right]}:price_{\left[\sum_{i=1}^n \left(1\sdot\frac{a_i}{b_i}\right)\right]}=\left(com\ den\right):1}}](/mediawiki/images/math/f/0/0/f00dda7f89566d9ac47b625af17a3eda.png)
![\scriptstyle{\color{blue}{price_{\left[\sum_{i=1}^n \left[\left(com\ den\right)\sdot\frac{a_i}{b_i}\right]\right]}\sdot1=price_{\left[\sum_{i=1}^n \left(1\sdot\frac{a_i}{b_i}\right)\right]}\sdot\left(com\ den\right)}}](/mediawiki/images/math/5/1/d/51d8b5f8757719a359d93bc158181a87.png)
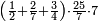
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left(1+\frac{1}{2}+\frac{2}{7}+\frac{3}{4}\right)\sdot\frac{25}{7}\sdot7&\scriptstyle=\frac{\left[\left(1\sdot28\right)+\left(\frac{1}{2}\sdot28\right)+\left(\frac{2}{7}\sdot28\right)+\left(\frac{3}{4}\sdot28\right)\right]\sdot\frac{25}{7}\sdot7}{28}\\&\scriptstyle=\frac{71\sdot\frac{25}{7}\sdot7}{28}\\&\scriptstyle=\frac{\left(253+\frac{4}{7}\right)\sdot7}{28}\\&\scriptstyle=63+\frac{11}{28}\\\end{align}}}](/mediawiki/images/math/e/0/1/e013c3e88a4b27189d077c82cfdc6c50.png)
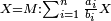
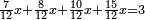
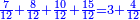
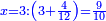 of a liṭra
of a liṭra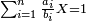
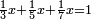
 golden coin
golden coin golden coin
golden coin golden coin
golden coin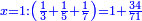
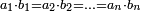
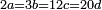




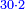 = the price of 30 liṭra at 2 dinar for a liṭra
= the price of 30 liṭra at 2 dinar for a liṭra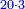 = the price of 20 liṭra at 3 dinar for a liṭra
= the price of 20 liṭra at 3 dinar for a liṭra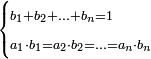
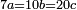
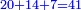
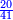 from the drug of 7 pašuṭ for a liṭra
from the drug of 7 pašuṭ for a liṭra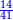 from the drug of 10 pašuṭ for a liṭra
from the drug of 10 pašuṭ for a liṭra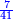 from the drug of 20 pašuṭ for a liṭra
from the drug of 20 pašuṭ for a liṭra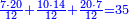
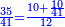
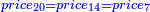
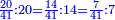
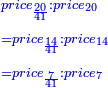
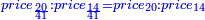
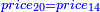
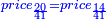
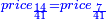
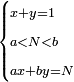
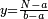
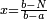
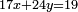
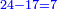
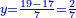
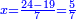
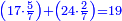
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left[17\sdot\left(24-19\right)\right]+\left[24\sdot\left(19-17\right)\right]&\scriptstyle=\left(17\sdot5\right)+\left(24\sdot2\right)\\&\scriptstyle=19\sdot7\\&\scriptstyle=19\sdot\left(24-17\right)\\\end{align}}}](/mediawiki/images/math/3/4/1/341324467d9752ef8c3407b4f7ac72d5.png)
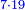
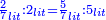
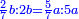
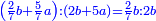
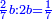
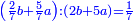
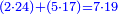
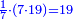
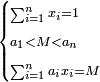
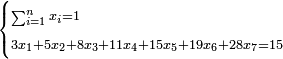
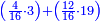
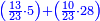
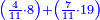
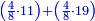
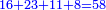
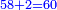
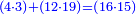
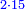
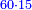
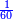 liṭra : liṭra = price of
liṭra : liṭra = price of 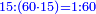
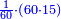
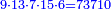
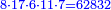


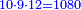
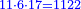
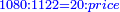
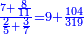
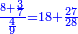
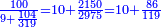
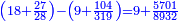
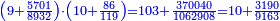
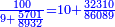

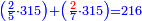
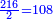
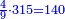
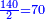

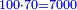
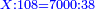


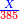
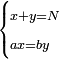
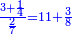
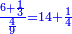
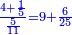
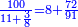
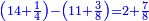
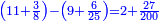
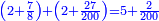
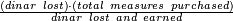
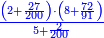
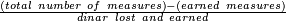
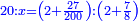
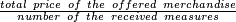
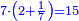
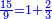
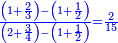
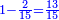
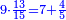

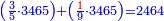
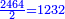
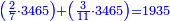
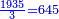
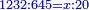
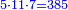
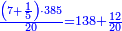
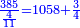
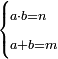
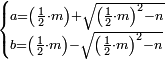
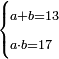
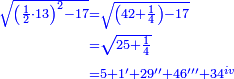
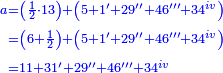
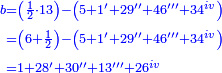

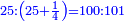
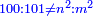
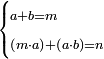
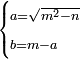
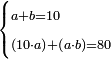
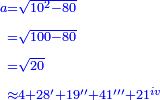
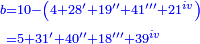

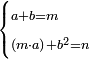
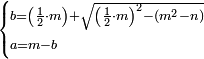
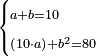
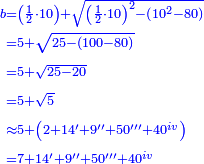
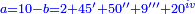
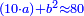
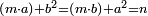
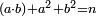
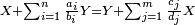
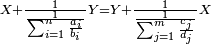
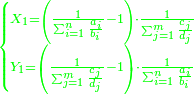
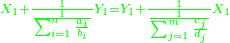
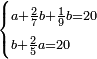
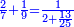
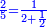
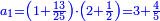
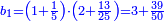
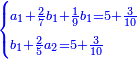
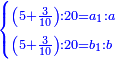
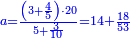
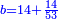
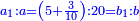
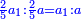
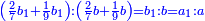
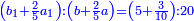
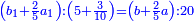
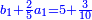
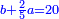
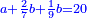
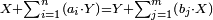
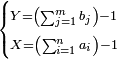
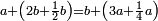
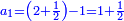
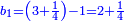
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle a_1+\left(2b_1+\frac{1}{2}b_1\right)&\scriptstyle=\left(a_1+b_1\right)+\left[\left(1+\frac{1}{2}\right)\sdot\left(2+\frac{1}{4}\right)\right]\\&\scriptstyle=\left(a_1+b_1\right)+\left(a_1\sdot b_1\right)\end{align}}}](/mediawiki/images/math/c/e/0/ce02beb0bbc4f5e43defa72dd19a6883.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle b_1+\left(3a_1+\frac{1}{4}a_1\right)&\scriptstyle=\left(b_1+a_1\right)+\left[\left(2+\frac{1}{4}\right)\sdot\left(1+\frac{1}{2}\right)\right]\\&\scriptstyle=\left(b_1+a_1\right)+\left(b_1\sdot a_1\right)\end{align}}}](/mediawiki/images/math/4/7/b/47b612d9c4d4aa33392a849bf024391b.png)
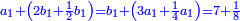
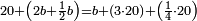
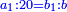

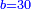
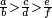
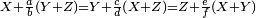
![\scriptstyle\begin{cases}\scriptstyle X=\frac{1}{\frac{e}{f}}+\left(\frac{1}{\frac{c}{d}}-\frac{1}{\frac{a}{b}}\right)+\left[\left(\frac{1}{\frac{a}{b}}-2\right)\sdot\left(\frac{1}{\frac{c}{d}}\sdot\frac{1}{\frac{e}{f}}\right)\right]\\\scriptstyle Y=X+2\sdot\left[\left(\frac{1}{\frac{c}{d}}-\frac{1}{\frac{a}{b}}\right)\sdot\left(\frac{1}{\frac{e}{f}}-1\right)\right]\\\scriptstyle Z=Y+2\sdot\left[\left(\frac{1}{\frac{a}{b}}-1\right)\sdot\left(\frac{1}{\frac{e}{f}}-\frac{1}{\frac{c}{d}}\right)\right]\end{cases}](/mediawiki/images/math/8/1/c/81cbe62888d95784d0bbfcb4105fc39f.png)
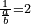
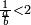
![\scriptstyle X=\frac{1}{\frac{e}{f}}+\left(\frac{1}{\frac{c}{d}}-\frac{1}{\frac{a}{b}}\right)-\left[\left(2-\frac{1}{\frac{a}{b}}\right)\sdot\left(\frac{1}{\frac{c}{d}}\sdot\frac{1}{\frac{e}{f}}\right)\right]](/mediawiki/images/math/b/f/d/bfd1b3276b2ebbb865dec8ac9cef35cc.png)
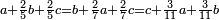
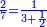
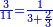
![\scriptstyle{\color{blue}{a=\left(3+\frac{2}{3}\right)+\left[\left(3+\frac{1}{2}\right)-\left(2+\frac{1}{2}\right)\right]+\left[\left[\left(2+\frac{1}{2}\right)-2\right]\sdot\left[\left(3+\frac{1}{2}\right)\sdot\left(3+\frac{2}{3}\right)\right]\right]=11+\frac{1}{12}}}](/mediawiki/images/math/c/f/f/cff44fec8c723d77da824bd8a360b890.png)
![\scriptstyle{\color{blue}{{\color{red}{b}}=\left(11+\frac{1}{12}\right)+2\sdot\left[\left[\left(3+\frac{1}{2}\right)-\left(2+\frac{1}{2}\right)\right]\sdot\left[\left(3+\frac{2}{3}\right)-1\right]\right]=16+\frac{{\color{red}{5}}}{12}}}](/mediawiki/images/math/5/5/9/559258e1a86b509f74a291629ccefd1f.png)
![\scriptstyle{\color{blue}{{\color{red}{c=\left(16+\frac{5}{12}\right)+2\sdot\left[\left[\left(2+\frac{1}{2}\right)-1\right]\sdot\left[\left(3+\frac{2}{3}\right)-\left(3+\frac{1}{2}\right)\right]\right]}}=16+\frac{11}{12}}}](/mediawiki/images/math/1/9/8/19892f980df8656c0a9c75053f76991e.png)
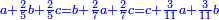
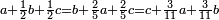
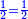
![\scriptstyle{\color{blue}{a=\left(3+\frac{2}{3}\right)+\left[\left(2+\frac{1}{2}\right)-2\right]=4+\frac{1}{6}}}](/mediawiki/images/math/f/b/1/fb1d5cdbe16dabcf73c9bdc309172786.png)
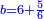

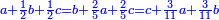
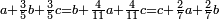
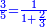
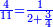
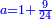
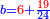

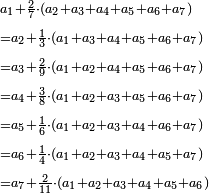
![\scriptstyle{\color{red}{7\sdot\left[\left(3-1\right)\sdot\left(9-2\right)\sdot\left(8-3\right)\sdot\left(6-1\right)\sdot\left(4-1\right)\sdot\left(11-2\right)\right]=}}](/mediawiki/images/math/3/c/a/3caf100ceba61fa1c2e9582117248d8e.png)







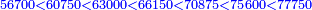
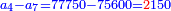
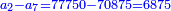
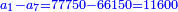
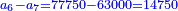
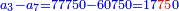
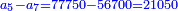

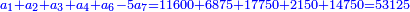
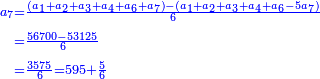
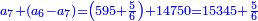
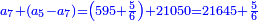
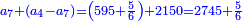
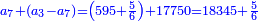
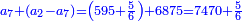
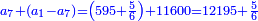
![\scriptstyle\begin{align}&\scriptstyle a_1+3\sdot\left(a_2+a_3+a_4+a_5\right)\\&\scriptstyle=a_2+\left[\left(3+\frac{1}{2}\right)\sdot\left(a_1+a_3+a_4+a_5\right)\right]\\&\scriptstyle=a_3+\left[\left(3+\frac{1}{3}\right)\sdot\left(a_1+a_2+a_4+a_5\right)\right]\\&\scriptstyle=a_4+\left[\left(3+\frac{2}{3}\right)\sdot\left(a_1+a_2+a_3+a_5\right)\right]\\&\scriptstyle=a_5+4\sdot\left(a_1+a_2+a_3+a_4\right)\\\end{align}](/mediawiki/images/math/4/7/f/47f8c287c74aff49ce2d0d59b4d9e685.png)
![\scriptstyle{\color{blue}{a_2+a_3+a_4+a_5={\color{red}{\left[\left(3+\frac{1}{2}\right)-1\right]\sdot\left[\left(3+\frac{1}{3}\right)-1\right]\sdot\left[\left(3+\frac{2}{3}\right)-1\right]\sdot\left(4-1\right)}}=46+\frac{2}{3}}}](/mediawiki/images/math/2/a/b/2ab2751be53db57fe2624d1405bf85b1.png)
![\scriptstyle{\color{blue}{a_1+a_3+a_4+a_5={\color{red}{\left(3-1\right)\sdot\left[\left(3+\frac{1}{3}\right)-1\right]\sdot\left[\left(3+\frac{2}{3}\right)-1\right]\sdot\left(4-1\right)}}=37+\frac{1}{3}}}](/mediawiki/images/math/4/a/a/4aa80d060f334cfd9b557e0e5a7a94ea.png)
![\scriptstyle{\color{blue}{a_1+a_2+a_4+a_5={\color{red}{\left(3-1\right)\sdot\left[\left(3+\frac{1}{2}\right)-1\right]\sdot\left[\left(3+\frac{2}{3}\right)-1\right]\sdot\left(4-1\right)}}=40}}](/mediawiki/images/math/a/9/5/a9535ba1c8192b69faab67353ae7122b.png)
![\scriptstyle{\color{blue}{a_1+a_2+a_3+a_5={\color{red}{\left(3-1\right)\sdot\left[\left(3+\frac{1}{2}\right)-1\right]\sdot\left[\left(3+\frac{1}{3}\right)-1\right]\sdot\left(4-1\right)}}=35}}](/mediawiki/images/math/5/8/5/585881b7ec85632ca99f7c69794aab11.png)
![\scriptstyle{\color{blue}{a_1+a_2+a_3+a_4={\color{red}{\left(3-1\right)\sdot\left[\left(3+\frac{1}{2}\right)-1\right]\sdot\left[\left(3+\frac{1}{3}\right)-1\right]\sdot\left[\left(3+\frac{2}{3}\right)-1\right]}}=31+\frac{1}{9}}}](/mediawiki/images/math/7/c/3/7c3923ac08aa422ff3649975509e6144.png)
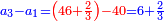
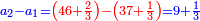
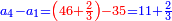
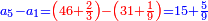
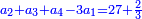
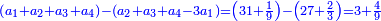
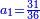
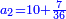
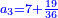
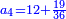
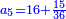
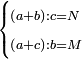
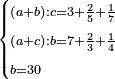
![\scriptstyle{\color{blue}{a_1=\left[\left(3+\frac{2}{5}+\frac{1}{7}\right)\sdot\left(7+\frac{2}{3}+\frac{1}{4}\right)\right]-1=27+\left(\frac{1}{3}\sdot\frac{1}{7}\right)}}](/mediawiki/images/math/2/4/a/24ac89a8bc196c329757a43259b62509.png)
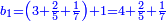
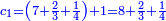
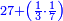
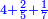
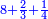
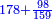
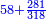


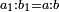
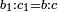
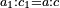
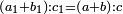
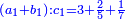
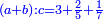
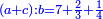
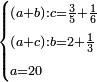
![\scriptstyle{\color{blue}{a_1=\left[\left(\frac{3}{5}+\frac{1}{6}\right)\sdot\left(2+\frac{1}{3}\right)\right]-1=\frac{2}{5}+\frac{1}{3}+\left(\frac{1}{3}\sdot\frac{1}{6}\right)}}](/mediawiki/images/math/c/c/e/cce0fb3dea3b1b8591c7b6a92a28dbec.png)
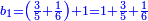
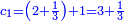
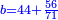
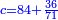
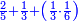
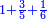
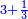
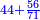
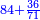
![\scriptstyle\left[\left(a+b\right):c\right]\times\left[\left(a+c\right):b\right]\ge1](/mediawiki/images/math/3/4/c/34c6c6fddec1cc00b952dd1493d52a60.png)
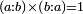
![\scriptstyle\left[\left(a+b\right):c\right]\times\left[\left(a+c\right):b\right]>1](/mediawiki/images/math/c/0/5/c05f889f9619525db245d62db2181b99.png)
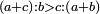
![\scriptstyle\left[\left(a+b\right):c\right]\times\left[c:\left(a+b\right)\right]=1](/mediawiki/images/math/0/4/7/047229efdad28e394dc896f6f01a860f.png)
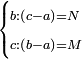
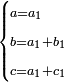
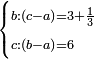
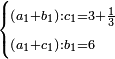
![\scriptstyle{\color{blue}{a_1=\left[\left(3+\frac{1}{3}\right)\sdot6\right]-1=19}}](/mediawiki/images/math/0/3/1/0315920f5be43158ca963f700a9a42e3.png)
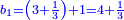
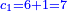
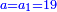
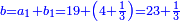
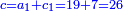
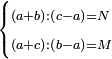
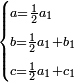
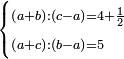
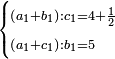
![\scriptstyle{\color{blue}{a_1=\left[\left(4+\frac{1}{2}\right)\sdot5\right]-1=21+\frac{1}{2}}}](/mediawiki/images/math/8/8/a/88a32084717210a422bc31efaed5b615.png)
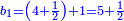
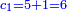
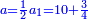
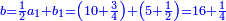
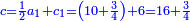
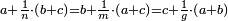
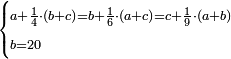
![\scriptstyle{\color{blue}{\begin{cases}\scriptstyle a_1={\color{red}{9+\left(6-4\right)+\left[\left(4-2\right)\sdot6\sdot9\right]}}=119\\\scriptstyle b_1={\color{red}{119+\left[2\sdot\left(6-4\right)\sdot\left(9-1\right)\right]}}=151\\\scriptstyle c_1={\color{red}{151+\left[2\sdot\left(4-1\right)\sdot\left(9-6\right)\right]}}=169\end{cases}}}](/mediawiki/images/math/8/e/5/8e5633fbe580c0321ababd2433e4b7df.png)
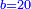
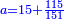
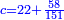
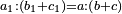
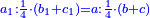
![\scriptstyle{\color{blue}{\left[a_1+\frac{1}{4}\sdot\left(b_1+c_1\right)\right]:a_1=\left[a+\frac{1}{4}\sdot\left(b+c\right)\right]:a}}](/mediawiki/images/math/b/3/e/b3ea4d14d39967c935284b3f3923b58a.png)
![\scriptstyle{\color{blue}{\left[b_1+\frac{1}{6}\sdot\left(a_1+c_1\right)\right]:b_1=\left[b+\frac{1}{6}\sdot\left(a+c\right)\right]:b}}](/mediawiki/images/math/8/a/4/8a46c8d9c47665462f52861a9406a59c.png)
![\scriptstyle{\color{blue}{\left[c_1+\frac{1}{9}\sdot\left(a_1+b_1\right)\right]:c_1=\left[c+\frac{1}{9}\sdot\left(a+b\right)\right]:c}}](/mediawiki/images/math/2/5/d/25d40d44f1a6e702b7a492eba92bdcce.png)
![\scriptstyle{\color{blue}{\left[a_1+\frac{1}{4}\sdot\left(b_1+c_1\right)\right]:\left[a+\frac{1}{4}\sdot\left(b+c\right)\right]=a_1:a}}](/mediawiki/images/math/1/d/0/1d02cdc9b5b4ccc9cc9d4538b84c9647.png)
![\scriptstyle{\color{blue}{\left[b_1+\frac{1}{6}\sdot\left(a_1+c_1\right)\right]:\left[b+\frac{1}{6}\sdot\left(a+c\right)\right]=b_1:b}}](/mediawiki/images/math/e/6/3/e6332e6ecf56d8ab7d5b640b6415cba1.png)
![\scriptstyle{\color{blue}{\left[c_1+\frac{1}{9}\sdot\left(a_1+b_1\right)\right]:\left[c+\frac{1}{9}\sdot\left(a+b\right)\right]=c_1:c}}](/mediawiki/images/math/b/5/5/b55fa575b1eb00daf9f55eb7b1fa5370.png)
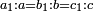
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\left[a_1+\frac{1}{4}\sdot\left(b_1+c_1\right)\right]:\left[a+\frac{1}{4}\sdot\left(b+c\right)\right]\\&\scriptstyle=\left[b_1+\frac{1}{6}\sdot\left(a_1+c_1\right)\right]:\left[b+\frac{1}{6}\sdot\left(a+c\right)\right]\\&\scriptstyle=\left[c_1+\frac{1}{9}\sdot\left(a_1+b_1\right)\right]:\left[c+\frac{1}{9}\sdot\left(a+b\right)\right]\\\end{align}}}](/mediawiki/images/math/e/e/a/eeabad9ee7424ab72577b83ed81a12e0.png)
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\left[a_1+\frac{1}{4}\sdot\left(b_1+c_1\right)\right]=\left[b_1+\frac{1}{6}\sdot\left(a_1+c_1\right)\right]=\left[c_1+\frac{1}{9}\sdot\left(a_1+b_1\right)\right]\\&\scriptstyle\longrightarrow\left[a+\frac{1}{4}\sdot\left(b+c\right)\right]=\left[b+\frac{1}{6}\sdot\left(a+c\right)\right]=\left[c+\frac{1}{9}\sdot\left(a+b\right)\right]\\\end{align}}}](/mediawiki/images/math/4/4/3/4439ecec09df4f31575c22f6e767af17.png)