Search Page

Category	Comment	Link	Annotated text
Elements/Elements II-1	a·∑bᵢ=∑(a·bᵢ)	ספר_המלכים#Sjh3	For every two numbers, such that one of them is divided into as many parts as there are, [the product of] the number that is not divided by the divided number is equal to the sum of its products by each part of the divided number. :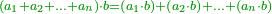$\scriptstyle{\color{OliveGreen}{\left(a_1+a_2+\ldots+a_n\right)\sdot b=\left(a_1\sdot b\right)+\left(a_2\sdot b\right)+\ldots+\left(a_n\sdot b\right)}}$ כל שני מספרים יחלק אחד מהם בחלקים כמו שיהיו הנה המספר שלא חולק במספר שחולק כמו הכאתו בכל חלקי המספר הנחלק כאשר יקובצו
Elements/Elements II-1	definition	ספר_המספר_/_אליהו_מזרחי#8mWV	It was already clarified in Euclid's Book of Elements, in the [second] section, in the first proposition that for any two straight lines, one of which is cut into segments as many as they may be, the sum of the surfaces generated from the whole straight line and each of the segments of the other straight line equals the surface generated from the whole straight line and the whole divided line. :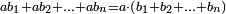$\scriptstyle ab_1+ab_2+\ldots+ab_n=a\sdot\left(b_1+b_2+\ldots+b_n\right)$ וזה שכבר התבאר בספר היסודות לאקלידס במאמר השלישי ממנו בתמונה הראשונה שכל שני קוים שנחלק אחד מהם לחלקים כמה שיהיו הנה השטח ההוא מהקו האחד כלו עם כל אחד מחלקי הקו האחר יחד הוא שוה לשטח ההווה מהקו האחד עם כל הקו הנחלק
Elements/Elements II-1	a·∑bᵢ=∑(a·bᵢ)	ספר_מעשה_חושב#4J1r	When there are two given numbers and one of them is divided into parts, as many as they may be, the product of the first number by the second is equal to the [sum of] the products of each of the parts of the first number by the second. :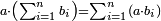$\scriptstyle a\sdot\left(\sum_{i=1}^n b_i\right)=\sum_{i=1}^n \left(a\sdot b_i\right)$ ב כאשר היו שני מספרים מונחים וחולק המספר האחד לחלקים כמה שיהיו הנה שטח המספר האחד בשני שוה לשטחי כל אחד מחלקי המספר האחד בשני מקובצים
Elements/Elements II-1	a·∑bᵢ=∑(a·bᵢ)	לקוטים_מספר_פראלוקא#t9Uk	If you have two numbers and you divide one of the two numbers, then you multiply each part by the second number, the total sum is the same as the product of the first number by the second. :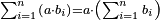$\scriptstyle\sum_{i=1}^n \left(a\sdot b_i\right)=a\sdot\left(\sum_{i=1}^n b_i\right)$ ‫156 אם יש לך ב' מספרים ותחלק א' מהב' מספרים ותכפול כל חלק על המספר השני הנה הסך העולה הוא כמו מה שיעלה מכפל המספר הראשון על השני
Elements/Elements II-1	10,2+3+5+2	לקוטים_מספר_פראלוקא#1Q9z	Example: the two numbers are 10 and 12 and we divide 12 to 2, 3, 5, 2, so their sum is 12. המשל הנה ב' מספרים והם י' וי"ב ונחלק י"ב על ב' ועל ג' ועל ה' ועל ב' והנה כלם י"ב
Elements/Elements II-1		ספר_החשבון_והמדות#fGS3	I say: if you divide any number into parts as you wish, [the sum of] the products of each of the parts by the whole number is equal to the square of the whole number. :$\scriptstyle{\color{OliveGreen}{\sum_{k=1}^n \left[\left(\sum_{i=1}^n a_i\right)\sdot a_k\right]=\left(\sum_{i=1}^n a_i\right)^2}}$ ואומר כל מספר שחלקת אותו לחלקים איך שרצית הנה כפל כל אחד מהחלקים על כל המספר מקובץ שוה למרובע כל המספר
Elements/Elements II-1	4,2+3+5	ספר_המספר_/_אליהו_מזרחי#1rE2	Example: if we divide the 10 into three parts randomly, one part of them is 2, the second is 3 and the third is 5. משל זה אם נחלק הי' לג' חלקים איך מה שקרה והיה החלק האחד מהם מספר ב' והשני מספר ג' והשלישי מספר ה'
Elements/Elements II-1	a·∑bᵢ=∑(a·bᵢ)	ספר_המספר_/_אליהו_מזרחי#me96	For every number divided into many parts randomly, the number that is generated from the product of a number by the whole given divided number is equal to the number generated from the sum of the products of that number by each part of the divided number. :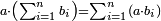$\scriptstyle a\sdot\left(\sum_{i=1}^n b_i\right)=\sum_{i=1}^n \left(a\sdot b_i\right)$ השנית שכל מספר נחלק לחלקים רבים איך מה שקרה הנה המספר ההווה מהכאת מספר מה עם המספר המונח הנחלק בכללו הוא שוה למספר ההווה מהכאת המספר ההוא עם כל אחד מחלקי המספר הנחלק כאשר יקובצו
Elements/Elements II-10	10,2	ספר_החשבון_והמדות#zIUc	Example: we have the number ten, we divide it into two halves, which are 5, and add to it another number 2, so it bacomes 12. דמיון יש לנו מספר מניינו עשרה וחלקנוהו לשני חצאים על ה' והוספנו עליו ‫33rמספר אחר ב' ונהיה י"ב
Elements/Elements II-10	(a+b)²+b²=2·((½a)²+((½a)+b)²)	לקוטים_מספר_פראלוקא#ijBn	If you divide any number into two equal parts, then add another number to the divided number, square it and add to it the square of the [number] you added, it is twice [the sum of] the square of the additional [number] plus half [the number] with the square of half [the number]. :$\scriptstyle\left(a+b\right)^2+b^2=2\sdot\left[\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2+\left(\frac{1}{2}\sdot a\right)^2\right]$ ‫165 אם תחלק איזה מספר על ב' חלקים שוים ואחר תוסיף מספר אחר על המספר המחולק ותרבענו ותוסיף על זה מרובע שהוספת יהיה ב' פעמים כמו כפל ממה שיעלה התוספת הנוסף על החצי עם מרובע החצי נוספים
Elements/Elements II-10	(a+b)²+b²=2·((½a)²+((½a)+b)²)	ספר_המלכים#CVU6	For any even number divided into half and another number is added to it, [the sum of] twice the product of half the number by itself and twice the product of half the number plus the additional [number] by itself is equal to [the sum of] the product of the [whole] number plus the additional [number] by itself and [the product] of the additional [number] by itself. :$\scriptstyle{\color{OliveGreen}{\left[2\sdot\left(\frac{1}{2}\sdot a\right)^2\right]+\left[2\sdot\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2\right]=\left(a+b\right)^2+b^2}}$ כל מספר זוג יחלק לחציים ונוסף בו מספר אחר הנה ההווה מהכאת חצי המספר בכמהו שני פעמים והכאת חצי המספר עם התוספת בכמהו שני פעמים הכהכאת המספר עם התוספת בכמהו והתוספת בכמהו
Elements/Elements II-10	12,8	לקוטים_מספר_פראלוקא#wuja	Example: we have 12, you divide it to 6 and 6, then add to 12 another number. Suppose that we add 8 to it. המשל יש לנו מספר י"ב ותחלקהו על ו'ו' ותוסיף על י"ב ‫148vמספר אחר ונניח כי נוסיף בם ח‫'
Elements/Elements II-10	10,2	ספר_המספר_/_אליהו_מזרחי#0WFg	Example: we have the number ten, we divide it into two halves and add to it the number 2, so it bacomes 12. דמיון יש לנו מספר עשרה וחלקנוהו לשני חציים והוספנו עליו מספר ב' ונהיה י"ב
Elements/Elements II-10	(a+b)²+b²=2·((½a)²+((½a)+b)²)	ספר_החשבון_והמדות#w9pW	If you divide any number into half and add to it another number, [the sum of] the square of the whole number plus the additional [number] and the square of the additional [number] is equal to twice [the sum of] the square of half the number and the square of half the number plus the additional [number] together. :$\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2+b^2=2\sdot\left[\left(\frac{1}{2}\sdot a\right)^2+\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2\right]}}$ עוד כל מספר שחלקת אותו לשני חציים והוספת עליו מספר אחר הנה מרובע המספר עם התוספת יחד ומרובע התוספת בעצמו הם כפל שני המרובעים שהם מרובע חצי המספר ומרובע חצי המספר עם התוספת יחד כאשר {{#annot:term|178,2083|Ycx9}}יחוברו{{#annotend:Ycx9}}
Elements/Elements II-10	(a+b)²+b²=2·((½a)²+((½a)+b)²)	ספר_המספר_/_אליהו_מזרחי#FJSe	Any number that you divide into half and add to it another number, [the sum of] the square of the [whole] number plus the additional [number] and the square of the additional [number] is equal to twice [the sum of] the square of half the number and the square of half the number plus the additional [number] when they are summed together. :$\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2+b^2=2\sdot\left[\left(\frac{1}{2}\sdot a\right)^2+\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2\right]}}$ עוד כל מספר שחלקת אותו לשני חצאים והוספת עליו מספר אחר הנה מרובע המספר עם התוספת יחד ומרובע התוספת בעצמו הם כפל שני המרובעים שהם מרובע חצי המספר ומרובע חצי המספר עם התוספת יחד כאשר יחוברו
Elements/Elements II-2	10,7+3	ספר_החשבון_והמדות#KF6o	Example: the number ten; we divide it into 7 and 3. דמיון המספר עשרה וחלקנוהו על ז' וג‫'
Elements/Elements II-2	∑ₖ((∑ᵢaᵢ)·aₖ)=(∑ᵢaᵢ)²	קצת_מענייני_חכמת_המספר#4EHv	If you divide any number into parts as you wish, [the sum of] the products of each of the parts by the whole number is equal to the square of the whole number. :$\scriptstyle{\color{OliveGreen}{\sum_{k=1}^n \left[\left(\sum_{i=1}^n a_i\right)\sdot a_k\right]=\left(\sum_{i=1}^n a_i\right)^2}}$ אחת כל מספר שחלקת אותו לחלקים איך שרצית הנה הכאת כל אח' מהחלקי' בכל המספר השוה למרובע הכל
Elements/Elements II-2	12,3+4+5	לקוטים_מספר_פראלוקא#Gj4L	Example: we wish to divide 12 into three parts 5, 3, 4. המשל נרצה לעשות מי"ב ג' חלקים ה' ג' ד‫'
Elements/Elements II-2	12,3+4+5	ספר_החשבון_והמדות#pdf0	Example: the number 12; we divide it into three, four and five. דמיון המספר י"ב וחלקנוהו על שלשה וארבעה וחמשה
Elements/Elements II-2	∑ₖ((∑ᵢaᵢ)·aₖ)=(∑ᵢaᵢ)²	לקוטים_מספר_פראלוקא#nMHc	If you have a number and you divide iy into parts as you wish, if you multiply each part by the divided number, then sum all the [products] they are equal to the divided number multiplied by itself. :$\scriptstyle\sum_{k=1}^n \left[\left(\sum_{i=1}^n a_i\right)\sdot a_k\right]=\left(\sum_{i=1}^n a_i\right)^2$ ‫157 אם יש לך מספר אחד ותחלק אותו לכ"כ חלקים שתרצה אם תכפול כל חלק על המספר המחולק ותקבץ כל החלקים יהיו שוים אל המספר המחולק כפול על עצמו
Elements/Elements II-2	12,3+4+5	ספר_המספר_/_אליהו_מזרחי#Nxlm	Example: the number 12, we divide it to three, four and five. דמיון זה המספר י"ב וחלקנוהו על שלשה וארבעה וחמשה
Elements/Elements II-2	∑ₖ((∑ᵢaᵢ)·aₖ)=(∑ᵢaᵢ)²	ספר_החשבון_והמדות#DxvK	For every number that you divide randomly into two parts, the sum of the products of each of the two parts by the whole number is equal to the square of the whole number. :$\scriptstyle{\color{OliveGreen}{\left[\left(a+b\right)\sdot a\right]+\left[\left(a+b\right)\sdot b\right]=\left(a+b\right)^2}}$ עוד כל מספר שחלקת אותו לשני חלקים איך שקרה הנה כפל כל אחד משני החלקים על כל המספר מקובץ שוה למרובע כל המספר
Elements/Elements II-2	∑ₖ((∑ᵢaᵢ)·aₖ)=(∑ᵢaᵢ)²	ספר_המספר_/_אליהו_מזרחי#mQeQ	Any number that you divide into parts as you wish, [the sum of] the products of each of the parts by the whole number is equal to the square of the whole number. :$\scriptstyle{\color{OliveGreen}{\sum_{k=1}^n \left[\left(\sum_{i=1}^n a_i\right)\sdot a_k\right]=\left(\sum_{i=1}^n a_i\right)^2}}$ והוא שכל מספר שחלקת אותו לחלקים איך שרצית הנה הכאת כל אחד מהחלקים עם כל המספר שוה למרובע כל המספר
Elements/Elements II-3	(a+b)·b=(a·b)+b²	קצת_מענייני_חכמת_המספר#PVyt	For any number divided into two parts as you wish, the product of the whole number by any of its two parts is equal to the product of the one part by the other plus the square of the part by which you multiplied the whole number. :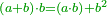$\scriptstyle{\color{OliveGreen}{\left(a+b\right)\sdot b=\left(a\sdot b\right)+b^2}}$ ב כל מספר שחלקת אותו לב' חלקים איך שקרה הנה הכאת המספר כלו עם כל אחד מב' חלקיו איזה שיהיה שוה להכאת החלק האחד עם האחר ולמרובע החלק אשר בו הכית כל המספר
Elements/Elements II-3	(a+b)·b=(a·b)+b²	לקוטים_מספר_פראלוקא#fYtF	If you divide any number into two parts, then multiply any of the two parts by the divided number and keep the product, so will be the result if you multiply the same part by itself, then add to it the product of the one part by the other. :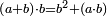$\scriptstyle\left(a+b\right)\sdot b=b^2+\left(a\sdot b\right)$ ‫158 אם תחלק איזה מספר על ב' חלקים ותכפול החלק שיהיה מב' החלקים על המספר המחולק ושמור העולה כך יעלה אם תכפול אותו חלק על עצמו ותוסיף בו העולה מהכפל מהחלק האחד על השני
Elements/Elements II-3	(a+b)·b=(a·b)+b²	ספר_מעשה_חושב#BvNU	When a number is divided into two parts, the product of the whole number by one of its parts is equal to the product of the one part by the other plus the square of the mentioned part. :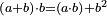$\scriptstyle \left(a+b\right)\sdot b=\left(a\sdot b\right)+b^2$ ד כאשר חולק מספר מה בשני חלקים הנה שטח כל המספר באחד מחלקיו שוה לשטח החלק האחד באחר ולמרובע החלק אשר זכרנו
Elements/Elements II-3	(a+b)·b=(a·b)+b²	ספר_המספר_/_אליהו_מזרחי#oIDS	For any number that you divide into two parts randomly, the product of the whole number by any of its two parts is equal to the product of the one part by the other plus the square of the part by which you have multiplied the whole number. :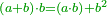$\scriptstyle{\color{OliveGreen}{\left(a+b\right)\sdot b=\left(a\sdot b\right)+b^2}}$ עוד כל מספר שחלקת אותו לשני חלקים איך שקרה הנה הכאת המספר כלו עם כל אחד משני חלקיו איזה שיהיה שוה להכאת החלק האחד עם השני ולמרובע החלק אשר הכית עם כל המספר
Elements/Elements II-3	10,3+7	ספר_החשבון_והמדות#zmnp	Example: the number ten, we divide it into two parts - three and seven. דמיון המספר עשרה חלקנוהו לשני חלקים על שלשה ושבעה
Elements/Elements II-3	(a+b)·b=(a·b)+b²	ספר_החשבון_והמדות#Eu5r	For any number divided into two parts as you wish, the product of the whole number by any of its two parts is equal to the product of the one part by the other plus the square of the part by which you multiplied the whole number. :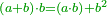$\scriptstyle{\color{OliveGreen}{\left(a+b\right)\sdot b= \left(a\sdot b\right)+b^2}}$ עוד כל מספר שחלקת אותו בשני חלקים איך שקרה הנה כפל המספר כולו על אחד משני חלקיו איזה שיהיה שוה לכפול החלק האחד על השני ולמרובע החלק משניהם אשר כפלת על כל המספר
Elements/Elements II-3	10,3+7	ספר_המספר_/_אליהו_מזרחי#CANO	Example: the number ten, we divide into two parts - three and seven. דמיון המספר עשרה חלקנוהו לשני חלקים על שלשה ושבעה
Elements/Elements II-3	12,4+8	לקוטים_מספר_פראלוקא#XIpE	Example: we have 12 and you divide it to 8 and 4. המשל אם יש לנו י"ב ותחלק אותו ח' ד‫'
Elements/Elements II-3	10,3+7	קצת_מענייני_חכמת_המספר#MLKI	Example: the number 10 is divided into two parts - 7 and 3. כמשל מספר הי' נחלק לב' חלקים לז' ולג‫'
Elements/Elements II-4	12,4+8	לקוטים_מספר_פראלוקא#HYCk	Example: we divide 12 to 4 and 8. המשל הנה נחלק ‫147vמספר י"ב על ד' ועל ח‫'
Elements/Elements II-4	10,3+7	ספר_החשבון_והמדות#hh0J	Example: the number ten; we divide it into three and seven. דמיון המספר עשרה חלקנוה על שלשה ושבעה
Elements/Elements II-4	(a+b)²=a²+b²+2(a·b)	ספר_המספר_/_אליהו_מזרחי#oC2j	For any number that you divide into two parts randomly, the square of the whole number is equal to [the sum of] the squares of the two parts and twice the product of the one part by the other. :$\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2=a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]}}$ עוד כל מספר שחלקת אותו לשני חלקים איך שקרה הנה מרובע כל המספר שוה לשני המרובעי' ההווים משני החלקים ולהכאת החלק האחד עם חברו פעמים
Elements/Elements II-4	(a+b)²=a²+b²+2(a·b)	ספר_המלכים#wUeW	For any number divided into [two] parts, whichever they may be, the product of the whole number by itself is equal to the sum of the products of each of the two parts by itself and double the product of one of the two parts by the other. :$\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2=a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]}}$ |style="width:45%; text-align:right;"|כל מספר יחלק בחלקים כמו שיהיו הנה הכאת המספר כלו בעצמו כמו הכאת כל אחד משני החלקים בעצמו וכפל הכאת אחד משני החלקים באחר כאשר יקובצו
Elements/Elements II-4	(a+b)²=a²+b²+2(a·b)	ספר_המספר_/_אליהו_מזרחי#TApz	For any number divided into two parts randomly, the square of the whole number is equal to [the sum of] the squares of the two parts and twice the product of the one part by the other. :$\scriptstyle\left(a+b\right)^2=a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]$ האחת שכל מספר נחלק לשנים חלקים איך מה שקרה הנה המרובע ההווה מן המספר כלו הוא שוה לשני המרובעים ההווים משני חלקיו עם כפל המספר ההווה מהכאת החלק האחד עם האחר
Elements/Elements II-4	(a+b)²=a²+b²+2(a·b)	קצת_מענייני_חכמת_המספר#v7Dx	For any number divided into two parts as you wish, the square of the whole number is equal to [the sum of] the squares of the two parts and twice the product of the one part by the other. :$\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2=a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]}}$ ג כל מספר שחלקת אותו לשני חלקים איך שקרה הנה מרובע כל המספר שוה לב' המרובעים ההווים מב' החלקים ולהכאת החלק האחד עם חבירו ב' פעמים
Elements/Elements II-4	10,3+7	ספר_המספר_/_אליהו_מזרחי#Ca24	Example: the number ten, we divide it to three and seven. דמיון המספר עשרה חלקנוהו על שלשה ושבעה
Elements/Elements II-4	(a+b)²=a²+b²+2(a·b)	ספר_החשבון_והמדות#q5ib	For any number divided into two parts as you wish, the square of the whole number is equal to [the sum of] the squares of the two parts and twice the product of the one part by the other. :$\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2=a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]}}$ עוד כל מספר שחלקת אותו לשני חלקים איך שקרה הנה מרובע כל המספר שוה לשני המרובעים ההוים משני החלקים ולכפל החלק האחד על חברו פעמים
Elements/Elements II-4	definition	ספר_האלזיברא#JPnC	When a straight line is cut randomly into two segments, the square on the whole line equals the sum of the two squares that are generated from the two segments plus twice the rectangle encompassed by the two segments. :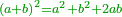$\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2=a^2+b^2+2ab}}$ כי כאשר נחלק קו ישר לב' חלקים איך שקרה הנה מרבע הקו כלו שוה לשני המרבעים ההווים משני החלקים ולכפל השטח הנצב הזויות אשר יקיפו בו שני החלקים
Elements/Elements II-4	reference	ספר_האלזיברא#Eeue	It was already clarified in [[ספר_היסודות_לאקלידס#Elements_II_4|'''Euclid, Elements, Book II, proposition 4''']] that: וכבר נתבאר ב'''תמונת הרביעית מן המאמר השני לאקלידס'''
Elements/Elements II-4	(a+b)²=a²+b²+2(a·b)	לקוטים_מספר_פראלוקא#lAxq	If you have a number and you divide it into two unequal parts, I say that if you sum the [parts] that are multiplied by themselves, then you multiply the smaller [part] by the greater, multiply the product by 2 and sum it with the reserved, the result is equal to the [original] number multiplied by itself. :$\scriptstyle\left(a+b\right)^2=a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]$ ‫169 אם יש לך מספר ותחלקהו על ב' חלקים בלתי שוים אומר כי אם תקבץ המספרי' המוכפלים על עצמם ואח"כ תכפול המספר הקטון על הגדול והעולה כפול על ב' ותקבץ זה עם השמור יעלה הכל כמו המספר כפול על עצמו
Elements/Elements II-4	10,3+7	קצת_מענייני_חכמת_המספר#OusC	Example: the number 10 is divided into 7 and 3. כמשל הי' נחלק לז' ולג‫'
Elements/Elements II-4	10,3+7	ספר_המספר_/_אליהו_מזרחי#6oZu	Example: if we divide the 10 into two parts randomly, one part of them is 3 and the other 7. משל זה אם נחלק הי' לשנים חלקים איך מה שקרה והיה החלק האחד מהם ג' והאחר ז'
Elements/Elements II-4	(a+b)²=a²+b²+2(a·b)	לקוטים_מספר_פראלוקא#lb40	If you divide any number into two and multiply each part by itself, you multiply also one [part] by the other and multiply [the product] by 2, then you sum all, the result is equal to the divided number multiplied by itself. :$\scriptstyle a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]=\left(a+b\right)^2$ ‫159 אם תחלק איזה מספר שיהיה על ב' ותכפול כל חלק על עצמו וג"כ כפול הא' על הב' וכפלם על ב' ותקבץ הכל הנה העולה יהיה שוה אל המספר המחולק כפול על עצמו
Elements/Elements II-4	(a+b)²=a²+b²+2(a·b)	ספר_מעשה_חושב#lUMx	When a number is added to a number, the square of the two numbers that are summed together is equal to [the sum of] the squares of these numbers and twice the product of the one by the other. :$\scriptstyle\left(a+b\right)^2=a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]$ ו כאשר נוסף על מספר מונח מספר מה הנה מרובע שני המספרים מחוברים שוה למרובעי המספרים ההם ולכפל שטח זה בזה
Elements/Elements II-5	10,3+7	ספר_החשבון_והמדות#zKhJ	Example: the number ten, we divide it to five and five, which are equal parts, then we divide it also to 7 and 3, which are unequal parts. דמיון המספר עשרה חלקנו לחמשה וחמשה שהם חלקים שוים גם חלקנוהו לז' וג' שהם חלקים בלתי שוים
Elements/Elements II-5	12,4+8	לקוטים_מספר_פראלוקא#pZPT	Example: we divide 12 into two equal parts 6 and 6, and into two unequal parts 4 and 8. המשל נחלק מספר י"ב לב' חלקים שוים ו'ו' ולב' חלקים בלתי שוים ד' וח‫'
Elements/Elements II-5	10,3+7	ספר_המספר_/_אליהו_מזרחי#zYJb	Example: the number ten, we divide it to five and five, which are equal parts, then we divide it also to seven and three, which are unequal parts. דמיון המספר עשרה חלקנוהו לחמשה וחמשה שהם חלקים שוים גם חלקנוהו לשבעה ושלשה שהם חלקים בלתי שוים
Elements/Elements II-5	(½(a+b))²=(a·b)+(b-½(a+b))²=(a·b)+(½(a+b)-a)²	קצת_מענייני_חכמת_המספר#9QNa	For any number divided into two equal parts and into two unequal parts, [the sum of] the product of one of the unequal parts by the other and the square of the difference between the two parts, i.e. between the equal part [= the half of the whole number] and the unequal [part] is equal to the square of half the [whole] number. :$\scriptstyle{\color{OliveGreen}{\left(a\sdot b\right)+\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]^2=\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2}}$ ד כל מספר כאשר תחלקהו לב' חלקים שוים ולב' חלקים בלתי שוים הנה הכאת החלק הא' עם חבירו מהחלקים הבלתי שוים ומרוב' מה שבין ב' חלקים ר"ל בין החלק השוה ובלתי שוה שוה למרובע חצי המספר
Elements/Elements II-5	(½(a+b))²=(a·b)+(b-½(a+b))²=(a·b)+(½(a+b)-a)²	ספר_החשבון_והמדות#43lj	For any number divided into two equal parts and into two unequal parts, [the sum of] the product of one of the unequal parts by the other and the square of the difference between the two parts, i.e. between the equal part [= the half of the whole number] and the unequal [part] is equal to the square of half the [whole] number. :$\scriptstyle{\color{OliveGreen}{\left(a\sdot b\right)+\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]^2=\left(a\sdot b\right)+\left[b-\left[\frac{1}{2}\sdot\left(a+b\right)\right]\right]^2=\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2}}$ עוד כל מספר כאשר תחלקהו לשני חלקים שוים ולשני חלקים בלתי שוים הנה כפל החלק האחד אל חברו מהחלקים הבלתי שוים ומרובע מה שבין שני ‫32vהחלקים ר"ל בין החלק השוה ובלתי שוה שוה למרובע חצי המספר
Elements/Elements II-5	(½(a+b))²=(a·b)+(b-½(a+b))²=(a·b)+(½(a+b)-a)²	ספר_המלכים#4PpZ	For any even number divided into halves and into [two] unequal parts, the product of half the [whole] number by itself is equal to [the sum of] the product of the greater part by the smaller [part] and the product of the excess of the half of the [whole] number over the smaller part by itself. :$\scriptstyle{\color{OliveGreen}{\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2=\left(a\sdot b\right)+\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]^2}}$ כל מספר זוג יחלק לחצאים ולחלקים מתחלפים הנה אשר יהיה מהכאת [חצי]‫M om. המספר בעצמו כמו ההווה מהכאת החלק הגדול בקטן עם הכאת מותר חצי המספר על החלק ההקטן [בכמהו]‫M וכמוהו
Elements/Elements II-5	10,3+7	קצת_מענייני_חכמת_המספר#41Hj	Example: the number 10 that is divided into 7 and 3. במש' הי' שנחלק לז' ולג‫'
Elements/Elements II-5	(½(a+b))²=(a·b)+(b-½(a+b))²=(a·b)+(½(a+b)-a)²	לקוטים_מספר_פראלוקא#24rA	If you divide any number into two equal parts and into two unequal parts, the product of the equal parts one by the other is as the product of the unequal parts one by the other, when you add to it the [square] of the difference between the [equal] part and the [unequal part]. ‫160 אם תחלק מספר אחד לב' חלקים שוים ולב' חלקים בלתי שוים הנה כל כך יעלה כפל החלקים השוים זה על זה כמו כפל החלקים הבלתי שוים זה על זה ותוסיף בם כפל היתרון שיש מהחלק האחד על האחר
Elements/Elements II-5	reference	ספר_האלזיברא#7B0h	[[ספר_היסודות_לאקלידס#Elements_II_5|'''Euclid, Elements, Book II, proposition 5''']]: the square formed by AZ, which is four measures, and is as the square of half [the number of] the things that is known to be 16, is equal to surface BH, which is equal to the right-angled surface encompassed by the two unequal segments, whose area is known to be 12, plus the square formed by ZB that is the difference between the two parts. :$\scriptstyle{\color{OliveGreen}{\left(a\sdot b\right)+\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-b\right]^2=\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2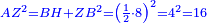}}$ :$\scriptstyle{\color{blue}{AZ^2=BH+ZB^2=\left(\frac{1}{2}\sdot8\right)^2=4^2=16}}$ והנה כפי מה שנתבאר ב'''תמו' החמישית מן המאמר השני לאקלידס'''
Elements/Elements II-5	(½(a+b))²=(a·b)+(b-½(a+b))²=(a·b)+(½(a+b)-a)²	ספר_המספר_/_אליהו_מזרחי#yKYx	For any number, when you divide it into two equal parts and into two unequal parts, [the sum of] the product of one of the unequal parts by the other and the square of the difference between the two parts, i.e. between the equal part [= the half of the whole number] and the unequal [part] is equal to the square of half the [whole] number. :$\scriptstyle{\color{OliveGreen}{\left(a\sdot b\right)+\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]^2=\left(a\sdot b\right)+\left[b-\left[\frac{1}{2}\sdot\left(a+b\right)\right]\right]^2=\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2}}$ עוד כל מספר כאשר תחלקהו לשני חלקים שוים ולשני חלקים בלתי שוים הנה הכאת החלק האחד עם חברו מהחלקים הבלתי שוים ומרובע מה שבין שני החלקים ר"ל בין החלק השוה ובלתי שוה שוה למרובע חצי המספר
Elements/Elements II-5	(½(a+b))²=(a·b)+(b-½(a+b))²=(a·b)+(½(a+b)-a)²	ספר_מעשה_חושב#AHZr	The product of half the given number by itself is equal to [the sum of] the product of a part of that number by the other part and the square of the difference between one of the [unequal] parts and half of the [whole] given number. ח השטח ההוה מחצי המספר המונח בעצמו שוה לשטח ההוה מחלק מה מהמספר ההוא בחלק השני ולמרובע יתרון אחד מן החלקים על חצי המספר המונח
Elements/Elements II-6	10,2	ספר_המספר_/_אליהו_מזרחי#bDvj	Example: the number ten, we divide it into two halves, which are five each, then we add two to the ten, they are 12. דמיון המספר עשרה וחלקנוהו לשני חצאים שהם כל חצי חמשה הוספנו על העשרה שנים והיו י"ב
Elements/Elements II-6	reference	ספר_האלזיברא#XaGL	[[ספר_היסודות_לאקלידס#Elements_II_6|'''Euclid, Elements, Book II, proposition 6''']] that the right-angled surface encompassed by the whole line with the addition and the addition, which is equal to surface ZD, whose area is 2 in our example, with the square formed by half the line, which is 16 in our example, both together are 36, equals the square of the line formed by half the line with the addition, which is line TB in our illustration. :$\scriptstyle{\color{OliveGreen}{\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2}}$ וכבר נתבאר ב'''תמונה הששית מן המאמר השני לאקלידס'''
Elements/Elements II-6	12,4	לקוטים_מספר_פראלוקא#qQuN	Example: we have 12, you divide it to 6 and 6, then add to 6 whichever number you wish. Suppose that we wish to add 4 to 6. המשל יש לנו מספר י"ב ותחלק אותו על ו"ו ותוסיף על ו' מספר איזה שתרצה ונניח כי נרצה להוסיף על ו' ד‫'
Elements/Elements II-6	10,2	ספר_החשבון_והמדות#yd9c	Example: the number ten, we divide it into two halves, which are five each, then we add two to the ten, they are 12. דמיון המספר עשרה וחלקנוהו לשני חצאים שהם כל חצי חמשה {{#annot:term|178,1206|GTDu}}הוספנו{{#annotend:GTDu}} על העשרה שנים והיו י"ב
Elements/Elements II-6	(a+b)·b+(½a)²=(½a+b)²	ספר_מעשה_חושב#vsiV	When a number is divided into two halves and a number is added to it, [the sum of] the product of the additional [number] by the whole number plus the additional [number] and the square of half the number is equal to the square of half the number and the additional [number] summed together. :$\scriptstyle\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2$ ה כאשר חולק מספר מה לחציין והוסף עליו מספר מה הנה שטח התוספת במספר כלו עם התוספת עם מרובע חצי המספר שוה למרובע חצי המספר והתוספת מקובצים
Elements/Elements II-6	reference	ספר_האלזיברא#BJrm	[[ספר_היסודות_לאקלידס#Elements_II_6|'''Euclid, Elements, Book II, proposition 6''']] that the right-angled surface encompassed by the whole line with the addition and the addition, which is equal to surface AW, whose area is known as 48, plus the square of half the line, whose area is known, which is 1, both together are 49, equals the square of the line formed by half the line with the addition, which is line AZ. :$\scriptstyle{\color{OliveGreen}{\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2}}$ וכבר נתבאר ב'''תמונה הששית ‫131vמן המאמר השני לאקלידס'''
Elements/Elements II-6	(a+b)·b+(½a)²=(½a+b)²	לקוטים_מספר_פראלוקא#77le	If you divide any number into two equal parts, then add an additional [number] to the divided number, multiply [the sum] by the additional [number] and add [the product] to the square of one of the parts, I say that it is equal to the square of half [the number] with the additional [number]. :$\scriptstyle\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2$ ‫161 אם תחלק איזה מספר לב' חלקים שוים ותוסיף בם א' מהחלקי' כפול על עצמו ותוסיף בם התוספת על כל המספר המחולק ותכפול אותו המספר אשר הוספת ותחברם עם כפל אחד מהחלקים אומר כי הוא שוה אל כפל המחצית עם התוספת
Elements/Elements II-6	(a+b)·b+(½a)²=(½a+b)²	קצת_מענייני_חכמת_המספר#nmaV	If we divide any number into half and add to it another number, [the sum of] the product of the whole number plus the additional [number] by the additional [number] and the square of half the number is equal to the square of half the number and the additional [number] together. :$\scriptstyle{\color{OliveGreen}{\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2}}$ ה כל מספר כאשר חלקנו אותו לחצי והוספת עליו מספר אחר הנה הכאת המספר כלו מחובר עם התוספ' בתוספת ומרובע חצי המספר שוה למרובע חצי המספר והתוספת ביחד
Elements/Elements II-6	(a+b)·b+(½a)²=(½a+b)²	ספר_החשבון_והמדות#A9xw	If you divide any number into half and add to it another number, [the sum of] the product of the whole number plus the additional [number] by the additional [number] and the square of half the number is equal to the square of half the number and the additional [number] together. :$\scriptstyle{\color{OliveGreen}{\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2}}$ עוד כל מספר כאשר חלקת אותו לחצאים והוספת עליו מספר אחר הנה כפל המספר כלו מקובץ עם התוספת בתוספת והמרובע ההוה מחצי המספר שוה למרובע חצי המספר והתוספת ביחד
Elements/Elements II-6	(a+b)·b+(½a)²=(½a+b)²	ספר_המספר_/_אליהו_מזרחי#tcs6	For any number, when you divide it into half and add to it another number, [the sum of] the product of the whole number plus the additional [number] by the additional [number] and the square of half the number is equal to the square of half the number and the additional [number] together. :$\scriptstyle{\color{OliveGreen}{\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2}}$ עוד כל מספר כאשר חלקת אותו לחצי והוספת עליו מספר אחר הנה הכאת המספר כלו מקובץ עם התוספת בתוספת והמרובע ההווה מחצי המספר שוה למרובע חצי המספר והתוספת ביחד
Elements/Elements II-6	(a+b)·b+(½a)²=(½a+b)²	ספר_המלכים#c7yY	For any number divided into two halves and another number is added to it, the product of half the number and the additional [number] together by itself is equal to [the sum of] the product of the [whole] number plus the additional [number] by the additional [number] and the product of half the original number by itself. :$\scriptstyle{\color{OliveGreen}{\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2=\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2}}$ כל מספר זוג יחלק לשני חצאים ויתוסף בו מספר אחר הנה הכאת חצי המספר עם התוספת בכמהו כהכאת המספר עם התוספת בתוספת והכאת חצי המספר הראשון בעצמו
Elements/Elements II-7	10,3+7	ספר_החשבון_והמדות#L1Xh	Example: the number ten, we divide it randomly to seven and three. דמיון המספר עשרה וחלקנוהו איך שקרה על שבעה ועל שלשה
Elements/Elements II-7	(a+b)²+a²=(2·(a+b)·a)+b²	ספר_החשבון_והמדות#hdYZ	For any number divided into two parts, the sum of the square of the whole number and the square of one of the parts is equal to twice the product of this part by the whole number plus the product of the other part by itself. :$\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2+a^2=2\sdot\left[\left(a+b\right)\sdot a\right]+b^2}}$ עוד כל מספר כשתחלקהו בשני חלקים איך שיקרה הנה המרובע ההוה מן המספר כלו והמרובע ההוה מאחד משני חלקים כאשר {{#annot:term|178,1216|tLsc}}התקבצו{{#annotend:tLsc}} שוים לכפל המספר כלו עם החלק הנזכר פעמים והמרובע ההוה מן החלק השני
Elements/Elements II-7	(a+b)²+a²=(2·(a+b)·a)+b²	לקוטים_מספר_פראלוקא#lBZs	If you have a number and you divide it into two unequal parts, you multiply the greater part by itself and multiply also the divided number by itself, then sum both products, the result is equal to the product of the greater number by the divided number multiplied by two, then you add to it the square of smaller part. :$\scriptstyle\left(a+b\right)^2+a^2=2\sdot\left[\left(a+b\right)\sdot a\right]+b^2$ ‫162 אם יש לך מספר ותחלקהו לב' חלקים בלתי שוים ותכפול החלק הגדול על עצמו גם תכפול המספר המחולק על עצמו ותחבר הב' הכפלות הנה העולה יהיה שוה אל כפל המספר הגדול על המספר המחולק ותכפלהו אח"כ על ב' גם תוסיף על זה כפל החלק הקטן ותחבר הכל יהיה שוה
Elements/Elements II-7	10,3+7	קצת_מענייני_חכמת_המספר#nE0O	Example: the number 10 is divided into 7 and 3. במשל הרי הי' נחלק לז' ולג‫'
Elements/Elements II-7	10,3+7	ספר_המספר_/_אליהו_מזרחי#VZVn	Example: the number ten, we divide it randomly to 7 and 3. דמיון המספר עשרה וחלקנוהו איך שקרה על ז' ועל ג‫'
Elements/Elements II-7	(a+b)²+a²=(2·(a+b)·a)+b²	ספר_המלכים#isjp	For any number divided into two parts, [the sum of] the product of the [whole] number by itself and [the product of] one of the two parts by itself is equal to twice the product of the [whole] number by the part that is multiplied by itself plus the [product of the] other part by itself. :$\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2+a^2=\left[2\sdot\left(a+b\right)\sdot a\right]+b^2}}$ כל מספר יחלק לשני חלקים [..] הנה הכאת המספר בכמוהו ואחד ‫59vמשני החלקים בכמוהו כמו ההווה מהכאת המספר בחלק המוכה בכמוהו שני פעמים והחלק השני בכמוהו
Elements/Elements II-7	(a+b)²+a²=(2·(a+b)·a)+b²	ספר_המספר_/_אליהו_מזרחי#WZG6	For any number, when you divide it into two parts randomly, [the sum of] the square of the whole number and the square of one of the two parts is equal to twice the product of the whole number by the mentioned part plus the square of the second part. :$\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2+a^2=2\sdot\left[\left(a+b\right)\sdot a\right]+b^2}}$ עוד כל מספר כאשר תחלקהו בשני חלקים איך שיקרה המרובע ההווה מן המספר כלו והמרובה ההווה מאחד משנים החלקים כאשר התקבצו שוים להכאת המספר כלו עם החלק הנזכר פעמים והמרובע ההווה מן החלק השני
Elements/Elements II-7	(a+b)²+a²=(2·(a+b)·a)+b²	קצת_מענייני_חכמת_המספר#DEFA	For any number divided into two parts, the sum of the square of the whole number and the square of one of the parts is equal to twice the product of this part by the whole number plus the product of the other part by itself :$\scriptstyle{\color{OliveGreen}{\left(a+b\right)^2+a^2=2\sdot\left[\left(a+b\right)\sdot a\right]+b^2}}$ ו כל מספר שתחלקהו בב' חלקים איך שקרה המרובע ההווה מהמספר כלו והמרובע ההווה מא' מב' אלו החלקים כאשר התקבצו שוה להכאת החלק הנזכ' עם המספר כלו ולהכאת החלק הב' הנשאר בעצמו
Elements/Elements II-7	12,4+8	לקוטים_מספר_פראלוקא#R7rS	Example: we wish to divide 12 to 4 and 8. המשל נרצה לחלק י"ב על ח' וד‫'
Elements/Elements II-7	definition	ספר_האלזיברא#cvaS	When a straight line is cut randomly into two segments, the sum of the squares on both segments equals twice the rectangle encompassed by both segments plus the square that is generated from the excess of the larger segment over the smaller segment. [ [[ספר_היסודות_לאקלידס#Elements_II_7|'''Euclid, Elements, Book II, proposition 7''']] ] :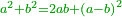$\scriptstyle{\color{OliveGreen}{a^2+b^2=2ab+\left(a-b\right)^2}}$ כי כאשר נחלק קו ישר ‫128rלשני חלקים איך שקרה הנה מרבעי שני החלקים שוים לכפל השטח הנצב הזויות אשר יקיפו בו שני החלקים ולמרבע ההוה ממותר החלק הגדול על הקטן
Elements/Elements II-8	(4·(a+b)·a)+b²=((a+b)+a)²	לקוטים_מספר_פראלוקא#TRuX	If you have a number and you divide it into unequal two parts, if you add one of the parts to the whole number, i.e. the divided number, [its square] is equal to the same part that you added multiplied by the whole number, then multiplied by four, when you add to it the square of the second part. :$\scriptstyle\left[\left(a+b\right)+a\right]^2=4\sdot\left[\left(a+b\right)\sdot a\right]+b^2$ ‫163 אם יש לך מספר ותחלקהו לב' חלקים בלתי שוים אם תוסיף א' מהחלקים על כל המספר ר"ל על המספר המחולק יהיה שוה אל אותו החלק אשר הוספת כפול על כל המספר אח"כ העולה תכפול על ד' ותוסיף על זה מרובע החלק השני
Elements/Elements II-8	10,3+7	קצת_מענייני_חכמת_המספר#9UoH	Example: the number 10 is divided into 7 and 3. במשל הי' נחלק לז' ולג‫'
Elements/Elements II-8	10,3+7	ספר_המספר_/_אליהו_מזרחי#pqrO	Example: we have the number ten, we divide it randomly to 3 and 7. דמיון יש לנו מספר עשרה וחלקנוהו איך שהזדמן על ג' ועל ז‫'
Elements/Elements II-8	12,4+8	לקוטים_מספר_פראלוקא#NtVp	Example: we wish to divide 12 to 4 and 8. המשל נרצה לחלק י"ב על ד' וח‫'
Elements/Elements II-8	(4·(a+b)·a)+b²=((a+b)+a)²	קצת_מענייני_חכמת_המספר#R68t	For any number divided into two parts as you wish, if you multiply the whole number by one of the parts four times, the sum of the product with the square of the other part is equal to the [square] of the whole number plus the one part :$\scriptstyle{\color{OliveGreen}{4\sdot\left[\left(a+b\right)\sdot a\right]+b^2=\left[\left(a+b\right)+a\right]^2}}$ ז כל מספר שחלקת אותו לב' חלקים איך שקרה אם הכית המספר כלו עם חלק אח' מהם ד' פעמים וקבצת הכל עם מרובע החלק הב' הנשאר היה שוה להכאת מספרו החלק הנזכר כאשר תחברם יחד
Elements/Elements II-8	10,3+7	ספר_החשבון_והמדות#AJOP	Example: we have the number ten, we divide it randomly to 3 and 7. דמיון יש לנו מספר מנינו העשרה וחלקנוהו איך שהזדמן על ג' ועל ז‫'
Elements/Elements II-8	(4·(a+b)·a)+b²=((a+b)+a)²	ספר_המלכים#Ocvs	For any number divided into two parts and one of the two parts is added to it, the product of the [whole] number plus the additional [part] by itself is equal to [the sum of] the product of the [whole] number by the additional [part] four times and the product of the other part by itself. :$\scriptstyle{\color{OliveGreen}{\left[\left(a+b\right)+a\right]^2=\left[4\sdot\left(a+b\right)\sdot a\right]+b^2}}$ כל מספר יחלק בשני חלקים ונוסף עליו כמו אחד משני החלקים הנה הכאת המספר עם התוספת בכמהו כהכאת המספר בתוספת ד' פעמים והכאת החלק האחר בכמהו
Elements/Elements II-8	(4·(a+b)·a)+b²=((a+b)+a)²	ספר_המספר_/_אליהו_מזרחי#LHo4	For any number, when you divide it into two parts randomly and you multiply the whole number by one of the two parts four times, then sum [the product] with the square of the other part [it] is equal to the [square] of the whole number plus the mentioned part when you sum them together. :$\scriptstyle{\color{OliveGreen}{4\sdot\left[\left(a+b\right)\sdot a\right]+b^2=\left[\left(a+b\right)+a\right]^2}}$ עוד כל מספר כאשר חלקת אותו בשני חלקים איך שיקרה והכית המספר כלו עם אחד משני חלקיו ארבעה פעמים וחברת אותו עם מרובע החלק הנשאר שוה למרובע ההווה מן המספר כלו והחלק הנזכר כאשר תחברם ביחד
Elements/Elements II-8	(4·(a+b)·a)+b²=((a+b)+a)²	ספר_החשבון_והמדות#EAD6	For any number divided into two parts as you wish, if you multiply the whole number by one of the parts four times, the sum of the product with the square of the other part is equal to the [square] of the whole number plus the one part. :$\scriptstyle{\color{OliveGreen}{4\sdot\left[\left(a+b\right)\sdot a\right]+b^2=\left[\left(a+b\right)+a\right]^2}}$ עוד כל מספר כאשר חלקת אותו בשני חלקים איך שיקרה וכפלת המספר כלו עם אחד משני חלקיו ארבעה פעמים ועם מרובע החלק הנשאר שוה למרובע ההוה מן המספר כלו והחלק הנזכר כאשר תחברם ביחד ותקח מרובעם
Elements/Elements II-9	a²+b²=2·((½·(a+b))²+(a-(½·(a+b)))²)	לקוטים_מספר_פראלוקא#E95L	If you divide any line into two equal parts and into two unequal parts, then you multiply each of the unequal parts [by itself] and sum them, they are twice [the sum of] the product of the equal parts plus the [square of] excess of the greater [part] over [half the number]. :$\scriptstyle a^2+b^2=2\sdot\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2+\left[a-\left[\frac{1}{2}\sdot\left(a+b\right)\right]\right]^2\right]$ ‫164 אם תחלק איזה קו לב' חלקים שוים ולב' חלקים בלתי שוים וכפול כל אחד מהחלקים בלתי שוים ותחברם הם כפל מהחלקים השוים נוסף בם יתרון החלק הגדול על הקטן
Elements/Elements II-9	a²+b²=2·((½·(a+b))²+(a-(½·(a+b)))²)	ספר_המספר_/_אליהו_מזרחי#ClRv	For any number that you divide into two equal parts and into two unequal parts, [the sum of] the two squares of the unequal parts is equal to twice [the sum of] the square of half the [whole] number and [the square] of the excess of the large part over the half [of the whole number]. :$\scriptstyle{\color{OliveGreen}{a^2+b^2=2\sdot\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2+\left[a-\left[\frac{1}{2}\sdot\left(a+b\right)\right]\right]^2\right]}}$ עוד כל מספר שחלקת אותו לשני חלקים שוים ושני חלקים בלתי שוים הנה שני המרובעים אשר יהיו מהחלקים הבלתי שוים הם כפל שני המרובעים אשר יהיו מחצי המספר ומהתוספת אשר לחלק הגדול על הה' שהוא המחצית
Elements/Elements II-9	10,3+7	ספר_המספר_/_אליהו_מזרחי#LnLo	Example: the number 10, we divide it into two equal parts, which are 5, and into two unequal parts, which are 7 and 3. דמיון המספר י' וחלקנוהו לשני חלקים שוים והם ה' ולשני חלקים בלתי שוים והם ז' ג‫'
Elements/Elements II-9	a²+b²=2·((½·(a+b))²+(a-(½·(a+b)))²)	ספר_החשבון_והמדות#CM8j	For any number divided into two equal parts and into two unequal parts, [the sum of] the squares of the unequal parts is equal to twice [the sum of] the square of half the [whole] number and the square of the difference between the large part and the half [of the whole number]. :$\scriptstyle{\color{OliveGreen}{a^2+b^2=2\sdot\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2+\left[a-\left[\frac{1}{2}\sdot\left(a+b\right)\right]\right]^2\right]}}$ עוד כל מספר שחלקת אותו לשני חלקים שוים ושני חלקים בלתי שוים הנה שני המרובעים אשר יהיו מהחלקים הבלתי שוים הם כפל שני המרובעים אשר יהיו מחצי המספר ומהתוספת אשר לחלק הגדול על המחצית
Elements/Elements II-9	12,4+8	לקוטים_מספר_פראלוקא#QBwh	Example: we wish to divide 12 into two equal parts 6 and 6 and into two unequal parts 8 and 4. המשל נרצה לחלק מספר י"ב לב' חלקי' שוים ו'ו' ולב' חלקים בלתי שוים ח' ד‫'
Elements/Elements II-9	a²+b²=2·((½·(a+b))²+(a-(½·(a+b)))²)	ספר_המלכים#g6A2	For any even number divided into two halves and into two unequal parts, [the sum of the products of] each of the two unequal parts by themselves is equal to [the sum of] twice the product of half the [whole] number by itself and twice the product of the excess of half the [whole] number over the smaller part by itself. :$\scriptstyle{\color{OliveGreen}{a^2+b^2=\left[2\sdot\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2\right]+\left[2\sdot\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]^2\right]}}$ כל מספר זוג יחלק בשני חצאים ובשני חלקים מתחלפים הנה כל אחד משני החלקים המתחלפים בכמהו כהכאת חצי המספר בכמהו שני פעמים והכאת מותר חצי המספר על החלק הקטן בכמהו שני פעמים
Elements/Elements II-9	10,3+7	ספר_החשבון_והמדות#O8o8	Example: we have the number ten, we divide it into two equal parts, which are 5, and into two unequal parts, which are 3 and 7. דמיון יש לנו מספר מנינו עשרה וחלקנוהו לשני חלקים שוים על ה' ושני חלקים בלתי שוים על ג' וז‫'
Elements/Elements-Introduction	a=b,a-c=b-c	ספר_המספר_/_אליהו_מזרחי#tNTC	For, when equal is subtracted from equals, then the remainders are necessarily equal, according to what is clarified in the introduction of the first section of Euclid's [book]. :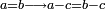$\scriptstyle a=b\longrightarrow a-c=b-c$ כי כאשר יחוסר מהשוים שוה יהיו הנשארים שוים בהכרח לפי מה שהתבאר בפתיחת המאמר הראשון מאקלידס
Elements/Elements-Introduction	a=b,a-c=b-c	ספר_המספר_/_אליהו_מזרחי#gaDw	This is because it was already clarified in the introduction of Euclid's book that when equal is subtracted from equals, then the remainders are equal :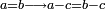$\scriptstyle a=b\longrightarrow a-c=b-c$ וזה שכבר התבאר בפתיחת ספר אקלידס כאשר חוסר מהשוים שוה יהיה הנשאר שוה
Elements/Elements IX-21	definition	ספר_המספר_/_אליהו_מזרחי#qiN5	When even numbers are summed, as many as they may be, their sum is an even number. הוא כאשר נקבצו מספרי זוגות כמה שיהיו הנה קבוצם מספר זוג
Elements/Elements IX-22	definition	ספר_המספר_/_אליהו_מזרחי#yrIb	When odd numbers are summed, as many as they may be, and their multitude is even, their sum is an even number. וכאשר נקבצו מספרים נפרדים כמה שיהיו והיה מספרם זוג הנה קבוצם מספר זוג
Elements/Elements IX-23	definition	ספר_המספר_/_אליהו_מזרחי#1A6m	When odd numbers are summed, as many as they may be, and their multitude is odd, their sum is an odd number. וכאשר נקבצו מספרים נפרדים כמה שיהיו והיה מספרם מפרד הנה קבוצם נפרד
Elements/Elements IX-28	definition	ספר_המספר_/_אליהו_מזרחי#RVMm	When an even number is multiplied by an odd number, or by an even number, then the product is even. :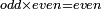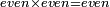$\scriptstyle odd\times even=even$; $\scriptstyle even\times even=even$ הוא שכאשר הוכה מספר זוג במספר נפרד או במספר זוג הנה המקובץ זוג
Elements/Elements IX-29	definition	ספר_המספר_/_אליהו_מזרחי#DYPK	When an odd number is multiplied by an odd number, then the product is odd. :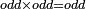$\scriptstyle odd\times odd=odd$ וכאשר הוכה מספר נפרד במספר נפרד הנה המקובץ נפרד
Elements/Elements V-15	(n·a)÷(n·b)=a÷b	ספר_המספר_/_אליהו_מזרחי#PIBA	For, it was already clarified in Euclid's Book of Elements, according to what was preceded in this section, that the given numbers have the same ratio as the ratio of their equimultiples. :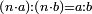$\scriptstyle\left(n\sdot a\right):\left(n\sdot b\right)=a:b$ וזה שכבר התבאר בספר היסודות לאקלידס לפי מה שקדם מן המאמר שמהמספרים המונחים הם יחס קצתם אל קצת הוא כיחס כפליהם קצתם אל קצת
Elements/Elements V-15	(n·a)÷(n·b)=a÷b	ספר_המספר_/_אליהו_מזרחי#wUJB	For, it was already clarified in Euclid's Book of Elements, in the fifth section, that any numbers, whose multiples are equal, have the same ratio as the ratio of their equimultiples. :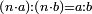$\scriptstyle\left(n\sdot a\right):\left(n\sdot b\right)=a:b$ וזה שכבר התבאר בספר היסודות לאקלידס במאמר החמישי ממנו שהמספרים אשר כפליהם שוים הנה יחס קצתם אל קצת כיחס כפליהם קצתם אל קצת
Elements/Elements V-9	definition	ספר_המספר_/_אליהו_מזרחי#2X92	For, any two magnitudes, which have the same ratio to the same magnitude, necessarily equal one another, according to what is clarified in Euclid's Book of Elements. :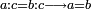$\scriptstyle a:c=b:c\longrightarrow a=b$ כי כל שני שעורים שיחסם אל שעור אחר בעצמו יחס אחד הנה הם שוים בהכרח לפי מה שהתבאר בספר היסודות לאקלידס
Elements/Elements VI-17	definition	ספר_האלזיברא#KlWg	It is already explained in {{#annot: reference | #Elements VI-17 | cH1a}}[[ספר_היסודות_לאקלידס#Elements_VI_17|'''Euclid, Elements, Book VI, proposition 17''']] that the product of the first by the last is as the product of the mean by its similar. :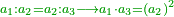$\scriptstyle{\color{OliveGreen}{a_1:a_2=a_2:a_3\longrightarrow a_1\sdot a_3=\left(a_2\right)^2}}$ וכבר נתבאר מ'''תמונת י"ז מן המאמר הששי לאקלידס'''{{#annotend:cH1a}} כי {{#annot: term | #multiplication, #הכאה | poG8}}הכאת ה{{#annotend:poG8}}ראשו' באחרון כמו הכאת האמצעי בדומה לו
Elements/Elements VI-17	reference	ספר_האלזיברא#cH1a	[[ספר_היסודות_לאקלידס#Elements_VI_17|'''Euclid, Elements, Book VI, proposition 17''']] that the product of the first by the last is as the product of the mean by its similar. :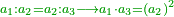$\scriptstyle{\color{OliveGreen}{a_1:a_2=a_2:a_3\longrightarrow a_1\sdot a_3=\left(a_2\right)^2}}$ וכבר נתבאר מ'''תמונת י"ז מן המאמר הששי לאקלידס'''
Elements/Elements VII-11	a÷b=c÷d→(c-a)÷(d-b)	ספר_המספר_/_אליהו_מזרחי#Iu2h	when two numbers are subtracted from two numbers and the ratio of the subtrahend to the subtrahend is the same as the ratio of the minuend to the minuend, then the [ratio of] the remainder to the remainder is the same as the ratio of the minuend to the minuend. ::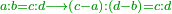$\scriptstyle{\color{OliveGreen}{a:b=c:d\longrightarrow\left(c-a\right):\left(d-b\right)=c:d}}$ וזה שכבר התבאר בספר היסודות לאקלידס במאמר השביעי ממנו בתמונת י"א שכאשר חוסרו משני מספרים ב' מספרים והיה יחס המחוסר אל המחוסר כיחס הכל אל הכל הנה יהיה הנשאר אל הנשאר כיחס הכל אל הכל
Elements/Elements VIII-11	definition	ספר_המספר_/_אליהו_מזרחי#sPcq	Its reason is also known from what was clarified in Euclid's Book of Elements, in the eighth section that for every two squares numbers the ratio of one of them to the other is as the duplicate ratio of that which the side has to the side. :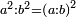$\scriptstyle a^2:b^2=\left(a:b\right)^2$ הנה סבתו ג"כ ידועה ממה שהתבאר בספר היסודו' לאקלידס במאמר הח' ממנו שכל שני מספרים מרובעים הנה יחס הא' מהם אל חברו הוא כיחס צלעו אל צלעו שנוי בכפל
Elements/Elements VIII-11	reference	ספר_האלזיברא#D3f5	[[ספר_היסודות_לאקלידס#Elements_VIII_11|'''Euclid, Elements, Book VIII, proposition 11''']] מתמונת י"א מן המאמר השמיני לאקלידס
Elements/Elements VIII-11	definition	ספר_האלזיברא#Nl0O	This is because the ratio of a square to a square is the same as the ratio of its side to its side duplicate. :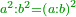$\scriptstyle{\color{OliveGreen}{a^2:b^2=\left(a:b\right)^2}}$ וזה מפני כי {{#annot: term | #ratio, #יחס | Eve2}}יחס{{#annotend:Eve2}} מרובע אל מרובע כיחס צלעו אל צלעו {{#annot: term | #duplicate, #שנוי | Q7dD}}שנוי{{#annotend:Q7dD}} ר"ל {{#annot: term | #multiplied, #כפול | G4iq}}כפול{{#annotend:G4iq}}
Elements/Elements VIII-11	definition	ספר_האלזיברא#QcHW	the ratio of a square to a square is as the ratio of its side to its side duplicated. [ [[ספר_היסודות_לאקלידס#Elements_VIII_11|'''Euclid, Elements, Book VIII, proposition 11''']] ] :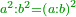$\scriptstyle{\color{OliveGreen}{a^2:b^2=\left(a:b\right)^2}}$ וזה כי מפני כי יחס מרבע אל מרבע כיחס צלעו אל צלעו שנוי
Elements/Elements VIII-12	reference	ספר_האלזיברא#jD6N	According to [[ספר_היסודות_לאקלידס#Elements_VIII_12|'''Euclid, Elements, Book VIII, proposition 12''']] מתמונת י"ב מן המאמר השמיני לאקלידס
Elements/Elements VIII-12	definition	ספר_האלזיברא#eDWE	This is because the ratio of a cube to a cube is the same as the ratio of its side to its side triplicate :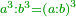$\scriptstyle{\color{OliveGreen}{a^3:b^3=\left(a:b\right)^3}}$ וזה מפני כי יחס מעקב אל מעקב כיחס צלעו אל צלעו {{#annot: term | #triplicate, #משולש | A27z}}משלש{{#annotend:A27z}}
Elements/Elements XIII-1	definition	המחומשים_והמעושרים#1Da2	Euclid proved that when a line is divided according to the ratio of a mean and two extremes, so that half the whole line is added to the larger segment, and all this is multiplied by itself, then the resulting square is equal to five times the square of half the line [Elements XIII.1]. ובאר אקלידס כי כאשר נחלק קו על יחס אמצעי ושתי קצוות שהחלק הגדול כאשר נוסף בארכו כמו חצי הקו כלו והוכה כל זה בעצמו המרובע ההוה מזה יהיה חמשה דמיוני המרובע ההוה מחצי הדבר
Elements/Elements XIII-10	definition	המחומשים_והמעושרים#w084	We do this since Euclid has explained that the line that cuts the fifth is on the line that cuts the sixth and the tithe, when they are set on one circle [Elements XIII,10]. ועשינו זה בעבור כי באר אוקלידס כי קו החותך החמישית על הקו החותך הששית והעשירית כאשר הונחו בעגולה אחת
Elements/Elements XIII-3	definition	המחומשים_והמעושרים#mhLN	Euclid has already explained [Elements XIII.3] that when line BH is divided by the ratio of a mean and two extremes, so that the greater part is equal to line DH, it is known that when a line is divided by the ratio of a mean and two extremes and we add half the greater part to the smaller part, then multiply the whole sum by itself, the square formed by the sum of the two is five times the product of [half] the greater part by itself. :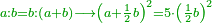$\scriptstyle{\color{OliveGreen}{a:b=b:\left(a+b\right)\longrightarrow\left(a+\frac{1}{2}b\right)^2=5\sdot\left(\frac{1}{2}b\right)^2}}$ ובאר אוקלידס שקו ב"ה כאשר חולק על יחס אמצעי ושני קצוות שהחלק הגדול הוא שוה אל קו ד"ה והוא ידוע כי כאשר נחלק קו אחד על יחס בעל אמצעי ושני קצוות ונוסיף על החלק הקטן חצי החלק הגדול ונכה הכל בעצמו שהמרובע ההוה משני אלו מקובצים יהיה חמשה דמיוני הכאת החלק הגדול בעצמו
Elements/Elements XIII-5	definition	המחומשים_והמעושרים#3lPz	It is known from what we have said, as Euclid said, that for every line divisible according to the ratio of a mean and two extremes, when another part equal to the larger portion is added to the line, then whole [line] is divisible according to the ratio of a mean and two extremes, and the larger portion of which is the original line [Elements XIII.5]. והוא ידוע מאשר אמרנו שאמרו אקלידס ואמר שכל קו שהוא על יחס אמצעי ושני קצוות ונוסף באורך הקו כמו החלק ‫60rהגדול וכל זה יחלק על יחס אמצעי ושני קצוות שהחלק הגדול הוא הקו הראשון
Elements/Elements XIII-9	definition	המחומשים_והמעושרים#ScqD	It he said in another place that when the side of a hexagon and the side of a decagon inscribed in the same circle are united in one line, then this whole line is divisible according to the ratio of a mean and two extremes, and the side of the hexagon is the larger portion [Elements XIII.9]. ואמר במקום אחר שכאשר קובצו צלע המשושה עם צלע המעושר אשר בעגולה אחת בקו אחד ישר יהיה כל הקו נחלק על יחס אמצעי ושני קצוות וצלע המשושה הוא החלק הגדול