Difference between revisions of "Find a Number Problems"
From mispar
(→Find One Number) |
(→Find Three Numbers) |
||
| Line 408: | Line 408: | ||
<div class="mw-collapsible mw-collapsed"><math>\scriptstyle\begin{cases}\scriptstyle a+b=c\\\scriptstyle a+c=100b\end{cases}</math><div class="mw-collapsible-content"> | <div class="mw-collapsible mw-collapsed"><math>\scriptstyle\begin{cases}\scriptstyle a+b=c\\\scriptstyle a+c=100b\end{cases}</math><div class="mw-collapsible-content"> | ||
{{#annotask: | {{#annotask: | ||
| − | [[category: #find | + | [[category: #find a number]] |
[[comment: a+b=c;a+c=100b]] | [[comment: a+b=c;a+c=100b]] | ||
}}</div></div><br> | }}</div></div><br> | ||
| Line 414: | Line 414: | ||
<div class="mw-collapsible mw-collapsed"><math>\scriptstyle\begin{cases}\scriptstyle a:b=2:3\\\scriptstyle b:c=3:4\\\scriptstyle\left(a^2\sdot a\right)+b^2=\left(12+\frac{1}{2}\right)\sdot c\end{cases}</math><div class="mw-collapsible-content"> | <div class="mw-collapsible mw-collapsed"><math>\scriptstyle\begin{cases}\scriptstyle a:b=2:3\\\scriptstyle b:c=3:4\\\scriptstyle\left(a^2\sdot a\right)+b^2=\left(12+\frac{1}{2}\right)\sdot c\end{cases}</math><div class="mw-collapsible-content"> | ||
{{#annotask: | {{#annotask: | ||
| − | [[category: #find | + | [[category: #find a number]] |
[[comment: (a²·a)+b²=12½c]] | [[comment: (a²·a)+b²=12½c]] | ||
}}</div></div><br> | }}</div></div><br> | ||
| Line 420: | Line 420: | ||
<div class="mw-collapsible mw-collapsed"><math>\scriptstyle\begin{cases}\scriptstyle\left(a+b\right):c=3+\frac{2}{5}+\frac{1}{7}\\\scriptstyle\left(a+c\right):b=7+\frac{2}{3}+\frac{1}{4}\\\scriptstyle b=30\end{cases}</math><div class="mw-collapsible-content"> | <div class="mw-collapsible mw-collapsed"><math>\scriptstyle\begin{cases}\scriptstyle\left(a+b\right):c=3+\frac{2}{5}+\frac{1}{7}\\\scriptstyle\left(a+c\right):b=7+\frac{2}{3}+\frac{1}{4}\\\scriptstyle b=30\end{cases}</math><div class="mw-collapsible-content"> | ||
{{#annotask: | {{#annotask: | ||
| − | [[category: #find | + | [[category: #find a number]] |
[[comment: (a+b)\c=3⅖⅐;(a+c)\b=7⅔¼;b=30]] | [[comment: (a+b)\c=3⅖⅐;(a+c)\b=7⅔¼;b=30]] | ||
}}</div></div><br> | }}</div></div><br> | ||
| Line 426: | Line 426: | ||
<div class="mw-collapsible mw-collapsed"><math>\scriptstyle\begin{cases}\scriptstyle\left(a+b\right):c=\frac{3}{5}+\frac{1}{6}\\\scriptstyle\left(a+c\right):b=2+\frac{1}{3}\\\scriptstyle a=20\end{cases}</math><div class="mw-collapsible-content"> | <div class="mw-collapsible mw-collapsed"><math>\scriptstyle\begin{cases}\scriptstyle\left(a+b\right):c=\frac{3}{5}+\frac{1}{6}\\\scriptstyle\left(a+c\right):b=2+\frac{1}{3}\\\scriptstyle a=20\end{cases}</math><div class="mw-collapsible-content"> | ||
{{#annotask: | {{#annotask: | ||
| − | [[category: #find | + | [[category: #find a number]] |
[[comment: (a+b)/c=⅗+⅙;(a+c)/b=2⅓;a=20]] | [[comment: (a+b)/c=⅗+⅙;(a+c)/b=2⅓;a=20]] | ||
}}</div></div><br> | }}</div></div><br> | ||
| Line 432: | Line 432: | ||
<div class="mw-collapsible mw-collapsed"><math>\scriptstyle\begin{cases}\scriptstyle b:\left(c-a\right)=3+\frac{1}{3}\\\scriptstyle c:\left(b-a\right)=6\end{cases}</math><div class="mw-collapsible-content"> | <div class="mw-collapsible mw-collapsed"><math>\scriptstyle\begin{cases}\scriptstyle b:\left(c-a\right)=3+\frac{1}{3}\\\scriptstyle c:\left(b-a\right)=6\end{cases}</math><div class="mw-collapsible-content"> | ||
{{#annotask: | {{#annotask: | ||
| − | [[category: #find | + | [[category: #find a number]] |
[[comment: b/(c-a)=3⅓;c/(b-a)=6]] | [[comment: b/(c-a)=3⅓;c/(b-a)=6]] | ||
}}</div></div><br> | }}</div></div><br> | ||
| Line 438: | Line 438: | ||
<div class="mw-collapsible mw-collapsed"><math>\scriptstyle\begin{cases}\scriptstyle\left(a+b\right):\left(c-a\right)=4+\frac{1}{2}\\\scriptstyle\left(a+c\right):\left(b-a\right)=5\end{cases}</math><div class="mw-collapsible-content"> | <div class="mw-collapsible mw-collapsed"><math>\scriptstyle\begin{cases}\scriptstyle\left(a+b\right):\left(c-a\right)=4+\frac{1}{2}\\\scriptstyle\left(a+c\right):\left(b-a\right)=5\end{cases}</math><div class="mw-collapsible-content"> | ||
{{#annotask: | {{#annotask: | ||
| − | [[category: #find | + | [[category: #find a number]] |
[[comment: (a+b)/(c-a)=4½;(a+c)/(b-a)=5]] | [[comment: (a+b)/(c-a)=4½;(a+c)/(b-a)=5]] | ||
}}</div></div><br> | }}</div></div><br> | ||
| Line 444: | Line 444: | ||
<div class="mw-collapsible mw-collapsed"><math>\scriptstyle\begin{cases}\scriptstyle a+\frac{1}{4}\sdot\left(b+c\right)=b+\frac{1}{6}\sdot\left(a+c\right)=c+\frac{1}{9}\sdot\left(a+b\right)\\\scriptstyle b=20\end{cases}</math><div class="mw-collapsible-content"> | <div class="mw-collapsible mw-collapsed"><math>\scriptstyle\begin{cases}\scriptstyle a+\frac{1}{4}\sdot\left(b+c\right)=b+\frac{1}{6}\sdot\left(a+c\right)=c+\frac{1}{9}\sdot\left(a+b\right)\\\scriptstyle b=20\end{cases}</math><div class="mw-collapsible-content"> | ||
{{#annotask: | {{#annotask: | ||
| − | [[category: #find | + | [[category: #find a number]] |
[[comment: a+¼(b+c)=b+⅙(a+c)=c+⅑(a+b);b=20]] | [[comment: a+¼(b+c)=b+⅙(a+c)=c+⅑(a+b);b=20]] | ||
}}</div></div><br> | }}</div></div><br> | ||
| Line 450: | Line 450: | ||
<div class="mw-collapsible mw-collapsed"><math>\scriptstyle\begin{cases}\scriptstyle a:b=b:c\\\scriptstyle a\sdot b\sdot c=1000\end{cases}</math><div class="mw-collapsible-content"> | <div class="mw-collapsible mw-collapsed"><math>\scriptstyle\begin{cases}\scriptstyle a:b=b:c\\\scriptstyle a\sdot b\sdot c=1000\end{cases}</math><div class="mw-collapsible-content"> | ||
{{#annotask: | {{#annotask: | ||
| − | [[category: #find | + | [[category: #find a number]] |
[[comment: a·b·c=1000;a\b\c]] | [[comment: a·b·c=1000;a\b\c]] | ||
}}</div></div><br> | }}</div></div><br> | ||
Revision as of 17:13, 9 October 2022
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | repeated subtraction | מלאכת_המספר#TEa8 | Question: if we subtract 12 from the double of any number, then we subtract another 12 from double the remainder also, and double the remainder is 12, how much is the original number?
:![\scriptstyle2\sdot\left[\left[2\sdot\left(2X-12\right)\right]-12\right]=12](/mediawiki/images/math/2/e/6/2e6830e9068e310a2b310a61c4dc1e73.png) שאילה אם מכפלו של אי זה מספר נקח י"ב ומכפל הנשאר נקח ג"כ י"ב אחרי' וכפל הנשאר יהיה י"ב כמה היה המספר הראשון
שאילה אם מכפלו של אי זה מספר נקח י"ב ומכפל הנשאר נקח ג"כ י"ב אחרי' וכפל הנשאר יהיה י"ב כמה היה המספר הראשון |
| word problem/find a number | repeated subtraction | ספר_חשבון#QPoG | If one asks you: a number, you subtract a tenth from it, then you subtract again a tenth from the remainder, and 100 are left.
:How much was the original number before subtracting the two tenths? : ![\scriptstyle X-\frac{1}{10}X-\left[\frac{1}{10}\sdot\left(X-\frac{1}{10}X\right)\right]=100](/mediawiki/images/math/c/a/9/ca950635d00da924119bda8eef8b09bd.png) אם ישאלך אדם חשבון שהסרות ממנו הי' ומן הנשאר הסרות ממנו העשירית פעם שנית ונשארו ק'
אם ישאלך אדם חשבון שהסרות ממנו הי' ומן הנשאר הסרות ממנו העשירית פעם שנית ונשארו ק'כמה היה כל החשבון בטרם שהסרת ממנו ב' העשיריות |
| word problem/find a number | repeated subtraction | מלאכת_המספר#j27H | Question: if the half of any amount plus one are subtracted, then the half of the remainder plus one, then the half of the remainder plus one, and one remains, how much is the original number?
שאילה אם מאי זה כמות ילקח חציו ואחד יותר ומהנשאר חציו ויותר אחד ומהנשאר חציו ויותר אחד ונשאר אחד כמה היה המספר הראשון
|}
:![\scriptstyle\left[\left[X-\left(\frac{1}{2}X+1\right)\right]-\left[\left[\frac{1}{2}\sdot\left[X-\left(\frac{1}{2}X+1\right)\right]\right]+1\right]\right]-\left[\left[\frac{1}{2}\sdot\left[\left[X-\left(\frac{1}{2}X+1\right)\right]-\left[\left[\frac{1}{2}\sdot\left[X-\left(\frac{1}{2}X+1\right)\right]\right]+1\right]\right]\right]+1\right]=1](/mediawiki/images/math/b/5/0/b50e38940b92660b687bec29a547c334.png) |
Contents
Find a Perfect Number
perfect number
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | perfect number | ספר_דיני_ממונות#x3Is | 109) If you want to find the second [perfect number] קט)MS L: om. ואם תרצה למצא השני |
| word problem/find a number | perfect number | ספר_דיני_ממונות#IXt8 | 108) Question: if you want to find a perfect number קח) שאלה אם תרצה למצא {{#annot:term|75|xt6c}}מספר שלם{{#annotend:xt6c}} נקרא בלשונם {{#annot:term|75|aiWm}}נומירו פירפיטו{{#annotend:aiWm}} |
| word problem/find a number | perfect number | ספר_דיני_ממונות#CaJp | 110) If you want to find the third [perfect number] קי)MS L: om. ואם ואם תרצה למצא השלישי |
Find One Number
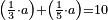
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | ⅓a+⅕a=10 | מלאכת_המספר#niUj | Suppose we want to find any whole, such that the sum of its third and its fifth together is ten.
: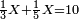 נניח שרצינו למצא אי זה כל שקבוץ שלישיתו וחמישיתו יחד הם עשרה
נניח שרצינו למצא אי זה כל שקבוץ שלישיתו וחמישיתו יחד הם עשרה |
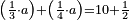
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | ⅓a+¼a=10½ | מלאכת_המספר#IQCS | Example for this: suppose the sum of a third and a quarter of the whole is equal to ten and a half and we wish to know the whole.
: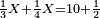 המשל לזה נניח קבוץ אחד משליש ורביע ששוה עשרה וחצי ורצינו לדעת הכל
המשל לזה נניח קבוץ אחד משליש ורביע ששוה עשרה וחצי ורצינו לדעת הכל |
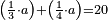
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | ⅓a+¼a=20 | מלאכת_המספר#Auzt | Example: we wish to find a number that the sum of its third and its quarter is 20.
: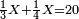 המשל רצינו למצא מספר שקבוץ שלישיתו ורביעיתו יהיה כ'
המשל רצינו למצא מספר שקבוץ שלישיתו ורביעיתו יהיה כ' |
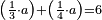
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | ⅓a+¼a=6 | מלאכת_המספר#m65t | Example: we wish to find a number, whose quarter and third are 6.
: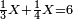 המשל רצינו למצא מספר אחד שרביעיתו ושלישיתו יהיה ו'
המשל רצינו למצא מספר אחד שרביעיתו ושלישיתו יהיה ו' |
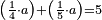
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | ¼a+⅕a=5 | מלאכת_המספר#0Nd6 | As the one who asks about the sum of a quarter and a fifth [of a whole], which is 5 integers, and we wish to know how much is the whole.
: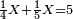 כמי שישאל על קבוץ רביע וחומש שהם ה' שלימי' ונרצה לדעת הכל כמה הוא
כמי שישאל על קבוץ רביע וחומש שהם ה' שלימי' ונרצה לדעת הכל כמה הוא |
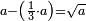
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a-⅓a=√a | ספר_האלזיברא#HmbP | Question: I want to find a number such that when its third is subtracted from it the remainder is the root of the original number
: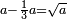 שאלה רציתי למצא מספר כאשר {{#annot: term | #to subtract, #חסר | rg2F}}חסר ממנו{{#annotend:rg2F}} שלישית הנשאר הוא שרש המספר כלו
שאלה רציתי למצא מספר כאשר {{#annot: term | #to subtract, #חסר | rg2F}}חסר ממנו{{#annotend:rg2F}} שלישית הנשאר הוא שרש המספר כלו |
![\scriptstyle\left[a-\left(\frac{2}{3}\sdot a\right)\right]^2=20](/mediawiki/images/math/0/2/0/020aa7d4628e7b55eaa289ac0c2211b9.png)
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | (a-⅓a)²=20 | ספר_האלזיברא#xJ4O | Question: I want to find a number such that when its third is subtracted from it, the square of the remainder is 20.
: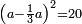 שאלה רציתי למצא מספר כאשר חסר ממנו שלישיתו מרבע הנשאר הוא מספר כ'
שאלה רציתי למצא מספר כאשר חסר ממנו שלישיתו מרבע הנשאר הוא מספר כ' |
![\scriptstyle\left[a\sdot\left(\frac{2}{3}\sdot a\right)\right]^2=36](/mediawiki/images/math/4/4/d/44d26474e128ec5582fe301dd2b9863a.png)
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | (a·⅔a)²=36 | ספר_ג'יבלי_אלמוקבאלא#IqWv | Find me a number, such that when it is multiplied by its two thirds, and the product is multiplied by itself, it yields 36.
:I ask: how much will the number be?
:![\scriptstyle\left[a\sdot\left(\frac{2}{3}\sdot a\right)\right]^2=36](/mediawiki/images/math/4/4/d/44d26474e128ec5582fe301dd2b9863a.png) תמצא לי מספר אחד שכשיוכה בשני שלישיו ועולה שני שלישי צינסו והעולה יוכה בעצמו
יעשה ל"ו
תמצא לי מספר אחד שכשיוכה בשני שלישיו ועולה שני שלישי צינסו והעולה יוכה בעצמו
יעשה ל"ואשאל כמה יבא להיות המספר |
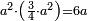
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a²·¾a²=6a | ספר_ג'יבלי_אלמוקבאלא#GJDy | Find me a number, such that when it is multiplied by itself, and the product is multiplied by its three quarters, it yields the same as 6 times the number.
:I ask: how much will this number be?
: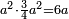 תמצא לי מספר אחד שכאשר הוכה בעצמו ומה שיעלה יוכה ב'''שני שלישיו''' יעשה כמו ו' דמיוני המספר האמור
תמצא לי מספר אחד שכאשר הוכה בעצמו ומה שיעלה יוכה ב'''שני שלישיו''' יעשה כמו ו' דמיוני המספר האמוראשאל כמה יהיה המספר האמור |
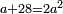
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a+28=2a² | ספר_האלזיברא#AZ3B | Question: we want to find a number such that when we add to it 28 the sum is twice its square
: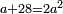 שאלה רצינו למצא מספר כאשר הוספנו עליו כ"ח {{#annot: term | #to be equal to, #שוה | hkKx}}יהיה שוה ל{{#annotend:hkKx}}שני דמיוני מרבעו
שאלה רצינו למצא מספר כאשר הוספנו עליו כ"ח {{#annot: term | #to be equal to, #שוה | hkKx}}יהיה שוה ל{{#annotend:hkKx}}שני דמיוני מרבעו |
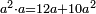
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a²·a=12a+10a² | ספר_ג'יבלי_אלמוקבאלא#FhTO | Find me a number, such that when it is multiplied by itself, and the product is multiplied by that number, it yields the same as the product of that number by 12, and that number multiplied by itself, then this product is multiplied by ten and this is added to the product by 12.
:I ask: how much will the number be?
: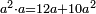 עשה לי החשבון תמצא לי מספר אחד שכאשר הוכה בעצמו ואותה ההכאה תוכה במספר ההוא יעשה כמו הכאת המספר האמור בי"ב ואח"כ להכות המספר האמור בעצמו ואותה ההכאה תוכה בעשרה ולחבר עם ההכאה שנעשתה בי"ב
עשה לי החשבון תמצא לי מספר אחד שכאשר הוכה בעצמו ואותה ההכאה תוכה במספר ההוא יעשה כמו הכאת המספר האמור בי"ב ואח"כ להכות המספר האמור בעצמו ואותה ההכאה תוכה בעשרה ולחבר עם ההכאה שנעשתה בי"באשאל כמה יבא להיות המספר האמור |
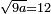
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | √(9a)=12 | ספר_ג'יבלי_אלמוקבאלא#TeOu | Find me a number, such that when it is multiplied by 9, the root of the product is 12.
:I ask: how much will the number be?
: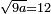 תמצא לי מספר אחד שכאשר יוכה בט' יהיה שרש העולה י"ב
תמצא לי מספר אחד שכאשר יוכה בט' יהיה שרש העולה י"באשאל כמה יבא להיות המספר |
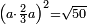
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | (a·⅔a)²=√50 | ספר_ג'יבלי_אלמוקבאלא#MvD8 | Find me a number, such that when it is multiplied by its two thirds, and that product is multiplied by itself, it yields the root of fifty.
:I ask: how much will the number be?
: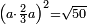 עשה לי זה החשבון תמצא לי מספר אחד שכאשר הוכה בשני שלישיו ואותה ההכאה תוכה בעצמה תעשה שרש חמשים
עשה לי זה החשבון תמצא לי מספר אחד שכאשר הוכה בשני שלישיו ואותה ההכאה תוכה בעצמה תעשה שרש חמשיםאשאל כמה יבא להיות המספר האמור |
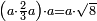
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | (a·⅔a)·a=a√8 | ספר_ג'יבלי_אלמוקבאלא#iQR6 | Find me a number, such that when it is multiplied by its two thirds, and this product is multiplied by that number, it yields the same as the product of that number by the root of 8.
:I ask: how much will the number be?
: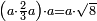 תמצא לי מספר אחד שכשיוכה בשני שלישיו ואותה ההכאה תוכה במספר האמור יעשה כמו הכאת המספר ההוא בשרש ח'
תמצא לי מספר אחד שכשיוכה בשני שלישיו ואותה ההכאה תוכה במספר האמור יעשה כמו הכאת המספר ההוא בשרש ח'אשאל כמה הוא כל אחד מהמספרי' |
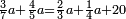
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | ³/₇a+⁴/₅a=⅔a+¼a+20 | ספר_מעשה_חושב#7YKC | Example: three-sevenths and four-fifths of the unknown number exceed two-thirds and a quarter of the unknown number by twenty and we wish to know how much is the number?
::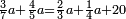 דמיון זה שיהיו ג' שביעיות וד' חמישיות המספר הנעלם מוסיפים על ב' שלישיות ורביעית המספר הנעלם עשרים ורצינו לדעת כמה המספר
דמיון זה שיהיו ג' שביעיות וד' חמישיות המספר הנעלם מוסיפים על ב' שלישיות ורביעית המספר הנעלם עשרים ורצינו לדעת כמה המספר |
| word problem/find a number | ³/₇a+⁴/₅a=⅔a+¼a+20 | ספר_דיני_ממונות#SkQW | 46) Question: three sevenths and four fifths of the unknown number exceed two thirds and a quarter of the unknown number by twenty.
:We wish to know: how much is the number?
: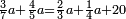 מו) שאלה ג' שביעיות וד' חמישיות המספר הנעלם מוסיפים על ב' שלישיות ורביעית המספר הנעלם כ'
מו) שאלה ג' שביעיות וד' חמישיות המספר הנעלם מוסיפים על ב' שלישיות ורביעית המספר הנעלם כ'רצינו לדעת כמה המספר הנעלם |
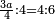
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | (3a/4)/4=4/6 | ספר_דיני_ממונות#mnbD | 43) Question: find me a number such that when multiplied by 3 then divided by 4 the ratio of the remainder to 4 is the same as the ratio of 4 to 6.
: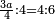 מג) שאלה תמצא לי מספר אשר כשתכפול על ג' ותחלק על ד' ומה שישאר יהיה יחסו אל ד' כיחס ד אל ו'
מג) שאלה תמצא לי מספר אשר כשתכפול על ג' ותחלק על ד' ומה שישאר יהיה יחסו אל ד' כיחס ד אל ו' |
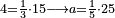
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | 4=⅓·15→a=⅕·25 | ספר_דיני_ממונות#RldY | 65) Question: if number 4 is a third of number 15 what is the fifth of 25? סה) שאלה אם מספר ד' הוא שליש מספר ט"ו מהו חומש כ"ה |
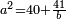
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a²=40+41\b | ספר_דיני_ממונות#aiR7 | 112) Question: find a number such that when you multiply it by itself the result is 40 and 41 parts of a fraction.
: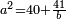 קיב)MS L: קי שאלה תמצא לי מספר אשר כשתכפלהו על עצמו יעלו מ' ומ"א חלקים מאיזה שבר שיזדמן
קיב)MS L: קי שאלה תמצא לי מספר אשר כשתכפלהו על עצמו יעלו מ' ומ"א חלקים מאיזה שבר שיזדמן |
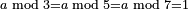
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a(mod)3=a(mod5)=a(mod7)=1 | ספר_דיני_ממונות#lQns | 168) Question: find me a number, such that if you divide it by 3, by 5, and by 7, 1 remains. קסח) שאלה בקש לי מספר שאם תחלקהו על ג' ועל ה ועל ז' ישאר א' |
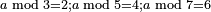
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a(mod)3=2,a(mod5)=4,a(mod7)=6 | ספר_דיני_ממונות#hx8d | 169) Question: if you are told that the remainder after casting out the threes is 2 etc.
:Do it this way:
:For instance, if it is said that when we divide it by 3, 2 remains; if its is divided by 5, 4 remains; and if it is divided by 7, 6 remains.
קסט) שאלה ואם אמר לך שנשאר בהשליכך ג"ג ב' או ג' עשה בדרך הזה עד"מ ואם אמר כשנחלקהו על ג' ישאר ב' ואם יחולק על ה' ישאר ד' ואם יחולק על ז' ישאר ו' |
Find Two Numbers
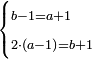
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | b-1=a+1;2(a-1)=b+1 | מלאכת_המספר#4BJp | Knowing the relation of two numbers that have the property that if we subtract one from the greater number and add it to the smaller number, the two numbers become equal; and if we subtract one from the smaller number and add it to the greater, the greater becomes double the smaller, or more if we wish ==== |style="width:45%; text-align:right;"|הפרק השני בידיעת התייחסות שני מספרי' שיש להם זה הטבע שאם נחסר אחד מהמספר הגדול ונוסיפהו על המספר הקטן יהיו הב' מספרי' שוים ואם נחסר אחד מהמספר הקטן ונוסיפהו בגדול יהיה הגדול כפל הקטן או יותר אם נרצה |
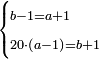
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | b-1=a+1;20(a-1)=b+1 | מלאכת_המספר#osY0 | In order to elaborate the explanation, we give another example: we assume two numbers, such that if we subtract one from the greater number and add it to the smaller, both numbers become equal; and if we subtract one from the smaller number and add it to the greater, the greater becomes twenty times the smaller. [ו]כדי לה[וסי]ף ביאור נעשה משל אחר בשנניח ב' מספר[ים] שאם נחסר אחד מהמספר הגדול [ו]נוסיפהו לקטן יהיה [ה]שני מספרי' שוים ואם נחסר אחד מהמספר הקטן ונוסיפהו בגדול יהיה הגדול עשרי' פעמי' בקטן |
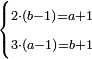
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | 2(b-1)=a+1;3(a-1)=b+1 | מלאכת_המספר#9M9M | The relation of two numbers such that if the greater gives one to the smaller, the smaller becomes double the greater; and if the smaller gives one to the greater, the greater becomes three times the smaller ==== |style="width:45%; text-align:right;"|הפרק הג' ביחס שני מספרי' שאם הגדול יתן אחד לקטן יהיה הקטן כפל הגדול ואם הקטן יתן אחד לגדול יהיה הגדול שלשה פעמי' יותר מהקטן |
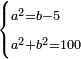
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a²=b-5;a²+b²=100 | ספר_ג'יבלי_אלמוקבאלא#a55J | Find me two numbers, such that when the first is multiplied by itself it yields the second minus 5, and when each of them is multiplied by itself, then both products are summed together, it yields 100.
:I ask: how much will each of the numbers be?
: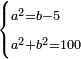 ואשים לך המשל ואומ' כן עשה לי זה החשבון תמצא לי שני מספרי' שכאשר יוכה הראשון בעצמו יעשה השני פחות ה'
ואשים לך המשל ואומ' כן עשה לי זה החשבון תמצא לי שני מספרי' שכאשר יוכה הראשון בעצמו יעשה השני פחות ה'ויוכו כל אחד מהם בעצמו ויחוברו אותם ההכאות יחד יעשה ק' ואשאל יבא כמה להיות כל אחד מהמספרים |
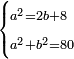
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a²=2b+8;a²+b²=80 | ספר_ג'יבלי_אלמוקבאלא#Ob3R | Find me two numbers such that the one multiplied by itself yields 2 times the second and 8 more;
:and when each of them is multiplied by itself, and the two products are summed together, they yield 80.
:I ask: how much will each number be?
: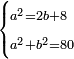 והנה המשל עשה לי זה החשבון תמצא לי ב' מספרי' שכאשר יוכה הראשון בעצמו יעשה ב' דמיוני השני וח' יותר
והנה המשל עשה לי זה החשבון תמצא לי ב' מספרי' שכאשר יוכה הראשון בעצמו יעשה ב' דמיוני השני וח' יותרומוכה כל אחד מהם בעצמו ויקובצו ב' ההכאו' יחד יעשו פ' אשאל כמה יבא להיות כל אחד מהמספרי' |
b=2a
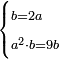
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | b=2a;a²b=9b | ספר_ג'יבלי_אלמוקבאלא#ZaKZ | Find me two numbers such that the one is double the other;
:and when the smaller is multiplied by itself, and the product is multiplied by the second number, it yields the same as the second, i.e. the larger, multiplied by 9.
:I ask: how much will each number be?
: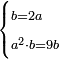 תמצא לי שני מספרים שהאחד יהיה {{#annot: term | #double, #כפל | HqHc}}כפל ה{{#annotend:HqHc}}שני
תמצא לי שני מספרים שהאחד יהיה {{#annot: term | #double, #כפל | HqHc}}כפל ה{{#annotend:HqHc}}שניוכשהוכה הקטון בעצמו ואותה ההכאה תוכה במספר השני יעשה כמו השני רצו' הגדול מוכה על ט' אשאל כמה יבא להיות כל אחד מהמספרים |
a:b=2:3
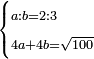
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a/b=⅔;4a+4b=√100 | ספר_ג'יבלי_אלמוקבאלא#FMUp | Find me two numbers such that one is a part of the other as 2 is of 3;
:and when each of them is multiplied by 4, and both products are summed together, they yield a root of 100.
:I ask: how much will each number be?
: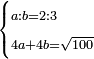 תמצא לי שני מספרים שיהיה חלק האחד מהאחר כמו שהוא ב' מג'
תמצא לי שני מספרים שיהיה חלק האחד מהאחר כמו שהוא ב' מג'וכשיוכה כל אחד בארבעה ויקובצו אלו ההכאות יחד יעשו שרש ק' אשאל כמה יבא להיות כל מספר מהם |
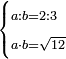
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a/b=⅔;ab=√12 | ספר_ג'יבלי_אלמוקבאלא#zNTn | Find me two numbers such that one is a part of the other as 2 is of 3;
:and if one is multiplied by the other, it yields a root of 12.
:I ask: how much will each number be?
: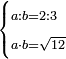 תמצא לי שני מספרים שיהיה חלק האחד מהאחר כמו שהוא ב' מג'
תמצא לי שני מספרים שיהיה חלק האחד מהאחר כמו שהוא ב' מג'ואם יוכה האחד באחר יעשה שרש מי"ב אשאל כמה יבא להיות כל אחד מהמספרים |
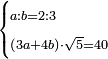
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a/b=⅔;(3a+4b)√5=40 | ספר_ג'יבלי_אלמוקבאלא#PB7l | Find me two numbers such that one is a part of the other as 2 is of 3;
:and when the first is multiplied by 3 and the second by 4, and both products are summed together and multiplied by the root of 5, it yields 40.
:I ask: how much will each number be?
: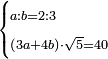 והנה המשל תמצא לי שני מספרים שיהיה חלק אחד מהם לאחר כמו שהוא ב' אל ג'
והנה המשל תמצא לי שני מספרים שיהיה חלק אחד מהם לאחר כמו שהוא ב' אל ג'וכשיוכה הראשון בשלשה והשני בארבעה ואלו שתי ההכאות מחוברים יחד ויוכה בשרש ה' יעשה מ' אשאל כמה יבא להיות כל אחד מהמספרי' |
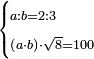
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a/b=⅔;ab√8=100 | ספר_ג'יבלי_אלמוקבאלא#mV9d | Find me two numbers such that one is a part of the other as 2 is of 3;
:and when the one is multiplied by the other, and the product is multiplied by the root of 8, it yields 100.
:I ask: how much will each number be?
: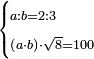 תמצא לי שני מספרי' שיהיה חלק האחד מהאחר כמו שב' הוא מג'
תמצא לי שני מספרי' שיהיה חלק האחד מהאחר כמו שב' הוא מג'וכשיוכה האחד באחר ואותה ההכאה תוכה בשרש ח' ועושה ק' אשאל כמה יבא להיות כל אחד מהמספרי' |
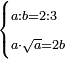
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a/b=⅔;a√a=2b | ספר_ג'יבלי_אלמוקבאלא#Jb23 | Find me two numbers such that the first is a part of the second as 2 is of 3;
:and when the first is multiplied by its root it yields the same as the product of the second by 2.
:I ask: how much will each number be?
: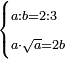 תמצא לי שני מספרים שיהיה הראשון חלק מהשני כמו שב' הוא מג'
תמצא לי שני מספרים שיהיה הראשון חלק מהשני כמו שב' הוא מג'וכשיוכה הראשון בשרש עצמו יעשה כמו הכאת השני בשנים אשאל כמה יבא להיות כל אחד מהמספרים |
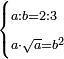
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a/b=⅔;a√a=b² | ספר_ג'יבלי_אלמוקבאלא#LtCT | Find me two numbers such that one is a part of the other as 2 is of 3;
:and when the first is multiplied by its root it yields the same as the product of the second by itself.
:I ask: how much will each number be?
: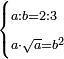 תמצא לי ב' מספרי' שיהיה האחד חלק מהאחר כמו ב' מג'
תמצא לי ב' מספרי' שיהיה האחד חלק מהאחר כמו ב' מג'ובהכות הראשו' בשרשו יעשה כמו הכאת השני בעצמו אשאל כמה יבא להיות כל אחד מן המספרים |
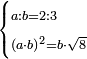
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a/b=⅔;(ab)²=b√8 | ספר_ג'יבלי_אלמוקבאלא#6dSA | Find me two numbers such that the first is a part of the second as 2 is of 3;
:and when the smaller is multiplied by the greater, and this product is multiplied by itself, it yields the same as the product of the second by the root of 8.
:I ask: how much will each number be?
: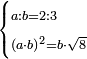 תמצא לי שני מספרים שיהיה הראשון חלק מהשני כמו שהוא ב' מג'
תמצא לי שני מספרים שיהיה הראשון חלק מהשני כמו שהוא ב' מג'ויוכה הקטון בגדול ואותה ההכאה תוכה בעצמה יעשה כמו הכאת השני בשרש ח' אשאל כמה יבא להיות כל אחד מהמספרי' |
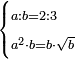
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a/b=⅔;a²b=b√b | ספר_ג'יבלי_אלמוקבאלא#DcQa | Find me two numbers such that the one is a part of the other as 2 is of 3;
:and when the first is multiplied by itself and this product is multiplied by the second, it yields the same as the product of the second by its root.
:I ask: how much will each number be?
: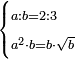 תמצא לי שני מספרי' שיהיה האחד חלק מהשני כמו שב' הוא מג'
תמצא לי שני מספרי' שיהיה האחד חלק מהשני כמו שב' הוא מג'ומוכה הראשון בעצמו ואותה ההכאה תוכה במספר השני יעשה 34vכמו הכאת השני בשרשו אשאל כמה יבא להיות כל אחד מהמספרי' |
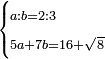
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a/b=⅔;5a+7b=16+√8 | ספר_ג'יבלי_אלמוקבאלא#qQCL | Find me two numbers such that the one is a part of the other as 2 is of 3;
:and when the first is multiplied by 5 and the second by 7, then both the products are summed together, it yields 16 and a root of 8.
:I ask: how much will each number be?
: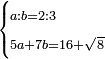 תמצא לי שני מספרי' שיהיה האחד מהאחר כמו שב' הוא מג'
תמצא לי שני מספרי' שיהיה האחד מהאחר כמו שב' הוא מג'ומוכה הראשון בה' והשני בז' ושתי אלו ההכאות יחוברו יחד יעשו י"ו ושרש ח' אשאל כמו' יבא להיות כל אחד מהמספרי' |
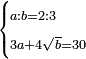
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a/b=⅔;3a+4√b=30 | ספר_ג'יבלי_אלמוקבאלא#37bI | Find me two numbers such that the one is a part of the other as 2 is of 3;
:and when the first is multiplied by 3 and the root of the second by 4, then both the products are summed together, it yields thirty.
:I ask: how much will each number be?
: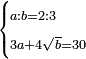 והנה המשל תמצא לי שני מספרי' שיהיה האחד חלק מאחר כמו שב' הוא מג'
והנה המשל תמצא לי שני מספרי' שיהיה האחד חלק מאחר כמו שב' הוא מג'ובהכות הראשון בג' ושרש השני בד' ויחוברו שתי אלו ההכאות יחד יעשה שלשים אשאל כמה יבא להיות כל אחד מהמספרי' |
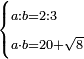
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a/b=⅔;ab=20+√8 | ספר_ג'יבלי_אלמוקבאלא#B6TE | Find me two numbers such that the first is a part of the second as 2 is of 3;
:and when the first is multiplied by the second it yields 20 and a root of 8.
:I ask: how much will each number be?
: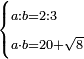 תמצא לי שני מספרים שיהיה הראשון חלק מהשני כמו שב' הוא מג'
תמצא לי שני מספרים שיהיה הראשון חלק מהשני כמו שב' הוא מג'ומוכה הראשון בשני יעשה כ' ושרש ח' אשאל כמה יבא להיות כל אחד מהמספרי' |
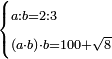
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a/b=⅔;(ab)b=100+\sqrt{8} | ספר_ג'יבלי_אלמוקבאלא#GBTu | Find me two numbers such that the first is a part of the other as 2 is of 3;
:and when the first is multiplied by the second, then this product is multiplied by the second, it yields 100 and a root of 8.
:I ask: how much will each number be?
: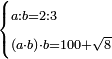 עשה לי החשבון תמצא לי שני מספרים שיהיה המספר ראשון חלק מהאחר כמו שב' הוא מג'
עשה לי החשבון תמצא לי שני מספרים שיהיה המספר ראשון חלק מהאחר כמו שב' הוא מג'ובהכות הראשון בשני ואותה ההכאה תוכה בשני יעשה מאה ושרש ח' אשאל כמה יבא להיות כל אחד מהמספרי' |
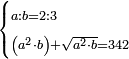
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a/b=⅔;a²b+\sqrt{a²b}=342 | ספר_ג'יבלי_אלמוקבאלא#oR0N | Find me two numbers such that the first is a part of the second as 2 is of 3;
:and if the first is multiplied by itself, then this product is multiplied by the second, and this product is summed with its root, it yields 342.
:I ask: how much will each number be?
: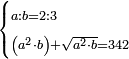 עשה לי זה החשבון תמצא לי שני מספרי' שיהיה הראשון חלק מהשני כמו שב' הוא מג'
עשה לי זה החשבון תמצא לי שני מספרי' שיהיה הראשון חלק מהשני כמו שב' הוא מג'ומוכה הראשון בעצמו ואותה ההכאה תכה בשני ותחובר זאת ההכאה עם שרשה יעשה שמ"ב אשאל כמה יבא להיות כל אחד מהמספרי' |
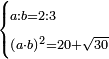
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a/b=⅔;(ab)²=20+√30 | ספר_ג'יבלי_אלמוקבאלא#9iel | [Find me two numbers] such that one is a part of the other as 2 is of 3;
:and when the first is multiplied by the second and this product is multiplied by itself, it yields 20 and a root of 20.
:I ask: how much will each number be?
: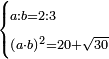 עשה לי זה החשבון שיהיה האחד חלק מהאחר כמו שב' הוא חלק מג'
עשה לי זה החשבון שיהיה האחד חלק מהאחר כמו שב' הוא חלק מג'ובהכות הראשון בשני ואותה ההכאה תוכה בעצמה יעשה כ' ושרש ל' אשאל כמה יבא להיות כל אחד מהמספרי' |
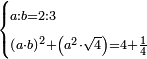
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a/b=⅔;(ab)²+a²√4=4¼ | ספר_ג'יבלי_אלמוקבאלא#jPKB | Find me two numbers such that one is a part of the other as 2 is of 3;
:and when the first is multiplied by the second and this product is multiplied by itself then summed with the product of the first multiplied by itself then by the root of 4, it yields 4 and a quarter.
:I ask: how much will each number be?
: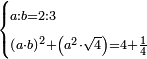 עשה לי זה החשבון תמצא לי שני מספרי' שיהיה הא' חלק מהאחר כמו שב' הוא מג'
עשה לי זה החשבון תמצא לי שני מספרי' שיהיה הא' חלק מהאחר כמו שב' הוא מג'ומוכה הראשון בשני וזאת ההכאה תוכה בעצמה ותחובר זאת ההכאה עם הכאת הראשון מוכה בעצמו ומה שיבא בשרש ד' יעשה ד' ורביע אשאל כמה יבא להיות כל אחד מהמספרי' |
![\scriptstyle\begin{cases}\scriptstyle a:b=2:3\\\scriptstyle3a+4b=\sqrt[3]{216}\end{cases}](/mediawiki/images/math/3/7/c/37c574e931d2b293ce8e7c05872dd409.png)
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a/b=⅔;3a+4b=³√216 | ספר_ג'יבלי_אלמוקבאלא#w4Ac | Find me two numbers such that one is a part of the other as 2 is of 3;
:and when the first is multiplied by 3 and the second by 4, and both products are summed together, they yield a cube root of 216.
:I ask: how much will each number be?
:![\scriptstyle\begin{cases}\scriptstyle a:b=2:3\\\scriptstyle3a+4b=\sqrt[3]{216}\end{cases}](/mediawiki/images/math/3/7/c/37c574e931d2b293ce8e7c05872dd409.png) והנה המשל תמצא לי ב' מספרי' שיהיה האחד חלק מהאחר כמו שב' הוא מג'
והנה המשל תמצא לי ב' מספרי' שיהיה האחד חלק מהאחר כמו שב' הוא מג'ומוכה הראשון בג' והשני בד' ויחוברו ב' אלו ההכאו' יחד יעשה שרש מעוק' מרי"ו אשאל כמה יבא להיות כל א' מהמספרי' |
a:b=3:4
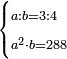
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a/b=¾;a²b=288 | ספר_ג'יבלי_אלמוקבאלא#7M0L | Find me two numbers such that the one is a part of the other as 3 is of 4;
:and when the smaller is multiplied by itself, and the product is multiplied by the larger, it yields 288.
:I ask: how much will each number be?
: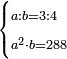 תמצא לי שני מספרים שיהיה האחד חלק מהאחר כמו שהוא ג' מד'
תמצא לי שני מספרים שיהיה האחד חלק מהאחר כמו שהוא ג' מד'וכשיוכה הקטן בעצמו ו{{#annot: term | #result, #יוצא | QU3I}}היוצא{{#annotend:QU3I}} תכה בגדול יעשה רפ"ח אשאל כמה כל אחד מהמספרי' |
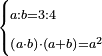
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a/b=¾;(ab)·(a+b)=a² | ספר_ג'יבלי_אלמוקבאלא#bWjS | Find me two numbers such that the one is a part of the other as 3 is of 4;
:and when the first is multiplied by the second, and the product is multiplied by the sum of both numbers together, it yields the same as the product of the larger by itself.
:I ask: how much will each number be?
: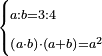 תמצא לי שני מספרים שיהיה חלק האחד מהאחר כמו שהוא ג' מד'
תמצא לי שני מספרים שיהיה חלק האחד מהאחר כמו שהוא ג' מד'וכאשר הוכה הראשון בשני ואותה ההכאה תוכה על מקובץ שני המספרי' יחד יעשה כמו הכאת הגדול בעצמו אשאל כמה יבא להיות כל אחד מהמספרי' |
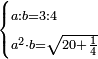
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a/b=¾;a²b=√(20¼) | ספר_ג'יבלי_אלמוקבאלא#4NoH | Find me two numbers such that one is a part of the other as 3 is of 4;
:and when the one is multiplied by itself, and this product is multiplied by the second, it yields a root of 20 and a quarter.
:I ask: how much will each number be?
: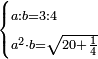 עשה לי זה החשבון תמצא לי שני מספרים שיהיה חלק האחד מהאחר כמו מה שהוא ג' מד'
עשה לי זה החשבון תמצא לי שני מספרים שיהיה חלק האחד מהאחר כמו מה שהוא ג' מד'וכשיוכה הראשון בעצמו ואותה ההכאה תכה בשני יעשה שרש כ' ורביע אשאל כמה יבא להיות כל אחד מהמספרים |
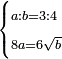
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a/b=¾;8a=6√b | ספר_ג'יבלי_אלמוקבאלא#8HYy | Find me two numbers such that the one is a part of the second as 3 is of 4;
:and the first multiplied by 8, yields the same as the root of the second multiplied by 6.
:I ask: how much will each number be?
: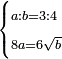 תמצא לי שני מספרי' שיהיה החלק האחד מהשני כמו שהוא ג' מד'
תמצא לי שני מספרי' שיהיה החלק האחד מהשני כמו שהוא ג' מד'וכן יעשה הראשון מוכה בח' כמו השני דהיינו שרשו מוכה בו' אשאל כמה יבא להיות כל אחד מהמספרים |
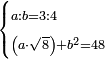
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a/b=¾;a√8+b²=48 | ספר_ג'יבלי_אלמוקבאלא#aGAJ | Find me two numbers such that the one is a part of the other as 3 is of 4;
:and if the first is multiplied by the root of 8, and the second is multiplied by itself, then both products are summed together, it yields 48.
:I ask: how much will each number be?
: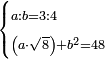 תמצא לי שני מספרי' שהאחד יהיה חלק מהאחר כמו שג' הוא מד'
תמצא לי שני מספרי' שהאחד יהיה חלק מהאחר כמו שג' הוא מד'ומוכה הראשון בשרש ח' והשני בעצמו ואותן שתי הכאות יחוברו יחד יעשו מ"ח אשאל כמה יבא להיות כל האחד מהמספרי' |
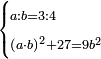
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a/b=¾;(ab)²+27=9b² | ספר_ג'יבלי_אלמוקבאלא#gmur | Find me two numbers such that the first is a part of the other as 3 is of 4;
:and the first multiplied by the second, and this product is multiplied by itself and 27 is added to it, yield the second number multiplied by itself and this product is multiplied by 9.
:I ask: how much will each number be?
: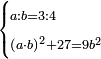 עשה לי זה החשבון תמצא לי שני מספרי' שיהיה הראשון חלק מהשני כמו שג' הוא מד'
עשה לי זה החשבון תמצא לי שני מספרי' שיהיה הראשון חלק מהשני כמו שג' הוא מד'ומוכה הראשון בשני ואותה ההכאה תוכה בעצמה ויחובר עמה כ"ז יעשה המספר השני בכפלו בעצמו ואותה ההכאה תוכה בט' אשאל כמה הוא כל אחד מהמספרים האמורי' |
![\scriptstyle\begin{cases}\scriptstyle a:b=3:4\\\scriptstyle\sqrt[3]{2a+3b}=8\end{cases}](/mediawiki/images/math/f/d/f/fdfeea3918f71a57781b72d247caef5c.png)
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a/b=¾;³√(2a+3b)=8 | ספר_ג'יבלי_אלמוקבאלא#q0Kk | Find me two numbers such that one is a part of the other as 3 is of 4;
:and when the one is multiplied by 2 and the other is multiplied by 3, and the two products are summed together their cube root is 8.
:I ask: how much will each number be?
:![\scriptstyle\begin{cases}\scriptstyle a:b=3:4\\\scriptstyle\sqrt[3]{2a+3b}=8\end{cases}](/mediawiki/images/math/f/d/f/fdfeea3918f71a57781b72d247caef5c.png) והנה המשל עשה לי זה החשבון תמצא לי ב' מספרי'
שיהיה הא' חלק מהאחר כמו שג' הוא מד'
והנה המשל עשה לי זה החשבון תמצא לי ב' מספרי'
שיהיה הא' חלק מהאחר כמו שג' הוא מד'ומוכה הראשון בב' והשני בג' ויקובצו ב' אלו ההכאו' יחד יהיה שרשם המעוקב ח' אשאל כמה יבא להיות כל א' מהמספרי' |
a:b=4:5
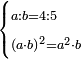
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a/b=⅘;(ab)²=a²b | ספר_ג'יבלי_אלמוקבאלא#Ukgo | Find me two numbers such that the first is a part of the second as 4 is of 5;
:and when the first is multiplied by the second, and this product is multiplied by itself, it yields the same as the product of the first by itself, then that product is multiplied by the second number.
:I ask: how much will each number be?
: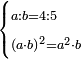 תמצא לי שני {{#annot: term | #proportional, #מתיחס | lK1I}}מספרים מתיחסים{{#annotend:lK1I}} שיהיה חלק הראשון מהשני כמו שהוא ד' מה'
תמצא לי שני {{#annot: term | #proportional, #מתיחס | lK1I}}מספרים מתיחסים{{#annotend:lK1I}} שיהיה חלק הראשון מהשני כמו שהוא ד' מה'וכשיוכה הראשון בשני ואותה ההכאה תוכה בעצמה ויעשה כמו שעושה הראשון מוכה בעצמו ואותה ההכאה תוכה במספר השני אשאל כמה יבא להיות כל אחד מהמספרים |
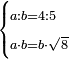
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a/b=⅘;ab=b√8 | ספר_ג'יבלי_אלמוקבאלא#roVS | Find me two numbers such that the first is a part of the second as 4 is of 5;
:and the one multiplied by the other yields the same as the product of the second by the root of 8.
:I ask: how much will each number be?
: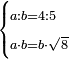 תמצא לי ב' מספרי' שיהיה הראשון חלק מהשני כמו שד' הוא מה'
תמצא לי ב' מספרי' שיהיה הראשון חלק מהשני כמו שד' הוא מה'ומוכה האחד באחר יעשה כמו הכאת השני בשרש ח' אשאל כמה יבא להיות כל אחד מהמספרי' |
a:b=3:5
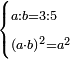
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a/b=⅗;(ab)²=a² | ספר_ג'יבלי_אלמוקבאלא#0dhl | Find me two numbers such that the first is a part of the second as 3 is of 5;
:and when the smaller is multiplied by the greater and the product is multiplied by itself, it yields the same as the product of the greater by itself.
:I ask: how much will each number be?
: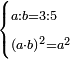 תמצא לי שני מספרים שיהיה חלק הראשון מהשני כמו שהוא ג' מה'
תמצא לי שני מספרים שיהיה חלק הראשון מהשני כמו שהוא ג' מה'וכאשר הוכה הקטון בגדול ומה שיעלה יוכה בעצמו יעשה כמו הכאת הגדול בעצמו אשאל כמה כל אחד מהמספרים |
![\scriptstyle\begin{cases}\scriptstyle a:b=3:5\\\scriptstyle\left[\left(a\sdot\sqrt{a}\right)+\left(b\sdot\sqrt{b}\right)\right]\sdot\sqrt{8}=100\end{cases}](/mediawiki/images/math/7/1/1/71187e61ee927d7bba48ce232ff213cc.png)
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a/b=⅗;(a√a+b√b)√8=100 | ספר_ג'יבלי_אלמוקבאלא#dp2A | Find me two numbers such that the one is a part of the other as 3 is of 5;
:and when each is multiplied by its root and both products are summed together, then the sum is multiplied by the root of 8, it yields 100.
:I ask: how much will each number be?
:![\scriptstyle\begin{cases}\scriptstyle a:b=3:5\\\scriptstyle\left[\left(a\sdot\sqrt{a}\right)+\left(b\sdot\sqrt{b}\right)\right]\sdot\sqrt{8}=100\end{cases}](/mediawiki/images/math/7/1/1/71187e61ee927d7bba48ce232ff213cc.png) תמצא לי שני מספרי' שיהיה חלק האחד מהאחר כמו שהוא ג' מה'
תמצא לי שני מספרי' שיהיה חלק האחד מהאחר כמו שהוא ג' מה'וכשיוכה כל אחד על שרשו ויחוברו שתי אלו ההכאות יחד וזה הסך יוכה בשרש ח' יעשה מאה אשאל כמה יבא להיות כל אחד מהמספרים |
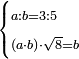
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a/b=⅗;ab√8=b | ספר_ג'יבלי_אלמוקבאלא#nOEQ | Find me two numbers such that the one is a part of the other as 3 is of 5;
:and when the one is multiplied by the other, then this product is multiplied by the the root of 8, it yields the same as the second number.
:I ask: how much will each number be?
: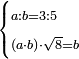 עשה לי זה החשבון תמצא לי ב' מספרי' שיהיה האחד חלק מהאחר כמו שהוא ג' מה'
עשה לי זה החשבון תמצא לי ב' מספרי' שיהיה האחד חלק מהאחר כמו שהוא ג' מה'וכשיוכה האחד באחר ואותה ההכאה תוכה בשרש ח' יעשה כמו המספר השני אשאל כמה הוא כל אחד מהמספרים |
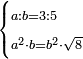
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a/b=⅗;a²b=b²√8 | ספר_ג'יבלי_אלמוקבאלא#YrhT | Find me two numbers such that the one is a part of the other as 3 is of 5;
:and the the first is multiplied by the other, then this product is multiplied by the second number, it yields the same as the product of the second by itself, then the product is multiplied by the root of 8.
:I ask: how much will each number be?
: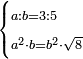 עשה לי זה החשבון תמצא לי שני מספרי' שיהיה האחד חלק מהאחר כמו שג' הם מה'
עשה לי זה החשבון תמצא לי שני מספרי' שיהיה האחד חלק מהאחר כמו שג' הם מה'ומוכה הראשון בעצמו ואותה ההכאה תוכה אשאל כמה יבא להיות כל אחד מהמספרי' |
![\scriptstyle\begin{cases}\scriptstyle a:b=3:5\\\scriptstyle a\sdot b=\sqrt[3]{729}\end{cases}](/mediawiki/images/math/0/5/a/05a756d12f1bd790b4653042daf26458.png)
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a/b=⅗;ab=³√729 | ספר_ג'יבלי_אלמוקבאלא#ai8Z | Find me two numbers such that one is a part of the other as 3 is of 5;
:and the one multiplied by the other yields a cube root of 729.
:I ask: how much will each number be?
:![\scriptstyle\begin{cases}\scriptstyle a:b=3:5\\\scriptstyle a\sdot b=\sqrt[3]{729}\end{cases}](/mediawiki/images/math/0/5/a/05a756d12f1bd790b4653042daf26458.png) והנה המשל תמצא לי ב' מספרי' שיהיה האחד חלק מהאחר כמו ג' מה'
והנה המשל תמצא לי ב' מספרי' שיהיה האחד חלק מהאחר כמו ג' מה'ומוכה הראשון בשני יעשה שרש מעו' מתשכ"ט אשאל כמה יבא להיות כל אחד מהמספרי' |
a:b=2:5
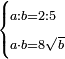
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a/b=⅖;ab=8√b | ספר_ג'יבלי_אלמוקבאלא#BstD | Find me two numbers such that the one is a part of the other as 2 is of 5;
:and when the first is multiplied by the second, it yields the same as the product of the root of the second by 8.
:I ask: how much will each number be?
: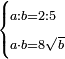 תמצא לי שני מספרי' שיהיה האחד חלק מהאחר כמו שב' הוא מה'
תמצא לי שני מספרי' שיהיה האחד חלק מהאחר כמו שב' הוא מה'וכשהוכה האחד בשני יעשה כמו הכאת שרש השני בח' אשאל כמה יבא להיות כל אחד מהמספרי' |
a:b=1:4
![\scriptstyle\begin{cases}\scriptstyle a:b=1:4\\\scriptstyle\left(a\sdot b\right)\sdot a=\sqrt[3]{216}\end{cases}](/mediawiki/images/math/1/7/1/171ce646462d735ef90bd02638d35efb.png)
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a/b=¼;aba=³√216 | ספר_ג'יבלי_אלמוקבאלא#nkyB | Find me two numbers such that one is a part of the other as 1 is of 4;
:and the one multiplied by the other, and this product is multiplied by the first, yields a cube root of 216.
:I ask: how much will each number be?
:![\scriptstyle\begin{cases}\scriptstyle a:b=1:4\\\scriptstyle\left(a\sdot b\right)\sdot a=\sqrt[3]{216}\end{cases}](/mediawiki/images/math/1/7/1/171ce646462d735ef90bd02638d35efb.png) והנה המשל תמצא לי שני מספרי' שיהיה אחד מהם חלק מהאחר כמו שא' הוא מד'
והנה המשל תמצא לי שני מספרי' שיהיה אחד מהם חלק מהאחר כמו שא' הוא מד'ומוכה הראשון בשני וההכאה ההיא תוכה בראשון יעשה שרש מעו' מרי"ו אשאל כמה יבא להיות כל אחד מהמספרי' |
a:b=1:3
![\scriptstyle\begin{cases}\scriptstyle a:b=1:3\\\scriptstyle\sqrt[3]{a}\sdot\sqrt[3]{b}=100\end{cases}](/mediawiki/images/math/6/b/6/6b684d922156985988350c4b2a4c248d.png)
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a/b=⅓;³√a³√b=100 | ספר_ג'יבלי_אלמוקבאלא#AP3O | Find me two numbers such that the one is a part of the second as 1 is of 3;
:and the cube root of the first multiplied by the cube root of the second yields 100.
:I ask: how much will each number be?
:![\scriptstyle\begin{cases}\scriptstyle a:b=1:3\\\scriptstyle\sqrt[3]{a}\sdot\sqrt[3]{b}=100\end{cases}](/mediawiki/images/math/6/b/6/6b684d922156985988350c4b2a4c248d.png) והנה המשל עשה לי זה החשבון תמצא לי 43rשני מספרי' שיהיה הראשון חלק מהשני כמו שא' הוא מג'
והנה המשל עשה לי זה החשבון תמצא לי 43rשני מספרי' שיהיה הראשון חלק מהשני כמו שא' הוא מג'ומוכה שרש מעו' מהראשון בשרש מעו' השני יעשה ק' אשאל כמה יבא להיות כל אחד מן המספרי' |
a:b=5:7
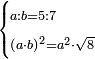
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a/b=⁵/₇;(ab)²=a²√8 | ספר_ג'יבלי_אלמוקבאלא#3fAj | Find me two numbers such that the one is a part of the other as 5 is of 7;
:and if the first is multiplied the second, then the product is multiplied by itself, it yields the same as the product of the smaller by itself, then the product multiplied by the root of 8.
:I ask: how much will each number be?
: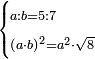 תמצא לי שני מספרי' שיהיה האחד חלק מהאחר כאשר ה' הוא מז'
תמצא לי שני מספרי' שיהיה האחד חלק מהאחר כאשר ה' הוא מז'ומוכה הראשון בשני ואותה ההכאה תוכה בעצמה יעשה כמו הכאת המספר הקטן בעצמו וההכאה ההיא תוכה בשרש ח' אשאל כמה יבא להיות כל אחד מהמספרי' |
Find Three Numbers
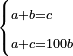
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a+b=c;a+c=100b | מלאכת_המספר#Q70A | Question: if there are three numbers, the [sum of the] first and the second is as the third, and the [sum of the] first and the third is as a hundred of the second. How much is each of the three numbers? שאילה אם יהיו ג' מספרי' והראשון והשני יהיו בכמות השלישי והראשון והשלישי כמאה מן השני כמה יהיה כל אחד מהשלשה מספרי' |
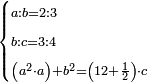
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | (a²·a)+b²=12½c | ספר_ג'יבלי_אלמוקבאלא#iH47 | Find me three numbers, such that the first is a part of the second as 2 is of 3, and the second is of the third as 3 is of 4.
:If the first is multiplied by itself, then the product is multiplied by the first number, and the second number is multiplied by itself, when both products are summed together, its yields the same as the product of the third number by 12 and a half.
: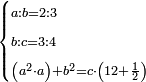 והנה המשל תמצא לי שלשה מספרים שיהיה חלק הראשון מהשני כמו שהוא ב' מג'
והנה המשל תמצא לי שלשה מספרים שיהיה חלק הראשון מהשני כמו שהוא ב' מג'והשני יהיה מהשלישי כמו שהוא ג' בד' ותכה הראשון בעצמו ואח"כ יוכה העולה במספר הראשון בעצמו ואח"כ יוכה המספר השני בעצמו וכשיחוברו יחד שתי אלו ההכאות יעשה כמו הכאת המספר השלישי בי"ב וחצי אשאל כמה יבא להיות כל אחד מהמספרים |
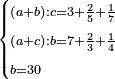
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | (a+b)\c=3⅖⅐;(a+c)\b=7⅔¼;b=30 | ספר_דיני_ממונות#OJ9R | 58) Question: when one number is added to a second number, their ratio to the third is 3 integers, 2-fifths and a seventh.
:When the first is added to the third, their ratio to the [second] is 7 integers, 2-thirds and a quarter.
:The second number is 30.
:We wish to know: how much is each of the rest?
נח) שאלה שיהיה מספר ראשון כשחובר אל מספר שני היה יחסו אל הג' ג' שלמים וב' חמישיות ושביעיות וכשחובר הראשון אל הג' היה יחסו הראשון ז' שלמים וב' שלישיות ורביעיות והמספר הב' ל' רצינו לדעת כמה כל א' מהנשארים |
| word problem/find a number | (a+b)\c=3⅖⅐;(a+c)\b=7⅔¼;b=30 | ספר_מעשה_חושב#odgb | Example: when one number is added to a second number, their ratio to the third is 3 integers, 2-fifths and a seventh.
::When the first is added to the third, their ratio to the second is 7 integers, 2-thirds and a quarter.
::The second number is 30.
::We wish to know: how much is each of the rest?
::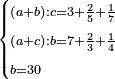 דמיון שיהיה מספר ראשון כשחובר אל מספר שני היה יחסו אל השלישי ג' שלמים וב' חמשיות ושביעית
דמיון שיהיה מספר ראשון כשחובר אל מספר שני היה יחסו אל השלישי ג' שלמים וב' חמשיות ושביעיתוכשחובר הראשון אל השלישי יהיה יחסו אל השניאל השני: P2271 הראשון ז' שלמים וב' שלישיות ורביעית והמספר השני שלשים ורצינו לדעת כמה כל אחד מהנשארים |
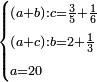
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | (a+b)/c=⅗+⅙;(a+c)/b=2⅓;a=20 | ספר_דיני_ממונות#gfLj | 59) Question: the ratio of the first and the second summed together to the third is 3-fifths plus a sixth.
:The ratio of the first and the third summed together to the second is 2 integers and a third.
:The first number is 20.
:We wish to know: how much is each of the remaining numbers?
נט) שאלה יהיה יחס הראשון עם השני מקובצים אל השלישי ג' חמישיות ושישית ויחס הראשון והג' מקובצים אל השני ב' שלמים ושלישית והמספר הראשון עשרים נרצה לדעת כמה כל א' מהמספרים הנשארים |
| word problem/find a number | (a+b)/c=⅗+⅙;(a+c)/b=2⅓;a=20 | ספר_מעשה_חושב#0XvG | Another example: the ratio of the first and the second summed together to the third is 3-fifths and a sixth.
::The ratio of the first and the third summed together to the second is 2 integers and a third.
::The first number is 20.
::We wish to know: how much is each of the remaining numbers?
::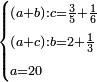 דמיון אחר יהיה יחס הראשון והשני מקובצים אל השלישי ג' חמשיות וששית
דמיון אחר יהיה יחס הראשון והשני מקובצים אל השלישי ג' חמשיות וששיתויחס הראשון והשלישי מקובצים אל השני ב' שלמים ושלישית והמספר הראשון עשרים ורצינו לדעת כמה כל אחד מ[ה]מספרים הנשארים |
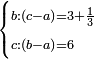
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | b/(c-a)=3⅓;c/(b-a)=6 | ספר_מעשה_חושב#353o | Example: the ratio of the second to what remains from the third when the first is subtracted from it is 3 integers and a third.
::The ratio of the third to what remains from the second when the first is subtracted from it is the number 6.
::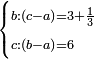 והמשל שיהיה יחס 82vהשני אל הנשאר מהשלישי כשחוסר ממנו הראשון ג' שלמים ושליש
והמשל שיהיה יחס 82vהשני אל הנשאר מהשלישי כשחוסר ממנו הראשון ג' שלמים ושלישויחס השלישי אל הנשאר מהשני כשחוסר ממנו הראשון מספר ו' |
| word problem/find a number | b/(c-a)=3⅓;c/(b-a)=6 | ספר_דיני_ממונות#73tk | 60) Question: the ratio of the second to what remains from the third when the first is subtracted from it is 3 integers and a third.
:The ratio of the third to what remains from the second when the first is subtracted from it is the number 6.
[ס)] שאלה שיהיה יחס הב' אל הנשאר מהג' כשחוסר ממנו הא' ג' שלמים ושליש ויחס הג' אל הנשאר מהב' כשחוסר ממנו הא' מספר ו' |
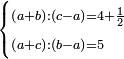
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | (a+b)/(c-a)=4½;(a+c)/(b-a)=5 | ספר_מעשה_חושב#UAnP | Example: the ratio of the first and the second summed together to what remains from the third when the first is subtracted from it is 4 integers and a half.
::The ratio of the first and the third summed together to what remains from the second when the first is subtracted from it is 5 integers.
::We wish to know: how much is each of the numbers that meet this condition?
::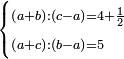 והמשל שיהיה יחס הראשון והשני מקובצים אל הנשאר [מהשלישי כשחוסר ממנו הראשון ד' שלמים וחצי
והמשל שיהיה יחס הראשון והשני מקובצים אל הנשאר [מהשלישי כשחוסר ממנו הראשון ד' שלמים וחציויחס הראשון והשלישי מקובצים אל הנשאר] מהשני כשחוסר ממנו הראשון הוא ה' שלמים ונרצה לדעת כמה כל המספרים שינהגו זה המנהג |
| word problem/find a number | (a+b)/(c-a)=4½;(a+c)/(b-a)=5 | ספר_דיני_ממונות#UcvZ | 61) Question: the ratio of the first and the second summed together to what remains from the third when the first is subtracted from it is 4 integers and a half.
:The ratio of the first and the third summed together to what remains from the second when the first is subtracted from it is 5 integers.
:We wish to know: how much is each of the numbers that meet this condition?
סא) שאלה שיהיה יחס הראשון והשני מקובצים אל הנשאר מהג' כשחוסר ממנו הראשון ד' שלמים וחצי ויחס הראשון והג' מקובצים אל הנשאר מהב' כשחוסר ממנו הראשון הוא ה' שלמים ונרצה לדעת כמה כל המספרים שינהגו זה המנהג |
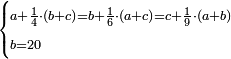
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a+¼(b+c)=b+⅙(a+c)=c+⅑(a+b);b=20 | ספר_מעשה_חושב#sryH | Example: the first with a quarter of the rest is equal to the second with a sixth of the rest and is also equal to the third with a ninth of the rest.
::The first is added to the greatest part of the rest and the third is added to the smallest part of the rest.
::The second number is 20.
::We wish to know: how much is each of the rest?
::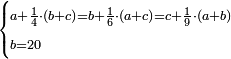 והמשל שיהיה הראשון עם רביעית הנשארים שוה אל השני עם ששית הנשארים
והמשל שיהיה הראשון עם רביעית הנשארים שוה אל השני עם ששית הנשאריםוהוא גם כן שוה אל השלישי עם תשיעית הנשארים וכבר התבאר לך במאמר הראשון מזה הספר שסדר אלו המספרים השלשה הוא על זאת ההדרגה אשר סדרנו רצוני שהראשון הוא אשר יתחבר עמו חלק יותר גדול מהנשארים והשלישי הוא אשר יתחבר עמו חלק יותר קטן מהנשארים והזכרתי לך זה למען לא תתבלבל בסדורם ויהיה המספר השני מהם כ' ורצינו לדעת כמה כל אחד מהנשארים |
| word problem/find a number | a+¼(b+c)=b+⅙(a+c)=c+⅑(a+b);b=20 | ספר_דיני_ממונות#HxDL | 62) Question: the first with a quarter of the rest is equal to the second with a sixth of the rest and is also equal to the third with a ninth of the rest.
:It has already been explained to you in the first section of this book that the order of these three numbers is according to this arrangement, meaning that the first is added to the greatest part of the rest and the [third] is added to the smallest part of the rest. I remind you this so that you will not be confused by the explanations.
:The second number is 20.
:We wish to know: how much is each of the rest?
סב) שאלה שיהיה הראשון עם רביעית הנשארים שוה אל השני עם שישית הנשארי' והוא ג"כ שוה אל השלישי עם תשיעית הנשארים כבר התבאר לך במאמ' הראשון מזה הספר שסדור אלו המספרים הג' הוא על זה הסדר אשר סדרוה רצוני שהראשון הוא אשר יתחבר המתחלק יותר גדול מן הנשארים והל' הוא אשר יתחבר עמו יותר קטן והנשארים והזכרתי זה לך למען לא תבלבל בביאורים והנה יהיה המספר השני מהם כ' ורצינו לדעת כמה כל א' מהנשארים |
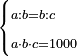
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | a·b·c=1000;a\b\c | ספר_דיני_ממונות#WgAN | 452) Question: we have three proportional numbers such that the ratio of the first to the second is as the ratio of the second to the third.
:If we multiply the first by the second, then multiply the result by the third it will be a thousand.
:How much are the proportional numbers?
116rתנב) שאלה יש לנו ג' מספרים יחסיים אשר יחס הא' אל הב' כיחס הב' אל הג' והנה נכפול הא' על הב' והעולה נכפול על ג' הוא אלף כמה הם המספרים היחסיים |
Find Six Numbers
six proportional numbers
| Category | Comment | Link | Annotated text |
|---|---|---|---|
| word problem/find a number | six proportional numbers | ספר_דיני_ממונות#Wrir | For example: we have six proportional numbers, the first is 2 and the sixth is 64.
::We wish to know which is the second.
דמיון זה יש לנו ו' {{#annot:term|994,1277|VUeX}}מספרים מתיחסים{{#annotend:VUeX}} הראשון ב' והו' ס"ד נרצה לדעת מהו השני |
| word problem/find a number | six proportional numbers | ספר_דיני_ממונות#FvyI | Example: the first is 2-[eighths] and the sixth is 256 integers. דמיון הראשון ב' שלישיות והו' רנ"ו שלמים |
| word problem/find a number | six proportional numbers | ספר_דיני_ממונות#fNcE | Example: we have six proportional numbers, the first of which is 2 and the sixth is 64. דמיון יש לנו ו' מספרים מתיחסים שהראשון ב' והו' ס"ד |
| word problem/find a number | six proportional numbers | ספר_דיני_ממונות#Yfpk | 111) Question: if you want to find a proportional number:
:For example: we have six proportional numbers, i.e. the ratio of the sixth to the fifth is the same as the ratio of the fifth to the fourth, and the same as the ratio of the fourth to the third, and the same as the ratio of the third to the second, and the same as the ratio of the second to the first.
:The first number is 2.
:The sixth is 2048.
:We wish to know how much is the second?
קיא)MS L: קט שאלה אם תרצה למצא {{#annot:term|994,2263|2xtB}}מספר יחסיי{{#annotend:2xtB}} הנקרא בלשונם {{#annot:term|994|DhLM}}נומירו פרופורציאונלי{{#annotend:DhLM}} דמיון זה יש לנו ו' {{#annot:term|994,2263|jjwV}}מספרים יחסיים{{#annotend:jjwV}} ר"ל שיחס הו' אל הה' כיחס הה' אל הד' וכיחס הד' אל הג' וכיחס הג' אל הב' וכיחס הב' אל הא' והמספר הא' ב' והו' ב' אלפים ומ"ח ונרצה לדעת מהו השני |