Difference between revisions of "Search Page"

From mispar
Jump to: navigation, search
Line 2: Line 2:
 
{{#annotask:
 
{{#annotask:
 
   [[wiki_text: %math%]]
 
   [[wiki_text: %math%]]
 +
  [[page: author="Abū Kāmil"]]
 
}}
 
}}

Revision as of 12:35, 6 September 2019

Category Comment Link Annotated text
extraction of root/addition of roots√10+√2חשבון_השטחים#zdrv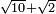\scriptstyle\sqrt{10}+\sqrt{2} ואם באת לחבר שורש עשרה עם שורש שנים
extraction of root/addition of roots√9+√4חשבון_השטחים#qIr6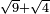\scriptstyle\sqrt{9}+\sqrt{4} ויהיו שני המספרים המרובעים תשעה וארבעה וכאשר תרצה לחבר שורש תשעה ושורש ארבעה עד שיהיו שורש למספר אחד
extraction of root/addition of roots√10+√2תחבולות_המספר#MvKXHe said: if we wish to sum up the root of ten with the root of two. :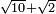\scriptstyle\sqrt{10}+\sqrt{2} אמ' ואם רצינו לחבר שרש עשרה עם שרש שנים
extraction of root/addition of roots√9+√4תחבולות_המספר#1OzLAs if you say: nine and four - we wish to sum their roots so that they become a root of a single number. :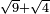\scriptstyle\sqrt{9}+\sqrt{4} כאלו תאמ' תשעה וארבעה ורצינו לחבר שרשיהם עד שיהיו שרש למספר אחד
extraction of root/addition of roots√18+√8תחבולות_המספר#H0sgHe said: if we wish to sum up the root of eighteen with the root of eight, so they become a root of a single number. :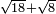\scriptstyle\sqrt{18}+\sqrt{8} ‫306vאמר ואם רצינו לחבר שרש שמנה עשר עם שרש שמנה עד שיהיו שרש למספר אחד
extraction of root/addition of roots√18+√8חשבון_השטחים#Pk5I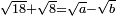\scriptstyle\sqrt{18}+\sqrt{8}=\sqrt{a}-\sqrt{b} וכאשר תרצה לחבר שרש שמנה עשר ושרש שמנה עד שיהיו שורש המספר האחד פחות שורש המספר האחר
quartic equation/biquadratic equation4(x²+8)=x⁴תחבולות_המספר#G1Mq[6] He said: the six problem is as if you are told: we add to a certain square [eight] dirham, then multiply the sum by four dirham and the result is the same as the product of the square [by itself]. :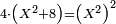\scriptstyle4\sdot\left(X^2+8\right)=\left(X^2\right)^2 אמ' והשאלה הששית כמו אם יאמרו לך הוספנו על התמונ' מרובע מה שלשה דרהמי והכינו המקובץ בארבעה דרהמי והיה העולה כמו הכאת א"ב בעצמו המרובע
quartic equation/biquadratic equation4(x²+8)=x⁴חשבון_השטחים#ZxMx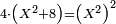\scriptstyle4\sdot\left(X^2+8\right)=\left(X^2\right)^2 אלגו תוסיף עליו שמנה אדרהם ותכה {{#annot:term|388,1217|vQSL}}המקובץ{{#annotend:vQSL}} על ארבעה אדרהם והיה כמו האלגו על עצמו
word problem/divide a numbera+b=10,20+a=n²,50-b=m²השאלות_החרשות/האלמות#XtSS13) If you are told: divide ten into two parts. :Add the one part to twenty and the sum has a root. :Subtract the other part from fifty and the remainder has a root. :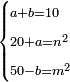\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle20+a=n^2\\\scriptstyle50-b=m^2\end{cases} יג ואם יאמרו לך עשרה תחלקהו לשני חלקים ותוסיף החלק האחד על עשרים ויהיה מה שיחזיק שרש ותגרע החלק האחר מחמשים ויחזיק הנשאר שרש
word problem/divide a numbera+b=10, 20+a=n²,50+b=m²השאלות_החרשות/האלמות#OLcA14) If you are told: divide ten into two parts, add the first part to twenty and it has a root; add the other part to fifty, and it has a root. :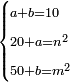\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle20+a=n^2\\\scriptstyle50+b=m^2\end{cases} יד ואם יאמרו לך תחלק עשרה לשני חלקים ותוסיף החלק האחד על עשרים ויחזיק שרש ותוסיף החלק האחר על חמשים ויחזיק שרש
word problem/divide a numbera+b=10, ab=21חשבון_השטחים#uEcKWe divided ten into two parts, then we multiplied the one [part] by the other and the result was 21. :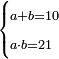\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle a\sdot b=21\end{cases} חלקנו עשרה לשני חלקים
והכינו האחד על האחר והיה עשרים ואחד
word problem/divide a numbera+b=10, 10²=6¼a²חשבון_השטחים#jgC7You divide ten into two parts, then multiply one of them by itself and multiply the ten by itself. :The product of ten by itself is the same as the product of one of the parts by itself 6¼ times. :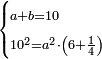\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle10^2=a^2\sdot\left(6+\frac{1}{4}\right)\end{cases} עשרה תחלקהו לשני חלקים
ותכה אחד מהם על עצמו ותכה העשרה על עצמו
ויהיה העולה מהכאת עשרה על עצמו כמו העולה מהכאת אחד החלקים על עצמו ששה פעמים ורביע
word problem/divide a numbera+b=10, (10/a·10/b)²=20¼חשבון_השטחים#eIQuIf you are told: we divided ten into two parts, then you divided the ten by each of the parts and multiplied the [one by the other and then the result by itself] and it yields 20¼ dirham. :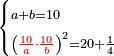\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle\left({\color{red}{\frac{10}{a}\sdot\frac{10}{b}}}\right)^2=20+\frac{1}{4}\end{cases} ואם יאמרו לך חלקנו עשרה לשני חלקים
וחלקת עשרה על כל חלק מהם והכית החלק האחד ממה שיעלה לחלק בעצמו והיה עשרים אדרהמי ורביע
word problem/divide a numbera+b=10, 40/a·40/b=100חשבון_השטחים#EWpjIf it is said: you divided ten into two parts, then you divided forty by each part of the two and multiplied the quotients one by the other and it yields 100 dirham. :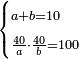\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle\frac{40}{a}\sdot\frac{40}{b}=100\end{cases} והוא ידוע ממה שאמרנו כי כאשר אמרו חלקת עשרה לשני חלקי‫'
וחלקת ארבעים על כל חלק מהשנים והכית מה שעלו אל החלקים האחד על האחר והיה מאה אהדרהמיש
word problem/divide a numbera+b=10, (b/a)²-(a/b)²=2חשבון_השטחים#YT0V[44] If you are told: you divided ten into two parts, then you divided each part by the other, multiplied each quotient by itself, subtracted the smaller [product] from the larger [product], and two dirham remain. :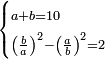\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle\left(\frac{b}{a}\right)^2-\left(\frac{a}{b}\right)^2=2\end{cases} ואם יאמרו לך חלקת עשרה לשני חלקים
וחלקת כל אחד מהם על האחר ומה שעלה לכל חלק הכית על עצמו וגרעת המעט מהרב ונשאר שני דרהמי
word problem/divide a numbera+b=10, b/a-a/b=5/6חשבון_השטחים#OWEq[43] If you are told: you divided ten into two parts, then you divided each part by the other, and subtracted the quotient of the smaller divided by the larger from the quotient of the larger divided by the smaller, and five-sixths of a dirham remain. :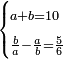\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle\frac{b}{a}-\frac{a}{b}=\frac{5}{6}\end{cases} ואם יאמרו לך חלקת עשרה לשני חלקים
וחלקת כל אחד מהם על האחר וגרעת מה שעלה לחלק מחלוקת המעט על הרב ממה שעלה לחלק מחלוקת הרב על המעט ונשאר חמשה ששיות מאדרהם
word problem/divide a numbera+b=10, a/b+b/a=√5חשבון_השטחים#t2znThis is as if we said: you divided ten into two parts, then divided each part by the other, and [the sum of the quotients] is the root of five. ::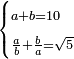\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle\frac{a}{b}+\frac{b}{a}=\sqrt{5}\end{cases} והוא כמו שאמרנו חלקת עשרה לשני חלקים
וחלקת כל אחד מהם על האחר ועלה שרש חמשה
word problem/divide a numbera+b=10, (a/b)²+(b/a)²=3חשבון_השטחים#BSCj[42] If you are told: you divided ten into two parts, then divided each part by the other, and multiplied each quotient of one part divided by the other by itself, and [the sum of the products] is three dirham. :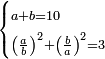\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle\left(\frac{a}{b}\right)^2+\left(\frac{b}{a}\right)^2=3\end{cases} ואם יאמרו לך עשרה חלקת לשני חלקים
וחלקת כל אחד מהם על האחר והכית כל אחד מהם שיעלו לחלק על האחר בעצמו ויהיה שלשה דרהמי
word problem/divide a numbera+b=10, a/b+b/a=√5חשבון_השטחים#BWTC[41] If you are told: you divided ten into two parts, then you divided each part by the other, and summed the quotients, and [the sum] is a root of five dirham. :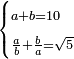\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle\frac{a}{b}+\frac{b}{a}=\sqrt{5}\end{cases} ואם יאמרו לך חלקת עשרה לשני חלקים
וחלקת כל חלק על האחר וקבצת מה שעלה לכל חלק ויהיה שרש חמשה דרהמי
word problem/divide a numbera+b=10, b²-(a·√8)=40חשבון_השטחים#6AdM[36] If you are told: you divided ten into two parts, then multiplied one part by itself and the other [part] by the root of eight, and subtracted the product of the part that is multiplied by the root of eight from the product of the part that is multiplied by itself, and forty dirham remain. :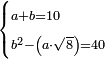\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle b^2-\left(a\sdot\sqrt{8}\right)=40\end{cases} ואם יאמרו לך עשרה חלקת אותם לשני חלקים
והכית החלק האחד על עצמו והאחר על שרש שמנה וגרעת המקובץ מהכאת החלק האחד בשרש שמנה מן המקובץ מהכאת החלק האחר על עצמו וישאר ארבעים דרהמי
word problem/divide a numbera+b=10, (a/b+b/a)·a=25-2aחשבון_השטחים#pQEIThis is like: you divided ten into two parts, then you divided each [part] by the the other [part], you summed the two quotients and multiplied [the sum] by one of the two parts of ten and [the result] is twenty five dirham minus two things. ::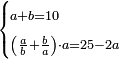\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle\left(\frac{a}{b}+\frac{b}{a}\right)\sdot a=25-2a\end{cases} והוא כמו שאמר עשרה חלקת אותו לשני חלקים
וחלקת כל אחד על האחר וקבצת מה שעלה לכל חלק והכית אותו על חלק אחד משני חלקי העשרה והיה כ"ה דרהמי פחות שני דברים והוא כ"ה פחות הדבר האחד
word problem/divide a numbera+b=10, (b/a+10)·b=69חשבון_השטחים#jitx[25] If you are told: you divided ten into two parts, then you divided the larger [part] by the smaller [part], and added the quotient to ten and multiplied the sum by the larger part and [the result] is sixty-nine dirham. :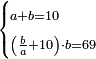\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle\left(\frac{b}{a}+10\right)\sdot b=69\end{cases} ואם יאמרו לך עשרה חלקת אותו לשני חלקים
וחלקת הגדול על הקטן והוספת מה שעלה לחלק על העשרה ותכה מה שיתקבץ על החלק הגדול ויהיה ששים ותשעה אדרהמי‫'
word problem/divide a numbera+b=10, (b/a+10)·a=46חשבון_השטחים#tH6B[24] If you are told: you divided ten into two parts, then you divided the larger [part] by the smaller [part], added the quotient to ten and multiplied the sum by the smaller part and [the result] is 46 dirham. :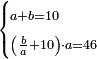\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle\left(\frac{b}{a}+10\right)\sdot a=46\end{cases} ואם יאמרו לך עשרה חלקת אותו לשני חלקים
וחלקת הגדול על הקטן והוספת העולה לחלק על עשרה והכית המקובץ על החלק הקטן והיה מ"ו אדרהמיש
word problem/divide a numbera+b=10, (a/b+b/a)·b=34חשבון_השטחים#Ch1h[23] If you are told: you divided ten into two parts, then you divided each part by the other, summed both quotients and multiplied [the sum] by one of the two parts of ten and [the result] is 34 dirham. :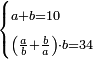\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle\left(\frac{a}{b}+\frac{b}{a}\right)\sdot b=34\end{cases} ואם יאמרו לך חלקת עשרה לשני חלקים
וחלקת כל אחד מהם על האחר וקבצת מה שעלה לחלק משניהם והכית אותו על החלק האחד משני חלקי העשרה והיה ל"ד אדרהמיש
word problem/divide a numbera+b=10, (b/a)·(b-a)=24חשבון_השטחים#4NOM[22] If you are told: you divide ten into two parts, then you divide one part by the other, and multiply the quotient by excess of the dividend over the divisor and [the result] is 24 dirham. :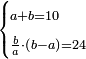\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle\frac{b}{a}\sdot\left(b-a\right)=24\end{cases} ואם יאמרו לך עשרה חלקת אותו לשני חלקים
וחלקת החלק האחד על האחר והכית מה שהגיע לחלק על ההבדל אשר יעדיף המספר הנחלק את המחלק ויהיה כ"ד דרהמי‫'
word problem/divide a numbera+b=10, (b/a+b)·a=30חשבון_השטחים#E7PV[19] If you are told: divide ten into two parts, then divide one part by the other, take the quotient and add it to the dividend and multiply the sum by the divisor and [the result] is thirty. :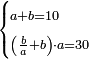\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle\left(\frac{b}{a}+b\right)\sdot a=30\end{cases} ואם יאמרו לך עשרה תחלקהו לשני חלקים
וחלק החלק האחד על האחר וקח המגיע לחלק והוסיפהו על המספר הנחלק והמקובץ תכהו על המחלק ויהיה שלשים
word problem/divide a numbera+b=10, a/b=4¼חשבון_השטחים#JKByAs the calculation in which it is said: we divide ten into two parts, then we divide one of them by the other and the result is four and a quarter. :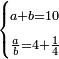\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle\frac{a}{b}=4+\frac{1}{4}\end{cases} כחשבון האומר בו חלקנו עשרה לשני חלקים
וחלקנו אחד מהם על האחר ועלה ארבעה ורביע
word problem/divide a numbera+b=10, (b/a)²·a=32חשבון_השטחים#2J8j[21] If you are told: you divide ten into two parts, then you divide one part by the other, and multiply the quotient by itself and by the divisor and [the result] is 32 dirham. :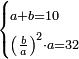\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle\left(\frac{b}{a}\right)^2\sdot a=32\end{cases} ואם יאמרו לך עשרה חלקת אותו לשני חלקים
וחלקת החלק האחד על האחר והכית מה שהגיע לחלק על עצמו ועל המחלק ויהיה ל"ב אדרהמי‫'
word problem/divide a numbera+b=10, (10+b/a)·(10-a/b)=107⅓חשבון_השטחים#pzmE[30] If you are told: you divided ten into two parts, then divided the larger [part] by the the smaller [part] and added the result to ten, divided the smaller [part] by the the larger [part] and subtracted the result from ten, and multiplied the [sum of each part] by the other and [the result] is one hundred and seven and [one]-third. :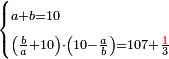\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle\left(\frac{b}{a}+10\right)\sdot\left(10-\frac{a}{b}\right)=107+\frac{{\color{red}{1}}}{3}\end{cases} ואם יאמרו חלקת עשרה לשני חלקים
וחלקת הרב על המעט והוספת העולה על העשרה וחלקת המעט על הרב וגרעת מה שעלה לחלק מן העשרה והכית האחד על האחר ויהיה מאה ושבעה ושני שלישיות
word problem/divide a numbera+b=10, (b/a+10)·(a/b+10)=122⅔חשבון_השטחים#zCoa[29] If you are told: divide ten into two parts, then divide the larger [part] by the the smaller [part] and add the result to ten, divide the smaller [part] by the the larger [part] and add the result to ten, and multiply the sum of each part by the other and [the result] is one hundred twenty-two dirham and two-thirds. :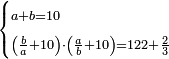\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle\left(\frac{b}{a}+10\right)\sdot\left(\frac{a}{b}+10\right)=122+\frac{2}{3}\end{cases} ואם יאמרו לך עשרה תחלקהו לשני חלקים
ותחלק הרב על המעט ותוסיף העולה על העשרה ותחלק המעט על הרב והוסיף העולה על העשרה ומה שיתקבץ מכל חלק תכה האחד על האחר ויהיה מאה ועשרים ושנים דרהמי ושני שלישים
word problem/divide a numbera+b=10, (a/b+b/a+10)·a=73חשבון_השטחים#bP5L[26] If you are told: we divided ten into two parts, then we divided the larger [part] by the smaller [part] and the smaller [part] by the larger [part], summed the quotients and added them to ten and multiplied the sum by the larger part and [the result] is seventy-three dirham. :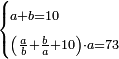\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle\left(\frac{a}{b}+\frac{b}{a}+10\right)\sdot a=73\end{cases} ואם יאמרו לך עשרה חלקנום לשני חלקים
וחלקנו הגדול על הקטן והקטון על הגדול וקבצת מה שעלה לכל חלק והוספתם על העשרה והכית המקובץ על החלק הגדול והיה שבעים ושלש דרהמי‫'
word problem/divide a numbera+b=10, 6a+⅓[(6a)/b]=56חשבון_השטחים#T9EL[11] If you are told: we divide ten into two parts, then we multiply one part by six, divide the product by the other part, take a third of the quotient and add it the product and [the result] is fifty-six. :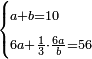\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle6a+\frac{1}{3}\sdot\frac{6a}{b}=56\end{cases} ואם יאמרו לך חלקנו עשרה לשני חלקים
והכינו החלק האחד על ששה וחלקנו מה שעלה מההכאה על החלק האחר ומה שעלה לחלק לקחנו ממנו השליש והוספנו על מה שעלה הכאת החלק האחד על ששה והיה חמשים וששה
word problem/divide a numbera+b=10, a/b-b/a=5/6חשבון_השטחים#as1Z3) Question. :If you are told: divide ten into two parts, then divide each one of them by the other and subtract one [quotient] from the other [quotient], and five-sixths of a dirham remain. :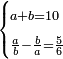\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle\frac{a}{b}-\frac{b}{a}=\frac{5}{6}\end{cases} ג) שאלה
ואם יאמרו לך עשרה חלקנום לשני חלקים
וחלקנו כל אחד מהם על האחר וגרענו האחד מן האחר ו{{#annot:term|936,1236|yzCK}}נשאר{{#annotend:yzCK}} חמשה ששיות מאדרהם
word problem/divide a numbera+b=10, a²-b²=80חשבון_השטחים#cOGN1) Question: if you are told: divide ten into two parts, then multiply each part by itself and subtract the product of the smaller from the product of the larger, and 80 remain. :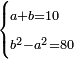\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle b^2-a^2=80\end{cases} א) שאלה ואם יאמרו לך תחלק עשרה לשני חלקים ותכה כל חלק על עצמו ותגרע הכאת החלק הקטן מהכאת החלק הגדול וישאר שמנים
word problem/divide a numbera+b=10, 10/a+10/b=6¼חשבון_השטחים#C69UIf you are told: you divided ten into two parts, then you divided the ten by each of the parts and [the sum of the quotients] is 6¼. :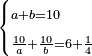\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle\frac{10}{a}+\frac{10}{b}=6+\frac{1}{4}\end{cases} ואם יאמרו לך חלקת עשרה לשני חלקים
וחלקת העשרה על כל חלק מהם ועלה ששה ורביע
word problem/divide a numbera+b=10, a²=1½abחשבון_השטחים#DmzfThe first problem of the six is: If you are told: divide ten into two parts, then multiply one part by the other and multiply the larger part by itself. The [product] of the part that is multiplied by itself is the same as the product of the one part by the other and as its half. :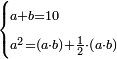\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle a^2=\left(a\sdot b\right)+\frac{1}{2}\sdot\left(a\sdot b\right)\end{cases} והשאלה הראשונה מן הששה היא אם יאמרו לך תחלק עשרה לשני חלקים ותכה החלק האחד על האחר ותכה החלק הגדול על עצמו ויהיה החלק המוכה על עצמו כמו הכאת החלק האחד על האחר וכמו חציו
word problem/divide a numbera+b=10, (a·b)/(b-a)=√6חשבון_השטחים#QOHt[35] If you are told: you divided ten into two parts, then you multiplied one [part] by the other and divided the product by the difference between the two parts of ten and the result is a root of six. :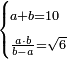\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle\frac{a\sdot b}{b-a}=\sqrt{6}\end{cases} ואם יאמרו לך חלקת עשרה לשני חלקים
והכית האחד על האחר וחלקת {{#annot:term|875,1216|AQjO}}מה שהתקבץ{{#annotend:AQjO}} על העודף משני חלקי העשרה ועלה שרש ששה
word problem/divide a numbera+b=10, (40/a)²·(40/b)²=625חשבון_השטחים#P3KnIf you are told: we divided ten into two parts, then you divided forty by each of the parts and multiplied each of the quotients by itself and they are 625. :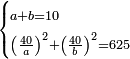\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle\left(\frac{40}{a}\right)^2+\left(\frac{40}{b}\right)^2=625\end{cases} ואם יאמרו לך חלקנו עשרה לשני חלקים
וחלקת על כל אחד מהם ארבעים ומה שעלו לחלקים הכית כל חלק על עצמו והיו תרכ"ה
word problem/divide a numbera+b=10, (a/b-b/a)·a=5חשבון_השטחים#Mlte[27] If you are told: you divided ten into two parts, then you divided each [part] by the the other [part] and took the difference between the two quotients and multiplied it by the [larger] part and [the result] is five dirham. :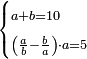\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle\left(\frac{a}{b}-\frac{b}{a}\right)\sdot a=5\end{cases} ואם יאמרו לך עשרה חלקת אותו לשני חלקים
וחלקת כל אחד על האחר ותקח הבדל השני חלקים שעלו לכל חלק מחלוקת האחד על האחר ותכהו על החלק האחד ויהיה חמשה דרהמי
word problem/divide a numbera+b=10, 50/a·40/b=125חשבון_השטחים#N2DJIf one says: we divided ten into two parts, then we divided fifty by one of the parts and forty by the other and multiplied the quotients one by the other and it yields 125. :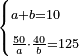\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle\frac{50}{a}\sdot\frac{40}{b}=125\end{cases} וגם כן התבאר מאשר אמרנו שאם יאמר אומר חלקנו עשרה לשני חלקי‫'
וחלקנו חמישי' על החלק האחד וארבעי' על האחר והכינו העולה לחלק האחד באחר והיה קכ"ה
word problem/divide a numbera+b=10, a·√10=b²חשבון_השטחים#w9sl[37] If you are told: you divided ten into two parts, then multiplied one part by the root of ten, and the other [part] by itself, and [the products] are equal. :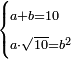\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle a\sdot\sqrt{10}=b^2\end{cases} ואם יאמרו לך עשרה חלקת לשני חלקים
והכית האחד בשרש עשרה והאחר על עצמו ויהיו שוים
word problem/divide a numbera+b=10, (a/b+a)·(b/a+b)=35חשבון_השטחים#xMD9[28] If you are told: you divided ten into two parts, then you divided the larger [part] by the smaller [part] and added the quotient to the larger [part], and you divided the smaller [part] by the larger [part] and added the quotient to the smaller [part] and multiplied one [sum] by the other and the result was thirty-five. :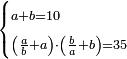\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle\left(\frac{a}{b}+a\right)\sdot\left(\frac{b}{a}+b\right)=35\end{cases} ואם אמרו לך עשרה חלקת אותו לשני חלקים
וחלקת הרב על המעט והוספת מה שעלה לחלק על הרב וחלקת המעט על הרב והוספת מה שעלה לחלק על המעט והכית האחד על האחר והיה שלשים וחמשה דרהמי‫'
word problem/divide a numbera+b=10, (b/a)·b=9חשבון_השטחים#5mDJ[20] If you are told: divide ten into two parts, then divide one part by the other, and multiply the quotient by the dividend and [the result] is nine dirham. :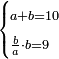\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle\frac{b}{a}\sdot b=9\end{cases} ואם יאמרו לך עשרה תחלקהו לשני חלקים
ותחלק החלק האחד על האחר ותכה המגיע לחלק על המספר הנחלק ויהיה תשעה דרהמי‫'
word problem/divide a numbera+b=10, b/a+a=5½חשבון_השטחים#KWTC[18] If you are told: we divided ten into two parts, then we divided one part by the other, and the sum of the quotient with the divisor is five and a half. :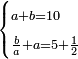\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle\frac{b}{a}+a=5+\frac{1}{2}\end{cases} ואם יאמרו לך עשרה דרהמי חלקנום לשני חלקים
וחלקנו החלק האחד על האחר ויהיה המגיע לחלק עם המחלק יהיה חמשה וחצי
word problem/divide a numbera+b=10, a/b+b/a=4¼חשבון_השטחים#nue7[2] If you are told: divide ten into two parts, then divide each of them by the other and [the sum of] the quotients is four and a quarter. :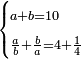\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle\frac{a}{b}+\frac{b}{a}=4+\frac{1}{4}\end{cases} ואם יאמרו לך עשרה תחלק אותו לשני חלקים ותחלק כל אחד מהם על האחר ויגיעו החלקי' ארבעה ורביע
word problem/divide a numbera+b=10, 10/a·10/b=6¼חשבון_השטחים#d6quIf you are told: we divided ten into two parts, then we divided the ten by each of the parts and multiplied the quotients one by the other and it yields 6¼. :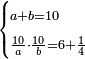\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle\frac{10}{a}\sdot\frac{10}{b}=6+\frac{1}{4}\end{cases} ואם יאמרו לך חלקנו עשרה לשני חלקי‫'
וחלקנו העשרה על כל חלק מהם והכינו מה שעלה לכל חלק האחד על האחר והיה ששה ורביע
word problem/divide a numbera+b=10, a+2√a=b-2√bחשבון_השטחים#tzY5If you are told: you divided ten into two parts, then you added to one part its two roots and subtracted from the other part its two roots and the parts became equal. :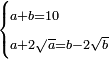\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle a+2\sqrt{a}=b-2\sqrt{b}\end{cases} ואם יאמרו לך עשרה חלקת אותם לשני חלקים
והוספת על החלק האחד שני שרשיו וגרעת מן החלק האחר שני שרשיו והשתוו החלקים
word problem/divide a numbera+b+c=10, a^2+b^2=c^2, ac=b^2חשבון_השטחים#FwR9If you are told: divide ten into three parts, then multiply the smaller by itself and the middle by itself and they are the same as the larger by itself. Multiply the smaller by the larger and it yields the same as the middle by itself. :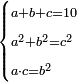\scriptstyle\begin{cases}\scriptstyle a+b+c=10\\\scriptstyle a^2+b^2=c^2\\\scriptstyle a\sdot c=b^2\end{cases} ואם יאמרו לך עשרה תחלקהו לשלשה חלקים
ותכה הקטן בעצמו והאמצעי בעצמו ויהיו כמו הגדול בעצמו
ותכה הקטון בגדול ויהיה כמו האמצעי בעצמו
word problem/divide a numbera+b=10, a²=9bחשבון_השטחים#X9cDWe divided ten into two parts, then we multiplied the smaller part by nine and the larger part by itself and the [products] were equal. :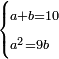\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle a^2=9b\end{cases} חלקנו עשרה לשני חלקים
והכינו החלק הקטן על תשעה והגדול על עצמו והיו שוים
word problem/divide a numbera+b=10, b/a=4חשבון_השטחים#PsKJDivide ten into two parts, then divide the larger part by the smaller part and the result is four. :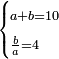\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle\frac{b}{a}=4\end{cases} תחלק עשרה לשני חלקים
ותחלק החלק הגדול על החלק הקטן ויגיע לחלק ארבעה
word problem/divide a numbera+b=10, ab=21תחבולות_המספר#Wntm[5] He said: the fifth problem is as if you are told: divide ten into two parts, such that when we multiply one part by the other the result is 21. :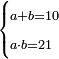\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle a\sdot b=21\end{cases} אמ' והשאלה החמישית כמו אם יאמרו לך תחלק עשרה לשני חלקים באופן שכאשר נכה החלק האחד באחר יעלה עשרים ורביע ואחד
word problem/divide a numbera+b=10, a²=9bתחבולות_המספר#7Ia4[4] He said: the fourth problem is as if you are told: divide ten into two parts, such that the product of the larger part by itself is the same as the product of the smaller part multiplied by nine. :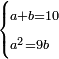\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle a^2=9b\end{cases} אמ' והשאלה הרביעית היא כמו אם יאמרו לך תחלק עשרה לשני חלקים באופן שיהיה העולה מהכאת החלק הגדול בעצמו כמו הכאת החלק הקטן בתשעה
word problem/divide a numbera+b=10, a²=1½abתחבולות_המספר#nJqx[1] He said: the first problem is as if you are told: divide ten into two parts, such that the product of the larger by itself is the same as one time and a half of the product of the one part by the other. :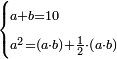\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle a^2=\left(a\sdot b\right)+\frac{1}{2}\sdot\left(a\sdot b\right)\end{cases} אמ' והשאלה הראשונה היא כמו אם יאמרו לך תחלק עשרה לשני {{#annot:term|606,1259|Vr9G}}חלקים{{#annotend:Vr9G}} באופן שתהיה הכאת החלק הגדול בעצמו כמו פעם וחצי מהעולה מהכאת החלק האחד באחר
word problem/divide a numbera+b=10, 10²=6¼a²תחבולות_המספר#LNn6[2] He said: and the second problem is as if you are told: divide ten into two parts, such that the product of ten by itself is the same as the product of one of the parts by itself 6¼ times. :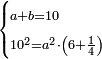\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle10^2=a^2\sdot\left(6+\frac{1}{4}\right)\end{cases} אמ' והשאלה השנית כמו אם יאמרו לך תחלק עשרה לשני חלקים באופן שיהיה העולה מהכאת עשרה בעצמו כמו הכאת העולה מהכא' אחד החלקי' בעצמו ששה פעמים ורביע
word problem/divide a numbera+b=10, b/a=4תחבולות_המספר#ogdI[3] He said: the third problem is as if you are told: divide ten into two parts, such that when you divide the larger part by the smaller part the quotient is four. :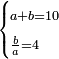\scriptstyle\begin{cases}\scriptstyle a+b=10\\\scriptstyle\frac{b}{a}=4\end{cases} אמ' והשאלה השלישית היא כמו אם יאמרו לך תחלק עשרה לשני חלקים באופן שכאשר תחלק החלק הגדול על החלק הקטן יגיע לחלק ארבעה
extraction of root/division of roots√10÷√2חשבון_השטחים#qjLW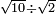\scriptstyle\sqrt{10}\div\sqrt{2} ואם יאמרו תחלק שורש עשרה על שורש שנים
extraction of root/division of roots√10÷√2תחבולות_המספר#pYYIIf it is said: divide ten by a root of two. :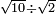\scriptstyle\sqrt{10}\div\sqrt{2} ואם אמרו תחלק שרש עשרה על שרש שנים
extraction of root/division of roots(2×√20)÷(3×√6)תחבולות_המספר#sCCwIf you are told: divide two roots of twenty by three roots of six. :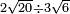\scriptstyle2\sqrt{20}\div3\sqrt{6} ואם אמר לך תחלק שנים שרשים מעשרים על שרשים שלשה מששה
extraction of root/division of roots(2×√20)÷(3×√6)חשבון_השטחים#cvXn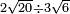\scriptstyle2\sqrt{20}\div3\sqrt{6} ואם יאמרו לך תחלק שנים שרשים מעשרים על שלשה שרשים מששה
extraction of root/division of roots√9÷√4תחבולות_המספר#1Gu9He said: if you are told: divide the root of nine by the root of four. :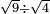\scriptstyle\sqrt{9}\div\sqrt{4} ‫305vאמ' ואם יאמרו לך תחלק שרש תשעה על שרש ארבעה
extraction of root/division of roots√9÷√4חשבון_השטחים#AVTk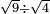\scriptstyle\sqrt{9}\div\sqrt{4} ואם יאמרו תחלק שורש תשעה על שורש ארבעה
Elements/Elements XIII-3definitionהמחומשים_והמעושרים#mhLNEuclid has already explained [Elements XIII.3] that when line BH is divided by the ratio of a mean and two extremes, so that the greater part is equal to line DH, it is known that when a line is divided by the ratio of a mean and two extremes and we add half the greater part to the smaller part, then multiply the whole sum by itself, the square formed by the sum of the two is five times the product of [half] the greater part by itself. :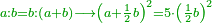\scriptstyle{\color{OliveGreen}{a:b=b:\left(a+b\right)\longrightarrow\left(a+\frac{1}{2}b\right)^2=5\sdot\left(\frac{1}{2}b\right)^2}} ובאר אוקלידס שקו ב"ה כאשר חולק על יחס אמצעי ושני קצוות שהחלק הגדול הוא שוה אל קו ד"ה והוא ידוע כי כאשר נחלק קו אחד על יחס בעל אמצעי ושני קצוות ונוסיף על החלק הקטן חצי החלק הגדול ונכה הכל בעצמו שהמרובע ההוה משני אלו מקובצים יהיה חמשה דמיוני הכאת החלק הגדול בעצמו
joint purchase problem/if you give mefive people, beastהשאלות_החרשות/האלמות#mYBB42) If you are told: five people gathered. :The first said to the second: if you give me half of what you have I will have the price of the beast. :The second said to the third: if you give me a third of what you have I will have the price of the beast. :The third said to the fourth: if you give me a quarter of what you have I will have the price of the beast. :The fourth said to the fifth: if you give me a fifth of what you have I will have the price of the beast :The fifth said to the first: if you give me a sixth of what you have I will have the price of the beast :How much is the price of the beast and how much does each of them have? :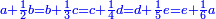\scriptstyle{\color{blue}{a+\frac{1}{2}b=b+\frac{1}{3}c=c+\frac{1}{4}d=d+\frac{1}{5}e=e+\frac{1}{6}a}} מב ואם יאמרו לך חמשה אנשים התקבצו ואמר הראשון לשני אם תתן לי החצי מאשר בידך יהיה לי ערך הבהמה
ואמר השני לשלישי אם תתן לי השלישית מאשר בידך יהיה לי ערך הבהמה
ואמר השלישי לרביעי אם תתן לי הרביעית מאשר בידך יהיה לי ערך הבהמה
ואמר הרביעי לחמישי אם תתן לי החמישית מאשר בידך יהיה לי ערך הבהמה
ואמר החמישי לראשון אם תתן לי ששית אשר בידך יהיה לי ערך הבהמה
כמה יהיה ערך הבהמה וכמה יהיה אלגו מכל אחד מהחמשה
equation/indeterminate equation10x-8-x²=n²השאלות_החרשות/האלמות#JrVS24) If you are told: a square that has a root, if you subtract it from its ten roots minus eight dirham, the remainder has a root. :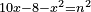\scriptstyle10x-8-x^2=n^2 כד ואם יאמרו לך אלגו שיחזיק שרש אם תגרעהו מעשרת שרשיו פחות שמנה שרשיו דרהמי יחזיק מה שישאר שרש
equation/indeterminate equationx²+x=n²,x²-x=m²השאלות_החרשות/האלמות#MUv822) If you are told: a square, if you add its root to it, the sum has a root; and if you subtract its root from it, the remainder has a root. :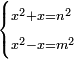\scriptstyle\begin{cases}\scriptstyle x^2+x=n^2\\\scriptstyle x^2-x=m^2\end{cases} כב ואם יאמרו לך אלגו אם תוסיף עליו שרשו יהיה למתקבץ שרש ואם תגרע ממנו שרשו יחזיק הנשאר שרש
equation/indeterminate equation2x+49-x²=n²השאלות_החרשות/האלמות#bkYa21) If you are told: a square, if you subtract it from its two roots plus 49 dirham, the remainder has a root. :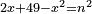\scriptstyle2x+49-x^2=n^2 כא ואם יאמרו לך אלגו אם תגרעהו משני שרשיו ומ"ט דרהמי יחזיק הנשאר שרש
equation/indeterminate equation8x+x²=n²,2x-x²=m²השאלות_החרשות/האלמות#62Ll20) If you are told: a square, if you add its eight roots to it, it has a root; and if you subtract it from its two roots, the remainder has a root. :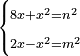\scriptstyle\begin{cases}\scriptstyle8x+x^2=n^2\\\scriptstyle2x-x^2=m^2\end{cases} כ ואם יאמרו לך אלגו אם תוסיף עליו שמנה שרשיו יחזיק שרש ואם תגרעהו משני שרשיו יהיה לנשאר שרש
equation/indeterminate equation8x+109-x²=n²השאלות_החרשות/האלמות#tMRx19) If you are told: a square, if you subtract it from its eight roots plus 109 dirham, it has a root. :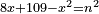\scriptstyle8x+109-x^2=n^2 יט ואם יאמרו לך אלגו אם תגרעהו משמנה שרשים וק"ט דרהמי יחזיק שרש
equation/indeterminate equation10+x²=n²,10-x²=m²השאלות_החרשות/האלמות#rWQ118) If you are told: a square, if you add it to ten, it has a root; and if you subtract it from ten, it has a root. :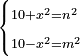\scriptstyle\begin{cases}\scriptstyle10+x^2=n^2\\\scriptstyle10-x^2=m^2\end{cases} יח ואם יאמרו לך אלגו אם תוסיפהו על עשרה יחזיק שרש ואם תגרעהו ‫70vמעשרה יחזיק שרש
equation/indeterminate equationx²+3x+1=n²,x²-(3x-2)=m²השאלות_החרשות/האלמות#43ha36) If you are told: a square that has a root, if you add to it its three roots and one dirham, it has a root; and if you subtract its three roots minus two dirham from it, the remainder has a root. :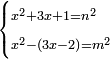\scriptstyle\begin{cases}\scriptstyle x^2+3x+1=n^2\\\scriptstyle x^2-\left(3x-2\right)=m^2\end{cases} לו ואם יאמרו לך אלגו שיחזיק שרש אם תוסיף עליו שלשת שרשיו ודרהם אחד יחזיק שרש
ואם תגרע ממנו שלשת שרשיו פחות שני דרהמי יחזיק מה שישאר שרש
equation/indeterminate equationx²-(x-1)=n²,x²-(1-x)=m²השאלות_החרשות/האלמות#Wdk537) If you are told: a square that has a root, if you subtract one dirham minus the root of the square from it, it has a root; [and if you subtract its root minus one dirham from it, it has a root]. :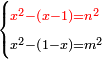\scriptstyle\begin{cases}\scriptstyle{\color{red}{x^2-\left(x-1\right)=n^2}}\\\scriptstyle x^2-\left(1-x\right)=m^2\end{cases} לז ואם יאמרו לך אלגו המחזיק שרש אם תגרע ממנו דרהם אחד פחות שרש האלגו יחזיק הנשאר שרש
equation/indeterminate equationx²+5=n²השאלות_החרשות/האלמות#rm8m1) When you are told: a square that has a root, if you add five to it, it has a root. How much is the square? :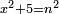\scriptstyle x^2+5=n^2 א כאשר יאמרו לך אלגו שמחזיק שרש אם תוסיף עליו חמשה יחזיק שרש כמה הוא האלגו
equation/indeterminate equationx²-10=n²השאלות_החרשות/האלמות#mV1w2) When you are told: a square that has a root, if you subtract ten dirham from it, what remains has a root. :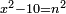\scriptstyle x^2-10=n^2 ב וכאשר יאמרו לך אלגו המחזיק שרש אם תגרע ממנו עשרה דרהמי יחזיק מה שישאר שרש
equation/indeterminate equationx²+3x=n²השאלות_החרשות/האלמות#L1j93) If you are told: a square that has a root, if you add three times its root to it, it has a root. How much is the square? :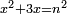\scriptstyle x^2+3x=n^2 ג ואם יאמרו לך אלגו המחזיק שרש אם תוסיף עליו שרשו שלשה פעמים יחזיק שרש כמה יהיה האלגו
equation/indeterminate equationx²-6x=n²השאלות_החרשות/האלמות#LfMV4) If you are told: a square that has a root, when we subtract six times its root from it, it has a root. :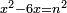\scriptstyle x^2-6x=n^2 ד ואם יאמרו לך אלגו מחזיק שרש כאשר גרענו ממנו שרשו ששה פעמים יחזיק שרש
equation/indeterminate equationx²+10x+20=n²השאלות_החרשות/האלמות#x5bu5) If you are told: a square that has a root, if you add to it ten times its root plus ten dirham, it has a root. :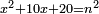\scriptstyle x^2+10x+20=n^2 ה ואם יאמרו לך אלגו המחזיק שרש אם תוסיף עליו עשרה פעמים שרשו ועשרה דרהמי יחזיק שרש
equation/indeterminate equationx²+x=n²,x²+1=m²השאלות_החרשות/האלמות#eNRx32) If you are told: a square that has a root, if you add its root to it, it has a root; and if you add to one dirham to it, it has a root. :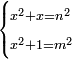\scriptstyle\begin{cases}\scriptstyle x^2+x=n^2\\\scriptstyle x^2+1=m^2\end{cases} לב ואם יאמרו לך אלגו המחזיק שרש אם תוסיף עליו שרשו יחזיק שרשו
ואם תוסיף עליו דרהם אחד יחזיק שרש
equation/indeterminate equationx²+(2-x)=n²,x²-(3-x)=m²השאלות_החרשות/האלמות#xP6r38) If you are told: a square that has a root, if you add two dirham minus the root of the square to it, it has a root; and if you subtract three minus the root of the square from it, it has a root. :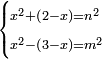\scriptstyle\begin{cases}\scriptstyle x^2+\left(2-x\right)=n^2\\\scriptstyle x^2-\left(3-x\right)=m^2\end{cases} לח ואם יאמרו לך אלגו המחזיק שרש אם תוסיף עליו שני דרהמי פחות שרש האלגו יחזיק שרש
ואם תגרע ממנו שלשה פחות שרש האלגו יחזיק שרש
equation/indeterminate equationx²-8x-30=n²השאלות_החרשות/האלמות#67aP6) If you are told: a square that has a root, if you subtract from it eight times its root and thirty dirham, the remainder has a root. :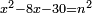\scriptstyle x^2-8x-30=n^2 ו ואם יאמרו לך אלגו המחזיק שרש אם תגרע ממנו שרשו שמנה פעמי' ושלשים דרהמי יחזיק מה שישאר שרש
equation/indeterminate equationx²+x+1=n²,x²+2x+2=m²השאלות_החרשות/האלמות#YEF939) If you are told: a square that has a root, if you add its root plus one dirham to it, it has a root; and if you add to the square its two roots plus two dirham, it has a root. :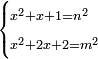\scriptstyle\begin{cases}\scriptstyle x^2+x+1=n^2\\\scriptstyle x^2+2x+2=m^2\end{cases} לט ואם יאמרו לך אלגו המחזיק שרש אם תוסיף עליו שרשו ודרהם אחד יחזיק שרש
ואם תוסיף על האלגו שני שרשיו ושני דרהמי יחזיק שרש
equation/indeterminate equationx²-5=n²,x²-5+√(x²-5)=m²השאלות_החרשות/האלמות#6x8t33) If you are told: a square that has a root, if you subtract five dirham from it, the remainder has a root; and if you add to the remainder its root, the sum has a root. :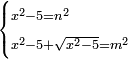\scriptstyle\begin{cases}\scriptstyle x^2-5=n^2\\\scriptstyle x^2-5+\sqrt{x^2-5}=m^2\end{cases} לג ואם יאמרו לך אלגו המחזיק שרש אם תגרע ממנו חמשה דרהמי יחזיק הנשאר שרש
ואם תוסיף על הנשאר שרשו יחזיק המקובץ שרש
equation/indeterminate equationx²+4x=n²,x²-(2x+1)=m²השאלות_החרשות/האלמות#1vZf34) If you are told: a square that has a root, if you add its four roots to it, it has a root; and if you subtract its two roots plus one dirham from it, the remainder has a root. :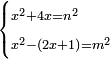\scriptstyle\begin{cases}\scriptstyle x^2+4x=n^2\\\scriptstyle x^2-\left(2x+1\right)=m^2\end{cases} לד ואם יאמרו לך אלגו שיחזיק שרש אם תוסיף עליו ארבעת שרשיו יחזיק שרש
ואם תגרע ממנו שני שרשיו ודרהם אחד יחזיק הנשאר שרש
equation/indeterminate equationx²+x=n²,x²+2x=m²השאלות_החרשות/האלמות#9AQM7) If you are told: a square that has a root, if you add its root to it, it has a root; and if you add its two roots to it, it has a root. :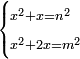\scriptstyle\begin{cases}\scriptstyle x^2+x=n^2\\\scriptstyle x^2+2x=m^2\end{cases} ז ואם יאמרו לך אלגו שיחזיק שרש אם תוסיף עליו שרשו יחזיק שרש ואם תוסיף עליו אלגו שני שרשיו יחזיק שרש
equation/indeterminate equationx²+x=n²,x²+3x=m²השאלות_החרשות/האלמות#5iEI8) If you are told: a square, if you add its root to it, it has a root; and if you add its three roots to it, it has a root. :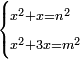\scriptstyle\begin{cases}\scriptstyle x^2+x=n^2\\\scriptstyle x^2+3x=m^2\end{cases} ח וכן אם יאמרו לך אלגו אם תוסיף עליו שרשו יחזיק שרש ואם תוסיף עליו שלשה שרשיו יחזיק שרש
equation/indeterminate equation49+x=n²,49+2x=m²השאלות_החרשות/האלמות#Y9ELIf you wish to know the number that when you add it to 49, it has a root; and if you add it to it twice, it has a root. :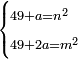\scriptstyle\begin{cases}\scriptstyle49+a=n^2\\\scriptstyle49+2a=m^2\end{cases} ואם רצית לדעת המספר שכאשר תוסיפהו על מ"ט יחזיק שרש ואם תוסיפהו עליו שני פעמים יחזיק שרש
equation/indeterminate equationx²-2x=n²,x²-3x=m²השאלות_החרשות/האלמות#65Jm9) If you are told: a square that has a root, if you subtract its two roots from it, the remainder has a root; and if you subtract its three roots from the square, the remainder has a root. :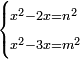\scriptstyle\begin{cases}\scriptstyle x^2-2x=n^2\\\scriptstyle x^2-3x=m^2\end{cases} ט וכן אם יאמרו לך מרובע המחזיק שרש אם תגרע ממנו שני שרשים יחזיק הנשאר שרש ואם תגרע מהמרובע שלשה שרשים יחזיק הנשאר שרש
equation/indeterminate equationx²-y=n²,x²-1½y=m²השאלות_החרשות/האלמות#CUHDWhen you wish to find a number that has a root, such that when you subtract from it another number, the remainder has a root; and if you subtract from it again the other number and its half, the remainder has a root. :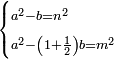\scriptstyle\begin{cases}\scriptstyle a^2-b=n^2\\\scriptstyle a^2-\left(1+\frac{1}{2}\right)b=m^2\end{cases} וכאשר תרצה למצוא מספר המחזיק שרש שכאשר תגרע ממנו מספר אחר יהיה לנשאר שרש ואם תגרע עוד ממנו כמו המספר האחר וכמו חציו יהיה לנשאר שרש
equation/indeterminate equationx-x²=n²השאלות_החרשות/האלמות#hdU110) If you are told: a square that has a root, if you subtract it from its root, the remainder has a root. :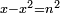\scriptstyle x-x^2=n^2 ‫67vי ואם יאמרו לך מרובע המחזיק שרש אם תגרעהו מן שרשו יהיה לנשאר שרש
equation/indeterminate equationx+x²=n²,x-x²=m²השאלות_החרשות/האלמות#Fofb11) If you are told: a square that has a root, if you add its root to it, it has a root; and if you subtract the square from its root, the remainder has a root. :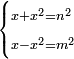\scriptstyle\begin{cases}\scriptstyle x+x^2=n^2\\\scriptstyle x-x^2=m^2\end{cases} יא ואם יאמרו לך מרובע המחזיק שרש אם תוסיף עליו שרשו יחזיק שרש ואם תגרע המרובע משרשו יהיה לנשאר שרש
equation/indeterminate equationx²-2x=n²,x²-2x+√(x²-2x)=m²השאלות_החרשות/האלמות#65Ct35) If you are told: a square that has a root, if you subtract its two roots from it, it has a root; and if you add to the remainder its root, it has a root. :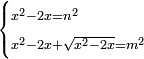\scriptstyle\begin{cases}\scriptstyle x^2-2x=n^2\\\scriptstyle x^2-2x+\sqrt{x^2-2x}=m^2\end{cases} לה ואם יאמרו לך אלגו המחזיק שרש אם תגרע ממנו שני שרשיו יחזיק שרש
ואם תוסיף על הנשאר שרשו יחזיק שרש
equation/indeterminate equationx²+y²=n²השאלות_החרשות/האלמות#Onda12) If you are told: divide five dirham into two parts, so that each part has a root. :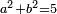\scriptstyle a^2+b^2=5 יב אם יאמרו לך חמשה דרהמי תחלקם לשני חלקים ולכל חלק שרש
equation/indeterminate equation3-x²=n²,2+x²=m²השאלות_החרשות/האלמות#6Zd315) If you are told: a square, if you subtract it from three dirham, the remainder has a root; and if you add it to two dirham, the sum has a root. :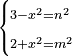\scriptstyle\begin{cases}\scriptstyle3-x^2=n^2\\\scriptstyle2+x^2=m^2\end{cases} טו ואם יאמרו לך מרובע אם תגרעהו משלשה דרהמי יחזיק הנשאר שרש ואם תוסיפהו על שני דרהמי יהיה למתקבץ שרש
equation/indeterminate equation10-x²=n²,20-x²=m²השאלות_החרשות/האלמות#EaVV16) If you are told: a square, if you subtract it from ten dirham, the remainder has a root; and if you subtract it from twenty, the remainder has a root. :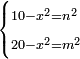\scriptstyle\begin{cases}\scriptstyle10-x^2=n^2\\\scriptstyle20-x^2=m^2\end{cases} יו ואם יאמרו לך אלגו אם תגרעהו מעשרה דרהמי יחזיק הנשאר שרש ואם תגרעהו מעשרים יחזיק הנשאר שרש
equation/indeterminate equation20+x²=n²,30+x²=m²השאלות_החרשות/האלמות#czE517) If you are told: a square, if you add it to twenty, it has a root; and if you add it to thirty, it has a root. :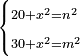\scriptstyle\begin{cases}\scriptstyle20+x^2=n^2\\\scriptstyle30+x^2=m^2\end{cases} יז ואם יאמרו לך אלגו אם תוסיפהו על עשרים יחזיק שרש ואם תוסיפיהו על שלשים יחזיק שרש
equation/indeterminate equationx²-4x=n²,x²-4x-2√(x²-4x)=m²השאלות_החרשות/האלמות#vAyv31) If you are told: a square, if you subtract its four roots from it, it has a root; and if you subtract from the remainder its two roots, it has a root. :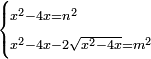\scriptstyle\begin{cases}\scriptstyle x^2-4x=n^2\\\scriptstyle x^2-4x-2\sqrt{x^2-4x}=m^2\end{cases} לא ואם יאמרו לך אלגו אם תוסיף עליו תגרע ממנו ארבעה שרשיו יחזיק שרש
ואם תגרע ואם תגרע מהנשאר שני שרשיו יחזיק שרש
equation/indeterminate equationx²+4x=n²,x²+4x+2√(x²+4x)=m²השאלות_החרשות/האלמות#2scj30) If you are told: a square that has a root, if you add its four roots to it, it has a root; and if you add to the sum its two roots, it has a root. :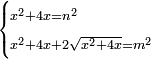\scriptstyle\begin{cases}\scriptstyle x^2+4x=n^2\\\scriptstyle x^2+4x+2\sqrt{x^2+4x}=m^2\end{cases} ל וכן אם יאמרו לך אלגו המחזיק שרש
אם תוסיף עליו ארבעת שרשיו יחזיק שרש
ואם תוסיף על המתקבץ שני שרשיו יחזיק שרש
equation/indeterminate equationx²+2x=n²,x²+2x+√(x²+2x)=m²השאלות_החרשות/האלמות#Csxg29) If you are told: a square that has a root, if you add two roots to it, it has a root; and if you add to the sum its root, it has a root. :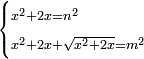\scriptstyle\begin{cases}\scriptstyle x^2+2x=n^2\\\scriptstyle x^2+2x+\sqrt{x^2+2x}=m^2\end{cases} כט כאשר יאמרו לך אלגו המחזיק שרש אם תוסיף עליו שני שרשים יחזיק שרש
ואם תוסיף על המקובץ שרשו יחזיק שרש
equation/indeterminate equationx²+3x=n²,x²+3x+6√(x²+3x)=m²השאלות_החרשות/האלמות#RKqA28) If you are told: a square that has a root, if you add its three roots to it, it has a root; and if you add to the sum its six roots, it has a root. :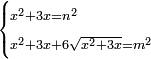\scriptstyle\begin{cases}\scriptstyle x^2+3x=n^2\\\scriptstyle x^2+3x+6\sqrt{x^2+3x}=m^2\end{cases} כח וכן אם יאמרו לך אלגו המחזיק שרש אם תוסיף עליו שלשת שרשיו יחזיק שרש
ואם תקבץ עם העולה ששת שרשיו יחזיק שרש
equation/indeterminate equationx²+2x=n²,x²+2x+3√(x²+2x)=m²השאלות_החרשות/האלמות#Xpj127) If you are told: a square that has a root, if you add its two roots to it, it has a root; and if you add to the sum its three roots, it has a root. :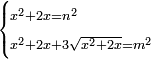\scriptstyle\begin{cases}\scriptstyle x^2+2x=n^2\\\scriptstyle x^2+2x+3\sqrt{x^2+2x}=m^2\end{cases} כז ואם יאמרו לך אלגו המחזיק שרש אם תוסיף עליו שני שרשיו יחזיק שרש
ואם תוסיף על המקובץ שלשת שרשיו יחזיק שרש
equation/indeterminate equation260-6x-x²=n²השאלות_החרשות/האלמות#63F726) If you are told: a square that has a root, if you subtract it from 260 minus six roots, the remainder has a root. :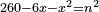\scriptstyle260-6x-x^2=n^2 כו ואם יאמרו לך אלגו המחזיק שרש אם תגרעהו מר"ס פחות ששה שרשים יחזיק הנשאר שרש
equation/indeterminate equationx²+1=10x-8השאלות_החרשות/האלמות#g7c725) If you are told: a square and one dirham equal ten roots minus eight dirham. :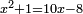\scriptstyle x^2+1=10x-8 כה ואם יאמרו לך אלגו ודרהם אחד ישוו עשרה שרשים פחות שמנה דרהמי
equation/indeterminate equationx²+2x=n²,x²-3x=m²השאלות_החרשות/האלמות#ltjx23) If you are told: a square, if you add its two roots to it, it has a root; and if you subtract its three roots from it, it has a root. :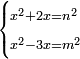\scriptstyle\begin{cases}\scriptstyle x^2+2x=n^2\\\scriptstyle x^2-3x=m^2\end{cases} כג ואם יאמרו לך אלגו אם תוסיף עליו שני שרשיו יחזיק שרש ואם תגרע ממנו שלשה שרשיו יחזיק שרש
algebraic operation/multiplication of algebraic expressions(10+x)×(10+x)חשבון_השטחים#aUXi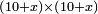\scriptstyle\left(10+x\right)\times\left(10+x\right) ואם יאמרו לך כמה יהיו עשרה אדרהמיש ודבר בעשרה אדרהמיש ודבר
algebraic operation/multiplication of algebraic expressions(10-x)×xחשבון_השטחים#TINt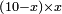\scriptstyle\left(10-x\right)\times x ואם יאמרו לך עשרה אדרהמיש פחות דבר אחד על דבר אחד
algebraic operation/multiplication of algebraic expressions3x×6חשבון_השטחים#6cOe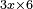\scriptstyle3x\times6 ואם יאמרו כמה יהיו שלשה דברים בששה אדרהמיש
algebraic operation/multiplication of algebraic expressions(10+x)×xחשבון_השטחים#mpes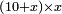\scriptstyle\left(10+x\right)\times x ואם יאמרו לך כמה יהיה עשרה אהדרמיש ודבר בדבר אחד
algebraic operation/multiplication of algebraic expressions2x×2xחשבון_השטחים#mF0Q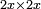\scriptstyle2x\times2x ואשים ענין זה בהכאת שני דברים בשני דברים
algebraic operation/multiplication of algebraic expressions(10+x)×(10-x)תחבולות_המספר#FNrCIf you are told: how much is the product of ten dirham plus a thing by ten dirham minus a thing? :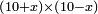\scriptstyle\left(10+x\right)\times\left(10-x\right) אמ' ואם יאמרו לך כמה יעלה מהכאת עשרה דרהמי ודבר בעשרה דרהמי פחות דבר
algebraic operation/multiplication of algebraic expressions(10+x)×(x-10)חשבון_השטחים#xrWT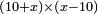\scriptstyle\left(10+x\right)\times\left(x-10\right) ואם יאמרו לך כמה יהיה עשרה אדרהמיש ודבר על דבר פחות עשרה אדרהמיש
algebraic operation/multiplication of algebraic expressions(10-x)×(10-x)תחבולות_המספר#wU5CIf you are told: how much is the product of ten dirham minus a thing by ten dirham minus a thing? :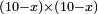\scriptstyle\left(10-x\right)\times\left(10-x\right) אמ' ואם יאמרו לך כמה יהיה מהכאת עשרה אדרהמי פחות דבר בעשרה אדרהמי פחות דבר
algebraic operation/multiplication of algebraic expressions(10+x)×xתחבולות_המספר#Dvm5If you are told: how much is the product of ten dirham plus a thing by one thing? :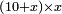\scriptstyle\left(10+x\right)\times x אמ' ואם יאמרו לך כמה יהיה מהכאת עשרה דרהמי ודבר בדבר אחד
algebraic operation/multiplication of algebraic expressions(10+x)×(10+x)תחבולות_המספר#e5FzIf you are told: how much is the product of ten dirham plus a thing by ten dirham plus a thing? :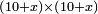\scriptstyle\left(10+x\right)\times\left(10+x\right) אמר ואם יאמרו לך כמה יעלה מהכאת עשרה דרהמי ודבר בעשרה דרהמי ודבר
algebraic operation/multiplication of algebraic expressions(10+⅔x)×(3-6x)חשבון_השטחים#EjPJ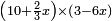\scriptstyle\left(10+\frac{2}{3}x\right)\times\left(3-6x\right) ואם יאמרו לך כמה יהיו עשרה אדרהמיש ושני שלישי דבר על שלשה אדרהמיש פחות ששה דברים
algebraic operation/multiplication of algebraic expressions(10+x)×(10-x)חשבון_השטחים#9LHU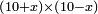\scriptstyle\left(10+x\right)\times\left(10-x\right) ואם יאמרו לך עשרה אדרהמיש ודבר על עשרה אדרהמיש פחות דבר
algebraic operation/multiplication of algebraic expressions3x×6תחבולות_המספר#NmR4If you are told: how much is the result of multiplying three things by six dirham? :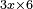\scriptstyle3x\times6 אמ' ואם יאמרו לך כמה יעלה מהכאת שלשה דברי' בששה דרהמי
algebraic operation/multiplication of algebraic expressions2x×2xתחבולות_המספר#AfDN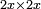\scriptstyle2x\times2x ונעמיד זה הענין בהכאת שני דברי' בשני דברים
algebraic operation/multiplication of algebraic expressions(10+x)×(x-10)תחבולות_המספר#Ga64If you are told: how much is the product of ten dirham plus a thing by a thing minus ten dirham? :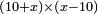\scriptstyle\left(10+x\right)\times\left(x-10\right) אמ' ואם יאמרו לך כמה העולה מהכאת עשרה דרהמי ודבר בדבר פחות עשרה דרהמי
algebraic operation/multiplication of algebraic expressions(10-x)×(10-x)חשבון_השטחים#w9JD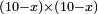\scriptstyle\left(10-x\right)\times\left(10-x\right) ואם יאמרו לך כמה יהיה עשרה אדרהמיש פחות דבר בעשרה אדרהמיש פחות דבר
algebraic operation/multiplication of algebraic expressions(10-x)×xתחבולות_המספר#EDhKIf you are told: how much is the product of ten dirham minus a thing by a thing? :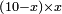\scriptstyle\left(10-x\right)\times x אמ' ואם יאמרו לך כמה יעלה מהכאת עשרה דרהמי {{#annot:term|879,1366|9fZc}}פחות{{#annotend:9fZc}} דבר אחד בדבר אחד
algebraic operation/multiplication of algebraic expressions(10+⅔x)×(3-6x)תחבולות_המספר#VDLnHe said: if you are told: how much is the product of ten dirham and two-thirds of a thing by three dirham minus six things? :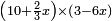\scriptstyle\left(10+\frac{2}{3}x\right)\times\left(3-6x\right) אמר ואם יאמרו לך כמה יהיה מהכאת עשרה דרהמי ושני שלישי דבר על שלשה דרהמי פחות ששה דברים
extraction of root/multiplication of roots(2×√10)×(½×√5)חשבון_השטחים#fTi5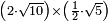\scriptstyle\left(2\sdot\sqrt{10}\right)\times\left(\frac{1}{2}\sdot\sqrt{5}\right) ואם יאמרו לך כמה יהיו הכאת שני שרשי עשרה על חצי שורש חמשה
extraction of root/multiplication of roots⅔×√9חשבון_השטחים#4FLj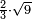\scriptstyle\frac{2}{3}\sdot\sqrt{9} וכאשר תרצה לקחת שני שלישי שורש תשעה
extraction of root/multiplication of roots½×√9חשבון_השטחים#FlzO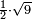\scriptstyle\frac{1}{2}\sdot\sqrt{9} וכאשר תרצה לקחת חצי שורש תשעה
extraction of root/multiplication of roots2×√16תחבולות_המספר#tRoEHe said: we give an example for this: when we wish to know the double root of sixteen. :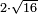\scriptstyle2\sdot\sqrt{16} אמ' ונניח {{#annot:term|197,1712|Ahnf}}דמיון לזה{{#annotend:Ahnf}} כאשר עשינו רצינו לדעת {{#annot:term|159,1230|j4A9}}כפל{{#annotend:j4A9}} שרש ששה עשר
extraction of root/multiplication of roots(2×√10)×(½×√5)תחבולות_המספר#FwABHe said: if you are told: how much is the product of two roots of ten by half a root of five? :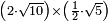\scriptstyle\left(2\sdot\sqrt{10}\right)\times\left(\frac{1}{2}\sdot\sqrt{5}\right) אמ' ואם יאמרו לך כמה יהיה מהכאת שני שרשי עשרה בחצי שרש חמשה
extraction of root/multiplication of roots√9×√4תחבולות_המספר#nTrHHe said: if you wish to know how much is the product of a root of nine by a root of four. :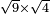\scriptstyle\sqrt{9}\times\sqrt{4} אמ' ואם תרצה לדעת כמה העולה מהכאת שרש תשעה בשרש ארבעה
extraction of root/multiplication of roots⅔×√9תחבולות_המספר#MSsUIf we wish to take two-thirds of a root of nine. :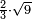\scriptstyle\frac{2}{3}\sdot\sqrt{9} ואם נרצה לקחת שני שלישי שרש תשעה
extraction of root/multiplication of roots½×√9תחבולות_המספר#UOpWHe said: when we wish to take half a root of nine. :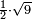\scriptstyle\frac{1}{2}\sdot\sqrt{9} אמ' וכאשר נרצה לקחת חצי שרש תשעה
extraction of root/multiplication of roots2×√16חשבון_השטחים#USTm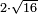\scriptstyle2\sdot\sqrt{16} ו{{#annot:term|197,1712|suQU}}דמיון זה{{#annotend:suQU}} כאשר רצינו לכפול שורש ששה עשר
extraction of root/multiplication of roots√9×√4חשבון_השטחים#WruF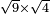\scriptstyle\sqrt{9}\times\sqrt{4} ואם תרצה להכות שורש תשעה על שורש ארבעה
equation/quadratic equation(x²+7)·√(3x²)=10x²חשבון_השטחים#dAZJIf you are told: a square, add to it seven dirham, then multiply the sum by a root of three times the square; it becomes ten times the square. :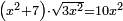\scriptstyle\left(x^2+7\right)\sdot\sqrt{3x^2}=10x^2 ואם יאמרו לך אלגו תוסיף עליו שבעה דרהמי ותכה המקובץ בשרש שלשה דמיוני האלגו ויהיה עשרה דמיוני האלגו
equation/quadratic equation[√(½x²)+3]·[√(⅓x²)+2]=20חשבון_השטחים#Y7kOIf you are told: a square, add three dirham to a root of its half, and two dirham to a root of its third, then multiply one [sum] by the other; it is twenty dirham. :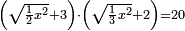\scriptstyle\left(\sqrt{\frac{1}{2}x^2}+3\right)\sdot\left(\sqrt{\frac{1}{3}x^2}+2\right)=20 ואם יאמרו לך אלגו תוסיף על שרש חציו שלשה דרהמי ועל שרש שלישיתו שני דרהמי ותכה האחד באחר ויהיה עשרים דרהמי
equation/quadratic equation[√(6x²)·√(5x²)]+10x²+20=(x²)²חשבון_השטחים#stdc[34] If you are told: a square, multiply a root of its six times by a root of its five times, then add ten times the square plus twenty dirham to the product and it is the same as [the product of] the square by itself. :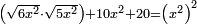\scriptstyle\left(\sqrt{6x^2}\sdot\sqrt{5x^2}\right)+10x^2+20=\left(x^2\right)^2 ואם יאמרו לך אלגו תרבה שרש מששה דמיוניו בשרש חמשה דמיוניו והוספת על מה שעלה מההכאה עשרה דמיוני האלגו ועשרים דרהמי יותר ויהיה כמו האלגו על עצמו
equation/quadratic equation[√(8x²)·√(3x²)]+20=(x²)²חשבון_השטחים#HcHI[33] If you are told: a square, multiply a root of eight times the square by a root of three times the square, then add twenty dirham to the result and it is the same as [the product of] the square by itself. :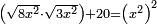\scriptstyle\left(\sqrt{8x^2}\sdot\sqrt{3x^2}\right)+20=\left(x^2\right)^2 ואם יאמרו לך אלגו תרבה שרש משמנה דמיוני האלגו בשרש משלשה דמיוני האלגו והוספת על העולה עשרים דרהמי ויהיה כמו האלגו על עצמו
equation/quadratic equation(x²-⅓x²)·3√(x²-⅓x²)=x²חשבון_השטחים#lFM5[15] If you are told: a square, we subtract its third from it, then multiply what remains by three roots of what remains from the square and the result is the square. :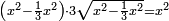\scriptstyle\left(x^2-\frac{1}{3}x^2\right)\sdot3\sqrt{x^2-\frac{1}{3}x^2}=x^2 ואם יאמרו לך אלגו גרענו ממנו שלישיתו והכינו הנשאר על שלשה שרשים מהנשאר מהאלגו וישוב האלגו
equation/quadratic equation3√x²+4√(x²-3√x²)=x²+4חשבון_השטחים#SNBo[17] If you are told: a square, its three roots and four roots of what remains from the square are the same as the square plus four dirham. :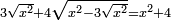\scriptstyle3\sqrt{x^2}+4\sqrt{x^2-3\sqrt{x^2}}=x^2+4 ואם יאמרו לך אלגו שלשת שרשיו וארבעה שרשים ממה שנשאר מהאלגו יהיה כמו האלגו וארבעה דרהמי' יותר
equation/quadratic equationa²+b²=c², ac=b², ab=10חשבון_השטחים#gGKeIf you are told: three unequal squares, if you multiply the smaller by itself and the mean by itself; they are as the greater by itself. If you multiply the smaller by the greater it is as the mean by itself. If you multiply the smaller by the mean it is ten dirham. :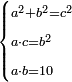\scriptstyle\begin{cases}\scriptstyle a^2+b^2=c^2\\\scriptstyle a\sdot c=b^2\\\scriptstyle a\sdot b=10\end{cases} ואם יאמרו לך שלשה אלגוש בלתי שוים
אם תכה הקטן בעצמו והאמצעי בעצמו יהיו כמו הגדול בעצמו
ואם תכה הקטון בגדול יהיה כמו האמצעי בעצמו
ואם תכה הקטן באמצעי יהיה עשרה דרהמי
equation/quadratic equationb²=3a², (a²+√a²)·(b²+√b²)=10b²חשבון_השטחים#nHFmIf you are told: two squares - one is three times the other; you add to each of them its root, then multiply the one by the other; it is ten times the greater square. :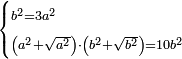\scriptstyle\begin{cases}\scriptstyle b^2=3a^2\\\scriptstyle\left(a^2+\sqrt{a^2}\right)\sdot\left(b^2+\sqrt{b^2}\right)=10b^2\end{cases} ואם יאמרו שני אלגוש והאחד שלשה דמיוני האחר הוספת על כל אחד מהם שרשו שלו והכית האחד באחר והיה עשרה דמיוני האלגו הגדול
equation/quadratic equation[x²+√(½x²)]²=4x²חשבון_השטחים#FvghIf you are told: a square, you add to it a root of its half, then multiply the result by itself; it becomes four times the square. :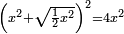\scriptstyle\left(x^2+\sqrt{\frac{1}{2}x^2}\right)^2=4x^2 ואם יאמרו לך אלגו הוספת עליו שרש חציו והכית העולה בעצמו ויהיה ארבעה דמיוני האלגו
equation/quadratic equation[x²+√(x²)+√(½x²)]²=5x²חשבון_השטחים#omooIf you are told: a square, add to it its root and a root of its half, then multiply the result by itself; it is five times the square. :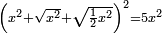\scriptstyle\left(x^2+\sqrt{x^2}+\sqrt{\frac{1}{2}x^2}\right)^2=5x^2 ואם יאמרו לך אלגו תוסיף עליו שרשו ושרש חציו ותכה המקובץ על עצמו ויהיה חמשה דמיוני האלגו
equation/quadratic equationx²+4√(x²)+√(½x²)+√(⅓x²)=10חשבון_השטחים#b04GIf you are told: a square, add to it its four roots plus a root of its half and a root of its third; it is ten dirham - how much is the square? :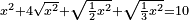\scriptstyle x^2+4\sqrt{x^2}+\sqrt{\frac{1}{2}x^2}+\sqrt{\frac{1}{3}x^2}=10 ואם יאמר לך אלגו תוסיף עליו ארבעה שרשיו ושרש חציו ושרש שלישיתו ויהיה עשרה דרהמי כמה הוא האלגו
equation/quadratic equation2√(x²)+√(½x²)+√(⅓x²)=20חשבון_השטחים#wOZVIf one says: a square whose two roots plus a root of its half and a root of its third are twenty dirham - how much is the square? :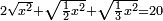\scriptstyle2\sqrt{x^2}+\sqrt{\frac{1}{2}x^2}+\sqrt{\frac{1}{3}x^2}=20 ואם יאמר אלגו אשר שני שרשיו ושרש חציו ושרש שלישיתו עשרים דרהמי כמה הוא האלגו
equation/quadratic equation[x²-(2√x²+10)]²=8x²חשבון_השטחים#aPQXIf you are told: a square, subtract its two roots and ten dirham from it, then multiply what remains by itself; it becomes eight times the square. :\scriptstyle\left[x^2-\left(2\sqrt{x^2}+10\right)\right]^2=8x^2 ואם יאמרו לך אלגו תגרע ממנו שני שרשיו ועשרה דרהמי ותכה מה שישאר בעצמו ויהיה שמנה דמיוני האלגו
equation/quadratic equation(√10·x²)/(2√3)=x²-10חשבון_השטחים#8OnPIf you are told: a square, multiply it by the root of ten, then divide the product by two plus the root of three; the quotient is the same as the square minus ten. :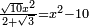\scriptstyle\frac{\sqrt{10}x^2}{2+\sqrt{3}}=x^2-10 ואם יאמרו לך אלגו תכהו בשרש עשרה ותחלק מה שיעלה על שנים ושרש שלשה ויעלה לאחד כל כך כמו שהוא האלגו פחות עשרה
equation/quadratic equation(x²+10)·√5=(x²)²חשבון_השטחים#hePu[38] If you are told: a square, you add to it ten dirham, then multiply the sum by a root of five and the result is the same as the product of the square by itself. :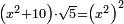\scriptstyle\left(x^2+10\right)\sdot\sqrt{5}=\left(x^2\right)^2 ואם יאמרו לך אלגו הוספת עליו עשרה דרהמי והכית המקובץ בשרש חמשה ויעלה כמו הכאת האלגו על עצמו
equation/quadratic equation[x²+√(3x²)]·√(2x²)=4x²חשבון_השטחים#lk6CIf you are told: a square, add to it a root of three times of it, then multiply the sum by a root of [twice] the square; it becomes four times the square. :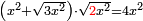\scriptstyle\left(x^2+\sqrt{3x^2}\right)\sdot\sqrt{{\color{red}{2}}x^2}=4x^2 ואם יאמרו לך אלגו תוסיף עליו שרש שלשה דמיוניו ותכה המקובץ בשרש האלגו יהיה ארבעה דמיוני האלגו
equation/quadratic equation[x²+√(x²)+√(½x²)]²=20חשבון_השטחים#OX0E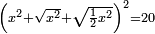\scriptstyle\left(x^2+\sqrt{x^2}+\sqrt{\frac{1}{2}x^2}\right)^2=20 ואם יאמרו לך אלגו הוסף עליו שרשו ושרש חציו ותכה המקובץ בעצמו ויהיה עשרים דרהמי
equation/quadratic equation2√(x²)+√(½x²)+√(⅓x²)=x²חשבון_השטחים#nPTXIf you are told: a square whose two roots plus a root of half the square and a root of its third are equal to the square - how much is the square? :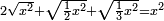\scriptstyle2\sqrt{x^2}+\sqrt{\frac{1}{2}x^2}+\sqrt{\frac{1}{3}x^2}=x^2 ואם יאמרו לך אלגו אשר שני שרשיו ושרש חצי האלגו ושרש שלישיתו ישוו האלגו כמה הוא האלגו
equation/quadratic equation3√x²+4√(x²-3√x²)=20חשבון_השטחים#tZ8i[13] If you are told: three roots of the square plus four roots of what remains from the square are twenty dirham. :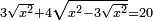\scriptstyle3\sqrt{x^2}+4\sqrt{x^2-3\sqrt{x^2}}=20 ואם יאמרו לך שלשה שרשים מהאלגו וארבעה שרשים ממה שנשאר מהאלגו יהיה עשרים דרהמי‫'
equation/quadratic equationx²·(x²+√10)=9x²חשבון_השטחים#XpMD[32] If you are told: a square, multiply it by itself plus a root of ten dirham and it becomes nine times the square. :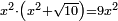\scriptstyle x^2\sdot\left(x^2+\sqrt{10}\right)=9x^2 ואם יאמרו לך אלגו תכהו על עצמו ושרש אחד מעשרה דרהמי ויהיה תשעה דמיוני האלגו
equation/quadratic equation√x²+√(√x²)+√(2√x²)+5√x²=10חשבון_השטחים#rWIeIf you are told: a square whose root and the root of its root, plus the root of its two roots, plus the root of five times the square are ten dirham. :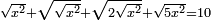\scriptstyle\sqrt{x^2}+\sqrt{\sqrt{x^2}}+\sqrt{2\sqrt{x^2}}+\sqrt{5x^2}=10 ואם יאמרו לך אלגו אשר שרשו ו{{#annot:term|2634|dE2e}}שרש שרשו{{#annotend:dE2e}} ושרש שני שרשיו ושרש חמשה דמיוני האלגו יהיה עשרה דרהמי
equation/quadratic equation3√x²+2√(x²-3√x²)=x²חשבון_השטחים#rq9x[16] If you are told: a square, its three roots and two roots of what remains are equal to the square. :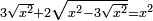\scriptstyle3\sqrt{x^2}+2\sqrt{x^2-3\sqrt{x^2}}=x^2 ואם יאמרו לך אלגו שלשת שרשיו ושני שרשי הנשאר ישוו האלגו
equation/quadratic equation[√(x²·2x²)+2]·x²=30חשבון_השטחים#uwLQ[40] If you are told: a square, you multiply it by its two times, extract the root of the product, add two dirham to it, then multiply the total by that square and the result is thirty dirham. :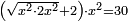\scriptstyle\left(\sqrt{x^2\sdot2x^2}+2\right)\sdot x^2=30 ואם יאמרו לך אלגו תכהו על {{#annot:term|387|piMO}}שני דמיוניו{{#annotend:piMO}} ותקח שרש העולה ותוסיף עליו שני דרהמי ותכה הכל באלגו ההוא ויהיה שלשים דרהמי
equation/quadratic equation(x²-⅓x²)·3√x²=x²חשבון_השטחים#ak8r[14] If you are told: we subtract from a square its third, then multiply what remains by three roots of the original square and the result is the original square. :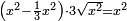\scriptstyle\left(x^2-\frac{1}{3}x^2\right)\sdot3\sqrt{x^2}=x^2 ואם יאמרו לך גרענו מן האלגו שלישיתו והכינו הנשאר על שלשה שרשים מהאלגו הראשון ושב האלגו הראשון
equation/quadratic equation[x²-(⅓x²+2)]²=x²+24חשבון_השטחים#lT08[12] If you are told: a square, you subtract its third and two dirham from it, then multiply what remains by itself and the result is the square plus 24 dirham. :\scriptstyle\left[x^2-\left(\frac{1}{3}x^2+2\right)\right]^2=x^2+24 ואם יאמרו לך אלגו גרעת ממנו שלישיתו ושני אדרהמיש ומה שנשאר הכית אותו על עצמו ושב האלגו וכ"ד אדרהמיש יותר
compound canonical equation/roots and numbers equal squares3x+4=x²חשבון_השטחים#qrpb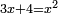\scriptstyle3x+4=x^2 והשרשים ומספרים שישוו אלגוש כמו אם יאמר שלשה שרשים וארבעה מספרים ישוו אלגו
compound canonical equation/roots and numbers equal squares3x+4=x²תחבולות_המספר#VKnlHe said: roots and numbers that are equal to a square is as saying three roots and four dirham are equal to a square. :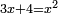\scriptstyle3x+4=x^2 אמ' שרשים ומספרים שישוו למרובע הוא כמו שיאמ' שלשה שרשים וארבעה דרהמי יהיו שוים למרובע
simple canonical equation/roots equal numbersx=4חשבון_השטחים#wMvnWhen the roots are equal to numbers, as if you say: the root is equal to four. :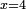\scriptstyle x=4 והשרשים שישוו מספרים כמו שתאמר שרש ישוה ארבעה
simple canonical equation/roots equal numbers5x=30תחבולות_המספר#jHg9As if one says: five roots are equal to thirty. :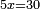\scriptstyle5x=30 כמו אם אמ' חמשה שרשים ישוו לשלשים
simple canonical equation/roots equal numbersx=4תחבולות_המספר#PaMjIf you are told: the roots of the square are equal to four numbers. :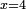\scriptstyle x=4 כי אם יאמרו לך שרשי המרובע ישוו לארבע' מספרי‫'
simple canonical equation/roots equal numbers½x=10חשבון_השטחים#0OjbIf you say: half a root is equal to ten. :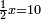\scriptstyle\frac{1}{2}x=10 וכמו אם תאמר חצי שרש ישוה עשרה
simple canonical equation/roots equal numbers5x=30חשבון_השטחים#1YGhAlso if you say: five roots are equal to thirty. :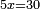\scriptstyle5x=30 וכמו אם תאמר חמשה שרשים ישוו שלשים
simple canonical equation/roots equal numbers½x=10תחבולות_המספר#e4m4If one says: half a root is equal to ten. :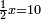\scriptstyle\frac{1}{2}x=10 ואם אמ' חמשה ושלשים חצי שרש ישוה לעשרה
divide a quantity problem/simple divisiontwo amounts of money between two groups of peopleחשבון_השטחים#YO6T[6] If you are told: we divide ten dirham among people. :Each one receives a thing. :Then we add to them four people and divide sixty dirham among all. :Each one of them receives five dirham more than each one of the former. :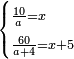\scriptstyle\begin{cases}\scriptstyle\frac{10}{a}=x\\\scriptstyle\frac{60}{a+4}=x+5\end{cases} ואם יאמרו לך חלקנו עשרה אדרהמיש על אנשים
ועלה לכל אחד דבר
והוספנו עליהם ארבעה אנשים וחלקנו עליהם ששים אדרהמיש
ועלה לאחד יותר ממה שעלה לאחד מהראשונים חמשה אדרהמיש
divide a quantity problem/simple divisiontwo amounts of money between two groups of peopleחשבון_השטחים#NF2x[8] This is as when you are told: we divide twenty dirham among people. :Each one receives a thing. :Then we add to them two people and divide sixty dirham among all. :Each one of them receives five dirham more than each one of the former. :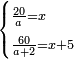\scriptstyle\begin{cases}\scriptstyle\frac{20}{a}=x\\\scriptstyle\frac{60}{a+2}=x+5\end{cases} והוא כי כאשר יאמרו לך עשרים אדרהמיש חלקנום על אנשים
והגיע לכל אחד מהם דבר
והוספנו עליהם שני אנשים וחלקנו עליהם ששים אדרהמיש
ועלה לאחד מהם יותר מאשר עלה לאחד מהראשונים בחמשה אדרהמיש
divide a quantity problem/simple divisiontwo amounts of money between two groups of peopleחשבון_השטחים#fCoU[7] If you are told: we divide sixty dirham [among people]. :Each one receives a thing. :Then we add to them three people and divide twenty dirham among all. :Each one of them receives twenty-six dirham less than each one of the former. :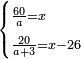\scriptstyle\begin{cases}\scriptstyle\frac{60}{a}=x\\\scriptstyle\frac{20}{a+3}=x-26\end{cases} ואם יאמרו לך חלקנו ששים אדרהמיש
ועלה לאחד דבר
והוספנו עליהם שלשה אנשים וחלקנו עליהם עשרים אדרהמיש
ועלה לאחד פחות מאשר עלה לאחד מהראשונים עשרים וששה אדרהמיש
divide a quantity problem/simple divisiontwo amounts of money between two groups of peopleחשבון_השטחים#65ve[9] If you are told: we divide ten dirham among people. :Each one receives a thing. :Then we add to them six people and divide forty dirham among all. :Each one of them receives as much as each one of the former equally. :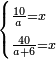\scriptstyle\begin{cases}\scriptstyle\frac{10}{a}=x\\\scriptstyle\frac{40}{a+6}=x\end{cases} ואם יאמרו לך חלקנו עשרה אדרהמיש על אנשים
והגיע לאחד דבר
והוספנו עליהם ששה אנשים וחלקנו בין כולם ארבעים אדרהמיש
והגיע לאחד מהם כמו שהגיע לאחד מהראשונים בשוה
divide a quantity problem/simple divisiontwo amounts of money between two groups of peopleחשבון_השטחים#0rxj[5] If you are told: we divide ten dirham among people. :Each one receives a thing. :Then we add to them four people and divide thirty dirham among all. :Each one of them receives four dirham less than each one of the former. :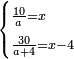\scriptstyle\begin{cases}\scriptstyle\frac{10}{a}=x\\\scriptstyle\frac{30}{a+4}=x-4\end{cases} ואם יאמרו לך חלקנו עשרה אדרהמיש על אנשים
ועלה לכל אחד מהם דבר
והוספנו עליהם ארבעה אנשים וחלקנו על כלם שלשים אדרהמיש
ועלה לכל אחד מהם פחות מאשר עלה לראשונים ארבעה אדרהמיש
divide a quantity problem/simple divisionsame amount of money between two groups of peopleחשבון_השטחים#K4Xr[4] If you are told: we divide fifty dirham among people. :Each one receives a thing. :Then we add to them three [people] and divide the fifty dirham among all. :Each one of the latter receives three dirham and three-quarters less than each one of the former. :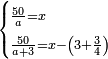\scriptstyle\begin{cases}\scriptstyle\frac{50}{a}=x\\\scriptstyle\frac{50}{a+3}=x-\left(3+\frac{3}{4}\right)\end{cases} שאלה ואם יאמרו לך חלקנו חמשים אדרהמיש על אנשים
ועלה לאחד דבר
והוספנו על האנשים עוד שלשה וחלקנו עליהם החמשים אדרהמיש
ועלה לכל אחד מהאחרונים פחות מאשר עלה לכל אחד מהראשונים שלשה אדרהמיש ושלשה רביעים
compound canonical equation/squares and numbers equal rootsx²+21=10xתחבולות_המספר#u4EAHe said: squares and numbers that are equal to roots is as if you say: when you sum twenty-one dirham with a certain square, they are equal to ten roots of the square. :\scriptstyle x^2+21=10x אמ' המרובעי' והמספרי' שישוו לשרשים הוא כאלו תאמ' כאשר תקבץ עם מרובע מה עשרים ואחד דרהמי יהיו שוים לעשרה משרשים מהמרובע
compound canonical equation/squares and numbers equal rootsx²+25=10xתחבולות_המספר#QWm3Example: one says: a square plus twenty-five [dirham] are equal to ten roots of the square. :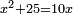\scriptstyle x^2+25=10x דמיון זה שיאמ' מרובע מה ועשרים וחמשה שרשים ישוו לעשרה שרשים מהמרובע
compound canonical equation/squares and numbers equal rootsx²+21=10xחשבון_השטחים#yRRf\scriptstyle x^2+21=10x והאלגוש והמספרים שישוו שרשים כאלו תאמר אלגוש ועשרים ואחד אדרהמיש ישוו עשרה שרשים
compound canonical equation/squares and numbers equal rootsx²+25=10xחשבון_השטחים#5rN4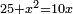\scriptstyle25+x^2=10x ו{{#annot: term | #to give an example, #משל | ZpYe}}אמשיל זה{{#annotend:ZpYe}} בשאילה אחרת ואניחנה שכ"ה אדרהמיש ואלגוש ישוו עשרה שרשים
compound canonical equation/squares and roots equal numbers½x²+5x=28חשבון_השטחים#XyaI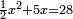\scriptstyle\frac{1}{2}x^2+5x=28 ואם אמרו לך חצי אלגוש וחמשה שרשים ישוו כ"ח אדרהמיש
נאמר כי כאשר {{#annot: term | #to add, #חבר | qgPe}}חברנו{{#annotend:qgPe}} על חצי האלגוש חמשה שרשי האלגוש יהיו כ"ח אדרהמיש
compound canonical equation/squares and roots equal numbersx²+10x=39חשבון_השטחים#BnUpSquares and roots are equal to numbers, it is as if you say: a square and ten roots are equal to thirty-nine dirham. :\scriptstyle x^2+10x=39 והאלגוש והשרשים שישוו מספרים הוא כאלו תאמר אלגו ועשרה שרשים ישוו תשעה ושלשים דרהמיש
compound canonical equation/squares and roots equal numbers3x²+15x=72תחבולות_המספר#HV5bExample: if one asks: three squares and 15 roots are equal to 72 dirham. :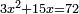\scriptstyle3x^2+15x=72 דמיון זה ששאל שלשה מרובעי' וט"ו שרשי' ישוו לע"ב דרהמי
compound canonical equation/squares and roots equal numbers2x²+10x=48חשבון_השטחים#cSpR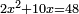\scriptstyle2x^2+10x=48 וזה כמו שתאמר שנים אלגוש ועשרה שרשים ‫2rישוו מ"ח אדרהמיש
compound canonical equation/squares and roots equal numbers½x²+5x=28תחבולות_המספר#FJRfLikewise, if one asks: half a square plus its five roots are equal to 28 dirham. :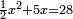\scriptstyle\frac{1}{2}x^2+5x=28 וכמו כן אם שאל השואל חצי מרובע וחמשה משרשיו ישוו לכ"ח דרהמי
compound canonical equation/squares and roots equal numbersx²+10x=39תחבולות_המספר#oMPaHe said: when squares and roots are equal to numbers, it is as if you say: the sum of one square and ten of its roots together is equal to thirty-nine dirham. :\scriptstyle x^2+10x=39 אמ' כאשר יהיו המרובעים והשרשים שוים למספרי' כאלו תאמ' המקובץ ממרובע מהאחד ועשרה משרשיו יחד ישוה לשלשים ותשעה דרהמי
simple canonical equation/squares equal numbers5x²=45חשבון_השטחים#yMV8Likewise, when five squares are equal to forty-five. :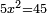\scriptstyle5x^2=45 וכן חמשה אלגוש ישוו חמשה וארבעים
simple canonical equation/squares equal numbersx²=16תחבולות_המספר#fCC4As if you are told: the square is equal to sixteen. :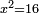\scriptstyle x^2=16 כמו אם יאמרו לך המרובע ישוה לששה עשר
simple canonical equation/squares equal numbers5x²=45תחבולות_המספר#C4DXIf one says: five squares are equal to forty-five. :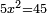\scriptstyle5x^2=45 כי אם אמ' חמשה מרובעי' ישוו לחמשה וארבעי‫'
simple canonical equation/squares equal numbersx²=16חשבון_השטחים#lI7wThe squares that are equal to numbers is as a square that equals sixteen. :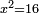\scriptstyle x^2=16 והאלגוש שישוו מספרים כמו אלגו שישוה שש עשרה
simple canonical equation/squares equal numbers⅓x²=27חשבון_השטחים#sOLHAlso if you say: a third of the square is equal to twenty-seven. :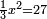\scriptstyle\frac{1}{3}x^2=27 וכן אם תאמר שלישית אלגו שוה ‫1vשבעה ועשרים
simple canonical equation/squares equal numbers⅓x²=27תחבולות_המספר#UsmiIf one says: a third of the square is equal to twenty-seven. :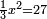\scriptstyle\frac{1}{3}x^2=27 ואם אמ' שלישית המרובע ישוה לשבעה ועשרים
simple canonical equation/squares equal rootsx²=5xתחבולות_המספר#EqMyFor example: if you are told; five roots are equal to one square. How much is the square? :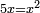\scriptstyle5x=x^2 {{#annot:term|197,1712|lPkF}}דמיון זה{{#annotend:lPkF}} אם אמרו לך חמשה שרשי' ישוו למרובע אחד כמה הוא המרובע
simple canonical equation/squares equal rootsx²=5xחשבון_השטחים#cbxXThe squares that are equal to roots is as if you say: a square equals five roots. :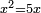\scriptstyle x^2=5x והאלגוש שישוו שרשים הוא כאלו תאמר אלגו ישוה חמשה שרשים
simple canonical equation/squares equal roots5x²=20xחשבון_השטחים#sJUhAs if you say: five squares equal twenty roots. :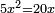\scriptstyle5x^2=20x וכמו שתאמר חמשה אלגוש ישוו עשרים שרשים
simple canonical equation/squares equal roots½x²=10xתחבולות_המספר#fayjAlso, if he says: half a square is equal to ten roots. :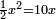\scriptstyle\frac{1}{2}x^2=10x וכן אם יאמ' חצי מרובע ישוה לעשרה שרשים
simple canonical equation/squares equal roots5x²=20xתחבולות_המספר#WDhUExample: if one asks: five squares are equal to twenty roots. :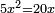\scriptstyle5x^2=20x דמיון זה אם ישאל חמשה מרובעי' ישוו לעשרים שרשים
simple canonical equation/squares equal roots½x²=10xחשבון_השטחים#N1ieLikewise, if it is said: half a square equals ten roots. :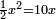\scriptstyle\frac{1}{2}x^2=10x וכמו כן אם יאמר חצי אלגו ישוה עשרה שרשים
extraction of root/subtraction of roots√9-√4תחבולות_המספר#YpmSHe said: when you wish to subtract a root of four from a root of nine, so that what remains is a root of a single number. :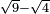\scriptstyle\sqrt{9}-\sqrt{4} אמ' וכאשר תרצה לגרוע שרש ארבעה משרש ששה תשעה עד שיהיה מה שישאר שרש למספר אחד
extraction of root/subtraction of roots√18-√8תחבולות_המספר#uKgYIf we want to subtract the root of eight from the root of eighteen. :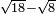\scriptstyle\sqrt{18}-\sqrt{8} ואם באנו לגרוע שרש שמנה משרש שמנה עשר
extraction of root/subtraction of roots√18-√8חשבון_השטחים#HW4Q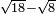\scriptstyle\sqrt{18}-\sqrt{8} ואם רצונך לגרוע שורש ח' משורש י"ח
extraction of root/subtraction of roots√9-√4חשבון_השטחים#e8VS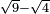\scriptstyle\sqrt{9}-\sqrt{4} וכאשר תרצה לגרוע שרש ארבעה משורש תשעה עד שיהיה מה שישאר משורש תשעה שורש מספר אחד פחות שורש מהמספר האחר
Retrieved from "http://mispar.ethz.ch/mediawiki/index.php?title=Search_Page&oldid=39201"