Difference between revisions of "Search Page"

From mispar
Jump to: navigation, search
Line 1: Line 1:
  
 
{{#annotask:
 
{{#annotask:
−
   [[wiki_text: %math%]]
+
   [[category: equation]]
 
   [[page: author="Abū Kāmil"]]
 
   [[page: author="Abū Kāmil"]]
 
}}
 
}}

Revision as of 12:36, 6 September 2019

Category Category Comment Link Annotated text
quartic equation/biquadratic equation4(x²+8)=x⁴תחבולות_המספר#G1Mq[6] He said: the six problem is as if you are told: we add to a certain square [eight] dirham, then multiply the sum by four dirham and the result is the same as the product of the square [by itself]. :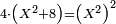\scriptstyle4\sdot\left(X^2+8\right)=\left(X^2\right)^2 אמ' והשאלה הששית כמו אם יאמרו לך הוספנו על התמונ' מרובע מה שלשה דרהמי והכינו המקובץ בארבעה דרהמי והיה העולה כמו הכאת א"ב בעצמו המרובע
quartic equation/biquadratic equation4(x²+8)=x⁴חשבון_השטחים#ZxMx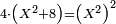\scriptstyle4\sdot\left(X^2+8\right)=\left(X^2\right)^2 אלגו תוסיף עליו שמנה אדרהם ותכה {{#annot:term|388,1217|vQSL}}המקובץ{{#annotend:vQSL}} על ארבעה אדרהם והיה כמו האלגו על עצמו
quadratic equation/canonical equationח.ל.ק./חלקtermחשבון_השטחים#rsWGהששה חלקים
quadratic equation/canonical equationtermחשבון_השטחים#hEUgהששה בקשות
canonical equation/compound canonical equationח.ב.ר./מחוברtermחשבון_השטחים#y7Ptמחוברים
canonical equation/compound canonical equationdefinitionחשבון_השטחים#FjYVושלשה {{#annot: term | #compound canonical equation, #מחובר | y7Pt}}מחוברים{{#annotend:y7Pt}} והם אלגוש ושרשים ישוו מספרים ואלגוש ומספרים ישוו שרשים ושרשים ומספרים ישוו אלגוש
equation/indeterminate equationx²+2x=n²,x²+2x+√(x²+2x)=m²השאלות_החרשות/האלמות#Csxg29) If you are told: a square that has a root, if you add two roots to it, it has a root; and if you add to the sum its root, it has a root. :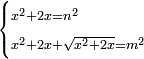\scriptstyle\begin{cases}\scriptstyle x^2+2x=n^2\\\scriptstyle x^2+2x+\sqrt{x^2+2x}=m^2\end{cases} כט כאשר יאמרו לך אלגו המחזיק שרש אם תוסיף עליו שני שרשים יחזיק שרש
ואם תוסיף על המקובץ שרשו יחזיק שרש
equation/indeterminate equationx²+3x=n²,x²+3x+6√(x²+3x)=m²השאלות_החרשות/האלמות#RKqA28) If you are told: a square that has a root, if you add its three roots to it, it has a root; and if you add to the sum its six roots, it has a root. :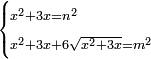\scriptstyle\begin{cases}\scriptstyle x^2+3x=n^2\\\scriptstyle x^2+3x+6\sqrt{x^2+3x}=m^2\end{cases} כח וכן אם יאמרו לך אלגו המחזיק שרש אם תוסיף עליו שלשת שרשיו יחזיק שרש
ואם תקבץ עם העולה ששת שרשיו יחזיק שרש
equation/indeterminate equationx²+2x=n²,x²+2x+3√(x²+2x)=m²השאלות_החרשות/האלמות#Xpj127) If you are told: a square that has a root, if you add its two roots to it, it has a root; and if you add to the sum its three roots, it has a root. :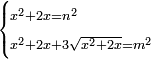\scriptstyle\begin{cases}\scriptstyle x^2+2x=n^2\\\scriptstyle x^2+2x+3\sqrt{x^2+2x}=m^2\end{cases} כז ואם יאמרו לך אלגו המחזיק שרש אם תוסיף עליו שני שרשיו יחזיק שרש
ואם תוסיף על המקובץ שלשת שרשיו יחזיק שרש
equation/indeterminate equation260-6x-x²=n²השאלות_החרשות/האלמות#63F726) If you are told: a square that has a root, if you subtract it from 260 minus six roots, the remainder has a root. :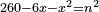\scriptstyle260-6x-x^2=n^2 כו ואם יאמרו לך אלגו המחזיק שרש אם תגרעהו מר"ס פחות ששה שרשים יחזיק הנשאר שרש
equation/indeterminate equationx²+1=10x-8השאלות_החרשות/האלמות#g7c725) If you are told: a square and one dirham equal ten roots minus eight dirham. :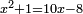\scriptstyle x^2+1=10x-8 כה ואם יאמרו לך אלגו ודרהם אחד ישוו עשרה שרשים פחות שמנה דרהמי
equation/indeterminate equation10x-8-x²=n²השאלות_החרשות/האלמות#JrVS24) If you are told: a square that has a root, if you subtract it from its ten roots minus eight dirham, the remainder has a root. :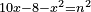\scriptstyle10x-8-x^2=n^2 כד ואם יאמרו לך אלגו שיחזיק שרש אם תגרעהו מעשרת שרשיו פחות שמנה שרשיו דרהמי יחזיק מה שישאר שרש
equation/indeterminate equationx²+2x=n²,x²-3x=m²השאלות_החרשות/האלמות#ltjx23) If you are told: a square, if you add its two roots to it, it has a root; and if you subtract its three roots from it, it has a root. :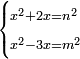\scriptstyle\begin{cases}\scriptstyle x^2+2x=n^2\\\scriptstyle x^2-3x=m^2\end{cases} כג ואם יאמרו לך אלגו אם תוסיף עליו שני שרשיו יחזיק שרש ואם תגרע ממנו שלשה שרשיו יחזיק שרש
equation/indeterminate equationx²+x=n²,x²-x=m²השאלות_החרשות/האלמות#MUv822) If you are told: a square, if you add its root to it, the sum has a root; and if you subtract its root from it, the remainder has a root. :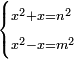\scriptstyle\begin{cases}\scriptstyle x^2+x=n^2\\\scriptstyle x^2-x=m^2\end{cases} כב ואם יאמרו לך אלגו אם תוסיף עליו שרשו יהיה למתקבץ שרש ואם תגרע ממנו שרשו יחזיק הנשאר שרש
equation/indeterminate equation2x+49-x²=n²השאלות_החרשות/האלמות#bkYa21) If you are told: a square, if you subtract it from its two roots plus 49 dirham, the remainder has a root. :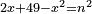\scriptstyle2x+49-x^2=n^2 כא ואם יאמרו לך אלגו אם תגרעהו משני שרשיו ומ"ט דרהמי יחזיק הנשאר שרש
equation/indeterminate equation8x+x²=n²,2x-x²=m²השאלות_החרשות/האלמות#62Ll20) If you are told: a square, if you add its eight roots to it, it has a root; and if you subtract it from its two roots, the remainder has a root. :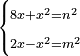\scriptstyle\begin{cases}\scriptstyle8x+x^2=n^2\\\scriptstyle2x-x^2=m^2\end{cases} כ ואם יאמרו לך אלגו אם תוסיף עליו שמנה שרשיו יחזיק שרש ואם תגרעהו משני שרשיו יהיה לנשאר שרש
equation/indeterminate equation8x+109-x²=n²השאלות_החרשות/האלמות#tMRx19) If you are told: a square, if you subtract it from its eight roots plus 109 dirham, it has a root. :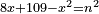\scriptstyle8x+109-x^2=n^2 יט ואם יאמרו לך אלגו אם תגרעהו משמנה שרשים וק"ט דרהמי יחזיק שרש
equation/indeterminate equation10+x²=n²,10-x²=m²השאלות_החרשות/האלמות#rWQ118) If you are told: a square, if you add it to ten, it has a root; and if you subtract it from ten, it has a root. :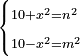\scriptstyle\begin{cases}\scriptstyle10+x^2=n^2\\\scriptstyle10-x^2=m^2\end{cases} יח ואם יאמרו לך אלגו אם תוסיפהו על עשרה יחזיק שרש ואם תגרעהו ‫70vמעשרה יחזיק שרש
equation/indeterminate equation20+x²=n²,30+x²=m²השאלות_החרשות/האלמות#czE517) If you are told: a square, if you add it to twenty, it has a root; and if you add it to thirty, it has a root. :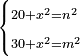\scriptstyle\begin{cases}\scriptstyle20+x^2=n^2\\\scriptstyle30+x^2=m^2\end{cases} יז ואם יאמרו לך אלגו אם תוסיפהו על עשרים יחזיק שרש ואם תוסיפיהו על שלשים יחזיק שרש
equation/indeterminate equation10-x²=n²,20-x²=m²השאלות_החרשות/האלמות#EaVV16) If you are told: a square, if you subtract it from ten dirham, the remainder has a root; and if you subtract it from twenty, the remainder has a root. :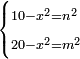\scriptstyle\begin{cases}\scriptstyle10-x^2=n^2\\\scriptstyle20-x^2=m^2\end{cases} יו ואם יאמרו לך אלגו אם תגרעהו מעשרה דרהמי יחזיק הנשאר שרש ואם תגרעהו מעשרים יחזיק הנשאר שרש
equation/indeterminate equation3-x²=n²,2+x²=m²השאלות_החרשות/האלמות#6Zd315) If you are told: a square, if you subtract it from three dirham, the remainder has a root; and if you add it to two dirham, the sum has a root. :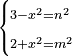\scriptstyle\begin{cases}\scriptstyle3-x^2=n^2\\\scriptstyle2+x^2=m^2\end{cases} טו ואם יאמרו לך מרובע אם תגרעהו משלשה דרהמי יחזיק הנשאר שרש ואם תוסיפהו על שני דרהמי יהיה למתקבץ שרש
equation/indeterminate equationx²+y²=n²השאלות_החרשות/האלמות#Onda12) If you are told: divide five dirham into two parts, so that each part has a root. :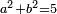\scriptstyle a^2+b^2=5 יב אם יאמרו לך חמשה דרהמי תחלקם לשני חלקים ולכל חלק שרש
equation/indeterminate equationx+x²=n²,x-x²=m²השאלות_החרשות/האלמות#Fofb11) If you are told: a square that has a root, if you add its root to it, it has a root; and if you subtract the square from its root, the remainder has a root. :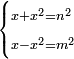\scriptstyle\begin{cases}\scriptstyle x+x^2=n^2\\\scriptstyle x-x^2=m^2\end{cases} יא ואם יאמרו לך מרובע המחזיק שרש אם תוסיף עליו שרשו יחזיק שרש ואם תגרע המרובע משרשו יהיה לנשאר שרש
equation/indeterminate equationx-x²=n²השאלות_החרשות/האלמות#hdU110) If you are told: a square that has a root, if you subtract it from its root, the remainder has a root. :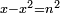\scriptstyle x-x^2=n^2 ‫67vי ואם יאמרו לך מרובע המחזיק שרש אם תגרעהו מן שרשו יהיה לנשאר שרש
equation/indeterminate equationx²-y=n²,x²-1½y=m²השאלות_החרשות/האלמות#CUHDWhen you wish to find a number that has a root, such that when you subtract from it another number, the remainder has a root; and if you subtract from it again the other number and its half, the remainder has a root. :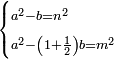\scriptstyle\begin{cases}\scriptstyle a^2-b=n^2\\\scriptstyle a^2-\left(1+\frac{1}{2}\right)b=m^2\end{cases} וכאשר תרצה למצוא מספר המחזיק שרש שכאשר תגרע ממנו מספר אחר יהיה לנשאר שרש ואם תגרע עוד ממנו כמו המספר האחר וכמו חציו יהיה לנשאר שרש
equation/indeterminate equationx²-2x=n²,x²-3x=m²השאלות_החרשות/האלמות#65Jm9) If you are told: a square that has a root, if you subtract its two roots from it, the remainder has a root; and if you subtract its three roots from the square, the remainder has a root. :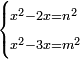\scriptstyle\begin{cases}\scriptstyle x^2-2x=n^2\\\scriptstyle x^2-3x=m^2\end{cases} ט וכן אם יאמרו לך מרובע המחזיק שרש אם תגרע ממנו שני שרשים יחזיק הנשאר שרש ואם תגרע מהמרובע שלשה שרשים יחזיק הנשאר שרש
equation/indeterminate equation49+x=n²,49+2x=m²השאלות_החרשות/האלמות#Y9ELIf you wish to know the number that when you add it to 49, it has a root; and if you add it to it twice, it has a root. :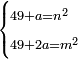\scriptstyle\begin{cases}\scriptstyle49+a=n^2\\\scriptstyle49+2a=m^2\end{cases} ואם רצית לדעת המספר שכאשר תוסיפהו על מ"ט יחזיק שרש ואם תוסיפהו עליו שני פעמים יחזיק שרש
equation/indeterminate equationx²+x=n²,x²+3x=m²השאלות_החרשות/האלמות#5iEI8) If you are told: a square, if you add its root to it, it has a root; and if you add its three roots to it, it has a root. :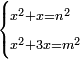\scriptstyle\begin{cases}\scriptstyle x^2+x=n^2\\\scriptstyle x^2+3x=m^2\end{cases} ח וכן אם יאמרו לך אלגו אם תוסיף עליו שרשו יחזיק שרש ואם תוסיף עליו שלשה שרשיו יחזיק שרש
equation/indeterminate equationx²+x=n²,x²+2x=m²השאלות_החרשות/האלמות#9AQM7) If you are told: a square that has a root, if you add its root to it, it has a root; and if you add its two roots to it, it has a root. :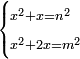\scriptstyle\begin{cases}\scriptstyle x^2+x=n^2\\\scriptstyle x^2+2x=m^2\end{cases} ז ואם יאמרו לך אלגו שיחזיק שרש אם תוסיף עליו שרשו יחזיק שרש ואם תוסיף עליו אלגו שני שרשיו יחזיק שרש
equation/indeterminate equationx²-8x-30=n²השאלות_החרשות/האלמות#67aP6) If you are told: a square that has a root, if you subtract from it eight times its root and thirty dirham, the remainder has a root. :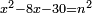\scriptstyle x^2-8x-30=n^2 ו ואם יאמרו לך אלגו המחזיק שרש אם תגרע ממנו שרשו שמנה פעמי' ושלשים דרהמי יחזיק מה שישאר שרש
equation/indeterminate equationx²+10x+20=n²השאלות_החרשות/האלמות#x5bu5) If you are told: a square that has a root, if you add to it ten times its root plus ten dirham, it has a root. :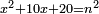\scriptstyle x^2+10x+20=n^2 ה ואם יאמרו לך אלגו המחזיק שרש אם תוסיף עליו עשרה פעמים שרשו ועשרה דרהמי יחזיק שרש
equation/indeterminate equationx²-6x=n²השאלות_החרשות/האלמות#LfMV4) If you are told: a square that has a root, when we subtract six times its root from it, it has a root. :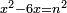\scriptstyle x^2-6x=n^2 ד ואם יאמרו לך אלגו מחזיק שרש כאשר גרענו ממנו שרשו ששה פעמים יחזיק שרש
equation/indeterminate equationx²+3x=n²השאלות_החרשות/האלמות#L1j93) If you are told: a square that has a root, if you add three times its root to it, it has a root. How much is the square? :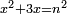\scriptstyle x^2+3x=n^2 ג ואם יאמרו לך אלגו המחזיק שרש אם תוסיף עליו שרשו שלשה פעמים יחזיק שרש כמה יהיה האלגו
equation/indeterminate equationx²-10=n²השאלות_החרשות/האלמות#mV1w2) When you are told: a square that has a root, if you subtract ten dirham from it, what remains has a root. :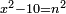\scriptstyle x^2-10=n^2 ב וכאשר יאמרו לך אלגו המחזיק שרש אם תגרע ממנו עשרה דרהמי יחזיק מה שישאר שרש
equation/indeterminate equationx²+5=n²השאלות_החרשות/האלמות#rm8m1) When you are told: a square that has a root, if you add five to it, it has a root. How much is the square? :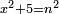\scriptstyle x^2+5=n^2 א כאשר יאמרו לך אלגו שמחזיק שרש אם תוסיף עליו חמשה יחזיק שרש כמה הוא האלגו
equation/indeterminate equationx²+(2-x)=n²,x²-(3-x)=m²השאלות_החרשות/האלמות#xP6r38) If you are told: a square that has a root, if you add two dirham minus the root of the square to it, it has a root; and if you subtract three minus the root of the square from it, it has a root. :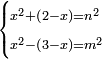\scriptstyle\begin{cases}\scriptstyle x^2+\left(2-x\right)=n^2\\\scriptstyle x^2-\left(3-x\right)=m^2\end{cases} לח ואם יאמרו לך אלגו המחזיק שרש אם תוסיף עליו שני דרהמי פחות שרש האלגו יחזיק שרש
ואם תגרע ממנו שלשה פחות שרש האלגו יחזיק שרש
equation/indeterminate equationx²-(x-1)=n²,x²-(1-x)=m²השאלות_החרשות/האלמות#Wdk537) If you are told: a square that has a root, if you subtract one dirham minus the root of the square from it, it has a root; [and if you subtract its root minus one dirham from it, it has a root]. :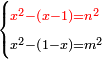\scriptstyle\begin{cases}\scriptstyle{\color{red}{x^2-\left(x-1\right)=n^2}}\\\scriptstyle x^2-\left(1-x\right)=m^2\end{cases} לז ואם יאמרו לך אלגו המחזיק שרש אם תגרע ממנו דרהם אחד פחות שרש האלגו יחזיק הנשאר שרש
equation/indeterminate equationx²+3x+1=n²,x²-(3x-2)=m²השאלות_החרשות/האלמות#43ha36) If you are told: a square that has a root, if you add to it its three roots and one dirham, it has a root; and if you subtract its three roots minus two dirham from it, the remainder has a root. :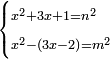\scriptstyle\begin{cases}\scriptstyle x^2+3x+1=n^2\\\scriptstyle x^2-\left(3x-2\right)=m^2\end{cases} לו ואם יאמרו לך אלגו שיחזיק שרש אם תוסיף עליו שלשת שרשיו ודרהם אחד יחזיק שרש
ואם תגרע ממנו שלשת שרשיו פחות שני דרהמי יחזיק מה שישאר שרש
equation/indeterminate equationx²+4x=n²,x²-(2x+1)=m²השאלות_החרשות/האלמות#1vZf34) If you are told: a square that has a root, if you add its four roots to it, it has a root; and if you subtract its two roots plus one dirham from it, the remainder has a root. :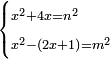\scriptstyle\begin{cases}\scriptstyle x^2+4x=n^2\\\scriptstyle x^2-\left(2x+1\right)=m^2\end{cases} לד ואם יאמרו לך אלגו שיחזיק שרש אם תוסיף עליו ארבעת שרשיו יחזיק שרש
ואם תגרע ממנו שני שרשיו ודרהם אחד יחזיק הנשאר שרש
equation/indeterminate equationx²-2x=n²,x²-2x+√(x²-2x)=m²השאלות_החרשות/האלמות#65Ct35) If you are told: a square that has a root, if you subtract its two roots from it, it has a root; and if you add to the remainder its root, it has a root. :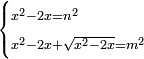\scriptstyle\begin{cases}\scriptstyle x^2-2x=n^2\\\scriptstyle x^2-2x+\sqrt{x^2-2x}=m^2\end{cases} לה ואם יאמרו לך אלגו המחזיק שרש אם תגרע ממנו שני שרשיו יחזיק שרש
ואם תוסיף על הנשאר שרשו יחזיק שרש
equation/indeterminate equationx²+x+1=n²,x²+2x+2=m²השאלות_החרשות/האלמות#YEF939) If you are told: a square that has a root, if you add its root plus one dirham to it, it has a root; and if you add to the square its two roots plus two dirham, it has a root. :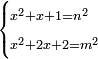\scriptstyle\begin{cases}\scriptstyle x^2+x+1=n^2\\\scriptstyle x^2+2x+2=m^2\end{cases} לט ואם יאמרו לך אלגו המחזיק שרש אם תוסיף עליו שרשו ודרהם אחד יחזיק שרש
ואם תוסיף על האלגו שני שרשיו ושני דרהמי יחזיק שרש
equation/indeterminate equationx²-5=n²,x²-5+√(x²-5)=m²השאלות_החרשות/האלמות#6x8t33) If you are told: a square that has a root, if you subtract five dirham from it, the remainder has a root; and if you add to the remainder its root, the sum has a root. :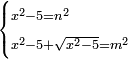\scriptstyle\begin{cases}\scriptstyle x^2-5=n^2\\\scriptstyle x^2-5+\sqrt{x^2-5}=m^2\end{cases} לג ואם יאמרו לך אלגו המחזיק שרש אם תגרע ממנו חמשה דרהמי יחזיק הנשאר שרש
ואם תוסיף על הנשאר שרשו יחזיק המקובץ שרש
equation/indeterminate equationx²+x=n²,x²+1=m²השאלות_החרשות/האלמות#eNRx32) If you are told: a square that has a root, if you add its root to it, it has a root; and if you add to one dirham to it, it has a root. :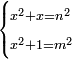\scriptstyle\begin{cases}\scriptstyle x^2+x=n^2\\\scriptstyle x^2+1=m^2\end{cases} לב ואם יאמרו לך אלגו המחזיק שרש אם תוסיף עליו שרשו יחזיק שרשו
ואם תוסיף עליו דרהם אחד יחזיק שרש
equation/indeterminate equationx²-4x=n²,x²-4x-2√(x²-4x)=m²השאלות_החרשות/האלמות#vAyv31) If you are told: a square, if you subtract its four roots from it, it has a root; and if you subtract from the remainder its two roots, it has a root. :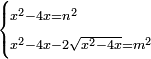\scriptstyle\begin{cases}\scriptstyle x^2-4x=n^2\\\scriptstyle x^2-4x-2\sqrt{x^2-4x}=m^2\end{cases} לא ואם יאמרו לך אלגו אם תוסיף עליו תגרע ממנו ארבעה שרשיו יחזיק שרש
ואם תגרע ואם תגרע מהנשאר שני שרשיו יחזיק שרש
equation/indeterminate equationx²+4x=n²,x²+4x+2√(x²+4x)=m²השאלות_החרשות/האלמות#2scj30) If you are told: a square that has a root, if you add its four roots to it, it has a root; and if you add to the sum its two roots, it has a root. :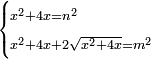\scriptstyle\begin{cases}\scriptstyle x^2+4x=n^2\\\scriptstyle x^2+4x+2\sqrt{x^2+4x}=m^2\end{cases} ל וכן אם יאמרו לך אלגו המחזיק שרש
אם תוסיף עליו ארבעת שרשיו יחזיק שרש
ואם תוסיף על המתקבץ שני שרשיו יחזיק שרש
equation/quadratic equation[x²-(⅓x²+2)]²=x²+24חשבון_השטחים#lT08[12] If you are told: a square, you subtract its third and two dirham from it, then multiply what remains by itself and the result is the square plus 24 dirham. :\scriptstyle\left[x^2-\left(\frac{1}{3}x^2+2\right)\right]^2=x^2+24 ואם יאמרו לך אלגו גרעת ממנו שלישיתו ושני אדרהמיש ומה שנשאר הכית אותו על עצמו ושב האלגו וכ"ד אדרהמיש יותר
equation/quadratic equation[√(x²·2x²)+2]·x²=30חשבון_השטחים#uwLQ[40] If you are told: a square, you multiply it by its two times, extract the root of the product, add two dirham to it, then multiply the total by that square and the result is thirty dirham. :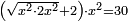\scriptstyle\left(\sqrt{x^2\sdot2x^2}+2\right)\sdot x^2=30 ואם יאמרו לך אלגו תכהו על {{#annot:term|387|piMO}}שני דמיוניו{{#annotend:piMO}} ותקח שרש העולה ותוסיף עליו שני דרהמי ותכה הכל באלגו ההוא ויהיה שלשים דרהמי
equation/quadratic equation(x²+10)·√5=(x²)²חשבון_השטחים#hePu[38] If you are told: a square, you add to it ten dirham, then multiply the sum by a root of five and the result is the same as the product of the square by itself. :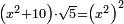\scriptstyle\left(x^2+10\right)\sdot\sqrt{5}=\left(x^2\right)^2 ואם יאמרו לך אלגו הוספת עליו עשרה דרהמי והכית המקובץ בשרש חמשה ויעלה כמו הכאת האלגו על עצמו
equation/quadratic equation3√x²+4√(x²-3√x²)=x²+4חשבון_השטחים#SNBo[17] If you are told: a square, its three roots and four roots of what remains from the square are the same as the square plus four dirham. :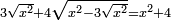\scriptstyle3\sqrt{x^2}+4\sqrt{x^2-3\sqrt{x^2}}=x^2+4 ואם יאמרו לך אלגו שלשת שרשיו וארבעה שרשים ממה שנשאר מהאלגו יהיה כמו האלגו וארבעה דרהמי' יותר
equation/quadratic equation3√x²+2√(x²-3√x²)=x²חשבון_השטחים#rq9x[16] If you are told: a square, its three roots and two roots of what remains are equal to the square. :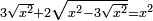\scriptstyle3\sqrt{x^2}+2\sqrt{x^2-3\sqrt{x^2}}=x^2 ואם יאמרו לך אלגו שלשת שרשיו ושני שרשי הנשאר ישוו האלגו
equation/quadratic equation(x²-⅓x²)·3√x²=x²חשבון_השטחים#ak8r[14] If you are told: we subtract from a square its third, then multiply what remains by three roots of the original square and the result is the original square. :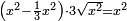\scriptstyle\left(x^2-\frac{1}{3}x^2\right)\sdot3\sqrt{x^2}=x^2 ואם יאמרו לך גרענו מן האלגו שלישיתו והכינו הנשאר על שלשה שרשים מהאלגו הראשון ושב האלגו הראשון
equation/quadratic equation[√(6x²)·√(5x²)]+10x²+20=(x²)²חשבון_השטחים#stdc[34] If you are told: a square, multiply a root of its six times by a root of its five times, then add ten times the square plus twenty dirham to the product and it is the same as [the product of] the square by itself. :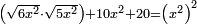\scriptstyle\left(\sqrt{6x^2}\sdot\sqrt{5x^2}\right)+10x^2+20=\left(x^2\right)^2 ואם יאמרו לך אלגו תרבה שרש מששה דמיוניו בשרש חמשה דמיוניו והוספת על מה שעלה מההכאה עשרה דמיוני האלגו ועשרים דרהמי יותר ויהיה כמו האלגו על עצמו
equation/quadratic equation[√(8x²)·√(3x²)]+20=(x²)²חשבון_השטחים#HcHI[33] If you are told: a square, multiply a root of eight times the square by a root of three times the square, then add twenty dirham to the result and it is the same as [the product of] the square by itself. :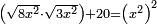\scriptstyle\left(\sqrt{8x^2}\sdot\sqrt{3x^2}\right)+20=\left(x^2\right)^2 ואם יאמרו לך אלגו תרבה שרש משמנה דמיוני האלגו בשרש משלשה דמיוני האלגו והוספת על העולה עשרים דרהמי ויהיה כמו האלגו על עצמו
equation/quadratic equation(x²-⅓x²)·3√(x²-⅓x²)=x²חשבון_השטחים#lFM5[15] If you are told: a square, we subtract its third from it, then multiply what remains by three roots of what remains from the square and the result is the square. :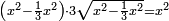\scriptstyle\left(x^2-\frac{1}{3}x^2\right)\sdot3\sqrt{x^2-\frac{1}{3}x^2}=x^2 ואם יאמרו לך אלגו גרענו ממנו שלישיתו והכינו הנשאר על שלשה שרשים מהנשאר מהאלגו וישוב האלגו
equation/quadratic equationa²+b²=c², ac=b², ab=10חשבון_השטחים#gGKeIf you are told: three unequal squares, if you multiply the smaller by itself and the mean by itself; they are as the greater by itself. If you multiply the smaller by the greater it is as the mean by itself. If you multiply the smaller by the mean it is ten dirham. :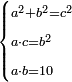\scriptstyle\begin{cases}\scriptstyle a^2+b^2=c^2\\\scriptstyle a\sdot c=b^2\\\scriptstyle a\sdot b=10\end{cases} ואם יאמרו לך שלשה אלגוש בלתי שוים
אם תכה הקטן בעצמו והאמצעי בעצמו יהיו כמו הגדול בעצמו
ואם תכה הקטון בגדול יהיה כמו האמצעי בעצמו
ואם תכה הקטן באמצעי יהיה עשרה דרהמי
equation/quadratic equationb²=3a², (a²+√a²)·(b²+√b²)=10b²חשבון_השטחים#nHFmIf you are told: two squares - one is three times the other; you add to each of them its root, then multiply the one by the other; it is ten times the greater square. :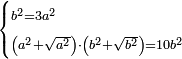\scriptstyle\begin{cases}\scriptstyle b^2=3a^2\\\scriptstyle\left(a^2+\sqrt{a^2}\right)\sdot\left(b^2+\sqrt{b^2}\right)=10b^2\end{cases} ואם יאמרו שני אלגוש והאחד שלשה דמיוני האחר הוספת על כל אחד מהם שרשו שלו והכית האחד באחר והיה עשרה דמיוני האלגו הגדול
equation/quadratic equation[x²+√(½x²)]²=4x²חשבון_השטחים#FvghIf you are told: a square, you add to it a root of its half, then multiply the result by itself; it becomes four times the square. :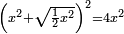\scriptstyle\left(x^2+\sqrt{\frac{1}{2}x^2}\right)^2=4x^2 ואם יאמרו לך אלגו הוספת עליו שרש חציו והכית העולה בעצמו ויהיה ארבעה דמיוני האלגו
equation/quadratic equation[x²+√(x²)+√(½x²)]²=5x²חשבון_השטחים#omooIf you are told: a square, add to it its root and a root of its half, then multiply the result by itself; it is five times the square. :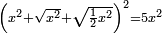\scriptstyle\left(x^2+\sqrt{x^2}+\sqrt{\frac{1}{2}x^2}\right)^2=5x^2 ואם יאמרו לך אלגו תוסיף עליו שרשו ושרש חציו ותכה המקובץ על עצמו ויהיה חמשה דמיוני האלגו
equation/quadratic equationx²+4√(x²)+√(½x²)+√(⅓x²)=10חשבון_השטחים#b04GIf you are told: a square, add to it its four roots plus a root of its half and a root of its third; it is ten dirham - how much is the square? :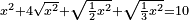\scriptstyle x^2+4\sqrt{x^2}+\sqrt{\frac{1}{2}x^2}+\sqrt{\frac{1}{3}x^2}=10 ואם יאמר לך אלגו תוסיף עליו ארבעה שרשיו ושרש חציו ושרש שלישיתו ויהיה עשרה דרהמי כמה הוא האלגו
equation/quadratic equation2√(x²)+√(½x²)+√(⅓x²)=20חשבון_השטחים#wOZVIf one says: a square whose two roots plus a root of its half and a root of its third are twenty dirham - how much is the square? :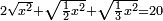\scriptstyle2\sqrt{x^2}+\sqrt{\frac{1}{2}x^2}+\sqrt{\frac{1}{3}x^2}=20 ואם יאמר אלגו אשר שני שרשיו ושרש חציו ושרש שלישיתו עשרים דרהמי כמה הוא האלגו
equation/quadratic equation[x²-(2√x²+10)]²=8x²חשבון_השטחים#aPQXIf you are told: a square, subtract its two roots and ten dirham from it, then multiply what remains by itself; it becomes eight times the square. :\scriptstyle\left[x^2-\left(2\sqrt{x^2}+10\right)\right]^2=8x^2 ואם יאמרו לך אלגו תגרע ממנו שני שרשיו ועשרה דרהמי ותכה מה שישאר בעצמו ויהיה שמנה דמיוני האלגו
equation/quadratic equation[x²+√(x²)+√(½x²)]²=20חשבון_השטחים#OX0E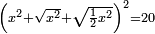\scriptstyle\left(x^2+\sqrt{x^2}+\sqrt{\frac{1}{2}x^2}\right)^2=20 ואם יאמרו לך אלגו הוסף עליו שרשו ושרש חציו ותכה המקובץ בעצמו ויהיה עשרים דרהמי
equation/quadratic equation2√(x²)+√(½x²)+√(⅓x²)=x²חשבון_השטחים#nPTXIf you are told: a square whose two roots plus a root of half the square and a root of its third are equal to the square - how much is the square? :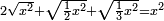\scriptstyle2\sqrt{x^2}+\sqrt{\frac{1}{2}x^2}+\sqrt{\frac{1}{3}x^2}=x^2 ואם יאמרו לך אלגו אשר שני שרשיו ושרש חצי האלגו ושרש שלישיתו ישוו האלגו כמה הוא האלגו
equation/quadratic equation√x²+√(√x²)+√(2√x²)+5√x²=10חשבון_השטחים#rWIeIf you are told: a square whose root and the root of its root, plus the root of its two roots, plus the root of five times the square are ten dirham. :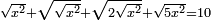\scriptstyle\sqrt{x^2}+\sqrt{\sqrt{x^2}}+\sqrt{2\sqrt{x^2}}+\sqrt{5x^2}=10 ואם יאמרו לך אלגו אשר שרשו ו{{#annot:term|2634|dE2e}}שרש שרשו{{#annotend:dE2e}} ושרש שני שרשיו ושרש חמשה דמיוני האלגו יהיה עשרה דרהמי
equation/quadratic equationx²·(x²+√10)=9x²חשבון_השטחים#XpMD[32] If you are told: a square, multiply it by itself plus a root of ten dirham and it becomes nine times the square. :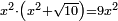\scriptstyle x^2\sdot\left(x^2+\sqrt{10}\right)=9x^2 ואם יאמרו לך אלגו תכהו על עצמו ושרש אחד מעשרה דרהמי ויהיה תשעה דמיוני האלגו
equation/quadratic equation3√x²+4√(x²-3√x²)=20חשבון_השטחים#tZ8i[13] If you are told: three roots of the square plus four roots of what remains from the square are twenty dirham. :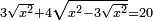\scriptstyle3\sqrt{x^2}+4\sqrt{x^2-3\sqrt{x^2}}=20 ואם יאמרו לך שלשה שרשים מהאלגו וארבעה שרשים ממה שנשאר מהאלגו יהיה עשרים דרהמי‫'
equation/quadratic equation(√10·x²)/(2√3)=x²-10חשבון_השטחים#8OnPIf you are told: a square, multiply it by the root of ten, then divide the product by two plus the root of three; the quotient is the same as the square minus ten. :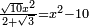\scriptstyle\frac{\sqrt{10}x^2}{2+\sqrt{3}}=x^2-10 ואם יאמרו לך אלגו תכהו בשרש עשרה ותחלק מה שיעלה על שנים ושרש שלשה ויעלה לאחד כל כך כמו שהוא האלגו פחות עשרה
equation/quadratic equation[√(½x²)+3]·[√(⅓x²)+2]=20חשבון_השטחים#Y7kOIf you are told: a square, add three dirham to a root of its half, and two dirham to a root of its third, then multiply one [sum] by the other; it is twenty dirham. :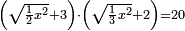\scriptstyle\left(\sqrt{\frac{1}{2}x^2}+3\right)\sdot\left(\sqrt{\frac{1}{3}x^2}+2\right)=20 ואם יאמרו לך אלגו תוסיף על שרש חציו שלשה דרהמי ועל שרש שלישיתו שני דרהמי ותכה האחד באחר ויהיה עשרים דרהמי
equation/quadratic equation[x²+√(3x²)]·√(2x²)=4x²חשבון_השטחים#lk6CIf you are told: a square, add to it a root of three times of it, then multiply the sum by a root of [twice] the square; it becomes four times the square. :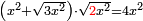\scriptstyle\left(x^2+\sqrt{3x^2}\right)\sdot\sqrt{{\color{red}{2}}x^2}=4x^2 ואם יאמרו לך אלגו תוסיף עליו שרש שלשה דמיוניו ותכה המקובץ בשרש האלגו יהיה ארבעה דמיוני האלגו
equation/quadratic equation(x²+7)·√(3x²)=10x²חשבון_השטחים#dAZJIf you are told: a square, add to it seven dirham, then multiply the sum by a root of three times the square; it becomes ten times the square. :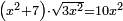\scriptstyle\left(x^2+7\right)\sdot\sqrt{3x^2}=10x^2 ואם יאמרו לך אלגו תוסיף עליו שבעה דרהמי ותכה המקובץ בשרש שלשה דמיוני האלגו ויהיה עשרה דמיוני האלגו
compound canonical equation/roots and numbers equal squares3x+4=x²תחבולות_המספר#VKnlHe said: roots and numbers that are equal to a square is as saying three roots and four dirham are equal to a square. :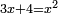\scriptstyle3x+4=x^2 אמ' שרשים ומספרים שישוו למרובע הוא כמו שיאמ' שלשה שרשים וארבעה דרהמי יהיו שוים למרובע
compound canonical equation/roots and numbers equal squaresbx+c=ax²חשבון_השטחים#VBedושרשים ומספרי' ישוו למרובעים
compound canonical equation/roots and numbers equal squares3x+4=x²חשבון_השטחים#qrpb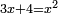\scriptstyle3x+4=x^2 והשרשים ומספרים שישוו אלגוש כמו אם יאמר שלשה שרשים וארבעה מספרים ישוו אלגו
compound canonical equation/roots and numbers equal squaresbx+c=ax²תחבולות_המספר#So10ושרשי' ומספרים שישוו למרובעים
simple canonical equation/roots equal numbersx=4תחבולות_המספר#PaMjIf you are told: the roots of the square are equal to four numbers. :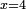\scriptstyle x=4 כי אם יאמרו לך שרשי המרובע ישוו לארבע' מספרי‫'
simple canonical equation/roots equal numbers½x=10תחבולות_המספר#e4m4If one says: half a root is equal to ten. :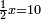\scriptstyle\frac{1}{2}x=10 ואם אמ' חמשה ושלשים חצי שרש ישוה לעשרה
simple canonical equation/roots equal numbers5x=30תחבולות_המספר#jHg9As if one says: five roots are equal to thirty. :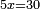\scriptstyle5x=30 כמו אם אמ' חמשה שרשים ישוו לשלשים
simple canonical equation/roots equal numbersbx=cתחבולות_המספר#qsBhושרשים שישוו למספרים
simple canonical equation/roots equal numbers5x=30חשבון_השטחים#1YGhAlso if you say: five roots are equal to thirty. :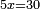\scriptstyle5x=30 וכמו אם תאמר חמשה שרשים ישוו שלשים
simple canonical equation/roots equal numbersx=4חשבון_השטחים#wMvnWhen the roots are equal to numbers, as if you say: the root is equal to four. :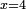\scriptstyle x=4 והשרשים שישוו מספרים כמו שתאמר שרש ישוה ארבעה
simple canonical equation/roots equal numbersbx=cחשבון_השטחים#1nZHושרשים ישוו מספרים
simple canonical equation/roots equal numbers½x=10חשבון_השטחים#0OjbIf you say: half a root is equal to ten. :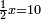\scriptstyle\frac{1}{2}x=10 וכמו אם תאמר חצי שרש ישוה עשרה
canonical equation/simple canonical equationפ.ש.ט./פשוטtermתחבולות_המספר#Zvsuהפשוטים
canonical equation/simple canonical equationdefinitionחשבון_השטחים#Ja1cהנה השלשה מהם {{#annot: term | #simple canonical equation, #נפרד | o3Jf}}נפרדים{{#annotend:o3Jf}} והם אלגוש ישוו שרשים והאלגו ישוו מספרים ושרשים ישוו מספרים
canonical equation/simple canonical equationפ.ר.ד./נפרדtermחשבון_השטחים#o3Jfנפרדים
compound canonical equation/squares and numbers equal rootsax²+c=bxחשבון_השטחים#iECfומרובעים ומספרי' ישוו לשרשים
compound canonical equation/squares and numbers equal rootsx²+25=10xחשבון_השטחים#5rN4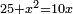\scriptstyle25+x^2=10x ו{{#annot: term | #to give an example, #משל | ZpYe}}אמשיל זה{{#annotend:ZpYe}} בשאילה אחרת ואניחנה שכ"ה אדרהמיש ואלגוש ישוו עשרה שרשים
compound canonical equation/squares and numbers equal rootsx²+25=10xתחבולות_המספר#QWm3Example: one says: a square plus twenty-five [dirham] are equal to ten roots of the square. :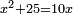\scriptstyle x^2+25=10x דמיון זה שיאמ' מרובע מה ועשרים וחמשה שרשים ישוו לעשרה שרשים מהמרובע
compound canonical equation/squares and numbers equal rootsx²+21=10xחשבון_השטחים#yRRf\scriptstyle x^2+21=10x והאלגוש והמספרים שישוו שרשים כאלו תאמר אלגוש ועשרים ואחד אדרהמיש ישוו עשרה שרשים
compound canonical equation/squares and numbers equal rootsax²+c=bxתחבולות_המספר#om8wומרובעי' ומספרי' שישוו לשרשים
compound canonical equation/squares and numbers equal rootsx²+21=10xתחבולות_המספר#u4EAHe said: squares and numbers that are equal to roots is as if you say: when you sum twenty-one dirham with a certain square, they are equal to ten roots of the square. :\scriptstyle x^2+21=10x אמ' המרובעי' והמספרי' שישוו לשרשים הוא כאלו תאמ' כאשר תקבץ עם מרובע מה עשרים ואחד דרהמי יהיו שוים לעשרה משרשים מהמרובע
compound canonical equation/squares and roots equal numbersx²+10x=39חשבון_השטחים#BnUpSquares and roots are equal to numbers, it is as if you say: a square and ten roots are equal to thirty-nine dirham. :\scriptstyle x^2+10x=39 והאלגוש והשרשים שישוו מספרים הוא כאלו תאמר אלגו ועשרה שרשים ישוו תשעה ושלשים דרהמיש
compound canonical equation/squares and roots equal numbersx²+10x=39תחבולות_המספר#oMPaHe said: when squares and roots are equal to numbers, it is as if you say: the sum of one square and ten of its roots together is equal to thirty-nine dirham. :\scriptstyle x^2+10x=39 אמ' כאשר יהיו המרובעים והשרשים שוים למספרי' כאלו תאמ' המקובץ ממרובע מהאחד ועשרה משרשיו יחד ישוה לשלשים ותשעה דרהמי
compound canonical equation/squares and roots equal numbers½x²+5x=28חשבון_השטחים#XyaI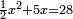\scriptstyle\frac{1}{2}x^2+5x=28 ואם אמרו לך חצי אלגוש וחמשה שרשים ישוו כ"ח אדרהמיש
נאמר כי כאשר {{#annot: term | #to add, #חבר | qgPe}}חברנו{{#annotend:qgPe}} על חצי האלגוש חמשה שרשי האלגוש יהיו כ"ח אדרהמיש
compound canonical equation/squares and roots equal numbers3x²+15x=72תחבולות_המספר#HV5bExample: if one asks: three squares and 15 roots are equal to 72 dirham. :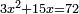\scriptstyle3x^2+15x=72 דמיון זה ששאל שלשה מרובעי' וט"ו שרשי' ישוו לע"ב דרהמי
compound canonical equation/squares and roots equal numbersax²+bx=cחשבון_השטחים#XqGpמרובעי' ושרשי' ישוו למספרים
compound canonical equation/squares and roots equal numbers½x²+5x=28תחבולות_המספר#FJRfLikewise, if one asks: half a square plus its five roots are equal to 28 dirham. :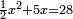\scriptstyle\frac{1}{2}x^2+5x=28 וכמו כן אם שאל השואל חצי מרובע וחמשה משרשיו ישוו לכ"ח דרהמי
compound canonical equation/squares and roots equal numbers2x²+10x=48חשבון_השטחים#cSpR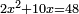\scriptstyle2x^2+10x=48 וזה כמו שתאמר שנים אלגוש ועשרה שרשים ‫2rישוו מ"ח אדרהמיש
compound canonical equation/squares and roots equal numbersax²+bx=cתחבולות_המספר#3sJZושרשים ומרובעי' שישוו למספרים
simple canonical equation/squares equal numbers⅓x²=27חשבון_השטחים#sOLHAlso if you say: a third of the square is equal to twenty-seven. :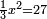\scriptstyle\frac{1}{3}x^2=27 וכן אם תאמר שלישית אלגו שוה ‫1vשבעה ועשרים
simple canonical equation/squares equal numbersx²=16חשבון_השטחים#lI7wThe squares that are equal to numbers is as a square that equals sixteen. :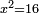\scriptstyle x^2=16 והאלגוש שישוו מספרים כמו אלגו שישוה שש עשרה
simple canonical equation/squares equal numbersx²=16תחבולות_המספר#fCC4As if you are told: the square is equal to sixteen. :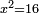\scriptstyle x^2=16 כמו אם יאמרו לך המרובע ישוה לששה עשר
simple canonical equation/squares equal numbers⅓x²=27תחבולות_המספר#UsmiIf one says: a third of the square is equal to twenty-seven. :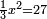\scriptstyle\frac{1}{3}x^2=27 ואם אמ' שלישית המרובע ישוה לשבעה ועשרים
simple canonical equation/squares equal numbers5x²=45תחבולות_המספר#C4DXIf one says: five squares are equal to forty-five. :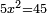\scriptstyle5x^2=45 כי אם אמ' חמשה מרובעי' ישוו לחמשה וארבעי‫'
simple canonical equation/squares equal numbersax²=cתחבולות_המספר#4O9Cומרובעי' שישוו למספרים
simple canonical equation/squares equal numbersax²=cחשבון_השטחים#kCXFואלאגוש ישוו מספרים
simple canonical equation/squares equal numbers5x²=45חשבון_השטחים#yMV8Likewise, when five squares are equal to forty-five. :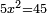\scriptstyle5x^2=45 וכן חמשה אלגוש ישוו חמשה וארבעים
simple canonical equation/squares equal roots½x²=10xחשבון_השטחים#N1ieLikewise, if it is said: half a square equals ten roots. :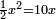\scriptstyle\frac{1}{2}x^2=10x וכמו כן אם יאמר חצי אלגו ישוה עשרה שרשים
simple canonical equation/squares equal rootsx²=5xחשבון_השטחים#cbxXThe squares that are equal to roots is as if you say: a square equals five roots. :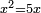\scriptstyle x^2=5x והאלגוש שישוו שרשים הוא כאלו תאמר אלגו ישוה חמשה שרשים
simple canonical equation/squares equal rootsax²=bxתחבולות_המספר#Udboשרשים שיהיו שוי' למרובעים
simple canonical equation/squares equal rootsax²=bxחשבון_השטחים#bTgPאלגוש ישוו שרשים
simple canonical equation/squares equal roots5x²=20xחשבון_השטחים#sJUhAs if you say: five squares equal twenty roots. :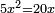\scriptstyle5x^2=20x וכמו שתאמר חמשה אלגוש ישוו עשרים שרשים
simple canonical equation/squares equal roots½x²=10xתחבולות_המספר#fayjAlso, if he says: half a square is equal to ten roots. :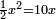\scriptstyle\frac{1}{2}x^2=10x וכן אם יאמ' חצי מרובע ישוה לעשרה שרשים
simple canonical equation/squares equal roots5x²=20xתחבולות_המספר#WDhUExample: if one asks: five squares are equal to twenty roots. :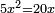\scriptstyle5x^2=20x דמיון זה אם ישאל חמשה מרובעי' ישוו לעשרים שרשים
simple canonical equation/squares equal rootsx²=5xתחבולות_המספר#EqMyFor example: if you are told; five roots are equal to one square. How much is the square? :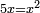\scriptstyle5x=x^2 {{#annot:term|197,1712|lPkF}}דמיון זה{{#annotend:lPkF}} אם אמרו לך חמשה שרשי' ישוו למרובע אחד כמה הוא המרובע
equation/unsolvable equationט.ע.י./מוטעהtermחשבון_השטחים#2srDמוטעה
equation/unsolvable equationכ.ז.ב./כוזבtermתחבולות_המספר#PMZLכוזבת
Retrieved from "http://mispar.ethz.ch/mediawiki/index.php?title=Search_Page&oldid=39202"