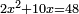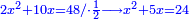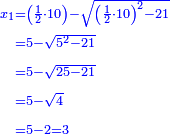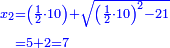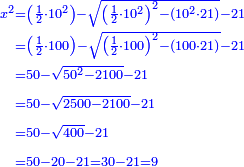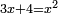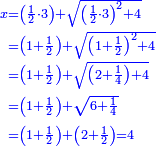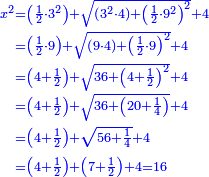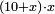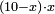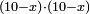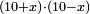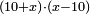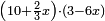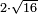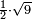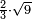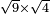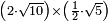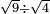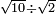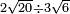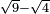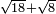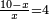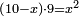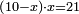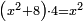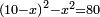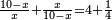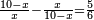Difference between revisions of "חשבון השטחים"
(→bx+c=ax2) |
|||
| Line 2,162: | Line 2,162: | ||
|- | |- | ||
| | | | ||
| + | == Addition of Roots == | ||
| + | |||
|style="text-align:right;"|בחבור השרשים האחד עם האחר | |style="text-align:right;"|בחבור השרשים האחד עם האחר | ||
|- | |- | ||
| Line 2,234: | Line 2,236: | ||
|- | |- | ||
| | | | ||
| + | == Subtraction of Roots == | ||
| + | |||
|style="text-align:right;"|בגרעון השרשים האחד מן האחר | |style="text-align:right;"|בגרעון השרשים האחד מן האחר | ||
|- | |- | ||
Revision as of 11:50, 3 February 2019
חשבון השטחים
| תחלת מה שצריך לדעת קורא זה הספר הוא שלשה חלקים אשר אמרם כבר מהומר אלבוארזמי[1] בספרו והם שרשים ראדיש ומרובעים אלגוש ומספרים קוונטאש | |
| והשורש הוא כל דבר שיתרבה על עצמו כמו האחד ומן האחד ולמעלה ושבריו ושברי שבריו עד אין להם סוף | |
| והאלגוש הוא המתקבץ מהתרבות זה השורש על עצמו שלם יהיה או נשבר | |
| והמנין הוא הצומח מאליו אשר לא יוכל יפול בו לא שם שורש ולא שם אלגו והוא המתיחס אל מה שבו מן האחדים | |
| ואלו השלשה חלקים כבר יהיה כל אחד מהם יהיה שוה לכל אחד מהחלקים הנשארים | |
| וכבר יהיה שישוה כמו השני חלקים שנשארו | |
| אם שיהיה שוה לכל אחד מהחלקי' מהנשארים | |
|
|
זה כמו שיאמרו לך אלגוש ישוו שרשים |
|
|
ואלאגו ישוו מספרים |
|
|
ושרשים ישוו מספרים |
| ואם שיהיה שוה החלק האחד לשני החלקים הנשארים | |
|
|
הוא כמו שתאמר מרובעים ושרשים ישוו למספרים |
|
|
ומרובעים ומספרים ישוו לשרשים |
|
|
ושרשים ומספרים ישוו למרובעים |
| ואלו הם ששה חלקים וצריך לבארם | |
Contentsax2=bx |
והאלגוש שישוו שרשים |
|
|
הוא כאילו תאמר אלגו ישוה חמשה שרשים |
| בעבור כי האלגו הוא שוה לחמשת שרשיו | |
| כי שורש האלגו יהיה לעולם כפי סכום השרשים מהאלגו ושוה אליהם והוא בזה המשל חמשה והאלגו עשרים וחמשה והוא כמו חמשה שרשיו[2] | |
| ועוד אבאר למה היה שורש האלגו כפי סכום השרשים ואשים ביאורו בזאת השאלה רצוני בזה המשל | |
| ואניח האלגו שטח מרובע עליו אבג"ד וצלעיו א"ב ב"ג ג"ד ד"א | |
| וכל אחד מצלעיו מרובה על אחד מסכום אורך זה השטח הוא שורש זה השטח האחר | |
| והעולה מכפל א"ב על אחד והוא קו ב"ה ויהיה שטח א"ה הוא שורש א"ג | |
| ושטח א"ג הוא כפי חמשה שרשיו | |
| ושטח א"ג חמשה כפלי שטח א"ה | |
| וחלק שטח א"ג לחמשה חלקים שוים ויהיו שטחי א"ה ט"ו ס"ז מ"ח ע"ג | |
| וקו ב"ג חמשה והוא שורש האלגו | |
| והאלגו הוא עשרים וחמשה ומש"ל | |
|
|
וכמו כן אם יאמר חצי אלגו ישוה עשרה שרשים |
| והאלגו כלו ישוה עשרים שרשים | |
|
|
הנה שרש האלגו עשרים |
|
|
והאלגו ארבע מאות |
|
|
וכמו שתאמר חמשה אלגו ישוו עשרים שרשים |
|
|
והאלגו ישוה ארבעה שרשים |
|
|
ושרש האלגו הוא ארבעה |
|
|
והאלגו הוא ששה עשר |
| וכן כמה שנרבה מהאלגו או שנחסר נשיבם לעולם לאלגו אחד | |
| וכן תעשה לכל מה שישובו מן השרשים אל האלגו | |
ax2=c |
והאלגוש שישוו מספרים |
|---|---|
|
|
כמו אלגו שישוה שש עשרה |
|
|
והנה הוא אלגו |
|
|
ושרשו ארבעה |
|
|
וכן חמשה אלגו ישוו חמשה וארבעים |
|
|
והאלגו האחד הוא חמישיתם והוא תשעה |
|
|
וכן אם תאמר שלישית אלגו ישוו שבעה ועשרים |
|
|
והאלגוש שמונים ואחד |
| וכן כל האלגוש איזה שיהיו יותר או פחות השיבם לעולם אל אלגו אחד | |
| וכן תעשה לאשר ישובו אליו מהמספרים | |
bx=c |
והשרשים שישוו מספרים |
|
|
כמו שתאמר שורש ישווה ארבעה |
|
|
והשורש הוא ארבעה |
|
|
והאלגוש שש עשרה |
|
|
וכמו אם תאמר חמשה שרשים ישוו שלשים |
|
|
והשורש ישווה ששה |
|
|
והאלגוש ששה ושלשים |
|
|
וכמו אם תאמר חצי שורש ישוה עשרה |
|
|
והשורש ישוה עשרים |
|
|
והאלגוש ארבע מאות |
| וכן כל השרשים איזה שיהיו יותר או פחות השיבם לעולם אל שורש אחד | |
| וכן תעשה לאשר ישובו אליו מהמספרים | |
| ותמצא אלו שלשה חלקים והם כמו שתאמר אלגוש ושרשי' ישוו מספרים ואלגוש ומספרים ישוו שרשים ושרשים ומספרים ישוו אלגוש | |
ax2+bx=c |
והאלגוש והשרשים שישוו מספרים |
|
|
הוא כאלו תאמר אלגוש ועשרה שרשים ישוו תשעה ושלשים דרהמיש |
| נאמר כי כאשר נחבר על האלגוש שרשיו העשרה ישוו תשעה ושלשים אדרהמיש | |
| ובזאת השאלה יש שנים אופנים | |
| האחד יראך שורש האלגו | |
| והאחר יראך האלגוש | |
| ועוד אבאר לך משפטיהן עם תמונות גימטריות יבינום חכמי הגימטריא אשר ישכילו בספר אוקלידס | |
| והאופן אשר יראך שורש האלגוש כבר אמרו מהומר אלבוארזמי בספרו | |
|
|
והוא שתקח לעולם חצי השרשים והוא בזאת השאלה חמשה ותרבם על עצמם ויהיו עשרים וחמשה |
|
|
והאלגוש תשעה |
|
|
והאופן אשר יראך האלגוש הוא שתרבה העשרה על עצמו ויהיה מאה ותרבם על הל"ט ויהיו ג' אלפים ותת"ק |
| וכן שנים אלגוש או שלשה או יותר או פחות השיבם לעולם אל אלגוש אחד והשיב עמו אשר תוכל מהשרשים ומהמספרים בדרך שהשיבות האלגוש | |
|
|
וזה כמו שתאמר שנים אלגוש ועשרה שרשים ישוו מ"ח אדרהמיש |
| נאמר ששני אלגוש כאשר נחברם ונקבצם על שרשיו עשרה מאחד מהם יהיה מ"ח אדרהמיש | |
| ויצטרך שתשיב השני אלגוש לאלגוש אחד | |
|
וכבר ידעת כי אחד משנים הוא החצי |
|
|
והשיב כל דבר אשר החזקת במבוקש אל חציו כאלו אמרת אלגוש וחמשה שרשים ישוו כ"ד אדרהמיש |
| ומשפטו כי כאשר תחבר על האלגוש שרשיו החמשה יהיו כ"ד | |
| וכבר הראיתיך כיצד תמצא השורש וכיצד תמצא האלגוש בשני האופני' האמורים | |
| ואם אמרו לך חצי אלגוש וחמשה שרשים ישוו כ"ח אדרהמיש | |
| נאמר כי כאשר חברנו על חצי האלגוש חמשה שרשי האלגוש יהיו כ"ח אדרהמיש | |
| וצריך שתשיב האלגוש שלך שלם והוא שתכפלהו ותכפול השרשים שיהיו עמו ויהיה האלגוש ועשרה שרשים ישוו נ"ו וכבר הראית מה לעשות לך עמהם | |
| והמשפט והסבה אשר בזה רצוני שאלגוש ועשרה שרשים שישוו ל"ט אדרהמיש | |
| הנה האופן הטיטולי אשר יראך השורש הוא שתשים שטח מרובע עליו אבג"ד | |
| ותחבר אליו השרשים אשר הנחת היותם עם האלגו והיו עשרה והם שטח אבו"ה | |
| וידוע כי קו ב"ה עשרה | |
| בעבור כי צלע א"ב משטח אבג"ד מורבה באחד יהיה שורש שטח אבג"ד והוא מרובה בעשרה יהיו עשרה שרשים משטח אבג"ד הנה קו ב"ה עשרה | |
| וכל שטח והג"ד שלשים ותשע בעבור כי הנחנו האלגוש ועשרה שרשיו והוא מהכאת קו ה"ג בקו ג"ד | |
| אבל קו ג"ד כמו קו ג"ב הנה הכאת קו ה"ג על קו ג"ב ל"ט | |
| וקו ה"ב עשרה ונחלק אותו לחציים על נקודת ח' ונוסף באורכו קו ג"ב | |
| ולכן יהיה השטח העולה מהכאת ה"ג בקו ב"ג עם מרובע ההווה מהכאת ח"ב על עצמו כמו מרובע ההוה מהכאת ח"ג על עצמו כמו שאמר אקלידס במאמר שיני בספרו | |
| אבל הכאת הקו ה"ג בקו ג"ב הנחנוה שלשים ותשע והכאת קו ח"ב על עצמו הוא עשרים וחמשה ומקובצם ששים וארבעה | |
| וכן יהיה הכאת קו ח"ג על עצמו ס"ד | |
| ושורש ששים וארבע הוא שמונה ולכן קו ח"ג שמונה | |
| וידוע שקו ח"ב חמשה | |
| וישאר קו ב"ג שלשה והוא שורש האלגוש | |
| והאלגוש תשעה | |
| ואם תרצה שאראך לעין מה שאמרתי עשה על קו ח"ג שטח מרובע והוא שטח חכנ"ג | |
| ותוציא קו א"ב ביושר עד נקודת ע' | |
| הנה קו ח"ג כמו קו נ"ג | |
| וקו ב"ג כמו קו ד"ג | |
| ישאר קו ב"ח כמו קו ד"נ | |
| ושטח ח"א כמו שטח א"נ | |
| אבל שטח ח"א כמו שטח מ"ה | |
| לכן שטח מ"ה כמו שטח א"נ | |
| ושטחי א"ח א"נ ד"ב השלשה שלשים ותשעה | |
| אבל שטח א"כ עשרים וחמשה בעבור כי הוא שוה להכאת ח"ב על עצמו | |
| הנה שטח כ"ג כלו ששים וארבעה | |
| וקו ח"ג שרשו והוא שמונה | |
| וקו ב"ח היה חמשה | |
| וישאר קו ג"ב שלשה ומש"ל | |
| ומשפט האופן אשר יראך האלגו הוא שתשים האלגוש קו א"ב | |
| ותחבר עמו עשרה שרשיו והוא קו ב"ג | |
| ויהיה קו א"ג שלשים ותשעה | |
| ואם תרצה לדעת כמות א"ב עשה על קו ב"ג שטח מרובע והוא שטח דהב"ג והוא מאה פעמים כמו קו א"ב מוכה על אחד מאחדיו | |
| בעבור כי קו ב"ג עשרה שרשים מקו א"ב | |
| ועשרה שרשים מהדבר מוכה על עצמו הוא כמו אותו הדבר מאה פעמים בי' מפני כי יחס | |
| ונשים קו א"מ מאה מן אשר בם קו א"ג שלשים ותשעה | |
| ונשלים שטח א"נ והנה הוא שלשת אלפים תת"ק בעבור כי קו א"ג שלשים ותשעה וקו | |
| ונמשיך קו ב"ח נכחי לא"מ | |
| ויהיה שטח א"ח שוה למרובע ב"ה כי הוא גם כן מאה פעמים כמו קו א"ב מוכה על אחד מאחדיו בעבור כי אורך קו א"מ מאה | |
| ויהיה מפני זה שטח ד"נ גם כן שלשת אלפים תת"ק והוא מהכאת קו ג"ה בקו ה"נ כי ה"ג כמו ה"ד | |
| והנה קו ג"נ מאה מפני שהוא שוה לא"מ | |
| ונחלק אותו לחציים על נקודת ל' | |
| וכבר נוסף על קו נ"ה ויהיה מפני זה שטח הכאת נ"ה על קו ה"ג ומרובע קו ג"ל יחד כמו מרובע קו ל"ה כמו שאמר אקלידס במאמר שיני מספרו | |
| אבל שטח נ"ה על ה"ג שלשת אלפים תת"ק | |
| ומרובע קו ג"ל שני אלפים ת"ק | |
| ונחברם יחד ויהיו ששת אלפים ות' והם כמו הכאת קו ל"ה על עצמו | |
| לכן יהיה קו ל"ה שמונים | |
| וקו ג"ה כמו קו ב"ג | |
| הנה כי קוי ל"ג ב"ג שמונים | |
| וכאשר נחסר קוי ב"ג ג"ל שהם שמונים מקוי א"ג ג"ל שהם שמונים ותשעה ישאר קו א"ב שהוא האלגוש תשעה ומש"ל
(א"מ) ארוך מאה א"ב עשירי' ב"ג של המרובע אל המרובע כיחס הצלע אל הצלע שינוי ושורש אם כן א"ב המרובע הוא עשירית העשירית מן המרובע ההוה מן כ"ג והוא ב"ה אם כן ב"ה באחד מאחדיו מאה דימיוני קו א"ב מוכה | |
ax2+c=bx |
והאלגוש והמספרים שישוו שרשים |
|
|
כאלו תאמר אלגוש ועשרים ואחד אדרהמיש ישוו עשרה שרשים |
| רצוני כי כאשר תחבר עם האלגו עשרים ואחד יהיה המחובר כמו עשרה שרשים מהאלגוש | |
| ובזאת החלוקה שני אופנים האחד יראך שורש האלגוש והאחר יראך האלגוש | |
| וכל אחד מהם יעשה בשני פנים האחד עם תוספת והאחד עם מגרעת | |
|
|
והאופן אשר יראך שורש האלגוש הוא שתקח חצי השרשים והם חמשה ותרבם על עצמם ויהיו עשרים וחמשה |
| והאלגוש תשעה | |
|
|
ואם תרצה הוסיף השנים על חצי השרשים ויהיו שבעה והוא שורש האלגו |
|
|
והאלגו ארבעים ותשעה |
| ודע כי כאשר תחצה השרשים באופן הזה ותרבם על עצמם ויהיה המתקבץ ממנו פחות מהאדרהמיש אשר עם האלגוש שאז מוטעה השאלה תשתנה החלוקה | |
| וכן פעמים יהיה כמו האדרהמיש בעצמם ויהיה שורש האלגו כמו חצי השרשים מבלי מגרעת ומבלי תוספת | |
| ועוד אבאר לך כל אשר אמרנו בזאת החלוקה עם תמונת גימטריאות | |
|
|
והאופן אשר אראך האלגו הוא אשר נרבה העשרה שרשים על עצמם ויהיה מאה ונרבה אלו המאה על עשרים ואחד ויהיו אלפיים ומאה |
| ואם תרצה תוסיף העשרים על החמישים ויהיו שבעים ותגרע מהם העשרים ואחד וישאר ארבעים ותשעה והוא האלגו | |
| וכן כל אשר יבא לידך משני אלגו או יותר או פחות השיבם לעולם אל אלגו אחד כמו שהראתיך באופן הראשון | |
| והמשפט שיראך כיצד אלגו וכ"א אדרהם ישוו כמו עשרה שרשים מהאלגו | |
| הנה האופן אשר יראך השרש שיוכל להיות האלגו יותר מהאדרהמיש אשר הנחנו עמו או פחות מהם | |
| ולא יוכל להיות האלגו כמו האדרמהיש כי אם בהיות הכאת חצי השרשים על עצמו כמו האדרמהיש אשר עם האלגו ויהיה מהאלגוש | |
| ואבאר כל זה ואראהו ואניח האדרמהיש אשר שמת עם האלגו שהם עשרים ואחד שיהיו יותר מהאלגו | |
| ואניח האלגו שטח מרובע עליו אבג"ד | |
| ונוסיף עליו העשרים ואחד והוא שטח אבה"ל וזה השטח גדול משטח אבג"ד כי כן הנחנוהו | |
| וקו ב"ל מפני זה גדול מקו ב"ד | |
| ושטח ה"ד עשרה שרשים משטח אבג"ד | |
| אם כן קו ל"ד עשרה | |
| ושטח ה"ב כ"א והוא שוה להכאת ל"ב בב"ד כי ב"ד שוה לב"א | |
| ונחלק קו ל"ד לחציים בנקודת ח' | |
| וכבר נחלק גם כן לשני חלקים בלתי שוים על נקודת ב' | |
| ולכן הכאת על ל"ב בב"ד עם מרובע ח"ב ישוו למרובע ח"ד כמו שאמר אקלידס בספרו במאמר השיני | |
| אבל הכאת קו ח"ד על עצמו עשרים וחמשה בעבור כי אורכו חמשה | |
| וקו ל"ב בב"ד עשרים ואחד כאמור | |
| וישאר מרובע קו ח"ב ארבעה וצלעו שנים | |
| אבל קו ח"ד הוא חמשה | |
| וישאר קו ב"ד הוא שלשה והוא שורש האלגוש | |
| והאלגוש תשעה | |
| ואם תרצה שאראך לעין מה שאמרתי אשים על קו ח"ד מרובע והוא שטח כ"ד | |
| ושטח כ"ד עשרים וחמשה כי קו ח"ד הוא חמשה | |
| ושטח ח"ג כמו שטח ח"ה בעבור כי קו ל"ח כמו קו ח"ד ושטח א"ח כמו שטח א"נ | |
| ולכן שטחי א"ח א"ד א"נ השלשה ישוו לשטח ה"ב שהוא מהכאת ל"ב בב"ד והוא עשרים ואחד | |
| ולכן ישאר שטח כ"א ארבעה | |
| והוא מרובע בעבור כי קו כ"נ כמו קו כ"ח וקו ח"ס כמו קו נ"מ | |
| וישאר קו כ"ס כמו קו כ"מ | |
| וקו מ"כ שנים והוא שוה לקו ח"ב | |
| אם כן קו ח"ב שנים | |
| וישאר קו ב"ד שלשה והוא שורש האלגוש | |
| והאלגוש תשעה ומש"ל | |
| ואבאר בזאת השאלה כאשר תקח חצי השרשים ויהיה העולה מהכאתם על עצמם יותר מהאדרהמיש שהנחת עם האלגוש שהם כ"א ופחות מן האלגוש | |
| ר"ל שאדרהמיש פחות מהאלגו | |
| ואשים האלגו שטח מרובע עליו אבג"ד | |
| ואחבר עמו העשרים ואחד והוא שטח אבה"ו | |
| ושטח א"ד גדול משטח א"ו כי כן הנחנו | |
| וקו ד"ב ארוך מקו ב"ו ושטח ה"ד עשרה שרשים משטח א"ד | |
| ולכן קו ד"ו עשרה | |
| והכאת קו ו"ב בב"ד הוא עשרים ואחד | |
| ותחלק קו ו"ד לחציים על נקודת ח' | |
| והנה הוא כבר נחלק לשני חלקים בלתי שוים על נקודת ב' | |
| ולכן יהיה הכאת ו"ב בב"ד והכאת ב"ח על עצמו יחד כמו הכאת ח"ד על עצמו כמו שאמר אקלידס במאמר שיני בספרו | |
| והכאת ח"ד על עצמו הוא עשרים וחמשה | |
| והכאת ו"ב בב"ד הוא עשרים ואחד | |
| וישאר הכאת קו ח"ב על עצמו ארבעה | |
| וקו ח"ב הוא שורש ארבע והוא שנים | |
| ותחברם עם קו ח"ד שהוא חמשה ויהיה קו ב"ד שבעה והוא שורש האלגוש | |
| והאלגוש ארבעים ותשעה | |
| הנה שביארנו לך כי כאשר הנחנו האלגוש פחות מהאדרהמיש שאז נוציאהו עם מגרעת | |
| וכאשר נניחיהו יותר מהאדרמהיש הנה אז נוציאהו עם התוספת | |
| ואם תרצה שאבאר לך לעין כל מה שאמרתי תצייר על קו ו"ח שטח מרובע עליו ו"נ | |
| ותוציא קו ח"נ על יושר עד נקודת כ' | |
| ושטח ב"נ כמו שטח נ"ה בעבור כי קו ל"נ שוה לקו נ"ח | |
| וקו ב"ח שוה לקו נ"ב כי שטח א"נ מרובע כמו שנבאר | |
| ושטח ו"נ הוא עשרים וחמשה | |
| ושטח א"ו עשרים ואחד | |
| וישאר שטח א"נ ארבעה | |
| והוא מרובע בעבור כי קו א"ב כמו קו א"ג | |
| וכ"ג כמו קו ב"ס מפני שקו כ"ג כמו קו ח"ד וח"ד כמו ח"ו וח"ו כמו ח"נ וח"נ כמו ב"ס הנה שקו ב"ס כמו קו כ"ג | |
| וישאר קו א"כ כמו קו א"ס | |
| ושטח א"נ מרובע וקו ס"נ שנים | |
| אבל קו ס"נ כמו קו ב"ח | |
| ויהיה קו ב"ח שנים | |
| ותחברם עם קו ח"ד שהוא חמשה ויהיה קו ב"ד שבעה והוא שורש האלגו | |
| והאלגוש ארבעים ותשעה | |
| ונתבאר עוד בזאת השאלה כי כאשר הכינו חצי השרשים על עצמם היה העולה יותר מהאדרמיש אשר שמת עם האלגו כמו שטח א"נ וזה מש"ל | |
| ועוד ביארנו כי כאשר הנחנו האלגו פחות מהאדרמהיש אשר עמו יצא המבוקש עם מגרעת | |
| ואם הנחנוהו יותר מהדרמהיש יצא המבוקש עם תוספת | |
| וביארתי עוד מה שנאמר בשתי צורות רצוני צורת הגירעון וצורת התוספת | |
| כאשר היה הכאת חצי השרשים על עצמו יותר מן האדרהמיש אשר הנחנוהו עם האלגוש | |
| ואבאר עוד כאשר יהיה העולה מהכאת חצי השרשים על עצמו שוה אל האדרמהיש אשר עם האלגוש שאז יהיה האלגו כמו האדרמהיש ממש ושורש האלגוש כמו חצי השרשים | |
| א"ח (אמ"פ) כבר יתבאר זה ביותר נקל וזה כי כאשר יהיה הכאת השרשי' על עצמם כמו האדרהמיש יחוייב שיהיה השרשי' האמצעיי ביחס בין האחד והאדרהמיש ואבאר ששרשים המרובעי אמצעיים ג"כ בין האחד והמרובע הנה האדרהמיש והמרובע שוים כי הדברי' אשר יחס שוה לדבר אחד הם שוים | |
| ואמשיל זה בשאילה אחרת ואניחנה שכ"ה אדרהמיש ואלגוש ישוו עשרה שרשים | |
| ואניח האלגוש שטח מרובע עליו אבג"ד | |
| ואחבר עמו הכ"ה אדרהמיש והם שטח אבה"ו | |
| וכל שטח ג"ו עשרה שרשים משטח אבג"ד | |
| וקו ד"ו עשרה | |
| וכאשר נחלק קו ד"ו לשני חציים על נקודת ח' לא ימלט הדבר מאחד משלשה ענינים | |
| אם שתפול נקודת ח' מלמעלה מנקודת ב' או למטה ממנה או בה | |
| ונניח ראשנה שתפול נקודת ח' למעלה | |
| אם יתכן זה הנה קו ד"ו נחלק לחציים על נקודת ח' | |
| ולשני חלקים בלתי שוים על נקודת ב' | |
| ולכן יהיה הכאת ד"ב בב"ו ומרובע ח"ב על עצמו ישוו להכאת ח"ו על עצמו כדמבואר בשני לאקלידס | |
| אבל הכאת ו"ח על עצמו הוא עשרים וחמשה בעבור כי הנחנוהו חצי ו"ד שהוא עשרה | |
| לכן הכאת ו"ב בב"ד עם מרובע ב"ח עשרים וחמשה | |
| אמ"פ [3] המעתיק אלו הם דברי הספר שהעתקתי ממנו במופת הזה ונראה לי שדבריו אינם מספיקים בזה אבל הראוי יותר שיאמר כי כאשר נפלה נקודת ח' החולקת למעלה מנקודת ב' אז האדרמהיש יותר מהאלגוש וכאשר תפול למטה ממנה יהיה האלגוש יותר מהאדרמהיש וזה כולו מבואר למעלה ונשאר שאם תפול עליה ובה בהכרח יהיו אז שוים | |
| עוד המשיך דבריו בדברים בלתי מתוקנים אצלי והם אלו | |
| וביארנו במה שאמרתי כי כאשר תרבה השרשים אשר ישוו האלגוש והמספרים בחלק הזה משלשה חלקים על עצמם ותקח חצי העולה ותרבהו על עצמו הנה יהיה כמו הכאת האדרמהיש על מה שעלה מהכאת השרשים על עצמם והאלגו הוא כמו האדרהמיש ומה שעלה מהכאת השרשים על עצמם והיה מחצי אשר עלה הכאת חצי השרשים על עצמו ותצא השאלה | |
| וכבר ביארנו כל אשר בזה האופן | |
| עד כאן | |
| ונראה לי כי היה רצונו של בעל הספר לבאר בזה המקום האופן השני מזאת החלוקה רצוני האופן אשר יראה לנו האלגוס כאשר ייעד למעלה ומופתו אבל נשמט מהספר אשר העתקתי ממנו | |
| ואבארהו בעבדי עוד על זה הספר בע"ה | |
bx+c=ax2 |
והשרשים ומספרים שישוו אלגוש |
|
|
כמו אם יאמר שלשה שרשים וארבעה מספרים ישוו אלגו |
| בזאת השאלה שני אופנים | |
| האחד יראך שורש האלגוש | |
| והאחר יראך האלגוש | |
| ועוד אבארם בתמונת גימטרייאות | |
|
|
והאופן אשר יראך השורש הוא אשר תחצה השרשים ויהיה אחד וחצי ותרבהו על עצמו ויהיו שנים ורביע |
| והאלגוש ששה עשר | |
|
|
והאופן אשר יראך האלגוש הוא שתרבה השלשה שרשים על עצמם ויהיה תשעה ותרבה אילו התשעה על הארבעה האדרהמיש אשר הנחת עם השרשים ויעלו ל"ו |
| וכאשר תניח מן האלגוש יותר או פחות השיבם תמיד אל אלגוש אחד כאשר עשינו בשאילה הראשנה | |
| והעלה בזאת השאלה שהיו שלשה שרשים וארבעה מספרים שוים אל האלגוש | |
| הנה האופן אשר יראך השורש הוא שתשים האלגוש שטח מרובע עליו אבג"ד והוא שלשה שרשים וארבעה מספרים | |
| והוא ידוע ממה שאמרנו שלשה שרשים וארבעה מספרים שוים אל האלגוש | |
| ונקח משטח א"ד שטח אהג"נ ונניחהו שלשה שרשים משטח א"ד והוא ידוע ממה שאמרנו שלשה שרשים | |
| ושטח ה"ד נשאר ארבעה מספרים | |
| ותחצה קו א"ה על נקודת ח' | |
| והנה לך קו א"ה נחלק לחציים על נקודת ח' ונוסף באורכו קו ב"ה ולכן הכאת א"ב בב"ה עם מרובע ה"ח ישוו להכאת ח"ב על עצמו כדמבואר בשני לאקלידס | |
| אבל הכאת א"ב בב"ה ארבעה בעבור כי קו א"ב שוה לקו ב"ד | |
| והכאת קו ה"ח על עצמו הוא שנים ורביע | |
| וחיבורם ששה ורביע | |
| וזה כי שטח א"נ א"נ שלשה שרשי ולכן שטח א"נ כמו העולה מהכאת א"ג משלש המספרי' ומהמא' (וא"ה) שלשה וה"ח אחד וחצי | |
| והנה שרשו שנים וחצי | |
| ולכן קו ח"ב שנים וחצי | |
| אבל קו ח"ה אחד וחצי | |
| ומפני זה יהיה כל קו א"ב ארבעה והוא שורש האלגוש | |
| והאלגו שש עשרה | |
| ולבאר הדבר יותר נניח על קו ח"ב שטח מרובע עליו ח"כ | |
| והוא ידוע שקו מ"ע כמו קו כ"ד | |
| בעבור כי קו א"ב כמו קו ב"ד | |
| וקו ב"ח כמו קו כ"ב | |
| ונשאר כ"ד כמו א"ח וא"ח כמו ח"ה וח"ה כמו מ"ע | |
| אם כן מ"ע כמו כ"ד | |
| ונניח קו מ"ט כמו קו נ"ד | |
| ולכן יהיה שטח ע"ט כמו שטח מ"ד | |
| ונשים שטח ה"כ משותף | |
| ויהיה שטח ה"ד כולו כמו שטח ע"ט מ"ב ושטח ה"ד ארבעה אם כן שטחי ע"ט מ"ב ארבעה | |
| והוא ידוע כי שטח ח"ט מרובע בעבור כי קו ב"ח כמו קו מ"ה וקו מ"ט כמו קו ה"ב | |
| וישאר קו ח"ה כמו קו ה"ט | |
| וקו ח"ה אחד וחצי | |
| ולכן שטח ח"ט שנים ורביע | |
| וכל שטח ח"כ ששה ורביע | |
| וקו ב"ח שנים וחצי וקו א"ח אחד וחצי וכל קו א"ב ארבעה והוא שורש האלגוש | |
| והאלגו ששה עשר | |
| ולזה האופן דרך אחרת | |
| והוא שנניח שטח מרובע עליו אבג"ד יהיה שלשה שרשים וארבעה מספרים | |
| ונבדיל מקו ג"א קו א"ח ונניחיהו אחד וחצי | |
| ונוציא קו ח"מ על נכחות הקו א"ב | |
| ושטח א"מ הוא שורש וחצי | |
| ונניח קו ע"ד אחד וחצי | |
| ונוציא ע"ט על נכחות ב"ד | |
| ושטח ע"ב הוא שורש וחצי | |
| וידוע כי שטח א"מ ושטח נ"ד ושטח נ"ב שלשה שרשים | |
| וישאר שטח ח"ע ארבעה מספרים וכמו שטח נ"ב | |
| ושטח נ"ב שנים ורביע | |
| ולכן יהיה שטח ע"ח ששה ורביע | |
| וקו ג"ח שנים וחצי | |
| וקו ח"א אחד וחצי | |
| וקו א"ג כלו ארבעה והוא שורש האלגו | |
| והאלגו ששה עשר ומש"ל | |
| ועלת האופן אשר יראך האלגוש | |
| הוא שנשים צלע האלגו קו א"ב והוא צלע שלשה שרשים וארבעה מספרים | |
| ויהיה קו ג"ב ממנו ארבעה מספרים | |
| וישאר קו א"ג שלשה שרשים מקו א"ב | |
| ונעשה על קו א"ג שטח מרובע עליו אגד"ה | |
| להיות יחס מרובע אל מרובע יחס צלע אל צלעו שינוי | |
| וידוע כי הוא כמו תשעה פעמים קו א"ב מוכה על אחד | |
| ונשים קו א"נ תשעה מאחדי קו א"ב | |
| ונשלים שטח א"ח ויהיה מפני זה שטח א"ח שוה למרובע א"ה | |
| ונמשיך קו ג"כ נכחי לקו ב"ח | |
| ונבדיל מקו א"ד קו א"ע שוה לקו א"נ | |
| ונוציא קו ע"ל נכחי לקו ד"ה | |
| והנה שטח ע"ג שוה לשטח א"כ | |
| וישאר שטח ע"ה שוה לשטח כ"ב | |
| אבל שטח כ"ב הוא שלשים ושש מפני כי קו ג"ב ארבעה וקו ג"כ השוה לקו א"נ תשעה ולכן שטח ע"ה גם הוא שלשים וששה | |
| וקו ע"א תשעה בעבור כי הוא שוה לקו א"נ | |
| ותחצה קו א"ע על נקודת מ' | |
| והנה כי קו ע"א נחלק לחצאים על נקודת מ' ונוסף בארכו קו ע"ד ולכן יהיה הכאת קו א"ד בקו ד"ע והכאת ע"מ על עצמו שוים להכאת ד"מ על עצמו כמבואר באקלידס במאמר שיני | |
| אבל הכאת א"ד בד"ע הוא כמו שטח ע"ה בעבור כי קו א"ד כמו קו ד"ה | |
| ושטח ע"ה הוא שלשים ושש | |
| הנה הכאת א"ד בד"ע הוא שלשים וששה | |
| והכאת ע"מ על עצמו הוא עשרים ורביע | |
| ותחברם יחד ויהיו חמישים ושש ורביע אם כן הכאת קו מ"ד על עצמו חמשים ושש ורביע | |
| ולכן יהיה קו מ"ד שבעה וחצי | |
| וקו א"מ ארבעה וחצי | |
| אם כן קו א"ד כלו שנים עשר והוא שוה לקו א"ג | |
| וקו ג"ב הוא ארבעה | |
| הנה כי קו א"ב ששה עשר והוא האלגו והוא מש"ל | |
| ואלו הששה חלקים אשר הגדנו בזה הספר וביארנו מלאכתם ועלותיהם | |
| הנה השלשה מהם נפרדים והם אלגוש ישוו שרשים והאלגו ישוו מספרים ושרשים ישוו מספרים | |
| ושלשה מחוברים והם אלגוש ושרשים ישוו מספרים ואלגוש ומספרים ישוו שרשים ושרשים ומספרים ישוו אלגוש | |
| והרבה מסופרי האלג'בר ואלמקאבלא לא יוכל להיות שלא יורוך קצת מהם | |
| ולכל חלק מאילו הששה חלקים שאלות אשר יורוך אותם בעלי המספר מהקובראמיינטו ומהקונפרונטאמיינטו | |
| ואתחיל ראשונה מהכאות הדברי' האחד באחר והדברים והמספרים על עצמם ועל הדברים ועל המספרים מלבד אילו אשר אמרנו ובענין אחר אשר לא יתכן בלעדי ידיעתו מי שירצה לקרות בספר הזה | |
| ואבאר לך באיזה צד יתרבו הדברים והם השרשים האחד באחד כאשר יהיו נפרדים או כאשר יהיו עם מספרים בין שיהיו נגרעים מהמספרים בין שיהיו המספרי' נגרעים מהם | |
| ובאיזה צד יתחברו אלו עם אלו | |
| וכיצד יגרע האחד מן האחר | |
| נגרעים מהם ובאיזה צד יתחברו כמ' שית' החלק הרביעי ב"ה מזה החלק הרביעי כמו שיתב' בו מזה תמ"ז מ"ז החלק הרביעי החלק הרביעי או | |
| וכאשר יהיו הדברים נוספים על המספרים יהיה החלק רביעי נוסף והחלק הרביעי אז הוא הכאת הדברי' זה עם זה והכאת המספרים האחד עם האחר | |
| בעבור כי כל שני מספרים שיוכו בשני מספרים אחרים לא יתכן מבלעדי שיתרבו ארבע פעמים | |
| והוא שיוכו שני המספרים הראשונים בכל אחד מן השנים המספרים האחרים ותהיה ההכאה ארבע פעמים | |
| וכאשר יהיו הדברים נגרעים מהמספרים יהיה החלק הרביעי נוסף והוא הכאת הדברים האחד באחר | |
| וכאשר היו האחד נוסף והאחר נגרע יהיה החלק הרביעי נגרע והוא הכאת הדברים האחד באחר | |
| וכאשר היו המספרים נגרעים מהדברים יהיה החלק הרביעי נוסף והחלק הרביעי אז הוא הכאת אחד המספרים באחר | |
| וכאשר היו אחד משני המספרים נוסף על הדברים והאחר נגרע מהדברים יהיה החלק הרביעי נגרע והוא הכאת אחד משני המספרים באחר | |
| וכאשר היו הדברים נוספי' על המספרי' ויהיה מספר אחד נגרע מהדברי' יהיה החלק הרביעי נגרע והוא הכאת הדברים נוספים במספר הנגרע | |
| וכבר הגדנו עם החלק רביעי מה הוא הראוי כפי מה שראיתי שבעלי המספר מתחילין עמו ובכפל | |
| ואפשר שיהיה החלק הרביעי מבלעדי אשר ספרנו אלא כי כלל הדבר שהכאת הנשנים האחד באחר תוספת והנשנה בנוסף נגרע והנוסף בנוסף נוסף | |
| ודע שהדברים בדברים אלגוש | |
| והדברים במספרים דברים ושרשים | |
| בעבור כי הדבר הוא השורש והשורש הוא הדבר והם שני שמות נופלים על ענין אחד | |
| ואם יאמרו לך כמה יהיה דבר אחד בעשרה אדרהמיש | |
| תאמר עשרה דברים | |
| וביאור זה שתשים הדבר בדמיון האחד ותכה האחד בעשרה ויהיו עשרה והם עשרה דברים | |
| ואם יאמרו כמה יהיו שני דברים על עשרה אהדרמיש | |
| תאמר עשרים | |
| וביאור זה שתשים השני דברים בדימיון שנים ממספר ותכה שנים בעשרה ויהיו עשרים דברים | |
| וכן כמה שתרצה מהדברים תשים לעולם כל דבר בדימיון האחר ותכה כל מספרי הדבר במספר האדרהמיש והעולה יהיו דברים | |
| בעבור כי כל מספר מהמספרים שיוכה במין אחד מהמינים יהיה כל אחד מהמינים בדמיון האחד | |
| אם היה דבר תשים אחד | |
| ואם היו שנים תשים שנים | |
| וכן אם היה אלגוש או דבר אחר איזה דבר שתרצה ותכהו על המספרים והעולה הוא מאותו המין | |
| ואשים לך על זה תמונה לבאר לך לעין אשר אמרתי | |
| ואם יאמרו לך כמה יהיה דבר על דבר | |
| תאמר אלגוש | |
| ואופנו שתשים הדבר בדימיון האחד ותכהו על אחד ויהיה אחד והוא אלגוש | |
| ואם יאמרו כמה יהיו שני דברים על שני דברים | |
| תאמר ארבעה אלגוש כמו שבארתי לך | |
| וכן שלשה דברים בשני דברים | |
| תכה שלשה בשנים ויהיו ששה אלגו | |
| וכן חצי דבר על חצי דבר | |
| יהיה רביע מאלגוש | |
| וכן כמה שתוסיף מהדברים או תגרע תשים כל דבר בדימיון האחד ותכה אילו האחדים עם האחדים האחרים והעולה מהם יהיה אלגוש | |
| ואשים לך על זה ענין אשר בו תבין משפט האלגוש והדבר | |
| ואשים ענין זה בהכאת שני דברים בשני דברים | |
| נניח קו א"ג שני דברים | |
| וקו ה"ג שני דברים | |
| והכינו קו א"ג בקו ג"ה והיה שטח א"ה | |
| ונאמר ששטח א"ה הוא ארבעה אלגוש | |
| ומופת זה שנחלק קו א"ג על מספר מה שבו מן הדברים ויהיו חלקיו א"ב ב"ג | |
| ותחלק קו ג"ה על מספר מה שבו מן הדברים ויהיו חלקיו ג"ד ד"ה | |
| ותוציא מנקודת ב' קו אחד עד ע' על נכחות קו ג"ה | |
| ותוציא מנקודת ד' קו נכחי לקו א"ג והוא קו ד"ח | |
| ונתחדשו מפני זה בשטח א"ה ד' מרובעים שוים והם מרובע ח"ב ומרובעי ב"ד וד"ע וח"ע | |
| וכל אחד מאילו המרובעים אלגו | |
| וכל אחד מקוי א"ב ב"ג ג"ד ד"ה מוכה באחד הוא דבר | |
| וזה הוא משפט האלגוש והדבר | |
| ושטח א"ה ארבעה אלגוש ומש"ל | |
| ואם יאמרו כמה יהיו שלשה דברים בששה אדרהמיש | |
| תשים השלשה דברים בדימיון שלשה ותכה שלשה בששה ויהיו שמונה עשרה והם שמנה עשר דברים | |
| ודימיון זה שנשים קו א"ב ששה מהמספרים | |
| וקו ב"ד שלשה דברים | |
| ותכה קו א"ב בב"ד ויהיה שטח א"ד | |
| ונאמר ששטח א"ד שמנה עשר דברים | |
| ומופת זה שנחלק קו א"ב שהוא ששה על מה שבו מן האחדים ויצאו ששה חלקים והם א"ג ג"ה ה"ו ו"ז ז"ח ח"ב | |
| ותחלק קו ד"ב אל מספר מה שבו מהדברים ויהיו חלקיו ב"ט ט"כ כ"ד | |
| marg.: אמ"פ זכור כי לא היה צריך לעשות קוי ב"ט ט"כ ד"כ שוים לקוי ב"ח ח"ז וה"ו בזה המופת כי לא התנה שיהיו דימיוני ה"ט רק דברי' לא אלגוש שהם מרובעים | |
| ותוציא מנקדות ג'ה'ו'ז'ח' קוים נכחיים לקו ב"ד והם קוי ג"ע ה"פ ו"נ ז"מ ח"ל | |
| ועוד תוציא מנקודות ט"כ שני קוים נכחיים לקו א"ב והם קוי ט"ק כ"ס | |
| ויהיה בשטח א"ד שמנה עשר שטחים שוים כמו שנגלה בתמונה כל שטח מהם שוה לשטח ח"ט | |
| ושטח ח"ט הוא מהכאת הדבר שהוא ב"ט באחד שהוא קו ב"ח | |
| ושטח ח"ט דבר | |
| ושטח א"ד כולו יהיה שמונה עשר דברי' | |
| וזהו משפט הכאת המספרים בדברים | |
| וזהו מה שאנו בבאורו | |
|
|
ואם יאמרו לך כמה יהיה עשרה אהדרמיש ודבר בדבר אחד |
| תאמר שהם עשרה דברים ואלגו | |
| ואופן מעשהו שתכה דבר בעשרה אדרהמיש ויהיו עשרה דברים | |
| ותכה דבר בדבר ויהיה אלגו | |
| ותקבצם ויהיו עשרה דברים ואלגוש אחד | |
| ואבארהו לך בזאת התמונה | |
| והוא שנניח קו א"ב עשרה דרהמיש | |
| וקו ב"ג דבר אחד | |
| ותכה קו א"ג בקו ב"ג ויצא שטח א"ד | |
| ונאמר ששטח א"ד עשרה דברים ואלגוש אחד | |
| ומופת זה שקו ב"ה כמו קו ג"ד | |
| וקו ג"ד כמו קו ב"ג | |
| אם כן קו ב"ה כמו קו ב"ג | |
| אבל קו ב"ג דבר אחד אם כן קו ב"ה דבר אחד | |
| וקו א"ב עשרה | |
| ושטח א"ה הוא מהכאת א"ב בקו ב"ה ולכן הנה הוא עשרה דברים | |
| ושטח ב"ד הוא אלגו כי הנה הוא מרובע והוא מהכאת ב"ג שהוא דבר על עצמו | |
| ויהיה כל שטח א"ד עשרה דברים ואלגו אחד והוא מה שאנחנו בבאורו | |
|
|
ואם יאמרו לך עשרה אדרהמיש פחות דבר אחד על דבר אחד |
| תאמר עשרה דברים פחות אלגו אחד | |
| ומעשהו שתכה עשרה אדרהמיש בדבר ויהיה עשרה דברים | |
| ותכה דבר על דבר ויהיה אלגו | |
| תגרעהו מהעשרה דברי' וישאר עשרה דברים פחות אלגו | |
| ואבאר זה בזאת התמונה | |
| והוא שנשים העשרה אדרהמיש קו א"ג | |
| ונניח קו ב"ג דבר אחד | |
| וישאר קו א"ב עשרה אדרהמיש פחות דבר | |
| ותכה קו א"ג בקו ב"ג ויצא שטח א"ד | |
| ונוציא מנקדת ב' קו נכחי לקו ג"ד והוא קו ב"ה | |
| ונאמר כי שטח א"ה עשרה דברים פחות אלגו | |
| ומופת זה כי היה שטח א"ד עשרה דברים בעבור כי הוא מהכאת קו א"ג שהוא עשרה בקו ג"ד שהוא דבר | |
| בעבור כי ג"ד שוה לב"ג | |
| ומרובע ב"ד אלגו בעבור כי הוא מהכאת קו ב"ג שהוא דבר בקו ג"ד השוה אליו | |
| ולכן ישאר שטח א"ה עשרה דברים פחות אלגו ומש"ל | |
|
|
ואם יאמרו לך כמה יהיו עשרה אדרהמיש ודבר בעשרה אדרהמיש ודבר |
| תאמר מאה אדרהמיש ואלגו ועשרים דברים | |
| ומעשיהו הוא שתכה עשרה על עשרה ויהיו מאה אדרהמיש | |
| עוד תכה עשרה על דבר ויהיו עשרה דברים | |
| וחזור ותכה דבר על עשרה אדרהמיש ויהיו עשרה דברים | |
| ותכה עוד דבר על דבר ויהיה אלגוש | |
| ותקבצם ויהיה כלו מאה אדרהמיש ואלגוש ועשרים דברים | |
| ואבאר זה בזאת התמונה | |
| והוא שנשים קו א"ב עשרה אדרהמיש ודבר | |
| וא"ג ממנו עשרה | |
| וג"ב דבר | |
| וכן תשים קו ב"ד עשרה דרהמיש ודבר | |
| ב"ה ממנו דבר | |
| וה"ד עשרה | |
| ותכה קו א"ב בקו ב"ד ויצא שטח א"ד | |
| ונאמר כי שטח א"ד מאה אדרהמיש ואלגוש ועשרים דברים | |
| ומופת זה שנוציא מנקודת ג' קו נכחי לקו ב"ד והוא קו ג"ח | |
| ונוציא מנקודת ה' קו נכחי לקו א"ב והוא קו ה"ז | |
| הנה שטח ג"ה מרובע | |
| וז"ח מרובע כמו שביאר זה אקלידס | |
| ושטח ג"ז כמו שטח ה"ח | |
| אבל שטח ז"ח מאה כי הוא הווה מהכאת א"ג שהוא עשרה בקו ה"ד שהוא גם כן עשרה | |
| ושטח ז"ג עשרה דברים כי הנה הוא מהכאת ב"ה שהוא דבר בקו א"ג שהוא עשרה | |
| ושטח ח"ה עשרה דברים בעבור כי הוא הוה מהכאת ב"ה שהוא דבר בקו ה"ד שהוא עשרה | |
| ושטח ג"ה המרובע הוא אלגו בעבור כי הוא מהכאת קו ג"ב שהוא דבר בקו ב"ה שהוא גם כן דבר | |
| ותקבץ הארבעה שטחים ויהיו כמו שטח א"ד והוא מאה אהדרהמיש
ואלגוש ועשרים דברים ומש"ל | |
|
|
ואם יאמרו לך כמה יהיה עשרה אדרהמיש פחות דבר בעשרה אדרהמיש פחות דבר |
| תאמר מאה אדרהמיש ואלגוש פחות עשרים דברים | |
| ואופן מעשיהו שתרבה עשרה אדרהמיש על עשרה אדרהמיש ויהיו מאה | |
| תכה דבר נגרע בעשרה אדרהמיש ויהיו עשרה דברים נגרעים | |
| עוד תשוב להכות עשרה אדרהמיש בדבר נגרע ויהיו עשרה דברים נגרעים | |
| ותרבה דבר נגרע בדבר נגרע ויהיה אלגו נוסף | |
| ותקבץ כל זה ויהיה מאה ואלגו פחות עשרים דברים | |
| ואבארהו לך בזאת התמונה | |
| והוא שתשים קו א"ב עשרה אדרהמיש פחות דבר שהוא ב"ג | |
| ונשים קו ג"ד עשרה | |
| וג"ה ממנו דבר | |
| ותכה קו א"ב שהוא עשרה אדרהמיש פחות דבר על קו ה"ד שהוא גם כן עשרה אדרהמיש פחות דבר ויהיה מרובע ז"ח | |
| ונאמר שמרובע ז"ח מאה אדרהמיש ואלגו פחות עשרים דברים | |
| ומופת זה שנשלים שטח א"ד | |
| ונוציא מנקודת ב' קו ישר נכחי לקו ג"ד והוא קו ב"ח | |
| ונוציא מנקודת ה' קו נכחי לקו א"ג והוא קו ה"ז | |
| ושטח א"ד מאה בעבור כי קו א"ג עשרה וג"ד עשרה | |
| ושטח ז"ג עשרה דברים בעבור כי קו א"ג עשרה וג"ה דבר | |
| וכן שטח ב"ד עשרה דברים בעבור כי קו ג"ד עשרה וקו ג"ב דבר | |
| ושטח מרובע ב"ה הוא אלגוש בעבור כי הוא מהכאת ב"ג שהוא דבר בג"ה שהוא גם כן דבר | |
| וישאר ה"ח עשרה דברים פחות אלגוס | |
| ושטח א"ה עשרה דברים | |
| ושטח ג"ז ושטח ה"ח יחד עשרים דברים פחות אלגוס | |
| ושטח א"ד הוא מאה | |
| וישאר שטח ז"ח מאה אדרהמיש ואלגו פחות עשרים דברים והוא מש"ל | |
| marg.: וזה כי נניח אלגו ב"ה משותף יחד יהיה א"כ מרובע ז"ח כמו מרובע א"ד עם מרובע ב"ה פחות כפל שטח א"ה | |
|
|
ואם יאמרו לך עשרה אדרהמיש ודבר על עשרה אדרהמיש פחות דבר |
| תאמר מאה אדרהמיש פחות אלגוש | |
| ואופן מעשהו שתכה עשרה על עשרה ויהיה מאה אדרהמיש | |
| ותכה הדבר הנוסף על עשרה ויהיה עשרה דברים נוספים | |
| ותכה הדבר הגורע על עשרה ויהיה עשרה דברים נגרעים | |
| ותחסר הנוספים כנגד הנגרעים וישארו מאה אדרהמיש | |
| ותכה הדבר הנוסף בדבר הגורע ויהיה אלגו גורע | |
| ותגרע מהמאה אדרהמיש וישארו מאה פחות אלגוש | |
| ואבאר זה בזאת התמונה | |
| והיא שנשים קו א"ב עשרה ודבר | |
| א"ג עשרה | |
| וג"ב דבר | |
| ונשים קו ב"ה עשרה דרהמיש פחות דבר | |
| קו ב"ד עשרה | |
| וקו ה"ד דבר | |
| ונכה קו א"ב שהוא עשרה אדרהמיש ודבר בקו ב"ה שהוא עשרה פחות דבר ויהיה שטח א"ה | |
| ונאמר ששטח א"ה הוא מאה אדרהמיש פחות אלגוש | |
| ומופת זה שנשלים שטח א"ד | |
| והנה שטח א"ד מאה אדרהמיש ועשרה דברים בעבור כי שטח א"ח מאה כי הוא מהכאת א"ג שהוא עשרה בג"ח שהוא גם כן עשרה | |
| ושטח ג"ד עשרה דברים בעבור כי הוא מהכאת ג"ב שהוא דבר בב"ד שהוא עשרה | |
| ויהיה כל שטח א"ד מאה אדרהמיש ועשרה דברים | |
| ושטח ז"ח כמו שטח ח"ב | |
| ותבדיל משטח ז"ח כמו שטח מ"ד המרובע והוא שטח כ"ח | |
| ויהיה מפני זה שטח כ"ד שנים מרובעים ושנים אלגוש | |
| וישאר שטח ז"ט כמו שטח מ"ב | |
| ויהיה שטח א"מ ושטח ז"ט מאה אדרהמיש פחות אלגוש בעבור כי שטח כ"ח אלגוש | |
| ולכן שטח א"ה יהיה מאה אדרהמיש פחות אלגוש | |
|
|
ואם יאמרו לך כמה יהיה עשרה אדרהמיש ודבר על דבר פחות עשרה אדרהמיש |
| תאמר אלגוש פחות מאה אדרהמיש | |
| ואופן מעשיהו שתכה הדבר (פחות עשרה אדרהמיש) על עצמו ויהיה אלגוש | |
| ותכה עשרה אדרהמיש נוספים על דבר ויהיה עשרה דברים נוספים | |
| ותכה הדבר על העשרה אדרהמיש נגרעים ויהיה עשרה דברים נגרעים | |
| ותשליך העשרה דברים הנוספים כנגד העשרה דברים הנגרעים וישאר אלגו | |
| ותכה העשרה אדרהמיש נוספים בעשרה אדרהמיש נגרעים ויהיה מאה אדרהמיש נגרעים | |
| ותגרעם מהאלגו וישאר אלגו פחות מאה אדרהמיש | |
| ואבאר זה בזאת התמונה | |
| והוא שתשים קו א"ב עשרה אדרהמיש ודבר | |
| א"ג עשרה | |
| וג"ב דבר | |
| ונניח קו ב"ה דבר פחות עשרה | |
| ב"ד הוא הדבר | |
| וד"ה עשרה | |
| ותכה קו א"ב שהוא עשרה אדרהמיש ודבר על קו ב"ה שהוא דבר פחות עשרה ויהיה השטח א"ה | |
| ונאמר ששטח א"ה אלגו פחות מאה אדרהמיש | |
| ומופת זה שנשלים שטח א"ד | |
| ויהיה שטח א"ד עשרה דברים ואלגוס בעבור כי קו א"ב עשרה אדרהמיש ודבר וקו ב"ד דבר | |
| ונוציא קו ג"ח נכחי לקו ב"ד | |
| ויהיה שטח ג"ד מרובע והוא אלגו' בעבור כי הוא מהכאת ג"ב שהוא דבר בב"ד שהוא גם כן דבר | |
| ויהיה שטח א"ח כמו שטח ח"ה בעבור כי קו ח"ג כמו קו ח"ד וקו א"ג כמו קו ה"ד | |
| ומפני זה יהיה שטח א"ח ושטח ג"ה יחד אלגוש | |
| אבל שטח כ"ח מאה בעבור כי א"ג כמו כ"ל וא"ג עשרה לכן כ"ל עשרה ול"ח כמו ה"ד וה"ד עשרה לכן ל"ח עשרה ולכן שטח כ"ח מאה | |
| וישאר שטח א"ה אלגו פחות מאה אדרהמיש ומש"ל | |
|
|
ואם יאמרו לך כמה יהיו עשרה אדרהמיש ושני שלישי דבר על שלשה אדרהמיש פחות ששה דברים |
| תאמר שלשים אדרהמיש פחות ארבעה אלגוש ופחות חמשים ושמנה דברים | |
| ואופן מעשיהו שתכה עשרה אדרהמיש על שלשה אדרהמיש ויהיו שלשים אדרהמיש | |
| ותכה שני שלישי דבר על שלשה אדרהמיש ויהיו שני דברים נוספים | |
| ותכה ששה דברים נגרעים על עשרה אדרהמיש ויהיו שישים דברים נגרעים | |
| ותשליך שני הדברים הנוספים כנגד השני דברים מן הנגרעים וישארו שלשים אדרהמיש פחות חמישים ושמנה דברים | |
| ותכה הששה דברים נגרעים על שני שלישי דבר הנוספים ויהיו ארבעה אלגוש נגרעים | |
| ותגרעם משלשים אדרהמיש וישארו שלשים אדרהמיש פחות ארבעה אלגו ופחות נ"ח דברים | |
| ואשר ביארתי והוספתי ביאור מכפל הדברים והמספרים האחד באחר הוא אשר ממנו תוכל לעשות כל אשר יפול מידך מזה השער | |
| וכאשר תרצה לכפול שורש ממספר ידוע או מאלגוש בלתי ידוע | |
| ורצוני בהכפלה הנה לקיחת שני שרשיו | |
| וכאשר תרצה שיהיו שני שרשי המספר הידוע או מהאלגוש הבלתי ידוע שורש מספר אחר או מאלגו אחר תניח השני שרשים בדמיון שנים ותכה שנים על שנים והעולה תכהו על המספר הידוע או על האלגו הבלתי ידוע | |
| וכאשר תרצה שלשה שרשים תכה שלשה על שלשה ועל האלגוש הבלתי ידוע או על המספר הידוע ויהיה שורש העולה שלשה שרשים מהמספר הידוע או מהאלגוש הבלתי ידוע | |
| וכאשר תרצה לחצות השורש תכה חצי על חצי ויהיה רביע ותכה רביע על האלגו הידוע או על הבלתי ידוע ויהיה שורש העולה מההכאה הוא חצי שורש המספר הידוע או מהבלתי ידוע | |
| וכן כל מה שתוסיף או תגרע מהשרשים כמו שאמרנו | |
|
|
ודמיון זה כאשר רצינו לכפול שורש ששה עשר |
| תכה שנים על שנים ויהיו ארבעה ותכה הארבעה בששה עשר ויהיו שישים וארבעה ושורשו הוא שמנה והם שני שרשי ששה עשר | |
| ואבאר זה בזאת התמונה | |
| והוא שנניח הששה עשר שטח מרובע עליו אבג"ד | |
| וקו ג"ד הנה הוא שורש מרובע א"ד | |
| וכאשר נרצה לכפול זה השטח נוציא קו ג"ד על יושר עד ה' | |
| ונשים ג"ה שוה לג"ד | |
| ויהיה קו ה"ד שני שרשים משטח א"ד | |
| וכאשר נרצה לדעת שורש איזה מספר הוא | |
| נשים על קו ה"ד שטח מרובע עליו ה"ז | |
| ונאמר ששטח ה"ז ארבעה דימיוני שטח ג"ב | |
| ומופת זה שנוציא קו ג"א על יושר עד נקודת ח' | |
| וקו א"ב על יושר עד נקודת ט' | |
| ויהיה בשטח ה"ז ארבעה מרובעים שוים והם מרובעים ג"ב ב"ח ח"ט ט"ג | |
| והוא מבואר שמרובע ה"ז ארבעה דימיוני מרובע ג"ב | |
| ומרובע ג"ב שש עשרה | |
| ולכן יהיה מרובע ה"ז ששים וארבע | |
| ויהיה קו ה"ד שורש ששים וארבע והוא שמנה ומש"ל | |
|
|
וכאשר תרצה לקחת חצי שורש תשעה |
| תכה חצי על חצי ויהיה רביע ותכהו על תשעה ויהיה שנים ורביע וקח שורשו והוא אחד וחצי והוא יהיה חצי שורש תשעה | |
|
|
וכאשר תרצה לקחת שני שלישי שורש תשעה |
| תכה שני שלישים על שני שלישים והם ארבע תשיעיות ותכם על תשעה ויהיו ארבעה ושורשו שנים והם שני שלישי שורש תשעה | |
| ואבאר לך זה בזאת התמונה | |
| והוא שנשים התשעה שטח מרובע עליו אבג"ד | |
| ויהיה קו ג"ד שורש תשעה והוא שורש שטח מרובע א"ד | |
| וכאשר נרצה לדעת שורש איזה מספר הוא | |
| נעשה על קו ז"ד שטח מרובע עליו כ"ז ל"ד | |
| ונאמר ששטח כ"ז ל"ד ארבע תשיעיות שטח ג"ב והם ארבעה ממספר | |
| ומופת זה שנוציא קו ז"כ על יושר עד נקודת ט' | |
| ותוציא מנקודת ה' קו ה"ח נכחי לקו ב"ד | |
| ותוציא מע' קו ע"פ נכחי לקו א"ב | |
| ובזה יעשו בשטח ג"ב תשעה שטחים שוים והם ה"ע ע"מ מ"ב מ"ט ט"ס כ"נ כ"פ פ"ז ז"נ | |
| ויהיה שטח ז"ל ארבעה מאילו התשעה השטחים וזה השטח יהיה ארבעה תשיעיות משטח ג"ב | |
| ושטח ג"ב תשעה | |
| ויהיה שטח ז"ל ארבעה | |
| וקו ז"ד שורש ארבעה ומש"ל | |
| וכל מה שיפול בידך מזה המין תעשה בו ככה | |
|
|
ואם תרצה להכות שורש תשעה על שורש ארבעה |
| תכה ארבעה על תשעה ויהיו שלשים ושש תקח שורשו והוא ששה והוא הכאת שורש תשעה על שורש ארבעה | |
| ואבאר זה בזאת התמונה | |
| והוא שתשים קו א"ב שורש תשעה | |
| וקו ב"ג שורש ארבעה | |
| וכאשר תרצה להכות קו א"ב על קו ב"ג תשים על קו א"ג שטח מרובע עליו א"ח | |
| ותוציא מנקודת ב' על קו ב"ג קו נכחי לקוי א"ה ג"ח והוא קו ב"ז | |
| וכל אחד מקוי א"ה ג"ח שורש תשעה ושורש ארבעה | |
| ונשים קו מ"ג שורש תשעה | |
| וישאר קו מ"ח שורש ארבעה | |
| ונוציא מנקודת מ' קו ישר נכחי לקוי א"ג ה"ח והוא קו מ"כ | |
| ויהיה שטח ע"א תשעה | |
| וקו ב"ע שורש תשעה | |
| ושטח ע"ח ארבעה | |
| וקו ז"ע שורש ארבעה כי ז"ע שוה לע"מ | |
| וקו ע"מ כמו קו ב"ג וע"ב כמו ע"כ | |
| ויחס מ"ע אל ע"כ כיחס ז"ע אל ע"ב | |
| ויחס ז"ע אל ע"ב כיחס שטח ז"כ אל שטח ע"א | |
| ולכן יהיה הכאת המספרים אשר בשטח ז"מ אל המספרים אשר בשטח ע"א כמו הכאת המספרים אשר בשטח ז"כ על עצמם | |
| וכבר ביאר זה אקלידס ואמר כי כאשר היו שלשה מספרים מתייחסים יהיה הכאת המספר הראשון בשלישי כמו הכאת השיני על עצמו | |
| אבל הכאת מה שבשטח ע"ח מהאחדים שהם ארבעה על אחדי שטח ע"א שהם תשעה יהיה שלשים ושש | |
| והכאת מה שבשטח ז"כ מהאחדים על עצמם יהיה כמו כן שלשים ושש | |
| ושטח ז"כ שורש שלשים ושש והוא ששה והוא הוה מהכאת שורש תשעה על שרש ארבעה בעבור כי קו כ"ע שרש תשעה וע"ז שרש ארבעה ומש"ל | |
|
|
ואם יאמרו לך כמה יהיו הכאת שני שרשי עשרה על חצי שורש חמשה |
| תסתכל שני שרשי עשרה שורש של איזה מספר הם על הדרך שהראיתיך | |
| ותמצא שהם שרש לארבעים | |
| ותחפש לאי זה המספר הוא שורש חצי שורש חמשה | |
| ותמצא שהוא שורש לאחד ורביע | |
| ויהיה כאלו שאלו כמה יהיה הכאת שורש ארבעים על שורש אחד ורביע | |
| ותכה ארבעים על אחד ורביע ויהיו חמישים | |
| ותאמר שורש חמישים הוא הכאת שני שרשי עשרה על חצי שורש חמשה | |
| ואניח לך על זה המעשה תמונה כוללת | |
| כל מספר שיוכה על מספר ונקח שורש העולה יהיה כמו הכאת שורש מספר אחד מהם לשרש מספר האחר | |
| משל זה שנשים ב"א שני מספרים ושורש ב"ג ושורש א"ד | |
| ונכה ב' על א' ויהיה ז' | |
| ונכה ג' על ד' ויהיה ח' | |
| ונאמר שח' כמו ה' שהוא שורש ז' | |
| ומופת זה שג' מוכה על עצמו היה ב' | |
| ומוכה על ד' היה ח' | |
| ויהיה יחס ג' אל ד' כיחס ח' אל א' | |
| והיה יחס ג' אל ד' כיחס ב' אל ח' | |
| ולכן יהיה יחס ב' אל ח' כיחס ח' אל א' | |
| והכאת ב' על א' יהיה כמו הכאת ח' על עצמו | |
| אבל הכאת ב' על א' הוא ז' | |
| והכאת ח' על עצמו יהיה כמו הכאת ה' על עצמו | |
| וח' כמו ה' ומש"ל | |
| וכמה שהוספתי וביארתי מזה המין בו השלמה | |
| גם דע כי כאשר תכה המחלק על העולה לחֶלק ישוב המספר שחלקת | |
| משל זה כאשר חלקת עשרה על שנים ויצא לכל חלק חמשה ותכה חמשה על שנים ויהיו עשרה והוא המספר הנחלק | |
| ואשים לזה המעשה תמונה כללית | |
| כל מספר שיהיה נחלק על מספר אחר יהיה הכאת העולה לכל חלק על המספר המחלק כמו מספר הנחלק | |
| משל זה שא' המספר הנחלק וב' הוא המחלק וחלקנו א' על ב' ועלה לכל חלק ג' | |
| ואומר שהכאת ב' על ג' הוא א' | |
| ומופת זה כי כבר נחלק א' על ב' ועלה הג' | |
| ולכן יהיה ג' בא' כל כך פעמים כמו שהוא בב' מן האחדים | |
| ויהיה מפני זה יחס ג' אל א' כיחס האחד אל ב' | |
| והכאת האחֵר על א' כהכאת ג' על ב' | |
| אבל הכאת האחד על א' הוא א' | |
| אם כן הכאת ב' על ג' הוא גם כן א' ומש"ל | |
|
|
ואם יאמרו תחלק שורש תשעה על שורש ארבעה |
| תחלק תשעה על ארבעה ויגיע לכל חלק שנים ורביע תקח שורשו והוא אחד וחצי והוא שורש תשעה מחולק על שורש ארבעה | |
|
|
ואם יאמרו תחלק שורש עשרה על שורש שנים |
| תחלק עשרה על שנים ויעלה אל החלק חמשה וקח שורשו | |
|
|
ואם יאמרו לך תחלק שנים שרשים מעשרים על שלשה שרשים מששה |
| תחפש שנים שרשים מעשרים לאיזה מספר הם שורש | |
| וידענו ממה שביארנו שהם שורש לשמנים | |
| ותחפש כמו כן שלשה שרשים מששה לאיזה מספר הם | |
| ותמצא שהם שורש לחמישים וארבעה | |
| ותחלק שמנים על חמישים וארבעה ויעלה אל החלק אחד וארבעה תשיעיות ושלישית התשיעית | |
| ושורש זה הוא מה שיעלה אל החלק מחלוקת שנים שרשים מעשרים על שלשה שרשים מששה | |
| וכן כל אשר יפול בידך מזה המין עשה כן כמעשה הזה | |
| ואמשיל לך מזה המין בתמונה כוללת | |
| והוא זה כל שני מספרים שיחלק האחד על האחר יהיה שורש העולה אל החלק כמו העולה מחלוקת שורש המספר הנחלק על שורש המספר המחלק | |
| משל זה שמספר א' נחלק על מספר ב' ועלה מספר ג' | |
| ושורש מספר א' הוא ח' | |
| ושורש מספר ב' הוא ד' | |
| וחלקנו ח' על ד' ועלה ע' | |
| ונאמר שע' הוא שורש ג' | |
| ומופת זה שא' נחלק על ב' ועלה ג' | |
| ויהיה מפני זה ג' ימנה א' במספר מה שבב' מן האחדים | |
| וכן יהיו אחדי ד' במספר דימיוני ע' בח' | |
| ואחד מוכה על אחד הוא אחד | |
| וד' מוכה על עצמו הוא ב' | |
| וע' מוכה על עצמו הוא מ' | |
| ומספר אחדי ב' יהיו כמו דימיוני מ' בא' | |
| אבל מספר אחדי ב' יהיה כמספר דימיוני ג' בא' | |
| הנה כי מספר דימיוני ג' בא' יהיה כמספר דימיוני מ' בא' | |
| וג' ישוה למ' וע' הוא שורש מ' הנה כי ע' שורש ג' ומש"ל | |
| הנה כי מספר דימיוני ג' בא' יהיה כמספר) דימיוני כי כבר התבאר א' (מ') בא' שאחדי ד' כמס[פר] דימיוני ע' בד' (בח') א"כ יחס האחד אל ד' כיחס ע' על ח' וכאשר היה זה כך המרובעי' ההוי' מהם מתיחסי' כמו שהתבאר באקליד' אם כן יחס האחד מוכה על אחד והוא אחד אל מרובע ד' והוא ב' כיחס מרובע ע' והוא מ' אל מרובע ח' והוא א'אם כן אחד (ב)ב' הם כמו דימיוני מ' בא' ו (אבל אחד בב' הם ג"כ כמו דימיוני ג' בא' וג' שוה למ') | |
Addition of Roots |
בחבור השרשים האחד עם האחר |
| וכאשר תרצה לחבר שורש מספר מהמספרים אל שורש מספר אחר עד שיחובר שורש איזה אלגוש | |
| הנה זה לא יתכן בכל מספר אבל יתכן בשני מספרים מרובעים | |
| רצוני במספרים המרובעים שיחזיקו שורש | |
| או בשני מספרים שכאשר נחלק האחד על האחר עלה אל החלק שורש וכאשר תכה האחד על האחר היה המקובץ שורש | |
| ובמספרי' אחרים מבלעדי אילו לא יתכן שתחבר שני שרשיהם עד שתשיבנה שורש אחד | |
| וכן בגרוע האחד מן האחר | |
| ואלו יהיו הרבה מבוארים | |
| ויהיו שני המספרים המרובעים תשעה וארבעה וכאשר תרצה לחבר שורש תשעה ושורש ארבעה עד שיהיו שורש למספר אחד | |
| תחבר תשעה וארבעה ויהיו י"ג ותכה תשעה על ארבעה ויהיו שלשים וששה וקח שני שרשיו והם שנים עשר תחברם עם שלש עשרה ויהיו עשרים וחמשה ושרשו חמשה והם שורש תשעה ושורש ארבעה מקובצים | |
| ואבאר זה בזאת התמונה | |
| וזה שנניח קו א"ב שורש תשעה | |
| וקו א"ג שורש ארבעה | |
| וכאשר נרצה לדעת קו ג"ב שורש איזה מספר הוא | |
| נעשה על קו ג"ב שטח מרובע עליו ג"ז | |
| ויהיה קו ג"ב שורש ג"ז | |
| ונעשה על קו א"ב שטח מרובע עליו אבכ"ל | |
| ונוציא א"כ על יושר עד נקודת ח' | |
| וקו ל"כ על יושר עד נקודת ע' | |
| ויהיה שטח כ"ב תשעה בעבור כי קו א"ב הוא שורש תשעה | |
| ושטח ע"ח ארבעה בעבור כי א"ג הוא שורש ארבעה וא"ג כמו ע"כ | |
| ושטח א"ע ששה כי הוא מהכאת שורש תשעה שהוא קו א"ב על שורש ארבעה שהוא קו א"ג | |
| ושטח ג"ז עשרים וחמשה | |
| וקו ג"ב הוא שורשו והוא חמשה ומש"ל | |
Subtraction of Roots |
בגרעון השרשים האחד מן האחר |
|
|
וכאשר תרצה לגרוע שרש ארבעה משורש תשעה עד שיהיה מה שישאר משורש תשעה שורש מספר אחד פחות שורש מהמספר האחר |
| תחבר התשעה עם הארבעה ויהיו ששה (שלושה) עשר ותכה
תשעה על ארבעה ויהיו שלשים ושנים (וששה) קח שני שרשיו והם שני' עשר ותחסרם מן השלשה עשר וישאר אחד ושורש האחד הוא יהיה הנשאר משורש תשעה בחסרך ממנו שורש הארבע והוא אחד ואבארהו לך בזאת התמונה והוא שנניח קו – א"ב שורש תשעה ושורש (וקו) א"ג שורש ארבעה וכאשר נגרע קו א"ג מקו א"ב ישאר קו ג"ב וכאשר נרצה לדעת מספר קו ג"ב שורש איזה מספר הוא נשים על קו א"ב (א"ג) שטח מרובע עליו א"מ ויהיה שטח א"מ ארבעה ותוציא קו ח"מ על יושר עד נ' וקו ה כ ז ג"מ על יושר עד כ' והוא ידוע כי מרובע מ"ז הוא מהכאת קו ג"ב על עצמו ושטח ח"כ שנים בעבור כי כל שטח א"ח א"כ – ח מ נ שששה כי הוא מהכאת קו א"ג שהוא שורש ארבעה בא"ה שהוא שורש תשעה ושטח א"ח (א"מ) ארבעה וישאר שטח ח"כ שנים ולזה יהיה שטח מ"ב שנים וישאר מרובע מ"ז אחד וקו מ"נ הוא ← ← שורשו והוא אחד וכבר היה קו מ"נ כמו כקו ג"ב ומש"ל א ג ב | |
|
|
וכאשר תרצה לחבר שרש שמנה עשר ושרש שמנה
עד שיהיו שורש המספר האחד (פחות שורש המספר האחר) זה המספר יתכן לחברו בעבור כי כאשר תתחלק שמנה עשר על שמנה יגיע לחלק שנים ורביע ומחזיק שורש ושורשו הוא אחד וחצי ואם תחלק שמנה על שמנה (עשר) יגיע לחלק ארבע תשיעיות ומחזיק שורש ושורשו הוא שני שלישים ואם תכה י"ח על ח' יהיו קו מ"ד (קמ"ד) ומחזיק שורש ושרשו י"ב וכל מספר שתחסר שתחבר שורשו אל שורש מספר אחר ויהיה משפטו זה המשפט יהיו שני שרשיהם מחוברים עד שיההיו שורש מספר אחר (אחד) וכאשר היה ספק* אחד *אולי הכוונה ל"משפט" ו"משפטים" מאלו הספקות אשר אמרנו אשר ימצאו במספרים יהיו השלשה בכתב-יד MS Paris נכתב "סגולה" ספיקות נמצאים וכאשר תרצה לדעת שורש איזה מספר במקום "ספק" ו"סגולות" במקום הוא תעשה כאשר אמרנו והוא שתחבר ח' עם י"ח ויהיו כ"ו – "ספוקות" ותשמרם ותכה ח' עליהם (על י"ח) ויהיו קמ"ד ותקח שני שרשיו והוא כ"ד ותחברם על הכ"ו ששמרת ויהיו נ' ושורשו הוא שורש ח' ושורש י"ח מקובצים ואם רצונך לגרוע שורש ח' משורש י"ח תגרע הכ"ד מהם מהכ"ו וישארו שנים ושורש שנים הוא שרש י"ח פחות (שורש) ח' ואם באת לחבר שורש עשרה עם שורש ש שנים זה לא יתכן לחברו ולא יתכן היותו שורש למספר אחר (אחד) בעבור כי כאשר תחלק עשרה על שנים יגיע לחלק חמש' והחמשה אינם מחזיקי' שורש וכאשר תחלק שנים על עשרה יגיע לחלק חומש ואין שורש לחומש ואם תכה שנים על עשרה יהיו עשרי' ואין שורש (ל)עשרים ואם תחברם כאשר הראתיך יהיו שנים שרשים מעשרים מחוברי' עם שני' עשר ושורשו הוא שורש עשרה ושורש שנים ואם בקשת לח לחסר האחר מן האחד תעשה כאשר אמרתי ויצא שנים עשר פחות שנים שרשים מעשרים ושורש הנשאר הוא שרש עשרה פחות שורש שנים והשאלה בזה יותר נכונה מהתשובה וראוי לך כאשר ישאלו ממך איזה דבר מזה הסוג שתהיה תשובתך עליה על דימיון אשר יוציאו עליך לפניך עדיף להשתמש בביטוי באגף השמאלי כפי שהוא בשוה כי כאשר תאמר שורש עשרה ושורש שנים יותר נכון מאשר בביטוי באגף הימני: מלאמר שנים עשר ושנים שרשים מעשרים ולקוח שורשו ויותר נכון לאמר בגרעון האחד מן האחר שורש עשרה פחות שורש שנים מלאמר שנים עשר פחות שני ש שרשים מעשרי' ולקוח שורש הנשאר שיהיה שורש עשרה פחות שורש שנים ושנים שרשים מעשרים יהיה שורש שמנים ועם אשר ביארתי מזה השלמה ואלו הששה בקשות אשר הראיתיך הנני עושה לך לכל חלק מהששה חלקים שאלה אשר כבר יורוך אותם חכמי האלגב"ר |
| והשאלה הראשנה מן הששה היא אם יאמרו לך תחלק עשרה לשנים חלקים ותכה האח' על האחר ותכה חלק הגדול על עצמו ויהיה החלק המוכה על עצמו כמו הכאת החלק האחד על האחר וכמו חציו | |
| והמעשה
בזה שנניח חלק הגדול דבר והחלק האחר עשרה פחות דבר ותכה דבר על עשרה פחות דבר ויהיו עשרה דברים פחות אלגו ותכה החלק הגדול על עצמו והוא דבר ויהיה אלגו וזה האלגו יהיה כמו עשרה דברי' פחות אלגו וכמו חצי זה ותכה עשרה דברים פחות אלגוס על אחד וחצי ויעלה חמשה עשר דברים פחות אלגו וחצי ואלו ישוו אלגוש ותניח החמשה עשר (דברים) עם האלגו איקובריאש וחצי עד שיהיו ט"ו דברים ותחבר האלגו וחצי עם האלגו ויהיה כלומ' ותאסוף אז שני אלגוס וחצי ישוו חמשה עשר דברי' ולכן האלגוס ← ישוה ששה דברי' והדבר ישוה ששה והוא החלק הגדול והחלק ← ← האחר יהיה ארבעה והוא הנשאר מעשרה וזאת השאלה א ← אראך לחלק הראשון מהששה חלקי' והוא אלגוש ישוו שרשים ואבאר זאת השאלה בתמונה מהתמונות והוא שנניח קו א"ב הסבר גיאומטרי: עשרה א"ג החלק הגדול וג"ב החלק הקטן ונכה קו א"ג על קו ג"ב ויהיה שטח ג"ד בעבור שהנחנו קו ג"ה כמו קו א"ג ב ג א ונכה קו א"ג על עצמו ויהיה שטח מרובע א"ה אבל שטח א"ה כמו שטח ג"ד וכמו חציו ולכן שט' קו ג"א יהיה כמו קו ג"ב וכמו חציו וקו א"ב כולו יהיה כמו קו ג"ב ← שני פעמי' וחצי אבל קו א"ב עשרה יהיה קו ב"ג ארבעה וקו א"ג ששה ומש"ל | |
| והשאלה השנית עשרה תחלקיהו לשני חלקי' ותכה אחד מהם על עצמו ותכה העשרה על עצמו (ויהיה) כמו העולה מהכאת אחד החלקים על עצמו ששה פעמי' ורביע | |
| והמעשה הזה שתשים החלק האחד דבר ותכהו על
עצמו והוא אלגו ותכה העשרה על עצמו ויהיה מאה ואלו המאה יהיה כמו האלגו ששה פעמי' ורביע ותכה האלגו על ששה ורביע ויהיה ששה אלגוש ורביע יישוו מאה והשיבם אל אלגו אחד והוא ארבע חלקי' מעשרים וחמשה והם ארבעה חומשי' מהחומש וקח מהמאה ארבע חומשי' מהחומש ויהיו י"ו ואלו הששה עשר ישוו אלגו ושורשו ארבע והוא החלק המבוקש וזאת ← השאלה הראתיך לחלק שיני מהששה חלקים שהוא אלגוש ישוו מספרים ואבאר לך בזאת התמונה והוא שנניח קו א"ב עשרה הסבר גיאומטרי: וג"ב המספר המבוקש ואכה קו א"ב שהוא עשרה על עצמו ויהיה מאה והוא שטח א"מ(ה) ואכה קו ג"ב שהוא החלק המבוקש על עצמו ויהיה מרובע ג"ד ושטח א"מ(ה) שהוא מאה (ש)הוא שש' מ פעמים ורביע מרובע ג"ד ותחלק מרובע ג"ד לארבע חלקים שוים כל אחד מהם שטח ב"ח ויהיה שטח א"מ(ה) כ"ה פעמים כמו שטח ח"ב ושטח א"מ מאה ושטח ב"ח ארבעה ← ד וג"ד שש עשרה וקו ג"ב ארבעה והוא החלק ח המבוקש ומש"ל | |
|
|
והשאלה השלישית תחלק עשרה לשני חלקים ותחלק החלק הגדול על החלק הקטן ויגיע לחלק ארבעה |
| והמעשה בזה
שנשים החלק הקטן דבר והגדול עשרה פחות דבר ותחלק עשרה פחות דבר על דבר ויגיע לחלק ארבעה כבר הראתיך כי כאשר תכה המגיע לחלק על המחלק שיעלה המספר המחולק אחרי כן תכה דבר על ארבעה ויהיו ארבעה דברי' ישוו עשרה פחות דבר ← ותכלול {איקוברא} העשרה עם הדבר עד שיהיו עשרה אדרה"מיש ותחבר דבר תכלול = איקוברא = תאסוף = add עם הארבע דברי' ויהיו עשרה ישוו חמשה דברי' והדבר ישווה ← שני אדרה"מיש (ותחבר דבר עם הארבע דברי' ויהיו עשרה ישוו חמ ← חמשה דברי' והדבר ישווה שני אדרה"מיש) וזאת ← השאלה הוצאתיה לחלק שלישי מהששה חלקי' והוא הדברי' ישוו מ מספרים ואבארה בזאת התמונה והוא שנניח קו א"ב עשרה הסבר גיאומטרי: וג"ב החלק הקטן וקו א"ג החלק הגדול וכאשר נחלק קו א"ג על קו ג"ב יעלה לחלק ארבעה וא"ג יהיה ארבעה כפלי ג"ב וא"ב יהיה ← א ג ב חמשה כפלי ג"ב וג"ב הוא חמישי' א"ב אבל ← א"ב עשרה וג"ב שנים ומש"ל | |
|
|
והשאלה הרביעית חלקנו עשרה לשני חלקיו והרבנו החלק הקטן על תשעה והגדול על עצמו והיו שוים |
| והמעשה בזה שנשים החלק
הגדול דבר והקטן עשרה פחות דבר ותכה דבר על עצמו והוא אל אלגוש ותכה עשרה פחות דבר על תשעה ויהיו תשעים פחות (עם) הדרה"מיש פחות תשעה דברי' ישוו אלגוש ותציעם {איקוברלוש ותאספם} עם התשעה ← דברי' ותוסיפם על האלגוש ויהיה אלגוש ותשעה דברי' ישוו תשעים תציע = איקוברלוש = תאסוף = add אדרה"מיש והאופן אשר נוציא לך הדבר ← הוא שתקח חצי הדברי' ויהיו ארבעה וחצי ותכם על עצמם ויהיו עשרים ורביע(ם) ותוסיפם על התשעים ויהיו מאה ועשר ורביע ושורשו הוא עשרה וחצי תגרע מהם מחצית השרשים שהוא ארבע וחצי וישאר ששה והוא הדבר והוא החלק הגדול ← והאופן אשר יוציא לך האלגוש הוא שתכה התשעה דברי' על עצמם ויהיו שמנים ואחד ותכם על התשעים ויהיה שבע' אלפים ומאתים ותשעים וקח מחציים (מחצית) שמונים ואחד ויהיה ארב ארבעים וחצי ותכם על עצמם ויהיה אלף תר"ם ורביע ותחב ותחברם עם ג * ט ב ז ויהיו שמנת אלפים ותשע מאות *הג' מסמנת אולי את המילה גלגל ושלשים ורביע ותקח שורשו והוא תשעים וארבע וחצי וגרעם מן הארבעים וחצי שהוא מחצית פ"א פ"א ומן התשעים שישוו האלגוש והשורש(ים) והם ק"ל וחצי וישאר ל"ו והם האלגוש וזאת השאלה הוצאתי לך לחלק הרביעי מהשלשה (שישה) חלקי' והוא האומר ← אלגוש ושרשים ישוו מספרים ואבארה לך בתמ בתמונה זו* והוא שנשי' קו ב"א עשרה וקו א"ג עשרה החלק הסבר גיאומטרי: הגדול וג"ב החלק הקטן והיה א"ג על עצמו כמו ג"ב על תשעה וא"ג על תשעה וג"ב על תשעה יחד הם תשעים ונניח א"ד תשעה וא"ג על עצמו ועל א"ד (ו)הוא כמו ד"ג על ג"א וד"ג על להיות א"ג ה"א (ג"א) יהיה תשעי' וקו ד"א תשעה ונחלק לחציים על נקודת ה' ונוסף על עצמו לאורכו קו א"ג והיה הכאת ד"ג על א"ג תשעים והכאת א"ה על כמו ג"ב עצמו יהיה עשרים ורביע ותקבצם עם תשעים ויהיו מאה על תשעה ועשר ורביע ולכן יהיה הכאת קו ה"ג על עצמו הוא ק"י ורביע ושרשו עשרה (וחצי) אם כן קו ה"ג עשרה וחצי אבל ה"א ארבע ← וחצי וישאר א"ג ששה והוא החלק הגדול וג"ב ארבעה והוא ← החלק הקטן ומש"ל | |
|
|
והשאלה החמישית חלקנו עשרה לשני חלקים והכינו האחד על האחר והיה עשרים ואחד |
| והמעשה בזה שנשים החלק האחד דבר וה'
והאחר עשרה פחות דבר ונכה (עשרה) דבר על עשרה פחות דבר ויהיה עשרה דברי' פחות אלגו ויישוו עשרים ואחד אדרה"מיש ותכלול העשרה (דברי') פחות אלגו עם האלגו והוסיף אותו על הע העשרים ואחד ויהיה אלגו ועשרים ואחד ישוו עשרה שרשים והאופן אשר נוציא לך הדבר הוא שתקח חצי הדברי' ויהיו חמשה ותכם על עצמם ויהיו עשרים וחמשה תגרע מהם העשרים ואחד וישארו ארבעה תקח שרשו והוא שנים ותגרעם מן החמשה וישארו שלשה והם החלק הקטן והחלק הגדול הוא הנשאר מעשרה ← והם שבעה ואם תרצה תוסיף השנים על חמשה ויהיו שבע' או והוא החלק הגדול והחלק הקטן הוא הנשאר מעשרה והוא שלשה והאופן אשר יוציא לך האלגוש הוא שתכה העשרה שרשים על עצמן ויהיו מאה ותכם על הכ"א(ה) אשר עם אלגוש ויהיה אלפים ומאה וקח חצי המאה והם חמישים ותכם על עצמם והם אלפים וחמש מאות תגרע מהם האלפיים (ומאה) וישארו ארבע מאות וקח שרשם והוא עשרים תגרעם מן החמישים שהם חצי מאה וישארו שלשים ותגרע מהם העשרים ואחד וישאר תשעה ויהיה אלגו והמעשה עם תוספת הוא שתוסיף העשרים על החמישי' ויהיו שבעי' ← או תגרע מהם העשרים ואחד ישארו ארבעי' ותשע והם האלגוש וזאת השאלה הוציאך אל החלק החמישי מהששה חלקים שהוא אלגוש ומספרים ישוו שרשים ואבאר זה בתמונה זו והוא שנניח קו א"ג על קו ב"ה (ג"ב) עשרים ואחד ותחלק קו א"ב לשני חציים הסבר גיאומטרי: על ה' ויהיה הכאת א"ג בא"ב בג"ב וה"ג על עצמו כמו הכאת ( ) א ה (ו) ג ב ה"ב על עצמו והכאת ה"ב על עצמו עשרים וחמשה וא"ג על ג"ב הוא עשרים ואחד וישאר ה"ג על עצמו ארבעה וה"ג יהיה שנים וה"ב היה חמשה וישאר ג"ב שלשה ויהיה א"ג ← ← שבעה ומש"ל | |
|
|
והשאלה הששית אלגוש תוסיף עליו שמנה אדרהמיש ותכה המקובץ על ארבעה אדרהמיש והיה כמו האלגוש על עצמו |
| והמעשה בזה שנשים האלגוש דבר ותחבר עמו שמונה
אדרהם ויהיה דבר ושמנה אדרה"מיש ותכם על ארבעה ויהיה ארבע' דברים ול"ב דרה"מיש והכה האלגוש והוא דבר על עצמו ויהיה אלגוש וישוה ל"ב דרה"ם וארבע דברי' והאופן אשר נוציא לך הדבר הוא שתקח מחצית הדברים ויהיה שנים ותכם על עצמם ויהיו ארבע' ותוסיפם על הל"ב ויהיו ל"ו תקח שרשו והוא ששה תוסיפם על מחצית השרשים וזהו שנים ויהיו שמנה והוא האלגו בעבור שהנחנו האלגוש דבר והאופן אשר יוציא האלגוש הוא שתכה הארבע שרשים על עצמם ויהיו ששה עשר ותכם על האדרה"מיש שהם ל"ב ויהיו תקי"ב וקח מחצית הא' (האלגוש?) ויהיו ח' ותכם על עצמם ויהיו ס"ד ותוסיפ' על התקי"ב ויהיו תקע"ו וקח שורשו והוא כ"ד ותחברם עם השמנה שהם מחצית הששה עשר ועם הל"ב ויהיו ס"ד והוא האלגוש ש שישוה השרשי' והמספרי' וקח שרשו והוא שמנה והוא המספר המבוקש וזאת השאלה הוצאתיך אל החלק מהחלקי' הששה והוא האומר מספרי' ושרשי' ישוו אלגוש ואבאר מזה בתמונה זו הסבר גיאומטרי: והוא שנשים האלגוש קו א"ב והשמנה אדרה"ם קו א"ג ונשים קו ב"ד האלגוש=דבר ארבע ונכה קו ג"ב בקו ב"ד ויהיה שטח ג"ד ותכה האלגוש הוא קו א"ב על עצמו ויהיה מרובע א"ה ושטח ג"ד הוא כמו שטח א"ה ות ותגרע שטח א"ד וישאר שטח מ"ה כמו שטח ג"מ ושטח ג"מ שלשים ושנים בעבור כי א"ג שמונה ז ה וא"מ שמנה ארבעה ולכן שטח מ"ה שלשי' ושנים ושטח מ"ה הוא מ ← מהכאת א"ז על ז"מ אם כן הכאת א"ז על ז"מ הוא שלשים ← ושנים וא"מ הוא ארבעה וחלקהו לשני חציים על ח' והכאת מ"ז על ← ז"א ומ"ח על עצמו יהיה כמו ח"ז על עצמו אבל מ"ח על עצמו ארבעה והכאת ח"ז על עצמו יהיה שלשי' ושש וח"ז יהיה ששה וא"ח שנים וא"ז שמנה והוא כמו א"ב וא"ב שמנה והוא האלגוש ← ומש"ל | |
|
|
שאלה ואם יאמרו לך תחלק עשרה לשני חלקי' ותכה כל חלק על עצמו ותגרע הכאת החלק הקטן מהכאת החלק הגדול וישאר שמנים |
| המעשה
בזה שתשים החלק הקטן דבר והגדול עשרה פחות דבר ותכה עשרה פחות דבר על עצמו ויהיה מאה דרה"מיש ואלגוש פחות עשרים דברים וישאר מאה דראה"מיש פחות עשרים דברים יהיו שמני' אדרה"מיש ותכלול המאה דרה"מי (ו)עם העשרי' הדברי' ותוסיפם על השמונים ויהיה עשרים דברי' ושמני' דרה"מיש ישוו מאה אדרה"מיש ← תגרע שמנים ממאה וישאר עשרים אדרה"מיש ישוו עשרי' דברי' והדב' ישווה אחד והוא החלק הקטן והגדול תשעה והוא מה שנשאר מן העשר' ← ואם נרצה נעשה החלק הגדול (עשרה) דבר והקטן עשרה פחות דבר תגרע מאה ואלגוש פחות עשרים דברים מאלגו וישאר עשרי' דברים פחות מאה אדרה"מיש (ותוסיפם על השמנים ויהיה מאה ושמנים אדרה"מיש) ותתכלול העשרים דברי' עם המאה אדרהמיש ותוסיפם על ← השמנים ויהיה מאה ושמנים אדרה"מיש ישווה עשרים דברי' והדבר ישוו ישווה תשעה והוא החלק הגדול והנשאר מהעשרה יהיה החלק הקטן ← והוא אחד ואם תרצה תחלק העשרה לשני חלקי' בחלוקה הנבדלת שיטה נוספת לפתרון: פתרון דיאופנטי מהחלוקה הנוהגת אותה בעלי המספר לחלוק בה העשרה ויתאמת בה המעשה ותדע החלק הגדול מהקטן ותלך ברוב מה שיפלו לפניך שיטה זו ניתנת לשימוש ברוב השאלות מהשאלות בקצרה וזה בחצית השרשים והוא שנניח החלק האחד דבר וחמשה והחלק האחר חמשה פחות (דבר) ותכה כל אחד מהם על ע' עצמו ותגרע העולה מהחלק הקטן מהעולה מהחלק הגדול וישאר עשרים דברים ישוו שמנים אדרה"מיש והדבר ישווה ארבע ← ותוסיף הארבע על החמשה והוא תשעה והוא החלק הגדול ותגרע ← הארבע מן החמשה וישאר אחד והוא החלק הגדול (הקטן) | |
|
|
ואם יאמרו לך עשרה תחלק אותו לשני חלקי' ותחלק כל אחד מהם על האחר ויגיעו החלקי' ארבע ורביע |
| והמעשה בזה שתשים החלק
האחד דבר והאחר עשרה פחות דבר ותכה דבר על עצמו ויהיה אלגוש ותכה עשרה פחות דבר על עצמו ויהיה מאה ואלגוש פחו' עשרים דברים ותחברם ויהיו מאה ושני אלגוש פחות עשרים דברי' ותשמרם ותכה החלק האחד על האחר והוא דבר על עשרה פחות דבר ויהיה עשרה דברי' פחות אלגוש ותכה על העולה אל החלקים והוא ארבע ורביע יהיה מ"ב דברים וחצי דבר פחות ארבע אלגוש ורביע אלגוש ישוו מאה אדרה"מיש ושני אלגו' פחות עשרים שרשים בעבור כי כל שני מספרי' שיחלקו כל אחד מהם על האחר יהיה הכאת כל אחד מהם על עצמן מחוברי' כמו הכאת האחד על האחר וההווה על החלק העולה מחלקות כל אחד מהם על האחר ועוד אבאר לך סבת זה אחר שאשלים חשבון השאלה כלל זה ניתן על ידי אל-ח'וארזמי ותכלול המאה אדרה"מיש ושני אלגוש עם העשרים דברי' ותוסיפ' על הארבעי' ושנים דברי' וחצי דבר פחות ארבעה אלגוש ורביע ישוו מאה אדרה"מיש ושני אלגוש ותכלול הס"ב דברי' וחצי עם הארבעה אלגוש ורביע ותוסיפם על המאה אדרה"מיש ושני אלגוש ויהיה מאה אדרה"מיש וששה אלגוש ורביע יישוו כ"ב (ס"ב) דברים וחצי והשיבם אל אלגוש אחד וכבר ידעת כי האלגוש מששה נרמול: ורביע אלגוש הוא ארבע ח(ו)משים מחומש (ותקח מכל אשר תחזיק ארבע חומשים מחומש) ותקח מכל אשר תחזיק ארבעה חומשים מחומש ויהיה אלגוש וששה עשר אדרה"מיש ישוה עשרה דברי' ומחצית ^ הדברים יהיה חמשה ותכם על עצמם ויהיה כ"ה ותגרע זכו' כי זה הוא מהם הי"ו וישאר תשעה ותקח שורשו והוא שלשה תגרעם ממחצית המכוון אשר השרשים שהוא חמשה וישאר שנים והוא החלק האחד והאחר יזכור תמיד שמנה ואם תרצה חלק העשרה לשני החלקים שהר בלעז קונפרו ← שהראיתיך אשר לא ינהגו החשבנים לחלוק בם העשרה ויתאמר נטאמי' בו יבי' confront, להקביל לך המעשה ולך בחצאת השרשים והוא שנשים החלק חמשה במה ישוה הדב' ודבר והאחר חמשה פחות דבר ותכה כל אחד מהם על עצמו ות ותחברם יחד ויהיה חמשי' אדרה"מיש ושני אלגוש ותכה חלק האחד על האחר ויהיה כ"ה אדרה"מיש פחות אלגוש ותכה על ארבע' ורביע ויהיה מאה ושש ורביע פחות ארבעה אלגוש ורביע אלגוש ישוו חמישים אדרה"מיש ושני אלגוש ותכללם עם הארבע אלגוש ורביע ותוסיפם על השני אלגוש וחמשי' ותגרע חמישי' כנגד חמישי' וישאר חמישי' ושש ורביע ישוו ששה אלגוש ורביע והאל והאלגוש ישווה תשעה (תשעה) והדבר הוא שורשו והוא שלשה ← ותגרעם מהחמשה ותוסיפם על חמשה בעבור שהנחנו החלק ← האחד חמשה פחות דבר והאחר חמשה ודבר ויהיה החלק האחד שמנה והאחר שנים כל מספר שיחלק האחד על האחר הנה המגיע אל החלק יהיה שוה לאשר יגיע אל החלק בחלקך העולה (מהכאת המספר על עצמו על העולה) מהכאת המספר הנחלק על – המחלק משל זה שמספר א' נחלק למספר ב' והגיע לחלק מספר ג' והכינו (א') על עצמו ויהיה ח' והכינו א' על ב' ויהיה ד' ונאמר שכאשר נחלק ח' על ד' יגיע ג' ומופת זה שא' נחלק על ב' ונהיה ג' הנה ב' ימנה א' בְשִעור מה שב"ג מן האחדים והאחד ימנה ג' בשעור מה שבג' מן האחדים ולכן יהיה האחד ימנה מט"ו מז' לאקליד' (היסודות vii, 15) ב' בשעור מה שימנה ג' (ב)א' וא' הוכה על עצמו והיה ח' והוכ' א ח על ב' והיה ד' ולכן יהיה ד' בח' ב ד מי"ח מז' כמו ב' בא' ושעור ב' בא' – ג ג לאקלי' (היסודות vii, 18) היה כמו שיעור האחד בג' אחד ושעור ד' בח' כשעור האחד בג' והאחד ימנה ג' בשיעור מה שבג' מן האחדים ויתבאר מזה שכאשר נחלק ח' על ד' עלה ג' ← והוא מש"ל כל שני מספרי' שיחלק כל אחד מהם על האחר הנה המגיע לחלק יהיה שוה לאשר יגיע לחלק בהחלק העול' מהכאת כל אחד מהמספרי' על עצמו על העולה מהכאת אחד המספרי' על האחר משל זה שמספר א' נחלק על מספר ב' ועלה ד' ומספר ב' נחלק על מספר א' ועלה ז' והוכה א' על עצמו ועלה ג' והוכה ב' על עצמו ועלה ח' והוכה א' על ב' ועל(ה) (ה)ע' ונאמר שמ' (שג') וח' כאשר נחלק כל אחד מהם על ע' יעלה ר"ד (ז' וד') מופת זה שא' נחלק על ב' ועל(ה) הע' (ד) וכאשר נחלק ג' על ע' יעלה ד' כמו שנתבאר בתמונה שלפניה וב' נחלק על ע' א' (ו)על(ה) ז' וב' הוכה על עצמו ועלה ח' וב' הוכה על א' והיה ע' וכאשר נחלק ח' על ע' יגיע ז' כמו שביארנו והוא מבואר שכאשר
נחלק ח' וג' על ע' יעלו ד"ז וכאשר
נכה ד' וז' על ע' יעלו ח' וג' וכבר
הוא מבואר שכל שני מספרים
שיחלק כל אחחד מהם על האחר הנה הכאת כל אחד על עצמו מחוברים יהיה כמו הכאת אחד המספרים על האחר ועל העולה לחלק מחלוקת כל אחד מהם על האחר והוא מש"ל כל שני מספרים שיחלק כל אחד מהם על האחר והוא משל יהיה הכאת מה שהגיע לחלקי' האחד על האחר אדרהם אחד לעולם משל זה שחלקנו מספר א' על מספר ב' והגיע ג' וחלקנו מספ' ב' על מספר א' ועלה ד' ונאמר שהכאת ג' על ד' אדרהם אחד המופת שא' נחלק על ב' ועלה ג' הנה שב' ימנה א' בשיעור מה שבג' מן האחדי' ושיעור האחד על ג' כשעור ב' אל א' וכאש ← וכאשר הפכנו יהיה שיעור א' אל ב' כשעור (האחד) ג' אל א' ו ← ועוד ב' נחלק על א' והיה ד' הנה שיעור א' אל ב' כשיעור האחד ← אל ד' וכבר היה יחס א' אל ד א ב ג ב' כיחס ג' אל אחד ולכן יחס האחד אל ד' כיחס ג' אל האחד ← והכאת ג' על ד' כמו הכאת האחד על עצמו והוא אחד ומש"ל ← … ואם תרצה תכוין חשבונך האמור במעשה אחר כזה ונשוב אל השאלה והיא כאשר אמרו לך עשרה חלקנום לשני חלקים וחלקנו כל אחד מהשני חלקים על האחד (האחר) ועל(ה) (ה)ארבעה ורביע תשים החלק האחד דבר והאחר עשרה פחות דבר פתרון (1): ותחלק עשרה פחות דבר (על דבר) ותכה הארבעה ורביע על דבר ויהיה ארבבעה דברים ורביע תגרע מהם עשרה פחות דבר (דבר) וישאר חמשה ורביע (דבר) פחות עשרה אדרה"מיש ותכה דבר על עצמו ויהיה אלגוש ותחלק אותו על עשרה אדרה"מיש פחות דבר דבר ויעלה חמשה דברים ורביע פחות עשרה אדרה"מיש וכבר ביארנו שכאשר נכה העולה על לחלק על המחלק שישוב השיעור הננחלק ונכה חמשה דברי' ורביע פחות עשרה אדרה"מיש על עשרה אדרה"מיש פחות דבר ויהיה ס"ב דברים וחצי פחות חמשה אלגוש ורביע ופחות מאה אדרה"מיש ישוו אלגוש ותכווניהו עמו ויהיה ששה אלגוש ורביע ומאה אדרה"מיש איקונפרונטלו confront, להקביל ישוו ס"ב דברי' וחצי ותעשה כאשר הראיתיך ויהיה החלק האחד שמנה והאחר שנים ולחשבון זה אופן אחר והוא שנשים החלק האחד דבר והאחר עשרה פחות דבר וחלק עשרה פחות פתרון (2): דבר על דבר ויעלה דינר אחד וכאשר תכה דינר על דבר יהיה דינר=מספר נעלם עשרה אדרה"מיש פחות דבר ותחלק דבר על עשרה פחות דבר ויעלה ארבע ורביע פחות דינר ותכה ארבע ורביע פחות דינ' ← על עשרה פחות דבר ויהיה נ"ב אדרה"מיש וחצי פחות (דינר על עשרה) חמשה דברי' ורביע פחות עשרה דינרין ישוו דבר ותכוין עמו כאשר אמר(תי) (כי) ויהיה עשרה דינרין (ודבר) ישוו נ"ב אדרה"מיש וחצי פחות חמשה דברי' ורביע (והדבר עשרה דינרין ישוו דבר) ותכוונהו עמו כ כאשר אמרתי ויהיה עשרה דינרי' ישוו נ"ב וחצי פחות ששה דברי' ורביע (והדינר) ישוו(ה) חמשה ורביע פחות חמשה שמיניות דבר וכבבר ידעת שכאשר נחלק עשרה אדרהמיש פחות דבר על דבר יעלה לחלק חמ חמשה ורביע פחות חמשה שמיניות דבר ותכה חמשה ורביע פחו' חמשה שמיניות דבר על דבר ויהיה חמשה דברי' ורביע פחות חמשה שמיניות (אלגוש) ישווה עשרה אדרה"מיש פחות אהדרמ"יש דבר דבר ותכוונהו עמו ויהיה ששה דברי' ורביע (ישוו חמשה שמיניות האלגוש ועשרה אדרהמיש) ← ותוסיף (ותכה) על דבר (ועל האדרהמיש) שתחזיק (אחד) (ו)שלשה חמישיותיו ויהיה (אלגוש וששה) עשרה אדרה"מיש ישוו עשרה דברי' ומחצית הדברי' יהיה חמשה ותכם על עצמם ויהיה כ"ה תגרע מהם הי"ו וישאר ט' תקח שורשו והוא ג' תגרעו ממחצית השרשי' שהוא חמש' וישאר שנים והוא החלק האחד והאחר שמנה וכבר ביארנו שכל ← שני מספרי' שיחלקו כל אחד מהם על האחר שהכאת העולה (על) (ה)חלקים האחד באחד יהיה אדרהם אחד ומה שעלה לשני החלקים בזאת השאלה ארבעה אהדרה"מיש ורביע ותשים האחד מה מהשנים דבר והאחר ארבעה ורביע פחות דבר ותכה אחד מהם פתרון (3): באחר ויהיה ארבעה דברי' ורביע פחות אלגוש ישוה אדרה"מיש אחד ותכוונהו עמו ויהיה הדבר אם תרצה ארבעה או אם תרצ תרצה רביע ותשוב להתחלת הששה (השאלה) ותאמר נשים החלק האחד מהשני או חלקי' דבר והאחר עשרה פחות דבר ותחלק עשרה פחות דבר על ד דבר ויעלה ארבעה ותכה ארבעה על דבר ויהיה ארבע דברים ישוו עשרה א(ד)דרה"מי(י)ש פחות דבר ותכוונהו עמו ויהיה הדבר שמנה (שנים) והוא החלק האחד מהשנים והאחר שנים (שמונה) | |
|
|
שאלה ואם יאמרו לך עשרה חלקנום לשני חלקים וחלקנו כל אחד מהם על האחר וגרענו האחד מן האחר ונשאר חמשה שישיות מאדרהם |
| והמעשה בזה שנשים החלק האחד דבר והאחר עשרה פחות
דבר ותכה דבר על עצמו ויהיה אלגוש ותכה עשרה פחות דבר על עצמו ויהיה מאה אהדר"מיש ואלגוש פחות עשרים דברים ותגרע האחד מן האחחר וישאר מאה אדרה"מיש פחות עשרים דברי' ותכה (אל) חלק האחד על האחר והוא דבר על עשרה פחות דבר ויהיה עשרה (דברים) פחות אלגוש ותכם על מה שנשאר מהשנים חלקים אחחר שגרענו חלק האחד מן האחר ויהיה חמשה שישיות אדרה"ם ויהיה שמנה דברי' ושליש פחות חמש' ששיות מאלגוש ויהיה עשרים ושמנה (דברי') ישוו מאה אדרה"מיש פחות עשרים שרשים ותאסוף המאה אדרה"מיש עם (העשרים) (ה)שרשים ותוסיפם על שמנה דברי' ושליש פחות חמשה שלישיות מאלגוש ויהיה עשרים ושמנה דברי' ושליש פחות חמשה שישיות מאלגוש ישוו מאה אדרה"מיש ותאסוף הדברי' עם חמשה שישיות מאלגו ותוסיפם על המאה אדרהמיש ויהיה מאה אדרהמיש וחמשה שישיות מאלגוש ישוו עשרים ושמנה דברי' ושליש ותשלים החמשה שישיות מאלגוש עד שיהיה אלגוש שלם והוא נרמול: שתוסיף עליהם (אחד ו)חמישיתם ותוסיף על כל דבר שתחזיק כמו (אחד ו)חמישיתו ויהיה אלגוש ומאה ועשרי' אדרה"מיש ישוו שלשי' וארבע דברים וקח מחצית השרשים והוא שבע עשרה ותכם על עצמם ותגרע מהעולה מאה ועשרים אדרה"מיש וישאר קס"ט ותקח שורשו והוא י"ג ותגרעם ממחצית הדברי' והם שבע עשר וישארו ארבעה והם החלק האחד מהשני חלקים והאחר הוא ש ששה ועלת זאת השאלה דומה לעלת השאלה שלפניה וההבדל בין שניהם הוא כי בשאלה הראשנה הוצרך לדעת הפכה לכל שני מספרים שיחלק כל אחד מהם על האחר שהכאת המגיע לחלקים כל אחד על עצמו מקובצים יהיה כמו כמו הכאת האחד מהם על האחר ועל מה שעלה לחלק מחלוקת כל אחד מהשני מספרי' על האחד וכבר ביארתי סבת זה ובשאלה הזאת נצטרך לדעת הסיבה לכל שני מספרי' שיוכה כל אחד משניהם על עצמו ונגרע האחד מן האחר ועל העודף אשר יעדיף בו בין אשר עלה לחלק מחלוקת כל אחד מהשני מספרי' על האחר ותוסיף עליה השאלה הר הראשנה ותצא עילת זאת השאלה יען שהיא דומה אליה והשלשה אופני' מהשאלה הראשנה תעשה גם כן בזאת השאלה | |
| שאלה ואם יאמרו לך חלקנו חמישים אדרה"מיש על אנשים ועלה לאחד דבר והוספנו על האנשים עוד שלשה וחלקנו עליהם החמישים אדרהמיש ועלה כל אחד מהאחרוני' פחות מאשר עלה לכל אחד מהראשונים שלשה אדרה"מיש ושלשה רביעית | |
| והמעשה בזה שתכה האנשי'
הראשוני' בשעור הגרעון אשר בין מה שעלה לכל אחד מהראשוני' ובין האחרוני' ומה שיעלה מן ההכאה (תחלוק) על מה שהעדיף מן האנשי' הראשוני' לשניי' ומה שיעלה לחלק תכה אותו על האנשי' השניים ומה שיעלה הוא המחלק ואשים לך עילת זה האופן והוא שנשים המספר המחולק והוא חמישי' אדרה"מיש שטח א"בג"ד והאנשים הראשוני' קו ג"ד ויעלה לכל אחד מהאנשים הראשוני' קו א"ג בעבור כי הכאת קו א"ג בקו ג"ד הוא שטח ג"ב וכאשרשר חלקנו שטח אב"ג"ד על ג"ד שהוא האנשים הראשוני' עלה לכל אחד מהם קו א"ג ותוסיף על האנשים הר הראשוני' והוא קו גד שלשה אנשים והוא קו דה ויהיה קו ג"ה האנשים הראשוני' ותשים ג"ז ה"ח חמשים ותחלקיהו על קו ג"ה שהוא האנשים הראשוני' ויעלה על קו גד והוא מה שיעלה לכל אחד מהאנשים השניים וקו א"ז יהיה שלשה ושלשה רביעי' בעבור כי הוא השיעור אשר בין מה שעלה לאחד מהראשונים ובין מה שעלה לאחד מהשניים ותכה האנשי' הראשוני' והם קו ז"מ כי הוא כמו ד"ג על קו א"ז שהוא היתרון בין מה שעלה לכל אחד מהראשוני' ובין כל אחד מהשניי' ויהיה שטח ב"ז ושטח ב"ו כמו שטח ד"ז בעבור כי שטח א"ד הוא כמו שטח ג"ח כי כל אחד משניהם חמישים ושטח ג"מ משותף ויש וישאר שטח ז" כמו שטח ד"ח וחלק שטח דח על קו ד"ה שהוא שלשה ושיעורו הוא ההבדל אשר בין האנשים הרא הראשוני' לשניי' ויעלה לחלק קו ר"מ והוא כמו קו ג"ז והוא מה שעלה לכל אחד מהראשוני' ויהיה שטח ג והוא חמישי' ומשל ואחר שזה מ ב א מבואר יתבאר העולה באופן זה שאנחנו נשים האנשים הראשו' ח מ ד דבר ותכהו על הגרעון שהוא שלש ושלשה רביעיות ויעלה שלשה דברים ושלשה רביעים ותחלקם על שלשה שהוא שיעור ההבדל אשר בין האנשים הראשונים ה ד ג לשניים ועלה לחלק דבר ורבוע ותכם על האנשים השניי' והם דבר ושליש ויהיה אלגוש ורביע ושלשה דברי' ושליש רביעיות דבר ישוו חמישים אדרה"מיש ותשיב כל דבר שתחזיק אל אלגוש אחד ויהיה אלגוש ושלש דברי' ישוו ארבעי' אדרה"מיש וקח מחצית הדברי' והוא אחד וחצי ותכם על עצמם ותוסיף העולה על הארבעי' ויהיה מ"ב ורביע וקח שרשו והוא ששה וחצי וג וגרע מהם הדברי' שהוא אחד וחצי וישאר חמשה והם האנשים הראשוני' | |
| ואם יאמרו לך חלקנו עשרה אדרהמיש על אנשים ועלה לכל אחד מהם דבר והוספנו עליהם ארבע אנשים וחלקנו על כלם שלשים אדרהמיש ועלה לכל אחד מהם פחות מאשר עלה לראשוני' ארבעה אדרהמיש | |
| והמעש' בזה שתכה האנשי' הראשוני' על הגרעון אשר בין הראשון והא
והאחרון ותוסיף על העולה מההכאה שעור ההבדל אשר בין המספר הנחלק ראשנה ובין השנייה ומה שיתקבץ חלק על ההבדל אשר בין האנשי' ההראשוני' וההשניי' והעולה תכה על האנשים השנייה ומה שיעלה הוא המספר הגדול ש שנחלק והוא בזאת השאלה שלשים ואשים לך על זה האופן והוא שנשים המספר הקטן הנחלק שהוא עשרה שטח א"ב ג"ד והאנשי' הראשוני' קו ג"ד ומה שעלה לאחד מן הראשוני' קו א"ג והוספנו על הראשוני' שהוא קו ג"ד ארבע' אנשים והוא קו ד"ה ויהיה קו ג"ה האנשי' השניי' ונשים שטח ג"ה ז"ח שלשים אדרה"מיש ותחלקיהו על קו ג"ה ויעלה קו ג"ז והוא מה שיעלה לאחד מהשניי' וישאר קו א"ז ארבע בעבור כי הוא שיעור ההבדל אשר בין מה שעלה לאחד מן הרא הראשוני' ובין אחד מהשניים ותכה האנשי' הראשונים והם קו ז"א השוה לקו ג"ד על קו ז"א ויהיה שטח ז"ב ב א ותוסיף על שטח ז"ב שיעור ההבדל אשר בין הש השלישית והעשרה והוא עשרים ויהיה ח מ ז שטח ד"ח והיה שטח ד"ח יותר משטח ז"ב בעשרים והוא יתרון השני מספרי' הנחלקים בעבור כי שטח א"ז ושטח ה ד ג גח שלישית ויהיה שטח ג"ח יותר משטח מ"א בעשרים ותגרע שטח ג"מ המשותף וישאר שטח ד"ח יותר גדול משטח ז"ב בעשרים ותחלק שטח ד"ח על קו ד"ה שהוא ארבעה ויעלה לחלק קו ר"מ ר"מ והוא כמו קו ג' והוא כמו מה שיעלה לאחד מהשנים ותכה קו ג"ז על קו ג"ה ויהיה שטח ג"ח והוא שלישית אדרהמיש ומש"ל ואחר שבארנו עילת זה האופן נשים האנשים הראשוני' דבר ותכה על ארבעה אדרהמיש שהוא מה שיגרע חלק השניים מחלק הראשוני' ויהיה ארבעה דברים ותוסיף עליהם עשרים אדרהמיש ותחלקם על יתרון ההבדל אשר בין האנשים הארשוני' לשניים והוא ארבעה ויגיע לחלק דבר וחמשה ותכם על האנששים השניים והם דבר וארבעה ויהיה אלגוש ותשעה דברים ועשרים יהיה המספר הגדול הנחלק והוא שלישית ותגרע העשרים מהשלשים וישאר אלגוש ותשעה דברי' ישוו עשרה יקח מחצית הדברי' ויהיו ארבעה וחצי ותכה על עצמם ויהיה עשרי' ורביע תוסיף עליהם העשרה אדרהמיש ויהיו שלשים ורביע תקח שורשו וה והוא חמשה וחצי תגרע מההם מחצית השרשים והוא אר ארבעה וחצי וישאר אחד והוא היה האנשים הראשונים | |
| ואם יאמרו לך חלקנו עשרה אדרהמיש על אנשים ועלה לכל אחד דבר והוספנו עליהם ארבעה אנשים וחלקנו עליהם ששים אדרה"מיש ועלה לאחד יותר ממה שעלה לאחד מן הראשונים חמשה אדרהמיש | |
| המעשה בזה שתכה הא
האנשים השניים על ההבדל אשר בין חלק האחד מן השנייה אל חלק אחד מהראשונים ותוסיף על העולה המספר הנחלק הקטן והמקובץ תגרע מהמספר הנחלק הגדול ומה שישאר תחלקיהו על יתרון האנשים הראשוני' והמגיע הוא הוא המספר הנחלק הקטן ואשים עילת זה האופן והוא שאשים המספר הנחלק הקטן שהוא עשרה שטח א"בג"ד והאנשי' הראשוני' קו ג"ד והוספנו על האנשים הראשוני' ארבעה אנשי' והם קו ד"ה ויהיה נ מ ויהיה קו ג"ה האנשים השניים ונניח שנים גה מל ששים ותחלקם על קו ג"ה שהוא האנשים השניי' ויעלה קו ג"ל והוא מה שיעלה לחלק לאנשים האחרוני' א ב ע ויהיה קו א"ל חמשה בעבור כי הוא יתרון החלק מאחד מהשניי' על חלק מאחד מהראשוני' ותכה ג ד ה האנשים השניים והם קו א"ע השוה לקו ג"ה על קו א"ל שהוא העודף ויהיה שטח א"ח ותוסיף עליו שטח ג"ב שהוא המספר הנחלק הקטן שהוא עשרה ומה שיתקבץ תגרעהו משטח ג"מ שהוא השטח הנחלק הגדול והוא ששים וישאר שטח ד"ע תחלקיהו על קו ב"ה שהוא ארבעה והוא יתרון האנשים השניים על הראשונים ויעלה קו ד"ב והוא שוה לקו א"ג וזהו החלק שהגיע לאחד מהראשוני' ותכהו על קו ג"ד שהוא האנשי' הראשוני' ויהיה שטח ג"ב עשרה ומש"ל ואחר שבארנו עלת זה האופן נשים האנשים השניים דבר וארבעה תכם על השיעור אשר בין החלק מאחד מהשניי' לראשוני' והוא חמשה ויעלה חמשה דברי' ועשרי' אדרה"מיש תוסיף עליה המספר הנחלק הקטן והוא עשרה ויקובץ חמשה דברי' ושלשים אדרה"מיש ותגרעם מהמספר הנחלק הגדול הוא ששי' אדרהמיש וישאר שלשי' אדרה"מיש פחות חמשה דברי' ותחלקם על יתרון האנשים השניי' על הראשוני' והוא ארבעה ויגיע לחלק שבעה וחצי פחות דבר ורביעיתם על האנשים הראשונים והם דבר ויהיה שבעה דברים פחות אלגוש ורביע ישוו המספר הנחלק הקטן והוא עשר' והשיב כל דבר שתחזיק אל אלגוש אחד ויהיה ששה דברי' פחות אלגוש ישוה שמנה ותשלים הדברי' עם האלגוש ותוסיפם על השמנה ויהיה אלגוש ושמנה ישוה ששה דברי' וקח מחצית הדברי' והוא שלשה ותכהו על עצמו ויהיה תשעה תגרע מהם השמנה שהם שלשה וישאר שנים והם האנשים הראשוני' ואם תרצה תוסיף האחד על מחצית השרשים ויקובץ ארבעה והם האנשים האחרוני' | |
| ואם יאמרו לך חלקנו ששי' אדרהמיש ועלה לאחד דבר והוספנו עליהם שלשה אנשים וחלקנו עליה' עשרים אדרהמיש ועלה לאחד פחות מאשר עלה לאחד מהראשונים עשרים וששה אדרה"מיש | |
| והמעשה בזה שנכה האנשי' הראשונים
בפחת החלק מהשניים שהוא כ"ו והעולה תגרע מהעודף משני מס מספרים הנחלקים שהוא ארבעים והנשאר תחלק על יתרון האנשים שהוא שלשה והמגיע תככה על האנשים השניים ומה שיעלה הוא ה המספר הנחלק הקטן ואשים עילת זה האופן והוא שנשים המספר הנחלק הגדול שהוא ששים אדרה"מיש שטח א"בג"ד והאנשים הראשוני' קו גד ומה שעלה לאחד מן הראשונים קו א"ג והוספנו על האנשים הראשונים שהוא קו גד שלשים אנשים והוא קו ד"ה ויהיה קו ג"ה שהוא האנשים השניים ונשים שטח ג"ה ח"ז עשרים וחלקם על קו ג"ה שהוא האנשים השניים ויהיה קו אז עשרים ושש בעבור א כי הוא יתרון החלק האחד על האחר ותכה האנשי' הרא הראשוני' והם קו ז"מ בקו א"ז ויהיה שטח י"ב תגרע ממנו יתרון שני המספרים הנחלקים שהוא ארבעים וישאר שטח ד"ח והוא ידוע כי שטח ז"ב הוא גדול משטח ד"ח בארבעים בעבור כי שטח א"ד הוא ששים ושטח ג"ח הוא עשרים והוא יעדיף בארבעים ותגרע שטח ז"ד ד מ ח המשותף וישאר שטח ז"ב יעדיף על שטח ד"ח בארבעים תחלקיהו על קו ד"ה שהוא שלשה ויעלה קו ד"מ השוה לקו ג"ז והוא המגיע לאחד מהאנשים האחרוני' ותכה קו ג"ו על גה שהוא האנשים השניי' ויהיה ג"ה שהוא המספר הנחלק הקטן שהוא עשרים ואחר שביארנו עילת זה האופן נניח האנשי' הראשוני' דבר ותכה אותו על גרעון חלק אחד שני מחלק האחד ראשון שהוא כ"ו אדרהמי ויהיה כ"ו דברים תגרע מהם יתרון שני המספרים הנחלקים והוא ארבעים וישאר כ"ו דברים פחות ארבעים אדרהמיש ותחלקם על יתרון האנשים שהוא שלשה ויעלה שמנה דברים ושני שלישי' פחות י"ג אדרהמיש ושליש ותכם על האנשים השניים והם דבר ושלשה ויהיה שמנה אלגוש ושני שלישי ושנים עשר דברים ושני שלישי דבר פחות ארבעים אדרהמיש ישוה המספר הנחלק הקטן והוא עשרים ותאספם עם הארבעים אדרה"מיש ותוסיפם על העשרי' אדרה"מיש ויהיו שמנה אלגוש ושני שלישי אלגוש וי"ב דברי' ושני שלישי דבר ישוו ששי' אדרה"מיש והשיב כל דבר שתחזיק לאלגוש אחד וכבר ידעת שהאלגוש משמנה אלגוש ושני שלישים אלגוש הוא שלשה חלקים מעשרים וששה חלקי' מאחד וקח מכל דבר שתחזיק שלשה דברי' מכ"ו חלקים ויהיה אלגוש ודבר וי"ב חלקים מכ"ו חלקים ישוה ששה וכ"ד חלקים מכ"ו חלקים מאדרהם ומחצית הדברים יהיה תשע עשרה חלקים מכ"ו חלקים בדבר ישוה ששה וכ"ד חלקים ותכם על עצמם ויהיה שלשה עשר חלקים מכ"ו חלקים מתרע"ו חלקים מאחד ותוסיפם על האדרה"מיש והם ששה וכ"ד חלקים מכ"ו יהיה שבעה וי"א חלקים מכ"ו וי"ג חלקים מתרע"ו וקח שרשו והוא שני אדרהמיש ויש חלקים מכ"ו וישאר שנים והם האנשים הראשונים | |
| ולאלה הארבעה שאלות ודומיהן יש שני אופני' והם דומים
לאופנים שונים אשר הראיתיך בחשבון האומר בו חלקנו עשרה לשני חלקים וחלקנו אחד מהם על האחר ועל הארבע ורביע והנה אראך אחד מהם למען תתלמד בו לאחרים והוא כי כאשר יאמרו לך עשרים אדרהמיש חלקנום על אנשים והגיע לכל אחד מהם דבר והוספנו עליהם שנים אנשים וחלקנו עליכם ששים אדרהמי"ש ועלה לאחד מהם יותר מאשר עלה לאחד מהראשונים בחמשה אדרהמיש והמעשהו שנשים האנשים הראשוני' דבר וחלק עליהם עשרים אדרהמי"ש ונוסיף על האנשים הראשונים שהם דבר שנים ויהיו דבר שנים הם האנשים האחרונים ותחלק ש ששים אדרהמי"ש על דבר ושנים הם האנשים האחרונים ותחלק על דבר ושנים יהיה שישים אדרהמיש והכאת דינר וחמשה על דבר ושנים יהיה ששים אדרהמיש והכאת ויגיע דינר ואחדחמשה עליהם דבר ושנים וכאשר תכה דינר וחמשה על דבר ושנים יהיה שלשים אדרהמיש וחמשה דברי' ודינר אחד ישוו ששים אדרהמיש ותגרע שלשים אדרהמיש וחמשה דברים מששים וישאר שלשים אדרהמיש פחות חמשה דברים ישוו שני דינרין והדינר ישוה ט"ו אדרהמי"ש פחות שני דברי' וחצי ותשוב אל השאלה הראשנה ותאמר תחלק עשרים אדרהמי"ש על דבר ויהיה ט"ו אדרהמיש פחו פחות שני דברי' וחצי ויהיה ט"ו דברי' פחות שני אלגוש וחצי ישוו עשרים אדרהמי"ש תשיב כל דבר שתחזיק אל אלגוש אחד וכבר ידעת ששני אלגוש משני אלגוש וחצי חמשה ותקח לכל דבר שתחזי' חמשה ויהיה ששה פחות אלגוש ישוה שמנה אדרהמיש ותאסוף הששה פחות אלגוש עם האלגוש ותוסיפיהו על השמונה אדרהמיש ויהיה אלגוש ושמנה אדרהמי"ש ישוה ששה דברים וקח מחצית הדברים והוא שלשה תכם על עצמם ויהיה תשעה תגרע מהם השמנה וישאר אחד תקח שורשו והוא אחד תגרעיהו ממחצית הדברים שהוא שלשה ושיאר שנים וההם האנשים הראשונים ואם תרצה תוסיף האחד על מחצית השרשים שהוא שלשה ויהיו ארבע והם האנשים השניים והבן זה | |
| ואם יאמרו לך חלקנו עשרה אדרהמי"ש על ענשים והגיע לאחד דבר והוספנו עליה' ששה אנשים וחלקנו בין כולם ארבעים אדרהמי"ש והגיע לאחד מהם כמו שהגיע לאחר מהראשוני' בשוה | |
| ומעשיהו שתכה המספר הנחלק הקטן על יתרון האנשים השניים על הראשונים
והעולה מההכאה תחלק על יתרון שני המספרי' הנחלקים ומה שיעלה הם האנשים הראשוני' ותכה המספר הנחלק הקטן והוא עשרה על יתרון האנשים שהוא ששה ויהיה ששים ותחלק ששים על יתרון שני המספרים הנחלקים שהוא שלשים ויעלה שנים והם האנשים הראשונים והוא ששה ויגיע לחלק חמשה תחלק עליהם המספר הנחלק הקטן שהוא עשרה ויגיע שנים והם האנשים הראש הראשונים וכבר הוא מבואר עלת זאת השאלה | |
| ולזאת השאלה פנים אחרים והוא שיחחס מספר האנשים הראשונים אל
האנשים השניים וכבר ידעת שחלק אחד מהראשוני' הוא עשרה וחלק אחד מהשניים הוא ארבעים ושיעור עשרה אצל ארבעים הוא הרביע והאנשים הראשוני' הם הרביע מהאנשי' השניים ותשים מהאנשי' הראשוני' דבר והאנשים השניים דבר וששה וכבר ידעת כי הרביע מדבר וששה הוא דבר ולכן תקח הרביע מדבר וששה ויהיה אדרהם וחצי ורביע דבר ישוה דבר ותגרע רביע דבר מדבר וישאר שלשה רביעי דבר דבר ישוו אחד וחצי והדבר שנים והם האנשים הראשונים | |
| ואם יאמרו לך עשרה בגדים קנום בין שני אנשים בשכר שבעים ושנים אדרהמי"ש וכל אחד לחלק בעצמו והיה שלשי' הנה שורש שלשי' הוא מה מה שעלה לחלק מהשני חלקי' | |
| וכאשר תרצה לדעת שיעור כל חלק מהשני חלקי' תעשה כמו שאמרנו והוא שנאמר שהחלק האחד חמשה ודבר והאחר חמשה פחות דבר
ותכה האחד באחד ויהיה כ"ה אדרהמי פחות אלגוש ותכה האחד באחד ויהיה כ"ה אדרהמי פחות אלגוש ותכה זה בשורש שלישי וכאשר תרצה זה תכה עשרים וחמשה אדרהמי פחות אלגוש בעצמו ויהיה תרכ"ה דרהמי ואלגוש אלגו פחות פחות חמישי' אלגוש ותכה זה בשלשי' אלגוש מאלגו וט"ו אלפי' ותש"נ אדרהמי פחות 1400 אלגוש ושורש זה ישוה מאה אדרהמיש ותכה מאה דרהמי' בעצמו ויהיה 10000 דרהמי ישוו שלשים אלגוש מאלגו וי"ח אלפים ותש"נ אדרהמי פחות 1900 אלגוש ותאסוף אוקבראשיש איקונפרונטאראש ותוסיף על כל דבר שתחזיק אלגוש אלגו ויהיה אלגו אלגו ורע"א אדרהמי ושני שלישית ישוה חמישי' אלגוש ותחצה האלגוש ויהיה כ"ה תכם בעצמם ויהיו תרכ"ה תגרע מהם הרע"א אדרהמ ושני שלישי' והנשאר שלישי' וש"ג ושליש ושרש זה כשיגרע מכ"ה ושרש הנשאר יתוסף על חמשה והוא החלק האחד וכשיגרע מחמשה הוא החלק האחר | |
| ואם יאמרו לך חלקנו עשרה לשני חלקי' וחלקת על כל אחד מהם ארבעי' ומה שעלו לחלק הכית כל חלק על עצמו והיו תרכ"ה | |
| וכאשר תחלק העשרה על כל חלק משני חלקי העשרה והעולה לחלק הכית כל חלק זה צריך שיהיה חצי שמינית מתרכ"ה והוא ל"ט וחצי שמינית בעבור כי עשרה עלה רביעית מ' וכאשר נכה רביע הדבר בעצמו יהיה חצי שמינית הדבר מוכה בעצמו וכבר ביארנו המעשה בזה | |
| וכאשר תרצה תוציא אילו השאלות [מ]שאלות אחרות רבות כפי אילו הדרכים וכפי אחרים כמו הם יתבאר המעשה בהם מהדרכים שאמרנו קודם ושהוספנו בזה הספר | |
| והתהילה לאל לבדו ית' וית' היכול אשר מאתו ההישרה |
Appendix: Bibliography
Kitāb fī al-Jābr wa'l-Muqābala (the first section) / by Abū Kāmil Shujāʽ Ibn Aslam Ibn Muḥammad ibn Shujāʽ (Egypt, ca. 850-930)
– Hebrew translation –
by Mordecai (Angelo) Finzi (Mantua, d. 1475)
Ḥeshbon ha-Sheṭaḥim (First Hebrew version)
Manuscripts:
- 1) Mantova, Comunita Israelitica MS ebr. 17/1 (IMHM: f 797), ff. 1r-44v (15th century; autograph)
- 2) München, Bayerische Staatsbibliothek, Cod. hebr. 225/2 (IMHM: f 1118), ff. 95r-154r (15th century)
Critical Edition (of the first section):
- Abu Kamil Shuja' ibn Aslam. The algebra of Abu Kamil: Kitab fi al-jabr wa'l-muqabala in a commentary by Mordecai Finzi. Ed. Martin Levey. Madison, Milwaukee, and London: The University of Wisconsin Press, 1966.
Bibliography:
- Lévy, Tony. 2007. L’algèbre arabe dans les textes hébraïques (II). Dans l’Italie des XVe et XVIe siècles, sources arabes et sources vernaculaires, Arabic Sciences and Philosophy 17, pp. 81-107.
- Yadegari, Mohammad. 1978. The Use of Mathematical Induction by Abū Kāmil Shujā‘ Ibn Aslam (850-930), Isis, vol. 69, no. 2 (Jun., 1978), pp. 259-262.
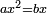
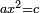
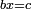
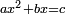
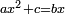
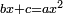
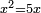
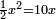
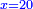
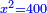
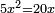

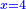
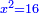
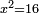
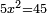
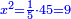
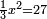
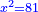
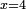
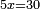
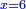
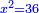
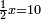

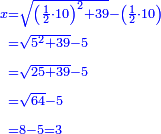
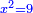
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle x^2&\scriptstyle=\left[\left(\frac{1}{2}\sdot10^2\right)+39\right]-\sqrt{\left(10^2\sdot39\right)+\left(\frac{1}{2}\sdot10^2\right)^2}\\&\scriptstyle=\left[\left(\frac{1}{2}\sdot100\right)+39\right]-\sqrt{\left(100\sdot39\right)+\left(\frac{1}{2}\sdot100\right)^2}\\&\scriptstyle=\left(50+39\right)-\sqrt{3900+50^2}\\&\scriptstyle=89-\sqrt{3900+2500}\\&\scriptstyle=89-\sqrt{6400}\\&\scriptstyle=89-80=9\\\end{align}}}](/mediawiki/images/math/a/a/9/aa93b426cdc117aedb59548f3a8f95b7.png)