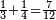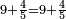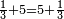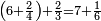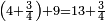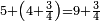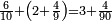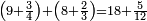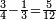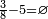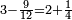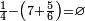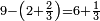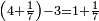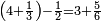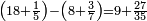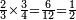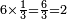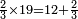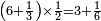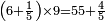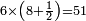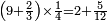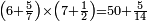Difference between revisions of "חשבון של שברים"

From mispar
Jump to: navigation, search
(→‎Appendix: Bibliography)
 
(69 intermediate revisions by the same user not shown)
Line 1: Line 1:
 +
{{#annotpage: time="1500-1600", peshat_title="00002052"}}
 
{|
 
{|
 
|-
 
|-
Line 67: Line 68:
 
|-
 
|-
 
|
 
|
−
|style="text-align:right;"|אבל אם תמצא ב' אותיות אלפין זו על גב זו ולא תמצא העברת קולמוס בנתיים אז הוא מרמז על שלימים
+
|style="text-align:right;"|אבל אם תמצא ב' <s>אותיות</s> אלפין זו על גב זו ולא תמצא העברת קולמוס בנתיים אז הוא מרמז על שלימים
 
|-
 
|-
 
|
 
|
 
|style="text-align:right;"|כזה ר"ל אחד שלם ול"ד  
 
|style="text-align:right;"|כזה ר"ל אחד שלם ול"ד  
 +
|-
 +
|}
 +
{|
 +
|-
 +
|
 +
== Addition of Fractions ==
 +
 +
|style="text-align:right;"|והא לך <s>לכפול</s> לחבר שברים בשברי'
 +
|-
 +
|Eight types
 +
|style="text-align:right;"|&#x202B;[ב]&#x202B;ח' עניינים
 +
|-
 +
|
 +
*<math>\scriptstyle\frac{1}{3}+\frac{1}{4}=\frac{7}{12}</math>
 +
|
 +
{|style="margin-left: auto; margin-right: 0px; text-align:center;"
 +
|-
 +
|<u>ז</u>||&nbsp;||rowspan="2"|ותמצא||<u>א</u>||&nbsp;||rowspan="2"|עם||<u>א</u>||&nbsp;
 +
|-
 +
|בא||&nbsp;||ד||&nbsp;||ג||&nbsp;
 +
|-
 +
|}
 +
|-
 +
|
 +
*<math>\scriptstyle9+\frac{4}{5}=9+\frac{4}{5}</math>
 +
|
 +
{|style="margin-left: auto; margin-right: 0px; text-align:center;"
 +
|-
 +
|<u>ד</u>||rowspan="2"|ט||rowspan="2"|ותמצא||<u>ד</u>||&nbsp;||rowspan="2"|עם||rowspan="2"|ט||&nbsp;
 +
|-
 +
|ה||ה||&nbsp;||&nbsp;
 +
|-
 +
|}
 +
|-
 +
|
 +
*<math>\scriptstyle\frac{1}{3}+5=5+\frac{1}{3}</math>
 +
|
 +
{|style="margin-left: auto; margin-right: 0px; text-align:center;"
 +
|-
 +
|<u>א</u>||rowspan="2"|ה||rowspan="2"|ותמצא||&nbsp;||rowspan="2"|ה||rowspan="2"|עם||<u>א</u>||&nbsp;
 +
|-
 +
|ג||&nbsp;||ג||&nbsp;
 +
|-
 +
|}
 +
|-
 +
|
 +
*<math>\scriptstyle\left(6+\frac{2}{4}\right)+\frac{2}{3}=7+\frac{1}{6}</math>
 +
|
 +
{|style="margin-left: auto; margin-right: 0px; text-align:center;"
 +
|-
 +
|<u>א</u>||rowspan="2"|ז||rowspan="2"|ותמצא||<u>ב</u>||&nbsp;||rowspan="2"|עם||<u>ב</u>||rowspan="2"|ו
 +
|-
 +
|ו||ג||&nbsp;||ד
 +
|-
 +
|}
 +
|-
 +
|
 +
*<math>\scriptstyle\left(4+\frac{3}{4}\right)+9=13+\frac{3}{4}</math>
 +
|
 +
{|style="margin-left: auto; margin-right: 0px; text-align:center;"
 +
|-
 +
|<u>ג</u>||rowspan="2"|גא||rowspan="2"|ותמצא||&nbsp;||rowspan="2"|ט||rowspan="2"|עם||<u>ג</u>||rowspan="2"|ד
 +
|-
 +
|ד||&nbsp;||ד
 +
|-
 +
|}
 +
|-
 +
|
 +
*<math>\scriptstyle5+\left(4+\frac{3}{4}\right)=9+\frac{3}{4}</math>
 +
|
 +
{|style="margin-left: auto; margin-right: 0px; text-align:center;"
 +
|-
 +
|<u>ג</u>||rowspan="2"|ט||rowspan="2"|ותמצא||<u>ג</u>||rowspan="2"|ד||rowspan="2"|עם||&nbsp;||rowspan="2"|ה
 +
|-
 +
|ד||ד||&nbsp;
 +
|-
 +
|}
 +
|-
 +
|
 +
*<math>\scriptstyle\frac{6}{10}+\left(2+\frac{4}{9}\right)=3+\frac{4}{90}</math>
 +
|
 +
{|style="margin-left: auto; margin-right: 0px; text-align:center;"
 +
|-
 +
|<u>ד</u>||rowspan="2"|ג||rowspan="2"|ותמצא||<u>ד</u>||rowspan="2"|ב||rowspan="2"|עם||<u>ו</u>
 +
|-
 +
|&#x202B;0ט||ט||&#x202B;0א||
 +
|-
 +
|}
 +
|-
 +
|
 +
*<math>\scriptstyle\left(9+\frac{3}{4}\right)+\left(8+\frac{2}{3}\right)=18+\frac{5}{12}</math>
 +
|
 +
{|style="margin-left: auto; margin-right: 0px; text-align:center;"
 +
|-
 +
|<u>ה</u>||rowspan="2"|חא||rowspan="2"|ותמצא||<u>ב</u>||rowspan="2"|ח||rowspan="2"|עם||<u>ג</u>||rowspan="2"|ט
 +
|-
 +
|בא||ג||ד
 +
|-
 +
|}
 +
|-
 +
|
 +
|
 +
|-
 +
|
 +
*The first type:
 +
|style="text-align:right;"|והא לך הדומיון אם תרצה לחבר עם יחד
 +
|-
 +
|
 +
|style="text-align:right;"|עשה כאשר אראך איה כפול אותו בשתי וערב ר"ל ב פ' ד דהיינו ח' כתוב ח' לפניך ואחר כך כפול השנית ג"כ בשתי וערב ג פ' ג דהיינו ט' וחבר ט' וח' שמצאת ותמצא ז"א כתוב אותו למעלה ואחר כך כפול הַב' אותיות התחתונות כגון ג פ' ד דהיינו ב"א כתוב תחת ז"א כזה דהיינו ז"א חלקים שתגיעו ב"א לשלם חסור ב"א ממנו דהיינו שלם וכתוב בצדו וישאר לך [ ] חלקים שמגיעי' ב"א לשלם כזה [ ]
 +
|-
 +
|
 +
*The second and third types - no need to elaborate
 +
|style="text-align:right;"|השער השני והשער השלישי אין [צריך] לכתוב
 +
|-
 +
|
 +
*The fourth type - the fractions are summed as in the first type, then the integers are summed together
 +
|style="text-align:right;"|השער הרביעי <s>עש</s> דהיינו ו שלימים עם עשה השברים בכפל שתי וערב כדלעיל ואחר כך חיבר השלימים יחד ותמצא מכוון
 +
|-
 +
|
 +
*The fifth and the sixth types - the integers are summed together, then the fractions are added
 +
|style="text-align:right;"|השער החמישי והשישי כפול השלימים יחד ואחר כך עשה השברים ג"כ להמניין
 +
|-
 +
|
 +
*The seventh type - as in the fourth type
 +
|style="text-align:right;"|השער השביעי חשוב כאשר הראתיך לעיל בשער הרביעי
 +
|-
 +
|
 +
*The eighth type - the integers are summed together, then the fractions are summed together, as in the first type
 +
|style="text-align:right;"|השער השמיני דהיינו עם חבור <s>כפול</s> השלימים בחיבור <s>בכפל</s> ותמצא זא ואחר כך כפול השברים כמו שעשית בראשונה ותמצא חא שלימים
 +
|-
 +
|A sum of three fractions
 +
|style="text-align:right;"|אבל כשתמצא ג' פ' שברים בשברים בבת אחת כגון א"ת לחבר
 +
|-
 +
|
 +
:Two of the fractions are summed together as in the first type, then the third fraction is added to the resulted sum
 +
|style="text-align:right;"|חשוב ב' שברים בשברים הראשונים והה' האחרונים כמו שהראתיך בראשונה ואחר כך חבר השלישי ג"כ לזה כגון א"ת לחשוב דומיון שלמעלה חשוב ב' הראשונות דהיינו בשתי וערב ותמצא ואחר כך תרצה לחבר עם כפול אותו בשתי וערב ותמצא ובזה תמצא ב שלימים או ומכוון
 +
|-
 +
|}
 +
{|
 +
|-
 +
|
 +
 +
== Subtraction of Fractions ==
 +
 +
|style="text-align:right;"|[והא לך לחסר שברים] משברים
 +
|-
 +
|Eight types
 +
|style="text-align:right;"|בח' עניינים
 +
|-
 +
|
 +
*<math>\scriptstyle\frac{3}{4}-\frac{1}{3}=\frac{5}{12}</math>
 +
|
 +
{|style="margin-left: auto; margin-right: 0px; text-align:center;"
 +
|-
 +
|<u>ה</u>||&nbsp;||rowspan="2"|ותשאר||<u>ג</u>||&nbsp;||rowspan="2"|מן||<u>א</u>||&nbsp;
 +
|-
 +
|בא||&nbsp;||ד||&nbsp;||ג||&nbsp;
 +
|-
 +
|}
 +
|-
 +
|
 +
*<math>\scriptstyle\frac{3}{8}-5=\varnothing</math>
 +
|
 +
{|style="margin-left: auto; margin-right: 0px; text-align:center;"
 +
|-
 +
|rowspan="2"|&nbsp;||rowspan="2"|אי אפשר <s>נמנה ולא תוכל לחסר ממנו</s>||<u>ג</u>||&nbsp;||rowspan="2"|מן||rowspan="2"|ה||&nbsp;
 +
|-
 +
|ח||&nbsp;||&nbsp;
 +
|-
 +
|}
 +
|-
 +
|
 +
*<math>\scriptstyle3-\frac{9}{12}=2+\frac{1}{4}</math>
 +
|
 +
{|style="margin-left: auto; margin-right: 0px; text-align:center;"
 +
|-
 +
|<u>א</u>||rowspan="2"|ב||rowspan="2"|ותשאר לך||&nbsp;||rowspan="2"|ג||rowspan="2"|מן||<u>ט</u>||&nbsp;
 +
|-
 +
|ד||&nbsp;||בא||&nbsp;
 +
|-
 +
|}
 +
|-
 +
|
 +
*<math>\scriptstyle\frac{1}{4}-\left(7+\frac{5}{6}\right)=\varnothing</math>
 +
|
 +
{|style="margin-left: auto; margin-right: 0px; text-align:center;"
 +
|-
 +
|rowspan="2"|&nbsp;||rowspan="2"|ג"כ לא תוכל לחסר ממנו||<u>א</u>||rowspan="2"|&nbsp;||rowspan="2"|מן||<u>ה</u>||rowspan="2"|ז
 +
|-
 +
|ד||ו
 +
|-
 +
|}
 +
|-
 +
|
 +
*<math>\scriptstyle9-\left(2+\frac{2}{3}\right)=6+\frac{1}{3}</math>
 +
|
 +
{|style="margin-left: auto; margin-right: 0px; text-align:center;"
 +
|-
 +
|<u>א</u>||rowspan="2"|ו||rowspan="2"|ותשאר לך||&nbsp;||rowspan="2"|ט||rowspan="2"|מן||<u>ב</u>||rowspan="2"|ב
 +
|-
 +
|ג||&nbsp;||ג
 +
|-
 +
|}
 +
|-
 +
|
 +
*<math>\scriptstyle\left(4+\frac{1}{7}\right)-3=1+\frac{1}{7}</math>
 +
|
 +
{|style="margin-left: auto; margin-right: 0px; text-align:center;"
 +
|-
 +
|<u>א</u>||rowspan="2"|א||rowspan="2"|ותשאר לך||<u>א</u>||rowspan="2"|ד||rowspan="2"|מן||&nbsp;||rowspan="2"|ג
 +
|-
 +
|ז||ז||&nbsp;
 +
|-
 +
|}
 +
|-
 +
|
 +
*<math>\scriptstyle\left(4+\frac{1}{3}\right)-\frac{1}{2}=3+\frac{5}{6}</math>
 +
|
 +
{|style="margin-left: auto; margin-right: 0px; text-align:center;"
 +
|-
 +
|<u>ה</u>||rowspan="2"|ג||rowspan="2"|ותשאר לך||<u>א</u>||rowspan="2"|ד||rowspan="2"|מן||<u>א</u>||&nbsp;
 +
|-
 +
|ו||ג||ב||&nbsp;
 +
|-
 +
|}
 +
|-
 +
|
 +
*<math>\scriptstyle\left(18+\frac{1}{5}\right)-\left(8+\frac{3}{7}\right)=9+\frac{27}{35}</math>
 +
|
 +
{|style="margin-left: auto; margin-right: 0px; text-align:center;"
 +
|-
 +
|<u>זב</u>||rowspan="2"|ט||rowspan="2"|ותשאר לך||<u>א</u>||rowspan="2"|חא||rowspan="2"|מן||<u>ג</u>||rowspan="2"|ח
 +
|-
 +
|הג||ה||ז
 +
|-
 +
|}
 +
|-
 +
|
 +
|style="text-align:right;"|והא לך הדומיון לחסר הח' חשבונות הרשומים למעלה על דרך זו
 +
|-
 +
|
 +
*The first type:
 +
|style="text-align:right;"|ובראשונה אם תרצה לחסר מן לעולם תקח בראשונה האות התחתון שבצד ימין והאות העליון שבצד שמאל בכפל
 +
דהיינו ג פ' ג הרי ט' <s>הט שמצאת כתוב</s> כתוב למעלה לפניך ואחר כך האחרים דהיינו א פ' ד כתוב אות הד' תחת הט' שמצאת [ ] כזה ואחר כך חסור האות התחתונה מהאות העליונה דהיינו ה' מן ט ותשאר ה כתוב <s>אותן</s> לפניך שלא תשכח ואחר כך כפול האותיות התחתונות דהיינו ג פ' ד הרי בא כתוב בא תחת ה' ותמצא מכוון
 +
|-
 +
|
 +
:Note: the line should not be forgotten lest the fractions will be considered as integers
 +
|style="text-align:right;"|והזהר בנפשך שתעבור בקולמוס ביניהם שלא תטעה ותאמר שהן שלימים כזה
 +
|-
 +
|
 +
*The second type - impossible to subtract integers from fractions
 +
|style="text-align:right;"|השנית השלימים מן לא תמצא לחסר ממנו
 +
|-
 +
|
 +
:But it is possible to subtract fractions from integers
 +
|style="text-align:right;"|אלא א"כ תהפוך אותו כגון מן ה' שלמים אז הוא אפשר
 +
|-
 +
|
 +
*The third type - the integer is converted to fractions
 +
|style="text-align:right;"|השלישית לחסר מן ג שלימים אז תשבר השלימים לשברי' <s>לשלישי'</s> כמו שתמצא בחסרון שתרצה לחסר דהיינו כל אחד לשנים עשר חלקי' ותמצא [ <s>מן</s> ] בראשונה חסור מן ותשאר לך דהיינו או או וד"ל
 +
|-
 +
|
 +
*The fourth type - impossible
 +
|style="text-align:right;"|הרביעית אי אפשר
 +
|-
 +
|
 +
*The fifth type - the fraction is subtracted from one unit taken from the integer, then the integer is subtracted from the remaining integer
 +
|style="text-align:right;"|החמישית עשה בעניין הזה מן ט שלימים קח אחד מִט' ושבור אותו בשברו דהיינו בשלישים כמו שתמצא בחיסור שתרצה לחסור והוא מן בראשון חסור מן ותשאר ואחר כך חסור ב מן ח ותשאר לך ו' ותמצא שנשאר לך מן הכל וד"ל
 +
|-
 +
|
 +
*The sixth type:
 +
|style="text-align:right;"|השישית לחסר ג מן חסור ג מן ד וישאר לך א ו והשברים נשארים כולם והוא וד"ל
 
|-
 
|-
 
|
 
|
−
|style="text-align:right;"|דמיהם חב דינרים עת' שהם רק ו' כמה הם מגיעין אז ערכיהו ז ג ח ב בשער הערך וכפול ו פ' חב ויעלה ח ו א חלקיהו בחשבון ו זג ותמצאם ד פ' זג ועוד ולדעת כמה אמות מכר זה שנתן ה' אמות עבור זהוב כפול החומש משישית דהיינו בא עם מניין אמות הבגד שהם 0 ג ויעלה 0 ו ג חלקיהו לחשבון זג ותמצאם ז ט פ' זג ועוד ואם תרצה לידע כמה מעות גובה ט' אמות היינו הד זהובים אם היו זג אז היו נמכרים בעד ה זהובים הג ליטר' פצן כשתערוך זהוב בעד ז' ליטראות כדלעיל עת' שהוא זב כמה הוא אז תערכיהו ב ז ג ה ג בשער הערך וכפול זב עם הג ויעלה ה ד ט חלקיהו ל ז ב בחשבון זג ותמצא הב פ' זג ועוד עשה מן אב ליטראות ג' זהו' וחברם עם הד ויהיו חד ויוותרו לך ד' ליטראות וגם נמצא שמעות הראשון כערך מעות השני לדעת מעות ואמות של השלישי המוכר אמה בעד ו' זהובים כפול חלק שישית מן 0ו והוא 0א עם 0ג והעולה הוא 00ג חלקיהו בחשבון זג ותמצא בו ח' פ' זג ועוד והוא מורה על ח' אמות ועוד מן האמה שמכר ולדעת כמה מעותיו ח' אמות יעלו חד זהו' אמה בעד ו' זהו' הנותרים אם היו זג היו נמכרים בעד בד ליטראות ז' ליטראות לזהוב עתה שהם ד' כמה הן נערכינו בשער הערך כזה ונאמר ונכפול ד' ז ג ב ד עם בד ויעלה ח ו א נחלקיהו בחשבון זג ונמצא [בו] ד' ד פ' זג ועוד נמצא שאין בין זה לזה במניין המעות והראשון מכר בא אמות ועוד מן האמה והשני מכר ט' אמו' ועוד ראובן שמעון לוי מן האמה והשלישי מכר ח' אמות ועוד מן האמה ו בא ט ח וזהו סימנם ועוד שאלו ראובן שמעון לוי רצו לתת בחבורה מ' ליטראות זהב לראשון יש לו זהב ששוה הליטרא ג' זהובים ולשני יש לו זהב ששוה הליטרא ה' זהובים ולשלישי יש לו זהב ששוה הליטרא ח' זהובים כמה ישים א כל אחד ליטרין שיתנו שוה בשוה תשובה עשה מספר המתחלק לְ ג ה ח כיצד כפול ג' על ה' ויעלה הא כפול הא פ' ח' ויעלה 0 ב א ה הסר מן 0 ב א וחברם יחד ויהיו טז וזהו המורה לדעת כמה ליטרין יתן כל אחד שיתנו סך שוה הראשון שזהבו שוה הליטרא ג' זהובים קח השליש מן 0 ב א וזהו 0ד כפול 0ד על 0ד מניין הליטרין ויעלה 0 0 ו א חלקיהו בחשבון ט ז כדלעיל ולשני כפול החומש מן 0 ב א עם 0ד לשלישי כפול השמינית מן 0 ב א עם 0ד וכבר הארכתי העניין הזה
+
*The seventh type:
−
הרי שיש לפניך ד' מטבעות ששוים מ' פשיטים הראשונה שוה (צריך להיות ) מן השני והנשאר מן השנייה הוא מן השלישית והשלישית שוה מן הראשונה והרביעית שוה מן השנייה לדעת כמה שוה כל אחת ואחת עשה כך הראשונה ששוה מן השני באיזה מספר תמצא שלימים בששה הוא ו' הוא א' הרי ד' מן ו' הוי אמר כאלו אמר הראשונה היא מן השני והשלישית ששוה מן הראשון אלו חלקים בכמה נמצאון במניין בא הוא הוא הוא א ב כלול יחד הרי ט' מן בא הוי כאלו אמר השלישית מן הראשונה והרביעי ששוה מן השני אין צריך ביאור דהא מבואר היטיב לדעת איך ימצאון החלקים חלוקים בפירוש הבן איזה חלקים הזכרנו בשאלה ובכל מקום שתמצא תמצא גם הזכרנו רביעית וחומש וכל אלו החלקים נמצאים במניין 0ו נמצאת מטבע שנייה 0ו מן 0ו 0ג וגם 0א כללם יחד והוא 0ד והיא מטבע הראשונה כמה עודף 0ו יותר על 0ד 0ב זהו שאמרנו בשאלה והנשאר מן השניי' עודף על
+
|style="text-align:right;"|השביעית לחסר מן חסור מן כמו שהראתיך  לעיל וזה אי אפשר לעשות קח א מן ד שלימים ושבור אותו בשברו דהיינו וכבר והוא ועכשיו חסור מן וישאר לך וד"ל
 +
|-
 +
|
 +
*The eighth type - the integers are summed together, then the fractions are summed together, as in the first type
 +
|style="text-align:right;"|השמינית לחסר מן לעולם תחסר בראשונה השברים מן השברים והוא מן אי אפשר קח א מן המושבר אותו בשברו דהיינו חמישיות וכבר הוא ותחסור מן על דרך זה ז פ' ו הוא בד כתוב אותן למעלה לפניך ואחר כך ג פ' ה הוא הא כתוב אותן תחתיה כזה וחסור ה"א מן ב"ד וישאר לך זב כתוב זב לפניך והעבר בד הא בקולמוס כזה ואחר כך כפול האותיות התחתונות והוא ז פ' ה הרי הג כתוב אותן תחת זב והעבר בקולמוס ביניהן כזה וד"ל
 +
|-
 +
|
 +
|style="text-align:right;"|אבל אם תרצה לחסר מן שכולן יש להן שם אחד דהיינו השברים יש להן שם אחד חסור האותיות העליונים זה מן זה והוא ה מן ז וישאר לך ב והתחתונות אינם צריכין לחסר והוא שנשאר לך וד"ל
 +
|-
 +
|
 +
|style="text-align:right;"|אם תרצה לחסר מן בראשונה חבור יחד כמו שהראתיך לעיל והוא ואחר כך חבור והוא ועכשיו חסור מן כמו שהראתיך לעיל בשתי וערב ותמצא או וד"ל
 +
|-
 +
|
 +
|style="text-align:right;"|והוא הדין תמצא לחסר בעניין הזה שאר חשבונות בהאי גוונא
 +
|-
 +
|}
 +
{|
 +
|-
 +
|
 +
 
 +
== Multiplication of Fractions ==
 +
 
 +
|style="text-align:right;"|והא לך לכפול שברים בשברים
 +
|-
 +
|Eight types
 +
|style="text-align:right;"|בח' עניינים'
 +
|-
 +
|
 +
*<math>\scriptstyle\frac{2}{3}\times\frac{3}{4}=\frac{6}{12}=\frac{1}{2}</math>
 +
|
 +
{|style="margin-left: auto; margin-right: 0px; text-align:center;"
 +
|-
 +
|<u>א</u>||rowspan="2"|או||<u>ו</u>||&nbsp;||rowspan="2"|הוא||<u>ג</u>||&nbsp;||rowspan="2"|פעמי'||<u>ב</u>||&nbsp;
 +
|-
 +
|ב||בא||&nbsp;||ד||&nbsp;||ג||&nbsp;
 +
|-
 +
|}
 +
|-
 +
|
 +
*<math>\scriptstyle6\times\frac{1}{3}=\frac{6}{3}=2</math>
 +
|
 +
{|style="margin-left: auto; margin-right: 0px; text-align:center;"
 +
|-
 +
|rowspan="2"|ב||rowspan="2"|או||<u>ו</u>||&nbsp;||rowspan="2"|הוא||<u>א</u>||&nbsp;||rowspan="2"|פעמי'||rowspan="2"|ו||&nbsp;
 +
|-
 +
|ג||&nbsp;||ג||&nbsp;
 +
|-
 +
|}
 +
|-
 +
|
 +
*<math>\scriptstyle\frac{2}{3}\times19=12+\frac{2}{3}</math>
 +
|
 +
{|style="margin-left: auto; margin-right: 0px; text-align:center;"
 +
|-
 +
|<u>ב</u>||rowspan="2"|בא||rowspan="2"|הוא||&nbsp;||rowspan="2"|טא||rowspan="2"|פעמי'||<u>ב</u>||&nbsp;
 +
|-
 +
|ג||&nbsp;||ג||&nbsp;
 +
|-
 +
|}
 +
|-
 +
|
 +
*<math>\scriptstyle\left(6+\frac{1}{3}\right)\times\frac{1}{2}=3+\frac{1}{6}</math>
 +
|
 +
{|style="margin-left: auto; margin-right: 0px; text-align:center;"
 +
|-
 +
|<u>א</u>||rowspan="2"|ג||rowspan="2"|הוא||<u>א</u>||&nbsp;||rowspan="2"|פעמי'||<u>א</u>||rowspan="2"|ו
 +
|-
 +
|ו||ב||&nbsp;||ג
 +
|-
 +
|}
 +
|-
 +
|
 +
*<math>\scriptstyle\left(6+\frac{1}{5}\right)\times9=55+\frac{4}{5}</math>
 +
|
 +
{|style="margin-left: auto; margin-right: 0px; text-align:center;"
 +
|-
 +
|<u>ד</u>||rowspan="2"|הה||rowspan="2"|הוא||&nbsp;||rowspan="2"|ט||rowspan="2"|פעמי'||<u>א</u>||rowspan="2"|ו
 +
|-
 +
|ה||&nbsp;||ה
 +
|-
 +
|}
 +
|-
 +
|
 +
*<math>\scriptstyle6\times\left(8+\frac{1}{2}\right)=51</math>
 +
|
 +
{|style="margin-left: auto; margin-right: 0px; text-align:center;"
 +
|-
 +
|rowspan="2"|אה||rowspan="2"|הוא||<u>א</u>||rowspan="2"|ח||rowspan="2"|פעמי'||&nbsp;||rowspan="2"|ו
 +
|-
 +
|ב||&nbsp;
 +
|-
 +
|}
 +
|-
 +
|
 +
*<math>\scriptstyle\left(9+\frac{2}{3}\right)\times\frac{1}{4}=2+\frac{5}{12}</math>
 +
|
 +
{|style="margin-left: auto; margin-right: 0px; text-align:center;"
 +
|-
 +
|<u>ה</u>||rowspan="2"|ב||rowspan="2"|הוא||<u>א</u>||rowspan="2"|פעמי'||rowspan="2"|ט||<u>ב</u>
 +
|-
 +
|בא||ד||ג
 +
|-
 +
|}
 +
|-
 +
|
 +
*<math>\scriptstyle\left(6+\frac{5}{7}\right)\times\left(7+\frac{1}{2}\right)=50+\frac{5}{14}</math>
 +
|
 +
{|style="margin-left: auto; margin-right: 0px; text-align:center;"
 +
|-
 +
|<u>ה</u>||rowspan="2"|&#x202B;0ה||rowspan="2"|הוא||<u>א</u>||rowspan="2"|ז||rowspan="2"|פעמי'||<u>ה</u>||rowspan="2"|ו
 +
|-
 +
|דא||ב||ז
 +
|-
 +
|}
 +
|-
 +
|
 +
|style="text-align:right;"|והא לך הדומיון ללכפול ח' שורות הרשומים לפניך על דרך זו
 +
|-
 +
|
 +
*The first type:
 +
|style="text-align:right;"|בראשונה אם תרצה לכפול פ' כפול האותיות העליוני למעלה יחד ואחר כך האותיות התחתונות ג"כ[ ] כזה כפול בראשונה ב פ' ג דהיינו האותיות העליונות מן השאילה ששאלתי והוא ו' ואחר כך האותיות התחתונות דהיינו ג פ' ד הרי ב"א כתוב למטה מה ו' כזה והעבר בקולמוס ביניהן וה"ה חשבון אחר בעניין הזה ודווקא השברי בשברים
 +
|-
 +
|
 +
*The second type:
 +
|style="text-align:right;"|השני' ו פ' כפול הַ ו' באות העליון וכתוב לפניך ואחר כך האותיות התחתונות אין אתה צריך לכפול אלא בהווייתו תהא כזה שרשמתי ו' פ א הוא א פעם ו' וכתוב הַג למטה מִ ו כזה הוא ב' שלימים
 +
|-
 +
|
 +
|style="text-align:right;"|ואם תרצה לשבור השלימים דהיינו ו' בשברו והוא חא ג"כ תוכל לחשוב בכפל כלעיל חא פ' א הוא חא ג כתוב למעלה ואחר כך ג פ ג ט הרי חא הוא וד"ל
 +
|-
 +
|
 +
*The third type - as the second type
 +
|style="text-align:right;"|השלישית כשנייה
 +
|-
 +
|
 +
*The fourth type:
 +
|style="text-align:right;"|הרביעית הוא פעמי' שבר השלימים בשברו דהיינו שלישים ותמצא ואחר כך חבור ג"כ לזה והוא ואמור פעמי' ועשה כראשון והוא וד"ל
 +
|-
 +
|
 +
*The fifth type:
 +
|style="text-align:right;"|החמישית הוא פעמי' ט כפול ו עם ט והוא דה ואחר כך כפול עם ט שלימים כמו שהראתיך לעיל בשער השני' ותמצא הוא וכבר מצאת דה ועכשיו תמצא ס"ה וה"ה תמצא לחשוב אם תשבר השלימי' לשברים לעשות מן ומן ט כל מה שתרצה שניים שלשי' רביעיות חמשיות וד"ל
 +
|-
 +
|
 +
*The sixth type - as the fifth type
 +
|style="text-align:right;"|השישית כחמישית
 +
|-
 +
|
 +
*The seventh type - as the fourth type
 +
|style="text-align:right;"|השביעית כרביעי
 +
|-
 +
|
 +
*The eighth type:
 +
|style="text-align:right;"|השמינית והוא פעמי' שבר הַו בשברו דהיינו ו' שביעיות והוא והַ תמצא יחד  ואחר כך שבר ג"כ ז בשברו דהיינו חציין והוא דא וכבר יש לך הרי עכשיו כפול פעמי' כפול זד עם הא והוא ה 0 ז ואחר כך כפול ז עם ב והוא דא והוא ובו תמצא 0ה שלים וד"ל
 +
|-
 +
|Whenever there is a product of integers and fractions by integers and fractions the integers should be converted into fractions
 +
|style="text-align:right;"|צריך אתה לידע כל מקו' שמגיע לידך חשבון שלימי' ושברים בשלימי' ושברים כמו שהראתיך שבור השלימים בשברו כלעיל ואחר כך תמצא החשבון מכוון
 +
|-
 +
|
 +
|style="text-align:right;"|אבל אם אתה תרצה לכפול שלימים בשלימים בראשונה ואחר כך שברים בשברים אז הוא בודאי טעות ו"א
 +
|-
 +
|}
 +
{|
 +
|-
 +
|
 +
 
 +
== Division of Fractions ==
 +
 
 +
|style="text-align:right;"|והא לך לחלוק שברים בשברים בחילוק
 +
|-
 +
|
 +
|style="text-align:right;"|אם תחלקו בחשבון יבא
 +
|-
 +
|
 +
|style="text-align:right;"|בחשבון יבא
 +
|-
 +
|
 +
:*Word Problem - Find a Number Problem - dividing ¾ into four fifths
 +
|style="text-align:right;"|אם ישאלך אדם ג' רביעיות אם תרצה לחלקו <s>לד' חלקים</s> לד' חמשיות כמה <s>לחלק</s> ד' חמשיות יש בו
 +
|-
 +
|
 +
|style="text-align:right;"|<s>חלק</s> תשיב לו ג' תשעה חלקי' מ
 +
|-
 +
|
 +
:*Word Problem - Divide a Quantity Problem - dividing 20 peraḥim among four brothers - three of the brothers will receive ¾ of the amount, i.e. 15 peraḥim
 +
|style="text-align:right;"|דהיינו אם יש בכאן עשרים פרחי' לחלק בין ד' אחים לג' אחי' יגיע ג' רביעיות והם ט"ו פרחי'
 +
|-
 +
|
 +
::Dividing the 15 peraḥim into five
 +
|style="text-align:right;"|ואם תרצה לחלק אלו ט"ו פרחי' שהם רביעיות עוד לב' חלקים יגיע לכל חלק מהם ג שהוא ג' חלקי' קטני' שהם ג' פרחי' מאלו העשרי' וכן עד"ז כולם
 +
|-
 +
|
 +
*The first type:
 +
|style="text-align:right;"|והא לך הדומיון לחלק שברים בשברים כגון הרוצה לחלק בחשבון חלוק אותו בשתי וערב על דרך זה לעולם קח בצד ימין העליון וכפול אותו עם אות התחתון שבצד שמאל וכתוב אותו למעלה לפניך ואחר כך כפול האות התחתון שבצד ימין וכפלתו באות העליון של שמאל
 +
|-
 +
|
 +
|style="text-align:right;"|כמשל כאמרך לכמה חלקי' שוים לְ יחלקו הַ או כאמרך אם תחלק השני שלישיו' לארבע חמשיות כמה תמצא באלו
 +
|-
 +
|
 +
|style="text-align:right;"|והא לך הדומיון בזה החשבון שרשמתי דהיינו בחשבון כפול ב פ ה הוא 0א תכתוב למעלה לפניך ואחר כך ג פ' ד הוא בא תכתוב למטה כזה
 +
|-
 +
|
 +
|style="text-align:right;"|אבל הרוצה '''לחסר''' בחשבון ג"כ כפלתו כלעיל ד פ' ג הוא בא תכתוב למעלה לפניך ואחר כך ה פ' ב 0א תכתוב למטה כזה והוא וד"ל
 +
|-
 +
|
 +
*The second type:
 +
|style="text-align:right;"|השנית והוא בחשבון כתוב לפניך כזה והוא מרמז על שלם ר"ל אחד חלק מאחת וכתוב לפניך כזה וכפולתו בשתי וערב כלעיל א פ' ב והוא ב תכתוב לפניך למעלה ואחר כך א פ' א הוא א תכתוב למטה כזה וד"ל
 +
|-
 +
|According to the writing conventions presented by the author:<br>
 +
Writing a zero or one below the number indicates an integer
 +
|style="text-align:right;"|השלישית אבל אם תרצה לחסר (לחלק) בחשבון ולא תרצה לעשות אלא בהווייתו תהא כזה דע כי הא' נחשב לפני האות שלמעלה ולא לפני האות שלמטה ולמטה עשה ציפור במקום אות התחתון כזה כפול א פ' ב הוא ב ואחר כך חבר 0' עם א והוא א' תכתוב למטה וד"ל
 +
|-
 +
|Note: the zero that indicates that the dividend is an integer should not be multiplied by the numerator of the divisor, for a product of zero is zero and therefore the denominator of the result will then be a zero, which will indicate erroneously that the result is an integer
 +
|style="text-align:right;"|והזהר בנפשך שלא תכפול הַ 0 עם הא כי 0 פ' א הוא 0 ואז תמצא והן ב שלימי' וד"ל
 +
|-
 +
|
 +
*The third type
 +
|style="text-align:right;"|השלישית לחלוק בחשבון זכור נא שתצטרך לחלוק אות העליון שבצד ימין עם האות התחתון שבצד שמאל והַ ה נחשב בלפני אות העליון כלעיל ואם תרצה לעשות למטה מהַ ה א כזה כפול ג פ' א הוא ג תכתוב למעלה ואחר כך ד פ' ה הוא 0ב והוא אבל אם תרצה לכתוב תחת הַה 0 כזה חבר ג עם 0 כלעיל והוא ג' ואחר כך ד פ' ה הרי 0ב וד"ל
 +
|-
 +
|
 +
*The fourth type - as the first type
 +
|style="text-align:right;"|הרביעית הוא בחשבון ועשה כבראשונה עשה הַ ג לשבעיות והם וכבר ב הרי הם בחשבון חשוב גב פ' גא הרי ט ט ב תכתוב למעלה ואחר כך ז פ' 0א הרי 0ז תכתוב למלמטה כזה ובו תמצא ד' פ' 0ז דהיינו ד' שלימי' וישאר לך טא דהיינו ד שלימי' וד"ל
 +
|-
 +
|
 +
*The fifth type - as the fourth type
 +
|style="text-align:right;"|החמישית והוא בחשבון כרביעית אך הזהר שתכתוב תחת הו' א' או 0' ועשה כמו שהראתיך לעיל
 +
|-
 +
|
 +
*The sixth type - as the second type
 +
|style="text-align:right;"|השישית והוא ב בחשבון שבר גא בשברו והוא וכבר שהם כתוב לפניך בחשבון חשוב אותו כחשבון השנית וכתוב דב 0 או א ואל תשכח לחבר עם 0' ולכפול עם א ותמצא וד"ל
 +
|-
 +
|
 +
*The seventh type - as the first type
 +
|style="text-align:right;"|השביעית והוא בחשבון שבר הַ ז בשברו וחשוב אותו כחשבון הראשון וד"ל
 +
|-
 +
|
 +
*The eighth type - as the first type
 +
|style="text-align:right;"|השמינית והוא בחשבון שבור השלימי' בשברם דהיינו מן טא עשה שלישים ומן א' עשה רביעיות וחשוב אותו כבראשון ותמצא מכוון וד"ל
 +
|-
 +
|}
 +
{|
 +
|-
 +
|
 +
 
 +
== Fractions of Fractions ==
 +
 
 +
|
 +
|-
 +
|The four basic operations with fractions of fractions
 +
|style="text-align:right;"|אם ישאלך אדם לחבור לו בארבע חשבונות הללו חציין שברים ל[ש ]
 +
|-
 +
|
 +
|style="text-align:right;"|כגון חצי שליש עם שאר שברים [ ] או שליש מרביעית עם שאר שברים
 +
|-
 +
|When fractions of fractions are involved - the simple fractions should be converted to the lower fractions, i.e. to fractions of fractions
 +
|style="text-align:right;"|שבור השברים בשברים קטנים דהיינו בשברו
 +
|-
 +
|
 +
|style="text-align:right;"|כגון אם ישאלך אדם תרצה לחבר עם (ו)שליש עשה מן השלישים חצי שלישים והן ב חצי שלישי' וכבר חצי שליש הרי הן ג חצי שלישים שהן עכשיו חבר עם כמו שהראתיך בחשבון בשברים בחיבור ותמצא או או ומכוון וד"[ל]
 +
|-
 +
|
 +
|style="text-align:right;"|הרוצה לחבר ועוד רביעית ועוד מרביעית עם (צריך להיות ) ועוד (צריך להיות ) משמינית עשה מן רביעי' ומן מרביעית כל אחד לששה עשר חלקי' דהיינו מרביעית * ותמצא סך הכל ואחר כך עשה * שהוא סך מהסך השני חד חלקי' ותמצא תתכתוב לפניך הקטון מכולם כזה עם ותמצא (צריך להיות ) והוא א' שלם (צריך להיות ) חלקי'
 +
|-
 +
|
 +
|style="text-align:right;"|ובכל השערים בכפל בחיבור בחיסור ובחילוק תעשה כלעיל וד"ל
 
|-
 
|-
 
|}
 
|}
−
והא לך לכפול לחבר שברים בשברי' [ב]ח' עניינים
 
−
עם ותמצא
 
−
עם ותמצא
 
−
עם ותמצא [ ]
 
−
עם ותמצא [ ]
 
−
עם ותמצא
 
−
עם ותמצא
 
−
(*) עם ותמצא * טעות, מסתדר עם במקום
 
−
עם ותמצא
 
−
והא לך הדומיון אם תרצה לחבר עם יחד עשה כאשר אראך איה כפול אותו בשתי וערב ר"ל ב פ' ד דהיינו ח' כתוב ח' לפניך ואחר כך כפול השנית ג"כ בשתי וערב ג פ' ג דהיינו ט' וחבר ט' וח' שמצאת ותמצא ז"א כתוב אותו למעלה ואחר כך כפול הַב' אותיות התחתונות כגון ג פ' ד דהיינו ב"א כתוב תחת ז"א כזה דהיינו ז"א חלקים שתגיעו ב"א לשלם ז א חסור ב"א ממנו דהיינו שלם וכתוב בצדו וישאר לך ב א [ ] חלקים שמגיעי' ב"א לשלם כזה [ ]
 
−
השער השני והשער השלישי אין [צריך] לכתוב
 
−
השער הרביעי עש דהיינו ו שלימים עם עשה השברים בכפל שתי וערב כדלעיל ואחר כך חיבר השלימים יחד ותמצא מכוון
 
−
השער החמישי והשישי כפול השלימים יחד ואחר כך עשה השברים ג"כ להמניין
 
−
השער השביעי חשוב כאשר הראתיך לעיל בשער הרביעי
 
−
השער השמיני דהיינו עם חבור כפול השלימים בחיבור בכפל ותמצא זא ואחר כך כפול השברים כמו שעשית בראשונה ותמצא חא שלימים
 
−
אבל כשתמצא ג' פ' שברים בשברים בבת אחת כגון א"ת לחבר חשוב ב' שברים בשברים הראשונים והה' האחרונים כמו שהראתיך בראשונה ואחר כך חבר השלישי ג"כ לזה כגון א"ת לחשוב דומיון שלמעלה חשוב ב' הראשונות דהיינו בשתי וערב ותמצא ואחר כך תרצה לחבר עם כפול אותו בשתי וערב ותמצא ובזה תמצא ב שלימים או ומכוון
 
−
[והא לך לחסר שברים] משברים בח' עניינים
 
−
מן ותשאר
 
−
מן אי אפשר נמנה ולא תוכל לחסר ממנו
 
−
מן ותשאר לך
 
−
מן ג"כ לא תוכל לחסר ממנו
 
−
מן ותשאר לך
 
−
מן ותשאר לך
 
−
מן ותשאר לך (צריך להיות )
 
−
מן ותשאר לך
 
−
והא לך הדומיון לחסר הח' חשבונות הרשומים למעלה על דרך זו
 
−
ובראשונה אם תרצה לחסר מן לעולם תקח בראשונה האות התחתון שבצד ימין והאות העליון שבצד שמאל בכפל
 
−
דהיינו ג פ' ג הרי ט' הט שמצאת כתוב כתוב למעלה לפניך ואחר כך האחרים דהיינו א פ' ד כתוב אות הד' תחת הט' שמצאת [ ] כזה ואחר כך חסור האות ט התחתונה מהאות העליונה דהיינו ה' מן ט ותשאר ה ד כתוב אותן לפניך שלא תשכח ואחר כך כפול האותיות התחתונות דהיינו ג פ' ד הרי בא כתוב בא תחת ה' ותמצא מכוון והזהר בנפשך שתעבור בקולמוס ביניהם שלא תטעה ותאמר שהן שלימים כזה
 
−
השנית השלימים מן לא תמצא לחסר ממנו אלא א"כ תהפוך אותו כגון מן ה' שלמים אז הוא אפשר
 
−
השלישית לחסר מן ג שלימים אז תשבר השלימים לשברי' לשלישי' כמו שתמצא בחסרון שתרצה לחסר דהיינו כל אחד לשנים עשר חלקי' ותמצא [ מן ] בראשונה * לחסר מן ב שלימים חסור מן ותשאר לך דהיינו או או וד"ל
 
−
הרביעית אי אפשר
 
−
החמישית עשה בעניין הזה מן ט שלימים קח אחד מִט' ושבור אותו בשברו דהיינו בשלישים כמו שתמצא בחיסור שתרצה לחסור והוא מן בראשון חסור מן ותשאר ואחר כך חסור ב מן ח ותשאר לך ו' ותמצא שנשאר לך מן הכל וד"ל
 
−
השישית לחסר ג מן חסור ג מן ד וישאר לך א ו והשברים נשארים כולם והוא וד"ל
 
−
השביעית לחסר מן חסור מן כמו שהראתיך  לעיל וזה אי אפשר לעשות קח א מן ד שלימים ושבור אותו בשברו דהיינו וכבר והוא ועכשיו חסור מן וישאר לך וד"ל
 
−
השמינית לחסר מן לעולם תחסר בראשונה השברים מן השברים והוא מן אי אפשר קח א מן המושבר אותו בשברו דהיינו חמישיות וכבר הוא ותחסור מן על דרך זה ז פ' ו הוא בד כתוב אותן למעלה לפניך ואחר כך ג פ' ה הוא הא כתוב אותן ב ד תחתיה כזה וחסור ה"א מן ב"ד וישאר לך זב כתוב ה א זב לפניך והעבר בד הא בקולמוס כזה ואחר כך כפול ז ב האותיות התחתונות והוא ז פ' ה הרי הג כתוב אותן תחת זב והעבר בקולמוס ביניהן כזה וד"ל
 
−
אבל אם תרצה לחסר מן שכולן יש להן שם אחד דהיינו השברים יש להן שם אחד חסור האותיות העליונים זה מן זה והוא ה מן ז וישאר לך ב והתחתונות אינם צריכין לחסר והוא שנשאר לך וד"ל
 
−
אם תרצה לחסר מן בראשונה חבור יחד כמו שהראתיך לעיל והוא ואחר כך חבור והוא ועכשיו חסור מן כמו שהראתיך לעיל בשתי וערב ותמצא או וד"ל והוא הדין תמצא לחסר בעניין הזה שאר חשבונות בהאי גוונא
 
−
והא לך לכפול שברים בשברים בח' עניינים'
 
−
פעמי' הוא או
 
−
פעמי' הוא או
 
−
פעמי' הוא
 
−
פעמי' הוא
 
−
פעמי' הוא
 
−
פעמי' הוא
 
−
פעמי' הוא
 
−
פעמי' הוא
 
−
והא לך הדומיון ללכפול ח' שורות הרשומים לפניך על דרך זו
 
−
בראשונה אם תרצה לכפול פ' כפול האותיות העליוני למעלה יחד ואחר כך האותיות התחתונות ג"כ[ ] כזה כפול בראשונה ב פ' ג דהיינו האותיות העליונות מן השאילה ששאלתי והוא ו' ואחר כך האותיות התחתונות דהיינו ג פ' ד הרי ב"א כתוב למטה מה ו' כזה והעבר בקולמוס ביניהן וה"ה חשבון אחר בעניין הזה ודווקא השברי בשברים
 
−
השני' ו פ' כפול הַ ו' באות העליון וכתוב לפניך ואחר כך האותיות התחתונות אין אתה צריך לכפול אלא בהווייתו תהא כזה שרשמתי ו' פ א הוא א פעם ו' וכתוב הַג למטה מִ ו כזה הוא ב' שלימים
 
−
ואם תרצה לשבור השלימים דהיינו ו' בשברו והוא חא ג"כ תוכל לחשוב בכפל כלעיל חא פ' א הוא חא ג כתוב למעלה ואחר כך ג פ ג ט הרי חא הוא וד"ל
 
−
השלישית כשנייה
 
−
הרביעית הוא פעמי' שבר השלימים בשברו דהיינו שלישים ותמצא ואחר כך חבור ג"כ לזה והוא ואמור פעמי' ועשה כראשון והוא וד"ל
 
−
החמישית הוא פעמי' ט כפול ו עם ט והוא דה ואחר כך כפול עם ט שלימים כמו שהראתיך לעיל בשער השני' ותמצא הוא וכבר מצאת דה ועכשיו תמצא ס"ה וה"ה תמצא לחשוב אם תשבר השלימי' לשברים לעשות מן ומן ט כל מה שתרצה שניים שלשי' רביעיות חמשיות וד"ל
 
−
השישית כחמישית
 
−
השביעית כרביעי
 
−
השמינית והוא פעמי' שבר הַו בשברו דהיינו ו' שביעיות והוא והַ תמצא יחד  ואחר כך שבר ג"כ ז בשברו דהיינו חציין והוא דא וכבר יש לך הרי עכשיו כפול פעמי' כפול זד עם הא והוא ה 0 ז ואחר כך כפול ז עם ב והוא דא והוא ובו תמצא 0ה שלים וד"ל
 
−
צריך אתה לידע כל מקו' שמגיע לידך חשבון שלימי' ושברים בשלימי' ושברים כמו שהראתיך שבור השלימים בשברו כלעיל ואחר כך תמצא החשבון מכוון אבל אם אתה תרצה לכפול שלימים בשלימים בראשונה ואחר כך שברים בשברים אז הוא בודאי טעות ו"א
 
−
והא לך לחלוק שברים בשברים בחילוק
 
−
אם תחלקו בחשבון יבא
 
−
בחשבון יבא אם ישאלך אדם
 
−
בחשבון יבא ג' רביעיות אם תרצה לחלקו
 
−
בחשבון יבא לד' חלקים לד' חמשיות כמה [  ] לחלק ד' חמשיות
 
−
בחשבון יבא יש בו חלק תשיב לו ג' תשעה חלקי' מ[ ]
 
−
ב בחשבון יבא דהיינו אם יש בכאן עשרים
 
−
בחשבון יבא פרחי' לחלק בין ד' אחים
 
−
בחשבון יבא לג' אחי' יגיע ג' רביעיות
 
−
והם ט"ו פרחי' ואם תרצה
 
−
והא לך הדומיון לחלק שברים בשברים כגון הרוצה לחלק לחלק אלו ט"ו פרחי' שהם בחשבון חלוק אותו בשתי וערב על דרך זה לעולם רביעיות עוד לב' חלקים קח בצד ימין העליון וכפול אותו עם אות התחתון שבצד יגיע לכל חלק מהם ג שמאל וכתוב אותו למעלה לפניך ואחר כך כפול האות שהוא ג' חלקי' קטני' שהם התחתון שבצד ימין וכפלתו באות העליון של שמאל ג' פרחי' מאלו העשרי'
 
−
והא לך הדומיון בזה החשבון שרשמתי דהיינו בחשבון וכן עד"ז כולם כפול ב פ ה הוא 0א תכתוב למעלה לפניך ואחר כמשל כאמרך לכמה חלקי' כך ג פ' ד הוא בא תכתוב למטה כזה שוים לְ יחלקו הַ אבל הרוצה לחסר (לחלק) בחשבון ג"כ כפלתו כלעיל ד פ' ג או כאמרך אם תחלק השני הוא בא תכתוב למעלה לפניך ואחר כך ה פ' ב שלישיו' לארבע חמשיות 0א תכתוב למטה כזה והוא וד"ל כמה תמצא באלו
 
−
השנית והוא בחשבון כתוב לפניך כזה והוא מרמז על שלם ר"ל אחד חלק מאחת וכתוב לפניך כזה וכפולתו בשתי וערב כלעיל א פ' ב והוא ב תכתוב לפניך למעלה ואחר כך א פ' א הוא א תכתוב למטה כזה וד"ל
 
−
השלישית אבל אם תרצה לחסר (לחלק) בחשבון ולא תרצה לעשות אלא בהווייתו תהא כזה דע כי הא' נחשב לפני האות שלמעלה ולא לפני האות שלמטה ולמטה עשה ציפור במקום אות התחתון כזה כפול א פ' ב הוא ב ואחר כך חבר 0' עם א והוא א' תכתוב למטה וד"ל והזהר בנפשך שלא תכפול הַ 0 עם הא כי 0 פ' א הוא 0 ואז תמצא והן ב שלימי' וד"ל
 
−
השלישית לחלוק בחשבון זכור נא שתצטרך לחלוק אות העליון שבצד ימין עם האות התחתון שבצד שמאל והַ ה נחשב בלפני אות העליון כלעיל ואם תרצה לעשות למטה מהַ ה א כזה כפול ג פ' א הוא ג תכתוב למעלה ואחר כך ד פ' ה הוא 0ב והוא אבל אם תרצה לכתוב תחת הַה 0 כזה חבר ג עם 0 כלעיל והוא ג' ואחר כך ד פ' ה הרי 0ב וד"ל
 
−
הרביעית הוא בחשבון ועשה כבראשונה עשה הַ ג לשבעיות והם וכבר ב הרי הם בחשבון חשוב גב פ' גא הרי ט ט ב תכתוב למעלה ואחר כך ז פ' 0א הרי 0ז תכתוב למלמטה כזה ובו תמצא ד' פ' 0ז דהיינו ד' שלימי' וישאר לך טא דהיינו ד שלימי' וד"ל
 
−
החמישית והוא בחשבון כרביעית אך הזהר שתכתוב תחת הו' א' או 0' ועשה כמו שהראתיך לעיל
 
−
השישית והוא ב בחשבון שבר גא בשברו והוא וכבר שהם כתוב לפניך בחשבון חשוב אותו כחשבון השנית וכתוב דב 0 או א ואל תשכח לחבר עם 0' ולכפול עם א ותמצא וד"ל
 
−
השביעית והוא בחשבון שבר הַ ז בשברו וחשוב אותו כחשבון הראשון וד"ל
 
−
השמינית והוא בחשבון שבור השלימי' בשברם דהיינו מן טא עשה שלישים ומן א' עשה רביעיות וחשוב אותו כבראשון ותמצא מכוון וד"ל
 
−
אם ישאלך אדם לחבור לו בארבע חשבונות הללו חציין שברים ל[ש ] כגון חצי שליש עם שאר שברים [ ] או שליש מרביעית עם שאר שברים שבור השברים בשברים קטנים דהיינו בשברו כגון אם ישאלך אדם תרצה לחבר עם (ו)שליש עשה מן השלישים חצי שלישים והן ב חצי שלישי' וכבר חצי שליש הרי הן ג חצי שלישים שהן עכשיו חבר עם כמו שהראתיך בחשבון בשברים בחיבור ותמצא או או ומכוון וד"[ל]
 
−
הרוצה לחבר ועוד רביעית ועוד מרביעית עם (צריך להיות ) ועוד (צריך להיות ) משמינית עשה מן רביעי' ומן מרביעית כל אחד לששה עשר חלקי' דהיינו מרביעית * ותמצא סך הכל ואחר כך עשה * שהוא סך מהסך השני חד חלקי' ותמצא תתכתוב לפניך הקטון מכולם כזה עם ותמצא (צריך להיות ) והוא א' שלם (צריך להיות ) חלקי' ובכל השערים בכפל בחיבור בחיסור ובחילוק תעשה כלעיל וד"ל
 
 
{|
 
{|
 
|-
 
|-
Line 206: Line 662:
 
|-
 
|-
 
|}
 
|}
 +
== Appendix: Bibliography ==
 +
'''''Anonymous'''''<br>
 +
'''''(Ḥeshbon shel Shevarim)'''''<br>
 +
 +
 +
'''Manuscript:'''<br>
 +
*Budapest, Magyar Tudományos Akadámia, Ms. Kaufmann A 520/15 (IMHM: f 15170), ff. 216; 219-229 (16th century)<br>
 +
:[https://www.nli.org.il/he/discover/manuscripts/hebrew-manuscripts/viewerpage?vid=MANUSCRIPTS&docid=PNX_MANUSCRIPTS990001919280205171-1#$FL53195257 Kaufmann A 520/15]

Latest revision as of 20:14, 12 July 2022

בטוב גדול אתחיל ד"א
Calculation of Fractions לכתוב חשבון של שברים
Division, Addition, Multiplication, Subtraction בחילוק ובחיבור ובכפל ובחיסור
והא לך שברים בחיסור
Eight types for each operation: ותמצא בו ח' שערי'
1) Fractions by fractions
 ראשונה דהיינו שברים בשברים
2) Integers by fractions
 ב דהיינו שלמים בשברים
3) Fractions by integers
 ג דהיינו שברים בשלמים
4) Integers and fractions by fractions
 ד שלמים ושברים בשברים
5) Integers and fractions by integers
 ה שלימים ושברים בשלימים
6) Integers by integers and fractions
 ו שלימים בשלימים ושברים
7) Fractions by integers and fractions
 ז שברים בשלימים ושברים
8) Integers and fractions by integers and fractions
 ח שלימים ושברים בשלימים ושברים
והא לך הדומיון
Two letters one above the other with a dividing line between them - indicate a fraction וידוע ליהוי לך כל מקום שתמצא ב' אותיות זו על גב זו והעברת קולמוס בנתיים
כזה מורה על ג רבעיות
אבל כשתמצא אות אחד אז הוא מרמז על שלימים
והוא הדין אם תמצא ב' אותיות זו על גב זו ודומין בצורותיהן
כזה והעברת קולמוס בנתיהן מרמזין חמשה חומשין
אבל אם תמצא ב' אותיות אלפין זו על גב זו ולא תמצא העברת קולמוס בנתיים אז הוא מרמז על שלימים
כזה ר"ל אחד שלם ול"ד

Addition of Fractions

 והא לך לכפול לחבר שברים בשברי'
Eight types ‫[ב]‫ח' עניינים
  • \scriptstyle\frac{1}{3}+\frac{1}{4}=\frac{7}{12}
ז   ותמצא א   עם א  
בא   ד   ג  
  • \scriptstyle9+\frac{4}{5}=9+\frac{4}{5}
ד ט ותמצא ד   עם ט  
ה ה    
  • \scriptstyle\frac{1}{3}+5=5+\frac{1}{3}
א ה ותמצא   ה עם א  
ג   ג  
  • \scriptstyle\left(6+\frac{2}{4}\right)+\frac{2}{3}=7+\frac{1}{6}
א ז ותמצא ב   עם ב ו
ו ג   ד
  • \scriptstyle\left(4+\frac{3}{4}\right)+9=13+\frac{3}{4}
ג גא ותמצא   ט עם ג ד
ד   ד
  • \scriptstyle5+\left(4+\frac{3}{4}\right)=9+\frac{3}{4}
ג ט ותמצא ג ד עם   ה
ד ד  
  • \scriptstyle\frac{6}{10}+\left(2+\frac{4}{9}\right)=3+\frac{4}{90}
ד ג ותמצא ד ב עם ו
‫0ט ט ‫0א
  • \scriptstyle\left(9+\frac{3}{4}\right)+\left(8+\frac{2}{3}\right)=18+\frac{5}{12}
ה חא ותמצא ב ח עם ג ט
בא ג ד
  • The first type:
 והא לך הדומיון אם תרצה לחבר עם יחד
עשה כאשר אראך איה כפול אותו בשתי וערב ר"ל ב פ' ד דהיינו ח' כתוב ח' לפניך ואחר כך כפול השנית ג"כ בשתי וערב ג פ' ג דהיינו ט' וחבר ט' וח' שמצאת ותמצא ז"א כתוב אותו למעלה ואחר כך כפול הַב' אותיות התחתונות כגון ג פ' ד דהיינו ב"א כתוב תחת ז"א כזה דהיינו ז"א חלקים שתגיעו ב"א לשלם חסור ב"א ממנו דהיינו שלם וכתוב בצדו וישאר לך [ ] חלקים שמגיעי' ב"א לשלם כזה [ ]
  • The second and third types - no need to elaborate
 השער השני והשער השלישי אין [צריך] לכתוב
  • The fourth type - the fractions are summed as in the first type, then the integers are summed together
 השער הרביעי עש דהיינו ו שלימים עם עשה השברים בכפל שתי וערב כדלעיל ואחר כך חיבר השלימים יחד ותמצא מכוון
  • The fifth and the sixth types - the integers are summed together, then the fractions are added
 השער החמישי והשישי כפול השלימים יחד ואחר כך עשה השברים ג"כ להמניין
  • The seventh type - as in the fourth type
 השער השביעי חשוב כאשר הראתיך לעיל בשער הרביעי
  • The eighth type - the integers are summed together, then the fractions are summed together, as in the first type
 השער השמיני דהיינו עם חבור כפול השלימים בחיבור בכפל ותמצא זא ואחר כך כפול השברים כמו שעשית בראשונה ותמצא חא שלימים
A sum of three fractions אבל כשתמצא ג' פ' שברים בשברים בבת אחת כגון א"ת לחבר
Two of the fractions are summed together as in the first type, then the third fraction is added to the resulted sum
 חשוב ב' שברים בשברים הראשונים והה' האחרונים כמו שהראתיך בראשונה ואחר כך חבר השלישי ג"כ לזה כגון א"ת לחשוב דומיון שלמעלה חשוב ב' הראשונות דהיינו בשתי וערב ותמצא ואחר כך תרצה לחבר עם כפול אותו בשתי וערב ותמצא ובזה תמצא ב שלימים או ומכוון

Subtraction of Fractions

 [והא לך לחסר שברים] משברים
Eight types בח' עניינים
  • \scriptstyle\frac{3}{4}-\frac{1}{3}=\frac{5}{12}
ה   ותשאר ג   מן א  
בא   ד   ג  
  • \scriptstyle\frac{3}{8}-5=\varnothing
  אי אפשר נמנה ולא תוכל לחסר ממנו ג   מן ה  
ח    
  • \scriptstyle3-\frac{9}{12}=2+\frac{1}{4}
א ב ותשאר לך   ג מן ט  
ד   בא  
  • \scriptstyle\frac{1}{4}-\left(7+\frac{5}{6}\right)=\varnothing
  ג"כ לא תוכל לחסר ממנו א   מן ה ז
ד ו
  • \scriptstyle9-\left(2+\frac{2}{3}\right)=6+\frac{1}{3}
א ו ותשאר לך   ט מן ב ב
ג   ג
  • \scriptstyle\left(4+\frac{1}{7}\right)-3=1+\frac{1}{7}
א א ותשאר לך א ד מן   ג
ז ז  
  • \scriptstyle\left(4+\frac{1}{3}\right)-\frac{1}{2}=3+\frac{5}{6}
ה ג ותשאר לך א ד מן א  
ו ג ב  
  • \scriptstyle\left(18+\frac{1}{5}\right)-\left(8+\frac{3}{7}\right)=9+\frac{27}{35}
זב ט ותשאר לך א חא מן ג ח
הג ה ז
והא לך הדומיון לחסר הח' חשבונות הרשומים למעלה על דרך זו
  • The first type:
 ובראשונה אם תרצה לחסר מן לעולם תקח בראשונה האות התחתון שבצד ימין והאות העליון שבצד שמאל בכפל

דהיינו ג פ' ג הרי ט' הט שמצאת כתוב כתוב למעלה לפניך ואחר כך האחרים דהיינו א פ' ד כתוב אות הד' תחת הט' שמצאת [ ] כזה ואחר כך חסור האות התחתונה מהאות העליונה דהיינו ה' מן ט ותשאר ה כתוב אותן לפניך שלא תשכח ואחר כך כפול האותיות התחתונות דהיינו ג פ' ד הרי בא כתוב בא תחת ה' ותמצא מכוון

Note: the line should not be forgotten lest the fractions will be considered as integers
 והזהר בנפשך שתעבור בקולמוס ביניהם שלא תטעה ותאמר שהן שלימים כזה
  • The second type - impossible to subtract integers from fractions
 השנית השלימים מן לא תמצא לחסר ממנו
But it is possible to subtract fractions from integers
 אלא א"כ תהפוך אותו כגון מן ה' שלמים אז הוא אפשר
  • The third type - the integer is converted to fractions
 השלישית לחסר מן ג שלימים אז תשבר השלימים לשברי' לשלישי' כמו שתמצא בחסרון שתרצה לחסר דהיינו כל אחד לשנים עשר חלקי' ותמצא [ מן ] בראשונה חסור מן ותשאר לך דהיינו או או וד"ל
  • The fourth type - impossible
 הרביעית אי אפשר
  • The fifth type - the fraction is subtracted from one unit taken from the integer, then the integer is subtracted from the remaining integer
 החמישית עשה בעניין הזה מן ט שלימים קח אחד מִט' ושבור אותו בשברו דהיינו בשלישים כמו שתמצא בחיסור שתרצה לחסור והוא מן בראשון חסור מן ותשאר ואחר כך חסור ב מן ח ותשאר לך ו' ותמצא שנשאר לך מן הכל וד"ל
  • The sixth type:
 השישית לחסר ג מן חסור ג מן ד וישאר לך א ו והשברים נשארים כולם והוא וד"ל
  • The seventh type:
 השביעית לחסר מן חסור מן כמו שהראתיך לעיל וזה אי אפשר לעשות קח א מן ד שלימים ושבור אותו בשברו דהיינו וכבר והוא ועכשיו חסור מן וישאר לך וד"ל
  • The eighth type - the integers are summed together, then the fractions are summed together, as in the first type
 השמינית לחסר מן לעולם תחסר בראשונה השברים מן השברים והוא מן אי אפשר קח א מן המושבר אותו בשברו דהיינו חמישיות וכבר הוא ותחסור מן על דרך זה ז פ' ו הוא בד כתוב אותן למעלה לפניך ואחר כך ג פ' ה הוא הא כתוב אותן תחתיה כזה וחסור ה"א מן ב"ד וישאר לך זב כתוב זב לפניך והעבר בד הא בקולמוס כזה ואחר כך כפול האותיות התחתונות והוא ז פ' ה הרי הג כתוב אותן תחת זב והעבר בקולמוס ביניהן כזה וד"ל
אבל אם תרצה לחסר מן שכולן יש להן שם אחד דהיינו השברים יש להן שם אחד חסור האותיות העליונים זה מן זה והוא ה מן ז וישאר לך ב והתחתונות אינם צריכין לחסר והוא שנשאר לך וד"ל
אם תרצה לחסר מן בראשונה חבור יחד כמו שהראתיך לעיל והוא ואחר כך חבור והוא ועכשיו חסור מן כמו שהראתיך לעיל בשתי וערב ותמצא או וד"ל
והוא הדין תמצא לחסר בעניין הזה שאר חשבונות בהאי גוונא

Multiplication of Fractions

 והא לך לכפול שברים בשברים
Eight types בח' עניינים'
  • \scriptstyle\frac{2}{3}\times\frac{3}{4}=\frac{6}{12}=\frac{1}{2}
א או ו   הוא ג   פעמי' ב  
ב בא   ד   ג  
  • \scriptstyle6\times\frac{1}{3}=\frac{6}{3}=2
ב או ו   הוא א   פעמי' ו  
ג   ג  
  • \scriptstyle\frac{2}{3}\times19=12+\frac{2}{3}
ב בא הוא   טא פעמי' ב  
ג   ג  
  • \scriptstyle\left(6+\frac{1}{3}\right)\times\frac{1}{2}=3+\frac{1}{6}
א ג הוא א   פעמי' א ו
ו ב   ג
  • \scriptstyle\left(6+\frac{1}{5}\right)\times9=55+\frac{4}{5}
ד הה הוא   ט פעמי' א ו
ה   ה
  • \scriptstyle6\times\left(8+\frac{1}{2}\right)=51
אה הוא א ח פעמי'   ו
ב  
  • \scriptstyle\left(9+\frac{2}{3}\right)\times\frac{1}{4}=2+\frac{5}{12}
ה ב הוא א פעמי' ט ב
בא ד ג
  • \scriptstyle\left(6+\frac{5}{7}\right)\times\left(7+\frac{1}{2}\right)=50+\frac{5}{14}
ה ‫0ה הוא א ז פעמי' ה ו
דא ב ז
והא לך הדומיון ללכפול ח' שורות הרשומים לפניך על דרך זו
  • The first type:
 בראשונה אם תרצה לכפול פ' כפול האותיות העליוני למעלה יחד ואחר כך האותיות התחתונות ג"כ[ ] כזה כפול בראשונה ב פ' ג דהיינו האותיות העליונות מן השאילה ששאלתי והוא ו' ואחר כך האותיות התחתונות דהיינו ג פ' ד הרי ב"א כתוב למטה מה ו' כזה והעבר בקולמוס ביניהן וה"ה חשבון אחר בעניין הזה ודווקא השברי בשברים
  • The second type:
 השני' ו פ' כפול הַ ו' באות העליון וכתוב לפניך ואחר כך האותיות התחתונות אין אתה צריך לכפול אלא בהווייתו תהא כזה שרשמתי ו' פ א הוא א פעם ו' וכתוב הַג למטה מִ ו כזה הוא ב' שלימים
ואם תרצה לשבור השלימים דהיינו ו' בשברו והוא חא ג"כ תוכל לחשוב בכפל כלעיל חא פ' א הוא חא ג כתוב למעלה ואחר כך ג פ ג ט הרי חא הוא וד"ל
  • The third type - as the second type
 השלישית כשנייה
  • The fourth type:
 הרביעית הוא פעמי' שבר השלימים בשברו דהיינו שלישים ותמצא ואחר כך חבור ג"כ לזה והוא ואמור פעמי' ועשה כראשון והוא וד"ל
  • The fifth type:
 החמישית הוא פעמי' ט כפול ו עם ט והוא דה ואחר כך כפול עם ט שלימים כמו שהראתיך לעיל בשער השני' ותמצא הוא וכבר מצאת דה ועכשיו תמצא ס"ה וה"ה תמצא לחשוב אם תשבר השלימי' לשברים לעשות מן ומן ט כל מה שתרצה שניים שלשי' רביעיות חמשיות וד"ל
  • The sixth type - as the fifth type
 השישית כחמישית
  • The seventh type - as the fourth type
 השביעית כרביעי
  • The eighth type:
 השמינית והוא פעמי' שבר הַו בשברו דהיינו ו' שביעיות והוא והַ תמצא יחד ואחר כך שבר ג"כ ז בשברו דהיינו חציין והוא דא וכבר יש לך הרי עכשיו כפול פעמי' כפול זד עם הא והוא ה 0 ז ואחר כך כפול ז עם ב והוא דא והוא ובו תמצא 0ה שלים וד"ל
Whenever there is a product of integers and fractions by integers and fractions the integers should be converted into fractions צריך אתה לידע כל מקו' שמגיע לידך חשבון שלימי' ושברים בשלימי' ושברים כמו שהראתיך שבור השלימים בשברו כלעיל ואחר כך תמצא החשבון מכוון
אבל אם אתה תרצה לכפול שלימים בשלימים בראשונה ואחר כך שברים בשברים אז הוא בודאי טעות ו"א

Division of Fractions

 והא לך לחלוק שברים בשברים בחילוק
אם תחלקו בחשבון יבא
בחשבון יבא
  • Word Problem - Find a Number Problem - dividing ¾ into four fifths
 אם ישאלך אדם ג' רביעיות אם תרצה לחלקו לד' חלקים לד' חמשיות כמה לחלק ד' חמשיות יש בו
חלק תשיב לו ג' תשעה חלקי' מ
  • Word Problem - Divide a Quantity Problem - dividing 20 peraḥim among four brothers - three of the brothers will receive ¾ of the amount, i.e. 15 peraḥim
 דהיינו אם יש בכאן עשרים פרחי' לחלק בין ד' אחים לג' אחי' יגיע ג' רביעיות והם ט"ו פרחי'
Dividing the 15 peraḥim into five
 ואם תרצה לחלק אלו ט"ו פרחי' שהם רביעיות עוד לב' חלקים יגיע לכל חלק מהם ג שהוא ג' חלקי' קטני' שהם ג' פרחי' מאלו העשרי' וכן עד"ז כולם
  • The first type:
 והא לך הדומיון לחלק שברים בשברים כגון הרוצה לחלק בחשבון חלוק אותו בשתי וערב על דרך זה לעולם קח בצד ימין העליון וכפול אותו עם אות התחתון שבצד שמאל וכתוב אותו למעלה לפניך ואחר כך כפול האות התחתון שבצד ימין וכפלתו באות העליון של שמאל
כמשל כאמרך לכמה חלקי' שוים לְ יחלקו הַ או כאמרך אם תחלק השני שלישיו' לארבע חמשיות כמה תמצא באלו
והא לך הדומיון בזה החשבון שרשמתי דהיינו בחשבון כפול ב פ ה הוא 0א תכתוב למעלה לפניך ואחר כך ג פ' ד הוא בא תכתוב למטה כזה
אבל הרוצה לחסר בחשבון ג"כ כפלתו כלעיל ד פ' ג הוא בא תכתוב למעלה לפניך ואחר כך ה פ' ב 0א תכתוב למטה כזה והוא וד"ל
  • The second type:
 השנית והוא בחשבון כתוב לפניך כזה והוא מרמז על שלם ר"ל אחד חלק מאחת וכתוב לפניך כזה וכפולתו בשתי וערב כלעיל א פ' ב והוא ב תכתוב לפניך למעלה ואחר כך א פ' א הוא א תכתוב למטה כזה וד"ל
According to the writing conventions presented by the author:

Writing a zero or one below the number indicates an integer

השלישית אבל אם תרצה לחסר (לחלק) בחשבון ולא תרצה לעשות אלא בהווייתו תהא כזה דע כי הא' נחשב לפני האות שלמעלה ולא לפני האות שלמטה ולמטה עשה ציפור במקום אות התחתון כזה כפול א פ' ב הוא ב ואחר כך חבר 0' עם א והוא א' תכתוב למטה וד"ל
Note: the zero that indicates that the dividend is an integer should not be multiplied by the numerator of the divisor, for a product of zero is zero and therefore the denominator of the result will then be a zero, which will indicate erroneously that the result is an integer והזהר בנפשך שלא תכפול הַ 0 עם הא כי 0 פ' א הוא 0 ואז תמצא והן ב שלימי' וד"ל
  • The third type
 השלישית לחלוק בחשבון זכור נא שתצטרך לחלוק אות העליון שבצד ימין עם האות התחתון שבצד שמאל והַ ה נחשב בלפני אות העליון כלעיל ואם תרצה לעשות למטה מהַ ה א כזה כפול ג פ' א הוא ג תכתוב למעלה ואחר כך ד פ' ה הוא 0ב והוא אבל אם תרצה לכתוב תחת הַה 0 כזה חבר ג עם 0 כלעיל והוא ג' ואחר כך ד פ' ה הרי 0ב וד"ל
  • The fourth type - as the first type
 הרביעית הוא בחשבון ועשה כבראשונה עשה הַ ג לשבעיות והם וכבר ב הרי הם בחשבון חשוב גב פ' גא הרי ט ט ב תכתוב למעלה ואחר כך ז פ' 0א הרי 0ז תכתוב למלמטה כזה ובו תמצא ד' פ' 0ז דהיינו ד' שלימי' וישאר לך טא דהיינו ד שלימי' וד"ל
  • The fifth type - as the fourth type
 החמישית והוא בחשבון כרביעית אך הזהר שתכתוב תחת הו' א' או 0' ועשה כמו שהראתיך לעיל
  • The sixth type - as the second type
 השישית והוא ב בחשבון שבר גא בשברו והוא וכבר שהם כתוב לפניך בחשבון חשוב אותו כחשבון השנית וכתוב דב 0 או א ואל תשכח לחבר עם 0' ולכפול עם א ותמצא וד"ל
  • The seventh type - as the first type
 השביעית והוא בחשבון שבר הַ ז בשברו וחשוב אותו כחשבון הראשון וד"ל
  • The eighth type - as the first type
 השמינית והוא בחשבון שבור השלימי' בשברם דהיינו מן טא עשה שלישים ומן א' עשה רביעיות וחשוב אותו כבראשון ותמצא מכוון וד"ל

Fractions of Fractions
The four basic operations with fractions of fractions אם ישאלך אדם לחבור לו בארבע חשבונות הללו חציין שברים ל[ש ]
כגון חצי שליש עם שאר שברים [ ] או שליש מרביעית עם שאר שברים
When fractions of fractions are involved - the simple fractions should be converted to the lower fractions, i.e. to fractions of fractions שבור השברים בשברים קטנים דהיינו בשברו
כגון אם ישאלך אדם תרצה לחבר עם (ו)שליש עשה מן השלישים חצי שלישים והן ב חצי שלישי' וכבר חצי שליש הרי הן ג חצי שלישים שהן עכשיו חבר עם כמו שהראתיך בחשבון בשברים בחיבור ותמצא או או ומכוון וד"[ל]
הרוצה לחבר ועוד רביעית ועוד מרביעית עם (צריך להיות ) ועוד (צריך להיות ) משמינית עשה מן רביעי' ומן מרביעית כל אחד לששה עשר חלקי' דהיינו מרביעית * ותמצא סך הכל ואחר כך עשה * שהוא סך מהסך השני חד חלקי' ותמצא תתכתוב לפניך הקטון מכולם כזה עם ותמצא (צריך להיות ) והוא א' שלם (צריך להיות ) חלקי'
ובכל השערים בכפל בחיבור בחיסור ובחילוק תעשה כלעיל וד"ל

Checking Methods of Operations with Fractions

 ועתה אכתוב לך מאזני צדק על השברים
The author states that he did not find other checking methods in all arithmetic books ולא מצאתי אחרת בכל ספרי חשבונות

Check - addition
והא לך הדומיון הרוצה לחבר עם
וכבר כתבתי לאיזה צד תפנה ת שתמצא החשבון והוא
ותרצה לידע אם חשבונך מכוון אם לאו כפול הַב אותיות התחתונות מן השאילה ומה שתמצא קח ממנו שלישיות כמה שתוכל ואחר כך קח ממנו רביעיות כמה שתוכל כזה ג פ' ד בא ראה מה השליש מן בא והוא ד תכפלתו עם הַ ב כי בשאילה תמצא ד פ' ב הוא ח' תכתוב לפניך ואחר כך ראה מה הרביעיות מן בא והוא ג' תכפלתו עם ג' כי בשאילה תמצא ג"כ ואמר ג פ' ג הוא ט' תכתוב תחת ח' כזה ח וחברתו יחד והוא * כמו שתמצאת כבר וזה ט * שהוא הוא בודאי יושר
ואם לא תמצא מכוון אז הוא ודאי טעות

Check - subtraction

 ומאזני צדק בחיסור
כגון הרוצה לחסר מן
כפלתו בשתי וערב כלעיל ג פ' ג ט תכתוב לפניך ואחר כך ב פ' ד הוא ח חסור ח מן ט ותשאר לך א' ואחר כך אמור ג פ' ד הוא בא תכתוב למטה מֵהַ א כזה
ומאזני צדק כלעיל בחיסור

Check - division

 ומאזני צדק בחילוק
ג"כ כמו בראשונה ובמקום שחסרת בחיסור ח מן ט חלק ח בחשבון ט ותמצא ומכוון וד"ל

Appendix: Bibliography

Anonymous
(Ḥeshbon shel Shevarim)


Manuscript:

  • Budapest, Magyar Tudományos Akadámia, Ms. Kaufmann A 520/15 (IMHM: f 15170), ff. 216; 219-229 (16th century)
Kaufmann A 520/15
Retrieved from "http://mispar.ethz.ch/mediawiki/index.php?title=חשבון_של_שברים&oldid=54939"