Difference between revisions of "עיר סיחון"
(→Chapter Nine – On Knowing the Fractions of Integer, whether in Multiplication, in Division, in Addition, or in Subtraction) |
(→Epilogue) |
||
| (339 intermediate revisions by the same user not shown) | |||
| Line 3: | Line 3: | ||
{| | {| | ||
|- | |- | ||
| − | | | + | |People come to Qiryat-Sefer, |
|style="text-align:right;"|‫<ref>50v</ref>אישים באו קרית ספר | |style="text-align:right;"|‫<ref>50v</ref>אישים באו קרית ספר | ||
|- | |- | ||
| − | | | + | |Where you can examine any number, |
|style="text-align:right;"|בה כל מספר תוכלו לבחון | |style="text-align:right;"|בה כל מספר תוכלו לבחון | ||
|- | |- | ||
| − | | | + | |I will tell you the name of the city, |
|style="text-align:right;"|את שם העיר אגיד לכם | |style="text-align:right;"|את שם העיר אגיד לכם | ||
|- | |- | ||
| − | | | + | |''For Ḥeshbon was the city of Siḥon'' [Numbers 21, 26]. |
| − | |style="text-align:right;"|על כי חשבון היא עיר סיחון | + | |style="text-align:right;"|על ''כי חשבון היא עיר סיחון''‫<ref group=note>במדבר כא, כו</ref> |
|- | |- | ||
| | | | ||
| − | == Introduction == | + | == <span style=color:green>Introduction</span> == |
| | | | ||
|- | |- | ||
|Said Yoseph b. rabi Moshe ha-Ṣarfati [= the French] Ish Ḥay: | |Said Yoseph b. rabi Moshe ha-Ṣarfati [= the French] Ish Ḥay: | ||
| − | |style="text-align:right;"|‫<ref>51r</ref><big>אמר</big> יוסף בר משה הצרפתי איש חי | + | |style="width:45%; text-align:right;"|‫<ref>51r</ref><big>אמר</big> יוסף בר משה הצרפתי איש חי |
|- | |- | ||
| − | |<span style= | + | |<span style=color:green>'''Arithmetic contains signs for the unity of God:'''</span> |
Since I have seen that arithmetic is a magnificent and extremely lovable science and the Creator, blessed be He, has placed the secret of His unity in the property of number [lit. calculation], | Since I have seen that arithmetic is a magnificent and extremely lovable science and the Creator, blessed be He, has placed the secret of His unity in the property of number [lit. calculation], | ||
|style="text-align:right;"|מאשר ראיתי כי {{#annot:term|365,1200|XQbO}}חכמת החשבון{{#annotend:XQbO}} היא חכמה מפארה ונחמדת עד מאד והיוצר ב"ה שם בתכונת החשבון סוד אחדותו | |style="text-align:right;"|מאשר ראיתי כי {{#annot:term|365,1200|XQbO}}חכמת החשבון{{#annotend:XQbO}} היא חכמה מפארה ונחמדת עד מאד והיוצר ב"ה שם בתכונת החשבון סוד אחדותו | ||
|- | |- | ||
| − | | | + | |My heart and kidneys urged me to write a book about it, as I extracted from studies of the ancient scholars in a clear language, clarified for every thinker, for its way is hidden and concealed and requires a broad knowledge as the entrance of a hall. |
|style="text-align:right;"|יעצוני לבי וכליותי לחבר ממנה ספר אחד כאשר אוציא <sup>מ</sup>מחקרי החכמים הקדומים בלשון גלוי ומבואר לכל משכיל למען אשר דרכה נסתר ונעלם וצריכה דעת רחבה בפתחו של אולם | |style="text-align:right;"|יעצוני לבי וכליותי לחבר ממנה ספר אחד כאשר אוציא <sup>מ</sup>מחקרי החכמים הקדומים בלשון גלוי ומבואר לכל משכיל למען אשר דרכה נסתר ונעלם וצריכה דעת רחבה בפתחו של אולם | ||
|- | |- | ||
| Line 36: | Line 36: | ||
|style="text-align:right;"|וארויח אנכי גם כן שתשמר החכמה בקרבי היטב בהוציאי אותה במלת לשוני ואזכה ללמוד וללמד | |style="text-align:right;"|וארויח אנכי גם כן שתשמר החכמה בקרבי היטב בהוציאי אותה במלת לשוני ואזכה ללמוד וללמד | ||
|- | |- | ||
| − | |A short rhyme of praise to God – asking him for a shelter and for turning a good thought into act | + | |<span style=color:green>'''A short rhyme of praise to God – asking him for a shelter and for turning a good thought into act'''</span> |
| − | + | | | |
| − | |||
| − | |||
| − | |||
|- | |- | ||
| − | | | + | |My Creator shall be my strength and refuge. |
| − | + | |style="text-align:right;"|ויוצרי יהיה לי למעוז ולמחסה | |
| − | |style="text-align:right;"|וקראתי שם זה הספר עיר סיחון על שם כי חשבון עיר סיחון | + | |- |
| + | |He shall link my good thought to an action. | ||
| + | |style="text-align:right;"|ומחשבתי הטובה יצרף אותה לי למעשה | ||
| + | |- | ||
| + | |For His wonderful mercy and grace. | ||
| + | |style="text-align:right;"|למען רחמיו וחסדו אשר נפלאו | ||
| + | |- | ||
| + | |And His expressions that are more than can be numbered. | ||
| + | |style="text-align:right;"|ועצמו מספר כל מעבריו | ||
| + | |- | ||
| + | |May his name be excellent and glorious forever. | ||
| + | |style="text-align:right;"|יהי שמו משובח לעד ומפואר לנצח | ||
| + | |- | ||
| + | |I named this book ʽIr Siḥon ''For Ḥeshbon was the city of Siḥon'' [Numbers 21, 26]. | ||
| + | |style="text-align:right;"|וקראתי שם זה הספר עיר סיחון על שם ''כי חשבון עיר סיחון''‫<ref group=note>במדבר כא, כו</ref> | ||
|- | |- | ||
| | | | ||
| − | == Table of Contents == | + | == <span style=color:green>Table of Contents</span> == |
| | | | ||
|- | |- | ||
| − | | | + | |This book is divided into eleven chapters: |
| − | |style="text-align:right;"|ונחלק הספר הזה לאחד עשר שערים | + | |style="width:45%; text-align:right;"|ונחלק הספר הזה לאחד עשר שערים |
|- | |- | ||
| | | | ||
| + | *The first chapter: on the foundation of all numbers and the nature of the one. | ||
|style="text-align:right;"|<big>השער</big> הראשון ביסוד המספר ותולדות האחד | |style="text-align:right;"|<big>השער</big> הראשון ביסוד המספר ותולדות האחד | ||
|- | |- | ||
| | | | ||
| + | *The second chapter: on the ranks of the numbers and the values of the digits used by the experts of this science. | ||
|style="text-align:right;"|<big>השער</big> השני במדרגות ‫<ref>51v</ref>המספר וסכום האותיות אשר ישתמשו בהם החכמים בזאת המלאכה | |style="text-align:right;"|<big>השער</big> השני במדרגות ‫<ref>51v</ref>המספר וסכום האותיות אשר ישתמשו בהם החכמים בזאת המלאכה | ||
|- | |- | ||
| | | | ||
| + | *The third chapter: on the addition of numerous numbers to each other. | ||
|style="text-align:right;"|<big>השער</big> השלישי ב{{#annot:term|154,1166|gszd}}מחברת{{#annotend:gszd}} {{#annot:term|35,1200|pm5x}}חשבונות{{#annotend:pm5x}} רבים זה עם זה | |style="text-align:right;"|<big>השער</big> השלישי ב{{#annot:term|154,1166|gszd}}מחברת{{#annotend:gszd}} {{#annot:term|35,1200|pm5x}}חשבונות{{#annotend:pm5x}} רבים זה עם זה | ||
|- | |- | ||
| | | | ||
| + | *The fourth chapter: on the subtraction of a small number from a greater number. | ||
|style="text-align:right;"|<big>השער</big> הרביעי ב{{#annot:term|155,1193|Chcd}}מגרעת{{#annotend:Chcd}} {{#annot:term|35,1200|cDwJ}}חשבון{{#annotend:cDwJ}} קטן מחשבון גדול | |style="text-align:right;"|<big>השער</big> הרביעי ב{{#annot:term|155,1193|Chcd}}מגרעת{{#annotend:Chcd}} {{#annot:term|35,1200|cDwJ}}חשבון{{#annotend:cDwJ}} קטן מחשבון גדול | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|<big>השער</big> החמישי ב{{#annot:term|156,1253|7voJ}}כפילת{{#annotend:7voJ}} הכאת האחדים על עצמן או על אחרים זולתם או ב{{#annot:term| | + | *The fifth chapter: on the multiplication of the units by each other, or by others, or on the multiplication of any number by itself, or by another number. |
| + | |style="text-align:right;"|<big>השער</big> החמישי ב{{#annot:term|156,1253|7voJ}}כפילת{{#annotend:7voJ}} הכאת האחדים על עצמן או על אחרים זולתם או ב{{#annot:term|185,1230|RIxQ}}כפול{{#annotend:RIxQ}} כל חשבון על עצמו או על חשבון אחר | ||
|- | |- | ||
| | | | ||
| + | *The sixth chapter: on the division of a great number by a smaller number. In this chapter I will also discuss the scales of multiplication, division, addition and subtraction. | ||
|style="text-align:right;"|<big>השער</big> הששי ב{{#annot:term|157,1221|h7Iv}}חלוקת{{#annotend:h7Iv}} חשבון גדול על חשבון קטן ממנו ובזה השער אדבר על מאזני הכפל והחלוק [והחבור]‫<ref>Vatican marg.</ref> והמגרעת | |style="text-align:right;"|<big>השער</big> הששי ב{{#annot:term|157,1221|h7Iv}}חלוקת{{#annotend:h7Iv}} חשבון גדול על חשבון קטן ממנו ובזה השער אדבר על מאזני הכפל והחלוק [והחבור]‫<ref>Vatican marg.</ref> והמגרעת | ||
|- | |- | ||
| | | | ||
| + | *The seventh chapter: on the extraction of the approximate root of the integer. | ||
|style="text-align:right;"|<big>השער</big> השביעי בלקיחת גדר המספר השלם היותר קרוב אליו | |style="text-align:right;"|<big>השער</big> השביעי בלקיחת גדר המספר השלם היותר קרוב אליו | ||
|- | |- | ||
| | | | ||
| + | *The eighth chapter: on the ratio of a number to another number. | ||
|style="text-align:right;"|<big>השער</big> השמיני במערכת חשבון אחד מחשבון אחר | |style="text-align:right;"|<big>השער</big> השמיני במערכת חשבון אחד מחשבון אחר | ||
|- | |- | ||
| | | | ||
| + | *The ninth chapter: on knowing the fractions of integers - their multiplication, division, addition, or subtraction. | ||
|style="text-align:right;"|<big>השער</big> התשיעי בידיעת חלקי השבר מן השלם בין בכפל בין בחלוק בחבור או במגרעת | |style="text-align:right;"|<big>השער</big> התשיעי בידיעת חלקי השבר מן השלם בין בכפל בין בחלוק בחבור או במגרעת | ||
|- | |- | ||
| | | | ||
| + | *The tenth chapter: on knowing the factors of square [numbers] that are inexpressible numbers by approximation. | ||
|style="text-align:right;"|<big>השער</big> העשירי בידיעת צלעות המרובעים מחשבון החרש והאלם על דרך קרוב | |style="text-align:right;"|<big>השער</big> העשירי בידיעת צלעות המרובעים מחשבון החרש והאלם על דרך קרוב | ||
|- | |- | ||
| | | | ||
| + | *The eleventh chapter: on nice rules, which are the anecdotes of this science. I will note in this chapter some profound difficult questions with the help of the God of Israel. | ||
|style="text-align:right;"|<big>השער</big> האחד עשר בכללים נחמדים והם פרפראות ‫<ref>52r</ref>החכמה הזאת וקצת מהשאלות העמוקות והקשות ואזכיר בשער הזה בעזרת אלהי ישראל | |style="text-align:right;"|<big>השער</big> האחד עשר בכללים נחמדים והם פרפראות ‫<ref>52r</ref>החכמה הזאת וקצת מהשאלות העמוקות והקשות ואזכיר בשער הזה בעזרת אלהי ישראל | ||
|- | |- | ||
| Line 92: | Line 114: | ||
| | | | ||
| − | == Chapter One – The Nature of the One and the Foundation of | + | == Chapter One – The Nature of the One and the Foundation of Numbers == |
| − | + | |style="width: 45%; text-align:right;"|<big>השער הראשון</big> בתולדות האחד ויסוד המספרים | |
|- | |- | ||
| | | | ||
| − | === Numeration === | + | === <span style=color:green>Numeration</span> === |
| | | | ||
|- | |- | ||
| | | | ||
| − | :*It is a known, clear and true thing that the one is not affected by | + | :*It is a known, clear and true thing that the one is not affected by multiplicity nor by change, but is the cause of any change and multiplicity. |
| − | |style="text-align:right;"|דבר ידוע ברור | + | |style="text-align:right;"|דבר ידוע ברור ואמיתי כי האחד איננו מקבל לא רבוי ולא שנוי אכן הוא סבת כל רבוי ושנוי |
|- | |- | ||
| | | | ||
| Line 111: | Line 133: | ||
| | | | ||
:Thereof every learned person may understand some hints regarding the secret of the unity of God the Glorious and Awful. | :Thereof every learned person may understand some hints regarding the secret of the unity of God the Glorious and Awful. | ||
| − | |style="text-align:right;"|ומזה יוכל להבין כל משכיל קצת רמיזות מסוד אחדות | + | |style="text-align:right;"|ומזה יוכל להבין כל משכיל קצת רמיזות מסוד אחדות השם הנכבד והנורא |
|- | |- | ||
| − | |<span style= | + | |<span style=color:green>The names of the numbers:</span> |
| | | | ||
|- | |- | ||
| − | !<span style= | + | !<span style=color:green>Units</span> |
| | | | ||
|- | |- | ||
| | | | ||
| − | * | + | *When we add one to one, which is the first combination, we call it "two". |
| − | |style="text-align:right;"|והנה כאשר {{#annot:term|178,1165|vicf}}נחבר{{#annotend:vicf}} אחד עם אחד והיא ההרכבה | + | |style="text-align:right;"|והנה כאשר {{#annot:term|178,1165|vicf}}נחבר{{#annotend:vicf}} אחד עם אחד והיא ההרכבה הראשונה נקרא זה שנים |
|- | |- | ||
| | | | ||
| − | * | + | *When we add one to the two, we call it "three". |
| − | |style="text-align:right;"|וכש{{#annot:term|178,1206|uPja}} נוסיף{{#annotend:uPja}} על השנים אחד נקרא זה שלשה | + | |style="text-align:right;"|וכש{{#annot:term|178,1206|uPja}} נוסיף{{#annotend:uPja}} על השנים אחד <s>והיא ההרכבה הראשונה</s> נקרא זה שלשה |
|- | |- | ||
| | | | ||
| − | * | + | *When we add one to the three, we call it "four". |
| − | |style="text-align:right;"|וכשנוסיף על | + | |style="text-align:right;"|וכשנוסיף על שלשה אחד נקרא זה ארבעה |
|- | |- | ||
| | | | ||
| − | * | + | *By adding one to the four we call it "five". |
| − | |style="text-align:right;"|וכן ב{{#annot:term|154,1207|83ML}}תוספת{{#annotend:83ML}} אחד על הארבעה | + | |style="text-align:right;"|וכן ב{{#annot:term|154,1207|83ML}}תוספת{{#annotend:83ML}} אחד על הארבעה נקרא זה חמשה |
|- | |- | ||
| | | | ||
| − | * | + | *By adding one to five it is called "six". |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ותוספת אחד על חמשה יקרא ששה |
|- | |- | ||
| | | | ||
| − | * | + | *By adding one to six it is called "seven". |
|style="text-align:right;"|ובתוספת אחד על ששה יקרא שבעה | |style="text-align:right;"|ובתוספת אחד על ששה יקרא שבעה | ||
|- | |- | ||
| | | | ||
| − | * | + | *By adding one to seven it is called "eight". |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ובתוס[פת] אחד על שבעה יקרא שמונה |
|- | |- | ||
| − | |||
| | | | ||
| + | *By adding one to eight it is called "nine". | ||
| + | |style="text-align:right;"|ובתוספת אחד על שמונה יקרא תשעה | ||
|- | |- | ||
| − | | | + | |These nine numbers are called "units". |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ואלה המספרים התשעה נקראים אחדים |
|- | |- | ||
| + | !<span style=color:green>Tens</span> | ||
| | | | ||
| − | + | |- | |
| − | + | |When we add one to nine, we call it ten, which is the beginning of the [rank of] tens. | |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וכאשר נוסיף אחד על תשעה ‫<ref>52v</ref>נקרא זה עשרה והוא ראשית כל חשבון עשרות |
|- | |- | ||
| | | | ||
| − | * | + | *Ten in the rank of tens is like one in the rank of units. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והנה העשרה בחשבון העשרות כמו האחד בחשבון האחדים |
|- | |- | ||
| | | | ||
| − | * | + | *When we have two tens, we call them "twenty". |
| + | |style="text-align:right;"|וכשיהיו לנו שני עשרות נקרא אותם עשרים | ||
| + | |- | ||
| + | | | ||
| + | *To three tens we call "thirty". | ||
|style="text-align:right;"|ונקרא לשלש עשרות שלשים | |style="text-align:right;"|ונקרא לשלש עשרות שלשים | ||
|- | |- | ||
| | | | ||
| − | * | + | *To four tens - "forty". |
|style="text-align:right;"|ולארבע עשרות ארבעים | |style="text-align:right;"|ולארבע עשרות ארבעים | ||
|- | |- | ||
| | | | ||
| − | * | + | *To five tens - "fifty". |
| − | |style="text-align:right;"|ולחמש חמשים | + | |style="text-align:right;"|ולחמש עשרות חמשים |
|- | |- | ||
| | | | ||
| − | * | + | *To six - "sixty". |
|style="text-align:right;"|ולשש ששים | |style="text-align:right;"|ולשש ששים | ||
|- | |- | ||
| | | | ||
| − | * | + | *To seven - "seventy". |
|style="text-align:right;"|ולשבע שבעים | |style="text-align:right;"|ולשבע שבעים | ||
|- | |- | ||
| | | | ||
| − | * | + | *To eight - "eighty". |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ולשמונה שמונים |
|- | |- | ||
| | | | ||
| − | *Ninety | + | *To nine - "Ninety". |
|style="text-align:right;"|ולתשע עשרות תשעים | |style="text-align:right;"|ולתשע עשרות תשעים | ||
| + | |- | ||
| + | |All these names are derived from the names of the units. | ||
| + | |style="text-align:right;"|וכל השמות האלה הם מושאלות משמות האחדים | ||
|- | |- | ||
| | | | ||
| − | : | + | :Ninety in the tens is like nine in the units. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והנה תשעים בעשרות כמו תשעה באחדים |
|- | |- | ||
| − | !<span style= | + | !<span style=color:green>Hundreds</span> |
| | | | ||
|- | |- | ||
| | | | ||
| − | :When we have ten tens we | + | :When we have ten tens we call them by an inclusive name a hundred, which is the beginning of the [rank of] hundreds, as one is the beginning of the units and ten is the beginning of the tens. |
|style="text-align:right;"|וכאשר יהיה לנו עשר עשרות נקרא להם בשם כולל מאה והוא ראשית חשבון המאות כמו האחד ראשית האחדים והעשרה ראשית העשרות | |style="text-align:right;"|וכאשר יהיה לנו עשר עשרות נקרא להם בשם כולל מאה והוא ראשית חשבון המאות כמו האחד ראשית האחדים והעשרה ראשית העשרות | ||
|- | |- | ||
| − | !<span style= | + | !<span style=color:green>Thousands</span> |
| | | | ||
|- | |- | ||
| | | | ||
| − | :When ten hundred are summed we call them | + | :When ten hundred are summed we call them by an inclusive name a thousand, which is the beginning of the thousands, as the hundred, which is the beginning of the hundreds. |
| − | |style="text-align:right;"|וכש{{#annot:term| | + | |style="text-align:right;"|וכש{{#annot:term|178,1216|WrFA}}יתקבצו{{#annotend:WrFA}} עשרה מאות נקרא להם בשם כולל אלף והוא ראשית האלפים כמו מאה ראשית המאות |
|- | |- | ||
| − | | | + | |?? |
| − | |style="text-align:right;"|אמנם | + | |style="text-align:right;"|אמנם למאת אמנם אין להם שם כולל עד שנגיע לעשר מאות שנקראו אלף כאמור |
|- | |- | ||
|But the thousands have no inclusive name. | |But the thousands have no inclusive name. | ||
| − | |style="text-align:right;"|וכן האלפים | + | |style="text-align:right;"|וכן האלפים אין להם שם כולל |
|- | |- | ||
| − | !<span style= | + | !<span style=color:green>The twelve names of numbers</span> |
| | | | ||
|- | |- | ||
| Line 222: | Line 253: | ||
| | | | ||
*Those are the nine names of the units; | *Those are the nine names of the units; | ||
| − | |style="text-align:right;"|ואלה הם תשעה שמות האחדים | + | |style="text-align:right;"|ואלה הם תשעה שמות ‫<ref>53r</ref>האחדים |
|- | |- | ||
| | | | ||
| Line 236: | Line 267: | ||
|style="text-align:right;"|ושם האלף | |style="text-align:right;"|ושם האלף | ||
|- | |- | ||
| − | | | + | |All numbers are derived from these twelve names. |
| − | |style="text-align:right;"|והנה כל המספרים ילקחו | + | |style="text-align:right;"|והנה כל המספרים יחלקו [ילקחו]<ref>marg.</ref> מאלה השנים עשר שמות |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|כי | + | :For, twenty, two hundred and two thousand are like two units, each in its own rank. |
| + | |style="text-align:right;"|כי עשרים ומאתים ואלפים הם כמו שני אחדים וכל אחד ואחד כפי מעלתו | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|וכן כאשר נאמר אחד עשר או שנים עשר | + | :Also when we say eleven [in Hebrew: "one-ten"], or twelve [in Hebrew: "two-ten"], these names consist of units and tens. |
| + | |style="text-align:right;"|וכן כאשר נאמר אחד עשר או שנים עשר הם שמות מורכבים מאחדים ועשרות | ||
|- | |- | ||
| − | | | + | |In this way all the numbers are generated and derived from these twelve separate names. |
| − | |style="text-align:right;"|ועל | + | |style="text-align:right;"|ועל דרך הזה יתילדו וילוו כל המספרים מאלו השנים עשר שמות המפורשים |
|- | |- | ||
|} | |} | ||
| Line 253: | Line 286: | ||
| | | | ||
| − | == Chapter Two – the | + | == Chapter Two – the Ranks of the Numbers and the Values of the Digits Used by the Experts of this Science == |
| − | + | |style="width:45%; text-align:right;"|<big>השער השני</big> ב{{#annot:term|203,1344|f28e}}מדרגות{{#annotend:f28e}} המספר ו{{#annot:term|217,1600|Ydqn}}סכום האותיות{{#annotend:Ydqn}} אשר ישתמשו בהם החכמים בזאת המלאכה | |
|- | |- | ||
| − | !The names of the ranks | + | !<span style=color:green>The names of the ranks</span> |
| | | | ||
|- | |- | ||
| − | |It was clarified in the | + | |It was clarified in the preceding chapter that all the names of numbers are derived from the nine names of the units until comes the tenth number which we call by one inclusive name. |
| − | |style="text-align:right;"|הנה התבאר בשער הקודם | + | |style="text-align:right;"|הנה התבאר בשער הקודם כי כל שמות המספרים הם מושאלים מתשע שמות האחדים עד אשר יבוא החשבון העשירי ונקרא לו בשם כולל |
|- | |- | ||
| − | | | + | |Therefore, the numbers are divided into ranks. |
|style="text-align:right;"|ומפני זה נחלקו המספרים למדרגות מדרגות | |style="text-align:right;"|ומפני זה נחלקו המספרים למדרגות מדרגות | ||
|- | |- | ||
| − | | | + | |The units are called "the first rank", the tens - "the second rank", the hundreds - "the third rank", the thousands - "the fourth rank", and so on endlessly. |
| − | |style="text-align:right;"|ויקראו | + | |style="text-align:right;"|ויקראו האחדים מדרגה ראשונה והעשרות מדרגה שנייה והמאות מדרגה שלישית והאלפים מדרגה רביעית וככה עד אין קץ |
| + | |- | ||
| + | |For every rank is the tenth of the following rank. | ||
| + | |style="text-align:right;"|כי כל {{#annot:term|203,1344|OdWT}}מדרגה{{#annotend:OdWT}} היא עשור המדרגה הבאה אחריה | ||
| + | |- | ||
| + | |According to this we call the tens of thousands "the fifth rank" and the hundreds of thousands "the sixth rank". | ||
| + | |style="text-align:right;"|ולפי זה נקרא לעשרת אלפים מדרגה חמישית ולמאה ‫<ref>53v</ref>אלף מדרגה ששית | ||
| + | |- | ||
| + | |This is the way of the ranks of the number. | ||
| + | |style="text-align:right;"|וזהו דרך מדרגות המספר | ||
|- | |- | ||
| | | | ||
| − | === The Positional Decimal System === | + | === <span style=color:green>The Positional Decimal System</span> === |
| | | | ||
|- | |- | ||
| − | |Since all the numbers are circulating by nine, for we find nine numbers in the rank of units, nine numbers in the rank of tens, and so on, in each rank there are nine numbers, it is | + | |Since all the numbers are circulating by nine, for we find nine numbers in the rank of units, nine numbers in the rank of tens, and so on, in each rank there are nine numbers, it is enough to write any small or large number with nine letters, each of which we consider as the units, that are up to nine. |
| − | |style="text-align:right;"|ובעבור כי כל החשבונות מתגלגלים על תשעה באשר נמצא | + | |style="text-align:right;"|ובעבור כי כל החשבונות מתגלגלים על תשעה באשר נמצא תשעה חשבונות ממדרגת אחדים ותשעה חשבונות ממדרגת עשרות וכן בכל המדרגות יש תשעה חשבונות בכל אחת מהן<br> |
| − | יספיק לכתוב כל חשבון קטן או גדול | + | יספיק לכתוב כל חשבון קטן או גדול בתשע אותיות שנחשוב כל אחת מהן כמו האחדים שהם עד תשעה |
| + | |- | ||
| + | !<span style=color:green>The numerals</span> | ||
| + | | | ||
|- | |- | ||
| − | + | |These are the digits used in this science: | |
|style="text-align:right;"|ואלה הם ה{{#annot:term|204,1332|phuN}}אותיות{{#annotend:phuN}} המשמשות בחכמה הזאת | |style="text-align:right;"|ואלה הם ה{{#annot:term|204,1332|phuN}}אותיות{{#annotend:phuN}} המשמשות בחכמה הזאת | ||
|- | |- | ||
| Line 294: | Line 339: | ||
|- | |- | ||
| − | ! | + | !<span style=color:green>tens</span> |
| − | + | | | |
|- | |- | ||
| − | | | + | |When we need to write the number ten, we do it this way: |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וכשהתצטרך לכתוב חשבון העשרה נעשה על הדרך הזה |
|- | |- | ||
| − | |Writing numbers with numerals, including zeroes or without them | + | |It is known that the tens are the second rank. |
| + | |style="text-align:right;"|בידוע כי העשרות הם המדרגה השנית | ||
| + | |- | ||
| + | |It was already explained that the ratio of the ten to the tens is [the same as] the ratio of the one to the units. | ||
| + | |style="text-align:right;"|וכבר התבאר כי יחס העשרה אל העשרות יחס האחד אל האחדים | ||
| + | |- | ||
| + | |Therefore, we only need to write the letter aleph [א] that indicates one and make a mark that this digit is in the second rank. | ||
| + | |style="text-align:right;"|על כן <sup>[אי]</sup> אנחנו צריכין כי אם לכתוב אות האלף המורה לאחד ולעשות היכר וסימן שהאות הזאת היא ממדרגה השנית | ||
| + | |- | ||
| + | |The arithmeticians agreed to make a mark indicating the ranks in the shape of a circle as this 0 and this shape is called sifra. | ||
| + | |style="text-align:right;"|והסכימו {{#annot:term|782,1328|0hSS}}חכמי החשבון{{#annotend:0hSS}} לעשות סימן היכר המדרגות בצורת עגול כדמות זה 0 וקוראים למורה הזאת סיפרא | ||
| + | |- | ||
| + | !<span style=color:green>Writing numbers with numerals, including zeroes or without them</span> | ||
| | | | ||
|- | |- | ||
| | | | ||
| − | *twenty | + | *When we want to write twenty, we write a zero first and after is 2, in the second rank, which indicates two tens. |
| − | |style="text-align:right;"|וכשנרצה לכתוב עשרים נכתוב {{#annot:term|205,1554|OR0i}}סיפרא{{#annotend:OR0i}} | + | |style="text-align:right;"|‫<ref>54r</ref>וכשנרצה לכתוב עשרים נכתוב {{#annot:term|205,1554|OR0i}}סיפרא{{#annotend:OR0i}} בתחלה ואחריה אות ב' במדרגה השנית ויורה זה שתי עשרות |
|- | |- | ||
| | | | ||
| − | *hundred | + | *When we want [to write] a hundred, we write two zeros, then the digit 1 in the third rank, and this indicates a hundred. |
| − | |style="text-align:right;"|וכאשר נבקש | + | |style="text-align:right;"|וכאשר נבקש מאה נכתוב שתים {{#annot:term|205,1554|iNJi}}סיפראש{{#annotend:iNJi}} ואות הא' במדרגה השלישית ויורה זה מאה |
|- | |- | ||
| − | + | |When we have units and tens, we write the units in the first rank and after it the tens in the second rank. | |
| − | |style="text-align:right;"|ולעולם כשיהיו לנו אחדים ועשרות נכתוב במדרגה הראשונה האחדים | + | |style="text-align:right;"|ולעולם כשיהיו לנו אחדים ועשרות נכתוב במדרגה הראשונה האחדים ואחריהם במדרגה השנית העשרות |
|- | |- | ||
| − | + | |If we do not have tens, only units and hundreds, we write the units in the first rank, a zero in the second [rank], and the hundreds in the third [rank]. | |
| − | |style="text-align:right;"|ואם | + | |style="text-align:right;"|ואם אין לנו עשרות כי אם אחדים ומאות נכתוב האחדים במדרגה הראשונה וספרא אחת בשנית והמאות בשלישית |
|- | |- | ||
| − | | | + | |Similarly, we write two or three zeros and so on endlessly, as we need according to the number. |
| − | |style="text-align:right;"|וכן נשים | + | |style="text-align:right;"|וכן נשים שתים או שלש סיפראש כאשר נצטרך לפי החשבון עד אין חקר |
| + | |- | ||
| + | |We always write each number in its rank. | ||
| + | |style="text-align:right;"|ונכתוב לעולם כל חשבון וחשבון במדרגתו | ||
|- | |- | ||
|} | |} | ||
| Line 325: | Line 385: | ||
| | | | ||
| − | == Chapter Three – Addition == | + | == Chapter Three – Addition of Numerous Numbers to Each Other == |
| − | |style="text-align:right;"|<big>השער השלישי ב{{#annot:term|154,1166|ZM9D}}מחברת{{#annotend:ZM9D}} רבים זה עם זה | + | |style="width:45%; text-align:right;"|<big>השער השלישי</big> ב{{#annot:term|154,1166|ZM9D}}מחברת{{#annotend:ZM9D}} חשבונות רבים זה עם זה |
|- | |- | ||
| − | !Written Addition | + | !<span style=color:green>Written Addition</span> |
| | | | ||
|- | |- | ||
| − | |<span style= | + | |<span style=color:green>'''Description of the procedure:'''</span> |
| | | | ||
|- | |- | ||
|The procedure of the addition of numbers is as follows: | |The procedure of the addition of numbers is as follows: | ||
| − | |style="text-align:right;"|{{#annot:term|469,1894|uQiQ}}דרך{{#annotend:uQiQ}} מחברת חשבונות כך | + | |style="text-align:right;"|{{#annot:term|469,1894|uQiQ}}דרך{{#annotend:uQiQ}} מחברת <sup>ה</sup>חשבונות כך הוא |
|- | |- | ||
| | | | ||
| − | *We write each number of the addition request one beneath the other, each in a row of its own, rank | + | *We write each number of the addition request one beneath the other, each in a row of its own, each rank beneath its corresponding rank, then we draw a line. |
| − | |style="text-align:right;"|נכתוב כל מספר ומספר מבקשת | + | |style="text-align:right;"|נכתוב כל מספר ומספר מבקשת החבור זה תחת זה כל אחד ואחד בטור בפני עצמו ממדרגה תחת מדרגה הדומה לה ואחר נעביר קו דיו |
|- | |- | ||
| | | | ||
*We start from the rank of units and sum all the units. | *We start from the rank of units and sum all the units. | ||
| − | |style="text-align:right;"|ונתחיל | + | |style="text-align:right;"|ונתחיל <sup>ב</sup>מדרגה הראשונה ו{{#annot:term|178,1210|gkYV}}נקבץ{{#annotend:gkYV}} כל האחדים |
|- | |- | ||
| | | | ||
| − | :*We write the sum under | + | :*We write the sum under the line, if it is less than ten. |
| − | |style="text-align:right;"|וה{{#annot:term|388,1217|AFvL}}מקובץ{{#annotend:AFvL}} נכתבנו תחת קו | + | |style="text-align:right;"|וה{{#annot:term|388,1217|AFvL}}מקובץ{{#annotend:AFvL}} נכתבנו תחת קו הדיו אם לא ‫<ref>54v</ref>יספיק לעשר |
|- | |- | ||
| | | | ||
:*If [the sum] is tens, we write a digit in the column of the second rank, as the number of the tens of the sum and we write a zero alone under the line. | :*If [the sum] is tens, we write a digit in the column of the second rank, as the number of the tens of the sum and we write a zero alone under the line. | ||
| − | |style="text-align:right;"|אמנם אם ילך בעשרות נכתוב אות בטורי המספר במדרגה | + | |style="text-align:right;"|אמנם אם ילך בעשרות נכתוב אות בטורי המספר במדרגה השניה כפי מספר עשרות המקובץ על עשרות המקובץ ונכתוב ספרא בלבד תחת קו הדיו |
|- | |- | ||
| | | | ||
| − | :*If the sum is [units] and tens, we should write [the units] under the line and in the second rank we write the number of the tens as is stated. | + | :*If the sum is [units] and tens, we should write [the units] under the line and in the second rank [we write] the number of the tens as is stated. |
| − | |style="text-align:right;"|ואם יעדיף המקובץ על עשרות אין אנחנו צריכים כי אם לכתוב תחת הקו העודף ההוא | + | |style="text-align:right;"|ואם יעדיף המקובץ על עשרות אין אנחנו צריכים כי אם לכתוב תחת הקו העודף ההוא והמדרגה השניה כפי מספר העשרות כאמור |
|- | |- | ||
| | | | ||
*We proceed this way and do with the rest of the ranks as we did with the rank of units, writing the sums of the ranks successively by the order beneath the line. | *We proceed this way and do with the rest of the ranks as we did with the rank of units, writing the sums of the ranks successively by the order beneath the line. | ||
| − | |style="text-align:right;"|ובדרך הזה נלך ונעשה גם כן כאשר עשינו | + | |style="text-align:right;"|ובדרך הזה נלך ונעשה גם כן כאשר עשינו ממדרגת האחדים מכל שאר המדרגות ונכתוב כל קבוץ המדרגות בזה אחר זה בסדור תחת קו הדיו |
|- | |- | ||
| | | | ||
*The [total] sum is what comes out from the sum of the ranks arranged under the line. | *The [total] sum is what comes out from the sum of the ranks arranged under the line. | ||
| − | |style="text-align:right;"|ומה שיצא מ{{#annot:term|154,1211|AtJO}} | + | |style="text-align:right;"|ומה שיצא מ{{#annot:term|154,1211|AtJO}}קבוץ{{#annotend:AtJO}} המדרגות מס<sup>ו</sup>דר תחת <sup>ה</sup>קו <s>הדיו</s> הוא ה{{#annot:term|388,1220|szGK}}מחובר{{#annotend:szGK}} |
|- | |- | ||
|When we sum a digit with a digit, we always consider each of them, in whichever rank they are, as if they are units, then we find their true meaning in their own rank. | |When we sum a digit with a digit, we always consider each of them, in whichever rank they are, as if they are units, then we find their true meaning in their own rank. | ||
| − | |style="text-align:right;"|ולעולם כשנחבר {{#annot:term|204,1332|OGlo}}אות{{#annotend:OGlo}} עם אות נחשוב כל אחת ואחת | + | |style="text-align:right;"|ולעולם כשנחבר {{#annot:term|204,1332|OGlo}}אות{{#annotend:OGlo}} עם אות נחשוב כל אחת ואחת באיזו מדרגה שתהיין כאלו הם אחדים ואחר נמצא אמיתתם במדרגתם |
|- | |- | ||
|Any thinker will understand that the reason for writing the number of tens of the sum of a certain rank in the following rank, is that every digit in the ranks is tenth of the next rank. | |Any thinker will understand that the reason for writing the number of tens of the sum of a certain rank in the following rank, is that every digit in the ranks is tenth of the next rank. | ||
| − | |style="text-align:right;"|וכל משכיל יבין כי טעם כתיבת מספר העשרות | + | |style="text-align:right;"|וכל משכיל יבין כי טעם [כתיבת מספר]‫<ref>Vatican om.</ref> העשרות מהתחבר באותיות המדרגה ההיא במדרגה הבאה אחריה הוא לפי שכל אות ואות מהמדרגות היא עשור מן המדרגה הבאה אחריה |
|- | |- | ||
| | | | ||
*If there is one or two ranks in the lines of the addend numbers, of which the whole column are zeros, zeros should be written correspondingly beneath the line as the number of these ranks. | *If there is one or two ranks in the lines of the addend numbers, of which the whole column are zeros, zeros should be written correspondingly beneath the line as the number of these ranks. | ||
| − | |style="text-align:right;"|ואם יהיה | + | |style="text-align:right;"|ואם יהיה בטור<sup>י</sup> מספר חשבונות החבור מדרגה אחת או שתים שכל טוריה סיפראש צריך לכתוב תחת קו הדיו סיפראש כאשר תבאנה במקומן כפי מספר המדרגות ההם |
|- | |- | ||
|In order that this mentioned addition operation will be better clarified to every person I shall discuss it by the experience way in the following calculations: | |In order that this mentioned addition operation will be better clarified to every person I shall discuss it by the experience way in the following calculations: | ||
| − | |style="text-align:right;"|ולמען אשר יתבאר | + | |style="text-align:right;"|ולמען ‫<ref>55r</ref>אשר יתבאר היטב אצל כל בני אדם מלאכת ה{{#annot:term|154,1208|xIzg}}חבור{{#annotend:xIzg}} הזאת הנזכרת אדבר ממנה [בדרך]‫<ref>Vatican om.</ref> הניסיון בחשבונות אלו |
|- | |- | ||
| | | | ||
*{{#annot:9208+3801|154|Hq9T}}We wish to know how much is the sum of nine thousand, two hundred and eight, with three thousand, eight hundred and one. | *{{#annot:9208+3801|154|Hq9T}}We wish to know how much is the sum of nine thousand, two hundred and eight, with three thousand, eight hundred and one. | ||
:<math>\scriptstyle9208+3801</math> | :<math>\scriptstyle9208+3801</math> | ||
| − | |style="text-align:right;"|בקשנו לידע כמה מחובר תשע אלפים ומאתים | + | |style="text-align:right;"|<big>בקשנו</big> לידע כמה מחובר תשע אלפים ומאתים ושמונה עם שלשת אלפים ושמונה מאות ואחד{{#annotend:Hq9T}} |
|- | |- | ||
| | | | ||
| Line 432: | Line 492: | ||
|- | |- | ||
|} | |} | ||
| − | | | + | |- |
| − | ::<span style=color: | + | | colspan="2"| |
| + | ::<span style=color:green>[Illustration of the procedure:]</span> | ||
::{| | ::{| | ||
|- | |- | ||
| − | |920<span style= | + | |920<span style=color:red>8</span>||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{8+1}}={\color{blue}{9}}}</math>||92<span style=color:red>0</span>8||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{0+0}}={\color{blue}{0}}}</math>||9<span style=color:red>2</span>08||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{2+8}}={\color{green}{1}}{\color{blue}{0}}}</math>||<span style=color:red>9</span>208||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{green}{1}}{\color{red}{+9+3}}={\color{blue}{13}}}</math>|| 9208 |
|- | |- | ||
| − | |<u>380<span style= | + | |<u>380<span style=color:red>1</span></u>||<u>38<span style=color:red">0</span>1</u>||<u>3<span style=color:red>8</span>01</u>||<u><span style=color:red>3</span>801</u>||<u> 3801</u> |
|- | |- | ||
| − | | ||   <span style= | + | | ||   <span style=color:#0000FF>9</span>||  <span style=color:#0000FF>0</span>9||<span style=color:#0000FF>10</span>09||<span style=color:#0000FF>13</span>009 |
|} | |} | ||
| − | + | ||
|- | |- | ||
| | | | ||
| − | :*<span style= | + | :*<span style=color:green>'''first rank: 9'''</span> |
::The sum of the first rank is smaller than ten, hence we write the result beneath the line, so it is 9. | ::The sum of the first rank is smaller than ten, hence we write the result beneath the line, so it is 9. | ||
|style="text-align:right;"|והנה {{#annot:term|388,1217|qKhT}}מקובץ{{#annotend:qKhT}} המדרגה הראשונה אינו מספיק לעשר ועל כן נכתוב העולה תחת קו הדיו והנה הוא ט‫' | |style="text-align:right;"|והנה {{#annot:term|388,1217|qKhT}}מקובץ{{#annotend:qKhT}} המדרגה הראשונה אינו מספיק לעשר ועל כן נכתוב העולה תחת קו הדיו והנה הוא ט‫' | ||
|- | |- | ||
| | | | ||
| − | :*<span style= | + | :*<span style=color:green>'''second rank: 0'''</span> |
| − | ::Since there is no digit but zeros in the second rank, we write one zero beneath the line, after the 9 that we wrote for the digits of the first rank. | + | ::Since there is no digit but zeros in the second rank, we write one zero beneath the line, after the 9 that we wrote for the sum of the digits of the first rank. |
| − | |style="text-align:right;"|וכאשר אין במדרגה | + | |style="text-align:right;"|וכאשר אין במדרגה השנייה אות כלל כי אם סיפראש לבדנה נכתוב תחת הקו סיפרא אחת אחר הט' שכתבנו בעבור חבור אותיות המדרגה הראשונה |
|- | |- | ||
| | | | ||
| − | :*<span style= | + | :*<span style=color:green>'''third rank: 0'''</span> |
| − | ::Since the sum of the third rank is ten, we write 1 beneath the lines of the numbers in the following fourth rank and | + | ::Since the sum of the third rank is ten, we write 1 beneath the lines of the numbers in the following fourth rank and a zero in the third [rank] beneath the line, next to the zero that we wrote after the 9. |
| − | |style="text-align:right;"|ובעבור שמקובץ המדרגה השלישית הוא עשר נכתוב תחת טורי חשבונות המספרים במדרגה הרביעית הבאה אחריה א' | + | |style="text-align:right;"|ובעבור שמקובץ המדרגה השלישית הוא עשר נכתוב תחת טורי חשבונות המספרים במדרגה הרביעית הבאה אחריה א' תחת קו הדיו סיפרא אחת בשלישית אצל הסיפרא שכתבנו אחר הט‫' |
|- | |- | ||
| | | | ||
| − | :*<span style= | + | :*<span style=color:green>'''fourth-fifth ranks: 13'''</span> |
::The sum of the fourth rank is thirteen, therefore we write 1 for the ten in the fifth rank; we place the rest, which is three, beneath the line next to the last zero and after the three we write the 1, from which we have formed the fifth rank. | ::The sum of the fourth rank is thirteen, therefore we write 1 for the ten in the fifth rank; we place the rest, which is three, beneath the line next to the last zero and after the three we write the 1, from which we have formed the fifth rank. | ||
| − | |style="text-align:right;"|והנה מקובץ המדרגה הרביעית הוא שלשה עשר ומפני זה נכתוב א' במדרגה חמישית בעבור העשרה ונשים העודף שהוא שלשה תחת הקו סמוך לסיפרא האחרונה | + | |style="text-align:right;"|והנה מקובץ המדרגה הרביעית הוא שלשה עשר ומפני זה נכתוב א' במדרגה חמישית בעבור העשרה ונשים העודף שהוא שלשה תחת הקו סמוך לסיפרא האחרונה ואחר אלו השלשה נכתוב הא' אשר חדשנו ממנה מדרגה חמישית |
|- | |- | ||
| − | |<span style= | + | |<span style=color:green>'''The sum: 13009'''</span> We find that the [total] sum is thirteen thousand and nine. |
| − | |style="text-align:right;"|ונמצא שה{{#annot:term|388,1220|ba1O}}מחובר{{#annotend:ba1O}} הוא שלשה עשר אלף ותשעה | + | |style="text-align:right;"|‫<ref>55v</ref>ונמצא שה{{#annot:term|388,1220|ba1O}}מחובר{{#annotend:ba1O}} הוא שלשה עשר אלף ותשעה |
|- | |- | ||
|} | |} | ||
| Line 474: | Line 535: | ||
== Chapter Four – Subtraction of a Small Number from a Greater Number == | == Chapter Four – Subtraction of a Small Number from a Greater Number == | ||
| − | |style="text-align:right;"|<big>השער הרביעי במגרעת חשבון קטן מחשבון | + | |style="width:45%; text-align:right;"|<big>השער הרביעי</big> במגרעת חשבון קטן מחשבון גדול |
|- | |- | ||
| − | !Written | + | !<span style=color:green>Written Subtraction</span> |
| | | | ||
|- | |- | ||
| − | |<span style= | + | |<span style=color:green>'''Description of the procedure:'''</span> |
| | | | ||
|- | |- | ||
| − | |When we wish to do so, we write the greater number in one line and the smaller beneath it in a | + | |When we wish to do so, we write the greater number in one line and the smaller number beneath it in a line, rank beneath rank. |
| − | |style="text-align:right;"|כשנבקש לעשות זה נכתוב | + | |style="text-align:right;"|כשנבקש לעשות זה נכתוב החשבון הגדול בטור אחד <s>זה</s> והחשבון הקטן תחתיה בטור מדרגה תחת מדרגה |
|- | |- | ||
| | | | ||
*We consider all the digits, in whichever rank they are, as if they are units. | *We consider all the digits, in whichever rank they are, as if they are units. | ||
| − | |style="text-align:right;"|והנה נחשוב כל האותיות כאלו | + | |style="text-align:right;"|והנה נחשוב כל האותיות כאלו הן אחדים באיזו מדרגה שתהיין |
|- | |- | ||
| | | | ||
| Line 495: | Line 556: | ||
| | | | ||
:*We write the remainder above it, if something remains. | :*We write the remainder above it, if something remains. | ||
| − | |style="text-align:right;"|ונכתוב | + | |style="text-align:right;"|ונכתוב עליה הנשאר אם ישאר ממנה כלום |
|- | |- | ||
| | | | ||
:*If there is no [remainder], we subtract it by writing a zero above it. | :*If there is no [remainder], we subtract it by writing a zero above it. | ||
| − | |style="text-align:right;"|ואם אין נמחקנה והוא שנרשום על ראשה | + | |style="text-align:right;"|ואם אין נמחקנה והוא שנרשום על ראשה ספרא |
|- | |- | ||
| | | | ||
*Then, we proceed with all the other ranks as the procedure in this rank, moving back from rank to rank until they are complete. | *Then, we proceed with all the other ranks as the procedure in this rank, moving back from rank to rank until they are complete. | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ואחר כן נעש<sup>ה</sup> מכל המדרגות האחרות כמעשה המדרגה הזאת ונלך אחור אחורנית ממדרגה למדרגה עד תומם |
|- | |- | ||
| | | | ||
:*If there is a digit in one of the ranks of the number in the bottom line [= subtrahend] that is greater than the corresponding digit in the upper line [= minuend], there is necessarily one digit in the number of the upper line that follows the [digit] that is in the rank in which we stand. | :*If there is a digit in one of the ranks of the number in the bottom line [= subtrahend] that is greater than the corresponding digit in the upper line [= minuend], there is necessarily one digit in the number of the upper line that follows the [digit] that is in the rank in which we stand. | ||
| − | |style="text-align:right;"|ואם תהיה אות באחת | + | |style="text-align:right;"|ואם תהיה אות באחת המדרגות מחשבון הטור השפל גדולה מהאות שכנגדה בטור העליון אמנם בהכרח יש אות אחת בטור החשבון העליון הסמוכה לזו אשר אנחנו עומדים במדרגתה מלאחריה |
|- | |- | ||
| | | | ||
::We do it in this way: we subtract 1 from the digit that follows this rank and write above it what remains from the digit from which we took the 1. If nothing remains from it, as there was only 1 there, we erase it. | ::We do it in this way: we subtract 1 from the digit that follows this rank and write above it what remains from the digit from which we took the 1. If nothing remains from it, as there was only 1 there, we erase it. | ||
| − | |style="text-align:right;"|נעשה על הדרך הזה נסיר א' מהאות שאחרי זאת המדרגה ונכתוב הנשאר מהאות ההיא אשר לקחנו הא' ממנה עליה ואם לא ישאר ממנה כלום כגון שלא היה שם כי אם א' נמחקנה | + | |style="text-align:right;"|נעשה על הדרך הזה נסיר א' מהאות [שאחרי זאת המדרגה ונכתוב הנשאר מהאות]‫<ref>marg.</ref> ההיא אשר לקחנו הא' ממנה עליה ואם לא ישאר ‫<ref>56r</ref>ממנה כלום כגון שלא היה שם כי אם א' נמחקנה |
|- | |- | ||
| | | | ||
| − | ::It is known that the 1 that we have is worth ten in relation to the preceding rank, hence, we consider the 1 as ten and add to this ten the number of the digit in the rank of the upper number, on which we stand. Now we have enough reserve to subtract the bottom digit from all this and we write the remainder above the corresponding upper digit. | + | ::It is known that the 1 that we have is worth ten in relation to the preceding rank, hence, we consider the 1 as ten and add to this ten the number of the digit in the rank of the upper number, on which we stand. Now we have enough reserve to subtract the bottom digit from all this and we write the remainder above the corresponding [upper] digit. |
| − | |style="text-align:right;"|ובידוע כי הא' הזאת שיש לנו היא שוה עשר בהקש אל המדרגה שלפניה לכן | + | |style="text-align:right;"|ובידוע כי הא' הזאת שיש לנו היא שוה עשר בהקש אל המדרגה שלפניה לכן נחשוב זאת הא' עשרה ונחחבר אל העשרה הזאת החשבון מהאות מהמדרגה העליונה אשר אנחנו עומדים עליה ויהיה לחשבון בעשרה הנזכרים כמו אחדים ועתה יספיק בריוח להסיר מכל זה האות התחתונה ונכתוב הנשאר על האות הראשונה שכנגדה |
|- | |- | ||
| | | | ||
*We proceed like this until we reach the first rank and what remains above the line of the upper number is the remainder of the subtraction. | *We proceed like this until we reach the first rank and what remains above the line of the upper number is the remainder of the subtraction. | ||
| − | |style="text-align:right;"|וכן נעשה תמיד עד שנגיע אל המדרגה הראשונה ומה שישאר על טור | + | |style="text-align:right;"|וכן נעשה תמיד עד שנגיע אל המדרגה <s>הזאת</s> הראשונה ומה שישאר על טור מספר החשבון העליון הוא נשאר מהמגרעת |
|- | |- | ||
| | | | ||
| − | :*Whenever we cannot subtract the bottom digit from the upper [digit], we give it supplement from the next rank by the aforesaid way, even if there are zeros separating between it and the following digit, or if we have to subtract the bottom digit from | + | :*Whenever we cannot subtract the bottom digit from the upper [digit], we give it supplement from the next rank by the aforesaid way, even if there are zeros separating between it and the following digit, or if we have to subtract the bottom digit from a zero that corresponds it in the upper line. |
| − | |style="text-align:right;"|והנה בכל עת אשר לא נוכל להסיר האות התחתונה מהעליונה נסייע לה מהמדרגה הבאה אחריה על הדרך האמור | + | |style="text-align:right;"|והנה בכל עת אשר לא נוכל להסיר האות התחתונה מהעליונה [נסייע לה]‫<ref>Vatican: כשיעלה</ref> מהמדרגה הבאה אחריה על הדרך האמור ואפי' היו סיפראש מפסיקות בינה ובין האות הבאה אחריה או שיש לנו להסיר האות התחתונה מסיפרא אשר תהיה כנגדה בטור העליון |
|- | |- | ||
| | | | ||
::We shift back by this way: we subtract 1 from the closest digit and write the remainder above it, if something remains from it, then we place this 1 above the preceding zero, so it becomes ten, we subtract 1 from it and 9 remains there above the zero. We place the 1 above the further preceding zero, so it is ten, we subtract 1 from it and nine remains above the zero. So on, we proceed until reaching the digit or the zero of the rank on which we stand, then we do as the aforementioned rule. | ::We shift back by this way: we subtract 1 from the closest digit and write the remainder above it, if something remains from it, then we place this 1 above the preceding zero, so it becomes ten, we subtract 1 from it and 9 remains there above the zero. We place the 1 above the further preceding zero, so it is ten, we subtract 1 from it and nine remains above the zero. So on, we proceed until reaching the digit or the zero of the rank on which we stand, then we do as the aforementioned rule. | ||
| − | |style="text-align:right;"|נשיב אחורנית על הדרך הזה שנסיר מהאות הקרובה א' ונכתוב עליה הנשאר אם ישאר ממנה כלום | + | |style="text-align:right;"|נשיב אחורנית על הדרך הזה שנסיר מהאות הקרובה <sup>א'</sup> ונכתוב עליה הנשאר אם ישאר ממנה כלום ונשים זאת הא' על הסיפרא ‫<ref>56v</ref>שלפניה ותהיה עשרה ונסיר מהם א' ונשאר שמה על הסיפרא ט' ונשים זאת הא' על הסיפרא הקודמת לזה ויהיו עשרה ונסיר מהם א' וישאר ט' על הסיפרא וכן נעשה לעולם עד שנגיע אל האות או אל הסיפרא מהמדרגה אשר אנחנו עומדים עליה ואז נעשה כמשפט האמור למעלה |
|- | |- | ||
| | | | ||
| − | *{{#annot:5083-92|155|ZVaI}}Example: we wish to subtract ninety- | + | *{{#annot:5083-92|155|ZVaI}}Example: we wish to subtract ninety-two from five thousand eighty-three. |
:<math>\scriptstyle5083-92</math> | :<math>\scriptstyle5083-92</math> | ||
| − | |style="text-align:right;"|המשל בזה בקשנו לגרוע מחמשת אלפים ושמונים ושלש | + | |style="text-align:right;"|<big>המשל בזה</big> בקשנו לגרוע מחמשת אלפים ושמונים ושלש תשעים ושנים{{#annotend:ZVaI}} |
|- | |- | ||
| | | | ||
:We write the two lines of the numbers according to this diagram: the greater number in the upper line and the smaller number in the bottom line correspondingly. | :We write the two lines of the numbers according to this diagram: the greater number in the upper line and the smaller number in the bottom line correspondingly. | ||
| − | |style="text-align:right;"|הנה נכתוב שני טורי החשבונות על זאת הצורה החשבון הגדול בטור העליון והחשבון | + | |style="text-align:right;"|הנה נכתוב שני טורי החשבונות על זאת הצורה החשבון הגדול בטור העליון והחשבון הקטון בטור שפל כנגדו |
|- | |- | ||
| | | | ||
| Line 567: | Line 628: | ||
|- | |- | ||
|} | |} | ||
| − | + | |- | |
| − | | | + | | colspan="2"| |
| − | + | ::<span style=color:green>[Illustration of the procedure:]</span> | |
| − | ::<span style=color: | ||
::{| | ::{| | ||
|- | |- | ||
| − | | ||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{5-1}}={\color{blue}{4}}}</math>||<span style= | + | | ||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{5-1}}={\color{blue}{4}}}</math>||<span style=color:blue>4</span>   ||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{10-1}}={\color{blue}{9}}}</math>||4<span style=color:#0000FF>9</span>||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{18-9}}={\color{blue}{9}}}</math>||49<span style=color:#0000FF>9</span>||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{3-2}}={\color{blue}{1}}}</math>||499<span style=color:#0000FF>1</span> |
|- | |- | ||
| − | |<span style= | + | |<span style=color:red>5</span>083||<span style=color:red>10</span>83|| <span style=color:red>18</span>3||   <span style=color:red>3</span>|| |
|- | |- | ||
| − | |  92||  92||  <span style= | + | |  92||  92||  <span style=color:red>9</span>2||   <span style=color:red>2</span>|| |
|} | |} | ||
| − | |||
|- | |- | ||
| | | | ||
| − | :*Since the digit in the | + | :*Since the digit in the last rank of the bottom line is greater that the corresponding digit in the upper line, we do as the aforesaid way: we subtract 1 from the last digit of the upper line, which is 5 that is next to the digit in the upper rank, on which we stand, after the zero, and 4 remains instead of the 5. |
::<math>\scriptstyle{\color{blue}{5-1=4}}</math> | ::<math>\scriptstyle{\color{blue}{5-1=4}}</math> | ||
| − | |style="text-align:right;"|ומאשר חשבון האות מהמדרגה | + | |style="text-align:right;"|ומאשר חשבון האות מהמדרגה האחרונה שבטור השפל גדול מחשבון האות אשר היא כנגדה בטור העליון נעשה על הדרך האמור ונסיר א' מהאות האחרונה מהטור העליון שהיא ה' הסמוכה לאות המדרגה העליונה שאנחנו עומדים עליה מאחריה אחר הסיפרא והנה ישאר ד' במקום הה‫' |
|- | |- | ||
| | | | ||
| − | :*The digit becomes ten when we place it above the zero; we subtract one from the ten and nine remains. | + | :*The digit 1 becomes ten when we place it above the zero; we subtract one from the ten and nine remains above the zero. |
::<math>\scriptstyle{\color{blue}{10-1=9}}</math> | ::<math>\scriptstyle{\color{blue}{10-1=9}}</math> | ||
| − | |style="text-align:right;"|ותהיה האות הזאת עשרה כשנשים אותה על הסיפרא ונסיר מהעשרה אחד וישאר | + | |style="text-align:right;"|ותהיה האות א' הזאת עשרה כשנשים אותה על הסיפרא ונסיר מהעשרה ‫<ref>57r</ref>אחד וישאר ט' על הסיפרא |
|- | |- | ||
| | | | ||
:*We place this one above the rank, on which we stand, which is 8, the total is eighteen. We subtract from it the last digit of the bottom line, which is 9; nine remains. We write it in its position above the 8. | :*We place this one above the rank, on which we stand, which is 8, the total is eighteen. We subtract from it the last digit of the bottom line, which is 9; nine remains. We write it in its position above the 8. | ||
::<math>\scriptstyle{\color{blue}{18-9=9}}</math> | ::<math>\scriptstyle{\color{blue}{18-9=9}}</math> | ||
| − | |style="text-align:right;"|ונשים האחד הזה על המדרגה אשר עמדנו בה שהיא ח' ויהיה בין הכל שמונה עשר נסיר מהם האות האחרונה | + | |style="text-align:right;"|ונשים האחד הזה על המדרגה אשר עמדנו בה שהיא ח' ויהיה בין הכל שמונה עשר נסיר מהם האות <s>ה</s> האחרונה שבטור השפל שהיא ט' וישאר תשעה ונכתוב במקומם על הח' ט‫' |
|- | |- | ||
| | | | ||
:*Then, we subtract the 2 of the bottom line from the corresponding 3 in the upper line and 1 remains. We write it above it. | :*Then, we subtract the 2 of the bottom line from the corresponding 3 in the upper line and 1 remains. We write it above it. | ||
::<math>\scriptstyle{\color{blue}{3-2=1}}</math> | ::<math>\scriptstyle{\color{blue}{3-2=1}}</math> | ||
| − | |style="text-align:right;"|אחרי כן נסיר הב' | + | |style="text-align:right;"|אחרי כן נסיר הב' שהיה מהטור השפל מהג' שכנגדה בטור העליון וישאר א' ונכתב<sup>נ</sup>ה עליה |
|- | |- | ||
|We find that the remainder is four thousand nine hundred and ninety-one. | |We find that the remainder is four thousand nine hundred and ninety-one. | ||
| Line 611: | Line 670: | ||
== Chapter Five – Multiplication of Units by Themselves or by Other Units and Multiplication of any Number by Itself or by Other == | == Chapter Five – Multiplication of Units by Themselves or by Other Units and Multiplication of any Number by Itself or by Other == | ||
| − | |style="text-align:right;"|<big>השער | + | |style="width:45%; text-align:right;"|<big>השער החמישי</big> בכפילת הכאת האחדים על עצמם או על אחדים אחרים ובכפול כל חשבון על עצמו או על אחר |
|- | |- | ||
|The meaning of this multiplication is to multiply one number by another: | |The meaning of this multiplication is to multiply one number by another: | ||
| Line 617: | Line 676: | ||
|- | |- | ||
| | | | ||
| − | * | + | *As if we say, for example: three times four, |
| − | |style="text-align:right;"|על דרך משל שלשה פעמים ארבעה | + | ::<math>\scriptstyle{\color{blue}{3\times4}}</math> |
| + | |style="text-align:right;"|כאשר נאמר על דרך משל שלשה פעמים ארבעה | ||
|- | |- | ||
|Or by itself: | |Or by itself: | ||
| Line 624: | Line 684: | ||
|- | |- | ||
| | | | ||
| − | * | + | *Three times three |
| − | |style="text-align:right;"| | + | :<math>\scriptstyle{\color{blue}{3\times3}}</math> |
| + | |style="text-align:right;"|שלשה פעמים שלשה | ||
|- | |- | ||
| | | | ||
| − | * | + | *Also ten times twenty |
| − | |style="text-align:right;"|וכן | + | :<math>\scriptstyle{\color{blue}{10\times20}}</math> |
| + | |style="text-align:right;"|וכן [עשר פעמים עשרים | ||
|- | |- | ||
| | | | ||
| − | *Or ten times ten <math>\scriptstyle{\color{blue}{10\times10}}</math> | + | *Or ten times ten |
| − | |style="text-align:right;"|או עשר פעמים עשר | + | :<math>\scriptstyle{\color{blue}{10\times10}}</math> |
| + | |style="text-align:right;"|או]‫<ref>Vatican om.</ref> עשר פעמים עשר | ||
|- | |- | ||
| | | | ||
| − | === Multiplication of Units by Units === | + | === <span style=color:green>Multiplication of Units by Units</span> === |
| | | | ||
|- | |- | ||
|It is true that regarding the multiplication of units alone there is no way in this science to find the result, therefore, one should memorize all the products of the units by themselves or by other units. | |It is true that regarding the multiplication of units alone there is no way in this science to find the result, therefore, one should memorize all the products of the units by themselves or by other units. | ||
| − | |style="text-align:right;"|ובאמת כי בכפילת האחדים לבדם לא נמצא דרך בחכמה הזאת למצוא ההווה ולפיכך צריך להזכיר ולהסדיר כל {{#annot:term|241,1838|SA5F}} | + | |style="text-align:right;"|ובאמת כי בכפילת האחדים לבדם לא נמצא דרך בחכמה הזאת למצוא ההווה ולפיכך צריך להזכיר ולהסדיר כל {{#annot:term|241,1838|SA5F}}כפילות{{#annotend:SA5F}} האחדים הן על עצמם <s>א</s>והן על אחדים אחרים והווייתן |
|- | |- | ||
|And these are: | |And these are: | ||
| Line 647: | Line 710: | ||
| | | | ||
:*Two times one is two | :*Two times one is two | ||
| − | |style="text-align:right;"|האחד שני פעמים שנים | + | |style="text-align:right;"|<big>האחד</big> שני פעמים שנים |
|- | |- | ||
| | | | ||
| Line 655: | Line 718: | ||
| | | | ||
:*Likewise, all the other numbers that are multiplied by one do not change or duplicated. | :*Likewise, all the other numbers that are multiplied by one do not change or duplicated. | ||
| − | |style="text-align:right;"|וכן כל המספרים האחרים ש{{#annot:term|358,1564|Smu2}}יכפלו {{#annotend:Smu2}}באחד לא יקבלו שום | + | |style="text-align:right;"|‫<ref>57v</ref>וכן כל המספרים האחרים ש{{#annot:term|358,1564|Smu2}}יכפלו{{#annotend:Smu2}} באחד לא יקבלו שום שנוי ורבוי |
|- | |- | ||
| | | | ||
| − | :*Two by two is four | + | :*Two by two is four. |
| − | |style="text-align:right;"|השנים בשנים ארבעה | + | |style="text-align:right;"|<big>השנים</big> בשנים ארבעה |
|- | |- | ||
| | | | ||
| − | :*Two by three is six | + | :*Two by three is six. |
|style="text-align:right;"|שנים בשלשה ששה | |style="text-align:right;"|שנים בשלשה ששה | ||
|- | |- | ||
| | | | ||
| − | :*Two by four is eight | + | :*Two by four is eight. |
|style="text-align:right;"|שנים בארבעה שמנה | |style="text-align:right;"|שנים בארבעה שמנה | ||
|- | |- | ||
| | | | ||
| − | :*Two by five is ten | + | :*Two by five is ten. |
|style="text-align:right;"|שנים בחמשה עשרה | |style="text-align:right;"|שנים בחמשה עשרה | ||
|- | |- | ||
| | | | ||
| − | :*Two by six is twelve | + | :*Two by six is twelve. |
|style="text-align:right;"|שנים בששה שנים עשר | |style="text-align:right;"|שנים בששה שנים עשר | ||
|- | |- | ||
| | | | ||
| − | :*Two by seven is fourteen | + | :*Two by seven is fourteen. |
|style="text-align:right;"|שנים בשבעה ארבעה עשר | |style="text-align:right;"|שנים בשבעה ארבעה עשר | ||
|- | |- | ||
| | | | ||
| − | :*Two by eight is sixteen | + | :*Two by eight is sixteen. |
|style="text-align:right;"|שנים בשמנה ששה עשר | |style="text-align:right;"|שנים בשמנה ששה עשר | ||
|- | |- | ||
| | | | ||
| − | :*Two by nine is eighteen | + | :*Two by nine is eighteen. |
| − | |style="text-align:right;"|שנים בתשעה | + | |style="text-align:right;"|שנים בתשעה <s>ארבעה</s> <sup>שמונה</sup> עשר |
|- | |- | ||
| | | | ||
| − | :*Three by three is nine | + | :*Three by three is nine. |
| − | |style="text-align:right;"|השלשה בשלשה תשעה | + | |style="text-align:right;"|<big>השלשה</big> בשלשה תשעה |
|- | |- | ||
| | | | ||
| − | :*Three by four is twelve | + | :*Three by four is twelve. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|השלשה בארבעה שנים עשר |
|- | |- | ||
| | | | ||
| − | :*Three by five is fifteen | + | :*Three by five is fifteen. |
|style="text-align:right;"|שלשה בחמשה חמשה עשר | |style="text-align:right;"|שלשה בחמשה חמשה עשר | ||
|- | |- | ||
| | | | ||
| − | :*Three by six is eighteen | + | :*Three by six is eighteen. |
|style="text-align:right;"|שלשה בששה שמנה עשר | |style="text-align:right;"|שלשה בששה שמנה עשר | ||
|- | |- | ||
| | | | ||
| − | :*Three by seven is twenty-one | + | :*Three by seven is twenty-one. |
|style="text-align:right;"|שלשה בשבעה עשרים ואחד | |style="text-align:right;"|שלשה בשבעה עשרים ואחד | ||
|- | |- | ||
| | | | ||
| − | :*Three by eight is twenty-four | + | :*Three by eight is twenty-four. |
| − | |style="text-align:right;"|שלשה | + | |style="text-align:right;"|שלשה בשמונה עשרים וארבעה |
|- | |- | ||
| | | | ||
| − | :*Three by nine is twenty-seven | + | :*Three by nine is twenty-seven. |
|style="text-align:right;"|שלשה בתשעה עשרים ושבעה | |style="text-align:right;"|שלשה בתשעה עשרים ושבעה | ||
|- | |- | ||
| | | | ||
| − | :*Four by four is sixteen | + | :*Four by four is sixteen. |
| − | |style="text-align:right;"|הארבעה בארבעה ששה עשר | + | |style="text-align:right;"|<big>הארבעה</big> בארבעה ששה עשר |
|- | |- | ||
| | | | ||
| − | :*Four by five is twenty | + | :*Four by five is twenty. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ארבעה בחמשה עשרים |
|- | |- | ||
| | | | ||
| − | :*Four by six is twenty-four | + | :*Four by six is twenty-four. |
| − | |style="text-align:right;"|ארבעה | + | |style="text-align:right;"|ארבעה בששה עשרים וארבעה |
|- | |- | ||
| | | | ||
| − | :*Four by | + | :*Four by seven is twenty-eight. |
| − | |style="text-align:right;"|ארבעה | + | |style="text-align:right;"|ארבעה בשבעה עשרים ושמונה |
|- | |- | ||
| | | | ||
| − | :*Four by eight is thirty-two | + | :*Four by eight is thirty-two. |
| − | |style="text-align:right;"|ארבעה | + | |style="text-align:right;"|ארבעה בשמונה שנים ושלשים |
|- | |- | ||
| | | | ||
| − | :*Four by nine is thirty-six | + | :*Four by nine is thirty-six. |
|style="text-align:right;"|ארבעה בתשעה ששה ושלשים | |style="text-align:right;"|ארבעה בתשעה ששה ושלשים | ||
|- | |- | ||
| | | | ||
| − | :*Five by five is twenty-five | + | :*Five by five is twenty-five. |
| − | |style="text-align:right;"|החמשה בחמשה עשרים וחמשה | + | |style="text-align:right;"|<big>החמשה</big> בחמשה עשרים וחמשה |
|- | |- | ||
| | | | ||
| − | :*Five by six is thirty | + | :*Five by six is thirty. |
|style="text-align:right;"|חמשה בששה שלשים | |style="text-align:right;"|חמשה בששה שלשים | ||
|- | |- | ||
| | | | ||
| − | :*Five by seven is thirty-five | + | :*Five by seven is thirty-five. |
| − | |style="text-align:right;"|חמשה בשבעה שלשים | + | |style="text-align:right;"|חמשה בשבעה שלשים וחמש |
|- | |- | ||
| | | | ||
| − | :*Five by eight is forty | + | :*Five by eight is forty. |
| − | |style="text-align:right;"|חמשה | + | |style="text-align:right;"|חמשה ‫<ref>58r</ref>בשמונה ארבעים |
|- | |- | ||
| | | | ||
| − | :*Five by nine is forty-five | + | :*Five by nine is forty-five. |
|style="text-align:right;"|חמשה בתשעה ארבעים וחמש | |style="text-align:right;"|חמשה בתשעה ארבעים וחמש | ||
|- | |- | ||
| | | | ||
| − | :*Six by six is thirty-six | + | :*Six by six is thirty-six. |
| − | |style="text-align:right;"|הששה בששה ששה ושלשים | + | |style="text-align:right;"|<big>הששה</big> בששה ששה ושלשים |
|- | |- | ||
| | | | ||
| − | :*Six by seven is forty-two | + | :*Six by seven is forty-two. |
|style="text-align:right;"|ששה בשבעה שנים וארבעים | |style="text-align:right;"|ששה בשבעה שנים וארבעים | ||
|- | |- | ||
| | | | ||
| − | :*Six by eight is forty-eight | + | :*Six by eight is forty-eight. |
| − | |style="text-align:right;"|ששה | + | |style="text-align:right;"|ששה בשמונה ש<sup>מו</sup>נה וארבעים |
|- | |- | ||
| | | | ||
| − | :*Six by nine is fifty-four | + | :*Six by nine is fifty-four. |
| − | |style="text-align:right;"|ששה בתשעה ארבעה | + | |style="text-align:right;"|ששה בתשעה ארבעה וחמישים |
|- | |- | ||
| | | | ||
| − | :*Seven by seven is forty-nine | + | :*Seven by seven is forty-nine. |
| − | |style="text-align:right;"|השבעה בשבעה | + | |style="text-align:right;"|<big>השבעה</big> בשבעה תשע וארבעים |
|- | |- | ||
| | | | ||
| − | :*Seven by eight is fifty-six | + | :*Seven by eight is fifty-six. |
| − | |style="text-align:right;"|שבעה | + | |style="text-align:right;"|שבעה בשמונה ששה וחמשים |
|- | |- | ||
| | | | ||
| − | :*Seven by nine is sixty-three | + | :*Seven by nine is sixty-three. |
|style="text-align:right;"|שבעה בתשעה שלשה וששים | |style="text-align:right;"|שבעה בתשעה שלשה וששים | ||
|- | |- | ||
| | | | ||
| − | :*Eight by eight is sixty-four | + | :*Eight by eight is sixty-four. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|<big>השמונה</big> בשמונה ארבעה וששים |
|- | |- | ||
| | | | ||
| − | :*Eight by nine is seventy-two | + | :*Eight by nine is seventy-two. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|שמונה בתשעה שנים ושבעים |
|- | |- | ||
| | | | ||
| − | :*Nine by nine is eighty-one | + | :*Nine by nine is eighty-one. |
| − | |style="text-align:right;"|התשעה בתשעה אחד | + | |style="text-align:right;"|<big>התשעה</big> בתשעה אחד ושמונים |
|- | |- | ||
|Thus, the whole method of multiplying the units is clear and nothing is missing. | |Thus, the whole method of multiplying the units is clear and nothing is missing. | ||
| − | |style="text-align:right;"|ובזה התבאר כל סדר | + | |style="text-align:right;"|<big>ובזה</big> התבאר כל סדר כפלת האחדים ולא נפקד מהם דבר |
|- | |- | ||
| | | | ||
| − | === Written Multiplication === | + | === <span style=color:green>Written Multiplication</span> === |
| | | | ||
|- | |- | ||
| − | |<span style= | + | |<span style=color:green>'''Description of the procedure:'''</span> |
| | | | ||
|- | |- | ||
| − | |When we wish | + | |When we wish to multiply a number by a number of other ranks we do it this way: |
| − | |style="text-align:right;"|וכאשר נבקש | + | |style="text-align:right;"|<big>וכאשר</big> נבקש לכפול החשבון על חשבון מהמדרגות האחרות נעשה על הדרך הזה |
|- | |- | ||
| | | | ||
| Line 821: | Line 884: | ||
|- | |- | ||
| | | | ||
| − | *We start from the first digit of the upper line and multiply all the upper digits by all the bottom | + | *We start from the first digit of the upper line and multiply all the upper digits by all the digits of the bottom line successively. |
| − | |style="text-align:right;"|והנה נתחיל באות הראשונה מהטור העליון | + | |style="text-align:right;"|והנה נתחיל באות הראשונה מהטור העליון ונכפול כל האותיות העליונות על כל אותיות הטור השפל ‫<ref>58v</ref>זו אחר זו |
|- | |- | ||
| | | | ||
*We write all the products beneath the line in the appropriate ranks, digit by digit, as required. | *We write all the products beneath the line in the appropriate ranks, digit by digit, as required. | ||
| − | |style="text-align:right;"|וכל ה{{#annot:term|241, | + | |style="text-align:right;"|וכל ה{{#annot:term|241,1564|yEhP}}נכפלים{{#annotend:yEhP}} נכתוב תחת הקו במדרגות הראויות להם אות תחת אות כאשר יצטרך |
|- | |- | ||
| | | | ||
*We always count how many ranks there are from the digit we multiply on the upper line to the multiplied digit of the bottom line, including these two digits: | *We always count how many ranks there are from the digit we multiply on the upper line to the multiplied digit of the bottom line, including these two digits: | ||
| − | |style="text-align:right;"|כי לעולם נמנה כמה מדרגות מהאות אשר נכפיל מהטור העליון עד | + | |style="text-align:right;"|כי לעולם נמנה כמה מדרגות מהאות אשר נכפיל מהטור העליון עד האות ה{{#annot:term|358,1564|GoLz}}נכפלות{{#annotend:GoLz}} שבטור השפל ושתי <sup>ה</sup>אותיות בכלל המנין |
|- | |- | ||
| | | | ||
:*If the product of a digit by another is equal to tens, we write a digit [that mark] the number of the tens according to the counted number of the ranks. | :*If the product of a digit by another is equal to tens, we write a digit [that mark] the number of the tens according to the counted number of the ranks. | ||
| − | |style="text-align:right;"|ואם יספיק כפל האות על חברתה לעשרות נכתוב אות | + | |style="text-align:right;"|ואם יספיק כפל האות על חברתה לעשרות נכתוב אות במספר העשרות כמספר מנין המדרגות |
|- | |- | ||
| | | | ||
:*If it does not reach ten, we write the product on the rank that is one less than the [counted] number [of the ranks]. | :*If it does not reach ten, we write the product on the rank that is one less than the [counted] number [of the ranks]. | ||
| − | |style="text-align:right;"|ואם לא יספיק לעשר נכתוב ה{{#annot:term|241,1564|Oq7Z}}נכפל{{#annotend:Oq7Z}} | + | |style="text-align:right;"|ואם לא יספיק לעשר נכתוב ה{{#annot:term|241,1564|Oq7Z}}נכפל{{#annotend:Oq7Z}} ממדרגה אחת פחותה מהמספר |
|- | |- | ||
| | | | ||
:*If it is equal to units and tens, we write the number of the tens according to the number of the ranks between the multiplied digits and the units one rank before that. | :*If it is equal to units and tens, we write the number of the tens according to the number of the ranks between the multiplied digits and the units one rank before that. | ||
| − | |style="text-align:right;"|ואם יעלה | + | |style="text-align:right;"|ואם יעלה הנכפל להיות בו אחדים ועשרות נכתוב העשרות כמספרן כמספר המדרגות שבין אות לאות והאחדים מדרגה אחת אחורנית |
|- | |- | ||
| | | | ||
| − | : | + | :When all the digits of the bottom line are multiplied by all the digits of the upper line according to the rule, we draw a line beneath the ranks of the [interim] products and we sum up all the digits in each rank, according to the addition procedure as explained above. |
| − | |style="text-align:right;"|וכשיכפלו כל אותיות הטור השפל בכל אותיות הטור העליון כמשפטן נעביר קו דיו תחת מדרגות | + | |style="text-align:right;"|וכשיכפלו כל אותיות הטור השפל בכל אותיות הטור העליון כמשפטן נעביר קו <s>ב</s>דיו תחת מדרגות הכפילה ונחבר ונקבץ כל האותיות מכל מדרגה ומדרגה כדרך עשיית החבור כאשר נתבאר במקומו במה שקדם |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | :The result is the [final] product. |
| + | |style="text-align:right;"|והעולה הוא ה{{#annot:term|241,1564|m9hV}}נכפל{{#annotend:m9hV}} | ||
| + | |- | ||
| + | |Now I will discuss the procedure of this chapter through examples: | ||
| + | |style="text-align:right;"|ועתה אדבר ממלאכת השער הזה על דרך הדמיון | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:902×246|156|JEg5}}<math>\scriptstyle902\times246</math> | + | *{{#annot:902×246|156|JEg5}}We wish to multiply nine hundred and two by two hundred and forty-six. |
| − | |style="text-align:right;"|בקשנו לכפול ולהכות שנים ותשע מאות על ששה וארבעים | + | :<math>\scriptstyle902\times246</math> |
| + | |style="text-align:right;"|<big>בקשנו</big> לכפול ולהכות שנים ותשע מאות על ששה וארבעים [ומאתים]‫<ref>Vatican marg.</ref>{{#annotend:JEg5}} | ||
|- | |- | ||
| | | | ||
| − | :{|class="wikitable" style="color:blue; text-align:center;" | + | ::We write them according to this diagram: |
| + | |style="text-align:right;"|‫[ונכתבם]‫<ref>Vatican om.</ref> על זאת הצורה | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
|- | |- | ||
|the lines of the numbers | |the lines of the numbers | ||
| Line 920: | Line 992: | ||
|} | |} | ||
|- | |- | ||
| + | | colspan="2"| | ||
| + | ::<span style=color:green>[Illustration of the procedure:]</span> | ||
| + | ::{| | ||
| + | |- | ||
| + | |90<span style=color:red>2</span>||rowspan="4"|<math>\scriptstyle\xrightarrow{{\color{red}{2\times6}}={\color{blue}{12}}}</math>||90<span style=color:red>2</span>||rowspan="4"|<math>\scriptstyle\xrightarrow{{\color{red}{2\times4}}={\color{blue}{8}}}</math>||90<span style=color:red>2</span>||rowspan="4"|<math>\scriptstyle\xrightarrow{{\color{red}{2\times2}}={\color{blue}{4}}}</math>||<span style=color:red>9</span>02||rowspan="4"|<math>\scriptstyle\xrightarrow{{\color{red}{9\times6}}={\color{blue}{54}}}</math>|| <span style=color:red>9</span>02 | ||
| + | |- | ||
| + | |24<span style=color:red>6</span>||<u>2<span style=color:red>4</span>6</u>||<u><span style=color:red>2</span>46</u>||<u>24<span style=color:red>6</span></u>||<u> 2<span style=color:red>4</span>6</u> | ||
| + | |- | ||
| + | | || <span style=color:#0000FF>12</span>|| 12||<span style=color:#0000FF>4</span>12||<span style=color:#0000FF>5</span>412 | ||
| + | |- | ||
| + | | || || <span style=color:#0000FF>8</span> || 8 || <span style=color:#0000FF>4</span>8  | ||
|} | |} | ||
| − | : | + | :::{| |
| − | ::{| | ||
|- | |- | ||
| − | + | |rowspan="4"|<math>\scriptstyle\xrightarrow{{\color{red}{9\times4}}={\color{blue}{36}}}</math>||  <span style=color:red>9</span>02||rowspan="4"|<math>\scriptstyle\xrightarrow{{\color{red}{9\times2}}={\color{blue}{18}}}</math>||   902 | |
|- | |- | ||
| − | + | |<u>  <span style=color:red>2</span>46</u>||<u>   246</u> | |
|- | |- | ||
| − | + | |<span style=color:#0000FF>3</span>5412||<span style=color:#0000FF>1</span>35412 | |
|- | |- | ||
| − | + | | <span style=color:#0000FF>6</span>48 || <span style=color:#0000FF>8</span>648  | |
|} | |} | ||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | :*<math>\scriptstyle{\color{blue}{2\times6=12}}</math> | + | :*When we multiply the digit 2 by the digit 6 beneath it in the bottom line, it is twelve. |
| − | |style="text-align:right;"|וכאשר | + | ::<math>\scriptstyle{\color{blue}{2\times6=12}}</math> |
| + | |style="text-align:right;"|‫<ref>59r</ref>וכאשר נכפל אות הבית על אות הו"ו אשר תחתיה בטור השפל יהיו שנים עשר | ||
| + | |- | ||
| + | | | ||
| + | ::The number of the ranks is two, so we write 2 in the first rank, for the two units, and after it, in the second rank, we write 1, for the ten. | ||
| + | |style="text-align:right;"|והנה מספר המדרגות שתים לכן נכתוב אות ב' במדרגה ראשונה כנגד שני האחדים ואחריה במדרגה שנית נכתוב א' כנגד העשרה | ||
| + | |- | ||
| + | | | ||
| + | :*When we multiply the mentioned digit 2 by the 4 in the bottom line, it is eight. | ||
| + | ::<math>\scriptstyle{\color{blue}{2\times4=8}}</math> | ||
| + | |style="text-align:right;"|וכאשר נכפיל אות הב' הנזכרת על הד' מהטור השפל יהיו שמונה | ||
| + | |- | ||
| + | | | ||
| + | ::The number of ranks is three, but since this product does not reach ten, we shift it one rank backwards and we write 8 for it in the second rank beneath the 1. | ||
| + | |style="text-align:right;"|ומספר המדרגות שלש ואולם באשר אין הכפלה ההיא מגעת לעשר נשים אותם מדרגה אחת אחורנית ונכתוב <s>ב'</s> כנגדן במדרגה השנייה ח' תחת הא‫' | ||
|- | |- | ||
| | | | ||
| − | :*<math>\scriptstyle{\color{blue}{2\ | + | :*When we multiply the mentioned digit by the 2 in the bottom line, it is four. |
| − | |style="text-align:right;"|וכאשר נכפיל | + | ::<math>\scriptstyle{\color{blue}{2\times2=4}}</math> |
| + | |style="text-align:right;"|וכאשר <sup>נכפיל</sup> את האות הנזכרת על הב' מהטור השפל יהיו ארבעה | ||
|- | |- | ||
| | | | ||
| − | : | + | ::Since this product does not reach ten, we write 4 for this four received now in the third rank after the 1 that is in the second rank. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וכאשר אין הכפלה הזאת מגעת לעשר נכתוב כנגד אלו הארבעה ד' במדרגה השלישית אשר נחדש עתה כשנכתבנה אחרי הא' שהיא במדרגה השנייה |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ובזה נשלם | + | :By this the multiplication of the digit of the first rank in the upper line by all the digits of the bottom line is complete. |
| + | |style="text-align:right;"|ובזה נשלם כפילת האות מהמדרגה הראשונה שבטור העליון על כל אותיות הטור השפל | ||
|- | |- | ||
| | | | ||
| + | :Now, we must also multiply the digit 9, which is the last rank of the upper line by all the digits of the bottom line: | ||
|style="text-align:right;"|ועתה אנחנו צריכים גם כן להכפיל אות הט' שהיא המדרגה האחרונה מהטור העליון על כל אותיות הטור השפל | |style="text-align:right;"|ועתה אנחנו צריכים גם כן להכפיל אות הט' שהיא המדרגה האחרונה מהטור העליון על כל אותיות הטור השפל | ||
|- | |- | ||
| | | | ||
| − | :*<math>\scriptstyle{\color{blue}{9\times6=54}}</math> | + | :*When we multiply this digit by the first digit of the bottom line, which is 6, the result is fifty-four. |
| − | |style="text-align:right;"|והנה | + | ::<math>\scriptstyle{\color{blue}{9\times6=54}}</math> |
| + | |style="text-align:right;"|והנה כשנכפל האות ההיא על אות המדרגה הראשונה ‫<ref>59v</ref>מהטור השפל שהיא ו' יעלה ארבעה וחמישים | ||
| + | |- | ||
| + | | | ||
| + | ::The number of the ranks is four, so we write 5 in the fourth rank, for [the fifty, and for] the four, we write another 4 beneath the 4 in the third rank. | ||
| + | |style="text-align:right;"|ומספר המדרגות הם ארבעה ולכן נכתוב במדרגה הרביעית ה' [כנגד]‫<ref>marg.</ref> [החמשים וכנגד]‫<ref>Vatican om.</ref> הארבעה נכתוב תחת הד' במדרגה השלישית ד' אחרת | ||
| + | |- | ||
| + | | | ||
| + | :*When we multiply this digit by the 4 in the bottom line, the result is thirty-six. | ||
| + | ::<math>\scriptstyle{\color{blue}{9\times4=36}}</math> | ||
| + | |style="text-align:right;"|וכאשר נכפול האות ההיא על הד' שבטור השפל יעלו ששה ושלשים | ||
| + | |- | ||
| + | | | ||
| + | ::The number of the ranks is five, so we write 3 in a fifth rank for the thirty, after the 5 that is written in the fourth rank, and for the six, we write 6 back beneath the preceding 5. | ||
| + | |style="text-align:right;"|ומספר המדרגות חמש ולכן נכתוב כנגד השלשים אחרי הה' [הכתובה]‫<ref>Vatican: וכנגדה</ref> במדרגה הרביעית ג' ונחדש עתה מדרגה חמישית וכנגד הששה נכתוב אחורנית תחת הה' הקדומה ו‫' | ||
|- | |- | ||
| | | | ||
| − | :*<math>\scriptstyle{\color{blue}{9\ | + | :*When we multiply the mentioned 9 by the last rank of the bottom line, which is 2, the result is eighteen. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{9\times2=18}}</math> |
| + | |style="text-align:right;"|וכש{{#annot:term|185,1230|qOaQ}}נכפיל{{#annotend:qOaQ}} אות הט' הנזכרת על המדרגה האחרונה שבטור השפל שהיא ב' יעלה שמנה עשר | ||
|- | |- | ||
| | | | ||
| − | : | + | ::The number of the ranks is six, so we write 1 in a sixth rank for the ten, and for the eight, we write 8 back beneath the preceding 3 that is in the fifth rank. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ומספר המדרגות שש ולכן נכתוב במדרגה ששית אשר נחדש א' כנגד עשרה וכנגד השמנה נכתוב ח' אחורנית תחת הג' הקדומה שהיא במדרגה <sup>ה</sup>חמישית |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ועם כל זה הוכפלו כל אותיות הטור העליון על אותיות הטור השפל כלנה אחת מהנה לא נעדרה | + | :By this all the digits of the upper line are multiplied by all the digits of the bottom line, none of them is missing. |
| + | |style="text-align:right;"|ועם כל זה הוכפלו כל אותיות הטור העליון על אותיות הטור <s>העליון על אותיות הטור</s> השפל כלנה אחת מהנה לא נעדרה | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ועתה נחל לקבץ כל האותיות שבכל מדרגה ומדרגה כמשפט מלאכת | + | :Now, we begin to sum up all the digits in each rank according to the addition procedure, after we draw a line beneath the [interim] products. We write beneath the line the result of addition: |
| + | |style="text-align:right;"|ועתה נחל לקבץ כל האותיות שבכל מדרגה ומדרגה כמשפט מלאכת החבור אחר אשר נעביר קו הדיו תחת הכפילה ונכתוב תחת הקו מה <s>שירצה</s> [שיצא]‫<ref>marg.</ref> מהחבור | ||
|- | |- | ||
| | | | ||
| − | :*first rank | + | :*It is known that the first rank resulting from this multiplication is 2. |
| − | |style="text-align:right;"|וידוע כי | + | |style="text-align:right;"|‫<ref>60r</ref>וידוע כי המדרגה הראשונה מהכפל הזאת תצא ב‫' |
|- | |- | ||
| | | | ||
| − | :*second rank | + | :*In the second [rank] it is 9. |
|style="text-align:right;"|ומהשנייה ט‫' | |style="text-align:right;"|ומהשנייה ט‫' | ||
|- | |- | ||
| | | | ||
| − | :*third rank | + | :*In the third [rank] is 8. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ומשלישית ח‫' |
|- | |- | ||
| | | | ||
| − | :*fourth rank: 1 | + | :*In the fourth rank: 1 remains, after we write the ten of the [sum of the] products in the following rank. |
|style="text-align:right;"|ומהרביעית תשאר א' אחרי כתבנו העשרה בכפילה במדרגה הבאה אחרי זאת | |style="text-align:right;"|ומהרביעית תשאר א' אחרי כתבנו העשרה בכפילה במדרגה הבאה אחרי זאת | ||
|- | |- | ||
| | | | ||
| − | :*fifth rank: 2 | + | :*In the fifth rank: 2 remains, after we write the ten in the following rank, which is the sixth. |
| − | |style="text-align:right;"|ומהמדרגה | + | |style="text-align:right;"|ומהמדרגה החמישית תשאר ב' אחרי כתבנו העשרה בכפילה במדרגה הבאה אחרי זאת שהיא ששית |
|- | |- | ||
| | | | ||
| − | :*sixth rank: 2 | + | :*In the sixth rank: we receive 2, since we add to it the ten we have left from the fifth rank that precedes it. |
| − | |style="text-align:right;"|ומהמדרגה הששית | + | |style="text-align:right;"|ומהמדרגה הששית יצא לנו ב' מאשר חברנו לה העשרה שנותר לנו מהמדרגה החמישית הקדומה אליה |
|- | |- | ||
| | | | ||
| − | : | + | :We find that the result is two hundred and twenty-one thousands, eight hundred and ninety-two. |
| − | |style="text-align:right;"|ונמצא | + | |style="text-align:right;"|ונמצא עולה מאתים ועשרים ואחד אלף ושמונה מאות ותשעים ושנים |
|- | |- | ||
| − | | | + | |This is the method and the procedure of the multiplication of all numbers rank by rank. |
|style="text-align:right;"|וככה הוא דרך וסדר כפילת כל החשבונות מערכה לקראת מערכה | |style="text-align:right;"|וככה הוא דרך וסדר כפילת כל החשבונות מערכה לקראת מערכה | ||
|- | |- | ||
| Line 1,011: | Line 1,124: | ||
== Chapter Six – Division of a Great Number by a Smaller Number == | == Chapter Six – Division of a Great Number by a Smaller Number == | ||
| − | |style="text-align:right;"|<big>השער הששי בחלוקת חשבון גדול על חשבון קטן ממנו | + | |style="width:45%;text-align:right;"|<big>השער הששי</big> בחלוקת חשבון גדול על חשבון קטן ממנו |
|- | |- | ||
| − | !Written Division | + | !<span style=color:green>Written Division</span> |
| | | | ||
|- | |- | ||
| − | |<span style= | + | |<span style=color:green>'''Description of the procedure:'''</span> |
| | | | ||
|- | |- | ||
| | | | ||
| − | *The one who wants to do this, writes the line of the greater number first, then he leaves a space of a whole line and write the smaller number in another line, corresponding to the first column of the greater number, each rank | + | *The one who wants to do this, writes the line of the greater number first, then he leaves a space of a whole line and write the smaller number in another line, corresponding to the first column of the greater number, each rank beneath to its similar. |
| − | |style="text-align:right;"|הרוצה לעשות זה יכתוב טור החשבון הגדול בתחלה ואחר יניח | + | |style="text-align:right;"|הרוצה לעשות זה יכתוב טור החשבון הגדול בתחלה ואחר יניח ר<sup>י</sup>וח וחלק כמלוא טור אחד ויכתוב החשבון הקטן בטור אחר כנגד הטור הראשון מהחשבון הגדול מדרגה תחת מדרגה הדומה לה |
|- | |- | ||
| | | | ||
| − | *Thereafter, he looks and sees how many times he can subtract the number of | + | *Thereafter, he looks and sees how many times he can subtract the number of the last rank in the line of the smaller number [= the divisor] from the digit on the last rank of the greater number [= the dividend] and he subtracts them from it. |
| − | |style="text-align:right;"|ואחר יביט ויראה כמה פעמים יוכל להוציא מספר | + | |style="text-align:right;"|ואחר יביט ויראה כמה [פעמים]‫<ref>Vatican om.</ref> יוכל להוציא מספר המדרגה האחרונה מטור החשבון הקטן מהאות מהמדרגה האחרונה שבטור החשבון הגדול ויוציאם ממנה |
|- | |- | ||
| | | | ||
:However, he should be wise and see if there is a number left, from which he can subtract all the other ranks in the line of the smaller number that precede the last one as the number of times he subtracts this last rank from the last digit in the line of the greater number. If he sees that there will be no number left that will be enough for it, he does not subtract it so many times, but as he sees that is enough to do what is said. | :However, he should be wise and see if there is a number left, from which he can subtract all the other ranks in the line of the smaller number that precede the last one as the number of times he subtracts this last rank from the last digit in the line of the greater number. If he sees that there will be no number left that will be enough for it, he does not subtract it so many times, but as he sees that is enough to do what is said. | ||
| − | |style="text-align:right;"|ואולם צריך שיחכם ויראה אם ישאר שם חשבון שיוכל להסיר ממנו כל המדרגות האחרות מטור החשבון הקטן הקדומות לזו האחרונה כמספר הפעמים אשר הסיר המדרגה הזאת | + | |style="text-align:right;"|ואולם צריך שיחכם ‫<ref>60v</ref>ויראה אם <s>ישוב שוב</s> [ישאר שם]‫<ref>marg.</ref> חשבון שיוכל להסיר ממנו כל המדרגות האחרות מטור החשבון הקטן הקדומות לזו האחרונה כמספר הפעמים אשר הסיר המדרגה האחרונה הזאת מהאות האחרונה מטור החשבון הגדול ואם ראה שלא ישאר שם חשבון שיספיק לזה שלא יסירנה כל כך פעמים אלא כאשר יראה שיספיק לעשות [מה שאמור]‫<ref>Vatican: מהשמור</ref> |
|- | |- | ||
| | | | ||
*As the number of times of subtraction he writes a digit corresponding them in the middle between the two lines of the smaller and greater numbers. | *As the number of times of subtraction he writes a digit corresponding them in the middle between the two lines of the smaller and greater numbers. | ||
| − | |style="text-align:right;"|וכמספר הפעמים אשר תהיה ההסרה יכתוב אות כנגדן באמצע שני טורי החשבונות הקטן והגדול | + | |style="text-align:right;"|וכמספר הפעמים אשר תהיה ההסרה יכתוב אות כנגדן <s>במ</s> באמצע שני טורי החשבונות הקטן והגדול |
|- | |- | ||
| | | | ||
*He counts from the last rank in the line of the greater number backwards according to the number of the ranks in the line of the smaller number and beneath the rank where the count ends he writes the number of times of subtraction. | *He counts from the last rank in the line of the greater number backwards according to the number of the ranks in the line of the smaller number and beneath the rank where the count ends he writes the number of times of subtraction. | ||
| − | |style="text-align:right;"|וימנה מהמדרגה האחרונה מטור החשבון הגדול כפי | + | |style="text-align:right;"|וימנה מהמדרגה האחרונה מטור החשבון הגדול כפי מנין המדרגות שבטור החשבון הקטן אחרנית והמדרגה אשר י<s>מ</s><sup>כ</sup>לה המנין שם יכתוב תחתיה מספר פעמי ה{{#annot:term|1679,155|You5}}הסרה{{#annotend:You5}} |
|- | |- | ||
| | | | ||
| − | *If there is anything left of the digit | + | *If there is anything left of the digit of the greater number after he subtracted from it, he writes the remainder above it. |
| − | |style="text-align:right;"|ואם | + | |style="text-align:right;"|ואם ישוב מהאות מהחשבון הגדול כלום אחרי מה שהסיר ממנה יכתוב עליה הנשאר |
|- | |- | ||
| | | | ||
| Line 1,049: | Line 1,162: | ||
| | | | ||
*Then, he subtracts all the other digits in the line of the smaller number that precede the digit of the last rank, one by one, from the digits that he finds written in the line of the greater number, as much as the times of subtraction from the last digit. | *Then, he subtracts all the other digits in the line of the smaller number that precede the digit of the last rank, one by one, from the digits that he finds written in the line of the greater number, as much as the times of subtraction from the last digit. | ||
| − | |style="text-align:right;"|ואחר יסיר כל שאר | + | |style="text-align:right;"|ואחר יסיר כל שאר אותיות המדרגות שבטור החשבון הקטן הקדומות לאות ‫<ref>61r</ref>המדרגה האחרונה זו אחר זו מהאותיות אשר ימצא עתה כתובות בטור החשבון הגדול כמספר פעמי ההסרה מהאות האחרונה |
|- | |- | ||
| | | | ||
| Line 1,057: | Line 1,170: | ||
| | | | ||
:If nothing is left of it, he writes a zero above its. | :If nothing is left of it, he writes a zero above its. | ||
| − | |style="text-align:right;"|ואם לא ישאר | + | |style="text-align:right;"|ואם לא ישאר שם כלום יכתוב עליה סיפרא |
|- | |- | ||
| | | | ||
| − | :*If he happens to have a digit in one rank of the line of the | + | :*If he happens to have a digit in one rank of the line of the smaller number that he can not subtract properly from the digit written in the line of the greater number, but there are still digits after the rank, on which he stands, he shifts to it from digits of those ranks, since it is known that each rank is ten times greater than the preceding rank, as is known in the previous chapters. Hence, he takes from their number as needed and writes what remains in its place and zeros, in places where nothing remains. |
| − | |style="text-align:right;"|ואם | + | |style="text-align:right;"|ואם הזדמן לו אות במדרגה אחת מהטור החשבון הקטן שלא יוכל להסיר אותה מהאות הכתובה בטור החשבון הגדול כראוי אבל אם יש שם עדין אותיות אחרי המדרגה שהוא עומד בה יחזור לה מהאותיות של אותן <sup>ה</sup>מדרגות לפי שידוע שכל מדרגה ומדרגה היא גדולה עשר פעמים מהמדרגה הקדומה כאשר נודע בשערים הקדומים לזה ויקח ממספרן כאשר יצטרך ויכתוב מה שישאר במקומות ההשארות וסיפרא וסיפרש במקומות אשר לא נשאר שם כלום |
|- | |- | ||
| | | | ||
| − | *After he completes the subtraction of all the digits in the line of the smaller number from the line of the greater number the same number of times, if that | + | *After he completes the subtraction of all the digits in the line of the smaller number from the line of the greater number the same number of times, he looks if what remains in the line of the greater number that is not divided yet is greater than the number of the line of the small number. If it is, he looks again, sees and measures how many times he can subtract the digit in the last rank of the line of the smaller number from the last digit of what is left in the line of the greater number and as the number of times he subtracts it from it so are the times he has to subtract the rest of the ranks in the line of the smaller number from what remains then in the line of the greater number. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ואחר אשר ישלים פעמי ההסרה מטור החשבון הגדול כל האותיות מטור החשבון הקטן במספר שוה זו כזו יעיין אם מה שנשאר בטור החשבון הגדול קיים שלא נתחלק [מספ]רו רב ממספר טור החשבון הקטן ואם הוא כן יחזור ‫<ref>61v</ref>ויביט ויראה וישום וישער כמה פעמים יוכל להסיר האות שבמדרגה האחרונה מטור החשבון הקטן מהאות האחרונה ממה שנשאר בטור החשבון הגדול וכמספר הפעמים אשר יסיר אותה ממנה כך פעמים יצטרך להסיר שאר המדרגות שבטור החשבון הקטן ממה שישאר אחרי כן בטור החשבון הגדול |
|- | |- | ||
| | | | ||
:Therefore, he should be careful first when looking for the value and evaluation to maintain his practice according to the rule and justice. | :Therefore, he should be careful first when looking for the value and evaluation to maintain his practice according to the rule and justice. | ||
| − | |style="text-align:right;"|לכן ישמור בתחלת הבטת השיעור והשומא שיכלכל מעשיו | + | |style="text-align:right;"|לכן ישמור בתחלת הבטת השיעור והשומא שיכלכל כל מעשיו כראוי במשפט וצדק |
|- | |- | ||
| | | | ||
| Line 1,077: | Line 1,190: | ||
| | | | ||
*He starts to count from the line of the greater number, from the digit at which he began to look in the second time, according to the number of the ranks in the line of the smaller number and beneath the rank where the count ends he writes the number of times of subtraction. | *He starts to count from the line of the greater number, from the digit at which he began to look in the second time, according to the number of the ranks in the line of the smaller number and beneath the rank where the count ends he writes the number of times of subtraction. | ||
| − | |style="text-align:right;"|ויתחיל למנות מטור החשבון הגדול מהאות אשר התחיל להביט בה שנית כפי | + | |style="text-align:right;"|ויתחיל למנות מטור החשבון הגדול מהאות אשר התחיל להביט בה שנית כפי מנין המדרגות שבטור החשבון הקטן אחורנית ובאותה מדרגה אשר תכלה מספרן שם יכתוב תחתיה מספר פעמי הסרת ההוצאה |
|- | |- | ||
| | | | ||
| Line 1,089: | Line 1,202: | ||
| | | | ||
*Afterwards, he examine if what is left in the line of the greater number is still greater than the number of the line of the smaller number. If it is so, he returns again and sees as we have done twice. | *Afterwards, he examine if what is left in the line of the greater number is still greater than the number of the line of the smaller number. If it is so, he returns again and sees as we have done twice. | ||
| − | |style="text-align:right;"|ואחרי זה יעיין אם רבה עדיין מה שנשאר בטור החשבון הגדול על מספר טור החשבון הקטן ואם הוא כן יחזור עוד ויביט כאשר עשינו זה פעמים | + | |style="text-align:right;"|ואחרי זה יעיין אם רבה עדיין ‫<ref>62r</ref>מה שנשאר בטור החשבון [הגדול]‫<ref>marg.</ref> על מספר טור החשבון הקטן ואם הוא כן יחזור עוד ויביט כאשר עשינו זה פעמים |
|- | |- | ||
| | | | ||
*He does it as many times until the number of what is left in the line of the greater number is smaller than the number in the line of the smaller number. | *He does it as many times until the number of what is left in the line of the greater number is smaller than the number in the line of the smaller number. | ||
| − | |style="text-align:right;"|ויעשה ככה הרבה פעמים עד שיהיה מה שישאר בטור החשבון הגדול מספרו | + | |style="text-align:right;"|ויעשה ככה הרבה פעמים עד שיהיה מה שישאר בטור החשבון הגדול מספרו מועט ממספר הטור מהחשבון הקטן |
|- | |- | ||
| | | | ||
| − | :*If it happens in the beginning of the examination that the number of the last digit of the ranks in the line of the smaller number is greater than the last digit in the line of the greater number, so that | + | :*If it happens in the beginning of the examination that the number of the last digit of the ranks in the line of the smaller number is greater than the last digit in the line of the greater number, so that he cannot subtract it from it even once, he should shift this whole digit one rank backwards and it becomes a number of tens in this rank, whereupon it will be enough to subtract the digit of the smaller number as many times from it. |
| − | |style="text-align:right;"|ואם יזדמן לו בתחלת | + | |style="text-align:right;"|ואם יזדמן לו בתחלת ההבטה שיגדל מספר אות האחרונה ממדרגת טור החשבון הקטן מהאות האחרונה שבטור החשבון הגדול עד שלא יוכל להוציאה ממנה אפילו פעם אחת ישים את כל האות ההיא <s>מ</s>מדרגה אחת אחור<sup>נית</sup> ותהיה <sup>היא</sup> מספר עשרות לאותה מדרגה ואם יספיק להוציא ממנה את האות מהחשבון הקטן הרבה פעמים |
|- | |- | ||
| | | | ||
::He thinks, looks and measures how many times he can subtract it from there, so that the remainder will be enough to subtract from it the other digits in the line of the smaller number the same number of times. | ::He thinks, looks and measures how many times he can subtract it from there, so that the remainder will be enough to subtract from it the other digits in the line of the smaller number the same number of times. | ||
| − | |style="text-align:right;"|ויחשוב ויביט וישום וישער כמה פעמים יוכל | + | |style="text-align:right;"|ויחשוב ויביט וישום וישער כמה פעמים יוכל להוציאה משם שיספיק הנשאר גם כן להוציא ממנו ככה פעמים האותיות האחרות שבטור החשבון הקטן |
|- | |- | ||
| | | | ||
*He always writes the number of times of subtraction in the middle between the two lines of the smaller and greater numbers as the number of the ranks of the smaller number. | *He always writes the number of times of subtraction in the middle between the two lines of the smaller and greater numbers as the number of the ranks of the smaller number. | ||
| − | |style="text-align:right;"|ולעולם יכתוב פעמי מספר ההסרה באמצע שני טורי החשבונות | + | |style="text-align:right;"|ולעולם יכתוב פעמי מספר ההסרה באמצע שני טורי החשבונות מהקטון והגדול כמספר המדרגות מהטור מהחשבון הקטן |
|- | |- | ||
| | | | ||
| − | *He starts to count their number from the digit that is in the rank at which he began to look for the subtraction in the line of the greater number. | + | *He starts to count their number back from the digit that is in the rank at which he began to look for the subtraction in the line of the greater number. |
| − | |style="text-align:right;"|ויתחיל מניית מספרן מהאות שבמדרגה אשר התחיל | + | |style="text-align:right;"|ויתחיל מניית מספרן אחורנית מהאות שבמדרגה אשר התחיל בו הבטת הסרת ההוצאה בטור החשבון הגדול |
|- | |- | ||
|The line that is formed between the two lines is the number of times that the line of the smaller number is in the line of the greater number. | |The line that is formed between the two lines is the number of times that the line of the smaller number is in the line of the greater number. | ||
| − | |style="text-align:right;"|והנה הטור המתהוה בין שני הטורים הוא מספר הפעמים אשר טור החשבון הקטן | + | |style="text-align:right;"|והנה הטור המתהוה בין שני הטורים הוא מספר ‫<ref>62v</ref>הפעמים אשר מספר טור החשבון הקטן הוא במספר טור החשבון הגדול |
|- | |- | ||
|What remains above the line of the greater number is the excess of the line of the greater number over the line of the smaller number after you have multiplied it by this number of times. | |What remains above the line of the greater number is the excess of the line of the greater number over the line of the smaller number after you have multiplied it by this number of times. | ||
| − | |style="text-align:right;"|ומה שנשאר על טור החשבון הגדול הוא מה שעודף | + | |style="text-align:right;"|ומה שנשאר על טור החשבון הגדול הוא מה שעודף עדין מספר הטור מהחשבון העליון על מספר הטור מהחשבון הקטן אחרי כפ<sup>י</sup>לת אותם פעמים עליו |
|- | |- | ||
| − | |This is the procedure | + | |This is the procedure of dividing a greater number by a smaller number. |
| − | |style="text-align:right;"|וכן הוא דרך | + | |style="text-align:right;"|וכן הוא דרך חלוקת החשבון הגדול על חשבון קטן ממנו |
|- | |- | ||
| − | |Since the skill of this chapter is very honorable and nice and it is very deep, I shall write in this chapter itself many calculations as an explanation of the method of this skill of division in order to guide and lead the student to understand all the aforementioned matters. | + | |Since the skill of this chapter is very honorable and nice and it is very deep, I shall write in this chapter itself many calculations as an explanation of the method of this skill of division in order to guide and lead the student to understand easily all the aforementioned matters. |
| − | |style="text-align:right;"|וכאשר מלאכת השער הזה היא נכבדת ונחמדת עד מאד והיא עמוקה הרבה לרוב אכתוב בשער הזה עצמו | + | |style="text-align:right;"|וכאשר מלאכת השער הזה היא נכבדת ונחמדת עד מאד והיא עמוקה הרבה לרוב אכתוב בשער הזה עצמו בבאור דרך מלאכת ה{{#annot:term|157,1221|gTvm}}חלוקה{{#annotend:gTvm}} הזאת מהרבה חשבונות כדי להדריך ולהתישר אל המתלמד שידין כל הענינים הנזכרים בנקלה |
|- | |- | ||
| | | | ||
*{{#annot:125÷11|157|PuIG}}We wish to divide one hundred and twenty-five by eleven. | *{{#annot:125÷11|157|PuIG}}We wish to divide one hundred and twenty-five by eleven. | ||
:<math>\scriptstyle125\div11</math> | :<math>\scriptstyle125\div11</math> | ||
| − | |style="text-align:right;"|בקשנו לחלק חמשה ועשרים ומאה על אחד עשר{{#annotend:PuIG}} | + | |style="text-align:right;"|<big>בקשנו</big> לחלק חמשה ועשרים ומאה על אחד עשר{{#annotend:PuIG}} |
|- | |- | ||
| | | | ||
:We write the two lines of the numbers according to this diagram: | :We write the two lines of the numbers according to this diagram: | ||
| − | |style="text-align:right;"|והנה נכתוב שני טורי | + | |style="text-align:right;"|והנה נכתוב שני טורי החשבונות על זאת הצורה |
|- | |- | ||
| | | | ||
:We write first the greater number, then we leave a space and write the smaller number in another line correspondingly. | :We write first the greater number, then we leave a space and write the smaller number in another line correspondingly. | ||
| − | |style="text-align:right;"|נכתוב החשבון הגדול בראשונה בטור אחד ואחר | + | |style="text-align:right;"|נכתוב החשבון הגדול בראשונה בטור אחד ואחר נניח ריוח כמלה טור ונכתוב כנגדו החשבון הקטן בטור אחר |
|- | |- | ||
| | | | ||
| Line 1,172: | Line 1,285: | ||
|- | |- | ||
|} | |} | ||
| − | | | + | |- |
| − | ::<span style=color: | + | | colspan="2"| |
| + | ::<span style=color:green>[Illustration of the procedure:]</span> | ||
::{| | ::{| | ||
|- | |- | ||
| − | | ||rowspan="5"|<math>\scriptstyle\xrightarrow{{\color{red}{1-\left({\color{blue}{1}}\times1\right)}}={\color{green}{0}}}</math>|| ||rowspan="5"|<math>\scriptstyle\xrightarrow{{\color{red}{2-\left(1\times1\right)}}={\color{green}{1}}}</math>|| ||rowspan="5"|<math>\scriptstyle\xrightarrow{{\color{red}{1-\left({\color{blue}{1}}\times1\right)}}={\color{green}{0}}}</math>|| <span style= | + | | ||rowspan="5"|<math>\scriptstyle\xrightarrow{{\color{red}{1-\left({\color{blue}{1}}\times1\right)}}={\color{green}{0}}}</math>|| ||rowspan="5"|<math>\scriptstyle\xrightarrow{{\color{red}{2-\left(1\times1\right)}}={\color{green}{1}}}</math>|| ||rowspan="5"|<math>\scriptstyle\xrightarrow{{\color{red}{1-\left({\color{blue}{1}}\times1\right)}}={\color{green}{0}}}</math>|| <span style=color:LimeGreen>0</span> ||rowspan="5"|<math>\scriptstyle\xrightarrow{{\color{red}{5-\left(1\times1\right)}}={\color{blue}{4}}}</math>|| 0  |
|- | |- | ||
| − | | ||<span style= | + | | ||<span style=color:LimeGreen>0</span>  ||0<span style=color:LimeGreen>1</span> ||01 ||01<span style=color:#0000FF>4</span> |
|- | |- | ||
| − | |<span style= | + | |<span style=color:red>1</span>25||1<span style=color:red>2</span>5||125||12<span style=color:red>5</span>||125 |
|- | |- | ||
| − | | || <span style= | + | | || <span style=color:#0000FF>1</span> || 1 || 1<span style=color:#0000FF>1</span>|| 11 |
|- | |- | ||
| − | | <span style= | + | | <span style=color:red>1</span>1|| 1<span style=color:red>1</span>|| <span style=color:red>1</span>1|| 1<span style=color:red>1</span>|| 11 |
|}<br> | |}<br> | ||
::<math>\scriptstyle\longrightarrow{\color{Violet}{\begin{align}&\scriptstyle11\ the\ result\\&\scriptstyle4\ the\ remainder\\\end{align}}}</math> | ::<math>\scriptstyle\longrightarrow{\color{Violet}{\begin{align}&\scriptstyle11\ the\ result\\&\scriptstyle4\ the\ remainder\\\end{align}}}</math> | ||
| − | + | ||
|- | |- | ||
| | | | ||
| − | :*When we look and take the 1 that is in the last rank of the line of the smaller number and the 1 that is in the last rank of the line of the greater number, we know | + | :*When we look and take the 1 that is in the last rank of the line of the smaller number and the 1 that is in the last rank of the line of the greater number, we know that we can subtract one from the other only once. |
| − | |style=" | + | |style="text-align:right;"|וכאשר נביט ונקח הא' שבמדרגה האחרונה מטור החשבון הקטן וגם הא' שבמדרגה ‫<ref>63r</ref>אחרונה מטור החשבון <s>הקטן</s> הגדול הנה ידענו שלא נוכל להסיר האחת מחברתה כי אם פעם אחת |
|- | |- | ||
| | | | ||
::Since the ranks of the line of the smaller number are two, we write 1 for this one time beneath the 2 that is in the line of the greater number, because it is second rank to the digit 1 of this same line, from which we start looking. | ::Since the ranks of the line of the smaller number are two, we write 1 for this one time beneath the 2 that is in the line of the greater number, because it is second rank to the digit 1 of this same line, from which we start looking. | ||
| − | |style="text-align:right;"|וכנגד הפעם הזאת כאשר מדרגות הטור מהחשבון הקטן הם | + | |style="text-align:right;"|וכנגד הפעם הזאת כאשר מדרגות הטור מהחשבון הקטן הם שתים נכתוב א' תחת הב' שבטור החשבון הגדול באשר היא מדרגה שנית גם כן לאות הא' מהטור ההוא עצמה אשר התחלנו ההבטה ממנה |
|- | |- | ||
| | | | ||
::As nothing remains from this 1, we write a zero above it. | ::As nothing remains from this 1, we write a zero above it. | ||
| − | |style="text-align:right;"|וכאשר לא נשאר כלום מהא' הזאת נכתוב | + | |style="text-align:right;"|וכאשר לא נשאר כלום מהא' הזאת נכתוב עליו סיפרא |
|- | |- | ||
| | | | ||
:*Then, we take the 1 that in the first rank of the line of the smaller number that precedes the other, with which we have started, in writing and we subtract it once also from the 2 that is in the line of the greater number; 1 remains above it. | :*Then, we take the 1 that in the first rank of the line of the smaller number that precedes the other, with which we have started, in writing and we subtract it once also from the 2 that is in the line of the greater number; 1 remains above it. | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אחרי כן נקח הא' שבמדרגה ראשונה מטור החשבון הקטן הקדומה במכתב אל האחרת אשר התחלנו בה ונסיר אותה גם כן פעם אחת מהב' שהיא בטור החשבון הגדול וישאר עליה א‫' |
|- | |- | ||
| | | | ||
:By that we have completed the subtraction of the digits in the line of the smaller number from the line of the greater number once of each equally. | :By that we have completed the subtraction of the digits in the line of the smaller number from the line of the greater number once of each equally. | ||
| − | |style="text-align:right;"|ובזה השלמנו {{#annot:term|1679,155|E95p}}הסרת{{#annotend:E95p}} האותיות שבטור החשבון הקטן מטור | + | |style="text-align:right;"|ובזה השלמנו {{#annot:term|1679,155|E95p}}הסרת{{#annotend:E95p}} האותיות שבטור החשבון הקטן מטור החשבון הגדול בשוה פעם האחת כפעם חברתה |
|- | |- | ||
| | | | ||
| − | :When we look at the remainder in the line of the greater number, we see that it is fourteen and this number is more than the number of the line of the digits of the smaller number, which is only eleven. | + | :When we look at the remainder in the line of the greater number, we see that it is [fourteen] and this number is more than the number of the line of the digits of the smaller number, which is only eleven. |
| − | |style="text-align:right;"|וכאשר נעיין הנותר בטור החשבון הגדול ראינו שהוא | + | |style="text-align:right;"|וכאשר נעיין הנותר בטור החשבון הגדול ראינו שהוא חמשה עשר והנה המספר הזה מרובה ממספר טור אותיות החשבון הקטן שאינו עולה רק אחד עשר |
|- | |- | ||
| | | | ||
:*Because of this, we take again the last 1 from the ranks in the line of the smaller number and subtract it once from the 1 that remains above the 2 in the line of the greater number. Then we write zero above it. | :*Because of this, we take again the last 1 from the ranks in the line of the smaller number and subtract it once from the 1 that remains above the 2 in the line of the greater number. Then we write zero above it. | ||
| − | |style="text-align:right;"|ובעבור זה נחזור | + | |style="text-align:right;"|ובעבור זה נחזור ונקח הא' האחרונה מהמדרגות שבטור החשבון הקטן ונסיר אותה פעם אחת מהא' אשר ‫<ref>63v</ref>נשארה על הב' שבטור החשבון הגדול ואחר נכתוב עליה סיפרא |
|- | |- | ||
| | | | ||
::For this subtraction one time, we write 1 beneath the 5, which is the first rank in the line of the greater number, since it is second to the digit, from which we started looking at the subtraction. | ::For this subtraction one time, we write 1 beneath the 5, which is the first rank in the line of the greater number, since it is second to the digit, from which we started looking at the subtraction. | ||
| − | |style="text-align:right;"|וכנגד פעם ההסרה הזאת נכתוב א' תחת הה' שהיא המדרגה הראשונה מטור החשבון הגדול באשר היא | + | |style="text-align:right;"|וכנגד פעם ההסרה הזאת נכתוב א' תחת הה' שהיא המדרגה הראשונה מטור החשבון הגדול באשר היא שנייה אל האות אשר התחלנו ממנה הבטת ההסרה |
|- | |- | ||
| | | | ||
| Line 1,227: | Line 1,341: | ||
| | | | ||
:Now it is visible and clear to the eye that what remains in the line of the greater number is much smaller than the number in the line of the smaller number. | :Now it is visible and clear to the eye that what remains in the line of the greater number is much smaller than the number in the line of the smaller number. | ||
| − | |style="text-align:right;"|ועתה נראה | + | |style="text-align:right;"|ועתה נראה ונכר לעין שמה שנשאר בטור החשבון הגדול מספר קטן מאד ממספר טור החשבון הקטן |
|- | |- | ||
| | | | ||
| Line 1,239: | Line 1,353: | ||
| | | | ||
:Therefore, we can say that we have found that the smaller number is eleven times in the greater number plus a remainder of four. | :Therefore, we can say that we have found that the smaller number is eleven times in the greater number plus a remainder of four. | ||
| − | |style="text-align:right;"|אם כן נוכל | + | |style="text-align:right;"|אם כן נוכל לאמר זאת מצאנו שהמספר הקטן הוא אחד עשר פעם במספר הגדול ועוד זולת זה עודף ארבעה |
|- | |- | ||
| | | | ||
*{{#annot:100÷9|157|u08O}}We wish to divide one hundred by nine. | *{{#annot:100÷9|157|u08O}}We wish to divide one hundred by nine. | ||
:<math>\scriptstyle100\div9</math> | :<math>\scriptstyle100\div9</math> | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|<big>ועוד בקשנו</big> לחלק מאה על ט‫'{{#annotend:u08O}} |
|- | |- | ||
| | | | ||
:We write them according to this diagram: | :We write them according to this diagram: | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|נכתבם על זאת הצורה |
|- | |- | ||
| | | | ||
| Line 1,287: | Line 1,401: | ||
|} | |} | ||
|- | |- | ||
| − | | | + | | colspan="2"| |
| − | ::<span style=color: | + | ::<span style=color:green>[Illustration of the procedure:]</span> |
::{| | ::{| | ||
|- | |- | ||
| − | | ||rowspan="5"|<math>\scriptstyle\xrightarrow{{\color{red}{10-\left({\color{blue}{1}}\times9\right)}}={\color{green}{1}}}</math>|| ||rowspan="5"|<math>\scriptstyle\xrightarrow{{\color{red}{10-\left({\color{blue}{1}}\times9\right)}}={\color{green}{1}}}</math>|| <span style= | + | | ||rowspan="5"|<math>\scriptstyle\xrightarrow{{\color{red}{10-\left({\color{blue}{1}}\times9\right)}}={\color{green}{1}}}</math>|| ||rowspan="5"|<math>\scriptstyle\xrightarrow{{\color{red}{10-\left({\color{blue}{1}}\times9\right)}}={\color{green}{1}}}</math>|| <span style=color:LimeGreen>0</span>  |
|- | |- | ||
| − | | ||<span style= | + | | ||<span style=color:LimeGreen>01</span> ||01<span style=color:#0000FF>1</span> |
|- | |- | ||
| − | |<span style= | + | |<span style=color:red>10</span>0||100||100 |
|- | |- | ||
| − | | || <span style= | + | | || <span style=color:#0000FF>1</span> || 1<span style=color:#0000FF>1</span> |
|- | |- | ||
| − | |  <span style= | + | |  <span style=color:red>9</span>||  <span style=color:red>9</span>||  9 |
|}<br> | |}<br> | ||
::<math>\scriptstyle\longrightarrow{\color{Violet}{\begin{align}&\scriptstyle11\ the\ result\\&\scriptstyle1\ the\ remainder\\\end{align}}}</math> | ::<math>\scriptstyle\longrightarrow{\color{Violet}{\begin{align}&\scriptstyle11\ the\ result\\&\scriptstyle1\ the\ remainder\\\end{align}}}</math> | ||
| − | + | ||
|- | |- | ||
| | | | ||
:*When we take the 9, which is the smaller number, we see that we cannot subtract it from the 1 that is in the third rank of the greater number. | :*When we take the 9, which is the smaller number, we see that we cannot subtract it from the 1 that is in the third rank of the greater number. | ||
| − | |style="text-align:right;"|וכאשר נקח הט' שהיא החשבון הקטן נראה שלא נוכל להסיר אותה מהא' שבמדרגה | + | |style="text-align:right;"|וכאשר נקח הט' שהיא החשבון הקטן ‫<ref>64r</ref>נראה שלא נוכל להסיר אותה מהא' שבמדרגה השלישית שהיא החשבון הגדול |
|- | |- | ||
| | | | ||
::Therefore, we shift the 1 to the zero that precedes it in writing, so it equals ten and from this ten we subtract 9; 1 remains above this zero. | ::Therefore, we shift the 1 to the zero that precedes it in writing, so it equals ten and from this ten we subtract 9; 1 remains above this zero. | ||
| − | |style="text-align:right;"|ועל כן נשים הא' על הסיפרא הקדומה לה במכתב ותהיה שוה עשר | + | |style="text-align:right;"|ועל כן נשים הא' על הסיפרא הקדומה לה במכתב ותהיה שוה עשר ומאלו העשר נסיר ט' וישאר א' על הספרא ההיא |
|- | |- | ||
| | | | ||
::We write 1 beneath it, for the one time that we have subtracted the 9 from the ten, as it is the first rank of the beginning of looking at the subtraction and the smaller number has only one rank. | ::We write 1 beneath it, for the one time that we have subtracted the 9 from the ten, as it is the first rank of the beginning of looking at the subtraction and the smaller number has only one rank. | ||
| − | |style="text-align:right;"|ונכתוב א' | + | |style="text-align:right;"|ונכתוב תחתיה א' כנגד פעם אחת שהסירונו הט' מהעשר באשר היא המדרגה [הראשונה]‫<ref>Vatican om.</ref> ל<sup>ה</sup>תחלת הבתות ההסרה ובחשבון הקטן אין בו גם כן כי אם מדרגה אחת |
|- | |- | ||
| | | | ||
::We write a zero above the 1 that we have shifted from its position. | ::We write a zero above the 1 that we have shifted from its position. | ||
| − | |style="text-align:right;"|ונכתוב סיפרא | + | |style="text-align:right;"|ונכתוב סיפרא על הא' אשר העתקנוה ממקומה |
|- | |- | ||
| | | | ||
| − | :*We look again to subtract the 9, which is the smaller number, from the 1 that is left above the zero in the line of the greater number. We should shift it to the other | + | :*We look again to subtract the 9, which is the smaller number, from the 1 that is left above the zero in the line of the greater number. We should shift it to the other preceding zero, so it equals ten. |
| − | |style="text-align:right;"|ואחר | + | |style="text-align:right;"|ואחר נחשוב עוד ונביט להסיר הט' שהוא החשבון הקטן מהא' שנשארה על הספרא בטור החשבון הגדול והנה אנחנו צריכים גם כן לשים אותה על הסיפרא האחרת הקדומה לה ותהיה שוה עשר |
|- | |- | ||
| | | | ||
::When we subtract from it 9 once, 1 remains above the first zero in the line if the greater number. | ::When we subtract from it 9 once, 1 remains above the first zero in the line if the greater number. | ||
| − | |style="text-align:right;"|וכשנסיר מהם | + | |style="text-align:right;"|וכשנסיר מהם הט' פעם אחת ישאר א' על הסיפרא הראשונה שבטור החשבון הגדול |
|- | |- | ||
| | | | ||
::For this one time that we have subtracted the 9 from the ten, we write 1 beneath the first zero, as it is first to the looking at the subtraction. | ::For this one time that we have subtracted the 9 from the ten, we write 1 beneath the first zero, as it is first to the looking at the subtraction. | ||
| − | |style="text-align:right;"|וכנגד הפעם | + | |style="text-align:right;"|וכנגד הפעם הזה שהסירונו הט' מהעשר נכתוב תחת הספרא הראשונה א' באשר היא ראשונה להבטת ההסרה |
|- | |- | ||
| | | | ||
| Line 1,339: | Line 1,453: | ||
*{{#annot:100÷12|157|E8oD}}We wish to divide one hundred by twelve. | *{{#annot:100÷12|157|E8oD}}We wish to divide one hundred by twelve. | ||
:<math>\scriptstyle100\div12</math> | :<math>\scriptstyle100\div12</math> | ||
| − | |style="text-align:right;"|עוד בקשנו לחלק מאה על שנים עשר{{#annotend:E8oD}} | + | |style="text-align:right;"|‫<ref>64v</ref><big>עוד בקשנו</big> לחלק מאה על שנים עשר{{#annotend:E8oD}} |
|- | |- | ||
| | | | ||
| Line 1,382: | Line 1,496: | ||
|} | |} | ||
|- | |- | ||
| − | | | + | | colspan="2"| |
| − | ::<span style=color: | + | ::<span style=color:green>[Illustration of the procedure:]</span> |
::{| | ::{| | ||
|- | |- | ||
| − | | ||rowspan="5"|<math>\scriptstyle\xrightarrow{{\color{red}{10-\left({\color{blue}{8}}\times1\right)}}={\color{green}{2}}}</math>|| ||rowspan="5"|<math>\scriptstyle\xrightarrow{{\color{red}{20-\left(8\times2\right)}}={\color{green}{4}}}</math>|| <span style= | + | | ||rowspan="5"|<math>\scriptstyle\xrightarrow{{\color{red}{10-\left({\color{blue}{8}}\times1\right)}}={\color{green}{2}}}</math>|| ||rowspan="5"|<math>\scriptstyle\xrightarrow{{\color{red}{20-\left(8\times2\right)}}={\color{green}{4}}}</math>|| <span style=color:LimeGreen>0</span>  |
|- | |- | ||
| − | | ||<span style= | + | | ||<span style=color:LimeGreen>02</span> ||02<span style=color:#0000FF>4</span> |
|- | |- | ||
| − | |<span style= | + | |<span style=color:red>10</span>0||100||100 |
|- | |- | ||
| − | | ||  <span style= | + | | ||  <span style=color:#0000FF>8</span>||  8 |
|- | |- | ||
| − | | <span style= | + | | <span style=color:red>1</span>2|| 1<span style=color:red>2</span>|| 12 |
| − | |} | + | |} |
::<math>\scriptstyle\longrightarrow{\color{Violet}{\begin{align}&\scriptstyle8\ the\ result\\&\scriptstyle4\ the\ remainder\\\end{align}}}</math> | ::<math>\scriptstyle\longrightarrow{\color{Violet}{\begin{align}&\scriptstyle8\ the\ result\\&\scriptstyle4\ the\ remainder\\\end{align}}}</math> | ||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
:*When we take 1, which is the last rank in the line of the smaller number and look to subtract it from the 1 that is in the third rank of the line of the greater number, we will not be able to subtract the 2 that precedes the 1 of the smaller number in writing from the zeros that remain there. | :*When we take 1, which is the last rank in the line of the smaller number and look to subtract it from the 1 that is in the third rank of the line of the greater number, we will not be able to subtract the 2 that precedes the 1 of the smaller number in writing from the zeros that remain there. | ||
| − | |style="text-align:right;"|והנה כאשר נקח | + | |style="text-align:right;"|והנה כאשר נקח האלף שהיא המדרגה האחרונה מטור החשבון הקטן ונביט להסיר אותו מהא' שבמדרגה השלישית בטור החשבון <s>הקטן ונביט להסיר אותה מהא' שבמדרגה השלישית בטור החשבון</s> הגדול והוא אחרי כן לא נוכל להסיר הב' הקדומה במכתב לפני הא' מהחשבון הקטן מהסיפרש אשר תשארנה שם |
|- | |- | ||
| | | | ||
| Line 1,414: | Line 1,526: | ||
| | | | ||
::Then, we look how many times we subtract the 1 of the smaller number from this ten: | ::Then, we look how many times we subtract the 1 of the smaller number from this ten: | ||
| − | |style="text-align:right;"|ואחר | + | |style="text-align:right;"|ואחר נביט כמה פעמים נסיר הא' מהחשבון הקטן מהעשר האלו |
|- | |- | ||
| | | | ||
::*If we subtract it nine times, only 1 remains from the whole ten, but then we will not have enough to subtract the 2 that is in the line of the smaller number also nine times from what remains in the line of the greater number, because the remainder is only ten, since the 1 is in the second rank, whereas nine times 2 is eighteen. | ::*If we subtract it nine times, only 1 remains from the whole ten, but then we will not have enough to subtract the 2 that is in the line of the smaller number also nine times from what remains in the line of the greater number, because the remainder is only ten, since the 1 is in the second rank, whereas nine times 2 is eighteen. | ||
| − | |style="text-align:right;"|והנה אם נסיר אותה תשע פעמים לא ישאר מכל העשר כי אם א' ולא יספיק לנו אחרי כן להסיר הב' שבטור החשבון הקטן גם כן תשע פעמים ממה שנשאר בטור החשבון העליון לפי שהנשאר אינו | + | |style="text-align:right;"|והנה אם נסיר אותה תשע פעמים <s>נסיר הא' מהחשבון הקטן מהעשר האלו והנה אם נסיר אותה</s> לא ישאר מכל העשר כי אם א' ולא יספיק לנו אחרי כן להסיר הב' שבטור החשבון הקטן גם כן תשע פעמים ממה שנשאר בטור החשבון העליון לפי שהנשאר אינו עולה רק עשר באשר הא' היא במדרגה שנית ותשע ‫<ref>65r</ref>פעמים ב' עולה שמונה עשר |
|- | |- | ||
| | | | ||
::Therefore we subtract the 1 from the ten that is above the zero in the second rank of the line of the greater number only eight times and 2 remains above that zero. | ::Therefore we subtract the 1 from the ten that is above the zero in the second rank of the line of the greater number only eight times and 2 remains above that zero. | ||
| − | |style="text-align:right;"|ומפני זה לא נסיר | + | |style="text-align:right;"|ומפני זה לא נסיר האלף מהעשר אשר על הסיפראש במדרגה שנית מטור החשבון הגדול כי אם שמונה פעמים וישאר ב' על הסיפרא הזאת |
|- | |- | ||
| | | | ||
::We write a zero above the 1 that is in the third rank, since we have shift it to the zero and nothing remains there. | ::We write a zero above the 1 that is in the third rank, since we have shift it to the zero and nothing remains there. | ||
| − | |style="text-align:right;"|ונכתוב סיפרא על הא' | + | |style="text-align:right;"|ונכתוב סיפרא על הא' שהיתה במדרגה השלישית שהרי שמנו אותה על הסיפרא ולא נשאר שם כלום |
|- | |- | ||
| | | | ||
::For the eight times of subtraction, we write 8 beneath the first zero, since the ranks of the smaller number are two and their counting starts from the second rank in the line of the greater number, as we have started the looking of this subtraction from there. | ::For the eight times of subtraction, we write 8 beneath the first zero, since the ranks of the smaller number are two and their counting starts from the second rank in the line of the greater number, as we have started the looking of this subtraction from there. | ||
| − | |style="text-align:right;"|וכנגד | + | |style="text-align:right;"|וכנגד שמונה פעמי <sup>ה</sup>הסרה נכתוב ח' תחת הסיפרא הראשונה באשר מדרגות החשבון הקטן הם שתים ומניינם מתחיל מהסיפרא מהמדרגה השניה שבטור החשבון הגדול לפי ששם התחלנו הבטת ההסרה הזאת |
|- | |- | ||
| | | | ||
:*Afterwards we subtract also the 2 of the smaller number eight times from what is left in the line of the greater number and we do it in this way: | :*Afterwards we subtract also the 2 of the smaller number eight times from what is left in the line of the greater number and we do it in this way: | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ואחרי זה נסיר גם כן הב' מהחשבון הקטן שמנה פעמים ממה שנשאר בטור החשבון הגדול ונעשה על הדרך הזה |
|- | |- | ||
| | | | ||
| Line 1,441: | Line 1,553: | ||
|- | |- | ||
| | | | ||
| − | ::*We subtract sixteen from them, which is the product of the times of the subtraction by 2; 4 remains from them above the zero | + | ::*We subtract sixteen from them, which is the product of the times of the subtraction by 2; 4 remains from them above the first zero. |
| − | |style="text-align:right;"|נסיר מהם ששה עשר שהוא העולה מכפל פעמי ההסרה על | + | |style="text-align:right;"|נסיר מהם ששה עשר שהוא העולה מכפל פעמי ההסרה על ב' וישאר מהם ד' על ראש הסיפרא הראשונה |
|- | |- | ||
| | | | ||
::*We write one zero in the place where the 2 that we have shifted to the first zero was written, since nothing remains there. | ::*We write one zero in the place where the 2 that we have shifted to the first zero was written, since nothing remains there. | ||
| − | |style="text-align:right;"|ונכתוב במקום | + | |style="text-align:right;"|ונכתוב במקום אשר היתה כתובה הב' אשר שמנו אותה על הסיפרא הראשונה סיפרא אחת לפי שלא נשאר שם כלום |
|- | |- | ||
| | | | ||
:The result of the division is that there are eight times twelve in one hundred and an excess of four. | :The result of the division is that there are eight times twelve in one hundred and an excess of four. | ||
| − | |style="text-align:right;"|והנה | + | |style="text-align:right;"|והנה ‫<ref>65v</ref>יצאה לנו החלוק שיש שמנה פעמים שנים עשר במאה ועודף עליהם ארבעה |
|- | |- | ||
| | | | ||
*{{#annot:901÷32|157|qhod}}We wish to divide nine hundred and one by thirty-two. | *{{#annot:901÷32|157|qhod}}We wish to divide nine hundred and one by thirty-two. | ||
:<math>\scriptstyle901\div32</math> | :<math>\scriptstyle901\div32</math> | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|<big>ועוד בקשנו</big> לחלק אחד ותשע מאות על שלשים ושתים{{#annotend:qhod}} |
|- | |- | ||
| | | | ||
:We write them according to this diagram: | :We write them according to this diagram: | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|נכתבים על זאת הצורה |
|- | |- | ||
| | | | ||
| Line 1,501: | Line 1,613: | ||
|- | |- | ||
|} | |} | ||
| − | | | + | |- |
| − | ::<span style=color: | + | | colspan="2"| |
| + | ::<span style=color:green>[Illustration of the procedure:]</span> | ||
::{| | ::{| | ||
|- | |- | ||
| − | | ||rowspan="6"|<math>\scriptstyle\xrightarrow{{\color{red}{9-\left({\color{blue}{2}}\times3\right)}}={\color{green}{3}}}</math>|| ||rowspan="6"|<math>\scriptstyle\xrightarrow{{\color{red}{10-\left({\color{blue}{2}}\times2\right)}}={\color{green}{6}}}</math>|| ||rowspan="6"|<math>\scriptstyle\xrightarrow{{\color{red}{26-\left({\color{blue}{8}}\times3\right)}}={\color{green}{2}}}</math>||<span style= | + | | ||rowspan="6"|<math>\scriptstyle\xrightarrow{{\color{red}{9-\left({\color{blue}{2}}\times3\right)}}={\color{green}{3}}}</math>|| ||rowspan="6"|<math>\scriptstyle\xrightarrow{{\color{red}{10-\left({\color{blue}{2}}\times2\right)}}={\color{green}{6}}}</math>|| ||rowspan="6"|<math>\scriptstyle\xrightarrow{{\color{red}{26-\left({\color{blue}{8}}\times3\right)}}={\color{green}{2}}}</math>||<span style=color:LimeGreen>0</span>  ||rowspan="6"|<math>\scriptstyle\xrightarrow{{\color{red}{21-\left({\color{blue}{8}}\times2\right)}}={\color{green}{5}}}</math>||0<span style=color:LimeGreen>0</span>  |
|- | |- | ||
| − | | || ||<span style= | + | | || ||<span style=color:LimeGreen>2</span>  ||2<span style=color:LimeGreen>2</span> ||22  |
|- | |- | ||
| − | | ||<span style= | + | | ||<span style=color:LimeGreen>3</span>  ||3<span style=color:#0000FF>6</span> ||36 ||36<span style=color:#0000FF>5</span> |
|- | |- | ||
| − | |<span style= | + | |<span style=color:red>9</span>01||901||901||901||901 |
|- | |- | ||
| − | | || <span style= | + | | || <span style=color:#0000FF>2</span> || 2 || 2<span style=color:#0000FF>8</span>|| 28 |
|- | |- | ||
| − | | <span style= | + | | <span style=color:red>3</span>2|| 3<span style=color:red>2</span>|| <span style=color:red>3</span>2|| 3<span style=color:red>2</span>|| 32 |
| − | |} | + | |} |
::<math>\scriptstyle\longrightarrow{\color{Violet}{\begin{align}&\scriptstyle28\ the\ result\\&\scriptstyle5\ the\ remainder\\\end{align}}}</math> | ::<math>\scriptstyle\longrightarrow{\color{Violet}{\begin{align}&\scriptstyle28\ the\ result\\&\scriptstyle5\ the\ remainder\\\end{align}}}</math> | ||
| − | + | ||
|- | |- | ||
| | | | ||
:*We see that if we subtract three times the 3 that is in the bottom line, which is the smaller number, from the 9 that is in the upper line, which is the greater number, we will not be able afterwards to compensate the other digit in the bottom line in order to subtract it from the zero, since nothing remains from the 9. | :*We see that if we subtract three times the 3 that is in the bottom line, which is the smaller number, from the 9 that is in the upper line, which is the greater number, we will not be able afterwards to compensate the other digit in the bottom line in order to subtract it from the zero, since nothing remains from the 9. | ||
| − | |style=" | + | |style="text-align:right;"|הנה אנחנו רואים שאם נסור הג' שבטור השפל שהוא החשבון הקטן מהט' אשר בטור העליון שהוא החשבון הגדול שלשה פעמים לא נוכל אחרי כן לעשות תשלום לאות האחרת שבטור השפל להסיר אותה מהסיפרא לפי שלא ישאר מאומה מהט‫' |
|- | |- | ||
| | | | ||
| − | ::Therefore we subtract it only twice and we write the 3 | + | ::Therefore we subtract it only twice and we write the remaining 3 above it. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אם כן לא נסירנה כי אם שני פעמים ונכתוב הג' הנותרת עליה |
|- | |- | ||
| | | | ||
::For these two times of subtraction, we write 2 beneath the zero, since the ranks of the bottom line are two and the zero is also second to the digit, from which we have started the subtraction. | ::For these two times of subtraction, we write 2 beneath the zero, since the ranks of the bottom line are two and the zero is also second to the digit, from which we have started the subtraction. | ||
| − | |style="text-align:right;"|וכנגד שני | + | |style="text-align:right;"|וכנגד שני פעמי ההסרה האלה נכתוב ב' תחת הסיפרא באשר מדרגות הטור השפל הם שתים והסיפרא גם כן היא שנית אל האות אשר התחלנו בה ההסרה |
|- | |- | ||
| | | | ||
:*Then we subtract the digit 2, which is the first rank in the bottom line, also twice from the zero that is in the upper line and we do it in this way: | :*Then we subtract the digit 2, which is the first rank in the bottom line, also twice from the zero that is in the upper line and we do it in this way: | ||
| − | |style="text-align:right;"|אחרי כן נסיר אות הב' שהיא המדרגה הראשונה שבטור השפל | + | |style="text-align:right;"|אחרי כן נסיר אות הב' שהיא המדרגה הראשונה שבטור השפל גם כן ב' פעמים מהסיפרא שבטור העליון והנה נעשה על דרך זה |
|- | |- | ||
| | | | ||
::*We take 1 from the 3 that remained above the 9 and 2 remains above it. | ::*We take 1 from the 3 that remained above the 9 and 2 remains above it. | ||
| − | |style="text-align:right;"|נקח א' | + | |style="text-align:right;"|נקח א' מהג' הנותרת על הט' וישאר עליה ב‫' |
|- | |- | ||
| | | | ||
::*We put the 1 that we took above the zero, so it equals ten. We subtract two times two from it; their product is four and 6 remains above the zero. | ::*We put the 1 that we took above the zero, so it equals ten. We subtract two times two from it; their product is four and 6 remains above the zero. | ||
| − | |style="text-align:right;"|והא' | + | |style="text-align:right;"|והא' שלקחנו נשים אותה ‫<ref>66r</ref>על הסיפרא ותהיה שוה עשר נסיר מהם ב' פעמים ב' העלה {{#annot:term|156,1253|0iJL}}כפילתם{{#annotend:0iJL}} ארבעה וישאר ו' על הסיפרא |
|- | |- | ||
| | | | ||
| − | :Now we have made a compensation by subtracting all the digits of the bottom line from the upper line an equal number of times for each. | + | :Now we have made a compensation by subtracting all the digits of the bottom line from the upper line an equal number of times [for each]. |
| − | |style="text-align:right;"|ועתה עשינו תשלום שהסירונו כל | + | |style="text-align:right;"|ועתה עשינו תשלום שהסירונו כל אותיות הטור השפל במספר פעמים שוה מהטור העליון |
|- | |- | ||
| | | | ||
:*Indeed, when we look at what is left in the upper line, we see that it is greater than the number of the bottom line, and because of this we should look again to subtract the 3, which is the last rank in the bottom line, from the 2 that is left in the last rank of the upper line. We do it in this way: | :*Indeed, when we look at what is left in the upper line, we see that it is greater than the number of the bottom line, and because of this we should look again to subtract the 3, which is the last rank in the bottom line, from the 2 that is left in the last rank of the upper line. We do it in this way: | ||
| − | |style="text-align:right;"|אכן כאשר נעיין | + | |style="text-align:right;"|אכן כאשר נעיין בטור העליון הנותר נראה שהוא רב יותר מספר מהטור השפל ומפני זה אנחנו צריכים לחזור ולהביט להסיר הג' שהיא המדרגה האחרונה שבטור השפל מהב' שנשארה לנו במדרגה האחרונה מהטור העליון ונעשה על דרך זה |
|- | |- | ||
| | | | ||
::*We shift the whole 2 to the 6 above the zero; they are twenty-six. | ::*We shift the whole 2 to the 6 above the zero; they are twenty-six. | ||
| − | |style="text-align:right;"|נשים הב' ההיא | + | |style="text-align:right;"|נשים הב' ההיא כולה על הו' אשר בראש הסיפרא ויהיו עשרים וששה |
|- | |- | ||
| | | | ||
::*Now, we measure how many times we can subtract the 3 from the twenty-six: we can subtract it eight times, which are twenty-four. | ::*Now, we measure how many times we can subtract the 3 from the twenty-six: we can subtract it eight times, which are twenty-four. | ||
| − | |style="text-align:right;"|ועתה נשום ונשער כמה | + | |style="text-align:right;"|ועתה [נשום]‫<ref>marg.</ref> ונשער כמה פעמים נוכל להסיר הג' מהששה ועשרים והנה נוכל להסיר אותה שמונה פעמים העולים עשרים וארבע |
|- | |- | ||
| | | | ||
::*When we subtract them from twenty-six, 2 remains above the 6. | ::*When we subtract them from twenty-six, 2 remains above the 6. | ||
| − | |style="text-align:right;"|כשנסיר אותם | + | |style="text-align:right;"|כשנסיר אותם מהששה ועשרים ישאר על הו' ב‫' |
|- | |- | ||
| | | | ||
| Line 1,569: | Line 1,682: | ||
|- | |- | ||
| | | | ||
| − | ::*For the eight times of subtraction, | + | ::*For the eight times of subtraction, I write 8 beneath the 1 that is the first rank of the upper line, since it is second to the rank, from which we have started looking at the subtraction. |
| − | |style="text-align:right;"|וכנגד | + | |style="text-align:right;"|וכנגד שמונה פעמי ההסרה אכתוב ח' תחת הא' שהיא המדרגה הראשונה מהטור העליון באשר היא שנייה אל המדרגה אשר התחלנו הבטת ההסרה ממנה |
|- | |- | ||
| | | | ||
:*Now, we subtract also the digit 2 of the bottom line eight times from what is left in the upper line. We do it in this way: | :*Now, we subtract also the digit 2 of the bottom line eight times from what is left in the upper line. We do it in this way: | ||
| − | |style="text-align:right;"|ועתה נסיר גם כן אות | + | |style="text-align:right;"|ועתה נסיר גם כן אות ב' ‫<ref>66v</ref>מהטור השפל שמונה פעמים ממה שנשאר בטור העליון ונעשה על הדרך הזה |
|- | |- | ||
| | | | ||
::*We shift the 2 that is left in the second rank of the upper line to the 1 that is in the first rank; they are twenty-one. | ::*We shift the 2 that is left in the second rank of the upper line to the 1 that is in the first rank; they are twenty-one. | ||
| − | |style="text-align:right;"|נשים הב' | + | |style="text-align:right;"|נשים הב' הנשארת לנו במדרגה השנייה מהטור העליון על הא' שבמדרגה ראשונה ממנה יהיו עשרים ואחד |
|- | |- | ||
| | | | ||
| Line 1,586: | Line 1,699: | ||
| | | | ||
::*We write a zero above the 2 that is written in the second rank, since we have shifted the whole of it to the first rank. | ::*We write a zero above the 2 that is written in the second rank, since we have shifted the whole of it to the first rank. | ||
| − | |style="text-align:right;"|ונכתוב סיפרא על הב' הכתובה | + | |style="text-align:right;"|ונכתוב סיפרא על הב' הכתובה בראש המדרגה השנית <s>בשאר</s> [באשר]‫<ref>marg.</ref> העתקנוה ממקומה ונשים אותה במדרגה הראשונה |
|- | |- | ||
| | | | ||
:This division is complete and we have found that the middle line is twenty-eight and what remains above the upper line is five. | :This division is complete and we have found that the middle line is twenty-eight and what remains above the upper line is five. | ||
| − | |style="text-align:right;"|ונשלמה החלוקה הזאת ומצאנו שהטור | + | |style="text-align:right;"|ונשלמה החלוקה הזאת ומצאנו שהטור ה<sup>א</sup>מצעי עולה שמונה ועשרים והנותר על הטור העליון חמשה |
|- | |- | ||
| | | | ||
*{{#annot:891÷40|157|chBm}}We wish to divide eight hundred and ninety-one by forty. | *{{#annot:891÷40|157|chBm}}We wish to divide eight hundred and ninety-one by forty. | ||
:<math>\scriptstyle891\div40</math> | :<math>\scriptstyle891\div40</math> | ||
| − | |style="text-align:right;"|ועוד בקשנו לחלק | + | |style="text-align:right;"|<big>ועוד בקשנו</big> לחלק שמונה מאות ותשעים ואחד על ארבעים{{#annotend:chBm}} |
|- | |- | ||
| | | | ||
| Line 1,634: | Line 1,747: | ||
|} | |} | ||
|- | |- | ||
| − | | | + | | colspan="2"| |
| − | ::<span style=color: | + | ::<span style=color:green>[Illustration of the procedure:]</span> |
::{| | ::{| | ||
|- | |- | ||
| − | | ||rowspan="4"|<math>\scriptstyle\xrightarrow{{\color{red}{8-\left({\color{blue}{2}}\times4\right)}}={\color{green}{0}}}</math>||<span style= | + | | ||rowspan="4"|<math>\scriptstyle\xrightarrow{{\color{red}{8-\left({\color{blue}{2}}\times4\right)}}={\color{green}{0}}}</math>||<span style=color:LimeGreen>0</span>  ||rowspan="4"|<math>\scriptstyle\xrightarrow{{\color{red}{9-\left(2\times4\right)}}={\color{green}{1}}}</math>||0<span style=color:LimeGreen>1</span>  |
|- | |- | ||
| − | |<span style= | + | |<span style=color:red">8</span>91||891||891 |
|- | |- | ||
| − | | || <span style= | + | | || <span style=color:#0000FF>2</span> || 2<span style=color:#0000FF>2</span> |
|- | |- | ||
| − | | <span style= | + | | <span style=color:red>4</span>0|| <span style=color:red>4</span>0|| 40 |
| − | |} | + | |} |
::<math>\scriptstyle\longrightarrow{\color{Violet}{\begin{align}&\scriptstyle22\ the\ result\\&\scriptstyle11\ the\ remainder\\\end{align}}}</math> | ::<math>\scriptstyle\longrightarrow{\color{Violet}{\begin{align}&\scriptstyle22\ the\ result\\&\scriptstyle11\ the\ remainder\\\end{align}}}</math> | ||
|- | |- | ||
| | | | ||
:*We subtract the 4 that is in the bottom line twice from the 8 that is in the upper line. | :*We subtract the 4 that is in the bottom line twice from the 8 that is in the upper line. | ||
| − | |style="text-align:right;"|ונסיר הד' שבטור השפל שתי פעמים מהח' | + | |style="text-align:right;"|ונסיר הד' שבטור השפל שתי פעמים מהח' שבטור העליון |
|- | |- | ||
| | | | ||
| Line 1,657: | Line 1,770: | ||
|- | |- | ||
| | | | ||
| − | ::For the two times of subtraction, we write 2 beneath the 9 that is in the upper line, since it is second rank to the digit, from which we have started the subtraction and in the bottom line there are also two ranks. | + | ::For the [two] times of subtraction, we write 2 beneath the 9 that is in the upper line, since it is second rank to the digit, from which we have started the subtraction and in the bottom line there are also two ranks. |
| − | |style="text-align:right;"|וכנגד | + | |style="text-align:right;"|וכנגד פעמי ההסרה נכתוב ב' תחת הט' שבטור העליון באשר היא מדרגה שנית אל האות אשר הנחלנו ממנה ההסרה ובטור השפל יש גם כן שתי מדרגות |
|- | |- | ||
| | | | ||
:*Again, we subtract the known 4 twice from the corresponding 9 in the upper line; 1 remains above it. | :*Again, we subtract the known 4 twice from the corresponding 9 in the upper line; 1 remains above it. | ||
| − | |style="text-align:right;"|עוד נשוב ונסיר הד' הנודעת | + | |style="text-align:right;"|‫<ref>67r</ref>עוד נשוב ונסיר הד' הנודעת מהט' שכנגדה בטור העליון שני פעמים וישאר עליה א‫' |
|- | |- | ||
| | | | ||
| Line 1,670: | Line 1,783: | ||
| | | | ||
:The result of the division is that in eight hundred and ninety-one there are twenty-two times forty and an excess of eleven. | :The result of the division is that in eight hundred and ninety-one there are twenty-two times forty and an excess of eleven. | ||
| − | |style="text-align:right;"|והנה | + | |style="text-align:right;"|והנה יצאתה אלינו החלוקה שיש בשמונה מאות <s>וש</s> ותשעים ואחד שנים ועשרים פעם ארבעים ועוד נוסף עליהם אחד עשר |
|- | |- | ||
| | | | ||
*{{#annot:321÷9|157|ERZO}}We wish to divide three hundred and twenty-one by nine. | *{{#annot:321÷9|157|ERZO}}We wish to divide three hundred and twenty-one by nine. | ||
:<math>\scriptstyle321\div9</math> | :<math>\scriptstyle321\div9</math> | ||
| − | |style="text-align:right;"|ועוד בקשנו לחלק שלש מאות ועשרים ואחד על תשעה{{#annotend:ERZO}} | + | |style="text-align:right;"|<big>ועוד בקשנו</big> לחלק שלש מאות ועשרים ואחד על תשעה{{#annotend:ERZO}} |
|- | |- | ||
| | | | ||
:We write them according to this diagram: | :We write them according to this diagram: | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ונכתוב אותם על זאת הצורה |
|- | |- | ||
| | | | ||
| Line 1,718: | Line 1,831: | ||
|} | |} | ||
|- | |- | ||
| − | | | + | | colspan="2"| |
| − | ::<span style=color: | + | ::<span style=color:green>[Illustration of the procedure:]</span> |
::{| | ::{| | ||
|- | |- | ||
| − | | ||rowspan="5"|<math>\scriptstyle\xrightarrow{{\color{red}{32-\left({\color{blue}{3}}\times9\right)}}={\color{green}{5}}}</math>|| ||rowspan="5"|<math>\scriptstyle\xrightarrow{{\color{red}{51-\left({\color{blue}{5}}\times9\right)}}={\color{green}{6}}}</math>|| <span style= | + | | ||rowspan="5"|<math>\scriptstyle\xrightarrow{{\color{red}{32-\left({\color{blue}{3}}\times9\right)}}={\color{green}{5}}}</math>|| ||rowspan="5"|<math>\scriptstyle\xrightarrow{{\color{red}{51-\left({\color{blue}{5}}\times9\right)}}={\color{green}{6}}}</math>|| <span style=color:LimeGreen>0</span>  |
|- | |- | ||
| − | | ||<span style= | + | | ||<span style=color:LimeGreen>05</span> ||05<span style=color:#0000FF>6</span> |
|- | |- | ||
| − | |<span style= | + | |<span style=color:red>32</span>1||321||321 |
|- | |- | ||
| − | | || <span style= | + | | || <span style=color:#0000FF>3</span> || 3<span style=color:#0000FF>5</span> |
|- | |- | ||
| − | |  <span style= | + | |  <span style=color:red>9</span>||  <span style=color:red>9</span>||  9 |
| − | |} | + | |} |
::<math>\scriptstyle\longrightarrow{\color{Violet}{\begin{align}&\scriptstyle35\ the\ result\\&\scriptstyle6\ the\ remainder\\\end{align}}}</math> | ::<math>\scriptstyle\longrightarrow{\color{Violet}{\begin{align}&\scriptstyle35\ the\ result\\&\scriptstyle6\ the\ remainder\\\end{align}}}</math> | ||
| − | |||
|- | |- | ||
| | | | ||
:*When we try to subtract the 9, which is the smaller number, from the 3 that is in the last rank of the upper line, we have to shift the whole 3 to the 2 that precedes it in writing; they are thirty-two. | :*When we try to subtract the 9, which is the smaller number, from the 3 that is in the last rank of the upper line, we have to shift the whole 3 to the 2 that precedes it in writing; they are thirty-two. | ||
| − | |style="text-align:right;"|וכאשר | + | |style="text-align:right;"|וכאשר נביט להסיר הט' שהיא החשבון הקטן מהג' שבמדרגה אחרונה מהטור העליון יצטרך לנו לשים את הג' כולה על הב' הקדומה לה במכתב ויהיו שלשים ושנים |
|- | |- | ||
| | | | ||
| − | ::We subtract the 9 from them three times, which are twenty-seven, | + | ::We subtract the 9 from them three times, which are twenty-seven, 5 is left from them above the 2. |
| − | |style="text-align:right;"|ונסיר מהם הט' שלש פעמים שעולים | + | |style="text-align:right;"|ונסיר מהם הט' שלש פעמים שעולים שבעה ועשרים וישאר מהם ה' על הב‫' |
|- | |- | ||
| | | | ||
::For these three times of subtraction, we write 3 beneath the 2 that is in the upper line, since we start the subtraction from this rank and in the bottom line there is only one rank. | ::For these three times of subtraction, we write 3 beneath the 2 that is in the upper line, since we start the subtraction from this rank and in the bottom line there is only one rank. | ||
| − | |style="text-align:right;"|וכנגד | + | |style="text-align:right;"|וכנגד שלשת פעמי ההסרה האלה תכתוב ג' תחת הב' שבטור העליון לפי שמאותה מדרגה אנחנו מתחילים ההסרה ואין בטור השפל כי <s>מד</s> אם ‫<ref>67v</ref>מדרגה אחת |
|- | |- | ||
| | | | ||
| Line 1,752: | Line 1,864: | ||
|- | |- | ||
| | | | ||
| − | :*Again, we subtract the 9 from the 5 that is left above the 2 in the upper line, but since we cannot subtract the 9 from the 5, we shift the whole 5 to the 1 | + | :*Again, we subtract the 9 from the 5 that is left above the 2 in the upper line, but since we cannot subtract the 9 from the 5, we shift the whole 5 to the 1; they are fifty-one. |
| − | |style="text-align:right;"|ונשוב עוד להסיר הט' מהה' הנשארת על הב' בטור העליון וכאשר לא נוכל להסיר | + | |style="text-align:right;"|ונשוב עוד להסיר הט' מהה' הנשארת על הב' בטור העליון וכאשר לא נוכל להסיר ט' מה' נשים כל הה' על הא' ויהיו חמישים ואחד |
|- | |- | ||
| | | | ||
| − | ::We subtract the 9 | + | ::We subtract the 9 five times, 6 is left from them above the first rank. |
| − | |style="text-align:right;"|והנה נסיר | + | |style="text-align:right;"|והנה נסיר הט' חמשה פעמים וישאר מהם ו' על המדרגה הראשונה |
|- | |- | ||
| | | | ||
::We write a zero above the 5, since nothing is left of it. | ::We write a zero above the 5, since nothing is left of it. | ||
| − | |style="text-align:right;"|ונכתוב סיפרא על הה' כאשר לא נשאר ממנה כלום | + | |style="text-align:right;"|ונכתוב סיפרא על הה' ד כאשר לא נשאר ממנה כלום |
|- | |- | ||
| | | | ||
::For the five times of subtraction, we write 5 beneath the first rank, from which we have started the subtraction, since in the bottom line there is only one rank. | ::For the five times of subtraction, we write 5 beneath the first rank, from which we have started the subtraction, since in the bottom line there is only one rank. | ||
| − | |style="text-align:right;"|וכנגד חמש | + | |style="text-align:right;"|וכנגד חמש פעמים ההסרה נכתוב ה' תחת המדרגה הראשונה שהתחלנו ההסרה ממנה כאשר אין בטור השפל כי אם מדרגה אחת |
|- | |- | ||
| | | | ||
:This division is complete and the middle line is thirty-five and what remains above the upper line is six. | :This division is complete and the middle line is thirty-five and what remains above the upper line is six. | ||
| − | |style="text-align:right;"|והנה | + | |style="text-align:right;"|והנה נגמרה החלוקה והטור האמצעי עולה ל"ה והנותר על הטור העליון ששה |
|- | |- | ||
| | | | ||
*{{#annot:583696÷764|157|2mgj}}We wish to divide five hundred and eighty-three thousand, six hundred and ninety-six by seven hundred and sixty-four. | *{{#annot:583696÷764|157|2mgj}}We wish to divide five hundred and eighty-three thousand, six hundred and ninety-six by seven hundred and sixty-four. | ||
:<math>\scriptstyle583696\div764</math> | :<math>\scriptstyle583696\div764</math> | ||
| − | |style="text-align:right;"|ועוד בקשנו לחלק חמש מאות | + | |style="text-align:right;"|<big>ועוד בקשנו</big> לחלק חמש מאות <sup>אלף</sup> ושמונים ושלשת אלפים ושש מאות ותשעים וששה על שבע מאות וששים וארבעה{{#annotend:2mgj}} |
|- | |- | ||
| | | | ||
| Line 1,824: | Line 1,936: | ||
|- | |- | ||
|} | |} | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | :<span style=color:green>[Illustration of the procedure:]</span> | ||
| + | :{| | ||
| + | |- | ||
| + | | ||rowspan="6"|<math>\scriptstyle\xrightarrow{{\color{red}{58-\left({\color{blue}{7}}\times7\right)=58-49=}}{\color{green}{9}}}</math>|| ||rowspan="6"|<math>\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{9-4=}}{\color{green}{5}}\\&\scriptstyle{\color{red}{43-\left({\color{blue}{7}}\times6\right)=43-42=}}{\color{green}{1}}\\\end{align}}</math>|| | ||
| + | |- | ||
| + | | || || <span style=color:LimeGreen>5</span>     | ||
| + | |- | ||
| + | | ||<span style=color:LimeGreen>09</span>    ||09<span style=color:LimeGreen>1</span>    | ||
| + | |- | ||
| + | |<span style=color:red>58</span>3696||583696||583696 | ||
| + | |- | ||
| + | | ||   <span style=color:#0000FF>7</span>  ||   <span style=color:#0000FF>7</span>   | ||
| + | |- | ||
| + | |   <span style=color:red>7</span>64||   7<span style=color:red>6</span>4||   76<span style=color:red>4</span> | ||
|} | |} | ||
| − | + | :::{| | |
| − | : | ||
| − | :{| | ||
|- | |- | ||
| − | + | |rowspan="6"|<math>\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{5-1=}}{\color{green}{4}}\\&\scriptstyle{\color{red}{11-3=}}{\color{green}{8}}\\&\scriptstyle{\color{red}{36-\left({\color{blue}{7}}\times4\right)=36-28=}}{\color{green}{8}}\\\end{align}}</math>|| <span style=color:LimeGreen>4</span>     | |
|- | |- | ||
| − | + | | 5<span style=color:LimeGreen>8</span>    | |
|- | |- | ||
| − | + | |091<span style=color:LimeGreen>8</span>   | |
|- | |- | ||
| − | + | |583696 | |
|- | |- | ||
| − | + | |   <span style=color:#0000FF>7</span>   | |
|- | |- | ||
| − | |   <span style= | + | |   <span style=color:red>7</span>64 |
|} | |} | ||
| − | |||
|- | |- | ||
| | | | ||
:The skill of what is required is much greater and deep than all we have mentioned and this is its description: | :The skill of what is required is much greater and deep than all we have mentioned and this is its description: | ||
| − | |style=" | + | |style="text-align:right;"|והנה המבוקש הזה מלאכתו רבה ועמוקה מכל <s>[..]</s> מה שזכרנו וזה תארו |
|- | |- | ||
| | | | ||
:*When we look to subtract the 7 that is in the bottom line from the 5 that is in the upper line, we cannot do so. | :*When we look to subtract the 7 that is in the bottom line from the 5 that is in the upper line, we cannot do so. | ||
| − | |style="text-align:right;"|הנה כשנביט להסיר | + | |style="text-align:right;"|הנה כשנביט להסיר ז' שבטור התחתון מהה' שבטור העליון לא נוכל |
|- | |- | ||
| | | | ||
| − | ::*Therefore, we shift it to the 8, which is the rank that precedes it in writing, and write a zero in its place, since nothing is left there. | + | ::*Therefore, we shift it to the [8], which is the rank that precedes it in writing, and write a zero in its place, since nothing is left there. |
| − | |style="text-align:right;"|ועל כן נשים אותה על | + | |style="text-align:right;"|‫<ref>68r</ref>ועל כן נשים אותה על הא' שהיא המדרגה הקד<sup>ו</sup>מה לה במכתב ונכתוב במקומה סיפרא באשר לא נשאר שם כלום |
|- | |- | ||
| | | | ||
::*The result is fifty-eight and when we measure how many times we shall subtract the 7 from it, we find that we can subtract only 7 times, so that we will be able to do the necessary rule with the remainder. | ::*The result is fifty-eight and when we measure how many times we shall subtract the 7 from it, we find that we can subtract only 7 times, so that we will be able to do the necessary rule with the remainder. | ||
| − | |style="text-align:right;"|והנה יעלו | + | |style="text-align:right;"|והנה יעלו חמישים ושמנה וכאשר נשום ונשער כמה פעמים נסיר מהם הז' נמצא שלא נוכל להוציאה כי אם שבעה פעמים כדי שנוכל לעשות מהנשאר המשפט הצריך |
|- | |- | ||
| | | | ||
::*Seven times 7 is forty-nine and when we subtract it from fifty-eight, 9 remains above the 8. | ::*Seven times 7 is forty-nine and when we subtract it from fifty-eight, 9 remains above the 8. | ||
| − | |style="text-align:right;"|והנה שבע | + | |style="text-align:right;"|והנה שבע פעמים ז' עולים תשע וארבעים וכשנסיר אותם משמנה וחמישים נשאר ט' על הח‫' |
|- | |- | ||
| | | | ||
::*We start counting three ranks of the bottom line back from this rank and the counting ends at 6 that is the third rank; we write 7 beneath it, for the seven times of subtraction. | ::*We start counting three ranks of the bottom line back from this rank and the counting ends at 6 that is the third rank; we write 7 beneath it, for the seven times of subtraction. | ||
| − | |style="text-align:right;"|ומהמדרגה הזאת נתחיל למנות שלש | + | |style="text-align:right;"|ומהמדרגה הזאת נתחיל למנות שלש המדרגות שבטור השפל אחורנית ויכלה מספרן בו' שהיא מדרגה שלישית ושם נכתוב תחתיה ז' כנגד שבע פעמי<s>ם</s> ההסרה |
|- | |- | ||
| | | | ||
:*Then, we subtract the 6 that is in the bottom line also 7 times from the 9; the result of the multiplication is forty-two. We do it in this way: | :*Then, we subtract the 6 that is in the bottom line also 7 times from the 9; the result of the multiplication is forty-two. We do it in this way: | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ואחרי כן נסיר הו"ו שבטור השפל גם כן שבעה <sup>ז'</sup> פעמים מהט' והעולה מ{{#annot:term|156,1230|90GV}}כפל{{#annotend:90GV}} זה על זה [הם ארבעים]‫<ref>Vatican: וארבעים</ref> ושנים ונעשה על הדרך הזה |
|- | |- | ||
| | | | ||
::*We subtract 4 from that 9 and write the remainder, which is 5, above it. | ::*We subtract 4 from that 9 and write the remainder, which is 5, above it. | ||
| − | |style="text-align:right;"|נסיר מהט' ההיא ד' ונכתוב עליה הנשאר שהוא ה' | + | |style="text-align:right;"|נסיר מהט' ההיא ד' ונכתוב עליה הנשאר שהוא ה‫' |
|- | |- | ||
| | | | ||
::*We shift the 4 to the 3, which is the rank that precedes in writing the rank above which the 9 is; they are forty-three. We find that 1 remains from them above the 3. | ::*We shift the 4 to the 3, which is the rank that precedes in writing the rank above which the 9 is; they are forty-three. We find that 1 remains from them above the 3. | ||
| − | |style="text-align:right;"|ונשים הד' על הג' שהיא מדרגה קדומה במכתב למדרגה | + | |style="text-align:right;"|ונשים הד' על הג' שהיא מדרגה קדומה במכתב למדרגה אשר היתה הט' עליה והנה יהיו ארבעים ושלש נמצא שישאר מהם א' על הג‫' |
|- | |- | ||
| | | | ||
:*Then, we subtract the 4 that is in the bottom line, which is the first rank of it, also 7 times; the result of the multiplication is twenty-eight. We do it in this way: | :*Then, we subtract the 4 that is in the bottom line, which is the first rank of it, also 7 times; the result of the multiplication is twenty-eight. We do it in this way: | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ואחר כך נסיר הד' שבטור השפל שהיא המדרגה הראשונה ממנה גם כן ‫<ref>68v</ref>שבע פעמים שעולה כפלתם שמונה ו<s>ארבעים</s><sup>עשרים</sup> ונעשה על הדרך הזה |
|- | |- | ||
| | | | ||
::*We take 1 from the 5 that is left in the upper line, in the fifth rank, and shift it to the 1 that is left above the 3 that precedes this rank; they are eleven. We subtract 3 from them; 8 remains above the 1. | ::*We take 1 from the 5 that is left in the upper line, in the fifth rank, and shift it to the 1 that is left above the 3 that precedes this rank; they are eleven. We subtract 3 from them; 8 remains above the 1. | ||
| − | |style="text-align:right;"|נקח א' מן הה' שנשארה לנו בטור העליון במדרגה חמישית ונשים אותה על הא' שנשארה על הג' הקדומה למדרגה הזאת ויהיו אחד עשר נסיר מהם ג' ישאר על הא' ח' | + | |style="text-align:right;"|נקח א' מן הה' שנשארה לנו בטור העליון במדרגה חמישית ונשים אותה על הא' שנשארה על הג' הקדומה למדרגה הזאת ויהיו אחד עשר נסיר <s>או</s>מהם ג' ישאר על הא' ח‫' |
|- | |- | ||
| | | | ||
::*We shift the 3 to the rank that precedes its rank in writing, which is 6; they are thirty-six. We subtract from them the product of 4 by 7, which is twenty-eight; 8 remains above the 6. | ::*We shift the 3 to the rank that precedes its rank in writing, which is 6; they are thirty-six. We subtract from them the product of 4 by 7, which is twenty-eight; 8 remains above the 6. | ||
| − | |style="text-align:right;"|נשים הג' על המדרגה הקדומה למדרגתה במכתב שהיא ו' ויהיו ששה ושלשים נסיר מהם כפל הד' על הז' שהם | + | |style="text-align:right;"|נשים הג' על המדרגה הקדומה למדרגתה במכתב שהיא ו' ויהיו ששה ושלשים נסיר מהם כפל הד' על הז' שהם שמנה ועשרים וישאר על הו' ח‫' |
|- | |- | ||
| | | | ||
:Now, we have completed the subtraction of all the digits of the bottom line from the upper line equally, each as many times as the other. | :Now, we have completed the subtraction of all the digits of the bottom line from the upper line equally, each as many times as the other. | ||
| − | |style="text-align:right;"|ועתה השלמנו להסיר כל אותיות הטור השפל מהטור העליון בשוה זו כזו האחת | + | |style="text-align:right;"|ועתה השלמנו להסיר כל אותיות הטור השפל מהטור העליון בשוה זו כזו האחת כפ[ע]ם חברתה |
| + | |- | ||
| + | | colspan="2"| | ||
| + | ::{| | ||
| + | |- | ||
| + | |rowspan="7"|<math>\scriptstyle\xrightarrow{\scriptstyle{\color{red}{48-\left({\color{blue}{6}}\times7\right)=48-42=}}{\color{green}{6}}}</math>|| <span style=color:LimeGreen>0</span>    ||rowspan="7"|<math>\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{6-3=}}{\color{green}{3}}\\&\scriptstyle{\color{red}{38-\left({\color{blue}{6}}\times6\right)=38-36=}}{\color{green}{2}}\\\end{align}}</math>|| 0<span style=color:LimeGreen>3</span>    | ||
| + | |- | ||
| + | | 4<span style=color:LimeGreen>6</span>   || 46    | ||
| + | |- | ||
| + | | 58   || 58<span style=color:LimeGreen>2</span>   | ||
| + | |- | ||
| + | |0918  ||0918   | ||
| + | |- | ||
| + | |583696||583696 | ||
| + | |- | ||
| + | |   7<span style=color:#0000FF>6</span> ||   7<span style=color:#0000FF>6</span>  | ||
| + | |- | ||
| + | |   7<span style=color:red>6</span>4||   76<span style=color:red>4</span> | ||
|} | |} | ||
| − | |||
::{| | ::{| | ||
|- | |- | ||
| − | + | |rowspan="7"|<math>\scriptstyle\xrightarrow{\scriptstyle{\color{red}{29-\left({\color{blue}{6}}\times4\right)=29-24=}}{\color{green}{5}}}</math>|| 03    | |
|- | |- | ||
| − | + | | 46<span style=color:LimeGreen>0</span>   | |
|- | |- | ||
| − | + | | 582   | |
|- | |- | ||
| − | + | |0918<span style=color:LimeGreen>5</span>  | |
|- | |- | ||
| − | + | |583696 | |
|- | |- | ||
| − | |   7<span style= | + | |   7<span style=color:#0000FF>6</span>  |
|- | |- | ||
| − | |    | + | |   <span style=color:red>7</span>64 |
|} | |} | ||
| − | |||
|- | |- | ||
| | | | ||
:When we examine what is left in the upper line, we see that it is much more than the number of the bottom line. | :When we examine what is left in the upper line, we see that it is much more than the number of the bottom line. | ||
| − | |style=" | + | |style="text-align:right;"|וכשנעיין במה שנשאר בטור העליון נראה שהוא רב מאד על מספר הטור השפל |
|- | |- | ||
| | | | ||
:*Therefore we look again to subtract the 7 that is in the bottom line from the 4 that is left in the upper line, in the fifth rank. | :*Therefore we look again to subtract the 7 that is in the bottom line from the 4 that is left in the upper line, in the fifth rank. | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|על כן נחזור ונביט להסיר ז' שבטור השפל מהד' שנשארה בטור העליון במדרגה חמישית |
|- | |- | ||
| | | | ||
::*We have to shift it to the 8 that is left above the preceding rank; they are forty-eight. | ::*We have to shift it to the 8 that is left above the preceding rank; they are forty-eight. | ||
| − | |style="text-align:right;"|והנה צריכים | + | |style="text-align:right;"|והנה אנחנו צריכים לשים אותה על הח' שנשארה על המדרגה הקדומה לזו יהיו שמנה וארבעים |
|- | |- | ||
| | | | ||
::*When we measure, we find that we can subtract the 7 six times from them, the product of which is forty-two, and when we subtract it from them, 6 remains above the 8. | ::*When we measure, we find that we can subtract the 7 six times from them, the product of which is forty-two, and when we subtract it from them, 6 remains above the 8. | ||
| − | |style="text-align:right;"|וכאשר נשום ונשער נמצא שנוכל להסיר הז' מהם שש פעמים שעולה | + | |style="text-align:right;"|וכאשר נשום ונשער נמצא שנוכל להסיר הז' מהם שש פעמים שעולה כפילתם שנים וארבעים ונמצא כשנסיר אותם מהם ישארו על הח' ו‫' |
|- | |- | ||
| | | | ||
::*We write a zero above the 4, since nothing is left of it. | ::*We write a zero above the 4, since nothing is left of it. | ||
| − | |style="text-align:right;"|ונכתוב סיפרא על הד' כאשר לא נשאר ממנה כלום | + | |style="text-align:right;"|ונכתוב סיפרא על הד' ‫<ref>69r</ref>כאשר לא נשאר ממנה כלום |
|- | |- | ||
| | | | ||
::*We start counting from the rank, above which we have wrote the 6, back by the three ranks of the bottom line, ending at the 9, which is the second rank of the upper line, and there we write 1 beneath it, for the six times of subtraction. | ::*We start counting from the rank, above which we have wrote the 6, back by the three ranks of the bottom line, ending at the 9, which is the second rank of the upper line, and there we write 1 beneath it, for the six times of subtraction. | ||
| − | |style="text-align:right;"|ומהמדרגה אשר כתבנו הו' עליה נחל לספור אחורנית השלש מדרגות שבטור השפל ויכלו בט' שהיא המדרגה השנית מהטור העליון ושם נכתוב תחתיה ו | + | |style="text-align:right;"|ומהמדרגה אשר כתבנו עתה הו' עליה נחל לספור אחורנית השלש מדרגות שבטור השפל ויכלו בט' שהיא המדרגה השנית מהטור העליון ושם נכתוב תחתיה ו"ו כנגד שש פעמי<s>ם</s> ההסרה |
|- | |- | ||
| | | | ||
| Line 1,944: | Line 2,084: | ||
| | | | ||
::*We subtract three from the 6 that is left in the fourth rank; 3 remains above the 6. | ::*We subtract three from the 6 that is left in the fourth rank; 3 remains above the 6. | ||
| − | |style="text-align:right;"|נסיר מהו' שנשארה | + | |style="text-align:right;"|נסיר מהו' שנשארה במדרגה רביעית שלשה וישאר על הו' ההיא שלשה <sup>ג‫'</sup> |
|- | |- | ||
| | | | ||
::*We shift the 3 that we have subtracted to the 8 that is left in the rank that precedes this rank; they are thirty-eight. When we subtract thirty-six from them, 2 remains above the 8. | ::*We shift the 3 that we have subtracted to the 8 that is left in the rank that precedes this rank; they are thirty-eight. When we subtract thirty-six from them, 2 remains above the 8. | ||
| − | |style="text-align:right;"|ונשים הג' אשר הסירונו מהם על הח' הנשארת לנו במדרגה הקדומה למדרגה הזאת ויהיו | + | |style="text-align:right;"|ונשים הג' אשר הסירונו מהם על הח' הנשארת לנו במדרגה הקדומה למדרגה הזאת ויהיו שמנה ושלשים כשנסיר מהם ששה ושלשים ישארו מהם ב' על הח‫' |
|- | |- | ||
| | | | ||
:*We have to further subtract the 4 that is in the bottom line also six times; their product is twenty-four. We do it in this way: | :*We have to further subtract the 4 that is in the bottom line also six times; their product is twenty-four. We do it in this way: | ||
| − | |style="text-align:right;"|עוד יש לנו | + | |style="text-align:right;"|עוד יש לנו להסיר הד' מהטור השפל גם כן שש פעמים והנה עולה כפלתם ארבעה ועשרים ונעשה על הדרך הזה |
|- | |- | ||
| | | | ||
::*We take the 2 that is left above the 8 and shift it to the 9 that is the rank that precedes this rank in writing; they are twenty-nine. We subtract twenty-four from them; 5 remains above the 9. | ::*We take the 2 that is left above the 8 and shift it to the 9 that is the rank that precedes this rank in writing; they are twenty-nine. We subtract twenty-four from them; 5 remains above the 9. | ||
| − | |style="text-align:right;"|נקח הב' | + | |style="text-align:right;"|נקח הב' הנשארת [לנו]‫<ref>marg.</ref> על הח' ונשים אותה על הט' שהיא המדרגה הקדומה במכתב לזאת המדרגה שהיתה הב' כתובה עליה ויהיו תשעה ועשרים כשנסיר מהם עשרים וארבע ישאר <sup>על</sup> הט' ה‫' |
|- | |- | ||
| | | | ||
| − | ::*We write a zero above the rank, in which the 2 is written, since nothing is left of it. | + | ::*We write a zero above the rank, in which the [2] is written, since nothing is left of it. |
| − | |style="text-align:right;"|ונכתוב סיפרא על המדרגה אשר | + | |style="text-align:right;"|ונכתוב סיפרא ‫<ref>69v</ref>על המדרגה אשר הד' כתובה עליה באשר לא נשאר ממנו כלום |
|- | |- | ||
| | | | ||
:By this, we have completed again the subtraction of the digits of the bottom line from the upper line equally, each the same number of times. | :By this, we have completed again the subtraction of the digits of the bottom line from the upper line equally, each the same number of times. | ||
| − | |style="text-align:right;"|ובזה השלמנו להסיר שנית אותיות הטור השפל מהטור העליון במספר שוה פעמים זו כזו | + | |style="text-align:right;"|ובזה השלמנו להסיר שנית אותיות הטור השפל מהטור העליון [במספר שוה פעמים זו כזו]‫<ref>marg.</ref> |
| − | | | + | |- |
| − | + | | colspan="2"| | |
::{| | ::{| | ||
|- | |- | ||
| − | |rowspan="8"|<math>\scriptstyle\xrightarrow{\scriptstyle{\color{red}{30-\left({\color{blue}{4}}\times7\right)=30-28=}}{\color{green}{2}}}</math>||  <span style= | + | |rowspan="8"|<math>\scriptstyle\xrightarrow{\scriptstyle{\color{red}{30-\left({\color{blue}{4}}\times7\right)=30-28=}}{\color{green}{2}}}</math>||  <span style=color:LimeGreen>0</span>   ||rowspan="8"|<math>\scriptstyle\xrightarrow{\scriptstyle{\color{red}{25-\left({\color{blue}{4}}\times6\right)=25-24=}}{\color{green}{1}}}</math>||  0<span style=color:LimeGreen>0</span>   |
|- | |- | ||
| − | | 03<span style= | + | | 03<span style=color:LimeGreen>2</span>  || 032   |
|- | |- | ||
| − | | 460  || 460  | + | | 460  || 460   |
|- | |- | ||
| − | | 582  || 582<span style= | + | | 582  || 582<span style=color:LimeGreen>1</span>  |
|- | |- | ||
| − | |09185 ||09185  | + | |09185 ||09185  |
|- | |- | ||
| − | + | |583696||583696 | |
|- | |- | ||
| − | |   76<span style= | + | |   76<span style=color:#0000FF>4</span>||   76<span style=color:#0000FF>4</span> |
| + | |- | ||
| + | |   7<span style=color:red>6</span>4||   76<span style=color:red>4</span> | ||
| + | |} | ||
| + | ::{| | ||
|- | |- | ||
| − | | | + | |rowspan="8"|<math>\scriptstyle\xrightarrow{\scriptstyle{\color{red}{16-\left({\color{blue}{4}}\times4\right)=16-16=}}{\color{green}{0}}}</math>||  00   |
| − | | | ||
| − | |||
| − | |||
|- | |- | ||
| − | | | + | | 032   |
| − | :When we examine what is left in the upper line, we find that it is still more than the number of the bottom line. | + | |- |
| − | |style=" | + | | 460<span style=color:LimeGreen>0</span>  |
| + | |- | ||
| + | | 5821  | ||
| + | |- | ||
| + | |09185<span style=color:LimeGreen>0</span> | ||
| + | |- | ||
| + | |583696 | ||
| + | |- | ||
| + | |   76<span style=color:#0000FF>4</span> | ||
| + | |- | ||
| + | |   764 | ||
| + | |} | ||
| + | ::<math>\scriptstyle\longrightarrow{\color{Violet}{\scriptstyle764\ the\ result}}</math> | ||
| + | |- | ||
| + | | | ||
| + | :When we examine what is left in the upper line, we find that it is still more than the number of the bottom line. | ||
| + | |style="text-align:right;"|‫[וכאשר נעיין בנשאר הטור העליון נמצא]‫<ref>marg.</ref> שמספרו מרובה עדין ממספר הטור השפל | ||
|- | |- | ||
| | | | ||
:*Therefore we should look again to subtract the 7 that is the last rank of the bottom line from the 3 that is left in the fourth rank. | :*Therefore we should look again to subtract the 7 that is the last rank of the bottom line from the 3 that is left in the fourth rank. | ||
| − | |style="text-align:right;"|ועל כן אנחנו צריכים עוד לחזור ולהביט ולהסיר הז' שהיא המדרגה האחרונה מהטור השפל מהג' | + | |style="text-align:right;"|ועל כן אנחנו צריכים עוד לחזור [ולהביט]‫<ref>marg.</ref> ולהסיר הז' שהיא <s>ד</s> המדרגה האחרונה מהטור השפל מהג' הנשארת לנו במדרגה הרביעית |
|- | |- | ||
| | | | ||
::*It is necessary to shift this 3 to the third rank that precedes it in writing, in which a zero is written; so the 3 equals thirty. | ::*It is necessary to shift this 3 to the third rank that precedes it in writing, in which a zero is written; so the 3 equals thirty. | ||
| − | |style="text-align:right;"|והנה מוכרח לשום את הג' הזאת על המדרגה השלישית הקדומה לה במכתב הכתוב | + | |style="text-align:right;"|והנה מוכרח לשום את הג' הזאת על המדרגה השלישית הקדומה לה במכתב הכתוב עליו סיפרא ותהיה שוה הג' שלשים |
|- | |- | ||
| | | | ||
::*We subtract the 7 4 times, for it will be enough for us to apply the necessary rule upon the remainder. | ::*We subtract the 7 4 times, for it will be enough for us to apply the necessary rule upon the remainder. | ||
| − | |style="text-align:right;"|ונסיר הז' ד' פעמים כי כן יספיק לנו לעשות בנשאר המשפט הצריך | + | |style="text-align:right;"|ונסיר מהם הז' ד' פעמים כי כן יספיק לנו לעשות בנשאר המשפט הצריך |
|- | |- | ||
| | | | ||
| Line 2,010: | Line 2,167: | ||
| | | | ||
::*When we subtract twenty-eight from thirty, 2 remains above the zero that is in the third rank. | ::*When we subtract twenty-eight from thirty, 2 remains above the zero that is in the third rank. | ||
| − | |style="text-align:right;"|והנה | + | |style="text-align:right;"|והנה כשנסיר שמנה ועשרים מהשלשים ישאר ב' על הסיפרא שהיא במדרגה השלישית |
|- | |- | ||
| | | | ||
::*We count from this rank back by the three ranks of the bottom line, ending at the first rank; we write beneath it the 4 times of subtraction. | ::*We count from this rank back by the three ranks of the bottom line, ending at the first rank; we write beneath it the 4 times of subtraction. | ||
| − | |style="text-align:right;"|ומהמדרגה הזאת נמנה אחורנית מספר | + | |style="text-align:right;"|ומהמדרגה הזאת נמנה אחורנית מספר השלש מדרגות שבטור השפל ויכלה מספרן במדרגה הראשונה והנה נכתוב תחתיה ד' פעמי ההסרה |
|- | |- | ||
| | | | ||
:*Then we have to subtract the 6 that in the bottom line also 4 times; their product is twenty-four. We do it in this way: | :*Then we have to subtract the 6 that in the bottom line also 4 times; their product is twenty-four. We do it in this way: | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|אחר זאת צריך גם כן שנסיר הו' שבטור השפל ארבעה פעמים שעולה כפילתם עשרים וארבע ונעשה על ‫<ref>70r</ref>הדרך הזה |
|- | |- | ||
| | | | ||
| − | ::*We shift the 2 that is left in the third rank to the | + | ::*We shift the 2 that is left in the third rank to the 5 that is left in the rank that precedes it in writing; they are twenty-five. |
| − | |style="text-align:right;"|נשים הב' | + | |style="text-align:right;"|נשים הב' הנשארת במדרגה השלישית על הה' הנשארת במדרגה הקדומה לה במכתב ויעלו חמשה ועשרים |
|- | |- | ||
| | | | ||
::*When we subtract twenty-four from them, 1 remains instead of the 5. | ::*When we subtract twenty-four from them, 1 remains instead of the 5. | ||
| − | |style="text-align:right;"|וכשנסיר מהם | + | |style="text-align:right;"|וכשנסיר מהם ארבע ועשרים ‫<sup>כ ד</sup> ישאר א' במקום הה‫' |
|- | |- | ||
| | | | ||
| Line 2,034: | Line 2,191: | ||
| | | | ||
:*We have to further subtract the 4 that is the first rank of the bottom line also 4 times; their product is sixteen. We do it in this way: | :*We have to further subtract the 4 that is the first rank of the bottom line also 4 times; their product is sixteen. We do it in this way: | ||
| − | |style="text-align:right;"|עוד אנחנו צריכים להסיר הד' שהיא | + | |style="text-align:right;"|עוד אנחנו צריכים להסיר אות הד' שהיא במדרגה הראשונה מהטור השפל גם כן ד' פעמים ועולה כפלתם ששה עשר ונעשה על זה הדרך |
|- | |- | ||
| | | | ||
::*We take the 1 that is left in the second rank, write above it a zero and shift it to the 6 that precedes this rank; they are sixteen. We subtract the product of 4 by 4 from them. | ::*We take the 1 that is left in the second rank, write above it a zero and shift it to the 6 that precedes this rank; they are sixteen. We subtract the product of 4 by 4 from them. | ||
| − | |style="text-align:right;"|נקח הא' הנשארת במדרגה השנית ונכתוב עליה סיפרא ונשים אותה על הו' הקדומה לזאת המדרגה יהיו ששה עשר | + | |style="text-align:right;"|נקח הא' הנשארת במדרגה השנית ונכתוב עליה סיפרא ונשים אותה על הו' הקדומה לזאת המדרגה יהיו ששה עשר ומהם נסיר כפילת הד' על הד‫' |
|- | |- | ||
| | | | ||
| Line 2,046: | Line 2,203: | ||
| | | | ||
:We find that the upper line is all gone in the divisions we made and the middle line that is created is the same as the line of the smaller number, no more and no less. | :We find that the upper line is all gone in the divisions we made and the middle line that is created is the same as the line of the smaller number, no more and no less. | ||
| − | |style="text-align:right;"|ונמצא שכל | + | |style="text-align:right;"|ונמצא שכל טור העליון הוא כלה ב{{#annot:term|157,1221|zfrI}}חלק<sup>ו</sup>ת{{#annotend:zfrI}} אשר עשינו והטור האמצעי אשר נתחדש הוא כטור החשבון הקטן לא פחות ולא יותר |
|- | |- | ||
| | | | ||
*{{#annot:583696÷1080|157|BBPT}}We wish to divide five hundred and eighty-three thousand, six hundred and ninety-six by one thousand and eighty. | *{{#annot:583696÷1080|157|BBPT}}We wish to divide five hundred and eighty-three thousand, six hundred and ninety-six by one thousand and eighty. | ||
:<math>\scriptstyle583696\div1080</math> | :<math>\scriptstyle583696\div1080</math> | ||
| − | |style="text-align:right;"|ועוד בקשנו לחלק חמש מאות ושמנים ושלשת אלפים ושש מאות ותשעים | + | |style="text-align:right;"|<big>ועוד בקשנו</big> לחלק חמש מאות <sup>אלף</sup> ושמנים ושלשת אלפים [ושש מאות ותשעים ושש]‫<ref>marg.</ref> על אלף ושמונים{{#annotend:BBPT}} |
|- | |- | ||
| | | | ||
:We write them according to this diagram: | :We write them according to this diagram: | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ונכתבם על זאת הצורה |
|- | |- | ||
| | | | ||
| Line 2,093: | Line 2,250: | ||
|- | |- | ||
|} | |} | ||
| − | + | |- | |
| − | | | + | | colspan="2"| |
| − | ::<span style=color: | + | ::<span style=color:green>[Illustration of the procedure:]</span> |
::{| | ::{| | ||
|- | |- | ||
| − | | ||rowspan="4"|<math>\scriptstyle\xrightarrow{{\color{red}{5-\left({\color{blue}{5}}\times1\right)=5-5=}}{\color{green}{0}}}</math>||<span style= | + | | ||rowspan="4"|<math>\scriptstyle\xrightarrow{{\color{red}{5-\left({\color{blue}{5}}\times1\right)=5-5=}}{\color{green}{0}}}</math>||<span style=color:LimeGreen>0</span>     ||rowspan="4"|<math>\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{8-4=}}{\color{green}{4}}\\&\scriptstyle{\color{red}{43-\left({\color{blue}{5}}\times8\right)=43-40=}}{\color{green}{3}}\\\end{align}}</math>||0<span style=color:LimeGreen>4</span>     |
|- | |- | ||
| − | |<span style= | + | |<span style=color:red">5</span>83696||583696|||583696 |
|- | |- | ||
| − | | ||   <span style= | + | | ||   <span style=color:#0000FF>5</span>  ||   <span style=color:#0000FF>5</span>   |
|- | |- | ||
| − | |  <span style= | + | |  <span style=color:red>1</span>080||  10<span style=color:red>8</span>0||  <span style=color:red>1</span>080 |
|} | |} | ||
::::{| | ::::{| | ||
|- | |- | ||
| − | |rowspan="5"|<math>\scriptstyle\xrightarrow{\scriptstyle{\color{red}{4-\left({\color{blue}{4}}\times1\right)=4-4=}}{\color{green}{0}}}</math>|| <span style= | + | |rowspan="5"|<math>\scriptstyle\xrightarrow{\scriptstyle{\color{red}{4-\left({\color{blue}{4}}\times1\right)=4-4=}}{\color{green}{0}}}</math>|| <span style=color:LimeGreen>0</span>    ||rowspan="5"|<math>\scriptstyle\xrightarrow{\scriptstyle{\color{red}{36-\left({\color{blue}{4}}\times8\right)=36-32=}}{\color{green}{4}}}</math>|| 0     |
|- | |- | ||
| − | |04    |||04<span style= | + | |04    |||04<span style=color:LimeGreen>04</span>   |
|- | |- | ||
|583696|||583696 | |583696|||583696 | ||
|- | |- | ||
| − | |   5<span style= | + | |   5<span style=color:#0000FF>4</span> |||   54<span style=color:#0000FF>0</span> |
|- | |- | ||
| − | |  10<span style= | + | |  10<span style=color:red>8</span>0|||  1080 |
|} | |} | ||
::<math>\scriptstyle\longrightarrow{\color{Violet}{\begin{align}&\scriptstyle540\ the\ result\\&\scriptstyle496\ the\ remainder\\\end{align}}}</math> | ::<math>\scriptstyle\longrightarrow{\color{Violet}{\begin{align}&\scriptstyle540\ the\ result\\&\scriptstyle496\ the\ remainder\\\end{align}}}</math> | ||
| − | + | ||
|- | |- | ||
| | | | ||
:*We see that we are able to subtract the 1 that is in the bottom line five times from the 5 that is in the upper line. | :*We see that we are able to subtract the 1 that is in the bottom line five times from the 5 that is in the upper line. | ||
| − | |style=" | + | |style="text-align:right;"|הנה אנחנו רואים שיש בידינו רשות להסיר הא' שבטור השפל חמש ‫<ref>70v</ref>פעמים מהה' שבטור העליון |
|- | |- | ||
| | | | ||
::*We do as we said and we write above it a zero, since nothing is left of it. | ::*We do as we said and we write above it a zero, since nothing is left of it. | ||
| − | |style="text-align:right;"|ונעשה | + | |style="text-align:right;"|ונעשה כדבר<sup>י</sup>נו ונכתוב עליו סיפרא באשר לא נשארה ממנה שארית |
|- | |- | ||
| | | | ||
::*We count four ranks back from this rank that is in the upper line, for the four ranks that are in the bottom line; their count ends in 6, which is in the same line. We write there 5, beneath it, for the five times of subtraction. | ::*We count four ranks back from this rank that is in the upper line, for the four ranks that are in the bottom line; their count ends in 6, which is in the same line. We write there 5, beneath it, for the five times of subtraction. | ||
| − | |style="text-align:right;"|ונמנה מהמדרגה הזאת שבטור העליון ארבע מדרגות אחורנית כנגד הארבע מדרגות שבטור השפל ויכלה | + | |style="text-align:right;"|ונמנה מהמדרגה הזאת שבטור העליון ארבע מדרגות אחורנית כנגד הארבע מדרגות שבטור השפל ויכלה מנינן בו' שבאותו טור ושם נכתוב תחתיה <sup>ה'</sup> כנגד חמש פעמי ההסרה |
|- | |- | ||
| | | | ||
:*Then, we have to subtract the 8 that is in the bottom line also 5 times; their product is forty. We do it in this way: | :*Then, we have to subtract the 8 that is in the bottom line also 5 times; their product is forty. We do it in this way: | ||
| − | |style="text-align:right;"|ואחרי זאת יש לנו להסיר הח' שבטור השפל גם כן ה' | + | |style="text-align:right;"|ואחרי זאת יש לנו להסיר הח' שבטור השפל גם כן ה' פעמים שכפילתם עולה ארבעים ונעשה על הדרך הזה |
|- | |- | ||
| | | | ||
| Line 2,143: | Line 2,300: | ||
| | | | ||
:By this, all the digits of the bottom line were subtracted from the upper line equally, each the same number of times. | :By this, all the digits of the bottom line were subtracted from the upper line equally, each the same number of times. | ||
| − | |style="text-align:right;"|ובזה הוסרו כל | + | |style="text-align:right;"|ובזה הוסרו כל האותיות הטור השפל מהטור העליון כל אחת ואחת מהן פעמים שוות |
|- | |- | ||
| | | | ||
:When we examine what is left in the upper line, we see that its number is more than the number of the bottom line. | :When we examine what is left in the upper line, we see that its number is more than the number of the bottom line. | ||
| − | |style="text-align:right;"|וכשנעיין הנותר בטור העליון נראה שמספרו מרובה | + | |style="text-align:right;"|וכשנעיין הנותר בטור העליון נראה שמספרו מרובה ממספר הטור השפל |
|- | |- | ||
| | | | ||
:*Therefore we look again to subtract the 1 that is in the bottom line 4 times from the 4 that is left in the fifth rank. | :*Therefore we look again to subtract the 1 that is in the bottom line 4 times from the 4 that is left in the fifth rank. | ||
| − | |style="text-align:right;"|ובעבור זה נחזור ונביט ונסיר הא' שבטור השפל ד' | + | |style="text-align:right;"|ובעבור זה נחזור ונביט ונסיר הא' שבטור השפל ד' פעמים מהד' שנשארה לנו במדרגה החמישית |
|- | |- | ||
| | | | ||
| Line 2,158: | Line 2,315: | ||
|- | |- | ||
| | | | ||
| − | ::* | + | ::*Count four ranks back; it ends in the second rank. We write there 4, beneath it, for the four times of subtraction. |
| − | |style="text-align:right;"|וממנה | + | |style="text-align:right;"|וממנה תמנה ארבע מדרגות אחורנית ויכלו במדרגה השנייה ושם ‫<ref>71r</ref>תכתוב תחתיה [ד']‫<ref>Vatican om.</ref> כנגד ארבעה פעמי ההסרה |
|- | |- | ||
| | | | ||
| − | :*We have to further subtract the 8 of the bottom line also 4 times; | + | :*We have to further subtract the 8 of the bottom line also 4 times; their product is thirty-two. We do it as follows: |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|עוד יש לנו להסיר גם כן הח' מהטור השפל ד' פעמים העולה כפלתם שנים ושלשים והנה נעשה כזה |
|- | |- | ||
| | | | ||
::*We take the 3 that is left in its place, in the fourth rank of the upper line, and shift it to the digit of the third rank, which is 6 that precedes it in writing; they are thirty-six. When we subtract thirty-two from them, 4 remains above the 6. | ::*We take the 3 that is left in its place, in the fourth rank of the upper line, and shift it to the digit of the third rank, which is 6 that precedes it in writing; they are thirty-six. When we subtract thirty-two from them, 4 remains above the 6. | ||
| − | |style="text-align:right;"|נקח הג' אשר נשארה במקומה בטור העליון במדרגה | + | |style="text-align:right;"|נקח הג' אשר נשארה במקומה בטור העליון במדרגה הרביעית ונשים אותה על אות המדרגה השלישית שהיא ו' הקדומה לה במכתב ויעלה ששה ושלשים וכשנסיר מהם שנים ושלשים ישאר על הו' ד‫' |
|- | |- | ||
| | | | ||
| − | ::* | + | ::*I write a zero above the 3, since nothing is left from it. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ואכתוב סיפרא על הג' באשר לא נשאר ממנה כלום |
|- | |- | ||
| | | | ||
:By this, all the digits of the bottom line were subtracted from the upper line again. | :By this, all the digits of the bottom line were subtracted from the upper line again. | ||
| − | |style="text-align:right;"|ובזה הוסרו כל אותיות הטור השפל מהטור העליון פעם | + | |style="text-align:right;"|ובזה הוסרו כל אותיות הטור השפל מהטור העליון כשוה פעם שניה |
|- | |- | ||
| | | | ||
| − | :When we examine what is left in the upper line, we see that its number is less than the number of the bottom line, and this is | + | :When we examine what is left in the upper line, we see that its number is less than the number of the bottom line, and this is your sign that the division is complete. |
| − | |style="text-align:right;"|והנה כאשר נעיין הנשאר בטור העליון נראה שהוא מועט במספרו ממספר הטור השפל | + | |style="text-align:right;"|והנה כאשר נעיין הנשאר בטור העליון נראה שהוא מועט במספרו ממספר הטור השפל וזה לך האות שנגמרה החלוקה |
|- | |- | ||
| | | | ||
| − | :The middle line generated from the number of the times of subtraction | + | :The middle line generated from the number of the times of subtraction is five hundred and forty. |
| − | |style="text-align:right;"|והטור האמצעי המתהוה ממספר פעמי | + | |style="text-align:right;"|והטור האמצעי המתהוה ממספר פעמי ההסרה עלה חמש מאות וארבעים |
|- | |- | ||
| | | | ||
| Line 2,189: | Line 2,346: | ||
|style="text-align:right;"|והנשאר על אותיות הטור העליון עולה ארבע מאות ותשעים ושש | |style="text-align:right;"|והנשאר על אותיות הטור העליון עולה ארבע מאות ותשעים ושש | ||
|- | |- | ||
| − | |Through all these many calculations I have mentioned the method of their division, every | + | |Through all these many calculations I have mentioned the method of their division, every wise man will be able to understand and learn the truths of doing this skill accurately. |
| − | |style="text-align:right;"|ומתוך כל אלו החשבונות הרבים שהזכרתי דרך חלוקתן בארוכה יוכל כל נבון | + | |style="text-align:right;"|ומתוך כל אלו החשבונות הרבים שהזכרתי דרך חלוקתן בארוכה יוכל כל נבון להבין ולהשכיל אמיתות עשיית המלאכה הזאת {{#annot:term|2483,2074|d2tL}}בדקדוק{{#annotend:d2tL}} |
| − | + | ||
| − | |||
|- | |- | ||
| | | | ||
| − | === Methods of Checking - Multiplication, Division, Addition, Subtraction === | + | === <span style=color:green>Methods of Checking - Multiplication, Division, Addition, Subtraction</span> === |
| | | | ||
|- | |- | ||
|Now, I should discuss in this chapter about the checking methods [lit. scales] of this division operation, as well as the checking methods [lit. scales] of the multiplication, addition and subtraction operations, as I promised at the beginning of this book, when mentioning the contents of its chapters. | |Now, I should discuss in this chapter about the checking methods [lit. scales] of this division operation, as well as the checking methods [lit. scales] of the multiplication, addition and subtraction operations, as I promised at the beginning of this book, when mentioning the contents of its chapters. | ||
| − | |style=" | + | |style="text-align:right;"|<big>ועתה אני צריך לדבר</big> בשער הזה מ{{#annot:term|353,1453|pDG1}}מאזני{{#annotend:pDG1}} ‫<ref>71v</ref>מלאכת החלוקה הזאת וממאזני מלאכת הכפל והחבור והמגרעת כאשר התאותי בהתחילי הספר הזה בהזכרת פרטי כללי שעריו |
|- | |- | ||
| | | | ||
| − | *<span style= | + | *<span style=color:green>'''Checking the result of division: multiplication'''</span> |
| | | | ||
|- | |- | ||
| | | | ||
| − | :I say that the most truthful and right | + | :I say that the most truthful and right scales are that whoever does the division operation multiplies the middle line that is generated from the number of the times of subtraction, according to the procedure of the multiplication operation, by the bottom line, which is the smaller number; then he takes all that remains above the upper line, if something remains there; adds it beneath the product, each digit beneath its corresponding rank; and sums it with the whole product. The line of the sum must be the same as the line of the greater number that he divided, each digit the same as its corresponding digit, ''if his deed is pure or upright'' [Proverbs 20, 11]. |
| − | |style="text-align:right;"|והנני אומר כי אין בכל ה{{#annot:term| | + | |style="text-align:right;"|והנני אומר כי אין בכל ה{{#annot:term|353,1453|ZHa7}}מאזנים{{#annotend:ZHa7}} יותר צדוקים וישרים כי אם כל מי שיעשה מלאכת חלוקתו שיכפיל ויכה במלאכת מעשה הכפילה הטור האמצעי המתהוה ממספר פעמי ההסרה על הטור השפל שהוא החשבון הקטן ואחר יקח כל מה שנותר למעלה בטור העליון אם נשאר שם כלום ויוסיף אותו תחת הכפילה כל אות ואות תחת מדרגה הראויה לה ואחרי כן יחבר ו{{#annot:term|178,1210|feiE}}יקבץ{{#annotend:feiE}} כל הכפילה ובהכרח צריך שתצא טור ה{{#annot:term|388,1211|EMLg}}קבוץ{{#annotend:EMLg}} והחבור כטור החשבון הגדול אשר חלק דומה כדומה מספר הטור האחד כמספר חברתה ''אם זך [ואם]‫<ref>marg.</ref> ישר פעולו''‫<ref group=note>משלי 2, יא</ref> |
|- | |- | ||
| | | | ||
| − | *<span style= | + | *<span style=color:green>'''Checking the result of multiplication: division'''</span> |
| | | | ||
|- | |- | ||
| | | | ||
| − | :Likewise, the | + | :Likewise, the scales of the multiplication operation are that he divides the result of multiplication by one of the two lines of the multiplied numbers and the result of division is the second line, if he goes the right way. |
| − | |style="text-align:right;"|וגם מאזני | + | |style="text-align:right;"|וגם מאזני <sup>הכפל</sup> הנה הם שיחלק העולה מהכפילה על אחת משני טורי {{#annot:term|608,1564|u4Sk}}החשבונות הנכפלים{{#annotend:u4Sk}} יצא לו בחלוק הטור השני אם בדרך ישר הוא הולך |
|- | |- | ||
| | | | ||
| − | *<span style= | + | *<span style=color:green>'''Checking the result of addition: subtraction'''</span> |
| | | | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|וכן כל מי | + | :Also, whoever adds two lines of numbers to each other, uses the subtraction operation: he subtracts one of the two lines from the sum and if his procedure is correct, he is left with the second line. |
| + | |style="text-align:right;"|וכן כל מי שחבר שני טורי חשבונות יחד זה עם זה יתעסק במלאכת המגרעת ויגרע מן המחובר אחד מן שני הטורים ‫<ref>72r</ref>וישאר לו הטור השני אם היה מעשהו באמונה | ||
|- | |- | ||
| | | | ||
| − | *<span style= | + | *<span style=color:green>'''Checking the result of subtraction: addition'''</span> |
| | | | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|ולפי | + | :According to our ways, we understand and learn that whoever subtracts a small number from a greater number, if he adds what is left for him to the line of the small number, the sum he receives is inevitably the same as the line of the greater number. |
| + | |style="text-align:right;"|ולפי דרכנו נבין ונלמוד שגם כן הגורע חשבון קטן מחשבון גדול שאם יחבר מה שנותר לו עם טור החשבון הקטן שבהכרח יצא לו המחובר טור אחד כטור החשבון הגדול זו כזו במספר שוות | ||
|- | |- | ||
| − | | | + | |By that the intention of everything I intended to explain in this chapter is clarified and it is time to finish with it and start with another. |
| − | |style="text-align:right;"|ועם זה התבארה כוונת כל מה | + | |style="text-align:right;"|ועם זה התבארה כוונת כל מה שהתכונתי לבאר בזה השער והגיע העת לפסוק בו ולהתחיל באחר |
|- | |- | ||
|} | |} | ||
| Line 2,241: | Line 2,399: | ||
== Chapter Seven – Extracting the Closest Root of Integer == | == Chapter Seven – Extracting the Closest Root of Integer == | ||
| − | |style="width: | + | |style="width: 45%; text-align:right;"|<big>השער השביעי</big> בלקיחת גדר {{#annot:term|20,1268|xrE0}}המספר השלם{{#annotend:xrE0}} היותר קרוב אליו |
|- | |- | ||
| − | |<span style=color: | + | |<span style=color:green>'''Definition of a square number:'''</span> {{#annot:definition|86|YpcZ}} Know that the product of every number by itself is called a number that has a root, whereas its root is the number that is multiplied by itself. |
| − | |style="text-align:right;"|תדע כי | + | |style="text-align:right;"|תדע כי כל כפל הכאת חשבון על עצמו הוא הנקרא מספר נגדר או [{{#annot:term|86,1837|6sNp}}נשרש{{#annotend:6sNp}}]‫<ref>Vatican: תשרש</ref> כאשר גדרו או שורשו הוא נכפל על עצמו{{#annotend:YpcZ}} |
|- | |- | ||
| | | | ||
| − | === One versus the integers === | + | === <span style=color:green>One versus the integers</span> === |
| | | | ||
|- | |- | ||
| | | | ||
| − | *For all integers | + | *For all integers, you find that when you multiply a number by itself, it, meaning the product, becomes greater than the original number. |
| − | |style="text-align:right;"|ובכל המספרים אשר יהיו {{#annot:term|20,1268|X06q}}שלמים{{#annotend:X06q}} תמצא לעולם כשתכפול המספר על עצמו שיתרבה | + | |style="text-align:right;"|ובכל המספרים אשר יהיו {{#annot:term|20,1268|X06q}}שלמים{{#annotend:X06q}} תמצא לעולם כשתכפול המספר על עצמו שיתרבה העולה מאשר היה המספר בתחלה |
|- | |- | ||
| | | | ||
| − | :Except for one | + | :Except for one, because when you multiply one by itself it is not affected by any change, but the result is one as it was originally without any multiplicity or change. |
| − | |style="text-align:right;"|חוץ מן המספר האחד כי כש{{#annot:term|185,1255|iesE}}תכה {{#annotend:iesE}}האחד על עצמו לא יקבל שום תמורה וחלוף אך יעלה אחד כאשר היה בתחלה | + | |style="text-align:right;"|חוץ מן המספר האחד כי כש[{{#annot:term|185,1255|iesE}}תכה{{#annotend:iesE}}]‫<ref>Vatican: תבוא</ref> האחד על עצמו לא יקבל שום תמורה וחלוף אך יעלה אחד כאשר היה בתחלה מבלתי רבוי ושנוי |
|- | |- | ||
| | | | ||
| − | :Therefore | + | :Therefore we can say that the number one is a square as well as the root of itself. |
| − | |style="text-align:right;"|ועל כן | + | |style="text-align:right;"|ועל כן נוכל לומר שמספר האחד הוא {{#annot:term|86,1836|rpzi}}נגדר{{#annotend:rpzi}} וגם כן הוא גדר עצמו |
|- | |- | ||
| | | | ||
| − | * | + | *The number one has another advantage over all other numbers: |
| − | |style="text-align:right;"|עוד | + | |style="text-align:right;"|עוד למספר האחד יתרון על שאר המספרים |
|- | |- | ||
| | | | ||
| − | :For all other numbers | + | :For all other numbers, when we take their extremes, [i.e.] the number that precedes them and the number that follows them, the sum of the two extremes is twice the mean number. |
| − | |style="text-align:right;"|שהנה כל המספרים זולתו | + | :<math>\scriptstyle{\color{OliveGreen}{\left(n-1\right)+\left(n+1\right)=2n}}</math> |
| + | |style="text-align:right;"|‫<ref>72v</ref>[שהנה]‫<ref>Vatican: שמנה</ref> כל המספרים זולתו שנקח שתי קצותיהם המספר שלפניהם והמספר שלאחריהם יהיה המחובר משני הקצוות {{#annot:term|387,1230|5j57}}כפל{{#annotend:5j57}} המספר האמצעי | ||
|- | |- | ||
| | | | ||
| − | : | + | :But, one does not have a preceding extreme. Its following extreme, which is two, is itself its double. |
| − | |style="text-align:right;"| | + | :<math>\scriptstyle{\color{blue}{2=2\sdot1}}</math> |
| + | |style="text-align:right;"|ולמספר האחד הנה אין לו קצה לפניו ועם הקצה שלאחריו שהוא שנים יספיק לכפלו | ||
|- | |- | ||
| − | | | + | |This is the virtue and superiority of one over all the other numbers. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וזה היא מעלה ורוממות האחד על שאר המספרים |
|- | |- | ||
| − | |There are other | + | |There are other things that have no place to be mentioned here. I have strayed from the purpose of the present chapter, when I needed to speak about the virtues of the number one, so now I will return to where I was at the beginning. |
| − | |style="text-align:right;"|ועוד דברים אחרים שאין | + | |style="text-align:right;"|ועוד דברים אחרים שאין מקומם להזכירם בזה והנה יצאתי מכוונת השער הזה באשר הוצרכתי לדבר במעלות מספר האחד ועתה אשוב אל אשר הייתי בתחלה |
|- | |- | ||
| | | | ||
| − | === | + | |
| + | === <span style=color:green>Square Nnumbers</span> === | ||
| | | | ||
|- | |- | ||
| | | | ||
| − | * | + | *I say regarding the roots that if you multiply a square number by a square number, the product is also a square number. |
| − | |style="text-align:right;"|ואומר בענייני ה{{#annot:term|439,1372|aqMn}}גדרים{{#annotend:aqMn}} שאם תכפול ותכה {{#annot:term|86,1836|xWd5}}מספר נגדר{{#annotend:xWd5}} על מספר נגדר יהיה | + | |style="text-align:right;"|ואומר בענייני ה{{#annot:term|439,1372|aqMn}}גדרים{{#annotend:aqMn}} שאם תכפול ותכה {{#annot:term|86,1836|xWd5}}מספר נגדר{{#annotend:xWd5}} על מספר נגדר יהיה הכפל גם כן חשבון נגדר |
|- | |- | ||
| | | | ||
| − | :<math>\scriptstyle a^2\times b^2=\left(a\times b\right)^2</math> | + | :When you want to know its root, you only need to extract the roots of the numbers you multiply by each other. Multiply the roots by each other and the result is the root of the third number. |
| − | |style="text-align:right;"|וכאשר תרצה לדעת גדרו אינך צריך | + | :<math>\scriptstyle{\color{OliveGreen}{a^2\times b^2=\left(a\times b\right)^2}}</math> |
| + | |style="text-align:right;"|וכאשר תרצה לדעת גדרו אינך צריך כן לקחת גדרי המספרים אשר {{#annot:term|185,1255|TnDR}}הכית{{#annotend:TnDR}} ו{{#annot:term|185,1230|57b8}}כפלת{{#annotend:57b8}} זה על זה ותכה ותכפול גדר האחד על חברו וההווה הוא גדר המספר השלישי | ||
|- | |- | ||
| | | | ||
| − | :<math>\scriptstyle{\color{blue}{4\times9=2^2\times3^2=\left(2\times3\right)^2=6^2=36}}</math> | + | :*Example: four is a square number and nine also. The product of the one by the other is thirty-six and it is also a square number. If we want to know its root, we extract the root of four, which is two, and the root of nine, which is three; we multiply them by each other; the result is six and this is the required. Because, when we multiply six by itself, it is thirty-six. |
| − | |style="text-align:right;"|דמיון הנה ארבעה | + | ::<math>\scriptstyle{\color{blue}{4\times9=2^2\times3^2=\left(2\times3\right)^2=6^2=36}}</math> |
| + | |style="text-align:right;"|<big>דמיון</big> הנה ארבעה מספר נגדר וגם תשעה והעולה מכפל האחד על חברו ששה ושלשים והנה הוא גם כן מספר נגדר ואם נבקש לדעת גדרו {{#annot:term|795,2073|FMAT}}נקח גדר{{#annotend:FMAT}} הארבעה שהוא שנים וכן {{#annot:term|439,1372|WdP4}}גדר{{#annotend:WdP4}} התשעה שהוא ‫<ref>73r</ref>שלשה ו{{#annot:term|185,1255|2Esg}}נכה{{#annotend:2Esg}} זה על זה יעלו ששה והוא המבוקש כי כאשר נכפול ששה על עצמו היה ששה ושלשים | ||
|- | |- | ||
| − | + | !<span style=color:green>Square ranks and non-square ranks</span> | |
| − | |||
| | | | ||
|- | |- | ||
| − | | | + | |<span style=color:green>'''Odd ranks have roots; even ranks have no root:'''</span> Know that the ranks of the numbers always follow this order one after the other: the first has a root, the second has no root, the third has a root, the fourth has no root, and so on endlessly. |
| − | |style="text-align:right;"|ותדע כי לעולם מדרגות החשבון הולכות על הסדר | + | |style="text-align:right;"|<big>ותדע</big> כי לעולם מדרגות החשבון הולכות על הסדר זו אחר זו בעניין זה שהראשונה היא {{#annot:term|86,1836|5yXg}}נגדרת{{#annotend:5yXg}} והשנייה איננה נגדרת והשלישית נגדרת והרביעית בלתי נגדרת וככה עד אין קץ |
|- | |- | ||
| | | | ||
| − | :* | + | :*By the root of the ranks, I mean that when you look at the first rank, which is the rank of units: its first number, which is one, has a root, as [explained] above. |
| − | |style="text-align:right;"|ורצוני | + | |style="text-align:right;"|ורצוני לומ' בגדר המדרגות הזה כי כשתסכל המדרגה הראשונה שהיא מדרגת האחדים מספרם הראשון שהוא אחד הוא נגדר כמו שקדם |
|- | |- | ||
| | | | ||
| − | :*The | + | :*The second rank, which is the rank of tens: its first number, which is ten, has no root. |
| − | |style="text-align:right;"|והמדרגה השנית | + | |style="text-align:right;"|והמדרגה השנית שהוא מדרגת העשרות מספרם הראשון שהוא עשר בלתי נגדר |
|- | |- | ||
| | | | ||
| − | :* | + | :*Also the third rank: its first number, which is a hundred, has a root. |
|style="text-align:right;"|וכן המדרגה השלישית מספרה הראשון שהוא מאה נגדר | |style="text-align:right;"|וכן המדרגה השלישית מספרה הראשון שהוא מאה נגדר | ||
|- | |- | ||
| | | | ||
| − | :*The first number | + | :*The fourth rank: its first number, which is a thousand, has no root. |
| − | |style="text-align:right;"|והמדרגה הרביעית | + | |style="text-align:right;"|והמדרגה הרביעית מספרה הראשון שהוא אלף הוא בלתי נגדר |
|- | |- | ||
| | | | ||
| − | : | + | :All the ranks follow this way. |
|style="text-align:right;"|ובדרך הזו הולכות המדרגות כלנה | |style="text-align:right;"|ובדרך הזו הולכות המדרגות כלנה | ||
|- | |- | ||
| | | | ||
| − | === Extracting roots - written procedure === | + | === <span style=color:green>Extracting roots - written procedure</span> === |
| | | | ||
|- | |- | ||
| − | |The procedure of | + | |The procedure for finding the unknown root of the known number is very complicated, with many aspects and different principles, and I cannot explain them with one rule for all numbers. |
| − | |style="text-align:right;"|ודרך מציאת הגדר הנעלם מהמספר הידוע היא עמוקה עד מאד ויש בה צדדים רבים ומדות נחלקות זו מזו ולא אוכל לפרש אותם דרך כלל אחד לכל המספרים | + | |style="text-align:right;"|<big>ודרך</big> מציאת הגדר הנעלם מהמספר הידוע כי היא עמוקה עד מאד ויש בה צדדים רבים ומדות נחלקות זו מזו ולא אוכל לפרש אותם דרך כלל אחד לכל המספרים |
| + | |- | ||
| + | |Therefore I write numerous various calculations and explain the way to extract the root of each of them at length and an intelligent person, who has wisdom in his heart should understand from them how to do so with other numbers. | ||
| + | |style="text-align:right;"|ועל כן אכתוב חשבונות הרבה בלתי דומים זה לזה ואבאר בארוכה בכל אחד מהם דרך להוציא גדרו ומהם יבין ‫<ref>73v</ref>כל משכיל ונבון אשר תנוח חכמה בלבו לעשות ככה במספרים אחרים זולתם | ||
|- | |- | ||
| − | | | + | | |
| − | |style="text-align:right;"| | + | *{{#annot:√225|439|Y95w}}We wish to know the root of two hundred and twenty-five. |
| + | :<math>\scriptstyle\sqrt{225}</math> | ||
| + | |style="text-align:right;"|<big>הנה בקשנו</big> לדעת גדר מאתים ועשרים וחמשה{{#annotend:Y95w}} | ||
|- | |- | ||
| | | | ||
| − | + | :We write it in the following diagram: | |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|נכתבם על זאת הצורה |
|- | |- | ||
| | | | ||
| Line 2,374: | Line 2,541: | ||
|} | |} | ||
|- | |- | ||
| − | | | + | | colspan="2"| |
| − | ::<span style=color: | + | ::<span style=color:green>[Illustration of the procedure:]</span> |
::{| | ::{| | ||
|- | |- | ||
| − | | ||rowspan="4"|<math>\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{2>1^2}}\\&\scriptstyle{\color{red}{2-{\color{blue}{1}}^2=}}{\color{green}{1}}\\&\scriptstyle{\color{red}{2\times1=}}{\color{blue}{2}}\\\end{align}}</math>|| ||rowspan="4"|<math>\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{12-\left(2\times{\color{blue}{5}}\right)=}}{\color{Orange}{2}}\\&\scriptstyle{\color{red}{{\color{Orange}{2}}5-{\color{blue}{5}}^2=}}{\color{green}{0}}\\\end{align}}</math>||<span style= | + | | ||rowspan="4"|<math>\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{2>1^2}}\\&\scriptstyle{\color{red}{2-{\color{blue}{1}}^2=}}{\color{green}{1}}\\&\scriptstyle{\color{red}{2\times1=}}{\color{blue}{2}}\\\end{align}}</math>|| ||rowspan="4"|<math>\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{12-\left(2\times{\color{blue}{5}}\right)=}}{\color{Orange}{2}}\\&\scriptstyle{\color{red}{{\color{Orange}{2}}5-{\color{blue}{5}}^2=}}{\color{green}{0}}\\\end{align}}</math>||<span style=color:LimeGreen>0</span>  ||rowspan="4"|<math>\scriptstyle\xrightarrow{\scriptstyle{\color{red}{\frac{1}{2}\sdot2=}}{\color{blue}{1}}}</math>||0   |
|- | |- | ||
| − | | ||<span style= | + | | ||<span style=color:LimeGreen>1</span>  ||1<span style=color:LimeGreen>00</span>||100 |
|- | |- | ||
| − | |<span style= | + | |<span style=color:red>2</span>25||225||225||225 |
|- | |- | ||
| − | | ||<span style= | + | | ||<span style=color:#0000FF><s>1</s>2</span> || 2<span style=color:#0000FF>5</span>|| <span style=color:#0000FF>1</span>5 |
| − | |} | + | |} |
::<math>\scriptstyle\longrightarrow{\color{Violet}{\scriptstyle15\ the\ root}}</math> | ::<math>\scriptstyle\longrightarrow{\color{Violet}{\scriptstyle15\ the\ root}}</math> | ||
| + | |- | ||
| | | | ||
| + | :*Then, we count the number of the ranks and we see that the last [rank] has a root, since it is third, therefore we start with it. | ||
| + | |style="text-align:right;"|ואחר נמנה מספר המדרגות וראינו שהאחרונה יש לה גדר באשר היא מדרגה שלישית ובעבור <s>ה</s>זה נתחיל ממנה | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | ::*It is 2. We look for the approximate root of 2; it is one, so write it beneath this 2. |
| + | |style="text-align:right;"|והנה [היא ב']‫<ref>Vatican om.</ref> נבקש הגדר היותר {{#annot:term|1614,1359|V5kt}}קרוב{{#annotend:V5kt}} אל ב' והנה הוא אחד נכתבנו תחת הב' ההיא | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | ::*We subtract its product by itself from it; 1 remains above it. |
| + | |style="text-align:right;"|ונסיר הכאתו על עצמו ממנה וישאר עליה א‫' | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | ::*We multiply twice the 1 that we wrote beneath the 2, and write the product back beneath the preceding rank. |
| + | |style="text-align:right;"|נכפול הא' שכתבנו תחת הב' פעמים ונכתוב העולה אחורנית תחת המדרגה הקדומה לזו | ||
|- | |- | ||
| | | | ||
| − | * | + | :::*So, we write 2 beneath the 2 of the second rank, and we write a zero above the 1 we wrote beneath the 2 of the last rank, or cross it out by a pen, as a sign that it is erased from there as if it were not written there. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ועל כן נכתוב ב' תחת הב' [מהמדרגה השנית ונכתוב סיפרא על הא' שכתבנו תחת הב']‫<ref>marg.</ref> מהמדרגה האחרונה או נעבור עליה קולמוס לסימן שתהיה נמחקת משם כאלו לא נכתבה |
|- | |- | ||
| | | | ||
| − | : | + | :::*Then, we shift the remaining 1 in the first rank from which we began, above the 2 that precedes it in writing; it is twelve. |
| + | |style="text-align:right;"|ואחרי זאת נשים הא' הנשארת במדרגה הראשונה להתחלתנו על הב' הקדומה לה במכתב יהיו שנים עשר | ||
|- | |- | ||
| | | | ||
| − | + | :*We examine how many times we can subtract the 2 from it, so that we will be able to subtract the product of the times of subtraction by themselves from the number that remains from it. | |
| + | |style="text-align:right;"|נעיין כמה פעמים נוכל להוציא מהם הב' עד שישאר מהם מספר שנוכל להסיר ממנו אחרי כן כמספר העולה מ{{#annot:term|156,1256|v6iU}}הכאות{{#annotend:v6iU}} מספר הפעמים ההם על <s>ע</s>עצמו | ||
|- | |- | ||
| − | | | + | | |
| + | ::*We find that if we subtract it five times it will be enough for the required and 2 remains in its place. | ||
| + | |style="text-align:right;"|‫<ref>74r</ref>והנה נמצא שיספיק לזה המבוקש אם נסירנה מהם חמש פעמים ותשאר הב' במקומה | ||
|- | |- | ||
| − | | | + | | |
| + | :::*We write a zero above the 1, as nothing is left of it. | ||
| + | |style="text-align:right;"|נכתוב סיפרא על הא' באשר [לא]‫<ref>Vatican: לה</ref> נשאר ממנה כלום | ||
|- | |- | ||
| − | | | + | | |
| − | + | :::*We write 5 beneath the first rank for the five times of subtraction. | |
| + | |style="text-align:right;"|ונכתוב ה' תחת המדרגה הראשונה בעד חמשת פעמי ההסרה | ||
|- | |- | ||
| − | |||
| | | | ||
| − | + | ::*Then we multiply the times of subtraction by themselves; the result is twenty-five. | |
| + | |style="text-align:right;"|ואחר נכה ונכפול מספר ההסרות על עצמו ויעלה חמשה ועשרים | ||
|- | |- | ||
| | | | ||
| − | {|style="margin-left: auto; margin-right: 0px;" | + | ::*We subtract it from the twenty-five that is in the line of the examined number and we find that it is all gone. |
| + | |style="text-align:right;"|נסיר אותם מחמשה ועשרים שבטור החשבון הנחקר ונמצא שכלה הכל | ||
| + | |- | ||
| + | | | ||
| + | :::*So, we write zero above the 5 and above the 2. | ||
| + | |style="text-align:right;"|ולכן נכתוב סיפרא על הה' ועל הב‫' | ||
| + | |- | ||
| + | | | ||
| + | ::*We create another line beneath it, which is 25. | ||
| + | |style="text-align:right;"|והנה חדשנו טור אחר תחתיו שהוא ה'ב‫' | ||
| + | |- | ||
| + | | | ||
| + | :*We subtract from 2 its half; 15 remains and this is the root of the sought number. | ||
| + | |style="text-align:right;"|נסיר מהב' חציה וישאר ה'א' והוא גדר המספר המבוקש | ||
| + | |- | ||
| + | | | ||
| + | ::For, if you multiply 15 by itself, you find the result is 225. | ||
| + | |style="text-align:right;"|כי אם תכפול ותכה ה'א' על עצמו תמצא שיצא [לך]‫<ref>marg.</ref> ה'ב'ב‫' | ||
| + | |- | ||
| + | | | ||
| + | *{{#annot:√925|439|k6sa}}We wish to know the approximate root of nine hundred and twenty-five. | ||
| + | :<math>\scriptstyle\sqrt{925}</math> | ||
| + | |style="text-align:right;"|<big>ועוד בקשנו</big> לדעת הגדר קרוב יותר אל תשע מאות ועשרים וחמשה{{#annotend:k6sa}} | ||
| + | |- | ||
| + | | | ||
| + | :This is its diagram: | ||
| + | |style="text-align:right;"|וזה היא צורתו | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px;" | ||
| + | |- | ||
| + | |0|| || | ||
| + | |- | ||
| + | |9||2||5 | ||
| + | |- | ||
| + | | ||6||0 | ||
| + | |} | ||
| + | |- | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px;" | ||
|- | |- | ||
|0|| || | |0|| || | ||
| Line 2,431: | Line 2,657: | ||
|} | |} | ||
|- | |- | ||
| − | | | + | | colspan="2"| |
| − | ::<span style=color: | + | ::<span style=color:green>[Illustration of the procedure:]</span> |
::{| | ::{| | ||
|- | |- | ||
| − | | ||rowspan="3"|<math>\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{\sqrt{9}=3}}\\&\scriptstyle{\color{red}{9-{\color{blue}{3}}^2=}}{\color{green}{0}}\\&\scriptstyle{\color{red}{2\times3=}}{\color{blue}{6}}\\\end{align}}</math>||<span style= | + | | ||rowspan="3"|<math>\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{\sqrt{9}=3}}\\&\scriptstyle{\color{red}{9-{\color{blue}{3}}^2=}}{\color{green}{0}}\\&\scriptstyle{\color{red}{2\times3=}}{\color{blue}{6}}\\\end{align}}</math>||<span style=color:LimeGreen>0</span>  ||rowspan="3"|<math>\scriptstyle\xrightarrow{\scriptstyle{\color{red}{2<6}}}</math>||0  ||rowspan="3"|<math>\scriptstyle\xrightarrow{\scriptstyle{\color{red}{\frac{1}{2}\sdot6=}}{\color{blue}{3}}}</math>||0   |
|- | |- | ||
| − | |<span style= | + | |<span style=color:red>9</span>25||925||925||925 |
|- | |- | ||
| − | | ||<span style= | + | | ||<span style=color:#0000FF><s>3</s>6</span> || 6<span style=color:#0000FF>0</span>|| <span style=color:#0000FF>3</span>0 |
| − | |} | + | |} |
::<math>\scriptstyle\longrightarrow{\color{Violet}{\begin{align}&\scriptstyle30\ the\ root\\&\scriptstyle25\ the\ remainder\\\end{align}}}</math> | ::<math>\scriptstyle\longrightarrow{\color{Violet}{\begin{align}&\scriptstyle30\ the\ root\\&\scriptstyle25\ the\ remainder\\\end{align}}}</math> | ||
| | | | ||
| Line 2,446: | Line 2,672: | ||
| | | | ||
:*Its last rank has a root, therefore we start from it. | :*Its last rank has a root, therefore we start from it. | ||
| − | |style="text-align:right;"|הנה יש למדרגתו | + | |style="text-align:right;"|הנה יש למדרגתו האחרונה גדר ולכן נתחיל ממנה |
|- | |- | ||
| | | | ||
| Line 2,454: | Line 2,680: | ||
| | | | ||
::*We subtract the 3 it; it is all gone, and nothing is left of it. Therefore we write a zero above it. | ::*We subtract the 3 it; it is all gone, and nothing is left of it. Therefore we write a zero above it. | ||
| − | |style="text-align:right;"|ונסיר {{#annot:term|241,1256|8xHy}}הכאת{{#annotend:8xHy}} הג' ממנה | + | |style="text-align:right;"|ונסיר {{#annot:term|241,1256|8xHy}}הכאת{{#annotend:8xHy}} הג' ממנה ותכלא ולא תשאר ממנה כלום ולכן נכתוב נכתוב עליה סיפרא |
|- | |- | ||
| | | | ||
::*We multiply the 3 twice, cross it out with a pen and write 6 one rank back. | ::*We multiply the 3 twice, cross it out with a pen and write 6 one rank back. | ||
| − | |style="text-align:right;"|נכפול הג' פעמים ונעביר עליה קולמוס ונכתוב ו' במדרגה אחת | + | |style="text-align:right;"|נכפול הג' פעמים ונעביר עליה קולמוס ונכתוב ו' במדרגה אחת אחרנית |
|- | |- | ||
| | | | ||
| − | :*We get the | + | :*We get the approximate root, because now we cannot subtract further 6 from 2 that is above it. So, we write a zero beneath the first rank, and we find that the line created is 60. |
| − | |style="text-align:right;"|והנה יצא אלינו הגדר הקרוב כי עתה לא נוכל עוד להסיר ו' מב' אשר על ראשה ומפני זה תחת המדרגה הראשונה ונמצא שהטור שנתחדש הוא סיפרא ו' | + | |style="text-align:right;"|והנה יצא אלינו הגדר הקרוב כי עתה לא נוכל עוד להסיר ו' מב' אשר על ראשה ומפני זה ‫<ref>74v</ref>נכתוב סיפרא תחת המדרגה הראשונה ונמצא שהטור שנתחדש הוא סיפרא ו‫' |
|- | |- | ||
| | | | ||
:*We subtract from the 6 its half; 30 remains and it is the required approximate root. | :*We subtract from the 6 its half; 30 remains and it is the required approximate root. | ||
| − | |style="text-align:right;"|נסיר מהו' חציה וישאר 0' ג' והוא הגדר הקרוב המבוקש | + | |style="text-align:right;"|נסיר מהו' חציה וישאר 0'ג' והוא הגדר הקרוב המבוקש |
| + | |- | ||
| + | | | ||
| + | ::For, if you multiply 30 by itself and put the remainder, which is 25, beneath it in the first line, you get 925. | ||
| + | |style="text-align:right;"|כי אם תכה ותכפול 0'ג' על עצמו ותשים תחתיו הנשאר בטור ראשון שהוא ה'ב' יצא לך ה'ב'ט‫' | ||
|- | |- | ||
| | | | ||
| − | : | + | *{{#annot:√7056|439|WCca}}We wish to know the root of seven thousand and fifty-six. |
| − | |style="text-align:right;"| | + | :<math>\scriptstyle\sqrt{7056}</math> |
| + | |style="text-align:right;"|<big>ועוד בקשנו</big> לדעת גדר שבעת אלפים וחמשים וששה{{#annotend:WCca}} | ||
|- | |- | ||
| | | | ||
| − | + | :We write it in the following diagram: | |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ונכתבים על זאת הצורה |
|- | |- | ||
| | | | ||
| Line 2,518: | Line 2,749: | ||
|- | |- | ||
| | | | ||
| − | ::<span style=color: | + | ::<span style=color:green>[Illustration of the procedure:]</span> |
| + | | | ||
| + | |- | ||
| + | | colspan="2"| | ||
::{| | ::{| | ||
|- | |- | ||
| − | | ||rowspan="6"|<math>\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{70>8^2}}\\&\scriptstyle{\color{red}{70-{\color{blue}{8}}^2=}}{\color{green}{6}}\\&\scriptstyle{\color{red}{2\times8=}}{\color{blue}{16}}\\\end{align}}</math>|| ||rowspan="6"|<math>\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{6-\left(4\times{\color{blue}{1}}\right)=}}{\color{green}{2}}\\&\scriptstyle{\color{red}{25-\left(4\times{\color{blue}{6}}\right)=}}{\color{green}{1}}\\&\scriptstyle{\color{red}{16-{\color{blue}{4}}^2=}}{\color{green}{0}}\\\end{align}}</math>|| <span style= | + | | ||rowspan="6"|<math>\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{70>8^2}}\\&\scriptstyle{\color{red}{70-{\color{blue}{8}}^2=}}{\color{green}{6}}\\&\scriptstyle{\color{red}{2\times8=}}{\color{blue}{16}}\\\end{align}}</math>|| ||rowspan="6"|<math>\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{6-\left(4\times{\color{blue}{1}}\right)=}}{\color{green}{2}}\\&\scriptstyle{\color{red}{25-\left(4\times{\color{blue}{6}}\right)=}}{\color{green}{1}}\\&\scriptstyle{\color{red}{16-{\color{blue}{4}}^2=}}{\color{green}{0}}\\\end{align}}</math>|| <span style=color:LimeGreen>0</span>  ||rowspan="6"|<math>\scriptstyle\xrightarrow{\scriptstyle{\color{red}{\frac{1}{2}\sdot16=}}{\color{blue}{8}}}</math>|| 0   |
|- | |- | ||
| − | | || || <span style= | + | | || || <span style=color:LimeGreen>20</span> || 20  |
|- | |- | ||
| − | | ||<span style= | + | | ||<span style=color:LimeGreen>06</span>  ||06<span style=color:LimeGreen>10</span>||0610 |
|- | |- | ||
| − | |<span style= | + | |<span style=color:red>70</span>56||7056||7056||7056 |
|- | |- | ||
| − | | || <span style= | + | | || <span style=color:#0000FF><s>8</s>6</span> || 16<span style=color:#0000FF>4</span>|| 164 |
|- | |- | ||
| − | | || <span style= | + | | || <span style=color:#0000FF>1</span>  || ||  <span style=color:#0000FF>8</span>  |
| − | |} | + | |} |
| + | |- | ||
| + | | | ||
::<math>\scriptstyle\longrightarrow{\color{Violet}{\scriptstyle84\ the\ root}}</math> | ::<math>\scriptstyle\longrightarrow{\color{Violet}{\scriptstyle84\ the\ root}}</math> | ||
| | | | ||
| Line 2,538: | Line 2,774: | ||
| | | | ||
:*The last rank of this number has no root, since it is fourth, therefore we shift it to the zero that precedes it in writing, so it is seventy. | :*The last rank of this number has no root, since it is fourth, therefore we shift it to the zero that precedes it in writing, so it is seventy. | ||
| − | |style="text-align:right;"|והנה | + | |style="text-align:right;"|והנה מדרגת המספר הזה האחרונה היא בלתי נגדרת באשר היא רביעית ועל כן נשים אותה על הסיפרא הקדומה לה במכתב ותהיה שבעים |
|- | |- | ||
| | | | ||
| − | ::*The root | + | ::*The approximate root of seventy is 8, whose product by itself is sixty-four. |
| − | |style="text-align:right;"|והגדר {{#annot:term|1614,1359|mIl2}}הקרוב{{#annotend:mIl2}} אל שבעים הוא | + | |style="text-align:right;"|והגדר {{#annot:term|1614,1359|mIl2}}הקרוב{{#annotend:mIl2}} אל שבעים הוא שמונה שעולה כפילתה על עצמו ששים וארבעה |
|- | |- | ||
| | | | ||
| Line 2,549: | Line 2,785: | ||
|- | |- | ||
| | | | ||
| − | ::*We write a zero above the last rank, as nothing is left of it. | + | :::*We write a zero above the last rank, as nothing is left of it. |
| − | |style="text-align:right;"|ונכתוב | + | |style="text-align:right;"|ונכתוב ספרא על המדרגה האחרונה באשר לא נשאר ממנה שם כלום |
|- | |- | ||
| | | | ||
| − | ::*For the approximation of seventy, we write 8 beneath the zero that is in the third rank. | + | ::*For the approximation root of seventy, we write 8 beneath the zero that is in the third rank. |
| − | |style="text-align:right;"|וכנגד הקרוב אל שבעים נכתוב ח' תחת הסיפרא | + | |style="text-align:right;"|וכנגד הגדר הקרוב אל שבעים נכתוב ח' תחת הסיפרא שבמדרגה השלישית |
|- | |- | ||
| | | | ||
::*Then we multiply the 8 twice; it is sixteen. We write it this way: | ::*Then we multiply the 8 twice; it is sixteen. We write it this way: | ||
| − | |style="text-align:right;"|אחרי זאת נכפול הח' פעמים | + | |style="text-align:right;"|אחרי זאת נכפול הח' פעמים שתהיה ששה עשר נכתוב אותם על דרך זה |
|- | |- | ||
| | | | ||
| Line 2,566: | Line 2,802: | ||
| | | | ||
:::*1 for the ten beneath the 8, which we cross it out with a pen. | :::*1 for the ten beneath the 8, which we cross it out with a pen. | ||
| − | |style="text-align:right;"|וא' כנגד העשרה תחת | + | |style="text-align:right;"|וא' כנגד העשרה תחת <sup>ה</sup>ח' ונעביר עליה קולמוס |
|- | |- | ||
| | | | ||
:*Afterwards we examine how many times we can subtract the 1 and the 6 from the 6 and the 5 that are above them, so that enough is left of them for the product of the times of subtraction by themselves. | :*Afterwards we examine how many times we can subtract the 1 and the 6 from the 6 and the 5 that are above them, so that enough is left of them for the product of the times of subtraction by themselves. | ||
| − | |style="text-align:right;"|אחרי כן נעיין כמה פעמים נוכל להסיר הא' והו' מהו' והה' אשר על ראשם בכדי שישאר מהם מספר שיספיק למה שיעלה מספר | + | |style="text-align:right;"|אחרי כן נעיין כמה פעמים נוכל ‫<ref>75r</ref>להסיר הא' והו' מהו' והה' אשר על ראשם בכדי שישאר מהם מספר שיספיק למה שיעלה מספר הכאות פעמי ההסרה על עצמם |
|- | |- | ||
| | | | ||
| − | ::*We find that we can subtract the 1 | + | ::*We find that we can subtract 4 times the 1 from the 6 that above it and 2 remains above it. |
| − | |style="text-align:right;"|והנה נמצא שנוכל להסיר הא' ד' פעמים מהו' אשר על ראשה וישאר עליה ב' | + | |style="text-align:right;"|והנה נמצא שנוכל להסיר הא' ד' פעמים מהו' אשר על ראשה וישאר עליה ב‫' |
|- | |- | ||
| | | | ||
::*Then we subtract the 6 also 4 times that are twenty-four, when we shift the 2 to the 5 that precedes it, so they are twenty-five and 1 remains above the 5. | ::*Then we subtract the 6 also 4 times that are twenty-four, when we shift the 2 to the 5 that precedes it, so they are twenty-five and 1 remains above the 5. | ||
| − | |style="text-align:right;"|ואחר נסיר גם כן הו' ד' | + | |style="text-align:right;"|ואחר נסיר גם כן הו' ד' פעמים שעולים עשרים וארבע כשנשים הב' על הה' שלפניה שיהיו עשרים וחמשה וישאר א' על הה‫' |
| + | |- | ||
| + | | | ||
| + | :::*We write a zero above the 2, as nothing is left of it. | ||
| + | |style="text-align:right;"|ונכתוב על הב' סיפרא באשר לא נשאר ממנה כלום | ||
| + | |- | ||
| + | | | ||
| + | :::*For the four times of subtraction we write 4 beneath the first rank. | ||
| + | |style="text-align:right;"|וכנגד ארבע פעמי ההסרה נכתו' ד' תחת המדרגה הראשונה | ||
|- | |- | ||
| | | | ||
| − | ::* | + | ::*Then, we multiply the 4 by itself; the result is sixteen. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ואחר נכה הד' על עצמו ויהיה ההווה ששה עשר |
|- | |- | ||
| | | | ||
| − | ::* | + | ::*We subtract it from the sixteen that is in the line of the examined number and we find that it is all gone. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ונסיר אותם מששה עשר שבטור החשבון הנחקר ונמצא שתכלה הכל |
|- | |- | ||
| | | | ||
| − | ::* | + | :::*So, we write zeros above the 6 and above the 1. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ולכן נכתוב על הו' ועל הא' סיפראש |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | :*The line that is generated is 164. |
| + | |style="text-align:right;"|והטור שנתחדש אצלינו הוא ד'ו'א‫' | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | ::*We take half the 6 and the 1 this way: |
| + | |style="text-align:right;"|נקח חצי הו' והא' על הדרך הזה | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | ::*We shift 1 above the 6; it is sixteen and its half is 8. |
| + | |style="text-align:right;"|שנשים הא' על הו' ויהיה ששה עשר ויהיה חציין ח‫' | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | :::*We write it be neath the 6. |
| + | |style="text-align:right;"|ונכתוב אותם תחת הו‫' | ||
|- | |- | ||
| | | | ||
| − | *{{#annot:√76543|439|p0o5}}<math>\scriptstyle\sqrt{76543}</math> | + | :*We find that the remainder is 84 and this is the root of the sought number. |
| − | |style="text-align:right;"|ועוד בקשנו לדעת הגדר | + | |style="text-align:right;"|ונמצא ש<sup>ה</sup>נשאר הוא ד'ח' והוא גדר המספר המבוקש |
| + | |- | ||
| + | | | ||
| + | ::For, if you multiply it by itself, you get one line, whose number is seven thousand and fifty-six. | ||
| + | |style="text-align:right;"|שהנה אם תכנו ותכפלנו על עצמו יצא לך טור אחד שמספרו שבעת אלפים וחמישים וששה | ||
| + | |- | ||
| + | | | ||
| + | *{{#annot:√76543|439|p0o5}}We wish to know the the approximate root of seventy-six thousand, five hundred and forty-three. | ||
| + | :<math>\scriptstyle\sqrt{76543}</math> | ||
| + | |style="text-align:right;"|<big>ועוד בקשנו</big> לדעת הגדר הקרוב שבעים וששה אלף וחמש מאות וארבעים ‫<ref>75v</ref>ושלשה{{#annotend:p0o5}} | ||
| + | |- | ||
| + | | | ||
| + | :This is its diagram: | ||
| + | |style="text-align:right;"|וזה היא צורתו | ||
|- | |- | ||
| | | | ||
| Line 2,645: | Line 2,906: | ||
|} | |} | ||
|- | |- | ||
| − | | | + | | colspan="2"| |
| − | ::<span style=color: | + | ::<span style=color:green>[Illustration of the procedure:]</span> |
::{| | ::{| | ||
|- | |- | ||
| − | | ||rowspan="5"|<math>\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{7>2^2}}\\&\scriptstyle{\color{red}{7-{\color{blue}{2}}^2=}}{\color{green}{3}}\\&\scriptstyle{\color{red}{2\times2=}}{\color{blue}{4}}\\\end{align}}</math>|| ||rowspan="5"|<math>\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{36-\left(7\times{\color{blue}{4}}\right)=}}{\color{green}{8}}\\&\scriptstyle{\color{red}{8-5=}}{\color{green}{3}}\\&\scriptstyle{\color{red}{55-{\color{blue}{7}}^2=}}{\color{green}{6}}\\&\scriptstyle{\color{red}{2\times7=}}{\color{blue}{14}}\\\end{align}}</math>||<span style= | + | | ||rowspan="5"|<math>\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{7>2^2}}\\&\scriptstyle{\color{red}{7-{\color{blue}{2}}^2=}}{\color{green}{3}}\\&\scriptstyle{\color{red}{2\times2=}}{\color{blue}{4}}\\\end{align}}</math>|| ||rowspan="5"|<math>\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{36-\left(7\times{\color{blue}{4}}\right)=}}{\color{green}{8}}\\&\scriptstyle{\color{red}{8-5=}}{\color{green}{3}}\\&\scriptstyle{\color{red}{55-{\color{blue}{7}}^2=}}{\color{green}{6}}\\&\scriptstyle{\color{red}{2\times7=}}{\color{blue}{14}}\\\end{align}}</math>||<span style=color:LimeGreen>03</span>    |
|- | |- | ||
| − | | ||<span style= | + | | ||<span style=color:LimeGreen>3</span>    ||3<span style=color:LimeGreen>86</span>   |
|- | |- | ||
| − | |<span style= | + | |<span style=color:red>7</span>6543||76543||76543 |
|- | |- | ||
| − | | ||<span style= | + | | ||<span style=color:#0000FF><s>2</s>4</span>   || 4<span style=color:#0000FF><s>7</s></span>   |
|- | |- | ||
| − | | || || <span style= | + | | || || <span style=color:#0000FF>14</span>   |
|} | |} | ||
| + | |- | ||
| | | | ||
| + | :*The last rank has a root, since it is fifth, so we start from it. | ||
| + | |style="text-align:right;"|הנה המדרגה האחרונה היא נגדרת באשר היא חמישית על כן נתחיל ממנה | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | ::*The approximate root of 7 is 2; we write it beneath it. |
| + | |style="text-align:right;"|והנה הגדר הקרוב אל ז' הוא ב' נכתבנה תחתיה | ||
|- | |- | ||
| | | | ||
| − | : | + | ::*We subtract from it the product of 2 by itself; 3 remains above the 7. |
| + | |style="text-align:right;"|נסיר ממנה הכאת הב' על עצמה וישאר על הז' <sup>ג‫'</sup> | ||
|- | |- | ||
| | | | ||
| − | + | ::*We multiply the 2 twice, cross it out with a pen and write the product, which is 4, one rank back, beneath the 6 that is the fourth rank. | |
| + | |style="text-align:right;"|נכפול הב' פעמים ונעביר עליה קולמוס ונכתוב העולה שהוא ד' במדרגה אחת אחרנית תחת הו' שהיא במדרגה הרביעית | ||
|- | |- | ||
| − | | | + | | |
| + | ::*Then, we shift the 3 that remains above the [7] to the rank that precedes it in writing; it is thirty-six. | ||
| + | |style="text-align:right;"|ואחר כן נשים הג' הנשארת לנו על הו' על המדרגה הקדומה לה במכתב יהיו ששה ושלשים | ||
|- | |- | ||
| − | | | + | | |
| + | :*We examine how many times we can subtract from it the 4 that we wrote beneath the four rank, so that enough is left of it for the product of the times of subtraction by themselves. | ||
| + | |style="text-align:right;"|נעיין כמה פעמים נוכל להסיר מהם הד' שכתבנו תחת המדרגה הרביעית בכדי שיספיק מה שישאר להסיר מספר הכאת פעמי ההסרה על עצמו | ||
|- | |- | ||
| − | | | + | | |
| + | ::*We find that we can subtract it only seven times that are twenty-eight. | ||
| + | |style="text-align:right;"|והנה <s>[.]</s> נמצא שלא נוכל להסיר אותה רק שבע פעמים העולים עשרים ושמונה | ||
|- | |- | ||
| − | | | + | | |
| − | | | + | ::*We subtract it from thirty-six; 8 remains above the 6. |
| + | |style="text-align:right;"|נסיר אותם מששה ושלשים ישאר על הו' ח‫' | ||
|- | |- | ||
| − | |||
| | | | ||
| − | + | :::*We write a zero above the 3 that was shifted from its place. | |
| + | |style="text-align:right;"|ונכתוב סיפרא <sup>על הג'</sup> באשר נעתקה ממקומה | ||
|- | |- | ||
| | | | ||
| − | + | :::*For the seven times of subtraction we write 7 beneath the third rank. | |
| + | |style="text-align:right;"|וכנגד שבע פעמי ההסרה נכתוב תחת המדרגה השלישית ז‫' | ||
|- | |- | ||
| − | | | + | | |
| + | ::*Then, we multiply 7 by itself; the result is forty-nine. | ||
| + | |style="text-align:right;"|אחרי כן נכה ונכפול ז' על עצמה [ויהיה העולה]‫<ref>Vatican om.</ref> ארבעים ותשעה | ||
|- | |- | ||
| − | | | + | | |
| + | ::*We subtract it from what remains in the line of the number this way: | ||
| + | |style="text-align:right;"|נסירה על הדרך הזה ממה שנשאר בטור המספר | ||
|- | |- | ||
| − | | | + | | |
| + | ::*We take 5 from the 8 that remains above the fourth rank; 3 remains above it. | ||
| + | |style="text-align:right;"|והנה נקח מהח' הנשארת ‫<ref>76r</ref><sup>על</sup> המדרגה הרביעית <sup>ה'</sup> וישאר עליה ג‫' | ||
|- | |- | ||
| − | | | + | | |
| − | + | ::*We shift the 5 to the 5 that precedes it in writing, which is the third rank; it is fifty-five. | |
| + | |style="text-align:right;"|ונשים הה' על הה' הקדומה לה במכתב שהיא המדרגה השלישית ויהיו חמשים וחמש | ||
|- | |- | ||
| − | | | + | | |
| + | ::*We subtract forty-nine from it; 6 remains above the 5. | ||
| + | |style="text-align:right;"|נסיר מהם תשע וארבעים ישארו על הה' ו‫' | ||
|- | |- | ||
| | | | ||
| − | :: | + | ::*Then, we multiply the seven times of subtraction twice; it is fourteen. |
| − | + | |style="text-align:right;"|אחרי זאת נכפול השבע פעמי ההסרה פעמים ויהיו ארבעה עשר | |
|- | |- | ||
| − | | | + | | |
| + | :::*We cross the 7 out with a pen. | ||
| + | |style="text-align:right;"|ונעביר הקולמוס על הז‫' | ||
|- | |- | ||
| − | | | + | | |
| + | ::*We write this way: | ||
| + | |style="text-align:right;"|ונכתבם על הדרך הזה | ||
|- | |- | ||
| − | | | + | | |
| + | :::*4 for the four beneath the 7 that we crossed out with a pen. | ||
| + | |style="text-align:right;"|ד' כנגד הארבעה תחת הז' אשר העברנו עליה קולמוס | ||
| + | |- | ||
| + | | | ||
| + | :::*1 for the ten beneath the 4 that is the fourth rank. | ||
| + | |style="text-align:right;"|וא' כנגד העשר תחת הד' שהיא תחת המדרגה הרביעית | ||
| + | |- | ||
| + | | | ||
| + | :*Thereafter, we write what remains in the line of the examined number in another place and make it a separate line; then we write beneath it what is obtained. | ||
| + | |style="text-align:right;"|ואחרי כן נעתיק במקום אחר מה שנשאר בטור המספר הנחקר ונעשה ממנו טור אחר לבדו ואחר נכתוב תחתיו מה שנתחדש | ||
|- | |- | ||
| − | |||
| − | |||
| − | |||
| | | | ||
| + | ::The line of what remains is 3643. | ||
| + | |style="text-align:right;"|והנה יהיה טור מה שנותר ג'ד'ו'ג‫' | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | ::We write beneath it in [another] line: 4 beneath the 4 that is in the second rank, and 5 beneath the 6; all this is what was obtained above. |
| + | |style="text-align:right;"|ונכתוב תחתיו בטור ד' תחת הד' שהיא המדרגה השנית וה' תחת הו' וכל זה הוא מה שנתחדש למעלה | ||
|- | |- | ||
| | | | ||
| − | + | :It is written in this form: | |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והנה יהיה המועתק על זאת הצורה |
|- | |- | ||
| | | | ||
| Line 2,725: | Line 3,023: | ||
{|style="margin-left: auto; margin-right: 0px;" | {|style="margin-left: auto; margin-right: 0px;" | ||
|- | |- | ||
| − | | || | + | | ||3||6|| |
|- | |- | ||
| − | | | + | |0||4||0||7 |
|- | |- | ||
| − | | | + | |3||6||4||3 |
|- | |- | ||
| − | + | | ||5||4||6 | |
| − | |||
| − | | || | ||
| − | |||
| − | |||
|} | |} | ||
|- | |- | ||
| Line 2,745: | Line 3,039: | ||
{|style="margin-left: auto; margin-right: 0px;" | {|style="margin-left: auto; margin-right: 0px;" | ||
|- | |- | ||
| − | | || | + | | ||ג||ו|| |
|- | |- | ||
| − | | | + | |0||ד||0||ז |
|- | |- | ||
| − | | | + | |ג||ו||ד||ג |
|- | |- | ||
| − | + | | ||ה||ד||ו | |
| − | |||
| − | | || | ||
| − | |||
| − | |||
|} | |} | ||
|- | |- | ||
|} | |} | ||
|- | |- | ||
| − | | | + | | colspan="2"| |
| − | ::<span style=color: | + | ::<span style=color:green>[Illustration of the procedure:]</span> |
::{| | ::{| | ||
|- | |- | ||
| − | + | |rowspan="4"|<math>\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{4+1=}}{\color{blue}{5}}\\&\scriptstyle{\color{red}{36-\left(6\times5\right)=6}}\\&\scriptstyle{\color{red}{6-2=}}{\color{green}{4}}\\&\scriptstyle{\color{red}{24-\left(6\times4\right)=}}{\color{green}{0}}\\&\scriptstyle{\color{red}{4-1=}}{\color{green}{3}}\\&\scriptstyle{\color{red}{10-4=}}{\color{green}{6}}\\&\scriptstyle{\color{red}{43-{\color{blue}{6}}^2=}}{\color{green}{7}}\\\end{align}}</math>|| <span style=color:LimeGreen>36</span> ||rowspan="4"|<math>\scriptstyle\xrightarrow{\scriptstyle{\color{red}{\frac{1}{2}\sdot54=}}{\color{blue}{27}}}</math>|| 36  | |
|- | |- | ||
| − | | | + | |<span style=color:LimeGreen>0407</span>||0407 |
|- | |- | ||
| − | | || | + | |3643||3643 |
|- | |- | ||
| − | |<span style= | + | | <span style=color:#0000FF>5</span>4<span style=color:#0000FF>6</span>|| <span style=color:#0000FF>27</span>6 |
| + | |} | ||
| + | ::<math>\scriptstyle\longrightarrow{\color{Violet}{\begin{align}&\scriptstyle276\ the\ root\\&\scriptstyle367\ the\ remainder\\\end{align}}}</math> | ||
|- | |- | ||
| − | | | + | | |
| + | ::*Now, we shift the 3 that is in the last rank of the upper line to the 6 that precedes it; it is thirty-six. | ||
| + | |style="text-align:right;"|והנה נשים הג' שבטור העליון במדרגה האחרונה על הו' הקדומה יהיו ששה ושלשים | ||
|- | |- | ||
| − | |||
| − | |||
| | | | ||
| + | :::*We write zero above the 3 that was shifted from its place. | ||
| + | |style="text-align:right;"|ונכתוב סיפרא על הג' באשר נעתקה ממקומה | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | :*We examine how many times we can subtract the digits of the bottom line from the upper line, so that we will be able to subtract the product of the times of subtraction by themselves from the number that remains of it. |
| + | |style="text-align:right;"|ונעיין כמה פעמים נוכל להסיר אותיות הטור השפל מהטור העליון בכדי שישאר ממנו אחרי כן מספר שנוכל ‫<ref>76v</ref>להסיר ממנו המספר שיעלה מהכאת פעמי ההסרה על עצמם | ||
|- | |- | ||
| | | | ||
| − | : | + | ::*We see that it is enough for that if we subtract it only 6 times. |
| + | |style="text-align:right;"|והוא נראה שיספיק לכל זה אם נסיר אותם ששה פעמים בלבד | ||
|- | |- | ||
| | | | ||
| − | + | ::*When we subtract the 5 six times that are thirty from the thirty-six, the 6 stays in its place. | |
| + | |style="text-align:right;"|וכשנסיר מהששה ושלשים הה' שש פעמים העולים שלשים תשאר הו' במקומה | ||
|- | |- | ||
| − | | | + | | |
| + | ::*We subtract also the 4 that is written beneath the second rank six times; the result is twenty-four. | ||
| + | |style="text-align:right;"|ואחרי זה נסיר הד' הכתובה תחת המדרגה השנית גם כן שש פעמים העולים עשרים וארבע | ||
|- | |- | ||
| − | | | + | | |
| + | ::*We do it this way: | ||
| + | |style="text-align:right;"|נעשה על הדרך הזה | ||
| + | |- | ||
| + | | | ||
| + | ::*We take 2 from the 6; 4 remains above it. | ||
| + | |style="text-align:right;"|נקח ב' מן הו' וישאר עליה ד‫' | ||
|- | |- | ||
| − | | | + | | |
| + | ::*We shift the 2 to the 4 that precedes this rank in writing; the result is twenty-four that are all gone. | ||
| + | |style="text-align:right;"|ונשים [הב']‫<ref>marg.</ref> על הד' הקדומה במכתב למדרגה הזאת ויעלו עשרים וארבע ויסופו ויכלו | ||
|- | |- | ||
| − | | | + | | |
| − | | | + | :::*We write zero above the 4, since nothing remains there. |
| + | |style="text-align:right;"|ונכתוב על הד' סיפרא באשר לא נשאר שם כלום | ||
|- | |- | ||
| − | |||
| | | | ||
| − | + | :::*For the six times of subtraction we write 6 beneath the first rank. | |
| + | |style="text-align:right;"|וכנגד שש פעמי ההסרה נכתוב ו' תחת המדרגה הראשונה | ||
|- | |- | ||
| | | | ||
| − | + | ::*We multiply the 6 by itself; the result is thirty-six. | |
| + | |style="text-align:right;"|ונכה הו' על עצמה תעלה ששה ושלשים | ||
|- | |- | ||
| − | | | + | | |
| + | ::*We subtract it from what is left in the upper line this way: | ||
| + | |style="text-align:right;"|נסירם ממה שנשאר בטור העליון על דרך זה | ||
|- | |- | ||
| − | | | + | | |
| + | ::*We subtract 1 from the 4 that is left above the third rank; 3 remains there. | ||
| + | |style="text-align:right;"|נסיר מן הד' הנשארת על המדרגה השלישית א' וישאר שמה ג‫' | ||
|- | |- | ||
| − | | | + | | |
| + | ::*We shift the 1 to the zero, which is above the second rank that precedes it; it is ten. | ||
| + | |style="text-align:right;"|נשים הא' על הסיפרא אשר על המדרגה השנית הקדומה לה ותהיה שוה עשר | ||
|- | |- | ||
| − | | | + | | |
| − | | | + | ::*We subtract four from it; 6 remains above the zero. |
| + | |style="text-align:right;"|נסיר מהם ארבעה וישאר על הסיפרא ו‫' | ||
|- | |- | ||
| − | | | + | | |
| − | + | ::*We shift the 4 to the first rank; it is forty-three. | |
| + | |style="text-align:right;"|נשים הד' על המדרגה הראשונה יעלו ארבעים ושלש | ||
|- | |- | ||
| | | | ||
| − | :: | + | ::*We subtract thirty-six from it; 7 remains above the 3 that is in the first rank. |
| − | + | |style="text-align:right;"|נסיר מהם הששה ושלשים ישארו ז' על הג' שבמדרגה הראשונה | |
|- | |- | ||
| − | | | + | | |
| + | :*The bottom line that is generated is 546. | ||
| + | |style="text-align:right;"|והנה הטור השפל אשר ‫<ref>77r</ref>נתחדש הוא ו'ד'ה‫' | ||
|- | |- | ||
| − | | | + | | |
| + | ::*We take half the 4 and the 5; 27 remains. | ||
| + | |style="text-align:right;"|נקח חצי הד' והה' ישאר ז'ב‫' | ||
|- | |- | ||
| − | | | + | | |
| + | :*We find that the remainder after all this is 276 and this is the approximate root of the sought number. | ||
| + | |style="text-align:right;"|נמצא מה שנשאר אחר כל זה ו'ז'ב' והוא הגדר היותר קרוב אל המספר המב<sup>ו</sup>קש | ||
|- | |- | ||
| − | |||
| − | |||
| − | |||
| | | | ||
| + | ::If you multiply 276 by itself and add what remains in the upper line, which is 365, you get the line of the number whose root you sought. | ||
| + | |style="text-align:right;"|ואם תכפול ו'ז'ב' <s>והוא הגדר היותר</s> על עצמו ותוסיף על כפילתו מה שנשאר בטור העליון שהוא ה'ו'ג' יצא לך טור המספר אשר דרשת גדרו | ||
|- | |- | ||
| | | | ||
| − | + | *{{#annot:√583696|439|gS7X}}We wish to know the root of five hundred and eighty-three thousand, six hundred and ninety-six. | |
| + | :<math>\scriptstyle\sqrt{583696}</math> | ||
| + | |style="text-align:right;"|<big>ועוד בקשנו</big> לדעת גדר חמש מאות ושמונים ושלשת אלפים ושש מאות ותשעים וששה{{#annotend:gS7X}} | ||
|- | |- | ||
| | | | ||
| − | + | :We write it in the following diagram: | |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ונכתבנו על זאת הצורה |
|- | |- | ||
| | | | ||
| Line 2,843: | Line 3,167: | ||
{|style="margin-left: auto; margin-right: 0px;" | {|style="margin-left: auto; margin-right: 0px;" | ||
|- | |- | ||
| − | | ||0|| | + | | ||0|| || || || |
|- | |- | ||
| − | | | + | | ||3||6|| || || |
|- | |- | ||
| − | | | + | |0||9||9||0|| || |
|- | |- | ||
| − | | | + | |5||8||3||6||9||6 |
| − | | | ||
|- | |- | ||
| − | |} | + | | || ||4|| || || |
| + | |- | ||
| + | | ||1||1||2|| || | ||
| + | |} | ||
| + | |- | ||
| + | |} | ||
| | | | ||
{|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| Line 2,859: | Line 3,187: | ||
{|style="margin-left: auto; margin-right: 0px;" | {|style="margin-left: auto; margin-right: 0px;" | ||
|- | |- | ||
| − | | ||0|| | + | | ||0|| || || || |
| + | |- | ||
| + | | ||ג||ו|| || || | ||
| + | |- | ||
| + | |0||ט||ט||0|| || | ||
|- | |- | ||
| − | | | + | |ה||ח||ג||ו||ט||ו |
|- | |- | ||
| − | | | + | | || ||ד|| || || |
|- | |- | ||
| − | | || | + | | ||א||א||ב|| || |
|} | |} | ||
|- | |- | ||
|} | |} | ||
| − | + | |- | |
| − | | | + | | colspan="2"| |
| − | + | ::<span style=color:green>[Illustration of the procedure:]</span> | |
| − | ::<span style=color: | ||
::{| | ::{| | ||
|- | |- | ||
| − | | ||rowspan=" | + | | ||rowspan="6"|<math>\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{58>7^2}}\\&\scriptstyle{\color{red}{58-{\color{blue}{7}}^2=}}{\color{green}{9}}\\&\scriptstyle{\color{red}{2\times7=}}{\color{blue}{14}}\\\end{align}}</math>|| ||rowspan="6"|<math>\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{9-\left(6\times{\color{blue}{1}}\right)=}}{\color{green}{3}}\\&\scriptstyle{\color{red}{33-\left(6\times{\color{blue}{4}}\right)=}}{\color{green}{9}}\\&\scriptstyle{\color{red}{9-3=}}{\color{green}{6}}\\&\scriptstyle{\color{red}{36-{\color{blue}{6}}^2=}}{\color{green}{0}}\\&\scriptstyle{\color{red}{2\times6=}}{\color{blue}{12}}\\\end{align}}</math>|| <span style=color:LimeGreen>0</span>     |
| + | |- | ||
| + | | || || <span style=color:LimeGreen>36</span>    | ||
|- | |- | ||
| − | | ||<span style= | + | | ||<span style=color:LimeGreen>09</span>    ||09<span style=color:LimeGreen>90</span>   |
|- | |- | ||
| − | |<span style= | + | |<span style=color:red>58</span>3696||583696||583696 |
|- | |- | ||
| − | | || <span style= | + | | || <span style=color:#0000FF><s>7</s>4</span>   || <s>74</s><span style=color:#0000FF><s>6</s></span>   |
| − | | | + | |- |
| − | : | + | | || <span style=color:#0000FF>1</span>    || 1<span style=color:#0000FF>12</span>   |
| − | + | |} | |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | :*Since the last rank of this number has no root, the 5 should be shifted to the 8 that precedes it in writing in the fifth rank; it is fifty-eight. |
| + | |style="text-align:right;"|באשר המדרגה האחרונה מהמספר הזה הוא בלתי נגדרת צריך ל<s>ה</s>שים את הה' על הח' הקדומה לה במכתב במדרגה חמישית ויעלו חמישים ושמונה | ||
|- | |- | ||
| | | | ||
| − | * | + | ::*The approximate root of this number [is 7], whose product by itself is forty-nine. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והגדר הקרוב אל המספר הזה שעולה הכאתו על עצמו הוא תשעה וארבעים |
|- | |- | ||
| | | | ||
| − | : | + | ::*When we subtract it from fifty-eight, 9 remains above the 8. |
| + | |style="text-align:right;"|וכשנסיר אותם מחמישים ושמונה ישארו על הח' ט‫' | ||
|- | |- | ||
| | | | ||
| − | + | :::*We write zero above the 5 that was shifted from its place. | |
| + | |style="text-align:right;"|ונכתוב סיפרא על הה' באשר נעתקה ממקומה | ||
|- | |- | ||
| − | | | + | | |
| + | :::*For the approximate root we write 7 beneath the 8. | ||
| + | |style="text-align:right;"|וכנגד הגדר הקרוב נכתוב ז' תחת הח‫' | ||
|- | |- | ||
| − | | | + | | |
| + | ::*[We] multiply the 7 twice, and cross it out with a pen; the product is fourteen. | ||
| + | |style="text-align:right;"|ויכפול הז' הזאת פעמים ונעביר עליה קולמוס והנה יהיה העולה ארבעה עשר | ||
|- | |- | ||
| − | | | + | | |
| − | + | :::*We write four for the four beneath the 3 that is the fourth rank and 1 for the ten beneath the 7 that we crossed out with a pen. | |
| + | |style="text-align:right;"|ונכתוב ד' כנגד הארבעה תחת הג' שהיא המדרגה ‫<ref>77v</ref>הרביעית וא' כנגד העשר תחת הז' אשר העברנו עליה הקולמוס | ||
|- | |- | ||
| − | |||
| | | | ||
| − | + | :*Now, we should [examine] how many times we can subtract the 1 and the 4 from what remains in the upper line, so that we will have enough to subtract the product of the times of subtraction by themselves from the remainder. | |
| + | |style="text-align:right;"|ועתה אנחנו צריכים [לעיין]‫<ref>Vatican om.</ref> כמה פעמים נוכל להסיר הא' והד' ממה שנשאר בטור המספר בכדי שיספיק לנו אחרי כן להסיר מהנשאר מספר הכרת פעמי ההסרה על עצמו | ||
|- | |- | ||
| | | | ||
| − | + | ::*We find that it is enough for us if we subtract it six times. | |
| + | |style="text-align:right;"|והנה נמצא שיספיק לנו אם נסיר אותם ששה פעמים | ||
|- | |- | ||
| − | | | + | | |
| + | ::*When we subtract the 1 six times from the 9, 3 remains above it. | ||
| + | |style="text-align:right;"|והנה כשנסיר הא' מהט' ששה פעמים ישאר עליה ג‫' | ||
|- | |- | ||
| − | | | + | | |
| + | ::*We also have to subtract the 4 six times; the product is twenty-four. | ||
| + | |style="text-align:right;"|וגם יש לנו להסיר הד' ששה פעמים שעלה כפלתם ארבע ועשרים | ||
|- | |- | ||
| − | | | + | | |
| − | + | ::*We do it this way: | |
| + | |style="text-align:right;"|ונעשה על הדרך הזה | ||
|- | |- | ||
| − | | | + | | |
| + | ::*We take the 3 that remains above the 9 and write a zero in its place. | ||
| + | |style="text-align:right;"|נקח הג' הנשארת לנו על הט' ונכתוב סיפרא במקומה | ||
|- | |- | ||
| | | | ||
| − | :: | + | ::*We shift it to the 3 that precedes it in the fourth rank; the result is thirty-three. |
| − | + | |style="text-align:right;"|ונשים אותה על הג' הקדומה לה במדרגה רביעית ויעלו שלש ושלשים | |
|- | |- | ||
| − | | | + | | |
| + | ::*When we subtract the twenty-four from it, 9 remains above the 3. | ||
| + | |style="text-align:right;"|כשנסיר מהם הארבע ועשרים ישארו על הג' ט‫' | ||
|- | |- | ||
| − | | | + | | |
| + | :::*For the six times of subtraction we write 6 beneath the third rank. | ||
| + | |style="text-align:right;"|וכנגד שש פעמי ההסרה נכתוב תחת המדרגה השלישית ו‫' | ||
|- | |- | ||
| − | |||
| − | |||
| − | |||
| | | | ||
| + | ::*When we multiply it by itself the result is thirty-six. | ||
| + | |style="text-align:right;"|וכשנכפול ונכה אותם על עצמם יעלו ששה ושלשים | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | ::*We subtract it from the line of the number this way: |
| + | |style="text-align:right;"|ונסיר אותם מטור המספר על הדרך [הזה]‫<ref>Vatican om.</ref> | ||
|- | |- | ||
| | | | ||
| − | * | + | ::*We take 3 from the 9 that is left in the fourth rank; 6 remains above it. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|נקח מן הט' הנשארת לנו במדרגה רביעית ג' וישארו עליה ו‫' |
|- | |- | ||
| | | | ||
| − | : | + | ::*We shift the 3 to the 6 that precedes it in the third rank; it is thirty-six, which is a product of the 6 by itself. |
| + | |style="text-align:right;"|נשים זאת הג' על הו' הקדומה לה במדרגה שלישית יעלו ששה ושלשים <s>אחד</s> [שהם]<ref>marg.</ref> כפילת הכאת הו' על עצמה | ||
|- | |- | ||
| | | | ||
| − | + | :::*We write a zero above the 6, for no remainder is left. | |
| + | |style="text-align:right;"|ו<sup>הנה</sup> נכתוב סיפרא על הו' באשר ‫<ref>78r</ref>לא נשארה ממנה שארית | ||
|- | |- | ||
| − | | | + | | |
| + | ::*Then, we double the six times of subtraction; it is twelve. | ||
| + | |style="text-align:right;"|אחרי זאת נכפול הששת פעמים ההסרה פעמים ויהיו שנים עשר | ||
|- | |- | ||
| − | | | + | | |
| + | ::*We write it this way: | ||
| + | |style="text-align:right;"|ונכתבם על הדרך הזה | ||
|- | |- | ||
| − | | | + | | |
| − | + | :::*2 beneath the 6 for the two and we cross it out by a pen. | |
| + | |style="text-align:right;"|ב' תחת הו' כנגד השתים ונעביר עליה קולמוס | ||
|- | |- | ||
| − | |||
| | | | ||
| − | + | :::*1 beneath the 4 that follows for the ten. | |
| + | |style="text-align:right;"|וא' תחת הד' שאחריה כנגד העשר | ||
|- | |- | ||
| | | | ||
| − | + | :*After all this, we write what remains in the line of the number in another place and make it a separate line; then we write beneath it what is obtained. | |
| + | |style="text-align:right;"|ואחר כל זה נעתיק במקום אחר מה שנשאר בטור המספר ונעשה ממנו טור אחד לבדו ואחר נכתוב תחתיו מה שנתחדש | ||
|- | |- | ||
| − | | | + | | |
| + | ::The line of what remains is 6096. | ||
| + | |style="text-align:right;"|והנה יהיה טור מה שנותר ו'ט'0ו‫' | ||
|- | |- | ||
| − | | | + | | |
| + | ::We write beneath it in another line: 2 beneath the 9, 5 beneath the zero, and 1 beneath the 6; all this is what was obtained above. | ||
| + | |style="text-align:right;"|ונכתוב תחתיו בטור אחר ב' תחת הט' וה' תחת הסיפרא וא' תחת הו' וכל זה הוא מה שנתחדש למעלה | ||
|- | |- | ||
| − | | | + | | |
| − | + | :It is written in this form: | |
| + | |style="text-align:right;"|והנה יהיה המועתק על זאת הצורה | ||
|- | |- | ||
| − | | | + | | |
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
|- | |- | ||
| | | | ||
| − | + | {|style="margin-left: auto; margin-right: 0px;" | |
| − | :: | ||
|- | |- | ||
| − | | || | + | |0|| || || |
|- | |- | ||
| − | | | + | |2|| ||1||0 |
|- | |- | ||
| − | | || | + | |6||0||9||6 |
| − | | | ||
| − | |||
| − | | | ||
|- | |- | ||
| − | | | + | |1||5||2||4 |
| − | | | + | |} |
|- | |- | ||
| + | |} | ||
| | | | ||
| − | + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | |
| − | |style="text-align: | ||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| − | | | + | | |
| + | {|style="margin-left: auto; margin-right: 0px;" | ||
|- | |- | ||
| − | | || ||& | + | |0|| || || |
|- | |- | ||
| − | | || | + | |ב|| ||א||0 |
|- | |- | ||
| − | | | + | |ו||0||ט||ו |
|- | |- | ||
| − | | || | + | |א||ה||ב||ד |
| − | + | |} | |
| − | |||
| − | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| − | | | + | | colspan="2"| |
| − | + | ::<span style=color:green>[Illustration of the procedure:]</span> | |
| + | ::{| | ||
|- | |- | ||
| − | | | + | |rowspan="4"|<math>\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{4+1=}}{\color{blue}{5}}\\&\scriptstyle{\color{red}{6-\left(4\times1\right)=}}{\color{green}{2}}\\&\scriptstyle{\color{red}{20-\left(4\times5\right)=}}{\color{green}{0}}\\&\scriptstyle{\color{red}{9-\left(4\times2\right)=}}{\color{green}{1}}\\&\scriptstyle{\color{red}{16-{\color{blue}{4}}^2=}}{\color{green}{0}}\\\end{align}}</math>||<span style=color:LimeGreen>0</span> <span style=color:LimeGreen>0</span> ||rowspan="4"|<math>\scriptstyle\xrightarrow{\scriptstyle{\color{red}{\frac{1}{2}\sdot152=}}{\color{blue}{76}}}</math>|| 36  |
| − | | | ||
|- | |- | ||
| − | | | + | |<span style=color:LimeGreen>2</span> <span style=color:LimeGreen>10</span>||2 10 |
| − | : | ||
| − | | | ||
|- | |- | ||
| − | | | + | |6096||6096 |
| − | |||
| − | | | ||
|- | |- | ||
| − | | | + | |1<span style=color:#0000FF>5</span>2<span style=color:#0000FF>4</span>|| <span style=color:#0000FF>76</span>4 |
| − | + | |} | |
| − | + | ::<math>\scriptstyle\longrightarrow{\color{Violet}{\scriptstyle764\ the\ root}}</math> | |
|- | |- | ||
| | | | ||
| − | :* | + | :*Now, we should examine how many times we can subtract the digits that we wrote beneath the first line, so that we will have enough afterwards to subtract the product of the times of subtraction by themselves from the remainder. |
| − | + | |style="text-align:right;"|ועתה יש לנו לעיין כמה פעמים נוכל להסיר האותיות שכתבנו תחת הטור הראשון ממנו בכדי שיספיק לנו אחרי כן להסיר מהנשאר כפל הכאת מספר ההסרות על עצמו | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | :* | + | ::*We find that it is enough for all this if we subtract it 4 times. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והנה נמצא שיספיק לכל זה אם נסירם ד' פעמים |
|- | |- | ||
| | | | ||
| − | ::* | + | ::*When we subtract four times the 1 that is the last rank of the bottom line from the 6 that is in the upper line above it, 2 remains above it. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והנה כשנסיר הא' שהיא המדרגה האחרונה מהטור השפל מהו' אשר בטור העליון על ראשה ארבעה פעמים ישאר עליו ב‫' |
|- | |- | ||
| | | | ||
| − | :: | + | ::*We have to subtract from the upper line also four times the 5 that is in the bottom line, the product of which is twenty. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וגם כן יש לנו להסיר ארבעה פעמים הה' אשר בטור השפל שעולה כפלתם עשרים ‫<ref>78v</ref>מהטור העליון |
|- | |- | ||
| | | | ||
| − | :* | + | ::*We do it this way: |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ונעשה על דרך זה |
|- | |- | ||
| | | | ||
| − | ::* | + | ::*We take the 2 the is left in the last rank of the upper line and shift it to the zero that precedes that rank; it is twenty and all is gone for the twenty of the product. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|נקח הב' הנשארת לנו במדרגה האחרונה מהטור העליון ונשים אותה על הסיפרא הקדומה למדרגה ההיא ויהיו עשרים ויסופו ויכלו בעד העשרים מהכפילה |
|- | |- | ||
| | | | ||
| − | ::: | + | :::*We write a zero above the 2 that we took, as it was shifted from its place. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ונכתוב על הב' אשר לקחנו סיפרא באשר נעתקה ממקומה |
|- | |- | ||
| | | | ||
| − | : | + | ::*Then, [we] subtract also four times the 2 that is in the bottom line from the 9 that is above it; 1 remains above it. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ואחרי זאת הסיר גם כן ארבעה פעמים הב' שבטור השפל מהט' אשר על ראשו וישאר עליה א‫' |
|- | |- | ||
| | | | ||
| − | : | + | :::*For the four times of subtraction we write 4 beneath the first rank of the upper line. |
| − | ::* | + | |style="text-align:right;"|והנה כנגד ארבעה פעמי ההסרה נכתוב תחת המדרגה הראשונה מהטור העליון ד‫' |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | :: | + | ::*When we multiply 4 by itself, it is sixteen. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וכאשר נכפול ונכה הד' על עצמה יהיה ההוא ששה עשר |
|- | |- | ||
| | | | ||
| − | :* | + | ::*We subtract it from the sixteen that is in the upper line, because 1 is left above the 9 in the second rank and the 6 in the first [rank]. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|נסירם מהששה עשר שבטור העליון שהרי נותרו א' על הט' במדרגה השנייה והו' שבראשונה |
|- | |- | ||
| | | | ||
| − | : | + | ::*We find that the whole upper line is gone, so we write zeros above the 6 and the 1 that above the 9. |
| − | :* | + | |style="text-align:right;"|ונמצא שיכלה כל הטור העליון ועל כן נכתוב סיפראש על הו' ועל הא' שבראש הט‫' |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | : | + | :*The bottom line that is generated is 1524. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והטור התחתון אשר נתחדש הוא ד'ב'ה'א‫' |
|- | |- | ||
| | | | ||
| − | :*1; | + | ::*We take half the 2, 5 and 1; the remainder is 764 and this is the sought root of the number. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|נקח חצי הב' והה' והא' ותהיה הנשאר ד'ו'ז' והוא הגדר מהמספר המבוקש |
|- | |- | ||
| | | | ||
| − | : | + | ::If you multiply 764 by itself, I promise you that the product is 583696. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ואם תכפול ד'ו'ז' על עצמו אני מבטיח לך שיצא מקבוץ ה{{#annot:term|241,1253|i2pU}}כפילה{{#annotend:i2pU}} ו'ט'ו'ג'ח'ה‫' |
|- | |- | ||
| | | | ||
| − | : | + | *{{#annot:√824464|439|nzC6}}We wish to know the root of this number, which is eight hundred and twenty-four thousand, four hundred and sixty-four. |
| − | |style="text-align:right;"| | + | :<math>\scriptstyle\sqrt{824464}</math> |
| + | |style="text-align:right;"|<big>ועוד בקשנו</big> לדעת גדר ‫<ref>79r</ref>המספר הזה שהוא שמונה מאות <sup>אלף</sup> ועשרים וארבעת אלף וארבע מאות וששים וארבעה{{#annotend:nzC6}} | ||
|- | |- | ||
| | | | ||
| − | : | + | :We write it in the following diagram: |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ונכתבם על זאת הצורה |
|- | |- | ||
| | | | ||
| − | + | :{|class="wikitable" style="color:blue; text-align:center;" | |
| − | |||
|- | |- | ||
| | | | ||
| − | + | {|style="margin-left: auto; margin-right: 0px;" | |
| − | |style=" | ||
|- | |- | ||
| − | | | + | | ||0||0|| || || |
| − | |||
| − | | | ||
|- | |- | ||
| − | | | + | |0||1||6||0||0||0 |
| − | |||
| − | | | ||
|- | |- | ||
| − | | | + | |8||2||4||4||6||4 |
| − | |||
| − | | | ||
|- | |- | ||
| + | | ||9||1||8||0||8 | ||
| + | |} | ||
| + | |- | ||
| + | |} | ||
| | | | ||
| − | : | + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" |
| − | + | |- | |
| − | |style= | + | | |
| + | {|style="margin-left: auto; margin-right: 0px;" | ||
| + | |- | ||
| + | | ||0||0|| || || | ||
| + | |- | ||
| + | |0||א||ו||0||0||0 | ||
| + | |- | ||
| + | |ח||ב||ד||ד||ו||ד | ||
| + | |- | ||
| + | | ||ט||א||ח||0||ח | ||
| + | |} | ||
| + | |- | ||
| + | |} | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | ::<span style=color:green>[Illustration of the procedure:]</span> | ||
| + | ::{| | ||
| + | |- | ||
| + | | ||rowspan="4"|<math>\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{82>9^2}}\\&\scriptstyle{\color{red}{82-{\color{blue}{9}}^2=}}{\color{green}{1}}\\&\scriptstyle{\color{red}{2\times9=}}{\color{blue}{18}}\\\end{align}}</math>|| ||rowspan="4"|<math>\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{14-\left(8\times{\color{blue}{1}}\right)=}}{\color{green}{6}}\\&\scriptstyle{\color{red}{64-\left(8\times{\color{blue}{8}}\right)=}}{\color{green}{0}}\\&\scriptstyle{\color{red}{64-{\color{blue}{8}}^2=}}{\color{green}{0}}\\\end{align}}</math>|| <span style=color:LimeGreen>00</span>   ||rowspan="4"|<math>\scriptstyle\xrightarrow{\scriptstyle{\color{red}{\frac{1}{2}\sdot18=}}{\color{blue}{9}}}</math>|| 00    | ||
|- | |- | ||
| − | | | + | | ||<span style=color:LimeGreen>01</span>    ||01<span style=color:LimeGreen>6000</span>||016000 |
| − | |style= | + | |- |
| + | |<span style=color:red>82</span>4464||824464||824464||824464 | ||
|- | |- | ||
| + | | || <span style=color:#0000FF><s>9</s>180</span> || <s>9</s>180<span style=color:#0000FF>8</span>||   <span style=color:#0000FF>9</span>08 | ||
|} | |} | ||
| − | { | + | ::<math>\scriptstyle\longrightarrow{\color{Violet}{\scriptstyle908\ the\ root}}</math> |
|- | |- | ||
| | | | ||
| − | + | :*Since the last rank of this number has no root, it should be shifted to the 2 that precedes it in writing that is the fifth ranke; it is eighty-two. | |
| − | + | |style="text-align:right;"|על אשר המדרגה האחרונה מהמספר הזה היא בלתי נגדרת צריך לשום אותה על הב' הקדומה לה במכתב שהיא המדרגה החמישית והנה יהיה שמנים ושנים | |
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | + | ::*Its approximate root is nine, since its product by itself is eighty-one. | |
| − | + | |style="text-align:right;"|והגדר היותר קרוב אליהם הוא תשעה כי כפל הכאתו על עצמו עולה אחד ושמונים | |
| + | |- | ||
| | | | ||
| + | ::*When we subtract it from it, 1 remains above the 2. | ||
| + | |style="text-align:right;"|והנה כשנסיר אותם מהם תשאר על הב' א‫' | ||
|- | |- | ||
| − | | | + | | |
| − | : | + | :::*We write a zero above the 2, as it was shifted from its place. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ונכתוב על הב' סיפרא באשר נעתקה ממקומה |
|- | |- | ||
| | | | ||
| − | :: | + | :::*We write 9 beneath that 2 for the nine, which is the approximate root and cross out the 9 with a pen. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והנה נכתוב תחת הב' ההיא ט' כנגד תשעה שהם הגדר היותר קרוב ואחר נעביר הקולמוס על הט‫' |
|- | |- | ||
| | | | ||
| − | :: | + | ::*We double it; it is eighteen. |
| − | + | |style="text-align:right;"|ונכפל אותה והיו שמנה עשר | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| − | | | + | | |
| − | : | + | ::*We write it this way: |
| − | + | |style="text-align:right;"|ונכתבם על הדרך הזה | |
| − | |||
| − | |||
| − | : | ||
| − | |style="text-align:right;"| | ||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | + | :::*1 beneath the fourth rank, for the ten. | |
| − | + | |style="text-align:right;"|א' תחת המדרגה הרביעית כנגד העשר | |
| − | |||
| − | |||
| − | |||
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | = | + | :::*8 for the eight one rank back. |
| − | + | |style="text-align:right;"|וח' כנגד השמנה במדרגה אחת אחורנית | |
| − | | | ||
|- | |- | ||
| | | | ||
| − | + | :::*Then, we write a zero beneath the second rank. | |
| − | + | |style="text-align:right;"|ואחרי זאת כתבנו סיפרא תחת המדרגה השנית | |
| − | |||
| − | |||
| − | |||
| − | |style="text-align:right;"| | ||
|- | |- | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| | | | ||
| + | :*Then we examine how many times we can subtract the digits of the created bottom line from what remains in the upper line, so that a number remains there from which we will be able to subtract the product of the times of subtraction by themselves. | ||
| + | |style="text-align:right;"|ואחר נעיין כמה פעמים נוכל להסיר אותיות הטור השפל המתחדש ממה שנשאר בטור העליון בכדי שישאר שם מספר ‫<ref>79v</ref>אחר זאת שנוכל להסיר ממנו כמספר העולה מכפילת פעמי ההסרות על עצמם | ||
|- | |- | ||
| − | |||
| − | |||
| | | | ||
| + | ::*We find that it is enough to subtract it eight times. | ||
| + | |style="text-align:right;"|והוא נמצא שיספיק להסיר אותם שמנה פעמים | ||
|- | |- | ||
| | | | ||
| − | * | + | ::*We do it this way: |
| − | : | + | |style="text-align:right;"|ונעשה על הדרך הזה |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | :* | + | ::*We take the 1 that is left in the upper line above the fifth rank and write zero above it, since we shift it from its place. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|נקח הא' הנשארת בטור העליון על המדרגה החמישית ונכתוב עליה סיפרא באשר נעתיקנה ממקומה |
|- | |- | ||
| | | | ||
| − | :* | + | ::*We shift it to the 4 that is left in the fourth rank that precedes it; it is fourteen. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ונשים אותה על הד' הנשארת במדרגה הרביעית הקדומה לה ויהיו ארבעה עשר |
|- | |- | ||
| | | | ||
| − | : | + | ::*We subtract from it eight times the 1 that beneath the fourth rank; 6 remains above the 4. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|נסיר מהם הא' שתחת המדרגה הרביעית שמנה פעמים וישאר על הד' ו‫' |
|- | |- | ||
| | | | ||
| − | * | + | ::*We also have to subtract eight times the 8 that is beneath the third rank; its product is sixty-four. |
| − | + | |style="text-align:right;"|וגם כן יש לנו להסיר הח' שתחת המדרגה השלישית שמונה פעמים שעולה כפלתם שישים וארבעה | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | :* | + | ::*We do it this way: |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ונעשה על הדרך הזה |
|- | |- | ||
| | | | ||
| − | : | + | :::We take the 6 left in the fourth rank and write a zero above it when we shift it from its place. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|נקח הו' הנשארת במדרגה הרביעית ונכתוב סיפרא עליה כאשר נעתיקנה ממקומה |
|- | |- | ||
| | | | ||
| − | : | + | :::We write it above the 4 in the third rank that precedes it; it is sixty-four and it is all gone when subtracting the product of 8. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ונשים אותה על הד' שהיא המדרגה השלישית הקדומה לה ויהיו שישים וארבעה ויכלו ויתמו בעבור הסרת פעמי הח‫' |
|- | |- | ||
| | | | ||
| − | + | :::We write a zero above the 4, because nothing remains of it. | |
| − | + | |style="text-align:right;"|ונכתוב על הד' ההיא סיפרא באשר לא נשאר ממנה כלום | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | : | + | :::For the eight times of subtraction we write 8 beneath the first rank. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וכנגד <sup>שמונה</sup> פעמי הסרת האותיות נכתוב תחת המדרגה הראשונה ח‫' |
|- | |- | ||
| | | | ||
| − | :* | + | ::*When we multiply 8 by itself the result is sixty-four. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וכאשר נכה ח' על עצמם יעלו שישים וארבעה |
|- | |- | ||
| | | | ||
| − | : | + | :::We subtract it from the sixty-four above it in the line of the number examined, because so far the 4 remains in the the first rank and the 6 in the second rank. Thus the entire upper line is gone. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|‫<ref>80r</ref>נסירם מהשישים וארבעה אשר על ראשם בטור המספר הנחקר כי הנה נשארו עד כה הד' שהיא המדרגה הראשונה והו' שהיא המדרגה השנית ובזה תכלה כל הטור העליון |
|- | |- | ||
| | | | ||
| − | : | + | :::So, we write zeros above the 4 and the 5. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ועל כן נכתוב סיפראש על הד' ועל הה‫' |
|- | |- | ||
| | | | ||
| − | :* | + | :*The bottom line that is generated is 1808. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והטור שנתחדש הוא ח'[0]ח'א‫' |
|- | |- | ||
| | | | ||
| − | :: | + | ::A half of 180 is 90. We find that what remains is 908 and this is the required root of the number. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וחצי סיפרא ח"א הוא 0ט' נמצא שיהיה הנותר אחרי זאת ח'0'ט' והוא גדר המספר המבוקש |
|- | |- | ||
| | | | ||
| − | : | + | :<span style=color:green>'''Check:'''</span> ''Try me herewith'' [Malachi 3, 10]: to multiply 908 by itself, for you will necessarily receive 824464 from the multiplication. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|''ובחנני נא בזאת''‫<ref group=note>מלאכי ג, י</ref> ונסני לכפול ח'0'ט' על עצמו כי בהכרח יצא לך מקבוץ ה{{#annot:term|241,1253|ARoF}}כפילה{{#annotend:ARoF}} ד'ו'ד'ד'ב'ח‫' |
|- | |- | ||
| | | | ||
| − | :<math>\scriptstyle | + | *{{#annot:√100|439|qY9w}}We also want the root of a hundred. |
| − | |style="text-align:right;"| | + | :<math>\scriptstyle\sqrt{100}</math> |
| + | |style="text-align:right;"|<big>ועוד בקשנו</big> שורש וגדר מאה{{#annotend:qY9w}} | ||
|- | |- | ||
| | | | ||
| − | + | :We write it in the following diagram: | |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|הנה נכתבה על זאת הצורה |
|- | |- | ||
| | | | ||
| − | : | + | :{|class="wikitable" style="color:blue; text-align:center;" |
| − | |||
|- | |- | ||
| | | | ||
| − | + | {|style="margin-left: auto; margin-right: 0px;" | |
| − | |style=" | ||
|- | |- | ||
| − | | | + | |0|| || |
| − | |||
| − | | | ||
|- | |- | ||
| − | | | + | |1||0||0 |
| − | | | ||
|- | |- | ||
| − | | | + | | ||1||0 |
| − | + | |} | |
| − | |||
|- | |- | ||
| + | |} | ||
| | | | ||
| − | + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | |
| − | |||
|- | |- | ||
| | | | ||
| − | + | {|style="margin-left: auto; margin-right: 0px;" | |
| − | |style=" | + | |- |
| + | |0|| || | ||
|- | |- | ||
| − | | | + | |א||0||0 |
| − | |||
| − | | | ||
|- | |- | ||
| − | | | + | | ||א||0 |
| − | + | |} | |
| − | |||
|- | |- | ||
| − | | | + | |} |
| − | |||
|- | |- | ||
| − | | | + | | colspan="2"| |
| − | + | ::<span style=color:green>[Illustration of the procedure:]</span> | |
| − | + | ::{| | |
|- | |- | ||
| − | | | + | | ||rowspan="3"|<math>\scriptstyle\xrightarrow{\scriptstyle{\color{red}{1-{\color{blue}{1}}^2=}}{\color{green}{0}}}</math>||<span style=color:LimeGreen>0</span>   |
| − | |||
| − | |style= | ||
|- | |- | ||
| − | | | + | |<span style=color:red>1</span>00||100 |
| − | : | ||
| − | | | ||
|- | |- | ||
| − | | | + | | || <span style=color:#0000FF>1</span>  |
| − | :<math>\scriptstyle{\color{ | + | |}<br> |
| − | + | ::<math>\scriptstyle\longrightarrow{\color{Violet}{\scriptstyle10\ the\ root}}</math> | |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | ::The third rank has a root, so we start with it. |
| + | |style="text-align:right;"|והנה המדרגה השלישית יש לה גדר ועל כן נתחיל ממנה | ||
|- | |- | ||
| | | | ||
| − | : | + | ::The root of 1 is one. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|כי גדר הא' הוא אחד |
|- | |- | ||
| | | | ||
| − | : | + | ::So, we write a zero above the 1, because it is gone when we subtract from it the product of the root by itself. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ולכן נכתוב סיפרא על הא' באשר תכלה כשנסיר ממנה הכאת הגדר על עצמו |
|- | |- | ||
| | | | ||
| − | :: | + | ::Since it is the root, we write 1 beneath the second zero. It indicates a ten there and this is the required root of the number. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וכנגד שהוא הגדר נכתוב א' תחת הסיפרא השנית ותהיה שוה שם עשר והוא גדר המספר המבוקש |
|- | |- | ||
| | | | ||
| − | : | + | *{{#annot:√400|439|2Rcj}}We wish to know the root of four hundred. |
| − | |style="text-align:right;"| | + | :<math>\scriptstyle\sqrt{400}</math> |
| + | |style="text-align:right;"|וכן רצינו לדעת שרש ארבע מאות{{#annotend:2Rcj}} | ||
|- | |- | ||
| | | | ||
| − | : | + | :We write it in the following diagram: |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ונכתבם על זאת הצורה |
|- | |- | ||
| | | | ||
| − | + | :{|class="wikitable" style="color:blue; text-align:center;" | |
| − | |style="text-align: | ||
|- | |- | ||
| | | | ||
| − | + | {|style="margin-left: auto; margin-right: 0px;" | |
| − | |style=" | ||
|- | |- | ||
| − | | | + | |0|| || |
| − | |||
| − | | | ||
|- | |- | ||
| − | | | + | |4||0||0 |
| − | |||
| − | | | ||
|- | |- | ||
| − | | | + | | ||2||0 |
| − | | | + | |} |
|- | |- | ||
| + | |} | ||
| | | | ||
| − | + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | |
| − | |||
|- | |- | ||
| | | | ||
| − | + | {|style="margin-left: auto; margin-right: 0px;" | |
| − | |style=" | ||
|- | |- | ||
| − | | | + | |0|| || |
| − | + | |- | |
| − | | | + | |ד||0||0 |
| + | |- | ||
| + | | ||ב||0 | ||
| + | |} | ||
| + | |- | ||
| + | |} | ||
|- | |- | ||
| − | | | + | | colspan="2"| |
| − | : | + | ::<span style=color:green>[Illustration of the procedure:]</span> |
| − | + | ::{| | |
|- | |- | ||
| − | | | + | | ||rowspan="3"|<math>\scriptstyle\xrightarrow{\scriptstyle{\color{red}{4-{\color{blue}{2}}^2=}}{\color{green}{0}}}</math>||<span style=color:LimeGreen>0</span>   |
| − | |||
| − | |style= | ||
|- | |- | ||
| − | | | + | |<span style=color:red>4</span>00||400 |
| − | |||
| − | | | ||
|- | |- | ||
| − | | | + | | || <span style=color:#0000FF>2</span>  |
| − | |style= | + | |} |
| + | ::<math>\scriptstyle\longrightarrow{\color{Violet}{\scriptstyle20\ the\ root}}</math> | ||
|- | |- | ||
| | | | ||
| − | : | + | ::It is known that the root of 4 is two. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וידוע כי גדר הד' שהוא שנים |
|- | |- | ||
| | | | ||
| − | :: | + | ::Therefore, we write a zero above the 4, because it is all gone, when you subtract from it the product of the root by itself. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ולכן ‫<ref>80v</ref>ולכן נכתוב סיפרא [על הד']‫<ref>Vatican om.</ref> באשר תכלה כלה כשתסיר ממנה הכאת הגדר על עצמו |
|- | |- | ||
| | | | ||
| − | : | + | ::For the two, which is the root, we write 2 beneath the second zero. It indicates twenty there, and this is the root of the number. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וכנגד השנים שהם הגדר נכתוב ניכתוב ב' תחת הסיפרא השנית ותהיה שוה שם עשרים והוא גדר המספר |
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{\ | + | *{{#annot:√4000|439|ZH6A}}If we wish to know the approximate root of four thousand. |
| − | |style= | + | :<math>\scriptstyle\sqrt{4000}</math> |
| + | |style="text-align:right;"|<big>ואם רצינו</big> לדעת הגדר הקרוב אל ארבעת אלפים{{#annotend:ZH6A}} | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | ::<span style=color:green>[Illustration of the procedure:]</span> | ||
| + | ::{| | ||
| + | |- | ||
| + | | ||rowspan="6"|<math>\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{40>6^2}}\\&\scriptstyle{\color{red}{40-{\color{blue}{6}}^2=}}{\color{green}{4}}\\&\scriptstyle{\color{red}{2\times6=}}{\color{blue}{12}}\\\end{align}}</math>|| ||rowspan="6"|<math>\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{4-\left(3\times{\color{blue}{1}}\right)=}}{\color{green}{1}}\\&\scriptstyle{\color{red}{10-\left(3\times{\color{blue}{2}}\right)=}}{\color{green}{4}}\\&\scriptstyle{\color{red}{4-1=}}{\color{green}{3}}\\&\scriptstyle{\color{red}{10-{\color{blue}{3}}^2=}}{\color{green}{1}}\\\end{align}}</math>|| <span style=color:LimeGreen>0</span>  ||rowspan="6"|<math>\scriptstyle\xrightarrow{\scriptstyle{\color{red}{\frac{1}{2}\sdot12=}}{\color{blue}{6}}}</math>|| 0   | ||
|- | |- | ||
| − | | | + | | || || <span style=color:LimeGreen>13</span> || 13  |
| − | : | ||
| − | | | ||
|- | |- | ||
| − | | | + | | ||<span style=color:LimeGreen>04</span>  ||04<span style=color:LimeGreen>41</span>||0441 |
| − | |||
| − | |style= | ||
|- | |- | ||
| − | | | + | |<span style=color:red>40</span>00||4000||4000||4000 |
| − | |||
|- | |- | ||
| − | | | + | | || <span style=color:#0000FF><s>6</s>2</span> || <s>6</s>2<span style=color:#0000FF>3</span>||  <span style=color:#0000FF>6</span>3 |
| − | |style= | ||
|- | |- | ||
| − | | | + | | || <span style=color:#0000FF>1</span>  || 1  || |
| − | |style= | ||
|} | |} | ||
| − | { | + | ::<math>\scriptstyle\longrightarrow{\color{Violet}{\begin{align}&\scriptstyle63\ the\ root\\&\scriptstyle31\ the\ remainder\\\end{align}}}</math> |
|- | |- | ||
| | | | ||
| − | + | ::We do this way: | |
| − | + | |style="text-align:right;"|נעשה על דרך זה | |
| − | |||
| − | |style="text-align:right;"| | ||
|- | |- | ||
| − | |||
| | | | ||
| + | ::The fourth rank has no root, so we write 4 above the zero that precedes it; it becomes forty. | ||
| + | |style="text-align:right;"|הנה המדרגה הרביעית היא בלתי נגדרת לפיכך נשים הד' על הסיפרא הקדומה לה ותהיה ארבעים | ||
|- | |- | ||
| | | | ||
| − | + | ::The closest [root] is six, because its product by itself is thirty-six. | |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והמרובע הקרוב אליהם הוא ששה כי כפילת הכאתו על עצמו תהיה לו שלשים וששה |
|- | |- | ||
| | | | ||
| − | : | + | ::4 remains above the third zero. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והנה ישארו ד' על הסיפרא השלישית |
|- | |- | ||
| − | | | + | | |
| − | |style="text-align:right;"| | + | ::We write a zero above the 4 that was in the fourth rank, when it was shifted from its place. |
| + | |style="text-align:right;"|ונכתוב סיפרא על הד' שהיתה במדרגה הרביעית כאשר נעתקה ממקומה | ||
|- | |- | ||
| | | | ||
| − | : | + | ::For the six, which is the closest root, we write 6 beneath the third zero. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וכנגד ששה שהם הגדר היותר קרוב נכתוב ו' תחת <sup>ה</sup>סיפרא השלישית |
|- | |- | ||
| − | | | + | | |
| − | |style="text-align:right;"| | + | ::Then, we multiply 6 twice and cross it out with a pen; it becomes twelve. |
| − | + | |style="text-align:right;"|אחרי זאת נכפול הו' פעמים ונעביר עליה קולמוס והנה יהיה ההוא שנים עשר | |
| − | |||
|- | |- | ||
| | | | ||
| − | + | ::We write 2 beneath the second zero for the two and 1 for the ten beneath the 6 [that was erased] with a pen. | |
| − | + | |style="text-align:right;"|נכתוב ב' כנגד השנים תחת הסיפרא השניה וא' כנגד העשר תחת הו' אשר הקולמוס עליה | |
| − | |||
| − | |style="text-align:right;"| | ||
|- | |- | ||
| − | |||
| | | | ||
| + | ::When we examine how many times we can subtract these 2 and 1 from what remains ubove the line, we find that three times are enough for us. | ||
| + | |style="text-align:right;"|וכאשר נעיין כמה פעמים נוכל להסיר הב' והא' ההמה מהנשאר למעלה ‫<ref>81r</ref>מן הטור נמצא שיספיק בשלשה פעמים | ||
|- | |- | ||
| | | | ||
| − | + | ::We do this way: | |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ונעשה בדרך הזה |
|- | |- | ||
| | | | ||
| − | : | + | ::We subtract the 1 beneath the third zero three times from the 4 remaining above it; 1 remains instead of it. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|<s>נקח הא' הנותרת במדרגה השלישית</s> נסיר הא' שתחת הסיפרא השלישית שלשה פעמים מהד' הנשארת על ראשה וישאר במקומה הא‫' |
| − | |||
| − | |||
| − | |||
|- | |- | ||
| − | | | + | | |
| − | |style="text-align:right;"| | + | ::We also have to subtract [three] times the 2, the product of which is six. |
| + | |style="text-align:right;"|וכן יש לנו להסיר הב' [שלשה]‫<ref>marg.</ref> פעמים שעולה כפילתם ששה | ||
|- | |- | ||
| | | | ||
| − | : | + | ::We do it this way: |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ונעשה בדרך [הזה‫]‫<ref>Vatican om.</ref> |
|- | |- | ||
| | | | ||
| − | : | + | ::We take the 1 remaining in the third rank and shift it above the second zero; it becomes ten. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|נקח הא' הנותרת במדרגה השלישית ונשים אותה על הסיפרא השנית ותהיה שוה עשר |
|- | |- | ||
| | | | ||
| − | : | + | ::We subtract the six from it; four remains there. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|נסיר מהם הששה ישארו שם ארבעה |
| − | | | + | |- |
| − | + | | | |
| + | ::We write zero above the 1 that is above the third rank, because it was shifted from its place. | ||
| + | |style="text-align:right;"|ונכתוב סיפרא על הא' שהיתה על המדרגה השלישית כי נעתקה ממקומה | ||
|- | |- | ||
| | | | ||
| − | + | ::For the three times of subtraction we write 3 beneath the zero that is in the first rank. | |
| − | + | |style="text-align:right;"|וכנגד שלשה פעמי ההסרה נכתוב תחת הסיפרא שבמדרגה הראשונה ג‫' | |
| − | |||
| − | |style="text-align:right;"| | ||
|- | |- | ||
| − | |||
| | | | ||
| + | ::When we multiply it by itself, it is nine. | ||
| + | |style="text-align:right;"|וכאשר נכפול ונכה אותה על עצמה יהיה ההוא תשעה | ||
|- | |- | ||
| | | | ||
| − | + | ::We subtract it from the upper line this way: | |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|נסיר אותם מהטור העליון בדרך זה |
|- | |- | ||
| | | | ||
| − | : | + | ::We take 1 from the 4 remaining in the second rank; 3 remains above it. |
| − | |style="text-align:right;"|נקח | + | |style="text-align:right;"|נקח א' מן הד' הנותרים במדרגה השנית וישארו עליה ג‫' |
|- | |- | ||
| | | | ||
| − | : | + | ::We shift the 1 to the zero that precedes its rank; it becomes ten. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ונשים הא' על הסיפרא הקדומה למדרגתה ותהיה שוה עשר |
|- | |- | ||
| | | | ||
| − | : | + | ::We subtract nine from it; 1 remains above that zero. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|נסיר מהם תשעה ישאר על הסיפרא ההיא א‫' |
|- | |- | ||
| | | | ||
| − | : | + | ::The bottom line that is generated is 123. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והטור אשר נתחדש הוא ג'ב'א‫' |
|- | |- | ||
| − | |||
| | | | ||
| + | ::A half of 12 is 6. | ||
| + | |style="text-align:right;"|וחצי ב'א' והוא ו‫' | ||
|- | |- | ||
| | | | ||
| − | : | + | ::We find that the required approximate root [is 63] |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ונמצא שתהיה הגדר הקרוב ‫<ref>81v</ref>המבוקש גדרו |
| + | |- | ||
| + | |The methods of calculating all these many numbers, which I have mentioned and extended the explanation for each of them [how] to extract its root or its approximate [root], are sufficient for you to apply their procedure to other cases you see, if you are wise. | ||
| + | |style="text-align:right;"|ובדרכי כל אלו החשבונות הרבים שהזכרתי והארכתי הביאור בכל אחד מהם למצוא גדרו או הקרוב אליו יספיק לך לעשות באחרים זולתם כתבניתם אשר אתה מראה אם נבון ואם חכם אתה | ||
|- | |- | ||
| − | |||
| − | |||
| − | |||
|} | |} | ||
{| | {| | ||
| Line 3,562: | Line 3,870: | ||
| | | | ||
| − | == | + | == Chapter Eight – the Ratio of a Number to Another Number == |
| − | |style="text-align:right;"| | + | |style="width:45%; text-align:right;"|<big>השער השמיני</big> במערכת חשבון אחד מחשבון אחר |
| + | |- | ||
| + | |The meaning of relation is to explain, when we have two known numbers or more, how we can find another number, whose ratio to one of them is the same as the ratio of this [given] number to the other [given number]. | ||
| + | |style="text-align:right;"|כוונת ההערכה הזאת היא לבאר כשיהיו לנו שני חשבונות ידועים או יותר באיזה דרך נוכל לחדש חשבון אחר שיהיה ערכו אל אחד מהם כערך האחד אל חברו | ||
| + | |- | ||
| + | |Know that the skill of this chapter is divided into four categories: | ||
| + | |style="text-align:right;"|ותדע כי מלאכת השער הזה היא נחלקת לארבעה חלקים | ||
|- | |- | ||
| − | |||
| | | | ||
| + | :<span style=color:green>'''Proportional Triad:'''</span> The first category is when we have two [known] numbers and we want to find a third number, whose ratio to one of them is the same as the ratio of one of them to the other. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a_1:a_2=a_2:a_3}}</math> | ||
| + | |style="text-align:right;"|<big>החלק האחד</big> הוא על דרך זה כשיהיו לנו שני חשבונות ונרצו לחדש ולמצוא חשבון שלישי שיהיה ערכו כל [אחד]‫<ref>Vatican om.</ref> מהם כערך כל האחד [מהם]‫<ref>marg.</ref> אל חברו | ||
|- | |- | ||
| | | | ||
| − | + | :<math>\scriptstyle{\color{OliveGreen}{a_3=\frac{\left(a_2\right)^2}{a_1}}}</math> | |
| − | | | + | | |
|- | |- | ||
| | | | ||
| − | :*<math>\ | + | :*The example: when we know the numbers four and six. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle4:6=6:x</math> |
| + | |style="text-align:right;"|המשל בזה כגון שתדע חשבון ארבעה וששה | ||
|- | |- | ||
| | | | ||
| − | : | + | ::It is known that when we relate six to four, it is the same and its half. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{6:4=\left[\left(1+\frac{1}{2}\right)\sdot4\right]:4}}</math> |
| + | |style="text-align:right;"|ובידוע כי כשנערוך חשבון ששה על חשבון ארבעה יהיה כמוהו ומחציתו | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{ | + | ::If we want to find a third number, whose ratio to six is the same as the ratio of six to four, we do it this way: |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{x:6=6:4}}</math> |
| + | |style="text-align:right;"|ואם נרצה לחדש חשבון שלישי שיהיה ערכו אל ששה ‫<ref>82r</ref>כערך ששה אל ארבעה נעשה על הדרך הזה | ||
|- | |- | ||
| | | | ||
| − | : | + | ::We take the number six, which is mean between the first known number and the third unknown number. We multiply it by itself; the product is thirty-six. We divide it by the first known number, which is four. We find it nine times in it. So, the ratio of nine to six is the same as the ratio of six to four. |
| − | |style="text-align:right;"|נחלק אותם על | + | ::<math>\scriptstyle{\color{blue}{x=\frac{6^2}{4}=\frac{36}{4}=9}}</math> |
| + | |style="text-align:right;"|נקח חשבון הששה שהוא אמצעי בין החשבון הראשון הידוע ובין השלישי הנעלם ונכפול ונכה אותו על עצמו ויהיה העולה ששה ושלשים נחלק אותם על חשבון הראשון הנודע שהוא ארבעה ומצאנו בהם תשע פעמים והנה תשעה ערכם אל ששה כערך ששה אל ארבעה | ||
|- | |- | ||
| | | | ||
| − | :<math>\scriptstyle{\color{ | + | :If we know the mean number and the last number, but we do not know the first number, we also multiply the mean by itself, then divide by the last known number and the result of division is the first number. |
| − | |style="text-align:right;"| | + | :<math>\scriptstyle{\color{OliveGreen}{a_1=\frac{\left(a_2\right)^2}{a_3}}}</math> |
| + | |style="text-align:right;"|ואם ידענו החשבון האמצעי והאחרון ונעלם ממנו החשבון הראשון נכפול גם כן האמצעי על עצמו ונחלקנו על החשבון האחרון הנודע והיוצא בחלוק הוא החשבון הראשון | ||
|- | |- | ||
| − | |||
| | | | ||
| + | ::According to this, when you know the numbers six and nine, but we do not know the [number] four: | ||
| + | ::<math>\scriptstyle x:6=6:9</math> | ||
| + | |style="text-align:right;"|ולפי זה כשתדע חשבון הששה והתשעה ולא נדע הארבעה | ||
|- | |- | ||
| | | | ||
| − | : | + | ::We multiply six by itself; the result is thirty-six. We divide it by nine that is known; we find it four times [in it]. So, four is the required [number]. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{x=\frac{6^2}{9}=\frac{36}{9}=4}}</math> |
| + | |style="text-align:right;"|נכפול הששה על עצמם יעלו ששה ושלשים נחלקם על התשעה הנודעים ונמצאנו ארבעה פעמים והנה הארבעה הוא המבוקש | ||
|- | |- | ||
| | | | ||
| − | : | + | :If we know the first and the third numbers, but we do not know the mean number, we multiply the two known numbers by each other, then we extract the root of the product and the required mean number is the root. |
| − | |style="text-align:right;"| | + | :<math>\scriptstyle{\color{OliveGreen}{a_2=\sqrt{a_1\sdot a_2}}}</math> |
| + | |style="text-align:right;"|ואם ידענו החשבון הראשון והשלישי ונעלם ממנו החשבון האמצעי נכפול ונכה השני חשבונות הנודעים זה על זה ונקח גדר העולה וכמספר הגדר הוא החשבון האמצעי המבוקש | ||
|- | |- | ||
| | | | ||
| − | : | + | ::According to this, when you know the numbers four and nine, but we do not know the mean [number]: |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle4:x=x:9</math> |
| + | |style="text-align:right;"|ועל זה הדרך תדע חשבון ‫<ref>82v</ref>הארבעה והתשעה ונעלם ממנו האמצעי | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{\ | + | ::We multiply four by nine; the result is thirty-six; its root is six and this is the required mean number. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{x=\sqrt{4\sdot9}=\sqrt{36}=6}}</math> |
| + | |style="text-align:right;"|נכפול ארבעה על תשעה ויעלו שלשים ושש וגדרם ששה והוא החשבון האמצעי המבוקש | ||
|- | |- | ||
| | | | ||
| − | : | + | :<span style=color:green>'''Rule of Three:'''</span> The second category is when we have three known numbers and we want to find a fourth number, whose ratio to the third is the same as the ratio of the first to the second. |
| − | |style="text-align:right;"| | + | :<math>\scriptstyle{\color{OliveGreen}{a_1:a_2=a_3:a_4}}</math> |
| + | |style="text-align:right;"|<big>החלק השני</big> כשיהיו לנו [שלשה]‫<ref>marg.</ref> חשבונות נודעים ונרצה לחדש חשבון רביעי שיהיה ערכו אל השלישי כערך הראשון אל <s>השלישי</s> השני | ||
|- | |- | ||
| | | | ||
| − | + | :<math>\scriptstyle{\color{OliveGreen}{a_4=\frac{a_2\sdot a_3}{a_1}}}</math> | |
| − | | | + | | |
|- | |- | ||
| | | | ||
| − | :<math>\ | + | :*As when we know the three numbers - six, ten and three - and I want to find a fourth number, whose ratio to three is the same as the ratio of ten to six. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle6:10=3:x</math> |
| + | |style="text-align:right;"|כגון שנדע החשבונות האלה השלשה ששה ועשרה ושלשה ואבקש למצוא חשבון רביעי שיהיה ערכו אל השלשה כערך העשרה אל הששה | ||
|- | |- | ||
| − | | | + | | |
| − | |style="text-align:right;"|והנה | + | ::We do as follows: we multiply ten and three by each other - both are called means, because they are between the first known number and the fourth unknown [number] - the result is thirty. We divide it by the first known number, which is six; we find it five times in it, so five is the required number, because the ratio of six to ten is the same as the ratio of three to five. |
| − | + | ::<math>\scriptstyle{\color{blue}{x=\frac{10\sdot3}{6}=\frac{30}{6}=5}}</math> | |
| − | + | |style="text-align:right;"|ונעשה ככה נכפול חשבון העשרה וחשבון השלשה זה על זה ושניהם נקראים אמצעיים לפי שהם נתונים בין החשבון <s>האמצעי</s> [הראשון]‫<ref>marg.</ref> הנודע ובין הרביעי הנעלם והנה הוא השלשים נחלקנו על החשבון הראשון הנודע שהוא ששה ונמצאו בו חמש פעמים והנה חמשה הוא החשבון המבוקש כי כערך ששה אל עשרה כן ערך שלשה אל חמשה | |
|- | |- | ||
| | | | ||
| − | + | :Likewise, if we know the two mean numbers and the fourth number, but the first number is unknown to us: we multiply the means by each other, then divide the product by the fourth known number; the result of division is the required. | |
| − | + | :<math>\scriptstyle{\color{OliveGreen}{a_1=\frac{a_2\sdot a_3}{a_4}}}</math> | |
| − | + | |style="text-align:right;"|וכן אם נדע השני חשבונות האמצעיים והחשבון הרביעי הנעלם ממנו החשבון הראשון נכפול האמצעיים זה על זה ונחלק ההווה על ‫<ref>83r</ref>החשבון הרביעי הנודע והיוצא בחלוק הוא המבוקש | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| − | |||
| | | | ||
| + | :If one of the two means is unknown to us: we multiply the first and the fourth numbers by each other, then divide the product by the known mean; the result of division is the unknown required number. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a_2=\frac{a_1\sdot a_4}{a_3}}}</math> | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a_3=\frac{a_1\sdot a_4}{a_2}}}</math> | ||
| + | |style="text-align:right;"|ואם יעלם ממנו אחד מהשנים האמצעיים נכפול החשבון הראשון והרביעי אלו על אלו ונחלק ההווה על האמצעי הנודע והיוצא בחלוק הוא החשבון המבוקש הנעלם | ||
|- | |- | ||
| | | | ||
| − | + | :<span style=color:green>'''Arithmetic proportion'''</span> The third category is when we want to write many numbers, such that the increment [between each two consecutive numbers] is the same. | |
| − | |style="text-align:right;"| | + | :<math>\scriptstyle{\color{OliveGreen}{a_2-a_1=a_3-a_2}}</math> |
| + | |style="text-align:right;"|<big>החלק השלישי</big> כשנרצה לכתוב ולחקוק חשבונות רבים מרחק האחד שוה <s>ו</s>למרחק חברו | ||
|- | |- | ||
| | | | ||
| − | :* | + | :*As 1; 2; 3; 4. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|כגון א'ב'ג'ד'ה'ו‫' |
|- | |- | ||
| | | | ||
| − | :*< | + | :*Or 2; 4; 6 etc. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|‫[או]‫<ref>Vatican om.</ref> ב'ד'ו' וכיוצא באלו |
| + | |- | ||
| + | |This category is clear and explained, thus, there is no need to elaborate on that. | ||
| + | |style="text-align:right;"|והחלק הזה דרכו גלוי ומבואר ואין צריך עוד להאריך בו | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{ | + | :<span style=color:green>'''Harmonic proportion'''</span> The fourth category: |
| − | |style="text-align:right;"| | + | :<math>\scriptstyle{\color{OliveGreen}{a_1:a_3=\left(a_2-a_1\right):\left(a_3-a_2\right)}}</math> |
| + | |style="text-align:right;"|<big>החלק הרביעי</big> | ||
|- | |- | ||
| | | | ||
| − | :*<math>\scriptstyle{\color{blue}{3\ | + | :*As these three digits, which are 3, 4, 6: the ratio of 3 to 6 is as the ratio of the interval from three to four to the interval from four to six - the interval from 3 to 4 is one and the interval from 4 to 6 is two; the ratio of 3 to 6 is as the ratio of one to two. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{3;\ 4;\ 6\longrightarrow3:6=1:2=\left(4-3\right):\left(6-4\right)}}</math> |
| + | |style="text-align:right;"|על אופן שלש אותיות אלו שהן ג'ד'ו' שערך ג' אל ו' כערך המרחק שמשלשה ועד ארבעה אל המרחק שמארבעה ועד ששה שהנה מרחק ג' מד' אחד ומרחק ד' מו' שנים וכערך האחד אל השנים כן ערך השלשה אל הששה | ||
|- | |- | ||
| | | | ||
| − | :<math>\scriptstyle{\color{ | + | :When we know the first and the last numbers, but we do not know the second number, we multiply one by the other, then divide the product by the sum of the two; we double the quotient and the result is the required. |
| − | |style="text-align:right;"| | + | :<math>\scriptstyle{\color{OliveGreen}{a_2=2\sdot\frac{a_1\sdot a_3}{a_1+a_3}}}</math> |
| + | |style="text-align:right;"|וכאשר נדע האות הראשונה והאחרונה ונעלמת ממנו האות השנית נכפול האחת אל חברתה ונחלק העולה על המחובר משתיהן והיוצא בחלוק נכפלנו והיוצא הוא המבוקש | ||
|- | |- | ||
| − | |||
| | | | ||
| + | ::According to this method, when we know the 3 and the 6 and we wish to know the mean, we multiply 3 by 6; it is eighteen. We divide it by the sum of the two, which is 9; we find it twice in it. We double it; it is four and so the mean should be 4. | ||
| + | ::<math>\scriptstyle{\color{blue}{2\sdot\frac{3\sdot6}{3+6}=2\sdot\frac{18}{9}=2\sdot2=4}}</math> | ||
| + | |style="text-align:right;"|ועל הדרך הזאת כשנדע הג' [והו']‫<ref>marg.</ref> ונרצה ‫<ref>83v</ref>לדעת האות האמצעית נכפול ג' על ו' יהיו שמנה עשר נחלקם על המחובר משניהם שהוא ט' נמצאנו שם שני פעמים נכפלם יהיו ארבעה וככה הוא משפט האמצעי להיות ד‫' | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | :If we know the first and the mean numbers, but we do not know the last, we multiply the first by the second, which is mean between the first that is known and the last that is unknown. We divide the product by the first number that is known, then we subtract from is the product of the difference between the first and the mean by itself; the result of division is the required. |
| + | :<math>\scriptstyle{\color{OliveGreen}{a_3=\frac{a_1\sdot a_2}{a_1-\left(a_2-a_1\right)}}}</math> | ||
| + | |style="text-align:right;"|ואם נדע האות הראשונה והאמצעית ולא נדע האחרונה נכפול הראשונה על השנייה שהיא אמצעית בין הראשונה הידועה ובין האחרונה הנעלמת והעולה נחלקנו על האות הראשונה הידועה אחר אשר נסיר ממנה [העולה מהכאת]‫<ref>Vatican om.</ref> המרחק שבין [הראשונה]‫<ref>Vatican om.</ref> [לאמצעית]‫<ref>Vatican: האמצעית</ref> [על עצמו]‫<ref>Vatican om.</ref> והיוצא מהחלוק הוא המבוקש | ||
|- | |- | ||
| | | | ||
| − | : | + | ::According to this, when we know the 3 and the 4, but we do not know the 6, we multiply the 3 by the 4; it is twelve. We divide it by the 3, after we subtract from it the product of the difference between it and the 4 by itself, which is one. We subtract it from the 3; 2 remains from it. We find this 2 six times in twelve; so the last third number is 6. |
| − | |style="text-align:right;"|ונמצא | + | ::<math>\scriptstyle{\color{blue}{\frac{3\sdot4}{3-\left(4-3\right)}=\frac{12}{3-1}=\frac{12}{2}=6}}</math> |
| + | |style="text-align:right;"|ולפי זה כשנודע הג' והד' ונעלמת ממנו הו' ונכפל ג' על ד' יהיו שנים עשר נחלקם על הג' אחר אשר נסיר ממנה [הכאת]‫<ref>Vatican om.</ref> המרחק שבינה ובין הד' [על עצמו]‫<ref>Vatican om.</ref> והנה הוא אחד נסיר אותו מהג' [ישאר]‫<ref>Vatican om.</ref> ממנה ב' ונמצא הב' הזאת ו' פעמים בשנים עשר וככה היא האות השלישית האחרונה ו‫' | ||
|- | |- | ||
| | | | ||
| − | : | + | :<math>\scriptstyle{\color{OliveGreen}{a_1=\frac{a_2\sdot a_3}{a_3+\left(a_3-a_2\right)}}}</math> |
| − | |||
| − | |||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{ | + | ::If we know the 4 and the 6, but we do not know the 3, we do this way: we multiply 4 by 6; it is twenty-four. We divide it by the sum of the third number with the difference between it and the 4, which is two. When we add it to the six, they are eight. When we divide twenty-four by it, we receive 3 times and so the first number should be 3. |
| − | |style="text-align:right;"|נכפול | + | ::<math>\scriptstyle{\color{blue}{\frac{4\sdot6}{6+\left(6-4\right)}=\frac{24}{6+2}=\frac{24}{8}=3}}</math> |
| + | |style="text-align:right;"|ואם ידענו הד' והו' ולא נדע הג' נעשה בדרך זאת נכפול הד' על הו' ויהיו ארבעה ועשרים נחלקם עם המחובר מהאות השלישית עם המרחק שבין הד' ובינה שהוא שנים וכש{{#annot:term|178,1165|m6K8}}נחברם{{#annotend:m6K8}} אל הששה יהיו שמנה וכשנחלק הארבע ועשרים עליהם ‫<ref>84r</ref>יצא לנו ה{{#annot:term|157,1223|hOsK}}חלוק{{#annotend:hOsK}} ג' פעמים וכן הוא משפט האות הראשונה להיות ג‫' | ||
|- | |- | ||
| − | | | + | |From these four categories [of proportions] explained you can understand and extract the proportions of all numbers you find, as the issue of each category is explained at length. |
| − | + | |style="text-align:right;"|ובאלו החלקים הארבעה המבוארים תוכל להבין ולהוציא כל ערכי החשבונות שתמצא כאשר התבאר בארוכה ענין כל חלק וחלק | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| − | |||
| − | |||
| − | |||
|} | |} | ||
{| | {| | ||
| Line 3,696: | Line 4,032: | ||
| | | | ||
| − | == | + | == Chapter Nine – On Knowing the Fractions of Integer, whether in Multiplication, in Division, in Addition, or in Subtraction == |
| − | |style="text-align:right;"| | + | |style="width:45%; text-align:right;"|<big>השער התשיעי</big> בידיעת חלקי ה{{#annot:term|15,1242|Rn7j}}שבר{{#annotend:Rn7j}} מן ה{{#annot:term|20,1268|c745}}שלם{{#annotend:c745}} בין בכפל בין בחלוק או ב{{#annot:term|154,1208|W34i}}חבור{{#annotend:W34i}} או במגרעת |
|- | |- | ||
| | | | ||
| − | ==== | + | === <span style=color:green>Introduction</span> === |
| − | |||
| − | |||
| − | |||
| | | | ||
|- | |- | ||
| − | | | + | |Know that the product of fractions by themselves or by other fractions is less than their sum. |
| − | + | :<math>\scriptstyle{\color{OliveGreen}{\frac{a}{b}\times\frac{c}{d}<\frac{a}{b}+\frac{c}{d}}}</math> | |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|תדע באמת כי כפילת הכאת השברים על עצמם או על שברים אחרים זולתם פחותה ממחברתם |
|- | |- | ||
| | | | ||
| − | : | + | ::For, when we say: multiply a quarter by a quarter, it is as if we say: take a quarter of the quarter, which is one part of sixteen of the whole. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|כי כאשר נאמר כפול והכה רביע על רביע הרי זה כאלו נאמר קח רביע הרביע שהוא חלק מששה עשר חלקים בשלם |
|- | |- | ||
| | | | ||
| − | : | + | ::And, if we say: add a quarter to a quarter, the sum is one half of a whole. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{\frac{1}{4}\times\frac{1}{4}=\frac{1}{16}<\frac{1}{2}=\frac{1}{4}+\frac{1}{4}}}</math> |
| + | |style="text-align:right;"|ואם נאמר חבר רביעית עם רביעית יהיה המחובר חצי שלם אחד | ||
|- | |- | ||
| − | | | + | |This rule of fractions is opposite to the rule of integers, since [the integers] increase when they are multiplied by themselves, or by others, more than they are increased by their summing. |
| − | : | + | :<math>\scriptstyle{\color{OliveGreen}{n+m<n\times m}}</math> |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ומנהג השברים הזה הפך מנהג השלמים כי הם יתרבו כאשר יו[כ]ו ויוכפלו על עצמם או על זולתם יותר משלא תרבה אותן מ[ח]ברתן |
| + | |- | ||
| + | |On the other hand, this [rule of fractions] is somewhat similar to the rule of the unit, that if we multiply it by itself the result is only one, while its sum with itself is two. | ||
| + | :<math>\scriptstyle{\color{blue}{1\times1<1+1}}</math> | ||
| + | |style="text-align:right;"|ואולם הם דומים למנהג <sup>מעשה</sup> האחד השלם במקצת שאם נכפלנו ונכנו בעצמו לא יעלה כי אם אחד ומחברתו עם עצמו תהיה שנים | ||
|- | |- | ||
| − | | | + | |Therefore, the number two is mean between all the other [integers] and [one and the fractions], since the sum of two with itself and its product by itself are both equal to four. |
| − | :<math>\scriptstyle{\color{blue} | + | :<math>\scriptstyle{\color{blue}{2+2=2\times2=4}}</math> |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ולזאת הושמו השנים אמצעיים בין שאר כל המספרים וביניהם ‫<ref>84v</ref>כי מחברת השנים [עם]‫<ref>Vatican om.</ref> עצמן וכפלת הכאתן בעצמן הכל עולה בשוה ארבעה ה{{#annot:term|388,1166|V2sT}}מחברת{{#annotend:V2sT}} כמו הכפילה |
|- | |- | ||
| | | | ||
| − | |||
| − | + | === <span style=color:green>Operations with fractions</span> === | |
| − | |||
| − | |||
| | | | ||
|- | |- | ||
| − | | | + | |In order that the practice in this chapter will be clear and known for all by elaborate explanation, I write various calculations of operations with fractions, from which the procedure in other cases can be known and learned. |
| − | + | |style="text-align:right;"|ובעבור אשר תהיה מלאכת השער הזה גלויה ומפורסמת לכל בביאור רחב אכתו<sup>ב</sup> מדרכי השברים חשבונות רבים עד שיודע וילמד [מהם לעשות]‫<ref>Vatican om.</ref> ככה באחרים זולתם | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | ==== <span style=color:green>Multiplication of fractions</span> ==== | |
| − | + | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | : | + | ===== <span style=color:green>Introduction</span> ===== |
| − | |||
| − | |||
| | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| − | | | + | |I shall start with their multiplication method, after I write a short introduction that needs to be clarified for the purpose of this craft. |
| − | + | |style="text-align:right;"|והנני מתחיל בדרך כפילת הכאתן אחר כי אכתוב מעט הקדמה שאני צריך לבאר אותה לצורך המלאכה הזאת | |
| − | |||
| − | | | ||
|- | |- | ||
| − | | | + | |I say here that the proper method for dealing with fractions is to find their common denominator, I mean to take an integer that has whole parts that are the same as the denominators that are needed. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ואומר בזה כי הדרך הישר בשברים לקחת בהם {{#annot:term|1163,1682|wryg}}מדומה{{#annotend:wryg}} רצוני לומר שיקח חשבון שלמים שימצאו בו חלקים שלמים כפי מספר השברים אשר יצטרך |
|- | |- | ||
| − | | | + | |The method of finding the common denominator: |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וככה הוא [לקיחת]‫<ref>Vatican: לחיקת</ref> המדומה |
|- | |- | ||
| − | |||
| | | | ||
| + | :When we want to find a number that has these fractions that are half, third, quarter, and one part of eleven: | ||
| + | |style="text-align:right;"|כשנרצה למצוא בו חשבון שיהיו בו {{#annot:term|15,1242|8HjB}}שברים{{#annotend:8HjB}} אלו שהם מחצית ושלישית ורביעית וחלק אחד מאחד עשר | ||
|- | |- | ||
| | | | ||
| − | + | ::Every scholar understands that the smallest of all numbers, in which we can find a half that is whole, is two, therefore we take two for the half. | |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והנה כל משכיל יבין כי החשבון הקדום שבכל החשבונות שנוכל למצוא בו חצי שתהיה שלימה הוא שנים ועל זה נקח בעבור המחצית שנים |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | ::As the half is derived from two, the third is derived from three, therefore we take three for it. |
| + | |style="text-align:right;"|וכמו שהמחצית יוצאת משנים כן תצא השלישית משלשה ולכן נקח בעבורה שלשה | ||
|- | |- | ||
| | | | ||
| − | : | + | ::When we multiply two by three, it is six; so six is the smallest number that has a half and a third of the integers. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וכשנכפול השנים בשלשה יהיו ששה והנה ששה הוא חשבון ‫<ref>85r</ref>הקרוב שיהיה בו מחצית ושלישית משלמים |
|- | |- | ||
| | | | ||
| − | : | + | ::When we multiply six by four, for the quarter that is derived from it, the result is twenty-four. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וכשנכפול הששה בארבעה בעבור הרביעית אשר תצא מהם יהיה העולה מהם עשרים וארבע |
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{ | + | :When we multiply it by eleven, for the other part that derived from it, the result is two hundred and sixty-four, and this is the common denominator that is required, for it has a half, third, quarter, and one part of eleven. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{2\sdot3\sdot4\sdot11=6\sdot4\sdot11=24\sdot11=264}}</math> |
| + | |style="text-align:right;"|וכשנ<sup>כ</sup>פול אותם באחד עשר כנגד החלק האחר שהוא מהם יהיה העולה מהם מאתים ושישים וארבעה <s>והנה</s> [והוא]‫<ref>marg.</ref> {{#annot:term|1163,1682|sJ8p}}החשבון המדומה{{#annotend:sJ8p}} המבוקש כי יש לו מחצית ושלישית ורביעית וחלק מהאחד עשר | ||
|- | |- | ||
| | | | ||
| − | : | + | :The same for all the others. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וכמוהו לכל האחרים זולתו |
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | ==== | + | ===== <span style=color:green>Multiplication of fractions by fractions</span> ===== |
| + | |||
| | | | ||
|- | |- | ||
| + | |<math>\scriptstyle{\color{OliveGreen}{\frac{a}{b}\times\frac{c}{d}=\frac{a\sdot c}{b\sdot d}}}</math><br> | ||
| + | <math>\scriptstyle{\color{OliveGreen}{\frac{a}{b}\times\frac{c}{d}=\frac{\left[\frac{a}{b}\sdot\left(b\sdot d\right)\right]\sdot\left[\frac{c}{d}\sdot\left(b\sdot d\right)\right]}{\left(b\sdot d\right)^2}}}</math> | ||
| | | | ||
| − | |||
|- | |- | ||
| − | |||
| | | | ||
| + | *{{#annot:⅘×⅘|17|yepM}}We wish to multiply four fifths by four fifths | ||
| + | :<math>\scriptstyle\frac{4}{5}\times\frac{4}{5}</math> | ||
| + | |style="text-align:right;"|<big>בקשנו</big> לכפול ארבע חמישיות בארבע חמישיות{{#annotend:yepM}} | ||
|- | |- | ||
| | | | ||
| − | + | ::It is known that the fifth is derived from five, which is the denominator, and its product by itself is twenty-five. | |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{5\sdot5=25}}</math> |
| + | |style="text-align:right;"|בידוע כי החמישית תצא מחמשה והוא המדומה והכאתו בעצמו עולה עשרים וחמשה | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | ::We multiply the number of the fifths, which is four, by itself; it is sixteen. |
| + | ::<math>\scriptstyle{\color{blue}{4\sdot4=16}}</math> | ||
| + | |style="text-align:right;"|ונכפול מספר החמישיות שהוא <s>מספר</s> <sup>ארבע</sup> <s>ב</s>על עצמו ויהיה ששה עשר | ||
|- | |- | ||
| | | | ||
| − | : | + | :The ratio of sixteen to twenty-five, which is the product of the denominator by itself, is three-fifths and a fifth of a fifth, and so is the ratio of their product to the whole. |
| − | |style="text-align:right;"| | + | :<math>\scriptstyle{\color{blue}{\frac{4}{5}\times\frac{4}{5}=\left(\frac{4}{5}\times\frac{4}{5}\right):1=16:25=\frac{3}{5}+\left(\frac{1}{5}\sdot\frac{1}{5}\right)}}</math> |
| + | |style="text-align:right;"|והנה ערך ששה עשר אל חמש ועשרים שהוא העולה מהכאת המדומה בעצמו שלש חמישיותיו וחמישית חמישית וככה הוא ערך היוצא מכפלתם אל השלם | ||
|- | |- | ||
| | | | ||
| − | : | + | *{{#annot:²/₄×¾|17|vUPh}}We wish to multiply two quarters by three quarters |
| − | |style="text-align:right;"| | + | :<math>\scriptstyle\frac{2}{4}\times\frac{3}{4}</math> |
| + | |style="text-align:right;"|<big>בקשנו</big> לכפול ולהכות שתי רביעיות על שלש רביעיות{{#annotend:vUPh}} | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{ | + | ::The denominator of the quarter is four, because it is derived from it, and its product by itself is sixteen. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{4\sdot4=16}}</math> |
| + | |style="text-align:right;"|מדומה הרביעית הנה הוא ארבעה כי ממנו תצא והכאתו על עצמו עולה ששה עשר | ||
|- | |- | ||
| | | | ||
| − | :<math>\scriptstyle{\color{blue} | + | ::When we multiply the two quarters by three, the result is six. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{2\sdot3=6}}</math> |
| + | |style="text-align:right;"|וכאשר נכפול השתי רביעיות בשלש ‫<ref>85v</ref>יהיו ששה | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | :Its ratio to the product of the denominator is a quarter and two-quarters of a quarter, and so is the ratio of their product to the whole. |
| + | :<math>\scriptstyle{\color{blue}{\frac{2}{4}\times\frac{3}{4}=\left(\frac{2}{4}\times\frac{3}{4}\right):1=6:16=\frac{1}{4}+\left(\frac{2}{4}\sdot\frac{1}{4}\right)}}</math> | ||
| + | |style="text-align:right;"|ערכם אל הכאת המדומה רביעיותו <s>בארבע חמישיות הנה המדומה</s> ושתי רביעיות רביעת אחת וככה הוא ערכם אל השלם | ||
|- | |- | ||
| − | |} | + | | |
| − | {| | + | *{{#annot:¾×⅘|17|EMJE}}We wish to multiply three quarters by four fifths. |
| + | :<math>\scriptstyle\frac{3}{4}\times\frac{4}{5}</math> | ||
| + | |style="text-align:right;"|<big>בקשנו</big> לכפול שלש רביעיות בארבע חמישיות{{#annotend:EMJE}} | ||
|- | |- | ||
| | | | ||
| − | + | ::The denominator of the quarter is four and the denominator of the fifth is five; the product of the one by the other is twenty. | |
| − | + | ::<math>\scriptstyle{\color{blue}{4\sdot5=20}}</math> | |
| − | + | |style="text-align:right;"|הנה המדומה הרביעית ארבעה ומדומה החמישית חמשה וכפלת האחד על חבירו תהיה עשרים | |
| − | |||
|- | |- | ||
| | | | ||
| − | + | ::Now, we multiply the number of the three-quarters by the number of the four-fifths; it is twelve. | |
| − | + | ::<math>\scriptstyle{\color{blue}{3\sdot4=12}}</math> | |
| + | |style="text-align:right;"|ועתה נכפול מספר השלש רביעיות במספר הארבע חמישיות יהיו שנים עשר | ||
| + | |- | ||
| | | | ||
| + | :The ratio of twelve to twenty, which is the product of one denominator by the other, is three-fifths, and this is the product of these mentioned fractions by each other - three-fifths of the whole. | ||
| + | :<math>\scriptstyle{\color{blue}{\frac{3}{4}\times\frac{4}{5}=12:20=\frac{3}{5}}}</math> | ||
| + | |style="text-align:right;"|וערך שנים עשר אל עשרים שהוא <sup>ה</sup>עולה מכפלת המדומה האחד על חבירו הוא שלש חמישיותיו וככה הוא העולה מכפילת השברים הנזכרים אלו על אלו שלש חמישיות השלם | ||
|- | |- | ||
| − | | | + | | |
| − | |style="text-align:right;"| | + | :Or, if we want, we operate in a different method: |
| + | |style="text-align:right;"|או אם נרצה נעשה בדרך אחרת | ||
|- | |- | ||
| − | | | + | | |
| − | |style="text-align:right;"| | + | ::We take one denominator for both by multiplying four by five; it is twenty and this is their common denominator. |
| + | ::<math>\scriptstyle{\color{blue}{4\sdot5=20}}</math> | ||
| + | |style="text-align:right;"|נקח מדומה אחד לשניהם ונכפול הארבעה בחמשה יהיו עשרים והוא המדומה לשניהם | ||
|- | |- | ||
| − | | | + | | |
| − | + | ::Its 3-quarters is fifteen. | |
| + | ::<math>\scriptstyle{\color{blue}{\frac{3}{4}\sdot20=15}}</math> | ||
| + | |style="text-align:right;"|והנה ג' רביעיותיו הם חמשה עשר | ||
|- | |- | ||
| − | | | + | | |
| − | |style="text-align:right;"| | + | ::Its four-fifths is sixteen. |
| + | ::<math>\scriptstyle{\color{blue}{\frac{4}{5}\sdot20=16}}</math> | ||
| + | |style="text-align:right;"|וארבע חמישיותיו הם ששה עשר | ||
|- | |- | ||
| − | | | + | | |
| − | |style="text-align:right;"| | + | ::We multiply one by the other; it is two hundred and forty. |
| + | ::<math>\scriptstyle{\color{blue}{15\sdot16=240}}</math> | ||
| + | |style="text-align:right;"|נכפול אלו על אלו יהיו מאתים וארבעים | ||
|- | |- | ||
| − | | | + | | |
| − | |style="text-align:right;"| | + | ::We multiply the denominator, which is twenty, by itself; it is four hundred. |
| + | ::<math>\scriptstyle{\color{blue}{20\sdot20=400}}</math> | ||
| + | |style="text-align:right;"|נכה המדומה שהוא עשרים ונכפול אותו על עצמו ויהיו ארבע מאות | ||
|- | |- | ||
| | | | ||
| − | + | :We take the ratio of two hundred and forty to it and we find that as the ratio of twelve to twenty so is the ratio of two hundred and forty to four hundred and this is the same. | |
| − | === | + | :<math>\scriptstyle{\color{blue}{\frac{3}{4}\times\frac{4}{5}=240:400=\frac{12}{20}}}</math> |
| − | + | |style="text-align:right;"|נעריך המאתים וארבעים אליהם ונמצא כי כערך שנים עשר אל <s>ארבעה</s> עשרים כן ערך מאתים ‫<ref>86r</ref>וארבעים אל ארבע מאות שוה בשוה והכל אחד | |
| + | |- | ||
| | | | ||
| + | *{{#annot:⁵/₇×⁷/₈|17|NoxQ}}We wish to multiply five sevenths by seven eighths. | ||
| + | :<math>\scriptstyle\frac{5}{7}\times\frac{7}{8}</math> | ||
| + | |style="text-align:right;"|<big>בקשנו</big> לכפול חמש שביעיות בשבע שמינית{{#annotend:NoxQ}} | ||
|- | |- | ||
| − | | | + | | |
| − | |style="text-align:right;"| | + | ::It is known that the denominator of the eighth is eight and of the seventh is seven; when we multiply them by each other, it is fifty-six. |
| + | ::<math>\scriptstyle{\color{blue}{7\sdot8=56}}</math> | ||
| + | |style="text-align:right;"|ידוע כי מדומה השמינית הוא שמונה והשביעית שבעה וכאשר נכה ונכפול אותם זה על זה יהיו חמשים וששה | ||
|- | |- | ||
| | | | ||
| − | + | ::Then, we multiply the number of the five-sevenths by the number of the seven-eighths, the result is 35. | |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{5\sdot7=35}}</math> |
| + | |style="text-align:right;"|ואחר כן נכפול מספר החמש שביעיות במספר השבע שמיניות ויעלו ל"ה | ||
|- | |- | ||
| | | | ||
| − | : | + | :Its ratio to fifty-six is five-eighths, or we can say that they are four-sevenths and three-eighth of a seventh. |
| − | |style="text-align:right;"| | + | :<math>\scriptstyle{\color{blue}{\frac{5}{7}\times\frac{7}{8}=35:56=\frac{5}{8}=\frac{4}{7}+\left(\frac{3}{8}\sdot\frac{1}{7}\right)}}</math> |
| + | |style="text-align:right;"|וערכם אל חמישים וששה חמש שמיני<s>נ</s>יותיו או נוכל לומר שהם ארבע שביעיותיו ושלשה שמינית שביעית | ||
|- | |- | ||
| | | | ||
| − | + | :In the other method: their common denominator is fifty-six. | |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ובדרך האחרת הנה המדומה האחד לשניהם הוא ששה וחמישים |
|- | |- | ||
| | | | ||
| − | : | + | ::Its five-sevenths is forty. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{\frac{5}{7}\sdot56=40}}</math> |
| + | |style="text-align:right;"|וחמש שביעיותיו הם ארבעים | ||
|- | |- | ||
| | | | ||
| − | + | ::Its seven-eighths is forty-nine. | |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{\frac{7}{8}\sdot56=49}}</math> |
| + | |style="text-align:right;"|ושבע שמיניותיו תשע וארבעים | ||
|- | |- | ||
| | | | ||
| − | : | + | ::Their product by each other is one thousand, nine hundred and sixty. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{40\sdot49=1960}}</math> |
| + | |style="text-align:right;"|וכפלתים זה על זה היא עולה אלף ותשע מאות וששים | ||
|- | |- | ||
| | | | ||
| − | + | ::The product of the denominator by itself is three thousand, one hundred and thirty-six. | |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{56\sdot56=3136}}</math> |
| + | |style="text-align:right;"|והכאת המדומה על עצמו עולה שלשת אלפים <sup>ומאה</sup> ושלשים וששה | ||
|- | |- | ||
| | | | ||
| − | + | :You find that when we take the ratio of one thousand, nine hundred and sixty to it, their ratio is equal to the ratio of thirty-five to fifty-six. | |
| − | |style="text-align:right;"| | + | :<math>\scriptstyle{\color{blue}{\frac{5}{7}\times\frac{7}{8}=1960:3136=\frac{35}{56}}}</math> |
| + | |style="text-align:right;"|ותמצא כאשר נעריך אליהם האלף ותשע מאות ושישים שיהיה מערכתם שוה למערכת שלשים וחמש אל חמישים וששה | ||
|- | |- | ||
| | | | ||
| − | + | :Both these ways are proper. | |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ושני הדרכים האלה כאחד טובים |
|- | |- | ||
| − | | | + | | |
| − | |style="text-align:right;"| | + | *{{#annot:⅘׳/₁₃|17|Wi3Z}}We wish to multiply four fifths by three parts of thirteen. |
| + | :<math>\scriptstyle\frac{4}{5}\times\frac{3}{13}</math> | ||
| + | |style="text-align:right;"|<big>בקשנו</big> לכפול ארבע חמישיות על שלשה חלקים משלשה עשר בשלם{{#annotend:Wi3Z}} | ||
|- | |- | ||
| | | | ||
| − | + | ::The denominator of the fifths is five and the denominator of the parts of thirteen is thirteen; and their product is sixty-five. | |
| − | + | ::<math>\scriptstyle{\color{blue}{5\sdot13=65}}</math> | |
| + | |style="text-align:right;"|הנה מדומה החמישיות ‫<ref>86v</ref>חמשה ומדומה החלקים משלשה עשר הוא שלשה עשר וכפלתם ששים וחמש | ||
| + | |- | ||
| | | | ||
| + | ::When we multiply the number of the four-fifths by the number of the three parts, it is twelve. | ||
| + | ::<math>\scriptstyle{\color{blue}{4\sdot3=12}}</math> | ||
| + | |style="text-align:right;"|וכאשר נכפול מספר הארבע חמישיות על מספר השלשה חלקים יהיו שנים עשר | ||
|- | |- | ||
| − | | | + | | |
| − | |style="text-align:right;"| | + | :So, it is twelve parts of sixty-five. We can consider it as two parts of thirteen plus two fifths of the part, or call it one-fifth minus one part of thirteen of it. |
| + | :<math>\scriptstyle{\color{blue}{\frac{4}{5}\times\frac{3}{13}=\frac{12}{65}=\frac{2}{13}+\left(\frac{2}{5}\sdot\frac{1}{13}\right)=\frac{1}{5}-\left(\frac{1}{13}\sdot\frac{1}{5}\right)}}</math> | ||
| + | |style="text-align:right;"|והנה שנים עשר חלקים מששים וחמש בשלם ונוכל לקחת אותם שני חלקים משלשה עשר ועוד שתי חמישיות חלק או נקראם חמישית אחת שלמה פחות ממנה חלק אחד משלשה עשר בה | ||
|- | |- | ||
| − | | | + | | |
| − | + | :In the other method it is known that their common denominator is sixty-five. | |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ובדרך האחרת ידוע כי המדומה לשניהם הוא שישים וחמש |
|- | |- | ||
| − | | | + | | |
| − | <math>\scriptstyle\ | + | ::Its four-fifths is fifty-two. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{\frac{4}{5}\sdot65=52}}</math> |
| + | |style="text-align:right;"|וארבע חמישיותיו המה חמשים ושתים | ||
|- | |- | ||
| − | | | + | | |
| − | |style="text-align:right;"| | + | ::Its three parts of thirteen is fifteen. |
| + | ::<math>\scriptstyle{\color{blue}{\frac{3}{13}\sdot65=15}}</math> | ||
| + | |style="text-align:right;"|ושלשת חלקי <sup>מ</sup>השלשה עשר המה חמשה עשר | ||
|- | |- | ||
| − | |<math>\scriptstyle{\color{blue}{\ | + | | |
| − | |style="text-align:right;"| | + | ::Their product by each other is seven hundred and eighty. |
| + | ::<math>\scriptstyle{\color{blue}{52\sdot15=780}}</math> | ||
| + | |style="text-align:right;"|וכפילתם מזה על זה הם שבע מאות ושמנים | ||
|- | |- | ||
| | | | ||
| − | + | ::The product of the denominator by itself is four thousand, two hundred and twenty-five. | |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{65\sdot65=4225}}</math> |
| + | |style="text-align:right;"|והכאת המדומה על עצמו היא ארבעת אלפים ומאתים ועשרים וחמש | ||
|- | |- | ||
| | | | ||
| − | + | :When we take the ratio of the seven hundred to it, we find that their ratio is equal to the ratio of twelve to sixty-five and this is the same. | |
| − | |style="text-align:right;"| | + | :<math>\scriptstyle{\color{blue}{\frac{4}{5}\times\frac{3}{13}=780:4225=\frac{12}{65}}}</math> |
| + | |style="text-align:right;"|וכאשר נערוך אליהם השבע מאות נמצא שיהיה ערכם שוה לערך שנים עשר אל שישים וחמש והכל אחד | ||
|- | |- | ||
| | | | ||
| − | *<math>\scriptstyle | + | *{{#annot:⁹/₁₅×¹¹/₁₇|17|YOwx}}We wish to multiply nine parts of fifteen by eleven parts of seventeen. |
| − | |style="text-align:right;"| | + | :<math>\scriptstyle\frac{9}{15}\times\frac{11}{17}</math> |
| + | |style="text-align:right;"|<big>בקשנו</big> לכפול תשע חלקים מחמשה עשר בשלם על אחד עשר עשר חלקים משבעה עשר בשלם{{#annotend:YOwx}} | ||
|- | |- | ||
| | | | ||
| − | + | ::We take ten as the denominator of the first and seventeen of the second. We multiply them by each other; the product is two hundred and fifty-five. | |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{15\sdot17=255}}</math> |
| + | |style="text-align:right;"|לקחנו מדומה האחד העשר והשני שבעה עשר ‫<ref>87r</ref>{{#annot:term|185,1230|Dkeb}}כפלנום{{#annotend:Dkeb}} זה על זה עלו מאתים וחמישים וחמש | ||
|- | |- | ||
| | | | ||
| − | + | ::We multiply also the nine parts by eleven; it is ninety-nine. | |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{9\sdot11=99}}</math> |
| + | |style="text-align:right;"|כפלנו גם כן התשע חלקים על האחד עשר היו תשעים ותשע | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|וככה | + | :Its ratio to two hundred and fifty-five is six parts of seventeen plus nine parts of fifteen of a part and so it is; or we can consider it as five parts of fifteen plus fourteen parts of seventeen of a part. |
| + | :<math>\scriptstyle{\color{blue}{\frac{9}{15}\times\frac{11}{17}=99:255=\frac{6}{17}+\left(\frac{9}{15}\sdot\frac{1}{17}\right)=\frac{5}{15}+\left(\frac{14}{17}\sdot\frac{1}{15}\right)}}</math> | ||
| + | |style="text-align:right;"|וערכם אל מאתים וחמישים וחמש ששה חלקים משבע עשרה בשלם ועוד תשע חלקים מחמשה עשר בחלק אחד מהם וככה הם מהשלם או נוכל לקחת אותם חמשה חלקים מחמש עשרה בשלם ועוד ארבעה עשר חלקים משבע עשרה בחלק אחד מהם | ||
|- | |- | ||
| | | | ||
| − | = | + | :In the other method: their common denominator is two hundred and fifty-five. |
| − | + | |style="text-align:right;"|ובדרך האחרת המדומה לשניהם הוא מאתים וחמשים וחמש | |
| + | |- | ||
| | | | ||
| + | ::Its nine parts of fifteen is one hundred and fifty-three. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{9}{15}\sdot255=153}}</math> | ||
| + | |style="text-align:right;"|ותשע חלקיו מחמשה עשר הם מאה וחמשים ושלשה | ||
|- | |- | ||
| − | | | + | | |
| − | |style="text-align:right;"| | + | ::Its eleven parts of seventeen is one hundred and sixty-five. |
| + | ::<math>\scriptstyle{\color{blue}{\frac{11}{17}\sdot255=165}}</math> | ||
| + | |style="text-align:right;"|ואחד עשר חלקיו משבע עשרה הם מאה וששים וחמש | ||
|- | |- | ||
| − | | | + | | |
| − | |style="text-align:right;"| | + | ::We multiply one by the other; the result is twenty-five thousand, two hundred and forty-five. |
| + | ::<math>\scriptstyle{\color{blue}{153\sdot165=25245}}</math> | ||
| + | |style="text-align:right;"|כפלנו החשבון האחד על חבירו עלו עשרים וחמש אלף ומאתים וארבעים וחמשה | ||
|- | |- | ||
| − | | | + | | |
| − | |style="text-align:right;"| | + | ::We multiply also the denominator by itself; the result is sixty-five thousand and twenty-five. |
| + | ::<math>\scriptstyle{\color{blue}{255\sdot255=65025}}</math> | ||
| + | |style="text-align:right;"|גם הכינו וכפלנו המדומה על עצמו עלה ששים וחמש אלף ועשרים וחמשה | ||
|- | |- | ||
| − | | | + | | |
| − | + | :When we take the ratio of twenty-five thousand, two hundred and forty-five to it, we find that their ratio is as the ratio of ninety-nine to the denominator, no more and no less. | |
| − | + | :<math>\scriptstyle{\color{blue}{\frac{9}{15}\times\frac{11}{17}=25245:65025=\frac{99}{255}}}</math> | |
| − | + | |style="text-align:right;"|וכאשר נערוך אליהם העשרים וחמש אלף ומאתים וארבעים וחמשה נמצא שערכם אליהם כערך תשעים ותשע אל המדומה לא פחות ולא יותר | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | *{{#annot:(⅔·¼·⅕)×(⁶/₇·⅛)|17|6SFy}}We wish to multiply two thirds of one quarter of a fifth by six sevenths of an eighth. | |
| − | + | :<math>\scriptstyle\left(\frac{2}{3}\sdot\frac{1}{4}\sdot\frac{1}{5}\right)\times\left(\frac{6}{7}\sdot\frac{1}{8}\right)</math> | |
| − | + | |style="text-align:right;"|<big>בקשנו</big> לכפול שתי שלישיות מרביעית חמישית על שש ‫<ref>87v</ref>שביעיות שמינית{{#annotend:6SFy}} | |
| − | | | ||
|- | |- | ||
| − | | | + | |This sought-after is more complicated to be extracted than the others mentioned, because its fractions are numerous. I shall present you the method to find it easily: |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|המבוקש הזה הוא קשה להוציאו מכל האחרים הנזכרים <s>בעבור</s> [באשר]‫<ref>marg.</ref> {{#annot:term|15,1438|2zQm}}נשבריהם{{#annotend:2zQm}} רבים ואכין לך הדרך למצוא אותו בנקלה |
|- | |- | ||
| − | | | + | | |
| − | <math>\scriptstyle | + | ::When we take three, for the third that is derived from it, and multiply it by four, since the quarter is derived from it, it is twelve. We multiply it by five, for the fifth; it is sixty and this is the denominator, in which you find a third, a quarte and a fifth. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{3\sdot4\sdot5=12\sdot5=60}}</math> |
| + | |style="text-align:right;"|הנה כאשר נקח שלשה בעבור השלישית היוצאת ממנו ונכפלנו בארבעה באשר תצא משם הרביעית יהיו שנים עשר נכפול אותם בחמשה בעבור החמישית יהיו שישים וזהו <sup>הוא</sup> המדומה שתמצא בו שלישית ורביעית וחמישית | ||
|- | |- | ||
| | | | ||
| − | + | ::Its fifth is twelve; its quarter is three; and its two-thirds two. We see and know clearly that two-thirds of a quarter of a fifth is two parts of sixty. | |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{\frac{2}{3}\sdot\frac{1}{4}\sdot\frac{1}{5}=\frac{\frac{2}{3}\sdot\left[\frac{1}{4}\sdot\left(\frac{1}{5}\sdot60\right)\right]}{60}=\frac{\frac{2}{3}\sdot\left(\frac{1}{4}\sdot12\right)}{60}=\frac{\frac{2}{3}\sdot3}{60}=\frac{2}{60}}}</math> |
| + | |style="text-align:right;"|והנה חמישיתו שנים עשר ורביעיתם שלשה ושתי שלישיתם שנים ואנחנו רואים ויודעים בבירור כי השתי שלישיות מרביעית חמישית הם שני חלקים [מששים]‫<ref>Vatican om.</ref> בשלם | ||
|- | |- | ||
| | | | ||
| − | : | + | ::We take also a denominator that has a seventh and an eighth; it is fifty-six. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{7\sdot8=56}}</math> |
| + | |style="text-align:right;"|נקח גם כן מדומה שיהיה בו שביעית שמינית ויהיה חמישים וששה | ||
|- | |- | ||
| | | | ||
| − | : | + | ::Its eighth is seven; and its six-sevenths is six. This six is parts of fifty-six. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{\frac{6}{7}\sdot\frac{1}{8}=\frac{\frac{6}{7}\sdot\left(\frac{1}{8}\sdot56\right)}{56}=\frac{\frac{6}{7}\sdot7}{56}=\frac{6}{56}}}</math> |
| + | |style="text-align:right;"|ושמיניתו שבעה ושש שביעיותיהם ששה והשש האלו הם חלקים [מחמשים]‫<ref>Vatican: מחמשה</ref> וששה בשלם | ||
|- | |- | ||
| | | | ||
| − | : | + | ::What we are asking for is as if we say to multiply two parts of sixty by six parts of fifty-six. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והם מבוקשינו הוא כמו אם אמרנו לכפול שני חלקים מששים על ששה חלקים מחמשים וששה |
|- | |- | ||
| − | | | + | | |
| − | |style="text-align:right;"| | + | ::So, we multiply one denominator by the other; it is three thousand, three hundred and sixty. |
| + | |style="text-align:right;"|ועל כן נכפול המדומה האחד על חבירו ויהיו שלשת אלפים ושלש מאות וששים | ||
|- | |- | ||
| | | | ||
| − | + | ::When we multiply the two parts by the six, it is twelve. | |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וכאשר נכפול השני חלקים על הששה יהיו שנים ‫<ref>88r</ref>עשר |
|- | |- | ||
| − | | | + | | |
| − | + | ::Its ratio to the product of one denominator by the other is a fifth of an eighth of its seventh. | |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והנה ערכם אל מספר הכאת המדומה האחד על חבירו חמישית שמינית ושביעיתו |
|- | |- | ||
| − | | | + | | colspan="2"| |
| − | + | :<math>\scriptstyle{\color{blue}{\left(\frac{2}{3}\sdot\frac{1}{4}\sdot\frac{1}{5}\right)\times\left(\frac{6}{7}\sdot\frac{1}{8}\right)=\frac{2}{60}\times\frac{6}{56}=\frac{2\sdot6}{60\sdot56}=\frac{12}{3360}=\frac{1}{5}\sdot\frac{1}{8}\sdot\frac{1}{7}}}</math> | |
| − | |||
|- | |- | ||
| | | | ||
| − | : | + | ::<span style=color:green>'''Check:'''</span> Because a seventh of the product is four hundred and eighty; its eighth is sixty, and twelve is a fifth of sixty. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{\frac{1}{5}\sdot\left[\frac{1}{8}\sdot\left(\frac{1}{7}\sdot3360\right)\right]=\frac{1}{5}\sdot\left(\frac{1}{8}\sdot480\right)=\frac{1}{5}\sdot60=12}}</math> |
| + | |style="text-align:right;"|כי שביעית {{#annot:term|241,1256|Ey7X}}מספר ההכאה{{#annotend:Ey7X}} הם ארבע מאות ושמונים ושמיניתם ששים והשנים עשר הנה הם חמישית שישים | ||
|- | |- | ||
| − | | | + | |You can also find it in the other way by taking a common denominator for both [products]. |
| − | + | |style="text-align:right;"|וגם כן תוכל למצוא אותו בדרך האחרת אם נקח מדומה אחד לשניהם | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| − | |the | + | |You will understand [what] to do through your wisdom, as you see in the previous examples. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ואתה תבין לעשות בחכמתיך כאשר אתה רואה במבוקשים הקדומים |
|- | |- | ||
| − | | | + | |Up to this point I have explained the method of multiplying the fractions by themselves or by other fractions. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|<big>עד הנה</big> [בארתי]‫<ref>Vatican: באתי</ref> וכללתי דרך הכאת כפילת השברים על עצמם או על שברים אחרים זולתם |
|- | |- | ||
| − | | | + | |Now I shall explain the method of multiplying integers by fractions, or integers and fractions by fractions alone, whether the fractions are of one type, or two types, or multiplying integers and fractions by integers and fractions, whether the fractions are of one type, or two types. Here is their explanation: |
| − | + | |style="text-align:right;"|ועתה אבאר דרכי כפלת הכאת שלמים על שברים או שלמים ושברים על שברים לבדם בין שיהיו השברים ממין אחד או משני מינים או כפילת שלמים ושברים על שלמים ושברים בין שהשברים הם ממין אחד או משני מינין וזה לך ביאורם | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | + | ||
| − | : | + | ===== <span style=color:green>Multiplication of integers by fractions</span> ===== |
| − | |||
| − | |||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
| + | |<math>\scriptstyle{\color{OliveGreen}{n\times\frac{a}{b}=\frac{n\sdot a}{b}}}</math> | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | :::<math>\ | + | *{{#annot:5×⁴/₆|17|chfZ}}Example of multiplying integers by fractions: we wish to multiply five integers by four sixths. |
| − | |style="text-align:right;"| | + | :<math>\scriptstyle5\times\frac{4}{6}</math> |
| + | |style="text-align:right;"|<big>דמיון</big> ל{{#annot:term|156,1253|QXoD}}כפילת{{#annotend:QXoD}} שלמים על שברים<br> | ||
| + | רצינו לכפול חמשה שלמים בארבע שישיות{{#annotend:chfZ}} | ||
|- | |- | ||
| | | | ||
| − | :: | + | ::The denominator of the sixths is six. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|הנה מדומה השישיות הוא ששה |
|- | |- | ||
| | | | ||
| − | :: | + | ::We multiply the five integers by the numerator of the four-sixths; it is twenty. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|נכפל מספר החמשה שלמים במספר הארבע ששיות יהיו עשרים |
|- | |- | ||
| | | | ||
| − | + | ::We divide it by the denominator; the result is three integers and two-sixths of one, which is its third. | |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{5\times\frac{4}{6}=\frac{5\sdot4}{6}=\frac{20}{6}=3+\frac{2}{6}=3+\frac{1}{3}}}</math> |
| + | |style="text-align:right;"|נחלקם על המדומה יעלו ‫<ref>88v</ref>שלשה שלמים ושתי שישיות אחד שהם שלישיתו | ||
|- | |- | ||
| − | | | + | |We can find it another way: |
| − | + | |style="text-align:right;"|ונוכל למצוא זה בדרך אחרת | |
| − | |||
| − | |style="text-align:right;"| | ||
|- | |- | ||
| + | |<math>\scriptstyle{\color{OliveGreen}{n\times\frac{a}{b}=\frac{\left(n\sdot b\right)\sdot a}{b^2}}}</math> | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | :: | + | ::We multiply the denominator, which is six, by the integer, which is five; it is thirty. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|נכפול המדומה שהוא ששה על מספר השלמים שהוא חמשה ויהיו שלשים |
|- | |- | ||
| | | | ||
| − | + | ::We multiply it by four-sixths; they are one hundred and twenty sixths of a sixth | |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|נכפול אותם על ארבע השישיות ויהיו מאה ועשרים ששיות ששית |
|- | |- | ||
| | | | ||
| − | : | + | ::The hundred and eight of them are three integers and the remaining twelve are two-sixths |
| − | ::<math>\scriptstyle\ | + | ::<math>\scriptstyle{\color{blue}{5\times\frac{4}{6}=\frac{\left(5\sdot6\right)\sdot4}{6\sdot6}=\frac{30\sdot4}{6\sdot6}=\frac{120}{6}\sdot\frac{1}{6}=\frac{108+12}{6}\sdot\frac{1}{6}=3+\frac{2}{6}}}</math> |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והמאה ושמנה מהם הם שלשה שלמים והשנים עשר הנשארים הם שני ששיות |
|- | |- | ||
| − | | | + | |We find that both ways lead to the same result. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ונמצא שני הדרכים האלה יוצאות אל כיוון אחד |
|- | |- | ||
| | | | ||
| − | : | + | |
| − | | | + | ===== <span style=color:green>Multiplication of integers and fractions by fractions of the same type</span> ===== |
| + | | | ||
|- | |- | ||
| + | |<math>\scriptstyle{\color{OliveGreen}{\left(n+\frac{a}{b}\right)\times\frac{c}{b}=\frac{\left[\left(n\sdot b\right)+a\right]\sdot c}{b^2}}}</math> | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
| − | | | + | | |
| − | |style="text-align:right;"| | + | *{{#annot:(3+⅘)×⅗|17|TGUm}}Example of multiplying integers and fractions by fractions of one type alone: we wish to multiply three integers and four-fifths by three-fifths. |
| + | :<math>\scriptstyle\left(3+\frac{4}{5}\right)\times\frac{3}{5}</math> | ||
| + | |style="text-align:right;"|<big>דמיון</big> לכפלת שלמים ושברים על שברים לבדם שהם ממין אחד<br> | ||
| + | רצינו לכפול שלשה שלמים וארבע חמישיות על שלש חמישיות{{#annotend:TGUm}} | ||
|- | |- | ||
| − | | | + | | |
| − | + | ::We take the denominator of the fifths; it is five. | |
| + | |style="text-align:right;"|לקחנו מדומה החמישיות חמשה | ||
|- | |- | ||
| | | | ||
| − | + | ::We multiply it by the three integers; they are fifteen-fifths. | |
| − | + | |style="text-align:right;"|כפלנו אותם על השלשה שלמים יהיו חמשה עשר חמישיות | |
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | + | ::We add the four-fifths to them; they are nineteen-fifths. | |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|{{#annot:term|178,1206|uiMr}}נוסיף{{#annotend:uiMr}} עליהם הארבע חמשיות ויהיו תשעה עשר חמשיות |
|- | |- | ||
| | | | ||
| − | : | + | ::We multiply them by the three-fifths; they are fifty-seven fifths of a fifth. |
| − | + | |style="text-align:right;"|נכפול אותם על השלש חמשיות ויהיו חמשים ושבע חמשיות חמישית | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | :: | + | ::The fifty of them are two integers and the remaining seven-fifths of a fifth are one fifth and two-fifths of a fifth. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והחמישים מהם הם שני שלמים והשבע חמישיות חמישית הנשארות הן הם חמישית אחת ושתי חמשיות חמישית |
|- | |- | ||
| + | | colspan="2"| | ||
| + | :<math>\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left(3+\frac{4}{5}\right)\times\frac{3}{5}&\scriptstyle=\left(\frac{5\sdot3}{5}+\frac{4}{5}\right)\sdot\frac{3}{5}=\left(\frac{15}{5}+\frac{4}{5}\right)\sdot\frac{3}{5}=\frac{15+4}{5}\sdot\frac{3}{5}=\frac{19}{5}\sdot\frac{3}{5}=\frac{57}{5}\sdot\frac{1}{5}=\left(\frac{50}{5}\sdot\frac{1}{5}\right)+\left(\frac{7}{5}\sdot\frac{1}{5}\right)\\&\scriptstyle=2+\left(\frac{7}{5}\sdot\frac{1}{5}\right)=2+\frac{1}{5}+\left(\frac{2}{5}\sdot\frac{1}{5}\right)\\\end{align}}}</math> | ||
| + | |- | ||
| + | |Another way: | ||
| + | |style="text-align:right;"|דרך אחרת | ||
| + | |- | ||
| + | |<math>\scriptstyle{\color{OliveGreen}{\left(n+\frac{a}{b}\right)\times\frac{c}{b}=\frac{n\sdot c}{b}+\frac{a\sdot c}{b^2}}}</math> | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | : | + | ::We multiply the three integers by the numerator of the three-fifths; they are nine-fifths. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{3\times\frac{3}{5}=\frac{3\sdot3}{5}=\frac{9}{5}}}</math> |
| + | |style="text-align:right;"|נכפול מספר השלש שלמים על מספר שלש [החמשיות]‫<ref>Vatican: החמישית</ref> ויהיו ‫<ref>89r</ref>תשעה חמישיות | ||
|- | |- | ||
| | | | ||
| − | :: | + | ::When we multiply the four-fifths also by the three-fifths, they are twelve-fifths of a fifth, which are two-fifths and two-fifths of a fifth. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{\frac{4}{5}\times\frac{3}{5}=\frac{4\sdot3}{5\sdot5}=\frac{12}{5}\sdot\frac{1}{5}=\frac{2}{5}+\left(\frac{2}{5}\sdot\frac{1}{5}\right)}}</math> |
| + | |style="text-align:right;"|וכשנכפול גם כן הארבע חמשיות על שלש חמשיות יהיו שנים עשר חמשיות חמישית שהן שתי חמשיות שלימות ושתי [חמשיות]‫<ref>Vatican om.</ref> חמישית | ||
|- | |- | ||
| | | | ||
| − | :: | + | ::With the nine-fifths we have the total is eleven-fifths and two-fifths of a fifth, which are two integers, one-fifth, and two-fifths of a fifth, as we found at first. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ותשע חמשיות שיש לנו הנה בין כלן אחד עשר חמשיות ושתי חמשיות חמישית שהן שני שלמים וחמישית אחת ושתי חמשיות חמשית כאשר נמצא בראשונה |
|- | |- | ||
| + | | colspan="2"| | ||
| + | :<math>\scriptstyle{\color{blue}{\left(3+\frac{4}{5}\right)\times\frac{3}{5}=\frac{9}{5}+\frac{2}{5}+\left(\frac{2}{5}\sdot\frac{1}{5}\right)=\frac{11}{5}+\left(\frac{2}{5}\sdot\frac{1}{5}\right)=2+\frac{1}{5}+\left(\frac{2}{5}\sdot\frac{1}{5}\right)}}</math> | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | ===== <span style=color:green>Multiplication of integers and fractions by fractions of different types</span> ===== | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
| + | |<math>\scriptstyle{\color{OliveGreen}{\left(n+\frac{a}{b}\right)\times\frac{c}{d}=\frac{\left[\left(n\sdot b\right)+a\right]\sdot c}{b\sdot d}}}</math> | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | :::<math>\scriptstyle | + | *{{#annot:(4+⅖)×¾|17|IoIr}}Example of multiplying integers and fractions by fractions that are not of one type: we wish to multiply four integers and two fifths by three quarters. |
| − | |style="text-align:right;"| | + | :<math>\scriptstyle\left(4+\frac{2}{5}\right)\times\frac{3}{4}</math> |
| + | |style="text-align:right;"|<big>דמיון</big>‫<ref>Vatican: דמין</ref> לכפול שלמים ושברים על שברים לבדם שאינם ממין אחד<br> | ||
| + | רצינו לכפול ארבעה שלמים ושתי חמשיות על שלש רביעיות{{#annotend:IoIr}} | ||
|- | |- | ||
| | | | ||
| − | + | ::We take the denominator of the fifths; it is five. | |
| − | + | |style="text-align:right;"|נקח מדומה החמישיות חמשה | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | :: | + | ::We multiply it by the four integers; it is twenty-fifths. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|נכפול אותו על הארבעה שלמים ויהיו עשרים [חמשיות |
|- | |- | ||
| | | | ||
| − | :::<math>\scriptstyle{\color{blue}{ | + | ::We add to them the two-fifths; they are twenty-two fifths. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{4+\frac{2}{5}=\frac{\left(4\sdot5\right)+2}{5}=\frac{20+2}{5}=\frac{22}{5}}}</math> |
| + | |style="text-align:right;"|נוסיף עליהם השתי חמשיות ויהיו עשרי']‫<ref>Vatican om.</ref> ושתים חמשיות | ||
|- | |- | ||
| | | | ||
| − | :: | + | ::We multiply them by the three-quarters; they are sixty-six quarters of a fifth. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{\frac{22}{5}\sdot\frac{3}{4}=\frac{22\sdot3}{4}\sdot\frac{1}{5}=\frac{66}{4}\sdot\frac{1}{5}}}</math> |
| + | |style="text-align:right;"|נכפול אותם על השלש רביעיות יהיו ששים [ושש]‫<ref>Vatican: ושתי</ref> רביעיות חמשית | ||
|- | |- | ||
| | | | ||
| − | :: | + | ::The denominator of the quarter is four. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והנה מדומה הרביעית הוא ארבעה |
|- | |- | ||
| − | |} | + | | |
| − | + | ::We multiply it by the denominator of the fifths; it is twenty. | |
| + | ::<math>\scriptstyle{\color{blue}{4\sdot5=20}}</math> | ||
| + | |style="text-align:right;"|נכנו על מדומה החמשיות ויהיו עשרים | ||
|- | |- | ||
| | | | ||
| − | === | + | ::We divide the sixty-six quarters by it; we find them three times in it, which are three integers and six-quarters of a fifth still remain indivisible that are one-fifth and two-quarters of a fifth. |
| − | + | ::<math>\scriptstyle{\color{blue}{\left(4+\frac{2}{5}\right)\times\frac{3}{4}=\frac{66}{20}=3+\left(\frac{6}{4}\sdot\frac{1}{5}\right)=3+\frac{1}{5}+\left(\frac{2}{4}\sdot\frac{1}{5}\right)}}</math> | |
| + | |style="text-align:right;"|נחלק עליהם הששים ושש רביעיות ונמצאם שם שלשה פעמים והם שלשה שלמים ונגדנה נשאר שם ששה רביעיות חמישית [שלא נתחלקו שהם חמישית]‫<ref>marg.</ref> אחת ושתי רביעיות חמישית | ||
| + | |- | ||
| + | |In another way: | ||
| + | |style="text-align:right;"|ובדרך אחרת | ||
| + | |- | ||
| + | |<math>\scriptstyle{\color{OliveGreen}{\left(n+\frac{a}{b}\right)\times\frac{c}{d}=\frac{n\sdot c}{d}+\frac{a\sdot c}{b\sdot d}}}</math> | ||
| | | | ||
|- | |- | ||
| − | |||
| − | |||
| − | |||
| − | |||
| | | | ||
| + | ::We multiply the four integers by three-quarters; they are twelve-quarters that are three integers. | ||
| + | ::<math>\scriptstyle{\color{blue}{4\sdot\frac{3}{4}=\frac{4\sdot3}{4}=\frac{12}{4}=3}}</math> | ||
| + | |style="text-align:right;"|נכפול הארבעה שלמים על השלשה הרביעיות ויהיו שנים עשר רביעיות שהם שלשה שלמים | ||
|- | |- | ||
| | | | ||
| − | + | ::Then, we multiply the two-fifths by the three-quarters; they are six-quarters of a fifth that are one-fifth and two-quarters of a fifth, as we found at first. | |
| − | :<math>\scriptstyle\ | + | ::<math>\scriptstyle{\color{blue}{\frac{2}{5}\sdot\frac{3}{4}=\frac{2\sdot3}{4}\sdot\frac{1}{5}=\frac{6}{4}\sdot\frac{1}{5}=\frac{1}{5}+\left(\frac{2}{4}\sdot\frac{1}{5}\right)}}</math> |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ואחר נכפול ‫<ref>89v</ref>השתי חמשיות על שלש הרביעיות ויהיו ששה רביעיות חמישית שהם [חמשית]‫<ref>Vatican: חמשיות</ref> אחת שלימה ושתי רביעיות חמישית כאשר מצאנו בתחלה |
|- | |- | ||
| | | | ||
| − | + | ||
| + | ===== <span style=color:green>Multiplication of integers and fractions by integers and fractions of the same type</span> ===== | ||
| | | | ||
|- | |- | ||
| + | |<math>\scriptstyle{\color{OliveGreen}{\left(n+\frac{a}{b}\right)\times\left(m+\frac{c}{b}\right)=\frac{\left[\left(n\sdot b\right)+a\right]\sdot\left[\left(m\sdot b\right)+c\right]}{b^2}}}</math> | ||
| | | | ||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | *{{#annot: | + | *{{#annot:(2+¾)×(3+²/₄)|17|lTDC}}Example of multiplying integers and fractions by integers and fractions of the same type: we wish to multiply two integers and three quarters by three integers and two quarters. |
| − | :<math>\scriptstyle\ | + | :<math>\scriptstyle\left(2+\frac{3}{4}\right)\times\left(3+\frac{2}{4}\right)</math> |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|<big>דמיון</big> לכפול שלמים ושברים על שלמים [ושברים]‫<ref>Vatican om.</ref> ששבריהם ממין אחד<br> |
| + | רצינו לכפול שני שלמים ושלש רביעיות על שלשה שלמים ושתי רביעיות{{#annotend:lTDC}} | ||
|- | |- | ||
| | | | ||
| − | : | + | ::The denominator of the quarters is four. |
| − | + | |style="text-align:right;"|הנה מדומה הרביעיות והוא ארבעה | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | : | + | ::So, we multiply it by the two integers; they are eight-quarters. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ועל כן נכפול אותם על השנים שלמים יהיו שמונה רביעיות |
|- | |- | ||
| | | | ||
| − | + | ::We add the three-quarters to them; they are eleven. | |
| − | :<math>\scriptstyle\ | + | ::<math>\scriptstyle{\color{blue}{\left(2\sdot4\right)+3=8+3=11}}</math> |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|נוסיף עליהם השלש רביעיות ויהיה מספרן אחד עשר |
| − | |||
|- | |- | ||
| | | | ||
| − | : | + | ::We also multiply the three integers by the denominator; they are twelve-quarters. |
| + | |style="text-align:right;"|וגם נכפול השלמים השלשה על המדומה ויהיו שנים עשר רביעיות | ||
| + | |- | ||
| | | | ||
| + | ::We add the two-quarters to them; their number is fourteen. | ||
| + | ::<math>\scriptstyle{\color{blue}{\left(3\sdot4\right)+2=12+2=14}}</math> | ||
| + | |style="text-align:right;"|נוסיף עליהם השתי רביעיות ויהיו מספרן ארבעה עשר | ||
|- | |- | ||
| | | | ||
| − | ::We | + | ::We multiply it by eleven; the result is one hundred and fifty and four-quarters of a quarter. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{11\sdot14=154}}</math> |
| + | |style="text-align:right;"|נכנו על האחד עשר ויעלו מאה וחמשים וארבעה רביעיות רביעית | ||
|- | |- | ||
| | | | ||
| − | ::We | + | ::We divide them by the product of the denominator by itself; the product is sixteen. |
| − | ::<math>\scriptstyle{\color{blue}{ | + | ::<math>\scriptstyle{\color{blue}{4^2=16}}</math> |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|נחלק אותם על הכאת<sup>ב'</sup> מספר<sup>א'</sup> המדומה על עצמו העולה ששה עשר |
|- | |- | ||
| | | | ||
| − | :: | + | ::We find them nine times in it that are nine integers; and ten-quarters of a quarter remain indivisible that are two-quarters and two-quarters of a quarter and this is the result of the multiplication. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ונמצאנו שם תשע פעמים והם תשע שלמים וישאר מהם שלא יתחלקו עשרה רביעיות רביעית שהן שתי רביעיות שלמות ושתי רביעיות רביעית וככה הוא היוצא מהכפילה הזאת |
|- | |- | ||
| + | | colspan="2"| | ||
| + | :<math>\scriptstyle{\color{blue}{\left(2+\frac{3}{4}\right)\times\left(3+\frac{2}{4}\right)=\frac{154}{16}=9+\left(\frac{10}{4}\sdot\frac{1}{4}\right)=9+\frac{2}{4}+\left(\frac{2}{4}\sdot\frac{1}{4}\right)}}</math> | ||
| + | |- | ||
| + | |Another method: | ||
| + | |style="text-align:right;"|דרך אחרת | ||
| + | |- | ||
| + | |<math>\scriptstyle{\color{OliveGreen}{\left(n+\frac{a}{b}\right)\times\left(m+\frac{c}{b}\right)=\left(n\sdot m\right)+\frac{\left(n\sdot c\right)+\left(m\sdot a\right)}{b}+\frac{a\sdot c}{b^2}}}</math> | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
| − | |||
| | | | ||
| + | ::We multiply the integers by the integers; they are six integers. | ||
| + | ::<math>\scriptstyle{\color{blue}{2\sdot3=6}}</math> | ||
| + | |style="text-align:right;"|‫<ref>90r</ref>נכפול השלמים על השלמים יהיו ששה שלמים | ||
|- | |- | ||
| | | | ||
| − | + | ::We multiply also the two integers by the two-quarters; they are four-quarters. | |
| − | : | + | ::<math>\scriptstyle{\color{blue}{2\sdot\frac{2}{4}=\frac{4}{4}}}</math> |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ונכפול גם כן השני שלמים על השתי רביעיות יהיו רביעיות ארבעה |
| − | |||
|- | |- | ||
| | | | ||
| − | :<math>\scriptstyle | + | ::Then, we multiply the three-quarters by the three integers; they are nine-quarters. |
| + | ::<math>\scriptstyle{\color{blue}{\frac{3}{4}\sdot3=\frac{9}{4}}}</math> | ||
| + | |style="text-align:right;"|ואחר נכפול השלש רביעיות על השלשה שלמים יהיו תשע רביעיות | ||
| + | |- | ||
| | | | ||
| + | ::We add them to the four-quarters we have, because they are all of the same type; they are thirteen-quarters. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{4}{4}+\frac{9}{4}=\frac{13}{4}}}</math> | ||
| + | |style="text-align:right;"|בחברם אל הארבעה רביעיות שיש לנו כי כלם הם ממין אחד והוא שלשה עשר רביעיות | ||
|- | |- | ||
| | | | ||
| − | :: | + | ::Then, we multiply the three-quarters by the two; they are six-quarters of a quarter that are one quarter and two-quarters of a quarter. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{\frac{3}{4}\sdot\frac{2}{4}=\frac{6}{4}\sdot\frac{1}{4}=\frac{1}{4}+\left(\frac{2}{4}\sdot\frac{1}{4}\right)}}</math> |
| + | |style="text-align:right;"|ואחרי זאת נכפול השלש רביעיות [על]‫<ref>Vatican: ועל</ref> השתים ויהיו ששה רביעיות רביעית שהן רביעית אחת שלימה ושתי רביעיות רביעית | ||
|- | |- | ||
| | | | ||
| − | ::We | + | ::We add the one quarter to the thirteen; they are fourteen-quarters. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{\frac{13}{4}+\frac{1}{4}=\frac{14}{4}}}</math> |
| + | |style="text-align:right;"|נוסיף הרביעית הזאת על השלשה עשר ויהיו ארבעה עשר רביעיות | ||
|- | |- | ||
| | | | ||
| − | :: | + | ::We divide them by the denominator, which is four; we find it three times there that are three integers. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|נחלקם על המדומה שהוא ארבעה ונמצאנו שם שלשה פעמים שהם שלשה שלמים |
|- | |- | ||
| | | | ||
| − | :: | + | ::We add them to the six; they are nine integers. |
| − | + | |style="text-align:right;"|נחברם אל הששה יהיו תשעה שלימים | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | : | + | ::Two-quarters still remain indivisible, plus the two-quarters of a quarter we have. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ועדנה ישארו שם שתי רביעיות שלא יתחלקו [ושתי]‫<ref>Vatican: השתי</ref> רביעיות רביעית שיש לנו |
|- | |- | ||
| − | + | | colspan="2"| | |
| − | + | :<math>\scriptstyle{\color{blue}{\left(2+\frac{3}{4}\right)\times\left(3+\frac{2}{4}\right)=6+\frac{14}{4}+\left(\frac{2}{4}\sdot\frac{1}{4}\right)=6+3+\frac{2}{4}+\left(\frac{2}{4}\sdot\frac{1}{4}\right)=9+\frac{2}{4}+\left(\frac{2}{4}\sdot\frac{1}{4}\right)}}</math> | |
|- | |- | ||
| − | | | + | |We find that this way leads to the same as the first [way]. |
| − | + | |style="text-align:right;"|והנה נמצא שהדרך הזאת <s>היא השתי רביעיות רביעית שיש לנו והנה נמצא שהדרך הזאת</s> היא מכוונת אל הראשונה | |
| − | |||
| − | |||
| − | |style="text-align:right;"| | ||
| − | |||
|- | |- | ||
| | | | ||
| − | : | + | |
| − | + | ===== <span style=color:green>Multiplication of integers and fractions by integers and fractions of different types</span> ===== | |
| − | |||
| | | | ||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| + | |<math>\scriptstyle{\color{OliveGreen}{\left(n+\frac{a}{b}\right)\times\left(m+\frac{c}{d}\right)=\frac{\left[\left(n\sdot b\right)+a\right]\sdot\left[\left(m\sdot d\right)+c\right]}{b\sdot d}}}</math> | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
| − | |||
| | | | ||
| + | *{{#annot:(5+⅔)×(2+³/₆)|17|NcZF}}Example of multiplying integers and fractions by integers and fractions that are not of the same type: we wish to multiply five integers and two thirds by two integers and three sixths. | ||
| + | :<math>\scriptstyle\left(5+\frac{2}{3}\right)\times\left(2+\frac{3}{6}\right)</math> | ||
| + | |style="text-align:right;"|<big>דמיון</big> לכפול שלמים ושברים על שלמים ושברים שאינם השברים ממין אחד<br> | ||
| + | רצינו לכפול חמשה שלמים ושתי שלישיות ‫<ref>90v</ref>על שני שלמיות ושלש ששיות{{#annotend:NcZF}} | ||
|- | |- | ||
| | | | ||
| − | + | ::It is known that the denominator of the third is three. | |
| − | + | |style="text-align:right;"|ידוע כי מדומה השלישיות הוא שלשה | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | :: | + | ::We multiply it by the five integers; they are fifteen-thirds. |
| − | + | |style="text-align:right;"|נכפול אותו על המספר החמשה שלמים ויהיו חמש עשרה שלישיות | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | :: | + | ::We add the two-thirds to them; their number is seventeen. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{\left(5\sdot3\right)+2=15+2=17}}</math> |
| + | |style="text-align:right;"|נוסיף עליהן השתי שלישיות יהי מספרן שבעה עשר | ||
|- | |- | ||
| | | | ||
| − | :: | + | ::It is also known that the denominator of the sixths is six. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וגם כן ידוע כי מדומה הששיות הוא ששה |
|- | |- | ||
| | | | ||
| − | :: | + | ::We multiply it by the two integers; they are twelve-sixths. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|נכפול אותם על השני שלמים ויהיו שנים עשר שישיות |
|- | |- | ||
| | | | ||
| − | :: | + | ::We add the three-sixths to them; their number is fifteen. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{\left(2\sdot6\right)+3=12+3=15}}</math> |
| + | |style="text-align:right;"|נוסיף עליהם השלש ששיות ויהיה מספרן חמשה עשר | ||
|- | |- | ||
| | | | ||
| − | ::We | + | ::We multiply one number by the other; they are two hundred and fifty-five. |
| − | ::<math>\scriptstyle{\color{blue}{ | + | ::<math>\scriptstyle{\color{blue}{17\sdot15=255}}</math> |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|נכה המספר האחד על חבירו ויהיו <s>העולה שמנה עשר</s> מאתים וחמשים וחמש |
|- | |- | ||
| | | | ||
| − | :: | + | ::Then, we multiply one denominator by the other; the product is eighteen. |
| − | ::<math>\scriptstyle{\color{blue}{ | + | ::<math>\scriptstyle{\color{blue}{3\sdot6=18}}</math> |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ואחרי זאת נכפול המדומה האחד על חבירו ויהיה העולה שמנה עשר |
|- | |- | ||
| | | | ||
| − | :: | + | ::We divide the two hundred and fifty-five by it; the result of division is fourteen and they are integers; three remain indivisible, which are three-thirds of a sixth, or we can call them three-sixths of a third and they are one sixth. |
| − | |style="text-align:right;"| | + | :<math>\scriptstyle{\color{blue}{\left(5+\frac{2}{3}\right)\times\left(2+\frac{3}{6}\right)=\frac{255}{18}=14+\left(\frac{3}{3}\sdot\frac{1}{6}\right)=14+\frac{1}{6}}}</math> |
| + | |style="text-align:right;"|נחלק עליהם המאתים וחמשים וחמש ויהיה היוצא בחלוק ארבעה עשר והנה הם שלמים ונשאר שם שלא נתחלק שלשה והם שלשה שלישיות שישית או נוכל לקרוא אותם שלש שישיות שלישית והן הם שישית אחת שלימה | ||
| + | |- | ||
| + | |Another method: | ||
| + | |style="text-align:right;"|דרך אחרת | ||
| + | |- | ||
| + | |colspan="2"| | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\left(n+\frac{a}{b}\right)\times\left(m+\frac{c}{d}\right)=\frac{\left[\left[n\sdot\left(b\sdot d\right)\right]+\left[\frac{a}{b}\sdot\left(b\sdot d\right)\right]\right]\sdot\left[\left[m\sdot\left(b\sdot d\right)\right]+\left[\frac{c}{d}\sdot\left(b\sdot d\right)\right]\right]}{\left(b\sdot d\right)^2}}}</math> | ||
|- | |- | ||
| | | | ||
| − | ::We | + | ::We look for a common denominator for both types of fractions: |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|נבקש מדומה אחד לשני מיני השברים |
|- | |- | ||
| | | | ||
| − | :: | + | ::We find it by multiplying three by six; it is eighteen. |
| − | ::<math>\scriptstyle{\color{blue}{ | + | ::<math>\scriptstyle{\color{blue}{3\sdot6=18}}</math> |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ונמצא זה כשנכפול שלשה בששה ויהיו שמנה עשר |
|- | |- | ||
| | | | ||
| − | : | + | ::We multiply this denominator by the five integers; they are ninety parts, every eighteen of which are one integer. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ונכפול המדומה הזה על החמשה שלמים ויהיו תשעים חלקים שכל שמונה עשר ‫<ref>91r</ref>מהם עולים שלם אחד |
|- | |- | ||
| | | | ||
| − | :: | + | ::For the two-thirds, we add two-thirds of the denominator to them, which is twelve; the number of these parts is one hundred and two. |
| − | ::<math>\scriptstyle{\color{blue}{\left( | + | ::<math>\scriptstyle{\color{blue}{\left(5\sdot18\right)+\left(\frac{2}{3}\sdot18\right)=90+12=102}}</math> |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והנה כנגד השתי שלישיות נוסיף עליהם <s>ה</s>שתי שלישיות המדומה שהם שנים עשר ויהיה מספר החלקים ההמה מאה ושנים |
|- | |- | ||
| | | | ||
| − | :: | + | ::We also multiply the denominator by the two integers; they are thirty-six parts. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וכמו כן נכפול המדומה על השני שלמים יהיו ששה ושלשים חלקים |
|- | |- | ||
| | | | ||
| − | :: | + | ::For the three-sixths, we add three-sixths of the denominator to them, which is nine; the number of these parts is forty-five. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{\left(2\sdot18\right)+\left(\frac{3}{6}\sdot18\right)=36+9=45}}</math> |
| + | |style="text-align:right;"|וכנגד השלש ששיות נוסיף עליהם שלש ששיות המדומה שהן תשעה ויהיה מספר החלקים האלה ארבעים [וחמשה]‫<ref>Vatican: ושמנה</ref> | ||
|- | |- | ||
| | | | ||
| − | :: | + | ::We multiply one number by the other; the result is four thousand, five hundred and ninety. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{102\sdot45=4590}}</math> |
| + | |style="text-align:right;"|נכפול המספר האחד על חבירו יהיה ההווה ארבעת אלפים וחמש מאות ותשעים | ||
|- | |- | ||
| | | | ||
| − | :: | + | ::We divide it by the product of the denominator by itself; the product is three hundred and twenty-four. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{18^2=324}}</math> |
| + | |style="text-align:right;"|נחלקם על {{#annot:term|241,1256|OjLW}}מספר הכאת{{#annotend:OjLW}} המדומה על עצמו העולה שלש מאות ועשרים וארבעה | ||
|- | |- | ||
| | | | ||
| − | ::We | + | ::The result of division is fourteen, which are integers, and fifty-four remain indivisible, which is a sixth of the product of the denominator by itself. We find the result of multiplication is fourteen integers and a sixth, as [found] at first. |
| − | + | :<math>\scriptstyle{\color{blue}{\left(5+\frac{2}{3}\right)\times\left(2+\frac{3}{6}\right)=\frac{4590}{324}=14+\frac{54}{324}=14+\frac{1}{6}}}</math> | |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ויהיה היוצא בחלוק ארבעה עשר והנה הם שלמים ונשאר שם שלא נתחלק חמשים וארבעה שהם ששית מספר הכאת מספר המדומה על עצמו נמצא היוצא מה{{#annot:term|156,1253|TXfT}}<sup>כ</sup>פילה{{#annotend:TXfT}} הזאת ארבעה עשר שלמים וששית שלם אחד כאשר בתחלה |
| + | |- | ||
| + | |All these ways are good and right for those who find knowledge. | ||
| + | |style="text-align:right;"|וכל הדרכים האלה הם טובים ונכוחים וישרים למוצאי דעת | ||
|- | |- | ||
| | | | ||
| − | + | ||
| − | : | + | ==== <span style=color:green>Division of fractions</span> ==== |
| − | |||
| − | |||
| | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| − | | | + | |Now I will start talking about the way of dividing the fractions by each other, or integers and fractions by integers and fractions. |
| − | + | |style="text-align:right;"|<big>ועתה אחל לדבר</big> בדרך חלוקת השברים אלו על אלו או שלמים ושברים על שלמים ושברים | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | : | + | ===== <span style=color:green>Division of fractions by fractions</span> ===== |
| − | + | ||
| − | |||
| − | |||
| | | | ||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| + | |<math>\scriptstyle{\color{OliveGreen}{\frac{a}{b}\div\frac{c}{d}=\frac{\frac{a}{b}\sdot\left(b\sdot d\right)}{\frac{c}{d}\sdot\left(b\sdot d\right)}}}</math> | ||
| | | | ||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | :: | + | *{{#annot:⅔÷²/₇|552|VpDd}}Example for dividing fractions by fractions: we wish to divide two thirds by two sevenths. |
| − | |style="text-align:right;"| | + | :<math>\scriptstyle\frac{2}{3}\div\frac{2}{7}</math> |
| + | |style="text-align:right;"|‫<ref>91v</ref><big>דמיון</big> בחלוקת שברים על שברים<br> | ||
| + | רצינו לחלק שני שלישיות על שני שביעיות{{#annotend:VpDd}} | ||
|- | |- | ||
| | | | ||
| − | :<span style=color: | + | ::We look for one denominator for both fractions: we multiply seven by three; it is twenty-one. |
| − | |style="text-align:right;"|וכאשר נבחן זה | + | ::<math>\scriptstyle{\color{blue}{3\sdot7=21}}</math> |
| + | |style="text-align:right;"|הנה נבקש מדומה אחד לשני השברים ונכפול שבעה בשלשה ויהיו עשרים ואחד | ||
| + | |- | ||
| + | | | ||
| + | ::Its two-thirds is fourteen. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{2}{3}\sdot21=14}}</math> | ||
| + | |style="text-align:right;"|ושתי [שלישיותיו]‫<ref>Vatican: שלישיות</ref> ארבעה עשר | ||
| + | |- | ||
| + | | | ||
| + | ::Its two-sevenths is six. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{2}{7}\sdot21=6}}</math> | ||
| + | |style="text-align:right;"|ושתי שביעיותיו ששה | ||
| + | |- | ||
| + | | | ||
| + | ::We divide the fourteen by it; the result of division is two and two remain undivided, which is a third of the six we divided. We find the result of division is two and a third. | ||
| + | :<math>\scriptstyle{\color{blue}{\frac{2}{3}\div\frac{2}{7}=\frac{14}{6}=2+\frac{2}{6}=2+\frac{1}{3}}}</math> | ||
| + | |style="text-align:right;"|והנה [נחלק]‫<ref>Vatican: נכפול</ref> הארבעה עשר עליהם והיוצא בחלוק הוא שנים והנשאר שלא נתחלק שנים והנה הם שלישית הששה אשר חלקנו עליהם ונמצא היוצא מהחלוקה הזאת שנים ושלישית | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | ===== <span style=color:green>Division of integers and fractions by integers and fractions</span> ===== | ||
| + | |||
| + | | | ||
| + | |- | ||
| + | |<math>\scriptstyle{\color{OliveGreen}{\left(n+\frac{a}{b}\right)\div\left(m+\frac{c}{d}\right)=\frac{\left[n\sdot\left(b\sdot d\right)\right]+\left[\frac{a}{b}\sdot\left(b\sdot d\right)\right]}{\left[m\sdot\left(b\sdot d\right)\right]+\left[\frac{c}{d}\sdot\left(b\sdot d\right)\right]}}}</math> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | *{{#annot:(4+⅔)÷(2+⅖)|552|eAW6}}Example for dividing integers and fractions by integers and fractions: we wish to divide four integers and two thirds by two integers and two fifths. | ||
| + | :<math>\scriptstyle\left(4+\frac{2}{3}\right)\div\left(2+\frac{2}{5}\right)</math> | ||
| + | |style="text-align:right;"|<big>דמיון</big> לחלק שלמים ושברים על שלמים ושברי‫'<br> | ||
| + | רצינו לחלק ארבעה שלמים ושתי שלישיות על [שני]‫<ref>Vatican om.</ref> שלימים ושתי חמשיות{{#annotend:eAW6}} | ||
| + | |- | ||
| + | | | ||
| + | ::The denominator of both is fifteen. | ||
| + | |style="text-align:right;"|והנה המדומה לשניהם הוא חמשה עשר | ||
| + | |- | ||
| + | | | ||
| + | ::So, we multiply it by the four integers; they are sixty parts. | ||
| + | |style="text-align:right;"|על כן נ<sup>כ</sup>פול אותו על הד' שלמים ויהיו ששים חלקים | ||
| + | |- | ||
| + | | | ||
| + | ::For the two-thirds, we add two-thirds of the denominator to them, which are ten; the number of the parts is seventy. | ||
| + | ::<math>\scriptstyle{\color{blue}{\left(4+\frac{2}{3}\right)\sdot15=\left(4\sdot15\right)+\left(\frac{2}{3}\sdot15\right)=60+10=70}}</math> | ||
| + | |style="text-align:right;"|ובעבור השתי שלישיות נוסיף עליהם שתי שלישיות המדומה שהם עשרה ויהיה מספר החלקים שבעים | ||
| + | |- | ||
| + | | | ||
| + | ::We also multiply the two integers by the denominator; it is thirty parts. | ||
| + | |style="text-align:right;"|וגם נכפול השני שלימים על המדומה ויהיו שלשים חלקים | ||
| + | |- | ||
| + | | | ||
| + | ::We add six to them, which are two-fifths of the denominator; their number is thirty-six. | ||
| + | ::<math>\scriptstyle{\color{blue}{\left(2+\frac{2}{5}\right)\sdot15=\left(2\sdot15\right)+\left(\frac{2}{5}\sdot15\right)=30+6=36}}</math> | ||
| + | |style="text-align:right;"|נוסיף עליהם ששה שהם שתי חמישיות המדומה ויהיה מספרם ששה ושלשים | ||
| + | |- | ||
| + | | | ||
| + | ::We divide the seventy by it; we find it two times in it, minus half a ninth of the divisor; or we say that the result of division is one time plus three-quarters and two-ninths minus a quarter of a ninth. | ||
| + | |style="text-align:right;"|נחלק עליהם מספר השבעים ונמצא שם שני פעמים פחות חצי תשיעית החשבון אשר ‫<ref>92r</ref>[חלקנו]‫<ref>Vatican: חלקקנו</ref> עליו או נאמר שהיוצא מהחלוקה הוא פעם אחת ועוד שלש <s>ועוד ש</s> רביעיות ושתי תשיעיות [פחות]‫<ref>marg.</ref> רובע תשיעית | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | :<math>\scriptstyle{\color{blue}{\left(4+\frac{2}{3}\right)\div\left(2+\frac{2}{5}\right)=\frac{70}{36}=2-\left(\frac{1}{2}\sdot\frac{1}{9}\right)=1+\frac{3}{4}+\frac{2}{9}-\left(\frac{1}{4}\sdot\frac{1}{9}\right)}}</math> | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | ==== <span style=color:green>Addition of fractions</span> ==== | ||
| + | | | ||
| + | |- | ||
| + | |After the ways of multiplying and dividing fractions have been clarified, it is also necessary to clarify the ways of adding them to each other and the way of subtracting smaller fractions from greater fractions | ||
| + | |style="text-align:right;"|<big>אחרי</big> אשר התבארו דרכי כפלות השברים וחלוקתם צריך לבאר גם כן דרכי מחברתם זה עם זה ודרך מגרעת שברים דקים וקטנים משברים גדולים מהם | ||
| + | |- | ||
| + | |Know that when we wish to know how much is the sum of known fractions with known fractions: | ||
| + | |style="text-align:right;"|ותדע כי כשנרצה לידע כמה מחברת שברים ידועים עם שברים ידועים | ||
| + | |- | ||
| + | |<math>\scriptstyle{\color{OliveGreen}{\frac{a}{b}+\frac{c}{d}=\frac{\left[\frac{a}{b}\sdot\left(b\sdot d\right)\right]+\left[\frac{c}{d}\sdot\left(b\sdot d\right)\right]}{b\sdot d}}}</math> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | *{{#annot:¾+⅚|677|Sh9x}}As we say for example: we sum three quarters with five sixths. How much is the result? | ||
| + | :<math>\scriptstyle\frac{3}{4}+\frac{5}{6}</math> | ||
| + | |style="text-align:right;"|כאשר נאמר על דרך משל חברנו שלש רביעיות עם חמש ששיות<br> | ||
| + | כמה העולה{{#annotend:Sh9x}} | ||
| + | |- | ||
| + | | | ||
| + | ::We do it this way: we take the common denominator of both; it is twenty-four. | ||
| + | |style="text-align:right;"|והנה נעשה על הדרך הזה נקח המדומה לשניהם והנה הוא עשרים וארבעה | ||
| + | |- | ||
| + | | | ||
| + | ::Its three-quarters is eighteen. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{3}{4}\sdot24=18}}</math> | ||
| + | |style="text-align:right;"|ושלש רביעיותיו שמנה עשר | ||
| + | |- | ||
| + | | | ||
| + | ::Its five-sixths is twenty. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{5}{6}\sdot24=20}}</math> | ||
| + | |style="text-align:right;"|וחמש ששיותיו עשרים | ||
| + | |- | ||
| + | | | ||
| + | ::We sum them together; it is thirty-eight. | ||
| + | ::<math>\scriptstyle{\color{blue}{18+20=38}}</math> | ||
| + | |style="text-align:right;"|נחברם זה עם זה יהיו שלשים ושמנה | ||
| + | |- | ||
| + | | | ||
| + | ::We take the twenty-four from it; fourteen remains from it, which is a whole half and half its sixth; or, if we wish the remainder is a half and a third of a quarter. | ||
| + | |style="text-align:right;"|ונקח מהם בעבור העשרים וארבע שלם אחד ונשאר מהם ארבעה עשר שהם חצי שלם אחד וחצי ששיתו או אם נרצה נקרא הנשאר חצי שלם ושלישית רביעיתו | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | :<math>\scriptstyle{\color{blue}{\frac{3}{4}+\frac{5}{6}=\frac{38}{24}=1+\frac{14}{24}=1+\frac{1}{2}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)=1+\frac{1}{2}+\left(\frac{1}{3}\sdot\frac{1}{4}\right)}}</math> | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | ==== <span style=color:green>Subtraction of fractions</span> ==== | ||
| + | | | ||
| + | |- | ||
| + | |When we wish to subtract from known fractions known fractions that are smaller than them and know the remainder. | ||
| + | |style="text-align:right;"|<big>וכאשר נבקש</big> לגרוע משברים ידועים שברים ידועים קטנים ודקים מהם ולדעת הנשאר | ||
| + | |- | ||
| + | |<math>\scriptstyle{\color{OliveGreen}{\frac{a}{b}-\frac{c}{d}=\frac{\left[\frac{a}{b}\sdot\left(b\sdot d\right)\right]-\left[\frac{c}{d}\sdot\left(b\sdot d\right)\right]}{b\sdot d}}}</math> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | *{{#annot:²/₄-⅕|678|tqJF}}As we say for example: we subtract one fifth from two quarters. How much is the remainder? | ||
| + | :<math>\scriptstyle\frac{2}{4}-\frac{1}{5}</math> | ||
| + | |style="text-align:right;"|כאשר נאמר על דרך משל גרענו משני ‫<ref>92v</ref>רביעיות חמישית אחד כמה הנשאר{{#annotend:tqJF}} | ||
| + | |- | ||
| + | | | ||
| + | ::We do as follows: we take a common denominator of both; it is 20. | ||
| + | |style="text-align:right;"|נעשה ככה נקח מדומה אחד לשניהם והנה הוא עשרים | ||
| + | |- | ||
| + | | | ||
| + | ::Its two-quarters is ten. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{2}{4}\sdot20=10}}</math> | ||
| + | |style="text-align:right;"|ושתי רביעיותיו הם עשרה | ||
| + | |- | ||
| + | | | ||
| + | ::Its one-fifth is four. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{1}{5}\sdot20=4}}</math> | ||
| + | |style="text-align:right;"|וחמישיתו הוא ארבעה | ||
| + | |- | ||
| + | | | ||
| + | ::We subtract four from the ten; six remains from it. | ||
| + | ::<math>\scriptstyle{\color{blue}{10-4=6}}</math> | ||
| + | |style="text-align:right;"|נסיר [מהעשרה ארבעה]‫<ref>Vatican: מהארבעה עשרה</ref> וישאר מהם ששה | ||
| + | |- | ||
| + | | | ||
| + | ::It is a quarter of the common denominator and a fifth of its quarter, and this is the ratio of the remainder to the unit. | ||
| + | :<math>\scriptstyle{\color{blue}{\frac{2}{4}-\frac{1}{5}=\frac{6}{20}=\frac{1}{4}+\left(\frac{1}{5}\sdot\frac{1}{4}\right)}}</math> | ||
| + | |style="text-align:right;"|והוא רביעית המדומה וחומש רביעיתו וככה ערך הנשאר אל השלם | ||
| + | |- | ||
| + | |By that everything I wanted to clarify in this chapter becomes clear. | ||
| + | |style="text-align:right;"|ובזה התבארו [כל]‫<ref>marg.</ref> מה שראיתי לבאר בשער הזה | ||
| + | |- | ||
| + | |Praise be to God, blessed be He. | ||
| + | |style="text-align:right;"|תהלה לאל [ברוך הוא]‫<ref>Vatican: ב"ה</ref> | ||
| + | |- | ||
| + | |} | ||
| + | {| | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | == Chapter Ten – Knowing the Square Roots of "Deaf" and "Mute" Numbers by Approximation == | ||
| + | |||
| + | |style="width: 45%; text-align:right;"|<big>השער העשירי</big> [בידיעת]‫<ref>Vatican: בידועת</ref> {{#annot:term|439,1464|AnW4}}צלעות{{#annotend:AnW4}} המרובעים מחשבון ה{{#annot:term|2370,1381|cS1r}}חרש{{#annotend:cS1r}} וה{{#annot:term|2370,1382|Kk7l}}אלם{{#annotend:Kk7l}} {{#annot:term|1613,2072|4eYJ}}על דרך קרוב{{#annotend:4eYJ}} | ||
| + | |- | ||
| + | | | ||
| + | === <span style=color:green>Introduction: square numbers and non-square numbers</span> === | ||
| + | |||
| + | | | ||
| + | |- | ||
| + | |<span style=color:green>'''Definition of a square number:'''</span> {{#annot:definition|86|ifI6}} Know that every number that has a root is called a square number and it is a "wise number". | ||
| + | |style="text-align:right;"|תדע כי כל מספר נגדר הוא נקרא מרובע והנה הוא מספר פקח {{#annotend:ifI6}} | ||
| + | |- | ||
| + | |The reason that it is called a "wise number" is that its root, which is the measure of each of the four sides of the square, can be truly found. | ||
| + | |style="text-align:right;"|וטעם היותו נקרא [{{#annot:term|86,1681|3xCB}}מספר פקח{{#annotend:3xCB}}]‫<ref>Vatican: מספר ופקח</ref> באשר גדרו שהוא מדת כל אחת ואחת מארבע {{#annot:term|325,1464|YlsD}}צלעות{{#annotend:YlsD}} המרובע יכול להמצא [באמתות]‫<ref>Vatican: באמיתית</ref> | ||
| + | |- | ||
| + | |Therefore, the numbers that do not have a real root are called deaf and mute, because their root cannot be found accurately only approximately | ||
| + | |style="text-align:right;"|ולזאת יקראו המספרים אשר אין להם גדר אמתי {{#annot:term|2370,1381|Efkq}}מספרים חרשים{{#annotend:Efkq}} ו{{#annot:term|2370,1382|jG3R}}אלמים{{#annotend:jG3R}} באשר לא יוכל כל נברא למצוא [גדרם]‫<ref>Vatican: גדרים</ref> בדקדוק כי אם {{#annot:term|1613,1611|9E0B}}בקירוב{{#annotend:9E0B}} | ||
| + | |- | ||
| + | |In every scientific discipline there are many secrets hidden and concealed from the hearts of men to be found. | ||
| + | |style="text-align:right;"|ובכל חכמה הרבה דברים נעלמים ונסתרים מלבות בני האדם למצאן | ||
| + | |- | ||
| + | |We also see this in the science of medicine, when physicians instruct to take a well-known herb root or stone to heal the sick person who carries them by their virtue, but no wise man can know the reason of the [healing] virtue of the stone, or the herb root, why it is so. | ||
| + | |style="text-align:right;"|והנה נראה זה גם כן בחכמת הרפואה שיצוו הרופאים לקחת שורש עשב ידוע או אבן ידועה להיותם מרפא בסגולה לחולה [הנושאם]‫<ref>Vatican: הנושאים</ref> ואין ‫<ref>93r</ref>כח בשום חכם לדעת טעם סגולת האבן או שרש העשב למה הוא ככה | ||
| + | |- | ||
| + | |Many things like these are known only to the Knower of all concealed things alone, blessed be He and blessed be His name. | ||
| + | |style="text-align:right;"|ודברים רבים כמו אלו אשר לא יודעו רק ליודע כל [נסתרות]‫<ref>Vatican: נסתרת</ref> לבדו ברוך הוא וברוך שמו | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === <span style=color:green>Sexagesimal fractions</span> === | ||
| + | |||
| + | | | ||
| + | |- | ||
| + | |Now, we return to the premises and say: since most ancients extracted the approximate roots of "deaf" or "mute" numbers by using the method of the astronomers, some of their methods should be introduced and explained first, before I discuss the extraction of roots [of non-square numbers]. | ||
| + | |style="text-align:right;"|ועתה נשוב אל הראשונות ונאמר כי לבעבור אשר רוב החכמים הקדומים הוציאו קרוב מדת צלעות המרובעים החרשים והאלמים על דרך חכמי המזלות [צריך]‫<ref>Vatican om.</ref> להקדים ולבאר קצת דרכיהם [בתחלה]‫<ref>Vatican om.</ref> בטרם שאדבר בדרך הוצאת מדת הצלעות | ||
| + | |- | ||
| + | |The astronomers divided the zodiac into twelve shapes that are called zodiacal signs. | ||
| + | |style="text-align:right;"|והנה חלקו חכמי המזלות הגלגל לשנים עשר צורות והמה נקראות מזלות | ||
| + | |- | ||
| + | |The reason for this division is that there is no number smaller than twelve that has as many whole parts [= divisors, in modern terminology] like it, for it has a half, a third, a quarter, a sixth, and half a sixth. | ||
| + | |style="text-align:right;"|וטעם החלוקה הזאת היא באשר אין מספר קטן פחות משנים עשר שיהיו לו חלקים רבים שלמים מבלי שבר כמוהו כי ימצא בו [חצי]‫<ref>Vatican: חצה</ref> ושלישית ורביעית ושישית וחצי שישית | ||
| + | |- | ||
| + | |They divided each zodiacal sign into thirty parts and called them degrees. | ||
| + | |style="text-align:right;"|וחלקו כל מזל לשלשים חלקים קראו אותם {{#annot:term|1970,1316|lmGW}}מעלות{{#annotend:lmGW}} | ||
| + | |- | ||
| + | |They divided it into this number, since there is no number smaller than it that has as many parts [= divisors] as it has, for it has a half, a third, a fifth, a sixth, and a tenth. | ||
| + | |style="text-align:right;"|ויחלקוהו למספר זה לפי שאין מספר פחות ממנו אשר ימצא בו חלקים רבים בלתי שבר כמוהו כי ימצא בו חצי ושלישית וחמשית וששית ועשירית | ||
| + | |- | ||
| + | |They divided each degree into sixty parts and called them primes. | ||
| + | |style="text-align:right;"|וחלקו כל {{#annot:term|1970,1316|DYe8}}מעלה{{#annotend:DYe8}} לששים ‫<ref>93v</ref>חלקים וקראו אותם ראשונים | ||
| + | |- | ||
| + | |This number has a half, a third, a quarter, a fifth, a sixth, and a tenth. | ||
| + | |style="text-align:right;"|ובמספר הזה ימצא בו חצי ושלישית ורביעית וחמשית וששית ועש<sup>י</sup>רית‫<ref>Vatican: וחלקו כל מעלה... ועשירית twice</ref> | ||
| + | |- | ||
| + | |They divided each prime into sixty seconds; each second into sixty thirds; and each third into sixty fourths. | ||
| + | |style="text-align:right;"|וחלקו כל ראשון לששים שניים וכל שני לששים שלישים וכל שלישי לששים רביעיים | ||
| + | |- | ||
| + | |And so on, they divided their fractions as needed, endlessly, each one is equal to sixty of the rank that follows it and sixty of each one are a unit of the preceding rank. | ||
| + | |style="text-align:right;"|וכן יחלקו חלקיהם כפי הצורך עד אין תכלית וכל אחד ואחד יהיה שוה ששים מהמדרגה השנייה לו וששים <sup>מ</sup>כל אחד ואחד יעלו אחד מהמדרגה הקודמת לו | ||
| + | |- | ||
| + | | | ||
| + | ==== <span style=color:green>Multiplication of Sexagesimal Fractions</span> ==== | ||
| + | |||
| + | | | ||
| + | |- | ||
| + | |I tell you that the degrees [act] as the integers: | ||
| + | |style="text-align:right;"|והנני מודיע לך [כי המעלות]‫<ref>Vatican om.</ref> הן הנה כמו השלמים | ||
| + | |- | ||
| + | |When we multiply degrees by degrees, the result of multiplication are always degrees. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\left(a\sdot60^0\right)\times\left(b\sdot60^0\right)=\left(a\sdot b\right)\sdot60^0}}</math> | ||
| + | |style="text-align:right;"|ולעולם כשנכפול מעלות על מעלות יהיה העולה מהכפלה מעלות | ||
| + | |- | ||
| + | |If we multiply them by other fractions, such as primes, seconds, or others, the type of these fractions always remains the same, their type does not change because of this multiplication. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\left(a\sdot60^0\right)\times\left(b\sdot\frac{1}{60^n}\right)=\left(a\sdot b\right)\sdot\frac{1}{60^n}}}</math> | ||
| + | |style="text-align:right;"|ואם נכפול אותם בחלקים אחרים כמו ראשונים או שניים או יותר לעולם יעמוד המין מהחלקים ההם בעצמו לא ישתנו ממינם בעבור הכפלה הזאת | ||
| + | |- | ||
| + | |The primes, the seconds, and all other types, follow the rule of the [simple] fractions. | ||
| + | |style="text-align:right;"|ואולם הראשונים או השניים או כל שאר המינין שאחריהן הנה משפטן כמשפט השברים | ||
| + | |- | ||
| + | | | ||
| + | ::As when we multiply a half by a half, the result is a quarter. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{1}{2}\times\frac{1}{2}=\frac{1}{4}}}</math> | ||
| + | |style="text-align:right;"|כי כמו שאם נכפול חצי על חצי יהיה העולה רביע | ||
| + | |- | ||
| + | |So, if we multiply seconds by seconds, the product is fourths. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a^{\prime\prime}\times b^{\prime\prime}=\left(a\sdot b\right)^{iv}}}</math> | ||
| + | |style="text-align:right;"|ככה אם נכפול חלקים שניים על חלקים שניים יהיה העולה מהכפלה רביעים | ||
| + | |- | ||
| + | |The product of seconds by primes is thirds. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a^{\prime\prime}\times b^\prime=\left(a\sdot b\right)^{\prime\prime\prime}}}</math> | ||
| + | |style="text-align:right;"|וכפלת שניים על הראשונים יהיה העולה שלישיים | ||
| + | |- | ||
| + | |The product of primes by primes is seconds. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a^\prime\times b^\prime=\left(a\sdot b\right)^{\prime\prime}}}</math> | ||
| + | |style="text-align:right;"|וכפלת הראשונים על ראשונים ‫<ref>94r</ref>יהיה העולה שניים | ||
| + | |- | ||
| + | |The product of seconds by thirds is fifths. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a^{\prime\prime}\times b^{\prime\prime\prime}=\left(a\sdot b\right)^{v}}}</math> | ||
| + | |style="text-align:right;"|ומכפלת שניים בשלישיים יהיה העולה חמשיים | ||
| + | |- | ||
| + | |The product of sixths by seconds, or fourths by fourths, is eighths. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a^{vi}\times b^{\prime\prime}=a^{iv}\times b^{iv}=\left(a\sdot b\right)^{viii}}}</math> | ||
| + | |style="text-align:right;"|וששים בשניים או רביעיים ברביעיים יהיה העולה שמניים | ||
| + | |- | ||
| + | |The product of seconds by fifths is sevenths. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a^{\prime\prime}\times b^{v}=\left(a\sdot b\right)^{vii}}}</math> | ||
| + | |style="text-align:right;"|ושניים בחמשיים יהיה העולה שביעיים | ||
| + | |- | ||
| + | |And so on for all according to the aforementioned method. | ||
| + | |style="text-align:right;"|וככה כלם על דרך זה האמור | ||
| + | |- | ||
| + | | | ||
| + | ===== <span style=color:green>Written procedure</span> ===== | ||
| + | |||
| + | | | ||
| + | |- | ||
| + | |I will give you a method for multiplying these mentioned fractions: | ||
| + | |style="text-align:right;"|ואכין לך דרך לכפילת החלקים <s>החלקים</s> הנזכרים האלה | ||
| + | |- | ||
| + | |When you wish to multiply a line of known fractions by a line of known fractions; in each line there are many higher and lower types, do as follows: take one of the two lines and convert all the higher types into the lowest type of that line. Add what you receive from the decomposing to the lowest type, because now they are all the same type. Apply the same procedure with the second line as well. | ||
| + | |style="text-align:right;"|כשתבקש לכפול טור אחד מחשבונות חלקים ידועים על טור אחד מחשבונות חלקים ידועים ויהיה בכל אחת מהטורים חלקים מהרבה מינים גדולים וקטנים תעשה ככה קח הטור האחד משתיהן ויצקת כל המינים הגדולים אל המין היותר קטן שבטור ההיא [וחבר אל שתיהם]‫<ref>Vatican: ועד</ref> המין הקטן אל מה שיעלה לך מה{{#annot:term|1561,1558|7pST}}התכה{{#annotend:7pST}} כי אז הם כלם ממין אחד כ"ד וכמעשה [הטור]‫<ref>Vatican om.</ref> הזאת תעשה הטור השנית גם כן מהטור השנית גם כן | ||
| + | |- | ||
| + | |We multiply one [line] by the other and see what type the result of multiplication should be, according to what was explained before. | ||
| + | |style="text-align:right;"|נכפול אלו על אלו ותראה <s>כי</s> איזה מין ראוי שיהיה היוצא מהכפלה על פי מה שיתבאר לפנים | ||
| + | |- | ||
| + | |Then, divide them by sixty many times, until you reach a type which you cannot divide by sixty. | ||
| + | |style="text-align:right;"|ואחר {{#annot:term|784,1259|Mgse}}חלק{{#annotend:Mgse}} אותם על ששים הרבה פעמים עד שתבא אל תכלית המין אשר לא תוכל לחלק אותם על ששים | ||
| + | |- | ||
| + | |Know that if there is any number left that cannot be divided in each division, the remainder is of the type of the divided number. | ||
| + | |style="text-align:right;"|ותדע אם ישאר שום מספר שלא נתחלק בכל חלוקה וחלוקה יהיה הנשאר ממין המספר המחלק | ||
| + | |- | ||
| + | |This multiplication technique is long as well as short, but it is well-guided. | ||
| + | |style="text-align:right;"|‫<ref>94v</ref>ודרך ה<sup>כ</sup>פילה הזאת היא ארוכה [ו]קצרה והיא סלולה ומיושבת בטוב | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | === <span style=color:green>Extracting Roots of Deaf Numbers</span> === | ||
| + | |||
| + | | | ||
| + | |- | ||
| + | |After clarifying and introducing what is appropriate for the art of this chapter, I will return to discuss the method of extracting the root a deaf square: | ||
| + | |style="text-align:right;"|ואחרי אשר בארתי והקדמתי מה שראוי למלאכת השער הזה אשוב לדבר בדרך הוצאת מדת הצלעות ממרובע שמספרו חרש | ||
| + | |- | ||
| + | |When we want to reach the required purpose, we look at the square that precedes the number we are examining, we find it as explained in chapter seven. We see how much is the excess over the preceding square. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{a^2+b}}</math> | ||
| + | |style="text-align:right;"|והנה כאשר נרצה לבא אל תכלית המבוקש הזה נעיין המרובע שעבר מהמספר אשר אנחנו חוקרים עליו ונגיע לדעת זה על פי מה שהתבאר בשער השביעי ונראה כמה העודף על המרובע שעבר | ||
| + | |- | ||
| + | | | ||
| + | *If it is less than its root, we do as follows: | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{b<a}}</math> | ||
| + | |style="text-align:right;"|ואם היה פחות מגדרו נעשה זאת | ||
| + | |- | ||
| + | | | ||
| + | :<span style=color:green>'''First approximation:'''</span> we convert the excess into primes by multiplying it by sixty, then dividing them by double the root of the preceding square. We add the quotient to the root and this is the approximate root. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\sqrt{a^2+b}\approx a+\left(\frac{60\sdot b}{2a}\right)^\prime}}</math> | ||
| + | |style="text-align:right;"|{{#annot:term|1562,1431|QhxO}}נשיב{{#annotend:QhxO}} העודף ראשונים והוא ש<sup>נכ</sup>פל שנכפול אותם בששים ואחר נחלקם על {{#annot:term|387,1230|UCaJ}}כפל{{#annotend:UCaJ}} הגדר מה<sup>מ</sup>רובע שעבר ומה שיצא בחלוק נוסיף אותו על הגדר [וככה יהיה מדת הצלעות בקרוב]‫<ref>Vatican om.</ref> | ||
| + | |- | ||
| + | | | ||
| + | :<span style=color:green>'''Second approximation:'''</span> if we want to correct it further, we multiply this [approximate] root by itself and see by how much the product exceeds over the number we are examining. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\left[a+\left(\frac{60\sdot b}{2a}\right)^\prime\right]^2-\left(a^2+b\right)}}</math> | ||
| + | |style="text-align:right;"|ואם נרצה {{#annot:term|1612,1387|XsfT}}לדקדק{{#annotend:XsfT}} אותה עוד נכפול ונכה המדה הזאת על עצמה ונראה מה {{#annot:term|420,1206|mYzg}}יוסיף ב{{#annotend:mYzg}}{{#annot:term|156,1256|8IVB}}הכאה{{#annotend:8IVB}} על החשבון אשר אנחנו חוקרים עליו | ||
| + | |- | ||
| + | | | ||
| + | :We examine the ratio of [the square of] the excess to double the [approximate] root we found: subtract this ratio from the [approximate] root and the remainder is a more accurate root than it was at first. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\sqrt{a^2+b}\approx a+\left(\frac{60\sdot b}{2a}\right)^\prime-\left[\frac{\left(\left(\frac{60\sdot b}{2a}\right)^\prime\right)^2}{2\sdot\left(a+\left(\frac{60\sdot b}{2a}\right)^\prime\right)}\right]}}</math> | ||
| + | |style="text-align:right;"|ונעיין מה ערך ה{{#annot:term|877,1207|updy}}תוספת{{#annotend:updy}} אל כפל [המדה]‫<ref>Vatican: המכה</ref> שמצאנו פעמים וכערך [ההוא]‫<ref>Vatican: הכאה</ref> תסיר מהמדה והנותר יהיה יותר מדה {{#annot:term|1614,1388|WRW2}}מדוקדקת{{#annotend:WRW2}} מאשר לא היתה בתחלה | ||
| + | |- | ||
| + | | | ||
| + | :<span style=color:green>'''Third approximation:'''</span> to correct it further, we do with the second [approximate] root as we did with the first [approximate] root, and what remains after subtracting the ratio of the excess to double the second [approximate] root from [the second approximate root] is the most accurate approximation. | ||
| + | |style="text-align:right;"|ו{{#annot:term|1612,1387|kaxo}}לדקדקה{{#annotend:kaxo}} יותר נעשה מהמדה הזאת השנית כאשר עשינו מהמדה הראשונה ‫<ref>95r</ref>ומה שישאר אחרי הסרת ערך ה{{#annot:term|877,1207|15Co}}תוספת{{#annotend:15Co}} ההכאה אל כפל המדה השנית פעמים ממנה יהיה מדה מדוקדקת מכלנה | ||
| + | |- | ||
| + | | | ||
| + | :From here on, do not trouble yourself to correct it even further, lest you dive into deep water and draw nothing in your hand. | ||
| + | |style="text-align:right;"|ומכאן ואילך אל תיגע עצמך לדקדק כי אולי תצלול במים אדירים וחרס יעלה בידך | ||
| + | |- | ||
| + | | | ||
| + | *If we find that the excess of the number over the preceding square is greater than the root of the preceding square, we proceed in another way: | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{b>a}}</math> | ||
| + | |style="text-align:right;"|ואם מצאנו שהעודף מהמספר על המרובע שעבר הוא יותר מגדר המרובע שעבר נעשה בדרך אחרת | ||
| + | |- | ||
| + | | | ||
| + | :We examine how much is the difference between our number and the next square. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{c^2-d}}</math> | ||
| + | |style="text-align:right;"|נעיין כמה המרחק ממספרנו ועד המרובע העתיד | ||
| + | |- | ||
| + | | | ||
| + | :<span style=color:green>'''First approximation:'''</span> we convert the difference into primes, then divide them by double the root of the next square. We subtract the quotient from the root of the next square and the remainder is the approximate root. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\sqrt{c^2-d}\approx c-\left(\frac{60\sdot d}{2c}\right)^\prime}}</math> | ||
| + | |style="text-align:right;"|ונשיב המרחק ראשונים ונחלקם על כפל [גדר]‫<ref>Vatican om.</ref> המרובע העתיד פעמים ומה שיצא בחלוק נגרע אותו מגדר המרובע העתיד והנשאר היא מדת הצלעות בקרוב | ||
| + | |- | ||
| + | | | ||
| + | :When we wish to correct it further, we do it in the previously explained way. | ||
| + | |style="text-align:right;"|וכשנבקש לדקדק אותה נעשה בדרך המבואר [בדקדוקיו]‫<ref>Vatican: בדק</ref> שלפנינו | ||
| + | |- | ||
| + | | | ||
| + | *If We find that the excess of our number over the preceding square is the same as its root, no less and no more, we call our number a "mean number" [<math>\scriptstyle{\color{OliveGreen}{a^2+a}}</math>]. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{b=a}}</math> | ||
| + | |style="text-align:right;"|והנה אם מצאנו העודף ממספרנו על המרובע שעבר שהוא בכגדרו לא פחות ולא יתר נקרא מספרינו ממוצע | ||
| + | |- | ||
| + | | | ||
| + | :If we want to extract the [approximate] root using the preceding square or the next square, it is the same [procedure], only that one procedure is by addition and the other procedure is by subtraction. | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\sqrt{a^2+a}=\sqrt{\left(a+1\right)^2-\left(a+1\right)}}}</math> | ||
| + | |style="text-align:right;"|ואם נרצה נוציא מדת הצלעות מהמרובע שעבר או מהמרובע שעתיד והכל יהיה שוה רק שמעשה האחד בתוספת ומעשה האחר במגרעת | ||
| + | |- | ||
| + | | | ||
| + | *<math>\scriptstyle{\color{OliveGreen}{b<a}}</math> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | ::{{#annot:√5|439|CVSH}}Example of a number, whose excess over the preceding square is less than the root of the square: We wish to know the measure of each side of the square that is five. | ||
| + | ::<math>\scriptstyle\sqrt{5}</math> | ||
| + | |style="text-align:right;"|<big>דמיון</big> במספר שהעודף על המרובע שעבר פחות מגדר המרובע ‫<ref>95v</ref>ההוא<br> | ||
| + | רצינו לדעת מדת כל {{#annot:term|439,1464|45q9}}צלע{{#annotend:45q9}} וצלע ממרובע שהוא חמשה{{#annotend:CVSH}} | ||
| + | |- | ||
| + | | | ||
| + | ::The excess of the preceding square is one. | ||
| + | |style="text-align:right;"|והנה העודף על המרובע שעבר הוא אחד | ||
| + | |- | ||
| + | | | ||
| + | ::We convert it into primes; they are sixty. | ||
| + | |style="text-align:right;"|נשיב אותו ראשונים ויהיו ששים | ||
| + | |- | ||
| + | | | ||
| + | ::We divide them by 4, which is double the root of the preceding square; the result of division is fifteen primes. | ||
| + | |style="text-align:right;"|נחלק אותם על הד' שהם כפל מהגדר מהמרובע שעבר פעמים ויהיה היוצא מהחלוקה חמשה עשר ראשונים | ||
| + | |- | ||
| + | | | ||
| + | ::We add them to the root of the preceding square; we find that the measure of each side [of the square] is approximately two integers and fifteen primes. | ||
| + | ::<math>\scriptstyle{\color{blue}{\sqrt{5}=\sqrt{2^2+1}\approx2+\left(\frac{60\sdot1}{2\sdot2}\right)^\prime=2+\left(\frac{60}{4}\right)^\prime=2+15^\prime}}</math> | ||
| + | |style="text-align:right;"|נוסיפם על הגדר מהמרובע שעבר ונמצא שיהיה מדה אחת לכל הצלעות שנים שלמים וחמשה עשר ראשונים בקרוב | ||
| + | |- | ||
| + | | | ||
| + | ::If we want to correct this root, we multiply the two integers and fifteen primes by themselves; they are five integers plus two hundred and twenty-five seconds, because it has already been explained that the product of primes by primes is seconds. | ||
| + | ::<math>\scriptstyle{\color{blue}{\left(2+15^\prime\right)^2=5+225^{\prime\prime}}}</math> | ||
| + | |style="text-align:right;"|ואם נרצה לדקדק המדה הזאת נכה ונכפול השנים שלימים וחמשה עשר ראשונים על עצמם ויהיו חמשה שלמים ומאתים ועשרים וחמש שניים כי מכפלת הראשונים על ראשונים כבר התבאר שיהיה העולה שניים | ||
| + | |- | ||
| + | | | ||
| + | ::Now, we should see what is the ratio of the excess over the five integers, which is two hundred and twenty-five seconds, to double the [approximate] root we have found; its ratio to it is as the ratio of one to seventy-two. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{\left(5+225^{\prime\prime}\right)-5}{2\sdot\left(2+15^\prime\right)}=\frac{225^{\prime\prime}}{2\sdot\left(2+15^\prime\right)}=\frac{1}{72}}}</math> | ||
| + | |style="text-align:right;"|ועתה יש לנו לראות הנוסף על החמשה שלמים שהוא מאתים ועשרים וחמש שניים איזה ערך הוא מכפלת המדה שמצאנו פעמים והנה ערכם אליה הוא כערך אחד משבעים ושנים | ||
| + | |- | ||
| + | | | ||
| + | ::Therefore, we convert all the fifteen primes we have into seconds; they are nine hundred seconds. | ||
| + | |style="text-align:right;"|ועל כן נשיב החמשה עשר ראשונים שיש לנו כלם שניים ויהיו תשע מאות שניים | ||
| + | |- | ||
| + | | | ||
| + | ::We divide them by seventy-two; we receive twelve from the division, and there are thirty-six seconds left that cannot be divided by seventy-two. | ||
| + | |style="text-align:right;"|ונחלק אותם על שבעים ושנים ותצא לנו החלוקה שנים עשר וישארו שלשים וששה שניים ‫<ref>96r</ref>שלא נתחלקו על השבעים ושנים | ||
| + | |- | ||
| + | | | ||
| + | ::We consider them as a half, which is their part of seventy-two, and this half is thirty thirds. We find that everything is divided by seventy-two; the result is twelve seconds and thirty thirds. | ||
| + | |style="text-align:right;"|ולכן נקח חצי האחד מהם שהיה חלק אחד מהשבעים ושנים ותהיה החצי שלשים שלישיים ונמצא שנחלק הכל על שבעים ושנים והיוצא הוא שנים עשר שניים ושלשים שלישיים | ||
| + | |- | ||
| + | | | ||
| + | ::We subtract them from the nine hundred seconds; eight hundred and eighty-seven seconds remain, plus thirty thirds, which is fourteen primes, forty-seven seconds, and thirty thirds; this root is more accurate than the first and its sign is 2, 14′, 47′′, 30′′′ and they are integers, primes, seconds and thirds. | ||
| + | |style="text-align:right;"|נסיר אותם מהתשע מאות שניים ישארו שמנה מאות ושמנים ושבעה שניים ושלשים [שלישיים שהם ארבעה עשר ראשונים וארבעי' ושבעה שניים ושלשים]‫<ref>marg.</ref> שלישיים וזא<sup>ת</sup> היא המדה {{#annot:term|1614,1388|Grmt}}המדוקדקת{{#annotend:Grmt}} יותר מבראשונה וסימן שלה ב' י"ד מ"ז ל' והנה הם שלמים ראשונים שניים שלישי<sup>י</sup>ם | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | ::<math>\scriptstyle{\color{blue}{\begin{align}\scriptstyle\sqrt{5}&\scriptstyle\approx\left(2+15^\prime\right)-15^\prime\sdot\frac{225^{\prime\prime}}{2\sdot\left(2+15^\prime\right)}=\left(2+15^\prime\right)-\left(15^\prime\sdot\frac{1}{72}\right)=2+900^{\prime\prime}-\left(\frac{900}{72}\right)^{\prime\prime}\\&\scriptstyle=2+900^{\prime\prime}-\left(12+\frac{36}{72}\right)^{\prime\prime}=2+900^{\prime\prime}-\left(12+\frac{1}{2}\right)^{\prime\prime}=2+900^{\prime\prime}-\left(12^{\prime\prime}+30^{\prime\prime\prime}\right)\\&\scriptstyle=2+887^{\prime\prime}+30^{\prime\prime\prime}=2+14^\prime+47^{\prime\prime}+30^{\prime\prime\prime}\\\end{align}}}</math> | ||
| + | |- | ||
| + | | | ||
| + | ::If we want to correct this [approximate] root further, multiply it by itself; you find that the excess over the examined number is 2 primes, [4]8 seconds, 44 thirds, 16 fourths, and 15 fifths. | ||
| + | |style="text-align:right;"|ואם נרצה לדקדק עוד זאת המדה תכה ותכפול אותה בעצמה ותמצא שיהיה העודף על החשבון הנחקר ב' ראשונים ע"ח שניים מ"ד שלישיים י"ו רביעיים ט"ו חמישיים | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | :::<math>\scriptstyle{\color{blue}{\left(2+14^\prime+47^{\prime\prime}+30^{\prime\prime\prime}\right)^2-5=2^\prime+48^{\prime\prime}+44^{\prime\prime\prime}+16^{iv}+15^v}}</math> | ||
| + | |- | ||
| + | | | ||
| + | ::See the ratio of [the square of] this excess to double the [approximate] root and subtract its ratio from the [approximate] root you have, as explained above. The remainder is a more accurate root than the previous roots. | ||
| + | |style="text-align:right;"|ותראה מ<sup>ה</sup> ערך הנוסף הזה אל כפל המדה פעמים וכערכו אליה תסיר מהמדה שיש לך כאשר התבאר למעלה ותהיה הנשאר מדה מדוקדקת מהאחרות הקודמות | ||
| + | |- | ||
| + | | | ||
| + | *<math>\scriptstyle{\color{OliveGreen}{b>a}}</math> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | ::{{#annot:√7|439|313V}}Example of a number, whose excess over the preceding square is greater than its root: We wish to know the measure of the sides of the square that is seven. | ||
| + | ::<math>\scriptstyle\sqrt{7}</math> | ||
| + | |style="text-align:right;"|<big>דמיון</big> במספר שהעודף על המרובע שעבר יתר מגדרו<br> | ||
| + | רצינו לדעת מדת הצלעות ממרובע שהוא שבעה{{#annotend:313V}} | ||
| + | |- | ||
| + | | | ||
| + | ::Since the excess over the preceding square is greater than its root, we see how much is the difference between our number and the next square: the difference is two, because this is the difference between seven and nine, which is the next square. | ||
| + | |style="text-align:right;"|ובאשר העודף על המרובע שעבר יותר מגדרו נראה כמה מרחק יש ממספרינו ‫<ref>96v</ref>ועד המרובע העתיד והנה המרחק הוא שנים כי ככה ירחוק שבעה מתשעה שהוא המרובע העתיד | ||
| + | |- | ||
| + | | | ||
| + | ::We convert it into primes; they are a hundred and twenty. | ||
| + | |style="text-align:right;"|{{#annot:term|1562,1431|N2KM}}נשיבם{{#annotend:N2KM}} ראשונים יהיו מאה ועשרים | ||
| + | |- | ||
| + | | | ||
| + | ::We divide them by double the next square, which is six; we find it twenty times there and they are primes. | ||
| + | |style="text-align:right;"|נחלקם על כפל גדר המרובע העתיד פעמים העולה ששה נמצאם שם עשרים פעמים והם ראשונים | ||
| + | |- | ||
| + | | | ||
| + | ::We subtract them from the root of the next square, which is three; two integers and forty primes remain and this is the root of the examined square approximately | ||
| + | |style="text-align:right;"|נסיר אותם מגדר המרובע העתיד שהוא שלשה וישאר שנים שלמים וארבעים ראשונים וזאת היא מדת צלעות המרובע הנחקר בקרוב | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | ::<math>\scriptstyle{\color{blue}{\sqrt{7}=\sqrt{9-2}=\sqrt{3^2-2}\approx3-\left(\frac{60\sdot2}{2\sdot3}\right)^\prime=3-\left(\frac{120}{6}\right)^\prime=3-20^\prime=2+40^\prime}}</math> | ||
| + | |- | ||
| + | | | ||
| + | ::When you want to correct this root, multiply it by itself. You find that the excess over the examined number is only six primes and forty seconds. | ||
| + | :::<math>\scriptstyle{\color{blue}{\left(2+40^\prime\right)^2-7=6^\prime+40^{\prime\prime}}}</math> | ||
| + | |style="text-align:right;"|וכאשר תרצה לדקדק המדה הזאת ותכנה בכפלה על עצמה תמצא שלא יהיה הנוסף על מספר המרובע הנחקר כי אם ששה ראשונים וארבעים שניים | ||
| + | |- | ||
| + | | | ||
| + | ::Finish the procedure as mentioned above. | ||
| + | |style="text-align:right;"|וגמור את המלאכה האמור למעלה | ||
| + | |- | ||
| + | | | ||
| + | *<math>\scriptstyle{\color{OliveGreen}{b=a}}</math> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | ::{{#annot:√6|439|nS0s}}Example of a number, whose excess over the preceding square is the same as the root of the preceding square: We wish to know the measure of the square that is six. | ||
| + | ::<math>\scriptstyle\sqrt{6}</math> | ||
| + | |style="text-align:right;"|<big>דמיון</big> במספר שהעודף על המרובע שעבר הוא כגדר המרובע ההוא שעבר<br> | ||
| + | רצינו לדעת מדת צלעות מרובע שהוא ששה{{#annotend:nS0s}} | ||
| + | |- | ||
| + | | | ||
| + | ::This square number is mean, so, we can extract the root using the preceding square, if we want, or using the next square; the result is the same, as one procedure is by addition and the other procedure is by subtraction. | ||
| + | ::<math>\scriptstyle{\color{OliveGreen}{\sqrt{a^2+a}=\sqrt{\left(a+1\right)^2-\left(a+1\right)}}}</math> | ||
| + | |style="text-align:right;"|והנה מספר המרובע הזה הוא ממוצע ואם נרצה נוכל להוציא המדה מהמרובע העבר או מהמרובע העתיד והכל יבוא אל כוון אחד כאשר יהיה מעשה האחד בתוספת ומעשה האחד במגרעת | ||
| + | |- | ||
| + | | | ||
| + | ::We extract it first using the preceding square, which is four: the excess is two, which is a hundred and twenty primes. | ||
| + | |style="text-align:right;"|ונוציאנה ‫<ref>97r</ref>בתחלה מהמרובע שעבר [שהוא ארבעה]‫<ref>Vatican om.</ref> והנה העודף שנים שהם מאה ועשרים ראשונים | ||
| + | |- | ||
| + | | | ||
| + | ::We divide them by double the root, which is four, we find it thirty times there and they are thirty primes. | ||
| + | |style="text-align:right;"|נחלקם על כפל הגדר שהוא [ארבעה נמצאם שם שלשים פעמים והם שלשים ראשוני | ||
| + | |- | ||
| + | | | ||
| + | ::We add them to the root, which is two and this is the first approximate root. | ||
| + | |style="text-align:right;"|נוסיפם על הגדר שהוא]‫<ref>Vatican om.</ref> שנים ותהיה זאת המדה הראשונה בקרוב | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | ::<math>\scriptstyle{\color{blue}{\sqrt{6}=\sqrt{4+2}=\sqrt{2^2+2}\approx2+\left(\frac{60\sdot2}{2\sdot2}\right)^\prime=2+\left(\frac{120}{4}\right)^\prime=2+30^\prime}}</math> | ||
| + | |- | ||
| + | | | ||
| + | ::If we extract the root using the next square, which is nine, we do it this way: the difference is three, which is a hundred and eighty primes. | ||
| + | |style="text-align:right;"|ואם נוציא המדה מהמרובע העתיד שהוא תשעה נעשה בדרך זה הנה המרחק שלשה שהם מאה ושמנים ראש<sup>ו</sup>נים | ||
| + | |- | ||
| + | | | ||
| + | ::We divide them by six, which is double the root of the next square, we find it thirty times there, and they are primes. | ||
| + | |style="text-align:right;"|נחלקם על ששה שהוא כפל הגדר המרובע העתיד נמצאנו שם שלשים פעם והם ראשונים | ||
| + | |- | ||
| + | | | ||
| + | ::We subtract them from three, which is the root of the next square; two integers and thirty primes remain, as we found first, when we extracted the root using the preceding square. | ||
| + | |style="text-align:right;"|נסיר אותם משלשה שהם גדר המרובע העתיד וישארו שנים שלמים ושלשים ראשונים <sup>כאשר מצאנו</sup> כאשר מצאנו בתחלה כאשר היינו מוצאים המדה מהמרובע [שעבר]‫<ref>Vatican om.</ref> | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | ::<math>\scriptstyle{\color{blue}{\sqrt{6}=\sqrt{9-3}=\sqrt{3^2-3}\approx3-\left(\frac{60\sdot3}{2\sdot3}\right)^\prime=3-\left(\frac{180}{6}\right)^\prime=3-30^\prime=2+30^\prime}}</math> | ||
| + | |- | ||
| + | | | ||
| + | ::The result is the same, therefore a number like this is called "mean". | ||
| + | |style="text-align:right;"|‫[והכל אחד ועל כן יקרא כל חשבון כזה ממוצע]‫<ref>Vatican om.</ref> | ||
| + | |- | ||
| + | | | ||
| + | ::If you want to correct the root, do as explained previously. | ||
| + | |style="text-align:right;"|ואם תרצה לדקדק המדות תעשה כאשר התבאר לפנים | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | == Chapter Eleven – Here I will Write Nice Rules of Arithmetic Methods for You == | ||
| + | |||
| + | |style="width: 45%; text-align:right;"|<big>השער האחד עשר</big> הנה אכתוב לך בזה כללים נחמדים בדרכי החשבון | ||
| + | |- | ||
| + | !<span style=color:green>Multiplication of a number by itself</span> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | *Know that when you wish to multiply a number by itself, whether that number is units alone, or there are tens with them, or tens alone: | ||
| + | |style="text-align:right;"|ותדע כי כאשר תרצה לכפול חשבון אחד על עצמו בין שיהיה החשבון ההוא אחדים בלבד או שיש עמהם עשרות או עשרות לבדן | ||
| + | |- | ||
| + | | | ||
| + | :*If it is a number that has a third [= divisible by 3], take its third, multiply it by itself, multiply its square by ten, and subtract its square from [the product]; the remainder is the required. | ||
| + | ::<math>\scriptstyle{\color{OliveGreen}{\left(3n\right)^2=\left[10\sdot\left[\frac{1}{3}\sdot\left(3n\right)\right]^2\right]-\left[\frac{1}{3}\sdot\left(3n\right)\right]^2}}</math> | ||
| + | |style="text-align:right;"|אם הוא מספר שיש לו שלישית קח שלישיתו והכה אותה על עצמה וכפול מרובעה עשרה פעמים והסר מהם מרובעה והנשאר הוא ‫<ref>97v</ref>המבוקש | ||
| + | |- | ||
| + | | | ||
| + | ::*Example: we wish to multiply six by six. | ||
| + | :::<math>\scriptstyle6^2</math> | ||
| + | |style="text-align:right;"|<big>דמיון</big> בקשנו לכפול שש על שש | ||
| + | |- | ||
| + | | | ||
| + | :::The third is two and its square is four. | ||
| + | |style="text-align:right;"|הנה השלישית שנים ומרובעו ארבעה | ||
| + | |- | ||
| + | | | ||
| + | :::We multiply is ten times; it is forty. | ||
| + | |style="text-align:right;"|נכפול אותה עשרה פעמים יהיו ארבעים | ||
| + | |- | ||
| + | | | ||
| + | :::We subtract four from it, which is a square of the third; thirty-six remains and this is the product. | ||
| + | |style="text-align:right;"|נסיר מהם ארבעה שהוא מרובע השלישית ישארו <sup>ששה</sup> ושלש<sup>י</sup>ם והוא הנכפל | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | ::<math>\scriptstyle{\color{blue}{6^2=\left(3\sdot2\right)^2=\left[10\sdot\left(\frac{1}{3}\sdot6\right)^2\right]-\left(\frac{1}{3}\sdot6\right)^2=\left(10\sdot2^2\right)-2^2=\left(10\sdot4\right)-4=40-4=36}}</math> | ||
| + | |- | ||
| + | | | ||
| + | :*If the number does not have a third but it exceeds by one over a multiple of three, we subtract [the one] and calculate [the square of] the multiple of three in the method explained, then we add the multiple of three and the number that follows it to our number and the sum is the required. | ||
| + | |style="text-align:right;"|ואם לא היה למספר שלישית אך עודף ממנו שלישיות אחד נסירנו משם ונחשוב המשולש בדרך המבואר ואחר נוסיף על חשבוננו המספר האחרון מהמשולש והמספר שאחריו אשר הסירונו והמחובר הוא המבוקש | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | ::<math>\scriptstyle{\color{OliveGreen}{\left(3n+1\right)^2=\left[\left[10\sdot\left[\frac{1}{3}\sdot\left(3n\right)\right]^2\right]-\left[\frac{1}{3}\sdot\left(3n\right)\right]^2\right]+3n+\left[\left(3n+1\right)\right]}}</math> | ||
| + | |- | ||
| + | | | ||
| + | ::*Example: we wish to multiply ten by itself. | ||
| + | :::<math>\scriptstyle10^2</math> | ||
| + | |style="text-align:right;"|<big>דמיון</big> בקשנו לכפול עשרה על עצמם | ||
| + | |- | ||
| + | | | ||
| + | :::We subtract one from it; nine remains and it is a product of three. | ||
| + | |style="text-align:right;"|נסיר מהם אחד וישארו תשעה והם משלשים | ||
| + | |- | ||
| + | | | ||
| + | :::We take three, which is its third; its square is nine. | ||
| + | |style="text-align:right;"|נקח שלשה שהוא שליש<sup>י</sup>תם והנה מרובעם תשעה | ||
| + | |- | ||
| + | | | ||
| + | :::It product by ten is ninety. | ||
| + | |style="text-align:right;"|וכפלתם עשרה פעמים הם תשעים | ||
| + | |- | ||
| + | | | ||
| + | :::We subtract the square of the third from it; eighty-one remains. | ||
| + | |style="text-align:right;"|ונסיר מהם מרובע השלישית וישארו שמונים ואחד | ||
| + | |- | ||
| + | | | ||
| + | :::We add nine and ten to it; the result is one hundred and this is the product. | ||
| + | |style="text-align:right;"|נוסיף עליהם תשע ועשרה יעלו מאה והוא הנכפל | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | ::<math>\scriptstyle{\color{blue}{\begin{align}\scriptstyle10^2&\scriptstyle=\left(9+1\right)^2=\left[\left(3\sdot3\right)+1\right]^2=\left[\left[10\sdot\left(\frac{1}{3}\sdot9\right)^2\right]-\left(\frac{1}{3}\sdot9\right)^2\right]+9+10=\left[\left(10\sdot3^2\right)-3^2\right]+9+10\\&\scriptstyle=\left[\left(10\sdot9\right)-9\right]+9+10=\left(90-9\right)+9+10=81+9+10=100\\\end{align}}}</math> | ||
| + | |- | ||
| + | | | ||
| + | :*If the number is one less than a multiple of three, we add [the one] and calculate [the square of the multiple of three] according to the rule, then we subtract [the multiple of three and] the number that precedes it from [the result] and the remainder is the required. | ||
| + | |style="text-align:right;"|ואם היה המספר פחות משלישיות אחד הוסיפנו עליו ו{{#annot:term|229,1269|0uI3}}נחשוב{{#annotend:0uI3}} אותו כמשפט ואחר נסיר ממנו החשבון שהוספנו עליו החשבון האחרון שלו והנשאר הוא המבוקש | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | ::<math>\scriptstyle{\color{OliveGreen}{\left(3n-1\right)^2=\left[\left[10\sdot\left[\frac{1}{3}\sdot\left(3n\right)\right]^2\right]-\left[\frac{1}{3}\sdot\left(3n\right)\right]^2\right]-\left(3n\right)-\left[\left(3n-1\right)\right]}}</math> | ||
| + | |- | ||
| + | | | ||
| + | ::*We wish to multiply eleven by itself. | ||
| + | :::<math>\scriptstyle11^2</math> | ||
| + | |style="text-align:right;"|<big>דמיון</big> בקשנו [לכפול]‫<ref>Vatican om.</ref> אחד עשר על עצמם | ||
| + | |- | ||
| + | | | ||
| + | :::We add one to it; it is twelve. | ||
| + | |style="text-align:right;"|‫<ref>98r</ref>נוסיף עליהם אחד ויהיו שנים עשר | ||
| + | |- | ||
| + | | | ||
| + | :::We calculate it by taking the third; its square is sixteen. | ||
| + | |style="text-align:right;"|{{#annot:term|229,1269|c5VF}}נחשבם{{#annotend:c5VF}} בדרך לקיחת השלישית והנה מרובעה ששה עשר | ||
| + | |- | ||
| + | | | ||
| + | :::Its product by ten is one hundred and sixty. | ||
| + | |style="text-align:right;"|וכפלתם בעשרה מאה וששים | ||
| + | |- | ||
| + | | | ||
| + | :::We subtract sixteen from it, which is the square of the third; one hundred and forty-four remains. | ||
| + | |style="text-align:right;"|נסיר מהם ששה עשר שהם מרובע השלישית ישארו מאה וארבעים וארבעה | ||
| + | |- | ||
| + | | | ||
| + | :::We subtract from it eleven and twelve, which are twenty-three; one hundred and twenty-one remains and this is the product. | ||
| + | |style="text-align:right;"|נסיר מהם אחד עשר ושנים עשר העולים עשרים ושלשה ישארו מאה ועשרים ואחד והוא הנכפל | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | ::<math>\scriptstyle{\color{blue}{\begin{align}\scriptstyle11^2&\scriptstyle=\left(12-1\right)^2=\left[\left(3\sdot4\right)-1\right]^2=\left[\left[10\sdot\left(\frac{1}{3}\sdot12\right)^2\right]-\left(\frac{1}{3}\sdot12\right)^2\right]-11-12\\&\scriptstyle=\left[\left(10\sdot4^2\right)-4^2\right]-11-12=\left[\left(10\sdot16\right)-16\right]-11-12\\&\scriptstyle=\left(160-16\right)-11-12=144-12-11=144-23=121\\\end{align}}}</math> | ||
| + | |- | ||
| + | !<span style=color:green>Multiplication of units and tens by units and tens</span> | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\left(10+a\right)\times\left(10+b\right)=\left[10\sdot\left[\left(10+a\right)+b\right]\right]+\left(a\sdot b\right)}}</math> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | ::*Another example: to know the product of eleven by eleven. | ||
| + | :::<math>\scriptstyle11\times11</math> | ||
| + | |style="text-align:right;"|<big>דמיון אחרת</big> לדעת כפלת האחד עשר על אחד עשר | ||
| + | |- | ||
| + | | | ||
| + | :::We consider this number as if it were written in two lines. | ||
| + | |style="text-align:right;"|הנה נחשוב שהמספר הזה נכתב בשני טורים | ||
| + | |- | ||
| + | | | ||
| + | :::We take the one of one line and add it to the other line; it is twelve. | ||
| + | |style="text-align:right;"|ונקח האחד מן הטור האחת ונחברם אל הטור האחרת ויהיו שנים עשר | ||
| + | |- | ||
| + | | | ||
| + | :::We multiply it by the remaining ten; it is a hundred and twenty. | ||
| + | |style="text-align:right;"|<sup>נ</sup>כפלם על העשרה הנשארים יהיו מאה ועשרים | ||
| + | |- | ||
| + | | | ||
| + | :::We add to it the product of the units by themselves; it is a hundred and twenty-one and this is the product. | ||
| + | |style="text-align:right;"|נוסיף עליהם הכאת האחדים על עצמם ויהיו מאה ועשרים ואחד והוא הנכפל | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | ::<math>\scriptstyle{\color{blue}{11\times11=\left[\left(11-1\right)\sdot\left(11+1\right)\right]+\left(1\sdot1\right)=\left(10\sdot12\right)+1=120+1=121}}</math> | ||
| + | |- | ||
| + | | | ||
| + | ::*Likewise if we wish to multiply fifteen by twelve. | ||
| + | :::<math>\scriptstyle15\times12</math> | ||
| + | |style="text-align:right;"|וככה אם נבקש לכפול חמשה עשר בשנים עשר | ||
| + | |- | ||
| + | | | ||
| + | :::We take the two and add it to fifteen; it is seventeen. | ||
| + | |style="text-align:right;"|נקח השנים ונשים אותם על החמשה עשר ויהיו שבעה עשר | ||
| + | |- | ||
| + | | | ||
| + | :::We multiply it by the remaining ten; it is a hundred and seventy. | ||
| + | |style="text-align:right;"|נכפלם על העשרה הנשארים יהיו מאה ושבעים | ||
| + | |- | ||
| + | | | ||
| + | :::We multiply the other two by five; it is ten. | ||
| + | |style="text-align:right;"|ונכה השנים האחרים על החמשה ויהיו עשרה | ||
| + | |- | ||
| + | | | ||
| + | :::We add it to a hundred and seventy; the product is a hundred and eighty. | ||
| + | |style="text-align:right;"|נחברם עם המאה ושבעים יהיה הנכפל מאה ושמנים | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | ::<math>\scriptstyle{\color{blue}{15\times12=\left[\left(12-2\right)\sdot\left(15+2\right)\right]+\left(2\sdot5\right)=\left(10\sdot17\right)+10=170+10=180}}</math> | ||
| + | |- | ||
| + | | | ||
| + | === <span style=color:green>Word Problems</span> === | ||
| + | |||
| + | | | ||
| + | |- | ||
| + | |Now, I shall start discussing and mentioning some of the difficult problems, extracting their solutions, and explaining each one of them at length. | ||
| + | |style="text-align:right;"|ועתה אתחיל לדבר ואזכיר קצת מהשאלות הקשות ‫<ref>98v</ref>ולהוציא תשובתן אאריך [הביאור]‫<ref>Vatican: וביאור</ref> כל אחת מהם | ||
| + | |- | ||
| + | !<span style=color:green>Find a Number Problem - Sums</span> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | *{{#annot:1-20|669|2heg}}Question: we summed all the successive numbers from one to twenty and it is the sum. How much is the sum? | ||
| + | :<math>\scriptstyle\sum_{i=1}^{20} i</math> | ||
| + | |style="text-align:right;"|<big>שאלה</big> חברנו כל {{#annot:term|2576,1835|ETrE}}המספרים הרצופים{{#annotend:ETrE}} מאחד עד עשרים והם הכלל כמה המחובר{{#annotend:2heg}} | ||
| + | |- | ||
| + | | | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\sum_{i=1}^n i=\left(n+1\right)\sdot\left(\frac{1}{2}\sdot n\right)}}</math> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | :We add one to the twenty and multiply [the result] by ten, which is half twenty; the product is two hundred and ten, and this is the required. | ||
| + | :<math>\scriptstyle{\color{blue}{\sum_{i=1}^{20} i=\left(20+1\right)\sdot\left(\frac{1}{2}\sdot20\right)=21\sdot10=210}}</math> | ||
| + | |style="text-align:right;"|הנה נוסיף על העשרים אחד ונכפלם [על]‫<ref>marg.</ref> עשרה שהוא חצי עשרים ויהי<sup>ה</sup> הנכפל מאתים ועשרה וככה המבוקש | ||
| + | |- | ||
| + | | | ||
| + | *{{#annot:1-11|669|pHD6}}If we want to know how much are the numbers summed up up to eleven. | ||
| + | :<math>\scriptstyle\sum_{i=1}^{11} i</math> | ||
| + | |style="text-align:right;"|ואם נרצה לדעת כמה עולים {{#annot:term|787,1220|my36}}המספרים המחוברים{{#annotend:my36}} על אחד עשר{{#annotend:pHD6}} | ||
| + | |- | ||
| + | | | ||
| + | :We add one to [the eleven] and multiply [the result] by half the eleven, which is five and a half; the product is sixty-six, and this is the sum. | ||
| + | :<math>\scriptstyle{\color{blue}{\sum_{i=1}^{11} i=\left(11+1\right)\sdot\left(\frac{1}{2}\sdot11\right)=12\sdot\left(5+\frac{1}{2}\right)=66}}</math> | ||
| + | |style="text-align:right;"|נוסיף עליו אחד יהיו שנים עשר נכפלם על חצי האחד עשר שהם חמשה וחצי ויהיה הנכפל ששים וששה וככה המחובר | ||
| + | |- | ||
| + | | | ||
| + | :There are other ways, but what I have wrote is the easiest and the most correct [way]. | ||
| + | |style="text-align:right;"|ויש [דרכים]‫<ref>Vatican: דמים</ref> אחרים ומה שכתבתי הוא היותר קל ונכון | ||
| + | |- | ||
| + | | | ||
| + | *{{#annot:aₙ, 1, 210|669|Xl23}}Reverse question: the sum of the successive numbers starting from one is 210. What is the last number of the summed [numbers]? | ||
| + | :<math>\scriptstyle\sum_{i=1}^{n} i=210</math> | ||
| + | |style="text-align:right;"|<big>נהפוך השאלה</big> ונאמר עלה המחובר ממספרים {{#annot:term|2576,1835|h4eV}}רצופים{{#annotend:h4eV}} המתחילים מאחד מאתים ועשרה<br> | ||
| + | איזה הוא המספר האחרון מהמחוברים{{#annotend:Xl23}} | ||
| + | |- | ||
| + | | | ||
| + | :<math>\scriptstyle{\color{OliveGreen}{\sum_{i=1}^{n} i=a\longrightarrow n^2+n=2a}}</math> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | ::We do as follows: we double two hundred and ten; it is four hundred and twenty. | ||
| + | |style="text-align:right;"|נעשה בדרך זה נכפול מאתים ועשרה פעמים ויהיו ארבע <sup>מאות</sup> ועשרים | ||
| + | |- | ||
| + | | | ||
| + | ::We take the closest root, whose extraction method was explained in chapter seven; we find that it is twenty and this is the last number of the summed numbers. | ||
| + | ::<math>\scriptstyle{\color{blue}{n^2+n=2\sdot210=420=20^2+20\longrightarrow n=20}}</math> | ||
| + | |style="text-align:right;"|נקח מהם הגדר היותר קרוב כאשר התבאר דרך לקיחתו בשער השביעי והנה נמצא שהוא עשרים והוא המספר האחרון מה{{#annot:term|787,1220|hrzp}}מחוברים{{#annotend:hrzp}} | ||
| + | |- | ||
| + | | | ||
| + | ::Thus, what remains from the number that has no root is twenty, as the number of the root. | ||
| + | |style="text-align:right;"|והנה נשאר מהמספר שהוא בלתי נגדר עשרים ‫<ref>99r</ref>כמספר הגדר | ||
| + | |- | ||
| + | | | ||
| + | :So should be in all the calculations that are similar to it and if not, then the one who asked has mistaken in his question, when he summed the numbers he made a mistake without a doubt. | ||
| + | |style="text-align:right;"|וכן ראוי שיהיה בכל החשבונות הדומים לזה ואם אין טעה השואל בשאלתו וכאשר חבר המספרים עשה בטעות בלי ספק | ||
| + | |- | ||
| + | !<span style=color:green>Triangulation Problem - Cane</span> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | *{{#annot:cane|655|q1uH}}Question: a cane 5 cubits tall, is standing next to a wall of the same height. | ||
| + | :If we lower its [top] two cubits down from the top of the wall, so that it will stand on a slope, how far will be the bottom end of the cane from the foot of the wall? | ||
| + | |style="text-align:right;"|<big>שאלה</big> [קנה]‫<ref>Vatican: הנה</ref> <sup>ה</sup>מדה ארוכה חמש אמות ועומדת זקופה בכותל אחת גבוה כמדתה<br> | ||
| + | אם [נשפיל]‫<ref>Vatican: השפל</ref> אותה מראש הכותל אמתיים כדי שתעמוד בשפוע כמה הרחיק ראש הקנה התחתון מיסוד הכותל{{#annotend:q1uH}} | ||
| + | |- | ||
| + | | | ||
| + | ::We do like this: we take the square of the five cubits; it is twenty-five. | ||
| + | |style="text-align:right;"|נעשה זאת נקח מרובע החמש אמות והם עשרים וחמש | ||
| + | |- | ||
| + | | | ||
| + | ::We take also the square of the three cubits that are left from there to the foot of the wall; it is nine. | ||
| + | |style="text-align:right;"|ונקח גם כן מרובע הג' אמות הנשארות משם ועד יסוד הכ<sup>ו</sup>תל והנה הוא ט‫' | ||
| + | |- | ||
| + | | | ||
| + | ::Its difference from twenty-five is sixteen. | ||
| + | |style="text-align:right;"|ומרחקו מעשרים וחמש ששה עשר | ||
| + | |- | ||
| + | | | ||
| + | ::The root of sixteen is four and so is the distance of the bottom end of the cane from the foot of the wall no more and no less. | ||
| + | |style="text-align:right;"|וגדר ששה עשר הוא ארבעה וככה מרחק ראש הקנה התחתון מיסוד הכותל בלתי תוספת ומגרעת | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | ::<math>\scriptstyle{\color{blue}{x=\sqrt{5^2-\left(5-2\right)^2}=\sqrt{5^2-3^2}=\sqrt{25-9}=\sqrt{16}=4}}</math> | ||
| + | |- | ||
| + | | | ||
| + | :If the difference between a square and a square is an inexpressible number, take its root approximately, as was explained in the preceding chapter, and this will be the measure of the distance from the bottom end of the cane to the foot of the wall. | ||
| + | |style="text-align:right;"|ואם היה החסרון <sup>מ</sup>מרובע אל מרובע מספר חרש ואלם תקח גדרו בקרוב כאשר התבאר בשער הקדום לזה וככה יהיה מדת מרחק מראש הקנה התחתון אל היסוד הכותל | ||
| + | |- | ||
| + | !<span style=color:green>Divide a Quantity Problem - Simple division</span> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | *{{#annot:WP|644|O1gy}}Question: I gave a messenger 30 dinar and one pašuṭ and ordered him to hire workers as much as his money allows, so that the payment of the one equals the payment of his friend, there will be no worker whose payment is one pašuṭ, and there will be no fractions in one's payment. | ||
| + | :We want to know how many workers he could hire. | ||
| + | :<math>\scriptstyle X^2=\left(12\sdot30\right)+1</math> | ||
| + | |style="text-align:right;"|<big>שאלה</big> נתתי לשלוחי שלש<sup>י</sup>ם דנרים ופשוט וצותי אותו שישכור פועלים כאשר יספיקו לו מעותיו ויהיה שכר האחד כשכר חברו ולא יהיה בהם ‫<ref>99v</ref>פועל ששכרו פשוט וגם לא יהיה בשכרו שום שברי שלם<br> | ||
| + | נרצה לדעת כמה פועלים יוכל לשכור{{#annotend:O1gy}} | ||
| + | |- | ||
| + | | | ||
| + | ::We convert all the dinar into pešuṭim and add the additional pašuṭ to them; they are three hundred and sixty-one pešuṭim. | ||
| + | |style="text-align:right;"|הנה {{#annot:term|1553,1431|NmWX}}נשיב{{#annotend:NmWX}} הדינרים כלם פשוטים ונחבר אליהם הפשוט הנוסף עליהם ויהיו שלש מאות וששים ואחד פשוטים | ||
| + | |- | ||
| + | | | ||
| + | ::We extract their root as the method of chapter seven; we find that it is nineteen. | ||
| + | ::<math>\scriptstyle{\color{blue}{X=\sqrt{\left(12\sdot30\right)+1}=\sqrt{361}=19}}</math> | ||
| + | |style="text-align:right;"|נקח גדרם בדרך השער השביעי ונמצא שהוא תשעה עשר | ||
| + | |- | ||
| + | | | ||
| + | ::We can answer that the messenger can hire nineteen workers at nineteen pešuṭim each no more and no less. | ||
| + | |style="text-align:right;"|ונוכל להשיב שיוכל לשכור השליח תשעה עשר פועלים ושכר כל אחד ואחד תשעה עשר פשוטים לא פחות ולא יתר | ||
| + | |- | ||
| + | !<span style=color:green>How much Problem - Wall</span> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | *{{#annot:WP|648|nyVk}}Question: a wall collapsed. It is rebuild with an extension, so that it will be higher than what it was by half the size it had at the beginning, and its sixth, and ninth. With the whole extension, its height was 50 cubits. How much was its original height? | ||
| + | :<math>\scriptstyle X+\frac{1}{2}X+\frac{1}{6}X+\frac{1}{9}X=50</math> | ||
| + | |style="text-align:right;"|<big>שאלה</big> חומה שנפלה והוספו עליה בבנין כדי שתהיה גבוה הרבה חצי מדתה מאשר היתה בתחלה וששיתה ותשיעתה עם כל זה והיתה מדת גבהה חמשים אמה כמה היתה מדתה בראשונה{{#annotend:nyVk}} | ||
| + | |- | ||
| + | | | ||
| + | ::<span style=color:green>'''False Position:'''</span> We take a denominator that has a half, a sixth, and a ninth. That is, we take two, since the half is derived from it, multiply it by six, for the sixth that is derived from it; the result is twelve. We multiply it also by nine for the ninth; the denominator is one hundred and eight. | ||
| + | ::<math>\scriptstyle{\color{blue}{2\sdot6\sdot9=12\sdot9=108}}</math> | ||
| + | |style="text-align:right;"|נקח מדומה שיהיה לו חצי וששית ותשיעית והוא שנקח שנים בעבור אשר יצאה מהם החצי ונכפול אותם בששה בעבור הששית אשר תצא מהם ויהיו שנים עשר ונכפול גם הם בתשעה בעבור התשיעית ויהיה המדומה מאה ושמנה | ||
| + | |- | ||
| + | | | ||
| + | ::*Its half is fifty-four. <math>\scriptstyle{\color{blue}{\frac{1}{2}\sdot108=54}}</math> | ||
| + | |style="text-align:right;"|ומחציתו חמשים וארבעה | ||
| + | |- | ||
| + | | | ||
| + | ::*Its sixth is eighteen. <math>\scriptstyle{\color{blue}{\frac{1}{6}\sdot108=18}}</math> | ||
| + | |style="text-align:right;"|וששיתו שמנה עשר | ||
| + | |- | ||
| + | | | ||
| + | ::*Its ninth is twelve. <math>\scriptstyle{\color{blue}{\frac{1}{9}\sdot108=12}}</math> | ||
| + | |style="text-align:right;"|ותשיעתו שנים ‫<ref>100r</ref>עשר | ||
| + | |- | ||
| + | | | ||
| + | ::The sum of all these parts is eighty-four. <math>\scriptstyle{\color{blue}{54+18+12=84}}</math> | ||
| + | |style="text-align:right;"|והמחובר מכל החלקים האלה עולה שמונים וארבעה | ||
| + | |- | ||
| + | | | ||
| + | ::We add it to the denominator; it is one hundred and ninety-two. | ||
| + | ::<math>\scriptstyle{\color{blue}{108+84=192}}</math> | ||
| + | |style="text-align:right;"|נוסיפם אל המדומה ויהיו מאה ותשעים ושנים | ||
| + | |- | ||
| + | | | ||
| + | ::<span style=color:green>'''Rule of Three:'''</span> So we take the ratio and say: as the ratio of a hundred and eight, which is the denominator, to a hundred and ninety-two, which results from adding all the mentioned parts to it, so is the ratio of the unknown original measure of the wall to fifty, which is the height now, after the extension of the construction. | ||
| + | ::<math>\scriptstyle{\color{blue}{108:192=X:50}}</math> | ||
| + | |style="text-align:right;"|והנה נעשה בדרך הערכין ונעריך ונאמר כערך מאה ושמנה שהוא המדומה אל מאה ותשעים ושנים שהוא העולה מתוספת החלקים הנזכרים עליו כן ערך מדת החומה אשר היתה בראשונה הנעלמת ממנו אל חמשים שהיא גבוהה עתה אחר התוספת בבנין | ||
| + | |- | ||
| + | | | ||
| + | ::When we multiply the first number by the fourth, it is five thousand and four hundred. | ||
| + | |style="text-align:right;"|וכאשר נכפול המספר הראשון על הרביעי יהיו חמשת אלפים וארבע מאות | ||
| + | |- | ||
| + | | | ||
| + | ::We divide it by the known mean, which is one hundred and ninety-two; we find it twenty-eight times in it and four parts remain that cannot be divided, which are parts of the one hundred and ninety-two by which we divided. | ||
| + | |style="text-align:right;"|נחלקם על האמצע הנודע שהוא מאה ותשעים ושנים נמצאנו שם שמנה ועשרים פעמים וישארו מהם עשרים וארבעה חלקים שלא נתחלקו והמה חלקים ממאה ותשעים ושנים בשלם אשר חלקנו עליו | ||
| + | |- | ||
| + | | | ||
| + | ::Therefore, we can answer that the measure of the height of the wall originally was twenty-eight cubits and four parts of one hundred and ninety-two in a cubit. | ||
| + | ::<math>\scriptstyle{\color{blue}{X=\frac{108\sdot50}{192}=\frac{5400}{192}=28+\frac{24}{192}}}</math> | ||
| + | |style="text-align:right;"|ועל כן נוכל להשיב כי מדת גבהות החומה בראשונה היתה שמונה ועשרים אמות ועשרים וארבעה חלקים ממאה ותשעים ושנים באמה | ||
| + | |- | ||
| + | | | ||
| + | :<span style=color:green>'''Check:'''</span> We examine if it is true in this way: | ||
| + | |style="text-align:right;"|ונבחן זה אם הוא אמת בדרך זאת | ||
| + | |- | ||
| + | | | ||
| + | ::We decompose all the cubits and convert each into the mentioned parts, then add the result to the twenty-four parts added to the cubits; the sum is five thousand and four hundred. | ||
| + | ::<math>\scriptstyle{\color{blue}{\left(28\sdot192\right)+24=5400}}</math> | ||
| + | |style="text-align:right;"|{{#annot:term|1562,1559|6FfN}}נתיך{{#annotend:6FfN}} כל האמות ונעשה מכל האחת ואחת החלקים הנזכרים ונחבר העולה אל עשרים וארבע החלקים העודפים על ‫<ref>100v</ref>האמות ויהיה המחובר חמשת אלפים וארבע מאות | ||
| + | |- | ||
| + | | | ||
| + | ::*Its half is two thousand and seven hundred. | ||
| + | :::<math>\scriptstyle{\color{blue}{\frac{1}{2}\sdot5400=2700}}</math> | ||
| + | |style="text-align:right;"|מחציתם אלפים ושבע מאות | ||
| + | |- | ||
| + | | | ||
| + | ::*Its sixth is nine hundred. | ||
| + | :::<math>\scriptstyle{\color{blue}{\frac{1}{6}\sdot5400=900}}</math> | ||
| + | |style="text-align:right;"|ששיתם תשע מאות | ||
| + | |- | ||
| + | | | ||
| + | ::*Its ninth is six hundred. | ||
| + | :::<math>\scriptstyle{\color{blue}{\frac{1}{9}\sdot5400=600}}</math> | ||
| + | |style="text-align:right;"|תשיעיתם שש מאות | ||
| + | |- | ||
| + | | | ||
| + | ::The sum is four thousand and two hundred. <math>\scriptstyle{\color{blue}{2700+900+600=4200}}</math> | ||
| + | |style="text-align:right;"|המחובר ארבעת אלפים ומאתים | ||
| + | |- | ||
| + | | | ||
| + | ::We add it to the five thousand and four hundred; it is nine thousand and six hundred. | ||
| + | ::<math>\scriptstyle{\color{blue}{5400+4200=9600}}</math> | ||
| + | |style="text-align:right;"|נוסיף זה על החמשת אלפים וארבע המאות ויהיו כתשע אלפים ושש מאות | ||
| + | |- | ||
| + | | | ||
| + | ::If you divide it by the number of parts of the whole cubit, you find it is fifty times there, as the number of cubits of the height of the wall now, after the extension of the construction. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{9600}{192}=50}}</math> | ||
| + | |style="text-align:right;"|ואם תחלקם על מספר חלקי האמה <s>גובה</s> השלמה תמצאנו שם חמשים פעמים כמכסת אמות גובה הח<sup>ו</sup>מה עתה אחרי תוספת הבנין | ||
| + | |- | ||
| + | | | ||
| + | *{{#annot:WP|648|V9HY}}Question: the town wall was 100 cubits high. Its third and its quarter had collapsed. | ||
| + | :How high is what remains? | ||
| + | :<math>\scriptstyle X=100-\left[\left(\frac{1}{3}\sdot100\right)+\left(\frac{1}{4}\sdot100\right)\right]</math> | ||
| + | |style="text-align:right;"|<big>שאלה</big> חומת העיר גבוה מאה אמה ונפרצו ממנה שלישיתה ורביעיתה<br> | ||
| + | כמה גובה הנשאר{{#annotend:V9HY}} | ||
| + | |- | ||
| + | | | ||
| + | ::<span style=color:green>'''False Position:'''</span> The denominator that has a third and a quarter is twelve. | ||
| + | |style="text-align:right;"|הנה המדומה שיש לו שלישית ורביעית הוא שנים עשר | ||
| + | |- | ||
| + | | | ||
| + | ::We take the mentioned parts from it and sum them up; it is seven. We subtract it from the denominator; five remain. | ||
| + | ::<math>\scriptstyle{\color{blue}{12-\left[\left(\frac{1}{3}\sdot12\right)+\left(\frac{1}{4}\sdot12\right)\right]=12-7=5}}</math> | ||
| + | |style="text-align:right;"|נקח ממנו החלקים הנזכרים ונחברם יהיו שבעה נסירם מהמדומה ישארו חמשה | ||
| + | |- | ||
| + | | | ||
| + | ::<span style=color:green>'''Rule of Three:'''</span> Now, we take the ratio and say: as the ratio of five to twelve so is the ratio of the unknown to one hundred. | ||
| + | ::<math>\scriptstyle{\color{blue}{5:12=X:100}}</math> | ||
| + | |style="text-align:right;"|ועתה נעריך ונאמר כערך חמשה אל שנים עשר כך ערך הנעלם אל מאה | ||
| + | |- | ||
| + | | | ||
| + | ::We multiply the first number by the fourth; it is five hundred. | ||
| + | ::<math>\scriptstyle{\color{blue}{X=\frac{5\sdot100}{12}=\frac{500}{12}=41+\frac{8}{12}=41+\frac{2}{3}}}</math> | ||
| + | |style="text-align:right;"|כפלנו החשבון הראשון על הרביעי ויהיו חמש מאות | ||
| + | |- | ||
| + | | | ||
| + | ::We divide it by the known mean; we find it forty-one times there and eight remain that cannot be divided, which are parts of twelve. So, the height of what remains is forty-one cubits and eight parts of twelve in a cubit, which are two-thirds. | ||
| + | |style="text-align:right;"|נחלקם על האמצעי הנודע נמצאנו שם ארבעים ואחד פעמים ונשארו מהם שמונה שלא נחלקו שהם חלקים משנים עשר וככה הוא גובה הנשאר ארבעים ואחת אמה ושמנה ‫<ref>101r</ref>חלקים משנים עשר באמה שהם שני שלישיות | ||
| + | |- | ||
| + | | | ||
| + | :<span style=color:green>'''Check:'''</span> When we examine it: | ||
| + | |style="text-align:right;"|וכאשר נבחן זה | ||
| + | |- | ||
| + | | | ||
| + | ::We convert the cubits into parts of twelve each; they are one thousand and two hundred. | ||
| + | ::<math>\scriptstyle{\color{blue}{100=\frac{1200}{12}}}</math> | ||
| + | |style="text-align:right;"|ונעשה מהאמה אמות אשר היו שם בראשונה חלקים משנים עשר מכל אחת ואחת יהיו אלף ומאתים | ||
| + | |- | ||
| + | | | ||
| + | ::*We take their third; it is four hundred. | ||
| + | :::<math>\scriptstyle{\color{blue}{\frac{1}{3}\sdot1200=400}}</math> | ||
| + | |style="text-align:right;"|נקח שלישיתם שהם ארבע מאות | ||
| + | |- | ||
| + | | | ||
| + | ::*And their quarter, which is three hundred. | ||
| + | :::<math>\scriptstyle{\color{blue}{\frac{1}{4}\sdot1200=300}}</math> | ||
| + | |style="text-align:right;"|ורביעיתם שהם שלש מאות | ||
| + | |- | ||
| + | | | ||
| + | ::The resulting sum is seven hundred. | ||
| + | ::<math>\scriptstyle{\color{blue}{400+300=700}}</math> | ||
| + | |style="text-align:right;"|והמחובר עולה שבע מאות | ||
| + | |- | ||
| + | | | ||
| + | ::We subtract it from one thousand and two hundred; five hundred remain, which are forty-one cubits and eight parts of twelve, as we stated. | ||
| + | ::<math>\scriptstyle{\color{blue}{1200=700=500}}</math> | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{500}{12}=41+\frac{8}{12}}}</math> | ||
| + | |style="text-align:right;"|נסיר אותם מהאלף ומאתים ישארו חמש מאות שהם ארבעים ואחת אמה ושמנה חלקים משנים עשר כאשר זכרנו | ||
| + | |- | ||
| + | !<span style=color:green>First from last Problem - Amount of grain</span> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | *{{#annot:WP|651|mKSQ}}Question: the landlord harvested his grain and gave a great heave offering by law from [what he collected] at first. | ||
| + | :Afterwards he gave the first tithe from what remained and from what remained then, he gave a second tithe, and he was left with 40 measures of grain. | ||
| + | :How much was the grain at first? | ||
| + | |style="text-align:right;"|<big>שאלה</big> בעל הבית שאסף תבואתו ותרם ממנו בתחלה תרומה גדולה כמשפט ואחרי כן הפריש מהנשאר מעשר ראשון ומהנשאר אחרי זאת הפריש מעשר שני ונשארו לו חמישים מדות חטה<br> | ||
| + | כמה היה הכרי בתחלה{{#annotend:mKSQ}} | ||
| + | |- | ||
| + | | colspan="2"| | ||
| + | :<math>\scriptstyle\left(X-\frac{2}{100}X\right)-\left[\frac{1}{10}\sdot\left(X-\frac{2}{100} X\right)\right]-\left[\frac{1}{10}\sdot\left[\left(X-\frac{2}{100}X\right)-\left[\frac{1}{10}\sdot\left(X-\frac{2}{100} X\right)\right]\right]\right]=50</math> | ||
| + | |- | ||
| + | | | ||
| + | ::It is known that our late rabbis said that the offering is half a hundred, which is one part of fifty. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{1}{2}\sdot100=50}}</math> | ||
| + | |style="text-align:right;"|ידוע כי התרומה אמרו רבותינו ז"ל שהיא תרי ממאה שהיא חלק אחד מהחמשים | ||
| + | |- | ||
| + | | | ||
| + | ::Therefore, we take the fifty and multiply it by ten for the first tithe that is subtracted from it; it is five hundred. | ||
| + | ::<math>\scriptstyle{\color{blue}{50\sdot10=500}}</math> | ||
| + | |style="text-align:right;"|על כן נקח חמשים ונכפלם בעשר בעבור המעשר ראשון היוצא ממנו ויהיו חמש מאות | ||
| + | |- | ||
| + | | | ||
| + | ::<span style=color:green>'''False Position:'''</span> We multiply it also by ten, for the second tithe; it is five thousand and it is the denominator. | ||
| + | ::<math>\scriptstyle{\color{blue}{500\sdot10=5000}}</math> | ||
| + | |style="text-align:right;"|ונכפול גם הם בעשר בעבור המעשר שני ויהיה חמשת אלפים והוא המדומה | ||
| + | |- | ||
| + | | | ||
| + | ::Hence, his offering is one hundred. | ||
| + | |style="text-align:right;"|והנה תרומתו מאה | ||
| + | |- | ||
| + | | | ||
| + | ::We subtract it; four thousand and nine hundred remain. | ||
| + | ::<math>\scriptstyle{\color{blue}{5000-100=4900}}</math> | ||
| + | |style="text-align:right;"|נסירנה ממנו ישארו ארבעת אלפים ‫<ref>101v</ref>ותשע מאות | ||
| + | |- | ||
| + | | | ||
| + | ::Its tithe is four hundred and ninety. | ||
| + | |style="text-align:right;"|מעשר שלהם ארבע מאות ותשעים | ||
| + | |- | ||
| + | | | ||
| + | ::We subtract it; four thousand four hundred and ten remain. | ||
| + | ::<math>\scriptstyle{\color{blue}{4900-\left(\frac{1}{10}\sdot4900\right)=4900-490=4410}}</math> | ||
| + | |style="text-align:right;"|נסיר אותו מהם ישארו ארבעת אלפים וארבע מאות ועשרה | ||
| + | |- | ||
| + | | | ||
| + | ::Its tithe is four hundred and forty-one | ||
| + | |style="text-align:right;"|מעשר שלהם ארבע מאות וארבעים ואחד | ||
| + | |- | ||
| + | | | ||
| + | ::We subtract it; three thousand nine hundred and sixty-nine remain. | ||
| + | ::<math>\scriptstyle{\color{blue}{4410-\left(\frac{1}{10}\sdot4410\right)=4410-441=3969}}</math> | ||
| + | |style="text-align:right;"|נסיר אותו מהם ישארו שלשת אלפים ותשע מאות [וששים ותשעה]‫<ref>Vatican: ותשעים וששה</ref> | ||
| + | |- | ||
| + | | | ||
| + | ::<span style=color:green>'''Rule of Three:'''</span> Now, we take the ratio and say: as the ratio of three thousand, nine hundred, and sixty-nine to five thousand so is the ratio of fifty to the unknown. | ||
| + | ::<math>\scriptstyle{\color{blue}{3969:5000=50:X}}</math> | ||
| + | |style="text-align:right;"|ועתה נעריך ונאמר כערך שלשת אלפים ותשע מאות ושש<sup>י</sup>ם ותשעה אל חמשת אלפים כן ערך חמשים אל הנעלם | ||
|- | |- | ||
| | | | ||
| − | ::We | + | ::We multiply the means; the result is two hundred and fifty thousand. |
| − | + | |style="text-align:right;"|כפלנו האמצעיים עלו מאתים וחמשים אלף | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | :: | + | ::We divide it by the first known number; we find it sixty-two times there, and three thousand nine hundred and twenty-two remained that cannot be divided, which are parts of three thousand nine hundred and sixty-nine by which we divided; and this was the amount of measures of grain that was at first, when the landlord began to give offering. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{X=\frac{50\sdot5000}{3969}=\frac{250000}{3969}=62+\frac{3922}{3969}}}</math> |
| + | |style="text-align:right;"|נחלקם על החשבון הראשון הנודע נמצאנו שם ששים ושתים פעמים ונשארו שלא נתחלקו שלשת [אלפים ותשע מאות ועשרים ושנים והם חלקים משלשת]‫<ref>Vatican om.</ref> אלפים ותשע מאות וששים ותשעה אשר חלקנו עליו וכזה היה סכום המדות אשר היו בכרי כשהתחיל בעל הבית לתרום | ||
|- | |- | ||
| + | !<span style=color:green>How much Problem - Amount of money</span> | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | :: | + | *{{#annot:WP|648|V202}}Question: Reuven demands from Shimon a hundred measures, which he says he owes him according to an oral [agreement]. |
| − | |style="text-align:right;"| | + | :Shimon says: I do not owe you a hundred measures, but as much as I owe you, with the same amount, and one-half of it, and a quarter of it, plus one will make a hundred. |
| + | :How much did he admit he owes him? | ||
| + | :<math>\scriptstyle X+X+\frac{1}{2}X+\frac{1}{4}X+1=100</math> | ||
| + | |style="text-align:right;"|<big>שאלה</big> ראובן תובע לשמעון מאה מנה שאומר שהוא חייב לו על פה<br> | ||
| + | ויאמר שמעון אליו אין אני חייב לך מאה מנה אבל כאותם שאני חייב לך ואחרים כמותם ומחציתם ורביעיתם ועם אחד יהיו מאה<br> | ||
| + | נרצה לדעת כמה הודה לו מתביעתו{{#annotend:V202}} | ||
|- | |- | ||
| | | | ||
| − | + | ::<span style=color:green>'''False Position:'''</span> We do as follows: we take a denominator that has a half and a quarter; we find it is eight. | |
| − | ::< | + | |style="text-align:right;"|ונעשה על דרך זה נקח מדומה שיש לו חצי ורביעית ‫<ref>102r</ref>והנה נמצא שמונה |
| − | |||
| − | |style="text-align:right;"| | ||
| − | |||
| − | |||
|- | |- | ||
| − | |||
| | | | ||
| + | ::We add the same; it is sixteen. We add also half the denominator, which is four; it is twenty; and its quarter, which is two; it is twenty-two. | ||
| + | ::<math>\scriptstyle{\color{blue}{8+8+\left[\left(\frac{1}{2}\sdot8\right)+\left(\frac{1}{4}\sdot8\right)\right]=16+4+2=20+2=22}}</math> | ||
| + | |style="text-align:right;"|נוסיף כמוהו יהיו ששה עשר וגם הוסיף מחצית המדומה שהיא ארבעה יהיו עשרים ורביעיתו שהוא שנים יהיו עשרים ושנים | ||
|- | |- | ||
| | | | ||
| − | + | ::<span style=color:green>'''Rule of Three:'''</span> Necessarily as the ratio of eight to twenty-two so is the ratio of the unknown to ninety-nine. | |
| − | + | ::<math>\scriptstyle{\color{blue}{8:22=X:99}}</math> | |
| − | : | + | |style="text-align:right;"|ובהכרח כערך שמנה אל עשרים ושנים כן ערך הנעלם אל תשעים ותשע |
| − | :<math>\scriptstyle | ||
| − | |style=" | ||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | :: | + | :::For it is known that the sum of the parts of the admission is only ninety-nine; and with one it is one hundred. <math>\scriptstyle{\color{blue}{99+1=100}}</math> |
| − | + | |style="text-align:right;"|כי בידוע כי המחובר מחלקי ההודאה עמה לא יעלה כי אם תשעה ותשעים ועם אחד הם מאה | |
| − | |style=" | ||
|- | |- | ||
| | | | ||
| − | :: | + | ::When we multiply the first number by the fourth, the result is seven hundred and ninety-two. |
| − | + | |style="text-align:right;"|וכאשר נכפול החשבון הראשון על הרביעי יעלו שבע מאות ותשעים ושנים | |
| − | |style="text-align:right;"|על | ||
|- | |- | ||
| | | | ||
| − | :: | + | ::We divide it by the known mean, which is twenty-two; the result of division is thirty-six and this is the number of measures he admitted that he owes him. |
| − | ::<math>\scriptstyle{\color{blue}{ | + | ::<math>\scriptstyle{\color{blue}{X=\frac{8\sdot99}{22}=\frac{792}{22}=36}}</math> |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|חלק<sup>נ</sup>והו על האמצעי הנודע שהוא עשרים ושנים יצא בחלוק ששה ושלשים וככה הוא מספר המנים שהודה שהוא חייב לו |
|- | |- | ||
| | | | ||
| − | : | + | :Examine it and you will find that it is true. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ובחון זה ותמצאהו באמת |
|- | |- | ||
| + | !<span style=color:green>Purchase Problem - Moneychanger</span> | ||
| | | | ||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | :: | + | *{{#annot:moneychanger|642|6Duv}}Question: a silversmith has sold to a moneychanger a silver chain that is worth three dinar of one coin or five dinar of another coin or seven dinar of yet another [coin]. |
| − | |style="text-align:right;"| | + | :The silversmith asked the moneychanger to pay him its price with these three coins an equal amount of each. |
| + | :How much is this amount? | ||
| + | :<math>\scriptstyle\frac{1}{3}X+\frac{1}{5}X+\frac{1}{7}X=1</math> | ||
| + | |style="text-align:right;"|<big>שאלה</big> צורף כסף שמכר לשולחני רתוקות כסף ערכה ממטבע אחד שלשה דינרים וממטבע אחר חמשה דינרים ומאחר חמשה דינרים<br> | ||
| + | ושאל הצורף לשולחני שיכוין לו בדמיו משלש המטבעות האלה מכל אחד חלק שוה<br> | ||
| + | ונבקש לדעת מספר החלק ההוא{{#annotend:6Duv}} | ||
|- | |- | ||
| | | | ||
| − | ::We | + | ::<span style=color:green>'''Common Denominator:'''</span> We investigate this way: we look for a denominator that has a third, a fifth, and a seventh; we find it is a hundred and five. |
| − | + | |style="text-align:right;"|ונחקור על דרך זה נבקש מדומה שיש לו שלישית וחמישית ושביעית והנה נמצא ‫<ref>102v</ref>מאה וחמש | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | ::Its | + | ::Its third is thirty-five; its fifth is twenty-one; and its seventh is fifteen. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|שלישיתו שלשים וחמשה וחמישיתו עשרים ואחד שביעיתו חמשה עשר |
|- | |- | ||
| | | | ||
| − | :: | + | ::The sum of all these parts is seventy-one and these are the fractions by which we have to divide each dinar. |
| − | ::<math>\scriptstyle{\color{blue}{ | + | ::<math>\scriptstyle{\color{blue}{\left(\frac{1}{3}\sdot105\right)+\left(\frac{1}{5}\sdot105\right)+\left(\frac{1}{7}\sdot105\right)=35+21+15=71}}</math> |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והמחובר מכל החלקים האלה שבעים ואחד והמה החלקים אשר נצטרך לחלק [כל]‫<ref>Vatican: אל</ref> דינר אליהם |
|- | |- | ||
| | | | ||
| − | :: | + | ::We divide the denominator by seventy-one; we find it there once and thirty-four parts remain that cannot be divided, which are parts of the seventy-one by which we divide the denominator. |
| − | ::<math>\scriptstyle{\color{blue}{ | + | ::<math>\scriptstyle{\color{blue}{X=\frac{105}{71}=1+\frac{34}{71}}}</math> |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והנה נחלק המדומה על שבעים ואחד נמצאנו שם פעם אחת וישארו שלא נתחלקו ארבעה ושלשים והמה חלקים מהשבעים ואחד אשר חלקנו עליהם המדומה |
|- | |- | ||
| | | | ||
| − | : | + | :So, the silversmith will take one dinar and thirty-four parts of seventy-one of a dinar from each coin. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וככה יקח הצורף מכל מטבע דינר אחד ושלשים וארבעה חלקים משבעים ואחד בדינר |
|- | |- | ||
| | | | ||
| − | :: | + | :<span style=color:green>'''Check:'''</span> I shall give you a route how to check it: |
| − | : | + | |style="text-align:right;"|ואתן לך מסלול ודרך איך תבחון זה |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| − | |||
| | | | ||
| + | ::Take the denominator, which is one hundred and five, and in order to convert all the coins to the coin of 3, we multiply it by them; they are three hundred and fifteen. | ||
| + | ::<math>\scriptstyle{\color{blue}{105\sdot3=315}}</math> | ||
| + | |style="text-align:right;"|תקח המדומה שהוא מאה וחמש וכדי ש{{#annot:term|1553,1431|HTld}}נשיב{{#annotend:HTld}} כל המטבעות ממטבע שלשה נכפלנו עליהם ויהיו שלש מאות וחמשה עשר | ||
|- | |- | ||
| | | | ||
| − | + | ::We divide them by five, in order to know how many parts of the coin of 5 are they; the result of division is sixty-three parts. | |
| − | + | ::<math>\scriptstyle{\color{blue}{\frac{315}{5}=63}}</math> | |
| − | : | + | |style="text-align:right;"|נחלקם על [חמשה]‫<ref>Vatican: חמשה עשר</ref> כדי שנדע כמה חלקים הם ממטבע חמשה יצא בחלוק ששים ושלשה חלקים |
| − | :<math>\scriptstyle | ||
| − | |style="text-align:right;"| | ||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | ::< | + | ::We divide the three hundred and fifteen by seven also, in order to know how many parts of the coin of 7 are they; the result of division is forty-five. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{\frac{315}{7}=45}}</math> |
| + | |style="text-align:right;"|גם נחלק שלש מאות וחמשה עשר על שבעה למען נדע כמה חלקים הם ממטבע שבעה יצא בחלוק ארבעים וחמשה | ||
|- | |- | ||
| | | | ||
| − | :: | + | ::When we sum all the parts of the three coins, which are 105, 63, 45, the result is two hundred and thirteen. |
| − | + | |style="text-align:right;"|וכאשר נחבר כל החלקים משלשת המטבעות שהם מאה וחמש וששים ושלשה וארבעים וחמשה ‫<ref>103r</ref>יעלו מאתים ושלשה עשר | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | :: | + | ::We divide them by seventy-one, which are the parts of the whole dinar; we find them there three times, which are three whole dinar. |
| − | ::<math>\scriptstyle{\color{blue}{ | + | ::<math>\scriptstyle{\color{blue}{\frac{\frac{315}{3}+\frac{315}{5}+\frac{315}{7}}{71}=\frac{105+63+45}{71}=\frac{213}{71}=3}}</math> |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|נחלקם על שבעים ואחד שהם [חלקי]‫<ref>Vatican: חלף</ref> הדינר השלם ונמצאם שם שלשה פעמים והנם שלשה דינרים שלימים |
|- | |- | ||
| | | | ||
| − | : | + | :Do likewise if you want to convert the whole amount to the coin of five or the coin of seven; and you will find the truth of this matter. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ועל הדרך הזה תעשה אם תרצה להשיב כל חשבון ממטבע חמשה או ממטבע שבעה ותמצא אמתת הדבר |
|- | |- | ||
| + | !<span style=color:green>Find a Number Problem</span> | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | : | + | *Question: a third, a fifth, and a seventh are summed together, how much is [their sum] in relation to the whole? |
| − | + | :<math>\scriptstyle\frac{1}{3}X+\frac{1}{5}X+\frac{1}{7}X</math> | |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|<big>שאלה</big> שלישית וחמישית ושביעית מחוברים איזה ערך הם מהשלם |
|- | |- | ||
| | | | ||
| − | : | + | ::<span style=color:green>'''Common Denominator:'''</span> We take one hundred and five as their denominator. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|לקחנו להם מאה וחמש למדומה |
|- | |- | ||
| − | |||
| | | | ||
| + | ::Its third is thirty-five; its fifth is twenty-one; its seventh is fifteen. | ||
| + | |style="text-align:right;"|שלישיתו חמשה ושלשים וחמישיתו עשרים ואחד ושביעיתו חמשה עשר | ||
|- | |- | ||
| | | | ||
| − | + | ::We sum up all; it is seventy-one. | |
| − | + | ::<math>\scriptstyle{\color{blue}{\left(\frac{1}{3}\sdot105\right)+\left(\frac{1}{5}\sdot105\right)+\left(\frac{1}{7}\sdot105\right)=35+21+15=71}}</math> | |
| − | : | + | |style="text-align:right;"|נחבר את כלם ויהיו שבעים ואחד |
| − | :<math>\scriptstyle\frac{1}{3} | ||
| − | |style="text-align:right;"| | ||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | :: | + | ::Its ratio to the denominator is four-sevenths, two-sevenths of a third, and one-third of one-fifth of a seventh. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{X=\frac{71}{105}=\frac{4}{7}+\left(\frac{2}{7}\sdot\frac{1}{3}\right)+\left(\frac{1}{3}\sdot\frac{1}{5}\sdot\frac{1}{7}\right)}}</math> |
| + | |style="text-align:right;"|והנה ערכם אל המדומה ארבע שביעי<sup>ו</sup>תיו ושתי שביעיות שלישיתו ושלישית ושלישית חמישית שביעיתו | ||
|- | |- | ||
| + | !<span style=color:green>Purchase Problem - Buy and Sell</span> | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | :: | + | *{{#annot:WP|641|dAOg}}Question: a buyer [bought] four fifths of a liṭra for one pašuṭ, and sold his possession at one pašuṭ for five ninths of a liṭra. |
| − | ::<math>\scriptstyle | + | :He earned 11 pešuṭim. |
| − | |style="text-align:right;"| | + | :How much was [his] money? |
| + | :<math>\scriptstyle\frac{4}{5}X-\frac{5}{9}X=11</math> | ||
| + | |style="text-align:right;"|<big>שאלה</big> הקונה ארבע חמישיות ליטרא בפשוט ומכר קנייתו בערך חמש תשיעיות ליטרא בפשוט והרויח אחד עשר פשוטים<br> | ||
| + | כמה היה הממון{{#annotend:dAOg}} | ||
|- | |- | ||
| | | | ||
| − | :: | + | ::<span style=color:green>'''Common Denominator:'''</span> The denominator that has a fifth and a ninth is forty-five. |
| − | :: | + | |style="text-align:right;"|הנה המדומה שיש לו חמישית ותשיעית הוא ארבעים וחמשה |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | : | + | ::Its four-fifths are thirty-six. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{\frac{4}{5}\sdot45=36}}</math> |
| + | |style="text-align:right;"|וארבע חמישיותיו ששה ושלשים | ||
|- | |- | ||
| | | | ||
| − | :< | + | ::Its five-ninths are twenty-five. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{\frac{5}{9}\sdot45=25}}</math> |
| + | |style="text-align:right;"|וחמש תשיעיותיו עשרים וחמש | ||
|- | |- | ||
| | | | ||
| − | :: | + | ::So is the amount of money. <math>\scriptstyle{\color{blue}{X=45}}</math> |
| − | + | |style="text-align:right;"|וככה הוא הממון | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | :: | + | :*If he says that he earned 22 pešuṭim. |
| − | ::<math>\scriptstyle{\color{blue}{\ | + | ::<math>\scriptstyle\frac{4}{5}X-\frac{5}{9}X=22</math> |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ואם אמר שהרויח עשרים ושנים פשוטים |
| + | |- | ||
| + | | | ||
| + | ::we multiply twenty-five times twenty-two. | ||
| + | ::<math>\scriptstyle{\color{blue}{25\sdot22}}</math> | ||
| + | |style="text-align:right;"|‫<ref>103v</ref>נכפול חמשה ועשרים שנים ועשרים פעמים | ||
|- | |- | ||
| | | | ||
| − | : | + | :*If he says that he earned 33 pešuṭim |
| − | ::<math>\scriptstyle | + | ::<math>\scriptstyle\frac{4}{5}X-\frac{5}{9}X=33</math> |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ואם אמר שהרויח שלשים ושלשה פשוטים |
|- | |- | ||
| | | | ||
| − | :: | + | ::We multiply them thirty-three times. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{25\sdot33}}</math> |
| + | |style="text-align:right;"|נכפלם שלשים ושלש פעמים | ||
|- | |- | ||
| | | | ||
| − | : | + | :And so on endlessly. |
| − | + | |style="text-align:right;"|וככה עד אין קץ | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| + | !<span style=color:green>Purchase Problem - Buy and Sell - Peanuts</span> | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
| − | |||
| | | | ||
| + | *{{#annot:WP|641|hmKB}}Question: a seller bought 20 liṭra of peanut for 20 dinar. | ||
| + | :Then he went and sold 10 liṭra of them at one dinar for five quarters of a liṭra. It turned out that he lost in doing so. | ||
| + | :Afterwards many buyers came and overcharged and he sold the remaining 10 liṭra at one dinar for three quarters of a liṭra. | ||
| + | :Now he comes to us and asks: did he gain or lose? | ||
| + | :<math>\scriptstyle\left(\frac{10}{\frac{5}{4}}+\frac{10}{\frac{3}{4}}\right)-20</math> | ||
| + | |style="text-align:right;"|<big>שאלה</big> סוחר קנה עשרים ליטראות בטנים בעשרים דינרים<br> | ||
| + | והלך ומכר מהן עשרה ליטרין לערך חמש רביעיות ליטרא בדינר ונמצא שהוא מפסיד בזה<br> | ||
| + | ואחרי כן באו הרבה קונים והפקיעו השערים ומכר העשרה ליטריין הנשארות לערך שלש רביעיות ליטרא בדינר<br> | ||
| + | ועתה בא אלינו לשאול אם הרויח או הפסיד או אם יצא הפסדו בשכרו{{#annotend:hmKB}} | ||
|- | |- | ||
| | | | ||
| − | + | ::We investigate this way: we convert the first 10 liṭra that he sold into quarters; they are forty. | |
| − | + | |style="text-align:right;"|והנה נחקור על דרך זה ונשיב העשר ליטראות הראשונות שמכר כלם רביעיות ויהיו ארבעים | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | ::< | + | ::We divide them by the 5-quarters that he sold for a dinar; we find them there eight times. We find that he sold the five for eight dinar. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{\frac{10}{\frac{5}{4}}=\frac{4\sdot10}{5}=\frac{40}{5}=8}}</math> |
| + | |style="text-align:right;"|נחלקם על החמש רביעיות שמכר בדינר נמצאם שם שמונה פעמים נמצא שה' מכרם בשמונה דינרים | ||
|- | |- | ||
| | | | ||
| − | :: | + | ::We convert also the other 10 liṭra into quarters, then divide them by the 3-quarters that he sold for a dinar; we find them there thirteen times, which are 13 dinar, and one-quarter remains that cannot be divided, which is a third of a dinar. |
| − | |style="text-align:right;"|שלישית | + | ::<math>\scriptstyle{\color{blue}{\frac{10}{\frac{3}{4}}=\frac{4\sdot10}{3}=\frac{40}{3}=13+\frac{1}{3}}}</math> |
| + | |style="text-align:right;"|נעשה כן [רביעיות]‫<ref>Vatican om.</ref> מהעשר ליטראות האחרונות ונחלקם על שלש רביעיות שמכר בדינר נמצא שם שלשה עשר פעמים שהם י"ג דינרים ועוד נשאר מהם שלא נתחלק רביעית אחת שהיא שלישית דינר | ||
|- | |- | ||
| | | | ||
| − | ::We | + | ::We add all this to the eight dinar; the sum is twenty-one dinar and four pešuṭim. |
| − | ::<math>\scriptstyle{\color{blue}{\ | + | ::<math>\scriptstyle{\color{blue}{\frac{10}{\frac{5}{4}}+\frac{10}{\frac{3}{4}}=8+\left(13+\frac{1}{3}\right)=21+\frac{4}{12}}}</math> |
| − | |style="text-align:right;"|נחבר | + | |style="text-align:right;"|נחבר כל זה אל ‫<ref>104r</ref>השמונה דינרים יהיו עשרים ואחד דינרים וארבעה פשוטים |
|- | |- | ||
| | | | ||
| − | :: | + | ::We find that he earned sixteen pešuṭim. |
| − | ::<math>\scriptstyle{\color{blue}{ | + | ::<math>\scriptstyle{\color{blue}{\left(21+\frac{4}{12}\right)-20=\frac{16}{12}}}</math> |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|נמצא שהרויח ששה עשר פשוטים |
|- | |- | ||
| − | !<span style=color: | + | !<span style=color:green>Partnership Problem - For the Same Time</span> |
| | | | ||
|- | |- | ||
| | | | ||
| − | *{{#annot: | + | *{{#annot:three partners|661|OJXh}}Question: three invested forty-six dinar - one contributed twelve dinar, the second contributed fifteen dinar, the third contributed nineteen dinar, and they earned together 20 dinar. How much should each one take [from the profit]? |
| − | + | :<math>\scriptstyle12+15+19=46</math> | |
| − | + | |style="text-align:right;"|<big>שאלה</big> שלשה שותפין בארבעים וששה דינרים חלק האחד שנים עשר דינרים וחלק השני חמשה עשר דינרים וחלק השלישי תשעה עשר דינרים והרויחו בין כלם עשרים דינרים כמה יקח כל אחד ואחד מהם{{#annotend:OJXh}} | |
| − | :<math>\ | ||
| − | |style="text-align:right;"|שאלה | ||
| − | כמה | ||
|- | |- | ||
| | | | ||
| − | ::<span style=color: | + | ::<span style=color:green>'''Rule of Three:'''</span> It is known that there is no doubt that each and every one will take the ratio to twenty as the ratio of his share to forty-six. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{x_i:20=a_i:46}}</math> |
| + | |style="text-align:right;"|ידוע כי אין ספק שכל אחד ואחד מהם יקח ערך מעשרים כערך חלקו אל הארבעים וששה | ||
|- | |- | ||
| | | | ||
| − | : | + | :You will find out this easily by the rule of four [lit. the rules of proportions]. |
| − | + | |style="text-align:right;"|ותברר זה במשפטי הערכין בנקלה | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| + | !<span style=color:green>Payment Problem - two workers, two different daily wages, the same actual payment</span> | ||
| | | | ||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | :: | + | *{{#annot:two workers|612|lLls}}Question: one hired Reuven and Shimon for 10 days to do a work for him any one of them in turns so that the work will not cease. |
| − | |style="text-align:right;"| | + | :He agreed with Reuven that if he will do the work alone the whole 10 days he would pay him 2 dinar and to Shimon he said that if he will do the work alone the whole days he would pay him 5 dinar. |
| + | :What they did? They did the work together so that when one was tired his friend replaced him and did the work while the other was resting and if the second was tired, the first returned to his work and the second was resting. | ||
| + | :Each one wrote how many days, or parts of days, he worked. | ||
| + | :They did so the whole ten days, and then when they came to the employer he paid both of them and gave each of them money equally. | ||
| + | :How much money did they receive and how many days did each of them work? | ||
| + | :<math>\begin{cases}\scriptstyle\frac{2}{10}R=\frac{5}{10}S\\\scriptstyle R+S=10\end{cases}</math> | ||
| + | |style="text-align:right;"|<big>שאלה</big> השוכר ראובן ושמעון שיעשו לו בין שניהם מלאכה עשרה ימים ולא תשבות המלאכה<br> | ||
| + | והתנה עם ראובן שאם יעסוק הוא [במלאכה לבדו כל העשרה ימים שיתן לו ב' דינרים<br> | ||
| + | ולשמעון אמר שאם יעסוק הוא]‫<ref>Vatican om.</ref> לבד במלאכה כל מספר הימים ההם שיתן לו חמשה דינרים<br> | ||
| + | מה עשו החזיקו שניהם במלאכה בדרך זה כשהאחד היה יגיע עומד חבירו תחתיו ועוסק במלאכה והוא שובת היה עיף השני הראשון חוזר למלאכתו והשני שובת וכל אחד ואחד כתב כמה ימים או חלקי ימים עבד<br> | ||
| + | ועשו זה כל העשרה ימים<br> | ||
| + | וכשבאו אל השוכר פרע את שניהם ונתן להם ‫<ref>104v</ref>מעות לכל אחד ואחד בשוה<br> | ||
| + | נרצה לדעת כמה מעות נטלו וכמה ימי עבודת כל אחד ואחד{{#annotend:lLls}} | ||
|- | |- | ||
| | | | ||
| − | : | + | ::We investigate this way: know that Reuven works five days for one dinar and Shimon is paid one dinar for two days only. The sum of the days of both is seven. |
| − | ::<math>\scriptstyle\ | + | ::<math>\scriptstyle{\color{blue}{5+2=7}}</math> |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והנה נחקור על דרך זה תדע כי ראובן יעבוד חמשה ימים בדינר ושמעון לא ישמש בדינר כי אם שני ימים והמחובר מימי שניהם הוא שבעה |
|- | |- | ||
| | | | ||
| − | :: | + | ::We divide the ten days by them; the result is one integer and three remain that cannot be divided. So the amount of money that each takes is one dinar and three-sevenths of a dinar. |
| − | ::<math>\scriptstyle{\color{blue}{ | + | ::<math>\scriptstyle{\color{blue}{\frac{10}{5+2}=\frac{10}{7}=1+\frac{3}{7}}}</math> |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|נחלקו העשרה ימים עליהם ויהיה היוצא אחד שלם ישארו שלשה שלא נתחלקו וככה הוא סכום המעות אשר יקח כל אחד מהם דינר ושלשה שביעיות דינר |
|- | |- | ||
| | | | ||
| − | : | + | ::Now we shall investigate how many are the working days of each by his payment according to the conditional ratio, so that they are summed up to ten days: |
| − | + | |style="text-align:right;"|ועתה נחקור כמה משפט ימי <s>כל</s> עבודת כל אחד ואחד בשכרו אשר לקח לפי ערך התנאי וצריך שיספיק בין שניהם לעשרה ימים | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | ::We | + | ::We do as follows: it is known that Reuven must work five days for one dinar, we ask to know how many days will he work for the three-sevenths of a dinar; we reach this knowledge by applying the rule of four [lit. the rules of the ratios]. |
| − | + | |style="text-align:right;"|ונעשה ככה בידוע כי ראובן חייב לעבוד בדינר אשר לקח חמשה ימים ונרצה לדעת כמה [ימים]‫<ref>Vatican om.</ref> יעבוד בעבור השלשה שביעיות מהדינר ונגיע לידיעת זה כאשר נעשה במשפטי הערכין | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | : | + | ::We convert the five days into sevenths; they are thirty-five. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{5=\frac{35}{7}}}</math> |
| + | |style="text-align:right;"|ונשיב החמשה ימים חלקי שביעיות ויהיו חמשה ושלשים | ||
|- | |- | ||
| − | |||
| | | | ||
| + | ::<span style=color:green>'''Rule of Three:'''</span> We take the ratio and say: as the ratio of three to seven, so is the ratio of the unknown to thirty-five. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{3}{7}:7=X:35}}</math> | ||
| + | |style="text-align:right;"|ונעריך ונאמר כערך שלשה אל שבעה כן ערך הנעלם אל חמשה ושלשים | ||
|- | |- | ||
| | | | ||
| − | + | ::We multiply the first number by the fourth; it is a hundred and five. | |
| − | + | |style="text-align:right;"|נכפול החשבון הראשון על הרביעי יהיו מאה וחמש | |
| − | |||
| − | |||
| − | |||
| − | |style="text-align:right;"| | ||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | ::We | + | ::We divide it by the known mean, which is seven; we find it there fifteen times that are parts of a seventh of a day; the result is two days and one-seventh of a day. |
| − | |style="text-align:right;"|והנה | + | ::<math>\scriptstyle{\color{blue}{\frac{\frac{3\sdot35}{7}}{7}=\frac{\frac{105}{7}}{7}=\frac{15}{7}=2+\frac{1}{7}}}</math> |
| + | |style="text-align:right;"|נחלקם על ‫<ref>105r</ref>האמצעי הנודע שהוא שבעה נמצאם שם חמשה עשר פעמים והנה הם חלקי שביעית יום העולים שני ימים ושביעית יום אחד | ||
|- | |- | ||
| | | | ||
| − | ::We | + | ::We find that Reuven's working days are seven days and one-seventh of a day. |
| − | ::<math>\scriptstyle{\color{blue}{\ | + | ::<math>\scriptstyle{\color{blue}{R=5+\left(2+\frac{1}{7}\right)=7+\frac{1}{7}}}</math> |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ונמצא כל <sup>ימי</sup> עבודת ראובן שבעה ימים ושביעית יום אחד |
|- | |- | ||
| | | | ||
| − | :: | + | ::It is known that Shimon must work two days for the dinar that he received. |
| − | + | |style="text-align:right;"|וידוע כי שמעון חייב לעבוד שני ימים בעבור הדינר שלקח | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | :: | + | ::When we convert the two days into sevenths, they are fourteen. |
| − | ::<math>\scriptstyle{\color{blue}{ | + | ::<math>\scriptstyle{\color{blue}{2=\frac{14}{7}}}</math> |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וכשנשיב [השני ימים]‫<ref>Vatican: הימים ושנים</ref> חלק<sup>י</sup> שביעיות יהיו ארבעה עשר |
|- | |- | ||
| | | | ||
| − | :: | + | ::<span style=color:green>'''Rule of Three:'''</span> As the ratio of the three-sevenths he took to seven, so is the ratio of the unknown to fourteen. |
| − | ::<math>\scriptstyle{\color{blue}{ | + | ::<math>\scriptstyle{\color{blue}{\frac{3}{7}:7=Y:14}}</math> |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והנה כערך השלשה שביעיות שלקח אל שבעה כן ערך הנעלם [אל]‫<ref>Vatican om.</ref> ארבעה עשר |
|- | |- | ||
| − | |||
| | | | ||
| + | ::We multiply the first [number] by the last; it is forty-two. | ||
| + | |style="text-align:right;"|כפלנו החשבון הראשון על האחרון היו ארבעים ושנים | ||
|- | |- | ||
| | | | ||
| − | + | ::We divide it by the known mean, which is seven; we find it there six times that are parts of sevenths of a day. | |
| − | :<math>\ | + | ::<math>\scriptstyle{\color{blue}{\frac{\frac{3\sdot14}{7}}{7}=\frac{\frac{42}{7}}{7}=\frac{6}{7}}}</math> |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|חלקנום על האמצעי הנודע שהוא שבעה נמצאם שם ששה פעמים והם חלק<sup>י</sup> שביעיות יום |
|- | |- | ||
| | | | ||
| − | :: | + | ::We find that Shimon's working days are two days and six-sevenths. |
| − | ::<math>\scriptstyle{\color{blue}{ | + | ::<math>\scriptstyle{\color{blue}{S=2+\frac{6}{7}}}</math> |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ונמצא כל ימי עבודת שמעון שני ימים ושש שביעיות יום |
|- | |- | ||
| | | | ||
| − | : | + | :<span style=color:green>'''Check:'''</span> When you sum up the number and the parts of the working days of both and make one day out of every seven parts, you find that they are exactly ten days. |
| − | |style="text-align:right;"| | + | :<math>\scriptstyle{\color{blue}{R+S=\left(7+\frac{1}{7}\right)+\left(2+\frac{6}{7}\right)=10}}</math> |
| + | |style="text-align:right;"|וכאשר תחבר מספר הימים והחלקים מעבודת שניהם ותעשה משבעה חלקים יום אחד תמצא שהם עשרה ימים בכיוון | ||
|- | |- | ||
| − | !<span style=color: | + | !<span style=color:green>Payment Problem - Messenger</span> |
| | | | ||
|- | |- | ||
| | | | ||
| − | *{{#annot: | + | *{{#annot:messenger|612|yWg7}}Question: I hired a messenger for 13 dinar and we agreed that he will walk for me from now on for 20 days 11 parsa [1 parsa = ca. 4 kilometers] a day, but the messenger embezzled or got injured and walked only 5 parsa a day for 7 days.<br> |
| − | + | :How much should his payment be according to the terms? | |
| − | + | :<math>\scriptstyle\frac{x}{7\sdot5}=\frac{13}{20\sdot11}</math> | |
| − | + | |style="text-align:right;"|<big>שאלה</big> שכרתי שליח אחד בשלשה עשר דינרים [והתנאתי]‫<ref>Vatican: והתאנתי</ref> עמו שילך לי מכאן ועד עשרים יום אחד עשר פרסאות בכל יום<br> | |
| − | : | + | והשליח מעל או שנאנס ולא הלך כי אם חמש פרסאות בכל יום עד ‫<ref>105v</ref>שבעה ימים<br> |
| − | + | נרצה לידע כמה משפט דמי שכרותו לפי התנאי{{#annotend:yWg7}} | |
| − | :<math> | ||
| − | |style="text-align:right;"|שאלה | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | ::We | + | ::We do it in this way: first we think as if the messenger would have walked five parsot the whole 20 days and we look how much should be his hiring payment. |
| − | + | |style="text-align:right;"|נעשה בדרך זאת בתחלה נחשוב כאלו הלך השליח החמש פרסאות כל העשרים יום ונראה מה יגיע אליו מהשכרות | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | ::We | + | ::<span style=color:green>'''Rule of Three:'''</span> We take the ratio and say: as the ratio of five to eleven, so is the ratio of the unknown to thirteen, which is the hiring payment. |
| − | ::<math>\scriptstyle{\color{blue | + | ::<math>\scriptstyle{\color{blue}{5:11=a:13}}</math> |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|והנה נעריך ונאמר כערך חמשה אל אחד עשר כן ערך הנעלם אל שלשה עשר שהוא ערך השכירות |
|- | |- | ||
| | | | ||
| − | :: | + | ::When we multiply the first number by the fourth, then divide by the known mean, we find that his hiring payment should be 5 dinar and 10 parts of 11 of a dinar. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{a=\frac{5\sdot13}{11}=5+\frac{10}{11}}}</math> |
| + | |style="text-align:right;"|כאשר נכפול החשבון הראשון על הרביעי ונחלק על האמצעי הנודע נמצא שיגיע אליו מהשכרות ה' דינרים וי' חלקים מי"א בדינר | ||
|- | |- | ||
| | | | ||
| − | :: | + | ::Since he walked five parsot for seven days only: |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ובעבור שלא הלך החמש פרסאות כי אם שבעה ימים |
|- | |- | ||
| | | | ||
| − | ::We | + | ::<span style=color:green>'''Rule of Three:'''</span> We take the ratio again and say: as the ratio of seven to twenty, so is the ratio of the unknown to 5 dinar and 10 parts of 11 of a dinar. |
| − | ::<math>\scriptstyle{\color{blue}{5 | + | ::<math>\scriptstyle{\color{blue}{7:20=X:\left(5+\frac{10}{11}\right)}}</math> |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|נחזור ונעריך ונאמר כערך שבעה אל עשרים כן ערך הנעלם אל ה' דינרים [וי']‫<ref>Vatican: ו'</ref> חלקים מי"א בדינר |
|- | |- | ||
| | | | ||
| − | :: | + | ::We multiply the first number, which is seven, by the fourth number, which is 5 dinar; it is 35. |
| − | + | |style="text-align:right;"|נכפול החשבון הראשון שהוא שבעה על החשבון הרביעי שהוא ה' דינרים ובו' יהיה ל"ה | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | ::We multiply | + | ::We multiply it also by the 10 parts; they are seventy parts. |
| − | |style="text-align:right;"|נכפול | + | |style="text-align:right;"|גם נכפול אותו על הי' חלקים יהיו שבעים חלקים |
|- | |- | ||
| | | | ||
| − | :: | + | ::When we have to divide the resulting product by the known mean, we return all to the same measure and convert the 35 into parts of 11; they are 385. |
| − | + | |style="text-align:right;"|וכאשר אנחנו צריכים לחלק העולה מהכפילה הזאת על האמצעי הנודע נשיב הכל ממתכונת אחת ונעשה מהל"ה חלקים מי"א ויהיו שפ"ה | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | ::We | + | ::We add to them the 70 parts, which are also parts of 11; they are 455. |
| − | + | |style="text-align:right;"|נחבר אליהם הע' חלקים שגם ‫<ref>106r</ref>הם המה חלקים מי"א ויהיו תנ"ה | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| | | | ||
| − | :: | + | ::Then we convert the known mean, which is twenty, into parts of 11; they are 220. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ואחרי זאת נשיב גם כן האמצעי הנודע שהוא עשרים חלקים מי"א יהיו ר"ך |
|- | |- | ||
| | | | ||
| − | :: | + | ::We divide 455 by them; we find them twice in them and 15 remain that cannot be divided, which are three-quarters of a part of eleven. |
| − | + | |style="text-align:right;"|נחלק תנ"ה עליהם נמצאם שם פעמים וישארו ט"ו שלא נתחלקו והם שלש רביעיות חלק אחד מהאחד עשר חלקים מר"ך שהוא השלם אשר חלקנו עליו | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| − | | | + | | colspan="2"| |
| − | + | ::<math>\scriptstyle{\color{blue}{X=\frac{7\sdot\left(5+\frac{10}{11}\right)}{20}=\frac{35+\frac{70}{11}}{20}=\frac{\frac{385+70}{11}}{20}=\frac{\frac{455}{11}}{20}=\frac{455}{220}=2+\frac{15}{220}=2+\left(\frac{3}{4}\sdot\frac{1}{11}\right)}}</math> | |
| − | ::<math>\scriptstyle{\color{blue}{\frac{3}{ | ||
| − | |||
|- | |- | ||
| | | | ||
| − | :: | + | ::Hence, the salary that the messenger will receive is two dinar and three-quarters of one part of eleven of a dinar. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וככה יקח השליח בשכרותו שני דינרים ושלש רביעיות חלק אחד מאחד עשר חלקים בדינר שלם |
|- | |- | ||
| + | !<span style=color:green>Divide a Quantity Problem - Proportional Division - Inheritance</span> | ||
| | | | ||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | :: | + | *{{#annot:inheritance|645|eycN}}Question: Jacob's four wives married him on the same day. On that day, he prepared for each of them a ketuba [= Jewish marriage contract] according the Jewish law. |
| − | :: | + | ::The name of the one is Leah and her ketuba amount is 4000 zehuvim [= golden coins]; |
| − | |style="text-align:right;"| | + | ::the name of the second is Zilpah and he ketuba amount is 3000 [zehuvim]; |
| + | ::the name of the third is Rachel and her ketuba amount is 2000 [zehuvim]; | ||
| + | ::and the name of the fourth is Bilhah and her ketuba amount is 1000 zehuvim. | ||
| + | :Later Jacob died and nothing was left of his property but 4000 zehuvim. | ||
| + | :The widows came to the court in order to divide the money that remained between them | ||
| + | |style="text-align:right;"|<big>שאלה</big> ארבעה נשי יעקב שנשאו לו ביום אחד ועשה לכל אח<sup>ת</sup> ואחת כתובה בו ביום כתקון חכמים<br> | ||
| + | שם האחת לאה וכתובתה [ארבעת]‫<ref>Vatican: שבעת</ref> אלפים זהובים<br> | ||
| + | ושם השנית זלפה וכתובתה שלשת אלפים<br> | ||
| + | ושם השלישית רחל וכתובתה אלפים<br> | ||
| + | ושם הרביעית בלהה וכתובתה אלף זהובים<br> | ||
| + | לימים מת יעקב ולא נשאר מנכסיו כי אם ארבעת אלפים זהובים<br> | ||
| + | באו האלמנות לבית דין לחלוק להן הממון הנשאר{{#annotend:eycN}} | ||
|- | |- | ||
| | | | ||
| − | :<span style=color: | + | :*<span style=color:green>The division according '''the sages of Israel''':</span> The late sages said that the court law is to divide the money between them in this way: |
| − | : | + | |style="text-align:right;"|ואמרו חכמים ז"ל שמשפט הבית דין לחלק להן הממון על דרך זה |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| − | |||
| | | | ||
| + | ::<span style=color:green>'''Bilhah:'''</span> They shall tell Bilhah whose ketuba has the smallest [amount] of all of them: You have no claim from the others except for a thousand gold coins and they too have a legal right on them, so take the fourth of the thousand, which is two hundred and fifty and go in peace and so each of them will take from it. | ||
| + | ::<math>\scriptstyle{\color{blue}{\frac{1}{4}\sdot1000=250}}</math> | ||
| + | |style="text-align:right;"|יאמרו <sup>א</sup>ל בלהה שכתובתה קטנה מכלנה אין לך ערעור בחברותיך כי אם באלף ‫<ref>106v</ref>זהובים וגם הנה יש להן משפט בהן על כן תקח רביעית האלף שהוא <s>מ</s>מאתים וחמשים ולכי לשלום וככה תקחן ממנו כל אחת מהן | ||
|- | |- | ||
| | | | ||
| − | + | ::<span style=color:green>'''Rachel:'''</span> Then, the court shall tell Rachel: You have no claim except for the two thousand that your two friends have a legal right on them too, and you have already taken your share from the one-thousand divided, so take the third of the other thousand required as a payment of your claim, which is three-hundred and thirty-three gold coins and one-third, and return to your home. We find that her total share is 583 gold coins and one-third. Likewise each of the two others will take three hundred and thirty-three gold coins and one-third from the second divided one thousand. | |
| − | + | |style="text-align:right;"|אחרי כן יאמרו גם כן ב"ד אל רחל אין לך ערעור רק על אלפים שיש לשתי חברותיך גם כן משפט בהן וכבר לקחת חלקך מהאלף המחולק על כן תקחי מהאלף אחר שצריך לתשלום תביעתך השלש שהוא שלש מאות ושלשים ושלשה זהובים ושליש זהוב ושובי לביתך ונמצא חלוקה בין הכל תקפ"ג זהובים ושליש זהוב וגם כן יקחו כל אחת משתיהן מאותו האלף השני הנחלק שלש מאות ושלשים ושלשה זהובים ושליש זהו‫' | |
| − | |||
| − | |style="text-align:right;"| | ||
| − | |||
| − | |||
|- | |- | ||
| − | | | + | | colspan="2"| |
| − | :: | + | ::<math>\scriptstyle{\color{blue}{\left(\frac{1}{4}\sdot1000\right)+\left(\frac{1}{3}\sdot1000\right)=250+\left(333+\frac{1}{3}\right)=583+\frac{1}{3}}}</math> |
| − | |||
|- | |- | ||
| | | | ||
| − | ::<span style=color: | + | ::<span style=color:green>'''Zilpah:'''</span> Then, they shall tell Zilpah: You have no claim except for the three-thousand that your friend Leah [too] has a legal right on them, and you have already taken your share from the two thousand divided, so we shall divide the one thousand required as a payment of your claim between the two [of you]. We find that the total share of Zilpah is one thousand eighty-three gold coins and one-third. |
| − | + | |style="text-align:right;"|ואחרי כן אמרו לזלפה אין לך תביעה רק בשלשת אלפים שיש ללאה חברתיך בהן משפט וכבר לקחת חלקך מהשני האלפים המחולקים [על כן]‫<ref>Vatican: עלך</ref> נחלק בין שתיהן האלף הצריך לתשלום תביעתך ונמצא שתהיה חלק זלפה בין הכל אלף [ושמנים]‫<ref>Vatican: ושלשים</ref> ושלשה זהובים ושליש זהוב | |
| − | |style="text-align:right;"| | ||
|- | |- | ||
| − | | | + | | colspan="2"| |
| − | + | ::<math>\scriptstyle{\color{blue}{\left(\frac{1}{4}\sdot1000\right)+\left(\frac{1}{3}\sdot1000\right)+\left(\frac{1}{2}\sdot1000\right)=\left(583+\frac{1}{3}\right)+500=1083+\frac{1}{3}}}</math> | |
| − | ::<math>\scriptstyle{\color{blue}{ | ||
| − | |||
|- | |- | ||
| | | | ||
| − | :: | + | ::<span style=color:green>'''Leah:'''</span> Leah is left with two thousand and eighty-three gold coins and a third. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ונשארו ללאה אלפים ושמנים ושלשה זהובים ושלישית זהוב |
|- | |- | ||
| − | | | + | | colspan="2"| |
| − | + | ::<math>\scriptstyle{\color{blue}{\left(\frac{1}{4}\sdot1000\right)+\left(\frac{1}{3}\sdot1000\right)+\left(\frac{1}{2}\sdot1000\right)+1000=\left(1083+\frac{1}{3}\right)+1000=2083+\frac{1}{3}}}</math> | |
| − | ::<math>\scriptstyle{\color{blue}{ | ||
| − | |||
|- | |- | ||
| | | | ||
| − | :: | + | :<span style=color:green>'''Check:'''</span> If you sum up [all] these parts according to the rule, you will find the result is four thousand. |
| − | |style="text-align:right;"| | + | :<math>\scriptstyle{\color{blue}{250+\left(583+\frac{1}{3}\right)+\left(1083+\frac{1}{3}\right)+\left(2083+\frac{1}{3}\right)=4000}}</math> |
| + | |style="text-align:right;"|ואם תחבר החלקים האלה ‫<ref>107r</ref>תמצא העולה ארבעת אלפים | ||
|- | |- | ||
| | | | ||
| − | :: | + | :*<span style=color:green>The division according to '''the arithmeticians''':</span> The arithmeticians divide this amount in a different way: |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle\frac{4000}{4000}X+\frac{3000}{4000}X+\frac{2000}{4000}X+\frac{1000}{4000}X=4000</math> |
| + | |style="text-align:right;"|<big>והנה</big> חכמי החשבון חולקים הממון הזה בדרך אחרת | ||
|- | |- | ||
| | | | ||
| − | :: | + | ::<span style=color:green>'''False Position:'''</span> They say that since Bilhah asks for a quarter of the amount, Rachel its half, Zilpah its three-quarters, and Leah its whole, we take a denominator that has a half and a quarter. We find it is eight. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ויאמרו כי בעבור שבלהה שואלת רביעית הממון ורחל חציו וזלפה שלש רביעיותיו [ולאה]‫<ref>Vatican: ולא</ref> כלו נקח מדומה שיהיה לו חצי ורביעית והנה נמצא שמנה |
|- | |- | ||
| | | | ||
| − | :: | + | ::Its quarter is two; its half is four; its three-quarters are six; the sum of all these parts with [the denominator] is twenty. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{8+\left(\frac{1}{4}\sdot8\right)+\left(\frac{1}{2}\sdot8\right)+\left(\frac{3}{4}\sdot8\right)=8+2+4+6=20}}</math> |
| + | |style="text-align:right;"|ורביעיתם שניים וחציים ארבעה ושלש רביעיותיהם ששה והמחובר מכל החלקים האלה עמו עולה עשרים | ||
|- | |- | ||
| | | | ||
| − | :: | + | ::<span style=color:green>'''Rule of Three:'''</span> As the ratio of twenty to four thousand, which is the amount that Jacob has left, so is the ratio of eight to the unknown share of Leah. |
| − | |style="text-align:right;"| | + | ::<math>\scriptstyle{\color{blue}{20:4000=8:X}}</math> |
| + | |style="text-align:right;"|והנה כערך עשרים אל ארבעת אלפים שהוא הממון הנשאר ליעקב ככה יהיה ערך שמנה אל חלק כתובת לאה הנעלם | ||
|- | |- | ||
| | | | ||
| − | :: | + | ::When we apply the rule of four [lit. the rule of proportions], we find that her share is one thousand and six hundred gold coins. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וכאשר נעשה כמשפט הערכין נמצא שתהיה חלקה אלף ושש מאות זהובים |
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue | + | ::<span style=color:green>'''Rule of Three:'''</span> As the ratio of twenty to four thousand, so is the ratio of six, which is three-quarters of the denominator, to the share of Zilpah. |
| − | | | + | ::<math>\scriptstyle{\color{blue}{20:4000=6:X}}</math> |
| + | |style="text-align:right;"|וכערך עשרים אל ארבעת אלפים ככה יהיה ערך ששה שהוא שלש רביעיות [המדומה]‫<ref>Vatican: ומדומה</ref> אל החלק שתקח זלפה בכתובתה | ||
|- | |- | ||
| | | | ||
| − | :: | + | ::When we examine by the rule of four, we find that her share is one thousand and two hundred gold coins. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|וכאשר נחקור במשפט הערכין נמצא שתהיה חלקה אלף ומאתים זהובים |
|- | |- | ||
| − | |||
| | | | ||
| + | ::<span style=color:green>'''Rule of Three:'''</span> We take the ratio and say: as the ratio of twenty to four thousand, so is the ratio of four, which is half the denominator, to the share of Rachel. | ||
| + | ::<math>\scriptstyle{\color{blue}{20:4000=4:X}}</math> | ||
| + | |style="text-align:right;"|ועם נעיין ונאמר כערך עשרים [אל]‫<ref>Vatican om.</ref> ארבעת אלפים כן ערך ארבעה שהוא חצי המדומה אל החלק שתקח רחל בכתובתה | ||
|- | |- | ||
| | | | ||
| − | + | ::We find that her share is eight hundred gold coins. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ::We find that her share is eight hundred gold coins. | ||
|style="text-align:right;"|‫<ref>107v</ref>ונמצא שיבואו לחלקה שמונה מאות זהובים | |style="text-align:right;"|‫<ref>107v</ref>ונמצא שיבואו לחלקה שמונה מאות זהובים | ||
|- | |- | ||
| | | | ||
| − | ::<span style=color: | + | ::<span style=color:green>'''Rule of Three:'''</span> We take the ratio and say: as the ratio of twenty to four thousand, so is the ratio of two to the share of Bilhah. |
::<math>\scriptstyle{\color{blue}{20:4000=2:X}}</math> | ::<math>\scriptstyle{\color{blue}{20:4000=2:X}}</math> | ||
|style="text-align:right;"|והנה גם כן נעריך ונאמר כערך עשרים אל ארבעת אלפים כן יהיה ערך שניים אל החלק אשר תקח בלהה בכתובתה | |style="text-align:right;"|והנה גם כן נעריך ונאמר כערך עשרים אל ארבעת אלפים כן יהיה ערך שניים אל החלק אשר תקח בלהה בכתובתה | ||
| Line 5,019: | Line 6,376: | ||
|- | |- | ||
| | | | ||
| − | :<span style=color: | + | :<span style=color:green>'''Check:'''</span> When you sum up all these four shares, you find that the result is four thousand precisely. |
:<math>\scriptstyle{\color{blue}{1600+1200+800+400=4000}}</math> | :<math>\scriptstyle{\color{blue}{1600+1200+800+400=4000}}</math> | ||
|style="text-align:right;"|וכאשר תחבר כל החלקים האלה ארבעתם תמצא שיהיו עולים ארבעת אלפים מכוונים | |style="text-align:right;"|וכאשר תחבר כל החלקים האלה ארבעתם תמצא שיהיו עולים ארבעת אלפים מכוונים | ||
|- | |- | ||
| − | !<span style=color: | + | !<span style=color:green>Motion Problem - Pursuit</span> |
| | | | ||
|- | |- | ||
| Line 5,038: | Line 6,395: | ||
| | | | ||
::We divide them by the excess of the parsot that the second walks in one day over the first, which is three; we find it forty times there, so he will catch up with him in forty [days]. | ::We divide them by the excess of the parsot that the second walks in one day over the first, which is three; we find it forty times there, so he will catch up with him in forty [days]. | ||
| − | |||
::<math>\scriptstyle{\color{blue}{X=\frac{10\sdot12}{15-12}=\frac{120}{3}=40}}</math> | ::<math>\scriptstyle{\color{blue}{X=\frac{10\sdot12}{15-12}=\frac{120}{3}=40}}</math> | ||
|style="text-align:right;"|נחלקם על יתרון הפרסאות שהולך השני מן הראשון ביום אחד שהם שלשה נמצאם שם ארבעים פעמים והנה ישיגנו בארבעים | |style="text-align:right;"|נחלקם על יתרון הפרסאות שהולך השני מן הראשון ביום אחד שהם שלשה נמצאם שם ארבעים פעמים והנה ישיגנו בארבעים | ||
|- | |- | ||
| | | | ||
| − | :<span style=color: | + | :<span style=color:green>'''Check:'''</span> You can check it when you calculate how many parsot the first had walked in fifty [days], because the second had walked in [forty] [days] as many as that. |
| − | :<math>\scriptstyle{\color{ | + | :<math>\scriptstyle{\color{OliveGreen}{50\sdot12=40\sdot15}}</math> |
|style="text-align:right;"|ותוכל לבחון זה כשתחשוב כמה פרסאות הלך השליח הראשון בחמשים יום כי ככה הלך השני בארבעה | |style="text-align:right;"|ותוכל לבחון זה כשתחשוב כמה פרסאות הלך השליח הראשון בחמשים יום כי ככה הלך השני בארבעה | ||
|- | |- | ||
| − | !<span style=color: | + | !<span style=color:green>Motion Problem- Encounter</span> |
| | | | ||
|- | |- | ||
| Line 5,062: | Line 6,418: | ||
| | | | ||
::We divide fifty, which is the distance, by them; we find them three times in it and two remain that cannot be divided. We consider them as one-eighth of sixteen. So, they will meet in three days and one-eighth of a day. | ::We divide fifty, which is the distance, by them; we find them three times in it and two remain that cannot be divided. We consider them as one-eighth of sixteen. So, they will meet in three days and one-eighth of a day. | ||
| − | |||
::<math>\scriptstyle{\color{blue}{X=\frac{50}{16}=3+\frac{2}{16}=3+\frac{1}{8}}}</math> days | ::<math>\scriptstyle{\color{blue}{X=\frac{50}{16}=3+\frac{2}{16}=3+\frac{1}{8}}}</math> days | ||
|style="text-align:right;"|נחלק חמשים שהוא המרחק עליהם נמצאם שם שלשה פעמים וישארו שנים שלא נתחלקו ונחשוב אותם שמינית ששה עשר והנה יתחבר זה עם זה בשלשה ימים ושמינית יום | |style="text-align:right;"|נחלק חמשים שהוא המרחק עליהם נמצאם שם שלשה פעמים וישארו שנים שלא נתחלקו ונחשוב אותם שמינית ששה עשר והנה יתחבר זה עם זה בשלשה ימים ושמינית יום | ||
|- | |- | ||
| − | !<span style=color: | + | !<span style=color:green>Find a Quantity Problem - Whole from Parts - Cane</span> |
| | | | ||
|- | |- | ||
| Line 5,075: | Line 6,430: | ||
|- | |- | ||
| | | | ||
| − | ::<span style=color: | + | ::<span style=color:green>'''False Position:'''</span> We do it like this: we take twelve as a denominator, because there is a third and a quarter in it. |
|style="text-align:right;"|נעשה כזאת נקח לנו שנים עשר למדומה יען ימצא השלישית ורביעית | |style="text-align:right;"|נעשה כזאת נקח לנו שנים עשר למדומה יען ימצא השלישית ורביעית | ||
|- | |- | ||
| Line 5,089: | Line 6,444: | ||
|- | |- | ||
| | | | ||
| − | ::<span style=color: | + | ::<span style=color:green>'''Rule of Three:'''</span> Now, we take the ratio and say: as the ratio of five to twelve so is the ratio of the two zeratot to the unknown. |
| − | ::<math>\scriptstyle{\color{ | + | ::<math>\scriptstyle{\color{OliveGreen}{5:12=2:X}}</math> |
|style="text-align:right;"|ועתה נעריך ונאמר כערך חמשה אל שנים עשר כן ערך השני זרתות אל הנעלם | |style="text-align:right;"|ועתה נעריך ונאמר כערך חמשה אל שנים עשר כן ערך השני זרתות אל הנעלם | ||
|- | |- | ||
| Line 5,099: | Line 6,454: | ||
|- | |- | ||
| | | | ||
| − | :<span style=color: | + | :<span style=color:green>'''Check:'''</span> You can check if this is true when you subtract a third and a quarter from twenty-four and you are left with ten, as the measure of the parts of the two whole zeratot that are seen above the mud. |
:<math>\scriptstyle{\color{blue}{\frac{24-\left[\left(\frac{1}{3}\sdot24\right)+\left(\frac{1}{4}\sdot24\right)\right]}{5}=\frac{10}{5}=2}}</math> | :<math>\scriptstyle{\color{blue}{\frac{24-\left[\left(\frac{1}{3}\sdot24\right)+\left(\frac{1}{4}\sdot24\right)\right]}{5}=\frac{10}{5}=2}}</math> | ||
|style="text-align:right;"|ותוכל לבחון זה אם הוא אמת כשתסיר מעשרים וארבעה שלישיתו ורביעיתו וישארו לך עשרה כשעור חלקי השני זרתות שלמות הנראות מעל הטיט | |style="text-align:right;"|ותוכל לבחון זה אם הוא אמת כשתסיר מעשרים וארבעה שלישיתו ורביעיתו וישארו לך עשרה כשעור חלקי השני זרתות שלמות הנראות מעל הטיט | ||
|- | |- | ||
| − | !<span style=color: | + | !<span style=color:green>Give and Take Problem - Earning and Spending</span> |
| | | | ||
|- | |- | ||
| Line 5,132: | Line 6,487: | ||
|style="text-align:right;"|ונמצא שהיו לו בשחרית אותו יום מחצית מאה וחמשים דינרים שהם שבעים וחמשה דינרים שנשארו לו מערב היום השלישי | |style="text-align:right;"|ונמצא שהיו לו בשחרית אותו יום מחצית מאה וחמשים דינרים שהם שבעים וחמשה דינרים שנשארו לו מערב היום השלישי | ||
|- | |- | ||
| − | | | + | | |
| − | :*Before he paid the tax of that day, he had one-hundred and seventy-five dinar. | + | :*Before he paid the tax of that day, he had one-hundred and seventy-five dinar. |
| − | ::<math>\scriptstyle{\color{blue}{100+75=175}}</math> | + | ::<math>\scriptstyle{\color{blue}{100+75=175}}</math> |
| − | |style="text-align:right;"|וקודם שפרע מכס היום ההוא היו לו מאה ושבעים וחמשה דינרים | + | |style="text-align:right;"|וקודם שפרע מכס היום ההוא היו לו מאה ושבעים וחמשה דינרים |
| − | |- | + | |- |
| − | | | + | | |
| − | ::We take their half; they are eighty-seven dinar and a half, which he had on the morning that remained for him from the evening of yesterday, which is the second day. | + | ::We take their half; they are eighty-seven dinar and a half, which he had on the morning that remained for him from the evening of yesterday, which is the second day. |
| − | ::<math>\scriptstyle{\color{blue}{\frac{1}{2}\sdot175=87+\frac{1}{2}}}</math> | + | ::<math>\scriptstyle{\color{blue}{\frac{1}{2}\sdot175=87+\frac{1}{2}}}</math> |
| − | |style="text-align:right;"|נקח מחציתם יהיו שמנים ושבעה דינרים וחצי שהיו לו בשחר שנשארו לו מאמש יום תמולו שהוא היום השני | + | |style="text-align:right;"|נקח מחציתם יהיו שמנים ושבעה דינרים וחצי שהיו לו בשחר שנשארו לו מאמש יום תמולו שהוא היום השני |
| − | |- | + | |- |
| − | | | + | | |
| − | :*We find that before paying the tax he had one-hundred eighty-seven dinar and a half. | + | :*We find that before paying the tax he had one-hundred eighty-seven dinar and a half. |
| − | ::<math>\scriptstyle{\color{blue}{100+\left(87+\frac{1}{2}\right)=187+\frac{1}{2}}}</math> dinar | + | ::<math>\scriptstyle{\color{blue}{100+\left(87+\frac{1}{2}\right)=187+\frac{1}{2}}}</math> dinar |
| − | |style="text-align:right;"|ונמצא שאז יהיו לו קודם פריעת המכס מאה ושמונים ושבעה דינרים וחצי | + | |style="text-align:right;"|ונמצא שאז יהיו לו קודם פריעת המכס מאה ושמונים ושבעה דינרים וחצי |
| − | |- | + | |- |
| − | | | + | | |
| − | ::We take their half; they are ninety-three dinar and nine pešuṭim, which he had on the morning that remained for him from the evening of the first day. | + | ::We take their half; they are ninety-three dinar and nine pešuṭim, which he had on the morning that remained for him from the evening of the first day. |
| − | ::in the evening he had: <math>\scriptstyle{\color{blue}{\frac{1}{2}\sdot\left(187+\frac{1}{2}\right)=93+\frac{9}{12}}}</math> | + | ::in the evening he had: <math>\scriptstyle{\color{blue}{\frac{1}{2}\sdot\left(187+\frac{1}{2}\right)=93+\frac{9}{12}}}</math> |
| − | |style="text-align:right;"|נקח חצים יהיו תשעה ושלשים דינרים ותשעה פשיטים משנים עשר בדינר שהיו לו בשחר הנשארים לו מערב יום ראשון | + | |style="text-align:right;"|נקח חצים יהיו תשעה ושלשים דינרים ותשעה פשיטים משנים עשר בדינר שהיו לו בשחר הנשארים לו מערב יום ראשון |
| − | |- | + | |- |
| − | | | + | | |
| − | :*We find that on that first day, before paying the tax he had one-hundred ninety-three dinar and nine pešuṭim. | + | :*We find that on that first day, before paying the tax he had one-hundred ninety-three dinar and nine pešuṭim. |
| − | ::<math>\scriptstyle{\color{blue}{100+\left(93+\frac{9}{12}\right)=193+\frac{9}{12}}}</math> | + | ::<math>\scriptstyle{\color{blue}{100+\left(93+\frac{9}{12}\right)=193+\frac{9}{12}}}</math> |
| − | |style="text-align:right;"|ונמצא שביום ההוא הראשון היו לו קודם פריעת המכס מאה ותשעים ושלשה דינרין ותשעה פשיטים | + | |style="text-align:right;"|ונמצא שביום ההוא הראשון היו לו קודם פריעת המכס מאה ותשעים ושלשה דינרין ותשעה פשיטים |
| + | |- | ||
| + | | | ||
| + | ::We take their half; they are ninety-six dinar and ten pešuṭim and a half; and so [is the amount of money] he brought. | ||
| + | |style="text-align:right;"|נקח חציים והם תשעים וששה דינרים ועשרה פשיטים וחצי פשוט וככה הביא | ||
|- | |- | ||
| − | | | + | | colspan="2"| |
| − | |||
::<math>\scriptstyle{\color{blue}{X=\frac{1}{2}\sdot\left(193+\frac{9}{12}\right)=96+\frac{10+\frac{1}{2}}{12}}}</math> | ::<math>\scriptstyle{\color{blue}{X=\frac{1}{2}\sdot\left(193+\frac{9}{12}\right)=96+\frac{10+\frac{1}{2}}{12}}}</math> | ||
| − | |||
|} | |} | ||
{| | {| | ||
| Line 5,169: | Line 6,526: | ||
| | | | ||
|- | |- | ||
| − | | | + | |Up to this point there have been many of the questions of many different types. |
| − | |style="text-align:right;"|<big>עד הנה</big> הרבה מן השאלות ממינים רבים ‫<ref>109v</ref>בלתי דומים זה לזה | + | |style="width:45%;text-align:right;"|<big>עד הנה</big> הרבה מן השאלות ממינים רבים ‫<ref>109v</ref>בלתי דומים זה לזה |
|- | |- | ||
| − | | | + | |I have explained the way to find the answer of each one at length, so that any wise man will be able to deduce from these answers to others. |
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ובארתי בכל אחת ואחת בארוכה דרך מציאת תשובתה וכל חכם לב יוכל לקחת מהתשובות האלה לזולתן |
|- | |- | ||
| − | | | + | |The time has come to end the words of this book that ''giveth goodly words'' [Genesis 49, 21] |
| − | |style="text-align:right;"|''הנותן אמרי שפר''‫<ref group=note>בראשית מט, כ"א</ref> | + | |style="text-align:right;"|והגיע ת[ור] לחתום פה עתה את דברי זה הספר ''הנותן אמרי שפר''‫<ref group=note>בראשית מט, כ"א</ref> |
|- | |- | ||
| − | | | + | |We will give praises, glories and songs to the Knower of all hidden things, because, they are not proper to others. |
| − | |style="text-align:right;"|ונערוך תושבחות ותהלות ושירות | + | |style="text-align:right;"|ונערוך תושבחות ותהלות ושירות ליודע כל נסתרות כי לא יאותו לזולתו |
|- | |- | ||
| − | | | + | |For ''the honor of his excellent majesty'' [Esther 1, 4]. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|style="text-align:right;"|בעבור ''יקר תפארת גדולתו''‫<ref group=note>אסתר א, ד</ref> | |style="text-align:right;"|בעבור ''יקר תפארת גדולתו''‫<ref group=note>אסתר א, ד</ref> | ||
|- | |- | ||
| − | | | + | |May his name be blessed and exalted. |
|style="text-align:right;"|יתברך ויתעלה שמו | |style="text-align:right;"|יתברך ויתעלה שמו | ||
|- | |- | ||
| − | | | + | |May He bestow us His compassion. |
|style="text-align:right;"|ויפיק אלינו חמלתו | |style="text-align:right;"|ויפיק אלינו חמלתו | ||
|- | |- | ||
| − | | | + | |May His kingdom be established upon us forever and ever. |
|style="text-align:right;"|ויכון עלינו לעולם ועד מלכותו | |style="text-align:right;"|ויכון עלינו לעולם ועד מלכותו | ||
|- | |- | ||
| − | | | + | |May He also shower water out of the wells of His salvation upon His congregation. |
|style="text-align:right;"|גם ישפיע לעדתו ממימי מעייני ישועתו | |style="text-align:right;"|גם ישפיע לעדתו ממימי מעייני ישועתו | ||
|- | |- | ||
| − | | | + | |May He hasten and quicken the day spoken of in the vision of Isaiah, his prophet, who wrote in his book: ''And in that day shall you say: 'Give thanks unto the Lord, call upon His name, declare His doings among the peoples, make mention that His name is exalted''' [Isaiah 12, 4]. |
|style="text-align:right;"|ימהר ויחיש יום יאמר חזות ישעיהו נביאו אשר כתב בספרו ''ואמרתם ביום ההוא הודו לי"י קראו בשמו הודיעו בעמים עלילותיו הזכירו כי נשגב שמו''‫<ref group=note>ישעיהו יב, ד</ref> | |style="text-align:right;"|ימהר ויחיש יום יאמר חזות ישעיהו נביאו אשר כתב בספרו ''ואמרתם ביום ההוא הודו לי"י קראו בשמו הודיעו בעמים עלילותיו הזכירו כי נשגב שמו''‫<ref group=note>ישעיהו יב, ד</ref> | ||
|- | |- | ||
| − | | | + | |Over and done. |
|style="text-align:right;"|תם ונשלם | |style="text-align:right;"|תם ונשלם | ||
|- | |- | ||
| − | | | + | |Praise be to the Creator of the world. |
|style="text-align:right;"|שבח לבורא עולם | |style="text-align:right;"|שבח לבורא עולם | ||
|- | |- | ||
| Line 5,244: | Line 6,595: | ||
:1) Ithaca (NY), Cornell University A 26/1 (IMHM: f 46122), ff. 3r-29v (15th century) | :1) Ithaca (NY), Cornell University A 26/1 (IMHM: f 46122), ff. 3r-29v (15th century) | ||
:2) Moscow, Russian State Library, Ms. Guenzburg 138/2 (IMHM: f 6818), ff. 23r-65v (15th century) | :2) Moscow, Russian State Library, Ms. Guenzburg 138/2 (IMHM: f 6818), ff. 23r-65v (15th century) | ||
| + | :[https://www.nli.org.il/he/discover/manuscripts/hebrew-manuscripts/viewerpage?vid=MANUSCRIPTS&docid=PNX_MANUSCRIPTS990000863450205171-1#$FL62183479 Guenzburg 138] | ||
:3) München, Bayerische Staatsbibliothek, Cod. hebr. 68/5 (IMHM: f 1131), ff. 346r-374v (Roma, 1552)<br> | :3) München, Bayerische Staatsbibliothek, Cod. hebr. 68/5 (IMHM: f 1131), ff. 346r-374v (Roma, 1552)<br> | ||
:[http://daten.digitale-sammlungen.de/~db/0010/bsb00103921/images/index.html?id=00103921&groesser=&fip=193.174.98.30&no=&seite=701 Cod.hebr. 68] | :[http://daten.digitale-sammlungen.de/~db/0010/bsb00103921/images/index.html?id=00103921&groesser=&fip=193.174.98.30&no=&seite=701 Cod.hebr. 68] | ||
Latest revision as of 08:39, 17 February 2023
Contents
- 1 Introduction
- 2 Table of Contents
- 3 Chapter One – The Nature of the One and the Foundation of Numbers
- 4 Chapter Two – the Ranks of the Numbers and the Values of the Digits Used by the Experts of this Science
- 5 Chapter Three – Addition of Numerous Numbers to Each Other
- 6 Chapter Four – Subtraction of a Small Number from a Greater Number
- 7 Chapter Five – Multiplication of Units by Themselves or by Other Units and Multiplication of any Number by Itself or by Other
- 8 Chapter Six – Division of a Great Number by a Smaller Number
- 9 Chapter Seven – Extracting the Closest Root of Integer
- 10 Chapter Eight – the Ratio of a Number to Another Number
- 11 Chapter Nine – On Knowing the Fractions of Integer, whether in Multiplication, in Division, in Addition, or in Subtraction
- 11.1 Introduction
- 11.2 Operations with fractions
- 11.2.1 Multiplication of fractions
- 11.2.1.1 Introduction
- 11.2.1.2 Multiplication of fractions by fractions
- 11.2.1.3 Multiplication of integers by fractions
- 11.2.1.4 Multiplication of integers and fractions by fractions of the same type
- 11.2.1.5 Multiplication of integers and fractions by fractions of different types
- 11.2.1.6 Multiplication of integers and fractions by integers and fractions of the same type
- 11.2.1.7 Multiplication of integers and fractions by integers and fractions of different types
- 11.2.2 Division of fractions
- 11.2.3 Addition of fractions
- 11.2.4 Subtraction of fractions
- 11.2.1 Multiplication of fractions
- 12 Chapter Ten – Knowing the Square Roots of "Deaf" and "Mute" Numbers by Approximation
- 13 Chapter Eleven – Here I will Write Nice Rules of Arithmetic Methods for You
- 14 Epilogue
- 15 Notes
- 16 Apparatus
- 17 Appendix I: Glossary of Terms
- 18 Appendix: Bibliography
| People come to Qiryat-Sefer, | [1]אישים באו קרית ספר |
| Where you can examine any number, | בה כל מספר תוכלו לבחון |
| I will tell you the name of the city, | את שם העיר אגיד לכם |
| For Ḥeshbon was the city of Siḥon [Numbers 21, 26]. | על כי חשבון היא עיר סיחון[note 1] |
Introduction |
|
| Said Yoseph b. rabi Moshe ha-Ṣarfati [= the French] Ish Ḥay: | [2]אמר יוסף בר משה הצרפתי איש חי |
| Arithmetic contains signs for the unity of God:
Since I have seen that arithmetic is a magnificent and extremely lovable science and the Creator, blessed be He, has placed the secret of His unity in the property of number [lit. calculation], |
מאשר ראיתי כי חכמת החשבון היא חכמה מפארה ונחמדת עד מאד והיוצר ב"ה שם בתכונת החשבון סוד אחדותו |
| My heart and kidneys urged me to write a book about it, as I extracted from studies of the ancient scholars in a clear language, clarified for every thinker, for its way is hidden and concealed and requires a broad knowledge as the entrance of a hall. | יעצוני לבי וכליותי לחבר ממנה ספר אחד כאשר אוציא ממחקרי החכמים הקדומים בלשון גלוי ומבואר לכל משכיל למען אשר דרכה נסתר ונעלם וצריכה דעת רחבה בפתחו של אולם |
| The people who are interested in the words of wisdom of this book will benefit much from its additional interpretation. | וירוחו בני אדם אשר נדב לבם אותם אל דברי החכמות בזה הספר מאד בתוספת הביאור |
| I myself will also benefit that the science will be preserved within me properly, when actualizing it by the phrasing of my language, and so I will gain learning as well as teaching. | וארויח אנכי גם כן שתשמר החכמה בקרבי היטב בהוציאי אותה במלת לשוני ואזכה ללמוד וללמד |
| A short rhyme of praise to God – asking him for a shelter and for turning a good thought into act | |
| My Creator shall be my strength and refuge. | ויוצרי יהיה לי למעוז ולמחסה |
| He shall link my good thought to an action. | ומחשבתי הטובה יצרף אותה לי למעשה |
| For His wonderful mercy and grace. | למען רחמיו וחסדו אשר נפלאו |
| And His expressions that are more than can be numbered. | ועצמו מספר כל מעבריו |
| May his name be excellent and glorious forever. | יהי שמו משובח לעד ומפואר לנצח |
| I named this book ʽIr Siḥon For Ḥeshbon was the city of Siḥon [Numbers 21, 26]. | וקראתי שם זה הספר עיר סיחון על שם כי חשבון עיר סיחון[note 2] |
Table of Contents |
|
| This book is divided into eleven chapters: | ונחלק הספר הזה לאחד עשר שערים |
|
השער הראשון ביסוד המספר ותולדות האחד |
|
השער השני במדרגות [3]המספר וסכום האותיות אשר ישתמשו בהם החכמים בזאת המלאכה |
|
השער השלישי במחברת חשבונות רבים זה עם זה |
|
השער הרביעי במגרעת חשבון קטן מחשבון גדול |
|
השער החמישי בכפילת הכאת האחדים על עצמן או על אחרים זולתם או בכפול כל חשבון על עצמו או על חשבון אחר |
|
השער הששי בחלוקת חשבון גדול על חשבון קטן ממנו ובזה השער אדבר על מאזני הכפל והחלוק [והחבור][4] והמגרעת |
|
השער השביעי בלקיחת גדר המספר השלם היותר קרוב אליו |
|
השער השמיני במערכת חשבון אחד מחשבון אחר |
|
השער התשיעי בידיעת חלקי השבר מן השלם בין בכפל בין בחלוק בחבור או במגרעת |
|
השער העשירי בידיעת צלעות המרובעים מחשבון החרש והאלם על דרך קרוב |
|
השער האחד עשר בכללים נחמדים והם פרפראות [5]החכמה הזאת וקצת מהשאלות העמוקות והקשות ואזכיר בשער הזה בעזרת אלהי ישראל |
Chapter One – The Nature of the One and the Foundation of Numbers |
השער הראשון בתולדות האחד ויסוד המספרים |
Numeration |
|
|
דבר ידוע ברור ואמיתי כי האחד איננו מקבל לא רבוי ולא שנוי אכן הוא סבת כל רבוי ושנוי |
|
והוא קדמון ואב לכל המספרים וכלם מתחדשים בעבורו כי הוא להם שורש ויסוד וממנו צומחים כל החשבונות |
|
ומזה יוכל להבין כל משכיל קצת רמיזות מסוד אחדות השם הנכבד והנורא |
| The names of the numbers: | |
| Units | |
|---|---|
|
והנה כאשר נחבר אחד עם אחד והיא ההרכבה הראשונה נקרא זה שנים |
|
וכש נוסיף על השנים אחד |
|
וכשנוסיף על שלשה אחד נקרא זה ארבעה |
|
וכן בתוספת אחד על הארבעה נקרא זה חמשה |
|
ותוספת אחד על חמשה יקרא ששה |
|
ובתוספת אחד על ששה יקרא שבעה |
|
ובתוס[פת] אחד על שבעה יקרא שמונה |
|
ובתוספת אחד על שמונה יקרא תשעה |
| These nine numbers are called "units". | ואלה המספרים התשעה נקראים אחדים |
| Tens | |
| When we add one to nine, we call it ten, which is the beginning of the [rank of] tens. | וכאשר נוסיף אחד על תשעה [6]נקרא זה עשרה והוא ראשית כל חשבון עשרות |
|
והנה העשרה בחשבון העשרות כמו האחד בחשבון האחדים |
|
וכשיהיו לנו שני עשרות נקרא אותם עשרים |
|
ונקרא לשלש עשרות שלשים |
|
ולארבע עשרות ארבעים |
|
ולחמש עשרות חמשים |
|
ולשש ששים |
|
ולשבע שבעים |
|
ולשמונה שמונים |
|
ולתשע עשרות תשעים |
| All these names are derived from the names of the units. | וכל השמות האלה הם מושאלות משמות האחדים |
|
והנה תשעים בעשרות כמו תשעה באחדים |
| Hundreds | |
|
וכאשר יהיה לנו עשר עשרות נקרא להם בשם כולל מאה והוא ראשית חשבון המאות כמו האחד ראשית האחדים והעשרה ראשית העשרות |
| Thousands | |
|
וכשיתקבצו עשרה מאות נקרא להם בשם כולל אלף והוא ראשית האלפים כמו מאה ראשית המאות |
| ?? | אמנם למאת אמנם אין להם שם כולל עד שנגיע לעשר מאות שנקראו אלף כאמור |
| But the thousands have no inclusive name. | וכן האלפים אין להם שם כולל |
| The twelve names of numbers | |
| For all the names of the numbers that are varied from one another are twelve no less and no more. | כי כל שמות המספרים החלוקים זה מזה הם שנים עשר לא פחות ולא יותר |
|
ואלה הם תשעה שמות [7]האחדים |
|
ושם העשרה |
|
ושם המאה |
|
ושם האלף |
| All numbers are derived from these twelve names. | והנה כל המספרים יחלקו [ילקחו][8] מאלה השנים עשר שמות |
|
כי עשרים ומאתים ואלפים הם כמו שני אחדים וכל אחד ואחד כפי מעלתו |
|
וכן כאשר נאמר אחד עשר או שנים עשר הם שמות מורכבים מאחדים ועשרות |
| In this way all the numbers are generated and derived from these twelve separate names. | ועל דרך הזה יתילדו וילוו כל המספרים מאלו השנים עשר שמות המפורשים |
Chapter Two – the Ranks of the Numbers and the Values of the Digits Used by the Experts of this Science |
השער השני במדרגות המספר וסכום האותיות אשר ישתמשו בהם החכמים בזאת המלאכה | ||||||||||
| The names of the ranks | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| It was clarified in the preceding chapter that all the names of numbers are derived from the nine names of the units until comes the tenth number which we call by one inclusive name. | הנה התבאר בשער הקודם כי כל שמות המספרים הם מושאלים מתשע שמות האחדים עד אשר יבוא החשבון העשירי ונקרא לו בשם כולל | ||||||||||
| Therefore, the numbers are divided into ranks. | ומפני זה נחלקו המספרים למדרגות מדרגות | ||||||||||
| The units are called "the first rank", the tens - "the second rank", the hundreds - "the third rank", the thousands - "the fourth rank", and so on endlessly. | ויקראו האחדים מדרגה ראשונה והעשרות מדרגה שנייה והמאות מדרגה שלישית והאלפים מדרגה רביעית וככה עד אין קץ | ||||||||||
| For every rank is the tenth of the following rank. | כי כל מדרגה היא עשור המדרגה הבאה אחריה | ||||||||||
| According to this we call the tens of thousands "the fifth rank" and the hundreds of thousands "the sixth rank". | ולפי זה נקרא לעשרת אלפים מדרגה חמישית ולמאה [9]אלף מדרגה ששית | ||||||||||
| This is the way of the ranks of the number. | וזהו דרך מדרגות המספר | ||||||||||
The Positional Decimal System |
|||||||||||
| Since all the numbers are circulating by nine, for we find nine numbers in the rank of units, nine numbers in the rank of tens, and so on, in each rank there are nine numbers, it is enough to write any small or large number with nine letters, each of which we consider as the units, that are up to nine. | ובעבור כי כל החשבונות מתגלגלים על תשעה באשר נמצא תשעה חשבונות ממדרגת אחדים ותשעה חשבונות ממדרגת עשרות וכן בכל המדרגות יש תשעה חשבונות בכל אחת מהן יספיק לכתוב כל חשבון קטן או גדול בתשע אותיות שנחשוב כל אחת מהן כמו האחדים שהם עד תשעה | ||||||||||
| The numerals | |||||||||||
| These are the digits used in this science: | ואלה הם האותיות המשמשות בחכמה הזאת | ||||||||||
| 1 2 3 4 5 6 7 8 9 |
| ||||||||||
| tens | |||||||||||
| When we need to write the number ten, we do it this way: | וכשהתצטרך לכתוב חשבון העשרה נעשה על הדרך הזה | ||||||||||
| It is known that the tens are the second rank. | בידוע כי העשרות הם המדרגה השנית | ||||||||||
| It was already explained that the ratio of the ten to the tens is [the same as] the ratio of the one to the units. | וכבר התבאר כי יחס העשרה אל העשרות יחס האחד אל האחדים | ||||||||||
| Therefore, we only need to write the letter aleph [א] that indicates one and make a mark that this digit is in the second rank. | על כן [אי] אנחנו צריכין כי אם לכתוב אות האלף המורה לאחד ולעשות היכר וסימן שהאות הזאת היא ממדרגה השנית | ||||||||||
| The arithmeticians agreed to make a mark indicating the ranks in the shape of a circle as this 0 and this shape is called sifra. | והסכימו חכמי החשבון לעשות סימן היכר המדרגות בצורת עגול כדמות זה 0 וקוראים למורה הזאת סיפרא | ||||||||||
| Writing numbers with numerals, including zeroes or without them | |||||||||||
|
[10]וכשנרצה לכתוב עשרים נכתוב סיפרא בתחלה ואחריה אות ב' במדרגה השנית ויורה זה שתי עשרות | ||||||||||
|
וכאשר נבקש מאה נכתוב שתים סיפראש ואות הא' במדרגה השלישית ויורה זה מאה | ||||||||||
| When we have units and tens, we write the units in the first rank and after it the tens in the second rank. | ולעולם כשיהיו לנו אחדים ועשרות נכתוב במדרגה הראשונה האחדים ואחריהם במדרגה השנית העשרות | ||||||||||
| If we do not have tens, only units and hundreds, we write the units in the first rank, a zero in the second [rank], and the hundreds in the third [rank]. | ואם אין לנו עשרות כי אם אחדים ומאות נכתוב האחדים במדרגה הראשונה וספרא אחת בשנית והמאות בשלישית | ||||||||||
| Similarly, we write two or three zeros and so on endlessly, as we need according to the number. | וכן נשים שתים או שלש סיפראש כאשר נצטרך לפי החשבון עד אין חקר | ||||||||||
| We always write each number in its rank. | ונכתוב לעולם כל חשבון וחשבון במדרגתו |
Chapter Three – Addition of Numerous Numbers to Each Other |
השער השלישי במחברת חשבונות רבים זה עם זה | |||||||||||||||||||
| Written Addition | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Description of the procedure: | ||||||||||||||||||||
| The procedure of the addition of numbers is as follows: | דרך מחברת החשבונות כך הוא | |||||||||||||||||||
|
נכתוב כל מספר ומספר מבקשת החבור זה תחת זה כל אחד ואחד בטור בפני עצמו ממדרגה תחת מדרגה הדומה לה ואחר נעביר קו דיו | |||||||||||||||||||
|
ונתחיל במדרגה הראשונה ונקבץ כל האחדים | |||||||||||||||||||
|
והמקובץ נכתבנו תחת קו הדיו אם לא [11]יספיק לעשר | |||||||||||||||||||
|
אמנם אם ילך בעשרות נכתוב אות בטורי המספר במדרגה השניה כפי מספר עשרות המקובץ על עשרות המקובץ ונכתוב ספרא בלבד תחת קו הדיו | |||||||||||||||||||
|
ואם יעדיף המקובץ על עשרות אין אנחנו צריכים כי אם לכתוב תחת הקו העודף ההוא והמדרגה השניה כפי מספר העשרות כאמור | |||||||||||||||||||
|
ובדרך הזה נלך ונעשה גם כן כאשר עשינו ממדרגת האחדים מכל שאר המדרגות ונכתוב כל קבוץ המדרגות בזה אחר זה בסדור תחת קו הדיו | |||||||||||||||||||
|
ומה שיצא מקבוץ המדרגות מסודר תחת הקו | |||||||||||||||||||
| When we sum a digit with a digit, we always consider each of them, in whichever rank they are, as if they are units, then we find their true meaning in their own rank. | ולעולם כשנחבר אות עם אות נחשוב כל אחת ואחת באיזו מדרגה שתהיין כאלו הם אחדים ואחר נמצא אמיתתם במדרגתם | |||||||||||||||||||
| Any thinker will understand that the reason for writing the number of tens of the sum of a certain rank in the following rank, is that every digit in the ranks is tenth of the next rank. | וכל משכיל יבין כי טעם [כתיבת מספר][12] העשרות מהתחבר באותיות המדרגה ההיא במדרגה הבאה אחריה הוא לפי שכל אות ואות מהמדרגות היא עשור מן המדרגה הבאה אחריה | |||||||||||||||||||
|
ואם יהיה בטורי מספר חשבונות החבור מדרגה אחת או שתים שכל טוריה סיפראש צריך לכתוב תחת קו הדיו סיפראש כאשר תבאנה במקומן כפי מספר המדרגות ההם | |||||||||||||||||||
| In order that this mentioned addition operation will be better clarified to every person I shall discuss it by the experience way in the following calculations: | ולמען [13]אשר יתבאר היטב אצל כל בני אדם מלאכת החבור הזאת הנזכרת אדבר ממנה [בדרך][14] הניסיון בחשבונות אלו | |||||||||||||||||||
|
בקשנו לידע כמה מחובר תשע אלפים ומאתים ושמונה עם שלשת אלפים ושמונה מאות ואחד | |||||||||||||||||||
|
והנה נכתוב אלו השני חשבונות בשני טורים על זאת הצורה | |||||||||||||||||||
|
| |||||||||||||||||||
| ||||||||||||||||||||
|
והנה מקובץ המדרגה הראשונה אינו מספיק לעשר ועל כן נכתוב העולה תחת קו הדיו והנה הוא ט' | |||||||||||||||||||
|
וכאשר אין במדרגה השנייה אות כלל כי אם סיפראש לבדנה נכתוב תחת הקו סיפרא אחת אחר הט' שכתבנו בעבור חבור אותיות המדרגה הראשונה | |||||||||||||||||||
|
ובעבור שמקובץ המדרגה השלישית הוא עשר נכתוב תחת טורי חשבונות המספרים במדרגה הרביעית הבאה אחריה א' תחת קו הדיו סיפרא אחת בשלישית אצל הסיפרא שכתבנו אחר הט' | |||||||||||||||||||
|
והנה מקובץ המדרגה הרביעית הוא שלשה עשר ומפני זה נכתוב א' במדרגה חמישית בעבור העשרה ונשים העודף שהוא שלשה תחת הקו סמוך לסיפרא האחרונה ואחר אלו השלשה נכתוב הא' אשר חדשנו ממנה מדרגה חמישית | |||||||||||||||||||
| The sum: 13009 We find that the [total] sum is thirteen thousand and nine. | [15]ונמצא שהמחובר הוא שלשה עשר אלף ותשעה | |||||||||||||||||||
Chapter Four – Subtraction of a Small Number from a Greater Number |
השער הרביעי במגרעת חשבון קטן מחשבון גדול | |||||||||||||||||||
| Written Subtraction | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Description of the procedure: | ||||||||||||||||||||
| When we wish to do so, we write the greater number in one line and the smaller number beneath it in a line, rank beneath rank. | כשנבקש לעשות זה נכתוב החשבון הגדול בטור אחד | |||||||||||||||||||
|
והנה נחשוב כל האותיות כאלו הן אחדים באיזו מדרגה שתהיין | |||||||||||||||||||
|
ונתחיל בראשונה באות המדרגה האחרונה אשר בחשבון הטור השפל ונגרוע אותה מהאות שכנגדה בטור מספר החשבון העליון | |||||||||||||||||||
|
ונכתוב עליה הנשאר אם ישאר ממנה כלום | |||||||||||||||||||
|
ואם אין נמחקנה והוא שנרשום על ראשה ספרא | |||||||||||||||||||
|
ואחר כן נעשה מכל המדרגות האחרות כמעשה המדרגה הזאת ונלך אחור אחורנית ממדרגה למדרגה עד תומם | |||||||||||||||||||
|
ואם תהיה אות באחת המדרגות מחשבון הטור השפל גדולה מהאות שכנגדה בטור העליון אמנם בהכרח יש אות אחת בטור החשבון העליון הסמוכה לזו אשר אנחנו עומדים במדרגתה מלאחריה | |||||||||||||||||||
|
נעשה על הדרך הזה נסיר א' מהאות [שאחרי זאת המדרגה ונכתוב הנשאר מהאות][16] ההיא אשר לקחנו הא' ממנה עליה ואם לא ישאר [17]ממנה כלום כגון שלא היה שם כי אם א' נמחקנה | |||||||||||||||||||
|
ובידוע כי הא' הזאת שיש לנו היא שוה עשר בהקש אל המדרגה שלפניה לכן נחשוב זאת הא' עשרה ונחחבר אל העשרה הזאת החשבון מהאות מהמדרגה העליונה אשר אנחנו עומדים עליה ויהיה לחשבון בעשרה הנזכרים כמו אחדים ועתה יספיק בריוח להסיר מכל זה האות התחתונה ונכתוב הנשאר על האות הראשונה שכנגדה | |||||||||||||||||||
|
וכן נעשה תמיד עד שנגיע אל המדרגה | |||||||||||||||||||
|
והנה בכל עת אשר לא נוכל להסיר האות התחתונה מהעליונה [נסייע לה][18] מהמדרגה הבאה אחריה על הדרך האמור ואפי' היו סיפראש מפסיקות בינה ובין האות הבאה אחריה או שיש לנו להסיר האות התחתונה מסיפרא אשר תהיה כנגדה בטור העליון | |||||||||||||||||||
|
נשיב אחורנית על הדרך הזה שנסיר מהאות הקרובה א' ונכתוב עליה הנשאר אם ישאר ממנה כלום ונשים זאת הא' על הסיפרא [19]שלפניה ותהיה עשרה ונסיר מהם א' ונשאר שמה על הסיפרא ט' ונשים זאת הא' על הסיפרא הקודמת לזה ויהיו עשרה ונסיר מהם א' וישאר ט' על הסיפרא וכן נעשה לעולם עד שנגיע אל האות או אל הסיפרא מהמדרגה אשר אנחנו עומדים עליה ואז נעשה כמשפט האמור למעלה | |||||||||||||||||||
|
המשל בזה בקשנו לגרוע מחמשת אלפים ושמונים ושלש תשעים ושנים | |||||||||||||||||||
|
הנה נכתוב שני טורי החשבונות על זאת הצורה החשבון הגדול בטור העליון והחשבון הקטון בטור שפל כנגדו | |||||||||||||||||||
|
| |||||||||||||||||||
| ||||||||||||||||||||
|
ומאשר חשבון האות מהמדרגה האחרונה שבטור השפל גדול מחשבון האות אשר היא כנגדה בטור העליון נעשה על הדרך האמור ונסיר א' מהאות האחרונה מהטור העליון שהיא ה' הסמוכה לאות המדרגה העליונה שאנחנו עומדים עליה מאחריה אחר הסיפרא והנה ישאר ד' במקום הה' | |||||||||||||||||||
|
ותהיה האות א' הזאת עשרה כשנשים אותה על הסיפרא ונסיר מהעשרה [20]אחד וישאר ט' על הסיפרא | |||||||||||||||||||
|
ונשים האחד הזה על המדרגה אשר עמדנו בה שהיא ח' ויהיה בין הכל שמונה עשר נסיר מהם האות | |||||||||||||||||||
|
אחרי כן נסיר הב' שהיה מהטור השפל מהג' שכנגדה בטור העליון וישאר א' ונכתבנה עליה | |||||||||||||||||||
| We find that the remainder is four thousand nine hundred and ninety-one. | ונמצא הנשאר ארבעת אלפים ותשע מאות ותשעים ואחד | |||||||||||||||||||
Chapter Five – Multiplication of Units by Themselves or by Other Units and Multiplication of any Number by Itself or by Other |
השער החמישי בכפילת הכאת האחדים על עצמם או על אחדים אחרים ובכפול כל חשבון על עצמו או על אחר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The meaning of this multiplication is to multiply one number by another: | כוונת הכפילה הזאת היא לכפול החשבון האחד על חבירו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כאשר נאמר על דרך משל שלשה פעמים ארבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Or by itself: | או על עצמו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
שלשה פעמים שלשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן [עשר פעמים עשרים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
או][21] עשר פעמים עשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Multiplication of Units by Units |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| It is true that regarding the multiplication of units alone there is no way in this science to find the result, therefore, one should memorize all the products of the units by themselves or by other units. | ובאמת כי בכפילת האחדים לבדם לא נמצא דרך בחכמה הזאת למצוא ההווה ולפיכך צריך להזכיר ולהסדיר כל כפילות האחדים הן על עצמם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| And these are: | ואלה הם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
האחד שני פעמים שנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ושלשה פעמים שלשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
[22]וכן כל המספרים האחרים שיכפלו באחד לא יקבלו שום שנוי ורבוי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
השנים בשנים ארבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
שנים בשלשה ששה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
שנים בארבעה שמנה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
שנים בחמשה עשרה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
שנים בששה שנים עשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
שנים בשבעה ארבעה עשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
שנים בשמנה ששה עשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
שנים בתשעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
השלשה בשלשה תשעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
השלשה בארבעה שנים עשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
שלשה בחמשה חמשה עשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
שלשה בששה שמנה עשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
שלשה בשבעה עשרים ואחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
שלשה בשמונה עשרים וארבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
שלשה בתשעה עשרים ושבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הארבעה בארבעה ששה עשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ארבעה בחמשה עשרים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ארבעה בששה עשרים וארבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ארבעה בשבעה עשרים ושמונה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ארבעה בשמונה שנים ושלשים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ארבעה בתשעה ששה ושלשים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
החמשה בחמשה עשרים וחמשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חמשה בששה שלשים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חמשה בשבעה שלשים וחמש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חמשה [23]בשמונה ארבעים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חמשה בתשעה ארבעים וחמש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הששה בששה ששה ושלשים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ששה בשבעה שנים וארבעים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ששה בשמונה שמונה וארבעים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ששה בתשעה ארבעה וחמישים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
השבעה בשבעה תשע וארבעים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
שבעה בשמונה ששה וחמשים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
שבעה בתשעה שלשה וששים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
השמונה בשמונה ארבעה וששים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
שמונה בתשעה שנים ושבעים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
התשעה בתשעה אחד ושמונים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Thus, the whole method of multiplying the units is clear and nothing is missing. | ובזה התבאר כל סדר כפלת האחדים ולא נפקד מהם דבר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Written Multiplication |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Description of the procedure: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| When we wish to multiply a number by a number of other ranks we do it this way: | וכאשר נבקש לכפול החשבון על חשבון מהמדרגות האחרות נעשה על הדרך הזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נכתוב שני החשבונות אשר נרצה לכפול אלה על אלה טור תחת טור ומדרגה תחת חברתה ונעביר תחת שני טורי החשבונות קו דיו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה נתחיל באות הראשונה מהטור העליון ונכפול כל האותיות העליונות על כל אותיות הטור השפל [24]זו אחר זו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכל הנכפלים נכתוב תחת הקו במדרגות הראויות להם אות תחת אות כאשר יצטרך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כי לעולם נמנה כמה מדרגות מהאות אשר נכפיל מהטור העליון עד האות הנכפלות שבטור השפל ושתי האותיות בכלל המנין | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם יספיק כפל האות על חברתה לעשרות נכתוב אות במספר העשרות כמספר מנין המדרגות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם לא יספיק לעשר נכתוב הנכפל ממדרגה אחת פחותה מהמספר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם יעלה הנכפל להיות בו אחדים ועשרות נכתוב העשרות כמספרן כמספר המדרגות שבין אות לאות והאחדים מדרגה אחת אחורנית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכשיכפלו כל אותיות הטור השפל בכל אותיות הטור העליון כמשפטן נעביר קו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והעולה הוא הנכפל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Now I will discuss the procedure of this chapter through examples: | ועתה אדבר ממלאכת השער הזה על דרך הדמיון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
בקשנו לכפול ולהכות שנים ותשע מאות על ששה וארבעים [ומאתים][25] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
[ונכתבם][26] על זאת הצורה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
[27]וכאשר נכפל אות הבית על אות הו"ו אשר תחתיה בטור השפל יהיו שנים עשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה מספר המדרגות שתים לכן נכתוב אות ב' במדרגה ראשונה כנגד שני האחדים ואחריה במדרגה שנית נכתוב א' כנגד העשרה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר נכפיל אות הב' הנזכרת על הד' מהטור השפל יהיו שמונה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומספר המדרגות שלש ואולם באשר אין הכפלה ההיא מגעת לעשר נשים אותם מדרגה אחת אחורנית ונכתוב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר נכפיל את האות הנזכרת על הב' מהטור השפל יהיו ארבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר אין הכפלה הזאת מגעת לעשר נכתוב כנגד אלו הארבעה ד' במדרגה השלישית אשר נחדש עתה כשנכתבנה אחרי הא' שהיא במדרגה השנייה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ובזה נשלם כפילת האות מהמדרגה הראשונה שבטור העליון על כל אותיות הטור השפל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועתה אנחנו צריכים גם כן להכפיל אות הט' שהיא המדרגה האחרונה מהטור העליון על כל אותיות הטור השפל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה כשנכפל האות ההיא על אות המדרגה הראשונה [28]מהטור השפל שהיא ו' יעלה ארבעה וחמישים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומספר המדרגות הם ארבעה ולכן נכתוב במדרגה הרביעית ה' [כנגד][29] [החמשים וכנגד][30] הארבעה נכתוב תחת הד' במדרגה השלישית ד' אחרת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר נכפול האות ההיא על הד' שבטור השפל יעלו ששה ושלשים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומספר המדרגות חמש ולכן נכתוב כנגד השלשים אחרי הה' [הכתובה][31] במדרגה הרביעית ג' ונחדש עתה מדרגה חמישית וכנגד הששה נכתוב אחורנית תחת הה' הקדומה ו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכשנכפיל אות הט' הנזכרת על המדרגה האחרונה שבטור השפל שהיא ב' יעלה שמנה עשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומספר המדרגות שש ולכן נכתוב במדרגה ששית אשר נחדש א' כנגד עשרה וכנגד השמנה נכתוב ח' אחורנית תחת הג' הקדומה שהיא במדרגה החמישית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועם כל זה הוכפלו כל אותיות הטור העליון על אותיות הטור | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועתה נחל לקבץ כל האותיות שבכל מדרגה ומדרגה כמשפט מלאכת החבור אחר אשר נעביר קו הדיו תחת הכפילה ונכתוב תחת הקו מה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
[33]וידוע כי המדרגה הראשונה מהכפל הזאת תצא ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומהשנייה ט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומשלישית ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומהרביעית תשאר א' אחרי כתבנו העשרה בכפילה במדרגה הבאה אחרי זאת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומהמדרגה החמישית תשאר ב' אחרי כתבנו העשרה בכפילה במדרגה הבאה אחרי זאת שהיא ששית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומהמדרגה הששית יצא לנו ב' מאשר חברנו לה העשרה שנותר לנו מהמדרגה החמישית הקדומה אליה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונמצא עולה מאתים ועשרים ואחד אלף ושמונה מאות ותשעים ושנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This is the method and the procedure of the multiplication of all numbers rank by rank. | וככה הוא דרך וסדר כפילת כל החשבונות מערכה לקראת מערכה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Chapter Six – Division of a Great Number by a Smaller Number |
השער הששי בחלוקת חשבון גדול על חשבון קטן ממנו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Written Division | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Description of the procedure: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הרוצה לעשות זה יכתוב טור החשבון הגדול בתחלה ואחר יניח ריוח וחלק כמלוא טור אחד ויכתוב החשבון הקטן בטור אחר כנגד הטור הראשון מהחשבון הגדול מדרגה תחת מדרגה הדומה לה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר יביט ויראה כמה [פעמים][34] יוכל להוציא מספר המדרגה האחרונה מטור החשבון הקטן מהאות מהמדרגה האחרונה שבטור החשבון הגדול ויוציאם ממנה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואולם צריך שיחכם [35]ויראה אם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכמספר הפעמים אשר תהיה ההסרה יכתוב אות כנגדן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וימנה מהמדרגה האחרונה מטור החשבון הגדול כפי מנין המדרגות שבטור החשבון הקטן אחרנית והמדרגה אשר י | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם ישוב מהאות מהחשבון הגדול כלום אחרי מה שהסיר ממנה יכתוב עליה הנשאר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם לא נשאר ממנה כלום יכתוב עליה סיפרא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר יסיר כל שאר אותיות המדרגות שבטור החשבון הקטן הקדומות לאות [38]המדרגה האחרונה זו אחר זו מהאותיות אשר ימצא עתה כתובות בטור החשבון הגדול כמספר פעמי ההסרה מהאות האחרונה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ובכל מקום יהיה זהיר לכתוב אחר ההסרה מה שישאר במקומו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם לא ישאר שם כלום יכתוב עליה סיפרא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם הזדמן לו אות במדרגה אחת מהטור החשבון הקטן שלא יוכל להסיר אותה מהאות הכתובה בטור החשבון הגדול כראוי אבל אם יש שם עדין אותיות אחרי המדרגה שהוא עומד בה יחזור לה מהאותיות של אותן המדרגות לפי שידוע שכל מדרגה ומדרגה היא גדולה עשר פעמים מהמדרגה הקדומה כאשר נודע בשערים הקדומים לזה ויקח ממספרן כאשר יצטרך ויכתוב מה שישאר במקומות ההשארות וסיפרא וסיפרש במקומות אשר לא נשאר שם כלום | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר אשר ישלים פעמי ההסרה מטור החשבון הגדול כל האותיות מטור החשבון הקטן במספר שוה זו כזו יעיין אם מה שנשאר בטור החשבון הגדול קיים שלא נתחלק [מספ]רו רב ממספר טור החשבון הקטן ואם הוא כן יחזור [39]ויביט ויראה וישום וישער כמה פעמים יוכל להסיר האות שבמדרגה האחרונה מטור החשבון הקטן מהאות האחרונה ממה שנשאר בטור החשבון הגדול וכמספר הפעמים אשר יסיר אותה ממנה כך פעמים יצטרך להסיר שאר המדרגות שבטור החשבון הקטן ממה שישאר אחרי כן בטור החשבון הגדול | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
לכן ישמור בתחלת הבטת השיעור והשומא שיכלכל כל מעשיו כראוי במשפט וצדק | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכמספר הפעמים אשר יוציא את האותיות שבטור החשבון הקטן מטור אותיות החשבון הגדול יכתוב אות אחת כנגדן באמצע שני טורי החשבונות הקטן והגדול | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויתחיל למנות מטור החשבון הגדול מהאות אשר התחיל להביט בה שנית כפי מנין המדרגות שבטור החשבון הקטן אחורנית ובאותה מדרגה אשר תכלה מספרן שם יכתוב תחתיה מספר פעמי הסרת ההוצאה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויזהר שלא ישכח לכתוב בכל מקום מהטור מהחשבון הגדול מה שישאר בו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
או לכתוב סיפרא על מקום הכליון אשר לא נשאר שם כלום | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחרי זה יעיין אם רבה עדיין [40]מה שנשאר בטור החשבון [הגדול][41] על מספר טור החשבון הקטן ואם הוא כן יחזור עוד ויביט כאשר עשינו זה פעמים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויעשה ככה הרבה פעמים עד שיהיה מה שישאר בטור החשבון הגדול מספרו מועט ממספר הטור מהחשבון הקטן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם יזדמן לו בתחלת ההבטה שיגדל מספר אות האחרונה ממדרגת טור החשבון הקטן מהאות האחרונה שבטור החשבון הגדול עד שלא יוכל להוציאה ממנה אפילו פעם אחת ישים את כל האות ההיא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויחשוב ויביט וישום וישער כמה פעמים יוכל להוציאה משם שיספיק הנשאר גם כן להוציא ממנו ככה פעמים האותיות האחרות שבטור החשבון הקטן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ולעולם יכתוב פעמי מספר ההסרה באמצע שני טורי החשבונות מהקטון והגדול כמספר המדרגות מהטור מהחשבון הקטן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויתחיל מניית מספרן אחורנית מהאות שבמדרגה אשר התחיל בו הבטת הסרת ההוצאה בטור החשבון הגדול | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The line that is formed between the two lines is the number of times that the line of the smaller number is in the line of the greater number. | והנה הטור המתהוה בין שני הטורים הוא מספר [42]הפעמים אשר מספר טור החשבון הקטן הוא במספר טור החשבון הגדול | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| What remains above the line of the greater number is the excess of the line of the greater number over the line of the smaller number after you have multiplied it by this number of times. | ומה שנשאר על טור החשבון הגדול הוא מה שעודף עדין מספר הטור מהחשבון העליון על מספר הטור מהחשבון הקטן אחרי כפילת אותם פעמים עליו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This is the procedure of dividing a greater number by a smaller number. | וכן הוא דרך חלוקת החשבון הגדול על חשבון קטן ממנו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Since the skill of this chapter is very honorable and nice and it is very deep, I shall write in this chapter itself many calculations as an explanation of the method of this skill of division in order to guide and lead the student to understand easily all the aforementioned matters. | וכאשר מלאכת השער הזה היא נכבדת ונחמדת עד מאד והיא עמוקה הרבה לרוב אכתוב בשער הזה עצמו בבאור דרך מלאכת החלוקה הזאת מהרבה חשבונות כדי להדריך ולהתישר אל המתלמד שידין כל הענינים הנזכרים בנקלה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
בקשנו לחלק חמשה ועשרים ומאה על אחד עשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה נכתוב שני טורי החשבונות על זאת הצורה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נכתוב החשבון הגדול בראשונה בטור אחד ואחר נניח ריוח כמלה טור ונכתוב כנגדו החשבון הקטן בטור אחר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר נביט ונקח הא' שבמדרגה האחרונה מטור החשבון הקטן וגם הא' שבמדרגה [43]אחרונה מטור החשבון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכנגד הפעם הזאת כאשר מדרגות הטור מהחשבון הקטן הם שתים נכתוב א' תחת הב' שבטור החשבון הגדול באשר היא מדרגה שנית גם כן לאות הא' מהטור ההוא עצמה אשר התחלנו ההבטה ממנה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר לא נשאר כלום מהא' הזאת נכתוב עליו סיפרא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אחרי כן נקח הא' שבמדרגה ראשונה מטור החשבון הקטן הקדומה במכתב אל האחרת אשר התחלנו בה ונסיר אותה גם כן פעם אחת מהב' שהיא בטור החשבון הגדול וישאר עליה א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ובזה השלמנו הסרת האותיות שבטור החשבון הקטן מטור החשבון הגדול בשוה פעם האחת כפעם חברתה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר נעיין הנותר בטור החשבון הגדול ראינו שהוא חמשה עשר והנה המספר הזה מרובה ממספר טור אותיות החשבון הקטן שאינו עולה רק אחד עשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ובעבור זה נחזור ונקח הא' האחרונה מהמדרגות שבטור החשבון הקטן ונסיר אותה פעם אחת מהא' אשר [44]נשארה על הב' שבטור החשבון הגדול ואחר נכתוב עליה סיפרא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכנגד פעם ההסרה הזאת נכתוב א' תחת הה' שהיא המדרגה הראשונה מטור החשבון הגדול באשר היא שנייה אל האות אשר התחלנו ממנה הבטת ההסרה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר נסיר גם כן הא' שבטור החשבון הקטן הראשונה פעם אחת מהה' שהיא המדרגה הראשונה מטור החשבון הגדול וישאר ד' על הה' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועתה נראה ונכר לעין שמה שנשאר בטור החשבון הגדול מספר קטן מאד ממספר טור החשבון הקטן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה מספר הטור האמצעית אשר חדשנו ממספר פעמי ההסרות עולה אחד עשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומה שנשאר בטור החשבון הגדול הוא ארבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אם כן נוכל לאמר זאת מצאנו שהמספר הקטן הוא אחד עשר פעם במספר הגדול ועוד זולת זה עודף ארבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועוד בקשנו לחלק מאה על ט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נכתבם על זאת הצורה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר נקח הט' שהיא החשבון הקטן [45]נראה שלא נוכל להסיר אותה מהא' שבמדרגה השלישית שהיא החשבון הגדול | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועל כן נשים הא' על הסיפרא הקדומה לה במכתב ותהיה שוה עשר ומאלו העשר נסיר ט' וישאר א' על הספרא ההיא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב תחתיה א' כנגד פעם אחת שהסירונו הט' מהעשר באשר היא המדרגה [הראשונה][46] להתחלת הבתות ההסרה ובחשבון הקטן אין בו גם כן כי אם מדרגה אחת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב סיפרא על הא' אשר העתקנוה ממקומה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר נחשוב עוד ונביט להסיר הט' שהוא החשבון הקטן מהא' שנשארה על הספרא בטור החשבון הגדול והנה אנחנו צריכים גם כן לשים אותה על הסיפרא האחרת הקדומה לה ותהיה שוה עשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכשנסיר מהם הט' פעם אחת ישאר א' על הסיפרא הראשונה שבטור החשבון הגדול | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכנגד הפעם הזה שהסירונו הט' מהעשר נכתוב תחת הספרא הראשונה א' באשר היא ראשונה להבטת ההסרה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ובזה נגמרה החלוקה הזאת ומצאנו שיש במאה אחד עשר פעמים תשעה ועוד אחד מוסף עליהם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
[47]עוד בקשנו לחלק מאה על שנים עשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתבם על זאת הצורה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה כאשר נקח האלף שהיא המדרגה האחרונה מטור החשבון הקטן ונביט להסיר אותו מהא' שבמדרגה השלישית בטור החשבון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ולפיכך צריך לנו להבין אחרית דבר מראשיתו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ובתחלת כל דבר נשים הא' שהיא החשבון העליון על הסיפרא הקדומה לה במכתב ותהיה שוה עשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר נביט כמה פעמים נסיר הא' מהחשבון הקטן מהעשר האלו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה אם נסיר אותה תשע פעמים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומפני זה לא נסיר האלף מהעשר אשר על הסיפראש במדרגה שנית מטור החשבון הגדול כי אם שמונה פעמים וישאר ב' על הסיפרא הזאת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב סיפרא על הא' שהיתה במדרגה השלישית שהרי שמנו אותה על הסיפרא ולא נשאר שם כלום | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכנגד שמונה פעמי ההסרה נכתוב ח' תחת הסיפרא הראשונה באשר מדרגות החשבון הקטן הם שתים ומניינם מתחיל מהסיפרא מהמדרגה השניה שבטור החשבון הגדול לפי ששם התחלנו הבטת ההסרה הזאת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחרי זה נסיר גם כן הב' מהחשבון הקטן שמנה פעמים ממה שנשאר בטור החשבון הגדול ונעשה על הדרך הזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נשים הב' שנשארה לנו במקום הסיפרא השנית על הסיפרא הראשונה ותהיה שוה שני עשרות שהם עשרים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נסיר מהם ששה עשר שהוא העולה מכפל פעמי ההסרה על ב' וישאר מהם ד' על ראש הסיפרא הראשונה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב במקום אשר היתה כתובה הב' אשר שמנו אותה על הסיפרא הראשונה סיפרא אחת לפי שלא נשאר שם כלום | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה [49]יצאה לנו החלוק שיש שמנה פעמים שנים עשר במאה ועודף עליהם ארבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועוד בקשנו לחלק אחד ותשע מאות על שלשים ושתים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נכתבים על זאת הצורה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה אנחנו רואים שאם נסור הג' שבטור השפל שהוא החשבון הקטן מהט' אשר בטור העליון שהוא החשבון הגדול שלשה פעמים לא נוכל אחרי כן לעשות תשלום לאות האחרת שבטור השפל להסיר אותה מהסיפרא לפי שלא ישאר מאומה מהט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אם כן לא נסירנה כי אם שני פעמים ונכתוב הג' הנותרת עליה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכנגד שני פעמי ההסרה האלה נכתוב ב' תחת הסיפרא באשר מדרגות הטור השפל הם שתים והסיפרא גם כן היא שנית אל האות אשר התחלנו בה ההסרה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אחרי כן נסיר אות הב' שהיא המדרגה הראשונה שבטור השפל גם כן ב' פעמים מהסיפרא שבטור העליון והנה נעשה על דרך זה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נקח א' מהג' הנותרת על הט' וישאר עליה ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והא' שלקחנו נשים אותה [50]על הסיפרא ותהיה שוה עשר נסיר מהם ב' פעמים ב' העלה כפילתם ארבעה וישאר ו' על הסיפרא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועתה עשינו תשלום שהסירונו כל אותיות הטור השפל במספר פעמים שוה מהטור העליון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אכן כאשר נעיין בטור העליון הנותר נראה שהוא רב יותר מספר מהטור השפל ומפני זה אנחנו צריכים לחזור ולהביט להסיר הג' שהיא המדרגה האחרונה שבטור השפל מהב' שנשארה לנו במדרגה האחרונה מהטור העליון ונעשה על דרך זה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נשים הב' ההיא כולה על הו' אשר בראש הסיפרא ויהיו עשרים וששה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועתה [נשום][51] ונשער כמה פעמים נוכל להסיר הג' מהששה ועשרים והנה נוכל להסיר אותה שמונה פעמים העולים עשרים וארבע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כשנסיר אותם מהששה ועשרים ישאר על הו' ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב סיפרא על המדרגה האחרונה מהטור העליון שהרי לא נשאר שם כלום | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכנגד שמונה פעמי ההסרה אכתוב ח' תחת הא' שהיא המדרגה הראשונה מהטור העליון באשר היא שנייה אל המדרגה אשר התחלנו הבטת ההסרה ממנה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועתה נסיר גם כן אות ב' [52]מהטור השפל שמונה פעמים ממה שנשאר בטור העליון ונעשה על הדרך הזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נשים הב' הנשארת לנו במדרגה השנייה מהטור העליון על הא' שבמדרגה ראשונה ממנה יהיו עשרים ואחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נסיר מהם כפל ח' על ב' שהוא ששה עשר וישאר מהם ה' על ראש הא' שהיא המדרגה הראשונה מהטור העליון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב סיפרא על הב' הכתובה בראש המדרגה השנית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונשלמה החלוקה הזאת ומצאנו שהטור האמצעי עולה שמונה ועשרים והנותר על הטור העליון חמשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועוד בקשנו לחלק שמונה מאות ותשעים ואחד על ארבעים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה נכתבם על זאת הצורה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונסיר הד' שבטור השפל שתי פעמים מהח' שבטור העליון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב עליה סיפרא באשר לא נשאר ממנה כלום | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכנגד פעמי ההסרה נכתוב ב' תחת הט' שבטור העליון באשר היא מדרגה שנית אל האות אשר הנחלנו ממנה ההסרה ובטור השפל יש גם כן שתי מדרגות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
[54]עוד נשוב ונסיר הד' הנודעת מהט' שכנגדה בטור העליון שני פעמים וישאר עליה א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכנגד שני פעמי ההסרה נכתוב ב' תחת הא' שהיא המדרגה הראשונה מהטור העליון באשר היא שנית אל אות הט' אשר התחלנו עתה ההסרה ממנה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה יצאתה אלינו החלוקה שיש בשמונה מאות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועוד בקשנו לחלק שלש מאות ועשרים ואחד על תשעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב אותם על זאת הצורה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר נביט להסיר הט' שהיא החשבון הקטן מהג' שבמדרגה אחרונה מהטור העליון יצטרך לנו לשים את הג' כולה על הב' הקדומה לה במכתב ויהיו שלשים ושנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונסיר מהם הט' שלש פעמים שעולים שבעה ועשרים וישאר מהם ה' על הב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכנגד שלשת פעמי ההסרה האלה תכתוב ג' תחת הב' שבטור העליון לפי שמאותה מדרגה אנחנו מתחילים ההסרה ואין בטור השפל כי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב סיפרא על מדרגת הג' כאשר לא נשאר ממנה כלום | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונשוב עוד להסיר הט' מהה' הנשארת על הב' בטור העליון וכאשר לא נוכל להסיר ט' מה' נשים כל הה' על הא' ויהיו חמישים ואחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה נסיר הט' חמשה פעמים וישאר מהם ו' על המדרגה הראשונה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב סיפרא על הה' ד כאשר לא נשאר ממנה כלום | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכנגד חמש פעמים ההסרה נכתוב ה' תחת המדרגה הראשונה שהתחלנו ההסרה ממנה כאשר אין בטור השפל כי אם מדרגה אחת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה נגמרה החלוקה והטור האמצעי עולה ל"ה והנותר על הטור העליון ששה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועוד בקשנו לחלק חמש מאות אלף ושמונים ושלשת אלפים ושש מאות ותשעים וששה על שבע מאות וששים וארבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה המבוקש הזה מלאכתו רבה ועמוקה מכל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה כשנביט להסיר ז' שבטור התחתון מהה' שבטור העליון לא נוכל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
[56]ועל כן נשים אותה על הא' שהיא המדרגה הקדומה לה במכתב ונכתוב במקומה סיפרא באשר לא נשאר שם כלום | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה יעלו חמישים ושמנה וכאשר נשום ונשער כמה פעמים נסיר מהם הז' נמצא שלא נוכל להוציאה כי אם שבעה פעמים כדי שנוכל לעשות מהנשאר המשפט הצריך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה שבע פעמים ז' עולים תשע וארבעים וכשנסיר אותם משמנה וחמישים נשאר ט' על הח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומהמדרגה הזאת נתחיל למנות שלש המדרגות שבטור השפל אחורנית ויכלה מספרן בו' שהיא מדרגה שלישית ושם נכתוב תחתיה ז' כנגד שבע פעמי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחרי כן נסיר הו"ו שבטור השפל גם כן שבעה ז' פעמים מהט' והעולה מכפל זה על זה [הם ארבעים][57] ושנים ונעשה על הדרך הזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נסיר מהט' ההיא ד' ונכתוב עליה הנשאר שהוא ה' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונשים הד' על הג' שהיא מדרגה קדומה במכתב למדרגה אשר היתה הט' עליה והנה יהיו ארבעים ושלש נמצא שישאר מהם א' על הג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר כך נסיר הד' שבטור השפל שהיא המדרגה הראשונה ממנה גם כן [58]שבע פעמים שעולה כפלתם שמונה ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נקח א' מן הה' שנשארה לנו בטור העליון במדרגה חמישית ונשים אותה על הא' שנשארה על הג' הקדומה למדרגה הזאת ויהיו אחד עשר נסיר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נשים הג' על המדרגה הקדומה למדרגתה במכתב שהיא ו' ויהיו ששה ושלשים נסיר מהם כפל הד' על הז' שהם שמנה ועשרים וישאר על הו' ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועתה השלמנו להסיר כל אותיות הטור השפל מהטור העליון בשוה זו כזו האחת כפ[ע]ם חברתה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכשנעיין במה שנשאר בטור העליון נראה שהוא רב מאד על מספר הטור השפל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
על כן נחזור ונביט להסיר ז' שבטור השפל מהד' שנשארה בטור העליון במדרגה חמישית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה אנחנו צריכים לשים אותה על הח' שנשארה על המדרגה הקדומה לזו יהיו שמנה וארבעים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר נשום ונשער נמצא שנוכל להסיר הז' מהם שש פעמים שעולה כפילתם שנים וארבעים ונמצא כשנסיר אותם מהם ישארו על הח' ו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב סיפרא על הד' [59]כאשר לא נשאר ממנה כלום | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומהמדרגה אשר כתבנו עתה הו' עליה נחל לספור אחורנית השלש מדרגות שבטור השפל ויכלו בט' שהיא המדרגה השנית מהטור העליון ושם נכתוב תחתיה ו"ו כנגד שש פעמי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אחרי כן יש לנו להסיר הו' שבטור השפל גם כן ששה פעמים שעולה כפלתם ששה ושלשים ונעשה על הדרך הזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נסיר מהו' שנשארה במדרגה רביעית שלשה וישאר על הו' ההיא שלשה ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונשים הג' אשר הסירונו מהם על הח' הנשארת לנו במדרגה הקדומה למדרגה הזאת ויהיו שמנה ושלשים כשנסיר מהם ששה ושלשים ישארו מהם ב' על הח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עוד יש לנו להסיר הד' מהטור השפל גם כן שש פעמים והנה עולה כפלתם ארבעה ועשרים ונעשה על הדרך הזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נקח הב' הנשארת [לנו][60] על הח' ונשים אותה על הט' שהיא המדרגה הקדומה במכתב לזאת המדרגה שהיתה הב' כתובה עליה ויהיו תשעה ועשרים כשנסיר מהם עשרים וארבע ישאר על הט' ה' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב סיפרא [61]על המדרגה אשר הד' כתובה עליה באשר לא נשאר ממנו כלום | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ובזה השלמנו להסיר שנית אותיות הטור השפל מהטור העליון [במספר שוה פעמים זו כזו][62] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
[וכאשר נעיין בנשאר הטור העליון נמצא][63] שמספרו מרובה עדין ממספר הטור השפל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועל כן אנחנו צריכים עוד לחזור [ולהביט][64] ולהסיר הז' שהיא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה מוכרח לשום את הג' הזאת על המדרגה השלישית הקדומה לה במכתב הכתוב עליו סיפרא ותהיה שוה הג' שלשים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונסיר מהם הז' ד' פעמים כי כן יספיק לנו לעשות בנשאר המשפט הצריך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב סיפרא על הג' באשר לא נשאר שם מאומה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה כשנסיר שמנה ועשרים מהשלשים ישאר ב' על הסיפרא שהיא במדרגה השלישית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומהמדרגה הזאת נמנה אחורנית מספר השלש מדרגות שבטור השפל ויכלה מספרן במדרגה הראשונה והנה נכתוב תחתיה ד' פעמי ההסרה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אחר זאת צריך גם כן שנסיר הו' שבטור השפל ארבעה פעמים שעולה כפילתם עשרים וארבע ונעשה על [65]הדרך הזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נשים הב' הנשארת במדרגה השלישית על הה' הנשארת במדרגה הקדומה לה במכתב ויעלו חמשה ועשרים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכשנסיר מהם ארבע ועשרים כ ד ישאר א' במקום הה' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועל הב' נכתוב סיפרא באשר לא נשאר ממנה כלום | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עוד אנחנו צריכים להסיר אות הד' שהיא במדרגה הראשונה מהטור השפל גם כן ד' פעמים ועולה כפלתם ששה עשר ונעשה על זה הדרך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נקח הא' הנשארת במדרגה השנית ונכתוב עליה סיפרא ונשים אותה על הו' הקדומה לזאת המדרגה יהיו ששה עשר ומהם נסיר כפילת הד' על הד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב על הו' סיפרא באשר לא נשאר שם כלום | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונמצא שכל טור העליון הוא כלה בחלקות אשר עשינו והטור האמצעי אשר נתחדש הוא כטור החשבון הקטן לא פחות ולא יותר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועוד בקשנו לחלק חמש מאות אלף ושמנים ושלשת אלפים [ושש מאות ותשעים ושש][66] על אלף ושמונים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתבם על זאת הצורה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה אנחנו רואים שיש בידינו רשות להסיר הא' שבטור השפל חמש [67]פעמים מהה' שבטור העליון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונעשה כדברינו ונכתוב עליו סיפרא באשר לא נשארה ממנה שארית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונמנה מהמדרגה הזאת שבטור העליון ארבע מדרגות אחורנית כנגד הארבע מדרגות שבטור השפל ויכלה מנינן בו' שבאותו טור ושם נכתוב תחתיה ה' כנגד חמש פעמי ההסרה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחרי זאת יש לנו להסיר הח' שבטור השפל גם כן ה' פעמים שכפילתם עולה ארבעים ונעשה על הדרך הזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נסיר ד' מהח' שבטור העליון ונשים הד' על המדרגה הקדומה במכתב אל הח' שהיא ג' והעולה ארבעים ושלש והארבעים יכלו ויתמו והג' תשאר במקומה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ובזה הוסרו כל האותיות הטור השפל מהטור העליון כל אחת ואחת מהן פעמים שוות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכשנעיין הנותר בטור העליון נראה שמספרו מרובה ממספר הטור השפל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ובעבור זה נחזור ונביט ונסיר הא' שבטור השפל ד' פעמים מהד' שנשארה לנו במדרגה החמישית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותכלה כלה ונכתוב במקומה סיפרא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וממנה תמנה ארבע מדרגות אחורנית ויכלו במדרגה השנייה ושם [68]תכתוב תחתיה [ד'][69] כנגד ארבעה פעמי ההסרה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עוד יש לנו להסיר גם כן הח' מהטור השפל ד' פעמים העולה כפלתם שנים ושלשים והנה נעשה כזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נקח הג' אשר נשארה במקומה בטור העליון במדרגה הרביעית ונשים אותה על אות המדרגה השלישית שהיא ו' הקדומה לה במכתב ויעלה ששה ושלשים וכשנסיר מהם שנים ושלשים ישאר על הו' ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואכתוב סיפרא על הג' באשר לא נשאר ממנה כלום | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ובזה הוסרו כל אותיות הטור השפל מהטור העליון כשוה פעם שניה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה כאשר נעיין הנשאר בטור העליון נראה שהוא מועט במספרו ממספר הטור השפל וזה לך האות שנגמרה החלוקה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והטור האמצעי המתהוה ממספר פעמי ההסרה עלה חמש מאות וארבעים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנשאר על אותיות הטור העליון עולה ארבע מאות ותשעים ושש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Through all these many calculations I have mentioned the method of their division, every wise man will be able to understand and learn the truths of doing this skill accurately. | ומתוך כל אלו החשבונות הרבים שהזכרתי דרך חלוקתן בארוכה יוכל כל נבון להבין ולהשכיל אמיתות עשיית המלאכה הזאת בדקדוק | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Methods of Checking - Multiplication, Division, Addition, Subtraction |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Now, I should discuss in this chapter about the checking methods [lit. scales] of this division operation, as well as the checking methods [lit. scales] of the multiplication, addition and subtraction operations, as I promised at the beginning of this book, when mentioning the contents of its chapters. | ועתה אני צריך לדבר בשער הזה ממאזני [70]מלאכת החלוקה הזאת וממאזני מלאכת הכפל והחבור והמגרעת כאשר התאותי בהתחילי הספר הזה בהזכרת פרטי כללי שעריו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנני אומר כי אין בכל המאזנים יותר צדוקים וישרים כי אם כל מי שיעשה מלאכת חלוקתו שיכפיל ויכה במלאכת מעשה הכפילה הטור האמצעי המתהוה ממספר פעמי ההסרה על הטור השפל שהוא החשבון הקטן ואחר יקח כל מה שנותר למעלה בטור העליון אם נשאר שם כלום ויוסיף אותו תחת הכפילה כל אות ואות תחת מדרגה הראויה לה ואחרי כן יחבר ויקבץ כל הכפילה ובהכרח צריך שתצא טור הקבוץ והחבור כטור החשבון הגדול אשר חלק דומה כדומה מספר הטור האחד כמספר חברתה אם זך [ואם][71] ישר פעולו[note 3] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וגם מאזני הכפל הנה הם שיחלק העולה מהכפילה על אחת משני טורי החשבונות הנכפלים יצא לו בחלוק הטור השני אם בדרך ישר הוא הולך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן כל מי שחבר שני טורי חשבונות יחד זה עם זה יתעסק במלאכת המגרעת ויגרע מן המחובר אחד מן שני הטורים [72]וישאר לו הטור השני אם היה מעשהו באמונה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ולפי דרכנו נבין ונלמוד שגם כן הגורע חשבון קטן מחשבון גדול שאם יחבר מה שנותר לו עם טור החשבון הקטן שבהכרח יצא לו המחובר טור אחד כטור החשבון הגדול זו כזו במספר שוות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| By that the intention of everything I intended to explain in this chapter is clarified and it is time to finish with it and start with another. | ועם זה התבארה כוונת כל מה שהתכונתי לבאר בזה השער והגיע העת לפסוק בו ולהתחיל באחר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Chapter Seven – Extracting the Closest Root of Integer |
השער השביעי בלקיחת גדר המספר השלם היותר קרוב אליו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Definition of a square number: Know that the product of every number by itself is called a number that has a root, whereas its root is the number that is multiplied by itself. | תדע כי כל כפל הכאת חשבון על עצמו הוא הנקרא מספר נגדר או [נשרש][73] כאשר גדרו או שורשו הוא נכפל על עצמו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
One versus the integers |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ובכל המספרים אשר יהיו שלמים תמצא לעולם כשתכפול המספר על עצמו שיתרבה העולה מאשר היה המספר בתחלה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חוץ מן המספר האחד כי כש[תכה][74] האחד על עצמו לא יקבל שום תמורה וחלוף אך יעלה אחד כאשר היה בתחלה מבלתי רבוי ושנוי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועל כן נוכל לומר שמספר האחד הוא נגדר וגם כן הוא גדר עצמו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עוד למספר האחד יתרון על שאר המספרים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
[75][שהנה][76] כל המספרים זולתו שנקח שתי קצותיהם המספר שלפניהם והמספר שלאחריהם יהיה המחובר משני הקצוות כפל המספר האמצעי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ולמספר האחד הנה אין לו קצה לפניו ועם הקצה שלאחריו שהוא שנים יספיק לכפלו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This is the virtue and superiority of one over all the other numbers. | וזה היא מעלה ורוממות האחד על שאר המספרים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| There are other things that have no place to be mentioned here. I have strayed from the purpose of the present chapter, when I needed to speak about the virtues of the number one, so now I will return to where I was at the beginning. | ועוד דברים אחרים שאין מקומם להזכירם בזה והנה יצאתי מכוונת השער הזה באשר הוצרכתי לדבר במעלות מספר האחד ועתה אשוב אל אשר הייתי בתחלה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Square Nnumbers |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואומר בענייני הגדרים שאם תכפול ותכה מספר נגדר על מספר נגדר יהיה הכפל גם כן חשבון נגדר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר תרצה לדעת גדרו אינך צריך כן לקחת גדרי המספרים אשר הכית וכפלת זה על זה ותכה ותכפול גדר האחד על חברו וההווה הוא גדר המספר השלישי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון הנה ארבעה מספר נגדר וגם תשעה והעולה מכפל האחד על חברו ששה ושלשים והנה הוא גם כן מספר נגדר ואם נבקש לדעת גדרו נקח גדר הארבעה שהוא שנים וכן גדר התשעה שהוא [77]שלשה ונכה זה על זה יעלו ששה והוא המבוקש כי כאשר נכפול ששה על עצמו היה ששה ושלשים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Square ranks and non-square ranks | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Odd ranks have roots; even ranks have no root: Know that the ranks of the numbers always follow this order one after the other: the first has a root, the second has no root, the third has a root, the fourth has no root, and so on endlessly. | ותדע כי לעולם מדרגות החשבון הולכות על הסדר זו אחר זו בעניין זה שהראשונה היא נגדרת והשנייה איננה נגדרת והשלישית נגדרת והרביעית בלתי נגדרת וככה עד אין קץ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ורצוני לומ' בגדר המדרגות הזה כי כשתסכל המדרגה הראשונה שהיא מדרגת האחדים מספרם הראשון שהוא אחד הוא נגדר כמו שקדם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והמדרגה השנית שהוא מדרגת העשרות מספרם הראשון שהוא עשר בלתי נגדר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן המדרגה השלישית מספרה הראשון שהוא מאה נגדר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והמדרגה הרביעית מספרה הראשון שהוא אלף הוא בלתי נגדר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ובדרך הזו הולכות המדרגות כלנה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Extracting roots - written procedure |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The procedure for finding the unknown root of the known number is very complicated, with many aspects and different principles, and I cannot explain them with one rule for all numbers. | ודרך מציאת הגדר הנעלם מהמספר הידוע כי היא עמוקה עד מאד ויש בה צדדים רבים ומדות נחלקות זו מזו ולא אוכל לפרש אותם דרך כלל אחד לכל המספרים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Therefore I write numerous various calculations and explain the way to extract the root of each of them at length and an intelligent person, who has wisdom in his heart should understand from them how to do so with other numbers. | ועל כן אכתוב חשבונות הרבה בלתי דומים זה לזה ואבאר בארוכה בכל אחד מהם דרך להוציא גדרו ומהם יבין [78]כל משכיל ונבון אשר תנוח חכמה בלבו לעשות ככה במספרים אחרים זולתם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה בקשנו לדעת גדר מאתים ועשרים וחמשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נכתבם על זאת הצורה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר נמנה מספר המדרגות וראינו שהאחרונה יש לה גדר באשר היא מדרגה שלישית ובעבור | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה [היא ב'][79] נבקש הגדר היותר קרוב אל ב' והנה הוא אחד נכתבנו תחת הב' ההיא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונסיר הכאתו על עצמו ממנה וישאר עליה א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נכפול הא' שכתבנו תחת הב' פעמים ונכתוב העולה אחורנית תחת המדרגה הקדומה לזו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועל כן נכתוב ב' תחת הב' [מהמדרגה השנית ונכתוב סיפרא על הא' שכתבנו תחת הב'][80] מהמדרגה האחרונה או נעבור עליה קולמוס לסימן שתהיה נמחקת משם כאלו לא נכתבה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחרי זאת נשים הא' הנשארת במדרגה הראשונה להתחלתנו על הב' הקדומה לה במכתב יהיו שנים עשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נעיין כמה פעמים נוכל להוציא מהם הב' עד שישאר מהם מספר שנוכל להסיר ממנו אחרי כן כמספר העולה מהכאות מספר הפעמים ההם על | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
[81]והנה נמצא שיספיק לזה המבוקש אם נסירנה מהם חמש פעמים ותשאר הב' במקומה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נכתוב סיפרא על הא' באשר [לא][82] נשאר ממנה כלום | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב ה' תחת המדרגה הראשונה בעד חמשת פעמי ההסרה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר נכה ונכפול מספר ההסרות על עצמו ויעלה חמשה ועשרים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נסיר אותם מחמשה ועשרים שבטור החשבון הנחקר ונמצא שכלה הכל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ולכן נכתוב סיפרא על הה' ועל הב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה חדשנו טור אחר תחתיו שהוא ה'ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נסיר מהב' חציה וישאר ה'א' והוא גדר המספר המבוקש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כי אם תכפול ותכה ה'א' על עצמו תמצא שיצא [לך][83] ה'ב'ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועוד בקשנו לדעת הגדר קרוב יותר אל תשע מאות ועשרים וחמשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה היא צורתו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה יש למדרגתו האחרונה גדר ולכן נתחיל ממנה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וגדרה הוא ג' נכתבנה תחתיה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונסיר הכאת הג' ממנה ותכלא ולא תשאר ממנה כלום ולכן נכתוב נכתוב עליה סיפרא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נכפול הג' פעמים ונעביר עליה קולמוס ונכתוב ו' במדרגה אחת אחרנית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה יצא אלינו הגדר הקרוב כי עתה לא נוכל עוד להסיר ו' מב' אשר על ראשה ומפני זה [84]נכתוב סיפרא תחת המדרגה הראשונה ונמצא שהטור שנתחדש הוא סיפרא ו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נסיר מהו' חציה וישאר 0'ג' והוא הגדר הקרוב המבוקש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כי אם תכה ותכפול 0'ג' על עצמו ותשים תחתיו הנשאר בטור ראשון שהוא ה'ב' יצא לך ה'ב'ט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועוד בקשנו לדעת גדר שבעת אלפים וחמשים וששה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתבים על זאת הצורה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה מדרגת המספר הזה האחרונה היא בלתי נגדרת באשר היא רביעית ועל כן נשים אותה על הסיפרא הקדומה לה במכתב ותהיה שבעים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והגדר הקרוב אל שבעים הוא שמונה שעולה כפילתה על עצמו ששים וארבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נסיר אותם משבעים ישארו ו' על הסיפרא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב ספרא על המדרגה האחרונה באשר לא נשאר ממנה שם כלום | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכנגד הגדר הקרוב אל שבעים נכתוב ח' תחת הסיפרא שבמדרגה השלישית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אחרי זאת נכפול הח' פעמים שתהיה ששה עשר נכתוב אותם על דרך זה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ו' כנגד הששה תחת המדרגה הקדומה לסיפרא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וא' כנגד העשרה תחת הח' ונעביר עליה קולמוס | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אחרי כן נעיין כמה פעמים נוכל [85]להסיר הא' והו' מהו' והה' אשר על ראשם בכדי שישאר מהם מספר שיספיק למה שיעלה מספר הכאות פעמי ההסרה על עצמם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה נמצא שנוכל להסיר הא' ד' פעמים מהו' אשר על ראשה וישאר עליה ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר נסיר גם כן הו' ד' פעמים שעולים עשרים וארבע כשנשים הב' על הה' שלפניה שיהיו עשרים וחמשה וישאר א' על הה' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב על הב' סיפרא באשר לא נשאר ממנה כלום | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכנגד ארבע פעמי ההסרה נכתו' ד' תחת המדרגה הראשונה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר נכה הד' על עצמו ויהיה ההווה ששה עשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונסיר אותם מששה עשר שבטור החשבון הנחקר ונמצא שתכלה הכל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ולכן נכתוב על הו' ועל הא' סיפראש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והטור שנתחדש אצלינו הוא ד'ו'א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נקח חצי הו' והא' על הדרך הזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
שנשים הא' על הו' ויהיה ששה עשר ויהיה חציין ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב אותם תחת הו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונמצא שהנשאר הוא ד'ח' והוא גדר המספר המבוקש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
שהנה אם תכנו ותכפלנו על עצמו יצא לך טור אחד שמספרו שבעת אלפים וחמישים וששה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועוד בקשנו לדעת הגדר הקרוב שבעים וששה אלף וחמש מאות וארבעים [86]ושלשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה היא צורתו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה המדרגה האחרונה היא נגדרת באשר היא חמישית על כן נתחיל ממנה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה הגדר הקרוב אל ז' הוא ב' נכתבנה תחתיה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נסיר ממנה הכאת הב' על עצמה וישאר על הז' ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נכפול הב' פעמים ונעביר עליה קולמוס ונכתוב העולה שהוא ד' במדרגה אחת אחרנית תחת הו' שהיא במדרגה הרביעית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר כן נשים הג' הנשארת לנו על הו' על המדרגה הקדומה לה במכתב יהיו ששה ושלשים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נעיין כמה פעמים נוכל להסיר מהם הד' שכתבנו תחת המדרגה הרביעית בכדי שיספיק מה שישאר להסיר מספר הכאת פעמי ההסרה על עצמו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נסיר אותם מששה ושלשים ישאר על הו' ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב סיפרא על הג' באשר נעתקה ממקומה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכנגד שבע פעמי ההסרה נכתוב תחת המדרגה השלישית ז' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אחרי כן נכה ונכפול ז' על עצמה [ויהיה העולה][87] ארבעים ותשעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נסירה על הדרך הזה ממה שנשאר בטור המספר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה נקח מהח' הנשארת [88]על המדרגה הרביעית ה' וישאר עליה ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונשים הה' על הה' הקדומה לה במכתב שהיא המדרגה השלישית ויהיו חמשים וחמש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נסיר מהם תשע וארבעים ישארו על הה' ו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אחרי זאת נכפול השבע פעמי ההסרה פעמים ויהיו ארבעה עשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונעביר הקולמוס על הז' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתבם על הדרך הזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ד' כנגד הארבעה תחת הז' אשר העברנו עליה קולמוס | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וא' כנגד העשר תחת הד' שהיא תחת המדרגה הרביעית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחרי כן נעתיק במקום אחר מה שנשאר בטור המספר הנחקר ונעשה ממנו טור אחר לבדו ואחר נכתוב תחתיו מה שנתחדש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה יהיה טור מה שנותר ג'ד'ו'ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב תחתיו בטור ד' תחת הד' שהיא המדרגה השנית וה' תחת הו' וכל זה הוא מה שנתחדש למעלה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה יהיה המועתק על זאת הצורה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה נשים הג' שבטור העליון במדרגה האחרונה על הו' הקדומה יהיו ששה ושלשים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב סיפרא על הג' באשר נעתקה ממקומה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונעיין כמה פעמים נוכל להסיר אותיות הטור השפל מהטור העליון בכדי שישאר ממנו אחרי כן מספר שנוכל [89]להסיר ממנו המספר שיעלה מהכאת פעמי ההסרה על עצמם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והוא נראה שיספיק לכל זה אם נסיר אותם ששה פעמים בלבד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכשנסיר מהששה ושלשים הה' שש פעמים העולים שלשים תשאר הו' במקומה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחרי זה נסיר הד' הכתובה תחת המדרגה השנית גם כן שש פעמים העולים עשרים וארבע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נעשה על הדרך הזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נקח ב' מן הו' וישאר עליה ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונשים [הב'][90] על הד' הקדומה במכתב למדרגה הזאת ויעלו עשרים וארבע ויסופו ויכלו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב על הד' סיפרא באשר לא נשאר שם כלום | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכנגד שש פעמי ההסרה נכתוב ו' תחת המדרגה הראשונה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכה הו' על עצמה תעלה ששה ושלשים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נסירם ממה שנשאר בטור העליון על דרך זה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נסיר מן הד' הנשארת על המדרגה השלישית א' וישאר שמה ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נשים הא' על הסיפרא אשר על המדרגה השנית הקדומה לה ותהיה שוה עשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נסיר מהם ארבעה וישאר על הסיפרא ו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נשים הד' על המדרגה הראשונה יעלו ארבעים ושלש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נסיר מהם הששה ושלשים ישארו ז' על הג' שבמדרגה הראשונה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה הטור השפל אשר [91]נתחדש הוא ו'ד'ה' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נקח חצי הד' והה' ישאר ז'ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נמצא מה שנשאר אחר כל זה ו'ז'ב' והוא הגדר היותר קרוב אל המספר המבוקש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תכפול ו'ז'ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועוד בקשנו לדעת גדר חמש מאות ושמונים ושלשת אלפים ושש מאות ותשעים וששה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתבנו על זאת הצורה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
באשר המדרגה האחרונה מהמספר הזה הוא בלתי נגדרת צריך ל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והגדר הקרוב אל המספר הזה שעולה הכאתו על עצמו הוא תשעה וארבעים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכשנסיר אותם מחמישים ושמונה ישארו על הח' ט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב סיפרא על הה' באשר נעתקה ממקומה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכנגד הגדר הקרוב נכתוב ז' תחת הח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויכפול הז' הזאת פעמים ונעביר עליה קולמוס והנה יהיה העולה ארבעה עשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב ד' כנגד הארבעה תחת הג' שהיא המדרגה [92]הרביעית וא' כנגד העשר תחת הז' אשר העברנו עליה הקולמוס | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועתה אנחנו צריכים [לעיין][93] כמה פעמים נוכל להסיר הא' והד' ממה שנשאר בטור המספר בכדי שיספיק לנו אחרי כן להסיר מהנשאר מספר הכרת פעמי ההסרה על עצמו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה נמצא שיספיק לנו אם נסיר אותם ששה פעמים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה כשנסיר הא' מהט' ששה פעמים ישאר עליה ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וגם יש לנו להסיר הד' ששה פעמים שעלה כפלתם ארבע ועשרים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונעשה על הדרך הזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נקח הג' הנשארת לנו על הט' ונכתוב סיפרא במקומה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונשים אותה על הג' הקדומה לה במדרגה רביעית ויעלו שלש ושלשים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כשנסיר מהם הארבע ועשרים ישארו על הג' ט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכנגד שש פעמי ההסרה נכתוב תחת המדרגה השלישית ו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכשנכפול ונכה אותם על עצמם יעלו ששה ושלשים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונסיר אותם מטור המספר על הדרך [הזה][94] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נקח מן הט' הנשארת לנו במדרגה רביעית ג' וישארו עליה ו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נשים זאת הג' על הו' הקדומה לה במדרגה שלישית יעלו ששה ושלשים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה נכתוב סיפרא על הו' באשר [96]לא נשארה ממנה שארית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אחרי זאת נכפול הששת פעמים ההסרה פעמים ויהיו שנים עשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתבם על הדרך הזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ב' תחת הו' כנגד השתים ונעביר עליה קולמוס | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וא' תחת הד' שאחריה כנגד העשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר כל זה נעתיק במקום אחר מה שנשאר בטור המספר ונעשה ממנו טור אחד לבדו ואחר נכתוב תחתיו מה שנתחדש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה יהיה טור מה שנותר ו'ט'0ו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב תחתיו בטור אחר ב' תחת הט' וה' תחת הסיפרא וא' תחת הו' וכל זה הוא מה שנתחדש למעלה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה יהיה המועתק על זאת הצורה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועתה יש לנו לעיין כמה פעמים נוכל להסיר האותיות שכתבנו תחת הטור הראשון ממנו בכדי שיספיק לנו אחרי כן להסיר מהנשאר כפל הכאת מספר ההסרות על עצמו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה נמצא שיספיק לכל זה אם נסירם ד' פעמים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה כשנסיר הא' שהיא המדרגה האחרונה מהטור השפל מהו' אשר בטור העליון על ראשה ארבעה פעמים ישאר עליו ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וגם כן יש לנו להסיר ארבעה פעמים הה' אשר בטור השפל שעולה כפלתם עשרים [97]מהטור העליון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונעשה על דרך זה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נקח הב' הנשארת לנו במדרגה האחרונה מהטור העליון ונשים אותה על הסיפרא הקדומה למדרגה ההיא ויהיו עשרים ויסופו ויכלו בעד העשרים מהכפילה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב על הב' אשר לקחנו סיפרא באשר נעתקה ממקומה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחרי זאת הסיר גם כן ארבעה פעמים הב' שבטור השפל מהט' אשר על ראשו וישאר עליה א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה כנגד ארבעה פעמי ההסרה נכתוב תחת המדרגה הראשונה מהטור העליון ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר נכפול ונכה הד' על עצמה יהיה ההוא ששה עשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נסירם מהששה עשר שבטור העליון שהרי נותרו א' על הט' במדרגה השנייה והו' שבראשונה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונמצא שיכלה כל הטור העליון ועל כן נכתוב סיפראש על הו' ועל הא' שבראש הט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והטור התחתון אשר נתחדש הוא ד'ב'ה'א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נקח חצי הב' והה' והא' ותהיה הנשאר ד'ו'ז' והוא הגדר מהמספר המבוקש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תכפול ד'ו'ז' על עצמו אני מבטיח לך שיצא מקבוץ הכפילה ו'ט'ו'ג'ח'ה' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועוד בקשנו לדעת גדר [98]המספר הזה שהוא שמונה מאות אלף ועשרים וארבעת אלף וארבע מאות וששים וארבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתבם על זאת הצורה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
על אשר המדרגה האחרונה מהמספר הזה היא בלתי נגדרת צריך לשום אותה על הב' הקדומה לה במכתב שהיא המדרגה החמישית והנה יהיה שמנים ושנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והגדר היותר קרוב אליהם הוא תשעה כי כפל הכאתו על עצמו עולה אחד ושמונים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה כשנסיר אותם מהם תשאר על הב' א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב על הב' סיפרא באשר נעתקה ממקומה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה נכתוב תחת הב' ההיא ט' כנגד תשעה שהם הגדר היותר קרוב ואחר נעביר הקולמוס על הט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכפל אותה והיו שמנה עשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתבם על הדרך הזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
א' תחת המדרגה הרביעית כנגד העשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וח' כנגד השמנה במדרגה אחת אחורנית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחרי זאת כתבנו סיפרא תחת המדרגה השנית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר נעיין כמה פעמים נוכל להסיר אותיות הטור השפל המתחדש ממה שנשאר בטור העליון בכדי שישאר שם מספר [99]אחר זאת שנוכל להסיר ממנו כמספר העולה מכפילת פעמי ההסרות על עצמם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והוא נמצא שיספיק להסיר אותם שמנה פעמים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונעשה על הדרך הזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נקח הא' הנשארת בטור העליון על המדרגה החמישית ונכתוב עליה סיפרא באשר נעתיקנה ממקומה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונשים אותה על הד' הנשארת במדרגה הרביעית הקדומה לה ויהיו ארבעה עשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נסיר מהם הא' שתחת המדרגה הרביעית שמנה פעמים וישאר על הד' ו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וגם כן יש לנו להסיר הח' שתחת המדרגה השלישית שמונה פעמים שעולה כפלתם שישים וארבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונעשה על הדרך הזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נקח הו' הנשארת במדרגה הרביעית ונכתוב סיפרא עליה כאשר נעתיקנה ממקומה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונשים אותה על הד' שהיא המדרגה השלישית הקדומה לה ויהיו שישים וארבעה ויכלו ויתמו בעבור הסרת פעמי הח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב על הד' ההיא סיפרא באשר לא נשאר ממנה כלום | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכנגד שמונה פעמי הסרת האותיות נכתוב תחת המדרגה הראשונה ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר נכה ח' על עצמם יעלו שישים וארבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
[100]נסירם מהשישים וארבעה אשר על ראשם בטור המספר הנחקר כי הנה נשארו עד כה הד' שהיא המדרגה הראשונה והו' שהיא המדרגה השנית ובזה תכלה כל הטור העליון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועל כן נכתוב סיפראש על הד' ועל הה' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והטור שנתחדש הוא ח'[0]ח'א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וחצי סיפרא ח"א הוא 0ט' נמצא שיהיה הנותר אחרי זאת ח'0'ט' והוא גדר המספר המבוקש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ובחנני נא בזאת[note 4] ונסני לכפול ח'0'ט' על עצמו כי בהכרח יצא לך מקבוץ הכפילה ד'ו'ד'ד'ב'ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועוד בקשנו שורש וגדר מאה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה נכתבה על זאת הצורה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה המדרגה השלישית יש לה גדר ועל כן נתחיל ממנה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כי גדר הא' הוא אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ולכן נכתוב סיפרא על הא' באשר תכלה כשנסיר ממנה הכאת הגדר על עצמו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכנגד שהוא הגדר נכתוב א' תחת הסיפרא השנית ותהיה שוה שם עשר והוא גדר המספר המבוקש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן רצינו לדעת שרש ארבע מאות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתבם על זאת הצורה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וידוע כי גדר הד' שהוא שנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ולכן [101]ולכן נכתוב סיפרא [על הד'][102] באשר תכלה כלה כשתסיר ממנה הכאת הגדר על עצמו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכנגד השנים שהם הגדר נכתוב ניכתוב ב' תחת הסיפרא השנית ותהיה שוה שם עשרים והוא גדר המספר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם רצינו לדעת הגדר הקרוב אל ארבעת אלפים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נעשה על דרך זה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה המדרגה הרביעית היא בלתי נגדרת לפיכך נשים הד' על הסיפרא הקדומה לה ותהיה ארבעים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והמרובע הקרוב אליהם הוא ששה כי כפילת הכאתו על עצמו תהיה לו שלשים וששה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה ישארו ד' על הסיפרא השלישית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב סיפרא על הד' שהיתה במדרגה הרביעית כאשר נעתקה ממקומה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכנגד ששה שהם הגדר היותר קרוב נכתוב ו' תחת הסיפרא השלישית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אחרי זאת נכפול הו' פעמים ונעביר עליה קולמוס והנה יהיה ההוא שנים עשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נכתוב ב' כנגד השנים תחת הסיפרא השניה וא' כנגד העשר תחת הו' אשר הקולמוס עליה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר נעיין כמה פעמים נוכל להסיר הב' והא' ההמה מהנשאר למעלה [103]מן הטור נמצא שיספיק בשלשה פעמים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונעשה בדרך הזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן יש לנו להסיר הב' [שלשה][104] פעמים שעולה כפילתם ששה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונעשה בדרך [הזה][105] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נקח הא' הנותרת במדרגה השלישית ונשים אותה על הסיפרא השנית ותהיה שוה עשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נסיר מהם הששה ישארו שם ארבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב סיפרא על הא' שהיתה על המדרגה השלישית כי נעתקה ממקומה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכנגד שלשה פעמי ההסרה נכתוב תחת הסיפרא שבמדרגה הראשונה ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר נכפול ונכה אותה על עצמה יהיה ההוא תשעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נסיר אותם מהטור העליון בדרך זה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נקח א' מן הד' הנותרים במדרגה השנית וישארו עליה ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונשים הא' על הסיפרא הקדומה למדרגתה ותהיה שוה עשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נסיר מהם תשעה ישאר על הסיפרא ההיא א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והטור אשר נתחדש הוא ג'ב'א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וחצי ב'א' והוא ו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונמצא שתהיה הגדר הקרוב [106]המבוקש גדרו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The methods of calculating all these many numbers, which I have mentioned and extended the explanation for each of them [how] to extract its root or its approximate [root], are sufficient for you to apply their procedure to other cases you see, if you are wise. | ובדרכי כל אלו החשבונות הרבים שהזכרתי והארכתי הביאור בכל אחד מהם למצוא גדרו או הקרוב אליו יספיק לך לעשות באחרים זולתם כתבניתם אשר אתה מראה אם נבון ואם חכם אתה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Chapter Eight – the Ratio of a Number to Another Number |
השער השמיני במערכת חשבון אחד מחשבון אחר |
| The meaning of relation is to explain, when we have two known numbers or more, how we can find another number, whose ratio to one of them is the same as the ratio of this [given] number to the other [given number]. | כוונת ההערכה הזאת היא לבאר כשיהיו לנו שני חשבונות ידועים או יותר באיזה דרך נוכל לחדש חשבון אחר שיהיה ערכו אל אחד מהם כערך האחד אל חברו |
| Know that the skill of this chapter is divided into four categories: | ותדע כי מלאכת השער הזה היא נחלקת לארבעה חלקים |
|
החלק האחד הוא על דרך זה כשיהיו לנו שני חשבונות ונרצו לחדש ולמצוא חשבון שלישי שיהיה ערכו כל [אחד][107] מהם כערך כל האחד [מהם][108] אל חברו |
|
|
|
|
המשל בזה כגון שתדע חשבון ארבעה וששה |
|
ובידוע כי כשנערוך חשבון ששה על חשבון ארבעה יהיה כמוהו ומחציתו |
|
ואם נרצה לחדש חשבון שלישי שיהיה ערכו אל ששה [109]כערך ששה אל ארבעה נעשה על הדרך הזה |
|
נקח חשבון הששה שהוא אמצעי בין החשבון הראשון הידוע ובין השלישי הנעלם ונכפול ונכה אותו על עצמו ויהיה העולה ששה ושלשים נחלק אותם על חשבון הראשון הנודע שהוא ארבעה ומצאנו בהם תשע פעמים והנה תשעה ערכם אל ששה כערך ששה אל ארבעה |
|
ואם ידענו החשבון האמצעי והאחרון ונעלם ממנו החשבון הראשון נכפול גם כן האמצעי על עצמו ונחלקנו על החשבון האחרון הנודע והיוצא בחלוק הוא החשבון הראשון |
|
ולפי זה כשתדע חשבון הששה והתשעה ולא נדע הארבעה |
|
נכפול הששה על עצמם יעלו ששה ושלשים נחלקם על התשעה הנודעים ונמצאנו ארבעה פעמים והנה הארבעה הוא המבוקש |
|
ואם ידענו החשבון הראשון והשלישי ונעלם ממנו החשבון האמצעי נכפול ונכה השני חשבונות הנודעים זה על זה ונקח גדר העולה וכמספר הגדר הוא החשבון האמצעי המבוקש |
|
ועל זה הדרך תדע חשבון [110]הארבעה והתשעה ונעלם ממנו האמצעי |
|
נכפול ארבעה על תשעה ויעלו שלשים ושש וגדרם ששה והוא החשבון האמצעי המבוקש |
|
החלק השני כשיהיו לנו [שלשה][111] חשבונות נודעים ונרצה לחדש חשבון רביעי שיהיה ערכו אל השלישי כערך הראשון אל |
|
|
|
|
כגון שנדע החשבונות האלה השלשה ששה ועשרה ושלשה ואבקש למצוא חשבון רביעי שיהיה ערכו אל השלשה כערך העשרה אל הששה |
|
ונעשה ככה נכפול חשבון העשרה וחשבון השלשה זה על זה ושניהם נקראים אמצעיים לפי שהם נתונים בין החשבון |
|
וכן אם נדע השני חשבונות האמצעיים והחשבון הרביעי הנעלם ממנו החשבון הראשון נכפול האמצעיים זה על זה ונחלק ההווה על [113]החשבון הרביעי הנודע והיוצא בחלוק הוא המבוקש |
|
ואם יעלם ממנו אחד מהשנים האמצעיים נכפול החשבון הראשון והרביעי אלו על אלו ונחלק ההווה על האמצעי הנודע והיוצא בחלוק הוא החשבון המבוקש הנעלם |
|
החלק השלישי כשנרצה לכתוב ולחקוק חשבונות רבים מרחק האחד שוה |
|
כגון א'ב'ג'ד'ה'ו' |
|
[או][114] ב'ד'ו' וכיוצא באלו |
| This category is clear and explained, thus, there is no need to elaborate on that. | והחלק הזה דרכו גלוי ומבואר ואין צריך עוד להאריך בו |
|
החלק הרביעי |
|
על אופן שלש אותיות אלו שהן ג'ד'ו' שערך ג' אל ו' כערך המרחק שמשלשה ועד ארבעה אל המרחק שמארבעה ועד ששה שהנה מרחק ג' מד' אחד ומרחק ד' מו' שנים וכערך האחד אל השנים כן ערך השלשה אל הששה |
|
וכאשר נדע האות הראשונה והאחרונה ונעלמת ממנו האות השנית נכפול האחת אל חברתה ונחלק העולה על המחובר משתיהן והיוצא בחלוק נכפלנו והיוצא הוא המבוקש |
|
ועל הדרך הזאת כשנדע הג' [והו'][115] ונרצה [116]לדעת האות האמצעית נכפול ג' על ו' יהיו שמנה עשר נחלקם על המחובר משניהם שהוא ט' נמצאנו שם שני פעמים נכפלם יהיו ארבעה וככה הוא משפט האמצעי להיות ד' |
|
ואם נדע האות הראשונה והאמצעית ולא נדע האחרונה נכפול הראשונה על השנייה שהיא אמצעית בין הראשונה הידועה ובין האחרונה הנעלמת והעולה נחלקנו על האות הראשונה הידועה אחר אשר נסיר ממנה [העולה מהכאת][117] המרחק שבין [הראשונה][118] [לאמצעית][119] [על עצמו][120] והיוצא מהחלוק הוא המבוקש |
|
ולפי זה כשנודע הג' והד' ונעלמת ממנו הו' ונכפל ג' על ד' יהיו שנים עשר נחלקם על הג' אחר אשר נסיר ממנה [הכאת][121] המרחק שבינה ובין הד' [על עצמו][122] והנה הוא אחד נסיר אותו מהג' [ישאר][123] ממנה ב' ונמצא הב' הזאת ו' פעמים בשנים עשר וככה היא האות השלישית האחרונה ו' |
|
|
|
|
ואם ידענו הד' והו' ולא נדע הג' נעשה בדרך זאת נכפול הד' על הו' ויהיו ארבעה ועשרים נחלקם עם המחובר מהאות השלישית עם המרחק שבין הד' ובינה שהוא שנים וכשנחברם אל הששה יהיו שמנה וכשנחלק הארבע ועשרים עליהם [124]יצא לנו החלוק ג' פעמים וכן הוא משפט האות הראשונה להיות ג' |
| From these four categories [of proportions] explained you can understand and extract the proportions of all numbers you find, as the issue of each category is explained at length. | ובאלו החלקים הארבעה המבוארים תוכל להבין ולהוציא כל ערכי החשבונות שתמצא כאשר התבאר בארוכה ענין כל חלק וחלק |
Chapter Nine – On Knowing the Fractions of Integer, whether in Multiplication, in Division, in Addition, or in Subtraction |
השער התשיעי בידיעת חלקי השבר מן השלם בין בכפל בין בחלוק או בחבור או במגרעת |
Introduction |
|
| Know that the product of fractions by themselves or by other fractions is less than their sum.
|
תדע באמת כי כפילת הכאת השברים על עצמם או על שברים אחרים זולתם פחותה ממחברתם |
|
כי כאשר נאמר כפול והכה רביע על רביע הרי זה כאלו נאמר קח רביע הרביע שהוא חלק מששה עשר חלקים בשלם |
|
ואם נאמר חבר רביעית עם רביעית יהיה המחובר חצי שלם אחד |
| This rule of fractions is opposite to the rule of integers, since [the integers] increase when they are multiplied by themselves, or by others, more than they are increased by their summing.
|
ומנהג השברים הזה הפך מנהג השלמים כי הם יתרבו כאשר יו[כ]ו ויוכפלו על עצמם או על זולתם יותר משלא תרבה אותן מ[ח]ברתן |
| On the other hand, this [rule of fractions] is somewhat similar to the rule of the unit, that if we multiply it by itself the result is only one, while its sum with itself is two.
|
ואולם הם דומים למנהג מעשה האחד השלם במקצת שאם נכפלנו ונכנו בעצמו לא יעלה כי אם אחד ומחברתו עם עצמו תהיה שנים |
| Therefore, the number two is mean between all the other [integers] and [one and the fractions], since the sum of two with itself and its product by itself are both equal to four.
|
ולזאת הושמו השנים אמצעיים בין שאר כל המספרים וביניהם [125]כי מחברת השנים [עם][126] עצמן וכפלת הכאתן בעצמן הכל עולה בשוה ארבעה המחברת כמו הכפילה |
Operations with fractions |
|
| In order that the practice in this chapter will be clear and known for all by elaborate explanation, I write various calculations of operations with fractions, from which the procedure in other cases can be known and learned. | ובעבור אשר תהיה מלאכת השער הזה גלויה ומפורסמת לכל בביאור רחב אכתוב מדרכי השברים חשבונות רבים עד שיודע וילמד [מהם לעשות][127] ככה באחרים זולתם |
Multiplication of fractions |
|
Introduction |
|
| I shall start with their multiplication method, after I write a short introduction that needs to be clarified for the purpose of this craft. | והנני מתחיל בדרך כפילת הכאתן אחר כי אכתוב מעט הקדמה שאני צריך לבאר אותה לצורך המלאכה הזאת |
| I say here that the proper method for dealing with fractions is to find their common denominator, I mean to take an integer that has whole parts that are the same as the denominators that are needed. | ואומר בזה כי הדרך הישר בשברים לקחת בהם מדומה רצוני לומר שיקח חשבון שלמים שימצאו בו חלקים שלמים כפי מספר השברים אשר יצטרך |
| The method of finding the common denominator: | וככה הוא [לקיחת][128] המדומה |
|
כשנרצה למצוא בו חשבון שיהיו בו שברים אלו שהם מחצית ושלישית ורביעית וחלק אחד מאחד עשר |
|
והנה כל משכיל יבין כי החשבון הקדום שבכל החשבונות שנוכל למצוא בו חצי שתהיה שלימה הוא שנים ועל זה נקח בעבור המחצית שנים |
|
וכמו שהמחצית יוצאת משנים כן תצא השלישית משלשה ולכן נקח בעבורה שלשה |
|
וכשנכפול השנים בשלשה יהיו ששה והנה ששה הוא חשבון [129]הקרוב שיהיה בו מחצית ושלישית משלמים |
|
וכשנכפול הששה בארבעה בעבור הרביעית אשר תצא מהם יהיה העולה מהם עשרים וארבע |
|
וכשנכפול אותם באחד עשר כנגד החלק האחר שהוא מהם יהיה העולה מהם מאתים ושישים וארבעה |
|
וכמוהו לכל האחרים זולתו |
Multiplication of fractions by fractions |
|
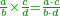
|
|
|
בקשנו לכפול ארבע חמישיות בארבע חמישיות |
|
בידוע כי החמישית תצא מחמשה והוא המדומה והכאתו בעצמו עולה עשרים וחמשה |
|
ונכפול מספר החמישיות שהוא |
|
והנה ערך ששה עשר אל חמש ועשרים שהוא העולה מהכאת המדומה בעצמו שלש חמישיותיו וחמישית חמישית וככה הוא ערך היוצא מכפלתם אל השלם |
|
בקשנו לכפול ולהכות שתי רביעיות על שלש רביעיות |
|
מדומה הרביעית הנה הוא ארבעה כי ממנו תצא והכאתו על עצמו עולה ששה עשר |
|
וכאשר נכפול השתי רביעיות בשלש [131]יהיו ששה |
|
ערכם אל הכאת המדומה רביעיותו |
|
בקשנו לכפול שלש רביעיות בארבע חמישיות |
|
הנה המדומה הרביעית ארבעה ומדומה החמישית חמשה וכפלת האחד על חבירו תהיה עשרים |
|
ועתה נכפול מספר השלש רביעיות במספר הארבע חמישיות יהיו שנים עשר |
|
וערך שנים עשר אל עשרים שהוא העולה מכפלת המדומה האחד על חבירו הוא שלש חמישיותיו וככה הוא העולה מכפילת השברים הנזכרים אלו על אלו שלש חמישיות השלם |
|
או אם נרצה נעשה בדרך אחרת |
|
נקח מדומה אחד לשניהם ונכפול הארבעה בחמשה יהיו עשרים והוא המדומה לשניהם |
|
והנה ג' רביעיותיו הם חמשה עשר |
|
וארבע חמישיותיו הם ששה עשר |
|
נכפול אלו על אלו יהיו מאתים וארבעים |
|
נכה המדומה שהוא עשרים ונכפול אותו על עצמו ויהיו ארבע מאות |
|
נעריך המאתים וארבעים אליהם ונמצא כי כערך שנים עשר אל |
|
בקשנו לכפול חמש שביעיות בשבע שמינית |
|
ידוע כי מדומה השמינית הוא שמונה והשביעית שבעה וכאשר נכה ונכפול אותם זה על זה יהיו חמשים וששה |
|
ואחר כן נכפול מספר החמש שביעיות במספר השבע שמיניות ויעלו ל"ה |
|
וערכם אל חמישים וששה חמש שמיני |
|
ובדרך האחרת הנה המדומה האחד לשניהם הוא ששה וחמישים |
|
וחמש שביעיותיו הם ארבעים |
|
ושבע שמיניותיו תשע וארבעים |
|
וכפלתים זה על זה היא עולה אלף ותשע מאות וששים |
|
והכאת המדומה על עצמו עולה שלשת אלפים ומאה ושלשים וששה |
|
ותמצא כאשר נעריך אליהם האלף ותשע מאות ושישים שיהיה מערכתם שוה למערכת שלשים וחמש אל חמישים וששה |
|
ושני הדרכים האלה כאחד טובים |
|
בקשנו לכפול ארבע חמישיות על שלשה חלקים משלשה עשר בשלם |
|
הנה מדומה החמישיות [133]חמשה ומדומה החלקים משלשה עשר הוא שלשה עשר וכפלתם ששים וחמש |
|
וכאשר נכפול מספר הארבע חמישיות על מספר השלשה חלקים יהיו שנים עשר |
|
והנה שנים עשר חלקים מששים וחמש בשלם ונוכל לקחת אותם שני חלקים משלשה עשר ועוד שתי חמישיות חלק או נקראם חמישית אחת שלמה פחות ממנה חלק אחד משלשה עשר בה |
|
ובדרך האחרת ידוע כי המדומה לשניהם הוא שישים וחמש |
|
וארבע חמישיותיו המה חמשים ושתים |
|
ושלשת חלקי מהשלשה עשר המה חמשה עשר |
|
וכפילתם מזה על זה הם שבע מאות ושמנים |
|
והכאת המדומה על עצמו היא ארבעת אלפים ומאתים ועשרים וחמש |
|
וכאשר נערוך אליהם השבע מאות נמצא שיהיה ערכם שוה לערך שנים עשר אל שישים וחמש והכל אחד |
|
בקשנו לכפול תשע חלקים מחמשה עשר בשלם על אחד עשר עשר חלקים משבעה עשר בשלם |
|
לקחנו מדומה האחד העשר והשני שבעה עשר [134]כפלנום זה על זה עלו מאתים וחמישים וחמש |
|
כפלנו גם כן התשע חלקים על האחד עשר היו תשעים ותשע |
|
וערכם אל מאתים וחמישים וחמש ששה חלקים משבע עשרה בשלם ועוד תשע חלקים מחמשה עשר בחלק אחד מהם וככה הם מהשלם או נוכל לקחת אותם חמשה חלקים מחמש עשרה בשלם ועוד ארבעה עשר חלקים משבע עשרה בחלק אחד מהם |
|
ובדרך האחרת המדומה לשניהם הוא מאתים וחמשים וחמש |
|
ותשע חלקיו מחמשה עשר הם מאה וחמשים ושלשה |
|
ואחד עשר חלקיו משבע עשרה הם מאה וששים וחמש |
|
כפלנו החשבון האחד על חבירו עלו עשרים וחמש אלף ומאתים וארבעים וחמשה |
|
גם הכינו וכפלנו המדומה על עצמו עלה ששים וחמש אלף ועשרים וחמשה |
|
וכאשר נערוך אליהם העשרים וחמש אלף ומאתים וארבעים וחמשה נמצא שערכם אליהם כערך תשעים ותשע אל המדומה לא פחות ולא יותר |
|
בקשנו לכפול שתי שלישיות מרביעית חמישית על שש [135]שביעיות שמינית |
| This sought-after is more complicated to be extracted than the others mentioned, because its fractions are numerous. I shall present you the method to find it easily: | המבוקש הזה הוא קשה להוציאו מכל האחרים הנזכרים |
|
הנה כאשר נקח שלשה בעבור השלישית היוצאת ממנו ונכפלנו בארבעה באשר תצא משם הרביעית יהיו שנים עשר נכפול אותם בחמשה בעבור החמישית יהיו שישים וזהו הוא המדומה שתמצא בו שלישית ורביעית וחמישית |
|
והנה חמישיתו שנים עשר ורביעיתם שלשה ושתי שלישיתם שנים ואנחנו רואים ויודעים בבירור כי השתי שלישיות מרביעית חמישית הם שני חלקים [מששים][137] בשלם |
|
נקח גם כן מדומה שיהיה בו שביעית שמינית ויהיה חמישים וששה |
|
ושמיניתו שבעה ושש שביעיותיהם ששה והשש האלו הם חלקים [מחמשים][138] וששה בשלם |
|
והם מבוקשינו הוא כמו אם אמרנו לכפול שני חלקים מששים על ששה חלקים מחמשים וששה |
|
ועל כן נכפול המדומה האחד על חבירו ויהיו שלשת אלפים ושלש מאות וששים |
|
וכאשר נכפול השני חלקים על הששה יהיו שנים [139]עשר |
|
והנה ערכם אל מספר הכאת המדומה האחד על חבירו חמישית שמינית ושביעיתו |
|
| |
|
כי שביעית מספר ההכאה הם ארבע מאות ושמונים ושמיניתם ששים והשנים עשר הנה הם חמישית שישים |
| You can also find it in the other way by taking a common denominator for both [products]. | וגם כן תוכל למצוא אותו בדרך האחרת אם נקח מדומה אחד לשניהם |
| You will understand [what] to do through your wisdom, as you see in the previous examples. | ואתה תבין לעשות בחכמתיך כאשר אתה רואה במבוקשים הקדומים |
| Up to this point I have explained the method of multiplying the fractions by themselves or by other fractions. | עד הנה [בארתי][140] וכללתי דרך הכאת כפילת השברים על עצמם או על שברים אחרים זולתם |
| Now I shall explain the method of multiplying integers by fractions, or integers and fractions by fractions alone, whether the fractions are of one type, or two types, or multiplying integers and fractions by integers and fractions, whether the fractions are of one type, or two types. Here is their explanation: | ועתה אבאר דרכי כפלת הכאת שלמים על שברים או שלמים ושברים על שברים לבדם בין שיהיו השברים ממין אחד או משני מינים או כפילת שלמים ושברים על שלמים ושברים בין שהשברים הם ממין אחד או משני מינין וזה לך ביאורם |
Multiplication of integers by fractions |
|
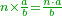
|
|
|
דמיון לכפילת שלמים על שברים רצינו לכפול חמשה שלמים בארבע שישיות |
|
הנה מדומה השישיות הוא ששה |
|
נכפל מספר החמשה שלמים במספר הארבע ששיות יהיו עשרים |
|
נחלקם על המדומה יעלו [141]שלשה שלמים ושתי שישיות אחד שהם שלישיתו |
| We can find it another way: | ונוכל למצוא זה בדרך אחרת |
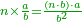
|
|
|
נכפול המדומה שהוא ששה על מספר השלמים שהוא חמשה ויהיו שלשים |
|
נכפול אותם על ארבע השישיות ויהיו מאה ועשרים ששיות ששית |
|
והמאה ושמנה מהם הם שלשה שלמים והשנים עשר הנשארים הם שני ששיות |
| We find that both ways lead to the same result. | ונמצא שני הדרכים האלה יוצאות אל כיוון אחד |
Multiplication of integers and fractions by fractions of the same type |
|
![\scriptstyle{\color{OliveGreen}{\left(n+\frac{a}{b}\right)\times\frac{c}{b}=\frac{\left[\left(n\sdot b\right)+a\right]\sdot c}{b^2}}}](/mediawiki/images/math/e/2/a/e2a27afe2a16c3b3df373989cb100803.png)
|
|
|
דמיון לכפלת שלמים ושברים על שברים לבדם שהם ממין אחד רצינו לכפול שלשה שלמים וארבע חמישיות על שלש חמישיות |
|
לקחנו מדומה החמישיות חמשה |
|
כפלנו אותם על השלשה שלמים יהיו חמשה עשר חמישיות |
|
נוסיף עליהם הארבע חמשיות ויהיו תשעה עשר חמשיות |
|
נכפול אותם על השלש חמשיות ויהיו חמשים ושבע חמשיות חמישית |
|
והחמישים מהם הם שני שלמים והשבע חמישיות חמישית הנשארות הן הם חמישית אחת ושתי חמשיות חמישית |
|
| |
| Another way: | דרך אחרת |
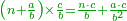
|
|
|
נכפול מספר השלש שלמים על מספר שלש [החמשיות][142] ויהיו [143]תשעה חמישיות |
|
וכשנכפול גם כן הארבע חמשיות על שלש חמשיות יהיו שנים עשר חמשיות חמישית שהן שתי חמשיות שלימות ושתי [חמשיות][144] חמישית |
|
ותשע חמשיות שיש לנו הנה בין כלן אחד עשר חמשיות ושתי חמשיות חמישית שהן שני שלמים וחמישית אחת ושתי חמשיות חמשית כאשר נמצא בראשונה |
|
| |
Multiplication of integers and fractions by fractions of different types |
|
![\scriptstyle{\color{OliveGreen}{\left(n+\frac{a}{b}\right)\times\frac{c}{d}=\frac{\left[\left(n\sdot b\right)+a\right]\sdot c}{b\sdot d}}}](/mediawiki/images/math/6/f/c/6fc4ddbcb93e9730ff64938575eebd7b.png)
|
|
|
דמיון[145] לכפול שלמים ושברים על שברים לבדם שאינם ממין אחד רצינו לכפול ארבעה שלמים ושתי חמשיות על שלש רביעיות |
|
נקח מדומה החמישיות חמשה |
|
נכפול אותו על הארבעה שלמים ויהיו עשרים [חמשיות |
|
נוסיף עליהם השתי חמשיות ויהיו עשרי'][146] ושתים חמשיות |
|
נכפול אותם על השלש רביעיות יהיו ששים [ושש][147] רביעיות חמשית |
|
והנה מדומה הרביעית הוא ארבעה |
|
נכנו על מדומה החמשיות ויהיו עשרים |
|
נחלק עליהם הששים ושש רביעיות ונמצאם שם שלשה פעמים והם שלשה שלמים ונגדנה נשאר שם ששה רביעיות חמישית [שלא נתחלקו שהם חמישית][148] אחת ושתי רביעיות חמישית |
| In another way: | ובדרך אחרת |
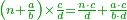
|
|
|
נכפול הארבעה שלמים על השלשה הרביעיות ויהיו שנים עשר רביעיות שהם שלשה שלמים |
|
ואחר נכפול [149]השתי חמשיות על שלש הרביעיות ויהיו ששה רביעיות חמישית שהם [חמשית][150] אחת שלימה ושתי רביעיות חמישית כאשר מצאנו בתחלה |
Multiplication of integers and fractions by integers and fractions of the same type |
|
![\scriptstyle{\color{OliveGreen}{\left(n+\frac{a}{b}\right)\times\left(m+\frac{c}{b}\right)=\frac{\left[\left(n\sdot b\right)+a\right]\sdot\left[\left(m\sdot b\right)+c\right]}{b^2}}}](/mediawiki/images/math/3/6/7/367d6ad38e7b5ffc9b90ef64917c17d2.png)
|
|
|
דמיון לכפול שלמים ושברים על שלמים [ושברים][151] ששבריהם ממין אחד רצינו לכפול שני שלמים ושלש רביעיות על שלשה שלמים ושתי רביעיות |
|
הנה מדומה הרביעיות והוא ארבעה |
|
ועל כן נכפול אותם על השנים שלמים יהיו שמונה רביעיות |
|
נוסיף עליהם השלש רביעיות ויהיה מספרן אחד עשר |
|
וגם נכפול השלמים השלשה על המדומה ויהיו שנים עשר רביעיות |
|
נוסיף עליהם השתי רביעיות ויהיו מספרן ארבעה עשר |
|
נכנו על האחד עשר ויעלו מאה וחמשים וארבעה רביעיות רביעית |
|
נחלק אותם על הכאתב' מספרא' המדומה על עצמו העולה ששה עשר |
|
ונמצאנו שם תשע פעמים והם תשע שלמים וישאר מהם שלא יתחלקו עשרה רביעיות רביעית שהן שתי רביעיות שלמות ושתי רביעיות רביעית וככה הוא היוצא מהכפילה הזאת |
|
| |
| Another method: | דרך אחרת |
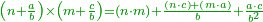
|
|
|
[152]נכפול השלמים על השלמים יהיו ששה שלמים |
|
ונכפול גם כן השני שלמים על השתי רביעיות יהיו רביעיות ארבעה |
|
ואחר נכפול השלש רביעיות על השלשה שלמים יהיו תשע רביעיות |
|
בחברם אל הארבעה רביעיות שיש לנו כי כלם הם ממין אחד והוא שלשה עשר רביעיות |
|
ואחרי זאת נכפול השלש רביעיות [על][153] השתים ויהיו ששה רביעיות רביעית שהן רביעית אחת שלימה ושתי רביעיות רביעית |
|
נוסיף הרביעית הזאת על השלשה עשר ויהיו ארבעה עשר רביעיות |
|
נחלקם על המדומה שהוא ארבעה ונמצאנו שם שלשה פעמים שהם שלשה שלמים |
|
נחברם אל הששה יהיו תשעה שלימים |
|
ועדנה ישארו שם שתי רביעיות שלא יתחלקו [ושתי][154] רביעיות רביעית שיש לנו |
|
| |
| We find that this way leads to the same as the first [way]. | והנה נמצא שהדרך הזאת |
Multiplication of integers and fractions by integers and fractions of different types |
|
![\scriptstyle{\color{OliveGreen}{\left(n+\frac{a}{b}\right)\times\left(m+\frac{c}{d}\right)=\frac{\left[\left(n\sdot b\right)+a\right]\sdot\left[\left(m\sdot d\right)+c\right]}{b\sdot d}}}](/mediawiki/images/math/6/c/0/6c0d626e6d84cbcd8358a58a669d70e7.png)
|
|
|
דמיון לכפול שלמים ושברים על שלמים ושברים שאינם השברים ממין אחד רצינו לכפול חמשה שלמים ושתי שלישיות [155]על שני שלמיות ושלש ששיות |
|
ידוע כי מדומה השלישיות הוא שלשה |
|
נכפול אותו על המספר החמשה שלמים ויהיו חמש עשרה שלישיות |
|
נוסיף עליהן השתי שלישיות יהי מספרן שבעה עשר |
|
וגם כן ידוע כי מדומה הששיות הוא ששה |
|
נכפול אותם על השני שלמים ויהיו שנים עשר שישיות |
|
נוסיף עליהם השלש ששיות ויהיה מספרן חמשה עשר |
|
נכה המספר האחד על חבירו ויהיו |
|
ואחרי זאת נכפול המדומה האחד על חבירו ויהיה העולה שמנה עשר |
|
נחלק עליהם המאתים וחמשים וחמש ויהיה היוצא בחלוק ארבעה עשר והנה הם שלמים ונשאר שם שלא נתחלק שלשה והם שלשה שלישיות שישית או נוכל לקרוא אותם שלש שישיות שלישית והן הם שישית אחת שלימה |
| Another method: | דרך אחרת |
|
| |
|
נבקש מדומה אחד לשני מיני השברים |
|
ונמצא זה כשנכפול שלשה בששה ויהיו שמנה עשר |
|
ונכפול המדומה הזה על החמשה שלמים ויהיו תשעים חלקים שכל שמונה עשר [156]מהם עולים שלם אחד |
|
והנה כנגד השתי שלישיות נוסיף עליהם |
|
וכמו כן נכפול המדומה על השני שלמים יהיו ששה ושלשים חלקים |
|
וכנגד השלש ששיות נוסיף עליהם שלש ששיות המדומה שהן תשעה ויהיה מספר החלקים האלה ארבעים [וחמשה][157] |
|
נכפול המספר האחד על חבירו יהיה ההווה ארבעת אלפים וחמש מאות ותשעים |
|
נחלקם על מספר הכאת המדומה על עצמו העולה שלש מאות ועשרים וארבעה |
|
ויהיה היוצא בחלוק ארבעה עשר והנה הם שלמים ונשאר שם שלא נתחלק חמשים וארבעה שהם ששית מספר הכאת מספר המדומה על עצמו נמצא היוצא מהכפילה הזאת ארבעה עשר שלמים וששית שלם אחד כאשר בתחלה |
| All these ways are good and right for those who find knowledge. | וכל הדרכים האלה הם טובים ונכוחים וישרים למוצאי דעת |
Division of fractions |
|
| Now I will start talking about the way of dividing the fractions by each other, or integers and fractions by integers and fractions. | ועתה אחל לדבר בדרך חלוקת השברים אלו על אלו או שלמים ושברים על שלמים ושברים |
Division of fractions by fractions |
|
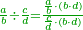
|
|
|
[158]דמיון בחלוקת שברים על שברים רצינו לחלק שני שלישיות על שני שביעיות |
|
הנה נבקש מדומה אחד לשני השברים ונכפול שבעה בשלשה ויהיו עשרים ואחד |
|
ושתי [שלישיותיו][159] ארבעה עשר |
|
ושתי שביעיותיו ששה |
|
והנה [נחלק][160] הארבעה עשר עליהם והיוצא בחלוק הוא שנים והנשאר שלא נתחלק שנים והנה הם שלישית הששה אשר חלקנו עליהם ונמצא היוצא מהחלוקה הזאת שנים ושלישית |
Division of integers and fractions by integers and fractions |
|
![\scriptstyle{\color{OliveGreen}{\left(n+\frac{a}{b}\right)\div\left(m+\frac{c}{d}\right)=\frac{\left[n\sdot\left(b\sdot d\right)\right]+\left[\frac{a}{b}\sdot\left(b\sdot d\right)\right]}{\left[m\sdot\left(b\sdot d\right)\right]+\left[\frac{c}{d}\sdot\left(b\sdot d\right)\right]}}}](/mediawiki/images/math/9/3/6/9368a096c2c1e1efcbf939db69b4dcda.png)
|
|
|
דמיון לחלק שלמים ושברים על שלמים ושברי' רצינו לחלק ארבעה שלמים ושתי שלישיות על [שני][161] שלימים ושתי חמשיות |
|
והנה המדומה לשניהם הוא חמשה עשר |
|
על כן נכפול אותו על הד' שלמים ויהיו ששים חלקים |
|
ובעבור השתי שלישיות נוסיף עליהם שתי שלישיות המדומה שהם עשרה ויהיה מספר החלקים שבעים |
|
וגם נכפול השני שלימים על המדומה ויהיו שלשים חלקים |
|
נוסיף עליהם ששה שהם שתי חמישיות המדומה ויהיה מספרם ששה ושלשים |
|
נחלק עליהם מספר השבעים ונמצא שם שני פעמים פחות חצי תשיעית החשבון אשר [162][חלקנו][163] עליו או נאמר שהיוצא מהחלוקה הוא פעם אחת ועוד שלש |
|
| |
Addition of fractions |
|
| After the ways of multiplying and dividing fractions have been clarified, it is also necessary to clarify the ways of adding them to each other and the way of subtracting smaller fractions from greater fractions | אחרי אשר התבארו דרכי כפלות השברים וחלוקתם צריך לבאר גם כן דרכי מחברתם זה עם זה ודרך מגרעת שברים דקים וקטנים משברים גדולים מהם |
| Know that when we wish to know how much is the sum of known fractions with known fractions: | ותדע כי כשנרצה לידע כמה מחברת שברים ידועים עם שברים ידועים |
![\scriptstyle{\color{OliveGreen}{\frac{a}{b}+\frac{c}{d}=\frac{\left[\frac{a}{b}\sdot\left(b\sdot d\right)\right]+\left[\frac{c}{d}\sdot\left(b\sdot d\right)\right]}{b\sdot d}}}](/mediawiki/images/math/d/c/a/dca3987ef7aba952f8772ebaef57fc89.png)
|
|
|
כאשר נאמר על דרך משל חברנו שלש רביעיות עם חמש ששיות כמה העולה |
|
והנה נעשה על הדרך הזה נקח המדומה לשניהם והנה הוא עשרים וארבעה |
|
ושלש רביעיותיו שמנה עשר |
|
וחמש ששיותיו עשרים |
|
נחברם זה עם זה יהיו שלשים ושמנה |
|
ונקח מהם בעבור העשרים וארבע שלם אחד ונשאר מהם ארבעה עשר שהם חצי שלם אחד וחצי ששיתו או אם נרצה נקרא הנשאר חצי שלם ושלישית רביעיתו |
|
| |
Subtraction of fractions |
|
| When we wish to subtract from known fractions known fractions that are smaller than them and know the remainder. | וכאשר נבקש לגרוע משברים ידועים שברים ידועים קטנים ודקים מהם ולדעת הנשאר |
![\scriptstyle{\color{OliveGreen}{\frac{a}{b}-\frac{c}{d}=\frac{\left[\frac{a}{b}\sdot\left(b\sdot d\right)\right]-\left[\frac{c}{d}\sdot\left(b\sdot d\right)\right]}{b\sdot d}}}](/mediawiki/images/math/5/1/3/5137933b83402870b3ff90ea3ed3d4c8.png)
|
|
|
כאשר נאמר על דרך משל גרענו משני [165]רביעיות חמישית אחד כמה הנשאר |
|
נעשה ככה נקח מדומה אחד לשניהם והנה הוא עשרים |
|
ושתי רביעיותיו הם עשרה |
|
וחמישיתו הוא ארבעה |
|
נסיר [מהעשרה ארבעה][166] וישאר מהם ששה |
|
והוא רביעית המדומה וחומש רביעיתו וככה ערך הנשאר אל השלם |
| By that everything I wanted to clarify in this chapter becomes clear. | ובזה התבארו [כל][167] מה שראיתי לבאר בשער הזה |
| Praise be to God, blessed be He. | תהלה לאל [ברוך הוא][168] |
Chapter Ten – Knowing the Square Roots of "Deaf" and "Mute" Numbers by Approximation |
השער העשירי [בידיעת][169] צלעות המרובעים מחשבון החרש והאלם על דרך קרוב |
Introduction: square numbers and non-square numbers |
|
| Definition of a square number: Know that every number that has a root is called a square number and it is a "wise number". | תדע כי כל מספר נגדר הוא נקרא מרובע והנה הוא מספר פקח |
| The reason that it is called a "wise number" is that its root, which is the measure of each of the four sides of the square, can be truly found. | וטעם היותו נקרא [מספר פקח][170] באשר גדרו שהוא מדת כל אחת ואחת מארבע צלעות המרובע יכול להמצא [באמתות][171] |
| Therefore, the numbers that do not have a real root are called deaf and mute, because their root cannot be found accurately only approximately | ולזאת יקראו המספרים אשר אין להם גדר אמתי מספרים חרשים ואלמים באשר לא יוכל כל נברא למצוא [גדרם][172] בדקדוק כי אם בקירוב |
| In every scientific discipline there are many secrets hidden and concealed from the hearts of men to be found. | ובכל חכמה הרבה דברים נעלמים ונסתרים מלבות בני האדם למצאן |
| We also see this in the science of medicine, when physicians instruct to take a well-known herb root or stone to heal the sick person who carries them by their virtue, but no wise man can know the reason of the [healing] virtue of the stone, or the herb root, why it is so. | והנה נראה זה גם כן בחכמת הרפואה שיצוו הרופאים לקחת שורש עשב ידוע או אבן ידועה להיותם מרפא בסגולה לחולה [הנושאם][173] ואין [174]כח בשום חכם לדעת טעם סגולת האבן או שרש העשב למה הוא ככה |
| Many things like these are known only to the Knower of all concealed things alone, blessed be He and blessed be His name. | ודברים רבים כמו אלו אשר לא יודעו רק ליודע כל [נסתרות][175] לבדו ברוך הוא וברוך שמו |
Sexagesimal fractions |
|
| Now, we return to the premises and say: since most ancients extracted the approximate roots of "deaf" or "mute" numbers by using the method of the astronomers, some of their methods should be introduced and explained first, before I discuss the extraction of roots [of non-square numbers]. | ועתה נשוב אל הראשונות ונאמר כי לבעבור אשר רוב החכמים הקדומים הוציאו קרוב מדת צלעות המרובעים החרשים והאלמים על דרך חכמי המזלות [צריך][176] להקדים ולבאר קצת דרכיהם [בתחלה][177] בטרם שאדבר בדרך הוצאת מדת הצלעות |
| The astronomers divided the zodiac into twelve shapes that are called zodiacal signs. | והנה חלקו חכמי המזלות הגלגל לשנים עשר צורות והמה נקראות מזלות |
| The reason for this division is that there is no number smaller than twelve that has as many whole parts [= divisors, in modern terminology] like it, for it has a half, a third, a quarter, a sixth, and half a sixth. | וטעם החלוקה הזאת היא באשר אין מספר קטן פחות משנים עשר שיהיו לו חלקים רבים שלמים מבלי שבר כמוהו כי ימצא בו [חצי][178] ושלישית ורביעית ושישית וחצי שישית |
| They divided each zodiacal sign into thirty parts and called them degrees. | וחלקו כל מזל לשלשים חלקים קראו אותם מעלות |
| They divided it into this number, since there is no number smaller than it that has as many parts [= divisors] as it has, for it has a half, a third, a fifth, a sixth, and a tenth. | ויחלקוהו למספר זה לפי שאין מספר פחות ממנו אשר ימצא בו חלקים רבים בלתי שבר כמוהו כי ימצא בו חצי ושלישית וחמשית וששית ועשירית |
| They divided each degree into sixty parts and called them primes. | וחלקו כל מעלה לששים [179]חלקים וקראו אותם ראשונים |
| This number has a half, a third, a quarter, a fifth, a sixth, and a tenth. | ובמספר הזה ימצא בו חצי ושלישית ורביעית וחמשית וששית ועשירית[180] |
| They divided each prime into sixty seconds; each second into sixty thirds; and each third into sixty fourths. | וחלקו כל ראשון לששים שניים וכל שני לששים שלישים וכל שלישי לששים רביעיים |
| And so on, they divided their fractions as needed, endlessly, each one is equal to sixty of the rank that follows it and sixty of each one are a unit of the preceding rank. | וכן יחלקו חלקיהם כפי הצורך עד אין תכלית וכל אחד ואחד יהיה שוה ששים מהמדרגה השנייה לו וששים מכל אחד ואחד יעלו אחד מהמדרגה הקודמת לו |
Multiplication of Sexagesimal Fractions |
|
| I tell you that the degrees [act] as the integers: | והנני מודיע לך [כי המעלות][181] הן הנה כמו השלמים |
| When we multiply degrees by degrees, the result of multiplication are always degrees.
|
ולעולם כשנכפול מעלות על מעלות יהיה העולה מהכפלה מעלות |
| If we multiply them by other fractions, such as primes, seconds, or others, the type of these fractions always remains the same, their type does not change because of this multiplication.
|
ואם נכפול אותם בחלקים אחרים כמו ראשונים או שניים או יותר לעולם יעמוד המין מהחלקים ההם בעצמו לא ישתנו ממינם בעבור הכפלה הזאת |
| The primes, the seconds, and all other types, follow the rule of the [simple] fractions. | ואולם הראשונים או השניים או כל שאר המינין שאחריהן הנה משפטן כמשפט השברים |
|
כי כמו שאם נכפול חצי על חצי יהיה העולה רביע |
| So, if we multiply seconds by seconds, the product is fourths.
|
ככה אם נכפול חלקים שניים על חלקים שניים יהיה העולה מהכפלה רביעים |
| The product of seconds by primes is thirds.
|
וכפלת שניים על הראשונים יהיה העולה שלישיים |
| The product of primes by primes is seconds.
|
וכפלת הראשונים על ראשונים [182]יהיה העולה שניים |
| The product of seconds by thirds is fifths.
|
ומכפלת שניים בשלישיים יהיה העולה חמשיים |
| The product of sixths by seconds, or fourths by fourths, is eighths.
|
וששים בשניים או רביעיים ברביעיים יהיה העולה שמניים |
| The product of seconds by fifths is sevenths.
|
ושניים בחמשיים יהיה העולה שביעיים |
| And so on for all according to the aforementioned method. | וככה כלם על דרך זה האמור |
Written procedure |
|
| I will give you a method for multiplying these mentioned fractions: | ואכין לך דרך לכפילת החלקים |
| When you wish to multiply a line of known fractions by a line of known fractions; in each line there are many higher and lower types, do as follows: take one of the two lines and convert all the higher types into the lowest type of that line. Add what you receive from the decomposing to the lowest type, because now they are all the same type. Apply the same procedure with the second line as well. | כשתבקש לכפול טור אחד מחשבונות חלקים ידועים על טור אחד מחשבונות חלקים ידועים ויהיה בכל אחת מהטורים חלקים מהרבה מינים גדולים וקטנים תעשה ככה קח הטור האחד משתיהן ויצקת כל המינים הגדולים אל המין היותר קטן שבטור ההיא [וחבר אל שתיהם][183] המין הקטן אל מה שיעלה לך מההתכה כי אז הם כלם ממין אחד כ"ד וכמעשה [הטור][184] הזאת תעשה הטור השנית גם כן מהטור השנית גם כן |
| We multiply one [line] by the other and see what type the result of multiplication should be, according to what was explained before. | נכפול אלו על אלו ותראה |
| Then, divide them by sixty many times, until you reach a type which you cannot divide by sixty. | ואחר חלק אותם על ששים הרבה פעמים עד שתבא אל תכלית המין אשר לא תוכל לחלק אותם על ששים |
| Know that if there is any number left that cannot be divided in each division, the remainder is of the type of the divided number. | ותדע אם ישאר שום מספר שלא נתחלק בכל חלוקה וחלוקה יהיה הנשאר ממין המספר המחלק |
| This multiplication technique is long as well as short, but it is well-guided. | [185]ודרך הכפילה הזאת היא ארוכה [ו]קצרה והיא סלולה ומיושבת בטוב |
Extracting Roots of Deaf Numbers |
|
| After clarifying and introducing what is appropriate for the art of this chapter, I will return to discuss the method of extracting the root a deaf square: | ואחרי אשר בארתי והקדמתי מה שראוי למלאכת השער הזה אשוב לדבר בדרך הוצאת מדת הצלעות ממרובע שמספרו חרש |
| When we want to reach the required purpose, we look at the square that precedes the number we are examining, we find it as explained in chapter seven. We see how much is the excess over the preceding square.
|
והנה כאשר נרצה לבא אל תכלית המבוקש הזה נעיין המרובע שעבר מהמספר אשר אנחנו חוקרים עליו ונגיע לדעת זה על פי מה שהתבאר בשער השביעי ונראה כמה העודף על המרובע שעבר |
|
ואם היה פחות מגדרו נעשה זאת |
|
נשיב העודף ראשונים והוא שנכפל שנכפול אותם בששים ואחר נחלקם על כפל הגדר מהמרובע שעבר ומה שיצא בחלוק נוסיף אותו על הגדר [וככה יהיה מדת הצלעות בקרוב][186] |
|
ואם נרצה לדקדק אותה עוד נכפול ונכה המדה הזאת על עצמה ונראה מה יוסיף בהכאה על החשבון אשר אנחנו חוקרים עליו |
|
ונעיין מה ערך התוספת אל כפל [המדה][187] שמצאנו פעמים וכערך [ההוא][188] תסיר מהמדה והנותר יהיה יותר מדה מדוקדקת מאשר לא היתה בתחלה |
|
ולדקדקה יותר נעשה מהמדה הזאת השנית כאשר עשינו מהמדה הראשונה [189]ומה שישאר אחרי הסרת ערך התוספת ההכאה אל כפל המדה השנית פעמים ממנה יהיה מדה מדוקדקת מכלנה |
|
ומכאן ואילך אל תיגע עצמך לדקדק כי אולי תצלול במים אדירים וחרס יעלה בידך |
|
ואם מצאנו שהעודף מהמספר על המרובע שעבר הוא יותר מגדר המרובע שעבר נעשה בדרך אחרת |
|
נעיין כמה המרחק ממספרנו ועד המרובע העתיד |
|
ונשיב המרחק ראשונים ונחלקם על כפל [גדר][190] המרובע העתיד פעמים ומה שיצא בחלוק נגרע אותו מגדר המרובע העתיד והנשאר היא מדת הצלעות בקרוב |
|
וכשנבקש לדקדק אותה נעשה בדרך המבואר [בדקדוקיו][191] שלפנינו |
|
והנה אם מצאנו העודף ממספרנו על המרובע שעבר שהוא בכגדרו לא פחות ולא יתר נקרא מספרינו ממוצע |
|
ואם נרצה נוציא מדת הצלעות מהמרובע שעבר או מהמרובע שעתיד והכל יהיה שוה רק שמעשה האחד בתוספת ומעשה האחר במגרעת |
|
|
|
|
דמיון במספר שהעודף על המרובע שעבר פחות מגדר המרובע [192]ההוא רצינו לדעת מדת כל צלע וצלע ממרובע שהוא חמשה |
|
והנה העודף על המרובע שעבר הוא אחד |
|
נשיב אותו ראשונים ויהיו ששים |
|
נחלק אותם על הד' שהם כפל מהגדר מהמרובע שעבר פעמים ויהיה היוצא מהחלוקה חמשה עשר ראשונים |
|
נוסיפם על הגדר מהמרובע שעבר ונמצא שיהיה מדה אחת לכל הצלעות שנים שלמים וחמשה עשר ראשונים בקרוב |
|
ואם נרצה לדקדק המדה הזאת נכה ונכפול השנים שלימים וחמשה עשר ראשונים על עצמם ויהיו חמשה שלמים ומאתים ועשרים וחמש שניים כי מכפלת הראשונים על ראשונים כבר התבאר שיהיה העולה שניים |
|
ועתה יש לנו לראות הנוסף על החמשה שלמים שהוא מאתים ועשרים וחמש שניים איזה ערך הוא מכפלת המדה שמצאנו פעמים והנה ערכם אליה הוא כערך אחד משבעים ושנים |
|
ועל כן נשיב החמשה עשר ראשונים שיש לנו כלם שניים ויהיו תשע מאות שניים |
|
ונחלק אותם על שבעים ושנים ותצא לנו החלוקה שנים עשר וישארו שלשים וששה שניים [193]שלא נתחלקו על השבעים ושנים |
|
ולכן נקח חצי האחד מהם שהיה חלק אחד מהשבעים ושנים ותהיה החצי שלשים שלישיים ונמצא שנחלק הכל על שבעים ושנים והיוצא הוא שנים עשר שניים ושלשים שלישיים |
|
נסיר אותם מהתשע מאות שניים ישארו שמנה מאות ושמנים ושבעה שניים ושלשים [שלישיים שהם ארבעה עשר ראשונים וארבעי' ושבעה שניים ושלשים][194] שלישיים וזאת היא המדה המדוקדקת יותר מבראשונה וסימן שלה ב' י"ד מ"ז ל' והנה הם שלמים ראשונים שניים שלישיים |
|
| |
|
ואם נרצה לדקדק עוד זאת המדה תכה ותכפול אותה בעצמה ותמצא שיהיה העודף על החשבון הנחקר ב' ראשונים ע"ח שניים מ"ד שלישיים י"ו רביעיים ט"ו חמישיים |
|
| |
|
ותראה מה ערך הנוסף הזה אל כפל המדה פעמים וכערכו אליה תסיר מהמדה שיש לך כאשר התבאר למעלה ותהיה הנשאר מדה מדוקדקת מהאחרות הקודמות |
|
|
|
|
דמיון במספר שהעודף על המרובע שעבר יתר מגדרו רצינו לדעת מדת הצלעות ממרובע שהוא שבעה |
|
ובאשר העודף על המרובע שעבר יותר מגדרו נראה כמה מרחק יש ממספרינו [195]ועד המרובע העתיד והנה המרחק הוא שנים כי ככה ירחוק שבעה מתשעה שהוא המרובע העתיד |
|
נשיבם ראשונים יהיו מאה ועשרים |
|
נחלקם על כפל גדר המרובע העתיד פעמים העולה ששה נמצאם שם עשרים פעמים והם ראשונים |
|
נסיר אותם מגדר המרובע העתיד שהוא שלשה וישאר שנים שלמים וארבעים ראשונים וזאת היא מדת צלעות המרובע הנחקר בקרוב |
|
| |
|
וכאשר תרצה לדקדק המדה הזאת ותכנה בכפלה על עצמה תמצא שלא יהיה הנוסף על מספר המרובע הנחקר כי אם ששה ראשונים וארבעים שניים |
|
וגמור את המלאכה האמור למעלה |
|
|
|
|
דמיון במספר שהעודף על המרובע שעבר הוא כגדר המרובע ההוא שעבר רצינו לדעת מדת צלעות מרובע שהוא ששה |
|
והנה מספר המרובע הזה הוא ממוצע ואם נרצה נוכל להוציא המדה מהמרובע העבר או מהמרובע העתיד והכל יבוא אל כוון אחד כאשר יהיה מעשה האחד בתוספת ומעשה האחד במגרעת |
|
ונוציאנה [196]בתחלה מהמרובע שעבר [שהוא ארבעה][197] והנה העודף שנים שהם מאה ועשרים ראשונים |
|
נחלקם על כפל הגדר שהוא [ארבעה נמצאם שם שלשים פעמים והם שלשים ראשוני |
|
נוסיפם על הגדר שהוא][198] שנים ותהיה זאת המדה הראשונה בקרוב |
|
| |
|
ואם נוציא המדה מהמרובע העתיד שהוא תשעה נעשה בדרך זה הנה המרחק שלשה שהם מאה ושמנים ראשונים |
|
נחלקם על ששה שהוא כפל הגדר המרובע העתיד נמצאנו שם שלשים פעם והם ראשונים |
|
נסיר אותם משלשה שהם גדר המרובע העתיד וישארו שנים שלמים ושלשים ראשונים כאשר מצאנו כאשר מצאנו בתחלה כאשר היינו מוצאים המדה מהמרובע [שעבר][199] |
|
| |
|
[והכל אחד ועל כן יקרא כל חשבון כזה ממוצע][200] |
|
ואם תרצה לדקדק המדות תעשה כאשר התבאר לפנים |
Chapter Eleven – Here I will Write Nice Rules of Arithmetic Methods for You |
השער האחד עשר הנה אכתוב לך בזה כללים נחמדים בדרכי החשבון |
| Multiplication of a number by itself | |
|---|---|
|
ותדע כי כאשר תרצה לכפול חשבון אחד על עצמו בין שיהיה החשבון ההוא אחדים בלבד או שיש עמהם עשרות או עשרות לבדן |
|
אם הוא מספר שיש לו שלישית קח שלישיתו והכה אותה על עצמה וכפול מרובעה עשרה פעמים והסר מהם מרובעה והנשאר הוא [201]המבוקש |
|
דמיון בקשנו לכפול שש על שש |
|
הנה השלישית שנים ומרובעו ארבעה |
|
נכפול אותה עשרה פעמים יהיו ארבעים |
|
נסיר מהם ארבעה שהוא מרובע השלישית ישארו ששה ושלשים והוא הנכפל |
|
| |
|
ואם לא היה למספר שלישית אך עודף ממנו שלישיות אחד נסירנו משם ונחשוב המשולש בדרך המבואר ואחר נוסיף על חשבוננו המספר האחרון מהמשולש והמספר שאחריו אשר הסירונו והמחובר הוא המבוקש |
|
| |
|
דמיון בקשנו לכפול עשרה על עצמם |
|
נסיר מהם אחד וישארו תשעה והם משלשים |
|
נקח שלשה שהוא שלישיתם והנה מרובעם תשעה |
|
וכפלתם עשרה פעמים הם תשעים |
|
ונסיר מהם מרובע השלישית וישארו שמונים ואחד |
|
נוסיף עליהם תשע ועשרה יעלו מאה והוא הנכפל |
|
| |
|
ואם היה המספר פחות משלישיות אחד הוסיפנו עליו ונחשוב אותו כמשפט ואחר נסיר ממנו החשבון שהוספנו עליו החשבון האחרון שלו והנשאר הוא המבוקש |
|
| |
|
דמיון בקשנו [לכפול][202] אחד עשר על עצמם |
|
[203]נוסיף עליהם אחד ויהיו שנים עשר |
|
נחשבם בדרך לקיחת השלישית והנה מרובעה ששה עשר |
|
וכפלתם בעשרה מאה וששים |
|
נסיר מהם ששה עשר שהם מרובע השלישית ישארו מאה וארבעים וארבעה |
|
נסיר מהם אחד עשר ושנים עשר העולים עשרים ושלשה ישארו מאה ועשרים ואחד והוא הנכפל |
|
| |
| Multiplication of units and tens by units and tens
|
|
|
דמיון אחרת לדעת כפלת האחד עשר על אחד עשר |
|
הנה נחשוב שהמספר הזה נכתב בשני טורים |
|
ונקח האחד מן הטור האחת ונחברם אל הטור האחרת ויהיו שנים עשר |
|
נכפלם על העשרה הנשארים יהיו מאה ועשרים |
|
נוסיף עליהם הכאת האחדים על עצמם ויהיו מאה ועשרים ואחד והוא הנכפל |
|
| |
|
וככה אם נבקש לכפול חמשה עשר בשנים עשר |
|
נקח השנים ונשים אותם על החמשה עשר ויהיו שבעה עשר |
|
נכפלם על העשרה הנשארים יהיו מאה ושבעים |
|
ונכה השנים האחרים על החמשה ויהיו עשרה |
|
נחברם עם המאה ושבעים יהיה הנכפל מאה ושמנים |
|
| |
Word Problems |
|
| Now, I shall start discussing and mentioning some of the difficult problems, extracting their solutions, and explaining each one of them at length. | ועתה אתחיל לדבר ואזכיר קצת מהשאלות הקשות [204]ולהוציא תשובתן אאריך [הביאור][205] כל אחת מהם |
| Find a Number Problem - Sums | |
|
שאלה חברנו כל המספרים הרצופים מאחד עד עשרים והם הכלל כמה המחובר |
|
|
|
|
הנה נוסיף על העשרים אחד ונכפלם [על][206] עשרה שהוא חצי עשרים ויהיה הנכפל מאתים ועשרה וככה המבוקש |
|
ואם נרצה לדעת כמה עולים המספרים המחוברים על אחד עשר |
|
נוסיף עליו אחד יהיו שנים עשר נכפלם על חצי האחד עשר שהם חמשה וחצי ויהיה הנכפל ששים וששה וככה המחובר |
|
ויש [דרכים][207] אחרים ומה שכתבתי הוא היותר קל ונכון |
|
נהפוך השאלה ונאמר עלה המחובר ממספרים רצופים המתחילים מאחד מאתים ועשרה איזה הוא המספר האחרון מהמחוברים |
|
|
|
|
נעשה בדרך זה נכפול מאתים ועשרה פעמים ויהיו ארבע מאות ועשרים |
|
נקח מהם הגדר היותר קרוב כאשר התבאר דרך לקיחתו בשער השביעי והנה נמצא שהוא עשרים והוא המספר האחרון מהמחוברים |
|
והנה נשאר מהמספר שהוא בלתי נגדר עשרים [208]כמספר הגדר |
|
וכן ראוי שיהיה בכל החשבונות הדומים לזה ואם אין טעה השואל בשאלתו וכאשר חבר המספרים עשה בטעות בלי ספק |
| Triangulation Problem - Cane | |
|
שאלה [קנה][209] המדה ארוכה חמש אמות ועומדת זקופה בכותל אחת גבוה כמדתה אם [נשפיל][210] אותה מראש הכותל אמתיים כדי שתעמוד בשפוע כמה הרחיק ראש הקנה התחתון מיסוד הכותל |
|
נעשה זאת נקח מרובע החמש אמות והם עשרים וחמש |
|
ונקח גם כן מרובע הג' אמות הנשארות משם ועד יסוד הכותל והנה הוא ט' |
|
ומרחקו מעשרים וחמש ששה עשר |
|
וגדר ששה עשר הוא ארבעה וככה מרחק ראש הקנה התחתון מיסוד הכותל בלתי תוספת ומגרעת |
|
| |
|
ואם היה החסרון ממרובע אל מרובע מספר חרש ואלם תקח גדרו בקרוב כאשר התבאר בשער הקדום לזה וככה יהיה מדת מרחק מראש הקנה התחתון אל היסוד הכותל |
| Divide a Quantity Problem - Simple division | |
|
שאלה נתתי לשלוחי שלשים דנרים ופשוט וצותי אותו שישכור פועלים כאשר יספיקו לו מעותיו ויהיה שכר האחד כשכר חברו ולא יהיה בהם [211]פועל ששכרו פשוט וגם לא יהיה בשכרו שום שברי שלם נרצה לדעת כמה פועלים יוכל לשכור |
|
הנה נשיב הדינרים כלם פשוטים ונחבר אליהם הפשוט הנוסף עליהם ויהיו שלש מאות וששים ואחד פשוטים |
|
נקח גדרם בדרך השער השביעי ונמצא שהוא תשעה עשר |
|
ונוכל להשיב שיוכל לשכור השליח תשעה עשר פועלים ושכר כל אחד ואחד תשעה עשר פשוטים לא פחות ולא יתר |
| How much Problem - Wall | |
|
שאלה חומה שנפלה והוספו עליה בבנין כדי שתהיה גבוה הרבה חצי מדתה מאשר היתה בתחלה וששיתה ותשיעתה עם כל זה והיתה מדת גבהה חמשים אמה כמה היתה מדתה בראשונה |
|
נקח מדומה שיהיה לו חצי וששית ותשיעית והוא שנקח שנים בעבור אשר יצאה מהם החצי ונכפול אותם בששה בעבור הששית אשר תצא מהם ויהיו שנים עשר ונכפול גם הם בתשעה בעבור התשיעית ויהיה המדומה מאה ושמנה |
|
ומחציתו חמשים וארבעה |
|
וששיתו שמנה עשר |
|
ותשיעתו שנים [212]עשר |
|
והמחובר מכל החלקים האלה עולה שמונים וארבעה |
|
נוסיפם אל המדומה ויהיו מאה ותשעים ושנים |
|
והנה נעשה בדרך הערכין ונעריך ונאמר כערך מאה ושמנה שהוא המדומה אל מאה ותשעים ושנים שהוא העולה מתוספת החלקים הנזכרים עליו כן ערך מדת החומה אשר היתה בראשונה הנעלמת ממנו אל חמשים שהיא גבוהה עתה אחר התוספת בבנין |
|
וכאשר נכפול המספר הראשון על הרביעי יהיו חמשת אלפים וארבע מאות |
|
נחלקם על האמצע הנודע שהוא מאה ותשעים ושנים נמצאנו שם שמנה ועשרים פעמים וישארו מהם עשרים וארבעה חלקים שלא נתחלקו והמה חלקים ממאה ותשעים ושנים בשלם אשר חלקנו עליו |
|
ועל כן נוכל להשיב כי מדת גבהות החומה בראשונה היתה שמונה ועשרים אמות ועשרים וארבעה חלקים ממאה ותשעים ושנים באמה |
|
ונבחן זה אם הוא אמת בדרך זאת |
|
נתיך כל האמות ונעשה מכל האחת ואחת החלקים הנזכרים ונחבר העולה אל עשרים וארבע החלקים העודפים על [213]האמות ויהיה המחובר חמשת אלפים וארבע מאות |
|
מחציתם אלפים ושבע מאות |
|
ששיתם תשע מאות |
|
תשיעיתם שש מאות |
|
המחובר ארבעת אלפים ומאתים |
|
נוסיף זה על החמשת אלפים וארבע המאות ויהיו כתשע אלפים ושש מאות |
|
ואם תחלקם על מספר חלקי האמה |
|
שאלה חומת העיר גבוה מאה אמה ונפרצו ממנה שלישיתה ורביעיתה כמה גובה הנשאר |
|
הנה המדומה שיש לו שלישית ורביעית הוא שנים עשר |
|
נקח ממנו החלקים הנזכרים ונחברם יהיו שבעה נסירם מהמדומה ישארו חמשה |
|
ועתה נעריך ונאמר כערך חמשה אל שנים עשר כך ערך הנעלם אל מאה |
|
כפלנו החשבון הראשון על הרביעי ויהיו חמש מאות |
|
נחלקם על האמצעי הנודע נמצאנו שם ארבעים ואחד פעמים ונשארו מהם שמונה שלא נחלקו שהם חלקים משנים עשר וככה הוא גובה הנשאר ארבעים ואחת אמה ושמנה [214]חלקים משנים עשר באמה שהם שני שלישיות |
|
וכאשר נבחן זה |
|
ונעשה מהאמה אמות אשר היו שם בראשונה חלקים משנים עשר מכל אחת ואחת יהיו אלף ומאתים |
|
נקח שלישיתם שהם ארבע מאות |
|
ורביעיתם שהם שלש מאות |
|
והמחובר עולה שבע מאות |
|
נסיר אותם מהאלף ומאתים ישארו חמש מאות שהם ארבעים ואחת אמה ושמנה חלקים משנים עשר כאשר זכרנו |
| First from last Problem - Amount of grain | |
|
שאלה בעל הבית שאסף תבואתו ותרם ממנו בתחלה תרומה גדולה כמשפט ואחרי כן הפריש מהנשאר מעשר ראשון ומהנשאר אחרי זאת הפריש מעשר שני ונשארו לו חמישים מדות חטה כמה היה הכרי בתחלה |
|
| |
|
ידוע כי התרומה אמרו רבותינו ז"ל שהיא תרי ממאה שהיא חלק אחד מהחמשים |
|
על כן נקח חמשים ונכפלם בעשר בעבור המעשר ראשון היוצא ממנו ויהיו חמש מאות |
|
ונכפול גם הם בעשר בעבור המעשר שני ויהיה חמשת אלפים והוא המדומה |
|
והנה תרומתו מאה |
|
נסירנה ממנו ישארו ארבעת אלפים [215]ותשע מאות |
|
מעשר שלהם ארבע מאות ותשעים |
|
נסיר אותו מהם ישארו ארבעת אלפים וארבע מאות ועשרה |
|
מעשר שלהם ארבע מאות וארבעים ואחד |
|
נסיר אותו מהם ישארו שלשת אלפים ותשע מאות [וששים ותשעה][216] |
|
ועתה נעריך ונאמר כערך שלשת אלפים ותשע מאות וששים ותשעה אל חמשת אלפים כן ערך חמשים אל הנעלם |
|
כפלנו האמצעיים עלו מאתים וחמשים אלף |
|
נחלקם על החשבון הראשון הנודע נמצאנו שם ששים ושתים פעמים ונשארו שלא נתחלקו שלשת [אלפים ותשע מאות ועשרים ושנים והם חלקים משלשת][217] אלפים ותשע מאות וששים ותשעה אשר חלקנו עליו וכזה היה סכום המדות אשר היו בכרי כשהתחיל בעל הבית לתרום |
| How much Problem - Amount of money | |
|
שאלה ראובן תובע לשמעון מאה מנה שאומר שהוא חייב לו על פה ויאמר שמעון אליו אין אני חייב לך מאה מנה אבל כאותם שאני חייב לך ואחרים כמותם ומחציתם ורביעיתם ועם אחד יהיו מאה |
|
ונעשה על דרך זה נקח מדומה שיש לו חצי ורביעית [218]והנה נמצא שמונה |
|
נוסיף כמוהו יהיו ששה עשר וגם הוסיף מחצית המדומה שהיא ארבעה יהיו עשרים ורביעיתו שהוא שנים יהיו עשרים ושנים |
|
ובהכרח כערך שמנה אל עשרים ושנים כן ערך הנעלם אל תשעים ותשע |
|
כי בידוע כי המחובר מחלקי ההודאה עמה לא יעלה כי אם תשעה ותשעים ועם אחד הם מאה |
|
וכאשר נכפול החשבון הראשון על הרביעי יעלו שבע מאות ותשעים ושנים |
|
חלקנוהו על האמצעי הנודע שהוא עשרים ושנים יצא בחלוק ששה ושלשים וככה הוא מספר המנים שהודה שהוא חייב לו |
|
ובחון זה ותמצאהו באמת |
| Purchase Problem - Moneychanger | |
|
שאלה צורף כסף שמכר לשולחני רתוקות כסף ערכה ממטבע אחד שלשה דינרים וממטבע אחר חמשה דינרים ומאחר חמשה דינרים ושאל הצורף לשולחני שיכוין לו בדמיו משלש המטבעות האלה מכל אחד חלק שוה |
|
ונחקור על דרך זה נבקש מדומה שיש לו שלישית וחמישית ושביעית והנה נמצא [219]מאה וחמש |
|
שלישיתו שלשים וחמשה וחמישיתו עשרים ואחד שביעיתו חמשה עשר |
|
והמחובר מכל החלקים האלה שבעים ואחד והמה החלקים אשר נצטרך לחלק [כל][220] דינר אליהם |
|
והנה נחלק המדומה על שבעים ואחד נמצאנו שם פעם אחת וישארו שלא נתחלקו ארבעה ושלשים והמה חלקים מהשבעים ואחד אשר חלקנו עליהם המדומה |
|
וככה יקח הצורף מכל מטבע דינר אחד ושלשים וארבעה חלקים משבעים ואחד בדינר |
|
ואתן לך מסלול ודרך איך תבחון זה |
|
תקח המדומה שהוא מאה וחמש וכדי שנשיב כל המטבעות ממטבע שלשה נכפלנו עליהם ויהיו שלש מאות וחמשה עשר |
|
נחלקם על [חמשה][221] כדי שנדע כמה חלקים הם ממטבע חמשה יצא בחלוק ששים ושלשה חלקים |
|
גם נחלק שלש מאות וחמשה עשר על שבעה למען נדע כמה חלקים הם ממטבע שבעה יצא בחלוק ארבעים וחמשה |
|
וכאשר נחבר כל החלקים משלשת המטבעות שהם מאה וחמש וששים ושלשה וארבעים וחמשה [222]יעלו מאתים ושלשה עשר |
|
נחלקם על שבעים ואחד שהם [חלקי][223] הדינר השלם ונמצאם שם שלשה פעמים והנם שלשה דינרים שלימים |
|
ועל הדרך הזה תעשה אם תרצה להשיב כל חשבון ממטבע חמשה או ממטבע שבעה ותמצא אמתת הדבר |
| Find a Number Problem | |
|
שאלה שלישית וחמישית ושביעית מחוברים איזה ערך הם מהשלם |
|
לקחנו להם מאה וחמש למדומה |
|
שלישיתו חמשה ושלשים וחמישיתו עשרים ואחד ושביעיתו חמשה עשר |
|
נחבר את כלם ויהיו שבעים ואחד |
|
והנה ערכם אל המדומה ארבע שביעיותיו ושתי שביעיות שלישיתו ושלישית ושלישית חמישית שביעיתו |
| Purchase Problem - Buy and Sell | |
|
שאלה הקונה ארבע חמישיות ליטרא בפשוט ומכר קנייתו בערך חמש תשיעיות ליטרא בפשוט והרויח אחד עשר פשוטים כמה היה הממון |
|
הנה המדומה שיש לו חמישית ותשיעית הוא ארבעים וחמשה |
|
וארבע חמישיותיו ששה ושלשים |
|
וחמש תשיעיותיו עשרים וחמש |
|
וככה הוא הממון |
|
ואם אמר שהרויח עשרים ושנים פשוטים |
|
[224]נכפול חמשה ועשרים שנים ועשרים פעמים |
|
ואם אמר שהרויח שלשים ושלשה פשוטים |
|
נכפלם שלשים ושלש פעמים |
|
וככה עד אין קץ |
| Purchase Problem - Buy and Sell - Peanuts | |
|
שאלה סוחר קנה עשרים ליטראות בטנים בעשרים דינרים והלך ומכר מהן עשרה ליטרין לערך חמש רביעיות ליטרא בדינר ונמצא שהוא מפסיד בזה |
|
והנה נחקור על דרך זה ונשיב העשר ליטראות הראשונות שמכר כלם רביעיות ויהיו ארבעים |
|
נחלקם על החמש רביעיות שמכר בדינר נמצאם שם שמונה פעמים נמצא שה' מכרם בשמונה דינרים |
|
נעשה כן [רביעיות][225] מהעשר ליטראות האחרונות ונחלקם על שלש רביעיות שמכר בדינר נמצא שם שלשה עשר פעמים שהם י"ג דינרים ועוד נשאר מהם שלא נתחלק רביעית אחת שהיא שלישית דינר |
|
נחבר כל זה אל [226]השמונה דינרים יהיו עשרים ואחד דינרים וארבעה פשוטים |
|
נמצא שהרויח ששה עשר פשוטים |
| Partnership Problem - For the Same Time | |
|
שאלה שלשה שותפין בארבעים וששה דינרים חלק האחד שנים עשר דינרים וחלק השני חמשה עשר דינרים וחלק השלישי תשעה עשר דינרים והרויחו בין כלם עשרים דינרים כמה יקח כל אחד ואחד מהם |
|
ידוע כי אין ספק שכל אחד ואחד מהם יקח ערך מעשרים כערך חלקו אל הארבעים וששה |
|
ותברר זה במשפטי הערכין בנקלה |
| Payment Problem - two workers, two different daily wages, the same actual payment | |
|
שאלה השוכר ראובן ושמעון שיעשו לו בין שניהם מלאכה עשרה ימים ולא תשבות המלאכה והתנה עם ראובן שאם יעסוק הוא [במלאכה לבדו כל העשרה ימים שיתן לו ב' דינרים |
|
והנה נחקור על דרך זה תדע כי ראובן יעבוד חמשה ימים בדינר ושמעון לא ישמש בדינר כי אם שני ימים והמחובר מימי שניהם הוא שבעה |
|
נחלקו העשרה ימים עליהם ויהיה היוצא אחד שלם ישארו שלשה שלא נתחלקו וככה הוא סכום המעות אשר יקח כל אחד מהם דינר ושלשה שביעיות דינר |
|
ועתה נחקור כמה משפט ימי |
|
ונעשה ככה בידוע כי ראובן חייב לעבוד בדינר אשר לקח חמשה ימים ונרצה לדעת כמה [ימים][229] יעבוד בעבור השלשה שביעיות מהדינר ונגיע לידיעת זה כאשר נעשה במשפטי הערכין |
|
ונשיב החמשה ימים חלקי שביעיות ויהיו חמשה ושלשים |
|
ונעריך ונאמר כערך שלשה אל שבעה כן ערך הנעלם אל חמשה ושלשים |
|
נכפול החשבון הראשון על הרביעי יהיו מאה וחמש |
|
נחלקם על [230]האמצעי הנודע שהוא שבעה נמצאם שם חמשה עשר פעמים והנה הם חלקי שביעית יום העולים שני ימים ושביעית יום אחד |
|
ונמצא כל ימי עבודת ראובן שבעה ימים ושביעית יום אחד |
|
וידוע כי שמעון חייב לעבוד שני ימים בעבור הדינר שלקח |
|
וכשנשיב [השני ימים][231] חלקי שביעיות יהיו ארבעה עשר |
|
והנה כערך השלשה שביעיות שלקח אל שבעה כן ערך הנעלם [אל][232] ארבעה עשר |
|
כפלנו החשבון הראשון על האחרון היו ארבעים ושנים |
|
חלקנום על האמצעי הנודע שהוא שבעה נמצאם שם ששה פעמים והם חלקי שביעיות יום |
|
ונמצא כל ימי עבודת שמעון שני ימים ושש שביעיות יום |
|
וכאשר תחבר מספר הימים והחלקים מעבודת שניהם ותעשה משבעה חלקים יום אחד תמצא שהם עשרה ימים בכיוון |
| Payment Problem - Messenger | |
|
שאלה שכרתי שליח אחד בשלשה עשר דינרים [והתנאתי][233] עמו שילך לי מכאן ועד עשרים יום אחד עשר פרסאות בכל יום והשליח מעל או שנאנס ולא הלך כי אם חמש פרסאות בכל יום עד [234]שבעה ימים |
|
נעשה בדרך זאת בתחלה נחשוב כאלו הלך השליח החמש פרסאות כל העשרים יום ונראה מה יגיע אליו מהשכרות |
|
והנה נעריך ונאמר כערך חמשה אל אחד עשר כן ערך הנעלם אל שלשה עשר שהוא ערך השכירות |
|
כאשר נכפול החשבון הראשון על הרביעי ונחלק על האמצעי הנודע נמצא שיגיע אליו מהשכרות ה' דינרים וי' חלקים מי"א בדינר |
|
ובעבור שלא הלך החמש פרסאות כי אם שבעה ימים |
|
נחזור ונעריך ונאמר כערך שבעה אל עשרים כן ערך הנעלם אל ה' דינרים [וי'][235] חלקים מי"א בדינר |
|
נכפול החשבון הראשון שהוא שבעה על החשבון הרביעי שהוא ה' דינרים ובו' יהיה ל"ה |
|
גם נכפול אותו על הי' חלקים יהיו שבעים חלקים |
|
וכאשר אנחנו צריכים לחלק העולה מהכפילה הזאת על האמצעי הנודע נשיב הכל ממתכונת אחת ונעשה מהל"ה חלקים מי"א ויהיו שפ"ה |
|
נחבר אליהם הע' חלקים שגם [236]הם המה חלקים מי"א ויהיו תנ"ה |
|
ואחרי זאת נשיב גם כן האמצעי הנודע שהוא עשרים חלקים מי"א יהיו ר"ך |
|
נחלק תנ"ה עליהם נמצאם שם פעמים וישארו ט"ו שלא נתחלקו והם שלש רביעיות חלק אחד מהאחד עשר חלקים מר"ך שהוא השלם אשר חלקנו עליו |
|
| |
|
וככה יקח השליח בשכרותו שני דינרים ושלש רביעיות חלק אחד מאחד עשר חלקים בדינר שלם |
| Divide a Quantity Problem - Proportional Division - Inheritance | |
|
שאלה ארבעה נשי יעקב שנשאו לו ביום אחד ועשה לכל אחת ואחת כתובה בו ביום כתקון חכמים שם האחת לאה וכתובתה [ארבעת][237] אלפים זהובים |
|
ואמרו חכמים ז"ל שמשפט הבית דין לחלק להן הממון על דרך זה |
|
יאמרו אל בלהה שכתובתה קטנה מכלנה אין לך ערעור בחברותיך כי אם באלף [238]זהובים וגם הנה יש להן משפט בהן על כן תקח רביעית האלף שהוא |
|
אחרי כן יאמרו גם כן ב"ד אל רחל אין לך ערעור רק על אלפים שיש לשתי חברותיך גם כן משפט בהן וכבר לקחת חלקך מהאלף המחולק על כן תקחי מהאלף אחר שצריך לתשלום תביעתך השלש שהוא שלש מאות ושלשים ושלשה זהובים ושליש זהוב ושובי לביתך ונמצא חלוקה בין הכל תקפ"ג זהובים ושליש זהוב וגם כן יקחו כל אחת משתיהן מאותו האלף השני הנחלק שלש מאות ושלשים ושלשה זהובים ושליש זהו' |
|
| |
|
ואחרי כן אמרו לזלפה אין לך תביעה רק בשלשת אלפים שיש ללאה חברתיך בהן משפט וכבר לקחת חלקך מהשני האלפים המחולקים [על כן][239] נחלק בין שתיהן האלף הצריך לתשלום תביעתך ונמצא שתהיה חלק זלפה בין הכל אלף [ושמנים][240] ושלשה זהובים ושליש זהוב |
|
| |
|
ונשארו ללאה אלפים ושמנים ושלשה זהובים ושלישית זהוב |
|
| |
|
ואם תחבר החלקים האלה [241]תמצא העולה ארבעת אלפים |
|
והנה חכמי החשבון חולקים הממון הזה בדרך אחרת |
|
ויאמרו כי בעבור שבלהה שואלת רביעית הממון ורחל חציו וזלפה שלש רביעיותיו [ולאה][242] כלו נקח מדומה שיהיה לו חצי ורביעית והנה נמצא שמנה |
|
ורביעיתם שניים וחציים ארבעה ושלש רביעיותיהם ששה והמחובר מכל החלקים האלה עמו עולה עשרים |
|
והנה כערך עשרים אל ארבעת אלפים שהוא הממון הנשאר ליעקב ככה יהיה ערך שמנה אל חלק כתובת לאה הנעלם |
|
וכאשר נעשה כמשפט הערכין נמצא שתהיה חלקה אלף ושש מאות זהובים |
|
וכערך עשרים אל ארבעת אלפים ככה יהיה ערך ששה שהוא שלש רביעיות [המדומה][243] אל החלק שתקח זלפה בכתובתה |
|
וכאשר נחקור במשפט הערכין נמצא שתהיה חלקה אלף ומאתים זהובים |
|
ועם נעיין ונאמר כערך עשרים [אל][244] ארבעת אלפים כן ערך ארבעה שהוא חצי המדומה אל החלק שתקח רחל בכתובתה |
|
[245]ונמצא שיבואו לחלקה שמונה מאות זהובים |
|
והנה גם כן נעריך ונאמר כערך עשרים אל ארבעת אלפים כן יהיה ערך שניים אל החלק אשר תקח בלהה בכתובתה |
|
ונמצא שתקח לחלקה ארבע מאות זהובים |
|
וכאשר תחבר כל החלקים האלה ארבעתם תמצא שיהיו עולים ארבעת אלפים מכוונים |
| Motion Problem - Pursuit | |
|
שאלה השולח ציר נאמן ללכת בארץ מרחק והוא הולך בכל יום ויום שנים עשר פרסאות אחר עשרה ימים נמלך המשלח להשיב השליח המהלך וישלח אחריו שליח אחר להשיבו שהוא הולך בכל יום חמשה עשר פרסאות [נרצה לידע בכמה ימים ישיגנו |
|
ונחקור בדרך זה נחשוב כמה פרסאות][246] הולך הראשון בטרם שנסע השני והנה הם מאה ועשרים |
|
נחלקם על יתרון הפרסאות שהולך השני מן הראשון ביום אחד שהם שלשה נמצאם שם ארבעים פעמים והנה ישיגנו בארבעים |
|
ותוכל לבחון זה כשתחשוב כמה פרסאות הלך השליח הראשון בחמשים יום כי ככה הלך השני בארבעה |
| Motion Problem- Encounter | |
|
שאלה ראובן קובע את דירתו [247]בעיר אחת בקצה המזרח ושמעון אחיו קובע דירתו באחת הערים בקצה המערב על ידי אגרות ששלחו זה לזה יעדו להם זמן שיצאו כל אחד מעירו ללכת לקראת אחיו ביום ראשון של חדש ניסן והמהלך אשר בין שתי העיירות חמשים פרסאות והנה ראובן הולך בכל יום שבע פרסאות ושמעון אחיו הולך בכל יום תשע פרסאות ונבקש לדעת בכמה ימים יתחברו זה עם זה |
|
ונעשה ככה נחבר פרסאות מהלך שניהם ביום אחד ויהיו ששה עשר |
|
נחלק חמשים שהוא המרחק עליהם נמצאם שם שלשה פעמים וישארו שנים שלא נתחלקו ונחשוב אותם שמינית ששה עשר והנה יתחבר זה עם זה בשלשה ימים ושמינית יום |
| Find a Quantity Problem - Whole from Parts - Cane | |
|
שאלה קנה הנעוצה בטיט היון שלישיתה ורביעיתה ונראית קומתה למעלה שני זרתות כמה אורך הקנה |
|
נעשה כזאת נקח לנו שנים עשר למדומה יען ימצא השלישית ורביעית |
|
ומחברת חלקים אלו ממנו יהיו שבעה |
|
נסיר אותם מהמדומה [248]ישארו חמשה |
|
ועתה נעריך ונאמר כערך חמשה אל שנים עשר כן ערך השני זרתות אל הנעלם |
|
כפלנו האמצעיים עלו עשרים וארבעה חלקנום על החשבון הראשון הנודע שהוא חמשה מצאנוהו שם ארבעה פעמים ונשארו מהם שלא נתחלק ארבעה והמה חמישיות וככה הוא אורך כל הקנה ארבעה זרתות וארבעה חמשיות זרת |
|
ותוכל לבחון זה אם הוא אמת כשתסיר מעשרים וארבעה שלישיתו ורביעיתו וישארו לך עשרה כשעור חלקי השני זרתות שלמות הנראות מעל הטיט |
| Give and Take Problem - Earning and Spending | |
|
שאלה שולחני שהביא ממון לעיר ידועה ובכל יום ויום הוא מרויח עד שכופל ממונו רק שצריך שיפרע למכס בכל יום מאה דינרין ונתעכב שם חמשה ימים |
|
ונעשה על זה הדרך בידוע כי ביום החמישי כשהשכים שלא היו לו רק חמישים דינרים וכפלם [249]והיו מאה ופרעם למכס ולא נשאר לו מאומה |
|
ובהכרח החמשים דינרים נשארו לו מערב היום הרביעי אחרי אשר פרע מכס אותו היום |
|
ונמצא שהיו לו בשחרית אותו יום מחצית מאה וחמשים דינרים שהם שבעים וחמשה דינרים שנשארו לו מערב היום השלישי |
|
וקודם שפרע מכס היום ההוא היו לו מאה ושבעים וחמשה דינרים |
|
נקח מחציתם יהיו שמנים ושבעה דינרים וחצי שהיו לו בשחר שנשארו לו מאמש יום תמולו שהוא היום השני |
|
ונמצא שאז יהיו לו קודם פריעת המכס מאה ושמונים ושבעה דינרים וחצי |
|
נקח חצים יהיו תשעה ושלשים דינרים ותשעה פשיטים משנים עשר בדינר שהיו לו בשחר הנשארים לו מערב יום ראשון |
|
ונמצא שביום ההוא הראשון היו לו קודם פריעת המכס מאה ותשעים ושלשה דינרין ותשעה פשיטים |
|
נקח חציים והם תשעים וששה דינרים ועשרה פשיטים וחצי פשוט וככה הביא |
|
| |
Epilogue |
|
| Up to this point there have been many of the questions of many different types. | עד הנה הרבה מן השאלות ממינים רבים [250]בלתי דומים זה לזה |
| I have explained the way to find the answer of each one at length, so that any wise man will be able to deduce from these answers to others. | ובארתי בכל אחת ואחת בארוכה דרך מציאת תשובתה וכל חכם לב יוכל לקחת מהתשובות האלה לזולתן |
| The time has come to end the words of this book that giveth goodly words [Genesis 49, 21] | והגיע ת[ור] לחתום פה עתה את דברי זה הספר הנותן אמרי שפר[note 5] |
| We will give praises, glories and songs to the Knower of all hidden things, because, they are not proper to others. | ונערוך תושבחות ותהלות ושירות ליודע כל נסתרות כי לא יאותו לזולתו |
| For the honor of his excellent majesty [Esther 1, 4]. | בעבור יקר תפארת גדולתו[note 6] |
| May his name be blessed and exalted. | יתברך ויתעלה שמו |
| May He bestow us His compassion. | ויפיק אלינו חמלתו |
| May His kingdom be established upon us forever and ever. | ויכון עלינו לעולם ועד מלכותו |
| May He also shower water out of the wells of His salvation upon His congregation. | גם ישפיע לעדתו ממימי מעייני ישועתו |
| May He hasten and quicken the day spoken of in the vision of Isaiah, his prophet, who wrote in his book: And in that day shall you say: 'Give thanks unto the Lord, call upon His name, declare His doings among the peoples, make mention that His name is exalted' [Isaiah 12, 4]. | ימהר ויחיש יום יאמר חזות ישעיהו נביאו אשר כתב בספרו ואמרתם ביום ההוא הודו לי"י קראו בשמו הודיעו בעמים עלילותיו הזכירו כי נשגב שמו[note 7] |
| Over and done. | תם ונשלם |
| Praise be to the Creator of the world. | שבח לבורא עולם |
Notes
Apparatus
- ↑ 50v
- ↑ 51r
- ↑ 51v
- ↑ Vatican marg.
- ↑ 52r
- ↑ 52v
- ↑ 53r
- ↑ marg.
- ↑ 53v
- ↑ 54r
- ↑ 54v
- ↑ Vatican om.
- ↑ 55r
- ↑ Vatican om.
- ↑ 55v
- ↑ marg.
- ↑ 56r
- ↑ Vatican: כשיעלה
- ↑ 56v
- ↑ 57r
- ↑ Vatican om.
- ↑ 57v
- ↑ 58r
- ↑ 58v
- ↑ Vatican marg.
- ↑ Vatican om.
- ↑ 59r
- ↑ 59v
- ↑ marg.
- ↑ Vatican om.
- ↑ Vatican: וכנגדה
- ↑ marg.
- ↑ 60r
- ↑ Vatican om.
- ↑ 60v
- ↑ marg.
- ↑ Vatican: מהשמור
- ↑ 61r
- ↑ 61v
- ↑ 62r
- ↑ marg.
- ↑ 62v
- ↑ 63r
- ↑ 63v
- ↑ 64r
- ↑ Vatican om.
- ↑ 64v
- ↑ 65r
- ↑ 65v
- ↑ 66r
- ↑ marg.
- ↑ 66v
- ↑ marg.
- ↑ 67r
- ↑ 67v
- ↑ 68r
- ↑ Vatican: וארבעים
- ↑ 68v
- ↑ 69r
- ↑ marg.
- ↑ 69v
- ↑ marg.
- ↑ marg.
- ↑ marg.
- ↑ 70r
- ↑ marg.
- ↑ 70v
- ↑ 71r
- ↑ Vatican om.
- ↑ 71v
- ↑ marg.
- ↑ 72r
- ↑ Vatican: תשרש
- ↑ Vatican: תבוא
- ↑ 72v
- ↑ Vatican: שמנה
- ↑ 73r
- ↑ 73v
- ↑ Vatican om.
- ↑ marg.
- ↑ 74r
- ↑ Vatican: לה
- ↑ marg.
- ↑ 74v
- ↑ 75r
- ↑ 75v
- ↑ Vatican om.
- ↑ 76r
- ↑ 76v
- ↑ marg.
- ↑ 77r
- ↑ 77v
- ↑ Vatican om.
- ↑ Vatican om.
- ↑ marg.
- ↑ 78r
- ↑ 78v
- ↑ 79r
- ↑ 79v
- ↑ 80r
- ↑ 80v
- ↑ Vatican om.
- ↑ 81r
- ↑ marg.
- ↑ Vatican om.
- ↑ 81v
- ↑ Vatican om.
- ↑ marg.
- ↑ 82r
- ↑ 82v
- ↑ marg.
- ↑ marg.
- ↑ 83r
- ↑ Vatican om.
- ↑ marg.
- ↑ 83v
- ↑ Vatican om.
- ↑ Vatican om.
- ↑ Vatican: האמצעית
- ↑ Vatican om.
- ↑ Vatican om.
- ↑ Vatican om.
- ↑ Vatican om.
- ↑ 84r
- ↑ 84v
- ↑ Vatican om.
- ↑ Vatican om.
- ↑ Vatican: לחיקת
- ↑ 85r
- ↑ marg.
- ↑ 85v
- ↑ 86r
- ↑ 86v
- ↑ 87r
- ↑ 87v
- ↑ marg.
- ↑ Vatican om.
- ↑ Vatican: מחמשה
- ↑ 88r
- ↑ Vatican: באתי
- ↑ 88v
- ↑ Vatican: החמישית
- ↑ 89r
- ↑ Vatican om.
- ↑ Vatican: דמין
- ↑ Vatican om.
- ↑ Vatican: ושתי
- ↑ marg.
- ↑ 89v
- ↑ Vatican: חמשיות
- ↑ Vatican om.
- ↑ 90r
- ↑ Vatican: ועל
- ↑ Vatican: השתי
- ↑ 90v
- ↑ 91r
- ↑ Vatican: ושמנה
- ↑ 91v
- ↑ Vatican: שלישיות
- ↑ Vatican: נכפול
- ↑ Vatican om.
- ↑ 92r
- ↑ Vatican: חלקקנו
- ↑ marg.
- ↑ 92v
- ↑ Vatican: מהארבעה עשרה
- ↑ marg.
- ↑ Vatican: ב"ה
- ↑ Vatican: בידועת
- ↑ Vatican: מספר ופקח
- ↑ Vatican: באמיתית
- ↑ Vatican: גדרים
- ↑ Vatican: הנושאים
- ↑ 93r
- ↑ Vatican: נסתרת
- ↑ Vatican om.
- ↑ Vatican om.
- ↑ Vatican: חצה
- ↑ 93v
- ↑ Vatican: וחלקו כל מעלה... ועשירית twice
- ↑ Vatican om.
- ↑ 94r
- ↑ Vatican: ועד
- ↑ Vatican om.
- ↑ 94v
- ↑ Vatican om.
- ↑ Vatican: המכה
- ↑ Vatican: הכאה
- ↑ 95r
- ↑ Vatican om.
- ↑ Vatican: בדק
- ↑ 95v
- ↑ 96r
- ↑ marg.
- ↑ 96v
- ↑ 97r
- ↑ Vatican om.
- ↑ Vatican om.
- ↑ Vatican om.
- ↑ Vatican om.
- ↑ 97v
- ↑ Vatican om.
- ↑ 98r
- ↑ 98v
- ↑ Vatican: וביאור
- ↑ marg.
- ↑ Vatican: דמים
- ↑ 99r
- ↑ Vatican: הנה
- ↑ Vatican: השפל
- ↑ 99v
- ↑ 100r
- ↑ 100v
- ↑ 101r
- ↑ 101v
- ↑ Vatican: ותשעים וששה
- ↑ Vatican om.
- ↑ 102r
- ↑ 102v
- ↑ Vatican: אל
- ↑ Vatican: חמשה עשר
- ↑ 103r
- ↑ Vatican: חלף
- ↑ 103v
- ↑ Vatican om.
- ↑ 104r
- ↑ Vatican om.
- ↑ 104v
- ↑ Vatican om.
- ↑ 105r
- ↑ Vatican: הימים ושנים
- ↑ Vatican om.
- ↑ Vatican: והתאנתי
- ↑ 105v
- ↑ Vatican: ו'
- ↑ 106r
- ↑ Vatican: שבעת
- ↑ 106v
- ↑ Vatican: עלך
- ↑ Vatican: ושלשים
- ↑ 107r
- ↑ Vatican: ולא
- ↑ Vatican: ומדומה
- ↑ Vatican om.
- ↑ 107v
- ↑ Vatican marg.
- ↑ 108r
- ↑ 108v
- ↑ 109r
- ↑ 109v
Appendix I: Glossary of Terms
| rank | מדרגה |
Appendix: Bibliography
Joseph Ben Moses Ṣarfati
Before 1384
‛Ir Siḥon
Manuscripts:
- 1) Ithaca (NY), Cornell University A 26/1 (IMHM: f 46122), ff. 3r-29v (15th century)
- 2) Moscow, Russian State Library, Ms. Guenzburg 138/2 (IMHM: f 6818), ff. 23r-65v (15th century)
- Guenzburg 138
- 3) München, Bayerische Staatsbibliothek, Cod. hebr. 68/5 (IMHM: f 1131), ff. 346r-374v (Roma, 1552)
- Cod.hebr. 68
- 4) Paris, Bibliothèque Nationale de France heb. 995/5 (IMHM: f 14680), ff. 297r-300v (16th century)
- heb. 995
- 5) Philadelphia, University of Pennsylvania, Schoenberg Collection Ljs 312 (IMHM: f 4795); (15th-16th century)
- LJS 312
- 6) St. Petersburg, Inst. of Oriental Studies of the Russian Academy B 176 (IMHM: f 53314); (18th century)
- 7) Vatican, Biblioteca Apostolica ebr. 397/3 (IMHM: f 475), ff. 51r-109v (Murcia, 1384/1385)
- Vat.ebr.397
- The transcript of the text is based on manuscript Vatican 397.
Bibliography:
- Steinschneider, Moritz. 1893-1901. Mathematik bei den Juden. Berlin-Leipzig-Frankfurt: Kaufmann, p. 188 (g101); repr. Hildesheim: G. Olms, 1964 and 2001.
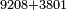
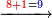
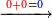
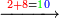
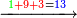
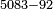
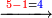
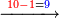
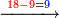
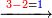
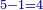
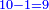
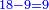



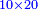
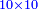
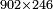
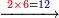
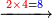
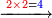
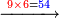
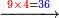
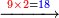
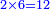
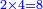


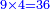

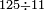
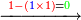
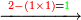
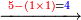

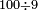


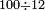

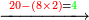

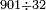
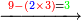
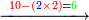

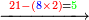

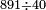
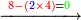
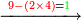

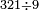



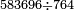

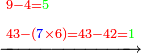
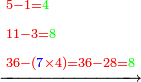
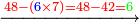
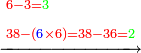
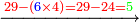
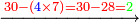
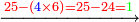
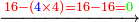

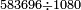
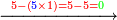
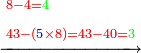
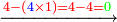
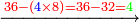
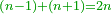

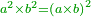
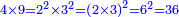
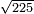
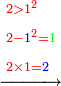
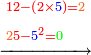
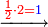
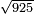
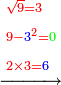



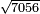
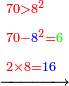
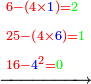


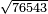
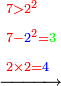
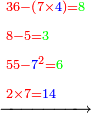
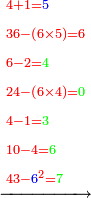
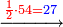

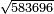
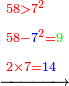
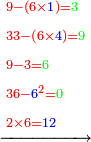
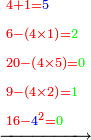

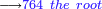
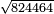
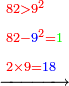
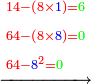

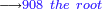
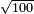
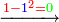
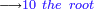
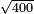


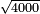
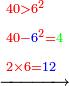
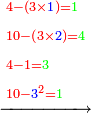

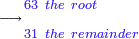
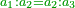
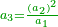
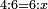
![\scriptstyle{\color{blue}{6:4=\left[\left(1+\frac{1}{2}\right)\sdot4\right]:4}}](/mediawiki/images/math/9/3/1/931ce1931ee11772930a388a4a1cd5e0.png)
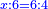
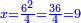
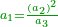
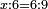
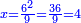
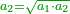
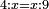
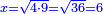
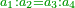
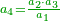
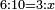
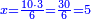
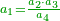
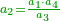
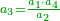
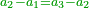

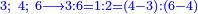
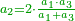
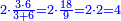
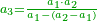
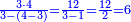
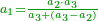
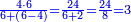

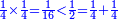


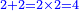
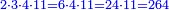
![\scriptstyle{\color{OliveGreen}{\frac{a}{b}\times\frac{c}{d}=\frac{\left[\frac{a}{b}\sdot\left(b\sdot d\right)\right]\sdot\left[\frac{c}{d}\sdot\left(b\sdot d\right)\right]}{\left(b\sdot d\right)^2}}}](/mediawiki/images/math/3/c/1/3c10d1507cb6b8db643f7eafc16665fc.png)
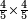
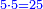
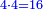
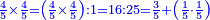
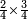

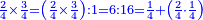
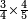
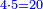
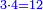
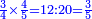


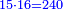
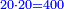
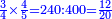
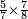
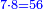
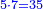
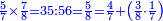
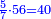
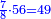
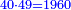
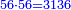
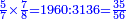
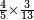
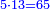

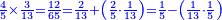
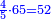

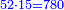
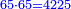

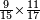
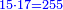
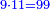
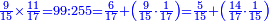

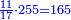
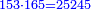
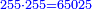
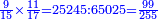
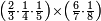
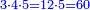
![\scriptstyle{\color{blue}{\frac{2}{3}\sdot\frac{1}{4}\sdot\frac{1}{5}=\frac{\frac{2}{3}\sdot\left[\frac{1}{4}\sdot\left(\frac{1}{5}\sdot60\right)\right]}{60}=\frac{\frac{2}{3}\sdot\left(\frac{1}{4}\sdot12\right)}{60}=\frac{\frac{2}{3}\sdot3}{60}=\frac{2}{60}}}](/mediawiki/images/math/8/f/1/8f11186204ccc044ba6fbebf2d4fc01c.png)
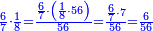
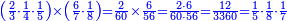
![\scriptstyle{\color{blue}{\frac{1}{5}\sdot\left[\frac{1}{8}\sdot\left(\frac{1}{7}\sdot3360\right)\right]=\frac{1}{5}\sdot\left(\frac{1}{8}\sdot480\right)=\frac{1}{5}\sdot60=12}}](/mediawiki/images/math/f/e/e/feebaeba6f09cbb35ca00b067dbe39c3.png)
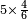
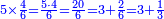
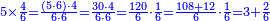
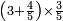
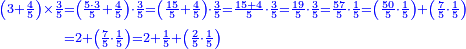
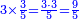
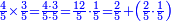
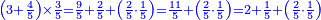
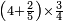
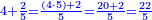
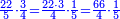
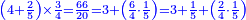
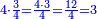
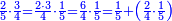
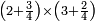

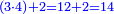
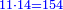
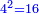
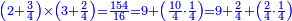
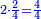

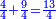
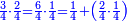
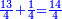
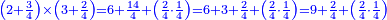
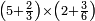
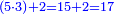
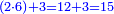
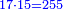
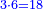
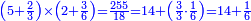
![\scriptstyle{\color{OliveGreen}{\left(n+\frac{a}{b}\right)\times\left(m+\frac{c}{d}\right)=\frac{\left[\left[n\sdot\left(b\sdot d\right)\right]+\left[\frac{a}{b}\sdot\left(b\sdot d\right)\right]\right]\sdot\left[\left[m\sdot\left(b\sdot d\right)\right]+\left[\frac{c}{d}\sdot\left(b\sdot d\right)\right]\right]}{\left(b\sdot d\right)^2}}}](/mediawiki/images/math/6/b/c/6bcbef6f88fa2678c13853f712cdc424.png)
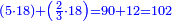
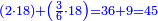
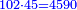
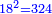

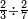
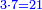
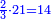
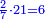
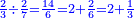
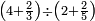
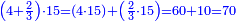
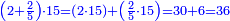
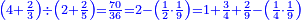
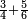
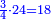
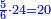

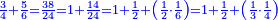
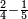


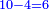
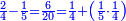
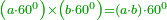
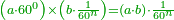
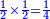
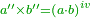


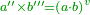
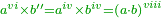
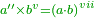
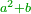
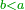

![\scriptstyle{\color{OliveGreen}{\left[a+\left(\frac{60\sdot b}{2a}\right)^\prime\right]^2-\left(a^2+b\right)}}](/mediawiki/images/math/d/1/8/d1884d02d5c52436853b8fa19a7b0990.png)
![\scriptstyle{\color{OliveGreen}{\sqrt{a^2+b}\approx a+\left(\frac{60\sdot b}{2a}\right)^\prime-\left[\frac{\left(\left(\frac{60\sdot b}{2a}\right)^\prime\right)^2}{2\sdot\left(a+\left(\frac{60\sdot b}{2a}\right)^\prime\right)}\right]}}](/mediawiki/images/math/3/0/e/30e5279dac9bf13aa0f31cfae39a398b.png)
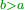
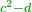

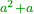 ].
].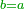
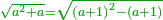
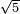
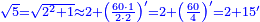
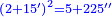
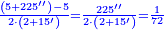
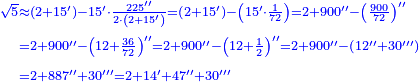
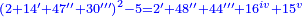
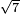
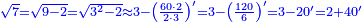
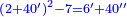
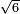
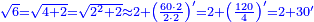
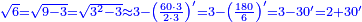
![\scriptstyle{\color{OliveGreen}{\left(3n\right)^2=\left[10\sdot\left[\frac{1}{3}\sdot\left(3n\right)\right]^2\right]-\left[\frac{1}{3}\sdot\left(3n\right)\right]^2}}](/mediawiki/images/math/8/7/b/87bdc32051b224513066e28e719f373b.png)
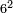
![\scriptstyle{\color{blue}{6^2=\left(3\sdot2\right)^2=\left[10\sdot\left(\frac{1}{3}\sdot6\right)^2\right]-\left(\frac{1}{3}\sdot6\right)^2=\left(10\sdot2^2\right)-2^2=\left(10\sdot4\right)-4=40-4=36}}](/mediawiki/images/math/3/8/d/38d1d5ec3932f81319dd5cf689ea938d.png)
![\scriptstyle{\color{OliveGreen}{\left(3n+1\right)^2=\left[\left[10\sdot\left[\frac{1}{3}\sdot\left(3n\right)\right]^2\right]-\left[\frac{1}{3}\sdot\left(3n\right)\right]^2\right]+3n+\left[\left(3n+1\right)\right]}}](/mediawiki/images/math/b/f/3/bf33f7d7d256c9cce1765e3f38e307be.png)
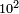
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle10^2&\scriptstyle=\left(9+1\right)^2=\left[\left(3\sdot3\right)+1\right]^2=\left[\left[10\sdot\left(\frac{1}{3}\sdot9\right)^2\right]-\left(\frac{1}{3}\sdot9\right)^2\right]+9+10=\left[\left(10\sdot3^2\right)-3^2\right]+9+10\\&\scriptstyle=\left[\left(10\sdot9\right)-9\right]+9+10=\left(90-9\right)+9+10=81+9+10=100\\\end{align}}}](/mediawiki/images/math/b/6/4/b644d352f59bcab6ac290785552438e0.png)
![\scriptstyle{\color{OliveGreen}{\left(3n-1\right)^2=\left[\left[10\sdot\left[\frac{1}{3}\sdot\left(3n\right)\right]^2\right]-\left[\frac{1}{3}\sdot\left(3n\right)\right]^2\right]-\left(3n\right)-\left[\left(3n-1\right)\right]}}](/mediawiki/images/math/4/2/4/424921fda72004011eee2ecd49af0392.png)
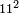
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle11^2&\scriptstyle=\left(12-1\right)^2=\left[\left(3\sdot4\right)-1\right]^2=\left[\left[10\sdot\left(\frac{1}{3}\sdot12\right)^2\right]-\left(\frac{1}{3}\sdot12\right)^2\right]-11-12\\&\scriptstyle=\left[\left(10\sdot4^2\right)-4^2\right]-11-12=\left[\left(10\sdot16\right)-16\right]-11-12\\&\scriptstyle=\left(160-16\right)-11-12=144-12-11=144-23=121\\\end{align}}}](/mediawiki/images/math/b/0/1/b0167e9801aca57699585726cc550144.png)
![\scriptstyle{\color{OliveGreen}{\left(10+a\right)\times\left(10+b\right)=\left[10\sdot\left[\left(10+a\right)+b\right]\right]+\left(a\sdot b\right)}}](/mediawiki/images/math/6/c/a/6ca9d98590fd0390228cb3a1b7607d13.png)
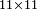
![\scriptstyle{\color{blue}{11\times11=\left[\left(11-1\right)\sdot\left(11+1\right)\right]+\left(1\sdot1\right)=\left(10\sdot12\right)+1=120+1=121}}](/mediawiki/images/math/e/a/1/ea13d6aefaefa54cb18f4c31e4c21646.png)
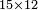
![\scriptstyle{\color{blue}{15\times12=\left[\left(12-2\right)\sdot\left(15+2\right)\right]+\left(2\sdot5\right)=\left(10\sdot17\right)+10=170+10=180}}](/mediawiki/images/math/2/e/0/2e0464051c8b288d93d7c642b5cb03ff.png)
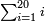
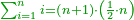
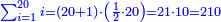
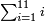
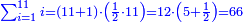
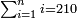
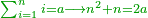
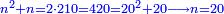
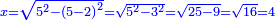
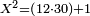
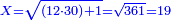
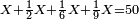

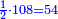
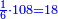
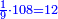

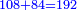
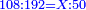
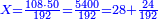
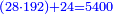
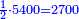
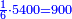
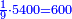


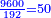
![\scriptstyle X=100-\left[\left(\frac{1}{3}\sdot100\right)+\left(\frac{1}{4}\sdot100\right)\right]](/mediawiki/images/math/0/6/4/064f6c9817381f7419d53dd1707a018a.png)
![\scriptstyle{\color{blue}{12-\left[\left(\frac{1}{3}\sdot12\right)+\left(\frac{1}{4}\sdot12\right)\right]=12-7=5}}](/mediawiki/images/math/9/9/4/994410b776b40d19b554ba92d759d4ae.png)

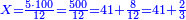
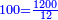
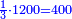
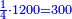


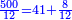
![\scriptstyle\left(X-\frac{2}{100}X\right)-\left[\frac{1}{10}\sdot\left(X-\frac{2}{100} X\right)\right]-\left[\frac{1}{10}\sdot\left[\left(X-\frac{2}{100}X\right)-\left[\frac{1}{10}\sdot\left(X-\frac{2}{100} X\right)\right]\right]\right]=50](/mediawiki/images/math/4/a/2/4a2924027b379bac5d8c351156314329.png)

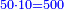
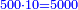

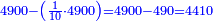
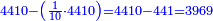


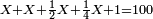
![\scriptstyle{\color{blue}{8+8+\left[\left(\frac{1}{2}\sdot8\right)+\left(\frac{1}{4}\sdot8\right)\right]=16+4+2=20+2=22}}](/mediawiki/images/math/5/a/3/5a39486b875ef2fbc83b16aa4a933d0a.png)
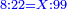
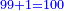
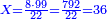
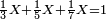
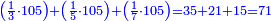
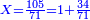
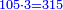
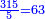
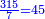
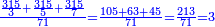
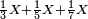
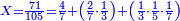
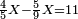
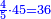
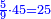
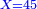
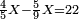

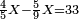

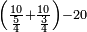
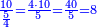
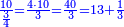
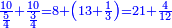
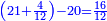
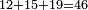

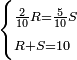
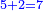
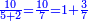
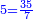
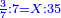
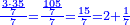
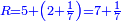
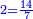
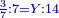
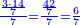
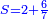
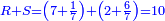
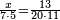

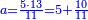
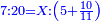
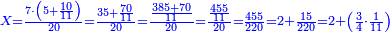
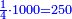


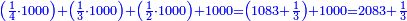
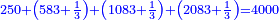
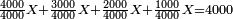
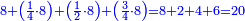





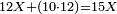

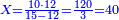

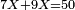
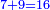
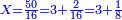 days
days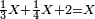
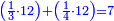
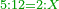
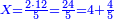 zeratot
zeratot![\scriptstyle{\color{blue}{\frac{24-\left[\left(\frac{1}{3}\sdot24\right)+\left(\frac{1}{4}\sdot24\right)\right]}{5}=\frac{10}{5}=2}}](/mediawiki/images/math/4/2/6/426ac9e6b1a5cfc0284b012d7d85c37b.png)
![\scriptstyle2\sdot\left[2\sdot\left[2\sdot\left[2\sdot\left(2X-100\right)-100\right]-100\right]-100\right]=100](/mediawiki/images/math/0/2/f/02f6b36951cd14a8b19a17e49a64a0b3.png)
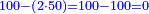
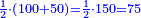
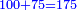
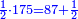
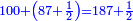 dinar
dinar