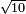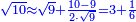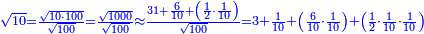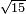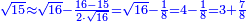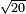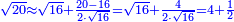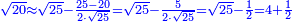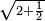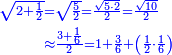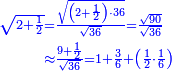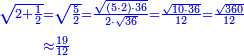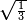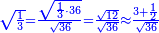Al-HAṢṢĀR - Arabic in Hebrew Characters
Contents
- 1 Chapter Six – Dividing a Small Number by a Larger Number
- 2 Chapter Seven – Division
- 3 Chapter Eight – Halving
- 4 Chapter Nine – Doubling
- 5 Chapter Ten – Extracting Roots
- 6 Multiplication of Fractions
- 6.1 Chapter One: Forms of Fractions
- 6.2 Chapter Two: Multiplication of Fraction by Integer
- 6.3 Chapter Three: Multiplication of Fraction and Fraction of Fraction by Integer
- 6.4 Chapter Four: Multiplication of Fraction of Fraction by Integer
- 6.5 Chapter Five: Multiplication of Two Different Fractions by Integer
- 6.6 Chapter Six: Multiplication of Fraction by Integer and Fraction
- 6.7 Chapter Seven: Multiplication of Fraction and Fraction of Fraction by Integer and Fraction
- 6.8 Chapter Eight: Multiplication of Fraction of Fraction by Integer and Fraction
- 6.9 Chapter Nine: Multiplication of Two Different Fractions by Integer and Fraction
- 6.10 Chapter Ten: Multiplication of Fraction by Integer and Fraction and Fraction of Fraction
- 6.11 Chapter Eleven: Multiplication of Fraction by Integer and Fraction of Fraction
- 6.12 Chapter Twelve: missing
- 6.13 Chapter Thirteen: Multiplication of Fraction and Fraction of Fraction by Integer and Fraction and Fraction of Fraction
- 6.14 Chapter Fourteen: Multiplication of Fraction and Fraction of Fraction by Integer and Fraction of Fraction
- 6.15 Chapter Fifteen: Multiplication of Fraction and Fraction of Fraction by Integer and Two Different Fractions
- 6.16 Chapter Sixteen: Multiplication of Fraction of Fraction by Integer and Fraction and Fraction of Fraction
- 6.17 Chapter Seventeen: Multiplication of Fraction of Fraction by Integer and Fraction of Fraction
- 6.18 Chapter Eighteen: Multiplication of Fraction of Fraction by Integer and Two Different Fractions
- 6.19 Chapter Nineteen: Multiplication of Two Different Fractions by Integer and Fraction and Fraction of Fraction
- 6.20 Chapter Twenty: Multiplication of Two Different Fractions by Integer and Fraction of Fraction
- 6.21 Chapter Twenty One: Multiplication of Two Different Fractions by Integer and Two Different Fractions
- 6.22 Chapter Twenty Two: Multiplication of Integer and Fraction by Integer and Fraction
- 6.23 Chapter Twenty Three: Multiplication of Integer and Fraction and Fraction of Fraction by Integer and Fraction and Fraction of Fraction
- 6.24 Chapter Twenty Four: Multiplication of Integer and Two Different Fractions by Integer and Two Different Fractions
- 6.25 Chapter Twenty Five: Multiplication of Integer and Two Different Fractions and Fraction of Fraction by Integer and Two Different Fractions and Fraction of Fraction
- 6.26 Chapter Twenty Six: Multiplication of Integer and Three Different Fractions by Integer and Three Different Fractions
- 6.27 Chapter Twenty Seven: Multiplication of Integer and Three Different Fractions and Fraction of Fraction
- 6.28 Chapter Twenty Eight: Multiplication of Fraction by Fraction
- 6.29 Chapter Twenty Nine: Multiplication of Fraction and Fraction of Fraction by Fraction
- 6.30 Chapter Thirty: Multiplication of Two Different Fractions by Fraction
- 6.31 Chapter Thirty One: Multiplication of Fraction and Fraction of Fraction by Fraction and Fraction of Fraction
- 6.32 Chapter Thirty Two: Multiplication of Two Different Fractions by Fraction and Fraction of Fraction
- 6.33 Chapter Thirty Three: Multiplication of Two Different Fractions by Two Different Fractions
- 6.34 Chapter Thirty Four: Multiplication of Fraction by Fraction of Fraction
- 6.35 Chapter Thirty Five: Multiplication of Three Different Fractions by Three Different Fractions
- 6.36 Chapter Thirty Six: Multiplication of Three Different Fractions and Fraction of Fraction by the Same
- 6.37 Chapter Thirty Seven: Multiplication of Fraction of Integer by Fraction of Integer
- 6.38 Chapter Thirty Eight: Multiplication of Fraction and Fraction of Fraction of Integer by Fraction and Fraction of Fraction of Integer
- 6.39 Chapter Thirty Nine: Multiplication of Different Fractions of Integer by Different Fractions of Integer
- 6.40 Chapter Forty: Multiplication of Fraction of Fraction of Integer by Fraction of Fraction of Integer
- 6.41 Chapter Forty One: Multiplication of Fraction of Integer and Fraction by Fraction of Integer and Fraction
- 6.42 Chapter Forty Two: Multiplication of Fraction of Integer and Fraction and Fraction of Fraction by the Same
- 6.43 Chapter Forty Three: Multiplication of Fraction of Integer and Two Different Fractions by the Same
- 6.44 Chapter Forty Four: Multiplication of Fraction of Integer and Fraction of Fraction by Fraction of Integer and Fraction of Fraction
- 6.45 Chapter Forty Five: Multiplication of Fraction of Fraction of Integer and Fraction by Fraction of Fraction of Integer and Fraction
- 6.46 Chapter Forty Six: Multiplication of Fraction of Fraction of Integer and Fraction and Fraction of Fraction by the Same
- 6.47 Chapter Forty Seven: Multiplication of Fraction of Fraction of Integer and Fraction of Fraction by the Same
- 6.48 Chapter Forty Eight: Multiplication of Fraction of Fraction of Integer and Two Different Fractions by Fraction of Fraction of Integer and Two Different Fractions
- 6.49 Chapter Forty Nine: Multiplication of Two Different Fractions of Integer and Fraction by Two Different Fractions of Integer and Fraction
- 6.50 Chapter Fifty: Multiplication of Two Different Fractions of Integer and Two Different Fractions by the Same
- 6.51 Chapter Fifty One: Multiplication of Fraction and Fraction of Fraction of Integer and Fraction and Fraction of Fraction by the Same
- 6.52 Chapter Fifty Two: Multiplication of Fraction of Fraction of Integer and Fraction of Fraction by the Same
- 6.53 Chapter Fifty Three: Multiplication of Fraction of Integer and Fraction of Integer by the Same
- 6.54 Chapter Fifty Four: Multiplication of Fraction of Integer and Fraction of Integer and Fraction by the Same
- 6.55 Chapter Fifty Five: Multiplication of Integer and Fraction and Integer and Fraction by the Same
- 6.56 Chapter Fifty Six: Multiplication of Integer and Two Different Fractions and Integer and Two Different Fractions and Integer by the Same
- 6.57 Chapter Fifty Seven: Multiplication of Integer and Fraction of Fraction and Integer and Fraction of Fraction and Integer by the Same
- 6.58 Chapter Fifty Eight: Multiplication of Fraction and Integer and Two Different Fractions and Integer and Fraction by the Same
- 6.59 Chapter Fifty Nine: Multiplication of Fraction and Fraction of fraction and Integer and Two Different Fractions and Integer and Fraction and Integer and Fraction and Fraction of Fraction by the Same
- 6.60 Chapter Sixty: Multiplication of Fractions
- 6.61 Chapter Sixty One: Multiplication of Fraction of Fraction of Integer and Fraction and Fraction of Fraction by the Same
- 6.62 Chapter Sixty Two: Multiplication of Fraction of fraction of Integer by the Same
- 6.63 Chapter Sixty Four:
- 6.64 Chapter Sixty Five: Multiplication of Fractions of Fractions by Fractions of Fractions
- 6.65 Chapter Sixty Six: Multiplication of Integer and Fraction of Fraction by Integer and Fraction of Integer
- 6.66 Chapter Sixty Seven: Multiplication of Integer and Fraction of Fraction and Fraction by the Same
- 6.67 Chapter Sixty Eight: Multiplication of Fraction of Fraction and Integer and Fraction of Fraction by the Same
- 6.68 Chapter Sixty Nine: Multiplication of Two Different Fractions and Integer and Fraction of Fraction and Integer and Fraction and Fraction of Fraction and Integer and Fraction of Fraction and Integer and Fraction
- 6.69 Chapter Seventy: Multiplication of Integer and Fraction by Integer and Fraction by Integer and Fraction and so on
- 6.70 Chapter Seventy One: Multiplication of Subtracted Fractions
- 6.71 Chapter Seventy Two: Multiplication of Reduced Fractions of Integers
- 7 Converting Fractions to Lower Fractions
- 8 Addition of Fractions
- 8.1 Chapter One – Adding One Fraction to Another
- 8.2 Chapter Two – Adding Two Fractions to Two Fractions
- 8.3 Chapter Three – Adding Fraction and Fraction of Fraction to Two Different Fractions
- 8.4 Chapter Four – Adding Fraction and Fraction of Fraction to Fraction and Fraction of Fraction
- 8.5 Chapter Five – Adding Integer and Fraction to Integer and Fraction
- 8.6 Chapter Six – Adding Integer and Fraction and Fraction of Fraction to Integer and Two Different Fractions
- 8.7 Chapter Seven – Adding Fraction of Integer to Integer
- 8.8 Chapter Eight – Adding Fraction of Integer to Fraction of Integer
- 8.9 Chapter Nine – Adding Fraction of Integer and Fraction to Fraction of Integer and Fraction
- 8.10 Addition of Unknown Amounts
- 9 Sums
- 10 Subtraction of Fractions
- 11 Division of Fractions
- 11.1 Division of the smaller by the larger
- 11.1.1 Division of Fraction and Fraction of fraction by Integer
- 11.1.2 Division of Two Different Fractions by Integer
- 11.1.3 Division of Fraction by Integer and Fraction
- 11.1.4 Division of Fraction by Integer and Fraction and Fraction of Fraction
- 11.1.5 Division of Fraction by Integer and Two Different Fractions
- 11.1.6 Division of Integer by Integer and Fraction
- 11.1.7 Division of Integer and Fraction by Integer and Fraction
- 11.1.8 Division of Fraction by Fraction
- 11.1.9 Division of Two Different Fractions by Fraction
- 11.1.10 Division of Fraction by Fraction and Fraction of Fraction
- 11.1.11 Division of Fraction by Two Different Fractions
- 11.1.12 Division of Fraction and Fraction of Fraction by Fraction and Fraction of Fraction
- 11.1.13 Division of Two Different Fractions by Two Different Fractions
- 11.1.14 Division of Fraction of Fraction by Integer and Fraction
- 11.1.15 Division of Fraction of Fraction by Integer and Fraction and Fraction of Fraction
- 11.1.16 Division of Fraction of Fraction by Integer and Two Different Fractions
- 11.1.17 Division of Fraction of Fraction by Fraction
- 11.1.18 Division of Fraction of Fraction by Fraction and Fraction of Fraction
- 11.1.19 Division of Fraction of Fraction by Two Different Fractions
- 11.2 Division of the larger by the smaller
- 11.2.1 Division of Integer by Fraction
- 11.2.2 Division of Integer by Fraction of Fraction
- 11.2.3 Division of Integer by Fraction and Fraction of Fraction
- 11.2.4 Division of Integer by Two Different Fractions
- 11.2.5 Division of Integer and Fraction by Fraction
- 11.2.6 Division of Integer and Fraction by Fraction of Fraction
- 11.2.7 Division of Integer and Fraction by Fraction and Fraction of Fraction
- 11.2.8 Division of Integer and Fraction by Two Different Fractions
- 11.2.9 Division of Integer and Fraction and Fraction of Fraction by Fraction
- 11.2.10 Division of Integer and Fraction and Fraction of Fraction by Fraction of Fraction
- 11.2.11 Division of Integer and Fraction and Fraction of Fraction by Fraction and Fraction of Fraction
- 11.2.12 Division of Integer and Fraction and Fraction of Fraction by Two Different Fractions
- 11.2.13 Division of Integer and Two Different Fractions by Fraction and Fraction of Fraction
- 11.2.14 Division of Integer and Two Different Fractions by Integer and Two Different Fractions
- 11.2.15 Division of Fraction by Fraction
- 11.2.16 Division of Fraction by Fraction of Fraction
- 11.2.17 Division of Fraction by Fraction and Fraction of Fraction
- 11.1 Division of the smaller by the larger
- 12 Completion of Fractions
- 13 Degrading
- 14 Extracting Roots of Integer and Fraction
- 15 Appendix I: Glossary of Terms
- 16 Appendix: Bibliography
Chapter Six – Dividing a Small Number by a Larger Number |
|
| only the end of the chapter survived | |
|
|
פארפעהא פי ידך תם אצֹרב אלתלאתה אלתי עלי ראס אלתמאניה פי אלסתה אלתי פי אלאמאם דאלך תמאנית עשר אלבאקי ארבעה פאגמל עליהא אלארבעה אלתי עלי אלסתה יכון דאלך תמאניה פאסקט מנהא סבעה אלבאקי ואחד פאצֹרבה פי אלאתנין ואגמל מא עליהא יכון דאלך תלאתה והו מסאוי לאלתלאתה אלתי רפעת פי ידך והו אלבאקי מן אלעדד אלמסמי וקד צחת אלמסאלה פאפהם תציב בחולאללה תעלי וחסן [...]ה |
Chapter Seven – Division |
אלבאב אלסאבע פי קסמת אלאעדאד בעצֹהא עלי בעצהא |
|---|---|
| Two kinds of division | אעלם אן הד אלבאב ינקסם קסמין: |
|
אחדא מנהא קסמת אלשי עלי גנסה |
|
ואלתאני קסמת אלשי עלי גיר גנסה |
|
פאמא קסמת אלשי עלי גנסה פהו אלעדד אלצחיח עלי אלעדד אלצחיח מתלה |
|
ואמא קסמת אלשי עלי גיר גנסה פהו קסמת אלצחיח עלי אלכסר |
| ואלמטלוב פי אלוגהין אנמא הו מא יגב ללואחד | |
| ואעלם אנך מתי ארדת אן תקסם עדד עלי עדד פהדא אלבאב יגתמל פי אלעדד וגוהא | |
|
|
פמן דאלך אן תסמי ואחד מן אלמקסום עליה ותאכוד תלך אלנסבה מן אלמקסום פמא כאן פהו יגב ללואחד |
|
ומתאל דאלך אקסם עשרין עלי ארבעה |
|
|
פתסמא ואחד מן ארבעה תגד דאלך רבעא פכד רבע אלעשרין ודאלך כמסה והו מא יכרג' מן אלקסמה והו אלואג'ב לכל ואחד מן אלארבעה |
|
|
ואלמעני אלתאני אן תרד אלמקסום ואלמקסום עליה אלי גזאً יתפקאן פיה |
|
|
[מע]ני לכל ואחד מנהמא רבעא פרדהמא אלי ארבעה תם תקסם רבע אלמקסום עלי רבע אלמקסום עליה פמא כרג פהו אלמטלוב |
|
ומתאל דאלך אקסם כמסה ותלאתין עלי כמסת עשר |
|
|
פלכל ואחדא מנהמא גזאً ישתרכאן פיה והו אלכמס פכד כמס אלכמסת עשר ודאלך תלאתה וכמס אלכמסה ותלאתין ודאלך סבעה פאקסמהא עלי אלתלאתה יכרג לך אתנאן ותלת והו מא יכרג מן קסמת אלכמסה ותלאתין עלי אלכמסת עשר |
| ואלנוע אלתאלת מן אלקסמה ינקסם קסמין: והו אמא אן יכון אלעדד אלמקסום עליה בגמלתה אולא מרכבאً או גיר מרכב | |
|
|
פאן כאן אולא גיר מרכב טלבת עדד תצֹרבה פי אלמקסום עליה בגמלתה פתסקטה מן אלעדד אלמקסום פיפני או יבקי מא הו אקל מן אלמקסום תם תסמי הד אלבאקי מן אלמקסום עליה ומא אגתמע פהו אלכארג מן אלקסמה |
|
ומתאל דאלך אקסם כמסין עלי אחדי עשר |
|
|
פקד עלמנא אן אלאחדי עשר עדד גיר מרכב לא יעדה אלא אלואחד פאטלב עדדאً תצרבה פי אלאחדי עשר פתסקט גמיע דאלך מן אלכמסין פיפני או יבקי מא הו אקל מן אלאחדי עשר תג'ד ארבעה פאצֹרבהא פי אלאחדי עשר בארבעה וארבעין אלבאקי סתה |
|
|
פתקסמהא עלי אלאחדי עשר ודאלך סתת אגזא מן אלאחדי עשר פאלכארג אדא ארבעה וסתת אגזא מן אחדי עשר |
|
|
ואדא כאן אלעדד מרכבא פ[חלה] אלאעדאדה אלתי תרכבת מ[נה] תם אקסם אלעדד אלמקסום עלי כל ואחדٍ מן הד אלאעדאד אלמדכורה תקסם אולא עלי אלאצגר מנהא ומא כרג' פי אלקסמה קסמת עלי אלאכבר מנה ומא כרג תקסמה עלי אלאכבר חתי תתם אלאעדאד אלמדכורה ממא עלי אלאגזא מנהא פהו אלמטלוב |
|
ומתאל דאלך אקסם סתין עלי תמאניה עשר |
|
|
פקד עלמת אן אלתמאנית עשר תרכבת מן אתנין פי תסעה פאקסם אלסתין עלי אלאתנין יכרג לך תלאתון פאקסם הד אלתלאתין עלי אלתסעה יכרג לך תלאתה ותבקי עלי תסעה תלאתה והי תלאתת אתסאע פיכון אלכארג תלאתה ותלאתת אתסאע |
written division |
פאן כתר אלעדד אלמקסום וכתרת מנאזלה פאקסמה בחרוף אלגבאר |
|
מתאל דאלך אקסם ארבעה וכמסין ותמן מאיה עלי תלאתה |
| פאנזל אלארבעה ואלכמסון ותמאן מאיה פי סטרא ואלתלאתה תחת אלעדד עלי הד אלצורה | |
| 8 5 4 3 |
| 854 | 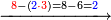 |
254 | 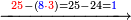 |
14 | 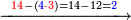 |
2 |
| 3 | 3 | 3 | 3 | |||
| 2 | 28 | 284 |
| תם אנזל אלעדד אלמקסום עליה תחת אלתמאניה אלתי הי אכר אלעדד מן אלמקסום תם אטלב עדדא תנזלה תחת אלתלאתה ותצרבה פיהא ותסקטה מן אלתמאניה תג'ד אתנין פאצֹרבה פי אלתלאתה תכון סתה פאסקטהא מן אלתמאניה אלבאקי אתנין פאנזלהא פי מכאן [אל]תמאניה בעד מא תנזל אלתמאניה תם תנקל אלתלאתה תחת אלכמסה פתכון תחת כמסה ועשרין פאטלב עדדא תצֹרבה פי אלתלאתה ותפני אלכמסה ואלעשרין ודאלך תמאניה פאצֹרבהא פי תלאתה בארבעה ועשרין ותנזל הד אלתמאניה תחת אלתלאתה ותכון מע אלאתנין פי סטרٍ תם אסקט אלכ'ד' ארבעה ועשרין מן אלכמסה ועשרין אלבאקי ואחד פאמחי אלכמסה ואלעשרין ואתבת ואחד פי מכאן אלכמסה תם תנקל אלתלאתה תחת מנזלה אכרי ממא תלי אלימין ודאלך תחת אלארבעה ומע אלארבעה ואחד מקסום פהי אד[.] ארבעת עשר פאטלב עדד תצֹרבה פי אלתלאתה תפני [מנ]ה אלארבעה עשר תגד ארבעה פאנזלהא תחת אלתלאתה ותכון מע אלתמאניה פי סטר תם אצֹרב הד אלארבעה פי אלתלאתה תכון אתני עשר פאסקטהא מן אלארבעה עשר אלבאקי אתנין פאקסמהא עלי אלתלאתה אלתי קסמת עליהא ודאלך תלתאן פיכון אלכארג' מן אלקסמה ארבעה ותמאניה ואתנאן ואתנאן עלי תלאתה והי ארבעה ותמאנון ומאיתין ותלתאן והדה צורתהא כדא | |
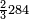
| |
|
פאן ארדת אמתחאן אלמסאלה פאטרח אלעדד אלמקסום סבעה סבעה והי מנטרחה |
|
|
תם אטרח אלכארג מן אלקסמה בטרח סבעה ותבקי מנה ארבעה פאצֹרבה[א] פי אלתלאתה אלתי קסמת עליהא תכון אתני עשר פאטרח מנהא סבעה אלבאקי כמסה פאגמל עליהא אלאתנין אלתי עלי אלתלאתה תכון סבעה מנטרחה |
|
פאן קאל קאיל אקסם סתה וארבעין וסבע מאיה ותמאנית אלאף ותסעין אלף עלי סתה ותלאתין |
| פאנזל אלעדד אלמקסום ואלמקסום עליה עלי הד אלצורה | |
| 9 8 7 4 6 3 6 | |
|
|
ואעלם אן אלסתה ואלתלאתון עדד מרכב מן ארבעה פי תסעה פאקסם אלעדד אלמדכור עלי ארבעה אלתי הי אקל אבדא עלי מא תקדם פי אלמסלה קבל האדא יכרג לך פי אלקסמה סתה ותמאנון וסתת מאיה וארבעה ועשרון אלפא ורבעין פאנזלהא עלי אלארבעה אלתי קסמת עליהא פאקסמהא עלי תסעה איצא עלי מא תקדם יכרג' לך פי אלקסמה ס[תה] ותלאתין][....] אתנין וארבעין וסבע מאיה ואלפאן ותבקי עלי אלתסעה תמאניה תם מד כטא ואגעל תחתה אלתסעה ואלארבעה ....] תלי אלימין ואגעל עלי אלתסעה אלתמאניה....] ועלי אלארבעה אלאתנין ואכתב אלעדד אלכארג' מע הדה אלאימא פי סטרٍ ויכון אלעדד ממא ילי אלימין ואלאימא ממא ילי אליסאר הכדא |
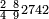
| |
| פיכון אלכארג' מן אלקסמה אתנין וארבעין וסבע מאיה ואלפין ותמאנית אתסאע ורבעיי תסע והי נצף אלתסע | |
| ואנמא קלנא רבעיי ליסהל עלינא פי אלאמתחאן | |
|
ואמתחאן הד אלמסלה אן תטרח אלעדד אלמקסום סבעה סבעה יבקי מנה ארבעה פארפעהא |
|
|
תם ארגע אלי אלעדד אלכארג פאטרח אלצחיח מנה כדאלך יבקי מנה כמסה פאצרבהא פי אלבאקי מן אלתסעה אדא טרחתהא ודאלך אתנאן פי כמסה תכ[ון] עשרה תבקי מנהא תלאתה פאג'מל עליהא אלבאקי מן אלתמאניה אלתי עלי אלתסעה ודאלך ואחד יכון דאלך ארבעה פאצרבהא פי אלארבעה אלתי הי אלאמאם תכון סת עשר אלבאקי מנהא בעד אלטרח אתנאן ועלי אלארבעה אתנין תכון ארבעה והו מסאוי ללארבעה אלתי בקית מן אלעדד אלמקסום פקד צחת אלמסאלה [........] אלאגזא מתאל א[חדי] עשר וסבע[ת] עשר פאלעמל פיהא עלי מא תדכר [.......] |
|
ומתאל דאלך אקסם סתה וסבעין ומיאתין עלי אחדי עשר פאנזל הד אלעדד אלמדכור פי סטרא עלי מא ת[קדם] [ת..... אלאחדי עשר תחת דאלך אלעדד תנזל [.....] אלדי הו עשרה תחת אלסבעה פ[תכון] אלאחדי [עשר] תחת סבעה ועשרין והדה צורתהא |
| 2 7 6 1 1 |
| 276 | 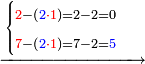 |
56 |  |
1 |
| 11 | 11 | 11 | ||
| 2 | 25 |
| תם אטלב עדדא תנזלה תחת אל[ואחד] אלדי הו ואחד והו איצֹא תחת אלסבעה פתצֹרבה פי אלואחד אלדי הו עשרה ופי אלואחד אלדי הו ואחד ויפני בדאלך [גמי]ע מא עלי ראסה תגד אתנין פאצֹרבהא פי אלואחד אלאכר תכון אתנין תם פי אלואחד אלאול תכון אתנין פאסקטהא מן אלסבעה אלבאקי כמסה פא[תבת]הא פי מכאן אלסבעה תם תנקל אלאחדי עשר תחת אלסתה ואטלב עדד תצֹרבה פי אלואחד אלאכר ותסקטה במא עלי ראסה ותצֹרבה איצֹא פי אלואחד אלדי עלי ראסה ותסקטה במא עליה פלא יבקי שיאً תגד כמסה פאצֹרבהא פי אלואחד אלאכר תכון כמסה אסקטהא מן אלכמסה אלתי עלי ראסהא תפני תם אצרב אלכמסה פי אלואחד [.....] בכמסה אסק[טהא] מן אלכמסה אלתי עלי [ראסהא] תפני תם אצֹרב אלכמסה פי אל[ואחד] אלאול בכמסה אסקטהא מן אלסתה אלתי עלי ראסהא תפני [וי]בקי ואחד פאנסבה אלי אלאחדי עשר ודאלך גזא מן [אחדי] עשר פקד כרג פי אלקסמה כמסה ועשרין וגז מן אחדי [עשר] והדה צורתהא | |
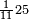
| |
|
ואמתחאן הד אלמסאלה אן תטרח אלסתה וסבעין ומאיתין אלמקסומה [סבעה] סבעה תבקי מנה תלאתה פארפעהא |
|
|
תם אטרח אלכמסה ועשרין אלתי כרגת מן אלקסמה סבעה סבעה תבקי מנהא ארבעה פאצֹרבהא פי אלאחדי עשר תבקי מן אלגמלה אתנין פאגמל עליהא אלגז אלדי עלי אלאחדי עשר בואחד תכון תלאתה והי מואפקה לאלתלאתה אלתי בקית מן אלעדד אלמקסום |
| ועלי הד אלמתאל הי אלקסמה עלי תלאתת עשר וסבעת עשר פאפהם תציב אן שא אללה תעלי במנה ופצלה |
Chapter Eight – Halving |
אלבאב אלתאמן פי תנציף אי עדדא שית |
|---|---|
|
אעלם אן הד אלבאב נוע מן אנואע אלקסמה פמתי ארדת אן תאכוד נצף עדד פאקסמה עלי [אתנין] פמא כרג' מן אלקסמה פהו נצף אלעדד אלמקסום |
|
ומתאל דאלך אדא ארדת תצף ארבעה וסתין וסבע מאיה ותמאנית אלאף |
| פאנזל אלעדד פי סטר עלי מא תקדם תם תנזל אולא אלארבעה תם אלסתה תם אלסבעה תם אלתמאניה עלי הד אלצורה | |
| 8 7 6 4 2 |
| 8764 | 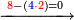 |
764 | 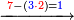 |
164 | 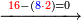 |
4 | 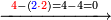 |
|
| 2 | 2 | 2 | 2 | |||||
| 4 | 43 | 438 | 4382 |
| תם תנזל אלאתנין תחת אלתמאניה אלתי הי אכר מנזלה תם אטלב עדדא תנזלה תחת אלאתנין תפני אלתמאניה פאסקטהא מן אלתמאניה אלתי עלי ראסהא תפני תם תנזל אלאתנין תחת אלסבעה ואטלב עדדא תצרבה פי אלאתנין תפני בה אלסבעה תגד אלתלאתה ויבקי ואחד פאתבתה פי מכאנה תם תנקל אלאתנין תחת אלסתה ומעהא ואחד מקדם פהמא אדאً תחת אלסתה עשר פאטלב עדדא תצרבה פי אלאתנין תפני בה אלסתת עשר תגד [תמאן] ותפני אלסתת עשר תם תנקל אלאתנין תחת אלארבעה ואטלב עדדא תצרבה פי אלאתנין תפני בה אלארבעה תגד אתנין פי אתנין בארבעה פקד כרג פי אלקסמה אתנין ותמאנון ותלת מאיה וארבעת אלאף והו נצף אלעדד אלמדכור | ||||||||||||||||||
|
ואעלם אן כל עדד יכון אולה פרדא פאן דאלך אלעדד ליס לה נצף צחיח אלא בכסר | |||||||||||||||||
|
ואעלם אנך מתי ארדת אן תאכוד תלת עדד פאקסמה עלי תלאתה | |||||||||||||||||
|
או רבעה פאקסמה עלי ארבעה | |||||||||||||||||
| ועלי הדא אלמתאל אלי עשרה | ||||||||||||||||||
Chapter Nine – Doubling |
אלבאב אלתאסע פי תצֹעיף אי עדד שית | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
אעלם אן הד אלבאב נוע מן אנואע אלג'מע והו גמע עדד אלי עדד אכר מתלה | |||||||||||||||||
|
מתאל דאלך אצֹעף ואחד ועשרין וארבע מאיה | |||||||||||||||||
| פאת'בתהא פי סטרٍ תם אתבת תחת דאלך אלסטר סטרא אכר מתלה תנזל כל גנס מע גנסה | ||||||||||||||||||
|
תם אבדא באלג'מע מן אלאחאד פאגמע אלואחד אלואחד יכון אתנין פאתבתהא עלי אלכט תם אגמע אלאתנין אלי אלאתנין תכון ארבעה תם אגמע אלארבעה אלי אלארבעה תכון תמאניה פיכון אלכארג עלי אלכט אתנין וארבעין ותמאן מאיה והו צֹעף אלואחד ועשרין וארבע מאיה | |||||||||||||||||
| תם אבדא תנזל אלואחד ועשרין וארבע מאיה תם מד כטא עלי הד אלצורה | ||||||||||||||||||
| 8 4 2 4 2 1 4 2 1 | ||||||||||||||||||
| אר[גע] אלי [...] | ||||||||||||||||||
Chapter Ten – Extracting Roots |
אלבאב אלעאשר פי אכד גדור אלאעדאד | |||||||||||||||||
| Square number - number that has a root | אעלם אן אלאעדאד אלמגדורה הי אלאעדאד אלמרבעה ואצֹלאעהא הי אלאגדאר | |||||||||||||||||
| ואעלם אן מראתב אלעדד מרתבה מנהא מגדורה ותא[ניה] ותאניה [גיר מגדורה] | ||||||||||||||||||
|
[...] מרתבת אלאחאד הי אול מרתבה מן מראתב אלאעדאד ואולהא אלואחד ולהא גדר ואחד | |||||||||||||||||
|
ואלמרתבה אלתאניה אלעשראת ואולהא עשרה וליס להא גדר | |||||||||||||||||
|
ואלמרתבה אלתאלתה אלמיון ואולהא אלמאיה ולהא גדר בעשרה | |||||||||||||||||
|
ואלמרתבה אלראבעה אלאלאף ואולהא אלאלף וליס להא גדר | |||||||||||||||||
|
ואלמרתבה אלכאמסה עשראת אלאלאף ולהא גדר וגדרהא מאיה | |||||||||||||||||
|
ועלי הד אלתרתיב מנזלה מגדורה ותאניה גיר מגדורה | |||||||||||||||||
written extraction of roots |
פאן ארדת אן תעלם כיף תאכוד גדר עדד מגדור | |||||||||||||||||
| description of the procedure | פאנזל דאלך אלעדד עלי מראתבה עלי מא תקדם תם אבדא מן אול מנזלה פלהא גדר ואלתאניה ליס להא גדר פאן כאן אכר מנזלה להא גדר פאבד[א] מנהא | |||||||||||||||||
|
ומתאל דאלך אדא ארדת אן תאכוד גדר כמסה ועשרין וסת מאיה | |||||||||||||||||
| תם אבדא מן אול מנזלה תג'ד לה ג'דרא ואלתאניה לא גִדר להא פאטלב עדדא תנזלה תחת אלסתה ותצֹרבה פי מתלה תפני בה אלסתה אלתי עלי ראסהא פתגד אתנין פאצרבהא פי מתלהא תכון ד' פאסקטהא מן אלסתה אלבאקי אתנין פאתבתהא פי מכאן אלסתה תם אצרב אל[אתנין] אלתי צֹרבת פי מתלהא תכון ארבעה קהקרהא אלי מא ילי אלימין ואנזלהא תחת אלאתנין תם אטלב עדדא תנזלה תחת אלכמסה תצרבה פי אלארבעה ותצֹרבה איצא פי מתלה פיפני בה גמיע דאלך אלעדד תגד כמסה פאצֹרבהא פי אלארבעה תכון עשרין פאסקטהא מן אלאתנין ואלעשרין אלבאקי אתנאן תם אצֹרב אל[כמס]ה פי נפסהא תכון כמסה ועשרין פאסקטהא מן אלכמסה ועשרין אלתי עלי ראסהא פתפני תם תנצף אלארבעה אלתי [.]צֹעפת תכון אתנין ואלכארג אד'אً כמסה ועשרין והו גדר אלעדד אלמטלוב | ||||||||||||||||||
| ||||||||||||||||||
|
פאן ארדת אן תאכוד גדר סתה ותסעין וסת מאיה ותלאתת אלאף | |||||||||||||||||
| 5 8 3 6 9 6 | ||||||||||||||||||
| תם עד אלמראתב תגדהא זוגא פמתי וגדתהא [זוגא פאתרך אכר מנזלה] לאנהא גיר מגדורה וארגע אלי אלתי תליהא אלי אלימין פא[ן כאן] עדד אלמרתאב פרדא פי אלמנזלה אלאכרה מגדורה פקד וגדת עדד הדא זוגא פאתרך אכר מנזלה ואנזל תחת אלתמאניה ואטלב עדדא תצֹרבה פי מתלה תפני בה תמאניה וכמסין תגד סבעה פאצֹרבהא פי מתלה תכון תסעה וארבעין פאסקטהא מן אלנ'ח' תמניה וכמסין אלבאקי תסעה תם אמחי אלתמניה וכמסין ואתבת אלתסעה מכאן אלתמניה תם אצעף אלסבעה תכון ארבעת עשר ותנקלהא מנזלה אלי מא ילי אלימין ודאלך אן תנזל אלארבעה תחת אלתמניה ואלואחד תחת אלתסעה | ||||||||||||||||||
| ||||||||||||||||||
| תם אטלב עדדא תנזלה תחת אלסתה פתצרבה פי אלואחד אלאכר פי אלארבעה ופי נפסהא ותסקט גמיע דאלך ממא עלי ראסה תגד סתה פאצרבהא פי אלואחד בסתה פאסקטהא מן אלתסעה אלבאקי תלאתה פאתבתהא פי מכאן אלתסעה תם אצרב אלסתה פי אלארבעה תכון ארבעה ועשרין [פאסקטהא מן אלתלאתה ותלאתין אלבאקי תסעה] [...] ארבעה תם אצרב אלסתה פי מתלהא [תכ]ון סתה ותלאתין פאסקטהא מן אלסתה ותסע[ין] אלתי עלי ראסהא אלבאקי סתון פאנזל צפרא עלי אלסתה ואלסתה עלי אלארבעה תם אצעף תכון אתני עשר פתנזל אלאתנין פי מוצע אלסתה ותקדם הד אלואחד אלדי הו עשרה מן אלאתני עשר אלי אלארבעה אלמתקדמה תכון כמסה תם קהקר גמיע דאלך מנזלה אלי מא ילי אלימין ודאלך אן תנזל אלאתנין תחת אלתסעה ואלכמסה תחת אלצפר ואלואחד תחת אלסתה | ||||||||||||||||||
| ||||||||||||||||||
| תם אטלב עדדא תנזלה תחת אלסתה אלתי הי אול מנזלה מן אלעדד אלמגדור פתצֹרבהא פי אלואחד אלאכר ופי אלכמסה ואלאתנין ופי נפסה פיפני בה גמיע מא יבקי מן אלעדד תגד ארבעה אצרבהא פי אלואחד בארבעה פאסקטהא מן אלסתה אלתי עלי ראסהא תבקי אתנין תם אצרב אלארבעה פי אתנין תכון תמאניה פאסקטהא מן אלתסעה אלתי עלי ראסהא יבקי ואחד פי מכאן אלתסעה תם אצֹרב אלארבעה פי נפסהא תכון סתת עשר פאסקטהא מן אלסת עשר אלתי עלי ראצהא תפני תם נצף גמיע מא אצעפת ודאלך אתנין ו[כמסון ומאה] [....] [ונצפהא] סתה וסבעין וארבעה [.....] פהו אדא ארבעה וסתין וסבע מאיה והו גדר אלעדד אלמ[......] | ||||||||||||||||||
| ||||||||||||||||||
|
[פאן ארדת אן תאכוד] גדר עדד יכון פי אולה צפרא פאעמ[ל] פי אלעדד עלי מא תקדם פי אכר אלגדור ואתבת אלאצפאר וכוד נצף עדדהא ונצף מא אצֹעפת ונצפה אלי אלאצפאר [יכון אלגדר] | |||||||||||||||||
|
ומתאל דאלך אדא ארדת אן תאכוד גדר עשרה אלאף | |||||||||||||||||
| פאנזל אלעשרת אלאף ארבעת אצפאר וואחד עלי מא תקדם פי צור אלגבאר והדה צורתהא | ||||||||||||||||||
| 1 0 0 0 0 | ||||||||||||||||||
|
|
תם עד אלמנאזל תגדהא פרדא פאבדא באכר מנזלה תם תקול אי עדד אצֹרבה פי מתלה ותסקט אלואחד פיפני תגד ואחד ומעה מן אלאצפאר ארבעה פכד נצפהא ודאלך אתנין פיכון אלגדר צפרין וואחדאﹰ | |||||||||||||||||
| ואד קד אתינא עלי מא קלנא מן הד אלאבואב אלעשרה פאנא נבדא אלאן בצֹרב אלכסור באלגבאר וקד בובת איצא אלכסור באתנין וסבעין באבא מכתצרה | ||||||||||||||||||
| כמל אללה אלחמד כתיראﹰ | ||||||||||||||||||
Multiplication of Fractions |
||||||||||||||||||
Chapter One: Forms of Fractions |
באב אלאול פי צור אלגבאר ואלכסור | |||||||||||||||||
| Simple fractions | אעלם אן אול אלכסור אלנצף ובעדה אלתלת ובעדה אלרבע ובעדה אלכמס ואלסדס ואלסבע ואלתמן ואלתסע ואלעשר פהדי אסמא בסאיט | |||||||||||||||||
|
|
פאדא ארדת אן תצוור אלגבאר נצפא פארסם אתנין ועליהא כטאً ועלי אלכט ואחד עלי הד אלצורה | |||||||||||||||||
|
|
ואלתלת תלאתה ועליהא ואחד עלי הדי אלצורה | |||||||||||||||||
|
|
ואן ארדת אלתלתין ג'עלת פי מכאן אלואחד אתנין פתכון תלתין | |||||||||||||||||
|
|
ואלרבע ואחד עלי ארבעה | |||||||||||||||||
|
|
ואלכמס ואחד עלי כמסה | |||||||||||||||||
|
|
וכדאלך אלי עשרה וואחד עלי עשרה | |||||||||||||||||
| ויכון בינהמא כטא עלי מא תקדם | ||||||||||||||||||
| ומן הד אלבסאיט איצ'א אלאגזא: | ||||||||||||||||||
|
|
גזאً מן אחדי עשר תנזל אחדי עשר ועליהא כטא ועלי אלכט ואחד | |||||||||||||||||
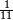
| ||||||||||||||||||
|
|
ואן כאן גזאין געלת מכאן אלואחד אתנין | |||||||||||||||||
|
|
ותסעת אגזא או עשרה יכון מכאן אלואחד עשרה פיכון עש[רה] אגזא מן אחדי עשר | |||||||||||||||||
| וכדאלך תפעל באלאגזא כלהא מתל תלאת עשר וסבעת עשר תנזל מקאם אלגז תם תמד עליה כטא ועלי אלכט עדד מא מעך מן אלאגזא | ||||||||||||||||||
| Fractions of fractions | תם תשתרך הד אלאסמא פיכון מנהא אסם מולף מן אתנין מתל נצף סדס פהו אלאסם מולף מן אלנצף ואלסדס פארסם מקאם אלסדס ומקאם אלנצף תחת כט ותכון אלסתה אולי ואלאתנין גזא ותנזל עלי אלאתנין ואחד כמא תרי | |||||||||||||||||
|
|
פהדא צורת נצף סדס | |||||||||||||||||
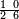
| ||||||||||||||||||
|
|
וכדאלך רבע אלסבע ארבעה וסבעה תחת אלכט עלי הד אלצורה | |||||||||||||||||
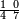
| ||||||||||||||||||
| פהד אלצורה הי כסר אלכסר | ||||||||||||||||||
| Fraction and fraction of fraction | פאן כאן מעך כסר וכסר כסר פאקסם אלמקאמין תחת אלכט וארסם עלי כל ואחד מנהא גזא מעלום | |||||||||||||||||
|
|
ומתאל דאלך לו קיל לך תלאתה אכמאס ותלת כמס | |||||||||||||||||
| פאנזל אלכמסה ואלתלאתה תחת כט וארסם עלי אלכט [...] תלאתה ועלי אלתלאתה ואחד עלי הד אלצורה | ||||||||||||||||||
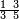
| ||||||||||||||||||
|
|
וכדאלך כמסה אסדאס ורבע סדס | |||||||||||||||||
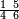
| ||||||||||||||||||
| אנזל אלארבעה עלי ואלסתה תחת כט וארסם עלי אלכט תלאתה ועלי אלסתה כמסה ועלי אלארבעה ואחד עלי הד אלצורה | ||||||||||||||||||
|
|
וכדאלך אשתראך אלאגזא מתל ארבעה מן תלאתת עשר ותלאתת אגזא מן אחדי עשר פי אלגז מן תלאתת עשר | |||||||||||||||||
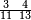
| ||||||||||||||||||
| פאנזל אלתלאתת עשר [ו]אלאחדי עשר תחת כט ועלי אלתלאתת עשר ארבעה ועלי אלאחדי עשר תלאתה פיכון ארבע אגזא מן תלאתת עשר ותלת אגזא מן אחדי עשר פי אלגז מן תלת עשר והדה צורתהא | ||||||||||||||||||
|
|
וכדאלך תשתרך פי תלאתת אסמא וארבע אסמא מתל תסעת אגזא מן אחדי עשר וסבעת אתסאע אלגז מן אחדי עשר וכמסת אסדאס תסע אלגז מן אחדי עשר ונצף סדס תסע אלגז מן אחדי עשר פמד כטא ואכתוב אלמקאם אלגז ובעדה מקאם אלתסע אלי מא ילי אליסאר ובעדה ובעדה מקאם אלתסע אלי מא ילי אליסאר ובעדה מקאם אלסדס ובעדה מקאם אלנצף תם אכתוב עלי כל ואחד מנהמא עדד אגזאיה ודאלך עלי אלאחדי עשר תסעה ועלי אלתסעה סבעה ועלי אלסתה כמסה ועלי אלאתנין ואחד עלי הד אלצורה | |||||||||||||||||
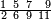
| ||||||||||||||||||
|
|
ומן הד אלכסור ארבעת אכמאס וכמסת אסדאס עשרת אגזא מן אחדי עשר כל ואחד מנהא מנסו[ב] אלי אלואחד פאנך תפרק אלכט בינהמא ולא יכון מתצלא עלי הד אלצורה | |||||||||||||||||
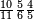
| ||||||||||||||||||
| ומן הד אלכסור [מא הו] מנסוב פי אללפט' מחדו[ד] אלואו והו אכד אלכסר מן אלכסר | ||||||||||||||||||
|
|
ומתאל דאלך תלאתת ארבאע ארבעת אכמאס כמסת אסדאס פצורת הד אלמתל צורת אלמתנאסבה באלואו ומד כטא" וארסם תחתה ארבעה תם אלכמסה תם אלסתה וארסם עלי כל ואחד מנהא עדד אלאגזא אלמדכורה וכדאלך עלי אלארבעה תלאתה ועלי כמסה ארבעה ועלי אלסתה כמסה והדה צורתהא | |||||||||||||||||
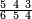
| ||||||||||||||||||
| ומ[ד] [ויכו....] פי הדא אכבר אמאם אלי מא ילי אליסאר וקד יאתי מן הד אלכסור מכתלף ומתנאסב | ||||||||||||||||||
|
|
מתל תלאתת ארבאע וארבעת אכמאס וכמסת אסדאס ונצף סדס ואנזל אלמכתלף כל ואחד מנהא תחת כט ואנזל אלמתנאסב תחת כט ואחד עלי מא תקדם והדה צורתהא | |||||||||||||||||
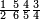
| ||||||||||||||||||
| ומנהא מא הו כסר אלכסר מנסוב אלי גיר ואחד מן אלכסור אלמכתלפה | ||||||||||||||||||
|
|
מתל תלאתת ארבאע וכמסת אסדאס ורבע תמן | |||||||||||||||||
| תחת כטא בדאתה והדה צורתהא | ||||||||||||||||||
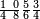
| ||||||||||||||||||
| עלי הד אלעמל קיאס מא יריד בעד הדא אן שא אללה תעלי | ||||||||||||||||||
Chapter Two: Multiplication of Fraction by Integer |
אלבאב אלתאני פי צרב אלכסר פי אלעדד אלצחיח | |||||||||||||||||
|
|
אדא קיל לך אצֹרב כמסה אסדאס פי עשרה | |||||||||||||||||
| פאנזל אלכמסתת אסדאס פי סטרא ואנזל תחתה פי סטרٍ אכר אלעשרה עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
|
|
תם אבדי באלסטר אלאעלי וכד אלכמסה אלתי עלי אלסתה ואצֹרבהא פי אלעשרה יכון גמיע דאלך כמסין פאקסמהא עלי אלסתה אלתי הי אלאמאם והי איצ'א תחת כטٍ יכרג' לך תמאניה וסדסאן והדה צורתהא | |||||||||||||||||
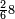
| ||||||||||||||||||
|
פאן ארדת אמתחאנהא פאטרח אלעשרה בטרח סבעה תבקי מנהא תלאתה פאצֹרבהא פי אלכמסה אלתי צרבת פיהא אלעשרה תכון כמסת עשר פאטרחהא סבעה אלבאקי ואחד | |||||||||||||||||
|
|
פאצרבה פי אלסתה אלתי הי אלאמאם ואגמל מא עלי ראצהא ודאלך אתנאן יכון דאלך תמאניה פאטרח מנהא סבעה אלבאקי ואחד והו מואפק ללגואב אלמרפוע | |||||||||||||||||
Chapter Three: Multiplication of Fraction and Fraction of Fraction by Integer |
אלבאב אלתאלת פי צֹרב אלכסר וכסר אלכסר פי אלעדד אלצחיח | |||||||||||||||||
|
|
אדא קיל לך אצֹרב כמסא" ונצף כמס פי אתני עשר | |||||||||||||||||
| פאנזל אלכמס ונצף כמס פי סטרא ואנזל אתני עשר פי סטרא תחתה עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
|
|
תם אבדא באלסטר אלאעלי פאצרב אלואחד אלדי עלי אלכמסה פי אלאתנין אלתי תחת אלכט ותג'מע אלי דאלך אלואחד אלדי עלי אלאתנין יכון דאלך תלאתה פאצֹרבהא פי אלאתני עשר תכון סתה ותלאתין פאקסמהא עלי אלאימא אלתי הי אתנין וכמסה יכרג לך אלמטלוב ודאלך תלאתה ותלאתת אכמאס והדה צורתהא | |||||||||||||||||
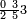
| ||||||||||||||||||
|
ואמתחאן הד אלמסאלה כמא תקדם פי עמלהא ודאלך אן תצֹרב אלואחד פי אלאתנין ותגמל מא עלי ראסהא עלי מא תקדם פי אלעמל יכון דאלך תלאתה תם אטרח מן אלאתני עשר סבעה אלבאקי כמסה פאצֹרבהא פי אלתלאתה אלתי בקית מן אלכט אלאעלי תכון כמסת עשר אטרחהא סבעה אלבאקי מנהא ואחד | |||||||||||||||||
|
|
תם ארג'ע אלי אלכארג פי אלגואב והו תלאתה פאצֹרבהא פי אלכמסה אלתי הי אלאמאם תכון כמסת עשר פיבקי מנהא בעד אלטרח ואחדאﹰ פאגמעה מע אלתלאתה אלתי עלי אלכמסה תכון ארבעה פאצֹרבהא פי אלאתנין אלדין המא אלאמאם אלתאני תכון תמאניה יבקי מנהא ואחד והו מואפק ללגואב | |||||||||||||||||
Chapter Four: Multiplication of Fraction of Fraction by Integer |
אלבאב אלראבע פי צֹרב כסר אלכסר פי אלעדד אלצחיח | |||||||||||||||||
|
|
אדא קיל לך אצֹרב תלת סבע פי כמסה ועשרין | |||||||||||||||||
| פאנזל אלתלת סבע פי סטר ואלכמסה ועשרין פי סטר[.] תחתה עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
|
|
תם אצֹרב אלואחד אלדי עלי [אלתלאתה] פי אלכמסה ועשרין פאקסמהא עלי אלאמאם [יכרג'] לך אלמטלוב ודאלך ואחד וסבע ותלת סבע כמא תבין | |||||||||||||||||
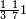
| ||||||||||||||||||
|
ואמתחאן הד אלמסאלה עלי מא תקדם פי עמלהא ודאלך אן תטרח אלכמסה ועשרין תבקי ארבעה פאצֹרבהא פי אלואחד אלדי עלי אלאמאם תכון ארבעה והו אלגואב בארבעה | |||||||||||||||||
|
|
תם ארגע אלי אלכארג והו ואחד פאצֹרבה פי אלסבע יכון טרחא ועלי אסמה ואחד פאצֹרבה פי אלתלאתה ואגמל מא עלי ראסהא תכון ארבעה והו אלמואפק ללג'וא[ב] | |||||||||||||||||
Chapter Five: Multiplication of Two Different Fractions by Integer |
אלבאב אלכאמס פי צֹרב אלכסרין אלמכתלפין פי אלעדד אלצחיח | |||||||||||||||||
|
|
אדא קיל לך אצרב תלאתה ארבאע וארבע אכמאס פי כמסת עשר | |||||||||||||||||
| פאנזל אלתלאתת ארבע ואלארבעת אכמאס פי סטראً ואנזל תחתה אלכמסה עשר עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
|
|
תם אבדא באלסטר אלאול פתצֹרב מא עלי אלארבעה פי אלאמאם אלדי הו אלכמסה ומא עלי אלכמסה פי אלאמאם אלדי הו ארבעה ותגמע אלארבעה אלצֹרבין פיכון דאלך ואחד ותלאתין פאצֹרבהא פי אלכמסת עשר יכון דאלך כמסה וסתין וארבע מאיה פאקסמהא עלי אלאמאם יכרג לך תלאתה ועשרין וכמס ורבע אלכמס עלי הד אלצורה | |||||||||||||||||
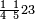
| ||||||||||||||||||
|
ואמתחאן הד אלמסאלה עלי מא תקדם פי צֹרבהא ודאלך אן תצֹרב אלתלאתה אלתי עלי אלארבעה פי אלכמסה אלתי תחת אלכט תכון כמסת עשר יבקי מנהא [ואחד תם אלד' אלתי עלי אלה' פי אלד' אלתי הו אלאמאם יכון י"ו יבקי מנהא] אתנאן פאצ'[רב]הא אלי אלואחד אלואחד אלמרפוע יכון דאלך תלאתה פאצֹרבהא פי אלואחד אלבאקי מן אלכמסת עשר יכון דאלך תלאתה והו אלג'ואב | |||||||||||||||||
|
|
תם ארג'ע אלי אלכארג' והו תלאתה ועשרין יבקי מנהא אתנאן פאצֹרבהא פי אלכמסה אלתי הי אלאמאם תכון עשרה יבקי מנהא תלאתה אגמל עליהא אלואחד אלדי עלי אלכמסה תכון ארבעה פאצֹרבהא פי אלארבעה אלתי הי אלאמאם תכון סתת עשר אלבאקי מנהא אתנא" ועלי ראסהא ואחד תכון תלאתה והי מואפקה ללג'ואב | |||||||||||||||||
Chapter Six: Multiplication of Fraction by Integer and Fraction |
אלבאב אלסאדס פי צרב אלכסר פי אלצחיח ואלכסר | |||||||||||||||||
|
|
אדא קיל לך אצֹרב תלאתת אכמאס פי תסעה ותלת | |||||||||||||||||
| פאנזל אלתלאתת אלאכמאס פי סטרא ואלתסעה ואלתלת פי סטר אכר תחתה עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
|
|
תם אצֹרב אלתסעה פי אלתלאתה ואגמל מא עלי ראצהא תכון תמאניה ועשרין פאצֹרבהא פי אלתלאתה אלתי עלי ראס אלכמסה תכון ארבעה ותמאנין פאקסמהא עלי אלאימה אלתי תחת אלכטוט יכרג לך אלמטלוב ודאלך כמסה ותלאתה אכמאס והדה צורתהא | |||||||||||||||||
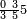
| ||||||||||||||||||
|
פאדא ארדת אלאמתחאן פאטרח אלתסעה יבקי מנהא אתנאן פאצרבהא פי אלתלאתה אלתי הי אל[אמאם] ואגמל מא עלי ראסהא תכון סבעה והו טרח פאצֹרבהא פי אלתלאת[ה] אלתי עלי אלכמסה תכון איצֹא טרחא וגואבהא טרח | |||||||||||||||||
|
|
תם ארגע אלי אלכארג' מן אלצֹרב והו כמסה ותלאתה אכמאס פאצֹרב אלכמסה אלצחאח פי אלכמסה אלתי הי אלאמאם תכון כמסה ועשרין אלבאקי ארבעה ועלי ראסהא תלאתה תכון סבעה והי מנטרחה פאצֹרבהא פי מקאם אלתלת יכון איצא טרחא וג'ואבהא בטרח פקד צחת אלמסאלה ואעלם אן צנאעה אלעמל פי כל מסאלה מתל צנאעה אלטרח | |||||||||||||||||
Chapter Seven: Multiplication of Fraction and Fraction of Fraction by Integer and Fraction |
אלבאב אלסאבע פי צרב אלכסר וכסר אלכסר פי אלצחיח ואלכסר | |||||||||||||||||
|
|
אדא קיל לך אצֹרב כמסת אסדאס ונצף סדס פי סתה ותלאתת אכמאס | |||||||||||||||||
| פאנזל אלכמסת אסדאס ונצף סדס פי סטרٍ ואלסתה ואלתלאתת אכמאס פי סטר ואחד תחתה עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
|
|
תם אבדא באלסטר אלאעלי פאצרב אלכמסה ואלאתנין ואגמל מא עלי ראסהא תכון אחדי עשר פארפעהא תם ארגע אלי אלכט אלאספל פאצֹרב אלסתה פי אלכמסה ואגמל מא עלי ראסהא תכון תלאתה ותלאתין פאצֹרבהא פי אלאחדי עשר אלמרפועה תכון תלאתה וסתין ותלת מאיה פאקסמהא עלי אלאימה יכרג' לך אלמטלוב ודאלך סתה וכמס סדס ונצף כמס סדס והדה צורתהא | |||||||||||||||||
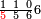
| ||||||||||||||||||
|
ואלאמתחאן פי הד אלמסאלה עלי מא תקדם [פי] צֹרבהא יבקי מן אלכט אלאעלי ארבעה ומן אלכט [אל]אספל כמסה תם אצֹרב אלארבעה אלתי בקית מן אלכט אלאספל פי אלכמסה תכון עשרין יבקי מנהא סתה והו אלגואב | |||||||||||||||||
|
|
תם ארגע אלי אלכארג והו סתה וכמס סדס ונצף כמס סדס פאצֹרבהא פי מקאם אלסדס תכון סתה ותלאתין אלבאקי מנהא ואחד פאצֹרבה פי אלכמסה ואג'מל מא עלי ראצהא תכון סתה פאצרבהא פי אתנין ואג'מל מא ראסהא תכון תלאתת עשר אלבאקי מנהא סתה מתל אלג'ואב | |||||||||||||||||
Chapter Eight: Multiplication of Fraction of Fraction by Integer and Fraction |
אלבאב אלתאמן פי צֹרב כסר אלכסר פי אלצחיח ואלכסר | |||||||||||||||||
|
|
אדא קיל לך אצֹרב תלת סבע פי עשרה ותלאתת אכמאס | |||||||||||||||||
| פאנזל אלתלת סבע פי סטרٍ ואלעשרה ותלאתת אכמאס פי סטרٍ אכר תחתה עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| תם אבדא באלסטר אלאספל פתצֹרב אלעשרה פי אלכמסה ואגמל מא עלי ראסהא תכון תלאתה וכמסין פתצֹרבהא פי אלואחד אלדי הו תלת סבע יכון תלאתה וכמסין פתקסמהא עלי אלאימה יכרג לך אלמטלוב ודאלך תלאתת אסבאע וכמסא סבע ותלתא סבע כמס עלי הד אלצורה | ||||||||||||||||||
|
| ||||||||||||||||||
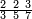
| ||||||||||||||||||
| ואמתחאן הד אלמסאלה עלי מא תקדם ואלגואב פיהא בארבעה טרח סבעה | ||||||||||||||||||
Chapter Nine: Multiplication of Two Different Fractions by Integer and Fraction |
אלבאב אלתאסע פי צֹרב אלכסרין אלמכתלפין פי אלצחיח ואלכסר | |||||||||||||||||
|
|
אדא קיל לך אצרב תלאתת ארבאע וארבע אכמאס פי כמסה וכמסת אסדאס | |||||||||||||||||
| פאנזל אלתלאתה אלארבאע ואלארבעת אלאכמאס פי סטרٍ עלי מא תקדם פי אלבאב אלאול פי צור אלכסור אלמכתלפה תם אנזל פי סטרٍ תחתה אלכמס ואלכמסת אסדאס עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| תם אבדא באלסטר אלאעלי פאצֹרב מא עלי אלארבעה פי אלכמסה ומא עלי אלכמסה פי אלארבעה ותג'מע אלצֹרבין יכון דאלך ואחדא ותלאתין פארפעהא תם ארג'ע אלי אלסטר אלא[ספ]ל פאצֹרב אלכמסה פי אלסתה ואג'מל מא עלי ראסהא יכון כמסה ותלאתין פאצֹרבהא פי אלואחד ואלתלאתין יכון דאלך כמסה ותמאנין ואלפא פאקסמהא עלי אלאימה יכרג לך אלמטלוב ודאלך תסעה וכמס[.] סדס ורבע כמס סדס והדה צורתהא | ||||||||||||||||||
|
| ||||||||||||||||||
| [added in the margin in Arabic digits] | 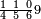
| |||||||||||||||||
| ואמתחאן הד אלמסאלה עלי צפת צֹרבהא ואלגואב פיהא בטרח וגמיע אלאמתחאן אנמא אקתצרת פיה עלי טרח סבעה | ||||||||||||||||||
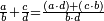
|
ואעלם אן אלכסרין אל מכתלפין חית מא אתאך מנהא שי פאנמא תאכוד מא עלי אלסטר אלאול ותצֹרבה פימא תחת אלכט אלתאני ותאכוד מא עלי אלכט אלתאני ותצרבה פי מא תחת אלכט אלאעלי ותג'מע אלצֹרבין ואלכסור אלמתנאסבה תאכוד מא עלי אכבר אמאם ותצֹרבה פי אלאמאם אלדי נסב אליה ותגמל מא עלי ראסה | |||||||||||||||||
Chapter Ten: Multiplication of Fraction by Integer and Fraction and Fraction of Fraction |
אלבאב אלעאשר פי צֹרב אלכסר פי אלצחיח ואלכס' וכס' אלכס' | |||||||||||||||||
|
|
אדא קיל לך אצרב תלאתה ארבאע פי כמסה וסבע אתמאן וסדס תמן | |||||||||||||||||
| פאנזל אלתלאתה ארבאע סטרٍ ואלכמסה וסבעת אתמאן וסדס תמן פי סטרא תחתה עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| תם אבדא באלסטר אלאספל ואצֹרב אלכמסה פי אלתמניה ואגמל מא עלי ראסהא יכון דאלך סבעה וארבעין ואצֹרבהא פי אלסתה ואגמל מא עלי ראסהא [ואצרבהא פי אלתלאתה אלתי עלי סטר אלעאלי] יכון דאלך תסעה וארבעין ותמאן מאיה פאקסמהא עלי אלאימה יכרג' לך אלמטלוב ודאלך ארבעה ותלאתת אתמאן וסדסא תמן ורבע סדס תמן והדה צורתהא | ||||||||||||||||||
|
| ||||||||||||||||||
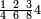
| ||||||||||||||||||
| ואמא אלאמתחאן פעלי צפת אלעמל ואלג'ואב פיהא באתנין פאפהם | ||||||||||||||||||
![\scriptstyle n+\frac{a_1}{b_1}+\left(\frac{a_2}{b_2}\sdot\frac{1}{b_1}\right)=\frac{\left[\left[\left(n\sdot b_1\right)+a_1\right]\sdot b_2\right]+a_2}{b_1\sdot b_2}](/mediawiki/images/math/c/9/d/c9db4fa0c85cc5f4c8ed8387974743ac.png)
|
ואעלם אנך מתי אתאך צחיח וכסר פאנמא אלעמל פיה אן תצֹרב אלצחיח פי אלכסר ותגמל מא עלי ראסה ומא אגתמע צֹרבתה פי מקאם אלכסר אלתאני וגמלת מא עלי ראסה | |||||||||||||||||
Chapter Eleven: Multiplication of Fraction by Integer and Fraction of Fraction |
אלבאב אלחאדי עשר פי צרב אלכס' פי אלצחיח וכסר אלכסר | |||||||||||||||||
|
|
אדא קיל לך אצֹרב כמסת אסדאס פי תמאניה וכמסת אסבאע תסע | |||||||||||||||||
| פאנזל אלכמסת אסדאס פי סטרٍ ואלתמאניה ואלכמסת אסבאע תסע פי סטרٍ תחתה עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
|
|
תם אבדא באלסטר אלאספל פאצֹרב אלתמאניה פי אלתסעה ומא אגתמע פי סבעה ותגמל מא עלי ראסהא יכון דאלך תסעה וכמס מאיה פאצֹרבהא פי אלכמסה אלתי עלי ראס אלסתה יגתמע לך כמסה וארבעין וכמס מאיה ואלפאן פאקסמהא עלי אלאימה יכרג לך אלמטלוב ודאלך סתה וסתת אתסאע וארבע אסבאע אלתסע וסדס סבע אלתסע והדה צורתה | |||||||||||||||||
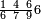
| ||||||||||||||||||
| ואלאמתחאן פיהא עלי צפת אלעמל ואלגואב פיהא בארבעה | ||||||||||||||||||
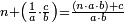
|
ואעלם אנה מתי אתאך צחיח וכסר כסר פאצֹרב אלצחיח אולא פי אלכסר אלאול ומא אג'תמע פי אלכסר אלתאני ותגמל מא עלי [ראסהא] | |||||||||||||||||
Chapter Twelve: missing |
||||||||||||||||||
Chapter Thirteen: Multiplication of Fraction and Fraction of Fraction by Integer and Fraction and Fraction of Fraction |
אלבאב אלתלאת עשר פי צֹרב אלכסר וכס' אלכס' פי אלצחיח ואלכס' וכס' אלכס' | |||||||||||||||||
|
|
מתאל דאלך אצֹרב כמסת אסדאס ונצף סדס פי תמאניה וכמסת אסבאע וכמס סבע | |||||||||||||||||
| פאנזל אלכמסת אסדאס ונצף סטרٍ תם אנזל תחתה אלתמאניה וכמסת אסבאע וכמס סבע פי סטרٍ עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| תם אבדי באלסטר אלאעלי פתצֹרב אלכמסה פי אלאתנין ואגמל מא עלי ראסהא יכון דאלך אחדי עשר תם ארגע אלי אלכט אלאספל פאצֹרב אלתמאניה פי אלסבעה ואגמל מא עלי ראסהא ואצֹרב אלמגתמע פי אלכמסה ואגמל מא עלי ראסהא יכון דאלך סתה ותלת מאיה פאצֹרבהא פי אלאחדי עשר אלמחפוטֹה אלתי כרגת מן אלסטר אלאול יכון דאלך סתה וסתין ותלאת מאיה ותלת אלאף פאקסמהא עלי אלאימה יכרג לך אלמטלוב ודאלך תמאניה ותלאתת אכמאס סדס סבע | ||||||||||||||||||
|
| ||||||||||||||||||
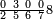
| ||||||||||||||||||
| וגואב הד אלמסאלה פי אלאמתחאן בסתה | ||||||||||||||||||
| ואעלם אנך אד וצלת פי אלאמתחאן פי כארג אלמסאלה אלי אן תצֹרב פי אלכמסה ותגמל מא עלי ראסהא פאלמגתמע אצֹרבה פי אלאתנין אלדין ליס עלי [ר]אסהא שי ואטרח מא מעך פאן ואפק פקד אצבת ואן [כאלף] ואכטית | ||||||||||||||||||
Chapter Fourteen: Multiplication of Fraction and Fraction of Fraction by Integer and Fraction of Fraction |
אלבאב אלראבע עשר פי צרב אלכס' וכס' אלכס' פי אלצחיח וכס' אלכס' | |||||||||||||||||
|
|
ומתאל דאלך אצֹרב כמסת אסדאס ונצף סדס פי תסעה וסדס סבע | |||||||||||||||||
| פאנזל אלכמסת אסדאס ונצף סדס פי סטרٍ ואלתסעה וסדס סבע פי סטרٍ תחתה עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| תם אעמל פי אלכמסה אסדאס ונצף סדס עלי מא תקדם יכון אלמג'תמע אחדי עשר פארפעהא תם ארגע ואעמל פי אלתסעה וסדס סבע עלי מא תקדם איצ'א יגתמע לך תסעה וסבעין ותלת מאיה פאצֹרבהא פי אלאחדי עשר יגתמע לך מן דאלך תסעה וסתין ומאיה וארבעה אלאף פאקסמהא עלי אלאימה יכרג לך אלמטלוב ודאלך תמאניה וסבע וכמסת אסדאס אלסבע וסדסא סדס אלסבע ונצף סדס סדס אלסבע פהדה צורתהא | ||||||||||||||||||
|
| ||||||||||||||||||
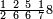
| ||||||||||||||||||
| ואלגואב פיהא באלאמתחן בארבעה | ||||||||||||||||||
Chapter Fifteen: Multiplication of Fraction and Fraction of Fraction by Integer and Two Different Fractions |
אלבאב אלכאמס עשר פי צרב אלכס' וכס' אלכס' פי אלצחיח ואלכסרין אלמכתלפין | |||||||||||||||||
|
|
ומתאל דאלך אצרב כמסת אסדאס ונצף סדס פי תמאניה ותסעת אעשאר ועשרת אעשאר אגזא מן אחדי עשר | |||||||||||||||||
| פאנזל אלכמסת אסדאס ונצף סדס פי סטר ואלתמאניה ואלתסעת אעשאר ואלעשרת אגזא מן אחדי עשר פי סטרא תחתה עלי הד אלצורה | ||||||||||||||||||
| [added in the margin, in Arabic digits] |
| |||||||||||||||||
| תם אעמל פי אלסטר אלאעלי עלי מא תקדם יכרג לך אחדי עשר תם ארג'ע אלסטר אלאספל פאצֹרב אלתמאניה פי אלעשרה ומא אג'תמע פי אלאחדי עשר יגתמע לך תמאנון ותמן מאיה פארפעהא תם אצרב אלתסעה פי אלאחדי עשר ואלעשרה פי אלעשרה יכון דאלך תסעה ותסעון ומאיה פאגמעהא אלי אלתמאניה ואלתמאן מאיה יכון דאלך | ||||||||||||||||||
|
| ||||||||||||||||||
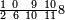
| ||||||||||||||||||
| ואלגואב פיהא בארבעה | ||||||||||||||||||
Chapter Sixteen: Multiplication of Fraction of Fraction by Integer and Fraction and Fraction of Fraction |
אלבאב אלסאדס עשר פי צרב כסר אלכסר פי אלצחיח ואלכסר וכסר אלכסר | |||||||||||||||||
|
|
מתאל דאלך אצֹרב תלתיי סבע פי סתה ותסעת אעשאר וארבע אכמאס אלעשר | |||||||||||||||||
| פאנזל אלתלתיי סבע פי סטרٍ ואנזל אלסתה ותסעת אעשאר וארבע אכמאס פי סטרٍ תחתה עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| תם אבדא באלסטר אלתאני פתצֹרב אלסתה פי אלעשרה ותגמל מא עלי ראסהא יכון דאלך תסעה וסתין תם אצרב אלתסעה וסתין פי אלכמסה אלתי תחת אלארבעה ואגמל מא עלי ראסהא יכון דאלך תסעה וארבעין ותלאת מאיה פאצֹרבהא פי אלאתנין אלדין עלי אלכט אלאעלי יכון דאלך תמאניה ותסעין וסת מאיה פאקסמהא עלי אלאימה יכרג לך אלמטלוב ודאלך סתה אעשאר וארבע אסבאע אלעשר וכמסא סבע אלעשר ותלתא כמס סבע אלעשר והדה צורתהא | ||||||||||||||||||
|
| ||||||||||||||||||
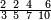
| ||||||||||||||||||
| ואלאמתחאן עלי מא תקדם ואלגואב בכמסה | ||||||||||||||||||
Chapter Seventeen: Multiplication of Fraction of Fraction by Integer and Fraction of Fraction |
אלבאב אלסאבע עשר פי צֹרב כסר אלכסר פי אלצחיח וכסר אלכסר | |||||||||||||||||
|
|
ומתאל דאלך אצֹרב תלאתת ארבאע אלתסע פי תמאניה וכמסת אסדאס אלסבע | |||||||||||||||||
| פאנזל אלתלאתה ארבאע אלתסע פי סטר ואנזל אלתמאניה וכמסת אסדאס אלסבע פי סטר תחתה עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| תם אבדא באלסטר אלאספל פתצרב אלתמאניה פי אלסבעה ומא אגתמע פי אלסתה ותגמל מא עלי ראסהא יכון דאלך ואחד וארבעין ותלת מאיה פאצֹרבהא פי אלתלאתה אלתי עלי אלכט אלאעלי יכון דאלך תלאתה ועשרין ואלפא פאקסמהא עלי אלאימה יכרג' לך אלמטלוב ודאלך סתת אתסאע ותלאתת אסדאס סבע אלתסע ותלאתת ארבאע סדס סבע אלתסע והדה צורתהא | ||||||||||||||||||
|
| ||||||||||||||||||
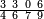
| ||||||||||||||||||
| וגואבהא בואחד | ||||||||||||||||||
Chapter Eighteen: Multiplication of Fraction of Fraction by Integer and Two Different Fractions |
אלבאב אלתאמן עשר פי צֹרב כסר אלכסר פי אלצחיח ואלכסרין אלמכתלפין | |||||||||||||||||
|
|
אדא קיל לך אצרב כמסת אסדאס אלתמן [פי סתה ותלאתת ארבאע וארבעת אכמאס] | |||||||||||||||||
| [פאנזל אלכמסה אסדאס אלתמן] פי סטר ואנזל אלעדד אלתאני פי סטרא תאני תחתה כמא תרי | ||||||||||||||||||
| ||||||||||||||||||
|
|
תם אבדא באלסטר אלאספל פתצֹרב אלסתה פי אלארבעה ומא אגתמע פי אלכמסה יכון דאלך מאיה ועשרין פארפעהא תם אצֹרב מא עלי אלארבעה פי אלכמסה ומא עלי אלכמסה פי אלארבעה ותגמע אלצרבין יכון דאלך ואחד וכמסין ומאיה | |||||||||||||||||
|
|
פאצרבהא פי אלכמסה אלתי עלי אלכט אלאעלי יכון דאלך כמסה וכמסין וסבע מאיה | |||||||||||||||||
| פאקסמהא עלי אלאימה יכרג' לך אלמטלוב ודאלך סתת אתמאן וסדס תמן ותלאתת אכמאס סדס אלתמן ותלאתת ארבאע כמס סדס אלתמן הכדא צורתהא | ||||||||||||||||||
|
| ||||||||||||||||||
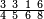
| ||||||||||||||||||
| ואלג'ואב פיהא בסתה באלאמתחאן | ||||||||||||||||||
Chapter Nineteen: Multiplication of Two Different Fractions by Integer and Fraction and Fraction of Fraction |
אלבאב אלתאסע עשר פי צֹרב אלכסרין אלמכתלפין פי אלצחיח ואלכסר וכסר אלכסר | |||||||||||||||||
|
|
ואדא קיל לך אצרב תלאתת ארבאע וארבעת אכמאס פי סתה וסבע אתמאן וסדס תמן | |||||||||||||||||
| פאנזל אל תלאתת ארבאע וארבעת אכמאס פי סטר [זאיד חתי לאכר אלדפה] עלי מא תקדם פי אלבאב אלאול פי צור אלכסור אלמכתלפה תם אבדא אנזל פי סטרٍ תחתה אלכמסה ואלכמסת אסדאס עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| תם אבדא באלסטר אלאעלי פאצֹרב מא עלי אלארבעה פי אלכמסה ומא עלי אלכמסה פי אלארבעה ותגמע אלצרבין יכון דאלך ואחד ותלאתין פארפעהא תם ארגע אלי אלסטר אלאספל פאצרב אלכמסה פי אלסתה ואגמל מא עלי ראצהא יכון כמסה ותלאתין פאצֹרבהא פי אלואחד ואלתלאתין יכון דאלך כמסה ותמאנין ואלפא" פאקסמהא עלי אלאימה יכרג' לך אלמטלוב ודאלך וכמס סדס ורבע | ||||||||||||||||||
|
| ||||||||||||||||||
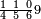
| ||||||||||||||||||
| ואמתחאן הד אלמסאלה עלי צפה צֹרבהא ואלגואב פיהא בטרח | ||||||||||||||||||
|
|
וגמיע אלאמתחאן אנמא אקתצרת פיה עלי טרח סבעה ואעלם אן אלכסרין אלמכתלפין חית מא אתאך מנהא שי פאנמא תאכוד מא עלי אלסטר אלאול ותצֹרבה פי מא תחת אלכט אלתאני ותאכוד מא עלי אלכט אלתאני ותצֹרבה פי מא תחת אלכט אלאול ותגמע אלצֹרבין ואלכסור אלמתנאסבה תאכוד פי סטרין ואנזל אלסתה וסבעה אתמאן וסדס אלתמן פי סטר תחתה עלי הד אלצורה | |||||||||||||||||
| ||||||||||||||||||
| תם אבדא באלסטר אלאעלי פאצֹרב עלי מא תקדם פי דאלך ואחד אלכסרין אלמכתלפין יגתמע לך ואחד ותלאתין פארפעהא תם ארגע אלי אלסטר אלאספל פאעמל פיה עלי מא תקדם פי אלצחיח ואלכסור אלמתנאסבה יגתמע לך מן דאלך ואחד | ||||||||||||||||||
|
| ||||||||||||||||||
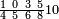
| ||||||||||||||||||
| ואלגואב פיהא בסתה | ||||||||||||||||||
Chapter Twenty: Multiplication of Two Different Fractions by Integer and Fraction of Fraction |
אלבאב אלמופי עשרין פי צרב אלכסרין אלמכתלפין פי אלצחיח וכסר אלכסר | |||||||||||||||||
|
|
אדא קיל לך אצֹרב תלאתה ארבאע וארבעת אכמאס פי סתה וסבע תמן | |||||||||||||||||
| פאנזל אלתלאתה ארבאע וארבעת אכמאס פי סטרין ואנזל תחתהא אלסתה וסבע תמן פי סטר עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| תם אבדא באלסטר אלאעלי פאצנע בה כמא צנעת באלכסרין אלמכתלפין יגתמע לך פיה ואחד ותלאתין פארפעהא תם ארגע אלי אלסטר אלאספל פאצנע בה כמא צנעת פי אלצחיח וכסר אלכסר יגתמע לך מנה סבעה וארבעין וארבע מאיה ועשרת אלאף פאקסמהא עלי אלאימה יכרג' לך אלמטלוב והו תסעת ותמנאן וארבעת אסבאע אלתמן וכמס סבע אלתמן ותלאתת ארבאע כמס סבע אלתמן כמא תרי | ||||||||||||||||||
|
| ||||||||||||||||||
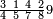
| ||||||||||||||||||
| ואלגואב פיהא בתלאתה | ||||||||||||||||||
Chapter Twenty One: Multiplication of Two Different Fractions by Integer and Two Different Fractions |
אלבאב אלחאדי ואלעשרין פי צֹרב אלכסרין אלמכתלפין פי אלצחיח ואלכסרין אלמכתלפין | |||||||||||||||||
|
|
אד'א קיל לך אצֹרב נצפא ותלתין פי כמסה וסתה אסבאע ותמאנית אתסאע | |||||||||||||||||
| פאנזל אלנצף ואלתלתין פי סטרין ואנזל תחתהא אלכמסה וסתת אסבאע ותמאנית אתסאע פי סטרין איצא עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| תם אבדא באלסטר אלאעלי ואצנע בה כמא תצנע באלכסרין אלמכתלפין יגתמע לך פיה פארפעהא תם ארגע אלי אלסטר אלאספל פאצנע בה כמא תצנע באלצחיח ואלכסרין אלמכתלפין יגתמע לך פיה כמסה ועשרין וארבע מאיה פאצרבהא פי אלסבעה אלמרפועה יגתמע לך מן דאלך כמסה וסבעון ותסע מאיה ואלפאן פאקסמהא עלי אלאימה ודאלך אן תצֹרב מקאם אלנצף פי מקאם אלתלת יכון סתה וסבעה ותסעה פאקסם עליהא אלעדד אלמדכור יכרג לך אלמטלוב ודאלך סבעה וסבעת אתסאע וכמסת אסבאע אלתסע וכמסת אסדאס סבע אלתסע כמא תרי | ||||||||||||||||||
|
| ||||||||||||||||||
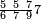
| ||||||||||||||||||
| והד אלמסאלה מטרוחה עלי אלאמתחאן | ||||||||||||||||||
Chapter Twenty Two: Multiplication of Integer and Fraction by Integer and Fraction |
אלבאב אלתאני ואלעשרין פי צֹרב אלצחיח ואלכסר פי אלצחיח ואלכסר | |||||||||||||||||
|
|
אדא קיל לך אצרב תלאתה וכמס פי סבעה ותלאתת אתמאן | |||||||||||||||||
| פאנזל אלתלאתה וכמסא פי סטרא ואלסבעה ואלתלאתת אתמאן פי סטרא תחתה עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
|
|
תם אבדא [באל]סטר אלאעלי פאצֹרב אלתלאתה פי אלכמסה ואג'מל מא עלי ראסהא יכון דאלך סתת עשר פארפעהא תם ארגע אלי אלסטר אלאספל פאצרב אלסבעה פי אלתמאניה ואגמל מא עלי ראסהא יכון דאלך תסעה וכמסון פאצֹרבהא פי אלסתת עשר אלמרפועה יגתמע לך מן דאלך ארבעה וארבעין ותסע מאיה פאקסמהא עלי אלאימה יכרג לך אלמטלוב ודאלך תלאתת ועשרין וארבעה אתמאן וארבעת אכמאס אלתמן כמא תרי | |||||||||||||||||
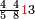
| ||||||||||||||||||
| וגואב אלמסאלה פיהא בסתה וצנאעתהא צנאעת אלעמל | ||||||||||||||||||
Chapter Twenty Three: Multiplication of Integer and Fraction and Fraction of Fraction by Integer and Fraction and Fraction of Fraction |
אלבאב אלתאלת ואלעשרין פי צרב אלצחיח ואלכס' וכס' אלכס' פי אלצחיח ואלכסר וכסר אלכסר | |||||||||||||||||
|
|
אדא קיל לך אצרב אתנין ותלאתת אכמאס ונצף כמס פי ארבעה וסבעת אתסאע וסתת אתמאן אלתסע | |||||||||||||||||
| פאנזל אלאתנין ותלאתת אכמאס ונצף כמס פי סטרٍ ואלארבעה וסבעה אתסאע וסתת אתמאן אלתסע פי סטרٍ תחתה עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| תם אבדא באלסטר אלאעלי פאצֹרב אלאתנין פי אלכמסה ואגמל מא עלי ראסהא יג'תמע לך מן דאלך סבעה ועשרון פארפעהא תם ארגע אלי אלסטר אלאספל פאצֹרב אלארבעה פי אלתסעה ואגמל מא עלי ראסהא ומא אגתמע צֹרבתה פי אלתמאניה וג'מלת מא עלי ראסהא יגתמע לך מן דאלך כמסון וארבע מאיה ותסעת אלאף פאקסמהא עלי אלאימה יכרג לך תלאת עשר ותסע ותמן תסע ובאקי אלאימה פארגה והדה צורתהא | ||||||||||||||||||
|
| ||||||||||||||||||
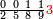
| ||||||||||||||||||
| והד אלמסאלה ענד אלאמתחאן מטרוחה | ||||||||||||||||||
Chapter Twenty Four: Multiplication of Integer and Two Different Fractions by Integer and Two Different Fractions |
באב ארבעה ועשרין פי צֹרב אלצחיח ואלכסרין אלמכתלפין פי אלצחיח ואלכסרין אלמכתלפין | |||||||||||||||||
|
|
אדא קיל לך אצרב סתה ותלתין ותלאתת אכמאס פי תסעה וכמסת אסדאס וסבעת אתמאן | |||||||||||||||||
| פאנזל אלעדד אלאול פי סטרין ואנזל אלעדד אלתאני פי סטר תחתה עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| תם אבדא באלסטר אלאעלי פאצרב אלסתה פי אלתלאתה ומא אגתמע פי אלכמסה יכון דאלך תסעין תם מא עלי אלתלאתה פי אלכמסה ומא עלי אלכמסה פי אלתלאתה ותגמע אלצֹרבין ותצֹיפה אלי אלתסעין יכון דאלך תסעת ומאיה פארפעהא תם ארגע אלי אלסטר אלאספל פאצרב אלתסעה פי אלסתה ומא אגתמע פי אלתמאניה ואצרב [איצ']א מא עלי אלסתה פי אלתמאניה ומא עלי אלתמאניה פי אלסתה ותגמע אלצרוב אלתלאתה יכון דאלך ארבעת עשר וכמס מאיה פאצרבהא פי אלתסעה ואלמאיה אלמרפועה יג'תמע לך סתה ועשרין וסתה וכמסין אלפא פאקסמהא עלי [אל]אימה יכרג לך אלמטלוב ודאלך סבעה וסבעין וסת אתמאן ותלאתת אסדאס אלתמן ותלת כמס סדס אל[תמן] והדה צורתהא | ||||||||||||||||||
|
| ||||||||||||||||||
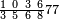
| ||||||||||||||||||
| אלגואב פיהא בכמסה | ||||||||||||||||||
Chapter Twenty Five: Multiplication of Integer and Two Different Fractions and Fraction of Fraction by Integer and Two Different Fractions and Fraction of Fraction |
באב כה פי צֹרב אלצחיח ואלכסרין אלמכתלפין ואלצחיח ואלכסרין אלמכתלפין | |||||||||||||||||
| אעלם אן הד אלבאב ינקסם קסמין: | ||||||||||||||||||
| אמא אן יכון כסר אלכסר מנסובא אלי ואחד מן אלכסרין | ||||||||||||||||||
| ואמא אן יכון מנסובא אלי כסר אכר | ||||||||||||||||||
| פאמא אן יכון מנסובא אלי ואחד מן כסור אלמסאלה | ||||||||||||||||||
|
|
ומתאל דאלך אצֹרב אתנין ותלאתת ארבאע וארבע אכמאס ונצף כמס פי סתה וסתת אסבאע ותסעת אעשאר ותלאתת אתמאן אלעשר פי סטרٍ תחתה עלי הד אלצורה | |||||||||||||||||
| ||||||||||||||||||
| תם אבדא באלסטר אלאעלי פאצֹרב אלאתנין פי אלארבעה אלתי הי אלאמאם ומא אגתמע פי אלכמסה ופי אלאתנין אלתי מע אלכמסה תחת אלכט יגתמע לך מן דאלך תמאנון תם תצרב אלתלאתה אלתי עלי אלארבעה פי אלכמסה תחת אלארבעה תם פי אלאתנין אלדין תחת אלכט ואגמל מא עלי ראסהא ואצֹרב אלמגתמע פי אלארבעה אלתי תחת אלכט אלאול יגתמע לך מן דאלך סתה ותלאתין פאגמעהא אלי אלתלאתין ואלתמאנין יכון דאלך סתה וארבעין ומאיה פארפעהא תם ארגע אלי אלכט אלאספל ואצרב אלסתה אלתי הי אלצחיח פי גמיע אלאימה אלתי תחת אלכטוט פי סטרהא עלי מא תקדם פי אלסטר אלאעלי יגתמע לך מן דאלך סתון ותלאת מאיה ותלאתת אלאף תם אצֹרב מא עלי אלסבעה פי אלעשרה ופי אלתמאניה יכון דאלך תמאנין וארבע מאיה תם אצרב מא עלי אלעשרה פי אלתמאניה ואגמל מא עלי ראסהא ואצרב פי אלסבעה יגתמע לך מן דאלך כמסה ועשרין וכמס מאיה פאגמעהא אלי אלתמאנין וארבע מאיה ואלסתין ותלאת מאיה ותלאתת אלאף יכון אלמגתמע כמסה וסתין ותלאתת מאיה וארבעת אלאף פאצֹרבהא פי אלדי כרג מן אלסטר אלאעלי יגתמע לך מן דאלך תסעין ומאיתין וסבעה ותלאתין אלפא וסתת מאית אלף פאקסמהא עלי אלאימה יכרג לך אל מטלוב ודאלך תמאניה ועשרון וארבעת אעשאר וארבעת אתמאן אלעשר וכמס סבע תמן אלעשר ורבע כמס סבע תמן אלעשר והדה צורתהא | ||||||||||||||||||
|
| ||||||||||||||||||
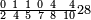
| ||||||||||||||||||
| ואלגואב פיהא בתלאתה | ||||||||||||||||||
| ואן שית מן הד אלמסאלה אדא צֹרבת אלצחיח פי מקאמאת אלכסור תם אצֹרב מא עלי אול אמאם פמא תחת גירה מן אלכטוט ותאכוד איצֹא מא עלי אלתאני ותצרבה פי אלאמאם אלאול ומא אגתמע צרבתה פי מקאם כסר אלכסר תם תאכוד מא עלי מקאם כסר אלכסר פתתרוך אלמקאם אלמנסוב אליה ותצרבה פי גירה כתרת אלמקאמאת או קלת | ||||||||||||||||||
| ואעלם אן אלכסור אלמכתלפה אנמא תנזלהא תחת כטוט מפתרקה פי סטר ואחד תם תאכוד מא עלי אול כטٍ ותתרך אלמקאם אלדי תחתה ותצֹרבה פי סאיר אלמקאמאת אלמתקדמה ענה תם תאכוד מא עלי אלכט אלתאני ותתרך אלמקאם אלדי תחתה ותצרבה פי אלמ[קאם] אלאול ופי באב אלמקאמאת אלמתקדמה לא תראעי בה פי אלצֹרב אלדי תחתה כטה פאן כאן מעך כסר אכדת מא עלי מקאם אלכסר ותרכת מא תחת אלכט אלדי הו עליה וצרבתה פי סאיר אלאסמי | ||||||||||||||||||
| ואלוגה אלתאני מן אלמסאלה אלמתקדמה והו אן יכון כסר אלכסר ליס ינסב אלי ואחד מן אלכסור אלמכתלפה | ||||||||||||||||||
|
|
ומתאל דאלך אצרב אתנין ותלת וכמס וסבע תמן מן תלאתה ותסע עשר וסדס אלגז מן אחדי עשר | |||||||||||||||||
| פאנזל אלאתנין ותלת כמס וסבע תמן פי סטרٍ תם אנזל תחתה פי סטר אכר אלתלאתה ואלתסע ואלעשר ואלסדס גז מן אחדי עשר כמא תרי | ||||||||||||||||||
| ||||||||||||||||||
| תם אבדא באלסטר אלאעלי פאצֹרב אלאתנין אלדין המא אלצחיח פי גמיע מקאמאת אלכסור אלתי פי סטר וארפעה תם תאכוד מא עלי אלתלאתה ותתרך אלצֹרב פי אלתלאתה ותצֹרב מא עליהא פי מא בקי מן אלמקאמאת תם תאכוד מא עלי אלכמסה ותתרך אלכמסה ותצֹרבה פי מא בקי מן אלמקאמאת אלתי תחת גירה מן אלמקאמאת תם תאכוד מא עלי אלסבעה ותתרך מא תחת אלכט אלדי הי עליה ולו כאנו תלאתת אימה ואכתר לא תצרבה פי ואחדא מנהא תם צֹרבה פי באקי אלמקאמאת אלתי [ת]חת כט גירה ואגמע דאלך כלה יגתמע לך מן דאלך תלאתה וארבעין ומאיה פארפעהא פהו אלדי כרג מן אלסטר אלאעלי תם ארגע אלי אלסטר אלאספל ותצֹרב אלתלאתה אלצחאח פי גמיע מקאמאת אלכסור ואחד בעד ואחד וארפעה תם אצֹרב מא עלי אלתסעה פי מא תחת אלכטוט גיר אלכט אלדי הו עליה וכדאלך תפעל באלעשרה תאכוד אלואחד אלדי הו עליהא ותתרך אלעשרה ותצֹרבה פי גיר דאלך מן אלמקאמאת וכדאלך תפעל פי אלואחד אלדי עלי אלסתה תתרך גמיע מא תחת אלכט אלדי הו עליה ותצֹרבה פי מא תחת אלכטוט אלבאקיה מן אלאימא ותגמע דאלך כלה יכון ארבעה וסתין ומאיה ותסעה עשר אלפא פאצרבה פי אלעדד אלדי כרג מן אלסטר אלאעלי יגתמע לך מן דאלך אתנין וכמסון וארבע מאיה ותמאניה וסתון אלפא וואחד וארבעון אלפא אלף פאקסמה עלי אלאימה יכרג לך תמאניה וגזאן מן אחדי עשר וכמסת אעשאר אלגז מן אחדי עשר וארבעת אכמאס סדס סבע תמן תסע עשר אלגז מן אחדי עשר עלי הדא אלצורה | ||||||||||||||||||
|
| ||||||||||||||||||
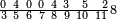
| ||||||||||||||||||
Chapter Twenty Six: Multiplication of Integer and Three Different Fractions by Integer and Three Different Fractions |
באב סתה ועשרין פי צרב צחיח ותלאתת כסור מכתלפה פי צחיח ותלאתת כסור מכתלפה | |||||||||||||||||
|
|
ומתאל דאלך אצרב אתנין ותלת וכמס וסדס פי ארבעה וסבע ותמן ותסע | |||||||||||||||||
| פאנזל הדין אלעדדין פי סטרין ואחדה תחת אכר כמא תרי | ||||||||||||||||||
| ||||||||||||||||||
| תם אבדא באלסטר אלאעלי פתצֹרב אלאתנין פי גמיע מקאמאת אלכסור אלתי תחת אלכטוט ודאלך פי תלאתה ומא אגתמע פי אלכמסה ומא אגתמע פי אלסתה ותרפעה תם תאכוד מא עלי אלתלאתה ותצֹרבה פי אלכמסה ואלסתה ותרפעה איצֹא תם תאכוד מא עלי אלסתה ותצֹרבה פי אלכמסה ואלתלאתה ותגמע הד אלצרוב אלארבעה יגתמע לך מן דאלך תלאתה וארבעין ומאיתין והו אלכארג מן אלסטר אלאעלי פארפעה תם ארגע אלי אלסטר אלאספל ותצנע בה מתל מא צנעת פי באלסטר אלאעלי מע צרובה כלהא יכון סבעה ומאיתין ואלפא פאצרבה פי אלדי כרג מן אלסטר אלאעלי יגתמע לך מן דאלך ואחד ותלת מאיה וסתה ותלאתון אלפא וכמס מאיאת אלפאً פאקסמהא עלי אלאימה יכרג לך אלמטלוב ודאלך אחדי עשר וסבעת אתסאע ותלאתת אתמאן אלתסע וסבע תמן אלתסע וכמסת אסדאס תמן תסע וכמסא סדס סבע תמן אלתסע והדה צורתהא | ||||||||||||||||||
|
| ||||||||||||||||||
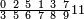
| ||||||||||||||||||
| וגואבהא בתלאתה ואלצנאעה פי אלאמתחאן ואלעמל פיהא ואחד | ||||||||||||||||||
Chapter Twenty Seven: Multiplication of Integer and Three Different Fractions and Fraction of Fraction |
באב סבעה ועשרין פי צֹרב אלצחיח ותלאתת כסור מכתלפה וכסר כסר | |||||||||||||||||
| אעלם אן קיאס הד אלבאב מתל קיאס צֹרב אלצחיח ואלכסרין וכסר אלכסר וכדאלך תתפרע מנה באבאן ועמלהא עלי מא תקדם פי אלכאמס ואלעשרין פמן פהמה ותדברה לם יתק יכפי יתק עליה מא יאתי בעדה מן אלכסור | ||||||||||||||||||
Chapter Twenty Eight: Multiplication of Fraction by Fraction |
באב תמניה ועשרון | |||||||||||||||||
|
|
אדא קיל לך אצֹרב סבעת אתמאן פי תסעת אעשאר | |||||||||||||||||
| פאנזל אלסבעה אתמאן פי סטר ואלתסעת אלאעשאר פי סטרٍ אכר תחתה עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
|
|
תם אצֹרב אלסבעה אלתי עלי אלתמאניה פי אלתסעה אלתי עלי אלעשרה יכון תלאתה וסתין פאקסמהא עלי אלאימה יכרג לך אלמטלוב ודאלך סבעת אעשאר וסבעת אתמאן אלעשר והדה צורתהא | |||||||||||||||||
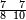
| ||||||||||||||||||
|
ואמתחאנהא כעמלהא ודאלך אן תאכוד מא עלי אלתמאניה והו טרח פתצֹרבה פי אלתסעה יכרג לך טרח | |||||||||||||||||
|
|
תם ארגע אלי אלכארג מן אלצֹרב והו סבעת אעשאר פסבעה טרח מצֹרובה פי תמאניה יכרג לך טרח תם ארגע אלי אלכארג ועלי ראסהא סבעה טרח [פ]אלכארג כלה טרח והו מואפק ללגואב | |||||||||||||||||
|
|
פאן קיל לך אצרב עשרת אגזא אחדי עשר פי אתני עשר גז מן תלאתת עשר | |||||||||||||||||
| פאנזלהא פי סטרא עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
|
|
תם אצֹרב אלעשרה אלתי עלי אלאחדי עשר פי אלאתני עשר אלתי עלי אלתלאתת עשר תכון עשרין ומאיה פאקסמהא עלי אלאימא יכרג לך אלמטלוב ודאלך עשרת אגזא מן תלאתת עשר ועשרת אגזא מן אחדי עשר פי אלגז מן תלאתה עשר והדה צורתהא | |||||||||||||||||
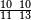
| ||||||||||||||||||
| וגואבהא ואחד | ||||||||||||||||||
Chapter Twenty Nine: Multiplication of Fraction and Fraction of Fraction by Fraction |
באב תסעה ועשרין פי צֹרב אלכסר וכסר אלכסר פי אלכסר | |||||||||||||||||
|
|
אדא קיל לך אצֹרב סתת אסבאע ותלת סבע ותמאנית אתסאע | |||||||||||||||||
| פאנזל אלתלאתת אלאסבאע ותלת סבע פי סטרٍ ואלתמאניה אלאתסאע פי סטרٍ תחתה עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
|
|
תם אבדא באלסטר אלאעלי פאצרבה אלסתה אלתי עלי אלסבעה פי אלתמאניה אלדי תחת אלכט ותגמל מא עלי ראסהא יכון דאלך סבעת עשר פאצֹרבהא פי אלתמאניה אלתי עלי אלתסעה פי אלסטר אלאספל יגתמע לך אתנין וכמסין ומאיה פאקסמהא עלי אלאימה יכרג לך אלמטלוב ודאלך סבעת אתסאע וסבע תסע ותלת סבע תסע והדה צורתהא | |||||||||||||||||
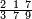
| ||||||||||||||||||
| וגואבהא בכמסה פאמתחן דאלך תגדה | ||||||||||||||||||
|
|
פאן קיל לך אצֹרב גזאً מן אחדי עשר ונצף גז מן אחדי עשר פי אתני עשר גז מן תלאתת עשר | |||||||||||||||||
| פאנזל אלגז מן אחדי עשר ונצף גז פי סטר ואלאתני עשר גזא מן תלאתת עשר פי סטרٍ תחתה עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
|
|
תם אבדא באלסטר אלאעלי עלי מא תקדם פאצרב אלואחד אלדי עלי אלאחדי עשר פי אלאתנין ואגמל מא עלי ראסהא תכון תלאתה פאצֹרבה פי אלאתני עשר תכון סתה ותלאתין פאקסמהא עלי אלאימה יכרוג לך אלמטלוב ודאלך גז מן תלאתת עשר וסבעת אגזא מן אחדי עשר פי אלגז מן תלאתה עשר כמא תרי | |||||||||||||||||
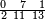
| ||||||||||||||||||
Chapter Thirty: Multiplication of Two Different Fractions by Fraction |
אלבאב אלמופי תלאתין פי צֹרב אלכסרין אלמכתלפין פי אלכסר | |||||||||||||||||
|
|
ומתאל דאלך אצֹרב תלתין וכמסת אסבאע פי עשרת אגזא מן אחדי עשר | |||||||||||||||||
| פאנזלהא עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
|
|
תם אגמל פי אלסטר אלאעלי עלי מא תקדם פי אלכסרין אלמכתלפין ודאלך אן תצֹרב מא עלי אלתלאתה פי אלסבעה ומא עלי סבעה פי אלתלאתה ותגמע אלצֹרבין יכון דאלך סתה ועשרין פאצרבהא פי אלעשרה אלתי עלי אלאחדי עשר יכון דאלך סתין ומיאתין פאקסם דאלך עלי אלאימה יכרג לך אלמטלוב ודאלך ואחד וגז מן אחדי עשר וסבעא גז מן אחדי עשר ותלתאً סבע אלגז מן אחדי עשר והדה צורתהא | |||||||||||||||||
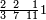
| ||||||||||||||||||
| ואלגואב פיהא בואחד | ||||||||||||||||||
Chapter Thirty One: Multiplication of Fraction and Fraction of Fraction by Fraction and Fraction of Fraction |
באב ואחד ותלאתין פי צֹרב אלכסר וכסר אלכסר פי אלכסר וכסר אלכסר | |||||||||||||||||
|
|
אדא קיל לך אצרב כמסה אסדאס ונצף סדס פי תסעה אעשאר וסבעת אתמאן אלעשר | |||||||||||||||||
| פאנזלה עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| תם אבדא באלסטר אלאעלי פאצֹרב אלכמסה פי אלאתנין ואגמל מא עלי ראסהא יכון דאלך אחדי עשר פארפעהא תם ארגע אלי אלסטר אלאספל פאצֹרב אלתסעה פי אלתמאניה ואגמל מא עלי ראסהא יכון תסעה וסבעין פאצרבהא פי אלאחדי עשר יכון תסעה וסתין ותמאן מאיה פאקסמהא עלי אלאימה יכרג לך תסע אעשאר וסדסא תמן אלעשר ונצף סדס תמן אלעשר ונצף סדס תמן אלעשר והדה צורתהא | ||||||||||||||||||
|
| ||||||||||||||||||
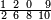
| ||||||||||||||||||
| ואלגואב פיהא איצֹא בואחד עלי עמל מא תקדם | ||||||||||||||||||
Chapter Thirty Two: Multiplication of Two Different Fractions by Fraction and Fraction of Fraction |
באב אתנין ותלאתין פי צֹרב אלכסרין אלמכתלפין פי אלכסר וכסר אלכסר | |||||||||||||||||
|
|
אדא קיל לך אצֹרב תלאתת ארבאע וארבעת אכמאס פי עשרת אגזא מן אחדי עשר ותמאנית אתסאע אלגז מן אחדי עשר | |||||||||||||||||
| פאנזלהא עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| תם אצנע באלסטר אלאעלי עלי מא תקדם פי אלכסרין אלמכתלפין יגתמע לך ואחד ותלאתון ואצנע באלסטר אלתאני עלי מא תקדם פי אלכסר וכסר אלכסר יגתמע לך תמאניה ותסעון פאצֹרבהא פי אלואחד ואלתלאתין אלמרפועה יכרג לך תמאניה ותלאתין ותלאתת אלאף פאקסמהא עלי אלאימה יכרג לך אלמטלוב ודאלך ואחד וכמסת אגזא מן אחדי עשר וסבעת אתסאע אלגז מן אחדי עשר וארבעת אכמאס תסע אלגז מן אחדי עשר ורבעא כמס תסע אלגז מן אחדי עשר והדה צורתהא | ||||||||||||||||||
|
| ||||||||||||||||||
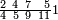
| ||||||||||||||||||
| והי מטרוחה כלהא | ||||||||||||||||||
Chapter Thirty Three: Multiplication of Two Different Fractions by Two Different Fractions |
באב תלאתה ותלאתין פי צֹרב אלכסרין אלמכתלפין פי אלכסרין אלמכתלפין | |||||||||||||||||
|
|
אד קיל לך אצֹרב תלתא ותלאתת אכמאס פי סבע ותסעין | |||||||||||||||||
| פאנזל אלמסלה פי סטרٍין עלי מא תקדם עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
|
|
תם אצנע באלסטר אלאעלי עלי מא תקדם פי אלכסרין אלמכתלפין יגתמע פיהא ארבעה עשר וכדאלך תפעל באלסטר אלתאני יגתמע פיה תלאתה ועשרין פאצרבהא פי אלארבעה עשר וכדאלך תפעל באלסטר אלתאני יגתמע פיה תלאתה ועשרין פאצֹרבהא פי אלארבעה עשר ואקסם עלי אלאימה יכרג לך אלמטלוב ודאלך תלאתת אתסאע וכמסא סבע אלתסע ותלת כמס סבע אלתסע כמא תרי | |||||||||||||||||
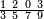
| ||||||||||||||||||
Chapter Thirty Four: Multiplication of Fraction by Fraction of Fraction |
באב ארבעה ותלאתין פי צֹרב כסרין מכתלפין וכסר כסר פי מתלה | |||||||||||||||||
| אדא קיל לך פהד אלמסאלה אנהא עלי וגהין אתנאן: | ||||||||||||||||||
| אמא אן יכון כסר אלכסר מנסובאً אלי ואחד מן אלכסור אלמכתלפה | ||||||||||||||||||
| או אלי גירהא | ||||||||||||||||||
| פאמא אן כאן מנסובא אלי ואחד מן אלכסור אלמכתלפה | ||||||||||||||||||
|
|
מתאל דאלך אצֹרב תלתין וכמסת אסבאע וסדס סבע פי סטרٍ אכמאס ותסעת אעשאר ותמאנית אתסאע אלעשר | |||||||||||||||||
| פאנזל אלתלתין וכמסת אסבאע וסדס סבע פי סטרٍ ואנזל אלארבעת אכמאס ואלתסעת אעשאר ותמאנית אתסאע אלעשר פי סטרٍ תחתה עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| תם אבדא באלסטר אלאעלי פאצֹרב אלאתנין פי סבעה ומא אגתמע פי אלסתה יכון דאלך ארבעה ותמאנין תם אצֹרב אלכמסה אלתי עלי ראס אלסבעה פי אלסתה ואגמל מא עלי ראסהא ואצרב פי אלתלאתה יכון דאלך תלאתה ותסעי[ן] פאגמעהא אלי אלארבעה ואלתמאניה תמאנין יכון דאלך סבעה וסבעין ומאיה פארפעהא תם ארגע אלי אלסטר אלאספל פאצֹרב אל ארבעה אלתי עלי אלכמסה פי אלעשרה ומא אגתמע פי אלתסעה יכון סתין ותלת מאיה תם אצֹרב אלתסעה אלתי עלי אלעשרה פי אלתסעה אלתי תחת אלכט ותגמל מא עלי ראצהא ומא אגתמע צֹרבתה פי אלכמסה יכון דאלך כמסה וארבעין וארבע מאיה פאגמעהא אלי אלסתין ותלאת מאיה יכון דאלך כמסה ותמאן מאיה פאצֹרבהא פי אלדי כרג מן אלסטר אלאעלי ותקסם אלמגתמע עלי אלאימה יכרג לך אתנאן וכמסת אעשאר ותסע עשר וסבע תסע עשר וסדס סבע תסע עשר כמא תרי | ||||||||||||||||||
|
| ||||||||||||||||||
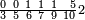
| ||||||||||||||||||
| והי מטרוחה פי אלאמתחאן | ||||||||||||||||||
| ואמא אלנוע אלתאני פהו אן יכון כסר [אלכסר] ליס ינסב אלי ואחד מן אלכסור אלמ[כתלפה] אלתי פי אלמסאלה | ||||||||||||||||||
|
|
ומתאל דאלך אצרב תלאתה ארבאע וארבע אכמאס ונצף סבע פי סבעת אתמאן ותמאנית אתסאע ו[תלת] עשר פאנזל אלמסאלה עלי הד אלצורה | |||||||||||||||||
| ||||||||||||||||||
| תם תאכוד מא עלי אלכט אלאול מן אלסטר אלאעלי ודאלך תלאתה פתצֹרבהא פי אלכמסה ומא אגתמע פי אלסבעה ומא אגתמע פי אלאתנין יכון דאלך עשרה ומיאתין פארפעהא איצֹא תם אצֹרב אלואחד אלדי עלי אלאתנין פי אלכמסה ואלארבעה יכון עשרין פאגמע הד אלתלאת צֹרוב תכון ארבעה וכמסין וארבע מאיה פארפעהא פהו אלכארג מן אלסטר אלאעלי תם ארגע אלי אלסטר אלאספל פאצנע בה מתל מא צנעת באלאול יגתמע לך פיה אתנין ותמאנון ותמן מאיה ותלאתת אלאף פאצֹרבהא פי אלדי כרג מן אלסטר אלאעלי פמא כאן אלמגתמע קסמתה עלי אלאימה יכרג לך פי אלקסמה אתנין ותסעת אעשאר ותסע עשר ותמנא תסע עשר ותמן תמן תסע אלעשר וכמס תסע תמן תמן תסע אלעשר והדה צורתהא הכדא | ||||||||||||||||||
|
| ||||||||||||||||||
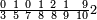
| ||||||||||||||||||
| ואלגואב פיהא בתלאתה ואלאמתחאן כאלעמל | ||||||||||||||||||
Chapter Thirty Five: Multiplication of Three Different Fractions by Three Different Fractions |
באב כמסה ותלאתין פי צֹרב תלאתת כסור מכתלפה פי תלאתת כסור מכתלפה | |||||||||||||||||
|
|
אדא קיל לך אצרב תלתין ותלאתת אכמאס וארבעת אסדאס פי כמסת אסבאע וסבעת אתמאן ותסעת אגזא מן אחדי עשר | |||||||||||||||||
| פאנזל הדין אלעדדין פי סטרין עלי הד אלצורה כמא תרי | ||||||||||||||||||
| ||||||||||||||||||
| תם תאכוד מא עלי אלכט אלאול מן אלסטר אלאעלי ותתרך אלמקאם אלדי תחתה ותצֹרבה פי אלמקאם אלתאני ואלתלאת תם תאכוד מא עלי אלכט אלתאני ותתרך אלמקאם אלדי תחתה ותצֹרבה פי מא בקי מן אלמקאמאת מתקדמהא ומתאכרהא תם תאכוד מא עלי אלכט אלתאלת ותתרך אלדי תחתה ותצֹרבה פי מא תחת גירה מן אלכטוט ותגמע הד אלצֹרוב אלתלאתה יכון דאלך ארבעה וסבעין ומאיה פארפעהא תם אצנע באלסטר אלאספל מא צנעת באלאעלי יגתמע לך פיה תלאתה ותמאנון וארבע מאיה ואלף פאצֹרבהא פי אלדי כרג מן אלסטר אלאעלי ומא אגתמע קסמתה עלי אלאימה יכרג' לך אלמטלוב ודאלך ארבעה וסבעת אגזא מן אחדי עשר ותמן אלגז מן אחדי עשר וארבעת אסבאע תמן אלגז מן אחדי עשר וארבעת אכמאס סדס סבע תמן אלגז מן אחדי עשר והדה צורתהא | ||||||||||||||||||
|
| ||||||||||||||||||
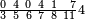
| ||||||||||||||||||
| ואלגואב טרח | ||||||||||||||||||
Chapter Thirty Six: Multiplication of Three Different Fractions and Fraction of Fraction by the Same |
באב סתה ותלאתין פי צֹרב תלאתת כסור מכתלפה וכסר כסר פי מתלהא | |||||||||||||||||
| אלעמל פי הד אלבאב עלי מא תקדם פי צֹרב אלכסרין וכסר אלכסר | ||||||||||||||||||
Chapter Thirty Seven: Multiplication of Fraction of Integer by Fraction of Integer |
באב סבעה ותלאתין פי צֹרב כסר אלעדד פי כסר אלעדד | |||||||||||||||||
|
|
ומתאל דאלך אצֹרב תלאתת ארבאע כמסה פי כמסה אסדאס סבעה | |||||||||||||||||
| פאנזל אלתלאתת אלארבאע אולא ואלכמסה בעדהא פי סטרٍ ואנזל אלכמסת אלאסדאס ואלסבעה בעדהא פי סטרٍ אכר תחתה עלי הד אלצורה כמא תרי | ||||||||||||||||||
| ||||||||||||||||||
|
|
תם אצֹרב אלתלאתה פי אלכמסה וארגע אלי אלסטר אלאספל ואצֹרב אלכמסה פי אלסבעה ואצֹרב אלמגתמע פי אלמגתמע ואקסם עלי אלאימא יכרג לך אלמטלוב ודאלך ואחד ועשרון וכמסת אסדאס ורבע סדס והדה צורתהא | |||||||||||||||||
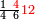
| ||||||||||||||||||
|
|
ואמתחאן הד אלמסאלה מתל אלעמל לא פרק בינהמא ודאלך אן תבדא באלסטר אלאעלי פתצֹרב אלתלאתה אלתי עלי ראס אלארבעה פי אלכמסה אלתי הי אלצחיח תכון כמסת עשר יבקי מנהא ואחד תם ארגע אלי אלסטר אלאספל פאצֹרב אלכמסה אלתי עלי ראס אלסתה פי אלסבעה יכון דאלך כמסה ותלאתין והי מטרוחה פאצֹרבהא פי אלואחד אלדי יבקי מן אלכט אלאעלי יכון דאלך טרחא פאלמסאלה אדא מטרוחה | |||||||||||||||||
|
|
תם ארגע אלי אלכארג מן אלמסאלה והו טרח פאצרבה פי אלסתה יכון טרחאً תם תאכוד אלכמסה אלתי עלי אלסתה פאצֹרבהא פי אלארבעה יכון דאלך עשרין ועלי אלארבעה ואחד יכון דאלך ואחד ועשרין | |||||||||||||||||
| פאלמסאלה אדאً בגמלתהא מטרוחה | ||||||||||||||||||
Chapter Thirty Eight: Multiplication of Fraction and Fraction of Fraction of Integer by Fraction and Fraction of Fraction of Integer |
באב תמאניה ותלאתין פי צֹרב כסר וכסר כסר אלעדד אלצחיח פי כסר וכסר כסר אלעדד אלצחיח | |||||||||||||||||
|
|
אדא קיל לך אצֹרב כמסת אסדאס ונצף סדס תמאניה פי תמאניה אתסאע וכמס תסע אתני עשר | |||||||||||||||||
| פאנזל אלכמסת אסדאס ונצף סדס תמאניה פי סטר תם אנזל אלתמאנית אתסאע וכמס תסע אתני עשר פי סטר תחתה עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
|
|
תם אבדא באלסטר אלאעלי פתצֹרב אלכמסה אלתי עלי אלסתה פי אלאתנין מקאם אלנצף ותגמל מא עליה יכון דאלך אחדי עשר פאצֹרבהא פי אלתמאניה אלצחיחה יכון דאלך תמאניה ותלאתין ותמאנין פארפעהא תם ארגע אלי אלסטר אלאספ[ל] פתצֹרב אלתמאניה פי אלכמסה ותגמל מא עלי ראסהא ות[ג]מל עלי[ה] אלואחד יכון דאלך ואחד וארבעין פאצֹרבהא פי אלאתנין עשר יגתמע לך מן דאלך אתנין ותסעין וארבע מאיה פאצֹרבהא פי אלתמאניה ואלתמאנון יגתמע לך מן דאלך סתה ותסעין ומיאתין ותלאתה וארבעון אלפאً פאקסמהא עלי אלאימה יכרג לך תמאנון ותסע ותלאתת אסדאס אלתסע ותלאתת אכמאס סדס אלתסע כמא תרי | |||||||||||||||||
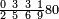
| ||||||||||||||||||
| וגואבהא וא[מתחאנהא] כמא תעמל [לא] פרק בינהמא | ||||||||||||||||||
Chapter Thirty Nine: Multiplication of Different Fractions of Integer by Different Fractions of Integer |
באב תסעה ותלאתין פי צֹרב כסרי אלעדד פי כסרי אלעדד | |||||||||||||||||
| ומתאל דאלך אצֹרב תלתין ותלאתת אכמאס תמאניה פי סתת אסבאע וכמסת אתסאע ארבעה | ||||||||||||||||||
|
|
פאנזל אלתלתין ואלתלאתת אלאכמאס תמאניה פי סטרٍ ואנזל תחתה אלסתת אלאסבאע ואלכמסת אלאתסאע ארבעה פי סטר אכר כמא תרי | |||||||||||||||||
| ||||||||||||||||||
| תם אבדא באלסטר אלאעלי פתעמל פי אלכסרין כמא תקדם פי אלכסרין אלמכתלפין ומא אגתמע צֹרבתה פי אלתמאניה וארפעה תם אצנע כדאלך באלסטר אלאספל פמא אגתמע צֹרבתה פי מא כרג מן אלסטר אלאעלי פמא אגתמע קסמתה עלי אלאימה יכרג לך אלמטלוב ודאלך סבעה וכמסין ותסעאן וסבעא תסע וכמסא סבע אלתסע ותלת כמס סבע אלתסע והדה צורתהא | ||||||||||||||||||
|
| ||||||||||||||||||
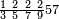
| ||||||||||||||||||
| וגואבהא באתנין ואלאמתחאן כאלעמל | ||||||||||||||||||
Chapter Forty: Multiplication of Fraction of Fraction of Integer by Fraction of Fraction of Integer |
באב אלמופי ארבעין פי צֹרב כסר כסר אלעדד פי כסר כסר אלעדד | |||||||||||||||||
|
|
ומתאל דאלך אצֹרב תלאתת ארבאע כמס תמאניה פי כמסת אסדאס סבע כמסת עשר | |||||||||||||||||
| פאנזל אלתלאתה ארבאע כמס תמאניה פי סטר וכמסת אסדאס סבע כמסה עשר פי סטר תחתה עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
|
|
תם אבדא באלסטר אלאעלי פתצֹרב אלתלאתה פי אלתמאניה ואחפט' מא אגתמע תם ארגע אלי אלסטר אלאספל ואצֹרב אלכמסה פי אלכמסת עשר פמא אגתמע צֹרבתה פי אלמחפוט' אלאול וקסמת מא כרג עלי אלאימה יכרג לך אלמטלוב ודאלך אתנין וסבע ובאקי אלאימה פארגה כמא תרי | |||||||||||||||||
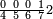
| ||||||||||||||||||
| ואלגואב פיהא בואחד | ||||||||||||||||||
| ומעני הד אלמסאיל אן תאכוד אלכסר מן כל עדדٍ פמא כאן צֹרבת [אחד]המא פי אלתאני עלי מא תקדם פי כל ואחד מנהא פי באבה | ||||||||||||||||||
Chapter Forty One: Multiplication of Fraction of Integer and Fraction by Fraction of Integer and Fraction |
באב ואחד וארבעין פי צרב כסר אלעדד ואלכסר פי מתלה | |||||||||||||||||
|
|
מתאל דאלך אצֹרב תלתיי כמסה וכמסת אסדאס פי סתת אסבאע תמאניה וארב[עת] אתסאע | |||||||||||||||||
| כמסה וכמסת אסדאס [פי] סטר ואנז[ל] ת[ח]תה סתת אסבאע תמאניה וארבעת אתסאע עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
|
|
תם אבדא באלסטר אלאעלי פתצֹרב אלכמסה אלתי הי אלצחיח פי אלסתה ותגמל מא עלי ראסהא יגתמע מן דאלך כמסה ותלאתין פאצרבהא פי אלאתנין אלדין עלי ראס אלתלאתה אלתי הי אול אלסטר יכון דאלך סבעין פארפעהא תם ארגע אלי אלסטר אלאספל פתצֹרב אלתמאניה פי אלתסעה ותגמל מא עלי ראסהא יכון דאלך סתה וסבעין פאצֹרבהא פי אלס[תה] אלדי עלי ראס אלסבע [יכון] דאלך סתה וכמסי[ן] וארבע מאיה פאצֹרבהא פי אלסבעין אלמרפועה פמא אגתמע קסמתה עלי אלאימה אלתי תחת אלכטוט יכרג לך אלמטלוב ודאלך תמאניה ועשרין ותסע וסבעא תסע וסדסא סבע תסע והדה הי צורתהא | |||||||||||||||||
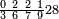
| ||||||||||||||||||
| ואלגואב פיהא בטרח ואלצנאעה כמא תעמל | ||||||||||||||||||
| ומעני הד אלמסאלה אן תאכוד מן אלכמסה וכמסת אסדאס תלתיהא ומן אלתמאניה וארבעה אתסאע סתת אסבאעהא ותצֹרב אלמגתמע פי אלמגתמע עלי מא תקדם תציב אן שא אללה תעלי | ||||||||||||||||||
Chapter Forty Two: Multiplication of Fraction of Integer and Fraction and Fraction of Fraction by the Same |
באב אתנין וארבעין פי צֹרב כסר אלעדד אלצחיח ואלכסר וכסר אלכסר פי נט'ירה | |||||||||||||||||
|
|
ומתאל דאלך אצֹרב תלאתת ארבאע כמסה וסתת אסבאע וסדס סבע פי סבעת אתמאן תלאתה ותלאתת אעשאר ותסע עשר | |||||||||||||||||
| פאנזל תלאתה ארבאע כמסה וסתת אסבאע וסדס סבע פי סטר עלי הד אלצורה ואלסבעת אתמאן תלאתה ואלתלאתת אלאעשאר ותסע עשר פי סטר תחתה כמא תרי | ||||||||||||||||||
| ||||||||||||||||||
|
|
תם אבדי באלסטר אלאעלי פאצֹרב אלכמסה אלתי הי אלצחיח פי אלסבעה ותגמל מא עלי ראסהא ומא אגתמע צֹרבתה פי אלסתה וגמלת מא עלי ראסהא ומא אגתמע צרבתה פי אלתלאתה אלתי עלי אלארבעה פי אול סטרٍ וארפע מא אגתמע ודאלך ואחד וארבעין וסבע מאיה והו אלכארג מן אלסטר אלאעלי תם ארגע אלי אלסטר אלאספל פתצרב אלתלאתה אלצחאח אלתי בין אלכטין פי אלעשרה ואגמל מא עלי ראסהא ואצֹרב מ[א אגת]מע פי אלסבעה ואגמל מא עליהא ואצרב מא אגתמע פי אלסבעה אלתי עלי ראס אלתמאניה יגתמע לך מן דאלך סתה ותלאתין ואלפאן פאצֹרבה פי אלדי כרג מן אלסטר אלאעלי פמא כרג קסמתה עלי אלאימה יכרג לך אלמטלוב ודאלך אתני עשר וסבעת אעשאר וסבעת אתסאע אלעשר וכמסת אסבאע תמן אלעשר וסדס סבע תמן תסע אלעשר ורבע סדס תמן אלעשר והדה צורתה | |||||||||||||||||
| ||||||||||||||||||
| ואלגואב פיהא בטרח ואלצנאעה ואחדה | ||||||||||||||||||
| ומעני הד אלמסאלה אנה אראד אן תאכוד מן כמסה וסתת אסבאע וסדס סבע תלאתת ארבאעהא ותאכוד איצֹא מן ת[לאתה] ותלאתת אעשאר סבעת אתמאנהא ותצרב אלכארג פי אלכארג | ||||||||||||||||||
Chapter Forty Three: Multiplication of Fraction of Integer and Two Different Fractions by the Same |
באב תלאתה וארבעין פי צרב כסר אלכסר ואלכסור אלמכתלפה פי מתלהא | |||||||||||||||||
|
|
אצֹרב נצף אתנין וכמס וסדס פי סבע תלאתה ותמן ותסע | |||||||||||||||||
| פאנזל אלנצף ואלאתנין וכמס וסדס פי סטר תם אנזל אלסבע ואלתלאתה ואלתמן ואלתסע פי סטר תחתה עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| תם אבדא באלסטר אלאעלי פתאכוד אלאתנין ואלכמס ואלסדס ותצֹרב בה כמא תקדם פי צרב אלצחיח ואלכסרין אלמכתלפין ומא אגתמע צרבתה פי אלואחד אלדי עלי אלאתנין פי אול אלכט יגתמע לך פיה ואחד וסבעין פאחפטהא תם אצנע כדאלך באלסטר אלתאני יגתמע מנה תלאתה ותלאתון ומאיתין פאצֹרבהא פי אלמחפוט' ואקסמהא עלי אלאימה יכרג לך אלמטלוב ודאלך ארבעה אתסאע וסבעה אתמאן אלתסע וסבעא תמן אלתסע וארבעת אסדאס סבע תמן אלתסע וכמס סדס סבע תמן אלתסע ונצף כמס סדס סבע תמן אלתסע והדה צורתהא | ||||||||||||||||||
|
| ||||||||||||||||||
| ||||||||||||||||||
| ואלגואב פיהא באתנין | ||||||||||||||||||
Chapter Forty Four: Multiplication of Fraction of Integer and Fraction of Fraction by Fraction of Integer and Fraction of Fraction |
באב ארבעה וארבעין פי צרב כסר אלעדד וכסר אלכסר פי כסר אלעדד וכסר אלכסר | |||||||||||||||||
|
|
אדא קיל לך אצֹרב סתת אסבאע כמסה ונצף סדס פי סבעה אתמאן תלאתה ותלאתת אכמאס אלתסע | |||||||||||||||||
| פאנזל אלסתה אסבאע ואלכמסה ונצף אלסדס פי סטרﹴ ואנזל תחתה פי סטר אכר אלסבעת אתמאן ואלתלאתה ואלתלאתת אכמאס אלתסע עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| תם אבדא באלסטר אלאעלי פאצרב אלכמסה פי אלסתה ומא אגתמע פי אלאתנין ותגמל מא עלי ראסהא ותגמל עלי אלמגתמע אלואחד ומא אגתמע צֹרבתה פי אלסתה אלתי עלי אלסבעה יכון גמיע דאלך סתה וסתון ותלת מאיה פארפעהא תם אצנע באלסטר אלאספל מתל מא צנעת באלסטר אלאעלי יגתמע לך סתה וסתין ותסע מאיה פאצֹרבהא פי אלמחפוט אלאול ומא אגתמע קסמתה עלי אלאימה יכרג לך אלמחפוט ודאלך אחדי עשר וסתת אתסאע ותמן אלתסע וכמסת אסבאע תמן אלתסע ותלאתת אסדאס סבע תמן אלתסע ותלאתת אכמאס סדס סבע תמן אלתסע והדה צורתהא | ||||||||||||||||||
|
| ||||||||||||||||||
| ||||||||||||||||||
| ואלגואב פיהא בטרח | ||||||||||||||||||
| ואלמעני פי ה[דה] אלמסאיל אנה אראד אן תאכוד מן אלכמסה ונצף סדס סתה אסבאעהא ויאכוד איצֹא מן אלתלאתה ותלאתת אכמאס אלתסע סבעה אתמאנהא ותצרב אלמגתמע פי אלמגתמע כמא תקדם | ||||||||||||||||||
Chapter Forty Five: Multiplication of Fraction of Fraction of Integer and Fraction by Fraction of Fraction of Integer and Fraction |
באב כמסה וארבעין פי צֹרב כסר כסר אלעדד ואלכסר פי כסר כסר אלעדד ואלכסר | |||||||||||||||||
|
|
אדא קיל לך אצֹרב תלתיי כמס תמאניה וסדס פי סטרﹴ ואנזל תחתה פי סטר אכר כמסת אסבאע תמן סתה ותסע כמא תרי | |||||||||||||||||
| ||||||||||||||||||
| תם אבדא באלסטר אלאעלי פאצֹרב אלתמאניה פי אלסתה ואגמל מא עלי ראצהא ומא אגתמע צֹרבתה פי אלאתנין אלתי עלי אלתלאתה פי אול כט יגתמע לך מן דאלך תמאניה ותסעין פארפעה תם אצנע כדאלך באלסטר אלאספל יגתמע לך פיה כמסה וסבעין ומאיתין פאצרבהא פי אלתמאניה ואלתסעין ואקסם מא אגתמע עלי אלאימה יכרג לך מן דאלך כמסה אתסאע ותמנא תסע וכמסת אסבאע תמן אלתסע וסדס סבע תמן אלתסע ותלת כמס סדס סבע תמן אלתסע והדה הי צורתהא | ||||||||||||||||||
|
| ||||||||||||||||||
| ||||||||||||||||||
| ואלגואב פיהא בטרח | ||||||||||||||||||
Chapter Forty Six: Multiplication of Fraction of Fraction of Integer and Fraction and Fraction of Fraction by the Same |
באב סתה וארבעין פי צֹרב כסר כסר אלעדד ואלכסר פי צֹרב כסר כסר אלעדד ואלכסר וכסר אלכסר | |||||||||||||||||
|
|
אדא קיל לך אצֹרב תלאתת ארבאע כמס סתה ותלאתת אגזא מן אחדי עשר וכמסת אסדאס אלגז מן אחדי עשר פי כמסת אסבאע תסע אתני עשר וסתת אגזא מן תלאתת עשר ותלאתת אכמאס אלגז מן תלאתת עשר | |||||||||||||||||
|
| ||||||||||||||||||
| פאנזלהא עלי הד אלצורה הכדא | ||||||||||||||||||
| ||||||||||||||||||
| תם תאכוד אלסתה אלתי בין אלכטין והו אלצחיח פתצֹרבה פי אלאחדי עשר ותגמל מא עלי ראצהא ותצרב מא אגתמע פי אלסתה אלתי תחת אלכט ותגמל מא עלי ראצהא פמא אגתמע צֹרבתה פי אלתלאתה אלתי עלי אלכט אלאול והי אלארבעה יגתמע לך מן דאלך סבעה וכמסין ומאיתין ואלף ותצנע הד אלצנאעה פי אלסטר אלאספל יכרג' לך כמסה ותסעין וארבע מאיה וסת אלאף פאצרבהא פי אלמחפוט אלאול ומא אגתמע קסמתה עלי אלאימה יכרג לך פי אלקסמה אתני עשר גז מן תלאתת עשר וגזאן מן אחדי עשר פי אלגז מן תלאת עשר וסבעת אתמאן תסע אלגז מן אחדי עשר פי אלגז מן תלת עשר וסבעא תמן תסע אלגז מן אחדי עשר פי אלגז מן [אחדי] עשר פי אלגז מן תלת עשר ותלאתת ארבאע כמס סדס סבע תמן תסע אלגז מן אחדי עשר פי אלגז מן תלאתת עשר והדה צורתה | ||||||||||||||||||
|
| ||||||||||||||||||
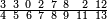
| ||||||||||||||||||
| וגואבהא בתלאתה | ||||||||||||||||||
Chapter Forty Seven: Multiplication of Fraction of Fraction of Integer and Fraction of Fraction by the Same |
באב סבעה וארבעין פי צרב כסר כסר אלעדד וכסר אלכסר פי נטירה | |||||||||||||||||
|
|
אדא קיל לך אצֹרב נצף כמס תסעה וכמס[ת] אסדאס פי תלאתת אתמאן תסע כמסה עשר ותלאתת אעשאר אלגז מן אחדי עשר | |||||||||||||||||
| פאנזלהא עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| תם אבדי באלסטר אלאעלי פאצֹרב אלתסעה פי אלסבעה אלתי תחת אלכט ומא אגתמע פי אלסתה ותגמל מא עלי ראסהא עלי מא תקדם פי צרב אלצחיח וכסר אלכסר ומא אגתמע צֹרבתה פי אלואחד אלדי עלי אלכט אלאול יגתמע לך מן דאלך תסעה וכמסין ותסע מאיה ואצֹרב פי אלעדד אלאול ואקסם מא אגתמע עלי אלאימה יכרג לך אלמטלוב ודאלך סתת אגזא מן אחדי עשר ועשר אלגז וסתת אתמאן עשר אלגז ותלאתת אסבאע תמן עשר אלגז וסדס סבע תמן עשר אלגז וכמס סדס סבע תמן עשר אלגז ונצף כמס סדס סבע תמן עשר אלגז והדה צורתהא | ||||||||||||||||||
|
| ||||||||||||||||||
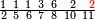
| ||||||||||||||||||
| ואלאמתחאן עלי מא תקדם אולא | ||||||||||||||||||
Chapter Forty Eight: Multiplication of Fraction of Fraction of Integer and Two Different Fractions by Fraction of Fraction of Integer and Two Different Fractions |
באב תמאניה וארבעין פי צֹרב כסר כסר אלעדד ואלכסרין אלמכתלפין פי כסר כסר אלעדד ואלכסרין אלמכתלפין | |||||||||||||||||
|
|
אדא קיל לך אצֹרב תלתיי כמס תמאניה ותלאתת אסדאס וארבעת אסבאע פי ארבעת אתסאע עשר תמאניה עשר וסתת אגזא מן אחדי עשר וכמסת אתמאן | |||||||||||||||||
| פאנזלה עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| תם תאתי אלי אלתמאניה ואלתלאתת אסדאס ואלארבעת אסבע תצנע בהא כמא צנעת באלצחיח ואלכסרין אלמכתלפין פמא אגתמע צֹרבתה פי אלאתנין אלדין עלי אלתלאתה יגתמע לך מן דאלך אתנין וסתין וסבע מאיה וכדאלך פאצנע באלסטר אלתאני יגתמע לך פיה תמאניה וארבעין וסבע מאיה וסתת אלאף פאצרבהא פי אלעדד אלאול ואקסם מא אגתמע עלי אלאימה יכרג לך אלמטלוב ודאלך ואחד ותלאתת אעשאר אלגז מן אחדי עשר ותלאתת אתסאע עשר אלגז מן אחדי עשר והדה צורתהא | ||||||||||||||||||
|
| ||||||||||||||||||
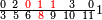
| ||||||||||||||||||
| אלגואב בטרח | ||||||||||||||||||
Chapter Forty Nine: Multiplication of Two Different Fractions of Integer and Fraction by Two Different Fractions of Integer and Fraction |
באב תסעה וארבעין פי צֹרב כסריי אלעדד ואלכסר פי נצֹירה | |||||||||||||||||
|
|
אדא קיל לך אצרב תלתין ותלאתת אכמאס תסעה וכמסת אסדאס פי תלאתת אסבאע וסבעת אתמאן אתני עשר וסבעת אתסאע | |||||||||||||||||
| פאנזלהא הכדא | ||||||||||||||||||
| ||||||||||||||||||
| פמענא פי אלסטר אלאול כסראן מכתלפאן וצחיח וכסר פאצנע באלכסרין אלמכתלפין עלי מא תקדם יגתמע מנה תסעה עשר ויבקי צחיח וכסר פאצנע בה כמא תקדם פי אלצחיח ואלכסר יגתמע פיה תסעה וכמסון פאצרבהא פי אלתסעת עשר יגתמע לך מן דאלך ואחד ועשרין ומאיה ואלף והדא הו אלכארג מן אלסטר אלאעלי פאחפטה תם אצנע באלסטר אלאספל כדאלך יגתמע מנה כמסת ותסעון ותלאת מאיה ותמאנית אלאף פאצֹרבהא פי אלמחפוט אלאול ואקסם מא אגתמע עלי אלאימה יכרג לך אלמטלוב ודאלך סבעה ומאיתין וארבע אתסאע ותמן תסע וכמסת אסבאע תמן תסע וסדסא סבע תמן אלתסע ותלת סדס תסע תמן אלתסע וסקטת אלכמסה אולא פי אלקסמה והדה צורתהא | ||||||||||||||||||
|
| ||||||||||||||||||
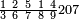
| ||||||||||||||||||
| ואלגואב פיהא בתמאניה ואלאמתחאן כאלעמל באב | ||||||||||||||||||
Chapter Fifty: Multiplication of Two Different Fractions of Integer and Two Different Fractions by the Same |
באב אלמופי כמסין פי צֹרב כסרי אלעדד ואלכסרין פי נט'ירה | |||||||||||||||||
|
|
ומתאל דאלך אצרב תלתין ותלאתת אכמאס סבעה ותלאתת ארבאע ותלאתת אכמאס פי כמסת אסדאס וכמסת אתמאן ארבעה וכמסת אסדאס ותסעת אעשאר | |||||||||||||||||
| פאנזל אלמסאלה עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| תם אנטר אלי אלאעלי תגדה כסרין מכתלפין וצחיחאﹰ וכסרין מכתלפין פתקסם אלסטר בקסמין תגעל אלקסם אלואחד אלכסרין אלמכתלפין תם תצנע באלקסם אלאול כמא תצנע באלכסרין אלמכתלפין פי אלבאב אלכמאס מן אלכסור יגתמע לך מן דאלך תסעה עשר פארפעהא תם אצנע באלקסם אלתאני כמא תצנע באלצחיח ואלכסרין אלמכתלפין פי אלבאב אלראבע ואלעשרין יגתמע מנה סבעה וסתין ומאיה פאצֹרבהא פי אלתסעה עשר יכון אלגמיע תלאתה וסבעין ומאיה ותלאתה אלאף והו אלכארג מן אלסטר אלאעלי תם אצנע באלסטר אלאספל כמא צנעת באלאעלי ה' יגתמע לך פיה תמאנון וארבעה ועשרין אלפא פאצרבהא פי אלמחפוט אלאול ואקסם מא כרג עלי אלאימה בעד אן תצרפהא אלי גירהא תרגע בעד אלתצריף עשרה תלאתת מראת ותסעה ותמאניה וסתה ואתנאן ואלעדד אלמקסום לה תמן ועשר פאקסם אולא עלי עשרה ותמאניה תם אקסם עלי בקית אלאימא יכרג לך תמאניה ותמאנין וארבעת אעשאר ותלאתת אעשאר עשר ותסעא עשר אלעשר וסדסאﹰ תסע עשר אלעשר ונצף סדס תסע עשר אלעשר והדה צורתהא | ||||||||||||||||||
|
| ||||||||||||||||||
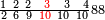
| ||||||||||||||||||
| גואבהא [....] | ||||||||||||||||||
Chapter Fifty One: Multiplication of Fraction and Fraction of Fraction of Integer and Fraction and Fraction of Fraction by the Same |
באב ואחד וכמסין פי צֹרב כסר וכסר כסר אלעדד וכסר וכסר כסר פי נט'ירה | |||||||||||||||||
|
|
ומתאל דאלך אדא קיל לך אצרב תלאתת אכמאס ונצף כמס ארבעה וסדס ונצף סדס פי סתת אסבאע וכמס סבע תלאתה וכמסת אגזא מן אחדי עשר וכמסת אתמאן אלגז מן אחדי עשר | |||||||||||||||||
|
| ||||||||||||||||||
| פאנזלהא עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| תם אבדא באלסטר אלאעלי תגד פיה כסר וכסר כסר פי כט ואחד ותגד ארבעה וכסרא וכסר כסר בעד דאלך פאקסם אלסטר בקסמין תגעל אלקסם אלואחד אלתלאתה אלאכמאס ונצף כמס פאצנע בה כמא צנעת פי אלבאב אלתלאת יגתמע לך פיה סבעה פארפעהא תם ארגע אלי אלקסם אלתאני מן אלסטר אלאעלי והו ארבעה וסדס ונצף סדס פאצנע בה כמא צנעת פי באב תלאתה ועשרין יכון אלמגתמע ואחד וכמסין פאצֹרבהא פי אלסבעה אלמרפעה יכון אלמגתמע סבעה וכמסין ותלת מאיה והו אלכארג מן אלסטר אלאעלי תם אצנע באלסטר אלאספל מתל דאלך יגתמע פיה תסעה וסבעין וכמס מאיה ותסעת אלאף פאצֹרבהא פי אלמחפוט אלאול ואקסם מא אגתמע עלי אלאימה בעד אן תצרפהא מא אצתטעת יכון אלכארג תסעה וגזין מן אחדי עשר וסבעת אעשאר אלגז מן אחדי עשר וסבעת אעשאר עשר אלגז וכמסת אתמאן עשר עשר אלגז ותלאתת אסדאס תמן עשר עשר אלגז מן אחדי עשר והדה צורתהא עלי הד אלצורה | ||||||||||||||||||
|
| ||||||||||||||||||
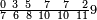
| ||||||||||||||||||
| ואלגואב פיהא כאלעמל | ||||||||||||||||||
Chapter Fifty Two: Multiplication of Fraction of Fraction of Integer and Fraction of Fraction by the Same |
באב אתנין וכמסין פי צֹרב כסר כסר אלעדד וכסר כסר פי נט'יר[ה] | |||||||||||||||||
|
|
אדא קיל לך אצֹרב תלתיי כמס תמאניה ורבע סדס פי תלאתת אסבאע תמן אתני עשר ונצף גז מן תלת עשר | |||||||||||||||||
| פאנזלהא עלי הד אלצורה כמא תרי | ||||||||||||||||||
| ||||||||||||||||||
| תם אלתפת אלסטר אלאעלי תגד פיה כסר כסר אולא וצחיחא וכסר כסר בעד דאלך פאצנע באלצחיח וכסר אל כסר כמא תקדם פי באבה יגתמע פיה תלאתה ותסעין ומאיה פאצֹרבהא פי אלאתנין אלדין עלי אלכט יכון דאלך תלאתה ותמאנין ותלאת מאיה והו אלכארג מן אלסטר אלאעלי ותעמל באלסטר אלתאני כדאלך יגתמע פיה תסעה ותלאתין ותסע מאיה פאצרבהא פי אלאול ואקסם עלי אלאימה בעד תצריפהא יכרג לך אלמטלוב ודאלך תמאנית אגזא מן תלאתת עשר ותסעת אעשאר אלגז מן תלת עשר וסבעת אתמאן עשר אלגז מן תלאתת עשר וסבע תמן עשר אלגז ונצף סדס סבע תמן עשר אלגז מן תלאתת עשר והדה צורתהא | ||||||||||||||||||
|
| ||||||||||||||||||
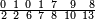
| ||||||||||||||||||
| ואלגואב פיהא בואחד | ||||||||||||||||||
Chapter Fifty Three: Multiplication of Fraction of Integer and Fraction of Integer by the Same |
באב תלאתה וכמסין פי צרב כסר אלעדד וכסר אלעדד ונט'ירה | |||||||||||||||||
|
|
ומתאל דאלך אצרב תלאתת אכמאס כמסה וכמסת אסדאס סבעה פי תלתיי ארבעה ונצף כמסה כמא תרי | |||||||||||||||||
| ||||||||||||||||||
| פהדה אלמסאלה כל כט מנהא מרכב מן אתנין מן מסאיל אלבאב אלתאסע ואלתלאתין פאדא קסמתה תקסם אלכסר אלאול כמא צנעת פי באב סבעה ועשרין פמא כרג צרבתה פי אלאמאם אלדי תחת אלכט אלתאני מן אלסטר אלאעלי יגתמע פיה תסעון תם אצנע באלקסם אלתאני כמא צנעת באלאול ומא אגתמע צֹרבתה פי אלאמאם אלדי תחת אלכט אלאול מן אלסטר אלאעלי יגתמע לך מן דאלך כמסה וסבעין ומאיה פאגמעהא אלי אלתסעין יכרג לך כמסה וסתין ומאיתין והו אלכארג מן אלסטר אלאעלי ואצנע כדאלך באלסטר אלאספל יגתמע פיה ואחד ותלאתין פאצֹרבהא פי אלעדד אלאול ואקסם עלי אלאימה יכרג לך כמסה וארבעין וסתת אעשאר וסדסא עשר ותלת סדס אלעשר והדה צורתהא | ||||||||||||||||||
|
| ||||||||||||||||||
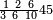
| ||||||||||||||||||
| וגואבהא בארבעה | ||||||||||||||||||
| ואן פי הד אלמסאלה וגהאן מן אלעמל אכץ מן הדא והו אן תאתי אלי אלסטר אלאעלי פתאכוד מן אלכמסה תלאתה אכמאסהא ודאלך תלאתה ומן אלסבעה כמסה אסדאסהא ודאלך כמסה וכמס אסדאס והו אלמטלוב מן אלסטר אלאעלי תם ארגע אלי אלסטר אלאספל פתאכוד מן אלכמסה נצפהא ודאלך אתנין ונצף ותאכוד מן אלארבעה תלאתיהא ודאלך אתנאן ותלתאן פתגמעהא אלי אלאתנין ונצף כמא ביינתה פי באב אלגמע יכון דאלך כמסה וסדסא פאצֹרבהא פי אלתמאניה וכמסת אסדאס כמא תקדם פי באב אתנין ועשרון יכרג לך אלמטלוב | ||||||||||||||||||
|
| ||||||||||||||||||
Chapter Fifty Four: Multiplication of Fraction of Integer and Fraction of Integer and Fraction by the Same |
באב ארבעה וכמסין פי צרב כסר אלצחיח וכסר אלצחיח ואלכסר פי נט'ירה | |||||||||||||||||
|
|
אדא קיל לך אצֹרב תלאתת אכמאס תלאתה ותלאתת ארבאע אתנין ותלתין פי ארבעה אכמאס אתנין וכמסת אסבאע תלאתה ונצף | |||||||||||||||||
| פאנזל אלמסאלה עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| פהד אלמסאלה כל סטר מנהא ינקסם קסמין אלאול מנהא תלאתת אכמאס ואלתלאתה והו כסר צחיח וכסר ואלקסם אלתאני אלתלאתת ארבאע פאצנע באלקסם אלאול עלי מא תקדם ומא אגתמע צֹרבתה פי אימת אלקסם אלתאני והו ארבעה ותלאתה יכון אלגמיע תמאניה ומאיה תם אצנע באלקסם אלתאני כמא תקדם פי צֹרב כסר אלצחיח ואלכסרין פי באב ואחד וארבעין פמא אגתמע צֹרבתה פי אמאם אלקסם אלאול והו כמסה יגתמע לך מן דאלך עשרון ומאיה פאגמעהא אלי אלתמאניה ומאיה יכון אלגמיע תמאניה ועשרין ומאיתין והו אלכארג מן אלסטר אלאעלי ואתבע הד אלצנאעה פי אלסטר אלאספל יגתמע פיה סבעה ותמאנון ומיאתין פאצֹרבה פי אלאול ואקסם עלי אלאימה יכרג לך אלמטלוב ודאלך כמסת עשר וכמסת אעשאר ותמאנית אעשאר אלעשר הכדא | ||||||||||||||||||
|
| ||||||||||||||||||
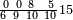
| ||||||||||||||||||
| אלגואב טרח | ||||||||||||||||||
| ואן שית פאצנע אלעמל אלתאני אלדי פי אלמסאלה קבל הדה פיכרגך אלעמל אלי הדא | ||||||||||||||||||
Chapter Fifty Five: Multiplication of Integer and Fraction and Integer and Fraction by the Same |
באב כמסה וכמסין פי צֹרב צחיח וכסר וצחיח פי מתלה | |||||||||||||||||
|
|
אדא קיל לך אצרב תלאתה ונצפא וכמסה ותלתא פי ארבעה ותלאתת ארבאע וסתה וארבעת אכמאס | |||||||||||||||||
| פאנזלהא עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| תם אבדא באלסטר אלאעלי תגד פיה צחיחאﹰ וכסרא וצחיחא וכסרא פאקסם אלסטר נצפין פיכון אלקסם אלאול אלתלאתה ואלנצף ואלקסם אלתאני כמסה ותלת פתצנע באלקסם אלאול עלי מא תקדם מן צרב אלצחיח ואלכסר ומא אגתמע צֹרבתה פי אמאם אלקסם אלתאני יכון דאלך ואחדא ועשרין תם אצנע באלקסם אלתאני עלי מא תקדם פי באבה ומא אגתמע צרבתה פי אמאם אלקסם אלאול יגתמע פיה אתנאן ותלאתון פאגמעהא אלי אלואחד ואלעשרין יכון דאלך תלאתה וכמסין והו אלכארג מן אלסטר אלאעלי ותצנע באלסטר אלתאני מתל מא צנעת באלסטר אלאול יגתמע פיה ואחד ותלאתין ומיאתין פאצֹרבה פי אלעדד אלאול ואקסם מא אגתמע עלי אלאימה יכרג לך אתנאן ומאיה ותלאתת ארבאע כמס סדס הכדא | ||||||||||||||||||
|
| ||||||||||||||||||
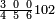
| ||||||||||||||||||
| וגואבהא טרח | ||||||||||||||||||
|
|
ואן שית פאגמע אלתלאתה ונצפא ואלכמסה ותלתא עלי מא בינתה פי באב גמע אלכסור יגתמע פיה תמאניה וכמסת אסדאס פארפעהא תם אגמע ארבעה ותלאתה ארבאע אלי סתה וארבעה אכמאס יכון דאלך אחדי עשר וכמסין ותלאתת ארבאע כמס פאצֹרבהא פי אלתמאניה וכמסת אסדאס עלי מא תקדם | |||||||||||||||||
|
| ||||||||||||||||||
| ומעני הד אלמסאלה אנה אראד אן יגמע אלצחיחין ואלכסרין מן אלכטין ותצרב אלמגתמע פי אלמגתמע | ||||||||||||||||||
|
|
ולהא מעני תאני ודאלך אנה אראד אן יאכוד ממא פי אלסטר אלאעלי מן אלכמסה ותלת נצפהא ותציפהא אלי אלתלאתה ותאכוד מן אלסטר אלאספל מן אלסתה וארבעה אכמאס תלאתה ארבאעהא פתצֹיפהא אלי אלארבעה ותצרבה פי אלאול | |||||||||||||||||
| פאעמל פי הד אלמסאלה אן תבדא באלסטר אלאעלי פתצֹרב אלתלאתה אלאול פי אלאמאם אלאול ומא אגתמע פי אלתאני פיכון דאלך תמאנית עשר תם אצרב אלכמסה פי אלתלאתה אלתי תליהא ותגמל מא עלי ראצהא ומא אגתמע צרבתה פי אלואחד אלדי עלי אלאתנין יכון דאלך סתת עשר פאגמעהא אלי אלתמאניה עשר יכון ארבעה ותלאתין והו אלכארג מן אלסטר אלאעלי פאחפט'ה תם אצנע באלסטר אלתאני כדאלך יגתמע פיה אתנין ותלאתין פאצֹרבה פי אלעדד אלאול אלמחפוט' ואקסם עלי אלאימה יכרג לך אלמטלוב ודאלך ואחד וכמסין ותלאתת אסדאס וכמסא סדס והדה צורתהא | ||||||||||||||||||
|
| ||||||||||||||||||
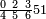
| ||||||||||||||||||
| אלגואב טרח | ||||||||||||||||||
Chapter Fifty Six: Multiplication of Integer and Two Different Fractions and Integer and Two Different Fractions and Integer by the Same |
באב סתה וכמסין פי צרב אלצחיח ואלכסרין אלמכתלפין פי צרב אלצחיח ואלכסרין אלמכתלפין ואלצחיח ואלכסרין אלמכתלפין פי אלצחיח פי מתלה | |||||||||||||||||
|
|
אדא קיל לך אצֹרב אתנין ותלאתין ותלאתת ארבאע תלאתה וארבעת אכמאס וכמסת אסדאס ארבעה פי ואחד ותלאתת אכמאס ונצף אתנין ותלאתת אגז[א] מן אחדי עשר ותסעת אעשאר תלאתה | |||||||||||||||||
|
| ||||||||||||||||||
| פאנזלהא עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| תם אנצור אלי אלסטר אלאעלי תגד פיה עדדא צחיחא פי תלאתת מואצע פי אולה ווסטה ואכרה פאקסם אלסטר אל אעלי עלי תלאתה אקסאם יכון אלאתנין אלאול מנה קסמא ואלכסראן מע אלתלאתה קסמא אכר ואלכסראן אלאכראן מע אלארבעה קסמא תאלתא פכל ואחד מן אלקסם אלתאני ואלתאלת אנמא אלמטלוב פיה אן תאכוד דאלך אלכסרין אלצחיח אלדי יליה ותגמע תלך אלאעדאד אלאתנין אלדין פי אול אלמסאלה פאלעמל פיהא עלי מא דכרנא אן תצנע באלקסם אלאוסט עלי מא תקדם פי אלבאב אלתאסע ואלתלאתין פמא אגתמע צרבתה פי אימת אלקסם יגתמע לך מן דאלך תלאתון וכמס מאיה ואלף תם תעמל באלקסם אלתאלת עלי מא תקדם פי אלבאב אלמדכור ומא אגתמע צרבתה פי אימת אלקסם אלתאני יגתמע לך מן דאלך אתנין וכמסין ותלת מאיה ואלף תם תאכוד אלאתנין אלדין פי אול אלמסאלה ותצֹרבהא פי אימת גמיע אלסטר יגתמע מן דאלך עשרין וסבע מאיה פאגמע הד אלצֹרוב אלתלאתה יכון דאלך אתנין וסת מאיה וארבעת אלאף והו אלכארג מן אלסטר אלאעלי תם אצנע כדאלך באלסטר אלאספל יגתמע פיה תסעין ותלאת מאיה וסבעת אלאף פאצרבהא פי אלעדד אלאול ואקסם מא אגתמע עלי אלאימה יכרג לך אלמטלוב ודאלך כמסה ותמאנון ותסעת אגזא מן אחדי עשר וסתת אעשאר אלגז וכמסת אסדאס עשר עשר אלגז מן אחדי עשר והדה צורתהא | ||||||||||||||||||
|
| ||||||||||||||||||
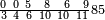
| ||||||||||||||||||
|
|
ולהד אלמסאלה וגה אכר והו אן תטלב פי אלמסאלה אן תציף אלאתנין אלאוליין מן אלסטר אלאעלי אלי אלכסרין אלדין בינהמא ותכון אלארבעה זאידה אלי אלגמע פקד אנקסם אלסטר איצא בתלאתת אקסאם אלקסם אלאול צחיח וכסראן וכדאלך אלקסם אלתאני ואלקסם אלתאלת צחיח מפרד | |||||||||||||||||
|
| ||||||||||||||||||
| פתצנע באלקסם אלאול עלי מא תקדם פי באב ארבעה ועשרין ומא אגתמע צרבתה פי אימת אלקסם אלתאני וכדאלך תצנע באלקסם אלתאלת עלי מא תקדם איצֹא מן אלבאב אלמדכור ומא אגתמע צֹרבתה פי אימת אלקסם אלאול תם תאכוד אלארבעה אלתי פי אכר אלסטר ותצרבהא פי אימת גמיע אלסטר כלה ותגמע הד אלצרוב אלתלאתה יכון דאלך תמאניה ותלאתין ותלת מאיה וארבעת אלאף פאצרבהא פי אלעדד אלאול ואקסם מא אגתמע עלי אלאימה יכרג לך אלמטלוב ודאלך תסעה ותסעין וסבעת אגזא מן אחדי עשר וכמסת אעשאר אלגז ותלאתת אסדאס עשר אלגז מן אחדי עשר כמא תרי | ||||||||||||||||||
|
| ||||||||||||||||||
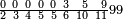
| ||||||||||||||||||
| וגואבהא בטרח | ||||||||||||||||||
| ופי אלוגה אלאול בטרח | ||||||||||||||||||
| וקד תנקסם הד אלמסאלה באקסאם אכר פמן פהם הדין אלקסמין פהם אלגרץ' פי כל מא יערץ' פי הדא | ||||||||||||||||||
Chapter Fifty Seven: Multiplication of Integer and Fraction of Fraction and Integer and Fraction of Fraction and Integer by the Same |
באב סבעה וכמסין פי צרב אלצחיח וכסר אלכסר ואלצחיח וכסר אלכסר ואלצחיח פי נט'ירה | |||||||||||||||||
|
|
אדא קיל לך אצרב אתנין ונצף כמס תלאתה ותלתיי סדס כמסה פי תלאתה ורבע סבע ארבעה וכמסת אסדאס תמן אתנין | |||||||||||||||||
|
| ||||||||||||||||||
| פצורהא הכדא עלי הדי אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| תם אקסם אלסטר אלאעלי בתלאתת אקסאם פתכון אלאתנאן אלאולאן ואלנצף כמס קסמא ואלתלאתה קסמא תאניא ואלתלתא סדס כמסה קסמא תאלתא פתצנע באלקסם אלתאני ואלתאלת עלי מא תקדם פי באב ארבעין ומא אגתמע מן אלתאני צרבתה פי אימת אלקסם אלתאני ותרפע דאלך תם תאכוד אלאתנין אלדין פי אול אלמסאלה פתצרבהא פי אימת אלסטר אלאעלי פמא אגתמע גמעתה מע אלמרפוע אלאול יכון דאלך ארבעה עשר וכמס מאיה ויכרג לך מן אלסטר אלתאני עלי מא תקדם ודאלך ארבעה וכמס מאיה וארבעת אלאף פתצרב אחד אל עדדין פי אלתאני ותקסם עלי אלאימה יכרג לך תסעה וכמסת אעשאר וסתת אתסאע אלעשר ותמנא תסע אלעשר וסדס סבע תמן תסע אלעשר והדה צורתהא | ||||||||||||||||||
|
| ||||||||||||||||||
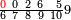
| ||||||||||||||||||
| וגואבהא אתנין | ||||||||||||||||||
|
|
ולהא מעני אכר ודאלך אן תקסם אלסטר אלאעלי בתלאתה אקסאם עלי גיר מא קסמת אולא תגעל אלקסם אלאול אתנין ונצף כמס ואלתאני תלאתה ותלתא כמס ואלתאלתה כמסה ותקסם אלסטר אלתאני עלי מא קסמת בה אלאול פיכון פי אלסטר אלאול אלקסם אלאול צחיח וכסר כסר וכדאלך אלתאני | |||||||||||||||||
|
| ||||||||||||||||||
| פתצנע בכל ואחד מנהא עלי מא תקדם פי צרב אלצחיח וכסר אלכסר ומא אגתמע מן אלקסם אלאול צֹרבתה פי אימת אלקסם אלתאני ומא אגתמע מן אלתאני צרבתה פי אימת אלאול תם תאכוד אלצחיח אלדי אכר אלמסאלה ותצרבה פי גמיע אימת אלסטר ותגמע דאלך כלה יכון תמאניה ותלאתין ותמאן מאיה ואלפא ומן אלסטר אלתאני ארבעה ותמאנין ומאיתין ואתני עשר אלפא פאצרבהא אכר אלעדדין פי אלתאני ואקסם עלי אלאימה יכרג לך תלאתה ותסעין ותלאתת אעשאר ותסעא עשר וארבע אתמאן תסע אלעשר ותסעא תמן תסע אלעשר וכמסת אסדאס סבע תמן תסע אלעשר והדה צורתהא הכדא | ||||||||||||||||||
|
| ||||||||||||||||||
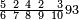
| ||||||||||||||||||
| וגואבהא בתלאתה | ||||||||||||||||||
Chapter Fifty Eight: Multiplication of Fraction and Integer and Two Different Fractions and Integer and Fraction by the Same |
באב תמאניה וכמסין פי צרב אלכסר ואלצחיח ואלכסרין אלמכתלפין ואלצחיח ואלכסר פי נצֹירה | |||||||||||||||||
|
|
אדא קיל לך אצֹרב תלאתת ארבאע כמסה ונצף וכמסת אסדאס תלאתה וכמס פי תלתיי ארבעה וסבע ותלאתת אתמאן אתנין ותלאתת אגזא מן אחדי עשר | |||||||||||||||||
|
| ||||||||||||||||||
| פאנזל אלמסאלה עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| תם אקסם אלסטר אלאעלי בקסמין יכון פי אלקסם אלואחד תלאתה ארבאע כמסה ונצף ופי אלקסם אלתאני כמסה אסדאס תלאתה וכמסין וכל ואחד מן הדין אלקסמין פי באב ואחד וארבעין [פתצנע] בכל קסם מנהא כמא תקדם פי באבה ותצרב מא כרג מן אלקסם אלאול פי אימת אלקסם אלתאני ומא כרג מן אלקסם אלתאני פי אימת אלקסם אלאול תגמע הדין אלצֹרבין יכון דאלך סבעין וסת מאיה ואלפאﹰ ומן אלסטר אלאספל תסעה וסבעין וסת מאיה וסת אלאף פאצרב אחד אלעדדין פי אלתאני ותקסם מא אגתמע עלי אלאימה יכרג כמסה ועשרין וגז מן אחדי עשר וכמסת אתסאע אלגז מן אחדי עשר וכמסת אתמאן תסע אלגז מן אחדי עשר וכמסת אסבאע תמן תמן תסע אלגז מן אחדי עשר והדי צורתהא עלי הד אלצורה | ||||||||||||||||||
|
| ||||||||||||||||||
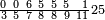
| ||||||||||||||||||
| וגואבהא בארבעה | ||||||||||||||||||
|
|
ולהד אלמסאלה וגה אכר והו אן תאכוד אלכמסת אלאסדאס מן אלקסם אלתאני ותציפהא אלי אלקסם אלאול יכון כסר עדד וכסרין מכתלפין והו מן באב תלאתה וארבעין ופי אלקסם אלתאני עדד וכסר והו מן באב אתנין ועשרין | |||||||||||||||||
| פתצנע בכל קסם עלי מא תקדם פי באבה ואלכארג מן אלקסם אלאול תצרבה פי אימת אלקסם אלתאני ואלכארג מן אלקסם אלתאני תצרבה פי אימת אלקסם אלאול ותגמע אלצֹרבין ותצנע כדאלך באלסטר אלאספל ותצרב אלמגתמע פי אלמגתמע ותקסם מא כרג עלי אלאימה יכרג לך אלמטלוב | ||||||||||||||||||
| ואעלם אן אלאצל פי הד אלמסאיל מתי קסמתהא בקסמין או תלאתה או ארבעה ואו כמסה או סתה או מא אגתמלת מן אלמעני תם צנעת בכל קסם עלי מא תקדם פי באבה או תאכוד אלמגתמע מן אלקסם אלאול ותצרבה פי אימת אלסטר אלמתקדמה כלהא ותאכוד אלמגתמע מן אלקסם אלתאני ותצרבה פי אלמתקדמה ואלמתאכרה וכדאלך תצנע באלתאלת ואלראבע ואלכאמס ואן כאן אכר אלאקסאם צחיחא פקט צרבתה פי גמיע אימת אלכסור כלהא ולא תבאלי הד אלקסם פי אי מוצע יכון פי אול אלמסאלה או פי וסטהא או פי אכרהא עלי הד אלאצל תפני גמיע מא תקדם מן אל כסור ומא תאכר מנהא | ||||||||||||||||||
| פצל | ||||||||||||||||||
|
|
וקד ינקסם הד אלמסאלה בקסמין אכרין אעני מסלת תמאניה וכמסין והו אן קד קסמת אולא בקסמין פכאן פי אלקסם תלאתת אקסאם כמסה ונצף ופי אלקסם אלתאני כמסת אסדאס תלאתה וכמסין פתאכוד אלנצף אלתאני אעני אלכסרין מן אלקסם אלאול ותציפהא אלי אלקסם אלתאני | |||||||||||||||||
|
|
פקד אקסם איצא בקסמין אלקסם אלאול תלאתת ארבאע כמסה והי מסאלה מן באב סבעה ותלאתין ופי אלקסם אלתאני נצף וכמסת אסדאס תלאתה וכמסין והי מסאלה מן באב תסעה וארבעין | |||||||||||||||||
| פתעמל בכל קסם עלי מא תקדם פי באבה ועלי מא שרטת פי הד אלבאב מן אלאצול ובאלסטר אלתאני מתל מא פעלת באלאול ותצרב אלמגתמע פי אלמגתמע ותקסם עלי אלאימה | ||||||||||||||||||
|
|
פאן קסמת הד אלמסאלה בתלאתה אקסאם פתגעל פי אלקסם אלאול תלאתת ארבאע פקט ופי אלקסם אלתאני כמסה ונצף והו מן באב אתנין ועשרין ופי אלקסם אלתאלת כמסת אסדאס תלאתה וכמס והו מן באב ואחד וארבעין | |||||||||||||||||
| פתעמל פי כל קסם עלי מא תקדם פי באבה ועלי אלשרוט אלתי שרטנא פי הד אלכתאב אלא אן אלקסם אלאול לם נביין פיה והו כסר פקט פתאכוד מא עלי ראסה ותצרבה פי באקי אלאימה וכדאלך מא אתאך מן אכר אלאקסאם כסר מפרד כאן אול אלמסאלה או וסטהא או אכרהא אנמא תאכוד מא עלי אלכט ותצֹרבה פי באקי אל אימה אלתי פי אלסטר מתקדמה ומתאכרה ותבני עלי מא תקדם | ||||||||||||||||||
|
|
וקד ינקסם הד אלבאב בתלאתת אקסאם אכר תגעל פי אלקסם אלאול תלאתה ארבאע כמסה וסדס מן באב סבעה ותלאתין ופי אלתאני נצף וכמסת אסדאס תלאתה והו מן באב תסעה ותלאתין ופי אלקסם אלתאלת כמסין
פתצנע פי כל [כסר] עלי מא תקדם פי באבה ופי אלכסר אלמפרד כמא דכרנא [ונתום] אלמסאלה עלי אלשרוט אלתי קדמנא פי הד אלבאב | |||||||||||||||||
|
|
וקד תנקסם הד אלמסאלה בתלאתת אקסאם אכרא והי אן תגמל אלקסם אלאול תלאתת ארבאע כמסה וקד דכרנאה פי אלקסם אלתאני נצפא וכמסת אסדאס והו מן באב תלאתה ותלאתין ופי אלקסם אלתאלת תלאתה ותלאתת אכמאס וקד דכרנא באבהא | |||||||||||||||||
| פתצנע פי כל קסם עלי מא תקדם פי באבה ועלי מא שרטנא פי הד אלבאב מן אלש[רוט] | ||||||||||||||||||
Chapter Fifty Nine: Multiplication of Fraction and Fraction of fraction and Integer and Two Different Fractions and Integer and Fraction and Integer and Fraction and Fraction of Fraction by the Same |
באב תסעה וכמסין פי צרב אלכסר וכסר אלכסר ואלצחיח ואלכסרין אלמכתלפין ואלצחיח ואלכסר ואלצחיח ואלכסר וכסר אלכסר פי נט'ירה | |||||||||||||||||
|
|
אדא קיל לך אצֹרב כמס אסדאס ונצף סדס תלאתה ותלאתת ארבאע וארבע אכמאס אתנין ותלאתת אתמאן ארבעה ותלאת אתסאע ותלתי תסע פי מתלהא | |||||||||||||||||
|
| ||||||||||||||||||
| פאנזל אלמסאלה עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| תם אקסם אלסטר אלאעלי בארבעה אקסאם תכון כמסת אסדאס ונצף סדס תלאתה קסם והו מן באב תמאניה ותלאתין ותכון תלאתת ארבאע וארבע אכמאס אתנין קסמא תאניא והו מן באב תסעה ותלאתין ותכון תלאתת אתמאן ארבעה ותלאתת אתסאע קסמא תאלתא והו מן באב ואחד וארבעין ויכון תלתי תסע קסמא ראבעא והו מן באב ארבעה פתעמל פי כל קסם עלי מא תקדם פי באבה פמא אגתמע מן כל קסם צֹרבתה פי סאיר אימת אלסטר ותפעל פי אלסטר אלתאני כדאלך ותצרב אלכארג פי אלכארג ומא אגתמע קסמתה עלי אלאימה יכרג לך אלמטלוב | ||||||||||||||||||
Chapter Sixty: Multiplication of Fractions |
באב סתין פי צרב אלכסר בחדף אלואו והו כסר מאכוד מן כסר | |||||||||||||||||
| וקד ינקסם הד אלבאב בקסמין מתצל ומנפצל | ||||||||||||||||||
| פאלמפצל הו אן תכון מקאמאת אלכסור פיה תתזאיד בואחד ואחד וכדאלך מא עלי כל מקאם יתזאיד בואחד ויכון אלדי עלי כל מקאם אקל מנה בואחד פהדא הו אלמתצל | ||||||||||||||||||
|
|
ומתאלה אדא קיל לך אצרב תלתיי תלאתת ארבאע ארבעה אכמאס כמסת אסדאס סתת אסבאע סבעת אתמאן תמאנית אתסאע תסעת אעשאר עשר אגזא מן אחדי עשר פי מתלה | |||||||||||||||||
|
| ||||||||||||||||||
| פחכם הד אלבאב אן תכון אלמקאמאת כלהא תחת כטא מן אלסטר אלאעלי ואלאספל עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| פלהד אלמסאלה וגהאן יריד אנך אלי שי ואחד מן אלכארג | ||||||||||||||||||
| פאלעמל אלואחד מן דאלך אנך תאכוד מא עלי אלאמאם אלאול והמא אתנאן ותצֹרבהמא פי מא עלי אלאמאם אלתאני ומא אגתמע צרבתה פי מא עלי אלתאלת ומא אגתמע צרבתה פי מא עלי אלראבע וכדאלך פי מא עלי אלכאמס ואלסאדס אלי אכרהא יגתמע פיה תמאן מאיה ותמאניה ועשרון אלפאﹰ וסת מאית אלף ותלאתת אלאף אלף וכדאלך יכרג מן אלסטר אלתאני פאצרב אלמגתמע פי אלמגתמע ואקסם עלי אלמגתמע יכרג לך אלמטלוב ודאלך ארבע אגזא מן אחדי עשר פי אלגז מן אחדי עשר והד אלעמל יצחבך פי גמיע הד אל[נוע] מתצלה ומנפצלה | ||||||||||||||||||
|
| ||||||||||||||||||
| ואלעמל אלתאני הו אן תאכוד מא עלי אול אמאם מן אלסטר אלאעלי ודאלך אתנין ותאכוד איצא מא עלי אול אמאם מן אלסטר אלאספל והמא אתנאן פתצרבהא פי אלאתנין אלאוליין יכון דאלך ארבעה ותקסמהא עלי אכר אמאם מן אלסטר אלאעלי עלי אכר אמאם מן אלסטר אלאספל יכון אלכארג מא דכרנא | ||||||||||||||||||
| ומעני הד אלמסאלה אן תאכוד ואחד פתקסמה באחדי עשר קסמא אלדי הו אכר אמאם מן אלסטר אלאעלי ועלי אכר אמאם מן אלסטר אלאספל פתאכוד מנהא עשרה אגזאיהא בעשר אגזא פתאכוד מנהא תסעה אגזאיהא בתסעה אגזא פתאכוד מנהא תמאנית אתסאעהא בתמאנית אגזא פתאכוד מנהא סבעת אתמאנהא בסבעת אגזא פתאכוד מנהא סתת אסבאעהא בסתת אגזא פתאכוד מנהא כמסת אסדאסהא בכמסת אגזא פתאכוד מנהא ארבעת א(כ)מאסהא בכמסת אגזא פתאכוד מנהא תלאתת ארבאעהא בתלאתת אגזא פתאכוד מנהא תלתיהא ודאלך גזאן פהו אלמטלוב מן אלסטר אלאעלי פתצרב גזין מן אחדי עשר פי גזין מן אחדי עשר עלי מא תקדם פי צרב אלכסר פי אלכסר פי באב תמאניה ועשרין | ||||||||||||||||||
|
| ||||||||||||||||||
| פצל | ||||||||||||||||||
| ואמא אלקסם אלתאני מן הד אלבאב והו אלמנפצל והו אן תכון אלמקאמאת לא תתזאיד בעדד ואחד ולא מא עלי ראסהא יתזאיד איצֹא בעדד ואחד פאנמא יצחבך פיה אלעמל אלאול מן הד אלמסאלה והו אן תאכוד מא עלי אלאמאם אלאול ותצרבה פי מא עלי אלתאני ומא אגתמע פי מא עלי אלתאלת ומא אגתמע פי מא עלי אלראבע אלי אכרהא ותעמל כדאלך באלסטר אלתאני ותצרב אלמגתמע פי אלמגתמע ותקסם עלי אלאימה | ||||||||||||||||||
|
|
ומתאל דאלך אצרב תלאתת אכמאס תלאתה אסבאע תסעת עשר פי תלתיי סתה אסבאע ארבעה אכמאס סבעת אתסאע | |||||||||||||||||
| פאנזלהא עלי הד אלצורה כמא תרי | ||||||||||||||||||
| ||||||||||||||||||
| תם אבדא באלסטר אלאעלי פתצרב מא עלי אלכט בעצה פי בעץ' יגתמע לך פיה תמאנית עשר ואצרב איצֹא מא עלי אלסטר אלאספל בעצֹה פי בעץ' יגתמע לך פיה סתה ותלאתין ותלאת מאיה פאצרבהא פי אלתמאנית עשר ותלאתת אסבאע סבע תסע תסע אלעשר וארבע ארבאע תסע תסע אלעשר ותלאתת אסבאע סבע תסע תסע אלעשר ותלאת אכמאס סבע סבע תסע תסע אלעשר וכמס כמס סבע סבע תסע תסע אלעשר כמא תרי | ||||||||||||||||||
|
| ||||||||||||||||||
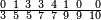
| ||||||||||||||||||
Chapter Sixty One: Multiplication of Fraction of Fraction of Integer and Fraction and Fraction of Fraction by the Same |
באב ואחד וסתין פי צרב אלכסור אלמכתלפה בחדף אלואו ואלצחיח ואלכסר וכסר אלכסר פי נט'ירה | |||||||||||||||||
|
|
אדא קיל לך אצרב תלאתת אכמאס ארבעת אסבאע תלאתה וכמסת אסדאס ונצף סדס פי תלתיי כמסת אסדאס סתה וסבעת אתמאן ותלתי תמן | |||||||||||||||||
|
| ||||||||||||||||||
| פאנזלהא עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| תם אקסם אלסטר אלאעלי בקסמין יכון פי אלקסם אלואחד אלכסר בחדף אלואו פי אול מסאלה פתעמל בה עלי מא תקדם פי באב סתין יגתמע לך אתני עשר ואלקסם אלתאני תלאתה וכמסת אסדאס ונצף סדס פתעמל בה כמא תקדם פי באב תלאתה ועשרין יגתמע פיה סבעה וארבעין פאצרבהא פי אלאתני עשר אלמרפועה יכון גמיע דאלך ארבעה וסתין וכמס מאיה פהו אלכארג מן אלסטר אלאעלי תם תתבע הד אלעמל פי אלסטר אלתאני ר' יגתמע פיה סבעון וסת מאיה ואלף פאצֹרבה פי אלעדד אלאול ואקסם עלי אלאימה יכרג לך אלמטלוב ודאלך כמסה ותסע וכמסת אתמאן אלתסע וכמסת אסבאע תמן אלתסע ותלת סבע תמן אלתסע
וגואבהא באתנין | ||||||||||||||||||
|
| ||||||||||||||||||
| פצל | ||||||||||||||||||
| פאן כאן פי מכאן כסר אלכסר כסראן מכתלפאן | ||||||||||||||||||
| פתעמל באלכסר אלאול אלדי הו בחדף אלואו כמא תקדם ותעמל באלצחיח ואלכסרין אלמכתלפין עלי מא תקדם פי באב ארבעה ועשרין ותצרב אלמגתמע פי אלמגתמע פמא כרג פהו אלכארג מן אלסטר אלאעלי וכדאלך תעמל באלתאני ותתום אלמסאלה כמא ביינת לך | ||||||||||||||||||
Chapter Sixty Two: Multiplication of Fraction of fraction of Integer by the Same |
באב אתנין וסתין פי צרב אלכסר וכסר אלכסר בחדף אלואו ואלצחיח פי נט'ירה | |||||||||||||||||
|
|
ומתאל דאלך אצֹרב תלתיי תלאתת ארבאע סתה פי תלאתה ארבאע ארבעה אתסאע תמאניה | |||||||||||||||||
| פאנזלהא עלי הד אלצורה כמא תרי | ||||||||||||||||||
| ||||||||||||||||||
Chapter Sixty Four: |
||||||||||||||||||
| [the beginning is missing] | ||||||||||||||||||
|
|
| |||||||||||||||||
| תם אבדא באלאול סטר פתצרב אלאתנין אלתי עלי אלכט אלאול פי אלסתה אלתי מעהא עלי כט ואחד תכון אתני עשר פארפעהא תם אצרב אלסתה אלתי הי אלצחיח פי אלארבעה ותגמל מא עלי ראסהא יכון סבעה ועשרון פאצרבהא פי אלאתני עשר תכון ארבעה ועשרין ותלאתת מאיה והו אלכארג מן אלסטר אלאעלי ותתבע הד אלצנאעה פי אלסטר אלתאני יגתמע פיה תמאניה ותמאנין ומאיתין פאצרבהא פי אלעדד אלאול ואקסם עלי אלאימה יכרג לך אלמטלוב ודאלך ארבעה וארבע אכמאס | ||||||||||||||||||
|
| ||||||||||||||||||
| וגואבהא באתנין | ||||||||||||||||||
| ואעלם אן הד אלמסאלה תשבה אלמסאלה אלתי פי באב ואחד וארבעין פאטלוב תגד | ||||||||||||||||||
Chapter Sixty Five: Multiplication of Fractions of Fractions by Fractions of Fractions |
באב כמסה וסתין פי צֹרב אלכסור אלמכתלפה בחדף אלואו | |||||||||||||||||
|
|
מתאל דאלך תלאתת ארבאע ארבעת אכמאס וכמסת אסדאס סתת אסבאע וסבעת אתמאן | |||||||||||||||||
|
| ||||||||||||||||||
| פאנזלהא עלי הד אלצורה כמא תרי | ||||||||||||||||||
| ||||||||||||||||||
| תם אבדא באלסטר אלאעלי תגד פיה תלאתה כטוט תחת כל כטא אמאמין פתאכוד מא עלי אלכט אלאול ותצרב אלאעדאד אלדי עליה בעצֹהא פי בעץ ומא אגתמע צרבתה פי באקי אימת אלסטר וכדאלך תצנע באלכט אלתאני ואלתאלת ותגמע אלצרוב אלתלאתה יכון דאלך תמאניה ועשרין וסתה וכמס מאיה וסתה ועשרין אלפא ומאיה אלף פאצרבהא פי אלעדד אלאול ואקסם עלי אלאימה יכרג לך ארבעה וסתת אלסבאע תסע אלעשר וסדס סבע תסע אלעשר | ||||||||||||||||||
|
| ||||||||||||||||||
| וגואבהא בטרח | ||||||||||||||||||
| ואן שית פי הד אלמסאלה אן תעמלהא באקרב מן הדא והו אן תאכוד מן אלארבעת אכמאס אלדי פי אול כט מן אלסטר אלאול תלאתת ארבאעהא ודאלך תלאתת אכמאס ומן אלסתת אסבאע כמסת אסדאסהא ודאלך כמסת אסבאע ותאכוד מן אלתמאנית אתסאע סבעת אתמאנהא ודאלך סבעת אתסאע פיכון מעך פי אלסטר אלאעלי תלאתת אכמאס וכמסת אסבאע וסבעת אתסאע והי תלאת כסור מכתלפה תם תרגע אלי אלסטר אלאספל פתאכוד מן אלתלאתת ארבאע תלתהא ודאלך נצף ותאכוד מן אלכמסת אסדאס ארבע אכמאסהא ודאלך תלתאן ותאכוד איצא מן אלסבעה אתמאן סתת אסבאעהא ודאלך תלאתת ארבאע פיכון פי אלסטר אלאספל תלאתת כסור מכתלפה והי נצף ותלתאן ותלאתת ארבאע פתעמל פי הד אלמסאלה עלי מא תקדם פי באב כמסה ותלאתון ואלכארג באלאול | ||||||||||||||||||
|
| ||||||||||||||||||
Chapter Sixty Six: Multiplication of Integer and Fraction of Fraction by Integer and Fraction of Integer |
באב סתה וסתין פי צֹרב אלצחיח ואלכסר וכסר אלכסר בחדף אלואו פי אלצחיח ואלכסר ואלצחיח | |||||||||||||||||
|
|
אדא קיל לך אצרב תלאתה ותלאתת אכמאס כמסת אסדאס פי ארבעה וסבעין תלאתה | |||||||||||||||||
| פאנזל אלמסאלה עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| תם תאכוד אלתלאתה אלצחאח אלתי פי אול אלמסאלה פתצֹרבהא פי אימת אלסטר פי אלכמסה אולא ומא אגתמע פי אלסתה ותנזלה אלי נאחיה תם תצֹרב מע עלי אלכט בעצֹה פי בעץ' ותצֹיפהא אלי אלעדד אלמרפוע יגתמע פיה כמסה ומאיה תם תרג'ע אלי אלסטר אלתאני פתצרב אלארבעה אלצחיחה פי מקאם אלסבע ותצֹרב אלאתנין אלדי עלי אלסבע פי אלתלאתה אלצחיחה ותגמע אלצרבין יגתמע לך פיה ארבעה ותלאתון פאצֹרב אכר אלעדדין פי אלתאני ואקסם עלי אלאימה יכרג לך סבעת עשר | ||||||||||||||||||
|
| ||||||||||||||||||
Chapter Sixty Seven: Multiplication of Integer and Fraction of Fraction and Fraction by the Same |
באב סבעה וסתין פי צרב אלצחיח ואלכסר וכסר אלכסר בחדף אלואו ואלכסר אלמפרד פי נט'ירה | |||||||||||||||||
|
|
ומתאל דאלך אצרב אתנין ותלאתת אסבאע תלאתת אכמאס ותלתין פי תלאתה ותלאתת ארבאע כמסת אסדאס ונצף | |||||||||||||||||
| פאנזלהא הכדא | ||||||||||||||||||
| ||||||||||||||||||
| תם אבדא באלסטר אלאעלי פתצֹרב אלאתנין אלדין פי אול אלמסאלה פי גמיע אלסטר תם תצרב מא עלי אלכט בעצֹה פי בעץ' ומא אגתמע פי אלאמאם אלדי תחת אלכט אלתאני תם תאכוד מא עלי אלכט אלכסר אלמפרד ותצרבה פי אימת אלכט אלאול ותגמע הד אלצֹרוב אלתלאתה תכון סבעה ותלאתת מאיה מן אלכט אל תאני תמאניה ותסעין ומאיה פאצרב אחדהמא פי אלתאני ואקסם עלי אלאימה יכרג לך אלמטלוב ודאלך אתני עשר ותלאתת אסבאע אלתמן וכמסא סבע אלתמן וכמל דאלך | ||||||||||||||||||
|
| ||||||||||||||||||
Chapter Sixty Eight: Multiplication of Fraction of Fraction and Integer and Fraction of Fraction by the Same |
באב תמאניה וסתין פי צֹרב כסר אלכסר בחדף אלואו ואלצחיח ואלכסר וכסר אלכסר בחדף פי נט'ירה | |||||||||||||||||
| אדא קיל לך אצרב תלאתת ארבאע ארבעה אכמאס אתנין ותלאתת אכמאס כמסת אסדאס פי מתלהא | ||||||||||||||||||
| פאנזלהא עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| תם תקסם אלכט אלאול מנהא בקסמין | ||||||||||||||||||
| פאמא אן תגעל אלאתנין אלדין המא אלצחיח והמא פי צדר אלמסאלה מן אלקסם אלאול ומן אלקסם אלתאני | ||||||||||||||||||
|
|
פאן געלתהא פי אלקסם אלתאני רגע אלקסם אלתאני מן באב סתה וסתין ואלאול מן באב סתין פתגעל פי כל ואחד מן הדין אלקסמין עלי מא תקדם פי באבה ומא אגתמע מן אלקסם אלאול צרבתה פי אימת אלקסם אלתאני ומא אגתמע מן אלקסם אלתאני צרבתה פי אימת אלקסם אלאול וגמעת אלצרבין וצנעת כדאלך באלסטר אלתאני וצרבת אלמגתמע פי אלמגתמע וקסמת עלי אלאימה יכרג לך אלמטלוב | |||||||||||||||||
|
| ||||||||||||||||||
|
|
פאן רדדת אלאתנין אלי אלקסם אלאול פיכון אלקסם אלקסם אלאול מן באב אתנין וסתין ואלקסם אלתאני מן באב סתין ותעמל עלי מא תקדם | |||||||||||||||||
| פאן לם יקסם אלמסאלה ובקית עלי חאלהא וארדת אן תאכוד מן אלאתנין ותלאתת אכמאס כמסת אסדאס תלאתת ארבאע ארבע אכמאסהא פתנזל אלמסאלה עלי חאלהא תם תצרב מא עלי אלכט בעצֹה פי בעץ' פתרפעה תם תצרב אלאתנין פי אלכמסה ומא אגתמע פי אלסתה ותצרב מא עלי אלכט אלאכר בעצֹה פי בעץ' ותצֹיפה אלי צרב אלאתנין פי אלאימה פמא אגתמע צרבתה פי אלעדד אלמרפוע אולא יגתמע מן דאלך תסע מאיה ומן אלתאני כדאלך פתצרב אחדהמא פי אלתאני ותקסם עלי אלאימה יכרג מן דאלך תסע מאיה ומן אלסטר אלתאני כדאלך יכרג אתנין ורבע | ||||||||||||||||||
|
| ||||||||||||||||||
| וגואבהא באתנין | ||||||||||||||||||
Chapter Sixty Nine: Multiplication of Two Different Fractions and Integer and Fraction of Fraction and Integer and Fraction and Fraction of Fraction and Integer and Fraction of Fraction and Integer and Fraction |
באב תסעה וסתין פי צרב אלכסרין אלמכתלפין ואלצחיח ואלכסר וכסר אלכסר בחדף אלואו ואלצחיח ואלכסר וכסר אלכסר בחדף אלואו ואלצחיח ואלכסר וכסר אלכסר בחדף אלואו ואלצחיח ואלכסר אלמפרד פי מתלה | |||||||||||||||||
| מתאל דאלך אדא קיל לך אצרב תלאתת ארבאע וכמסת אסדאס ארבעה ותלאתת אכמאס סתה אסבאע תלאתה וכמסת אסדאס ונצף סדס ארבעה וסבעת אתמאן תמאנית אתסאע תלאתה ונצף פי מתלהא | ||||||||||||||||||
| פאנזלהא עלי הד אלצורה כמא תרי | ||||||||||||||||||
|
| |||||||||||||||||
| ואעלם אן הד אלמסאלה לא תנעמל עלי חיאלהא אלא אן תרדהא אלי מעני אכצר מן גמיע מא דכרנא מן אלכסר | ||||||||||||||||||
|
|
ולהד אלמסאלה מעאני כתירה פאכרהא אן אלתלאתה ונצפא אלתי אכר אלמסאלה סבעת אתמאן תמאנית אתסאעהא פהד אלמסאלה מן באב ארבעה וסתין ותטלב איצא מן אלארבעה אלתי הי אלצחיח כמסה אסדאס ונצף סדסהא פהדה מסאלה מן באב תמאניה ותלאתין ותטלב איצֹא מן אלתלאתה אלתי הי אלצחיח תלאתת אכמאס סתה אסבאעהא פהדי מסאלה מן באב אתנין וסתין ותטלב איצא מן אלארבעה אלתי הי אלצחיח כמסת אסדאסהא ותלאתת ארבאעהא פהדה מסאלה מן באב תסעה ותלאתין ותריד אן תגמע הדה כלה ותצֹרבה פי מתלה או פי גירה | |||||||||||||||||
|
| ||||||||||||||||||
| פאלעמל פי הד אלמסאלה אן תעמל פי כל קסם קסמנא בה אלמסאלה ודכרנא באבהא עלי מא דכרנא פי באבה ומא אגתמע מנה צרבתה פי אימת אלאקסאם אלבאקיה ותגמע אלצֹרוב כלהא ותעמל עלי מא תקדם | ||||||||||||||||||
| וכדאלך אן שית אן תקסם הד אלמסאלה פגייר הד אלאקסאם פתעמל בכל קסם עלי מא תקדם פי באבה | ||||||||||||||||||
| ואעלם אן הד אלמסאלה להא אכתר מן עשרין וגהא מן אלעמל גמיע מא יכד בעד הדא אן שא אללה תעלי | ||||||||||||||||||
Chapter Seventy: Multiplication of Integer and Fraction by Integer and Fraction by Integer and Fraction and so on |
אלבאב אלמופי סבעין פי צרב אלעדד ואלכסר פי אל עדד ואלכסר פי אלעדד ואלכסר ומא אגתמע פי עדד וכסר אלי מא לא נהאיה לה | |||||||||||||||||
|
|
ומתאל דאלך אדא קיל לך אצרב ואחד ונצפא פי ואחד ותלת פי ואחד ורבע פי ואחד וכמס פי ואחד וסדס פי ואחד וסבע פי ואחד ותמן פי ואחד ותסע פי ואחד ועשר פהדי תסע מסאיל מן צחיח וכסר | |||||||||||||||||
|
| ||||||||||||||||||
| פאנזלהא עלי הד אלצורה | ||||||||||||||||||
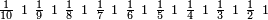
| ||||||||||||||||||
| תם תאכוד אלואחד אלדי פי אול אלמסלה ותצרבה פי אלאתנין אלתי הי מקאם אלכסר ותגמל מע עלי ראסהא כמא תקדם פי באב אלעדד ואלכסר פי אלעדד ואלכסר יכון דאלך תלאתה פאתבתהא תחתהא ותצנע באלתאניה כדאלך יגתמע פיה ארבעה פאתבתהא תחתהא ותגמע לדי אלמסאלה אלתאניה כמסה ופי אלראבעה סתה ופי אלכאמסה סבעה ופי אלסאדסה תמאניה ופי אלסאבעה תסעה ופי אלתאמנה עשרה ופי אלתאסעה אחדי עשר פאצרב הד אלאעדאד בעצהא פי בעץ' פמא אגתמע קסמתה עלי אלאימה יכרג לך אלמטלוב ודאלך כמסה ונצף | ||||||||||||||||||
|
| ||||||||||||||||||
| ואן שית אכדת אול מסאלה והי ואחד ונצף פתצֹרבהא אנצאפא תכון תלאתת אנצאף פאצֹרבהא פי אלואחד ותלת תכון ארבע אנצאף פאצרבה פי אלואחד ורבע תכון כמסת אנצאף אצרבהא פי ואחד וכמס תכון סתת אנצאף אצֹרבהא פי ואחד וסדס תכון סבעת אנצאף אצרבהא פי ואחד וסבע תכון תמאנית אנצאף אצרבהא פי ואחד ותמן תכון תסעת אנצאף אצרבהא פי ואחד ותסע תכון עשרת אנצאף אצרבהא פי ואחד ועשר תכון אחדי עשר נצפא פתצרבהא אחאד תכון כמסה ונצפא | ||||||||||||||||||
|
| ||||||||||||||||||
Chapter Seventy One: Multiplication of Subtracted Fractions |
באב ואחד וסבעין פי צֹרב אלכסור באלאסתתנא | |||||||||||||||||
| אדא קיל לך אצֹרב תלאתת ארבאע אלא סדסא פי ארבעת אכמאס אלא תלתא | ||||||||||||||||||
| פאנזלהא עלי הד אלצורה | ||||||||||||||||||
|
| |||||||||||||||||
| פהד אלמסאלה תחתמל מעניאן: | ||||||||||||||||||
|
|
אחדהא אנה אראד אן תאכוד תלאתה ארבאע ותסקט מנהא סדסא ואחדא ותרפע אלבאקי תם תאכוד ארבע אכמאס ואחד ותסקט מנה תלת ואחדא ותצרב אלבאקי פי אל באקי | |||||||||||||||||
| פוגה אלעמל פי הד אלוגוה אן תצרב מא עלי ראס אלארבעה פי אלסתה תכון תמאניה עשר והו אלמטלוב מן אלסטר אלאעלי תם תצרב אלסטר אלאספל אעני מא עלי אלכמסה פי אלתלאתה תכון אתני עשר ותצרב מא עלי אלתלאתה פי אלכמסה ותסקטה מן אלאתני עשר אלבאקי סבעה פאצרבהא פי אלארבעת עשר אלמחפוטה ואקסם עלי אלאימה יכרג לך תסעאן ותלאתת אתמאן אלתסע ותלאתת אכמאס תמן אלתסע | ||||||||||||||||||
|
| ||||||||||||||||||
|
|
ואמא אלוגה אלתאני פהו אן תאכוד תלאתת ארבאע ואחד ותסקט מנהא תלתהא ותצרב אלבאקי פי אלבאקי | |||||||||||||||||
| פוגה אלעמל פי הד אלבאב אן תצרב אלתלאתה פי אלסתה תכון תמנית עשר ותאכוד מא עלי אלסתה ותצרבה פי מא עלי אלארבעה והי תלאתה ותסקטהא מן אלתמנית עשר יכון אלבאקי כמסת עשר ותפעל באלסטר אלתאני כדאלך יכון דאלך תמאניה פתצרבהא פי אלבאקי מן אלסטר אלאעלי יכרג לך עשרין ומאיה פאקסמהא עלי אלאימה יכרג אלמטלוב תלאתה | ||||||||||||||||||
|
| ||||||||||||||||||
Chapter Seventy Two: Multiplication of Reduced Fractions of Integers |
באב אתנין וסבעין פי צרב כסר אלעדד באלאסתתנא | |||||||||||||||||
| אדא קיל לך אצרב תלאתת ארבאע כמסת | ||||||||||||||||||
| פאנזלהא עלי הד אלצורה | ||||||||||||||||||
|
| |||||||||||||||||
| פהד אלמסאלה תחתמל תלת וגוה | ||||||||||||||||||
|
|
ודאלך אנה אראד תאכוד מן אלכמסה תלאתת ארבאעהא | |||||||||||||||||
| פאלעמל פי הד אלוגה אן תצרב אלתלאתה אלתי עלי אלארבעה פי אל כמסה ומא אגתמע פי אלסתה אלתי הי אלאמאם אלתאני יכון דאלך תסעין תם תאכוד אלואחד אלדי עלי אלסתה פתצרבה פי אלכמסה ומא אגתמע פי אלארבעה אלתי הי אלאמאם אלאול יכון דאלך עשרין פאסקטהא מן אלתסעין אלבאקי סבעין ואלבאקי מן אלסטר אלתאני בהד אלעמל תלאתה ותלאתין פאצרבהא פי אלסבעין ואקסם מא אגתמע עלי אלאימה יכרג לך ארבעה וסתת אתמאן ונצף תמן | ||||||||||||||||||
|
| ||||||||||||||||||
|
|
ואלוגה אלתאני אנה אראד אן תאכוד תלאתת ארבאע אלכמסה ותסקט מנהא סדסהא ותאכוד איצא ארבעת אכמאס אלתלאתה ותסקט מנהא רבעהא ותצרב אלבאקי פי אלבאקי | |||||||||||||||||
| פוגה אלעמל אן תצרב אלתלאתה פי אלכמסה ומא אגתמע פי אלסתה תכון תסעין עלי מא תקדם תם תאכוד אלואחד אלדי עלי אלסתה ותצֹרבה פי אלכמסה ומא אגתמע פי אלתלאתה אלתי עלי ראס אלכמסה תכון כמסת עשר פאסקטהא מן אלתסעין אלבאקי כמסה וסבעין ואלבאקי מן אלסטר אלתאני בהד אלעמל סתה ותלאתין פתצרב אלעדדין אחדהא פי אלתאני ותקסם עלי [אלאימה] | ||||||||||||||||||
|
| ||||||||||||||||||
|
|
ואלוגה אלתאלת אן תאכוד תלאתת ארבאע אלכמסה ותסקט מנהא סדסא ואחדא ותאכוד איצֹא ארבעת אכמאס אלתלאתה ותסקט מנהא רבעא ואחד ותצרב אלבאקי פי אל[באקי] | |||||||||||||||||
| פוגה אלעמל אן תצרב אלתלאתה פי אלכמסה ומא אגתמע פי אלסתה כמא תקדם פי אלוגה אלאול יכון תסעין תם תצרב אלואחד אלדי עלי אלסתה פי אלארבעה אלתי הי אלאמאם ותסקטהא מן אלתסעין אלבאקי סתה ותמאנ[ין] ואלבאקי מן אלסטר אלתאני בהד אלעמל תלאתה וארבעין פאצרב אחד אלעדדין פי אלתאני ואקסם עלי אלאימה יכרוג לך אלמטלוב | ||||||||||||||||||
|
| ||||||||||||||||||
| ואד קד אתינא מן צרב אלכסור עלי פיה כפאיה למן תדברהא ועלם אלמראד מנהא ממא לא יסע אחד גהלהא ותרכנא אלתטויל ואלתשגיב ומא דכרנא יקא[ד] עליה גמיע אלחסאב ואללה אלמופק לאלצואב פלנבדא בצרב אלכסור והו באב חסן כתיר אלמנפעה מן גמיע אלכסור | ||||||||||||||||||
| פתפהם גמיעה ואללה אלמופק לאלצואב במנה וקותה | ||||||||||||||||||
Converting Fractions to Lower Fractions |
באב צרף אלכסור בעצהא אלי בעץ' | |||||||||||||||||
| אעלם אן הד אלבאב אנמא מענאה אן תרוד אלכסר מן אסם אלי אסם אכר אמא אד[א] מנה פי אלגז או אכבר ואמא אלאחסן פיהא אן תצרף אלכסור כלהא אלי אדק גז והו אן תרוד אלאתלאת ארבאעא או אכמאסא או אעשארא ואן תרוד אלאסדאס אסבאעאﹰ פהו אחסן אלי אן תדפע אליה צֹרורה ענד גמע אלכסור או טרחהא וסנביינהא פי מכאנהא אן שא אללה תעלי | ||||||||||||||||||
Simple fraction to simple fraction |
באב מנה אכר מן אלצרף והו צרף אלכסר אלי אלכסר | |||||||||||||||||
|
|
אדא קיל לך כמסת אסדאס כם סבע תכון | |||||||||||||||||
| פאנזל אלכמסת אסדאס פי סטר ואנזל מקאם אלסבע והו סבעה פי סטר תחתה ומוד כטא בינהמא עלי הד אלצורה | ||||||||||||||||||
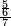
| ||||||||||||||||||
|
|
תם אצרב אלכמסה אלדי עלי אלסתה פי אלסבעה אלתי תחת אלכט אלאספל יכון דאלך כמסה ותלאתין פאקסמהא עלי אלסתה אלתי הי אלאמאם פי אלכט אלאעלי פמא כרג קסמתה עלי אלסבעה אלתי הי מקאם אלסבע יכרג לך פי אלקסמה כמס אסבאע וכמסת אסדאס אלסבע | |||||||||||||||||
|
|
ואן קאל תלאתת אתמאן כם תסע תכון | |||||||||||||||||
|
|
פאצרב אלתלאתת עדד אלאתמאן פי אלתסעה אלתי תריד אן תצרף אליהא אלאתמאן תכון סבעה ועשרין פאקסמהא עלי אלתמאניה אלתי הי מקאם אלתמן תכרג תלאתה פאלתלאתה אלכארגה הי אתסאע ואלתלאתה אל באקיה הי אתמאן אלתסע | |||||||||||||||||
| ואעלם אן גמיע עמל הד אלבאב אמא אן תאכוד עדד אלכסר אלמצרוף אליה פתצרובה אבדא פי מקאם אלמצרוף אולא ומא כרג עלי מקאם אלכסר אלמצרוף אליה והד אלעמל עאם פי גמיע באב אלצרף | ||||||||||||||||||
|
|
פאן קאל תסעה אעשאר כם גז מן אחדי עשר תכון | |||||||||||||||||
|
|
פאצרב תסעה פי אחדי עשר ותקסם מא כרג עלי אלעשרה אולא ומא כרג עלי אלאחדי עשר יכרג תסע אגזא מן אחדי עשר ותסעת אעשאר אלגז מן אחדי עשר | |||||||||||||||||
Fraction and fraction of fraction to fraction |
באב מנה אכר | |||||||||||||||||
|
|
אדא קיל לך כמסת אסדאס ונצף סדס כם עשר יכון | |||||||||||||||||
| פאנזל אלמסאלה עלי הד אלצורה | ||||||||||||||||||
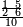
| ||||||||||||||||||
|
|
תם אצנע באלכמסת אסדאס ונצף סדס עלי מא תקדם פי באב אלכסור יגתמע לך פיהא אחדי עשר פאצרבהא פי אלעשרה ואקסם מא אגתמע עלי אימת אלסטר אלאעלי תם מא כרג עלי אלעשרה יכרג לך אלמטלוב ודאלך תסעת אעשאר וסדס אלעשר | |||||||||||||||||
|
|
פאן קאל כמסת אתמאן ותלת תמן כם גז מן תלאתת עשר תכון | |||||||||||||||||
| פאנזל אלכמסת אתמאן ותלת תמן פי סטר ואנזל תחתה פי סטרא אכר מקאם אלגז מן תלאתה עשר תחת כטא עלי הד אלצורה | ||||||||||||||||||
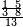
| ||||||||||||||||||
| תם אצנע באלכמסת אתמאן ותלת תמן כמא תקדם ומא אגתמע צרבתה פי אלתלאתה עשר יגתמע מן דאלך תמניה ומיאתין פאקסמהא עלי אלאימה אלכט אלאעלי ומא כרג עלי אלתלאתת עלי יכרג תמאנית אגזא מן תלאתת עשר וכמסת אתמאן אלגז ותלת תמן אלגז מן תלאתת עשר | ||||||||||||||||||
|
| ||||||||||||||||||
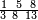
| ||||||||||||||||||
Fraction and fraction to fraction |
באב מנה אכר | |||||||||||||||||
|
|
אדא קיל לך תלתאן וכמסת אסדאס כם עשר יכון פיהא | |||||||||||||||||
|
|
פהד אלמסאלה יגתמע פיהא מן אלאעשאר אכתר מן עשרה לאן אלתלתין אדא צרפתהא אסדאס תכון ארבע אסדאס ומעני פי אלכסר אלתאני כמסת אסדאס מענא תסעת אסדאס | |||||||||||||||||
| פאדא אראדת אן תצרף הד אלמסאלה אעשאר פאנזל אלתלתין ואלכמסת אסדאס פי סטר ואנזל תחתה מקאם אלעשר פי סטר אכר עלי הד אלצורה הכדא | ||||||||||||||||||
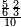
| ||||||||||||||||||
|
|
תם אצנע באלתלתין וכמסת אסדאס עלי מא תקדם מן צרב אלכסרין אלמכתלפין ומא אגתמע צרבתה פי אלעשרה יכרוג לך כמסת עשר עשרא והו ואחד ונצף | |||||||||||||||||
Fraction of fraction to fraction of fraction |
באב מנה אכר | |||||||||||||||||
|
|
אדא קיל לך תלת כמס כם רבע כמס יכון | |||||||||||||||||
| פהד אלמסאלה ישתרך פיהא אלכמס פי אלוגהין פי אלמצרוף ואלמצרוף אליה פאצקט לפט' אלכמס מן אלוגהין מתי אתפקא אבדא | ||||||||||||||||||
|
|
תם תקול תלת כם רבע יכון | |||||||||||||||||
|
|
פתעמל עלי מא תקדם פי אלבאב אלאול מן אלצרף יכרג לך רבע ותלת | |||||||||||||||||
|
|
באלנסבה אלי כמס ואחד מן תלך אלאכמאס אלתי אסקטנא דכרהא פיכון אדא כמס ותלת רבע כמס | |||||||||||||||||
|
|
וכדאלך אן קאל רבע סבע כם כמס סבע | |||||||||||||||||
|
|
פתסקט אלסבע באלסבע אבדא תם תקול רבע כם כמס תכון יכרג לך רבע כמס פהו כמס סבע ורבע כמס סבע | |||||||||||||||||
|
|
פאן קאל כמס תמן כם סבע תסע תכון | |||||||||||||||||
| פאנזל כמס אלתמן פי סטר ואנזל תחתה סבע אלתסע עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
|
|
תם תאכוד אלואחד אלדי הו אלכמס מן אלסטר אלאעלי פתצרבה פי אימת אלסטר אלאספל ומא אגתמע קסמתה עלי אלאימה אלסטר אלאעלי יכרג לך סבע תסע וארבעת אתמאן סבע [תסע] ותלאתת אכמאס תמן סבע תסע | |||||||||||||||||
Fractions of fractions to fraction |
באב מנה אכר | |||||||||||||||||
|
|
אדא קיל לך תלאתת ארבאע כמס וכמסת אסדאס סבע וסבעת אתמאן תסע כם עשר יכון פיהא | |||||||||||||||||
| פאנזלהא עלי הד אלצורה כמא תרי | ||||||||||||||||||
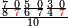
| ||||||||||||||||||
| פתעמל פי הד אל[מסאל]ה אעני פי אלסטר אלאעלי עלי מא תקדם פי צרב אלתלת כסור אלמכתלפה פי מתאלהא ודאלך אן תאכוד אלתלאתה אלתי עלי אלכט מן אלסטר אלאול פתצרבהא פי אלאימה אלתי תחת אלכט אלתאני תצרב אולא פי אלואחד ומא אגתמע צרבתה פי אלתאני ומא אגתמע צרבתה פי אלכט אלתאלת ותרפעה תם תאכוד מא עלי אלכט אלאוסט פתצרבה פי אימת אלאול ומא אגתמע פי אימת אלכט אלתאלת תם תאכוד מא עלי אלכט אלתאלת ותצרבה פי אימת אלכט אלתאני ומא אגתמע פי אלאול ותגמע הד אלצרוב אלתלאתה ותצרבהא פי אלעשרה | ||||||||||||||||||
|
| ||||||||||||||||||
| ואד קד ביינא מן צרב אלכסור מא פיה כפאיה למן יתדברהא פלנבדא אלאן בגמע אלכסור ובעדה איצא בטרחהא ותתבע פיהא טריק אלאכתצאר ונתרך אלתטויל מע מא ינט'אף אליהא מן שכלהא ממא יחתאג אליה פי אלגמע אן שא אללה תעלי | ||||||||||||||||||
Addition of Fractions |
||||||||||||||||||
Chapter One – Adding One Fraction to Another |
אלבאב אלאול מנהא ודאלך גמע אלכסור בעצ'הא אלי בעץ' | |||||||||||||||||
|
אדא קיל לך אגמע תלאתת ארבאע אלי ארבעת אכמאס | |||||||||||||||||
| פאנזל אלתלאתה אלארבע ואלארבעת אלאכמאס פי סטר ואחד עלי הד אלצורה | ||||||||||||||||||
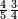
| ||||||||||||||||||
|
|
תם אצרב מא עלי אלכט אלאול פי מא תחת אלתאני ומא עלי אלכט אלתאני פי מא תחת אלכט אלאול עלי מא תקדם פי צרב אלכסרין אלמכתלפין ותגמע אלצרבין יכון דאלך ואחד ותלאתין פאקסמהא עלי אלאימה עלי אלארבעה ומא כרג עלי אלכמסה יכרג לך אלמטלוב ודאלך ואחד וכמסאן ותלאתת ארבאע אלכמס | |||||||||||||||||
| ואמתחאנהא עלי מא תקדם מן צרב אלכסור עלי הד אלעמל פיהא | ||||||||||||||||||
| ולהא וגהא אכר והו אן תצרב אלתלאתת ארבאע אל כמס תכון תלאתת אכמאס ותלאתת ארבאע אלכמס פתגמעהא אלי אלארבעה אכמאס תכון סבעת אכמאס אסקט מנהא כמסה בואחד תבקי כמסאן ותלאתת ארבאע אלכמס ואלמגתמע מנהא אדא ואחד וכמסאן ותלאת ארבאע אלכמס | ||||||||||||||||||
|
| ||||||||||||||||||
Chapter Two – Adding Two Fractions to Two Fractions |
באב גמע אלכסרין אלי אלכסרין | |||||||||||||||||
|
אדא קיל לך אגמע תלאתת ארבאע וארבעת אכמאס אלי כמסת אסדאס וסתת אסבאע | |||||||||||||||||
| פאנזל אלתלאתת ארבאע ואלארבעת אכמאס פי סטר ואנזל תחתה פי סטר אלכמסת אסדאס ואלסתת אסבאע עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| תם תצנע באלסטר אלאעלי עלי מא תקדם פי צרב אלכסרין אלמכתלפין פי באבהא יגתמע מן דאלך [ו]אחד ותלאתין פאצרבהא פי אימת אלסטר אלאספל תם תצנע באלסטר אלאספל כמא תקדם פי אלסטר אלאעלי ומא אגתמע צרבתה פי אלסטר אלאעלי יגתמע לך מן דאלך עשרין וארבע מאיה ואלף פאגמעהא אלי אלעדד אלמחפוט אלאול יכון דאלך אתנין ועשרין וסבע מאיה ואלפין פאקסמהא עלי אלאימה יכרג מן אלקסמה תלאתה וסבע וארבע אסדאס אלסבע ונצף כמס סדס אלסבע | ||||||||||||||||||
|
| ||||||||||||||||||
| פצל | ||||||||||||||||||
| ואעלם אן גמיע אלעמל פי גמע אלכסור או אלצחיח ואלכסר בעצהא אלי בעץ פאלאצל פיהא אן תצנע בכל עדד כמא עמלת בה פי באבה פי אלצרב פמא אגתמע מן דאלך צרבתה פי אימת אלסטר אלאעלי ובעד דאלך תגמע הדין אלעדדין ותקסמה עלי אלאימה פאן כנת פי אלטרח טרחת אחד הדין אלעדדין מן אלאכר וקסמת אלבאקי עלי אלאימה ואן כנת פי אלקסמה קסמת אחד הדין אלעדדין עלי אלתאני יכרוג לך אלמטלוב וסנביין מן אלמקסום מנהא עלי צאחבה פי באב אלקסמה | ||||||||||||||||||
| ואעלם אן הד אלעמל יצחבך פי אלגמע ואלטרח ואלגבר פי בעץ אלמסאיל וכדאלך פי אלחט ואלקסמה | ||||||||||||||||||
Chapter Three – Adding Fraction and Fraction of Fraction to Two Different Fractions |
באב גמע אלכסר וכסר אלכסר אלי אלכסרין אלמכתלפין | |||||||||||||||||
| [the chapter appears twice in the manuscript] | ||||||||||||||||||
|
אדא קיל לך אגמע כמסת אסדאס ונצף סדס אלי סבעת אתמאן ותמאנית אתסאע | |||||||||||||||||
| פאנזל אלמסאלה עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| תם אצנע באלכמסת אסדאס ונצף סדס עלי מא תקדם פי צרב אלכסר וכסר אלכסר ומא אגתמע צרבתה פי אימת אלסטר אלאספל יגתמע מן דאלך אתנין ותסעין וסבע מאיה פאחפטהא תם אצנע באלכסרין עלי מא תקדם פי באבהא ומא אגתמע צרבתה פי אימת אלכט אלאעלי יגתמע מן דאלך ארבעה ועשרין וכמס מאיה ואלף פאגמעה אלי אלמחפוט אלאול יגתמע מן דאלך סתת עשר ותלאת מאיה ואלפאן פאקסמהא עלי אלאימה יכרג לך אתנאן וסתת אתסאע ותמן תסע | ||||||||||||||||||
|
| ||||||||||||||||||
Chapter Four – Adding Fraction and Fraction of Fraction to Fraction and Fraction of Fraction |
באב גמע אלכסר וכסר אלכסר אלי אלכסר וכסר אלכסר | |||||||||||||||||
|
אדא קיל לך אגמע כמסת אגזא מן אחדי עשר ותלאתת ארבאע אלגז מן אחדי עשר אלי עשרת אגזא מן תלת עשר ותמאנית אתסאע אלגז מן תלת עשר | |||||||||||||||||
| פאנזלהא עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| תם תצנע בכל סטר מנהא עלי מא תקדם פי באבה ומא אגתמע מן אלסטר אלאעלי צרבתה פי אימת אלסטר אלתאני ומא אגתמע פי אימת אלסטר אלאספל צרבתה פי אימת אלסטר אלאעלי ותגמע אלצרבין ותקסמה עלי אלאימה יכרג לך ואחד וארבעת אגזא מן תלת עשר וסבעת אגזא מן אחדי עשר פי אלגז מן תלת עשר וארבעת אתסאע אלגז ותלאתת ארבאע תסע אלגז מן אחדי עשר פי אלגז מן תלאתת עשר | ||||||||||||||||||
|
| ||||||||||||||||||
Chapter Five – Adding Integer and Fraction to Integer and Fraction |
באב גמע אלצחיח ואלכסר אלי אלצחיח ואלכסר | |||||||||||||||||
|
אדא קיל לך אגמע אתנין ונצף אלי תלאתה וכמסין | |||||||||||||||||
| פאנזלהא עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| תם תצנע בכל סטר מנהא עלי מא תקדם פי באב אתנין ועשרין פי צרב אלצחיח ואלכסר פי אלצחיח ואלכסר ומא אגתמע לך מן אלסטר אלאעלי צרבתה פי אלכמסה אלתי הי אמאם אלכט אלאספל ומא אגתמע איצא מן אלכט אלאספל צרבתה פי אלאתנין אלתי הי אמאם אלכט אלאעלי ואגמע אלצרבין יכון תסעה וכמסין פאקסמהא עלי אלאימה יכרג לך אלמטלוב ודאלך כמסה וארבעה אכמאס ונצף כמס | ||||||||||||||||||
|
| ||||||||||||||||||
| ואן שית פא[צף] אלאתנין אלי אלתלאתה תכון כמסה תם אגמע נצפא אלי כמס עלי מא תקדם תכון ארבעת אכמאס ונצף כמס פאצפהא אלי אלכמסה תכון כמסה וארבעה אכמאס ונצף כמס | ||||||||||||||||||
|
| ||||||||||||||||||
Chapter Six – Adding Integer and Fraction and Fraction of Fraction to Integer and Two Different Fractions |
באב גמע אלצחיח ואלכסר וכסר אלכסר אלי אלצחיח ואלכסרין אלמכתלפין | |||||||||||||||||
|
אדא קיל לך אגמע תמאניה וכמסה אסדאס ונצף סדס אלי סתה וכמסת אסבאע ועשר[ה] אגזא מן אחדי עשר | |||||||||||||||||
| פאנזלהא עלי הד אלצורה הכדא | ||||||||||||||||||
| ||||||||||||||||||
| תם אבדא באלסטר אלאעלי פאצרב אלתמאניה פי אלסתה ואגמל מא עלי ראסהא פמא כרג צרבתה פי אימת אלסטר אלאספל ותחפטה תם תרגע אלי אלסטר אלאספל פתצרב אלסתה פי אלסבעה ומא אגתמע פי אלאחדי עשר ואלכמסה פי אלאחדי עשר ואלעשרה פי אלסבעה ותגמע הד אלצרוב אלתלאתה פמא אגתמע מנהא צרבתה פי אימת אלסטר אלאעלי וגמעת אלי אלמחפוט אלאול וקסמת אלכל עלי אלאימה יכרג לך סת עשר וכמסת אגזא מן אחדי עשר וסתת אסבאע אלגז מן אחדי עשר ותלאתת אסדאס סבע אלגז ונצף סדס סבע אלגז מן אחדי עשר | ||||||||||||||||||
|
| ||||||||||||||||||
Chapter Seven – Adding Fraction of Integer to Integer |
באב מנה אכר | |||||||||||||||||
|
אגמע תלאתת ארבאע כמסה אלי סתה | |||||||||||||||||
| פאנזל אלמסאלה עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
|
|
תם אצנע אלתלאתה אלתי עלי אלכט פי אלכמסה ואצרב אלסתה פי אלארבעה ואקסם עלי ארבעה יכרג לך תסעה ותלאתה ארבאע | |||||||||||||||||
|
|
ואן שית פכד תלאתת ארבאע אלכמסה ודאלך תלאתה ותלאתת ארבאע פאגמעהא אלי אלסתה | |||||||||||||||||
Chapter Eight – Adding Fraction of Integer to Fraction of Integer |
באב מנה אכר | |||||||||||||||||
|
אגמע תלתיי סבעה אלי סבעת אתמאן תסעה | |||||||||||||||||
| פאנזל אלמסאלה עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| תם אצנע פי הד אלמסאלה כמא תקדם פי באב צרב כסר אלעדד ודאלך באן תצרב אלאתנין פי אלסבעה ומא אגתמע צרבתה פי אמאם אלכט אלאספל תם תצרב איצא אלסבעה אלתי הי אלאתמאן פי אלסבעה ומא אגתמע פי אמאם אלכט אלאעלי ותגמע אלצרבין ותקסם עלי אלאימה יכרג לך אלמטלוב ודאלך אתני עשר וארבעת אתמאן ותלת אלתמן | ||||||||||||||||||
|
| ||||||||||||||||||
|
|
ואן שית פאצרב תלתין פי סבעת תכרג לך ארבעה ותלתאן תם אצרב סבעת אתמאן פי תסעת יכרג לך סבעה וסבעה אתמאן פאגמעהא אלי אלארבעה ואלתלתין עלי מא תקדם | |||||||||||||||||
Chapter Nine – Adding Fraction of Integer and Fraction to Fraction of Integer and Fraction |
באב מנה אכר | |||||||||||||||||
|
אגמע תלאתת ארבאע כמסה ונצף אלי כמסת אסדאס סתה ותלת | |||||||||||||||||
| פאנזלהא עלי הד אלצורה | ||||||||||||||||||
| ||||||||||||||||||
| תם אצנע בכל סטרא מן הד אלמסאלה עלי מא תקדם פי באב ואחד וארבעין ומא אגתמע מן כל סטר מנהא צרבת אלכארג פי אלסטר אלאעלי פי אימת אלסטר אלאספל ואלכארג מן אלסטר אלאספל תצרבה פי אימת אלסטר אלאעלי וגמעת אלצרבין וקסמת עלי אלאימה יכרג לך אלמטלוב תסעה ותלאתת אתמאן וסדס תמן ותלת סדס תמן | ||||||||||||||||||
|
| ||||||||||||||||||
Addition of Unknown Amounts |
באב מערפת אעדאד מן גיר עלמהא | |||||||||||||||||
|
|
אדא קיל לך אגמע מן מאל תלתה ורבעה ואעלם כם אלמגתמע | |||||||||||||||||
|
|
פהד אלמסאלה כאנה קאל אגמע תלתא אלי רבע | |||||||||||||||||
|
|
פתעמל עלי מא תקדם יכרוג לך תלאתת אסדאס ונצף סדס | |||||||||||||||||
|
|
פאן קיל לך אגמע מן עשרת דראהם תלתהא ורבעהא ואעלם כם אלמגתמע | |||||||||||||||||
|
|
פהד אלמסאלה כאנה קאל אצרב תלתא ורבעא פי עשרה | |||||||||||||||||
|
|
פתעמל עלי מא תקדם יכרג כמסה וכמס [אסדאס] | |||||||||||||||||
|
|
ואן שית פאגמע תלתא אלי רבע ואצרב מא כרג פי אלעשרה | |||||||||||||||||
|
|
פאן קיל אגמע מן עשרת דראהם תלתהא ורבעהא וכמס מא בקי | |||||||||||||||||
| פאלעמל פי הד אלמסאלה אן תקדם אלתלת מן תלאתה ואלרבע מן ארבעה תם תצרב אלתלאתה פי אלארבעה תכון אתני עשר פאתכדהא אמאמא תם תאכוד מן אלאתני עשר תלתהא ורבעהא ודאלך סבעה אלבאקי מן אלאתני עשר כמסה פתאכוד מנהא כמסהא לקולה וכמס מא בקי ודאלך ואחד פתציפה אלי אלסבעה תכון תמאניה פאצרבהא פי אלעשרת דראהם ואקסם מא אגתמע עלי אלאתני עשר אלתי הי אלאמאם יכרג לך סתה ותלתאן | ||||||||||||||||||
|
| ||||||||||||||||||
| ואן שית סמית אלעשרה מן אלאתני עשר ותאכוד תלך אלנסבה מן אלתמאניה | ||||||||||||||||||
|
| ||||||||||||||||||
|
|
פאן קאל אגמע מן עשרת דראהם תלתהא ורבעהא ודרהמא פאצרב תלתא ורבעא פי עשרה פמא כרג זידת עליה דרהמא | |||||||||||||||||
| ואן שית פאקים אלתלת ואלרבע מן אתני עשר פתאכוד תלתהא ורבעהא ודאלך סבעה פאצרבהא פי אלעשרה תכון סבעין תם אצרב אלדרהם פי אלאתני עשר ואגמלה עלי אלסבעין יכון דאלך אתנין ותמאנין פאקסמהא עלי אלאתני עשר אלתי הי אלאמאם יכרג לך סתה וכמסת אסדאס | ||||||||||||||||||
|
| ||||||||||||||||||
|
|
ולו קאל פי הד אלמסאלה תלתהא ורבעהא אלא דרהמא | |||||||||||||||||
|
|
כנת תסקט אלאתני עשר מן אלסבעין פמא בקי קסמתה עלי אלאימה יכרג ארבע וכמסת אסדאס | |||||||||||||||||
Word Problems: How Much or How Many |
באב מנה אכר והו מן גמע אלאמואל | |||||||||||||||||
|
פאן קאל לך מאלאً גמעת תלתה ורבעה פכאן ואחד ועשרין דרהמא | |||||||||||||||||
| פאלעמל פי הד אלמסאלה אן תקים אלתלת ואלרבע מן אלאתני עשר תם תאכוד מן אלאתני עשר תלתהא ורבעהא ודאלך סבעה פנסבת הד אלסבעה מן אלאתני עשר אלתי הי אלאמאם כנסבת אלואחד ואלעשרין מן אלמאל אלמטלוב | ||||||||||||||||||
|
| ||||||||||||||||||
|
|
פאצרב אלאתני עשר פי אלואחד ואלעשרין ותקסם מא כרג עלי אלסבעה יכרג לך סתה ותלאתין והו אלמאל | |||||||||||||||||
|
ואן שית פאעמלהא באלגבר | |||||||||||||||||
|
|
ודאלך אן תגמל אלמאל שיא פתאכוד מנה תלתה ורבעה ודאלך תלאתת אסדאס ונצף סדס חתי יכון שיא תאמא | |||||||||||||||||
|
|
תגד דאלך בצרבה פי ואחד וכמסת אסבאע | |||||||||||||||||
|
|
ונסבתה פי באב גבר אלכסור פתצרב ואחד וכמסת אסבאע פי ואחד ועשרין יכרג לך סתה ותלאתין והו אלמאל | |||||||||||||||||
|
ואן שית פאעמלה באלכפאת | |||||||||||||||||
|
ודאלך אן תתכד אי עדד שית אמאמא פאנה יגוז דאלך פתעמל אלכפת אלואחדה תלאתה פתאכוד תלתהא ורבעהא ודאלך ואחד ותלאתת ארבאע פקאבל בהא אלואחד ואלעשרין תגדהא אקל מנהא פקד אכטאת פי כפת תלאתה תסעת עשר ורבע נאקצה פאחפט הד אלכטא | |||||||||||||||||
|
| ||||||||||||||||||
|
תם תאכוד כפה תאניה ולתכון ארבעה פתאכוד תלתהא ורבעהא ודאלך אתנאן ותלת פקאבל בהא אלואחד ואלעשרין פקד אכטאת פי כפת ארבעה פתמאנית עשר ותלתאן נאקצה | |||||||||||||||||
|
| ||||||||||||||||||
| פאצרב כט אלכפת אלאולי אלדי הו תסעת עשר ורבע פי אלכפת אלתאניה אלתי הי ארבעה יכון דאלך סבעה וסבעין פאחפטהא תם אצרב כט אלכפת אלתאניה אלתי הי תמאנית עשר ותלתאן פי אלכפת אלאולי אלתי הי תלאת יגתמע מן דאלך סתה וכמסון פאטרחהא פי מן אלסבעה ואלסבעין אלבאקי ואחד ועשרון תם אטרח אקל אלכטין מן אכתרהא אלבאקי תלאתת אסדאס ונצף סדס פאקסם עליהא אלואחד ואלעשרין יכרג לך סתה ותלאתין והו אלמאל וסנביין הדא פי באבהא אן שא אללה תעלי | ||||||||||||||||||
|
| ||||||||||||||||||
| באב מנה אכר | ||||||||||||||||||
|
פאן קאל מאלא גמעת תלתה ורבעה ונצף מא בקי פכאן עשרת דראהם כם אלמאל | |||||||||||||||||
| פאלעמל פי דאלך אן תקים אלתלת ואלרבע ואלנצף מן ארבעה ועשרין פתאכוד תלתהא ורבעהא בארבעת עשר תסקטהא מן אלארבעה ואלעשרין תבקי עשרה פתאכוד נצפהא לקולה ונצף מה בקי בכמסה פתציפהא אלי אלארבעה עשר תכון תסעת עשר פאתכדהא אמאמא תם אצרב אלעשרה פי אלארבעה ואלעשרין ותקסם מא אגתמע עלי אלאימה יכרג אתני עשר ואתני עשר גזא מן תסעת עשר תלתהא ורבעהא ונצף מא בקי | ||||||||||||||||||
|
| ||||||||||||||||||
|
פתעמל עלי מא תקדם פאן כאן אלכארג עשרה פקד צח אלעמל | |||||||||||||||||
|
| ||||||||||||||||||
|
ואן שית פאעמל באלגבר | |||||||||||||||||
| ודאלך אן תגעל אלמאל שיא פתאכוד תלתה ורבעה ונצף מא בקי ודאלך ארבעת אסדאס ותלאתת ארבאע סדס שי פהו יפעל עשרה | ||||||||||||||||||
|
| ||||||||||||||||||
|
|
פתקול בכם תגבר ארבעת אסדאס ותלאתת ארבאע סדס חתי יכון ואחד תגד דאלך פצרבה פי ואחד וכמסת אגזא מן תסעת עשר | |||||||||||||||||
|
|
פתצרב ואחד וכמסת אגזא מן תסעת עשר פי עשרה פמא אגתמע פהו אלמאל | |||||||||||||||||
|
ואן שית פאעמלהא באלכפאת | |||||||||||||||||
|
ודאלך אן תאכוד מן סתה ותאכוד תלתהא ורבעהא ונצף מא בקי | |||||||||||||||||
|
| ||||||||||||||||||
|
יכון דאלך סתה ותלתא פתקאבל בהא אלעשרה פקד אכטאת פי כפת תמאניה בתלאתה ותלתין נאקצה | |||||||||||||||||
|
| ||||||||||||||||||
| פתצרב כט אלכפה אלאולא אלדי הו כמסה ורבע פי אלכפת אלתאניה אלתי הו תמאניה תכון אתנין וארבעין תם תצרב כט אלכפה אלתאניה אלתי הי תלאתה ותלתאן פי אלכפת אלאולא אלתי סתה תכון אתנין ועשרין פאסקטהא מן אתנין וארבעין אלבאקי עשרון תם אטרח אקל אלכטין מן אכתרהא פי באב אלטרח יכרג אלמטלוב אתני עשר ואתני עשר גז מן תסעת עשר והו אלמאל | ||||||||||||||||||
|
| ||||||||||||||||||
|
ואן שית פתאכוד מן ואחד תלתה ורבעה ונצף מא בקי יכון דאלך ארבעת אסדאס ותלאתת ארבאע סדס פנסבת ארבעת אסדאס ותלאתת ארבאע סדס מן ואחד כנסבת עשרה מן אלמטלוב פהדה ארבע אעדאד מתנאסבה אלאולי מנהא ארבע אסדאס ותלאתת ארבאע סדס ואלתאני ואחד ואלתאלת עשרה ואלראבע מגהול | |||||||||||||||||
|
| ||||||||||||||||||
|
|
פתצרוב אלתאני והו ואחד פי אלתאלת והו עשרה ותקסם אלגמיע עלי אלאול והו מן באב ארבעה אסדאס ותלאתת ארבאע סדס וסנביין הד אלקסמה פי באב קסמת אלכסור אן שא אללה תעלי | |||||||||||||||||
| באב מנה אכר | ||||||||||||||||||
|
מאלאً גמעת תלתה ורבעה ודרהמא פכאן כמסת עשר דרהמא כם אלמאל | |||||||||||||||||
|
|
פאלעמל פיה אן תסקט אלדרהם מן אלכמסה עשר אלבאקי ארבעת עשר | |||||||||||||||||
|
פכאנה קאל מאלא גמעת תלתה ורבעה אלא דרהמין פכאן ארבעת עשר | |||||||||||||||||
|
|
פתעמל עלי מא תקדם יכרג אלמאל ארבעה ועשרין | |||||||||||||||||
|
ואן קאל מאלא גמעת תלתה ורבעה אלא דרהמין פכאן אתני עשר | |||||||||||||||||
|
|
פתזיד אלדרהמין עלי אלאתני עשר תכון ארבעת עשר | |||||||||||||||||
|
פכאנה קאל מאלא גמעת תלתה ורבעה פכאן ארבעת עשר פתעמל עלי מא תקדם | |||||||||||||||||
|
ואן קאל מאלא גמעת תלתה וארבעת דראהם וכמסה אלא דרהמי[ן] פכאן עשרת דראהם | |||||||||||||||||
|
|
פמעך ארבעת דראהם זאידה ודרהמי[ן] נאקצה פאסקט אלדרהמין אלנאקצה מן אלארבעת דראהם אלזאידה אלבאקי דרהמאן זאידה פתסקטהא מן אלעשרה אלבאקי תמאניה | |||||||||||||||||
|
פכאנה קאל מאלא גמעת תלתה וכמסה פכאן תמאניה דראהם | |||||||||||||||||
|
|
פתפעל עלי מא תקדם יכרג אלמאל כמסת עשר | |||||||||||||||||
|
פאן קאל מאל גמעת כמסה וסתת דראהם וסדסה אלא תמאניה דראהם פכאן תמאנית דראהם | |||||||||||||||||
|
|
פאסקט מן אלתמאניה דראהם אלסת אלדראהם אלבאקי דרהמאן והי נאקצה | |||||||||||||||||
|
פכאנה קאל מאל גמעת כמסה וסדסה אלא דרהמין פכאן תמאניה פתעמל עלי מא תקדם | |||||||||||||||||
|
ואעלם אנה מתי כאנת אלדראהם אלמפרוצה מע אלתלת ואלסדס אולא גז אלמפרוצה זאידה פאסקטהא מן אלעדד אלדי דכר אנה אגתמע לה מן אלאגזא | |||||||||||||||||
|
פאן כאנת נאקצה פזדהא תם אלעמל בעד דאלך עלי מא תקדם | |||||||||||||||||
| באב מנה אכר | ||||||||||||||||||
|
מאלא גמעת תלתה ורבעה וצרבתה פי מתלה פעאד אלמאל | |||||||||||||||||
| פאקם אלתלת ואלרבע מן אתני עשר תם תאכוד תלתהא ורבעה ודאלך סבעה פאצרבהא פי מתלהא תכון תסעת וארבעין והו אלמאל תם אצרב אלאתני עשר פי מתלהא ואקסם עלי אלאמאם יכרג פי אלקסמה אתנאן וסתת אסבאע וארבעה אסבאע אלסבע | ||||||||||||||||||
|
| ||||||||||||||||||
|
ואן שית פאעמלהא באלגבר | |||||||||||||||||
| ודאלך אן תגעל אלמאל שיא פתאכוד תלתה ורבעה ודאלך תלאתה אסדאס שי ונצף סדס שי פתצרבהא פי מתלהא תכון תלאתת אסבע מאל ונצף תמן תסע מאל פהדא יעדל שיא פתגבר ותקאבל יכרג לך אלמאל אלדי דכרנאה | ||||||||||||||||||
|
| ||||||||||||||||||
|
ולו קאל מאלא גמעת תלתה ורבעה וצרבתה פי מתלה פעאד אלמאל ומתל תלתה | |||||||||||||||||
| פאקם אלתלת ואלרבע מן אתני עשר תם תאכוד תלתהא ורבעהא ודאלך סבעה פתסקט פאצרבהא פי מתלהא תכון סבעה וארבעין פהו אלאמאם תם אצרב אלאתני עשר פי מתלהא ואגמל מא אגתמע תלתיה יכון דאלך ארבעין ומאיתין פאקסמה עלי אלאמאם יכרג לך אלמאל ודאלך ארבעה וסתת אסבאע וסבעא סבע | ||||||||||||||||||
|
| ||||||||||||||||||
|
ואן קאל מאלא גמעת תלתה וכמסה ואכדת רבע מא גמעת ונצף מא בקי פכאן אחדי עשר | |||||||||||||||||
| פאקם אלתלת ואלכמס ואלרבע מן סתין ואסתגני ען אקאמת אלנצף אד הו מוגוד פי אלרבע פתאכוד מן אלסתין תלתהא וכמסהא ודאלך אתני ותלאתין אלבאקי מן אלסתין תמאניה פתאכוד נצפהא בארבעת עשר ותאכוד רבע אלאתנין ואלתלאתין אלדי גמעת אולא בתמאניה פתציפה אלי אלארבעת עשר תכון אתנין ועשרין פהו אלאמאם תם אצרב אלאחדי עשר פי אלסתין ואקסם עלי אלאמאם יכרג לך תלאתון | ||||||||||||||||||
|
| ||||||||||||||||||
|
|
ואן שית פאקסם אלאתנין ואלעשרין עלי אלאחדי עשר ומא כרג קסמת עליה אלסתין | |||||||||||||||||
|
|
ואן שית קסמת אלסתין עלי אתנין ועשרין ומא כרג צרבתה פי אלאחדי עשר | |||||||||||||||||
|
ואן קאל מאלא גמעת נצפה ותלת מא בקי ורבע מא בקי וכמס מא בקי פכאן עשרין דרהמא | |||||||||||||||||
|
|
פאקם אלתלת ואלרבע ואלכמס מן סתין פתאכוד נצפהא בתלאתין ותאכוד תלת מא בקי בעשרה אלבאקי עשרין ותאכוד רבע מא בקי בכמסה אלבאקי כמסת עשר ותאכוד כמסהא בתלאתה תם תגמע אלתלאתין מע אלעשרה ואלכמסה ואלתלאתה ותגמע דאלך כלה יכון תמאניה וארבעין פהו אלאמאם תם אצרב אלעשרין פי אלתלאתין ותקסם מא אגתמע עלי אלאמאם יכרג לך אלמטלוב ודאלך כמסה ועשרין | ||
|
|
ואן שית קסמת אלעשרין עלי תמאניה וארבעין פמא כרג צרבתה פי אלסתין | ||
|
|
ואן שית קסמת אלתמאניה ואלארבעין עלי אלעשרין יכרג אתנאן וכמסאן פאקסם אלסתין עליהא יכרג לך אלמטלוב אפהם תציב | ||
Find a Number Problem - Two Unknowns |
באב מנה אכר | ||
|---|---|---|---|
|
|
עדדאן מכתלפאן גמעת תלת אחדהא אלי רבע אלתאני פכאן סתה | ||
| פהד אלמסאלה מסאלתא להא צואבאת כתירה | |||
|
|
פאחד אלצואב אן תאכוד מן אלסת[ה] כם שית פתגעלה תלת אחד אלעדדין יכון אלבאקי מן סתה רבע אלעדדין | ||
|
|
יכון אלבאקי תלת אלתאני | ||
|
|
ואן געלת אלמאכוד מן אלסתה רבע אחד אלעדדין יכון אלבאקי תלת אלתאני פכאנך אכדת מן אלסתה אתנין פתגעלה תלת אחד אלעדדין פתכון אלאתנין תלת אלסתה תם אסקט אלאתנין מן אלסתה אלבאקי ארבעה פהו רבע אלתאני פאלעדד אלתאני אדא סתת עשר פאחד אלעדדין סתה ואלתאני סתת עשר | ||
|
|
ואן שית פיכון אחד אלעדדין תסעה ואלתאני אתני עשר | ||
|
|
או יכון אחד אלעדדין תמאניה ואלתאני אתני עשר | ||
|
|
או יכון אחד אלעדדין תלאתה ואלתאני עשרין | ||
|
|
או יכון אחד אלעדדין ארבעה ואלתאני כמסת עשר | ||
Sums |
באב מן אלגמע איצא | ||
|
|
אדא קיל לך אגמע מן ואחד אלי עשרה עלי תואלי אלעדד | ||
|
|
פאעמל ואחד עלי אלעשרה יכון אחדי עשר פאצרבהא פי נצף אלעשרה והו כמסה תכון כמסה וכמסין והו אלמטלוב | ||
| פצל | |||
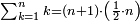
|
ואעלם אנה מתי קיל לך אגמע מן ואחד אלי עדדٍ פאגמל ואחד עלי אלעדד ותצרב אלגמיע פי נצף אלעדד אלאול פמא אגתמע פהו אלמטלוב | ||
|
|
פאן קאל אגמע מן כמסה אלי עשרה | ||
| פאגמע אולא מן ואחד אלי עשרה עלי מא תקדם יכון כמסה וכמסין תם אסקט ואחד אבדא מן אלכמסה אלבאקי ארבעה פאגמע מן ואחד אלי ארבעה תכון עשרה פאסקטהא מן אלכמסה ואלכמסין אלבאקי כמסה וארבעין והו אלדי יגתמע מן כמסה אלי עשרה | |||
|
| |||
| באב מנה אכר | |||
|
|
אגמע מן ואחד אלי עדד מגהול עלי תואלי אלעדד פיבלג כמסה וכמסין כם אלעדד אלמגהול | ||
| קיאסה אן תצרב אלכמסה ואלכמסין פי אתנין אבדא תכון עשרה ומאיה פאחפטהא תם תאכוד נצף אלואחד אלדי בדאת אלגמע מנה ודאלך נצף פאצרבה פי מתלה יכון רבעאً פאגמלה עלי אלעשרה ואלמאיה יכון עשרה ומאיה ורבע פתאכוד גדרה וסנביין דאלך פי באב אלגדר יכון עשרה ונצפאً פאסקט מנהא אלנצף אלדי צרבתה פי מתלה אלבאקי עשרה והו אלעדד אלמגהול | |||
|
| |||
|
ואן שית באלגבר | ||
|
|
פאגעל אלעדד שיא פתגמל עליה ואחדא יכון ואחדא ושיאً פאצרבה פי נצף אלשי אלדי הו אלעדד אלאול יכון נצף מאל ונצף שי יעדל כמסה וכמסין | ||
|
|
פתגבר אלמאל בצרבה פי אתנין ותצרב גמיע אלמעאדלה פי אתנין יכון מעך מאל ושי יעדל מאיה ועשרה פקד כרגת אלי אלוגה אלראבע מן וגוה אלגבר פתעמל עלי מא תקדם פי מוצעה | ||
Odds |
באב מנה אכר | ||
|
|
אגמע מן ואחד אלי תסעת עשר עלי תואלי אלאפראד | ||
|
|
קיאסה אן תגמל ואחד אבדא עלי אלתסעה עשר יכון עשרין פתאכוד נצפהא ודאלך עשרה פאצרבהא פי מתלהא יכון מאיה והו אלדי יכרג מן ואחד אלי תסעה עשר עלי תואלי אלאפראד | ||
| פצל | |||
| ולו קאל פי הד אלמסאלה מן ואחד אלי עשרה או אלי אתני עשר עלי תואלי אלאפראד לם יגז לאן אלעשרה מן אלעדד אלזוג וליסת מן אלעדד אלפרד | |||
|
|
פאן קאל אגמע מן ואחד אלי עדד מגהול פרדٍ עלי תואלי אלעדד פאגתמע סתה ותלאתין כם אלעדד אלפרד | ||
|
|
קיאסה אן תאכוד גדר אלסתה ואל תלאתין ודאלך סתה פאצעפהא תכון אתני עשר פאסקטהא ואחדא אלבאקי אחדי עשר והו אלעדד אלפרד אלדי גמע אליה | ||
|
ואן שית פאגעל אלעדד שיאً פתגמל עליה ואחדא יכון ואחד ושיא פתאכוד נצפה ודאלך נצף ואחד ונצף שי פאצרבה פי מתלה יכון רבע מאל ונצף שי ורבע ואחדא פהדא יעדל סתה ותלאתין | ||
|
|
פתסקט רבע ואחדא מן אלסתה ואלתלאתין אלבאקי כמסה ותלאתין ותלאתת ארבאע פמעך רבע מאל ונצף שי יעדל כמסה ותלאתין ותלאתת ארבאע | ||
|
|
פתגד רבע אלמאל ודאלך בצרבה פי ארבעה פתצרב גמיע אלמעאדלה פי ארבעה יכון מאלא ושאיין יעדל מאיה ותלאתה וארבעין פקד כרגת אלי אלצרב אלראבע מן אלגבר פתעמל עלי מא תקדם יכרג אלשי אחדי עשר והו אלעדד אלמגהול | ||
|
|
ואן שית אן תצרב סתה ותלאתין פי ארבעה אבדא ותאכוד גדרהא כרג גדרהא ותסקט מנה ואחדא | ||
| ואעלם אנך מתי עמלת הד אלמסאלה בוגה אלגדר פכרגת אלמסאלה גיר מנטלקה פאן אלעמל כטא | |||
Evens |
באב מנה אכר | ||
|
|
אגמע מן אתנין אלי עשרה עלי תואלי אלאזואג | ||
| פאעמל אלאתנין עלי אלעשרה אבדא תכון אתני עשר פתאכוד נצפהא ותצרבה פי נצף אלעשר[ה] יכון דאלך תלאתין והו אלעדד אלדי תריד | |||
|
| |||
|
|
ואן שית פכד רבע אלאתנין עשר ואצרבה פי אלעשרה או תאכוד רבע אלעשרה ותצרבה פי אלאתני עשר | ||
|
|
פאן קאל אגמע מן סתה אלי אתני עשר עלי תואלי אלאזואג | ||
| קיאסה אן תגמע מן אתנין אלי אתני עשר תכון אתנין וארבעין תם תסקט מן אלסתה אתנין אלבאקי ארבעה פאגמע מן אתנין אלי ארבעה תכון סתה פאסקטהא מן אתנין וארבעין אלבאקי סתה ותלאתין והו אלעדד אלמטלוב | |||
|
| |||
|
|
פאן קאל אגמע מן אתנין אלי עדד זוג עלי תואלי אלאזואג פאגתמע תלאתון כם אלעדד אלדי גמעת אליה | ||
| קיאסה אן תצרב אלתלאתין פי ארבעה אבדא תכון מאיה ועשרין תם תאכוד נצף אלאתנין אבדא פתצרבה פי מתלה יכון ואחד פאגמלה עלי אלמאיה ועשרין יכון ואחד ועשרין ומאיה פתאכוד גדרהא ודאלך אחדי עשר והו אלעדד אלמגהול | |||
|
| |||
|
ואן שית פאגעל אלעדד שיא ואתנין פתאכוד נצפהא ודאלך נצף שי וואחד פתצרבה פי נצף שי יכון רבע מאל ונצף שי יעדל תלאתין | ||
|
|
פתגבר ותקאבל יכרג אלשי עשרה והו מא ארדת | ||
Squares |
באב מנה אכר | ||
|
|
אגמע מן מרבע ואחד אלי מרבע עשרה עלי תואלי אלעדד | ||
|
|
קיאסה אן תגמע מן ואחד אלי עשרה עלי מא תקדם יכון כמסה וכמסין תם תאכוד תלתיי אלעשרה בזיאדת תלת ואחד אבדא יכון סבעה פאצרבהא פי אלכמסה ואלכמסין יכון כמסה ותמאנין ותלאת מאיה והו מא ארדת | ||
|
|
פאן קאל אגמע מן מרבע כמסה אלי מרבע אתני עשר | ||
| פאגמע אולא מן מרבע ואחד אלי מרבע אתני עשר פמא אגתמע פאחפטה תם אסקט ואחד אבדא מן אלכמסה אלבאקי ארבעה פתגמע מן מרבע [ו]א[ח]ד אלי מרבע ארבעה פמא אגתמע אסקטה מן אלמחפוט אלאול פמא כרג הו אלמט[לוב] | |||
|
| |||
Squares of Evens |
באב מנה אכר | ||
|
|
אגמע מן מרבע אתנין אלי מרבע עשרה עלי תואלי אלאזואג | ||
|
|
קיאסה אן תגמע מן אתנין אלי עשרה תכון תלאתין תם תאכוד תלתיי אלעשרה בזיאדת תלתיי ואחד והו סבעה ותלת פתצרבה פי אלתלאתין תכון עשרין ומאיתין והו מא ארדת | ||
| ואן שית פתאכוד מן אלתלאתין תלתהא תכון עשרין תם זיד עלי אלעשרה ואחד יכון אחדי עשר פאצרבהא פי אלעשרין | |||
|
| |||
Squares of Odds |
|||
|
|
פאן קאל אגמע מן מרבע ואחד אלי מרבע תסעה עלי תואלי אלפרד | ||
| קיאסה אן תגמל עלי תסעה אתנין יכון אחדי עשר תם אגמל עלי אלתסעה ואחד יכון עשרה פכד נצפהא ואצרבה פי נצף אלאחדי עשר ומא אגתמע צרבתה פי תלתי תסעה יכון דאלך כמסה וסתין ומאיה והו מא ארדת | |||
|
| |||
| ואן שית פאגמע מן ואחד אלי תסעה יכון כמסה ועשרין פאסקט מנהא תלתהא בזיאדת סדס ואחד יבקי סת עשר ונצף | |||
|
| |||
|
|
ואן שית פאגמל עלי אלתסעה ואחד ותצרב מא אגתמע פי נצף אלתסעה ומא אגתמע מן תלת אלתסעה בזיאדת תלתיי ואחד פמא אגתמע פהו מא ארדת | ||
|
|
ואן שית פתאכוד נצף אלתסעה ותרפעה תם תאכוד תלת אלתסעה בזיאדת תלתיי ואחד ותרפעה איצא תם תגמל עלי אלתסעה ואחד יכון עשרת תם אצרב אלארבעה ונצף פי תלאתה ותלתין ומא אגתמע פי אלעשרה | ||
Cubics |
באב מנה אכר | ||
|
|
אגמע מן מכעב ואחד אלי מכעב עשרה | ||
|
|
אלעמל פי דאלך אן תגמע מן ואחד אלי עשרה עלי תואלי אלעדד יכון כמסה וכמסין פאצרבהא פי מתלהא והו מא ארדת | ||
|
|
פאן קאל אגמע מן מכעב ארבעה אלי מכעב עשרה | ||
| פאסקט מן אלארבעה ואחד אלבאקי תלאתה תם אגמע מן מכעב ואחד אלי מכעב עשרה ואגמ[ע] איצא מן מכעב ואחד אלי מכעב תלאתה ואסקט אלאקל מן אלאכתר פמא בקי פהו אלמטלוב | |||
|
| |||
|
|
פאן קאל אגמע מן מכעב ואחד אלי מכעב עדד מגהול פבלג כמסה ועשרין ותלאתת אלאף כם אלעדד אלמגהול | ||
|
|
פתעמל עלי מא תקדם יכרג לך עשרה | ||
| פצל | |||
| ואעלם אנך מתי כאן פי הד אלבאב אלעדד אלמפרוץ ליס לה גדר פאן אלמסאלה כטא | |||
| ואן שית פאעמלה באלגבר כמא תקדם פי אצל אלעמל אולא | |||
Cubics of Evens |
באב מנה אכר | ||
|
|
אגמע מן מכעב אתנין אלי מכעב עשרה עלי תואלי אלאזואג | ||
| פאגמע אולא מן אתנין אלי עשרה עלי מא תקדם יכרג תלאתין פאצרבהא פי צעפהא תכון אלפא ותמן מאיה והו מא ארדת | |||
|
| |||
|
|
פאן קאל אגמע מן מכעב אתנין אלי מכעב עדד מגהול עלי תואלי אלאזואג יבלג אלפא ותמן מאיה כם אלעדד אלמגהול | ||
|
|
אלעמל פי דאלך אן תאכוד נצף אלעדד אלמפרוץ ותאכוד גדר יכון תלאתין | ||
|
|
פכאנה קיל לך גמע מן אתנין אלי עדד זוג עלי תואלי אלאזואג יבלג תלאתין כם אלעדד אלזוג | ||
| פתעמל [על]י מא תקדם יכרג אלעדד עשרה פאפהם תציב | |||
Geometrical Progression of Doubles – Squares of Chessboard |
אלקול פי תצאעיף ביות אלשטרנג וגמע מא פיהא | ||
| אדא ארדת אן תצעף ביות אלשטרג וגמיע מא פיהא עלי א[ן] יכון פי אלביות אלאול ואחד ופי אלתאני אתנין ופי אלתאלת ארבעה ופי אלראבע תמאניה ופי אלכאמס סתת עשר וכדאלך תצעיף אלעדד לכל בית אלי אן תסתופי גמיע אלארבעה וסתין בית | |||
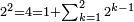
|
פאדא ארדת דאלך פאגעל מא פי אלבית אלאול אתנין | ||
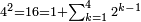
|
פאצרבהא פי מתלהא תכון סת עשר והו מא פי אלבית אלראבע וגמיע מא קבלה בזיאדת ואחד | ||
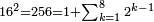
|
תם תצרב אלסתה עשר פי מתלהא תכון סתה וכמסין ומאיתין והו מא פי אלבית אלתאמן וגמיע מא קבלה בזיאדת ואחד | ||
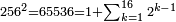
|
תם תצרב סתה וכמסין פי מתלהא ומיאתין תכון סתה ותלאתין וכמס מאיה וכמסה | ||
| 65536 | |||
| וגמיע מא קבלה בזיאדת ואחד | |||
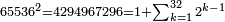
|
תם תצרב אלסאדס עשר פי מתלה יכון אלכארג סתה ותסעין ומיאתין וסבעה וסתין אלפא ותסע מאית אלפא וארבעה ותסעין אלפא אלף ומיאתין אלפאً אלף וארבעת אלאף אלפא אלף והדא צורתהא הכדא | ||
| 4294967296 | |||
| והו מא פי אלבית אלתאני ואלתלאתין וגמיע מא קבלה בזיאדת ואחד | |||
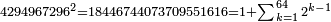
|
תם תצרב אלתאני ואלתלאתין פי מתלה יכון אלכארג סתת עשר וסת מאיה וואחד וכמסין אלפא וכמס מאית אלפא ותסעת אלאף אלף וסבע מאית אלפא אלף ותלאתה וסבעין אלף מכררה כמס מראת וארבע מאית אלף מכררה ארבע מראת וסבע מאית אלףً אלף מכררה ארבע מראת וסבע מאית אלפא אלף מכררה ארבע מראת וסתה וארבעין אלף מכררה כמס מראת וארבע מאית אלף מכררה כמס מראת ותמנת עשר אלף מכררה סת מראת
הדה צורתהא | ||
| 18446744073709551616 | |||
| והו מא פי ביות אלשטרנג אלארבעה ואלסתין בזיאדת ואחד פאסקט מנהא אלואחד יכון אול אלמסאלה כמסה עשר פאפהם גמיע דאלך תציב אן שא אללה תעלי | |||
Subtraction of Fractions |
באב אלטרח | ||
| אעלם אן גמיע מא [צרף] פי באב אלגמע מן אלאעמאל פתצרף פי באב אלטרח מתאל דאלך אדא ארדת אן תטרח עדדא וכסרא מן עדדא וכסראً פאנך תצנע באלעדד ואלכסר עלי מא תקדם פי באב אל צרב ומא אגתמע צרבתה פי אימת אלסטר אלאספל תם תרפעה אלי נאחיה תם תצנע איצא באלסטר אלאעלי עלי מא תקדם פי באב אלצרב ומא אגתמע צרבתה פי אימת אלסטר אלאעלי פמא אגתמע טרחת מנה אלעדד אלאול אלמרפוע פמא בקי קסמתה עלי אלאימה פמא כרג פהו אלמטלוב | |||
|
|
מתאל דאלך אדא קיל לך אטרח רבעא מן כמס אסדאס | ||
| פאנזל אלרבע פי סטר ואנזל אלכמסת אלאסדאס פי סטר אכר תח[תה] עלי הד אלצורה | |||
| |||
|
|
תם אצרב אלואחד אלדי עלי אלכט אלאעלי פי אלסתה אלתי הי אלאמאם מן אלכט אלאספל תכון סתה פאחפטהא תם אצרב אלכמסה אלתי עלי אלכט אלאספל פי אלארבעה אלתי הי אמאם אלכט אלאעלי תכון עשרין פאסקט מנהא אלסתה אלבאקי ארבעת עשר פאקסמה עלי אלאימה יכרג לך אלמטלוב ודאלך תלאתת אסדאס ונצף סדס | ||
|
|
פאן קאל אטרח ארבע אכמאס ונצף סדס מן עשרת אגזא מן אחדי עשר | ||
| פאנזל אלמסאלה עלי הד אלצורה | |||
|
|
| ||
| תם אצנע באלסטר אלאעלי ואלסטר אלאספל כמא תקדם פי צרב אלכסר וכסר אלכסר ומא אגתמע מן אלכט אלאעלי צרבתה פי אימת אלכט אלאספל ומא אגתמע פי אלכט אלאספל צרבתה פי אימת אלכט אלאעלי ותסקט אלאקל מן אלאכתר ומא בקי קסמתה עלי אלאימה יכרג לך אלמטלוב ודאלך ארבע אתמאן אלעשר וארבע אסדאס תמן אלעשר | |||
|
| |||
|
|
פאן קאל אטרח ארבע אכמאס ותלת מן סתת אסבאע ותלאתת אתמאן | ||
| פאנזלהא עלי הד אלצורה | |||
| |||
| תם אצנע באלסטר אלאעלי ואלאספל עלי מא תקדם מן צרב אלכסרין אלמכתלפין ומא אגתמע מן אלסטר אלאעלי צרבתה פי אימת אלסטר אלאספל ומא אגת[מע] איצא מן אלסטר אלאספל צרב[תה] פי אימת אלסטר אלאעלי תם תטרח מא כרג מן אלכט אלאעלי מן אלכארג מן אלכט אלאספל פמא בקי קסמתה עלי אלאימה יכרג לך אלמטלוב | |||
Subtraction of Integer and Fraction from Integer and Fraction/s |
באב מנה אכר | ||
|
|
אדא קיל לך אטרח כמסה ותלתא מן סבעה ותלאתת ארבאע | ||
| כמא פאנזלהא עלי הד אלצורה | |||
| |||
| תם אצנע באלכט אלאעלי ואלכט אלאספל כמא צנעת פי צרב אלצחיח ואלכסר ותצרב אלכארג מן אלכט אלאעלי פי אמאם אלכט אלאספל וכדאלך מא כרג מן אלכט אלאספל צרבתה פי אמאם אלכט אלאעלי תם תסקט אלאקל מן אלאכתר אלבאקי תסעה ועשרין פאקסמהא עלי אלאימה יכרג אתנאן וסדסאן ונצף סדס | |||
|
| |||
|
|
פאן קאל אטרח נצפא וגז מן אחדי עשר וכמסת אסדאס ומן תמאניה ותסעת אעשאר | ||
| פאנזל אלמסאלה עלי הד אלצורה | |||
| |||
| תם אצנע באלסטר אלאעלי עלי מא תקדם פי אלכסור אלמכתלפה ומא אגתמע צרבתה פי אמאם אלכט אלאספל תם תצנע באלסטר אלאספל עלי מא תקדם פי אלצחיח ואלכסר ומא אגתמע צרבתה פי אמאם אלאעלי פמא אגתמע טרחת מנה אלאקל פמא בקי קסמתה עלי אלאימה יכרג לך אלמטלוב | |||
|
| |||
Subtraction of Fraction of Integer from Fraction of Integer |
באב מנה אכר | ||
|
|
אדא קיל לך אטרח תלאתת ארבאע כמסה מן סבעת אתמאן תסעה | ||
| פאנזל אלמסאלה עלי הד אלצורה | |||
| |||
|
|
תם אצרב אלתלאתה פי אלכמסה ומא אגתמע צרבתה פי אלתמ[אניה] אלתי הי אמאם אלכט אלאספל פארפעה תם אצרב אלסבעה פי אלסתה ומא אגתמע פי אלארבעה אלתי הי אמאם אלכט אלאעלי פמא אגתמע טרחת מנה אלמרפוע אלאול ומא בקי קסמתה עלי אלאימה יכרג לך אלמטלוב | ||
Subtraction of Fraction of Integer and Fraction from Fraction of Integer |
באב מנה אכר | ||
|
|
אטרח תלאתת ארבאע כמסה ונצף מן כמסת אסדאס סבעה | ||
| פאנזלהא עלי הד אלצורה כמא תרי פי מא בעד דאלך | |||
| |||
|
|
תם אצנע באלסטר אלאעלי עלי מא תקדם פי צרב אלכסור פי באב ואחד וארבעין ומא אגתמע צרבתה פי אמאם אלסטר אלאספל ומא אגתמע פי אלסטר אלאספל צרבתה פי אימת אלסטר אלאעלי פמא אגתמע טרחת מנה אלעדד אלאול ומא בקי קסמתה עלי אלאימה יכרוג לך אלמטלוב כמא ארדת | ||
Subtraction of Unknown Amounts |
באב מן אלטרח אכר | ||
|
|
אטרח מן עשרת דראהם תלתהא ורבעהא ואעלם כם בקי | ||
| פאלעמל פי דאלך אן תקים אלתלת ואלרבע מן אתני עשר תם תטרח מנהא תלתהא ורבעהא אלבאקי כמסה נסבת אלכמסה מן אלאתני עשר אלדי הו אלמקאם כנסבת אלמטלוב מן אלעשרה פאצרב אלכמסה פי אלעשרה ואקסם מא אגתמע עלי אתני עשר יכרג ארבעה וסדס והו אלבאקי מן אלעשרה | |||
|
| |||
| ואן שית צרבת תלתאً ורבעאً פי עשרה פמא כרג טרחתה מן אלעשרה פמא בקי פהו אלמטלוב | |||
|
|
ואן שית פי אלעמל אלאול קסמת אלכמסה עלי אלאתני עשר וצרבת מ[א כרג] פי אלעשרה או קסמת אלעשרה עלי אלאתני עשר וצרבת מא כרג פי אלכמסה | ||
| באב | |||
|
|
פאן קאל אטרח מן עשרת דראהם תלתהא ורבעהא ותלאתת דראהם ואעלם מא בקי | ||
| פאקם אלתלת ואלרבע מן אתני עשר פהו אלאמאם תם תאכוד תלתה ורבעה ותסקטה מן אלאתני עשר אלבאקי כמסה פאצרבהא פי אלעשרה תכון כמסין פארפעהא תם תאכוד אלתלאתת דראהם אלמדכורה פתצרבהא פי אלאתני עשר כרג ואחד וסדס והו אלבאקי | |||
|
| |||
|
|
ואן שית קסמת אלכמסין עלי אלאמאם פמא כרג טרחת מנה אלתלאתה | ||
| ואן שית צרבת תלתא ורבעא פי עשרה ומא כרג גמלת עליה תלאתה וטרחת אלגמיע מן עשרה והכדא תעמל פי גמיע מן הד אלאמור הכדא | |||
| באב מנה אכר | |||
|
|
פאן קאל אטרח מן עשרת דראהם תלתהא ורבעהא אלא דרהמין | ||
| פאקם אלתלת ואלרבע מן אתני עשר תם אטרח תלתהא ורבעהא אלבאקי כמסה פאצרבהא פי אלעשרה תכון כמסין פאחפטהא תם אצרב אלדרהמין פי אלאתני עשר ואגמלהא עלי אלכמסין תכון ארבעה וסבעין פאקסמהא עלי אלאמאם אלדי הו אלאתני עשר יכרג סתה וסדס הו אלבאקי | |||
|
| |||
| ואן שית צרבת תלתא ורבעא פי עשרה ומא כרג טרחת מנה אלדרהמין ומא בקי סקטתה מן אלעשרה פאלבקי הו אלמטלוב | |||
Word Problems: First from Last |
באב מנה אכר | ||
|
מאלא טרחת תלתה ורבעה פבקי עשרה כם אלמאל | ||
|
|
פאקסם אלתלת ואלרבע מן אתני עשר תם אסקט מנהא תלתהא ורבעהא אלבאקי כמסה והו אלאמאם תם אצרב אלעשרה פי אלאתני עשר ואקסם מא אגתמע עלי אלאמאם יכרג ארבעה ועשרין והו אלמאל | ||
|
ואן שית באלגבר | ||
|
|
פאגעל אלמאל שיא פאטרח תלתה ורבעה אלבאקי סדסא שיא ונצף סדס שיא פהדא יעדל עשרה | ||
|
|
פנקול בכם אלגבר סדס ונצף סדס חתי יכון ואחד פנגד דאלך בצרבה פי אתנין וכמסין | ||
|
|
פתצרב אלעשרה פי אתנין וכמסין יכון ארבעה ועשרין והו אלמאל | ||
|
ואן שית באלכפאת | ||
|
ודאלך אן תתכד אי עדדא שית אמאמא פכאנך אכדת אתני עשר פתסקט מנהא תלתהא ורבעהא אלבאקי כמסה פקאבל בהא אלעשרה פקד אכטאת פי כפת אתני עשר בכמסה נאקצה | ||
|
תם תאכוד כפתאً אכרי מן תמאניה עשר פתסקט תלתהא ורבעהא אלבאקי מנהא סבעה ונצף נאקצה | ||
|
| |||
| פאצרב כט אלכפת אלאולי אלדי הו כמסה פי אלכפה אלתאניה אלתי תמאנית עשר יכון דאלך תסעין תם אצרב כט אלכפה אלתאניה והו אתנאן ונצף פי אלכפה אלאולי אלתי הי אתני עשר תכון תלאתין פאסקטהא מן אלתסעין אלבאקי סתין ואסקט אקל אלכטין מן אכתרהא אלבאקי אתנין ונצף פאקסם עליהא אלסתין יכרג ארבעה ועשרין והו אלמאל | |||
|
| |||
| פצל | |||
|
ואעלם אנה מתי כאן אלכטאן נאקצא[ן] פאסקט אקל אלצרב מן אכתרהמא פמא בקי קסמת עליה אלבאקי מן אלצרבין | ||
|
| |||
|
וכדאלך תפעל אדא כאן אלכטאן נאקצאן | ||
|
פאן כאן אחד אלכטין נאקצין פאן כאן אחד אלכטאן זאידאً ואלאכר נאקצא פאגמע אלצרבין ואגמע איצא אלכטין ואקסם גמיע אלצרבין עלי גמיע אלכטין פמא כרג פהו אלמטלוב | ||
|
| |||
| פצל אכר | |||
|
ואעלם אנה אדא כאן אלכטין נאקצאן פאלמאל אכתר מן כל ואחד מן אלכפין | ||
|
ואן כאן אלכטאן זאידין פאלמאל אקל מן כל ואחד מן אלכפתין | ||
|
ואן כאן אחד אלכטא זאידא ואלאכר נאקצא פאלמאל בין אלכפתין ואעלם דאלך | ||
| באב מנה אכר | |||
|
מאלא טרחת תלתה ודרהמא ורבעה ודרהמין וכמסה ותלאתת דראהם פבקי עשרה כם אלמאל | ||
| פאקם אלתלת ואלרבע מן סתין תם אטרח תלתהא ורבעהא וכמסהא אלבאקי תלאתת עשר והו אלאמאם תם אגמע אלדראהם כלהא ודאלך סתה פאגעלהא עלי אלעשרה תכון סת עשר פאצרבהא פי אלסתין ואקסם אלמגתמע עלי אלאמאם יכרג לך אלמטלוב ותלאתה וסבעון ואחדי עשר גז מן תלאתת עשר | |||
|
| |||
| פצל | |||
|
ואעלם אן אלדראהם אדא כאנת זאידתא פזדהא עלי אלדראהם אלבאקיה | ||
|
ואן כאנת נאקצה פאנקצהא מן אלדראהם אלבאקיה | ||
| תם אלעמל עלי מא תקדם פי באב אלטרח | |||
|
ואמא פי באב אלגמע פאדא כאנת אלדראהם אלמפרוצה מע אלתלת ואלרבע ואלגז אלמדכור זאידה פאנקצהא מן אלעדד אלמדכור ואן כאנת אלדראהם נאקצה פזדהא עלי מא תקדם | ||
| באב עלי מא תקדם פי אול אלמסאלה מן טרח אלאמואל | |||
|
מאלא טרחת תלתה וצרבת מא בקי פי מתלה פעאד אלמאל | ||
|
אלעמל פי דאלך אן תקים אלתלת מן תלאתה פאסקט תלתהא אלבאקי אתנין ונצף מא בקי אלבאקי ואחד פאצרב אלואחד אלבאקי פי אלאתנין אלזאידה תכון אתנין תכון אתנין פהו אלאמאם תם אצרב אלתלאתה פי מתלהא ואקסם עלי אלאמאם יכרג ארבעה ונצף והו אלמאל | ||
|
| |||
|
פאן קאל מאלא דהב תלתה וצרבת מא בקי פי מתלה פכאן סתת אמתאל אלמאל ותלתיי תלתה | ||
|
|
פאקם אלתלת מן תלאתה פתדהב תלתה אלבאקי אתנין פאצרבהא פי מתלהא תכון ארבעה פהו אלאמאם תם אצרב אלתלאתה פי מתלהא ומא אגתמע פי סתה ותלאתין יכון סתין פאקסמהא עלי אלאמאם יכרג כמסה והו אלמאל אלמטלוב תציב | ||
Word Problems: Whole from Parts |
באב מנה אכר | ||
|
ודאלך מן אלקצב קצבתא פי אלחמא תלתהא ופי אלמא רבעהא ופוק אלמא עשרת אשבאר | ||
|
פהדה אלמסאלה כקולך מאל דהב תלתה ורבעה פבקי עשרה | ||
|
|
פתעמל עלי מא תקדם יכרג ארבעה ועשרין והו טול אלקצבה | ||
|
ולו קאל קצבתא פי אלחמא תלתהא ודראעאן ופי אלמא רבעהא ותלאתת אדרע ופוק אלמא עשרת אדרע | ||
|
פהד אלמסאלה כקולך מאלא טרחת תלתה ודרהמין ורבעה ותלאתת דראהם יבקי עשרה | ||
|
|
פתעמל עלי מא תקדם יכרג אלמטלוב טול אלקצבה סתה ותלאתין | ||
|
פאן קאל פי ראסה תלתה ופי דנבה רבעה ופי וסטה עשרת אריטאל כם זינת אלחות | ||
|
פהדא כקולך מאל טרחת תלתה ורבעה פבקי עשרה | ||
|
|
פתעמל עלי מא תקדם יכרג ארבעה ועשרין והי זינת אלחות | ||
|
וכדאלך לו קאל תלתה וארטאל ורבעה וארטאל | ||
| פאן הד אלמסאיל כלהא אנמא תכרג מן הד אלבאב | |||
Division of Fractions |
באב מן אלקסמה | ||
| אעלם אן הד אלבאב יגרי מגרי אלגמע ואלטרח ומענאה אן יציר אלמקסום ואלמקסום עליה מן גנס ואחד ואן תרדהא גמיעא אלי אדק כסר פי אלמסאלה תם תקסם בעד דאלך אחדהא עלי אלתאני פמא כרג פהו מא כרג ללואחד | |||
| והד אלמסאלה תנקסם קסמין: | |||
Division of the smaller by the larger |
קסמת קליל עלי כתיר ותסמא אלתסמיה | ||
| ואלקסם אלתאני קסמת אלקליל עלי אלכתיר עלי אלקליל | |||
| ונבדא בקסמת אלקליל עלי אלכתיר כמא ביינא פי אלעדד אלצחיח | |||
|
|
מתאלה אקסם תלת דרהם עלי ארבעה רגאל | ||
| פאנזלהא עלי הד אלצורה | |||
| |||
|
|
תם תאכוד אלתי הי מקאם אלצחיח פתצרבהא פי מקאם אלתלת מן אלסטר אלאעלי תכון אתני עשר פהו אלאמאם תם תסמי אלואחד אלדי עלי אלתלאתה מן אתני עשר יכון נצף סדס פאלואגב לכל ואחד מן אלארבעה ונצף סדס אלדרהם | ||
| פצל | |||
| ואעלם אן צרב גמיע מא פי אלסטר אלאספל מן אלעדד אדא צרבתה פי מקאמאת אלכסור מן אלסטר אלאעלי פאן אלמגתמע מן דאלך הו אלאמאם אלדי נקסם עליה תם אן כנת תקסם כסרא עלי עדד פתאכוד מא עלי אלכסר ותקסמה עלי אלאמאם כמא פעלת פי הד אלמסאלה ומא יאתי בעדהא | |||
|
|
מתאל דאלך אדא קיל לך אקסם כמסת אסדאס עלי תמאניה | ||
| פאנזל אלמסאלה עלי הד אלצורה | |||
| |||
|
|
תם אצרב אלתמאניה פי אלסתה תכון תמאניה וארבעין פסמי מנהא אלכמסה תכון כמס אסדאס אלתמן פהו אלכארג מן אלקסמה | ||
|
|
פאן קאל אקסם כמסת אגזא מן אחדי עשר עלי סבעה | ||
| פאנזל אלמסאלה עלי הד אלצורה | |||
| |||
|
|
תם אצרב אלסבעה פי אלאחדי עשר יכון סתה וסבעין פהו אלאמאם תם סמי מנהא אלכמסה תכון כמס אסבאע אלגז מן אחדי עשר | ||
| ואן שית כמסה אגזא מן אחדי עשר פי אלסבע | |||
| פצל | |||
| ואקרב מא תעמל פי הד אלבאב אן תרד אלצחיח אבדא מקאם כסר תחת אלכט אלאעלי ותנסב אליהא גמיעא אלכסר אלמקסום | |||
|
|
מתאלה אקסם סבעת אתסאע עלי סבעת עשר | ||
| פאנזל אלמסאלה עלי הד אלצורה | |||
| |||
|
|
תם תאכוד אלסבעה עשר פתרדהא מקאם כסר תחת אלכט אלאעלי אלי מא ילי אלימין צורת גמיע דאלך סבעת אתסאע אלגז מן סבעת עשר עלי הד אלצורה | ||
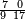
| |||
Division of Fraction and Fraction of fraction by Integer |
באב קסמת אלכסר וכסר אלכסר עלי אלצחיח והי תסמייה | ||
|
|
מתאלה אקסם כמסת אסדאס ונצף סדס עלי כמסה | ||
| פאנזל אלמסאלה עלי הד אלצורה | |||
| |||
|
|
תם אבדא באלסטר אלאספל פתצרב אלכמסה אלתי פיה פי אימת אלסטר אלאעלי פי אלסתה ומא אגתמע פי אלאתנין יכון סתין והו אלאמאם תם ארגע אלי אלסטר אלאעלי פתצרב אלכמסה אלתי עלי אלסתה פי אלאתנין ותגמל מא עלי ראסהא יכון אחדי עשר פסמיהא מן אלאמאם אלדי הו סתון תכרג עשרה וכמסת אסדאס אלעשר פאפהם דאלך | ||
|
|
פאן קאל אקסם עשר אגזא מן אחדי עשר ותלאתת אכמאס אלגז מן אחדי עשר עלי תלאתה וסתין | ||
| פאנזלהא עלי הד אלצורה | |||
| |||
| תם אצרב אלתלאתה ואלסתין פי אלאחדי עשר ומא אגתמע פי אלכמסה יכון גמיע דאלך כמסה וסתין וארבע מאיה ותלאתת אלאף פהו אלאמאם תם אצרב אלעשרה פי אלכמסה ואגמל מא עלי ראסהא יכון תלאתה וכמסין פסמיהא מן אלאמאם יכרג תסע אלגז מן אחדי עשר ותלאתת אסבאע תסע אלגז מן אחדי עשר ותלאתת אכמאס סבע תסע אלגז מן אחדי עשר | |||
|
| |||
Division of Two Different Fractions by Integer |
באב קסמת אלכסרין אלמכתלפין עלי אלצחיח והי תסמיה | ||
|
|
מתאלה אקסם תלאתת אכמאס וסבעת אתמאן עלי סתה | ||
| פאנזלהא עלי הד אלצורה | |||
| |||
| תם אבדא באלסטר אלאספל פאצרב אלסתה אלתי הי אלצחיח פי אימת אלסטר אלאעלי תצרב אולא פי אלכמסה ומא אגתמע פי אלתמאניה יכון דאלך ארבעין ומיאתין והו אלאמאם תם אצנע באלסטר אלאעלי כמא תצנע באלסטרין אלמכתלפין ודאלך אן תצרב מא עלי אלכמסה והו תלאתה פי אלתמאניה כמא תצנע באלכסרין אלמכתלפין ודאלך אן תצרב מא עלי אלכמסה והו תלאתה פי אלתמאניה תכון ארבעה ועשרין ותצרב איצא מא עלי אלתמאניה פי אלכמסה ודאלך סבעה פי כמסה יכון כמסה ותלאתין פאגעלהא אלי אלארבעה ואלעשרין יכון תסעה וכמסין פסמיהא מן אלאמאם יכרג לך עשראן ותלאתת אתמאן אלעשר ותלתא תמן אלעשר | |||
|
| |||
| ואן שית פאגמע תלאתה אכמאס אלי אלסבעה אתמאן יכון גמיע דאלך ואחד ותלאתין ותלאתת אתמאן וארבעת אכמאס אלתמן תם סמי ואחד מן אלסתה אלמקסום עליהא תגד סדסא פאצרב סדסאً מן ואחד פי תלאתת אכמאס וסבעת אכמאס אלתמן פמא כרג פהו אלמטלוב | |||
|
| |||
|
|
ואן שית פאצרב סדסאً פי תלאתת אכמאס וסבעת אתמאן פמא כרג פהו אלמטלוב והכדא פי אלגמיע | ||
Division of Fraction by Integer and Fraction |
באב קסמת אלכסר עלי אלצחיח ואלכסר | ||
|
|
אקסם סתת אסבאע עלי כמסה ונצף | ||
| פאנזל אלמסאלה עלי הד אלצורה | |||
| |||
|
|
תם אבדא באלסטר אלאספל פתצרב אלכמסה פי אלאתנין ותגמל מא עלי ראסהא יכון אחדי עשר פאצרבהא פי אלסבעה אלתי הי מקאם אלכסר פי אלסטר אלאעלי יכון סבעה וסבעין והו אלאמאם תם אצרב אלסתה אלתי עלי אלסבעה פי אלסטר אלאעלי פי אלאתנין אלתי הי מקאם אלכסר פי אלסטר אלאספל תכון אתני עשר פסמיהא מן אלאמאם פמא כרג פהו אלמטלוב | ||
|
|
ואן שית פסמי ואחד מן כמסה ונצף תגד גזאً מן אחדי עשר פי סתת אסבאע פמא כרג פהו אלמטלוב | ||
| פצל | |||
| אעלם אנך אדא ארדת אן תקסם ואחד עלי עדד פסמי אלואחד מן אלעדד פמא כאנת אלתסמיה פהו אלכארג מן אלקסמה | |||
|
|
מתאל דאלך אקסם ואחד עלי תלאתה פסמי ואחד מן אלתלאתה תגדה תלתא פתלת הו אלכארג מן אלקסמה | ||
| פאן קסמת ואחד עלי עדד וכסר פאצרב אלואחד פי מקאם אלכסר וארפעה פהו אלמסמי תם אצרב אלעדד פי מקאם כסרא ואגמל אלכסר אלמדכור פמא אגתמע סמית מנה אלעדד אלמרפוע פמא כאן פהו אלכארג מן אלקסמה | |||
|
|
מתאלה אקסם ואחד עלי תלאתה ותלת | ||
|
|
פאצרב אלואחד פי מקאם אלתלת יכון תלאתה פארפעהא תם אצרב אלתלאתה פי מקאם אלתלת תכון תסעה פאגמל עליהא אלתלת אלמדכור יכון עשרה פסמי מנהא אלתלאתה יכרג תלאתת אעשאר והו מא יכרג מן קסמת ואחד עלי תלאתה ותלת | ||
| ומענאה אן תרד אלמקסום ואלמקסום עליה אלי גנס ואחד מן אדק כסר פי אלמסאלה תם תקים אלואחד עלי אלתאני | |||
|
|
מתאל דאלך אכר אקסם ואחד על[י] תלאתה ורבע | ||
|
|
פצייר אלואחד ארבאעא יכון ארבעה תם צייר אלסתה ורבעא ארבעא תכון כמסה ועשרין פסמי מנהא אלארבעה תכון ארבעת אכמאס אלכמס והו מא יכרג מן קסמת ואחד עלי סתה ורבע | ||
|
|
תם תרגע אלי אלמסאלה פתקול אקסם ואחדא עלי כמסה ונצף | ||
|
|
פצייר אלואחד אנצאפא יכון אתנין תם צייר אלכמסה ואל נצף אנצאפא יכון אחדי עשר פסמי אתנין מן אחדי עשר ודאלך גזאן מן אחדי עשר | ||
|
|
פתצרבהא פי אלסתת אסבאע פמא כרג פהו אלמטלוב מן קסמת סתת אסבאע עלי כמסה ונצף פאפהם תציב | ||
| באב מנה אכר | |||
|
|
אקסם עשר אגזא מן אחדי עשר עלי סתה ותלתין | ||
| פאנזלהא עלי הד אלצורה | |||
| |||
|
|
תם אבדא באלסטר אלאספל פאצרב אלסתה פי אלתלאתה ואגמל מא עלי ראסהא יכון עשרין פאצרבהא פי אלאחדי עשר אלתי הי אלאמאם פי אלסטר אלאעלי תכון עשרין ומאיתין פהו אלאמאם תם אצרב אלעשרת אלתי עלי אלאחדי עשר פי אלתלאתה אלתי הי אלאמאם פי אלכט אלאספל יכון תלאתין פסמיהא מן אלאמאם יכרג גז מן אחדי עשר ונצף גז מן אחדי עשר והי תסמיה | ||
|
|
ואן שית פסמי ואחד מן סתה ותלאתין תגד עשרה ונצף עשר פאצרב עשרה ונצף עשר פי עשרה אגזא מן אחדי עשר פמא כרג פהו אלמטלוב | ||
Division of Fraction by Integer and Fraction and Fraction of Fraction |
באב קסמת אלכסר עלי אלצחיח ואלכסר וכסר אלכסר | ||
|
|
אדא קיל לך אקסם ארבעה אכמאס עלי תלאתה וסתת אסבאע ונצף סבע | ||
| פאנזלהא עלי הד אלצורה | |||
| |||
|
|
תם אבדא באלסטר אלאספל פתצרב אלתלאתה פי אלסבעה ותגמל מא עלי ראסהא יגתמע מן דאלך כמסה וכמסין פאצרבהא פי אלכמסה אלתי הי אלאמאם פי אלסטר אלאעלי יכון כמסה וסבעין ומיאתין פהו אלאמאם תם אצרב אלארבעה אלתי עלי אלכמסה פי אלסטר אלאעלי פי מקאמאת אלכסור פי אלסטר אלאספל יכון סתה וכמסין פסמיהא מן אלאמאם פמא כרג פהו אלמטלוב ודאלך גזאן מן אחדי עשר וכמס אלגז מן אחדי עשר | ||
Division of Fraction by Integer and Two Different Fractions |
באב קסמת אלכסר עלי אלצחיח ואלכסרין אלמכתלפין והי תסמיה | ||
|
|
אדא קיל לך אקסם סתת אגזא מן תלאתת עשר עלי ארבעה ותלת וסתת אגזא מן אחדי עשר | ||
| פאנזל אלמסאלה עלי הד אלצורה כמא תרי | |||
| |||
|
|
תם אבדא באלסטר אלאספל פתפעל בה כמא תפעל פי צרב אלצחיח ואלכסרין אלמכתלפין ודאלך אן תצרב אלארבעה פי אלתלאתה ומא אגתמע פי אלאחדי עשר תם תצרב מא עלי אלאחדי עשר פי אלתלאתה ומא עלי אלתלאתה פי אלאחדי עשר ותגמע אלצרוב אלתלאתה תכון ואחד וסתין ומאיה פאצרבהא פי אלתלאתת עשר אלתי הי מקאם אלכסר מן אלסטר אלאעלי יכון תלאתה ותסעין ואלפין פהו אלאמאם תם תאכוד אלסתה אלתי עלי אלתלאתת עשר פי אלסטר אלאעלי פתצרבהא פי מקאם אלכסור פי אלכט אלאספל יגתמע לך מן דאלך תמאניה ותסעין ומאיה פסמיהא מן אלאמאם ודאלך גזאן מן תלאתה ועשרין וגזאן מן תלאתת עשר פי אלגז מן תלאתה ועשרין וסבעא אלגז [מן] תלאתת עשר פי אלגז מן תלאתה ועשרין | ||
Division of Integer by Integer and Fraction |
באב קסמת אלצחיח עלי אלצחיח ואל כסר והי תסמיה | ||
|
|
אדא קיל לך אקסם אתנין עלי אתנין ונצף | ||
| פאנזל אלאתנין פי סטראً ואנזל אלכמסה ואלנצף פי סטרא תחתה עלי הד אלצורה | |||
| |||
|
|
תם אבדא באלסטר אלאספל פתצרב אלכמסה פי אלאתנין ותגמל מא עלי ראסהא יכון אחדי עשר והו אלאמאם תם אצרב אלאתנין אלדין פי אלסטר אלאעלי פי אלאתנין אלדין המא מקאם אלכסר פי אלסטר אלאספל פמא אגתמע סמיתה מן אלאמאם תכרג ארבע אגזא מן אחדי עשר פי אתנין פמא כרג פהו אלמטלוב | ||
Division of Integer and Fraction by Integer and Fraction |
באב קסמת אלצחיח ואלכסר עלי אלצחיח ואלכסר | ||
|
|
אדא קיל לך אקסם סתה ורבעא עלי תמאניה ותלת | ||
| פאנזלהא עלי הד אלצורה | |||
| |||
|
|
תם אבדא באלסטר אלאספל פתצרב אלתמאניה פי אלתלאתה ותגמל מא עלי ראסהא תכון כמסה ועשרין פאצרבהא פי אמאם אלסטר אלאעלי והו ארבעה תכון מאיה פהו אלאמאם תם ארגע אלי אלסטר אלאעלי פתצרב אלסתה פי אלארבעה ותגמל מא עלי ראסהא תכון כמסה ועשרין פאצרבהא פי אמאם אלכט אלאספל אלדי הו תלאתה תכון כמסה וסבעין פסמיהא מן אלאמאם אלדי הו מאיה יכרג תלאתת ארבאע פאפהם ותרי ותדבר | ||
| והד אלאבואב אלמתקדמה אנמא הי תסמיה אן תקול אקסם כדא עלי כדא או סמי כדא מן כדא אדא כאן אלמקסום מן אלמקסום עליה | |||
Division of Fraction by Fraction |
באב קסמת אלכסר עלי אלכסר | ||
|
|
אדא קיל לך אקסם תלתא עלי תלאתה ארבאע | ||
| פאנזלהא עלי הד אלצורה | |||
| |||
|
|
תם אבדא באלסטר אלאספל פתצרב אלתלאתה אלתי עלי אלארבעה פי אמאם אלכט אלאעלי והו תלאתה יכון תסעה פארפעהא פהו אלאמאם תם תאכוד אלואחד אלדי עלי מקאם אלכסר פי אלסטר אלאעלי פתצרבה פי אלארבעה אלתי הי מקאם אלכסר פי אלסטר אלאספל יכון דאלך ארבעה פסמיהא מן אלאמאם יכרג ארבעת אתסאע | ||
|
|
פאן קאל אקסם תלאתת אכמאס עלי סבעת אתסאע | ||
| פאנזלהא עלי הד אלצורה | |||
| |||
|
|
תם אבדא באלסטר אלאספל פתצרב אלסבעה פי אלכמסה אלתי הי אמאם אלכט אלאעלי יכון כמסה ותלאתין והו אלאמאם תם אצרב אלתלאתה אלתי עלי אלכמסה פי אלתסעה אלתי אמאם אלכט אלאספל יכון סבעה ועשרין פסמיהא מן אלאמאם יכרג כמסת אסבאע וכמסא סבע | ||
|
|
ולו קאל אקסם גזאין מן תלאתת עשר עלי תסעת אעשאר | ||
| פאנזל אלמסאלה עלי הד אלצורה | |||
| |||
|
|
תם אצרב אלתסעה פי אלתלאתה עשר יכון אלאמאם תם אצרב אלאתנין פי אלעשרה וסמי מנהא אלאמאם יכרג גזאן מן תלאתה עשר ותסמי אלגז מן תלאתת עשר | ||
|
|
פאן קאל אקסם כמסת אגזא מן אחדי עשר עלי תסעת אגזא מן סבעת עשר | ||
| פאנזלהא עלי הד אלצורה | |||
| |||
|
|
תם באלסטר אלאספל פתצרב אלתסעה פי אלאחדי עשר יכון אלאמאם תם אצרב אלכמסה פי אלסבעת עשר וסמיה מן אלאמאם פמא כרג פהו מא ארדת ודאלך תסעת אגזא מן אחדי עשר וארבעת אתסאע אלגז מן אחדי עשר | ||
Division of Two Different Fractions by Fraction |
באב קסמת אלכסרין עלי אלכסר ותסמי אלתסמיה | ||
|
|
אדא קיל לך אקסם תלתא וסבעא עלי עשרת אגזא מן אחדי עשר | ||
| פאנזלהא עלי הד אלצורה | |||
| |||
|
|
תם אבדא באלסטר אלאספל פתצרב אלעשרה פי אימת אלסטר אלאעלי יכון עשרה ומאיתין פהו אלאמאם תם אפעל באלסטר אלאעלי תפעל באלכסר[ין] אלמכתלפין יגתמע פיה עשרה פאצרבהא פי אלאחדי עשר וסמי מא כרג מן אלאמאם יכרג כמסה אעשאר וסבע עשר ותלתא סבע עשר ואן שית תלאת אסבאע ותלת סבע | ||
Division of Fraction by Fraction and Fraction of Fraction |
באב קסמת אלכסר עלי אלכסר וכסר אלכסר והי תסמיה | ||
|
|
אדא קיל לך אקסם תלתין עלי תסעה אעשאר וכמסת אתמאן אלעשר | ||
| פאנזל אלמסאלה אדא עלי הד אלצורה כמא תרי | |||
| |||
|
|
תם אבדא באלסטר אלאספל פתפעל בה כמא תפעל באלכסר וכסר אלכסר יגתמע פיה סבעה וסבעון פאצרבהא פי אלתלאתה אלתי הי אמאם אלסטר אלאעלי יכון ואחד ותלאתין ומאיתין פהו אלאמאם תם אצרב אלאתנין אלדין פי אלסטר אלאעלי פי אימת אלסטר אלאספל יכון סתין ומא[יה] פסמיהא מן אלאמאם יכרג סבעת אגזא מן אחדי עשר וארבעת אסבאע אלגז מן אחדי עשר ותלת סבע אלגז מן אחדי עשר | ||
Division of Fraction by Two Different Fractions |
באב קסמת אלכסרין עלי אלכסרין והו תסמיה | ||
|
|
מתאל דאלך אקסם סבעת אתסאע עלי תלאתת ארבאע סבעת אתמאן | ||
| פאנזל אלמסאלה עלי הד אלצורה | |||
| |||
|
|
תם אבדא באלסטר אלאספל תעמל בה כמא תעמל באלכסרין אלמכתלפין יגתמע פיה אתנין וכמסין פאצרבהא פי אלאמאם אלדי פי אלסטר אלאעלי והו תסעה יכון דאלך תמאניה וסתין וארבע מאיה פהו אלאמאם תם אצרב אלסבעה עלי אלתסעה פי אימת אלסטר אלאספל והי ארבעה ותמאניה יכון ארבעה ועשרין ומאיתין פסמיהא מן אלאמאם יכרג סת אגזא מן תלאתת עשר ותסעא גז מן תלאתת עשר | ||
Division of Fraction and Fraction of Fraction by Fraction and Fraction of Fraction |
באב קסמת אלכסר וכסר אלכסר עלי אלכסר וכסר אלכסר והי תסמיה | ||
|
|
אדא קיל לך אקסם ארבע אתסאע ונצף תסע עלי סבעה אתמאן ותלת תמן | ||
| פאנזלהא עלי הד אלצורה | |||
| |||
|
|
תם אבדא באלסטר אלאספל פתעמל בה כמא תעמל באלכסר וכסר אלכסר ומא אגתמע צרבתה פי אימת אלסטר אלאעלי יכון סתה ותסעין ותלאתת מאיה פהו אלאמאם תם אצנע באלסטר אלאעלי כמא תקדם פי צרב אלכסר וכסר אלכסר ומא אגתמע צרבתה פי אימת אלסטר אלאספל תכון סתת עשר ומיאתין פסמיהא מן אלאמאם יכרג סת אגזא מן אחדי עשר | ||
Division of Two Different Fractions by Two Different Fractions |
באב קסמת אלכסרין אלמכתלפין עלי אלכסרין אלמכתלפין | ||
|
|
והי תסמיה אדא קיל לך אקסם תלתין ותלאתת אכמאס עלי תסעת אעשאר ועשרת אגזא מן אחדי עשר | ||
| פאנזלהא עלי הד אלצורה | |||
| |||
|
|
תם אבדא באלסטר אלאספל פתעמל בה כמא תעמל באלכסרין אלמכתלפין יכון דאלך סתה ותסעין ומאיה פאצרבהא פי אימת אלסטר אלאעלי יכון דאלך כמסה ותמאנין ותסע מאיה ואלפין והו אלא[מאם] יכרג לך אלמטלוב ודאלך תסעה ותלאתין גז ומאיה גז מן תסעה ותסעין ומאיה וכמס אלגז מן תסעה ותסעין ומאיה ותלתא כמס אלגז מן תסעה ותסעין ומאיה והד צורתהא | ||
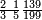
| |||
Division of Fraction of Fraction by Integer and Fraction |
באב קסמת כסר אלכסר עלי אלצחיח ואלכסר והי תסמיה | ||
|
|
אדא קיל לך אקסם סבעת אתמאן אלתסע עלי תלאתה ונצף | ||
| פאנזלהא עלי הד אלצורה | |||
| |||
|
|
תם אבדא באלסטר אלאספל פתצרב אלתלאתה פי אלאתנין ותגמל מא עלי ראסהא יכון סבעה פאצרבהא פי אמאם אלסטר אלאעלי יכון דאלך ארבעה וכמס מאיה והו אלאמאם תם אצרב אלסבעה אלתי עלי אלכט אלאעלי פי אלאתנין מקאם אלכסר פי אלסטר אלאספל יכון דאלך ארבעת עשר פסמיהא מן אלאמאם יכון תמן תסע | ||
Division of Fraction of Fraction by Integer and Fraction and Fraction of Fraction |
באב קסמת כסר אלכסר עלי אלצחיח ואלכסר וכסר אלכסר והי תסמיה | ||
|
|
אדא קיל לך אקסם תסעת אעשאר אלגז מן תלאתת עשר עלי סתה ותלאתת אתמאן ותלת תמן | ||
| פאנזלהא עלי הד אלצורה כמא תרי | |||
| |||
| תם אבדא באלסטר אלאספל פתתבע עמל צרב אלצחיח ואלכסר ואלכסר וכסר אלכסר יגתמע פיה ארבעה ועשרין ומאיה פאצרבהא פי אימת אלכט אלאעלי יכון דאלך עשרין ועשרין אלפא והו אלאמאם תם אצרב אלתסעה אלתי עלי אלכט אלאעלי פי אימת אלכט אלאספל יכון סתת עשר ומיאתין פסמיהא מן אלאמאם יכרג גז מן אחדי עשר פי אלגז מן תלאתת עשר וכמסת אעשאר אלגז מן אחדי עשר פי אלגז מן תלאתת עשר ותלאתת אסבאע עשר אלגז פי אלגז | |||
|
| |||
Division of Fraction of Fraction by Integer and Two Different Fractions |
באב קסמת כסר אלכסר עלי אלצחיח ואלכסרין אלמכתלפין והי תסמיה | ||
|
|
אדא קיל לך אקסם תלאתת אכמאס אלסבע עלי ואחד וכמסת אסדאס ותלתין | ||
| פאנזלהא עלי הד אלצורה | |||
| |||
|
|
תם אעמל באלסטר אלאספל כמא תקדם עלי אלכסרין פי עמל אלצחיח ואלכסרין אלמכתלפין ומא אגתמע צרבתה פי אימת אלסטר אלאעלי יכון אלגמיע כמסה וסבעין וכמס מאיה ואלפאً והו אלאמאם תם אצרב אלתלאתה אלתי עלי אלכט אלאעלי פי אימת אלסטר אלאספל יכון ארבעה וכמסין פסמיהא מן אלאמאם יכרג סבעא תסע וארבעת אכמאס כמס סבע אלתמן | ||
Division of Fraction of Fraction by Fraction |
באב קסמת כסר אלכסר עלי אלכסר והו תסמיה | ||
|
|
אדא קיל לך אקסם כמסת אתסאע אלעשר עלי תלאתה אכמאס | ||
| פאנזלהא עלי הד אלצורה | |||
| |||
|
|
תם אצרב אלתלאתה אלתי עלי אלכט אלאעלי פי אימת אלכט אלאעלי יכון דאלך סבעין ומיאתין פהו אלאמאם תם אצרב אלכמסה אלתי עלי אלכט אלאעלי פי אמאם אלכט אלאספל יכון כמסה ועשרין פסמיהא מן אלאמאם יכון תמאנית אתסאע אלעשר ותלת תסע אלעשר | ||
Division of Fraction of Fraction by Fraction and Fraction of Fraction |
באב קסמת כסר אלכסר עלי אלכסר וכסר אלכסר והי תסמיה | ||
|
|
אקסם תלאתת ארבאע אלכמס עלי תלאתה אסדאס ונצף אלסדס | ||
| פאנזלהא הכדא | |||
| |||
|
|
תם אצנע באלסטר אלאספל כמא תקדם פי אלכסר וכסר אלכסר ומא אגתמע צרבתה פי אימת אלסטר אלאעלי יכון דאלך מאיה וארבעין והו אלאמאם תם אצרב אלתלאתה אלתי עלי אלכט אלאעלי פי מקאמאת אלסטר אלאספל תכון סתה ותלאתין פסמיהא מן אלאמאם יכון עשראן וארבע אתסאע אלעשר | ||
Division of Fraction of Fraction by Two Different Fractions |
באב קסמת כסר אלכסר עלי אלכסרין אלמכתלפין והי אלתסמיה | ||
|
|
אדא קיל לך אקסם נצף סבע עלי תלאתת ארבאע ותלאתת אכמאס | ||
| פאנזלהא עלי הד אלצורה | |||
| |||
|
|
תם אצנע באלסטר אלאספל כמא תפעל באלכסרין אלמכתלפין ומא אגתמע צרבתה פי אימת אלסטר אלאעלי יכון דאלך תמאניה וסבעין ותלאתת מאיה פהו אלאמאם תם אצרב אלואחד אלדי עלי אלכט אלאעלי פי אימת אלסטר אלאספל ותסמי מא אגתמע מן אלאמאם יכרג תלאתת אסבאע אלתסע וסדס סבע אלתסע | ||
| ופי מא קדמנא מן קסמת אלקליל עלי אלכתיר אלדי הו אלתסמיה כפאיה יסתדל בה עלי גמיע מא יריד מן אשיא מנה והוא קיל פי הד אלמסאיל אלמתקדמה אקסם או סמי כל דאלך גאיז פיהא והד אלבאב יסמיה אהל אלח[סאב] תסמיה אלכסור ונתבע בעד הד אלבאב קסמת אלכתיר עלי אלקלי והי קסמת אלכסור בעצהא עלי בעץ ענד אהל אלחסאב ונתבע פיה אלמסאיל עלי חסב מא קדמנא | |||
Division of the larger by the smaller |
באב קסמת אלכתיר עלי אלקליל | ||
| אעלם אן הד אלבאב גמיע אעמאלה מסאניה לגמיע אעמאל אלבאב אלמתקדם | |||
| ודאלך אן נבדא אולא באלסטר אלאספל פנתבע פיה אלעמל עלי מא תקדם פי באב אלצרב פמא אגתמע צרבתה פי אימת אלסטר אלאעלי יכון הד אלמגתמע אלדי עליה אלקסמה תם אצ[נע] באלסטר אלאעלי עלי מא תקדם פי באבה ומא אגתמע צרבתה פי אימת אלסטר אלאספל פמא אגתמע קסמתה עלי אלאמאם פמא כרג פהו אלמטלוב | |||
| והד אלעמל יצחבך פי גמיע מא יאתי בעד הדא אן שא אללה תעלי | |||
Division of Integer by Fraction |
באב קסמת אלצחיח עלי אלכסר | ||
|
|
אדא קיל לך אקסם עשרה עלי כמס | ||
| פאנזלהא הכדא | |||
| |||
|
|
תם אצרב אלכמסה פי אלעשרה ואקסם עלי אלאמאם יכרג דאלך כמסון והו אלכארג מן אלקסמה | ||
| ומעני הד אלמסאלה אדא וגב לכמס עשרה כם יגב ללואחד אלצחיח פאלמטלוב מן אלקסמה אבדא אנמא הו מא יגב ללואחד | |||
| והד אלבאב איצא ינקסם קסמין: אמא אן יכון קסמת אלצחיח עלי אלגז ואחד | |||
| או עלי אגזא כתירה | |||
| פאן קסמת עלי גז ואחד פאצרב אלצחיח פי מקאם דאלך אלגז פמא כרג פהו אלכארג מן אלקסמה והו אלואגב ללואחד | |||
| ואן כאנת אלקסמה עלי אגזא צרבת אלצחיח פי מקאם דאלך אלגז וקסמת מא אגתמע עלי עדד אלאגזא פמא כרג פהו אלואגב ללואחד | |||
|
|
פאן קאל אקסם סתה עלי תסע | ||
|
|
פאצרב סתה פי תסעה יכון ארבעה וכמסין והו אלכארג מן אלקסמה | ||
|
|
וכדאלך לו קאל אקסם עשרין עלי עשר | ||
|
|
פאצרב אלעשרין פי מקאם אלעשר יכון מאיתין והו אלכארג מן אלקסמה | ||
| ואמא קסמת אלצחיח עלי אלאגזא | |||
|
|
מתאלה אקסם סתה עלי תלתין | ||
| פאנזלהא עלי הד אלצורה | |||
| |||
|
|
תם אצרב אלסתה פי אלתלאתה ואקסם עלי אלאתנין יכרוג לך תסעה | ||
|
|
ולו קאל אקסם תסעה עלי תלאתה אתמאן | ||
| פאנזלהא עלי הד אלצורה | |||
| |||
|
|
תם אצרב אלסתה פי אלתמאניה ואקסם עלי אלתלאתה יכרג ארבעה ועשרין | ||
|
|
ולו קאל אקסם כמסת עשר עלי עשרת אגזא מן אחדי עשר | ||
| פאנזלהא עלי הד אלצורה | |||
| |||
|
|
תם אצרב אלאחדי עשר פי אלכמסה עשר ואקסם מא כרג עלי אלעשרה יכון דאלך סת עשר ונצפא | ||
| פאסתכראג הד אלאמאם אלדי יקסם עליה פי גמיע הד אלנוע אנמא הו אן תאכוד אלאגזא אלתי עלי אלכט אלאספל פתתכדהא אמאמא בעד צרבהא פי אימת אלסטר אלאעלי עלי מא תקדם | |||
Division of Integer by Fraction of Fraction |
באב קסמת אלצחיח עלי כסר אלכסר | ||
| אעלם אן גמיע אלעמל פי הד אלבאב ואלבאב אלדי תקדם עמל ואחד | |||
| והו ינקסם קסמין: אנמא אן יכון אלכסר אלמקסום עליה גזא ואחדא או אגזא | |||
| פאן כאן גזא ואחדא פאן צרב אלעדד אלמקסום פי מקאם אלכסר והו אלכארג מן אלקסמה | |||
| ואן כאן אלכסר אלמקסום אגזא פאנך תצרב אלעדד אלמקסום פי מקאמאת תלך אלכסור ותקסם מא אגתמע עלי עדד אלאגזא פמא כרג פהו אלמטלוב | |||
|
|
מתאל פי אלקסמה עלי גז ואחד אקסם עשרה עלי תלת כמס | ||
| פאנזלהא עלי הד אלצורה | |||
| |||
|
|
תם אצרב אלעשרה פי אימת אלסטר אלאספל פמא כרג פהו אלכארג מן אלקסמה ודאלך כמסון ומאיה | ||
| ואן כאן אצל אלעמל אן תקסם אלמאיה ואלכמסין עלי אלואחד אלדי עלי אלתלאתה לאכן אלקסמה עלי אלואחד לא תתגזא כמא אן אלצרב פי ואחד לא יתצאעף פאסקטנא נחן לפט אלקסמה עלי ואחד ואיצא פאן אלמטלוב פי אלקסמה אנמא הו מא יגב ללואחד אדא כאנו גמאעה וקסם עליהם עדד פאדא קסם אלעדד עלי ואחד אעטי דאלך אלעדד כלה ללואחד ואסתגנינא ען לפט אלצרב ואלקסמה פיה | |||
| ואמא אלקסמה עלי אלאגזא מן הד אלבאב | |||
|
|
פמתאלה אקסם תסעה עלי תלתיי תמן | ||
| פאנזל אלמסאלה עלי הד אלצורה | |||
| |||
|
|
תם אצרב תסעה פי אימת אלסטר אלאספל ומא אגתמע קסמתה עלי אלאתנין אלדין המא אלתלתאן יכרג תמאניה ומאיה | ||
|
|
ולו קאל אקסם תסעה עשר עלי תלאתת ארבאע כמס | ||
| פאנזל אלמסאלה עלי הד אלצורה | |||
| |||
|
|
תם אצרב תסעה פי אימת אלסטר אלאספל ומא אגתמע עלי הד אלצורה תם אצרב אלתסעת עשר פי אמאם אלכט אלאספל תם תקסם מא אגתמע עלי אלתלאתה אלתי הי אלארבאע יכרג סתה ועשרון ומאיה ותלתאן פאפהם | ||
Division of Integer by Fraction and Fraction of Fraction |
באב קסמת אלצחיח עלי אלכסר וכסר אלכסר | ||
|
|
אדא קיל לך אקסם ארבעה עלי תלאתה אכמאס ותלת כמס | ||
| פאנזלהא עלי הד אלצורה | |||
| |||
|
|
תם אבדא באלסטר אלאספל פתפעל בה כמא פעלת פי באב אלכסר וכסר אלכסר ודאלך באן תצרב אלתלאתה אלתי עלי אלכמסה פי אלתלאתה אלתי הי אלמקאם אלכסר ותגמל מא עלי ראסהא יכון דאלך עשרה פהו אלאמאם תם אצרב אלארבעה אלמקסומה פי מקאם אלסטר אלאספל יכון סתין פאקסמהא עלי אלאמאם יכרג סתה והו אלכארג מן אלקסמה | ||
|
|
פאן קיל לך אקסם כמסה עלי עשרה אגזא מן אחדי עשר ונצף אלגז מן אחדי עשר פאנזלהא עלי הד אלצורה | ||
| |||
|
|
תם אבדא באלסטר אלאספל פתצרב אלעשרה פי אלאתנין ותגמל מא עלי ראסהא יכון ואחד ועשרין והו אלאמאם תם אצרב אלכמסה פי אלאחדי עשר ופי אלאתנין ותקסם מא אגתמע עלי אלאמאם יכרג כמסה וסבע ותלתא סבע | ||
Division of Integer by Two Different Fractions |
באב קסמת אלצחיח עלי אלכסרין אלמכתלפין | ||
|
|
אקסם תמאניה עלי תלת ותלאתת ארבאע | ||
| פאנזלהא עלי הד אלצורה | |||
| |||
|
|
תם אצנע באלסטר אלאספל כמא תפעל באלכסרין אלמכתלפין יגתמע פיה תלאתת עשר פהו אלאמאם תם אצרב אלתמאניה פי אימת אלסטר אלאספל ותקסם עלי אלאמאם יכרג סבעה וכמסת אגזא מן תלאתת עשר | ||
|
|
פאן קאל אקסם עשרה עלי תלאתת אכמאס ותלאתת אתמאן | ||
| פאנזלהא עלי הד אלצורה | |||
| |||
|
|
תם אצנע באלסטר אלאספל כמא תקדם פי אלכסרין אלמכתלפין תכון תסעה ותלאתין פהו אלאמאם תם תצרב אלעשרה פי מקאמאת אלכסר פי אלכט אלאספל יכון דאלך ארבע מאיה פאקסמהא עלי אלאמאם יכרג עשרה ותלאתת אגזא מן תלאתת עשר ותלת גז מן תלת עשר | ||
Division of Integer and Fraction by Fraction |
באב קסמת אלצחיח ואלכסר עלי אלכסר | ||
| אדא ארדת אן תקסם צחיחא וכסרא עלי כסר | |||
| פאנזל אלמסאלה פי סטרין אלמקסום פי אלסטר אלאעלי ואלמקסום עליה פי אלסטר אלאספל תם תצנע באלסטר אלאעלי עלי מא תקדם פי באבה פי צרב אלצחיח ואלכסר ומא אגתמע צרבתה פי אמאם אלכט אלאספל אנמא אלמטלוב פיה מקאם אלכסר אלדי פי דאלך אלסטר וכדאלך פי גמיע מא יאתי בעדה תצרב אלעדד אלדי עלי מקאם אלכסר מן אלכט אלאספל והו עדד אלאגזא פי אמאם אלסטר אלאעלי פמא אגתמע פהו אלאמאם פאקסם עליה אלעדד אלאול | |||
|
|
מתאלה אקסם כמסת עשר ונצפא עלי כמסה אסדאס | ||
| פאנזלהא עלי הד אלצורה | |||
| |||
|
|
תם אצרב אלכמסה אלתי עלי אלכט אלאספל פי אמאם אלכט אלאעלי תכון עשרה והו אלאמאם תם ארגע אלי אלכט אלאעלי פתצנע בה כמא תקדם פי צרב אלצחיח ואלכסר ודאלך אן תצרב אלכמסה עשר פי אלאתנין ותגמל מא עלי ראסהא יכון ואחד ותלאתין פאצרבה פי אמאם אלכט אלאספל יכון סתה ותמאנין ומאיה פאקסמהא עלי אלאמאם יכרג תמאנית עשר וסתת אעשאר | ||
|
|
פאן קאל אקסם עשרין ורבע עלי תלאתת אכמאס | ||
| פאנזלהא עלי הד אלצורה | |||
| |||
|
|
תם אצרב אלתלאתה אלתי עלי אלכט אלאספל פי אמאם אלכט אלאעלי יכון אתני עשר פהו אלאמאם אלדי יקסם עליה תם ארגע אלי אלכט אלאעלי פתצרב אלעשרין פי אלארבעה ותגמל מא עלי ראסהא ותצרבה פי אמאם אלכט אלאספל יכון דאלך כמסה וארבע מאיה פאקסמהא עלי אלאמאם יכרג לך תלאתה ותלאתין וארבע אסדאס ונצף סדס | ||
Division of Integer and Fraction by Fraction of Fraction |
באב קסמת אלצחיח ואלכסר עלי כסר אלכסר | ||
|
|
אדא קיל לך אקסם כמסה ותלת עלי תלאתת ארבאע כמס | ||
| פאנזלהא עלי הד אלצורה | |||
| |||
|
|
תם אצרב אלתלאתה אלתי עלי אלכט אלאספל פי אלתלאתה אלתי הי אמאם אלכט אלאעלי יכון תסעה והו אלאמאם תם ארגע אלי אלסטר אלאעלי פתצרב אלכמסה פי אלתלאתה ותגמל מא עלי ראסהא יכון סת עשר פאצרבהא פי אימת אלכט אלאספל יכון גמיע דאלך עשרין ותלת מאיה פאקסמהא עלי אלאמאם יכרג לך כמסה ותלאתי[ן] וכמסת אתסאע | ||
|
|
פאן קאל אקסם תמאניה ותלאתת אגזא מן תלת עשר עלי תלאתת אכמאס אלסבע | ||
| פאנזלהא עלי [הד] אלצורה | |||
| |||
|
|
תם אצרב אלתלאתה אלתי עלי אלכט אלאספל פי אלתלאתת עשר אלתי עלי אלכט אלאספל פי אלתלאתה עשר אלתי הי אמאם אלכט אלאעלי יכון תסעה ותלאתין והו אלאמאם תם אצרב אלתמאניה פי אלתלאתה עשר ותגמל מא עלי ראסהא ומא אגתמע צרבתה פי אימת אלסטר אלאספל יכון דאלך כמסה וארבעין וסבע מאיה ותלאתת אלאף פאקסמהא עלי אלאמאם יכרג לך סתה ותסעין ותלת גז מן תלאתת עשר | ||
Division of Integer and Fraction by Fraction and Fraction of Fraction |
באב קסמת אלצחיח ואלכסר עלי אלכסר וכסר אלכסר | ||
|
|
אדא קיל לך אקסם סתה ונצפא עלי ארבעת אכמאס ונצף כמס | ||
| פאנזל אלמסאלה עלי הד אלצורה | |||
| |||
|
|
תם אבדא באלסטר אלאספל פתצנע בה כמא תצנע פי צרב אלכסר וכסר אלכסר יכון דאלך תסעה פאצרב פי מקאם אלכסר פי אלסטר אלאעלי יכון תמאנית [עשר] והו אלאמאם תם ארגע אלי אלסטר אלאעלי פתעמ[ל] בה כמא תקדם פי צרב אלכסר ומא אגתמע צרבתה פי אימת אלסטר אלאספל יכון תלאתין ומ[איה] אקסם עלי אלאמאם יכרג לך סבעה ותסעאן | ||
Division of Integer and Fraction by Two Different Fractions |
באב קסמת אלצחיח ואלכסר עלי אלכסרין | ||
|
|
אדא קיל לך אקסם ע[שר]ה ותלתא עלי כמס וסדס | ||
| פאנזלהא כמא תרי | |||
| |||
| תם אצנע באלסטר אלאספל כמא תקדם פי אלכסרין יגתמע פיה אחדי עשר פאצרבהא פי מקאם אלתלת מן אלכט אלאעלי יכון תלאתה ותלאתין והו אלאמאם תם אצרב אלעשרה פי אלתלאתה ואגמל מא עלי ראצהא ואלדי יגתמע לך צרבתה פי אימת אלכט אלאספל יכון דאלך תלאתין ותסע מאיה פאקסמהא עלי אלאמאם יכרג תמאניה ועשרין וגז מן אחדי עשר | |||
|
| |||
Division of Integer and Fraction and Fraction of Fraction by Fraction |
באב קסמת אלצחיח ואלכסר וכסר אלכסר עלי אלכסר | ||
|
|
אדא קיל לך אקסם ארבעה ותלאתת אתמאן ונצף תמן עלי תלאתת אכמאס | ||
| פאנזלה[א] עלי הד אלצורה | |||
| |||
| תם אבדא באלסטר אלאספל פתצרב אלתלאתה אלתי עלי אלכמסה פי אימת אלכט אלאעלי תכון תמאניה וארבעין והו אל[א]מאם תם ארגע אלי אלסטר אלאעלי פתצנע בה כמא צנעת פי צרב אלצחיח ואלכסר וכסר אלכסר ודאלך אן תצרב אלארבעה פי אלתמאניה ותגמל מא עלי ראסהא והי תלאתה ותצרב אלמגתמע פי אלאתנין ותגמל מא עלי ראצהא יכון ואחד ותסעין פאצרבהא פי אלכמסה אלתי הי מקאם אלכסר פי אלכט אלאספל יכון כמסה וכמסין ותלת מאיה פאקסמהא עלי אלאמאם יכרג לך פי אלקסמה סבעה ותלאתה אתמאן וסדס תמן | |||
|
| |||
Division of Integer and Fraction and Fraction of Fraction by Fraction of Fraction |
באב קסמת אלצחיח ואלכסר וכסר אלכסר עלי כסר אלכסר | ||
|
|
אדא קיל לך אקסם אתנין וסתת אסבאע ותלתיי סבע עלי ארבעת אכמאס אלסדס | ||
| פאנזלה עלי הדה אלצורה כמא תרי פי מא יאתי בעד | |||
| |||
| תם תאכוד אלארבעה אלתי עלי אל[כט] אלאספל פתצרבהא פי אימת אלכט אלאעלי יכון דאלך ארבעה ותמאנין והו אלאמאם תם אצנע באלסטר אלאעלי כמא תקדם פי צרב אלצחיח ואלכסר וכסר אלכסר פמא אגתמע צרבתה פי אימת אלכט אלאספל יכון דאלך סתין ותמן מאיה ואלפא פאקסמהא עלי אלאמאם יכרג לך אתנין ועשרין וסבע | |||
|
| |||
Division of Integer and Fraction and Fraction of Fraction by Fraction and Fraction of Fraction |
באב קסמת אלצחיח ואלכסר וכסר אלכסר עלי אלכסר וכסר אלכסר | ||
|
|
אדא קיל לך אקסם תסעה וכמסת אסדאס ורבע סדס עלי סבע ונצף סבע | ||
| פאנזלהא עלי הד אלצורה | |||
| |||
|
|
תם אבדא באלסטר אלאספל פתצרב אלואחד אלדי עלי אלסבעה פי אלאתנין ותגמל מא עלי ראצהא ומא אגתמע צרבתה פי אימת אלסטר אלאעלי יכון דאלך אתנין וסבעין והו אלאמאם תם תצנע באלסטר אלאעלי כמא תקדם פי באבה ומא אגתמע צרבתה פי אימת אלסטר אלאספל יכון דאלך תמאנית עשר ותלאתת מאיה ותלאתת אלאף פאקסמהא עלי אלאמאם יכרג לך סתה וארבעין וסתת אתמאן אלתסע | ||
Division of Integer and Fraction and Fraction of Fraction by Two Different Fractions |
באב קסמת אלצחיח ואלכסר וכסר אלכסר עלי אלכסרין אלמכתלפין | ||
|
|
אדא קיל לך אקסם תלאתה ותלאתת אעשאר ונצף אלעשר עלי תלאתת ארבאע ותלאתת אגזא מן אחדי עשר | ||
| פאנזלהא עלי הד אלצורה | |||
| |||
| תם אצנע באלסטר אלאספל כמא צנעת באלסטרין אלמכתלפין יגתמע פיה כמסה וארבעין פאצרבהא פי אימת אלכט אלאעלי יכון תסע מאיה והו אלאמאם תם ארגע אלי אלכט אלאעלי פתצרב אלתלאתה אלתי הי אלצחיח פי אלעשרה ותגמל מא עלי ראסהא ומא אגתמע צרבתה פי אלאתנין ותגמל מא עלי ראסהא יכון דאלך אתנין וכמסין וכמס מאיה ותלאתת אלאף פאקסמהא עלי אלאמאם יכרג תלאתה ותלאתין וכמסת אסבאע וארבע אכמאס אלסבע | |||
|
| |||
Division of Integer and Two Different Fractions by Fraction and Fraction of Fraction |
באב קסמת אלצחיח ואלכסרין עלי אלכסר וכסר אלכסר | ||
|
|
אדא קיל לך אקסם תמאניה ותלאתת אגזא מן אחדי עשר וכמסת אסבאע עלי כמסת אתמאן ותלת תמן | ||
| פאנזלהא עלי הד אלצורה | |||
| |||
|
|
תם אבדא באלסטר אלאספל פתצרב פי אלכמסה אלתי עלי אלתמאניה פי אלתלאתה ותגמל מא עלי ראסהא יכון סתת עשר פאצרבהא פי אימת אלסטר אלאעלי פהו אלאמאם תם ארגע אלי אלסטר אלאעלי פתעמל בה כמא תקדם פמא אגתמע צרבתה פי אימת אלסטר אלאספל יכון דאלך תמאניה וסת מאיה וסת עשר אלפא פאקסמהא עלי אלאמאם יכרג תלת עשר וכמסת אגזא מן אחדי עשר וסבעא תמן אלגז מן אחדי עשר | ||
Division of Integer and Two Different Fractions by Integer and Two Different Fractions |
באב קסמת אלצחיח ואלכסרין עלי אלכסרין | ||
|
|
אדא קיל אקסם עשרה וסתת אגזא מן תלת עשר וסבעת אתמאן עלי תסעת אעשאר וסבעת אגזא מן אחדי עשר | ||
| פאנזלהא עלי הד אלצורה כמא תרי | |||
| |||
| תם אבדא באלסטר אלאספל פתעמל בה עלי מא תקדם ומא אגתמע צרבתה פי אימת אלסטר אלאעלי יכון דאלך סתה וסבעין וכמס מאיה וסבעת עשר אלפא והו אלאמאם תם אצנע באלסטר אלאעלי עלי מא תקדם ומא אגתמע צרבתה פי אימת אלסטר אלאספל יכון דאלך תסעין וסת מאיה ותסעת ועשרין אלפא ומאיה אלף אקסם עלי אלאמאם יכרג סבעה וארבעת אגזא מן תלאתת עשר ותמנא גז מן תלאתת עשר פי אלגז מן תלאתת עשר פי אלגז מן תלאתת עשר | |||
|
| |||
Division of Fraction by Fraction |
באב קסמת אלכסר עלי אלכסר | ||
|
|
מתאל דאלך אקסם סתת אסבאע עלי תלאתת אתמאן | ||
| פאנזלה עלי הד אלצורה | |||
| |||
|
|
תם אבדא באלסטר אלאספל פתצרב אלתלאתה אלדי עלי אלתמאניה פי אלסבעה אלתי הי אלאמאם אלסטר אלאעלי יכון ואחד ועשרין והו אלאמאם תם אצרב אלסתה אלתי עלי אלכט אלאעלי פי אלתמאניה אלתי תחת אלכט אלאספל יכון תמאניה וארבעין פאקסמהא עלי אלאמאם יכרג אתנאן וסבעאן | ||
Division of Fraction by Fraction of Fraction |
באב קסמת אלכסר עלי כסר אלכסר | ||
|
|
אקסם תסעת אעשאר עלי תלתיי סבע | ||
| פאנזלהא עלי הד אלצורה | |||
| |||
|
|
תם אבדא באלסטר אלאספל פתצרב אלאתנין פי אלעשרה אלתי הי אמאם אלכט אלאעלי תכון עשרין והו אלאמאם תם אצרב אלתסעה אלתי עלי אלכט אלא[על]י פי אימת אלכט אלאספל תכון תסעה ותמ[אני]ן ומאיה פאקסמהא עלי אלאמ[א]ם יכרג תסעה וארבעה אעשאר ונצף עשר | ||
Division of Fraction by Fraction and Fraction of Fraction |
באב קסמת אלכסר עלי אלכסר וכסר אלכסר | ||
|
|
אקסם אתני עשר גז מן תלאתת עשר עלי תמן ותל[ת] תמן | ||
| פאנזלהא עלי הד אלצורה | |||
| |||
|
|
תם אצנע באלסטר אלאספל עלי מא תקדם פי אלכסר וכסר אלכסר ומא אגתמע צרבתה פי אמאם אלכט אלאעלי יכון אתנין וכמסין והו אלאמאם תם תאכוד אלאתני עשר אלתי עלי אלכט אלאעלי ותצרבהא פי אימת אלכט אלאספל יכון תמאניה ותמאנין ומאתין פאקסמהא עלי אלאמאם יכרג כמסת וסבעת אגזא מן תלת עשר | ||
| באב | |||
|
|
תם תאכוד תלתיי ארבעה ונצף ודאלך תלת פתקסם תלאתה ותלאתת ארבאע יכרג ואחד ורבע והו אלמטלוב | ||
| ואעלם אן אלעמל פגמע הד אלמסאיל אן תצנע בכל שי מנהא עלי מא תקדם פי באבה ותצרב אלכארג מן אלסטר אלאספל פי אימת אלסטר אלאעלי יכון אגתמאע הו אלאמאם תם תצרב אלכארג מן אלסטר אלאעלי פי אימת אלסטר אלאספל ואקסם [מא] אגתמע עלי אלאמאם יכרג מא ארדת | |||
| באב מנה אכר | |||
|
|
אקסם עשרה עלי סבעת אתמאן כמסה ותלת אלא תלת אתנין ורבע | ||
| פוגה אלעמל פי דאלך אן תאכוד מן אלאתני[ן] ורבע תלתהא ומן אלכמסה ותלת סבעת אתמאנהא ותסקט אלאקל מן אלאכבר פמא בקי קסמת עליה אלעשרה פמא כרג פהו אלמטלוב | |||
| באב מנה אכר | |||
|
|
אקסם תלאתת ארבאע תלאתת אכמאס תסעה עלי תלאתת אעשאר ומא כרג קסמתה עלי תלתיי סבעה אלא קסמת אתנין ותמן עלי סבעה אתמאן ונצף תמן | ||
| יכרג אתנאן וכמס ותלת כמס תם תאכוד תלתיי אלסבעה ודאלך ארבעה ותלתאן פאסקט מנהא אלאתנין וכמס ותלת כמס אלבאקי אתנאן וכמסאן פאצרבהא פי אלתלאתה אעשאר יכון דאלך סבעה אעשאר וכמס עשר תם תאכוד מן אלתסעה תלאתת ארבאע תלאתת אכמאסהא ודאלך ארבעה ונצף עשר | |||
|
| |||
|
|
פכאנה קאל אקסם ארבעה ונצף עשר עלי סבעת אעשאר וכמס עשר | ||
| פתעמל עלי מא תקדם יכרג כמסה וכמסת אתמאן פאפהם תציב | |||
| באב מנה אכר | |||
|
|
אקסם מאיה עלי אתנין ומא כרג עלי נצף ומא כרג עלי ארבעה ומא כרג עלי תלת ומא כרג עלי תלאתת ארבא[ע] ומא כרג עלי כמסה ואעלם כם [יג]ב ל[אלמאיה] מן אלכמסה | ||
| פאלעמל פי דאלך אן תצרב אתנין פי נצף יכון ואחד פאצרבה פי אלארבעה יכון ארבעה פאצרבה פי תלת יכון ואחד ותלת ואצרבה פי תלאתת ארבאע י[כון] ואחד פאצרבה פי כמסה יכון כמסה פאקסם עליהא אלמאיה יכר[ג] עשרין והו מא ארדת פאפהם | |||
|
| |||
Completion of Fractions |
באב גבר אלכסור | ||
| אעלם אן הד אלבאב כ[ת]יר אלמנפעה פי גמיע אעמאל אלחסאב ולא סימא מן אראד עמל אל[גבר] ואלמקאבלה פתצרבה פי כל מסאלה מן גמיע אעמאלהא אלא אליסיר | |||
|
|
אדא קיל לך בכם תגבר תלת חתי יכון ואחד | ||
|
|
פהד אלמסאלה אנמא אלמטלוב מנה[א] אי עדד תצרבה פי תלאתה פיכון אלכארג מן אלצרב ואחד פאלעמל פי הד אלמסאלה אן תקסם ואחד עלי תלת יכרג תלאתה וה[ד] אלעדד אלדי אדא צרבת פיה [תלאתה] כא[ן] אלכארג ואחדא והו אל[עמ]ל פי גמיע הד אלבאב קל[י]לאً וכתירא | ||
|
|
ואן שית פאנך פקד עלמת אדא צרבת תלתא פי עדד פאן אלכארג תלת דאלך אלעדד פאלואחד אדא הו תלת דאלך אלעדד אלמטלוב | ||
|
|
ואן שית ציירת אלואחד אתלאתא תכון תלאתת אתלאת פאקסמהא עלי תלת יכרג תלאתה | ||
|
|
ואן קאל בכם תגבר תלאתת ארבאע חתי יכון ואחד | ||
|
|
פאקסם ואחד עלי תלאתה ארבאע פמא כרג פהו מא ארדת ודאלך ואחד ותלת | ||
|
|
ואן קאל בכם תגבר תלאתת אגזא מן אחדי עשר | ||
|
|
פאקסם ואחד עלי תלאתה אגזא מן אחדי עשר יכרג תלאתה ותלתאן והו מא ארדת | ||
| ולו קאל פי הד אלמסאלה חתי תכון אתנאן או תלאתה או כמסה קסמת דאלך אלעדד אלואחד עלי אלכסר אלמגבור | |||
|
|
ומתאלה לו קאל בכם תגבר תלתין חתי יכונא ארבעה | ||
|
|
פאקסם ארבע[ה] עלי תלתין יכרג סתה ארבעה כמא קאל | ||
| ולו קאל בכם תגבר ואחד ונצפא חתי יכון אתנין ונצפא או תלאתה ותלתא חתי תכון כמסה או סתה אנמא מא הו אכתר מן אלעדד אלמפרוט אולא קסמת אלעדד עלי אלעדד אלאול אלמפרוט פמא כרג פאצרבה פי אלעדד תגד אלעדד אלאול | |||
|
|
ומתאל דאלך לו קאל בכם תגבר אתני[ן] ונצפא חתי תכו[ן] סתה | ||
|
|
פאקסם אלסתה עלי אלאתנין ונצף יכרג אתנין וכמסא פתקו[ל] בצרבהא פי אתנין וכמסין פי מא תגבר באתנין ונצף חתי תכון סתה ואלעלה פי דאלך אן כ[ל] עדדין יקסם אחדהא עלי אלתאני פאן אלדי יכרג מן אלקסמה אדא צרבתה פי אלעדד אלמקסום עליה עאד אלעדד וקד ביין דאלך אבו כ[א]מ[ל] פי כתאבה | ||
| פצל | |||
| אעלם אן אלגבר לא יכון אלא מן אלקליל אלי אלכתיר | |||
| מתל אן תגבר תלתא חתי יכון ואחד או ארבעא או כמסת אסדאס או סתת אסבאע או עשרת אגזא מן אחדי עשר ויגוז פי הד אלמסאיל אן תקול חתי יכון ואחד או ואחד ונצף או אתנין או תלאתה או מא הו אכתר מן אלכסר אלמפרוט | |||
| וכדאלך יגוז אן תגבר כסרא אלי כסר אדא כאן אלכסר אלתאני אכתר מן אלאול | |||
|
|
מתאל אן תקול בכם תגבר תלתא חתי יכון נצפא | ||
|
|
פהדא יגוז פתקסם נצף עלי תלת עלי מא תקדם יכרג ואחד ונצף פתצרב ואחד ונצף מן תלאתה חתי יכון נצפאً | ||
|
|
וכדאלך בכם תגבר כמסין חתי תכון כמסת אעשאר | ||
|
|
פתצרבהא פי ואחד ורבע | ||
|
|
ולו קאל בכם תגבר תלתין חתי יכונאן נצפאً לם תוגבר לאן אלתלתין אכתר מן אלנצף ולא ינגבר כתיר מן קליל לאן אלגבר הו אלזיאדה פי אלשי חתי יצל אלי אלגבר אלדי תריד אן תוצלה אליה וליס ימכן אן תזיד פי תלתין חתי יכונא נצפא | ||
Degrading |
באב אלחט אעלם הו כלאף אלגבר | ||
|
|
מתאלה אדא קיל לך בכם תחט ואחד חתי יכון נצפא | ||
|
|
עלי ואחד פמא כרג פאצרבה פי אלואחד ינחט אלואחד פירגע נצפא ודאלך נצפא | ||
|
|
ולו קאל בכם תחט אתנין ונצפא חתי יכונא ואחד | ||
|
|
פאדא ארדת דאלך קסמת ואחד עלי אתנין ונצף פמא כרג פתצרבה פי דאלך ודאלך כמסאן | ||
|
|
ולו קאל בכם תחט סתה ורבעא חתי יכונא ואחדא | ||
|
|
פאקסם ואחד עלי סתה ורבע יכרג ארבע אכמאס אלכמס ינחט חתי יכון ואחד | ||
|
|
ולו קאל בכם תחט תמאניה ונצפא חתי תכון אתנין ונצפא | ||
|
|
פאקסם אלאתנין ונצפא עלי תמאניה ונצף יכרג כמסת אגזא מן סבעה עשר פתצרבהא פי כמס אגזא מן סבעת עשר תנחט חתי תכון אתנין ונצפא | ||
| פצל | |||
| ואעלם אן אלחט לא יכון אלא מן אלכתיר אלא אלקליל ולא יגוז אן יכון מן אלקליל אלי אלכתיר וקד באן פי אלגבר | |||
Extracting Roots of Integer and Fraction |
באב אסתכראג אלגדור פי אלעדד אלצחיח ואלגדור פי אלעדד אלצחיח ואלכסור | ||
| וקד תקדם פי צדר אלכתאב כיף יסתכרג גדר אלעדד אלצחיח אלמגדור | |||
| ונריד אן נביין פי הד אלבאב אסתכראג גדר אלכסור אלמגדורה וגיר אלמגדורה | |||
|
|
אדא קיל לך כם גדר רבע פאנזל אלרבע עלי הד אלצורה | ||

| |||
|
|
תם תאכוד גדר אלמקאם ודאלך אתנין פאתכדהא אמאמאً תם תאכוד גדר אלואחד אלדי עלי אלכט ודאלך ואחד פתקסמה עלי אלאמאם יכרג לך נצף והו גדר רבע | ||
|
|
פאדא צרבת נצפאً פי נצף כאן רבעא | ||
Extracting Roots of Fraction and Fraction of Fraction |
באב מנה אכר | ||
|
|
אדא קיל לך כם גדר ארבעת אתמאן ונצף תמן | ||
| פאנזל אלארבעת אתמאן ונצף תמן פי סטר עלי הד אלצורה | |||
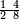
| |||
|
|
תם תצרב אלאתנין אלדין המא אלאמאם פאחפטה תם ארגע ואצרב אלארבעה אלתי עלי אלתמאניה פי אלאתנין ותגמל מא עלי ראצהא תכון תסעה פתאכוד גדרהא ודאלך תלאתה פאקסמהא עלי אלאמאם יכרוג תלאתת ארבאע והו מא ארדת | ||
|
|
ואן קאל כם גדר סתה אתסאע ורבע תסע | ||
| פאנזל אלסת אתסאע ורבע תסע עלי הד אלצורה | |||
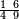
| |||
|
|
תם אצרב אלאמאם פי אלאמאם יכון סתה ותלאתין פתאכוד גדרהא ודאלך סתה והו אלאמאם תם אצרב אלסתה פי אלארבעה ואגמל מא עלי ראסהא יכון כמסה ועשרין פתאכוד גדרהא בכמסה פאקסמהא עלי אלאמאם יכרג כמס אסדאס והו מא ארדת | ||
|
|
ואן קאל כם גדר סתה אתמאן ותמן תמן | ||
| פאנזלהא עלי הד אלצורה | |||
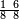
| |||
|
|
תם אצרב אלתמאניה פי אלתמאניה ואגמל מא עלי ראסהא יכון תסעה וארבעין פתאכוד גדרהא ודאלך סבעה פאקסמהא עלי אלאמאם יכרג סבעת את[מאן] והו מא ארדת | ||
| ואעלם אן אלעמל פי הד אלמסאיל מתל אלעמל פי אלכסר וכסר אלכסר | |||
Extracting Roots of Fraction and Fraction of Fraction and Fraction of Fraction of Fraction |
באב מנה אכר | ||
|
|
אדא קיל לך כם גדר סבעת אתסאע וארבע אתמאן אלתסע ונצף תמן אלתסע | ||
| פאנזלהא עלי הד אלצורה | |||
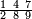
| |||
|
|
תם אצרב אלאימה אלתי תחת אלכט בעצהא פי בעץ ולם יכון ללמגתמע גדר פליס ללמסאלה גדר מנטק ואצל אלעמל פי הד אלמסאיל מן טריק אלמקאם אן תטלב אקל עדד לה נצף ותמן ותסע ודאלך אן תצרב הד אלמקאמאת בעצהא פי בעץ ותאכוד גדר מא כרג פמא כאן פהו אלמקאם תם תאכוד מן אלמקאם אלכסר אלמדכור פמא כאן ארדת גדרה וקסמתה עלי גדר אלמקאם פהו אלמטלוב | ||
| ואן לם יכון ללמקאם גדר פליס ללמסאלה גדר ואן לם יכון איצא ללאגזא גדר פליס ללמסאלה גדר מנטק | |||
| באב מנה אכר | |||
|
|
אדא קיל לך כם גדר תסעה אגזא מן אחדי עשר וגז מן אחדי עשר | ||
| פאנזלהא עלי הד אלצורה | |||
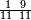
| |||
|
|
תם תצרב אלאחדי עשר אלואחד פי אלתאניה ותאכוד גדר מא כרג יכון אחדי עשר והו אלאמאם תם אצרב אלתסעה אלתי עלי אלאחדי עשר פי אלאחדי עשר אלתאניה ותגמל מא עלי ראצהא יכון דאלך מאיה פתאכוד גדרהא בעשרה פאקסמהא עלי אלאמאם יכרג עשר אגזא מן אחדי עשר והו מא ארדת | ||
| פצל | |||
| ואעלם אנה אדא כאן פי אלמסאלה אמאמאן מתמאתלא[ן] פתאכוד אחדהא פתגעלה אלאמאם תם תעמל פי באקי אלמסאלה עלי מא תקדם | |||
|
|
מתאלה אדא קיל לך כם כם גדר כמסה אסבאע וסבע סבע | ||
| פאנזלהא עלי הד אלצורה | |||
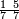
| |||
|
|
פפי הד אלמסאלה אמאמאן מתמאתלאן והו סבעה וסבעה פתאכוד אחדהמא פתתכדה אמאמא תם תצרב אלכמסה אלתי עלי אלסבעה אלאולי פי אלסבעה אלתאניה ותגמל מא עלי ראצהא יכון סתה ותלאתין פתאכוד גדרהא ודאלך סתה פאקסמהא עלי אלאמאם אלדי הו סבעה יכרג סתת אסבאע והו מא ארדת | ||
| פאן כאן פי אלמסאלה תלאת מקאמאת אתנין מתמאתלאן ואלתאלת לה גדר פתאכוד גדר דאלך אלאמאם אלתאלת אלמכאלף ללאתנין פמא כאן געלתה מע אחד אלאמאמין אלמתמאתלין תחת כט פתתכדהא אימה תקסם עליהא ותעמל פי באקי אלמסאלה עלי מא תקדם | |||
|
|
מתאלה כם גדר תסע וארבע אתמאן אלתסע וארבע אתמאן תמן אלתסע | ||
| פאנזלהא עלי הד אלצורה | |||
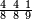
| |||
|
|
פהד אלמסאלה פיהא אמאמאן מתמאתלאן והמא תמאניה ותמאניה ואמאמאן אכר והו תסעה פתאכוד גדר תסעה ודאלך תלאתה ותאכוד אכר אלאמאמין אלמתמאתלין ודאלך תמאניה ויכון מעך אמאמאן ללקסמה והמא תלאתה תלאתה ותמאניה תם אצרב אלואחד אלדי עלי אלתסעה פי אלתמאניה אלתי תליהא ותגמל מא עלי ראסהא פמא אגתמע צרבתה פי אלתמאניה אלתאניה ותגמל מא עלי ראצהא יכון מאיה פכד גדרהא ודאלך עשרה פאקסמהא עלי אלאימה יכרג תלאתת אתמאן ותלת תמן | ||
| פאן כאן מעך ארבעת אימה אמאמאן מתמאתלאן ואתנאן מתמאתלאן איצא פתאכוד אכר אלאמאמין אלמתמאתלין ואחד אלאמאמין פתגעל הדין אלמאכודין אמאמין תקסם עליהא תם תתבע אלמסאלה אלי אכרהא | |||
|
|
ומתאלה כם גדר עשרה אגזא מן אחדי עשר וארבע אגזא מן אחדי עשר פי אלגז מן אחדי עשר וכמסת אסבאע אלגז מן אחדי עשר פי אלגז מן אחדי עשר וארבעת אסבאע סבע אלגז מן אחדי עשר פי אלגז מן אחדי עשר | ||
| פאנזלהא עלי הד אלצורה | |||
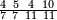
| |||
|
|
פהד אלמסאלה פיהא ארבע אימה אתנאן מתמאתלאן והמא אחדי עשר ואחדי עשר ואלאכראן מתמאתלאן והמא סבעה וסבעה פתאכוד אלאחדי עשר אלואחד ואלסבעה אלואחד יכון אלאמאם אחדי עשר וסבעה תם אצרב מא עלי אלאחדי עשר אלאול פי אלתאניה ותגמל מא עלי ראסהא ותצרב מא אגתמע פי אלסבעת אלאולי ותגמל מא עלי ראצהא ותצרב מא אגתמע פי אלסבעה אלתאניה ותגמל מא עלי ראצהא יכון דאלך כמסה ועשרין וסת מאיה וכמסת אלאף פתאכוד גדרהא ודאלך כמסה וסבעין פאקסמה עלי אלאימה יכרג לך עשרת אגזא מן אחד עשר וכמסת אסבאע אלגז מן אחדי עשר והו מא ארדת | ||
| פאן כאן פי אלמסאלה ארבע אימה אתנין מנהא מתמאתלאן ואלאתנין אלאכראן מכתלפאן פאצרב אחד אלמכתלפין פי אלתאני פאן אגתמע מנהא עדד לה גדר פאלמסאלה מגדורה פתאכוד גדר מא אגתמע מן אלצרב ותתכדה אמאמא מע אחד אלאמאמין אלמתמאתלין ותעמל פי אלבאקי עלי מא תקדם | |||
|
|
ומתאלה כם גדר כמסת אתסאע וסבעת אתסאע תסע וכמסת אתמאן תסע תסע ונצף תמן תסע תסע | ||
| פאנזלהא עלי הד אלצורה | |||
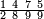
| |||
|
|
פהד אלמסאלה פיהא אמאמאן מתסאויאן ואמאמאן מכתלפאן פאצרב אחד אלאמאמין אלמכתלפין פי אלתאני ואלתאלת ואלאתנין פי תמאניה תכון סתה עשר פתאכוד גדרהא ודאלך ארבעה ותאכוד אחד אלאמאמין אלמתסאויין ודאלך תסעה פתגעל הדין אלעדדין אימה והמא ארבעה ותסעה תם תעמל עלי מא תקדם פי צרב אלכסר וכסר אלכסר יכרג ואחד וארבע[ין] ותמן מאיה פכד גדרהא ודאלך תסעה ועשרין פאקסמהא עלי אלאימה יכרג סבעת אתסאע ורבע תסע והו מא ארדת | ||
Extracting Roots of Integer and Fraction |
באב אסתכראג גדר אלעדד אלצחיח ואלכסר | ||
|
|
אדא קיל לך כם גדר אתנין ורבע | ||
| פאנזלהא עלי הד אלצורה | |||
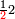
| |||
|
|
תם תאכוד גדר אלארבעה אלתי הי אלאמאם ודאלך אתנין פארפעהא תם אצרב אלאתנין פי אלארבעה ותגמל מא עלי ראצהא יכון תסעה פכד גדרהא ודאלך תלאתה פאקסמה עלי אלאמאם יכרג ואחד ונצף והו מא ארדת | ||
| פצל | |||
| אעלם אנה אדא כאן מקאם אלכסר גדר פיושך אן יכון ללמסלה גדר מנטק | |||
| באב מנה אכר | |||
|
|
אדא קיל לך כם גדר אחדי עשר ותסע | ||
| פאנזלהא עלי הד אלצורה | |||
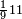
| |||
|
|
תם תאכוד גדר אלתסעה ותתכדה אמאמאً ודאלך תלאתה תם אצרב אלאחדי עשר פי אלתסעה ותגמל מא עלי ראצהא ותאכוד גדר מא כרג יכון עשרה פאקסמה עלי אלאמאם יכרג תלאתה ותלת והו מא ארדת | ||
| ואעלם אן גמיע אלעמל פי הד אלבאב אנמא הו אן תאכוד גדר מקאם אלכסר ותתכדה אמאמא תם תצרב אלצחיח פי מקאם אלכסר ותגמל מא עלי ראסה ותאכוד גדר אלמגתמע ותקסמה עלי אלאמאם פאפהם אעמלה עלי מא תקדם פי צרב אלעדד ואלכסר | |||
|
|
אדא קיל לך כם גדר ארבעת אתמאן ותמן תמן | ||
| פאנזלהא עלי הד אלצורה | |||
![\scriptstyle\frac{1\ 4}{8\ 8}\left[4\right]](/mediawiki/images/math/1/e/2/1e219180ba2e21dd61f2ba9115680150.png)
| |||
|
|
תם אנטור אלאימה תגדהא אתנין מתמאתלין פתאכוד אחדהא ותתכדה אמאמא עלי מא תקדם תם תצנע באלמסאלה עלי מא תקדם פי צרב אלצחיח ואלכסר וכסר אלכסר ומא אגתמע אכדת גדרה וקסמתה עלי אלאמאם יכרג אתנין ותמן | ||
| ולו לם תכון אלאימה מתמאתלה צרבת אחדהא פי אלתאני ואכדת גדר אלמגתמע ותעמל עלי מא תקדם ופי מא דכר מן הד אלבאב כפאיה [אלקי]אס עליה מא יאתי בעדה ונתבעה באכראג גדר אלאעדאד | |||
Approximations |
באב אסתכראג אלגדור אלצם | ||
Approximations of Integers |
|||
|
|
אדא קיל לך כם גדר כמסה | ||
|
פתאכוד אקרב עדד מרבע אלי אלכמסה תגד ארבעה תסקטהא מן אלכמסה אלבאקי ואחד פסמי דאלך אלואחד מן צעף גדר אלארבעה יכון רבעא פאעלמה עלי גדר אלארבעה הו אתנאן ורבע והו גדר כמסה פתקרבת | ||
|
|
פאדא אצרבת אתנין ורבעא פי מתלהא כאן דאלך כמסה ונצף תמן פקד וקע אלתקריב פנצף תמן זאיד | ||
|
ואן שית אן תקרב אלעמל אכתר מן הדא פאנך תצעף אלאתנין ורבעא תכון ארבעה ונצף פסמי מנהא אלנצף תמן יכון דאלך תמן תסע פאסקטה מן אלרבע אלדי מע אלאתנין ורבע יבקי אתנין ותסעאן ותמן תסע | ||
|
|
פאדא צרבתה פי מתלה כאן דאלך כמסה ותמן תמן תסע תסע והו אקרב מן כמסה ונצף תמן | ||
|
ולו ארדת אקרב מן הדא לאצעפת אלאתנין ותסעין ותמן תסע ותסמי דאלך אלתמן תם תסע תסע פמא אסקטת מן אלאתנין ותסעין ותמן תסע פהו אקרב מן אלאול | ||
| באב מנה אכר | |||
|
|
אדא קיל לך כם גדר עשרה | ||
|
|
פתנטר אקרב עדד מגהול מגדור אלי אלעשרה תגדה תסעה פתסקטהא מן אלעשרה אלבאקי ואחד פתסמיה מן צעף גדר אלתסעה יכון דאלך תלאתה וסדסא והו גדר אלעשרה בתקריב | ||
| ואן שית פאצרב אלעשרה פי אי עדד שית לה גדר פכאנך צרבתהא פי מאיה יכון אלמגתמע אלפא פתאכוד גדרהא עלי מא תקדם באלתקריב יכון דאלך ואחד ותלאתין וסתת אעשאר ונצף עשר פאקסמה עלי גדר אלמאיה תכון תלאתה ועשרא וסתת אעשאר אלעשר ונצף עשר אלעשר והדא אקרב מן סדס | |||
|
| |||
|
|
פאן קאל כם גדר כמס[ת] עשר | ||
|
|
פתאכוד אקרב עדד מרבע אלי אלכמסה עשר ודאלך סתת עשר פאסקט מנהא אלכמסת עשר אלבאקי ואחד פסמיה מן צעף גדר אלסת עשר ודאלך תמאניה יכון תמנא פאסקטה מן אלארבעה אלתי הי גדר אלסתת עשר יכון תלאתה וסבעה אתמאן והו גדר אלסת עשר בתקריב | ||
|
|
פאן קאל כם גדר עשרין | ||
| פתאכוד אן שית אלסתה עשר ואן שית אלכמסה ואלעשרין לאן אלעשרין ואסטה בין הדין אלעדדין אלמרבעין | |||
|
|
פכאנך אכדת אלסת עשר פאסקטהא מן אלעשרין אלבאקי ארבעה פסמיהא מן צעף גדר אלסתה עשר יכון נצפאً פאצפה אלי גדר אלסתה עשר יכון ארבעה ונצפא והו גדר אלעשרין בתקריב | ||
|
|
ואן שית אכדת אלכמסה ואלעשרין פאסקט מנהא אלעשרין אלבאקי כמסה פסמיהא מן צעף גדר אלכמסה ואלעשרין יכון נצפאً פתסקט מן גדר אלכמסה ואלעשרין אלבאקי ארבעה ונצף והו גדר אלעשרין בתקריב | ||
Approximations of Integers and Fractions |
באב מנה אכר | ||
|
|
אדא קיל לך כם גדר אתנין ונצף | ||
|
|
פמקאם אלנצף מן הד אלמסאלה ליס לה גדר פאתכדה אמאמא תם צייר אלאתנין ואלנצף אנצאפא תכון כמסה פאצרבהא פי אלאתנין תכון עשרה פתאכוד גדר אלעשרה [עלי] מא תקדם תכון תלאתה וסדסא פאקסמהא עלי אלאתנין יכרג ואחד ותלאתת אסדאס ונצף סדס | ||
|
|
ואן שית פאצרב אלאתנין ונצף פי אי עדד מרבע שית יכון לה נצף פכאנך קד צרבתהא פי סתה ותלאתין יכון תסעין פתאכוד גדרהא יכון תסעה ונצפא פאקסמה עלי גדר אלסתה ואלתלאתין יכרג וא[ח]ד ותלאתת אסדאס ונצף סדס | ||
|
|
ואן שית אדא ציירת אלאתנין ונצף אנצאפא יכון כמסה וצרבתה[א] פי אתנין תכון עשרה פאצרב הד אלעשרה פי אלסתה ואלתלאתין תכון סתין ותלאתת מאיה פתאכוד גדרהא ודאלך תסעת עשר בתקריב פאקסמהא עלי פ[..] אתני עשר פמא כרג פהו אלמטלוב | ||
Approximations of Fractions |
באב מנה אכר | ||
|
|
אדא קיל לך כם גדר תלת | ||
|
|
פאצרב תלתא פי סתה ותלאתין תכון אתני עשר פתאכוד יכון תלא[ת.......] [תל]את[ה] ונצף בתקריב פאקסמהא עלי | ||
Appendix I: Glossary of Terms
| rank | מנזלה, מרתבה |
Appendix: Bibliography
Kitāb al-Bayān / by Abū Bakr al-Haṣṣār (Morocco, 12th century)
– Arabic in Hebrew Characters –
Manuscript:
- Cambridge, University Library Add. 1222 (IMHM: f 17085) (16th-17th century)
Bibliography:
- Aballagh, Mohamed and Ahmed Djebbar. 1987. Découverte d’un écrit mathématique d’al-Hassâr (XIIe siècle): le livre I du Kāmil, Historia Mathematica 14, pp.147–158.
- Kunitzsch, Paul. 2003. A New Manuscript of Abū Bakr al-Hassār's Kitāb al-Bayān, Suhayl (Barcelona), vol. 3, pp. 187-192.
- Suter, Heinrich. 1901. Das Rechenbuch des Abu Zakarija el-Hassar, Bibliotheca Mathematica, vol. 2, pp. 12-40.
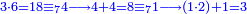
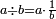
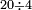
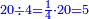
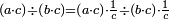
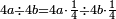
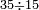
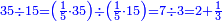
![\scriptstyle\left[a+\left(b\sdot p\right)\right]\div p=b+\frac{a}{p}](/mediawiki/images/math/2/8/0/2801589a692a7665684083b20992e117.png)
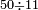
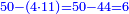
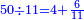
![\scriptstyle\left[\left[a+\left(b\sdot c\right)\right]\sdot d\right]\div\left(c\sdot d\right)=\left[a+\left(b\sdot c\right)\right]\div c=b+\frac{a}{c}](/mediawiki/images/math/7/a/6/7a6804ae701a16b5de85728a97dab776.png)
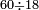
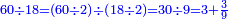
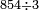
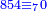
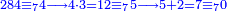
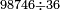
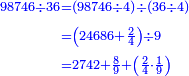
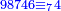
![{\color{blue}{\begin{align}\scriptstyle2742\equiv_75&\scriptstyle\longrightarrow5\sdot\left(9\equiv_72\right)=10\equiv_73\\&\scriptstyle\longrightarrow\left[3+\left(8\equiv_71\right)\right]\sdot4=4\sdot4=16\equiv_72\\&\scriptstyle\longrightarrow2+2=4\\\end{align}}}](/mediawiki/images/math/8/d/c/8dc6b0ac7dd55983c580e1b5e84eded0.png)
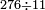
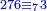
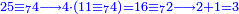
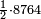
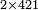
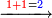
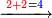
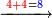
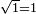
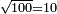
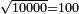
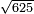
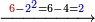
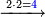
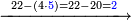
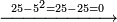
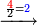
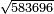
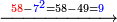
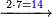
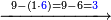
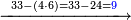

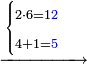
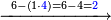
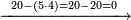
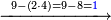
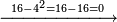
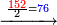
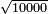

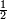
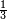
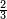

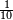
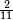
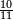
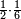
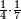
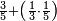
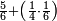
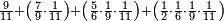
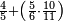
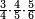
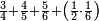
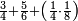
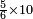
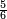
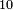
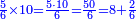
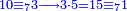
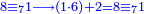
![\scriptstyle\left[\frac{1}{5}+\left(\frac{1}{2}\sdot\frac{1}{5}\right)\right]\times12](/mediawiki/images/math/3/8/d/38d26a85ea2cfc361c9a8a6775ab9e5b.png)
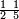
![{\color{blue}{\begin{align}\scriptstyle\left[\frac{1}{5}+\left(\frac{1}{2}\sdot\frac{1}{5}\right)\right]\times12&\scriptstyle=\frac{\left[\left(1\sdot2\right)+1\right]\sdot12}{2\sdot5}\\&\scriptstyle=\frac{3\sdot12}{2\sdot5}=\frac{36}{2\sdot5}\\&\scriptstyle=3+\frac{3}{5}\\\end{align}}}](/mediawiki/images/math/3/1/5/315d5d022b1a029a34ee326d33c9cdf6.png)
![\scriptstyle{\color{blue}{12\equiv_75\longrightarrow5\sdot\left[\left(1\sdot2\right)+1\right]=5\sdot3=15\equiv_71}}](/mediawiki/images/math/2/b/9/2b95ff353e77d810fd7e65fdf20efff0.png)
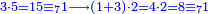
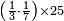
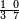
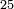
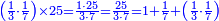

![\scriptstyle{\color{blue}{1\sdot7\equiv_70\longrightarrow\left[\left(0+1\right)\sdot3\right]+1=4}}](/mediawiki/images/math/a/2/9/a29d829f1ef4b74f8244365d33476b81.png)
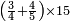
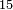
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{3}{4}+\frac{4}{5}\right)\times15&\scriptstyle=\frac{\frac{\left[\left(4\sdot4\right)+\left(3\sdot5\right)\right]\sdot15}{4}}{5}=\frac{\frac{31\sdot15}{4}}{5}=\frac{\frac{465}{4}}{5}\\&\scriptstyle=23+\frac{1}{5}+\left(\frac{1}{4}\sdot\frac{1}{5}\right)\\\end{align}}}](/mediawiki/images/math/e/0/2/e02c951279ca4d6416f487cbb7448f1d.png)
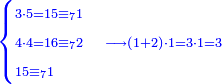
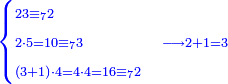
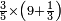

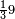
![{\color{blue}{\begin{align}\scriptstyle\frac{3}{5}\times\left(9+\frac{1}{3}\right)&\scriptstyle=\frac{\left[\left(9\sdot3\right)+1\right]\sdot3}{3\sdot5}=\frac{28\sdot3}{3\sdot5}=\frac{84}{3\sdot5}\\&\scriptstyle=5+\frac{3}{5}\\\end{align}}}](/mediawiki/images/math/7/6/e/76efcdba7e07b7cc48ff2735b3781d8a.png)
![\scriptstyle{\color{blue}{9\equiv_72\longrightarrow\left[\left(2\sdot3\right)+1\right]\sdot3=7\sdot3\equiv_70}}](/mediawiki/images/math/c/b/c/cbcab0861c35c2c6ff619da37f20e428.png)
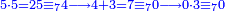
![\scriptstyle\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\times\left(6+\frac{3}{5}\right)](/mediawiki/images/math/7/3/9/739d727bdcdfb4c09f59bba584125807.png)
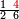
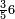
![{\color{blue}{\begin{align}\scriptstyle\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\times\left(6+\frac{3}{5}\right)&\scriptstyle=\frac{\left[\left(5\sdot2\right)+1\right]\sdot\left[\left(6\sdot5\right)+3\right]}{6\sdot2\sdot5}\\& \scriptstyle=\frac{11\sdot33}{6\sdot2\sdot5}=\frac{363}{6\sdot2\sdot5}\\&\scriptstyle=6+\left(\frac{1}{5}\sdot\frac{1}{6}\right)+\left(\frac{1}{2}\sdot\frac{1}{5}\sdot\frac{1}{6}\right)\\\end{align}}}](/mediawiki/images/math/3/8/a/38a51c94c6541b7355d9e3ecebc5c8c8.png)
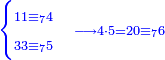
![{\color{blue}{\begin{align}&\scriptstyle6\sdot6=36\equiv_71\\&\scriptstyle\longrightarrow\left[\left[\left(1\sdot5\right)+1\right]\sdot2\right]+1=\left(6\sdot2\right)+1=13\equiv_76\\\end{align}}}](/mediawiki/images/math/f/8/a/f8a07f569708ec00bb2191045b644d30.png)
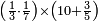
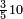
![\scriptstyle{\color{blue}{\left(\frac{1}{3}\sdot\frac{1}{7}\right)\times\left(10+\frac{3}{5}\right)=\frac{\left[\left(10\sdot5\right)+3\right]\sdot1}{2\sdot7\sdot5}=\frac{53\sdot1}{3\sdot7\sdot5}=\frac{53}{3\sdot7\sdot5}=\frac{3}{7}+\left(\frac{2}{5}\sdot\frac{1}{7}\right)+\left(\frac{2}{3}\sdot\frac{1}{5}\sdot\frac{1}{7}\right)}}](/mediawiki/images/math/3/a/8/3a8bcf262628cc83ea853c9c206d7ac4.png)
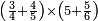
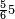
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{3}{4}+\frac{4}{5}\right)\times\left(5+\frac{5}{6}\right)&\scriptstyle=\frac{\left[\left(3\sdot5\right)+\left(4\sdot4\right)\right]\sdot\left[\left(5\sdot6\right)+5\right]}{4\sdot5\sdot6}=\frac{31\sdot35}{120}=\frac{1085}{120}\\&\scriptstyle=9+\left(\frac{1}{5}\sdot\frac{1}{6}\right)+\left(\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{6}\right)\\ \end{align}}}](/mediawiki/images/math/e/c/7/ec701144ce8008fc694d9be2cd4c7d0c.png)
![\scriptstyle\frac{3}{4}\times\left[5+\frac{7}{8}+\left(\frac{1}{6}\sdot\frac{1}{8}\right)\right]](/mediawiki/images/math/f/f/e/ffe897c7d6abf4185f4ffb7c669d3ce1.png)

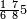
![{\color{blue}{\begin{align}\scriptstyle\frac{3}{4}\times\left[5+\frac{7}{8}+\left(\frac{1}{6}\sdot\frac{1}{8}\right)\right]&\scriptstyle=\frac{\left[\left[\left[\left(5\sdot8\right)+7\right]\sdot6\right]+1\right]\sdot3}{4\sdot8\sdot6}=\frac{\left[\left(47\sdot6\right)+1\right]\sdot3}{4\sdot8\sdot6}=\frac{849}{4\sdot8\sdot6}\\&\scriptstyle=4+\frac{3}{8}+\left(\frac{2}{6}\sdot\frac{1}{8}\right)+\left(\frac{1}{4}\sdot\frac{1}{6}\sdot\frac{1}{8}\right)\\\end{align}}}](/mediawiki/images/math/b/d/a/bda492b4ae77d2a95d39f662fa56c8dc.png)
![\scriptstyle\frac{5}{6}\times\left[8+\left(\frac{5}{7}\sdot\frac{1}{9}\right)\right]](/mediawiki/images/math/e/5/f/e5f35b79321220d2b908e6078c54c785.png)
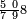
![{\color{blue}{\begin{align}\scriptstyle\frac{5}{6}\times\left[8+\left(\frac{5}{7}\sdot\frac{1}{9}\right)\right]&\scriptstyle=\frac{\left[\left(8\sdot9\sdot7\right)+5\right]\sdot5}{6\sdot7\sdot9}\\&\scriptstyle=\frac{509\sdot5}{6\sdot7\sdot9}=\frac{2545}{6\sdot7\sdot9}\\&\scriptstyle=6+\frac{6}{9}+\left(\frac{4}{7}\sdot\frac{1}{9}\right)+\left(\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\\ \end{align}}}](/mediawiki/images/math/f/c/e/fcec7b72d0e06fe04eb8983c04dd518f.png)
![\scriptstyle\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\times\left[8+\frac{5}{7}+\left(\frac{1}{5}\sdot\frac{1}{7}\right)\right]](/mediawiki/images/math/b/7/f/b7f33a721f2cc7aa748520999089bce0.png)
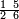
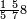
![{\color{blue}{\begin{align}\scriptstyle\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\times\left[8+\frac{5}{7}+\left(\frac{1}{5}\sdot\frac{1}{7}\right)\right]&\scriptstyle=\frac{\left[\left(5\sdot2\right)+1\right]\sdot\left[\left[\left[\left(8\sdot7\right)+5\right]\sdot5\right]+1\right]}{6\sdot2\sdot7\sdot5}=\frac{11\sdot306}{6\sdot2\sdot7\sdot5}=\frac{3366}{6\sdot2\sdot7\sdot5}\\&\scriptstyle=8+\left(\frac{3}{5}\sdot\frac{1}{6}\sdot\frac{1}{7}\right)\\ \end{align}}}](/mediawiki/images/math/7/a/6/7a6daef3bb982001d33702fc786ec7f7.png)
![\scriptstyle\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\times\left[9+\left(\frac{1}{6}\sdot\frac{1}{7}\right)\right]](/mediawiki/images/math/9/6/a/96a8fdd4fab69e58c8a676b813acc28d.png)
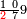
![{\color{blue}{\begin{align}\scriptstyle\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\times\left[9+\left(\frac{1}{6}\sdot\frac{1}{7}\right)\right]&\scriptstyle=\frac{\left[\left(5\sdot2\right)+1\right]\sdot\left[\left(9\sdot6\sdot7\right)+1\right]}{6\sdot2\sdot6\sdot7}=\frac{11\sdot379}{6\sdot2\sdot6\sdot7}=\frac{4169}{6\sdot2\sdot6\sdot7}\\&\scriptstyle=8+\frac{1}{7}+\left(\frac{5}{6}\sdot\frac{1}{7}\right)+\left(\frac{2}{6}\sdot\frac{1}{6}\sdot\frac{1}{7}\right)+\left(\frac{1}{2}\sdot\frac{1}{6}\sdot\frac{1}{6}\sdot\frac{1}{7}\right)\\\end{align}}}](/mediawiki/images/math/3/6/6/36644bab12a199342111b9f24f031816.png)
![\scriptstyle\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\times\left(8+\frac{9}{10}+\frac{10}{11}\right)](/mediawiki/images/math/8/c/a/8ca9548a897d46b48ef337cafe7ed47c.png)
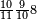
![{\color{blue}{\begin{align}\scriptstyle\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\times\left(8+\frac{9}{10}+\frac{10}{11}\right)&\scriptstyle=\frac{\left[\left(5\sdot2\right)+1\right]\sdot\left[\left(8\sdot10\sdot11\right)+\left[\left(9\sdot11\right)+\left(10\sdot10\right)\right]\right]}{6\sdot2\sdot10\sdot11}\\&\scriptstyle=\frac{11\sdot\left(880+199\right)}{6\sdot2\sdot10\sdot11}=\frac{11\sdot1079}{6\sdot2\sdot10\sdot11}\\&\scriptstyle=\frac{11869}{6\sdot2\sdot10\sdot11}\\&\scriptstyle=8+\frac{10}{11}+\left(\frac{9}{10}\sdot\frac{1}{11}\right)+\left(\frac{1}{2}\sdot\frac{1}{6}\sdot\frac{1}{10}\sdot\frac{1}{11}\right) \\\end{align}}}](/mediawiki/images/math/0/6/3/06372ae078954714837e756d0a2b80b0.png)
![\scriptstyle\left(\frac{2}{3}\sdot\frac{1}{7}\right)\times\left[6+\frac{9}{10}+\left(\frac{4}{5}\sdot\frac{1}{10}\right)\right]](/mediawiki/images/math/4/c/0/4c07b959f75b107b9a85f4431149a854.png)
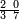
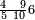
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{2}{3}\sdot\frac{1}{7}\right)\times\left[6+\frac{9}{10}+\left(\frac{4}{5}\sdot\frac{1}{10}\right)\right]&\scriptstyle=\frac{\left[\left[\left[\left(6\sdot10\right)+9\right]\sdot5\right]+4\right]\sdot2}{3\sdot7\sdot10\sdot5}\\&\scriptstyle=\frac{\left[\left(69\sdot5\right)+4\right]\sdot2}{3\sdot7\sdot10\sdot5}\\&\scriptstyle=\frac{349\sdot2}{3\sdot7\sdot10\sdot5}=\frac{698}{3\sdot7\sdot10\sdot5}\\&\scriptstyle=\frac{6}{10}+\left(\frac{4}{7}\sdot\frac{1}{10}\right)+\left(\frac{2}{5}\sdot\frac{1}{7}\sdot\frac{1}{10}\right)+\left(\frac{2}{3}\sdot\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{10}\right) \\\end{align}}}](/mediawiki/images/math/8/2/5/82543f38b14e8aaf62d62c55946b66c0.png)
![\scriptstyle\left(\frac{3}{4}\sdot\frac{1}{9}\right)\times\left[8+\left(\frac{5}{6}\sdot\frac{1}{7}\right)\right]](/mediawiki/images/math/d/f/e/dfe926298d98140474daec8e3ef52953.png)
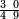
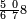
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{3}{4}\sdot\frac{1}{9}\right)\times\left[8+\left(\frac{5}{6}\sdot\frac{1}{7}\right)\right]&\scriptstyle=\frac{\left[\left(8\sdot7\sdot6\right)+5\right]\sdot3}{4\sdot9\sdot6\sdot7}=\frac{341\sdot3}{4\sdot9\sdot6\sdot7}=\frac{1023}{4\sdot9\sdot6\sdot7}\\&\scriptstyle=\frac{6}{9}+\left(\frac{3}{6}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)+\left(\frac{3}{4}\sdot\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{9}\right) \\\end{align}}}](/mediawiki/images/math/f/3/7/f37e913ddb9cce95043ccf8a105e3e1a.png)
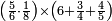
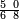
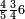
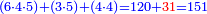
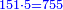
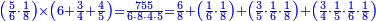
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{3}{4}+\frac{4}{5}\right)\times\left(5+\frac{5}{6}\right)&\scriptstyle=\frac{\left[\left(3\sdot5\right)+\left(4\sdot4\right)\right]\sdot\left[\left(5\sdot6\right)+5\right]}{4\sdot5\sdot6}=\frac{31\sdot35}{4\sdot5\sdot6}=\frac{1085}{4\sdot5\sdot6}\\&\scriptstyle=9+\left(\frac{1}{5}\sdot\frac{1}{6}\right)+\left(\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{6}\right)\\\end{align}}}](/mediawiki/images/math/a/e/7/ae7780933847701a6859a98fd52770ec.png)
![\scriptstyle\left(\frac{3}{4}+\frac{4}{5}\right)\times\left[6+\frac{7}{8}+\left(\frac{1}{6}\sdot\frac{1}{8}\right)\right]](/mediawiki/images/math/1/d/e/1de58acd88921baf39cf31c2001274d7.png)
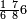
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{3}{4}+\frac{4}{5}\right)\times\left[6+\frac{7}{8}+\left(\frac{1}{6}\sdot\frac{1}{8}\right)\right]&\scriptstyle=\frac{\left[\left(3\sdot5\right)+\left(4\sdot4\right)\right]\sdot\left[\left[\left[\left(6\sdot8\right)+7\right]\sdot6\right]+1\right]}{4\sdot5\sdot8\sdot6}=\frac{31\sdot331}{4\sdot5\sdot8\sdot6}=\frac{10261}{4\sdot5\sdot8\sdot6}\\&\scriptstyle=10+\frac{5}{8}+\left(\frac{3}{6}\sdot\frac{1}{8}\right)+\left(\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{6}\sdot\frac{1}{8}\right)\\\end{align}}}](/mediawiki/images/math/8/f/b/8fb9ba18f268e735cd411785fabf8243.png)
![\scriptstyle\left(\frac{3}{4}+\frac{4}{5}\right)\times\left[6+\left(\frac{1}{7}\sdot\frac{1}{8}\right)\right]](/mediawiki/images/math/a/0/8/a08d4959f373c7157cdca395fae419df.png)
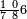
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{3}{4}+\frac{4}{5}\right)\times\left[6+\left(\frac{1}{7}\sdot\frac{1}{8}\right)\right]&\scriptstyle=\frac{\left[\left(3\sdot5\right)+\left(4\sdot4\right)\right]\sdot\left[\left(6\sdot7\sdot8\right)+1\right]}{4\sdot5\sdot7\sdot8}=\frac{31\sdot{\color{red}{337}}}{4\sdot5\sdot7\sdot8}=\frac{10447}{4\sdot5\sdot7\sdot8}\\&\scriptstyle=9+\frac{2}{8}+\left(\frac{4}{7}\sdot\frac{1}{8}\right)+\left(\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\right)+\left(\frac{3}{4}\sdot\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\right)\\\end{align}}}](/mediawiki/images/math/3/3/d/33de834409e84ec3dd73390bc33f531a.png)
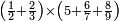
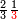
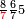
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{1}{2}+\frac{2}{3}\right)\times\left(5+\frac{6}{7}+\frac{8}{9}\right)&\scriptstyle=\frac{\left[\left(1\sdot3\right)+\left(2\sdot2\right)\right]\sdot\left[\left(5\sdot7\sdot9\right)+\left[\left(6\sdot9\right)+\left(8\sdot7\right)\right]\right]}{2\sdot3\sdot7\sdot9}\\&\scriptstyle=\frac{7\sdot425}{6\sdot7\sdot9}\\&\scriptstyle=\frac{2975}{6\sdot7\sdot9}\\&\scriptstyle=7+\frac{7}{9}+\left(\frac{5}{7}\sdot\frac{1}{9}\right)+\left(\frac{5}{6}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/0/7/8/078fee08b98b37284c822e832858d309.png)
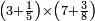
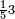
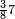
![{\color{blue}{\begin{align}\scriptstyle\left(3+\frac{1}{5}\right)\times\left(7+\frac{3}{8}\right)&\scriptstyle=\frac{\left[\left(3\sdot5\right)+1\right]\sdot\left[\left(7\sdot8\right)+3\right]}{5\sdot8}\\&\scriptstyle=\frac{16\sdot59}{5\sdot8}\\&\scriptstyle=\frac{944}{5\sdot8}\\&\scriptstyle=23+\frac{4}{8}+\left(\frac{4}{5}\sdot\frac{1}{8}\right)\\\end{align}}}](/mediawiki/images/math/2/7/a/27aaee9e1e9b2481e825ace93dadddd0.png)
![\scriptstyle\left[2+\frac{3}{5}+\left(\frac{1}{2}\sdot\frac{1}{5}\right)\right]\times\left[4+\frac{7}{9}+\left(\frac{6}{8}\sdot\frac{1}{9}\right)\right]](/mediawiki/images/math/1/9/4/194f683354067debfa65dc8b696fb706.png)
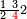
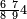
![{\color{blue}{\begin{align}\scriptstyle\left[2+\frac{3}{5}+\left(\frac{1}{2}\sdot\frac{1}{5}\right)\right]\times\left[4+\frac{7}{9}+\left(\frac{6}{8}\sdot\frac{1}{9}\right)\right]&\scriptstyle=\frac{\left[\left[\left[\left(2\sdot5\right)+3\right]\sdot2\right]+1\right]\sdot\left[\left[\left[\left(4\sdot9\right)+7\right]\sdot8\right]+6\right]}{5\sdot2\sdot8\sdot9}\\&\scriptstyle=\frac{27\sdot{\color{red}{350}}}{5\sdot2\sdot8\sdot9}\\&\scriptstyle=\frac{9450}{5\sdot2\sdot8\sdot9}\\&\scriptstyle=13+\frac{1}{9}+\left(\frac{1}{8}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/e/c/7/ec718eb3efd310145d3edde04461d7a4.png)
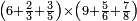
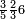
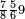
![{\color{blue}{\begin{align}\scriptstyle\left(6+\frac{2}{3}+\frac{3}{5}\right)\times\left(9+\frac{5}{6}+\frac{7}{8}\right)&\scriptstyle=\frac{\left[\left(6\sdot3\sdot5\right)+\left[\left(2\sdot5\right)+\left(3\sdot3\right)\right]\right]\sdot\left[\left(9\sdot6\sdot8\right)+\left[\left(5\sdot8\right)+\left(7\sdot6\right)\right]\right]}{3\sdot5\sdot6\sdot8}\\&\scriptstyle=\frac{\left(90+{\color{red}{19}}\right)\sdot514}{3\sdot5\sdot6\sdot8}\\&\scriptstyle=\frac{109\sdot514}{3\sdot5\sdot6\sdot8}\\&\scriptstyle=\frac{56026}{3\sdot5\sdot6\sdot8}\\&\scriptstyle=77+\frac{6}{8}+\left(\frac{3}{6}\sdot\frac{1}{8}\right)+\left(\frac{1}{3}\sdot\frac{1}{5}\sdot\frac{1}{6}\sdot\frac{1}{8}\right)\\\end{align}}}](/mediawiki/images/math/1/f/3/1f33124a438c6f585a342baf0469d665.png)
![\scriptstyle\left[2+\frac{3}{4}+\frac{4}{5}+\left(\frac{1}{2}\sdot\frac{1}{5}\right)\right]\times\left[6+\frac{6}{7}+\frac{9}{10}+\left(\frac{3}{8}\sdot\frac{1}{10}\right)\right]](/mediawiki/images/math/c/a/5/ca56729c1329c7234d2a3479bc3a4064.png)
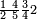
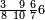
![{\color{blue}{\begin{align}&\scriptstyle\left[2+\frac{3}{4}+\frac{4}{5}+\left(\frac{1}{2}\sdot\frac{1}{5}\right)\right]\times\left[6+\frac{6}{7}+\frac{9}{10}+\left(\frac{3}{8}\sdot\frac{1}{10}\right)\right]\\&\scriptstyle=\frac{\left[\left(2\sdot4\sdot5\sdot2\right)+\left(3\sdot5\sdot2\right)+\left[\left[\left(4\sdot2\right)+1\right]\sdot4\right]\right]\sdot\left[\left(6\sdot7\sdot10\sdot8\right)+\left(6\sdot10\sdot8\right)+\left[\left[\left(9\sdot8\right)+3\right]\sdot7\right]\right]}{4\sdot5\sdot2\sdot7\sdot10\sdot8}\\&\scriptstyle=\frac{\left(80+30+36\right)\sdot\left(3360+480+525\right)}{4\sdot5\sdot2\sdot7\sdot10\sdot8}\\&\scriptstyle=\frac{146\sdot4365}{4\sdot5\sdot2\sdot7\sdot10\sdot8}=\frac{637290}{4\sdot5\sdot2\sdot7\sdot10\sdot8}\\&\scriptstyle=28+\frac{4}{10}+\left(\frac{4}{8}\sdot\frac{1}{10}\right)+\left(\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{10}\right)+\left(\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{10}\right)\\ \end{align}}}](/mediawiki/images/math/7/1/1/7112f896f7c0e92a69532d9670e76c71.png)
![\scriptstyle\left[2+\frac{1}{3}+\frac{1}{5}+\left(\frac{1}{7}\sdot\frac{1}{8}\right)\right]\times\left[3+\frac{1}{9}+\frac{1}{10}+\left(\frac{1}{6}\sdot\frac{1}{11}\right)\right]](/mediawiki/images/math/2/6/7/2674bbca8a320135a18e2259c80cbc80.png)
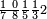
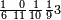
![{\color{blue}{\begin{align}&\scriptstyle\left[2+\frac{1}{3}+\frac{1}{5}+\left(\frac{1}{7}\sdot\frac{1}{8}\right)\right]\times\left[3+\frac{1}{9}+\frac{1}{10}+\left(\frac{1}{6}\sdot\frac{1}{11}\right)\right]\\&\scriptstyle=\frac{\left[\left(2\sdot3\sdot5\sdot7\sdot8\right)+\left(1\sdot5\sdot7\sdot8\right)+\left(1\sdot3\sdot7\sdot8\right)+\left(1\sdot3\sdot5\right)\right]\sdot\left[\left(3\sdot9\sdot10\sdot6\sdot11\right)+\left(1\sdot10\sdot6\sdot11\right)+\left(1\sdot9\sdot6\sdot11\right)+\left(1\sdot9\sdot10\right)\right]}{3\sdot5\sdot7\sdot8\sdot9\sdot10\sdot6\sdot11}\\&\scriptstyle=\frac{{\color{red}{2}}143\sdot19164}{3\sdot5\sdot7\sdot8\sdot9\sdot10\sdot6\sdot11}\\&\scriptstyle=\frac{41068452}{3\sdot5\sdot7\sdot8\sdot9\sdot10\sdot6\sdot11}\\&\scriptstyle=8+\frac{2}{11}+\left(\frac{5}{10}\sdot\frac{1}{11}\right)+\left(\frac{3}{9}\sdot\frac{1}{10}\sdot\frac{1}{11}\right)+\left(\frac{4}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\sdot\frac{1}{11}\right)+\left(\frac{4}{5}\sdot\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\sdot\frac{1}{11}\right) \\\end{align}}}](/mediawiki/images/math/b/6/2/b62c095fdeb61b91a6575f69c90fddd6.png)
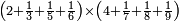
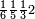
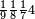
![{\color{blue}{\begin{align}&\scriptstyle\left(2+\frac{1}{3}+\frac{1}{5}+\frac{1}{6}\right)\times\left(4+\frac{1}{7}+\frac{1}{8}+\frac{1}{9}\right)\\&\scriptstyle=\frac{\left[\left(2\sdot3\sdot5\sdot6\right)+\left(1\sdot5\sdot6\right)+\left(1\sdot6\sdot3\right)+\left(1\sdot5\sdot3\right)\right]\sdot\left[\left(4\sdot7\sdot8\sdot9\right)+\left(1\sdot8\sdot9\right)+\left(1\sdot9\sdot7\right)+\left(1\sdot8\sdot7\right)\right]}{3\sdot5\sdot6\sdot7\sdot8\sdot9}\\&\scriptstyle=\frac{243\sdot2207}{3\sdot5\sdot6\sdot7\sdot8\sdot9}\\&\scriptstyle=\frac{536301}{3\sdot5\sdot6\sdot7\sdot8\sdot9}\\&\scriptstyle=11+\frac{7}{9}+\left(\frac{3}{8}\sdot\frac{1}{9}\right)+\left(\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{5}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{2}{5}\sdot\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right) \\\end{align}}}](/mediawiki/images/math/c/d/d/cddecc42bb5310fd2c096a1ec3946404.png)
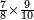

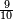
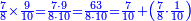

![\scriptstyle{\color{blue}{7\equiv_70\longrightarrow\left[\left(7\sdot8\right)+7\right]\equiv_70}}](/mediawiki/images/math/f/d/8/fd84b5e686ee3e9296cf52634425bc2c.png)
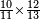
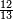

![\scriptstyle\left[\frac{6}{7}+\left(\frac{1}{3}\sdot\frac{1}{7}\right)\right]\times\frac{8}{9}](/mediawiki/images/math/f/9/7/f97a19d668836f661a08889fa51e299c.png)
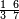

![{\color{blue}{\begin{align}\scriptstyle\left[\frac{6}{7}+\left(\frac{1}{3}\sdot\frac{1}{7}\right)\right]\times\frac{8}{9}&\scriptstyle=\frac{\left[\left(6\sdot3\right)+1\right]\sdot8}{7\sdot3\sdot9}\\&\scriptstyle=\frac{1{\color{red}{9}}\sdot8}{7\sdot3\sdot9}=\frac{152}{7\sdot3\sdot9}\\&\scriptstyle=\frac{7}{9}+\left(\frac{1}{7}\sdot\frac{1}{9}\right)+\left(\frac{2}{3}\sdot\frac{1}{7}\sdot\frac{1}{9}\right) \\\end{align}}}](/mediawiki/images/math/f/8/8/f88e40f0dbbb9a56aa6e39b2188dfad7.png)
![\scriptstyle\left[\frac{1}{11}+\left(\frac{1}{2}\sdot\frac{1}{11}\right)\right]\times\frac{12}{13}](/mediawiki/images/math/b/3/1/b3108e0fc4b9e093af19900912f9dbb5.png)
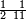
![{\color{blue}{\begin{align}\scriptstyle\left[\frac{1}{11}+\left(\frac{1}{2}\sdot\frac{1}{11}\right)\right]\times\frac{12}{13}&\scriptstyle=\frac{\left[\left(1\sdot2\right)+1\right]\sdot12}{2\sdot11\sdot13}\\&\scriptstyle=\frac{3\sdot12}{2\sdot11\sdot13}=\frac{36}{2\sdot11\sdot13}\\&\scriptstyle=\frac{1}{13}+\left(\frac{7}{11}\sdot\frac{1}{13}\right) \\\end{align}}}](/mediawiki/images/math/a/2/b/a2b5da24ca73b2be5d2d8ecb6b8497e4.png)
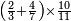
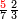
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{2}{3}+\frac{4}{7}\right)\times\frac{10}{11}&\scriptstyle=\frac{\left[\left(2\sdot7\right)+\left(4\sdot3\right)\right]\sdot10}{3\sdot7\sdot11}\\&\scriptstyle=\frac{26\sdot10}{3\sdot7\sdot11}=\frac{260}{3\sdot7\sdot11}\\&\scriptstyle=1+\frac{1}{11}+\left(\frac{2}{7}\sdot\frac{1}{11}\right)+\left(\frac{2}{3}\sdot\frac{1}{7}\sdot\frac{1}{11}\right) \\\end{align}}}](/mediawiki/images/math/2/8/e/28e9ee51835dfac6f6564b3922bff0e6.png)
![\scriptstyle\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\times\left[\frac{9}{10}+\left(\frac{7}{8}\sdot\frac{1}{10}\right)\right]](/mediawiki/images/math/5/7/8/5781c5536b7840a71d28f8ec3a3dcbdc.png)
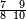
![{\color{blue}{\begin{align}\scriptstyle\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\times\left[\frac{9}{10}+\left(\frac{7}{8}\sdot\frac{1}{10}\right)\right]&\scriptstyle=\frac{\left[\left(5\sdot2\right)+1\right]\times\left[\left(9\sdot8\right)+7\right]}{6\sdot2\sdot10\sdot8}\\&\scriptstyle=\frac{11\sdot79}{6\sdot2\sdot10\sdot8}\\&\scriptstyle=\frac{869}{6\sdot2\sdot10\sdot8}\\&\scriptstyle=\frac{9}{10}+\left(\frac{2}{6}\sdot\frac{1}{8}\sdot\frac{1}{10}\right)+\left(\frac{1}{2}\sdot\frac{1}{6}\sdot\frac{1}{8}\sdot\frac{1}{10}\right) \\\end{align}}}](/mediawiki/images/math/c/9/2/c9226ed09a339b06f56117e6c694d429.png)
![\scriptstyle\left(\frac{3}{4}+\frac{4}{5}\right)\times\left[\frac{10}{11}+\left(\frac{8}{9}\sdot\frac{1}{11}\right)\right]](/mediawiki/images/math/d/d/e/dde0eb7bd402c0e93bfdac59da3033c0.png)
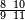
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{3}{4}+\frac{4}{5}\right)\times\left[\frac{10}{11}+\left(\frac{8}{9}\sdot\frac{1}{11}\right)\right]&\scriptstyle=\frac{\left[\left(3\sdot5\right)+\left(4\sdot4\right)\right]\sdot\left[\left(10\sdot9\right)+8\right]}{4\sdot5\sdot11\sdot9}\\&\scriptstyle=\frac{31\sdot98}{4\sdot5\sdot11\sdot9}\\&\scriptstyle=\frac{3038}{4\sdot5\sdot11\sdot9}\\&\scriptstyle=1+\frac{5}{11}+\left(\frac{7}{9}\sdot\frac{1}{11}\right)+\left(\frac{4}{5}\sdot\frac{1}{9}\sdot\frac{1}{11}\right)+\left(\frac{2}{4}\sdot\frac{1}{5}\sdot\frac{1}{9}\sdot\frac{1}{11}\right)\\\end{align}}}](/mediawiki/images/math/c/6/9/c69916756c50aa52fe46494953c5b4a1.png)
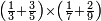
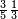
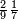
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{1}{3}+\frac{3}{5}\right)\times\left(\frac{1}{7}+\frac{2}{9}\right)&\scriptstyle=\frac{\left[\left(1\sdot5\right)+\left(3\sdot3\right)\right]\sdot\left[\left(1\sdot9\right)+\left(2\sdot7\right)\right]}{3\sdot5\sdot7\sdot9}\\&\scriptstyle=\frac{14\sdot23}{3\sdot5\sdot7\sdot9}\\&\scriptstyle=\frac{3}{9}+\left(\frac{2}{5}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)+\left(\frac{1}{3}\sdot\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/1/3/e/13ea58f02e9ba4a165dc9ee796195bad.png)
![\scriptstyle\left[\frac{2}{3}+\frac{5}{7}+\left(\frac{1}{6}\sdot\frac{1}{7}\right)\right]\times\left[\frac{4}{5}+\frac{9}{10}+\left(\frac{8}{9}\sdot\frac{1}{10}\right)\right]](/mediawiki/images/math/8/9/c/89c984e9a2e8e2ca9db67ecc3cae4f93.png)
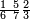
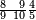
![{\color{blue}{\begin{align}&\scriptstyle\left[\frac{2}{3}+\frac{5}{7}+\left(\frac{1}{6}\sdot\frac{1}{7}\right)\right]\times\left[\frac{4}{5}+\frac{9}{10}+\left(\frac{8}{9}\sdot\frac{1}{10}\right)\right]\\&\scriptstyle=\frac{\left[\left(2\sdot7\sdot6\right)+\left[\left[\left(5\sdot6\right)+1\right]\sdot3\right]\right]\sdot\left[\left(4\sdot10\sdot9\right)+\left[\left[\left(9\sdot9\right)+8\right]\sdot5\right]\right]}{3\sdot7\sdot6\sdot5\sdot10\sdot9}\\&\scriptstyle=\frac{\left(84+93\right)\sdot\left(360+445\right)}{3\sdot7\sdot6\sdot5\sdot10\sdot9}\\&\scriptstyle=\frac{177\sdot805}{3\sdot7\sdot6\sdot5\sdot10\sdot9}\\&\scriptstyle=2+\frac{5}{10}+\left(\frac{1}{9}\sdot\frac{1}{10}\right)+\left(\frac{1}{7}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)+\left(\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)\\\end{align}}}](/mediawiki/images/math/4/7/8/478f0d34f978314485b7af5194e14530.png)
![\scriptstyle\left[\frac{3}{4}+\frac{4}{5}+\left(\frac{1}{2}\sdot\frac{1}{7}\right)\right]\times\left[\frac{7}{8}+\frac{8}{9}+\left(\frac{1}{3}\sdot\frac{1}{10}\right)\right]](/mediawiki/images/math/b/a/6/ba6de07c368359996ed40f8c820d9fd7.png)
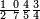
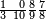
![{\color{blue}{\begin{align}&\scriptstyle\left[\frac{3}{4}+\frac{4}{5}+\left(\frac{1}{2}\sdot\frac{1}{7}\right)\right]\times\left[\frac{7}{8}+\frac{8}{9}+\left(\frac{1}{3}\sdot\frac{1}{10}\right)\right]\\&\scriptstyle=\frac{\left[\left(3\sdot5\sdot7\sdot2\right)+\left(4\sdot4\sdot7\sdot2\right)+\left(1\sdot5\sdot4\right)\right]\sdot\left[\left(7\sdot9\sdot10\sdot3\right)+\left(8\sdot8\sdot10\sdot3\right)+\left(1\sdot9\sdot8\right)\right]}{4\sdot5\sdot2\sdot7\sdot8\sdot9\sdot3\sdot10}\\&=\scriptstyle\frac{\left(210+{\color{red}{224}}+20\right)\sdot3882}{4\sdot5\sdot2\sdot7\sdot8\sdot9\sdot3\sdot10}=\frac{454\sdot3882}{4\sdot5\sdot2\sdot7\sdot8\sdot9\sdot3\sdot10}\\&\scriptstyle=2+\frac{9}{10}+\left(\frac{1}{9}\sdot\frac{1}{10}\right)+\left(\frac{2}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)+\left(\frac{1}{8}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)+\left(\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)\end{align}}}](/mediawiki/images/math/b/a/8/ba8b7fdfaa8c471d0df6754e125eb720.png)
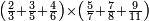
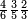
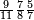
![{\color{blue}{\begin{align}&\scriptstyle\left(\frac{2}{3}+\frac{3}{5}+\frac{4}{6}\right)\times\left(\frac{5}{7}+\frac{7}{8}+\frac{9}{11}\right)\\&\scriptstyle=\frac{\left[\left(2\sdot5\sdot6\right)+\left(3\sdot3\sdot6\right)+\left(4\sdot3\sdot5\right)\right]\sdot\left[\left(5\sdot8\sdot11\right)+\left(7\sdot7\sdot11\right)+\left(9\sdot7\sdot8\right)\right]}{3\sdot5\sdot6\sdot7\sdot8\sdot11}\\&\scriptstyle=\frac{174\sdot1483}{3\sdot5\sdot6\sdot7\sdot8\sdot11}\\&\scriptstyle=4+\frac{7}{11}+\left(\frac{1}{8}\sdot\frac{1}{11}\right)+\left(\frac{4}{7}\sdot\frac{1}{8}\sdot\frac{1}{11}\right)+\left(\frac{4}{5}\sdot\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{11}\right)\\\end{align}}}](/mediawiki/images/math/6/9/0/69098024d773e68e31c4ee11e07bf8bb.png)
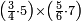
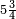
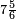
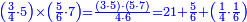
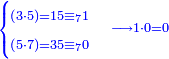
![{\color{blue}{\scriptstyle\begin{cases}\scriptstyle21\equiv_70\longrightarrow0\sdot6=0\\\scriptstyle\left[\left(5\sdot4\right)+1\right]=20+1=21\equiv_70\end{cases}}}](/mediawiki/images/math/6/2/2/622e8d902b48d728aa1dfbd5ec7e0e5e.png)
![\scriptstyle\left[\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\sdot8\right]\times\left[\left[\frac{8}{9}+\left(\frac{1}{5}\sdot\frac{1}{9}\right)\right]\sdot12\right]](/mediawiki/images/math/1/6/0/1600fa727c35dec4f3c4ad5a9afdabb3.png)
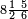
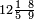
![{\color{blue}{\begin{align}&\scriptstyle\left[\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\sdot8\right]\times\left[\left[\frac{8}{9}+\left(\frac{1}{5}\sdot\frac{1}{9}\right)\right]\sdot12\right]\\&\scriptstyle=\frac{\left[\left[\left(5\sdot2\right)+1\right]\sdot8\right]\sdot\left[\left[\left(8\sdot5\right)+1\right]\sdot12\right]}{6\sdot2\sdot9\sdot5}\\&\scriptstyle=\frac{\left(11\sdot8\right)\sdot\left(41\sdot12\right)}{6\sdot2\sdot9\sdot5}=\frac{88\sdot492}{6\sdot2\sdot9\sdot5}\\&\scriptstyle=\frac{43296}{6\sdot2\sdot9\sdot5}\\&\scriptstyle=80+\frac{1}{9}+\left(\frac{3}{6}\sdot\frac{1}{9}\right)+\left(\frac{3}{5}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/c/6/b/c6b4ccf19bbae67ace95379874184ca7.png)
![\scriptstyle\left[\left(\frac{2}{3}+\frac{3}{5}\right)\sdot8\right]\times\left[\left(\frac{6}{7}+\frac{5}{9}\right)\sdot4\right]](/mediawiki/images/math/5/1/a/51a5f2c5f34e3fd50333a6ab3d89872a.png)
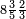
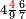
![{\color{blue}{\begin{align}\scriptstyle\left[\left(\frac{2}{3}+\frac{3}{5}\right)\sdot8\right]\times\left[\left(\frac{6}{7}+\frac{5}{9}\right)\sdot4\right]&\scriptstyle=\frac{\left[\left[\left(2\sdot5\right)+\left(3\sdot3\right)\right]\sdot8\right]\sdot\left[\left[\left(6\sdot9\right)+\left(5\sdot7\right)\right]\sdot4\right]}{3\sdot5\sdot7\sdot9}\\&\scriptstyle=57+\frac{2}{9}+\left(\frac{2}{7}\sdot\frac{1}{9}\right)+\left(\frac{2}{5}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)+\left(\frac{1}{3}\sdot\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/9/2/d/92ddfbb150ccc848723b03123cc5074e.png)
![\scriptstyle\left[\left(\frac{3}{4}\sdot\frac{1}{5}\right)\sdot8\right]\times\left[\left(\frac{5}{6}\sdot\frac{1}{7}\right)\sdot15\right]](/mediawiki/images/math/0/5/f/05f9355bfe0fc140027cb8b0dd02c1ec.png)
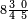
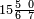
![\scriptstyle{\color{blue}{\left[\left(\frac{3}{4}\sdot\frac{1}{5}\right)\sdot8\right]\times\left[\left(\frac{5}{6}\sdot\frac{1}{7}\right)\sdot15\right]=\frac{\left(3\sdot8\right)\sdot\left(5\sdot15\right)}{4\sdot5\sdot6\sdot7}=2+\frac{1}{7}}}](/mediawiki/images/math/5/4/f/54f19d884fd4f3d92b4474809d32db29.png)
![\scriptstyle\left[\frac{2}{3}\sdot\left(5+\frac{5}{6}\right)\right]\times\left[\frac{6}{7}\sdot\left(8+\frac{4}{9}\right)\right]](/mediawiki/images/math/d/b/0/db0965fa4c8a446b7ce40af91705900c.png)
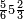
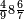
![{\color{blue}{\begin{align}\scriptstyle\left[\frac{2}{3}\sdot\left(5+\frac{5}{6}\right)\right]&\scriptstyle\times\left[\frac{6}{7}\sdot\left(8+\frac{4}{9}\right)\right]\\&\scriptstyle=\frac{\left[\left[\left(5\sdot6\right)+5\right]\sdot2\right]\sdot\left[\left[\left(8\sdot9\right)+4\right]\sdot6\right]}{3\sdot6\sdot7\sdot9}\\&\scriptstyle=\frac{\left(35\sdot2\right)\sdot\left(76\sdot6\right)}{3\sdot6\sdot7\sdot9}\\&\scriptstyle=\frac{70\sdot456}{3\sdot6\sdot7\sdot9}\\&\scriptstyle=28+\frac{1}{9}+\left(\frac{2}{7}\sdot\frac{1}{9}\right)+\left(\frac{2}{6}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\end{align}}}](/mediawiki/images/math/9/1/1/911130a3716d56d9f4ebd916ad18277c.png)
![\scriptstyle\left[\frac{3}{4}\sdot\left[5+\frac{6}{7}+\left(\frac{1}{6}\sdot\frac{1}{7}\right)\right]\right]\times\left[\frac{7}{8}\sdot\left[3+\frac{3}{10}+\left(\frac{1}{9}\sdot\frac{1}{10}\right)\right]\right]](/mediawiki/images/math/e/d/2/ed219e497be7d0951c74faa4e0f2f7d7.png)
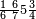
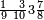
![{\color{blue}{\begin{align}&\scriptstyle\left[\frac{3}{4}\sdot\left[5+\frac{6}{7}+\left(\frac{1}{6}\sdot\frac{1}{7}\right)\right]\right]\times\left[\frac{7}{8}\sdot\left[3+\frac{3}{10}+\left(\frac{1}{9}\sdot\frac{1}{10}\right)\right]\right]\\&\scriptstyle=\frac{\left[\left[\left[\left[\left(5\sdot7\right)+6\right]\sdot6\right]+1\right]\sdot3\right]\sdot\left[\left[\left[\left[\left(3\sdot10\right)+3\right]\sdot9\right]+1\right]\sdot7\right]}{4\sdot7\sdot6\sdot8\sdot10\sdot9}\\&\scriptstyle=\frac{741\sdot20{\color{red}{8}}6}{4\sdot7\sdot6\sdot8\sdot10\sdot9}\\&\scriptstyle=12+\frac{7}{10}+\left(\frac{7}{9}\sdot\frac{1}{10}\right)+\left(\frac{5}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)\\&\scriptstyle+\left(\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)+\left(\frac{2}{4}\sdot\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)\\\end{align}}}](/mediawiki/images/math/3/e/e/3ee63b98ef44cdbf48007edf4130d132.png)
![\scriptstyle\left[\frac{1}{2}\sdot\left(2+\frac{1}{5}+\frac{1}{6}\right)\right]\times\left[\frac{1}{7}\sdot\left(3+\frac{1}{8}+\frac{1}{9}\right)\right]](/mediawiki/images/math/0/0/4/004e700b6414538394bc342a34fa598e.png)
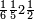
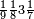
![{\color{blue}{\begin{align}&\scriptstyle\left[\frac{1}{2}\sdot\left(2+\frac{1}{5}+\frac{1}{6}\right)\right]\times\left[\frac{1}{7}\sdot\left(3+\frac{1}{8}+\frac{1}{9}\right)\right]\\&\scriptstyle=\frac{\left[\left[\left(2\sdot5\sdot6\right)+\left(1\sdot6\right)+\left(1\sdot5\right)\right]\sdot1\right]\sdot\left[\left[\left(3\sdot8\sdot9\right)+\left(1\sdot9\right)+\left(1\sdot8\right)\right]\sdot1\right]}{2\sdot5\sdot6\sdot7\sdot8\sdot9}\\&\scriptstyle=\frac{71\sdot233}{2\sdot5\sdot6\sdot7\sdot8\sdot9}\\&\scriptstyle=\frac{4}{9}+\left(\frac{7}{8}\sdot\frac{1}{9}\right)+\left(\frac{2}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{4}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{1}{5}\sdot\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{1}{2}\sdot\frac{1}{5}\sdot\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/7/b/0/7b0289eb4701221c90b38244df7e39d8.png)
![\scriptstyle\left[\frac{6}{7}\sdot\left[5+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\right]\times\left[\frac{7}{8}\sdot\left[3+\left(\frac{3}{5}\sdot\frac{1}{9}\right)\right]\right]](/mediawiki/images/math/5/f/5/5f53be0be7aff5af1d6d8efd389472f7.png)
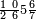
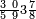
![{\color{blue}{\begin{align}&\scriptstyle\left[\frac{6}{7}\sdot\left[5+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\right]\times\left[\frac{7}{8}\sdot\left[3+\left(\frac{3}{5}\sdot\frac{1}{9}\right)\right]\right]\\&\scriptstyle=\frac{\left[\left[\left(5\sdot6\sdot2\right)+1\right]\sdot6\right]\sdot\left[\left[\left(3\sdot9\sdot5\right)+3\right]\sdot7\right]}{2\sdot5\sdot6\sdot7\sdot8\sdot9}\\&\scriptstyle=\frac{366\sdot966}{2\sdot5\sdot6\sdot7\sdot8\sdot9}\\&\scriptstyle=11+\frac{6}{9}+\left(\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{5}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{3}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{3}{5}\sdot\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/5/9/d/59d429ff3a33e1c19a03416be95ae4c3.png)
![\scriptstyle\left[\left(\frac{2}{3}\sdot\frac{1}{5}\right)\sdot\left(8+\frac{1}{6}\right)\right]\times\left[\left(\frac{5}{7}\sdot\frac{1}{8}\right)\sdot\left(6+\frac{1}{9}\right)\right]](/mediawiki/images/math/9/a/0/9a08cbb7c870dbf982d1d194761990fe.png)
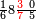
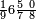
![{\color{blue}{\begin{align}&\scriptstyle\left[\left(\frac{2}{3}\sdot\frac{1}{5}\right)\sdot\left(8+\frac{1}{6}\right)\right]\times\left[\left(\frac{5}{7}\sdot\frac{1}{8}\right)\sdot\left(6+\frac{1}{9}\right)\right]\\&\scriptstyle=\frac{\left[\left[\left(8\sdot6\right)+1\right]\sdot2\right]\sdot\left[\left[\left(6\sdot9\right)+1\right]\sdot5\right]}{3\sdot5\sdot6\sdot7\sdot8\sdot9}\\&\scriptstyle=\frac{98\sdot275}{3\sdot5\sdot6\sdot7\sdot8\sdot9}\\&\scriptstyle=\frac{5}{9}+\left(\frac{2}{8}\sdot\frac{1}{9}\right)+\left(\frac{5}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{2}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{3}{5}\sdot\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{1}{3}\sdot\frac{1}{5}\sdot\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/e/0/a/e0a145b0f36d2ec2e48d31fb61e80e87.png)
![\scriptstyle{\left[\left(\frac{3}{4}\sdot\frac{1}{5}\right)\sdot\left[6+\frac{3}{11}+\left(\frac{5}{6}\sdot\frac{1}{11}\right)\right]\right]\times\left[\left(\frac{5}{7}\sdot\frac{1}{9}\right)\sdot\left[12+\frac{6}{13}+\left(\frac{3}{8}\sdot\frac{1}{13}\right)\right]\right]}](/mediawiki/images/math/8/a/a/8aa44881aad0cb08461e477dc815f423.png)
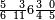
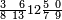
![{\color{blue}{\begin{align}&\scriptstyle{\left[\left(\frac{3}{4}\sdot\frac{1}{5}\right)\sdot\left[6+\frac{3}{11}+\left(\frac{5}{6}\sdot\frac{1}{11}\right)\right]\right]\times\left[\left(\frac{5}{7}\sdot\frac{1}{9}\right)\sdot\left[12+\frac{6}{13}+\left(\frac{3}{8}\sdot\frac{1}{13}\right)\right]\right]}\\&\scriptstyle{=\frac{\left[\left[\left[\left[\left(6\sdot11\right)+3\right]\sdot6\right]+5\right]\sdot3\right]\sdot\left[\left[\left[\left[\left(12\sdot13\right)+6\right]\sdot8\right]+3\right]\sdot5\right]}{4\sdot5\sdot6\sdot7\sdot8\sdot9\sdot11\sdot13}}\\&\scriptstyle{=\frac{1257\sdot6495}{4\sdot5\sdot6\sdot7\sdot8\sdot9\sdot11\sdot13}}\\&\scriptstyle{=\frac{12}{13}+\left(\frac{2}{11}\sdot\frac{1}{13}\right)+\left(\frac{8}{9}\sdot\frac{1}{11}\sdot\frac{1}{13}\right)+\left(\frac{7}{8}\sdot\frac{1}{9}\sdot\frac{1}{11}\sdot\frac{1}{13}\right)+\left(\frac{2}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{11}\sdot\frac{1}{13}\right)}\\&\scriptstyle{+\left(\frac{3}{5}\sdot\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{11}\sdot\frac{1}{13}\right)+\left(\frac{3}{4}\sdot\frac{1}{5}\sdot\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{11}\sdot\frac{1}{13}\right)}\\\end{align}}}](/mediawiki/images/math/0/d/4/0d4f113e1ba8bae2f383da3f025a7bd3.png)
![\scriptstyle\left[\left(\frac{1}{2}\sdot\frac{1}{5}\right)\sdot\left[9+\left(\frac{5}{6}\sdot\frac{1}{7}\right)\right]\right]\times\left[\left(\frac{3}{8}\sdot\frac{1}{9}\right)\sdot\left[15+\left(\frac{3}{10}\sdot\frac{1}{11}\right)\right]\right]](/mediawiki/images/math/c/1/9/c194b62459d0d62bff13d93cbe5d9e5e.png)
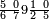
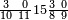
![{\color{blue}{\begin{align}&\scriptstyle\left[\left(\frac{1}{2}\sdot\frac{1}{5}\right)\sdot\left[9+\left(\frac{5}{6}\sdot\frac{1}{7}\right)\right]\right]\times\left[\left(\frac{3}{8}\sdot\frac{1}{9}\right)\sdot\left[15+\left(\frac{3}{10}\sdot\frac{1}{11}\right)\right]\right]\\&\scriptstyle=\frac{\left[\left(9\sdot7\sdot6\right)+5\right]\sdot\left[\left[\left(15\sdot10\sdot11\right)+3\right]\sdot3\right]}{2\sdot5\sdot6\sdot7\sdot8\sdot9\sdot10\sdot11}\\&\scriptstyle=\frac{{\color{red}{383\sdot4}}959}{2\sdot5\sdot6\sdot7\sdot8\sdot9\sdot10\sdot11}\\&\scriptstyle=\frac{6}{11}+\left(\frac{2}{10}\sdot\frac{1}{11}\right)+\left(\frac{6}{8}\sdot\frac{1}{10}\sdot\frac{1}{11}\right)+\left(\frac{3}{7}\sdot\frac{1}{8}\sdot\frac{1}{10}\sdot\frac{1}{11}\right)\\&\scriptstyle+\left(\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{10}\sdot\frac{1}{11}\right)+\left(\frac{1}{5}\sdot\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{10}\sdot\frac{1}{11}\right)+\left(\frac{1}{2}\sdot\frac{1}{5}\sdot\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{10}\sdot\frac{1}{11}\right)\\\end{align}}}](/mediawiki/images/math/9/1/e/91e92469bd141a51c4311d010cd8be44.png)
![\scriptstyle\left[\left(\frac{2}{3}\sdot\frac{1}{5}\right)\sdot\left(8+\frac{3}{6}+\frac{4}{7}\right)\right]\times\left[\left(\frac{4}{9}\sdot\frac{1}{10}\right)\sdot\left(18+\frac{6}{11}+\frac{5}{8}\right)\right]](/mediawiki/images/math/9/7/d/97d9dfda0018e2b0241f56adec4bb691.png)
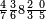
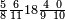
![{\color{blue}{\begin{align}&\scriptstyle\left[\left(\frac{2}{3}\sdot\frac{1}{5}\right)\sdot\left(8+\frac{3}{6}+\frac{4}{7}\right)\right]\times\left[\left(\frac{4}{9}\sdot\frac{1}{10}\right)\sdot\left(18+\frac{6}{11}+\frac{5}{8}\right)\right]\\&\scriptstyle=\frac{\left[\left[\left(8\sdot6\sdot7\right)+\left[\left(3\sdot7\right)+\left(4\sdot6\right)\right]\right]\sdot2\right]\sdot\left[\left[\left(18\sdot11\sdot8\right)+\left[\left(6\sdot8\right)+\left(5\sdot11\right)\right]\right]\sdot4\right]}{3\sdot5\sdot6\sdot7\sdot8\sdot9\sdot10\sdot11}\\&\scriptstyle=\frac{762\sdot6748}{3\sdot5\sdot6\sdot7\sdot8\sdot9\sdot10\sdot11}\\&\scriptstyle=1+\left(\frac{3}{10}\sdot\frac{1}{11}\right)+\left(\frac{3}{9}\sdot\frac{1}{10}\sdot\frac{1}{11}\right)+{\color{red}{\left(\frac{1}{6}\sdot\frac{1}{9}\sdot\frac{1}{10}\sdot\frac{1}{11}\right)+\left(\frac{2}{5}\sdot\frac{1}{6}\sdot\frac{1}{9}\sdot\frac{1}{10}\sdot\frac{1}{11}\right)}}\\\end{align}}}](/mediawiki/images/math/1/d/6/1d62a84e37546b6c93ffff78d904fbf2.png)
![\scriptstyle\left[\left(\frac{2}{3}+\frac{3}{5}\right)\sdot\left(9+\frac{5}{6}\right)\right]\times\left[\left(\frac{3}{7}+\frac{7}{8}\right)\sdot\left(12+\frac{7}{9}\right)\right]](/mediawiki/images/math/b/b/8/bb89089481d6771d64a646f1b2604e99.png)
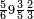
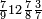
![{\color{blue}{\begin{align}\scriptstyle\left[\left(\frac{2}{3}+\frac{3}{5}\right)\sdot\left(9+\frac{5}{6}\right)\right]&\scriptstyle\times\left[\left(\frac{3}{7}+\frac{7}{8}\right)\sdot\left(12+\frac{7}{9}\right)\right]\\&\scriptstyle=\frac{\left[\left[\left(2\sdot5\right)+\left(3\sdot3\right)\right]\sdot\left[\left(9\sdot6\right)+5\right]\right]\sdot\left[\left[\left(3\sdot8\right)+\left(7\sdot7\right)\right]\sdot\left[\left(12\sdot9\right)+7\right]\right]}{3\sdot5\sdot6\sdot7\sdot8\sdot9}\\&\scriptstyle=\frac{\left(19\sdot59\right)\sdot8395}{3\sdot5\sdot6\sdot7\sdot8\sdot9}\\&\scriptstyle=\frac{1121\sdot8395}{3\sdot5\sdot6\sdot7\sdot8\sdot9}\\&\scriptstyle=207+\frac{4}{9}+\left(\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{5}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{2}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{1}{3}\sdot\frac{1}{6}\sdot\frac{1}{{\color{red}{7}}}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/5/a/6/5a65c45bc35f911330675814126e0a36.png)
![\scriptstyle\left[\left(\frac{2}{3}+\frac{3}{5}\right)\sdot\left(7+\frac{3}{4}+\frac{3}{5}\right)\right]\times\left[\left(\frac{5}{6}+\frac{5}{8}\right)\sdot\left(4+\frac{5}{6}+\frac{9}{10}\right)\right]](/mediawiki/images/math/b/4/9/b497ed9da24bcbdf311fe9fdd582187b.png)
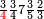
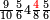
![{\color{blue}{\begin{align}&\scriptstyle\left[\left(\frac{2}{3}+\frac{3}{5}\right)\sdot\left(7+\frac{3}{4}+\frac{3}{5}\right)\right]\times\left[\left(\frac{5}{6}+\frac{5}{8}\right)\sdot\left(4+\frac{5}{6}+\frac{9}{10}\right)\right]\\&\scriptstyle=\frac{\left[\left(2\sdot5\right)+\left(3\sdot3\right)\right]\sdot\left[\left(7\sdot4\sdot5\right)+\left[\left(3\sdot5\right)+\left(3\sdot4\right)\right]\right]\sdot\left[\left(5\sdot8\right)+\left(5\sdot6\right)\right]\sdot\left[\left(4\sdot6\sdot10\right)+\left[\left(5\sdot10\right)+\left(9\sdot6\right)\right]\right]}{3\sdot4\sdot5\sdot5\sdot6\sdot6\sdot8\sdot10}\\&\scriptstyle=\frac{\left(19\sdot167\right)\sdot24080}{2\sdot6\sdot8\sdot9\sdot10\sdot10\sdot10}\\&\scriptstyle=\frac{\frac{\frac{3173\sdot24080}{10}}{8}}{2\sdot6\sdot9\sdot10\sdot10}\\&\scriptstyle=88+\frac{4}{10}+\left(\frac{3}{10}\sdot\frac{1}{10}\right)+\left(\frac{2}{9}\sdot\frac{1}{10}\sdot\frac{1}{10}\right)+\left(\frac{2}{6}\sdot\frac{1}{9}\sdot\frac{1}{10}\sdot\frac{1}{10}\right)+\left(\frac{1}{2}\sdot\frac{1}{6}\sdot\frac{1}{9}\sdot\frac{1}{10}\sdot\frac{1}{10}\right)\\\end{align}}}](/mediawiki/images/math/1/e/1/1e1394cd7adf66817eca7fc89468920a.png)
![\scriptstyle\left[\left[\frac{3}{5}+\left(\frac{1}{2}\sdot\frac{1}{5}\right)\right]\sdot\left[4+\frac{1}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\right]\times\left[\left[\frac{6}{7}+\left(\frac{1}{5}\sdot\frac{1}{7}\right)\right]\sdot\left[3+\frac{5}{11}+\left(\frac{5}{8}\sdot\frac{1}{11}\right)\right]\right]](/mediawiki/images/math/b/8/6/b86a2bf3e89b5176cfd5c7970fa56c64.png)
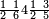
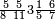
![{\color{blue}{\begin{align}&\scriptstyle\left[\left[\frac{3}{5}+\left(\frac{1}{2}\sdot\frac{1}{5}\right)\right]\sdot\left[4+\frac{1}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\right]\times\left[\left[\frac{6}{7}+\left(\frac{1}{5}\sdot\frac{1}{7}\right)\right]\sdot\left[3+\frac{5}{11}+\left(\frac{5}{8}\sdot\frac{1}{11}\right)\right]\right]\\&\scriptstyle=\frac{\left[\left[\left(3\sdot2\right)+1\right]\sdot\left[\left(4\sdot2\sdot6\right)+\left(1\sdot2\right)+1\right]\right]\sdot\left[\left[\left(6\sdot5\right)+1\right]\sdot\left[\left(3\sdot8\sdot11\right)+\left(5\sdot8\right)+5\right]\right]}{2\sdot2\sdot5\sdot5\sdot6\sdot7\sdot8\sdot11}\\&\scriptstyle=\frac{\left(7\sdot51\right)\sdot9579}{2\sdot2\sdot5\sdot5\sdot6\sdot7\sdot8\sdot11}\\&\scriptstyle=\frac{357\sdot9579}{2\sdot2\sdot5\sdot5\sdot6\sdot7\sdot8\sdot11}\\&\scriptstyle=9+\frac{2}{11}+\left(\frac{7}{10}\sdot\frac{1}{11}\right)+\left(\frac{7}{10}\sdot\frac{1}{10}\sdot\frac{1}{11}\right)+\left(\frac{5}{8}\sdot\frac{1}{10}\sdot\frac{1}{10}\sdot\frac{1}{11}\right)+\left(\frac{3}{6}\sdot\frac{1}{8}\sdot\frac{1}{10}\sdot\frac{1}{10}\sdot\frac{1}{11}\right)\\\end{align}}}](/mediawiki/images/math/e/5/6/e56643c9f84dc78adb14a69f37f030c3.png)
![\scriptstyle\left[\left(\frac{2}{3}\sdot\frac{1}{5}\right)\sdot\left[8+\left(\frac{1}{4}\sdot\frac{1}{6}\right)\right]\right]\times\left[\left(\frac{3}{7}\sdot\frac{1}{8}\right)\sdot\left[12+\left(\frac{1}{2}\sdot\frac{1}{13}\right)\right]\right]](/mediawiki/images/math/b/d/3/bd39d71c41ffa67e9904a9b88747ee73.png)
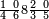
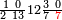
![{\color{blue}{\begin{align}&\scriptstyle\left[\left(\frac{2}{3}\sdot\frac{1}{5}\right)\sdot\left[8+\left(\frac{1}{4}\sdot\frac{1}{6}\right)\right]\right]\times\left[\left(\frac{3}{7}\sdot\frac{1}{8}\right)\sdot\left[12+\left(\frac{1}{2}\sdot\frac{1}{13}\right)\right]\right]\\&\scriptstyle=\frac{\left[\left[\left(8\sdot4\sdot6\right)+1\right]\sdot2\right]\sdot\left[\left[\left(12\sdot2\sdot13\right)+1\right]\sdot3\right]}{2\sdot3\sdot4\sdot5\sdot6\sdot7\sdot8\sdot13}\\&\scriptstyle=\frac{\left(193\sdot2\right)\sdot939}{2\sdot3\sdot4\sdot5\sdot6\sdot7\sdot8\sdot13}\\&\scriptstyle=\frac{38{\color{red}{6}}\sdot939}{2\sdot3\sdot4\sdot5\sdot6\sdot7\sdot8\sdot13}\\&\scriptstyle=\frac{8}{13}+\left(\frac{9}{10}\sdot\frac{1}{13}\right)+\left(\frac{7}{8}\sdot\frac{1}{10}\sdot\frac{1}{13}\right)+\left(\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\sdot\frac{1}{13}\right)+\left(\frac{1}{2}\sdot\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{10}\sdot\frac{1}{13}\right)\\\end{align}}}](/mediawiki/images/math/8/5/4/854a6dca900f5d89cd943146eb8ceecd.png)
![\scriptstyle\left[\left(\frac{3}{5}\sdot5\right)+\left(\frac{5}{6}\sdot7\right)\right]\times\left[\left(\frac{2}{3}\sdot4\right)+\left(\frac{1}{2}\sdot5\right)\right]](/mediawiki/images/math/9/e/f/9efa063bb7945eb7d7c881b90eeae9c3.png)
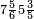
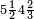
![{\color{blue}{\begin{align}\scriptstyle\left[\left(\frac{3}{5}\sdot5\right)+\left(\frac{5}{6}\sdot7\right)\right]\times\left[\left(\frac{2}{3}\sdot4\right)+\left(\frac{1}{2}\sdot5\right)\right]&\scriptstyle=\frac{\left[\left[\left(3\sdot5\right)\sdot6\right]+\left[\left(5\sdot7\right)\sdot5\right]\right]\sdot\left[\left[\left(2\sdot4\right)\sdot2\right]+\left[\left(1\sdot5\right)\sdot3\right]\right]}{2\sdot3\sdot5\sdot6}\\&=\scriptstyle\frac{\left(90+175\right)\sdot31}{2\sdot3\sdot5\sdot6}\\&\scriptstyle=\frac{265\sdot31}{2\sdot3\sdot5\sdot6}\\&\scriptstyle=45+\frac{6}{10}+\left(\frac{2}{6}\sdot\frac{1}{10}\right)+\left(\frac{1}{3}\sdot\frac{1}{6}\sdot\frac{1}{10}\right)\\\end{align}}}](/mediawiki/images/math/3/7/3/373bd6b248896cb5730aef7b122a2ca6.png)
![{\color{blue}{\begin{align}\scriptstyle\left[\left(\frac{3}{5}\sdot5\right)+\left(\frac{5}{6}\sdot7\right)\right]\times\left[\left(\frac{2}{3}\sdot4\right)+\left(\frac{1}{2}\sdot5\right)\right]&\scriptstyle=\left[3+\left(5+\frac{5}{6}\right)\right]\sdot\left[\left(2+\frac{2}{3}\right)+\left(2+\frac{1}{2}\right)\right]\\&\scriptstyle=\left(8+\frac{5}{6}\right)\sdot\left(5+\frac{1}{6}\right)\\\end{align}}}](/mediawiki/images/math/0/c/4/0c43bb54b91614d12040e6bc6015dbbf.png)
![\scriptstyle\left[\left(\frac{3}{5}\sdot3\right)+\left[\frac{3}{4}\sdot\left(2+\frac{2}{3}\right)\right]\right]\times\left[\left(\frac{4}{5}\sdot2\right)+\left[\frac{5}{7}\sdot\left(3+\frac{1}{2}\right)\right]\right]](/mediawiki/images/math/a/c/9/ac90cb543446e9ef209b88692cd48240.png)
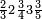
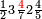
![{\color{blue}{\begin{align}&\scriptstyle\left[\left(\frac{3}{5}\sdot3\right)+\left[\frac{3}{4}\sdot\left(2+\frac{2}{3}\right)\right]\right]\times\left[\left(\frac{4}{5}\sdot2\right)+\left[\frac{5}{7}\sdot\left(3+\frac{1}{2}\right)\right]\right]\\&\scriptstyle=\frac{\left[\left[\left(3\sdot3\right)\sdot4\sdot3\right]+\left[\left[3\sdot\left[\left(2\sdot3\right)+2\right]\right]\sdot5\right]\right]\sdot\left[\left[\left(4\sdot2\right)\sdot7\sdot2\right]+\left[\left[5\sdot\left[\left(3\sdot2\right)+1\right]\right]\sdot5\right]\right]}{2\sdot3\sdot4\sdot5\sdot5\sdot7}\\&\scriptstyle=\frac{\left(108+120\right)\sdot287}{2\sdot3\sdot4\sdot5\sdot5\sdot7}\\&\scriptstyle=\frac{228\sdot287}{2\sdot3\sdot4\sdot5\sdot5\sdot7}\\&\scriptstyle=15+\frac{5}{10}+\left(\frac{8}{10}\sdot\frac{1}{10}\right)\\\end{align}}}](/mediawiki/images/math/a/1/c/a1c642a81a9370d65bc005f53f27a0d4.png)
![\scriptstyle\left[\left(3+\frac{1}{2}\right)+\left(5+\frac{1}{3}\right)\right]\times\left[\left(4+\frac{3}{4}\right)+\left(6+\frac{4}{5}\right)\right]](/mediawiki/images/math/d/c/e/dce671800feba457094cdfcc90b5a6f2.png)
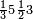
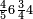
![{\color{blue}{\begin{align}&\scriptstyle\left[\left(3+\frac{1}{2}\right)+\left(5+\frac{1}{3}\right)\right]\times\left[\left(4+\frac{3}{4}\right)+\left(6+\frac{4}{5}\right)\right]\\&\scriptstyle=\frac{\left[\left[\left[\left(3\sdot2\right)+1\right]\sdot3\right]+\left[\left[\left(5\sdot3\right)+1\right]\sdot2\right]\right]\sdot\left[\left[\left[\left(4\sdot4\right)+3\right]\sdot5\right]+\left[\left[\left(6\sdot5\right)+4\right]\sdot4\right]\right]}{2\sdot3\sdot4\sdot5}\\&\scriptstyle=\frac{\left(21+32\right)\sdot231}{2\sdot3\sdot4\sdot5}\\&\scriptstyle=\frac{53\sdot231}{2\sdot3\sdot4\sdot5}\\&\scriptstyle=102+\left(\frac{3}{4}\sdot\frac{1}{5}\sdot\frac{1}{6}\right)\\\end{align}}}](/mediawiki/images/math/0/d/f/0df87612be93f8cdf3d4e4d9d9e15960.png)
![\scriptstyle\left[\left(3+\frac{1}{2}\right)+\left(5+\frac{1}{3}\right)\right]\times\left[\left(4+\frac{3}{4}\right)+\left(6+\frac{4}{5}\right)\right]=\left(8+\frac{5}{6}\right)\sdot\left[11+\frac{2}{5}+\left(\frac{3}{4}\sdot\frac{1}{5}\right)\right]](/mediawiki/images/math/e/4/b/e4bae6fc372c9c55f04ef46407ef928d.png)
![\scriptstyle\left[3+\left[\frac{1}{2}\sdot\left(5+\frac{1}{3}\right)\right]\right]\times\left[4+\left[\frac{3}{4}\sdot\left(6+\frac{4}{5}\right)\right]\right]](/mediawiki/images/math/3/e/2/3e22d62d8b8a2cb5d6852ad408fcd2a3.png)
![{\color{blue}{\begin{align}&\scriptstyle\left[3+\left[\frac{1}{2}\sdot\left(5+\frac{1}{3}\right)\right]\right]\times\left[4+\left[\frac{3}{4}\sdot\left(6+\frac{4}{5}\right)\right]\right]\\&\scriptstyle=\frac{\left[\left(3\sdot2\sdot3\right)+\left[\left[\left(5\sdot3\right)+1\right]\sdot1\right]\right]\sdot\left[\left(4\sdot4\sdot5\right)+\left[\left[\left(6\sdot5\right)+4\right]\sdot3\right]\right]}{2\sdot3\sdot4\sdot5}\\&\scriptstyle=\frac{\left(18+16\right)\sdot{\color{red}{18}}2}{2\sdot3\sdot4\sdot5}\\&\scriptstyle=\frac{34\sdot{\color{red}{18}}2}{2\sdot3\sdot4\sdot5}\\&\scriptstyle=51+\frac{3}{6}+\left(\frac{2}{5}\sdot\frac{1}{6}\right)\\\end{align}}}](/mediawiki/images/math/7/5/e/75e3aad2eae1e72ee54ea30604d5100a.png)
![\scriptstyle\left[2+\left[\left(\frac{2}{3}+\frac{3}{4}\right)\sdot3\right]+\left[\left(\frac{4}{5}+\frac{5}{6}\right)\sdot4\right]\right]\times\left[1+\left[\left(\frac{3}{5}+\frac{1}{2}\right)\sdot2\right]+\left[\left(\frac{3}{11}+\frac{9}{10}\right)\sdot3\right]\right]](/mediawiki/images/math/e/3/8/e381ac62d5a0863c6a7d62fd8b4c2b73.png)
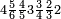
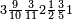
![{\color{blue}{\begin{align}&\scriptstyle\left[2+\left[\left(\frac{2}{3}+\frac{3}{4}\right)\sdot3\right]+\left[\left(\frac{4}{5}+\frac{5}{6}\right)\sdot4\right]\right]\times\left[1+\left[\left(\frac{3}{5}+\frac{1}{2}\right)\sdot2\right]+\left[\left(\frac{3}{11}+\frac{9}{10}\right)\sdot3\right]\right]\\&\scriptstyle=\frac{\left[\left(2\sdot3\sdot4\sdot5\sdot6\right)+\left[\left[\left(2\sdot4\right)+\left(3\sdot3\right)\right]\sdot3\sdot5\sdot6\right]+\left[\left[\left(4\sdot6\right)+\left(5\sdot5\right)\right]\sdot4\sdot3\sdot4\right]\right]}{2\sdot3\sdot4\sdot5\sdot5\sdot6\sdot10\sdot11}\\&\scriptstyle\sdot\frac{\left[\left(1\sdot5\sdot2\sdot11\sdot10\right)+\left[\left[\left(3\sdot2\right)+\left(1\sdot5\right)\right]\sdot2\sdot11\sdot10\right]+\left[\left[\left(3\sdot10\right)+\left(9\sdot11\right)\right]\sdot3\sdot5\sdot2\right]\right]}{2\sdot3\sdot4\sdot5\sdot5\sdot6\sdot10\sdot11}\\&\scriptstyle=\frac{\left(720+1530+{\color{red}{2}}352\right)\sdot7390}{2\sdot3\sdot4\sdot5\sdot5\sdot6\sdot10\sdot11}\\&\scriptstyle=\frac{4602\sdot7390}{2\sdot3\sdot4\sdot5\sdot5\sdot6\sdot10\sdot11}\\&\scriptstyle=85+\frac{9}{11}+\left(\frac{6}{10}\sdot\frac{1}{11}\right)+{\color{red}{\left(\frac{8}{10}\sdot\frac{1}{10}\sdot\frac{1}{11}\right)}}+\left(\frac{5}{6}\sdot\frac{1}{10}\sdot\frac{1}{10}\sdot\frac{1}{11}\right)\\\end{align}}}](/mediawiki/images/math/a/2/2/a22f0b40d3e4bade724e159ec01b77e2.png)
![\scriptstyle\left[\left(2+\frac{2}{3}+\frac{3}{4}\right)+\left(3+\frac{4}{5}+\frac{5}{6}\right)+4\right]\times\left[\left(1+\frac{3}{5}+\frac{1}{2}\right)+\left(2+\frac{3}{11}+\frac{9}{10}\right)+3\right]](/mediawiki/images/math/d/7/7/d77f14b6a5c47d1358f27996043a6568.png)
![{\color{blue}{\begin{align}&\scriptstyle\left[\left(2+\frac{2}{3}+\frac{3}{4}\right)+\left(3+\frac{4}{5}+\frac{5}{6}\right)+4\right]\times\left[\left(1+\frac{3}{5}+\frac{1}{2}\right)+\left(2+\frac{3}{11}+\frac{9}{10}\right)+3\right]\\&\scriptstyle=\frac{\left[\left[\left[\left(2\sdot3\sdot4\right)+\left[\left(2\sdot4\right)+\left(3\sdot3\right)\right]\right]\sdot5\sdot6\right]+\left[\left[\left(3\sdot5\sdot6\right)+\left[\left(4\sdot6\right)+\left(5\sdot5\right)\right]\right]\sdot3\sdot4\right]+\left(4\sdot3\sdot4\sdot5\sdot6\right)\right]}{2\sdot3\sdot4\sdot5\sdot5\sdot6\sdot10\sdot11}\\&\scriptstyle\sdot\frac{\left[\left[\left[\left(1\sdot5\sdot2\right)+\left[\left(3\sdot2\right)+\left(1\sdot5\right)\right]\right]\sdot11\sdot10\right]+\left[\left[\left(2\sdot11\sdot10\right)+\left[\left(3\sdot10\right)+\left(9\sdot11\right)\right]\right]\sdot5\sdot2\right]+\left(3\sdot5\sdot2\sdot11\sdot10\right)\right]}{2\sdot3\sdot4\sdot5\sdot5\sdot6\sdot10\sdot11}\\&\scriptstyle=\frac{4338\sdot9100}{2\sdot3\sdot4\sdot5\sdot5\sdot6\sdot10\sdot11}\\&\scriptstyle=99+\frac{7}{11}+\left(\frac{5}{10}\sdot\frac{1}{11}\right)+\left(\frac{3}{6}\sdot\frac{1}{10}\sdot\frac{1}{11}\right)\\\end{align}}}](/mediawiki/images/math/5/4/9/549bcb46bcf0cf5a8ba2a5103f647256.png)
![\scriptstyle\left[2+\left[\left(\frac{1}{2}\sdot\frac{1}{5}\right)\sdot3\right]+\left[\left(\frac{2}{3}\sdot\frac{1}{6}\right)\sdot5\right]\right]\times\left[3+\left[\left(\frac{1}{4}\sdot\frac{1}{7}\right)\sdot4\right]+\left[\left(\frac{5}{6}\sdot\frac{1}{8}\right)\sdot2\right]\right]](/mediawiki/images/math/c/0/b/c0bc2ad5bc456adaef584d86297ba6fa.png)
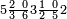
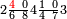
![{\color{blue}{\begin{align}&\scriptstyle\left[2+\left[\left(\frac{1}{2}\sdot\frac{1}{5}\right)\sdot3\right]+\left[\left(\frac{2}{3}\sdot\frac{1}{6}\right)\sdot5\right]\right]\times\left[3+\left[\left(\frac{1}{4}\sdot\frac{1}{7}\right)\sdot4\right]+\left[\left(\frac{5}{6}\sdot\frac{1}{8}\right)\sdot2\right]\right]\\&\scriptstyle=\frac{\left[\left(2\sdot2\sdot5\sdot3\sdot6\right)+\left(1\sdot3\sdot3\sdot6\right)+\left(2\sdot5\sdot2\sdot5\right)\right]\sdot\left[\left(3\sdot4\sdot7\sdot6\sdot8\right)+\left(1\sdot4\sdot6\sdot8\right)+\left(5\sdot2\sdot4\sdot7\right)\right]}{2\sdot3\sdot4\sdot5\sdot6\sdot6\sdot7\sdot8}\\&\scriptstyle=\frac{514\sdot4504}{2\sdot3\sdot4\sdot5\sdot6\sdot6\sdot7\sdot8}\\&\scriptstyle=9+\frac{5}{10}+\left(\frac{6}{9}\sdot\frac{1}{10}\right)+\left(\frac{2}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)+\left(\frac{{\color{red}{2}}}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)\\\end{align}}}](/mediawiki/images/math/0/2/c/02c5ce17699d754127dc39d1c30e5c78.png)
![\scriptstyle\left[\left[2+\left(\frac{1}{2}\sdot\frac{1}{5}\right)\right]+\left[3+\left(\frac{2}{3}\sdot\frac{1}{6}\right)\right]+5\right]\times\left[\left[3+\left(\frac{1}{4}\sdot\frac{1}{7}\right)\right]+\left[4+\left(\frac{5}{6}\sdot\frac{1}{8}\right)\right]+2\right]](/mediawiki/images/math/5/8/d/58d515ef7eab036fb7989bff254d93db.png)
![{\color{blue}{\begin{align}&\scriptstyle\left[\left[2+\left(\frac{1}{2}\sdot\frac{1}{5}\right)\right]+\left[3+\left(\frac{2}{3}\sdot\frac{1}{6}\right)\right]+5\right]\times\left[\left[3+\left(\frac{1}{4}\sdot\frac{1}{7}\right)\right]+\left[4+\left(\frac{5}{6}\sdot\frac{1}{8}\right)\right]+2\right]\\&\scriptstyle=\frac{\left[\left[\left[\left(2\sdot2\sdot5\right)+1\right]\sdot3\sdot6\right]+\left[\left[\left(3\sdot3\sdot6\right)+2\right]\sdot2\sdot5\right]+\left(5\sdot2\sdot5\sdot3\sdot6\right)\right]\sdot\left[\left[\left[\left(3\sdot4\sdot7\right)+1\right]\sdot6\sdot8\right]+\left[\left[\left(4\sdot6\sdot8\right)+5\right]\sdot4\sdot7\right]+\left(2\sdot4\sdot7\sdot6\sdot8\right)\right]}{2\sdot3\sdot4\sdot5\sdot6\sdot6\sdot7\sdot8}\\&\scriptstyle=\frac{1838\sdot12284}{2\sdot3\sdot4\sdot5\sdot6\sdot6\sdot7\sdot8}\\&\scriptstyle=93+\frac{3}{10}+\left(\frac{2}{9}\sdot\frac{1}{10}\right)+\left(\frac{4}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)+\left(\frac{2}{{\color{red}{7}}}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)+\left(\frac{5}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)\\\end{align}}}](/mediawiki/images/math/9/4/c/94c20b2a3252b17e780757bc921f45b0.png)
![\scriptstyle\left[\left[\frac{3}{4}\sdot\left(5+\frac{1}{2}\right)\right]+\left[\frac{5}{6}\sdot\left(3+\frac{2}{5}\right)\right]\right]\times\left[\left[\frac{2}{3}\sdot\left(4+\frac{1}{7}\right)\right]+\left[\frac{3}{8}\sdot\left(2+\frac{3}{11}\right)\right]\right]](/mediawiki/images/math/f/4/c/f4cf264503d356d541b3d10d3eb20358.png)
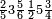
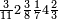
![{\color{blue}{\begin{align}&\scriptstyle\left[\left[\frac{3}{4}\sdot\left(5+\frac{1}{2}\right)\right]+\left[\frac{5}{6}\sdot\left(3+\frac{2}{5}\right)\right]\right]\times\left[\left[\frac{2}{3}\sdot\left(4+\frac{1}{7}\right)\right]+\left[\frac{3}{8}\sdot\left(2+\frac{3}{11}\right)\right]\right]\\&\scriptstyle=\frac{\left[\left[\left[\left[\left(5\sdot2\right)+1\right]\sdot3\right]\sdot6\sdot5\right]+\left[\left[\left[\left(3\sdot5\right)+2\right]\sdot5\right]\sdot4\sdot2\right]\right]\sdot\left[\left[\left[\left[\left(4\sdot7\right)+1\right]\sdot2\right]\sdot8\sdot11\right]+\left[\left[\left[\left(2\sdot11\right)+3\right]\sdot3\right]\sdot3\sdot7\right]\right]}{2\sdot3\sdot4\sdot5\sdot6\sdot7\sdot8\sdot11}\\&\scriptstyle=\frac{1670\sdot6679}{2\sdot3\sdot4\sdot5\sdot6\sdot7\sdot8\sdot11}\\&\scriptstyle=25+\frac{1}{11}+\left(\frac{5}{9}\sdot\frac{1}{11}\right)+\left(\frac{5}{8}\sdot\frac{1}{9}\sdot\frac{1}{11}\right)+\left(\frac{5}{8}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{11}\right)+\left(\frac{6}{7}\sdot\frac{1}{8}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{11}\right)\\\end{align}}}](/mediawiki/images/math/b/4/a/b4af2d9d8a81bddde25a75bb9c41da17.png)
![\scriptstyle\left[\frac{3}{4}\sdot\left(5+\frac{1}{2}+\frac{5}{6}\right)\right]+\left(3+\frac{2}{5}\right)](/mediawiki/images/math/a/c/e/acecb390fc0818208bdef56b4ec27ea2.png)
![\scriptstyle\left[\frac{3}{4}\sdot\left(5+\frac{1}{2}\right)\right]+\left[\frac{5}{6}\sdot\left(3+\frac{2}{5}\right)\right]](/mediawiki/images/math/6/7/5/67534e00cbb539b268b6717f73a4575d.png)
![\scriptstyle\left(\frac{3}{4}\sdot5\right)+\left[\frac{1}{2}+\left(\frac{5}{6}\sdot3\right)+\frac{2}{5}\right]](/mediawiki/images/math/3/b/9/3b9344a22345da2575ba536d259c151b.png)
![\scriptstyle\frac{3}{4}+\left(5+\frac{1}{2}\right)+\left[\left(\frac{5}{6}\sdot3\right)+\frac{2}{5}\right]](/mediawiki/images/math/7/3/5/735797f15ed2029fb6ad60ec4c0d953b.png)
![\scriptstyle\left(\frac{3}{4}\sdot5\right)+\left[\frac{1}{2}+\left(\frac{5}{6}\sdot3\right)\right]+\frac{2}{5}](/mediawiki/images/math/b/6/0/b60bb4a84559b8b8daa82e5f123aac40.png)
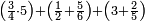
![\scriptstyle\left[\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\sdot3\right]+\left[\left(\frac{3}{4}+\frac{4}{5}\right)\sdot2\right]+\left[\frac{3}{8}\sdot\left(4+\frac{3}{9}\right)\right]+\left(\frac{2}{3}\sdot\frac{1}{9}\right)](/mediawiki/images/math/6/a/e/6ae04398de7ca6ddeaaac8ce8271944a.png)
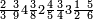
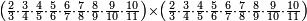
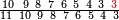
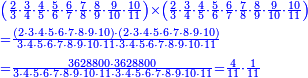
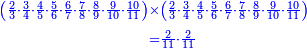
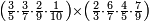
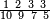
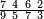
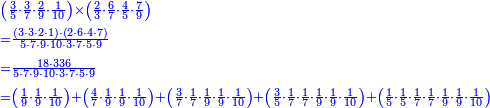
![\scriptstyle\left[\left(\frac{3}{5}\sdot\frac{4}{7}\right)\sdot\left[3+\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\right]\times\left[\left(\frac{2}{3}\sdot\frac{5}{6}\right)\sdot\left[6+\frac{7}{8}+\left(\frac{2}{3}\sdot\frac{1}{8}\right)\right]\right]](/mediawiki/images/math/2/5/5/2550673eb8dc78a12727d2d5dc0b5427.png)
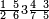
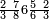
![{\color{blue}{\begin{align}&\scriptstyle\left[\left(\frac{3}{5}\sdot\frac{4}{7}\right)\sdot\left[3+\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\right]\times\left[\left(\frac{2}{3}\sdot\frac{5}{6}\right)\sdot\left[6+\frac{7}{8}+\left(\frac{2}{3}\sdot\frac{1}{8}\right)\right]\right]\\&\scriptstyle=\frac{\left[\left(3\sdot4\right)\sdot\left[\left(3\sdot6\sdot2\right)+\left[\left(5\sdot2\right)+1\right]\right]\right]\sdot\left[\left(2\sdot5\right)\sdot\left[\left(6\sdot8\sdot3\right)+\left[\left(7\sdot3\right)+2\right]\right]\right]}{5\sdot7\sdot6\sdot2\sdot3\sdot6\sdot8\sdot3}\\&\scriptstyle=\frac{\left(12\sdot47\right)\sdot1670}{5\sdot7\sdot6\sdot2\sdot3\sdot6\sdot8\sdot3}\\&\scriptstyle=\frac{564\sdot1670}{5\sdot7\sdot6\sdot2\sdot3\sdot6\sdot8\sdot3}=5+\frac{1}{9}+\left(\frac{5}{8}\sdot\frac{1}{9}\right)+\left(\frac{5}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{1}{3}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/b/6/c/b6cb616b1530825777c28b7b1b1e51ef.png)
![\scriptstyle\left[\left(\frac{2}{3}\sdot\frac{3}{4}\right)\sdot6\right]\times\left[\left(\frac{3}{4}\sdot\frac{4}{7}\right)\sdot8\right]](/mediawiki/images/math/b/b/5/bb5eed5e9b25166de1f36bb9904c0f62.png)
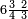
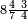
![\scriptstyle\left[\left(\frac{2}{3}\sdot\frac{6}{9}\right)\sdot\left(6+\frac{3}{4}\right)\right]\times\left[\left(\frac{3}{4}\sdot\frac{8}{9}\right)\sdot\left(2+\frac{2}{5}\right)\right]](/mediawiki/images/math/f/a/4/fa4daab5fb3c530e96d4f4be1abe9aec.png)
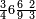
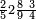
![{\color{blue}{\begin{align}\scriptstyle\left[\left(\frac{2}{3}\sdot\frac{6}{9}\right)\sdot\left(6+\frac{3}{4}\right)\right]\times\left[\left(\frac{3}{4}\sdot\frac{8}{9}\right)\sdot\left(2+\frac{2}{5}\right)\right]&\scriptstyle=\frac{\left[\left(2\sdot6\right)\sdot\left[\left(6\sdot4\right)+3\right]\right]\sdot\left[\left(3\sdot8\right)\sdot\left[\left(2\sdot5\right)+2\right]\right]}{3\sdot4\sdot4\sdot5\sdot9\sdot9}\\&\scriptstyle=\frac{\left(12\sdot27\right)\sdot288}{3\sdot4\sdot4\sdot5\sdot9\sdot9}\\&\scriptstyle=\frac{324\sdot288}{3\sdot4\sdot4\sdot5\sdot9\sdot9}\\&\scriptstyle=4+\frac{4}{5}\\\end{align}}}](/mediawiki/images/math/5/6/6/566930c75890cd2119d9c600444e7d16.png)
![\scriptstyle\left[\left(\frac{3}{4}\sdot\frac{4}{5}\right)+\left(\frac{5}{6}\sdot\frac{6}{7}\right)+\left(\frac{7}{8}\sdot\frac{8}{9}\right)\right]\times\left[\left(\frac{2}{3}\sdot\frac{3}{4}\right)+\left(\frac{4}{5}\sdot\frac{5}{6}\right)+\left(\frac{6}{7}\sdot\frac{7}{8}\right)\right]](/mediawiki/images/math/9/d/7/9d786b3054d18765a05eec5c1fbeed6c.png)
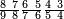
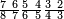
![{\color{blue}{\begin{align}&\scriptstyle\left[\left(\frac{3}{4}\sdot\frac{4}{5}\right)+\left(\frac{5}{6}\sdot\frac{6}{7}\right)+\left(\frac{7}{8}\sdot\frac{8}{9}\right)\right]\times\left[\left(\frac{2}{3}\sdot\frac{3}{4}\right)+\left(\frac{4}{5}\sdot\frac{5}{6}\right)+\left(\frac{6}{7}\sdot\frac{7}{8}\right)\right]\\&\scriptstyle=\frac{\left[\left(3\sdot4\sdot6\sdot7\sdot8\sdot9\right)+\left(5\sdot6\sdot4\sdot5\sdot8\sdot9\right)+\left(7\sdot8\sdot4\sdot5\sdot6\sdot7\right)\right]\sdot\left[\left(2\sdot3\sdot5\sdot6\sdot7\sdot8\right)+\left(4\sdot5\sdot3\sdot4\sdot7\sdot8\right)+\left(6\sdot7\sdot3\sdot4\sdot5\sdot6\right)\right]}{3\sdot4\sdot4\sdot5\sdot5\sdot6\sdot6\sdot7\sdot7\sdot8\sdot8\sdot9}\\&\scriptstyle=\frac{126528\sdot{\color{red}{38640}}}{3\sdot4\sdot4\sdot5\sdot5\sdot6\sdot6\sdot7\sdot7\sdot8\sdot8\sdot9}\\&\scriptstyle=4+\left(\frac{6}{7}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)+\left(\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)\\\end{align}}}](/mediawiki/images/math/4/c/9/4c9ef24dc53cc235a4f3bf6621f0ff05.png)
![{\color{blue}{\begin{align}\scriptstyle\left[\left(\frac{3}{4}\sdot\frac{4}{5}\right)+\left(\frac{5}{6}\sdot\frac{6}{7}\right)+\left(\frac{7}{8}\sdot\frac{8}{9}\right)\right]&\scriptstyle\times\left[\left(\frac{2}{3}\sdot\frac{3}{4}\right)+\left(\frac{4}{5}\sdot\frac{5}{6}\right)+\left(\frac{6}{7}\sdot\frac{7}{8}\right)\right]\\&\scriptstyle=\left(\frac{3}{5}+\frac{5}{7}+\frac{7}{9}\right)\sdot\left(\frac{1}{2}+\frac{2}{3}+\frac{3}{4}\right)\\\end{align}}}](/mediawiki/images/math/5/c/3/5c39f4220139e746ad60abc153e7f8b0.png)
![\scriptstyle\left[3+\left(\frac{3}{5}\sdot\frac{5}{6}\right)\right]\times\left[4+\left(\frac{2}{7}\sdot3\right)\right]](/mediawiki/images/math/8/2/1/821afa9bbf7e8492c07babae03f19a28.png)
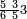
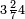
![{\color{blue}{\begin{align}\scriptstyle\left[3+\left(\frac{3}{5}\sdot\frac{5}{6}\right)\right]\times\left[4+\left(\frac{2}{7}\sdot3\right)\right]&\scriptstyle=\frac{\left[\left(3\sdot5\sdot6\right)+\left(3\sdot5\right)\right]\sdot\left[\left(4\sdot7\right)+\left(2\sdot3\right)\right]}{5\sdot6\sdot7}\\&\scriptstyle=\frac{105\sdot34}{5\sdot6\sdot7}=17\\\end{align}}}](/mediawiki/images/math/2/4/8/2480334fd55cecc7e413ff0287fd47df.png)
![\scriptstyle\left[2+\left(\frac{3}{7}\sdot\frac{3}{5}\right)+\frac{2}{3}\right]\times\left[3+\left(\frac{3}{4}\sdot\frac{5}{6}\right)+\frac{1}{2}\right]](/mediawiki/images/math/b/a/0/ba08b2bb8f498724f17c160ad860406d.png)
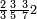
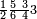
![{\color{blue}{\begin{align}\scriptstyle\left[2+\left(\frac{3}{7}\sdot\frac{3}{5}\right)+\frac{2}{3}\right]\times\left[3+\left(\frac{3}{4}\sdot\frac{5}{6}\right)+\frac{1}{2}\right]&\scriptstyle=\frac{\left[\left(2\sdot7\sdot5\sdot3\right)+\left(3\sdot3\sdot3\right)+\left(2\sdot7\sdot5\right)\right]\sdot\left[\left(3\sdot4\sdot6\sdot2\right)+\left(3\sdot5\sdot2\right)+\left(1\sdot4\sdot6\right)\right]}{2\sdot3\sdot4\sdot5\sdot6\sdot7}\\&\scriptstyle=\frac{307\sdot198}{2\sdot3\sdot4\sdot5\sdot6\sdot7}\\&\scriptstyle=12+\left(\frac{3}{7}\sdot\frac{1}{8}\right)+\left(\frac{2}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\right)\\\end{align}}}](/mediawiki/images/math/a/8/8/a88aa1260c3682802538adb6e18336cd.png)
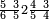
![\scriptstyle\left[\left(\frac{3}{4}\sdot\frac{4}{5}\right)+\left[2+\left(\frac{3}{5}\sdot\frac{5}{6}\right)\right]\right]\times\left[\left(\frac{3}{4}\sdot\frac{4}{5}\right)+\left[2+\left(\frac{3}{5}\sdot\frac{5}{6}\right)\right]\right]](/mediawiki/images/math/d/b/7/db784fab4d130d581737adb53b770169.png)
![\scriptstyle\left[\left[\left(\frac{3}{4}\sdot\frac{4}{5}\right)\sdot2\right]+\left(\frac{3}{5}\sdot\frac{5}{6}\right)\right]\times\left[\left[\left(\frac{3}{4}\sdot\frac{4}{5}\right)\sdot2\right]+\left(\frac{3}{5}\sdot\frac{5}{6}\right)\right]](/mediawiki/images/math/a/b/a/aba1152702b7d2136b6cb1bc55f7c89b.png)
![{\color{blue}{\begin{align}&\scriptstyle\left[\left(\frac{3}{4}\sdot\frac{4}{5}\right)\sdot\left[2+\left(\frac{3}{5}\sdot\frac{5}{6}\right)\right]\right]\times\left[\left(\frac{3}{4}\sdot\frac{4}{5}\right)\sdot\left[2+\left(\frac{3}{5}\sdot\frac{5}{6}\right)\right]\right]\\&\scriptstyle=\frac{\left[\left(3\sdot4\right)\sdot\left[\left(2\sdot5\sdot6\right)+\left(3\sdot5\right)\right]\right]\sdot\left[\left(3\sdot4\right)\sdot\left[\left(2\sdot5\sdot6\right)+\left(3\sdot5\right)\right]\right]}{4\sdot5\sdot5\sdot6\sdot4\sdot5\sdot5\sdot6}\\&\scriptstyle=\frac{900\sdot900}{4\sdot5\sdot5\sdot6\sdot4\sdot5\sdot5\sdot6}\\&\scriptstyle=2+\frac{1}{4}\\\end{align}}}](/mediawiki/images/math/2/6/8/26826ae00950321c79516b7e12fa669e.png)
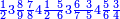
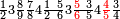
![\scriptstyle\left[\left(\frac{3}{4}+\frac{5}{6}\right)\sdot4\right]+\left[\left(\frac{3}{5}\sdot\frac{6}{7}\right)\sdot3\right]+\left[\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\sdot4\right]+\left[\left(\frac{7}{8}\sdot\frac{8}{9}\right)\sdot\left(3+\frac{1}{2}\right)\right]](/mediawiki/images/math/5/3/8/538da8dac450b21a7ff9d132c742ce50.png)
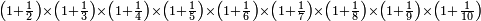
![{\color{blue}{\begin{align}&\scriptstyle\left(1+\frac{1}{2}\right)\times\left(1+\frac{1}{3}\right)\times\left(1+\frac{1}{4}\right)\times\left(1+\frac{1}{5}\right)\times\left(1+\frac{1}{6}\right)\times\left(1+\frac{1}{7}\right)\times\left(1+\frac{1}{8}\right)\times\left(1+\frac{1}{9}\right)\times\left(1+\frac{1}{10}\right)\\&\scriptstyle=\frac{\left[\left(1\sdot2\right)+1\right]\sdot\left[\left(1\sdot3\right)+1\right]\sdot\left[\left(1\sdot4\right)+1\right]\sdot\left[\left(1\sdot5\right)+1\right]\sdot\left[\left(1\sdot6\right)+1\right]\sdot\left[\left(1\sdot7\right)+1\right]\sdot\left[\left(1\sdot8\right)+1\right]\sdot\left[\left(1\sdot9\right)+1\right]\sdot\left[\left(1\sdot10\right)+1\right]}{2\sdot3\sdot4\sdot5\sdot6\sdot7\sdot8\sdot9\sdot10}\\&\scriptstyle=\frac{3\sdot4\sdot5\sdot6\sdot7\sdot8\sdot9\sdot10\sdot11}{2\sdot3\sdot4\sdot5\sdot6\sdot7\sdot8\sdot9\sdot10}\\&\scriptstyle=5+\frac{1}{2}\\\end{align}}}](/mediawiki/images/math/c/4/d/c4d4a5158b5d7f0889a0c66a58f80cb4.png)
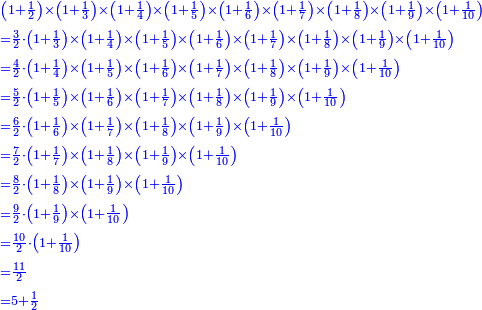
 minus
minus 
 minus
minus 
 الا
الا 
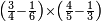
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{3}{4}-\frac{1}{6}\right)\times\left(\frac{4}{5}-\frac{1}{3}\right)&\scriptstyle=\frac{\left[\left(3\sdot6\right)-\left(1\sdot4\right)\right]\sdot\left[\left(4\sdot3\right)-\left(1\sdot5\right)\right]}{3\sdot4\sdot5\sdot6}\\&\scriptstyle=\frac{\left(18-4\right)\sdot\left(12-5\right)}{3\sdot4\sdot5\sdot6}\\&\scriptstyle=\frac{14\sdot7}{3\sdot4\sdot5\sdot6}\\&\scriptstyle=\frac{2}{9}+\left(\frac{3}{8}\sdot\frac{1}{9}\right)+\left(\frac{3}{5}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/e/6/7/e67595574e4a7f85c1ec0f1a1e261903.png)
![\scriptstyle\left[\frac{3}{4}-\left(\frac{1}{6}\sdot\frac{3}{4}\right)\right]\times\left[\frac{4}{5}-\left(\frac{1}{3}\sdot\frac{4}{5}\right)\right]](/mediawiki/images/math/a/e/4/ae4ff6ee9ccb7e44b1386662f2fe7ed1.png)
![{\color{blue}{\begin{align}\scriptstyle\left[\frac{3}{4}-\left(\frac{1}{6}\sdot\frac{3}{4}\right)\right]\times\left[\frac{4}{5}-\left(\frac{1}{3}\sdot\frac{4}{5}\right)\right]&\scriptstyle=\frac{\left[\left(3\sdot6\right)-\left(1\sdot3\right)\right]\sdot\left[\left(4\sdot3\right)-\left(1\sdot4\right)\right]}{3\sdot4\sdot5\sdot6}\\&\scriptstyle=\frac{\left(18-3\right)\sdot8}{3\sdot4\sdot5\sdot6}\\&\scriptstyle=\frac{15\sdot8}{3\sdot4\sdot5\sdot6}\\&\scriptstyle=\frac{120}{3\sdot4\sdot5\sdot6}\\&\scriptstyle=\color{red}{\frac{1}{3}}\\\end{align}}}](/mediawiki/images/math/9/1/f/91f3baa991818d4d0f7d8d424e5864ba.png)
 minus
minus 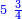
 minus
minus 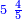
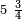
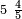
![\scriptstyle\left[\left(\frac{3}{4}\sdot5\right)-\left(\frac{1}{6}\sdot5\right)\right]\times\left[\left(\frac{4}{5}\sdot3\right)-\left(\frac{1}{4}\sdot3\right)\right]](/mediawiki/images/math/4/d/0/4d0df47dc57fcfe2ae9c244e13efc5c6.png)
![{\color{blue}{\begin{align}\scriptstyle\left[\left(\frac{3}{4}\sdot5\right)-\left(\frac{1}{6}\sdot5\right)\right]\times\left[\left(\frac{4}{5}\sdot3\right)-\left(\frac{1}{4}\sdot3\right)\right]&\scriptstyle=\frac{\left[\left(3\sdot5\sdot6\right)-\left(1\sdot5\sdot4\right)\right]\sdot\left[\left(4\sdot3\sdot4\right)-\left(1\sdot3\sdot5\right)\right]}{4\sdot4\sdot5\sdot6}\\&\scriptstyle=\frac{\left(90-20\right)\sdot33}{4\sdot4\sdot5\sdot6}=\frac{70\sdot33}{4\sdot4\sdot5\sdot6}\\&\scriptstyle=4+\frac{6}{8}+\left(\frac{1}{2}\sdot\frac{1}{8}\right)\\\end{align}}}](/mediawiki/images/math/2/3/4/2344143242860faa47919da665df41eb.png)
![\scriptstyle\left[\left(\frac{3}{4}\sdot5\right)-\left[\frac{1}{6}\sdot\left(\frac{3}{4}\sdot5\right)\right]\right]\times\left[\left(\frac{4}{5}\sdot3\right)-\left[\frac{1}{4}\sdot\left(\frac{4}{5}\sdot3\right)\right]\right]](/mediawiki/images/math/d/9/a/d9a6878ee6eb1ba00eb46382912dc1b1.png)
![{\color{blue}{\begin{align}\scriptstyle\left[\left(\frac{3}{4}\sdot5\right)-\left[\frac{1}{6}\sdot\left(\frac{3}{4}\sdot5\right)\right]\right]\times\left[\left(\frac{4}{5}\sdot3\right)-\left[\frac{1}{4}\sdot\left(\frac{4}{5}\sdot3\right)\right]\right]&\scriptstyle=\frac{\left[\left(3\sdot5\sdot6\right)-\left(1\sdot5\sdot3\right)\right]\sdot\left[\left(4\sdot3\sdot4\right)-\left(1\sdot4\sdot3\right)\right]}{4\sdot4\sdot5\sdot6}\\&\scriptstyle=\frac{\left(90-15\right)\sdot36}{4\sdot4\sdot5\sdot6}=\\&\scriptstyle\frac{75\sdot36}{4\sdot4\sdot5\sdot6}\\\end{align}}}](/mediawiki/images/math/1/5/0/1507be477172a0b25f4bcc0e666d13e8.png)
![\scriptstyle\left[\left(\frac{3}{4}\sdot5\right)-\frac{1}{6}\right]\times\left[\left(\frac{4}{5}\sdot3\right)-\frac{1}{4}\right]](/mediawiki/images/math/c/0/e/c0ea2f1eede67f376f403c8953b1890a.png)
![{\color{blue}{\begin{align}\scriptstyle\left[\left(\frac{3}{4}\sdot5\right)-\frac{1}{6}\right]\times\left[\left(\frac{4}{5}\sdot3\right)-\frac{1}{4}\right]&\scriptstyle=\frac{\left[\left(3\sdot5\sdot6\right)-\left(1\sdot4\right)\right]\sdot\left[\left(4\sdot3\sdot4\right)-\left(1\sdot5\right)\right]}{4\sdot4\sdot5\sdot6}\\&\scriptstyle=\frac{\left(90-4\right)\sdot43}{4\sdot4\sdot5\sdot6}\\&\scriptstyle=\frac{86\sdot43}{4\sdot4\sdot5\sdot6}\\\end{align}}}](/mediawiki/images/math/c/9/d/c9d661e2970d60a81899d862a4a21e0c.png)
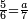
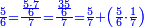
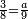
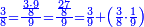
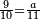
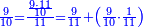
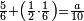
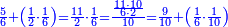
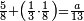
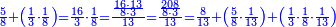
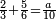
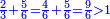
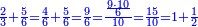
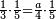
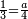
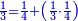
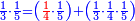
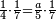
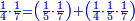
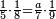
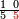
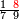
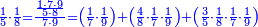
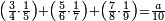
![\scriptstyle{\color{blue}{\left(\frac{3}{4}\sdot\frac{1}{5}\right)+\left(\frac{5}{6}\sdot\frac{1}{7}\right)+\left(\frac{7}{8}\sdot\frac{1}{9}\right)=\frac{\frac{\left[\left(3\sdot6\sdot7\sdot8\sdot9\right)+\left(5\sdot4\sdot5\sdot8\sdot9\right)+\left(7\sdot4\sdot5\sdot6\sdot7\right)\right]\sdot10}{4\sdot5\sdot6\sdot7\sdot8\sdot9}}{10}}}](/mediawiki/images/math/2/b/e/2beb0345b73012dfbd98191c56958b10.png)
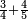
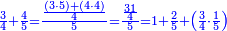
![\scriptstyle{\color{blue}{\frac{3}{4}+\frac{4}{5}=\left[\frac{3}{5}+\left(\frac{3}{4}\sdot\frac{1}{5}\right)\right]+\frac{4}{5}=\frac{7}{5}+\left(\frac{3}{4}\sdot\frac{1}{5}\right)=1+\frac{2}{5}+\left(\frac{3}{4}\sdot\frac{1}{5}\right)}}](/mediawiki/images/math/d/4/b/d4b56f6a049595d4effb8ea40a738abb.png)
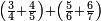
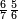
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{3}{4}+\frac{4}{5}\right)+\left(\frac{5}{6}+\frac{6}{7}\right)&\scriptstyle=\frac{\left[\left[\left(3\sdot5\right)+\left(4\sdot4\right)\right]\sdot6\sdot7\right]+\left[\left[\left(5\sdot7\right)+\left(6\sdot6\right)\right]\sdot4\sdot5\right]}{4\sdot5\sdot6\sdot7}\\&\scriptstyle=\frac{\left(31\sdot6\sdot7\right)+\left[\left[\left(5\sdot7\right)+\left(6\sdot6\right)\right]\sdot4\sdot5\right]}{4\sdot5\sdot6\sdot7}\\&\scriptstyle=\frac{\left(31\sdot6\sdot7\right)+1420}{4\sdot5\sdot6\sdot7}\\&\scriptstyle=\frac{2722}{4\sdot5\sdot6\sdot7}\\&\scriptstyle=3+\frac{1}{7}+\left(\frac{4}{6}\sdot\frac{1}{7}\right)+\left(\frac{1}{2}\sdot\frac{1}{5}\sdot\frac{1}{6}\sdot\frac{1}{7}\right)\\\end{align}}}](/mediawiki/images/math/a/9/7/a97a2e378d0394dfa29d03e90716d3db.png)
![\scriptstyle\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]+\left(\frac{7}{8}+\frac{8}{9}\right)](/mediawiki/images/math/4/c/4/4c4b65fa69c305cfcc4cb5e5a2e49e9e.png)
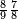
![{\color{blue}{\begin{align}\scriptstyle\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]+\left(\frac{7}{8}+\frac{8}{9}\right)&\scriptstyle=\frac{\left[\left[\left(5\sdot2\right)+1\right]\sdot8\sdot9\right]+\left[\left[\left(7\sdot9\right)+\left(8\sdot8\right)\right]\sdot2\sdot6\right]}{2\sdot6\sdot8\sdot9}\\&\scriptstyle=\frac{792+1524}{2\sdot6\sdot8\sdot9}\\&\scriptstyle=\frac{2316}{2\sdot6\sdot8\sdot9}\\&\scriptstyle=2+\frac{6}{9}+\left(\frac{1}{8}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/d/b/6/db6a560dc18a1b9d1aa86592461eda3d.png)
![\scriptstyle\left[\frac{5}{11}+\left(\frac{3}{4}\sdot\frac{1}{11}\right)\right]+\left[\frac{10}{13}+\left(\frac{8}{9}\sdot\frac{1}{13}\right)\right]](/mediawiki/images/math/1/1/1/111cfe95df77cdc573d3d8c3a15e0491.png)
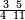
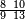
![{\color{blue}{\begin{align}\scriptstyle\left[\frac{5}{11}+\left(\frac{3}{4}\sdot\frac{1}{11}\right)\right]+\left[\frac{10}{13}+\left(\frac{8}{9}\sdot\frac{1}{13}\right)\right]&\scriptstyle=\frac{\left[\left[\left(5\sdot4\right)+3\right]\sdot13\sdot9\right]+\left[\left[\left(10\sdot9\right)+8\right]\sdot11\sdot4\right]}{4\sdot9\sdot11\sdot13}\\&\scriptstyle=1+\frac{4}{13}+\left(\frac{7}{11}\sdot\frac{1}{13}\right)+\left(\frac{4}{9}\sdot\frac{1}{11}\sdot\frac{1}{13}\right)+\left(\frac{3}{4}\sdot\frac{1}{9}\sdot\frac{1}{11}\sdot\frac{1}{13}\right)\\\end{align}}}](/mediawiki/images/math/e/7/4/e747c873d43060966b5a81302034c04b.png)
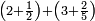
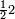
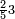
![\scriptstyle{\color{blue}{\left(2+\frac{1}{2}\right)+\left(3+\frac{2}{5}\right)=\frac{\left[\left[\left(2\sdot2\right)+1\right]\sdot5\right]+\left[\left[\left(3\sdot5\right)+2\right]\sdot2\right]}{2\sdot5}=\frac{59}{2\sdot5}=5+\frac{4}{5}+\left(\frac{1}{2}\sdot\frac{1}{5}\right)}}](/mediawiki/images/math/2/9/4/294398e2e2cc3dcbac6fb23f957fbce5.png)
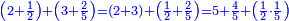
![\scriptstyle\left[8+\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]+\left(6+\frac{5}{7}+\frac{10}{11}\right)](/mediawiki/images/math/5/5/2/5526b3773d4250a1b558ca73bb605f6c.png)
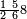
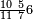
![{\color{blue}{\begin{align}\scriptstyle\left[8+\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]+\left(6+\frac{5}{7}+\frac{10}{11}\right)&\scriptstyle=\frac{\left[\left[\left[\left[\left(8\sdot6\right)+5\right]\sdot2\right]+1\right]\sdot7\sdot11\right]+\left[\left[\left(6\sdot7\sdot11\right)+\left(5\sdot11\right)+\left(10\sdot7\right)\right]\sdot6\sdot2\right]}{2\sdot6\sdot7\sdot11}\\&\scriptstyle=16+\frac{5}{11}+\left(\frac{6}{7}\sdot\frac{1}{11}\right)+\left(\frac{3}{6}\sdot\frac{1}{7}\sdot\frac{1}{11}\right)+\left(\frac{1}{2}\sdot\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{11}\right)\\\end{align}}}](/mediawiki/images/math/5/1/5/515a8c1a15185a11b458c54d79c93225.png)
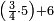

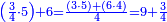
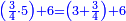
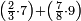
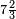
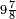
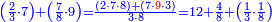
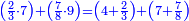
![\scriptstyle\left[\frac{3}{4}\sdot\left(5+\frac{1}{2}\right)\right]+\left[\frac{5}{6}\sdot\left(6+\frac{1}{3}\right)\right]](/mediawiki/images/math/3/8/c/38c6011f1c3aa05525cc220db0b08a58.png)
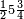
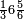
![{\color{blue}{\begin{align}\scriptstyle\left[\frac{3}{4}\sdot\left(5+\frac{1}{2}\right)\right]+\left[\frac{5}{6}\sdot\left(6+\frac{1}{3}\right)\right]&\scriptstyle=\frac{\left[\left[\left[\left(5\sdot2\right)+1\right]\sdot3\right]\sdot6\sdot3\right]+\left[\left[\left[\left(6\sdot3\right)+1\right]\sdot5\right]\sdot4\sdot2\right]}{2\sdot3\sdot4\sdot6}\\&\scriptstyle=9+\frac{3}{8}+\left(\frac{1}{6}\sdot\frac{1}{8}\right)+\left(\frac{1}{3}\sdot\frac{1}{6}\sdot\frac{1}{8}\right)\\\end{align}}}](/mediawiki/images/math/8/c/6/8c644ca7a889c17ffa935c0536595957.png)
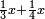
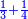
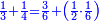
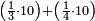
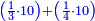
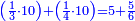
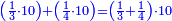
![\scriptstyle\left(\frac{1}{3}\sdot10\right)+\left(\frac{1}{4}\sdot10\right)+\left[\frac{1}{5}\sdot\left[10-\left(\frac{1}{3}\sdot10\right)-\left(\frac{1}{4}\sdot10\right)\right]\right]](/mediawiki/images/math/e/b/f/ebf3b0cdd50dbf66d5b3f14c7e905873.png)
![{\color{blue}{\begin{align}&\scriptstyle\left(\frac{1}{3}\sdot10\right)+\left(\frac{1}{4}\sdot10\right)+\left[\frac{1}{5}\sdot\left[10-\left(\frac{1}{3}\sdot10\right)-\left(\frac{1}{4}\sdot10\right)\right]\right]\\&\scriptstyle=\frac{\left[\left[\frac{1}{3}\sdot\left(3\sdot4\right)\right]+\left[\frac{1}{4}\sdot\left(3\sdot4\right)\right]+\left[\frac{1}{5}\sdot\left[\left(3\sdot4\right)-\left[\frac{1}{3}\sdot\left(3\sdot4\right)\right]-\left[\frac{1}{4}\sdot\left(3\sdot4\right)\right]\right]\right]\right]\sdot10}{\left(3\sdot4\right)}\\&\scriptstyle=\frac{\left[\left(\frac{1}{3}\sdot12\right)+\left(\frac{1}{4}\sdot12\right)+\left[\frac{1}{5}\sdot\left[12-\left(\frac{1}{3}\sdot12\right)-\left(\frac{1}{4}\sdot12\right)\right]\right]\right]\sdot10}{12}\\&\scriptstyle=\frac{\left[7+\left[\frac{1}{5}\sdot\left(12-7\right)\right]\right]\sdot10}{12}\\&\scriptstyle=\frac{\left[7+\left(\frac{1}{5}\sdot5\right)\right]\sdot10}{12}\\&\scriptstyle=\frac{\left(7+1\right)\sdot10}{12}\\&\scriptstyle=\frac{8\sdot10}{12}\\&\scriptstyle=6+\frac{2}{3}\\\end{align}}}](/mediawiki/images/math/c/6/f/c6f585541a08c6943761aff6d63e76b3.png)
![\scriptstyle{\color{blue}{\left(\frac{1}{3}\sdot10\right)+\left(\frac{1}{4}\sdot10\right)+\left[\frac{1}{5}\sdot\left[10-\left(\frac{1}{3}\sdot10\right)-\left(\frac{1}{4}\sdot10\right)\right]\right]=\frac{8\sdot10}{12}=\frac{10}{12}\sdot8}}](/mediawiki/images/math/b/3/a/b3a5646cf2b3c1e4b4b88dc82f247f60.png)
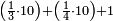
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{1}{3}\sdot10\right)+\left(\frac{1}{4}\sdot10\right)+1&\scriptstyle=\frac{\left[\left[\left(\frac{1}{3}\sdot12\right)+\left(\frac{1}{4}\sdot12\right)\right]\sdot10\right]+\left(1\sdot12\right)}{12}\\&\scriptstyle=\frac{\left(7\sdot10\right)+\left(1\sdot12\right)}{12}\\&\scriptstyle=\frac{70+12}{12}\\&\scriptstyle=\frac{82}{12}\\&\scriptstyle=6+\frac{5}{6}\\\end{align}}}](/mediawiki/images/math/9/d/e/9de4ec09be455f756cd745a865bcee14.png)
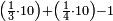
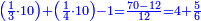
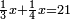
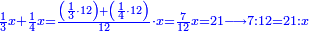
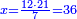
![\scriptstyle{\color{blue}{\frac{1}{3}x+\frac{1}{4}x=\frac{3}{6}x+\left(\frac{1}{2}\sdot\frac{1}{6}\right)x=\left[\frac{3}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\sdot x=21}}](/mediawiki/images/math/a/b/f/abf85e08fa67d4be08fd1afee16d2fbe.png)
![\scriptstyle{\color{blue}{\left[\frac{3}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\sdot a=1\longrightarrow a=1+\frac{5}{7}}}](/mediawiki/images/math/2/9/e/29ee0b3a8e3f9f2d9bc81aa0baf39980.png)
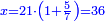
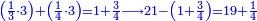
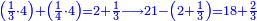
![\scriptstyle{\color{blue}{x=\frac{\left[\left(19+\frac{1}{4}\right)\sdot4\right]-\left[\left(18+\frac{2}{3}\right)\sdot3\right]}{\left(19+\frac{1}{4}\right)-\left(18+\frac{2}{3}\right)}=\frac{77-56}{\frac{3}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)}=\frac{21}{\frac{3}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)}=36}}](/mediawiki/images/math/6/2/8/628b03d73de1aa9586820e6f70b458b2.png)
![\scriptstyle\frac{1}{3}x+\frac{1}{4}x+\left[\frac{1}{2}\sdot\left[x-\left(\frac{1}{3}x+\frac{1}{4}x\right)\right]\right]=10](/mediawiki/images/math/0/9/0/09094cbf4bca71b2ab0b2f4f26a1599b.png)
![{\color{blue}{\begin{align}\scriptstyle x&\scriptstyle=\frac{24\sdot10}{\left(\frac{1}{3}\sdot24\right)+\left(\frac{1}{4}\sdot24\right)+\left[\frac{1}{2}\sdot\left[24-\left[\left(\frac{1}{3}\sdot24\right)+\left(\frac{1}{4}\sdot24\right)\right]\right]\right]}\\&\scriptstyle=\frac{24\sdot10}{14+\left[\frac{1}{2}\sdot\left(24-14\right)\right]}\\&\scriptstyle=\frac{24\sdot10}{14+\left(\frac{1}{2}\sdot10\right)}\\&\scriptstyle=\frac{24\sdot10}{14+5}\\&\scriptstyle=\frac{24\sdot10}{19}\\&\scriptstyle=12+\frac{12}{19}\\\end{align}}}](/mediawiki/images/math/8/e/2/8e214e2346aa94142039ee6e51b84cc9.png)
![\scriptstyle{\color{blue}{\left[\frac{1}{3}\sdot\left(12+\frac{12}{19}\right)\right]+\left[\frac{1}{4}\sdot\left(12+\frac{12}{19}\right)\right]+\left[\frac{1}{2}\sdot\left[\left(12+\frac{12}{19}\right)-\left[\left[\frac{1}{3}\sdot\left(12+\frac{12}{19}\right)\right]+\left[\frac{1}{4}\sdot\left(12+\frac{12}{19}\right)\right]\right]\right]\right]=10}}](/mediawiki/images/math/d/7/e/d7ee7eec4964b01f69ec98180a658e3e.png)
![\scriptstyle{\color{blue}{\frac{1}{3}x+\frac{1}{4}x+\left[\frac{1}{2}\sdot\left[x-\left(\frac{1}{3}x+\frac{1}{4}x\right)\right]\right]=\left[\frac{4}{6}+\left(\frac{3}{4}\sdot\frac{1}{6}\right)\right]x=10}}](/mediawiki/images/math/9/b/8/9b83d19691d0f0a583b6af03da545911.png)
![\scriptstyle{\color{blue}{\left[\frac{4}{6}+\left(\frac{3}{4}\sdot\frac{1}{6}\right)\right]\sdot a=1\longrightarrow a=1+\frac{5}{19}}}](/mediawiki/images/math/9/6/7/967ee9547ff2bd3e6824d92760d04aaa.png)
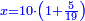
![\scriptstyle{\color{blue}{\left(\frac{1}{3}\sdot6\right)+\left(\frac{1}{4}\sdot6\right)+\left[\frac{1}{2}\sdot\left[6-\left[\left(\frac{1}{3}\sdot6\right)+\left(\frac{1}{4}\sdot6\right)\right]\right]\right]{\color{red}{=4+\frac{3}{4}\longrightarrow10-\left(4+\frac{3}{4}\right)=5+\frac{1}{4}}}}}](/mediawiki/images/math/4/2/3/42379a4e3667a41943db87d7b55fb183.png)
![\scriptstyle{\color{blue}{{\color{red}{\left(\frac{1}{3}\sdot8\right)+\left(\frac{1}{4}\sdot8\right)+\left[\frac{1}{2}\sdot\left[8-\left[\left(\frac{1}{3}\sdot8\right)+\left(\frac{1}{4}\sdot8\right)\right]\right]\right]=}}6+\frac{1}{3}\longrightarrow10-\left(6+\frac{1}{3}\right)=3+\frac{2}{3}}}](/mediawiki/images/math/b/6/a/b6a7326e40a51f1b9b971022e91108c1.png)
![\scriptstyle{\color{blue}{x=\frac{\left[\left(5+\frac{1}{4}\right)\sdot8\right]-\left[\left(3+\frac{2}{3}\right)\sdot6\right]}{\left(5+\frac{1}{4}\right)-\left(3+\frac{2}{3}\right)}=\frac{42-22}{\left(5+\frac{1}{4}\right)-\left(3+\frac{2}{3}\right)}=\frac{20}{\left(5+\frac{1}{4}\right)-\left(3+\frac{2}{3}\right)}=12+\frac{12}{19}}}](/mediawiki/images/math/6/d/5/6d5c4634c9fb4a838f9417bdb1d0a4b9.png)
![\scriptstyle{\color{blue}{\left(\frac{1}{3}\sdot1\right)+\left(\frac{1}{4}\sdot1\right)+\left[\frac{1}{2}\sdot\left[1-\left[\left(\frac{1}{3}\sdot1\right)+\left(\frac{1}{4}\sdot1\right)\right]\right]\right]=\frac{4}{6}+\left(\frac{3}{4}\sdot\frac{1}{6}\right)\longrightarrow\left[\frac{4}{6}+\left(\frac{3}{4}\sdot\frac{1}{6}\right)\right]:1=10:x}}](/mediawiki/images/math/4/4/5/445ad22065f2cc72ab3fdb31af4b9c91.png)
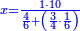
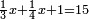
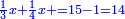
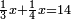
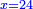
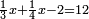
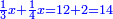
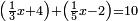
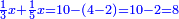
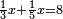
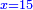
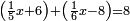
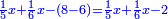
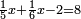
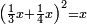
![\scriptstyle{\color{blue}{x=\frac{12^2}{\left[\left(\frac{1}{3}\sdot12\right)+\left(\frac{1}{4}\sdot12\right)\right]^2}=\frac{12^2}{7^2}=\frac{12^2}{49}=2+\frac{6}{7}+\left(\frac{4}{7}\sdot\frac{1}{7}\right)}}](/mediawiki/images/math/a/2/3/a231e7caed858e8722ac84130f9cb4a4.png)
![\scriptstyle{\color{blue}{\left(\frac{1}{3}x+\frac{1}{4}x\right)^2=\left[\left[\frac{3}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]x\right]^2=\left[\frac{3}{{\color{red}{9}}}+\left(\frac{1}{2}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)\right]x^2=x}}](/mediawiki/images/math/3/2/c/32c74213ca28aace5e89faa6a8950425.png)
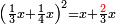
![\scriptstyle{\color{blue}{x=\frac{12^2+\left(\frac{2}{3}\sdot12^2\right)}{\left[\left(\frac{1}{3}\sdot12\right)+\left(\frac{1}{4}\sdot12\right)\right]^2}=\frac{240}{7^2}=\frac{240}{4{\color{red}{9}}}=4+\frac{6}{7}+\left(\frac{2}{7}\sdot\frac{1}{7}\right)}}](/mediawiki/images/math/c/3/e/c3e66c0eca1e8e7731231a5887771dcb.png)
![\scriptstyle\left[\frac{1}{4}\sdot\left(\frac{1}{3}x+\frac{1}{5}x\right)\right]+\left[\frac{1}{2}\sdot\left[x-\left(\frac{1}{3}x+\frac{1}{5}x\right)\right]\right]=11](/mediawiki/images/math/4/e/4/4e44ec3b676fd08257ac8ed3890d89bb.png)
![{\color{blue}{\begin{align}&\scriptstyle x=\frac{11\sdot60}{\left[\frac{1}{4}\sdot\left[\left(\frac{1}{3}\sdot60\right)+\left(\frac{1}{5}\sdot60\right)\right]\right]+\left[\frac{1}{2}\sdot\left[60-\left[\left(\frac{1}{3}\sdot60\right)+\left(\frac{1}{5}\sdot60\right)\right]\right]\right]}\\&\scriptstyle=\frac{11\sdot60}{\left(\frac{1}{4}\sdot32\right)+\left[\frac{1}{2}\sdot\left(60-32\right)\right]}\\&\scriptstyle=\frac{11\sdot60}{8+\left(\frac{1}{2}\sdot{\color{red}{2}}8\right)}\\&\scriptstyle=\frac{11\sdot60}{8+14}\\&\scriptstyle=\frac{11\sdot60}{22}=30\\\end{align}}}](/mediawiki/images/math/c/3/6/c36efa46ffabc03091c48220f0a06117.png)
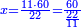
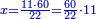
![\scriptstyle\frac{1}{2}x+\left[\frac{1}{3}\sdot\left(x-\frac{1}{2}x\right)\right]+\left[\frac{1}{4}\sdot\left[x-\left[\frac{1}{2}x+\left[\frac{1}{3}\sdot\left(x-\frac{1}{2}x\right)\right]\right]\right]\right]+\left[\frac{1}{5}\sdot\left[x-\left[\frac{1}{2}x+\left[\frac{1}{3}\sdot\left(x-\frac{1}{2}x\right)\right]+\left[\frac{1}{4}\sdot\left[x-\left[\frac{1}{2}x+\left[\frac{1}{3}\sdot\left(x-\frac{1}{2}x\right)\right]\right]\right]\right]\right]\right]\right]=20](/mediawiki/images/math/f/0/8/f084d8fb8895bc719d9d091d4cd15afb.png)
![\scriptstyle{\color{blue}{x\scriptstyle=\frac{20\sdot60}{30+\left[\frac{1}{3}\sdot\left(60-30\right)\right]+\left[\frac{1}{4}\sdot\left[60-\left[30+\left[\frac{1}{3}\sdot\left(60-30\right)\right]\right]\right]\right]+\left[\frac{1}{5}\sdot\left[60-\left[30+\left[\frac{1}{3}\sdot\left(60-30\right)\right]+\left[\frac{1}{4}\sdot\left[60-\left[30+\left[\frac{1}{3}\sdot\left(60-30\right)\right]\right]\right]\right]\right]\right]\right]}}}](/mediawiki/images/math/4/5/a/45a86b2ca30b8abb1a72ed6de2996dfa.png)
![{\color{blue}{\begin{align}&\scriptstyle=\frac{20\sdot60}{30+10+\left(\frac{1}{4}\sdot20\right)+\left[\frac{1}{5}\sdot\left[60-\left[30+10+\left(\frac{1}{4}\sdot20\right)\right]\right]\right]}\\&\scriptstyle=\frac{20\sdot60}{30+10+5+\left[\frac{1}{5}\sdot\left[60-\left(30+10+5\right)\right]\right]}\\&\scriptstyle=\frac{20\sdot60}{30+10+5+\left(\frac{1}{5}\sdot15\right)}\\&\scriptstyle=\frac{20\sdot60}{30+10+5+3}\\&\scriptstyle=\frac{20\sdot60}{48}=25\\\end{align}}}](/mediawiki/images/math/d/6/b/d6bcd8ceafadf1f59a2129a4f8a7691f.png)
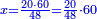
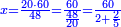
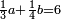
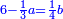
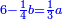
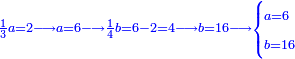
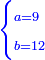
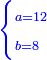
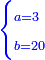
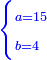
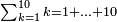
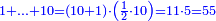
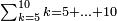
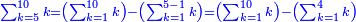
![\scriptstyle{\color{blue}{5+\ldots+10=\left(1+\ldots+10\right)-\left[1+\ldots+\left(5-1\right)\right]=\left(1+\ldots+10\right)-\left(1+\ldots+4\right)=55-10=45}}](/mediawiki/images/math/2/5/c/25c40160eeda3e15cfea8cf849f3d265.png)
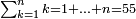
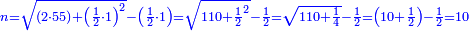
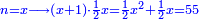
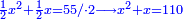
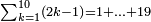
![\scriptstyle{\color{blue}{1+\ldots+19=\left[\frac{1}{2}\sdot\left(19+1\right)\right]^2=\left(\frac{1}{2}\sdot20\right)^2=10^2=100}}](/mediawiki/images/math/5/0/c/50c60912af82352d0e1898f1cacb47ec.png)
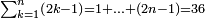
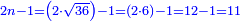
![\scriptstyle{\color{blue}{2n-1=x\longrightarrow\left[\frac{1}{2}\sdot\left(x+1\right)\right]^2=\left(\frac{1}{2}x+\frac{1}{2}\right)^2=\frac{1}{4}x^2+\frac{1}{2}x+\frac{1}{4}=36}}](/mediawiki/images/math/e/4/b/e4b6eaea1b12db82244bd0620f99eec4.png)
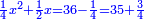
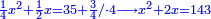
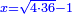
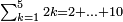
![\scriptstyle{\color{blue}{2+\ldots+10=\left[\frac{1}{2}\sdot\left(10+2\right)\right]\sdot\left(\frac{1}{2}\sdot10\right)=\left(\frac{1}{2}\sdot12\right)\sdot\left(\frac{1}{2}\sdot10\right)=30}}](/mediawiki/images/math/f/5/1/f51017e663db1fbe93036073b3ec2211.png)
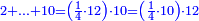
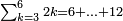
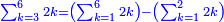
![\scriptstyle{\color{blue}{6+\ldots+12=\left(2+\ldots+12\right)-\left[2+\ldots+\left(6-2\right)\right]=\left(2+\ldots+12\right)-\left(2+\ldots+4\right)=42-6=36}}](/mediawiki/images/math/6/9/4/694f6202ac26b2f6ff5c8632696c15ad.png)
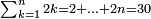
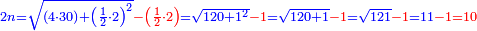
![\scriptstyle{\color{blue}{2n=x\longrightarrow\left[\frac{1}{2}\sdot\left(x+2\right)\right]\sdot\frac{1}{2}x=\left(\frac{1}{2}x+1\right)\sdot\frac{1}{2}x=\frac{1}{4}x^2+\frac{1}{2}x=30}}](/mediawiki/images/math/9/1/f/91fc38496a268bfcbdbdb682bd17d225.png)
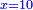
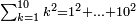
![\scriptstyle{\color{blue}{\sum_{k=1}^{10} k^2=\left(\sum_{k=1}^{10} k\right)\sdot\left[\left(\frac{2}{3}\sdot10\right)+\frac{1}{3}\right]}}](/mediawiki/images/math/c/8/4/c84c0a4d7aaca911422cca587a2083b8.png)
![\scriptstyle{\color{blue}{1^2+\ldots+10^2=\left(1+\ldots+10\right)\sdot\left[\left(\frac{2}{3}\sdot10\right)+\frac{1}{3}\right]=55\sdot7=385}}](/mediawiki/images/math/1/4/c/14c05a4d5f2912d4c244acd5ddec0341.png)
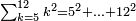
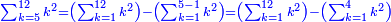
![\scriptstyle{\color{blue}{5^2+\ldots+12^2=\left(1^2+\ldots+12^2\right)-\left[1^2+\ldots+\left(5-1\right)^2\right]=\left(1^2+\ldots+12^2\right)-\left(1^2+\ldots+4^2\right)}}](/mediawiki/images/math/6/e/2/6e28e0321dba374bfb1c4c0834652ebb.png)
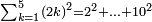
![\scriptstyle{\color{blue}{2^2+\ldots+10^2=\left(2+\ldots+10\right)\sdot\left[\left(\frac{2}{3}\sdot10\right)+\frac{2}{3}\right]=30\sdot\left(7+\frac{1}{3}\right)=220}}](/mediawiki/images/math/b/d/c/bdc2fb35e6fa4d1c08c8a80df3158906.png)
![\scriptstyle{\color{blue}{2^2+\ldots+10^2=\left[\frac{2}{3}\sdot\left(2+\ldots+10\right)\right]\sdot\left(10+1\right)=\left(\frac{2}{3}\sdot30\right)\sdot11=20\sdot11=220}}](/mediawiki/images/math/6/d/6/6d60d79678b2c4e72273b16dc467b0c0.png)
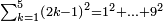
![\scriptstyle{\color{blue}{1^2+\dots+9^2=\left[\frac{1}{2}\sdot\left(9+2\right)\right]\sdot\left[\frac{1}{2}\sdot\left(9+1\right)\right]\sdot\left(\frac{2}{3}\sdot9\right)=\left(\frac{1}{2}\sdot11\right)\sdot\left(\frac{1}{2}\sdot10\right)\sdot\left(\frac{2}{3}\sdot9\right)=165}}](/mediawiki/images/math/7/f/0/7f00cbc70541208fd798b35b74453c11.png)
![{\color{blue}{\begin{align}\scriptstyle1^2+\dots+9^2&\scriptstyle=\left[\left(1+\ldots+9\right)-\left[\left[\frac{1}{3}\sdot\left(1+\ldots+9\right)\right]+\frac{1}{6}\right]\right]{\color{red}{\sdot\left(9+1\right)}}\\&\scriptstyle=\left[25-\left[\left(\frac{1}{3}\sdot25\right)+\frac{1}{6}\right]\right]{\color{red}{\sdot10}}\\&\scriptstyle=\left(16+\frac{1}{2}\right){\color{red}{\sdot10}}\\\end{align}}}](/mediawiki/images/math/f/2/1/f2199ae09e14b2138d90639dafa9f21d.png)
![\scriptstyle{\color{blue}{1^2+\dots+9^2=\left(9+1\right)\sdot\left(\frac{1}{2}\sdot9\right)\sdot\left[\left(\frac{1}{3}\sdot9\right)+\frac{2}{3}\right]}}](/mediawiki/images/math/5/0/2/5022b8b5b367884f124d8bc23c855d1d.png)
![\scriptstyle{\color{blue}{1^2+\dots+9^2=\left(\frac{1}{2}\sdot9\right)\sdot\left[\left(\frac{1}{3}\sdot9\right)+\frac{2}{3}\right]\sdot\left(9+1\right)=\left(4+\frac{1}{2}\right)\sdot\left(3+\frac{2}{3}\right)\sdot10}}](/mediawiki/images/math/3/2/9/329c377a60c5e1b9e9ba99a6ee2b47d8.png)
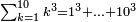
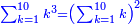
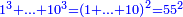
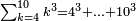
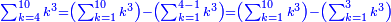
![\scriptstyle{\color{blue}{4^3+\ldots+10^3=\left(1^3+\ldots+10^3\right)-\left[1^3+\ldots+\left(4-1\right)^3\right]=\left(1^3+\ldots+10^3\right)-\left(1^3+\ldots+3^3\right)}}](/mediawiki/images/math/9/c/a/9ca7b7c29df04d1aa0dccbbb8015ee3b.png)
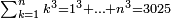
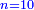
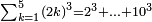
![\scriptstyle{\color{blue}{\sum_{k=1}^{5} \left(2k\right)^3=\left[\sum_{k=1}^{5} \left(2k\right)\right]\sdot\left[2\sdot\sum_{k=1}^{5} \left(2k\right)\right]}}](/mediawiki/images/math/3/4/a/34a235f959489f67963c301d247db10e.png)
![\scriptstyle{\color{blue}{2^3+\ldots+10^3=\left(2+\ldots+10\right)\sdot\left[2\sdot\left(2+\ldots+10\right)\right]=30\sdot\left(2\sdot30\right)=1800}}](/mediawiki/images/math/4/6/4/46426cf626cc98ae66f4116784811d40.png)
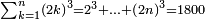

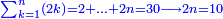
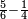
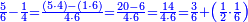
![\scriptstyle\frac{10}{11}-\left[\frac{4}{5}+\left(\frac{1}{2}\sdot\frac{1}{5}\right)\right]](/mediawiki/images/math/a/0/2/a02336007e9bb0f486bfcaadb4e67bca.png)
![\scriptstyle\frac{9}{10}+\left(\frac{3}{4}\sdot\frac{1}{10}\right)-\left[\frac{7}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)\right]](/mediawiki/images/math/8/5/1/851b4268ae804ae5e1a8deac3f796057.png)
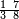
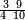
![{\color{blue}{\begin{align}\scriptstyle\frac{9}{10}+\left(\frac{3}{4}\sdot\frac{1}{10}\right)-\left[\frac{7}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)\right]&\scriptstyle=\frac{\left[\left[\left(9\sdot4\right)+3\right]\sdot8\sdot3\right]-\left[\left[\left(7\sdot3\right)+1\right]\sdot10\sdot4\right]}{3\sdot4\sdot8\sdot10}\\&\scriptstyle=\left(\frac{4}{8}\sdot\frac{1}{10}\right)+\left(\frac{4}{6}\sdot\frac{1}{8}\sdot\frac{1}{10}\right)\\\end{align}}}](/mediawiki/images/math/9/b/3/9b39eed76a4c1904307aa89452b54d66.png)
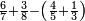
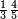
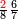
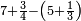
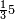
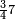
![{\color{blue}{\begin{align}\scriptstyle7+\frac{3}{4}-\left(5+\frac{1}{3}\right)&\scriptstyle=\frac{\left[\left[\left(7\sdot4\right)+3\right]\sdot3\right]-\left[\left[\left(5\sdot3\right)+1\right]\sdot4\right]}{4\sdot3}\\&\scriptstyle=\frac{29}{4\sdot3}\\&\scriptstyle=2+\frac{2}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\\\end{align}}}](/mediawiki/images/math/d/8/b/d8b5d52972a9253146f2d08538599729.png)
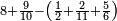
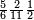
![\scriptstyle\frac{9}{10}{\color{red}{\left[8\right]}}](/mediawiki/images/math/d/6/5/d65cd29970434412a23cd371014def78.png)
![{\color{blue}{\scriptstyle8+\frac{9}{10}-\left(\frac{1}{2}+\frac{2}{11}+\frac{5}{6}\right)=\frac{\left[\left[\left(8\sdot10\right)+9\right]\sdot2\sdot11\sdot6\right]-\left[\left[\left(1\sdot11\sdot6\right)+\left(2\sdot2\sdot6\right)+\left(5\sdot2\sdot11\right)\right]\sdot10\right]}{2\sdot6\sdot10\sdot11}}}](/mediawiki/images/math/b/2/1/b21a18673e469e93e762a53af50863d7.png)
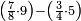
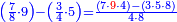
![\scriptstyle\left(\frac{5}{6}\sdot7\right)-\left[\frac{3}{4}\sdot\left(5+\frac{1}{2}\right)\right]](/mediawiki/images/math/b/8/3/b83fb9285fa6009f204f26bd4f70c9ae.png)
![\scriptstyle{\color{blue}{\left(\frac{5}{6}\sdot7\right)-\left[\frac{3}{4}\sdot\left(5+\frac{1}{2}\right)\right]=\frac{\left(7\sdot5\sdot4\sdot2\right)-\left[\left[\left(5\sdot2\right)+1\right]\sdot3\sdot6\right]}{2\sdot4\sdot6}}}](/mediawiki/images/math/e/a/f/eaf3530d0a5c315a5bf14139fa4dba10.png)
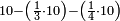
![\scriptstyle{\color{blue}{10-\left(\frac{1}{3}\sdot10\right)-\left(\frac{1}{4}\sdot10\right)=\frac{\left[12-\left(\frac{1}{3}\sdot12\right)-\left(\frac{1}{4}\sdot12\right)\right]\sdot10}{12}=\frac{5\sdot10}{12}=4+\frac{1}{6}}}](/mediawiki/images/math/7/b/0/7b023ec3d1f7c6d55dd82e346ccb59b3.png)
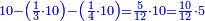
![\scriptstyle 10-\left[\left(\frac{1}{3}\sdot10\right)+\left(\frac{1}{4}\sdot10\right)+3\right]](/mediawiki/images/math/c/f/2/cf2bd8909cfb411c03b2ea3f9fc9b40f.png)
![{\color{blue}{\begin{align}\scriptstyle10-\left[\left(\frac{1}{3}\sdot10\right)+\left(\frac{1}{4}\sdot10\right)+3\right]&\scriptstyle=\frac{\left[\left[12-\left(\frac{1}{3}\sdot12\right)-\left(\frac{1}{4}\sdot12\right)\right]\sdot10\right]-\left(3\sdot12\right)}{12}\\&\scriptstyle=\frac{\left(5\sdot10\right)-\left(3\sdot12\right)}{12}\\&\scriptstyle=\frac{50-\left(3\sdot12\right)}{12}\\&\scriptstyle=\frac{14}{12}\\&\scriptstyle=1+\frac{1}{6}\\\end{align}}}](/mediawiki/images/math/9/6/c/96c423dd602007bdccb0fe75e85d597a.png)
![{\color{blue}{\scriptstyle10-\left[\left(\frac{1}{3}\sdot10\right)+\left(\frac{1}{4}\sdot10\right)+3\right]=\frac{50}{12}-3}}](/mediawiki/images/math/6/c/5/6c574bef393f751f0b1389f41c0e0d8d.png)
![\scriptstyle10-\left[\left(\frac{1}{3}\sdot10\right)+\left(\frac{1}{4}\sdot10\right)-2\right]](/mediawiki/images/math/c/5/5/c55fd60a314d17d0af06c011228f7c69.png)
![{\color{blue}{\begin{align}\scriptstyle10-\left[\left(\frac{1}{3}\sdot10\right)+\left(\frac{1}{4}\sdot10\right)-2\right]&\scriptstyle=\frac{\left[\left[12-\left(\frac{1}{3}\sdot12\right)-\left(\frac{1}{4}\sdot12\right)\right]\sdot10\right]+\left(2\sdot12\right)}{12}\\&\scriptstyle=\frac{\left(5\sdot10\right)+\left(2\sdot12\right)}{12}\\&\scriptstyle=\frac{50+\left(2\sdot12\right)}{12}\\&\scriptstyle=\frac{74}{12}\\&\scriptstyle=6+\frac{1}{6}\\\end{align}}}](/mediawiki/images/math/7/9/6/7968cc5340cc70a4d4073c6fe719c941.png)
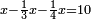
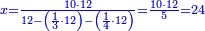
![\scriptstyle{\color{blue}{x-\frac{1}{3}x-\frac{1}{4}x=\left[\frac{2}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]x=10}}](/mediawiki/images/math/d/7/e/d7eced8a372f1155019b2ba68f9cbf3c.png)
![\scriptstyle{\color{blue}{\left[\frac{2}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\sdot a=1\longrightarrow a=2+\frac{2}{5}}}](/mediawiki/images/math/a/1/5/a1510445ab9d35842c983633a69ca022.png)
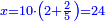
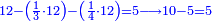
![\scriptstyle{\color{blue}{18-\left(\frac{1}{3}\sdot18\right)-\left(\frac{1}{4}\sdot18\right)=7+\frac{1}{2}\longrightarrow\left[10-\left(7+\frac{1}{2}\right)=2+\frac{1}{2}\right]}}](/mediawiki/images/math/6/a/0/6a090c02a158c17a77b0356e5119c4f6.png)
![\scriptstyle{\color{blue}{x=\frac{\left(5\sdot18\right)-\left[\left(2+\frac{1}{2}\right)\sdot12\right]}{5-\left(2+\frac{1}{2}\right)}=\frac{90-30}{2+\frac{1}{2}}=\frac{60}{2+\frac{1}{2}}=24}}](/mediawiki/images/math/1/1/9/11942b410cc814c48c2d53dc5bd80852.png)
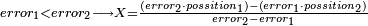
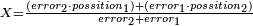
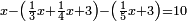
![\scriptstyle{\color{blue}{x=\frac{\left[10+\left(3+3\right)\right]\sdot60}{60-\left[\left(\frac{1}{3}\sdot60\right)+\left(\frac{1}{4}\sdot60\right)+\left(\frac{1}{5}\sdot60\right)\right]}=\frac{\left(10+6\right)\sdot60}{13}=\frac{16\sdot60}{13}=73+\frac{11}{13}}}](/mediawiki/images/math/3/d/7/3d717bfbdb0827fcfb54b098a395b51e.png)
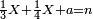 - vice versa:
- vice versa: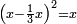
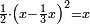
![\scriptstyle{\color{blue}{x=\frac{3^2}{\frac{1}{2}\sdot\left[3-\left(\frac{1}{3}\sdot3\right)\right]\sdot\left[3-\left(\frac{1}{3}\sdot3\right)\right]}=\frac{9}{\left(\frac{1}{2}\sdot2\right)\sdot2}=\frac{9}{1\sdot2}=\frac{9}{2}=4+\frac{1}{2}}}](/mediawiki/images/math/e/9/8/e98e31aada62b432c168a5843aee62f0.png)
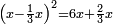
![\scriptstyle{\color{blue}{x=\frac{3^2\sdot\left(6+\frac{2}{3}\right)}{\left[3-\left(\frac{1}{3}\sdot3\right)\right]^2}=\frac{60}{2^2}=\frac{60}{4}=15}}](/mediawiki/images/math/e/4/3/e43a545eabdb35e0c4135f275d231a15.png)
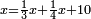
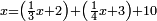
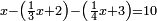
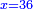
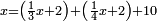
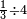

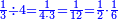
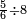

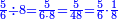
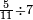
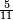

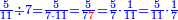
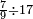

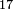

![\scriptstyle\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\div5](/mediawiki/images/math/f/3/5/f35247a33fdf18d5e069da1dd98835fe.png)

![\scriptstyle{\color{blue}{\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\div5=\frac{\left(5\sdot2\right)+1}{5\sdot6\sdot2}=\frac{11}{60}=\frac{1}{10}+\left(\frac{5}{6}\sdot\frac{1}{10}\right)}}](/mediawiki/images/math/4/9/7/4975680573c957c07c91e1915bc2958c.png)
![\scriptstyle\left[\frac{10}{11}+\left(\frac{3}{5}\sdot\frac{1}{11}\right)\right]\div63](/mediawiki/images/math/9/b/0/9b0959a66fde808099c9dfefd633a000.png)
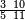
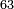
![{\color{blue}{\begin{align}\scriptstyle\left[\frac{10}{11}+\left(\frac{3}{5}\sdot\frac{1}{11}\right)\right]\div63&\scriptstyle=\frac{\left(10\sdot5\right)+3}{63\sdot11\sdot5}\\&\scriptstyle=\frac{53}{3465}\\&\scriptstyle=\left(\frac{1}{9}\sdot\frac{1}{11}\right)+\left(\frac{3}{7}\sdot\frac{1}{9}\sdot\frac{1}{11}\right)+\left(\frac{3}{5}\sdot\frac{1}{7}\sdot\frac{1}{9}\sdot\frac{1}{11}\right)\\\end{align}}}](/mediawiki/images/math/4/b/d/4bdba511e4156c37e25ce63a137a08b7.png)
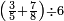
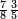
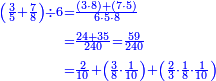
![\scriptstyle{\color{blue}{\left(\frac{3}{5}+\frac{7}{8}\right)\div6=\left[1+\frac{3}{8}+\left(\frac{4}{5}\sdot\frac{1}{8}\right)\right]\div6=\left[1+\frac{3}{8}+\left(\frac{4}{5}\sdot\frac{1}{8}\right)\right]\sdot\frac{1}{6}}}](/mediawiki/images/math/0/e/6/0e60e4654a1cb8557d438aaeb04b2670.png)
![\scriptstyle{\color{blue}{\left(\frac{3}{5}+\frac{7}{8}\right)\div6=\left[\left(\frac{3}{5}+\frac{7}{8}\right)\right]\sdot\frac{1}{6}}}](/mediawiki/images/math/4/5/7/457660597915a0e44233bcf46f94dcf3.png)
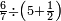
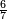
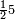
![{\color{blue}{\begin{align}\scriptstyle\frac{6}{7}\div\left(5+\frac{1}{2}\right)&\scriptstyle=\frac{6\sdot2}{\left[\left(5\sdot2\right)+1\right]\sdot7}\\&\scriptstyle=\frac{12}{11\sdot7}=\frac{12}{77}\\\end{align}}}](/mediawiki/images/math/f/d/4/fd4dd364f4c2d341283cf107461e6389.png)
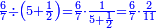
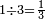
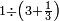
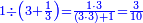
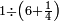
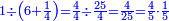
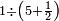
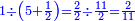
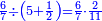
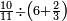
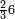
![{\color{blue}{\begin{align}\scriptstyle\frac{10}{11}\div\left(6+\frac{2}{3}\right)&\scriptstyle=\frac{10\sdot3}{\left[\left(6\sdot3\right)+2\right]\sdot11}\\&\scriptstyle=\frac{30}{20\sdot11}=\frac{30}{220}\\&\scriptstyle=\frac{1}{11}+\left(\frac{1}{2}\sdot\frac{1}{11}\right)\\\end{align}}}](/mediawiki/images/math/e/6/0/e60b5b6d619069eb0767fd33e8ded154.png)
![\scriptstyle{\color{blue}{\frac{10}{11}\div\left(6+\frac{2}{3}\right)=\frac{10}{11}\sdot\left[\frac{1}{10}+\left(\frac{1}{2}\sdot\frac{1}{10}\right)\right]}}](/mediawiki/images/math/8/3/9/83939baf4266a8aef3a5c3523bc501ec.png)
![\scriptstyle\frac{4}{5}\div\left[3+\frac{6}{7}+\left(\frac{1}{2}\sdot\frac{1}{7}\right)\right]](/mediawiki/images/math/5/7/b/57b7577cb03e6f202ca23aa4cd5ee3c2.png)
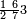
![{\color{blue}{\begin{align}\scriptstyle\frac{4}{5}\div\left[3+\frac{6}{7}+\left(\frac{1}{2}\sdot\frac{1}{7}\right)\right]&\scriptstyle=\frac{4\sdot2\sdot7}{\left[\left[\left[\left(3\sdot7\right)+6\right]\sdot2\right]+1\right]\sdot5}\\&\scriptstyle=\frac{56}{55\sdot5}=\frac{56}{275}\\&\scriptstyle=\frac{2}{11}+\left(\frac{1}{5}\sdot\frac{1}{11}\right)+{\color{red}{\left(\frac{1}{5}\sdot\frac{1}{5}\sdot\frac{1}{11}\right)}}\\\end{align}}}](/mediawiki/images/math/1/f/f/1ff9ab42134d06611ed1f848a14cbe37.png)
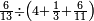
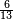
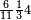
![{\color{blue}{\begin{align}\scriptstyle\frac{6}{13}\div\left(4+\frac{1}{3}+\frac{6}{11}\right)&\scriptstyle=\frac{6\sdot3\sdot11}{\left[\left(4\sdot3\sdot11\right)+\left(1\sdot11\right)+\left(6\sdot3\right)\right]\sdot13}\\&\scriptstyle=\frac{198}{161\sdot13}\\&\scriptstyle=\frac{198}{2093}\\&\scriptstyle=\frac{2}{23}+\left(\frac{2}{13}\sdot\frac{1}{23}\right)+\left(\frac{2}{7}\sdot\frac{1}{13}\sdot\frac{1}{23}\right)\\\end{align}}}](/mediawiki/images/math/2/b/2/2b2eed3f968f12c278902cd48c776b6b.png)
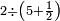

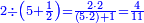
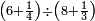
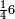
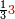
![\scriptstyle{\color{blue}{\left(6+\frac{1}{4}\right)\div\left(8+\frac{1}{3}\right)=\frac{\left[\left(6\sdot4\right)+1\right]\sdot3}{\left[\left(8\sdot3\right)+1\right]\sdot4}=\frac{25\sdot3}{25\sdot4}=\frac{75}{100}=\frac{3}{4}}}](/mediawiki/images/math/c/a/f/caf07083151be12b2c2217d125d96f03.png)
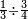
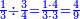
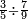
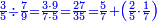
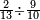
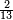
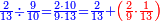
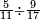
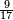
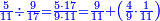
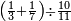
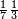
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{1}{3}+\frac{1}{7}\right)\div\frac{10}{11}&\scriptstyle=\frac{\left[\left(1\sdot7\right)+\left(1\sdot3\right)\right]\sdot11}{10\sdot3\sdot7}\\&\scriptstyle=\frac{10\sdot11}{210}\\&\scriptstyle=\frac{5}{10}+\left(\frac{1}{7}\sdot\frac{1}{10}\right)+\left(\frac{2}{3}\sdot\frac{1}{7}\sdot\frac{1}{10}\right)\\&\scriptstyle=\frac{3}{7}+\left(\frac{{\color{red}{2}}}{3}\sdot\frac{1}{7}\right)\\\end{align}}}](/mediawiki/images/math/4/3/4/434a0c270496bc3bb59941519493d9be.png)
![\scriptstyle\frac{2}{3}\div\left[\frac{9}{10}+\left(\frac{5}{8}\sdot\frac{1}{10}\right)\right]](/mediawiki/images/math/d/d/2/dd244e384f4422a279cba9537b8b864b.png)
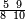
![{\color{blue}{\begin{align}\scriptstyle\frac{2}{3}\div\left[\frac{9}{10}+\left(\frac{5}{8}\sdot\frac{1}{10}\right)\right]&\scriptstyle=\frac{2\sdot10\sdot8}{\left[\left(9\sdot8\right)+5\right]\sdot3}\\&\scriptstyle=\frac{160}{77\sdot3}\\&\scriptstyle=\frac{160}{231}\\&\scriptstyle=\frac{7}{11}+\left(\frac{4}{7}\sdot\frac{1}{11}\right)+\left(\frac{1}{3}\sdot\frac{1}{7}\sdot\frac{1}{11}\right)\\\end{align}}}](/mediawiki/images/math/5/5/0/5506c727a7033a2c435bb6de55cea262.png)
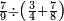
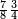
![\scriptstyle{\color{blue}{\frac{7}{9}\div\left(\frac{3}{4}+\frac{7}{8}\right)=\frac{7\sdot4\sdot8}{\left[\left(3\sdot8\right)+\left(7\sdot4\right)\right]\sdot9}=\frac{224}{52\sdot9}=\frac{224}{468}=\frac{6}{13}+\left(\frac{2}{9}\sdot\frac{1}{13}\right)}}](/mediawiki/images/math/7/7/a/77ac664fb41ac9e289545f47dc187fc9.png)
![\scriptstyle\left[\frac{4}{9}+\left(\frac{1}{2}\sdot\frac{1}{9}\right)\right]\div\left[\frac{7}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)\right]](/mediawiki/images/math/8/a/1/8a111107fc608a5ae9f5d99f4f2ec182.png)
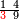
![\scriptstyle{\color{blue}{\left[\frac{4}{9}+\left(\frac{1}{2}\sdot\frac{1}{9}\right)\right]\div\left[\frac{7}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)\right]=\frac{\left[\left(4\sdot2\right)+1\right]\sdot8\sdot3}{\left[\left(7\sdot3\right)+1\right]\sdot9\sdot2}=\frac{216}{396}=\frac{6}{11}}}](/mediawiki/images/math/3/c/c/3ccc74df6aac408d8a4b1919e2a05f57.png)
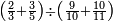
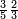
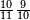
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{2}{3}+\frac{3}{5}\right)\div\left(\frac{9}{10}+\frac{10}{11}\right)&\scriptstyle=\frac{\left[\left(2\sdot5\right)+\left(3\sdot3\right)\right]\sdot10\sdot11}{\left[\left(9\sdot11\right)+\left(10\sdot10\right)\right]\sdot3\sdot5}\\&\scriptstyle=\frac{2090}{19{\color{red}{9}}\sdot3\sdot5}\\&\scriptstyle=\frac{2090}{2985}\\&\scriptstyle=\frac{139}{199}+\left(\frac{1}{199}\sdot\frac{1}{5}\right)+\left(\frac{2}{3}\sdot\frac{1}{5}\sdot\frac{1}{199}\right)\\\end{align}}}](/mediawiki/images/math/d/f/d/dfd53ecc4322b35842a3a98cee5bd2ba.png)
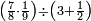
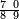
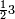
![\scriptstyle{\color{blue}{\left(\frac{7}{8}\sdot\frac{1}{9}\right)\div\left(3+\frac{1}{2}\right)=\frac{7\sdot2}{\left[\left(3\sdot2\right)+1\right]\sdot8\sdot9}=\frac{14}{7\sdot8\sdot9}=\frac{14}{504}=\frac{{\color{red}{2}}}{8}\sdot\frac{1}{9}}}](/mediawiki/images/math/7/a/d/7adbf80e250786445dbcf0ed0cec9c7a.png)
![\scriptstyle\left(\frac{9}{10}\sdot\frac{1}{13}\right)\div\left[6+\frac{3}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)\right]](/mediawiki/images/math/4/5/1/451bee3fb541e81d2eb989739ad43640.png)
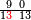
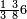
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{9}{10}\sdot\frac{1}{13}\right)\div\left[6+\frac{3}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)\right]&\scriptstyle=\frac{9\sdot8\sdot3}{\left[\left[\left[\left(6\sdot8\right)+3\right]\sdot3\right]+1\right]\sdot10\sdot13}\\&\scriptstyle=\frac{216}{1{\color{red}{5}}4\sdot10\sdot13}\\&\scriptstyle=\frac{216}{20020}\\&\scriptstyle=\left(\frac{1}{11}\sdot\frac{1}{13}\right)+\left(\frac{5}{10}\sdot\frac{1}{11}\sdot\frac{1}{13}\right)+\left(\frac{3}{7}\sdot\frac{1}{10}\sdot\frac{1}{11}\sdot\frac{1}{13}\right)\\\end{align}}}](/mediawiki/images/math/1/0/b/10b24d24cf3eb30fc32379fdec06e9d3.png)
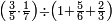
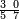
![\scriptstyle\frac{2}{3}\frac{5}{6}\left[1\right]](/mediawiki/images/math/d/1/4/d148e41627110c39037e7310620178f2.png)
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{3}{5}\sdot\frac{1}{7}\right)\div\left(1+\frac{5}{6}+\frac{2}{3}\right)&\scriptstyle=\frac{3\sdot6\sdot3}{\left[\left(1\sdot6\sdot3\right)+\left(5\sdot3\right)+\left(2\sdot6\right)\right]\sdot5\sdot7}\\&\scriptstyle=\frac{54}{1575}\\&\scriptstyle=\left(\frac{2}{7}\sdot\frac{1}{9}\right)+\left(\frac{4}{5}\sdot\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{{\color{red}{9}}}\right)\\\end{align}}}](/mediawiki/images/math/b/7/f/b7fd8fc9392c3bc9cecae0666e1660cb.png)
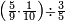
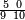
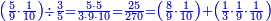
![\scriptstyle\left(\frac{3}{4}\sdot\frac{1}{5}\right)\div\left[\frac{3}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]](/mediawiki/images/math/e/2/6/e2635a129664cacdecfb3781e889b1cc.png)
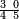
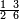
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{3}{4}\sdot\frac{1}{5}\right)\div\left[\frac{3}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]&\scriptstyle=\frac{3\sdot6\sdot2}{\left[\left(3\sdot2\right)+1\right]\sdot4\sdot5}\\&\scriptstyle=\frac{36}{140}\\&\scriptstyle=\frac{2}{10}+\left(\frac{4}{{\color{red}{7}}}\sdot\frac{1}{10}\right)\\\end{align}}}](/mediawiki/images/math/d/0/0/d00ee2083a8c91466b2710578fe519a4.png)
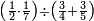
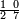
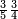
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{1}{2}\sdot\frac{1}{7}\right)\div\left(\frac{3}{4}+\frac{3}{5}\right)&\scriptstyle=\frac{1\sdot4\sdot5}{\left[\left(3\sdot5\right)+\left(3\sdot4\right)\right]\sdot2\sdot7}\\&\scriptstyle=\frac{1\sdot4\sdot5}{27\sdot2\sdot7}\\&\scriptstyle=\frac{1\sdot4\sdot5}{378}\\&\scriptstyle=\left(\frac{3}{7}\sdot\frac{1}{9}\right)+\left(\frac{{\color{red}{2}}}{6}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/1/d/e/1def78d99ada374b6c0c951985b0b127.png)
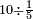
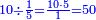
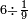
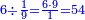
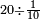
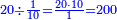
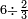
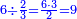
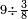


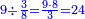
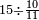
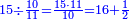
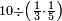
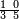
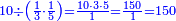
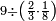
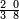
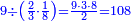
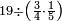
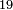
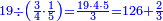
![\scriptstyle4\div\left[\frac{3}{5}+\left(\frac{1}{3}\sdot\frac{1}{5}\right)\right]](/mediawiki/images/math/9/c/8/9c8ab85302d51c8c896d8f72077ae8fd.png)
![\scriptstyle{\color{blue}{4\div\left[\frac{3}{5}+\left(\frac{1}{3}\sdot\frac{1}{5}\right)\right]=\frac{4\sdot5\sdot3}{\left(3\sdot3\right)+1}=\frac{60}{10}=6}}](/mediawiki/images/math/f/d/f/fdf853e7cb387a4a045f5680f3209519.png)
![\scriptstyle5\div\left[\frac{10}{11}+\left(\frac{1}{2}\sdot\frac{1}{11}\right)\right]](/mediawiki/images/math/3/2/f/32feea03a00ca4a14965e14d179083f7.png)
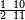
![{\color{blue}{\begin{align}\scriptstyle5\div\left[\frac{10}{11}+\left(\frac{1}{2}\sdot\frac{1}{11}\right)\right]&\scriptstyle=\frac{5\sdot11\sdot2}{\left(10\sdot2\right)+1}\\&\scriptstyle=\frac{5\sdot11\sdot2}{21}\\&\scriptstyle=5+\frac{1}{7}+\left(\frac{2}{3}\sdot\frac{1}{7}\right)\\\end{align}}}](/mediawiki/images/math/9/e/d/9edb196d56bc985a2828acd9d0a0ef5f.png)
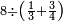
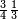
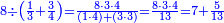
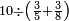
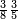
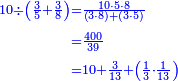
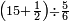
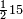
![{\color{blue}{\begin{align}\scriptstyle\left(15+\frac{1}{2}\right)\div\frac{5}{6}&\scriptstyle=\frac{\left[\left(15\sdot2\right)+1\right]\sdot6}{5\sdot2}\\&\scriptstyle=\frac{31\sdot6}{5\sdot2}\\&\scriptstyle=\frac{186}{10}\\&\scriptstyle=18+\frac{6}{10}\\\end{align}}}](/mediawiki/images/math/4/0/7/407aecd9cd097112cccf6e3be3777d2e.png)
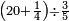
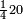
![{\color{blue}{\begin{align}\scriptstyle\left(20+\frac{1}{4}\right)\div\frac{3}{5}&\scriptstyle=\frac{\left[\left(20\sdot4\right)+1\right]\sdot5}{3\sdot4}\\&\scriptstyle=\frac{405}{12}\\&\scriptstyle=33+\frac{4}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\\\end{align}}}](/mediawiki/images/math/d/7/d/d7da79ef9310e2cbb6e0d240f07eced1.png)
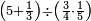
![{\color{blue}{\begin{align}\scriptstyle\left(5+\frac{1}{3}\right)\div\left(\frac{3}{4}\sdot\frac{1}{5}\right)&\scriptstyle=\frac{\left[\left(5\sdot3\right)+1\right]\sdot4\sdot5}{3\sdot3}\\&\scriptstyle=\frac{16\sdot4\sdot5}{9}\\&\scriptstyle=\frac{320}{9}\\&\scriptstyle=35+\frac{5}{9}\\\end{align}}}](/mediawiki/images/math/d/1/8/d1810d01b9dbdcace60dc26faf53dc9f.png)
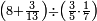
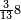
![{\color{blue}{\begin{align}\scriptstyle\left(8+\frac{3}{13}\right)\div\left(\frac{3}{5}\sdot\frac{1}{7}\right)&\scriptstyle=\frac{\left[\left(8\sdot13\right)+3\right]\sdot5\sdot7}{3\sdot13}\\&\scriptstyle=\frac{3745}{39}\\&\scriptstyle=96+\left(\frac{1}{3}\sdot\frac{1}{13}\right)\\\end{align}}}](/mediawiki/images/math/9/8/c/98c74b876baf3df1923654c8c87c3cfc.png)
![\scriptstyle\left(6+\frac{1}{2}\right)\div\left[\frac{4}{5}+\left(\frac{1}{2}\sdot\frac{1}{5}\right)\right]](/mediawiki/images/math/a/b/8/ab8d988d4f4fc8d6fd5641aaf3c0ae9f.png)
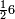
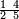
![{\color{blue}{\begin{align}\scriptstyle\left(6+\frac{1}{2}\right)\div\left[\frac{4}{5}+\left(\frac{1}{2}\sdot\frac{1}{5}\right)\right]&\scriptstyle=\frac{\left[\left(6\sdot2\right)+1\right]\sdot5\sdot2}{\left[\left(4\sdot2\right)+1\right]\sdot2}\\&\scriptstyle=\frac{130}{9\sdot2}\\&\scriptstyle=\frac{130}{18}\\&\scriptstyle=7+\frac{2}{9}\\\end{align}}}](/mediawiki/images/math/5/4/4/54469364d81013ae62dca780fe4fd1b1.png)
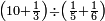
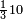
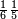
![\scriptstyle{\color{blue}{\left(10+\frac{1}{3}\right)\div\left(\frac{1}{5}+\frac{1}{6}\right)=\frac{\left[\left(10\sdot3\right)+1\right]\sdot5\sdot6}{\left[\left(1\sdot6\right)+\left(1\sdot5\right)\right]\sdot3}=\frac{930}{11\sdot3}=\frac{930}{33}=28+\frac{{\color{red}{2}}}{11}}}](/mediawiki/images/math/4/e/b/4eb8045d1236448f1573f53dfed50708.png)
![\scriptstyle\left[4+\frac{3}{8}+\left(\frac{1}{2}\sdot\frac{1}{8}\right)\right]\div\frac{3}{5}](/mediawiki/images/math/3/2/d/32d11722e462ccb9eb7450bb533cbc0c.png)
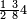
![\scriptstyle{\color{blue}{\left[4+\frac{3}{8}+\left(\frac{1}{2}\sdot\frac{1}{8}\right)\right]\div\frac{3}{5}=\frac{\left[\left[\left[\left(4\sdot8\right)+3\right]\sdot2\right]+1\right]\sdot5}{3\sdot8\sdot2}=\frac{71\sdot5}{48}=\frac{355}{48}=7+\frac{3}{8}+\left(\frac{1}{6}\sdot\frac{1}{8}\right)}}](/mediawiki/images/math/2/e/1/2e1e893e31a4359aacb7c4ffbb7f8ab4.png)
![\scriptstyle\left[2+\frac{6}{7}+\left(\frac{2}{3}\sdot\frac{1}{7}\right)\right]\div\left(\frac{4}{5}\sdot\frac{1}{6}\right)](/mediawiki/images/math/e/3/b/e3b6d865fd628df8725345bed9550838.png)
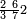
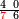
![\scriptstyle{\color{blue}{\left[2+\frac{6}{7}+\left(\frac{2}{3}\sdot\frac{1}{7}\right)\right]\div\left(\frac{4}{5}\sdot\frac{1}{6}\right)=\frac{\left[\left[\left[\left(2\sdot7\right)+6\right]\sdot3\right]+2\right]\sdot5\sdot6}{4\sdot7\sdot3}=\frac{1860}{84}=22+\frac{1}{7}}}](/mediawiki/images/math/2/7/1/271fd8b64cd98eb5af0364510c8109dc.png)
![\scriptstyle\left[9+\frac{5}{6}+\left(\frac{1}{4}\sdot\frac{1}{6}\right)\right]\div\left[\frac{1}{7}+\left(\frac{1}{2}\sdot\frac{1}{7}\right)\right]](/mediawiki/images/math/c/a/c/cac708cd096182197de710a38d627540.png)
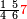
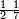
![{\color{blue}{\begin{align}\scriptstyle\left[9+\frac{5}{6}+\left(\frac{1}{4}\sdot\frac{1}{6}\right)\right]\div\left[\frac{1}{7}+\left(\frac{1}{2}\sdot\frac{1}{7}\right)\right]&\scriptstyle=\frac{\left[\left[\left[\left(9\sdot6\right)+5\right]\sdot4\right]+1\right]\sdot7\sdot2}{\left[\left(1\sdot2\right)+1\right]\sdot6\sdot4}\\&\scriptstyle=\frac{3318}{72}\\&\scriptstyle=46+\left(\frac{6}{8}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/4/f/6/4f635b61896cc6c3d9eb4c6d759a87e7.png)
![\scriptstyle\left[3+\frac{3}{10}+\left(\frac{1}{2}\sdot\frac{1}{10}\right)\right]\div\left(\frac{3}{4}+\frac{3}{11}\right)](/mediawiki/images/math/d/5/0/d50f89556f17cf14018f8175b13f65fe.png)
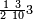
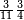
![{\color{blue}{\begin{align}\scriptstyle\left[3+\frac{3}{10}+\left(\frac{1}{2}\sdot\frac{1}{10}\right)\right]\div\left(\frac{3}{4}+\frac{3}{11}\right)&\scriptstyle=\frac{\left[\left[\left[\left(3\sdot10\right)+3\right]\sdot2\right]+1\right]\sdot4\sdot11}{\left[\left(3\sdot11\right)+\left(3\sdot4\right)\right]\sdot10\sdot2}\\&\scriptstyle{\color{red}{=\frac{2948}{45\sdot10\sdot2}}}\\&\scriptstyle{\color{red}{=\frac{2948}{900}}}\\&\scriptstyle{\color{red}{=3+\frac{2}{10}+\left(\frac{7}{10}\sdot\frac{1}{10}\right)+\left(\frac{5}{9}\sdot\frac{1}{10}\sdot\frac{1}{10}\right)}}\\\end{align}}}](/mediawiki/images/math/c/0/4/c04be682816921a58f8410bf84818684.png)
![\scriptstyle\left(8+\frac{3}{11}+\frac{5}{7}\right)\div\left[\frac{5}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)\right]](/mediawiki/images/math/e/5/1/e51880c2c718f84daf210b6c68fb1a69.png)
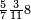
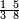
![{\color{blue}{\begin{align}\scriptstyle\left(8+\frac{3}{11}+\frac{5}{7}\right)\div\left[\frac{5}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)\right]&\scriptstyle=\frac{\left[\left(8\sdot11\sdot7\right)+\left(3\sdot7\right)+\left(5\sdot11\right)\right]\sdot8\sdot3}{\left[\left(5\sdot3\right)+1\right]\sdot11\sdot7}\\&\scriptstyle=\frac{16608}{16\sdot11\sdot7}\\&\scriptstyle=\frac{16608}{1232}\\&\scriptstyle=13+\frac{5}{11}+{\color{red}{\left(\frac{2}{8}\sdot\frac{1}{11}\right)}}+\left(\frac{2}{7}\sdot\frac{1}{8}\sdot\frac{1}{11}\right)\\\end{align}}}](/mediawiki/images/math/2/7/a/27a35d885dca08c5d073f787f5378709.png)
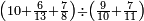
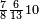
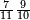
![{\color{blue}{\begin{align}\scriptstyle\left(10+\frac{6}{13}+\frac{7}{8}\right)\div\left(\frac{9}{10}+\frac{7}{11}\right)&\scriptstyle=\frac{\left[\left(10\sdot13\sdot8\right)+\left(6\sdot8\right)+\left(7\sdot13\right)\right]\sdot10\sdot11}{\left[\left(9\sdot11\right)+\left(7\sdot10\right)\right]\sdot13\sdot8}\\&\scriptstyle=\frac{129690}{17576}\\&\scriptstyle=7+\frac{4}{13}+{\color{red}{\left(\frac{12}{13}\sdot\frac{1}{13}\right)}}+\left(\frac{2}{8}\sdot\frac{1}{13}\sdot\frac{1}{13}\sdot\frac{1}{13}\right)\\\end{align}}}](/mediawiki/images/math/d/4/b/d4bc7551a0ab72e5a62163cd99e51b9b.png)
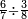

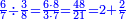
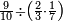
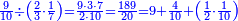
![\scriptstyle\frac{12}{13}\div\left[\frac{1}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)\right]](/mediawiki/images/math/a/8/e/a8e55ff0cbe3a1bbc2b04795da66cd11.png)
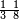
![\scriptstyle{\color{blue}{\frac{12}{13}\div\left[\frac{1}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)\right]=\frac{12\sdot8\sdot3}{\left[\left(1\sdot3\right)+1\right]\sdot13}=\frac{288}{52}=5+\frac{7}{13}}}](/mediawiki/images/math/3/8/3/383b059504fac1676fb11bca94866215.png)
![\scriptstyle\left[\frac{3}{5}\sdot\left(6+\frac{1}{4}\right)\right]\div\left[\frac{2}{3}\sdot\left(4+\frac{1}{2}\right)\right]](/mediawiki/images/math/9/0/f/90f436caad26a7b1c6dd52057663f3a4.png)
![\scriptstyle{\color{blue}{\left[\frac{3}{5}\sdot\left(6+\frac{1}{4}\right)\right]\div\left[\frac{2}{3}\sdot\left(4+\frac{1}{2}\right)\right]=\left(3+\frac{3}{4}\right)\div3=1+\frac{1}{4}}}](/mediawiki/images/math/7/d/9/7d94c4cf5abf2b3ca33a98f5bbc1fb84.png)
![\scriptstyle10\div\left[\left[\frac{7}{8}\sdot\left(5+\frac{1}{3}\right)\right]-\left[\frac{1}{3}\sdot\left(2+\frac{1}{4}\right)\right]\right]](/mediawiki/images/math/1/b/7/1b7f16e412d991a2e6ac44c44e98d15a.png)
![\scriptstyle\left[\left[\left(\frac{3}{4}\sdot\frac{3}{5}\right)\sdot9\right]\div\frac{3}{10}\right]\div\left[\left(\frac{2}{3}\sdot7\right)-\left[\left(2+\frac{1}{8}\right)\div\left[\frac{7}{8}+\left(\frac{1}{2}\sdot\frac{1}{8}\right)\right]\right]\right]](/mediawiki/images/math/5/d/0/5d035686f0d758ca5d6e74040f716d33.png)
![{\color{blue}{\begin{align}&\scriptstyle\left[\left[\left(\frac{3}{4}\sdot\frac{3}{5}\right)\sdot9\right]\div\frac{3}{10}\right]\div\left[\left(\frac{2}{3}\sdot7\right)-\left[\left(2+\frac{1}{8}\right)\div\left[\frac{7}{8}+\left(\frac{1}{2}\sdot\frac{1}{8}\right)\right]\right]\right]=\\&\scriptstyle=\left[4+\left(\frac{1}{2}\sdot\frac{1}{10}\right)\right]\div\left[\frac{3}{10}\sdot\left[\left(4+\frac{2}{3}\right)-\left[2+\frac{1}{5}+\left(\frac{1}{3}\sdot\frac{1}{5}\right)\right]\right]\right]\\&\scriptstyle=\left[4+\left(\frac{1}{2}\sdot\frac{1}{10}\right)\right]\div\left[\frac{3}{10}\sdot\left(2+\frac{2}{5}\right)\right]\\&\scriptstyle=\left[4+\left(\frac{1}{2}\sdot\frac{1}{10}\right)\right]\div\left[\frac{7}{10}+\left(\frac{1}{5}\sdot\frac{1}{10}\right)\right]\\\end{align}}}](/mediawiki/images/math/b/9/2/b929f740991d70e5bfb1c8bdea920c15.png)
![\scriptstyle\left[4+\left(\frac{1}{2}\sdot\frac{1}{10}\right)\right]\div\left[\frac{7}{10}+\left(\frac{1}{5}\sdot\frac{1}{10}\right)\right]=5+\frac{5}{8}](/mediawiki/images/math/a/b/c/abc6480763890132d71e1f7bd4b5d5c2.png)
![\scriptstyle\left[\left[\left[\left[\left(100\div2\right)\div\frac{1}{2}\right]\div4\right]\div\frac{1}{3}\right]\div\frac{3}{4}\right]\div5](/mediawiki/images/math/0/c/e/0ce5a89a17928644be23031e62662c90.png)
![{\color{blue}{\begin{align}\scriptstyle\left[\left[\left[\left[\left(100\div2\right)\div\frac{1}{2}\right]\div4\right]\div\frac{1}{3}\right]\div\frac{3}{4}\right]\div5&\scriptstyle=100\div\left[\left[\left[\left[\left(2\sdot\frac{1}{2}\right)\sdot4\right]\sdot\frac{1}{3}\right]\sdot\frac{3}{4}\right]\sdot5\right]\\&\scriptstyle=100\div\left[\left[\left[\left(1\sdot4\right)\sdot\frac{1}{3}\right]\sdot\frac{3}{4}\right]\sdot5\right]\\&\scriptstyle=100\div\left[\left[\left(4\sdot\frac{1}{3}\right)\sdot\frac{3}{4}\right]\sdot5\right]\\&\scriptstyle=100\div\left[\left[\left(1+\frac{1}{3}\right)\sdot\frac{3}{4}\right]\sdot5\right]\\&\scriptstyle=100\div\left(1\sdot5\right)\\&\scriptstyle=100\div5=20\\\end{align}}}](/mediawiki/images/math/8/b/c/8bce1c36060f1ae22620f343fb3d9505.png)
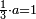
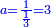
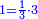
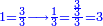
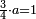
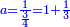
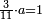
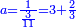
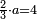
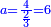
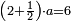
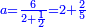
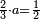
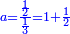
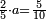
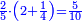
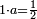
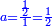
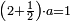
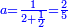
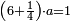
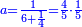
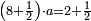
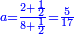
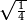
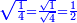
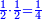
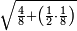
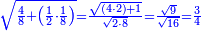
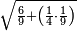
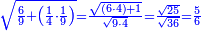
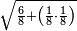
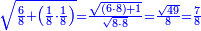
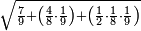
![\scriptstyle{\color{blue}{\sqrt{\frac{7}{9}+\left(\frac{4}{8}\sdot\frac{1}{9}\right)+\left(\frac{1}{2}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)}=\frac{\sqrt{\left[\left[\left(7\sdot8\right)+4\right]\sdot2\right]+1}}{\sqrt{9\sdot8\sdot2}}}}](/mediawiki/images/math/a/5/2/a525cee0c08425bbe4ff1360ead65180.png)
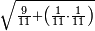
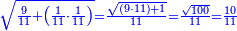
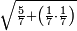
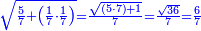
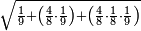
![{\color{blue}{\begin{align}\scriptstyle\sqrt{\frac{1}{9}+\left(\frac{4}{8}\sdot\frac{1}{9}\right)+\left(\frac{4}{8}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)}&\scriptstyle=\frac{\sqrt{\left[\left[\left(1\sdot8\right)+4\right]\sdot8\right]+4}}{\sqrt{9}\sdot8}\\&\scriptstyle=\frac{\sqrt{100}}{3\sdot8}=\frac{10}{3\sdot8}\\&\scriptstyle=\frac{3}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)\\\end{align}}}](/mediawiki/images/math/6/d/c/6dcf8b683d1129d406d816f629e5a971.png)
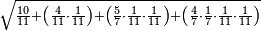
![{\color{blue}{\begin{align}&\scriptstyle\sqrt{\frac{10}{11}+\left(\frac{4}{11}\sdot\frac{1}{11}\right)+\left(\frac{5}{7}\sdot\frac{1}{11}\sdot\frac{1}{11}\right)+\left(\frac{4}{7}\sdot\frac{1}{7}\sdot\frac{1}{11}\sdot\frac{1}{11}\right)}\\&\scriptstyle=\frac{\sqrt{\left[\left[\left[\left[\left(10\sdot11\right)+4\right]\sdot7\right]+5\right]\sdot7\right]+4}}{11\sdot7}\\&\scriptstyle=\frac{\sqrt{5625}}{11\sdot7}=\frac{75}{11\sdot7}\\&\scriptstyle=\frac{10}{11}+\left(\frac{5}{7}\sdot\frac{1}{11}\right)\\\end{align}}}](/mediawiki/images/math/d/0/a/d0a59e45fce2a700b4db03b098b7a970.png)
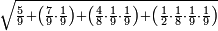
![{\color{blue}{\begin{align}&\scriptstyle\sqrt{\frac{5}{9}+\left(\frac{7}{9}\sdot\frac{1}{9}\right)+\left(\frac{4}{8}\sdot\frac{1}{9}\sdot\frac{1}{9}\right)+\left(\frac{1}{2}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{9}\right)}\\&\scriptstyle=\frac{\sqrt{\left[\left[\left[\left[\left(5\sdot9\right)+7\right]\sdot8\right]+4\right]\sdot2\right]+1}}{\sqrt{2\sdot8}\sdot9}\\&\scriptstyle=\frac{\sqrt{841}}{\sqrt{16}\sdot9}=\frac{29}{4\sdot9}\\&\scriptstyle=\frac{7}{9}+\left(\frac{1}{4}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/8/6/6/866310e1a130f10685a4e4766ed5f465.png)
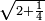
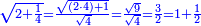
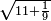
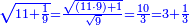
![\scriptstyle\sqrt{\left[4\right]+\frac{4}{8}+\left(\frac{1}{8}\sdot\frac{1}{8}\right)}](/mediawiki/images/math/a/8/e/a8e4e4c1d5bce29afa692163270e21b3.png)

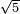
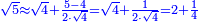
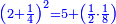
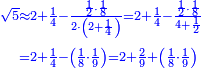
![\scriptstyle{\color{blue}{\left[2+\frac{2}{9}+\left(\frac{1}{8}\sdot\frac{1}{9}\right)\right]^2=5+\left(\frac{1}{8}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{9}\right)}}](/mediawiki/images/math/c/7/e/c7ecbb64983979bd2585829b2ff90688.png)
![\scriptstyle{\color{blue}{\sqrt{5}\approx2+\frac{2}{9}+\left(\frac{1}{8}\sdot\frac{1}{9}\right)-\frac{\frac{1}{8}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{9}}{2\sdot\left[2+\frac{2}{9}+\left(\frac{1}{8}\sdot\frac{1}{9}\right)\right]}}}](/mediawiki/images/math/0/2/a/02af5e239bfa7e479b8d4fc3237bda47.png)