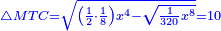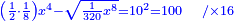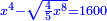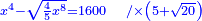המחומשים והמעושרים
Contents[hide]
Introduction |
|
| Abū Kāmil: after explaining what needs explanation of the restoration and confrontation relating to numbers according to our predecessors, by knowledge and wisdom of them, in addition to what was written by those who are well versed in geometry, who know Euclid's Elements and other books. | אמר אבו כאמל אחר אשר ביארנו מה שצריך ביאור מן הנתלה במספרי' מהאסיפה וההשואה דילקובראמיינטו אידיל קונפרונטאמיינטו על הקודמים לנו וזה בידיעה ובחכמה בהם מוסף על מה שכתבו הבקיאים בגמטרייא שידעו ספר האוקלידס וספרים אחרים |
| Here, this book will further define and explain: | הנה נניח עוד ונבאר בספרנו זה |
|
שעור כל צלע מצלעות כל אחד מהמחומשים והמעושרים אשר צלעותיהם שוות וזויותיהם שוות אשר תקיף לכל אחד מהם עגולה ידועה או יקיף כל אחד מהם אל עגולה ידועה |
| ושעור קוטר העגולה אשר תקיף אל המחומש ואל המעושר ידוע שוה הצלעות והזויות או שיקיפו כל אחד מהם אל עגולה ידועה | |
| ושעור הקו החותך חלק אחד מחמשה עשר חלקים ממקיף העגולה | |
| ושעור כל צלע מצלעות המחומש והמעושר שהם שוי הצלעות והזויות כאשר היו ידועי השעור | |
| ושעור צלעות המשולשים ידועי השעור כאשר היו במחומשים ובמעושרים שוי הצלעות והזויות | |
| ודברים אחרים בלעדי אלו נבאר בספרנו זה אשר הוציאו אותם הקודמים בטורח רב ויעידו על זה בעלי המספר והגימטרייא אשר בזמננו זה ואשר כתבו לנו דבריהם מן הקודמים בידיעת המספר והגימטריאה | |
| ויעזרנו השם היכול לחבר הראוי מזה ולישר מה שנניח על הכנתו וישתבח היוצר ויחונן |
Finding the side of a pentagon that is circumscribed by a circle |
|
| I start by extracting the size of a fifth of the circumference of a circle whose diameter is known. | ואתחיל בהוצאת שעור חמשית קו העגולה אשר קטרה ידוע |
|
|
|
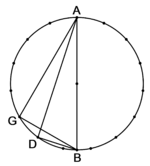
| This is that we suppose the known circle is circle ABHG. | וזה שנניח העגולה הידועה עגלת א"בה"ג |
| Its diameter is ten and it is line CH.
|
וקטרה הוא עשרה במספר והוא קו ח"ה |
| In it there is a regular pentagon enclosed by the circle, which is pentagon ABHG. | ובתוכה מחומש שוה הצלעות והזויות תקיף בו העגולה והוא מחומש אבה"ג |
| When you wish to know the size of each side of this pentagon: | וכאשר תרצה לדעת שעור כל צלע מצלעות זה המחומש |
| We draw line GLD that cuts two fifth of the circle's circumferential line. | נוציא קו גל"ד והוא קו חותך שני חומשי קו המקיף העגולה |
We suppose line HD is a thing [ ]. ].
|
ונניח קו ה"ד דבר |
| It is known that line HL is tenth of the square.
|
והוא ידוע שקו ה"ל עשירית האלגו |
| Since the product of HD by itself is the same as the product of CH by HL.
|
בעבור כי הכאת ה"ד בעצמו היא כמו הכאת ח"ה בה"ל |
| Also line GL is a root of the square minus a tenth of a tenth of a square of the square.
|
וקו ג"ל שרש האלגו פחות עשירית העשירית מאלגו אלגו |
| Line GL is the same as line LD.
|
וקו ג"ל כמו קו ל"ד |
| Line GD is a root of four squares minus two-fifths of a square of a square.
|
ויהיה קו ג"ד שרש מארבעה אלגוש פחות שני חומשי עשירית מאלגו אלגו |
| It is known that [the product of] AB by GD plus [the product of] AB by itself is the same as the product of GD by itself.
|
והוא ידוע שא"ב בג"ד וא"ב בעצמו יהיו כמו הכאת ג"ד בעצמו |
| Since the product of AB by GD plus [the product of] AG by BD is the same as the product of AD by BG.
|
בעבור כי הכאת א"ב בג"ד וא"ג בב"ד יהיו כמו הכאת א"ד בב"ג |
| [The product of] AG by BD is the same as [the product of] AB by itself.
|
וא"ג בב"ד הוא כמו א"ב בעצמו |
| [The product of] AD by BG is the same as [the product of] GD by itself.
|
וא"ד בב"ג הוא כמו ג"ד בעצמו |
| [The product of] GD by itself is four squares minus two-fifths of a tenth of a square of a square.
|
וג"ד בעצמו הוא ארבעה אלגוש פחות שני חומשי עשירית מאלגו אלגו |
| Subtract from it the product of AB by itself, which is a square; three squares minus [two-fifths] of a tenth of a square of a square remains equal to the product of AB by GD. | ותגרע ממנו הכאת א"ב בעצמו והוא אלגו ישאר שלשה אלגוש פחות חמישית עשירית מאלגו אלגו ישוה להכאת א"ב בג"ד |
|
| |
| Divide three squares minus [two-fifths] of a tenth of a square of a square by line AB, which is a thing; the result is line GD, which is three things minus [two-fifths] of a tenth of a cube. | ותחלק שלשה אלגוש פחות חמישית עשירית מאלגו אלגו על קו א"ב והוא דבר ויעלה קו ג"ד שלשה דברים פחות חמישית עשירית ממעוקב בעצמו |
|
| |
| So, it is nine squares plus one part of 625 parts of a cube-cube minus six parts of 25 parts of a square of a square equals four squares minus two-fifths of a tenth of a square of a square.
|
ויהיו תשעה אלגוש וחלק אחד מתרכ"ה חלקים ממעוקב מעוקב פחות ששה חלקים מכ"ה חלקים מאלגו אלגו ישוו ארבעה אלגוש פחות שני חומשי עשירית מאלגו אלגו |
| Confrontation: Confront them; it is a fifth of a square of a square equals five squares and one part of 625 parts of a cube-cube.
|
ותנכח עמהם ויהיה חמישית האלגו אלגו ישוה חמשה אלגוש וחלק אחד מתרכ"ה חלקים ממעוקב מעוקב |
| Divide everything you have by a square.
|
ותחלק כל הדברים שתחזיק על אלגו |
| The result is five dirham plus one part of 625 of a square of a square equals a fifth of a square.
|
ויעלה חמשה אדרהמי וחלק אחד מתרכ"ה מאלגו אלגו ישוה חמישית האלגו |
| Normalization: Complete your square, so it becomes a [whole] square of a square, by multiplying it by 625.
|
ותשלים האלגו שלך עד שיהיה אלגו אלגו והוא שתכהו בתרכ"ה |
| It is a square of a square plus 3125 dirham equals 125 squares.
|
ויהיה אלגו אלגו ושלשת אלפים וקכ"ה אדראהמי ישוו קכ"ה אלגוש |
| Halve [the number of] the squares; it is 62 and a half. | ותחצה האלגוש ויהיו ס"ב וחצי |
| Multiply it by itself; it is 3906 and a quarter. | ותכה אותם בעצמם ויהיה שלשת אלפים ותתק"ו ורביע |
| Subtract 3125 from it; 781 and a quarter remains. | תגרע מהם ג' אלפים וקכ"ה וישאר תשפ"א ורביע |
| We subtract its root from 62 and a half. | ושרש נגרע מס"ב וחצי |
| The root of the remainder is line HD, which is one of the sides of the pentagon. | ושרש הנשאר הוא קו ה"ד שהוא אחד מהצלעות מהמחומש |
|
| |
| Q.E.D. | והוא מה שרצינו לבאר |
Finding the tithe of the circle when the fifth of the circle is known |
|
| When we wish to know the size of the line that cuts a tithe of a known circle, when the line that cuts a fifth of the circle is known: | וכאשר רצינו לדעת שעור הקו החותך עשירית עגולה ידועה וידענו הקו החותך חמישית העגולה |
|
|
|
| We suppose its circumferential line is ABGDHC. | נניח הקו המקיף בה אבגדה"ח |
| We suppose its diameter, which is line AC, is ten.
|
ונניח קוטרה עשרה במספר והוא קו א"ח |
| We draw on its half five equal lines, each of which cuts a tithe of the circle, these lines are: AB, BG, GD, DH, HC. | ונניח בחצייה חמשה קוים שוים וכל אחד מהם חותך עשירית העגולה והם קוי א"ב ב"ג ג"ד ד"ה ה"ח |
| It is known that line DC cuts a fifth of this circle. | והוא ידוע כי קו ד"ח הוא קו חותך לחמישית מזאת העגולה |
| We have already explained that when it is multiplied by itself, it is sixty-two and a half minus a root of 781 and a quarter.
|
וכבר בארנו כי כשהוכה בעצמו הוא ששים ושנים וחצי פחות שרש מתשפ"א ורביע וקו א"ג בעצמו |
| The product of AG by DC plus [the product of] GD by AC is the same as [the product of] AD by GC.
|
והכאת א"ג בד"ח וג"ד בא"ח יהיו כמו א"ד בג"ח |
| AG is the same as DC.
|
וא"ג כמו ד"ח |
| The product of DC by itself plus [the product of] GD by AC is the same as the product of GC by itself.
|
והכאת ד"ח בעצמו וג"ד בא"ח יהיה הכאת ג"ח בעצמו |
| Line GD cuts a tithe of the circle. | וקו ג"ד הוא קו חותך עשירית זאת העגולה |
We suppose it is a thing [ ]. ].
|
ונניחהו דבר |
| Multiply it by line AC, which is the diameter of the circle and it is ten; it is ten things.
|
ותכה אותו בקו א"ח שהוא קוטר העגולה והוא עשרה ויהיה עשרה דברים |
| Multiply line DC by itself; it is 62 and a half minus a root of 781 and a quarter.
|
ותכה קו ד"ח בעצמו ויהיה ס"ב וחצי פחות שרש מתשפ"א ורביע |
| [The product of] line GC [by itself] is 62 and a half plus ten things minus a root of 781 and a quarter.
|
ויהיה קו ג"ח בס"ב וחצי ועשרה דברים פחות שרש מתשפ"א ורביע |
| Add to it the product of AG by itself, which is 62 and a half minus a root of 781 and a quarter; it is 125 dirham plus ten things minus a root of 31[25] dirham. | ותוסיף עליהם הכאת א"ג בעצמו והוא ס"ב וחצי פחות שרש מתשפ"א ורביע ויהיה קכ"ה אדרהמיש ועשרה דברים פחות שרש משלשת אלפים ומאה דרהמיש |
|
| |
| Confrontation: Confront them; it is after the confrontation a root of 3125 dirham minus 25 equals ten things.
|
ותנכח עמהם ויהיה אחרי הנכוחות שרש משלשת אלפים ומאה וקכ"ה אדרהמיש פחות כ"ה ישוה עשרה דברים |
| The thing equals a root of 31 and a quarter minus two and a half and it is line GD that cuts a tithe of the circle.
|
והדבר ישוה שרש מל"א ורביע פחות שנים וחצי והוא קו ג"ד שהוא קו חותך עשירית העגולה |
| Q.E.D. | והוא מה שרצינו לבאר |
Finding the side of a pentagon that circumscribes the circle |
|
| When you wish to know the size of the line that cuts a fifth part of the regular pentagon that circumscribes the circle: | וכאשר תרצה לדעת שעור הקו החותך חמשי חלק אחד מהמחומש השוה הצלעות והזויות אשר יקיף אל עגולה ידועה |
|
|
|
| We suppose the diameter of the circle is ten. | ונניח קוטר העגלה עשרה |
| We construct on it a cyclic regular pentagon, which is pentagon ABGDZ. | ונעשה עליה מחומש שוה הצלעות והזויות והוא מחומש אבגד"ז |
| It is known that line TC cuts a fifth of the circle. | והוא ידוע כי קו ט"ח חותך חמישית העגלה |
| We have already explained that when it is multiplied by itself it is 62 and a half minus a root of 781 and a quarter.
|
וכבר בארנו כי כשהוכה בעצמו הוא ס"ב וחצי פחות שורש מתשפ"א ורביע |
| The square of TL is fifteen and five-eighths minus a root of forty-eight, a quarter, and five-eighths of an eighth.
|
ומרובע ט"ל חמשה עשר וחמשה שמיניות פחות שרש ארבעים ושמנה ורביע וחמשה שמיניות משמינית |
| Subtract it from the square of line TH, which is half the diameter and its square is twenty-five; the square of line HL remains nine, a quarter, an eighth and a root of 48, a half, a quarter and five-eighths of an eighth. | תגרעם ממרובע קו ט"ה שהוא חצי הקוטר ומרובעו עשרים וחמשה וישאר מרובע קו ה"ל תשעה ורביע ושמינית ושרש ממ"ח וחצי ורביע וחמשה שמיניות משמינית |
|
| |
We suppose line AB, which is one of the sides of the pentagon that circumscribes the circle, is a thing [ ] and its square is a square [ ] and its square is a square [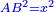 ]. ].
|
ונניח קו א"ב שהוא צלע אחד מצלעות המחומש שיקיף בעגולה דבר ומרובעו אלגו |
| The ratio of this square to the square of line BH, which is twenty-five, is as the ratio of the square of TC, which is the line that cuts a fifth of the pentagon that circumscribes the circle, which is 62 and a half minus a root of 781 and a quarter, to the square of HL, which is nine, a quarter, an eighth, and a root of 48, a half, a quarter and five-eighths of an eighth. | ושעור זה האלגו ממרובע קו ב"ה שהוא עשרים וחמשה כמו שעור מרובע ט"ח שהוא קו חותך חמשית המחומש המקיף בעגולה והוא ס"ב וחצי פחות שרש מתשפ"א ורביע ממרובע ה"ל והוא תשעה ורביע ושמינית ושרש ממ"ח וחצי ורביע וחמשה שמיניות משמינית משמינית |
|
| |
| It is nine squares and three-eighths of a square plus a root of 48, six-eighths, and five-eighths of an eighth squares of a square; and this is equal to the square of KH [multiplied] by the square of TC, which is 1562 and a half minus a root of 488281 and a quarter. | ויהיה תשעה אלגוש ושלשה שמיניות מאלגו ושרש ממ"ח וששה שמיניות וחמשה שמיניות משמינית מאלגו אלגו וזה ישוה מרובע כ"ה במרובע ט"ח והוא אלף ותקס"ב וחצי פחות שרש מתפ"ח אלפים ורפ"א ורביע |
|
| |
| Normalization: Convert everything you have to a square, by multiplying it by a fifth plus a fifth of a fifth minus a root of twenty parts of 625 parts of a dirham.
|
ותשיב כל דבר שתחזיק אל אלגו והוא שתכה אותו בחמישית וחמישית מחמישית פחות שרש מעשרים חלקים מתרכ"ה חלקים מאדרהם |
| Multiply nine squares and three-eighths of a square plus a root of 48, three-quarters, and five-eighths of an eighth squares of a square, by a fifth plus a fifth of a fifth minus a root of twenty parts of 625 parts of a unit; it is a square. | ותכה תשעה אלגוש ושלשה שמיניות מאלגו ושרש ממ"ח אלגוש אלגו ושלשה רביעים מאלגו אלגו וחמשה שמיניות משמינית מאלגו אלגו בחמישית וחמישית מחמישית פחות שרש מעשרים חלקים מתרכ"ה חלקים מאחד ויהיה אלגו |
|
| |
| Multiply 1562 and a half minus a root of 488281 and a quarter by a fifth plus a fifth of a fifth minus a root of twenty parts of 625 parts of a unit; it is 375 dirham plus a root of 15625 minus a root of [78]125 dirham minus a root of 28[1]25 dirham, which is 500 minus a root of 200000. | ותכה אלף תקס"ב וחצי פחות שרש מתפ"ח אלפי' ורפ"א ורביע בחמישית וחמישית החמישית פחות שרש מעשרים חלקים מתרכ"ה חלקים מאחד ויהיה שע"ה אדרהמיש ושרש מט"ו אלפים ותרכ"ה פחות שרש מתת"ע אלף וקכ"ה אדרהמי ופחות שרש מכ"ח אלפי' וכ"ה אדרהמי' וזה הוא ת"ק פחות שרש ממאתים אלף |
|
| |
| The root of this remainder is line AB, which is one of the sides of the regular pentagon that circumscribes the known circle, whose diameter is ten. | ושרש זה הנשאר הוא קו א"ב שהוא צלע אחד מהמחומש שוה הצלעות והזויות המקיף בעגולה ידועה אשר קוטרה עשרה במספר |
| It has already been clarified that the square of line AB, which is one part of the pentagon, is 500 minus two roots of two hundred thousand. Understand this. | וכבר התבאר שמרובע קו א"ב שהוא חלק אחד מהמחומש הוא ת"ק פחות שני שרשים ממאתים אלף והבן זה |
Finding the side of a decagon that circumscribes the circle |
|
| When you wish to know the size of the line that cuts a tithe part of the regular decagon that circumscribes the circle: | וכאשר תרצה לדעת שעור קו החותך עשירית המעושר השוה הצלעות והזויות המקיף בעגולה ידועה |
|
|
|
| Construct a circle whose diameter is ten. | תעשה עגולה יהיה קוטרה עשרה במספר |
| Construct on it a decagon that circumscribes the circle, which is decagon ABGDESCQZM. | ותעשה עליה מעושר אחד שיקיף בעגלה והוא מעושר אבג"ד ע"ס צ"ק ז"מ |
| We wish to know the size of line AB, which is one side of the decagon. | ונרצה לדעת שעור קו א"ב שהוא צלע אחד מהמעושר |
| It is already known that line TC cuts a tithe of the decagon of the circle. | כבר הוא ידוע שקו ט"ח הוא קו חותך עשירית המעושר אשר בעגולה |
| We have explained that it is a root of 31 and a quarter minus two and a half.
|
ובארנו שהוא שרש מל"א ורביע פחות שנים וחצי |
| Line TL is its half, which is a root of seven, a half, a quarter, and half an eighth minus one and a quarter.
|
וקו ט"ל הוא חציו והוא שרש משבעה וחצי ורביע וחצי שמינית פחות אחד ורביע |
| Its square is nine, a quarter, and an eighth minus a root of 48, a half, a quarter and five-eighths of an eighth.
|
ומרובעו הוא תשעה ורביע ושמינית פחות שרש ממ"ח וחצי ורביע וחמשה שמיניות משמינית |
| Subtract it from the square of TH, which is twenty-five; the square of HL remains, which is fifteen, five-eighths, and a root of 48, a half, a quarter and five-eighths of an eighth. | ותגרעם ממרובע ט"ה והוא עשרים וחמשה וישאר מרובע ה"ל חמשה עשר וחמשה שמיניות ושרש ממ"ח וחצי ורביע וחמשה שמיניות משמינית |
|
| |
| The square of TC is thirty-seven and a half minus a root of 781 and a quarter.
|
ומרובע ט"ח שלשים ושבע וחצי פחות שרש מתשפ"א ורביע |
We suppose line AB is a thing [ ] which is one side of the decagon that circumscribes the circle, and its square is a square [ ] which is one side of the decagon that circumscribes the circle, and its square is a square [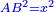 ]. ].
|
ונניח קו א"ב דבר והוא צלע אחד מצלעות המעושר אשר יקיף בעגולה ומרובעו אלגו |
| The ratio of the square to the square of TC, which is thirty-seven and a half minus a root of 781 and a quarter, is the same as the ratio of the square of KH, which is twenty-five, to the square of HL, which is fifteen, five-eighths, and a root of 48, a half, a quarter and five-eighths of an eighth. | ויחס האלגו אל מרובע ט"ח שהוא שלשים ושבע וחצי פחות שרש מתשפ"א ורביע הוא כיחס מרובע כ"ה שהוא עשרים וחמשה אל מרובע ה"ל שהוא חמשה עשר וחמשה שמיניות ושרש ממ"ח וחצי ורביע וחמשה שמיניות משמינית |
|
| |
| Multiply it by the square of AB, which is a square; it is 15 squares and 5-eighths of a square plus a root of 48, 3-quarters, and 5-eighths of an eighth squares of a square equals the square of KH [multiplied] by the square of TC, which is 937 and a half minus a root of 488281. | ותכה אותם במרובע א"ב שהוא אלגו ויהיה ט"ו אלגוש וה' שמיניות מאלגו ושרש ממ"ח אלגוש מאלגו וג' רביעים מאלגו אלגו וה' שמיניות משמינית מאלגו אלגו ישוה מרובע כ"ה במרובע ט"ח והוא תתקל"ז וחצי פחות שרש מתפ"ח אלפים ורפ"א |
|
| |
| Normalization: Convert everything you have to a square, by multiplying everything you have by two-fifths of a fifth minus a root of four-fifths of one part of 625 parts of a unit. | ותשיב כל דבר שתחזיק אל אלגו והוא שתכה כל מה שתחזיק בשני חמישיות מחמישית האחד פחות שרש מארבעה חמישיות מחלק אחד מתרכ"ה חלקים מאחד |
|
| |
| It is a square equals 75 dirham and a root of 625 dirham minus a root of 3125 minus a root of 1125, which is one hundred dirham minus a root of eight thousand and this is the square of line AB, which is one side of the decagon that circumscribes the known circle, whose diameter is ten.
|
ויהיה אלגו ישוה ע"ה דרהמי ושרש מתרכ"ה דרהמי פחות שרש משלשת אלפים וקכ"ה ופחות שרש מאלף וקכ"ה אדרהמי וזה הוא מאה דרהמי פחות שרש משמנת אלפים והוא מרובע קו א"ב שהוא צלע אחד מהמעושר אשר יקיף בעגולה ידועה אשר קוטרה עשרה |
| Q.E.D. | והוא מה שרצינו לבאר |
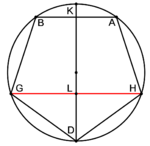
Finding the diameter of a circle that circumscribes a pentagon |
|
| When you wish to know the size of the diameter of a circle that circumscribes a known regular pentagon: | וכאשר תרצה לדעת שעור קוטר עגולה המקפת במחומש ידוע שוה הצלעות והזויות |
|
|
|
| We suppose the known pentagon is pentagon ABGDH. | נניח המחומש הידוע מחומש אבגד"ה |
| We suppose each of its sides is ten. | ונניח כל צלע ממנו עשרה במספר |
| There is a circle that circumscribes it, whose diameter is line KLD. | ועליו עגולה תקיף בו וקטרה קו כל"ד |
| To know its diameter: | ולדעת קטרה |
We draw line HG and suppose it is a thing [ ]. ].
|
שנוציא קו ה"ג ונשימהו דבר |
| We explain that its product by AB, which is ten, plus [the product of] AB by itself equals the product of HG by itself:
|
ונבאר שהכאתו בא"ב שהוא עשרה וא"ב בעצמו הוא שוה להכאת ה"ג בעצמו |
| The product of HG, which is a thing, by AB, which is ten, is ten things.
|
והכאת ה"ג בעצמו שהוא דבר בא"ב שהוא עשרה יהיה עשרה דברים |
| [The product of] AB by itself is one hundred.
|
וא"ב בעצמו מאה |
| [The product of] HG by itself is a square.
|
וה"ג בעצמו אלגו |
| So, it is a square equals ten things and one hundred dirham.
|
ויהיה אלגו ישוה עשרה דברים ומאה דרהמי |
| The thing equals five and a root of 125 and this is line HG.
|
והדבר ישוה חמשה ושרש מקכ"ה והוא קו ה"ג |
| Its half is two dirham, a half and a root of 31 and a quarter and this is line HL.
|
וחציו שני דרהמי וחצי ושרש מל"א ורביע והוא קו ה"ל |
| Multiply it by itself; it is 37 and a half plus a root of 781 and a quarter.
|
תכה אותו בעצמו ויהיה ל"ז וחצי ושרש מתשפ"א ורביע |
| Subtract it from [the product of] HD by itself, which is one hundred; the remainder is 62 and a half minus a root of 781 and a quarter, which is a square of line DL. | תגרעם מה"ד בעצמו שהוא מאה ישאר ס"ב וחצי פחות שרש מתשפ"א ורביע והוא מרובע קו ד"ל |
|
| |
We suppose the diameter of the circle, which is line KLD, is a thing [ ] and its square is a square [ ] and its square is a square [ ]. ].
|
ונניח קטר העגולה שהוא קו כל"ד דבר ומרובעו אלגו |
| The ratio [of the square] of DK to the square of HD, which is one hundred, is the same as the ratio of the square of HD to the square of LD, which is 62 and a half minus a root of 781 and a quarter. | ויחס ד"כ אל מרובע ה"ד שהוא מאה הוא כיחס מרובע ה"ד אל מרובע ל"ד והוא ס"ב וחצי פחות שרש מתשפ"א ורביע |
|
| |
| Multiply it by a square; it is 62 squares and a half minus a root of 781 and a quarter squares of a square equals the square of HD, which is ten thousand.
|
ותכה אותו באלגו ויהיה ס"ב אלגוש וחצי פחות שרש מתשפ"א ורביע אלגו אלגו ישוה רביע מרובע מה"ד בעצמו והוא עשרת אלפים |
| Normalization: Convert everything you have to a square, by multiplying everything you have by a fifth of a tenth plus a root of one part and a quarter of one part of 15625 parts of a unit. | ותשיב כל דבר שתחזיק אל אלגו והוא שתכה כל מה שתחזיק באלגו מחמישית אחת מעשירית אחד ושרש מחלק אחד ורביע מט"ו אלפים ותרכ"ה חלקים מאחד |
|
| |
| It is a square equals two hundred and a root of eight thousand, so it is clear that the square of a diameter of the circle, which is line KLD is two hundred and a root of eight thousand.
|
ויהיה אלגו ישוה מאתים ושרש שמנת אלפים וכבר התבאר כי מרובע קוטר העגולה שהוא קו כל"ד הוא מאתים ושרש משמנת אלפים |
| Q.E.D. | וזה מה שרצינו לבאר |
Finding the diameter of an inscribed circle that is contained in a pentagon |
|
| When we wish to know the diameter of the inscribed circle that is contained in the known regular pentagon ABGDH, each of its sides is ten: | וכאשר נרצה לדעת קוטר העגולה המקפת במחומש אבגד"ה הידוע שוה הצלעות והזויות והוא שכל צלע מצלעותיו עשרה במספר |
|
|
|
| The center of the circle is point M. | ומרכז העגולה נקדת מ' |
| Half its diameter [= radius of the inscribed circle] is line KM. | וחצי קוטרה קו כ"מ |
| Half the diameter [= radius] of the circumscribing circle is line AM. | וחצי קטר העגולה המקפת במחומש הוא קו א"מ |
| We have explained that the square of its diameter is two hundred and a root of eight thousand.
|
ובארנו כי מרובע קטרו הוא מאתים ושרש משמנת אלפים |
| The square of AM, which is half the diameter, is fifty and a root of [five hundred].
|
ומרובע א"מ שהוא חצי הקטר יהיה חמשים ושרש מחמישית |
| Subtract from it the square of AK, which is twenty-five; the square of KM remains, which is half the diameter of the inscribed circle in this pentagon, which is twenty-five and [a root of 500]. | תגרע מהם מרובע א"כ והוא עשרים וחמשה ישאר מרובע כ"מ והוא חצי קוטר העגולה הנופלת בזה המחומש והוא עשרים וחמשה וחלק אחד מת"ק |
|
| |
| The square of the diameter of the inscribed circle in your pentagon is one hundred and a root of eight thousand.
|
ומרובע קטר העגולה אשר נפל המחומש שלך בתוכה הוא מאה ושרש שמונת אלפים |
| Q.E.D. | וזה הוא מה שרצינו לבאר |
| If you wish, multiply one side of the pentagon by itself, then subtract it from the product of the diameter of the circumscribing circle by itself, extract the root of the remainder, and the result is the diameter of the inscribed circle. | ואם תרצה תכה צלע אחד מהמחומש בעצמו ותגרעהו מהכאת הקטר מהעגולה אשר נפלה על זה המחומש בעצמו ותקח שרש הנשאר והיוצא הוא קוטר העגולה אשר נפלה תוך המחומש |
| This method is drawn from a regular figure. | וזה האופן יצא מצורה שות הצלעות והזויות |
| When we wish to know the size of the diameter of the inscribed circle that is contained in a known regular pentagon, each of its sides is ten, by a different procedure from the one we explained above: | וכאשר נרצה לדעת שעור קוטר עגולה מקפת במחומש ידוע שוה הצלעות והזויות וכל צלע ממנו עשרה במספר בזולת המעשה אשר בארנו קודם |
| It is known from Euclid's words that for any line that cuts a part of the circle, the ratio of this line to the line that cuts a part of another circle equal to the part that the said line cuts from the said circle is the same as the ratio of the diameters of the circles to each other. | יהיה ידוע ממה שאמר אוקלידס שכל קו יחתוך חלק אחד מהעגולה יהיה יחס זה הקו אל הקו אשר יחתוך מעגולה אחרת חלק שוה כמו החלק אשר חתך הקו האמור מהעגולה האמורה כיחס קטרי העגולות האחד באחר |
| We have already explained concerning the circle whose diameter is ten, that the square of the line that cuts a fifth of this circle is 62 and a half minus a root of 781 and a quarter. | וכבר בארנו כי העגולה אשר קטרה עשרה יהיה מרובע הקו החותך חמישית זאת העגולה ס"ב וחצי פחות שרש מתשפ"א ורביע |
| It is known from what we said that the ratio of one hundred to 62 and a half minus a root of 781 and a quarter is the same as the ratio of the square, which is the square of the diameter of the unknown inscribed circle of the pentagon, each side of which is ten, which we assumed to be a thing, to one hundred, which is the square of the diameter of the circumscribing circle of the known pentagon.
|
והוא ידוע ממה שאמרנו כי יחס המאה אל הס"ב וחצי פחות שרש מתשפ"א ורביע יהיה כיחס האלגו שהוא מרובע קטר קטר העגולה בלתי ידועה אשר יקיף בה המחומש אשר כל חלק ממנו עשרה בעבור כי הח הנחנוהו דבר ממאה והוא מרובע קטר העגולה המקפת אל המחומש הידוע |
| Multiply one hundred by one hundred; it is ten thousand.
|
ותכה מאה במאה יהיה עשרת אלפים |
| Multiply the square by 62 and a half minus a root of 781 and a quarter; it is 62 and a half squares minus a root of 781 and a quarter squares of a square equals ten thousand.
|
ותכה אלגו בס"ב וחצי פחות שרש מתשפ"א ורביע ויהיה ס"ב אלגוש וחצי אלגו פחות שרש מתשפ"א ורביע מאלגו אלגו וישוה עשרת אלפים |
| Normalization: Convert everything you have to a square, by multiplying everything you have by a fifth of a tenth plus a root of one part and a quarter of one part of [15]625 parts of a unit. | ותשיב כל דבר שתחזיק אל אלגו והוא שתכה כל דבר שתחזיק בחמישית העשירית מאחד ושרש חלק אחד ורביע חלק מכ"ה אלפים ותרכ"ה חלקים מאחד |
|
| |
| It is a square equals two hundred dirham and a root of eight thousand and this is the square of the diameter of the inscribed circle contained in the pentagon, each side of which is ten.
|
ויהיה אלגו ישוה מאתים דרהמי ושרש משמנת אלפים והוא מרובע קטר העגולה המקפת במחומש כאשר היה כל צלע ממנו עשרה |
Finding the diameter of a circle that is inscribed by a pentagon |
|
| When we wish to draw in a known regular pentagon, each side of which is ten, an inscribed circle contained by the pentagon: | וכן כאשר נרצה לעשות במחומש ידוע שוה הצלעות והזויות וכל צלע ממנו הוא עשירית עגלה אשר יקיף בה המחומש |
| We have already explained concerning the circle, whose diameter is ten, that the square of each side of the pentagon surrounding the circle is 500 minus a root of two hundred thousand. | וכבר בארנו כי עגולה אשר יהיה קוטרה עשרה יהיה המרובע מכל צלע מהמחומש המקיף בעגולה ת"ק פחות שרש ממאתים אלף |
| I say that [the ratio of one hundred] to the part of the pentagon, which is 500 minus a root of two hundred thousand, is as [the ratio] of the square, which is the square of the required [diameter of the] unknown circle, to the diameter of the known circle, which is one hundred.
|
ואומר ויהיה החלק מהמחומש מת"ק פחות שרש ממאתים אלף יהיה אלגו והוא מרובע העגולה הבלתי ידועה המבוקש כקטרה אל קטר העגולה הידועה והוא מאה |
| Multiply one hundred by one hundred; it is ten thousand.
|
ותכה מאה במאה ויהיה עשרת אלפים |
| Multiply the square by 500 minus a root of two hundred thousand; it is 500 squares minus a root of two hundred thousand squares of a square equals ten thousand dirham.
|
ותכה אלגו בת"ק פחות שרש ממאתים אלף ויהיה ת"ק אלגוש פחות שרש ממאתים אלף אלגו אלגו ישוה עשרת אלפים דרהמי |
| Normalization: Convert everything you have to a square, by multiplying everything you have by a tenth of a tenth plus a root of one part of 12500 parts of a unit. | ותשיב כל דבר שתחזיק אל אלגו והוא שתכה כל מה שתחזיק בעשירית העשירית מאחד ושרש חלק אחד מי"ב אלפים ות"ק חלקים מאחד |
|
| |
| The square equals one hundred and a root of eight thousand and this is the square of the diameter of the inscribed circle contained by the pentagon, each side of which is ten.
|
ויהיה האלגו ישוה מאה ושרש משמנת אלפים והוא מרובע הקטר מן העגולה אשר נפלה בזה המחומש אשר כל צלע מצלעיו עשרה |
Finding the diameter of a circle that is inscribed by a decagon |
|
| When we wish to construct in a known regular decagon, each side of which is ten, an inscribed circle contained by the decagon: | וכן כאשר נרצה לעשות על מעושר ידוע שוה הצלעות והזויות אשר כל צלע ממנו הוא עשירית העגולה המקפת בזה המעושר |
| We have already explained concerning the circle, whose diameter is ten, that the [side] of the decagon inscribed in it is a root of 31 and a quarter minus two and a half. | וכבר בארנו כי עגלה שיהיה קטרה עשרה שעגלת המעושר אשר נפל בתוכה הוא שרש מל"א ורביע פחות שנים וחצי |
We suppose the diameter of the circle is a thing [ ]. ].
|
ונניח קטר העגולה דבר |
| Say that the ratio of the thing to ten is the same as the ratio of ten to the root of 31 and a quarter minus two and a half.
|
ותאמר כי יחס הדבר אל עשרה יהיה כמו יחס העשרה אל שרש ל"א ורביע פחות שנים וחצי |
| Multiply ten by ten; it is a hundred.
|
ותכה ותכה עשרה בעשרה יהיה מאה |
| Multiply a thing by a root of 31 and a quarter minus two and a half; it is a root of 31 squares and a quarter minus two things and a half. | ותכה דבר בשרש מל"א ורביע פחות שנים וחצי ויהיה שרש מל"א אלגו ורביע פחות שני דברים וחצי |
|
| |
| Restore it with two things and a half; it equals a root of 31 squares and a quarter. | ותאספם עם השני דברים וחצי ישוה שרש מל"א אלגו ורביע |
|
| |
| Multiply one hundred dirham plus [two] thing[s] and a half by themselves; it is ten thousand dirham plus six squares and a quarter and 500 things equals 31 squares and a quarter. | ותכה מאה דרהמי ודבר וחצי בעצמו ויהיה עשרת אלפים אדרהמי וששה אלגוש ורביע ות"ק דברים ישוה ל"א אלגו ורביע |
|
| |
| Confront them; the thing is ten plus a root of 500 and this is the root of the diameter of the inscribed circle of the decagon, each side of which is ten.
|
ותנכחם עמהם ויהיה הדבר עשרה ושרש מת"ק והוא שרש קטר עגלת המעושר אשר כל צלע מצלעותיו עשרה |
| When we wish to construct a circle circumscribed about a known regular decagon, each side of which is ten: | וכן כאשר נרצה לעשות במעושר ידוע שוה הצלעות והזויות אשר כל צלע ממנו עשרה עגולה אחת תקיף בזה המעושר |
| We have already explained concerning the circle, whose diameter is ten, that the square of the side of the circumscribed decagon is one hundred minus a root of eight thousand. | וכבר בארנו כי עגלה אשר קוטרה עשרה יהיה מרובע הקו אשר הוא חלק אחד מהמעושר שנפל עליו הוא מאה פחות שרש משמנת אלפים |
| I say that the ratio of one hundred minus a root of eight thousand to one hundred is the same as its ratio to the square.
|
ואומר כי יחס מאה פחות שרש משמנת אלפים אל מאה יהיה כיחסם אל אלגו |
| Multiply it by itself; it is ten thousand.
|
תכה אותם בעצמם יהיו עשרת אלפים |
| Multiply one hundred minus a root of eight thousand by a square; it is ten thousand times one hundred squares minus a root of eight thousand squares of a square equals ten thousand.
|
ותכה מאה פחות שרש משמנת אלפים באלגו ויהיה עשרת אלפים פעם מאה אלגוש פחות שרש משמנת אלפים אלגו אלגו ישוה עשרת אלפים |
| Normalization: Reduce everything you have into one square by multiplying it by half a tenth plus a root of one part of 500.
|
ותשיב כל אשר תחזיק אל אלגו והוא שתכה אותו בחצי עשירית אחד ושרש חלק אחד מת"ק חלקים מאחד |
| The square is equal to 50 plus a root of two hundred thousand and this is the square of the diameter of the circle circumscribed about the decagon.
|
ויהיה האלגו ישוה ת"ק ושרש ממאתים אלף והוא מרובע קטר העגולה אשר נפלה חוץ מן המעושר בעצמו |
| We have already explained that if the diameter is ten plus a root of 500, its square is a hundred plus a root of two hundred thousand. | וכבר בארנו שאם הקוטר הוא עשרה ושרש מת"ק יהיה מרובעו מאה ושרש ממאתים אלף |
| Subtract a hundred from it, which is the product of one side of the [inscribed] decagon by itself; the remainder is 500 plus a root of two hundred thousand, and this is the diameter of the circle circumscribed about the decagon. | תגרע מהם מאה והוא הכאת צלע אחד מהמעושר בעצמו ישאר ת"ק ושרש ממאתים אלף ושרש זה הוא קטר העגולה אשר נפלה חוץ מזה המעושר |
| I will explain the reason for this procedure: | ואניח סבת זה האופן |
| It is because when a regular figure is circumscribed about a circle and inscribed in a circle, [the sum of] the product of one of the sides [of that figure] by itself and the product of the diameter of the inscribed circle by itself equals the product of the diameter of the circumscribed circle by itself. | והוא כי כל תמונה שות הצלעות והזויות אשר תקיף בעגולה ותקיף בה עגולה הנה הכאת אחת הצלעות בעצמה והכאת קטר העגולה אשר נפלה פנימה בעצמו יהיו שתי אלו ההכאות יחד כמו הכאת קטר העגולה המקפת בתמונה בעצמו |
|
|
|
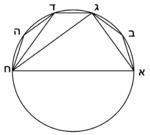
| Example: We draw an equilateral triangle, let it be the triangle ABG. | דמיון זה שנעשה משולש שוה הצלעות והזויות והוא משולש אב"ג |
| In the triangle the inscribed circle CZL. | ובתוכו עגולה יקיף בה המשולש עליה חז"ל |
| Another circle ABG is circumscribed about the triangle, the diameter of which is line AD. | ותקיף למשולש עגולה אחרת עליה אב"ג וקטרה קו א"ד |
| The diameter of the inscribed circle is line KE. | וקטר העגלה הפנימית מהמשולש הוא קו כ"ע |
| I say that [the sum of] the product of AG by itself and KE by itself is the same as the product of AD by itself. | ואומר שהכאת א"ג בעצמו וכ"ע בעצמו יהיו כמו הכאת א"ד בעצמו |
| Proof: We draw a perpendicular line bisecting the inner circle, from line AG, at point L, which is where the line is tangent to the inner circle. | מופת זה שנוציא מקו א"ג מנקדת ל' ממנו והוא המקום אשר ימשש בו זה הקו אל העגולה הפנימית קו אחד על זוית נצבה יחלק העגולה הפנימית |
| It is known that it passes through the center of the two circles. | והוא ידוע שיעבור על מרכז שתי העגולות |
| We extend it to the point of intersection with circle CZL, let it be line LZ. | ונוציאהו עד שיעבור אל מקיף זאת העגולה היא עגולת חז"ל והוא קו ל"ז |
| This line is the same as the diameter of the CZL circle and is equal to the line KE. | ויהיה זה הקו כמו קטר עגולת חז"ל והוא שוה לקו כ"ע |
| We attach point Z to point D by line ZD. | ונדביק נקדת ז' בנקדת ד' עם קו ז"ד |
| We attach point D to point G by line GD. | ונדביק ד' בג' עם קו ג"ד |
| Line AN is equal to line MD.
|
ויהיה קו א"מ שווה לקו מ"ד |
| Line ML is equal to line MZ.
|
וקו מ"ל כמו קו מ"ז |
| Angle AML is the same as angle DMZ.
|
וזוית אמ"ל כמו זוית דמ"ז |
| Line DZ is the same as line AL.
|
וקו ד"ז כמו קו א"ל |
| AL is the same as LG.
|
וא"ל כמו ל"ג |
| Angle GLZ is the same as [angle] DZL.
|
וזוית גל"ז כמו דז"ל |
| Triangle AML is the same as triangle DMZ.
|
ומשולש אמ"ל כמו משולש דמ"ז |
| The angles of the one are equal to the angles of the other. | וזויות האחד כמו זויות האחר |
| Angle ALM is the same as angle MZD.
|
וזוית אל"מ כמו זוית מז"ד |
| Line ZD is equal to line LG.
|
וקו ז"ד יהיה שוה לקו ל"ג |
| וכבר בארנו שהם שוים ושנדבקו שני ראשי כל אחד מהם קו משני קוים אלו עם קוי ז"ל וד"ג | |
| Line ZL is equal to line DG.
|
ויהיה קו ז"ל שוה לקו ד"ג |
| Multiply AG by itself and GD by itself; [their sum] is the same as the product of AD by itself.
|
ותכה א"ג בעצמו וג"ד בעצמו ויהיה כמו הכאת א"ד בעצמו |
| Since angle AGD is a right angle.
|
בעבור כי זוית אג"ד נצבת |
| DG is the same as LZ.
|
וד"ג הוא כמו ל"ז |
| LZ is the same as KE.
|
ול"ז כמו כ"ע |
| The [sum of the] product of AG by itself and the product of KE by itself is the same as the product of AD by itself.
|
והנה הכאת א"ג בעצמו וכ"ע בעצמו יהיו כמו הכאת א"ד בעצמו |
| Q.E.D. | והוא מה שרצינו לבאר |
Finding the side of a pentadecagon that is circumscribed by a circle |
|
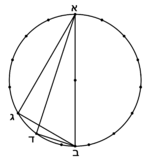
| When we define a regular pentadecagon shape that is circumscribed by a circle whose diameter is ten, its sides and angles are equal, and we wish to know the size of each of its sides. | וכאשר נניח תמונה בעלת חמש עשרה זויות שוות תקיף בה עגולה אשר קטרה עשרה והיא שות הצלעות והזויות ונרצה לדעת שעור כל צלע ממנה |
|
|
|
| We suppose the known circle is circle ABG. | נניח העגולה הידועה עגולת אב"ג |
| Its diameter is AB. | וקטרה א"ב |
|
ונעשה בתוכה צלע אחד יחתוך המעושר שלה והוא חלק וחצי מאחד מהחמשה עשר והוא קו ב"ד |
|
וכבר בארנו שהוא שרש מל"א ורביע פחות שנים וחצי |
|
וקו א"ד הוא תשלומה והוא קו חותך שני חמשי העגולה |
|
|
והוא ס"ב וחצי ושרש מתשפ"א הנלקח שרשו |
| וארשום בזאת העגולה קו חותך הששית והוא קו ב"ג והוא קו חותך שני חלקים וחצי מהחמש עשרה והוא חותך מחמשה | |
|
וקו א"ג הוא תשלומה והוא קו חותך שלישית העגולה |
|
|
והוא שרש מע"ה |
| ותכה קו ב"ד והוא שרש מל"א ורביע פחות שנים וחצי בקו א"ג והוא שרש מע"ה ויהיה שרש מאלפיים ושמ"ג וחצי ורביעית פחות שרש מתס"ח וחצי ורביע | |
|
| |
| ותגרעם מהכאת קו א"ד בקו ב"ג והוא אלף ותקס"ב וחצי ושרש מת' אלפים ופ"א אלפים ורפ"א ורביע הלקוח שרשו | |
| ותוסיף עליו שרש מתס"ח וחצי ורביע ותגרע מכל זה שרש מאלפים ושמ"ג וחצי ורביעית והוא כמו הכאת קו א"ב בקו ג"ד | |
| ומה שישאר תחלקהו על קו א"ב והוא עשרה ויעלה קו ג"ד חמשה עשר וחמשה שמיניות ושרש ממ"ח ושלשה רביעים וחמשה שמיניות משמינית לקוח שרשו ושרש מארבעה דרהמי וחצי ושמינית וחצי שמינית פחות שרש מכ"ג ושלשה שמיניות וחצי שמינית | |
| ונדביק הוצאת ג"ד בעבור שתבינהו תקח שרש ממ"ח ושלשה רביעים וחמשה שמיניות משמינית פור לו מאש סירקאנו ויהיה ששה ונ"ט דקים וט"ו שניים ומ"ו שלישיים . תוסיפם על ט"ו ושלשה שמיניות ויהיה ויהיה כ"ב ול"ו דקים ומ"ה שניים ומ"ו שלישיים . ותקח השרשו ויהיה לו מאש סירקאנו ארבעה ומ"ה דקים וי"ט שניים ושליש אחד . ותוסיף עליו שרש מד' וחמשה שמיניות וחצי שמינית פור לו מאש סירקאנו והוא שנים וט' דקים ונ"ד שניים וי"ב שלישיים תגרע מהם שרש מכ"ג ושלשה שמיניות וחצי שמינית והוא ארבעה דרהמי ונ' דקים וכ"ח שניים וכ"ה שלישיים וישאר שנים וד' דקים ומ"ה שניים והוא קו ג"ד פור לו מאש סירקאנו | |
| Q.E.D. | והוא מה שרצינו לבאר |
Finding the height of an equilateral triangle |
|
| If you are told: an equilateral triangle whose area is ten, how much is its height? | ואם יאמרו לך משלש שוה הצלעות והזויות עשרה במספר כמה יהיה קטרו |
|
ונניח המשולש אב"ג |
|
וקטרו א"ד |
We wish to know the size of AD that is the height of 
|
ונרצה לדעת שעור א"ד שהוא קטר המשולש מאב"ג |
We suppose it is a thing [ ]. ].
|
נניחהו דבר |
|
|
ויהיה קו ד"ג שרש משלישית האלגו |
|
וכל חלק מהמשולש מאב"ג שרש מאלגו ושליש |
|
ושעור משלש אב"ג שרש משלישית אלגו אלגו |
|
וקוטרו דבר |
|
|
ויהיה דבר ושרש משלישית אלגו אלגו ישוה עשרה |
| Normalization:
|
ותשלים שרש משלישית אלגו אלגו עד שיהיה שרש אלגו אלגו והוא אלגו והשלימך אותו הוא שתכה אותו בשרש שלשה ותכה כל מה שתחזיק בשרש משלשה |
|
|
ויהיה אלגו ושרש שלשה אלגוש ישוה שרש משלש מאות |
| ותחצה שרש משלשה אלגוש ויהיה שרש משלשה רביעים תכה אותו בעצמו ויהיה שלשה רביעים | |
|
| |
| Q.E.D. | והוא מה שרצינו לבאר |
Finding the length of a rectangle that is encompassed by an equilateral triangle |
|
| If you are told: an equilateral triangle, each side of which is ten, inside it a rectangle, whose area is ten, how much is the length of the rectangle? | ואם יאמרו לך משלש שוה הצלעות והזויות כל חלק ממנו עשרה ובתוכו מרובע ארוך נצב הזויות ושעורו עשרה כמה יהיה אורך המרובע |
For example, we define the triangle as 
|
דמיון זה שנשים משולש משלש אב"ג |
| The rectangle in it is rectangle HZCT | והמרובע ארוך שנפל בתוכו מרובע הזח"ט |
| We wish to know the size of line CH, which is the length of the rectangle. | ורצינו לדעת שעור קו ח"ה שהוא אורך המרובע |
|
ונשימהו דבר |
|
ויהיה קו ב"ח שרש משלישית האלגו |
|
וכן הוא קו ט"ג שרש משלישית אלגו |
|
ישאר קו ח"ט עשרה פחות שרש מאלגו ושליש |
|
תכה אותו בקו ה"ח והוא דבר יהיה עשרה פחות שרש מאלגו אלגו ושלישית מאלגו אלגו ישוה עשרה דרהמי |
|
ותאסוף הדברי' עם שרש מאלגו אלגו ושלישית מאלגו אלגו ותוסיפם על האדרהמיש |
|
|
ותכה עשרה דרהמי ושרש מאלגו אלגו ושלישית אלגו אלגו ישוה עשרה דברים |
| Normalization:
|
ותשיב כל הדברים דבר אשר תחזיק אל שרש אלגו אלגו והוא אלגו וזה שנכה אותו בשרש משלשה רביעיות תכה כל מה שתחזיק בשרש משלשה רביעיות |
|
|
ויהיה אלגו ושרש מע"ה דרהמי ישוה שרש מע"ה דרהמי אלגוש |
|
|
ותחצה שרש מע"ה ויהיה שרש מי"ח וחצי ורביע תכה אותו בעצמו ויהיה י"ח וג' רביעים |
Finding the side of a square that is contained in an equilateral triangle |
|
| If you are told: an equilateral triangle ABG, inside it a square CLEM, the measure of [the sum of] the triangle and the square is ten, how much is each side of the square CLEM and how much are the areas of the triangle and the square? | ואם יאמרו לך משלש שוה הצלעות והזויות עליו אב"ג ובתוכו מרובע נצב הזויות ושוה הצלעות עליו חלע"מ ושעור המשולש והמרובע עשרה כמה יהיה כל חלק ממרובע חלע"מ וכמה יהיה שעור המשולש והמרובע |
|
ולדעת זה נשים כל חלק מהמרובע דבר |
|
ויהיה שעורו אלגו |
|
וישאר שעור משולש אב"ג עשרה פחות אלגו |
|
ושעור המרובע אלגו |
|
וישאר שעור משלשי בל"ח ומע"ג ואח"ע עשרה פחות שני אלגוש |
|
והנחנו כל חלק מהמרובע דבר ויהיה קו מ"ע |
|
וקו מ"ג שרש שלישית אלגו |
|
|
ושעור משלש מע"ג |
|
וקו ל"ב שרש שלישית אלגו אלגו |
|
וקו א"ט שרש משלשה רביעיות מאלגו |
|
|
ושעור משלש אח"ע שרש משמינית אלגו אלגו וחצי שמיני' אלגו אלגו |
|
ויהיה משלש מע"ג ומשלש חב"ל ומשלש חע"א שרש משלישית אלגו אלגו ושרש משמינית אלגו אלגו וחצי שמינית מאלגו אלגו וישוו עשרה פחות שני אלגוש |
| Normalization: Complete a root of a third of a square of a square, so it becomes a root of a square [of a square], which is a square, by multiplying it by a root of three:
|
ותשלים שרש משלישית אלגו אלגו עד שיהיה שרש מאלגו והוא אלגו והשלימך אותו הוא שתכה אותו בשרש משלשה |
|
|
תכה שרש שלישית אלגו אלגו בשרש משלשה יהיה שרש מאלגו אלגו והוא אלגו |
|
|
ותכה שרש שמינית אלגו אלגו וחצי שמינית מאלגו אלגו בשרש שלשה ויהיה שרש מחצי אלגו אלגו וחצי שמינית אלגו אלגו והוא שלשה רביעים מאלגו |
|
|
ויהיה אלגו ושלשה רביעים מאלגו |
|
|
ותכה עשרה פחות שני אלגוש בשרש שלשה יהיה שרש משלש מאות פחות שרש מי"ב אלגו אלגו |
|
|
ויהיה אלגו ושלשה רביעי אלגו ישוה שרש משלש מאות פחות שרש מי"ב אלגו אלגו |
|
ותשלים שרש משלש מאות עם שרש מי"ב אלגו אלגו ותוסיפהו על אלגו ושלשה רביעים |
|
|
ויהיה אלגו ושלשה רביעים ושרש מי"ב אלגו אלגו ישוה שרש משלש מאות |
| Normalization: Convert everything you have to a square, by multiplying everything you have by a root of 3072 parts of 20449 minus 28 parts of 143.
|
ותשיב כל דבר שתחזיק אל אלגו והוא שתכה כל מה שתחזיק בשרש משלשת אלפים וע"ב חלקים מעשרים אלף ותמ"ט חלקים מאחד פחות כ"ח חלקים מקמ"ג דרהמי |
|
|
ויהיה אלגו ישוה שרש ממ"ה דרהמי ואלף ושצ"ה חלקים מכ"ה אלפים ותמ"ט חלקים מאחד פחות שרש מי"א דרהמי ועשרת אלפי' ורס"א חלקים מכ' אלף ותמ"ט חלקים מאדרהם |
Which is the area of sqaure CLEM in 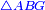
|
והוא שעור מרובע חלע"מ אשר במשולש אב"ג |
| תגרעהו מעשרה ומה שישאר הוא שעור משולש אב"ג | |
| ואם תרצה תאמר כי שעור המרובע ששה וק"ב חלקים מקל"ב חלקים מאחד פחות שרש מיא מי"א אדרהמי ועשרת אלפים ורס"א חלקים מעשרים אלפים ותמ"ט חלקים מדרהם אחד | |
| ושעור המשולש שלשה ומ"א חלקים מקמ"ג חלקים מאחד ושרש מי"א ועשרת אלפים ורס"א חלקים מעשרים אלפי' ותמ"ט חלקים מאחד |
Finding each side of a pentagon that is encompassed by a square |
|
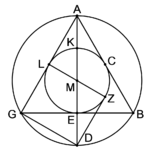
| ואם יאמרו לך מרובע שוה הצלעות והזויות נצבות וכל צלע ממנו עשרה והוא מרובע אבג"ד | |
| ועשינו בו מחומש אחד כמו זאת התמונה והוא מחומש אהחז"מ | |
| ורצינו לדעת כל צלע מצלעות המחומש כמה יהיה שעורו | |
| ולדעת זה נניח החלק האחד מהמחומש והוא קו א"ה דבר | |
| וישאר קו ח"ב עשרה פחות שרש מעש מדבר | |
| וקו ג"ז חצי אלגו | |
| וקו ב"ה עשרה פחות דבר | |
| ותכה כל אחד מהם בעצמו ותקבצם ויהיה מאתים דרהמי ואלגו וחצי אלגו פחות עשרים שרשים ופחות שרש ופחות שרש ממאתים אלגוש ישוה אלגו | |
| ותנכחהו עמו ויהיה קו א"ה שהוא צלע אחד מהמחומש מאתים ושרש מש"כ אלפים כשילקח שרש זה ויגרע מעשרים ושרש מן מאתים | |
| Q.E.D. | וזה הוא מה שרצינו לבאר |
| ואני מרדכי הכותב מה שמצאתי מלה במלה העתקתי אבל לא הבינותי כלל מזאת התמונה | |
| גם נראה לי כי הצורה הראויה לבאר היא שיהיה גם המחומש שוה הצלעות והזויות יקיף בו המרובע כמו זאת התמונה השניה | |
| ואחרי זה מדי השלימי לרשום זאת התמונה השניה הבינותי בה והנה המרובע הוא המקיף במחומש הוא מרובע ארוך לא מרובע אמתי | |
| ונראה שלא יתכן לעשות מרובע אמתי יקיף במחומש שוה הצלעות והזויות כי אם כמו זאת התמונה השלישית אשר פניה דורכות מול פני התמונה הראשונה אשר נעתקה מן הספר הלועז | |
| וחשבתי ראשונה שהתמונה היתה משובשת בספר ובאתי לישרה כאשר יישרתי הרבה מן התמונות האחרות וישתבח השם שפתח עיני כן יראני נפלאות בתורתו אכיר' |
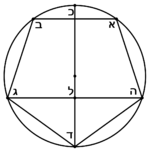
Finding each side of a regular pentagon whose area is fifty spans |
|
| If you are told: a regular pentagon whose area is fifty spans, how much is each of its sides? | ואם יאמרו לך מחומש שוה הצלעות והזויות שעורו חמשים זרתות כמה יהיה כל חלק ממנו |
| דמיון זה שנניח המחומש מחומש אבגד"ה | |
| ומרכז העגולה אשר יקיף בה זה המחומש נקדת מ' | |
| ונוציא קוי א"מ מ"ב מ"ג מ"ד מ"ה | |
| והוא ידוע שנחלק זה המחומש למשולשים שוים והם אמ"ב במ"ג גמ"ד דמ"ה המ"א | |
| ויהיה משלש המ"ד עשרה במספר | |
| וכבר בארנו במה שאמרנו קודם בזה הספר שיהיה כאשר נניח מחומש שוה הצלעות והזויות כל חלק ממנו עשרה יהיה מרובע הקטר מהעגלה אשר תקיף בו מאתים ושרש משמנת אלפים | |
| וידוע ממה שאמרנו שכאשר נרצה לדעת קטר עגולה מקפת במחומש ידוע שנכה חלק אחד מהמחומש בעצמו ונכפלהו ונשמרהו . ונכה חלק אחד מהמחומש בעצמו והעולה נכה בעצמו ונקח ארבעה חמשיו ומה שיצא תקח שרשו והעולה תוסיפהו על מה ששמרת ואשר יתקבץ תקח שרשו והעולה יהיה קטר העגולה | |
| וכאשר נניח זה כן נניח קו ה"ד דבר והוא חלק אחד מהמחומש ויהיה מרובע קטר העגולה כפי מה שבארנו שני אלגוש ושרש מארבעה חמשים מאלגו אלגו | |
| ומרובע חצי קטרה והוא קו ה"מ הוא חצי אלגו ושרש חצי עשירית מאלגו אלגו | |
| ונוציא עמוד ממשולש המ"ד וידוע שיפול בנקדת חצי קו ה"ד והוא קו מ"ח | |
| ויהיה קו ה"ח חצי דבר תכה אותו בעצמו יהיה רביע אלגו | |
| תגרעהו ממרובע קו ה"מ והוא חצי אלגו ושרש מחצי עשירית אלגו אלגו וישאר מרובע קו מ"ח רביע אלגו ושרש מחצי עשירית מאלגו אלגו | |
| תכה אותו בקו ה"ח והוא חצי דבר ויהיה חצי שמינית מאלגו אלגו ושרש משני חלקים מש"כ חלקים מאלגו אלגו אלגו אלגו ישוה עשרה מוכה בעצמו והוא מאה | |
| Normalization: Complete half an eighth of a square of a square, so it becomes a whole square of a square, by multiplying it by sixteen, then multiply everything you have by 16.
|
ותשלים חצי שמינית מאלגו אלגו עד שיהיה אלגו אלגו והוא שתכה אותו בששה עשר תכה כל אשר תחזיק בי"ו |
| It is a square of a square plus a root of four-fifths of square-square-square-square equals 1600.
|
ויהיה אלגו אלגו ושרש מארבעה חמשים מאלגו אלגו אלגו אלגו ישוה אלף ות"ר |
| Normalization: Convert everything you have to a square of a square, by multiplying everything you have by five minus a root of twenty.
|
ותשיב כל מה שתחזיק אל אלגו אלגו וזה שתכה כל דבר שתחזיק בחמשה פחות שרש מעשרים |
| It is a square of a square equals eight thousand minus a root of fifty-one thousand of thousand and two hundred thousand.
|
ויהיה אלגו אלגו ישוה שמנת אלפים פחות שרש מחמשים ואחד אלף אלפים ומאתים אלף |
| תקח שרש זה והיוצא יהיה כל חלק מהמחומש | |
|
ואם יאמרו לך מעושר שוה הצלעות והזויות שעורו מאה מהמספר כמה יהיה כל חלק ממנו |
|
דמיון זה שנניח המעושר מעושר אב"ג דה"ו זחט"ל |
|
ומרכז העגולה אשר תקיף לזאת העגולה נקדת מ' |
|
והוא ידוע שנחלק לעשרה משולשים שוים |
|
ויהיה משולש זמ"ו עשרה |
| וכבר בארנו קודם זה שכאשר נניח מעושר שוה הצלעות והזויו' כל חלק ממנו עשרה שקוטר העגולה אשר תקיף לזה המעושר יהיה עשרה ושרש מת"ק | |
| ויהיה ידוע מאשר אמרנו כי כאשר נרצה לדעת קוטר עגולה תקיף למעושר ידוע שתכה חלק אחד מהמעושר בעצמו והעולה בחמשה ותקח שרש העולה ותוסיפהו על חלק אחד מהמעושר והיוצא יהיה הוא קוטר העגולה | |
| ואחר שמבואר הוא זה ממה שאמרנו נניח קו ז"ו דבר והוא חלק אחד מהמעושר ויחוייב שיהיה קוטר העגולה דבר ושרש מחמשה אלגוש | |
|
וחצי הקטר והוא קו ז"מ חצי דבר ושרש מאלגו ורביע |
| והוא ידוע מאשר אמרנו שאמרו אקלידס ואמר שכל קו שהוא על יחס אמצעי ושני קצוות ונוסף באורך הקו כמו החלק הגדול הגדול וכל זה יחלק על יחס אמצעי ושני קצוות שהחלק הגדול הוא הקו הראשון | |
| יהיה ידוע מאשר אמרנו שכאשר חלקו קו על יחס אמצעי ושני קצוות שהחלק הגדול ממנו הוא החלק הקטן מהקו הראשון | |
| ואמר במקום אחר שכאשר קובצו צלע המשושה עם צלע המעושר אשר בעגולה אחת בקו אחד ישר יהיה כל הקו נחלק על יחס אמצעי ושני קצוות וצלע המשושה הוא החלק הגדול | |
|
וקו ז"ו צלע המעושר |
|
וקו ז"מ הוא צלע המשושה |
| וכאשר הנחנו שני אלו הקוים קו אחד יהיה קו כבר נחלק על יחס בעל אמצעי ושני קצוות כמו קו זמ"ו | |
| וכאשר נניח ז"ו דבר ונגרעהו מז"מ ונוסיף על מה שישאר חצי קו ז"ו ותכה מה שיתקבץ בעצמו יהיה כמו חמשה דמיוני מרובע חצי קו ז"ו כפי מה שכתב אוקלידס . ותכה קו ז"ו בעצמו והעולה בחמשה ותקח שרשו ותוסיפהו על חצי קו ז"ו והוא חצי דבר יעלה קו ז"מ | |
|
וכבר התבאר כי קו ז"מ חצי דבר ושרש מאלגו ורביע |
| ותוציא עמוד משולש זמ"ו והוא קו מ"ס והוא ידוע שיפול על נקדת אמצע קו ז"ו והוא ז"ס | |
|
ותכה קו ז"מ בעצמו והוא חצי דבר ושרש מאלגו ורביע ויהיה אלגו וחצי ושרש מאלגו אלגו ורביע אלגו אלגו |
|
ותכה קו ז"ס והוא חצי דבר בעצמו ויהיה רביעית אלגו |
| תגרעהו מאלגו וחצי ושרש מאלגו אלגו ורביעית אלגו אלגו וישאר אלגו ורביע ושרש מאלגו אלגו ורביעית אלגו אלגו | |
|
| |
| ושרש זה הוא קו מ"ס | |
| תכה אותו בקו ז"מ והוא חצי דבר יהיה רביעית אלגו אלגו וחצי שמינית מאלגו אלגו ושרש מחמשה חלקים מס"ד חלקים מאלגו אלגו אלגו אלגו ישוה מאה דרהמי | |
| Normalization: Complete a quarter of a square of a square and half an eighth of a square of a square, so it becomes a whole square of a square, by multiplying it by three and a fifth, then multiply everything you have by three and a fifth.
|
ותשלים רביע אלגו אלגו וחצי שמינית מאלגו אלגו עד שיהיה אלגו אלגו והוא שנכה אותו בשלשה וחומש תכה כל דבר שתחזיק בשלשה וחומש |
| It is a square [of a square] plus a root of four-fifths of square-square-square-square equals 320 dirham.
|
יהיה אלגו ושרש מארבעה חומשים מאלגו אלגו אלגו אלגו ישוה ש"כ דרהמי |
| Normalization:Convert everything you have to a square of a square, by multiplying everything by [five] minus a root of twenty.
|
ותשיב כל דבר שתחזיק אל אלגו אלגו והוא שתכה כל דבר שתחזיק בשרש מחמשה פחות שרש מעשרים |
| It is a square of a square equals 1600 minus [a root of two] thousand of thousand and 48 thousand.
|
ויהיה אלגו אלגו ישוה אלף ות"ר פחות שני שרשים מאלף אלפים ומ"ח אלפים |
| ושרש זה הוא קו ז"ו שהוא חלק אחד מהמעושר | |
| Q.E.D. | והוא מה שרצינו לבאר |
Finding the side of a regular pentagon that contains a triangle, whose area is ten |
|
| If you are told: a regular pentagon ABGDH, it [contains] a triangle BHD whose measure is ten, how much will be Line DH, which is [the base of] the triangle and one side of the pentagon? | ואם יאמרו לך מחומש אבגד"ה שוה הצלעות והזויות שעורו הוא משולש בה"ד שהוא עשרה כמה יהיה קו ד"ה שהוא דומה למשלש וחלק אחד מהמחומש |
Knowing this is that we suppose line HD is a thing [ ]. ].
|
וידיעת זה הוא שנניח קו ה"ד דבר |
| Euclid has already explained that when line BH is divided by the ratio of a mean and two extremes, so that the greater part is equal to line DH, it is known that when a line is divided by the ratio of a mean and two extremes and we add half the greater part to the smaller part, then multiply the whole sum by itself, the square formed by the sum of the two is five times the product of [half] the greater part by itself.
|
ובאר אוקלידס שקו ב"ה כאשר חולק על יחס אמצעי ושני קצוות שהחלק הגדול הוא שוה אל קו ד"ה והוא ידוע כי כאשר נחלק קו אחד על יחס בעל אמצעי ושני קצוות ונוסיף על החלק הקטן חצי החלק הגדול ונכה הכל בעצמו שהמרובע ההוה משני אלו מקובצים יהיה חמשה דמיוני הכאת החלק הגדול בעצמו |
| We divide line BH by the ratio of a mean and two extremes at point M. | ונחלק קו ב"ה על יחס אמצעי ושני קצוות על נקדת מ' |
| We suppose the greater part as line HM. | ונשים החלק הגדול קו ה"מ |
| Let line MH equal to line HD. | ויהיה קו מ"ה שוה לקו ה"ד |
| We divide line MH into two parts at point L. | ונחלק קו מ"ה לשני חלקים על נקדת ל' |
| והכאת ב"ל בעצמו יהיה חמשה דמיוני הכאת ל"ה בעצמו | |
|
והכאת ה"ל בעצמו הוא רביעית אלגו |
| בעבור שעשינו קו ה"ד דבר | |
|
ויהיה קו מ"ה דבר |
|
ול"ה חצי דבר |
|
והכאת ל"ב בעצמו הוא אלגו ורביע |
|
וקו ב"ל הוא שרש מאלגו ורביע |
|
וקו ל"ה חצי דבר |
|
וקו ב"ה חצי דבר ושרש מאלגו ורביע |
| ונוציא עמוד במשולש בה"ד והוא קו ב"ח | |
|
ויהיה קו ה"ח חצי דבר |
|
תכה אותו בעצמו יהיה רביעית אלגו |
| תגרעהו מהכאת ב"ה בעצמו והוא אלגו וחצי ושרש מאלגו אלגו ורביעית אלגו אלגו וישאר אלגו ורביעית ושרש מאלגו אלגו ורביעית אלגו אלגו | |
| ושרש זה הוא קו ב"ח | |
| תכה אותו בקו ה"ח והוא חצי דבר ויהיה רביעית אלגו אלגו וחצי שמינית מאלגו אלגו ושרש מחמשה חלקים מס"ד חלקים מאלגו אלגו אלגו אלגו ישוה מאה דרהמי | |
| Normalization: Complete a quarter of a square of a square and half an eighth of a square of a square, so it becomes a whole square of a square, by multiplying it by three and a fifth, then multiply everything you have by three and a fifth.
|
ותשלים רביעית רביעית אלגו אלגו וחצי שמינית מאלגו אלגו עד שיהיה אלגו אלגו וזה בשנכה אותו בשלשה וחומש וכאשר הוכה כל דבר שתחזיק בשלשה וחומש |
| It is a square of a square plus a root of four-fifths of square-square-square-square equals 320 dirham.
|
יהיה אלגו אלגו ושרש מארבעה חומשים מאלגו אלגו אלגו אלגו ישוה שכ"ב שכ"ד דרהמי |
| Normalization: Complete everything, [so it becomes a whole] square of a square, by multiplying it by five minus a root of twenty.
|
ותשיב כל דבר אל אלגו אלגו והוא שתכה אותו בחמשה פחות שרש מעשרים |
| It is a square of a square equals 1600 dirham minus a root of [two] thousand of thousand and 48 thousand.
|
יהיה אלגו אלגו ישוה אלף ות"ר פחות שרש מאלף אלפים ומ"ח אלפים |
| Its root is line DH. | ושרש זה הוא קו ד"ה |
| והוא משולש בה"ד מזה המחומש שאמרנו שהוא דומה לזמ"ו מהמעושר שאמרנו בתמונה שקדמה לזאת | |
| ואם יאמרו לך שעור משלש אב"ה עשרה כמה יהיה קו ב"ה | |
|
ידיעת זה הוא שנניח קו ב"ה דבר |
| ובאר אקלידס כי כאשר נחלק קו על יחס אמצעי ושתי קצוות שהחלק הגדול כאשר נוסף בארכו כמו חצי הקו כלו והוכה כל זה בעצמו המרובע ההוה מזה יהיה חמשה דמיוני המרובע ההוה מחצי הדבר | |
| ונניח קו ב"ה דבר וכאשר הכינו חציו בעצמו ומה שיצא בחמשה יהיה אלגו ורביעית | |
|
ויהיה נודע מאשר אמרנו שקו א"ה שרש מאלגו ורביע פחות חצי דבר |
|
ויעלה הקטר על קו ב"ה והוא א"ע |
|
ותכה קו א"ה בעצמו יהיה אלגו וחצי פחות שרש מאלגו אלגו ורביע אלגו אלגו |
|
ותכה קו ה"ע בעצמו והוא חצי דבר ויהיה רביע אלגו |
| ותגרעהו ממנו ישאר אלגו ורביע פחות שרש מאלגו אלגו ורביע אלגו אלגו | |
|
| |
|
ושרש זה יהיה קו א"ע שהוא עמוד משלש אב"ה |
| תכה אותו בקו ה"ע והוא חצי דבר יהיה רביע אלגו אלגו וחצי שמינית מאלגו אלגו פחות חמשה חלקים מס"ד חלקים מאלגו אלגו אלגו אלגו ושרש זה ישוה שעור משולש אב"ה והוא עשרה | |
|
| |
|
|
תכה אותם בעצמם יהיה מאה ישוה רביע אלגו אלגו וחצי שמינית מאלגו אלגו פחות שרש מחמשה חלקים מס"ד חלקים מאלגו אלגו אלגו אלגו |
| Normalization: Complete a quarter of a square of a square, so it becomes a whole square of a square, by multiplying it by three and a fifth, then multiply everything you have by three and a fifth.
|
ותשלים רביע אלגו אלגו עד שיהיה אלגו אלגו והוא שנכה אותו בשלשה וחומש תכה כל מה שתחזיק בשלשה בשלשה וחומש |
| It is a square of a square minus a root of four-fifths of square-square-square-square equals 320.
|
ויהיה אלגו אלגו פחות שרש מארבעה חומשים מאלגו אלגו אלגו אלגו ישוה ש"כ |
| Normalization: Complete it, so it becomes a whole square of a square, by multiplying it by five plus a root of twenty, then multiply everything you have by five plus a root of twenty.
|
תשלימהו עד שיהיה אלגו אלגו שלם והוא שתכה אותו בחמשה ושרש מעשרים ותכה כל דבר שתחזיק בחמשה ושרש מעשרים |
| It is a square of a square equals 1600 dirham plus a root of [two] thousand of thousand and 48 thousand.
|
ויהיה אלגו אלגו ישוה אלף ת"ר דרהמי ושרש מאלף אלפי' ומ"ח אלפים |
| Its root is line BH. | ושרש זה הוא קו ב"ה |
| Q.E.D. | והוא מה שרצינו לבאר |
Finding the line that cuts a fifth of the circle that circumscribes a decagon |
|
| If you are told: a regular decagon ABGDHWZCTK and the measure of triangle KTC is ten. | ואם יאמרו לך מעושר אב"ג דה"ו זחט"כ שוה הצלעות והזויות ושעור משלש כט"ח עשרה במספר |
| How much will be Line KC, which is a line that cuts a fifth of the circle that circumscribes the decagon? | כמה יהיה קו כ"ח שהוא קו חותך חמישית העגולה המקפת בזה המעושר |
| To know this we suppose line KC is a thing.
|
ולדעת זה נניח קו כ"ח דבר |
We have already explained that when we assume the line that cuts a fifth of the circle is a thing [ ], the square of its diameter is two squares plus a root of four-fifths of a square of a square [ ], the square of its diameter is two squares plus a root of four-fifths of a square of a square [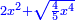 ]. ].
|
וכבר בארנו שכאשר נניח קו חותך חמישית העגולה דבר יהיה מרובע קטרה שני אלגוש ושרש מארבעה חומשים מאלגו אלגו |
Hence, the square of half the diameter is half a square plus a root of half a tenth of a square of a square [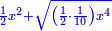 ] ]
|
ויהיה מרובע חציו של הקטר חצי אלגו ושרש מחצי עשירית מאלגו אלגו |
| When you subtract it from the line that cuts the fifth [of the circle], which is a square, the square of KT remains half a square minus a root of half a tenth of a square of a square. | תגרעהו ממרובע קו החותך החמישית והוא אלגו ישאר מרובע כ"ט חצי אלגו פחות שרש מחצי עשירית מאלגו אלגו |
|
| |
| We do this since Euclid has explained that the line that cuts the fifth is on the line that cuts the sixth and the tithe, when they are set on one circle. | ועשינו זה בעבור כי באר אוקלידס כי קו החותך החמישית על הקו החותך הששית והעשירית כאשר הונחו בעגולה אחת |
| Subtract from it the square of KM by itself; the square of TM, which is the height of triangle KTC, remains a quarter of a square minus a root of half a tenth of a square of a square. | תגרע ממנו מרובע כ"מ בעצמו ורביע אלגו ישאר מרובע ט"מ שהוא עמוד משלש כט"ח ורביע אלגו פחות שרש מחצי עשירית מאלגו אלגו |
|
| |
| Multiply it by the square of KM, which is a quarter of a square; the result is half an eighth of a square of a square minus a root of one part of 320 parts of a square-square-square-square. | תכה אותו במרובע כ"מ והוא רביעית אלגו ויהיה חצי שמינית מאלגו אלגו פחות שרש מחלק אחד מש"כ חלקים מאלגו אלגו אלגו אלגו |
|
| |
| Its root is equal to the area of triangle MTC, which is ten.
|
ושרש זה ישוה שעור משולש מט"ח והוא עשרה במספר |
| Multiply ten by itself; it is one hundred equals half an eighth of a square of a square minus a root of one part of 320 parts of a square-square-square-square.
|
ותכה העשרה בעצמם יהיה מאה ישוה חצי שמינית מאלגו אלגו פחות שרש חלק אחד מש"כ חלקים מאלגו אלגו אלגו אלגו |
| Normalization: Complete half an eighth of a square of a square, so it becomes a whole square of a square, by multiplying it by sixteen, then multiply everything you have by sixteen.
|
ותשלים חצי שמינית מאלגו אלגו עד שיהיה אלגו אלגו שלם והוא שתכה אותו בשש עשרה אחר זה תכה כל אשר תחזיק בשש עשרה |
| It is a square of a square minus a root of four-fifths of a square-square-square-square equals 1600.
|
ויהיה אלגו אלגו פחות שרש מארבעה חומשים מאלגו אלגו אלגו אלגו ישוה אלף ות"ר |
| Normalization: Complete it, so it becomes a whole square of a square, by multiplying it by five plus a root of twenty, then multiply everything you have by five plus a root of twenty.
|
ותשלימהו עד שיהיה אלגו אלגו שלם והוא שתכה אותו בחמשה ושרש מעשרים ותכה כל דבר שתחזיק בחמשה ושרש מעשרים |
| It is a square of a square equals eight thousand plus a root of fifty-one thousand of thousand and two hundred thousand.
|
יהיה אלגו אלגו ישוה שמנת אלפים ושרש מחמשים ואחד אלף אלפים ומאתים אלף |
| Its root is line KC, which is the line that cuts a fifth of the circle that circumscribes the decagon. | ושרש זה הוא קו כ"ח שהוא קו חותך חמישית העגולה המקפת במעושר |
| Q.E.D. | והוא מה שרצינו לבאר |
Appendix: Bibliography
The second section: on pentagons and decagons / by Abū Kāmil Shujāʽ Ibn Aslam Ibn Muḥammad ibn Shujāʽ (Egypt, ca. 850-930)
– Hebrew translation –
by Mordecai (Angelo) Finzi (Mantua, d. 1475)
ha-Meḥumashim ve-ha-Meʽusharim
Manuscripts:
- 1) Mantova, Comunita Israelitica MS ebr. 17/2 (IMHM: f 797), ff. 51v-62r (15th century; autograph)
- Abu Kamil Shudeya, Algebra
- 2) 2) München, Bayerische Staatsbibliothek, Cod. hebr. 225/2 (IMHM: f 1118), ff. 155r-165v (15th century)
- Mathematische Abhandlungen, vielleicht von Mordechai Finzi (1445-1473)
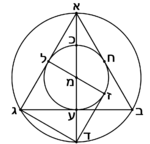
The transcript is based mainly on manuscript Mantova 17

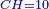
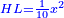
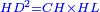
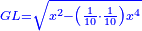
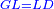
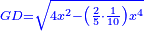

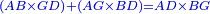
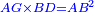
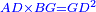
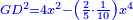
![\scriptstyle{\color{blue}{AB\times GD=GD^2-AB^2=\left[4x^2-\left(\frac{2}{5}\sdot\frac{1}{10}\right)x^4\right]-x^2=3x^2-\left(\frac{{\color{red}{2}}}{5}\sdot\frac{1}{10}\right)x^4}}](/mediawiki/images/math/8/b/1/8b11a53f782838601e3efd3ad7f081aa.png)
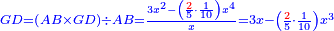
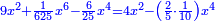
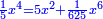
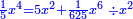
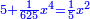
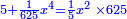
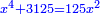
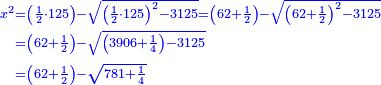

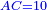
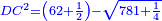
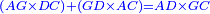

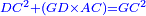
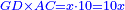
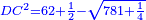
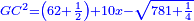
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle GC^2+AG^2&\scriptstyle=\left[\left(62+\frac{1}{2}\right)+10x-\sqrt{781+\frac{1}{4}}\right]+\left[\left(62+\frac{1}{2}\right)-\sqrt{781+\frac{1}{4}}\right]\\&\scriptstyle=125+10x-\sqrt{31{\color{red}{25}}}\\\end{align}}}](/mediawiki/images/math/9/8/2/9822f19f92d1b1c8f9bb710cfeb26976.png)
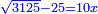



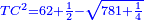
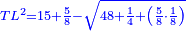
![\scriptstyle{\color{blue}{HL^2=TH^2-TL^2=25-\left[15+\frac{5}{8}-\sqrt{48+\frac{1}{4}+\left(\frac{5}{8}\sdot\frac{1}{8}\right)}\right]=9+\frac{1}{4}+\frac{1}{8}-\sqrt{48+\frac{1}{2}+\frac{1}{4}+\left(\frac{5}{8}\sdot\frac{1}{8}\right)}}}](/mediawiki/images/math/2/1/9/2190ac522aaa34320d29a990047bf634.png)
![\scriptstyle{\color{blue}{BH^2:AB^2=25:x^2=\left[9+\frac{1}{4}+\frac{1}{8}-\sqrt{48+\frac{1}{2}+\frac{1}{4}+\left(\frac{5}{8}\sdot\frac{1}{8}\right)}\right]:\left[62+\frac{1}{2}-\sqrt{781+\frac{1}{4}}\right]=HL^2:TC^2}}](/mediawiki/images/math/a/e/8/ae86d07e0f1acbc0c66197d4d5566bd9.png)
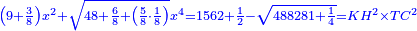
![\scriptstyle{\color{blue}{\times\left[\frac{1}{5}+\left(\frac{1}{5}\sdot\frac{1}{5}\right)-\sqrt{\frac{20}{625}}\right]}}](/mediawiki/images/math/d/6/5/d65ca6d857f9646b2148a939cb929e8b.png)
![\scriptstyle{\color{blue}{\left[\left(9+\frac{3}{8}\right)x^2+\sqrt{48+\frac{3}{4}+\left(\frac{5}{8}\sdot\frac{1}{8}\right)}x^4\right]\times\left[\frac{1}{5}+\left(\frac{1}{5}\sdot\frac{1}{5}\right)-\sqrt{\frac{20}{625}}\right]=x^2}}](/mediawiki/images/math/f/f/5/ff5f0c3d9bba526e17bab3dd05df3503.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left[1562+\frac{1}{2}-\sqrt{488281+\frac{1}{4}}\right]\times\left[\frac{1}{5}+\left(\frac{1}{5}\sdot\frac{1}{5}\right)-\sqrt{\frac{20}{625}}\right]&\scriptstyle=375+\sqrt{15625}-\sqrt{{\color{red}{78}}125}-\sqrt{28{\color{red}{1}}25}\\&\scriptstyle=500-\sqrt{200000}\end{align}}}](/mediawiki/images/math/1/b/4/1b4d40d2c2f34aecc04c4caa17f821a3.png)



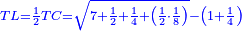
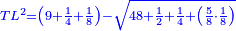
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle HL^2=TH^2-TL^2&\scriptstyle=25-\left[\left(9+\frac{1}{4}+\frac{1}{8}\right)-\sqrt{48+\frac{1}{2}+\frac{1}{4}+\left(\frac{5}{8}\sdot\frac{1}{8}\right)}\right]\\&\scriptstyle=\left(15+\frac{5}{8}\right)+\sqrt{48+\frac{1}{2}+\frac{1}{4}+\left(\frac{5}{8}\sdot\frac{1}{8}\right)}\end{align}}}](/mediawiki/images/math/2/9/6/2962597864819f0d8c2d8e8456f7f581.png)
![\scriptstyle{\color{blue}{AB^2:TC^2=x^2:\left[\left(37+\frac{1}{2}\right)-\sqrt{781+\frac{1}{4}}\right]=25:\left[\left(15+\frac{5}{8}\right)+\sqrt{48+\frac{1}{2}+\frac{1}{4}+\left(\frac{5}{8}\sdot\frac{1}{8}\right)}\right]=KH^2:HL^2}}](/mediawiki/images/math/9/d/2/9d27d2b6aefa9477194ea8ac754b5a70.png)
![\scriptstyle{\color{blue}{\left(15+\frac{5}{8}\right)x^2+\sqrt{\left[48+\frac{3}{4}+\left(\frac{5}{8}\sdot\frac{1}{8}\right)\right]x^4}=\left(937+\frac{1}{2}\right)-\sqrt{488281+{\color{red}{\frac{1}{4}}}}=KH^2\times TC^2}}](/mediawiki/images/math/5/a/e/5ae4ec3c030bb52afba668d79fd4e4f0.png)
![\scriptstyle{\color{blue}{\left(15+\frac{5}{8}\right)x^2+\sqrt{\left[48+\frac{3}{4}+\left(\frac{5}{8}\sdot\frac{1}{8}\right)\right]x^4}=\left(937+\frac{1}{2}\right)-\sqrt{488281+{\color{red}{\frac{1}{4}}}}\quad/\times\left[\left(\frac{2}{5}\sdot\frac{1}{5}\right)-\sqrt{\frac{4}{5}\sdot\frac{1}{625}}\right]}}](/mediawiki/images/math/5/2/4/5248570fa3878c00480e4a1ab67a09e8.png)


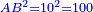
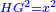

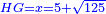
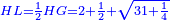
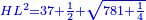
![\scriptstyle{\color{blue}{DL^2=HD^2-HL^2=100-\left[37+\frac{1}{2}+\sqrt{781+\frac{1}{4}}\right]=62+\frac{1}{2}-\sqrt{781+\frac{1}{4}}}}](/mediawiki/images/math/c/2/2/c22b06ab4b97b581a086014862a2a966.png)
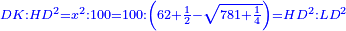

![\scriptstyle{\color{blue}{\left(62+\frac{1}{2}\right)x^2-\sqrt{\left(781+\frac{1}{4}\right)x^4}=10000\quad/\times\left[\left(\frac{1}{5}\sdot\frac{1}{10}\right)+\sqrt{\frac{1}{15625}+\left(\frac{1}{4}\sdot\frac{1}{15625}\right)}\right]}}](/mediawiki/images/math/1/6/b/16bd297418792932031338d669404232.png)
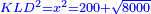


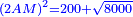


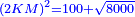

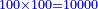
![\scriptstyle{\color{blue}{\left(62+\frac{1}{2}\right)x^2-\sqrt{\left(781+\frac{1}{4}\right)x^4}=10000\quad/\times\left[\left(\frac{1}{5}\sdot\frac{1}{10}\right)+\sqrt{\frac{1}{{\color{red}{1}}5625}+\left(\frac{1}{4}\sdot\frac{1}{{\color{red}{1}}5625}\right)}\right]}}](/mediawiki/images/math/d/b/e/dbef416c5474ef4a04a4c16c080d6b4b.png)
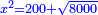
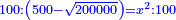

![\scriptstyle{\color{blue}{500x^2-\sqrt{200000x^4}=10000\quad/\times\left[\left(\frac{1}{10}\sdot\frac{1}{10}\right)+\sqrt{\frac{1}{12500}}\right]}}](/mediawiki/images/math/0/c/5/0c5a738ac33affa1e3cc645ffe2d072d.png)
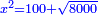
![\scriptstyle{\color{blue}{x:10=10:\left[\sqrt{\left(31+\frac{1}{4}\right)x^2}-\left(2+\frac{1}{2}\right)x\right]}}](/mediawiki/images/math/3/1/1/311f5831248c33ac4db896faf6ee09b9.png)
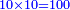
![\scriptstyle{\color{blue}{x\times\left[\sqrt{31+\frac{1}{4}}-\left(2+\frac{1}{2}\right)\right]=\sqrt{\left(31+\frac{1}{4}\right)x^2}-\left(2+\frac{1}{2}\right)x}}](/mediawiki/images/math/7/2/4/724cb1eb45dec6f360e16882ff557273.png)
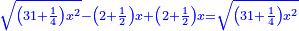
![\scriptstyle{\color{blue}{\left[100+\left(2+\frac{1}{2}\right)x\right]^2=10000+\left(6+\frac{1}{4}\right)x^2+500=\left(31+\frac{1}{4}\right)x^2}}](/mediawiki/images/math/a/b/4/ab41cf2bbe71bb3414a1674f707e1050.png)
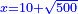
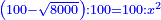
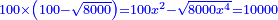
![\scriptstyle{\color{blue}{\times\left[\left(\frac{1}{2}\sdot\frac{1}{10}\right)+\sqrt{\frac{1}{500}}\right]}}](/mediawiki/images/math/9/2/a/92a5dbee2553393894d0c236fa46cab1.png)
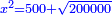
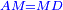
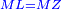
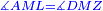
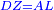
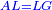
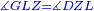

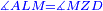
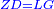
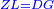
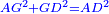

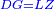
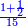 of the circle
of the circle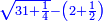
 of the circle
of the circle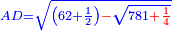
 of the circle
of the circle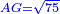
![\scriptstyle{\color{blue}{BD\times AG=\left[\sqrt{31+\frac{1}{4}}-\left(2+\frac{1}{2}\right)\right]\times\sqrt{75}=\sqrt{2343+\frac{1}{2}+\frac{1}{4}}-\sqrt{468+\frac{1}{2}+\frac{1}{4}}}}](/mediawiki/images/math/1/f/8/1f8d1db8faf8216536084660e9051b10.png)
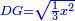
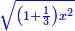
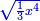
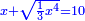

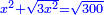

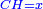
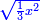
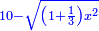
![\scriptstyle{\color{blue}{\left[10-\sqrt{\left(1+\frac{1}{3}\right)x^2}\right]\times x=10{\color{red}{x}}-\sqrt{\left(1+\frac{1}{3}\right)x^4}=10}}](/mediawiki/images/math/8/b/0/8b09abc30b587b24b5514354fe729094.png)
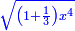 to the dirham
to the dirham 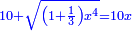
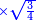
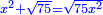
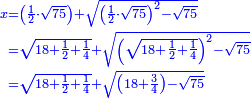
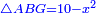
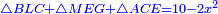
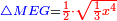
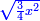
![\scriptstyle{\color{blue}{\triangle ACE=\sqrt{\left[\frac{1}{8}+\left(\frac{1}{2}\sdot\frac{1}{8}\right)\right]x^4}}}](/mediawiki/images/math/8/0/9/809e20dc64711b1ce0bbcab792d03783.png)
 =
=![\scriptstyle{\color{blue}{\sqrt{\frac{1}{3}x^4}+\sqrt{\left[\frac{1}{8}+\left(\frac{1}{2}\sdot\frac{1}{8}\right)\right]x^4}=10-2x^2}}](/mediawiki/images/math/0/1/4/0149304215ba5b7609ba5904ad16feec.png)
![\scriptstyle{\color{blue}{\sqrt{\frac{1}{3}x^4}+\sqrt{\left[\frac{1}{8}+\left(\frac{1}{2}\sdot\frac{1}{8}\right)\right]x^4}=10-2x^2\quad/\times\sqrt{3}}}](/mediawiki/images/math/e/4/0/e40997d2862ec23d8d7bf25eb788baba.png)
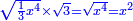
![\scriptstyle{\color{blue}{\sqrt{\left[\frac{1}{8}+\left(\frac{1}{2}\sdot\frac{1}{8}\right)\right]x^4}\times\sqrt{3}=\sqrt{\left[\frac{1}{2}+\left(\frac{1}{2}\sdot\frac{1}{8}\right)\right]x^4}=\frac{3}{4}x^2}}](/mediawiki/images/math/2/2/e/22eaa3d3520b283c9bf86b67c12507e7.png)
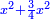
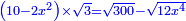
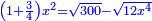
 by adding it to
by adding it to 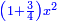
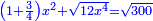
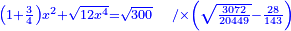
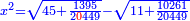
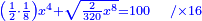
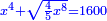
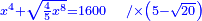
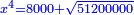
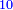
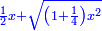
![\scriptstyle{\color{blue}{\left[\frac{1}{2}x+\sqrt{\left(1+\frac{1}{4}\right)x^2}\right]^2=\left(1+\frac{1}{2}\right)x^2+\sqrt{\left(1+\frac{1}{4}\right)x^4}}}](/mediawiki/images/math/8/c/1/8c1e5d219b677d860bbee2f7cd5d1ecc.png)
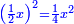
![\scriptstyle{\color{blue}{ZM^2-ZS^2=\left[\left(1+\frac{1}{2}\right)x^2+\sqrt{\left(1+\frac{1}{4}\right)x^4}\right]-\frac{1}{4}x^2=\left(1+\frac{1}{4}\right)x^2+\sqrt{\left(1+\frac{1}{4}\right)x^4}}}](/mediawiki/images/math/3/b/1/3b1ba672f98868d86835c9fb64c485ad.png)
![\scriptstyle{\color{blue}{\left[\frac{1}{4}+\left(\frac{1}{2}\sdot\frac{1}{8}\right)\right]x^4+\sqrt{\frac{5}{64}x^8}=100\quad/\times\left(3+\frac{1}{5}\right)}}](/mediawiki/images/math/0/2/1/021761890d2680028c7e66e02b34db6e.png)
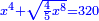

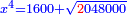
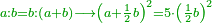
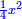
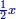
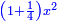
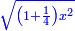
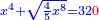
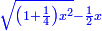
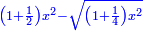
![\scriptstyle{\color{blue}{AH^2-HE^2=\left[\left(1+\frac{1}{2}\right)x^2-\sqrt{\left(1+\frac{1}{4}\right)x^2}\right]-\frac{1}{4}x^2=\left(1+\frac{1}{4}\right)x^2-\sqrt{\left(1+\frac{1}{4}\right)x^2}}}](/mediawiki/images/math/2/b/5/2b531f158b7f32caaec594e04888f31b.png)
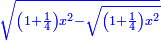
![\scriptstyle{\color{blue}{AE\times HE=\sqrt{\left(1+\frac{1}{4}\right)x^2-\sqrt{\left(1+\frac{1}{4}\right)x^2}}\times\frac{1}{2}x=\sqrt{\left[\frac{1}{4}+\left(\frac{1}{2}\sdot\frac{1}{8}\right)\right]x^4-\sqrt{\frac{5}{64}x^8}}=\triangle ABH=10}}](/mediawiki/images/math/d/e/8/de84a7c65c041482be57e60f7923debc.png)
![\scriptstyle{\color{blue}{\left[\frac{1}{4}+\left(\frac{1}{2}\sdot\frac{1}{8}\right)\right]x^4-\sqrt{\frac{5}{64}x^8}=10^2=100}}](/mediawiki/images/math/2/1/2/212ba190bb7f01a89c401974e036ab32.png)
![\scriptstyle{\color{blue}{\left[\frac{1}{4}+\left(\frac{1}{2}\sdot\frac{1}{8}\right)\right]x^4-\sqrt{\frac{5}{64}x^8}=100\quad/\times\left(3+\frac{1}{5}\right)}}](/mediawiki/images/math/a/5/a/a5af102f0ffa7218d1d5dea7cbc0fc73.png)
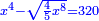


![\scriptstyle{\color{blue}{KT^2=x^2-\left[\frac{1}{2}x^2+\sqrt{\left(\frac{1}{2}\sdot\frac{1}{10}\right)x^4}\right]=\frac{1}{2}x^2-\sqrt{\left(\frac{1}{2}\sdot\frac{1}{10}\right)x^4}}}](/mediawiki/images/math/1/1/e/11e54bb085431c45ad131c0719b45ca5.png)
![\scriptstyle{\color{blue}{TM^2=KT^2-KM^2=\left[\frac{1}{2}x^2-\sqrt{\left(\frac{1}{2}\sdot\frac{1}{10}\right)x^4}\right]-\frac{1}{4}x^2=\frac{1}{4}x^2-\sqrt{\left(\frac{1}{2}\sdot\frac{1}{10}\right)x^4}}}](/mediawiki/images/math/1/1/3/11309aaf7f4546c8fc73b50d88fd7e4a.png)
![\scriptstyle{\color{blue}{TM^2\times KM^2=\left[\frac{1}{4}x^2-\sqrt{\left(\frac{1}{2}\sdot\frac{1}{10}\right)x^4}\right]\times\frac{1}{4}x^2=\left(\frac{1}{2}\sdot\frac{1}{8}\right)x^4-\sqrt{\frac{1}{320}x^8}}}](/mediawiki/images/math/5/a/b/5abfb020c96d442a4cda1453f1327e8d.png)