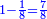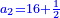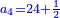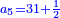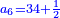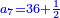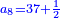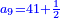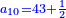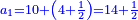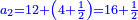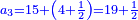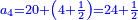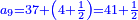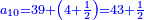Chapter Seven - Fractions
|
המין הז' בשברים
|
| Which includes all the types [of arithmetical operations]
|
והוא דמות כל המינים כלם
|
Conversion of fractions
|
|
| I say first that it requires the knowledge to convert fractions to fractions or to convert two fractions or more to one fraction.
|
ואומר בראשונה כי צורך גדול לזה הוא ידיעת המרת שברים בשברים או הפך שני שברים או יותר לשבר אחד
|
| Converting fractions to fractions
|
|
| Fractions to fractions:
|
אמנם שברים בשברים
|
- As if you say: we convert quarters to sixths.
|
כאלו תאמר נמיר רביעיות לשישיות
|
- Divide the 6 of the sixths by the 4 of the quarters; the result is one and a half. So, the quarter is one-sixth and a half [of a sixth].
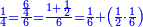
|
הנה אז תחלוק הו' של שישיות על הד' מהרביעיות ויצא אחד וחצי והנה שישית וחצי הוא הרביע
|
- Or, we say: we convert quarters to thirds of quarters.
|
או נאמר נמיר רביעיות לשלישי רביעיות
|
- We multiply 3 by 4 of the 3-quarters; it is 12. We divide it by 4 of the quarters; the result is three. So, the quarter is 3 of three-quarters.
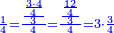
|
נכפול ג' בד' של ג' רביעיות ויהיו י"ב נחלקם על ד' של רביעיות ויצאו שלשה והנה הרביעית הוא ג' שלישי רביעיות
|
- Or, we say: we convert the quarters to thirds of fifths.
|
או שנאמר נמיר הרביעיות בשלישי חמישיות
|
- We multiply 3 by 5; the result is 15. We divide it by 4; the result is 3 and 3-quarters. So, the quarter is 3-fifths and 3-quarters of a fifth.
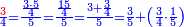
|
נכפול הג' בה' ויעלו ט"ו נחלקם על ד' ויצאו ג' וג' הרביעיות והנה הרביע הוא ג' חמישיות ועוד ג' רביעיות חמישיות
|
| Converting two fractions to one fraction
|
|
| Or, if we wish to convert two fractions to one fraction as close as possible.
|
או שנרצה להפך שני שברים לשבר אחד יותר קרוב שאפשר
|
- Example: we wish to know the fraction that is the least common multiple shared by tenths and eighteenths.
|
והנה המשל רצינו לדעת שבר ראשון שבו ישתתפו עשיריות בשמונה עשיריות
|
| First, one should look for their least common multiple, as follows:
|
והנה בתחלה ראוי לבקש [5]המספר הראשון שבו ישתתפו ויהיה כזה
|
| First, we should know is they share a common factor that counts both and look for it.
|
בתחלה נדע אם הם משתתפים למספר ימנה אותו נבקש אותו
|
| If they share two common factors, we look for the greater.
|
ואם משתתפים בשני מספרים נבקש היותר גדול
|
- Ten and 18 share two as a common factor that counts both. We know that it counts ten by 5 and 18 by 9.
|
והנה העשרה והי"ח משתתפים בשנים אשר ימנה אותם ונדע במה ימנה לעשרה בה' ולי"ח בט'
|
- We multiply 10 by 9 [or 18 by 5]; it is ninety and this is the least common multiple shared by ten and 18.

|
ואחר נכפול הי' בט' ויהיו תשעים ולי"ח בה' והוא יהיה המספר הראשון שבו ישתתפו העשרה או הי"ח
|
- The tenth is 9 [parts of] ninety, by which two counts 18.
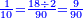
|
ועתה הנה העשירית יהיה הט' מתשעים שבו מנה השנים לי"ח
|
- The eighteenth is [5] [parts of] ninety, by which 2 counts ten.
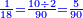
|
והח' עשיריות יהיה הט' מתשעים שבו מנה הב' לעשרה
|
| Converting three fractions to one fraction
|
|
| If there are three types of fractions.
|
ואם היו ג' מיני שברים
|
- As if you say: the tenth, the twelfth, and the eighteenth.
|
כאלו תאמר העשירית והשתים עשיריות והח' עשירית
|
- First, we look for the least common multiple shared by the tenth and the twelfth.
|
הנה בתחלה נבקש מספר ראשון שישתתפו בו העשירית והשתים עשירית
|
- We find it by looking for their greatest common divisor; it is two, because it counts 10 by 5 and 12 by 6.
|
ונמצא אותו בבקש המספר הגדול שימנה אותם והנה הוא השנים בכאן כי ימנה לעשרה בה' ולי"ב בשש
|
- Thus, 5 and 6 are the least numbers of the ratio 10:12.
|
והנה הה' והו' אלה יהיו השני מספרים אשר הם הפחות מספרים אשר על היחס הי' והי"ב
|
- So, if you multiply 10 by 6, or 12 by 5, the result is 60 and it is the least common multiple shared by 10 and 12.

|
ולכן אם תכפול העשר בו' או הי"ב בה' יעלו ס' והוא יהיה המספר הקרוב שישתתפו בו הי' והי"ב
|
- Look also for the greatest common divisor of 60 and 18; it is 6, because it counts 60 by 10 and 18 by 3.
|
עוד ראה המספר הגדול שימנה לס' האלו ולי"ח והוא הו' כי ימנה לס' בי' ולי"ח בג'
|
- Multiply 60 by 3; the result is 180 and it is the least common multiple shared by the three of them.
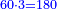
|
תכפול הס' בג' ויעלו ק"ף והוא המספר הראשון שישתתפו בו שלשתם
|
- If you want to know how much is the tenth, [multiply] 6 that counts 12 by 3 that counts 18; the result is 18 and it is the tenth.
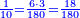
|
ואם תרצה לדעת כמה הוא העשירית ממנו הו' המונה לי"ב בג' המונה לי"ח ויעלו י"ח והוא העשירית
|
- For the twelfth, multiply 5 that counts 10 by 3 that counts 18; the result is 15 and it is the twelfth.
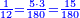
|
ואמנם השתים עשירית כפול הה' המונה לעשרה בג' המונה לי"ח ויעלו ט"ו והוא יהיה השתים עשירית
|
- The eighteenth is 10 that counts 60.
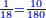
|
ואמנם הח' עשירית הוא יהיה הי' המונה לס'
|
- As the sixtieth is 3 that counts 18, if we wish to know it, although the intention here is only for the three former fractions that are the tenth, the twelfth, and the eighteenth.
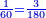
|
כמו שהשישימית יהיו הג' המונים לי"ח אם רצינו לדעת אותו אלא שאין המכוון בכאן אלא בשלשת השברים הראשונים שהם הי' והי"ב והי"ח
|
| Know that if they do not share a common divisor, then the least common multiple of the fractions is found by multiplying one by the other.
|
ודע כי אם לא ישתתפו המספרים במספר ימנה אותם הנה אז ימצא המספר שישתתפו בו השברים בכפול הא' על האחר
|
- As if you say: fifths and sixths - nothing counts them except for 1.
|
כאלו תאמר חמישיות ושישיות שאין דבר שימנם אלא האחד
|
- The least common multiple of these [fractions] is 30 that is generated from the product of 5 by 6.
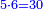
|
הנה המספר הראשון שימצאו בו אלה השרשים הוא השלשים הבא מכפילת הה' בו'
|
- The fifth is the denominator that is the six.
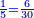
|
ואז החמישית הוא שם השבר ר"ל הששה
|
- The sixth is the denominator of the other fraction, i.e. the five.
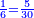
|
והשישית הוא בא משם השבר האחר ר"ל החמשה
|
| If there are three numbers that do not share a common divisor:
|
ואם היו ג' מספרים בלתי משתתפים במונה
|
- As if you say: 3, 4, 5. Their least common multiple is found by multiplying 3 by 4; it is 12, then 5 by 12; it is 60 and this is the number in which these fractions are found.
|
כאלו תאמר הג' והארבעה והחמשה הנה המספר שישתתפו בו ימצא בכפול הג' בד' ויהיו י"ב ואחר הה' בי"ב ויהיו ס' והנה המספר שמצאו השברים האלו
|
- The third [is found] by multiplying 4 [by 5].
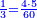
|
והנה השלישית בכפול הד'
|
- The quarter is found by multiplying 3 by 5.
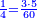
|
וימצא הרביע בכפול הג' בה'
|
- The fifth is found by multiplying 3 by 4.
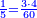
|
וימצא החומש בכפול הג' בד'
|
| Now, we will discuss the mentioned operations with fractions.
|
ועתה נדבר במינים הנאמרים ה בשברים
|
| We will start with the addition operation as usual.
|
ונתחיל בקיבוץ כמנהג
|
The First Type: Addition of fractions
|
המין הא' בקיבוץ השברים
|
| Two fractions with no common denominator
|
|
![\scriptstyle{\color{OliveGreen}{\frac{a}{b}+\frac{c}{d}=\frac{\left[a\sdot\left[\frac{1}{b}\sdot\left(b\sdot d\right)\right]\right]+\left[c\sdot\left[\frac{1}{d}\sdot\left(b\sdot d\right)\right]\right]}{b\sdot d}}}](/mediawiki/images/math/c/7/8/c7895df3cbba962a7df6ccafc823a3fc.png)
|
| We start with addition of two fractions, such that there is no number that counts both.
|
ונתחיל בקיבוץ שני שברים שלא ימצא להם מספר שימנם
|
- We give an example: we wish to sum two thirds with 3 quarters.
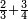
|
ונשים משל לזה רצינו לקבץ ב' שלישיות בג' רביעיות
|
|
|
- We seek the least common multiple of 3 and 4. Since no number counts them other than one, it is found only by multiplying one of them by the other; it is 12.
|
הנה נבקש מספר ראשון שישתתפו בו הג' והד' [6]ולפי שאין דבר שימנם אלא האחד לא ימצא אלא בכפול אחד מהם באחר ויהיו י"ב
|
-
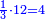
|
והנה השליש הוא ד'
|
- As we said, we multiply the two that is the number of the thirds by 4; it is 8 and this is the two-thirds.
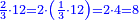
|
כמו שאמרנו נכפול השנים ממספר השלישיות בד' ויהיו ח' והם השני שלישיות
|
-
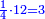
|
עוד הרביע הוא ג'
|
- We multiply the 3 that is the number of the quarter by 4 it; it is 9 and this is the 3-quarters.
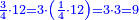
|
נכפול בהם הג' ממספר הרביעיות ויהיו ט' והנה הג' רביעיות
|
- We sum up 8 and 9; it is 17 parts of 12. We divide it by 12; the result is one integer and 5 parts of 12 remain and this is the sum.
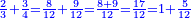
|
נקבץ הח' והט' ויהיו י"ז חלקים מי"ב נחלקים על י"ב ויצא אחד שלם וישארו עוד ה' חלקים מי"ב וזהו העולה
|
| Three fractions with no common denominator
|
|
![\scriptstyle{\color{OliveGreen}{\frac{a}{b}+\frac{c}{d}+\frac{g}{h}=\frac{\left[a\sdot\left[\frac{1}{b}\sdot\left(b\sdot d\sdot h\right)\right]\right]+\left[c\sdot\left[\frac{1}{d}\sdot\left(b\sdot d\sdot h\right)\right]\right]+\left[g\sdot\left[\frac{1}{h}\sdot\left(b\sdot d\sdot h\right)\right]\right]}{b\sdot d\sdot h}}}](/mediawiki/images/math/e/b/3/eb31c18467b571d3dda496f6914b79db.png)
|
| If we want to sum three fractions.
|
ואם נרצה לקבץ ג' שברים
|
- As if you say: 2-thirds, 3-quarters and 4-fifths.
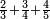
|
כאלו תאמר שני שלישיות וג' רביעיות וד' חמישיות
|
- Since no [number] counts these fractions, except for one, their least common multiple is found only by multiplying 3 by 4; it is 12, and this by 5; it is sixty and this is the whole whose fractions we seek for.
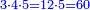
|
הנה לפי שלא ימנה לשברים הללו אלא האחד הנה לא ימצא מספר ראשון שישתתפו בו אלא בכפול הג' בד' והיו י"ב וזה בה' והיו שישים וזה יהיה דמות השלם אשר נבקש שבריו
|
- The third is found by multiplying 4 by 5, which is twenty.
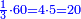
|
והנה השל[י]ש ימצא בכפול הד' בה' שהוא עשרים
|
- The two-thirds are found by multiplying two by twenty; it is 40.
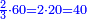
|
ושני השלישים ימצא בכפול השנים בעשרים ויהיו מ'
|
- The quarter is found by multiplying 3 by 5; it is 15.
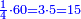
|
והרביעי יהיה בכפול הג' בה' ויהיו ט"ו
|
- The 3-quarters are [found] by multiplying 3 by 15; the result is 45.
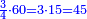
|
וג' הרביעיות יהיו בכפול [הג' בט"ו ויעלו מ"ה
|
- The fifth is found by multiplying 3 by 4; it is 12.
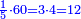
|
והחמשי ימצא בכפול הג' בד' ויהיו י"ב
|
- The 4-fifths are [found] by multiplying 4 by 12; it is 48.
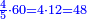
|
וד' החמשיות בכפול][7] הד' בי"ב ויהיו מ"ח
|
- Now, we sum up 40, 45, and 48; the result is 133.
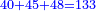
|
ועתה נקבץ המ' והמ"ה והמ"ח ויעלו קלח"ג
|
- We divide it by 60, which is the whole; the result is two integers and 13 parts of 60.
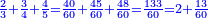
|
ונחלק אותו על הס' שהוא דמות השלם ויצא שנים שלמים ועוד י"ג חלקים מס'
|
| From this you deduce for four [fractions] and more.
|
ומזה תבין לד' שרשים או יותר
|
| If there is a number that counts both, or if one counts the other, you can do as said above.
|
ואמנם אם ימצא לשברים מספר שימנם בו שימנה האחד לאחר הנה יכול היית לעשות כדין הנאמרים למעלה
|
| Yet, then their multiple will not be the least common multiple of these fractions, which is more appropriate, since it is the smallest and the intellect comprehend it quickly as well as its fractions. Therefore, it is better to look for their least common multiple.
|
אלא שלא יהיה השלם ההוא המספר הראשון שישתתפו בו אותם השברים שהוא היותר נאות לפי שהוא ראשון ומספר יותר קטן והשכל יקיף בו ובשבריו יותר מהרה ולזה ראוי לבקש להם המספר הראשון שישתתפו לשלם
|
| Two fractions, the denominator of one of them is a divisor of the other
|
|
![\scriptstyle{\color{OliveGreen}{\frac{a}{b}+\frac{c}{d\sdot b}=\frac{\left[a\sdot\left[\frac{1}{b}\sdot\left(b\sdot d\right)\right]\right]+c}{b\sdot d}}}](/mediawiki/images/math/c/5/0/c508caaff04ccc2a6abc0776fa43bd51.png)
|
| First, the example for this is of two fractions, such that one counts the other:
|
ויהיה המשל בתחלה לזה בשני שברים שימנה האחד לאחר
|
- As if you say: we wish to sum up two-thirds with 4-ninths.
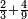
|
כאלו תאמר רצינו לקבץ שני שלישיות בד' תשיעיות
|
- Since 3 counts 9 by 3, we define the whole as 9.
|
ולפי שהג' מונה לט' בג' נשים השלם הט'
|
- The third is 3, as the number by which it counts the 9.
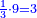
|
ויהיה השליש ג' כמספר אשר הוא מונה בו לט'
|
- We multiply it by 2, which is the number of the thirds; the result is 6, which are the 2-thirds.
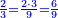
|
נכפול אותו בשני ממספר השלישיות יעלו ו' והם הב' שלישיות
|
- We add it to 4-ninths; the result is ten.
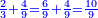
|
ונקבץ אותם לד' מהתשיעיות יעלו עשרה
|
- We divide it by 9; the result is one integer and one-ninth.
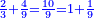
|
נחלק אותם על הט' יצא אחד שלם ועוד תשיעית אחד
|
| Two fractions with common divisor
|
|
![\scriptstyle{\color{OliveGreen}{\frac{a}{b\sdot g}+\frac{c}{d\sdot g}=\frac{\left[a\sdot\left[\frac{1}{b\sdot g}\sdot\left(b\sdot d\sdot g\right)\right]\right]+\left[c\sdot\left[\frac{1}{d\sdot g}\sdot\left(b\sdot d\sdot g\right)\right]\right]}{b\sdot d\sdot g}}}](/mediawiki/images/math/b/f/1/bf19fb80e190649be13c951e1940036c.png)
|
| If one does not count the other, but there is another number that counts both:
|
ואם לא ימנה הא' לאחר אבל ימצא מספר אחר שימנה אותם
|
- As if you say: we wish to sum up 3-quarters with 4-sixths.
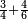
|
כאלו תאמר רצינו לקבץ ג' רביעיות בד' שישיות
|
- 2 counts both and it is their greatest common divisor - [it counts] 4 by 2 and 6 by 3.
|
שימנה אותם הב' והוא היותר גדול שימנם אמנם לד' בב' ולו' בג'
|
- We find their least common multiple by multiplying 4, the denominator of the quarter, by the divisor of 6, which is 3; the result is 12.
|
הנה אז נמצא המספר הראשון שישתתפו בו בכפול הד' משם הרביע במספר המונה לששיות שהיה ג' ויעלו י"ב
|
- Or, by multiplying 6, the denominator of the sixths, by the divisor of 4, which is 2.
|
או בכפול הו' משם השישיות במספר המונה לד' שהיה ב'
|
- This is the whole.

|
והוא יהיה דמות השלם
|
- Then, we find the quarter in 3, by which 2 counts 6.
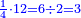
|
ואחר נמצא הרביע משם הג' שמנה בו הב' לו'
|
- The 3-quarters by multiplying 3 by 3; the result is 9.
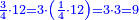
|
וג' רביעיות בכפול הג' בג' ויעלו ט'
|
- We find also the sixth in 2, by which 2 counts 4.
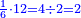
|
וכן נמצא השישית משם השנים שמנה בו השנים לד'
|
- The 4-[sixths] by multiplying 2 by 4; it is 8.
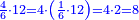
|
וד' חמישיות בכפול הב' בד' ויהיו ח'
|
- We sum up 8 and 9; it is 17. We divide it by 12; the result is one integer and 5 parts of 12 of the whole.
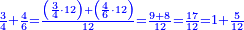
|
ונקבץ הח' והט' ויהיו י"ז ונחלק אותו על הי"ב ויצא אחד שלם ועוד ה' חלקים מי"ב בשלם
|
| From this and from what we have said at first concerning the foundations of the discussion on fractions you may learn and know how to proceed if there are three types of fractions or more.
|
ומזה וממה שאמרנו בתחלה ביסודות לדבר בשברים תשכיל ותדע איך תעשה אם יהיה השברים ג' מינים או יותר
|
The Second Type: Subtraction of fractions
|
המין הב' במגרעת השברים
|
| The intention in this is to subtract fractions from integers or fractions from fractions that are larger than them.
|
הכוונה בו לגרוע שברים משלמים או שברים משברים גדולים מהם
|
| Fractions from integers
|
|
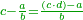
|
|
- The first example: we subtract five-eighths from one integer.
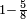
|
ויהיה [8]המשל תחלה נגרע חמש שמיניות מאחד שלם
|
- It is clear when we convert the whole integer to eighths; they are eight. We subtract from them 5; 3 remain.
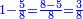
|
הנה אז מבואר בעשותינו השלם כלו שמיניות ויהיו שמונה נגרע מהם הה' וישארו ג'
|
| Fractions with the same denominator
|
|
It is also clear when subtracting fractions from similar fractions.
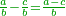
|
ואמנם בגרוע שברים משברים דומים גם הוא מבואר
|
- For, if we wish to subtract 3-eighths from 5-eighths:
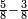
|
כי אם נרצה לגרוע ג' שמיניות מה' שמיניות
|
- 2-eighths remain.
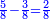
|
ונשאר ב' שמיניות
|
| Fractions with different denominators
|
|
![\scriptstyle{\color{OliveGreen}{\frac{a}{b}-\frac{c}{d}=\frac{\left[a\sdot\left[\frac{1}{b}\sdot\left(b\sdot d\right)\right]\right]-\left[c\sdot\left[\frac{1}{d}\sdot\left(b\sdot d\right)\right]\right]}{b\sdot d}}}](/mediawiki/images/math/d/0/9/d0943c4416f582ab13803553e211310e.png)
|
|
| What requires a study is when the fractions are different.
|
אמנם מה שיש בו עיון הוא בשהם שברים מתחלפים
|
- We wish to subtract 2-quarters from 6-eighths.
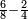
|
כיצד רצינו לגרוע ב' רביעיות מו' שמיניות
|
- We must look for their common multiple and this is found by multiplying one denominator by the other, which are 4 and 8; it is 32.
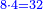
|
הנה אז נצטרך לבקש המספר שישתתפו בו שני השברים וזה ימצא בכפול שם השבר באחר שהם ד' וח' והוא ל"ב
|
- The quarter is the name of the one fraction; it is 8. 2-quarters are 16.
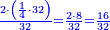
|
ולפי שהרביע הוא שם השבר האחד והוא ח' וב' זה הרביעיות והוא י"ו
|
- The eighth is the name of the other fraction; it is 4. 6-eighths are 24.
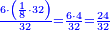
|
והשמינית הוא שם השבר האחר והוא ד' וו' שמיניו' הם כ"ד
|
- When we subtract 16 from 24, 8 remain; they are parts of 32 of the whole, and this is its quarter.
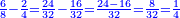
|
הנה בגרענו הי"ו מהכ"ד ישארו ח' והם חלקים מל"ב בשלם שהם רביעיתם
|
| If the denominators of the fractions are numerous, their common multiple is very large and the calculation with it is more difficult.
|
אמנם אם רבו שמות המספרים השברים והנה המספר שישתת[פ]ו בו יהיה גדול מאד ויכבד העיון בו
|
- The denominator of one fraction is a divisor of the other
|
|
![\scriptstyle{\color{OliveGreen}{\frac{a}{b\sdot d}-\frac{c}{b}=\frac{a-\left[c\sdot\left[\frac{1}{b}\sdot\left(b\sdot d\right)\right]\right]}{b\sdot d}}}](/mediawiki/images/math/8/a/2/8a28dd28f4e8c1ffea1a486dbe9f9dbe.png)
|
|
| When one fraction counts the other fraction:
|
וימנה השבר האחד לשבר האחר
|
- As if you say: we wish [to subtract] 4-eighths from 12-sixteenths.
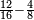
|
כאלו תאמר רצינו ד' שמיניות מי"ב שש עשיריות
|
- The number that is a common multiple of them, by multiplication of the denominator of one fraction by the other, is 128, but this is a great number that contains the divisor.
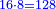
|
והנה המספר שישתתפו בו על דרך כפילת שם השבר באחר יהיה קכ"ח והוא מספר גדול להקיפו שכל המונה
|
- So, we should know by which number 8 counts 16; it is by 2.
|
הנה אז ראוי שנדע באי זה מספר ימנה
הח'][9] לי"ו והוא בב'
|
- We multiply the 4-eighths by the two, which is the divisor; they are 8.
|
ונכפול הד' מהשמיניות בשנים המונים ויהיו ח'
|
- We subtract them from 12; 4 remain and they are parts of 16, which is a quarter.
|
ונגרע אותם מי"ב וישארו ד' והם חלקים מי"ו שהם רביעיתם
|
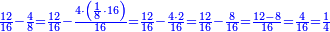
|
| Two fractions with common divisor
|
|
![\scriptstyle{\color{OliveGreen}{\frac{a}{b\sdot g}-\frac{c}{d\sdot g}=\frac{\left[a\sdot\left[\frac{1}{b\sdot g}\sdot\left(b\sdot d\sdot g\right)\right]\right]-\left[c\sdot\left[\frac{1}{d\sdot g}\sdot\left(b\sdot d\sdot g\right)\right]\right]}{b\sdot d\sdot g}}}](/mediawiki/images/math/c/c/f/ccf25ba4246eeb10ca46180c0f136558.png)
|
|
| If one fraction does not count the whole of the other fraction, but it counts its divisors, i.e. there is one number that counts both.
|
ואם אמנם לא ימנה השבר האחד לאחר בכללו אבל ימנהו בחלקיו ר"ל שימצא מספר אחד שימנה לשניהם
|
- As if you say: we wish to subtract 4-twelfths from 14-sixteenths.
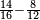
|
כאלו תאמ' רצינו לגרוע ח' שנים עשיריות מי"ד ו' עשיריות
|
- We look for their greatest [common] divisor, which is 4; it divides 12 by 3 and 16 by 4.
|
הנה אז נבקש המספר היותר גדול שימנם והוא הד' והנה ימנה לי"ב בג' ולי"ו בד'
|
- We multiply 12 by 4, or 16 by 3; the result is 48.
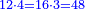
|
ונכפול הי"ב בד' או הי"ו בג' ויעלו מ"ח
|
- Its [twelfth] is [4] and its 4-twelfths are 32.
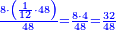
|
והנה השש עשיריות הוא וח' שנים עשיריות הוא ל"ב
|
- Its sixteenths is 3 and its 14-sixteenths are 42.
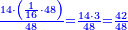
|
ואמנם הו' עשיריות הוא הג' וי"ד ו' עשיריו' הוא מ"ב
|
- When we subtract 32 from 42, 10 remain and they are parts of 48.
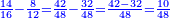
|
ועתה כשנגרע הל"ב מהמ"ב ישארו שם י' והם חלקים ממ"ח
|
If you want to reduce the resulting fraction, look for the greatest number that divides it. Divide the numerator and the denominator by its and the result is the reduced number related to the former.
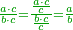
|
ואם תרצה עוד להקטין שם היוצא הנה בקש עוד המספר הגדול שימנם ותחלוק עליו שם המספר היוצא ושם מספר השבר ויצא מספר יותר קטן מיוחס לראשון
|
- The example: we find the greatest number that divides ten and 48; it is two. We divide ten by it; the result is 5. We also divide 48 by it; the result is 24. So, 10 parts of 48 are the same as the five parts of 24 we have just received.
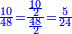
|
והמשל בזה עוד הנה נדע אי זהו המספר הגדול שימנה לעשרה ולמ"ח והנה בכאן הוא השנים ונחלוק עליו העשרה ויצאו ה' וכן נחלוק המ"ח עליו ויצאו כ"ד והנה הי' חלקים ממ"ח הם כמו חמשה חלקים מכ"ד שיצאו לנו באחרונה
|
| Check: the correctness of this type is checked by adding what we subtracted to the result and it should be equal to the greater number from which we subtracted, as is the case with integers.
|
ואמנם אמיתת זה המין יבחן בשוב לקבץ מה שגרענו עם היוצא ויהיה שוה למספר הגדול שגרענו ממנו כענין בשלמים
|
The Third Type: Multiplication of fractions
|
המין הג' בכפילת השברים
|
| Multiplying a fraction by a fraction of an integer
|
|
The meaning is that you multiply a fraction by the ratio of a fraction to the whole.
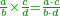
|
הנה הכוונה שתכפול שבר מה ביחס שבר מה אל השלם
|
- As if you say: we multiply once a quarter of 1 by a quarter.
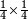
|
כאלו תאמר נכפול רביע א' ברביע פעם
|
- The procedure is that you multiply a quarter by a quarter, i.e. 4 by 4; it is 16. Multiply one by one; the product is 1. So, the result is one part of 16, which is equal to a quarter of a quarter.
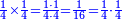
|
והמעשה בו שתכפול הרביע ברביע ר"ל ד' על ד' ויהיו י"ו ותכפול האחד באחד ויעלה א' והנה העולה יהיה אחד מי"ו שוה רביע מרביע
|
- Therefore, if you want, say that the result of multiplication of a quarter by a quarter is a quarter of a quarter.
|
לכן אם תרצה תאמר בכפילת רביע ברביע שהעולה הוא רביע מרביע
|
- You say the same about the product of a quarter by a third, which is quarter of a third.
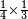
|
וכן תאמר בכפילת רביע בשליש שהוא רביע משליש
|
Many have wondered how it is that the multiplication of integers increases, while the multiplication of fractions decreases.
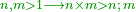 
|
ורבים תמהו איך הכפילה בשלמים מרבה ומוסיף והכפילה בשברים גורע ופוחת
|
| The truth is that the decreasing and the deficit do not happen due to the multiplication as it increases.
|
והאמת כי הפחת והגרעון לא קרה לי מפני הכפילה מסבת זה מוסיף
|
- If you wish to multiply two-thirds by 4-fifths.
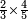
|
כיצד אם רצית לכפול שני שלישיות בד' חמישיות
|
- From the multiplication side it increases.
|
הנה מצד הכפילה הולך ומוסיף
|
- Because we multiply 2 by 4; the result is 8.
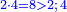
|
הוא כי נכפול הב' בד' ויעלו ח'
|
- But, the decreasing occurs from the aspect of the fractions, because we decompose this product into parts.
|
אבל החסרון קרה מצד השברים כי נשבור העולה הזה פעמים
|
- Once when we mention the thirds and second when we mention the fifths, so from this side the 8 that we increased are necessarily parts of 15 that we got from multiplying three by five, i.e. by decomposing both.
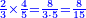
|
אחד בזכרנו שלישיות והב' בזכרנו חמישיות עד שמזה הצד יתחייב כי הח' שנתרבו לנו יהיו חלקים מט"ו שיצא לנו מכפילת השלש בחומש ר"ל משבירת שניהם
|
- I should show you this in the first example we gave, which is the multiplication of a quarter by a quarter:
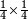
|
ומן הדין הוא זה כמו שאראך במשל הראשון שהמשלנו שהוא כפילת רביע ברביע
|
- Because the result is a quarter of a quarter and that is because if we were to multiply one by a quarter the result would be a quarter and since we only multiplied it by a quarter, the result is necessarily a quarter of a quarter.
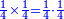
|
כי העולה הוא רביע מרביע וזה כי לו אנחנו שכפלנו אחד ברביע מה יהיה העולה רביע אחד ולפי שאנחנו לא כפלנו בו אלא רביע בהכרח שיהיה העולה רביע מרביע
|
| From this you can understand that in the multiplication of numbers there is a mean and two extremes: because the multiplication of integers by integers increases, the multiplication of fractions by fractions decreases, and the multiplication of 1 by itself neither increases nor decreases.
|
ומזה תבין כי יש בכפילת המספרים דמות אמצע ושתי קצוות וזה כי כפילת הרבים השלמים בשלמים מוסיף וכפילת שברים בשברים גורע וכפילת הא' בעצמו לא יוסיף ולא יגרע
|
| Hence, one is the beginning of the integers and the end of the fractions.
|
והנה האחד ראשית השלמים וסוף השברים
|
| Metaphor This is similar to what happens in nature, because when a man stands in deep water, he sees his image upside down in the water, i.e. his head down and his feet up - the feet are the beginning of the man on dry land and the end of man's reflection in the water. The higher the man's head on land, the lower the reflection of the man's head in the water.
|
והנה ידמה זה למה שהיה בטבע כי כשיעמוד אדם על מים עמוקים הנה יראה צורתו במים הפוכה ר"ל ראשו למטה ורגליו למעלה והרגל ראשית האדם אשר בחרבה וסוף צורת האדם אשר במים וכמו שכל מה שיגאה ראש האדם אשר בחרבה כן ישפל ראש כל צורת האדם אשר במים
|
| Similarly, as the integers are increasing their inverse fractions are decreasing.
|
כן כל מה שיתרבו המספרים השלמים יחסרו השברים הנגדים לו
|
- As when we take the two, it increases the one to its double, so when we take the half, which is its inverse, since it is one of two, it decreases the one by half.
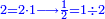
|
כיצד אם לקחנו השנים שנתרבה על האחדות בכדי כפלו כן כשלקחנו החצי שהוא נגדי לו לפי שהוא אחד משנים גרע מהאחדות החצי
|
- Also, as when we take the three, we find that it increases the one three times, so when we take the third, it decreases the one by three times, until it becomes its third.
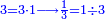
|
וכן כשנקח השלשה הנה נמצא כי הוסיף על האחד שלשה כפלים כן כשנקח השליש גרע מהאחד שלשה חסרונות עד ששב לשלישיותו
|
- And so on for the others.
|
וכן בשאר
|
Therefore, you find that the ratio of integer multiples to one is the same as the ratio of one to the fractions that are the inverse of those integers.

|
והנה תמצא לזה כי יחס הכפלים השלמים אל האחד כיחס האחד אל השברים הנגדים לשלמים ההם
|
- This is because the ratio of two to one is the same as the ratio of 1 to a half.
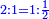
|
וזה כי יחס השנים אל האחד הוא כיחס הא' אל החצי
|
- Also, the ratio of 3 to 1 is the same as the ratio of 1 to a third.
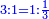
|
וכן יחס הג' אל הא' הוא כיחס הא' אל השליש
|
- And so on endlessly.
|
וכן לאין סוף
|
| Therefore, [one] is mean from the aspect of ratio.
|
אם כן הוא אמצעי ביחס
|
| Multiplication of fractions by integers
|
|
| The multiplication of fractions by integers is easy to know.
|
ואמנם כפילת השברים בשלמים נקל לדעתו
|
You find it by multiplying the number of integers by the numerator, then divide the product by the denominator and this is the result.

|
ותמצאהו בכפול מספר השלמים במספר השברים והעולה תחלקהו על שם השבר והוא יהיה העולה
|
- We wish to multiply 2-thirds by 4 integers.
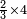
|
כיצד רצינו לכפול ב' שלישיות בד' שלמים
|
- We multiply 4 by two; the result is 8. We divide it by the denominator, which is three; we receive two integers and two-thirds.
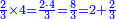
|
הנה נכפול הד' על השנים ויעלו ח' נחלקהו על שם השבר שהוא שלש ויצא לנו שני שלמים ושני שלישיות
|
| Multiplication of fractions by fractions of fractions
|
|
| The multiplication of fractions by fractions of fractions is also easy.
|
וכן כפילת שברים בשברי שברים יהיה נקל
|
Since you convert the fractions of fractions into one fraction.
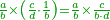
|
אחרי אשר תשיב השברי שברים לשם שבר אחד
|
- We wish to multiply two-thirds by 3-quarters of one-third.
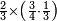
|
כיצד רצינו לכפול שני שלישיות בג' רביעיות שליש אחד
|
- First, we convert 3-quarters of one-third into one fraction: we find it by multiplying 4 of the quarters by 3 of the thirds; the result is 12.
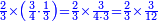
|
הנה בהתחלה נשיב הג' רביעיו' שליש אחד לשבר אחד ונמצאהו בכפול ד' של רביעיות בג' של שליש ויעלו י"ב
|
- Its third is 4, as we said, and its 3-quarters are 3. So, they are 3 parts of 12.
|
והנה השליש הוא ד' כמו שאמרנו וג' רביעיות הם ג' אם כן הם ג' חלקים מי"ב
|
- Now, multiply two-thirds by three parts of 12 as we said and this is the result of multiplication of the fraction of fraction that we demonstrated.
|
ועתה תכפול השני שלישיות בשלש חלקים מי"ב כפי מה שאמרנו והוא יהיה העולה מכפילת השבר בשבר השבר שהמשלנו
|
| Check: the check of this type is by division as in the case of integers and the result is the [multiplicand].
|
ומופת זה המין הוא החלוקה כענין בשלמים ויצא היוצא
|
The Fourth Type: Division of fractions
|
המין הד' בחלוקת השברים
|
| Division of fractions by fractions
|
|
When we want this, we divide the numerator by the numerator as well as the denominator by the denominator and the result is the denominator of the resulting fraction.
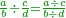
|
הנה כשרצינו זה נחלוק מספר השברים על מספר השברים וכן שם השבר על השבר ויצא שם השבר השלם היוצא
|
- We wish to divide six-eighths by two-quarters.
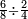
|
כיצד רצינו לחלק ששה שמיניות בשני רביעיות
|
- We divide six by two; the result is 3. We also divide 8 by 4; the result is two. Therefore, the result of division is 3 parts of two of the whole, which is one and a half.
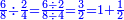
|
והנה נחלק הששה לשנים ויצאו ג' וכן נחלק הח' על הד' ויצאו שנים ויהיה היוצא בחלוקה ג' חלקים משנים השלם שהוא אחד וחצי
|
Check: multiplication
- The proof for this is that when we multiply one and a half by two quarters, the result is 3-quarters, which is the same as 6-eighths.
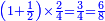
|
והמופת על זה כי כשנכפול אחד וחצי בשני רביעיות יצאו ג' רביעיות שהוא כמו הו' שמיניות
|
| Man should be more puzzled by this and say: how do we say that the thing can give what it does not have?
|
והנה בזה יתמה האדם יותר ואומר איך נאמר שיוכל לתת הדבר מה שאין לו
|
- How can we say that 3-eighths give one integer and a half that it does not have?
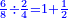
|
ואיך נאמר שיתן הו' שמיניות אחד שלם וחצי והוא אין לו
|
- The contentment of the mind is that we said: If we were to divide 8-eighths, which is one integer, into 4-quarters, which is also one, what would be the result? Eight-eighths, which is one, because when dividing 1 by 1 the result is one.
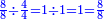
|
אמנם התיישבות הנפש בזה הוא שנאמר לו אלו חלקנו ח' שמיניות שהוא אחד שלם לד' רביעיות שהוא אחד גם כן מה היה היוצא שמונה שמיניות שהוא אחד כי בחלוקת א' על א' יצא אחד
|
- Now, if we divide 8-eighths by half the 4-quarters, which are two-quarters, the result of the division should be twice the result [of division] by 4-quarters; so it is two.
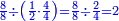
|
ועתה אם חלקנו הח' שמיניות על חצי הד' רביעיות שהוא שני רביעיות אינו דין שיצא בחלוקה כפלים מאשר היה יוצא לד' רביעיות ויהיו שנים
|
- As if you were to divide them by double the 4-quarters, which are two, the result of the division would be one half.
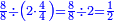
|
כמו שאלו חלקת אותם על כפל הד' רביעיות שהם שנים היוצא בחלוקה חצי אחד
|
- Since we do not divide 8-eighths here, but 3-quarters, which is 6-eighths, we have to subtract from the result of division, which is two, a quarter of it, so 1 and a half remain, as we have done.
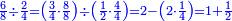
|
והנה לפי שלא חלקנו בכאן ח' שמיניות אבל ג' רביעיותיו שהם ו' שמיניות אינו דין שנגרע מהיוצא בחלוקה שהיו שנים הרביע מהם וישארו א' וחצי כמו שעשינו
|
| We return to the refutation of this doubt that we mentioned: how can a thing give what it does not have and I say that the thing does not give by division what it does not have, because the division is by the numerators, not by denominators as we have said concerning the multiplication of fractions.
|
ונשוב להתיר הספק שאמרנו שאיך יתן דבר מה שאין לו ואומר כי בחלוקה לא יתן דבר מה שאין לו כי החלוקה הוא במספרים לא בשמות השברים כמו שאמרנו בכפילת השברים
|
- So, when we divide 6-eighths by 2-quarters, the 6 gives the two only what it has, which is 2 to each.
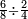
|
והנה כשחלקנו הו' שמיניות על הב' רביעיות הנה לא נתן הו' לשנים אלא מה שיש לו והוא ב' לכל אחד
|
- But, because the receiving fractions, which are the two-quarters, fall short by half of what the whole receives, the result gives them twice of what the whole receives [from division].
|
אבל מפני שהשברים המקבלים שהם שני הרביעיות קצרה ידם במחצה מהכיל מה שיקבל השלם הושב להם היוצא כפל מהיוצא לשלם
|
| Metaphor: It happens to them as it happens to a man who feeds his animals each day one portion of barley for each, yet one of the animals is sick and can eat one portion only every two days instead of every day. It seems as if [this animal] is given more than the other animals, but in fact this is not true, it is only in relation to what it eats.
|
ויקרה להם כמו שקרה לאיש אחד שהיה מחלק לאיש מדה אחד של שעורים לכל אחד מבהמותיו ליום אחד והנה בהמה אחת מהן היתה חולה ושבורה ולא הכילה לאכלה מדה אחת ביום אחד אבל בשני ימים והיה לה כאלו נתנו לה לחם משנה מאשר לשאר הבהמות אע"ף שבאמת אינו כן אבל היה בה בהתייחסות אכלה
|
- That is the case here: if we were to divide the 8-eighths by a whole 1, it would receive all those 8-eighths.
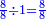
|
וכזה הענין כאן אלו חלקנו הח' שמיניות לא' שלם היה יוצא לו כל אותם הח' שמיניות
|
- Now, when we divide them by 2-quarters, which is one half, they necessarily need twice as much as a whole one needs.
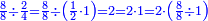
|
ועתה כשחלקנו אותם על ב' רביעיות שהוא חצי אחד בהכרח שיספיקו להם כפל ממה שיספיקו לאחד השלם
|
- It is as if they receive twelve-eighths, which is 1 and a half.
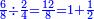
|
ויהיה כאלו נפל להם שנים עשרה שמיניות שהוא א' וחצי
|
| It is in relation to their deficiency compared to one, but not in actu.
|
וזהו בהתייחסות אל חסרונם הא' אבל לא בשלוח
|
The Fifth Type: Proportions [of fractions]
|
המין הה' בערכין
|
| This is clear from what we said about integers, as well as from that we know that this type consists of multiplication and division and as their verification, so is the verification here.
|
הנה זה מבואר ממה שדברנו בשלמים וממה שידענו שזה המין מורכב מכפילה וחלוקה וכפי האמות בהם ככה ימצא האימות בזה
|
The Sixth Type: Roots of fractions
|
המין הו' בשרשי השברים
|
| Know that the issue of roots of fractions is similar to the issue of roots of integers.
|
דע כי ענין השרשים בשברים דומה לעניינים בשלמים
|
| I have already said that the one is the beginning of the integers and the end of the fractions.
|
וכבר אמרתי כי האחד הוא ראש השלמים וסוף השברים
|
As one is a square number [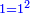 ] and if you wish to find the next integer square, you should find a pair, or pairs, of numbers between them - [the number of the pairs between ] and if you wish to find the next integer square, you should find a pair, or pairs, of numbers between them - [the number of the pairs between 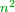 and and 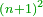 is] as the number of the preceding squares, so is the case of the fractions. is] as the number of the preceding squares, so is the case of the fractions.
|
והנה כמו שהאחד מספר מרובע ואם תרצה לדעת המרובע הסמוך בשלמים תצטרך לשום ביניהם זוג מספרים או זוגי מספרים כמספר המרובעים שעברו כן הענין בשברים
|
[= the number of pairs of fractions between two consecutive squares 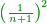 and and 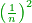 is equal to the number of the preceding squares] is equal to the number of the preceding squares]
|
|
- Because, between 1, which is the first square and the first square fraction there is one pair of fractions: between one and a quarter that are squares, there is one pair of fraction, which is a half and a third.
|
כי בין האחד שהוא המרובע הראשון להם ובין השבר המרובע הראשון זוג שברים אחד וזה כי בין האחד והרביע שהם מרובעים הנה יש ביניהם זוג שברים והוא החצי והשליש
|
- Between a quarter and a ninth there are two pairs of [fractions] as the number of the preceding [squares], which are a fifth, a sixth, a seventh, and an eighth.
|
וכן בין הרביע והתשיעית שני זוגי מספרים כמספרים שעברו והם החמישית והשישית והשביעית והשמינית
|
- As two, which is next to one, is the root of four, which is the square that is follows the first, so the half, which is one of two, is the root of a quarter.
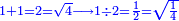
|
וכמו שהשנים הסמוך אל האחד הוא שורש הארבעה שהוא המרובע הסמוך לראשון כן החצי שהוא אחד מהשנים הוא שורש הרביע
|
- As two squares [
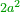 ] and three [ ] and three [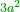 ] do not have a root, because two and three do not have a root, also there is no root for two times 4 [ ] do not have a root, because two and three do not have a root, also there is no root for two times 4 [ ], nor to 3 times 4 [ ], nor to 3 times 4 [ ], so there is no root for two-quarters [ ], so there is no root for two-quarters [ ] nor to 3-quarters [ ] nor to 3-quarters [ ]. ].
|
וכמו שאין לשני מרובעים ולא לשלשה שורש כי אין לשנים ולא לשלשה שרש כן אין לשני פעמים ד' ולא לג' פעמים ד' שורש כן אין לשני רביעיות ולא לג' רביעיות שורש
|
| Because the multiplication of a non-square number by a square number generates a non-square [number], just as [the multiplication of] a square number by a square generates a square.
|
כי מכפילת מספר בלתי מרובע במספר מרובע יולד בלתי מרובע כמו שממספר מרובע במרובע יולד מרובע
|
- The product of 4 by 9 is 36 and it is a square number.
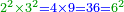
|
וזה כי מכפילת הד' בט' יעלו ל"ו והוא מספר מרובע
|
- The product of 4 by 16 is 64, which is also a square number.
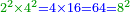
|
וכן מכפילת הד' בי"ו יעלו ס"ד והוא גם כן מספר מרובע
|
- And so on.
|
וכן תמיד
|
- In general, I say that if you want to know the fractions that have a root, look at the integers that have a root and derive their name for the fractions and they will [have a root].

|
ובכללו אומר כי אם תרצה לדעת השברים אשר יהיה להם שורש הנה ראה השלמים אשר להם שורש וגזור מהם שם לשברים והם יהיו
|
- 4 has a root and a quarter has also a root.
|
כיצד הד' יש לו שורש וכן הרביע יש לו שורש
|
- 9 has a root and so does the ninth.
|
ועוד הט' יש לו שורש וכן התשיעית
|
- 16 has a root and one part of 16 has a root also.
|
ועוד הי"ו יש לו שורש וכן אחד מי"ו יש לו שורש
|
- I further say that just as two is the root of 4, so the half, which is one of two, is the root of a quarter.
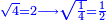
|
ועוד אומר כי כמו שהשנים הוא שורש הד' כן החצי שהוא אחד משנים שורש הרביע
|
- Also, just as three is the root of nine, so the third is the root of a ninth.
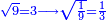
|
וכן כמו שהשלש הוא שורש התשעה כן השליש הוא שורש התשיעית
|
- And so on endlessly.
|
וכן לעולם
|
- Know that what I said, that there is no square between a square and a square - as if you say between 1 and 4, or between 4 and 9, as well as between 1 and a quarter, or between a quarter and a ninth - must be understood for integers, or fractions - each type by itself.
|
ודע כי זה שאמרתי כי לא ימצא מרובע בין מרובע למרובע כאלו תאמ' בין הא' והד' ובין הד' והט' וכן בין הא' והרביע או בין הרביע [10]והתשיעית צריך שיובן בשלמים או בשברים כל אחד בפני עצמו
|
[= between 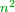 and and 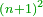 or between or between 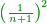 and and 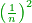 ] ]
|
|
- Among the numbers of the type of integers and fractions there are infinitely many squares
|
אבל בשברים שלמים כבר ימצאו לבלתי תכלית
|
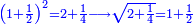
|
כיצד כשתכפול האחד והחצי באחד והחצי יעלו שנים ורביע והנה אין לו שורש
|
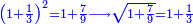
|
והנה כשנכפול אחד ושליש באחד ושליש יעלו [אחד שלם][11] וז' תשיעיות יש לו גם כן שורש
|
| Similarly for 1+¼ and so on
|
וכן באחד ורביע או אחד וחמישית ולאין תכלית
|
| Why there are no roots for non-square numbers
|
|
|
|
וא"ת והלא המספר סמוך זה לזה וכיון שהאחד ושליש [חסר][12] תחת שני תשיעיות משורש השנים והאחד והחצי הוסיף ממנו רביע והנה בין יחסר ב' תשיעיות או יוסיף רביע אפש אפשר שנמצא מספר שישתוה כפילתו למספר השנים ויהיה שורש לו
|
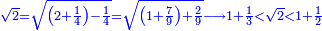
|
A number a so that 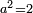 exists in potentia, but not in actu: exists in potentia, but not in actu:
|
נשוב ונאמר כי האמת כי ימצא בכח אבל לא בפועל
|
| It exists in potentia since it is continuous, but it does not exists in actu since it is separated into numbers
|
ואמנם נמצא בכח מצד שהוא מדובק ולא ימצא בפעל מצד שנפרד והיה למספר
|
- Reference to Ibn Rushd [middle commentary on the Physics VI.12 ?]: every line is divisible at any of its point, but if it is divided in actu at a certain point, it is indivisible at the point next to it
|
והיה זה כענין שיאמר ן' רשד כי כל קו אפשר שיתחלק בכל נקודה ממנו ואמנם כשנתחלק בפועל באחד נמנע בסמוכה לה
|
- It is possible: since it is continuous
|
ואמנם אפשר מצד שהוא מדובק
|
- it is possible to construct a quadrilateral whose area is 2, hence it has to have sides, and these sides can be formed as equal - thus they represent the root of 2
|
לפי שאפשר שנעשה מרובע שיהיה תשבורת שנים ובהכרח שימצא לו צלעות ואפשר לעשותן שוות והוא השורש
|
- It is impossible: from the aspect of the numbers
|
ואמנם נמנע השורש מצד המספר
|
- It is impossible that the root of 3 will be an integer:
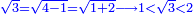
|
לפי ששורש השלשה במשל אפ אי אפשר שיהיה שלם כי האחד יגרע והשני יוסיף
|
- It is also impossible that the root of 3 will be an integer and fraction:
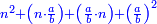 → →
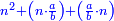 can be integers can be integers
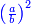 cannot be an integer → cannot be an integer →
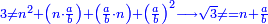
|
וגם א"א שימצא בשלם [.] ושבר לפי שכ[ש]נכפול השלם בשלם וגם השלם בשבר אפשר שיצא מזה שלם
אבל כשנכפול השבר בשבר היוצא יהיה שבר השבר והוא לא יתחבר עם השבר וכ"ש עם השלם לשיצא מכלם שורש שלם
|
| All the types of arithmetical operations are enough for solving simple problems
|
הנה אלה המינים יספיקו באשר הם בשאלות הפשוטות
|
| For solving complex problems these techniques should be combined
|
ואמנם במורכבות צריך להרכיב בהם בדרכים הנאמרים
|
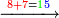
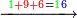

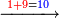

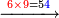
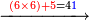
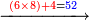

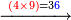
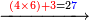
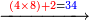
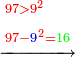
![\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{163-\left[\left(9\times8\right)+\left(8\times9\right)\right]=19}}\\&\scriptstyle{\color{red}{19-7=}}{\color{green}{12}}\\&\scriptstyle{\color{red}{71-{\color{blue}{8}}^2=}}{\color{green}{7}}\\\end{align}}](/mediawiki/images/math/4/c/3/4c3b888f90580d8f25d52a1e9038e7ce.png)
![\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{127-\left[\left(9\times6\right)+\left(6\times9\right)\right]=19}}\\&\scriptstyle{\color{red}{19-10=}}{\color{green}{9}}\\&\scriptstyle{\color{red}{108-\left[\left(6\times8\right)+\left(8\times6\right)\right]=12}}\\&\scriptstyle{\color{red}{12-4=}}{\color{green}{8}}\\&\scriptstyle{\color{red}{42-{\color{blue}{6}}^2=}}{\color{green}{6}}\\\end{align}}](/mediawiki/images/math/d/0/6/d0631e355c2dbb91f8884a7e8683c343.png)
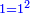 ] and if you wish to find the next integer square, you should find a pair, or pairs, of numbers between them - [the number of the pairs between
] and if you wish to find the next integer square, you should find a pair, or pairs, of numbers between them - [the number of the pairs between 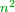 and
and 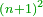 is] as the number of the preceding squares, so is the case of the fractions.
is] as the number of the preceding squares, so is the case of the fractions.
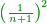 and
and 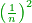 is equal to the number of the preceding squares]
is equal to the number of the preceding squares]
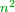 and
and 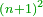 or between
or between 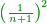 and
and 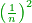 ]
]
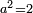 exists in potentia, but not in actu:
exists in potentia, but not in actu:
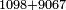
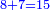
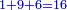

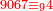
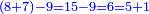


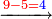
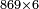
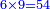
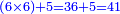
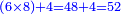
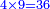

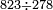
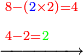
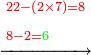
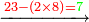

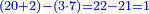
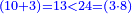
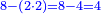

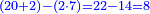


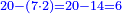
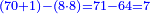



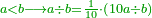
![\scriptstyle{\color{OliveGreen}{a<b\longrightarrow a\div b=\frac{1}{10}\sdot\left[\frac{1}{10}\sdot\left(10a\div b\right)\right]}}](/mediawiki/images/math/d/e/2/de2406622e6bb7fbf22fa4d0ddedcd57.png)
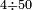
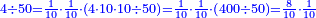
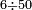
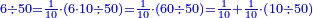
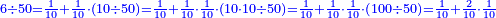
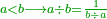
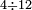
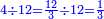
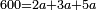
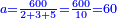



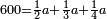
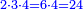
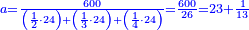
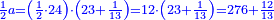
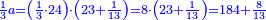
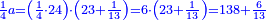
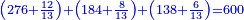
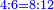
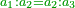

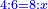
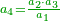
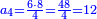
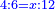
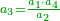
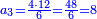

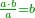
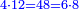
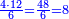
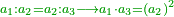
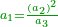 ;
; 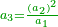
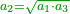
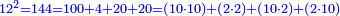
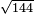

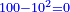
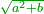
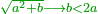
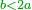 ], we could have given one more than what we have extracted in the first [approximate] root.
], we could have given one more than what we have extracted in the first [approximate] root.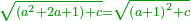
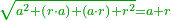

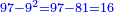
![\scriptstyle{\color{blue}{163-\left[\left(8\sdot9\right)+\left(9\sdot8\right)\right]=163-\left(72+72\right)=163-144=19}}](/mediawiki/images/math/2/9/c/29cfac2135d16c9d2d3f6d54b3376990.png)
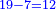

![\scriptstyle{\color{blue}{127-\left[\left(6\sdot9\right)+\left(9\sdot6\right)\right]=127-108=19}}](/mediawiki/images/math/1/6/b/16b63602d05272830b592d86968b42d8.png)
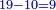
![\scriptstyle{\color{blue}{108-\left[\left(6\sdot8\right)+\left(8\sdot6\right)\right]=108-96=12}}](/mediawiki/images/math/0/2/7/027683a888e17e8f6ed4e2465ce9540b.png)
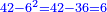
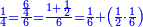
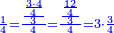
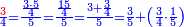

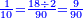
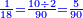

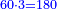
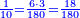
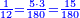
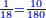
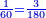
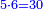
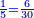
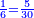
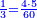
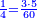
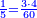
![\scriptstyle{\color{OliveGreen}{\frac{a}{b}+\frac{c}{d}=\frac{\left[a\sdot\left[\frac{1}{b}\sdot\left(b\sdot d\right)\right]\right]+\left[c\sdot\left[\frac{1}{d}\sdot\left(b\sdot d\right)\right]\right]}{b\sdot d}}}](/mediawiki/images/math/c/7/8/c7895df3cbba962a7df6ccafc823a3fc.png)
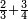
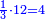
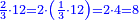
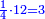
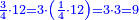
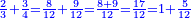
![\scriptstyle{\color{OliveGreen}{\frac{a}{b}+\frac{c}{d}+\frac{g}{h}=\frac{\left[a\sdot\left[\frac{1}{b}\sdot\left(b\sdot d\sdot h\right)\right]\right]+\left[c\sdot\left[\frac{1}{d}\sdot\left(b\sdot d\sdot h\right)\right]\right]+\left[g\sdot\left[\frac{1}{h}\sdot\left(b\sdot d\sdot h\right)\right]\right]}{b\sdot d\sdot h}}}](/mediawiki/images/math/e/b/3/eb31c18467b571d3dda496f6914b79db.png)
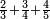
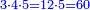
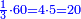
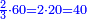
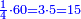
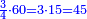
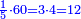
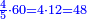
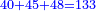
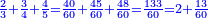
![\scriptstyle{\color{OliveGreen}{\frac{a}{b}+\frac{c}{d\sdot b}=\frac{\left[a\sdot\left[\frac{1}{b}\sdot\left(b\sdot d\right)\right]\right]+c}{b\sdot d}}}](/mediawiki/images/math/c/5/0/c508caaff04ccc2a6abc0776fa43bd51.png)
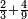
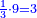
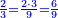
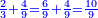
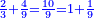
![\scriptstyle{\color{OliveGreen}{\frac{a}{b\sdot g}+\frac{c}{d\sdot g}=\frac{\left[a\sdot\left[\frac{1}{b\sdot g}\sdot\left(b\sdot d\sdot g\right)\right]\right]+\left[c\sdot\left[\frac{1}{d\sdot g}\sdot\left(b\sdot d\sdot g\right)\right]\right]}{b\sdot d\sdot g}}}](/mediawiki/images/math/b/f/1/bf19fb80e190649be13c951e1940036c.png)
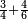

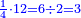
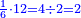
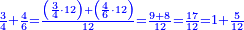
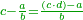
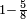
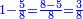
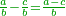
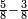
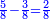
![\scriptstyle{\color{OliveGreen}{\frac{a}{b}-\frac{c}{d}=\frac{\left[a\sdot\left[\frac{1}{b}\sdot\left(b\sdot d\right)\right]\right]-\left[c\sdot\left[\frac{1}{d}\sdot\left(b\sdot d\right)\right]\right]}{b\sdot d}}}](/mediawiki/images/math/d/0/9/d0943c4416f582ab13803553e211310e.png)
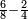
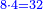
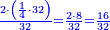
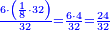
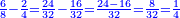
![\scriptstyle{\color{OliveGreen}{\frac{a}{b\sdot d}-\frac{c}{b}=\frac{a-\left[c\sdot\left[\frac{1}{b}\sdot\left(b\sdot d\right)\right]\right]}{b\sdot d}}}](/mediawiki/images/math/8/a/2/8a28dd28f4e8c1ffea1a486dbe9f9dbe.png)
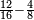
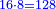
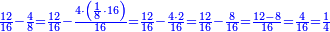
![\scriptstyle{\color{OliveGreen}{\frac{a}{b\sdot g}-\frac{c}{d\sdot g}=\frac{\left[a\sdot\left[\frac{1}{b\sdot g}\sdot\left(b\sdot d\sdot g\right)\right]\right]-\left[c\sdot\left[\frac{1}{d\sdot g}\sdot\left(b\sdot d\sdot g\right)\right]\right]}{b\sdot d\sdot g}}}](/mediawiki/images/math/c/c/f/ccf25ba4246eeb10ca46180c0f136558.png)
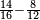
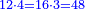
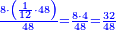
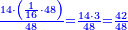
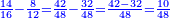
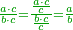
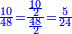
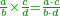
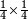
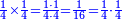
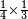
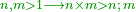

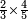
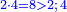
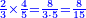
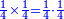
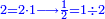
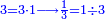

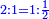
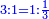

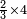
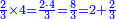
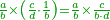
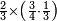
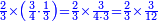
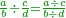
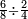
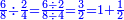
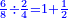
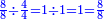
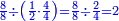
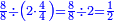
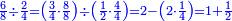
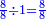
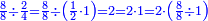
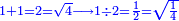
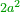 ] and three [
] and three [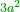 ] do not have a root, because two and three do not have a root, also there is no root for two times 4 [
] do not have a root, because two and three do not have a root, also there is no root for two times 4 [ ], nor to 3 times 4 [
], nor to 3 times 4 [ ], so there is no root for two-quarters [
], so there is no root for two-quarters [ ] nor to 3-quarters [
] nor to 3-quarters [ ].
].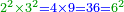
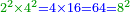

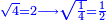
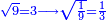
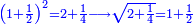
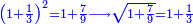
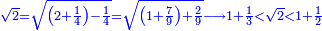
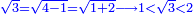
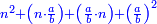 →
→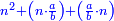 can be integers
can be integers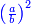 cannot be an integer →
cannot be an integer →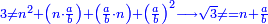
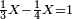
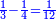
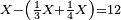
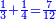
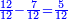

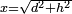
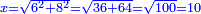
![\scriptstyle\left[\left[X-\left(\frac{1}{2}X+\frac{1}{2}\right)\right]-\left[\left[\frac{1}{2}\sdot\left[X-\left(\frac{1}{2}X+\frac{1}{2}\right)\right]\right]+\frac{1}{2}\right]\right]-\left[\frac{1}{2}\sdot\left[\left[X-\left(\frac{1}{2}X+\frac{1}{2}\right)\right]-\left[\left[\frac{1}{2}\sdot\left[X-\left(\frac{1}{2}X+\frac{1}{2}\right)\right]\right]+\frac{1}{2}\right]\right]+\frac{1}{2}\right]=1](/mediawiki/images/math/f/2/8/f28c22c40aef6283c27e81473fabdc88.png)
![\scriptstyle{\color{blue}{8-\left(\frac{1}{2}\sdot8\right)-\left[\frac{1}{2}\sdot\left(\frac{1}{2}\sdot8\right)\right]-\left[\frac{1}{2}\sdot\left[\frac{1}{2}\sdot\left(\frac{1}{2}\sdot8\right)\right]\right]=1}}](/mediawiki/images/math/b/a/8/ba8943378c2c9e86a2338e7f2544dd64.png)
![\scriptstyle{\color{blue}{\left[\left[8-\left[\left(\frac{1}{2}\sdot8\right)+\frac{1}{2}\right]\right]-\left[\left[\frac{1}{2}\sdot\left[8-\left[\left(\frac{1}{2}\sdot8\right)+\frac{1}{2}\right]\right]\right]+\frac{1}{2}\right]\right]-\left[\frac{1}{2}\sdot\left[\left[8-\left[\left(\frac{1}{2}\sdot8\right)+\frac{1}{2}\right]\right]-\left[\left[\frac{1}{2}\sdot\left[8-\left[\left(\frac{1}{2}\sdot8\right)+\frac{1}{2}\right]\right]\right]+\frac{1}{2}\right]\right]+\frac{1}{2}\right]=\frac{1}{8}}}](/mediawiki/images/math/1/b/1/1b150b9f34880a4ea8f9c389cb845ea5.png)