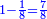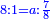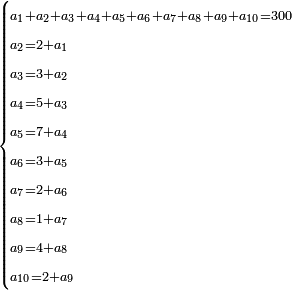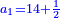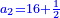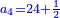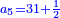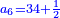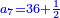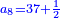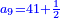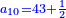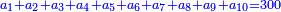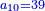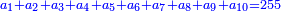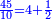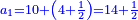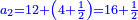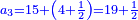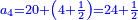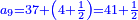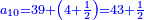קצור המספר
From mispar
Contents
[hide]| [1]קצור המספר מהרב ר' יהודה ן' בירגה | |
Prologue |
|
| Commercial and social needs of arithmetic: | |
| Since the selling of lands in the land of Israel depends on the number of the years after Jubilee [Leviticus 25, 14-16] and the redemption of the Hebrew maid [depends] on the number of years before the seventh [year] [Maimonides, Mishneh Torah, Sefer Qinyan, Hilḵot ʽAvadim 4, 6], so a person should study arithmetic lest a person would [cheat] his fellowman. | אחר אשר מכירת הקרקעות בארץ תלויה במספר שנים אחר היובל[note 1] וכן אמה העבריה בפריון במספר שנים קודם השביעי[note 2] הנה ראוי לאדם להתחבר בחכמת המספר לבל יונו איש את עמיתו |
| The author states that he writes on the subject in outline form | אכתוב לך בו ראשי פרקים |
Discussion on the nature of one |
|
| I say that the one that is without essence is equivalent to the being; hence, it belongs in actu to the ten categories and its meaning is in the nature of each category. | ואומר כי האחד אשר הוא חוץ לנפש הנה הוא נרדף לנמצא ולזה ימצא בפועל במאמרות העשרה ויהיה הוראתו בטבע מאמ' מאמ' |
| The [one] that is in essence belongs to the category of quantity. | ואשר הוא בנפש הוא מאמ' הכמות |
| It follows necessarily that that which is in essence exists in actu and that which is without essence is in potentia. | והנה בהכרח שמה שימצא בנפש בפועל שיהיה מציאותו חוץ לנפש בכח |
|
והאפשרות לפחות כי כל פועל נפשי אשר לא ימצא חוץ לנפש כלל הנה הוא פועל בדוי וזה הכח |
|
והאפשרות בדברים הוא הכח אשר בהם להתפרד במחשבה מפני חלוף ענין נמצא בו וכן כח בהם להתחבר במחשבה מפני דמיון מה שימצא בדברים |
| Indeed, when the essence is separated, the one is compared to what is apart of it, i.e. this thing is limited individual in itself within something of the rest of the beings | אמנם כאשר תפריד הנפש הנה יהיה האחד נאמ' בהקש אל אשר הוא חוץ ממנו כלומ' זה דבר מוגבל ונפרד בפני עצמו בדבר מה משאר הנמצאות בענין שנאמ' אחת היא יונתי תמתי[note 3] |
| When the essence is summed, the one is with regard to its parts, i.e. all these parts are one and a whole in some sense | וכאשר תחבר הנפש הנה יהיה האחד נאמ' בהקש אל חלקיו כלומ' אלה החלקים כלם הם אחד ושלם בצד מה כענין שנאמ' והיה המשכן אחד[note 4] |
|
והנה המפרשים הבינו פי' הפסוק הייחוד[note 5] כפי העניין הראשון לפי שהם הבינו כי אותם השמות רומזים לסבת הסבות כלם |
|
אמנם המקובלים שקבלו כי הם רומזים לשפע מושפע מאתו ית' בספירות ותארי מדות פירשו אותו כפי הענין השני |
|
ואמנם אחדות סבת הסבות כלם הנה למה שאין בו אפשרות להתחלק לדברים שונים כי אינו מורכב ולא להתחבר כי אין דומה לו להיותו מתחבר עמו הנה אותו האחדות אינו מתחלק ואינו מתרבה ואין כח בנפש לפעול בו זה |
|
ולזה נאמ' עליו בזוהר אנת הוא אחד ולא בחשבון[note 6] |
| However, the unity of the existences is by God. | ואמנם אחדות הנמצאות מאתו ית' |
| Since every existence of them is somewhat similar to at least one other existence, as they exist […] they have the potentiality to increase and be multiplied through their unity. | לפי שכל נמצא מהם יש לו דמיון מה עם נמצא אחד לפחות בהיותם נמצאים אפי' שיהיה זה בהם בקדימה ואיחור הנה באחדותם כח להתרבות ולהכפל |
| Since they are one, although in their essential form they are separate and distinct from each other, and because they have some diversity, they have the potentiality to be divided and separated, even though they are one in form. | ולהיותם למספר אחד אע"ף שבצורתם העצמית יהיו נפרדים ונבדלי' וגם לפי שבהם חילוף מה יש בהם כח להתחלק ולהפרד אע"ף שהם אחדים בצורה בו |
Definition of Number |
|
| Therefore, the number counts all things, as the number ten, for example counts 10 people but also 10 horses. | לזה המספר מונה כל הדברים כי הי' מהמספר ד"מ ימנה לי' מהאנשים וכן ימנה לי' מהסוסים |
| Hence, the number is a sum of undetermined units; | והנה המספר הוא קבוץ אחדים בלתי רמוזים |
| the essence is its agent and the units are its subject. | והיה הנפש כפועל לו והאחדות כנושא |
Numeration |
|
| Since sometimes the measurement becomes measured and the number numbered, people count with their fingers, and the fingers are ten as the number of the countings. | ולפי שלפעמים תשוב הממד[2] מדוד והמספר ספור ויקרה לאנשים שימנו באצבעותיהם והיה האצבעות עשרה כמספר הספירות |
|
הנה כל האנשים הסכימו לעשות עד עשרה כלל אחד ועשרה פעמים זה כלל שני [3]ועשרה פעמים הכלל השני כלל שלישי וכן תמיד מהרכבת העשרה מהכלל הקודם יולד כלל אחד |
|
וסדר הכללים הוא זה אחדים עשרות מאות אלפים עשרת אלפים מאת אלפים אלף אלפים עשרת אלפי אלפים מאת אלפי אלפים אלף אלפי אלפים וכזה עד אין קץ |
|
והנה עשו מכל ג' כללים סדר אחד לפי שבשלשה נמצא התחלה ואמצע ותכלית |
The arithmetical opperations |
|
|
ואמנם מפעל הנפש בחבר הנפרדים היה מין אחד מהמספר שנקרא הקיבוץ |
|
ומפעל הנפש בהפרדה היה מין שני מהמספר שיקרא המגרעת |
|
ומפעל הנפש בהכפילה הדברים היה מין שלישי מהמספר שיקרא הכפילה |
|
ומפעל הנפש בהפריש הכפלים נמצא מין ד' והוא החלוקה |
|
ומפעל הנפש בהכפל כפלים או חלקיהם על מספר מה כאשר תכפול על מספר אחר היה מין חמישי והוא הערכים |
|
ומפעל הנפש בהפריש הכפלים במספר האחדים אשר בכל כפל נמצא מין ששי שנקרא השרשים |
| Those are the types [of arithmetical operations] | ואלה המינים |
|
אם שיהיה עסקם במספרים שלמים ומזה הצד כלם סוג אחד ויקרא השלמים |
|
ואם שיעסקו בשברי מספרים ויהיו כלם סוג אחד ונקרא שברים |
| The [fractions] are called a type of [operation] by itself - so there are seven types [of operations] | וכבר קראו לזה מין בפני עצמו ושלמו בו במספר ז' מינים |
Chapter One - Addition |
|
| The first type is addition - the meaning is to sum two or three numbers or more and calculate their sum. | המין הא' בקיבוץ הכוונה בו לקבץ שני מספרים או שלשה או יותר לידע סכום מניינם |
Written Addition |
|
| Description of the procedure: | |
|
והנה ראוי שיסודרו כל כלל מהם תחת הכלל הדומה לו כיצד אחדים תחת אחדים ועשרות תחת עשרות וכן השאר |
|
ואחר תתחיל לקבץ מהאחדים כלם ותכתבם במקומם |
|
ואם יעלו מהם עשרות תקבצם עם העשרות אם היו שם עשרות |
|
ואם יעלו מהם עשרות ומאות תקבץ העשרות עם העשרות והמאות עם המאות |
|
ואם אין שם עשרות או מאות תכתבם בפני עצמם |
|
וכל זה בשערך העשרות שעלו מן האחדים כאלו הם אחדים בתוך מדרגת העשרות כמו שאתה משער העשרות לאחדים במדרגתם וכן המאות שעלו מהם בתוך מדרגת המאות |
|
ויהיה המשל בזה רצינו לקבץ אלף ותשעים ושמונה עם תשעת אלפים ושישים ושבעה |
- [Illustration of the procedure:]
1098 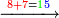
1098 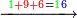
1098 
1098 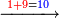
1098 9067 9067 9067 9067 9067 5 65 165 10165
|
והנה החלונו באחדים ואמרנו שמונה ושבעה הרי הם ט"ו | ||||||||||||||||
|
נכתוב הה' אחדים תחת האחדים והעשרה נחשוב אותו כאלו הוא אחד בתוך העשרות | ||||||||||||||||
|
ונקבץ אותו עם התשעה והששה עשרות ויעלו י"ו | ||||||||||||||||
|
נכתוב הו' במדרגת העשרות והעשר שהוא עשר עשרות נכתוב אותו בפני עצמו במדרגת המאות ונחשוב אותו כאלו הוא אחד ר"ל מאה אחת | ||||||||||||||||
|
עוד נקבץ האלפים והיו עשרה | ||||||||||||||||
|
והנה לפי שאין שם אחדי אלפים נכתוב במדרגתם ספרא ונכתוב העשר במדרגתם | ||||||||||||||||
| Eventually [the final result is] as in this diagram | והיו שם לאחר הכל כמו שהוא בצורה הזאת | ||||||||||||||||
| |||||||||||||||||
Methods of checking |
|||||||||||||||||
|
ואם עשית אמת בזה הנה כשתגרע אחד מהמספרים הראשונים מהמקובץ יצא המספר האחר | ||||||||||||||||
|
כי כן דרך כל מורכב מפשוטים כי כשתמצא הפשוט האחד בפני עצמו הנה בהכרח שימצא השני בעצמו כמו שנתבאר בפילוסופיא [בחכמה הטבעית] | ||||||||||||||||
|
ויש מי שבקש מופת לדעת אם טעה בקבץ המספרים בהשליך אותיות הנקבצים ט'ט' והחזיק בנשאר וככה ישאר בכלל העולה אחרי השליך אותיותיו ט'ט' | ||||||||||||||||
|
כיצד מן השטה העליונה לא נשאר דבר כי הלכו להם ט'ט' | ||||||||||||||||
|
ומן השטה התחתונה נשארו ד' | ||||||||||||||||
|
והנה ג"כ נשארו ד' מהכלל העולה | ||||||||||||||||
|
והטעם בזה הוא כי אין קבוץ שני המספרים יחד דבר אחר זולתי השליך הם תשיעיות שהם ממין אחד | ||||||||||||||||
|
כיצד כשקבצנו הח' והז' מהאחדים והיו ט"ו הנה כתבנו באחדים חמשה ועם העשרות אחד הרי ו' והפלנו מהט"ו ט' | ||||||||||||||||
|
וכן כשקבצנו העשרות ועלו י"ו הנה כתבנו בעשרות ששה ובמאות אחד והפלנו ט' | ||||||||||||||||
| וכן כשקבצנו האלפים העלנו תשעה וכתבנו א' | |||||||||||||||||
|
והנה א"כ אין הפרש בין המספרים הנקבצים [ו]הכלל העולה זולתי אלה התשיעיות וא"כ והפיל אותם ישארו שוים | ||||||||||||||||
|
לפי שמהשוים כשנפיל שוים ישארו שוים | ||||||||||||||||
|
הנה כשנפיל עוד התשיעיות הנקבצים מהאחדים והעשרות והמאות וכו' מהמספרים הנקבצי' וכן נפיל אותם הכלל העולה כמו כן הנה ראוי שיהיה השאר בהם שוים | ||||||||||||||||
|
ומזה המשפט תבין הטעם ג"כ בגרעון | ||||||||||||||||
|
כי המספר הנגרע והמספר הנשאר מקובצים ישתוו למספר אשר גרעת ממנו | ||||||||||||||||
| Thus, the subtraction is potentially inverse operation to addition. | וא"כ הנה הגרעון מתהפך לקבוץ בכח | ||||||||||||||||
| The reason for casting out by 9 as a check of a multiplication procedure: In the multiplication the reason is that any product of nines is a sum of nines. | ובכפילה הנה הטעם הוא כי התשיעיות בכל מספר שיוכפלו יעלה מהם תשיעיות | ||||||||||||||||
Therefore, what remains from the multiplied numbers is exactly the resulting product of the excess of one of the numbers over nine by the excess of the other number [over nine] and this is what should remain from the total product after casting out the nines. 
|
וא"כ לא ישאר במספרים הנכפלים אלא מה שיעלה מכפילת העודף על תשיעיות בזה המספר בעודף במספר השני וזהו מה שראוי שישאר בכלל העולה מהכפילה אחר הפלת תשעיותיו | ||||||||||||||||
| From the multiplication rule you understand the reason of division, for they are inverse operations, like the addition and subtraction. | וממשפט הכפילה תבין הטעם בחלוקה כי שניהם מתהפכים בענין הקבוץ והגרעון | ||||||||||||||||
Chapter Two - Subtraction |
|||||||||||||||
| The second type is subtraction - when we wish to subtract a number from a greater number. | המין הב' במגרעת הנה כשנרצה לגרוע מספר ממספר יותר ממנו | ||||||||||||||
Written Subtraction |
|||||||||||||||
| Description of the procedure: | |||||||||||||||
|
נסדרם תחלה כל מדרגה תחת הדומה לה | ||||||||||||||
|
ונתחיל לגרוע ממדרגת האחדים | ||||||||||||||
|
והנה אם האחדים אשר במספר הגדול היו יותר מהאחדים אשר במספר הקטן נגרע מהם אחדי המספר הקטן והשאר נכתוב אותו תחת מדרגותם | ||||||||||||||
|
ואם היו להפך הנה אז נקח אחד מאחדי העשרות מהמספר הגדול ונתיכהו לאחדים ויהיה לעשרה עם אחדי המספר הגדול ואז נגרע מהם אחדי המספר הקטן ונכתוב השאר תחת מדרגתם והנה אז ישארו עשרות המספר הגדול חסרים האחד אשר לקחנו מהם | ||||||||||||||
|
ואם אין במדריגת העשרות שום עשר לקחת ממנו עשר אחד לשום על אחדיו ויש במדריגת המאות שום מאה הנה נקח משם שום מאה אחד ונתיך אותו לעשרותיו שהם עשרה במדרגת העשרות ונקח מהם עשר אחד ונשארו שם תשעה ונכתוב אותם שם והעשר שלקחנו משם נשים אותו על אחדיו ואז נגרע מהם האחדים של המספר הקטן | ||||||||||||||
|
ויהיה המשל לזה רצינו לגרוע ממאה ושבעה חמישים ותשעה | ||||||||||||||
|
|||||||||||||||
|
הנה לפי שאין בו בשבעה לגרוע ממנו התשעה וגם לא מצינו במדרגת העשרות של מספר גדול שום עשר הנה נקח המאה אשר לו ויהיה לעשרה במדרגת העשרות ונקח מהם אחד לשום על האחדים ונשארו שם תשעה ואחר גרענו מהשבעה עם העשרה תשעה ונשארו שמונה | ||||||||||||||
|
עוד נגרע מאשר מהתשעה שנשארו במדרגת העשרות החמשה עשרות של המספר הקטן וישארו תחתיהם ארבעה | ||||||||||||||
|
ואמנם המאה לא נשאר מהם דבר כבר עשינו אותו עשרות | ||||||||||||||
|
אם כן הנשאר מן הכל הוא ח' וארבעים | ||||||||||||||
Method of checking |
|||||||||||||||
|
ואם עשית חשבון אמיתי בזה הנה כשתשוב לקבץ שני המספרים התחתונים ר"ל המספר אשר גרענו והמספר הנשאר יעלה המספר הג' והוא הגדול אשר גרענו ממנו |
Chapter Three - Multiplication |
|
| The third type is multiplication - the meaning is to multiply a number by units, or by units and tens, or by units, tens and hundreds of another number and so on endlessly. | המין הג' בכפילה הנה הכוונה בזה לכפול מספר מה במספר אחדי מספר אחד או אחדים ועשרות או אחדים ועשרות ומאות וכן אפשר שתוסיף עד אין תכלית |
Written Multiplication |
|
| Description of the procedure: | |
| When you wish to multiply them, arrange them according to their ranks. | והנה כשתרצה לכפול אותם תסדרם במדרגתם כמשפט |
|
ותתחיל לכפול המספר ההוא שרצית לכפול אותו כל מדרגה ומדרגה ממנו כמספר האחדים אשר במספר האחר |
|
והנה אם מכפילת אחדיו יעלו גם עשרות אז תכתוב האחדים במדריגתם והעשרות עם העשרות אחר שתחשבם לאחדים בתוכם |
|
וכן תעשה אם מכפילת האחדים בעשרות יעלו גם מאות תכתוב העשרות במקומם והמאה בתוך המאות בחשבך אותו לאחדים בתוכם |
|
|
|
והנה המשל בזה רצינו לכפול שמונה מאות ושישים ותשעה במספר אחדי ששה שיש במספר אחר |
- [Illustration of the procedure:]
6 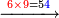
6 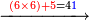
6 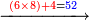
6 869 869 869 869 4 14 5214
|
ונתחיל לכפול מאחדיו ונאמ' ששה פעמים תשעה הם נ"ד |
|
נכתוב הד' ונשמור הה' ונחשוב אותם לה' |
|
ואחר נכפול הששה בשישים שהם במדרגתם נחשבים לששה יעלו ל"ו נחבר אליהם החמשה שחשבנו אותם מהחמישים ויעלו מ"א |
|
נכתוב האחד במדרגת העשרות ונשמור המ' ונחשוב אותם לד' |
|
ואחר תכפול הו' שמנה בשש מאות אשר במדרגתם הם נחשבים לשמונה ויעלו מ"ח נחבר אליהם הד' ששמרנו ויעלו נ"ב |
|
נכתוב השנים במדרגת המאות והחמישים אחריהם במדרגת אלפים בחשבנו אותם שם לחמשה כמו שהוא בזאת הצורה |
|
ואמנם אם היה הכפילה במספר אחדים ועשרות של מספר מה |
|
כאלו תאמר שרצינו לכפול אותם הח' מאות ושישים ותשעה במספר אחדים ועשרות של ארבעים וששה |
- [Illustration of the procedure:]
46 
46 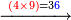
46 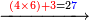
46 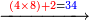
46 869 869 869 869 869 5214 5214 5214 5214 6 76 3476
|
הנה נכפול אותם בתחלה בכמו ו' האחדים אשר עשינו בתחלה ונכתוב העולה כל מדרגה ומדרגה במקומה |
|
ואחר נשוב לכפול אותם בארבעים אחר חשבנו אותם לד' במקומם |
|
ונתחיל מהתשעה אחדים ויעלו ל"ו |
|
ונכתוב הו' תחת האחד שהיה בכפילת הששה בתחלה |
|
לפי ששוה הוא כפילת אחדים בעשרות שהיה כפילת הו' מהמ"ו ב[...]בשישים מהתתס"ט לכפילת עשרות באחדים שזהו כפילת המ' בט' |
|
ובכפילה הזאת לא תמצא אחדים לפי שכפילת עשרות בכל דבר יעלו עשרות או יותר |
|
ונשמור הל' מהל"ו |
|
ונשוב לכפול המ' בס' ובחשבנו אם אותם אחדים במקומם יעלו כ"ד נחבר ג' מהל' יעלו כ"ז |
|
נכתוב הז' שהם מאות תחת השנים שהיו באותה מדרגה בתחלה |
|
וישאר עשרים שהם שנים ונשמור אותו |
|
נכפול עוד הארבעים בח' מאות בחשבנו אותם לאחדים ויעלו ל"ב ונחבר אליהם שנים מהעשרים ששמרנו ויעלו ל"ד |
|
תכתוב הד' תחת הה' מהאלפים והשלשים אחריהם חשובים לג' |
|
ואחר תקבץ סך הכל כמשפט ויעלו ל"ט אלף ותשע מאות ושבעים |
| Do the same if the ranks are multiple. | וכזה תעשה אם המדרגות יהיו רבות |
Method of checking |
|
|
ואם עשית אמת הנה כשתחלוק היוצא על כל אחד מהמספרים הנכפלים זה על זה יצא השני |
Calculating the number of ranks in a product of two numbers |
|
| And if you wish to know up how many ranks will the ranks of the product rise, count the ranks of both multiplied numbers and sum them together, then subtract one rank. | ואם תרצה לדעת עד כמה מדרגות יעלו מדריגות הכפילה הנה מנה מדריגות שני המספרים הנכפלים זה עם זה ותקבצם יחד והסר מדריגה אחת |
|
לפי שהאחדות אינו מרבה דבר |
| The remainder are the ranks of the number resulted from the multiplication. | והנשאר הם יהיו מדריגות המספר היוצא מהכפילה |
|
ואמנם אם יתחברו מהמדרגות האחרונות מהנכפלים בהכאתם ומהמדריגות הסמוכות להם עד עשרה הנה אז המדרגות העולות מהכפילה יהיו כמספר מדריגות שני המספרים הנכפלים זה על זה מבלי הסר מהם שום מדרגה |
Chapter Four - Division |
||||||||||||||||||||
| The fourth type is division | המין הד' בחלוקה | |||||||||||||||||||
Dividing a large number by a smaller one |
||||||||||||||||||||
| The first meaning of dividing integers is to divide a large number by a number smaller than it, in such a way that each [digit] of the small number is given an equal part. | הכוונה הראשונה בו בחלוקה בשלמים לחלק מספר גדול על מספר יותר קטן ממנו בענין שיגיע לכל אחד מהמספר הקטן חלק שוה לאחר | |||||||||||||||||||
Written Division |
||||||||||||||||||||
| Description of the procedure: | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| The procedure is as follows: | והמעשה בזה יהיה כן | |||||||||||||||||||
| Arrange the numbers by their ranks successively as the rule. | סדר ב' המספרים במדריגתם זה תחת זה כמשפט | |||||||||||||||||||
|
והנה אם האות האחרונה שבמספר הגדול יותר כוללת מהאות האחרונה של מספר הקטן | |||||||||||||||||||
|
תתחיל החלוק ממנה ועליה ר"ל מהאות האחרונה של מספר גדול על האות האחרונה של המספר הקטן ותן לי ממנה היותר פעמים שתוכל | |||||||||||||||||||
|
ובלבד שתשאיר בה להשלים עמו מהאות הסמוכה לה לאות הסמוכה לאחרונה מהמספר הקטן אם יצטרך לו | |||||||||||||||||||
|
וכן אם יהיה שם יותר אותיות שישאר בה או בשנית לה להשלים עמו באות השלישית ממנה לאחרונה אשר מהמספר הקטן אם יצטרך אליו | |||||||||||||||||||
|
והנה המשל בזה רצינו לחלק שמונה מאות ועשרים ושלשה למאתים ושבעים ושמונה | |||||||||||||||||||
| ||||||||||||||||||||
|
והתחלנו מהאות האחרונה מהמספר הרב שהוא שמונה לחלקו על האות האחרונה מהמספר המעט שהיה שנים | |||||||||||||||||||
|
והנה מן הדין היה שנתן לו ד' אלא כשנתן לו ככה מהאות הסמוכה לאחרונה מהרב שהוא שנים לאות הסמוכה לאחרונה מהמעט שהוא שבעה הנה לא יהיה בו די | |||||||||||||||||||
|
והכוונה היתה שיקבלו כלם חלקים שוים על כן לא נתן מהח' לשנים ארבעה ולא גם כן נתן לו ג' | |||||||||||||||||||
|
לפי שאע"ף שיספיק השנים עם מה שישאר מהשמונה שהם ב' אחדים שיהיו נחשבים לעשרים ושנים לתת לשבעה לשלש לכ"א וגם ישאר שם אחד | |||||||||||||||||||
|
הנה לא יהיה די בשלש מהמספר הרב לתת לשמנה מהמספר המעט שלש לכל אחד מהם | |||||||||||||||||||
|
ואפילו שיוריד אליו האחד שנשאר על השנים ויהיו י"ג לפי שיותר הוא ג' פעמים שמנה שהוא כ"ד | |||||||||||||||||||
|
על כן לא נתן מהשמנה לשנים אלא שנים ונכתוב אותם במדרגה הראשונה | |||||||||||||||||||
|
לפי שראוי למנות מדרגות המספר אשר נחלק עליו מהמדרגה האחרונה מהמספר אשר נחלק ממנו למפרע | |||||||||||||||||||
|
אם היה בה מספר די לחלק ממנו על המספר האות האחרונה מהמספר המעט כמו שיש בכאן בשמונה די לחלק על השנים | |||||||||||||||||||
|
ובמקום שיכלה שם תכתוב מה שיעלה בחלוקה | |||||||||||||||||||
|
ואם אין די במה שכתו' במדרגה האחרונה ההיא לתת למספר אשר הוא למדרגה התחתונה ותצטרך להעתיק אותה ממקומה ולחושבה לעשרות במדרגה הסמוכה לה כדי לחלק ממנה הנה אז תמנה מהמדרגה השנית לה ר"ל מהאות הסמוכה לה למפרע ובמקום שיכלה שם תכתוב היוצא בחלוק | |||||||||||||||||||
|
ומדרך זה תדע מתחלת החלוקה לכמה מדרגות יעלה היוצא בחלוק | |||||||||||||||||||
|
ועתה נשלם דרך החלוקה במשל שהמשלנו ונאמר כי כבר יצא לה בחלוק שנים וכשנמנה מדריגות הנחלק עליו מהמדריגה האחרונה מהמחולק למפרע הנה יכלו במדרגה הראשונה שהיא מדרגת האחדים על כן נכתוב שם השנים תחת הג' ועל הח' במה שביניהם | |||||||||||||||||||
|
והנה כשנתן לשנים האחרונים שנים לכל אחד יעלו ד' נגרע אותם מהח' ישארו ד' | |||||||||||||||||||
|
נתן כך לשבעה יעלו י"ד | |||||||||||||||||||
|
ולפי שאין בשנים הסמוכים לח' די לזה נקח מד' שנשארו מהח' שנים והשנים הנשארים נכתבם על הח' | |||||||||||||||||||
|
והנה השנים שלקחנו יהיו נחשבים לכ' על השנים ויהיו הכל כ"ב | |||||||||||||||||||
|
נגרע מהם הי"ד וישארו ח' | |||||||||||||||||||
|
עוד נצטרך לקחת שנים מאלה השמונה לשום על הג' וישארו ו' ונכתבם על הב' | |||||||||||||||||||
|
והב' שלקחנו נורידם על הג' ויהיו שם הכל כ"ג | |||||||||||||||||||
|
נגרע מהם שני פעמים שמונה וישארו שם שבעה נכתבם על הג' | |||||||||||||||||||
|
והנה תמצא בזה כי יצא לכל אחד בחלוקה שנים ונשארו לחלק רס"ז | |||||||||||||||||||
|
וכן תעשה גם שיהיו המספר הרב רבות ומדרגות המספר המעט מעטות עד שיצא בחלוקה שתים או שלש מדרגות | |||||||||||||||||||
|
אלא שראוי שתדע שאם כבר חלקת משום מדרגה מהמספר הרב או אפי' שלא חלקת אלא שאין במדרגה ההיא כדי לתת ממנה אלא בהעתיק אותה ממקומה הנה תשים בחלוקה סיפרא לומר שאין נמצא דבר במתחלק לחלק באותה מדריגה | |||||||||||||||||||
|
ולהרגילך בזה נמשיל עוד משל אחד בזה | |||||||||||||||||||
|
ויהיה המספר המתחלק מאתים וארבעת אלפים ושש מאות ושתים עשרה והנחלק עליו מאתים ושמונים ותשעה | |||||||||||||||||||
| ||||||||||||||||||||
|
והנה כבר היינו יכולים לתת משנים העליונים לשנים התחתונים אחד אלא שלא יהיה דבר בסיפרא הסמוכה לו לתת לח' הסמוכה לשנים התחתונים | |||||||||||||||||||
|
והנה צריכין אנחנו להעתיק השנים ממקומם על הסיפרא ויהיו עשרים | |||||||||||||||||||
|
ונחלק ממנו על השנים ולא נוכל לתת עשרה כי אין בחלוק יותר מאחדים ולא גם כן נוכל לתת בזה המספר לתת תשעה ולא עוד אלא שמונה כי לא יהיה די בארבעה לחלק ככה לשמונה אבל ראוי שנתן שבעה | |||||||||||||||||||
|
ולפי שמדרגות המספר אשר נחלק עליו הם שלשה וכשנמנה כמספרם למפרע מהספרא שהועתק אליו השנים העליונים יכלה אל המדרגה השלישית שהוא מדרגת המאות הנה ראוי לכתו' שם אלו הז' היוצאים בחלוקה | |||||||||||||||||||
|
ואז נשוב ונאמר כי שבעה פעמים שנים הם י"ד נגרע אותם מהעשרים ישארו ששה | |||||||||||||||||||
|
ולפי ששבעה פעמים שמונה הם נ"ו ויצטרך הד' אשר אצל הספרא להוריד אליה הו' הנשארים על הספרא | |||||||||||||||||||
|
נכתוב סיפרא על הסיפרא ויהיו על הד' ס"ד נגרע מהם הנ"ו ישארו שמונה על הד' | |||||||||||||||||||
|
ועוד לפי שז' פעמים ט' הם ס"ג ויצטרך הששה להוריד אליהם מהשמונה ששה הנה נשארו שם שנים ונכתבם על הד' | |||||||||||||||||||
|
והנה הו' שהורדנו על הו' יעלו לשם ס"ו נגרע מהם הס"ג ישארו שם שלשה ונכתבם על הששה | |||||||||||||||||||
|
ונעשה סימן במדרגת הסיפרא לומר שכבר חלקנו ממנה | |||||||||||||||||||
|
ואע"ף שהיה נשאר לשם די לחלק אין ראוי לעשותו אלא בהורידו מאותה מדרגה לסמוכה התחתונה ממנה כ"ש כשישאר דבר שאין בו די לחלק או לא דבר כמו שהוא בכאן | |||||||||||||||||||
|
ונשוב לחלק מהשנים שנשארו על הד' על השנים התחתונים | |||||||||||||||||||
|
ודי היה בזה לתת להם אחד אלא שלא יהיה די בג' הסמוכים להם לתת כמו זה לח' הסמוכי' לשנים התחתונים | |||||||||||||||||||
|
ונצטרך להוריד השנים העליונים ממדרגתם על הג' הסמוכים להם והיו שם כ"ג | |||||||||||||||||||
|
ונכתוב ספרא סמוך לז' לומ' לא מצאנו במדרגת השנים העליוני' דבר לחלק משם | |||||||||||||||||||
|
ונרשום סימן תחת הד' לומ' כבר חלקנו משם ספרא כי לא מצאנו דבר יותר | |||||||||||||||||||
|
ונשוב לחלק הכ"ג לשנים והנה לא נוכל לתת תשעה וכ"ש יותר לפי שלא ישאר מהכ"ג להשלים עם האחד לשמונה | |||||||||||||||||||
|
לכן נתן להם שמונה ויעלו י"ו נגרע אותם מכ"ג ישארו שם ז' | |||||||||||||||||||
|
ולפי שח' פעמים ח' הוא ס"ד נצטרך להוריד על האחד כל אותם השבעה וישאר שם ספרא על הכ"ג | |||||||||||||||||||
|
ויהיו ע"א על הא' נגרע ס"ד מהם ישאר גם כן שם שבעה | |||||||||||||||||||
|
ולפי שנצטרך להורידם על השנים לספק לח' פעמים ט' שהם ע"ב נכתוב ספרא על האחד גם כן | |||||||||||||||||||
|
ואחר שהורדנו אותם על השנים והיו ע"ב נגרע מהם ע"ב מכפילת ח' פעמים ט' ולא ישאר גם לשם דבר ונכתוב ספרא על השנים | |||||||||||||||||||
|
והנה כבר חלקנו כל המספר ולא נותר עד אחד | |||||||||||||||||||
|
ונאמין זה לפי שהגיע מדרגות החלוקה עד מדרגות האחדי' וגם כן לפי שכבר חלקנו מדרגות מספר הששה למספר השנים התחתוני' והם שוים במדרגתם | |||||||||||||||||||
| ואין מקום לחלק עוד ממדרגה פחותה ממנה לשנים לפי שהם ממדרגה גדולה | ||||||||||||||||||||
| וזה כפי המכוון הראשון בחלוקה שאמרנו | ||||||||||||||||||||
| ||||||||||||||||||||
Method of checking |
||||||||||||||||||||
|
ואם עשית באמת החלוקה הנה כשתכפול התש"ח היוצאים בחלוקה על הרס"ט אשר חלקת עליהם יהיה העולה שוה למאתים וארבעת אלפים ותרי"ב שחלקת אותם | |||||||||||||||||||
|
ובזה תבחין כל חלוקה שתעשה אלא שראוי שתדע שאם נשארו לחלק שום מספרים על המספר הנחלק שראוי שתקבצם עם העולה מהכפילה ואז ישתוה למספר הנחלק | |||||||||||||||||||
|
ויש מי שבקש מופת לדעת אם טעה בקבוץ המספרים בהשליך אותיות הנקבצים ט'ט' ואחזיק בנשאר וככה ישאר בכלל העולה אחרי השליך אותיותיו ט'ט' | |||||||||||||||||||
|
כיצד מהשטה הראשונה לא נשאר דבר כי אם הלכו להם ט'ט' | |||||||||||||||||||
|
ומן השטה התחתונה נשארו ד' | |||||||||||||||||||
|
והנה אם כן נשארו ד' מהכלל העולה | |||||||||||||||||||
|
והטעם בזה הוא כי אין קבוץ שני המספרים יחד דבר אחר זולתם השליך התשיעיות שהם ממין אחד | |||||||||||||||||||
|
כיצד כשקבצנו הח' והז' מהאחדים והיו ט"ו הנה כתבנו באחדים חמשה ועם העשרות אחד והפלנו מהט"ו ט' | |||||||||||||||||||
|
וכן כשקבצנו העשרות ועלו י"ו הנה כתבנו בעשרות ששה ובמאות א' והפלנו והפלנו ט' | |||||||||||||||||||
|
וכן כשקבצנו האלפים הפלנו ט' וכתבנו א' | |||||||||||||||||||
|
והנה אין הפרש בין המספרים הנקבצים לכלל העולה זולתי אלה התשיעיות | |||||||||||||||||||
|
ואם כן בהפיל אותם ישארו שוים שמהשוים כשנפיל שוים ישארו שוים | |||||||||||||||||||
|
כשנפיל עוד התשיעיות הנקבצים מהאחדים והעשרות והמאות וכו' מהמספרים הנקבצים וכן נפיל אותם מהכלל העולה כמו כן הנה ראוי שיהיה הנשאר בהם שוים | |||||||||||||||||||
| From this rule you can understand the reason of subtraction also, because the sum of the subtrahend and the remainder is equal to the subtracted number. | ומזה המשפט תבין הטעם גם כן בגרעון כי המספר הנגרע והמספר הנשאר מקובצים ישתוו למספר אשר גרעת ממנו | |||||||||||||||||||
| Therefore, subtraction is inverse of addition in potentia. | ואם כן יהיה הגרעון מתהפך לקבוץ בכח | |||||||||||||||||||
| The reason of multiplication is that the product of nines by any number is nines. | ובכפילה הנה הטעם הוא כי התשיעיות בכל מספר שיוכפלו יעלה מהם תשיעיות | |||||||||||||||||||
| So, the remainder from the multiplied numbers is only the product of the excess over the nines in one number by the excess over the nines in the second number and this is what should remain from the total result of multiplication after casting out its nines. | ואם כן לא נשאר במספרים הנכפלים אלא מה שעלה [מכ]פילת העודף על תשיעיות בזה המספר בעודף מתשיעיות במספר ה[שני] וזהו מה שראוי שישאר בכלל העולה מהכפילה אחר הפלת תשעיותיו | |||||||||||||||||||
| From the rule of multiplication you can understand the reason of division, because they are inverses, as matter of addition and subtraction. | וממשפט הכפילה תבין הטעם בחלוקה כי שניהם מתהפכים כענין הקבוץ והגרעון | |||||||||||||||||||
Dividing a small number by a larger one |
||||||||||||||||||||
| The second meaning of division is to divide a small number by a number greater than it | הכוונה השנית בחלוקה לחלק מספר קטן על מספר גדול ממנו | |||||||||||||||||||
| Since it is [a division] of integers it is included in the [discussion of] integers, even though the resulting quotient is fractions. | כיון שזה בשלמים אע"פ שהחלוקה יצא בשברים נמצא זה בתוך השלמים | |||||||||||||||||||
| We say that the people got used in this [kind of] division to multiply the smaller number by ten, then they divide the result by the larger number, if the product is greater than it, and the result of the division is tenths.
|
ונאמר כי האנשים הרגילו בחלוקה זאת לכפול המספר הקטן בעשרה והיוצא יחלקו על המספר הרב אם היוצא יותר ממנו והיוצא בחלוקה יהיו עשיריות | |||||||||||||||||||
| If multiplying by ten is not enough to divide by the greater number, or if there is something left to divide after multiplying by ten, then multiply it by ten again and the result is tenths of tenths and so on.
|
ואם אין די בכפול בעשרה לחלק על מספר הרב או אם ישאר דבר לחלק אחר הכפילה בעשרה הנה תכפול אותם עוד בעשרה ויהיה היוצא עשיריות של עשיריות וכן תמיד | |||||||||||||||||||
|
ומשל לאחד רצינו לחלק ד' על חמישים | |||||||||||||||||||
|
הנה עשינו אותם עשיריות עדין אין די נעשה אותם עוד עשיריות יהיו ד' מאות נחלקים על החמישים יצא לכל אחד שמונה והם עשיריות של עשיריות | |||||||||||||||||||
|
| ||||||||||||||||||||
|
[ומ]של לשני רצינו לחלק ששה על חמישים | |||||||||||||||||||
|
עשינו אותם עשיריות היו ששים חלקנו אותם על החמישים יצא לכל אחד א' וישארו שם עשרה | |||||||||||||||||||
|
| ||||||||||||||||||||
|
נעשם עוד עשיריות ויהיו מאה נחלקם על חמישים יצא לכל אחד שנים והם עשיריות של עשיריות | |||||||||||||||||||
|
| ||||||||||||||||||||
| Since this division is unnatural, I say that we divide the larger number by the smaller one and the resulting number is the name of the fraction resulting from the division.
|
ואמנם לפי שהחלוק הזה בלתי טבעי אני אומר כי נחלוק המספר הגדול על הקטן והמספר היוצא יהיה שם השבר היוצא בחלוק | |||||||||||||||||||
|
המשל בזה נרצה לחלק ד' על י"ב | |||||||||||||||||||
|
הנה נהפך המשפט ונחלק הי"ב על הד' ויצא בחלוקה שלשה ואומר כי שם השבר אשר יצא בחלוקה הוא שליש | |||||||||||||||||||
|
וכן הוא כי כשנעשה הד' שלישים כלם יהיו י"ב שלישים וכשנחלקם לי"ב יצא לכל אחד שליש | |||||||||||||||||||
| וכזה בכל מה שיביאך אליו החלוקה | ||||||||||||||||||||
Dividing a number to unequal parts |
||||||||||||||||||||
| The third meaning of division is to divide a certain number by another number of unequal parts | הכוונה הג' בחלוקה לחלק מספר מה על מספר אחר לחלקים בלתי שוים | |||||||||||||||||||
|
ויהיה משל בזה רצינו לחלק שש מאות על ג' בענין שיצא לראשון ביחס השנים ולשני ביחס השלשה ולשלישי ביחס הה' | |||||||||||||||||||
|
ואז ראוי שנקבץ היחסים כלם ויגיע מהם עשרה נחלוק עליהם השש מאות יצא לכל אחד שישים | |||||||||||||||||||
|
נכפיל זה ביחס השנים ויעלו ק"כ וזה מה שראוי לראשון | |||||||||||||||||||
|
עוד נכפול זה בג' ויעלו ק"ף וזה מה שראוי לשני | |||||||||||||||||||
|
עוד נכפול זה בה' יעלו ש' וזה מה שראוי לג' | |||||||||||||||||||
|
וכן אם אמרנו לחלקם על ג' ויהיה לראשון יחס החצי ולשני יחס השליש ולשלישי יחס הרביע | |||||||||||||||||||
|
הנה נדרוש מספר ימצאו בו היחסים כלם ונמצאהו כשנכפול החצי בשליש ויהיה ו' וזה בד' ויגיע כ"ד | |||||||||||||||||||
|
ונקבץ החצי והשליש והרביע ויעלו כ"ו | |||||||||||||||||||
|
ואחר נחלוק הו' מאות עליהם יצא לכל אחד כ"ג וחלק מי"ג | |||||||||||||||||||
|
ונקח חצי הכ"ד שהוא י"ב ונכפול אותו בכ"ג וחלק מי"ג ויעלו רע"ו וי"ב חלקים מי"ג וזהו מה שראוי לראשון | |||||||||||||||||||
|
| ||||||||||||||||||||
|
עוד נקח שליש הכ"ד והם שמונה ונכפול אותו בכ"ג וחלק מי"ג ויעלו קפ"ד וח' חלקים מי"ג וזהו מה שראוי לשני | |||||||||||||||||||
|
| ||||||||||||||||||||
|
עוד נקח רביע הכ"ד והם ו' ונכפול אותו בכ"ג וחלק מי"ג ויעלו קל"ח וו' חלקים מי"ג | |||||||||||||||||||
|
| ||||||||||||||||||||
|
וכשתקבץ הכל יעלו הו' מאות | |||||||||||||||||||
Chapter Five - Proportions |
|
| The fifth type is on ratios. | המין הה' בערכים |
| The intention in it is to know the ratio of what is partly unknown, relying on our knowledge of another ratio the is similar to it. | הכוונה בו לדעת ערך מה שנעלם קצתו מפני ידיעתנו ערך אחר דומה לו בכללו |
| The Rule of Three | |
|---|---|
| The ratio is found in actu between four terms.
|
והנה הערך ימצא בפעל בין ד' גבולים |
|
כאלו תאמר כי ערך הד' אל הו' הוא כערך הח' אל הי"ב |
| Proportional Triad | |
| It is found in potentia by three terms, when the two of them that are means are the same in affect.
|
וימצא בכח בג' גבולים כאשר השנים מהם האמצעיים אחדים [בחמר] נפעל |
|
כאלו תאמר כי ערך הד' אל הו' הוא כערך הו' אל הט' |
| The proportional triad as a special case of the rule of three, in which the two means are equal: | |
| Thus, the mean is one name in actu, i.e. in form, but is numerous in potentia, i.e. as the number of the proportional numbers. | והנה האמצעי שם אחד בפעל ר"ל בצורה רבים בכח ר"ל כמספר הנערכים |
| Therefore, the rule is applied on four proportional numbers, and the three proportional numbers are considered as four, as we have said. | לכן המשפט נעשה בד' נערכים ומשם יובן הג' נערכים שהם ד' כמו שאמרנו |
| The Rule of Three | |
|
והנה כשנודע לנו הערך האחד כאלו תאמר ערך הד' אל הו' ומהערך האחר נדע גבול אחר ונעלם גבול אחד ממנו כאלו תאמ' שנעלם הי"ב |
|
|
|
|
הנה אז נכפול הגבול השני מהערך הראשון שהוא ששה בגבול הראשון מהערך השני שהוא ח' ויעלו מ"ח |
|
נחלוק אותו על הגבול הראשון שהיה ד' ויצא בחלוקה י"ב והוא המבוקש בו |
|
נשים הנעלם מהערך השני הוא ח' |
|
|
|
|
הנה אז נכפול הגבול הראשון מהראשון שהוא הד' בגבול השני מהערך השני שהוא הי"ב ויעלו מ"ח |
|
נחלוק אותו על הו' ויצאו ח' והוא הנעלם המבוקש |
| Argumentation | |
| The reason for that is: | והסבה בזה הוא |
| For every four proportional numbers, the product that is generated from the multiplication of the first by the fourth is equal to the product that is generated from the multiplication of the second by the third.
|
כל ד' מספרים נערכים הנה המשוטח הבא מכפילת הראשון ברביעי שוה למושטח הבא מכפילת השני בשלישי |
| Also, the area of every quadrilateral is the product of its sides one by the other. | ועוד כי תשבורת כל מושטח הוא בא מכפילת הצלעות זה בזה |
| Furthermore, for every quadrilateral that we know its area and one of its sides, we can deduce its the other side by dividing the area by the known [side] and the result is the size of the unknown side as was explained in Euclid's [Elements, Book VII, definitions].
|
ועוד כל מושטח אשר ידענו התשבורת שלו וידענו צלע אחד מצלעיו הנה ידענו הצלע האחר בחלקנו התשבורת ההיא על השטח הנודע ויצא מספר הצלע הנעלם כמו שיתבאר כל זה באוקלידס ועליו |
| [= a composite number is the product of its divisors one by the other. If the composite number and one of its divisors are known, then the other divisor can be deduced] | |
|
ועתה כאשר כפלנו הראשון שהיה ד' ברביעי שהיה י"ב ועלה מ"ח הנה לנו מושטח מה שהוא שוה למושטח השני הנעשה מהשני שהוא ו' בשלישי שהוא ח' |
|
אם כן מושטח ו' בח' הוא מ"ח ולפי שנודע לנו מזה המושטח הצלע הא' שהוא הו' נחלוק עליו המושטח שהיה מ"ח ויצא ח' והוא הצלע השני ממנו נודע |
| Proportional Triad | |
|
וכן במשל האחר מן הג' המספרים הנערכים כי ידענו שהמושטח הבא מן הראשון בשלישי שוה למושטח השני בעצמו |
|
כי הנה אם נעלם המספר הראשון או השלישי הנה נכפול השני בעצמו ונדע תשבורת הראשון בשלישי ונחלק התשבורת על הראשון אם היה הוא נודע או על השלישי אם הוא הנודע ויצא לנו הנעלם |
|
ואמנם אם נעלם השני הנה נכפול הראשון על השלישי ויצא לנו תשבורת השני על עצמו נבקש שורש אותו התשבורת והוא יהיה המספר השני |
Chapter Six - Roots |
|
| The sixth type is on roots. | המין הו' בשרשים |
| Know that it is said that a number is a root of another number, if when you multiply it by itself, the result is the same as the other number no more and no less. | דע כי מספר שרשי למספר אחר יאמר כאשר תכפול אותו בעצמו ויעלה לכמו אותו המספר האחר בלא תוספת ומגרעת |
| It is said to be a square number if such a root number is found for it. | ויאמר מספר מרובע על מי שימצא לו מספר שרשי כזה |
| Know that every number is a root, but not every number is a square. | ודע כי כל מספר הוא שורש ואין כל מספר הוא מרובע |
|
אבל כל המספרים מרובעים זוגי מספר במספר כמספר המרובעים שעברו עד המרובע האחרון מהם |
|
כיצד הא' הוא שורש עצמו ומרובע בעצמו והד' הוא מספר מרובע הנה ביניהם זוגי מספרים שהם הא' והשלש כמספר המרובעים שעברו שהיה הוא האחד |
|
עוד הט' הוא מספר מרובע והנה בין הד' והט' זוגי מספרים שנים והם הה' והו' והז' והח' כמספר המרובעים שעברו עד הט' שהם שנים והם הא' והד' |
|
עוד הי"ו הוא מספר מרובע הנה בין הט' והי"ו זוגי מספרים ג' והם הי' והי"א והי"ב והי"ג והי"ד והט"ו כמספר המרובעים שעברו עד הי"ו והם ג' הא' והד' והט' |
|
וכן לעולם |
|
ועוד דע כי המרובע הראשון הוא נפרד והשני זוג והשלישי נפרד והרביעי זוג וכן לעולם |
|
וזה כענין שרשיהם כי שורש המרובע הנפרד הוא נפרד ושורש המרובע הזוג הוא זוג |
|
וכשתכפול הנפרד בנפרד יעלה נפרד והזוג בזוג יעלה זוג |
|
והנה סדר השרשים אחד נפרד ואחד זוג תמיד |
|
כי הא' שורש הא' והוא נפרד והב' שורש הד' והוא זוג והג' שורש הט' והוא נפרד וכן תמיד |
|
עוד דע כי מדרגות השורש ראוי להיות בחצי מדרגות המרובע ועוד חצי מדרגה |
|
וזה כי כבר אמרנו בהכפלה כי נדע המדרגות העולות מכפילת כל מספר במספר בקבץ מדרגתם והסר מהם אחד |
|
ולפי שבשרשים מדרגות הנכפלים שוים לפי שהוא נכפל בעצמו ראוי אם כן להיות מדרגות השורש חצי מדרגות המרובע ועוד מדרגה אחת בשניהם שהוא חצי מדרגה לכל אחד |
|
על כן לא יתכן לבקש שורש למדרגות שום מרובע כשיהיו זוגות כי לא יתכן להיות חצי מדרגה אלא בשרשים שמדרגתם נפרדים שבהם כי ימצא חצי מדרגה וכשנוסיף מדרגה אחרת ימצא בהם מדרגה שלמה |
|
ואם כן בכל מספר שמדרגתם זוגות ראוי להוריד האות האחרונה מהם לסמוכה לה ואז יהיו מדרגתם נפרדות ויהיה חצי מדרגתם עם החצי מדרגה שנוסיף מדרגות שלמות והם יהיו מדרגות השורש |
|
והנה נתחיל למנות מהמדרגה העליונה עד חצי המדרגות למפרע ושם נכתוב המדרגה העליונה מהשורש ועד שם יגיע |
|
עוד דע כי כשנחשב חשבונות במספרים הנה כל מה שנקרב אל הפשוטים ואל האחדים יהיה יותר ידוע לנו מהמתרחקים מהם |
|
ולזה חבור אחדים מה עם אחדים כמעט שהוא מושכל ראשון |
|
ואינו כן במספרים הרחוקים המורכבים כי נצטרך למלאכה לדעתו |
| Thus, when wishing to find the root of a square number, the extraction of the root should be executed one part after the other instead of seeking the whole root at once | ולזה כשנתור לדעת שורש כל מספר מרובע אין ראוי לנו לבקש השורש כלו ביחד אבל חלק אחר חלק עד תומם |
Extracting roots - written procedure |
|
| Description of the procedure: | |
|---|---|
| Therefore, first we start looking for the root of the digit in the highest rank, if their number is odd, and if their number is even, lower it to the preceding [rank] and it becomes tens there. | ולכן נתחיל לבקש תחלה שורש האות אשר במדרגה העליונה אם הם נפרדות ואם הם זוגות תורידה אל הסמוכה לה ותעשה שם עשרות |
| Look for a root number, such that when you multiply it by itself, the product is the same as [the number in the said rank], or as [close] as possible, and write it in its rank according to the rule I told you. | ובקש מספר שרשי שכשתכפלהו על עצמו יעלה כמוהו או כל מה שאפשר ממנו ותכתבהו במדרגתה כמשפט שאמרתי לך |
| Write the remainder above that rank and make a mark there to indicate that we have already divided there. | ותכתוב הנשאר באותה מדרגה עליה ורשום שם סימן לומר כבר חלקנו משם |
| Know that the product of any number by itself is the same as [the sum of] the products of each of its ranks by itself and by the others. | עוד דע כי כפולת כל מספר בעצמו הוא כמו כפולת מדרגותיו כל אחת בעצמה ובאחרת |
|
ומשל לזה רצינו לכפול י"ב על י"ב והם קמ"ד הרי הוא כמו כפילת העשר שבמדרגה העליונה עם העשר האחר והוא ק' וכמו כן כפילת השנים על השנים והם ד' וכמו כפילת העשר העליונים בשנים התחתונים שהם כ' ועוד כפילת השנים העליונים בעשר התחתונים שהם כ' אחרים והנה כשתקבץ הכל יעלו קמ"ד |
|
| |
|
והנה דרך בקשת שורש קמ"ד |
| ראוי אם כן להיות בזה אחר שמדרגותיו נפרדים נבקש שורש המאה והוא עשר ונכתוב א' במדרגה השנית כי היא חצי המדרגות ועוד חצי מדרגה ולא נשאר דבר בק'. ואחר נאמ' אי זה מספר הוא אשר כשנכפול אותו בעשרה והעשרה בו יכלול המ' או קרוב שאפשר ממנו וכשנכפול אותו על עצמו יכלול הד' עם מה שישאר מהמ' אם יהיה שם נשאר כי בזה ישלם כפילת כל מדרגותיו כמו שאמרנו ונמצא כי הוא השנים נכתוב אותו סמוך לאחד וזה כי כשנכפול בו העשרה יהיו עשרים. וכשנכפול אותו בעשרה יהיו עשרים אחרים הרי המ' נכללים וכשנכפול אותו בעצמו יעלו ד' וכשנקבץ הכל יעלו קמ"ד הרי ששרשם הוא י"ב | |
| The same way for a large number, with numerous ranks | ומזה תשכיל ותדע לעשות אפי' שיהיו המדרגות רבות |
Extracting roots of non-square numbers
|
|
| Since not every number is a square, a remainder may be left [at the end of the extraction procedure] above the dividend number after we have subtracted the square from it. | ולפי שאין כל מספר הוא מרובע הנה כבר ישאר מספר מה על המספר הנחלק אחר שהוצאנו ממנו המרובע |
| Although [this case] should be investigated [in the section] on fractions [because the remainder is a fraction], as [the given number to be extracted] is an integer, it is discussed here. | והנה אע"פ שזה ראוי לעיין בו בשברים הנה לפי שהוא בשלמים נדבר בו בכאן |
| I say that the remainder is necessarily less than double the [approximate] root.
|
ואומר כי בהכרח שישאר שם פחות מכפל השורש |
|
ועוד אחר שאלו היה נשאר שם יותר היינו יכולין לתת אחד יותר ממה שהוצאנו בשורש הראשון |
|
כי לא יתרבה בזה מכפילת השורש השני הזה אלא האחד בשורש הראשון והשורש הראשון באחד והאחד בעצמו והנה די בנשאר לזה |
| Now, when we want to include this remainder by adding a certain fraction to the [approximate] root, we look for a fraction, such that when we multiply it by the [approximate] root and the [approximate] root by it, and it by itself, it includes the remainder, and this is the [new approximate] root.
|
ועתה כשנבקש לכלול הנותר הזה בהוסיפנו חלק מה על השרש הנה נראה איזה שבר הוא אשר כשנכפול אותו בשורש והשורש בו והוא בעצמו יכלול הנשאר והוא יהיה השורש |
| If you do not find such fraction, look for an approximate [fraction]. | ואם לא תמצא שבר כזה בקש הקרוב אליו |
|
ויהיה משל אחד לזה רצינו לדעת שורש תשע מאות ושבעים ושלשה אלפים ומאה ושמונים ושנים |
- [Illustration of the procedure:]
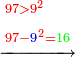
![\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{163-\left[\left(9\times8\right)+\left(8\times9\right)\right]=19}}\\&\scriptstyle{\color{red}{19-7=}}{\color{green}{12}}\\&\scriptstyle{\color{red}{71-{\color{blue}{8}}^2=}}{\color{green}{7}}\\\end{align}}](/mediawiki/images/math/4/c/3/4c3b888f90580d8f25d52a1e9038e7ce.png)
![\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{127-\left[\left(9\times6\right)+\left(6\times9\right)\right]=19}}\\&\scriptstyle{\color{red}{19-10=}}{\color{green}{9}}\\&\scriptstyle{\color{red}{108-\left[\left(6\times8\right)+\left(8\times6\right)\right]=12}}\\&\scriptstyle{\color{red}{12-4=}}{\color{green}{8}}\\&\scriptstyle{\color{red}{42-{\color{blue}{6}}^2=}}{\color{green}{6}}\\\end{align}}](/mediawiki/images/math/d/0/6/d0631e355c2dbb91f8884a7e8683c343.png)
0 01 0109 16 1627 162786 973182 973182 973182 973182 9 98 986
|
ולפי שמדרגותיו זוגות נוריד הט' על הז' ויעלו צ"ז |
|
נבקש שורש שבהכפלו יגיע לזה או היותר שאפשר ממנו והוא יהיה תשעה |
|
נקח חצי המדרגות שהם עד מספר הז' כי המדרגת הט' אין למנות אותה שכבר הורדנו אותו ממדרגתו והם שתים וחצי ונוסיף חצי מדרגה עוד ויהיו שלשה מדרגות |
|
אם כן תחת מספר האחד נכתוב הט' שיצא לנו לשורש |
|
נכפול אותו בעצמו יגיע פ"א |
|
נגרע אותו מצ"ז ישארו שם י"ו |
|
נכתוב האחד שהוא העשרה על הט' והששה על הז' |
|
ונרשום סימן על הז' שכבר שרשנו משם ואין לבקש משם עוד שורש |
|
עוד נשוב לשרש מהשלשה ונוריד עליו הששה שנשארו על השבעה וגם האחד שנשאר על הט' ויחשבו עליו לקס"ג |
|
ונאמר אי זהו המספר שכשנכפול אותו בט' והט' בו יכלול הקס"ג וכשנכפול אותו בעצמו יכלול האחד אשר אצלו עם מה שישאר מהעליונים ממנו ונאמר כי הוא השמונה כי אם נתן ט' לא יספיק לכל |
|
והנה הח' כפול בט' הם ע"ב והט' בח' ע"ב הם קמ"ד |
|
נגרע אותם מהקס"ג ישארו י"ט |
|
נקח מהם ז' להוריד על האחד לכלכל משם לח' כשנכפלם בעצמם וישארו שם י"ב |
|
נכתוב השנים על השלשה והעשר שהוא אחד על הששה |
|
ונכתוב סיפרא על האחד שנשאר על הט' העליונה |
|
והנה לנו על האחד אשר בחשבון עם הז' שהורדנו עליו ע"א נגרע ממנו ח' פעמים ח' שהוא ס"ד ישארו שם שבעה ונכתבם עליו |
|
ונשים סימן על השלשה לומ' כבר [4]שרשנו משם |
|
ונשוב עוד לשרש ממדרגות האחד ר"ל ממה שנשאר עליו והוא ז' עם כל הנשאר למעלה ממנו שכשהורדנו עליו יהיו קכ"ז |
|
ונאמר איזהו מספר אשר כשנכפול אותו בט' והט' בו יכלול הקכ"ז האלה או היותר ממנו שאפשר וכשנכפול אותו בח' והח' בו יכלול השמונה הסמוכים לו עם מה שנשאר למעלה או היותר שאפשר וכשנ[כ]פול אותו על עצמו יכלול השנים עם מה שנשאר במדרגות אשר למעלה או כל מה שאפשר מהם ונאמ' כי הוא מספר הששה |
|
ונכתבם במדרגת האחדים והנה אין עוד שורש אחר זה |
|
ונאמר כי |
|
נגרע אותם מקכ"ז ישארו י"ט |
|
נגרע מהם עשרה להוריד על הט' הסמוכים לכלכל לח' התחתונים כשנכפלם בששה והששה בהם ישארו שם ט' |
|
נכתבם על הז' ונכתוב סיפרא על האותיות העליונות שנשארו על הששה |
|
והנה העשרה שהורדנו על הח' יעלה לשם עם השמונה לק"ח נגרע מהם צ"ו מכפילת ו' על הח' והח' על הו' ישארו שם י"ב |
|
ולפי שנצטרך להוריד ד' על הב' לכלכל לו' כשנכפלם בעצמם ישארו לשם ח' |
|
ונכתבם על הח' |
|
עוד הנה הד' שהורדנו על השנים עם השנים עלו למ"ב נגרע מהם ששה פעמים ששה שהם ל"ו ישארו שם ששה שנכתבם על הב' |
| והנה יצא תתקפ"ו ונשארו עוד תתקפ"ו אחרים שלא מצאנו שורש בשלמים שיכללם על כן נבקש אותו בשברים ונאמ' איזהו מספר אשר כשנכפול אותו בתתקפ"ו והתתקפ"ו בו ונכפול אותו בעצמו יכלול זה ונאמר כי הוא החצי בקרוב אלא שחסר לנו רביע לכלכל לכפילת החצי על עצמו | |
| Check: multiplying the root by itself - and adding the remainder to the product | ויבחן המעשה הנה כאשר [תכפול] השורש היוצא על עצמו שראוי להשתוות למספר אשר בקשת שורשו כשתחבר אל הכפילה הנשאר על המספר שבקשת שורשו |
Chapter Seven - Fractions |
המין הז' בשברים |
| Which includes all the types [of arithmetical operations] | והוא דמות כל המינים כלם |
Conversion of fractions |
|
| I say first that it requires the knowledge to convert fractions to fractions or to convert two fractions or more to one fraction. | ואומר בראשונה כי צורך גדול לזה הוא ידיעת המרת שברים בשברים או הפך שני שברים או יותר לשבר אחד |
| Converting fractions to fractions | |
|---|---|
| Fractions to fractions: | אמנם שברים בשברים |
|
כאלו תאמר נמיר רביעיות לשישיות |
|
הנה אז תחלוק הו' של שישיות על הד' מהרביעיות ויצא אחד וחצי והנה שישית וחצי הוא הרביע |
|
או נאמר נמיר רביעיות לשלישי רביעיות |
|
נכפול ג' בד' של ג' רביעיות ויהיו י"ב נחלקם על ד' של רביעיות ויצאו שלשה והנה הרביעית הוא ג' שלישי רביעיות |
|
או שנאמר נמיר הרביעיות בשלישי חמישיות |
|
נכפול הג' בה' ויעלו ט"ו נחלקם על ד' ויצאו ג' וג' הרביעיות והנה הרביע הוא ג' חמישיות ועוד ג' רביעיות חמישיות |
| Converting two fractions to one fraction | |
| Or, if we wish to convert two fractions to one fraction as close as possible. | או שנרצה להפך שני שברים לשבר אחד יותר קרוב שאפשר |
|
והנה המשל רצינו לדעת שבר ראשון שבו ישתתפו עשיריות בשמונה עשיריות |
| First, one should look for their least common multiple, as follows: | והנה בתחלה ראוי לבקש [5]המספר הראשון שבו ישתתפו ויהיה כזה |
| First, we should know is they share a common factor that counts both and look for it. | בתחלה נדע אם הם משתתפים למספר ימנה אותו נבקש אותו |
| If they share two common factors, we look for the greater. | ואם משתתפים בשני מספרים נבקש היותר גדול |
|
והנה העשרה והי"ח משתתפים בשנים אשר ימנה אותם ונדע במה ימנה לעשרה בה' ולי"ח בט' |
|
ואחר נכפול הי' בט' ויהיו תשעים ולי"ח בה' והוא יהיה המספר הראשון שבו ישתתפו העשרה או הי"ח |
|
ועתה הנה העשירית יהיה הט' מתשעים שבו מנה השנים לי"ח |
|
והח' עשיריות יהיה הט' מתשעים שבו מנה הב' לעשרה |
| Converting three fractions to one fraction | |
| If there are three types of fractions. | ואם היו ג' מיני שברים |
|
כאלו תאמר העשירית והשתים עשיריות והח' עשירית |
|
הנה בתחלה נבקש מספר ראשון שישתתפו בו העשירית והשתים עשירית |
|
ונמצא אותו בבקש המספר הגדול שימנה אותם והנה הוא השנים בכאן כי ימנה לעשרה בה' ולי"ב בשש |
|
והנה הה' והו' אלה יהיו השני מספרים אשר הם הפחות מספרים אשר על היחס הי' והי"ב |
|
ולכן אם תכפול העשר בו' או הי"ב בה' יעלו ס' והוא יהיה המספר הקרוב שישתתפו בו הי' והי"ב |
|
עוד ראה המספר הגדול שימנה לס' האלו ולי"ח והוא הו' כי ימנה לס' בי' ולי"ח בג' |
|
תכפול הס' בג' ויעלו ק"ף והוא המספר הראשון שישתתפו בו שלשתם |
|
ואם תרצה לדעת כמה הוא העשירית ממנו הו' המונה לי"ב בג' המונה לי"ח ויעלו י"ח והוא העשירית |
|
ואמנם השתים עשירית כפול הה' המונה לעשרה בג' המונה לי"ח ויעלו ט"ו והוא יהיה השתים עשירית |
|
ואמנם הח' עשירית הוא יהיה הי' המונה לס' |
|
כמו שהשישימית יהיו הג' המונים לי"ח אם רצינו לדעת אותו אלא שאין המכוון בכאן אלא בשלשת השברים הראשונים שהם הי' והי"ב והי"ח |
| Know that if they do not share a common divisor, then the least common multiple of the fractions is found by multiplying one by the other. | ודע כי אם לא ישתתפו המספרים במספר ימנה אותם הנה אז ימצא המספר שישתתפו בו השברים בכפול הא' על האחר |
|
כאלו תאמר חמישיות ושישיות שאין דבר שימנם אלא האחד |
|
הנה המספר הראשון שימצאו בו אלה השרשים הוא השלשים הבא מכפילת הה' בו' |
|
ואז החמישית הוא שם השבר ר"ל הששה |
|
והשישית הוא בא משם השבר האחר ר"ל החמשה |
| If there are three numbers that do not share a common divisor: | ואם היו ג' מספרים בלתי משתתפים במונה |
|
כאלו תאמר הג' והארבעה והחמשה הנה המספר שישתתפו בו ימצא בכפול הג' בד' ויהיו י"ב ואחר הה' בי"ב ויהיו ס' והנה המספר שמצאו השברים האלו |
|
והנה השלישית בכפול הד' |
|
וימצא הרביע בכפול הג' בה' |
|
וימצא החומש בכפול הג' בד' |
| Now, we will discuss the mentioned operations with fractions. | ועתה נדבר במינים הנאמרים |
| We will start with the addition operation as usual. | ונתחיל בקיבוץ כמנהג |
The First Type: Addition of fractions |
המין הא' בקיבוץ השברים |
| Two fractions with no common denominator | |
|
| |
| We start with addition of two fractions, such that there is no number that counts both. | ונתחיל בקיבוץ שני שברים שלא ימצא להם מספר שימנם |
|
ונשים משל לזה רצינו לקבץ ב' שלישיות בג' רביעיות |
|
|
|
הנה נבקש מספר ראשון שישתתפו בו הג' והד' [6]ולפי שאין דבר שימנם אלא האחד לא ימצא אלא בכפול אחד מהם באחר ויהיו י"ב |
|
והנה השליש הוא ד' |
|
כמו שאמרנו נכפול השנים ממספר השלישיות בד' ויהיו ח' והם השני שלישיות |
|
עוד הרביע הוא ג' |
|
נכפול בהם הג' ממספר הרביעיות ויהיו ט' והנה הג' רביעיות |
|
נקבץ הח' והט' ויהיו י"ז חלקים מי"ב נחלקים על י"ב ויצא אחד שלם וישארו עוד ה' חלקים מי"ב וזהו העולה |
| Three fractions with no common denominator | |
|
| |
| If we want to sum three fractions. | ואם נרצה לקבץ ג' שברים |
|
כאלו תאמר שני שלישיות וג' רביעיות וד' חמישיות |
|
הנה לפי שלא ימנה לשברים הללו אלא האחד הנה לא ימצא מספר ראשון שישתתפו בו אלא בכפול הג' בד' והיו י"ב וזה בה' והיו שישים וזה יהיה דמות השלם אשר נבקש שבריו |
|
והנה השל[י]ש ימצא בכפול הד' בה' שהוא עשרים |
|
ושני השלישים ימצא בכפול השנים בעשרים ויהיו מ' |
|
והרביעי יהיה בכפול הג' בה' ויהיו ט"ו |
|
וג' הרביעיות יהיו בכפול [הג' בט"ו ויעלו מ"ה |
|
והחמשי ימצא בכפול הג' בד' ויהיו י"ב |
|
וד' החמשיות בכפול][7] הד' בי"ב ויהיו מ"ח |
|
ועתה נקבץ המ' והמ"ה והמ"ח ויעלו קל |
|
ונחלק אותו על הס' שהוא דמות השלם ויצא שנים שלמים ועוד י"ג חלקים מס' |
| From this you deduce for four [fractions] and more. | ומזה תבין לד' שרשים או יותר |
| If there is a number that counts both, or if one counts the other, you can do as said above. | ואמנם אם ימצא לשברים מספר שימנם בו שימנה האחד לאחר הנה יכול היית לעשות כדין הנאמרים למעלה |
| Yet, then their multiple will not be the least common multiple of these fractions, which is more appropriate, since it is the smallest and the intellect comprehend it quickly as well as its fractions. Therefore, it is better to look for their least common multiple. | אלא שלא יהיה השלם ההוא המספר הראשון שישתתפו בו אותם השברים שהוא היותר נאות לפי שהוא ראשון ומספר יותר קטן והשכל יקיף בו ובשבריו יותר מהרה ולזה ראוי לבקש להם המספר הראשון שישתתפו לשלם |
| Two fractions, the denominator of one of them is a divisor of the other | |
|
| |
| First, the example for this is of two fractions, such that one counts the other: | ויהיה המשל בתחלה לזה בשני שברים שימנה האחד לאחר |
|
כאלו תאמר רצינו לקבץ שני שלישיות בד' תשיעיות |
|
ולפי שהג' מונה לט' בג' נשים השלם הט' |
|
ויהיה השליש ג' כמספר אשר הוא מונה בו לט' |
|
נכפול אותו בשני ממספר השלישיות יעלו ו' והם הב' שלישיות |
|
ונקבץ אותם לד' מהתשיעיות יעלו עשרה |
|
נחלק אותם על הט' יצא אחד שלם ועוד תשיעית אחד |
| Two fractions with common divisor | |
|
| |
| If one does not count the other, but there is another number that counts both: | ואם לא ימנה הא' לאחר אבל ימצא מספר אחר שימנה אותם |
|
כאלו תאמר רצינו לקבץ ג' רביעיות בד' שישיות |
|
שימנה אותם הב' והוא היותר גדול שימנם אמנם לד' בב' ולו' בג' |
|
הנה אז נמצא המספר הראשון שישתתפו בו בכפול הד' משם הרביע במספר המונה לששיות שהיה ג' ויעלו י"ב |
|
או בכפול הו' משם השישיות במספר המונה לד' שהיה ב' |
|
והוא יהיה דמות השלם |
|
ואחר נמצא הרביע משם הג' שמנה בו הב' לו' |
|
וג' רביעיות בכפול הג' בג' ויעלו ט' |
|
וכן נמצא השישית משם השנים שמנה בו השנים לד' |
|
וד' חמישיות בכפול הב' בד' ויהיו ח' |
|
ונקבץ הח' והט' ויהיו י"ז ונחלק אותו על הי"ב ויצא אחד שלם ועוד ה' חלקים מי"ב בשלם |
| From this and from what we have said at first concerning the foundations of the discussion on fractions you may learn and know how to proceed if there are three types of fractions or more. | ומזה וממה שאמרנו בתחלה ביסודות לדבר בשברים תשכיל ותדע איך תעשה אם יהיה השברים ג' מינים או יותר |
The Second Type: Subtraction of fractions |
המין הב' במגרעת השברים |
| The intention in this is to subtract fractions from integers or fractions from fractions that are larger than them. | הכוונה בו לגרוע שברים משלמים או שברים משברים גדולים מהם |
| Fractions from integers | |
|
|
|
|
ויהיה [8]המשל תחלה נגרע חמש שמיניות מאחד שלם |
|
הנה אז מבואר בעשותינו השלם כלו שמיניות ויהיו שמונה נגרע מהם הה' וישארו ג' |
| Fractions with the same denominator | |
| It is also clear when subtracting fractions from similar fractions.
|
ואמנם בגרוע שברים משברים דומים גם הוא מבואר |
|
כי אם נרצה לגרוע ג' שמיניות מה' שמיניות |
|
ונשאר ב' שמיניות |
| Fractions with different denominators | |
|
|
|
| What requires a study is when the fractions are different. | אמנם מה שיש בו עיון הוא בשהם שברים מתחלפים |
|
כיצד רצינו לגרוע ב' רביעיות מו' שמיניות |
|
הנה אז נצטרך לבקש המספר שישתתפו בו שני השברים וזה ימצא בכפול שם השבר באחר שהם ד' וח' והוא ל"ב |
|
ולפי שהרביע הוא שם השבר האחד והוא ח' וב' זה הרביעיות והוא י"ו |
|
והשמינית הוא שם השבר האחר והוא ד' וו' שמיניו' הם כ"ד |
|
הנה בגרענו הי"ו מהכ"ד ישארו ח' והם חלקים מל"ב בשלם שהם רביעיתם |
| If the denominators of the fractions are numerous, their common multiple is very large and the calculation with it is more difficult. | אמנם אם רבו שמות המספרים השברים והנה המספר שישתת[פ]ו בו יהיה גדול מאד ויכבד העיון בו |
|
|
|
|
|
| When one fraction counts the other fraction: | וימנה השבר האחד לשבר האחר |
|
כאלו תאמר רצינו ד' שמיניות מי"ב שש עשיריות |
|
והנה המספר שישתתפו בו על דרך כפילת שם השבר באחר יהיה קכ"ח והוא מספר גדול להקיפו שכל המונה |
|
הנה אז ראוי שנדע באי זה מספר ימנה
הח'][9] לי"ו והוא בב' |
|
ונכפול הד' מהשמיניות בשנים המונים ויהיו ח' |
|
ונגרע אותם מי"ב וישארו ד' והם חלקים מי"ו שהם רביעיתם |
|
| |
| Two fractions with common divisor | |
|
|
|
| ואם אמנם לא ימנה השבר האחד לאחר בכללו אבל ימנהו בחלקיו ר"ל שימצא מספר אחד שימנה לשניהם | |
|
|
כאלו תאמ' רצינו לגרוע ח' שנים עשיריות מי"ד ו' עשיריות |
| הנה אז נבקש המספר היותר גדול שימנם והוא הד' והנה ימנה לי"ב בג' ולי"ו בד' | |
|
|
ונכפול הי"ב בד' או הי"ו בג' ויעלו מ"ח |
|
|
והנה השש עשיריות הוא וח' שנים עשיריות הוא ל"ב |
|
|
ואמנם הו' עשיריות הוא הג' וי"ד ו' עשיריו' הוא מ"ב |
|
|
ועתה כשנגרע הל"ב מהמ"ב ישארו שם י' והם חלקים ממ"ח |
|
ואם תרצה עוד להקטין שם היוצא הנה בקש עוד המספר הגדול שימנם ותחלוק עליו שם המספר היוצא ושם מספר השבר ויצא מספר יותר קטן מיוחס לראשון |
|
|
והמשל בזה עוד הנה נדע אי זהו המספר הגדול שימנה לעשרה ולמ"ח והנה בכאן הוא השנים ונחלוק עליו העשרה ויצאו ה' וכן נחלוק המ"ח עליו ויצאו כ"ד והנה הי' חלקים ממ"ח הם כמו חמשה חלקים מכ"ד שיצאו לנו באחרונה |
| Check: addition | ואמנם אמיתת זה המין יבחן בשוב לקבץ מה שגרענו מן עם היוצא ויהיה שוה למספר הגדול שגרענו ממנו כענין בשלמים |
Multiplication of fractions |
המין הג' בכפילת השברים |
| Multiplying a fraction by a fraction of an integer | |
|
|
הנה הכוונה שתכפול שבר מה ביחס שבר מה אל השלם |
|
|
כאלו תאמר נכפול רביע א' ברביע פעם |
|
|
והמעשה בו שתכפול הרביע ברביע ר"ל ד' על ד' ויהיו י"ו ותכפול האחד באחד ויעלה א' והנה העולה יהיה אחד מי"ו שוה רביע מרביע |
|
לכן אם תרצה תאמר בכפילת רביע ברביע שהעולה הוא רביע מרביע |
|
וכן תאמר בכפילת רביע בשליש שהוא רביע משליש |
How come the multiplication of integers is adding while the multiplication of fractions is reducing
|
ורבים תמהו איך הכפילה בשלמים מרבה ומוסיף והכפילה בשברים גורע ופוחת |
| The multiplication [of the numerators] is not the reason why the product of the fractions is smaller than the fractions themselves | והאמת כי הפחת והגרעון לא קרה לי מפני הכפילה מסבת זה מוסיף |
|
|
כיצד אם רצית לכפול שני שלישיות בד' חמישיות |
|
הנה מצד הכפילה הולך ומוסיף |
|
|
הוא כי נכפול הב' בד' ויעלו ח' |
| The decreasing is from the aspect of the denominators - the product of the numerators is divided twice | אבל החסרון קרה מצד השברים כי נשבור העולה הזה פעמים |
|
|
אחד בזכרנו שלישיות והב' בזכרנו חמישיות עד שמזה הצד יתחייב כי הח' שנתרבו לנו יהיו חלקים מט"ו שיצא לנו מכפילת השלש בחומש ר"ל משבירת שניהם |
|
|
ומן הדין הוא זה כמו שאראך במשל הראשון שהמשלנו שהוא כפילת רביע ברביע |
|
|
כי העולה הוא רביע מרביע וזה כי לו אנחנו שכפלנו אחד ברביע מה יהיה העולה רביע אחד ולפי שאנחנו לא כפלנו בו אלא רביע בהכרח שיהיה העולה רביע מרביע |
| In the multiplication of numbers there is a mean between two extremes: | ומזה תבין כי יש בכפילת המספרים דמות אמצע ושתי קצוות |
|
וזה כי כפילת הרבים השלמים בשלמים מוסיף |
|
וכפילת שברים בשברים גורע |
|
וכפילת הא' בעצמו לא יוסיף ולא יגרע |
| One - the beginning of the integers and the end of the fractions | והנה האחד ראשית השלמים וסוף השברים |
|
והנה ידמה זה למה שהיה בטבע כי כשיעמוד אדם על מים עמוקים הנה יראה צורתו במים הפוכה. ר"ל ראשו למטה ורגליו למעלה. והרגל ראשית האדם אשר בחרבה וסוף צורת האדם אשר במים |
|
וכמו שכל מה שיגאה ראש האדם אשר בחרבה כן ישפל ראש כל צורת האדם אשר במים |
| Similarly, a the integers are rising their corresponding fractions are getting smaller | כן כל מה שיתרבו המספרים השלמים יחסרו השברים הנגדים לו |
|
|
כיצד אם לקחנו השנים שנתרבה על האחדות בכדי כפלו כן כשלקחנו החצי שהוא נגדי לו לפי שהוא אחד משנים גרע מהאחדות החצי |
|
|
וכן כשנקח השלשה הנה נמצא כי הוסיף על האחד שלשה כפלים כן כשנקח השליש גרע מהאחד שלשה חסרונות עד ששב לשלישיותו וכן בשאר |
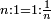
|
והנה תמצא לזה כי יחס הכפלים השלמים אל האחד כיחס האחד אל השברים הנגדים לשלמים ההם |
|
|
וזה כי יחס השנים אל האחד הוא כיחס הא' אל החצי |
|
|
וכן יחס הג' אל הא' הוא כיחס הא' אל השליש וכן לאין סוף |
|
אם כן הוא אמצעי ביחס |
| Multiplication of fractions by integers | |
| is easy | ואמנם כפילת השברים בשלמים נקל לדעתו |
|
|
ותמצאהו בכפול מספר השלמים במספר השברים והעולה תחלקהו על שם השבר והוא יהיה העולה |
|
|
כיצד רצינו לכפול ב' שלישיות בד' שלמים |
|
|
הנה נכפול הד' על השנים ויעלו ח' נחלקהו על שם השבר שהוא שלש ויצא לנו שני שלמים ושני שלישיות |
| Multiplication of fractions by fractions of fractions | |
| is easy | וכן כפילת שברים בשברי שברים יהיה נקל |
| Converting the fraction of fraction to one fraction |
אחרי אשר תשיב השברי שברים לשם שבר אחד |
|
|
כיצד רצינו לכפול שני שלישיות בג' רביעיות שליש אחד |
|
|
הנה בהתחלה נשיב הג' רביעיו' שליש אחד לשבר אחד ונמצאהו בכפול ד' של רביעיות בג' של שליש ויעלו י"ב והנה השליש הוא ד' כמו שאמרנו וג' רביעיות הם ג' אם כן הם ג' חלקים מי"ב ועתה תכפול השני שלישיות בשלש חלקים מי"ב כפי מה שאמרנו והוא יהיה העולה מכפילת השבר בשבר השבר שהמשלנו |
| Check: division | ומופת זה המין הוא החלוקה כענין בשלמים ויצא היוצא |
Division of fractions |
המין הד' בחלוקת השברים |
| Division of fractions by fractions |
הנה כשרצינו זה נחלוק מספר השברים על מספר השברים. וכן שם השבר על השבר ויצא שם השבר השלם היוצא |
|
|
כיצד רצינו לחלק ששה שמיניות בשני רביעיות |
|
|
והנה נחלק הששה לשנים ויצאו ג' וכן נחלק הח' על הד' ויצאו שנים ויהיה היוצא בחלוקה ג' חלקים משנים השלם שהוא אחד וחצי |
| Check: multiplication | והמופת על זה |
|
|
כי כשנכפול אחד וחצי בשני רביעיות יצאו ג' רביעיות שהוא כמו הו' שמיניות |
| How could the fraction produce more than what it contains? [= how come the result of the division of fractions is greater than the dividend?] | והנה בזה יתמה האדם יותר ואומר איך נאמר שיוכל לתת הדבר מה שאין לו |
Demonstration: 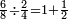
|
ואיך נאמר שיתן הו' שמיניות אחד שלם וחצי והוא אין לו |
|
|
אמנם התיישבות הנפש בזה הוא שנאמר לו אלו חלקנו ח' שמיניות שהוא אחד שלם לד' רביעיות שהוא אחד גם כן מה היה היוצא שמונה שמיניות שהוא אחד כי בחלוקת א' על א' יצא אחד |
|
|
ועתה אם חלקנו הח' שמיניות על חצי הד' רביעיות שהוא שני רביעיות אינו דין שיצא בחלוקה כפלים מאשר היה יוצא לד' רביעיות ויהיו שנים |
|
|
כמו שאלו חלקת אותם על כפל הד' רביעיות שהם שנים היוצא בחלוקה חצי אחד |
|
|
והנה לפי שלא חלקנו בכאן ח' שמיניות אבל ג' רביעיותיו שהם ו' שמיניות אינו דין שנגרע מהיוצא בחלוקה שהיו שנים הרביע מהם וישארו א' וחצי כמו שעשינו |
| Division of the numerators not a division of the denominators | ונשוב להתיר הספק שאמרנו שאיך יתן דבר מה שאין לו ואומר כי בחלוקה לא יתן דבר מה שאין לו כי החלוקה הוא במספרים לא בשמות השברים כמו שאמרנו בכפילת השברים |
|
והנה כשחלקנו הו' שמיניות על הב' רביעיות הנה לא נתן הו' לשנים אלא מה שיש לו והוא ב' לכל אחד |
|
אבל מפני שהשברים המקבלים שהם שני הרביעיות קצרה ידם במחצה מהכיל מה שיקבל השלם הושב להם היוצא כפל מהיוצא לשלם |
| Metaphor: a man feeds his animals each day one portion of barley for each, yet one of the animals is sick and can eat one portion only every two days instead each day. It seems as if this animal was given more than the rest of the animals, but in fact this is not true, it is only because it could not eat the whole portion | ויקרה להם כמו שקרה לאיש אחד שהיה מחלק לאיש מדה אחד של שעורים לכל אחד מבהמותיו ליום אחד והנה בהמה אחת מהן היתה חולה ושבורה ולא הכילה לאכלה מדה אחת ביום אחד אבל בשני ימים והיה לה כאלו נתנו לה לחם משנה מאשר לשאר הבהמות |
|
|
וכזה הענין כאן אלו חלקנו הח' שמיניות לא' שלם היה יוצא לו כל אותם הח' שמיניות |
|
|
ועתה כשחלקנו אותם על ב' רביעיות שהוא חצי אחד בהכרח שיספיקו להם כפל ממה שיספיקו לאחד השלם |
|
|
ויהיה כאלו נפל להם שנים עשרה שמיניות שהוא א' וחצי |
The fractions are related to the one as whole (e. g.  - eight parts of eight) and not as the absolute one - eight parts of eight) and not as the absolute one
|
וזהו בהתייחסות אל חסרונם הא' אבל לא בשלוח |
Proportions of fractions |
המין הה' בערכין |
| The subject is clear from the discussion on proportions of integers | הנה זה מבואר ממה שדברנו בשלמים |
| This type consists of multiplication and division | וממה שידענו שזה המין מורכב מכפילה וחלוקה |
| Check: the same as for integers | וכפי האמות בהם ככה ימצא האימות בזה |
Roots of fractions |
המין הו' בשרשי השברים |
| The issue of roots of fractions is similar to the issue of roots of integers | דע כי ענין השרשים בשברים דומה לעניינים בשלמים |
| One - the beginning of the integers and the end of the fractions | וכבר אמרתי כי האחד הוא ראש השלמים וסוף השברים |
|
|
והנה כמו שהאחד מספר מרובע |
The number of pairs of numbers between two consecutive squares 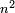 and and 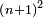 is equal to the number of squares preceding is equal to the number of squares preceding 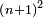 [i.e. n] [i.e. n]
|
ואם תרצה לדעת המרובע הסמוך בשלמים תצטרך לשום ביניהם זוג מספרים או זוגי מספרים כמספר המרובעים שעברו |
The same for fractions: [the number of pairs of fractions between two consecutive squares 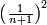 and and 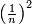 is equal to the number of squares succeeding is equal to the number of squares succeeding 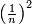 [i.e. n] [i.e. n]
|
כן הענין בשברים |
|
כי בין האחד שהוא המרובע הראשון להם ובין השבר המרובע הראשון זוג שברים אחד וזה כי בין האחד והרביע שהם מרובעים הנה יש ביניהם זוג שברים והוא החצי והשליש |
|
וכן בין הרביע והתשיעית שני זוגי מספרים כמספרים שעברו והם החמישית והשישית והשביעית והשמינית |
|
|
וכמו שהשנים הסמוך אל האחד הוא שורש הארבעה שהוא המרובע הסמוך לראשון כן החצי שהוא אחד מהשנים הוא שורש הרביע |
|
וכמו שאין לשני מרובעים ולא לשלשה שורש כי אין לשנים ולא לשלשה שרש |
|
כן אין לשני פעמים ד' ולא לג' פעמים ד' שורש כן אין לשני רביעיות ולא לג' רביעיות שורש |
|
כי מכפילת מספר בלתי מרובע במספר מרובע יולד בלתי מרובע |
|
כמו שממספר מרובע במרובע יולד מרובע |
|
|
וזה כי מכפילת הד' בט' יעלו ל"ו והוא מספר מרובע |
|
|
וכן מכפילת הד' בי"ו יעלו ס"ד והוא גם כן מספר מרובע וכן תמיד |
|
|
ובכללו אומר כי אם תרצה לדעת השברים אשר יהיה להם שורש הנה ראה השלמים אשר להם שורש וגזור מהם שם לשברים והם יהיו |
|
כיצד הד' יש לו שורש וכן הרביע יש לו שורש |
|
ועוד הט' יש לו שורש וכן התשיעית |
|
ועוד הי"ו יש לו שורש וכן אחד מי"ו יש לו שורש |
|
|
ועוד אומר כי כמו שהשנים הוא שורש הד' כן החצי שהוא אחד משנים שורש הרביע |
|
|
וכן כמו שהשלש הוא שורש התשעה כן השליש הוא שורש התשיעית וכן לעולם |
|
ודע כי זה שאמרתי כי לא ימצא מרובע בין מרובע למרובע |
|
כאלו תאמ' בין הא' והד' ובין הד' והט' |
|
וכן בין הא' והרביע או בין הרביע [10]והתשיעית |
| צריך שיובן בשלמים או בשברים כל אחד בפני עצמו | |
|
אבל בשברים שלמים כבר ימצאו לבלתי תכלית |
|
|
כיצד כשתכפול האחד והחצי באחד והחצי יעלו שנים ורביע והנה אין לו שורש |
|
|
והנה כשנכפול אחד ושליש באחד ושליש יעלו [אחד שלם][11] וז' תשיעיות יש לו גם כן שורש |
| Similarly for 1+¼ and so on | וכן באחד ורביע או אחד וחמישית ולאין תכלית |
| Why there are no roots for non-square numbers | |
| וא"ת והלא המספר סמוך זה לזה וכיון שהאחד ושליש [חסר][12] תחת שני תשיעיות משורש השנים והאחד והחצי הוסיף ממנו רביע והנה בין יחסר ב' תשיעיות או יוסיף רביע | |
|
| |
A number a so that 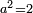 exists in potentia, but not in actu: exists in potentia, but not in actu:
|
נשוב ונאמר כי האמת כי ימצא בכח אבל לא בפועל |
| It exists in potentia since it is continuous, but it does not exists in actu since it is separated into numbers | ואמנם נמצא בכח מצד שהוא מדובק ולא ימצא בפעל מצד שנפרד והיה למספר |
|
והיה זה כענין שיאמר ן' רשד כי כל קו אפשר שיתחלק בכל נקודה ממנו ואמנם כשנתחלק בפועל באחד נמנע בסמוכה לה |
|
ואמנם אפשר מצד שהוא מדובק |
|
לפי שאפשר שנעשה מרובע שיהיה תשבורת שנים ובהכרח שימצא לו צלעות ואפשר לעשותן שוות והוא השורש |
|
ואמנם נמנע השורש מצד המספר |
|
לפי ששורש השלשה במשל |
|
וגם א"א שימצא בשלם אבל כשנכפול השבר בשבר היוצא יהיה שבר השבר והוא לא יתחבר עם השבר וכ"ש עם השלם לשיצא מכלם שורש שלם |
| All the types of arithmetical operations are enough for solving simple problems | הנה אלה המינים יספיקו באשר הם בשאלות הפשוטות |
| For solving complex problems these techniques should be combined | ואמנם במורכבות צריך להרכיב בהם בדרכים הנאמרים |
Word Problems |
|
| Give and Take Problem - filling/draining a cistern | |
|---|---|
|
כיצד אדם שאל שאלה אחת בור רק יש לי גובהו י"ב אמות ובכל לילה מתמלא שלישיתו וביום הסמוך יחסר רביעיתו בכמה ימים עם לילותיהם י |
|
והנה זאת [השאלה][13] מורכבת מהמגרעת והכפילה |
|
|
וזה כי בתחלה צריך שנגרע הרביע מהשליש וישאר אחד משנים עשר |
| ואחר נכפול זה בי"ב ויהיו י"ב ובאותן הימים | |
| First From Last Problem - Money | |
|
עוד שנית ממון היה לי בכיס ולקחתי שלישיתו ורביעיתו ונשארו י"ב כמה היה |
|
הנה זאת השאלה תשוב אל הקיבוץ ואל המגרעת ואל הערכים |
|
|
אל הקיבוץ כיצד נקבץ השלישית והרביעית והיו ז' מי"ב בשלם |
|
|
|
|
נעריך ונאמר אם כל שאר החלקים חוץ מהשליש והרביע שהם ה' שוים י"ב השליש והרביע שהם ז' כמה יהיו שוים |
|
|
נכפול ז' בי"ב ויעלו פ"ד נחלקם על הה' ויצאו י"ו וד' חמישיות והוא מספר השליש והרביע |
|
|
נקבצם עם הי"ב והיו כ"ח וד' חמישיות והוא היה הממון [14]אשר בכיס |
| There are problems that consist of two wisdoms and two types of arithmetical operations | ויש מורכבת משני חכמות ומשני מינים |
| Triangulation Problem | |
|
כיצד שאל אחד כותל יש לי שגובהו ח' אמות וסביבותיה נהר או חפירה יש ברחבה ו' אמות כמה צריך להיות גובה הסולם להניחו סמוך לחפירה ויספיק לעלות לגבהה של כותל |
|
זאת השאלה תצטרך לחכמת ההנדסה[15] שתודיע לנו כי המרובע הסולם שהוא יתר הזוית הנצבה שוה לשני מרובעים הנעשים האחד מהחפירה והשני מהכותל |
|
|
ואחר שהודיענו זה נכפול הו' בעצמו שהוא החפירה ויעלו ל"ו וכן נכפול הכותל בעצמו שהוא ח' ויעלו ס"ד ונקבץ הל"ו אל הס"ד ועלו מאה ונקח שרשם והוא עשרה והוא יהיה גובה הסולם |
| Another question that consists of proportional numbers | עוד מורכבת ממספר מה וממספרים מתייחסים |
| Find a Number Problem | |
|
כמו ששאל אחד איזהו מספר אשר כשנשליך חציו ועוד חצי אחד ומן הנשאר חציו ועוד חצי אחד וישאר אחד ב[ע]ינו |
|
|
הנה בתחלה נבקש מספר שימצא החצי וחצי החצי וחצי חצי החצי וזה ימצא באשר נאמר כי החצי ימצא בשנים וחצי החצי בד' וחצי חצי החצי בח' והנה כשנשליך מח' החצי וחצי החצי וחצי חצי החצי ישאר אחד א"כ מכל ח' ישאר אחד בזה הדרך |
| ואמנם כשנשליך מח' החצי ועוד חצי אחד ומן הנשאר החצי ועוד חצי אחד ומהנשאר החצי ועוד חצי אחד ישאר בינינו שמינית אחת | |
|
|
ועתה צריכין אנחנו לחבר לזה המספר מספר אחר שהשליך החצי וחצי החצי וחצי חצי החצי ישארו ז' שמיניות להשלים הנשאר לאחד שלם |
|
ונמצא אותו בערכים שנאמר אם במספר שמונה ישאר אחד באיזה מספר ישארו שבעה שמיניות |
|
|
ויצא לנו שהוא מספר השבעה |
|
|
א"כ בקבצנו מספר הז' הזה אל מספר הח' יעלו ט"ו והוא יהיה המספר המבוקש |
| Divide a Quantity Problem | |
|---|---|
|
[שאלה אם היו לנו עשרה קבין לחם והם שוים שלש מאות זהובים וזה הקבים אינם שוים או הלחם לא היה שוה |
|
ואין אנו יודעים כמה שוה הקב הראשון אלא ידענו שהקב הב' שוה ב' זהובי' יותר מהראשון |
|
והקב הג' ג' זהובים יותר מהקב הב' |
|
והקב הד' ה' זהובים יותר מהקב הג' |
|
והקב הה' ז' יותר מהקב הד' |
|
והקב הו' ג' זהובים יותר מהקב הה' |
|
והקב הז' ב' זהובי' יותר מהקב הו' |
|
והקב הח' א' זהוב יותר מהקב הז' |
|
והקב הט' ד' זהובי' יותר מהקב הח' |
|
והקב הי' ב' זהובים יותר מהקב הט' |
|
הנה נרצה לידע כמה שוה כל א' וא' מהם |
|
|
|
|
|
הנה אומ' שהקב האחד ישוה י"ד זהובי' וחצי |
|
|
והשני י"ו וחצי |
|
|
והשלישי י"ט וחצי |
|
|
והד' כ"ד וחצי |
|
|
והחמישי ל"א וחצי |
|
|
והששי ל"ד וחצי |
|
|
והשביעי ל"ו וחצי |
|
|
והשמיני ל"ז וחצי |
|
|
והתשיעי מ"א וחצי |
|
|
והעשירי מ"ג וחצי |
|
|
ויעלה כל זה לשלש מאות זהובים שהיו שוים כלם אבל שלא היו שוים כל קב מהם לכל קב מהם |
|
|
והדרך אשר בו תעשה זה הוא כי נשים במשל שישוה הקב הראשון י' זהובים |
|
|
וכפי הנחתינו ישוה הב' י"ב |
|
|
והשלישי ט"ו |
|
|
והרביעי כ' |
|
|
והה' [כ"ז] |
|
|
והו' ל' |
|
|
הז' ל"ב |
|
|
והשמיני ל"ג |
|
|
והתשיעי ל"ז |
|
|
והעשירי ל"ט |
|
|
תחבר כל זה תחבר רנ"ה |
|
|
ראה מה שחסר עד השלש מאות והוא מ"ה זהובים |
|
|
נחלק אלו המ"ה על הי' קבים ויפול לכל קב ד' זהובים וחצי |
| הנה תחבר אלו הד' זהובים וחצי מאלו המספרים הסמוכים וחצי אשר הזכרתי ויצא שישוה | |
|
|
הקב הראשון י"ד והחצי |
|
|
והשני י"ו וחצי |
|
|
והשלישי י"ט וחצי |
|
|
והד' כ"ד וחצי |
|
|
והחמישי ל"א וחצי |
|
|
והששי ל"ד וחצי |
|
|
והשביעי ל"ו וחצי |
|
|
והשמיני ל"ז וחצי |
|
|
והתשיעי מ"א וחצי |
|
|
והעשירי מ"ג וחצי |
|
|
והנה תחבר כל זה ויתחבר שלש מאות |
| יש מי שמבקש מופת לדעת אם טעה בקבוץ המספרים][16] | |
| ת"ם של"ע ת"ם |
Notes
[Expand]
Apparatus
[Expand]
Appendix I: Glossary of Terms
[Expand]
Appendix: Bibliography
Judah Ibn Verga
Spain, c. 1450
Qiṣṣur ha-Mispar
Manuscripts:
- 1) Jerusalem, The National Library of Israel Ms. Heb. 8°2000 (IMHM: B 753 (8°2000)), ff. 1r-3v (Amsterdam, 17th century)
- 2) London, British Library Add. 27107/5 (IMHM: f 5782), ff. 32v-43v (cat. Margo. 1016, 5); (16th-17th century)
- Ḳitsur sefer ha-mispar
- 3) London, British Library Add. 27107/13 (IMHM: f 5782), ff. 162r-174v (cat. Margo. 1016, 13); (16th-17th century)
- 4) Paris, Bibliothèque Nationale de France heb. 1005/19 (IMHM: f 30347), ff. 100r-110r (15th-16th century)
- 5) Paris, Bibliothèque Nationale de France heb. 1005/21 (IMHM: f 30347), ff. 118v-120r (15th-16th century)
- 6) Paris, Bibliothèque Nationale de France heb. 1087/1 (IMHM: f 15039), ff. 1r-8v (16th century)
- heb. 1087/1
- 7) St. Petersburg, Inst. of Oriental Studies of the Russian Academy C 76/7 (IMHM: f 69233), ff. 112v-122v (15th-16th century)
- The transcript of the text is based on manuscript Paris 1005.
Bibliography:
- Steinschneider, Moritz. 1893–1901. Mathematik bei den Juden. Berlin-Leipzig-Frankfurt: Kaufmann, p. 196 (h62); repr. Hildesheim: G. Olms, 1964 and 2001.
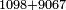
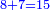
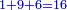

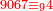
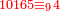
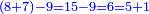
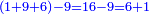


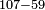
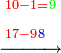
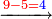
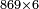
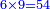
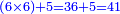
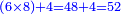
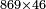
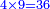
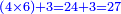

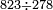
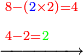
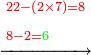
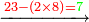

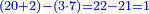
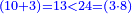
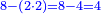

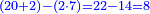

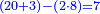
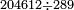
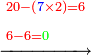
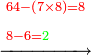

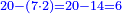
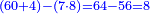
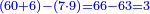
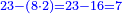
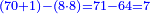
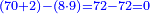
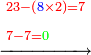
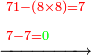


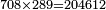

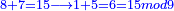
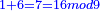
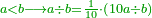
![\scriptstyle{\color{OliveGreen}{a<b\longrightarrow a\div b=\frac{1}{10}\sdot\left[\frac{1}{10}\sdot\left(10a\div b\right)\right]}}](/mediawiki/images/math/d/e/2/de2406622e6bb7fbf22fa4d0ddedcd57.png)
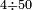
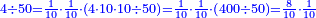
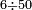
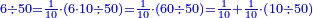
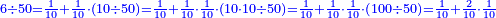
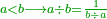
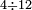
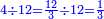
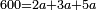
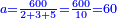



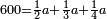
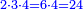
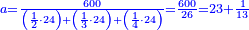
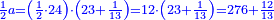
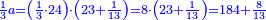
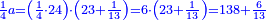
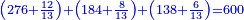
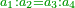
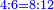
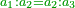

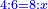
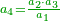
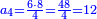
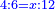
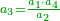
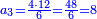

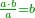
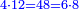
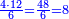
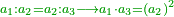
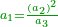 ;
; 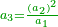
 ] and 4 is a square number - between them there is one pair of numbers, which are [2] and 3 - as the number of the squares before [4], which is one.
] and 4 is a square number - between them there is one pair of numbers, which are [2] and 3 - as the number of the squares before [4], which is one.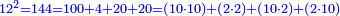
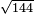
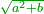
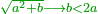
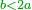 ], we could have given one more than what we have extracted in the first [approximate] root.
], we could have given one more than what we have extracted in the first [approximate] root.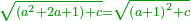
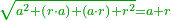
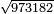

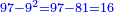
![\scriptstyle{\color{blue}{163-\left[\left(8\sdot9\right)+\left(9\sdot8\right)\right]=163-\left(72+72\right)=163-144=19}}](/mediawiki/images/math/2/9/c/29cfac2135d16c9d2d3f6d54b3376990.png)
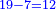

![\scriptstyle{\color{blue}{127-\left[\left(6\sdot9\right)+\left(9\sdot6\right)\right]=127-108=19}}](/mediawiki/images/math/1/6/b/16b63602d05272830b592d86968b42d8.png)
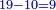
![\scriptstyle{\color{blue}{108-\left[\left(6\sdot8\right)+\left(8\sdot6\right)\right]=108-96=12}}](/mediawiki/images/math/0/2/7/027683a888e17e8f6ed4e2465ce9540b.png)
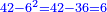
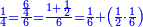
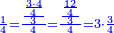
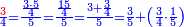

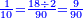
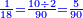

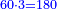
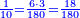
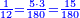
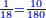
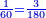
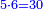
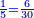
![\scriptstyle{\color{OliveGreen}{\frac{a}{b}+\frac{c}{d}=\frac{\left[a\sdot\left[\frac{1}{b}\sdot\left(b\sdot d\right)\right]\right]+\left[c\sdot\left[\frac{1}{d}\sdot\left(b\sdot d\right)\right]\right]}{b\sdot d}}}](/mediawiki/images/math/c/7/8/c7895df3cbba962a7df6ccafc823a3fc.png)
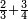
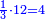
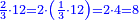
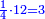
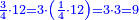
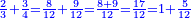
![\scriptstyle{\color{OliveGreen}{\frac{a}{b}+\frac{c}{d}+\frac{g}{h}=\frac{\left[a\sdot\left[\frac{1}{b}\sdot\left(b\sdot d\sdot h\right)\right]\right]+\left[c\sdot\left[\frac{1}{d}\sdot\left(b\sdot d\sdot h\right)\right]\right]+\left[g\sdot\left[\frac{1}{h}\sdot\left(b\sdot d\sdot h\right)\right]\right]}{b\sdot d\sdot h}}}](/mediawiki/images/math/e/b/3/eb31c18467b571d3dda496f6914b79db.png)
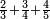
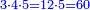
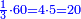
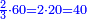
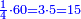
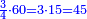
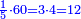
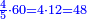
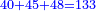
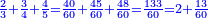
![\scriptstyle{\color{OliveGreen}{\frac{a}{b}+\frac{c}{d\sdot b}=\frac{\left[a\sdot\left[\frac{1}{b}\sdot\left(b\sdot d\right)\right]\right]+c}{b\sdot d}}}](/mediawiki/images/math/c/5/0/c508caaff04ccc2a6abc0776fa43bd51.png)
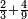
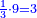
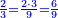
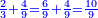
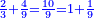
![\scriptstyle{\color{OliveGreen}{\frac{a}{b\sdot g}+\frac{c}{d\sdot g}=\frac{\left[a\sdot\left[\frac{1}{b\sdot g}\sdot\left(b\sdot d\sdot g\right)\right]\right]+\left[c\sdot\left[\frac{1}{d\sdot g}\sdot\left(b\sdot d\sdot g\right)\right]\right]}{b\sdot d\sdot g}}}](/mediawiki/images/math/b/f/1/bf19fb80e190649be13c951e1940036c.png)
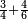

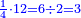
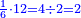
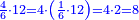
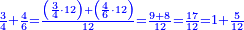
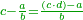
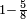
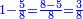
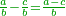
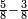
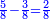
![\scriptstyle{\color{OliveGreen}{\frac{a}{b}-\frac{c}{d}=\frac{\left[a\sdot\left[\frac{1}{b}\sdot\left(b\sdot d\right)\right]\right]-\left[c\sdot\left[\frac{1}{d}\sdot\left(b\sdot d\right)\right]\right]}{b\sdot d}}}](/mediawiki/images/math/d/0/9/d0943c4416f582ab13803553e211310e.png)
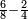
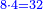
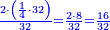
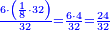
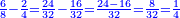
![\scriptstyle{\color{OliveGreen}{\frac{a}{b\sdot d}-\frac{c}{b}=\frac{a-\left[c\sdot\left[\frac{1}{b}\sdot\left(b\sdot d\right)\right]\right]}{b\sdot d}}}](/mediawiki/images/math/8/a/2/8a28dd28f4e8c1ffea1a486dbe9f9dbe.png)
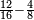
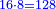
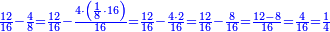
![\scriptstyle{\color{OliveGreen}{\frac{a}{b\sdot g}-\frac{c}{d\sdot g}=\frac{\left[a\sdot\left[\frac{1}{b\sdot g}\sdot\left(b\sdot d\sdot g\right)\right]\right]-\left[c\sdot\left[\frac{1}{d\sdot g}\sdot\left(b\sdot d\sdot g\right)\right]\right]}{b\sdot d\sdot g}}}](/mediawiki/images/math/c/c/f/ccf25ba4246eeb10ca46180c0f136558.png)
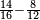
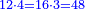
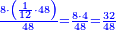
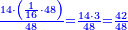
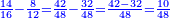
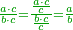
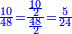
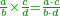
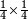
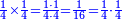
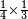
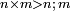
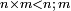
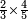
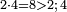
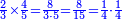
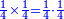
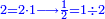
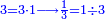
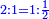
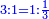

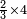
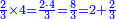
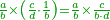
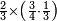
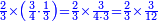
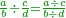
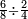
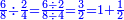
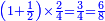
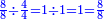
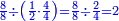
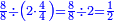
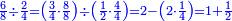
 is half of a whole, therefore it receives twice of what the whole receives from division
is half of a whole, therefore it receives twice of what the whole receives from division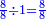
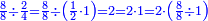
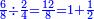
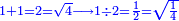
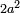 and for
and for 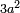

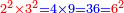
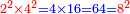
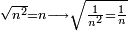
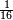 has a root
has a root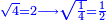
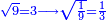
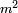 between
between 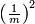 between
between  and 1 or between
and 1 or between 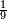 and
and 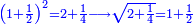
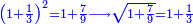
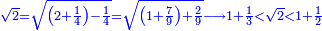
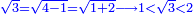
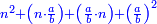 →
→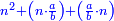 can be integers
can be integers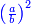 cannot be an integer →
cannot be an integer →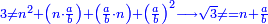
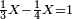
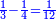
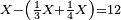
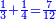
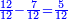

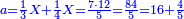
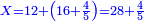
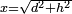
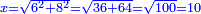
![\scriptstyle\left[\left[X-\left(\frac{1}{2}X+\frac{1}{2}\right)\right]-\left[\left[\frac{1}{2}\sdot\left[X-\left(\frac{1}{2}X+\frac{1}{2}\right)\right]\right]+\frac{1}{2}\right]\right]-\left[\frac{1}{2}\sdot\left[\left[X-\left(\frac{1}{2}X+\frac{1}{2}\right)\right]-\left[\left[\frac{1}{2}\sdot\left[X-\left(\frac{1}{2}X+\frac{1}{2}\right)\right]\right]+\frac{1}{2}\right]\right]+\frac{1}{2}\right]=1](/mediawiki/images/math/f/2/8/f28c22c40aef6283c27e81473fabdc88.png)
![\scriptstyle{\color{blue}{8-\left(\frac{1}{2}\sdot8\right)-\left[\frac{1}{2}\sdot\left(\frac{1}{2}\sdot8\right)\right]-\left[\frac{1}{2}\sdot\left[\frac{1}{2}\sdot\left(\frac{1}{2}\sdot8\right)\right]\right]=1}}](/mediawiki/images/math/b/a/8/ba8943378c2c9e86a2338e7f2544dd64.png)
![\scriptstyle{\color{blue}{\left[\left[8-\left[\left(\frac{1}{2}\sdot8\right)+\frac{1}{2}\right]\right]-\left[\left[\frac{1}{2}\sdot\left[8-\left[\left(\frac{1}{2}\sdot8\right)+\frac{1}{2}\right]\right]\right]+\frac{1}{2}\right]\right]-\left[\frac{1}{2}\sdot\left[\left[8-\left[\left(\frac{1}{2}\sdot8\right)+\frac{1}{2}\right]\right]-\left[\left[\frac{1}{2}\sdot\left[8-\left[\left(\frac{1}{2}\sdot8\right)+\frac{1}{2}\right]\right]\right]+\frac{1}{2}\right]\right]+\frac{1}{2}\right]=\frac{1}{8}}}](/mediawiki/images/math/1/b/1/1b150b9f34880a4ea8f9c389cb845ea5.png)