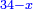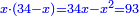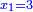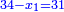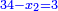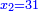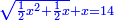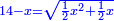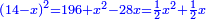השאלות החרשות/האלמות
ContentsPrologue |
|
| In the name of God | בשם השם |
| Abū Kāmil said: after we have completed inferring the summary of much of them | אמר אבו כאמל אחר שהשלמנו להוציא מה שהיה קצור מהרבה מהם |
| and commenting on words of the geometricians of our time and the ancients regarding to: | ונעיר על זה המהנדסים אשר בזמננו זה ומאשר חברו לנו דבריהם מהקודמים |
|
מהקוים המחתכים המחומש והמעושר אשר תקיף לכל אחד מהם עגולה ידועה או שתקיף לשניהם עגולה ידועה |
|
והוצאת קטר העגולה המקפת במחומש ובמעושר הידועים או כשיקיפו בעגולה מחומש ומעושר ידועים |
|
והוצאת שעור קו חלק אחד מחלקי מקיף העגולה הידועה |
|
והוצאת שעור צלעות המחומש והמעושר שוי הצלעות והזויות כאשר היה שעורם ידוע וצלעות המשולשים ידועי השעור כאשר היו במחומש או במעושר שוה הצלעו' והזיות |
| and more, that we explained in our book. | ויותר מזה שבארנו בספרנו זה |
| Now, I shall explain many of the indeterminate problems, that were inferred by the arithmeticians, each by itself. | ועתה אבאר הרבה מהשאלות החרשות נ' האלמות שהוציאום החשבנים כל דבר בעצמו |
| That is to say, they will be solved through many methods, by straight knowledge, in ways that consist of techniques used by the arithmeticians. | רצוני שהוצאתם היה בדרכים רבים וידיעה ישרה ובפנים מורכבים מאופנים נהוגים בין החשבנים |
| Those techniques were deprived of proofs, that should have been done. | והם אופנים משוללים ממופתים היה ראוי לעשות עליהם |
| Many of them are derived from proper speculation and good skill. | ומהם אשר הוצאו עם עיון טוב ומלאכה נאותה והרבה מהם |
| Praised be the Lord, for every praise, for he is informer of every knowledge. | ומשובח יהיה היוצר על כל שבח כי הוא המודיע כל ידיעה |
| I shall further explain much of what was given by the arithmeticians in their books, which they solved by the techniques of restoration and confrontation [algebra], in order that the reader will understand them properly. | ואבאר עוד הרבה מאשר הניחום החשבנים בספריהם ועשו אותם עם האופנים מאלגבר ואלמוקאבלה בעבור שיבינם הקורא הבנה טובה |
Indeterminate Problems |
|
|
א כאשר יאמרו לך אלגו שמחזיק שרש אם תוסיף עליו חמשה יחזיק שרש כמה הוא האלגו |
|
זאת השאלה אלמת |
|
ולה דרכים רבים ונאמר אנחנו שנים מהם ואיך ייעשו להיותם מובנים לך לעשות איזה מהם שתרצה |
|
והדרך האחת היא שתניח האלגו שלך אלגו המחזיק שרש ושרשו הוא דבר |
|
ותוסיף עליו חמשה יותר ויהיה אלגו וחמשה יותר וצריך שיחזיק שרש |
|
וכבר ידעת כי שרשו יותר מדבר בעבור כי האלגו היה שרשו דבר |
|
ותשים שרשו דבר ומספר |
|
יהיה מאותו המספר אלגו כשיוכה בעצמו יהיה פחות מהחמשה הנוספים |
|
ונשימיהו דבר ודרהם אחד |
|
ותכה זה בעצמו ויהיה אלגו ודרהם אחד ושני דברים ישוה אלגו וחמשה דרהמי |
|
ותגרע אלגו ודרהם אחד מאלגו וחמשה דרהמי וישאר שני דברים ישוו ארבעה דרהמי |
|
והדבר שנים והם שרש האלגו |
|
והאלגו ארבעה דרהמי |
|
וכשתוסיף עליו חמשה יהיה תשעה דרהמי ושרשו שלשה |
|
ואם תניח שרשו דבר ושני דרהמי |
|
ותכהו בעצמו יהיה אלגו וארבעה דרהמי וארבעה דברים ישוו אלגו וחמשה דרהמי |
|
תגרע אלגו וארבעה דרהמי מאלגו וחמשה דרהמי ישאר ארבעה דברים ישוו דרהם אחד |
|
והדבר ישוה רביע דרהם והוא שרש האלגו |
|
והאלגו חצי שמינית מדרהם |
|
וכשתוסיף עליו חמשה דרהמי יהיה חמשה וחצי שמינית ושרשו שני דרהמי ורביע |
|
ואם תרצה תניח שרש האלגו דבר וחצי דרהם |
|
או דבר ודרהם אחד ושני שלישים |
|
או איזה מספר שתרצה אחר שיהיה המספר שתוסיף על הדבר כאשר הוכה בעצמו יהיה פחות מחמשה דרהמי |
|
וכן כל אשר תשאל מזה ייעשה כמעשה הזה |
|
ב וכאשר יאמרו לך אלגו המחזיק שורש אם תגרע ממנו עשרה דרהמי יחזיק מה שישאר שרש |
|
זאת השאלה אלמת |
|
וכבר ידעת כי שרש מאלגו דבר |
|
ושרש מאלגו פחות עשרה דרהמי הוא פחות מדבר |
|
ותניחהו דבר פחות דרהם אחד |
|
או פחות שני דרהמי |
|
או פחות אלגו |
|
תוסיף מהמספר והשברים או מהשברים |
|
ונניחהו דבר פחות דרהם אחד |
|
ותכה אותו בעצמו ויהיה אלגו ודרהם אחד פחות שני דברים |
|
ויהיה אלגו וי"א דרהמי פחות שני דברים ישוה אלגו |
|
איאימיינטה השני דברים ותוסיפם על האלגו ותגרע אלגו מאלגו וישאר י"א דרהמי ישוו שני דברים |
|
|
והדבר חמשה וחצי והוא שרש האלגו |
|
|
והאלגו שלשים ורביע |
|
|
וכאשר תגרע מהם עשרה דרהמי ישאר עשרים ורביע |
|
|
ושרשו ארבעה וחצי |
|
ואם תניח שרש האלגו שלך פחות עשרה דרהמי דבר פחות שני דרהמי |
|
|
|
ותכה אותו בעצמו ותכונהו עם המחובר מהכאת אלגו פחות עשרה דרהמי |
|
|
יהיה שרש האלגו שלשה וחצי |
|
|
והאלגו י"ב ורביע |
|
|
ואם תגרע מהם עשרה ישאר שנים ורביע |
|
|
ושרשו אחד וחצי |
|
ואם תניח המספר הנמשך לדבר כאשר תכה אותו בעצמו יתקבץ יותר מהדרהמי הנמשכים אל האלגו אחד |
|
תדע כי שרש האלגו פחות אותו המספר יהיה אז אותו המספר מהדבר פחות אותו הדבר |
|
בעבור כי שרש האלגו פחות עשרה יהיה אותו המספר הנמשך לדבר פחות דבר |
|
וכן הכאת המספר מהדבר פחות מהמספר בעצמו כמו הכאת הדבר פחות אותו המספר בעצמו |
|
ג ואם יאמרו לך אלגו המחזיק שרש אם תוסיף עליו שרשו שלשה פעמים יחזיק שרש כמה יהיה האלגו |
|
זאת השאלה אלמת |
|
תניח שרש האלגו ושלשה דברים דבר ודרהם אחד |
|
או דבר וחצי דרהם |
|
או דבר ואדרהם אחד על האלגו והוא בזאת השאלה שלשה דברים |
|
ונניחהו דבר ודרהם אחד |
|
|
ותכה אותו בעצמו |
|
|
יהיה אלגו ודרהם אחד ושני דברים ישוה אלגו ושלשה דברים |
|
|
ותגרע אלגו ושני דברים מאלגו ושלשה דברים |
|
|
ישאר דבר אחד ישוה דרהם אחד והוא שרש האלגו |
|
|
והאלגו דרהם אחד |
|
|
ואם תוסיף עליו שלשה פעמי' שרשו יהיה ארבעה דרהמי |
|
|
ושרשו שנים |
|
ד ואם יאמרו לך אלגו מחזיק שרש כאשר גרענו ממנו שרשו ששה פעמים יחזיק שרש |
|
זאת השאלה אלמת |
|
וידיעתה הוא שנניח האלגו אלגו |
|
|
ונגרע ממנו שרשו ששה פעמים וישאר אלגו פחות ששה שרשיו |
|
|
ושרשו[1] פחות מהדבר |
|
אם כן תניחהו דבר פחות ארבעה דרהמי |
|
או פחות חמשה |
|
או פחות שלשה וחצי |
|
או פחות מהמספר שתרצה אחר שיהיה יותר מהחצי מהששה דברים הנמשכים אל האלגו |
|
ונניחיהו דבר פחות ארבעה דרהמי |
|
|
ונכה אותם בעצמם |
|
|
ויהיה אלגו וי"ו דרהמי פחות שמנה דברי' ישוה אלגו פחות ששה דברים |
|
|
|
|
ותנכחהו עמו ויהיה הדבר שמנה |
|
|
והאלגו הוא ששים וארבעה |
|
|
תגרע מהם שרשו ששה פעמים והוא מ"ח ישארו י"ו |
|
|
ושרשו ארבעה |
|
ה ואם יאמרו לך אלגו המחזיק שרש אם תוסיף עליו עשרה פעמים שרשו ועשרה דרהמי יחזיק שרש |
|
זאת השאלה אלמת |
|
וידיעתה שתניח האלגו שלך אלגו |
|
|
ותוסיף עליו שרשו עשרה פעמי' ועשרי' דרהמי אחד |
|
יהיה שרש זה דבר ומספר |
|
שכאשר הוכה בעצמו יהיה המתקבץ מן ההכאה בדברי' פחות מהעשרה ובדרהמי יהיה יותר מהעשרים דרהמי
ולא יעבור שיהיה פחות משניהם רצוני מהעשרה ומהעשרים ולא יותר משניהם |
|
|
|
|
בעבור כי כאשר תכונוהו עם מה שיתקבץ מההכאה האלגו והעשרה דברים והעשרים דרהמי |
|
ישאר דבר ודרהמי אחד ישוה הדבר |
|
אחר תניחהו דבר וארבעה דרהמי וחצי |
|
|
ותכה זה בעצמו |
|
|
ויהיה אלגו ותשעה דברים ועשרים דרהמי ורביע ישוה אלגו ועשרה דברים ועשרים דרהמי |
|
|
|
|
ותכונם עמו ויהיה הדבר הוא רביע דרהם והוא שרש האלגו |
|
|
והאלגו חצי שמינית |
|
|
ואם תוסיף עליו שרשו עשרה פעמים ועשרים דרהמי יהיה עשרים ושנים וחצי וחצי שמינית |
|
|
ושרש זה ארבעה דרהמי וחצי ורביע |
|
ו ואם יאמרו לך אלגו המחזיק שרש אם תגרע ממנו שרשו שמנה פעמי' ושלשים דרהמי יחזיק מה שישאר שרש |
|
זאת השאלה אלמת |
|
וידיעתה שתניח האלגו שלך אלגו |
|
|
תגרע ממנו שרשו שמנה פעמים ושלשים דרהמי וישאר אלגו פחות שמנה דברים ופחות שלשים דרהמי |
|
ושרשו פחות מדבר |
|
וננחיהו דבר פחות חמשה דרהמי |
|
או פחות ששה |
|
או פחות מהמספר שתרצה שיהיה יותר מחצי השמנה דברים הנשנים באלגו |
|
ואם תרצה תניח שרשו מספר פחות דבר ויהיה המספר יותר מחצי הדברים הנשנים באלגו |
|
ונניחהו דבר פחות חמשה דרהמי |
|
|
ותכה אותו בעצמו |
|
|
ויהיה אלגו וכ"ה דרהמיש פחות עשרה דברים ישוה אלגו פחות שמנה דברים ושְלֹשִים דרהמי |
|
ותכונהו עמו ויהיה הדבר ישוה כ"ו וחצי והוא שרש האלגו |
|
|
והאלגו תשנ"ו דרהמי ורביע |
|
|
ותסיר ממנו שרשו שמנה פעמי' ושלשים דרהמי וישאר תק"ו ורביע |
|
|
ושרשו כ"ו וחצי |
|
ז ואם יאמרו לך אלגו שיחזיק שרש אם תוסיף עליו שרשו יחזיק שרש ואם תוסיף עליו אלגו שני שרשיו יחזיק שרש |
|
זאת השאלה אלמת |
|
ותעשה אותה כמעשה |
|
שתחפש מספר שיחזיק שרש ואם תוסיף עליו מספר אחר יחזיק שרש ואם תוסיף עליו שני שרשיו יחזיק שרש |
|
וכאשר מצאת אותו המספר תחלקהו על המספר הנוסף והעולה יהיה שרש האלגו |
|
|
והמספר המחזיק שרש אחד והמספר הנוסף כ"ד ומ"ח |
|
|
וכבר ידעת כי בהוסיפך על אחד מ"ח יהיה מ"ט ושרשו שבעה |
|
|
ואם תוסיף כ"ד על האחד יהיה כ"ה ושרשו חמשה |
|
|
ואם בקשת לדעת כמה היה האלגו תחלק האחד על כ"ד ויעלה שלישית משמינית והוא שרש האלגו |
|
|
והאלגו חלק אחד מתקע"ו חלקים באחד |
|
|
ואם תוסיף עליו שרשו והוא שלישית משמינית וחלק אחד מתקע"ו יחזיק שרש ושרשו חמשה חלקים מכ"ד |
|
|
ואם תוסיף באלגו שני שרשיו והוא חצי ששית וחלק אחד מתקע"ו ומחזיק שרש ושרשו שבעה חלקים מכ"ד |
|
והאלגו ששית משמינית |
|
ואם תרצה תניח המספר המושג או המחופש שמחזיק שרש מ"ט והחלק הנוסף ק"כ ור"מ |
|
|
ואתה יודע כי כשתוסיף על מ"ט ק"כ יהיה קס"ט ושרשו י"ג |
|
|
ואם תוסיף עליו ר"מ יהיה רפ"ט ושרשו י"ז |
|
|
וכאשר תרצה לדעת שעור האלגו תחלק מ"ט על ק"כ ויעלה לחלק חומש אחד ושמינית אחד וחצי ששית והוא שרש האלגו |
|
|
והאלגו אלפיים ות"א חלקים מי"ד אלפים ות' באחד |
| ואם תוסיף עליו שרשו והוא חמשת אלפים ותת"פ מי"ד אלפים ות' יהיה שמנת אלפים ורפ"א מי"ד אלפים ות' ויחזיק שרש ושרשו צ"א חלקים מק"כ | |
|
| |
| ואם תוסיף על האלגו שני שרשיו והוא י"א אלפים ותש"ס מי"ד אלפים ות' יהיה י"ד אלפים ות' ויחזיק שרש ושרשו קי"ט מק"כ | |
|
| |
|
ח וכן אם יאמרו לך אלגו אם תוסיף עליו שרשו יחזיק שרש ואם תוסיף עליו שלשה שרשיו יחזיק שרש |
|
ואם תוסיף עליו שלשה פעמים שעור האלגו יחזיק שרש ואמרנו זה בעבור כי משולש השרשים הוא משלשה שרשים |
|
|
והמספר הנשאל אשר מחזיק שרש אחד והמספר הנוסף עליו שמנה וכ"ד |
|
|
ותחלק האחד על שמנה יעלה שמינית אחד והוא שרש האלגו |
|
|
והאלגו שמינית השמינית |
|
|
ואם תוסיף עליו שרשו והוא שמינית יהיה שמינית ושמינית השמינית ויחזיק שרש ושרשו שלשה שמיניות |
|
|
ואם תוסיף עליו שלשה שרשים והוא שלשה שמיניות יהיה שלשה שמיניות ושמינית השמינית ויחזיק שרש ושרשו חמשה שמיניות |
|
ואם תרצה תניח המספר המחזיק שרש קס"ט והמספר הנוסף עליו ק"כ וש"ס |
|
|
וזה כי כשתוסיף על קס"ט ק"כ יהיה רפ"ט ומחזיק שרשו ושרשו הוא שבעה עשר |
|
|
ואם תוסיף עליו ש"ס יהיה תקכ"ט ומחזיק שרש ושרשו שלשה ועשרים |
|
|
ואם רצונך לדעת שעור המרובע תחלק קס"ט על ק"כ ויעלה אחד ומ"ט חלקים מק"כ והוא שרש המרובע |
|
|
והמרובע יהיה אחד שלם וי"ד אלפים וקס"א חלקי' מי"ד אלפים ות' באחד |
| ואם תוסיף עליו שרשו יעלה שלשה שלמים ותרע"ו אלפים ותתק"כ חלקים מאלף אלפים ותשכ"ח אלפים באחד ומחזיק שרש ושרשו הוא אחד וק"א חלקי' מק"כ באחד | |
|
| |
| ואם תוסיף עליו שלשת שרשיו והם ארבעה דרהמי ועשרים ושבעה חלקים מק"כ באחד יהיה ששה דרהמי ושלשת אלפי' חלקי' מי"ד אלפים ות' ומחזיק שרש ושרשו אחד ונ"ט מק"כ | |
|
| |
| There are many ways to solve this problem and its similar | ולזאת השאלה ולדומים אליה דרכים רבים |
| Explanation: the reason for the extraction of these numbers | ועתה אבאר לך הסבה בהוצאת אלו המספרים |
|
למען תהיה לך למאזנים לכל אלו האופנים |
Know that for any square that has a root, if you add to it its two roots plus one dirham, [the sum] has a root and its root is as the root of the original square plus one. 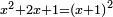
|
דע כי כל מרובע המחזיק שרש אם תקבץ עמו שני שרשיו ואדרהם אחד יחזיק שרש ושרשו הוא כמו שרש המרובע הראשון עם תוספת אחד |
| And when you wish to find a number that has a root, such that when you add to it another number, [their sum] has a root, and when you add to it twice the number that you added at the first time, or thrice, or four times, or as many times as you wish, the sum has a root:
|
וכאשר תבקש למצוא מספר מהמספרים שיחזיק שרש וכאשר תוסיף עליו מספר מה אחר יחזיק שרש וכאשר תוסיף עליו שני פעמים המספר שהוספת בראשונה |
|
תניח המרובע שלך מרובע |
|
|
ותקבץ עמו שנים משרשיו ואדרהם אחד ויהיה העולה יחזיק שרש ושרשו הוא דבר ואדרהם אחד |
|
|
ואם תרצה להוסיף על המרובע כשעור המספר הראשון תקבץ עמו ארבעה שרשים ושנים דרהמי ואם תרצה שלשה פעמים או ארבעה תקח כפי זה |
|
ואם לקחת כשעור המספר יהיה מרובע וארבעה שרשים ושנים דרהמי ותכונהו עמהם |
|
|
ויהיה דבר ישוה רביעית אדרהם והוא שרש המרובע |
|
|
והמרובע הוא חצי שמינית |
|
|
ונהיה כאלו הנחנו המספר הנוסף עליו שני דברים ודרהם אחד ויהיה אדרהם אחד וחצי בעבור כי הדבר הוא רביע דרהם |
|
והדרהם ששה עשר |
|
|
ויהיה מפני זה האדרהם וחצי עשרים וארבעה חלקים |
|
|
והוא המספר שכאשר תוסיף אותו על האחד יחזיק שרש |
|
|
ואם תוסיפהו שני פעמים והוא מ"ח יחזיק גם כן שרש ותשוה אחר זה כאשר בארתי לך |
| Another method | ואם תרצה תעשה לזאת השאלה דרך אחרת |
|
תניח שרש המרובע והארבעה דברים ושני דרהמי דבר ודרהם אחד ושני שלישי דרהם |
|
|
ותכה זה השרש בעצמו |
|
ויהיה מרובע ושני דרהמי ושבע תשיעיות מדרהם ושלשה דברים ושליש דבר ישוו מרובע וארבעה דברים ושני דרהמי ותכונם יחד |
|
|
ויהיה הדבר דרהם אחד ושתות והוא שרש המרובע |
|
|
והמרובע יהיה מ"ט חלקים מל"ו חלקים באדרהם והוא החלק הנשאל שיחזיק שרש |
|
|
ואם רצית לדעת המספר שכאשר תוסיפהו על מ"ט יחזיק שרש ואם תוסיפהו עליו שני פעמים יחזיק שרש |
|
הנה ידעת שהנחת המספר הראשון הנוסף שני שרשים ודרהם אחד וכבר בארנו שהשרש הוא דרהם אחד ושתות והאדרהם ל"ו חלקים ויהיו שני השרשים ואדרהם שלשה ושליש |
|
|
ותכה שלשה ושליש בל"ו ויהיה ק"כ |
|
|
והוא המספר שכאשר תוסיפהו על מ"ט יחזיק שרש |
|
|
ואם תוסיף על מ"ט שני פעמים ק"כ והוא ר"מ יחזיק שרש ותעשה כאשר בארתי |
|
ט וכן אם יאמרו לך מרובע המחזיק שרש אם תגרע ממנו שני שרשים יחזיק הנשאר שרש ואם תגרע מהמרובע שלשה שרשים יחזיק הנשאר שרש |
|
וזאת השאלה חרשת[2] |
|
ותעשה אותה כמעשה הזה |
|
שתבקש מספר שיחזיק שרש וכאשר תגרע ממנו מספר אחר יהיה הנשאר יחזיק שרש ואם תגרע ממנו אותו המספר וכמו חציו יהיה הנשאר יחזיק שרש |
|
|
בעבור כי שלשת השרשים כמו שני המספרים וחצי יותר |
|
וכאשר תמצא אותו המספר תחלקהו על חצי המספר הנגרע והעולה לחלק יהיה שרש המרובע |
|
וחלקת על חצי המספר הנגרע בעבור כי המספר הנגרע עלה במחשבת המספרים כפי שני שרשי המרובע והחצי עלה כפי שרש המרובע |
|
|
והמספר הנגרע שיחזיק שרש כ"ה והמספר הנגרע ממנו הוא י"ו |
|
|
כאשר תגרע מכ"ה י"ו ישאר תשעה ומחזיק שרש והוא שלשה |
|
|
וכאשר תגרע מהם כ"ד ישאר אחד ושרשו אחד |
|
|
וכאשר תרצה לדעת שעור המרובע תחלק כ"ה על שמנה ויעלה לחלק שלשה ושמינית והוא שרש המרובע |
|
|
והמרובע תשעה וששה שמיניות ושמינית השמינית |
| ותגרע ממנו שני שרשיו והוא ששה ורביע וישאר שלשה וחצי ושמינית השמינית ומחזיק שרש והוא אחד ושבעה שמיניות | |
|
| |
| ותגרע מהמרובע שלשת שרשיו שהם תשעה ושלשה שמיניות ישאר שלשה שמיניו' ושמינית השמינית ויחזיק שרש והוא חמשה שמיניות | |
|
| |
| The extraction of these numbers is already obvious from what was shown, | והוצאת המספרים האלה כבר תהיה נגלית מאשר הראינו לך |
| but, it will be further taught in order that it will be memorized properly. | אבל אשכילך עוד עליהם למען יכנס הדבר בלבך היטב |
Know that for any number that has a root, if you subtract from it its two roots minus one dirham, the remainder has a root and its root is as the root of the original square minus one dirham.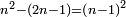
|
דע כי כל מספר המחזיק שרש כאשר תגרע ממנו שני שרשיו פחות דרהם אחד יהיה לנשאר שרש ושרשו יהיה כמו שרש המרובע פחות דרהם אחד |
| And when you wish to find a number that has a root, such that when you subtract from it another number, the remainder has a root, and if you subtract from it again the other number and its half, the remainder has a root:
|
וכאשר תרצה למצוא מספר המחזיק שרש שכאשר תגרע ממנו מספר אחר יהיה לנשאר שרש ואם תגרע עוד ממנו כמו המספר האחר וכמו חציו יהיה לנשאר שרש |
|
תניח המרובע שלך מרובע |
|
|
ותגרע ממנו שני שרשיו פחות דרהם אחד וישאר מרובע ודרהם אחד פחות שני שרשים ושרשו הוא דבר פחות דרהם אחד |
|
|
ותגרע מזה המרובע שני שרשיו פחות דרהם אחד ועוד כמו חציו וישאר מרובע ודרהם וחצי פחות שלשה דברים |
|
|
|
ותכוין עמהם כמו שבארתי לך ויהיה הדבר שני דרהמי וחצי והוא שרש המרובע |
|
|
והמרובע ששה ורביע והוא כ"ה חלקים מארבעה בדרהם |
|
|
ונניח המספר הנגרע ממנו שני שרשים פחות דרהם אחד והוא ארבעה דרהמי |
|
וכל דרהם ארבעה חלקי' |
|
|
ויהיו שש עשרה |
|
|
והנה יהיה המספר המבוקש אשר יחזיק שרש כ"ה והמספר הנגרע ממנו י"ו והמספר השני הנגרע כ"ד |
|
ותעשה מהנשאר בשאלה כאשר הראיתיך |
|
והנה תוכל לעשות לזאת השאלה ולדומים אליה דרכים אחרים כרצונך כאשר בארתי לך |
|
י ואם יאמרו לך מרובע המחזיק שרש אם תגרעהו מן שרשו יהיה לנשאר שרש |
|
זאת השאלה חרשת |
|
ונניח המרובע מרובע |
|
ונגרעהו משרשו והוא דבר וישאר דבר פחות מרובע וצריך שיחזיק שרש |
|
תניח שרשו איזה שתרצה מהדברים אם תרצה יהיה דבר או אם תרצה יהיה יותר או אם תרצה יהיה פחות |
|
ותנחיהו דבר |
|
|
ותכהו בעצמו |
|
|
ויהיה מרובע ישוה דבר פחות מרובע |
|
ותכוין עמו כאשר אמרתי ויהיה הדבר ישוה חצי דרהם והוא שרש המרובע |
|
|
והמרובע רביעי דרהם |
|
ואם נניח שרשו שני דברים |
|
|
יעלה הדבר ישוה חמישית דרהם |
|
|
והמרובע חמישית מחמישית דרהם |
|
|
ותגרעהו משרשו והוא חמישית דרהם וישאר ארבעה חֳמשים מחמישית דרהם ויחזיק שרש והוא שני חומשים מחמישית דרהם |
|
יא ואם יאמרו לך מרובע המחזיק שרש אם תוסיף עליו שרשו יחזיק שרש ואם תגרע המרובע משרשו יהיה לנשאר שרש |
|
זאת השאלה חרשת |
|
ותעשה אותה כמעשה |
|
שתבקש מספר שיחזיק שרש ואם תקבץ עמו מספר אחר יחזיק שרש ואם תגרע המספר הראשון המחזיק שרש מהמספר האחר הנוסף יחזיק הנשאר שרש |
|
וכאשר תמצא זה המספר תחלקהו על המספר הנוסף והעולה לחלק יהיה שרש המרובע |
|
|
והמספר המחזיק שרש ארבעה והמספר הנוסף חמשה |
|
|
וכאשר תוסיף על ארבעה חמשה יהיה תשעה ומחזיק שרש ושרשו שלשה |
|
|
וכאשר תגרע הארבעה מהחמשה ישאר אחד ומחזיק שרש והוא אחד |
|
|
וכאשר תרצה לדעת שעור המרובע תחלק ארבעה על חמשה ויעלה לחלק ארבעה חומשים והוא שרש המרובע |
|
|
והמרובע יהיה שלשה חומשים וחמישית מחמישית |
|
ובארתי לך הנה המלאכה להוציא אלו המספרים |
|
וכבר בארתי במה שעבר עד הנה |
|
שאם נניח מרובע שיחזיק שרש |
|
|
ואם תגרעהו משני שרשיו ואדרהם אחד ישאר שני שרשים ואדרהם אחד פחות מרובע |
|
אחר זה נניח שרשו דבר פחות דרהם אחד |
|
ושניתי האדרהם בדבר בעבור שיעלה בהכאה דרהם אחד וכאשר תכוין עמו ישאר מרובע ישוה דבר |
|
|
אחר זה תכה דבר פחות דרהם אחד בעצמו |
|
|
ויהיה מרובע ואדרהם אחד פחות שני דברים ישוה שני דברים ואדרהם אחד פחות מרובע |
|
ותכוין עמו ויהיה מרובע ישוה שני דברי' |
|
|
והדבר שנים |
|
|
והמרובע ארבעה והוא המספר המחזיק שרש |
|
|
והמספר האחר הוא ארבעה ואדרהם אחד והוא חמשה |
|
ואם נניח שרש המרובע חצי דבר ואדרהם אחד |
|
ותכהו בעצמו ותכונהו עם העולה מהכאת שני דברי' ודרהם אחד פחות מרובע |
|
|
יעלה המספר המחזיק שרש ששה עשר |
|
והמספר האחר חמשה ושני דברים ויהיה שרש המרובע ששה עשר חלקים מס"ה חלקים באחד |
| Similar cases should be solved by this procedure, or by any chosen method | וכל מה שיפול בידך מזה האופן תעשהו במעשה הזה ותקח הדרך אשר תבחר |
| Another method | ועתה אבאר לך זאת השאלה בהבנת דרך אחרת |
Know that for every number that is divided into two parts, each of which has a root 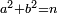 , and into two other parts that have no root: , and into two other parts that have no root:
|
דע כי כל מספר שיחלק לשני חלקים באופן שיהיה לכל חלק שרש ולשני חלקים אחרים שלא יהיה להם אטימו |
| It will be explained now: | ועתה אבאר לך זה למען תבינהו |
|
יב אם יאמרו לך חמשה דרהמי תחלקם לשני חלקים ולכל חלק שרש |
|
|
וכבר ידעת שאחד החלקים הוא אחד והאחר ארבעה |
|
וכאשר תרצה לחלקם לשני חלקים אחרים בלעדי אלו החלקים באופן שיהיה לכל חלק שרש |
|
|
תקח שרש החלק האחד ותוסיף עליו דבר ותכהו בעצמו והיוצא יהיה החלק האחד |
|
|
ותגרעהו מחמשה וישאר החלק האחר |
|
|
ולקחנו החלק האחד והוא אחד |
|
|
ושרשו אחד |
|
|
הוספנו עליו דבר ויהיה אחד ודבר אחד הכינו אותו בעצמו והיה מרובע ודרהם אחד ושני דברים והוא החלק האחד משני החלקים המבוקשים |
|
ותגרעהו מן החמשה וישאר ארבעה פחות מרובע ופחות שני דברים והוא החלק האחר וצריך שיחזיק שרש |
|
וכבר ידענו ששרשו פחות משני דרהמי |
|
ונניחיהו שני דברי' פחות דבר ושני שלישי |
|
|
והכינום בעצמם |
|
|
ויהיה ארבעה דרהמי ואלגו ושבעה תשיעיות מאלגו פחות חמשה דברים ושליש דבר ישוה ארבעה דרהמי פחות אלגו ופחות שני דברים |
|
ותכוין עמו כאשר ידעת ויהיה הדבר דרהם אחד וחמישית אחד |
|
|
והנחנו שרש החלק האחד מהשנים דבר ודרהם אחד ויהיה שרש החלק האחד שני דרהמי וחמישית |
|
|
ותכהו בעצמו ויהיה ארבעה דרהמי וארבעה חומשים וחמישית החמישית והוא החלק האחד אשר בקשת |
|
|
והאחר הוא הנשאר מהחמשה והוא ארבעה חומשי החומש |
|
ואם תרצה לחלק אותו לשנים חלקים אחרים זולת אלו החלקים |
|
תניח החלק הקטן שרש מארבעה דרהמי פחות אלגו ופחות שני דברים ושנים דרהמי פחות שני דברים |
|
ותכם בעצמם ותכונהו עם המתקבץ מהכאת ארבעה דרהמי פחות אלגו ופחות שני דברים |
|
ותעשה כאשר אמרתי לך |
|
|
ויהיה שרש החלק האחד שנים דרהמי ושלשה חלקים משלשה עשר |
|
|
ושרש החלק האחר שנים חלקים מי"ג |
|
ותכה כל אחד משניהם בעצמו |
|
|
ויהיה החלק האחד ארבעה דרהמי וי"ב חלקים מי"ג חלקים באחד ותשעה חלקים מקס"ט |
| All cases of this type should be solved by this procedure. | וכן תעשה לכל אשר יבוא לך מזה המין תעשה עמו כמעשה הזה ויחזיק מהחלקים כמה שתרצה |
|
והוא שלעולם תקח שרש האחד מהשני חלקים ותוסיף עליו דבר ותכה זה בעצמו והיוצא הוא האחד מהשני חלקים אשר בקשת |
|
ותגרעהו מהמספר אשר תרצה לחלק לשני חלקים אשר לכל חלק מהם שרש והנשאר הוא החלק האחר והוא מספר שיחזיק שרש הנשנה לו אלגו ודבר |
|
|
ותקח שרש המספר ותשנה לו אשר תרצה מהדברים אחר אשר לא יכוונו כאשר תכם בעצמם |
|
|
ותכוין עמו החלק שהוא מספר המחזיק שרש נשנה מהאלגו ודבר ויעלו לך מן החלקים עד אין להם תכלית |
|
יג ואם יאמרו לך עשרה תחלקהו לשני חלקים ותוסיף החלק האחד על עשרים ויהיה מה שיחזיק שרש ותגרע החלק האחר מחמשים ויחזיק הנשאר שרש |
|
זאת השאלה חרשת |
|
ומעשהו שנניח החלק האחד אלגו פחות עשרים |
|
|
באופן שכאשר תוסיפיהו על עשרים יחזיק שרש והוא אלגו |
|
|
ושרשו דבר |
|
|
והחלק האחר יהיה הנשאר מהעשרה והוא שלשים פחות אלגו |
|
ותגרעם מן החמשים וישאר אלגו ועשרים דרהמי וצריך שיחזיק שרש |
|
וכאשר תבקש לדעתו תניח האלגו יותר מעשרים ופחות משלשים כי זה המספר לו אופנים רבים |
|
והאופן האחד שתניח שרש האלגו חמשה ושתות |
|
|
והאלגו יהיה כ"ו ושני שלישים ורביע תשיעית |
|
|
ותגרע ממנו עשרים דרהמי וישאר ששה ושני שלישים ורביע תשיעית והוא אחד מהשני חלקים |
|
|
וכאשר תוסיפהו על עשרים יחזיק שרש ושרשו חמשה ושתות |
|
|
והחלק האחר יהיה מה שישאר מהעשרה והוא שלשה דרהמי ורביע וחצי תשיעית |
|
|
וכאשר תגרעם מחמשים ישאר מ"ו ושני שלישים ורביע תשיעית ומחזיק שרש ושרשו הוא ששה דרהמי וחצי ושליש |
|
וכאשר נרצה לדעת איך נניח שרש המרובע חמשה ושתות |
|
תניח שרש מאלגו ועשרים דרהמי דרהם אחד ושני שלישי ודבר אחד |
|
|
ותכם בעצמם |
|
|
ויהיה שני דרהמי ושבעה תשיעיות ואלגו ושלשה דברים ושלישית דבר ישוה אלגו ועשרים דרהמי |
|
ותכוין עמו ויהיה הדבר חמשה ושתות |
| If another solution is desired - one should proceed as is said in the previous solution | ואם תרצה אופן אחר זולת זה תעשה כאשר אמרתי לך קודם זה |
|
יד ואם יאמרו לך תחלק עשרה לשני חלקים ותוסיף החלק האחד על עשרים ויחזיק שרש ותוסיף החלק האחר על חמשים ויחזיק שרש |
|
זאת השאלה חרשת |
|
ומלאכתו שנניח החלק האחד אלגו פחות עשרים דרהמי |
|
|
באופן שכאשר תוסיפהו על עשרים יחזיק שרש |
|
|
והחלק האחר הנשאר מן העשרה יהיה שלשים פחות אלגו |
|
וכשתוסיפם על החמשים יהיו שמנים דרהמי פחות אלגו וצריך שיחזיק שרש |
|
כאלו אמר תחלק שמנים לשני חלקים ולכל חלק שרש |
Problems of this type should be solved by this procedure - through finding a number that can be divided into two parts, each of which has a root: 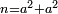
|
וכאשר יפלו לפניך שאלות מזה המין תעשה כמעשה הזה עד שיעלה לך מספר שתחלקהו לשני חלקים ויחזיק כל חלק שרש אם הניח מספר שיוכל להתחלק |
| If the given number cannot be divided like this - the problem cannot be solved. | ואם לאו השאלה היא לא יתכן שתגיע אל תכלית |
|
ותחלק השמנים לשני חלקים ולכל חלק שרש ותניח אחד החלקים יותר מעשרי' ופחות משלשים |
| This problem has many solutions, endlessly. | ולזה הדרך אופנים רבים עד אין מספר |
| The procedure for extracting any desired solution is the one described before. | והמלאכה להוציא איזה אופן שתרצה מהם היא כפי מה שאמרתי לך קודם |
|
|
ואחד מהאופנים שתשים החלק האחד כ"ו דרהמי ול' חלקים מרפ"ט |
|
|
והחלק האחר הנשאר משמנים והוא נ"ג ורנ"ט חלקים מרפ"ט חלקים באחד |
| When you wish to know the measure of each of the parts of ten: | וכאשר תרצה לדעת שעור כל חלק מן העשרה |
|
|
תגרע מהחלק ראשון מהשמנים עשרים וישאר ששה דרהמי ושלשים חלקים מרפ"ט והוא החלק ראשון מהעשרה |
|
|
והחלק האחר הוא הנשאר מעשרה והוא שלשה דרהמי ורנ"ט חלקים מרפ"ט חלקים באחד |
|
|
וכאשר נוסיף החלק הגדול משני חלקי העשרה על עשרים יהיה עשרים ושש ושלשים חלקים מרפ"ט ומחזיק שרש והוא חמשה דרהמי ושלשה חלקים משבעה עשר |
|
|
וכאשר נוסיף החלק הקטן מן העשרה על החמשים יהיה חמשים ושלשה דרהמי ורנ"ט חלקים מרפ"ט ומחזיק שרש והוא שבעה דרהמי וחמשה חלקים משבעה עשר |
|
טו ואם יאמרו לך מרובע אם תגרעהו משלשה דרהמי יחזיק הנשאר שרש ואם תוסיפהו על שני דרהמי יהיה למתקבץ שרש |
|
זאת השאלה חרשת |
|
|
ומעשהו שתקבץ השנים עם השלשה ויהיו חמשה |
|
תחלקם לשני חלקים יחזיק כל חלק שרש |
|
ותניח החלק האחד יותר משנים ופחות משלשה |
|
|
ותגרע השנים מהחלק האחד ומה שישאר יהיה המרובע |
|
ואם תרצה תניח האלגו עשרים ושלשה חלקים מקס"ט חלקים באחד |
|
ואם תרצה תניחהו קמ"ו מקס"ט |
|
ואם תרצה תניחהו תל"א חלקים מתרכ"ה חלקים באחד |
|
והנה תוכל לעשות זאת השאלה והדומים אליה כפי האופנים אשר תבחר כאשר בארתי לך לפנים |
|
יו ואם יאמרו לך אלגו אם תגרעהו מעשרה דרהמי יחזיק הנשאר שרש ואם תגרעהו מעשרים יחזיק הנשאר שרש |
|
זאת השאלה חרשת |
|
ומעשהו שתניח האלגו שלך עשרה דרהמי פחות אלגו |
|
ואם תרצה עשרים דרהמי פחות אלגו |
|
ותניחהו כן בעבור כי כאשר תגרעהו מאחד מהם ישאר אלגו ומחזיק שרש והוא דבר |
|
ונניחהו עשרה דרהמי פחות אלגו |
|
|
וכאשר תגרעהו מן עשרה ישאר אלגו |
|
ואם תגרעהו מעשרים ישאר אלגו ועשרה דרהמי וצריך שיחזיק שרש |
|
|
וכבר ידעת ששרשו יותר מדבר |
|
ונניח שרשו דבר ושני דרהמי |
|
או דבר ושלשה |
|
או אשר תרצה מהמספרים כאשר בארתי לך לפנים |
|
אחר שיהיה כאשר הכינו אותו בעצמו ונכוין עמהם אלגו ועשרה דרהמי |
|
|
יהיה האלגו פחות מעשרה דרהמי |
|
ותניחהו דבר ושני דרהמי |
|
|
ותכהו בעצמו |
|
|
יהיה אלגו וארבעה דרהמי וארבעה דברים ישוה אלגו ועשרה דרהמי |
|
ותכוין עמו ויהיה שרש האלגו אדרהם אחד וחצי |
|
|
והאלגו שנים דרהמי ורביע |
|
|
והנחנו האלגו עשרה דרהמי פחות אלגו |
|
|
ויהיה האלגו המבוקש שבעה דרהמי וחצי ורביע |
|
|
ואם נגרעהו מעשרה ישאר שנים ורביע ושרשו אחד וחצי |
|
ואם הנחנו שרש מאלגו מעשרה דרהמי דבר ושלשה דרהמי |
|
|
יהיה האלגו תשעה דרהמי וחצי ושליש וחמשה ששיות הששית |
| The solutions defined in this problem and in its similar are more than any number. | והאופנים הם שתניח בזאת השאלה ובדומים אליה יותר מאשר הוא המספר |
|
יז ואם יאמרו לך אלגו אם תוסיפהו על עשרים יחזיק שרש ואם תוסיפיהו על שלשים יחזיק שרש |
|
זאת השאלה חרשת |
|
ומעשהו שנניח האלגו אלגו פחות עשרים דרהמי |
|
או אם תרצה אלגו פחות שלשים |
|
ונניחהו אלגו פחות עשרים דרהמי |
|
|
ובתוספתו על עשרים יעלה אלגו |
|
|
ושרשו דבר |
|
ונוסיפהו על שנים ויהיה אלגו ועשרה דרהמי וצריך שיחזיק שרש |
|
|
ויהיה האלגו יותר מעשרים |
|
ותניח שרשו דבר ואדרהם אחד' |
|
|
ותכם בעצמם |
|
ותכונהו עם המתקבץ מהכאת אלגו ועשרה דרהמי ויהיה המרובע עשרים דרהמי ורביע |
|
|
ותגרע ממנו עשרי' דרהמי וישאר רביע אחד והוא המרובע המבוקש |
|
ואם תוסיפהו על עשרים יחזיק שרש |
|
ואם תרצה תאמר האלגו ע"ה דרהמי וחצי שמינית |
|
|
אם תוסיפהו על עשרים יחזיק שרש ושרשו תשעה דרהמי וחצי ורביע |
|
|
ואם תוסיפהו על שלשים יחזיק שרש והוא עשרה דרהמי ורביע |
| This problem and its similar have many solutions. | ולזאת השאלה ולדומים אליה אופנים רבים |
|
יח ואם יאמרו לך אלגו אם תוסיפהו על עשרה יחזיק שרש ואם תגרעהו מעשרה יחזיק שרש |
|
וכאשר ישתוו השני מספרים בזאת השאלה ונניח אחד מהשני מספרים שיחלקו לשני חלקים לכל חלק שרש אז תחזיק מהאופנים מה שלא יסופרו |
|
ואם לא יתחלק לשני חלקים שיחזיק כל חלק שרש תהיה השאלה חרשת זולת שום אופן |
|
|
ותחלק העשרה לשני חלקים ולכל חלק שרש |
|
|
והוא אחד ותשעה |
|
|
ותקח שרשי אחד ותשעה ויהיו ארבעה ותכם בעצמם ויהיה ששה עשר תגרע מהם העשרה וישאר ששה והוא האלגו אשר כאשר תוסיפהו על העשרה יחזיק שרש ואם תגרעהו מן העשרה יחזיק שרש |
|
|
והמשפט בזאת השאלה הוא עולה בעבור כי כאשר תגרע האלגו שהוא ששה מעשרה ישאר ארבעה |
|
|
והארבעה הם מהכאת העודף מאחד משני החלקים על שרש החלק האחר אין שיבוש |
|
יט ואם יאמרו לך אלגו אם תגרעהו משמנה שרשים וק"ט דרהמי יחזיק שרש |
| (½roots)²+numbers | וכאשר יקרה לפניך שאלה כזאת תכה מחצית השרשים בעצמם ותוסיפהו על האדרהמי |
|
ואם יתחלק המקובץ מהם לשני חלקים ויחזיק כל חלק שרש תהיה השאלה נשלמת ותחזיק מהאופנים הרבה אשר לא יוכלו להמנות |
|
ואם לא יתחלק המתקבץ מהם לשני חלקים ולכל חלק מהם שרש תהיה השאלה חרשת בזולת שום אופן |
|
|
ותכה מחצית השרשים בעצמם ויהיו ששה עשר ותוסיפם על ק"ט ויהיה קכ"ה |
|
|
ותחלק קכ"ה לשני חלקים שיחזיק כל חלק שרש |
|
ואם תרצה תניח החלק האחד כ"ה והאחר מאה |
|
ואם תרצה תניח האחד ארבעה והאחר קכ"א |
| One can divide it into whichever two parts one wishes, as stated and explained above | ואם תרצה תחלקהו לשני חלקים אחרי' כאשר אמרתי ובארתי |
|
ותשוב ותקח החלק האחד מאיזה משני חלקי' שתרצה ותוסיפהו על המרובע |
|
|
אחר תקח כ"ה ותוסיפהו על המרובע ויהיה אלגו וכ"ה |
|
|
ונאמר אלגו וכ"ה דרהמי ישוו שמנה דברים וק"ט דרהמי |
|
|
ותגרע כ"ה מק"ט |
|
|
וישאר אלגו ישוה שמנה דברים ופ"ד דרהמי |
| ומחצית הדברים יהיה ארבעה תכם בעצמם ויהיו ששה עשר | |
|
| |
| The reason for this procedure: | והמשפט למה הוצאנוה בזה המעשה |
the division of the sum into two parts, each of which has a root: 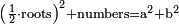
|
וחלקנום לשני חלקים לכל חלק שרש |
is because if: 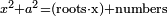
|
בעבור כי כשהוספנו החלק האחד על האלגו והשוינו עמו הדברים והדרהמי אשר במספרנו |
| then:
|
וחצינו הדברים והכינום בעצמם והוספנוהו על המספר או גרענו המספר ממנו יהיה המתקבץ ממנו או הנשאר הוא החלק האחר |
|
|
ויהיה מה שישאר מהשרשים והדרהמי אחר גרעון האלגו מהמספר יהיה החלק הנוסף עליו אלגו |
|
|
ותשוב ותקח שרש המאה והוא עשרה ותוסיף עליהם מחצית השרשים והוא ארבעה ויהיו ארבעה עשר והוא שרש האלגו |
|
|
והאלגו קצ"ו |
|
|
ותגרעהו משמנה שרשיו וק"ט דרהמי והם רכ"א וישאר כ"ה ושרשו חמשה |
|
|
ואם לקחנו החלק האחד והוא מאה דרהמי והוספנום על האלגו |
|
|
ונכוין המתקבץ עם שמנה שרשיו וק"ט דרהמי |
|
|
יהיה האלגו פ"א |
|
|
ואם לקחנו החלק האחר והוא ארבעה והוספנוהו על האלגו |
|
|
ונכוין עמו שמנה שרשיו וק"ט |
|
|
יהיה המרובע רכ"ה |
|
|
ואם תרצה ל"ו ואם תרצה ארבעה |
| The solutions of this problem are numerous. | והאופנים לזאת השאלה הם רבים |
|
כ ואם יאמרו לך אלגו אם תוסיף עליו שמנה שרשיו יחזיק שרש ואם תגרעהו משני שרשיו יהיה לנשאר שרש |
|
זאת השאלה חרשת |
|
וחכמתה |
|
שנניח השמנה שרשים הנוספים באלגו ששה עשר דברים וס"ד דרהמי |
|
באופן שיהיה למתקבץ שרש ושרשו דבר ושמנה דרהמי |
| If other is defined it is possible provided that [the sum] has a root. | ואם הנחנו אחר זולת זה יעבר אחר זה שיהיה שיחזיק שרש |
|
וכאשר הנחנו השמנה שרשים י"ו דברים וס"ד דרהמי |
|
הנה אז תדע כי כל שרש שני דברים ושמנה דרהמי |
|
והשני שרשי' ארבעה דברים וי"ו דרהמי |
|
והוא כמו שיאמר אלגו אם תגרעהו מארבעה שרשיו וששה עשר יחזיק מה שישאר שרש |
|
ותעשה כאשר אמרתי |
|
|
ויהיה האלגו שלשים ושש והוא האלגו |
|
ותשוב ותאמר כבר הנחנו שרש האלגו שני דברים ושמנה דרהמי ועשרים דברים |
|
|
ותחלק ל"ו על עשרים יעלה דרהם אחד וארבעה חומשי' והוא שרש האלגו המבוקש |
|
|
והאלגו שלשה דרהמי וחמשית וחומש החמישית |
| ואם תוסיף עליהם שמנה שרשיו והוא ארבעה עשר דרהמי ושני חומשים יהיה שבעה עשר ושלשה חומשים וחומש החמישית ושרשו ארבעה וחומש | |
|
| |
| ואם תגרע מהאלגו שהוא שלשה דרהמי וחמישית וחומש החמישית משני שרשיו שהם שלשה דרהמי ושלשה חומשים ישאר חומש אחד וארבעה חומשים מחמישית ושרשו שלשה חומשים | |
|
| |
|
ואם תעשה זה באופן החלק האחר יהיה האלגו דרהם אחד |
| This problem can be resolved by many solutions. | והיטב תוכל לעשות לזאת השאלה באופנים רבים |
|
כא ואם יאמרו לך אלגו אם תגרעהו משני שרשיו ומ"ט דרהמי יחזיק הנשאר שרש |
|
אם תרצה תעשה כאשר אמרתי |
|
ואם תרצה תכה שני השרשים בעצמם והיוצא יהיה האלגו |
|
והסיבה למה עשינו כזה בעבור כי המ"ט מחזיקים שרש |
| If the number have no root - proceeding as explained previously | ואם לא יחזיק המספר שרש תשוב למעשה הראשון שבארתי לך קודם זאת השאלה |
| Since this procedure is possible only for a number that has a root, and it involves many solutions, not one. | כי זה המעשה לא יתכן כי אם במספר שיחזיק שרש ולא יחזיק אופן אחד כי אם רבים |
| The first solving procedure of this problem and its similar has many solutions. | והמעשה הראשון לזאת השאלה ולדומים אליה יהיה באופנים רבים |
|
כב ואם יאמרו לך אלגו אם תוסיף עליו שרשו יהיה למתקבץ שרש ואם תגרע ממנו שרשו יחזיק הנשאר שרש |
|
זאת השאלה חרשת |
|
ותעשה אותה כמעשה |
|
שתבקש מספר שיחזיק שרש וכאשר תקבץ עמו מספר אחר יחזיק שרש ואם תגרע ממנו אותו המספר יחזיק שרש |
|
וכאשר מצאת אותו המספר תחלק אותו על המספר הנוסף ומה שיעלה לחלק יהיה שרש המרובע |
|
|
והמספר המחזיק שרש הוא כ"ה והמספר הנוסף עליו כ"ד והמספר הנגרע כ"ד |
|
|
וכבר ידעת כי כאשר תוסיף כ"ד על כ"ה יהיה מ"ט ושרשו שבעה |
|
|
וכאשר תגרע כ"ד מכ"ה ישאר אחד ושרשו אחד |
|
|
ואם תבקש לדעת שעור האלגו תחלק כ"ה על כ"ד ויהיה אחד ושלישית השמינית והוא שרש האלגו |
|
|
והאלגו אחד ושני שלישים וחלק אחד מתקע"ו באחד |
|
|
ואם תוסיף עליו שרשו והוא אחד ורביע ושתות יהיה שנים דרהמי ושמינית אחד וחלק אחד מתקע"ו ומחזיק שרש והוא אחד ושליש ושמינית |
|
|
ואם תגרע ממנו שרשו והוא אחד ושליש ושמינית ישאר כ"ה חלקים מתקע"ו חלקים באחד ומחזיק שרש והוא שמינית אחד וחצי ששית |
|
ואם תרצה תניח המספר המבוקש המחזיק שרש קס"ט והמספר הנוסף ק"כ והמספר הנגרע ממנו ק"כ |
|
|
ואתה יודע כי כשתוסיף על קס"ט ק"כ יהיה למתקבץ שרש והוא שבעה עשר |
|
|
וכאשר תגרע מהם ק"כ יהיה לנשאר שרש והוא שבעה |
|
|
וכאשר תרצה לדעת שעור האלגו תחלק קס"ט על ק"כ ויעלה לחלק אחד וחמישית אחד ושמינית אחד וחצי שתות והוא שרש האלגו |
|
|
והאלגו אחד וי"ד אלפים וקס"א מי"ד אלפים ות' באחד |
|
|
ואם תוסיף באלגו שרשו שהוא אחד וחמישית ושמינית וחצי שמינית ושתות אחד יהיה שלשה דרהמי וחמשת אלפים ותרמ"א חלקים מי"ד אלפים ות' חלקים באחד ומחזיק שרש והוא אחד ועשרה חלקים מק"כ |
|
|
ואם תגרע ממנו שרשו שהוא אחד וחמישית ושמינית וחצי שתות ישארו שמנת אלפים ורפ"א מי"ד אלפים ות' ומחזיק שרש והוא צ"א חלקים מק"כ |
| This problem and its similar have many solutions. | ולזאת השאלה ולדומים אליה אופנים רבים |
| The extraction of these numbers or those desired, for there are solutions as many as one wishes - is already explained. | וכבר בארתי לך המלאכה בהוצאת אלו המספרים או אשר תרצה מהם כי הם מחזיקים אופנים רבים כרצונך |
| The extraction of these numbers is further explained: | ואני אשכילך עוד בהוצאת אלו המספרים למען יחכם בהם לבבך |
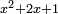 has a root has a root
|
כבר הודעתיך שכל אלגו שיחזיק שרש כאשר תוסיף עליו שני שרשיו ודרהם אחד יחזיק שרש |
|
|
אחר זה תגרע מהאלגו שני שרשיו ודרהם אחד |
|
ותאמר שני שרשיו ודרהם אחד יהיה המספר המבוקש |
|
|
וישאר אלגו פחות שני שרשים ודרהם אחד וכבר ידעת ששרשו פחות מדבר |
|
וננחיהו דבר פחות שני דרהמי |
|
|
ותכהו בעצמו |
|
|
ויהיה אלגו וארבעה דרהמי פחות ארבעה דברים ישוה אלגו פחות שני שרשים ודרהם אחד |
|
ותכונהו עמו ויהיה הדבר ישוה שני דרהמי וחצי והוא שרש האלגו |
|
|
והאלגו ששה ורביע |
|
|
ונניח המספר הנוסף עליו שני שרשים ודרהם אחד והוא ששה בעבור כי השרש הוא שנים וחצי |
|
|
ויהיה המספר המבוקש ששה ורביע והמספר הנוסף ששה והמספר הנגרע ששה |
|
תשיבם לרביעיות |
|
|
ויהיה המספר המבוקש כ"ה והמספר הנוסף כ"ד והמספר הנגרע כ"ד |
|
ואם נניח שרש האלגו פחות שני דברים ודרהם אחד דבר פחות דרהם וחצי תכהו בעצמו |
|
|
ויהיה אלגו ושני דרהמי ורביע פחות שלשה דברים ישוה אלגו פחות דבר ודרהם אחד |
|
ותכונהו עמו ויהיה הדבר ישוה שלשה דרהמי ורביע |
|
|
ותכנהו עמו ויהיה הדבר שלשה עשר והוא שרש האלגו המבוקש |
|
|
שיחזיק שרש והוא קס"ט כל ששה עשר ממנו אחד |
|
|
והמספר הנוסף עליו הוא שני שרשים ודרהם אחד והוא ששה וחצי בעבור כי השרש שלשה דרהמי ורביע |
|
כל דרהם ששה עשר חלקים |
|
|
ויהיה זה ק"כ חלקים |
| proceeding with the following as shown | ותעשה בנמשך כאשר הראיתי לך |
|
כג ואם יאמרו לך אלגו אם תוסיף עליו שני שרשיו יחזיק שרש ואם תגרע ממנו שלשה שרשיו יחזיק שרש |
|
וצריך שתבקש מספר שיחזיק שרש וכאשר תוסיף עליו מספר מה אחר יחזיק שרש וכאשר תגרע ממנו כמו המספר הנוסף וכמו חציו יחזיק הנשאר שרש |
|
בעבור כי שלשת השרשים הם שני השרשים וכמו חציים |
|
|
וכאשר מצאת אותו המספר תחלקהו על חצי המספר הנוסף או על שלישית המספר הנגרע והעולה לחלק יהיה שרש המרובע |
|
|
והמספר המחזיק שרש קכ"א והמספר הנוסף עליו מ"ח |
|
|
וכאשר תרצה לדעת שעור המספר תחלק קכ"א אם תרצה על מחצית המ"ח או אם תרצה על שליש הע"ב |
|
|
והאלגו כ"ה ורביעית הששית וחלק אחד מתקע"ו באחד |
|
|
ואם תוסיף עליו שני שרשיו שהם עשרה דרהמי וחצי ששית ויהיה ל"ה דרהמי ושלשה רביעי ששית וחלק אחד מתקע"ו ומחזיק שרש והוא חמשה דרהמי וחצי ושלישית השמינית |
|
|
ואם תגרע מהאלגו שלשת שרשיו שהם ט"ו ושמינית אחד ישאר עשרה ושתות ושמינית וחלק אחד מתקע"ו ומחזיק שרש והוא שלשה ושמינית וחצי ששית |
|
ואם תרצה תניח המספר המבוקש שיחזיק שרש מ"ט והמספר הנגרע מ"ח |
|
|
ותחלק מ"ט על ששה עשר ועלה לחלק שלשה וחצי שמינית והוא שרש האלגו |
|
|
והאלגו תשעה ושלשה שמיניות וחלק אחד מרנ"ו |
|
ואם תרצה תניח המספר המחזיק שרש תרכ"ה והמספר הנוסף של"ו |
|
|
ותחלק תרכ"ה על מחצית של"ו או על שלישית תק"ד והוא קס"ח ויעלה לחלק שלשה ושני שלישים ורביע השביעית ושמינית השביעית והוא שרש האלגו |
|
|
והאלגו שלשה עשר דרהמי וקמ"א חלקים מקפ"ט וכ"ה חלקים מכ"ח אלפים ורכ"ד |
|
|
ואם תוסיף עליו שני שרשיו והם שבעה דרהמי וצ"ד חלקים מקפ"ט יהיה כ"א דרהמי ומ"ז חלקים מקס"ח חלקים וכ"ה חלקים מכ"ח אלפים ורכ"ד חלקים ומחזיק שרש והוא ארבעה דרהמי וק"ג חלקים מקס"ג חלקים מאחד |
|
|
ואם תגרע מהאלגו שלשת שרשיו ישאר שני אדרהמי וקי"ד חלקים מקס"ח וכ"ה חלקים מכ"ח אלפים ורכ"ד חלקים מאחד ומחזיק שרש והוא דרהם אחד וק"ט מקס"ח חלקים באחד |
| The reason for the extraction of these numbers is explained above. | וסבת הוצאת אלו המספרים תהיה מבוארת ממה שבארנו קודם |

|
וכבר הראיתי לך שכל אלגו שיחזיק שרש והוא דבר ודרהם אחד |
|
תניח המספר הנוסף על האלגו שני דברים ודרהם אחד והמספר הנגרע ממנו שלשת שרשיו ודרהם אחד וחצי |
|
|
ותגרע מהאלגו שלשת שרשיו ודרהם וחצי וישאר אלגו פחות שלשה שרשים ודרהם אחד |
|
ותניח שרשו ושני דברים פחות שני דרהמי |
|
|
ותכם בעצמם |
|
|
ויהיה אלגו וארבעה דרהמי פחות ארבעה דברים ישוה אלגו פחות שלשה דברים ודרהם אחד וחצי |
|
ותכונם עמהם ויהיה הדבר חמשה וחצי |
|
|
והאלגו שלשים ורביע |
|
|
ונניח המספר הנוסף עליו שני דברים ודרהם אחד והוא שנים עשר |
|
|
ונניח המספר הנגרע ממנו שלשה דברים ודרהם וחצי והוא שמנה עשר |
|
השיבם רביעיות |
|
|
ויהיה המספר המבוקש שיחזיק שרש קכ"א והמספר הנוסף מ"ח |
| proceeding with the procedure as stated. | ותעשה בפעולתם כמו שאמרתי לך |
|
כד ואם יאמרו לך אלגו שיחזיק שרש אם תגרעהו מעשרת שרשיו פחות שמנה דרהמי יחזיק מה שישאר שרש |
| (½roots)²-numbers | כאשר יקרה לך שאלות ככה תכה מחצית השרשים בעצמם והמתקבץ תגרע ממנו האדרהמי |
|
ומה שישאר אם יתחלק לשני חלקים שיחזיק כל חלק שרש הנה תחזיק השאלה רבים מהאופנים כמה שתרצה |
|
ואם לא יתחלק לשני חלקים שיחזיק כל חלק שרש הנה לא יהיה לשאלה אופן ולא מלאכה |
|
ואם כאשר תכה מחצית השרשים בעצמו יצא כמו שעור הדרהמי או פחות מהם לא היתה השאלה נכונה |
|
|
ונכה מחצית השרשים בעצמם בזאת השאלה והוא חמשה ויהיה עשרים וחמשה תגרע מהם שמנה הדרהמי וישאר שבעה עשר |
|
|
ואם תרצה תאמר אלגו וששה עשר דרהמי ישוה עשרה שרשים פחות שמנה דרהמי |
|
|
ואם תרצה תאמר אלגו ודרהם אחד ישוה עשרה שרשים פחות שמנה |
|
|
והוא כאלו תאמר אלגו וששה עשר דרהמי ישוה עשרה שרשים פחות שמנה דרהמי |
|
|
ויהיה האלגו אם תרצה ל"ו |
|
|
ואם תרצה יהיה שמנה עשר |
|
כה ואם יאמרו לך אלגו ודרהם אחד ישוו עשרה שרשים פחות שמנה דרהמי |
|
|
יהיה האלגו אם תרצה אחד |
|
|
ואם תרצה יהיה שמנים ואחד |
|
כו ואם יאמרו לך אלגו המחזיק שרש אם תגרעהו מר"ס פחות ששה שרשים יחזיק הנשאר שרש |
| (½roots)²+numbers | וכאשר תפול לפניך שאלה כזאת תכה מחצית השרשים בעצמם ותוסיפם על הדרהמי |
|
ומה שיתקבץ אם יתחלק לשני חלקים שיחזיק כל חלק שרש תהיה השאלה אז בעלת אופנים כמה שתרצה |
|
ואם לא יתחלק ככה תהיה השאלה חרשת בזולת האופן |
|
|
אחר זה הנה הכאת מחצית השרשים בעצמם בזאת השאלה היא תשעה כי מחציתם שלשה תוסיפם על ר"ס ויהיה רס"ט |
|
|
ותאמר אם תרצה אלגו וקס"ט ישוו ר"ס דרהמי פחות ששה דברים |
|
|
ואם תרצה תאמר אלגו ומאה דרהמי ישוו ר"ס פחות ששה דברים |
|
|
ויהיה האלגו מ"ט דרהמי |
|
|
ואם אמרת אלגו ומאה דרהמי ישוו ר"ס דרהמי פחות ששה דברים |
|
|
יהיה האלגו מאה דרהמי |
|
כז ואם יאמרו לך אלגו המחזיק שרש אם תוסיף עליו שני שרשיו יחזיק שרש ואם תוסיף על המקובץ שלשת שרשיו יחזיק שרש |
|
מלאכתו שתניח האלגו שלך אלגו |
|
|
תוסיף עליו שני שרשיו ויהיה אלגו ושני שרשים |
|
|
ויחזיק שרש והוא דבר וחצי |
|
והסבה למה הנחתי שרשו דבר וחצי |
|
|
בעבור כי שלשת השרשים כמו שני השרשים וכמו חציים |
|
|
ותכה דבר וחצי בעצמו |
|
|
ויהיה שני אלגו ורביע ישוה אלגו ושני שרשים |
|
ותכונהו עמו ויהיה שרש האלגו דרהם אחד ושלשה חומשים |
|
|
והאלגו שני דרהמי ושני חומשים ורביע חומש החומש |
|
|
ואם תוסיף עליו שני שרשיו והם שלשה וחמשית יהיה חמשה דרהמי ושלשה חומשי' וארבעה חומשי החומש |
|
|
והוא ידוע כי שרשו כמו שרש האלגו הראשון וכמו חציו והוא שני דרהמי ושני חמישיות |
|
|
ושני השרשים כמו האלגו וכמו רביעיתו |
|
|
והוא מחויב שיהיו שלשת שרשים מחמשה דרהמי ושלשה חומשים ורביע חומש מחמישית כמו שהוא האלגו ורביעיתו יותר והוא שבעה וחומש |
|
|
וכאשר תוסיפם על חמשה דרהמי ושלשה חומשים וארבעה חומשי החומש יהיה שנים עשר וארבעה חומשים וארבעה חומשי החומש |
|
|
והוא ידוע כי שרשו הוא כמו שרש אחד וחצי מחמשה ושלשה חומשים וארבעה חומשי החומש והוא שלשה דרהמיש ושלשה חומשים |
|
|
והוא ראוי שיהיו ארבעה שרשים וחצי מי"ב וארבעה חומשים וארבעה חומשי החומש שיהיו כמו האלגו וכמו רביעיתו יותר והוא י"ו וחומש |
|
|
וכאשר תוסיפם על י"ב וארבעה חומשים וארבעה חומשי החומש יהיה כ"ט וארבעה חומשי החומש |
|
|
והוא ידוע כי שרשו הוא כמו שרש אחד וחצי מי"ב וארבעה חומשי' וארבעה חומשי החומש והוא חמשה דרהמי ושני חומשים |
| וכן אם תוסיף מה שתרצה מהשרשים על המתיחס אליו שאשר יתקבץ ממנו יחזיק שרש כמו שנאמר | |
|
|
כי כאשר נוסיף על כ"ט וארבעה חומשי החומש ששת שרשיו ושלשה רביעי השרש יהיה למתקבץ מהם שרש והוא כמו שרש וחצי מכ"ט וארבעה חומשים מחומש והוא שמנה עשר |
|
|
וכאשר תוסיף על המתקבץ עשרת שרשיו ושמינית השרש יחזיק המתקבץ מהם שרש והוא כמו שמנה עשר וכמו חציו שהם כ"ז |
| וכן ימשכו כל אשר תרצה מההוספות כמו זה האופן כאשר תניח התוספת מתיחס לשאלה כאלו אמרנו שיחס השאלה הוא שששת שרשיו הם כמו שני השרשים וכמו חצים והולכים ומתוספים עד אין להם סוף | |
|
כח וכן אם יאמרו לך אלגו המחזיק שרש אם תוסיף עליו שלשת שרשיו יחזיק שרש ואם תקבץ עם העולה ששת שרשיו יחזיק שרש |
|
מלאכתו שתניח האלגו שלך אלגו |
|
|
תוסיף עליו שלשת שרשיו ויהיה האלגו ושלשה שרשים |
|
|
ושרשו שני דברים |
|
|
והסיבה בהניחנו שרשו שני דברים הוא בעבור כי ששת השרשים כמו שלשה שרשים |
|
|
ותכה שני דברים בשני דברים |
|
|
ויהיה ארבעה אלגוש ישוו אלגו ושלשה דברים |
|
ותכונהו עמו ויהיה הדבר ישוה דרהם אחד והוא שרש האלגו |
|
|
והאלגו דרהם אחד |
| וכמו זה ימשך מה שתרצה מההוספות כפי יחס השאלה | |
|
|
נאמר כי כאשר תוסיף על מה שהתקבץ שנים עשר שרשים יחזיק שרש |
| ואם תוסיף על המקובץ שרשו יחזיק שרש | |
|
|
וכאשר תוסיף על זה המקובץ עשרי' וארבעה שרשיו יחזיק המתקבץ שרש |
|
ואם תוסיף מ"ח שרשים יחזיק שורש |
|
ואם תוסיף צ"ו שרשים יחזיק שרש |
| וכמעשה הזה יעלו כל מה שיפלו לפניך מזה המין כאשר יניחו השרשים השניים יותר מהראשונים | |
| ואם יונחו פחות מהראשונים לא יצאו עם זה המעשה | |
| אבל להם דרכים אחרים יצאו בהם והם אלו | |
|
כט כאשר יאמרו לך אלגו המחזיק שרש אם תוסיף עליו שני שרשים יחזיק שרש ואם תוסיף על המקובץ שרשו יחזיק שרש |
|
ולידיעתו תניח האלגו שלך אלגו |
|
|
ותוסיף עליו שני שרשיו ויהיה אלגו ושני שרשי' |
|
ותוסיף על הנקבץ שרשו והוא שרש האלגו ושני שרשים ויהיה אלגו ושני שרשי' ושרש האלגו ושני שרשים וצריך שיחזיק שרש |
|
|
ונניח שרשו דבר וחצי דרהם |
|
|
ותכהו בעצמו |
|
|
ויהיה אלגו ודבר ורביעית דרהם ישוה אלגו ושני דברים ושרש מאלגו ושני שרשים |
|
|
ותגרע אלגו ושרש מאלגו ושני שרשים |
|
|
וישאר שרש ושרש מאלגו ושני שרשים ישוו רביעית דרהם |
|
|
ותגרע שרש מרביעית דרהם |
|
|
ישאר רביעית דרהם פחות שרש ישוה שרש מאלגו ושני שרשי' |
|
|
ותכה רביעית דרהם פחות שרש בעצמו |
|
|
ויהיה חלק מי"ו ואלגו פחות חצי דבר ישוה אלגו ושני שרשים |
|
ותכונהו עמו ויהיה השרש רביעית העשירית |
|
|
והאלגו חלק אחד מאלף ות"ר |
|
והנחנו השרש דבר וחצי דרהם כדי שישחתו האלגוש וישארו דברים ישוו למספרים |
|
ל וכן אם יאמרו לך אלגו המחזיק שרש אם תוסיף עליו ארבעת שרשיו יחזיק שרש |
|
וידיעתו שתניח האלגו שלך אלגו |
|
|
ותוסיף עליו ארבעת שרשיו ויהיה אלגו וארבעה דברים |
|
|
ותוסיף על אלגו וארבעה דברים שני שרשיו ושרש ארבעה אלגוש וי"ו דברים ויהיה אלגו וארבעה דברים ושרש מארבעה אלגוש וי"ו דברים |
|
|
ותגרע אלגוש ושני דברים מאלגו וארבעה דברים |
|
|
וישאר דרהם אחד ישוה שני דברים ושרש מארבעה אלגוש וי"ו דברים |
|
|
ותגרע שני הדברים מהדרהם |
|
|
וישאר דרהם אחד פחות שני דברים ישוה שרש מארבעה אלגוש וי"ו דברים |
|
|
ותכה דרהם אחד פחות שני דברים בעצמו |
|
|
ויהיה דרהם אחד וארבעה אלגוש פחות ארבעה שרשים ישוה ארבעה אלגוש וי"ו דברים |
|
ותכוין עמו ויהיה הדבר חצי עשירית מדרהם |
|
|
והאלגו חלק אחד מארבע מאות |
| Whichever of this species that you have, apply the procedure on its root, until you find it by reduction, when it remains that things are equal to numbers. | וכל אשר יפול בידך מזה המין תעשה מלאכה בשרשו עד שכאשר מצאת אותו עם הכוון ישאר דברים ישוו מספרים |
| This procedure is very useful. | וזאת המלאכה גדולת התועלת די מוגו אפרוביגו |
|
לא ואם יאמרו לך אלגו אם תגרע ממנו ארבעה שרשיו יחזיק שרש ואם תגרע מהנשאר שני שרשיו יחזיק שרש |
|
ולידיעת זה תניח האלגו שלך אלגו |
|
|
ותגרע ממנו ארבעה שרשיו וישאר אלגו פחות ארבעה דברים |
|
|
ויחזיק שרש והוא חצי דבר |
|
|
והסיבה למה הנחתי חצי הדבר בעבור כי היו שני שרשים חצי הארבעה |
|
|
ותכה חצי דבר בעצמו |
|
|
ויהיה רביע אלגו ישוה אלגו פחות ארבעה אלגוש |
|
ותכונהו עמו ויהיה שרש האלגו חמשה ושליש |
|
|
והאלגו עשרים ושמנה וארבעה תשיעיות |
| The ratio of the roots in this question and its similar is treated as in the preceding question. | וזאת השאלה והדומים אליה יתנהג בה יחס השרשים כאשר נהגנו בשאלה שקדמה לה |
We say that when you subtract from the remainder its root, it has a root; and if you subtract from that remainder half of its root, it has a root; then a quarter of its root; an eighth of its root; half the eighth of its root - each of the subtracted numbers are half their preceding numbers, for two roots and half the four roots 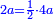
|
נאמר כי כאשר תגרע מהנשאר שרשו יחזיק שרש ואם תגרע מהנשאר חצי שרשו יחזיק שרש וכן רביעית שרשו ושמינית שרשו וחצי שמינית שרשו כל אחד מאלו המספרים הנגרעים חצי המספרים הנגרעים שהם קודמים אליו בעבור כי שני השרשים חצי הארבעה השרשים |
| Whichever of this species that you have, solve it by this method when the secondary roots are less than the primary roots. | וכל אשר יפול לפניך מזה המין תעשהו עם זה האופן כאשר הניחו השרשים השניים פחות מהראשונים |
|
לב ואם יאמרו לך אלגו המחזיק שרש אם תוסיף עליו שרשו יחזיק שרשו ואם תוסיף עליו דרהם אחד יחזיק שרש |
|
וידיעתו שתניח האלגו שלך אלגו |
|
ותוסיף עליו שרשו ויהיה אלגו ודבר ויחזיק שורש |
|
ותוסיף על האלגו אדרהם אחד ויהיה אלגו ודרהם אחד ויחזיק שורש |
|
|
ותשוב ותניח שרש האלגו ודבר |
|
|
ושרש מאלגו ודרהם אחד פחות חצי דרהם |
|
|
ותכם בעצמם |
|
|
ויהיה אלגו ודרהם ורביע פחות שרש מאלגו ודרהם אחד ישוה אלגו ודבר |
|
|
ותגרע אלגו מאלגו |
|
|
וישאר דרהם אחד ורביע פחות שרש מאלגו ודרהם אחד ישוה שרש |
|
ותאסוף האדרהם ורביע עם שרש מאלגו ודרהם אחד ותוסיפם על השרש |
|
|
ויהיה שרש ושרש מאלגו ודרהם אחד ישוה דרהם ורביע |
|
|
ותגרע השרש מדרהם ורביע |
|
|
ישאר דרהם ורביע פחות דבר ישוה שרש מאלגו ודרהם אחד |
|
|
ותכה האדרהם ורביע פחות דבר בעצמו |
|
|
ויהיה אדרהם וחצי וחצי שמינית פחות שני שרשים וחצי ישוה אלגו ודרהם אחד |
|
ותכונהו עמהם ויהיה הדבר ישוה תשעה חלקים מארבעים והוא שרש האלגו |
|
|
והאלגו פ"א חלקים מאלף ות"ר |
|
והנחנו שרשו אלגו ודרהם פחות חצי דרהם למען ישאר אחר הכוון שרשים ישוו לדרהם אחד |
|
לג ואם יאמרו לך אלגו המחזיק שרש אם תגרע ממנו חמשה דרהמי יחזיק הנשאר שרש ואם תוסיף על הנשאר שרשו יחזיק המקובץ שרש |
|
וידיעתו שתניח האלגו שלך אלגו |
|
ותגרע ממנו חמשה דרהמי וישאר אלגו פחות חמשה דרהמי |
|
ותוסיף על אלגו פחות חמשה דרהמי שרשו והוא שרש האלגו פחות חמשה דרהמי ויהיה אלגו פחות חמשה דרהמי ושרש מהאלגו פחות חמשה דרהמי |
|
ותניח שרשו דבר |
|
|
ותכהו בעצמו |
|
|
ויהיה אלגו ורביע דרהם פחות שרש ישוה אלגו פחות חמשה דרהמי והוא שרש מאלגו פחות חמשה דרהמי |
|
ותאסוף זה האלגו עם החמשה וזה יהיה עם השרש ותוסיף החמשה על אלגו ורביע דרהם והשרש אלגו |
|
|
ויהיה השרש אלגו וחמשה דרהמי ורביע מהדברים ישוה שרש האלגו פחות חמשה דרהמי |
|
|
ותכה חמשה דרהמי ורביע הדברי' בעצמם |
|
|
ויהיה עשרים ושבעה דרהמי וחצי וחצי שמינית ואלגו פחות עשרה שרשים וחצי שרש ישוה אלגו פחות חמשה דרהמי |
|
ותכוין עמהם ויהיה הדבר ישוה שלשה דרהמי ושבעה עשר חלקים מקפ"ט והוא שרש האלגו |
|
|
והאלגו תשעה דרהמי וק"ג חלקים מקס"ח חלקים וקכ"א חלקים מכ"ח אלפים ורכ"ד חלקים באחד |
| Check:
|
וכאשר תגרע ממנו חמשה ישאר ארבעה דרהמי וק"ג חלקים מקס"ח וקכ"א חלקים מכ"ח אלפים ורכ"ד |
|
|
ותוסיף עליו שרשו שהוא שני דרהמי וכ"ה חלקים מקס"ח וקכ"א חלקים מכ"ח אלפים ורכ"ד ויחזיק שורש והוא שני דרהמי ומאה דרהמי מקס"ח חלקים |
|
לד ואם יאמרו לך אלגו שיחזיק שורש אם תוסיף עליו ארבעת שרשיו יחזיק שרש ואם תגרע ממנו שני שרשיו ודרהם אחד יחזיק הנשאר שרש |
|
וידיעתו שתניח האלגו שלך אלגו |
|
ותוסיף עליו ארבעת שרשיו ויהיה אלגו וארבעה שרשי' ויחזיק שרש |
|
ותגרע מהאלגו שני שרשיו ודרהם אחד וישאר אלגו פחות שני שרשים ודרהם אחד ויחזיק שרש |
|
ותניח שרשו כמו שאבאר לך בכוון שלא יתכן להיות שרש אחד מאלגו וארבעה דברים פחות שלשה דרהמי |
|
|
ותכהו בעצמו |
|
|
ויהיה אלגו ותשעה דרהמי וארבעה שרשים פחות ששה שרשים מאלגו וארבעה דברים ישוו אלגו פחות שני שרשים ודרהם אחד |
|
ותכוין עמו ויהיה אלגו וששה שרשים ועשרה דרהמי ישוה אלגו וששה שרשים מאלגו וארבעה דברים |
|
|
וששה שרשים מאלגו וארבעה דברים שרש מל"ו אלגוש וקמ"ד דברים |
|
|
ותגרע אלגו מאלגו |
|
|
וישאר ששה שרשים ועשרה דרהמי ישוה שרש מל"ו אלגוש וקמ"ד דברים |
|
ותכוין בהם ויהיה הדבר ישוה ארבעה דרהמי ושתות והוא שרש האלגו |
|
|
והאלגו שבעה עשר דרהמיש ורביע התשיעית |
|
לה ואם יאמרו לך אלגו המחזיק שרש אם תגרע ממנו שני שרשיו יחזיק שרש ואם תוסיף על הנשאר שרשו יחזיק שרש |
|
וידיעתו שתניח האלגו שלך אלגו |
|
ותגרע ממנו שני שרשיו וישאר אלגו פחות שני שרשים |
|
ותוסיף עליו שרשו ויהיה אלגו פחות שני שרשים ושרש האלגו פחות שני שרשים ויחזיק שרש |
|
ותניח שרשו דבר פחות דרהם אחד וחצי |
|
|
ותכם בעצמם |
|
|
ויהיה אלגו ושני דרהמי ורביע פחות שלשה שרשים ישוה אלגו פחות שני שרשים ושרש מאלגו פחות שני שרשים |
|
ותכוין בהם ויהיה אחר הכוון דבר ושרש מאלגו פחות שני שרשים ישוו שני דרהמי ורביע |
|
|
ותגרע דבר משני דרהמי ורביע |
|
|
ישאר שני דרהמי ורביע פחות דבר ישוה שרש מאלגו פחות שני שרשים |
|
|
ותכה שני דרהמי ורביע פחות דבר בעצמו |
|
|
ויהיה חמשה דרהמי וחצי שמינית ואלגו פחות ארבעה דברים וחצי דבר ישוה אלגו פחות שני שרשים |
|
ותכוין עמהם ויהיה הדבר שני דרהמי ורביע עשירית והוא שורש האלגו |
|
|
והאלגו ארבעה ועשירית אחד מחלק אחד מאלף ת"ר |
| Check:
|
ותגרע ממנו שני שרשיו והם ארבעה וחצי עשירית ישאר חצי עשירית וחלק אחד מאלף ת"ר |
|
|
ותוסיף עליו שרשו והוא חומש אחד ורביעית העשירית יהיה רביע אחד ורובע העשירית וחלק אחד מאלף ת"ר ומחזיק שרש והוא חצי ורביע העשירית |
|
לו ואם יאמרו לך אלגו שיחזיק שרש אם תוסיף עליו שלשת שרשיו ודרהם אחד יחזיק שרש ואם תגרע ממנו שלשת שרשיו פחות שני דרהמי יחזיק מה שישאר שרש |
|
וידיעתו שתניח האלגו שלך אלגו |
|
ותוסיף עליו שלשת שרשיו ודרהם אחד ויהיה אלגו ושלשה שרשים ודרהם אחד ויחזיק שרש |
|
ותגרע מהאלגו שלשת שרשיו פחות שני דרהמי וישאר אלגו ושני דרהמי פחות שלשה שרשים ומחזיק שרש |
|
ותניח שרשו שרש מאלגו ושלשה שרשים ודרהם אחד פחות שלשה דרהמיש |
|
|
ותכם בעצמם |
|
|
ויבא אלגו ושלשה שרשים ועשרה דרהמי פחות שרש מל"ו אלגוש ול"ו דרהמי וק"ח דברים ישוו אלגו ושני דרהמי פחות שלשה שרשים |
|
|
|
|
ותכוין עמהם ויהיה אחר הכוון ששה דברים ושמנה דרהמי ישוה שרש מל"ו אלגוש ול"ו דרהמיש ור"ח דברים |
|
|
ותכה ששה דברים ושמנה דרהמי בעצמם |
|
|
ויהיה ל"ו אלגוש וצ"ו דברי' וס"ד דרהמי ישוו ל"ו אלגו ול"ו דרהמי וק"ח דברים |
|
|
|
|
ותכוין עמהם ויהיה הדבר שני דרהמי ושליש אחד והוא שרש האלגו |
|
|
והאלגו חמשה דרהמי וארבעה תשיעיות |
| Check:
|
ואם תוסיף עליו שלשת שרשיו ודרהם אחד יהיה שלשה עשר דרהמי וארבעה תשיעיות ושרשו ג' דרהמי ושני שלישים |
|
|
ואם תגרע ממנו שלשת שרשיו פחות שנים דרהמי ישאר ארבעה תשיעיות ושרשו שנים שלישיות |
|
לז ואם יאמרו לך אלגו המחזיק שרש אם תגרע ממנו דרהם אחד פחות שרש האלגו יחזיק הנשאר שרש |
|
וידיעתו שתניח האלגו שלך אלגו |
|
ותוסיף עליו דרהם אחד פחות שרש האלגו ויהיה אלגו ודרהם אחד פחות שרש האלגו ומחזיק שרש |
|
ואם תגרע מהאלגו דרהם אחד פחות שרש האלגו ישאר אלגו ושרש פחות דרהם אחד ומחזיק שרש |
|
ותניח שרש האלגו אלגו ודרהם אחד פחות דבר ודרהם אחד פחות שרש האלגו ושרש פחות דרהם אחד |
|
|
ותכהו בעצמו |
|
|
ויהיה אלגו ושרש פחות שני שרשים מאלגו ושרש פחות דרהם אחד ישוה אלגו ודרהם אחד פחות שרש |
|
ותאספם עם השרש ותוסיפהו עם האלגו ושרש |
|
ותאסוף האחד עם שני שרשים מאלגו ושרש פחות דרהם אחד ותוסיפהו על האלגו ודרהם אחד |
|
|
ותגרע אלגו מאלגו |
|
|
וישאר דרהם אחד ושרש מאלגו ושרש פחות דרהם אחד ישוו שני דברים |
|
|
ותגרע דרהם אחד משני דברים |
|
|
וישאר שני דברים פחות דרהם אחד ישוה שני שרשים מאלגו ושרש פחות דרהם אחד |
|
|
וחציו |
|
|
שהוא דבר פחות חצי דרהם ישוה שרש מאלגו ושרש פחות דרהם אחד |
|
|
ותכה דבר פחות חצי דרהם בעצמו |
|
|
ויהיה אלגו ורביע דרהם פחות דבר ישוה אלגו ושרש פחות דרהם אחד |
|
|
|
|
ותכוין עמהם ויהיה הדבר חמשה שמיניות מדרהם והוא שרש האלגו |
|
|
והאלגו שלשה שמיניות ושמינית אחד משמינית |
|
לח ואם יאמרו לך אלגו המחזיק שרש אם תוסיף עליו שני דרהמי פחות שרש האלגו יחזיק שרש ואם תגרע ממנו שלשה פחות שרש האלגו יחזיק שרש |
|
ולידיעת זה תשים האלגו שלך אלגו |
|
ותוסיף עליו שני דרהמי פחות שרש ויהיה אלגו ושני דרהמי פחות שרש ויחזיק שרש |
|
ותגרע ממנו שלשה פחות שרש וישאר אלגו ושרש פחות שלשה דרהמי ויחזיק שרש |
|
ותניח שרש האלגו ושני דרהמי פחות שרש מדרהם אחד ושרש מאלגו ושרש פחות שלשה דרהמי |
|
ותכהו בעצמו ויהיה אלגו ושרש פחות שני דרהמי ושני שרשים מאלגו פחות שלשה דרהמי ישוה אלגו ושנים דרהמי פחות שרש |
|
|
|
ותאסוף האלגו ושני דרהמי עם השרש ותוסיפיהו עם האלגו ושרש פחות שני דרהמי
ותגרע אלגו מאלגו וישאר שני שרשים ושרש מאלגו ושרש פחות שלשה דרהמי ישוה ארבעה דרהמי |
|
ותגרע שני השרשים מהארבעה דרהמיש ישאר ארבעה דרהמי פחות שני שרשים ישוה שנים שרשים מאלגו ושרש פחות שלשה דרהמי |
|
ותקח חציו והוא שני דרהמי פחות שרש ישוה אלגו ושרש פחות שלשה דרהמי |
|
ותכה שני דרהמי פחות דבר בעצמו ויהיה ארבעה דרהמי ואלגו פחות ארבעה דברים ישוה אלגו ושרש פחות שלשה דרהמי |
|
|
|
ותכוין בהם ויהיה הדבר ישוה דרהם אחד ושני חומשים |
|
והאלגו דרהם אחד וארבעה חומשים וארבעה חומשים מחומש |
|
לט ואם יאמרו לך אלגו המחזיק שרש אם תוסיף עליו שרשו ודרהם אחד יחזיק שרש ואם תוסיף על האלגו שני שרשיו ושני דרהמי יחזיק שרש |
|
וידיעתו שתניח האלגו שלך אלגו |
|
ותוסיף עליו שרשו ודרהם אחד ויהיה אלגו ושרש ודרהם אחד ויחזיק שרש |
|
ותוסיף על האלגו שני שרשיו ושני דרהמי ויחזיק שרש |
|
ותניח שרשו חצי דרהם ושרש מאלגו ושרש ודרהם אחד ישוה אלגו ושני שרשים ושני דרהמי |
|
ותגרע אלגו ושרש ודרהם אחד ורביע מאלגו ושני שרשים ושני דרהמי וישאר דבר ושלשה רביעי דרהם |
|
ותכהו בעצמו ויהיה אלגו ודבר וחצי וחצי דרהם וחצי שמינית ישוה אלגו ושרש ושני דרהמי |
|
|
|
ותכוין בהם ויהיה הדבר שבעה שמיניות והוא שרש האלגו |
|
והאלגו חמשה שמיניות ושמינית השמינית |
Word Problems |
|
|
מ) ואם יאמרו לך ארבעה אנשים התקבצו יחד לקנות בהמה אחת ואמר הראשון לשלשה אם תתנו לי החצי מאשר תחזיקו יהיה לי ערך הבהמה |
|
| |
|
וידיעת זה שתניח אל האחד דבר ולשני דינר אחד ולשלישי דרהם אחד ולרביעי פלס אחד |
|
ואמר הראשון שמחזיק דבר אל השלשה תנו לי החצי מאשר לכם ואקבצהו עם אשר לי ויהיה לי ערך הבהמה |
|
ומחצית אשר להם הוא חצי דינר וחצי דרהם וחצי פלס וכאשר קובצו עם הדבר אשר הוא מחזיק יהיה דבר וחצי דינר וחצי דרהם וחצי פלס והוא ערך הבהמה |
|
ואמר השני אשר לו דינר אחד לשלשה תנו לי השלישית מאשר לכם ואקבצהו עם אשר לי ויהיה לי ערך הבהמה |
|
ושלישית אשר להם הוא שלישית דבר ושלישית דרהם ושלישית פלס וכאשר קובצו עם הדינר אשר לו יהיו בידו דינר אחד ושלישית דבר ושלישית דרהם ושלישית פלס והוא ערך הבהמה |
|
וזה יהיה שוה לדבר וחצי דינר וחצי דרהם וחצי פלס |
|
|
|
ותכוין בהם ויהיה זה שתגרע שלישית דבר מדבר שלם וישאר שני שלישי דבר |
|
ותגרע שליש דרהם מחצי דרהם וישאר ששית דרהם |
|
ותגרע שליש פלס מחצי פלס וישאר ששית פלס |
|
ותגרע חצי גאקיש מדינר אחד וישאר חצי דינר ישוה שני שלישי דבר[3] ושתות דרהם ושתות פלס[4] |
|
והדינר ישוה דבר ושליש דבר ושליש דרהם ושליש אלפלס |
|
ורביע דינר ישוה שליש דבר וחצי שתות דרהם וחצי שתות פלס |
|
וחמישית דינר ישוה חמישית דבר וחמישית שלישית הדבר וחמישית שלישית דרהם וחמישית שלישית פלס |
|
ותניח ערך הבהמה דבר וחצי דינר וחצי דרהם וחצי אלפלס |
|
ותגרע חצי הדינר מערך הבהמה ותניח במקומו חצי אשר ישוה הדינר והוא שני שלישי דבר ושתות דרהם ושתות אלפלס ויהיה ערך הבהמה דבר ושני שלישים מדבר ושני שלישי דרהם ושני שלישי אלפלס |
|
| |
|
וכבר הסירונו מספר הדינר והנחנו במקומו דבר ושליש דבר ושליש דרהם ושליש פלס |
|
ואמר השלישי אשר לו דרהם אחד תנו לי הרביעית מאשר לכם ואקבצהו עם אשר לי ויהיה לי ערך הבהמה |
|
ורביעית אשר להם הוא רביעית הדבר ורביעית דינר ורביעית פלס וכאשר תקבצם עם האדרהם אשר לו יהיו ותסיר סך הדינר ותניח במקומו אשר ישוה רביעית הדינר כמבואר למעלה יהיו אז מה שבידו שלישית דבר ורביעית דבר ודרהם וחצי שתות דרהם ושליש אלפלס והוא ערך הבהמה ויהיה שוה לדבר ושני שלישי דבר ושני שלישי דרהם ושני שלישי אלפלס |
|
| |
|
|
|
ותכוין בהם והוא שתגרע שלישית דבר ורביעית דבר מדבר ושני שלישי דבר ושליש פלאס משני שלישי פלאס וישאר דבר וחצי ושתות ושליש פלאס |
|
ותגרע שני שלישי דרהם מדרהם וחצי שתות וישאר רביע ושתות דרהם ישוה דבר וחצי שתות דבר ושליש פלאס |
|
והדרהם ישוה שני דברים ושלשה חומשי דבר וארבעה חומשי אלפלאס |
|
ותסיר השני שלישי דרהם מערך הבהמה ותשים במקומם שני שלישים ממה ששוה הדרהם והוא דבר ושליש ושני חומשי דבר ושליש וחומש אלפלאס ויהיה ערך הבהמה שלשה דברים ושני חומשי דבר ופלס אחד וחומש |
|
| |
|
וכבר לקחנו הדרהם ושמנו במקומו שני דברים ושלשה חומשי דבר וארבעה חומשי אלפלאס |
|
ותגרע שלישית הדרהם אשר הוא בערך הדינר ותניח במקומו שלישית מה שישוה הדרהם והוא שני שלישי דבר וחומש דבר וחומש אלפלאס ושלישית חומש אלפלאס ויהיה ערך הדינר שני דברים וחומש ושלשה חומשי אלפלאס |
|
| |
|
הנה התבאר שיחזיק הראשון דבר |
|
והשני והוא אותו מהדינר יחזיק שני דברים וחומש ושלשה חומשי אלפלס |
|
והשלישי והוא אותו מהדרהם יחזיק שני דברים ושלשה חומשי דבר וארבעה חומשי אלפלס |
|
וערך הבהמה יהיה שלשה דברים ושני חומשי דבר ופלס אחד וחומש |
|
ואמר האיש הרביעי המחזיק אלפלס אחד אל השלשה תנו לי החמישית ממה שבידכם ואקבצהו עם אשר לי ויהיה לי ערך הבהמה |
|
וחמישית אשר להם הוא דבר וארבעה חומשי חמישית דבר וחמישית אלפלס ושני חומשי חמישית אלפלס וכאשר קבצנום עם האלפלס אשר הוא מחזיק יהיה לו אלפלס אחד וחמישית אלפלס ושני חומשי חמישית אלפלאס ודבר וארבעה חומשי חמשית דבר וישוה כל זה ערך הבהמה שהוא שלשה דברים ושני חומשי דבר ופלס אחד וחומש |
|
| |
|
|
|
תגרע פלס וחומש מפלס וחומש ושני חומשי חמשית פלס וישאר שני חומשי חמישית פלס |
|
ותגרע דבר וארבעה חומשי חמישית דבר משלשה דברים ושני חומשי דבר וישאר שני דברים וחומש וחמישית חמישית הדבר וישוה שְני חומשי חמשית אלפלס |
|
והפלס ישוה עשרים ושמנה דברים |
|
ונניח הדבר אחד והוא מה שמחזיק הראשון |
|
והשני תשעה עשר בעבור כי הוא שלשה חומשים ממה שמחזיק הרביעי וכמו הכפל מאשר יחזיק הראשון ושני חומשיו יותר |
|
והשלישי עשרים וחמשה בעבור כי הוא ארבעה חומשי מאשר לרביעי וכמו הכפל מהראשון ושלשה חומשי יותר |
|
וערך הבהמה שלשים ושבע בעבור כי הוא כמו אשר לרביעי וכמו החומש וכמו שלשה דימיוני אשר לראשון וכמו חמישיתו |
| This procedure is the one that is known to the arithmeticians and it is a complete understanding, except that it is very subtle and the number is extracted with great difficulty. | וזה המעשה הוא אשר ידעו אותו בעלי המספר ביניהם והיא הבנה שלימה זולת שהיא מאד דקה ובקושי גדול יצא החשבון |
| I solve this with a direct procedure and full understanding: | וכבר אוצאוהו לאור אני עם [נ"ר אם] המלאכה ישרה והבנה שלימה |
|
וזה שנניח כל אשר יחזיקו דרהם אחד |
|
ונניח שיהיה לאחד מזה הדרהם דבר |
|
וישאר לשלשה דרהם פחות דבר |
|
וכאשר נקבץ חציים עם אשר לראשון שהוא דבר יהיה ערך הבהמה חצי דבר וחצי דרהם |
|
ותניח לשני דינר אחד |
|
וכאשר נקבץ שלישית הדרהם עם הדינר יהיה ערך הבהמה שני שלישיות מדינר ושלישית אדרהם וישוה ערך הבהמה מהחלק האחד שהיה חצי דבר וחצי דרהם |
|
ותגרע שליש דרהם מחצי דרהם וישאר שני שלישי דינר ישוה חצי דבר וששית דרהם |
|
והדינר שלשה רביעי דבר ורביע דרהם |
|
והוסר שם הדינר ונשאר במקומו שלשה רביעי דבר ורביע דרהם |
|
ותניח לשלישי דינר אחד |
|
וישאר לשלשה דרהם אחד פחות דינר |
|
וכאשר קבצנו רביעיתו עם אשר לשלישי שהוא דינר אחד יהיה ערך הבהמה שלשה רביעי דינר ורביעית דרהם וישוה ערך הבהמה מהחלק האחד שהוא חצי דבר וחצי דרהם |
|
ותגרע רביעית דרהם מחצי דרהם וישאר חצי דבר ורביע דרהם ישוה שלשה רביעי דינר |
|
והדינר ישוה שני שלישי דבר ושליש דרהם |
|
ויהיה כל אשר לשלשה שני דברים ורביע ושתות דבר ושליש ורביע דבר ושליש ורביע דרהם |
|
וכבר הנחנו לארבעתם דרהם אחד ומפני זה ישאר לרביעי רביע ושתות מדרהם פחות שני דברים ורביע ושתות דבר |
|
ואמר זה האיש הרביעי אל השלשה המחזיקים שני דברים ורביע ושתות דבר ושליש ורביע דרהם תנו לי החומש מאשר לכם ואקבצנו עם אשר לי ויהיה לי ערך הבהמה |
|
והחומש אשר להם הוא כ"ט חלקים מס' חלקים בדבר וז' חלקים מס' בדרהם |
|
וכאשר תקבצהו עם אשר לו שהוא רביע ושתות מדרהם פחות שני דברים ורביע ושתות מדבר יהיה אשר יחזיק הרביעי ל"ב חלקים מששים בדרהם אחד פחות דבר וחמישים וששה חלקים מששים חלקים בדבר והוא ערך הבהמה וישוה לערך מהחלק האחד שהוא חצי דבר וחצי דרהם |
|
| |
|
|
|
ותכוין בהם ויהיה אחר הכיון שלישית העשירית מדרהם ישוה שְנֵי דברים ושלישית דבר ועשירית דבר |
|
והדרהם ישוה ע"ג דברים |
|
ותניח שווי הדרהם ע"ג והוא כל אשר מחזיקים ארבעתם |
|
ושווי הדבר אחד והוא מה שיש לראשון |
|
ואשר לשני יהיה תשע עשרה בעבור כי היה לו כדי אשר ישוה רביע דרהם ושלשה רביעי דבר |
|
ולשלישי עשרים וחמשה בעבור כי היה לו כדי שליש דרהם ושני שלישי דבר |
|
ולרביעי כ"ח בעבור כי היה לו כדי רביע ושתות דרהם פחות שני דברים ורביעי ושתות דבר |
|
ואם תרצה תקבץ אשר לראשון ולשיני ולשלישי ויהיה מ"ה ותגרעם מע"ג ויהיה מה שישאר אשר לאיש הרביעי והוא כ"ח |
|
וערך הבהמה ל"ז בעבור כי הונח חצי מה ששוה דרהם וחצי מה שיש לראשון |
| From now on you will be able to apply this procedure to whatever that falls into your hands of this kind and its mysteries will be solved. | ומעתה תוכל לעשות כמעשה הזה כל אשר יפול בידך מזה האופן ויצא לאור תעלומותיו |
|
מא) ואם יאמרו לך חמשה אנשים התקבצו יחד לקנות אלפאגה אחת ואמר הראשון לשיני ולשלישי תנו לי החצי מאשר לכם ויהיה לי כדי לקנותה |
|
| |
|
ולדעת זה נניח לראשון דבר ולשני דינר אחד ולשלישי דרהם אחד |
|
ולא נצטרך בזאת השאלה ולדומים אליה כדי להוציא החשבון ליותר מאילו השלשה מינים |
|
אחר כן אמר הראשון המחזיק דבר לשני ולשלישי המחזיקים דינר ודרהם תנו לי החצי מאשר לכם ואקבצהו עם אשר לי ויהיה לי ערך הבהמה |
|
והחצי מאשר מחזיקים הוא חצי דינר וחצי דרהם ולכן יהיה לו דבר אחד וחצי דינר וחצי דרהם והוא ערך הבהמה |
|
ואמר השני אשר לו דינר אחד לשלישי ולרביעי תנו לי שלישית החלק מאשר לכם ועם אשר לי שהוא דינר אחד אחזיק ערך הבהמה שֵיהַיַה דבר אחד וחצי דינר וחצי ודרהם |
|
ותגרע מערך הבהמה דינר אחד וישאר דבר אחד וחצי דרהם פחות חצי דינר והוא שליש מה שיחזיקו השלישי והרביעי |
|
ותכהו בשלשה ויהיה שלשה דברים ודרהם אחד וחצי פחות דינר וחצי והוא כל אשר יחזיקו השלישי והרביעי |
|
ותגרע אשר לשלישי שהוא דרהם אחד וישאר מה שהוא לרביעי והוא שלשה דברים וחצי דרהם פחות דינר אחד וחצי |
|
ואמר השלישי המחזיק דרהם אחד לרביעי ולחמישי תנו לי רביעית אשר לכם ועם אשר לי יהיה לי ערך הבהמה והוא דבר אחד וחצי דינר וחצי דרהם |
|
ותגרע מערך הבהמה אשר לשלישי שהוא דרהם אחד וישאר דבר וחצי דינר פחות חצי דרהם והוא רביעית אשר לרביעי ולחמשי |
|
ותכהו בארבעה ויהיה ארבעה דברים ושני דינרים פחות שני דרהמי והוא כל אשר לרביעי ולחמישי |
|
ותגרע מהם מה שיש לרביעי שהוא שלשה דברים וחצי דרהם פחות דינר אחד וחצי וישאר מה שיש לחמשי דבר אחד ושלשה דינרים וחצי פחות שני דרהם וחצי |
|
ואמר הרביעי המחזיק שלשה דברים וחצי דרהם פחות דינר אחד וחצי לחמישי ולראשון המחזיקים שני דברים ושלשה דינרים וחצי פחות שני דרהמי וחצי תנו לי החמישית מאשר לכם ועם אשר לי יהיה בידי כמו ערך הבהמה |
| וחמישית אשר להם הוא שני חומשי דבר ושבעה עשיריות דינר פחות חצי דרהם
וכאשר תקבצם עם אשר לו יהיה בידו שלשה דברים ושני חומשים פחות ארבעה חומשי דינר | |
|
| |
|
|
והוא שוה לערך הבהמה מהחלק האחר שיהיה דבר וחצי דינר וחצי דרהם |
|
|
|
|
ותכוין בהם ויהיה הדרהם יהיה שוה ארבעה דברים וארבעה חומשי דבר פחות שני דינרים ושלשה חומשי דינר |
|
ותגרע חצי הדרהם אשר בערך הבהמה ותניח במקומו חצי מה ששוה הדרהם והוא שני דברים ושני חומשי דבר פחות דינר אחד ושלשה עשירית מדינר ויהיה ערך הבהמה שלשה דברים ושני חומשי דבר פחות ארבעה חומשי דינר |
|
והנה אשר לראשון הוא דבר |
|
ואשר לשני הוא דינר אחד |
|
ולשלישי ארבעה דברים וארבעה חומשי דבר פחות שני דינרים ושלשה חומשי דינר |
|
ולרביעי חמשה דברים ושני חומשי דבר פחות שני דינרים וארבעה חומשי דינר |
|
והסבה למה הנחנו ככה לרביעי הוא בעבור שהיה לרביעי שלשה דברים וחצי פחות דינר אחד וחצי ותגרע חצי דרהם מאשר בידו ותניח במקומו החצי ממה ששוה הדרהם |
|
וצריך הוא כפי מה שביארנו לחמישי עשרה דינרי' פחות אחד עשרה דברים |
|
ואמר לראשון ולשני אשר להם דבר אחד ודינר אחד תנו לי הששית מאשר לכם ואקבצנו עם אשר לי ויהיה לי ערך הבהמה והששית מאשר להם הוא ששית דבר וששית דינר ויהיה מה שיחזיק החמישי עשרה דינרים ושתות פחות עשרה דברים וחמשה ששיות הדבר והוא ערך הבהמה |
|
| |
|
|
וישוה לערך הבהמה מהחלק האחר שהוא ג' דברים ושני חומשי דבר פחות ארבעה חומשי דינר |
|
|
|
ותכוין בהם ויהיו אחרי זה הכיון הדבר ארבעים ושבעה והוא אשר לראשון |
|
והדינר ששים ואחד והוא אשר לשני |
|
ואשר לשלישי ששים ושבעה בעבור כי הוא ארבעה דימיונים וארבעה חומשים ממה שיש לראשון פחות שני דמיונים ושלשה חומשים ממה שיש לשני |
|
ולרביעי שמונים ושלשה בעבור כי לו חמשה דימיונים ושני חומשים ממה שיש לראשון פחות שני דימיונים וארבעה חומשים ממה שיש לשני |
|
ולחמישי תשעים ושלשה בעבור כי הוא עשרה דימיונים מאשר לשני פחות אחד עשר דימיוני אשר אל הראשון |
|
וערך הבהמה קי"א בעבור כי הוא שלשה דימיונים ושני חומשים מאשר לראשון פחות ארבעה חומשים מאשר לשני |
| ואם בקשת להוציא אשר לרביעי ואשר לחמישי אחר זה המעשה | |
|
הנה כבר ידעת שאשר לראשון מ"ז |
|
ואשר לשני ס"א |
|
ואשר לשלישי ס"ז |
|
ותגרע מה שיש לשני מערך הבהמה וישאר חמישים ותכם בשלשה ויהיה ק"נ ותגרע מהם מה שיש לשלישי והוא ס"ז ישאר אשר לרביעי פ"ג |
|
ואם בקשת לדעת אשר לחמישי תגרע מה שיש לשלישי מערך הבהמה וישאר מ"ד ותכם ארבעה ויהיה קעו ותגרע מהם מה שיש לרביעי והוא פ"ג וישאר צ"ג והוא מה שיש לחמישי |
|
ואם תרצה תניח לראשון דבר אחד |
|
ולשני דינר אחד |
|
ולשלישי דרהם אחד |
|
ולרביעי אלפלס אחד |
| ולא יצטרך לזאת השאלה ולדומים אליה כדי להוציא החשבון ליותר מאילו הארבעה מינים | |
|
ואמר הראשון לשני ולשלישי תנו לי החציה אשר לכם ואקבצהו עם אשר לי ויהיה עימי ערך הבהמה ויהיה ערך הבהמה דבר וחצי דינר וחצי דררהם |
|
ואמר השני לשלישי ולרביעי תנו לי שלישית אשר לכם ועם אשר לי יהיה לי ערך הבהמה ויהיה ערכה מזה החלק דינר ושליש דרהם ושליש אלפלס |
|
|
וישוה לערך הבהמה מהחלק האחר שהוא דבר וחצי דינר וחצי דרהם |
|
|
|
ותכוין בהם ויהיה האלפלס ישוה שלשה דברים וחצי דרהם פחות דינר וחצי והוא אשר לרביעי |
|
ותניח לחמישי אלפלס אחד |
|
ואמר השלישי אשר לו דרהם אחד לרביעי ולחמישי אשר להם אלפלס אחד ושלשה דברים וחצי דרהם פחות שני דינרים וחצי תנו לי רביעית אשר לכם ועם אשר לי יהיה ערך הבהמה ורביעית אשר להם היא שלשה רביעי דבר ורביעית אלפלס ושמינית דרהם פחות ג' שמיניות מדינר וכאשר קובצו עם הדרהם אשר לו יהיה בידו כמו ערך הבהמה ויהיה ערך הבהמה מזה החלק דרהם אחד ושמינית אחד מדרהם ורביע אלפלס ושלשה רביעי דבר פחות שלשה שמיניות מדינר |
|
| |
|
|
ויהיה שוה לערך הבהמה מהחלק הראשון שהוא דבר וחצי דינר וחצי דרהם |
|
|
|
ותכוין בהם ויהיה אלפלס ישוה דבר ושלשה דינרי' וחצי פחות שני דרהמי וחצי והוא אשר לחמישי |
| ותעשה הנשאר מן השאלה כפי מה שהראתיך | |
|
מב) ואם יאמרו לך חמשה אנשים התקבצו ואמר הראשון לשני אם תתן לי החצי מאשר בידך יהיה לי ערך הבהמה ואמר השני לשלישי אם תתן לי השלישית מאשר בידך יהיה לי ערך הבהמה |
|
ולדעת זה תניח לראשון דבר |
|
ולשני דינר אחד |
|
ולשלישי דרהם אחד |
|
ואמר הראשון אשר בידו דבר אחד לשני אשר בידו דינר אחד אם תתן לי החצי מאשר לך יהיה לי ערך האלפאגה ויהיה ערך הבהמה דבר וחצי דינר |
|
ואמר השני אשר בידו דינר אחד לשלישי אשר בידו דרהם אחד אם תתן לי השלישית מאשר לך יהיה לי ערך הבהמה ויהיה ערך הבהמה מזה החלק דינר אחד ושלישית דרהם |
|
|
ויהיה שוה לערך הבהמה מהחלק האחד שהיה דבר וחצי דינר |
|
|
|
ותכוין בהם ויהיה הדרהם ישוה שלשה דברים פחות דינר אחד וחצי והוא אשר לשלישי |
|
ותניח לרביעי דרהם אחד |
|
ואמר השלישי אשר לו שלשה דברים פחות דינר וחצי לרביע אשר לו דרהם אחד אם תתן לי הרביעית מאשר לך יהיה ערך הבהמה ויהיה ערך הבהמה מזה החלק שלשה דברים ורביע דרהם פחות דינר וחצי |
|
|
וישוה ערך הבהמה והחלק האחד שהוא דבר וחצי דינר |
|
|
|
ותכוין עמו ויהיה הדרהם ישווה שמונה דינרים פחות שמנה דברים והוא אשר לרביעי |
|
ותניח לחמישי דרהם אחד |
|
ואמר הרביעי אשר לו שמנה דינרים פחות שמנה דברים לחמישי אשר לו דרהם אחד אם תתן לי החמישית מאשר לך יהיה לי ערך הבהמה ויהיה ערך הבהמה מזה החלק שמנה דינרים וחמשית דרהם פחות שמנה דברים |
|
|
ויהיה שוה לערך הבהמה והחלק האחר שהוא דבר וחצי דינר |
|
|
|
ותכוין בהם ויהיה הדרהם ישוה מ"ה דברים פחות ל"ז דינרים וחצי והוא מה שיש לחמישי |
|
ואמר לראשון אשר לו דבר אם תתן לי הששית מאשר בידך יהיה לי ערך הבהמה והששית מהראשון הוא ששית דבר ונקבציהו עם מה שמחזיק ויהיה ערך הבהמה מזה החלק מ"ה דברים וששית דבר פחות ל"ז דינרים וחצי |
|
|
ויהיה שוה לערך הבהמה מהחלק האחר שהוא דבר וחצי דינר |
|
|
|
|
ותכוין בהם ויהיה אחר הכוון מ"ד דברים וששית דבר ישוה ל"ח דינרים |
|
והשיבם כלם ששיות ויהיה הדבר רכ"ח והוא אשר לראשון |
|
והדינר רס"ה והוא אשר לשיני |
|
ולשלישי שלשה דברים פחות דינר אחד וחצי והוא רפ"ו וחצי |
|
והשיבם כלם חצאים ויהיה הדבר והוא אשר לראשון תנ"ו |
|
ויהיה הדינר והוא מה שיש לשני תק"ל |
|
ויהיה אשר לשלישי תקע"ג |
|
ולרביעי שמנה דינרים פחות שמנה דברים ויהיה תקצ"ב |
|
ולחמישי מ"ה דברים פחות ל"ז דינרים וחצי והוא תרמ"ה |
|
ויהיה ערך הבהמה תתקכ"א |
|
מג) ואם יאמרו לך ארבעה אנשים התקבצו לקנות בהמה אחת ואמר הראשון לשני אם תתן לי דרהם אחד יהיה לי הכפל ממה שנשאר לך |
|
ולדעת זה תניח לראשון דבר |
|
ולשני דינר אחד |
|
וכאשר לקח הראשון מהשני דרהם אחד יהיה לראשון דבר ודרהם אחד ויהיה כמו הכפל ממה שנשאר לשני והוא שני דברים פחות שני דרהמי |
|
|
|
ותכוין בהם ויהיה הדינר ישוה חצי דבר ודרהם וחצי והוא אשר לשני |
|
ותניח לשלישי דינר אחד |
|
וכאשר לקח ממנו השני שני דרהמי יהיה לשני חצי דבר ושלשה דרהמי וחצי ויהיה שוה לשלשה דימיוני מה שנשאר לשלישי והוא שלשה דינרים פחות ששה דרהמי |
|
|
|
ותכוין בהם וישוה הדינר שתות דבר ושלשה דרהמי ושתות והוא אשר לשלישי |
|
ונניח לרביעי דינר אחד |
|
וכאשר לקח ממנו השלישי שלשה דרהמי יהיה לו שתות דבר וששה דרהמי ושתות וישוה ארבעה דימיונים ממה שנשאר לרביעי והוא ארבעה דינרים פחות שנים עשר דרהמי |
|
|
|
ותכוין בהם ויהיה שוה הדינר שלישית השמינית מדבר וארבע דרהמי ורביע ושתות ושמינית דרהם והוא אשר לרביעי |
|
וכאשר לקח מהראשון ארבעה דרהמי יהיה לו שמנה דרהמי וי"ג חלקים מכ"ד חלקים בדרהם ושלישית השמינית מדבר וישוה לחמשה דימיונים מאשר נשאר לראשון והוא חמשה דברים פחות עשרים דרהמי |
|
ותכוון בהם יהיה הדבר ישוה לחמשה דרהמי ותשעים חלקים מקי"ט חלקים מאחד והוא אשר לראשון |
|
ולשני החצי ממה שיש לראשון ודרהם אחד וחצי יותר ויהיה ארבעה דרהמי ומ"ה חלקים מקי"ט |
|
ולשלישי הששית ממה שיש לראשון ושלשה דרהמי ושתות יותר והוא ארבעה דרהמי וט"ו חלקים מקי"ט חלקים בדרהם |
|
ולרביעי שליש השמינית מאשר לראשון וארבעה דרהמי ושתות ושמינית והוא ארבעה דרהמי וצ"ג חלקים מקי"ט חלקים בדרהם |
|
מד) ואם יאמרו לך אלגו בין שלשה אנשים לאחד החצי ולשני השליש ולשלישי השתות והרויחו האלגו ביניהם והחזיר אשר לו החצי המחצית מחלקו |
|
ולדעת זה נניח האלגו דבר ודינר אחד ודרהם אחד אידיו נ"א איגאנו נראה לי |
|
והרויח בעל החצי דבר |
|
ובעל השליש דינר אחד |
|
ובעל השתות דרהם אחד |
|
והשיב בעל החצי חצי דבר |
|
והשיב בעל השליש שלישית הדינר |
|
והשיב בעל השתות ששית דרהם |
|
והתקבץ מאשר השיבו חצי דבר ושלישית דינר וששית דרהם |
|
וחלקו אותו ביניהם לשליש והמגיע לכל אחד מהם שתות דבר ותשיעית דינר וחצי תשיעית דרהם |
| וקבצוהו כל אחד מהם עם מה שנשאר להם | |
|
ויהיה לבעל החצי שני שלישי דבר ותשיעית דינר וחצי תשיעית דרהם |
|
וישוה לחצי האלגו שהוא חצי דבר וחצי דינר וחצי דרהם |
|
|
|
|
ותכוין בהם ויהיה הדבר ישוה שני דינרים ושליש ושני דרהמי ושני שלישיות |
|
וצריך שיהיה האלגו שלשה דינרים ושליש ושלשה דרהמי ושני שלישים |
|
ושב חציו והוא דינר ושתות ודרהם ושליש |
|
וכל מה שהשיבו דינר אחד וחצי ודרהם וחצי |
|
וחלקוהו לשליש לכל אחד חצי דינר וחצי דרהם |
|
ויהיה לבעל הדינר אשר לו שלישית האלגו והוא דינר ותשיעית דינר ודרהם ושני תשיעיות דרהם |
|
|
|
|
ותכוין בהם ויהיה הדינר ישוה י"ג דרהמיש והוא מה שהרויח בעל השלישית |
|
|
והדבר שני דינרים ושליש ושני דרהמיש ושני שלישים והוא שלשים ושלשה והוא מה שהרויח בעל החצי |
|
|
והרויח בעל השתות דרהם אחד והוא אחד |
|
|
וצריך מבלי טורח כאשר תנסהו שתכהו בששה פעמים ויהיה מה שהרויח בעל החצי קצ"ח ובעל השלישית ע"ח ובעל השתות ששה והאלגו כולו רפ"ב |
| וכמעשה הזה יעשוהו בעלי החשבון ביניהם והיא הבנה שלימה אלא שתתדקדק ביותר על מי שיעשהו במספר רב אם יניחו האנשים הרבה ואוציאהו אני לחפשי עם מלאכה ישרה והבנה מובנת | |
|
והוא שנניח האלגו דבר |
| ואשר הרויח כל אחד מהם מן אלגו ואחר מה שהשיבו כפי הנחתנו מדרהמי שליש וחלקוהו לִשְלִיש ועלה לכל אחד מהם וקבצהו עם מה שנשאר לו ויהיה לכל אחד | |
|
ובנקלה תדע שאשר נשאר לבעל החצי אחר שהשיב החצי ממה שהרויח חצי דבר פחות דרהם |
|
ומה ששב הוא חצי דבר פחות דרהם אחד |
|
ולשלישי שב שתות דבר פחות דרהם אחד |
|
ומה ששב אחד משלשים בדבר חמשה דרהמי |
|
ויהיה כל אשר השיבו חצי דבר וחמישית דבר פחות דרהם אחד וז' עשיריות מדרהם |
|
|
וה' שביעיות מדרהם והוא כל האלגו |
|
וכאשר תרצה לדעת כמה הרויח בעל החצי דבר פחות שני דרהמי והוא ארבעה דרהמי וה' שביעיות מדרהם |
|
והרויח בעל השליש חצי דבר פחות דרהם אחד וחצי והוא דרהם אחד וו' שביעיות מדרהם |
|
ומה שהרויח בעל השתות חמישית דבר פחות דרהם אחד וחומש והוא שביעית דרהם |
|
ותניח כל דרהם מ"ב חלקים |
|
ויהיה האלגו רפ"ב |
|
ומה שהרויח בעל החצי קצ"ח |
|
ומה שהרויח בעל השליש ע"ח |
|
ומה שהרויח בעל השתות ששה |
Garments |
|
|
מה) ואם יאמרו לך עשרה בגדים ערך הבגד הראשון דרהם אחד וערך כל אחד מן האחרים יוסיפו האחד על האחר דרהם אחד השני יעדיף על הראשון דרהם אחד והשלישי יעדיף על השני דרהם אחד וכן כל האחרים כמה יהיה ערך כלם |
|
|
וכבר תדע כי ערך הבגד הראשון דרהם אחד והעשירי עשרה דרהמי |
|
|
וערך השני שנים והתשיעי תשעה |
|
|
וערך השלשי שלשה והשמיני שמנה |
|
והנה הערך מכל אחד מאלו הזוגות אחד עשר |
|
|
וכמו כן יהיה ערך כל הזוגות כאלו והם חמשה זוגות ותכה אחד עשר בחמשה ויהיה נ"ה וככה ערך עשרת הבגדים |
|
מו) ואם יאמרו לך ערך הבגד הראשון אחד ויוסיף ערך כל אחד מהנשארים שנים על ערך חבירו כמה יהיה ערך כלם |
|
|
הנה יהיה ערך הבגד העשירי י"ט |
|
|
בעבור כי הוסיף השני על הראשון שנים |
|
|
והשלישי על השני שנים |
|
|
ויוסיף השלישי על הראשון ארבעה |
|
|
והרביעי על הראשון ששה |
|
|
והעשירי יוסיף על הראשון י"ח |
|
|
וכפי זה יהיה ערך הראשון עם העשירי מקובצים עשרים |
|
|
ותכה עשרים בחמשה ויהיה מאה וככה יהיה ערך עשרת הבגדים |
|
מז) ואם יאמרו לך עשרה בגדים ערך הראשון שלשה דרהמים ויוסיף ערך האחרים האחד על האחר ארבעה ארבעה כמה יהיה ערך כלם |
|
|
והמעשה בזה כאשר ביארתי והוא שתכה יתרון האחד על האחר והוא ארבעה במספר הבגדים פחות אחד ויהיה ל"ו ותוסיף עליהם שלשה והוא ערך הבגד הראשון ויתקבץ ל"ט |
| ויהיה ערך הראשון והעשירי ארבעים [5]ושנים וכן ערך התשיעי והשני יהיה ארבעים ושנים ובדרך הזה יהיה ערך כל שני בגדים מהם ותכה מ"ב בחמשה ויהיה מאתים ועשר וככה ערך כל הבגדים | |
|
| |
Group of People |
|
|
מח) ואם יאמרו לך חבורה מאנשים עלו להרויח והרויח הראשון דרהם אחד והרויח כל אחד מהם יותר מאשר לפניו דרהם אחד והיה כל אשר הרויחו שלש מאות כמה היו האנשים מהחבורה |
|
ולדעת זה תניח מספר אנשי החבורה דבר |
|
וצריך שירויחו בין כל שנים מהם כפי הסדר האמור בבגדי' דבר ודרהם אחד |
|
ותכה דבר ודרהם אחד בחצי דבר ויהיה חצי אלגו וחצי דבר והוא כל מה שהרויחו ויהיה שוה שלש מאות דרהמי |
|
|
|
ותכוין עמהם ויהיה הדבר עשרים וארבעה וככה מספר אנשי החבורה |
|
מט) ואם יאמרו לך חבורה מאנשים והראשון הרויח שני דרהמי והוסיף כל אחד על אשר לפניו שלשה והיה כל מה שהרויחו מאה ועשרים ושש כמה יהיה מספר החבורה |
|
|
ולדעת זה תניח כמו שבארתי לך בבגדים שתכה מה שיותיר כל אחד במספר החבורה פחות אחד ויהיה שלשה דברים פחות שלשה דרהמי ותוסיף עליו מה שהרויח הראשון והוא שנים ויהיה שלשה דברים פחות דרהם אחד |
|
|
ויהיה מה שהרויח הראשון והאחרון שלשה דברים ודרהם אחד והוא מה שהרויח כל |
|
|
ותכה זה במספר החבורה ויהיה אלגו וחצי וחצי דבר והוא כל מה שהרויחה החבורה והוא ישוה קכ"ו דרהמי |
|
|
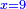
|
ותכוין עמהם ויהיה הדבר תשעה והוא מספר החבורה |
|
נ) ואם יאמרו לך חבורה מאנשים שהרויח הראשון דרהם אחד והוסיף כל אחד על אשר לפניו אחד דרהם וקבצו כל אשר הרויחו יחד וחלקוהו בשוה ועלה לחלק לכל אחד מהם עשרה דרהמי |
|
וכבר בארנו שכל אשר הרויחו הוא חצי אלגו וחצי דבר |
|
|
וחלקנוהו על מספר החבורה והוא דבר ויגיע לחלק עשרה דרהמי |
|
[6]נא) ואם יאמרו לך חבורה אשר שני שלישיתיה הרויח הראשון דרהם אחד והוסיפו |
|
ולדעת זה נשים מספר החבורה דבר |
| ושני שלישם הרויח הראשון דרהם אחד והוסיפו בשני דרהם | |
|
וצריך כפי מה שבארנו שיהיה כל אשר הרויחו ארבעה תשיעיות מאלגו |
|
|
ואנו נחלקם על מספר החבורה שהוא דבר ויצא ארבעה דרהמי |
|
|
ותכה ארבעה דרהמי בדבר ויהיה ארבעה דברים ישוו ארבעה תשיעיות מאלגו |
|
|
והאלגו ישוה |
|
|
והדבר ישוה תשעה והם מספר החבורה |
|
נב) ואם יאמרו לך חבורה ששלשת רביעיה עלו להרויח והרויח הראשון שני דרהמי והוסיפו האחרים בשלשה רביעים וכאשר שבו חלקום כל אשר הרויחו בין כל החבורה בשוה והגיע לכל אחד מהם עשרים וארבעה דרהמי כמה יהיה מספר החבורה |
|
ולדעת זה תניח מספר החבורה דבר |
|
ועלו שלשת רביעיה להרויח והם שלשה רביעי דבר |
| והרויח הראשון שנים דרהמי והוסיפו בשלשה שלשה רביעים | |
|
וצריך כפי מה שבארנו שיהיה כל אשר הרויחו שלשת רביעי הדבר ששה שמיניות מאלגו ושלשת רביעי שמינית האלגו ושלשה שמיניות מדבר |
|
|
ותחלקהו על מספר החבורה שהוא דבר |
|
|
ויהיה עשרים וארבעה דברים ישוה שלשה רביעי אלגו ושלשה שמיניות מדבר |
|
|
|
ותכוין עמהם ויהיה הדבר עשרים ושמנה והוא מספר החבורה |
|
נג) ואם יאמרו לך חבורה ששני שלישיה יצאו להרויח והרויח הראשון מהם דרהם אחד והוסיפו בשני דרהמי והשלישית הנשאר הרויח הראשון מהם שנים דרהמי והוסיפו בארבעה וקבצו כל מה שהרויחו כל אנשי החבורה וחלקוהו |
|
ולדעת זה תניח מספר החבורה דבר |
| ויצאו [7]שני שלישיה להרויח והם שלישי דבר והרויח הראשון דרהם אחד ונתוספו בשני דרהמי | |
|
וצריך לפי מה שבארנו שיהיה מה שהרויחו שני השלישים ארבעה תשיעיות מאלגו |
| והשליש האחר הרויח הראשון מהם שני דרהמי ונתוספו הארבעה | |
|
וצריך כפי מה שבארנו שיהיה מה שהרויח השלישית שתי תשיעיות מאלגו |
|
ותקבצם עם אשר הרויחו השני שלישים והוא ארבעה תשיעיות ויהיה כל אשר הרויחו כל אנשי החבורה שני שלישיות מאלגו |
|
ותחלקהו על מספר החבורה שהוא דבר ויהיה עשרים |
|
ותכה עשרים בדבר ויהיה עשרים דברים ישוו שני שלישי אלגו |
|
והאלגו ישוה שלשים דברים |
|
והדבר שלשים והוא מספר החבורה |
|
נד) ואם יאמרו לך חבורה מאנשים יצאו להרויח והרויח הראשון דרהם אחד ונתוספו באחד וכאשר שבו קבצו יחד כל מה שהרויחו כלם וחלקוהו ביניהם בשוה והגיע לכל אחד מהם כמו שני שלישי מספר החבורה |
|
וצריך |
|
שיהיה כמו שבארנו כל מה שהרויחו בם חצי אלגו וחצי דבר |
|
|
ונחלקהו על מספר החבורה והוא דבר ויהיה שני שלישי דבר |
|
|
ותכה שני שלישי דבר בדבר ויהיה שני שלישי אלגו ישוה חצי אלגו וחצי דבר |
|
|
והדבר ישוה שלשה דרהמי והוא מספר החבורה |
|
נה) ואם יאמרו לך חבורה שיצאו ארבעה שרשיה וחצי שרש להרויח והרויח הראשון דרהם אחד ונתוספו באדרהם אחד וכאשר שבו חלקו מה שהרויחו בין כל החבורה בשוה והגיע לכל אחד מהם עשרה דרהמי וחצי כמה יהיה מספר החבורה |
|
ולדעת זה תניח מספר החבורה |
|
ויצאו ארבעת שרשיו וחצי והוא ארבעה דברי' וחצי |
| והריוח הראשון דרהם אחד ונתוספו באדרהם אחד | |
|
וצריך שיהיה מה שהרויחו כפי מה שבארנו עשרה אלגוש ושמינית מאלגו ושני דברים ורביע דבר |
|
|
ונחלקם על מספר החבורה והוא אלגו ויצא לחלק עשרה דרהמי וחצי |
|
|
ותכה עשרה דרהמי וחצי באלגו ויהיה עשרה אלגוש וחצי ישוו עשרה אלגוש ושמינית מאלגו ושני דברים ורביע |
|
|
|
ותכוין עמהם ויהיה הדבר [8]ששה |
|
והאלגו שלשים וששה והוא מספר החבורה |
|
נו) ואם יאמרו לך שלשים אנשים הרויח הראשון דרהם אחד ונתוספו בדבר אחד והיה כל אשר הרויחו אלף ושלש מאות ושלשים וחמשה בכמה נתוספו כל אחד על האחר אשר לפניו |
|
ולדעת זה תניח השני שהוסיף על הראשון בדבר אחד והשלישי על השני בדבר אחד והרביעי על השלישי בדבר אחד וכן עד האחרון |
|
ותעשה בהם כאשר בארתי והוא שתכה מה |
|
ותוסיף עליו מה שהרויח הראשון והוא דרהם אחד ויהיה כ"ט דברים ושני דרהמי והוא מה שהרויח כל |
|
ותכם בחמש עשרה שהוא מחצית החבורה ויהיה שלשים דרהמי ותל"ה דברים והוא כל אשר הרויחו א"י אלוגלו ויהיה אלף ושלש מאות ושלשים וחמשה דרהמי |
|
|
|
ותכוין עמהם ויהיה הדבר שלשה והוא |
Motion Problems |
|
|
נז) ואם יאמרו לך שלחתי איש אחד מן העיר וצויתיו שילך [ביום ראשון][9] ואחר זה שלחתי איש אחר וצויתיו שילך [ביום ראשון][10] |
|
וידיעת זה היא שתניח מספר הימי' הראשונים שהלך האיש הראשון דבר |
|
וצריך כפי מה שבארנו בחבורה שיהיה מספר הפרסאות שהלך חצי אלגו וחצי דבר |
|
ויהיה מה שהלך השני מהימים דבר פחות פ"ד ימים |
|
וצריך שיהיה מספר הפרסאות כפי מה שבארנו בחבורה אלגו ושבעה אלפים וחמשים וששה פחות קס"ח דברים ויהיה שוה חצי אלגו וחצי דבר |
|
|
|
ותכוין עמהם ויהיה הדבר מאתים ושמנים ושמנה והוא מה שהלך האיש הראשון |
|
והלך השני מאתים וארבעה ימים |
|
[11]נח) ואם יאמרו לך צויתי לראשון שילך ביום ראשון פרסא אחת ושיוסיף בכל יום פרסא אחת והלך שמנה ימים וצויתי לשני שילך בכל יום הראשון פרסא אחת ושיוסיף בכל יום שלשה פרסאות |
|
ולדעת זה תניח מספר הימים שהלך הראשון דבר |
|
וצריך כפי מה שבארנו בחבורה שיהיה מספר הפרסאות חצי אלגו וחצי דבר |
|
ויהיה מה שהלך השני מן הימים דבר פחות שמנה |
|
וצריך שיהיה מספר פרסותיו אלגו וחצי ומאה דרהמי פחות כ"ד דברים וחצי והוא ישוה חצי אלגו וחצי דבר |
|
|
|
ותכוין עמהם ויהיה הדבר עשרים ימים והוא מה שהלך הראשון |
|
ומה שהלך השני הוא שנים עשר ימים |
|
נט) ואם יאמרו לך איש אחד עלה מן העיר וצויתי ושלחתי לאיש אחר אחר זה וצויתיו שילך בכל יום שרש מספר הפרסאות שיפגע בהם הראשון |
|
וידיעתו שתניח מה שהלך הראשון מן הפרסאות אלגו |
|
וצריך שיהיה מספר הימים שהלך חצי עשירית מאלגו |
|
והאיש השני הלך פחות מהראשון בחמשה עשר ימים ויהיה מספר ימיו חצי עשירית מאלגו פחות ט"ו ימים |
|
ותכם במה שהלך בכל יום והוא דבר בעבור שצוה ללכת בכל יום שרש מספר הפרסאות שימצאהו בהם ומספר הפרסאות הוא אלגו ושרשו דבר ויהיה חצי עשירית ממעוקב דיקוביקא בלעז פחות חמשה עשר דברים ישוה אלגו |
|
|
|
ותכוין עמהם ויהיה אלגו ישוה שלש מאות דרהמי ועשרים דברים |
|
והדבר ישוה שלשים והוא שרש מספר הפרסאות שהלך הראשון |
|
ותכם בעצמם ויהיה תשע מאות פרסאות |
|
ותחלקם על הפרסאות שהלך בכל יום והם עשרים ויעלה לחלק מ"ה ימים והם ימי השני |
|
ס) ואם יאמרו לך איש אחד עלה מן העיר וצויתיו שילך בכל יום עשרים פרסאות והלך מ"ה ימים ושלחתי אחר זה אחר וצויתיו שילך בכל יום שרש מאשר הלך הראשון מהימים שימצאהו בהם |
|
וידיעתו שתניח בכל יום שרש מאשר הלך הראשון מהימים אלגו |
|
ויהיה מספר פרסותיו שהלך עשרים אלגוש |
|
[12]ויהיה מספר ימי השני אלגו פחות מ"ה ימים |
|
ותכם במה שהלך כל יום והוא דבר והנה קוביקא פחות מ"ה דברים ישוה עשרים אלגו |
|
|
|
ותכוין עמהם ויהיה הדבר עשרים ושנים והוא שרש הימים שהלך הראשון |
|
ותכם בעצמם ויהיה תפ"ד והם הימים שהלך הראשון |
|
ותכם בעשרים ויהיה תשעה אלפים ותר"פ והוא מספר הפרסאות שהלך |
|
ומספר אשר מהשני ת"מ |
|
ותכם בפרסאות שהלך כל יום והם כ"ב ויהיו תשעה אלפים ותר"פ |
Buy and Sell Problems |
|
|
סא ואם יאמרו לך אונקיא אחת בעד עשרים דרהמי ואונקיא אחת בעד ט"ו דרהמי ואונקיא בעד עשרה ואמרו לך תקח מהכל אונקי' אחת בעד י"ח דרהמי |
|
זאת השאלה היא חרשת |
|
וידיעתה שתקח דבר מהאונקיא שהיא בעד עשרה דברים מהדרהמי ודבר מהאונקיא שהיא בעד ט"ו דברים מהדרהמי |
|
וישאר מהאונקיא אונקיא פחות שני דברים |
|
ומהדרהמי י"ח דרהמי פחות כ"ה דברים |
|
ותקח מאונקיא שהיא בעד עשרים אונקיא פחות שני דברים בעד עשרים דרהמי פחות ארבעים דברים |
|
ויהיה י"ח דרהמי פחות כ"ה דברים ישוה עשרים דרהמי פחות ארבעים דברים |
|
|
|
ותכוין עמהם ויהיה הדבר ישוה שני שלישי החומש |
|
ומאשר היא בעד ט"ו מכל אחת ב' מט"ו מאונקיא |
|
|
|
ואם תרצה תקח דבר מהאונקיא שהיא בעד עשרה דברים מהדרהמי |
|
ותקח שני דברים מהאונקיא שהיא בעד ט"ו דברים מהדרהמי |
|
וישאר ערך האונקיא י"ח דרהמי פחות ארבעים דברים |
|
ומהאונקיא אונקיא פחות שלשה דברים |
|
וקנה בהם מהאונקיא שהיא בעד עשרים דרהמי בעד עשרים דרהמי פחות שני דברים |
|
|
והדבר ישוה י"ו דרהמי פחות ארבעים דברים |
|
|
|
ותכוין עמהם ויהיה הדבר עשרה ותקח מהאונקיא שהיא בעד עשרה עשירית אחד מאונקיא |
|
ומאשר היא בעד ט"ו חמישית אחד מאונקיא |
|
ומאשר היא בעד עשרים שבעה עשיריות מאונקיא וחצי וחומש מאונקיא |
|
[13]סב ואם יאמרו לך ליט' אחת בעד חמשה דרהמי וליט' אחת בעד ארבעה דרהמי ועשרה ליט' בעד דרהם אחד תקח מהכל ליט' אחת בעד שני דרהמי |
|
זאת השאלה היא חרשת |
|
וידיעתו שתניח דבר מהליט' שהיא בעד חמשה דרהמי בעד חמשה דברים מהשני דרהמי |
|
ודבר מהליט' שהיא בעד ארבעה דרהמי בעד ארבעה דברים משני הדרהמי |
|
וישאר משני הדרהמי שני דרהמי פחות תשעה דברים |
|
|
ישוה עשרה דרהמי פחות חמישית דבר |
|
|
|
ותכוין עמהם ויהיה הדבר ט' מפ"ח בליט' |
|
ואם תרצה תקח מהליט' שהיא בעד חמשה דברים דבר בחמשה דברים משני הדרהמי |
|
וישאר משני הדרהמי שני דרהמי פחות כ"ה דברים |
|
ומהליט' ליט' פחות ששה דברים |
|
ותקח מאשר הוא עשרה ליט' בעד דרהם אחד עם עשרה דרהמי פחות שלשה חומשי דבר |
|
|
ויהיה אז שני דרהמי פחות כ"ה דברי' ישוה עשרה דרהמי פחות שני חומשי דבר |
|
|
|
ותכוין עמו ויהיה הדבר י"ט מרמ"ד והוא מה שקנה מהליט' אשר בעד חמשה דרהמי |
|
וקנה מהליט' אשר בעד ארבעה דרהמי צ"ה מרפ"ד בליט' |
|
ואם תרצה תקח מהליט' שהיא בעד חמשה ג' מעשרה בליט' ושני חומשים מעשירית הליט' בעד דרהם אחד וחצי וחומש |
|
ומהליט' שהיא בעד ארבעה דרהמי שלשה מחמשים בליט' בעד חמשה דרהמי ושנים מחמשים באדרהם |
|
ומהליט' שהיא עשרה ליט' בעד דרהם אחד שלשה חומשים מליט' בעד שלשה מחמשים בדרהם |
|
סג ואם יאמרו לך קניתי בעד עשרה דרהמי חטה לחשבון הקאפיזיש בעד דרהם אחד וקניתי עם שלשה דרהמי גולגולאן לחשבון בלתי ידוע |
|
וידיעתו שתקנה ל' קאפיזיש מחטה בעד עשרה דרהמי לחשבון שלשה קאפיזיש בעד דרהם אחד |
|
וקניתי עם שלשה דרהמי גולגולאן לחשבון דבר אחד בעד דרהם אחד ויהיה שלשה דברים |
|
ושלשת הדברים לחשבון שלשה דרהמי ויעלה שוויו דבר |
|
וישאר מהקרן ומהריוח שבעה עשר [14]פחות דבר והוא שווי החטה כאשר מכרוהו בכלל הגולגולאן |
|
תכה דבר אחד בי"ז דרהמי פחות דבר ויהיה י"ז דברים פחות אלגו ישוה שלשים |
|
וכוין עמו ויהיה הדבר אם תרצה ט"ו ואם תרצה שנים ואמור הכלל מהגולגולאן אם תרצה ט"ו קאפיזיש ואם תרצה שנים |
| וכאשר יקרה לפניך שאלה כזאת או דומה אליה אם יחלק הקרן והריוח או הקרן פחות | |
|
סד ואם יאמרו לך קאפיזיש בלתי ידועים שוויים צ"ג דרהמי אלא |
|
וידיעתו שתניח שווי הקאפיז דבר |
|
ישאר מספר הקאפיזיש ל"ד פחות דבר |
|
תכה דבר בל"ד פחות דבר יהיה ל"ד דברים פחות אלגו ישוה צ"ג דרהמי |
|
|
|
ותכוין ויהיה הדבר שלשה והוא שווי הקאפיז |
|
והקאפיזיש ל"א |
|
ואם תרצה תניח הקאפיזיש שלשה |
|
ושווי הקאפיז ל"א |
|
סה ואם יאמרו לך קאפיזיש בלתי ידועים מכר הראשון בעד דרהם אחד והוסיפו בדרהם אחד ולקח שרש הכל והוסיפהו על מספרו ויצא י"ד |
|
חכמתו שתניח מספר הקאפיזיש דבר |
|
וצריך שיהיה שוויו כפי מה שבארנו בחבורות חצי אלגו וחצי דבר |
|
ושרשו נוסף על דבר יהיה י"ד |
|
ותגרע דבר מי"ד ישאר י"ד פחות דבר ישוה שרש מחצי אלגו וחצי דבר |
|
תכה י"ד פחות דבר בעצמו יהיה[15] קצ"ו דרהמי' ואלגו פחות כ"ח דברים ישוה חצי אלגו וחצי דבר |
|
|
|
ותכוין בהם ויהיה הדבר שמנה והם הקאפיזיש |
Notes
- ↑ marg.: ר"ל שרש הנשאר
- ↑ top: נ' אלמת
- ↑ דבר: MS Ma דבר
וחצי דרהם - ↑ פלס: MS Ma
טורניש[פלס] - ↑ 84v
- ↑ 84v
- ↑ 85r
- ↑ 85v
- ↑ marg.
- ↑ marg.
- ↑ 112r
- ↑ 112v
- ↑ 113r
- ↑ 113v
- ↑ יהיה: MS M ויעלה
Appendix: Bibliography
Kitāb Masā’il allatī hiya ghair Maḥdūda (The third section on indeterminate equations) / by Abū Kāmil Shujāʽ Ibn Aslam Ibn Muḥammad ibn Shujāʽ (Egypt, ca. 850-930)
– Hebrew translation –
by Mordecai (Angelo) Finzi (Mantua, d. 1475)
Ḥeshbon ha-ʽAgulah (ha-Sheʼelot ha-Ḥershot ve-ha-ʼIlmot)
Manuscripts:
- 1) Mantova, Comunita Israelitica MS ebr. 17/3 (IMHM: f 797), ff. 63v-85v; 112r-113v (15th century; autograph)
- Abu Kamil Shudeya, Algebra
- 2) München, Bayerische Staatsbibliothek, Cod. hebr. 225/3 (IMHM: f 1118), ff. 166v-191v (15th century)
- Mathematische Abhandlungen, vielleicht von Mordechai Finzi (1445-1473)
Bibliography:
- Lévy, Tony. 2007. L’algèbre arabe dans les textes hébraïques (II). Dans l’Italie des XVe et XVIe siècles, sources arabes et sources vernaculaires, Arabic Sciences and Philosophy 17, pp. 81-107.
- Schub, Pincus and Martin Levey. 1968. Book on Indeterminate Problems of abū Kāmil (850-930), Centaurus 13, pp. 91-94.
- ———. 1970. Indeterminate Problems of abū Kāmil (850-930), Atti della Accademia Nazionale dei Lincei, Memorie della classe di scienze fisiche, matematiche e naturali, ser. VIII, vol. X, no.2, pp. 23-96.
- Sesiano, Jacques. 1977. Les Méthodes d'analyse indéterminée chez Abū Kāmil, Centaurus 21, pp. 89-105.
- Yadegari, Mohammad. 1978. The Use of Mathematical Induction by Abū Kāmil Shujā‘ Ibn Aslam (850-930), Isis, vol. 69, no. 2 (Jun., 1978), pp. 259-262.
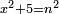
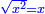 ].
].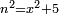
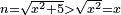
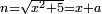
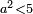

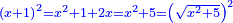
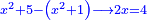
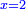
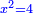
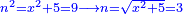

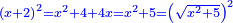
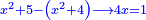
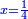
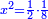



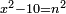
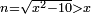
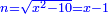
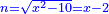
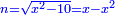 [?]
[?]
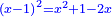
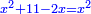

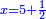
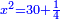
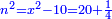
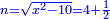

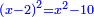
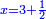
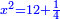
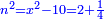
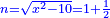
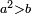
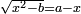
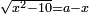
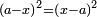
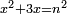

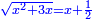

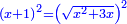
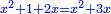
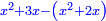
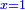
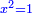
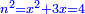
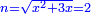
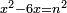

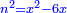
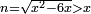


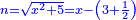
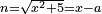 such that
such that 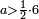

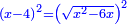
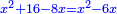
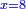
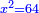
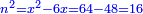
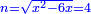
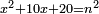
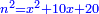
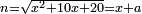
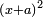
 will be less or more than 10
will be less or more than 10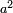 will be less or more than 20
will be less or more than 20
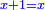 [?]
[?]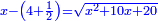
![\scriptstyle{\color{blue}{\left[x+\left(4+\frac{1}{2}\right)\right]^2=\left(\sqrt{x^2+10x+20}\right)^2}}](/mediawiki/images/math/3/1/b/31bd255e6e7a11bf85ebfb7791d7591b.png)
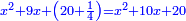

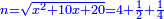
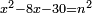
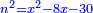
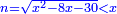
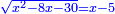
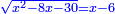
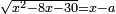 for any number greater than half the eight roots of the square:
for any number greater than half the eight roots of the square: 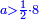
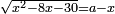 for any number greater than half the eight roots of the square:
for any number greater than half the eight roots of the square: 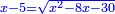
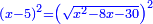
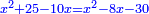


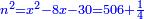
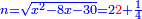
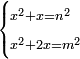
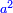 , such that:
, such that: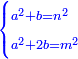
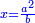
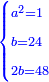


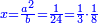
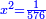
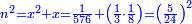
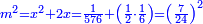
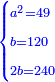
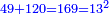

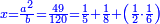
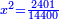
![\scriptstyle{\color{blue}{n^2=x^2+x=\frac{2401}{14400}+\left[\frac{1}{5}+\frac{1}{8}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]=\frac{2401}{14400}+\frac{5880}{14400}=\frac{8281}{14400}=\left(\frac{91}{120}\right)^2}}](/mediawiki/images/math/7/3/f/73f3712df4c06c99e4c853174d081e93.png)
![\scriptstyle{\color{blue}{m^2=x^2+2x=\frac{2401}{14400}+2\sdot\left[\frac{1}{5}+\frac{1}{8}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]=\frac{2401}{14400}+\frac{11760}{14400}=\frac{14161}{14400}=\left(\frac{119}{120}\right)^2}}](/mediawiki/images/math/3/8/e/38e44d8ed23af2b16b990463f051dbb4.png)
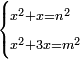
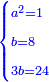
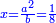
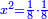
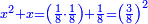
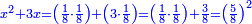
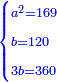
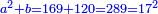
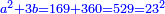
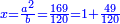
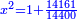
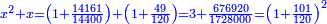
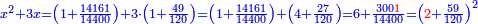
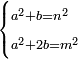
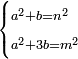
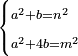
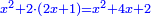
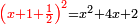 ]
]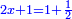
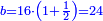
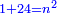
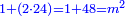
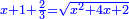
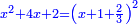
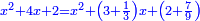
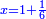
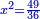
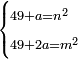
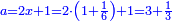
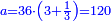
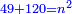
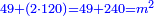
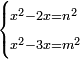
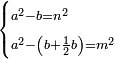
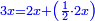
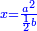
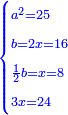
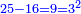
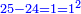
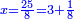
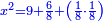
![\scriptstyle{\color{blue}{x^2-2x=\left[9+\frac{6}{8}+\left(\frac{1}{8}\sdot\frac{1}{8}\right)\right]-\left(6+\frac{1}{4}\right)=3+\frac{1}{2}+\left(\frac{1}{8}\sdot\frac{1}{8}\right)=\left(1+\frac{7}{8}\right)^2}}](/mediawiki/images/math/c/0/3/c03a1cf27555e36dcbecb26ac89bc566.png)
![\scriptstyle{\color{blue}{x^2-3x=\left[9+\frac{6}{8}+\left(\frac{1}{8}\sdot\frac{1}{8}\right)\right]-\left(9+\frac{3}{8}\right)=\frac{3}{8}+\left(\frac{1}{8}\sdot\frac{1}{8}\right)=\left(\frac{5}{8}\right)^2}}](/mediawiki/images/math/2/f/f/2ffcf247f479965c00a42cb9a8e7da3e.png)
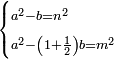
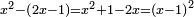
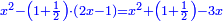
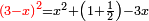 ]
]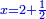
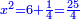
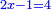
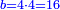
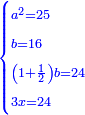
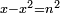
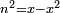 should have a root
should have a root or more or less
or more or less
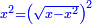
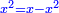
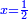
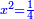

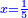
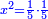
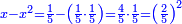
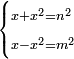
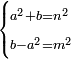
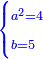
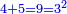
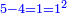
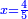
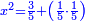
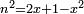
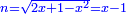
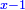 was chosen - in order that squares equal roots will remain after equalizing.
was chosen - in order that squares equal roots will remain after equalizing.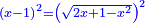
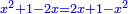
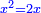
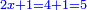
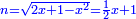
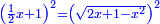
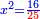
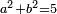
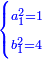
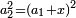
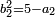
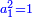
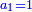
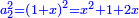
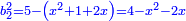 should have a root
should have a root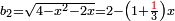
![\scriptstyle{\color{blue}{\left[2-\left(1+\frac{1}{3}\right)x\right]^2=\left(\sqrt{4-x^2-2x}\right)^2}}](/mediawiki/images/math/4/5/a/45a9ecfa777c43d1e88b562b4a56ba4d.png)
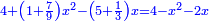
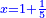
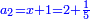
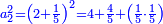
![\scriptstyle{\color{blue}{b_2^2=5-\left[4+\frac{4}{5}+\left(\frac{1}{5}\sdot\frac{1}{5}\right)\right]=\frac{4}{5}\sdot\frac{1}{5}}}](/mediawiki/images/math/6/4/e/64e0e6c4fa14315a7a248466f7d88902.png)
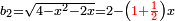
![\scriptstyle{\color{blue}{\left[2-\left(1+\frac{1}{2}\right)x\right]^2=\left(\sqrt{4-x^2-2x}\right)^2}}](/mediawiki/images/math/d/5/2/d5242221c565a5101c58589c2a027d2b.png)
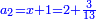
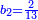
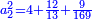
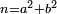
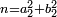 ]
]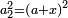
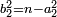 , which is a number that has a root, and this number is of the type of a number minus a square and roots.
, which is a number that has a root, and this number is of the type of a number minus a square and roots.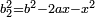 ]
]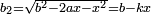
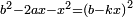
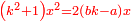
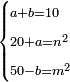
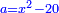

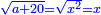
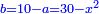
 which should have a root
which should have a root , for this number has many manners.
, for this number has many manners.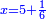
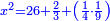
![\scriptstyle{\color{blue}{a=x^2-20=\left[26+\frac{2}{3}+\left(\frac{1}{4}\sdot\frac{1}{9}\right)\right]-20=6+\frac{2}{3}+\left(\frac{1}{4}\sdot\frac{1}{9}\right)}}](/mediawiki/images/math/8/5/5/85534b870bf3086a19ef6900f48dd7e2.png)
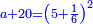
![\scriptstyle{\color{blue}{b=10-a=10-\left[6+\frac{2}{3}+\left(\frac{1}{4}\sdot\frac{1}{9}\right)\right]=3+\frac{1}{4}+\left(\frac{1}{2}\sdot\frac{1}{9}\right)}}](/mediawiki/images/math/d/8/f/d8f46212272c5cee1c22a34e2aafc751.png)
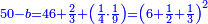
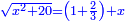
![\scriptstyle{\color{blue}{\left[\left(1+\frac{2}{3}\right)+x\right]^2=\left(\sqrt{x^2+20}\right)^2}}](/mediawiki/images/math/7/4/2/742cfd93289928b83418cc7a1610bf43.png)
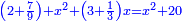
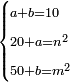
 which should have a root
which should have a root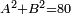
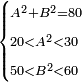
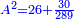
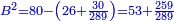
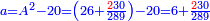
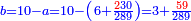
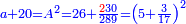
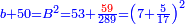
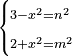

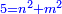
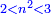

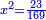
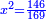
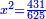
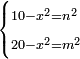

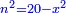
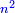 from 10 or from 20, the remainder will be a square
from 10 or from 20, the remainder will be a square 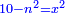
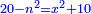 which should have a root
which should have a root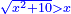


 according to what was explained before.
according to what was explained before.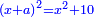

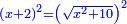
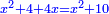
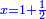

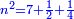
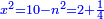
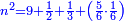
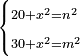
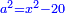
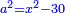

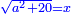
 which should have a square
which should have a square

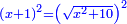

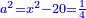
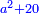 has a root
has a root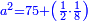
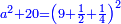
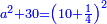
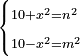
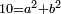
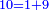
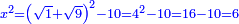
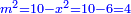
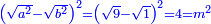
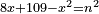
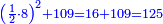
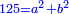

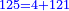
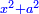
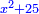
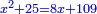
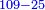
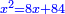
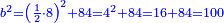
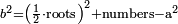
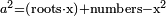
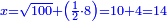
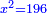
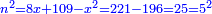
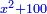
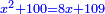
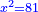
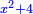
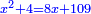
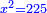
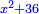
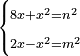




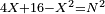
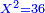

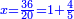
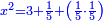
![\scriptstyle{\color{blue}{8x+x^2=\left(14+\frac{2}{5}\right)+\left[3+\frac{1}{5}+\left(\frac{1}{5}\sdot\frac{1}{5}\right)\right]=17+\frac{3}{5}+\left(\frac{1}{5}\sdot\frac{1}{5}\right)=\left(4+\frac{1}{5}\right)^2}}](/mediawiki/images/math/8/6/1/861834c2507163fc3c2737d99ce02c8f.png)
![\scriptstyle{\color{blue}{2x-x^2=\left(3+\frac{3}{5}\right)-\left[3+\frac{1}{5}+\left(\frac{1}{5}\sdot\frac{1}{5}\right)\right]=\frac{1}{5}+\left(\frac{4}{5}\sdot\frac{1}{5}\right)=\left(\frac{3}{5}\right)^2}}](/mediawiki/images/math/c/f/a/cfa723873960216653ec6f59eda554bd.png)
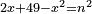
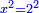
 has a root.
has a root.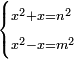
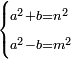
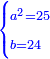
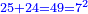
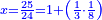
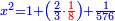
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle x^2+x&\scriptstyle=\left[1+\left(\frac{2}{3}{\color{red}{\sdot\frac{1}{8}}}\right)+\frac{1}{576}\right]+\left[1+\left({\color{red}{\frac{1}{3}\sdot\frac{1}{8}}}\right)\right]\\&\scriptstyle=2+\frac{1}{8}+\frac{1}{576}\\&\scriptstyle=\left(1+\frac{1}{3}+\frac{1}{8}\right)^2\\\end{align}}}](/mediawiki/images/math/5/6/d/56d14289ccf7d76f5e6462c83f3b8c92.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle x^2-x&\scriptstyle=\left[1+\left(\frac{2}{3}{\color{red}{\sdot\frac{1}{8}}}\right)+\frac{1}{576}\right]-\left[1+\left({\color{red}{\frac{1}{3}\sdot\frac{1}{8}}}\right)\right]\\&\scriptstyle=\frac{25}{576}\\&\scriptstyle=\left[\frac{1}{8}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]^2\\\end{align}}}](/mediawiki/images/math/1/0/2/1023184bd08076aa5d7a4e36c8adb92f.png)
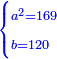
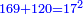
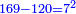
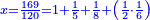
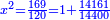
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle x^2+x&\scriptstyle=\left(1+\frac{14161}{14400}\right)+\left[1+\frac{1}{5}+\frac{1}{8}+\left({\color{red}{\frac{1}{2}\sdot\frac{1}{6}}}\right)\right]\\&\scriptstyle=3+\frac{5641}{14400}\\&\scriptstyle=\left(1+\frac{{\color{red}{101}}}{120}\right)^2\\\end{align}}}](/mediawiki/images/math/e/4/5/e45d90dbccba0d80ca6f93a2140b98f7.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle x^2-x&\scriptstyle=\left(1+\frac{14161}{14400}\right)-\left[1+\frac{1}{5}+\frac{1}{8}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\\&\scriptstyle=\frac{8281}{14400}\\&\scriptstyle=\left(\frac{91}{120}\right)^2\\\end{align}}}](/mediawiki/images/math/0/e/0/0e0fcd4ce69481670817c51b34875b61.png)
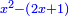
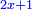 is the sought number
is the sought number 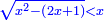
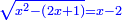
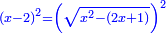
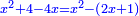
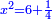
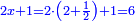
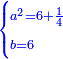
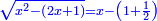

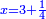
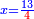
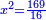
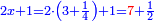
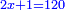
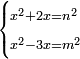
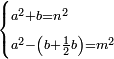
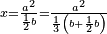
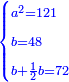
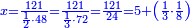
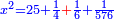
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle x^2+2x&\scriptstyle=\left(25+\frac{1}{4}{\color{red}{+}}\frac{1}{6}+\frac{1}{576}\right)+\left[10+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\\&\scriptstyle=35+{\color{red}{\frac{1}{2}}}+\frac{1}{576}\\&\scriptstyle=\left(5+\frac{1}{2}+\frac{1}{3}{\color{red}{+}}\frac{1}{8}\right)^2\\\end{align}}}](/mediawiki/images/math/3/a/1/3a1924d32e7dfbe5d646aa6d14bec759.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle x^2-3x&\scriptstyle=\left(25+\frac{1}{4}{\color{red}{+}}\frac{1}{6}+\frac{1}{576}\right)-\left(15+\frac{1}{8}\right)\\&\scriptstyle=10+\frac{1}{6}+\frac{1}{8}+\frac{1}{576}\\&\scriptstyle=\left[3+\frac{1}{8}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]^2\\\end{align}}}](/mediawiki/images/math/e/1/2/e1265f8c2485d8ee8f7daf6dd1de44af.png)
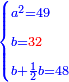
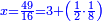
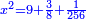
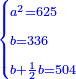
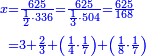
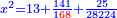
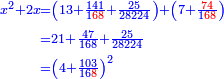
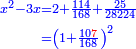
![\scriptstyle\begin{cases}\scriptstyle x^2+2x+1=n^2\\\scriptstyle x^2-\left[3x+\left(1+\frac{1}{2}\right)\right]=m^2\end{cases}](/mediawiki/images/math/0/f/8/0f807ab541011f16cb21bd6c3494d4f7.png)
![\scriptstyle{\color{blue}{x^2-\left[3x+\left(1+{\color{red}{\frac{1}{2}}}\right)\right]}}](/mediawiki/images/math/b/d/a/bdae3ffbff309541b227e49897d292a2.png)
![\scriptstyle{\color{blue}{\sqrt{x^2-\left[3x+\left(1+\frac{1}{2}\right)\right]}={\color{red}{x}}-2}}](/mediawiki/images/math/0/2/9/029ebb28798fbc22c3e2a27a27934f82.png)
![\scriptstyle{\color{blue}{\left(x-2\right)^2=\left[\sqrt{x^2-\left[3x+\left(1+\frac{1}{2}\right)\right]}\right]^2}}](/mediawiki/images/math/9/a/9/9a9d1c0a71141e98baae0647c34cd8b6.png)
![\scriptstyle{\color{blue}{x^2+4-4x=x^2-\left[3x+\left(1+\frac{1}{2}\right)\right]}}](/mediawiki/images/math/9/5/a/95a9026e7ab16b93cf84dae19794c754.png)
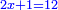
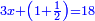
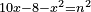
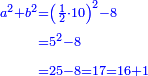
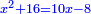
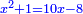
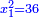
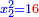
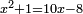
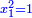
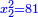
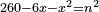
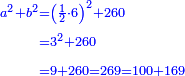
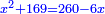
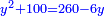
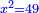
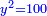
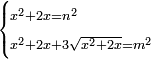
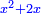
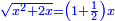
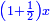 :
: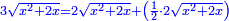
![\scriptstyle{\color{blue}{\left[\left(1+\frac{1}{2}\right)x\right]^2=\left(\sqrt{x^2+2x}\right)^2}}](/mediawiki/images/math/2/a/9/2a9a5a2d20c7ebeaecaa0398783aa000.png)
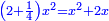
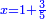
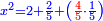
![\scriptstyle{\color{blue}{x^2+2x=\left[2+\frac{2}{5}+\left(\frac{4}{5}\sdot\frac{1}{5}\right)\right]+\left(3+\frac{1}{5}\right)=5+\frac{3}{5}+\left(\frac{4}{5}\sdot\frac{1}{5}\right)}}](/mediawiki/images/math/0/c/e/0ce207462169165bac229f56bebe1530.png)
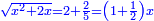
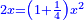
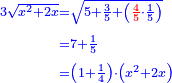
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle x^2+2x+3\sqrt{x^2+2x}&\scriptstyle=\left[5+\frac{3}{5}+\left(\frac{4}{5}\sdot\frac{1}{5}\right)\right]+\left(7+\frac{1}{5}\right)\\&\scriptstyle=12+\frac{4}{5}+\left(\frac{4}{5}\sdot\frac{1}{5}\right)\\\end{align}}}](/mediawiki/images/math/1/a/6/1a664bd141c828130fd4ef3346659174.png)
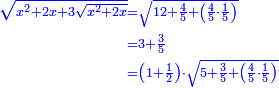
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left(4+\frac{1}{2}\right)\sdot\sqrt{12+\frac{4}{5}+\left(\frac{4}{5}\sdot\frac{1}{5}\right)}&\scriptstyle=16+\frac{1}{5}\\&\scriptstyle=\left(1+\frac{1}{4}\right)\sdot\left[12+\frac{4}{5}+\left(\frac{4}{5}\sdot\frac{1}{5}\right)\right]\\\end{align}}}](/mediawiki/images/math/0/6/0/060b83483ca4c4d4c4fb40cb06c9cc26.png)
![\scriptstyle{\color{blue}{\left(16+\frac{1}{5}\right)+\left[12+\frac{4}{5}+\left(\frac{4}{5}\sdot\frac{1}{5}\right)\right]=29+\left(\frac{4}{5}\sdot\frac{1}{5}\right)}}](/mediawiki/images/math/e/e/6/ee60d81ab41aa4bb558d48486fc39b85.png)
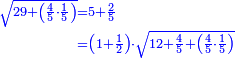
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\sqrt{\left[29+\left(\frac{4}{5}\sdot\frac{1}{5}\right)\right]+\left(6+\frac{3}{4}\right)\sdot\sqrt{29+\left(\frac{4}{5}\sdot\frac{1}{5}\right)}}\\&\scriptstyle={\color{red}{8+\frac{1}{10}}}\\&\scriptstyle=\left(1+\frac{1}{2}\right)\sdot\sqrt{29+\left(\frac{4}{5}\sdot\frac{1}{5}\right)}\\\end{align}}}](/mediawiki/images/math/8/6/c/86cbd7a190d31ea76d18cc835d46f3da.png)
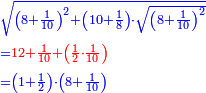
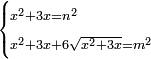

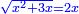
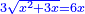



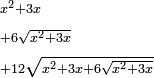

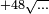 has a root
has a root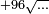 has a root
has a root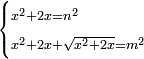
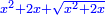 should have a root
should have a root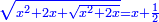
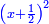
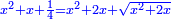
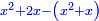
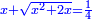
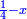
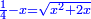
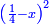
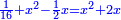
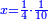
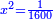
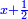 in order that the square will be consumed and it will remain that things are equal to numbers.
in order that the square will be consumed and it will remain that things are equal to numbers.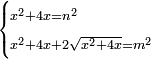

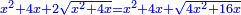
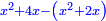
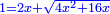
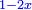
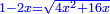
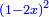
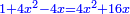
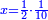
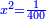
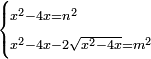
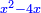
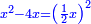
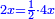
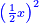
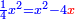
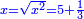

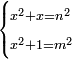
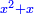 has a root
has a root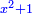 has a root
has a root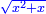
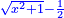
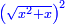
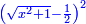
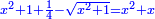
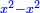
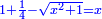
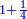 :
: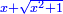
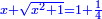
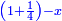

![\scriptstyle{\color{blue}{\left[\left(1+\frac{1}{4}\right)-x\right]^2}}](/mediawiki/images/math/6/2/3/62332aef2a5a9624e4ab59ca021e31c1.png)
![\scriptstyle{\color{blue}{\left[1+\frac{1}{2}+\left(\frac{1}{2}\sdot\frac{1}{8}\right)\right]+{\color{red}{x^2}}-\left(2+\frac{1}{2}\right)x=x^2+1}}](/mediawiki/images/math/f/4/c/f4cd4ffdc0feb70c72098e45fcad2869.png)
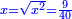
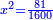
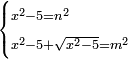
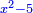 [has a root]
[has a root]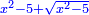 [has a root]
[has a root]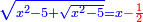
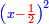
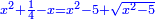
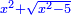 :
: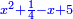

![\scriptstyle{\color{blue}{\left[\left(5+\frac{1}{4}\right){\color{red}{-x}}\right]^2}}](/mediawiki/images/math/4/3/f/43f47b686d52f2889c7996e0073a603f.png)
![\scriptstyle{\color{blue}{\left[27+\frac{1}{2}+\left(\frac{1}{2}\sdot\frac{1}{8}\right)\right]+x^2-\left(10+\frac{1}{2}\right)x=x^2-5}}](/mediawiki/images/math/3/9/c/39ccbb61bd637555f60dffa6cf396d6b.png)
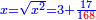
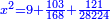
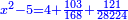
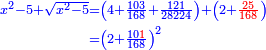
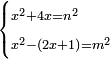
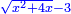
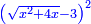

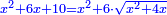

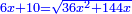
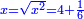
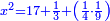
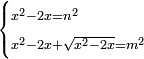
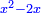 [has a root]
[has a root]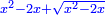 has a root
has a root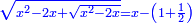
![\scriptstyle{\color{blue}{\left[x-\left(1+\frac{1}{2}\right)\right]^2}}](/mediawiki/images/math/5/f/8/5f8d19774c352dc1124735a1eaf8fa56.png)
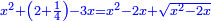
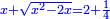
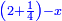
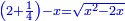
![\scriptstyle{\color{blue}{\left[\left(2+\frac{1}{4}\right)-x\right]^2}}](/mediawiki/images/math/0/1/9/019c627ee6e6cae3878a7e9f9f3477c3.png)
![\scriptstyle{\color{blue}{\left[5+\left(\frac{1}{2}\sdot\frac{1}{8}\right)\right]+x^2-\left(4+\frac{1}{2}\right)x=x^2-2x}}](/mediawiki/images/math/6/4/4/64444adb089b048df9b1775978433545.png)
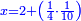
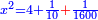
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle x^2-2x&\scriptstyle=\left(4+\frac{1}{10}+\frac{1}{1600}\right)-\left[4+\left(\frac{1}{2}\sdot\frac{1}{10}\right)\right]\\&\scriptstyle=\left(\frac{1}{2}\sdot\frac{1}{10}\right)+\frac{1}{1600}\\\end{align}}}](/mediawiki/images/math/3/f/2/3f289b579249ff810d92d3e23a11a86f.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle x^2-2x+\sqrt{x^2-2x}&\scriptstyle=\left[\left(\frac{1}{2}\sdot\frac{1}{10}\right)+\frac{1}{1600}\right]+\left[\frac{1}{5}+\left(\frac{1}{4}\sdot\frac{1}{10}\right)\right]\\&\scriptstyle=\frac{1}{4}+\left(\frac{1}{4}\sdot\frac{1}{10}\right)+\frac{1}{1600}\\&\scriptstyle=\left[\frac{1}{2}+\left(\frac{1}{4}\sdot\frac{1}{10}\right)\right]^2\\\end{align}}}](/mediawiki/images/math/b/b/f/bbf2af77af72890fa0fae5b8bfefbf72.png)
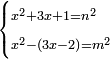
 has a root
has a root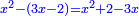 has a root
has a root
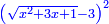


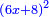
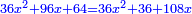
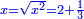
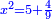
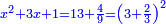
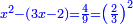
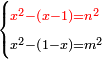
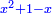 has a root
has a root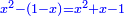 has a root
has a root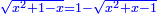
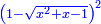
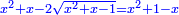
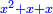
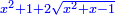

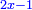

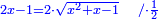
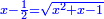
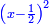

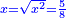
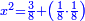
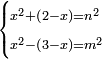
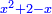 has a root
has a root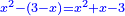 has a root
has a root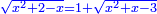
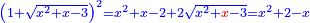
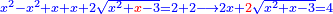


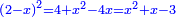
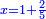
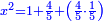
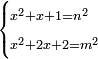
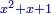
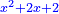 has a root
has a root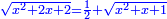
![\scriptstyle{\color{blue}{\left(x^2+2x+2\right)-\left[\left(x^2+x+1\right)+\frac{1}{4}\right]=x+\frac{3}{4}}}](/mediawiki/images/math/0/0/1/001debd2f5a29140f6dcd1edd66bd010.png)
![\scriptstyle{\color{blue}{\left(x+\frac{3}{4}\right)^2\longrightarrow x^2+\left(1+\frac{1}{2}\right)x+\left[\frac{1}{2}+\left(\frac{1}{2}\sdot\frac{1}{8}\right)\right]=x^2+x+{\color{red}{1}}}}](/mediawiki/images/math/7/3/f/73f31418f3f186d2bd7040380625d920.png)
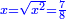
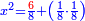
![\scriptstyle{\color{blue}{a+\left[\frac{1}{2}\sdot\left(b+c+d\right)\right]=b+\left[\frac{1}{3}\sdot\left(a+c+d\right)\right]=c+\left[\frac{1}{4}\sdot\left(a+b+d\right)\right]=d+\left[\frac{1}{5}\sdot\left(a+b+c\right)\right]}}](/mediawiki/images/math/a/e/4/ae49ae680d8337711b8246237b23fc23.png)
 ], the third a dirham [
], the third a dirham [ ], and the fourth a fals [
], and the fourth a fals [ ]
]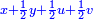
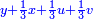
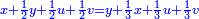
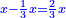
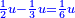
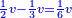
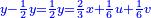
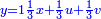
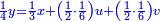
![\scriptstyle{\color{blue}{\frac{1}{5}y=\left[\frac{1}{5}+\left(\frac{1}{5}\sdot\frac{1}{3}\right)\right]x+\left(\frac{1}{5}\sdot\frac{1}{3}\right)u+\left(\frac{1}{5}\sdot\frac{1}{3}\right)v}}](/mediawiki/images/math/8/2/c/82ca068b5c2d020ba1dd90ba8e01b1c4.png)
![\scriptstyle{\color{blue}{x+\frac{1}{2}y+\frac{1}{2}u+\frac{1}{2}v=x+\left[\frac{2}{3}x+\frac{1}{6}u+\frac{1}{6}v\right]+\frac{1}{2}u+\frac{1}{2}v=1\frac{2}{3}x+\frac{2}{3}u+\frac{2}{3}v}}](/mediawiki/images/math/6/a/4/6a4db9ea14a01086466f9c2a966b7df0.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle u+\frac{1}{4}x+\frac{1}{4}y+\frac{1}{4}v=u+\frac{1}{4}x+\left[\frac{1}{3}x+\left(\frac{1}{2}\sdot\frac{1}{6}\right)u+\left(\frac{1}{2}\sdot\frac{1}{6}\right)v\right]+\frac{1}{4}v&\scriptstyle=\left(\frac{1}{3}+\frac{1}{4}\right)x+\left[1+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]u+\frac{1}{3}v\\&\scriptstyle=1\frac{2}{3}x+\frac{2}{3}u+\frac{2}{3}v\\\end{align}}}](/mediawiki/images/math/4/2/e/42e6cf6349bc90828f1577908f11ce24.png)
![\scriptstyle{\color{blue}{\left[\left(1+\frac{2}{3}\right)-\left(\frac{1}{3}+\frac{1}{4}\right)\right]x+\left(\frac{2}{3}-\frac{1}{3}\right)v=\left[1+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]x+\frac{1}{3}v}}](/mediawiki/images/math/0/f/a/0fa8392cf6b231033609e8643afb272a.png)
![\scriptstyle{\color{blue}{\left[\left[1+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]-\frac{2}{3}\right]u=\left(\frac{1}{4}+\frac{1}{6}\right)u=\left[1+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]x+\frac{1}{3}v}}](/mediawiki/images/math/1/5/7/157283267fca1c6514a6d9c2f28bdd9e.png)
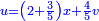
![\scriptstyle{\color{blue}{1\frac{2}{3}x+\frac{2}{3}u+\frac{2}{3}v=1\frac{2}{3}x+\frac{2}{3}\sdot\left[\left(2+\frac{3}{5}\right)x+\frac{4}{5}v\right]+\frac{2}{3}v=1\frac{2}{3}x+\left[\left(1+\frac{1}{3}+\frac{2}{5}\right)x+\left(\frac{1}{3}+\frac{1}{5}\right)v\right]+\frac{2}{3}z=3\frac{2}{5}x+1\frac{1}{5}v}}](/mediawiki/images/math/a/1/f/a1fb8803247242e39d9378bad214a106.png)
![\scriptstyle{\color{blue}{y=1\frac{1}{3}x+\frac{1}{3}u+\frac{1}{3}v=1\frac{1}{3}x+\frac{1}{3}\sdot\left[\left(2+\frac{3}{5}\right)x+\frac{4}{5}v\right]+\frac{1}{3}v=1\frac{1}{3}x+\left[\left(\frac{2}{3}+\frac{1}{5}\right)x+\left[\frac{1}{5}+\left(\frac{1}{3}\sdot\frac{1}{5}\right)\right]v\right]+\frac{1}{3}v=2\frac{1}{5}x+\frac{3}{5}v}}](/mediawiki/images/math/2/3/7/23741bcc8733db3716de35ab4e50406f.png)
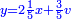
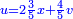
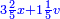
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle v+\frac{1}{5}x+\frac{1}{5}y+\frac{1}{5}u&\scriptstyle=v+\frac{1}{5}\sdot\left[x+\left(2\frac{1}{5}x+\frac{3}{5}v\right)+\left(2\frac{3}{5}x+\frac{4}{5}v\right)\right]=v+\left[\left[1+\left(\frac{4}{5}\sdot\frac{1}{5}\right)\right]x+\left[\frac{1}{5}+\left(\frac{2}{5}\sdot\frac{1}{5}\right)\right]v\right]\\&\scriptstyle=\left[1+\left(\frac{4}{5}\sdot\frac{1}{5}\right)\right]x+\left[1+\frac{1}{5}+\left(\frac{2}{5}\sdot\frac{1}{5}\right)\right]v=3\frac{2}{5}x+1\frac{1}{5}v\\\end{align}}}](/mediawiki/images/math/7/d/d/7dd362ed87d4a2270322a9c0f05c344b.png)
![\scriptstyle{\color{blue}{\left[1+\frac{1}{5}+\left(\frac{2}{5}\sdot\frac{1}{5}\right)\right]v-1\frac{1}{5}v=\frac{2}{5}\sdot\frac{1}{5}v}}](/mediawiki/images/math/0/9/9/09989998647008c8d2372f3168f32be9.png)
![\scriptstyle{\color{blue}{3\frac{2}{5}x-\left[1+\left(\frac{4}{5}\sdot\frac{1}{5}\right)\right]x=\left[2+\frac{1}{5}x+\left(\frac{1}{5}\sdot\frac{1}{5}\right)\right]x=\frac{2}{5}\sdot\frac{1}{5}v}}](/mediawiki/images/math/b/1/6/b16ac80f3e90ed3b72162ad72172972d.png)

![\scriptstyle{\color{blue}{y=2\frac{{\color{red}{1}}}{5}x+\frac{3}{5}v=\left[\left(2+\frac{1}{5}\right)\sdot1\right]+\left(\frac{3}{5}\sdot28\right)=19}}](/mediawiki/images/math/4/1/6/41672b3160b07d1f0444759c9e134669.png)
![\scriptstyle{\color{blue}{u=2\frac{3}{5}x+\frac{4}{5}v=\left[\left(2+\frac{3}{5}\right)\sdot1\right]+\left(\frac{4}{5}\sdot28\right)=25}}](/mediawiki/images/math/4/b/d/4bd1b033a6e077153401f1c04decaf98.png)
![\scriptstyle{\color{blue}{3\frac{{\color{red}{2}}}{5}x+1\frac{1}{5}v=\left[\left(3+\frac{2}{5}\right)\sdot1\right]+\left(1+\frac{1}{5}\sdot28\right)=37}}](/mediawiki/images/math/b/7/3/b7370c63a604bb49053b22f5ca109738.png)
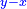 ]
]![\scriptstyle{\color{blue}{x+\left[\frac{1}{2}\sdot\left(y-x\right)\right]=\frac{1}{2}x+\frac{1}{2}y}}](/mediawiki/images/math/2/4/0/24025f6b2232950c37bb11369a0f6810.png)
![\scriptstyle{\color{blue}{u+\left[\frac{1}{3}\sdot\left(y-u\right)\right]=\frac{2}{3}u+\frac{1}{3}y=\frac{1}{2}x+\frac{1}{2}y}}](/mediawiki/images/math/a/0/b/a0b98375081da140457151a8e0b019f6.png)
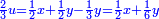
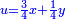
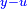 ]
]![\scriptstyle{\color{blue}{u+\left[\frac{1}{4}\sdot\left(y-u\right)\right]=\frac{3}{4}u+\frac{1}{4}y=\frac{1}{2}x+\frac{1}{2}y}}](/mediawiki/images/math/1/9/d/19dec3eaf471ac9e8daaf84403d733e4.png)
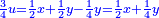
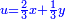
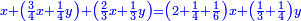
![\scriptstyle{\color{blue}{y-\left[\left(2+\frac{1}{4}+\frac{1}{6}\right)x+\left(\frac{1}{3}+\frac{1}{4}\right)y\right]=\left(\frac{1}{4}+\frac{1}{6}\right)y-\left(2+\frac{1}{4}+\frac{1}{6}\right)x}}](/mediawiki/images/math/a/2/6/a2691d3f0fb50d154b99ca2c08db9a88.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left[\left(\frac{1}{4}+\frac{1}{6}\right)y-\left(2+\frac{1}{4}+\frac{1}{6}\right)x\right]+\left[\frac{1}{5}\sdot\left[\left(2+\frac{1}{4}+\frac{1}{6}\right)x+\left(\frac{1}{3}+\frac{1}{4}\right)y\right]\right]&\scriptstyle=\left[\left(\frac{1}{4}+\frac{1}{6}\right)y-\left(2+\frac{1}{4}+\frac{1}{6}\right)x\right]+\left(\frac{29}{60}x+\frac{7}{60}y\right)\\&\scriptstyle=\frac{32}{60}y-1\frac{56}{60}x=\frac{1}{2}x+\frac{1}{2}y\\\end{align}}}](/mediawiki/images/math/a/e/2/ae254deae444402c0cd66416e0a4c109.png)
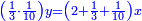
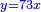
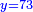
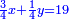
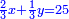
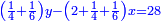
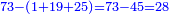
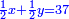
![\scriptstyle{\color{blue}{a+\left[\frac{1}{2}\sdot\left(b+c\right)\right]=b+\left[\frac{1}{3}\sdot\left(c+d\right)\right]=c+\left[\frac{1}{4}\sdot\left(d+e\right)\right]=d+\left[\frac{1}{5}\sdot\left(e+a\right)\right]=e+\left[\frac{1}{6}\sdot\left(a+b\right)\right]}}](/mediawiki/images/math/5/8/5/585b26c7e0cd60e4dccb5bca434fdf76.png)
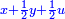
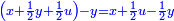
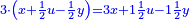
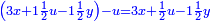
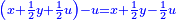
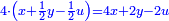
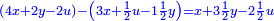
![\scriptstyle{\color{blue}{\left(3x+\frac{1}{2}u-1\frac{1}{2}y\right)+\left[\frac{1}{5}\sdot\left(2x+3\frac{1}{2}y-2\frac{1}{2}u\right)\right]=\left(3x+\frac{1}{2}u-1\frac{1}{2}y\right)+\left(\frac{2}{5}x+\frac{7}{10}y-\frac{1}{2}u\right)=3\frac{2}{5}x-\frac{4}{5}y}}](/mediawiki/images/math/c/c/2/cc24eac01997a563f9ab3c068a225348.png)
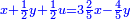
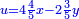
![\scriptstyle{\color{blue}{x+\frac{1}{2}y+\left[\frac{1}{2}\sdot\left(4\frac{4}{5}x-2\frac{3}{5}y\right)\right]=x+\frac{1}{2}y+2\frac{2}{5}x-1\frac{3}{10}y=3\frac{2}{5}x-\frac{4}{5}y}}](/mediawiki/images/math/1/c/6/1c6511ff0c9f871f25351150b0c944b9.png)
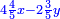
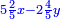
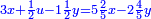
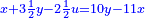
![\scriptstyle{\color{blue}{\left(10y-11x\right)+\left[\frac{1}{6}\sdot\left(x+y\right)\right]=\left(10y-11x\right)+\left(\frac{1}{6}x+\frac{1}{6}y\right)=10\frac{1}{6}y-10\frac{5}{6}x}}](/mediawiki/images/math/4/b/5/4b5bff47c6fa51131d2d5b61515724f9.png)
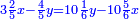
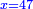
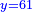
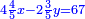
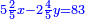
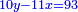
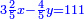
![\scriptstyle{\color{blue}{\left[3\sdot\left(111-61\right)\right]-67=\left(3\sdot50\right)-67=150-67=83}}](/mediawiki/images/math/1/a/b/1ab76e2903cc032f3b28c3647428efbb.png)
![\scriptstyle{\color{blue}{\left[4\sdot\left(111-67\right)\right]-83=\left(4\sdot44\right)-83=176-83=93}}](/mediawiki/images/math/8/e/a/8ea766d7ea4583c39e7fbb524c2be9b2.png)



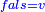
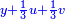
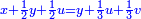
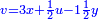
![\scriptstyle{\color{blue}{u+\left[\frac{1}{4}\sdot\left[\left(3x+\frac{1}{2}u-{\color{red}{1}}\frac{1}{2}y\right)+v\right]\right]=u+\left(\frac{3}{4}x+\frac{1}{4}v+\frac{1}{8}u-\frac{3}{8}y\right)=1\frac{1}{8}u+\frac{1}{4}v+\frac{3}{4}x-\frac{3}{8}y}}](/mediawiki/images/math/b/1/7/b1747cf13f2963a349c298e4df5d443d.png)
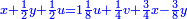
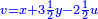
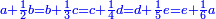
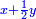
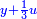
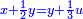
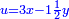
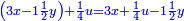
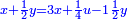
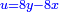
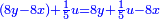
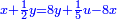
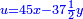
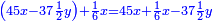
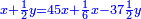
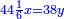

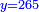
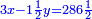

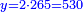
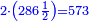
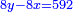
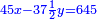
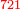
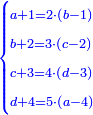
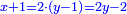
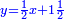
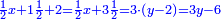
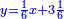
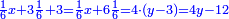
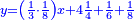
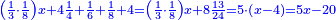
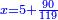
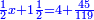
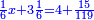
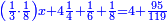
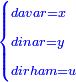
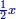
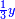
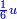
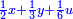
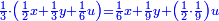
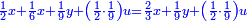
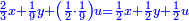
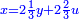
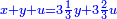
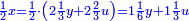
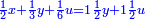
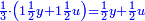
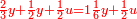
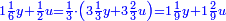
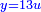
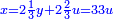
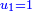
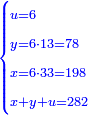
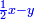
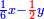
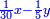
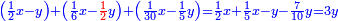
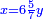
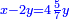
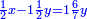
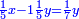
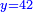
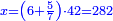
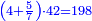
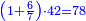
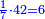
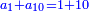
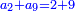
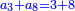
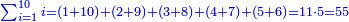
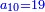
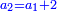
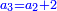
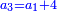
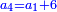
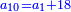
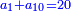
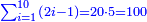
![\scriptstyle{\color{blue}{a_{10}=\left[d\sdot\left(n-1\right)+a_1\right]=\left[4\sdot\left(10-1\right)\right]+a_1=36+3=39}}](/mediawiki/images/math/e/9/0/e905399335c1776803fe8d7e6d16fa25.png)
![\scriptstyle{\color{blue}{\sum_{i=1}^{10} \left[3+4\sdot\left(i-1\right)\right]=\left(a_1+a_{10}\right)+\left(a_2+a_9\right)+\ldots=42+42+\ldots=42\sdot5=210}}](/mediawiki/images/math/7/4/8/748bdd83320ff5515cfa7a4468aa3fb0.png)
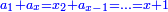
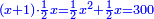
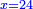
![\scriptstyle{\color{blue}{a_x=\left[d\sdot\left(n-1\right)\right]+a_1=\left[3\sdot\left(x-1\right)\right]+2=\left(3x-3\right)+2=3x-1}}](/mediawiki/images/math/7/4/d/74d1079352eaf54969dbae4659e12d62.png)
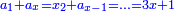
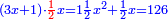
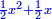
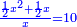
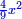
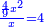
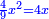
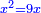
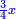
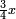 =
= 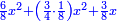
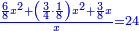
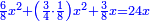
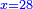
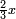 =
= 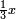 =
= 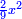
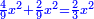
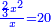
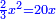
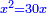
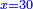
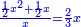
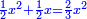
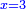
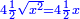
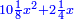
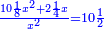
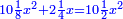
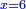
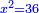
![\scriptstyle{\color{blue}{a_{30}=a_n=\left[d\sdot\left(n-1\right)\right]+a_1=\left[x\sdot\left(30-1\right)\right]+1=29x+1}}](/mediawiki/images/math/0/6/1/061949fcfa835cf5dc3c4f08f1a38a6a.png)
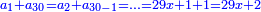
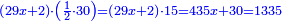
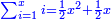
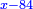



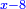
![\scriptstyle{\color{blue}{\sum_{i=1}^{x-8} \left[1+\left(3i-3\right)\right]=1\frac{1}{2}x^2+100-24\frac{1}{2}x=\frac{1}{2}x^2+\frac{1}{2}x}}](/mediawiki/images/math/f/b/5/fb500d80de828336751b348a7084bab6.png)
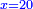
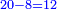
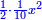
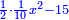
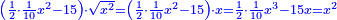
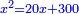
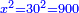
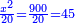
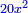
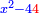

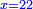
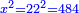
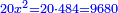


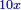 ] and a thing [
] and a thing [ ].
].
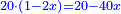
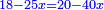
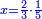
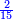
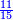
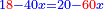
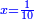

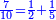

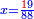
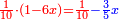
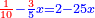
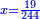
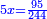
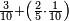 for
for 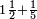
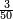 for
for 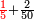
 for
for 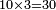 qafiz for 10 dirham
qafiz for 10 dirham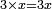 for 3 dirham
for 3 dirham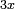 for
for 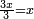 dirham
dirham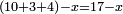 dirham
dirham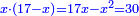
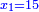 qafiz of sesame
qafiz of sesame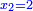 qafiz of sesame
qafiz of sesame