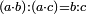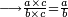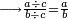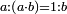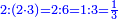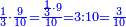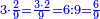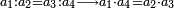Sums
|
|
- To know the numbers that are set in succession.
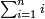
|
לידע מספרים מונחים על סדר המספר
|
- Such as: 1; 2; 3; 4; 5; 6; 7; 8; 9; 10
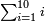
|
כגון אבג"ד ה"ו זחט"י
|
|
|
- Multiply the last number, which is ten, by its half plus one half.
![\scriptstyle{\color{blue}{\sum_{i=1}^{10} i=10\sdot\left[\left(\frac{1}{2}\sdot10\right)+\frac{1}{2}\right]}}](/mediawiki/images/math/c/0/f/c0fdc71237cda523c5f4225f91df85b5.png)
|
תכה מהמספר האחרון שהוא העשרה בחציו וחצי א'
|
|
|
- Or add to it one, then multiply it by its half without the addition - they are 55 and so is their sum.
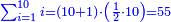
|
או הוסיף עליו אח' והכהו בחציו בלי תוספ' ויהיו נ"ה וככה קבוצם
|
|
|
- If you wish, multiply the last number, which is 10, by itself, the result is 100, add to it the root, which is 10, they are 110, take their half and it is the required.
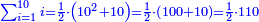
|
ואם תרצה הכה המספר האחרון בעצמו שהוא י' יעלה ק' הוסיף עליו מספר השרש שהוא הי' יהיו ק"י קח חציים והוא המבוקש
|
- Numbers that were summed successively and the result is a known number.
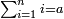
|
חשבון שחובר על הסדר ועלה מספר ידוע
|
- Such as the number 55, how much is the last number?
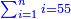
|
כגון מספר נ"ה כמה הוא מספר האחרון
|
|
|
- Multiply it by 2, they are 110, you will find it contains a square and its root together, then the question is true and its root is the last number.
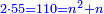
|
תכפלהו בב' יהיו ק"י תמצא בו מרובע וגדרו באחת ואז השאלה אמתית וגדרו הוא סוף המספר
|
- If you wish, add a quarter to its double, then extract the root of the total, subtract the root of the quarter, which is a half, and the remainder is the required.
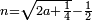
|
ואם תרצה הוסיף רביע אחד על כפלו וקח גדר הכל ותפיל גדר הרביע והוא החצי והנשאר הוא המבוקש
|
- If the numbers that are given in succession do not start from 1.
|
ואם המספרים המונחים על סדר המספר לא יתחילו מהא'
|
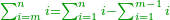
|
|
- As saying: from 5 to 10.
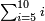
|
כאמרך מה' עד י'
|
- Know their sum from 1 to ten - it is 55; know their sum for 1 to 4 that precedes 5 - it is 10. Subtract it from 55, 45 remains and this is their sum.

|
דע קבוצם מא' עד עשרה הוא נ"ה ודע קבוצם מא' עד ד' שהוא קודם ה' יהיו י' הפלים מהנ"ה ישארו מ"ה וככה קבוצם
|
- Numbers that were summed from a known number.
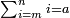
|
חשבון שחובר מתחלת מספר ידוע
|
- As saying: from 5 and the sum is 45, how much is the last number?
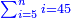
|
כאמרך מה' ועלה מ"ה כמה הוא סוף המספר
|
- Know their sum of the units from 1 to the number that precedes 5, which is 4 - it is 10. Add it to 45, they are 55. Know [up to] which number it is summed according to the previous way, it is 10 and it is the last number.
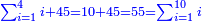
|
דע קבוץ האחדים שמא' עד המספר הקודם לה' שהוא הד' יהיו י' הוסיפם על המ"ה יהיו נ"ה דע מאיזה מספר נתחברו ע"ד הקודם והוא י' וזהו סוף המספר
|
- We know the 10, which is [the last] summed number, and that the sum is 45, but the 5 is unknown.
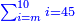
|
ידענו הי' שהוא המספר שהנקבץ עד מ"ה ונעלם הה'
|
- Know [the sum] from 1 to 10, which is 55.
|
תדע מהא' עד י' שהוא נ"ה
|
- Know until what number the sum is the excess of this sum over 45, which is 10, according to the previous way; it is 4 and this is the number that precedes the required.
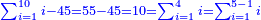
|
ותדע עד איזה מספר נקבץ קבוץ היתרון על המ"ה שהוא י' ע"ד הקודם והוא ד' והמספר שלאחריו הוא המבוקש
|
|
|
Arithmetic progression
|
|
|
|
ואם הם על יחס מספרי וזה על ג' מינים או התחלתם שוה לתוספתם או פחות או יותר
|
|
|
ואם התחלתם שוה לתוספתם יתחילו מהאח' או לא יתחילו
|
- Example:
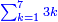
|
כגון מספרי ג' ו' ט' י"ב ט"ו י"ח כ"א שתוספת אלו על אלו שוה למספר הראשון והוא הג'
|
|
|
יש בזה ב' דרכים:
|
-
- Example:
![\scriptstyle{\color{blue}{3+6+9+12+15+18+21=\left[\left(\frac{1}{2}\sdot{7}\right)+\frac{1}{2}\right]\sdot{21}=4\sdot{21}}}](/mediawiki/images/math/7/1/3/71350e31457692457563708b3881ec83.png)
|
הראשון שתקח חצי כמות המדרגות בתוספת חצי ז' שהוא במשלינו זה ד' ותכהו במספר האחרון שהוא הכ"א יעלה פ"ד
|
-
- Example:
![\scriptstyle{\color{blue}{3+6+9+12+15+18+21=\left[\frac{1}{2}\sdot\left(3+21\right)\right]\sdot{7}=\left(\frac{1}{2}\sdot{24}\right)\sdot{7}=12\sdot{7}}}](/mediawiki/images/math/0/2/e/02e542d23f66274e0b78bdf4ab7081c0.png)
|
והב' שתחבר הראשון עם האחרון יהיו כ"ד ותקח חצים והוא י"ב ותכם במנין המדרגות והוא ז' יעלה פ"ד
|
|
|
ואם התחלתם פחות מתוספתם
|
- Example:
![\scriptstyle{\color{blue}{\sum_{k=1}^8 \left[\left[2\sdot\left(k-1\right)\right]+1\right]}}](/mediawiki/images/math/7/a/d/7ad45aa9fb63dddfd4194e85bbaac96c.png)
|
כגון א'ג' ה'ז' ט' י"א י"ג ט"ו שתוספתם שנים והתחלתם מהאחד
|
-
- Example:
![{\color{blue}{\begin{align}\scriptstyle1+3+5+7+9+11+13+15&\scriptstyle=\left[\left[\left(2-1\right)+15\right]\sdot\left[\left(\frac{1}{2}\sdot{8}\right)+\frac{1}{2}\right]\right]-\left[\left(2-1\right)\sdot{8}\right]\\&\scriptstyle=\left[\left(1+15\right)\sdot\left(4+\frac{1}{2}\right)\right]-\left(1\sdot{8}\right)\\&\scriptstyle=\left[16\sdot\left(4+\frac{1}{2}\right)\right]-8=72-8\\\end{align}}}](/mediawiki/images/math/1/1/b/11b77d5c87bf9d959c8549e24258096b.png)
|
נוסיף המגרעת שהוא אחד על המספר האחרון שהוא ט"ו יהיו י"ו ונכם בחצי המדרגות בתוספת חצי שהם ד' וחצי יעלה ע"ב נגרע מהם הכאת המגרעת עם כל המדרגות שהוא הכאת האח' בח' שהם מנין המדרגות יעלה ח' נגרעם מהע"ב ישארו ס"ד וככה קבוצם
|
-
- Example:
![\scriptstyle{\color{blue}{1+3+5+7+9+11+13+15=\left[\frac{1}{2}\sdot\left(1+15\right)\right]\sdot{8}=\left(\frac{1}{2}\sdot{16}\right)\sdot{8}=8\sdot{8}}}](/mediawiki/images/math/9/b/b/9bb5e90d5282d4952e471fa649e02ee1.png)
|
ואם תרצה להשתמש בדרך הב' שנחבר הא' עם הט"ו יהיו י"ו ונקח חציים שהוא ח' ותכם במנין המדרגות שהם ח' יהיו ז' ס"ד וככה קבוצם
|
|
|
ואם יותר מתוספתם
|
- Example:
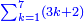
|
כגון מספרי ה'ח' י"א י"ד י"ז כ' כ"ג
|
-
- Example:
![{\color{blue}{\begin{align}\scriptstyle5+8+11+14+17+20+23&\scriptstyle=\left[\left[\left(5-3\right)+23\right]\sdot\left[\left(\frac{1}{2}\sdot{7}\right)+\frac{1}{2}\right]\right]-\left(5-3\right)\\&\scriptstyle=\left[\left(2+23\right)\sdot\left[\left(\frac{1}{2}\sdot{7}\right)+\frac{1}{2}\right]\right]-2\\&\scriptstyle=\left[25\sdot\left[\left(\frac{1}{2}\sdot{7}\right)+\frac{1}{2}\right]\right]-2=100-2\\\end{align}}}](/mediawiki/images/math/2/7/6/2763bf8d6beb4c2cd198a3e747c87e0c.png)
|
תוסיף היתר על התוספת שהוא ב' על המספר האחרון שהוא כ"ג יהיו כ"ה הכם בחצי המדרגות בתוספת חצי יהיו ק' גרע התוספת שהוא ב' ישאר צ"ח וככה קבוצם
|
-
- Example:
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle5+8+11+14+17+20+23&\scriptstyle=\left[\frac{1}{2}\sdot\left[\frac{23-5}{3}+1\right]\right]\sdot\left(5+23\right)\\&\scriptstyle=\left[\frac{1}{2}\sdot\left[\frac{18}{3}+1\right]\right]\sdot\left(5+23\right)\\&\scriptstyle=\left(\frac{1}{2}\sdot{7}\right)\sdot\left(5+23\right)\\\end{align}}}](/mediawiki/images/math/e/3/3/e338f6fb48010cfe5efd298d2313c405.png)
|
ואם תרצה חסר הראשון שהו' הה' מן האחרון שהוא כ"ג ישארו י"ח תחלקהו על מספר תוספתם שהוא ג' והיוצא תוסיף עליו א' יהיו שבעה ושמרם אח"כ חבר הראשון והאחרון והכם בחצי השבעה
|
-
- Example:
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle5+8+11+14+17+20+23&\scriptstyle=\left(\frac{23-5}{3}+1\right)\sdot\left[\frac{1}{2}\sdot\left(5+23\right)\right]\\&\scriptstyle=\left(\frac{18}{3}+1\right)\sdot\left[\frac{1}{2}\sdot\left(5+23\right)\right]\\&\scriptstyle=7\sdot\left[\frac{1}{2}\sdot\left(5+23\right)\right]\\\end{align}}}](/mediawiki/images/math/9/7/e/97ea12068c5e9d1ae4cbedac69b6b2d2.png)
|
או תקח חציים ותכם עם השבעה וככה קבוצם
|
|
|
ואם תרצה תדע אם המספר שממנו צמיחתם שוה לתוספתם
|
- Example:
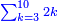
|
כגון מספרי ו' ח' י' י"ב י"ד י"ו י"ח כ'
|
|
תדע מנין המדרגות שממספר שממנו צמיחתם עד המספר האחרון ותדע קבוץ המספרים על דרך הקודם ושמרהו ואח"כ תדע מנין המדרגות שהם מהמספר שממנו צמיחתם עד המספר הקודם לראשון מדרגה אחת ותדע קבוצם על דרך הקודם ותגרע זה מהשמור
|
|
|
ואם המספר שממנו צמיחתם פחות מתוספתם
|
- Example:
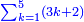
|
כגון מספרי ה'ח' י"א י"ד י"ז
|
|
תדע מנין המדרגות שמהמספר שממנו צמיחתם עד המספר האחרון ותוסיף המגרעת על המספר האחרון ותדע מנין קבוצם ע"ד הקודם תכה חצי כמות המדרגות בתוספת חצי עמו ותגרע מהעולה הכאת המגרע' עם מנין המדרגות שמהמספר שממנו צמיחתם עד המספר האחרון ושמור הנשאר אח"כ תדע מנין המדרגות שמהמספר שממנו צמיחתם עד המדרגה הקודמת למספר המדרגה הראשונה ותחבר עמו מספר המגרעת עם כל המדרגות ותכהו עם חצי המדרגות בתוספת חצי ותגרע מהעולה הכאת המגרעת עם כל המדרגות שמהמספר שממנו צמיחתם עד המדרגה הקודמת למספר הראשון והנשאר תגרעהו מהשמור והוא המבוקש
|
|
|
ולידע מנין המדרגות וגם לידע אם המספר הא' שממנו צמיחתם שוה לתוספתם תחלק המספר האחרון על מספר תוספתם
|
|
|
ואם יצא בחילוק שוה מה שיצא בחילוק הוא מספר המדרגות שמהמספר שממנו צמיחתם עד המספר האחרון והתחלתם שוה לתוספתם
|
|
|
ואם נותר שום מספר מה שיצא בחילוק בתוספת אחת הוא מספר המדרגות שמהמספר שממנו צמיחתם עד המספר האחרון והנותר הוא המספר שממנו צמיחתם והבן
|
|
|
ואם המספר האחרון הוא אשר רצית לידע הכה המותר עם מספר המדרגות חסר אחת והוסיף על העולה מספר הראשון והבן
|
|
|
ויש דרכים אחרים מיוחדים בנושא מיוחד וג"כ עניינים אחרים לידע שאלות החשבון וכו'
|
|
|
Multiplication of Fractions
|
הכאת השברים
|
Multiply the numerator by the numerator, then relate [the product] to the product of the denominator by the denominator.
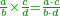
|
שתכה הכמות עם הכמות וניחסהו אל הכאת האיכות עם האיכות
|
Or we multiply the product of the denominators by itself, then we relate to it the result of multiplication of the products of the numerator of one by the denominator of the other.
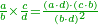
|
או נכה העולה מהכאת האיכות בפני עצמו ונייחס אליו הכאת העולה מהכאת כמות האח' עם איכות חבירו זה בזה
|
Likewise, if fractions of fractions, and fractions of fractions of fractions and so on endlessly are related to integers: we multiply all the numerators by each other, then the product by the integers, whether they are integers or fractions of fractions of integers, then multiply the denominators by their order and relate the product to the product of the numerators by each other.
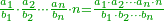
|
וכן אם היו מיוחסים אל שלמים שברי שברים ושברי שברי שברים וכן עד אין תכלית נכה כל האיכיות זה בזה ומה שיתקבץ עם השלימים ואם היו שלמים אחדים או שברי שברים של שלמים תחזור ותכה כל הכמיות על הסדר ותיחס ואם תרצה המקובץ אל הכאת האיכות זה בזה
|
| If you want to sum products of numbers:
|
ואם תרצה לקבץ מספרים מוכים
|
- For instance: you wish to know the sum of the product of two quarters by 2-sixths with the product of 4-fifths by 5-sixths, without having to multiply first then to sum, and still the total result is exact.
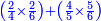
|
כגון שרצית לידע קבוץ הכאת שני רביעיות עם ב' ששיות עם קבוץ הכאת ד' חומשיות עם ה' ששיות מבלתי שתצטרך תחלה להכות ואח"כ לקבץ אבל יצא הכל מתוקן ביחד
|
|
|
|
- Multiply all the denominators by each other; the result is 720, keep it.
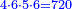
|
תכה האיכיות כלם זה בזה יעלה תש"כ ותשמרם
|
- Multiply the numerator of the first by the denominator of the second; it is 120.
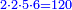
|
אח"כ תכה כמות הראשונים עם איכות השניים יהיו ק"ך
|
- [Multiply] the numerator of the second by the denominator of the first; the result is 480.
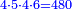
|
וכמות השניים עם איכות הראשונים יעלה ת"ף
|
- Add it to 120; it is 600.

|
חברם אל ק"ך יהיו ת"ר
|
- Relate it to 720; it is 600 parts of 720, which is 5-sixths and so is the sum of the product of these with the product of these.
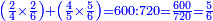
|
יחסם אל תש"כ יהיו ת"ר חלקים מתש"כ והם ה' שישיות וככה העולה מקבוץ הכאת אלו עם קבוץ הכאת אלו
|
| In this way, as many as the numbers are, you multiply the numerators of the whole number by all the denominators.
|
וכן על דרך זה ירבו המספרים מה שירבו תכה כמיות כל המספר עם כל האיכיות
|
- For instance: you wish to know the product of [the sum of] two quarters with two sixths by the sum of 4-fifths with 5-sixths, without having to sum them, then to multiply them, and still the total result is exact.
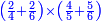
|
כגון שרצית לידע כמה העולה מהכאת הב' רביעיות עם שני ששיות עם קבוץ ד' חומשיות עם ה' ששיות בזול' שתקבצם ואח"כ להכותם אבל יצא הכל מתוקן בפעם אחת
|
- Arrange them as follows:
|
תסדרם ככה
|
|
|
|
- Multiply the numerator of the first by the denominator of the second, the denominator of the third, and the numerator of the fourth; it is 300, keep it.
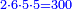
|
תכה כמות הראשון עם אכות הב' ואיכות הג' וכמות הד' יהיו ש' ושמרם
|
- Multiply the numerator of the first by the denominator of the second, the numerator of the third, and the denominator of the fourth; it is 288, keep it.
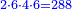
|
אח"כ תכה כמות הראשון עם איכות הב' וכמות הג' ואיכות הד' יהיו רפ"ח ושמרם
|
- Multiply the numerator of the second by the denominator of the first, the denominator of the third, and the numerator of the fourth; it is 200, keep it.
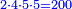
|
אח"כ תכה כמות הב' עם איכות הראשון ועם איכות הג' וכמות הד' יהיו ק"ק ושמרם
|
- Multiply the numerator of the second by the denominator of the first, the numerator of the third, and the denominator of the fourth; it is 192.
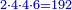
|
אח"כ תכה כמות הב' עם איכות הראשון וכמות הג' ואיכות הד' יהיו קצ"ב
|
- Sum the four reserved; the result is 980.
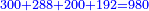
|
חבר הד' השמורים יעלה תתק"ף
|
- Multiply the denominators by each other; the result is 720.
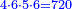
|
ותכה המורים זה בזה עד כלותם יעלה תש"כ
|
- Relate the 980 to it and this is the product of the sum of 2-quarters with two sixths by the sum of 4-fifths with five sixths.
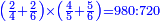
|
יחס התתק"ף אליהם הוא העולה מהכאת קבוץ ב' רביעיות עם שני ששיות עם קבוץ ד' חומשיות עם חמשה ששיות
|
|
|
Methods of checking
|
מאזנים
|
Divide the result of the multiplication by one of the multiplied fractions, whichever you want, and the result of division is the other fraction.
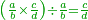
|
שתחלק העולה מההכאה על השב' אחד מהמוכים איזה שתרצה ויעלה השבר האחר בחלוקה
|
- Like this: we multiply 2-quarters by 2-sixths; the result is 4 parts of 24.
|
כיצד הכינו ב' רביעיות עם ב' ששיות ועלה ד' חלקים מכ"ד
|
- We divide them by the 2-quarters; the result of division is two sixths.
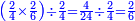
|
נחלקם על הב' רביעיות יצא בחילוק שני ששיות
|
| The division procedure will be explained in its place with God's help.
|
ודרך החלוק יתבאר במקומו בעה"ו
|
Other scales: multiply the difference between the smaller fraction and 1 by the other. We sum the result with the primary product and [the sum] is equal to the greater fraction.
![\scriptstyle{\color{OliveGreen}{\left[\left(1-\frac{c}{d}\right)\times\frac{a}{b}\right]+\left(\frac{a}{b}\times\frac{c}{d}\right)=\frac{a}{b}}}](/mediawiki/images/math/7/4/4/744b88e33933bda6d8cf81e3fa9253ba.png)
|
מאזנים אחרים שתכה ההב' שבין השבר הקטן עד תשלום הא' שלם עם חבירו ונקבץ העולה עם העולה מהכאה ראשונה וישוה לשבר הגדול
|
- In this example, we multiply 2-quarters by 2-sixths; the result is 4 parts of 24.
|
במשל זה הכינו ב' רביעיות עם ב' ששיות ועלה ד' חלקים מכ"ד
|
- We take the smaller fraction, which is 2-sixths, the difference between it and the unit is 4-sixths.
|
לקחנו השבר הקטן והוא הב' ששיות וההבדל שבינו ובין השלם ד' ששיות
|
- We multiply it by 2-quarters, which is the greater fraction; the result is 8 parts of 24.
|
הכינום עם ב' רביעיות שהוא השבר הגדול ועלה ח' חלקים מכ"ד
|
- We sum it with the 4 parts of 24, which is the primary product; [the sum] is 12 parts of 24 that are 2-quarters.
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left[\left(1-\frac{2}{6}\right)\times\frac{2}{4}\right]+\left(\frac{2}{4}\times\frac{2}{6}\right)&\scriptstyle=\left(\frac{4}{6}\times\frac{2}{4}\right)+\frac{4}{24}\\&\scriptstyle=\frac{8}{24}+\frac{4}{24}=\frac{12}{24}=\frac{2}{4}\\\end{align}}}](/mediawiki/images/math/8/5/e/85e0d0186ccbd8de9315c4c355b58d33.png)
|
קבצנו אותם עם הד' חלקים מכ"ד שהיא ההכאה הראשונה והם י"ב חלקים מכ"ד והם הב' רביעיות
|
- If you want to verify that they are indeed 2-quarters, arrange them as follows:
|
ואם תרצה לאמת אם הם בעצמם הב' רביעיות סדרם ככה
|
|
|
|
Cross-multiply the numerator of the one by the denominator of the other and [the result] is equal to the product of the denominator of the one by the numerator of the other. Understand [this].
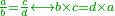
|
ותכה אלכסונות כמות הא' עם איכות חבירו וישו' העולה מהכאת כמות האחד עם איכות חבירו והבן
|
|
|
מאזנים אחרים נקח כמות השבר היוצא מהכאת השברים המוכים ונבקש מספר שיהי' יחסו אליו יחס השבר האח' מהשברים המוכים איזה שתרצה ואם היחס מספר המבוקש אל איכות השבר היוצא מהכאת השברים המוכים שוה אל יחס השבר הנשאר צדקת
|
- In our example: we multiply the 2-quarters by 2-sixths; the result is 4 parts of 24.
|
במשלינו זה הכינו הב' רביעיות עם הב' ששיות ועלה ד' חלקים מכ"ד
|
- We look for a number, to which the 4 that is the numerator resulting from the product of the multiplied fractions is related by the ratio of 2-quarters or 2-sixths.
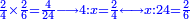
|
נבקש מספר שיהיה מיוחס אליו הד' שהוא הכמות היוצא מהכאת השברים המוכי' יחס ב' רביעיות או ב' ששיות
|
|
|
ודרך ידיעת זה הוא שנסדרם ככה
|
|
|
|
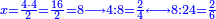
|
ונכה האלכסונות שהם ד' עם ד' יעלה י"ו נחלקם על השנים שהוא איכות הב' רביעיות יעלה ח' ונשים אותו תחת הד' הב' נמצא שארבעה מח' הוא יחס הב' רביעיות וניחס מספר המבוק' שהוא הח' אל איכות השבר היוצא מההכאה שהוא כ"ד ונמצא שהם ב' ששיות ממנו וזהו השבר האחד הנשאר
|
- Example:
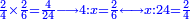
|
ואם תרצה לעשות המאזנים בהכ' שתבקש מספר שיהיה יחסו הד' אליו כיחס הב' שישיות
|
|
|
וזה בשנסדרם ככה
|
|
|
|
- Cross-multiply the 6 by the 4; the result is 24.
|
ותכה האלכסון שהוא הו' עם הד' יעלה כ"ד
|
- Divide it by 2; the quotient is 12. Write it beneath the 4.
|
חלקם על הב' יעלה י"ב בחלוקה ותשימים תחת הד'
|
- Take the 12 and relate it to the 24, of which it is 2-quarter, and this is the other fraction itself.
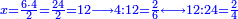
|
ותקח הי"ב ותיחסם אל הכ"ד והם ב' רביעיו' ממנו והוא בעצמו השבר האחר
|
|
|
Subtraction of Fractions
|
דרך החסור
|
|
|
ועתה נתחיל לבאר דרך החסור בע"ה ואו' שהדרך היותר כולל הוא שתכה כמות האחד עם איכות חבירו וכמות האחר עם איכות חבירו וחסר זה מזה והנשאר [תיחס] אל הכאת האיכות
|
|
|
או תחלקהו על המורים ע"ד הקודם בשתעשה להם כלילת יופי והוא המבוקש
|
- Example:
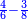
|
דרך משל רצינו לחסר ג' שמניות מד' ששיות כזה הצורה
|
|
|
|
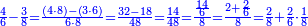
|
תכה כמות הג' עם איכות הד' יהיו י"ח ותכה הכמות האחר עם איכות חבירו יהיו ל"ב תחסר מהם י"ח ישאר י"ד ותכה האיכיות והם הח' בו' יהיו מ"ח והם י"ד חלקים ממ"ח או תחלק הי"ד על הו' יעלה ב' וישארו ב' והם שני שמניות וב' ששיות וככה צורתם
|
|
|
|
|
|
והוא הנשאר מחסור הג' שמניות מד' ששיות
|
![\scriptstyle{\color{blue}{\frac{4}{6}-\frac{3}{8}=1-\left[\frac{3}{8}+\left(1-\frac{4}{6}\right)\right]=1-\left(\frac{3}{8}+\frac{2}{6}\right)=1-\frac{34}{48}=\frac{14}{48}}}](/mediawiki/images/math/e/6/c/e6c3bf2ae9c4471daa25e36009354632.png)
|
דרך אחרת שתשלים השבר הגדול שהוא ד' ששיות לא' שלם והנה השלמנום בשני ששיות קבצנום עם השבר הקטן והוא הג' שמניות יעלה ל"ד חלקים ממ"ח השלמנום לאח' שלם בי"ד חלקי' ממ"ח והוא המבוקש
|
![\scriptstyle{\color{blue}{\frac{4}{6}-\frac{3}{8}=\left[\frac{4}{6}+\left(1-\frac{3}{8}\right)\right]-1=\left(\frac{4}{6}+\frac{5}{8}\right)-1=\left(1+\frac{14}{48}\right)-1=\frac{14}{48}}}](/mediawiki/images/math/c/8/e/c8e205993be6c43b6e513b1a1e954a51.png)
|
ואם תרצה קבץ החסר מהשבר הקטן והוא הג' שמניות השלמנום לאח' שלם בה' שמניות נקבצו עם הד' ששיות ועלה א' שלם וי"ד חלקים ממ"ח והשלכנו האחד השלם ומה שישאר הוא המבוקש
|
Methods of checking
|
מאזנים
|
|
|
שתקבץ הנשאר מחיסור השבר מהשבר עם השבר הגדול והעולה מקבוצם חסר ממנו הקטן והנשאר ממנו אם היה כפל הנשאר מהחסור צדקת
|
- Example:
![{\color{blue}{\begin{align}\scriptstyle\left[\frac{4}{6}+\left(\frac{4}{6}-\frac{3}{8}\right)\right]-\frac{3}{8}&\scriptstyle=\left(\frac{4}{6}+\frac{14}{48}\right)-\frac{3}{8}\\&\scriptstyle=\frac{276}{288}-\frac{3}{8}\\&\scriptstyle=\frac{1344}{2304}\\&\scriptstyle=2\sdot\frac{14}{48}=2\sdot\left(\frac{4}{6}-\frac{3}{8}\right)\\\end{align}}}](/mediawiki/images/math/8/7/2/8728716975997ba60a517668eccbd8ac.png)
|
במשלינו זה קבצנו הי"ד חלקים ממ"ח עם הד' ששיות ועלה רע"ו חלקי' מרפ"ח חסרנו מהם הג' שמניות ונשאר אלף ושמ"ד חלקים מהאלפים וש"ד והם כפל הי"ד חלקים ממ"ח
|
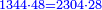
|
והמופת שתשי' ה[כ"]ד חלקים ממ"ח והאלף ושמ"ד חלקים מאלפים וש"ד בזאת הצורה
|
|
|
|
|
|
ותכה האלכסונות ויהיו שוים
|
|
|
מאזנים אחרים שתקבץ הנשאר מחיסור השבר מהשבר עם השבר הקטן ואם ישוה לגדול צדקת
|
- Example:
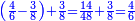
|
הרי קבצנו הי"ד חלקים ממ"ח עם הג' שמניות ועלה ד' ששיות
|
|
|
מאזנים אחרים חסר הנשאר מהשבר הגדול והנשאר אם ישוה לקטן דע שצדקת
|
- Example:
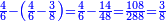
|
במשלינו זה חסרנו הארבעה עשר חלקים ממ"ח מד' ששיות ישארו ק"ח חלקים מרפ"ח והם הם הג' שמיניות
|
|
|
והמופת שתסדרם ככה
|
|
|
|

|
ותכה האלכסונות ויהיו שוים ודי למבין
|
|
|
מאזנים אחרים חסר הנשאר מהשבר הגדול והנשאר אם שוה לקטן דע שצדקת
|
|
|
במשלינו זה חסרנו הי"ד חלקים ממ"ח מד' ששיות ישארו ק"ח חלקים מרפ"ח והם הם הו' שמיניות
|
Combined Subtraction
|
|
![{\color{OliveGreen}{\begin{align}&\scriptstyle\left(\frac{a_1}{b_2}+\frac{a_2}{b_2}+\cdots+\frac{a_n}{b_n}\right)-\left(\frac{c_1}{d_2}+\frac{c_2}{d_2}+\cdots+\frac{c_m}{d_m}\right)\\&\scriptstyle=\frac{\sum_{k=1}^n \left[a_k\sdot\left(\prod_{i=1,i\neq k}^n b_i\right)\sdot\left(\prod_{i=1}^m d_i\right)\right]-\sum_{k=1}^m \left[c_k\sdot\left(\prod_{i=1,i\neq k}^m d_i\right)\sdot\left(\prod_{i=1}^n b_i\right)\right]}{\prod_{k=1}^n b_k\sdot\prod_{i=1}^m d_i}\\\end{align}}}](/mediawiki/images/math/4/d/c/4dcd5d89beb5c0da5e72607633288b70.png)
|
ואולם אם רצית לחסר שברים רבים משברים רבים מבלתי שתצטרך לקבץ תחלה ואח"כ לחסרם הנה תוכל להשתמש בזה הדרך
|
- Example:
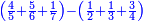
|
|
- Multiply all the denominators by each other, the result is 5040

|
תכה כל האיכיות זה בזה יעלה 5040
|
- Multiply the [each] numerator of the subtrahend by all the denominators except its denominator, the result is 7980
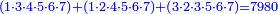
|
ותכה כמות השבר הנחסר עם כל איכיות זולת איכותו וכן כל איכות הכמות מהנחסר יעלה 7980
|
- Do the same with all the numerators [of the minuend], the result is 8952
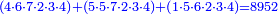
|
וכן תעשה לכל הכמיות אשר יוחסרו השברים מהם ויעלה ח' אלפים ותתקנ"ב
|
|
ותחסר מהם הז' אלפים ותתק"ף ישארו תתקע"ב והם תתקע"ב חלקים מה' אלפים ומ'
|
![{\color{OliveGreen}{\begin{align}&\scriptstyle\left(\frac{a_1}{b_1}-\frac{c_1}{d_1}\right)+\left(\frac{a_2}{b_2}-\frac{c_2}{d_2}\right)+\cdots+\left(\frac{a_n}{b_n}-\frac{c_n}{d_n}\right)\\&\scriptstyle=\frac{\sum_{k=1}^n \left[a_k\sdot\left(\prod_{i=1,i\neq k}^n b_i\right)\sdot\left(\prod_{i=1}^m d_i\right)\right]-\sum_{k=1}^n \left[c_k\sdot\left(\prod_{i=1,i\neq k}^n d_i\right)\sdot\left(\prod_{i=1}^n b_i\right)\right]}{\prod_{k=1}^n b_k\sdot\prod_{i=1}^n d_i}\\\end{align}}}](/mediawiki/images/math/8/d/3/8d3aec6a4bbf87b62d0cbba13d6ac7d2.png)
|
ואולם אם רצית לדעת העולה מכל הנשארים מחסרונו' שברים רבים משברים רבים מבלתי שתצטרך לחסרם תחלה ואח"כ לקבצם
|
- Example:
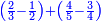
|
לחסר החצי מב' שלישיות וג' רביעיות מד' חומשיות
|
|
|
|
|
נכה האיכיות יעלו ק"כ
|
|
נכה כמות השבר הנחסר מהראשון עם כל האיכיות חוץ מאיכותו והם ס'
|
|
גם נכה כמות השבר הנחסר מהב' עם כל האיכיות זולת אכותו והם צ'
|
|
קבצם עם הס' הם ק"נ
|
|
אח"כ הכה השבר הגדול אשר ממנו יחוסר הקטן מהמין הראשון עם כל איכות זולת מאיכותו וכן כמות השבר הגדול אשר ממנו ויחוסר הקטן מהמין הב' וקבצהו עם הראשון והם קע"ו
|
|
נחסר מהם הק"נ וישארו כ"ו והם כ"ו חלקים מק"נ
|
![{\color{OliveGreen}{\begin{align}&\scriptstyle\left(\frac{a_1}{b_1}\times\frac{a_2}{b_2}\times\cdots\times\frac{a_n}{b_n}\right)-\left(\frac{c_1}{c_1}\times\frac{c_2}{c_2}\times\cdots\times\frac{c_m}{d_m}\right)\\&\scriptstyle=\frac{\left[\left(\prod_{i=1}^n a_i\right)\sdot\left(\prod_{j=1}^m d_j\right)\right]-\left[\left(\prod_{j=1}^m c_j\right)\sdot\left(\prod_{i=1}^n b_i\right)\right]}{\prod_{i=1}^n b_i\sdot\prod_{j=1}^m d_j}\\\end{align}}}](/mediawiki/images/math/4/6/f/46fa9a817ecbb4234aa0243bd14a7c22.png)
|
ואולם אם רצית לדעת הנשאר מחסור העולה מהכאת השברים אחדים עם שברים מבלתי שתצטרך לדעת העולה מהכאת השברים ההם
|
- Example:
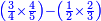
|
כמו עד"מ רצית לדעת מחיסור העולה מהכאת החצי עם ב' שלישיות מהעולה מהכאת הג' רביעיות עם ד' חומשיות מבלתי שתצטרך להכות החצי עם הב' שלישיות והג' רביעיות עם הד' חומשיות הנה יסודרו בזה הדרך
|
|
|
|
|
נכה כל האיכיו' והם ק"כ
|
|
ונכה השברים הנחסרים הכמות עם הכמות והעולה עם איכות השברים הגדולים אשר יוחסרו הקטנים מהם והם מ'
|
|
ונכה כמות השברים הגדולים הכמות עם הכמות והעולה עם כל איכיות השברים הקטנים והם ע"ב
|
|
נחסר מהם מ' ישארו ל"ב והם ל"ב חלקים מק"כ
|
![{\color{OliveGreen}{\begin{align}&\scriptstyle\left(\frac{a_1}{b_1}-\frac{c_1}{d_1}\right)\times\left(\frac{a_2}{b_2}-\frac{c_2}{d_2}\right)\\&\scriptstyle=\frac{\left[\left(a_1\sdot d_1\right)-\left(c_1\sdot b_1\right)\right]\times\left[\left(a_2\sdot d_2\right)-\left(c_2\sdot b_2\right)\right]}{b_1\sdot d_1\sdot b_2\sdot d_2}\\\end{align}}}](/mediawiki/images/math/a/5/7/a57b58619cb3cdaff8f457f98a6a022f.png)
|
ואולם אם רצית לדעת העול' מהכאת הנשאר מחיסור שברים מה משברים מה עם הנשאר מחיסור השברים מה משברים מה מבלתי שתצטרך לדעת הנשארים מהחסורים ההם כלל
|
- Example:
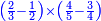
|
כמו עד"מ אם רצית לדעת העולה מהכאת הנשאר מחסור החצי מב' שלישיו' עם הנשאר מחיסור הג' רביעיות מהד' חמשיות הנה יסודרו ע"ז הדרך
|
|
|
|
![{\color{blue}{\scriptstyle\left(\frac{2}{3}-\frac{1}{2}\right)\times\left(\frac{4}{5}-\frac{3}{4}\right)=\frac{\left[\left(2\sdot2\right)-\left(1\sdot3\right)\right]\times\left[\left(4\sdot4\right)-\left(3\sdot5\right)\right]}{3\sdot2\sdot5\sdot4}}}](/mediawiki/images/math/3/c/c/3cc16132d344c4acfadd35fb7d6cbd3a.png)
|
נכה האיכיות והם ק"כ
|
|
|
אח"ז נחסר העולה מהכאת אלכסון א"ג מהכאת אלכסון ב"ב והנשאר נשמרהו
|
|
|
גם נחס' העול' מהכאת אלכסון ג"ה מהעולה מהכאת אלכסון ד"ד והנשאר נשמרהו
|
|
|
ואח"ז נכה הנשאר עם הנשאר וההווה נייחסהו אל השמור הראשון וההוה הוא העולה מהכאת הנשאר מחסור החצי מהב' שלישיו' עם הנשאר מחסור הג' רביעיות מד' חמשיות
|
![{\color{OliveGreen}{\begin{align}&\scriptstyle\left[\left(\frac{a_1}{b_1}\times\frac{c_1}{d_1}\right)+\left(\frac{a_2}{b_2}\times\frac{c_2}{d_2}\right)+\cdots+\left(\frac{a_n}{b_n}\times\frac{c_n}{d_n}\right)\right]-\\&\scriptstyle-\left[\left(\frac{a_{n+1}}{b_{n+1}}\times\frac{c_{n+1}}{d_{n+1}}\right)+\left(\frac{a_{n+2}}{b_{n+2}}\times\frac{c_{n+2}}{d_{n+2}}\right)+\cdots+\left(\frac{a_{n+m}}{b_{n+m}}\times\frac{c_{n+m}}{d_{n+m}}\right)\right]\\&\scriptstyle=\frac{\left[\sum_{k=1}^n \left[\left(a_k\sdot c_k\right)\sdot\prod_{i=1,i\neq k}^{n+m} \left(b_i\sdot d_i\right)\right]\right]-\left[\sum_{k={n+1}}^{n+m} \left[\left(a_k\sdot c_k\right)\sdot\prod_{i=1,i\neq k}^{n+m} \left(b_i\sdot d_i\right)\right]\right]}{\prod_{i=1}^{n+m} b_i\sdot\prod_{i=1}^{n+m} d_i}\\\end{align}}}](/mediawiki/images/math/8/9/2/892a36331b9e37d892c0a0ee6c19faa1.png)
|
ואולם אם רצית לדעת הנשאר מחסור העולה מקבוץ העולה מהכאות שברים מהעולה מקבוץ העולים מהכאת שברים מה מבלתי שתצטרך להכות ואח"ז לקבץ ואח"ז לחסר אבל יצאו לך שלשתן בפעם אחת
|
- Example:
![{\color{blue}{\scriptstyle\left[\left(\frac{1}{2}\times\frac{2}{3}\right)+\left(\frac{3}{4}\times\frac{4}{5}\right)\right]-\left[\left(\frac{3}{7}\times\frac{4}{5}\right)+\left(\frac{2}{3}\times\frac{1}{4}\right)\right]}}](/mediawiki/images/math/b/b/d/bbd1d7fd145240388f8000054956bb7f.png)
|
עד"מ רצית להכות חצי עם ב' שלישיו' וג' רביעיות עם ד' חמשיות וג' שביעיות עם ד' חמשיות וב' שלישיות עם ג' רביעיות ואח"ז לקבץ העולה מהכאת החצי עם הב' שלישיות עם העולה מהכאת ג' רביעיות עם ד' חמשיו' והעולה מהכאת הג' שביעיות עם ד' חמשיות עם העולה מהכאת הב' שלישיות עם הרביע אח"ז לחסר ההוה מהקבוץ מההוה מהקבוץ לדעת הנשאר הנה יסודרו על זה הסדר
|
|
|
|
|
נכה כל האיכיות והם נ' אלף ות'
|
|
נכה כמות הב' שברים הראשונים זה עם זה והעולה עם כל האיכיות על הסדר הזה חוץ מאיכיותיו והם י"ו אלף ות"ת
|
|
גם נכה כמות הב' שברים השניי' העול' עם כל האכיות על הסדר חוץ אכיותיו והם ל' אלף ור"מ
|
|
ונקבצם עם י"ו אלפים ות"ת והם מ"ז אלף ומ' ונשמרם
|
|
אח"ז נכה הב' שברים מהשלישיי' זה עם זה והעולה עם האכיות כולם חוץ מאכיותיהם והם י"ז אלף ור"פ
|
|
גם נכה כמות הב' שברים הרביעיים זה עם זה והעולה עם כל האיכיות חוץ מאכיותיהן והם ח' אלפים ות'
|
|
נקבצם עם הי' אלף ור"פ והם כ"ה אלף ותר"פ
|
|
נחסרם מהשמור הב' וישארו כ"א אלף ש"ס והם כ"א אלף ש"ס [..] נ' אלף ות"ת
|
Division
|
|
Dividing a large number by a smaller number
|
|
| Dividing a certain amount among people, giving each one twice as much as his friend
|
כאשר תרצה לחלק מספר מה אל אנשים מה ולתת לכל אח' כפל חבירו
|
- Example: dividing 100 among four people, giving each one twice as much as his friend
|
כגון שתרצה לחלק ק' אל ד' אנשים ולתת לכל אחד כפל חבירו
|
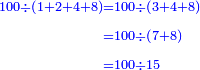
|
ככה תעשה דע א' כמה יתחבר וזה שחלק הא' נקחהו כמו שהוא אח' והחלק ב' הרי ג' והחלק ג' ד' הרי ז' והחלק הד' ח' הרי ט"ו חלק ק' על ט"ו והיוצא הוא חלק הראשון ולדעת הב' כפלהו בו כן לעולם
|
|
|
ומזה תבין לכל השאלות שבזה המין והבן
|
Small number by a larger number
|
לחלק מספר מעט על מספר רב
|
| The method: dividing the larger number by the smaller number
|
תחלק הרב על המעט
|
- If there is no remainder - the result is the denominator:
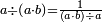
|
אם יתחלק לו לשלמים בלתי תוספת ומגרע' הנה היוצא בחלק בצמצום הוא מורה החלק אשר הם כל השברים הנשאלים יחד מהשלם
|
- Example:
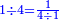
|
ר"ל שאם יצא בחלוק ד' הנה יבא לו רביעית הא' ובדומה לזה
|
- If the remainder is 1:
![\scriptstyle a\div\left[\left(a\sdot b\right)+1\right]=\frac{1}{\left[\left(a\sdot b\right)\div a\right]+1}+\left(\frac{1}{\left[\left(a\sdot b\right)\div a\right]+1}\sdot\frac{a-1}{\left(a\sdot b\right)+1}\right)](/mediawiki/images/math/8/4/0/840986bc829b9c0631a46fea168fe09c.png)
|
ואם לא יתחלק כלו לשלמים וישאר שום מספר הנה נוסי' אח' ועלה יוצא בחלוק ונחסר הנשאר מהמספר אשר חלקו ועליו ומה שישא' הם חלקים מכל המורים
|
- Example:
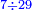
|
המשל רצינו לחלק ז' על כ"ט
|
![{\color{blue}{\begin{align}\scriptstyle7\div29&\scriptstyle=\frac{1}{\left[\left(29-1\right)\div7\right]+1}+\left(\frac{1}{\left[\left(29-1\right)\div7\right]+1}\sdot\frac{7-1}{29}\right)\\&\scriptstyle=\frac{1}{4+1}+\left(\frac{1}{4+1}\sdot\frac{6}{29}\right)\\&\scriptstyle=\frac{1}{5}+\left(\frac{1}{5}\sdot\frac{6}{29}\right)\\\end{align}}}](/mediawiki/images/math/7/a/6/7a69fe025577e0f20f925c87624417be.png)
|
נעשה ההפך נחלק הכ"ט על הז' יצא בחלוק ד' ובשביל שנשאר א' בלא נוסי' על הד' א' ויהיה ה' והוא ה' ונחסר הא' מז' ישארו ו' והם ו' חלקים מכ"ט בחמישית נוסף שהעלה חמישי' שיש בידינו
|
- If the remainder is greater than 1:
![\scriptstyle a\div\left[\left(a\sdot b\right)+c\right]=\frac{1}{\left[\left(a\sdot b\right)\div a\right]+1}+\left(\frac{1}{\left[\left(a\sdot b\right)\div a\right]+1}\sdot\frac{a-c}{\left(a\sdot b\right)+c}\right)](/mediawiki/images/math/1/0/c/10c67f4a03765d28d7de9dbe21d73433.png)
|
ואם תרצה שיצאו לך חלקים יותר
|
- Example:
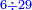
|
חלק הכ"ט על הו'
|
![{\color{blue}{\begin{align}\scriptstyle6\div29&\scriptstyle=\frac{1}{\left[\left(29-5\right)\div6\right]+1}+\left(\frac{1}{\left[\left(29-5\right)\div6\right]+1}\sdot\frac{6-5}{29}\right)\\&\scriptstyle=\frac{1}{4+1}+\left(\frac{1}{4+1}\sdot\frac{1}{29}\right)\\&\scriptstyle=\frac{1}{5}+\left(\frac{1}{5}\sdot\frac{1}{29}\right)\\\end{align}}}](/mediawiki/images/math/2/4/6/2465c314f8c1caf95b9e720b4d017ec4.png)
|
יצא בחלוק ד' וישארו ה' נוסי' א' על הד' ויהיו ה' ונחסר הה' אל הו' כאמור וישאר א' והעולה הוא ה' א' וחמישית ה' א' וחלק מכ"ט מחמישית חמישית אחד וזו צורתם
|
|
|
|
Check: conversion of fractions 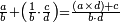
|
והמופת שנעשם פריטה
|
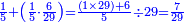
|
שתכה הא' בה' ותשא מה שעל ראש' ותכה הכל עם הכ"ט ותשא מה שעל ראשם ותחלק הכל לכל המורים זולת הכ"ט ויצא לך מספ' הז' שלם בלי תוספת ומגרעת
|
|
|
ואם לא יהיה במורים המספר אשר תרצה לחלק עליו המספר האחד
|
- the last sentence is unclear
|
כגון אם רצית לחלק ו' לכ"ז שיבא לו חמישי' אח' בכ"ז ותחלקהו על כל המורי' זולתו ויצא לך בשוה המספר
|
Division of Fractions [= Converting Fractions]
|
מין החלוק מן השברים
|
- Example:

|
רצית לחלק ג' רביעיות על שני חמישיות
|
|
|
|
![{\color{blue}{\begin{align}\scriptstyle\frac{3}{4}&\scriptstyle=\frac{2}{5}\sdot\frac{3\sdot5}{4\sdot2}\\&\scriptstyle=\frac{2}{5}\sdot\frac{15}{8}\\&\scriptstyle=\frac{2}{5}\sdot\left(1+\frac{7}{8}\right)\\&\scriptstyle=\frac{2}{5}+\frac{7}{4\sdot5}\\&\scriptstyle=\frac{2}{5}+\frac{7}{20}\\&\scriptstyle=\frac{2}{5}+\left[\frac{1}{5}+\left(\frac{3}{4}\sdot\frac{1}{5}\right)\right]=\frac{3}{5}+\left(\frac{3}{4}\sdot\frac{1}{5}\right)\\\end{align}}}](/mediawiki/images/math/f/9/6/f96aade01caac4e8ac0e5e38a88af98e.png)
|
הכה הב' עם הד' יהיו ח' אח"כ הכה הג' עם הה' יהיו ט"ו חלק הט"ו על הח' יצא א' שלם הרי יצא לנו שני חמישיות ונשארו ז' יחסם על הכ' שהו' הכאת האיכות עם האיכות יעלה ז' מכ' אח"כ חלקם על החומש ויצא חומש אח' וג' רביעיות חומש חברהו עם הב' חמישיות והיוצא הוא המבוקש והוא ג' חמישיות וג' רביעיות החומש האח'
|
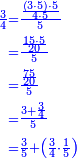
|
דרך אחר נכה הג' עם הה' כמות המחלק עם איכות המחלק יעלה ט"ו והכה הט"ו עם איכות המחלק שהוא הה' יעלה ע"ה וזהו המחולק אח"כ נכה האיכיות והם כ' נחלק עליהם הע"ה יצאו ג' וג' רביעיות ולהיות שהמחולק הוא חמישיות ידענו שהג' וג' רביעיות חמשיות וג' רביעיות החומש
|
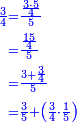
|
דרך אחר נכה כמות המחולק עם איכות המחלק יהיו ט"ו נחלקם על איכות המחולק יצאו ג' וג' רביעיות ולהיות שהמחול' הוא חמישי' ידענו שהג' וג' רביעיות הם ג' חמשיות וג' רביעיות החומש
|
Methods of checking
|
מאזנים
|
|
|
תכה החלק עם המחלק אם הוא שוה למחולק צדקת
|
- Example:
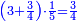
|
במשלינו זה הכינו הג' וג' רביעיו' עם החמישי' ועלה ג' רביעיות והוא הוא בעצמו המחולק
|
- Example:
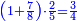
|
או נכה א' וז' שמיניות עם ב' חמישיות ויעלה בעצמו הג' רביעיות
|
![\scriptstyle{\color{blue}{\left(1+\frac{7}{8}\right)\sdot\frac{2}{5}=\frac{2}{5}+\left(\frac{7}{8}\sdot\frac{2}{5}\right)=\frac{2}{5}+\left[\frac{1}{5}+\left(\frac{3}{4}\sdot\frac{1}{5}\right)\right]=\frac{3}{5}+\left(\frac{3}{4}\sdot\frac{1}{5}\right)=\left(3+\frac{3}{4}\right)\sdot\frac{1}{5}}}](/mediawiki/images/math/6/1/0/6103c77a142273f502b27e272a7e4b89.png)
|
וזה שא' וז' שמיניות כשיוחס אל הב' חמישיות שהם א' וז' שמיניות כמותם ר"ל הא' הוא ב' חמישיות וז' שמיניו' הם ז' שמיניות של ב' חמישיו' שהוא חומש א' וג' רביעיו' החומש עם הב' חומשים שבידינו הם ג' רביעיות וג' רביעיו' החומש וא"כ הכל שוה לאמרנו ג' וג' רביעיות ויחסנו אותם לחומש או א' וז' שמיניות ויחסנו אותם לב' חמישיו' וזה מבואר בעין השכל והבן
|
|
|
מאזנים אחרים שתמצא המספ' המתיחס כמות המחלק אליו יחס כמות המחלק אל איכותו ואם המספר ההוא מתיחס אל איכות המחולק יחס כמו' החלק אל איכותו דע שצדקת
|
- Example:
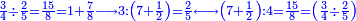
|
במשלינו זה חלקנו הג' רביעיות על הב' חמשיות ויצא א' וז' שמיניות שהם ט"ו שמיניות בקשנו מספר שתיחס כמות המחולק שהוא הג' אליו יחס כמות המחלק אל איכותו שהוא הב' אל הה' ומצאנו שהוא ז' וחצי והנה יחס הז' וחצי אל הד' שהוא איכות המחולק כיחס כמות החלק שהוא הט"ו אל איכותו שהוא ח' וזה מבואר בעין השכל
|
|
|
וג"כ אם תרצה לעשותו בזה הדרך בג' וג' רביעיות ותבקש ביחס החמישית לבד גם עשה תעשה ויכול תוכל כי הכל דבר א' כמו שביארנו וגלינו
|
|
|
ואם תרצה לעשות המאזנים בהפך והוא שתראה המסופר שיהיה יחס כמות המחולק אליו כיחס כמות המחלק אל איכותו
|
|
|
ואם המספר ההוא מתחלק אל איכות המחולק כיחס כמות המחלק אל איכותו ידענו שצדקנו
|
- Example:
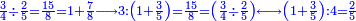
|
במשלינו זה בקשנו מספר שיהיה יחס כמות מחולק אליו שהוא ג' כיחס כמות החלק אל איכותו שהוא הט"ו עם הח' ומצאנו שהוא א' וג' חמישיות שהם ח' שמיניות ויחסם אל הד' הוא כיחס הב' אל הה' שהוא כמות המחלק אל אכותו והבן זה מאד כי הובן בתכלית
|
Combined Division
|
|
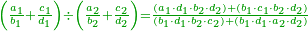
|
|
|
|
ואולם אם רצית לחלק קבוץ הב' שלישיות וג' רביעיו' על קבוץ שני שביעיות וששית מבלתי שתצטרך לקבץ תחלה ואח"כ לחל' הנה יסודרו על זה הדרך
|
|
|
|
|
ונכה איכות השבר הראשון עם איכות השבר הב' והעולה עם איכות הג' והעולה עם כמו' הד' והם פ"ד
|
|
גם נכה איכות השבר הראשון עם איכות השבר הב' והעול' עם כמות הג' והעול' עם איכות הד' והם קמ"ד ונשמרם
|
|
נחברם אל הפ"ד והם רכ"ח ונשמרם
|
|
אח"ז נכה איכות הד' עם איכות הג' והעולה עם אכות הב' והעולה עם כמות הראשון והם של"ו
|
|
גם נכה איכות הרביעי עם איכות הג' והעולה עם כמות הב' והעולה עם איכות הראשו' והם שע"ח
|
|
חברם אל השל"ו הם תשי"ד
|
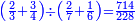
|
נחלקם על הרכ"ח השמורים והיוצא הוא ההווה מחלוק הב' שלישיו' וג' רביעיו' על הב' שביעיות וששית
|
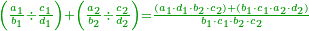
|
|
|
|
ואולם אם רצית לקבץ היוצא מחלוק הג' רביעיות על הב' שלישיות עם היוצא מחלוק הב' שביעיו' על הו' מבלתי שתצטרך לחלק תחלה ואח"כ לקבץ
|
|
נכה כמות השבר הראשון עם איכות הב' ועם איכות הג' ועם כמות הד' והם נ"ו ונשמרם
|
|
אח"ז נכה כמות השבר הראשון עם איכות הב' וכמות הג' ואיכות הד' והם צ"ו
|
|
גם נכה כמות השבר הד' עם איכות הג' וכמות הב' ואיכות הראשו' והם ס"ג
|
|
נחברם אל הצ"ו והם קנ"ט
|
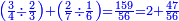
|
נחלקם על הנ"ו השמורים והיוצא הוא ב' שלמים ומ"ה חלקים מנ"ו והוא המבוקש מקבוץ היוצאים מחלוק הג' רביעיות על הב' שלישיו' ומחלוק הב' שביעיו' על הו'
|
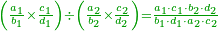
|
|
|
|
ואולם אם רצית לחלק העולה מהכאת הב' שלישיו' עם הג' רביעי' על העולה מהכאת הב' שביעיו' עם הששי' מבלתי שתצטר' להכות תחלה ואח"כ לחלק
|
|
נכה כמות הראשו' עם הב' והעול' עם איכות הג' ואיכות הד' והם רנ"ב ונשמרם
|
|
אח"ז נכה כמות השבר הד' עם כמו' השבר הג' והעולה עם איכות הראשו' והב' והם כ"ד
|
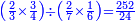
|
תחלק עליהם הרל"ב והיוצא הוא ההווה מחלוק העולה מהכאת הב' שלישיו' עם הג' רביעיו' על העולה מהכאת הב' שביעי' על הו'
|
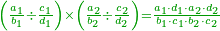
|
|
|
|
ואולם אם רצית להכות היוצא מחלוק הג' רביעיות על הב' שלישיות עם היוצא מחלוק הב' שביעית על הו' מבלתי שתצטרך לחלק תחלה ואח"כ להכות
|
|
נכה כמות הראשון עם איכות הב' ואיכות הג' וכמות הד' והם נ"ו ונשמרם
|
|
אח"ז נכה האכות הראשון עם כמות הב' ועם כמות הג' ועם איכות הד' והם ק"ח
|
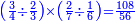
|
נחלקם על הנ"ו השמורים והיוצא הוא ההווה מהכאת היוצא מחלוק הג' רביעיו' על הב' שלישיו' עם היוצא מחלוק הב' שביעיו' על הששית
|
![\scriptstyle{\color{OliveGreen}{\left(\frac{a_1}{b_1}-\frac{c_1}{d_1}\right)\div\left(\frac{a_2}{b_2}-\frac{c_2}{d_2}\right)=\frac{\left[\left(a_1\sdot d_1\right)-\left(c_1\sdot b_1\right)\right]\times\left(b_2\sdot d_2\right)}{\left[\left(a_2\sdot d_2\right)-\left(c_2\sdot b_2\right)\right]\times\left(b_1\sdot d_1\right)}}}](/mediawiki/images/math/d/e/1/de19fec67919b87194e6104febf0c88d.png)
|
|
|
|
ואולם אם רצית לחלק הנשאר מחצור הב' שלישיות מג' רביעיות על הנשאר מחסור הששית מהב' שביעיות מבלתי שתצטרך לחסר ראשונה ואח"כ לחלק
|
|
נכה כמות הראשון עם איכות הב' והעולה נחסרהו מהכאת כמות השני עם איכות הראשון והנשאר נכהו עם איכות הג' ואיכות הד' והם מ"ב
|
|
אח"ז נכה כמות הד' עם איכות הג' והעולה נחסרהו מהעולה מהכאת כמות הג' עם איכות הד' והנשאר נכהו עם איכות הב' ועם איכות הראשון והם ס'
|
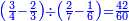
|
נחלקם על המ"ב השמורים והיוצא הוא ההווה מחלוק הנשאר מחסור הב' שלישיו' מהג' רביעיות על הנשאר מחיסור הו' מהב' שביעיות
|
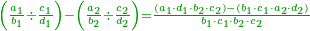
|
|
|
|
ואולם אם רצית לחסר היוצא מחלוק הג' רביעיו' על הב' שלישיו' מהיוצא מחילוק הב' שביעיו' על הו' מבלתי שתצטרך לחלק ראשונה ואח"כ לחסרם
|
|
נכה כמות הראשון עם איכות הב' ואיכות הג' וכמו' הד' והם נ"ו וזהו השמור הראשון
|
|
אח"כ נכה איכות הראשון עם הב' והעולה עם איכות הג' ועם איכות הד' והם ס"ג ונשמרם וזהו השמור הב'
|
|
אח"ז נכה איכות הד' עם כמות הג' ועם איכות הב' ועם כמות הראשו' והם צ"ו
|
|
נחסר מהם הס"ג שהוא השמור הב' והנשאר שהוא הל"ג
|
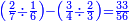
|
ניחסם אל השמור הראשון שהוא הנ"ו וההווה הוא ההוה מחסור היוצא מחלוק הג' רביעיות על הב' שלישיות מהיוצא מחלוק הב' שביעיות על הששית וש'מ'ל'
|
Cubic Roots
|
|
Cubic Roots of Integers
|
מעוקב השלמים
|
| Description of the extraction procedure:
|
תסדר הטור הדרוש כל אח' כפי מדרגתו
|
- Marking every three ranks with a dividing line
|
ובסוף כל ג' אותיות תשים קו
|
- The procedure starts from the leftmost dividing line:
|
ותתחיל מהקו האחרון
|
- Finding the highest digit of the root - based on the rule:
![\scriptstyle{\color{OliveGreen}{\sqrt[3]{a^3+r}\approx a}}](/mediawiki/images/math/d/0/8/d08276a0299fcd67809bb7e55f5c8068.png)
|
ונכתוב שם מספר שיוכה בדרך עקוב ויחוסר מהמספר שעליו עם עזר המדרגות הקודמו' ויקרא היסוד הראשון
|
- Finding the second highest digit of the root - based on the rule:
![\scriptstyle{\color{OliveGreen}{\sqrt[3]{\left(10a\right)^3+3\sdot\left[\left(10a\right)^2\sdot b\right]+3\sdot\left(10a\sdot b^2\right)+b^3}=\sqrt[3]{\left(10a+b\right)^3}=10a+b}}](/mediawiki/images/math/d/5/9/d598b308f04b6a0d930b9301f3c9d44c.png)
|
אח"ז תכתוב במקום הקו הקודמת יסוד ב' ושיוכה עם העולה מהכאת הראשון בג' והעול' עם היסוד הראשון והב' יחד והעולה שיחוסר מהמספר שני לו עם עזר הנמשכים לו גם תכה היסוד הב' באופ' מעוקב והעולה תחסרהו מהמספר שעליו עם עזר המספרים הקודמים לו
|
- Finding the third highest digit of the root - based on the previous rule
|
אח"ז נכתו' במקום הקו הקודמת יסו' ג' שיוכה עם העולה מהכאת הראשון והב' יחד עם מספר הג' והעולה עם היסוד הראשון והב' והג' ויחוס' מהמרב' הב' עם עזר המדרגות הנמשכים לו גם נכה היסוד הג' באופן מעוקב והעולה נחסרהו מן המספר שעליו עם עזר המספרים הקודמים לו
|
|
|
וכן תמיד בסדר הזה
|
Approximating the root of a non-cubic number
|
|
|
|
|
- Adding triplets of zeros to the right of the number
|
וכאשר הגענו אל מדרגת האחדים ממנו ונשארו מספרים על המספר הדרוש ותרצה לדעת עוד יסודו הקרוב נוסיף על המדרגו' המונחות מצד האחדים ג' סיפראש או ששה או ט' או מה שתרצה לבד שתוסיפהו ג'ג'
|
- Applying the above procedure
|
ואח"ז נעשה מה שקד' מהדרך למציאות היסוד עד שתגיע למדרגה הראשונה מהסיפראש
|
- Erasing from the result one third of the number of zeros added in the first step
|
אח"ז נקח כל היסודות ונסדרם בטור אח' על סדר המדרגות ונשליך מהם במספר שליש הסיפראש
|
- Converting the result to sexagesimal fractions:
- Considering the result as degrees
|
ונקח היסודות האחדות והם מעלות
|
- Multiplying the remainder by 60 and erasing three zeros from the product - the remainder are minutes
|
אח"ז נכה הנשלכים בס' והעולה נשליך מהם כמספר ג' הסיפראס ונקח הנשארים והם ראשונים
|
- So on until all the zeros added in the first step are erased
|
וכן נעשה תמיד עד שיכלה הסיפראש
|
- Summing up all the resulted sexagesimal fractions as the approximate cubic root
|
ואז נחבר הכל יהיה הוא היסוד הקרוב
|
|
|
דרך אחר למספר שאין בו יסוד מעוקב
|
- Adding triplets of zeros to the right of the number
|
שתוסיף סיפראש כמה שתרצה ובלבד שיהיו נוספים בתוספת ג'ג'
|
- Applying the above procedure
|
ונשתמש עם הדרך הקודם בעינו עד שנגיע לסיפרא הראשונה
|
- Converting the result to sexagesimal fractions: if 3n is the number of zeros added to the right of the given number, 60n should be placed as the denominator of the result in the first step of the procedure
|
אח"ז נקח כל היסודות המסודרות תחת מספר הדרוש ונכהו בס' והעולה בס' וזה עד שתהיינ' הסיפראש היוצאות בראש הטור העולה מההכאות בכמות שליש הסיפראש
|
- Erasing the zeros added in the first step and dividing the result by 60
|
אח"ז נשליך הסיפראש ונחלק הנשאר על ס' והנשאר יהיה מאיכות השברים המחולקים
|
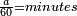
|
ר"ל שאם הוכו פעם אחת לבד יהיו ראשונים
|
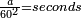
|
ואם ב' שניים
|
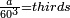
|
ואם ג' שלישיים
|
|
|
והיוצא הוא ממין הקודם למין ז' המחולקים ר"ל שאם היו ראשונים היוצא מהחלוקה מעלות ואם היו שניים היוצא מהחלוקה ראשונים וכן תמיד
|
Cubic Roots of Fractions
|
יסוד השברים המעוקבים
|
|
|
אם הכמות והאיכות מעוקב תקח מעוקב הכמות ותיחסהו אל מעוקב האיכות
|
|
|
ואם אינם מעוקבים או האיכות לבד בלתי מעוקב נכה האיכות בדרך עקוב ונכה הכמות עם העולה מהכאת האיכות בעצמו אח"ז ניחס יסוד השמור הב' שהוא הכאת הכמות עם העולה מהכאת האיכות בעצמו אל השמור הראשון שהוא העולה מהכאת האיכות בדרך עקוב
|
|
|
ואם איכותם נעקב נבקש יסוד הכמות הקרוב והיוצא ניחסהו אל מעוקב האיכות
|
- Example:
![\scriptstyle\sqrt[3]{\frac{a^3+r}{3^3}}=\frac{\sqrt[3]{a^3+r}}{\sqrt[3]{3^3}}\approx\frac{1}{3}a](/mediawiki/images/math/d/e/4/de4eae3e3c0d1c88d454625601a90f44.png)
|
ר"ל שאם היה מעוקבו ג' היה היחס הוא השליש וכן תמי'
|
| Integers and fractions - converting the integers into an improper fraction
|
ואולם בשלמים ושברים יחד נתיך השלמים לשברים ונעשה הדרך הקודם בעינו
|
Divisibility of a Number
|
|
3; 6; 9
|
|
| To find out if a given number has a third, a sixth, or a ninth [= if 3, 6, or 9 are divisors of the number]
|
לידע אם יש שלישי' או ששי' או ט' מספר מה מבלי שברים
|
- Summing the numerals of the given number as units and casting nines from the sum
|
תדע ראשונה אם יש לו תשיעי' וזה יודע כשתחבר רשמי מספר החשבון כאלו הם אחדים
|
- If there is no remainder - the number has a ninth and a third [= divisible by 9 and 3]
|
ואם יושלך לט"ט בידוע שיש לו תשיעיות וג"כ שלישי'
|
- If the given number is even - it has a sixth [= divisible by 6] as well
|
וג"כ ששית אם המספר זוג ואם נפרד לאו
|
- If the remainder is 3 or 6 - it does not have a ninth [= not divisible by 9], but it has a third [= divisible by 3], and if this number is even, it has also a sixth [= divisible by 6]
|
ואם ישארו ו' או ג' יהיה לו שלישי' וג"כ ששית אם הוא זוג אבל לא תשיעית
|
2; 4; 8
|
|
| To find out if a given number has a half, a quarter, or an eighth [= if 2, 4, or 8 are divisors of a the number]
|
ואם תרצה לידע אם יש לו מחצית או ד' או שמינית
|
- If the given number is odd - it does not have any of these fractions [= not divisible by 2, 4, or 8]
|
אם חשבון נפרד אין לו שום אחד מהם
|
- If the given number is even - it has a half [= divisible by 2]
|
ואם זוג בידוע שיש לו חצי
|
- Casting out eighths from the sum of the numerals of the given number received through to the following procedure:
![\scriptstyle number\;of\;the\;type:\;2a+10b+\left[\left(2c-1\right)\sdot100\right]\longrightarrow the\;sum:\;2a+2b+4\sdot\left(2c-1\right)](/mediawiki/images/math/6/9/2/692097c3efc92180cde84cf4d0489077.png)
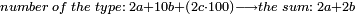
|
ולידע אם לא ג"כ רביעית ושמיני' קח המספר אשר במעלה הראשונה לצד ימין כמו שהיא ואשר בשנייה כפול ואם אין שם מספר לא תקח כלום ואשר בשלישית אם הוא נפרד כפלהו בד' ואם הוא זוג או סיפרא לא תקח כלום וכן מהמעלה הג' ולמעלה תניח אותו לא תקח כלום וקבץ כל מה שקבצת עד המעלה הג' עד"ז
|
- If there is no remainder - the number has an eighth [= divisible by 8]
|
אם יושלך באלו לח' יש לו שמינית וכ"ש רביעי'
|
- If the remainder is 4 - it has a quarter [= divisible by 4] alone
|
ואם ישארו ד' יש לו ד' לבד
|
- If the remainder is a number other than 4 - it has no quarter [= not divisible by 4]
|
ואם נותר מספר אחר אין לו אפי' רביעית
|
7
|
|
| To find out if a given number has a seventh [= if 7 is a divisor of a given number]
|
ואם תרצה לידע אם יש לו שביעי'
|
|
|
יש בזה דרכים:
|
- Multiplying each of the numbers 1, 3, 2, 6, 4, 5 by the numeral in the corresponding rank by the order, then summing the numerals of the products - if there is no remainder after casting out the sevenths - the given number has a seventh [= divisible by 7], otherwise it does not
|
הראשון שתניח אלו האותיות א'ג'ב'ו'ד'ה' על סדר המדרגות חלילה ותכה כל א' מאלו האותיות במדרגה שכנגדה וחשב כל האחדים והשלך השביעיות ואם יושלך לז' יש לו שביעית ואם לאו לאו
|
- Another procedure: multiplying the leftmost digit of the given number by 3, adding the product to the digit in the preceding rank on the right and casting out sevens from the sum, then multiplying the remainder by 3, adding the product to the preceding rank on the right and casting out sevens from the sum, and so on repeatedly - if there is no final remainder, the given number has a seventh [= divisible by 7]
|
הב' שתכה הרושם האחרון שלצד שמאל בג' וחברהו לאשר תמצא במעלה שלפניו ותשליכה לז' והנשאר תחברהו לאשר לפניו ותכה הנשאר מהשלכת השביעיו' בג' וחברהו לאשר תמצא לפניו וכן תמיד עד המדרגה הראשונה ואם יושלך ז'ז' יש לו שביעית
|
- If one of the numerals is a zero the interim remainder is multiplied by 3 and the procedure continues as described
|
ואם לא תמצא שם מספר כי אם סיפרא תכה הנשאר בג' וכן בכל ספרא וספרא תכה הנשאר בג' עד שיכלו כל סיפראים וכן תמיד
|
11
|
|
| To find out if a given number has 11th [= if 11 is a divisor of a given number]
|
ולידע אם לו י"א ר"ל אם יושלך לי"א
|
- Subtracting the numeral in the highest rank of the given number from the numeral in the previous rank, then subtracting the remainder from the preceding numeral and so on repeatedly
|
תחסר האחרון שלצד שמאל מאשר לפניו והנשאר מאשר לפני פניו וכן תמיד
|
- If there is no remainder - the number has an 11th [= divisible by 11], otherwise it is not
|
ואם יושלך הכל יש לו י"א ואם לאו לאו
|
- If one of the numerals is a zero or if it is smaller than the subtrahend, 11 is added to this numeral and the procedure continues as described
|
ואם לא תמצא שם מספר או מספר קטן ממנו שלא תוכל לחס' ממנו והנשאר תוסיף עליו הי"א ותחסר מהכל זה המספר וכן תמיד
|
13
|
|
| To find out if a given number has 13th [= if 13 is a divisor of a given number]
|
אם יש לו י"ג
|
- [Multiplying the leftmost digit of the number by 3], casting out thirteens from the product, subtracting the remainder from the preceding rank then multiplying the result of subtraction by 3 again and so on
|
תכה הרושם האחרון בג' והוציאוהו י"ג י"ג והנשאר הוציאוהו מאשר תמצא במעלה אשר לפניו והנשאר כפלהו שנית בג' והוציאוהו י"ג י"ג והנשאר הוציאוהו מאשר לפניו וכן תמיד עד תכליתם
|
- If there is no remainder - the number has a 13th [= divisible by 13]
|
ואם יצא הכל יושלך לי"ג
|
- If one of the numerals is smaller than the subtrahend, 13 is added to this numeral and the procedure continues as described
|
ואם יחסר בשום מעלה שלא תמצא שם די להוציא אשר צויתיך הוסיף י"ג והוציא מהנתחבר אשר עליך להוציא והנשאר כפלהו בג' והוציאוהו י"ג י"ג ואם יצא יש לו י"ג ואם לאו לאו
|
General technique
|
דרך כולל כל
|
| Adding the leftmost digit to the second leftmost digit and casting out the [potential divisor] in question from the sum, then adding the remainder to the digit in the preceding rank as tens and casting out the [potential divisor] again from the sum, and so on
|
שתחבר המספר האחרון עם אשר לפניו בשתחברהו לעשרות והב' לאחדים ותשליכהו למספר אשר תרצה להשליכו והנשאר חשבהו לעשרות וחברהו לאשר תמצא במעלה שלפניו והוציאהו למספר אשר תרצה להוציא וכן תמיד על הסדר הזה
|
Geometric Shapes
|
|
Square
|
|
- Example: finding the area or the diagonal of a square both sides of which are 10
|
אם מרובע נכון שיש בצלעיו עשר על עשר ד"מ ורצית לידע שטחו או אלכסונו
|
- The area of a square = the product of its two sides
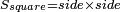
|
תעשה בזה הדרך: תכה הצלע עם חבירו כאח' וזהו שטחו
|
- The diagonal of a square:
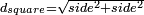
|
ותכה הב' צלעות כל אחת בפני עצמו וגדר של מקובצם הוא האלכסון
|
- The side of a square, when its area is given:
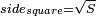
|
ואם ידעת השטח גדרו והוא הצלע
|
- The side of a square, when its diagonal is given:
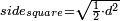
|
ואם ידעת האלכסון גדר חצי הכאתו הוא הצלע
|
Rectangle
|
|
- Example: finding the area of a rectangle of 10 in length and 5 in width
|
אבל במרובע ארוך שיש לצלעיו י' באורך וה' ברוחב עד"מ
|
- The area of a rectangle = the product of its two sides
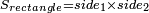
|
בידיעת ב' צלעיו תכה זה עם זה כאחת זהו שטחו
|
- The side of a rectangle, when the area and one of the sides are given:
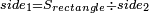
|
ובידיעת שטחו וצלע א' תחלק השטח על הצלע הידוע ויצא הצלע הנעלם
|
- The diagonal of a rectangle:
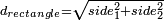
|
ובידיעת ב' צלעיו ותכה זה בפני עצמו וזה בפני עצמו וגדר מקובצם הוא האלכסון
|
- The side of a rectangle, when the diagonal and one of the sides are given:
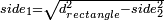
|
ובידיע' האלכסון וצלע א' תוציא הכאת הצלע מהכאת האלכסון וגדר הנשאר הוא הצלע האחר
|
Triangle
|
בשבירת המשולש
|
| Relying on Euclid
|
יש דרכים רבים אבל מה שנ"ר יותר כולל הוא מה שנתבא' בכח דברי אקדידס החכם מתוך הקדמה אח' ובקיום זאת ההקדמה נוליד המבוקש בע"ה
|
- The square of the diagonal of a given rectangle is equal to sum of the squares of both its sides
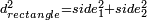
|
וזה ששם נתבאר שקוטר המרובע ר"ל אלכסונו הוא כפל מרובע ב' הצלעים כשיוכה זה בפני עצמו וזה בפני עצמו הוא שוה להכאת האלכסון בעצמו
|
- Example: finding the area of an equilateral triangle whose sides are equal to 10
|
ובזה ההקדמה יתבאר לך כשיש משולש בצורה הזאת
|
|
|
|
|
ונסכים שהוא שוה הג' הצלעות ושיש בכל צלע עשר
|
| Finding the area by dividing the triangle into two identical triangles
|
הנה ידיעת שבריו הוא שתחלקהו במחשבתך לב' משולשים שוים וזה שתרשום בזוית א' קו ישר ובהכרח יחלוק הקו ר"ל קו ג"ב לשני חצאין ובזה הרי ידענו שצלע אחד יש בו ה' והאלכסון עשר כפי מה שהונח
|
|
|
ובהוצאת הצלע האח' יתחייב כפי ההקדמ' שהנחנו שתוציא הכאת הצלע מהכאת האלכסון וגדר הנשאר הוא הצלע האחר
|
|
|
ואיכות החיוב מבואר כיון שהאלכסון בהכאתו שוה להכאת שני צלעיו כל אח' בפני עצמו א"כ יתחייב בהכרח כשתוציא הכאת הצלע האח' מהאלכסון שגדר הנשאר הוא האלכסו'
|

|
ועשינו כן שהכינו הה' והיה כ"ה והכינו הי' והיה ק' חסרנו הכ"ה מהק' ונשארו ע"ה וגדרם הוא הצלע האחר בקשנו גדרם ע"ד הקירוב כמו שהודעתיך בשער הקידום הדרך היותו נקל כזו והיותר מדוייק ומצאנו ששרשם הוא הוא ח' וב' רביעיות וג' רביעיות רביעית
|
![\scriptstyle{\color{blue}{S_{triangle}=5\sdot\left[8+\frac{2}{4}+\left(\frac{3}{4}\sdot\frac{1}{4}\right)\right]=43+\frac{1}{4}+\left(\frac{3}{4}\sdot\frac{1}{4}\right)}}](/mediawiki/images/math/3/7/4/374d0caf4ae58e88ea8696d9aec06b3a.png)
|
הכינום עם ה' שהוא הצלע הא' ויצא מ"ג שלמים ורביעי' וג' רביעיות רביעית והוא שטח המשולש
|
|
|
לפי שהאלכסון חולק המרובע לב' חצאים וחצי זהו חצי המשולש וחציו האחר הוא חצי המשולש ר"ל החלקים מהמשולש אשר חלקנו צלעו בזוית אח' ודי למבין
|
Euclidean Propositions
|
|
Euclid's Elements, Book II, Propositions 1-8 - [Arithmetical Version]
|
|
| Propositions that are of great need for arithmetic from the words of the wise Euclid in Book II and they are 9 propositions
|
הקדמות צריכין צורך גדול למספר מדברי אקלידס החכם במא' הב' והם ט' הקדמות
|
- 1) Euclid, Elements, Book II, propositions 2: If you divide any number into parts as you wish, [the sum of] the products of each of the parts by the whole number is equal to the square of the whole number
![\scriptstyle\sum_{k=1}^n \left[\left(\sum_{i=1}^n a_i\right)\sdot a_k\right]=\left(\sum_{i=1}^n a_i\right)^2](/mediawiki/images/math/2/a/1/2a190390030d9c138d548197fab10837.png)
|
אחת כל מספר שחלקת אותו לחלקים איך שרצית הנה הכאת כל אח' מהחלקי' בכל המספר השוה למרובע הכל
|
- Proof: the whole contains nothing but its parts and the product of the whole by the whole is equal to the product of the whole by each of its parts
|
המופת שאין בכלל זולת חלקיו והכאת הכלל בכלל הוא כהכאת הכלל בכל חלקיו וזה מבואר
|
- 2) Euclid, Elements, Book II, proposition 3: For any number divided into two parts as you wish, the product of the whole number by any of its two parts is equal to the product of the one part by the other plus the square of the part by which you multiplied the whole number.
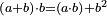
|
ב' כל מספר שחלקת אותו לב' חלקים איך שקרה הנה הכאת המספר כלו עם כל אחד מב' חלקיו איזה שיהיה שוה להכאת החלק האחד עם האחר ולמרובע החלק אשר בו הכית כל המספר
|
- Proof: the product of the whole by one of its parts is equal to the product of the part by itself and by the other part, since the whole consists of both of them
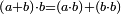
|
מופתו כי הכלל כשהכית אותו עם איזה חלק הוא כאלו הכית אותו החלק בעצמו ועם החלק האחר כיון שזה הכלל מורכב מהם
|
- Example: the number 10 is divided into two parts - 7 and 3.
|
כמשל מספר הי' נחלק לב' חלקים לז' ולג'
|
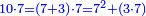
|
הנה הכאת הי' בז' כאלו הכית הז' בעצמו ועם הכת הג' אחר שהז' והג' הם חלקי' הי' ואין בכלל זולת חלקיו
|
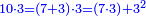
|
וכן כאשר הכית הי' בג' הרי הוא כאלו הכית הג' עם הז' ועמו בעצמו כגון שהם ר"ל הג' והז' הם הם בעצמם מקובצים מספר הי' וזה מבואר מאד
|
- 3) Euclid, Elements, Book II, proposition 4: For any number divided into two parts as you wish, the square of the whole number is equal to [the sum of] the squares of the two parts and twice the product of the one part by the other.
![\scriptstyle\left(a+b\right)^2=a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]](/mediawiki/images/math/7/2/7/727b0c35fd93a7a347bed8413905049f.png)
|
ג' כל מספר שחלקת אותו לשני חלקים איך שקרה הנה מרובע כל המספר שוה לב' המרובעים ההווים מב' החלקים ולהכאת החלק האחד עם חבירו ב' פעמים
|
- Proof:
![\begin{align}\scriptstyle\left(a+b\right)^2&\scriptstyle=\left[a\sdot\left(a+b\right)\right]+\left[b\sdot\left(a+b\right)\right]\\&\scriptstyle=\left[a^2+\left(a\sdot b\right)\right]+\left[b^2+\left(a\sdot b\right)\right]\\&\scriptstyle=a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]\\\end{align}](/mediawiki/images/math/a/7/e/a7ec26694f08b055373189269d468fa1.png)
|
מופתו כי הכאת הכלל עם הכלל כאלו הכית הב' חלקים עם הכלל והכאת החלק והא' עם הכלל הוא כאלו הכית החלק בעצמו ועם החלק האח' וג"כ בחלק האח' שהכית אותו בכלל כאלו הכית בעצמו ועם החלק הא' כיון שאין בכלל זולת חלקיו והרי אלו החלקים הם חלקי זה המספר הגדול
|
- Example: the number 10 is divided into 7 and 3.
|
כמשל הי' נחלק לז' ולג'
|
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle
10^2&\scriptstyle=\left(7\sdot10\right)+\left(3\sdot10\right)\\&\scriptstyle=\left[7^2+\left(7\sdot3\right)\right]+\left[3^2+\left(3\sdot7\right)\right]\\&\scriptstyle=3^2+7^2+\left[2\sdot\left(3\sdot7\right)\right]\\\end{align}}}](/mediawiki/images/math/e/d/c/edc28fc524ac369e81faec0eab87cfa6.png)
|
הכאת הי' בעצמו הוא כאלו הכית הז' עם הי' והג' עם הי' הכאת הז' עם הי' כאלו הכית הז' בעצמו ועם הג' כיון שהז' והג' הם חלקי הי' והכאת הג' בי' כאלו הכית הג' בז' ועם הג' הרי ב' פעמים הכינו הג' עם הז' וג"כ הכינו הז' בעצמו והג' בעצמו ושוה הכל למרובע הי' ומבואר הוא מאד למסתכל בעין השכל
|
- 4) Euclid, Elements, Book II, proposition 5: For any number divided into two equal parts and into two unequal parts, [the sum of] the product of one of the unequal parts by the other and the square of the difference between the two parts, i.e. between the equal part [= the half of the whole number] and the unequal [part] is equal to the square of half the [whole] number.
![\scriptstyle\left(a\sdot b\right)+\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]^2=\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2](/mediawiki/images/math/6/2/4/6240a40a1b55eec2eca043f4e2218ca7.png)
|
ד' כל מספר כאשר תחלקהו לב' חלקים שוים ולב' חלקים בלתי שוים הנה הכאת החלק הא' עם חבירו מהחלקים הבלתי שוים ומרוב' מה שבין ב' חלקים ר"ל בין החלק השוה ובלתי שוה שוה למרובע חצי המספר
|
- Proof:
![\scriptstyle\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a=b-\left[\frac{1}{2}\sdot\left(a+b\right)\right]](/mediawiki/images/math/b/0/e/b0e26ef8336bd37ea2dc5ea7d13ed5fe.png)
|
מופתו המספר שנחלק לב' חלקים בלתי שוים מה שנגרע מהמספר הקטן מהחצי הוא מיותר במספר הגדול על החצי
|
- Example: the number 10 that is divided into 7 and 3.
|
במש' הי' שנחלק לז' ולג'
|

|
מה שנגרע הג' מהה' שהוא ב' הז' יותר מהה' זה המספר בעצמו שהם הב'
|
![\begin{align}\scriptstyle a\sdot b&\scriptstyle=a\sdot\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]+\left[b-\left[\frac{1}{2}\sdot\left(a+b\right)\right]\right]\right]\\&\scriptstyle=a\sdot\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]+\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]\right]\\\end{align}](/mediawiki/images/math/3/c/c/3cc1957606b0ead5eb951b5585bef540.png)
|
וא"כ כשאנו מכים המספר הקטן בגדול הוא כאלו הכינו המספר הקטן בחצי המספר והתוספת כיון שהתוספת והחצי הם חלקי החלק הגדול
|
![\scriptstyle\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2=\left[\frac{1}{2}\sdot\left(a+b\right)\right]\sdot\left[a+\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]\right]](/mediawiki/images/math/0/7/1/0715bf55a8d43cbdfa4205e649097a2e.png)
|
והכאת החצי עצמו הוא כאלו הכינו החצי עם המספר הקטן ועם התוספת כיון שהתוספת והמספר הקטן הם חלקי החצי
|
![\scriptstyle\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]^2=\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]\sdot\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]\right]-\left[a\sdot\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]\right]](/mediawiki/images/math/4/4/3/4439c64a1a40d88eb65eca7693b2e920.png)
|
והוא מבואר שההכא' בין הכאת החצי בתוספת בין הכאת המספר הקטן בתוספת הוא הכאת התוספת בתוספת וע"כ כהכאת התוספת בעצמו
|
![\scriptstyle\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2=\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]^2+\left(a\sdot b\right)](/mediawiki/images/math/1/4/b/14b17150edc445172d80441ffc56150b.png)
|
ואם נוסיפהו על מרובע הקטן בגדול הוא מרוב' החצי בהכאת
|
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle5^2&\scriptstyle=\left(5\sdot3\right)+\left(5\sdot2\right)\\&\scriptstyle=\left(3\sdot5\right)+\left[\left(3\sdot2\right)+2^2\right]\\&\scriptstyle=\left(3\sdot7\right)+2^2\\&\scriptstyle=\left(3\sdot7\right)+\left(5-3\right)^2\\\end{align}}}](/mediawiki/images/math/0/4/5/045c6411c7de6ffda0eec8a7d9df0b56.png)
|
במשל הכאת הז' בג' הוא כאלו הכינו הג' בה' ובב' והכאת הה' בעצמו הוא כאלו הכינו הג' בה' והה' בב' שהם התוספת וההבדל שבין זאת ההכאה להכאת הג' בב' הוא הכאת הב' בעצמם וזה מבואר מאד
|
- 5) Euclid, Elements, Book II, proposition 6: If we divide any number into half and add to it another number, [the sum of] the product of the whole number plus the additional [number] by the additional [number] and the square of half the number is equal to the square of half the number and the additional [number] together.
![\scriptstyle\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2](/mediawiki/images/math/a/0/b/a0b403dd8b7c15a5cb1dc47a5f8ca5bb.png)
|
ה' כל מספר כאשר חלקנו אותו לחצי והוספת עליו מספר אחר הנה הכאת המספר כלו מחובר עם התוספ' בתוספת ומרובע חצי המספר שוה למרובע חצי המספר והתוספת ביחד
|
- Proof:
![\scriptstyle\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2=\left(\frac{1}{2}\sdot a\right)^2+\left[b\sdot\left(\frac{1}{2}\sdot a\right)\right]+\left[b\sdot\left[\left(\frac{1}{2}\sdot a\right)+b\right]\right]](/mediawiki/images/math/7/5/8/758d2201b39249424cb4d658762bd95f.png)
|
מופתו כי כשהוספנו על החצי מספר מה הנה יתוסף על מרובע החצי הכאת התוספת בחצי והכאת התוס' בחצי מחובר עם התוספת
|
- Example:
![\scriptstyle\left(5+2\right)^2=5^2+\left(2\sdot5\right)+\left[2\sdot\left(5+2\right)\right]](/mediawiki/images/math/1/2/3/123699a4976836521e4fa0f9f56218c6.png)
|
וזה כי אמרנו ה' פעמים ה' הם כ"ה ואמרנו ז' שלז' הרי נתוסף הכאת הב' שהם התוספת בה' והכאת הב' בז' שהוא מחובר עם התוספת והחצי
|
![\begin{align}\scriptstyle\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2&\scriptstyle=\left(\frac{1}{2}\sdot a\right)^2+\left[b\sdot\left[\left(\frac{1}{2}\sdot a\right)+\left(\frac{1}{2}\sdot a\right)+b\right]\right]\\&\scriptstyle=\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2\\\end{align}](/mediawiki/images/math/2/5/1/251974ee9075190da8b9dc79563ff0f5.png)
|
וזהו בעצמו מה שאנו עושין כשאנו מוסיפין התוספת במספר כלו לפי שהמספ' חציו ועם התוספת שאנו מוסיפין עליו ומהל' הכאת התוספת עם החצי ואע"כ עם החצי והתוספת מחובר או הכאתו עם כל המספר והתוספת ביחד והבן
|
- 6) Euclid, Elements, Book II, proposition 7: For any number divided into two parts, the sum of the square of the whole number and the square of one of the parts is equal to twice the product of this part by the whole number plus the product of the other part by itself
![\scriptstyle\left(a+b\right)^2+a^2=2\sdot\left[\left(a+b\right)\sdot a\right]+b^2](/mediawiki/images/math/5/e/f/5ef738b800e1b84fc257df70a83fb86b.png)
|
ו' כל מספר שתחלקהו בב' חלקים איך שקרה המרובע ההווה מהמספר כלו והמרובע ההווה מא' מב' אלו החלקים כאשר התקבצו שוה להכאת החלק הנזכ' עם המספר כלו ולהכאת החלק הב' הנשאר בעצמו
|
- Proof:
![\scriptstyle\left(a+b\right)^2=a^2+b^2+\left[2\sdot\left(a+b\right)\right]](/mediawiki/images/math/4/d/6/4d6ae9d470a2827afd617df98dd97974.png)
|
מופתו כבר התבאר בהקדמה ג' שהכאת הכלל בעצמו הוא הכאת חלקיו כל אחת בפני עצמו והכאת החלק הא' עם חבירו ב' פעמים
|
![\begin{align}\scriptstyle2\sdot\left[\left(a+b\right)\sdot a\right]+b^2&\scriptstyle=2a^2+\left[2\sdot\left(a\sdot b\right)\right]+b^2\\&\scriptstyle=a^2+\left[a^2+\left[2\sdot\left(a\sdot b\right)\right]+b^2\right]\\&\scriptstyle=\left(a+b\right)^2+a^2\\\end{align}](/mediawiki/images/math/c/2/f/c2fe7ee2c8c60da164b571e70406a5a9.png)
|
וא"כ כשאנו מכין החלק הנז' אשר הוספנו מרובעו למרובע המספר כלו עם המספר כלו ב' פעמים הרי אנו מכין אותו בעצמו ב' פעמים ועם החלק הא' ב' פעמי' ואח"כ אנו מוסיפין מרובע החלק הב' הנשאר והכאת הכלל בעצמו הוא הכאת החלק בעצמו פעם א' וכל אח' עם חבירו ב' פעמים הרי נותר הנה הכאת חלק אחד בעצמו פעם אח' אנו מוסיפין זה על מרובע הכלל כדי שיהיה שוה
|
- Example: the number 10 is divided into 7 and 3.
|
במשל הרי הי' נחלק לז' ולג'
|
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left[2\sdot\left(3\sdot10\right)\right]+7^2&\scriptstyle=\left[2\sdot\left(3\sdot7\right)\right]+\left(2\sdot3^2\right)+7^2\\&\scriptstyle=10^2+3^2\\\end{align}}}](/mediawiki/images/math/1/c/0/1c021025c0e975ce0233ebd9770b7392.png)
|
הנה הכאת הג' בי' ב' פעמים הוא הכאת הג' בז' ב' פעמים והכאת הג' בעצמו ב' פעמים ואח"כ אנו מכין הז' בעצמו נותר לנו על מרובע הכלל הכאת הג' בעצמו פעם אחד לכן אנו מוסיפין אותו על מרובע הכלל כדי שישוו
|
- 7) Euclid, Elements, Book II, proposition 8: For any number divided into two parts as you wish, if you multiply the whole number by one of the parts four times, the sum of the product with the square of the other part is equal to the [square] of the whole number plus the one part
![\scriptstyle4\sdot\left[\left(a+b\right)\sdot a\right]+b^2=\left[\left(a+b\right)+a\right]^2](/mediawiki/images/math/f/6/2/f62f5f20431f619df80a01a1d97e57cf.png)
|
ז' כל מספר שחלקת אותו לב' חלקים איך שקרה אם הכית המספר כלו עם חלק אח' מהם ד' פעמים וקבצת הכל עם מרובע החלק הב' הנשאר היה שוה להכאת מספרו החלק הנזכר כאשר תחברם יחד
|
- Proof: based on two propositions
|
המופת יתבאר בב' הקדמות
|
- I) For any number divided into two parts as you wish, [the sum of] the product of one part by the whole number and the [square] of the other part is equal to the sum of the product of the other part by the whole number and the [square] of the one part
![\scriptstyle\left[a\sdot\left(a+b\right)\right]+b^2=\left[b\sdot\left(a+b\right)\right]+a^2](/mediawiki/images/math/f/0/5/f052cf921b4ee55e1ca01f6021885458.png)
|
אחת כל מספר שחלקת אותו לב' חלקים כי איך שקרה הנה הכאת החלק עם כל הכלל והחלק הנשאר בעצמו כאשר תקבצם שוה להכאת החלק הנשאר בכלל והכאת החלק הא' בעצמו כאשר תקבצם
|
- Example:
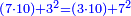
|
במשל הי' נחלק לז' ולג' הנה הכאת הז' בי' והכאת הג' בעצמו שוה להכאת הג' בי' והכאת הז' בעצמו
|
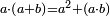
|
וזה כי הכאת החלק בכלל הוא כאלו הכית אותו בעצמו ועם החלק האחד הנשאר כי אין הכלל זולת חלקיו
|
![\scriptstyle\left[a\sdot\left(a+b\right)\right]+b^2=a^2+\left(a\sdot b\right)+b^2](/mediawiki/images/math/8/f/6/8f6de5615e58347da74d4e00628a1c66.png)
|
ואח"כ כשאנו מכין החלק הנשא' בעצמו הרי עשינו ג' הכאות הכאת כל חלק בפני עצמו והכאת החלק הא' באחר
|
![\scriptstyle\left[b\sdot\left(a+b\right)\right]+a^2=b^2+\left(a\sdot b\right)+a^2](/mediawiki/images/math/3/3/1/331e5719b87be662c7b73c4dbcd44eaa.png)
|
וג"כ כאשר הפכנו הענין זה בעצמו אנו עושין
|
- Example:
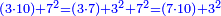
|
המשל כי הכאת הג' בי' הוא כאלו הג' בז' ועמו בעצמו וכשהכינו הז' בעצמם עשינו בזה ג' הכאות הכאת הז' בעצמו והכאת הג' בעצמו והכאת הג' בז' כן ג"כ כשאנו מכין הז' בי' ואח"כ הג' בעצמו אלו הג' הכאות בעצמם אנו עושין הכאת הג' בעצמם והכאת הז' בעצמם והכאת הג' בז' וזה מבואר
|
- II) For any number whose square is known and we want to know the square of another number, we add [to the known square] twice the product of difference [between the two numbers] by the number [whose square is] known plus [the square] of the difference
![\scriptstyle b^2=a^2+2\sdot\left[a\sdot\left(b-a\right)\right]+\left(b-a\right)^2](/mediawiki/images/math/0/8/8/088cad58241d957f9f3c27b451de0ab5.png)
|
ההקדמה הב' כי כל מספר שנודע לנו מרובעו ונרצה לידע מרובע מספר אחר הנה נוסף עליו הכאת התוספת במספ' הנודע ב' פעמים והתוספת בעצמו פעם אחת
|
- Example:
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle17^2&\scriptstyle=10^2+2\sdot\left[10\sdot\left(17-10\right)\right]+\left(17-10\right)^2\\&\scriptstyle=10^2+2\sdot\left(10\sdot7\right)+7^2\\\end{align}}}](/mediawiki/images/math/6/7/7/67731d828dc38dc51514d914a547e881.png)
|
במשל נודע לנו מרובע הי' ורצינו לידע מרובע הי"ז הנה נכה הז' בי' ב' פעמים ועם עצמו פעם אחת ונוסיפהו על מרובע הי' והוא העולה מהכאת י"ז בעצמו
|
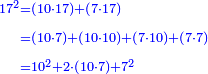
|
והסב' כשאנו אומרים י"ז פעמים הוא כאמרנו י' פעמים י"ז וז' פעמים י"ז וכשאנו אומרים י' פעמים י"ז כאלו אמרנו ז' פעמים י' וי' פעמים ז' וכשאנו אומרי' ז' פעמים י"ז כאלו אמרנום ז' פעמים י' וז' פעמים ז' נמצאו בזה ד' הכאות הכאת הי' בי' והכאת הז' בי' ב' פעמים והכאת הז' בעצמם
|
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle10^2&\scriptstyle=17^2-2\sdot\left(10\sdot7\right)-7^2\\&\scriptstyle=17^2-2\sdot\left[10\sdot\left(17-10\right)\right]-\left(17-10\right)^2\\\end{align}}}](/mediawiki/images/math/9/a/4/9a4a30b469c46bcbb14480005742377f.png)
|
וכשיש לנו י' פעמים י' חסר לנו הכאת הז' שהוא התוספת בי' שהוא המספר אשר נודע מרובעו ב' פעמים והכאת הז' שהוא התוספת בעצמו
|
![\scriptstyle4\sdot\left[\left(a+b\right)\sdot a\right]+b^2=\left[\left(a+b\right)+a\right]^2](/mediawiki/images/math/f/6/2/f62f5f20431f619df80a01a1d97e57cf.png)
|
בזה יובנו דברי ההקדמה הנזכ' הנה כשהכית החלק בכלל ד' פעמים ואח"כ החלק הנשאר בעצמו שוה להכאת המספר והתוספת כשיחוברו
|
![\scriptstyle b^2+\left[a\sdot\left(a+b\right)\right]=a^2+\left[b\sdot\left(a+b\right)\right]](/mediawiki/images/math/7/e/e/7eea030d1d0b98bc71555403dc241abd.png)
|
וזה כי הכאת החלק הנשאר בעצמו כאשר יחובר אל הכאת החלק האח' בכלל שוה כאשר המירונו שנעשה ההפך
|
![\begin{align}\scriptstyle4\sdot\left[\left(a+b\right)\sdot a\right]+b^2&\scriptstyle=3\sdot\left[a\sdot\left(a+b\right)\right]+\left[a\sdot\left(a+b\right)\right]+b^2\\&\scriptstyle=3\sdot\left[a\sdot\left(a+b\right)\right]+\left[b\sdot\left(a+b\right)\right]+a^2\\\end{align}](/mediawiki/images/math/6/9/a/69a38eddd17c3f2cd5ee01abd642fef1.png)
|
וא"כ הד' פעמים שהכינו בכלל נקח אחד מהם וישארו ג' ותחבר זאת ההכאת אל הכאת החלק הנשאר בעצמו הוא כאלו החלק האח' בכלל וזה החלק שאנו מכין אותו בכלל נכה אותו בעצמו וא"כ יש לו ג' הכאות החלק בכלל והכאת אחרת של החלק האחר בכלל והכאת החלק האח' בעצמו
|
- Based on the first proposition proved above [Elements, Book II, propositions 1-2]
![\scriptstyle\sum_{k=1}^n \left[\left(\sum_{i=1}^n a_i\right)\sdot a_k\right]=\left(\sum_{i=1}^n a_i\right)^2](/mediawiki/images/math/2/a/1/2a190390030d9c138d548197fab10837.png)
|
וכבר ביארנו בהקדמה הראשונה שהכאת המספר שנתחלק בעצמו כאלו הכינו אותו עם כל חלקיו
|
![\begin{align}\scriptstyle4\sdot\left[\left(a+b\right)\sdot a\right]+b^2&\scriptstyle=3\sdot\left[a\sdot\left(a+b\right)\right]+\left[a\sdot\left(a+b\right)\right]+b^2\\&\scriptstyle=3\sdot\left[a\sdot\left(a+b\right)\right]+\left[b\sdot\left(a+b\right)\right]+a^2\\&\scriptstyle=2\sdot\left[a\sdot\left(a+b\right)\right]+\left[a\sdot\left(a+b\right)\right]+\left[b\sdot\left(a+b\right)\right]+a^2\\&\scriptstyle=2\sdot\left[a\sdot\left(a+b\right)\right]+\left(a+b\right)^2+a^2\\&\scriptstyle=\left[\left(a+b\right)+a\right]^2\\\end{align}](/mediawiki/images/math/b/3/5/b35a5226568e484fafd988c80c4828c2.png)
|
וא"כ מהג' פעמים שהכינו החלק בכלל נחסר אחת ונחבר עמה הכאת החלק האח' במספר שנתחל' והרי יש לנו מרובע המספר שנתחלק כלו נשאר לנו ב' פעמים הכאת החלק במספר שנתחלק ב' פעמים והכאת זה החלק בעצמו וזהו מה שאנו צריכין להוסיף על מרובע המספר שנתחלק כמו שביארנו
|
Other Propositions
|
הקדמות אחרות
|
1) Euclid, Elements, Book VII, proposition 17: For numbers [multiplied by] the same multiplier, the ratio of a [product] to a [product] is equal to the ratio of a [number] to a [number]
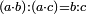
|
החלקים אשר כפליהם שוים הנה ייחס קצתם אל קצתם כיחס חלק קצתם אל קצת
|
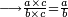
|
וא"כ יתחייב מזה שכל חלק מהשברים כאשר יכפל כמותו ואיכותו שוה הפעמי' הנה הוא השבר הראשון בעינו
|
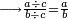
|
וכן אם תחלק כמותו ואכותו לחלקים שוים ותיחס חלק הכמות עם חלק האיכות הוא השבר הראשון בעינו
|
| 2) the product of a fraction by a fraction is a fraction of fraction
|
ב' הכאת השבר עם השבר הוא כאמרנו נקח השבר השבר
|
3) For any number multiplied by any number, the ratio of the multiplied number to the product is equal to the ratio of one to the multiplier
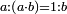
|
ג' שכל מספר נכפל בכפלים כמ' שיהיו המספר הנכפל יחסו אל המספר העולה מכפליו כערך הא' אל הכפלים שבו נכפל
|
- Example:
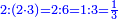
|
כמו מספר הב' שהוכה בג' ועלה ו' יחסו אל הו' כיחס האחד אל שלשה שהוא שליש
|
4) 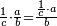
|
ד' כאשר תרצה לקחת מהשברים מה חלק מה הנה נקח מכמות השברים המונחים לפני החלק הדרוש וניחסהו אל האיכות
|
- Example:
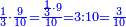
|
אם רצית שליש הט' עשיריות קח שליש הט' והם ג' יחסים אל האיכו' והם עשיריות יהיו ג' עשיריות
|
5) 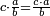
|
ה' שכאשר תרצה לכפול שברים מונחים באיזה כפלים שיהיו נכפול הכמו' וניחסהו אל האיכות
|
- Example:
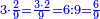
|
רצית להכות ב' תשיעיות בג' תכה הב' בג' הם ו' יחסם אל האיכות יהיו ו' תשיעיות
|
6) Euclid, Elements, Book VII, proposition 17: For any number multiplied by two numbers, the ratio of the two products one to the other is equal to the ratio of the two numbers one to the other
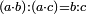
|
ו' כל מספר יוכו בו ב' מספרים יחס השטח האחד אל האח' כיחס הב' מספרים בעצמם הא' מהם אל הב'
|
7) Euclid, Elements, Book VII, proposition 19: For any four proportional numbers, the product of the first by the fourth is equal to the product of the second by the third
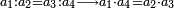
|
ז' ד' מספרים מתיחסם הכאת הראשון בד' שוה להכאת הב' בג'
|
8) Euclid, Elements, Book II, proposition 1: For any number multiplied by any number, their product is equal to [the sum of] the products of the multiplied number by each part of the multiplier number, divided into parts as you wish
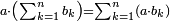
|
ח' כל מספר יוכה עם מספר מה איזה מספר היה הנה העולה מהם שוה לעולה מהכאת המספר המוכה עם כל אחד מחלקי המספר המכה על איזה חלקים שיחלק
|
| A short paragraph – philosophical observation concerning the meaning of the mean term
|
זכירה האמצעי בבחינתו בעצמו אינו נגדיי ובבחינות טובו הוא נגדיי לא' מהקצוות והוא נסתר כמו מרכז העגולה אף ליודעי חכמת השיעור והוא האמצעי בערך אלינו ולא בערך הדבר ועל כן הוא נסתר כי האמצעי בערך הדבר ידוע לבעלי חכמת השיעור והתיקון בהרחיק מהקצווי הפחות ולא תשער זה ע"ד כולל זולת התורה האלהית הקדושה שאינה משוערת מהשכל האינושי וזה אמת על כל פנים
|
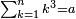
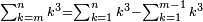
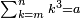
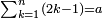
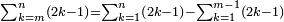
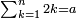
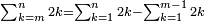
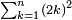
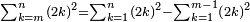
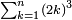
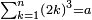
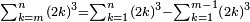
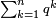
![\scriptstyle\sum_{k=1}^n q^k=q^n+\left[\frac{1}{q-1}\sdot\left(q^n-q\right)\right]](/mediawiki/images/math/8/5/2/8520ba5c791c1bd274691b5900880769.png)
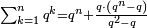
![{\color{OliveGreen}{\begin{align}&\scriptstyle\left(\frac{a_1}{b_2}+\frac{a_2}{b_2}+\cdots+\frac{a_n}{b_n}\right)-\left(\frac{c_1}{d_2}+\frac{c_2}{d_2}+\cdots+\frac{c_m}{d_m}\right)\\&\scriptstyle=\frac{\sum_{k=1}^n \left[a_k\sdot\left(\prod_{i=1,i\neq k}^n b_i\right)\sdot\left(\prod_{i=1}^m d_i\right)\right]-\sum_{k=1}^m \left[c_k\sdot\left(\prod_{i=1,i\neq k}^m d_i\right)\sdot\left(\prod_{i=1}^n b_i\right)\right]}{\prod_{k=1}^n b_k\sdot\prod_{i=1}^m d_i}\\\end{align}}}](/mediawiki/images/math/4/d/c/4dcd5d89beb5c0da5e72607633288b70.png)
![{\color{OliveGreen}{\begin{align}&\scriptstyle\left(\frac{a_1}{b_1}-\frac{c_1}{d_1}\right)+\left(\frac{a_2}{b_2}-\frac{c_2}{d_2}\right)+\cdots+\left(\frac{a_n}{b_n}-\frac{c_n}{d_n}\right)\\&\scriptstyle=\frac{\sum_{k=1}^n \left[a_k\sdot\left(\prod_{i=1,i\neq k}^n b_i\right)\sdot\left(\prod_{i=1}^m d_i\right)\right]-\sum_{k=1}^n \left[c_k\sdot\left(\prod_{i=1,i\neq k}^n d_i\right)\sdot\left(\prod_{i=1}^n b_i\right)\right]}{\prod_{k=1}^n b_k\sdot\prod_{i=1}^n d_i}\\\end{align}}}](/mediawiki/images/math/8/d/3/8d3aec6a4bbf87b62d0cbba13d6ac7d2.png)
![{\color{OliveGreen}{\begin{align}&\scriptstyle\left(\frac{a_1}{b_1}\times\frac{a_2}{b_2}\times\cdots\times\frac{a_n}{b_n}\right)-\left(\frac{c_1}{c_1}\times\frac{c_2}{c_2}\times\cdots\times\frac{c_m}{d_m}\right)\\&\scriptstyle=\frac{\left[\left(\prod_{i=1}^n a_i\right)\sdot\left(\prod_{j=1}^m d_j\right)\right]-\left[\left(\prod_{j=1}^m c_j\right)\sdot\left(\prod_{i=1}^n b_i\right)\right]}{\prod_{i=1}^n b_i\sdot\prod_{j=1}^m d_j}\\\end{align}}}](/mediawiki/images/math/4/6/f/46fa9a817ecbb4234aa0243bd14a7c22.png)
![{\color{OliveGreen}{\begin{align}&\scriptstyle\left(\frac{a_1}{b_1}-\frac{c_1}{d_1}\right)\times\left(\frac{a_2}{b_2}-\frac{c_2}{d_2}\right)\\&\scriptstyle=\frac{\left[\left(a_1\sdot d_1\right)-\left(c_1\sdot b_1\right)\right]\times\left[\left(a_2\sdot d_2\right)-\left(c_2\sdot b_2\right)\right]}{b_1\sdot d_1\sdot b_2\sdot d_2}\\\end{align}}}](/mediawiki/images/math/a/5/7/a57b58619cb3cdaff8f457f98a6a022f.png)
![{\color{OliveGreen}{\begin{align}&\scriptstyle\left[\left(\frac{a_1}{b_1}\times\frac{c_1}{d_1}\right)+\left(\frac{a_2}{b_2}\times\frac{c_2}{d_2}\right)+\cdots+\left(\frac{a_n}{b_n}\times\frac{c_n}{d_n}\right)\right]-\\&\scriptstyle-\left[\left(\frac{a_{n+1}}{b_{n+1}}\times\frac{c_{n+1}}{d_{n+1}}\right)+\left(\frac{a_{n+2}}{b_{n+2}}\times\frac{c_{n+2}}{d_{n+2}}\right)+\cdots+\left(\frac{a_{n+m}}{b_{n+m}}\times\frac{c_{n+m}}{d_{n+m}}\right)\right]\\&\scriptstyle=\frac{\left[\sum_{k=1}^n \left[\left(a_k\sdot c_k\right)\sdot\prod_{i=1,i\neq k}^{n+m} \left(b_i\sdot d_i\right)\right]\right]-\left[\sum_{k={n+1}}^{n+m} \left[\left(a_k\sdot c_k\right)\sdot\prod_{i=1,i\neq k}^{n+m} \left(b_i\sdot d_i\right)\right]\right]}{\prod_{i=1}^{n+m} b_i\sdot\prod_{i=1}^{n+m} d_i}\\\end{align}}}](/mediawiki/images/math/8/9/2/892a36331b9e37d892c0a0ee6c19faa1.png)
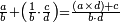
![\scriptstyle{\color{blue}{\left(1+\frac{7}{8}\right)\sdot\frac{2}{5}=\frac{2}{5}+\left(\frac{7}{8}\sdot\frac{2}{5}\right)=\frac{2}{5}+\left[\frac{1}{5}+\left(\frac{3}{4}\sdot\frac{1}{5}\right)\right]=\frac{3}{5}+\left(\frac{3}{4}\sdot\frac{1}{5}\right)=\left(3+\frac{3}{4}\right)\sdot\frac{1}{5}}}](/mediawiki/images/math/6/1/0/6103c77a142273f502b27e272a7e4b89.png)
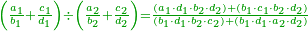
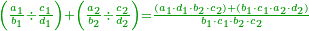
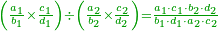
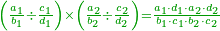
![\scriptstyle{\color{OliveGreen}{\left(\frac{a_1}{b_1}-\frac{c_1}{d_1}\right)\div\left(\frac{a_2}{b_2}-\frac{c_2}{d_2}\right)=\frac{\left[\left(a_1\sdot d_1\right)-\left(c_1\sdot b_1\right)\right]\times\left(b_2\sdot d_2\right)}{\left[\left(a_2\sdot d_2\right)-\left(c_2\sdot b_2\right)\right]\times\left(b_1\sdot d_1\right)}}}](/mediawiki/images/math/d/e/1/de19fec67919b87194e6104febf0c88d.png)
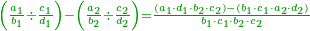
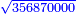
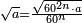
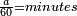
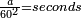
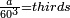
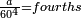
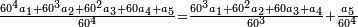
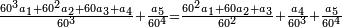
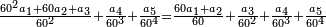
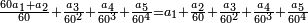
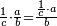
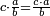
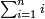
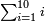
![\scriptstyle{\color{OliveGreen}{\sum_{i=1}^{n} i=n\sdot\left[\left(\frac{1}{2}\sdot n\right)+\frac{1}{2}\right]}}](/mediawiki/images/math/1/5/c/15c33ef94f6705e49da83967f0dddc21.png)
![\scriptstyle{\color{blue}{\sum_{i=1}^{10} i=10\sdot\left[\left(\frac{1}{2}\sdot10\right)+\frac{1}{2}\right]}}](/mediawiki/images/math/c/0/f/c0fdc71237cda523c5f4225f91df85b5.png)
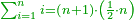
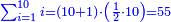
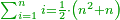
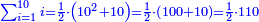
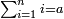
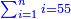
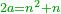
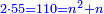
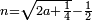
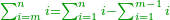
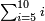

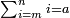
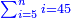
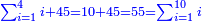
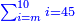
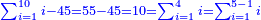
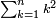
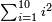
![\scriptstyle{\color{OliveGreen}{\sum_{i=1}^{n} i^2=\left(\sum_{i=1}^{n} i\right)\sdot\left[\left(\frac{2}{3}\sdot n\right)+\frac{1}{3}\right]}}](/mediawiki/images/math/3/d/e/3de704868bfb9b9a142ddf62d83bc112.png)
![\scriptstyle{\color{blue}{\sum_{i=1}^{10} i^2=\left(\sum_{i=1}^{10} i\right)\sdot\left[\left(\frac{2}{3}\sdot10\right)+\frac{1}{3}\right]=55\sdot7=385}}](/mediawiki/images/math/2/b/a/2ba3acc98bcbd3f147ab927dd9b48811.png)
![\scriptstyle{\color{OliveGreen}{\sum_{i=1}^n i^2=\left(\sum_{i=1}^n i\right)\sdot\left[\left[\frac{2}{3}\sdot\left(n-1\right)\right]+1\right]}}](/mediawiki/images/math/e/d/f/edf214156fd7c4c3ddb575a93911d0d1.png)
![\scriptstyle{\color{blue}{\sum_{k=1}^{10} k^2=\left(\sum_{k=1}^{10} k\right)\sdot\left[\left[\frac{2}{3}\sdot\left(10-1\right)\right]+1\right]}}](/mediawiki/images/math/8/b/c/8bcfe13faadb2a38abc83f12f8d0a1f5.png)
![\scriptstyle{\color{OliveGreen}{\sum_{i=1}^{11} i^2 =\left(\sum_{i=1}^{n} i\right)\sdot\left[\left[\frac{2}{3}\sdot \left(n+1\right)\right]-\frac{1}{3}\right]}}](/mediawiki/images/math/f/2/0/f20ca72a0b35535ef76c3017d54e7fa1.png)
![\scriptstyle{\color{blue}{\sum_{i=1}^{11} i^2 =\left(\sum_{i=1}^{11} i\right)\sdot\left[\left[\frac{2}{3}\sdot \left(11+1\right)\right]-\frac{1}{3}\right]}}](/mediawiki/images/math/e/a/c/eacacb7ee0f3d70ddd583f3e4ece1220.png)
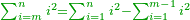
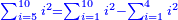
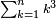
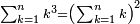
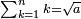
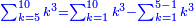
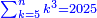
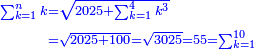
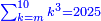
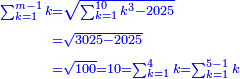
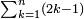
![\scriptstyle\sum_{k=1}^n \left(2k-1\right)=\left[\left[\frac{1}{2}\sdot\left(2n-1\right)\right]+\frac{1}{2}\right]^2](/mediawiki/images/math/2/0/a/20a10f45b8fb2803558c0f0ac0863baf.png)
![\scriptstyle\sum_{k=1}^n \left(2k-1\right)=\left[\frac{1}{2}\sdot\left[\left(2n-1\right)+1\right]\right]^2](/mediawiki/images/math/5/a/e/5aea89765e5b1ca007b6a29bcd89ad23.png)
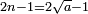
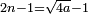
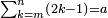
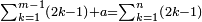
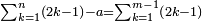
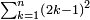
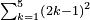
![\scriptstyle{\color{OliveGreen}{\sum_{k=1}^5\left(2k-1\right)^2=\left[\left[\sum_{k=1}^5\left(2k-1\right)\right]\sdot\left[\left[\frac{2}{3}\sdot\left(2k - 1\right)\right]+\frac{2}{3}\right]\right]-\left(\frac{1}{3}\sdot{n}\right)}}](/mediawiki/images/math/2/9/d/29db1261f226bb7b721a3f178cba0119.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle1^2+3^2+5^2+7^2+9^2&\scriptstyle=\left[25\sdot\left[\left(\frac{2}{3}\sdot9\right)+\frac{2}{3}\right]\right]-\left(\frac{1}{3}\sdot5\right)\\&\scriptstyle=\left[25\sdot\left(6+\frac{2}{3}\right)\right]-\frac{5}{3}\\&\scriptstyle=\left(166+\frac{2}{3}\right)-\left(1+\frac{2}{3}\right)\\\end{align}}}](/mediawiki/images/math/b/0/8/b08e33a0a47a1a7b8e436f6454e1b72a.png)
![\scriptstyle\sum_{k=1}^n\left(2k-1\right)^2=\left[\frac{2}{3}\sdot\left(2n-1\right)\right]\sdot\left[\left(\frac{1}{2}\sdot{2n}\right)\sdot\left[\frac{1}{2}\sdot\left(2n+1\right)\right]\right]](/mediawiki/images/math/0/f/f/0fff5ef7079ae6041ccc689021793eba.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle1^2+3^2+5^2+7^2+9^2&\scriptstyle=\left(\frac{2}{3}\sdot{9}\right)\sdot\left[\left(\frac{1}{2}\sdot{10}\right)\sdot\left(\frac{1}{2}\sdot{11}\right)\right]\\&\scriptstyle=6\sdot\left[5\sdot\left(5+\frac{1}{2}\right)\right]\\&\scriptstyle=6\sdot\left(27+\frac{1}{2}\right)\\\end{align}}}](/mediawiki/images/math/f/5/d/f5dcabb49970f94b25d1fdce8e5f2300.png)
![\scriptstyle\sum_{k=1}^n\left(2k-1\right)^2=\left[\left[\frac{1}{3}\sdot\left(2n-1\right)\right]+\frac{1}{3}\right]\sdot\left[\left[\frac{1}{2}\sdot\left(2n-1\right)\right]\sdot\left(2n+1\right)\right]](/mediawiki/images/math/1/8/0/180efc8336febcd78cf422e3ad4bcffa.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle1^2+3^2+5^2+7^2+9^2&\scriptstyle=\left[\left(\frac{1}{3}\sdot{9}\right)+\frac{1}{3}\right]\sdot\left[\left(\frac{1}{2}\sdot{9}\right)\sdot{11}\right]\\&\scriptstyle=\left(3+\frac{1}{3}\right)\sdot\left[\left(4+\frac{1}{2}\right)\sdot{11}\right]\\&\scriptstyle=\left(3+\frac{1}{3}\right)\sdot\left(49+\frac{1}{2}\right)\\\end{align}}}](/mediawiki/images/math/6/0/9/60955d508d3254ce3f60a7e449331225.png)
![\scriptstyle\sum_{k=1}^n\left(2k-1\right)^2=\left[\left[\sum_{k=1}^n\left(2k-1\right)\right]-\left[\left[\frac{1}{3}\sdot\left[\sum_{k=1}^n\left(2k-1\right)\right]\right]+\frac{1}{6}\right]\right]\sdot\left[\left(2n-1\right)+1\right]](/mediawiki/images/math/5/0/0/50047de1bf6b9c919695eba1bf725342.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle1^2+3^2+5^2+7^2+9^2&\scriptstyle=\left[25-\left[\left(\frac{1}{3}\sdot25\right)+\frac{1}{6}\right]\right]\sdot\left(9+1\right)\\&\scriptstyle=\left(16+\frac{1}{2}\right)\sdot10\\\end{align}}}](/mediawiki/images/math/0/d/a/0daf25c46daaf25a3c61b5df1b649d7e.png)
![\scriptstyle\sum_{k=1}^n\left(2k-1\right)^2=\left[\left[\left[\frac{1}{3}\sdot\left(2n-1\right)\right]+\frac{2}{3}\right]\sdot\left[\frac{1}{2}\sdot\left(2n-1\right)\right]\right]\sdot\left[\left(2n-1\right)+1\right]](/mediawiki/images/math/a/d/b/adb1bb3e07fcabe1b6c7c69f6daa94a2.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle1^2+3^2+5^2+7^2+9^2&\scriptstyle=\left[\left[\left(\frac{1}{3}\sdot9\right)+\frac{2}{3}\right]\sdot\left(\frac{1}{2}\sdot9\right)\right]\sdot\left(9+1\right)\\&\scriptstyle=\left[\left(3+\frac{2}{3}\right)\sdot\left(4+\frac{1}{2}\right)\right]\sdot{10}\\&\scriptstyle=\left(16+\frac{1}{2}\right)\sdot10\\\end{align}}}](/mediawiki/images/math/f/5/3/f5355a7c79aa5a0dbe9e2918fd9861f2.png)
![\scriptstyle\sum_{k=1}^n\left(2k-1\right)^2=\left[\frac{1}{6}\sdot\left(2n-1\right)\right]\sdot\left[\left[\left(2n-1\right)+1\right]\sdot\left[\left(2n-1\right)+2\right]\right]](/mediawiki/images/math/f/e/b/feb317aa5cefd1faf574f19ef56e947b.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle1^2+3^2+5^2+7^2+9^2&\scriptstyle=\left(\frac{1}{6}\sdot9\right)\sdot\left[\left(9+1\right)\sdot\left(9+2\right)\right]\\&\scriptstyle=\left(1+\frac{1}{2}\right)\sdot\left(10\sdot11\right)\\&\scriptstyle=\left(1+\frac{1}{2}\right)\sdot110\\\end{align}}}](/mediawiki/images/math/5/2/c/52c00c09074229b7c54ae68d9fe9c29c.png)

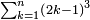
![\scriptstyle\sum_{k=1}^n\left(2k-1\right)^3=\left[2\sdot\left[\sum_{k=1}^n\left(2k-1\right)\right]^2\right]-\left[\sum_{k=1}^n\left(2k-1\right)\right]](/mediawiki/images/math/6/5/8/65823a460b2de27e8feedacdfdf349a9.png)
![\scriptstyle\sum_{k=1}^n\left(2k-1\right)^3=\left[\left[\sum_{k=1}^n\left(2k-1\right)\right]-\frac{1}{2}\right]\sdot\left[2\sdot\left[\sum_{k=1}^n\left(2k-1\right)\right]\right]](/mediawiki/images/math/8/f/4/8f409617cfa059237d6a827c819a1ce1.png)
![\scriptstyle2n-1=\sqrt{4\sdot\left[\sqrt{\left(\frac{1}{2}\sdot{a}\right)+\left(\frac{1}{2}\sdot\frac{1}{8}\right)}+\sqrt{\frac{1}{2}\sdot\frac{1}{8}}\right]}-1](/mediawiki/images/math/d/f/4/df492255476351651b70c1d786cdf13c.png)
![\scriptstyle\left[\sum_{k=1}^n\left(2k-1\right)^3\right]-a=\sum_{k=1}^{m-1}\left(2k-1\right)^3](/mediawiki/images/math/4/2/3/4235edc55463ec745e3854894246fc7c.png)
![\scriptstyle\sum_{k=1}^n 2k =\left[\left(\frac{1}{2}\sdot{2n}\right)+1\right]\sdot\left(\frac{1}{2}\sdot{2n}\right)](/mediawiki/images/math/b/3/c/b3c797cef133fc955b53e577cfc0df9b.png)
![\scriptstyle\sum_{k=1}^n 2k =\left[\frac{1}{2}\sdot\left(2n+2\right)\right]\sdot\left(\frac{1}{2}\sdot{2n}\right)](/mediawiki/images/math/6/9/8/698ed5658cba23e5158e4b7ed63ebe74.png)
![\scriptstyle\sum_{k=1}^n 2k=\left(\frac{1}{4}\sdot{2n}\right)\sdot\left[2\sdot\left(n+1\right)\right]](/mediawiki/images/math/1/b/8/1b8ba31e73cad7843c250ad7269936e9.png)
![\scriptstyle\sum_{k=1}^n 2k=\left[\frac{1}{4}\sdot\left[2\sdot\left(n+1\right)\right]\right]\sdot{2n}](/mediawiki/images/math/0/f/f/0ff2fb05a727e2bfb836dc9ea50d674b.png)
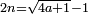
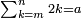
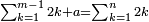
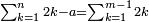
![\scriptstyle\sum_{k=1}^n\left(2k\right)^2=\left[\left[\frac{2}{3}\sdot\left(2n\right)\right]+\frac{2}{3}\right]\sdot\left[\sum_{k=1}^n 2k\right]](/mediawiki/images/math/2/4/e/24e7a797b4d2d27e51f5e15fa262fb84.png)
![\scriptstyle\sum_{k=1}^n\left(2k\right)^2=\left[\frac{2}{3}\sdot\left[\sum_{k=1}^n 2k\right]\right]\sdot\left(2n+1\right)](/mediawiki/images/math/5/4/4/544594f2cf374d660a5c1b76e01ad767.png)
![\scriptstyle\sum_{k=1}^n\left(2k\right)^2=\left[\frac{1}{6}\sdot\left(2k\right)\right]\sdot\left[\left(2n+1\right)\sdot\left(2n+2\right)\right]](/mediawiki/images/math/e/9/f/e9f225dd4bee7e082395c8e182194dbf.png)
![\scriptstyle\sum_{k=1}^n\left(2k\right)^3=2\sdot\left[\sum_{k=1}^n 2k\right]^2](/mediawiki/images/math/c/a/5/ca5a0885b4cc27ac492aff8cea6401f7.png)
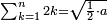
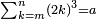
![\scriptstyle\left[\sum_{k=1}^{m-1}\left(2k\right)^3\right]+a=\sum_{k=1}^n\left(2k\right)^3](/mediawiki/images/math/1/6/4/164c3f8e4790341bab9cbd735d31341e.png)
![\scriptstyle\left[\sum_{k=1}^n\left(2k\right)^3\right]-a=\sum_{k=1}^{m-1}\left(2k\right)^3](/mediawiki/images/math/0/d/3/0d345f00c161b3e09955222514268939.png)
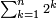
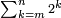
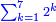
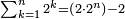
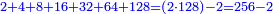
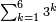
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle3+9+27+81+243+729&\scriptstyle=729+\left[\frac{1}{3-1}\sdot\left(729-3\right)\right]\\&\scriptstyle=729+\left[\frac{1}{2}\sdot\left(729-3\right)\right]\\&\scriptstyle=729+363\\\end{align}}}](/mediawiki/images/math/9/d/1/9d1cb2311ab1e4355462049e2132bce8.png)
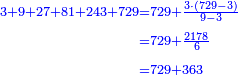
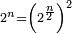
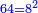
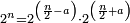
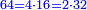
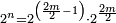
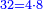
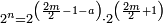

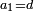
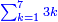
![\scriptstyle S_n=\left[\left(\frac{1}{2}\sdot{n}\right)+\frac{1}{2}\right]\sdot{a_n}](/mediawiki/images/math/7/e/b/7eb29b904d71df29333e671ce5c26ce9.png)
![\scriptstyle{\color{blue}{3+6+9+12+15+18+21=\left[\left(\frac{1}{2}\sdot{7}\right)+\frac{1}{2}\right]\sdot{21}=4\sdot{21}}}](/mediawiki/images/math/7/1/3/71350e31457692457563708b3881ec83.png)
![\scriptstyle S_n=\left[\frac{1}{2}\sdot\left(a_1+a_n\right)\right]\sdot{n}](/mediawiki/images/math/6/c/e/6ced82d8579ff576f2e054b5fcf35161.png)
![\scriptstyle{\color{blue}{3+6+9+12+15+18+21=\left[\frac{1}{2}\sdot\left(3+21\right)\right]\sdot{7}=\left(\frac{1}{2}\sdot{24}\right)\sdot{7}=12\sdot{7}}}](/mediawiki/images/math/0/2/e/02e542d23f66274e0b78bdf4ab7081c0.png)
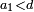
![\scriptstyle{\color{blue}{\sum_{k=1}^8 \left[\left[2\sdot\left(k-1\right)\right]+1\right]}}](/mediawiki/images/math/7/a/d/7ad45aa9fb63dddfd4194e85bbaac96c.png)
![\scriptstyle S_n=\left[\left[\left(d-a_1\right)+a_n\right]\sdot\left[\left(\frac{1}{2}\sdot{n}\right)+\frac{1}{2}\right]\right]-\left[\left(d-a_1\right)\sdot{n}\right]](/mediawiki/images/math/3/f/f/3ff2e4d770df846fcab47b2dccceff6a.png)
![{\color{blue}{\begin{align}\scriptstyle1+3+5+7+9+11+13+15&\scriptstyle=\left[\left[\left(2-1\right)+15\right]\sdot\left[\left(\frac{1}{2}\sdot{8}\right)+\frac{1}{2}\right]\right]-\left[\left(2-1\right)\sdot{8}\right]\\&\scriptstyle=\left[\left(1+15\right)\sdot\left(4+\frac{1}{2}\right)\right]-\left(1\sdot{8}\right)\\&\scriptstyle=\left[16\sdot\left(4+\frac{1}{2}\right)\right]-8=72-8\\\end{align}}}](/mediawiki/images/math/1/1/b/11b77d5c87bf9d959c8549e24258096b.png)
![\scriptstyle{\color{blue}{1+3+5+7+9+11+13+15=\left[\frac{1}{2}\sdot\left(1+15\right)\right]\sdot{8}=\left(\frac{1}{2}\sdot{16}\right)\sdot{8}=8\sdot{8}}}](/mediawiki/images/math/9/b/b/9bb5e90d5282d4952e471fa649e02ee1.png)
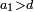
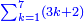
![\scriptstyle S_n=\left[\left[\left(a_1-d\right)+a_n\right]\sdot\left[\left(\frac{1}{2}\sdot{n}\right)+\frac{1}{2}\right]\right]-\left(a_1-d\right)](/mediawiki/images/math/2/b/8/2b8fcfdc05f6b50d1cfe407caaaa766b.png)
![{\color{blue}{\begin{align}\scriptstyle5+8+11+14+17+20+23&\scriptstyle=\left[\left[\left(5-3\right)+23\right]\sdot\left[\left(\frac{1}{2}\sdot{7}\right)+\frac{1}{2}\right]\right]-\left(5-3\right)\\&\scriptstyle=\left[\left(2+23\right)\sdot\left[\left(\frac{1}{2}\sdot{7}\right)+\frac{1}{2}\right]\right]-2\\&\scriptstyle=\left[25\sdot\left[\left(\frac{1}{2}\sdot{7}\right)+\frac{1}{2}\right]\right]-2=100-2\\\end{align}}}](/mediawiki/images/math/2/7/6/2763bf8d6beb4c2cd198a3e747c87e0c.png)
![\scriptstyle S_n=\left[\frac{1}{2}\sdot\left[\frac{a_n-a_1}{d}+1\right]\right]\sdot\left(a_1+a_n\right)](/mediawiki/images/math/0/2/3/02339f609fa5841082be779504961e6e.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle5+8+11+14+17+20+23&\scriptstyle=\left[\frac{1}{2}\sdot\left[\frac{23-5}{3}+1\right]\right]\sdot\left(5+23\right)\\&\scriptstyle=\left[\frac{1}{2}\sdot\left[\frac{18}{3}+1\right]\right]\sdot\left(5+23\right)\\&\scriptstyle=\left(\frac{1}{2}\sdot{7}\right)\sdot\left(5+23\right)\\\end{align}}}](/mediawiki/images/math/e/3/3/e338f6fb48010cfe5efd298d2313c405.png)
![\scriptstyle S_n=\left[\frac{a_n-a_1}{d}+1\right]\sdot\left[\frac{1}{2}\sdot\left(a_1+a_n\right)\right]](/mediawiki/images/math/7/7/a/77ab42c88377250e93905a9de38d5b53.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle5+8+11+14+17+20+23&\scriptstyle=\left(\frac{23-5}{3}+1\right)\sdot\left[\frac{1}{2}\sdot\left(5+23\right)\right]\\&\scriptstyle=\left(\frac{18}{3}+1\right)\sdot\left[\frac{1}{2}\sdot\left(5+23\right)\right]\\&\scriptstyle=7\sdot\left[\frac{1}{2}\sdot\left(5+23\right)\right]\\\end{align}}}](/mediawiki/images/math/9/7/e/97ea12068c5e9d1ae4cbedac69b6b2d2.png)
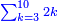
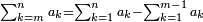
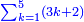
![\begin{align}\scriptstyle\sum_{k=m}^n a_k&\scriptstyle=\left[\left[\left[\left(\frac{1}{2}\sdot{n}\right)+\frac{1}{2}\right]\sdot\left[a_n+\left(d-a_1\right)\right]\right]-\left[\left(d-a_1\right)\sdot{n}\right]\right]\\&\scriptstyle-\left[\left[\left[\left[\frac{1}{2}\sdot\left(m-1\right)\right]+\frac{1}{2}\right]\sdot\left[a_{m-1}+\left(d-a_1\right)\right]\right]-\left[\left(d-a_1\right)\sdot\left(m-1\right)\right]\right]\\\end{align}](/mediawiki/images/math/6/f/a/6fad7e2bfe24280171b3616cdc04176a.png)
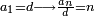
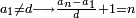
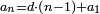
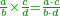
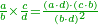
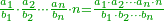
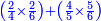
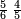
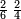
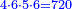
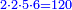
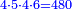

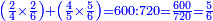
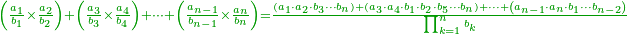
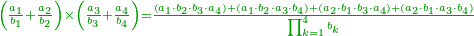
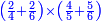
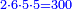
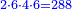
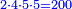
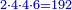
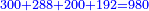
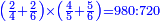
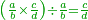
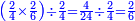
![\scriptstyle{\color{OliveGreen}{\left[\left(1-\frac{c}{d}\right)\times\frac{a}{b}\right]+\left(\frac{a}{b}\times\frac{c}{d}\right)=\frac{a}{b}}}](/mediawiki/images/math/7/4/4/744b88e33933bda6d8cf81e3fa9253ba.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left[\left(1-\frac{2}{6}\right)\times\frac{2}{4}\right]+\left(\frac{2}{4}\times\frac{2}{6}\right)&\scriptstyle=\left(\frac{4}{6}\times\frac{2}{4}\right)+\frac{4}{24}\\&\scriptstyle=\frac{8}{24}+\frac{4}{24}=\frac{12}{24}=\frac{2}{4}\\\end{align}}}](/mediawiki/images/math/8/5/e/85e0d0186ccbd8de9315c4c355b58d33.png)

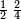
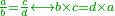
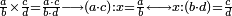
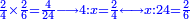
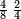
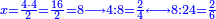
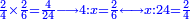
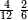
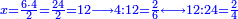
![\scriptstyle{\color{OliveGreen}{\frac{a_1}{b_1}+\frac{a_2}{b_2}+\cdots+\frac{a_n}{b_n}=\frac{\sum_{k=1}^n \left[a_k\sdot\left(\prod_{i=1,i\neq{k}}^n b_i\right)\right]}{\prod_{k=1}^n b_k}}}](/mediawiki/images/math/1/3/3/1337a9ba8d106c26c238d334902374d3.png)
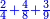
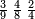
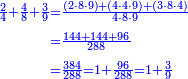
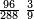
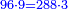
![\scriptstyle{\color{OliveGreen}{\left(1-\frac{a}{b}\right)>\frac{c}{d}\longrightarrow\frac{a}{b}+\frac{c}{d}=1-\left[\left(1-\frac{a}{b}\right)-\frac{c}{d}\right]}}](/mediawiki/images/math/b/3/2/b32cf3f9474b989e5929f34080038680.png)
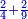
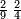
![\scriptstyle{\color{blue}{\frac{2}{4}+\frac{2}{9}=1-\left[\left(1-\frac{2}{4}\right)-\frac{2}{9}\right]=1-\left(\frac{2}{4}-\frac{2}{9}\right)=1-\frac{10}{36}=\frac{26}{36}}}](/mediawiki/images/math/0/e/2/0e2cedbf95ca5b6bddddcae39fa9909d.png)
![\scriptstyle\left(1-\frac{a}{b}\right)<\frac{c}{d}\longrightarrow\frac{a}{b}+\frac{c}{d}=\left[\frac{c}{d}-\left(1-\frac{a}{b}\right)\right]+1](/mediawiki/images/math/2/3/b/23bbd8921616da524fc3fde8faaa736a.png)
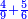
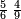
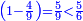
![{\color{blue}{\begin{align}\scriptstyle\frac{4}{9}+\frac{5}{6}&\scriptstyle=\left[\frac{5}{6}-\left(1-\frac{4}{9}\right)\right]+1\\&\scriptstyle=\left(\frac{5}{6}-\frac{5}{9}\right)+1=\frac{15}{54}+1\\\end{align}}}](/mediawiki/images/math/b/8/3/b832bf542a265805123046bfc3938e4f.png)
![\scriptstyle\left[1-\left[\left(\frac{a}{b}+\frac{c}{d}\right)-1\right]\right]<\frac{e}{f}\longrightarrow\frac{a}{b}+\frac{c}{d}+\frac{e}{f}=\left[\frac{e}{f}-\left[1-\left[\left(\frac{a}{b}+\frac{c}{d}\right)-1\right]\right]\right]+1+1](/mediawiki/images/math/5/f/5/5f58f0fc1f597d89cfba5b8077ac5d14.png)
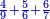
![\scriptstyle{\color{blue}{1-\left[\left(\frac{4}{9}+\frac{5}{6}\right)-1\right]=1-\frac{15}{54}=\frac{39}{54}<\frac{6}{7}}}](/mediawiki/images/math/f/8/5/f85b885efdc3f0514b4f44ae45b3fa1d.png)
![{\color{blue}{\begin{align}\scriptstyle\frac{4}{9}+\frac{5}{6}+\frac{6}{7}&\scriptstyle=\left[\frac{6}{7}-\left[1-\left[\left(\frac{4}{9}+\frac{5}{6}\right)-1\right]\right]\right]+1+1\\&\scriptstyle=\left[\frac{6}{7}-\left(1-\frac{15}{54}\right)\right]+1+1=\left(\frac{6}{7}-\frac{39}{54}\right)+1+1=\frac{51}{378}+1+1\\\end{align}}}](/mediawiki/images/math/c/d/e/cdebc53de8f329986a30edf1e24b47e8.png)
![\scriptstyle\left[1-\left[\left(\frac{a}{b}+\frac{c}{d}\right)-1\right]\right]>\frac{e}{f}\longrightarrow\frac{a}{b}+\frac{c}{d}+\frac{e}{f}=1-\left[\left[1-\left[\left(\frac{a}{b}+\frac{c}{d}\right)-1\right]\right]-\frac{e}{f}\right]+1](/mediawiki/images/math/9/a/6/9a68f052cc089fdb1ff27bc33029e921.png)
![\scriptstyle\left[\left(1-\frac{a}{b}\right)-\frac{c}{d}\right]<\frac{e}{f}\longrightarrow\frac{a}{b}+\frac{c}{d}+\frac{e}{f}=\left[\frac{e}{f}-\left[\left(1-\frac{a}{b}\right)-\frac{c}{d}\right]\right]+1](/mediawiki/images/math/c/7/b/c7b0abf4f3f738c224c245168150911e.png)
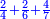
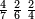
![{\color{blue}{\begin{align}\scriptstyle\frac{2}{4}+\frac{2}{6}+\frac{4}{7}&\scriptstyle=\left[\frac{4}{7}-\left[\left(1-\frac{2}{4}\right)-\frac{2}{6}\right]\right]+1\\&\scriptstyle=\left(\frac{4}{7}-\frac{4}{24}\right)+1\\&\scriptstyle=\frac{68}{168}+1\\\end{align}}}](/mediawiki/images/math/e/3/0/e305979eab5de24c68114c367db9d38c.png)
![\scriptstyle\left[\left(1-\frac{a}{b}\right)-\frac{c}{d}\right]>\frac{e}{f}\longrightarrow\frac{a}{b}+\frac{c}{d}+\frac{e}{f}=1-\left[\left[\left(1-\frac{a}{b}\right)-\frac{c}{d}\right]-\frac{e}{f}\right]](/mediawiki/images/math/2/3/7/23755dccf0f300bf22db1e74a43d08af.png)
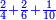
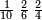
![\scriptstyle{\color{blue}{\left[\left(1-\frac{2}{4}\right)-\frac{2}{6}\right]=\frac{4}{24}>\frac{1}{10}}}](/mediawiki/images/math/9/5/9/95982f33557fe5e67d22f1647f93e6d1.png)
![{\color{blue}{\begin{align}\scriptstyle\frac{2}{4}+\frac{2}{6}+\frac{1}{10}&\scriptstyle=1-\left[\left[\left(1-\frac{2}{4}\right)-\frac{2}{6}\right]-\frac{1}{10}\right]\\&\scriptstyle=1-\left(\frac{4}{24}-\frac{1}{10}\right)\\&\scriptstyle=1-\frac{16}{240}=\frac{224}{240}\\\end{align}}}](/mediawiki/images/math/c/1/d/c1d9fe254b1d290f39e0ee75cd68cd47.png)
![\scriptstyle\left[1-\left[\frac{c}{d}-\left(1-\frac{a}{b}\right)\right]\right]<\frac{e}{f}\longrightarrow\frac{a}{b}+\frac{c}{d}+\frac{e}{f}=\left[\left[\frac{e}{f}-\left[1-\left[\frac{c}{d}-\left(1-\frac{a}{b}\right)\right]\right]\right]+1\right]+1](/mediawiki/images/math/8/e/e/8eecfed88c0a67a691054eae0d4909a3.png)
![\scriptstyle\left[1-\left[\frac{c}{d}-\left(1-\frac{a}{b}\right)\right]\right]>\frac{e}{f}\longrightarrow\frac{a}{b}+\frac{c}{d}+\frac{e}{f}=\left[1-\left[\left[1-\frac{c}{d}-\left(1-\frac{a}{b}\right)\right]-\frac{e}{f}\right]\right]+1](/mediawiki/images/math/4/5/3/4533d780746631e4aff63be214c944bd.png)
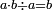

![\scriptstyle\left(a\sdot b\right)\div\left(c\sdot b\right)=\left[\left(a\sdot b\right)\div b\right]\div\left[\left(c\sdot b\right)\div b\right]=a\div c](/mediawiki/images/math/1/f/6/1f640630efc6327e2613d04c8a08c8b4.png)
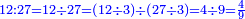
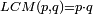
![\scriptstyle LCM\left[\left(a\sdot b\right),b\right]=a\sdot b](/mediawiki/images/math/1/2/d/12ddf85b96efa3da388f95e80169e9df.png)
![\scriptstyle LCM\left[\left(a\sdot b\right),\left(c\sdot b\right)\right]=\left(a\sdot b\right)\sdot c=a\sdot\left(c\sdot b\right)](/mediawiki/images/math/b/6/f/b6ff88df5070f7c498ae873b6e2b3a65.png)
![\scriptstyle\sum_{k=1}^n \frac{a_k}{b_k}=\frac{\sum_{k=1}^n \left[\frac{a_k}{b_k}\sdot LCM\left(b_1,b_2,\cdots,b_n\right)\right]}{LCM\left(b_1,b_2,\cdots,b_n\right)}](/mediawiki/images/math/1/9/0/19031c8dff61d5ec20ee45e37072ee97.png)
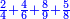
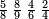
![\scriptstyle{\color{blue}{ LCM\left(4,6\right)=LCM\left[\left(2\sdot2\right),\left(3\sdot2\right)\right]=2\sdot6=3\sdot4=12}}](/mediawiki/images/math/9/0/5/9056c902fb8aa7dc6a2a29b8851ab72a.png)
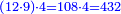
![{\color{blue}{\begin{align}\scriptstyle\frac{2}{4}+\frac{4}{6}+\frac{8}{9}+\frac{5}{8}&\scriptstyle=\frac{\left[2\sdot\left(432\div4\right)\right]+\left[4\sdot\left(432\div6\right)\right]\left[8\sdot\left(432\div9\right)\right]+\left[5\sdot\left(432\div8\right)\right]}{432}\\&\scriptstyle=\frac{216+288+384+270}{432}\\&\scriptstyle=\frac{1158}{432}\\&\scriptstyle=2+\frac{294}{432}\\\end{align}}}](/mediawiki/images/math/e/5/d/e5dc8fb590548b49c6115d7108886a21.png)
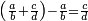
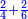
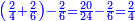
![\scriptstyle\left[\left(\frac{a}{b}+\frac{c}{d}\right)+\left(1-\frac{a}{b}\right)\right]-1=\frac{c}{d}](/mediawiki/images/math/8/b/b/8bb79c6340b5cc89864d498428993391.png)
![\scriptstyle{\color{blue}{\left[\left(\frac{2}{4}+\frac{2}{6}\right)+\left(1-\frac{2}{4}\right)\right]-1=\left(\frac{20}{24}+\frac{2}{4}\right)-1=\left(1+\frac{2}{6}\right)-1=\frac{2}{6}}}](/mediawiki/images/math/8/6/4/864f6f2c6f571bc0ab5f55cc4be9614b.png)
![\scriptstyle{\color{blue}{\left[\left(\frac{2}{4}+\frac{2}{6}\right)+\left(1-\frac{2}{6}\right)\right]-1=\left(\frac{20}{24}+\frac{4}{6}\right)-1=\left(1+\frac{3}{6}\right)-1=\frac{3}{6}=\frac{2}{4}}}](/mediawiki/images/math/0/7/b/07b6760ec6933235d33f343d19528d64.png)
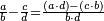
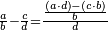
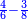
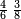
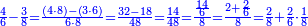
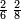
![\scriptstyle\frac{a}{b}-\frac{c}{d}=1-\left[\frac{c}{d}+\left(1-\frac{a}{b}\right)\right]](/mediawiki/images/math/b/2/4/b24bfd0510e6ab40f48d3e033ed858a3.png)
![\scriptstyle{\color{blue}{\frac{4}{6}-\frac{3}{8}=1-\left[\frac{3}{8}+\left(1-\frac{4}{6}\right)\right]=1-\left(\frac{3}{8}+\frac{2}{6}\right)=1-\frac{34}{48}=\frac{14}{48}}}](/mediawiki/images/math/e/6/c/e6c3bf2ae9c4471daa25e36009354632.png)
![\scriptstyle\frac{a}{b}-\frac{c}{d}=\left[\frac{a}{b}+\left(1-\frac{c}{d}\right)\right]-1](/mediawiki/images/math/f/9/5/f95a8308ffae0282af046f7093f4a050.png)
![\scriptstyle{\color{blue}{\frac{4}{6}-\frac{3}{8}=\left[\frac{4}{6}+\left(1-\frac{3}{8}\right)\right]-1=\left(\frac{4}{6}+\frac{5}{8}\right)-1=\left(1+\frac{14}{48}\right)-1=\frac{14}{48}}}](/mediawiki/images/math/c/8/e/c8e205993be6c43b6e513b1a1e954a51.png)
![\scriptstyle\left[\frac{a}{b}+\left(\frac{a}{b}-\frac{c}{d}\right)\right]-\frac{c}{d}=2\sdot\left(\frac{a}{b}-\frac{c}{d}\right)](/mediawiki/images/math/f/6/f/f6fefbda7339158ecd0c846ae39dcb26.png)
![{\color{blue}{\begin{align}\scriptstyle\left[\frac{4}{6}+\left(\frac{4}{6}-\frac{3}{8}\right)\right]-\frac{3}{8}&\scriptstyle=\left(\frac{4}{6}+\frac{14}{48}\right)-\frac{3}{8}\\&\scriptstyle=\frac{276}{288}-\frac{3}{8}\\&\scriptstyle=\frac{1344}{2304}\\&\scriptstyle=2\sdot\frac{14}{48}=2\sdot\left(\frac{4}{6}-\frac{3}{8}\right)\\\end{align}}}](/mediawiki/images/math/8/7/2/8728716975997ba60a517668eccbd8ac.png)
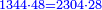
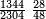
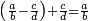
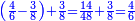
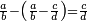
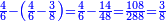
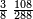

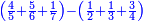
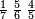
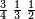

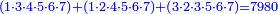
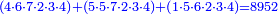
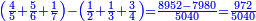
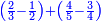
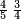
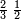
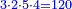
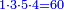



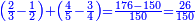
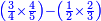



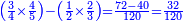
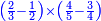
![{\color{blue}{\scriptstyle\left(\frac{2}{3}-\frac{1}{2}\right)\times\left(\frac{4}{5}-\frac{3}{4}\right)=\frac{\left[\left(2\sdot2\right)-\left(1\sdot3\right)\right]\times\left[\left(4\sdot4\right)-\left(3\sdot5\right)\right]}{3\sdot2\sdot5\sdot4}}}](/mediawiki/images/math/3/c/c/3cc16132d344c4acfadd35fb7d6cbd3a.png)
![{\color{blue}{\scriptstyle\left[\left(\frac{1}{2}\times\frac{2}{3}\right)+\left(\frac{3}{4}\times\frac{4}{5}\right)\right]-\left[\left(\frac{3}{7}\times\frac{4}{5}\right)+\left(\frac{2}{3}\times\frac{1}{4}\right)\right]}}](/mediawiki/images/math/b/b/d/bbd1d7fd145240388f8000054956bb7f.png)
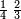
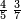

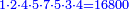

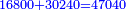
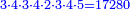

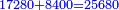
![\scriptstyle{\color{blue}{\left[\left(\frac{1}{2}\times\frac{2}{3}\right)+\left(\frac{3}{4}\times\frac{4}{5}\right)\right]-\left[\left(\frac{3}{7}\times\frac{4}{5}\right)+\left(\frac{2}{3}\times\frac{1}{4}\right)\right]=\frac{47040-25680}{50400}=\frac{21360}{50400}}}](/mediawiki/images/math/e/d/2/ed2d7d05282e05bd340152ee2627e47b.png)
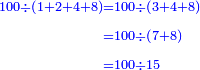
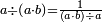
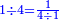
![\scriptstyle a\div\left[\left(a\sdot b\right)+1\right]=\frac{1}{\left[\left(a\sdot b\right)\div a\right]+1}+\left(\frac{1}{\left[\left(a\sdot b\right)\div a\right]+1}\sdot\frac{a-1}{\left(a\sdot b\right)+1}\right)](/mediawiki/images/math/8/4/0/840986bc829b9c0631a46fea168fe09c.png)
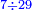
![{\color{blue}{\begin{align}\scriptstyle7\div29&\scriptstyle=\frac{1}{\left[\left(29-1\right)\div7\right]+1}+\left(\frac{1}{\left[\left(29-1\right)\div7\right]+1}\sdot\frac{7-1}{29}\right)\\&\scriptstyle=\frac{1}{4+1}+\left(\frac{1}{4+1}\sdot\frac{6}{29}\right)\\&\scriptstyle=\frac{1}{5}+\left(\frac{1}{5}\sdot\frac{6}{29}\right)\\\end{align}}}](/mediawiki/images/math/7/a/6/7a69fe025577e0f20f925c87624417be.png)
![\scriptstyle a\div\left[\left(a\sdot b\right)+c\right]=\frac{1}{\left[\left(a\sdot b\right)\div a\right]+1}+\left(\frac{1}{\left[\left(a\sdot b\right)\div a\right]+1}\sdot\frac{a-c}{\left(a\sdot b\right)+c}\right)](/mediawiki/images/math/1/0/c/10c67f4a03765d28d7de9dbe21d73433.png)
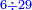
![{\color{blue}{\begin{align}\scriptstyle6\div29&\scriptstyle=\frac{1}{\left[\left(29-5\right)\div6\right]+1}+\left(\frac{1}{\left[\left(29-5\right)\div6\right]+1}\sdot\frac{6-5}{29}\right)\\&\scriptstyle=\frac{1}{4+1}+\left(\frac{1}{4+1}\sdot\frac{1}{29}\right)\\&\scriptstyle=\frac{1}{5}+\left(\frac{1}{5}\sdot\frac{1}{29}\right)\\\end{align}}}](/mediawiki/images/math/2/4/6/2465c314f8c1caf95b9e720b4d017ec4.png)
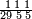
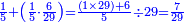

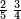
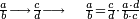
![{\color{blue}{\begin{align}\scriptstyle\frac{3}{4}&\scriptstyle=\frac{2}{5}\sdot\frac{3\sdot5}{4\sdot2}\\&\scriptstyle=\frac{2}{5}\sdot\frac{15}{8}\\&\scriptstyle=\frac{2}{5}\sdot\left(1+\frac{7}{8}\right)\\&\scriptstyle=\frac{2}{5}+\frac{7}{4\sdot5}\\&\scriptstyle=\frac{2}{5}+\frac{7}{20}\\&\scriptstyle=\frac{2}{5}+\left[\frac{1}{5}+\left(\frac{3}{4}\sdot\frac{1}{5}\right)\right]=\frac{3}{5}+\left(\frac{3}{4}\sdot\frac{1}{5}\right)\\\end{align}}}](/mediawiki/images/math/f/9/6/f96aade01caac4e8ac0e5e38a88af98e.png)
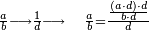
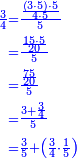
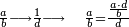
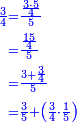
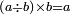
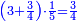
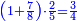
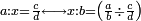
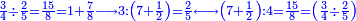
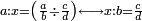
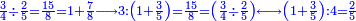
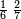
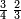
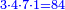
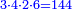
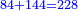
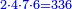
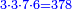

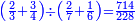
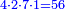

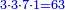
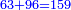
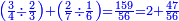
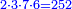
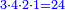
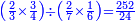
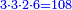
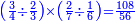
![\scriptstyle{\color{blue}{\left[\left(3\sdot3\right)-\left(4\sdot2\right)\right]\times\left(7\sdot6\right)=42}}](/mediawiki/images/math/0/d/8/0d89936b5ff51b49bdc00487eb7c653f.png)
![\scriptstyle{\color{blue}{\left[\left(2\sdot6\right)-\left(7\sdot1\right)\right]\times\left(4\sdot3\right)=60}}](/mediawiki/images/math/f/5/3/f53c691e6d1f9e0d0e83791f40284745.png)
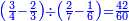


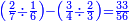


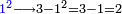
![\scriptstyle{\color{blue}{\left[\left[2\sdot\left(10\sdot1\right)\right]+8\right]\sdot8=\left(20\sdot8\right)+8^2}}\longrightarrow\begin{cases}\scriptstyle25-\left(2\sdot8\right)=25-16=9\\\scriptstyle96-8^2=96-64=32\\\end{cases}](/mediawiki/images/math/a/9/f/a9f7eabc5555111b4522c93eed224456.png)
![\scriptstyle{\color{blue}{\left[\left[2\sdot\left(10\sdot18\right)\right]+8\right]\sdot8=\left(360\sdot8\right)+8^2}}\longrightarrow\begin{cases}\scriptstyle32-\left(3\sdot8\right)=32-24=8\\\scriptstyle88-\left(6\sdot8\right)=88-48=40\\\scriptstyle407-8^2=343\\\end{cases}](/mediawiki/images/math/d/7/f/d7f2bbeb20231f2ab938cf9792628905.png)
![\scriptstyle{\color{blue}{\left[\left[2\sdot\left(10\sdot188\right)\right]+9\right]\sdot9=\left(3760\sdot9\right)+9^2}}\longrightarrow\begin{cases}\scriptstyle34-\left(3\sdot9\right)=34-27=7\\\scriptstyle73-\left(7\sdot9\right)=73-63=10\\\scriptstyle100-\left(6\sdot9\right)=100-54=46\\\scriptstyle460-9^2=379\\\end{cases}](/mediawiki/images/math/3/5/1/3517971bd85a7323e71ba300e2d6d57f.png)
![\scriptstyle{\color{blue}{\left[\left[2\sdot\left(10\sdot1889\right)\right]+1\right]\sdot1=\left(37780\sdot1\right)+1^2}}\longrightarrow\begin{cases}\scriptstyle3-\left(3\sdot1\right)=0\\\scriptstyle7-\left(7\sdot1\right)=0\\\scriptstyle9-\left(7\sdot1\right)=9-7=2\\\scriptstyle20-\left(8\sdot1\right)=20-8=12\\\scriptstyle20-1^2=19\\\end{cases}](/mediawiki/images/math/b/7/d/b7dd2ab18a6a35395477255c19a54e0c.png)
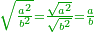
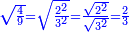
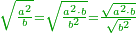
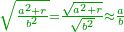
![\scriptstyle{\color{OliveGreen}{\sqrt[3]{a^3+r}\approx a}}](/mediawiki/images/math/d/0/8/d08276a0299fcd67809bb7e55f5c8068.png)
![\scriptstyle{\color{OliveGreen}{\sqrt[3]{\left(10a\right)^3+3\sdot\left[\left(10a\right)^2\sdot b\right]+3\sdot\left(10a\sdot b^2\right)+b^3}=\sqrt[3]{\left(10a+b\right)^3}=10a+b}}](/mediawiki/images/math/d/5/9/d598b308f04b6a0d930b9301f3c9d44c.png)
![\scriptstyle\sqrt[3]{\frac{a^3}{b^3}}=\frac{\sqrt[3]{a^3}}{\sqrt[3]{b^3}}=\frac{a}{b}](/mediawiki/images/math/5/5/2/55215afa0eb94bb987abf8d5f12510eb.png)
![\scriptstyle\sqrt[3]{\frac{a^3}{b}}=\sqrt[3]{\frac{a^3\sdot b^2}{b^3}}=\frac{\sqrt[3]{a^3\sdot b^2}}{\sqrt[3]{b^3}}](/mediawiki/images/math/3/3/2/33204800e2b4f562b39489f20f0de4a7.png)
![\scriptstyle\sqrt[3]{\frac{a^3+r}{b^3}}=\frac{\sqrt[3]{a^3+r}}{\sqrt[3]{b^3}}\approx\frac{a}{b}](/mediawiki/images/math/6/3/0/6303290fa0ad7148d6224aa7abafea0c.png)
![\scriptstyle\sqrt[3]{\frac{a^3+r}{3^3}}=\frac{\sqrt[3]{a^3+r}}{\sqrt[3]{3^3}}\approx\frac{1}{3}a](/mediawiki/images/math/d/e/4/de4eae3e3c0d1c88d454625601a90f44.png)
![\scriptstyle number\;of\;the\;type:\;2a+10b+\left[\left(2c-1\right)\sdot100\right]\longrightarrow the\;sum:\;2a+2b+4\sdot\left(2c-1\right)](/mediawiki/images/math/6/9/2/692097c3efc92180cde84cf4d0489077.png)
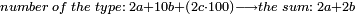
![\scriptstyle a^2=\left[10\sdot\left(\frac{1}{3}\sdot a\right)^2\right]-\left(\frac{1}{3}\sdot a\right)^2](/mediawiki/images/math/6/6/9/669d098149df5c68b5fe9e475df8e3d8.png)
![{\color{blue}{\begin{align}\scriptstyle9^2&\scriptstyle=\left[10\sdot\left(\frac{1}{3}\sdot9\right)^2\right]-\left(\frac{1}{3}\sdot9\right)^2\\&\scriptstyle=\left(10\sdot3^2\right)-3^2\\&\scriptstyle=\left(10\sdot9\right)-9=90-9=81\\\end{align}}}](/mediawiki/images/math/a/0/5/a05938d1c8da86fbca93ed63bda34c69.png)
![\scriptstyle\left(a-1\right)^2=\left[\left[10\sdot\left(\frac{1}{3}\sdot a\right)^2\right]-\left(\frac{1}{3}\sdot a\right)^2\right]-\left(a-1\right)-a](/mediawiki/images/math/c/2/c/c2cdd5e9b41a5d2fead0db29924624d1.png)
![{\color{blue}{\begin{align}\scriptstyle8^2&\scriptstyle=\left[\left[10\sdot\left(\frac{1}{3}\sdot9\right)^2\right]-\left(\frac{1}{3}\sdot9\right)^2\right]-8-9\\&\scriptstyle=\left[\left(10\sdot3^2\right)-3^2\right]-17\\&\scriptstyle=\left[\left(10\sdot9\right)-9\right]-17\\&\scriptstyle=\left(90-9\right)-17=81-17=64\\\end{align}}}](/mediawiki/images/math/5/b/6/5b66675eabee21e384ccae59f006fbd8.png)
![\scriptstyle\left(a+1\right)^2=\left[\left[10\sdot\left(\frac{1}{3}\sdot a\right)^2\right]-\left(\frac{1}{3}\sdot a\right)^2\right]+\left(a+1\right)+a](/mediawiki/images/math/0/2/1/021c5965b811b3a4f60d24984894eb93.png)
![{\color{blue}{\begin{align}\scriptstyle7^2&\scriptstyle=\left[\left[10\sdot\left(\frac{1}{3}\sdot6\right)^2\right]-\left(\frac{1}{3}\sdot6\right)^2\right]+7+6\\&\scriptstyle=\left[\left(10\sdot2^2\right)-2^2\right]+13=36+13=49\\\end{align}}}](/mediawiki/images/math/9/f/5/9f54d91d891994b1eb68fb3cd7bac69a.png)
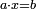
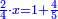
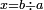
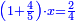
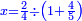
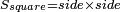
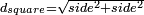
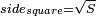
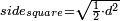
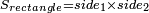
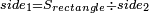
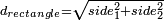
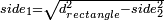
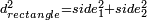
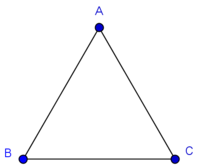
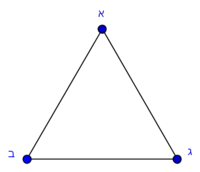
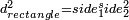

![\scriptstyle{\color{blue}{S_{triangle}=5\sdot\left[8+\frac{2}{4}+\left(\frac{3}{4}\sdot\frac{1}{4}\right)\right]=43+\frac{1}{4}+\left(\frac{3}{4}\sdot\frac{1}{4}\right)}}](/mediawiki/images/math/3/7/4/374d0caf4ae58e88ea8696d9aec06b3a.png)
![\scriptstyle\sum_{k=1}^n \left[\left(\sum_{i=1}^n a_i\right)\sdot a_k\right]=\left(\sum_{i=1}^n a_i\right)^2](/mediawiki/images/math/2/a/1/2a190390030d9c138d548197fab10837.png)
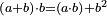
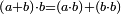
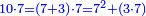
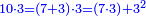
![\scriptstyle\left(a+b\right)^2=a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]](/mediawiki/images/math/7/2/7/727b0c35fd93a7a347bed8413905049f.png)
![\begin{align}\scriptstyle\left(a+b\right)^2&\scriptstyle=\left[a\sdot\left(a+b\right)\right]+\left[b\sdot\left(a+b\right)\right]\\&\scriptstyle=\left[a^2+\left(a\sdot b\right)\right]+\left[b^2+\left(a\sdot b\right)\right]\\&\scriptstyle=a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]\\\end{align}](/mediawiki/images/math/a/7/e/a7ec26694f08b055373189269d468fa1.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle
10^2&\scriptstyle=\left(7\sdot10\right)+\left(3\sdot10\right)\\&\scriptstyle=\left[7^2+\left(7\sdot3\right)\right]+\left[3^2+\left(3\sdot7\right)\right]\\&\scriptstyle=3^2+7^2+\left[2\sdot\left(3\sdot7\right)\right]\\\end{align}}}](/mediawiki/images/math/e/d/c/edc28fc524ac369e81faec0eab87cfa6.png)
![\scriptstyle\left(a\sdot b\right)+\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]^2=\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2](/mediawiki/images/math/6/2/4/6240a40a1b55eec2eca043f4e2218ca7.png)
![\scriptstyle\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a=b-\left[\frac{1}{2}\sdot\left(a+b\right)\right]](/mediawiki/images/math/b/0/e/b0e26ef8336bd37ea2dc5ea7d13ed5fe.png)

![\begin{align}\scriptstyle a\sdot b&\scriptstyle=a\sdot\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]+\left[b-\left[\frac{1}{2}\sdot\left(a+b\right)\right]\right]\right]\\&\scriptstyle=a\sdot\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]+\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]\right]\\\end{align}](/mediawiki/images/math/3/c/c/3cc1957606b0ead5eb951b5585bef540.png)
![\scriptstyle\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2=\left[\frac{1}{2}\sdot\left(a+b\right)\right]\sdot\left[a+\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]\right]](/mediawiki/images/math/0/7/1/0715bf55a8d43cbdfa4205e649097a2e.png)
![\scriptstyle\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]^2=\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]\sdot\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]\right]-\left[a\sdot\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]\right]](/mediawiki/images/math/4/4/3/4439c64a1a40d88eb65eca7693b2e920.png)
![\scriptstyle\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2=\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]^2+\left(a\sdot b\right)](/mediawiki/images/math/1/4/b/14b17150edc445172d80441ffc56150b.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle5^2&\scriptstyle=\left(5\sdot3\right)+\left(5\sdot2\right)\\&\scriptstyle=\left(3\sdot5\right)+\left[\left(3\sdot2\right)+2^2\right]\\&\scriptstyle=\left(3\sdot7\right)+2^2\\&\scriptstyle=\left(3\sdot7\right)+\left(5-3\right)^2\\\end{align}}}](/mediawiki/images/math/0/4/5/045c6411c7de6ffda0eec8a7d9df0b56.png)
![\scriptstyle\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2](/mediawiki/images/math/a/0/b/a0b403dd8b7c15a5cb1dc47a5f8ca5bb.png)
![\scriptstyle\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2=\left(\frac{1}{2}\sdot a\right)^2+\left[b\sdot\left(\frac{1}{2}\sdot a\right)\right]+\left[b\sdot\left[\left(\frac{1}{2}\sdot a\right)+b\right]\right]](/mediawiki/images/math/7/5/8/758d2201b39249424cb4d658762bd95f.png)
![\scriptstyle\left(5+2\right)^2=5^2+\left(2\sdot5\right)+\left[2\sdot\left(5+2\right)\right]](/mediawiki/images/math/1/2/3/123699a4976836521e4fa0f9f56218c6.png)
![\begin{align}\scriptstyle\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2&\scriptstyle=\left(\frac{1}{2}\sdot a\right)^2+\left[b\sdot\left[\left(\frac{1}{2}\sdot a\right)+\left(\frac{1}{2}\sdot a\right)+b\right]\right]\\&\scriptstyle=\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2\\\end{align}](/mediawiki/images/math/2/5/1/251974ee9075190da8b9dc79563ff0f5.png)
![\scriptstyle\left(a+b\right)^2+a^2=2\sdot\left[\left(a+b\right)\sdot a\right]+b^2](/mediawiki/images/math/5/e/f/5ef738b800e1b84fc257df70a83fb86b.png)
![\scriptstyle\left(a+b\right)^2=a^2+b^2+\left[2\sdot\left(a+b\right)\right]](/mediawiki/images/math/4/d/6/4d6ae9d470a2827afd617df98dd97974.png)
![\begin{align}\scriptstyle2\sdot\left[\left(a+b\right)\sdot a\right]+b^2&\scriptstyle=2a^2+\left[2\sdot\left(a\sdot b\right)\right]+b^2\\&\scriptstyle=a^2+\left[a^2+\left[2\sdot\left(a\sdot b\right)\right]+b^2\right]\\&\scriptstyle=\left(a+b\right)^2+a^2\\\end{align}](/mediawiki/images/math/c/2/f/c2fe7ee2c8c60da164b571e70406a5a9.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left[2\sdot\left(3\sdot10\right)\right]+7^2&\scriptstyle=\left[2\sdot\left(3\sdot7\right)\right]+\left(2\sdot3^2\right)+7^2\\&\scriptstyle=10^2+3^2\\\end{align}}}](/mediawiki/images/math/1/c/0/1c021025c0e975ce0233ebd9770b7392.png)
![\scriptstyle4\sdot\left[\left(a+b\right)\sdot a\right]+b^2=\left[\left(a+b\right)+a\right]^2](/mediawiki/images/math/f/6/2/f62f5f20431f619df80a01a1d97e57cf.png)
![\scriptstyle\left[a\sdot\left(a+b\right)\right]+b^2=\left[b\sdot\left(a+b\right)\right]+a^2](/mediawiki/images/math/f/0/5/f052cf921b4ee55e1ca01f6021885458.png)
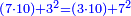
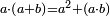
![\scriptstyle\left[a\sdot\left(a+b\right)\right]+b^2=a^2+\left(a\sdot b\right)+b^2](/mediawiki/images/math/8/f/6/8f6de5615e58347da74d4e00628a1c66.png)
![\scriptstyle\left[b\sdot\left(a+b\right)\right]+a^2=b^2+\left(a\sdot b\right)+a^2](/mediawiki/images/math/3/3/1/331e5719b87be662c7b73c4dbcd44eaa.png)
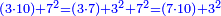
![\scriptstyle b^2=a^2+2\sdot\left[a\sdot\left(b-a\right)\right]+\left(b-a\right)^2](/mediawiki/images/math/0/8/8/088cad58241d957f9f3c27b451de0ab5.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle17^2&\scriptstyle=10^2+2\sdot\left[10\sdot\left(17-10\right)\right]+\left(17-10\right)^2\\&\scriptstyle=10^2+2\sdot\left(10\sdot7\right)+7^2\\\end{align}}}](/mediawiki/images/math/6/7/7/67731d828dc38dc51514d914a547e881.png)
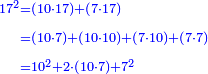
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle10^2&\scriptstyle=17^2-2\sdot\left(10\sdot7\right)-7^2\\&\scriptstyle=17^2-2\sdot\left[10\sdot\left(17-10\right)\right]-\left(17-10\right)^2\\\end{align}}}](/mediawiki/images/math/9/a/4/9a4a30b469c46bcbb14480005742377f.png)
![\scriptstyle b^2+\left[a\sdot\left(a+b\right)\right]=a^2+\left[b\sdot\left(a+b\right)\right]](/mediawiki/images/math/7/e/e/7eea030d1d0b98bc71555403dc241abd.png)
![\begin{align}\scriptstyle4\sdot\left[\left(a+b\right)\sdot a\right]+b^2&\scriptstyle=3\sdot\left[a\sdot\left(a+b\right)\right]+\left[a\sdot\left(a+b\right)\right]+b^2\\&\scriptstyle=3\sdot\left[a\sdot\left(a+b\right)\right]+\left[b\sdot\left(a+b\right)\right]+a^2\\\end{align}](/mediawiki/images/math/6/9/a/69a38eddd17c3f2cd5ee01abd642fef1.png)
![\begin{align}\scriptstyle4\sdot\left[\left(a+b\right)\sdot a\right]+b^2&\scriptstyle=3\sdot\left[a\sdot\left(a+b\right)\right]+\left[a\sdot\left(a+b\right)\right]+b^2\\&\scriptstyle=3\sdot\left[a\sdot\left(a+b\right)\right]+\left[b\sdot\left(a+b\right)\right]+a^2\\&\scriptstyle=2\sdot\left[a\sdot\left(a+b\right)\right]+\left[a\sdot\left(a+b\right)\right]+\left[b\sdot\left(a+b\right)\right]+a^2\\&\scriptstyle=2\sdot\left[a\sdot\left(a+b\right)\right]+\left(a+b\right)^2+a^2\\&\scriptstyle=\left[\left(a+b\right)+a\right]^2\\\end{align}](/mediawiki/images/math/b/3/5/b35a5226568e484fafd988c80c4828c2.png)