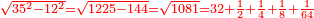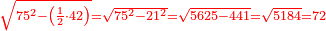Part Two: Multiplication
|
החלק השני מהספר הראשון
|
|
|
הפרק הראשון לכפול מספר על מספר
|
|
|
הרוצה לכפול מספר על מספר ראוי שיהיה הלוח הזה שגור בפיו כי בזה יהיה זריז לכפול מספר פלוני על מספר פלוני מא' עד ט'
|
|
|
ואם יהיה המספר אשר ירצה לכפול על מספר אחר כל אחד ממדרגה אחת או מאיזו מדרגה שיורה יקח דמיון לכל אחד ממדרגת האחדים ויכפול זה על זה כאלו הם אחדים ויראה העולה ואח"כ יקח לכל האחד מספר במדרגתו שאם היה האחד עשרות והאחר מאות נקח בעד העשרות שנים ובעד המאות שלשה ונחברם ויהיו חמשה אח"כ נשליך לעולם אחד והשאר יורה לנו העולה מאיזה מדרגה הוא
|
- Example: we wish to multiply eighty by five hundred.
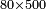
|
דמיון זה רצינו לכפול שמנים על חמש מאות
|
|
|
לקחנו דמיונם מהאחדים בעד השמני' שמנה ובעד החמש מאות חמשה וכפלנו חמשה על שמנה ויצא לנו הסכום ארבעים
|
|
|
עוד לקחנו בעד המאות שלשה ובעד השמנים שנים כי הם מהמדרגה השנית חברנום ונהיו חמשה השלכנו אחד ונשארו ארבעה ואלה הארבעה הם מדרגת האלפים
|
|
|
וידענו מזה שהארבעים אשר יצאו כשכפלנו השמנים על החמש מאות הם ארבעים אלף
|
|
|
אולם כשתרצה לכפול שני מספרים על שני מספרים צריך שנכתוב אותן כל אחד במדרגתו ושנכפול אותן ארבעה פעמים כל אחד מהטור שלמטה עם כל אחד מהטור שלמעלה ונכתוב המספר המונח בטור הראשון והמספר אשר נרצה לכפול עליו בטור התחתון ונתחיל לכפול אחדי התחתון על אחדי העליון וההוה נכתוב אותו למטה במדרגת האחדים וזה אם לא הגיע לעשרות
|
|
|
אבל אם הגיע לעשרות נוציא העשרות מהם ונשמרם והנשארים אשר לא הגיעו לכלל העשרה נכתוב במדרגת האחדים
|
|
|
עוד נכפול האחדים שלמטה עם מדרגת העשרות שלמעלה ואשר יהיה נחבר גם מספר העשרות ששמרנו עם אחדי זה הכפל כי אע"פ שהם עשרות אבל מה שיצא מהם יהיה כאלו הם עשרות ואחדים כי על דמיון האחדים אנו כופלים הכל והאחדים אשר יתקבצו מזה הכפל נכתבם במדרגת העשרות והעשרות אם יהיו נכתבם במדרגה השלישית
|
|
|
אחר נראה העולה והוא חשבון כפל המספר ההוא
|
- Example: we wish to multiply twenty-five by forty-three.
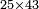
|
דמיון רצינו לכפול עשרים וחמשה על ארבעים ושלשה
|
|
|
כזה
|
| |
|
2 |
5
|
| |
|
4 |
3
|
| |
2 |
1 |
5
|
| |
8 |
6 |
|
| 1 |
0 |
7 |
5
|
|
|
|
|
|
כפלנו הה' על הג' ונהיו ט"ו גרענו העשירית ושמרנוה נשארו ה' וכתבנום במדרגת האחדים
|
|
|
עוד כפלנו הה' על הד' ונהיו עשרים ומפני שלא יצאו מזה אחדים כתבנו העשירית האחת לבד ששמרנו במקום העשרות והעשרים כתבנום במדרגה השלישית
|
|
|
עוד כפלנו הב' על הג' ונהיו ששה ומפני שלא יצאו גם בכאן אחדים כתבנו במקום האחדים סיפרא והששה כתבנום במקום העשרות
|
|
|
עוד כפלנו העשרים על הארבעי' ונהיו שמנה מאות וכתבנום במדרגה השלישית כי כל אחד מהכפולים היו ממדרגה שנית ובהשלכת האחד נשארו שלשה
|
|
|
אחר כן קבצנום ונהיו אלף ושבעים וחמשה
|
|
|
ואם נרצה לכפול שלשה מספרים על שלשה מספרים אז ראוי שנכפלם תשעה פעמים בזה הסדר
|
- Example: we wish to multiply three hundred forty-eight by two hundred thirty-five.
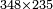
|
דמיון רצינו לכפול שלש מאות וארבעים ושמנה על מאתים ושלשים וחמשה
|
|
|
כתבנו אותם בצורה הזאת
|
| |
|
3 |
4 |
8
|
| |
|
2 |
3 |
5
|
| |
1 |
8 |
8 |
0
|
| |
9 |
4 |
0 |
|
| 7 |
0 |
5 |
|
|
| 8 |
1 |
7 |
8 |
0
|
|
|
|
|
|
כפלנו הח' על הה' ונהיו ארבעים ומפני שאין כאן אחדים כתבנו סיפרא במדרגת האחדים ושמרנו העשרות הארבעה
|
|
|
עוד כפלנו הג' על הח' ונהיו כ"ד שמרנו שתי עשרות ועם הארבעה שהם אחדיו חברנו הארבעה אשר שמרנו ונהיו שמנה וכתבנום במדרגת העשרות
|
|
|
עוד כפלנו הב' על הח' ונהיו י"ו שמרנו העשירית האחת וחברנו עם אחדיו שהם הששה את השתי עשרות שהיו שמורות לנו ונהיו ח' וכתבנום במדרגת המאות והעשירית האחת אשר שמרנו עתה כתבנוה במדרגת האלפים
|
|
|
הנה כבר כפלנו הח' על כל אחד ואחד מהמספרים שבטור הראשון השלשה
|
|
|
עוד שבנו לכפול הד' עם כל אחד ואחד מהם וכפלנוה תחלה עם הה' ונהיו עשרים ומפני שלא יצאו אחדים כתבנו ספרא במדרגת העשרות שהיא מדרגת אחדיו כי המספרים שכפלנו הם ממדרגה הראשונה והשנית והעשרים שהם שני עשרות שמרנום
|
|
|
עוד כפלנו הד' עם הג' ונהיו י"ב שמרנו העשירית האחת וחברנו עם השנים שהם אחדיו השני עשרות שהיו שמורות לנו ונהיו ד' כתבנום במדרגת המאות לפי שהמספרים שכפלנו הם במדרגה השניה
|
|
|
עוד כפלנו הארבעה עם הב' ונהיו ח' חברנו גם העשירית השמורה לנו עמם ונהיו ט' כתבנום במדרגת האלפים לפי שהמספרים אשר כפלנו היו ממדרגה השנית והשלישית
|
|
|
הנה כבר כפלנו גם הד' שבטור השפל עם כל אחד ואחד מהשלש מספרים שבטור העליון
|
|
|
עוד נשוב לכפול הג' עם כל אחד ואחד מן שלשת המספרים העליונים כפלנו אותו עם ה' והיה ט"ו הוצאנו העשירית ושמרנוה והה' כתבנום למטה במדרגת המאות כי שני המספרים האלה מדרגותם הם הראשונה והשלישית
|
|
|
עוד כפלנו אותם עם ג' ונהיו ט' חברנו גם העשירית השמורה ונהיו י' ולא היו לשם אחדים ולכן כתבנו במדרגת האלפים ספרא והעשירית אנו שומרים אותה
|
|
|
עוד הכינו אותם עם שנים ונהיו ו' חברנו גם העשירית השמורה עמם ונהיו ז' וכתבנום במדרגת הרבבות כי שני המספרים האלה הם במדרגה השלישית
|
|
|
אחרי כן קבצנו שלשה הסכום כמשפט ונהיו פ"א אלף ושבע מאות ושמנים
|
|
|
דמיון אחר במספר שיש לו ספרא
|
- We wish to multiply a hundred and five by two hundred and twenty-four.
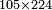
|
רצינו לכפול מאה וחמשה על מאתים ועשרים וארבעה
|
|
|
כתבנו אותם ככה בזאת הצורה
|
| |
|
2 |
2 |
4
|
| |
|
1 |
0 |
5
|
| |
1 |
1 |
2 |
0
|
| |
0 |
0 |
0 |
|
| 2 |
2 |
4 |
|
|
| 2 |
3 |
5 |
2 |
0
|
|
|
| |
|
ב |
ב |
ד
|
| |
|
א |
0 |
ה
|
| |
א |
א |
ב |
0
|
| |
0 |
0 |
0 |
|
| ב |
ב |
ד |
|
|
| ב |
ג |
ה |
ב |
0
|
|
|
|
|
כפלנו הה' על הד' ונהיו כ' ומפני שאין שם אחדים כתבנו סיפרא במדרגת האחדים והשתי עשרות שמרנום
|
|
|
עוד כפלנו הה' עם הב' ונהיו י' ומפני שאין שם אחדים כתבנו הב' עשרות השמורות במדרגת העשרות וזאת העשירית שמרנוה
|
|
|
עוד כפלנו הה' עם ב הב' ונהיו י' ומפני שאין שם אחדים כתבנו למטה העשירית אשר שמרנו במדרגת המאות וזאת העשירית במדרגת האלפים
|
|
|
עוד שבנו להכות כל אחד משלשה המספרים העליונים עם הסיפרא וכתבנו סיפרא במדרגת העשרות וכן במדרגת המאות וכן במדרגת האלפים
|
|
|
עוד שבנו לכפול הא' עם הד' ונהיה ד' וכתבנוהו במדרגת המאות כי שני המספרים הנכפלים היו מהמדרגה הראשונה והשלישית
|
|
|
עוד כפלנו הא' עם הב' ונהיו ב' וכתבנום במדרגת האלפים כי שני המספרים הכפולים היה האחד מהמדרגה השנית והאחר מהמדרגה השלישית
|
|
|
עוד כפלנו הא' עם השנים ונהיו ב' וכתבנום במדרגת הרבבות כי שני המספרים הכפולים היה כל אחד מהמדרגה השלישית
|
|
|
אחר כן קבצנו העולה מהם והם כ"ג אלף וחמש מאות ועשרים
|
|
|
אמר מרדכי ראיתי להודיעך הכפל הזה בדרך אחרת נקלה מצאתיה אצל חכמי הישמעלים והוא שתעשה כל סך הנכפלים בשטה אחת מבלתי שתצטרך אל יותר מזה
|
|
|
וככה תעשה תשים המספר אשר תרצה לכפול עליו בשטה העליונה כמנהג
|
|
|
עוד שים המספר אשר תרצה לכפול אותו עליו בשטה השפלה כל מדרגה כנגד הדומה לה
|
|
|
ואחר כן החל לכפול האחדים על האחדים ותכתוב העולה למטה
|
|
|
ואם יעלו עשרות תפוש אותם בלבך ותכתוב האחדים לבדם למטה
|
|
|
עוד תכפול האחדים שבשטה השפלה עם העשרות שבשטה העליונה כאלו הם אחדים על אחדים והעשרות אשר תפשת בלבך מהחשבון הראשון חשוב אותם אחדים וחברם עם אלה
|
|
|
גם תכפול האחדים שהם בשטה העליונה עם העשרות שהם בשטה השניה וחבר הכל ותכתוב העולה למטה
|
|
|
ואם עלו עשרות והטעם מדרגה עליונה מזאת תפוס בלבך
|
|
|
גם תכפול האחדים שבשטה השפלה עם המאות שבשטה העליונה
|
|
|
וכן האחדים שבשטה העליונה עם המאות שבשטה השפלה
|
|
|
גם העשרות שבשטה השפלה עם העשרות שבשטה העליונה
|
|
|
והכלל המדרגות אשר בקבוצן תהיינה שוות הסך
|
|
|
כי הראשונה עם השלשה יעשו ד' וככה השלישית עם הראשונה והשנית עם השנית
|
|
|
גם הראשונה עם הרביעית יעשו חמשה וככה השנית עם השלישית
|
|
|
וככה תעשה עד אין קץ ואשר יהיה תחבר המספר שהיה במדרגה שחשבנוה עשרות שתפשת בלבך עמם וכתבם למטה והוא הסך המבוקש
|
- Example: we wish to multiply three hundred and forty-eight by two hundred and thirty-five.
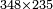
|
דמיון רצינו לכפול שלש מאות וארבעים ושמנה על מאתים ושלשים וחמשה
|
|
|
כזה
|
|
|
|
|
|
כפלנו הח' על הה' ונהיו מ' ובעבור שלא נשארו אחדים כתבנו גלגל במדרגה הראשונה והמ' תפשנום בלבנו ארבע
|
|
|
עוד כפלנו ח' עם ג' והיו כ"ד גם ד' עם ה' כי הם שוה המדרגות והיו כ' חברנום עם הכ"ד והיו מ"ד גם חברנו עמהם הד' שתפשנו בלבנו היו מ"ח וכתבנו למטה במדרגת העשרות ח' והמ' תפשנו בלבנו ד'
|
|
|
עוד כפלנו ח' עם ב' והיו י"ו גם ג' עם ה' והיו ט"ו גם ד' עם ג' והיו י"ב כי כל אלה שוה המדרגות והם מ"ג חברנו עמהם הד' שתפשנו בלבנו והם מ"ז כתבנו הז' במדרגת המאות והד' שהם המ' תפשנו בלבנו
|
|
|
עוד כפלנו ד' עם ב' והיו ח' גם כפלנו ג' עם ג' והיו ט' גם חברנו הד' שתפשנו בלבנו עמם והיו כ"א כתבנו הא' במדרגת האלפים והכ' תפשנו אותם בלבנו שנים
|
|
|
עוד כפלנו ג' עם ב' והיו ו' חברנו עמהם הב' שתפשנו בלבנו והיו ח' כתבנו הח' במדרגת הרבבות
|
|
|
וידענו מזה שהסך העולה מכפל השטה השפלה על השטה העליונה הם שמנים ואחת אלפים ושבע מאות ושמנים
|
|
|
וכבר נהגו בעלי החשבון לכפול בדרך שלישית
|
|
|
והוא שתקח שלישית המספר ותכפלהו על עצמו וההוה הוא מרובעו ותקח כדומה לו ממדרגה הבאה אשר היא יותר עליונה ממנה ותוציא מזאת המדרגה מרובע השלישית והנשאר הוא המבוקש
|
- Example: we wish to know the square of 9.
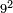
|
דמיון רצינו לדעת מרובע ט'
|
|
|
ולקחנו שלישיתו וכפלנו אותו על עצמו ונהיה ט' לקחנו דמיונו ממדרגה הבאה העליונה ממנה והיה צ' הוצאנו ממנו הט' שהוא מרובע השלישית ונשארו פ"א והוא המבוקש
|
|
|
ואם רצית לכפול מספר שאין לו שלישית אתה לוקח שלישית המספר היותר קרוב אליו ותרבע אותו ותעשה כמשפט אחר תעיין ואם המספר אשר לקחת שלישיתו הוא יותר פחות מהמספר המבוקש קבץ שני המספרים והוסיפם על הסך וההוה הוא המבוקש
|
- Example: we wish to know the square of ten.
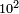
|
דמיון רצינו לדעת מרובע עשרה
|
|
|
וזה אין לו שלישית והמספר הקרוב אליו אשר יש לו השלישית הוא התשעה והוא פחות ממנו לקחנו מרובע שלישיתם והוא ט' ולקחנו דמיונם מהמדרגה הבאה והוא צ' גרענו ממנו הט' ונשארו פ"א ומפני שהמספר אשר לקחנו השלישית ממנו הוא פחות מהמספר המבוקש קבצנו שני המספרים הט' עם הי' ונהיו י"ט הוספנום על הפ"א ונהיו ק' והוא מרובע העשרה
|
|
|
אבל אם היה המספר אשר לקחנו השלישית ממנו יותר מהמספר המבוקש אנו מקבצים שני המספרים וגורעים אותם מהסך והנשאר הוא המבוקש
|
- Example: we wish to know the square of 11.
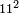
|
דמיון רצינו לדעת מרובע י"א
|
|
|
ומפני שאין לו שלישית והמספר הקרוב אליו שיש לו שלישית הוא הי"ב והוא יותר ממנו לקחנו שלישיתו וכפלנוהו במספר המרובע ולקחנו דמיונו במדרגה הבאה והוא ק"ס גרענו ממנו הי"ו שהוא מרובע השלישית ונשארו קמ"ד ומפני שהמספר אשר לקחנו השלישית ממנו שהוא י"ב הוא יותר מהמספר המבוקש מרובעו שהוא י"א קבצנו שתיהן ונהיו כ"ג וגרענו אותם מן קמ"ד ונשארו קכ"א וזהו המבוקש שהוא מרובע י"א
|
|
|
אמר מרדכי מצאתי דרך נכבד בענין הכפל בדרך החמישיות והוא כי כאשר תרצה לכפול מספר על עצמו תקח חמישיתו ותכפלהו על עצמו ותעלהו במעלה הבאה הסמוכה לה אחר תכפול אותה על שנים וחצי והוא המבוקש
|
- Example: we wish to multiply sixty by sixty.
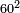
|
דמיון רצינו לכפול ששים על ששים
|
|
|
וחמישיתו י"ב כפלנום על עצמם נהיו קמ"ד העלנו אותם במדרגה הבאה הסמוכה להם ונהיו אלף וארבע מאות וארבעים כפלנום על ב' וחצי ונהיו ג' אלפים ת"ר וזהו המבוקש
|
- Another example: we wish to multiply fifty by fifty.
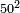
|
דמיון אחר רצינו לכפול חמשים על חמשים
|
|
|
וחמישיתו עשרה כפלנוהו על עצמו ונהיה מאה העלינוהו אל המדרגה הסמוכה לה ונהיו אלף כפלנום על ב' וחצי ונהיו ב' אלפים וחצי וזהו המבוקש
|
|
|
ואם רצית לכפול מספר על עצמו ואין לו חמישית תעיין המספר הקרוב אליו שיש לו חמישית אם מלפניו אם מלאחריו ולא יעבור ההפרש לעולם על שנים
|
|
|
ואם היה המספר אשר יש לו חמישית הקרוב אל מספרך קודם ממספרך באחד תחשבהו בדרך שהזכרתי ראשונה על המספר שיש לו חמישית אחר תחבר מספרך עם המספר שיש לו החמשית ותוסיפהו על הסך והוא המבוקש
|
|
|
ואם היה ההפרש שנים תכפול מספרך אחר שתחברהו עם המספר שיש לו חמישית עם שנים ואחר תוסיפנו על הסך והוא המבוקש
|
|
|
אמנם אם המספר שיש לו החמשית הוא אחר מספרך תחשוב חשבונך על המספר שיש לו החמישית אחר תחבר מספרך עם המספר פעם אחת אם ההפרש אחד או תכפול אותו עם ב' אחר שחברתו אם ההפרש שנים ותגרעהו מהסך והנשאר הוא המבוקש
|
- Example: we wish to multiply 11 by 11.
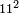
|
דמיון רצינו לכפול י"א על י"א
|
|
|
והנה זה המספר אין לו חמשית והמספר הקרוב אליו אשר יש לו חמישית הוא העשרה וכפלנו אותו בדרך החמישיות ועלו ק' אחר חברנו הי' שיש לו החמישית עם הי"א שהוא מספרינו פעם אחת מפני שההפרש בין שמספרנו ובין י' הוא אחד ונהיו כ"א חברנו עם הק' ונהיו קכ"א וזהו המבוקש
|
|
|
דמיון אחר במספר שההפרש שנים
|
- We wish to multiply 12 by 12.
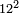
|
רצינו לכפול י"ב על י"ב
|
|
|
והנה זה המספר אין לו חמישית והמספר הקרוב לו בעל החמשית הוא העשירי' כפלנוהו בדרך החמישיות ונהיו ק' אחר חברנו הי' שיש לו החמישית עם הי"ב שהוא מספרנו ונהיו כ"ב ומפני שההפרש שנים כפלנום ב' פעמים ונהיו מ"ד וחברנום עם הק' והיו קמ"ד וזהו המבוקש
|
|
|
דמיון אחר במספרים אשר המספר שיש לו חמשית הקרוב אליו הוא אחריהם כי הדמיונים אשר עשינו היה בהיותו לפניהם
|
- We wish to multiply 14 by 14.
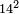
|
רצינו לכפול י"ד על י"ד
|
|
|
והנה זה המספר אין לו חמישית ראינו המספר אשר יש לו חמישית הקרוב אליו והוא ט"ו כפלנום בדרך החמישיות ועלה רכ"ה אחר חברנו את המספר הזה שיש לו חמישית עם מספרינו שהוא י"ד פעם אחת מפני שההפרש אחד והיה כ"ט גרענום מן הסך מפני כי המספר אשר יש לו החמישית היה אחרי מספרנו ונשארו קצ"ו וזהו המבוקש
|
|
|
דמיון במספר כזה שההפרש אשר בינו ובין אשר יש לו החמישית שנים
|
- We wish to multiply 13 by 13.
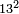
|
רצינו לכפול י"ג על י"ג
|
|
|
וזה המספר אין לו חמישית והמספר הקרוב אליו שיש לו החמישית הוא החמשה עשר כפלנוהו בדרך החמישיות והיה רכ"ה אחר חברנו זה המספר שיש לו החמישית עם י"ג שהוא מספרנו ונהיו כ"ח כפלנום על ב' מפני שההפרש אשר בין שני המספרים ב' ונהיו נ"ו גרענום מן רכ"ה מפני שהמספר שיש לו החמישית הוא אחרי מספרנו ונשארו קס"ט וזהו המבוקש
|
|
|
ואם תרצה לכפול מספר על מספר שהם רחוקים מהכלל בשווי האחד חסר ממנו והאחר מוסיף עליו אתה יכול לכפול הכלל על עצמו אחר תרבע המספר היתר והחסר ותגרעהו מחשבון הכלל וההוה הוא המבוקש
|
- Example: we wish to multiply twenty-five by thirty-five.
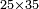
|
דמיון רצינו לכפול כ"ה על ל"ה
|
|
|
והכלל ל' והה' בתוספת וחסרון כפלנו הכלל ונהיו תת"ק אחר כפלנו הה' ונהיה כ"ה גרענום מהתת"ק ונשארו תתע"ה והוא המבוקש
|
|
|
אמר מרדכי עם היות שאמרנו שאם היו המספרים שתים על שתים אתה צריך לכפלם ארבעה על ארבעה ר"ל ארבעה פעמים צריך אתה לדעת שאם היה כללם אחד יספיק לכפלם שלש פעמים
|
|
|
כגון הרוצה לכפול י"ג על י"ד והנה כלל שניהם עשרה תחבר שני הפרטים ויהיו ז' ותכפול ז' פעמים י' נהיו ע' וי' פעמים י' הרי ק' וג' פעמים ד' הרי י"ב והעולה קפ"ב וזהו המבוקש
|
|
|
מאזנים על הכפל בדרך הט'
|
|
|
תחשוב הטור העליון כולו כאלו הם אחדים והשליכם ט' ט' והשאר שמרהו וזה יקרא השמור הראשון
|
|
|
עוד תעשה כן בטור השפל והשאר יקרא השמור השני
|
|
|
תכפול השמור הראשון על השמור השני ואשר יהיה השליכהו ט' ט' והשאר שמרהו וזה יקרא השמור השלישי
|
|
|
אחר תעיין הטור השלישי השפל אשר יקרא הסך ותחשבהו כאלו הם אחדים והשליכם ט' ט' והשאר עיין ואם הוא שוה לשמור השלישי אפשר שחשבונך יהיה אמת ואם לאו דע בודאי שטעית
|
|
|
מאזנים בדרך השבעה
|
|
|
עיין מספרי הטור הראשון ותתחיל מהיותר כולל ותחשבהו עשרות ואשר בצדו אחדים והשליכם ז' ז' ואשר ישאר חשבהו עשרות ואשר בצדו אחדים והשליכם עוד ז' ז' ואשר ישאר עוד חשבהו עשרות ואשר בצדו אחדים והשליכם עוד ז' ז' ואשר ישאר עוד חשבהו עשרות ואשר בצדו אחדים והשליכם ז' ז' וכן תעשה עד שתגיע למעלת האחדים ואשר ישאר שמרהו וזה יקרא השמור הראשון
|
|
|
עוד תקח מספרי הטור השני ועשה כמשפט הזה ואשר ישאר יקרא השמור השני
|
|
|
אחר תכפול השמור השני על השמור הראשון ואשר יהיה השליכהו ז' ז' והשאר יקרא השמור השלישי
|
|
|
אחר כן תעיין מספרי הטור השפל השלישי אשר יקרא הסך ועשהו כמשפטי הטורים העליונים ועיין הנשאר ואם הוא שוה לשמור השלישי אפשר שחשבונך יהיה אמת ואם לאו דע בודאי שטעית
|
Word Problems
|
מקום השאלות
|
- 1)
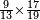
|
א כמה ט' חלקים מי"ג הכפולים על י"ז חלקים מי"ט
|
|
|
כי אלה אין להם ערך מדובר לכן ראוי שתדע איך תכפול ומה תעשה
|
- common denominator:
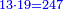
|
ראוי שנדע בתחלה המורה והנה נכפל י"ג על י"ט יהיו רמ"ז והוא המורה
|
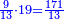
|
אח"כ נקח לכל אחד מט' חלקים י"ט נהיו קע"א והוא המספר האחד
|
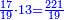
|
עוד נקח לכל אחד מי"ז חלקי' י"ג נהיו רכ"א
|
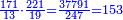
|
נכפול זה על זה נהיו ל"ז אלפים תשצ"א חלקנו אותם על רמ"ז ועלו קנ"ג
|
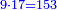
|
והנה העולה מכפל ט' בי"ז גם כן קנ"ג
|
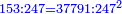
|
וערך זה אל רמ"ז כערך המספר הראשון [ר"ל מספר ל"ז אלפים תשצ"א] אל מרובע רמ"ז והוא המבוקש
|
|
|
ואם תרצה לדקדקו חלק קנ"ג על י"ט יהיה העולה ח' חלקים מי"ג וישאר שבר א' שהוא שבר חלק מי"ט
|
|
|
או אם תרצה חלקנו זה קנ"ג על י"ג ויהיו י"א חלקים שלימים מי"ט וי' נשברים שי"ג מהם עושה חלק אחד מי"ט
|
| How Much Problem - road
|
|
- 2) Question: a road, we add to it its quarter and its fifth and the sum is 10 miles.
- How long is the road?
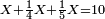
|
ב שאלה דרך חברנו אליה רביעיתה וחמשיתה והיתה י' מילין
כמה היתה הדרך
|
- False Position - common denominator:
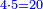
|
נשים המורה כ' כי ד' פעמי' ה' הם כ'
|
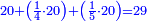
|
ורביעיתו וחמשיתו הם ט' נחברם עם המורה נהיו כ"ט
|
- Rule of Four:
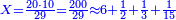
|
נכפול הכ' עם הי' ונהיו ר' נחלקם על כ"ט ונהיו ו' מילין וחצי מיל ושליש מיל וחלק אחד מט"ו בקרוב וככה היא הדרך
|
|
|
ג שאלה לקחנו תשיעית ממון ועשיריתו וחלק אחד מי"א ממנו
כמה הוא כל זה מערך הממון
|
|
|
והנה זה נקל הוא מי שידע לחבר השברים כאשר כתבנו בחבורם
וכן נעשה נבקש מורה והוא שנכפול ט' על י' ונהיו צ' עוד צ' על י"א ונהיו תתק"ץ וזהו המורה
ותשיעיתו ק"י ועשיריתו צ"ט וחלק אחד י' ממנו צ' והכל מחוברי' רצ"ט
וערך רצ"ט אל תתק"צ ככה אלה מערך הממון חלקנו אותם אל צ' שהוא חלק אחד מאחת מי"א ונהיו ג' חלקי' מי"א וכ"ט חלקי' מצ' שהם שלישית חלק מי"א פחות משהו
|
| How Much Problem - Money
|
|
- 4) Question: an amount of money, we add to it its half, its third, its fifth, and its sixth and the sum is 60.
- How much is the amount of money?
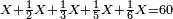
|
ד שאלה ממון הוספנו עליו מחציתו שלישיתו חמשיתו וששיתו ובין הכל היו ס'
כמה היה הממון
|
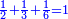
|
ידענו שהחצי והשלישית והששית הוא אחד שלם
|
- False Position:
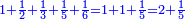
|
ונחשב שהיה לו אחד והיה לו עתה שנים וחמשית
|
- Rule of Four:
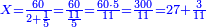
|
נחלק הס' על הב' וחמשית וכך היה הממון
והנה תשיב הב' שלימי' אל חמשיות מפני שיש לנו חמשית ונחבר גם החמשית שיש לנו עמם ונהיו י"א חמשיות
נכפול ה' על ס' ונהיו ש' והוא המורה
נחלקם על י"א והיה החלק כ"ז וג' חלקי' מי"א וככה היה הממון
|
| How Many Problem - horses
|
|
- 5) Question: a riding man saw a man pulling horses and said to him: where are you leading these 100 horses?
- He answered him: these and other like them and a half of them and a quarter of them with the horse you ride are 100.
- How much were the horses?
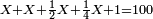
|
ה שאלה אדם רוכב ראה איש מושך סוסים וא"ל אנה אתה מוליך אלה הק' סוסים
והשיב לו אלה ואחרים כמותם ומחציתם ורביעיתם ועם הסוס שאתה רוכב הם ק'
כמה היו הסוסים
|
- subtracting the rider's horse:
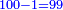
|
הנה נוציא הסוס שרוכב זה ונשארו צ"ט
|
- converting to fourths - False Position:
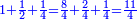
|
יש לנו שנים ומחצית ורביעית ומפני שיש לנו רביעית נשיב הכל לרביעיות והנה הב' שלימי' הם ח' רביעיות והמחצית ב' הרי י' נחבר גם הרביעיות שיש לנו עמם נהיו י"א רביעיות
|
- Rule of Four:
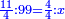
|
אחר נשיב אותם אל הערכים ונכתוב אם הי"א רביעיות נתנו צ"ט הד' רביעיות שהוא האחד השלם כמה יתנו'
|
- the number of horses:
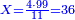
|
נכפל האמצעיים שהם הד' על הצ"ט ונחלקם על י"א שהוא הקצה נהיו ל"ו וככה מספר הסוסים
|
| Buy and Sell Problem
|
|
- 6) Question: a man bought 24 liṭra for 24 dinar. He sold 12 [of them] at 1¼ liṭra for one dinar, and the [other] 12 liṭra at (1‒¼) liṭra for one dinar.
- We want to know: did he earn or lose?
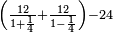
|
ו שאלה אדם קנה כ"ד ליט' בכ"ד דינ' ומכר הי"ב ליט' ורביע ליט' בדינר והי"ב ליט' מכר ליט' פחות רביע ליט' בדינר
נבקש לדעת אם הרויח או הפסיד
|
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left(\frac{12}{1+\frac{1}{4}}+\frac{12}{1-\frac{1}{4}}\right)-24&\scriptstyle=\left(\frac{4\sdot12}{5}+\frac{4\sdot12}{3}\right)-24\\&\scriptstyle=\left(\frac{48}{5}+\frac{48}{3}\right)-24\\&\scriptstyle=\left[\left(9+\frac{1}{2}+\frac{1}{10}\right)+16\right]-24\\&\scriptstyle=\left(25+\frac{1}{2}+\frac{1}{10}\right)-24=1+\frac{1}{2}+\frac{1}{10}\\\end{align}}}](/mediawiki/images/math/5/e/3/5e3a2961b99ecea99fbb5358aff1322e.png)
|
נשיב הי"ב ליט' הראשוני' לרביעיות ונהיו מ"ח
נחלקם על ה' כי ה' רביעיות מכר בדינר ונהיו ט' וחצי ועשירית ואלה הם הדינ' שלקח מהי"ב ליט' הראשונים
עוד נכה הי"ב ליט' האחרוני' בד' כי ליט' פחות רביע מכר בדינ' ונהיו מ"ח נחלקם על ג' מפני שהליט' פחות רביע הם ג' רביעיות ונהיו י"ו ואלה הם הדינ' שלקח מהי"ב ליט' האחרונים
נחבר שני הממונות נהיו כ"ה וחצי ועשירית נוציא כ"ד דינ' של הקרן נשאר דינר וחצי ועשירית וזהו הריוח
|
| Buy and Sell Problem
|
|
- 7) Question: a man bought three fifths of a liṭra for one pašuṭ, then he sold four sevenths of a liṭra for one pašuṭ and he earned one pašuṭ.
- How much money did he have originally?
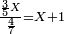
|
ז שאלה אדם קנה ג' חמשיות ליט' בפשוט ומכר ד' שביעיות ליט' בפשוט והרויח פשוט
כמה היה ממונו
|
- common denominator:
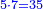
|
נבקש המורה והוא ל"ה
|
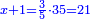
|
וג' חמשיותיו כ"א
|
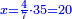
|
וד' שביעיותיו כ'
|
- Check: the profit is one pašuṭ
|
והממון היה כ' פשוטי' כי בכל פשוט ירויח חלק אחד מכ' בפשוט וכשימכור של כ' פשוטי' ירויח פשוט אחד
|
| Buy and Sell Problem
|
|
- Question: a man bought 9/17 parts of a liṭra for one pašuṭ, then he sold 10/19 parts [of a liṭra] for one pašuṭ and he earned one pašuṭ.
- How much was the money?
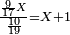
|
שאלה אדם קנה ט' חלקים מי"ז חלקי' ליטר' בפשוט ומכר י' חלקי' מי"ט בפשוט והרויח פשוט
כמה היה הממון
|
- common denominator:
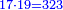
|
נבקש המורה והוא שנכפול י"ז על י"ט ונהיו שכ"ג
|
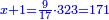
|
וידוע כי ט' חלקי' מי"ז הם קע"א וככה היה הממון
|
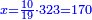
|
וי' חלקי' מי"ט הם ק"ע
|
- Check: the profit is one pašuṭ
|
והנה הרויח הפשוט
|
| How Much Problem - Money
|
|
- 8) Question: an amount of money, we sum its third, its quarter, and its fifth and the sum is 30.
- How much is the amount of money?
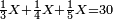
|
ח שאלה ממון חברנו שלישיתו רביעיתו חמשיתו והיו ל'
כמה הוא כל הממון
|
- False Position - common denominator:

|
נבקש המורה והוא ס'
|
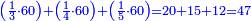
|
ושלישיתו כ' ורביעיתו ט"ו וחמשיתו י"ב וכלם מ"ז
|
- Rule of Four:
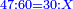
|
הנה כערך מ"ז אל ס' כן ערך ל' אל כל הממון
|
|
|
ונכתו' ככה אם המ"ז יתנו ס' הל' כמה יתנו
|
|
|
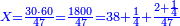
|
נכפול האמצעיים כך ונהיו אלף ת"ת נחלקם על הקצה שהוא המ"ז נהיה החלק ל"ח ורביעית וב' חלקי' ורביע חלק ממ"ז
|
| Partnership Problem - For the Same Time
|
|
- 9) Question: five people - the first gave 6 dinar, the second 7 dinar, the third 8 [dinar], the fourth 9 dinar, and the fifth 10 dinar.
- They earned a total of 11 dinar.
- How much should each of them take [from the profit]?
|
ט שאלה אם אנשים ה' נתן האחד ו' דינ' והשני ז' דינ' והשלישי ח' והרביעי ט' דינ' והחמשי י' דינ'
והרויחו בין הכל י"א דינ'
כמה יקח כל אחד מהם
|
|
|
הנה אלה הי"א דינ' הרויחו אותם כל הדינ' מקובצי' ונראה אותם כמה הם
אח"כ נשיב אותם אל הערך של כל אחד ואחד וכפי ערך ממונו ככה יקח
|
- the sum of the given dinar:
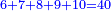
|
והנה הדינרי' מקובצי' הם מ' דינ'
|
|
|
ונכתו' הערך של הראשון ככה
|
|
|
- Rule of Four:
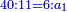
|
אם המ' דינ' הרויחו י"א הו' כמה ירויחו
|
- the owner of the 6 dinar
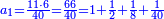
|
נכפול האמצעיים ונהיו ס"ו ונחלקם על מ' שהוא הקצה ונהיה החלק האחד אחד וחצי ושמינית וחלק אחד ממ' וככה יקח בעל הו' דינר
|
|
|
עוד נכתו' הערך של השני ככה
|
|
|
- Rule of Four:
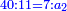
|
אם המ' דינ' הרויחו י"א הז' דינ' כמה ירויחו
|
- the owner of the 7 dinar
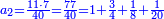
|
נכפל האמצעיים ונהיו ע"ז נחלקם על הקצה שהוא המ' ונהיה החלק האחד אחד וג' רביעיות ושמינית וחלק א' מכ' וככה יקח בעל הי' הז' דינ'
|
|
|
עוד נכתו' הערך של השלישי ככה
|
|
|
- Rule of Four:
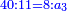
|
אם המ' דינ' הרויחו י"א דינ' הח' דינ' כמה ירויחו
|
- the owner of the 8 dinar
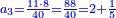
|
נכפל האמצעיים ונהיו פ"ח נחלקם על המ' שהוא הקצה ונהיה החלק האחד ב' וחמשית וככה יקח בעל הח' דינ'
|
|
|
עוד נכתו' הערך של הרביעי ככה
|
|
|
- Rule of Four:
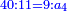
|
אם המ' דינ' הרויחו י"א הט' דינ' כמה ירויחו
|
- the owner of the 9 dinar
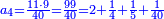
|
נכפול האמצעיים ונהיו צ"ט נחלקם על המ' שהוא הקצה ונהיה החלק האחד ב' ורביעית וחמשית וחלק אחד ממ' וככה יקח בעל הט' דינ'
|
|
|
עוד נכתו' הערך של החמשי ככה
|
|
|
- Rule of Four:
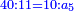
|
אם המ' דינ' הרויחו י"א הי' כמה ירויחו
|
- the owner of the 10 dinar
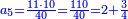
|
נכפול האמצעיים ונהיו ק"י נחלקם על מ' שהוא הקצה ונהיה החלק הא' ב' וג' רביעיות וככה יקח בעל הי' דינ'
|
-
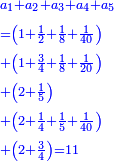
|
וכשתקבץ כל החלקי' שיקחו הכל תמצאם י"א לא פחות ולא יתר
|
|
דרך אחרת למצוא זה
|
- converting the profit of 11 dinar into pešuṭim, then dividing by 40 and multiplying by the number of dinar given by each
|
תעשה הי"א דינ' שהם הריוח כלם פשוטי' ותחלקם על מ' ותראה כמה ריוח יגיע לכל דינר מהמ'
|
- multiplying by 6 = the share of the owner of the 6 dinar
|
והריוח ההוא תכפול אותו עם הו' ואשר יהיה ככה יגיע לבעל הו'
|
- multiplying by 7 = the share of the owner of the 7 dinar
|
עוד תכפול אותו עם הז' ואשר יהיה ככה יגיע לבעל הז'
|
|
וכן תעשה עם הח' והט' והי'
|
- 10) Question: the buyer had three [kinds of] coins.
- He went to the seller to buy one liṭra of silk.
- The first coin was worth 3 dinar.
- The second coin was worth 4 dinar.
- The third coin was worth 6 dinar.
- The buyer said: give me one liṭra of silk and take from my three coins equally so that you will take the value of the liṭra
- How much should he take from each coin?
|
י שאלה יש אצל הקונה שלשה מטבעים
והלך אצל המוכר לקנות ליט' אחת משי
והמטבע האחת היתה שווה ג' דינ'
והמטבע השנית היתה שוה ד' דינ'
והמטבע השלישי' היתה שוה ו' דינ'
ואמ' הקונה תן לי ליט' משי וקח מג' מטבעותי בשווי עד שתקח מה ששוה הליט'
כמה יקח מכל מטבע ומטבע
|
- common denominator:
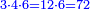
|
נבקש המורה והוא ע"ב כי כפל ג' על ד' י"ב וכפל י"ב על ו' ע"ב
|
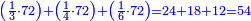
|
ושלישיתו כ"ד ורביעיתו י"ח וששיתו י"ב והכל נ"ד וזהו הדינ'
|
- he will take from each coin:
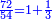
|
נחלק המורה שהוא ע"ב על נ"ד ונהיה החלק האחד אחד ושליש וככה יקח מכל מטבע
|
- Converting the dinar into 12 perutot
- he will take from each coin:
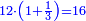 perutot perutot
|
והנה נעשה הדינ' י"ב פרוטו' ויקח י"ו פרוטות מכל מטבע
|
- 3 dinar from the coin of 3 dinar =
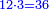 perutot perutot
|
ואם תרצה לדעת איך הוא כך תחשוב שרוצה לקחת ל"ו פרוטות ממטבע ששוה ג' דינ'
|
- 16 perutot from the coin of 3 dinar
|
ולקח ממנו י"ו פרוטות
|
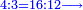
- + 16 perutot from the coin of 4 dinar =
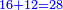 perutot from the coin of 3 dinar perutot from the coin of 3 dinar
|
וכשלקח עוד י"ו פרוטות ממטבע ששוה ד' דינ' כאלו לקח י"ב פרוטו' ממטבע ששוה ג' דינ' כערך הד' אל הג' נחבר הי"ב עם הי"ו ונהיו כ"ח
|
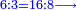
- + 16 perutot from the coin of 4 dinar =
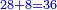 perutot from the coin of 3 dinar perutot from the coin of 3 dinar
|
עוד כשלקח י"ו פרוטות ממטבע ששוה ו' דינ' הוא כאלו לקח ח' פרוטו' ממטבע ששוה ג' דינ' כערך הג' אל הו' נחבר הח' עם הכ"ח ונהיו ל"ו וזהו המבוקש
|
| Payment Problem - constructing a shelf
|
|
- 11) Question: a man agreed with a craftsman to construct for him a shelf of 6 in length and 6 in width and he will pay him 8 dinar.
- He constructed for him [a shelf of] 3 in length and 3 in width.
- How much should he pay him?
|
יא שאלה אדם התנה עם אומן לבנות לו אצטבא ו' באורך ו' וו' ברוחב ויתן לו ח' דינ'
והוא בנה לו ג' בארך וג' ברחב
כמה יתן לו
|
- He will be paid a quarter
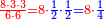
|
אין ספק כי יתן לו הרביעית שהוא ב' דינ' כי כפל חצי על חצי הוא רביעית אחד
|
- If he had constructed a half of the length by the whole width or half of the width by the whole length, he would have been paid a half of the payment
|
שאלו היה בונה כל האורך עם חצי הרוחב או ההפך היה נותן לו המחצית
|
- If he agreed with him to construct for him [a shelf of] 5 in length, 6 in width, and 7 in height and he will pay him 8 dinar.
- He constructed for him [a shelf of] 4 in length, 5 in width, and 6 in height.
- How much should he pay him?
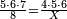
|
אבל אם התנה עמו שיבנה לו ה' בארך ו' ברוחב ז' בגובה ויתן לו ח' דינ'
והוא בנה ד' בארך וה' ברחב וו' בגובה
כמה יתן לו
|
|
|
אז ראוי שנחבר כל מספרי התנאי ונשיבם אל הערכים וכן מספרי הבניין
|
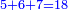
|
חברנו תחלה מספרי התנאי ונהיו י"ח
|
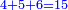
|
עוד חברנו מספרי הבניין ונהיו ט"ו
|
- Rule of Four:
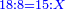
|
ועשינו הערך ככה אם אם הי"ח יתנו ח' דינ' הט"ו כמה יתנו
|
|
|
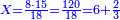
|
כפלנו האמצעיים ונהיו ק"כ חלקנום על הי"ח שהוא הקצה ונהיה החלק ו' וב' שלישיות וככה יקח
|
| Payment Problem - three workers, three different daily wages, the same actual payment
|
|
- 12) Question: a man hired three brothers - Reuven, Shimon and Levi - for two days so that one of them will work with him.
- If Reuven will work with him the whole two days he will pay him 6 dinar.
- If Shimon will work alone he will pay him 4 dinar.
- If Levi will work alone he will pay him 3 dinar.
- They worked a total of two days together.
- Finally, he paid each of them an equal share.
- How much is the share of each of them and how many hours did each of them work?
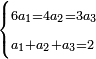
|
יב שאלה אדם אחד שכר ג' אחים ראובן שמעון לוי לעבוד אחד מהם עמו ב' ימי'
ואם יעבוד ראובן עמו כל הב' ימי' יתן לו ו' דינ'
ואם יעבוד שמעון לבדו יתן לו ד' דינ'
ואם יעבוד לוי לבדו יתן לו ג' דינ'
עתה בין הכל עבדו ב' ימי'
ובאחרונה פרע לכל חלק שוה
כמה פרע כל אחד ואחד וכמה שעות עבד כל אחד ואחד
|
- common denominator:

|
נבקש המורה והוא ע"ב כי כפל ו' על ד' הם כ"ד ואלה על ג' הם ע"ב
|
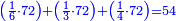
|
וששיתו ושלישיתו ורביעיתו הם נ"ד
|
- each of them will be paid
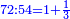 dinar dinar
|
הנה כערך ע"ב אל נ"ד ככה יקח מהדינרי' וערך ע"ב אל נ"ד הוא אחד ושליש וככה יקח כל אחד ואחד
|
- calculating the working hours of each:
|
נבקש לדעת כמה שעות עבד כל אחד ואחד
|
- the dinar should be converted into thirds
|
ונשיבהו אל הערכים ונשיב הדינ' שלישיות מפני השליש שעודף על הדינר
|
- 1 day = 12 hours
|
והיום י"ב שעות
|
- Rule of Four:
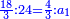
|
ונעשה ערך ראובן כך אם הי"ח שלישיות כ"ד שעות הד' שלישיות כמה יתנו
|
- Reuven worked:
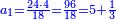 hours hours
|
נכפול האמצעיים ונהיו צ"ו נחלקם על י"ח ונהיה החלק ה' שעות ושליש וככה עבד ראובן
|
|
|
- Rule of Four:
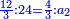
|
ונעשה ערך שמעון כך אם הי"ב שלישיות כ"ד שעות הד' שלישיות כמה יתנו
|
|
|
- Shimon worked:
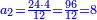 hours hours
|
כפלנו האמצעיים והם צ"ו חלקנום על י"ב ונהיה החלק ח' שעות וככה עבד ראובן שמעון
|
- Rule of Four:
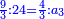
|
ונעשה ערך לוי כך אם הט' שלישיות יתנו כ"ד שעות הד' שלישיות כמה יתנו
|
|
|
- Shimon worked:
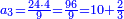 hours hours
|
כפלנו האמצעים ונהיו צ"ו חלקנום על ט' ונהיה החלק י' שעות וב' שלישיים וככה עבד לוי
|
-
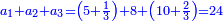 hours = 2 days hours = 2 days
|
חבר כל השעות שעבדו שלשתם ותמצאם כ"ד שעות שהם ב' ימים
|
|
|
הזה בסוף השאלה הט' עיין הטב
|
| Boiling Problem
|
|
- 13) Question: a man was boiling 6 measures of a beverage and he wanted that one third will remain. One measure was evaporated while cooking, then one measure overflow and four measures remained.
- He wants to [reduce] them [as planned for the original amount]
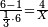
|
יג שאלה אדם אחד היה מבשל משקה ו' מדות ורצה שישאר השליש ונחסרה המדה האחת בבשול אחר נשפכה מדה אחת ונשארו הד' מדות
ורוצה להשיבם להשאירם כמשפט הראשון
|
- Rule of Four:
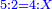
|
נשיבם אל הערכים ככה אם הה' מדות יתנו ב' הד' כמה יתנו
|
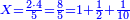
|
נכפל האמצעיים ונהיו ח' נחלקם על הקצה שהוא הה' ונהיה החלק אחד וחצי ועשירית וככה ראוי שישאר
|
- 14) Question: a sheet of 100 cubits long.
- Reuven began to measure it from one end and Shimon from the other end.
- Reuven measures 10 cubit in one hour and Shimon [measures] 12 [cubit in one hour]
- When will they meet?
|
יד שאלה יריעה ק' אמות
והתחיל למנותה ראובן מן הקצה האחד ושמעון מן הקצה האחר
וראובן מונה י' אמות בשעה ושמעון י"ב
מתי יפגשו
|
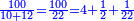 hours hours
|
נחבר שני המניינים אשר הם כ"ב אמות בשעה ונחלק הק' אמות עליהם ונהיה החלק ד' וחצי וחלק אחד מכ"ב
וידענו שבד' שעות וחצי וחלק מכ"ב בשעה יפגשו שניהם על המניין
|
- the number of cubits measured by Reuven
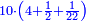
|
ואם תרצה לדעת כמה אמות מנה ראובן תכפול י' בד' וחצי וחלק א' מכ"ב ואשר יעלה כן מספר האמות אשר מנה ראובן
|
- the number of cubits measured by Shimon
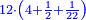
|
וכן אם תרצה לדעת כמה מנה שמעון תכפול תכפול הד' שעות וחצי וחלק מכ"ב על י"ב ואשר יעלה כך מספר האמות אשר מנה שמעון
|
| Shared Work Problem - Draining a Vessel - Barrel
|
|
- 15) Question: a full barrel has three taps
- If the first is opened the barrel is drained in half a day.
- If the second is opened it is drained in a third of a day.
- If the third is opened it is drained in a quarter of a day.
- If you opened all three taps together, in how many hours will the barrel to be drained?
|
טו שאלה חבית מליאה יש בה ג' נקבים
אם תפתח הא' יכלה החבית בחצי היום
ואם תפתח השנית יכלה בשלישית יום
ואם תפתח השלישית יכלה ברביעית יום
ואם פתחת השלשה נקבים ביחד בכמה שעות יכלה החבית
|
- day = 12 hours
|
אתה צריך לדעת כי היום י"ב שעות
|
- barrel = 48 measures
|
וכן החבית כמה מדות מכילה ונניח שמכילה מ"ח מדות
|
- through the first tap it is drained in
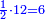 hours hours
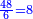 measures in one hour measures in one hour
|
והנה בפתיחת הנקב האחד יכלה בו' שעות שהם ח' מדות בשעה
|
- through the second tap it is drained in
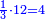 hours hours
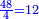 measures in one hour measures in one hour
|
ובפתיחת הנקב השני יכלה בד' שעות שהם י"ב מדות בשעה
|
- through the third tap it is drained in
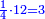 hours hours
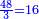 measures in one hour measures in one hour
|
ובפתיחת הנקב הג' יכלה בג' שעות שהם י"ו מדות בשעה
|
- through all three taps in one hour:
 measures measures
|
תחבר כל המדות אשר יכלו בשעה אחת והם ל"ו
|
- the barrel is drained through all three taps in
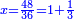 hours hours
|
תחלק המ"ח על הל"ו יהיה אחד ושליש והנה בשעה אחת ושליש תכלה הכל
|
- Rule of Four:
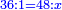
|
ונעשה הערכים ככה אם הל"ו שעה אחת המ"ח על כמה יהיה
|
|
|
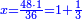
|
נכפול האמצעיים והם מ"ח נחלקם על הקצה שהם ל"ו ונהיה החלק אחד ושלישית
|
| Find a Quantity Problem - Whole from Parts Problem - Lance
|
|
- 16) Question: a lance, a half of it is in the water, a third of it is in the soil, and up above [the water] it is 6 cubits long.
- What is the length of the lance?
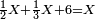
|
טז שאלה רומח חציו במים שלישיתו בעפר ולמעלה ו' אמות
כמה גבהות כל הרומח
|
- False Position - common denominator:

|
נבקש המורה והוא ו'
|
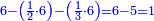
|
וחציו ושלישיתו ה' נגרעם מן הו' ונשארו א'
|
- the length of the lance:
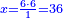
|
נכפול הו' עם הו' שהם האמצעיים ונחלקם על הא' שהוא הקצה נהיה ל"ו וככה גובה הרומח
|
- Check:
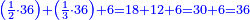
|
וחציו י"ח ושלישיתו י"ב הרי ל' ולמעלה ו'
|
- Rule of Four:
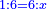
|
ונעשה הערך כך אם הא' יתנו ו' הו' כמה יתנו
|
| Find a Quantity Problem - Whole from Parts Problem - Tree
|
|
- 17) Question: a tree, a fifth of it is [ingrained] in the soil, a sixth of it is in the water, and up above the water it is 7 cubits long.
- What is the height of the tree?
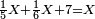
|
יז שאלה אילן חמשיתו בעפר וששיתו במים ולמעלה מהמים ז' אמות כמה גבהות כל האילן
|
- False Position - common denominator:

|
הנה המורה ל'
|
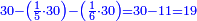
|
וחמשיתו וששיתו י"א נגרעם מל' שהוא המורה נשארו י"ט
|
- the height of the tree:
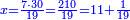
|
נכפול האמצעיים שהם הז' בל' נהיו ר"י נחלקם על י"ט ונהיו י"א חלקים וחלק אחד מי"ט וככה גבהות האילן
|
- Rule of Four:

|
ונעשה הערך כך
|
|
|
| Triangulation Problem - Two towers
|
|
- 18) Question: there are two towers, the height of one is 60 cubits and the height of the other is 40 cubits.
- The distance between them is 50 cubits.
- At the top of each tower sits a bird.
- Between them a water pool.
- The birds are flying at the same speed, going down and drinking at the same time, then taking off at the same time.
- How far is the pool from the base of each tower?
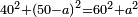
|
יח שאלה אם היו שני מגדלים גובה הא' ס' אמה וגובה השני מ' אמה
והמרחק שביניהם נ' אמה
ובראש כל מגדל צפור יושב
ובין המגדלים בריכת מים
ועפים הצפרים בהתעופפות שוה ויורדים ושותים בזמן שוה ועולים בזמן שוה
כמה מרחק הבריכה מיסוד כל מגדל
|
- denominator:

|
נחבר מרובע מ' שהוא אלף ת"ר עם מרובע נ' שהוא אלפים ות"ק נהיו ד' אלפי' ק'
אח"כ נקח מרובע ס' שהוא ג' אלפי' ות"ר ונגרעם משתי המרובעים הנזכרים שהם ד'ק' ונשארו ת"ק והוא המורה
|
- the distance between the pool and the tower whose height is 60 cubits:
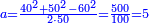
|
נכפול גם מרחק שני המגדלים שהוא נ' על ב' ונהיו ק' נחלקם המורה עליהם ונהיו ה' וככה מרחק הבריכה מן המגדל שגובהו ס' אמו'
|
- the distance between the pool and the other tower:

|
ומהמגדל האחר המ"ה אמות הנשארות
|
| Joint Purchase Problem - If You Give Me - Buying a Fish
|
- 19) Question: three men went to the market to buy a fish.
- The first said: I will give all of what I have and you will give a half of what you have and we will buy the fish.
- The second said: I will give all of what I have and you will give a third of what you have and we will buy the fish.
- The third said: I will give all of what I have and you will give a quarter of what you have and we will buy the fish.
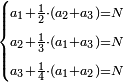
|
יט שאלה ג' אנשים אשר הלכו בשוק לקנות דג אחד
האחד אמר אני אתן כל מה שיש לי ואתם תנו החצי ממה שיש לכם ונקנה הדג
אמר השני אני אתן כל מה שיש לי ואתם תנו שליש ממה שיש לכם ונקנה הדג
אמר הג' אני אתן כל מה שיש ואתם תנו הרביע ממה שיש לכם ונקנה הדג
|
|
|
כתוב דבר הקונים החצי והרביע כזה
|
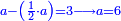
|
אח"כ תאמר מהו כאשר תקח חציו ממנו ישאר ג' כמספר הקונים והנה הוא ו' כתוב אותו תחת הב'
|
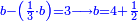
|
עוד תאמר מהו כאשר תקח שלישיתו ממנו ישאר ג' כמספר הקונים והנה הוא ד' וחצי כתוב אותו תחת הג'
|
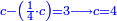
|
עוד תאמר מהו כאשר תקח רביעיתו ממנו ישאר ג' כמספר הקונים והנה הוא ד' תכתבהו תחת הד'
|
|
|
| 4 |
4 |
6
|
| |
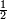 |
|
|
- common denominator:
![\scriptstyle{\color{blue}{\left(2\sdot6\right)+\left[2\sdot\left(4+\frac{1}{2}\right)\right]+\left(2\sdot4\right)=12+9+8=29}}](/mediawiki/images/math/4/b/6/4b603e8d3bbbfa2a95c54b43550e6b90.png)
|
כפול הכל עם הב' ותאמר ב' פעמי' ו' הם י"ב
עוד ב' פעמי' ד' וחצי הם ט'
עוד ב' פעמי' ד' הם ח'
חבר הכל הם כ"ט וזהו המורה
|
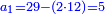
|
כפול הראשון שהוא י"ב עם ב' וחסרהו מן המורה נשארו ה' וכך יש לראשון בכיסו
|
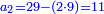
|
כפול השני שהוא ט' עם הב' וחסרהו מן המורה נשארו י"א וכך יש לשני בכסו
|
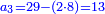
|
כפול השלישי שהוא ח' עם ב' וחסרהו מן המורה ונשארו י"ג וכך יש לשלישי בכסו
|
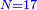
|
נמצא שקנו הדג בי"ז
|
|
ואם תרצה לבחון זה
|
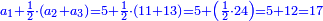
|
תביט כי הראשון נתן כל מה שיש לו והיו ה' והם נתנו החצי שיש להם ומה שיש להם הם כ"ד כי השני יש לו י"א והג' י"ג והחצי י"ב תחברם עם הה' והוא י"ז והוא מחיר הדג
|
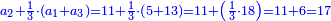
|
עוד השני נתן כל אשר לו והם י"א והראשון והשלישי נתנו השליש ממה שיש להם והם ו' כי לשניהם י"ח לראשון ה' ולשלישי י"ג חבר הי"א עם הו' ונהיו י"ז והוא מחיר הדג
|
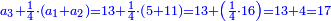
|
עוד השלישי נתן כל אשר לו והם הי"ג והראשון עם השני נתנו ד' שהוא הרביע ממה שיש להם כי לראשון ה' ולשני י"א והם י"ז והוא מחיר הדג
|
| Divide a Quantity Problem - Proportional Division – Promissory Note
|
|
- 20) Question: four men issued a promissory note with a man.
- The first [was promised] that if he would work with him for a month, he will pay him 10 zehuvim.
- The second [was promised] that if he would work with him for a month, he will pay him 5 zehuvim which are a half.
- The third [was promised] that if he would work with him for a month, he will pay him 3⅓ zehuvim which are a third.
- The fourth [was promised] that if he would work with him for a month, he will pay him 2½ zehuvim which are a quarter.
- They all worked a whole month, but he did not pay any one and died.
- All that he had were only 10 zehuvim
|
כ שאלה אדם אחד הוציאו עליו שטר חוב ד' אנשים
הראשון שאם יעבוד עמו חדש ימי' יתן לו י' זהובי'
והשני שאם יעבוד עמו חדש ימים יתן לו ה' זהובים שהם מחציתם
והשלישי שאם יעבוד עמו חדש ימים יתן לו ג' זהובים ושליש שהם שלישיתם
והד' שאם יעבוד עמו חדש ימים יתן לו ב' זהובים וחצי שהוא רביעיתם
ועבדו כלם החדש בשלימות ולא פרע לשום אחד ומת
ולא נמצא לו יותר מי' זהובים בכל אשר היה לו
|
- The division according to the arithmeticians: each one receives his proportional share
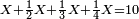
|
הנה חכמי החשבון יתנו לכל אחד כפי ערך ממונו
|
- False Position - common denominator:
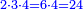
|
והנה המורה כ"ד כי תכפול הב' על הג' והם ו' עוד הו' על הד' הם כ"ד ובזה ימצאו כל החלקי' הנשארי' ונשים האחד השלם כ"ד כי הוא המורה
|
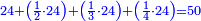
|
וכשתחבר אליו חציו ושלישיתו ורביעיתו יהיה בין הכל נ'
|
- converting the zehuvim into pešuṭim [1 zahuv = 12 pešuṭim]:
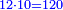
|
ונעשה הי' זהובים ק"כ פשוטי' מי"ב פשוטי' בזהוב
|
- Rule of Four:

|
ונעשה ערך הראשון כך אם הנ' יתנו לו כ"ד הק"כ מה יתנו לנו
|
|
|
- the share of the owner of the 10 zehuvim:

|
נכפול האמצעיים ונהיו ב' אלפים תת"פ נחלקם על הנ' שהוא הקצה נהיה החלק נ"ז פשוטים וחצי פשוט ועשירית פשוט וזהו חלק הראשון בעל הי' זהובים
|
- Rule of Four:
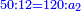
|
ונעשה ערך השני כך אם הנ' יתנו לנו י"ב הק"כ מה יתנו לנו
|
|
|
- the share of the owner of the 5 zehuvim:
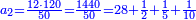
|
נכפול האמצעיים ונהיו אלף ת"מ נחלקם על הנ' שהוא הקצה ועלו כ"ח פשוטי' וחצי פשוט וחמשית פשוט ועשרית פשוט וזהו החלק השני בעל הה' זהובים
|
- Rule of Four:
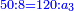
|
ונעשה ערך השלישי ככה אם הנ' יתנו ח' הק"כ כמה יתנו
|
|
|
- the share of the owner of the 3⅓ zehuvim:
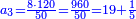
|
נכפול האמצעיים ונהיו תתק"ס נחלקם על הנ' שהוא הקצה יהיו י"ט פשוטי' וחמשית פשוט וזהו חלק השלישי בעל ג' זהובים ושליש
|
- Rule of Four:
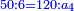
|
ונעשה ערך הרביעי ככה אם הנ' יתנו ו' הק"כ כמה יתנו
|
|
|
- the share of the owner of the 2½ zehuvim:
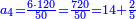
|
נכפול האמצעיים ונהיו תש"כ נחלקם על הנ' שהוא הקצה ונהיו י"ד פשוטי' וב' חמשיות פשוט וזהו חלק הרביעי בעל הב' זהובי' וחצי
|
-
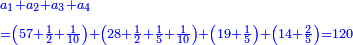
|
וכשתחבר כל כל אלה החלקים יעלו ק"כ פשוטי' שהם י' זהובי'
|
|
|
ואם לא תרצה להשיב הכל אל הערכים מפני הטורח תעשה כך אחר שידעת חלק הראשון מן הערכי' תן מחציתו לשני ושלישיתו לשלישי ורביעיתו לרביעי ושוה יהיה זה וזה
|
|
|
וכן תוכל אתה לעשות שאלות אחרות עד אין קץ ותוכל להשיב עליהם אם תדע ואם תדע הכללים שהקפנו בהם בזה החבור ולא הזכרתי דרך מציאות שרשי המרובעים הנה כי אינם צורך בזה החבור ואחרתים עד מקומם ושם אבארם אם יחפוץ הנותן ליעף כח
|
|
|
תם ונשלם שבח לבורא עולם אבגדה גם
|
The Second Book of this Treatise Discusses Geometry
|
[1]הספר השני מזה החבור המדבר בחכמת המדות
|
[The First Section]
|
|
Chapter One of the First Section of the Second Book
|
הפרק הראשון מהחלק הראשון מהספר השני
|
|
|
אמר מרדכי קודם שנדבר על חכמת המדות ראוי לבאר שמות שנשתמשו בהם בעלי זאת המלאכה והחכמה כי לכל חכמה שמות מיוחדות נשתמשו בהם בעלי החכמה ההיא מורות בענינים באותה החכמה בלתי הענינים אשר יורו בזולת החכמה ההיא להיות שהם הסכמיים וכאשר הניחו בזולת החכמה ההיא על מה שהניחו כן יוכלו להעתיקם ממה שהניחום למה שהניחום בחכמה מיוחדת אם על דרך השאלה או על דרך הספוק או על דרך ההעתקה ולפעמים גם ע"ד השתוף הגמור ולכן ראוי למחבר ספר אם ירצה להיות דבריו מובנים לבאר תחילה השמות אשר נשתמשו בם בעלי החכמה ההיא וכן עשה גם החכם אקלידס בספר היסודות אשר ביאר בהצעת כל מאמר דברים הצריכים באותו מאמר
|
|
|
ונאמר שכשתשמע הנה נקדה תבין שתורה על דבר שאין לו שעור כלל לא ארך ולא רחב ולא עומק והיא נמצאת בראש הקו כי היא תכליתו וכן היא אשר תמצא באמצע הקו כשתשער רמיזה היא תכלית חצי הקו והיא בעצמה ראש חצי הקו האחר
|
| The line is a length with no breadth drawn between two points that are its limits.
|
והקו הוא אורך בלא רחב נמשך בין שתי נקדות אשר הן תכליותיו
|
| The surface is a breadth stretched between lines, which has only length and breadth and its limits are the lines.
|
והשטח הוא הרחב המתוח בין הקוים ויש לו אורך ורחב לבד ותכליותיו הם הקוים
|
| The plane angle is that which is encompassed by two straight lines.
|
והזוית השטוחה היא אשר יקיפו בה שני קוי' ישרי'
|
| Among the angles there are right angles, acute angles and obtuse angles.
|
והזוית ממנה נצבת וממה חדה וממנה נרוחת
|
| The right angle is [generated] when a straight line falls on a straight line and makes the two angles on its either sides equal.
|
והזוית הנצבת היא כשיפול הקו הישר על קו ישר וישים השתי זויות אשר משתי צדדיו שוות כזה ┴
|
| The acute angle is the one that is smaller than it.
|
והחדה היא אשר היא יותר קטנה מזאת
|
| The obtuse angle is the one that is greater than it.
|
והנרוחת היא אשר היא יותר גדולה מזאת
|
| When a line falls on a line and makes the two angles on its either sides equal, it is called perpendicular.
|
והקו אשר יפול על הקו ויעשה שתי הזויות אשר משתי צדדיו שוות יקרא עמוד
|
| The line on which it stands is called base.
|
והקו שהוא עומד עליו יקרא תושבת
|
|
|
והקוים הנכחיים הם אשר כשיוצאו לכל א' משני צדדים ואפילו ללא תכלית לא יפגשו
|
|
|
והתמונה השטחית תחלק אל ישרת הקוים ואל בלתי ישרת הקוים
|
|
|
והתמונה הישרת קוים היא אשר יקיפו בה ג' קוים או יותר
|
|
|
ואשר יקיפו בה ג' קוים לא יותר תקרא משולש
|
|
|
ואשר יקיפו בה ד' קוים תקרא מרובע
|
|
|
ואשר יקיפו בה ה' קוים תקרא מחומש
|
|
|
וכן כל כיוצא בזה
|
|
|
והקוים אשר יקיפו בתמונה יקראו צלעות
|
| The triangle is divided into three species:
|
והמשולש יחלק אל שלשה מינים
|
| One is called equilateral, which is the one whose three sides are equal.
|
הא' יקרא שוה הצלעות והוא אשר שלש צלעותיו שוים
|
| The second is called isosceles, which is the one whose two sides are equal and the third is unequal, whether it is longer than both, or shorter than both.
|
והשני יקרא שוה השוקים והוא אשר תהיינה שתי צלעותיו שוות והשלישית בלתי שוה אם יותר ארוכה מכל אחת מהן או יותר קצרה מכל אחת מהן
|
| The third is called scalene, which none [of its sides] is equal to the other.
|
והשלישי יקרא מתחלף הצלעות והוא אשר אין אחת שוה לחברתה
|
|
|
עוד [2]המשולש יחלק אל נצב הזויות והוא אשר זויתו האחת נצבת כזה
|
|
|
ואל נרוחת הזוית והוא שזויתו האחת מרווחת כזה
|
|
|
ואל חד הזויות והוא אשר שלש זויותיו חדות
|
|
|
ובעל הד' צלעות יחלק אל מרובע שוה הצלעות ואל בלתי שוה הצלעות
|
|
|
עוד השוה הצלעות יחלק אל מה שהוא נצב הזויות ויקרא שוה הצלעות נצב הזויות כזה
|
|
|
ואל מה שהוא בלתי נצב הזויות כזה ויקרא מעויין
|
|
|
עוד הבלתי שוה הצלעות יחלק אל מה שהוא שתי צלעותיו הנכוחיים שוים וזויותיו נצבות ויקרא מרובע ארוך כזה
|
|
|
ואל כל ששתי צלעותיו שוות אבל אין זויותיו נצבות ויקרא דומה למעויין כזה
|
|
|
ואל זולת אלה ויקרא הנוטה
|
|
|
והוא ארבע תמונות יתבארו בזה החבור
|
|
|
והתמונה הבלתי ישרת הקוים השטוחה תחלק אל עגולה וחצי עגולה
|
|
|
והעגולה היא תמונה יקיף בה קו אחד בתוכה נקדה כל הקוים היוצאים ממנה אל המקיף שוים
|
|
|
והנקדה ההיא תקרא מרכז העגולה
|
|
|
והקו אשר יצא ממקיף העגולה ויעבור על המרכז יקרא מיתר
|
|
|
והחתיכה אשר תושבתה במיתר יקרא קשת
|
|
|
וחצי העגולה היא אשר יקיף בה חצי הקו המקיף והאלכסון
|
|
|
וחתיכת העגולה היא תמונה תקיף בה היתר והקשת ותחלק לשני מינים אם שהיא קטנה מחצי עגולה או גדולה הימנה
|
| The area of the shape is the right-angled quadrilateral parts, whose length is as their width, or those that are equal to them, that are filling the shape.
|
ותשבורת התמונה הוא החלקים המרובעים נצבי הזויות אשר ארכם כרחבם או השוים להם הממלאים את התמונה הדרושים על התמונה
|
| The multiplication is the product of a side by a side, or of a straight line by a curve, or of a number by a number.
|
וההכאה היא כפל צלע בצלע או קו ישר בקו קשתי או מספר במספר
|
| Euclid has already explained in a book that he wrote about the measurement of land that the plane geometry is based on four things: directions, points, lines, and angles; and it also has species and types.
|
וכבר ביאר אקלידס בספר אחד שחבר במדידת הארץ כי חכמת המדות השטוחה היא מיוסדת מארבעה דברים מהפאות ומהנקודות ומהקוים ומהזויות וגם כן היא מקבלת סוגים ומינים
|
| The directions are east, west, north, and south.
|
והפאות הם מזרח ומערב וצפון ודרום
|
| The points are those that you regard as a beginning or a sign of a thing.
|
והנקדות הם אשר תקח אותם התחלה או סימן לדבר
|
| The lines are ten: straight line, base, top, perpendicular, parallel line, diagonal, legs, perimeter, diameter, and hypotenuse.
|
והקוים הם י' קו ישר ותושבת וראש ועמוד וקו נכחי וקטר ושוקים ומקיף ואלכסון ומיתר
|
| The straight line is that which is drawn straightly from both its ends that are two points.
|
והקו הישר הוא הנמשך על יושר משתי תכליותיו שהם שתי נקדות
|
| The base is a straight line on which another straight line stands and makes the two angles on both its sides right angles
|
והתושבת היא קו ישר אחד עומד עליו קו ישר אחר ועושה השתי זויות אשר משני צדדיו נצבות
|
| The top is the line that stands above the base.
|
והראש הוא הקו העומד על התושבת
|
| The perpendicular is a line that goes down from the top to the base and makes the two angles on both its sides right angles.
|
והעמוד הוא הקו היורד מהראש אל התושבת ועושה השתי זויות אשר משתי צדדיו נצבות
|
| The parallel line is a line that stands in parallel to another line and the distances of their extremes that are at right angles are equal.
|
והקו הנכחי הוא קו עומד נכח קו אחר ומרחקי קצותיהם אשר על זויות נצבות שוים
|
| The diagonal is a line that is drawn from the one of the vertices of the quadrilaterals and their like to another vertex.
|
והקטר הוא הקו הנמשך מזויות המרובעים וכיוצא בהם עם הזוית האחרת
|
| The legs
|
והשוקים הם קוים ישרים יורדים מקצות הארץ עד שתי קצות התושבת
|
| The perimeter
|
והמקיף הוא הקו הסובב במרחק שהוא המרכז עד הקו ההוא והקוים היוצאים אליו מהמרכז שוים
|
| The diameter
|
והאלכסון הוא [3]קו יוצא מהמקיף ועובר על מרכזו ויוצא אל המקיף מהצד האחר וחולק את המקיף בשני חלקים שוים
|
| The hypotenuse
|
והמיתר הוא הקו הישר אשר תחת הזוית הנצבת
|
|
|
והזויות הם ג' נצבת חדה ונרוחת
|
|
|
הנצבת היא כאשר יעמוד קו ישר על קו ישר ויעשה הזויות אשר משני צדדיו שוות כל אחת תקרא נצבת
|
|
|
והזוית אשר היא קטנה מזאת תקרא חדה
|
|
|
ואשר היא גדולה מזאת תקרא נרוחת
|
|
|
סוגי המדידה הם שלש מהארבעה קוים הישרי' ומדידת התמונה ר"ל תשבורת התמונות ומדידת הגופנים
|
|
|
מדידת הקוים הישרים היא אשר ימדדו על יושר באורך לבד וזה יקרא מדידה מספרית
|
|
|
מדידת תשבורת התמונות הוא אשר יש לו אורך ורחב ועובי כי ממנו יודע מדידת הגופנים ויקרא גם כן מעוקב
|
|
|
ומיני המדידה הם חמשה המרובע והמשולש והמעוין והנוטה והעגולות
|
|
|
והתמונות י"ח
|
|
|
אם תמונות המרובעים ב' מרובע נכחי הצלעות ונצב הזויות
|
|
|
ואם תמונות המשולשים משולש שוה הצלעות ומשולש שוה השוקים ומשולש מתחלף הצלעות ומשולש נצב הזויות ומשולש נרוח הזויות ומשולש חד הזויות
|
|
|
ואם תמונות המעויינים ב' המעויין והדומה למעויין
|
|
|
ואם תמונות הנוטים הם ד' נוטה נצב הזויות נוטה שוה השוקים נוטה חד הזויות נוטה נרוח הזויות
|
|
|
ואם תמונות העגולות ד' העגולה וחצי העגולה וחתיכת העגולה מחציה ומעלה וחתיכת העגולה הקטנה שהיא קטנה ממנה
|
Chapter Two
|
הפרק השני
|
|
|
דע כי המשולש הוא שרש ופנה לכל התמונות השטחיות ישרות הקוים כי ממנו חוברו ואליו יותכו כאשר הודיע זה ניקומאכוש הגיהרשיני במאמר השני מספר הארתימישיקא שחבר
|
|
|
ולכן מי שידע למדוד המשולשים ידע למדוד כל התמונות בכפל תשבורת המשולש במספר אשר יולידו התמורה אם הם שוים ואם היו בלתי שוים יהיה זה בקבוץ תשבורת כל המשולשי' אשר יולידוהו ומפני זה היה מספיק להודיע מדידת המשולש למנין לבד אבל מפני שהמדה והשעור אשר נשער בה מרובעת ארכה כרחבה
|
|
|
כי תשבורת התמונות הם משוערות על האמות המרובעות כאשר הודענו מן גדרה
|
|
|
והמשולש בעצמו לא יתאמת מנינו רק בהצטרפו אל המרובע כי המופת שיובא עליו בהקשה אל המרובע לכן ראוי שנודיע מדידת המשולשים [נ' המרובעים] תחלה אח"כ נודיע דרכי המשולשים והשאר
|
|
|
וקודם זה נודיע שכל מוסכל לא יגיע אלא בידוע ולכן עלו כל הדרושים אל המושכלות הראשונות או אל אחד מהמינים אשר הם ידועים בעצמם
|
|
|
וידוע כי כשנדרוש למצוא תשבורת תמונה איזו שתהיה קודם שנמצאנה היא מוסכלת אצלנו
|
|
|
ולכן ראוי להגיעה לנו בידוע והידוע אשר יגיע לנו היא ידיעת חלק ממנה אם צלעות מצלעותיה או עמוד ותושבת וזולת זה
|
|
|
ואם גם אלה הם מוסכלים אז תגיע לנו האמה אשר ימדדו בה ולכן ראוי להודיע [4]שהאמה הזאת ידועה אשר תגיע לנו ידיעת המוסכלים מהנמדדים היא אורך לבד בלי מרחב ואינה אמה מרובעת כאשר הם אמות התשבורת כי גם המרובעת תכליותיה הם הקוים אשר הם אורך לבד והם המגבילים אותה
|
|
|
ומהנה אתחיל לבאר איך ימדדו המרובעים ונתחיל ממרובע שוה הצלעות נצב הזויות כי הוא כשרש לשאר המרובעים אחרי שהמעויין ידמה לו בשווי הצלעות והארוך בהתיצבות הזויות
|
|
|
ועוד כי אמת התשבורת היא מרובעת הצלעות שוים והזויות
|
|
|
והיתה זאת אמת התשבורת כי זאת תודיע לנו השעור של התמונה והדבר אשר יודיע שעור הדבר ראוי שיהיה שוה נודע וידוע שהזויות הנצבות הם שוות לעולם מה שאין כן החדה והנרוחת כי יקבלו הפחות והיתר והדבר אשר יקבל הפחות והיתר הוא בלתי מוגבל והבלתי מוגבל הוא בלתי ידוע והבלתי ידוע בעצמו איך יהיה סבה לזולתו
|
|
|
הדבור על מדידת המרובע שוה הצלעות נצב הזויות
|
|
|
ראוי שתדע בכלל כי כל בעל ארבעה צלעות נצב הזויות הארבעה הנה הכאת צלעו האחד בצלעו האחר ככה תשברתו
|
|
|
והיה זה סבה להיות שמרובע צלעו האחד שוה להכאת צלעו הא' בצלעו השני
|
|
|
דמיון מרובע אבג"ד הוא שוה הצלעות כי נשים כל א' מצלעותיו עשר אמות והנה מרובע צלעו האחד מאה אמה וככה הוא תשברתו כי הם מאה אמות מרובעות נצבות הזויות כל אמה מהן מרובעת דומה אל המרובע הגדול
|
|
|
המופת על זה נחלק כל צלע ממנו על עשר אמות בעשרה נקדות ונגיע מכל נקדה מהצלע האחד קו על הצלע הנכחי לו הנה יהיו הקוים נכוחיים האחד לחברו ולצלעו המרובע הגדול כי מרחקי קצותיהם אשר הם על זויות נצבות שוים אם כן קו ה"ו נכחי אל קו א"ד וקו ב"ל נכחי אל קו א"ב
|
|
|
ונאמר תחלה כי קו א"ד נפל על שני קוי א"ב וב"ל הנכוחיים
|
|
|
הנה ישרת שתי הזויות הפנימיות אשר בצד אחד שוות לשתי נצבות וזוית א' היא נצבת אם כן גם זוית ב' היא נצבת על כל פנים [5]והתמונות הנכחיות הצלעות יהיו זויותיהם המומרות שוות א"כ גם זוית ה' נצבת וגם הזוית הנשארת מזה המרובע הקטן שהוא האמה נצבת
|
|
|
עוד קו ו"ה נפל על קו א"ב והקו הישר אשר יפול על קו ישר הנה ב' הזויות אשר בצדו אם נצבות או שוות לשתי נצבות וזוית ה' נצבת אם כן גם הזוית אשר בצדו נצבת ומזה יתבאר כי גם על ד' זויות האמות נצבות וכן יתבארו כל הי' אמות אשר בטור הא'
|
|
|
עוד קו ב"ל נחתך בקו ה"ו וב' הקוים אשר יחתכו זויותיהם המקבילות שוות א"כ גם זוית האמה הראשונה אשר בטור הב' השמאלית נצבת וכנגדה נצבת וכן יתבארו כל האמות אשר בתשבורת הזאת ולהיותם שוי הצלעות יתבאר מחלוקת כל צלע השוה לחלקים וכשתחסר מן השוים יהיה הנשאר שוים והב' דברים השוים לדברים שוים גם הם שוים
|
|
|
וזאת המדידה נכונה בבעלות ד' הנצבות הזויות הד' ר"ל שתכפול צלעו הא' על צלעו השני המקיפו' בזוית א' ולמצוא התשבורת
|
|
|
דמיון בבעלת ד' צלעות נצב הזויות הד' נכוחי הצלעות אשר צלעה הא' י' וצלעה האחרת ה' כזה הנה כפילת הה' על הי' הם נ' וזהו התשבורת של זאת התמונה ומופתה כמופת הקודם
|
|
|
אבל אם היתה התמונה שוה הצלעות ולא היתה נצבת הזויות ולא יתכן שימדד במדידת צלעותיה כי זה יביא לטעות גדולה
|
|
|
דמיון יש לנו מרובע שוה הצלעות ובלתי נצב הזויות עליו אבג"ד ויהיה כל א' מצלעיו י' אמות הנה אם תכפול צלעו הא' בצלעו השני אז אם תקח מרובע צלעו הא' יעלה ק' ואין זה תשבורת המרובע הזה
|
|
|
המופת נוציא ב' קוטרים מזויותיו הא' קוטר א"ג והב' קטר ב"ד ויהיה קטר א"ג י"ו אמה וקטר ב"ד י"ב אמה ויחתכו על נקדת ה' הנה נעשה שטח נכוחי הצלעות נצב הזויות אשר צלעו אחת כקטר הארוך וצלעו האחרת כקטר הקצר ויהיה כל צלע נכוחי לקטר הדומה לו כי שתי הקטרים יחתכו על זויות נצבות כאשר נראה המופת במדידתו ונכתוב עליו ה' ו' ז' ח' הנה נחלק השטח הנצב הזויות לד' חלקים שוים עם קטרי המרובע הקטן אשר אין זויותיו נצבות
|
|
|
עוד כל חלק מהד' חלקים נחלק לשני חלקים שוים עם צלעות המרובע הקטן לא פחות ולא יתר
|
|
|
ותשבורת השטח הנצב הזויות הוא בכפל צלעו האחד על השני וצלעו הא' הוא י"ו אמה כי [6]הוא שוה לקטר הארוך מהמרובע וצלעו השנית הוא י"ב אמה כי הוא שוה לקטר הקצר מהמרובע וכפל י"ו על י"ב הם קצ"ב וזהו תשבורת השטח הנצב הזויות אשר הוא כפל תשבורת המרובע אשר בתוכו
|
|
|
ואם כן תשבורת המרובע הם צ"ו אמות אשר בתוכו ואלו היינו נשענים על כפל צלעותיו היה יוצא ק' אמה וזאת שגיאה גדולה
|
|
|
ולכן אמרו בעלי השעור שזה המרובע יהיה נמדד בכפילת מחצית קטרו הא' על קטרו השני והוא תשברתו
|
|
|
המופת על המדידה הזאת ידוע שכאשר יהיה שוה הצלעות הנה שני קטריו יחתכו על זויות נצבות כי כל קטר הוא מחלק אותו לשני משולשים שוה השוקים והקטר תושבת שני המשולשים וכאשר יצא הקטר האחד מזוית משולש שוה השוקים אשר התושבת היא מיתרה עד הזוית האחרת ממשולש שוה השוקים שזאת התושבת היא מיתר גם אותה תחלק התושבת לשני חלקי' שוים [7] ועל זויות נצבות וכפילת כל הקוטר בכל הקטר יהיה תשבורת המרובע החיצון אשר הוא כפלו לכן מרובע חציו בכולו הוא מחצית זה שהוא תשבורת המרובע הזה ולכן אמרו כשתמצא מרובע שוה הצלעות בין שיהיה נצב הזויות בין שלא יהיה לא תמנה אותו כי עם מדידת האלכסונים ולא תטעה לעולם כי להכיר האדם הזוית הנצבת מהבלתי נצבת אינו בקלות ולכן ראוי להשמר מן הטעות
|
|
|
ואם היה המרובע שוה הצלעות נצב הזויות ולא ידעת צלעו או רצית למדדו מקטרו האחד תקח מרובעו ותחלקהו על שני חלקים והחלק האחד הוא תשבורת המרובע ההוא ושרש החלק הוא אורך צלעו
|
|
|
דמיון מרובע אשר עליו אבג"ד שוה הצלעות נצב הזויות והיה מרובע קטרו ר' תחלק הר' לשני חלקים יהיה החלק הא' ק' והוא תשבורת המרובע ושרש הק' שהם י' הם אורך צלעו וכן אם אינו שוה הצלעות אבל הוא נצב הזויות יהיה הקטר ידוע אליך והצלע האחד ורצית למדדו משתי אלה תקח מרובע הקטר ותגרע ממנו מרובע הצלע הידוע והנשאר הוא מרובע הצלע הנשאר תקח שרשו והוא אורך הצלע תכה אותו עם הצלע הידוע והוא תשבורת המרובע
|
|
|
דמיון מרובע ארוך אשר עליו אבג"ד והיה צלע א"ב י' אמות וקטר א"ג י"ב אמות
|
|
|
לקחנו מרובע הקטר והוא קמ"ד אמות גרענו ממנו ק' אמה שהוא מרובע הצלע הידוע שהוא י' אמות ונשארו מ"ד אמות ושרשם ו' אמות ושני שלישי אמה פחות משהו שהוא אורך הצלע השני הכינו הו' ושני שלישי' פחות משהו עם הי' ונהיו ס"ו אמות ושני שלישים פחות משהו והוא תשבורת המרובע
|
|
|
המופת על שתי [8]על שתי אלו המדידות ידוע שהקטר הוא חילק את שני המרובעים האלה על שני משלשים שוים נצבי הזויות להיות שהם נכוחיי הצלעות והקטר משותף בשניהם וזוית אחת בכל משלש נצבת והקטר הוא מיתר הזוית הנצבת לכל משולש מהם וכבר התבאר בחכמת המדות שהמשולש הנצב הזוית שני המרובעים אשר יהיו מהצלעות המקיפות בזוית הנצבת שוות למרובע ההוה מהצלע שהוא מיתר לזוית הנצבת א"כ כשתגרע מהשוה לשנים האחד ישאר השני ושרשו הוא המבוקש הנולד מנפילתו בחברו אשר יקיף עמו בזוית הנצבת הוא תשבורת המרובע ההוא
|
|
|
ואם היתה תשבורת המרובע ידועה לך וידעת גם צלעו האחד ולא ידעת גם צלעו השני תחלק תשבורת המרובע על הצלע הידוע ויצא לך הצלע האחר הבלתי ידוע
|
|
|
דמיון היה מרובע תשברתו ק' אמה וצלעו האחר י' אמה תחלק תשברתו שהוא הק' אמה על י' ויצא לך החלק י' ומזה ידעת שגם צלעו האחר י' אמות והמרובע הזה שוה הצלעות
|
|
|
וכן אם היה תשברתו ק' אמה וצלעו הא' כ' אמה תחלק הק' על הכ' ויצא לך החלק ה' והוא צלעו האחר ומזה ידעת שהוא שטח נכחי הצלעות אשר יקרא מרובע ארוך
|
|
|
המופת על זה כי התשבורת הוא מספר נולד מכפילת חלקי הצלע האחד בחלקי הצלע האחר והמספר הנכפל במספר אחר ימצא באותה תולדה המספר האחר בכמות המספר האחר וכן האחר בזה וכשידעת כמות מספר האחד והתולדת אם תחלק התולדת על כמות המספר הנודע ידענו המספר אשר ימצא בכמות המספר הנודע ובהתקבצו כפעמי המספר הנודע נהיה התולדת
|
|
|
ולכן חלקנו תשבורת המרובע על צלעו הנודע והוא יודיע לנו צלעו הבלתי נודע
|
|
|
ואם היה המרובע שוה הצלעות ובלתי נצב הזויות והוא אשר יקרא מעויין והיה קטרו הא' י"ו אמה וקטרו הב' י"ב אמה כמה יהיה צלעו תחלק כל קטר לשני חלקים וקח מכל אחד מרובע החלק האחר ותחבר שני המרובעי' כאלו הם מספר אחד וקח השרש והוא צלע המרובע ההוא
|
|
|
דמיון חלקנו קטר י"ו על ח' ח' ולקחנו מרובע ח' שהם ס"ד וכן קטר הי"ב על ו' ו' ולקחנו מרובע הו' שהם ל"ו חברנו הס"ד עם הל"ו ונהיו ק' ושרשו י' והוא צלע המרובע
|
|
|
המופת על זה כי כל צלע מצלעי זה המרובע יהיה קטר לשטח נכחי הצלעות נצב הזויות אשר צלעו הא' ח' וצלעו השני ו' כאשר הודענו במדידת המרובע הזה ומרובע הקטר ראוי להיותו שוה לשני מרובעי כי הוא מיתר למשלש בזויתו הנצבת ולכן ישוה זה צלע המרובע לשני ש שני מרובעי חציי קטריו
|
|
|
ואם שאל השואל מעויין שקטרו האחד [9]שקטרו האחד י"ו אמה וצלעו י' אמה כמה קטרו האחד תקח מרובע מחצית הקטר הידוע שהוא ח' ומרובעו ס"ד
ותגרעהו ממרובע הצלע שהוא ק' ונשאר שהוא ל"ו הוא מרובע חצי הקטר האחר תקח שרשו והוא ו' והוא מחצית
הקטר כפלהו והוא י"ב והוא הקטר האחר
|
|
|
המופת על זה ידוע שמחצית כל קטר משניהם עומד על הקטר האחר על זויות נצבות ומחצית הקטר הידוע עם מחצית הקטר הבלתי ידוע וצלע המרובע יעשו משלש נצב הזויות והצלע יהיה מיתר הזוית הנצבת ומרובע הצלע שהוא מיתר לזוית הנצבת ישוה לשני מרובעי שתי הצלעות הנשארות שהם וחציי הקטרים וכאשר תגרע מרובע הצלע הא' המקיף בזוית נצבת אשר הוא בזה מחצית הקטר ממרובע צלע המרובע שהוא המיתר לזוית הנצבת ישאר מרובע חצי הקטר האחר שהוא המקיף האחר לזוית הנצבת ושרשו הוא חצי הקטר ואם תכפלהו תמצא כל הקטר
|
|
|
ובכאלה השאלות תוכל להוציא גם אתה שאלות אחרות ולהשיב עליהן
|
|
|
ומהנה נכנס בבאור מדידת המשולשי' למיניהם אחר נבאר מדידת הנוטים כי לא נוכל לבאר מדידת הנוטים ראשונה למדידת המשולשים אחר שהמשולשים הם יסוד לנוטים כי כל נוטה יחלק לשני משולשים מתחלפים או ליותר מזה וכאשר תדע מדידת המשולשים למיניהם יגיע לך בקלות ידיעת מדידת הנוטים
|
Chapter Three on the Measuring of the Various Triangles
|
הפרק השלישי במדידת המשולשים למיניהם
|
|
|
כבר ידעת שהמשולשים נחלקו לשוי הצלעות ולשוי השוקים ולמתחלפי הצלעות
|
|
|
ונקדים לבאר תחלה דרכי המשלש השוה הצלעות כי בו יפול העמוד במחצית התושבת בכל צלע שתרצה להוציאו אחר נדבר על המשלשים האחרים
|
|
|
ונאמר בתחלה כי הדבר הכולל לכל המשלשים במדידתם הוא שתכפול העמוד במחצית התושבת או כל התושבת במחצית העמוד וההוה הוא תשבורת המשלש המבוקש
|
|
|
ומפני זה ראוי להודיע בתחלה איך יצא העמוד בכל משלש ומשלש עד שיהיה ידוע כי בו יגיע לנו תשבורת המשלש המוסכלת
|
|
|
ונאמר כי במשלש השוה הצלעות לעולם יפול העמוד במחצית התושבת אחר שג' זויותיה הם חדות לעולם וג' צלעותיה שוות וארצה בעמוד הקו הנופל מזוית ראש המשלש אשר יקרא גובה התמונה על תושבתה על זויות נצבות
|
|
|
המשל בזה משלש אב"ג שוה הצלעות ועמוד אשר יצא מראש המשלש אשר הוא נקדת א' על תושבתה יפול בנקדת ד' ואומר שנקדת ד' היא מחצית התושבת
|
|
|
המופת בזה העמוד חולק את המשלש לשני משלשים אשר שתי צלעות כל משולש ממנו שוות לשתי הצלעות מהאחר כל אחד [10]לגילו צלע א"ג שוה לצלע א"ב ועמוד א"ד צלע משותף לשתיהן וזוית אד"ב שוה לזוית אד"ג כי שתיהן נצבות אם כן צלע ג"ד שוה לצלע ד"ב וצלע ג"ד וד"ב הם מחוברים הם כל התושבת אם כן כל אחת מהן היא מחצית התושבת
|
|
|
והמופת אשר תשבורת כל משלש הוא כפילת העמוד בחצי תושבת או כל התושבת בחצי העמוד אם במשולש שוה הצלעות או במשלש שוה השוקים אשר הוצאת עמודו על צלעו המתחלפת הוא זה כי המופת אשר הורה במשלש שוה הצלעות הוא בעצמו יורה זה על שוה השוקים כאשר הוצאת עמודו על צלעו המתחלפת כי כאשר הוצאת העמוד על מחצית התושבת אח"כ הוצאת קו על קצה התושבת נכחי אל העמוד עוד הוצאת קו מראש העמוד הנכחי אל מחצית התושבת כבר נהיה שטח נכחי הצלעות אשר צלעו האחת העמוד וצלעו האחר מחצית התושבת
|
|
|
והשטח הזה שוה למשלש הנזכר כי צלע המשלש הנז' הוא קטר לנכחי הצלעות הנז' ומחלק אותו לשני המשלשים שוים והמשולש האחד הוא מחצית כל המשלש הנזכר אם כן כל שטח הנכחי הצלעות אשר הוא נחלק לשני משולשים הוא שוה לכל המשלש הנז' ותשבורת השטח הנכחי הצלעות הוא כפילת צלעו האחת בצלעו האחרת וצלעו האחת היא עמוד המשלש וצלעו האחרת היא מחצית תושבת המשלש אם כן תשבורת המשלש הוא כפילת העמוד בחצי תושבתו אחר שהוא שוה לשטח הנכחי הצלעות
|
|
|
המשל בזה משלש אב"ג הוא שוה הצלעות או השוקים ועמודו הוא קו א"ד והוצאנו על קצה מחצית תושבת המשלש הזה קו ב"ה על נקדת ב' נכחי לקו א"ד ועל נקדת ה' הוצאנו קו א"ה נכחי לקו ד"ב
|
|
|
הנה אומר כי שטח א"ד ה"ב הנכחיי הצלעו' שוה למשלש אב"ג
|
|
|
המופת בזה כי זוית אה"ב שוה לזוית אד"ב כי שתיהן נצבות והקטר שהוא צלע המשלש שהוא א"ב חלק את השטח לשני משלשים שוים אחר שהוא קו ישר ונפל על שני קוים נכוחיים שם את שתי הזויות המומרות שוות אם כן זוית ב"ד היא שוה לזוית בא"ה וקטר א"ב משותף אם כן משלש הא"ב שוה למשלש אב"ד ומשלש אב"ד הוא חצי שטח הנכחי הצלעות שהוא שטח ה"אד"ב והוא חצי משלש אב"ג אם כן שטח ה"אב"ד שוה למשולש אב"ג ושטח נכחי הצלעות הנצב הזויות כפילת צלעו האחת בצלעו האחרת היא תשברתו אם כן גם תשבורת משלש אב"ג הוא כפילת צלע נכחי הצלעות האחת שהוא עמוד המשלש בצלעו האחרת שהוא מחצית תושבת המשולש וזמש"ל
|
|
|
ואם המופת שבכפילת מחצית העמוד על [11]על כל התושבת נמצא התשבורת הוא זה אם תרצה מהכלל הידוע שכל חשבון כפולת חציו בחשבון אחר כלו הוא בכפולת כלו כמחצית אותו החשבון
|
|
|
ואם תרצה נביא מופת מחכמת המדות והוא זה משלש אב"ג שוה הצלעות ונוציא מנקדת ח' ממנו עמוד אל תושבת ב"ג והוא קו א"ד ונסמן במחציתו נקדת ה' ונוציא מנקדת ה' שני קוים דבקים על יושר נכוחיים ושוים לתושבת ב"ג והם ה"ז ה"ח ונגיע קוי ח"ב ז"ג הנה אומר כי שטח ב"ג ז"ח הנכחיי הצלעות שוה למשלש אב"ג
|
|
|
המופת כי נוטה ט"ב ב"ג משותף לשטח ב"ג ז"ח ולמשלש אב"ג ונשאר משלש חט"ב כמשלש אט"ה כי זוית חט"ב שוה לזוית הט"א וזוית אה"ט שוה לזוית בח"ט וצלע א"ה שוה לצלע ב"ח כי שתיהם מחצית העמוד אם כן משלש חט"ב שוה למשלש אט"ה וכן משלש בז"ג שוה למשלש אב"ה וההנהגה אחת א"כ נוטה ט"ב ב"ג עם שני משולשי חט"ב בז"ג שהם כל השטח נכחי הצלעות שוה לנוטה ט"ב ב"ג עם שני משולשי אט"ה אב"ה שהם כל משלש אב"ג אם כן משלש אב"ג שוה לשטח נכחי הצלעות ב"ג ז"ח ותשבורת השטח הנכחי הצלעות הוא הכאת צלעו האחד שהוא שוה למחצית העמוד של המשולש בצלעו האחר שהוא שוה לכל תושבת המשולש אם כן גם תשבורת המשולש שהוא שווה לו הוא הכאת מחצית העמוד בכל התושבת וזה מש"ל
|
|
|
וכן זה המופת בעצמו יורה על משלש שוה השוקים כאשר הוצאת העמוד על צלעו המתחלפת
|
|
|
הנה כבר ידעת שכשיבא בידך הן משלש שוה הצלעות הן שוה השוקים תכפול העמוד במחצי' התושבת או ההפך ותמצא התשבורת
|
|
|
ולדעת העמוד מהצלע הן במשלש שוה הצלעות או במשולש שוה השוקים
תעשה כן תקח מרובע חצי התושבת ותגרעהו ממרובע הצלע ואשר ישאר יקח שרשו והוא העמוד
|
|
|
המופת על זה כי צלע המשולש הוא מיתר הזוית הנצבת אשר יקיפו בה העמוד ומחצית התושבת והתבאר בחכמת השעור כי מרובע הצלע אשר היא מיתר הזוית הנצבת[12] ותקח שרש הנשאר תמצא את צלע האחרת
|
|
|
אולם בעלי השעור נתנו כללים אחרים במדידת המשולש השוה הצלעות כדי להקל על המחשב ואמרו לעולם תקח מט"ו בצלעו י"ג והוא העמוד או תהיה מרבע את הצלע והוצא ממנו הרביעית וקח שתי הרביעיות הג' והוא עמוד המשולש הזה
|
|
|
ואלה הכללים וכדומה להם יצאו מהמופת הנז'
|
|
|
ומה שאמרנו בענין משלש שוה השוקים הוא כשהוצאת עמודו על צלעו המתחלפת אבל אם הוצאת אותו על צלע אחד מצלעותיו דע שיש לו שני משפטים אחרים נבארם כשנבאר [13]משפטי המשלש שמתחלף הצלעות
|
| If we wish to measure a scalene triangle, we should extract its height on its side first and to know its distance from one of the sides, for the height that we extract in the equilateral triangle and in the isosceles triangle always falls on the middle of the base, yet this height that is drawn in the scalene triangle does not fall on the middle [of the base] at all, but it is far from one side and close to the other side.
|
אם נרצה לשער המשלש המתחלף הצלעות תחלה ראוי להוציא עמודו על צלעו המתחלפת ולדעת מרחקו מאחת הצלעות כי העמוד אשר הוצאנו במשלש השוה הצלעות ובמשולש שוה השוקים הוא נופל במחצית התושבת לעולם אבל אין העמוד הזה היוצא במשולש המתחלף הצלעות יוצא על המחצית כלל אבל הוא רחוק מהצלע האחת והוא קרוב אל הצלע השנית
|
| We call its distance from the first side "the close distance" and we call its distance from the far side "the far distance".
|
ומרחקו מהצלע האחת אנו קוראים אותו המרחק הקרוב ומרחקו מהצלע הרחוק אנו קוראים אותו המרחק הרחוק
|
| After we know the position of the height on one of the sides, we can then announce the length of its height.
|
ואחר שנדע גבול מעמדו באחת מהצלעות אז נביא להודיע אורך עמודו
|
- Let us say the triangle ABG is a scalene triangle, whose side AB is 20 cubits, side AG is 18 cubits, and side GB is, on which we draw the height, which is the base, is 16 cubits.
|
ונאמר משלש אב"ג מתחלף הצלעות אשר צלע א"ב ממנו עשרים אמה וצלע א"ג ממנו י"ח אמה וצלע ג"ב ממנו אשר עליו נוציא את העמוד והוא התושבת י"ו אמה
|
- We wish to know the distance of the height from its position to side אג, which is the short [distance].
|
ונרצה לדעת גבול מעומד העמוד מצלע א"ג אשר הוא הקצר
|
- We already know that the length of this side is 18 cubits.
|
וכבר ידענו שאורך הצלע הזה י"ו אמה
|
- We take its square, it is 324.
|
נקח מרובעו הוא שכ"ד
|
- We add to it the square of the base, which is 256; the result is 580.
|
ונחבר אליו מרובע התושבת שהוא רנ"ו ויהיו תק"ף
|
- Then, we subtract the square of AB, which is the longer side, from 580; we already know that it is 20, and its square is 400; we subtract it from 580; the remainder is 180.
|
אחר נגרע מן תק"ף מרובע א"ב אשר הוא הצלע הארוך וכבר ידענו שהוא כ' ומרובעו הוא ת' נגרעם מן תק"ף נשארו ק"פ
|
- We take its half; it is 90
|
נקח מחציתם והם צ'
|
|
|
ונחלק אותם על התושבת שארכה י"ו ונהיה החלק הא' ה' וחצי ושמינית וזהו גבול מעמד העמוד מן הצלע הקצר על התושבת
|
|
|
ואם רצינו לדעת גבול מעמדו מן הצלע הארוך נקח מרובעו שהוא ת' ונחבר אותו עם מרובע התושבת שהוא רנ"ו ושניהם תרנ"ו נגרע מאלה מרובע הצלע הקצר שהוא שכ"ד נשארו של"ב נקח מחציתם והם קצ"ו ונחלקם על התושבת שהם י"ו ונהיה י"ו שליש וחלק אחד מכ"ד וזהו גבול מעמד העמוד מן הצלע הארוך על התושבת
|
|
|
עוד נמשיל במשלש מתחלף הצלעות משל אחד על חשבון שלם ר"ל שיצא גבול מעמד עמודו על התושבת באחדים שלמים מבלתי חלק
|
|
|
ונאמר משלש אב"ג אשר צלע א"ג ממנו י"ג וצלע א"ב ממנו ט"ו וצלע ב"ג ממנו אשר הוא התושבת י"ד ורצינו לדעת גבול מעמד העמוד על התושבת מהצלע הקצר שהוא א"ג ממנו
|
|
|
חברנו אל מרובע הצלע הזה מרובע התושבת ונהיו שס"ה גרענו מזה המרובע מהצלע הארוך אשר הוא רכ"ה ונשארו ק"מ לקחנו חצים והם ע' חלקנום על י"ד שהוא חותך התושבת והיה החלק האחד ה' וזהו גבול מעמד העמוד מן הצלע הקצר
|
|
|
ואם תרצה לדעת גבול מעמדו מן הצלע הארוך נחבר מרובעו עם מרובע התושבת ונהיו תכ"א הוצאנו מהם מרובע הצלע הקצר שהוא קס"ט נשארו רנ"ב לקחנו חצים והם קכ"ו וחלקנום על י"ד שהוא התושבת היה החלק הא' ט' וזהו גבול [14]מעמד העמוד מן הצלע הארוך
|
|
|
המופת על זה כבר התבאר בחכמת השעור שמרובע הצלע אשר הוא מיתר זוית חדה הוא פוחת מן מרובעי שתי צלעות הנשארות בכפל שטח הנצב הזויות אשר יקיף בו התושבת כלו עם מקום מעמד העמוד מאותו הצד ולכן כאשר תחבר מרובע הצלע עם מרובע התושבת ותוציא מהם מרובע הצלע הנשאר ישאר בכפל הנצב הזויות אשר יקיף בו כל התושבת והחלק אשר יצא עליו העמוד מאותו הצד ולכן נחלק אותו לשנים והחלק האחד נחלקהו על התושבת אחרי שהסך הוא כפל ואשר יצא הוא מקום מעמד העמוד על אותו הצד
|
|
|
המשל בזה המשלש אשר ציירנו ידענו שצלע א"ג ממנו הוא י"ג אמה ומרובעו קס"ט והתושבת י"ד אמה ומרובעה קצ"ו ושתי המרובעים שס"ה וצלע א"ב אשר הוא ט"ו אמה ומרובעו רכ"ה יהיה פוחת משני המרובעים הנזכרי' בכפל השטח הנצב הזויות אשר יקיף בו ג"ד בג"ב א"כ כאשר גרענו רכ"ה משס"ה ישאר ק"מ והוא ככפל השטח הנצב הזויות אשר יקיף בו ג"ד בג"ב ומפני שהוא כפל לקחנו חציו והוא ע' והוא כשטח הנצב הזויו' אשר יקיף ג"ד בג"ב חלקנוהו על התושבת שהוא י"ד וידענו שהחלק האחד ממנו הוא מקום מעמד העמוד מאותו הצד והחלק הוא ה' ומזה ידענו שמרחק העמוד מאותו הצלע הוא ה'
|
|
|
ואחר שידענו גבול מעמדו נבא לדעת ארכו וכן נעשה נגרע מרובע החלק מן התושבת אשר עומד עליו העמוד ממרובע הצלע הדבק בו ואשר ישאר הוא מרובע העמוד
|
|
|
המשל בזה המשלש גרענו מרובע ה' שהוא כ"ה ממרובע הצלע הדבק בו ואשר ישאר הוא מרובע העמוד גרענו כ"ה ממרובע הצלע הדבק בו שהוא קס"ט ושרשו י"ב והוא אורך העמוד
|
|
|
וכן אם רצינו לדעת אותו מהחלק האחר מהתושבת אשר הוא ט' ומרובעו פ"א גרענו אותו ממרובע הצלע הדבק בו אשר הוא רכ"ה נשארו קמ"ד ושרשו י"ב והוא אורך העמוד
|
|
|
והמופת על זה כי מרובע כל צלע מהם שוה עם מרובע העמוד והחלק מן התושבת הדבק בו מפני שהוא מיתר לזוית הנצבת כל א' במשלשו כי כאשר הוצאת העמוד כבר נחלק המשלש לשני משלשים וכאשר גרעת מרובע החלק מן התושבת וממרובע הצלע הדבק בו נשאר במרובע הצלע מרובע העמוד וכשלקחת שרשו מצאת אורך העמוד
|
|
|
הנה בארנו מדידת כל המשלשים למיניהם והבדלם מצד הצלעות
|
|
|
ואעפ"י שבמדות האלה יכללו גם מתחלפי הזויות כי המשלש שוה השוקים לא ימלט מהיותו חד הזויות ואם נצב הזויות או נרוח גם ככה המתחלף הצלעות אמנם בעבור שיש להם מדות מיוחדות [15]גם מפני הזויות נבארם ואין זה צורך
|
|
|
ונאמר כי המשלש הנצב הזויות אין צורך להוציא עמודו על צלעו שהוא מיתר הזוית הנצבת כי כל אחת משתי צלעותיו המקיפות בזוית הנצבת הן עמודיו ולכן אם תכה אחד מהצלעות הנזכרות בצלעו האחרת המקפת עמו הזוית הנצבת תמצא תשברתו
|
|
|
והמופת על זה ידוע ממה שבארנו במשלשים הקודמים
|
|
|
עוד המשלש הנרוח הזוית אין הכרח להוציא עמודו על צלעו שהוא מיתר הזוית הנרוחת לבד
|
|
|
אבל אם רצית להוציאו בדרך זו אשר אורה לך
|
|
|
כבר התבאר בחכמת השעור שמרובע מיתר הזוית הנרוחת עודף על מרבעי שתי הצלעות המקיפות בה בכפל התושבת אשר עליה הצלע בקו היוצא חוצה מקצה התושבת הנזכרת עד מקום נפילת העמוד פעמים
|
|
|
המשל בזה משלש אב"ג נרוחת הזויות וזוית אג"ב ממנו היא הנרוחת אומר שמרובע א"ב שהוא מיתר הזוית הנרוחת עודף על מרובע צלע א"ג וג"ב בכפל בג"ד פעמים
|
|
|
ודרך הוצאת העמוד הזה במשלש הזה כך נשים הזוית הנרוחת אשר עליה ג' וצלע ג"א ד' אמות וצלע ב"ג י"ג אמה וצלע א"ב שהוא מיתר הזוית ט"ו אמה ומרובע ט"ו מוסיף על מרובע י"ג ומרובע ד' אשר הם קפ"ה אמה מ' אמה ואם תחלק מחצית התוספת על אחת מהצלעות יצא לך מרחק העמוד חוצה מן הצלע ההוא עד"מ חלקנו מחצית המ' אשר הוא התוספת והם כ' על קו ג"א אשר הוא ד' אמות ויצא החלק ה' וידענו מזה שהעמוד נפל חוצה מן צלע ג"א ה' אמות והוא קו ג"ד והעמוד עליה עמוד א"ד ואם תחלק אותו על קו ב"ג אשר ארכו י"ג אמה יצא החלק האחד שבעים ואחד חלקים מי"ג והוא מרחק העמוד היוצא חוצה מן ג"ב והעמוד עליו
|
Chapter Four on the Measuring of the Various Trapezoids
|
הפרק הרביעי במדידת הנוטים למיניהם
|
|
|
הנוטה הוא תמונה בעלת ד' צלעות שאינה לא מרובע ולא נכחי הצלעות ארוך ולא מעויין ולא דומה למעויין והם מינים רבים אעפ"י שכלם נכללים בד' יש מהם ג' ששתי צלעותיו המקבילות שוות והראש והתושבת בלתי שוות אבל הם נכחיות כזה ויש מהם ששתי הצלעות שוות והראש והתושבת בלתי שוות ולא נכחיות כזה ויש מהם ששתי הצלעות הדבקות מהם שוות האחת לחברתה כזה וכן השתי צלעות האחרות
|
|
|
ויש מהם חד הזוית כזה ויש מהם שאין צלע הא' שוה עם האחר כזה ויש מהם נצב הזויות כזה ויש מהם נצב הזוית האחת כזה ויש מהם נרוח הזוית כזה ויש מהם תמונות עקלקלות זולת אלו לכן ראוי לך שאתן דרך הצריכה לנו במדידתם
|
| Height and area of an isosceles trapezium
|
|
|
|
ואחל מהנוטה אשר שתי צלעותיו שוות ואינם נכוחיות והראש והתושבת בלתי שוות אבל [16]הם נכוחיות
|
|
|
ונאמר אם היה נוטה אבג"ד וצלע א"ב ח' אמות וצלע ד"ג י"ח אמות ושני צלעי א"ד ב"ג כל אחד מי"ג אמה ותרצה למצוא תשברתו תעשה כך
|
|
|
תגרע הראש מהתושבת ומהמותר תקח מחציתו ומנה כמה הוא מזאת התושבת האחת וסמן שם נקדה
|
|
|
עוד מנה כמה הוא מזוית התושבת האחרת וסמן שם נקדה
|
|
|
דמיון גרענו הח' מן הי"ח ונשארו י' לקחנו מחציתם והם ה'
|
|
|
מנינו כן מזוית ג' וסמננו שם נקדת ה'
|
|
|
עוד מנינו כן מזוית ד' וסמננו שם נקדת ז' הגענו א"ה וב"ז וידענו עמודי זאת התמונה
|
|
|
רצינו לדעת ארך העמודים וכפלנו הצלע שהם י"ג על עצמם והיו קס"ט
|
|
|
הוצאנו מהם כ"ה שהוא מרובע ה' נשארו קמ"ד
|
|
|
לקחנו גדרם והם י"ב וידענו שארך העמוד הם י"ב
|
|
|
חברנו הראש עם התושבת והם כ"ו ולקחנו מחציתם והם י"ג
|
|
|
וכפלנום עם העמוד שהם י"ב והיו קנ"ו וזהו תשבורת הנוטה הזה
|
|
|
המופת על זה ידוע שמחצית העודף יהיה מהצד האחד ומחציתו מהצד האחר עד שיוציאו העמודים עליהם וצלע א"ד הוא מיתר הזוית הנצבת ולכן מרבעו שוה למרובע העמוד עם תושבת משלש אד"ה ותושבת משלש אד"ה ה' ומרבעו כ"ה תגרעהו ממרובע הצלע אשר הוא קס"ט נשאר קמ"ד וגדרו י"ב והוא ארך העמוד
|
|
|
וידוע שתשבורת משלש אד"ה הוא כפילת העמוד בחצי ד"ה וכן תשבורת משלש בז"ג הוא כפילת העמוד ז"ג אם כן תשבורת שני משולשים האלה הוא כפילת העמוד ד"ה ותשבורת השטח הנצב הזויות והוא שטח אבה"ז הנה הוא כפילת העמוד בתושבת ה"ז אם כן כפילת ד"ז עם העמוד הוא תשבורת נוטה אבג"ד
|
|
|
ויתבאר גם כן זה בצורה אחרת מהמופת
|
|
|
והוא יש לנו נוטה אבג"ד שוה השוקים וצלע א"ב שוה לצלע ג"ד וכל אחת מהן בעלת י"ג אמות וצלע א"ג ו' אמות וצלע ב"ד י"ו אמות ונרצה למצוא התשבורת והעמוד
|
|
|
אוציא קו נכחי א"ה לקו ג"ד ואוציא עמוד א"ז על קו ב"ד אם כן שטח אהג"ד הוא נכחי הצלעות וא"כ א"ב שוה לה"ד וג"ד לא"ה ולפי שב"ד י"ו אמו' וה"ד ו' אמו' א"כ ב"ה הנשארת תהיה י' אמות ולפי שמשלש אב"ה שוה השוקים וכל אחת מצלעותיו ידועה יהיה א"כ גם עמוד א"ז ידוע והוא י"ב אמות כאשר קדם ידיעתו ונחלק צלעי אבג"ד באמצע על נקדת ח"ט ונוציא עמוד בח"ל מט"נ על קו ב"ד
|
|
|
אם כן משלש אב"ח שוה למשלש בח"ל
|
|
|
ומשלש דמ"ט שוה למשלש גנ"ט
|
|
|
לכן אם נוסיף בשתוף בעל שש צלעות א"ח ל"נ ט"ד ישוה שטח כ"ל מ"נ הנכחי הצלעות לנוטה אבג"ד
|
|
|
ולפי שא"ב שוה לב"ל
|
|
|
וה"מ שוה לג"נ
|
|
|
אם כן א"ב ד"מ שוים לב"ל נ"ג
|
|
|
וכשיתוסף עליהם בשתוף א"ד ל"נ יהיו שני' ב"מ ל"נ שהם שני פעמים כ"מ שוה לשני [17]א"ד ב"ג ושני א"ד ב"ג ידועים כי הם כ"ב אמות א"כ גם נ"מ פעמים כ"ב ויהיה כ"מ י"א אמות אבל גם כ"ל י"ב אמות ונוטה אבג"ד שוה לשטח כ"ל מ"נ הנכחי בצלעות א"כ יהיה תשברתו קל"ב אמות כתשבורת
הנכחי הצלעות
|
| Height and area of an acute trapezium
|
|
|
|
ואם רצית למדוד נוטה חד הזוית כגון נוטה אבג"ד והזוית אשר אצל ב' חדה וצלע א"ב י"ג אמות וצלע ג"ד כ' אמות וצלע א"ד ו' אמות וצלע ב"ג כ"ז אמות ותרצה למצוא התשבורת והעמוד כך תעשה
|
|
|
תגרע הו' אמות מן הכ"ז אמות וישארו כ"א אמות ובהיות צלעות משלש החד הזויות ידועות והם י"ג וכ"א וכ' יודע גם ארך א"ז העמוד שהוא י"ב אמות כמו שידענו זה מקודם ותחבר עם הו' אמות כ"ז אמות ויהיה מחציתו י"ו אמות וחצי כפלם עם העמוד ויהיו קצ"ח והם תשבורת הנוטה
|
|
|
והמופת על זה אוציא קו א"ה נכחי לקו ג"ד ואוציא א"ז עמוד ולפי שא"ה כ' אמות וג"ה ו' אמות אם כן ב"ה הנשאר כ"א אמות ולפי שקו א"ז העמוד במשלש אב"ה החד הזויות הוא י"ב אמות וצלעי א"ב ג"ד נחלקים באמצע על נקדת ח' וט' ובח"ל הוא העמוד גם מט"נ כמו שהראנו בצורה הזאת הקודמת לזה יראה שנוטה אבג"ד שוה לשטח כ"ל מ"נ נכחי הצלעות וקוי ב"ג א"ד ביחד הם כפל כ"מ וכ"מ הוא י"ו אמות וחצי וכ"ל הוא י"ב אמות כי כן הוא קו א"ז א"כ תשבורת הנוטה הזה הוא קצ"ח אמות
|
| Height and area of an obtuse trapezium
|
|
|
|
אם רצית למדוד נוטה נרוח הזויות כמו נוטה אבג"ד והזוית אשר אצל ב' נרוחת והיה צלע א"ב י"ג אמות וצלע ג"ד כ' אמות וצלע א"ג ו' אמות וצלע ב"ד י"ז אמות כזה
|
|
|
תגרע הו' אמות מהי"ז אמות וישארו י"א אמות ובהיות צלעי המשלש נרוח הזוית ידועות י"ג וי"ז וכ' ימצא גם העמוד שהוא י"ב תחבר הי"ז עם הו' הם כ"ג ומחצית זה הם י"א וחצי תכפלם על י"ב יהיו קל"ח והוא תשבורת הנוטה הזה
|
|
|
והמופת על זאת המדידה אוציא עמוד א"ה ואוציא קו א"ז נכחי לקו ג"ד יהיה א"כ קו א"ז כ' אמות וקו ז"ד ו' אמות ואם כן קו ב"ז הנשאר יהיה י"א אמות ולכן לפי שמשלש אב"ז הוא נרוח הזוית יהיה קו א"ח י"ב אמות וכן לפי מה שהתבאר למעלה השטח אשר יהיה מב"ד א"ג ביחד ומא"ה הוא כפל נוטה אבג"ד אם כן תשבורת הנוטה הזה הוא קל"ח אמות
|
| Height and area of a scalene quadrilateral
|
|
|
|
ואם רצית למדוד נוטה אבג"ד ולא יהיה צלע מצלעותיה נכוחי והזוית אשר אצל ג' נצבת ויהיה כל צלע מצלעותיה ידוע אם צלע א"ב י"ג אמות ואם ב"ג י' אמות ואם ג"ד כ' אמות [18]ואם ד"א י"ז אמות כזה תעשה כך
|
|
|
תכפול הי' אמות על הכ' אמות ויהיו ר' וקח מחציתם והוא ק' ועוד תכפול הי' על עצמם ויהיו ק' והכ' על עצמם ויהיו ת' וחברם ויהיו ת"ק והי"ג על עצמם ויהיו קס"ט חברם עם הת"ק ויהיו תרס"ט גרע מהם מרובע י"ז וישארו ש"פ קח חציים והוא ק"צ כפלם על עצמם ויהיו ל"ו אלפי' וק'
|
|
|
חלקם על ת' ויהיה החלק ע"ב וחמישית
|
|
|
תגרעם מן קס"ט ישארו צ"ו וחצי וחמישית ועשירית
|
|
|
כפלם על ת"ק ויהיו מ"ח אלף ות'
|
|
|
קח גדרם ויהיו רכ"א וקח מחציתם ויהיה ק"י והוא תשבורת משלש אב"ד
|
|
|
אבל גם תשבורת משולש בג"ד ק' אמות אם כן תשבורת נוטה אבג"ד ר"י אמות
|
|
|
המופת על המדידה הזאת נגיע קו ב"ד ואעמיד עליה עמוד קו א"ה ולפי שכל אחד מצלעי ב"ג ג"ד הם ידועות וזוית שאצל ג' נצבת אם כן משלש בג"ד יהיה ידוע ויהיה גם מרובע ב"ד ידוע והוא ת"ק אמות אבל גם מרובע א"ב ידוע א"כ מרובעי א"ב ב"ד ידועים והם יותר ממרובע א"ד אם כן זוית אב"ד תהיה חדה ואם כן מרובעי א"ב ב"ד גדולים ממרובע א"ד בכפל השטח הנצב הזויות אשר יקיפו בו קוי א' ב"ה פעם אחת ידוע והוא גדר מרובע ב"ד על מרובע ב"ה אם כן גם מרובע ד"ב על מרובע ב"ה ידוע ומרובע ב"ד ידוע א"כ גם מרובע ב"ה ידוע אבל גם מרובע ה"א על מרובע ב"ד וגדרו הוא השטח אשר יקיפו ב"ד א"ה א"כ גם השטח אשר יקיפו בו ב"ד ד"ה ידוע והוא כפל משלש אב"ד אם כן גם משלש אב"ד ידוע אבל גם משלש בג"ד ידוע ולכן כל בעלת ד' צלעות אבג"ד ידועה
|
|
|
והיות גם העמוד היוצא מנקדת א' על קו ב"ד ידוע הנה אני מביא עליו המופת יהיה נוטה עליו אבג"ד וכל אחת מצלעותיו תהיה ידועה וזוית בג"ד נצבת
|
|
|
והיות העמוד היוצא מנקדת א' על קו ג"ד ידוע אוציא אם על קו ג"ד עמוד א"ז ועל קו א"ז עמוד ב"ח ועל קו ב"ד עמוד א"ה והוא מבואר כי קו ב"ד ידוע וא"ה העמוד אשר עליה לפי שגם ב"א א"ד הם ידועים ולפי שזוית גב"ד שוה לזוית בט"א אבל גם זוית בג"ד הנצבת שוה לזוית אה"ט הנצבת אם כן יחס א"ה אל ה"ט ויחס ג"ד אל ג"ב ידוע א"כ גם יחס א"ה אל ה"ט ידוע וא"ה ידוע אם כן גם ה"ט ידוע והם מקיפים בזוית נצבת אם כן גם א"ט ידוע ולפי שכל אחת מב"ה ה"ט ידוע אם כן גם השטח נצב הזויות ידוע אשר יקיפו בו בט"ה ויהיה שוה לשטח אשר יקיפו בו אט"ח והזוית אשר אצל כל אחת מה"ח נצבת אם כן גם ח"ט ידוע ולכן יהיה גם א"ח ידוע אבל גם ח"ז שוה לב"ג אם כן גם א"ז כולו יהיה ידוע ויהיה אופן המעשה כן
|
|
|
אם צלע א"ב יהיה י"ג אמו' ואם צלע ב"ג י' אמות ואם צלע ג"ד כ' אמות ואם צלע ד"א י"ז אמו' [19]ונרצה למצוא התשבורת הנז' ויהיה אם עמוד א"ה בכח צ"ו וחצי וחמש יתחלק א' מט"ו ואם ב"ה יהיה בכח ע"ב וחמש ואם ב"ד יהיה בכח ת"ק ולפי שאם צלע ג"ד היא כ' אמות ואם ג"ב היא עשר אמות א"כ מרובעם יהיה ת' אמות וק' אמות ועשה כך
|
|
|
ראה כיחס ת' אל הק' מה היחס אל צ"ו ורביעית וחמישית ותמצא שהוא אל כ"ד וחמישית
|
|
|
וכן מרבע ה"ט וכפל הע"ב על כ"ד וחמישית וקח גדר ההוה וכפלהו בשנים וההוה הוא ככפל השטח הנצב הזוית אשר יקיפו בו ב"ה ונוסיף מרובע ב"ה ב"ט כלומר מרובע ע"ב וחמישית וכ"ד וחמישית מחוברים ונדע כ"ט בכח שהוא ק"פ וחבר קצ"ו וחצי וחמישית ועשירית והכ"ד וחמישיתו ויעלה קכ"ד וכפל הק"ף על הכ"ד וחמישית יהיה בכח ד' אלפים שכ"ו וחלקם על הקכ"א יהיה ל"ו ונגרע מקכ"א בכח ל"ו בכח וישארו כ"ה בכח שהם ה' באורך ותוסיף כל שעור ב"ג והוא י' אמות וההוה ט"ו וזהו שעור העמוד ואם ה"ט בכח כ"ד וחמישית ואם ח"ט באורך ו' ואם באורך י"א
|
|
|
ואם תרצה למדוד נוטה אבג"ד אשר הזוית שאצל ג' נצבת ויהיה צלע א"ב י"ג אמות וצלע ב"ג י' אמות וצלע ג"ד ח' אמות וצלע א"ד כ"ה אמות כזה ותרצה למצוא תשברתו תעשה כן תכפול הי' על עצמם יעלו ק' גם הח' על עצמם יעלו ס"ד תחברם יעלו קס"ד גם תכפול הי"ג על עצמם יעלו קס"ט חברם עמם יעלו של"ג גם כפול הכ"ה על עצמם יעלו תרכ"ה גרע של"ג ישארו רצ"ב קח חציים והם קמ"ו כפלם על עצמם יעלו כ"א אלף שי"ו חלקם על קס"ד יהיה החלק קכ"ט וק"ס חלקים מקס"ד באחד גרעם מן קס"ט ישארו ל"ט וד' חלקים מן קס"ד באחד כפלם על קס"ד יעלו ו' אלפים ות' וגדרו פ' וחציים מ' ויהיה תשבורת משולש אב"ד מ' אמות אבל גם תשבורת משולש בג"ד כן מ' אמות אם כן תשבורת כל נוטה אבג"ד פ' אמות
|
|
|
והמופת על המדידה הזאת נגיע ב"ד ויהיה תשבורת משולש בג"ד ידוע ומרובע ב"ד יהיה קס"ד אמות אבל גם מרובע א"ב קס"ט אמות א"כ מרובע א"ב ב"ד ככפל השטח הנצב הזויות שהם של"ג אמות והם פחותים ממרובע א"ד אם כן זוית אב"ד נרוחת ואוציא עמוד א"ה על ד"ב בהוציאי אותו עד ה' א"כ מרובע א"ד יותר גדול ממרובעי א"ב ב"ד ככפל השטח הנצב הזויו' אשר יקיפו בו קוי ב"ה ידוע לכן גם השטח הנצב הזויות אשר יקיפו בו ב"ד ב"ה יהיה ידוע ויהיה גדר מרובע ב"ד על ב"ה א"כ מרובע ב"ד על מרובע ב"ה ידוע אבל גם מרובע ב"ד גם מרובע ה"ב הנשאר ידוע והזוית אשר אצל ה' נצבת א"כ גם מרובע א"ה ידוע לכן גם מרובע א"ה על מרובע ב"ד ידוע ויהיה גדרו השטח הנצב הזויות אשר יקיפו בו א"ה ב"ד אם כן גם שטח הנצב הזוית אשר יקיפו בו א"ה ב"ד ידוע וחציו הוא משלש אב"ד שהוא מ' אמות כמו שזכרנו [20]אם כן גם משלש אב"ד ידוע לכך גם כל בעל ד' צלעות אבג"ד יהיה ידוע
|
Chapter Five on Knowing the Round Shapes
|
הפרק החמישי בידיעת התמונות העגולות
|
|
|
דע שהעגולה היא קו אחד בתוכה נקדה שכל הקוי' היוצאים ממנה אל המקיף שוים
|
|
|
והנה בזה השער יכנסו מדידת העגולה השלימה אשר גדרנוה ומדידת חתיכות העגולה וחתיכות העגולה ג' מינים
|
|
|
הא' הוא חצי העגולה
|
|
|
השני יותר מחציה
|
|
|
השלישי פחות מחציה
|
|
|
ונחל במדידת העגולה השלימה אחר נדבר במדידת חתיכותיה ונאמר כי תשבורת העגולה היא בשתכה את מחצית קטרה במחצית הקו המקיף אותה והנה ערך הקו המקיף אותה ר"ל את העגולה מקטרה כערך כ"ב אל הז' נמצא שהקו המקיף הוא בערך ג' ושביעית וזה לפי דעת חכמי המדות המדקדקים בחכמה הזאת
|
|
|
אמנם בטלמיוס עשה כל חשבונותיו בספר המג'יסטי על חשבון שיהיה הקטר שלישית הקו המקיף כי חלק את העגולה על ש"ס מעלות והקטר על ק"כ מעלות ואעפ"י שאין יחס בין הקטר שהוא קו ישר לקו המקיף שהוא קו עגול אבל היחס יפול במספר לא בשעור
|
|
|
ואם רצית למצוא תשבורת העגולה מהמקיף לבד תקח מרובע הקו המקיף וזה בשתכה אותו על עצמו וההוה תכה אותם על ז' וההוה קח מהם חלק א' מפ"ח והוא תשבורת העגולה
|
|
|
המשל בזה הכינו כ"ב על עצמם והם תפ"ד כפלנום ז' פעמים והם ג' אלפים ושפ"ח לקחנו מהם חלק מפ"ח והם ל"ח וחצי והוא תשבורת העגולה
|
|
|
דמיון אחר אם רצית למצוא תשבורת העגולה מהמקיף לבד תוסיף על המקיף חציו ורביעיתו וההוה הוא תשבורת העגולה
|
|
|
המשל בזה הוספנו על הקו המקיף שהוא כ"ב אמות חציו ורביעיתו שהם י"ו אמות וחצי ההוה ל"ח וחצי והם תשבורת העגולה
|
|
|
ואם רצית תשבורת העגולה מהקטר לבד מבלתי שתביט אל הקו המקיף כפול מרובע הקטר על י"א וחלק העולה על י"ד והעולה הוא תשבורת העגולה וזה על חשבון חכמי המדות
|
|
|
ובטלמיוס אמר במקום אחר כי ערך הקו המקיף אל כל האלכסון והוא ג' וח' חלקי' מששים באחד
|
|
|
ואין הפרש בין זה החשבון ובין חשבון חכמי המדות רק דבר מועט שאינו מזיק בחשבון לכן סמכנו את חשבוננו על דעת חכמי המדות
|
|
|
עוד אם רצית למצוא תשבורת העגולה מהקטר לבד תקח הקטר וכפלהו על הקו המקיף וקח מההוה רביעיתו והוא תשבורת העגולה
|
|
|
המשל בזה הקטר ז' והקו המקיף כ"ב כפלנו זה על זה וההוה קנ"ד ורביעיתו ל"ח וחצי והוא תשבורת העגולה
|
|
|
הנה כבר בארנו דרך תשבורת מדידת העגולה
|
|
|
[21]ומעתה נחל לבאר דרך מדידת חתיכותיה ונאמר כי מקצת העגולה היא מקפת מן קצת הקו המקיף את העגולה ומקו ישר יקרא המיתר והוא המשוך מקצה הקו המקיף אותה עד קצהו האחר
|
|
|
וכאשר יצא ממחצית המיתר קו על זוית נצבת אל המקיף יקרא החץ
|
|
|
ועיין אל כל חתיכה ואם החצי יהיה כמחצית המיתר דע שהחתיכה היא חצי עגולה
|
|
|
ואם יהיה קצר ממחצית היתר דע שהחתיכה היא פחותה מחצי העגולה
|
|
|
ואם הוא יותר ארוך ממחצית היתר החתיכה היא גדולה ממחצית העגולה
|
|
|
וכאשר היתה החתיכה חצי עגולה ורצית לדעת תשברתה תכפול חצי היתר שהוא אלכסון החצי עם חצי הקו המקיף אותה וההוה הוא תשבורת מחצית העגולה כי מחצית הקו המקיף העגולה שהיא החתיכה הוא רביע הקו המקיף כל העגולה השלימה
|
|
|
וכאשר הכית מחצית הקטר ברביע העגולה תמצא תשבורת כל העגולה
|
|
|
וכאשר תכה מחצית הקטר ברביע העגולה תמצא תשבורת חצי העגולה
|
|
|
כי כל חשבון שתכה חציו בכולו יהיה ההוה מחצית הכאת כלו
|
|
|
ואם תכה חציו בחציו ההוה רביע הכאת כלו בכולו
|
|
|
המשל בזה עגולה שלימה אשר הקו המקיף אותה כ"ב אמות ידענו שקטרה ז' אמות רצינו למצוא תשברתה
|
|
|
הכינו מחצית הקטר שהוא ג' וחצי על מחצית הקו המקיף שהוא י"א אמות וההוה ל"ח וחצי ידענו מזה שתשבורת העגולה ל"ח וחצי אמות
|
|
|
רצינו לדעת תשבורת מחצית העגולה הזאת לקחנו מחצית הקו המקיף אותה שהוא ה' וחצי והכינו אותם עם מחצית הקטר שהוא ג' וחצי וההוה י"ט ורביע והוא תשבורת חצי העגולה
|
|
|
המשל בזה חצי עגולה שיהיה קטרה י"ד אמות והחץ ז' אמות
|
|
|
תקח מרובע הקטר והוא קצ"ו אמות ותכפלהו בי"א ההוה ב' אלפים קנ"ז קח החלק האחד מכ"ח שהם ע"ז אמות והם תשבורת חצי העגולה
|
|
|
ואם רצית למצוא את תשבורתה מהחץ תעשה כך תקח מרובע החץ ותכפלהו על י"א ותקח שביעיתו והוא תשבורת חצי העגולה
|
|
|
המשל בזה קח מרובע החץ שהוא ז' ומרובעו מ"ט כפלהו על י"א ההוה תקל"ט ושביעיתו ע"ז והוא תשבורת חצי העגולה
|
|
|
עוד חצי עגולה אשר קטרה ז' אמות וחצה חצי הקטר שהוא ג' וחצי והקו המקיף י"א אמות ותרצה לדעת תשברתה תעשה כך תכפול הז' אמות של הקטר עם הי"א אמות של הקו המקיף וההוה ע"ז אמות קח רביעיתם והם י"ט אמות ורביע והם תשבורת חצי העגולה
|
|
|
ובאופן אחר תעשה כך תקח מרובע הקטר שהוא ז' אמות ומרובעו מ"ט כפלם על י"א וההוה תקל"ט קח חלק א' מכ"ח והוא י"ט אמות ורביע וזהו התשבורת
|
|
|
[22]רצינו למצוא תשבורת חתיכת עגולה פחות מחציה ובזה הוא הכרח למצוא קטר כל העגולה אשר זאת החתיכה ממנה וככה נעשה
|
|
|
כבר התבאר בספר היסודות לאקלידס כי כל עגולה יפלו בה שני מיתרים ויחתכו זה את זה יהיה חלק המיתר בחברו האחר ככפל חלק המיתר השני בחברו
|
|
|
וכאשר רצינו למצוא אלכסון העגולה אשר זו החתיכה נחצבת ממנו נעבירהו חותך המיתר על זויות נצבות ויחתכהו באמצע כפי מה שהתבאר בספר היסודות לאקלידס
|
|
|
ונכפול חצי המיתר על מחציתו וההוה ממנו ראוי שיהיה כמו ההוה מחץ החתיכה הזאת על שארית האלכסון
|
|
|
וכאשר ידענו כמות אורך החץ נכפלהו על מספר שיהיה ההוה מכפלו כמו ההוה ממחצי' המיתר על מחציתו והמספר אשר כפלנו אותו עליו יחד עם החץ יהיה שעור אלכסון
|
|
|
המשל בזה יהיה חתיכת עגולה פחות מחציה חתיכת א"ב ויהיה מיתרה ח' אמות וחצה ב' אמות והוא ג"ד חותך על זויות נצבות את המיתר
|
|
|
ובהכרח שיחתוך אותו אל חצאים וכשנוציאנו עד מקיף העגולה כאשר נשלים אותה יעבור על מרכז העגולה
|
|
|
והנה חתך המיתר על ד' ד' אם כן כשנעריך חצי המיתר על חציו ההוה י"ו וכבר הנחנו החץ ב' נעריך אותו על מספר שיהיה ההוה י"ו ואין מספר כזה זולתי הח' וידענו שהחסר מן החץ עד תשלום האלכסון הם ח' חברנום עם החץ ביחד והיו י' והוא אורך כל האלכסון ונעשה חצו בה ונשלים העגולה ונאמר שנוציא שני קוים מנקדת ח' שהוא חצי האלכסון ומרכז העגולה אל נקדת א' ונקדת ב' ונכה מחצית הקטר שהוא ח"ג במחצית הקשת המקיף את החתיכה והוא קשת א"ג וההוה הוא תשבורת המשולש אשר שתי צלעותיו ח"א ח"ב ותושבתו קשת אב"ג
|
|
|
אחר כך נכה מחצית המיתר בעמוד המשולש הוא קו א"ד וההוה הוא תשבורת המשולש ישר הקוים
|
|
|
נגרע התשבורת מתשבורת המשולש אשר תושבותיו קשת אב"ג ואשר ישאר הוא תשבורת החתיכה הדרושה
|
|
|
וכאשר רצינו לדעת זאת המדידה באופן אחר מבלתי שנצטרך להוציא כל אלכסון העגולה נחבר המיתר והחץ ונקח חציים ונכה אותם עם החץ גם נכה חצי המיתר על עצמו ונקח מהכאת חצי המיתר על עצמו חלק א' מן ארבעה עשר ונוסיף אותם על הכאת חצי המיתר והחצי עם החץ והוא התשבורת
|
|
|
כגון מיתר י"ב עם חץ ד' שהם י"ו וחציים ח' נכה בד' הם ל"ב וחצי המיתר על עצמו הם ל"ו חלקו מי"ד ב' אמות וחצי וחלק מי"ד נוסיפם [23]על הל"ב אמות יהיה תשבורת החתיכה ל"ד אמות וחצי וחלק א' מי"ד
|
|
|
נרצה למצוא תשבורת חתיכת העגולה אשר היא גדולה מחציה
|
|
|
והחתיכה הזאת היא קשת אב"ג עם מיתר א"ג
|
|
|
ותוכל לדעת התשבורת כשתמצא קטר העגולה אשר זאת החתיכה היא חתיכה ממנה ותהיה כופל חצי הקטר בחצי הקשת ותהיה מוסיף עליו תשבורת המשולש אשר תושבתו המיתר וראשו מרכז העגולה וההוה הוא תשבורת החתיכה
|
|
|
ונעמוד על ידיעת האלכסון כן נקח מרובע חצי המיתר ונחלקהו על החץ ונוסיף העולה על החץ וההוה הוא אלכסון העגולה אשר זאת החתיכה נחתכה ממנה
|
|
|
המשל בזה יהיה חתיכת העגולה קשת אב"ג והמיתר א"ג וארכו י"ב אמות והחץ ב"ד וארכו ח' אמות
|
|
|
לקחנו מרובע חצי היתר שהוא ל"ו וחלקנוהו על החץ שהוא ח' ועלה החלק ד' אמות וחצי הוספנום על החץ והם י"ב אמות וחצי וידענו שהאלכסון הוא י"ב אמות וחצי
|
|
|
רצינו למצוא את התשבורת ולקחנו חצי הקטר שהוא ו' אמות ורביע וכפלנו אותו על חצי הקשת וההוה שמרנוהו
|
|
|
אחר כך מצאנו תשבורת המשולש שתשברתו א"ג ועמודו ה"ד ושתי צלעותיו הם א"ה ג"ה ומצאנוהו כן ידענו שאורך כל א' מצלעותיו השתים הוא כארך חצי הקטר ולכן יהיה מרובע הצלע כמרובע העמוד ומרובע מחצי' המיתר כי הוא תושבת לזוית הנצבת ואחרי שמרובע מחצית המיתר ל"ו נגרעהו ממרובע הצלע שהוא ל"ט אמות וחלק א' מי"ו נשארו ג' אמות וחלק א' מי"ו והם מרובע ארך העמוד
|
|
|
כפלנו העמוד עם מחצי' התושבת שהם ו' אמות וההוה הם י"ח אמות ושלישית וחלק מל' גם אחד מק"כ והוא תשבורת משלש אה"ג
|
|
|
הוספנו על השמור וההוה הוא תשבורת החתיכה הנזכרת
|
|
|
ואם רצינו למצוא התשבורת הזאת מבלי שנצטרך להוציא האלכסון נעשה כך
|
|
|
נכה המיתר עם החץ וההוה נכה אותו עם י"א ומן ההוה נקח חלק א' מי"ד והוא תשבורת החתיכה הזאת
|
|
|
המשל בזה חתיכת עגולה גדולה מחציה היא קשת אב"ג ומיתרה א"ג וארכו כ"ד אמות והחץ י"ו אמות
|
|
|
הכינו החץ עם המיתר ההוה שפ"ד אמות הכינו שפ"ד עם י"א ההוה ד' אלפים ורכ"ד לקחנו מהם חלק א' מהי"ד וההוה ש"א אמות וחצי ושביעית וחלק מי"ד והוא תשבורת החתיכה הנזכרת
|
|
|
אמר מרדכי בעבור שאלה המדידות אנו צריכים למצוא כמות הקשת המקפת בחתיכו' העגולה וזה מתבאר בלוחות המיתרים והקשתות כי בידיעת המיתר נדע הקשת גם בידיעת הקשת נדע המיתר כמו שביאר זה בטלמיוס במאמר א' מספר האלמג'יסטי
|
מאגיסטי ואין מדרך חבורנו זה לכתוב בו לוחות ראיתי להמציא לך דרך לדעת הקשתות מבלי שתצטרך
אל הלוחות ההם ואומר אם חתכת העגולה תהיה פחות מחציה ותרצה לדעת כמות הקשת המקיף אותה תעשה
כך לעולם . תחבר המיתר על החץ ותגרע מהם רביעיתם וקח מהנשארים רביעיתם והוסף עליהם וההוה
53
כי מהם התהוו ואליהם יותכו וכבר ידעת מדידת המשולשים למיניהם . וכאשר תרצה למדוד
תמונה רבת הזויות תוציא קו ישר מכל זוית מזויותיו אל מרכז התמונה ואז תחלק למשלשי'
בכמות הזויות . וכאשר תמדוד כל המשלשים ותקבץ מנינם המקובץ הוא תשבורת התמונה ההיא ואם
אחד מי"ב וההוה שנ"ח ושליש והם תשבורת התמונה
ואם רצית למדוד תמונה בעלת שמנה זויות תעשה כך
תכפול הצלע על עצמו וההוה כפלהו על כ"ט וקח ששיתו
54
עצמו וההוה כפלהו על מ"ה ומההוה קח רביעיתם וככה תשבורת התמונה . המשל יש לנו תמונת א'ב'ג'ד'ה'ו'ז'
ח'ט'י' י"א י"ב וכל צלע מצלעותיה י' אמות כפלנו הצלע על עצמו היו ק' כפלנום
על מ"ה וההוה ד' אלפים ת"ק לקחנו רביעיתם והם אלף קכ"ה וככה תשברתם
היא זוית של בעלת ה' זויות וא"כ שוה לב"ד א"ב קו א"ד ונחלקהו על יחס אמצעי ושני קצוות והחלק הגדול הוא קו א"ב
וקו א"ג הוא חצי א"ד אם כן המרובע ההוה משני קוי ב"א א"ג הוא כפלים ממרובע א"ג . ואומר אחוק מחומש אבגדה"ו
אשר כל אחד מצלעותיו י' אמות וארצה למצוא תשברתו אקח מרכז העגולה המקפת את התמונה והיא ז' ואגיע
55
לצלע בעלת ז' זויות ונגיע קוי ב"א א"ג אם כן משלש אב"ג שוה הצלעות אם כן מרובע א"ד הוא ג' כפלי מרבע
ד"ב א"ב יחס ד"א אל ד"ב בכח כיחס מט' אל ח' בקירוב ובאורך יחס ד"א אל א"ב כיחס ז' אל ד' ויהיה ב"ג כפל
ב"ד אם כן יחס אל ד"א כיחס ח' אל ז' . ואם תרצה למדוד תמונה בעלת ז' זויות אחוק תמונת אבגדהו"ז
ט' זויות ידוע וכבר התבאר בקוי העגולה כי קו ז"ה הוא שלישית ה"מ בקרוב אם כן מרובע ה"מ הוא ט' כפלי מרובע
ה"ז לכן מרובע מ"ז הוא ח' כפלי מרובע ה"ז ובחצי העגולה יתחייב להיות הזויות אשר אצל ז' נצבת אם כן יחס מרובע מ"ז
אל מרובע ז"ה כיחס רפ"ט אל ל"ו בקרוב אם כן יחס מ"ז אל ז"ה כיחס י"ז אל ו' בקרוב לכן יחס מרובע ה"ז אל משולש
[The Second Section on the Division of Plane Shapes]
|
|
The First Chapter of the Second Section of the Second Book on the Division of Plane Shapes
|
הפרק הראשון מהחלק השני מהספר השני בחלוקת התמונו' השטחיות
|
| We start with the triangles
|
ונחל מהמשלשים
|
| If you wish to divide an isosceles triangle into two equal parts, draw a perpendicular from one of its vertices to the base, by dividing the angle into two equal parts, so the triangle is divided into two equal triangles
|
אם רצית לחלוק משולש שוה הצלעות לשני חלקים שוים אוציא עמוד מזוית אחד מזויותיו אל התושבת וזה בשתחלוק הזוית אל שני חלקים שוים ואז יהיה המשולש נחלק לשני משלשים שוים
|
| Do so if the triangle is equilateral triangle, draw a perpendicular from the vertex opposite to its base to the base.
|
וככה תעשה אם המשולש שוה ותוציא מזויתו שהיא מיתר התושבת עמוד אל התושבת
|
|
|
גם אם רצית לחלקו ביותר משני חלקים תחלק התושבת בשיווי לחלקים שתרצה ותוציא מכל חלק מהם קו ישר אל הזוית כלומר אל ראש המשולש ואז יחלק המשולש בשעור חלקי התושבת
|
- The proof of this division has already been clarified in Euclid's VI.1
|
ומופת זה התבאר בתמונה הא' ממאמר ו' לאקלידס
|
|
|
דמיון רצינו לחלק משולש אב"ג לשני חלקים שוים חלקנו התושבת שהוא ב"ג על נקדת ד' לשני חלקים שוים והוצאנו עמוד מנקדת ד' אל ראש המשולש שהוא א' ובזה נחלק לשני משולשים שוים
|
|
|
ואם רצינו לחלקו על ג' חלקנו התושבת על ג' חלקים שוים והם א"ד ד"ה ה"ג אחר הוצאנו ד"א ה"א ובזה נחלק על שלשה חלקים שוים
|
|
|
גם ככה תעשה אם רצית לחלקו יותר מזה
|
|
|
אמנם אם רצית לחלק המשולש הנזכר לב' חלקים שוים מהצד האחד עד שיהיה החלק משולש והאחד נוטה
|
|
|
כגון משולש אב"ג ונחלקהו על משולש אד"ה ועל נוטה ד"הב"ג נעשה כך נחלק הצלע האחד על נקדה שיהיה מרובע החלק האחד כפל מרובע החלק השני ונוציא מהנקודה ההיא קו נכוחי לתושבת המשולש ונגיעהו על הצלע האחד ואז נחלק המשלש לשני חלקים שוים משלש אד"ה ונוטה ד"הב"ג
|
|
|
והמופת על זה כבר ביאר אקלידס בתמונת י"ח ממאמר ו' שכל שני משלשים דומים יחס המשולש אל המשולש כיחס צלעו אל צלעו הנכחי לו שנוי
|
|
|
וידוע שהמשלש הגדול והוא המשולש אב"ג דומה אל המשולש הקטן והוא משולש אד"ה
|
|
|
כי הזוית אשר אצל ח' משותפת לשני המשולשי'
|
|
וזוית אד"ה שוה לזוית אב"ג כי הם שתי זויות המומרות אשר על קוים נכוחיים כשנפל עליהם קו ישר והחיצונה [25]שוה לשכנגדה
|
|
|
גם ככה זוית אה"ד שוה לזוית אג"ב לזה הענין עצמו
|
|
|
אם כן מיתרי הזויות השוות מתיחסות יחס א"ב אל א"ד כיחס א"ה אל ה"ג וכיחס ד"ה אל ב"ג אם כן שני המשולשים דומים ולכן יהיה יחס משלש אב"ג אל משלש אד"ה כיחס צלע א"ב אל צלע א"ד שנוי וזה היחס מי"ו מח' בעצמו הוא יחס צלע מרובע א"ב אל מרובע צלע א"ד כי כאשר תכפול יחס הצלע אל הצלע בעצמו והוא אשר יקרא היחס שנוי יהיה הנולד יחס המרבע אל מרבע
|
|
|
דמיון אם צלע א"ב ו' אמות וצלע א"ד ב' אמות יהיה יחס ב' אל ו' כיחס השלישית אל האחד וכאשר תקח יחס השלישית אל האחד שנוי וזה כשתכפול השלישית על השלישית יהיה הנולד תשיעית וזהו יחס המשלש הקטן אל המשלש הגדול
|
|
|
גם ככה כשתקח מרובע ו' שהוא הצלע האחד הוא ל"ו ומרובע ב' שהוא צלע המשולש האחד ד' יהיה יחס ד' אל ל"ו יחס התשיעית אל האחד והוא המשלש הקטן אל הגדול
|
|
|
על כן כשתרצה לחלק המשולש לשני חלקים שוים נחלק צלע א"ב על נקודה והיא ד' עד שיהיה מרובע צלע א"ב כפל מרובע א"ד וכאשר עשינו כן הוצאנו מנקדת ד' קו נכחי לקו ב"ג והוא ד"ה ובזה נחלק המשלש לשני חלקים שוים החלק האחד משלש אד"ה והשני נוטה ד"ה ב"ג
|
|
|
דמיון שתקח מנקדת א' אשר היא ראש המשולש ה' חלקים מז' בו פחות עשירית השביעית
|
|
|
המשל שקו א"ב ז' אמות ומרובעו מ"ט ונמדוד מנקדת א' ה' אמות פחות עשירית השביעית ונסמן שם נקדה ויהיה מרובע הקו אשר הוא מנקדת א' עד הנקדה אשר סמננו כ"ד אמות וחצי והוא מחצית התשבורת של המשלש הגדול
|
|
|
ידענו מזה שהמשולש הקטן הוא חצי המשולש הגדול ונשאר הנוטה חציו אחר
|
|
|
ואם רצית לחלקו לג' חלקים עד שיהיו שני נוטים ומשולש א' חלק צלע הגדול על ו' ומנה מנקדת א' שהוא ראש המשולש ה' וחמישית בקרוב וסמן שם נקדה והיא ב' והוצא מזאת הנקודה קו נכחי לתושבת המשולש הגדול והוא ב"ג והנה יחלק אל משלש קטן ואל נוטה ויהיה הקטן שלישית המשולש הגדול
|
|
|
עוד תחלק הנוטה בשני חצאים וזה כשנחלק תושבת המשולש הגדול לשני חלקים שוים ונסמן שם נקדה והיא ז' עוד נחלק תושבת המשולש הקטן כן ונגיע קו ישר מנקדה אל נקדה או נחלק הנוטה לשני חלקים שוים
|
|
|
ואם רצית לחלקו לשני משלשים שוים ולנוטה מנה מראש המשולש אשר הוא חלקים פחות מעט מט' בצלע וסמן שם נקדת ד' והוצא נקדת קו נכחי מנקדת ד' אל תושבת המשולש הגדול והוא קו ד"ה ויהיה המשלש הקטן שני חלקים מהמשולש הגדול ונשאר נוטה ד"ה ב"ג החלק השלישי ומשלש אד"ה שני חלקים תחלק תושבת ד"ה לחצאים על נקדת ז' והוצא ממנו קו אל ראש המשולש הנה נחלק המשלש הקטן לשנים ונמצא כל המשולש הגדול נחלק לג' [26]חלקים שוים לשני משלשי אד"ז אז"ה ולנוטה ד"ה ב"ה וזה במשלש שוה הצלעות או שוה השוקים שתהיה צלע המתחלפ' תושבת המשולש
|
|
|
ואם היה המשולש שוה הצלעות או שוה השוקים ולא תהיה הצלע המתחלפת תושבת המשולש ותרצה לחלקו בשני חלקים שוים
|
|
|
דמיון משלש אב"ג מתחלף הצלעות או משולש דא"ז שוה השוקים ואין התושבת צלע המתחלפת ונרצה לחלקם בשני חלקים או בג' תמצא תשבורת כל המשולש כמו שהודעתיך במדידת המשולשים אח"כ תסמן בצלעו האחת נקדה ונחלקהו אל משולש נצב הזויות ואל נוטה עד שיהיה תשבורת המשולש נצב הזויות חציו או שלישיתו כפי מה שתבקש והשאר ישארו הנוטה וכבר הודעתיך מדידת כל אלה
|
The Second Chapter on the Division of the quadrilateral and the Circle
|
הפרק השני בחלוקת התמונות המרובעות והעגולה
|
| You already know the types of the quadrilateral shapes and how they are divided into square, rhombus, parallelogram and scalene quadrilateral; and the scalene quadrilaterals are divided into various types.
|
כבר ידעת מיני התמונות המרובעות ואיך יחלק אל שוה הצלעות נצב הזויות ואל שוה הצלעות ובלתי נצב הזויות ואל מרובע ארוך בלתי נצב הזויות שוה הצלעות הנכחיות ואל נוטה והנוטה מינים רבים
|
| Division of a square into parts
|
|
| I shall start with the square, as it precedes them by nature and by degree
|
ואחל מהמרובע שוה הצלעות נצב הזויות כי הוא הקודם בטבע ומעלה מהם
|
| I say that if you wish to divide the square ABGD into two [equal] parts, divide DG into two halves at point Z, and draw a line from point Z parallel to each of the sides AD and BG, hence the square is divided into two equal part
|
ואומר אם תרצה לחלק מרבע אבג"ד שוה הצלעות נצב הזויות לשני חלקי' תחלק צלע ד"ג לשני חצאים על נקדת ז' ותוציא מנקדת ז' צלע נכחי לכל אחת מצלעות א"ד ב"ג ובזה יחלק המרובע לשני חלקים שוים
|
- The proof of this division has already been clarified in Euclid's VI.1 that the ratio of the sides of the parallelograms, whose heights are the same magnitude, to one another is as the ratio of their bases to one another.
|
והמופת על זה החלוק כבר התבאר בתמונת א' ממאמר ו' מאקלידס שהצלעות נכחיי הצלעות כאשר היה גבהותם בשעור אחד הנה יחס קצתם אל קצתם כיחס תושבותיהם קצתם אל קצת
|
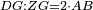
|
ויחס ד"ג אל ז"ג כפל א"ב
|
|
ד"ז מחצית ד"ג
|
|
גם ככה ז"ג מחצית ד"ג
|
|
|
ובזה המופת בעצמו יחלק גם מצלע א"ד אל ב"ג וכן תעשה אם רצית לחלקו לג' חלקים ויותר
|
|
|
ואם רצית לחלקו מהזויות תגיע זוית א' אל זוית ג' ויחלק המרבע לשנים חלקים
|
- The proof of this division:
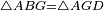
|
והמופת על החלוקה הזאת כי שני משלשי אב"ג אג"ד שוים
|
|
כי צלע א"ב שוה לצלע ד"ג
|
|
וצלע ב"ג לצלע א"ד
|
|
וזוית אב"ג שוה לזוית אד"ג
|
|
|
והתושבת משותפת
|
|
|
אם כן שני המשולשים שוים
|
|
|
ואם רצית לחלקו לשלשה חלקים שוים בדרך הראשונה כבר ידעת דרכו אמנם בזאת הדרך השנית תעשה כך תקח מהצלע ב' שלישיו ותגיע הזוית עד הנקודה וככה תעשה מהצלע האחר ויחלק המרובע לג' חלקי' שוים
|
|
|
דמיון רצינו לחלק מרבע אבג"ד לשלשה חלקים מדרך הזויות ויהיה כל צלע מצלעותיו י' אמות
|
|
|
לקחנו מצלע ד"ג ו' חלקים ושני שלישי חלק עד נקדת ה' והגענו א"ה והנה משולש [27]אד"ה נצב הזויות לשלישית המרובע גם ככה עשינו מנקדת ב' חלקנוהו ו' חלקים ושני שלישי חלק עד נקדת ז' והגענו ג"ז והנה משולש גז"ב נצב הזויות השלישית האחד ונשאר א"ה ז"ג הנכחי הצלעות השלישית האחר
|
- The proof of this division:
|
והמופת על זה החלוק כבר התבאר בתמונת ל"ו ממאמר א' מאיקלידס שהשטחים הנכחיי הצלעות מהמשולשים שהם על תושבות שוות ובמה שבין שני קוים נכוחיים יהיה השטח הנכחי הצלעות כפל המשולש
|
|
|
והנה תושבת א"ז ה"ג מחצית תושבת משולש גב"ז וראוי שיהיו שוים ועוד כי שטח א"ז ה"ג שוה לשטח ב"ט ה"ג הנכחי הצלעות ונצב הזויות כי הם תושבת אחת ובמה שבין קוים הנכוחיים ושטח א"ז ה"ג שלישית מרובע אבג"ד כי כן יחס תושבתו אל תושבתו א"כ שטח א"ז ה"ג שלישית כל המרובע ושני המשולשים שוים
|
|
|
כי צלע א"ד כמו צלע ב"ג
|
|
|
וצלע ד"ה כמו צלע ב"ז
|
|
וזוית אד"ה שוה לזוית גב"ז
|
|
|
הנה אם כן מרובע אבג"ד נחלק לג' חלקים שוים
|
|
|
ואם רצית לחלקו לד' חלקים אם מן הדרך הראשונה תוכל לחלקו בשני אופנים האחד שתחלק צלע המרובע על ד' חלקים שוים על א"ה ועל ה"ז ועל ז"ח ועל ח"ב ותגיע ח"ט ז"כ ח"ל ויחלק המרובע לד' חלקים שוים
|
- The proof of this division:
|
והמופת על החלוקה הזאת בארתיו בחלוקתו לשני חלקים
|
|
|
והאופן השני שתחלקהו מהאורך לשני חלקים עוד מהרחב תחלקהו ויחלק לד' חלקים שוים
|
|
|
דמיון רצינו לחלק מרבע אבג"ד לד' חלקים חלקנו צלע א"ב לשני חלקים על נקדת ה' והגענו ה"ז ויפול נכחי לא"ד ולב"ג ויחלק המרובע לב' חלקים
|
|
|
עוד חלקנו צלע א"ד לשנים על נקדת ח' והגענו ויפול נכחי לא"ב ולד"ג ויחלק המרובע על ד' חלקים
|
- The proof of this division:
|
והמופת על החלוקה הזאת כי מרובע אהה"ב שוה למרובע חבד"ז כי צלע א"ה שוה לצלע א"ח כי כשתחסר מן השוה שוה יהיה הנשאר שוה ולצלע ח"ב וב"ה כי הם נכחיי הצלעות וכן לג' המרובעים הנשארים אם כן כל מרובע אבג"ד נחלק לד' מרובעים דומים למרובע אבג"ד
|
|
|
ואם רצית לחלקו לג' חלקים מדרך השנית כלומר מדרך הזויות תגיע ב' אלכסוניו ויחלק לד' חלקים שוים וכל חלק יהיה משולש שוה השוקים
|
|
|
דמיון רצינו לחלק מרבע אבג"ד לד' חלקים שוים מדרך הזויות
|
|
|
הוצאנו אלכסון א"ג ואלכסון ב"ד ויחלק המרובע לד' משולשים משולש אה"ב ומשולש בה"ג ומשולש גה"ד ומשולש דה"א
|
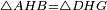
|
והנה משולש אה"ב שוה למשולש דה"ג
|
|
כי זוית אה"ב לזוית דה"ג
|
|
וזוית אב"ה שוה לזוית הד"ג
|
|
וצלע א"ב שוה לצלע ד"ג בעצמו
|
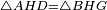
|
ולזה ישוה משולש אה"ד אל משולש בה"ג
|
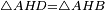
|
ומשולש אה"ד ישוה למשולש אה"ב
|
|
כי צלע א"ד ישוה לצלע א"ב
|
|
וצלע א"ב משותף
|
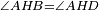 as both are right angles. as both are right angles.
|
וזוית אה"ב שוה לזוית אה"ד כי שתיהן נצבות
|
|
|
ואמרי שהם שוה השוקים כי צלע המרובע הגדול מחצית הקצר וחציי הקטרים הכל שוים
|
|
|
[28]הנה כבר בארנו משפטי חלוקת המרובע השוה הצלעות נצב הזויות וזה המשפט בעצמו אל הנכחי הצלעות הנצב הזויות הנקרא ארוך כזה כי הוא שוה עמו בכל הדרכים ומופתיו כמופתיו
|
- If you wish to divide an equilateral quadrilateral that is not right-angled, like this, into two [equal] parts:
|
ואם רצית לחלק המרובע שהוא שוה הצלעות אך הוא בלתי נצב הזויות כזה לשני חלקים
|
|
|
מדרך הראשונה תחלק צלע א"ב לשני חלקים על נקדת ה' ותוציא מנקדת ה' קו נכחי לקו א"ד ולקו ב"ג והוא קו ה"ז ובזה נחלק המרובע לשני חלקים שוים
|
- The proof of this division:
|
והמופת על החלוקה הזו כי א"ה כמו ה"ב
|
|
וא"ד כמו ב"ג
|
|
וה"ז משותף
|
|
וזוית דא"ה שוה לזוית זה"ב
|
|
וזוית אד"ז שוה לזוית הז"ג
|
|
וזוית אה"ז שוה לזוית הב"ג
|
|
וזוית אז"ד שוה לזוית בג"ז
|
- The area of one equal to [the area of] the other.
|
והשטח האחד שוה לחברו
|
|
|
וככה תעשה אם רצית לחלקו בג' וד' חלקים
|
|
|
גם אם רצית לחלקו מצלע א"ד חלקהו בכזה הדרך בעצמו ומאלה המופתים בעצמם
|
|
|
ואם רצית לחלקו מן דרך הזויות אם רצית לחלקו בשני חלקים שוים תגיע אלכסון א"ג ויחלק על שני חלקים שוים
|
- The proof of this division:
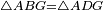
|
והמופת על החלוקה הזאת כי משולש אב"ג שוה למשולש אד"ג
|
|
צלע א"ב כמו צלע ד"ג
|
|
וצלע א"ד כמו צלע ב"ג
|
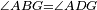 since they are sides of the same base. since they are sides of the same base.
|
וזוית אב"ג שוה לזוית אד"ג כי הם מיתרי תושבת אחת
|
- Therefore the two triangles are equal and they are the two parts of the quadrilateral.
|
אם כן שני המשולשים שוים והם שני חלקי המרובע
|
- Do likewise if you wish to divide it by using diagonal BD, relying on this same proof.
|
גם ככה תעשה אם רצית לחלקו מאלכסון ב"ד בכזה המופת בעצמו
|
|
|
ואם רצית לחלקו לשלשה חלקים שוים אם מהדרך הראשונה חלק צלע א"ב לג' חלקים שוים על א"ה ה"ז וז"ב והוצא קו ה"ח נכוחי לא"ד וקו ז"ט נכוחי לב"ג ויחלק המרובע לג' חלקים שוים וכן אם רצית לחלקו לד' חלקים ויותר
|
- The proof of this division:
|
והמופת על החלוקה הזאת כי צלע א"ד שוה לצלע ה"ח
|
|
וצלע ה"ח שוה לצלע ז"ט
|
|
וצלע ז"ט שוה לצלע ב"ג
|
|
וצלע א"ה שוה לצלע ה"ז ז"ב
|
|
וזוית הא"ד שוה לזויות זה"ח בז"ט
|
|
וזוית אד"ח שוה לזוית הח"ט זט"ג
|
|
וזוית הח"ד שוה לזויות זט"ח בג"ט
|
|
|
אם כן גם השטחים נכחיי הצלעות שוים והם ג' חלקי המרובע
|
|
|
ואם רצית לחלקו מדרך השנית עשה כך חלק צלע ד"ג ויהיה מנקדת ד' עד נקדת ה' שני שלישי הצלע ותגיע א"ה עוד חלק צלע א"ב ויהיה מנקדת ב' עד נקדת ז' שני שלישי הצלע ותגיע ג"ז ובזה נחלק המרובע לג' חלקים שוים
|
- The proof of this division:
|
והמופת על החלוקה הזאת כי יחס משולש אד"ה אל שטח א"ז ה"ג נכחי הצלעות כחצי יחס תושבתו אל תושבתו כי הם בין שני קוים נכוחיים
|
|
|
וכן יחס משולש גב"ז אל שטח א"ז ה"ג לזאת הסבה בעצמה וחצי יחס תושבתו על תושבתו כמוהו אם כן שני המשולשים והשטח שלשה חלקים שוים והם חלקי המרובע
|
|
|
ואם רצית לחלקו לד' חלקי' שוים תחלק צלע א"ב לשני חלקים שוים על נקדת ה' גם ככה תחלק צלע ד"ג על נקדת ו' ותגיע א"ז וג"ה עוד תחלק א"ה לשני חלקים שוים על נקודת ח' גם תחלק ז"ג על נקדת ט' ותגיע ח"ט ובזה נחלק המרובע אל ארבעה [29]חלקים שוים
|
- The proof of this division:
|
והמופת על החלוקה הזאת לפי שתושבת משולש אד"ז בתושבת שטח א"ה ז"ג נכחי הצלעות והם בין שני קוים נכחיים יהיה השטח הזה כפל כל אחד ממשולשי אד"ז גב"ה וכאשר חלקנו זה לשני
חלקים שוים לשטח א"ח ז"ט ולשטח ח"ה ט"ג יהיה כל אחד מהשטחים שהם חלקי השטח האחד שוה לכל אחד מהמשולשים ושני השטחים עם שני המשולשים הם כל חלקי המרובע הנה נחלק כל המרובע לד' חלקים שוים
|
|
|
עוד אם רצית לחלקו לארבעה חלקים שוים
|
- The proof of this division:
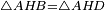
|
והמופת על החלוקה הזאת כי משולש אה"ב שוה למשולש אה"ד
|
|
צלע א"ב שוה לצלע א"ד
|
|
|
וצלע א"ה משותף
|
|
וזוית דא"ה שוה לזוית הא"ב
|
- Because
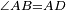
|
לפי שצלע א"ב שוה לצלע א"ד
|
|
|
וצלע א"ג משותף
|
|
ותושבת ב"ג שוה לתושבת ד"ג
|
|
תהיה זוית דא"ג שוה לזוית גא"ב
|
|
|
וזוית גא"ד וגא"ב הן זויות דא"ה והא"ב
|
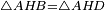
|
אם כן משולש אה"ב שוה למשולש אה"ד
|
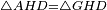
|
ומשולש אה"ד שוה למשולש גה"ד
|
|
לפי שצלע א"ד שוה לצלע ג"ד
|
|
|
וצלע ד"ה משותף
|
|
וזוית אד"ה שוה לזוית הד"ג
|
|
|
לפי שצלע א"ד ממשולש אד"ב שוה לצלע ד"ג ממשולש דב"ג
|
|
|
וצלע ד"ב משותף
|
|
|
ותושבת א"ב שוה לתושבת ב"ג
|
- Therefore
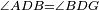
|
אם כן זוית אד"ב שוה לזוית בד"ג
|
|
|
וזויות אד"ב ובד"ג הן זויות אד"ה והד"ג
|
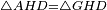
|
אם כן משולש אה"ד שוה למשולש גה"ד
|
|
|
ובזה הדרך בעצמו יתבאר שמשולש גד"ה שוה למשולש גה"ב אם כן המשולשים הד' שהם כל חלקי המרובע שוים
|
|
|
ואם רצית לחלק מדרך אחרת עשה כך
|
|
|
דמיון רצינו לחלק מרובע אבג"ד לד' חלקים חלקנו צלע א"ד על נקדת ה' והיא חצי הצלע גם חלקנו צלע ב"ג לשני חצאים על נקדת ז' גם חלקנו צלע א"ב לשני חציים על נקדת ה' גם חלקנו צלע ד"ג לשני חצאים על נקדת ט' אחר כך הגענו ה"ז ח"ט ויפגשו על נקדת כ' ויחלק המרובע לד' חלקים שוים
|
- The proof of this division:
|
והמופת על החלוקה הזאת לפי שצלע ה"ז נכחי לצלע ד"ג כי מרחק תושבתו של כל א' מהם שוה
|
|
|
ותושבת ג"ט שוה לתושבת ט"ד
|
|
|
יהיה מרובע ג"ז כ"ט שוה למרובע ט"ב ה"ד
|
|
|
ולפי שצלע ח"ט נכחי לצלע א"ד
|
|
|
ותושבת ד"ה שוה לתושבת ה"א
|
|
|
יהיה מרובע ט"כ ה"ד שוה למרובע ה"כ ח"א
|
|
|
ובזה הדרך בעצמו ישוה להם מרובע ח"ב ז"כ ואלה ד' מרובעי' הם כל חלקי המרובע הגדול והם שוים
|
|
|
ודרך חלוקת זה המרובע הבלתי נצב הזויות הוא דרך חלוקת המרובע הארוך הבלתי נצב הזויות הנכחי הצלעות ומופתיו כמופתיו
|
|
|
ומעתה נבאר חלוקת הנוטים כי הם מינים הרבה
|
|
|
ונחל מן הנוטה אשר צלעיו שוים וראשו ותושבתו בלתי שוים וראשו נכח תושבתו והוא אשר יקרא משולש חתוך הראש כזה
|
|
|
ויש ממנו נצב הזויות אך אין ראשו נכח תושבתו
|
|
|
וכאשר רצינו לחלק נוטה אבג"ד שראשו נכח תושבתו ושתי צלעותיו שוים לשני חלקים שוים
|
|
|
נחלק צלע א"ב לשני חלקים שוים על נקדת ה' וכן [30]נחלק צלע ג"ד על נקדת ז' ונגיע ה"ז ויחלק נוטה אבג"ד לשני חלקים שוים
|
- The proof of this division:
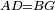
|
והמופת על החלוקה הזאת לפי שצלע א"ד שוה לצלע ב"ג
|
|
|
ותושבת ד"ז לתושבת ז"ג
|
|
|
וראש א"ה לראש ה"ב
|
|
|
וצלע ה"ז הוא משותף
|
|
|
אם כן נוטה א"ה ד"ז שוה לנוטה ה"ב ז"ג והם כל נוטה אבג"ד והנה נחלק לשני חלקים שוים
|
|
|
ואם רצית לחלקו לג' חלקים שוים והיה הראש כמו מחצית התושבת תחלק התושבת לשני חלקים שוים על נקדת ז' ותגיע א"ז ב"ז ויחלק הנוטה לג' משולשים שוים
|
- The proof of this division:
|
והמופת על החלוקה הזאת ששטח א"ב ד"ז נכחי הצלעות והוא כפל משולש אד"ז כי הם על תושבת אחת ובין שני קוים נכוחיים וכפל משלש אד"ז שוה לשני משולשי אד"ז אז"ב עוד שח"ט א"ב ג"ז שוה לכפל משולש בז"ג לסבה הזאת בעצמה וכפל משולש בז"ג שוה לשני משולשי אז"ב בז"ג א"כ גם ג' המשלשים שוים כי כשתפיל אב"ז המשותף ישאר משלש אד"ז שוה למשלש בז"ג והם כל חלקי הנוטה
|
|
|
אמנם אם ראש הנוטה איננו במחצית התושבת אבל עודף עליו ותרצה לחלק אותו בשלשה חלקים שוים או יהיה פוחת ממנו תעשה כך
|
|
|
תמצא תשברתו אחר כך חלק מספר התשבורת לג' חלקים וככה יהיה חלוקתו כלומר מספר שלישית השברים הוא שלישית הנוטה וככה כל חלק וחלק וככה תחלק את הנוטה שהוא נצב הזויות ואין ראשו נכח תושבתו
|
|
|
גם אם רצית לחלק העגולה לשני חלקים שוים תוציא אלכסון העגולה ובעברה על המרכז תחלק לשני חלקים שוים
|
|
|
והמופת על החלוקה הזאת כי קשת חצי העגולה שוה לקשת חציה האחר והאלכסון משותף אם כן התמונה האחת שוה לאחרת
|
|
|
ואם רצית לחלקה לג' חלקים שוים או ליותר כמה חלקים שתרצה תחלק העגולה כמספר החלקי' שתרצה ותסמן נקדות כמספר החלקים על העגולה אח"כ הוצא מכל נקודה קו ישר אל המרכז והנה נחלקה העגולה על מספר החלקים שרצית
|
- The proof of this division:
|
והמופת על החלוקה הזאת כי הקשתות שוות והקוים שוים כי הם יוצאים מהמקיף אל המרכז ואם כן נחלקה העגולה אל משלשים שוים אשר תושבותם קשתות שוות מהעגולה
|
The Third Section on the Measuring of Solids
|
החלק השלישי במדידת הגופנים
|
The First Chapter
|
הפרק הראשון
|
|
|
דע שהגופנים הם אשר יש להם אורך ורחב וגובה
|
|
|
ויש מהם אשר יקרא מחודד וכל תושבותיו משולשים כזה והיא תמונה אשר תעלה בגובהה ותכלה אל נקדה אחת
|
|
|
ויש מהם אשר תושבתו מרובע וצדדיו משולשים כזה ויפלו בגבהם אל נקדה ויש מהם שתושבתם עולה בשטח עגול ויכלה בגבהו אל נקדה כזה
|
|
|
[31]ויש מהם שתושבתם רבת הזויות ותכלה אל נקדה ויש מהם שתושבתם משולש וראשם משלש וצדדיהם המרובעים עולים על צד זוית נצבת כזה
|
|
|
ויש שאינם עולים על נקדה אבל נפסקים קודם שיגיעו אל הנקדה כזה
|
|
|
ויש מהם תמונת הכדור כזה
|
| the volume of a cube
|
|
|
|
ונחל לפרש מדידת התמונה שתושבתה מרובע וראש המרובע וצדדיה מרבעים עולים על זויות נצבות ואומר שזאת התמונה אם היא שוה ארכה ורחבה וגבהה מדידתה כן נכפול ארכה על רחבה וההוה נכפלהו על גבהה וככה מדידת זאת התמונה והיא הנקראת מעוקב
|
|
|
דמיון ארכה עשרה גבהה עשרה ורחבה עשרה כפלנו י' על י' ההוה ק' עוד כפלנו י' על ק' ההוה אלף והוא מדידת זאת התמונה
|
|
|
ואם הצד הא' מן הג' יותר מהאחרים או כל אחד לא ישוה לחברו גם כן ככה נמדדהו
|
|
|
דמיון האורך י' והרחב ט"ו והגובה כ' נכפול י' על ט"ו ההוה ק"נ נכפלם על כ' ההוה ג' אלפים וזאת היא מדידתה
|
|
|
ודע שהאמה אשר בה אנו מודדי' התמונות הגופניות היא אמה אורך ואמה רחב ואמה גובה וזאת תקרא אמה מוגשמת ואלכסון אלה התמונות יוצא מזויות אחת אשר בראשה אל נכח הזוית אשר בתושבתה
|
|
|
דמיון אם יצא בראשה מזויות מזרחי' צפונית יגיע בתושבתה אל זוית מערבית דרומית ומדידת אורך האלכסון כך
|
| the diagonal of a cube
|
|
|
|
דמיון בצורת המעוקב אשר כל צלע מצלעותיו י' נקח מרובע אלכסון התושבת ונחברהו עם מרובע הגובה ונקח שרשו והוא אורך האלכסון המבוקש
|
|
|
וידוע שמרובע אלכסון התושבת הוא ר' ונחברהו עם מרובע הגובה שהוא ק' עלו ש' ונקח שרשם והם י"ו ורביע וחלק א' מט"ו בקרוב
|
|
|
גם ככה נמדוד אלכסון התמונות אשר ארכם יותר מרחבם כשנמצא אלכסון התושבת ונחבר מרובעו עם מרובע הגובה ונקח השרש והוא אורך אלכסון התמונה
|
|
|
וכאשר נרצה למצוא אלכסון התושבת נחבר מרובע צלע התושבת הארוך עם מרובע צלעו הקצר ונקח השרש והוא ארך אלכסון התושבת
|
|
|
ואם היתה התמונה צדדיה בלתי עולים על זויות נצבות אבל דומים למעויין או תהיינה מעויינות תמדוד תושבתה כמו שידעת במדידת הצורות האלה אחר כך מה שיצא כפלהו על הגובה והוא מדידת זאת התמונה כאלה
|
|
|
ואם היתה תושבתה משולש וראשה משולש וצדדיה מרובעים תמצא תשבורת המשולש אשר הוא תושבתה ותכפול אותו על הגובה והעולה היא מדידת זאת התמונה בלבד שיהיה משלש ראשה עם משולש תושבתה שוים
|
|
|
גם אם היתה תושבת התמונה וראשה מחומשים שוים או משושים שוים ויתר מאלה תמצא תשבורת [32]התושבת וכפלהו על הגובה והעולה היא התמונה המבוקשת
|
|
|
ואם היתה תושבת התמונה עגולה וראש עגולה שוה לה תמצא תשבורת העגולה ותכפלהו על הגובה והעולה הוא מדידת התמונה ההיא
|
|
|
אך אם התמונה עולה בהדרגה וכלה אל נקדה אם תושבתה משולש תמצא תשבורת התושבת וכפלהו על שלישית הגובה והעולה הוא מדידת זאת התמונה
|
|
|
וככה אם תושבתה מרובעת או מחומשת וכדומה להם שתכפול לעולם תשבורת התושבת עם שליש הגובה או כל הגובה עם שליש תשבורת התושבת והעולה הוא המבוקש וכן אם תושבתה עגולה תמצא תשבורת העגולה וכפלה על שלישית הגובה או על כפל אורך הגובה על שלישית התשבורת של התושבת והעולה הוא המבוקש
|
|
|
ולדעת איך נמצא גובה התמונה אודיעך ענינו פה
|
|
|
דע שהגובה הוא עמוד יוצא מתושבת התמונה אל ראשה על זויות נצבות
|
|
|
ואם היתה תושבת התמונה עגולה נקח חצי קטרה ונכפלה על עצמה עוד נקח גובה הצד ונכפלהו על עצמו ונוציא מרובע חצי קטרה ממרובע הצד והנשאר נקח גדרו והוא אורך הגובה
|
|
|
דמיון עגולה חצי קטרה ו' ומרובעו ל"ו וגובה הצד י' ומרובעו ק' גרענו ל"ו מן ק' ונשארו ס"ד לקחנו שרשם והם ח' וככה אורך הגובה
|
|
|
ואם היתה התושבת של התמונה משלש שוה הצלעות תוציא עמוד מראש משלש התושבת אל תושבתו ותחלקהו לשני חלקי' ובמקום שיתחלק שם הוא מחצית העמוד וסמן שם נקדה
|
|
|
עוד תחלק צלע משלש התושבת לשני חלקים שוים ובמקום שיתחלק הוא מחצית הצלע וסמן שם נקדה אח"כ ראה מה בין נקדת מחצית העמוד לנקדת מחצית הצלע וקח מרובעו וגרעהו ממרובע גובה צד התמונה וקח שרש הנשאר והוא גובה התמונה אך אם תושבת התמונה הוא מחומש שוה הצלעות והזויות או משושה והכלל רב הזויות
|
|
|
וכן מרובע שוה הצלעות והוא שתקח מחצית כל הצלעות ותקבצם יחד ותחלק על המחצית ההוא מרבע התושבת והיוצא מן החלוקה תרבעהו ותוציא את מרובעו ממרובע גובה הצד והנשאר בידך קח גדרו והוא גובה התמונה ההיא
|
|
|
ואם לא היו הצלעות שוות כלומר צלעות התושבת גם לא הזויות אתה צריך למצוא גובה על יד בלי מעשה ואז תמצא תשבורת כל המשלשים הבלתי שוים אשר התושבת נחלקת עליהם בהוציאך קוים מזויותיה אל מרכזה ותחברם ותכפול על שלישית הגובה וההוה הוא המבוקש אך אם התמונה אינה כלה אל נקדה אבל כלה אל שטח משלש או מרובע או זולת אלה בתמונה אשר תושבתה לבד שהראש קטן מן התושבת יש לה דרכים אחרי' יתבארו פה
|
|
|
וזאת התמונה תקרא חתוכת הראש לפי שאם תוציא צדדיה למעלה תכלה אל מחודד וכבר בארנו לך משפטי המחודד
|
|
|
והנה זאת התמונה תחלק אל שני מחודדים אל המחדד הגדול אשר כלה אל נקדה ואל [33]המחדד הקטן שראש התמונה חתוכת הראש תושבת לו ועולה אל הנקודה
|
|
|
ואם היתה תושבת בעלת ד' צלעות וככה הראש תוציא אורך הצדדים עד הנקודה למעלה ואתה יכול למדוד המחודד הגדול כמו שידעת
|
|
|
עוד תמדוד המחודד הקטן וגרעהו מהגדול והנשאר הוא מדידת התמונה חתוכת הראש
|
|
|
ולכן צריך להודיעך איך תמצא ארך הצדדים אשר הם מראש התמונה מחוץ עד הנקודה
|
|
|
דמיון תמונת אבג"ד חתוכת הראש ותושבתה קו א"ב והוא ו' אמות וראשה ג"ד והוא ד' אמות וגובה העמוד אשר באמצע והוא קו ה"ז י' אמות כפול הראש לכל הגובה יעלה מ' אמות חלק אותם על ב' אשר הם יתרון התושבת על הראש יהיו כ' והוא אורך קו ה"ט הנשאר מהגובה
|
|
|
רצית למצוא ארך הצדדים אשר הם למעלה מהראש עד הנקודה תקח מרובע כ' שהם ארך ה"ט והם ת' ומרובע ב' שהם אורך ג"ה והם ד' וחברם עם ת' והם ת"ד גם גדרם שהם כ' אמות ועשירית אמה בקרוב והם אורך צלע ג"ט שהוא מחוץ
|
|
|
ואם רצית למצוא אורך כל צלע המחודד שהוא צלע א"ט תקח מרובע קו ז"ט שארכו ל' ומרובעו תת"ק גם מרובע חצי התושבת שהוא קו א"ז והוא ג' אמות ומרובעו ט' חברם עם תת"ק יעלו תתק"ט קח גדרם והוא ל' ועשירית א' וחלק אחד מל' והוא אורך כל התשבורת של הצלע
|
|
|
תמצא תשבורת תושבת המחודד הגדול שהוא ו' על ו' אמות וההוה ל"ו כפלם עם שלישית הגובה שהם י' כי כל הגובה הם ל' וההוה ש"ס והוא מדידת המחודד הגדול
|
|
|
עוד תשוב למדוד המחודד הקטן שתושבתו ד' על ד' ותשברתה הם י"ו כפלם עם ו' וב' שלישיות שהם שליש גבהו וההוה ק"ו וב' שלישיות תגרעם מן ש"ס שהם מדידת המחודד הגדול ישארו רנ"ג ושלישית אחד והוא מדידת התמונה חתוכת הראש המבוקשת
|
|
|
אך מפני שהחשבון קשה מעט נתנו בעלי החשבון דרך אחרת קצרה מזאת והוא שתקח מרובע התושבת והוא ל"ו ומרובע הראש והוא י"ו ותכפול גדר הראש בגדר התושבת וההוה כ"ד תחבר הל"ו והי"ו והכ"ד והעולה ע"ו כפלם עם שלישית הגובה שהם ג' ושליש ההוה רכ"ג ושליש והוא מדידת התמונה חתוכת הראש
|
|
|
ואם היתה תושבת התמונה עגולה וכן ראשה
|
|
|
כגון תמונה אשר תושבתה עגולה וקטר העגולה ד' אמות וראש העגולה וקטרה ב' אמות המרובע ד' אשר הוא קטר התושבת והוא י"ו ומרובע ב' שהוא קטר הראש והוא ד' וכפול ב' בד' הרי ח' והכל כ"ח גרע רביעיתם וחלק אחד מי"ד נשארו כ"ב כפלם עם ד' שהוא שלישית הגובה יעלו ס"ח והוא מדידת התמונה הזאת
|
|
|
ולפעמים ימצא כלי אחד מחובר משתי תמונות כזאת התמונה הנזכרת שיהיו שני ראשיו עגולות קטנות ואמצעיתו רחב כזאת התמונה הנזכרת
|
|
|
ותמדוד כל אחת מן חלקי הכלי השנים בפני עצמו כמו שידעת וחבר שניהם וככה מדידת הכלי
|
|
|
ואם היה תושבת התמונה וראשה [34]משלשים שוי הצלעות אך צלעות התושבת גדולות מצלעות הראש
|
|
|
כגון תמונה שתושבתה משלש שוה הצלעו' כל אחת מצלעותיו ד' אמות וגבהו ו' אמות אתה יודע כי תשבורת משלש התושבת כ"ח פחות ב' שביעיו' האחד בקירוב וגדר המספר הזה ה' אמות וב' שביעיות
|
|
|
ואתה יכול לדעת הרביע מחלק רבוע המשלשים ותמצא רבוע משלש הראש ז' אמות פחות חצי שביעית וגדר המספר הזה שנים וד' שביעיות אמה וחצי שביעית חבר תשבורת שני המשלשים ויהיו ל"ד אמות וט' חלקים מי"ד באמה הוסף עליהם גדר משלש התושבת בגדר משלש הראש ויהיו י"ד אמה פחות שביעית על דרך קירוב יהיה הכל מ"ח וחצי מונה אותו בשליש הגובה והוא ב' יהיה הכל צ"ז והוא מדידת חתוכת הראש
|
|
|
ועל הדרך הזה תדע מדידת כל תמונה חתוכת הראש אשר תושבתה מחומש או תמונה אחרת והוא שתהיה יודע השני ראשים בתשברתם ותוסיף עליהם רבוע גדר תשבורת הראש בגדר תשבורת התושבת ותכלול הכל ותכפול אותו בשליש הגובה ותמצא מדידת התמונה ההיא
|
|
|
והנה אתן לך דמיון בתמונות הרבה כדי שתרגיל את עצמך במדידתם
|
| the volume of a pyramid with a square base
|
|
|
|
תמונה מחודדת תושבתה מרובע נמדדה כך
|
|
|
יהיה כל אחד מצלעות התושבת מכ"ד אמות וצלעות המחודד מי"ח אמות תקח מרובע הכ"ד וההוה תקע"ו קח מחציתם והם רפ"ח גם קח מרובע הי"ח וההוה שכ"ד תגרע מאלה הרפ"ח נשארו ל"ו קח גדרם והם ו' וזהו שעור עמוד המחודד ולפי שהעמוד הוא ו' נקח שלישיתו הם ב' ותכהו עם התקע"ו וההוה אלף קנ"ב וזהו תשבורת המחודד
|
| A pyramid, whose base is a square, each of the sides of its base is 12 cubits, and its inclinations are 36 cubits; we wish to find its perpendicular. We do as follows:
|
מחודד שתושבתו מרובע אשר כל אחת מצלעות תושבתו בעל י"ב אמות וצלעות גבהותו מל"ו אמות ונרצה למצוא העמוד נעשה כך
|
|
|
נכפול צלע התושבת כלומ' הי"ב על עצמם וההוה קמ"ד
|
|
|
עוד נכפול הצלע האחד על עצמו וההוה קמ"ד
|
|
|
נחברם ביחד ההוה רפ"ח
|
|
|
נקח גדרם והם י"ו גם תוספת מעט וכך הוא קטר התושבת
|
|
|
נקח מחצית הי"ו והם ח' וחצי
|
|
|
ונכפלם על עצמם ההוה ע"ב ורביע
|
|
|
עוד נכפול הל"ו שהם צלע גבהותו על עצמם ההוה אלף רצ"ו
|
|
|
נגרע מאלה הע"ב ורביע וישארו אלף רכ"ד עם תוספת מעט שבם
|
|
|
ונקח גדרם וההוה ל"ה עם תוספת מעט שבו וכן הוא אורך העמוד
|
|
|
תכה אלה עם הקמ"ד שהם תשבורת התושבת ההוה ה' אלפים ומ'
|
|
|
נקח שלישית אלה ההוה אלף תר"פ וכן הוא תשבורת המוגשם
|
|
|
ולמה אנו לוקחים השלישית כי כל מוגשם נחלק לג' מחודדים כשהם שוה הגובה ותושבותיהם [35]משולשים ואנו עשינו חשבוננו על מוגשם נכחי השטחים והמוגשם הנכחי נחלק לב' מגודרים וכל מגודר של עמוד של המחודד הוא ג' כפלי מחצית המחודד המונח והוא בעל תושבת מרובעת כן הראה זה במופת אקלידס במאמר השני
|
| the volume of a truncated pyramid with a square base
|
|
| A truncated square pyramid, i.e. whose top is truncated, the sides of its bottom base are ten cubits, the sides of its upper base are 2 cubits, and its inclinations are 9 cubits; we measure it as follows:
|
מחודד מזונב כלומר חתוך הראש מרבע אשר צלעות תושבתו מעשר אמות וצלעות הראש מב' אמות וצלעות גבהותו מט' אמות נמדוד אותו כן
|
- Subtract the two cubits of the sides of the upper base from the sides of the bottom base; the remainder is 8.
|
תגרע השני אמות של צלעות הראש מצלעות של התושבת וישארו ח'
|
- Multiply it by itself; it is 64.
|
תכפלם על עצמם ויהיו ס"ד
|
- We take its half; it is 32.
|
נקח מחציתם והם ל"ב
|
- We multiply also the 9 by itself; it is 81.
|
גם נכפול הט' על עצמם ויהיו פ"א
|
- We subtract 32 from it; the remainder is 49.
|
נגרעם מאלה הל"ב ישארו מ"ט
|
- We extract its root; it is 7 and this is the perpendicular.
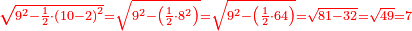
|
נקח גדרם והם ז' וכן הוא העמוד
|
- Since the perpendicular is 7 cubits, we find the volume of the solid as follows:
|
ולפי שהעמוד ז' אמות נמצא תשבורת המוגשם כן
|
- We add the 2 of the upper base to the 10 of the bottom base; it is 12.
|
נחבר הב' של הראש עם הי' של התושבת ויהיו י"ב
|
- We take its half; it is 6.
|
ונקח חציים והם ו'
|
- We multiply it by itself; the result is 36.
|
נכפלם על עצמם ויהיו ל"ו
|
- Then, subtract 2 of the upper base from 10; the remainder is 8.
|
אחר כך תגרע מהי' הב' של הראש וישארו ח'
|
- We take its half; it is 4.
|
ונקח חציים והם ד'
|
- We multiply it by itself; the result is 16.
|
ונכפלם על עצמם ויהיו י"ו
|
- We take its third; it is 5 and one third.
|
ונקח שלישיתם יהיו ה' ושליש
|
- Add it to the 36; it is 41 and a third.
|
הוסף אלה על הל"ו ויהיו מ"א ושליש
|
- Multiply it by 7; the result is 289 and one third; and this is the volume.
|
כפלם על הז' ויהיו רפ"ט ושליש וכן הוא התשבורת
|
![\scriptstyle{\color{red}{\begin{align}\scriptstyle\left[\left[\frac{1}{2}\sdot\left(2+10\right)\right]^2+\frac{1}{3}\sdot\left[\frac{1}{2}\sdot\left(10-2\right)\right]^2\right]\sdot7&\scriptstyle=\left[\left(\frac{1}{2}\sdot12\right)^2+\frac{1}{3}\sdot\left(\frac{1}{2}\sdot8\right)^2\right]\sdot7\\&\scriptstyle=\left[6^2+\frac{1}{3}\sdot4^2\right]\sdot7\\&\scriptstyle=\left[36+\left(\frac{1}{3}\sdot16\right)\right]\sdot7\\&\scriptstyle=\left[36+\left(5+\frac{1}{3}\right)\right]\sdot7\\&\scriptstyle=\left(41+\frac{1}{3}\right)\sdot7=289+\frac{1}{3}\end{align}}}](/mediawiki/images/math/6/9/a/69a20480af90dcf2089eeee70a314aff.png)
|
|
| the volume of a pyramid with a right-angled triangular base
|
|
| If you wish to measure a pyramid whose base is a right-angled triangle, it is not necessary to investigate the inclinations in order to find the perpendicular, because it has a right angle.
|
אם תרצה למדוד מחודד אשר תושבתו משולש נצב אינו הכרח לחקור על צלעות הגבהות למצוא העמוד בהיותו בעל זוית נצבת
|
- Let the perpendicular be 25 cubits, if one side of the right angle of the triangle's base is 4 cubits and the other is 5 cubits, do this:
|
ויהיה אם העמוד כ"ה אמות ואם הראשונה שאצל הזוית שאצל תושבת המשולש ד' אמות ואם האחרת ה' אמות תעשה כך
|
- Multiply 4 by 5; the result is 20.
|
כפול הד' על הה' ההוה כ'
|
- Take its half; it is 10.
|
קח חציים והם י'
|
- Multiply this by the 25, which is the perpendicular; the result is 250.
|
כפלם על כ"ה שהוא העמוד ההוה ר"נ
|
- Take its third; it is 41 and two thirds.
![\scriptstyle{\color{red}{\frac{1}{6}\sdot\left[\left[\frac{1}{2}\sdot\left(4\sdot5\right)\right]\sdot25\right]=\frac{1}{6}\sdot\left[\left(\frac{1}{2}\sdot20\right)\sdot25\right]=\frac{1}{6}\sdot\left(10\sdot25\right)=\frac{1}{6}\sdot250=41+\frac{2}{3}}}](/mediawiki/images/math/0/4/f/04f865b5ce2da6db54aa2c9f9c8d9272.png)
|
קח שישיתם והם מ"א וב' שלישים
|
| Due to the reason that I mention, which is that every prism whose base is a triangle, which is half a square, is divided into three pyramids that have triangular bases, so is this prism.
|
בעבור הסבה שאזכור והיא כל מגודר אשר תושבתו משלש בחצי מרבע הוא נחלק לג' מחודדים בעלי תושבות משולשים וכן המגודר הזה
|
- As Euclid has shown in Book XII.
|
כן הראה במופת אקלידס במאמר השני
|
| The [triangular] prism is a half of a square [prism] and is divided into three pyramids, the result is six, [which is] a half and a third.
|
והמגודר הוא חצי מרובע ונחלק לג' מחודדים ההוה הוא ו' וחצי ושליש
|
| The pyramid with a triangular base is necessarily a sixth of the square [prism], so we take one sixth.
|
ובהכרח שהמחודד בעל תושבת משלשי שלה ששית תושבת מהמרובע ונקח הששית
|
| the volume of a pyramid with an isosceles triangular base
|
|
- If the triangle is isosceles, the legs are 12 cubits, the base is 8 cubits, the inclinations are 25 cubits, and you wish to measure the pyramid, do as follows:
|
ואם המשולש שוה השוקים ויהיו השוקים מי"ב אמות והתושבת ח' אמות וצלעות הגבהות מכ"ה אמות ותרצה למדוד המחודד תעשה כך
|
- Divide the base, which is 8 cubits, into halves; the result is 4.
|
תחלק התושבת שהוא ח' אמות לחצאין ההוה ד'
|
- Multiply it by itself; the result is 16.
|
כפלם על עצמם ההוה י"ו
|
- Multiply one of the sides by itself, that is 12 by itself; the result is 144.
|
וכפול אחת הצלעות על עצמו כלומר הי"ב על עצמם ההוה קמ"ד
|
- Subtract the square of 4 from it, which is 16; the remainder is 128.
|
גרע מאלה מרובע ד' שהם י"ו ישארו קכ"ח
|
- Extract the root, which is 11, a quarter, one part of 22, and one part of 44. This is the measure of the perpendicular on the base of the isosceles triangle.

|
קח גדרם שהם י"א ורביע וחלק מכ"ב וחלק ממ"ד וזהו השעור של העמוד אשר על תושבת המשלש שוה השוקים
|
- If you wish to find the area, do as follows: multiply the perpendicular by the base, i.e. 11, a quarter, one part of 22, and one part of 44 by 8; the result is 90 and one part of 22.
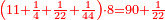
|
ואם תרצה למצא התשברת תעשה כך תכפול העמוד על התושבת כלו' י"א ורביע וחלק מכ"ב וחלק ממ"ד על הח' ההוה צ' וחלק מכ"ב
|
- Multiply it by perpendicular of the pyramid.
|
כפלם על עמוד המחודד
|
- You find it as follows: since for every triangle we take a half of the perpendicular to the base, we take a half of the 11, one quarter, one part of 22, and one part of 44; the result is 5, a half, an eighth, one part of 44, and one part of 88.
|
ותמצאנו כך לפי שבכל [36]משולש אנו לוקחים חצי עמוד התושבת נקח חצי הי"א ורביע וחלק מכ"ב וחלק ממ"ד והם ה' וחצי ושמינית וחלק ממ"ד וחלק מפ"ח
|
- We Multiply this by itself; the result is 32 and one part of 44.
|
נכפלם על עצמם וההוה ל"ב וחלק ממ"ד
|
- We multiply also the inclination, which is 25, by itself; the result is 625.
|
גם נכפול צלעות הגבהות על עצמם שהם כ"ה ההווה תרכ"ה
|
- Subtract the 33 and [one part of 44]; the remainder is 593.
|
תגרע הל"ב ורביע ההוה תקצ"ג
|
- We extract its root; the result is 24, a quarter and an eighth with a remainder and this is the measure of the perpendicular.
![\scriptstyle{\color{red}{\begin{align}\scriptstyle\sqrt{25^2-\left[\frac{1}{2}\sdot\left(11+\frac{1}{4}+\frac{1}{22}+\frac{1}{44}\right)\right]^2}&\scriptstyle=\sqrt{25^2-\left(5+\frac{1}{2}+\frac{1}{8}+\frac{1}{44}+\frac{1}{88}\right)^2}\\&\scriptstyle=\sqrt{625-\left(32+\frac{1}{44}\right)}=\sqrt{593}\\&\scriptstyle=24+\frac{1}{4}+\frac{1}{8}+\end{align}}}](/mediawiki/images/math/7/3/b/73b076e764e8db382fbe97b1df814204.png)
|
נקח גדרם והם כ"ד ורביע ושמיני' עם התוספת מעט וזהו שעור העמוד
|
- Multiply it by the area of the triangle, i.e. the 90 and one part of 22; the result is 2199.
|
כפול אלה על תשבורת המשולש כלו' הצ' וחלק מכ"ב ההוה אלפים וקצ"ט
|
- We take from this a sixth of the square; the result is 367 and a half; and this is the volume of the pyramid.
|
נקח מאלה ששית המרובע וההוה שס"ו וחצי וזהו תשבורת המחודד
|
| the volume of a pyramid with an obtuse-angled triangular base
|
|
|
|
ואם המחודד יהיה נרוח הזויות ויהיה תושבת משולש נרוח הזויות תכפול תשבורת המשלש נרוח הזויות עם העמוד ונקח השליש וישאר לך תשבורת המחודד
|
|
|
וכן אם יהיה חד הזויות
|
| the volume of a pyramid with a right-angled triangular base
|
|
|
|
מחודד שתושבתו משלש נצב הזויות ויהיה עמוד ו' אמות ותושבתו ח' אמות והמיתר לזוית הנצבת י' אמות והמחודד כל אחת מצלעותיו י"ג אמות ונרצה למצוא עמודו
|
|
|
נעשה כך נמצא בתחלה אלכסון העגולה המקפת המשולש שיהיה י' אמות שהוא המיתר לזוית הנצבת ואקח חצייה והם ה' ואכפלם על עצמם וההוה כ"ה גם אכפול הי"ג של צלע הגבהו' על עצמם וההוה קס"ט ואגרע מאלה הכ"ה וישארו קמ"ד ואקח גדרם והם י"ב והתשבורת נמצאה וכן בתחלה אמצא תשבורת המשולש והוא כ"ד אמות ואקח שלישית העמוד שהוא עמוד המחודד והם ד' כפלם על תשבורת התושבת ויהיו צ"ו אמות וכן הוא תשבורת המחודד
|
| the volume of a pyramid with an equilateral triangular base
|
|
|
|
מחודד העומד על משולש שוה הצלעות נמדדהו כך
|
|
|
יהיה כל צלע מצלעות התושבת מל' אמות וצלעות הגבהות ב' אמות
|
|
|
כפול הל' על עצמם וההוה תק"ת נקח שלישיתם והם ש' גם נכפול הת' על עצמם ההוה ת' ומאלה אגרע הש' נשארו ק' וקח גדרם והם י' וזהו אורך העמוד
|
|
|
ולפי שהעמוד י' אמות ימצא התשבורת כן נכפול הל' על עצמם ההוה תת"ק נקח מאלה השלישית והעשירית והוא ש"צ נקח שלישית אלה והוא ק"ל נכפול אלה על י' שהוא שעור העמוד ההוה אלף וש' וזהו תשבורת המחודד
|
| the volume of a pyramid with a pentagonal base
|
|
|
|
מחודד על תושבת בעלת ה' זויות אשר כל אחת מצלעות התושבת מי"ב אמות וצלעות הגבהות מל"ה אמות ונרצה למצוא העמוד וגם תשבורת המחודד
|
|
|
אחוק על הבעל ה' זויות אשר הקו המקיף ס"ג אמות ואם כן האלכסון יהיה כ' אמות קח מאלה חציים והם י' וכפלם על עצמם עלו ק' עוד [37]כפול הל"ה אמות של גבהות הצלעות על עצמם יעלו אלף רכ"ה גרע מאלה הק' ישארו אלף קכ"ה קח גדרם והם ל"ג וחצי וחלק מכ"ב עם תוספת וזהו אורך העמוד
|
|
|
כפול תשבורת התושבת הבעלת ה' זויות וכן תעשה מן הי"ב אמות של התוספת קח חציים והם ו' וכפלם על עצמם וההוה ל"ו עוד נכפול חצי האלכסון שהם י' על עצמם וההוה ק' גרע מאלו הל"ו ונשארו ס"ד קח גדרם והם ח' והוא שעור העמוד של המשולש כפלם עם התושבת שהם י"ב יעלה צ"ו קח חציים והם מ"ח והם תשבורת המשלש כפול אלה ה' פעמים אחרי שהם ה' משולשים ויהיו ר"מ אמות כפול אלה על העמוד שהוא ל"ג וחצי וחלק מכ"ב יעלו ח' אלפים ונ' ומאלה קח ששיתם אחרי שהם ששה מגודרים ההוה אלף שמ"א וב' שלישים וזהו תשבורת המחודד
|
|
|
ונוכל למצוא גם בלתי חקיקת העגולה את האלכסון לפי שצלע המחומש יש לו כח על צלע המשושה ועל צלע המעושר נקח חצי הצלע כלומר חצי הי"ב ויהיו ו' נכפלם על עצמם יעלו ל"ו גם נכפול הי"ב על עצמם יעלו קמ"ד גרע מאלה הל"ו נשארו ק"ח קח גדרם והוא י' אמות ושליש וחלק מט"ו וזהו שעור צלע בעל שש הזויות גם זהו שעור הארך מן המרכז
|
| the volume of a pyramid with a hexagonal base
|
|
| The measuring of a hexagonal [pyramid] is the same, without requiring the diagonal
|
ויהיה גם מדידת בעל השש זויות כך בלתי שאדרוש את האלכסון
|
- For example, let a hexagonal pyramid, each side of which is 12 cubits, the inclinations are 35 cubits, and we wish to find the perpendicular and the volume of the pyramid, we do as follows:
|
כגון שיהיה מחודד בעל שש זויות ויהיה כל א' מהצלעות מי"ב אמות וצלעות הגבהות מל"ה אמות ונרצה למצוא העמוד ותשבורת המחודד נעשה כך
|
- We multiply 12 by itself; the result is 144.
|
נכפול הי"ב על עצמם יעלו קמ"ד
|
- 35 by its self; the result is 1225
|
והל"ה על עצמם יעלו אלף רכ"ה
|
- Subtract 144 from it; the remainder is 1081
|
גרע מאלה הקמ"ד יעלו אלף פ"א
|
- We extract its root; it is 32 cubits, a half, a quarter, an eighth, and one part of 64; we know that this is the measure of the perpendicular
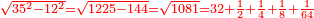
|
נקח גדרם והוא ל"ב אמות וחצי ורביע ושמינית וחלק מס"ד וידענו שזהו שעור העמוד
|
|
|
כפול אותו על תשבורת בעל השש וקח אותו כך לפי שבעל השש זויות יש לו ו' משולשים שוי הזויות קח תשבורת המשלש האחד וכפלהו ו' פעמים ותמצא תשבורת בעל הו' זויות
|
|
|
ועשה כן במשלש השוה הצלעות תכה צלעו הראשון על עצמו יעלה קמ"ד נקח השליש והם מ"ח גם העשירית יהיו י"ד ושליש וחלק מט"ו חברם יהיו ס"ב ושליש וחלק מט"ו כפול אלה ו' פעמים אחרי שהם ו' משולשים יעלו שע"ד ורביע וחלק מט"ו כפול אלה על העמוד שהם ל"ב וחצי ורביע ושמינית וחלק מס"ד יעלו י"ב אלף תי"ד ושליש קח ששיתם שהוא ששית המגודר יעלו ב' אלפים ונ"ב ושליש והם שעור המחודד
|
| the volume of a pyramid with an octagonal base
|
|
- A pyramid whose base is octagonal and we wish to measure it
|
מחודד אשר תושבתו בעל ח' זויות ונרצה למדוד אותה
|
|
|
יהיה מחודד אשר כל צלע מצלעות תושבתו מי' אמות וצלעות גבהותו מט"ו אמות
|
|
|
ואם תרצה למצוא העמוד ותשבורת המחודד תעשה כך קח חצי צלע התושבת של בעל ח' זויות כלו' מהי' חציים [38]וההוה ה' וכפלם על עצמם וההוה כ"ה כפלם בשנים וההוה נ' קח גדרם והוא ז' אמות וחלק מי"ד הוסף על אלה חצי צלע בעל שמנה תושבות שהם ה' ויהיה הסך י"ב וחלק מי"ד כפלם על עצמם ההוה קמ"ו עם תוספת מעט וכפול חצי הצלע על עצמו ההוה כ"ה חברם עם הקמ"ו וההוה קע"א גרע קי"ז וישארו נ"ד קח גדרם והם שבע ושליש וכן הוא שעור העמוד
|
|
|
והתשבורת של המחודד תמצאהו ככה
|
|
|
קח תשבורת תושבת בעל הח' זויות וכפלה עם העמוד ושלישית ההוה הוא אלף וקפ"א וזהו שעור אמות תשבורת מחודד בעל ח' זויות
|
|
|
מחודד משולש בעל מגבעות על תושבת קשתות קטנות מחצי העגולה מן הקצה אל הקצה ומיתר הקשת שבתושבת כל אחת י' אמות והעמודים הנופלים רחב ב' אמות וצלעות הגבהות מב' אמות
|
|
|
ונעשה כך נקח חצי מיתר אחת שבתושבת ויהיו ה' נכפלם על עצמם יעלו כ"ה והמיתר האחר שהוא י' נכפלהו על עצמו וההוה ק' גרע מאלה הכ"ה וישארו ע"ה קח גדרם והם ה' וחצי ושמינית וחלק א' מי"ו וכך הוא השעור שמראש המשולש עד התושבת והוא העמוד נקח חציים והם ד' ורביע וחלק מי"ו וחלק מל"ב כפלם על עצמם ההוה י"ו וחצי ורביעית ותשיעית עם תוספת מעט וזהו שעור חצי התושבת כפול הה' על עצמם ההוה כ"ה והסך ביחד יהיו מ"ג וחצי ורביעית ותשיעית קח גדרם והוא ו' וחצי ותשיעית וכן הוא ממרכז העגולה המקפת המשלש
|
|
|
וכשתרצה למצוא העמוד תעשה כן כפול הו' וחצי ותשיעית על עצמם ההוה מ"ג אמות וחצי ורביעית ותשיעי' גם כפול צלעות הגבהות שהם כ' על עצמם ההוה ת' גרע מאלה המ"ג וחצי ורביעית ותשיעית ישארו שנ"ו וחלק מי"ח קח גדרם והוא י"ח וחצי ורביעית ותשיעית וכן הוא שעור העמוד כפלהו עם תושבת המשולש וכך תקחהו הה' שהם מחצית התושבת על עמוד תושבת המשולש שהם ה' וחצי ושמינית וחלק א' מי"ו ההוה מ"ג וחצי וכן הוא שעור אמות התשבורת המשולש כפלם על י"א וחצי ורביע ותשיעית ההוה תת"כ עם תוספת מעט וזהו תשבורת המשולש
|
|
|
ומזה ראוי להוציא המגרעות וכן תעשה תחבר התושבת והעמוד הי' והב' וההוא י"ב אמות כפלם עם עמוד המחודד שהם י"א וחצי ורביע ותשיעית ההוה רכ"ו אמות כפלם על ג' לפי ששם ג' מגרעות ההוה תרע"ט וכל התשלום הוא תת"כ אמות נגרע מאלה התרע"ט ונשארו קמ"א נקח מאלה הששית ההוה כ"ג ושלישים ב' אחרי שהם מהמגודר הם כ"ג וב' שלישים וזהו תשבורת התמונה
|
|
|
וכבר התבאר במאמר הי"ב מספר היסודות שכל מגודר שתושבתו משולשת יחלק לג' מחודדים שוים
|
|
|
[39]וידוע שכל מחודד הוא שלישית המגודר כשיהיו בעלי צלעות שוות וגובה שוה
|
|
|
ומבואר מזה שכל מחודד שיהיה על איזו תמונה שיהיה הוא שלישית המוגשם הנכחי שתושבתו שוה לתושבתו וגבהו הוא שוה לגבהו
|
|
|
התמונה הנקראת בלשון יון מישקו והיא תמונה שהיא מתחלפת הצלעות צלעות התושבת גם הראש נמדדה כך
|
|
|
הגובה יהיה נ' אמות
|
|
|
ואם תושבת התמונה צלעה האחת הגדולה בעלת כ"ד אמות והקטן בעל י"ו אמות
|
|
|
ואם הראש הצלע הגדולה בעלת י"ב אמות ואם הקטנה בעלת ח' אמות נחבר הצלעו' הגדולו' של הראש ושל התושבת כלומר הי"ב הכ"ד ההוה ל"ו וכן חברתי הצלעות הקטנות של הראש ושל התושבת כלומר הי"ו והח' וההוה כ"ד קח חצי הל"ו וההוה י"ח וכן חצי הכ"ד וההוה י"ב כפול אלה על י"ח וההוה רי"ו ועוד נגרע מן הצלע הגדולה הי"ב מן הכ"ד וישארו י"ב נקח חציים והם ו' נגרע צלע הראש מן התושבת כלומ' הצלע הקטן והם הח' מן הי"ו וישארו ח' נקח חציים ויהיו ד' כפלם על ו' ההוה כ"ד קח השלישית והם ה' ונוסיפם על הרי"ו ויהיו יחד רכ"ד כפלם על הגובה שהם נ' ההוה י"א אלף ר' והם שעור תשבורת זאת התמונה
|
|
|
וכן נמדדהו גם אם היה בעל משפטים אחרים
|
Chapter Two on the Measuring of the Spheres and Round Solids
|
הפרק השני במדידת הכדורים והגופים העגולים
|
|
|
הכדור גדרו אקלידס במאמר אחד עשר מספר היסודות שהוא אשר יעבור חצי עגולה כאשר יקויים קו הקוטר בשני צירים עד שלא יסורו וסבבה הקשת אשר היא חצי הקו המקיף עד שתשוב אל מקומם והוא מוגשם העגול ומרכז הכדור ומרכז העגולה אחת
|
| the volume and the surface of a sphere
|
|
|
|
והכדור יתכן למדוד התשבורת של השטח המקיף אותו לבד גם יתכן למדוד תשבורת כל גופו
|
|
|
וכאשר נרצה למצוא תשבורת השטח תרבע את קטר הכדור ותכפול את המרובע הזה ג' פעמים ושביעית פעם ויעלה בידך משיחת שטח הכדור כפלהו בשתות הקטר ויעלה בידך תשבורת גוף הכדור
|
|
|
כגון ז' אמות כדור בקטרו והקו המקיף כ"ב אמות ונרצה למצוא תשבורת גופו נעשה כך נכפול הקטר על עצמו ויעלו מ"ט וכשתכפול זה המרובע ג' פעמים ושביעית פעם יהיה קנ"ד והן אמות שטח הכדור כפול אותן בשתות הקטר והוא א' ושתות יהיה ק"פ פחות שלש והוא תשבורת הכדור הזה
|
|
|
דרך אחרת כדור אשר קטרו ז' אמות והקו המקיף כ"ב [40]אמות ונרצה למצוא תשבורת גופו נעשה כך נכפול הקטר על עצמו וההוה מ"ט עוד נכפול אלה על הקטר שהם ז' יעלו שמ"ג אמות נכפול אלה י"א פעם יהיו ג' אלפים תשע"ג אמות נחלקם על כ"א ויעלה החלק האחד קע"ט וב' שלישים וכן שעור תשבורת גוף הכדור
|
|
|
ואם תרצה למדוד השטח תעשה כך נמצא לעולם הקטר והם במשלינו ז' ונכפלם עם המקיף שהם כ"ב ההוה קנ"ד וכן הוא תשבורת שעור שטח הכדור
|
|
|
אם תרצה למדוד האויר המוקף בכדור תמדוד לפי הביאור אשר הקדמנו במדידת הכדור בלתי עובי הכתלים
|
|
|
כגון שיהיה אורך קטר האויר מהכדור ח' אמות ועובי שתי הכתלים ב' אמות כפול הח' אמות של קטר האויר על עצמם יעלו ס"ד כפול אלה עוד על הח' של הקטר יעלו תקי"ב אמו' כפלם על י"א יעלו ה' אלפים תרל"ב חלקם על כ"א יעלו רפ"ח אמות ושביעית וחלק מן כ"א וזהו תשבורת אויר הכדור
|
| the volume of a hemisphere
|
|
|
|
אם תרצה למדוד חצי כדור תמדדהו לפי באור מדידת הכדור והנקבצים תחלקם על מ"ב
|
|
|
דמיון הקטר ז' אמות והקו המקיף כ"ב אמות ותרצה למצוא תשבורת גופני של חצי הכדור תעשה כן כפול הז' אמות של הקטר על עצמם ההוה מ"ט כפול עוד אלה על הז' אמות של הקטר ההוה שמ"ג כפול אלה על י"א וחלק העולה על מ"ב וההוה פ"ט אמות וחצי ושליש וכן הוא שעור חצי הכדור
|
|
|
אם תרצה למדוד אויר חצי הכדור תמדדהו לפי הביאור אשר קדם במדידת תשבורת חצי הכדור בלתי עובי הכתלים
|
|
|
דמיון יהיה קטר אויר חצי הכדור י' אמות ועובי שתי הכתלים ד' אמות כפל י' אמות קטר האויר לבד על עצמם וההוה ק' עוד כפול הק' על הי' הנזכרים ההוה אלף כפלם על י"א ההוה אלפים י"א חלקם על מ"ב ההוה רס"א אמות וחצי ושלישית חלק מי"ד וזהו שעור אמות אויר חצי הכדור
|
| the volume of a quarter of a sphere
|
|
|
|
אם תרצה למדוד רביע הכדור תמדוד לפי הבאור שהקדמנו במדידת חצי הכדור והנקבצים חלקם על פ"ד
|
|
|
דמיון קטר הרביע עם עובי ב' כתלים ד' אמות כפלם על עצמם ההוה קצ"ו כפול אלה על י"ד של הקטר הנזכר ההוה ב' אלפים תשמ"ד כפלם על י"א ההוה ל' אלף וקפ"ד חלקם על פ"ד וקח החלק האחד וההוה הוא שנ"ט ושלישית וכן הוא שעור רביע הכדור
|
|
|
אם תרצה למדוד אויר הרביע הנז' ולמצוא תשברתו הגופני תמדוד לפי הביאור הנזכר [41]במדידת הרביע בלתי עובי הכתלים כלומר הי' אמות של קטר האויר ויהיו ק' עוד כפול הק' על הי' ההוה אלף כפול האלף על י"א ההוה י"א אלפים חלקם על פ"ד ההוה ק"ל אמות וחצי ושליש וחלק מי"ב וחלק מכ"ח וכן הוא שעור מדידת אויר ורביע גרעם מהשנ"ט ושליש הנחברים וישארו רכ"ח אמות ורביע ושמינית וזהו תשבורת המבוקש
|
|
|
אם רצית למדוד בריכה מעוגלת כדוריית והיא חצי כדור כבר הראיתיך מדידתו במדידת חצי הכדור
|
| the volume of a spherical segment smaller than a hemisphere
|
|
|
|
אך אמנם אם היא פחותה מחצי כדור וזה תדעהו כשיהיה עמקה פחות מחצי רחב פיה תמדדה כך כגון בריכה שרוח בפיה ו' אמות ושליש ועמקה ב' אמות
|
|
|
תמצא את קטרה בראשונה כמו שלמדת בפרק החמישי במדידת התמונות העגולות והפחותות מחצי עגולה וכשתחשוב את קטר הבריכה הזו תמצאנו שהוא ז' אמו' כפול הב' שהם עמק הבריכה על הז' שהם קטר הכדור יהיו י"ד כפלם ג' פעמים ושביעית פעם יהיו מ"ד והוא מדידת שטח הבריכה כפול אותו בשתות הקטר והוא א' ושתות יעלו נ"א ושליש וזהו תשבורת גוף הבריכה
|
| the volume of a spherical segment larger than a hemisphere
|
|
|
|
ואם היתה הבריכה יותר מחצי כדור וזה תדעהו כשיהיה העומק יותר ממחצית רחב פיה
|
|
|
כגון בריכה שרחב פיה ו' אמות ושליש ועמקה ה' אמות כשתבקש לדעת קטר הכדור הנחצבת ממנה תמצאנו ז' תכפול העומק שהם ה' אמות בז' אמות הקטר ההוה ל"ה
|
|
|
כפלם ג' פעמים ושביעית פעם יהיו ק"י וזהו מדידת שטח הבריכה כפול אותה בשתות הקטר יהיו קכ"ח ושליש וזהו תשבורת גוף הבריכה
|
| the volume of a cylinder
|
|
|
|
אם רצית למדוד גוף נקרא בלשון יון קלידירו והוא גוף ארוך מעוגל שוה הרחב ראשו לתושבתו
|
|
|
דמיון גוף כזה אשר ארכו נ' אמות והקטר ז' אמות והמקיף כ"ב אמות ונמצא מהמקיף כמו שאנו עושים במדידת העגולה התשבורת והוא ל"ח אמות וחצי כפול אלה על האורך שהם נ' ההוה אלף תתקכ"ה והוא תשבורת הגוף הזה
|
| the volume of a cone
|
|
|
|
אם רצית למדוד אצטוונא מחודדת תעשה כך
|
|
|
דמיון אצטוונא שקטר תושבתה ז' אמות והעמוד היורד מראשה ל' אמות נמדד התושבת מהקטר הו' אמות של גובה העמוד השליש והוא י' ונכפלם על הל"ח וחצי ההוה שפ"ה אמות וזהו תשבורת הגוף של האצטוונא הנזכרת
|
|
|
אם רצית למצוא תשבורת אצטוונ' מחודדת [42]מקשיית ויש לו תושבת העגולה אשר הקטר מ"ב אמות וצלעות גבהות האצטוונא כל אחת[43] מע"ה אמות ותרצה למצא העמוד תמצאהו כך
|
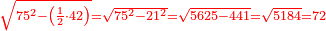
|
קח גובה הצלעות אשר הם ע"ה אמות וכפלם על עצמם וההווה ה' אלפים תרכ"ה וחצי קטר התושבת אשר הם כ"א כפלם על עצמם וההווה תמ"א גרעם מה' אלפים תרכ"ה נשארו ה' אלפים קח גדרם הם ע"ב וזהו ארך העמוד של האצטוונה
|
|
|
ותמצא גם תשברת העגלה והם אלף פ"ו אמות
|
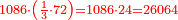
|
כפלם עם שלישית העמוד שהם כ"ד ההווה כ"ו אלף ס"ד וזהו תשברת גוף האצטוונא
|
|
|
ואם תרצה למצא תשברת שטחה קח חצי קטר התושבת שהם כ"א וכפלם על העמוד שהם ע"ב ההווה אלף תקי"ב כפל אלה על כ"ב ההווה ל"ג אלף רס"ד קח שביעית אלה ההווה ד' אלפים תשנ"ה בקרוב וכן הוא תשברת שטח האצטוונא
|
| the volume of a truncated cone
|
|
|
|
אם תרצה למדד אצטוונא מזונבת כלומר חתוכת הראש שהקטר היותר גדול שלה י' אמות והקטן ד' אמות והארך ל' אמות ותרצה למצא תשברת גופה תעשה כך
|
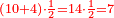
|
תחבר שני הקטרים הי' והד' וההווה י"ד וקח חציים והם ז' ונחשבהו קטר
|
|
|
ונמצא תשברת [44]העגלה אשר קטרה ז' כמו שידעת ויהיה ל"ח אמות וחצי
|
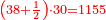
|
תכפלם על הל' אמות של הארך וההווה אלף קנ"ה אמות והוא תשברת גוף האצטוונא
|
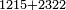
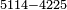
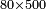
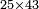
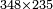
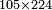
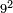
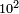
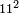
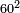
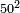
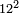
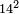
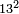
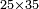
![\scriptstyle\sum_{k=1}^n \left[\left(\sum_{i=1}^n a_i\right)\sdot a_k\right]=\left(\sum_{i=1}^n a_i\right)^2](/mediawiki/images/math/2/a/1/2a190390030d9c138d548197fab10837.png)
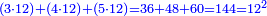
![\scriptstyle\left[\left(a+b\right)\sdot a\right]+\left[\left(a+b\right)\sdot b\right]=\left(a+b\right)^2](/mediawiki/images/math/9/c/9/9c9305cbc3ba9b0e4edc1ee228e83fa9.png)

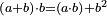
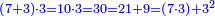
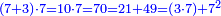
![\scriptstyle\left(a+b\right)^2=a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]](/mediawiki/images/math/7/2/7/727b0c35fd93a7a347bed8413905049f.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle
3^2+7^2+\left[2\sdot\left(3\sdot7\right)\right]&\scriptstyle=9+49+\left(2\sdot21\right)=9+49+42\\&\scriptstyle=100=10^2\\&\scriptstyle=\left(3+7\right)^2\\\end{align}}}](/mediawiki/images/math/8/4/8/8485bf1fc7542ef51ab16602c07e9c8b.png)
![\scriptstyle\left(a\sdot b\right)+\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]^2=\left(a\sdot b\right)+\left[b-\left[\frac{1}{2}\sdot\left(a+b\right)\right]\right]^2=\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2](/mediawiki/images/math/c/e/d/ceda777c2ea9424440ecf784d4535ff0.png)
![\scriptstyle{\color{blue}{\scriptstyle\left(3\sdot7\right)+\left[\left(\frac{1}{2}\sdot10\right)-3\right]^2=\left(3\sdot7\right)+\left(5-3\right)^2}}](/mediawiki/images/math/0/3/d/03dfdce3ec288d58b8f094e10b1397f2.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left(3\sdot7\right)+\left[7-\left(\frac{1}{2}\sdot10\right)\right]^2&\scriptstyle=\left(3\sdot7\right)+\left(7-5\right)^2\\&\scriptstyle=\left(3\sdot7\right)+2^2\\&\scriptstyle=21+4=25=5^2=\left(\frac{1}{2}\sdot10\right)^2\\\end{align}}}](/mediawiki/images/math/3/9/8/398cace15239fa9433c0a2f9fcf38677.png)
![\scriptstyle\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2](/mediawiki/images/math/a/0/b/a0b403dd8b7c15a5cb1dc47a5f8ca5bb.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left[2\sdot\left(10+2\right)\right]+\left(\frac{1}{2}\sdot10\right)^2&\scriptstyle=\left(2\sdot12\right)+5^2\\&\scriptstyle=24+25\\&\scriptstyle=49=7^2=\left(5+2\right)^2\\&\scriptstyle=\left[\left(\frac{1}{2}\sdot10\right)+2\right]^2\\\end{align}}}](/mediawiki/images/math/6/0/9/6096e9f7553e21c7650a3ee7d05439b9.png)
![\scriptstyle\left(a+b\right)^2+a^2=2\sdot\left[\left(a+b\right)\sdot a\right]+b^2](/mediawiki/images/math/5/e/f/5ef738b800e1b84fc257df70a83fb86b.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle10^2+7^2&\scriptstyle=100+49=149\\&\scriptstyle=140+9\\&\scriptstyle=\left[2\sdot\left(7\sdot10\right)\right]+3^2\\\end{align}}}](/mediawiki/images/math/5/a/0/5a0e68f34ec6e37d68c92ab618338648.png)
![\scriptstyle4\sdot\left[\left(a+b\right)\sdot a\right]+b^2=\left[\left(a+b\right)+a\right]^2](/mediawiki/images/math/f/6/2/f62f5f20431f619df80a01a1d97e57cf.png)
![\scriptstyle{\color{blue}{\scriptstyle\left[4\sdot\left(10\sdot7\right)\right]+3^2=280+9=289=17^2=\left(10+7\right)^2}}](/mediawiki/images/math/2/d/9/2d930b3cf54ef8cfc52718dc74fc4c81.png)
![\scriptstyle a^2+b^2=2\sdot\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2+\left[a-\left[\frac{1}{2}\sdot\left(a+b\right)\right]\right]^2\right]](/mediawiki/images/math/5/e/8/5e87deb6f6b5cec598e43b4b3374a25c.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle7^2+3^2&\scriptstyle=58=2\sdot\left(25+4\right)=2\sdot\left(5^2+2^2\right)\\&\scriptstyle=2\sdot\left[5^2+\left(7-5\right)^2\right]\\&\scriptstyle=2\sdot\left[\left(\frac{1}{2}\sdot10\right)^2+\left[7-\left(\frac{1}{2}\sdot10\right)\right]^2\right]\\\end{align}}}](/mediawiki/images/math/6/0/e/60e2c8e906170cf2be7705524d6f41d4.png)
![\scriptstyle\left(a+b\right)^2+b^2=2\sdot\left[\left(\frac{1}{2}\sdot a\right)^2+\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2\right]](/mediawiki/images/math/b/7/d/b7dd112f5309b8cd4f778bd6269c21f3.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left(10+2\right)^2+2^2&\scriptstyle=12^2+2^2\\&\scriptstyle=144+4=148=2\sdot74=2\sdot\left(25+49\right)\\&\scriptstyle=2\sdot\left(5^2+7^2\right)=2\sdot\left[5^2+\left(5+2\right)^2\right]\\&\scriptstyle=2\sdot\left[\left(\frac{1}{2}\sdot10\right)+\left[\left(\frac{1}{2}\sdot10\right)+2\right]^2\right]\\\end{align}}}](/mediawiki/images/math/0/3/e/03e712da00104b0b92112fed9e8e4c88.png)
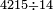
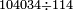
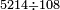
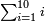
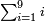
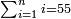
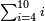
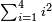
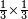
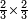
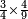
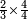
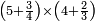
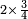
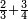
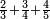
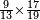
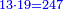
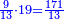
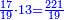
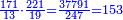
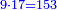
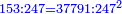
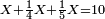
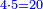
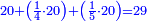
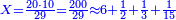
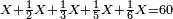
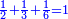
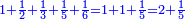
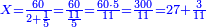
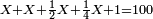
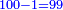
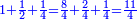
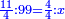
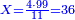
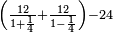
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left(\frac{12}{1+\frac{1}{4}}+\frac{12}{1-\frac{1}{4}}\right)-24&\scriptstyle=\left(\frac{4\sdot12}{5}+\frac{4\sdot12}{3}\right)-24\\&\scriptstyle=\left(\frac{48}{5}+\frac{48}{3}\right)-24\\&\scriptstyle=\left[\left(9+\frac{1}{2}+\frac{1}{10}\right)+16\right]-24\\&\scriptstyle=\left(25+\frac{1}{2}+\frac{1}{10}\right)-24=1+\frac{1}{2}+\frac{1}{10}\\\end{align}}}](/mediawiki/images/math/5/e/3/5e3a2961b99ecea99fbb5358aff1322e.png)
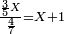
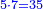
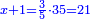
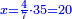
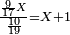
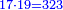
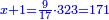
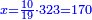
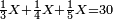

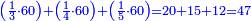
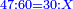
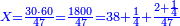
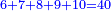
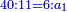
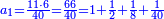
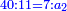
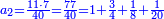
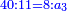
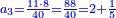
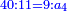
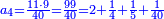
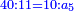
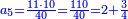
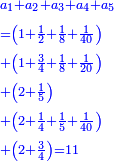
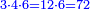
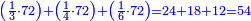
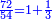
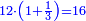 perutot
perutot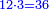 perutot
perutot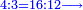
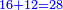 perutot from the coin of 3 dinar
perutot from the coin of 3 dinar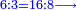
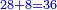 perutot from the coin of 3 dinar
perutot from the coin of 3 dinar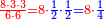
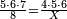
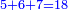
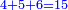
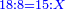
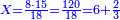
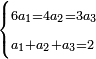

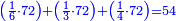
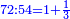 dinar
dinar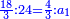
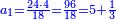 hours
hours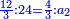
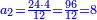 hours
hours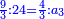
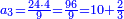 hours
hours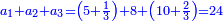 hours = 2 days
hours = 2 days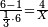
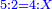
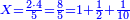
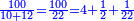 hours
hours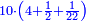
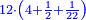
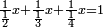
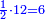 hours
hours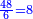 measures in one hour
measures in one hour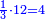 hours
hours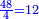 measures in one hour
measures in one hour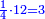 hours
hours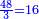 measures in one hour
measures in one hour measures
measures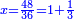 hours
hours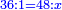
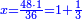
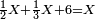

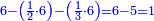
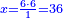
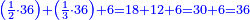
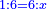
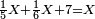

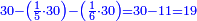
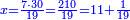

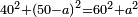

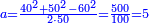

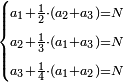
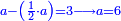
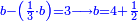
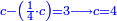
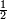
![\scriptstyle{\color{blue}{\left(2\sdot6\right)+\left[2\sdot\left(4+\frac{1}{2}\right)\right]+\left(2\sdot4\right)=12+9+8=29}}](/mediawiki/images/math/4/b/6/4b603e8d3bbbfa2a95c54b43550e6b90.png)
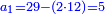
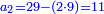
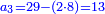
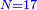
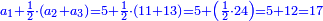
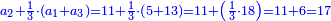
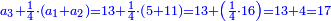
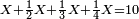
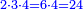
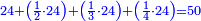
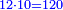


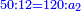
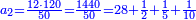
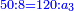
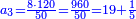
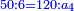
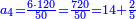
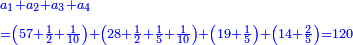
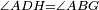
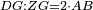
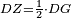
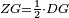
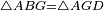
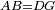
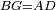
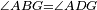
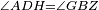
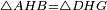
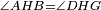
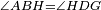
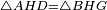
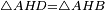
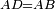
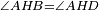 as both are right angles.
as both are right angles.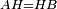
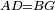
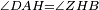
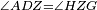
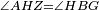
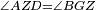
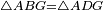
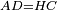
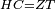
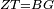
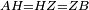
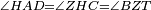
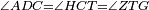
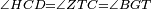
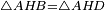
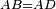
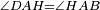
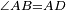
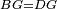
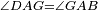
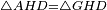
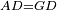
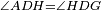
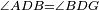
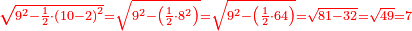
![\scriptstyle{\color{red}{\begin{align}\scriptstyle\left[\left[\frac{1}{2}\sdot\left(2+10\right)\right]^2+\frac{1}{3}\sdot\left[\frac{1}{2}\sdot\left(10-2\right)\right]^2\right]\sdot7&\scriptstyle=\left[\left(\frac{1}{2}\sdot12\right)^2+\frac{1}{3}\sdot\left(\frac{1}{2}\sdot8\right)^2\right]\sdot7\\&\scriptstyle=\left[6^2+\frac{1}{3}\sdot4^2\right]\sdot7\\&\scriptstyle=\left[36+\left(\frac{1}{3}\sdot16\right)\right]\sdot7\\&\scriptstyle=\left[36+\left(5+\frac{1}{3}\right)\right]\sdot7\\&\scriptstyle=\left(41+\frac{1}{3}\right)\sdot7=289+\frac{1}{3}\end{align}}}](/mediawiki/images/math/6/9/a/69a20480af90dcf2089eeee70a314aff.png)
![\scriptstyle{\color{red}{\frac{1}{6}\sdot\left[\left[\frac{1}{2}\sdot\left(4\sdot5\right)\right]\sdot25\right]=\frac{1}{6}\sdot\left[\left(\frac{1}{2}\sdot20\right)\sdot25\right]=\frac{1}{6}\sdot\left(10\sdot25\right)=\frac{1}{6}\sdot250=41+\frac{2}{3}}}](/mediawiki/images/math/0/4/f/04f865b5ce2da6db54aa2c9f9c8d9272.png)

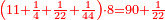
![\scriptstyle{\color{red}{\begin{align}\scriptstyle\sqrt{25^2-\left[\frac{1}{2}\sdot\left(11+\frac{1}{4}+\frac{1}{22}+\frac{1}{44}\right)\right]^2}&\scriptstyle=\sqrt{25^2-\left(5+\frac{1}{2}+\frac{1}{8}+\frac{1}{44}+\frac{1}{88}\right)^2}\\&\scriptstyle=\sqrt{625-\left(32+\frac{1}{44}\right)}=\sqrt{593}\\&\scriptstyle=24+\frac{1}{4}+\frac{1}{8}+\end{align}}}](/mediawiki/images/math/7/3/b/73b076e764e8db382fbe97b1df814204.png)