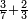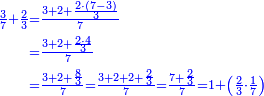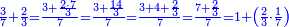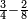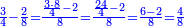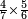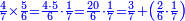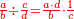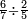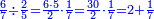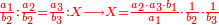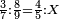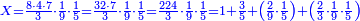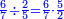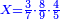- Since there are two zeros at the beginning of the top row, write under the line two zeros corresponding to them as their number.
|
ולפי שבתחלת השורה העליונה שתי סיפרות תשים בתחלת השורה העליונ' בעדן תחת הקו שתי סיפרו' כמספרן
|
- Complete this row by multiplying the next upper digit that follows them, which is 5:
|
ותשלים השורה ההיא מכפל המספר העליון הבא אחריהן והוא ה5
|
- Multiply the 5 by the zero that is in the first rank of the bottom number; it is zero. Place it after the two mentioned zeros, which is the third rank that [precedes] the fourth rank. It follows that its row starts from the third rank.

|
ותכפול ה5 בסיפרא שהיא אשר במעלה הראשונה מהמספר התחתון ויהיה סיפרא ותשימנה אחר השתי סיפרות הנזכרות שהיא המעלה השלישית הדומה למעלה הרביעית והנה בא על מתכונתו ששורתו מתחלת במעלה הג' שהיא מעלתו
|
- Then say: multiply 5 by 2; it is 10. Place the zero after the mentioned zeros.
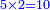
|
ותאמ' אח"כ כפול 5 ב-2 הוא 10 תשים סיפרא אחר הסיפרות הנזכרות
|
- Keep the 10 as one, to add it to the product of 5 by 9, which is 45; the total sum is 46. Place the 6 after all the zeros and keep the 4.
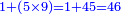
|
ותשמור ה-10 לאחד לחברו עם כפל 5 ב-9 שהוא 45 ויהיה הכל 46 ותשים ה6 אחר כל הסיפרות ותשמור ה-4
|
- When you multiply the 5 by the zero that follows the 9, do not put zero, since you have 4 in your hand, so place it instead after the 6.
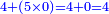
|
וכאש' תכפול ה5 בסיפרא הבאה אחר ה9 לא תשים סיפרא אחר היות בידך 4 ותשימם במקומה אחר ה6
|
- When you multiply the 5 by the following zero, [place] a zero after the 4, since you have nothing in your hand.

|
אכן כאש' תכפול ה5 בסיפרא הנמשכת לא תשים סיפרא אחר ה4 אחר שאין בידך מאומה
|
- Multiply 5 by 4; the result is 20. Put a zero and keep the 2.
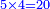
|
ותכפול 5 ב-4 ויעלו 20 תשים סיפרא ותשמר 2
|
- Multiply 5 by 5; they are 25 and with the 2 that you have the total sum is 27. Put 7 and after it put 2, because the multiplication of the upper digit by all the bottom digits is complete.
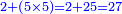
|
ותכפול 5 ב5 ויהיו 25 ועם ה2 אשר בידך יהיה עם הכל 27 שים 7 ותשים אחריהם 2 כי כבר נשלם כפל המספר העליון בכל המספרים התחתונים
|
- Since you find [a zero] after the upper 5 that was multiplied, the rule requires to multiply it by all the bottom digits and make of it one line.
|
ואחרי היותך מוצא אחר ה5 העליון הנכפל כבר היה הדין נותן לכפלה עם כל המספרים התחתונים ולעשות ממנו שורה אחת
|
- But, there is no need for this, only that you start with the 7 that is after it and make its line provided that the line of the 7 starts from the fifth rank, which is its rank as mentioned.
|
ואין צורך אלא שתתחיל מה7 אשר אחריה ותעשה שורתו בלבד שתתחיל שורת ה7 מהמעלה הה' אשר היא מעלתו כנזכר
|
- In order not to be mistaken, place a zero at the beginning of the line of the 7, for the upper zero that is between the 5 and 7, whose rank is the fifth rank.
|
אכן כדי שלא תטעה תשים בראש שורת ה7 במעלה סיפרא בעד הסיפרא העליונה אשר בין הה' וה7 אשר מעלתה המעלה ה5
|
- Complete the line by multiplying the 7 that follows it by all the bottom digits:
|
ותשלים השורה בכפל ה7 הבאה אחריה בכל הרשמים התחתונים
|
- Say: the product of 7 by zero is zero. Put another zero.

|
ותאמ' כפל 7 בסיפרא הוא סיפרא ותשים סיפרא אחרת
|
- Say also: the product of 7 by 2 is 14. Place 4, which are the units, after the mentioned zeros and keep the 1.
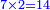
|
ותאמר עוד כפל 7 [ב2 ויעלו 14 תשים 4 שהם האחדים אחר הסיפרות הנזכרות ותשמור הא'
|
- Say also: the product of 7 by 9 is 63; plus the one that we have the result is 64. We put the 4 and keep the 6 as units.
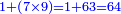
|
ותאמר עוד כפל 7 ב9] ב9 ויעלה 63 ועוד האחד אשר בידינו יעלה 64 נשים ה4 ונשמר ה6 לאחדים בידינו
|
- We say also: the product of 7 by zero is zero. Since we have a 6, we do not put a zero, but we put the 6 that we have in its place.
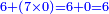
|
ונאמר עוד כפל 7 בסיפרא היה עולה סיפרא אכן להיות בידינו ה6 לא נשים סיפרא אבל נשים ה6 אשר בידינו למקומה
|
- We say: the product of 7 by zero is zero. We put a zero, as we do not have units at all.

|
ונאמר כפל 7 בסיפרא עולה סיפרא ונשים סיפרא אחר שאין בידינו אחדים כלל
|
- We say: the product of 7 by 4 is 28. We put 8 and keep the 2.
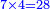
|
ונאמר כפל 7 ב4 עולה 28 נשים 8 ותשמור 2
|
- We say: the product of 7 by 5 is 35; plus the two that we have the result is 37. We put the 7 and after it the 3, because the multiplication of the 7 by all the bottom digits is complete.
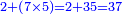
|
ונאמר כפל 7 ב5 עולה 35 ועם השנים אשר בידינו יעלו 37 נשים 7 ואחריהם 3 כי כבר נשלם כפל זה ה7 על כל הרשמי' התחתונים
|
- Since there are two zeros after the 7 in the upper line, in order not to be mistaken, we put two zeros corresponding their rank at the beginning of the line of the 9 that follows them.
|
ואחר היות שתי סיפרות בשורה העליונה אחר ה7 כדי שלא נטעה נשים שתי סיפרות כנגד מעלתן בהתחלת שורת ה9 הבא אחריהן
|
- Again we say: the product of 9 by zero is zero. Put a zero after the two zeros that we placed at the beginning of this line.

|
ושוב נאמ' כפל 9 בסיפרא הוא סיפרא ותשים סיפרא אחר השתי סיפרות כאשר שמנו בג[ת]חלת שורה זו
|
- We say: the product of 9 by 2 is 18. We put 8 after the three mentioned zeros and keep the one.

|
ונאמר כפל 9 ב2 עולה 18 נשים 8 אחר השלשה סיפרות הנזכרות ונשמור אחד
|
- We say: the product of 9 by 9 is 81 and since we have 1, the result is 82. We put the 2 and keep the 8.
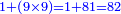
|
ונאמר כפל 9 ב7 ב9 עולה 18 81 ואחר שהיה בידינו 1 יעלו 82 נשים 2 ונשמור 8
|
- We say: the product of 9 by zero is zero. We put the 8 that we have in its place.
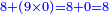
|
ונאמר כפל 9 בסיפרא הוא סיפרא ונשים ה8 אשר בידינו במקומה
|
- We say: the product of 9 by zero is zero. We put it, as we have nothing in our hands.

|
ונאמר כפל 9 בסיפרא הוא סיפרא ונשימה אחר שאין בידינו דבר שוב
|
- We say: the product of 9 by 4 is 36. We put 6 and keep the 3.
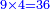
|
ונאמר כפל 9 ב4 עולה 36 נשים 6 ונשמור 3
|
- We say: the product of 9 by 5 is 45; plus the 3 that we have the result is 48. We put the 8 and after it the 4, because the multiplication of the 9 by all the bottom digits is complete.
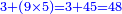
|
ונאמר כפל 9 ב5 עולה 45 ו3 אשר בידינו יעלו 48 ונשים 8 ואחריהן 7 [4] כי כבר נשלם כפל 9 זה בכל הרשמים התחתונים
|
- Since the upper digits were already multiplied by all the bottom [digits], we draw a line beneath all the lines and sum all the lines that were generated from their products, i.e. the three lines between the lines.
|
ואחרי אשר כבר נכפלו ר"ל הרשמים העליונים עם כל התחתונים נרשום תחת כל השורות קו דיו ונחבר כל השורות שנתחדשו מכפליהן ר"ל ה3 שורות אשר בין הקוים להנה
|
- We receive that the result of the multiplication of the two questioned numbers one by the other is 486463564860000.
|
יעלה בידינו שכפל הב' מספרים הנשאלים זה בזה עלה 486463564860000
|
Check
|
|
- Division: If you want to check if you did it right or not, divide the great number resulting from the multiplication by one of the two multiplied numbers, so the result of division is the other [multiplied number]. But if it is lacking or exceeding, know that you have erred in one of the operations of multiplication or division.
|
ואם תרצה לבחון אם עשית כדין אם לאו יתחלק זה המספר הגדול העולה מהכפל לאחד מהב' מספרים הנכפלים ויצא בחילוק האחר ולא ישאר דבר ואם יחסר או יעדיף דע לך שטעית באחד המעשים בכפל או בחילוק
|
Reason: Procedure
|
|
| The reason for starting the line of multiplication of each upper digit by the bottom [digits] from its corresponding rank:
|
הטעם בהתחלת שורת כפל כל מספר עליון בתחתונים מהמעלה הדומה לו
|
- Because, e.g. if the upper number is of the hundreds, which is the third rank, when we multiply it by the units of the bottom number, the result is of the hundreds.
|
כי על ד"מ אם המספר העליון הוא מאות שהוא במעלה הג' כשנכפלם באחדי המספר התחתון יהיה העולה מאות
|
- If it is of the thousands, which is the fourth [rank], the result is of the thousands.
|
ואם יהיה אלפים שהוא בד' יהיה העולה אלפים
|
- Therefore, the units resulting from the first multiplication are in the third rank, which corresponds to the rank [of the upper number], and the tens resulting from this multiplication are units of the subsequent rank, as explained in the beginning of the book, in the explanation of the ranks. So, you keep them as units to add them to the next [product].
|
לכן כאשר יהיו [...] אחדים העולי' מהכפל הראשון ההוא במעלה הג' שהיא המעלה הדומה למעלתו והעשרות העולות מזה הכפל הם אחדים במעלה הבאה אחריהן כמו שנתבאר בתחלת הספר בפי' המעלות לכן תשמרם לאחדים לחברם עם הבא אחריהן
|
- When we multiply the upper number by the second of the bottom [digits], the result are tens of hundreds, which are thousands, if the upper [number] is of the hundreds.
|
וכשנכפול מספר עליון זה באשר במעלה השנית מהתחתונים יהיו העולה עשירי מאות שהם אלפים אם העליון הוא מאות
|
- If it is of the thousands, these tens are tens of thousands, so we place them in the rank that follows the one that we place at the beginning of this line and we add to them the reserved from the previous multiplication.
|
ואם הוא אלפים יהיו העשרות האלה עשרות אלפים לכן נשימהו במעלה הנמשכת לאשר שמנו בתחלת שורה זו ונחבר להם השמור בידינו מהכפל הקודם
|
- And so on, forever it rises rank by rank, until it is clear from what is said that the place of the units resulting from the multiplication of each upper digit by a bottom [digit] is the rank whose decimal position is as the [sum] of the ranks of both upper and bottom digits that are multiplied by each other minus one.
|
וכן לעולם כאשר יתרחק יעלה מעלה אחר מעלה עד שיצא לנו מזה ברור מה שאמרנו כי אחדי כפל כל מספר עליון בתחתון יהיה מקום האחדים העולים מהכפל ההוא במעלה אשר מנין מדרגותיה כמנין מעלות שני רשמים האלו הנכפלים זה בזה העליון והתחתון יחד חסר אחת
|
- If one of them is in the first rank, we have explained that the place [of the product] is in the rank that corresponds the rank [of the other multiplied digit]
|
וזה שאם האחד מהם במעלה הראשונה הרי ביארנו שמקומו הוא במעלה הדומה למעלתו
|
- If it is in the second rank, [the product] rises one rank above the rank of the other [multiplied] digit as explained.
|
ואם יהיה בשנית יעלה מעלה אחת על מעלות המספר האחר כמנין מעלותיו כמו שביארנו
|
- If it is in the third [rank], [the product] rises by two.
|
ואם הוא בג' יעלה שתים
|
- And so on it exceeds over the ranks of the second [multiplied] digit by the number of the ranks [of the first multiplied digit] minus one.
|
וכן יוסיף לעולם על מעלות המספר האחר כמנין מעלותיו כמו שביארנו ואם הוא בג' יעלה שתים וכן יוסיף לעולם על מעלות המספר האחר כמנין מעלותיו חסר אחת
|
- Hence, the rank of the units resulting from the multiplication is as [the sum of] the ranks of both digits that are multiplied one by the other minus 1 and all this is clear by reason.
|
והנה יהיה מעלות אחדי העולים מהכפל כמעלות שני הרשמים הנכפלים זה בזה חסר אחת וכל זה ברור בטעם
|
Reason: Check
|
וטעם הבחינה
|
| Multiplication is the inverse operation of division.
|
הוא כי הכפל הוא הפך החילוק
|
| Practical illustration: dividing a given amount of money between a certain number of people equally
|
|
| When a certain known number of people receive a known amount of money each
|
כי כאשר למין מה ממספר אנשים ידועים ועלה לכל אחד מהם מנין ממון ידוע
|
- The total [amount of] money is the product of the number of people multiplied by the amount of money that each of them receives.
|
הרי יש בכל הממון כפלי ממספר האנשים כמספר הממון העולה לכל אחד מהן
|
- Or, if you want to say: the product of the money that each of them gets multiplied by the number of people. All is the same.
|
או אם תרצה לומר כפלי הממון שיצא לכל אחד מהם כמספר האנשים ההם והכל אחד
|
For example: if we divide 12 golden coins between 3 people [equally], each of them receives 4.
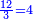
|
כי המשל אם חלקנו 12 זהובים ל3 אנשים עלה לכל אחד מהם 2 4
|
- For, twelve is a product of 3 by 4, or 4 by 3.
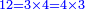
|
הרי השנים עשר הם כפל 3 ב4 או ה4 ב3
|
- Thus, if we divide these 12 between 4 people, each receives 3
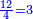
|
ואם נחלק 2 12 אלו ל3 ל4 אנשים יעלה לכל אחד מהם ג'
|
- and if between 3 [people], each receives 4
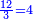
|
ואם לג' יעלה לכל אחד מהם 4
|
| Hence, when we divide the result of multiplication by one of the multiplied numbers, the result of division is the second [multiplicand] no more and no less.
|
הרי שכאשר נחלק העולה מהכפל לאחד מהמספרים הנכפלים יצא השני בחילוק בלי תוספת ומגרעת
|
| So, the check of the multiplication operation is by division, and the check of the division operation is by multiplication and this is an obvious thing.
|
הרי שבחינת הכפל בחילוק וכן בחינת החילוק בכפל וזה דבר ברור
|
|
|
Chapter Four: Division
|
הפרק הרביעי בחילוק
|
written division
|
|
|
|
|
| When you wish to divide a large number by a smaller number
|
כאשר תרצה לחלק מספר גדול למספר קטן
|
description of the procedure
|
|
| We place them one above the other orderly: the greater above, we call it the dividend; the smaller beneath, we call it the divisor [lit. by which it is divided].
|
ונשימם זה על זה על הסדר הגדול למעלה נקראנוהו המתחלק והקטן למטה וקראנוהו אשר נחלק עליו
|
| Put every rank beneath its corresponding and
|
ותשים כל מעלה תחת בת גילה
|
| These two lines should be spaced, i.e. leave a space between them, in order to put the result of division between them, as will be explained in the [description of the] division [procedure].
|
ויהיו שתי שורות אלו מרווחות [..] ר"ל שתשים ריוח בין זו לזו לשים ביניהם היוצא בחילוק כאשר יתבאר בחילוק
|
- See how many times the last bottom digit to the left can be extracted from the last digit of the upper [number].
|
וראה המספר האחרון התחתון אשר לצד שמאל כמה פעמים יצא מהמספר האחרון אשר בעליון
|
- If it is not even once in it, as it is smaller than it, see how many times it can be extracted from the last [digit] and the one that precedes it, considering the last [digit] as tens and the one that precedes it as units. The number of these times is called the result of division.
|
ואם איננו בו אפי' פעם אחת שהוא קטן ממנו ראה כמה פעמים יצא מזה האחרון ומאשר לפניו בקחתך האחרון לעשרות ואשר לפניו לאחדים ומנין פעמים אלו הוא הנקרא היוצא בחילוק
|
- Know that you have to extract the digits that precede the last bottom digit as many times from the upper one that precedes the last digit or digits, from which you extract the multiples of the last bottom digit, as the number of times that you extract the last bottom digit from the last upper digit or digits.
|
ודע שיש לך להוציא כ"כ פעמים המספרים אשר לפני האחרון התחתון מאשר לפני האחרון או האחרונים העליונים אשר הוצאת מהם כפלי האחרון התחתון כפעמים אשר הוצאת האחרון התחתון מהאחרון העליו' או האחרונים
|
- When there is a remainder from the last digit or digits, consider them as tens or hundreds, according to their relation to the present rank, [subtract from them] as the multiples that you subtract the last bottom digit from the last upper digit or digits.
|
[וכאשר נשאר מהאחרון או מהאחרונים בקחתך אותם לעשרות ולמאות כפי ערכם אל המעלה הזאת ככפלים אשר הוצאת האחרון התחתון מן האחרון העליון או האחרונים]
|
- If there is not enough, do not subtract from the last digit as much as these multiples, for you always have to subtract each [bottom digit] from its corresponding upper digit as many times as you subtract the last [bottom digit] from the last [upper] digit or digits.
|
[ואם אין בו] לא תוציא לאחרון ככל הכפלים ההם כי לעולם יש לך להוציא כל אחד כל פעמים מהעליון הראוי לו כפעמים אשר תוציא האחרון מן האחרון או מן האחרונים
|
- You should know that whenever you wish to subtract the bottom digit from the upper digit and you do not find in its corresponding rank enough [to subtract] its multiples, if there is in the one that follows the consecutive [rank], you can subtract from it, provided that you keep the positional value of the ranks, so that every digit is tens to its preceding and hundreds to the one that precedes its preceding and so on according to this relation.
|
א[כן] יש לך לדעת כי בכל עת שתרצה להוציא התחתון מהעליון ואין דיו לכופליו כאשר תמצא במעלה הראויה לו שאם יש בנמשך אחר הנמשך תוכל להוציא ממנו ובלבד שתשמור לעולם ערך המעלות שכל מספר הוא במעלה שלפניו לעשרות ואשר לפני פניו למאות וכן לעולם על הערך הזה
|
- Interim result: After you know the multiples of which you can subtract each of the bottom digits from the corresponding upper rank or ranks,
|
ואחר שתדע הכפלים אשר תוכל להוציא כל אחד מהמספרים התחתונים מהמעלה או מעלות הראויות להם מהעליונים
|
- i.e. for example, if the last bottom [digit] is subtracted from the [seventh] [upper] rank and the one that precedes the last is subtracted from the sixth [rank] and the one that precedes the preceding is subtracted from the fifth, until they are complete.
|
ר"ל כי עד"מ אם האחרון התחתון לקח מהמעלה הו' התחתון ואשר לפני האחרון יקח מו' ואשר לפני פניו מהה' עד כלותם
|
- in the rank that they end, i.e. where the first bottom digit is to be subtracted as many times from that rank according to the order explained - place the number of the multiples that are subtracted corresponding to that rank, beneath the upper digit.
|
ובמעלה אשר יכלו ר"ל שהראשון התחתון יש לו לקחת בפעם ההיא מהמעלה ההיא על סדר שביארנו כנגד המעלה ההיא תשים מנין הכפלים אשר לקחו ותשימם תחת המספר העליון
|
- Interim remainder: When there is a remainder from the upper digit, place the remainder above it, so that this remainder will be in front of your eyes to be used as tens or hundreds for the preceding [digit] and the one that precedes the preceding, as explained.
|
וכאשר ישאר שום דבר משום מספר עליון תשים עליו השארית ושארית זה יהיה לעולם בין עיניך להועיל ממנו לעשרות או למאות לאשר לפניו ולפני פניו כמו שביארנו
|
- Repeated division: When all the bottom [digits] to be subtracted from their corresponding [upper digits] are complete, if there is a remainder in the upper number that is as the bottom number or more, we divide it again as in the beginning: We see how many times the last bottom digit can be subtracted from the last digit or digits of this remainder, as we have done in the beginning with the whole number, and the preceding and the one that precedes the preceding, all by the same multiples, each from its corresponding [upper digit].
|
וכאשר תמו כל התחתונות לקחת מן הראויות להם אם נשאר עוד במספר העליון כמספר התחתון או יותר ממנו נשוב לחלקו עליו כבתחלה ונראה כמה פעמים יצא האחרון התחתון מהאחרון או אחרוני שארית זו כמו שעשינו בתחלה בכל המספר ואשר לפניו מאשר לפניו לכולם כפלים שווים כל אחד מהראוי לו
|
- Last interim division: We always repeate [the division] time and time again, until the time comes when each of the bottom [digits] are subtracted from its very rank, i.e. the units from the units, the tens from the tens and the number of multiples is placed at that time in the first rank.
|
וכן נשוב לעולם פעם אחר פעם עד הגיע עת יקח כל אחד מהתחתונים ממעלתו ממש ר"ל האחדי' מהאחדים והעשרות מהעשרות ומספר הכפלים יושם בעת ההיא במעלה הראשונה
|
- We do not divide again, because what remains then is less than the bottom number.
|
ולא נשוב עוד לחלק כי לא ישאר אז כי אם הפחות מהמספר התחתון
|
- The less cannot be divided by the more into integers but only into fractions.
|
והפחות על הרב לא יוכל לחלק לשלמים כי אם לשברים
|
- We will mention further in this chapter how it will be divided into fractions.
|
ועוד נזכיר בפרק זה איך יתחלק לשברים
|
- The decimal place of the interim result: Always remember to place each time the result of division of that time, i.e. the multiples that you subtract at that time, corresponding to the rank from which the first bottom digit is subtracted, i.e. the [digit] that is in the first rank, if there is a number there, or if there is only a zero there - see from where it should be subtracted, if there is a number there, and place there the result of division of that time.
|
וזכור לעולם שתשים בכל פעם היוצא בחילוק בפעם ההיא ר"ל לפעמים הכפלים אשר תוציא בפעם ההיא כנגד המעלה אשר משם [יקח] המספר הראשון התחתון ר"ל אשר יהיה במעלה הראשונה אם יהיה שם מספר [ואף אם לא יהיה שם מספר] כי אם סיפרא תראה מהיכן היה לו ראוי ליקח אם היה שם מספר כי אם סיפרא ושם תשים היוצא בחילוק בפעם ההיא
|
- It turns out that when we want to know from which rank a certain bottom digit should be subtracted, we should see from which rank the last bottom digit should be subtracted at that time, then count the number of the ranks from there to the right, as the number of the ranks that this bottom digit is far to the right from the last bottom digit - where they end it should be subtracted from the upper digit.
|
ויצא לנו מכך כי כאשר נרצה לידע אי זה מקום ראוי לקחת ממנו שום מספר מהתחתונים בשום פנים שנראה מאי זו מעלה לקחת לאחרון שבתחתונים בפעם ההיא ותמנה משם לצד ימין מנין מעלות כמספר מעלות מרחק המספר ההוא התחתון [לצד ימין מהמספר האחרון התחתון] ובמקום שיכלו מהעליונות משם יקח
|
- Likewise, when you wish to know in which rank to place the result of division each time, see from which rank the last bottom digit was subtracted at that time, count from there to the right, as the number of the bottom digits, and where this counting ends, place the result of division at that time. From that very rank the digit that is in the first rank of the bottom number is subtracted at that time.
|
גם כאשר תרצה לידע באיזה מקום תשים היוצא בחילוק בכל פעם ראה מאיזה מקום לקח האחרון התחתון בפעם ההיא ומנה משם לצד ימין כמנין רשמי התחתון וכאשר תכלה המנין ההוא שם תשים היוצא בחלוק בפעם ההיא ומהמעלה ההיא בעצמה יקח המספר אשר במעלה הראשונה בטור התחתון בעת ההיא
|
example
|
המשל
|
We wish to divide 4380408998 by a smaller number, which is 46079.
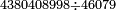
|
רצינו לחלק 4380408998 על מספר קטן ממנו והוא 46079
|
- We put them in two spaced lines orderly one on top of the other like this:
|
נשימם בשני טורים מרווחים זה על זה על הסדר כזה
|
|
|
| 0
|
| 01
|
| 13
|
| 054
|
| 00290102
|
| 23324924
|
| 0744193751
|
| 4380408998
|
| 95063
|
| 46079
|
|
|
|
|
[אמ' משה זה טעות אבל האמת הוא כי היוצא בחלוק לכל א' [...] הוא זה 95000 שלמים נוסף על השברים]
|
- We say: 4, which is the last bottom digit, can be subtracted once from the last upper digit.
|
ונאמ' מה שהוא המספר האחרון העליון יוכל לצאת 4 שהוא המספר האחרון התחתון פעם אחת
|
- But, we cannot subtract 6 that precedes the last bottom digit from 4 that precedes the last upper digit
|
אכן מד' אשר לפני האחרון העליון שהוא אשר לפני האחרון התחתון לא נוכל לצאת 6 שהוא אשר לפני האחרון התחתון
|
- Therefore, we do not subtract from there [= the last upper digit], but we subtract from the last two [upper] digits, which are 43.
|
לכן לא נוציא משום [משם] דבר אבל נוציא מהשנים האחרונים שהם 43
|
- We say: how many times 4 is in 43?
|
ונאמר 43 כמה פעמים יש 4
|
- We do not say ten, since if the 3 that in this rank could have taken 10, it would have taken it from the last digit, which is ten in relation to this rank.
|
ולא נאמר עשרה שהג' שמהמעלה הזאת היה יכול לקחת 10 היה לוקח מהאחרון אחרון שהוא 10 בערך המעלה הזאת
|
- Therefore, we say: only 9.
|
לכן לא נאמ' כי אם 9
|
- The bottom line has 5 digits, hence we count 5 ranks to the right from the upper 3, from which we subtract. They end in the zero and we place beneath it the 9 resulting from the division, which is the number of times that we have to subtract the bottom digits from the upper digits at this time, each from its corresponding rank, as mentioned.
|
והנה השורה התחתונה היא 5 רשמים לכן לא נמנה מהג [3] העליון אשר לוקח משם 5 מעלות לצד ימין ויכלו בסיפרא ונשים תחתיה אלו ה9 היוצאים בחילוק שהוא מספר הכפלים אשר לנו להוציא התחתונים מהעליונים בפעם הזאת כל אחד מהמעלה הראויה לו כנזכר
|
|
|
ונאמר ב2 אין די ל5 ניקח מ27 ויהיו בו ה' פעמים ונשימהו תחת השלישית כי שם יכלו ה7 מעלות לצד ימין שהם כמנין מעלות השורה התחתונה
|
-
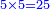
|
ונאמר 5 ב5 הם 25
|
- We subtract the 5 from the 7; 2 remains.
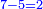
|
נסיר הה' מהז' ישארו שנים
|
- We subtract the 2 from the 2; nothing remains.

|
ונסיר הב' מהב' ולא ישאר דבר
|
-
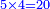
|
ונאמ' ה' בד' הם כ'
|
|
|
ולא נקח אחדים
|
|
|
אכן הב' עשרות נקחם מהב' אשר שמנו עתה על הז' ולא ישאר דבר
|
- We say also: 5 by 9 are 45.
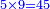
|
עוד נאמר ה' בט' הם מ"ה
|
|
|
נסיר הה' מהו' כי היא מעלה הראויה לו כנזכר וישאר א'
|
|
|
ונסיר הד' מהד' ולא ישאר דבר הנה לנו שכלה כל החשבון
|
[the last step is missing  ] ]
|
ולהיות לנו בזה היוצא בחלוק מעלות חלקות מהמספר הן בתחלה הן באמצע נשים ספרות במקומם כי זה מעשה הסיפרות ותועלתם כאשר הזכרנו
|
|
|
והנה יצא לנו שכאשר חלקנו העולה מהכפל באחת הנכפלים יצא השני בלי תוספת ומגרעת ובלי שארית כלל
|
|
|
וכן אם תחלקנה לחבירתה תצא חבירתה בחילוק כאשר בא בזאת הצורה
|
|
|
| 0
|
| 1
|
| 020
|
| 0838 000
|
| 03011100141
|
| 486463564860000
|
| 5400920
|
| 90070500
|
|
|
|
|
ולא ראיתי להאריך בזה עוד והכל מבואר למבין
|
reason: procedure
|
|
| The reason for the decimal place of the interim result of division: this decimal place is set according to the rank of the dividend from which the multiple of the rightmost digit of the divisor was subtracted
|
וטעם מקום הנחת היוצא בחילוק הוא כי כפי המדרגה אשר ממנה לקח המספר הראשון הם הפעמים אשר לקחו
|
|
|
ר"ל שאם חלקנו שש מאות לג' אחדים
|

|
הנה יגיע לכל אחד ב' והמדרגה אשר ממנה לקח היא מדרגת המאות הנה השנים אשר יצאו בחלוק היא הם מאותה המדרגה והם מאתים
|
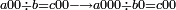
|
ואם היו שם עוד אלפים בעליון ועשרות בתחתון הנה הפעמים אשר יגיעו לאחדים מהמאות יגיעו לעשרות מהאלפים
|
- As the tens are tens in relation to the units, so the thousands are tens in relation to the hundreds; and as the hundreds are in relation to the units, so the thousands are in relation to the tens, and the tens of thousands are in relation to the hundreds
|
כי כמו שהעשרות הם עשרות לאחדים [ככה האלפים הם עשרות למאות הנה כאשר הגיע לאחדים מהמאות] מהמאות יגיעו לעשרות מהאלפים וכן למאות מהעשרות אלפים וכן לעולם כי כמו שזה עולה לאשר כמותו כן עולה זה
|
- The rank of the division by units is the rank of the dividend - thus, if the units were extracted from the hundreds, the tens will be extracted from the thousands, and the hundreds will be extracted from the tens of thousands
|
כבר ביארנו כי מדרגת הפעמים אשר הגיעו לאחדים היא מרוחק המדרגה אשר ממנו לקח והיא בעצמה המדרגה אשר לקחו העשרות מהאלפים והמאות מהעשרות אלפים וכן כולם
|
| The multiple of a certain digit of the divisor should be extracted from the rank of the dividend that is placed in relation to the rank from which the multiple of the divisor's units was extracted, as the decimal position of that certain digit of the divisor in relation to its units
|
ר"ל שכל אחד מהתחתונות מדרגתה הראויה לקחת ממנה היא מרוחקת לצד שמאל [מהמדרגה אשר לקחו ממנה האחדים כמספר המדרגות אשר היא מהאחדים] מהאחדים
|
- If the units of the divisor were extracted from the hundreds of the dividend, then the hundreds of the divisor, that are on the third rank in relation to the units of the divisor, should be taken from the tens of thousands of the dividend, that are on the third rank in relation to the hundreds of the dividend
|
ר"ל כמספר אשר זה התחתון לצד שמאל מהאחדים ר"ל כמספר אשר זה התחתון לצד שמאל מהאחדים שהרי המאות מדרגתם היא שלישית לצד שמאל מהאחדים וכן העשרות אלפים אשר ראוי לו לקחת מהם בקחת האחדים מהמאות כאשר זכרנו גם הם שלישיים לצד שמאל מהמאות אשר היא המדרגה אשר ממנה לקחו האחדים והקש על זה ובזה נכלל טעם כל המעשה
|
reason: check
|
וטעם הבחינה
|
| The reason for the checking procedure: multiplication is the inverse operation of division
|
כי הכפל הוא הפך החילוק
|
- The meaning of division: finding out how many times the small number is in the larger number
|
ר"ל שהחילוק הוא לידע כמה פעמים המספר הקטון במספר הגדול
|
- The meaning of multiplication: [finding out] how much is the sum of the multiples of a given number for a given number of times
|
והכפל הוא כמה סך כפלי מספר ידוע פעמים ידועים
|
|
|
וכן אם בחלקנו כ' לה' יעלה לכל אחד ד'
או לד' לכל אחד ה'
הנה כ' הוא כפל ד' בה' שהם המספר אשר חלקנו עליו והיוצא בחילוק
|
|
|
ואם חלקנו כ"א לד' כמה יעלה לכל אחד ה' וישאר א'
ולזה כאשר כפלנו ד' בה' ויעלה כ' הוספנו עליהם הא' הנשאר יעלה הכל כ"א שהוא כמספר המתחלק וכל זה ברור
|
| Finding the proper fraction of the remainder from division - reference to the section on fractions
|
וכאשר תרצה לחבר המעט הנשאר על המספר התחתון, שהוא גדול ממנו או שום אחד מספר קטן על מספר אחד גדול ממנו תמצא בחלק הב' בפרק הא' במאמ' האחדות אשר בו דרך כולל לכל המספרים בין יהיו להם מורים בין אם יהיו פשוטים
|
divisibility of a number
|
|
| To give you an inclusive method for dividing a large number by a smaller number and vice versa, I use the technique of the ancients: to extract the denominators of the number by which you want to divide, whether it is the smaller number or the greater number; that is to consider the numbers of which it is composed, if it is not a prime number.
|
אכן לתת לך דרך כולל בין לחלק רב למעט או בהפך דרכתי דרך הראשונים והוא שתוציא המורים מהחשבון אשר תרצה לחלק עליו אם מועט אם הרבה והוא ל[ראו'] המספרים אשר הוא מורכב מהם אם איננו פשוט
|
3; 6; 9
|
|
| First, if you want to know if it has a third, a sixth, or a ninth [= if 3, 6, or 9 are divisors of the number]:
|
ראשונה אם תרצה לדעת אם יש לו שלישית או שישית או תשיעית מבלי שברים
|
- six: See, if the first digit that is in the first rank is an odd number, then you know that the number does not have a sixth [= not divisible by 6].
|
עיין אם האות הראשונה אשר במעלה הא' מהחשבון הוא נפרד תדע שאין לו שישית
|
- If it is an even number, know that if it has a third [= divisible by 3], it has also a sixth [= divisible by 6], otherwise it has not.
|
ואם הוא סזוג [אז] דע שאם יהיה לו שלישית יהיה לו ג"כ שישית ואם לאו לאו
|
- nine and three: Every [number] that it has a ninth [= divisible by 9], has also a third [= divisible by 3], but not vice versa.
|
וכל שיש לו תשיעית יש לו ג"כ שלישית ולא יתהפך
|
- To know if a number has a ninth or a third, consider all the digits of the number as if they are of the first rank, i.e. sum them as units and cast out the nines from this sum
|
ולדעת אם יש למספר תשיעית או שלישית הבט כל רשמי מספרי החשבון כאלו היו כולם מהמעלה הראשונה ר"ל שתחברם כלם כאלו היו אחדים וחסר כל ט' ט' שבחבור ההוא
|
- No remainder - If it is consumed by the nines, know that it has a ninth [= divisible by 9] and it certainly has a third [= divisible by 3].
|
ואם יצא כולו תשיעיות תדע שיש לו תשיעית וכ"ש שלישית
|
- The reminder is 6 or 3 - if 6 or 3 remains, it has a third [= divisible by 3], but it does not have a ninth [not divisible by 9].
|
ואם ישארו ו' או ג' יהיה לו שלישית לא תשיעית
|
- The reminder is a number other than 3 - if another number remains, such as 4 or 5 and the like, it does not even have third [= not divisible by 3].
|
ואם ישאר מספר אחר כמו ד' או ה' או הדומה להם אין לו אפי' שלישי'
|
| Reasons
|
|
- The reason that we consider all the digits of the number as units, without considering their ranks, is that every [unit of] a certain rank is ten [units of] the preceding rank, therefore when subtracting nine from the ten [of a certain rank] the remainder belongs to the preceding rank, and so on repeatedly. We find that after casting out the nines [their ranks] are the same.
|
הטעם מה שא[נו] לוקחים כל רשמי המספרים לאחדים בלי עיון אל מעלותיהן הוא לפי שכל מעלה היא עשר בערך אל אשר לפניה בהסר מהעשרה תשע ישאר כמותה וכן כולם
נמצא שלאחר הסרת התשיעיות כלם שוים
|
- We say that if the first digit is an odd number, it does not have a sixth [= 6 is not a divisor of the number], since the whole number is odd, and an odd number is indivisible by an even number, i.e. it is not a product of an even number multiplied by an odd number and all the more so by an even number.
|
ואמרנו שאם הרושם הראשון הוא מספר נפרד שאין לו שישית הוא לפי שכל החשבון בכללו הוא נפרד שאין לו שישית הוא לפי שכל החשבון בכללו הוא נפרד והחשבון הנפרד לא נחלק לשלמים אל חשבון זוג ר"ל שאינו מורכב מחשבון זוג אפי' עם הנפרד כ"ש עם הזוג
|
- We say that if it is an even number that has a third [= divisible by three], it has also a sixth [= divisible by six], since the whole number that consists of an even number multiplied by 3 is an even number. For if it were an odd number, it were a product of an odd number by an odd number, but as the number that consists of the 3 is even, it is divisible by double the 3, i.e. by six, so it has a sixth.
|
ואמרנו שאם הוא זוג שאם יש לו שלישית יש לו ג"כ שישית הוא לפי שמאחר שהחשבון בכללו זוג מספר כפלי הג' ג' אשר בו הוא זוג שאם היה נפרד הנה היה מורכב מנפרד בנפרד והיה כולו בנפרד ואחר שהחשבון אשר בו הג' ג' הוא זוג א"כ הוא נחלק לזוגי ג' ר"ל לששה ששה והנה יש לו שישית על השלימות וזה מבואר
|
2; 4; 8
|
|
| To find out if a given number has a half, a quarter, or an eighth [= if 2, 4, or 8 are divisors of a the number]
|
ואם תרצה לדעת אם יש לו מחצית, או רביעית, או שמינית
|
| Considering its units:
|
ראה הרושם הראשון
|
| If it is an odd number, it does not have a half, a quarter or an eighth [not divisible by 2, 4, or 8] - from the same reason mentioned above concerning the sixth [= 6 as a divisor]
|
אם הוא חשבון נפרד, הנה אין לו אח' מהם, מהטעם שאמרנו בשישית
|
- two: if it is an even number or 0 - then the whole number is even, for the tens and up are even - therefore it has a half [= divisible by 2]
|
ואם הוא זוג, או 0', הרי כל החשבון בכללו זוג, כי העשרות ומהם ולמ[ע]לה כלם זוג אחדים וא"כ בידוע שיש לו מחצית
|
- four and eight: if it is an even number or 0
|
ולדעת אם יש לו ג"כ רביעית ושמינית
|
The digits of the whole number are summed according to the following procedure:
- for a number of the type
![\scriptstyle2a+10b+\left[100\sdot\left(2c-1\right)\right]](/mediawiki/images/math/8/b/e/8bee57b5ad3455a444ccbebe707bbcec.png)
- → the sum is
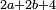
- for a number of the type
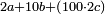
- → the sum is
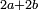
|
קח המספר אשר במעלה הראשונה כמו שהוא ואשר בשנייה כפול, אם יש שם מספר ואשר בשלישי', אם הוא נפרד, קח בעבורו ד' אחדים
ואם הוא זוג, או 0, לא תקח בעבורו מאומה וכן מהמעלה השלישית ולמעלה לא תקח דבר
|
- Considering the remainder after casting out eights from this sum
|
וחבר כל אשר לקחת והשלך אותו ח' ח'
|
- No remainder - the number has an eighth and a quarter [= divisible by 8 and 4]
|
ואם יצא הכל, הנה יש לו שמינית ורביעית
|
- The remainder is 4 - the number has a quarter [= divisible by 4]
|
ואם ישאר [ארבעה] יש לו רביעית לבד
|
- The remainder is a number other than 4 - the number does not have an eighth or a quarter [=not divisible by 4 or 8]
|
ואם ישאר חשבון אחר, אין לו לא שמינית ולא רביעית
|
| The reason for doubling the digit of the tens in the sum: when extracting eight from each ten the remainder is two
|
וטעם אומרנו שנקח אשר במעלה השנית כפול, הוא לפי שהם עשרות ומכל עשר, כאשר תסיר ח', ישארו ב', הרי שישאר לנו מכל עשר שנים, לכן אנו כופלים כל העשרות ולכך אנו לוקחים אותם כפולות
|
| The reason for not taking any digit for an even number of hundreds in the sum: every even number of hundreds is divisible by 8 (for example: 200÷8=25)
|
ואשר במעלה השלישית הם מאות וכל זוגי מאות יש להם שמינית, כי שמינית מאתים הוא כ"ה, לכן לא נקח בעבור זוגי המאות דבר
|
| The reason for taking 4 for an odd number of hundreds in the sum: when extracting eights from one hundred the remainder is four - 100-(12·8)=100-96=4
|
אך אם יש שם מאה נפרד, אחר הסרת זוגי המאות, נקח בעבורו ד', כי בהסיר שמיניות המאה, שהם י"ב שמיניות, שהם עולים לצ"ו, ישארו ד'
|
| No need to take any thing for the ranks that are higher than the hundreds - because all of them are an even number of hundreds and therefore are divisible by 8
|
ומהמעלה השלישית ולמעלה לא תקח דבר, כי כלם הם זוגי מאות ויש להם שמינית כמו שביארנו
|
7
|
|
| To find out if a given number has a seventh [= if 7 is a divisor of a given number]
|
ואם תרצה לדעת אם יש לו שביעית
|
| Considering the final remainder from the following procedure: multiplying the leftmost digit of the number by 3, adding the product to the digit in the preceding rank on the right and casting out sevens from the sum. Multiplying the remainder by 3, adding the product to the preceding rank on the right and casting out sevens from the sum, and so on repeatedly
|
ראה הרושם האחרון אשר לצד שמאל וכפלהו בג' וחברהו לאשר תמצא במעלה לאשר לפניה והסר לעולם השביעיות והנשאר כפלהו בג' וחברהו עם אשר תמצא אשר לפניה ואם לא תמצא שם מספר כי אם 0', כפלהו פעם שנית בג' וכן על כל 0' וחברהו עם אשר תמצא לפניו והשלך לעולם הז' ז'
|
- If there is no remainder - the number has a seventh [= divisible by 7]
|
ואם יצא הכל לשביעיות, הרי ידענו שיש לו שביעית
|
|
ואם לאו לאו
|
| The reason for multiplying each rank by 3 and adding the product to the preceding rank: [the unit of] every rank is ten [units of] the preceding rank and when subtracting 7 from 10 the remainder is 3. Therefore, each unit is valued 3 in the preceding rank after subtracting 7 from it
|
הטעם מה שאנו כופלים כל מעלה בג' לחברו לאש' לפניה, הוא לפי שכל מעלה היא עשר בערך אשר לפניה ובהסר מהם הז' [ישארו ג', הנה כל אחד הוא כשלש בערך אשר לפניו, אחרי הסרת הז']
|
5; 10
|
|
| To find out if a given number has a tenth, or a fifth [= if 10, or 5 are divisors of a given number]
|
ואם תרצה לדעת אם יש לו עשירית, או חמישית
|
- If the digit of the units is zero - the whole number is tens and therefore it has a tenth and a fifth [= divisible by 10 and 5]
|
אם הרושם הראשון הוא 0, הנה הכל עשרות, [כי אם המאות ומשם ולמעלה הכל הוא עשרות] והנה יש לו עשירית גם חמישית
|
- If the digit of the units is 5 - the number has a fifth [= divisible by 5]
|
ואם הוא ה', הנה יש לו חמישית לבד
|
- If the digit of the units is other than 0 or 5 - it does not have a fifth [= not divisible by 5]
|
ואם הוא מספר אחר גם חמישית אין לו
|
11
|
|
| To find out if a given number has 11th [= if 11 is a divisor of a given number]
|
ואם תרצה לדעת אם יש לו י"א
|
| Meaning: completely divisible by 11 - no remainder is left when casting out by elevens
|
פי' אם יתחלק לי"א על השלימות והוא שיושלך כלו י"א י"א ולא ישאר דבר וכיוצא בזה הוא מה שאמרנו בכל המורים העוברים
|
| Subtracting the numeral in the highest rank of the given number from the numeral in the previous rank, then subtracting the remainder from the preceding numeral and so on repeatedly
|
ראה הרושם האחרון והוצא ה1' מאשר תמצא במעלה אשר לפניו והנשאר הוציאנו מה שתמצא מאשר לפני פניו וכן עד הגיעו לראש
|
- If there is no remainder - the number has an 11th [= divisible by 11]
|
ואם יצא הכל, יש לו י"א י"א
|
|
ואם לאו לאו
|
| If one of the numerals is a zero or if it is smaller than the subtrahend, 11 is added to this numeral and the procedure continues as described
|
ואם בשום מקום תמצא סיפרא, או שום מספר קטן במנין, שלא תוכל להוציא ממנו אשר צוויתיך, הוסיף י"א על הנמצא שם סיפרא 0, וכן או שמונה חשבון קטן ומהכל תוציא אשר ציויתיך והנשאר מאשר לפניו, כן לעולם
|
| The reason for the procedure: every rank is ten times the preceding rank, therefore when taken with the preceding rank these are tens and units
|
הטעם כי כל מספר הוא עשרה בערך במעלה אשר לפניו, לכן כאשר תקחנו לעשרות ואשר לפניו לאחדים זה בזה, הרי כל מה שלקחת הם י"א י"א
|
| The reason for adding 11 to a small number is that 11 will be extracted anyway in this procedure
|
ואשר הוא לפי אמרנו ולהוסיף אות י"א באשר לפניו, כאשר לא תמצא שם די מחסורו, הוא לפי שאם נוסיף כמה י"א י"א בחשבוננו, לא יעלה ולא יוריד, כי הוא בעצמו יושלך לי"א י"א, ר ג"כ יצא אחר התוספת ואם לאו לאו וזה מבואר
|
13
|
|
| To find out if a given number has 13th [= if 13 is a divisor of a given number]
|
ואם תרצה לדעת אם יש לו י"ג
|
| Multiplying the leftmost digit of the number by 3, casting out thirteens from the product, subtracting the remainder from the preceding rank then multiplying the result of subtraction by 3 again and so on
|
ראה הרושם האחרון וכפלהו בג' והוצא הי"ג י"ג אשר בו והנשאר הוציאהו מאשר תמצא במעלה אשר לפניו והנשאר כפלהו שנית בג' והוצא הי"ג אשר בו והנשאר כפלהו שנית בג' והוצא הג' אשר בו והנשאר הוציאהו מאשר לפניו וכן לעולם עד תכליתם
|
- If there is no remainder - the number has a 13th [= divisible by 13]
|
ואם יצא הכל יש לו י"ג
|
|
ואם לאו לאו
|
| If there is a small number in one of the ranks so that 13 cannot be extracted in the above procedure: 13 should be add to the preceding rank then the small number should be subtracted from the sum and the procedure can continue
|
וכאשר יחסר בשום פנים מעלה, שלא תמצא די להוציא אשר ציויתיך, הוסף י"ג והוצא [מהמתחבר אשר עליך להוציא והנשאר כפלהו בג' והוצא] הי"ג י"ג והנ' הוציאהו מאשר לפניו וכן לעולם
|
| The reason for the procedure: every number is ten times its value in the preceding rank, so for each 13 subtracted - the 3 units are subtracted from the preceding rank
|
הטעם כי כל מספ' הוא עשרה כערך אשר במעלה הקודמת וכאשר תסירנו ותסיר ג' שכמותו מהמעלה הקודמת שהי' לה לאחדים, הרי כל אשר הוצאת הוא עשרות וג' ואחדים על כל עשר, מספר הנה כל מספר הוא י"ג י"ג
|
| Adding 13 to a small number will not harm the procedure for the same reason noted above regarding 11
|
גם התוספת אש' ציויתיך להוסיף מהי"ג לא יזיק בהוצאת הי"ג, כאשר הזכרנו בהוספת הי"א בהמצאת מורה הי"א וזה מבואר
|
general rules
|
|
- If the numbers 2-11, 13 are not [divisors] of a given number - any [divisor] of the given number is not divisible by these numbers
|
והמספר אשר לא תמצא לו אחד מהמורים הנזכרים ותרצה לידע אם יש לו מורה אחר המורה הזה, אשר תבקש הוא שלא יהיה לו שום מורה מהמורים
|
- The reason: if one of these numbers was a [divisor] of the [divisor], then this [divisor] could not have been a [divisor] of the given number, for if it were a [divisor] of the given number then its own [divisor] should have been the [divisor] of the given number also
|
הטעם שאם היה לו שום מורה מהם, בידוע שאינו מורה לזה החשבון, שאם הוא מורה לזה החשבון, הנה לחשבון ג"כ יש לו המורה אשר לזה המורה ואתה לא מצאתו
|
- 21 is a [divisor] → 7 and 3 are also [divisors]
|
המשל אם יקח כ"א, הנה אם כ"א הוא מורה לחשבון, הנה יש לחשבון מורי זה המורה, ר"ל שביעית ושלישית וכבר ידעת שאין לחשבונך אחד מהם, לכן לא יהיה לו כ"א
|
- If 1; 2; 3; …; n-1 are not [divisors] of a given number a, and a<n2 - then n is not a [divisor] of a
|
גם אם מספר אשר בקשת לו כל המורים העוברים זה אחר זה ולא מצאתם, אם הוא פחות ממרובע המורה הסמוך אשר תרצה לבקש, אינך צריך לבקשו, כי איננו לו מורה אם לא מורה אחר בעולם, כי בידוע שהוא מספר פשוט
|
- The reason: if n is a [divisor] of a and a<n2, then there is b<n, so that a=b·n, but b cannot be a [divisor] of a according to the condition that 1; 2; 3; …; n-1 are not [divisors] of a → contradiction
|
הטעם שאם היה לו זה המורה הפשוט הסמוך אשר אתה מבקש ואין צריך לומר אחר גדול ממנו, הנה להיות חשבונך פחות ממרובעו, הנה הפעמים אשר יהיה בו המורה ההוא יהיה מספרם פחות ממספר המורה בעצמו וגם מספר הפעמים יהיה לו למורה, כי כל דבר הנחלק למספר מה ויצא בחילוק מספר מה ולא נשאר דבר, הנה שניהם לו מורים, כי כאשר יתחלק לאשר יוצא עתה בחילוק, יצא בחלוק אשר נחלקו עליו עתה ולא ישאר דבר ואולם להיות מספר פעמים אלו פחות ממספר מורה המבוקש, הלא הם כאחד המורים הקודמים וא"כ היה לו אחד מהמורים הקודמים ואתה לא מצאתם הרי זה שקר
|
- 1; 2; 3; …; 16 are not [divisors] of a → if a is divided by 17, 17 times or more, then a≥172 = 289; and if it is divided by 17, 16 times or less, then one of the numbers smaller than 17 is a [divisor] of a → contradiction
|
המשל אם בקשת עד י"ז ולא מצאת ותרצה לבקש אם יש לו י"ז ומספרך שהוא פחות מרפ"ט, שהוא ממרובע י"ז, הנה בידוע שאם היה יוצא לי"ז י"ז, שהפעמים אשר בו י"ז י"ז הם פחות מי"ז, שאם היו י"ז לא או יותר, הרי חשבונך היה כמרובע י"ז, או גדול ממנו והוא קטן
ואם הפעמים האלה אשר י"ז בו הם פחות מי"ז, המשל י"ו ומשם ולמטה, הנה היה לו רביעית, או אחד מהמורים הקודמים, שהרי יתחלק למספר פעמים אלו ג"כ ויצא בחילוף הי"ז וזה שקר, שהרי לא מצאת לו אחד מהעוברים
|
- If 1; 2; 3; …; n-1 are not [divisors] of a given number a, and a≥n2
|
ואולם כאשר יהיה חשבונך כמרובע המורה הנמשך אשר תבקש, או גדול ממנו ותרצה לדעת אם תמצא לו זה המורה הסמוך
|
- If there is an integer m, so that a÷n=m → then n and m are [divisors] of a
|
ואם יתחלק אליו לשלימים מבלי שארית הוא לו למורה צדק גם היוצא בחילוק
|
- Otherwise - n is not a [divisor] of a
|
ואם לאו לאו
|
Repetitive division of a number by its [divisors]
|
|
- Dividing a number by a known [divisor] and receiving an integer as a result
|
וכאשר ידעת שיש לו שום מורה, חלק המספר כולו לזה המורה ותחלק אליו לשלימים והיוצא בחילוק
|
- The [divisor] and the result of the division are both [divisors] of the number
|
ואם לא תרצה לבקש יותר, הנה אלו השני מספרים, ר"ל המורה אשר חלקת עליו והיוצא בחילוק הם הם מוריו
|
- Dividing the result of division by its [divisor] - this [divisor] must be also a [divisor] of the given number itself
|
אכן אם היוצא בחילוק הוא חשבון גדול ותרצה לבקש לו מורה ג"כ, עשה כדרכים הנזכרים
|
|
|
ואולם דע שהמורים אשר לא מצאת לחשבון הגדול, לא תמצאם ג"כ לזה היוצא בחילוק וזה ברור ואין לך לבקש אחד מהם כי אם הדומה לאשר מצאת, או למעלה ממנו, אם מצאת לו מורה, חלקנו עליו והיוצא בחילוק יהיה מורה שלישי
|
- Dividing the second result of division by its divisor, and so on
|
ואם זה ג"כ גדול ותרצה לבקש לו ג"כ מורה אחר, עשה כנזכר וחלקנו על המורה אשר ידעת אשר הוא למורה לו והיוצא בחילוק יהיה לו למורה רביעי
|
|
|
ואם תרצה תוכל ל[...] לבקש עוד חמישי, או שישי, או זולתם
|
|
|
המשל רצינו לחלק 2447235 על 50335084800
|
- Are 3, 6, 9 [divisors] of 50335084800?
|
נוציא [....] המורים לזה החשבון הגדול אשר רצינו לחלק עליו ונראה ראשונה אם יש לו ג', או ששה, או ט'
|
- the first digit is 0 → if 3 or 9 are [divisors] of 50335084800 then 6 is also its [divisor]
|
ואחר שהרושם הראשון הוא 0, ידענו שאם יש לו ג', או ט', יש לו ג"כ ששה
|
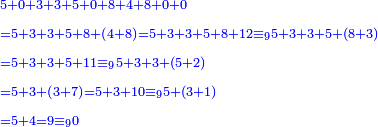
|
ולדעת אם יש לו ג', או ט', נחברם כלם כאלו הם אחדים
ונאמ' ח' עם ד' הם י"ב, נוציא מהם הט' ישארו [.] ג'
ועם 8 הם י"א, נסיר הט', ישארו ב'
ועם ה' יהיו ז' ועם הג' יהיו עשרה, נסיר ט', ישארו א'
ועם הג' יהיו ד' ועם הה' יהיו כולם ט' ט', הרי יצא החשבון לט' ט'
|
- →3, 6, 9 are [divisors] of 50335084800
|
וידענו שיש לו ט' וג', גם ו' לסבה שזכרנו ונקח מהם אשר תרצה
|
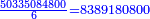
|
ועל דרך משל, נקח למורה ו' ונחלקנו על ו' ויצא בחלוקם 8389180800
|

- the first digit is 0
- →3, 6, 9 are [divisors] of 8389180800
|
ואחר שהיוצא בחילוק הוא חשבון גדול, נבקש לו מורה ונעשה לזה כאשר לחשבון הראשון ויצא הכל לט' ט'
ואחר שהרושם הראשון סיפרא
ויש לו ט', יש לו ג"כ ו' וכ"ש ג'
|
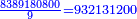
|
ונקח ט' למורה ונחלק זה החשבון לט' ויצא בחילו' 932131200
|
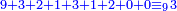
- the first digit is 0
- →3, 6 are [divisors] of 8389180800
|
ונעשה לזה כאשר עשינו לקודמים וישארו ג'
הנה יש לו ג'
ג"כ ו' להיות הראשונה סיפרא
|

|
ונקח למורה ג' ונחלקנו עליו ויצא בחילוקם 310710400
|
- Since 9 is not a [divisor] of 8389180800 → 3 is not a [divisor] of 310710400
|
ואחר שהקודם לא היה לו ט', בידוע שלזה אין לו אפי' ג'
הטעם לפי שזה שלישית הקודם ואם לזה היה לו שלישית הקודם ואם לזה היה לו שלישית, הנה שלישיתו, ר"ל שלישית זה שהיה שלישית הראשון, הוא לראשון שלישית שלישית, שהוא תשיעית ולא מצאנוהו
|
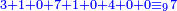
|
וכן הוא האמת, כאשר תחברם ותוציא הט' ט' ישארו ז'
|
- Are 2, 4, 8 [divisors] of 310710400?
|
ונעיין אם יש לו ב' וד', או ח'
|
- the first digit is 0 → 2 is a [divisor] of 310710400
|
ואחר שהראשון סיפרא, בידוע שיש לרוב לו ב'
|
- the first digit is 0; the second digit is 0; the third digit is an even number
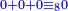
- → 4 and 8 are [divisors] of 310710400
|
ולדעת אם יש לו ד', או ח', היה לנו לקחת אשר [במעלה] הראשונה ולא מצאנו שם כי אם 0 ולא נקח דבר כי אם בשנית, היה לנו לכופלו ולא מצאנו שם כי אם 0, לא נקח דבר והשלישית אחר שהוא זוג, אין לנו לקחת בעבורה דבר ולא ממנה ולמעלה
הנה יש לו ח' וד' וב'
|
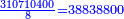
|
ונקח למורה אשר נחפוץ מהם, המשל ח' ונחלקנו לח' ויצא בחילוק 38838800
|
- the first digit is 0; the second digit is 0; the third digit is an even number
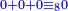
- → 4 and 8 are [divisors] of 38838800
|
ולזאת ג"כ יש לה שמינית ורביעית וחצי לסבה הנזכרת
|
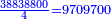
|
ונקח א' מהם, המשל ד' וחלקנו עליו ויצא בחילוק 9709700
|
- the first digit is 0; the second digit is 0; but the third digit is an odd number

- → only 2 and 4 are [divisors] of 9709700
|
ולזאת אין לה שמינית, כי הראשונה והשנית הם 0 ולא נקח בעבורם דבר והשלישית היא ז' שהוא נפרד ונקח בעבורו ד'
הנה שאין לו כי אם ד' וב'
|
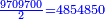
|
ונקח אחד מהם, המשל ב' ונחלקנו עליו ויצא בחילוק 4854850
|
- Since 8 is not a [divisor] of 9709700 → 4 is not a [divisor] of 4854850
|
מאחר שזו היא מחצית הראשונה, אין לנו רביעית, לפי שלא היה לראשונה שמינית, כי רביעית זו היא רביעית חצי הראשונה שהוא שמינית
|
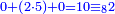
|
וכן תמצאנו בבחינה שאין לו רביעית, כי בראשונה אין מספר וכל השניה היא עשרה והשלישית היא זוג ולא נקח דבר בעבורה, הרי שאין בידינו כי אם עשר, נסיר ח', ישארו ב', הרי שאין לו כי אם חצי
|
- Are 5, 10 [divisors] of 4854850?
|
ואם לא תרצה לקחתו שנית למורה, [עיין] אם יש לו עשר, או ה'
|
- the first digit is 0
- → 5, 10 are [divisors] of 4854850
|
ואחר שהראשונה 0, בידוע שיש לו [עשר וגם] ה'
|
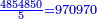
|
ונקח אחד מהם, המשל ה' ונחלקנו עליו ויצא בחילוק 970970
|
- the first digit is 0
- → 5, 10 are [divisors] of 970970
|
וגם זה, אחר שהראשונה 0, יש לה י', גם ה'
|
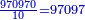
|
ונקח עד"מ העשרה ונחלקנו לי' ויצא בחילוק 97097
|
- the first digit is not 0
- → 5, 10 are not [divisors] of 97097
|
ואחר שהראשונה אינה לא ה' ולא 0, אין לו לא ה' ולא עשרה
|
- Is 7 [divisor] of 97097?
|
ונראה אם יש לו שביעית
|
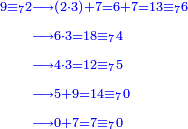
- → 7 is a [divisor] of 97097
|
ומהט' האחרון נסיר שבעה, ישארו שנים
ונכפלהו בג', יהיו ו' ונחברם לז' אשר לפניו, יהיו י"ג, נסיר הז', ישארו ו'
נכפלהו בג', יהיו י"ח, נסיר מהם י"ד, שני שביעיות, ישארו ד'
ואחר שבמעלה שלפני זאת אין שם חשבון כי אם 0, נכפול אלו הד' בג', יהיו י"ב, נסיר ז', ישארו חמשה
נחברם לט' שלפני זאת, יהיו י"ד והם שביעיות, גם הראשונה ז', הנה יצא הכל ז' ז'
הנה יש לו שביעית
|
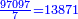
|
ונקחנו למורה ונחלקנו עליו ויצא בחילוק 13871
|
- Is 7 a [divisor] of 13871?
|
ונשוב לראות ונעיין אם יש לזה ג"כ ז'
|
- the remainder 4
- → 7 is not a [divisor] of 13871
|
ונמצא שישארו ד'
הנה אין לו ז'
|
- Is 11 a [divisor] of 13871?
|
ונראה אם יש לו י"א
|
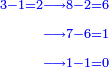
- → 11 is a [divisor] of 13871
|
ונחסר הא' האחרון מהג' שלפניו וישארו ב'
נסירם מהח' שלפניהם, ישארו ו'
נסירם מהז' שלפניהם, ישאר א'
נסירם מהא' שלפניו ולא ישאר דבר, הרי יש לו י"א
|
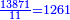
|
ונקחנו למורה ונחלקנו עליו ויצא בחילוק 1261
|
- Is 11 a [divisor] of 1261?
|
ונשוב לראות אם יש לו הי"א
|
- the remainder 7
- → 11 is not a [divisor] of 1261
|
ונמצא שישארו ז'
הנה אין לו י"א
|
- Is 13 a [divisor] of 1261?
|
ונעיין אם יש לו י"ג
|
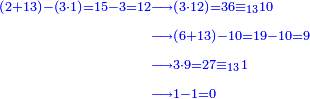
- → 13 is a [divisor] of 1261
|
ונכפול הא' אחרון בג' ולא נוכל להסירם מהב' שלפניהם, לכן נוסיף עליהם י"ג ויהיו ט"ו, נסיר הג', ישארו י"ב
ונכפלם בג' ויהיו ל"ו, נסיר כ"ו שהם י"ג י"ג, ישארו י'
[ולא נוכל להסירם מהו' שלפניהם ונוסיף עליהם י"ג ויהיה י"ט, נסיר מהם י', ישארו] ישארו ט'
נכפלם בג', יהיו כ"ז, נסיר כ"ו, ישאר א'
נסירנו מהא' הראשון ולא ישאר דבר
הרי יש לו י"ג
|
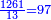
|
נקחנו למורה ונחלקנו עליו ויצא בחילוק 97
|
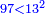
- the numbers 1-12 are not [divisors] of 97
- → 13 is not a [divisor] of 97
|
ואחר שזה החשבון הוא פחות ממרובע י"ג, אינך צריך לעיין עוד אם יש לו [הי"ג] י"ג וכ"ש מורה גדול ממנו ולא אחד מהקודמים, אשחר שלא נמצא לראשונים, לכן נקחנו בעצמו למורה
|
|
|
הנה יצאו לנו מורים לזה החשבון והחשבון הקטן אשר רצינו לחלק לזה החשבון הגדול היה 2447235 ונחלקנו לאלו המורים ונשימם זה אחר זה כרצוננו, כי זה לא יזיק, כי אין מוקדם ומאוחר במורים ותחלק כל החשבון למורה האחרון אשר לצד שמאל והנשאר שים תחתיו והיוצא בחילוק חלק לאשר לפניו וכן לעולם, עד אשר יכלה המספר ויגיע למקום שהיוצא בחילוק יהיה פחות מהמורה אשר לפניו, כי אז תשים זה היוצא תחת המורה הזה אשר לפניו וכבר כלית כל מלאכתך
|
|
|
ואם יכלו המורים והמספר לא יכלה וזה יקרה כאשר היה המספר המתחלק גדול מהמספר אשר רצינו לחלק עליו, אשר הורכב מהמורים ההם, פי' שיצאו ממנו המורים ההם, אז היוצא בחילוק בחלקך למורה הראשון תשימנו מבחוץ והם שלמים וכאשר עשינו זה המעש', ר"ל כשחלקנו מספרינו למורים אלו להיות המתחלק קטן מהמספר אשר רצינו לחלק עליו, אשר הוא [מע]ל המורים, יכלה המספר והמה לא יכלו
|

|
ויצא לנו כי כאשר נחלק 2447235 על 50335084800, שהיוצא בחילוק הוא ש[נ]י חמישיות חצי רביעית שמינית שלישית תשיעית שישית, פי' כי כאשר עשינו האח' השלם ו' חלקים וא' מאלו הו' ט' וא' מאלו ה[.] הט' ג' וא' מאלו הג' ח' וא' מהח' א' ד' וא מהד' ב' וא' מב' אלו חמשה, שיוצא לכל אחד מאחדי המספר הגדול אשר חלקנו עליו, שתי חלקים חלק זה מהחלקים האחרונים האלו ה[.....]
ועוד יצא בחלוקנו זה ה' עשיריות חלק זה פי'[ה'][עשיריות] ה[חמיש]ית חצי רביעית שמינית שלישית תשיעית שישית
ועוד שביעית עשירית חמישית חצי רביעית וכו'
ועוד ד' חלקים מי"א מז' מי' מה' וכו'
ועוד [ט' חלקים מי"ג מי"א מז' מי' מה' וכו'
ועוד כ"ב] כ"ב חלקים מצ"ז מי"ג מי"א מז' מי' מה' וכו'
|
|
|
| 97 |
13 |
11 |
7 |
10 |
5 |
2 |
4 |
8 |
3 |
9 |
6
|
| 22 |
9 |
4 |
1 |
5 |
2 |
|
|
| Receiving reduced fractions from the division operation - both the dividend and the divisor are divided by a common divisor
|
ואם תרצה שיצאו לך חלקים נאותים יותר, תעיין לעולם כאשר תחלק המספר למורים, אם למספר הזה יש שום אחד מהמורים ההם
|
|
|
המשל במספרינו וזה המתחלק שיש לו תשיעית ותשים המורה ההוא האחרון לצד שמאל ותחלק עליו ראשונה ולא ישאר דבר לשום תחתיו וגם ליוצא בחילוק נעיין אם יש לו א' מהמורים הנותרים ונשימנו לפני זה אשר חלקנו עליו ונחלק [עליו ולא ישאר [.] דבר
|
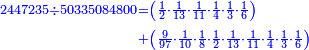
|
וכן נעשה לעולם בענין שיצא לנו בחלקינו זה] זה המספר הקטן הנזכר לגדול, שהיוצא לכל א' הוא חצי חלק מי"ג מי"א מד' מג' מו' ועוד ט' חלקים מצ"ז מי' מח' מחצי וכו' הכל כמו שהוא בצורה הזאת:
|
|
|
| 9 |
5 |
7 |
97 |
10 |
8 |
2 |
13 |
11 |
4 |
3 |
6
|
| |
9 |
|
|
1 |
|
|
| Both division procedures are correct - the division that is based on the divisors of the given number and ends with reduced fractions is more proper and therefore is called perfect beauty
|
ואלו שני המעשים הכל אחד, אלא שבמעשה השני חלקים יותר נאותים
ולחלוקה על המורים עליו השגחה זו נקרא לו כלילת יופי, לפי שהוא לעשות מהפרטים כללים יפים ונאותים
|
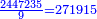
|
וכ[די להרחיב הענין ו]לבארו בפי' אמשול משל לחלוקנו זה והוא כי המספר המתחלק יש לו תשיעית, לכן שמנו הט' האחרון וחלקנוהו עליו ולא נשאר דבר, על כן לא שמנו תחתיו דבר ויצא לנו בחלוק 271915
|
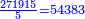
|
ויש לזה היוצא בחילוק חמישית, לכן שמנו הה' לפני הט' וחלקנו עליו ולא נשאר דבר ויצא [לזה] היוצא בחלוק 54383
|
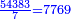
|
ויש לו שביעית, לכן שמנו מיד ל[פני] המורים הנזכרים הז' וחלקנוהו עליו ולא נשאר דבר ויצא בחילוק [7769]
|
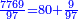
|
ואין לו שום אחד מהמורים הנותרים, לכן נשים אשר נרצה ושמנו היותר גדול והוא הצ"ז וחלקנו עליו ונשאר ט' ושמנוהו תחתיו ויצא בחילוק 80
|
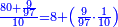
|
ויש לו עשירית לכן שמנו מיד ה10 וחלקנום עליו ולא נשאר דבר ויצא בחלוק ח'
|
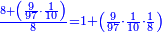
|
ויש לו שמינית, לכן שמנו מיד הח' וחלקנום עליו ולא נשאר דבר ויצא בחלוק
|
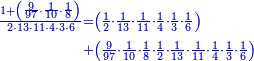
|
ואחר שהוא פחות משום אחד מהמורים הנותרים, אין לנו עוד לחלק, אבל נשימהו תחת המורה אשר נשים מיד לפני המושמים הנזכרים ושמנו הב' ושמנו תחתיו זה הא' אשר יצא באחרונה בחלוק ואחר שמנו המורים הנותרים כאשר הזדמן
|
| The general rule: dividing the dividend by the divisors of the given divisor [= the number by which the dividend should be divided]
|
הכלל העולה מהדברים הוא שכאשר נרצה לחלק שום מספר גדול, או קטן, על מספר אחר גדול ממנו, או קטן ממנו, שנוציא מורה המספר אשר רצינו לחלק עליו ונשים אותם כפי המזדמן זה אחר זה, או אם ירצה ישגיח בהנחתם, יען יצאו החלקים יותר נאותים כאשר ביארנו ונחלק המספר המתחלק על המורה האחרון אשר לצד שמאל והנשאר נשים תחתיו והיוצא נחלק לאשר לפניו וכן לעולם
|
- The dividend is smaller than the divisor
|
ואם היה המתחלק קטן מאשר חלקנו עליו, יכלה המספר והמה לא יכלו
|
|
|
וכאשר יכלה, יהיה היוצא בחילוק פחות מהמורה אשר לפני המורים אשר חלקנו כבר עליהם, לכן אין לנו לחלק זה היוצא המעט על זה המורה הרב ממנו, אבל שימהו תחתיו
|
- The dividend is larger than the divisor
|
ואם היה המספר המתחלק גדול מאשר רצינו לחלק עליו, יכלו המורים והמספר לא יכלה והיוצא מן החלוק האחרון [....] נשימהו חוץ לצורה והם השלמים אשר יצאו בחלוק ואשר בתוך הצורה תחת המורים הם השברים ושברי שברים, אשר יצאו בחלוק מוסף על השלימים הנזכרים
|
|
|
וכדי להרחיב הענין אעשה משל אחר, המשל רצינו לחלק 3123740520 על 216
|
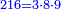
|
והנה מורה זה המספר הקטן, אשר רצינו לחלק עליו, הם אלו | 3 | 8 | 9
|
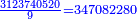
|
וחלקנו מספרינו זה הגדול על הט' ולא נשאר דבר ויצא בחילוק 347082280
|
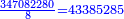
|
וחלקנום [על הח'] ולא נשאר דבר ויצא בחילוק 43385285
|
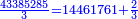
|
[וחלקנום על הג' ויצא לנו בחלוק הזה האחרון 14461761 והם] והם השלמים ונשארו ב' ושמנום תחת הג' והם השברים היוצאים בחילוק, הנוספים על השלמים
|
|
|
ואם גם עתה בזה החילוק האחרון לא היה נשאר דבר, לא היינו שמים תחתיו דבר וכיון שלא נמצא דבר תחת המורים, לא היו יוצאים בחילוק שברים כלל, כי אם השלמים לבד וזה יקרה כאשר החשבון אשר חלקנו עליו יהיה ראוי להיות מורה לחשבון המתחלה
|
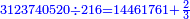
|
ואולם במשלנו זה אח' אשר נשארו בחלוק האחרון ב', יש לו ג"כ שברים ושמנום תחת הג' ויצא לנו כי כאשר חלקנו 3123740520 על 216 שיות עד שיגיע לכל אחד מהם 14461761 שלמים וב' שלישיות, כאשר בא בזאת הצורה
|
|
|
|
| Checking the extraction the divisors: multiplying them one by one
|
ואם רצית לבחון הוצאת המורים ההיתה כתקנה, כפול הראשון בשני והעולה בשלישי והעולה ברביעי וכן לכלם עד כלותם ואם יצא לך מזה החשבון המספר הראשון בלי תוספת ומגרעת, תדע שיצאו כתקנם ואם לאו לאו
|

|
המשל בצורה הנזכרת: אם רצינו לידע אם המורי' יצאו על היושר, נכפול ט' בח', יהיו ע"ב, נכפלים בג', יעלו 216 והנה כלו המורים ויצא החשבון בעל המורים בעינו
|
| Checking the division by the divisors: multiplying the result by the divisors
|
ואם תרצה לידע אם חלקת המספר על המורים על היוש'
|
- There are integers in the final result
|
אם יש שם שלמים כפול השלמים במורה הא' ההוא וכל המקובץ כפלהו במורה השני והוסף על העולה אשר תמצא תחתיו וכפול הכל על המורה [..] השלישי והוסף עליו אשר תמצא תחתיו וכן תעשה לעולם עד כלותם ואם ככלות המורים יצא לנו המספר המתחלק, הלא מעשיך אמת ויציב ואם לאו לאו
|
- There are no integers in the final result
|
ואם אין שם שלמים, קח אשר תמצא ראשונה תחת המורה הקודם אשר תמצא תחתיו דבר וכפלהו במורה הסמוך לו לצד שמאל וחבר הנמצא תחתיו עם העולה וכפול הכל על המורה הנמשך הנמשך והוסף אשר תחתיו וכן לעולם עד כלותם ואם אז יצא החשבון המתחלק בעינו, הנה [נכון] ואם לאו לאו
|
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left(14461761+\frac{2}{3}\right)\sdot3\sdot8\sdot9&\scriptstyle=\left[\left(14461761\sdot3\right)+2\right]\sdot8\sdot9\\&\scriptstyle=\left(43385283+2\right)\sdot8\sdot9\\&\scriptstyle=43385285\sdot8\sdot9\\&\scriptstyle=347082280\sdot9=3123740520\\\end{align}}}](/mediawiki/images/math/a/7/b/a7bae6e6f9c8c1a40897743e0bc1e090.png)
|
ונכפול השלמים בג' שהוא המורה הראשון ויעלה 43385283
נחבר לזה הב' אשר תחת המורה הזה ויעלה הכל 43385285
נכפלם על הח' שהוא המורה השני ויעלה 347082280
ואחר שלא נמצא תחת זה המורה דבר, לא נוסיף עליהם דבר
ונשוב ונכפלם בט' שהוא המורה השלישי ויצא לנו החשבון המתחלק בעינו שהוא 3123740520
|
|
|
עוד אמשול זה בדרך קצרה בצורה הקודמת לזאת, אשר אין שם שלמים ביוצא בחילוק כי אם שברים לבד:
|
|
|
המשל בתמונה זו
|
|
|
| 9 |
5 |
7 |
97 |
10 |
8 |
2 |
13 |
11 |
4 |
3 |
6
|
| |
9 |
|
1 |
|
|
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\left[\left(\frac{1}{2}\sdot\frac{1}{13}\sdot\frac{1}{11}\sdot\frac{1}{4}\sdot\frac{1}{3}\sdot\frac{1}{6}\right)+\left(\frac{9}{97}\sdot\frac{1}{10}\sdot\frac{1}{8}\sdot\frac{1}{2}\sdot\frac{1}{13}\sdot\frac{1}{11}\sdot\frac{1}{4}\sdot\frac{1}{3}\sdot\frac{1}{6}\right)\right]\sdot50335084800\\&\scriptstyle=\left[\left(1\sdot8\sdot10\sdot97\right)+9\right]\sdot7\sdot5\sdot9\\&\scriptstyle=\left[\left(8\sdot10\sdot97\right)+9\right]\sdot7\sdot5\sdot9\\&\scriptstyle=\left[\left(80\sdot97\right)+9\right]\sdot7\sdot5\sdot9\\&\scriptstyle=\left(7760+9\right)\sdot7\sdot5\sdot9\\&\scriptstyle=7769\sdot7\sdot5\sdot9\\&\scriptstyle=54383\sdot5\sdot9\\&\scriptstyle=271915\sdot9=2447235\\\end{align}}}](/mediawiki/images/math/a/d/b/adb9721e698eac41a3204cb448b3301f.png)
|
ונקח הראשון אשר תחת הב' שהוא המורה הראשון אשר נמצא תחתיו דבר ונכפלהו בח' שהוא המורה הסמוך ויעלה ח' ואחר שאין תחתיו דבר, לא נוסיף עליהם דבר ונכפלם בי' שהוא המורה הסמוך ויעלה פ' ואחר שלא נמצא תחתיו דבר, נשוב ונכפלם בלי תוספת על הצד שהוא המורה הסמוך ויעלה 7760, נחבר אליהם הט' אשר תמצא תחתיו ויעלה 7769 ונכפלם בז' ויעלה 54383 ונשוב ונכפלם בה' ויעלה 271915 ונכפלם בט' שהוא המורה האחרון ויצא לנו החשבון המתחלק בעינו והוא 2447235 והנה [נכון הנה אמת]
|
| The reason for dividing the dividend by the divisors of the divisor: since the divisor by which the dividend should be divided is a product of all its divisors
|
[וטעם הוצאת המורים וחלקנו עליהם המספר כנזכר הוא כי אחר שהמספר] עליהם המספר כנזכר הוא כי אחר שהמספר אשר רצינו לחלק עליו הוא מורכב מאלו המורים כמוהו כמוהם
|
|
|
ר"ל כי מי שיחלק א' על מאה עד"מ, הנה יגיע ממנו לכל א' מהמאה חלק עליו ממאה שבו, פי' שנעשה הא' השלם אשר רצינו לחלק [מאה חלקים שוים ויגיע לכל א' מהמאה אשר רצינו לחלק עליהם] עליהם הא' הראשון חלק א' מהם
|
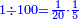
|
ואחר שחשבון הק' אשר רצינו לחלק [עליהם] הא' חלק א' מהם ואחר שחשבון יש לו חמישית וחמישיתו הוא כ', נמצא שכל א' מהמאה הוא חלק א' מכ' מחמישית שבמאה וכאשר נעשה א' שלם ק' אקלימים חלקים, הנה כל אחד מהם הוא חלק אחד מק' שבשלם שבשלם וגם הוא חלק א' מעשרים מחמישית השלם, הרי שאמרנו חלק א' מק' שבשלם כאומרנו חלק אחד מכ' מחמישית שבשלם
|
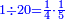
|
ולסבה זו בעינה יהיה אומרנו רביעית חמישית כאומרנו חלק א' מכ', לפי שעשרים יש לו חמישית וחמישיתו ד', נמצא שעשרים מורכב מה' וד' ושהאחד הוא חמישית רביעית, או רביעית חמישית, כי הכל א', הרי לנו ש שאמרנו רביעית חמישית כאומרנו חלק א' מכ' שבשלם
|
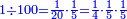
|
[ואולם אמרנו חלק אחד מכ' מה' שבשלם הוא כאמרנו חלק א' מק' שבשלם כאשר] כאשר ביארנו, הנה יצא לנו שאומרנו רביעית חמישית חמישית הוא כאומרנו חלק א' מק' שבשלם
|
|
|
ובדמיון זה בכל חשבון מורכב ממורים כמה שיהיו
|
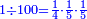
|
ואם כאשר חלקנו א' שלם לק', הגיע לכל א' מהם חלק אחד מק' שבשלם, שהוא רביעית חמישית החמישית
|
|
|
ואם חלקנו על ק' ב' שלמים
|
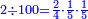
|
יגיע לכל א' ב' רביעיות חמישיות חמישית
|
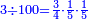
|
ואם ג' ג'
|
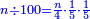
|
הרי [הרי] כי מספר השלמים אשר נחלק אל ק' מספר הרביעיות חמישיות חמישית שיגיעו לכל אחד מהם וזה ברור
|
|
|
ולזה אם רצינו לחלק ע' על ק'
|
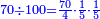
|
ידענו שיגיע לכל אחד מהם ע' רביעיות חמישיות חמישית והרי הוא כאלו שמנו המורים כזה הסדר, ושמנו הע' רביעיות תחת המורה האחרון:
|
|
|
|
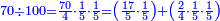
|
ואחר שיש בידיך 70 רביעיות חמשיות חמשית, אם בקשנו לדעת כמה חמשיות חמישית הם, הרי הוא כאלו היו בידינו ע' רביעיות ורצינו לדעת כמה שלמים הם וזה יודע בחלקנו אותם לד', לפי שכל ד' רביעיות הם א' שלם וכן כל ד' רביעיות חמישית [חמישית חמישית הם חמישית חמישית שלם, לכן נחלק אלו הע' רביעיות חמישית] חמישית והנשאר יהיה מהמין הראשון, ר"ל רביעיות חמישיות חמישית ולזה ראוי לנו לשים היוצא בחלוק, שהוא י"ז, תחת הה' אשר הוא המורה אשר לפניו והנשאר שהוא תחת הד' שהוא המורה אשר לפניו והנשאר, שהוא ב', תחת הד' שהוא המורה האחרון אשר חלקנו עליו כזה:
הנה ידענו כי כאשר חלקנו ע' על ק', שהגיע לכל אחד מהם י"ז חמישיות חמישית וב' רביעיות חמשית חמישית
|
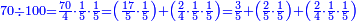
|
ואחר שיש בידינו י"ז חמישיות חמישית, ידענו שהם שלשה חמישיות שלמות ויותר, לפי שכל חמש חמשיות חמישית הם חמישית אחד, כמו שחמש חמשיות שלם הן שלם וראוי לנו לידע כמה חמישיות שלמות הן, לכן נחלקם על הה' ויצא לנו בחלוק ג', שהוא ג' חמישיות שלימות, לכן נשימם תחת הה' הראשון והב' השני והנשארים הם ממין במינם כבתחלה, ר"ל חמישיות חמישית, לכן שמנום תחת הה' השני כזה:
|
|
|
ואם אלו הג' אשר תחת המורה הראשון היה כמותו, או גדול ממנו, ר"ל שהיה ה' או יותר, היה העולה לשלם, או לשלימים, כי כל חמש חמשיות הן שלם אחד והיה ראוי לנו לחלק אותן על ה' והיוצא בחילוק היו שלימים והנשאר היה חמישיות כאשר בתחלה
|
|
|
אכן אחר שהוא קטן מהמורה, ר"ל שהוא פחות מה' שהוא המורה שהוא המורה הראשון, אין כאן שלם כלל ואין לנו לעשות שום חלוק, אבל כבר השגנו מבוקשנו והוא כי כאשר חלקנו ע' על ק', שהגיע לכל אחד מהם ג' חמישיות וב' חמישיות חמישית וב' רביעיות חמישית חמישית
|
|
|
הכלל העולה מאלו מהדברים שהמחלק ע' על ק' יגיע לכל אחד ע' חלקים מק' חלקים בשלם
|
Checking the extraction of the divisors

|
ואחר שמאה הוא מורכב מאלו השלשה מספרים, ר"ל מה' וה' וד' וזה כי כאשר כפלנו הא' בחבירו והעולה בנשאר, עולה ק', פי' כי כפל ה' בה' הוא כ"ה וכאשר כפלנום בד', יעלו ק' וזאת היא בחינת הוצאת המורים אשר הזכרנו למעלה, כי בכפול זה בזה והעולה באחר וכן לעולם עד כלותם ויצא לנו החשבון הראשון, ידענו שהחשבון ההוא מורכב מאלו ה[ב'] מספרים
|
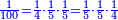
|
ואחר היות הק' מורכב מה' הד', כך הוא אומרנו חלק מק' שבשלם כאומרנו רביעית חמישית חמישית רביעית חמישית, או כאומרנו חמישית חמישית רביעית, כי הכל אחד
|
| The arrangement of the fractions of the division result can be changed - in order to receive proper reduced fractions
|
ומטעם אחר על זה אמרנו שבידינו לסדר המורים זה אחר זה כפי המזדמן, אם בהשגחה, כדי שיצאו השברים היותר שלמים שיוכל והיותר נאותים
|
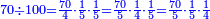
|
וזה כי כאשר אמרנו שהמחלק ע' על המאה יגיע לכל אחד ע' רביעיות חמישית חמישית, היינו יכולים לומר ע' חמשיות רביעית חמישית, או ע' חמישיות חמישית רביעית
|
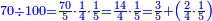
|
ואחר שבידינו לסדרם כחפצנו, ראוי לסדרם ולהשגיח בסדורו
וזה כי כאשר רצינו לחלק אלו הע' לאלו המורים, אחר שהעין יש לו חמישית שהוא א' מאלו המורים, ראוי לנו לחלקם ראשונה על הה' ונשימנו אחרון, כדי שלא ישאר דבר לשים תחתנו ויצא בחילוק י"ד
ואם היה להם רביעית, היה ראוי לחלקם על ד' ולשומו לפני האחרון
ואם היה לו ה' לה'
אכן שאין לו אחד מהם, נסדר אלו השני המורים הנשארים כפי המזדמן
וע'ד'מ' נחלק אלו היד לד' ונשימהו לפני האחרון ויצא בחילוק ג' ואחר שהוא פחות מהה' שהוא המורה האח', נשימהו תחתיו והב' הנשארים נשימם תחת הד' שהוא המורה השני [אשר] נחלקנו עליו כזה:
|
|
|
|
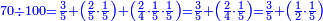
|
והנה יצאו לנו חלקים יותר נאותים, כי יותר נאות הוא לומר ג' חמישיות [ושני רביעיות חמישית], שהן חצי חמישית, כאשר בא בצורה הזאת, מאומרנו ג' חמישיות ושני חמישיות חמישית וב' רביעיות חמישית חמישית
|
| Check: converting the fractions
|
וידוע הוא כי בחינת זה הוא להשיבם כלם מהמין הראשון, ר"ל חמישיות רביעית חמישית, כפי צורה זו האחרונה, או רביעית חמישית חמישית, כפי הצורה הקודמת וזה יקרא פריטה כאשר יתבאר בחלק השני
|
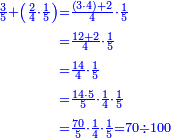
|
ואחר שיש לו חמישיות שלמות, גם רביעיות חמישית, נשיבם כלם ראשונה רביעיות חמישית
וידוע כי כל חמישית שלמה היא ד' רביעיותיה, פי' ד' רביעית חמישית, כמו שכל שלם ד' רביעיות שלם, הרי לנו כי כל אחד מאלו הג' חמישיות שלימות היא ד' רביעיות חמישית ולדעת כמה הם נכפול ג', שהוא מספר החמישיות, בד' שהוא המורה הבא אחריו ויעלה י"ב, הרי לנו שהג' חמישיות הם י"ב רביעיות חמישית
ומצאנו תחתיו שנים שהם מזה המין, פי' שהם רביעיות חמישיות, נחברם אליהם ויהיו י"ד רביעיות חמישית
וכאש' נרצה לדעת כמה חמישיות רביעית חמישית הם, נכפלם בה' שהוא המורה הבא אחריהם ויעלו כלם ע'
ואם תחת זה המורה היה נמצא דבר, זה היה ג"כ חמישיות רביעית חמישית והיינו מחברים אותם אליהם
אכן אחר שלא נמצא תחתיו דבר וכבר כלו המורים, כבר כלינו מעשינו
ואחר שעלה לחשבוננו הראשון, פי' לעין [ע'], שהוא החשבון הקטן אשר רצינו לחלק על הק' שהוא בעל אלו המורים מבלי תוספת ומגרעת, ידענו כי כל מעשינו בצדק ובמשפט
|
| Division of a large number by a smaller number, with a result of integers and fractions
|
הרי לנו מבוארים טעמי' כל הנזכר, גם המעשה, גם הבחינות וביאור הכל בכלל ובפרט
|
|
|
וכדי להתלמד, אביא משל אחר, שיהיה המתחלק על אלו הק' גדול מהם, כדי שיצאו שם שברים גם שלמים:
|
|
|
המשל רצינו לחלק ק"מ על ק'
|
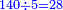
|
ואחר שאלו הק"מ, שהם החשבון אש' רצינו לחלק, יש לה כל אלו המורים, נשים אשר נחפוץ אחרון ונחלקנו עליו, המשל על הה' ויצא ושבא בחילוק כ"ח ולא נשאר דבר
|
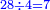
|
ואחר שיש להם רביעית, נחלקם על הד' ונשימנו לפני האחרון ויצא בחילוק ז'
|
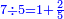
|
ואחר שהם כמורה הנשאר וגדול ממנו, נחלקם עליו ויצא בחילוק א', שהוא א' שלם, כי כבר שלמו המורים ונשימנו מחוץ והב' הנשארים נשימם תחתיו כזה:
|
|
|
|
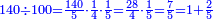
|
הרי לנו כי כאשר חלקנו ק"מ על ק', שעולה לכל 1 ואחד מהמאה ק"מ חלקים ממאה שבשלם, שהם ק"מ חמישיות רביעית חמישית, שהם כ"ח רביעיות חמישיות, שהם ז' חמישיות שלמות, שהם א' שלם וב' חמישיות
|
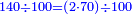
|
וכמו שזה החשבון המתחלק הזה כפל החשבון המתחלק ראשונה
|
![\scriptstyle{\color{blue}{1+\frac{2}{5}=\frac{7}{5}=2\sdot\left[\frac{3}{5}+\left(\frac{2}{4}\sdot\frac{1}{5}\right)\right]=2\sdot\left[\frac{3}{5}+\left(\frac{1}{2}\sdot\frac{1}{5}\right)\right]}}](/mediawiki/images/math/3/6/e/36eeba3351620eebf8c50f917db3a94e.png)
|
כן היוצא בחילוק, שהוא א' שלם וב' חמישיות, שהם ז' חמישיות, הוא כפל היוצא בחילוק ראשונה, שהיה ג' חמישיות וב' רביעיות חמישית פי' ג' חמישיות וב' רביעיות חמישית פי' שלשה חמישיות וחצי חמישית
|
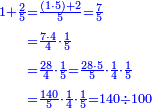
|
הנה כל המעשה ברור ומבורר, גם הבחינה והיא להשיב הכל לקדמותו וזה כי האחד נשיבהו חמשיות שלמות וזה בכופלנו אותו בה', שהוא המורה על החמישיות, ויהיו ה' ונחבר אליהם הב' הנמצא תחתיו שהם ג"כ חמישיות שלימות וזה בכפלנו אותו בה' שהוא המורה על החמישיות ויהיו ה' ונחבר אליהם הב' הנמצא תחתיו, שהם ג"כ חמשיות שלמות, [יהיו כלם ז' חמישיות שלמות]
וכאשר נרצה להשיבם רביעיות חמישית, נכפלם בד' ויהיו כ"ח רביעיות חמישית ואחר שלא נמצא תחתיו דבר, לא נחבר אליהם דבר
עוד נשיבם חמישיות רביעית חמישית וזה בכפלנו אותו בה' ויעלה ק"מ חמישיות רביעית חמישית והנה כלו המורים ואין תחתיו דבר לחבר על העולה
|
|
|
ויצא לנו כחשבוננו הראשון שוה בשוה וב[דרך זה] תעשה כפל המספרי' הנשארים, הן למעשה, הן לבחינה
|
|
|
Chapter Five: Proportions
|
הפרק הה'
|
Rule of Four
|
|
For the ratio that a known number has to [a known number], if you want to know for another known number, to which number it has this same ratio:
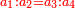
|
אם תרצה לדעת הערך שיש למספר ידוע למספר ידוע אחר אצל איזה מספר יש לו אותו הערך בעצמו
|
- For example, the ratio of 5, which number has the same ratio?

|
המשל הערך לה' אצל איזה מספר יש לו אותו הערך בעצמו
|
- Example: For the ratio that 5 is to 7, 10 is in the same ratio to which number?
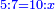
|
המשל הערך שיש לה' אצל ז' אצל מי יש לי' זה הערך
|
- Or, which number has the same ratio to 14?
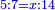
|
או אצל י"ד למי שיש לו זה הערך
|
| To understand it briefly I will give them an order:
|
וכדי להבינו בקוצר אשים להם סדר
|
When we say: the ratio that 5 is to 7 - the 5 is called "first" [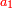 ] and the 7 [is called] "second" [ ] and the 7 [is called] "second" [ ], since the 5 is related to 7. ], since the 5 is related to 7.
|
והוא כי כאשר נאמ' הערך שיש לה' אצל ז' נקרא הה' ראשון והז' שני לפי שהה' הוא הנערך אצל ז'
|
- If you say: to which number does 10 has this ratio? What we relate to it is missing, which is the second of the others.
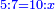
|
והנה אם תאמר אצל מי יש ערך זה לי' יחסר אשר אליו אנו מעריכים שהוא השני מהאחרים
|
- If we say: which number has this ratio to 14? the related is missing, which is the first of the others.
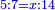
|
ואם נאמר למי יש זה הערך אצל י"ד יחסר הנערך שהוא הראשון מהאחרים
|
| This is the rule: the related of those that are first and of those that are last is called first, and that to which it is related, is called second.
|
זה הכלל כי לנערך הן מן הראשונים הן מן האחרונים נקרא ראשון ולאשר מעריך אצלו נקרא שני
|
- When you wish to know the unknown:
|
וכאשר תרצה לדעת הנעלם
|
- If you have the first of the two that are last, but the second of those that are last is unknown: we multiply the first [of those that are last] by the second of the first two that are known, then divide by that which remains of the three that are known, i.e. by the first of those that are first; the result of division is the unknown.
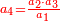
|
אם יש בידך הראשון מן השנים האחרונים ונעלם השני שבאחרונים נכפול אותו הראשון [בשני] מן השנים הראשונים הידועים וחלקנו לנשאר מהג' הידועים ר"ל לראשון שבראשונים והיוצא בחילוק הוא הנעלם
|
- If you have the second of those that are last, but the first is unknown: multiply the second [of those that are last], which is known, by the first of those that are first, then divide the product by the second of those that are first; and the result of division is the required unknown.
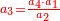
|
ואם היה בידך השני שבאחרונים ונעלם הראשון כפול אותו השני הידוע בראשון שבראשונים והעולה חלקהו לשני שבראשונים והיוצא בחילוק הוא הנעלם המבוקש
|
|
|
וכאשר תחלק העולה על השני שבראשונים או על הראשון אם תרצה תוציא המורים אם זה הראשון או השני אשר תחלק עליו הוא חשבון גדול והיוצא בין שלמים ושברים הוא המבוקש הנעלם
|
| This is the rule: always multiply the first of these by the second of the others and divide the product by what remains of those that are known; the result of division is the unknown.
|
זה הכלל לעולם תכפול הראשון מאלו בשני מאלו והעולה תחלק על הנשאר מהידועים והיוצא בחילוק הוא הנעלם
|
- Example: if we say: the ratio of 3 to 7 - 5 has this ratio to whom?
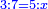
|
המשל אם אמרנו הערך שיש לג' אצל הז' לה' אצל מי יש לו זה הערך בעצמו
|
|
|
ונשימם לו על זה כזה
|
|
|
|
- We know the related of those that are last, which is called first, it is 5. We multiply it by the second of those that are first, which is 7; the result is 35. We divide it by what remains of those that are known, which is 3; the result of division is 11 integers and 2-thirds and this is the required unknown.
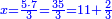
|
הנה ידענו הנערך שבאחרונים והוא הנקרא ראשון והוא הה' ונכפלנו בשני שבראשונים והוא הז' ויעלו ל"ה ונחלקנו לנשאר מהידועים והוא הג' ויצא בחילוק י"א שלמים [וב' שלישיות וזהו הנעלם המבוקש
|
- Meaning: the ratio that 3 is to 7 is that same ratio that 5 is to 11 and 2-thirds.
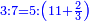
|
פי' כי הערך אשר לג' אצל הז' הוא הערך בעצמו אשר לה' אצל י"א וב' שלישיות] וב' שלישיות
|
- It is clear that as 7 is twice 3 plus its third, which is 1, so is 11 and 2-thirds twice 5 plus its third, which is 1 and 2-thirds.
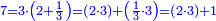 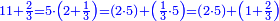
|
וזה ברור שכמו שז' הוא כפל ג' ועוד שלישיתם שהוא א'
כן י"א וב' שלישיות הוא כפל ה' ועוד שלישיתו שהוא א' וב' שלישיות
|
|
ואם אמרו הערך אשר לג' אצל ז' אצל י"א וב' שלישיות למי יש לו זה הערך
|
|
|
נשימם בצורה הזאת
|
|
|
|
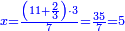
|
הנה הנעלם הוא הנערך שהוא הראשון שבאחרונים והידוע שבהם הי"א וב' שלישיות והוא השני שבהם לכן נכפלנו בראשון שבראשונים שהוא הג' ויעלה ל"ה ונחלקם לנשאר מהידועי' והוא הז' ויצא בחלוקה
|
| Written calculation
|
זה הכלל נקרא להם שם ונסדרם מין תחת מינו ונכפלם מין בשאינו מינו שהם האלכסונים ונחלקנו למינו היוצא בחילוק הוא הנעלם המבוקש
|
|
|
ואם הם בעצמם היה להם שינוי בשמות אשר בהם נודע איזה מינו או שאינו מינו לא נצטרך לקרוא להם שם חדש
|
- Exchange Problem - Currencies: If 3 golden dinar are worth 50 silver dinar, how many silver dinar will 11 golden dinar be worth?
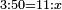
|
המשל אם ג' דינרי זהב שוים נ' דינרי כסף י"א דינרי זהב כמה דינרי כסף שוים
|
|
|
נסדרם מין תחת מינו הזהב תחת הזהב כזה
|
|
|
|
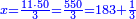
|
ונכפול למין בשאינו מינו שהם הזהב והכסף והם הי"א בנ' שהם האלכסונים ויעלה 550 ונחלקם על מינו פי' על ג' של זהב ויצא בחילוק 183 ושליש שהם הדינרי כסף הנעלמים
|
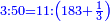
|
הרי לנו שאם שלשה דינרי זהב שוים נ' של כסף י"א דינרי זהב שוים 183 דינרי כסף ועוד שליש דינר כזה
|
|
|
|
- Exchange Problem - Currencies: If 3 golden dinar are worth 50 silver dinar, how many [golden dinar] will 183⅓ silver dinar be worth?
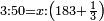
|
ואם השאלה היתה להפך שנעלם לנו הזהב כאומרנו ואם ג' דינרי זהב שוים נ' של כסף 183 דינרי כסף ושליש דינר כמה שוים
|
|
|
נשימם מין על מינו כזה
|
|
|
|
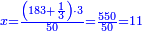
|
ונכפול מין בשאינו מינו פי' הכסף בזהב שהם האלכסונים ויעלו 550 ונחלקם על מינו שהוא הכסף הנשאר והוא הנ' ויצא בחילוק י"א והם דינרי זהב הנעלמים והכל עולה לענין אחד
|
The reason for the solution of the first example: 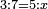
|
הטעם כי כאשר אמרנו הערך שיש לג' אצל ז' לה' אצל מי שיש לו זה הערך
|
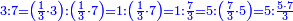
|
הנה ידענו שהערך שיש לג' אצל ז' יש לאחד שהוא שליש הג' אצל שליש [הז' פי' שאם הג' על דרך משל שליש הז' הנה האחד הוא שליש שלישית הז' וזה ברור ואחר שידענו שערך א' אצל שליש ז' הוא] ז' הוא כערך ג' אצל ז' שהוא הערך הנשאל ושליש ז' הוא ז' שלישיות הנה ידענו שזה הערך בעצמו יש לה' אצל ה' פעמים ז' שלישיות ולדעת כמה שלישיות הם יש לנו לכפול ה' בז' והעולה הם שלישיות ולדעת כמה שלמים הם חלקנום על הג'
|
The reason for the solution of the second example: 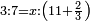
|
וכן בדמיון השני כי אחר שידענו ערך ג' אצל ז' ורצינו לידע למי יש לו זה הערך בעצמו אצל י"א וב' שלישיות הרי הוא כאלו ידענו ערך ז' אצל ג' ונרצה לידע לי"א וב' שלישיות אצל מי יש לו זה הערך והנה הטעם ברור שהרי שב כדמיון הראשון בעינו אכן כדי להרחיב ביאור אבארנו בעודו בעינו
|
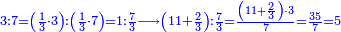
|
ואומר כי אחר שידענו שהערך שיש לג' אצל ז' הוא הערך בעצמו שיש לאחד, שהוא שליש הג', אצל ז' שלישיות, שהם שליש הז' כאשר ביארנו, א"כ לכל שבעה שלישיות אשר בי"א וב' שלישיות הנערך אליהם הוא א' וכמספר כמה ז' שלישיות יש בהם, כך הוא המספר אחדי הנערך אליהם הנעלם ולדעת כמה שלמים ז' שלישיות יש בי"א וב' שלישיות, נדע תחלה כמה שלישיות הוא וזה יודע בכפלהו אותם בג', לכן כפלנום בג' ועלה ל"ה, הנה ידענו שיש בהם [ל"ה] שלישיות ולדעת כמה פעמים יש בהם ז' שלישיות, חלקנום על ז' ויצא לנו ה' והוא המספר הפעמים אשר יש ז' שלישיות בי"א וב' שלישיות
|
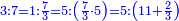
|
וכבר ידענו שהנערך אצל כל ז' שלישיות הוא א' שלם, א"כ הנערך אצל ה' פעמים ז' שלישיות הוא ה' שלמים ואולם ידענו שהי"א וב' שלישיות הוא ה' פעמים ז' שלישיות, א"כ הנערך אליהם הוא ה' שלמים
|
| The reasons for the solutions of the exchange problems:
|
ועוד במשלי הדינרים
|
- The first problem:
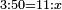
|
כי כאשר ידענו שג' דינרי זהב שוים נ' של כסף
|
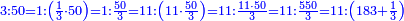
|
נודע שדינר זהב אחד, שהוא שוה שליש נ' דינרים של כסף, שהוא חמישים שלישי דינר ונודע מזה שהי"א דינרי זהב שוים י"א פעמים נ' שלישי דינר כסף ולדעת כמה שלישים הם, כפלנו הי"א בנ' ועלה 550, הנה ידענו שהי"א דינרי זהב שוים 550 שלישי דינר כסף ולדעת כמה דינרי כסף הם, חלקנום על ג' ויצא 183 ושליש והם הדינרי כסף ששוים הי"א דינרי זהב וזה ברור
|
- The second problem:
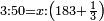
|
ועוד אבארנו במשל השני והוא כי ביודעינו שג' דינרי זהב שוים נ' דינרי כסף, כל דינרי זהב שוה נ' שלישי דינר כסף, כמו שביארנו
|
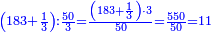
|
וא"כ כל נ' שלישי דינר, אשר בק'פ'ג' ושליש, שוה דינר זהב ולדעת כמה פעמים יש בהם נ' שלישי דינר, נדע תחלה כמה שלישי דינר הם וזה יודע בכפלנו אותם בג' כאש' עשינו ועלו 550 והם שלישי דינר וכל נ' מהם שוים דינר זהב, א"כ בחלקנום אותם על נ' כאשר עשינו, נדע כמה דינרי זהב שוים, שהוא כמספר היוצא בחלוקו, הוא י"א וכל זה ברור
|
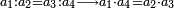
|
והנה יתבאר מכל הנזכר במעט עיון כי כל ד' מספרים נערכים, כפל הראשון מאלו בשני מן האחרים ככפל השני בראשון מן האחרים
|
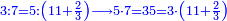
|
כי בדמיון הראשון כפל הה' בז', שהוא ל"ה, ככפל הג' בי"א וב' שלישיות, אשר היה הנעלם
|
Therefore, when one of the numbers is unknown, the product of the first number of one of the two ratios by the second number of the other ratio is equal to the product of the unknown number by the remaining known number
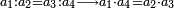
|
ולזה, כאש' נעלם אחד מהם, איזה מהם שיהיה, כפלנו מהנודעים הראשון מאלו בשני מאלו וידענו שזה בעצמו הוא כפל הנעלם בנשאר מהנודעים ולזה בחלקנו אותו לנודע, יצא הנעלם
|
Rule of Three
|
|
Sometimes the proportional numbers are only three, i.e. the mean is the first of those that are last and the second of those that are first.
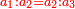
|
ולפעמים לא יהיו המספרים הנערכים כי אם ג' פי' שהאמצעי יהיה ראשון לאחרונים ושני לראשונים
|
We have already explained that for every four proportional numbers the product of the first of those by the second of those is as the product of the first of those by the second of thos, i.e. the product of the first by the last is as the product of the two means by each other.

|
ואולם כבר ביארנו שכל ד' מספרים נערכים כפל הראשון מאלו בשני מאלו ככפל הראשון מאלו בשני מאלו פי' כפל הראשון באחרון ככפל הב' האמצעיים זה בזה
|
When they are only three, the mean stands instead of the two means, which are the second of those that are first and the first of those that are last, so the product of the first by the third, which is the second of those that are last, is as the product of the mean by itself, which is both first [of those that are last] and second [of those that are first], as we explained.
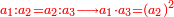
|
ואולם כשהם ג' לבד האמצעי עומד במקום השנים האמצעיי' שהוא שני לראשונים וראשון לאחרונים א"כ כפל הראשון בשלישי שהוא השני מהאחרונים ככפל האמצעי בעצמו שהוא ראשון ושני כאשר ביארנו
|
- When the mean and one of the others are known, the unknown is extracted, for we multiply the mean by itself , then divide [the product] by the other that is known and the result is the unknown.
|
ולזה בהודע האמצעי ואחד מן האחרים יודע הנעלם כי נכפול האמצעי בעצמו ונחלקנו לאחר הנודע ויצא הנעלם
|
- When the two [extremes] are known, the mean is extracted, by multiplying the two that are known [one by the other] and the product is as the product of the mean by itself, i.e. as its square.
|
גם בהודע השנים יודע האמצעי וזה בהכפל השנים הנודעים והעולה הוא ככפל האמצעי בעצמו פי' שהוא כמרובע
|
- The mean is the root - we extract the root of this number by finding a number whose product by itself is as this product and the resulting root is the unknown mean.
|
והאמצעי הוא השרש ונוציא שורש זה המספר שהוא לבקש מספר שכפלו על עצמו עולה כפי החשבון והשרש אשר יצא הוא האמצעי הנעלם
|
| The method of extracting the roots is very difficult and there are numbers whose real root is never known only approximately, so I have assigned a special chapter to this and it is the next chapter.
|
ודרך הוצאת השרשים הוא קשה מאד ויש מספרים אשר לא יודע בהם שרש אמיתי לעולם כי בקירוב על זה הקצתי לו פרק לעצמו והוא הפרק הבא אחר זה
|
| Example for the three proportional numbers:
|
דמיון הג' מספרים נערכים
|
- As we say: the ratio of 2 to 4 is as the ratio of 4 to 8

|
הוא כאומרנו הערך אשר לב' אצל הד' כערך ד' אצל ח'
|
- 4 is the mean, instead of the two [means], which is the second of those that are first and the first of those that are last.
|
שהד' האמצעי הוא במקום שנים שהוא שני מן הראשונים וראשון מן האחרונים
|
- If one of the extremes is unknown, such as 2, whereas 4 and 8 are known:
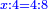
|
ואם הנעלם מהקצוות המשל הב' ונודע הד' והח'
|
- Meaning that one asks: Who has the ratio to 4, as the ratio of 4 to 8?
|
כלומר ששאל השואל למי יש ערך אצל ד' כערך אשר לד' אצל שמונה
|
- Exchange Problem - Currencies: Or if he says: How many golden dinar are worth 4 silver dinar, if 4 golden dinar are worth [8] silver dinar?
|
או שאמ' כמה דינרי זהב שוים ד' דינרי כסף אם ד' דינרי זהב שוים אחד דינרי כסף
|
- We know that the product of 4 by 4, which is the mean, that is 16 is as the product of the known 8 by the unknown
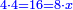
|
הנה ידענו שכפל ד' בד' שהוא האמצעי שהוא שהם י"ו שהוא ככפל ח' הידוע בנעלם
|
- Thus, we divide it by 8 and the result of division, which is 2, is the unknown.
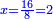
|
לכן נחלקם על הח' והיוצא והוצרך בחלוק והוא ב' הוא הנעלם
|
- If 2 and 4 are known, and 8 is unknown:
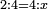
|
וכן אם נודעו השנים והד' ונעלם הח'
|
- That is, one asks: the ratio of 2 to 4 - 4 has this ratio to whom?
|
ששאל השואל הערך אשר לב' אצל ד' אצל מי יש לד' זה הערך
|
- Exchange Problem - Currencies: Or, if he asks: If 2 golden dinar are worth 4 silver dinar, how many silver dinar will 4 golden dinar be worth?
|
או ששאל אם שני דינרי זהב שוים ד' דינרי כסף ד' דינרי זהב כמה דינרי כסף שוים
|
- We multiply 4 by itself; the result is 16. We divide it by [2]; the result of division is [8] and this is the unknown.
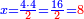
|
נכפול הד' בעצמו ויעלה י"ו ונחלקם על הח' ויצא בחילוק ב' והוא הנעלם
|
- If the unknown is 4, which is the mean that stands instead of the two [means], whereas 2 and 8, the first and the last, are known:
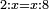
|
ואם היה הנעלם הד' שהוא האמצעי העומד במקום שנים והנודעים הב' והח' ראשון ואחרון
|
- We multiply 2 by 8; the result is 16 and it is the product of the unknown mean by itself, as we have explained; the 16 is the square of the mean.
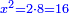
|
נכפול הב' בח' ויעלה י"ו וזה כפל האמצעי הנעלם בעצמו כמו שביארנו ואלו הי"ו הם מרובע האמצעי
|
- The mean is its root - the root of 16 is 4.
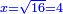
|
והאמצעי הוא שרושם ושרש י"ו הוא ד'
|
| Everything is explained in these examples.
|
והכל מבואר בדמיונות אלו
|
| If 16 is a number, whose root extraction is difficult for us, or it is impossible for us to know its real root, only by approximation, we proceed in the extraction of the root as explained in chapter six that is assigned to it.
|
ואם זה הי"ו היה החשבון אשר יקשה עלינו בקשת שרשו או שהוא נמנע בחקנו לידע שרשו האמיתי כי אם בקרוב נדרוך בבקשת השרש ההוא כמו שיתבאר בפרק ו' זה אשר הקציתי לו
|
Comparing Fractions
|
השער השלישי בהשואה
|
| Definition: Comparing fractions is when you have fractions of various types that are not related to each other at all, i.e. the type of these fractions is not the type of fractions of the others.
|
ההשואה היא כאשר יהיו לך שברים ממינים שונים בלתי נקשרים זה בזה כלל ר"ל שאין אלו שברי שברים אלו
|
- Example: if you have two integers, 3-eighths and 2-quarters of an eighth, 4-fifths, 6-sevenths and 3-eighths of a sevenths, like this, and you wish to convert all of them into one type.
![\scriptstyle\left[2+\frac{3}{8}+\left(\frac{2}{4}\sdot\frac{1}{8}\right)\right]\quad\frac{4}{5}\quad\left[\frac{6}{7}+\left(\frac{3}{8}\sdot\frac{1}{7}\right)\right]](/mediawiki/images/math/2/f/5/2f5db2cd7e551020181114628b7f1a51.png)
|
המשל אם היו בידיך שני שלמים ועוד וג' שמינית וב' רביעיות שמינית ועוד ד' חמישיות ועוד ו' שביעיות וג' שמיניות שביעית כזה ותרצה להשיבם כלם ממין אחד
|
|
|
|
- First we fractionalize the 2 integers plus the 3-eighths and the 2-quarters of an eighth, then the 4-fifths and then the 6-sevenths, since they are related to the 6-sevenths and the 3-eighths of a seventh, for the related also need fractionalizing.
|
ונעשה תחלה פריטה לב' שלמים וג' שמיניות וב' רביעיות שמינית ועוד ד' חמישיות ועוד ו' שביעיות אחרי היותם נקשרים גם לו' שביעיות וג' שמיניות שביעית כי גם הם נקשרים וצריכים פריטה
|
- We start by saying: 2 units, how many eighths are they? This is known by multiplying them by 8; they are 16. We add to them the 3 that is beneath [the 8] and the total is 19.
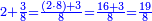
|
ונתחיל לומר ב' אחדים כמה שמיניות הם וזה יודע בהכפלם בח' יהיו י"ו ונחבר להם הג' אשר תחתיו יהיו כלם י"ט
|
- We convert them further to quarters of an eighth by multiplying them by 4; the result is 76. Then we add to them the 2 that is beneath [the 4]; the result is 78 quarters of an eighth.
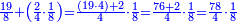
|
עוד נשיבם רביעיות שמיני' וזה יהיה בהכפלם כלם בד' יעלו ע"ו ונחבר להם הב' אשר תחתיו יעלו ע"ח רביעיות שמינית
|
- We also fractionalize the 6-sevenths plus 3-eighths of a seventh by saying: 6-sevenths, how many eighths of a seventh are they? This is known by multiplying them by 8; they are 48. We add to them the 3 that is beneath [the 8]; the result is 51 eighths of a seventh.
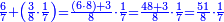
|
עוד נפרוט הו' שביעיות וג' שמיניות שביעית ונאמרו ו' שביעיות שלמות כמה שלמות שמיניות שביעית הם וזה יודע בהכפלם בח' ויעלו מ"ח ונחבר להם הג' אשר תחתיו ועלו נ"א שמיניות שביעית
|
- It is as if we were asked to convert 78 quarters of an eighth, 4 fifths, and 51 eighths of a seventh into one type. Like this:
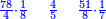
|
והרי הוא כאלו שאלו לנו להשיב למין אחד עין ע"ח רביעיות שמינית וד' חמישיות ונ"א שמיניות שביעית שביעי כזה
|
|
|
|
- Since we have different denominators and different fractions, we should explain how to convert all of them into one type without changing them, i.e. that they will all be fractions of the same denominators.
|
ואחרי היות בידינו מורים משונים ושברים משונים ראוי לנו לבאר איך נשיבם כלם ממין אחד מבלתי שינוי ביניהם ר"ל שיהיו כלם שברים ממורים אחדים
|
- First, I will explain that the order of the denominators neither increases nor decreases:
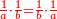
|
וקודם זה אציע שסדור המורים אינו מעלה ומוריד
|
- Because, the seventh of an eighth, for instance, is the the same as the eighth of a seventh, since each is a part of 56, which is the number that consists of these denominators and this is clear.
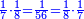
|
כי כך הוא שביעית שמינית עד"מ כמו שמינית שביעית כי כל אחד מהם הוא חלקנו מנ"ו בשלם שהוא המספר אשר הוא מורכב מאלו המורים וזה ברור
|
- So, when we have, for example, 3-sevenths and 4-eighths

|
לכן כאשר היה לנו עד"מ ג' שביעיות וד' שמינית
|
- We convert all of them into sevenths of an eighth, which are eighths of a seventh
|
נשיבם כלם שביעיות שמינית שהוא שמיניות שביעית
|
- This is done by multiplying the 3 that are the number of the sevenths by 8; they are 24 eighths of a seventh.
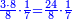
|
וזה יעשה בכפול הג' שברי השביעיות בח' ויהיו כ"ד שמיניות שביעיות
|
- This is clear, since every seventh is 8-eighths of a seventh, as each integer is eight eighths.
|
וזה ברור כי כל שביעיות הוא ח' שמיניות שביעית כמו שכל שלם הוא שמונה שמיניות השלם
|
- We do the same with the 4-eighths: we convert them into sevenths of an eighth by multiplying the 4, which is the number of the fractions, by 7, which is the denominator of the seventh; the result is 28.
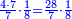
|
וכן נעשה לד' שמיניות שנשיבם לשביעיות שמינית והוא בכפול הד' שהוא מספר השברים בז' שהוא מורה השביעיות ויעלו כ"ח
|
- They are 28 sevenths of an eighth and the others are 24 eighths of a seventh, so all are of the same type, as we said that there is no difference between saying a seventh of an eighth and saying an eighth of a seventh.
|
והם כ"ח שביעיות שמינית והאחרות עלו כ"ד שמיניות שביעית הנה כלם ממין אחד כמו שהזכרנו שאין חלוף בין אומרנו שביעית שמינית לאומרנו שמינית שביעית
|
After explaining the premise, we return to our first procedure, which is multiplying each numerator of the fractions that we have by the denominators of the others successively, thus each fraction will be of all the denominators, so they are of the same type, for the order of the denominators forward or backward does not matter.
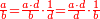 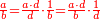
|
ואחר שהצענו הצעה זו נשוב למעשינו הראשון והוא לכפול כל מספר שברים אשר בידינו במורי חברותיה זה אחר זה וכן לכלם ואז תהיה כל אחד שברים מכל המורים והנה הם שוים כי סדור המורים בקדימה ואיחור לא יזיק
|
|
ונתחיל במעשינו ונאמר 78 רביעיות שמינית כאשר נכפלם בה' שהוא מורה החמישיות יעלו 390 חמישיות רביעית שמינית
|
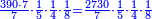
|
עוד נכפול זה המחובר בז' שהוא מורה השביעית ויעלו 2730 שביעיות חמישיות רביעית שמינית
|
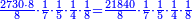
|
עוד נכפול כל זה בח' שהוא המורה השמיניות ויעלו 21840 שמיניות שביעיות חמישיות רביעיות שמיניות וזהו העולה מה78 רביעיות שמיניות
|
|
עוד נכפול הד' שהוא ד' חמישיות בכל מורי חברותיה זה אחר זה ונאמר ד בח' הם [ל"ב] שמיניות חמשית
|
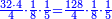
|
עוד נכפלם בד' יהיו 128 רביעיות שמיניות חמישית
|
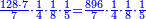
|
ונכפלם בז' יהיה 896 שביעיות רביעית שמינית חמישית
|
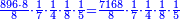
|
עוד נכפלם בח' 8 יעלו 7168 שמיניות שביעית רביעית שמינית חמישית
|
|
עוד נכפול הנ"א שהם נ"א שמיניות שביעית בה' יעלו 255 חמישיות שמיניות שביעית
|
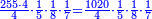
|
נכפלם בד' יעלו 1020 רביעית חמישיות שמיניות שביעית
|
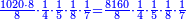
|
עוד נכפלם בח' יעלו 8160 שמיניות רביעיות חמישית שמינית שביעית
|
|
|
הרי כלם ממין אחד כי המורים שוים כי הסדר אינו מעלה ומוריד כאשר ביארנו
|
| Beware lest you make a mistake when doing this comparison, not to add what is beneath the denominators to the product of the numerators by the denominators, for this is done only in fractionalization, when we want to sum all the mentioned related fractions and convert them to the lowest fraction.
|
והשמר לך מאד פן תטעה בעשותך השואה זו לחבר לעולה מכפל השברים במורים מה שנמצא תחת המורי' כי זה לא יעשה כי אם בפריטה לבד שאנו רוצים לחבר כל השברים הנזכרים הנקשרים ולפרטם למין הפרוטות
|
- Example: converting different kinds of coins (peraḥim, zehuvim, peruṭot) to the currency of the lowest value (peruṭot)
|
המשל במי שיש לו פרחים וזהובים ופרוטות שרוצה להשיב הפרוטות שיש לו או להשיב הפרחים זהובים ר"ל לראות כמה זהובים יעלו ולחבר לעולה הזהובים אשר היו בידו ואחר כך להשי' כל הזהובים פרוטות ולחבר עמהם הפרוטות אשר בידו ויהיה אז הכל מחובר ונפרט
|
|
|
אבל ההשואה אין בה חבור כלל כי אם לעשות כל שברים מהם ממין האחדים לכן לא יחברם כלל וזה מבואר בטעם
|
|
|
ולזה שמתי להם שמות שונים מורי' על הענין ברמז
|
- Hašavah (equalization) = converting fractions that are related together into one type of fractions by multiplying each of these fractions by the denominators of the others. The intention is not to sum the fractions together, but only to equalize their denominators
|
כי להחזרת השברים הבלתי נקשרות למין אחד בהכאת כל אחד מהם במורי חברותיה, קראתי השואה שאין כונתינו חבור כלל כי אם ההשואה לבד
|
- Periṭah (fractionalization) = converting fractions that are related together into the lowest type of fractions
|
ולהשבת השברים הנקשרים כלם יחד למין השברים הגרועים מהם קראתי פריטה
|
- Two reasons for the use of the term periṭah:
|
לשתי כוונות
|
- 1) the root is used for converting different kinds of coins to the currency of the lowest value (peruṭot) and for converting the general to particular (peraṭim)
|
האחת שהוא כפורט ועושה מהפרחים וזהובים ופרוטות פרוטות וכמשיב הכללים לפרטים
|
- 2) reminding of the details (peraṭ) that should be considered in the procedure - i.e. the numerators that are written beneath the denominators
|
והכונה השנית היא כי בשם זה יזכר שיש לו לקחת עמו הפרט והעוללות אשר ימצא תחת המורים
|
| When multiplication and fractionalization are needed - the fractionalization should be applied first, and then the multiplication
|
ובכל מספר שצריך הכאה עם הפריטה, יעשה קודם הפריטה לבעלי ההכאה ואחר ההכאה
|
|
|
לכן בכל מקום אשר נזכיר ונצוה לעשות פריטה רצוננו ואחריה ההכאה, אם הוצרך איליה, או אשר מהם יצטרך, שאם יהיה לך מספר מורכב מהשברים הצריכים הכאה ועם הצריכים פריטה
|
|
|
המשל: ג' רביעיות מב' חמישיות וג' רביעיות חמישיות מד' ששיות ושלישית ששית, תשימם על הסדר כזה:
|
|
|
|
|
ותעשה פריטה לד' שביעיות ושלישית שישית והוא שתכפול הד' בג' ותחבר להם האחד אשר תחתיו ויעלו י"ג שלישיות ששית
|
|
וכן תעשה לב' חמישיות וג' רביעיות חמישית ויעלו י"א רביעיות חמישית
|
![\scriptstyle{\color{blue}{\frac{3}{4}\sdot\left[\frac{2}{5}+\left(\frac{3}{4}\sdot\frac{1}{5}\right)\right]\sdot\left[\frac{4}{6}+\left(\frac{1}{3}\sdot\frac{1}{6}\right)\right]=\frac{3}{4}\sdot\left(\frac{11}{4}\sdot\frac{1}{5}\right)\sdot\left(\frac{13}{3}\sdot\frac{1}{6}\right)}}](/mediawiki/images/math/2/c/4/2c44639491e6830397006b9f964ce49d.png)
|
וישוב מספרך כאלו אמרו ג' רביעיות מי"ח רביעיות חמישית מי"ג שלישיות שישית כזה
|
|
|
|
| The numerators are multiplied after the fractionalization
|
ואחר עשותך פריטה זו כנזכר, תעשה ההכאה והוא לתת סבות להכות הג', שהם השברים האחרונים במספר השברים, לא במורים השברים וגם לזה ירשמו בשם ההכאה, כי בהכאה יבא השבר והשבר הוא תחת המורה, כמו שהנשבר הוא שפל ובזוי עם
|
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\frac{3}{4}\sdot\left[\frac{2}{5}+\left(\frac{3}{4}\sdot\frac{1}{5}\right)\right]\sdot\left[\frac{4}{6}+\left(\frac{1}{3}\sdot\frac{1}{6}\right)\right]&\scriptstyle=\frac{3}{4}\sdot\left(\frac{11}{4}\sdot\frac{1}{5}\right)\sdot\left(\frac{13}{3}\sdot\frac{1}{6}\right)\\&\scriptstyle=\frac{3\sdot11\sdot13}{4}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{3}\sdot\frac{1}{6}\\&\scriptstyle=\frac{33\sdot13}{4}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{3}\sdot\frac{1}{6}\\&\scriptstyle=\frac{429}{4}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{3}\sdot\frac{1}{6}\\\end{align}}}](/mediawiki/images/math/e/9/0/e90e6a029b0f349d92e33d74057d39fc.png)
|
ותתחיל להכות ולומר שלשה בי"א הם ל"ג ול"ג בי"ג הם 429, הרי עלו כל השברים הנשאלים 429 רביעית חמישית שלישית שישית, כזה:
|
|
|
|
| Then the product is divided by the denominators
|
ותחלק אלו ה429 למורים אלו, ר"ל לד' והיוצא לד' האחר והיוצא לה' וכן לכלם עד כלותם
|
| The remainder of division by a certain denominator is written beneath that denominator
|
וכאשר ישאר דבר בשום חלוקה מהן, תשימהו תחת המורה ההוא
|
| The most beautiful arrangement: dividing firstly by the denominator the division by which generates the smallest remainder, preferably dividing first by the divisors of the product if there are any among the denominators and placing these denominators at the end [to the right] starting from the largest to the smallest
|
וככלות החשבון קודם כלות המורים ויצא לך בחלוק על אחד מהן פחות מהמורה אשר לפניו, תשים אותו היוצא תחת המורה הזה אשר לפני. ואז תדע כמה שישיות, או כמה שלישיות שישיות הן. וזה נקרא כלילת יופי כמו שנזכר למעלה, לפי שהוא לעשות מהפרטים כללים, יען יהיו השברים יותר גדולים ויותר יפים
|
|
|
והיופי האמיתי כשתעיין בתחלה המספר המתחלק, אם יש לו שום אחד מהמורים ההם ואותו תשים אחרון וכן בשנית ביוצא וכן בשלישית וכן לעולם
|
| For equalization purpose only, there is no need to divide by the denominators
|
ולא תעשה זה כי אם כאשר ישאלו לך כמה עולים חלקים אלו הנשארות, אכן אם עשית זה לצורך ההשואה, או לצורך אחד מהשערים הבאים, לא תחלקהו על המורים כלל, כי לא כתבתיו כאן, כי אם ללמדך על המעשה ואם אין זה מקומו ונזכר כבר במקומות אחרים
|
|
ובעשותך זה בדמיוננו זה ר"ל שתחלק ה429 על הד' שהוא המורה האחרון, יצא בחילוק 107 וישאר א' ותשימהו תחתיו
|
|
[ותחלק זה היוצא לד' הקודם לו יצא בחלוק כ"ו וישארו ג' תשימם תחתיו
|
|
ותחלק זה היוצא לה' ויצא בחלוק ה' וישאר א' ותשימהו תחתיו
|
|
ותחלק] ותחלק ה' אלו על הג' ויצא א' וישארו ב' ותשימם תחתיו
|
|
|
וזה הא' אם היה גדול מהו' מדות שהוא המורה אשר לפני אלו הסמוך להם היה לנו לחלקם עליו והיוצא בחלוק היה שלימים
|
|
|
אחר שהוא ראשון וכבר כלו המורים והנשאר הינו שמים אותו תחתיו והיה שישיות שלמות
|
Chapter One: Addition
|
הפרק האחד עשר בחבור
|
| Summing fractions with integers or fractions with fractions
|
בחיבור ובו מאמ' האמרה והאחדות
|
|
|
כאשר תרצה לחבר שברים עם שלמים ושברים, [או] עם שברים ממין אחר
|
| The procedure: the numbers are converted to the lowest type of fraction, then their numerators are multiplied, and they are equalized; at the end the numerators are summed and the result is divided by the denominators
|
בתחלה תפרוט כל אחד מהמספרים לבדו אשר יצטרך פריטה, גם תכה הצריך להכאה, ואחר שתפרוט וכל אחד מהם הצריך להם, או לאחד מהם, ר"ל לפריטה או להכאה, תשוה המספרים אחד אל אחד, עד שיהיו כלם ממין אחד והעולה בכל אחד מהם חבר הכל יחד, ר"ל מספר השברים וחלקנו על כל המורים אשר לכל אחד השברים
|
|
|
כי ע'ד'מ' אם במשלנו אשר עשינו בהשואה בתחלת השער הג' שאלו לך שתחברם ותאמ' כמה הם
|
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\left[2+\frac{3}{8}+\left(\frac{2}{4}\sdot\frac{1}{8}\right)\right]+\frac{4}{5}+\left[\frac{6}{7}+\left(\frac{3}{8}\sdot\frac{1}{7}\right)\right]\\&\scriptstyle=\left(\frac{21840}{8}\sdot\frac{1}{7}\sdot\frac{1}{5}\sdot\frac{1}{4}\sdot\frac{1}{8}\right)+\left(\frac{7168}{8}\sdot\frac{1}{7}\sdot\frac{1}{4}\sdot\frac{1}{8}\sdot\frac{1}{5}\right)+\left(\frac{8160}{8}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{8}\sdot\frac{1}{7}\right)\\&\scriptstyle=\frac{37168}{8}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{8}\sdot\frac{1}{7}\\\end{align}}}](/mediawiki/images/math/3/f/a/3fabdb3522b40d4fd287ccee0cba4b71.png)
|
היה לך לעשות כל אשר עשינו הפריטה לכל אחד וההשואה לכלם, עד שיגיעו לאשר הגיעו
והוא שהשנים השלמים וג' שמיניות וב' רביעיות שמינית עלו ל21840 [שמיניות שביעית חמשית רביעית שמינית
והד' חמשיות עלו ל8160] מכל המורים
ואחר עשותך כל זה, היה לך לחבר יחד כל מספרי השברים, ר"ל ה21840 עם ה7168 ועם ה8160 ויעלו 37168 והם מהה' מורים הנזכרים, ר"ל ה8 וה4 והה' והז' והח', שהם כל מורי המספרים הראשונים
|
- The order of the denominators in the sum is unimportant
|
ותשימם על הסדר כאשר תרצה, או בהשגחה כאשר הזכרנו בפרק הרביעי, כדי שיצאו החלקים יותר נאותים ושם תמצאנו מבואר באר הטב
|
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\left[2+\frac{3}{8}+\left(\frac{2}{4}\sdot\frac{1}{8}\right)\right]+\frac{4}{5}+\left[\frac{6}{7}+\left(\frac{3}{8}\sdot\frac{1}{7}\right)\right]\\&\scriptstyle=\frac{37168}{8}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{8}\sdot\frac{1}{7}\\&\scriptstyle=\frac{4646}{7}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{8}\\&\scriptstyle=\left(\frac{663}{4}\sdot\frac{1}{5}\sdot\frac{1}{8}\right)+\left(\frac{5}{7}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{8}\right)\\&\scriptstyle={\color{red}{\left(\frac{165}{5}\sdot\frac{1}{8}\right)+\left(\frac{3}{4}\sdot\frac{1}{5}\sdot\frac{1}{8}\right)+\left(\frac{5}{7}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{8}\right)}}\\&\scriptstyle=\frac{33}{8}+\left(\frac{3}{4}\sdot\frac{1}{5}\sdot\frac{1}{8}\right)+\left(\frac{5}{7}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{8}\right)\\&\scriptstyle=4+\frac{1}{8}+\left(\frac{3}{4}\sdot\frac{1}{5}\sdot\frac{1}{8}\right)+\left(\frac{5}{7}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{8}\right)\\\end{align}}}](/mediawiki/images/math/c/f/f/cff900155b4478d71bf101689365b48b.png)
|
ולהיות לזה החשבון 37168 המתחלק שמינית, שהוא אחד מהמורים, נשימנו אחרון, ר"ל הראשון
ונחלק חשבונננו זה עליו, ר"ל 7 ויצא בחילוק 663 [נ' 3] וישארו ה' ונשימם תחתיו
ונחלקם על הד' ויצא בחילוק ל"ג ולא ישאר דבר
ונחלקם אלו הל"ג היוצאים בחילוק על הח' שהוא המורה הנשאר ויצא בחלוק ד' ד' והם שלמים לפי שכבר כלו כל המורים ונשימם מחוץ וישאר א' והוא שמינית שלימה ונשימה תחת כזה:
|
|
|
|
|
|
הנה עלה בידינו שכאשר חברנו השנים שלמים וג' שמיניות וב' רביעיות שמינית עם ד' חמישיות ועם ו שביעיות וג' שמיניות שביעית, שעלה הכל ד' שלמים ושמינית אחת וג' רביעיות חמישית שמינית וה' שביעיות רביעית חמישית שמינית והקש על זה
|
|
|
והה' והוא הטעם אם אמרו לך מספרים רבים והיו בהם שצריכין ג"כ הכאה קודם השיווי, שתעשה להם ג"כ ההכאה קודם השיווי ואחר כך ההשוואה וא'ח'כ' החבור כנזכר
|
- If its is asked how many of a certain type of fractions is the sum
- If the certain type of fractions is one of the given denominators of the sum - then this denominator is placed first among the denominators of the sum
|
ואולם אם לא שאלו לך בסתם כמה הם
|
- Example: how many fifths is the above sum?
|
אבל אמרו לך ע'ד'מ' כמה חמישיות הם, אחר שזה הה' הוא במורים, אינך צריך לעשות פועל חדש, כי אם שתשים הה' הראשון מהמורים כזה:
|
|
|
|
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\left[2+\frac{3}{8}+\left(\frac{2}{4}\sdot\frac{1}{8}\right)\right]+\frac{4}{5}+\left[\frac{6}{7}+\left(\frac{3}{8}\sdot\frac{1}{7}\right)\right]\\&\scriptstyle=4+\frac{1}{8}+\left(\frac{3}{4}\sdot\frac{1}{5}\sdot\frac{1}{8}\right)+\left(\frac{5}{7}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{8}\right)\\&\scriptstyle=4+\left(\frac{25}{8}\sdot\frac{1}{5}\sdot\frac{1}{5}\right)+\left(\frac{3}{4}\sdot\frac{1}{8}\sdot\frac{1}{5}\right)+\left(\frac{5}{7}\sdot\frac{1}{4}\sdot\frac{1}{8}\sdot\frac{1}{5}\right)\\\end{align}}}](/mediawiki/images/math/1/9/6/196fa95f6efe1a7855af3737ee476de9.png)
|
ויעלה בידך ד' שלמים כ"ה שמיניות חמישית חמישית וג' רביעיות שמינית חמישית וה' שביעיות רביעית שמינית חמישית והכל אחד ודי למבין
|
- If the certain type of fractions is not one of the given denominators of the sum
|
אכן אם אמרו לך להחזירם ממין אחר שאינו במורי'
|
- Example: how many ninths is the above sum?
|
המשל שאמרו לך כמה תשיעיות הן
|
- Conversion: after fractionalizing, multiplying, and equalizing - multiplying the result by the denominator of the specific fraction required (9 in the above example) - then dividing by the denominators of the given fractions
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\left[2+\frac{3}{8}+\left(\frac{2}{4}\sdot\frac{1}{8}\right)\right]+\frac{4}{5}+\left[\frac{6}{7}+\left(\frac{3}{8}\sdot\frac{1}{7}\right)\right]\\&\scriptstyle=\frac{37168}{8}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{8}\sdot\frac{1}{7}\\&\scriptstyle=\frac{37168\sdot9}{8}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\\&\scriptstyle=\frac{334512}{8}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\\&\scriptstyle=\frac{41814}{4}\sdot\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\\&\scriptstyle=\left(\frac{10453}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{2}{4}\sdot\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)\\&\scriptstyle={\color{red}{\left(\frac{2090}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{2}{4}\sdot\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)}}\\&\scriptstyle=\left(\frac{298}{8}\sdot\frac{1}{9}\right)+\left(\frac{4}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{2}{4}\sdot\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)\\&\scriptstyle=\frac{37}{9}+\left(\frac{2}{8}\sdot\frac{1}{9}\right)+\left(\frac{4}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{2}{4}\sdot\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)\\&\scriptstyle=4+\frac{1}{9}+\left(\frac{2}{8}\sdot\frac{1}{9}\right)+\left(\frac{4}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{2}{4}\sdot\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/f/4/f/f4f0b709e2439e0d86aab99b15f87642.png)
|
זה יקרא מאמר ההמרה והוא שאחרי עשותך הפריטה וההכאה וההשואה, קודם שתחלקם למורים הנזכרים, תכפול כל חשבון השברים, ר"ל ה37168, בזה המורה אשר רצו להחליפם אליו, ר"ל הט', שהוא המורה התשיעית ויעלו 334512 ונשים הט' למורה ראשון וכל המורים האחרי' אחריו, אם כאשר יזדמן, אם בהשגחה
ובחלקנו ראשונה לח' ויצא בחילוק 41814 ולא ישאר דבר
ונחלק זה היוצא לד' ויצא בחילוק 10453 וישארו ב' ונשימם תחתיו
ונחלקנו לז' ויצא בחילוק 298 וישארו ד' ונשימם תחתיו
ונחלק זה היוצא על הח' ויצא בחילוק ל"ז וישארו ב' ונשימם תחתיו
ונחלק זה היוצא על הט' ויצא בחילוק ד' והם שלמים וישאר א' ונשימהו תחתיו והנה המרנו החלקים, ר"ל השברים, לתשיעית וחלקי תשיעית
|
| The rule of conversion
|
כלל זה מאמר זה הוא שכאשר ישאלו לך על חלקי' ידועים שונים ובלתי שונים, שתמירם למין אחר, בין אם יאמרו לך לשבר, או לשבר שבר
|
- Example: converting to
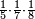
|
כמו שיאמרו לך השיבם לחמישיות שביעית שמינית, או הדומה לזה
|
| Fractionalizing, multiplying, and equalizing the given fractions, then summing the resulted fractions and multiplying the sum by the denominator of the fraction into which the sum should be converted
|
יש לך לעשות תחלה פריטה והכאה והשואה לשברים, אם היו שונים, ושוב תחברם יחד ושוב תכפלם כלם ביחד על המורה, או המורים אשר רוצים שתמירם אליהם
|
- Example: converting to
 → multiplying by 5 → multiplying by 5
|
ר"ל שאם אמרו לך שתמירם לחמישיות, תכפלם בה' לבד
|
- Example: converting to
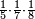 → multiplying by 8, 7, and 5 → multiplying by 8, 7, and 5
|
ואם אמרו לך לחמישיות שביעית שמינית, תכפלם בח' והעולה בז' והעולה בה'
|
| The denominators of the fractions into which the sum should be converted are written first in the final result, then the denominators of the given summed fractions
|
ואחר עשותך כל זה, תשים מורה, או מורה ההמרה, ראשונה לצד ימין על הסדר שנשאל הח' תחלה ואחריו הז' ואחריו הה' ושוב תסדר אחריהם מורה שבידך, כפי המזדמן, או בהשגחה, ותחלק על כלם המספר אשר עלה לידיך מכפל מספר שבריך במורה ,או מורי ההמרה וכל זה ברור בטעם
|
|
|
כי לעולם אם תכפול אשר בידך במורים מונחים, הנה יהיה למקובץ מורים אלו מוספים על מוריו הראשונים ולכן כאשר תרצה לעשות להם כלילת יופי, ר"ל להשיב שברים אלו הנפרטות לכללים וחלקים יפים, יש לך לסדר עם מוריו הראשונים אלו המורים אשר הוכפלו בהם והסדר לא יזיק ולפי ששאלו כמה חלקים הם מהמורים האלו, לכן נשימם ראשונה במלאכה
|
| ha-Aḥdut (unification) - converting the sum of fractions into one fraction (one denominator)
|
אכן אם יאמרו לך להשיבם לחלק אחר הגדול שאיפשר, לכן נקראה האחדות והוא ענין נכבד, כי ממנו יצא לנו לחלק מעט על רב ולחדש מורים ב בעצמינו, מבלי הוצאת מורי המספר שרצינו לחלק עליו, או גם להוסיף על מוריו
|
|
|
לזה הקצתי לו מאמר לבדו ואכתבנו בזה הפרק, לפי שהוא כעין חבור
|
|
|
וקראתי לו שם שם האחדות, לפי שאנו רוצים לעשותם חלק אחד אם איפשר ואם הוא בלתי איפשר
|
|
|
ואם הוא בלתי איפשר, יש לנו להוסיף אחד במלאכה כאש' יתבאר
|
| The term aḥdut has two meaning, as will be explained below
|
לב' כוונות אלו קראתי לו שם האחדות
|
Summing fractions to one fraction
|
מאמר האחדות
|
|
|
אם רצית להשיב שברים שוים שוים או שונים לחלק אחד אם איפשר או לגדול שאיפשר
|
|
|
המשל שני חמישיות מב' תשיעיות מב' שלמים ועוד שמינית אחת ושני תשיעיות שביעית שמינית מרביעית ושתי ששיות רביעית
|
|
|
תשימם על הסדר כזה
|
|
|
|
| The order of the operations: fractionalization, multiplication, equalization, and summing
|
תעשה להם פריטה והכאה והשוואה וחיבור
|
|
|
וכדי להרגילך עוד במעשה אעשה אחת אחת
|
- We fractionalize the quarter and the two sixths of a quarter: we multiply 1 by 6; the are 6; we add to them the units that are beneath them, i.e. the 2; the result is 8 sixths of a quarter.
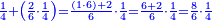
|
נעשה פריטה לרביעית ושתי שישיות רביעית
נכפול א' בו' יהיו ו' ונחבר להם הפרט אשר נמצא תחתיו ר"ל הב' יעלו ח' שישיות רביעית
|
- We fractionalize the seventh and the 2-ninths of a seventh of an eighth: we multiply 1 by 7 then we multiply them further by 9; they are 63; we add to them the two; the result is 65 ninths of a seventh of an eighth.
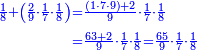
|
עוד נעשה פריטה לשביעית וב' תשיעיות שביעית שמינית
נכפול א' בז' נכפלם עוד בט' יהיו ס"ג ונחבר להם השנים ויעלו ס"ה תשיעיות שביעיות שמינית
|
![\scriptstyle{\color{blue}{\left[\frac{1}{8}+\left(\frac{2}{9}\sdot\frac{1}{7}\sdot\frac{1}{8}\right)\right]\sdot\left[\frac{1}{4}+\left(\frac{2}{6}\sdot\frac{1}{4}\right)\right]=\left(\frac{65}{9}\sdot\frac{1}{7}\sdot\frac{1}{8}\right)\sdot\left(\frac{8}{6}\sdot\frac{1}{4}\right)}}](/mediawiki/images/math/9/8/9/989a1bcb49b832461aa0a175792074ba.png)
|
והרי הוא כאלו אמרו ס"ה תשיעיות שביעית שמינית מח' שישיות רביעית כזה
|
|
|
|
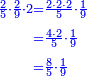
|
עוד נעשה הכאה לשני מספרי' שבידינו
ונתחיל במספ' הראשון: ונאמ ב' בב' הם ד', נכפלם עוד בשני השלמים, יהיו ח' חמישיות תשיעית שלימה כזה
|
|
|
|
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\left[\frac{1}{8}+\left(\frac{2}{9}\sdot\frac{1}{7}\sdot\frac{1}{8}\right)\right]\sdot\left[\frac{1}{4}+\left(\frac{2}{6}\sdot\frac{1}{4}\right)\right]\\&\scriptstyle=\left(\frac{65}{9}\sdot\frac{1}{7}\sdot\frac{1}{8}\right)\sdot\left(\frac{8}{6}\sdot\frac{1}{4}\right)\\&\scriptstyle=\frac{65\sdot8}{9}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{6}\sdot\frac{1}{4}\\&\scriptstyle=\frac{520}{9}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{6}\sdot\frac{1}{4}\\\end{align}}}](/mediawiki/images/math/a/d/9/ad962ba769fbe462ffd2b8f8cea6f6f1.png)
|
עוד נכה במספר השני השמונה ששיות רביעית בס"ה ויעלו 520 תשיעיות שביעית שמינית שישית רביעית כזה:
|
|
|
|
|
|
ונעשה ההשואה לאלו השני מספרים:
|
|
|
ואחר היות בכל אחת מהם מורה הט' פעם אחת, לא נכפול בו שום אחד מהמספרים ולא נסדרהו כי אם פעם אחת, כאשר הזכרתי בסוף השער הג'
|
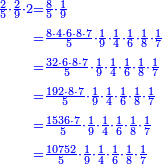
|
ונכפול הח' חמישיות תשיעיות בכל מורה המספר האחר, זולתי הט' כאשר התבאר ונאמר שמונה בד' יעלה ל"ב
נכפלם בו', יעלו 192
נכפלם בח', יעלו 1536
נכפלם בז', יעלו 10752
|
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\left[\frac{1}{8}+\left(\frac{2}{9}\sdot\frac{1}{7}\sdot\frac{1}{8}\right)\right]\sdot\left[\frac{1}{4}+\left(\frac{2}{6}\sdot\frac{1}{4}\right)\right]\\&\scriptstyle=\frac{520}{9}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{6}\sdot\frac{1}{4}\\&\scriptstyle=\frac{520\sdot5}{9}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{6}\sdot\frac{1}{4}\sdot\frac{1}{5}\\&\scriptstyle=\frac{2600}{9}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{6}\sdot\frac{1}{4}\sdot\frac{1}{5}\\\end{align}}}](/mediawiki/images/math/2/7/1/2711897ee7dc16819dc9f0d50ba83e5b.png)
|
עוד נשוב לכפול ה520, שהם מספ' השברים האחרים, בה' שהוא מורה חבריהם ולא בט' כנזכר ויעלו 2600 נסדרם זה על זה כזה:
|
|
|
|
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\left(\frac{2}{5}\sdot\frac{2}{9}\sdot2\right)+\left[\left[\frac{1}{8}+\left(\frac{2}{9}\sdot\frac{1}{7}\sdot\frac{1}{8}\right)\right]\sdot\left[\frac{1}{4}+\left(\frac{2}{6}\sdot\frac{1}{4}\right)\right]\right]\\&\scriptstyle=\left(\frac{10752}{5}\sdot\frac{1}{9}\sdot\frac{1}{4}\sdot\frac{1}{6}\sdot\frac{1}{8}\sdot\frac{1}{7}\right)+\left(\frac{2600}{9}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{6}\sdot\frac{1}{4}\sdot\frac{1}{5}\right)\\&\scriptstyle=\left(\frac{13352}{7}\sdot\frac{1}{8}\sdot\frac{1}{6}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/e/8/2/e827db0c5e3aac4f7c828927829ec6b6.png)
|
ונחברם יחד יעלו 13352
נסדר כל המורים, ר"ל כל מורי שני המספרי' בלתי הט', שלא נשימנו כי אם פעם אחת, ונשים מספרינו תחת המורה האחרון, לפי שהוא שברים נפרטות מכל אלו המורים
והרי זה כאלו שאלו לנו 13352 שביעיות שמינית שישית רביעית חמישית תשיעית, איזה חלק הם, אם הם חלק אחד ממש, או החלק הגדול שאפשר
|
| Definition of the common denominator: first we examine which number has all these denominators alone, i.e. that is compound of them and this number is called the common denominator [lit. the mother of the denominators], for it gave tham birth and they came out from it.
|
נעיין תחלה איזהו המספר שהוא בעל אלו המורים כלם לבדם ר"ל שהוא מורכב מהם ונקרא למספר הזה אם המורים כי היא ילדתם וממנה יצאו
|
| This is known by multiplying all the denominators one by the other and the product by another and so on until they end.
|
וזה יודע בכפול כל המורים אחד באחד והעולה באחר וכן כלם עד כלותם:
|
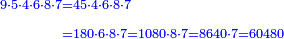
|
ונאמ' ט' בה' יעלו מ"ה, נכפלם בד', יעלו [180, נכפלם בו', יעלו 1080, נכפלם בח', יעלו] 8640, נכפלם בז', יעלו 60480
|
|

|
ולזאת קרינו אם המורים למספר השברים, ר"ל שנחלק ה68480 ל13352 ואם יתחלק כלו לשלימים, בלי תוספת ומגרעת, הנה היוצא בחילוק בצמצום הוא מורה החלק, אשר הם כל השברים הנשאלים יחד מהשלם, ר"ל רביעית אחד, או הדומ' לו
|
| Dividing the common denominator by the summed numerator
|
|
- No remainder:
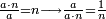
|
ואם לא יתחלק כלו לשלמים בלי תוספת ומגרעת, הנה היוצא בחלוק בצמצום הוא מורה החלק, אשר הם כל השברים הנשאלים יחד מהשלם, ר"ל רביעית אחת, או הדומה לו
|
- There is a remainder:
![\scriptstyle\frac{\left(a\sdot n\right)+r}{a}=n+\frac{r}{a}\longrightarrow\frac{a}{\left(a\sdot n\right)+r}=\frac{1}{n+1}+\frac{a-r}{\left(n+1\right)\sdot\left[\left(a\sdot n\right)+r\right]}](/mediawiki/images/math/b/9/2/b92d1354c49c317f8eb727d0819e6f80.png)
|
ואם לא יתחלק כלו לשלמים וישאר שום מספר
|
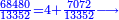
|
כמשלינו זה, שיצא בחילוק ד' ונשאר 7072
|
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\left(\frac{2}{5}\sdot\frac{2}{9}\sdot2\right)+\left[\left[\frac{1}{8}+\left(\frac{2}{9}\sdot\frac{1}{7}\sdot\frac{1}{8}\right)\right]\sdot\left[\frac{1}{4}+\left(\frac{2}{6}\sdot\frac{1}{4}\right)\right]\right]\\&\scriptstyle=\left(\frac{13352}{7}\sdot\frac{1}{8}\sdot\frac{1}{6}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{9}\right)\\&\scriptstyle=\frac{13352}{68480}\\&\scriptstyle=\frac{1}{4+1}+\frac{13352-7072}{5\sdot68480}\\&\scriptstyle=\frac{1}{5}+\left(\frac{6280}{7}\sdot\frac{1}{8}\sdot\frac{1}{6}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{9}\sdot\frac{1}{5}\right)\\\end{align}}}](/mediawiki/images/math/8/2/c/82c4adbc763288a7ace55ff6dc9136dc.png)
|
נוסיף א' על היוצא בחילוק ויהיה ה' והוא מורה החלק הגדול שאפשר, ר"ל חמשית אחת
עוד נחסר ה7072 הנשארים מה13352 אשר חלקנו עליו וישאר 6280, שהוא חלקים מכל המורים מזה החלק, ר"ל מחמישית אחת
ר"ל שיצא לנו שכל השברים הנשאלים הם חמישית אחת ו6280 שביעיות שמינית שישית רביעית חמישית תשיעית חמישית כזה:
|
|
|
|
| The order of the denominators of compound fractions of fractions is unimportant, but the denominator of the simple fraction should be placed separately, on the right
|
[ואם תרצה לעשות לשברים אלו כלילת יופי, ר"ל לחלקם על המורים, תסדרם] תסדרם כפי שהם עתה, או כפי המזדמן, או בהשגחה כנזכר למעלה ובלבד שתניח הה' ראשון לצד ימין עם הא' אשר תחתיו, כי זה אין בידיך לשנותו וכל האחרים נקשרים בו, ר"ל שהם כלם שברים ושברי שברים ממנו, ר"ל מחמשית מהשלם
|
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\left(\frac{2}{5}\sdot\frac{2}{9}\sdot2\right)+\left[\left[\frac{1}{8}+\left(\frac{2}{9}\sdot\frac{1}{7}\sdot\frac{1}{8}\right)\right]\sdot\left[\frac{1}{4}+\left(\frac{2}{6}\sdot\frac{1}{4}\right)\right]\right]\\&\scriptstyle=\frac{1}{5}+\left(\frac{6280}{7}\sdot\frac{1}{8}\sdot\frac{1}{6}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{9}\sdot\frac{1}{5}\right)\\&\scriptstyle=\frac{1}{5}+\left(\frac{6280}{8}\sdot\frac{1}{5}\sdot\frac{1}{4}\sdot\frac{1}{6}\sdot\frac{1}{9}\sdot\frac{1}{7}\sdot\frac{1}{5}\right)\\&\scriptstyle=\frac{1}{5}+\left(\frac{785}{5}\sdot\frac{1}{4}\sdot\frac{1}{6}\sdot\frac{1}{9}\sdot\frac{1}{7}\sdot\frac{1}{5}\right)\\&\scriptstyle=\frac{1}{5}+\left(\frac{157}{4}\sdot\frac{1}{6}\sdot\frac{1}{9}\sdot\frac{1}{7}\sdot\frac{1}{5}\right)\\&\scriptstyle=\frac{1}{5}+\left(\frac{39}{6}\sdot\frac{1}{3}\sdot\frac{1}{3}\sdot\frac{1}{7}\sdot\frac{1}{5}\right)+\left(\frac{1}{4}\sdot\frac{1}{6}\sdot\frac{1}{3}\sdot\frac{1}{3}\sdot\frac{1}{7}\sdot\frac{1}{5}\right)\\&\scriptstyle=\frac{1}{5}+\left(\frac{6}{3}\sdot\frac{1}{3}\sdot\frac{1}{7}\sdot\frac{1}{5}\right)+\left(\frac{3}{6}\sdot\frac{1}{3}\sdot\frac{1}{3}\sdot\frac{1}{7}\sdot\frac{1}{5}\right)+\left(\frac{1}{4}\sdot\frac{1}{6}\sdot\frac{1}{3}\sdot\frac{1}{3}\sdot\frac{1}{7}\sdot\frac{1}{5}\right)\\&\scriptstyle=\frac{1}{5}+\left(\frac{2}{3}\sdot\frac{1}{7}\sdot\frac{1}{5}\right)+\left(\frac{3}{6}\sdot\frac{1}{3}\sdot\frac{1}{3}\sdot\frac{1}{7}\sdot\frac{1}{5}\right)+\left(\frac{1}{4}\sdot\frac{1}{6}\sdot\frac{1}{3}\sdot\frac{1}{3}\sdot\frac{1}{7}\sdot\frac{1}{5}\right)\\\end{align}}}](/mediawiki/images/math/d/e/1/de140719bae84adbb3f37634029381d9.png)
|
ונחלקם תחלה לח' ויצא בחלוק 785 ולא ישאר דבר
ונחלק זה היוצא לה' ויצא בחילוק 157 ולא ישאר דבר
ונחלקם לד' ויצא בחילוק ל"ט וישאר א' ונשימנו תחתיו
ונחלקם לו' ויצא בחילוק ו' וישארו ג'
[ונ]תיך הט', ר"ל שנעשה ממנו ב' מורים, שהם ג' ג', כי כך הוא שלישית שלישית, כמו תשיעית ועוד אדבר בזה בכלל האחרון ב"ה י"ת
ונחלק הו', אשר יצאו בחלוק באחרונה, על האחד מהם, ר"ל על הג' ויצא בחילוק ב' ולא ישאר דבר
ואלו הב', אחר שהוא מספר קטן משאר המורים, אין לנו עוד לחלקם, רק להשימם תחת המורה הסמוך אשר נשים לפניהם ויהיו הג' השני כדי שלא ישכח ונשימם תחתיו
ונסדר עוד הט [הו'] המורה הנשאר לפניהם ולפניו הה' ראשונה ונשים תחתיו הא', אשר היה תחתיו, שהוא המורה היותר חלק גדול הגדול שאיפשר אשר בקשנו
הנה יצא לנו שהשברים הנשאלים יעלו חמשית א' שלמה וב' שלישיות שביעית חמישית וג' ששיות שלישית שלישית שביעית חמישית ורביעית שישית שלישית שלישית שביעית חמישית כזה
|
|
|
|
|
|
והקש על זה
|
The reason that if there is no remainder the result is
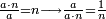
|
וטעם אומרנו שאם לא ישאר דבר, שהיוצא בחילוק בעצמו הוא מורה החלק אשר השברים מהשלם
|
The portions of the denominators are the portions of their common denominator in one unit
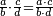
|
הוא לפי שאמרנו אלו החלקים מאלו המורים הוא כאלו אמרנו כ"כ מחלקי אם המורים בשלם
|
|
|
ר"ל כי ע'ד'מ' אם היו לנו ב' שלישיות רביעית
|
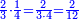
|
הוא כאומרנו שני חלקים מי"ב בשלם, שהיא אם אלו המורים, ר"ל שהוא מורכב מהם, שכפל ג' בד' עולה י"ב
|
|
|
וכן אומרנו ג' רביעיות חצי שלישית
|
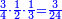
|
היא כאומרנו ג' חלקים מכ"ד בשלם, שהוא אם שלש מורים אלו וזה ברור
|
| The fractions are fractions of fractions of their common denominator in one unit
|
ועוד נחבר בפ' הרביעי מהחלק הא' הנה ידענו שאלו השברים הם חלקים מחלקי האם בשלם
|
|
|
ואם הם היה שלישיתם, הם שלישית השלם
|
|
|
ואם רביעיתם, רביעית
|
|
|
ואם כמותם הם א' שלם
|
|
|
וע'ד'מ' אם מספר השברים היה חמישית האם, ר"ל חמישית השלם, בחלקנו האם עליהם היה היוצא בחלוק ה' ולא היה נשאר דבר
|
|
|
ואם היה רביעית, יצאו ד'
|
|
|
הרי לנו שהיוצא בחילוק הוא המורה החלק אשר השברים מהשלם וזה ברור בטעם, כאשר נתחלק הכל ולא נשאר דבר
|
The reason that if there is a remainder the result is
![\scriptstyle\frac{\left(a\sdot n\right)+r}{a}=n+\frac{r}{a}\longrightarrow\frac{a}{\left(a\sdot n\right)+r}=\frac{1}{n+1}+\frac{a-r}{\left(n+1\right)\sdot\left[\left(a\sdot n\right)+r\right]}](/mediawiki/images/math/b/9/2/b92d1354c49c317f8eb727d0819e6f80.png)
|
ולברר טעם אומרנו שכאשר נשאר שם דבר, שנוסיף א' על היוצאות וכו', אביא משל אח':
|
|
|
המשל היו בידינו ג' רביעיות שביעית
|
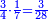
|
ר"ל שלשה חלקים מכ"ח, שהוא אם המורים בשלם
|
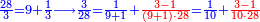
|
ואם נחלק אלו הכ"ח אל הג', יצאו ט' בחילוק וישאר א'
נוסיף א' על הט' היוצא בחילוק, יעלה עשרה, המורה על העשירית
|

|
ואם החלקים הראשונים היו ג' חלקים מל' באחד, היו עשירית אחד בצמצום, כי בחלקנו הל' בשלשה היו יוצאים ולא היה נשאר דבר ואז היו עשירית שלמה כמו שביארנו
|
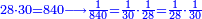
|
אכן להיותם ג' חלקים מכ"ח בשלם יותר מעשירית אחת ולדעת כמה הם יותר, נכפול הכ"ח בל' ויעלו 840 והנה אומרנו חלק אחד מ840 בשלם הוא כאומרנו חלק אחד מל' מכ"ח בשלם, או חלק אחד מכ"ח מל' בשלם, כי הם המורים אשר מהם הורכב וכל זה נתבאר הטב בפרק הד' מהחלק הא'
|
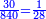
|
וא"כ הל' חלקים מה840 בשלם הם חלק אחד מכ"ח בשלם
|
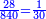
|
וכן הכ"ח חלקים מ840 בשלם הם חלק אחד מל' בשלם
|
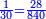
|
הרי לנו שהחלק אחד מל' בשלם הוא כ"ח חלקים מ840 בשלם
|
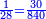
|
וכן החלק מכ"ח בשלם הוא ל' חלקים מ840
|
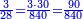
|
נמצא שהג' חלקי' מכ"ח בשלם הוא ג' פעמים ל', שהם 90 חלקים מ840 בשלם
|
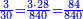
|
והג' חלקים מל' בשלם הם ג' פעמים הם כ"ח שהם פ"ד חלקים מ840
|
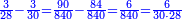
|
הנה יעדפו עליהם ו' חלקים מ840 בשלם, ר"ל ו' חלקים מל' מכ"ח בשלם, כי הם מוריו
|
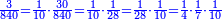
|
וכל ג' חלקים מאלו הם עשירית הל', שהם, ר"ל שהם הל', הם חלקי א' מכ"ח בשלם כמו שנתבאר, א"כ כל שלשה מהם הם עשירית [חלק מכ"ח בשלם, ר"ל חלק מכ"ח מעשירית בשלם, שהוא] הל' שהם ר"ל הל' הם חלקי א' מכ"ח בשלם כמו שנתבאר א"כ כל שלשה מהם הם עשירית הל' חלק מכ"ח בשלם ר"ל חלק מכ"ח מעשירית בשלם שהוא רביעית שביעית עשירית מהשלם
|
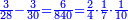
|
והששה הנוספות, אשר מצאנו לג' חלקים מכ"ח אשר היו בידינו, על הג' חלקים מל', אשר מצאנו לג' חלקים, היו עשירית שלמה, יעלו א"כ ב' רביעיות שביעית עשירית
|
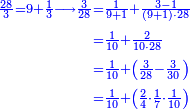
|
הרי לנו שכאשר חלקנו הכ"ח, שהוא האם, על הג', שהיו מספר החלקים, ויצא ט' ונשאר א', שכאשר הוספנו אחד על הט' ועלה י' והורה עשירית, שנשאר לנו לתוספת ב' רביעיות שביעית עשירית, שהם התוספת אשר למספר אשר חלקנו עליו, שהיה ג' על השארית שהיה א', ר"ל שאלו הב' הם חלקים מהמורים, שהיו רביעית שמינית מהמורה שנתחדש, שהוא עשירית וכל זה ברור בטעם למבין והקש על זה
|
| Dividing a small number by a greater number - without [divisors] or with [divisors]
|
ויצא לנו מזה שהרוצה לחלק מעט על רב, שיוכל לחלקו בלי הוצאת המורים, או בהוצאת המורים ויצאו לנו ג"כ החלק היותר גדול שאיפשר בשם אחד
|
| The method is very effective for division of a prime number (that has no [divisors]), such as 101
|
וזה יועיל מאד כאשר אנו רוצים לחלק למספר פשוט, כמו ק"א, או כדומה לו, שאין לו מורים
|
- Two examples - with divisors and without divisors
|
וכדי לבאר הענין יפה יפה, אביא שני משלים: אחד עם הוצאת המורים ואחד מבלי הוצאת המורים
|
- Example with divisors:
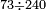
|
המשל רצינו לחלק 73 על 240
|

|
והנה מוריו הם אלו ו' ח' ה', כי מהם מורים הוא מורכב והוא האם
|
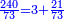
|
ונחלק האם, שהוא המספר הגדול אשר רצינו לחלק עליו, על המספר הקטן, ר"ל ה73, אשר הוא המספר אשר רצינו לחלק עליו על המספר הקטן, ר"ל ה73, אשר הוא המספר אשר רצינו לחלק ויצא בחילוק ג' וישארו כ"א
|
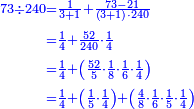
|
נוסיף א' על היוצא, יהיה ד' והוא המורה החלק גדול והוא רביעית אחת ונשימנו ראשונה ונשים תחתיו א', עוד נשים הכ"א הנותרים מהע"ג, שהוא החשבון אשר חלקנו עליו עתה, ישארו נ"ב והם מוסיפים על הרביעית, ר"ל שהעולה שיצא לנו בחלוק ה73 המספר הקטן על ה240, שהוא המספר הגדול, רביעית אחת ונ"ב חלקים מ240 מרביעית
או אם תרצה, תקח מורה במקומו ותאמר רביעית אחת ונ"ב חמישיות שמינית שישית רביעית
ואם תרצה תעשה להם כלילת יופי ויעלו רביעית אחת וחמישית רביעית וד' שמיניות שישית חמישית רביעית והקש על זה
|
- Example without divisors - illustrating that the procedure can be used repeatedly until reaching to a simple fraction (whose numerator is 1) -
|
ועוד אעשה משל אחר מאשר אין לו מורים כלל
|
|
|
ושם אאריך, שאנו יכולים לעשות מעשינו זה פעם אחר פעם עד כלות המספר והגיעו לחלק אחד, כי גם לזה קראתיו אחדות, כי יגיעם כלם לאחד ואפי' בין כל המורים למורה האחרון, נוכל להכניס מורה חדש ככל חפצנו
|
- Example without divisors:
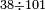
|
המשל לחלק ל"ח לק"א, כי זה המספר, ר"ל ק"א
|

|
ונחלק הק"א לל"ח [ויצאו בחלוק ב' וישארו כ"ה
|
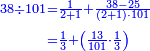
|
נוסיף א' על הב', יהיו ג' ונשימהו למורה ראשון ונשים תחתיו א' ונגרע השארית מהל"ח אשר] אשר חלקנו עליו עתה וישארו י"ג
ואם לא היו כ"כ, הינו שמים למורה שני הק"א והינו שמים זה השארית, ר"ל אלו הי"ג, תחתיו והינו אומרים שהמחלק ל"ח על ק"א, שיגיע לכל אחד מהם שלישית אחת וי"ג חלקים מק"א משלישית שלמה
|
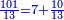
|
אכן להיותם הרבה וכדי שנמצא חלקים יותר נאותות, נשוב לחלק הק"א לאלו הי"ג ויצא בחילוק ז' וישאר י'
|
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle38\div101&\scriptstyle=\frac{1}{3}+\frac{13}{101}\sdot\frac{1}{3}\\&\scriptstyle=\frac{1}{3}+\frac{1}{3}\sdot\left[\frac{1}{7+1}+\frac{13-10}{\left(7+1\right)\sdot101}\right]\\&\scriptstyle=\frac{1}{3}+\frac{1}{3}\sdot\left[\frac{1}{8}+\frac{3}{8\sdot101}\right]\\&\scriptstyle=\frac{1}{3}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)+\left(\frac{3}{101}\sdot\frac{1}{3}\sdot\frac{1}{8}\right)\\\end{align}}}](/mediawiki/images/math/d/d/3/dd32f95b035bc980c80c4385a7b505f0.png)
|
ונשים זה הז' בתוספת אחד והוא ח' למורה שני ונשים תחתיו א' ונשים הי', שהם השארית מהי"ג אשר חלקנו עליהם עתה וישארו ג'
ואם תרצה, כבר כלית כל מלאכתך ותשים הק"א למורה שלישי ותשים למורה שלישי ותשים אלו הג' תחתיו שהם השארית הנשארה
|
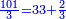
|
אכן אם תרצה עוד להכפל המעשיך, יען תגיע לאחדות גמורה, ר"ל שלא יהיו שם מנין שברים כי אם אחד אחד, תשוב תחלק הק"א על אלו הג' ויצא בחילוק ל"ג וישארו ב'
|
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle38\div101&\scriptstyle=\frac{1}{3}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)+\left(\frac{3}{101}\sdot\frac{1}{3}\sdot\frac{1}{8}\right)\\&\scriptstyle=\frac{1}{3}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)+\left[\frac{1}{3}\sdot\frac{1}{8}\sdot\left[\frac{1}{33+1}+\frac{3-2}{\left(33+1\right)\sdot101}\right]\right]\\&\scriptstyle=\frac{1}{3}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)+\left[\frac{1}{3}\sdot\frac{1}{8}\sdot\left[\frac{1}{34}+\frac{1}{34\sdot101}\right]\right]\\&\scriptstyle=\frac{1}{3}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)+\left(\frac{1}{3}\sdot\frac{1}{8}\sdot\frac{1}{34}\right)+\left(\frac{1}{3}\sdot\frac{1}{8}\sdot\frac{1}{34}\sdot\frac{1}{101}\right)\\\end{align}}}](/mediawiki/images/math/9/e/8/9e81c6f384212f9effbf03c4791a0698.png)
|
ונוסיף א' על הל"ג ויהיו ל"ד ונשימם למורה שלמי ונשים א' תחתיו ונחסר אלו שני הנשארים מהג' אשר חלקנו עליהם עתה וישאר א' וכבר הגענו לאחדות הגמור וכלינו מלאכתנו מכל וכל ונשים ק"א למורה [...] ונשים א' תחתיו
|
|
|
הרי לך שלש צורות שכלם אמיתיות ותוכל להשיב כאשר תרצה מהם וכן היה הרשות בידך לעשות זה פעם אחר פעם, [כאשר [..] מחלק אם המורים, כבמשל הא', ונשים כל המורים המתחדשים פעם אחר פעם זה] זה אחר זה כ"א תחת כל אחד
|
| Aḥdut (unification)- reminder for placing 1 [as a numerator of the simple fractions] beneath each denominator
|
כי לכל זה יועיל שם האחדות, שלא תשכח מלשים א' תחת כל מורה מתחדש ואחר תשים האם עצמה, או מוריה במקומה
|
- If the unification is complete - [the final fraction is simple i.e. its numerator is 1] - placing 1 beneath the last denominator
|
ותחת האחרון א', אם הגעת לאחדות הגמורה
|
- If the unification is incomplete - placing the remainder beneath the last denominator
|
ואם אין, תשים תחתיו הנשאר באחרונה, אחרי הסירך הנשאר מהמספר אשר אתה מחלק עליו בעת ההיא באחרונה [.]השארית האחרונה ההיא תשים תחת המורה האחרון אשר לאם
|
- The option to continue the procedure when the remainder is greater than 1, by dividing the denominator by the remainder
|
ואם יהיה רב ממנו, תעשה מהם כלילת יופי, רצוני לומר לחלק השארית הא' ההיא על המורה האחרון והיוצא שלפניו והנשאר תשים תחתיו וכן לעולם עד כלותו וכל זה מבואר ונכפל פעמים רבות
|
|
|
וגם בכל מספר אחר, אשר חלקת הכל למורים, אם תראה שאשר שמת תחת המורה האחרון הוא מספר רב ותרצה להמציא בין כל המורים הראשונים זה האחרון אשר לצד שמאל משום מורה מחודש, או מורים, חלק המורה האחרון על אשר תחתיו
|
|
|
כאשר עשית במה שבין הצורה השנית והשלישית, שהרי הק"א היה המורה האחרון בצורה הראשונה ולפי שמצאת הי"ג, שהם מספר רב, תחתיו, המצאת המורה הח' ששמת שני והוא שלישי בידך, שבא בצורה השנית
|
|
|
וכן עשית פעם אחת מהצורה השנית לשלישית והמצאת מורה אחר והוא הל"א ושמת הק"א רביעי
|
- The procedure continues considering the common denominator - the last denominator to the left
|
ובלבד שלא תעשה זה כי אם למורה האחרון אשר לצד שמאל וכל זה מבורר בטעם הראשון למבין
|
- Considering other divisors - fractionalizing the common denominator
|
ואם תרצה להוציא המורים בין המורים האמצעיים, תצטרך להוציא המורים לכל המורה האחרון אשר לצד שמאל והאם ההיא תחלק למנין השברים, אשר היו תחת המספר המורים ההם, אחרי עשות להם פריטה, אם כבר נתחלק להם המספר וכל זה ברור בטעם
|
|
|
כי אחר שהוצאת האם למורים האם, הרי שבו כלם כמורה אחד ואתה מבקש בין הראשונים ובינו מורה, או מורים אחדים ואחר שהמצאת המורים אשר רצית, תשים האם הזאת אחריהם לצד שמאל, או המורים אשר הורכבה מהם, זה אחר זה במקומה, כי הכל אחד ודי למבין
|
| Checking the unification: fractionalization
|
ואם תרצה לבחון מעשיך, עשה פריטה לכל אלו השברים אשר באו לך
|
- Division of a small number by a greater number: if one of the denominators is the given large number by which the smaller number should be divided - dividing the numerator which is the result of the fractionalization by all the denominators except for the large number - the result of division should be the small number divided originally
|
ואם יש במוריך אלו המספר הגדול אשר רצית לחלק עליו, ר"ל הק"א במשל האחרון, חלק זה העולה מהשברים הנפרטים על כל שאר המורים מבלעדיו זה אחר זה, או על אמם ויצא לך באחרונה כמנין המספר הקטן אשר רצית לחלק ולא נשאר דבר בשום חלוקה מאלו, הנה מעשיך אמת ונכון, ואם לאו, דע שטעית
|
- A sum of fractions: dividing the numerators by the unified denominators
|
גם במשל הראשון, אם יש במוריך אלו הם המורים הראשונים, או המורים עצמם, חלק כל מספר השברים הנפרטות על שאר המורים שנתחדשו במלאכת האחדות, או על אמם ואם לא ישאר לעולם דבר ויצא באחרונה כמספר הקטן אש' רצית לחלק, או כשברים הנפרטים במשל ראש המאמר, הנה אמת הנה נכון ואם לאו דע שטעית
|
| If the large number or the common denominator does not appear as a denominator in the final result - multiplying the numerators of the result by this large number or the common denominator and dividing the product by the other denominators - the result of division should be the small number to be divided, or the original numerators
|
ואם אין במלאכתך זאת, ר"ל במוריך, לא אם המורים ולא המורים עצמם, כפול כל המספר השברים הנפרטים בחשבון הגדול אשר רצית לחלק עליו, אם באם המורים מהחלקים הנשאלים, כבמשל הראשון אשר בראש זה המאמר, אם במספר הגדול אשר רצית לחלק עליו, כבמשל השני והעולה חלקנו לכל מוריך אלו, או לאמם ואם יצא כמספר השברים הנפרטים הנשאלים במשל הראשון, או כמספר הקטן אשר רצית לחלק במשל השני, מבלי שארית כלל, הנה אמת ואם לאו שקר
|
| Checking the above three examples:
|
וקודם התחילי בטעם בחינה זאת, כדי להרגילך במעשה, אעשה בחינה בכל אחד משלשת המשלים הנזכרים:
|
|
|
הנה פריטת המשל הראשון
|

|
היה 7 ב3 21, 23 ב3 69, 69 ב6 414 וה3 הם 417 וב4 1668, 1668 ו1 1669, 5 1669 8345, 8345 ב8 66760 והנה עלה בידינו שהפריטה היא 66760
|
|
|
ואם לא היו בידינו כל המורים הראשונים, היו כופלים זה בכל המורים הראשונים והעולה היינו מחלקים אל כל שמונת מורים אלו אחד אחד אחד, או לאמם והיא יוצא מספר פריטת השברים הנשאלים והיא 13352
|
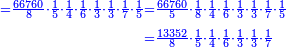
|
אכן אחרי היות בידינו כל המורים הראשונים, ר"ל כל מורה השברים הנשאלים ואל יטעך שאין כאן הט', שהרי במקומו ג' ג', שהם מוריו
ונחלוק זה אשר עלה לנו מפריטתינו זאת, ר"ל ה66760, למורים שנתחדשו במלאכתינו, ר"ל לה' הראשון לבדו, כי לא נתחדשו עוד ויצא בחילוק 13352, שהוא מספר פריטת השברים הנשאלים ולא נשאר דבר והנה אמת
|
|
|
ובמשל השני
|

|
הוא הפריטה א' בה' ה', וא' ו'
ו'בו' ל"ו, בח' 288
ו4 292
נחלקם לד', שהוא המורה המתחדש, יצא בחילוק מבלי שארית 73, שהוא המספר הקטן שרצינו לחלק והנה אמת
|
|
|
ובמשל השלישי
|
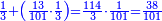
|
בצורה הראשונה, הנה הפריטה עולה 114, נחלקם לג', שהוא המורה המתחדש, יצאו הל"ח, שהוא המספר הקטן אשר רצינו לחלק
|
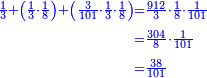
|
ובצורה השנית הפריטה 912, נחלקם לג' ולח', שהם המורים החדשי', תחלה לג', יצא 304, נחלקם לח' ויצאו הל"ח
|
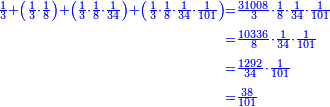
|
ובצורה השלישית הפריטה 31008, נחלקם לג', יצא 10336, נחלקם לח', יצא 1292, נחלקם לל"ד, שהוא המורה הנשאר מהמורים החדשים, יצא הל"ח והנה אמת
|
| The reason for checking the unification by fractionalization: fractionalizing means finding the numerator of the fraction that consists of all the denominators - the original denominators and the renewed denominators - therefore by dividing this numerator by the renewed denominators the original numerator will be received
|
וטעם בחינה זה הוא ברור, כי כשיש במורינו המורי' הראשונים, או האם או האם, או המספר הגדול אשר רצינו לחלק עליו, הנה הפריטה היא מספר שברים מכל המורים חדשים גם שנים וזה ברור כמו שנתבאר פעמים רבות
|
|
|
כי הפריטה הוא להשיבם פרוטות כי הפריטה הוא מספר שברים מכל המורים, שהוא המין האחרון והוא נקשר בכל המורים וכאשר נחלקם על המורים המתחדשים, הוא כעושה כלילת יופי, כי הסדר לא יזיק ואחר שנתחלק על כל החדשים ולא נשאר דבר, הנה יצאו מן הכלל והיוצא באחרונה הם שברים מהמורים הראשונים, או מאמם כבראשונה, או מהמספר הגדול
|
|
|
ר"ל שהל"ח שיצאו לנו, אחר שחלקנו הפריטה במורים החדשי' ויצאו הם מן הכלל, הם חלקים מק"א חלקים בשלם, כי לכל אחד מהל"ח יעלה לכל אחד חלק אחד מק"א בשלם ומהל"ח ל"ח
|
| The reason for multiplying the fractionalized numerator by the original denominators, if the original denominators do not appear in the final result after it was fractionalized: multiplying by the original denominators means further fractionalizing the numerator to be a numerator of the original denominators as well
|
וטעם אומרנו שאם אין המורים הראשונים, או אמם, או המספר הגדול במורינו, שנכפול הפריטה במורים הראשונים, או באמם, או במספר הגדול ונחלקנו בכל המורים, שיצא מבלי שארית כמספר פריטת השברים הנשאלים במשל הראשון, או כמספר הקטן במשל השני, הוא לפי שהפריטה היא שברים מכל אלו המורים וכאשר אנו כופלים אותה במורים הראשונים, או באמם, או במספר הגדול, הוא שאנו פורטים אותה עוד לשברי שברים מהראשונים
|
|
|
ר"ל כי אם יש בידינו ג' רביעיות שמינית ע'ד'מ'
|
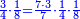
|
אם נכפלם בז', היוצא שביעית רביעית שמינית וזה נתברר פעמים רבות
|
| Therefore, the product by the original denominators is a numerator of a fraction that consists of the renewed denominators as well as the original denominators and when divided by the renewed denominators, the result of division should be a numerator of a fraction that consists of the original denominators - the original numerator
|
והנה במעשינו היוצא אחר הכפל יהיו שברים מכל אלו המורים אשר לנו ומהראשונים, או מאמם, או מהמספר הגדול שהוספנו עליהם עתה וכאשר נחלקנו למורינו, ר"ל מבלתי הראשונים אשר הוספנו עתה, או מבלתי אמם, או מבלתי המספר הגדול אשר הוספנו עתה, כי להן לא נחלקם, ישאר היוצא שברים מהמורים הראשונים, או מאמם, או מהמספר הגדול
|
|
|
והנה אם היוצא היה כמספר פריטת השברים הנשאלים במשל הראשון, או כמספר הקטן בשני, הנה שב כבתחלה והנה כל מעשינו אמת ויציב
|
- Note: if the denominator or the large number [by which the small number is divided] is a prime number (such as 101) - it cannot be converted or be absent after the unification procedure, since it has no divisors and therefore cannot be divided by another number without a remainder
|
ודע כי המספר הפשוט, ר"ל אם היה המספר הגדול מספר פשוט, שאין לו מורים, כבמשל השלישי שהוא קי"א, כי לעולם לא יעדר ולא יומר וזה ברור, כי הוא לא יתחלק לשום מספר בשלימות מבלי שארית, אחר שהוא פשוט
|
Chapter Six: Roots
|
הפרק הששי בשרשים
|
The procedure: fractionalization and multiplication if needed, multiplication by the denominators, extracting the root as in the case of the integers, then reducing and arranging the denominators
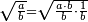
|
גם בזה תצטרך לעשות לשבריך פריטה, גם הכאה, או מה שיצטרכו מהם והיוצא תשוב תכפול אותו בכל המורים אחד אחד זה אחר זה, או באמם
|
|
|
ושמור נפשך מאד שמר, שלא תחבר לו הנמצא תחת המורי', כי זה לא יעשה כי אם בפריטה
|
|
|
ומכל העולה הוצא השרש ככל כמעשיך בשלימים והשלימים היוצאים בשרש הם חלקים משלם מאלו המורים
|
|
|
ואם תרצה, [עשה להם] כלילת יופי והשברים היוצאים בשרש הם שברים מחלק אחד מכל אלו המורים בשלם
|
|
|
המשל רצינו לדעת שרש ד' שישיות מד' שלמים וה' תשיעיות כזה:
|
|
|
|
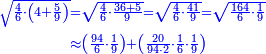
|
ויצאו 94 שלימים שהם 94 שישיות תשיעיות נפרוט הד' שלימים ונכפול אותם בט', יעלו 36 ועם ה5, יהיו 41, נכם בד', יעלו 164 שישיות תשיעית כזה
ויצאו 94 שלימים, שהם 94 שישיות תשיעיות ונשארו 20
|
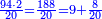
|
ואם רצית להתקרב אל האמת, כפול השרש שהוא 94 וחלקם עליהם
ויעלה בדרך האחדות והוא שנחלק כפל ה94, שהוא 188, ל20 ועלו ט' ונשארו ח'
|
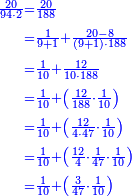
|
הוספנו א' מעל הט', היה 10, שהוא מורה עשירית אחת ונחסר הח' הנותרים מן ה20, נשארו י"ב, שהם חלקים מ188 ומעשירית
ומורה ה188 והם 47 [874] והנה הי"ב הם י"ב רביעיות חלק ממ"ז בעשירית כזה
נעשה להם כלילת יופי והוא שנחלקם לד', יצאו ג' ולא ישאר דבר ואחר שהם פחות מהמ"ז, נשימם תחתיו כזה:
|
|
|
|
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\sqrt{\frac{4}{6}\sdot\left(4+\frac{5}{9}\right)}&\scriptstyle\approx\left(\frac{94}{6}\sdot\frac{1}{9}\right)+\left(\frac{20}{94\sdot2}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)\\&\scriptstyle=\left(\frac{94}{6}\sdot\frac{1}{9}\right)+\left[\left[\frac{1}{10}+\left(\frac{3}{47}\sdot\frac{1}{10}\right)\right]\sdot\frac{1}{6}\sdot\frac{1}{9}\right]\\&\scriptstyle=\left(\frac{94}{6}\sdot\frac{1}{9}\right)+\left(\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)+\left(\frac{3}{47}\sdot\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)\\&\scriptstyle=1+\frac{6}{9}+\left(\frac{4}{6}\sdot\frac{1}{9}\right)+\left(\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)+\left(\frac{3}{47}\sdot\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)\\&\scriptstyle=1+\frac{2}{3}+\left(\frac{4}{6}\sdot\frac{1}{9}\right)+\left(\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)+\left(\frac{3}{47}\sdot\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/3/2/1/3215f7c5e43f2a2b4b1ac3306f8da535.png)
|
הנה עלה לנו כל השרש 94 ועשירית וג' חלקים מ47 מעשירית וכל אלו הם חלקים משישית תשיעית כנזכר
א"כ השרש היוצא הוא 94 שישיות תשיעית ועשירית שישית תשיעית וג' חלקים ממ"ז מעשירית שישית תשיעית כזה:
ונעשה כלילת יופי ל94 ויעלה א' לשלם וזהו שלם באמת ועוד ו' תשיעיות, שהם שני שלישיות ועוד ד' תשיעיות שישיות ויש לנו עוד עמהם עשירית שישית תשיעית וג' חלקים ממ"ז מעשירית ששית תשיעית כזה:
|
|
|
|
|
|
וזהו השרש הקרוב
|
Check:
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left[\left(\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)+\left(\frac{3}{47}\sdot\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)\right]^2&\scriptstyle=\frac{2500}{47}\sdot\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\sdot\frac{1}{47}\sdot\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\\&\scriptstyle\left(\frac{4}{9}\sdot\frac{1}{47}\frac{1}{47}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)+\left(\frac{1}{6}\sdot\frac{1}{9}\sdot\frac{1}{47}\sdot\frac{1}{47}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/3/7/c/37c2f73a3ca36b19e555b950edca459f.png)
|
ואם תרצה לבחון אותו, כפול אותו על עצמו וראה אם יתקרב לנשאל, שהוא 146 שישיות תשיעית בתוספת אחד, בכמו מרובע השברים אשר הוספנו על שרש השברים הראשון אשר הוצאנו והעשירית שישית תשיעית וג' חלקי' ממ"ז מעשירית שישית תשיעית, שמרובעם, ר"ל כפלם בעצמם אחר הפריטה, יעלה 2500 חלקים ממ"ז מעשירית שישית תשיעיות ממ"ז מעשירית תשיעית
וכאשר תעשה להם כלילת יופי, יעלה ד' תשיעיות ממ"ז ממ"ז משישית תשיעית ושישית מתשיעית ממ"ז ממ"ז מששית תשיעית
|
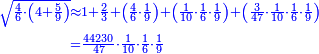
|
והנה פריטת זה השרש יעלה 44230 חלקים מחלק ממ"ז מעשירית משישית תשיעית
|
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left[1+\frac{2}{3}+\left(\frac{4}{6}\sdot\frac{1}{9}\right)+\left(\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)+\left(\frac{3}{47}\sdot\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)\right]^2&\scriptstyle=\left(\frac{44230}{47}\sdot\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)^2\\&\scriptstyle=\frac{44230}{47}\sdot\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\sdot\frac{44230}{47}\sdot\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\\&\scriptstyle=\frac{1956292900}{47}\sdot\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\sdot\frac{1}{47}\sdot\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\\\end{align}}}](/mediawiki/images/math/b/c/d/bcdd152e8b9660a0cf72e65b28eb952a.png)
|
וכאשר נכפול זה על עצמו הוא כאומרנו 44230 חלקים מחלק מ"ז מעשירית שישית תשיעית [מ442300 חלקים מחלק מ"ז מעשירית ששית תשיעית כזה] כזה:
| |
47 |
10 |
6 |
9
|
| 47 |
10 |
6 |
9 |
44230
|
| 44230
|
ונכה ה44230 ויעלה 1956292900 חלקים מחלק מ"ז מעשירית שישית תשיעית מחלק מ"ז מעשירית תשיעית בשלם כזה
|
|
|
| 47 |
10 |
6 |
9 |
47 |
10 |
6 |
9
|
| 1956292900
|
|
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\left[1+\frac{2}{3}+\left(\frac{4}{6}\sdot\frac{1}{9}\right)+\left(\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)+\left(\frac{3}{47}\sdot\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)\right]^2\\&\scriptstyle=\frac{1956292900}{47}\sdot\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\sdot\frac{1}{47}\sdot\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\\&\scriptstyle=\left(\frac{164}{6}\sdot\frac{1}{9}\right)+\left[\left(\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)+\left(\frac{3}{47}\sdot\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)\right]^2\\&\scriptstyle\left(\frac{164}{6}\sdot\frac{1}{9}\right)+\left(\frac{4}{9}\sdot\frac{1}{47}\frac{1}{47}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)+\left(\frac{1}{6}\sdot\frac{1}{9}\sdot\frac{1}{47}\sdot\frac{1}{47}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/7/4/6/7464f65fea982e7b530ca03f0c62dd8f.png)
|
ונעשה להם כלילת יופי, ר"ל שנחלקנו לכל המורים האלו, עד הגיענו אל הט' והו', המורים הראשונים ובהיגיענו שם נדע כמה שישית תשיעיות יעלה, אם יגיע למספר הנשאל שהוא 164 שישיות תשיעית ועוד מרובע השברים הנוספים הנזכרים כנזכר ואשר עלינו זה עלה 164 שישיות תשיעית ועוד ד' תשיעיות ממ"ז ממ"ז [נ' ד'] משישית תשיעית וזה התוספת שוה ממש למרובע השברים הנוספים בשרש על שרש השברים אשר יצא ראשונה והיה כל מלאכתך אמת
|
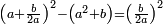
|
ויצא לנו עוד מזה, שנתאמת מה שאמרנו בפ"ז מהחלק הא', שכאשר נחלק הנשאר על כפל השרש מבלי תוספת אחר, שיעדף המרובע האחרון על החשבון הנשאל כמרובע השברי' הנוספים וכן יהיה בכל פעם ופעם דוק ותשכח
|
The reason for multiplying the numerator by the denominators: so that the denominator will be a square - the product of the denominators by themselves
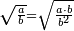
|
וטעם אמרנו שאחר הפריטה נכה המספר הפריטה בכל המורים הוא כדי שיהיה זה המרובע חלקים מאלו המורים פעמים, ר"ל נשנים
|
|
שאם היו רביעיות, יהיו עתה רביעיות רביעית
|
|
ואם היו חמישיות רביעית, יהיו עתה חמישיות רביעית חמישית רביעית וכן לעולם
|
|
|
והוצרכנו לזה לפי שמורי השרש לעולם הם נשנים במורי המרובע
|
|
וזה שאם השרש ע'ד'מ' ב' רביעיות, יהיה המרובע ד' רביעיות [רביעית]
|
|
ואם יהיה השרש ב' חמישיות רביעית, יהיה המרובע ד' חמישיות רביעית חמישית רביעית
|
| Multiplication of fractions by fractions means fractions of fractions: 2 quarters by 2 quarters is 2 quarters of 2 quarters
|
והטעם בזה לפי שהכפל בשברים שהוא אומרנו ע'ד'מ' כפל ב' רביעיות בב' רביעיות, הוא כאומרנו ב' רביעיות מב' רביעיות, כמו שביארנו למעלה
|
- How much quarters of quarters there are in 2 quarters of 2 quarters? - 2×2
|
ולדעת כמה רביעיות רביעית הם, יש לנו להכות הב' בב'
|
When calculating the square of a given fraction, the numerator is multiplied by itself, as in the calculation of the square of an integer the integer is multiplied by itself
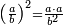
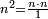
|
ר"ל המספר שברי השרש בעצמם, כדרכנו במרובע השלמים, [כי מרובע השלמים במרובע השלמים] כמספר החלקים והשינוי בהם
|
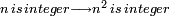
|
כי בשלמים מספר השרש ומספר המרובע הם ממין אחד, ר"ל שהם שלימים
|
|
|
ולזה יהיה לעולם גדול המרובע מהשרש
|
|
|
וכן כל כפל מספר שלם במספר
|
|
|
ואף אם יהיה כפל שלימים בשברים
|
The numerator is growing by multiplication, but the type of number does not change

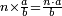
|
וזה לפי שהמספר מתרבה בכפל והמין אינו משתנה
|
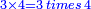
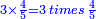
|
כי כאשר תאמר ע'ד'מ' כפול ג' שלמים בד' שלימים, או בד' חמישיות, הוא כאומרך כפול ג' פעמים ד' שלימים, או ד' חמישיות, הנה שהמספר מתרבה והדין לא ישתנה
|
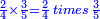
|
אבל בשברים אומרנו כפול ב' רביעיות בג' חמישיות הוא כאומרנו שני רביעיות פעם
|

|
ואם אומרנו כפול רביעית אחת בג' חמישיות הוא כאומרנו ג' חמישיות רביעית פעם והוא ג' חמישיות רביעית
|
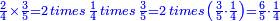
|
ואולם אומרנו שני רביעיות, יהיה בב' פעמים רביעית פעם וכל פעם הוא ג' חמישיות רביעית, הנה הב' רביעיות יהיו ו' חמישיות רביעית
|
| The number is increasing through the multiplication of the numerator by the numerator
|
וכן לעולם יתרבה המספר בכפל [מספר השברים במספר] משבר השברים
|
The product of the numerators is a fraction whose denominator is a product of the denominator of one of the numbers by the denominator of the other number
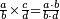
|
ויהיה העולה מכל שני מורי שני המספרים הנכפלים יחד, כבמשלנו זה שהם חמישיות רביעיות
|
Hence the numerator of the square is a square of the numerator of the root
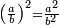
|
ולזה יהיה מספר שברי המרובע כמרובע מספר שברי השרש כדרכו בשלם שוה בשוה
|
| The denominator of the square is a square of the denominators of the root
|
אבל כי המורים נשנים, לפי שאנו כופלים השרש בכמותו ומורי שניהם יהיה כפל מורי האחר, כי שוים הם במורים וכל זה ברור בטעם
|
| This is illustrated in the calculation of area
|
גם זה יתבאר בשאנו כופלים בשטח:
|
| The area of 4 length and 3 width = 4×3
|
כי כאשר אנו או[מרי]ם בשטח ג' פעמים ד', הוא כאומרנו שיש בארך ד'
|
| The area of 4 length and 1 width = 4×1=4
|
ואלו לא היה ברחבו כי אם א', לא היו כי אם ד'
|
| Area consists of one [dimension] of length and one [dimension] of breadth
|
לפי שכל אחד שאנו אומרים בשטח, הוא שיהיה לו א' באורך וא' ברוחב
|
| Body consists of one [dimension] of length, one [dimension] of breadth, and one [dimension] of height
|
וכן בגשם: א' באורך וא' ברוחב ואחד בגובה
|
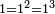
|
לזה לא יתרבה מרובע האחד ולא גם המעוקב, כי אומרנו אחד בשטח הוא כאומרנו אחד מרובע וכן בגשם מעוקב
|
| 4 length and 3 width = 3 stripes of 4 length = 3×4
|
וכאשר היו ד' באורך וג' ברוחב, הרי הם ג' רצועות של ד' ד' והוא כאומרנו ג' פעמים ד' ול וכן לעולם
|
| The meaning of multiplying fraction by fraction
|
אבל כשא[א]נו כופלים שבר בשבר
|

|
המשל ג' רביעיות בד' חמישיות הוא כאומרנו שארכו ד' חמישיות השלם ורחבו ג' רביעיות השלם
|

|
ואם ארכו אחד שלם היה ג' רביעיות שלם כי מן השלם המרובע חסר הרביע שנפצל מרחבו וזה מובן במעט עיון
|
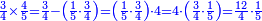
|
אבל לפי שמארכו נפצל ג"כ חמישיתו, הנה הוא כמי שהסיר מהג' רביעיות חמישיתם ונשארו ד' חמישיותיהם, הנה השטח הוא ד' חמישיות מג' רביעיות [וכל חמישית מהם היא חמישית ג' רביעיות, שהוא כשלש רביעיות חמישית, כי כך הוא חמישית רביעית כרביעית חמישית, א"כ הד' החמישיות מג' רביעיות הם ד' פעמים] הם ד' פעמים ג' רביעיות רביעיות חמישית, שהם י"ב
|
- If the denominator is a square, there is no need to multiply the numerator by the denominator, when extracting the root of the fraction
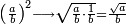
|
ולזה אנו כופלים בהכאה מספר השברים במספר השברים וכן בשרש והכל עולה לענין אחד
|
|
|
ואחר שביארנו שמורי המרובע הם נשנים ממורי השרש ומספר שברי המרובע הוא כמרובע מספר שברי השרש, נתבא' שאם היו לזה המרובע מורים נכפלים, ר"ל ד'ד', או ה'ה' וכדומה לזה, שלא היינו צריכים לכפול במוריום, כי אם להוציא השרש לבד מהמספר שב[..]ו כ[ער]ך בשלמים ומורי השרש היוצא היו חצי מוריו המרובע ונחלקנו אליהם, ר"ל לחצי מוריו
|
-
|
וכן אפי' אם לא היו כלם כפולים, אבל שכל אחד מאשר אינם בו פעמים הוא כפול, ר"ל כי אם הם כפולים בעצמם, ר"ל שהם מרובעים, כד', או כט', תקח שרש המורה ההוא אשר למרובע במקומו למורה השרש, ר"ל הב' במקום ד' והג' במקו' הט'. וזה שהרי בידיך לשום כמורי המרובע במקום הד' השנים, או במקום הט' ג'ג' ותקח אחד מהם בשרש וכל זה ברור
|
| This issue is explained in a special chapter on factorization at the end of the book
|
ויתבאר עוד במאמ' ההתכה, אשר בכלל אשר ייעדתי לשום בסוף הספר
|
- If some of the denominators are squares and some are not squares, those that are not squares should be multiplied by the numerator
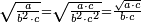
|
ואם יהיו שם מאלו ומאלו, תכפול מספר שברי המרובע באשר אינם נכפלים ולא מרובעים ותוסיפם על חצי הנכפלים ושרשי המורים המרובעים אשר לקחת במקומם ועליהם תחלק השלימים היוצאים בשרש והשברים היוצאים בשרש הם חלקים מחלק אחד מאלו המורים, אשר להם תחלק שלימי השרש והכל נתבאר במעשה ובטעם
|
In order to avoid confusion, the author instructs to multiply the numerators by the denominators in any case, even if the denominators are squares
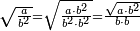
|
אכן כדי שלא לבלבלך בזה לראות אם הם נכפלים ולקחת חציים, או לקחת מהמרובעים שתים במקומם, ציויתיך צויתיך לכפלו בכלם ויהיו לו, ר"ל למרובע הנשאל, כפל המורים אשר לו עתה ונחלק מספר [62]שברי השרש לאשר לו בתחלה, שהם חצי מאשר לו עתה
|
| If one is not well versed in the procedure, it is better for him to make an effort, even if it is needlessly, in order to avoid confusion
|
וטוב שתטרח ואם לו לצורך, כדי שלא תתבלבל, אם אינך בקי במלאכה
|
|
But, if one is skilled, he can skip this, in order to make the procedure easier for himself
|
ואם ראית בעצמך, שאתה ראוי להיות שצו ש'צ' כהן הנושא כפיו, תוכל להקל מעליך העבודה ואתה רשאי ולא אני
|
General Rules for Operations with Fractions
|
|
|
|
ואחר אש' השלמנו הו' פרקים אשר בשערים, נתחיל בכל אשר ייעדנו שהוא מועיל לכלם
|
Finding the Common Denominator
|
|
| The rule that is useful for all fractions.
|
הכלל המועיל לכל השברים
|
| If you wish to solve all the issues of the chapters on fractions perfectly, seek for one great denominator that includes all the numbers, i.e. a common denominator for all their denominators in question, by which you will clearly find everything you want, i.e. you will be able to find through this common denominator how much is the quarter, the fifth, or any of the fractions you need.
|
אם תרצה להוציא כל ענייני פרקי השברים על השלימות תבקש לכל המספרים מורה א' גדול כולל אותם ר"ל אם כל מוריהם ושם תמצא כל מבוקשך בברור ר"ל שתוכל למצוא במורה ההוא כמה הוא הרביעית והחמישית או כל מה שתצטרך בכל השברים ההם
|
- For example, if we say: sum 3-quarters of a ninth with 4-fifths of a ninth and 7-fifths of a seventh.
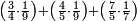
|
כי המשל אם אמרנו חבר ג' רביעיות תשיעית עם ד' חמישיות תשיעית עם 7 חמישיות שביעית
|
- The great denominator of these numbers is, as said, the common denominator of these 4 denominators, which is by multiplying one by the other and the product by the other until they end; it is 1260.

|
הנה מורה החשבונים הגדול אשר אמרתי הוא אם ד' מורים אלו והוא בהכפל זה בזה והעולה באחר עד תומם ויהיה 1260
|
- We consider one integer as 1260 parts.
|
והוא שעשינו האחד השלם 1260 חלקים
|
- The ninth is 140, which is the product of 3 of the mentioned denominators, i.e. their common denominator.

|
והנה תשיעית הוא ק"מ והוא ככפל הג' מורים הנזכרים ר"ל באמם
|
- A quarter of the ninth is a quarter of it; it is 35 and it is the common denominator of the mentioned denominators, i.e. the product of 5 by 7.
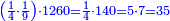
|
ורביעית התשיעית יהיה ברביעית זה והוא ל"ה והוא אם המורים הנזכרים ר"ל ככפל ה' בז'
|
- 3 quarters of the ninth are three times 35, which is 105.

|
והג' רביעיות התשיעית יהיו שלשה פעמים ל"ה שהם 105
|
- The seventh is the common denominator of the three that remain; it is 180.

|
ושביעית המורה הוא אם השלשה הנשארים והם 180
|
- A fifth of one-seventh is a fifth of it; it is 36 and it is the common denominator of the remaining.
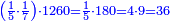
|
וחמישית שביעית הוא חמישית זה והוא ל"ו והוא אם הנשארים
|
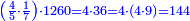
|
והד' חמישיות שביעית הם ד' פעמים ל"ו או אם תרצה לומר ד' פעמים כפל הב' מורים זה בזה ר"ל ט' בד' שהוא ל"ו והעולה יהיה 144
|
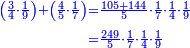
|
[63]ותחברם עם הה'10 שעלו הג' רביעיות תשיעית יעלו 249 ב0ובא חלקים בשלם כי זה מורה הוא מספר המורה הגדול אשר לקחת וכל חלק מאלו הוא חלק מכל אלו המורים
|
|
|
וזה כי 140 הם תשיעיות אחד
|
|
|
ול"ה שהם רביעיתם הם רביעית תשיעית
|
|
|
והה' שהם שביעית הל"ה הם שביעית רביעית תשיעית
|
|
|
והא' שהוא חמישית הה' הוא חמישית תשיעית רביעית שביעית
|
|
|
א"כ אלו ה249 הם חמישיות תשיעית רביעית שביעית
|
|
|
ואם תרצה לידע מה המה אלה הנה אחר שכל ה' מהם הם תשיעיות רביעית תשיעית תחלקם לה' והיוצא יהיו שביעיות רביעית תשיעית
|
|
|
ואם נשאר דבר הוא כבתחלה חמישיות תשיעית רביעית שביעית
|
|
|
ומהשביעית רביעיות תשיעית וכאשר תחלק לז' יהיה היוצא רביעיות תשיעיות
|
|
|
וכשתחלק זה היוצא לד' יהיה היוצא תשיעית
|
|
|
וכשתחלקנו לט' ה יהיה היוצא שלימים
|
| The order of the denominators is unimportant
|
וכל זה אי המעשה הנזכר למעלה עין בעין כמו שנרמז בצורות הרמוזות מחוץ לספר כי הסדר לא יזיק דוק ותשכח
|
|
|
והנה העולה מחבור השברים הנשאלות על כל א' מהדרכים כי הכל אחד הוא שביעית אחת ורביעית שביעית וד' תשיעיות רביעית שביעית וד' חמישיות תשיעית רביעית שביעית והקש על זה בכל שאר הפרקים
|
Completion of Fractions
|
מאמר ההשלמה
|
| Completion is used when subtracting fractions or fractions of fractions from fractions or fractions of fractions, in the procedure of extraction of roots for instance
|
ההשלמה הוא כאשר יש בידינו שבורים ידועים, או שברי שברים ואנו צריכים לגרעם משברים, או שברי שברים אחרים, שיש בידינו ממיניהם וזה יקרה בהוצאת השרשים, כמו כפי שנכתב בפ' ו' מזה החלק
|
The need to find the completion of fractions from integer or from a larger fraction - adding the completion to the subtracted in the subtraction procedure, relying on the following principle:
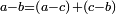
|
ולפעמים השברי שברים הנגרעי' הם רבים מאשר יגרע מהם, אכן יש שם שברי רבים, או שלימים, למלאת די מחסורנו, לכן אנו צריכים לידע, כאשר נקח השלם, או השבר הגדול, להוציא ממנו שברי שברים אלו, שנדע בקלות הנשאר מהשלם, או מהשבר הגדול [ההוא, אחר שהוצאנו ממנו, שזה הוא מה שחסרים אלו השברי שברים מאחד שלם או שבר גדול] להוציא ממנו שברי שברים אלו שנדע בקלות הנשאר מהשלם או מהשבר הגדול להוציא ממנו שברי שברים אלו שנדע בקלות הנשאר מהשלם או מהשבר הגדול ההוא אחר שהוצאנו ממנו שזה הוא מה שחסרים אלו השברי ה' שברים מאחד שלם או שבר גדול וזוהי השלמתן לאחד
|
|
|
ואחר שנדע השלמתן לאחד, אם היו לנו שברי שברים ממינם, כאשר נגרע מהם, אלא שהיו מעט אשר בידינו, נחבר זאת ההשלמה עמהן והמחובר יהיה הנשאר
|
|
|
המשל רצינו לגרוע ז' תשיעיות וה' שביעיות תשיעית וג' רביעיות שביעית תשיעית מג' שלמים וה' תשיעיות ושלש שביעיות תשיעית
|
|
|
הנה להיות הג' רביעיות רב מהב', גם הה' שביעיות מהג', גם הז' תשיעיות מהה', נצטרך לקחת אחד שלם למלאת די מחסורינו וישארו ב' שלמים
|
| The completion is the remainder from subtracting the given number from the whole
|
ולדעת כמה ישאר ממנו אחר קחתנו ממנו די ספקנו, נצטרך להשלימם לאחד שלם וההשלמה הוא השארית וזה ברור בטעם
|
|
|
וזאת ההשלמה נחברנה עם השברים, אשר היו לנו ולא היה בהם די ספקנו, כי להם משפט הגאולה והמחובר הוא הנשאר
|
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle
\left[3+\frac{5}{9}+\left(\frac{3}{7}\sdot\frac{1}{9}\right)+\left(\frac{2}{4}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\right]-\left[\frac{7}{9}+\left(\frac{5}{7}\sdot\frac{1}{9}\right)+\left(\frac{3}{4}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\right]\\&\scriptstyle=\left[\left(3-1\right)+\frac{5}{9}+\left(\frac{3}{7}\sdot\frac{1}{9}\right)+\left(\frac{2}{4}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\right]+\left[1-\left[\frac{7}{9}+\left(\frac{5}{7}\sdot\frac{1}{9}\right)+\left(\frac{3}{4}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\right]\right]\\&\scriptstyle=\left[2+\frac{5}{9}+\left(\frac{3}{7}\sdot\frac{1}{9}\right)+\left(\frac{2}{4}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\right]+\left[\frac{1}{9}+\left(\frac{1}{7}\sdot\frac{1}{9}\right)+\left(\frac{1}{4}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\right]\\&\scriptstyle=2+\frac{6}{9}+\left(\frac{4}{7}\sdot\frac{1}{9}\right)+\left(\frac{3}{4}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/b/a/a/baa9c24e903e00db5154a21ab2a825b6.png)
|
ונאמר ג' רביעיות שביעית תשיעית בכמה יהיו שביעית תשיעית, ברביע אחד, נשים א' תחתיהם
עוד נאמר הרי השלמנו [לשביעית תשיעית אחד וחמש שביעיות תשיעית שהיו לנו, הרי ו' ובכמה ישלומו לתשיעית אחד] לתשיעית אחד שלמה, באחד נשימנו תחתיו
ונאמר הרי השלמנו לתשיעית שלמה וז' שיש בידינו, הרי כאן ח', בכמה ישלמו לשלם, באחד, נשים תחתיהם א'
הרי לנו שנשאר מהאחד השלם תשיעית אחת ושביעית תשיעית ורביעית שביעית תשיעית ונחברם עם אשר בעליונה ויעלה שנשאר בידינו ב' שלימים וו' תשיעיות וד' רביעיות שביעית תשיעית [וג' רביעיות שביעית תשיעית] וכל זה ברור בטעם
|
The written procedure of completion: writing the numerator of the complement under the fraction to be complete; e.g. 1 under ¾ to indicate that ¼ is its complement
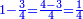
|
וכדי להקל מעליך המעשה, אתן לך כלל כי לאחרון אשר לצד שמאל, אשר שם יתחיל הצורך, נשים תחתיו כדי השלמת מספר שבריו למורה אשר עליו שוה בשוה
|
|
|
ר"ל הג' רביעיות בכמה ישלימו הג' לד', שהוא המורה אשר עליו, בא', נשימנו תחתיו ובכל האחרים, עד אשר נמצא מקום רב, אשר משם נקח האחד אשר הוצרכנו
|
|
|
לעולם נשים תחת מספר השברים כדי השלמתן למורה אשר עליהם חסר אחד והוא האחד אשר הושלם כבר באשר אחריו לצד שמאל
|
| Another solving method - similar to the subtraction of integers - borrowing one unit from a fraction of a higher type, and marking the loan with a dot as a reminder
|
ואם היינו רוצים, היינו עושים כדרך שאנו עושי' בשלימי' ולא נצטרך להשלמה כלל
|
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle
\left[3+\frac{5}{9}+\left(\frac{3}{7}\sdot\frac{1}{9}\right)+\left(\frac{2}{4}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\right]-\left[\frac{7}{9}+\left(\frac{5}{7}\sdot\frac{1}{9}\right)+\left(\frac{3}{4}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\right]\\&\scriptstyle=\left[3+\frac{5}{9}+\left(\frac{3}{7}\sdot\frac{1}{9}\right)+\left[\left(\frac{4}{4}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)+\left(\frac{2}{4}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\right]\right]-\left[\frac{7}{9}+\left(\frac{6}{7}\sdot\frac{1}{9}\right)+\left(\frac{3}{4}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\right]\\&\scriptstyle=\left[3+\frac{5}{9}+\left[\left(\frac{7}{7}\sdot\frac{1}{9}\right)+\left(\frac{3}{7}\sdot\frac{1}{9}\right)\right]+\left(\frac{3}{4}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\right]-\left[\frac{8}{9}+\left(\frac{6}{7}\sdot\frac{1}{9}\right)\right]\\&\scriptstyle=\left[3+\left(\frac{9}{9}+\frac{5}{9}\right)+\left(\frac{4}{7}\sdot\frac{1}{9}\right)+\left(\frac{3}{4}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\right]-\left(1+\frac{8}{9}\right)\\&\scriptstyle=3+\frac{6}{9}+\left(\frac{4}{7}\sdot\frac{1}{9}\right)+\left(\frac{3}{4}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)-1\\&\scriptstyle=2+\frac{6}{9}+\left(\frac{4}{7}\sdot\frac{1}{9}\right)+\left(\frac{3}{4}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/4/5/b/45b4d274eb40b7256c8d56e8c488795c.png)
|
והוא שנאמ' ברביעיות, שהוא אחרון, ג' מב' לא יוכלו לצאת כלו, הא' ממקום השביעיות אשר לפניו ונשים נקודה על מספר השביעיות אשר לנו לגרוע, כדי שנזכור להסירו עמהם בהגיענו שם, כדרך שאנו עושים בשלימים להוסיף על הנגרעים א' בשביל הנקודה ונסירה כלו ממינו
ואחר שלוינו האחד ושמנו זה הנקודה, נקח בעד זה האחד כמורה שהוא ד' ונאמ' ד' וב' הם ו', נסיר מהם הג', ישארו ג'
ונאמר ה' שביעיות ונקודה הם ו', לא נוכל להסירם מהג', נשים נקודה על הז' תשיעיות אשר לנו לגרוע ונאמר זה האחד הוא ז' כמורה וג', הרי י', נסיר מהם ו', ישארו ד'
עוד נאמר ז' ונקודה הם שמונה, לא יצאו מה', נשים נקודה מחוץ במקום הראוי לשלימים, אם היו לנו שלימים ונאמר זה האחד הוא ט' כמורה וה', הרי י"ד, נסיר מהם ח', ישארו [ו',
עוד נסיר הנקודה, שהוא א' שלם, מהג' שלימים, ישארו ב'] ב' שלימים והנה כל המעשה אחד והכל ברור בטעם ודי למבין
|
Discussion on the Decomposing and Composing of Fractions
|
מאמר התכת השברים והרכבתן או שתיהן יחד
|
- Sometimes there is a need to convert denominators to other denominators when equalizing and reducing, therefore I thought to explain how one denominator is decomposed into two denominators.
|
לפי שלפעמים יצטרך להשיב מורים למורים אחרים בהשואה ובכלילת יופי להוציאם מן הכלל ראיתי לבאר איך יותך מורה אחד לשני מורים
|
- This is when the denominator is composed.
|
וזהו כאשר המורה מורכב
|
- Such as 6, which is composed of 2 and 3, so we remove it and replace it with 2, 3.

|
כו' שהוא מורכב מב' וג' שנסירהו ונשים תחתיו ב'ג'
|
- Also 3, 3 instead of 9.

|
וכן בעד ט' ג' ג'
|
- And 2, 4 instead of 8.

|
ובעד ח' ב' ד'
|
- The rule: the product of the replacing denominators is the same as the removed [original denominator]
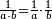
|
זה הכלל שכפל המורים המושמים תחתיו יהיה כמו המוסר
|
- Sometimes we do the opposite that we replace the 2 with one, i.e. we [remove] the 2 and the 4 and replace them with 8.
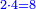
|
ולפעמים נעשה להפך שנשים הב' אחד ר"ל שנשים הב' והד' ונשים תחתיו הח' וכן בכללן
|
- This as placing the common denominator instead of the denominators, or the denominators instead of the common denominator.
|
וזהו כמו לשים האם תחת המורים או המורים תחת האם
|
- Other times both is needed
|
ולפעמים נצטרך הכל
|
- Such as when we have 6, 4 and we need 3,8.

|
כגון שיש בידינו ו' ד' ואנו צריכים ג' ח'
|
- Or, when we have 3, 4 and we need 6, 2.

|
או שיש בידינו ג' ד' ואנו צריכים ו' ב'
|
| The rule:
|
זה הכלל
|
- If what we place is one instead of numerous, this number should be the same as te product of the denominators multiplied by each other.
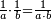
|
אם אשר שמנו הוא א' במקום רבים צריך שיהיה מספרו ככפל המורים זה בזה
|
- If numerous instead of one, their product by each other should be the same as the removed number.
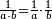
|
ואם רבים תחת אחד שיהיה כפלם זה בזה כמספר המוסר
|
- If numerous instead of numerous, their product by each other [should be the same as the product of the others by each other]
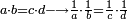
|
ואם רבים במקום רבים שיעלה כפל אלו זה בזה ודי למבין
|
| rank
|
מדרגה, מעלה
|
| dividend
|
המתחלק
|
| divisor
|
אשר נחלק עליו
|
| quotient
|
היוצא בחילוק
|
| common denominator
|
אם המורים
|
| treatise
|
קצור, קיצור
|
| book
|
ספר (ה), ספרי
|
| section
|
חלק (ה... ב)
|
| chapter
|
כלל
|
| chapter
|
פרק (ה / ה.. ב), פרקי ה, פרקים (ב / ה)
|
| chapter
|
שער (ה / ה... ב), שערים
|
| discussion
|
מאמר (ה)
|
|
|
בחלק ה... בפרק ה... ממנו
|
| introduction
|
מבוא ב, מבוא ל
|
| introduction
|
הקדמה
|
| to preface
|
אקדים
|
| word
|
תיבה, הברותיו
|
| letter
|
אות
|
| language
|
בלשון
|
| alien tongue
|
לשון נכרי
|
| Hebrew language
|
לשון עברי
|
| number
|
מספר (ה), מספרים, מספרינו, מספרך, מספרם, מספרן
|
|
|
חשבון (ה), חשבונך, חשבוננו, החשבונים
|
| number
|
מנין
|
| digit
|
אות (ה), אותיות, רושם, רשמים, רושם ה, רשמי ה
|
| digit
|
מספר, מספרים, מספרי ה
|
| zero
|
סיפרא, סיפרות, ספרות
|
| prime number
|
מספר פשוט, פשוט, פשוטים
|
| odd
|
נפרד, חשבון נפרד, החשבון הנפרד, מספר נפרד, הנפרדים, נפרדת
|
| even
|
זוג, חשבון זוג, זוגי (ה), מספר זוגי
|
| pair
|
זוגי
|
| unit
|
אחד, אחדים, אחדי (ה), ידות
|
| units
|
אחדים, אחדי (ה)
|
| units
|
הפרט
|
| product of tens, none-units
|
כלל
|
| tens
|
עשרות, עשרי
|
| hundreds
|
מאות
|
| thousands
|
אלפים
|
| ten thousand
|
רבבה, רבבות
|
| millions
|
חשבונות
|
| rank
|
דרגה
|
|
|
מדרגה, מדרגת ה, מדרגתה ה, מדרגות, מדרגתם, מדרגותיה, מדרגותיו
|
|
|
מעלה (ה), מעלות (ה), מעלת ה, מעלתה, מעלתו, מעלתן, מעלותיו, מעלותיהן
|
| empty rank
|
מעלה חלקה ממספר, מעלה החלקה ממספר, מעלות חלקות מהמספר
|
| positional value (relation)
|
ערך המעלות
|
| positional value
|
בערך (ב / ה), כערך, ערך מקום ה, בערך המעלה, בערך מעלת ה
|
| decimal place
|
מקום (ה), מקום הנחת, מקום ההנחה, מקומו ה, מקומו הוא ב
|
| place
|
מקום (ה / ש), מקומו, מקומות
|
| place holding
|
שמירת המדרגות
|
| line
|
קו, קוים
|
| point, dot
|
נקודה, נקדה, נקודות, נקדות
|
| row, line
|
שורה, שורות, שורת (ה / ה... מה), שורתו
|
|
|
טור (ה), טורים
|
| surface
|
שטח
|
| body
|
גשם
|
| cube
|
מעוקב, המעוקב
|
| stripe
|
רצועות של
|
| length
|
ארך, אורך, באורך, ארכו
|
| width
|
רוחב, רחבו, ברוחב
|
| height
|
גובה
|
| addition
|
|
| addition
|
חבור, חיבור
|
|
|
בחברך אליהם ה
|
|
|
לחבר (ל / על ה / עמהם ה / ... עם / ה... על ה / כל ה / יחד כל), לחברו (ל / עם, עמו), לחברם (עם / עם ה), לחבירו עם
|
|
|
חבר ( ... עם / ה... ל / ה... עם / הכל יחד)
|
|
|
חברהו (ל / עם), חברם ל, חברם עם ה, חברנו ה... עם, חברת אותם
|
|
|
יחבר ה... עם
|
|
|
יחברם
|
|
|
מחברים (אותו עליהם / אותם אליהם)
|
|
|
נחבר (אליהם / אליהם ה / ל / להם ה / ה... ל / ... עמהן)
|
|
|
נחברנה עם ה, נחברהו אל ה
|
|
|
נחברם (אליהם / אליהם ה / יחד / ל / להם ה / עם / כלם)
|
|
|
תחבר (אליהם ה / להם ה / לו ה)
|
|
|
תחברם (יחד / יחד ... עם / כלם / עם ה)
|
|
|
תחברנו (עם / עם ה / ל)
|
| to be summed
|
מחובר, מחוברות יחד
|
| sum
|
המתחבר, המחובר
|
| sum
|
המקובץ
|
| sum
|
סך
|
| summed
|
המקובץ (מ / מה)
|
| summed
|
מחובר עם ה
|
|
|
עלה חיבורם, עלה מחבורם, עולה חיבורם, העולה מהחיבור, העולה מחבור ה
|
| addition
|
תוספת (אשר ל / בהם / ה / על ה)
|
| to add
|
להוסיף (אותו על ה / אחד / מה / על ה / ... ב), להוסיפו (על ה / עליו), להוסיפם על ה
|
|
|
הוסיף ...על ה, הוסיף עליו זה התוספת
|
|
|
הוסף (על ה / עליו)
|
|
|
הוספנו (על / עליהם / ... מעל ה / ... על ה / עליהם ה)
|
|
|
הוספנוהו על ה
|
|
|
יוסיף לעולם על
|
|
|
מוסיפים (... ב / עליו)
|
|
|
נוסיף (ב / עליהם / עליו / ... ב / ... על / ... על ה / ה...על ה / ה... עם ה)
|
|
|
נוסיפנו
|
|
|
תוסיף (עליו / ... על / ה... על), תוסיפם על, תוסיפנו על ה
|
|
|
המתוסף ב, המתוסף עתה ב, המתוסף על ה
|
|
|
יתוסף ב, נתוסף, ניתוסף ב, ניתוסף דבר ב, נתוספו (ב / לו... על), מתוסף
|
|
|
בהוספת ה
|
| added
|
מוסף על ה, מוספים על
|
|
|
נוסף, נוספות, נוספים (ב... על / ב... על ה / על ה), נוספת ב... על
|
|
|
תוסף ב
|
|
|
יוסיף ב
|
|
|
מוסיף (על / על ה)
|
|
|
קיבוץ כל השורות יחד
|
| plus
|
בתוספת (ה)
|
| by addition
|
לתוספת
|
| addition
|
מתוספת ב
|
| additive, additional
|
היה לתוספת, היו לתוספת
|
| subtraction
|
|
| subtraction
|
המגרעת
|
| to subtract
|
ונסור ה
|
| subtraction
|
בהסר מה
|
|
|
לגרוע (... מ), לגרעם מ
|
|
|
גרע (... ממנו / ממנו ה)
|
|
|
נגרע (ה... מה / מהם)
|
|
|
הנגרעים
|
|
|
יגרע (מהם)
|
|
|
החסרו מ
|
|
|
חסרון (מ), החסרון אשר ב... מה, חסרונו
|
|
|
לחסר (מה / ... מ / ה... מ), לחסרו (מ / מן ה), לחסרם מה
|
|
|
לחסו' ... מ
|
|
|
חסר מ, חסר ... מ
|
|
|
חסרם מ
|
|
|
חסרנו (ה / מ / ממנו / ממנו ה)
|
|
|
חסרת
|
|
|
יחסר (כ / מ / מה / ממנו כ / ... מ / ... מה / ... כ / ה... מה)
|
|
|
יחסר יותר
|
|
|
יחסרהו מ
|
|
|
נחסר (ה / אלו ... מה / ה...מה / ה... מן ה / ... מה)
|
|
|
נחסרה
|
|
|
נחסרנו (מה), נחסרנו לעולם מה, נחסרהו לעולם מה
|
|
|
נחסרם זה מזה
|
|
|
תחסר (ה / מה / מהם ה / הכל מה), תחסרנו ממנו
|
|
|
מחוסר
|
|
|
מחסרים, מחסרים עתה מה
|
|
|
מן ... חסר ה
|
|
|
חסרים אלו ה... מ
|
| minus
|
חסר, חסר אחת
|
|
|
אשר חסרנו ממנו
|
|
|
אשר חסרת, אשר חסרת ממנו
|
|
|
יחסר מעלה ממקום ה
|
|
|
בהסיר, בהסר מהם ה, להסירו, להסירם מה, הסירך ה
|
| to subtract
|
הסיר מה, הסר, הסרת (ה)
|
|
|
נסיר (ה / ... מה / ה ... מה / ה... מ / מה / מהם / מהם ה / ממנו ה)
|
|
|
נסירה (ממנו / כלו ממינו), נסירהו
|
|
|
נסירם (מה / ממנה)
|
|
|
נסירנו מה
|
|
|
תסיר (ה / מהם / ... מה), תסירנה, תסירנו
|
| subtraction
|
הוצאת... מ
|
|
|
להוציא (מה / ממנו / ... מ / ה... מה)
|
|
|
להוציאו מהם
|
|
|
להוציאם (מה / מהם ה)
|
|
|
הוצא (ה / מ / ה... מ)
|
|
|
הוצאנו ממנו
|
|
|
הוצאת (מהם / ה... מה / ה... מן)
|
|
|
הוציא... מה
|
|
|
הוציאהו מ
|
|
|
הוציאנו (מה)
|
|
|
יוציא כל ה
|
|
|
מוציאים מה
|
|
|
נוציא (כל / מ / מה / מהם ה / ה... מה / ... מ)
|
|
|
נוציאם מה
|
|
|
נוציאנו (מ / מה / מאשר על)
|
|
|
תוציא (ה... מן / ... מ)
|
|
|
להוציא כ"כ פעמים המספרים
|
| to be subtracted, to be consumed
|
ויצא כל זה ה, יצא הכל
|
|
|
לא תוציא ל
|
| to subtract
|
תוציאנו מה
|
|
|
ומהכל תוציא אשר
|
|
|
אשר עליו להוציא
|
| to be subtracted
|
לצאת (ה / כלו / מהם / מאשר על), יצא, יצאו (מ / ... מ)
|
|
|
בלי תוספת ומגרעת, מבלי תוספת ומגרעת
|
|
|
מבלי תוספת, מבלי תוספת ה
|
|
|
לבד בלי תוספת אחד כלל
|
|
|
ואם יחסר או יעדיף
|
| Multiplication
|
|
| multiplication of fractions
|
הכאה, הכאת ... ב
|
|
|
להכות (ה... ב)
|
|
|
הכה (אותן / ... ב)
|
|
|
נכה (ב / ה / ה... ב), נכם ב
|
|
|
תכה הצריך להכאה
|
|
|
לעשות הכאה, נעשה הכאה ל, עשה להם הכאה, תעשה להם ג"כ ההכאה
|
|
|
ונכם זה בזה
|
|
|
הוכה (ב), הוכה... על, הוכו, הוכתה בהם
|
|
|
לבעלי ההכאה
|
| product
|
כפל (ב / ה / עם / ... ב / ... על / ... עם / ה... ב / ה... על / זה ה... ב / ... זה בזה / ה... זה בזה / כל ה)
|
|
|
כפליהן, כפלו על
|
| product
|
המחובר
|
| product
|
מקובץ
|
| product
|
אשר עלה לידיך מכפל ... ב
|
| multiplying
|
בהכפל (ה / ... ב), בכופלנו אותו ב, בכפול (אותו ב / ה... ב / ... אחד באחד / אותם זה בזה / ... ב), הכפלו ב, הכפלם (ב / כלם ב)
|
|
|
בכפול זה בזה, בהכפל זה בזה
|
| to multiply
|
כפלת ה... ב
|
|
|
בכפלנו אותו ב
|
|
|
לכפול (ב / בהם / בהם ה / ה / ה ... ב / ה... עם / ... ב / ... על / כל ה... בהם / כל ה.... עם ה)
|
|
|
לכפלה עם, לכפלו (ב / בכלם), לכפלם ב
|
|
|
כופל ב, כופלים (אותה ב / אותו / ב / ה / כל ה / ... ב / ה... ב)
|
|
|
כפול (אותו ב / אותו... ב / ... ב / ... על / ה... ב / ה... על / ... פעמים)
|
|
|
כפלהו (ב / שנית ב), כפלהו אותם ב
|
|
|
כפלו (ב / על / עם / ... ב)
|
|
|
כפלם זה בזה
|
|
|
כפלנו (אותם ב / בהם / ה... ב / ... ב / ... על)
|
|
|
כפלנוהו ב
|
|
|
כפלנום ב
|
|
|
כפלת
|
|
|
נכפול (אותם ב / ב / בהם / בו / זה ב / אותו... ב / ... ב / ... על / ה... ב)
|
|
|
נכפלהו ב, נכפלו... עם
|
|
|
נכפלם (ב / על ה / עוד ב / ... ב)
|
|
|
נכפלנו (ב / בהם)
|
|
|
תכפול (אותו ב / בו / ה... ב / ה... עם / ... ב / ... בו / ... על / ... ב... פעמים)
|
|
|
תכפלם (ב / ... על ה)
|
|
|
תכפלנו (ב / בהם)
|
| to multiply
|
כופלים בהכאה ... ב
|
|
|
כפל אלו זה בזה
|
|
|
כפלו ב... פעמים
|
| product by itself
|
כפלתו בעצמו
|
|
|
כפלו (בעצמו / על עצמו)
|
|
|
כפל... בעצמו, כפל ... על עצמו, כפל ה... בעצמו
|
|
|
כפל... בעצמם, כפל ה... על עצמם
|
|
|
ככפלו לעצמו
|
|
|
לכפול על כולם ועל עצמו
|
|
|
כופלים ה... בכמותו
|
|
|
כפול אותו על עצמו, כפול ... על עצמם
|
|
|
כפלם בעצמם
|
|
|
כפלנו ... על עצמם, כפלנוהו בעצמו, כפלנוהו על עצמו
|
|
|
נכפול (על עצמו / ... על עצמו / ה... על עצמו / ה... בעצמו / זה על עצמו)
|
|
|
נכפלנו (בעצמו / על עצמו)
|
|
|
תכפול (ה... בעצמו / אותו ה... על עצמו)
|
|
|
תכפלנו על עצמו
|
|
|
כפולים בעצמם
|
| multiple
|
כפלי (ה / מ), כפלים
|
| multiplied
|
כפול, כפולים
|
|
|
פעמים כפל ה... זה בזה
|
|
|
כפל הכפלים ההם
|
|
|
לכופליו
|
|
|
כופלו
|
|
|
אנו לוקחים אותם כפולות
|
| to be multiplied
|
הוכפל ה, הוכפלה בה, הוכפלו בהם, יוכפל כפלים ב
|
| product
|
עולה מהכפל, העולה מהכפל (ה / הזה), העולים מהכפל (... ב / ה... ב), העולים בכפל, העולות מזה הכפל, העולה מכפלו עם ה, העולה מכפלם
|
|
|
שעלה בכפל
|
|
|
תעלה מ...
|
|
|
היוצא אחר הכפל
|
|
|
נכפלו, נכפלו בהם
|
|
|
הכפלים, מנין הכפלים
|
|
|
כפול, כפולים
|
|
|
נכפל, נכפלים ב
|
|
|
הנכפל, הנכפלים, מספרים הנכפלים, המספרים הנכפלים, הנכפלים זה בזה
|
|
|
נכפל פעמים רבות
|
|
|
אשר אינם נכפלים
|
| to be duplicate
|
ישנו (ב / בהם), נשנים (ב / מ)
|
| duplicated
|
כפול, נכפלים
|
| to duplicate
|
לכפלו, ישנך
|
| duplication
|
כפל ה
|
| duplication
|
השינוי
|
| double
|
כפול, כפל (ה), כפלו
|
| doubling
|
כפל
|
| to double
|
כפול (ה), כפלת ה, נכפול ה, תכפול, תכפלנו
|
| Division
|
חלוקה, לחלוקה על ה... עליו, חלוקת ה, חלוק (ה), חילוק (ב / ה / ... ב), בחילוק, בחילוק על ה, חלוקנו, בחלוקנו ל, בחלקך ל, בחלקנו (אותו ל / ה / ה... ל / ה... עליהם / אותו ל / אותם ל / ... ל), בחלקינו... ל
|
|
|
בחלקנום אותם על
|
|
|
לחלק (ל / ... ל / ... על / ה... ל / ה... עליהם / אותן על / אליהם אלו ה / עליהם / על הכל)
|
|
|
לחלקה עתה להם, לחלקו (ב / ל / על / עליו)
|
|
|
לחלקם (ל / להם / על / על ה / עליהם / עליו / ראשונה על ה)
|
|
|
חלק (ל / עליו / ה... ל / ה... על / ה... עליהם / זה ה... על / אליו זה ה / ... על)
|
|
|
חלקהו ל
|
|
|
חלקם (ל / עליהם)
|
|
|
חלקנו (אותו על / ה / ה... ב / ה... על / ל / על / על ה / עליהם ה / עליו / ... ל / ... על / ... על ה)
|
|
|
חלקנוהו (על / על ה / עליו), חלקנום (ב / ל / על / על ה / עליו)
|
|
|
חלקת (ה... על ה / הכל ל)
|
|
|
יחלק ... על
|
|
|
מחלקים (אותו ל / אל / ... ל)
|
|
|
נחלוק ... ל
|
|
|
נחלק (אלו ה / אליהם / אליהם ה / ה / ל / לו / על / עליה / עליהם / עליהם ה / עליו / ... ל / ...על / ה... ל / ה... על / ה... על ה / אלו ה... ל / אלו ה... אל ה)
|
|
|
נחלק זה החשבון ל, נחלק חשבוננו זה עליו, נחלק מספרינו על
|
|
|
נחלק זה היוצא ל, נחלק זה היוצא על ה
|
|
|
נחלקם (ל / על / על ה / עליהם / עליו / תחלה ל)
|
|
|
נחלקם על מינו, נחלקנו למינו
|
|
|
נחלקנו (אליהם / ב / ל / על / עליו)
|
|
|
תחלק (... ל / ... על ה / על ה / עליו / ה... ל / ה... על / ה... על ה); תחלק (ל / עליהם); תחלק על כלם ה, תחלק כל החשבון ל, תחלק אליו לשלימים
|
|
|
תחלקה
|
|
|
תחלקם ל
|
|
|
תחלקנה ל
|
|
|
תחלקנו (ל / על)
|
|
|
יתחלק ל, יתחלק ... ל, יתחלקו
|
|
|
המחלק ... על
|
|
|
נחלק ל
|
|
|
נתחלק הכל
|
|
|
נתחלק על כל ה, נתחלק להם המספר
|
|
|
בחלוקה הראשונה
|
|
|
חלקתי הספר לב' חלקים
|
|
|
אשר אתה מחלק עליו
|
|
|
אשר רצינו לחלק (על ה / עליהם / עליהם ה / עליו / ל), שרצינו לחלק (עליו)
|
|
|
אשר רצית לחלק (עליו)
|
|
|
אשר תרצה לחלק (עליו)
|
|
|
אשר חלקנו (עליהם / עליו), שחלקנו עליהם
|
|
|
אשר חלקת עליו
|
|
|
אשר חלקת עליהם
|
|
|
אשר חלקנו כבר עליהם
|
|
|
אשר נחלק (אל / עליו), אשר נחלקו עליו
|
|
|
אשר תחלק עליו
|
|
|
עליהם תחלק ה
|
|
|
אשר להם תחלק
|
|
|
המתחלק (ל), החשבון המתחלק, המספר המתחלק, מספר המתחלק
|
| quotient
|
היוצא מן החלוק ה, היוצא בחלוק, היוצא בחילוק, היוצא בחלוקו, היוצאים בחלוק, היוצאים בחילוק
|
|
|
יוצאים בחילוק
|
|
|
יצא בחלוק, יצא בחילוק, יצא בחילוק (ה / ל), יצא לנו בחלוק, יצא זה בחלוק ה, יצא בחילוק ה... ל, יצאו בחלוק, יצא ה... בחילוק, יצאו... בחילוק, יצא בו בחלוק
|
|
|
יצא בחלוקה, יצא מהחלוקה
|
|
|
יצא בחלוקנו, יצא בחלוקם, יצא בחילוקם
|
|
|
העולה שיצא לנו בחלוק ה ... על ה
|
|
|
תצא ... בחילוק
|
|
|
יצא בחילוק מבלי שארית, היוצא בחילוק בצמצום, היוצא בחלוק בצמצום
|
|
|
יצא בחילוק לכל אחד
|
|
|
יצא בחילוק מספר מה
|
|
|
אשר יוצא עתה בחילוק
|
|
|
אשר יצא לנו בחילוק, אשר יצא בחילוק באחרונה, אשר יצא באחרונה בחלוק
|
|
|
אשר יצאו בחילוק, אשר יצאו בחלוק, אשר יצאו בחלוק באחרונה, שיצאו בחילוק
|
|
|
יצא לך בחלוק על
|
|
|
יצאו בחלוק
|
|
|
ויצא ... בחלוק, ויצא בחילו'
|
|
|
עלה בחלוק
|
| factor, divisor
|
מורה (ל / לו), מורים (ל), מורי, מוריו
|
| part, divisor
|
חלקיו
|
| true divisor
|
מורה צדק
|
| indivisible
|
לא נחלק לשלמים אל חשבון, לא יוכל להתחלק עליו, שלא יוכל להתחלק לשלמים, לא יתחלק כלו לשלמים
|
|
|
לא יתחלק לשום מספר בשלימות מבלי שארית
|
| divisible
|
יתחלק כלו לשלימים, הנחלק למספר מה, יתחלק אליו לשלימים מבלי שארית
|
| divisible by two
|
יש לו מחצית, יש לו ב'
|
| divisible by three
|
יש לו שלישית, יהיה לו שלישית, יש לו ג', היה לו שלישית
|
| divisible by four
|
יש לו רביעית, יש לו ד', יש לה רביעית, יש להם רביעית, יש לחשבון רביעית, היה להם רביעית, היה לו רביעית
|
| indivisible by four
|
אין לו רביעית, אין לנו רביעית
|
| divisible by five
|
יש לו חמישית, יש לו חמישיות שלמות, יש לזה ה... חמישית, היה לו ה'
|
| divisible by six
|
יש לו שישית
|
| indivisible by six
|
אין לו שישית
|
| divisible by seven
|
יש לו שביעית
|
| indivisible by seven
|
אין לו ז'
|
| divisible by eight
|
יש לה שמינית, יש לו שמינית, יש לו ח', יש להם שמינית
|
| indivisible by eight
|
אין לה שמינית
|
| divisible by nine
|
יש לו תשיעית, יש לו ט', יש למספר תשיעית
|
| divisible by ten
|
יש לו עשירית, יש לו עשר, יש לה י'
|
| divisible by eleven
|
יש לו י"א, יש לו הי"א, יתחלק לי"א על השלימות
|
| indivisible by eleven
|
אין לו י"א
|
| divisible by thirteen
|
יש לו י"ג, יש לו הי"ג
|
| divisible by seventeen
|
יש לו י"ז
|
|
|
יצא הכל לשביעיות
|
|
|
יצא הכל ז' ז'
|
|
|
השלך לעולם הז' ז'
|
|
|
השלך אותו ח' ח'
|
| casting out by nines
|
הסרת התשיעיות, חסר כל ט' ט', תוציא הט' ט'
|
| to be cast out by nines
|
יצא הכל לט' ט', יצא החשבון לט' ט', יצא כולו תשיעיות
|
| to be cast out by 11
|
יושלך כלו י"א י"א, יושלך לי"א י"א
|
| to cast out by 13
|
הוצא הי"ג י"ג, הוצאת הי"ג
|
| to be cast out by 13
|
יוצא לי"ז י"ז
|
| to extract the factors
|
תוציא המורים מ
|
| to extract the factor
|
המצאת מורה ה
|
| fractions
|
|
| integer
|
שלמים, שלימים, מספר שלם
|
| fraction
|
שבר, שברים (מ / מה), שבורים, שברי (ה), שבריהם
|
| fraction
|
חלק מ, חלקים (מ / מה), חלקי (ה)
|
| fraction of fraction
|
שברי שברים (מ), שבר שבר
|
| fractional
|
הנשבר
|
| portion
|
שברים מ
|
| part
|
חלק (ה / מ), חלקים מ, חלק אחד מ, חלקי ה, חלקיו
|
|
|
חלקים מחלק, חלקים מחלק מ
|
|
|
ב... חלקים בשלם
|
|
|
מ... חלקים בשלם
|
|
|
חלקי... בשלם; חלקי... מ... בשלם
|
|
|
חלקים משלם מ, חלקים מ... בשלם; חלקים מ... שבשלם; חלקים מה ... בשלם
|
|
|
חלקים מ... באחד
|
|
|
חלקים מחלקי ה... בשלם; חלקים מ... חלקים בשלם; חלקים מ... חלקים מ... שלם
|
|
|
חלק מ... ב; חלק מ... בשלם; חלק מ... שבשלם; חלק ... מ... בשלם; חלק ... מ... שבשלם
|
|
|
אחד מ... בשלם; חלק א' מ; חלק אחד מ... בשלם; חלק אחד מ... שבשלם; חלק א' מ... שבשלם
|
|
|
חלק א' מ... מ... שב; חלק א' מ... מ... השלם; חלק אחד מ... מ... בשלם; חלק אחד מ... מ... שבשלם
|
|
|
השברים מהשלם
|
| numerator
|
מספר השברים, מספר שברים, מספר שברי (ה), מספר שבריו, מספר שבריך, מספר המורה, מספר החלקים, מנין שברים, מנין השברים, שברים מה
|
|
|
החלק על המורים
|
| denominator
|
מורה (ה), מורהו, מורים (ל), מורי (ה), מוריה, מוריו (ה), מוריך, מורינו, המורה החלק, מורה החלק
|
|
|
הוצאת המורים, הוצאת מורי ה
|
| to extract the denominator
|
להוציא המורים (ל), הוצא את מוריו, נוציא מורה ה, נוציא מורי ה, נוציא מוריו, נוציא המורים ל, תוציא המורים
|
| to be extracted
|
יצאו ממנו המורים
|
|
|
לקחתו ... למורה, בקחתך אותם למורים
|
|
|
נקח למורה, נקח ... למורה, נקח מוריהם, נקחם למורים, נקחנו למורה
|
|
|
תקח מורה, תקחם למורים
|
|
|
לוקחים מתחלה ה... למורה
|
|
|
נשים ה... למורה, נשים... למורה, נשימם למורה
|
| common denominator
|
אם, אם המורים, אם כל מוריהם, אם אלו המורים, אם המורים כלם, אם ... מורים, האם (ה), אמם
|
| to extract a common denominator
|
הוצאת האם למורים, נוציא אם כל המורים
|
| in reduction
|
בצמצום
|
| reduced
|
שלמים
|
|
|
כלילת יופי, ובכלילת יופי
|
|
|
בעשותך כלילת יופי
|
|
|
לעשות לשברים אלו כלילת יופי
|
|
|
לעשות לה כלילת יופי, לעשות להם כלילת יופי
|
|
|
נעשה כלילת יופי ל, נעשה להם כלילת יופי, נעשה לו כלילת יופי (על)
|
|
|
עשה להם כלילת יופי
|
|
|
תעשה להם כלילת יופי, תעשה מהם כלילת יופי
|
|
|
הוא כעושה כלילת יופי
|
|
|
עשותנו להם כלילת יופי שהן
|
| unification
|
אחדות, לעשות בדרך האחדות
|
| completion
|
ההשלמה, השלמתם, השלמתן (ל / לאחד)
|
| to complete
|
השלמנו (ה / ל), להשלימם לאחד שלם, המשלימות אותו לאחד שלם
|
| to be completed
|
הושלם כבר ב, ישלומו ל, ישלמו ל, ישלימו ה... ל, שלמו ה
|
|
|
כדי השלמת מספר
|
| complement
|
המשלים אותו כ, השלמתו (ל / לאחד), השלמתם (ל / לאחד)
|
| complement
|
מה שיש מה... עד תשלום
|
| complement
|
קצתו האחר
|
| to finish
|
השלמת ל, נשלים ה, תשלים (ל / לשורה / השורה)
|
| decomposing
|
התכה, התכת השברים
|
| to decompose
|
התיכנו אותו, נתיך ה
|
|
|
יותך ...ל
|
| composing
|
הרכבתן
|
| composed
|
מורכב, מורכב מ, מורכב מהם
|
| factorization
|
פריטה, פריטת (ה), פריטתינו, פריטתה, פריטת השברים, מספר פריטת השברים
|
|
|
חלקי הפריטה
|
| fractionalizing
|
כפורט
|
| to fractionalize
|
לפרטם ל
|
|
|
לעשות פריטה, עשות להם פריטה, נעשה פריטה ל, עשה הפריטה ל, נעשה תחלה פריטה ל, תעשה פריטה ל
|
|
|
עשה פריטה לכל אלו השברים
|
|
|
פורטים אותה עוד ל
|
|
|
נפרטות (מ), נפרטים, החלקים הנפרטו' השברים הנפרטות, השברים הנפרטים
|
|
|
נפרוט (ה)
|
|
|
נפרטו, נפרט (ה)
|
|
|
תפרוט
|
| conversion
|
המרה
|
|
|
המרנו ה... ל, תמירם אליהם, תמירם ל, תמירם למין אחר
|
|
|
מורה המרה, מורי ההמרה
|
|
|
החזרת השברים, חזרת השלימים לחלקים
|
|
|
השבת השברים, להשיבם פרוטות
|
|
|
משיב הכללים לפרטים
|
| to convert
|
להחזירם מ
|
| to convert
|
להחליפם אליו
|
|
|
להשיב ה, להשיבם, להשיבם לחלק אחר
|
|
|
להשיב למין אחד
|
|
|
להשיב כלם מהמין, להשיב הכל ממין השברי', להשיבם כלם מהמין הראשון
|
|
|
להשיבם כלם ממין אחד
|
|
|
להשיב ... לכללים
|
|
|
להשיב שברים... לחלק אחד
|
|
|
להשיב מורים למורים אחרים
|
|
|
נשיבם, נשיבם ל, נשיבם כלם, נשיבם כלם ממין אחד, נשיבם עוד
|
|
|
נשיב ראשונה ה... ל
|
|
|
השיבם ל, נשיבהו, תשיבם, תושיבם
|
|
|
נשיבם כלם ראשונה
|
|
|
להשיב הכל לקדמותו
|
| to be converted
|
ישובו, ישוב הכל מ, שב
|
| comparing fractions
|
השואה, השוואה, ההשואה שעשינו
|
|
|
בעשותך השואה זו, לעשות בזה ההשואה
|
|
|
נעשה ההשואה ל, נעשה להם השוואה, תעשה ההשואה, אשר עשינו בהשואה
|
|
|
להשוות ... עם, להשוותם, נשוה, תשוה ה... אחד אל אחד
|
|
|
לעשות תחלה פריטה והכאה, לעשות לשבריך פריטה גם הכאה, לעשות לכל א' מ... פריטה והכאה, לעשות שני המעשים ר"ל הפריטה והכאה, עשותנו הפריטה וההכאה לכל אחד מהם
|
|
|
נעשה פריטה והכאה ל, נעשה לה הכאה גם פריטה, נעשה ל... פריטה והכאה, נעשה לכל אחד פריטה והכאה
|
|
|
עשותך הפריטה וההכאה וההשואה, עשותנו הפריטה וההכאה וההשוואה
|
| extraction of roots
|
|
| root
|
שרש (ה), שרשו, שרשים, שרשנו, שרשי ה
|
| square
|
מרובע (ה), מרובעו, מרובעם, מרובעים
|
| none square
|
ולא מרובעים
|
| cube
|
מעוקב ה
|
| to extract the root
|
ולקחת חציים
|
| extracted root
|
השרש אשר הוצאת, שרש ה... אשר הוצאנו
|
|
|
הוצאת השרשים
|
| to extract a root
|
להוציא השרש, להוציא שורש, הוצא השרש, נוציא שורש, נוציא שרשו
|
|
|
לבקש שרש
|
|
|
בקשנו שרש, בקשת השרש, בקשת שרשו
|
|
|
לדעת שרש, לדעת שרשו
|
|
|
לידע שרש, לידע שרשו, לידע שרשו האמיתי
|
|
|
לקחתו השרש
|
|
|
נקח שרשו
|
|
|
מרובע השרש
|
|
|
בעל השרש
|
|
|
השרש היוצא
|
|
|
השרש המתוסף
|
|
|
השרש המחוסר, השרש הזה המחוסר
|
|
|
נעשה מהכל שרש אחת
|
|
|
השרש הקרוב
|
|
|
אשר לא יודע בהם שרש אמיתי לעולם כי בקירוב
|
|
|
היה זה השרש אמיתי
|
|
|
יהיה שרש קרוב מאד אל האמת
|
|
|
בקרוב
|
|
|
אין זה שרש אמיתי
|
|
|
הקרוב
|
|
|
אשר בשרשו, אשר יצאו בשרש
|
|
|
שלימי השרש, השלימים היוצאים בשרש, השלמים אשר יצאו בשרש
|
|
|
השברים היוצאים בשרש
|
|
|
השרש בעצמו
|
|
|
אשר בקשנו שרשו
|
|
|
כשורש בעינו, שהוא כמו השרש
|
| Proportions
|
|
| proportion, ratio
|
ערך, ערכים, ערכי ה
|
|
|
הערך ל
|
|
|
ערך ... אצל, הערך שיש ל... אצל, הערך שיש ל... אצל ה
|
|
|
הערך אשר ל... אצל, הערך אשר ל... אצל ה
|
|
|
הערך שיש ל... אצל
|
|
|
כערך ... אצל, כערך אשר ל... אצל
|
|
|
הערך בעצמו יש ל... אצל, הערך בעצמו שיש ל... אצל
|
|
|
הוא הערך בעצמו אשר ל... אצל
|
|
|
למי יש ערך אצל, למי יש זה הערך אצל
|
|
|
אצל מי יש ערך זה ל, אצל מי יש לו זה הערך
|
|
|
אצל מי יש ל... זה הערך
|
|
|
אצל ... למי יש לו זה הערך
|
|
|
ל... אצל מי יש לו זה הערך, ל... אצל מי יש לו זה הערך בעצמו
|
|
|
למי יש לו זה הערך בעצמו אצל
|
|
|
אצל איזה מספר יש לו אותו הערך בעצמו
|
| rule of three
|
הג' מספרים נערכים
|
| related, proportional
|
הנערך, הנערך אליהם, הנערך אצל (כל), נערכים
|
| to relate
|
לקשרם יחד
|
| mean
|
האמצעי, האמצעיים
|
| first term
|
ראשון, הראשון שב, ראשון ל
|
| second term
|
שני, שני שבהם, שני ל, השני מה
|
| related
|
נערך, הנערך, הנערך אצל
|
| related
|
נקשר ב, נקשרות, נקשרים (בו / ...ל / זה בזה / זו בזו)
|
| unrelated
|
הבלתי נקשרות
|
| what we relate to it
|
אשר אליו אנו מעריכים
|
|
|
אשר מעריך אצלו
|
| relation to
|
ערכם אל ה
|
| in relation to
|
בערך (ה)
|
| according to this relation
|
על הערך הזה
|
| to remain
|
ישאר (ב / ה / דבר / לנו מ / ממנו), ישארו, נשאר (ב / מ / מה / דבר / על ה / עוד ב), נשארו (ב / עוד... ב)
|
| remainder
|
הנשאר (ב / מ / מה), הנשארים (מה), הנשארות, הנשארת
|
| remainder
|
שארית (ה / מה), השארית הנשארה, שאריתנו
|
| to remain
|
נותר (דבר)
|
| remainder
|
הנותר, הנותרים (מה)
|
|
|
נשאר לנו (ב) / בידינו
|
|
|
אין שם דבר
|
|
|
תשאר מל
|
|
|
שנשארו בחלוקה
|
| to be left
|
ישארו לנו ל
|
| to result
|
יבא ה
|
| to result
|
יצא (ה / כ / ל / לך / תחת ה), יצאו (ה / לנו), יוצאות, יוצאים, תצא ה
|
|
|
יצא באחרונה, יצא לך באחרונה
|
| to result
|
נספק
|
| to result
|
יעלה (כ / ל / הכל / מ / ש), יעלו, עולים (ל), עולה (ה / הכל / ל / מה), עלה (הכל / ל), עלו (ה / ל)
|
| result
|
היוצא (ב / מ / מה / באחרונה / לנו), היוצאים
|
| result
|
העולה (מ / מה), אשר יעלה
|
|
|
העולה לכל אחד מהן
|
| to result
|
הגיע ל... מה, יגיע ל, יגיעו ל... מה, אשר הגיעו ל
|
| to receive, to obtain
|
יצא לך מ, יצא לנו (כי / ה / מזה / מזה ש / מכך כי), שיוצא ל, יצאו לך, יצאו לנו, ויצא לנו עוד מזה ש, היוצא ל
|
|
|
עלה לנו (כל ה / מ)
|
| to receive, to obtain
|
הגיע לכל א', הגיע לכל אחד מהם, יגיע לכל א', יגיע לכל אחד, יגיע לכל א' מה, יגיע לכל אחד מהם, יגיעו לכל אחד מהם, יגיע ממנו לכל א' מה
|
|
|
יצא לכל אחד מהם
|
|
|
עלה לכל אחד מהם, יעלה לכל אחד, יעלה לכל אחד מהם
|
|
|
יעלה בידך, עלה בידינו ש, יעלה בידינו ש
|
| keep
|
נשמור, שומר ש, שמור (ה / ... על ה), תשמור (ה / ה... ל)
|
|
|
השמור, השמור בידינו מה, השמורים
|
|
|
תשמר (ה... ל)
|
|
|
נשמר ה... לאחדים בידינו
|
|
|
תשמרם לאחדים ל
|
|
|
לשמור משמרתי
|
| to beware, to be careful
|
שמר, השמר לך, שמור נפשך
|
| to write
|
אכתבנו ב, כתבתי (עליה), כתבתיו
|
| to be written
|
נכתב ב
|
|
|
כמו שכתו' למעלה
|
| written
|
הרשום, הרשומה
|
| noted
|
הרשומים
|
| to want
|
ירצה (ל), נרצה (ל) , רוצה ל, רוצים (ל / ש), רצה ב, רצו ל, רצינו (ל), רצית ל, תרצה (ל)
|
|
|
מי שירצה
|
|
|
רצונך ל, רצוננו
|
| הרוצה ל
|
| as one wish
|
כרצונך, כרצונו, כרצוננו
|
|
|
נחפוץ (מהם)
|
|
|
כחפצנו, ככל חפצנו, בחפצם
|
| to find
|
למצוא ב
|
|
|
מוצא, מצאנו (שם / תחתיו), מצאנוהו, מצאת (ב / ה / לו / מ / שם), מצאתו, מצאתם, מצינו
|
|
|
נמצא (לו / ש / שם / תחת / תחתיו), נמצאנו שם
|
|
|
תמצא (ב / לפניו / עליהם / על ראשו / תחתיו / לו / שם / ... תחת ה), תמצאם, תמצאנו
|
|
|
הנמצא (ב / תחת ה / תחתיו), הנמצאת שם, הנמצאים (ב)
|
|
|
לא נמצא ל
|
|
|
אשר נמצא תחתיו דבר
|
|
|
היה נמצא דבר זה
|
|
|
אשר מצאנו ל
|
|
|
אשר לא מצאת ל
|
|
|
אשר תמצא אשר לפניה
|
| to be found
|
ימצא (על ראשו / תחת ה), נמצא (ב / תחת ה / תחתיו)
|
| to be found
|
הנמצא ב
|
|
|
תמצא לכל אחד מהמספרים שום מורה
|
|
|
מה שתמצא מ
|
|
|
אשר לא תמצא לו
|
|
|
אין צריך כי אם ל
|
|
|
תחוש (ל / להם), אל תחוש ל, לא נחוש ל
|
|
|
אינך צריך לחוש מה
|
|
|
לרשום, ארשום
|
ורשום קו דיו תחתיהן, ותרשום קו דיו תחתיהן
נרשום קו דיו עליהם
תרשום קו דיו תחת
נרשום תחת כל השורות קו דיו
ונרשום קו על כל הנשאר
תרשום קו על הכל
ונרשום על... קו דיו
ותשרט קו דיו על
to place, to put לשום (ב / ה / תחתיו), לשומו לפני ה, לשומם (במקומה / ... ב), לשים (ביניהם ה / עמהם ה / תחתנו / ... תחת), לשים במקום, לשים ... במקום על
to place, to putt תניח ה... עם ה
to be placed הונח
to define לשום כ ... ה, לשים אותה עצמה ל, שם ה, שמת (ה)
to be placed הושמו ה... במקומם, יושם ... ב
defined, positioned המושם, המושמים (ב)
positioning בהנחתם
placing הנחת ה
ובהשימך (ה), להשימם תחת ה, לשום ב... ל
נשים (... אחר ה / ... ב / אותם / ה / עליו / ה... על ה / לפני / לפניהם / ... לפניו / ה... לפניו / ... לפניהם / ה... לפני ה / עמהם ה / תחת / תחתיה אלו ה / תחתיו / תחתיו ה / תחתיהם / ... תחת ה / ... תחתיהם / ... תחתיו / ה... תחת ה)
נשים המספרים זה על זה
נשימה (תחת)
נשימהו (ב / ל / עליו / חוץ ל / לפני ה / תחת ה / תחתיו)
נשימם (ב / עליה / עליהם / עליו / על ה / עם / זו על זו / זה אחר זה / תחת ה / תחתיו / ה... תחת ה / מחוץ / במקומו / במקוצו עם ה / לו על זה / ... על)
נשימנו (לפני / לפני ה / לפניהם / מחוץ / עליהם / עליו / על ה / תחת ה / תחתיו)
נשימם ראשונה ב
שים (ה / ה... ל / על / אותו תחת ה / תחת ה / תחתיו)
שימהו (על ה / תחתיו)
שימם ב
שמים (ל / לפניהם / תחתיו / אותו תחתיו / ... תחתיו),
שמנו (ב / ה / ה... לפני ה / ה... תחת ה / תחתיו / במקומו / מיד ה / זה ה)
שמנוהו תחתיו
שמנום תחת ה
שמנוהו מעלה אחת לפניהם
שמת (אותו / בהם / תחת ה / תחתיו / ... ב / שם ה)
תשים (... אחר / ... אחר ה / אחריהם / ב / ב... תחת / בראש / ה... ל / ה ... על / ה... תחת ה / לפניהם / ... לפניהם / ... לפני ה / ... כנגד / על ה / עליו ה / תחת ה / ... תחת / ... תחת ה / תחתיו /תחתיו ה)
תשי' לעולם ה
תשים ריוח בין זו לזו
תשימה
תשימהו (תחת ה / תחתיו)
תשימם (ב / עמהם / תחת ה / תחתיו / במקומה אחר ה)
תשימנה אחר ה
תשימנו (ב / על ה / מבחוץ)
נשים ... בעד ה... במקומה
נשים ה... למקומה, נשים במקומו, נשים ... במקומם
נשים ...ל... במקומה
נשים נקודה (על / על ה)
נשים נקדה תחתיה, ונשים תחתיה נקדה
נשים נקודה מחוץ במקום ה
שים נקדה אחת על ה
ותשים עליה נקודה אחת בעדו
ותשים ... אחת תחת הקו בעד ה
ותשים נקדה אחת (עליה / תחת ה)
תשים תחתיה נקדה, תשים תחתיה נקודה
תשימם לשארית תחת הקו
תשים בעד כל סיפרא שב
order, arrangement סדור ה
by the order, successively על הסדר ש
to arrange לסדר (ה... זה אחר זה / עם), לסדרם, מסדרים, נסדר (... לפניהם), נסדרהו, נסדרם (זה על זה), תסדר ה
הסדר, בסדר, כסדרם
לשים ה... בסדר
אשים להם סדר
ישים ... זו על זו על הסדר
נשימם על הסדר, נשימם ... על הסדר זה אחר זה,
נשימם זה על זה על הסדר, נשימם ב... זה על זה על הסדר
שמנו ה... כזה הסדר
תשים ה... זה על זה על הסדר
תשימם על הסדר
על סדר שביארנו
ישגיח ב
להשגיח בסדורו
בהשגחה
כפי המזדמן
כאשר הזדמן, כאשר יזדמן
שעלו בידך משום מעלה
to have ולהיות לנו ב, היה ל, היה להם, היה לו, היה לנו, היו ל, היו לך, היו לנו, יהיה לו, יהיה לך, יהיו להם, יהיו לו, יהיו לך, יש ל, יש לה, יש לו (ה), יש לך, יש לנו
owner of, having בעל (ה / אלו ה)
to have אשר להם, אשר לו, אשר לך, אשר לנו
בידינו, בידך
אשר היו בידו, אשר בידו
יש בידיך, יש בידך ה, יש בידינו, יש בידינו מ
שיש בידינו
שבידך, שבידיך, שבידינו
אשר בידך, אשר בידינו, אשר היו בידינו
כל אשר בידינו
להיות בידינו ה
היות בידך, היות בידינו
היה בידך ה, היו בידיך, היו בידך, יהיו בידך
היה בידינו, היה בידינו ה, היו בידינו
בידיך ל, בידינו ל
כאלו היו בידינו
כאלו יש לנו בידינו
והנה עלה בידינו ש
not having אין ל, איננו לו
אין לו
אין בידך מאומה
to discuss אדבר בזה ב
saying אומרו, אמרנו, אומרנו (כי / ש)
אומרנו... כאומרנו
כאומרנו (ש), הוא כאומרנו ש, היא כאומרנו, שהוא כאומרנו
והנה אומרנו, והוא כי אומרנו, וזה כי אומרנו, שהוא אומרנו
הוא כאומרך
כך הוא אומרנו
to say לומר (ש), לו' ש, אומר כי, אומרים ש, אמרנו (ב / כי / ש / ב... ש), אמרו (לך ב / לך ש / לנו), אמרתי, יאמרו לך (ל), נאמר (ב), תאמר (ש)
to say כאשר אמרנו, כאשר אמרתי
לאומרם
רצוני לומר
כאלו אמרו, כאלו אמרו לנו, כאלו אמרנו
הוא כאלו אמרו ש, והרי הוא כאלו אמרו, הוא כאלו אמרו לנו, והרי הוא כאלו אמרו לנו
אומרים ב
נאמרו
to note, to mention הזכירו, הזכרנו (ב / למעלה כי), הזכרתי (ב), זכרנו, נזכיר (ב)
above mentioned הנזכר למעלה
זכר לדבר
mentioned הנזכר, הנזכרת, הנזכרים, הנזכרות, הנזכרים
as mentioned כנזכר, כנזכרים ב, כנזכר למעלה
כמו שנזכר, כמו שהזכרנו (ב / ש), כמו שנזכר למעלה, ונזכר כבר ב
יזכר ש
to remember זכור לעולם (כי / ש)
נזכור ל
to forget תשכח (מ), תשכחהו, תשכחם
to be forgotten (שלא) ישכח
name שם (ה), שמות, ששמה
to name, to call יקראו, נקרא (ל / לו), נקראנוהו, קראנו לזה, קראנוהו, קראתי (לו), קראתיו, קרינו ... ל
to be called יקרא, נקרא (ה / ... מה), נקראה (ה), הנקראים, הנקרא
to denominate ותקרא לו שם מ
to denote שמתי להם
designation ברמז
to seek
לבקש (לו), לבקשו, לבקש אחד מהם
בקשת, בקשנו (ל), מבקשים ל, מבקש, תבקש (ל)
נבקש מספר (ל / ש / אשר), תבקש מספר
לבקש מורים ל, נבקש מורים ל, נבקש עוד מורים ל
לבקש לו מורה, נבקש לו מורה, נבקש לו מורים
נבקש מורה, תבקש מורי ה
אשר בקשת לו כל המורים
sought-after המבוקש, הוא המבוקש
sought-after מבוקשך, מבוקשנו, מבוקשינו
to ask for לבקש
to loan
לוינו האחד, נלוה אחד מ, נלוה אחד מה, נלוה א' מ, תלוה אחד מה
אשר ממנו לוית האחד, אשר ממנה לוית האחד
זה האחד אשר לוית
היות לווה ממנה
to examine לעיין, נעיין (אם), עיין (אם / ה), תעיין
clarification ברור
check, examination בחינה (ב / ש), בחינת (ה), בחינות
to check, to examine לבחון (אותו), אבחן, בחנהו
to be examined להבחן ב
להבחין אם עשית כדין וכשורה
לבחון אם עשית כדין אם לאו
להבחין מעשיך, לבחון מעשיך
examine it carefully דוק, דוק ותשכח
to explain להטעים
reason טעם (ב / ה / בזה / כי / ש / כל ה), טעמי', טעמו ב, טעמיהם
by reason בטעם
reason לסבה (ה / ש), בסבת
proof מופת, מופתי (ה / כל), מופתיהם, מופתיו
example דמיון, דמיוננו, דמיונות
example משל (ב / ש / בזה / לזה ב / על / על ה), משלים, משלי (ה), משלינו (ה), במשלנו, כבמשל, כבמשלנו, כמשלינו זה ש
for example ועל דרך משל, על ד"מ
to give example, to demonstrate אביא משל (... ל), אביא ... משלים, אמשול, אמשול משל ל
form, diagram צורה (ה), צורות, צורת ה, צורות מספרים
figure צורות
בא בזאת הצורה, בא בצורה הזאת
זאת הצורה ה
כפי צורה זו, כפי הצורה, כמו שהוא בצורה הזאת
בצורה (ה / הזאת / הנזכרת)
diagram בתמונה
to ask ישאלו לך (על... ש), שאל, שאלו לך (ש), שאלו לנו (כמה / ל), שאלו (כמה), שואל, שאל השואל
question שאלה, שאלתנו
in question, to be asked נשאל, הנשאל, הנשאל לנו, הנשאלים, הנשאלות, שנשאל
to answer יענו כי
to answer ולהשיב... ל, תשיב ... ש
answer תשובה
משפט אחד להנה
method, way בדרך (ה / ש), ובדרך זה, דרכים, דרכי ה, דרכם, כדרכו ב, כדרכנו, על דרך ה, ע"ד
על הצד ש
to proceed, to walk דרכתי, נדרוך ב
to go, to proceed בלכתך ל, ללכת, לך אל ה, נלך ל, תלך ל
skill, procedure מלאכה, מלאכתך, מלאכת ה, מלאכתינו
procedure, technique מעשה (ה), מעשהו, מעשיך (ב), מעשינו, מעשים (ב)
operation במעשיו
to do, to proceed
עשותך, עשותך כל זה
בעשותינו זה, בעשותך זה
לעשות (זה), לעשותו
אעשה, יעשו, נעשה (ל / לכל אחד / ממנו), נעשנו, עושים (ב), עשה, עשינו (לכל אחד מהם), עשית (ב / זה ל), תעשה (ה / ל / להם)
to be done יעשה (... ב)
וכן תעשה, וכן תעשה לעולם ש, ועשה כן לעולם
וכן תעשה עד תומם
וכן נעשה לעולם בטעם
נעשה במעשה
לעשות כל אשר עשינו ה
לעשות מעשינו זה, עושים מעשינו, עשינו זה המעש'
מעשינו ה
במעשינו
כמעשינו ב
נעשה לזה כאשר ל, נעשה לזה כאשר עשינו ל
נעשה בתוספת, נעשה בתוספת א' על
נעשה להפך ש
לעשות ממנו שורה אחת, יעשה ממנה שורה אחת, תעשה ממנו שורה שנית, תעשה שורתו
תעשה אחד מ2 דברים
עשה כדרכים
כמו שעשית ל... עם ה
כמו שעשינו בתחלה ב
תעשה זה ( ... ל)
to make נעשה ממנו, עושה מה, תעשה ממנו
לעשותם חלק אחד
נעשה א' שלם... חלקים, עשינו האחד השלם ... חלקים
נעשה הא' השלם
עשינו ... חלקים שוים, עשינו מהם... חלקים שוים
עשינו אותו ...חלקים, עשינו אותם ... חלקים שוים
לעשות כל שברים מהם ממין האחדים
לעשות מהפרטים כללים
לעשות בעד כל סיפרא מהן סיפרא אחת
אעשה משל אחר (מ)
action, operation פועל
to repeat the procedure להכפל (ה / זה ה), להכפיל (המעשה / המעשים)
המכפיל פעמי המעשה
repetitive procedure בהכפל (ה)
end, complete תמו כל ה
end, complete כלה... ה, כלה ה, יכלה ה, יכלו (ה), יכלו ב, יכלו מה, כלו ה, כלו אלו ה
תכלה המנין
כלות ה, ככלות ה
עד כלות ה, עד כלותם, עד כלותו
כלינו מעשינו
כלית כל מלאכתך, כלית כל מלאכתך על השלמות
כלינו כל מלאכתנו, כלינו מלאכתנו מכל וכל
to be gone כלה כל ה
equalizing השיווי
to equalize נשוום יחד
to be equalized הושווה (ל)
to be equal
שוה (ל / ממש ל), יהיה שוה ל, שוים (ה / בכל), שוים הם ב
השוה ל
equal שוים, שווים, שוות, שוה לכלם
explanation פי' ה
explanation ביאור (הכל)
explained מפורש ב
to explain לבאר (איך / ה), לבארו ב, אבאר, אבארנו (ב / בטעם), ביארנו כי / ש, נבאר זה ב
וזה מה שרצינו לבאר
כמו שבארנו, כמו שביארנו, כמו שביארנו ב, כמו שביארנו למעלה
כאשר ביארנו, כאשר ביארנו ב, כאשר ביארנו למעלה
וכן ביארנוהו למעלה
הרי ביארנו ש, הנה ביארנו כי
כבר ביארנו כי, כבר ביארנו ש
שביארנו
כאשר אבאר ב
כאשר ביאר ב
יתבאר בש, יתבאר עוד ב, נתבאר
כאשר התבאר, כאשר יתבאר (ב)
כמו שיתבאר (ב), כמו שנתבאר (ב)
כמו שנתבאר פעמים רבות כי
כמו שנתבאר למעלה
וכל זה יתבאר מעשהו ב
ועוד נתבאר איך, ועוד נתבאר אחר זה איך
וכל זה נתבאר הטב ב
מבואר באר הטב
להרחיב ביאור אבארנו בעודו בעינו
והנה יתבאר מ... כי
מבואר כי
מבוארים
וזה מבואר
והכל מבואר למבין
וכל זה מבואר, והכל מבואר ב
וזה מבואר בטעם
וכל זה מבואר בטעם ובצורה, הוא מבואר בטעם ובצורה
על דרך ברור
to clarify ולברר
to be made clear נתברר
it is clear נתבא' ש
clear, certain, evident ברור (כי), וזה ברור (ב / כי / ש), הוא ברור כי
ברור ומבורר
וזה דבר ברור, וכל זה ברור, והכל ברור
וזה ברור בטעם
והוא ברור במעשה ובטעם
כי הכל ברור המעשה והטעם
וכל זה תראה ברור ומפורש בטעם
וכל זה מבורר בטעם הראשון למבין
וכל זה ברור בטעם, וכל זה ברור בטעם למבין, והכל ברור בטעם ודי למבין
ודי למבין
ובזה תראה ברור מה שאמרתי ש
והכל נתבאר במעשה ובטעם
to become עולה לעשר מאשר לפניה, עולה עשר ידות מאשר לפניה
בערך אל אשר לפניה
בערך אשר לפניה, בערך אשר לפניו
to be able to
יוכל ל, יוכלו ל, יכולים ל, יכולנו ל, נוכל ל, תוכל ל
as much / great as possible היותר שנוכל, היותר שתוכל (ל), היותר ... שיוכל
to be able to היה הרשות בידך ל
to take בקחת ה... מה, בקחתך (אותם ל / ה... ל)
ליקח (... מה), לקחת (אותם מ / מן ה / מה... במקומם / מה / מהם / ממנה / משם / ה... מ / ה... מה / ה... מהם / ... מה / ל / בעבורה), לקחתו (מ)
יקח (ה / מ / כל אחד מה), יקחו (מ / מה)
לוקח (מה / משם), לוקחים משם
לקח (ה / מה / ה... מה), לקחו (ה / כל ה / כלם / ממנה ה / ה... מה)
לקחנו (... ל / ... מהם / ה... ל / ה... מ / ה... מהם / משם ל) , לקחנוהו ל
נקח (ה / כל ה / ל / לו מה / מ / מה / מהם / מהם ה / עוד / ...ה / ה... מה / ... מה / ... מהם / משם ה / משם... ל), ניקח מ
נקח (בעבור / בעבורו / בעבורם / בעד זה), נקחם מה, נקחנו בעצמו ל
קח (ה / ... מה / בעבורו), קחתנו (אלו ה / ממנו), תקח (בעבורו / ה... ל / ... ל), תקחנו ל
to be taken ויקחו מ
אשר יש לנו לקחת משם
מקום לקיחתם
should אשר לך ל, אשר לנו ל, היה לו ל, היה לך ל, היה לנו ל, יהיה לו ל, יש לו ל, יש לך ל, יש לנו ל, עליך ל, עלינו ל
should not אין לנו ל, אין לנו עוד ל, אין לנו ל... כלל, אין לנו ל... כי אם
should צריך ש
should
ראוי ל, ראוי לו ל, ראוי לנו ל, ולזה ראוי לנו ל
should be ראויין להיות
לא תחדל מ
ומהכל
ושמת שם נקודה
לא תמצא שם
ויהיה לעש' במעלה זו
ואם במקום הנקודה
ואם לא יהיה במעלה שאחר שום מספר
דבר שכלתה כבר ה
מהמעלה אשר הנקדה תחתיה אם יש שם מספר
ולא נקודה שכבר נשלם
יצא כלו בהם בשוה
לצאת
במעלה שאחר זו
תשוב כבתחלה
הם באמצע
? והנה בא על מתכונתו ש
to be היות (ב / ה), היותם
to be להיות (ה / ל), להיותה, להיותו ב, להיותם, היותך, בהיותך, היותם, היה, היו, היינו, הינו, שהיו, יהיו (ה), יהיה (ב / ה / כ), תהיה, היתה, יהא
אינך
to become וישוב
to become יהיה (ל / ב... ל / ל... על ה / לנו ל), יהיו (ל / לנו ל), הוא ל
to become היה בידך ל, יהיה ל... בידך, היו ל... בידך, יהיו ל... בידך
אשר הם ל... בידך
נעביר עליו
to cross out with a pen נעביר עליו הקולמוס, נעביר עליו קולמוס, נעביר קולמוס על ה, תעבור הקולמוס על ה
שעבר עליו הקולמוס
to begin, to start להתחיל מה, אחל ל, נתחיל (ב / ל), תתחיל (ל / מה)
מתחילות מה
וקודם התחילי ב
יתחיל ה
beginning התחלת, תחלת ה, בתחלת ה, מתחלת ב
beginning ראש ה, בראש זה ה
end סוף ה, בסוף ה
end תכליתם
הדומה ל, הדומה לה, הדומה לו, הדומה להם, הדומה לזה
כדומה לו, כדומה לזה
ודומיהן
כאלו דומים ל
need to צריך (ל), צריכים (ל), הצריכים, צריכין, צריך אתה לעולם ל, הצריך להם
to be needed הוצרך אליה, הוצרך מ
צורך
לצורך (ה)
no need לו לצורך, אין צורך, ואין צורך אלא ש, שאין לו צורך ל
הוצרכנו, הוצרכנו לזה
יצטרך ל, נצטרך ל, נצטרך הכל, תצטרך ל
אשר מהם יצטרך, אשר יצטרך מהם, אשר מהן יצטרך ל
אשר יצטרך, אשר תצטרך
מה שיצטרכו מהם
כל מה שתצטרך
by how much בכמה הוא
כמה ... יעלו, כמה יעלו
כמה פעמים יצא (מה / ה... מה)
כמה פעמים יש
כמה כפלי כפלים
כי כבר נשלם
נשלם
נשלמה
כמה יעלה לכל אחד
כמה שיהיו מהם
כמה... הם / כמה ... הן / כמה הם
כמה ... יש ב, כמה ... יש בהם
כמה הוא ה
בכמה יהיו
בכמה
כמה הם יותר
כמה פעמים ה... ב
כמה פעמים יש בהם
נדע תחלה כמה ... הוא, נדע תחלה כמה ... הם
נדע כמה ....יעלה
to know לידע (אם / כלם / ל / מה / באיזה / כמה), לדעת (אם / ה / כי / ש / כמה / מה / מאיזו)
דע (כי / ש / לך ש), דע לך ש, ידע כי, ידעו, ידענו (ה / כי / ש), ידעת (כי / ש), ידעתי, נדע (אם / כמה / ש), תדע (ה / כי ה / ש / כמה)
נדע בקלות ה... מה
ביודעינו ש
וזה יודע, יודע ב, יודע ה
נודע (ה / ש / מזה שה), נודעים, נודעו ה, הנודעים
הידוע
אשר בהם נודע
בהודע ה
ואין דעתך
אין דעתינו ל
מיודעים
knowledge ידיעות
דעת, דעתי, מדעתי, מדעתנו
ידע יודע ה
אשר לא יודע
it is known בידוע ש, וידוע הוא כי, וידוע כי, ידוע הוא ... כי
to be unknown נעלם לנו ה, נעלם ה
known הידוע, הידועים, ידועים, מספר ידוע
unknown הנעלם, נעלם (ה / ממנו), הוא הנעלם, הנעלמים
to dictate נותן ל
to mistake, to err טעינו, טעית (ב), נטעה, תטעה (ב / ל / מל)
mistake, error טעות, טעיות
to mislead יטעך ש
to think לחשוב כי, אחשוב זאת
to explain, to introduce להציע, אציע ש, הצענו
premise הצעה, הצעות
to rise יעלה מעלה אחר מעלה
to reach יעלה... ל
to exceed by יעלה ... על, יעלה
to exceed יעדף ה... על ה... כ, יעדפו עליהם
exceeding עודף על ה, העודף (ב... על ה), העודפים, העודפים (ב... על ה), מוסיפים על ה
excess יותר על
to exceed יותר על ה
to exceed by יהיה יותר על ה ... ב
excess עודף
with excess לתוספת
plus עם תוספת
to increase יעלה, מעלה
to increase יתרבה, יתרבה המספר ב, מתרבה (בכפל)
to decrease יוריד, מוריד
אינו מעלה ומוריד
to be missing יחסר... מה, חסר ב... מה
to be lessened יחסר
to fall short of היו למגרעת, יחסר
deficit חסרון
with deficit למגרעת
to continue, to keep תוסיף ל
inverse operation הפך ה, הפכים, להפכו
to be inverted יתהפך
amount מנין
people אנשים, אנשי, איש
spacious מרווחות, מרווחים
when ever בכל עת ש
enough די
to be enough די ב, די ל
not enough ואין די, ואין בו די, אין די ל, אין דיו ל, אין שם כדאי ל, ואין ב... כדאי ל, אין ... כדי, ולא יהיה בו די ל
and that is it ודי
sufficiency ספקנו, די ספקנו
benefit תועלתם
to be useful יועיל
beneficial, useful מועיל ל, מועילים ל
to apportion להועיל ממנו ל
to harm יזיק, מזיק
? בשום פנים
to count מונה, נמנה מה, תמנה (מ / מה / משם)
to indicate להראות, להורות, הורה, המורה על ה, מורה לנו ש, מורי' על ה
to confuse לבלבלך בזה
יבלבל עליך
יתבלבל (ב), נתבלבל, תתבלבל
to be able יוכל ל, יוכלו ל
ויקח ... פעמים
להתחלק עליו לשלמים
to discuss נדבר
consideration עיון אל
study עיון
learning בלומדי, לומדם
to learn ללמוד ב, להתלמד, תתלמד
to teach ללמדך על
to bring הבאתי ב, יגיעם כלם ל
הנה לנו ש
to elaborate להאריך בזה עוד, אאריך
to elaborate להרחיב ה
to give לתת לך, אתן לך, יתנו
general, inclusive כולל
ancients הראשונים
to consider as הבט... כאלו
to consider as לוקחים ... לאחדים
all are the same כלם שוים
מה שאמרנו ב
to reach בהגיענו שם, בהיגיענו שם, הגיענו אל ה, הגיעו ל, הגענו (אל / ל), הגעת ל, יגיע (אליהם / ל), יגיעו ל, תגיע ל
to be contained in בו, יהיה בו ה, אשר ב, אשר בו
contradiction בחילוף
so is וכן הוא ה, כן הוא
they themselves הם הם
total היה הכל, יהיה הכל, יהיו הכל, יהיו כולם
in order that יען
were it ההיתה
as they are כמות שהם
the same as כך הוא... כמו
as כדרך שה
at present אשר בנתים
at once ברגע
with little במעט
בכל עת
large הרבה
with respect to על ה
לכופלו
to achieve השגנו
to attain תשיגנה
to be attained שבא ב, אשר באו לך
to indicate המורה על ה
to denominate לקרוא להם שם, נקרא להם שם
diagonal האלכסונים
difference שינוי ב
to stand עומד
to be difficult יקשה עלינו
difficult קשה
effort עמל
effort יגיעה
to exert oneself, to endeavor ניגע
to ease, to make it easy להקל ה... מעלינו, להקל מעליך (ה), להקל מעלינו (ה), להקל עלינו ה
to assign הקצתי לו, הקציתי לו
extreme הקצוות
money ממון
golden זהב, אלו של זהב, של זהב, מזהב
silver כסף, של כסף, אלו של כסף
dinar דינר, דינרי, דינרים
peraḥim פרחים
zehuvim, golden coin זהובים
peruṭot פרוטות
zuzim זוזים
to lower להורידם, הורדנום (ב' מעלות), מורידים (אותם), מורידין ה, נוריד, נורידנו, נורידם (מעלה אחת), תורידם (מעלה אחת)
lowering הורדה, הורדת מעלה, הורדתם
to be lowered יורדו, ירד
disappeared נעדרת
to come close to, to approach להתקרב (אל האמת / מאד), יתקרב אל (האמת), יתקרב ל... ב, נתקרבת אל (האמת), תתקרב אליו
to come closer to להתקרב יותר אל (האמת), להתקרב עוד אל (האמת / השרש), יתקרב מאד מאד, מתקרב יותר, נתקרב יותר אל (האמת), תתקרב יותר אל ה
to be close to קרוב אל (האמת)
יתקרב אל האמת לחסרון
יתקרב אל האמת לתוספת
יתרחק מן האמת, יתרחק מן האמת ב
רחוקו מן האמת מ, ריחוקו מן האמת
difference מרחק (... מ / ה... מה), מרחקו מ, מרחקם מ, רחוקו מ, רחוקם, ריחוק, ריחוקים, ריחוקם מה
difference הרחקתם מ
to become distanced from אשר נתרחקו מ, שנתרחקו מה, יתרחק, תתרחק, מרוחקת ... מה
distance מרוחק ה
בכל מאויו
באחד המעשים ב
to require יחייב
given מונח ל
side, factor צלעות
generation הולדה
to generate לחדש, חדשנו
to be generated נתחדש, נתחדש מ, נתחדשו (ב / מ), יתחדש
created attained, המתחדש, מתחדש, המתחדשים
created מחודש
to invent, to create להמציא, אמציא, המצאת, המצאת ה
invention המצאות
to instruct נצוה ל, צוינו ל, ציויתי ל, ציויתיו, צוויתיך, ציויתיך ל, צויתיך ל
meaning, instruction הוראה, הוראת
indicator מורי
ומ"מ
as necessary בכל הצורך
too much יותר מדאי
portion of קצת ה
smaller portion מעוטו
greater portion רובו
portion חלקי ה, חלקים
to hurry חששתי ל
to investigate לדקדק, דקדקתי
to be satisfied למסתפק ב
thing דבר, דברים
any thing שום דבר
matter דברים
issue, matter ענין, ענייני ה, עניינים
concerning, in the matter of בענין ש
type מין (ה / מה מ), מינים, מינה, מינו, מינם, מיניהם, מיני
שהוא ממינו, אשר ממינו
שאינו מינו
מין בשאינו מינו
מין על מינו
to be eliminated יתבטל
observation השגחה
to wonder תתמה ש
to remove הסרנו אותו מהם
change שינוי ביניהם
no difference between אין חלוף בין ... ל
forward בקדימה
backward ואיחור
intention כונה, כוונות, כונתינו, כוונתי, בכוונה מכוונה
lowest הגרועים מהם
לקחת עמו ה
detail פרט
gleanings? עוללות
to be marked by ירשמו ב
beauty היופי
true האמיתי, אמיתיות
ואותו
ועל דרך היופי
to be difficult תכבד ה
work עבודה
האמרה
plus עם ה, ועוד (ה)
to be gone יצא
it follows that ויצא מזה כי
to become possible יצא לנו ל
to derive ממנה יצאו
to find out יצא לנו ש
להוציאם מן הכלל, יצאו מן הכלל, ויצאו הם מן הכלל
to assign הקצתי לו
like כעין
descendant ילדתם
to change לשנותו
נחבר ב
to consist of הורכב מה
to be composed הורכב, הורכבה מהם
to insert להכניס
to be converted שבו כלם
to be absent יעדר
to be converted יומר
to distinguish, to separate תבחין בין ה... ל
high גבוהים
to be verified נתאמת
truth אמת
הנה אמת, הנה אמת הנה נכון, הנה נכון הנה אמת
והנה כל מעשינו אמת, הנה כל מעשינו אמת ויציב, הלא מעשיך אמת ויציב, הנה מעשיך אמת ונכון
כל מעשינו בצדק ובמשפט
false שקר
absurd שקר
rule דין, הוא הדין, כלל (ה / ... ל / כי / ש)
the rule requiresהיה הדין נותן
to change משתנה, ישתנה
time פעם, פעמים, פעמי ה
כפעם בפעם, פעם בפעם
every time בכל פעם, בכל פעם ופעם
time after time פעם אחר פעם
greatest number of times מספר הרב הפעמים, היותר פעמים מב, יותר רב פעמים
to split שנפצל מ, מ... נפצל
to understand להבנה, להבין, להבינו
understanding הבנות, הבנתי
understandable מובן
to designate ייעדתי ל, ייעדנו
to see לראות (אם / ... ב), אראה, נראה (אם / כמה), ראה (אם / ה), ראית ... ש, תראה (ב / ש)
היה נראה ש
to consider ראה ל, ראיתי ל
to bother תטרח
to actualize להוציא
to be determined נרמז ב, נרמז ש
determined רמוז ב, הרמוזות
deduce from this והקש על זה, והקש על זה ב
to happen, to occur יקרה (ב / כאשר)
נביאנו
אינו כלל
?זה פירושם
שבא הכל כאלו
for panic לבהלה
for naught לבטלה
to fill, to fulfill למלאת, מלאתיו, תמלא
to satisfy למלאת את
to train להרגילך ב, להרגילך עוד ב
style, form בסגנון
removed המוסר
מספרו
one and the same והנה כל ה... אחד, אחד בעצמו
והכל עולה לדרך אחד
והכל עולה לסך אחד
והכל עולה לענין אחד
to shorten ולקצר
to contrive לתחבל
half חצי ה, חצי מ, חצאין, חצאי, חציו, מחצית ה
to reverse בהפוך ה... ל, הפוך ה
to return חזרו ל, תחזור ל
to return להחזירו ל
to return נשוב (ו / ל / עוד), תשוב (ל)
meaning כלומר ש
meaning פי' (כי / ש)
wise חכם, חכמים
Sages of the Gentiles חכמי הגוים
science חכמה, חוכמות, חכמתם
mathematics חכמת הלימודיות
natural science חכמת הטבע
arithmetic חכמת המספר, במספר
philosophers מתפלספים
rational soul נפשם משכלת
rationalism התבוניות, תבונה
rational concept המושכלות
intellect שכלו, שכלי, שכלנו
subject נושאיהם
essence עצמים
accident מקרים
straightness יושר
to raise תעלה
a while כמה
to reveal לגלות
treasures מצפוניה
to grasp, to take hold החזיקתני
to influence תאצילני
to translate להשיבו ב
to elaborate בהרחבת
| to long
|
חשקתיך
|
| desire
|
תאותך
|
| to grant
|
ולתת את
|
| request
|
שאלתך
|
| trouble
|
טרדות ה
|
| to allow
|
מסכימות ל, מסכימים
|
| to engage in
|
להתעסק ב
|
| to live
|
יחיו
|
| in the eyes
|
בעיני, בעיניהם
|
| master
|
אלופים
|
| possible
|
איפשר
|
| heart
|
לבם
|
| attached
|
נקשר
|
| succeed
|
יכשר
|
| to rule over
|
להשתרר
|
| to overcome
|
ולנצח
|
| time
|
זמן
|
| years
|
שנות
|
| youth
|
זמן הנערות
|
| maturity
|
זמן הבחרות
|
| less and more
|
בפחות וביתר
|
| senseless
|
תפל
|
| defect
|
דופי
|
| mockery
|
התול
|
| slander
|
לעז
|
| to ridicule
|
לעגו
|
| to joke
|
יתלוצצו
|
| to encourage
|
החזיקו יד
|
| to be told
|
יסופר
|
| engagement
|
עסקם ב
|
| simple things
|
פשוטות
|
| perceptible
|
מושגות ב
|
| outstanding, prominent
|
מסויימים
|
| to encamp
|
חונים
|
| division by division
|
דגלים דגלים
|
| path by path
|
שבילים שבילים
|
| wanderer
|
נעים ונדים
|
| to sway
|
מתנודדים
|
| to rob
|
יגזלו מ
|
| to steal
|
יגנוב ה
|
| to deceive
|
להונות, יונה
|
| to exploit
|
ולעשוק
|
| poverty
|
עוני
|
| glory
|
הודם
|
| might
|
מאודם
|
| business
|
מסחרים
|
| to eat
|
יאכל
|
| word
|
דברו
|
| to strengthen
|
להחזיק
|
| to raise up
|
להקים
|
| pedantic
|
מדקדקים
|
| to eliminate
|
לכלות
|
| guilt
|
אשם
|
| to be careful
|
נזהר מ
|
| pegs
|
יתדות
|
| to emanate
|
אצל
|
| friend
|
רעהו
|
| to choose
|
בחר מ
|
| bad luck
|
רוע מזלו
|
| to be well with
|
טוב לו
|
| to continue
|
ולהתמיד
|
| righteousness
|
צדקו
|
| to carve
|
לחקוק אותו
|
| forever
|
לנצח
|
| affection
|
וחבתן
|
| to overpower
|
גברה
|
| to tearing down, to break
|
פרצתי
|
| definition
|
גדר ה
|
| humility
|
ענוה
|
| order
|
סדור
|
| to stand
|
קמתי בפניהם
|
| to give honor to
|
אחלוק הכבוד
|
| to be enriched
|
להעשר
|
| emanation
|
סידורה
|
| to compose
|
חברתי
|
| goodness
|
טוב
|
| to weaken
|
מחלישים
|
| to come
|
באתי ל
|
| wonderful and fearful things
|
נפלאות ונוראות
|
| lights
|
אורות
|
| to inform
|
יודיעו
|
| argument
|
טענות
|
| apology
|
התנצלותי
|
| virtue
|
מעלה
|
| to leave
|
עזב את ה
|
| queens
|
גבירות
|
| to expand
|
מרבות
|
| boughs and branch
|
סנסנים ופארות
|
| fruit
|
פירות
|
| extended his hand
|
פשט ידו ב
|
| humiliating
|
כמבזה
|
| to grasp
|
אחז את
|
| hidden
|
צפון
|
| concealed
|
נעלם
|
| to admit
|
יעיד על עצמו
|
| to admit
|
להודות כי
|
| today
|
היום
|
| to estimate
|
אומדים
|
| foundation
|
יסוד, יסודה
|
| building
|
בניינה, בניינם
|
| consists of
|
הבנויות על ה
|
| room
|
חדרים
|
| to open
|
לפתוח
|
| entrance
|
פתח
|
| lenient and stringent
|
קל וחומר
|
| strong
|
חזק, חזקות, חזקים
|
| to be held
|
מוחזקות בידיהם, ומוחזק
|
| right
|
נכונים
|
| known, recognized
|
מפורסם, מפורסמים
|
| to rely
|
נשענים
|
| pronoun
|
|
|
|
אני, אנו, הננו, אתה, הוא (ה), היא, הם (מ), המה, הן, הנה
|
|
|
והוא גם הוא
|
|
|
אותו ה, אותה ה, מאותה ה
|
|
|
ההיא (בעצמה), ההוא, ההם, ההן
|
| which are / is
|
שהוא, שהיא, שהם, שהן, שהוא ה, והוא ש, שהנו
|
|
|
שיהיו שם
|
|
|
שזהו
|
|
|
זה (ה / הוא / ש), זו (ה), זאת (ה / היא), וזהו, וזוהי
|
|
|
זה... וזה
|
|
|
אלו (ה / הם / הם ה / אשר / ש), אלה, האלה, האלו
|
| of these
|
מאלו, מאלו ומאלו
|
| of them
|
שבהם, מהם, מהן, מאלו, ממנו
|
|
|
הוא ב
|
|
|
כזה
|
|
|
מזה ה
|
|
|
לזה, לזאת
|
|
|
אשר
|
|
|
אשר הם
|
| itself / themselves
|
עצמה, עצמו, עצמם, בעצמה (ה), בעצמו, בעצמם
|
| by itself
|
בפני עצמו, לעצמו
|
| by our selves
|
בעצמינו
|
| your self
|
בעצמך
|
| any, certain
|
שום, שום ה, משום
|
| certain
|
איזה
|
| certain
|
מה
|
| every one
|
כל אחד (ש)
|
| every
|
כל
|
| every… of them
|
כל... מהם
|
| every thing
|
כל דבר, הכל
|
| some thing
|
דבר מה
|
| all
|
הכל, כל (ה), כל אשר, כלם, כל זה, כולה, כלה, היה כלה, בכל, יהיו כלם, כולם
|
| all of
|
כולם מה
|
| each
|
כל, כל ... מהם, כל ... ו... מהם, בכל ... ו...
|
|
|
כ"א, כל אחד, כל אחת, כל א' (מ), כל אחד מ, כל אחד מאלו ה, כל אחד מה, כל אחד מהם, כל אחת מהם
|
| one of
|
אחד (ה / מ / מה / מהם), א' מה
|
| for each
|
על כל, לכולם
|
| by each other
|
זו בזו
|
| to each other
|
זה לזה
|
| one after the other
|
זה אחר זה
|
| for each
|
לכל
|
|
|
וכל ש
|
| the rest
|
שאר (ה), כל שאר ה, כבשאר ה
|
| both
|
שניהם, שתיהן
|
|
|
או
|
|
|
גם, וכן, וכן כולם, וכן כלם, וכן לכלם, וכן בכללן, וכן ב
|
|
|
גם ה... גם ה, הן ... הן, הן ל... הן ל, הן מן .... הן מן ...
|
|
|
בין ש... או ש
|
|
|
בין... בין אם
|
|
|
בין ... או
|
|
|
או ... או
|
|
|
הן ... או
|
|
|
בה, בו, בהם, בכלן
|
|
|
זה אשר
|
|
|
אשר ב, יהיה ב, אשר בו (ה), אשר היו ב
|
|
|
אשר מה
|
|
|
בזה... ובזה
|
| which
|
איזה ... הם, איזהו ה
|
| by which
|
ממנו
|
| from which
|
אשר ממנה, אשר ממנו
|
| that
|
מה ש
|
| that
|
הוא ש, הוא אשר
|
| what
|
מה ש
|
| who
|
מי ש
|
| whichever
|
איזה מהם שיהיה
|
|
|
זה בזה
|
| which
|
איזה, אי זה
|
| which is
|
שזהו
|
| which is
|
והוא כי
|
| which is of
|
שהוא מ
|
| the same as
|
הוא כ
|
|
|
כמי ש
|
|
|
כי כך הוא
|
|
|
והנה, הנה, הנה ה
|
|
|
הנה ש
|
| by this
|
בזה
|
| one by one
|
אחד אחד
|
| negative clause
|
|
| without
|
בלי, מבלי, מבלי... כלל, בלי... כלל
|
| without
|
מבלתי (ה), בלתי
|
|
|
בלא
|
| not
|
בלתי
|
|
|
בלתי ... כלל
|
|
|
אין ... דבר
|
|
|
אין לך ל... דבר
|
|
|
אין בה... כלל כי אם
|
|
|
אין ... כלל, אין... כלל כי אם ה... לבד
|
|
|
אינו כי אם
|
|
|
אין... כי אם, אינו... כי אם, אינך... כי אם
|
|
|
אין ב... כי אם; אין שם ... כי אם
|
|
|
אין אנו ... אלא
|
|
|
אין אנו... כלל, אינך ... כלל
|
|
|
אין לו, אין לו... כלל
|
|
|
אין לו כי אם
|
|
|
אין לך... כי אם
|
|
|
אין בידיך כי אם
|
|
|
אין בידיך ל
|
|
|
אין בידינו ... כלל
|
|
|
ואין לו ל... כי אם; אין לך ל... כי אם, אין לנו ל... כי אם
|
|
|
אין לך ... כי עם
|
|
|
לא... כלל כי אם
|
|
|
לא... כי אם
|
|
|
לא... כלל
|
|
|
לא ... לעולם
|
|
|
לא... כל
|
|
|
לא ... דבר
|
|
|
לא ... מאומה
|
|
|
לא ... שום
|
|
|
ואלו לא היה ב... כי אם
|
|
|
אין בכאן
|
|
|
לא... שום דבר
|
|
|
לא... אלא
|
|
|
אין מ... ל
|
| even not
|
אף לא
|
| not even
|
אין גם
|
|
|
לא ... אפי', לא... אפילו
|
|
|
אין ה... ולא ה
|
|
|
אין ... לא ... ולא
|
|
|
לא ... ולא, לא... ולא גם
|
| do not
|
ואל, אין, אינו, אינך
|
| is / are not
|
אינה, איננו, אינו, אינם
|
| not
|
לאו
|
| at all
|
בשום פנים
|
| at all
|
כלל
|
| no, there is no
|
אין, אין ב, אין ה, אין זה, אין כאן ה
|
| is / are not
|
אינם (מ), אינו, איננו
|
|
|
אין בה, אין בו, אינו ב, אינו בה, איננו בו, אינם בו, אין ... ב
|
|
|
אם לא, ואם לאו
|
|
|
ואם לאו לאו
|
| neither… nor
|
לא... ולא
|
|
|
לא היה לו
|
|
|
אין ל, ואין לנו ל
|
|
|
אין לו אחד מהם, אין לו שום אחד מה
|
|
|
עוד, ועוד
|
|
|
הרי, הרי ש, הרי לך, הרי לנו (כי / ש), והרי, שהרי
|
|
|
הרי הוא כאלו, הרי זה כאלו
|
|
|
כי אם
|
|
|
ככה
|
|
|
כמה
|
| indeed
|
אכן
|
|
|
ככה
|
|
|
בעבור ה
|
|
|
שאינו ראשון, שאינו ראשון לו
|
|
|
בעת ההיא, בפעם ההיא
|
|
|
הם מ
|
|
|
את, אותם
|
| Prepositions
|
|
| after
|
אחר (ה), אחר ש, אחר אשר, אחרי, אחרי אשר, אחרי ש, שאחרי ה, אחר זה, אחריה (ה), אחריו (ה), אחריהם, אחריהן
|
| before
|
לפני ה, לפניהם, לפניו (ה), שלפני ה, שלפניהם, קודם (ה / זה / ש)
|
| before
|
טרם
|
| by
|
והוא ב, בש, וזה ב, וזה בש, וזה יהיה ב, בזה
|
| between
|
בין ה, בין כל ה, מה שבין ה, בין ה...ובינו, בין... ל, בין ה... וה, בין ה... להנה, ביניהם
|
| among
|
בהם
|
| with, plus
|
עם, עם ה, עמו, עמהם
|
|
|
שעמו, אשר עמהם
|
| bellow
|
למטה (מהם)
|
|
|
לשמאל, לצד שמאל (מה), לצד שמאלי
|
|
|
הימין
|
|
|
לימין, לצד ימין (מה)
|
|
|
לצד ימין מהמקום
|
| above
|
למעלה
|
| above, on
|
מעל ה, על (ה / הכל), עליהם, עליהן, עליו, על ראש, על ראשו, על ראשם
|
| beneath
|
תחת ה, תחתיהם, תחתיהן, תחתיו
|
|
|
זו תחת זו
|
| out of
|
ומתוך
|
| until
|
עד, עד ש, עד אשר
|
|
|
כנגד ה, כנגד אותה ה, כנגדה
|
| in
|
אשר היה ב, בזה
|
| in
|
בתוך ה
|
| for
|
בעד ה, בעדה, בעדו, בעדן
|
| for
|
שהי' לה ל, יהיה לו ל, לו, הוא ל, הוא לו ל
|
| for
|
בשביל (ה)
|
| from
|
ממנה, ממנו
|
| except
|
מלבד
|
| except
|
בלתי ה, זולתי (ה), מזולת ה, זולתם
|
| except
|
מבלעדיו
|
| or
|
או
|
|
|
לבדו, כל אחד לבדו
|
|
|
יהיה עם הכל
|
| it is all the same
|
הכל אחד, הכל א'
|
|
|
כולל, כולל אותם
|
| so much, so an so
|
כ"כ
|
|
|
ואליהם
|
|
|
על ידי
|
|
|
להם
|
|
|
בכלל ובפרט
|
|
|
אלא ש
|
|
|
בפעם הזאת
|
|
|
מאשר
|
|
|
באשר
|
| corresponding
|
כנגד (ה), נגדו
|
| for
|
בעד ה
|
|
|
לפעמים
|
|
|
ג"כ
|
|
|
א"כ
|
| i.e.
|
ר"ל, ר"ל ש, ר"ל כי, ר"ל אשר
|
|
|
ר"ל ע'ד'מ' ש
|
|
|
עד"מ, ע'ד'מ'
|
| etc.
|
וכו'
|
| all the more so
|
כ"ש
|
| also
|
ג"כ
|
| adjectives
|
|
| many
|
רבות, רבים
|
| many
|
הרבה
|
| numerous
|
רבים
|
| more than
|
רבים מ
|
| few
|
כמה
|
| few
|
קצת
|
| few
|
מצומצמות
|
|
|
האחד, האחת
|
|
|
אחרון, אחרונה, אחרונים, אחרון ל
|
| other
|
חבירו, חבירתה, חבר, חברותיה, חבריהם, חברתה
|
| other
|
אחר, אחרת, אחרות, אחרים
|
| other
|
זולתו, זולתם
|
| better that
|
וטוב ש
|
| more
|
יותר
|
| greater, more than
|
יותר (מ / מה / ממנו)
|
| much greater
|
הרבה מאד יותר מה
|
| great
|
רב, הרבה
|
| greater
|
רב, רב מאד מה, רב (מה / ממנו), מספר רב, המספר הרב
|
| great/greater
|
הגדול (ב), הגדולה, גדולה (מה), גדולים (מהם), הגדולים
|
|
|
גדול (מ / מה / מהם / ממנו), גדול ה... מה
|
| greatest
|
גדול שאיפשר, הגדול שאפשר, הגדול שאיפשר, היותר גדול שאיפשר
|
|
|
היותר שאפשר, היותר שאיפשר, היותר שאפש' מ
|
|
|
יותר גדולים, יותר גדול מה
|
| small
|
מעט, מועט
|
| little
|
הקטן
|
| smaller
|
קטן, קטון, קטנה, קטן (מ / מה / מהם / ממנו), קטנים, קטן במנין
|
| smaller
|
מעט, המספר המעט
|
| smaller, less than
|
פחות (מ / מה / ממנו), הפחות מה
|
| inferior
|
שפל
|
| upper
|
עליון, עליונה, עליונים
|
| bottom
|
תחתון, תחתונה, תחתונים, תחתונות
|
| last
|
אחרון (שב), אחרונה, אחרונים, אחרונו'
|
| first
|
קודם
|
| first
|
ראש
|
| first, former
|
ראשון (מאלו / מה / מן / מן ה / שב), ראשונה (מה), המספר הראשון, החשבון הראשון, ראשונים, הראשונים
|
| second
|
שני (ב / ל / לו / מאלו / מה / מן / שב), ב' מאלו, שנית (מה)
|
| third
|
שלישי, שלישית (ל), שלישיים ל
|
| fourth
|
רביעי, רביעית
|
| fifth
|
חמישית
|
| sixth
|
שישית
|
| prior
|
מוקדם
|
| latter
|
מאוחר
|
| preceding
|
העובר, העוברים, אשר לפניו, הקודמת, הקודמים
|
| preceding
|
אשר לפני (ה), אשר לפניו, אשר לפניה, אשר לפניהם, שלפני זאת, שלפניו, שלפניהם
|
|
|
אשר לפני פניו
|
|
|
לאשר לפניו ולפני פניו
|
| preceding, previous
|
הקודם (לו / לזה), קודם, הקודמת, קודמת (ל), קודמים
|
| previous
|
שעבר
|
| next to
|
סמוך, הסמוך ל, הסמוך להם, הסמוך לו
|
| following, succeeding
|
הנמשך, הנמשך אליו, הנמשכת ל, נמשך אחר הנמשך
|
| following
|
הבא אחריו, הבא אחריהם, הבא אחריהן, הבא אחר זה, הבאה, הבאה אחריה, הבאה אחריהן, הבאה אחר ה, הבאים, הבאים אחריה
|
|
|
שאחר ה
|
|
|
העולה
|
| itself
|
בעינו, בעינה
|
| very, itself
|
ממש
|
| other, another
|
אחר, אחרת, אחרים
|
| others
|
אחרים, האחרות
|
| short
|
קצר, קצרה
|
| correct
|
נכון, נכונה
|
| correct
|
אמת
|
| various
|
שונים
|
| indifferent
|
בלתי שונים
|
| different
|
משונים, שונים
|
| corresponding
|
אשר כנגדו
|
| corresponding
|
בת גילה
|
| worthy of
|
ראוי ל
|
| appropriate
|
הראוי ל, הראויה ל, הראוי לו, הראויה לו, הראויות להם
|
| appropriate
|
נאות, נאותים, נאותות
|
| new, renewed
|
חדש, חדשים
|
| absolute
|
גמור, גמורה
|
| well versed in
|
בקי ב
|
| entitled
|
רשאי
|
| easy
|
קלה
|
| necessary
|
מחוייב
|
| given
|
מונחים
|
| important
|
נכבד
|
| beautiful, proper
|
יפים
|
| nice
|
יפים
|
| nice
|
הנאה
|
| thin
|
רזה
|
| poor
|
דלה
|
| despicable
|
בזויה
|
| despicable
|
נקלה
|
| included
|
נכלל
|
| whole
|
כולו
|
| whole
|
השלם, שלם, שלימה, שלמה, שלמות, שלמים
|
| the whole
|
כל ה... בכללו, בכללו
|
| possible
|
איפשר
|
| impossible
|
בלתי איפשר, נמנע
|
| adverb
|
|
| there is/are
|
יש, יש ב, יש... ב , יש ב... ה, יש בכל ה, יש שם
|
| from there
|
משם
|
| vice versa
|
בהפך, להפך ש
|
| again
|
שוב
|
| little
|
במעט, המעט ה, מעט, במיעוט
|
| there
|
שם (ה)
|
| here
|
כאן, בכאן
|
| now
|
עתה (ש)
|
| so far, until now
|
עד הנה
|
| at the beginning
|
מתחלה
|
| in the middle
|
באמצע
|
| at first
|
ראשונה
|
| approximately
|
בקרוב
|
| already
|
כבר
|
| also
|
גם
|
| downward
|
ולמטה
|
| upwards
|
ולמעלה, למעלה ממנו
|
| et cetera
|
וכיוצא בזה
|
| successively
|
זה אחר זה
|
| precisely
|
עין בעין
|
| perfectly
|
על השלימות
|
| properly
|
יפה יפה
|
| vaguely
|
בסתם
|
| truly, really
|
באמת
|
| truly, really
|
ממש
|
| clearly
|
ברור, בברור
|
| closely, carefully
|
הטב
|
| inversely
|
יהיה להפך
|
| immediately
|
מיד
|
| correctly
|
כתקנה, כתקנם, על היושר
|
| equally
|
בשוה, שוה בשוה
|
| briefly
|
בקוצר
|
| surely
|
הלא, הלא הם, הן
|
| so on endlessly
|
כן לעולם, וכן לעולם, וכן יהיה לעולם
|
| only
|
רק
|
| only
|
לבד
|
| only
|
כי אם
|
| alone
|
לבד, לבדה, לבדם
|
| together
|
יחד, ביחד, כלם ביחד, כל ה... יחד
|
| very
|
מאד
|
| even
|
אפי'
|
| even if
|
ואם, אף אם
|
| instead
|
תחת, תחתיו
|
| instead
|
במקום (ה), במקומה, במקומו, במקומם
|
| such as
|
כגון ש
|
| as
|
כמו (ה / ש / שה / שהוא ה / שהן); כמוה, כמוהו, כמוהם, כמונו, כמותם
|
|
|
כמות (שהם / שהן); כמותה, כמותו
|
|
|
אשר כמותו, שכמותו
|
| as
|
כפי (ה / ש / שהם)
|
| as
|
כאשר
|
| as much as
|
כל מה ש (... יותר)
|
| so
|
כן, וכן
|
| so
|
כך הוא (ה)
|
| always
|
לעולם
|
| ever
|
בעולם, לעולם
|
| henceforth
|
מכאן ואילך
|
| then
|
ואז, אז
|
| then, afterwards
|
ואחר כך, וא'ח'כ', אח"כ
|
| afterwards
|
אחר כן, אחרי כן, ואחר
|
| further
|
עוד
|
| furthermore
|
ועוד (ש)
|
| therefore
|
ולכך, לכן, על כן
|
| therefore
|
לזה, על זה
|
| provided that, so long as
|
ובלבד ש
|
| until the end
|
עד תומם
|
| once
|
פעם אחת
|
| twice
|
פעמי', פעמים, ב' פעמים
|
| outside
|
מחוץ ל
|
| altogether
|
מכל וכל
|
| lastly
|
באחרונה
|
| first, at first, firstly
|
ראשונה ב, תחלה, בתחלה
|
|
|
כבראשונה, כבתחלה
|
| how
|
איך
|
| how many, how much
|
כמה (הם / ... הם / ... הן)
|
| where
|
מאיזה מקום, מהיכן
|
| when
|
בעת (ה)
|
| when
|
כאשר, כש
|
| why
|
למה
|
| which
|
מאי זה, מאי זו, מאיזו
|
| conjunction
|
|
| in order to
|
כדי ש, כדי ל
|
| but
|
אבל, אין זה... אבל
|
| but
|
אך
|
| but
|
ואולם
|
| since
|
וכיון ש
|
| since
|
אכן ש
|
| since
|
אחר היות (ב / ה / ... ב / שם), אחרי היות, אחרי היותם
|
| since
|
להיות (ה)
|
| since, because
|
אחרי, אחר ש, ואחרי ש, אחר אשר, מאחר ש, ומאחר שכן, כי אחר ש
|
| because
|
זה היה ל
|
| because
|
יען
|
| because
|
כי, זה כי, וזה ש, והוא כי
|
| since
|
עם היות ש
|
| since
|
לפי ש
|
| since
|
אחרי, אחר ש
|
| as if
|
כאלו, הוא כאלו
|
| if
|
אם, ואם, שאם
|
| whether… or
|
בין אם... בין אם, בין אם... או
|
|
|
אם... אז
|
|
|
או ... או
|
|
|
אם... או
|
|
|
אם ... אם, אם... ואם
|
| even though
|
ואם
|
| lest
|
פן
|
| Scripture and Other Sources
|
|
| living soul [Genesis 2, 7]
|
נפש חיה
|
| going up and down [Genesis 28, 12]
|
זה עולה וזה יוריד
|
| soul has longed for [Genesis 34, 8]
|
נפשך חשקה ב, חשקה נפשם
|
| of beautiful form, and fair to look upon [Genesis 39, 6]
|
יפה תאר ונחמד מראה
|
| when angry [Genesis 49, 6]
|
באפם
|
| with their will they hamstrung a bull [Genesis 49, 6]
|
וברצונם יעקרו שור
|
| gave them a rule [Exodus 15, 25]
|
ישימו חוק
|
| his hands were in faith [Exodus 17, 12]
|
והיו ידיו אמונה
|
| he has sinned and is guilty [Leviticus 5, 23]
|
יחטא ואשם
|
| lie down, and none shall make you afraid [Leviticus 26, 6]
|
זה ישכיב וזה יחריד
|
| He shall not alter it, nor change it [Leviticus 27, 10]
|
לבל יחליף וימיר
|
| Are there few or many [Numbers 13, 18]
|
אם מעטים ואם רבים
|
| remained alive of those men [Numbers 14, 38]
|
מן האנשים חיו
|
| not of my own devising [Numbers 16, 28]
|
כי לא מלבי
|
| our soul loathe [Numbers 21 5]
|
קצה נפשם ב
|
| no way to turn either to the right or to the left [Numbers 22, 26]
|
ימין ושמאל אין לנטות
|
| between your eyes [Deuteronomy 6, 8]
|
בין עיניך
|
| sufficient for his needs, which he is lacking [Deuteronomy 15, 8]
|
מחסורך אשר יחסר לך
|
| sufficient for his need [Deuteronomy 15, 8]
|
די מחסורו, די מחסורנו, די מחסורינו
|
| birthright entitlement [Deuteronomy 21, 17]
|
כמשפט הבכורה
|
| shall be helpless [Deuteronomy 28, 32]
|
אין לאל ידו
|
| whose heart turns away [Deuteronomy 29, 17]
|
אשר לבו פונה
|
| to keep His commandments and His statutes and His ordinances [Deuteronomy 30, 16]
|
מחזיק במצותיו ואל משפטיו וחקותיו
|
| crooked and twisted [Deuteronomy 32, 5]
|
עקש ופתלתול
|
| controlled or strengthened [Deuteronomy 32, 36]
|
עצורה ועזובה
|
| the rock in which they trusted [Deuteronomy 32, 37]
|
צור בו חסיו
|
| The dwelling-place of God [Deuteronomy 33, 27]
|
לאלוהי מעונה
|
| there stood not a man against them [Joshua 21, 42]
|
ולא יעמוד איש בפניהן
|
| The wisest of her princesses answer her [Judges 5, 29]
|
חוכמות שרותיה תענינה
|
| whosoever is fearful and trembling [Judges 7, 3]
|
ירא וחרד
|
| the love of his soul [Samuel I 20, 17]
|
אהבת נפש
|
| they quench my coal [Samuel II 14, 7]
|
ומכבים אש גחלתי
|
| beans and lentils [Samuel II 17, 28]
|
פולי' ועדשים
|
| I have kept the ways of the Lord [Samuel II 22, 22]
|
שומר דרכי אל
|
| go here or there [Kings I, 2, 42]
|
אנה ואנה
|
| as a reed is shaken in the water [Kings I 14, 15]
|
כאשר בתוך המים ינוד הקנה
|
| hopping between two ideas [Kings I 18, 21]
|
על שתי הסעיפים פוצח [פוסח]
|
| as a lodge in a garden of cucumbers [Isaiah 1, 8]
|
וכמקשה המלונה
|
| to increase to government [Isaiah 9, 6]
|
ארבה המשרה
|
| as one who gathers ears of grain [Isaiah 17,5]
|
כמקלט שבלים
|
| berries at the top of the uppermost bough [Isaiah 17, 6]
|
גרגרים מראש אמיר
|
| two or three berries [Isaiah 17, 6]
|
ב' ג' גרגרים
|
| thrust in a sure place [Isaiah 22, 25]
|
תקוע במקום נאמן
|
| as with the buyer, so with the seller [Isaiah 24, 2]
|
כמוכרים כקונים
|
| fierce people [Isaiah 33, 19]
|
עם נועז
|
| tent that shall not fall, whose pegs shall never be moved [Isaiah 33, 20]
|
אהל בל יצען בל יסע יתדותיו
|
| by them, they shall live, and altogether therein is the life of my spirit [Isaiah 38, 16]
|
עליהם יחיו ולכל בהם חיי רוח
|
| Since thou art precious in My eyes and honorable and I loved thee [Isaiah 43, 4]
|
מאשר יקרת בעיני נכבדת ואני אהבתיך
|
| Let them present their witnesses, and they shall be deemed just [Isaiah 43, 9]
|
יתנו עידיהם ואותי יצדיקו
|
| let them hear, and say "it is true" [Isaiah 43, 9]
|
ישמיעו ויאמרו אמת
|
| I am bereaved and solitary, exiled and rejected [Isaiah 49, 21]
|
סורה וגזלה גלמודה ושכולה
|
| ear to hear according to the teachings [Isaiah 50, 4]
|
אזן לשמוע כלימודים
|
| justify the righteous [Isaiah 53, 11]
|
צדק תצדיק
|
| with transgressors he was counted [Isaiah 53, 12]
|
ואת פושעים לא מנה
|
| choose what I desire [Isaiah 56, 4]
|
בחרו באשר חפצו
|
| remove the obstacles [Isaiah 57, 14]
|
להרים מכשול
|
| foolish, they know Me not [Jeremiah 4, 22]
|
הסכלים אשר לא ידעו
|
| How do you say, "We are wise" [Jeremiah 8, 8]
|
ואם כה יאמרו חכמים
|
| with a pen of iron, and with the point of a diamond [Jeremiah 17, 1]
|
בלוח ברזל בצפורן שמיר
|
| the near and the far [Jeremiah 25, 26]
|
אם קרוב ואם רחוק
|
| there is none that care for her [Jeremiah 30, 17]
|
דורש אין לה
|
| the right of redemption [Jeremiah 32, 7]
|
משפט הגאולה
|
| become a derision [Jeremiah 48, 39]
|
יהיה להם לשחוק
|
| each one would go [Ezekiel 1, 9/12]
|
ילכו איש אל
|
| and shall be as though they had not been [Obadiah 1, 16]
|
והיו כלא היו
|
| his soul is not upright [Habakkuk 2, 4]
|
לא ישרה נפשך
|
| as the apple of the eye [Psalms 17, 8]
|
בבבת עין ואישון
|
| they open their lips, they shake their head [Psalms 22, 8]
|
יניע בראש ובשפה יפטיר
|
| despised by the people [Psalms 22, 7]
|
בזוי עם
|
| The Lord helped them [Psalms 37, 40]
|
יעזרם אלהים
|
| their health is sound [Psalms 73, 4]
|
ובריא אולם
|
| He humbles this one and elevates that one [Psalms 75, 8]
|
זה ישפיל וזה ירים
|
| after the stubbornness of their heart, they might walk in their own counsels [Psalms 81, 13]
|
ועריהן יגזור לבם בשרירות
|
| the work of our hands establish it [Psalms 90, 17]
|
ומעשה ידיהו כוננה
|
| their help and their shield [Psalms 115, 9]
|
עזרם ומגינם
|
| laud Him, all peoples [Psalms 117, 1]
|
ישבחוהו לאומים
|
| thousands and ten thousands [Psalms 144, 13]
|
מאליפות מרובבות
|
| his hope is in the Lord [Psalms 146 5]
|
ואשר על יי שברו
|
| His wisdom is beyond reckoning [Psalms 147, 5]
|
ובתבונתם אין מספר
|
| When it is still in its greenness, it will not be plucked [Job 8, 12]
|
לא נקטף עודנו באבו
|
| the tents prosper [Job 12, 6]
|
אהלים ישליו
|
| hint [Job 15, 12]
|
רזום ירמזון
|
| breach upon breach [Job 16, 14]
|
פרץ על פני פרץ
|
| For the years that are few will come [Job 16, 22]
|
שנות מספר יאתיו
|
| When his desire has been filled sufficiently [Job 20, 22]
|
למלאת ספקו
|
| is hidden from the eyes of all living [Job 28, 21]
|
נעלמה מעיני כל חי
|
| who is a teacher like Him [Job, 36, 22]
|
ומי כמוהו מונה
|
| bars and doors [Job 38, 10]
|
בריח ודלתים
|
| He imparted to her understanding [Job 39, 17]
|
וחלק לו בבינה
|
| Its ways are ways of pleasantness [Proverbs 3, 17]
|
דרכיה דרכי נועם
|
| those who hold it fast are happy [Proverbs 3, 18]
|
ותומכם מאושר
|
| He winks with his eyes, scraps with his feet and points with his fingers [Proverbs 6, 13]
|
קורץ בעיניו מולל ברגליו מורה באצבעותיו
|
| of great understanding, but he who is quick-tempered [Proverbs 14, 29]
|
מקוצר רוח ותבונה
|
| a high wall [Proverbs 18, 11]
|
חומה נשגבה
|
| trustworthy man [Proverbs 28, 20]
|
איש אמונה
|
| removes falsehood and the lying word [Proverbs 30, 8]
|
מרחקת שוא ודבר כזב
|
| Many women have done valiantly [Proverbs 31, 29]
|
רבות בנות עשו חיל
|
| built as a model [Song of Songs 4, 4]
|
בנוי לתלפיות
|
| honey and milk are under thy tongue [Song of Songs 4, 11]
|
תחת לשונה דבש וחלב
|
| That which is crooked cannot be straightened and that which is missing [Ecclesiastes 1, 15]
|
מעוות לא תוכל לתקן וחסרון
|
| increase vanity [Ecclesiastes 6, 11]
|
הבל מרבים
|
| For it is not out of wisdom that you have asked concerning this [Ecclesiastes 7, 10]
|
כי לא מחכמה שאל על זאת
|
| for God made man straight, but they sought many intrigues [Ecclesiastes 7, 29]
|
והאלהים עשה אותם ישר והמה בקשו חשבונות רבים
|
| advantage to one who has a tongue [Ecclesiastes 10, 11]
|
יתרון לבעל הלשון
|
| which will succeed [Ecclesiastes 11, 6]
|
אי זה יכשר
|
| childhood and youth [Ecclesiastes 11, 10]
|
ילדות ושחרות
|
| listened and sought out [Ecclesiastes 12, 9]
|
אזון וחקור
|
| knowledge and understanding [Daniel 1, 17]
|
במדע ובהשכל
|
| when the transgressors have been destroyed [Daniel 8, 23]
|
להיתם פשע
|
| to purify, and whiten [Daniel 11, 35]
|
יתברר ויתלבן, מבררים ומלבנים
|
| weakened the hands [Ezra 4, 4]
|
מרפים ידי
|
| Kohen who raises his hands [Mishnah, Berakhot 5:4]
|
כהן הנושא כפיו
|
| regard himself [Mishnah, Pesachim 10]
|
ובראות עצמו
|
| understand foreign languages, in that foreign language [Mishnah, Megillah 2]
|
ללעוזות בלעז
|
| has not seen the luminaries in his life [Mishnah, Megillah 4]
|
ומימיו לא ראה מאורות
|
| build him a house [Mishnah, Bava Metzia 8:9]
|
להעמיד הבית
|
| the time has come [Mishnah, Tamid 1]
|
הגיע עת
|
| a single handful does not satisfy a lion [Talmud Bavli, Berakhot, 3, 2]
|
אין הקומץ משביע את הארי
|
| True and Trustworthy [Talmud, Berakhot 12a, 23]
|
אמת ואמונה
|
| these and those agree [Talmud, Berakhot 36a]
|
אלו ואלו מודים
|
| do not accept authority [Talmud, Berakhot 48a]
|
בלתי מקבלים מרות
|
| that which is earlier is earlier, and that which is later is later [Talmud, Pesachim 6b]
|
להקדים את המוקדם ולאחר את המאוחר
|
| the work of Heaven [Talmud, taanit 23a:3]
|
למלאכת השמים
|
| for the sake of Heaven [Talmud, Taanit 24a]
|
לשום שמים
|
| chops down the saplings [Talmud, Chagigah 15a]
|
מקצץ בנטיעות
|
| standing that includes no reverence [Talmud, Kiddushin 32b]
|
קימה שאין בה הדור
|
| to include Torah scholars [Talmud, Kiddushin 57a]
|
את לרבות תלמידי חכמים
|
| imparted flavor derived from imparted flavor [Talmud, Chulin 111b]
|
בר נותן טעם
|
| thanking and praising [Talmud, Niddah 31a]
|
מודה ומשבח
|
| to prohibit or to permit [Jerusalem Talmud, Ketubot 11a]
|
פעם לאסור ופעם להתיר
|
| even though there is no explicit proof for this matter [Tosefta, Berakhot 1]
|
ואם אין ראיה לדבר זכר לדבר
|
| her daughter and her sister [Tosefta, Yevamot 4, 5]
|
בתה ואחותה
|
| house be wide open [Pirkei Avot 1]
|
בית פתוח לרוחה
|
| Some ascended and some descended [Pirke de Rabbi Eliezer 35]
|
אלו יורדים ואלו עולים
|
| Love upsets the natural order [Bereishit Rabbah 55]
|
אהבה מקלקלת את השורה
|
| finger joints [Bamidbar Rabbah 11]
|
וקשרי אצבעות
|
| as a pupil before his master [Bamidbar Rabbah 20]
|
כתלמיד לפני רבו
|
| vessels of belief [Devarim Rabbah 8]
|
כלי אומנותה
|
| tithing by guesswork [Pirkei Avot 1:16]
|
לעשר אומדות
|
| to clarify the uncertain [Sefer ha-Mitzvot l'Rasag, Positive Commandments 97, 15]
|
לברר את המסופק
|
| Whosoever wants it may come [Mishneh Torah, Torah Study 3]
|
ויבא מי שירצה
|
| says: no, when it is no, and yea, when it is yea [Mishnah Torah, Human Dispositions 5]
|
אומרת על הן הן ועל לאו לאו
|
| the pillars having been erected [Mishnah Torah, Tefillin Mezuzah and Torah Scroll 6]
|
ולהעמיד עמודים
|
| change their appointed charge [Mishneh Torah, Blessing 10]
|
וישנו את תפקידם
|
| to build foundations [Mishneh Torah, Sabbath 1, 18]
|
לבנות יסודות
|
| the law requires that [Mishneh Torah, Divorce 2]
|
היה הדין נותן ש
|
| all kinds of seeds [Mishneh Torah, Diverse Species 1, 8]
|
וכל מיני זרעונים
|
| known and heralded [Mishneh Torah, Repentance 4]
|
ידועים ומפורסמים
|
| drachmas or zuzim [Maimonides on Mishnah Peah 8:5]
|
זוזים ודרכמונים
|
| defective comprehension [Maimonides, Guide for the Perplexed, 1, 36, 5]
|
קוצר השגתי
|
| necessary or impossible [Maimonides, Guide for the Perplexed, 2, 14, 5]
|
ולמחוייב ולנמנע
|
| pin upon which everything hangs [Maimonides, Guide for the Perplexed, 3, intro. 4]
|
יתד שהכל תלוי בו
|
| that relation between you and Him [Maimonides, Guide for the Perplexed, 3, 51, 6]
|
היחס אשר בינו לבינה
|
| set us apart from those who go astray [Siddur Sefarad, Ashrei]
|
הבדילו מן התועים
|
| delightful sapling [Siddur, Purim, Shabbat Zachor 56]
|
נטע נעמן
|
| How many degrees of good [Pesach Haggadah, Magid, Dayenu]
|
כמה מעלות טובות
|
| to render halachic decisions [Sefer ha-Midot, Codifiers of the Law]
|
ולהורות הוראות
|
| to show strength [Ibn Ezra on Genesis 10:8]
|
להראות גבורות
|
| lying in an out of the way corner [Rabbeinu Bahya, Devarim 33:4]
|
מונח בקרן זוית
|
| ruling, self-glorification [Duties of the Heart, Sixth Treatise on Submission 10]
|
השררה והגדולה
|
| left no manner of doubt [Sefer Kuzari 2]
|
והניח את הספק
|
| with the help of the One who dwells in the [heavenly] abodes [Ralbag on Chronicles II 36:22]
|
בעזרת שוכן מעונים
|
| It is whole and complete
|
תם ונשלם
|
| Glory to God, the Creator of the world
|
ת"ל בורא עולם
|
| Knower of the truth
|
יודע האמת
|
| Knower of the hidden
|
יודע הנסתרות
|
| prayer leader
|
ש'צ'
|
|
|
ב"ה י"ת
|
|
|
יעקב בן החכם ר' יצחק קנפנטון, ר' יעקב קפנתון ז"ל
|
|
|
ר' יואל ן' דאוד
|
|
|
אוקלידס
|



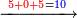
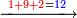

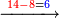
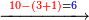
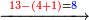
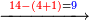
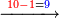
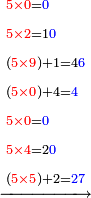
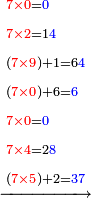
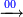
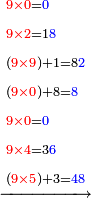
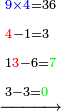
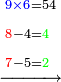
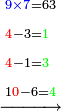
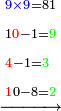
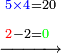
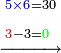
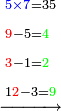
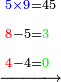
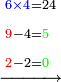
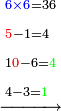
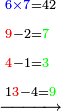
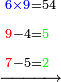
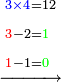
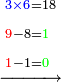
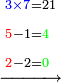
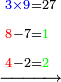
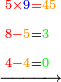
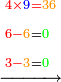
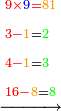
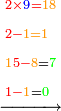
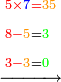
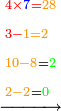
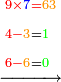
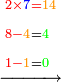
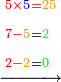
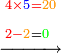
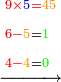
 ]
]
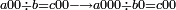
 ] and the 7 [is called] "second" [
] and the 7 [is called] "second" [ ], since the 5 is related to 7.
], since the 5 is related to 7.
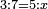
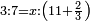
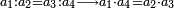
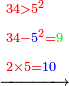
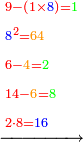
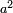 in the multiple of a product of tens by itself
in the multiple of a product of tens by itself 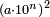 is always an odd number (2n-1)
is always an odd number (2n-1)
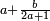 ] when the remainder is the same as the [approximate] root or greater, improves the approximation, as I explained, but if one repeats the procedure [
] when the remainder is the same as the [approximate] root or greater, improves the approximation, as I explained, but if one repeats the procedure [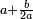 ], one does not need this addition, because by repeating the procedure one approaches [the truth] very closely even without adding 1. It is better not to add it, so as to maintain a standard form of procedure and prevent confusion.
], one does not need this addition, because by repeating the procedure one approaches [the truth] very closely even without adding 1. It is better not to add it, so as to maintain a standard form of procedure and prevent confusion.
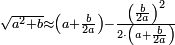
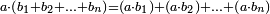
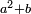 is the square of the subtrahend
is the square of the subtrahend
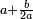 instead of the previous approximation
instead of the previous approximation 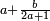 , even if b≥a, in order to avoid confusion
, even if b≥a, in order to avoid confusion
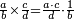
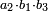 ]
]
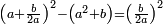
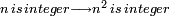
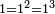
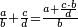
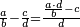
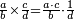
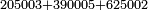
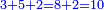
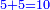
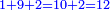
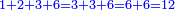
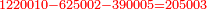
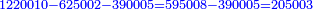
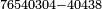

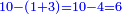
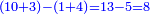
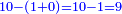
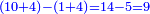
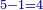
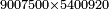

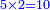
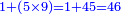
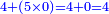
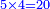
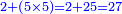

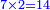
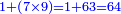
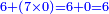
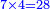
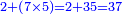


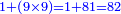
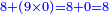
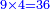
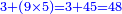
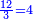
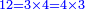
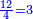
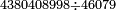
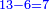

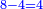
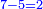
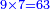

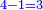
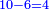

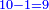
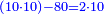

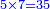
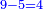
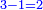

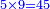
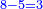
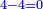
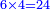
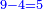

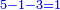
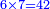

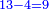
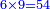
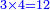

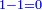
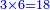

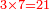
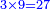



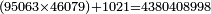
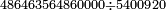
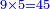


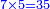
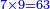
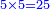
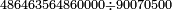
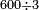


![\scriptstyle2a+10b+\left[100\sdot\left(2c-1\right)\right]](/mediawiki/images/math/8/b/e/8bee57b5ad3455a444ccbebe707bbcec.png)
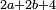
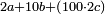
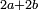
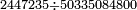
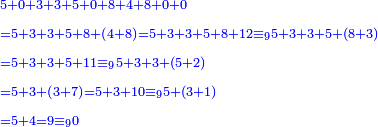
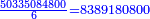

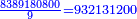
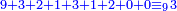

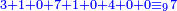
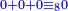
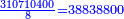
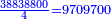

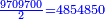
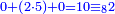
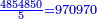
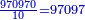
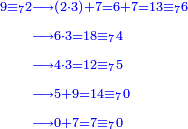
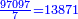
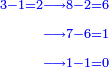
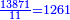
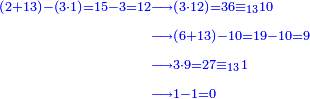
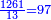
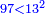

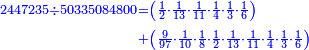
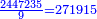
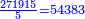
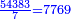
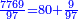
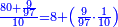
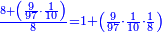
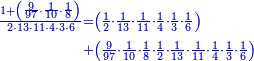
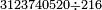
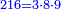
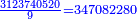
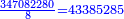
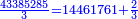
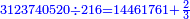

![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left(14461761+\frac{2}{3}\right)\sdot3\sdot8\sdot9&\scriptstyle=\left[\left(14461761\sdot3\right)+2\right]\sdot8\sdot9\\&\scriptstyle=\left(43385283+2\right)\sdot8\sdot9\\&\scriptstyle=43385285\sdot8\sdot9\\&\scriptstyle=347082280\sdot9=3123740520\\\end{align}}}](/mediawiki/images/math/a/7/b/a7bae6e6f9c8c1a40897743e0bc1e090.png)
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\left[\left(\frac{1}{2}\sdot\frac{1}{13}\sdot\frac{1}{11}\sdot\frac{1}{4}\sdot\frac{1}{3}\sdot\frac{1}{6}\right)+\left(\frac{9}{97}\sdot\frac{1}{10}\sdot\frac{1}{8}\sdot\frac{1}{2}\sdot\frac{1}{13}\sdot\frac{1}{11}\sdot\frac{1}{4}\sdot\frac{1}{3}\sdot\frac{1}{6}\right)\right]\sdot50335084800\\&\scriptstyle=\left[\left(1\sdot8\sdot10\sdot97\right)+9\right]\sdot7\sdot5\sdot9\\&\scriptstyle=\left[\left(8\sdot10\sdot97\right)+9\right]\sdot7\sdot5\sdot9\\&\scriptstyle=\left[\left(80\sdot97\right)+9\right]\sdot7\sdot5\sdot9\\&\scriptstyle=\left(7760+9\right)\sdot7\sdot5\sdot9\\&\scriptstyle=7769\sdot7\sdot5\sdot9\\&\scriptstyle=54383\sdot5\sdot9\\&\scriptstyle=271915\sdot9=2447235\\\end{align}}}](/mediawiki/images/math/a/d/b/adb9721e698eac41a3204cb448b3301f.png)
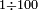
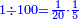
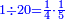
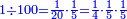
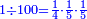
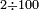
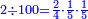
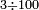
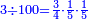
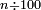
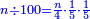
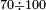
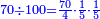
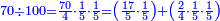
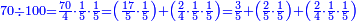

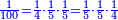
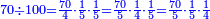
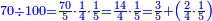
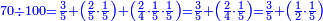
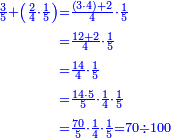
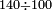
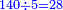
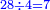
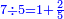
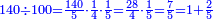
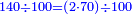
![\scriptstyle{\color{blue}{1+\frac{2}{5}=\frac{7}{5}=2\sdot\left[\frac{3}{5}+\left(\frac{2}{4}\sdot\frac{1}{5}\right)\right]=2\sdot\left[\frac{3}{5}+\left(\frac{1}{2}\sdot\frac{1}{5}\right)\right]}}](/mediawiki/images/math/3/6/e/36eeba3351620eebf8c50f917db3a94e.png)
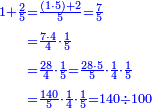
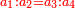

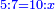
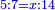
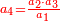
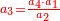
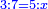
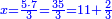
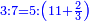
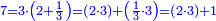
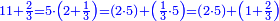
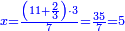
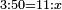
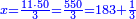
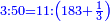
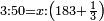
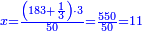
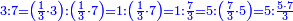
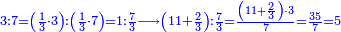
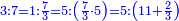
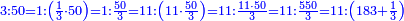
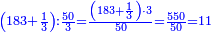
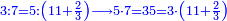
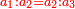

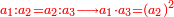
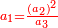
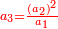
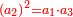


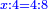
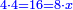
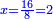
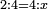
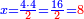
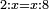
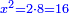
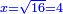
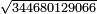
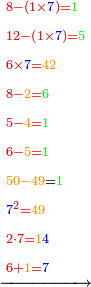

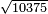
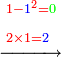
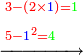

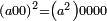
![\scriptstyle\left(ab0\right)^2=\left(a^2\right)0000+\left[2\sdot\left[\left(a\sdot b\right)000\right]\right]+\left(b^2\right)00](/mediawiki/images/math/1/e/9/1e9176dee0a4f90f16fd369b7e96c83b.png)
![\scriptstyle\left(a0b0\right)^2=\left(a^2\right)000000+\left[2\sdot\left[\left(a\sdot b\right)00000\right]\right]+\left(b^2\right)00](/mediawiki/images/math/d/5/0/d50616d9b65871ed420ee55dfd27d175.png)
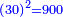
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left(30+5\right)^2&\scriptstyle=\left(35\right)^2=35\sdot35\\&\scriptstyle=\left(30\sdot30\right)+\left(5\sdot30\right)+\left(30\sdot5\right)+\left(5\sdot5\right)\\&\scriptstyle=\left(30\right)^2+\left[\left[2\sdot\left(5\sdot30\right)+5^2\right]\right]\\\end{align}}}](/mediawiki/images/math/f/8/4/f84beea6c2e936cfe6ad5b09eb21f3a6.png)
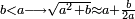
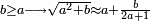

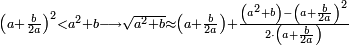
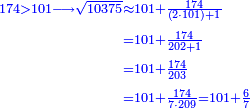
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle10375-\left(101+\frac{6}{7}\right)^2&\scriptstyle=10375-\left[10374+\frac{6}{7}+\left(\frac{1}{7}\sdot\frac{1}{7}\right)\right]\\&\scriptstyle=\frac{6}{7}\sdot\frac{1}{7}\\&\scriptstyle\longrightarrow\left(101+\frac{6}{7}\right)^2<10375\\\end{align}}}](/mediawiki/images/math/3/4/6/346cf9ca90fc49ad270cfd4bfa318118.png)

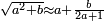
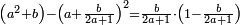
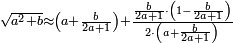
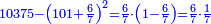
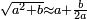
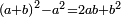
![\scriptstyle\left(a+\frac{b}{2a}\right)^2\approx a^2+\left[2\sdot\left(a\sdot\frac{b}{2a}\right)\right]=a^2+b](/mediawiki/images/math/b/5/5/b55de2a98bec366440918e6f0fb41b25.png)
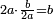
![\scriptstyle\left(a+\frac{b}{2a}\right)^2-\left[\left(a+\frac{b}{2a}\right)-\frac{\left(\frac{b}{2a}\right)^2}{2\sdot\left(a+\frac{b}{2a}\right)}\right]^2=\frac{\left(\frac{b}{2a}\right)^2}{2\sdot\left(a+\frac{b}{2a}\right)}\sdot\left[\left[2\sdot\left(a+\frac{b}{2a}\right)\right]-\frac{\left(\frac{b}{2a}\right)^2}{2\sdot\left(a+\frac{b}{2a}\right)}\right]](/mediawiki/images/math/9/2/0/9209b3c0a16707778f4b1641468bfe6e.png)
![\scriptstyle\frac{\left(\frac{b}{2a}\right)^2}{2\sdot\left(a+\frac{b}{2a}\right)}=\frac{\left(\frac{b}{2a}\right)^2}{\left[2\sdot\left[\left(a+\frac{b}{2a}\right)-\frac{\left(\frac{b}{2a}\right)^2}{2\sdot\left(a+\frac{b}{2a}\right)}\right]\right]+\left[2\sdot\frac{\left(\frac{b}{2a}\right)^2}{2\sdot\left(a+\frac{b}{2a}\right)}\right]}](/mediawiki/images/math/1/1/f/11f2b1739c847db8c1b239929b98c221.png)
![\scriptstyle\left[\left(a+\frac{b}{2a}\right)-\frac{\left(\frac{b}{2a}\right)^2}{2\sdot\left(a+\frac{b}{2a}\right)}\right]^2-\left(a^2+b\right)=\left[\frac{\left(\frac{b}{2a}\right)^2}{2\sdot\left(a+\frac{b}{2a}\right)}\right]^2](/mediawiki/images/math/d/c/b/dcbaac2fd64464c42636e8a0f325ec94.png)
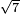
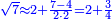
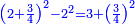
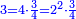
![\scriptstyle{\color{blue}{\left(2+\frac{3}{4}\right)^2-7=\left[7+\left(\frac{3}{4}\right)^2\right]-7=\left(\frac{3}{4}\right)^2=\frac{9}{4}\sdot\frac{1}{4}=\frac{2}{4}+\left(\frac{1}{4}\sdot\frac{1}{4}\right)}}](/mediawiki/images/math/e/e/4/ee4b6356d625ccfa4fb96cdad3e3dbb2.png)
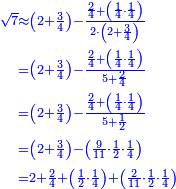
![\scriptstyle{\color{blue}{\left(2+\frac{3}{4}\right)^2-\left[2+\frac{2}{4}+\left(\frac{1}{2}\sdot\frac{1}{4}\right)+\left(\frac{2}{11}\sdot\frac{1}{2}\sdot\frac{1}{4}\right)\right]^2=\left[\left(\frac{9}{11}\sdot\frac{1}{2}\sdot\frac{1}{4}\right)\sdot\left[2\sdot\left(2+\frac{3}{4}\right)\right]\right]-\left(\frac{9}{11}\sdot\frac{1}{2}\sdot\frac{1}{4}\right)^2}}](/mediawiki/images/math/d/1/c/d1c9c0ef367e01eee2593758313a172f.png)
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\left(\frac{9}{11}\sdot\frac{1}{2}\sdot\frac{1}{4}\right)\sdot\left[2\sdot\left(2+\frac{3}{4}\right)\right]\\&\scriptstyle=\left(\frac{9}{11}\sdot\frac{1}{2}\sdot\frac{1}{4}\right)\sdot\left(5+\frac{1}{2}\right)\\&\scriptstyle=\left(\frac{9}{11}\sdot\frac{1}{2}\sdot\frac{1}{4}\right)\sdot\left[\left[2\sdot\left[2+\frac{2}{4}+\left(\frac{1}{2}\sdot\frac{1}{4}\right)\left(\frac{2}{11}\sdot\frac{1}{2}\sdot\frac{1}{4}\right)\right]\right]+\left[2\sdot\left(\frac{9}{11}\sdot\frac{1}{2}\sdot\frac{1}{4}\right)\right]\right]\\&\scriptstyle=\frac{2}{4}+\left(\frac{1}{4}\sdot\frac{1}{4}\right)\\\end{align}}}](/mediawiki/images/math/f/5/1/f5144add645e7e66dfc8f0ddf4f6c98f.png)
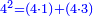
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\left(\frac{9}{11}\sdot\frac{1}{2}\sdot\frac{1}{4}\right)\sdot\left[2\sdot\left(2+\frac{3}{4}\right)\right]\\&\scriptstyle=\left(\frac{9}{11}\sdot\frac{1}{2}\sdot\frac{1}{4}\right)\sdot\left[2\sdot\left[\left[2+\frac{2}{4}+\left(\frac{1}{2}\sdot\frac{1}{4}\right)\left(\frac{2}{11}\sdot\frac{1}{2}\sdot\frac{1}{4}\right)\right]\right]+\left(\frac{9}{11}\sdot\frac{1}{2}\sdot\frac{1}{4}\right)\right]\\\end{align}}}](/mediawiki/images/math/3/2/0/320a8a4cab2af8d8e5ae350b51f9b562.png)
![\scriptstyle\left(a+\frac{b}{2a}\right)^2-\left(a^2+b\right)=\left(\frac{b}{2a}\right)^2=\frac{\left(\frac{b}{2a}\right)^2}{2\sdot\left(a+\frac{b}{2a}\right)}\sdot\left[2\sdot\left(a+\frac{b}{2a}\right)\right]](/mediawiki/images/math/8/2/f/82f5c2dca7525d3f86ef921b8c06665a.png)
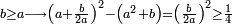
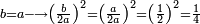
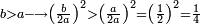
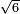
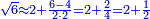
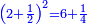
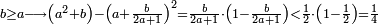
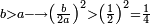
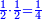
![\scriptstyle\left(1-\frac{n}{m}\right)>\frac{n}{m}\longrightarrow\frac{1}{4}-\left[\frac{n}{m}\sdot\left(1-\frac{n}{m}\right)\right]=\left(\frac{1}{2}-\frac{n}{m}\right)^2](/mediawiki/images/math/3/4/7/3471d2335b0094a14c822c09e6ea93f4.png)
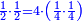
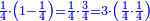
![\scriptstyle{\color{blue}{\left(\frac{1}{2}\sdot\frac{1}{2}\right)-\left[\frac{1}{4}\sdot\left(1-\frac{1}{4}\right)\right]=\frac{1}{4}\sdot\frac{1}{4}}}](/mediawiki/images/math/e/5/6/e56017f8b5d12e1a06c185b2e08165c8.png)
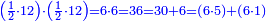
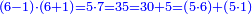
![\scriptstyle{\color{blue}{\left[\left(\frac{1}{2}\sdot12\right)\sdot\left(\frac{1}{2}\sdot12\right)\right]-\left[3\sdot\left(12-3\right)\right]=\left(6\sdot6\right)-\left(3\sdot9\right)=36-27=9=3^2}}](/mediawiki/images/math/d/c/8/dc8d1bb404f25dfbdd1aac97a111a3f7.png)
![\scriptstyle{\color{blue}{\left(\frac{1}{2}\sdot12\right)\sdot\left(\frac{1}{2}\sdot12\right)=6\sdot6=\left(6\sdot3\right)+\left(6\sdot3\right)=\left[2\sdot\left(3\sdot3\right)\right]+\left[2\sdot\left(3\sdot3\right)\right]}}](/mediawiki/images/math/7/7/3/773f982d49f1f7eabb2749d468f5842d.png)
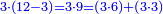
![\scriptstyle\frac{1}{4}n^2-\left[m\sdot\left(n-m\right)\right]=\left[\left(\frac{1}{2}n\right)\sdot\left(\frac{1}{2}n\right)\right]-\left[m\sdot\left(n-m\right)\right]=\left[\left(\frac{1}{2}n\right)-m\right]^2](/mediawiki/images/math/d/f/f/dff4f9ed570e017e0796e90ef9835089.png)
![\scriptstyle{\color{blue}{\left[\left(\frac{1}{2}\sdot12\right)\sdot\left(\frac{1}{2}\sdot12\right)\right]-\left[3\sdot\left(12-3\right)\right]=3^2=\left(\frac{1}{4}\sdot12\right)^2}}](/mediawiki/images/math/6/2/e/62e5daa2fbcb3de5524af1ce6bab01ba.png)
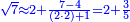
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle7-\left(2+\frac{3}{5}\right)^2&\scriptstyle=7-\left[6+\frac{3}{5}+\left(\frac{4}{5}\sdot\frac{1}{5}\right)\right]\\&\scriptstyle=\frac{1}{5}+\left(\frac{1}{5}\sdot\frac{1}{5}\right)\\&\scriptstyle=\frac{6}{5}\sdot\frac{1}{5}\\&\scriptstyle=\frac{3}{5}\sdot\frac{2}{5}\\&\scriptstyle=\frac{3}{5}\sdot\left(1-\frac{3}{5}\right)\\\end{align}}}](/mediawiki/images/math/4/f/e/4fe5a34ebab76fb7f26f2e84e3738899.png)
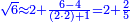
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle6-\left(2+\frac{2}{5}\right)^2&\scriptstyle=6-\left[5+\frac{3}{5}+\left(\frac{4}{5}\sdot\frac{1}{5}\right)\right]\\&\scriptstyle=\frac{1}{5}+\left(\frac{1}{5}\sdot\frac{1}{5}\right)\\&\scriptstyle=\frac{6}{5}\sdot\frac{1}{5}\\&\scriptstyle=\frac{2}{5}\sdot\frac{3}{5}\\&\scriptstyle=\frac{2}{5}\sdot\left(1-\frac{2}{5}\right)\\\end{align}}}](/mediawiki/images/math/6/c/d/6cdaff275080e1af87d6ff164bb216f1.png)
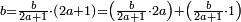
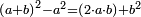
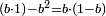
![\scriptstyle{\color{blue}{\left(\frac{1}{3}\sdot1\right)=\left(\frac{1}{3}\sdot\frac{1}{3}\right)+\left(\frac{2}{3}\sdot\frac{1}{3}\right)=\left(\frac{1}{3}\sdot\frac{1}{3}\right)+\left[\frac{1}{3}\sdot\left(1-\frac{1}{3}\right)\right]}}](/mediawiki/images/math/a/9/a/a9abd966f023033e08f139de78734678.png)
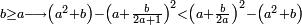
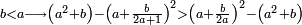
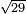
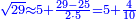
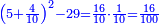
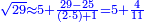
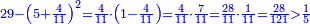
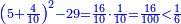
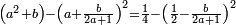
![\scriptstyle\left(a+\frac{b}{2a}\right)^2-\left(a^2+b\right)=\frac{1}{4}-\left[\left(\frac{1}{2}-\frac{b}{2a}\right)^2+\left[2\sdot\frac{b}{2a}\sdot\left(\frac{1}{2}-\frac{b}{2a}\right)\right]\right]](/mediawiki/images/math/6/0/1/60162fb94c8df6119d9a732b6cf94953.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle29-\left(5+\frac{4}{11}\right)^2&\scriptstyle=\frac{4}{11}\sdot\frac{7}{11}\\&\scriptstyle=\frac{1}{4}-\frac{2+\frac{1}{4}}{11^2}\\&\scriptstyle=\frac{1}{4}-\left[\left(1+\frac{1}{2}\right)\sdot\frac{1}{11}\right]^2\\&\scriptstyle=\frac{1}{4}-\left(\frac{1}{2}-\frac{4}{11}\right)^2\\\end{align}}}](/mediawiki/images/math/e/0/7/e07cc09c88a7b076c0cf7996b50938b2.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left(5+\frac{4}{10}\right)^2-29&\scriptstyle=\left(\frac{4}{10}\right)^2\\&\scriptstyle=\frac{16}{100}\\&\scriptstyle=\frac{1}{4}-\frac{9}{100}\\&\scriptstyle=\frac{1}{4}-\left[\left(\frac{1}{2}-\frac{4}{10}\right)^2+\left[2\sdot\frac{4}{10}\sdot\left(\frac{1}{2}-\frac{4}{10}\right)\right]\right]\\\end{align}}}](/mediawiki/images/math/b/2/8/b28812f579e6cbbe14cdbb6454a3fd3d.png)
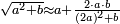
![\scriptstyle\sqrt{a^2+b}\approx\left[a+\frac{2\sdot a\sdot b}{\left(2a\right)^2+b}\right]+\frac{2\sdot\left[a+\frac{2\sdot a\sdot b}{\left(2a\right)^2+b}\right]\sdot\frac{b^3}{\left[\left(2a\right)^2+b\right]^2}}{\left[2\sdot\left[a+\frac{2\sdot a\sdot b}{\left(2a\right)^2+b}\right]\right]^2+\frac{b^3}{\left[\left(2a\right)^2+b\right]^2}}](/mediawiki/images/math/7/2/1/72191ee00d85c68740fcb61a7d024e38.png)
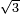
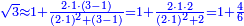
![\scriptstyle{\color{blue}{3-\left(1+\frac{4}{6}\right)^2=\frac{2^3}{\left[\left(2\sdot1\right)^2+2\right]^2}=\frac{8}{6}\sdot\frac{1}{6}}}](/mediawiki/images/math/8/4/0/84003fda2d08d250632a602206672d45.png)
![\scriptstyle{\color{blue}{\sqrt{3}\approx\left(1+\frac{4}{6}\right)+\frac{2\sdot\left(1+\frac{4}{6}\right)\sdot\left(\frac{8}{6}\sdot\frac{1}{6}\right)}{\left[2\sdot\left(1+\frac{4}{6}\right)\right]^2+\left(\frac{8}{6}\sdot\frac{1}{6}\right)}=1+\frac{112}{153}}}](/mediawiki/images/math/b/8/7/b87b5b0f88656891e814164d14c78dc4.png)
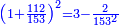
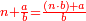
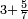
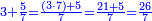
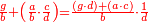
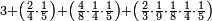
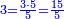
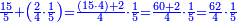
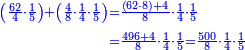
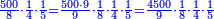
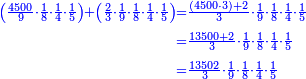
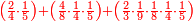
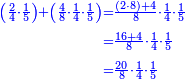
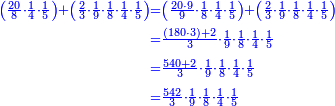
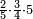
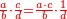


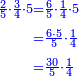
![\scriptstyle\left[\frac{2}{4}+\left(\frac{3}{5}\sdot\frac{1}{4}\right)\right]\sdot\left[\left(\frac{3}{7}\sdot\frac{1}{8}\right)+\left(\frac{4}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\right)\right]\sdot\left(\frac{3}{9}\sdot\frac{1}{10}\right)\sdot4](/mediawiki/images/math/3/8/7/387896d3f82f552dba69fe6e4ba31825.png)
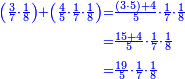
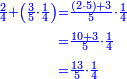
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\left[\frac{2}{4}+\left(\frac{3}{5}\sdot\frac{1}{4}\right)\right]\sdot\left[\left(\frac{3}{7}\sdot\frac{1}{8}\right)+\left(\frac{4}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\right)\right]\sdot\left(\frac{3}{9}\sdot\frac{1}{10}\right)\sdot4\\&\scriptstyle=\left(\frac{13}{5}\sdot\frac{1}{4}\right)\sdot\left(\frac{19}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\right)\sdot\left(\frac{3}{9}\sdot\frac{1}{10}\right)\sdot4\\\end{align}}}](/mediawiki/images/math/5/1/5/515cdf218fb76746a29bffe0fa8b9ca9.png)
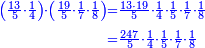
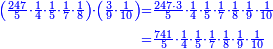
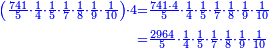
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\left[\frac{2}{4}+\left(\frac{3}{5}\sdot\frac{1}{4}\right)\right]\sdot\left[\left(\frac{3}{7}\sdot\frac{1}{8}\right)+\left(\frac{4}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\right)\right]\sdot\left(\frac{3}{9}\sdot\frac{1}{10}\sdot4\right)\\&\scriptstyle=\frac{2964}{5}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\\&\scriptstyle=\frac{2964}{4}\sdot\frac{1}{5}\sdot\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\\&\scriptstyle=\frac{741}{5}\sdot\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\\&\scriptstyle=\left(\frac{148}{4}\sdot\frac{1}{2}\sdot\frac{1}{7}\sdot\frac{1}{5}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)+\left(\frac{1}{5}\sdot\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)\\&\scriptstyle=\left(\frac{37}{7}\sdot\frac{1}{2}\sdot\frac{1}{5}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)+\left(\frac{1}{5}\sdot\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)\\&\scriptstyle=\left(\frac{5}{5}\sdot\frac{1}{2}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)+\left(\frac{1}{2}\sdot\frac{1}{7}\sdot\frac{1}{5}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)+\left(\frac{1}{5}\sdot\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)\\&\scriptstyle=\left(\frac{1}{2}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)+\left(\frac{2}{7}\sdot\frac{1}{5}\sdot\frac{1}{2}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)+\left(\frac{1}{5}\sdot\frac{1}{4}\sdot\frac{1}{7}\sdot\frac{1}{5}\sdot\frac{1}{2}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)\\\end{align}}}](/mediawiki/images/math/2/b/d/2bd03844fe84eaf9f6b4f6d4c7725be7.png)
![\scriptstyle\left[2+\frac{3}{8}+\left(\frac{2}{4}\sdot\frac{1}{8}\right)\right]\quad\frac{4}{5}\quad\left[\frac{6}{7}+\left(\frac{3}{8}\sdot\frac{1}{7}\right)\right]](/mediawiki/images/math/2/f/5/2f5db2cd7e551020181114628b7f1a51.png)
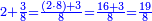
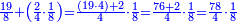
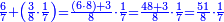
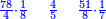
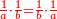
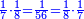

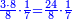
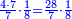
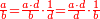
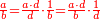
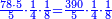
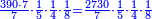
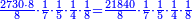
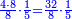
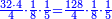
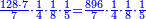
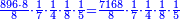
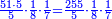
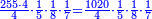
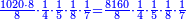
![\scriptstyle\frac{3}{4}\sdot\left[\frac{2}{5}+\left(\frac{3}{4}\sdot\frac{1}{5}\right)\right]\sdot\left[\frac{4}{6}+\left(\frac{1}{3}\sdot\frac{1}{6}\right)\right]](/mediawiki/images/math/3/6/6/36625e7aca77358ba4aba9749ff2d22f.png)
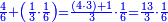
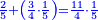
![\scriptstyle{\color{blue}{\frac{3}{4}\sdot\left[\frac{2}{5}+\left(\frac{3}{4}\sdot\frac{1}{5}\right)\right]\sdot\left[\frac{4}{6}+\left(\frac{1}{3}\sdot\frac{1}{6}\right)\right]=\frac{3}{4}\sdot\left(\frac{11}{4}\sdot\frac{1}{5}\right)\sdot\left(\frac{13}{3}\sdot\frac{1}{6}\right)}}](/mediawiki/images/math/2/c/4/2c44639491e6830397006b9f964ce49d.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\frac{3}{4}\sdot\left[\frac{2}{5}+\left(\frac{3}{4}\sdot\frac{1}{5}\right)\right]\sdot\left[\frac{4}{6}+\left(\frac{1}{3}\sdot\frac{1}{6}\right)\right]&\scriptstyle=\frac{3}{4}\sdot\left(\frac{11}{4}\sdot\frac{1}{5}\right)\sdot\left(\frac{13}{3}\sdot\frac{1}{6}\right)\\&\scriptstyle=\frac{3\sdot11\sdot13}{4}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{3}\sdot\frac{1}{6}\\&\scriptstyle=\frac{33\sdot13}{4}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{3}\sdot\frac{1}{6}\\&\scriptstyle=\frac{429}{4}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{3}\sdot\frac{1}{6}\\\end{align}}}](/mediawiki/images/math/e/9/0/e90e6a029b0f349d92e33d74057d39fc.png)
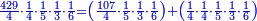
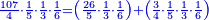
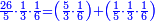
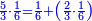
![\scriptstyle{\color{blue}{\frac{3}{4}\sdot\left[\frac{2}{5}+\left(\frac{3}{4}\sdot\frac{1}{5}\right)\right]\sdot\left[\frac{4}{6}+\left(\frac{1}{3}\sdot\frac{1}{6}\right)\right]=\frac{1}{6}+\left(\frac{2}{3}\sdot\frac{1}{6}\right)+\left(\frac{1}{5}\sdot\frac{1}{3}\sdot\frac{1}{6}\right)+\left(\frac{3}{4}\sdot\frac{1}{5}\sdot\frac{1}{3}\sdot\frac{1}{6}\right)+\left(\frac{1}{4}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{3}\sdot\frac{1}{6}\right)}}](/mediawiki/images/math/e/b/b/ebbd0a763e3002706acf0da028cd5659.png)

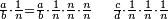
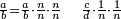

![\scriptstyle\left[2+\frac{3}{8}+\left(\frac{2}{4}\sdot\frac{1}{8}\right)\right]+\frac{4}{5}+\left[\frac{6}{7}+\left(\frac{3}{8}\sdot\frac{1}{7}\right)\right]](/mediawiki/images/math/1/0/f/10fe63879aceb251d84882daff3b8503.png)
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\left[2+\frac{3}{8}+\left(\frac{2}{4}\sdot\frac{1}{8}\right)\right]+\frac{4}{5}+\left[\frac{6}{7}+\left(\frac{3}{8}\sdot\frac{1}{7}\right)\right]\\&\scriptstyle=\left(\frac{21840}{8}\sdot\frac{1}{7}\sdot\frac{1}{5}\sdot\frac{1}{4}\sdot\frac{1}{8}\right)+\left(\frac{7168}{8}\sdot\frac{1}{7}\sdot\frac{1}{4}\sdot\frac{1}{8}\sdot\frac{1}{5}\right)+\left(\frac{8160}{8}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{8}\sdot\frac{1}{7}\right)\\&\scriptstyle=\frac{37168}{8}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{8}\sdot\frac{1}{7}\\\end{align}}}](/mediawiki/images/math/3/f/a/3fabdb3522b40d4fd287ccee0cba4b71.png)
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\left[2+\frac{3}{8}+\left(\frac{2}{4}\sdot\frac{1}{8}\right)\right]+\frac{4}{5}+\left[\frac{6}{7}+\left(\frac{3}{8}\sdot\frac{1}{7}\right)\right]\\&\scriptstyle=\frac{37168}{8}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{8}\sdot\frac{1}{7}\\&\scriptstyle=\frac{4646}{7}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{8}\\&\scriptstyle=\left(\frac{663}{4}\sdot\frac{1}{5}\sdot\frac{1}{8}\right)+\left(\frac{5}{7}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{8}\right)\\&\scriptstyle={\color{red}{\left(\frac{165}{5}\sdot\frac{1}{8}\right)+\left(\frac{3}{4}\sdot\frac{1}{5}\sdot\frac{1}{8}\right)+\left(\frac{5}{7}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{8}\right)}}\\&\scriptstyle=\frac{33}{8}+\left(\frac{3}{4}\sdot\frac{1}{5}\sdot\frac{1}{8}\right)+\left(\frac{5}{7}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{8}\right)\\&\scriptstyle=4+\frac{1}{8}+\left(\frac{3}{4}\sdot\frac{1}{5}\sdot\frac{1}{8}\right)+\left(\frac{5}{7}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{8}\right)\\\end{align}}}](/mediawiki/images/math/c/f/f/cff900155b4478d71bf101689365b48b.png)
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\left[2+\frac{3}{8}+\left(\frac{2}{4}\sdot\frac{1}{8}\right)\right]+\frac{4}{5}+\left[\frac{6}{7}+\left(\frac{3}{8}\sdot\frac{1}{7}\right)\right]\\&\scriptstyle=4+\frac{1}{8}+\left(\frac{3}{4}\sdot\frac{1}{5}\sdot\frac{1}{8}\right)+\left(\frac{5}{7}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{8}\right)\\&\scriptstyle=4+\left(\frac{25}{8}\sdot\frac{1}{5}\sdot\frac{1}{5}\right)+\left(\frac{3}{4}\sdot\frac{1}{8}\sdot\frac{1}{5}\right)+\left(\frac{5}{7}\sdot\frac{1}{4}\sdot\frac{1}{8}\sdot\frac{1}{5}\right)\\\end{align}}}](/mediawiki/images/math/1/9/6/196fa95f6efe1a7855af3737ee476de9.png)
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\left[2+\frac{3}{8}+\left(\frac{2}{4}\sdot\frac{1}{8}\right)\right]+\frac{4}{5}+\left[\frac{6}{7}+\left(\frac{3}{8}\sdot\frac{1}{7}\right)\right]\\&\scriptstyle=\frac{37168}{8}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{8}\sdot\frac{1}{7}\\&\scriptstyle=\frac{37168\sdot9}{8}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\\&\scriptstyle=\frac{334512}{8}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\\&\scriptstyle=\frac{41814}{4}\sdot\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\\&\scriptstyle=\left(\frac{10453}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{2}{4}\sdot\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)\\&\scriptstyle={\color{red}{\left(\frac{2090}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{2}{4}\sdot\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)}}\\&\scriptstyle=\left(\frac{298}{8}\sdot\frac{1}{9}\right)+\left(\frac{4}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{2}{4}\sdot\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)\\&\scriptstyle=\frac{37}{9}+\left(\frac{2}{8}\sdot\frac{1}{9}\right)+\left(\frac{4}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{2}{4}\sdot\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)\\&\scriptstyle=4+\frac{1}{9}+\left(\frac{2}{8}\sdot\frac{1}{9}\right)+\left(\frac{4}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{2}{4}\sdot\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/f/4/f/f4f0b709e2439e0d86aab99b15f87642.png)
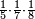
 → multiplying by 5
→ multiplying by 5![\scriptstyle\left(\frac{2}{5}\sdot\frac{2}{9}\sdot2\right)+\left[\left[\frac{1}{8}+\left(\frac{2}{9}\sdot\frac{1}{7}\sdot\frac{1}{8}\right)\right]\sdot\left[\frac{1}{4}+\left(\frac{2}{6}\sdot\frac{1}{4}\right)\right]\right]](/mediawiki/images/math/e/2/5/e2537ec7557a116d21369f6f61831a30.png)
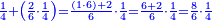
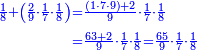
![\scriptstyle{\color{blue}{\left[\frac{1}{8}+\left(\frac{2}{9}\sdot\frac{1}{7}\sdot\frac{1}{8}\right)\right]\sdot\left[\frac{1}{4}+\left(\frac{2}{6}\sdot\frac{1}{4}\right)\right]=\left(\frac{65}{9}\sdot\frac{1}{7}\sdot\frac{1}{8}\right)\sdot\left(\frac{8}{6}\sdot\frac{1}{4}\right)}}](/mediawiki/images/math/9/8/9/989a1bcb49b832461aa0a175792074ba.png)
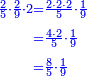
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\left[\frac{1}{8}+\left(\frac{2}{9}\sdot\frac{1}{7}\sdot\frac{1}{8}\right)\right]\sdot\left[\frac{1}{4}+\left(\frac{2}{6}\sdot\frac{1}{4}\right)\right]\\&\scriptstyle=\left(\frac{65}{9}\sdot\frac{1}{7}\sdot\frac{1}{8}\right)\sdot\left(\frac{8}{6}\sdot\frac{1}{4}\right)\\&\scriptstyle=\frac{65\sdot8}{9}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{6}\sdot\frac{1}{4}\\&\scriptstyle=\frac{520}{9}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{6}\sdot\frac{1}{4}\\\end{align}}}](/mediawiki/images/math/a/d/9/ad962ba769fbe462ffd2b8f8cea6f6f1.png)
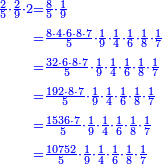
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\left[\frac{1}{8}+\left(\frac{2}{9}\sdot\frac{1}{7}\sdot\frac{1}{8}\right)\right]\sdot\left[\frac{1}{4}+\left(\frac{2}{6}\sdot\frac{1}{4}\right)\right]\\&\scriptstyle=\frac{520}{9}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{6}\sdot\frac{1}{4}\\&\scriptstyle=\frac{520\sdot5}{9}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{6}\sdot\frac{1}{4}\sdot\frac{1}{5}\\&\scriptstyle=\frac{2600}{9}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{6}\sdot\frac{1}{4}\sdot\frac{1}{5}\\\end{align}}}](/mediawiki/images/math/2/7/1/2711897ee7dc16819dc9f0d50ba83e5b.png)
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\left(\frac{2}{5}\sdot\frac{2}{9}\sdot2\right)+\left[\left[\frac{1}{8}+\left(\frac{2}{9}\sdot\frac{1}{7}\sdot\frac{1}{8}\right)\right]\sdot\left[\frac{1}{4}+\left(\frac{2}{6}\sdot\frac{1}{4}\right)\right]\right]\\&\scriptstyle=\left(\frac{10752}{5}\sdot\frac{1}{9}\sdot\frac{1}{4}\sdot\frac{1}{6}\sdot\frac{1}{8}\sdot\frac{1}{7}\right)+\left(\frac{2600}{9}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{6}\sdot\frac{1}{4}\sdot\frac{1}{5}\right)\\&\scriptstyle=\left(\frac{13352}{7}\sdot\frac{1}{8}\sdot\frac{1}{6}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/e/8/2/e827db0c5e3aac4f7c828927829ec6b6.png)
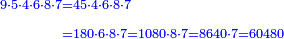

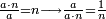
![\scriptstyle\frac{\left(a\sdot n\right)+r}{a}=n+\frac{r}{a}\longrightarrow\frac{a}{\left(a\sdot n\right)+r}=\frac{1}{n+1}+\frac{a-r}{\left(n+1\right)\sdot\left[\left(a\sdot n\right)+r\right]}](/mediawiki/images/math/b/9/2/b92d1354c49c317f8eb727d0819e6f80.png)
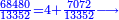
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\left(\frac{2}{5}\sdot\frac{2}{9}\sdot2\right)+\left[\left[\frac{1}{8}+\left(\frac{2}{9}\sdot\frac{1}{7}\sdot\frac{1}{8}\right)\right]\sdot\left[\frac{1}{4}+\left(\frac{2}{6}\sdot\frac{1}{4}\right)\right]\right]\\&\scriptstyle=\left(\frac{13352}{7}\sdot\frac{1}{8}\sdot\frac{1}{6}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{9}\right)\\&\scriptstyle=\frac{13352}{68480}\\&\scriptstyle=\frac{1}{4+1}+\frac{13352-7072}{5\sdot68480}\\&\scriptstyle=\frac{1}{5}+\left(\frac{6280}{7}\sdot\frac{1}{8}\sdot\frac{1}{6}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{9}\sdot\frac{1}{5}\right)\\\end{align}}}](/mediawiki/images/math/8/2/c/82c4adbc763288a7ace55ff6dc9136dc.png)
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\left(\frac{2}{5}\sdot\frac{2}{9}\sdot2\right)+\left[\left[\frac{1}{8}+\left(\frac{2}{9}\sdot\frac{1}{7}\sdot\frac{1}{8}\right)\right]\sdot\left[\frac{1}{4}+\left(\frac{2}{6}\sdot\frac{1}{4}\right)\right]\right]\\&\scriptstyle=\frac{1}{5}+\left(\frac{6280}{7}\sdot\frac{1}{8}\sdot\frac{1}{6}\sdot\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{9}\sdot\frac{1}{5}\right)\\&\scriptstyle=\frac{1}{5}+\left(\frac{6280}{8}\sdot\frac{1}{5}\sdot\frac{1}{4}\sdot\frac{1}{6}\sdot\frac{1}{9}\sdot\frac{1}{7}\sdot\frac{1}{5}\right)\\&\scriptstyle=\frac{1}{5}+\left(\frac{785}{5}\sdot\frac{1}{4}\sdot\frac{1}{6}\sdot\frac{1}{9}\sdot\frac{1}{7}\sdot\frac{1}{5}\right)\\&\scriptstyle=\frac{1}{5}+\left(\frac{157}{4}\sdot\frac{1}{6}\sdot\frac{1}{9}\sdot\frac{1}{7}\sdot\frac{1}{5}\right)\\&\scriptstyle=\frac{1}{5}+\left(\frac{39}{6}\sdot\frac{1}{3}\sdot\frac{1}{3}\sdot\frac{1}{7}\sdot\frac{1}{5}\right)+\left(\frac{1}{4}\sdot\frac{1}{6}\sdot\frac{1}{3}\sdot\frac{1}{3}\sdot\frac{1}{7}\sdot\frac{1}{5}\right)\\&\scriptstyle=\frac{1}{5}+\left(\frac{6}{3}\sdot\frac{1}{3}\sdot\frac{1}{7}\sdot\frac{1}{5}\right)+\left(\frac{3}{6}\sdot\frac{1}{3}\sdot\frac{1}{3}\sdot\frac{1}{7}\sdot\frac{1}{5}\right)+\left(\frac{1}{4}\sdot\frac{1}{6}\sdot\frac{1}{3}\sdot\frac{1}{3}\sdot\frac{1}{7}\sdot\frac{1}{5}\right)\\&\scriptstyle=\frac{1}{5}+\left(\frac{2}{3}\sdot\frac{1}{7}\sdot\frac{1}{5}\right)+\left(\frac{3}{6}\sdot\frac{1}{3}\sdot\frac{1}{3}\sdot\frac{1}{7}\sdot\frac{1}{5}\right)+\left(\frac{1}{4}\sdot\frac{1}{6}\sdot\frac{1}{3}\sdot\frac{1}{3}\sdot\frac{1}{7}\sdot\frac{1}{5}\right)\\\end{align}}}](/mediawiki/images/math/d/e/1/de140719bae84adbb3f37634029381d9.png)
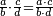
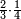
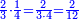
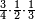
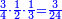
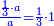
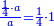
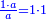
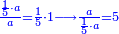
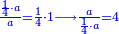
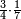
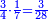
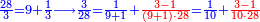

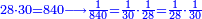
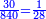
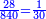
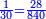
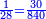
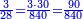
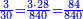
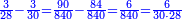
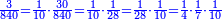
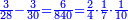
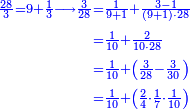
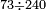

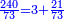
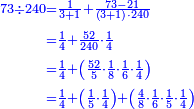
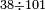

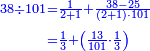
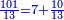
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle38\div101&\scriptstyle=\frac{1}{3}+\frac{13}{101}\sdot\frac{1}{3}\\&\scriptstyle=\frac{1}{3}+\frac{1}{3}\sdot\left[\frac{1}{7+1}+\frac{13-10}{\left(7+1\right)\sdot101}\right]\\&\scriptstyle=\frac{1}{3}+\frac{1}{3}\sdot\left[\frac{1}{8}+\frac{3}{8\sdot101}\right]\\&\scriptstyle=\frac{1}{3}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)+\left(\frac{3}{101}\sdot\frac{1}{3}\sdot\frac{1}{8}\right)\\\end{align}}}](/mediawiki/images/math/d/d/3/dd32f95b035bc980c80c4385a7b505f0.png)
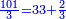
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle38\div101&\scriptstyle=\frac{1}{3}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)+\left(\frac{3}{101}\sdot\frac{1}{3}\sdot\frac{1}{8}\right)\\&\scriptstyle=\frac{1}{3}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)+\left[\frac{1}{3}\sdot\frac{1}{8}\sdot\left[\frac{1}{33+1}+\frac{3-2}{\left(33+1\right)\sdot101}\right]\right]\\&\scriptstyle=\frac{1}{3}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)+\left[\frac{1}{3}\sdot\frac{1}{8}\sdot\left[\frac{1}{34}+\frac{1}{34\sdot101}\right]\right]\\&\scriptstyle=\frac{1}{3}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)+\left(\frac{1}{3}\sdot\frac{1}{8}\sdot\frac{1}{34}\right)+\left(\frac{1}{3}\sdot\frac{1}{8}\sdot\frac{1}{34}\sdot\frac{1}{101}\right)\\\end{align}}}](/mediawiki/images/math/9/e/8/9e81c6f384212f9effbf03c4791a0698.png)

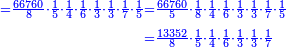

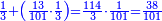
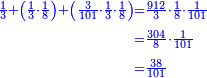
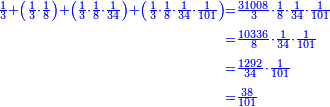
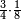
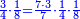
![\scriptstyle\left[\left[\frac{8}{9}+\left(\frac{3}{7}\sdot\frac{1}{5}\sdot\frac{1}{9}\right)\right]\sdot\left(\frac{5}{6}\sdot3\right)\right]-\left[\left[\frac{3}{4}+\left(\frac{2}{5}\sdot\frac{1}{4}\right)\right]\sdot\frac{2}{9}\right]](/mediawiki/images/math/d/6/d/d6d3383d94cc0c6f1b9eabdd1be5711c.png)
![\scriptstyle{\color{blue}{\left[\frac{3}{4}+\left(\frac{2}{5}\sdot\frac{1}{4}\right)\right]\sdot\frac{2}{9}=\frac{34}{5}\sdot\frac{1}{4}\sdot\frac{1}{9}}}](/mediawiki/images/math/7/4/b/74b8c93d7ed6516a0fe4bd7b5c8adb2a.png)
![\scriptstyle{\color{blue}{\left[\frac{8}{9}+\left(\frac{3}{7}\sdot\frac{1}{5}\sdot\frac{1}{9}\right)\right]\sdot\left(\frac{5}{6}\sdot3\right)=\frac{4245}{7}\sdot\frac{1}{5}\sdot\frac{1}{9}\sdot\frac{1}{6}}}](/mediawiki/images/math/d/c/f/dcf61fe7fff902138bbf8445996648a3.png)

![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left[\frac{3}{4}+\left(\frac{2}{5}\sdot\frac{1}{4}\right)\right]\sdot\frac{2}{9}&\scriptstyle=\frac{34\sdot6\sdot7}{7}\sdot\frac{1}{6}\sdot\frac{1}{5}\sdot\frac{1}{4}\sdot\frac{1}{9}\\&\scriptstyle=\frac{1428}{7}\sdot\frac{1}{6}\sdot\frac{1}{5}\sdot\frac{1}{4}\sdot\frac{1}{9}\\\end{align}}}](/mediawiki/images/math/3/c/a/3cadc8744997613d5d60f8e779e311ce.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left[\frac{8}{9}+\left(\frac{3}{7}\sdot\frac{1}{5}\sdot\frac{1}{9}\right)\right]\sdot\left(\frac{5}{6}\sdot3\right)&\scriptstyle=\frac{4245\sdot4}{4}\sdot\frac{1}{7}\sdot\frac{1}{5}\sdot\frac{1}{9}\sdot\frac{1}{6}\\&\scriptstyle=\frac{16980}{4}\sdot\frac{1}{7}\sdot\frac{1}{5}\sdot\frac{1}{9}\sdot\frac{1}{6}\\\end{align}}}](/mediawiki/images/math/a/4/4/a44a2f3628574707f8e2ec57544d3306.png)
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\left[\left[\frac{8}{9}+\left(\frac{3}{7}\sdot\frac{1}{5}\sdot\frac{1}{9}\right)\right]\sdot\left(\frac{5}{6}\sdot3\right)\right]-\left[\left[\frac{3}{4}+\left(\frac{2}{5}\sdot\frac{1}{4}\right)\right]\sdot\frac{2}{9}\right]\\&\scriptstyle=\left(\frac{16980}{4}\sdot\frac{1}{7}\sdot\frac{1}{5}\sdot\frac{1}{9}\sdot\frac{1}{6}\right)-\left(\frac{1428}{7}\sdot\frac{1}{6}\sdot\frac{1}{5}\sdot\frac{1}{4}\sdot\frac{1}{9}\right)\\&\scriptstyle=\frac{15552}{4}\sdot\frac{1}{7}\sdot\frac{1}{5}\sdot\frac{1}{9}\sdot\frac{1}{6}\\&\scriptstyle=2+\left(\frac{2}{7}\sdot\frac{1}{5}\right)\\\end{align}}}](/mediawiki/images/math/a/a/3/aa3e06c8bc5151dd6518572edac92e1f.png)
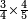
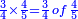
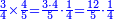
![\scriptstyle\left[\left[\frac{4}{7}\sdot\left(\frac{5}{9}\sdot\frac{1}{8}\right)\right]\right]\times\left[\left(\frac{3}{5}\sdot\frac{1}{9}\right)\sdot\left(\frac{2}{3}\sdot5\right)\right]](/mediawiki/images/math/8/e/1/8e1455aa8265c18c2b288e543c19aede.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left[\left[\frac{4}{7}\sdot\left(\frac{5}{9}\sdot\frac{1}{8}\right)\right]\right]\times\left[\left(\frac{3}{5}\sdot\frac{1}{9}\right)\sdot\left(\frac{2}{3}\sdot5\right)\right]&\scriptstyle=\frac{4}{7}\sdot\left(\frac{5}{9}\sdot\frac{1}{8}\right)\sdot\left(\frac{3}{5}\sdot\frac{1}{9}\right)\sdot\left(\frac{2}{3}\sdot5\right)\\&\scriptstyle=\frac{600}{7}\sdot\frac{1}{9}\sdot\frac{1}{8}\sdot\frac{1}{5}\sdot\frac{1}{9}\sdot\frac{1}{3}\\\end{align}}}](/mediawiki/images/math/2/7/9/279e5ba209dfc6b135b1d0320cc51fd7.png)
![\scriptstyle{\color{blue}{\left[\left[\frac{4}{7}\sdot\left(\frac{5}{9}\sdot\frac{1}{8}\right)\right]\right]\times\left[\left(\frac{3}{5}\sdot\frac{1}{9}\right)\sdot\left(\frac{2}{3}\sdot5\right)\right]=\frac{600}{7}\sdot\frac{1}{9}\sdot\frac{1}{8}\sdot\frac{1}{5}\sdot\frac{1}{9}\sdot\frac{1}{3}=\frac{5}{9}\sdot\frac{1}{7}\sdot\frac{1}{9}}}](/mediawiki/images/math/0/c/0/0c059d28324ce62c3bdb1bf7ea1de18c.png)
![\scriptstyle\left[\frac{3}{4}+\left(\frac{2}{3}\sdot\frac{1}{4}\right)\right]\div\left[\left[\frac{4}{9}+\left(\frac{5}{6}\sdot\frac{1}{9}\right)\right]\sdot\frac{2}{3}\right]](/mediawiki/images/math/a/0/b/a0bf54c86fb59c4b365c62aeb651544d.png)
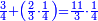
![\scriptstyle{\color{blue}{\left[\frac{4}{9}+\left(\frac{5}{6}\sdot\frac{1}{9}\right)\right]\sdot\frac{2}{3}=\frac{58}{6}\sdot\frac{1}{9}\sdot\frac{1}{3}}}](/mediawiki/images/math/1/0/d/10d30a962745577ac136a3f6ac85a875.png)
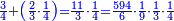
![\scriptstyle{\color{blue}{\left[\frac{4}{9}+\left(\frac{5}{6}\sdot\frac{1}{9}\right)\right]\sdot\frac{2}{3}=\frac{58}{6}\sdot\frac{1}{9}\sdot\frac{1}{3}=\frac{232}{6}\sdot\frac{1}{9}\sdot\frac{1}{3}\sdot\frac{1}{4}}}](/mediawiki/images/math/b/c/f/bcf7cf3cc51650dd0b6d9982861ca94f.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left[\frac{3}{4}+\left(\frac{2}{3}\sdot\frac{1}{4}\right)\right]\div\left[\left[\frac{4}{9}+\left(\frac{5}{6}\sdot\frac{1}{9}\right)\right]\sdot\frac{2}{3}\right]&\scriptstyle=\left(\frac{594}{6}\sdot\frac{1}{9}\sdot\frac{1}{3}\sdot\frac{1}{4}\right)\div\left(\frac{232}{6}\sdot\frac{1}{9}\sdot\frac{1}{3}\sdot\frac{1}{4}\right)\\&\scriptstyle=\frac{594}{232}\\\end{align}}}](/mediawiki/images/math/b/2/7/b274c6c7c71f0ead2db15a4b0ed35e7d.png)

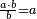
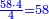
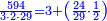
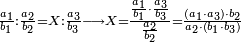
![\scriptstyle\left[\frac{3}{4}\sdot\left(3-\frac{1}{4}\right)\right]:\left[\frac{4}{5}\sdot\left(5-\frac{1}{5}\right)\right]=\left[\frac{5}{6}\sdot\left(6-\frac{1}{6}\right)\right]:X](/mediawiki/images/math/0/6/b/06b938d3936d7baec8744616f4c89a6b.png)
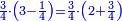
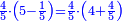
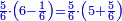
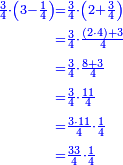
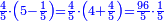
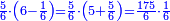
![\scriptstyle{\color{blue}{\left[\frac{3}{4}\sdot\left(3-\frac{1}{4}\right)\right]:\left[\frac{4}{5}\sdot\left(5-\frac{1}{5}\right)\right]=\left[\frac{5}{6}\sdot\left(6-\frac{1}{6}\right)\right]:X\longleftrightarrow\left(\frac{33}{4}\sdot\frac{1}{4}\right):\left(\frac{96}{5}\sdot\frac{1}{5}\right)=\left(\frac{175}{6}\sdot\frac{1}{6}\right):X}}](/mediawiki/images/math/8/3/b/83b408ca60c0b13f2ca139ce6acc9004.png)
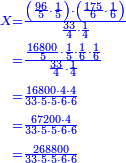

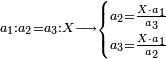
![\scriptstyle{\color{blue}{\left[9+\left(\frac{1}{3}\sdot\frac{1}{11}\right)+\left(\frac{4}{6}\sdot\frac{1}{3}\sdot\frac{1}{11}\right)\right]\sdot\left(\frac{33}{4}\sdot\frac{1}{4}\right)}}](/mediawiki/images/math/3/f/d/3fdd6f57b0fcf48e26dd34013c0017e7.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left[9+\left(\frac{1}{3}\sdot\frac{1}{11}\right)+\left(\frac{4}{6}\sdot\frac{1}{3}\sdot\frac{1}{11}\right)\right]\sdot\left(\frac{33}{4}\sdot\frac{1}{4}\right)&\scriptstyle=\left(\frac{1792}{6}\sdot\frac{1}{3}\sdot\frac{1}{11}\right)\sdot\left(\frac{33}{4}\sdot\frac{1}{4}\right)\\&\scriptstyle=\frac{59136}{4}\sdot\frac{1}{4}\sdot\frac{1}{6}\sdot\frac{1}{3}\sdot\frac{1}{11}\\\end{align}}}](/mediawiki/images/math/b/e/d/bedbd8fc417aa4d3a5f99b2c4ee6417b.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\frac{\left[9+\left(\frac{1}{3}\sdot\frac{1}{11}\right)+\left(\frac{4}{6}\sdot\frac{1}{3}\sdot\frac{1}{11}\right)\right]\sdot\left(\frac{33}{4}\sdot\frac{1}{4}\right)}{\frac{96}{5}\sdot\frac{1}{5}}&\scriptstyle=\frac{\frac{59136}{4}\sdot\frac{1}{4}\sdot\frac{1}{6}\sdot\frac{1}{3}\sdot\frac{1}{11}}{\frac{96}{5}\sdot\frac{1}{5}}\\&\scriptstyle=\frac{59136\sdot5\sdot5}{4\sdot4\sdot6\sdot3\sdot11\sdot96}\\&\scriptstyle=\frac{1478400}{4\sdot4\sdot6\sdot3\sdot11\sdot2\sdot8\sdot6}\\&\scriptstyle=\frac{1478400}{11\sdot3\sdot4\sdot8\sdot4\sdot2\sdot6\sdot6}\\&\scriptstyle=\frac{1478400}{8448\sdot6\sdot6}\\&\scriptstyle=\frac{1478400}{8448}\sdot\frac{1}{6}\sdot\frac{1}{6}\\&\scriptstyle=\frac{175\sdot8448}{8448}\sdot\frac{1}{6}\sdot\frac{1}{6}\\&\scriptstyle=\frac{175}{6}\sdot\frac{1}{6}\\\end{align}}}](/mediawiki/images/math/9/e/6/9e6f1f061c8d339fa999f4e213dac3e0.png)
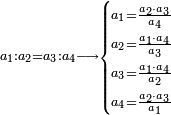
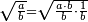
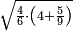
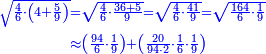
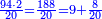
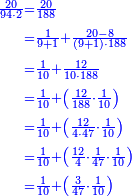
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\sqrt{\frac{4}{6}\sdot\left(4+\frac{5}{9}\right)}&\scriptstyle\approx\left(\frac{94}{6}\sdot\frac{1}{9}\right)+\left(\frac{20}{94\sdot2}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)\\&\scriptstyle=\left(\frac{94}{6}\sdot\frac{1}{9}\right)+\left[\left[\frac{1}{10}+\left(\frac{3}{47}\sdot\frac{1}{10}\right)\right]\sdot\frac{1}{6}\sdot\frac{1}{9}\right]\\&\scriptstyle=\left(\frac{94}{6}\sdot\frac{1}{9}\right)+\left(\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)+\left(\frac{3}{47}\sdot\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)\\&\scriptstyle=1+\frac{6}{9}+\left(\frac{4}{6}\sdot\frac{1}{9}\right)+\left(\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)+\left(\frac{3}{47}\sdot\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)\\&\scriptstyle=1+\frac{2}{3}+\left(\frac{4}{6}\sdot\frac{1}{9}\right)+\left(\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)+\left(\frac{3}{47}\sdot\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/3/2/1/3215f7c5e43f2a2b4b1ac3306f8da535.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left[\left(\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)+\left(\frac{3}{47}\sdot\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)\right]^2&\scriptstyle=\frac{2500}{47}\sdot\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\sdot\frac{1}{47}\sdot\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\\&\scriptstyle\left(\frac{4}{9}\sdot\frac{1}{47}\frac{1}{47}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)+\left(\frac{1}{6}\sdot\frac{1}{9}\sdot\frac{1}{47}\sdot\frac{1}{47}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/3/7/c/37c2f73a3ca36b19e555b950edca459f.png)
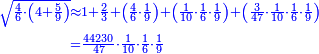
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left[1+\frac{2}{3}+\left(\frac{4}{6}\sdot\frac{1}{9}\right)+\left(\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)+\left(\frac{3}{47}\sdot\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)\right]^2&\scriptstyle=\left(\frac{44230}{47}\sdot\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)^2\\&\scriptstyle=\frac{44230}{47}\sdot\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\sdot\frac{44230}{47}\sdot\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\\&\scriptstyle=\frac{1956292900}{47}\sdot\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\sdot\frac{1}{47}\sdot\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\\\end{align}}}](/mediawiki/images/math/b/c/d/bcdd152e8b9660a0cf72e65b28eb952a.png)
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\left[1+\frac{2}{3}+\left(\frac{4}{6}\sdot\frac{1}{9}\right)+\left(\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)+\left(\frac{3}{47}\sdot\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)\right]^2\\&\scriptstyle=\frac{1956292900}{47}\sdot\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\sdot\frac{1}{47}\sdot\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\\&\scriptstyle=\left(\frac{164}{6}\sdot\frac{1}{9}\right)+\left[\left(\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)+\left(\frac{3}{47}\sdot\frac{1}{10}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)\right]^2\\&\scriptstyle\left(\frac{164}{6}\sdot\frac{1}{9}\right)+\left(\frac{4}{9}\sdot\frac{1}{47}\frac{1}{47}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)+\left(\frac{1}{6}\sdot\frac{1}{9}\sdot\frac{1}{47}\sdot\frac{1}{47}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/7/4/6/7464f65fea982e7b530ca03f0c62dd8f.png)
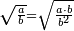
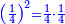
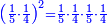
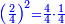
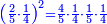
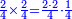
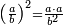
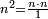
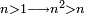
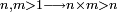
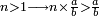

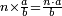
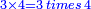
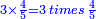
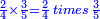

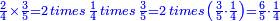
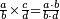
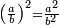


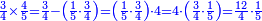
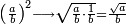
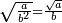
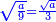
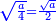
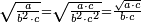
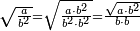
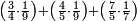


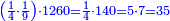


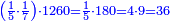
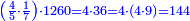
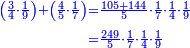
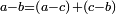
![\scriptstyle\left[3+\frac{5}{9}+\left(\frac{3}{7}\sdot\frac{1}{9}\right)+\left(\frac{2}{4}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\right]-\left[\frac{7}{9}+\left(\frac{5}{7}\sdot\frac{1}{9}\right)+\left(\frac{3}{4}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\right]](/mediawiki/images/math/c/9/c/c9c6d9287898412880ce3955aec5dcbf.png)
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle
\left[3+\frac{5}{9}+\left(\frac{3}{7}\sdot\frac{1}{9}\right)+\left(\frac{2}{4}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\right]-\left[\frac{7}{9}+\left(\frac{5}{7}\sdot\frac{1}{9}\right)+\left(\frac{3}{4}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\right]\\&\scriptstyle=\left[\left(3-1\right)+\frac{5}{9}+\left(\frac{3}{7}\sdot\frac{1}{9}\right)+\left(\frac{2}{4}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\right]+\left[1-\left[\frac{7}{9}+\left(\frac{5}{7}\sdot\frac{1}{9}\right)+\left(\frac{3}{4}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\right]\right]\\&\scriptstyle=\left[2+\frac{5}{9}+\left(\frac{3}{7}\sdot\frac{1}{9}\right)+\left(\frac{2}{4}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\right]+\left[\frac{1}{9}+\left(\frac{1}{7}\sdot\frac{1}{9}\right)+\left(\frac{1}{4}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\right]\\&\scriptstyle=2+\frac{6}{9}+\left(\frac{4}{7}\sdot\frac{1}{9}\right)+\left(\frac{3}{4}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/b/a/a/baa9c24e903e00db5154a21ab2a825b6.png)
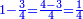
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle
\left[3+\frac{5}{9}+\left(\frac{3}{7}\sdot\frac{1}{9}\right)+\left(\frac{2}{4}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\right]-\left[\frac{7}{9}+\left(\frac{5}{7}\sdot\frac{1}{9}\right)+\left(\frac{3}{4}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\right]\\&\scriptstyle=\left[3+\frac{5}{9}+\left(\frac{3}{7}\sdot\frac{1}{9}\right)+\left[\left(\frac{4}{4}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)+\left(\frac{2}{4}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\right]\right]-\left[\frac{7}{9}+\left(\frac{6}{7}\sdot\frac{1}{9}\right)+\left(\frac{3}{4}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\right]\\&\scriptstyle=\left[3+\frac{5}{9}+\left[\left(\frac{7}{7}\sdot\frac{1}{9}\right)+\left(\frac{3}{7}\sdot\frac{1}{9}\right)\right]+\left(\frac{3}{4}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\right]-\left[\frac{8}{9}+\left(\frac{6}{7}\sdot\frac{1}{9}\right)\right]\\&\scriptstyle=\left[3+\left(\frac{9}{9}+\frac{5}{9}\right)+\left(\frac{4}{7}\sdot\frac{1}{9}\right)+\left(\frac{3}{4}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\right]-\left(1+\frac{8}{9}\right)\\&\scriptstyle=3+\frac{6}{9}+\left(\frac{4}{7}\sdot\frac{1}{9}\right)+\left(\frac{3}{4}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)-1\\&\scriptstyle=2+\frac{6}{9}+\left(\frac{4}{7}\sdot\frac{1}{9}\right)+\left(\frac{3}{4}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/4/5/b/45b4d274eb40b7256c8d56e8c488795c.png)



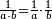
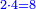


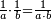
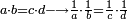
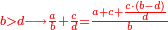
 ], it is part of all the denominators, the greater and the smaller, [i.e. b and d].
], it is part of all the denominators, the greater and the smaller, [i.e. b and d].