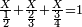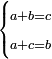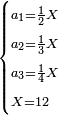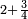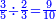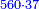Introduction
|
|
| The previous arithmetic books were written overly at length
|
אמר המחבר בראותי אריכות דברי החכמים הקדומים מחברי ספרי המספר
|
| The astronomical, geometrical and musical doctrines as well as the arithmetical teachings were not explained properly in those books
|
ושהסדרים והלמודים ההכרחיים בחכמת התכונה וההנדסה ויחסי המוסיקא אינם מבוארים בספרים ההם אלא בקושי גדול
|
|
|
וכן ג"כ בז' מיני שלמים כמו בשברים ובשרשים וביחסי המספרים
|
| Teaching using shortcuts and comprehensive methods is preferable to the student as well as the teacher, since lengthiness of words and loquacity are exhausting
|
ולהיות הלמוד שהוא בדרכים הקצרים והכוללים יותר נבחר כן ללומד כמו למלמד
|
|
|
כי כל אריכות דברים ולהג הרבה יגיעת בשר[1]
|
| The author: Yiẓḥaq b. R. Moshe ʽEli ha-Sefaradi [= the Spanish] from the city of Oriola of the kingdom of Aragon
|
לכן אני יצחק בכ"ר משה עלי נ"ע הספרדי ממדינת אוריאולה ממלכות ארגון
|
| Isaac wrote his book at the request of his friends who studied astronomy and geometry because they used those methods with a great difficulty and bother
|
לבקשת קצת אוהבי המעיינים בחכמת התכונה וההנדסה למה שהיה פועלם בקשי ובטורח גדול בדרכים ההם
|
| He composed a short treatise that encompasses all necessary arithmetic knowledge, and thus saves lengthy talks that are ineffectual and cause a waste of time
|
נערתי חצני וחברתי זה החבור הקצר כולל כל מה שהוא הכרחי בזאת המלאכה מלאכת המספר הנקראת ארישמטיקה כפי מה שחנני השם וכפי יד אלהי הטובה עלי
|
|
|
וחברתי בו ד' דרכים כוללים וקצרים בכל ז' מיני המספר וסגולותיו ומציאות היחסים בכל מה שהוא אפשרי במלאכה הזאת
|
|
|
וזה בדרכים מופתיים ונאהבים למשכילים באופן שכל מי שישתדל לעיין בזה הספר הקצר יקיף בכל מה שהוא הכרחי בזאת המלאכה וינצל מהאריכות הבלתי מועיל ומהפסד הזמן וישיג בו בכל מה שלבו חפץ כי הוא לחכמות הלמודיות כאור נגה הולך ואור עד נכון[2] ובעזר השם ב"ה אתחיל ואומר
|
Table of content
|
הספר הזה יחלק לשלשה מאמרים
|
|
|
במאמר הראשון נדבר בז' מיני המספר
|
|
|
במאמר השני נדבר בדרכים ויחסים ושאלות ותשובות הצריכות במלאכת הזאת
|
|
|
במאמר השלישי נדבר בקצת דרכים והתחלות משותפות למלאכת המספר וההנדסה
|
|
|
המאמר הא' יחלק לד' כללים
|
|
|
בכלל הא' נדבר בגדר מלאכת המספר וגדר המספר והאחדות וקצת התחלות צריכות אליה ומנין מיני המספר
|
|
|
בכלל השני נדבר בששה מיני המספר השלמים
|
|
|
בכלל השלישי נדבר בז' מיני השברים ואפני רבוע השברים בחכמת התכונה
|
|
|
בכלל הרביעי נדבר בדרכים מישרים למציאות שרשי המספרים המרובעים והמעוקבים
|
|
|
הכלל הא' מהמאמר הא' בגדר מלאכת המספר וגדר המספר והאחדות וקצת התחלות הצריכות אליה ומנין מיני המספר
|
|
|
הכלל הב' יחלק לששה פרקים
|
|
|
הפרק הראשון נדבר בו מהמין הראשון מהמספר שהוא הקבוץ
|
|
|
הפרק השני במין השני שהוא חסור
|
|
|
הפרק השלישי מהמין השלישי שהוא הכפול ודרכים כוללים בידיעת המספר השלמים
|
|
|
הפרק הרביעי במין הרביעי שהוא חלוק באמצע
|
|
|
הפרק החמישי במין החמשי שהוא הרבוע וקצת מסגלותיו
|
|
|
הפרק הששי במין הששי שהוא המחלק
|
|
|
הכלל הג' מהמאמר הראשון ויתחלק לשמנה פרקים
|
|
|
הפרק הראשון בדרכים מישירי בענייני הנחת השברים וגדרם וסדרם
|
|
|
הפרק השני בקבוץ השברים
|
|
|
הפרק השלישי בחסור השברים
|
|
|
הפרק הרביעי בכפול השברים
|
|
|
הפרק החמשי בחלוק השברים באמצע
|
|
|
הפרק הששי ברבוע השברים
|
|
|
הפרק השביעי באופני רבוע השברים בחכמת התכונה
|
|
|
הפרק השמני מהחלק השברים
|
|
|
הכלל הד' מהמאמר הראשון ויתחלק לד' פרקים
|
|
|
הפרק הא' בנתינת דרכים מישירים למציאות שרשי המספרים המרובעים או היותר קרובים למספרים הבלתי מרובעים
|
|
|
הפרק השני במציאות שרשי המספרים בשברים לבד או בשברים ושלמים יחד
|
|
|
הפרק השלישי בנתינת דרך אחד כולל למצא בו שרשי המספרים על דרך תוספת הסיפרש
|
|
|
הפרק הד' בדרכים מישירים למציאות שרשי המספרים המעוקבים או היותר קרובים למספרים הבלתי מעקבים
|
|
|
המאמר השני יתחלק בשני כללים
|
|
|
בכלל הראשון נדבר בדרכים ויחסים כוללים בזאת המלאכה
|
|
|
בכלל השני נדבר בקצת שאלות ותשובות מישירות בעיון ובמעשה בזאת המלאכה
|
|
|
הכלל הא' מהמאמר השני יחלק לשמנה פרקים
|
|
|
הפרק הראשון ביחסי המספרים מהשלמים
|
|
|
הפרק השני בדרכים מישירים למציאות יחסי המספרים השברים
|
|
|
הפרק הג' בדרכים מישירים למציאות המחולק ביחסי השברים
|
|
|
הפרק הרבעי בנתינת משל א' כולל לכל חלקי הלמוד במחלק ובמחולק בידיעת יחסי השברים
|
|
|
הפרק החמשי בידיעת יחסי הד' מספרים המתיחסים בשתי המלאכות וההנדסה
|
|
|
הפרק הששי בידיעת יחסי כל ג' מספרים המתיחסים
|
|
|
הפרק הז' בידיעת יחס הששה מספרים המתיחסים
|
|
|
הכלל השני מהמאמ' השני ויחלק לד' פרקים
|
|
|
הפרק הראשון בידיעת חלוף המדות והמשקלים והמשורות והמטבעות לפי חלוף מקומם
|
|
|
הפרק השני בידיעת התיחסות שני מספרים שיש להם זאת הסגולה שאם נחסר א' מהמספר הגדול והוספנוהו על הקטן יהיו שווים ואם בהפך יהיה הגדול הפך הקטן או יותר כפי שנרצה
|
|
|
הפרק הג' ביחס שני מספרים שאם הגדול יתן אחד לקטן יהיה הקטן הגדול ואם בהפך יהיה הגדול ג' פעמים
|
|
|
הפרק הד' שבידיעת קבוץ ב' חלקים מתחלפים מאי זה כל או יותר איך נדע הכל
|
|
|
הפרק הה' בנתינת דרכים כוללים לידיעת איזה מספר בלתי ידוע בדרך המתנגדים
|
|
|
הפרק הששי בלמוד החבורות
|
|
|
הפרק הז' בקצת שאלות ותשובות
|
|
|
המאמר השלשי נדבר בו בקצת התחלות מההנדסה ויתחלק לג' כללים
|
|
|
הכלל הראשון בידיעת השעור הקוויי
|
|
|
הכלל השני בידיעת השעור השטחיי
|
|
|
הכלל השלישי בידיעת השעור הגשמי
|
|
|
הכלל הראשון מהמאמר השלישי יתחלק לג' פרקים
|
|
|
הפרק הראשון בקצת התחלות ההנדסה וגדר הקו ובידיעת השעור הקוויי בגבה
|
|
|
הפרק השני בידיעת השעור הקוויי במישור
|
|
|
הפרק השלישי בידיעת השעור הקוויי בעמק
|
|
|
הכלל השני מהמאמר השלישי בידיעת השעור השטחי ויתחלק לה' פרקים
|
|
|
פרק א' בידיעת שעור השטח המשלש השוה הזויות
|
|
|
הפרק השני בידיעת שעור שטח המשלש שוה הצלעות
|
|
|
הפרק השלשי בידיעת שעור שטח המשלש מתחלף הצלעות
|
|
|
הפרק הד' בידיעת שעור שטח המרובע ושטח הרבוע
|
|
|
הפרק הה' בידיעת שעור שטח העגול לפי סברת החכמים
|
|
|
הכלל השלישי מהמאמר השלשי ובו פרק א' והוא בידיעת שעור אי זה גשם שיהיה
|
Book One: Numbers
|
|
Section one: Introduction to Arithmetic – Definitions and Principles
|
הכלל הראשון מהמאמר הראשון בגדר מלאכת המספר גדר המספר והאחדות וקצת התחלות צריכות אליה ומנין מיני המספר
|
| Necessary preliminary definitions:
|
|
- Definition of arithmetic: arithmetic is a craft that teaches to count many units, their differences and properties that are easily applied by memory.
|
מלאכת המספר היא מלאכה תורה למנות הרבה אחדים והבדליהם וסגולתם ובנקלה יקויימו בזכירה
|
- Definition of unit: unit is a foundation and the first part of the number, every number consists of it, but it is apart from every number.
|
אחדות הוא יסוד וחלק ראשון מהמספר וכל מספר יורכב ממנו אבל הוא חוץ לכל מספר
|
|
|
כי שנים או שלשה לא יצויירו בלתי האחד
|
|
|
כי השנים אינם אלא כפל האחד
|
|
|
והשלשה אינם אלא שלוש האחד
|
|
|
אבל האחד יצוייר בלתי שיצויירו שנים או שלשה
|
- Definition of number: number is defined as a sum of units
|
ולכן יגדר המספר בשהוא קבוץ אחדים
|
The Positional Decimal System
|
|
|
|
והראשון שצריך שתדע שתמונות המספר עשרה והם אלו: 1 2 3 4 5 6 7 8 9 0
|
|
|
התמונה הראשונה או האות או הסימן כמו שתרצה לקרוא לה תורה אחד השנית שתים והשלישית שלשה וכן כסדר עד תשעה
|
- Zero
|
והעשירית תקרא סיפרא ואינה שוה דבר בעצמה אבל היא להוראת מקום מקנה יותר כמות לאות הנמשכת אליה
|
| The written ranks [= decimal places] and their writing order
|
ואלה התמונות צריך שיכתבו כמו שהן בכאן כסדר
|
- 1) Units
|
והמקום הראשון שבטור יקרא מקום של אחדים בעבור שירמוז לאחדים בין שתהיה הראשונה תשעה או אי זה שתהיה מהן
|
- 2) Tens
|
והמקום השני שבטור יקרא מקום של עשרות
|
- 3) Hundreds
|
והמקום השלישי יקרא מקום של מאות
|
- 4) Thousands
|
והמקום הרבעי של אלפים
|
- 5) Tens of Thousands
|
והמקום החמשי של עשרת אלפים
|
- 6) Hundreds of Thousands
|
והששי של מאות אלפים
|
- 7) Thousands of Thousands
|
והשביעי של אלף אלפים
|
- 8) Tens Thousands of Thousands
|
והשמני של עשרות אלף אלפים
|
- 9) Hundreds Thousands of Thousands
|
והתשיעי של מאות אלף אלפים
|
- 10) Thousands Thousands of Thousands
|
והמקום העשירי שבטור יקרא מקום של אלף אלפי אלפים בעבור שתרמוז אליהם
|
| Every rank is ten times the preceding rank
|
וכן מעשרה לעשרה כי כל מעלה או מדרגה עולה יותר מהקודמת לה מנין עשרה וכן אל לא תכלית אם נרצה
|
| The numerals in the written ranks
|
א"כ התמונות הנזכרות ר"ל האותיות לפי מקומם כך יהיה הוראתם בדרך זה שהאחד במקום האחדים ישווה אחד ובמקום העשרות עשרה ובמקום המאות מאה ובמדרגת האלפים אלף וכן בסדר ממדרגה למדרגה
|
|
|
וכן שנים במקום האחדים שוה שנים ובמקום העשרות עשרים ובמקום המאות מאתים ובמקום האלפים אלפים
|
|
|
וכן בסדר ממדרגה למדרגה ממעלה למעלה
|
- Every number is either units, or product of ten, or composed from both
|
וכל מספר לא ימנע מאחד משלשה דרכים או שיהיה אחדים או כללים או מורכב משניהם
|
|
|
והאחדים הוא כל מספר שהוא פחות מעשרה
|
|
|
והכללים הוא מספר ששוה עשרות או מאות או זולת זה מהמדרגות
|
|
|
ומורכב משניהם הוא כל מספר שיש בו אחדים וכללים יחד
|
| List of the seven arithmetical operations: subtraction, doubling, halving, multiplication, division, and extracting roots of square and cubic numbers
|
ודע שמיני מלאכת המספר הם שבעה והם קבוץ חסור כפול חלוק באמצע רבוע חלוק מציאות עקרי המספרים המרובעים והמעוקבים
|
Section Two: Integers
|
הכלל השני מהמאמר הראשון
|
|
|
ויתחלק לשבעה פרקים
|
Chapter One: Addition
|
הפרק הראשון במין הראשון מהמספר והוא הקבוץ
|
| Definition of the addition operation: addition is summing two numbers or more to one inclusive number.
|
קבוץ הוא חבור שני מספרים או יותר במספר אחד כולל לכולם
|
| Written Addition
|
|
Description of the procedure:
- In this species we are able to write as much lines as we wish.
|
במין הזה נוכל לכתוב כל הטורים שנרצה
|
- The units should be written corresponding to the units, the tens corresponding to the tens, the hundreds corresponding to the hundreds and so on, every rank corresponding to its similar.
|
וצריך לכתוב האחדים כנגד האחדים והעשרות כנגד העשרות ומאות כנגד מאות וכן כסדר מדרגה כנגד כל מדרגה הדומה לה
|
- Then the numerals are summed as units.
|
ואחר כך יקובצו כל האותיות האחדים
|
| The sum of two digits - three options:
|
והקבוץ הזה לא ימנע מהיותו אחד משלש דרכים כמו שידעת
אם שיהיה מאחדים או מעשרות או מורכב משניהם
|
- The sum of the digits in the rank is equal to units
|
ואם יהיה מאחדים נכתוב אותו בטור האחדים
|
- The sum of the digits in the rank is equal to tens
|
ואם יהיה מעשרות נכתוב סיפרא ונעביר עשרה או עשרות אל המדרגה הראשונה הנמשכת אחריה שהיא מדרגת העשרות
|
- The sum of the digits in the rank is equal to units and tens
|
ואם יהיו אחדים ועשרות יחד נכתוב האחדים תחת האחדים כאמור והעשרות במדרגת העשרות ובסדר הזה בכל מדרגה ומדרגה שיהיה
|
|
כפי הנראה בצורה הזאת
|
-
|
| ג ד ב ה
|
| ב ו ט ח
|
| ה 0 ב ד א
|
|
|
| Check: casting out by 9
|
והמופת על זה שנשליך המקובץ ט' ט' והנשאר נשמור אותו וכן נעשה בנקבץ ואם הנותר משניהם שוה א"כ הקבוץ היה אמיתי ואם לא אינו אמתי וזה יספיק במין הראשון
|
Chapter Two: Subtraction
|
הפרק השני במין חסור
|
| Definition of the subtraction operation: the subtraction is knowing the remainder of any number after a number that is smaller than it was subtracted from it.
|
חסור הוא ידיעת הנשאר מאי זה מספר שיהיה כשיוסר ממנו מספר אחד פחות ממנו
|
| Written Subtraction
|
|
| Description of the procedure:
|
ויעשה בדרך זה נכתוב השני מספרים בשני טורים הגדול למעלה והקטן למטה מסודרים כל מדרגה תחת המדרגה הדומה לה עד תשלום כל המדרגות שיהיו
|
| Subtracting a digit from a digit - three options:
|
ובזה המין צריך לעיין בשלשה דברים
|
|
|
או האות האחד מהמספר העליון תהיה שוה לאות האחר מהמספר התחתון או יותר או פחות
|
- The digit of the subtracted is equal to the digit in the corresponding rank of the subtrahend
|
ואם יהיו שוות נכתוב למטה מהם סיפרא לאות שלא נשאר דבר כמי שמחסר ששה מששה שלא ישאר דבר
|
- The digit of the subtracted is larger than the digit in the corresponding rank of the subtrahend
|
ואם האות העליון יהיה יותר נחסר מה שלמטה מהמדרגה של מעלה ונכתוב הנותר כמי שמחסר חמשה מששה שישאר אחד
|
- The digit of the subtracted is smaller than the digit in the corresponding rank of the subtrahend:
- the corresponding digit of the result = the digit of the subtracted + the complement of ten of the subtrahend's digit
|
ואם העליון יהיה פחות מאותו שלמטה נעיין האות שלמטה כמה יש עד עשרה ומה שיהיה נחבר אותו עם האות העליון שכנגדו וחבור אלו השנים יקרא מותר ונכתוב אותו למטה תחת האות העליון
|
- then one is added to the succeeding digit of the subtrahend
|
וכשנרצה לחסר האות הנמשכת אליה מהעליונה שכנגדה צריך להוסיף אחד על האות התחתונה הנמשכת
|
- the same as adding one to loaning one from the succeeding digit of the subtracted
|
וזה הפעל הכרחי בעבור שהאות העליונה הקודמת היתה פחותה מהתחתונה וזה התוספת מהאחד שאמרנו הוא כמו שאם חסרנו אחד מהאות הסמוכה לעליונה הפחותה מהתחתונה שכנגדה ובזה הדרך נעשה עד שיגמר כל הטור
|
|
כפי הנראה בזאת הצורה
|
-
|
|
| 4282 |
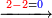 |
4282
|
| 2432 |
2432
|
| |
0
|
|
וצריך שתדע כמו שאמרנו שבעבור שהאות העליונה שוה לתחתונה כשיחוסר האחת מהאחרת לא נשאר דבר ולכן כתבנו סיפרא
|
| 4282 |
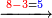 |
4282
|
| 2432 |
2432
|
| |
50
|
|
ובמדרגה השנית בעבור שהאות העליונה היא שוה יותר מהתחתונה נראה כמה יש מהתחתונה עד תשלום העליונה וידענו שהם ה' ולכן כתבנו ה' למטה
|
| 4282 |
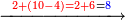 |
4282
|
| 2432 |
2432
|
| |
850
|
|
ואח"כ במדרגה השלישית בעבור שהאות התחתונה שוה יותר מהעליונה נדע כמה יש ממנה ר"ל מהתחתונה עד תשלום עשרה וידענו שהם ו' ונחבר אליהם האות העליונה שהיא ב' ויהיה קבוץ שניהם ח' והוא המותר ונכתוב אותו תחת הד'
|
| 4282 |
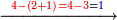 |
4282
|
| 2432 |
2432
|
| |
1850
|
|
ואח"כ בב' שהיא במדרגה הרביעית נוסיף אחד ויהיה ג' ונחסרם מהד' שהוא האות העליון וישאר למטה א'
|
|
|
וכסדר הזה צריך לעשות ואם ירבו המדרגות
|
|
|
והמופת על זה נחבר אותו המספר שחסרנו מהעליון עם המותר
|
| Check: addition
|
ואם יהיה למספר העליון כמו מספר העולה מחבור המותר עם המספר שחסרנו דע כי החסור שעשינו הוא אמתי ואם לא אינו אמתי וזה מספיק במין השני
|
Chapter Three: Doubling
|
הפרק השלישי במין השלישי והוא הכפול ודרכים כוללים למציאות המספרים השלמים
|
| Definition of the doubling operation: doubling is summing any two numbers that are equal.
|
כפול הוא קבוץ אי זה שני מספרים שיהיו שווים
|
| starting from the units
|
וגם בזה המין ראוי שנתחיל מהאחדים
|
| Description of the procedure:
|
ואי זה מספר שיהיה נכתוב אותו למטה כסדר כפל כל מדרגה ומדרגה בזה הדרך
|
- double the digit is less than ten
|
שאם יהיה הכפל מאי זו מדרגה שתהיה פחות מעשרה נכתוב אותו
|
- double the digit is equal to ten
|
ואם יהיה הכפל עשרה שלמים נכתוב סיפרא וישאר בידינו אחד להוסיף על כפל האות הנמשכת אליה
|
- double the digit is more than ten
|
ואם יהיה יותר מעשרה נכתוב מה שיהיה יותר והעשרה נעבירם למדרגה הנמשכת כמו שעשינו במין הקבוץ לא פחות ולא יותר
|
|
כפי הנראה בצורה הזאת
|
-
|
|
| the doubles: 2; 2×2=4; 2×4=8
|
והמין הזה נוכל להתחיל מהאחד שכפלו הב' וכפול הב' ד' וכפול ד' ח'
|
| Perfect Numbers
|
ובדרך הכפול הזה ימצאו המספרים השלמים
|
| Definition of a perfect number: the definition of a perfect number is any number that generated from the sum of all its divisors, so that when all its divisors are summed they produce it neither less nor more
|
וגדר מספר השלם הוא כל מספר שיבנה מקבוץ כל חלקיו שכשילקח כל אחד מחלקיו ויקובצו יבנו אותו לא פחות ולא יתר
|
for a prime number 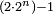
|
והמספר השלם ימצא בדרך זה בשנקח כפל אחד מזה המין ונעיין אם כפלו פחות אחד יהיה מספר ראשון
|
the number ![\scriptstyle2^n\sdot\left[\left(2\sdot2^n\right)-1\right]](/mediawiki/images/math/b/e/d/bed5e2c1c4b911a165a80a26323b01e6.png) is a perfect number is a perfect number
|
ואם יהיה מספר ראשון אז נכה אותו הכפל שלקחנו עם כפלו פחות אחד והעולה מהכאה זו הוא מספר שלם
|
| definition of a prime number: every number that is not resulting from a product of any number
|
וגדר המספר הראשון הוא כל מספר שלא יצא מהכאת שום מספר
|
- example: 7; 31; 3
|
כמו ז' או ל"א או ג'
|
- 6 is the perfect number in the rank of units:
![\scriptstyle{\color{blue}{2\sdot\left[\left(2\sdot2\right)-1\right]=2\sdot3=6}}](/mediawiki/images/math/4/a/d/4ad7cfaee668178995b5434ddc6e77ea.png)
|
המשל לקחנו הכפל הראשון מזה המין שהוא ב' ובעבור שכפלו פחות אחד הוא ג' והוא מספר ראשון נכה הכפל הראשון שהוא ב' בכפלו פחות אחד שהוא ג' ויצאו ששה שהוא מספר שלם וזהו המספר השלם שבמדרגת האחדים
|
| in each rank there is only one perfect number
|
כי בכל מדרגה יש מספר אחד שלם לא יותר
|
|
|
וימצא בדרך האמור וזה מספיק במין השלישי הזה
|
| Check: halving
|
והמופת במין הזה הוא בשנעשה המין הד' שהוא חלוק באמצע
|
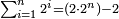
|
ולזה המין יש סגלה אחרת שמי שירצה לדעת העולה מכל הנכפל יכפול האחרון ויסיר אחד ויהיה שוה לכל הנכפל והנה לך צורתו
|
| |
|
|
1
|
| |
|
|
2
|
| |
|
|
4
|
| |
|
|
8
|
| |
|
1 |
6
|
| |
|
3 |
2
|
| |
|
6 |
4
|
| |
1 |
2 |
8
|
| |
2 |
5 |
6
|
| |
5 |
1 |
2
|
| 1 |
0 |
2 |
4
|
| 2 |
0 |
4 |
8
|
| 4 |
0 |
9 |
6
|
| 8 |
1 |
9 |
2
|
|
|
| |
|
|
א
|
| |
|
|
ב
|
| |
|
|
ד
|
| |
|
|
ח
|
| |
|
א |
ו
|
| |
|
ג |
ב
|
| |
|
ו |
ד
|
| |
א |
ב |
ח
|
| |
ב |
ה |
ו
|
| |
ה |
א |
ב
|
| א |
0 |
ב |
ד
|
| ב |
0 |
ד |
ח
|
| ד |
0 |
ט |
ו
|
| ח |
א |
ט |
ב
|
|
|
Chapter Six: Division
|
הפרק הששי במין הששי שהוא החלוק
|
| Definition of the division operation: dividing any number into equal parts as the number of units in the divisor
|
חלוק הוא חלוקת אי זה מספר שיהיה בכך חלקים שוים כמספר האחדים שבמחלק
|
|
|
ובמין הזה צריך שנתחיל באות ששוה יותר ונכתוב המחלק תחת המחולק בשנניח מקום פנוי בין המחלק והמחולק שנכתוב בו החלק המבוקש לכל אחד מחלקי המחלק
|
|
|
ובעבור שהחלוק אינו אלא לדעת כמה פעמים ימצא המחלק במחולק לכן צריך שנעיין כמה פעמים ימצא אות המחלק באות המחולק ומספר אותם הפעמים צריך שנכתוב במקום הפנוי שהנחנו
|
|
המשל נרצה לחלק קמ"ד לשמנה תעשה כך כצורה הזאת
|
-
|
|
|
|
וצריך שתדע כי כשאות המחולק פחות מהמחלק כמו בזה המשל אז נקח ב' אותיות מהמחולק ונקח היותר גדולה בשם עשרה והאחרת בשם אחדות
|
|
|
כמו שאתה רואה בזאת הצורה
|
| |
 |
06
|
| 144 |
144
|
| |
1
|
| 8 |
8
|
|
הא' בשם עשרה והד' בשם ארבעה וקבוצם י"ד ונאמר כמה פעמים ימצא ח' בי"ד וראינו שימצא פעם אחת ונשארו ששה והאחד שמנו בשם חלק שהיא א' תחת הד' והו' שנשארו כתבנו על הד' של המחולק ובעבור שמהי"ד לא נשארו יותר מו' כתבנו על הא' מהמחולק 0' והו' הנשארים יהיו עשרות להבא
|
| |
 |
0
|
| 06 |
060
|
| 144 |
144
|
| 1 |
18
|
| 8 |
8
|
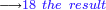
|
וא"כ נשארו עדיין לחלק ס"ד ונחלקם בח' ויהיו ח' לחלק ונכתוב אותם תחת הד' הראשון של המחולק ונאמר ח' פעמים ח' הם ס"ד וכשנחסרם מהמחולק שהם ס"ד לא ישאר דבר ולכן כתבנו 0' על הו' ו0' על הד'
|
- the divisor consists of one digit [= units] alone
|
ובדרך הזה צריך בכל המדרגות ואם ירבו מאד וכל זה כשיהיה המחלק אות אחת בלבד
|
|
|
ודע כי כשאות החלק יבא תחת אחדי המחולק אז נדע שלא נשאר יותר לחלק וזה יובן בשלמים
|
|
|
ואם ישאר דבר תיחסהו למחלק וכאותו היחס מחלקי שלם אחד יהיה לכל חלק מהמחלק או תהפך כל א' וא' מהנשארים לכל כך חלקים כמו האחדים שיש במחלק ואחר נחלקם במחלק ואז לא ישאר דבר לחלק
|
|
|
המשל בזה שאם המחלק יהיה ח' והנשאר לחלק היו ג' ניחס הג' לח' ויהיה היחס ג' שמניות או נעשה מכל א' מג' הנשארים ח' חלקים ויהיו כ"ד חלקים ונחלקם על המחלק שהם ח' ויבא לכל חלק ג' שמניות ובדרך הזה תעשה בכל עת שישאר לך דבר לחלק
|
- the divisor consists of two digits [= units and tens]
|
ואם יהיה המחלק מב' אותיות נכתוב אותו תחת המחולק במדרגה השוה יותר בהניחנו מקום פנוי כאמור
|
|
|
וצריך שתדע עוד שאם המחלק יהיה מב' אותיות שהאותיות הנגדיות מהמחולק צריך שבפעלתנו נקח האחת כמו אחדים והאחרת כמו עשרות
|
- the divisor consists of three digits = units, tens and hundreds
|
ואם המחלק יהיה מג' אותיות הנגדיות מהמחולק תהיה האחת כמו אחדים והב' כמו עשרות והג' כמו מאות
|
|
|
וכן בסדר הזה ואם ירבו ירבו השמות
|
|
|
וראשונה נעיין האות השמאלית מהמחלק כמה פעמים ימצא באות הראשון שבמחולק וכל כך פעמים שימצא בו כך נכתבהו בשם חלק במקום הפנוי על אות אחדי המחלק בתנאי זה שהכאת החלק באות הימנית מהמחלק יספיק לחסר אותה מהאות הימנית של המחולק בעזר האות השמאלית שבצדה למה שהשתי אותיות של המחולק נעזרות לעולם וזה הכרחי בכל מדרגות החלוק ואז נחסרם מהמחולק
|
|
|
ואם שתי האותיות של המחולק היו פחות מאותיות המחלק נכתוב 0' בשם חלק
|
|
|
ונעבור לבאות ואז צריך שנקח השתי אותיות מהמחולק מצד שמאל בשם אות שמאלית מהמחלק והאחרת בשם אות ימנית ומאלו השתי אותיות מהמחולק מצד שמאל נעיין כמה פעמים אפשר לחסר מהן השמאלית מהמחלק ושכל כך פעמים יחסר האות הימנית מהמחלק מהימנית מהמחולק
|
|
|
וכדרך זה עד כלות כל אותיות המחולק כאמור למעלה
|
|
|
כי כונת החלוק אינו אלא שהאות שנשים בשם חלק שכל כך פעמים שיחסר שמאלית המחלק משמאלית המחולק שכל כך פעמים יחסר ימנית המחלק מימנית המחולק ויותר אם יהיו
|
|
כנראה בצורה הזאת
|
-
|
|
| |
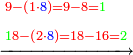 |
0
|
| |
12
|
| 9876 |
9876
|
| |
8
|
| 12 |
12
|
|
ונניח שנרצה לחלק ט' אלפים ותתע"ו בי"ב חלקים בעבור שהמחלק הוא משתי אותיות נקח השתי אותיות אחרונות מהמחולק שהם ח'ט' הח' בשם אחדים והט' בשם עשרות שהם צ"ח על י"ב ונעיין כמה פעמים אפשר לחסר האות השמאלי של המחלק שהיא א' מאות השמאלית מהמחולק שהוא ט' ונראה שימצא בה ט' פעמים האמנם למה שאמרנו שכל כך פעמים כמו שימצא שמאלית המחלק בשמאלית המחולק שכל כך פעמים צריך לחסר ימנית המחלק מימינית המחולק וזה אינו מספיק לכן כתבנו ח' בשם חלק וחסרנו אותם מהט' וישאר א' על הט' ונאמר ח' פעמים ב' שהם י"ו כשנחסרם מי"ח ישארו ב' על הח' וסיפרא על הא' מהמחולק
|
| 0 |
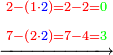 |
00
|
| 12 |
123
|
| 9876 |
9876
|
| 8 |
82
|
| 12 |
12
|
|
ועתה נחזור ונקח הב' והז' הב' בשם שמאלי והז' בשם ימיני כאמור ונסדרם כמו שסדרנו בב' אותיות הראשונות בשנאמר כמה פעמים אפשר לחסר שמאלית המחלק שהיא א' משמאלית המחולק שהיא ב' ונמצא שאפשר שיחסר ב' פעמים וג"כ נמצא שימינית המחלק שהיא ב' אפשר שיחסר שני פעמים מימינית המחולק שהיא ז' ולכן כתבנו ב' בשם חלק והכינו הב' מהחלק על הא' שהיא אות שמאלית מהמחלק ויעלו ב' ונחסרם מהב' שהיא שמאלית המחולק וישאר 0' עוד נכה הב' שהיא החלק על הב' שהיא ימנית המחלק ויעלו ד' ונחסרם מהז' וישאר ג' על הז'
|
| 00 |
 |
000
|
| 123 |
1230
|
| 9876 |
9876
|
| 823 |
823
|
| 12 |
12
|
|
ויהיה ו' ימינית המחולק וג' שמאלית המחולק ונעיין כמה פעמים אפשר לחסר א' שהוא שמאלית המחלק מהג' שהיא שמאלית המחולק ומצאנו שג' פעמים ובקשנו ג"כ אם ימצא הב' שהיא ימנית המחלק כל כך פעמים בימינית של המחולק ומצאנו שכן ולכן כתבנו ג' בשם חלק והכינו ג' בא' ועלה לג' ונוציאם מהג' של המחולק המחולק וישאר 0' וגם כן נכה הג' של החלק על ימינית המחלק שהיא ב' ויעלו ו' ונחסרם מהו' שהיא ימינית המחולק וישאר 0' ונכתוב 0' על הו'
|

|
והנה נחלק הכל ויהיה החלק תתכ"ג
|
|
|
והמופת על זה הוא שנכה החלק במחלק ואם יהיה שוה למחולק הוא אמת ואם לאו נחזור שנית לחשבוננו
|
|
|
ומופת אחר שנחסר התשעיות מהמחלק בצד אחד ומהחלק לצד אחר ונכה הנשאר מהשנים שלא יעלה לט' ונוציא ג"כ התשיעיות ומה שלא יעלה לט' נשמרהו ונשליך ג"כ המחולק לתשיעיות ונראה הנשאר שלא הגיע לט' ואם לא נשאר דבר בלתי מתחלק אז נראה אם הנשאר מהתשיעיות המחולק שוה לשמור הרי טוב ואם לא טעינו אמנם אם נשאר דבר בלתי מתחלק נשליך ג"כ המתחלק לתשיעיות והנשאר חסריהו מהנשאר מטור המתחלק או נוסיפהו על הנשאר הראשון שהוא השמור ונראה ואם יהיה שוה לנשאר מההכאה הוא אמת ואם לא אינו אמת
|
|
|
ואם יהיה המחלק יותר משתי אותיות נעשה בדרך זה בעצמו לא פחות ולא יתר שכל כך פעמים כמו שימצא שמאלית המחלק בשמאלית המחולק כל כך פעמים נחסר ימינית המחלק מימינית המחולק וכל כך פעמים אות הג' של המחלק מאות הג' מהמחולק והד' ג"כ אם יהיה מד'
|
|
|
וכן אם ירבו האותיות הרבה מאד נעשה כסדר הזה
|
|
|
וזה יספיק בו' מיני השלמים
|
|
|
ונדבר עתה מו' מיני השברים ומסגולותיהם בעה"ו
|
Section Three: Fractions
|
הכלל השלישי מהמאמר הראשון
|
|
|
ויתחלק לשמנה פרקי'
|
Chapter One: Introduction on Fractions
|
הפרק הראשון בדרכים מישירים באופני הנחת השברים וגדרם וסדורם
|
|
|
ואחר שדברנו מו' מיני השלמים עתה צריך שנדבר בו' מיני השברים
|
|
|
וצריך שתדע כי כמו שיש ו' מיני שלמים כן ג"כ יש ו' מיני שברים
|
|
|
וקודם שנדבר מהם צריך שנאמר מהו שבר ואיך יסודר בכתיבתו ובאי זה חשבון ישבר
|
| definition of fraction = any part that is taken from an integer
|
השבר הוא אי זה חלק שילקח מהשלם
|
|
|
כמו חצי או שליש או רביע וכדומה
|
|
|
ואיך יסודרו בכתיבתם הוא זה בעבור שבכל שבר ושבר יצויירו שני עניינים ר"ל כמות המתדבק וכמות המתחלק
|
|
|
המשל כשנאמר ב' שלישיות או שלש רבעיות
|
|
|
הב' והג' הם כמות מתחלק בעבור שמדברים מהמספר כי המספר הוא כמות מתחלק
|
|
|
והשלישיות והרביעיות כמות מתדבק בעבור שמדברים מחלק או חלקים מאיזה כל שיהיה ולכן רומזים לכמות מתדבק
|
|
|
ובעבור שהשברים יוכללו בשני מיני הכמה כאמור לכן צריך שיכתב כל שבר ושבר בשתי אותיות האחת לרמוז על הכמה מתדבק והשני על הכמה המתחלק
|
|
|
והאות הרומזת לכמה המתחלק נכתוב למעלה ותחתיה קו אחד
|
|
|
והאות הרומזת לכמה המתדבק נכתוב תחתי הקו
|
|
|
המשל אם נרצה לכתוב שני שלישיות
|
|
|
נכתוב ב' ותחת הב' קו אחד ותחת הקו ג' כמו שיראה בצורה זו
|
|
|
|
|
|
והאות העליונה שהיא ב' או מה שיהיה תרמוז לכמות רבוי השברים כמו א' ב' ג' ד' ה' וכל מה שתרצה
|
|
|
והאות התחתונה שהיא ג' כל מה שיהיה תרמוז לשם החלק כמו חצי או שליש או רביע או חמישית או מה שיהיה מחלקי השלם
|
|
|
כי השלם יחלק לשני חצאים ולג' שלישיות ולד' רביעיות ולה' חמישיות ולו' ששיות וכן מכל החלקים שנרצה לחלק בהם השלם
|
|
|
וצריך שתדע כי כמו שהשליש הוא א' מג' חלקי השלם כן השלם לא יחלק בשלישיות יותר משלש ולא רביעיות יותר מד' ולא בחמישיות יותר מה' וכן כלם כסדר הזה
|
|
|
והשברים יכתבו בדרך זה
|
|
|
שאם תכתוב חצי שלם כתוב כך
|
|
|
|
|
|
והשלשית תכתוב כך
|
|
|
|
|
|
והרבעית כך
|
|
|
|
|
|
וג' רביעיות תכתוב כך
|
|
|
|
|
|
וד' חמשיות תכתוב כך
|
|
|
|
|
|
וכן כל מה שתרצה כסדר הזה
|
Chapter Two: Addition of Fractions
|
הפרק השני בקבוץ השברים
|
| Definition of the addition of fractions = conversion of two types of fractions or more to integers, or to one type of fractions, or to integers and one type of fractions together
|
והוא השבת ב' מיני שברים או יותר לשלמים או למין אחד מהשברים או לשלמים ומין אחד מן השברים יחד
|
|
|
ונעשה בדרך זה נכתוב כל השברים שנרצה
|
|
|
כמי שרוצה לחבר או לדעת קבוץ חצי ושליש ורביע
|
|
|
או מה שיהיה כנראה בצורה זו
|
|
|
הראשון שצריך בזה המין הוא למצא חשבון אחד שימצאו בו כל אלה השברים וימצא בדרך זה בשנכה ב' על ג' והעולה משניהם נכה בד' וכן כסדר הזה נכה לעולם כל העולה מהכאת כל האותיות העוברות עם הנמשכת אליהן עד שנשלים כל הטור התחתון ר"ל כל האותיות שהן תחת הקו והעולה מכל אלה ההכאות הוא החשבון שימצאו בו כל השברים באי זה מין שיהיה ממיני השברים
|
- common denominator:
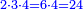
|
והחשבון שימצאו בו כל השברים הכתובים בזאת הצורה שלמעלה הוא כ"ד והוא בדרך זה נכה ב' על ג' ויעלו ו' וכל זה ר"ל הו' על הד' ויהיו לכ"ד
|
|
|
ובזה החשבון ימצאו חצי ושליש ורביע ולזה החשבון ר"ל כ"ד יש להם מקום של שלם
|
|
|
כי כמו שמהשלם יקח אדם אי זה חלק שירצה כך מזה החשבון של כ"ד שהם במקום השלם נקח אי זה חלק שנרצה
|
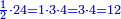
|
ולכן נקח החצי והשליש והרביע בזה הדרך נתחיל לקחת החצי בזה הדרך שהאות שנמצאת על קו החצי שהיא א' נכהו באות ג' שהיא תחת הא' הרומזת השליש ויהיו ג' ואלו הג' נכם על ד' שהיא תחת א' הרומזת הרביע ויהיו י"ב שהוא חצי של אותו החשבון שאמרנו
|
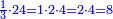
|
ואח"כ נקח השליש בדרך זה שנכה אות השליש שהיא על הקו עם האות של החצי שהיא תחת הקו ויהיה המוכה ב' ונכה הב' על ד' ויעלה ח' שהוא השליש של זה החשבון
|
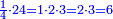
|
ואח"כ נכה הא' שהיא על ד' על הב' שהיא תחת הקו הרומזת החצי ויהיה ב' ואלו הב' נכה אותם בג' שהם תחת הקו הרומזת השליש ויעלו לו' שהם רביע זה החשבון ר"ל הכ"ד
|
- numerator:
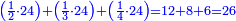
|
א"כ יש לנו ג' חשבונות שהם חצי ושליש ורביע שהם י"ב וח' וו' וקבוץ כלם כ"ו
|
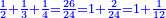
|
והשלם שיוחסו אליו אלו הכ"ו הוא כ"ד ולכן נחלק הכ"ו בכ"ד ויצא א' שלם וישארו ב' שלא נחלקו וניחס אותם לחשבון כ"ד ונמצא שהם חלק א' מי"ב של שלם א' וזהו העולה מג' שברים האמורים למעלה א"כ העולה מהשברים האמורים הוא אחד שלם וחלק אחד מי"ב חלקי השלם
|
|
|
וכדי שיובן יותר טוב נעשה משל אחד
|
|
|
ונניח שנרצה לקבץ ב' שלישיים וג' רביעיים וד' חמישיים וה' ששיים
|
|
|
שצורתם היא זאת
|
- common denominator:
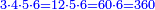
|
הראשון שצריך שנמצא הוא החשבון שהוא במקום שלם ר"ל שימצאו בו כל אלו השברים ונעשה כך נכה כל האותיות שתחת הקוים בזה הדרך ראשנה נכה ג' בד' ויהיו י"ב ואלו הי"ב נכם בה' ויעלו ששים ונכה ששים בו' ויעלו ש"ס וזהו המספר שבו ימצאו כל אלו השברים והוא מקום שלם ויקרא ג"כ מחלק
|
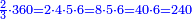
|
ועתה צריך שנוציא ממנו כל השברים ונעשה בדרך זה וראשנה נוציא השבר הראשון מהצורה האמורה שהוא שני שלישיות בדרך זה בשנקח הב' שהם על הג' ונכם בד' ויהיו ח' ואלו הח' נכם על ה' שהיא תחת ד' ויהיו מ' ומ' נכה בו' שהיא תחת הה' ויעלו ר"מ וזה המספר יקרא שני שלישיים של מחלק ר"ל של אותו המחלק שאמרנו שהוא במקום שלם
|
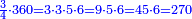
|
ואח"כ נוציא הג' רביעיות בדרך זה בשנקח הג' שהיא על הד' ונכהו בכל האותיות התחתונות זולת האות שתחתיה שהיא ד' בדרך זה ג' על ג' ויהיו ט' וט' על ה' ויהיו מ"ה ומ"ה על ו' ויעלו ר"ע והוא החשבון שיורה על ג' רביעיות
|
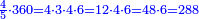
|
ואח"כ נוציא הד' חמישיות בדרך זה בשנקח הד' שהיא על ה' ונכה בכל האותיות התחתונות זולת הה' שהיא תחת הד' בדרך זה נכה ד' בג' ויהיו י"ב וי"ב בד' ויעלו מ"ח ומ"ח בו' ויעלו רפ"ח וזהו החשבון שיורה על ד' חמישיות
|
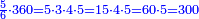
|
ואח"כ נוציא הה' ששיות בשנקח ה' שהיא על ו' ונכהו בכל האותיות התחתונות זולת הו' שתחתיה בדרך זה ה' על ג' יעלה ט"ו וט"ו על ד' יעלה סמך וס' בה' יעלה ש' וזהו החשבון שיורה על ה' ששיות
|
- numerator:
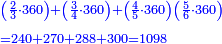
|
והנה כבר הוצאנו כל השברים שאמרנו ועתה צריך שנקבץ כל אלה השברים שאמרנו ונעשה בדרך זה נקח החשבון הר"מ והר"ע והרפ"ח והש' ונחבר הכל ויהיה קבוצם אלף וצ"ח וזהו קבוץ כל השברים שאמרנו
|
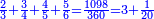
|
וכל זה הקבוץ נחלק בש"ס שהוא המחלק והוא במקום שלם כמו שאמרנו ויצאו ג' שלמים וחלק אחד מעשרים החלקים של שלם אחד וזהו קבוץ כל השברים שאמרנו והנה לך צורתו
|
|
|
ובעבור שאמרנו שקבוץ כל הצורה האמורה למעלה עולה לג' שלמים וחלק אחד מעשרים חלקים משלם א' צריך עתה שנבאר איך מצאנו אותו החלק מכ' חלקי השלם ואיך ימצאו כל הדומים דע כי לאחר שיחלק אי זה חשבון שיהיה באחר וישאר אי זה חשבון שלא יחלק להיותו פחות מהחלק אז ניחסהו למחלק ויחס שימצא ביניהם אותו היחס יש לו עם שלם אחד
|
|
|
המשל כבר ראית שבצורה שלמעלה נשארו י"ח שלא נחלקו בעבור שהיו פחות מהמחלק שהוא ש"ס לכן בקשנו היחס שיש בין הי"ח והש"ס ומצאנו שהוא יחס האחד לעשרים ולכן אמרנו למעלה שהוא אחד מכ' חלקי השלם והדרך למצא היחס הזה בנקלה דע אלו השני מספרים י"ח למעלה וש"ס למטה ונעיין בכמה חלקים אפשר לחלק הי"ח ובכל כך חלקים נחלק הש"ס
|
|
|
המשל כי כמו שהי"ח יחלקו בג' חלקים ויצאו ו' כך הש"ס יחלקו בג' חלקים ויצאו ק"ך ונחזור ונחלק הו' בג' חלקים ויצאו שנים ונחלק הק"ך בג' גם כן יצאו מ' עוד נחלק הב' באמצע ויצא א' וגם המ' באמצע ויצאו כ' אם כן יהיה אחד מכ' חלקי השלם ובדרך זה ניחס כל שני מספרים שבכל כך חלקים שיחלק האחד יחלק השני והנה לך צורתו
|
|
|
וצריך שתדע שבזה המין ר"ל הקבוץ אפשר לקבץ הרבה חלופים משברים מה שאינו כן במינים האחרים כי בכל מין מהם צריך חלוף שני שברים בלבד מה שאינו כן בזה המין וזה מספיק במין הזה
|
Chapter Six: Multiplication of Fractions
|
הפרק השישי מרבוע השברים
|
|
|
וכבר גדרנוהו ולא יקרה אלא באחד מחמשה פנים
|
- 1) Integers by fractions
|
הא' שלם או שלמים לבד עם שבר לבד
|
- 2) Integers and fractions by fractions
|
ב' שלם או שלמים ושברי' יחד עם שבר לבד
|
- 3) Integers and fractions by integers
|
ג' שלם או שלמים ושבר יחד עם שלם או שלמים לבד
|
- 4) Integers and fractions by integers and fractions
|
ד' שלם או שלמים ושבר יחד עם שלם ושבר יחד
|
- 5) Fractions by fractions
|
ה' שבר לבד בשבר לבד
|
| 1) Integers by fractions
|
וראשונה מהפן האחד שהיא משלם או שלמים לבד עם שבר לבד
|
|
|
המשל נרצה לרבע ד' שלמים בב' שלישיות
|
- denominator: 3
|
ונעשה כן נניח ב' מספרים משני צדדים בדרך זה וראשונה נעשה המחלק בדרך זה שנקח המספר שלמטה מהקו והוא יהיה המחלק והוא ג' בזאת הצורה
|
- numerator:

|
אח"כ נרבע הד' שלמים בב' שהם על הקו ויהיו ח' ואלו הח'
|
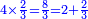
|
נחלקם במחלק שאמרנו שהם ג' ויבאו שני שלמים וב' שלישיות וזהו הרבוע מד' שלמים האמורים בב' שלישיות
|
| 2) Integers and fractions by fractions
|
ומשל הפן השני שהוא שלם או שלמים ושבר יחד עם שבר לבד
|
|
|
כמי שרוצה לרבע ד' וחצי עם שני שלישיות
|
- denominator:

|
ראשונה נעשה המחלק בדרך זה שנרבע הב' שהם תחת הא' על הג' שהיא תחת הב' ויעלה לו' ואלו הו' הם המחלק
|
- numerator:
![\scriptstyle{\color{blue}{\left[\left(4\sdot2\right)+1\right]\sdot2=\left(8+1\right)\sdot2=9\sdot2=18}}](/mediawiki/images/math/f/6/7/f6776cd569ed49e4aa40be43566a259b.png)
|
ואח"כ נרבע הד' שלמים בב' שהיא מצדו שהיא תחת הא' ויעלה לח' ונחבר עליהם הא' שהיא על הב' ויהיו ט' וזהו המספר של זה הצד ונכה הט' עם הב' של הצד האחד ויעלו י"ח
|
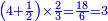
|
ואל הי"ח נחלקם על המחלק שהם ו' ויבא לכל חלק ג' ואלו הג' הם הרבוע העשוי מד' שלמים וחצי עם שני השלישיות
|
| 3) Integers and fractions by integers
|
ומשל לפן השלישי שהוא או שלם או שלמי' ושבר יחד עם שלם או שלמים לבד
|
|
|
כמי שרוצה לרבע ד' שלמים ושליש אחד על ו' שלמים
|
- denominator: 3
|
ובעבור שאין בכאן אלא מין אחד משברים בלבד לכן יהיה הג' שהיא תחת הא' הוא המחלק
|
|
|
ותשמור כלל זה שבכל מקום שלא יהיה אלא מין אחד משברים יהיה המספר שהוא תחת קו השבר המחלק
|
- numerator:
![\scriptstyle{\color{blue}{\left[\left(4\sdot3\right)+1\right]\sdot6=\left(12+1\right)\sdot6=13\sdot6=78}}](/mediawiki/images/math/1/d/9/1d9b723c3e6844776f2e70d9c40e3d4c.png)
|
ואחר שנתננו דרך המחלק נכה הד' שלמים שאמרנו על ג' שהיא תחת הא' ויהיו י"ב ונוסיף לו הא' שעל הג' ויהיו י"ג ואלו הי"ג נכם על הו' השלמים שאמרנו ע"ח
|
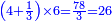
|
ואלו הע"ח נחלקם בג' שהוא המחלק שאמרנו ויבאו כ"ו מהחלוקה וזה הוא הרבוע מד' שלמים ושלם אחד על ו' שלמים
|
| 4) Integers and fractions by integers and fractions
|
ומשל הפן הד' השלם או שלמים ושבר יחד עם שלם או שלמי' מצד א' יחד
|
|
|
כמי שרוצה לרבע זה המספר
|
- denominator:

|
קודם כל דבר שנעשה המחלק כן והוא רבוע האותיות שתחת קוי השברים אח"כ נקח הד' שהיא תחת הג' ונכה אותה על הב' שהיא תחת הא' ויהיו ח' וזהו המחלק ונשמור אותו בפני עצמו
|
- numerator:
![\scriptstyle{\color{blue}{\left[\left(4\sdot4\right)+3\right]\sdot\left[\left(2\sdot2\right)+1\right]=\left(16+3\right)\sdot\left(4+1\right)=19\sdot5=95}}](/mediawiki/images/math/b/2/f/b2f0b8a3dfc87ea96c0d2ca487f51a03.png)
|
ואח"כ נכה הד' השלמים על הד' שהיא תחת הג' שבצדה ויעלה לי"ו ונוסיף עמהם הג' שעל הד' שבצדם ויעלה לי"ט ונשמרם ונעבור לצד האחר ונכה הב' שלמים בב' שתחת הא' שבצדה ויעלו לד' ונוסיף עמהם הא' שעל הב' שבצדם ויעלו ה' ונשמרם ג"כ א"כ יש לנו ג' דברים הראשון המחלק והשני שהשלמים שמצד אחד החזרנו אותם למין השברים שבצדם ועלו י"ט והשלישי שהשלמי' שמצד האחד החזרנום למין השברים שבצדם ועלו כלם ה' ועתה נכה הה' עם הי"ט ויעלו צ"ה
|
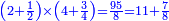
|
ונחלקם על המחלק האמור שהוא ח' ויבא מהחלוקה י"א שלמי' וז' שמניות וזו ההכאה שרצינו
|
| 5) Fractions by fractions
|
ומשל הפן הה' שהוא רבוע שבר עם שבר
|
|
|
כמי שרוצה לרבע
|
- denominator:
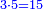
|
נוציא המחלק שהוא הכאת האותיות שתחת הקוים שהם ג' וה' ויעלה ט"ו ונשמור אותו
|
- numerator:
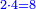
|
ואחר נכה האותיות שעל הקוים שהם ב' וד' ויעלו ח'
|
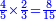
|
ואלו השמנה נחלקם במחלק שהוא ט"ו שבעבור שהמחלק יותר מהמחולק כיחס המחולק אל המחלק ומצאנו ח' חלקים מט"ו של שלם אחד וזהו הרבוע מב' שלישיות וד' חמישיות
|
|
|
והמופת ממין רבוע השברים הוא זה שנחלק הרבוע שעשינו מהשני צדדים על אחד מהצדדים ויצא הצד האחד ואם לא אינו אמת ובעבור שמופת הרבוע הוא בחלק ועדיין לא דברנו בחלוק השברים לכן לא הרחבנו בו עד שנדבר מחלוק השברים הנמשך לזה
|
Chapter Eight: Division of Fraction
|
הפרק השמיני והוא מחלק השברים
|
|
|
וכבר ידעת גדרו והמין הזה יקרה בשמנה פנים
|
- 1) Fractions by fractions
|
האחד שבר בשבר
|
- 2) Fractions by integers
|
הב' שבר בשלם
|
- 3) Fractions by integers and fractions
|
השלשי שבר בשלם ושבר
|
- 4) Integers and fractions by integers and fractions
|
הד' שבר ושלם בשבר ושלם
|
- 5) Integers by fractions
|
הה' שלם בשבר
|
- 6) Integers and fractions by fractions
|
הו' שלם ושבר בשבר
|
- 7) Integers and fractions by integer
|
הז' שלם ושבר בשלם
|
- 8) Integers by integers and fractions
|
הח' שלם בשלם ושבר
|
| 1) Fractions by fractions
|
הפן הראשון שהוא חלוק שבר בשבר
|
|
|
כמי שרוצה לחלק ג' רביעיות בב' שלשיות נכתוב כל אחד בצד חברו בצורה הזאת
|
- denominator:
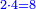
|
וקודם כל דבר נעשה המחלק כן שנכה ב' שהיא על ג' על ד' שהיא תחת ג' ויעלה ח' וזהו המחלק
|
- numerator:

|
ואחר צריך שנעשה המחולק בדרך זה שנכה הג' שהיא על ד' בג' שהיא תחת ב' ויעלה ט' וזהו המחולק
|
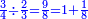
|
ואח"כ נחלק המחולק במחלק ויצא אחד שלם ושמינית שלם וזהו חלוק ג' רבעיות בשני שלישיות כמו שרצינו
|
| 2) Fractions by integers
|
השני שהוא חלוק שבר בשלם
|
|
|
נכתוב כל אחד בצד חברו כמו שעשינו בפן הראשון בדרך זה
|
|
|
נניח שרצינו לחלק ג' שמניות בשני שלמים בצורה זו
|
- denominator:
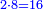
|
וראשונה נעשה המחלק בדרך זה נניח השלם שהוא ב' על ח' שהוא תחת ג' ויעלה י"ו וזהו המחלק
|
- numerator: 3
|
ואחר כך נעשה המחולק כך שנקח הג' שהיא על ח' והוא המחולק
|
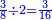
|
ונחלק זה המחולק שהוא ג' בי"ו שהוא המחלק ויצאו ג' חלקים מי"ו חלקים של שלם אחד וזהו מה שרצינו
|
| 3) Fractions by integers and fractions
|
השלישי שהוא שבר בשלם ושבר
|
|
|
כמי שרוצה לחלק ב' שלישיות בד' שלמים וחצי
|
- denominator:
![\scriptstyle{\color{blue}{\left[\left(4\sdot2\right)+1\right]\sdot3=\left(8+1\right)\sdot3=9\sdot3=27}}](/mediawiki/images/math/e/8/e/e8e4a046900922c7247cf2a2064e18a7.png)
|
ונעשה המחלק בדרך זה שנכה ד' על ב' שהוא תחת הא' ויעלה ח' ונוסיף עליהם הא' שהוא על הב' ויהיו ט' ואלה הט' נכה אותם על ג' שהיא תחת הב' שבצד הא' ויעלו כ"ז וזהו המחלק
|
- numerator:

|
ונעשה המחולק בדרך זה שנכה הב' שהיא על ג' על הב' שהיא תחת הא' שבצד הא' ויעלה ד' וזהו המחולק
|
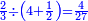
|
ונחלקהו במחלק שהוא כ"ז ויצא מהחלוקה ד' חלקים מכ"ז חלקים של שלם וזה הוא מה שרצינו
|
| 4) Integers and fractions by integers and fractions
|
הרביעי שהוא שבר ושלם בשבר ושלם נכתוב כל אחד כאמור למעלה
|
|
|
כמי שרוצה לחלק ט וחצי בג' וד' חמשיות וצורתו היא זאת
|
- denominator:
![\scriptstyle{\color{blue}{\left[\left(5\sdot3\right)+4\right]\sdot2=\left(15+4\right)\sdot2=19\sdot2=38}}](/mediawiki/images/math/5/a/2/5a22144368ac484b03473dc5faaf74b3.png)
|
ונעשה המחלק בדרך זה שנכה ג' על ה' שהיא תחת ד' שבצדה ויעלה טו ונוסיף עוד ד' שהיא על ה' על טו ויהיו י"ט ואלו נכם על ב' שהיא תחת א' שבצד האחר ויעלו ל"ח וזהו המחלק ונשמור אותו
|
- numerator:
![\scriptstyle{\color{blue}{\left[\left(9\sdot2\right)+1\right]\sdot5=\left(18+1\right)\sdot5=19\sdot5=95}}](/mediawiki/images/math/8/2/1/82111221272aefe0d07464888b030a03.png)
|
ונעשה המחולק בדרך זה שנכה ט' על ב' שתחת הא' שבצדה ויעלה י"ח ונוסיף עוד א' שעל הב' שבצדה ויעלו י"ט ואלו נכה אותם על ה' שתחת הד' שבצד האחר ויעלו צ"ה וזהו המחולק
|
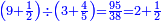
|
ואח"כ נחלק המחולק במחלק שאמרנו ויצא מהחלוקה ב' שלמים וחצי וזהו מה שרצינו
|
| 5) Integers by fractions
|
החמישי שהוא שלם בשבר
|
|
|
נכתבם כאמור כמי שרוצה לחלק י"ב בד' תשיעיות וזהו צורתו
|
- denominator: 4
|
ובזה הפן המחלק הוא האות שהיא על הקו ולכן המחלק הנה הוא ד' שעל הט'
|
- numerator:
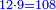
|
והמחולק יהיה מה שיעלה מהכאת הי"ב שלמים על הט' שתחת הד' וא"כ המחולק הוא ק"ח
|
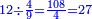
|
ונחלקם בד' שהוא המחלק ויהיו כ"ז בחלוקה וזהו מה שרצינו
|
| 6) Integers and fractions by fractions
|
הששי שהוא שלם ושבר בשבר
|
|
|
נכתוב כל א' כאמור המשל נרצה לחלק ד' ושליש אחד בה' ששיות והנה לך צורתו:
|
- denominator:

|
ונעשה המחלק כך שנכה ה' שהיא על ו' בג' שתחת הא' שבצדו האחר ויעלה ט"ו וזהו המחלק ונשמור אותו
|
- numerator:
![\scriptstyle{\color{blue}{\left[\left(4\sdot3\right)+1\right]\sdot6=\left(12+1\right)\sdot6=13\sdot6=78}}](/mediawiki/images/math/1/d/9/1d9b723c3e6844776f2e70d9c40e3d4c.png)
|
ואחר שנעשה המחולק בדרך זה שנכה ד' על ג' שתחת הא' שבצדה ויעלו י"ב ונוסיף א' שהיא על ג' שבצדה ויהיו י"ג ונכם בו' שתחת הה' שבצד האחר ויעלו ע"ח וזהו המחולק
|
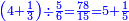
|
ונחלקהו במחלק שהוא ט"ו ויצא מהחלוקה ה' שלמים וא' חמישית וזה הוא מה שרצינו בזה הפן
|
| 7) Integers and fractions by integer
|
השביעי שהוא שלם ושבר בשלם
|
|
|
נכתבם כאמור המשל רצינו לחלק ג' ושלישיות בד' וצורתו היא זאת
|
- denominator:

|
ראשונה נעשה המחלק כך שנכה הד' על ג' שהיא תחת הא' שבצד האחד ויעלה י"ב וזהו המחלק בפן הזה
|
- numerator:
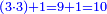
|
ונעשה המחולק בדרך זה שנכה הג' שלמים על ג' שהיא תחת הא' שבצדה ויהיה ט' ונוסיף עליו הא' שעל הג' שבצדה ויעלו עשרה וזהו המחולק
|
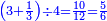
|
ונחלקהו במחלק שהוא י"ב ויצאו ה' ששיות וזהו מה שרצינו
|
| 8) Integers by integers and fractions
|
השמיני שהוא שלם בשלם ושבר
|
|
|
נכתוב כל אחד כאמור המשל שנרצה לחלק נ' בשנים וחצי וזאת היא צורתו
|
- denominator:
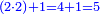
|
וראשונה נעשה המחלק בדרך זה נכה ב' על ב' שתחת הא' שבצדה ויעלה ד' ונוסיף הא' שעל הב' שבצדה ויעלה ה' וזהו המחלק ונשמור אותו
|
- numerator:

|
ואחר נעשה המחולק בדרך זה שנכה הנ' על ב' שהיא תחת הא' מהצד האחר ויעלה ק' וזהו המחולק
|
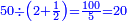
|
ונחלקהו במחלק שהוא ה' ויצא מהחלוקה כ' לכל אחד מהשנים השלמים של המחלק
|
|
|
ואחר נתן לכל שבר הראוי לו ביחס מה שנתננו לשלם המשל במין זה שחלקנו נ' בב' וחצי ויצא מהחלוקה כ' לכל שלם
|
|
|
א"כ נאמ' אם לכל אחד מהשלמים ראוי כ' לחצי ראוי שיהיו עשרה ובדרך זה ראוי לחלק החמישים וזהו מה שרצינו
|
|
|
והמופת לכל מיני החלוק הוא שנכה המחלק בחלק ואם יעלה כמו המחולק שוה בשוה אז נדע שהחלוק אמתי המשל כבר ידעת שהחלק האחרון מזה המין היה כ' והמחלק היה שנים וחצי ולכן אם תכה שנים וחצי בכ' יעלו לחמשים
|
|
|
וזה המופת כולל לכל הח' פנים שאמרנו מזה המין שהוא חלוק וזהו מה שרצינו
|
Section Four: Roots
|
הכלל הד' מהמאמר הראשון
|
|
|
ויתחלק לד' פרקים
|
Chapter One: Extracting and Approximation of Square Roots of Integers
|
הפרק הראשון בנתינת דרכים מישירים למציאות שרשי המספרים המרובעים או היותר קרובים למספרים הבלתי מרובעים
|
|
|
ואחר שדברנו מששת מיני המספר מהשלמים גם מהשברים שהם כוללים לכל מה שיצטרך במלאכת המספר עתה צריך שנדבר מדרכים מישירים למציאות שרשי המספרים המרובעים והמעוקבים בעבור שהם הכרחיים ומועילים בחכמות הלמודיות
|
|
|
ולכן ראוי שנאמ' ראשונה מהו גדר שרש המספר
|
|
|
וקודם כל דבר צריך שתדע שיש שני מיני שרשי מספר כוללים
|
|
|
הראשון שרש המרובע
|
|
|
והשני יקרא שרש המעוקב
|
|
|
וראשונה נדבר בשרש המרובע
|
|
|
ואם כן גדר שרש המרובע הוא מספר אחד שכשיוכה בעצמו מוליד אותו
|
|
|
ולכן שנים הם שרש ד' בעבור שכשיוכה בעצמו יוליד ד'
|
|
|
גדר אחד שהוא מספר אחד שכשיוכה בעצמו מוליד מספר מרובע אם כן כל מספר מוכה בעצמו מוליד מספר שיש לו שרש ומספר כזה יקרא מרובע
|
|
|
כמו ב' פעמים ב'
|
|
|
או ה' פעמים ה'
|
|
|
או י' פעמים י' וכן מהאחרים
|
|
|
צריך שתדע שכל מרובע מוכה על אי זה מרובע שיהיה יוליד מרובע
|
|
|
המשל ד' שיש להם שרש מוכה על ט' שגם כן יש לו שרש יולידו ל"ו ששרשם ו'
|
|
|
ואם כשיחולק המחולק במחלק החלק יהיה מרובע או אם יוכה המחולק במחלק יוליד מההכאה ההיא מרובע
|
|
|
המשל י"ח מחולק בח' יצאו והשרש מאלו אחד וחצי אם נכה י"ח על ח' יצאו קמ"ד ושרש המספר הזה הוא י"ב ואע"פ שאין שרש לי"ח ולח'
|
|
|
ומכאן יתחייב שצריך שתדע שכל המדרגות אין להם שרש אלא אותם שמהכאת אחרים בעצמם יולדו
|
|
|
כמו טור האחדים שהוא הטור הראשון יש לו שרש שאינו מאחד אלא מהכאתו בעצמו כי פעם אחד אחד הוא א'
|
|
|
והטור השני שהוא עשרות אין לו שרש כי לא ימצא שום מספר שבהכאתו בעצמו יוליד אותו
|
|
|
והטור השלישי שהוא מאות יש לו שרש כי מהכאת עשרה בעצמו יולד ק'
|
|
|
והטור הרביעי שהוא אלף אין לו שרש כי אין שם מספר שבהכאתו יולד הוא
|
|
|
והטור הה' שהוא עשרת אלפים יש לו שרש כי המאה מוכה בעצמו יולידהו כי ק' פעמים ק' יולידו עשרת אלפים
|
|
|
וכן אפשר לומ' מהטורים האחרים עד בלתי תכלית באופן שכל ההבדלי' שבסדר המספר יהיו נפרדים ימצא להם שרש כמו א' ג' ה' ז' כלומ' במדרגת האחדות ואם תרצה לומ' כן מהמאות ובמדרגת עשרות האלפים ובהבדל האלף אלפים וכן מכל המדרגות האחדות שהם נפרדות כאמור
|
|
|
וההבדלים או מדרגות שיהיו זוגות אין להם שרש כמו מדרגת הב' הרומזת לעשרות או מ' מדרגת הד' הרומזת לאלפים או מדרגת הו' הרומזת למאות האלפים וכן מכל המדרגות האחרות מהזוגות
|
|
|
ובשברי התכונה או אי זה שיהיו הוא בהפך
|
|
|
כי השברים התכונים ראשונים אין להם שרש
|
|
|
אבל אותם שיצאו מאחרים יש להם שרש
|
|
|
כמו הראשונים שבשברים בעבור שיש להם מקום ראשון אין להם שרש
|
|
|
אבל השניים יש להם מקום שני בשברים יש להם שרש כי מהכאת הראשונים בעצמם יולדו
|
|
|
והשלישיים שבמקום שלישי יעמדו אין להם שרש כי לא יולדו מהכאת אחרים בעצמם
|
|
|
והרבעיים שיש להם מקום הד' יש להם שרש כי מהכאת השניים בעצמם יולדו וכן מהאחרים בדרך זה
|
|
|
וכן יעשה משברי הסוגים האחרים ר"ל שאינם מהתכונה כשיהיו מההנדסה או מאיזו חכמה שיהיו
|
|
|
כמו חציים שלשיים וחמשיות וששיות והדומים בעבור שלא יולדו מאחדים ואלו יקראו מהבדל ראשון או שברים ראשונים לכן אין להם שרש
|
|
|
אבל כל מספר שיוכה בעצמו יקרא שבירה שנייה ולכן יש לו שרש
|
|
|
כמו מהכאת חצי בעצמו שיוליד רביעית שיקרא חצי של חצי
|
|
|
ומהכאת השלשית בעצמו שיוליד ט' שיקרא שלשית של שלשית
|
|
|
ומהכאת החמישית בעצמו שיולד כ"ה ויקרא חמישית החמישית
|
|
|
אבל העשירית והאחד עשירית והשלשה עשירית וארבע עשירית והדומים אין להם שרש כי הם שברים ראשונים ולא יולדו מהאחרים
|
|
|
אבל העשירית מעשירית והאחד עשירית מא' עשירית ושלשה עשירית משלשה עשירית וארבעה עשירית מארבע עשירית וחמשה עשירית מחמשה עשירית וכן מהדומים יש להם שרש
|
|
|
האמנם השברים שמההבדל השלישי שיש להם מקום שלשי אין להם שרש כמו חצי מחצי של חצי או שלשה עשיריות משלשה עשיריות של שלשה עשיריות וכן כל הדומים
|
|
|
א"כ כל השברים שלא יולדו מהכאת אחרים יקראו שברים של הבדל ראשון ואין להם שרש
|
|
|
אבל אותם שמהכאת אחרים בעצמם ראשונה יולדו יקראו שברים מהבדל שני ויש להם שרש
|
|
|
א"כ דבר מבואר הוא בשלמים שאותם ההבדלים שיש להם שרש הם אותם שיהיו נפרדים בטורים אבל בשברים הוא בהפך שהזוגות יש להם שרש ולנפרדים לא
|
|
|
ואחר ידיעת אלה העניינים כשנרצה למצא שרש אי זה מספר שיהיה נסדרהו בהבדלותיו ר"ל מדרגותיו כלומ' מקומותיו גם אותיותיו
|
|
|
ובעבור שלעולם ראוי להתחיל מההבדל הנפרד לכן צריך ראשונה להבחין אם ההבדלים יהיו זוגות או נפרדים
|
|
|
ואם יהיו נפרדים תשים תחת ההבדל האחרון מספר אחד שמנה בעצמו יעשה המספר שוה למספר שעליו או פחות היותר קרוב שאפשר שימצא אם לא ימצא שוה
|
|
|
ואם ההבדלים יהיו זוגות יושם תחת האות ר"ל ההבדלים שקודם ההבדל ר"ל האחרונה מספר אחד שכשיוכה בעצמו יוליד מספר שוה או פחות היותר קרוב שאפשר שימצא למספר שעליו אם לא ימצא לו שוה ויחוסר מאותו שעליו ומחברו
|
|
|
ואם לא ישאר מאומה אז נכתוב עליהם 0'
|
|
|
ואם ישאר יכתב מה שישאר באות הקודמת שהיא הימנית ואחר יוכפל ויושם בהבדל הנמשך אליו ובהבדל השלישי יושם מספר אחד שמוכה בנכפל ומחוסר מאותו שעל הנכפל ואחר כך מוכה בעצמו ומחוסר מהמספר שעליו יהיה יותר קרוב לבטל המספר של מעלה משום מספר אחר
|
|
|
ואם לא ישאר יותר הבדל אז יהיה המספר הראשון והשלשי שרש המספר שלמעלה
|
|
|
ואם יהיו יותר אותיות ר"ל הבדלים נכפול האות השלישית מהתחתונות ואח"כ נסייע הכפל הראשון אות אחת לפנים ונכפול הכפלים הראשוניים ואחר הכפל השני נניח מספר אחד שכשיוכה בנכפלים ובעצמו ימחוק כל מה שלמעלה כאמור
|
|
|
ואם יהיו יותר הבדלים ר"ל אותיות יוכפל המספר האחרון ויונח מספר אחר שכשיוכה בנכפלים הצריכים לסיע ממקומם ללכת מדרגה אחרת יותר קודם ההכאה ובעצמו ימחוק כל מה שלמעלה כאמור וכן צריך להעשות עד שיגמר כל הטור באופן שלעולם המספר שהוא אחד הנכפל יוכה בנכפלים ובעצמו
|
|
|
המשל שנניח מספר אחד שנרצה לבקש שרשו והוא ה"בוה"ו
|
| |
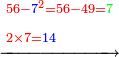 |
07
|
| 5625 |
5625
|
| 7 |
74
|
| |
1
|
|
ובעבור שההבדלים הם זוגות צריך שנתחיל באות שקודם האחרונה שהיא ו'
וצריך שנניח מספר אחד שיוכה בעצמו יוליד מספר שוה או פחות היותר קרוב שאפשר שימצא בשלא ימצא מספר שוה לאותו שלמעלה שהוא ו"ה
והמספר היותר קרוב לו"ה הוא ז' כי כשיוכה בעצמו יוליד מ"ט וכשיוסרו מהמספר שלמעלה שהוא ו'ה' ישארו ז' ואלו הז' שישארו נשימם על הו' שהיא אחת מאותיות ו"ה ועל הה' נשים 0'
והז' ששמנו למטה לשרש נכפול אותם ויהיו י"ד והעשרה נשים תחת הז' ונמחוק הז' והד' ננחם במקו' הנמשך שהוא תחת הב'
|
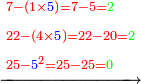 |
0
|
| 2
|
| 0700
|
| 5625
|
| 745
|
| 1
|
|
ואח"כ תחת האות האחרת הנמשכת נשים מספר אחד שהוא ה' שכשיוכה בנכפל ובעצמו ימחוק או יבטל אותו שלמעלה באופן זה בהכות הה' באחד שהוא העשרה מהכפל יוליד ה' שכשיוסרו מאותו שלמעלה שהוא ז' ישארו ב' על ז'
ואחר נכה הה' הנזכרים בד' ויהיו כ' שכשיוסרו משלמעלה שהוא כ"ב ישארו ב' על הב' ונכתוב 0' על הב' העליון שהיה במקום יוד לבית הנמשכת
אח"כ נכה הה' בעצמה ויהיו לנו כ"ה שכשיוסרו משלמעלה שהוא כ"ה לא ישאר כלום ואז יהיה לנו שרש המספר ה"ז כמו שנראה זאת הצורה הראשונה ובעבור שלא נשאר כלום נכתוב 0"0 על ב' ועל ה' וזה מה שרצינו זו היא הצורה הראשונה
|
Chapter Four: Extracting and Approximation of Cubic Roots of Numbers
|
הפרק הרביעי בנתינת דרכים מישירים למציאות שרש המספרים המעוקבי' או היותר קרובים למספרים הבלתי מעוקבים
|
|
|
ושרש מעוקב מאי זה מספר שיהיה הוא מספר אחד שכשיוכה במרובע ויוליד מספר אחר יקרא מספר מעקב
|
|
|
כמו ב' שהם שרש מעקב של ח' בעבור שהכאת הב' במרובעם שהם ד' יולידו ח' שהוא מספר מעקב של ב'
|
|
|
וכן ג' הם שרש מעקב כ"ז בעבור שהכאת ג' במרובעם שהוא ט' יוליד כ"ז שהוא מספר מעקב של ג'
|
|
|
וכן אלף הוא מספר מעקב של יו"ד כי הוא נולד בהכאת י' במרובעם שהוא ק' וכן מן האחרים
|
| The cubic square of the units should be memorized
|
ודע ששרש מעקב לא ימצא בזאת התחבולה שנאמ' אם לא שיהיה יותר מתשעה [ר"ל השרש] וכל אותם שהם פחותים מי' צריך שיודעו על פה בהכרח אם כן אתה לא תוכל למצא שרש מספר בתחבולה אם לא שיהיה מאלף ומעלה
|
|
|
ולהבין השרש הזה הוא הכרחי לדעת מה הם המדרגות שיש להם שרש מעקב
|
|
|
וצריך שתדע שאין לכל המדרגות שרש אלא לאותם שיולדו מהכאה מעוקבת
|
|
|
כי המדרגה הראשונה מהמספר שהוא מדרגת האחדות יש לו שרש מעקב כי האחד מוכה בעצמו באופן מעוקב יוליד אחד שהוא מספר מעוקב
|
|
|
והמדרגה השנית שהיא מדרגת העשרות אין לה שרש מעקב כי לא ימצא מספר אחר שמוכה בעצמו באופן מעקב יוליד עשרה
|
- hundreds - no cubic roots
|
והמדרגה השלישית שהיא מדרגת המאות אין לה שרש מעוקב כי לא ימצא מספר אחר שמוכה בעצמו יולידהו
|
- thousands - have cubic roots
|
אבל המדרגה הד' שהיא מדרגת האלפים יש לה שרש כי יולד מההכאה המעקבת מהעשרה
|
- tens of thousands - no cubic roots
|
והמדרגה הה' שהיא עשרת אלפים אין לה שרש מעקב לסבה הנזכרת
|
- hundreds of thousands - no cubic roots
|
והמדרגה הו' שהיא מאת אלפים אין לה ג"כ שורש מעוקב וסבה הנזכרת
|
- thousands of thousands - have cubic roots
|
והמדרגה הז' שהיא אלף אלפים יש לה שרש מעוקב כי יולד מההכאה המעוקבת מהמאה
|
| the first rank and the ranks that are a product of thousand (every fourth rank) have square roots; in other ranks there are no square roots
|
וכן ראוי שיובן בכל המספרים האחדים והוא שלא ימצא שרש מעקב אלא במדרגת האחדים והאלפים
|
Written calculations
|
|
|
|
ואחר שידעת כל זה אם תרצה להוציא זה השרש נכתוב המספר שנרצה בין שיהיה אלף או יותר מאלפים ונרשום האותיות העושות האלפים בשנתחיל מהאחדים
|
|
|
ודע שהאותיות המורות השרש הם האחדים והאלפים ואלף אלפים ואלף אלפי אלפים ואלף אלפי אלפי אלפים וכן כסדר הזה כלומ' כל האלפים בדרך הזה ר"ל האחדים והאות הד' לה כשימנה עמה והאות הז' והי' והי"ג והי"ו והי"ט והכ"ב והכ"ה וכן מהדומות ארבעה כי אלו הם המורות על בעלה השרש המעוקב
|
|
|
ואחר ידיעת אלו האותיות המורות אלפים נתחיל לעקב ר"ל לבקש השרש המעוקב מהאות האחרונה מהמורות אלפים בשנכתוב תחתיה אות אחת שכשיוכה בעצמו באופן מעוקב יעשה מספר שוה לאותה שלמעלה הימינה או פחות היותר קרוב שאפשר שימצא אם לא ימצא שוה ונחסרהו משלמעלה ממנו
|
|
|
והאות הזאת תקרא תחת המשולשת ואח"כ נשלשה ר"ל שנרצה אותה יותר ממה שהיה ג' פעמים
|
|
|
המשל אם יהיו ב' נחזירם ז' ונכתוב אותם במקום שלשי אליה ר"ל לתחת המשלשת לצד הימין והתחת המשלשת נסיעה אות אחת לאחור ונרשום הראשונה
|
|
|
ובמקום הסמוך למשלשת אחריה נכתוב אות אחרת ויקרא אות נמצאת שכשיוכה במשולשת ובתחת משלשת ובעצמה באופן מעקב יוליד מספר שוה או היותר קרוב שאפשר למספר שעליהם ונחסרם ממה שלמעלה מהם
|
|
|
ואם הטור יהיה יותר באותיות נשלש האות הנמצאת והמשלשת שלה נכתוב במקום השלשי לה בדרך המוזכר שלמעלה והיא ר"ל הנמצאת נרשום אותה ונסיעה אות אחת לאחור והמשולשות האחרות והתחת משולשות נסיעם כל אחת לאחור אות אחת ונרשום הראשונות ונבקש אות אחרת נמצאת שמוכה בכל המשלשות והתחת משלשות ובעצמה באופן מעוקב יוליד מספר שוה או היותר קרוב שאפשר לשלמעלה מהם ונחסרהו מהם וזה הדרך יהיה לנו תמיד ואם ירבו האותיות מאד מאד
|
|
|
וצריך שתדע שאם המשלשת תהיה ב' אותיות ר"ל אחדים ועשרות האחדים נכתוב כנזכר ר"ל במקום והעשרות נכתוב במקום השלישי לאחדים מצד שמאל אליה שהוא מקום רשימת התחת משלשת וכן לעולם
|
|
|
ודע שכל אות נמצאת בשתפעול פעולתה ויהיו יותר אותיות תחזור היא תחת משלשת
|
|
|
המשל נרצה לדעת השרש המעקב של י"ב אלף וקסב
|
|
|
וזו היא צורתו
| |
0 |
0 |
0 |
|
| 0 |
ד |
ה |
ב |
0
|
| א |
ב |
א |
ו |
ז
|
|
|
|
|
| |
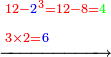 |
04
|
| 12167 |
12167
|
| 2 |
226
|
|
ולפי מה שאמרנו למעלה לא ימצא בזה המספר אלא שני מקומות בעלי שרשים מעקבים והם האחדים והאלפים ונתחיל במקום האלפים שהוא ב' וא' עמה והוא המקום האחרון המעוקב מזה המספר ונכתוב ב' תחתיו בעבור שלא נמצא מספר יותר קרוב לב"א שיקבל הכאה מעוקבת אלא ב'
א"כ נכה ב' בעצמם באופן מעוקב ויוליד ח' ונחסרם מב"א וישארו ד' על ב' ונכתוב 0' על הא'
ואחר נשלש הב' ויהיו ו' ונכתוב אותה תחת האות השלישית לב' שהיא תחת הו' העליונה ונרשום הב' ונסיעה אות אחת לאחור ונשימה אצל המשלשת ובמקום שהיתה שלישית אליה חזרה שניה אליה מצד שמאל
|
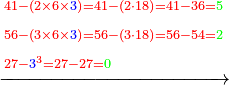 |
000
|
| 04520
|
| 12167
|
| 2263
|
|
ואחר המשולשת נכתוב ג' שמוכת במשולשת שהיא ו' יוליד י"ח ואלו הי"ח נכם בתחת משלשת שהיא ב' ויהיו ל"ו ונחסרם ממ"א שהם על הב' וישארו ה' על הא' ו0' על הד'
ואחר נכה הג' הנזכרת שהיא האות הנמצאת במשולשת שהיא ו' ויוליד י"ח וכל זה נכה בג' ויוליד נ"ד ונחסרם מהמספר שהוא על המשלשת שהוא נ"ו וישארו ב' על הו' ו0' על הה'
ואחר נכה הג' הנזכרת בעצמה באופן מעוקב ויוליד כ"ז ונחסרם ממה שלמעלה מהם שהם כ"ז ולא ישאר ולא מאומה ולכן נכתבם על הב' ועל הז' ז'
|
![\scriptstyle\longrightarrow{\color{Violet}{the\ result\ \sqrt[3]{12167}=23}}](/mediawiki/images/math/5/4/5/545f29847e0149872f407d5a9d9b295d.png)
|
וא"כ ידענו שהמספר הזה הוא מעוקב ושרש כ"ג
|
|
|
ומשל אחר אם יקרה באופן אחר נניח שנרצה לדעת השרש המעוקב מתקע"א אלף ותשפ"ז
|
|
|
וזאת היא צורתו
| |
0 |
0 |
|
|
|
| |
א |
א |
0 |
0 |
|
| 0 |
ה |
ט |
ג |
ב |
0
|
| ה |
ז |
א |
ז |
ח |
ז
|
|
|
|
|
| |
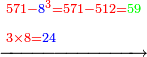 |
059
|
| 571787 |
571787
|
| 8 |
884
|
| |
2
|
|
ובעבור שבזאת הצורה לא ימצא אלא במקומות בעלי שרש נתחיל באחרון שהוא א' ונכתוב תחתיו מספר אחד שמוכה בעצמו באופן מעוקב יוליד מספר היותר קרוב אליו והוא ח' שאין שם מספר יותר קרוב בעבור שמוכה בעצמו באופן מעוקב יוליד מספר היותר קרוב אליו והוא ח' שאין שם מספר יותר קרוב
בעבור שמוכה בעצמו באופן מעוקב יעשה תקי"ב ונחסרם מתקע"א שהם על הח' וישארו נ"ט הט' נכתוב על הא' והה' על הז'
ונשלש הח' ויהיו כ"ד ונכתוב הד' באות השלישית לח' שהיא תחת משלשת והעשרים הנרמזים בכ' נכתוב תחת א' שכתבנו למטה בראשונה ונרשום אותה ר"ל הח' ונסיעה לאחור מדרגה א' ויהיו למטה ג' אותיות הב' למטה כנגד הט העליונה והח' תחת הז' והד' תחת הח'
|
![\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{59-\left(8\times2\times{\color{blue}{3}}\right)=59-\left(8\sdot6\right)=59-48=}}{\color{green}{11}}\\&\scriptstyle{\color{red}{117-\left[\left(8\times4\times{\color{blue}{3}}\right)+\left(3\times2\times{\color{blue}{3}}\right)\right]=}}\\&\scriptstyle{\color{red}{117-\left[\left(8\sdot12\right)+\left(3\sdot6\right)\right]=}}\\&\scriptstyle{\color{red}{117-\left(96+18\right)=117-114=}}{\color{green}{3}}\\&\scriptstyle{\color{red}{38-\left(3\times4\times{\color{blue}{3}}\right)=38-\left(3\sdot12\right)=38-36=}}{\color{green}{2}}\\&\scriptstyle{\color{red}{27-{\color{blue}{3}}^3=27-27=}}{\color{green}{0}}\\\end{align}}](/mediawiki/images/math/2/5/6/25659b3c9703b5f4b750226970caf7e4.png) |
00
|
| 1100
|
| 059320
|
| 571787
|
| 8843
|
| 2
|
|
ונכתוב עוד אחר הד' אות חדשה ויקרא אות נמצאת ויהיה רביעית שישוה כל כך שכשיוכה על הג' התחתונות ובעצמה באופן מעקב יוליד מספר שוה לכל האותיות העליונות או היותר קרוב שאפשר ולא ימצא אות יותר ראויה לזה מהג' ולכן נכתוב ג' תחת הז' במדרגה הראשונה
ודרך ההכאות יהיה זה נכה הג' שכתבנו באות השוה שהיא ב' ויעלה ו' ואלו הו' נכה במשלשת שהיא ח' ויעלו מ"ח ואלו המ"ח נחסרם מהאותיות שעל הב' שהם נ"ט וישארו י"א
ונחזור ונכה הג' פעם שנית על הד' שהיא אות האחדים מהשלוש הראשון על הח' ויעלה י"ב ואלו הי"ב נכה על הח' ויעלו צ"ו
ואח"כ נכה הג' הנזכר בב' הנזכרת ויעלה ו' ונחזור ונכה אלו הו' על הג' ויהיו י"ח
ואלו הי"ח עם הצ"ו יעלה קי"ד ואלו הקי"ד נחסרם מהג' אותיות העליונות שעל הח' שהם קי"ז וכשנחסר מהם קי"ד ישארו ג' ונכתוב הג' על הז' ונכתוב סיפרא על כל אחת מהב' אלפים
ונחזור ונכה הג' פעם שלישי על הד' שהיא אות מהאחדים מהמשלשת ויוליד י"ב ואלו נכם עם הג' בעצמה ויעלו ל"ו ונחסרם מהאותיות שעל הד' שהם ל"ח וישארו ב' ונכתוב אותם על הח' העליונה ונכתוב סיפרא על הג'
ופעם ד' נכה הג' בעצמה באופן מעוקב ויעלה כ"ז ונחסרם מהאותיות שעל הג' שהם כ"ז ולא ישאר דבר
|
![\scriptstyle\longrightarrow{\color{Violet}{the\ result\ \sqrt[3]{571787}=83}}](/mediawiki/images/math/c/b/4/cb4c1436cb7a06ebcd99307287954f67.png)
|
אם כן לא נשאר דבר אחר הוצאת השרש הזה יראה שזה המספר הוא מעוקב שלם ושרשו הוא פ"ג
|
|
|
וכדי להוסיף ביאור נעשה משל אחר והנה לך צורתו
| |
|
|
0 |
|
|
|
|
| |
|
|
ב |
|
|
|
|
| |
|
א |
ו |
0 |
|
|
|
| |
א |
ו |
ד |
א |
0 |
0 |
|
| 0 |
ד |
ב |
ז |
ה |
ה |
ו |
0
|
| א |
ב |
ח |
א |
ב |
ט |
0 |
ד
|
|
|
|
|
| |
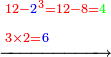 |
04
|
| 12812904 |
12812904
|
| 2 |
226
|
|
ולפי מה שאמרנו יש במספר הזה ג' מקומות בעלי שרשי מעוקבים הראשון הוא מקום האחדים והשני מקום האלפים והג' מקום האלף אלפים
ובעבור שלעולם צריך להתחיל במקום האחרון א"כ נתחיל מהב' שהוא מקום האלף אלפים ומקום האחרון ונכתוב תחתיה ב' כי לא ימצא מספר אחד שמוכה בעצמו באופן מעוקב יהיה יותר קרוב לי"ב שהם על הב' מב'
ולכן נכה הב' באופן מעוקב ויוליד ח' ונחסרם מי"ב וישארו ד' ונכתוב אותם על הב' שבטור העליון שהיא מקום האחרון ונכתוב 0' על הא'
ונשלש הב' ויהיו ו' ונכתוב אותה תחת האות השלישית אל הב' שהיא תחת הא' העליונה ונסיע הב' התחתונה מדרגה אחת לאחור כאמור למעלה ונרשום הב' הראשונה התחתונה
|
 |
0
|
| 164
|
| 04275
|
| 12812904
|
| 226339
|
| 26
|
|
ואח"כ נכתוב אות אחת אצל הו' שהיא האות המשולשת באופן שכשיוכה בו' שהיא המשולשת ובב' שהיא תחת המשלשת ובעצמה באופן מעוקב יוליד מספר שוה לכל האותיות העליונות שעליהן או היותר קרוב שאפשר ובעבור שלא ימצא מספר יותר קרוב נכתו' ג' אצל הז'
ואח"כ נעשה ההכאות בדרך זה שנכה הג' באות המשלשת שהיא ו' ויהיו י"ח ואלו הי"ח נכם על הב' שאצלה והיא התחת משלשת ויהיו ל"ו ונחסרם מהאותיות שעל הב' שהם מ"ח וישארו י"ב ונכתוב ב' על ח' וא' על ד'
ונחזור ונכה הג' על ו' ויהיו י"ח ואלו הי"ח נכם בג' עצמו שהיא האות הנמצאת ויהיו נ"ד ואלו נחסרם מהאותיות שעל הו' שהם קכ"א וישארו ס"ז ונכתוב ז' על א' וו' על ב' ו0' על הא'
ונחזור ונכה הג' בעצמו באופן מעוקב ויוליד כ"ז ונחסרם מהאותיות שעליה וישארו ה' על הב' וד' על הז'
ואח"כ נשלש הג' ויהיו ט' ונכתוב אותם במקום השלשי אליה שהוא תחת ה0' והמשולשת שהיא ג' נרשום אותה ונסיעה למקום הסמוך אליה ויעמוד תחת הט' העליונה וג"כ הו' נרשום אותה ונסיעה אות אחת אצלה ויעמוד תחת הה' העליונה והב' ג"כ נסיעה למקום הסמוך אליה ויעמוד תחת הה' העליונה
|
![\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{64-\left(2\times6\times{\color{blue}{4}}\right)=64-\left(2\sdot24\right)=64-48=}}{\color{green}{16}}\\&\scriptstyle{\color{red}{165-\left[\left(3\times6\times{\color{blue}{4}}\right)+\left(2\times9\times{\color{blue}{4}}\right)\right]=}}\\&\scriptstyle{\color{red}{165-\left[\left(3\sdot24\right)+\left(2\sdot36\right)\right]=}}\\&\scriptstyle{\color{red}{165-\left(72+72\right)=165-144=}}{\color{green}{21}}\\&\scriptstyle{\color{red}{219-\left[\left(4\times6\times{\color{blue}{4}}\right)+\left(3\times9\times{\color{blue}{4}}\right)\right]=}}\\&\scriptstyle{\color{red}{219-\left[\left(4\sdot24\right)+\left(3\sdot36\right)\right]=}}\\&\scriptstyle{\color{red}{219-\left(96+108\right)=219-204=}}{\color{green}{15}}\\&\scriptstyle{\color{red}{150-\left(4\times9\times{\color{blue}{4}}\right)=150-\left(4\sdot36\right)=150-144=}}{\color{green}{6}}\\&\scriptstyle{\color{red}{64-{\color{blue}{4}}^3=64-64=}}{\color{green}{0}}\\\end{align}}](/mediawiki/images/math/e/b/e/ebe0f4df388bc732084130a719026f81.png) |
0
|
| 02
|
| 0160
|
| 164100
|
| 04275560
|
| 12812904
|
| 2263394
|
| 26
|
|
ואחר כך נכתוב עוד אות אחת שכשיוכה באותיות הד' התחתונות ובעצמה באופן מעוקב יולידו מספר שוה לכל האותיות שלמעלה או פחות היותר קרוב שאפשר שימצא ובעבור שלא ימצא מספר יותר קרוב לד' לכן נכתוב ד'
ונעשה ההכאות בדרך זה שנכה ד' שהיא האות הנמצאת על ו' שהיא המשולשת ראשונה ויעלה כ"ד ואלו נכם בב' ויעשה מ"ח ואלו נחסרם מהאותיות שעל הב' שהם ס"ד וישארו י"ו ונכתוב ו' על ד' וא' על ו'
ופעם שנית נכה הד' הנזכר במשולשת הראשונה שהיא ו' ויעלה כ"ד ואלו נכם בג' שהיא תחת המשלשת השנית שהיא תחת ט' ויהיו ע"ב
ופעם שלשית נכה הד' על ט' ויעלו ל"ו ונכם בב' ויהיו ע"ב
ואלו עם הע"ב שלמעלה יהיו קמ"ד ונחסרם מהאותיות שהם על הו' שהיא המשלשת הראשונה שהם קס"ה וישארו כ"א והא' נכתוב על הה' והעשרים שהם ב' על ו' ו0' על הא'
ופעם ד' נכה הד' על הו' שהיא המשולשת הראשונה ויהיו כ"ד ואלו נכם על ד' עצמה ויהיו צ"ו
ופעם חמשית נכה הד' על הט' שהיא המשולשת הב' ויהיו ל"ו ואלו נכם על הג' שהיא תחת המשולשת השנית ויוליד ק"ח
ונחברם עם צ"ו ויהיו ר"ד ונחסרם מהאותיות שהם על הג' שהם רי"ט וישארו ט"ו
ופעם ששית נכה הד' הנזכר במשולשת השנית שהם ט' ויעלה ל"ו ואלו נכם בד' בעצמה ויעשה קמ"ד ונחסרם מהאותיות שעל הט' שהם קן וישארו ו' ונכתוב אותם על ה0' ונכתוב 0' על הה' ו0' על הא'
ופעם ז' ואחרונה נכה הד' הנזכרת בעצמה באופן מעוקב ויעשה ס"ד ונחסרם מהאותיות שעליה שהם ס"ד ולא ישאר דבר ולכן נכתוב 0' על הד' העליונה ועל הו' העליונה
|
![\scriptstyle\longrightarrow{\color{Violet}{the\ result\ \sqrt[3]{12812904}=234}}](/mediawiki/images/math/7/b/1/7b16bd7f1fdac314a617c85aee43a714.png)
|
ובעבור שלא נשאר שום דבר לכן נקראהו מעוקב ושרשו הוא רל"ד
|
| Check: multiplying the result by itself three times
|
והמופת לזה שנכה השרש בעצמו באופן מעוקב ויוליד המספר הראשון וזהו מה שרצינו
|
Chapter Two: Proportions of Fractions – finding the common denominator
|
הפרק השני בדרכים מישירים במציאות יחסי המספרים השברים
|
|
|
האמנם בשברים צריך לדעת שני דברים והם מציאות המחלק ומציאות המחולק ומציאות המחלק יודע בדרך זה שנעיין המספר הראשון מהשלשה שאמרנו כי לא ימנע מאחד מאלו הה' דרכים הראשון אם שיהיה הראשון שבר לבד והאחרים שלמים הג' או הראשון שבר ושלם יחד ואחדים או בא זה מהם שבר הד' או הראשון שבר ושלם יחד והאחרים שלמים הה' או הראשון שלם ובאחד מהאחרים או בשניהם שבר וראשונה מהראשון
|
|
|
המשל אם נרצה לדעת אם ב' שלישיות שוים ז' שלמים וד' תשיעיות כמה שוים ד' שלשה עשריות
|
|
|
והנה לך צורתם
|
- denominator:
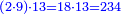
|
וראשונה נוציא המחלק שנכה הב' שהיא על ג' בט' שהיא תחת הד' ויעלו י"ח וכל זה נכה על י"ג שהוא תחת ד' ויעלה רלד וזהו המחלק
|
|
|
ומשל אחר לזה המין אם שני שלישיות שוות ד' וחצי כמה שוים ו'
|
|
|
והנה לך צורתו
|
- denominator:

|
ונעשה המחלק כך נכה הב' שעל הג' על ב' שהיא תחת א' ויהיו ד' וזהו המחלק
|
|
|
הדרך השני או יהיה הראשון שבר לבד והאחרים שלמים
|
|
|
המשל אם שני שלישיות שוות ח' כמה שווים ט'
|
|
|
והנה לך צורתו
|
|
|
וימצא המחלק כך שנקח הב' שהיא על הג' כי הוא לבד המחלק בעבור שלא נצטרך במחלק בזה המין למספרים האחדים ר"ל הב' האחרונים אלא כשיהיה באחד מהם או בשניהם שבר או שברים
|
|
|
הדרך הג' או יהיה הראשון שבר ושלם יחד ובאחד מהאחרים אי זה שיהיה או בשניהם שבר לבד או שבר ושלם יחד
|
|
|
המשל אם ה' וב' שלשיות שוות ו' וג' רביעיות כמה שוים ח' וה' שנים עשריות
|
|
|
וזו צורתו
|
- denominator:
![\scriptstyle{\color{blue}{\left[\left[\left(5\sdot3\right)+2\right]\sdot4\right]\sdot12=\left[\left(15+2\right)\sdot4\right]\sdot12=\left(17\sdot4\right)\sdot12=68\sdot12=816}}](/mediawiki/images/math/b/e/6/be6fd06595fca39aacff31a9abeeba9f.png)
|
ולמצוא המחלק נכה ה' על ג' שתחת ב' מצדה ויעלה ט"ו ונוסיף הב' שעל הג' ויעלו י"ז ואלו נכם בד' שהיא תחת ג' של מספר ב' ויעלו ס"ח ואלו נכם בי"ב שהם תחת ה' שהוא המספר הג' ויעלו תתי"ו וזהו המחלק
|
|
|
וצריך שתדע שהי"ז שעלו הכאת ה' בג' מצדה והוספת הב' שעל הג' ואח"כ הכינו אותם בד' שתחת הג' של מספר שני ועלו ס"ח שאם לא היה עוד שבר במספר הג' זה לבדו ר"ל הס"ח היה המחלק
|
|
|
וכן הוא הדין אם השבר יהיה במספר השלשי ולא יהיה במספר השני
|
|
|
הדרך הד' או הראשון שבר ושלם יחד והאחרים שלמים
|
|
|
המשל אם ה' וב' שביעיות שוות ד' כמה שוים עשרים
|
|
|
וזו היא צורתו
|
- denominator:

|
ונמצא המחלק כך נכה הה' בז' מצדה שהיא תחת הב' ויעלו ל"ה ונוסיף הב' שעל הז' ויהיו ל"ז וזהו המחלק ובעבור שהשני מספרים האחרים הם שלמים אינם מצטרכים במחלק כאמור
|
|
|
הדרך הה' או הראשון שלם ובאחד מהאחרים או בשתיהם שבר לבד או שבר ושלם
|
|
|
המשל אם כ' שוים ט"ו וה' חלקים מל"ז כמה שוים ה' וב' שביעיות
|
|
|
וזאת היא צורתו
|
- denominator:
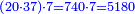
|
ונוציא המחלק כך נכה הראשון שהוא הכ' השלמים בל"ז שתחת הה' מהמספר השני ויעלו תש"מ ואלו נכם על ז' שתחת ב' של מספר ג' ויעלו ה' אלפים וק"ף וזהו המחלק
|
|
|
ואם לא יהיה שבר אלא באחד מהמספרי' האחרים נכה הראשון השלם באותו השבר שתחת הקו והוא יהיה המחלק
|
|
|
וזה יספיק במה שהוא המחלק ועתה נדבר במחולק בע"ה
|
Chapter Three: Proportions of Fractions – finding the numerator
|
הפרק השלשי בדרכים מישירים במציאות המחולק ביחסי השברים
|
|
|
וצריך שתדע שהמחולק יקרה באחד מו' דרכים
|
|
|
הדרך הראשון אם שכל א' משני המספרים האחרונים יהיה שבר לבד והב' או משני מספרים יהיו שלמים והג' או שכל אחד מהשני מספרים יהיה שלם ושבר ביחד והד' או אחד מהשני מספרים יהיה שלם ושבר ביחד והאחר שבר לבד והה' או אחד מהם שלם ושבר יחד והאחד שלם וה' או האחד יהיה שלם והאחר שבר וראשונה מהדרך הראשון
|
|
|
המשל אם ב' שלישיות שוות ד' תשיעיות כמה שוים ד' חלקים מי"ג
|
|
|
והנה לך צורתו
|
|
|
ונבקש המחולק כך בזה המין שנכה המספר שהוא על הקו של הא' מן האחרונים על המספר שהוא על קו המספר האחר וזאת ההכאה נשמור אותה ונכה עוד במספר שתחת קו המספר הראשון וזהו המחולק
|
|
|
ואם המספר הראשון יהיה שלם לבד אז יהיה המחולק מה שעלה מההכאה הראשונה מהשני מספרים האחרונים כמו שאמרנו בענין המחלק כי אין אנו צריכים שלמים אלא לשברים שתחת הקוים על שני המספרים האחרונים וכן בענין המחולק אין אנו צריכים מהראשון אם יהיה שלם שום הכאה אלא כשיהיה שבר ואז ממה שתחת הקו שלו
|
- numerator:
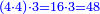
|
ויהיה המחולק בזה המשל מ"ח שכך עולה ד' של אחד מהאחרונים על ד' של האחר שהיא י"ו וי"ו על ג' מהמספר הראשון והוא מ"ח כאמור
|
|
|
הדרך השני או השני מספרים יהיו שלמים
|
|
|
המשל אם ב' שלישיות שוות ח' כמה שוים ט'
|
|
|
והנה לך צורתו
|
|
|
ונמצא המחולק ככה שנכה השם באחר באחר והעולה נכהו בשבר שתחת הקו של המספר הראשון
|
- numerator:
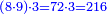
|
המשל נכה ח' על ט' ועלו ע"ב ואלו נכה אותם בג' ועלו רי"ו וזהו המחולק
|
|
|
הדרך הג' או שכל א' מהשני מספרים יהיה שלם ושבר אחד
|
|
|
המשל אם ה' וב' שלישיות שוות ו' וג' רביעיות כמה שוים ח' וה' חלקים מי"ב
|
|
|
והנה צורתו
|
|
|
ונוציא המחולק כך שנכה כל א' מהשלמים מהמספרי' האחרונים במה שתחת הקו שבצדו ונוציא עוד מה שעל הקו שבצדו ואחר נכה העולה מהב' מספרים זה על זה ונכה עוד זו ההכאה באות שתחת הקו של מספר ראשון וזהו המחולק
|
|
|
ואם המספר הראשון יהיה שלא יספיקו למחולק הכאות המספרים האחרונים כמו שאמרנו
|
- numerator:
![\scriptstyle{\color{blue}{\left[\left[\left(6\sdot4\right)+3\right]\sdot\left[\left(8\sdot12\right)+5\right]\right]\sdot3=\left[\left(24+3\right)\sdot\left(96+5\right)\right]\sdot3=\left(27\sdot101\right)\sdot3=2727\sdot3=8181}}](/mediawiki/images/math/3/3/e/33e6307a5615be5658beefa98b9c1160.png)
|
והמשל לזאת הצורה נכה ו' בד' שבצדם ויעלו כ"ד ונוסיף ג' שעל הקו ויעלו כ"ז עוד נכה ח' מהמספר האחרון על י"ב שבצדו ויעלו צ"ו ונוסיף ה' שעל הקו ויעלו כלם ק"א ועוד נכה ק"א על כ"ז ויעלו אלפים ותשכ"ז ואלו נכם באות שתחת קו המספר הראשון ויהיו ח' אלפים וקפ"א וזהו המחולק
|
|
|
ואם לא היה שבר במספר הראשון היה המחולק אלפים ותשכ"ז שהיא הכאת השני מספרים אחרונים כאמור
|
|
|
הדרך הד' או אחד מהשני מספרים האחרונים יהיה שלם ושבר יחד והאחר שבר לבד
|
|
|
המשל אם אחד שוה ד' חמישיות כמה שוים שנים וחצי
|
|
|
והנה צורתו
|
|
|
ונוציא המחולק בדרך זה שמהצד שימצא השלם עם השבר נכה השלם בשבר שתחת הקו שבצדו ונוסיף עליו מה שעל הקו שבצדו וכל זה נכהו במספר האחר מהאחרונים שהוא על הקו וזהו המחולק
|
|
|
ואם היה במספר הראשון שבר היינו מכים עמו כל זאת ההכאה האמורה
|
- numerator:
![\scriptstyle{\color{blue}{\left[\left(2\sdot2\right)+1\right]\sdot4=\left(4+1\right)\sdot4=5\sdot4=20}}](/mediawiki/images/math/9/4/3/9438da687c558cf44b88afb73ca06ee9.png)
|
המשל לזאת הצורה נכה ב' שלמי' בב' שהוא שבר שבצדה ויעלה ד' ונוסיף א' שעל הקו ויעלו ה' ואלו נכם בד' שהיא על הה' ויעלו כ' וזהו המחולק
|
|
|
ואם היה שבר במספר הראשון הוצרכנו להכות אלו הכ' באות שהיא תחת הקו של מספר ראשון
|
|
|
הדרך הה' או יהיה אחד מהמספרים האחרונים שלם ושבר יחד והאחר שלם לבד
|
|
|
המשל אם שני שלישיות שוות ד' וחצי כמה שוים ששה
|
|
|
וזה צורתו
|
|
|
ונבקש המחולק ככה שנכה השלם עם המספר שתחת הקו שהוא מצדו ונוסיף מה שלמעלה הימנו וכל זה נכה עם השלם היחידי שהוא מהצד האחר וכל זה נכה עוד עם המספר שהוא תחת הקו שבמספר הראשון אם יהיה בו שבר
|
|
|
ואם לא יהיה בו שבר אלא שלם לבד אינו צריך יותר הכאה
|
- numerator:
![\scriptstyle{\color{blue}{\left[\left[\left(4\sdot2\right)+1\right]\sdot6\right]\sdot3=\left[\left(8+1\right)\sdot6\right]\sdot3=\left(9\sdot6\right)\sdot3=54\sdot3=162}}](/mediawiki/images/math/5/8/e/58ef7f28670af1c26a23f2c27ed973e1.png)
|
והמשל לצורה נעשה המחולק בדרך זה שנכה הד' על הב' * ויעלה ט' וזה נכה על הו' שהוא השלם מהמספר השלשי ויעלה נ"ד וזה היה * ויעלה ח' ונוסיפ המחולק אם לא היה במספר הראשון שבר אבל בעבור שיש בו שבר נכה עליו הא' שעל הקו הנ"ד שיש בידינו על האות שתחת תחת הקו של אותו שבר שהוא ג' ויעלה קס"ב וזה יהיה אז המחולק
|
|
|
הדרך הו' או יהיה אחד מהמספרים האחרונים שבר לבד והאחר שלם לבד
|
|
|
המשל אם ט' שוים ב' שלישיות כמה שוים ח'
|
|
|
וזו היא צורתו
|
|
|
ונוציא המחולק כך שאי זה שיהיה מהשני מספרים האחרונים שלם נכה אותו עם המספר שעל הקו שהוא ג"כ מהאחרונים וזהו המחולק בעבור שאין שום שבר במספר הראשון
|
|
|
אבל אם יהיה בו שבר בין שיהיה לבדו בין שיהיה עם שלם אז נכה זאת ההכאה עם המספר שהוא תחת הקו וכל זה אז יהיה המחולק
|

|
המשל לצורה זו נעשה המחולק כך שנכה הח' שהיא אחד מהאחרונים על ב' שהוא על ג' ויעלה ט' וזהו המחולק י"ו
|
|
|
אבל אם יהיה במספר הראשון שבר נוסיף להכות האמורים
|
|
|
וצריך שתדע שבזה המין ר"ל אם כך שוים כך כמה שוים כך כלומ' סוג היחסים האמורים לא ימצאו יותר דרכים מאותם שאמרנו בין במחלק בין במחולק ואחר שיהיו בידינו המחלק והמחולק נחלק במחולק המחלק ויצא לנו מספר שביעי* והוא מה שבקשנו ואם כן יש לנו עתה ד' מספרים מתיחסים באופן רביעי שהיחס שימצא בין הראשון והשני אותו יחס ימצא בין השלישי והרביעי
|
|
|
ומופת נחליף היחסים בדרך זה והוא שנקח הג' מספרים בזה הסדר והוא שנעשה מהמספר הג' שיש בידינו מספר ראשון ומהמספר הרביעי נעשה שני ומהמספר הראשון שלשי ונסדרם כמו שלמעלה ונאמ' אם זה שוה זה כמה שוה זה ואם יצא לנו במספר הד' בסדר זה המספר שהיה שני בסדר הראשון אז נדע שהמספר הרביעי שיצא בסדר הראשון היה אמתי ואם לא לא וזה מספיק בזה הלימוד
|
Chapter Four: Proportions of Fractions – finding the fourth number
|
הפרק הרביעי בנתינת משל אחד כולל לכל אופני הלמוד במחלק ובמחולק בידיעת יחסי השברים
|
|
|
וכדי להוסיף ביאור נתן משל לכל חלקי הלמוד ביחד ר"ל מהמחלק והמחולק והמופת שלהם וזה באחד מן הדרכים שאמרנו
|
|
|
והוא זה אם שוים כמה שוים ו'
|
- denominator:

|
וראשונה נוציא המחלק כך שנכה הב' שהיא על הג' מהמספר הראשון על ב' שהיא תחת א' של מספר שני ויהיו ד' וזהו המחלק ונשמור אותו
|
- numerator:
![\scriptstyle{\color{blue}{\left[\left[\left(4\sdot2\right)+1\right]\sdot6\right]\sdot3=\left[\left(8+1\right)\sdot6\right]\sdot3=\left(9\sdot6\right)\sdot3=54\sdot3=162}}](/mediawiki/images/math/5/8/e/58ef7f28670af1c26a23f2c27ed973e1.png)
|
ואחר נעשה המחולק כך שנכה ד' מהמספר השני על ב' שהיא תחת הא' שבצדה ויעלה ח' ונוסיף עוד הא' שעל הב' מהמספר השני ויעלה ט' ואלו נכם עוד על ו' שהוא מספר שלשי ויעלה נ"ד עוד נכם על ג' שהיא תחת ב' של מספר ראשון ויעלה קס"ב וזהו המחולק
|
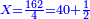
|
ונחלק אלו במחלק שהוא ד' ויצא מהחלוק מ' וחצי וזהו המספר הד' ששוים ו' המבוקש
|
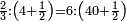
|
והיחס שיש בין שתי שלישיות לד' וחצי וזהו המספר הד' ששוים למ' וחצי
|
|
|
והמופת לדעת אם זה אמת נסדרם ככה ונאמר אם ו' שוים מ' וחצי כמה שוים
|
- denominator:
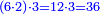
|
נעשה המחלק כך נכה המספר הראשון שהוא ו' על ב' שהיא תחת הא' של מספר שני יהיו י"ב ואלו הי"ב נכם בג' שהיא תחת ב' של מספר שלשי ויעלה ל"ו וזהו המחלק
|
- numerator:
![\scriptstyle{\color{blue}{\left[\left(40\sdot2\right)+1\right]\sdot2=\left(80+1\right)\sdot2=81\sdot2=162}}](/mediawiki/images/math/b/e/b/bebc782632c636f73d7f310f70b46727.png)
|
ואחר נעשה המחולק בדרך זה נכה המ' שהוא מהמספר השני על ב' שהיא תחת א' שבצדה ויעלה פ' ונוסיף א' שהיא על ב' של מספר שני ויעלה פ"א ונכם בב' שעל הג' של מספר שלשי ויעלה קס"ב וזהו המחולק
|
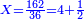
|
ונחלקהו בל"ו שהוא המחלק ויצא מהחלוק ואלו הד' וחצי היה המספר השני של סדר ראשון שאמרנו וזה המופת יורה שהסדר הראשון שעשינו היה אמתי
|
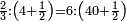
|
א"כ אם ב' שלישיות שוות ד' וחצי הו' שוים מ' וחצי וזה מה שרצינו
|
|
|
ומשל אחר להוסיף ביאור אם ט' שוים כמה שוים ח'
|
- denominator:
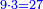
|
ונעשה המחלק בשנכה הט' שהוא המספר הראשון על הג' שתחת ב' מהמספר השני ויעלה כ"ז וזהו המחלק
|
- numerator:

|
ונעשה המחולק ככה בשנכה הח' שהוא מספר שלשי בב' שעל הג' של מספר שני ויעלה י"ו וזהו המחולק
|
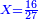
|
ונחלק הי"ו על כ"ז שהוא המחלק ויצא מהחלוק י"ו חלקים מכ"ז בשלם וזהו המספר הרביעי שרצינו לדעת
|
|
|
ולמופת זה נאמ' אם ח' שוים י"ו כמה שוים ט'
|
- denominator:
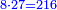
|
ונעשה המחלק בשנכה הח' שהוא מספר ראשון מזה הסדר על כ"ז שתחת י"ו של מספר שני ויעלה רי"ו וזהו המחלק ונשמור אותו
|
- numerator:
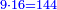
|
והמחולק נעשה בשנכה הט' על י"ו שהוא על הקו של מספר שני ויעלו קמ"ד וזהו המחולק
|
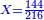
|
ונחלקהו במחלק שהוא רי"ו ויצא מהחלוק קמ"ד חלקים מרי"ו חלקים של שלם והנה לך צורתו ואם יהיה זה שוה לב' שלישיות של מספר שני של סדר ראשון מה שעשינו הוא אמת
|
|
|
ומופת שהם שוים שני שלישיות הוא זה שנכתוב ב' שלישיות בדרך זה והמספר שרצינו לדעת אם הוא ב' שלישיות נכתוב כנגדו כמו שאתה רואה ואח"כ כל אות עם סותרו ואם ב' ההכאות יהיו שוות השברים הם שוים כמו שאמרנו וא"כ הסדר שעשינו הוא אמתי וזה מה שרצינו
|
|
|
דע שזה המופת מהשברים שעשינו הוא כולל לכל שני שברים כשנרצה לדעת אם הם שוים וזה מה שרצינו
|
Chapter Five: finding the whole from a given sum of its part using double false position
|
הפרק החמישי בנתינת דרכים כוללים לדעת אי זה מספר שיהיה בלתי ידוע בדרך המתנגדים
|
|
|
וזה יודע בג' דרכים כוללים בעבור שבהם יעשו כאלה היחסים וזולתם אי זה שיהיו ויקראו דרכי המתנגדות
|
|
|
והראשון הוא זה נניח שרצינו למצא אי זה כל שקיבוץ שלישיתו וחמישתו יחד הם עשרה
|
- false position (1):
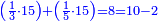
|
וקודם כל דבר נבקש אי זה מספר שימצאו בו אלו השברים [והמספר שנמצא בו אלו הנזכרים הוא ט"ו] וקבוץ שלישיתו וחמישיתו יחד הוא ח' ואלו הם פחות מהמבוקש שנים
|
- false position (2):
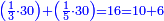
|
ונקח מספר אחר שהוא ל' ונראה שקבוץ שלישיתו וחמישיתו הוא י"ו וא"כ יהיו יותר מהמבוקש ו'
|
- denominator:
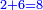
|
ועתה נניח כל זה בדרך צורה כן והראשון שצריך שנבקש יחד הם היותר והפחות שהם ב' וו' וזה יהיה המחלק ונשמור אותו
|
- numerator:
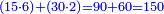
|
ואחר נעשה המחולק כן שנכה המתנגדים כל אחד עם נגדו כמו ט"ו עם ו' ויעלה צ' ונכה עוד ל' עם ב' ויעלה ס' ונחבר צ' עם ס' ויהיו ק"ן
|
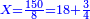
|
ונחלקם במחלק שהוא ח' ויצא מהחלוקה י"ח וג' רביעיות וזהו המספר שקבוץ שלישיתו וחמישיתו יחד יוד וזה מה שרצינו בדרך הראשון
|
|
|
הדרך הב' והוא שהשני מספרים שאנו צריכים בדרך הזה למצא בהם השברים המבוקשים צריך שיהיה כל אחד פחות מקבוץ ה' חלקים הכל המבוקשים
|
|
|
המשל רצינו למצא מספר שקבוץ שלישיתו ורביעיתו יהיה כ'
|
- false position (1):
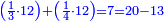
|
נבקש מספר אחד שימצא בו שליש ורביע והוא י"ב וקבוץ שלישיתו ורביעתו ז' א"כ הוא פחות מקבוץ השברים י"ג
|
- false position (2):
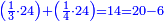
|
ונקח עוד מספר אחר שימצא בו שליש ורביע והוא כ"ד וקבוץ שלישיתו ורביעיתו הם י"ד אם כן הוא פחות מהמבוקש ו'
|
|
|
ואח"כ נאמר י"ב פחות י"ג וכ"ד פחות ו'
|
|
|
וכמו שלמעלה עשינו מחלק מהיותר והפחות בכאן צריך שנעשה מחלק מהפחות ומהפחות והם י"ג וו'
|
- denominator:
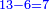
|
וכמו שלמעלה קבצנו היותר והפחות לעשות המחלק בכאן צריך שנחסר לעשות המחלק ואכ"כ נחסר ו' מי"ג וישארו ז' וזהו המחלק ונשמור אותו
|
- numerator:
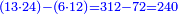
|
ואחר נכה המתנגדים כאמור למעלה והם י"ג עם כ"ד ויעלו שי"ב ונכה עוד ו' עם י"ב ויעלו ע"ב ונחסר ע"ב משי"ב וישארו לך ר"מ וזהו המחולק
|
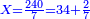
|
ונחלק במחלק שהוא ז' ויצא מהחלוקה ל"ד וב' שביעיות והנה לך צורתו
|
|
|
הדרך השלישי והוא שכל אחד משני המספרים שברים נבקש השברים צריך שיהיה יותר
|
|
|
המשל רצינו למשול מספר אחד שרביעיתו ושלישיתו יהיה ו'
|
- false position (1):
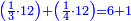
|
נבקש מספר שימצא בו שליש ורביע והוא י"ב וקבוץ שלישיתו ורביעיתו הוא אחד יותר מהמבוקש
|
- false position (2):
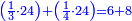
|
ונבקש ג"כ מספר שהוא כ"ד והוא ח' יותר מהמבוקש ונחסר היותר קטן מהגדול והגדול הוא ח' והקטן הוא א'
|
- denominator:
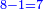
|
ונחסר א' מח' וישארו ז' וזהו המחלק
|
- numerator:
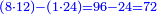
|
ויעשה המחולק כן נכה המתנגדים הח' על הי"ב ויעלו צ"ו ונכה הא' על הכ"ד ויעלו כ"ד ונחסר כ"ד מצ"ו וישארו ע"ב
|
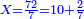
|
ונחלקם במחלק שהוא ז' ויצא מחלוקתו וזהו המספר שלישיתו ורביעיתו מקובץ באחד שוה ששה [והנה] זאת היא צורתו
|
|
|
למוד אחר מיחסים אם ישאל שואל אם כששוה מדת הקמח י"ב לבנים גזר המלך שית[נו] ח' ליטרין לחם בלבן כששוה המדה י"א לבנים כמה ראוי שיתנו לפי אותו היחס
|
|
|
נעשה כן שנניח דרושינו זה [על] שרש התיחסות הג' מספרים וזה בשנסדר המספר הראשון על שווי האחרון ר"ל לשווי הי"א לבנים והמספר השני נסדר על שווי הראשון ר"ל שווי הי"ב והמספר השלישי כמות הלחם ונאמר א"כ י"ב שוים י"א כמה שוים ח' ונשלים הלמוד כמו שהוא כתוב בדרכי היחסים וזה מה שרצינו
|
|
|
שאלה אם כשהשקל שוה מ' לבנים ואדם אחד יש לו חתיכת זהב שוקל ה' שקלים ורוצה להחליף ממנו כל כך שקלים שהנשארים יהיו שוים ללבנים ר"ל כמות השקלים הנשארים לו ככמות הלבנים שלקח מהחלוק
|
|
|
נעשה כן נקח שווי השקל שהוא מ' לבנים ונוסיף א' ויהיו מ"א ונחלק מאה במ"א ויבאו ב' וי"ח ממ"ג של שקל וכל כך שקלים צריך להחליף וזה מה שרצינו
|
Chapter Seven: Word Problems
|
הפרק השביעי בקצת שאלות ותשובות
|
|
|
שאלה אם מכפלו של אי זה דבר נקח י"ב ומכפל הנשאר נקח גם י"ב אחרים וכפל הנשאר יהיה י"ב כמה היה המספר הראשון
|
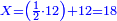
|
התשובה נקח מהמספר הידוע שהוא י"ב חציו ונחבר אליו המספר המוסד שהוא הי"ב והם י"ח וזה המספר שבקשנו תחלה
|
|
|
ובדרך זה נוכל לומר כל מספר שיהיה בין של שלמים בין של שברים בין מעט בין רב
|
|
|
שאלה אם מאיזה כמות ילקח חציו ואחד יותר ומהנשאר חציו ויותר אחד ומהנשאר שלישית חציו ויותר אחד ונשאר אחד כמה היה המספר הראשון
|
|
|
התשובה נקח האחד שנשאר באחרונה ויותר א' ונכפול אותם ויהיו ד' ונוסיף אותם עליהם עוד אחד ויהיו י"א ונכפלם ויהיו כ"ב וזהו המספר הראשון שנשאל עליו ובדרך זה תוכל לעשות ואע"פ שתוסיף בכל פעם במקום האחד שנים או שלשה או מה שתרצה
|
- Shared Work Problem - Draining a Vessel - Barrel - with three holes. Through one hole it is drained in a half of a day. Through the second hole, it [is drained] in a two thirds of a day. Through the third hole, it [is drained] in a three quarters of a day. When it is drained through the three holes together, how long will it take [the barrel] to be drained?
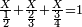
|
שאלה אם יהיה חבית אחת ויהיו לה שלשה נקבים שבאחד יורק בחצי היום ובנקב השני בב' שלישי היום ובנקב השלישי בג' רביעי יום כשיורק בשלשה הנקבים יחד בכמה זמן יורק
|
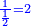
|
תשובה נאמר כן באותו נקב שיורק בחצי יום יורקו שנים ביום אחד
|
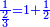
|
ובנקב שיורק בב' שלישי יום יורקו ביום אחד אחת וחצי
|
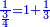
|
ובנקב שיורק בג' רביעיות יורקו ביום אחד חבית אחת ושליש
|
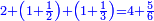
|
ועתה נחבר כל אלו הג' מספרים ויהיה קבוצם ד' חביות וה' ששיות
|
|
|
ואח"כ נאמר בדרך שכך שוה כך כמה שוה כך
|
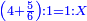
|
אם ד' חביות וה' ששיות של חבית שוות יום אחד כמה שוה חבית אחת
|
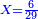
|
ונשלים הדרך וימצא ששות ו' חלקים כ"ט מיום אחד
|
|
|
שאלה אם יהיו ג' מספרים וראשון ושני יהיו בכמות השלישי וראשון ושלישי בכמות מן השני כמה יהיה שוה כל אחד מהשלשה מספרים
|
|
|
התשובה נניח שאלו השלשה מספרים הם חלקי דבר אחד ונניח עוד שהמספר הראשון והשני הם חצי אותו דבר והשלישי הוא חציו האחד ונאמר אם ראשון ושלישי הם מאה מהשני יראה שהשני הוא אחד ממאה ואחד מחלקי הכל ואם הראשון עם השני הם חצי הכל א"כ נאמר שההבדל שיש בין חלק אחד ממאה ואחד מחלקי הכל ובין חצי הכל הוא שווי המספר הראשון אבל ההבדל הוא צ"ט חלקים ממאתים ושנים מהכל אם כן נאמר שהמספר הראשון הוא צ"ט חלקים מר"ב מהכל ואם הכל הוא ר"ב יהיה המספר השני ב' שהוא חלק אחד ממאה ואחד מהכל הנזכר שהוא ר"ב ובעבור שהמספר השלישי הוא חצי הכל והכל הוא ר"ב אם כן יהיה המספר השלישי מאה ואחד שהוא חצי הכל וזה מה שרצינו ועתה יש לנו שלשה מספרים הראשון צ"ט והשני ב' והשלישי ק"א ואם נחבר המספר הראשון והשלישי יעלה ר' שהם מאה מהשני ובזה הדרך נוכל לעשות מכל המספרי' המתיחסים בזה היחס ואם היו יותר או פחות וזה מה שרצינו בזה
|
|
|
שאלה אם יהיו שלשה אנשים בחברה אחת וחצי הריוח יהיה ראוי לא' ושלישית הריוח לשני ורביעית הריוח לשלישי והריוח יהיה י"ב כמה יבא לכל אחד מהם
|
|
|
התשובה צריך שתדע שאם נתן לא' החצי מזה המספר ר"ל הי"ב ושלישיתו לאחד ורביעיתו לאחר לא יספיקו ולכן צריך שתעשה בדרך זה שלמי שראוי החצי יקח פחות וכן השני והשלישי ויהיה בדרך זה שנקח אי זה מספר שנרצה שימצאו בו חצי ושלישי ורבע כמו י"ב או כ"ד או ל"ו או אי זה שיהיה ונקח חציו ושלישיתו ורביעיתו ונקבצם יחד וזה הקבוץ יקרא מספר ראשון והריוח יהיה מספר שני וכל אחד מחלקי המספר המקובץ יהיה מספר שלישי וכשיהיו בידינו אלו המספרים נסדרם בדרך שאם זה שוה זה
|
|
|
המשל שנאמר אם כל המקובץ שוה ככל הריוח כמה שוה ו' וחצי
|
|
|
ר"ל אם י"ג שוים י"ב כמה שוים ו' ושליש היחס ונמצא ששוה ה' וז' מי"ג ואחר נחזור ונאמר אם כל המקובץ ששוה שוה כל הריוח כמה שוה השליש ר"ל אם י"ג שוים י"ב כמה שוים ד' ונמצא ששוים ג' וט' מי"ג ונחזור עוד ונאמר אם כל המקובץ שוה כל הריוח כמה שוה הרובע ר"ל אם י"ג שוים י"ב כמה שוים ג' ונמצא ששוים וזה מה שרצינו
|
|
|
שאלה איך יחלקו עשרה בשני חלקים שהאחד נחלק לאחד וי' מי"ג שיצאו מהחלוקה ה'
|
|
|
ולדעת זה צריך שנקדים שתי הקדמות כוללות
|
|
|
ההקדמה הראשונה היא שכמו שכל מחולק נחלק במחלק יוליד החלק כן ג"כ כשנחלק המחולק על החלק יוליד המחלק
|
|
|
ההקדמה השנית היא שמספר החלק ומספר היחס המחולק למחלק שוים
|
|
|
המשל אם נחלק י' על ב' יהיה החלק ה' ומספר יחס המחולק למחלק ה' כי י' הם ה' פעמים ב' וזהו יחס המחולק למחלק וא"כ המחולק הוא ביחס ה' והחלק ה' בלתי היחס וא"כ במה שיש לכל אחד שם של ה' הם שוים וזה מה שרצינו
|
|
|
התשובה היא שנקח במחשבתנו חלק אחד מעשרה בלתי ידוע ויהיה שמו דבר אחד והי' בלתי דבר אחד יהיה המחולק ולפי ההקדמה השנית יהיה שוה לה' שהוא החלק וא"כ אם י' בלתי דבר אחד שוה לה' עם דבר אחד יהיה יותר מה' דבר אחד ובעבור שיהיו שוים החלק והמחולק נוסיף דבר אחד על הה' שהוא החלק ויהיו ו' ואחר שהמחולק והחלק הם שוים נחלק המחולק על החלק ויצא מהחלק שבקשנו שהוא א' ושני שלישיות וזהו הדבר האחד הבלתי ידוע שלקחנו מהעשרה ומה שנשאר עד תשלום י' שהם ח' ושליש המחולק והם ג"כ העשרה בלתי דבר שיהיה ג"כ מספר בלתי ידוע כמו שאמרנו ועתה אם נחלק ח' ושליש א' ושני שלישיות יבא לחלק ה' ואלו השני מספרים המחולק והמחלק הם עשרה וזהו מה שרצינו וכמו שאמרנו בעשרה להיות החלק ה' נוכל לומר גם כן אי זה מספר שנרצה בשנשמור היחסים הראויים לאותו מספר כמו שעשינו בזה המשל כי כמו שלקחנו לחלק ה' מי' נקח לחלק כ"ז משלשים ונעשה כאמור ותמצא באותו דרך שהמחלק הוא והמחלק כ"ח והחלק כ"ז כמו שידעתו וזהו מה שרצינו לזה
|
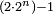
![\scriptstyle2^n\sdot\left[\left(2\sdot2^n\right)-1\right]](/mediawiki/images/math/b/e/d/bed5e2c1c4b911a165a80a26323b01e6.png) is a perfect number
is a perfect number
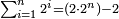
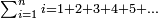
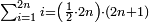
![\scriptstyle\sum_{i=1}^{2n-1} i=\left[\left[\frac{1}{2}\sdot\left(2n-1\right)\right]+\frac{1}{2}\right]\sdot\left(2n-1\right)](/mediawiki/images/math/e/5/f/e5f7eed9ad497158078a947782b7d590.png)
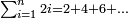
![\scriptstyle\sum_{i=1}^n 2i=2+4+6+\ldots=\left(\frac{1}{2}\sdot2n\right)\sdot\left[\left(\frac{1}{2}\sdot2n\right)+1\right]](/mediawiki/images/math/a/8/2/a82f446b63509836f1780f83ae5e3f46.png)
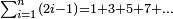
![\scriptstyle\sum_{i=1}^n \left(2i-1\right)=1+3+5+7+\ldots=\left[\left[\frac{1}{2}\sdot\left(2n-1\right)\right]+\frac{1}{2}\right]^2](/mediawiki/images/math/4/b/7/4b709fc93951248c53ba452ce06603dc.png)
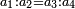
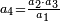
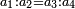
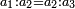
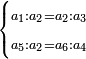
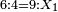
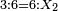
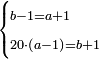
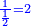
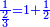
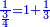
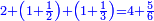
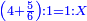
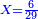
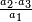
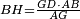
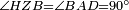
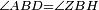
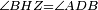
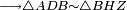
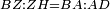
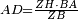
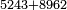
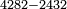
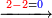
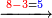
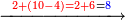
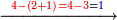
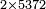
![\scriptstyle{\color{blue}{2\sdot\left[\left(2\sdot2\right)-1\right]=2\sdot3=6}}](/mediawiki/images/math/4/a/d/4ad7cfaee668178995b5434ddc6e77ea.png)
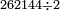
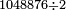
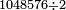
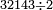
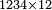
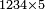
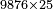
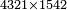
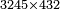
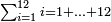
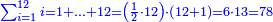
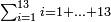
![\scriptstyle{\color{blue}{\sum_{i=1}^{13} i=1+\ldots+13=\left[\left(\frac{1}{2}\sdot13\right)+\frac{1}{2}\right]\sdot13=\left[\left(6+\frac{1}{2}\right)+\frac{1}{2}\right]\sdot13=7\sdot13=91}}](/mediawiki/images/math/9/c/e/9ceefc6ebbbdf0e0aca92452d5ae2149.png)
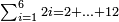
![\scriptstyle{\color{blue}{\sum_{i=1}^6 2i=2+\ldots+12=\left(\frac{1}{2}\sdot12\right)\sdot\left[\left(\frac{1}{2}\sdot12\right)+1\right]=6\sdot\left(6+1\right)=6\sdot7=42}}](/mediawiki/images/math/9/7/8/978a671a457a4cc584dd6a7ba9ad5c41.png)
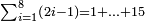
![\scriptstyle{\color{blue}{\sum_{i=1}^8 \left(2i-1\right)=1+\ldots+15=\left[\left(\frac{1}{2}\sdot15\right)+\frac{1}{2}\right]^2=\left[\left(7+\frac{1}{2}\right)+\frac{1}{2}\right]^2=8^2=64}}](/mediawiki/images/math/b/1/4/b14585548b5c68a04f29b88716c0bc65.png)
![\scriptstyle a<b<10\longrightarrow a\times b=\left(10\sdot a\right)-\left[\left(10-b\right)\sdot a\right]](/mediawiki/images/math/0/8/f/08f332539dacd4cdb6b5d5486e9e076e.png)
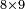
![\scriptstyle{\color{blue}{8<9<10\longrightarrow8\times9=\left(10\sdot8\right)-\left[\left(10-9\right)\sdot8\right]=80-\left(1\sdot8\right)=80-8=72}}](/mediawiki/images/math/a/d/a/ada688c8cf4727a759a5ff8758b8791c.png)
![\scriptstyle a<b<10\longrightarrow a\times b=\left(10\sdot b\right)-\left[\left(10-a\right)\sdot b\right]](/mediawiki/images/math/6/a/e/6aeb543ebf851f38f0e5cd03c35b0477.png)
![\scriptstyle{\color{blue}{8<9<10\longrightarrow8\times9=\left(10\sdot9\right)-\left[\left(10-8\right)\sdot9\right]=90-\left(2\sdot9\right)=72}}](/mediawiki/images/math/1/2/f/12f368ec55a5ad7b76fdc2460670353e.png)
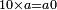
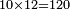
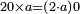
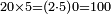
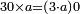
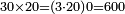
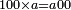
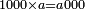
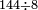


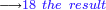
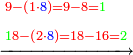
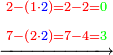








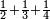
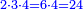
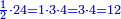
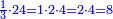
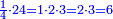
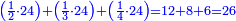
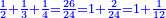
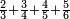
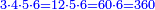
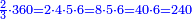
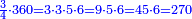
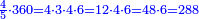
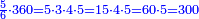
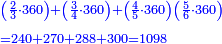
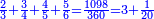
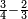



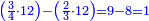
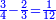
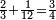
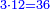
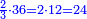
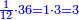
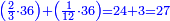
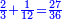
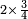
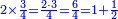
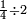
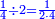
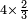

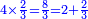
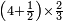

![\scriptstyle{\color{blue}{\left[\left(4\sdot2\right)+1\right]\sdot2=\left(8+1\right)\sdot2=9\sdot2=18}}](/mediawiki/images/math/f/6/7/f6776cd569ed49e4aa40be43566a259b.png)
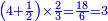
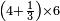
![\scriptstyle{\color{blue}{\left[\left(4\sdot3\right)+1\right]\sdot6=\left(12+1\right)\sdot6=13\sdot6=78}}](/mediawiki/images/math/1/d/9/1d9b723c3e6844776f2e70d9c40e3d4c.png)
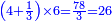
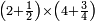
![\scriptstyle{\color{blue}{\left[\left(4\sdot4\right)+3\right]\sdot\left[\left(2\sdot2\right)+1\right]=\left(16+3\right)\sdot\left(4+1\right)=19\sdot5=95}}](/mediawiki/images/math/b/2/f/b2f0b8a3dfc87ea96c0d2ca487f51a03.png)
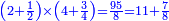
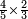
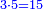
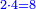
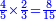
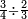

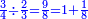
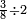
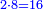
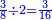
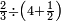
![\scriptstyle{\color{blue}{\left[\left(4\sdot2\right)+1\right]\sdot3=\left(8+1\right)\sdot3=9\sdot3=27}}](/mediawiki/images/math/e/8/e/e8e4a046900922c7247cf2a2064e18a7.png)

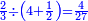
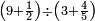
![\scriptstyle{\color{blue}{\left[\left(5\sdot3\right)+4\right]\sdot2=\left(15+4\right)\sdot2=19\sdot2=38}}](/mediawiki/images/math/5/a/2/5a22144368ac484b03473dc5faaf74b3.png)
![\scriptstyle{\color{blue}{\left[\left(9\sdot2\right)+1\right]\sdot5=\left(18+1\right)\sdot5=19\sdot5=95}}](/mediawiki/images/math/8/2/1/82111221272aefe0d07464888b030a03.png)
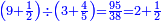
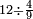
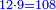
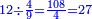
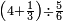

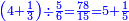
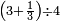
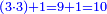
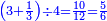
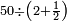
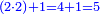

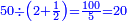
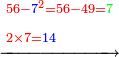
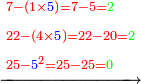
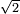
![\scriptstyle2^3=2\sdot2^2=2\sdot4=8\longrightarrow\sqrt[3]{8}=2](/mediawiki/images/math/d/6/a/d6a25a0e3295cb972ba58ad4251c3a45.png)
![\scriptstyle3^3=3\sdot3^2=3\sdot9=27\longrightarrow\sqrt[3]{27}=3](/mediawiki/images/math/2/c/9/2c9f0aa3f25282fafe4c76ae8e2c191a.png)
![\scriptstyle10^3=10\sdot10^2=10\sdot100=1000\longrightarrow\sqrt[3]{1000}=10](/mediawiki/images/math/d/b/7/db752fe191a69252d969a11fa49648b0.png)
![\scriptstyle\sqrt[3]{12167}](/mediawiki/images/math/a/b/c/abc38f531fb13e4a1ec9492e6194fa3a.png)
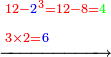
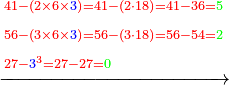
![\scriptstyle\longrightarrow{\color{Violet}{the\ result\ \sqrt[3]{12167}=23}}](/mediawiki/images/math/5/4/5/545f29847e0149872f407d5a9d9b295d.png)
![\scriptstyle\sqrt[3]{571787}](/mediawiki/images/math/3/e/8/3e8cc95dfa131c676806e901de31e5fc.png)
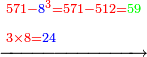
![\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{59-\left(8\times2\times{\color{blue}{3}}\right)=59-\left(8\sdot6\right)=59-48=}}{\color{green}{11}}\\&\scriptstyle{\color{red}{117-\left[\left(8\times4\times{\color{blue}{3}}\right)+\left(3\times2\times{\color{blue}{3}}\right)\right]=}}\\&\scriptstyle{\color{red}{117-\left[\left(8\sdot12\right)+\left(3\sdot6\right)\right]=}}\\&\scriptstyle{\color{red}{117-\left(96+18\right)=117-114=}}{\color{green}{3}}\\&\scriptstyle{\color{red}{38-\left(3\times4\times{\color{blue}{3}}\right)=38-\left(3\sdot12\right)=38-36=}}{\color{green}{2}}\\&\scriptstyle{\color{red}{27-{\color{blue}{3}}^3=27-27=}}{\color{green}{0}}\\\end{align}}](/mediawiki/images/math/2/5/6/25659b3c9703b5f4b750226970caf7e4.png)
![\scriptstyle\longrightarrow{\color{Violet}{the\ result\ \sqrt[3]{571787}=83}}](/mediawiki/images/math/c/b/4/cb4c1436cb7a06ebcd99307287954f67.png)
![\scriptstyle\sqrt[3]{12812904}](/mediawiki/images/math/0/7/a/07aafd0c5fd061d54bb34d4011050183.png)

![\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{64-\left(2\times6\times{\color{blue}{4}}\right)=64-\left(2\sdot24\right)=64-48=}}{\color{green}{16}}\\&\scriptstyle{\color{red}{165-\left[\left(3\times6\times{\color{blue}{4}}\right)+\left(2\times9\times{\color{blue}{4}}\right)\right]=}}\\&\scriptstyle{\color{red}{165-\left[\left(3\sdot24\right)+\left(2\sdot36\right)\right]=}}\\&\scriptstyle{\color{red}{165-\left(72+72\right)=165-144=}}{\color{green}{21}}\\&\scriptstyle{\color{red}{219-\left[\left(4\times6\times{\color{blue}{4}}\right)+\left(3\times9\times{\color{blue}{4}}\right)\right]=}}\\&\scriptstyle{\color{red}{219-\left[\left(4\sdot24\right)+\left(3\sdot36\right)\right]=}}\\&\scriptstyle{\color{red}{219-\left(96+108\right)=219-204=}}{\color{green}{15}}\\&\scriptstyle{\color{red}{150-\left(4\times9\times{\color{blue}{4}}\right)=150-\left(4\sdot36\right)=150-144=}}{\color{green}{6}}\\&\scriptstyle{\color{red}{64-{\color{blue}{4}}^3=64-64=}}{\color{green}{0}}\\\end{align}}](/mediawiki/images/math/e/b/e/ebe0f4df388bc732084130a719026f81.png)
![\scriptstyle\longrightarrow{\color{Violet}{the\ result\ \sqrt[3]{12812904}=234}}](/mediawiki/images/math/7/b/1/7b16bd7f1fdac314a617c85aee43a714.png)
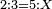
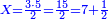
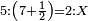
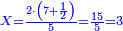
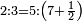
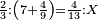
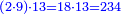
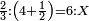
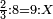
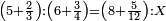
![\scriptstyle{\color{blue}{\left[\left[\left(5\sdot3\right)+2\right]\sdot4\right]\sdot12=\left[\left(15+2\right)\sdot4\right]\sdot12=\left(17\sdot4\right)\sdot12=68\sdot12=816}}](/mediawiki/images/math/b/e/6/be6fd06595fca39aacff31a9abeeba9f.png)
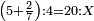

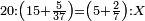
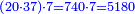
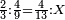
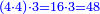
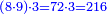
![\scriptstyle{\color{blue}{\left[\left[\left(6\sdot4\right)+3\right]\sdot\left[\left(8\sdot12\right)+5\right]\right]\sdot3=\left[\left(24+3\right)\sdot\left(96+5\right)\right]\sdot3=\left(27\sdot101\right)\sdot3=2727\sdot3=8181}}](/mediawiki/images/math/3/3/e/33e6307a5615be5658beefa98b9c1160.png)
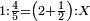
![\scriptstyle{\color{blue}{\left[\left(2\sdot2\right)+1\right]\sdot4=\left(4+1\right)\sdot4=5\sdot4=20}}](/mediawiki/images/math/9/4/3/9438da687c558cf44b88afb73ca06ee9.png)
![\scriptstyle{\color{blue}{\left[\left[\left(4\sdot2\right)+1\right]\sdot6\right]\sdot3=\left[\left(8+1\right)\sdot6\right]\sdot3=\left(9\sdot6\right)\sdot3=54\sdot3=162}}](/mediawiki/images/math/5/8/e/58ef7f28670af1c26a23f2c27ed973e1.png)
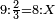

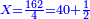
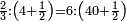
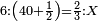
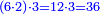
![\scriptstyle{\color{blue}{\left[\left(40\sdot2\right)+1\right]\sdot2=\left(80+1\right)\sdot2=81\sdot2=162}}](/mediawiki/images/math/b/e/b/bebc782632c636f73d7f310f70b46727.png)
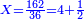
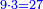
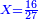
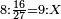
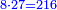
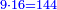
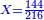
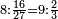
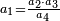
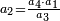
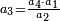
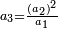
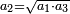
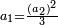
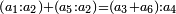
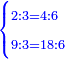
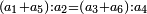

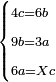

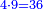
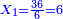

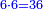

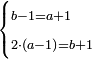
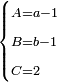

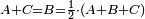

![\scriptstyle\begin{align}\scriptstyle C&\scriptstyle=\left(A+C\right)-A\\&\scriptstyle=\left[\frac{1}{2}\sdot\left(A+B+C\right)\right]-\left[\frac{1}{3}\sdot\left(A+B+C\right)\right]\\&\scriptstyle=\left(\frac{1}{2}-\frac{1}{3}\right)\sdot\left(A+B+C\right)\\&\scriptstyle=\frac{1}{6}\sdot\left(A+B+C\right)\\\end{align}](/mediawiki/images/math/7/7/a/77aa161a1aeee2a190f0bf30e79ea6ed.png)
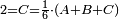
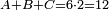
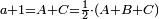
![\scriptstyle a=\left[\frac{1}{2}\sdot\left(A+B+C\right)\right]-1=\left(\frac{1}{2}\sdot12\right)-1=5](/mediawiki/images/math/1/5/e/15e5878b000cfc94c7af54ca81c6ff3a.png)
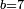
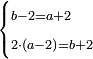
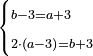
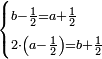
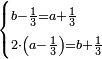
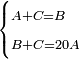
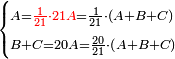
![\scriptstyle\begin{align}\scriptstyle C&\scriptstyle=\left(A+C\right)-A\\&\scriptstyle=\left[\frac{1}{2}\sdot\left(A+B+C\right)\right]-\left[\frac{1}{21}\sdot\left(A+B+C\right)\right]\\&\scriptstyle=\left(\frac{1}{2}-\frac{1}{21}\right)\sdot\left(A+B+C\right)\\&\scriptstyle=\frac{19}{42}\sdot\left(A+B+C\right)\\\end{align}](/mediawiki/images/math/f/5/2/f52cf75a882cc3288802493ce7b1ad5f.png)
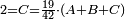
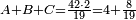
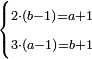
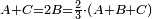
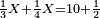
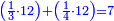
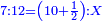
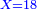
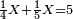
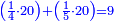
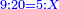
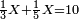
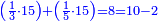
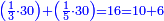
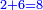
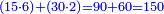
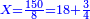
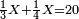
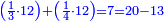
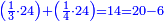
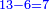
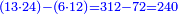
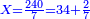
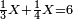
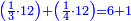
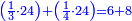
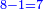
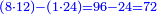
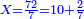
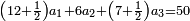
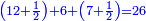
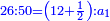
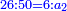
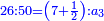
![\scriptstyle2\sdot\left[\left[2\sdot\left(2X-12\right)\right]-12\right]=12](/mediawiki/images/math/2/e/6/2e6830e9068e310a2b310a61c4dc1e73.png)
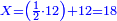
![\scriptstyle\begin{align}&\scriptstyle\left[\left[X-\left(\frac{1}{2}X+1\right)\right]-\left[\left[\frac{1}{2}\sdot\left[X-\left(\frac{1}{2}X+1\right)\right]\right]+1\right]\right]\\&\scriptstyle-\left[\left[\frac{1}{2}\sdot\left[\left[X-\left(\frac{1}{2}X+1\right)\right]-\left[\left[\frac{1}{2}\sdot\left[X-\left(\frac{1}{2}X+1\right)\right]\right]+1\right]\right]\right]+1\right]\\&\scriptstyle=1\\\end{align}](/mediawiki/images/math/b/a/e/bae2ae7c214bb9c33b783f1eb83909e8.png)