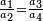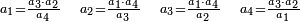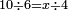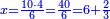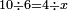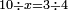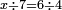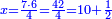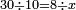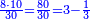ספר יסודי התבונה ומגדל האמונה
Contents
[hide]- 1 Introduction
- 2 Book One – the Foundations of Wisdom
- 2.1 Prologue
- 2.2 Foundation One – Mathematics
- 2.2.1 Introduction
- 2.2.2 Section One – Arithmetic
- 2.2.2.1 Introduction
- 2.2.2.2 Part One – Theoretical Arithmetic
- 2.2.2.3 Part Two – Practical Arithmetic
- 2.2.2.3.1 Numeration
- 2.2.2.3.2 The fundamental arithmetical operations
- 2.2.2.3.3 Multiplication of a Number by a Number
- 2.2.2.3.4 Division
- 2.2.2.3.5 Subtraction
- 2.2.2.3.6 Multiplication of Fractions
- 2.2.2.3.7 Division of Fractions
- 2.2.2.3.8 Subtraction of Fractions
- 2.2.2.3.9 Addition of Fractions
- 2.2.2.3.10 Converting of Fractions
- 2.2.2.3.11 Completion of Fractions
- 2.2.2.4 Business Arithmetic
- 2.2.3 Section Two – Geometry
- 2.2.4 Section Three – Music
- 3 Notes
- 4 Apparatus
- 5 Appendix: Bibliography
| זה ספר יסודי התבונה ומגדל האמונה | |
|---|---|
| The book was translated from Arabic to Hebrew by the Spanish sage Abraham bas Ḥiyya ha-Nasi | שנעתק מכתב ערבית ללשון הקדש על ידי הנשיא החכם ר' אברהם ב"ר חייא ז"ל הספרדי |
Introduction |
פתח הספר |
| According Bar Ḥiyya, the following two verses represent the order of studying the sciences | |
| It is written: Thus says the Lord: Let not the wise man boast of his wisdom, nor the brave man boast of his bravery, nor the rich man boast of his riches. But let him that boasts exult in this, that he understands and knows me, for I am the Lord Who practices grace, justice and righteousness on the earth; for in these things I delight, says the Lord.[Jeremiah 9, 22-23] | כתוב כֹּה אָמַר יְהוָה אַל-יִתְהַלֵּל חָכָם בְּחָכְמָתוֹ וְאַל-יִתְהַלֵּל הַגִּבּוֹר בִּגְבוּרָתוֹ וְאַל-יִתְהַלֵּל עָשִׁיר בְּעָשְׁרוֹ. כִּי אִם-בְּזֹאת יִתְהַלֵּל הַמִּתְהַלֵּל הַשְׂכֵּל וְיָדֹעַ אוֹתִי כִּי אֲנִי יְהוָה עֹשֶׂה חֶסֶד ומִשְׁפָּט וּצְדָקָה בָּאָרֶץ כִּי-בְאֵלֶּה חָפַצְתִּי נְאֻם-יְהוָה [note 1] |
| וכתוב תחלת חכמה יראת י' ודעת קדושים בינה[note 2] | |
| וכתוב ויאמר לאדם הן יראת י' היא חכמה וסור מרע בינה[note 3] | |
| Bar Ḥiyya asks why the verses in Jeremiah warn one from praising himself for his wisdom, but allow him the be praised for the knowledge of God | ויכול אדם לשאול על הכתובים האלה איך אמר הכתוב אל יתהלל חכם בחכמתו הזהירו להלל עצמו |
| There are no wisdom and intelligence without the knowledge of God | וידוע וברור הוא לכל אדם שאין חכמה ובינה אלא בדעת אלהים |
| The one who has the knowledge of God should be called wise | והיודע דעת אלהים ראוי הוא להקרא חכם כמו שפרש בכתוב השני ודעת קדושים בינה |
| The two biblical verses supposedly contradict each other: the wise should not praise himself for his wisdom, but one should praise himself for his wisdom | וזה דומה למי שאומר אל יתהלל חכם בחכמתו אבל יתהלל אדם בחכמה ונראה שני הכתובים מכחישין וסותרין זה את זה |
| Ber Ḥiyya discusses the question at length not because it is a difficult question but since it is and issue of wisdom | ואנו משיבים על השאלה הזו ומאריכים בה לא מפני שהשאלה קשה אלא מפני שהוא דבר חכמה ונאה לו לאדם להאריך ולהתעסק בדבר חכמה |
| Wisdom is said in two senses: | ואנו פותחים ראשונה ואומרים כי מלת חכמה נאמרת על שני ענינים |
|
על החכמה שהיא חכמה ממש שאומר עליה הכתוב והחכמה מאין תמצא[note 4] והיא מדע כל הנמצאות על אומד תבניתן ותוכן יצירתם ואומן נתינתן |
|
והוצרכנו לשום בגדר החכמה ג' חוצצים כדי להכניס בגדר הזה ג' מעלות |
|
ויהיה אומד תבנית הנמצאות מכניס בגדר הזה החכמה מעיינת בצורת הנמצאות תבנית גופן כחכמת המנין והדומה לה |
|
ותוכן יצירתם מכניס בו החכמה המעיינת בגופי הנמצאות וסדר יצירתם ככל החכמות המדברות על בנין שמים וארץ ושאר כל היצורים |
|
ואומן נתינתם מכניס בו החכמה המעולה על כל החכמות והיא חכמת התורה נתונה ליראי השם |
|
והמעלות האלה השלוש מסורות כנגד ג' מעלות האמת והאמונה אשר בחכמה |
|
כי החכמה המעיינת בתכליתי הנמצאות וצורתן החיצונה מעיינת בדבר שהדעת מקפת לו מכל צדדין ואין לו מחלוקת בין החכמה והאמת בו מוחזק ואין בו ספקה |
|
והחכמה המעיינת ביצירת הנמצאות וצורתן התיכונה היא חוקרת ובוחנת על דברים נסתרים מהעין ומחוששי הגוף ואין הדעת שולטת עליהם אלא מדרך הסברא ובין אנשי החכמה בה מחלוקות גדולות והאדם רשאי להחזיק בדברי מי שיראו לו דבריו מהחכמה לראית בינתו והישר בעיניו ואין עליו חטא ואשמה ויכול להוציא הוצאה מלבו ולהוסיף ולגרוע בדרך בינתו ולא יהיה במעשה הזה סר מדרך החכמה |
|
והחכמה המעיינת בדברי הקדש היא חכמה מקובלת מרוח הקדש וחוקרת על דברים שאין הדעת מגעת אליהם מעוצם פלואתם ורב נגהם כאשר אין העין יכולה להביט אל מאור השמש בחצי השמים לפי שאורו בהיר וחזק מאור עין האדם |
|
על דרך הזו היא מעלת החכמה שלוש מעלות והגדר אשר שמנו לחכמה כוללם והחכמות האלה נקראות חכמת שכלנית וחכמת השכל |
|
ואת הענין השנית אשר החכמה נאמרת עליו בלשון הקדש היא חכמת האומנות והמלאכות שאדם קונה אותם ולומד לעשותם מבינת לבו כמו שנאמר ויעשו כל חכם לב[note 5] וכל אשה חכמת לב[note 6] כל זה על עושי המלאכה החכמה באמונתי (?) |
|
וגדר החכמה הזו היא כח שאדם יכול להוציא בו במעשה ידיו כל הצורות והתמונות העומדות בתוך לבו ומפני זה נקראת חכמת לב וחכמה עמלנית |
| These two types of wisdom are acquired by man through his rational soul | והאדם קונה שתי החכמות האלה בכח נפשו הדברנית |
| God gave man three souls, or one soul with three faculties: | כי הקב"ה מסר באדם ג' נפשות או נפש אחת שיש לה ג' כוחות אי זה מהן תצרה לג (?) הענין בו אחד במקום הזה וחכמי הגוים מתחלקים בו |
The faculty by which man grows, become fruitful, eat, drink, and desires. By this faculty, a man resembles the field crops and plants |
והנפש האחת מג' היא הכח אשר בו האדם צמח וגדל ופרה ורבה ואוכל ושותה ומתאוה לכל תאוות העולם הזה ובכח הזה הוא דומה לצמח האדמה ולגדולי הארץ |
The faculty of vitality, anger, jealousy, and motion from one place to another. By this faculty, a man resembles the animals and beasts |
והנפש השנית יש לה כוח החיים החמה והקנאה והגבורה והתנועה והטלטול ממקום למקום והאדם דומה בכוח זה לחיות ולבהמות |
The faculty by which a person distinguishes between good and bad, disgrace and praise, truth and false, right and wrong. Thus, the person departs from the animals and resembles the angels. Through this faculty, a man speaks and thinks. |
והנפש השלישית בה יכול אדם להב[ח]ין בין טוב לרע בכל עניני העולם ובין הגנאי והשבח במעשי בני האדם ולהבדיל בין האמת ובין השקר בכל הענינים המובנים בלב ולהכיר הנכון מהכזב בדברת האדם ובדמות האלה נפרד מהחיות ונבדל מהבהמות ודומה למלאכים וגדודי עולם עליוני |
|
ואין משמע הוגה ומדבר בכאן ההגיון היוצא על פה והדבור הנשמע על הלשון אבל הגיון הלב והנפש ודבורם כי מצינו מלת ההגיון נאמר על ההרהורין והמחשבות שבתוך הלב ועל הענינים הנרשמין והנקשרים בנפש |
|
ובכוח הנפש הזו נתקיים גדר האדם ונגבל תחומו המכונן את יצירתו והנותן סמני ההפרש בינו ובין בעלי החיים והוא החי הדובר המת |
|
והחי הוא הכלל הגדול הכונס אותו עם שאר בעלי החיים |
|
והדובר סימן חוצץ בינו ובין כלל הבהמות והחיות והעופות ובין כל החיים שאינם דוברים ומכניסו בכלל המלאכים |
|
והמת סימן אחר חוצץ בינו ובין המלאכים ומכניסו בכלל הבהמות ושאר בעל החיים אשר סוף חיותם למות |
|
ויהיה הדובר בכאן אמור על דבור הלב ועל הבינה שהוא דומה למלאכים בדבורם ועל אשר בו אדם יכול לדבר ולהבין ואלו לא היה פירושו כך לא היה האלם נכנס בגדר האדם מפני שאינו מדבר בפיו והוא נקרא אדם ונכנס בגדר האדם מפני שהוא מבין בלבו |
|
וכן דובר באיכת אתה יכול לאמרו על מה שהוא מדבר באותה שעה ועל מה שעתיד לדבר וכן פירוש כל מה אשר אני דובר כל מה שאני מדבר לך מעתה שאני עתיד לדבר |
|
וכן המת האמור בגדר הזה הבן ממנו שסופו למות ואתה מוצא מלת מת אמורה בלשון הקודש על ב' ענינים |
| The human rational soul is the superior and the ruler of the two other souls. The person whose soul behaves in the right way and its virtues subdue the two other souls is a man who is praised in all his acts. | והנפש הדברנית אשר באדם היא המעולה והשולטת על שתי נפשות אחרות והאדם אשר נפשו הזאת נוהגת על דרכה ועל נכונה ותהיינה מדותיה גוברות על שתי נפשות הנשארות הוא האדם המשובח המפואר בכל מעשיו |
| Each one of the three souls has good virtues by which it is praised and vices by which it is condemned: | וכל נפש ונפש מאלו ג' נפשות יש לה מדות טובות שהיא מתהללת ומדות רעות שהיא מתגנה בהם |
|
ונמצא מהלל הנפש הצמחה היא הצדקות והענוה ושיהיה אדם שולט בראותו ומונע עצמו מתאוות רעות וקניינין מגונים |
|
ומדותיה הרעות כל מה שהוא חלוף הדבר הזה ושיהיה האדם נוטה לתאוות העולם ובוצע להם |
A person cannot control his desire if he has no sufficiency and property in order to stay away from bad possessions |
ואין אדם יכול לשלוט בתאותו אם לא יהיה לו עושר וממון שיהיה יכול להרחיק עצמו מקנינים רעים כי העני המוצרך והרעב נזקק מרב דלותו ועניותו ודחקו לכנס בכל קנין שהוא בא אל ידו אם טוב ואם רע |
|
וכן הנפש החיה יש לה מדות טובות וכנגדה מדות רעות |
|
ומדותיה הרעות אם לא תהיה נשמעת לנפש ההוגה ונכנעת אליה ותהיה הנפש הצמחה לוכדת עליה נכנעת לה |
|
ותהיינה מדותיה הטובות שתהיה שומעת לנפש ההוגה ומקבלת עצמה ושולטת על הנפש הצמחה ושוברת גסותה |
| The vegetative soul is metaphorically compared to a bad tempered beast wishing to eat everything infront of it. | וכל החכמים המשילו הנפש הצמחה לבהמה רעה גסת רוח אשר רצונה לאכול ולהריק כל אשר לפניה |
| The vital soul is metaphorically compared to a bridle on the mouth of that beast, for keeping it away from its lust and leading it to the desired place, and a goad to instruct and guide it. | והמשילו נפש החיה למתג ורסן בפי הבהמה הזאת ואם לא יהיה כח במתג ורסן הזה וחוזק למנעה מתאותה לא יוכל אדם לרכוב הבהמה הגסה ולחסום פיה ולהנהיגה למקום שירצה |
|
ומשם היתה לנפש החיה צריכה לכח וגבורה ותהיה מהללה ופארה הגבורה |
|
והנפש הדברנית צריכה לשני מידות טובות |
|
כדי שתהיה במין האחד מנהגת שתי נפשות האחרות ונותנת להם עצה ותושיה לשמש הגוף בכל צרכי העולם הזה ולתקן על כוחות הגוף ועל מלאכות ואומניות שהם מעסקי העולם והכתוב קרא למדות האלה חכמה |
|
והמין השני הוא המדות שהיא מתקנת בהם עצמה ומייצרת בהם כל כוחות נפשיות אשר באדם וקונה בהם זכות העולם הבא וטובותיו ובמדות האלה יכולה להביט אל כל דבר מופלא ומעולה ממנה והכתוב קרא למין הזה השכל |
| ותמצא לנפש ההוגה שתי מהללות והן חכמה והשכל | |
|
ובא הכתוב ואמר אל יתהלל חכם בחכמתו[note 15] כלומר אל יתהלל אדם במדות נפשו ההוגה המיסרת בהן כח הגוף |
|
אבל רשאי אדם להתהלל בהשכל והיא מדת נפשו ההוגה שהיא מיסרת בהן את עצמה ומבטת על העולם העליון ואין לו להתהלל בהשכל אם לא ידביק לו דעת אלהים מפני שאין אדם יכול להגיע אליה וחכמת לבו אם לא יעזרנו המקום ברוח הקודש לקבל דברי הנביאים הבאה מרוח הקודש |
|
וכל חכמה בלעדיה אינה ראויה להשתבח בה מפני שהיא קנין בני אדם ואיש הקונה אותה ואין מתעסק וטורח בדברי תורה וזריז לעשותן הוא כעור באפלה ותועה בין הכרמים ואינו יודע למצוא הדרך וללכת אל עיר |
|
והקונה יראת השם ותלמוד תורה ואחר יעיין בשאר החכמות ילך בדרך ישרה וימצא אחרית טוב וזהו שאמר הכתוב ראשית חכמה יראת יהוה[note 18] |
|
והירא את השם ועוסק בתורה חייב להתהלל בחלקו ולהדות לקונו ויהיה יודע כי הקב"ה עושה חסד עם האדם ונותן לו דעת ובינה להבין החכמה |
|
ולא אמר אל יתהלל בחכמה
שלא יאמר אדם החכמה שקניתי חכמתי היא ובתבונתי הגעתי אליה |
| Intellect is superior to sufficiency, which is superior to strength, which is superior to wisdom | והמעיין בו עיון יפה יכול לטעון עליו ויאמר כי בפירוש הזה אתה נותן החכם עודף על הגבור כי החכמה מפארת הנפש הדברנית והגבורה מפארת הנפש הבהמית ועושר מפאר הנפש הצמחית ואם אין החכם יכול להתהלל בפאר נפשו הדברנית כל שכן שאין רשאי להתהלל בפאר נפשו הבהמית וכל שכן בפאר נפשו הצמחה המתאוה |
| Strength, sufficiency and craft are attributed also to animals; therefore, it is obvious that a person should not praise himself for these virtues | ועוד שגנאי הדבר שיהיה אדם מתהלל בדבר הנמשל בו כבהמה וצמחי האדמה
כי הגבורה והכח נמצאות בארי ונמר יתר מהאדם וקנין וצבירת מצוי בנמלה ובדבורה וגם המלאכה מצוי בעכביש ובתלעה וברוב עופות וחיות ולא הוצרך הכתוב להזהיר על זאת שאין אדם בער וכסיל שיתהלל באלו המדות |
| Since sufficiency is superior to strength, which is superior to wisdom and wisdom is a virtue of the rational soul, all these virtues are associated to the rational soul and the bible warns man not to praise himself for them | אבל הזהיר הכתוב אדם מתהלל במדת נפשו ההוגה ותהיה הגבורה והחכמה והעושר ממדות נפשו ההוגה |
| Wisdom precedes strength, which precedes sufficiency, which precedes intellect, which is the essence of all wisdoms: A person first acquires wisdom; when increasing his wisdom he obtains strength; when increasing his strength he becomes self-sufficient; then, reaching the depth of wisdom, he becomes endowed with intellect. On top of all these wisdoms lies the knowledge of God, as a tower built upon them. | ויהיה אדם בתחלתן קונה חכמה וכשהוא מוסיף על קנין החכמה ומתגבר בה נקרא גבור והמעדיף על זה נקרא עשיר |
| The types of wisdom of the sages in this world are based on four foundations corresponding to the four expressions in the verse from Jeremiah mentioned in the beginning of the introduction | ואנו מוצאין החכמות אשר בידי החכמים בעולם הזה בראיות על ד' יסודות כנגד ד' שמות שקראם הכתוב בפסוק אשר פתחנו בו |
| The belief in God and the study of his Holy Scriptures, for which one is allowed to praise himself, are the tower built upon these four foundations | ואמונת השם ותלמוד תורתו אשר הרשה לנו הכתוב להתהלל בה מקיימת היסודות האלו אשר על ד' פנות החכמה והוא המגדל הבנוי עליהם |
| From the prohibition to be praised for those virtues it is concluded that one is allowed learn them and be engaged with them. | ומתוך שאסר הכתוב להתהלל במדות האלה אנו רואים שהתירם ללמדם ולהתעסק בהן |
| The purpose of the treatise is to state and reveal these types of wisdom in short | ומפני זה באתי בחבור הזה להודיע ולגלות ענייני החכמות האלה בדרך קצרה לפי עניות דעתי ודלות בינתי |
| The work is divided to two sections: | ואני מחלק החבור הזה לב' מאמרות |
|
המאמר הראשון יתפרש בו יסודי התבונה שהתנה עליהם הכתוב מתחלת הפסוק עד השכל וידוע אותי[note 30] |
|
והמאמר השני יתברר בו מגדל המפרש בפסוק הזה מן כי אני יהוה עושה[note 31] עד סוף הפסוק |
| I. The First Section: the Foundations of Wisdom | והמאמר הראשון מתחלק לד' חלקים ויקרא כל חלק וחלק מהם יסוד כנגד יסודות החכמה |
|
היסוד הראשון בפירוש חכמת המוסר וחכמת המדבר והיסוד הזה קראו הכתוב חכמה ועומדים עליו ה' עמודים |
|
העמוד הראשון בחכמת המנין אשר היא נקרא בלשון ערבי עלם אלעדד |
|
העמוד השני בחכמת השעור הנקרא בלשון ערבי אלהנדסה |
|
העמוד השלישי בחכמת הנגון הנקרא עלם אלתאליף |
|
העמוד הד' בחכמת הכוכבים עלם אלנג'ום |
|
העמוד החמישי בחכמת הדבר הנקרא אלמנטיק |
| וכל אחד מהעמודים האלה נחלקים לשערים ויהיו נזכרים בתחלת כל עמוד ועמוד מהם | |
|
היסוד השני מפרש חכמת היצירות החוקרת על כל הנמצאות ומבארת תוכן מציאותם ודרך בריאתם וקראה הכתוב גבורה |
| והעמודים הסמוכים עליה שמונה | |
|
העמוד הראשון חוקר על כללות נבראות ותחלת החכמה הזאת ועקרה אשר ממנו |
|
העמוד השני חוקר על כל גופות הפשוטות שאין מתחלפות בשמים וכוכבים |
|
העמוד השלישי חוקר על הכוננות וההפסד הבא על הנמצא תחת השמים |
|
העמוד הרביעי חוקר על פנות היצירה הארבעה ועל הדומה להם |
|
העמוד החמישי חוקר על גופות מתחלפות אשר תוכן כברן ככסף וזהב ודומה להם |
|
העמוד השישי חוקר על צמח האדמה |
|
העמוד השביעי חוקר על בעלי החיים |
|
העמוד השמיני חוקר נפש האדם וגופו הגופנית והרוחנית |
| וכל העמודים נחלקים לשערים | |
|
היסוד השלישי חוקר על חכמה האינשית והחכמה המדנית הנקרית עושר ועמודיה ג' |
|
העמוד הראשון מפרש דרך שמוש האדם בעצמו |
|
העמוד השני מבאר דרך שמושו בינו לבין ביתו ועבדיו |
|
העמוד השלישי מבאר דרך עצות המלך ורוזני המדינות |
|
היסוד הרביעי מפרש חכמת האלהית שקורין לה חכמי הגוים חכמת החכמות |
| ויש להם שני עמודים | |
|
העמוד האחד מדבר על כל העניינים הנסדרים בראש החכמות אשר לפניה המסורים שם על דרך קבלה והחכמה הזאת נותנת להם אות ומופת |
|
העמוד השני חוקר על האחדות האלהית ועל האור הבהיר ועל כל הנמצאות אשר אינן גופות ולא גלם ואינם נצרכות לגוף ולגלם ככל צבאי עולם העליון |
| While there is no need for studying the Holy Scriptures in order to acquire all previous types of wisdom, theology could be understood correctly only from the Holy Scriptures. | והכתוב קרא לחכמה הזו נקראת בשני שמות האלו אלא להודיעך כי על כל החכמות אשר לפניה אי אתה צריך בלימודם אל תלמוד התורה והחכמה הזו אין אדם מבינה על דרכה הנכונה אלא מהתורה וכתבי הקדש |
| The above introduction concentrates on the principles of the first section of the work. The explanation to the parts of the second section was supposed to be given later on at the beginning of the second section, which is now lost, or was not completed | זהו מספר יסודי המאמר הראשון ועמודיו ואני מאחר פירוש חלקי המאמר השני עד הגיעו אליו בעזרת השם |
Book One – the Foundations of Wisdom |
|
Prologue |
|
| Bar Ḥiyya asks his readers not to blame him for entering a narrow place not fitting for walking and endangering himself in losing his way by writing the book | ואל יאשימוני רבותי המסתכלים בדברי אלה ואהיה בעיניהם כמו שהכניס עצמו ממצוק ובמקום צר שאינו ראוי ללכת בו ומסתכן בעצמי בצאתי מדרכי ואני מגלה להם את סודי |
| He explains that he did not engage in it voluntarily for his own sake, but because many of the distinguished men of his time, whose advice he must accept, brought him to do so, since in the whole land of France there was no book written in Hebrew about these types of wisdom. By their instruction, he translated it from Arabic books to Hebrew according to his own understanding. | ולא לרצוני נכנסתי ולא לכבודי להחזיק לי טובה אבל רבים מגדולי דורי שאני חייב לקבל עצתם הביאוני בכל זה מפני שלא היה בכל ארץ צרפת מהחכמות האלו ספר כתוב בלשון עברית ועל פיהם העתקתים מספרי ישמעאל אל לשון הקדש בהשגת ידי |
| Bar Ḥiyya states that every man has to teach his learning according to his own understanding and aim to God | וכל אדם חייב להורות מתלמודו כפי בינתו אחד המרבה ואחד הממעיט ושיכוון לבו לשמים |
| He begs his reader to acquit him and to gracefully correct every mistake and error found in the book both linguistically and in terms of content | ואני מפייס מכל הקורא בחבור הזה שידינני לכף זכות כתכתב בצדק תשפט עמתך[note 33] |
| Lastly, he asks God to help him, save him from sin, and to bestow him his grace | וכמו כך אני מתחנן לפני צורי ומבקש מלפניו להיות בעוזרי ולהצילנו מחטא ועון ויתן חנו עלי בעיניו ובעיני כל חסידיו כי הכל בידיו ואין צור מבלעדיו |
Foundation One – Mathematics |
|
Introduction |
|
| Mathematics is divided into three sciences: | החבור הזה מיוסד על שלושה עמודים |
|
העמוד הראשון מן היסוד הראשון מחובר בחכמת המספר הנקראה בלשון יון ארתמאטיקה |
|
והעמוד השני בחכמת השיעור הנקראה גיאומטריא בלשון יון |
|
והעמוד השלישי בחכמת הנגון הנקראה בלשון יון מושיקא |
Section One – Arithmetic |
העמוד הראשון מפרש חכמת המנין |
|---|---|
Introduction |
|
| וחכמת הזאת נקראת בלשון יון ארתמטיקה | |
| וכל חכמי האומות לומדים אותה תחלת כל החכמות מפני שדיעות בני האדם מקבלות את החכמה הזאת מילדותם | |
| ואי אתה מוצא אדם שאין מבין ממנה מעט | |
| וכל הלמד אותה אינו צריך בבינתה אל עוזר מחכמה אחרת מפני שהחכמה הזאת קרובה אל הלב וגלוייה | |
| Arithmetic consists of two parts: | והיא מתחלקת לשני חלקים |
|
החלק האחד על המנין מדרך שהוא נמצא בדעות ועומדת צורתו בלבות החכמים לא מדרך שהוא בדברים הנמנין בו ועומד בגדודי עולם ובכל הנמצאים בו ואנו קוראים לחלק הזה חכמת המספר |
|
והחלק השני מעיין במנין מדרך שהוא עומד בכל הנמצאות בעולם והוא מונה אותם ובו האדם יכול לחשוב כל עסקיו וקניניו ומפני זה אנו קוראים לה חכמת החשבון |
| ואנו מתחילים לבאר את שני החלקים האלה בענין זה החבור | |
Part One – Theoretical Arithmetic |
החלק הראשון בחכמת המספר |
Introduction - Preliminary definitions |
|
|
הוי יודע כי המספר הזה או המנין הזה הוא רבוי הנקבץ מהאחדים |
|
ומשמע האחדות בכאן הוא ענין הנמצא באחד אשר בו הוא נקרא אחד והאחדות היא משכללת את צורת האחד ומקיימת תבניתו ומפני שאנו מעיינים במספר הנוצר בלב הביאנו בגדרו האחדות שהיא נוצרת בלב ולא הביאנו האחד שהוא נמצא חוצה מהלב |
| one is not a number - it is the foundation and the cause of all numbers | ומתוך שגדר המספר הוא רבוי הנקבץ מהאחדים או מן החד אתה רואה כי זה האחד והאחדות אינה מספר אבל אתה אומר כי האחד הוא מן המספר והוא עקר המספר ואינו מספר וכן הוא סופר את המספרים ואינו מספר |
|
וכדומה לו תיבות אלף בית אשר הן עקר לשון הקודש ובהן נבנה כל לשון ויובן כל דבר אמור בלשון והן מן הלשון ואינם לשון כי אינם משמיעים ענין מעניני העולם אשר הלשון מחוה ומלמד אותם וכל ענין אינו נשמע אלא בהם והם מן הלשון ואינו לשון כן האחד מן המספר ואינו מספר |
|
והאות המעידה על המספר ומפרשת אותו ונותנת בו סימן אשר הוא משכלל אותו |
| Every number is half of the sum of the numbers on either side | כי כל מספר הוא מחצית שני צדיו הצד העודף עליו והצד החסר וכן הוא מחצית שני צדי צדיו עד תכלית כל צדיו |
| ואתה מבין האות הזה מן העשרה על דרך המשל הצד אשר לפניה העודף הוא י"א והצד אשר מאחריה החסר ממנה הוא ט' ואתה מוצא העשרה מחצית שני הצדדים האלה בהתקבצם יחד וכן הוא מחצית שני צדי צדדיה שהם י"ב וח' ומחצית שני צדי צדי צדדיה שהם י"ג וז' וכן עד תכלית כל צדדיה ובענין הזה תמצא כל המספר מחצית ב' צדיו עד סופן | |
| והאחד מפני שאינו מספר אין אתה מוצא לו ב' צדדים ומפני שהוא פשוט בלי מתחלק אתה מוצא אותה מחצית צדו האחד והוא השנים אשר האחד מחציתו והוא מחצית לדבר אחד מענין אחד ולא מחצה לשני דברים ולא על שני ענינים | |
Classification of numbers |
חלקי המספר |
| Two types of numbers – odd and even | והמספר נחלק לב' חלקים ראשונים והם הזוג והנפרד |
| Even Number - any number that is divisible [by two] | הזוג הוא המספר הנחלק בנתים |
| Odd Number - any number that is indivisible [by two] | והנפרד הוא המספר שאינו יכול ליחלק בנתים |
| ומסמני הזוג שכל חלקיו שהוא נחלק אליהם הם שנים בדמותם | |
| אם החלק האחד יהיה זוג השני יהיה זוג | |
| ואם האחד יהיה נפרד גם השני יהיה נפרד | |
| אבל הנפרד הוא שכל חלקיו לעולם אינם שוים לא במנינם ולא בדמותם אבל האחד לעולם זוג והשני נפרד | |
| ואתה יכול לחלק את הזוג בנתים לשני חלקים שוים במספרם ואי אתה יכול לחלק את הנפרד לשני חלקים שוים במספרם | |
| אבל אם אתה מדקדק בחלוקם ומקריב אותם מן השוה אתה מוצא חלק אחד מוסיף על השני אחד או גורע ממנו אחד כגון ט' כשאתה מחלק אותה לה' חלקים ולד' | |
| Classification of even numbers | חלקי הזוג |
| והזוג נחלק לשני חלקים ראשונים והם זוג הזוג וזוג הנפרד ויתילד ביניהם חלק שלישי והוא זוג הזוג והנפרד | |
|
וזוג הזוג כמו ד' ח' י"ו הוא המספר הבא מכפילת הזוג הראשון פעם אחת או יותר מאחת |
|
וזוג הנפרד כמו ו' י"ד י"ח הוא המספר הבא מכפילת הנפרד פעם אחת |
|
וזוג הזוג והנפרד כמו י"ב כ"ד ל"ו הוא המספר הבא מכפילת המספר הנפרד פעמים שיהיה מספרם זוג |
| ומסימני זוג הזוג אם אתה מחלקו בנתים יהיו שני חלקיו זוג | |
| וכן כל אחד מחלקיו אם אתה מחלק בנתים יהיו חלקיו זוגות | |
| וכן חלקי חלקיו עד שאתה מגיע אל הזוג הראשון והוא שנים | |
| כגון מספר י"ו אם תחלקהו בנתים יהיו ב' חלקיו ח' ח' | |
| ואם תחלק עוד את חלקים האלה יהיו חלקיהם ד' ד' | |
| ועוד הם נחלקים לב' ב' שהוא הזוג הראשון | |
| ואתה קורא למספר הזה ולכל בתריו הבאים מחלוקם בנתים זוג הזוג עד הגיעם אל הזוג הראשון שהוא שנים | |
| ומסימני זוג הנפרד הוא הנחלק בנתים לשני נפרדות פעם אחת בלבד כגון י"ד, נ"ח | |
| ומסמני זוג הזוג והנפרד שהוא נחלק בנתים וחלקיו נחלקים בנתים ואינו מגיע בחלוקו אל הזוג הראשון | |
| כמספר י"ב שהוא נחלק בנתים לו"ו והם נחלקים לג"ג | |
| ואתה מוצא בחלק הזה סימני זוג הזוג והנפרד ודומה לזוג הזוג בחלקו בנתים למספר שהוא זוג והוא דומה לזוג הנפרד בהגיעו אל מנין נפרד בסוף בתריו | |
| ובענין שהוא דומה לזוג הזוג הוא נפרש מזוג הנפרד ובענין הדומה לזוג הנפרד נפרש מזוג הזוג | |
| והוא דומה לכל אחד מהם בענין אחד | |
| וקראו את זוג הזוג בשם הזה מפני שאין מונה אותו מספר שאינו זוג והוא מונה אותו פעם זוגות | |
| ונקרא השני זוג הנפרד מפני שהזוג מונה אותו נפרד פעמים והנפרד מונה אותו זוג פעמים | |
| ונקרא זוג הזוג והנפרד מפני שהזוגות המונין לו מהן מונה זוגים פעמים ומהן נפרדים פעמים | |
| Classification of odd numbers | חלקי הנפרד |
|
והנפרד נחלק לשני חלקים לנפרד ראשון ולנפרד שני הנפרד הראשון הוא כל נפרד שאחד לבדו מונה אותו ואין אתה מוצא מספר שיהיה משלים את מנינו בלתי האחד לבדו כגון ג' ה' ז' י"א וכדומה להן |
|
והנפרד השני הוא כל מספר שאתה מוצא מספר שיהיה מונה אותו ולא יהיה המספר הזה כי אם בנפרדות |
| כגון ט' ט"ו כ"א ודומה להם כי מספר ט' תמצא מספר ג' מונה אותו ג' פעמים וכן ה' מונה ט"ו וכן ז' לכ"א ג' פעמים וכן ג' מונה לט"ו בה' פעמים ומונה לכ"א בז' פעמים | |
| וקורין לחלק הזה נפרד הנפרד מפני שכל מספר שהוא מונה אותו הוא נפרד פעמים נפרדות | |
(i.e. has no common divisor with this number) |
ואתה מוצא לנפרד הזה חלק שלישי והוא המספר שהוא שני לגבי עצמו וראשון לגבי מספר אחד ואי אתה מוצא החלוק הזה אלא בין שני מספרים נפרדים כשאתה מקיש אחד מהם אל חברו |
| example: 9 and 25 | כגון שני מספרים ט' וכ"ה אשר כל אחד מהם שני בפני עצמו מפני שיש לכל אחד מהם מספר שהוא מונה אותו ואין אתה מוצא מנין שהם מתחברים בו שהוא מונה לשניהם |
| כי התשעה תמצא שלשה מונה אותו ואינו מונה למספר כ"ה | |
| וכן מספר כ"ה חמשה מונה אותו ואינו מונה למספר ט' | |
| ואין ג' (ב'?) המספרים האלה דומים למספרי ט"ו וכ"א כאשר זכרנו למעלה אשר יש להם מנין שהוא מונה לשניהם והוא ג' | |
| 2 is a prime number | ואין אתה מוצא בזוג מספר ראשון לבד מהשנים אשר הוא תחלת המנין ואין המספר מונה אותן כי אם אחד |
| והן נקראים ראשון על ב' פנים מפני שהאחד לבדו מונה אותן ומפני שהן ראשון המנין | |
| Other classifications of numbers | חלקי המספר בדרך אחרת |
| Three types of numbers | והמספר נחלק מדרך אחרת וג' חלקים |
| למלא ועודף וחסר | |
|
והמספר המלא הוא אשר חלקיו המונין אותו ממלאים אותו ואין עודפים עליו ולא פוחתים ממנו |
| כגון מספר ו' אשר חלקיו שתות ושליש וחצי ואי אתה מוצא לו חלק אחר וכשאתה מקבץ שתיתו ושלישו וחציו תמצא בהן ששה לא פחות ולא יותר ודומה לו מספר כ"ח | |
|
והמספר העודף הוא אשר חלקיו עודפים על מספרו |
| כמו י"ב אשר אתה מוצא בהן כמו אחד מי"ב וגם שתות ושליש ורביע וחצי וכשאתה כולל כל החלקים האלה יהיה המספר י"ו ויהיה יותר על המספר אשר הם חלקין (חלקיו?) והוא י"ב | |
|
המספר החסר הוא אשר אין חלקיו ממלאים את מספרו |
| כמספר י"ד אשר תמצא לו חלק אחד מי"ד וגם יש לו שביע ויש לו חצי ואי אתה מוצא בו יותר מאלו ג' חלקים וכשאתה מצרפם יחד יגיע מספרם עד עשרה ולא יותר והוא חסר מי"ד אשר הם חלקיה | |
| והמשילו החכמים המספר המלא לאדם ישר ותמים | |
| והמספר העודף המשילו לאדם שיש לו אברים עודפים כגון מי שיש לו שש אצבעות בידיו וברגליו | |
| והמספר החסר המשילו לאדם שהוא פחות אחד מאבריו או יש לו ד' אצבעות בידיו וברגליו | |
| וכאשר המספרים העודפים והפוחתים רבים בכל מעלות המספר והמספר המלא מופלא ומעט כי אי אתה מוצא ממנו כי אם אחד במעלת האחדים ובמעלת העשרות ואחד במעלת המאות ויש מעלות שאי אתה מוצא בו מספר מלא | |
| כן בני האדם אתה מוצא בהם רבים המוסיפים על מדותם ויוצאים מקצתם וכן תמצא רבים החסרים והגרועים בבני אדם | |
| Types of numbers in relation to other numbers | חלקי המספר מדרך הקשתו |
| והמספר זה נחלק למספר רב ומספר מעט | |
| Small number | והמספר המעט |
|
נקרא חלק אל המספר הרב אם יהיה מונה אותו על השלמות |
|
והוא נקרא מקצת למספר הרב אם לא ישלימנו במנותו אבל ישאיר מעט שאינו יכול למנותו מפני שאינו כמוהו |
| כמספר ג' והוא נקרא חלק ממספר י"ב מפני שהוא מונה אותו ד' פעמים ומשלימו | |
| ונקרא מקצת המספר ח' מפני שאין משלים אותו במנותו אבל הוא משיייר ממנו ב' שהן המעט מג' והם מקצת ח' | |
| large number | והמספר הרב |
|
נקרא כפלים למעט אם יהיה המעט מונה אותו |
|
ואם אינו מונה אותו יקרא הרב עודף על המעט ואינו נקרא כפלים לו |
|
וכל שני מספרים שיש להם מספר שהוא מונה לשניהם נקראים מספרים נאותים |
| השני מספרים ט"ו וכ"ה אשר הם נאותים זה לזה כמספר (במספר ?) ה' שהוא מונה לשניהם ומשלים אותם והוא מונה למספר ט"ו ג' פעמים, ולמספר כ"ה ה' פעמים והוא חלק לשניהם לאחד שלישית ולשני חמישית | |
|
וכל שני מספרים שאין להם מספר שיהיה מונה אותם זולתי האחד שאינו המספר נקרים מספרים נכריים זה מזה |
| כשני מספרים ח' וי"ה וכדומה להם | |
Classification of ratios |
|
|
וכל מספר שאתה מקיש אותו אל מספר יכול יהיה המספר המוקש אליו שוה לו במנותו |
| וההקשה הזאת נקראת ישרה ושקולה | |
| כשאתה מקיש י' אל י' או ק' אל ק' | |
| ואין בהקשה הזאת חלקים רבים אבל היא באה לעולם על דרך אחת | |
|
ויכול תהיה ההקשה אל מספר עודף עליו או פוחת ממנו והיא נקראת הקשה נחלפת |
| ויש חלקים רבים כפי רוב תוספת או החסרון | |
| ואעפ"כ היא עומדת על ה' שרשים שהן אבות לכל החלקים המתחלקים מהם | |
| ואלה ה' חלקים נחלקים לשני ענינים | |
| Two types involve with co-prime numbers: | הענין האחד הוא בין מספרים נכריים וכוללים להם שני שרשים |
|
האחד כשאתה מקיש מספר אל מספר אחד שהוא עודף עליו או פוחת ממנו שני חלקים או ג' ואין ביניהם חלק שיהיה מונה לשניהם |
| כמספר ה' אל מספר ז' אשר ביניהן ב' והוא שני חלקים לשניהם מפני שהוא שני חמישי הה' ושני שביעי הז' | |
|
והשרש השני מההקשה הזאת כל מספר שיהיה מוקש אל כפלו ועוד שני חלקים ממנו או ג' |
| כמספר ה' אל מספר י"ב אשר הוא כפלו וב' חמישיות וכיוצא בדמיונות האלו כגוף המוסיף ג' כפלים וחלקים או יותר או פחות מזה | |
| וכל ההקשה הזאת אינה משמשת באחת מן החכמות אלא בצד רחוק | |
| Three types involve with numbers that have a common divisor: | וענין השני משרשי ההקשה בין שני מספרים נאותים וכוללים לה ג' שרשים |
|
הראשון מהם הקשת מספר אל מספר שהוא מוסיף עליו או פוחת ממנו חלק אחד |
| כמספר ו' אל מספר ח' או ט' | |
|
והשני מוסיף עליו או פוחת כפל |
| כשאתה מקיש מספר ו' אל מספר י"ב | |
|
והשלישי מורכב משניהם והוא הקשת מספר אל כפלו וחלק אחד |
| כמספר ו' אל ט"ו אשר הוא כפלו וחצי כפלו | |
| וכשאתה שונה החלק הראשון בין ג' מספרים יש פעמים שתהיה ביניהם מוצא החלק השני | |
| כגון מספרים האלה והם ו' ח' י"ב | |
| אם אתה מקיש ו' אל ח' תמצאנו מוסיף שליש | |
| ואם תקיש ח' אל י"ב תמצאנו מוסיף מחצית | |
| ואם תקיש ו' אל י"ב תמצאנו כפלו | |
| וכן אם אתה מקיש העודף אל פוחת כמו הקשתך י"ב אל ח' ואחר כן ח' אל ו' ולבסוף י"ב אל ו' תמצא הענין אחד | |
| אלא שאתה בהקשת הפוחת אל העודף עולה בהקשה ובהקשת העודף אל הפוחת יורד בהקשה | |
| Importance of ratios - sign for the material bodies | וברבוי ההקשות האלה רמז לחכמי המספר הוציאו ממנו אות על כל גדודי העולם שהם נבראים על סוד ההקשה הנאותה |
| ואתה מוצא כל צלעי הנבראות מוקשים בשעורם על השרש הזה | |
| ושבחו החכמים המעיינים בחכמות החצוניות ההקשה הזאת שבח גדול | |
| והוא פתח חכמת הנגון ועליה נבנה כל יסודה אשר אתה רואה בעמוד השלישי מן היסוד הזה בע"ה | |
| Types of numbers in relation to their own parts | סדרי המספר בהקשת חלקיו אליו |
|
וכל מספר שיש לו חלק החלק מונה אותו כמנין החלק עצמו או כמנין חלק אחד מחלקיו |
|
והמספר אשר חלקו מונה אותו במספרו נקרא מספר רבוע מפני שצלעו האחת שוה לצלעו השנית |
|
|
וכשאתה שונה את צלעו כמנינה יתקבץ המספר הרבוע |
|
|
כמספר ד' וט' וי"ו וכדומה להן |
|
ואשר חלקו מונה אותו כמנין חלק אחד מחלקיו יקרא מספר שטוח ויש לו שני צלעים |
|
|
כמספר ט"ו אשר צלעו האחת ג' והשנית ה' |
| וכשאתה שונה צלעו כמנין הצלע השנית יתקבץ מספרו השטוח שהוא ט"ו | |
|
וכל מספר שאתה מונה אותו באחד לבדו נקרא מספר ארוך |
| מפני שהוא צלע עצמו ואין לו צלע שני כי אם האחד שאינו מספר | |
| והמספר הרבוע דומה לשטוח המרובע בגופי הגלמים | |
| והמספר השטוח דומה לשטוח שאינו מרובע אבל ארכו מוסף על רחבו | |
| והמספר הארוך דומה לקו אשר יש לו אורך בלבד ואין לו רוחב | |
| וכל הענין הזה תראהו מפורש בחכמת השיעור | |
| the square numbers are formed in sequence by the series of the odd numbers |
וכל המספרים הרביעים הם נמצאים על סדרן מקבוץ האחד אשר הוא הריבוע הראשון עם המספרים הנפרדים על סדרם |
|
|
והענין הזה אם אתה מקבץ האחד שהוא הרבוע הראשון אל השלש שהן תחלת הנפרדות ואתה מוצא הריבוע השני והוא ד' אשר צלעו ב' |
|
|
ואם אתה מוסיף על ריבוע השני המספר הנפרד השני והוא ה' יהיה הכל ט' והוא הריבוע השלישי שצלעו ג' |
|
|
וכן אם אתה מוסיף על הריבוע השלישי הנפרד השלישי והוא ז' יצא לך הרביעי והוא י"ו |
|
|
וכן על הסדר הזה לעולם אתה מוסיף על הריבוע המספר הנפרד אשר במעלתו ויצא לך הריבוע התלוי אליו ועד אין סוף |
| the five types of ratios depend on the equivalence ratio, created from it, and return to it, as the square numbers are created from the odd numbers | וכן אתה מוצא חמשת ההקשות המנין אשר הן נחלפות תלויות בהקשה הישרה וחוזרות אליה כשאתה מתיר את הקשרם כאשר המספרים הנפרדים קושרים את הריבוע במספר |
| sample table of ratios | והנה אני מצייר לך צורת אחת תראה בה שש ההקשות אשר הם עם הנחלפות עם הישרה סדורות בשלשה מספרים בכל הקשה והקשה כדי שתבין הענין הזה |
Three rules of reducing the ratios successively to equality:
|
ואם אתה רוצא להתיר הקשה נחלפת עם ישרה אתה פוחת ראש מספריו מהשני והנשאר אחר הפחת חבר עם השני ופחות מן השלישי וישאר בידך שלשה שהן שוין או מוקשין על שרש אחד שהוא קרוב אל השוה כגון הקשת החלק אשר היא המעלה השלישית בצורה הזאת ומספריה ד' ו' ט' |
| לוח שש ההקשות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| analogy between the returning of the five ratios to the equivalence ration and the gradual stage of refraining from desire: overcoming one make the next stage easier, until the level of righteousness is reached |
והחכמים נוהגים מזה רמז על האדם אם הוא מכריח עצמו וכובש יצרו מתאוות העולם פעם אחת יהיה זריז פעם אחרת להכריח יותר עד שיעלה לגדר התמימות וחסד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולבעלי החכמה הזאת בענין הזה טעמים נאים ונכוחים במוסר הנפש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן יש להם בענין הראשון בסדור המספרים אשר הם רבועים רמז גדול על שבח האחד שהוא יסוד המספר והוא העקר והסוד לכל בריות העולם יהיה השם המיוחד האמתי אשר לא יוגדר כי הוא מחוייב המציאות ואין סבה למציאותו יתברך שמו לעד ולנצח | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| theoretical arithmetic versus practical arithmetic: Theoretical arithmetic – rational wisdom inquiring the number – its form and definitions – as understood by the heart [= theoretically] |
וכל אשר הקדמנו למעלה מצורת המנין וגדריו הוא מן החכמה השכלנית ומעיינת במנין מהדרך שהוא עומד בלב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Part Two – Practical Arithmetic |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Practical arithmetic – wisdom that investigates number as it is realized in earthly affairs and businesses, for there is nothing in this world that does not use number, is not counted by number, and coincide with it from all aspects | וחכמת החשבון אשר אנו באים עתה לדבר עליה בחלק הזה היא מעיינת במנין מדרך שהוא נופל על כל עניני העולם הזה ועל עסקיו כי אין לך דבר בעולם הזה שאין המנין משמש ומונה אותו וחופף אליו מכל צדדיו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Numeration |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The Twelve Names that Form Every Number | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכל המנין כלו נכלל בשנים עשר שמות תשעה מהם הם חוזרין חלילה עליו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והתשעה שמות הם האחדים והם המעלה הראשונה מהם עד תשעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והג' שמות הן לג' מעלות המנין אחר האחדים והם העשרות והמאות והאלפים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואלו הארבע הם עקר מעלות המנין אשר הם חוזרין עליו ומקיפין אותו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כי כל מעלה אשר עולה אל האלפים שמה חצוב משלושת המעלות אשר לפניה אלפי אלפים ועשרות אלפי אלפים ומאות אלפי אלפים ואלפי אלפי אלפים וכן למעלה מזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וחכמי החשבון קורין לכל מעלה ומעלה מהמעלות האלה בלשון ישמעאל אוש בסמך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ופירושו בלשוננו מענין יסוד ואנו קורין לו בלשון הקדש אוש בשין והוא חצוב מן אושיא יחיטו[note 34] ואושיא שאמרו רבותינו בתלמוד והוא משמע יסוד ומפני זה אנו אומרים אוש האחדים אחד אוש העשרות שנים ואוש המאות שלשה כאלו היינו אומרים יסוד מעלת האחדים אחד וכן העשרות והמאות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The fundamental arithmetical operations |
וחכמי המנין מתעפקים (מתעסקים?) בחשבון על ענינים רבים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ראשונה הם צריכים לחשוב מנין במנין | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ושנית לחלק מנין אל מנין | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ושלישית לדעת קצב מנין ממנין | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ורביעית לפחות מנין מן מנין | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וחמישית לספות מנין אל מנין | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וששית להשלים מנין במנין | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ושביעית להשיב מנין אל מנין | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובזה הענין הם צריכים לחלק את האחד ולעיין בחלקיו איך הם נחשבים זה בזה ונמשלים זה עם זה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואנו נותנים כללות לכל אחד מענינים האלה בדרך החבור הזה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והמבין צורת הענינים האלה נקרא מבין בחכמת החשבון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והממהר בחשבון ומקבץ אותו נחוץ נקרא זריז במלאכת החשבון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואינו נקרא על זה חכם בה ומבין | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה דרך הבינה יכול אדם ללומדה וללמדה בספר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והמלאכה והזריזות בה אינה נלמדת מספר כי בינה ממעשה הלב והמלאכה ממעשה ידים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Multiplication of a Number by a Number |
דרך חשבון מנין במנין | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Repeating one number as many times as the number of units that are in the second number. | הוא שיהיה האדם שונה מספר אחד פעמים שיהיה מנינם כמנין האחדים אשר במספר השני | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Any number multiplied once does not increase, and is as its former amount. | וכל מספר שאתה מונה אותו פעם אחת אינו נוסף והוא עומד במנינו הראשון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ומפני זה אנו אומרים האחד הנחשב על אחד הוא אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והשנים על האחד הוא שנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכן כל מנין שאתה מונה אותו באחד כמו כן אין אתה משנה אותו במספרו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תחשוב אותו בשנים אתה כופל אותו ומוצא כפלים מהמספר הראשון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תחשוב אותו בשלש תמצא בו שלשה מהמספר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן עד העשרה אשר אם תחשוב אותם בעשרה יהיו מאה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והרוצה לחשוב מספר במספר למעלה מן העשרה הוא צריך שיהיה חשבון מעלת האחדים על האחדים סדור בפיו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם יבא לחשוב שאר המעלות אחת אל אחת יעמיד המספר אשר משני המעלות בדמותו ממעלת האחדים ויחשוב אותם כאלו הם אחדים ויחזיק המנין שמור בידו ואח"כ ידע אוש אחד מן המעלות וירחק מהמעלה השנית כמנין אוש המעלה האחת והמעלה אשר יגיע אליה היא מעלת החשבון אשר שמר בידו האחדים מן המעלה ההיא והעשרות מן המעלות אשר באות אחריה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכאלו היית רוצה לחשוב שש מאות בד' אלפים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
אתה נוהג בהם ראשונה מנהג האחדים ותחשוב ששה בד' ויהיו כ"ד ואתה שומר המספר הזה עמך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וקח אוש המאות שהוא ג' ומנה מן האלפים ג' מעלות והמעלה שמגיע אליה היא מעלת החשבון השמור והיא מעלת מאות האלפים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן אם אתה מונה אוש האלפים והוא ארבעה ממעלת המאות אתה מגיע כמו כן אל מעלת מאות האלפים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ותדע מכאן כי האחדים מהמספר אשר שמרת הם מן המעלה הזאת ומן מעלת אלפי האלפים אשר אחריהם הם עשרותיו מפני זה אתה אומר כי מספר כ"ד אשר אמרת הם אלפי אלפים ת' אלף כי אחדיו הם ארבעה ועשרותיו הם שנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואתה יכול לדעת מעלת המספר הנכלל על דרך אחר והוא שתהיה חושב אושי שני המעלות ותדע מנין אושיהם והפחות מהם אחד והשאר יהיה מעלת המספר הנכלל כאלו היית לוקח בדמוי הזה אוש המאות והוא ג' ותחשוב אותו עם אוש האלפים והוא ארבעה ויהיה הכל שבעה ותפחות ממנו אחד לאוש וישארו בידך ששה וזה המספר הוא אוש מאות (אלפי) אלפים אשר היא מעלת הנכלל בחשבון כאשר חשבת למעלה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וחכמי המנין יודעים מכאן מאי זה טעם אתה משליך מן שתי האושות בהתקבצם אחד לאוש ותמצא מעלת החשבון הנכלל והטעם הזה הוא מפני האחד שעולה בחשבון האוש לכאן ולכאן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואיש המעיין היטב בענין הזה יבין את הטעם ואינו צריך לפירוש אחר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Division |
דרך חלוק מנין על מנין והוצאת קצב מנין מן מנין | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חלוק מנין על מנין הוא שתחלק מנין רב על מעט | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והוצאת קצב מנין מן מנין כשאתה מחלק מנין מעט אל רב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ומפני שהענין דומין זה לזה מצד אחד נתפרשו שניהם בשער אחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והרוצה לדעת קצב מנין מן מנין יעיין בשני המספרים אם מעט מהם מונה את הרב ידע כי המעט הוא חלק מן הרב קצוב שמו מן המספר אשר הוא מונה אותו בו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון מי שהוא רוצה לדעת קצב מספר ט"ו ממספר ק"פ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הוא יודע כי מספר ט"ו מונה את ק"פ י"ב פעמים ומשם הוא יודע כי ט"ו הוא חלק אחד מי"ב מן ק"פ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם אין המעט מונה את הרב יכול יהיה ביניהם מספר שיהיה לשניהם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם הוא כן ידע כמה פעמים מונה הוא למעט וכמה הוא מונה לרב וכדרך שני המספרים יהיה קצב שני המספרים הראשונים אחד מן אחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון הרוצה לומר קצב ט"ו מן מאה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אתה יודע כי מספר אשר הוא מונה לשניהם הוא ה' ותמצא המספר הזה מונה למספר ט"ו ג' פעמים ולמספר ק' הוא מונה אותו כ' פעמים וכקצב ג' מכ' כן ט"ו ממספר ק' והוא עשור וחצי עשור | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ועוד על דרך אחרת קח החלק הנמצא לשניהם ביחד וכקצב החלק מן החלק כן קצב המספר מן המספר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואתה מוצא לשני מספרים האלה חומש וחמישית ט"ו הוא ג' וחמישית ק' הוא כ' וכמו קצב ג' מן כ' כן קצב ט"ו מן ק' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם שני המספרים יהיו נוכריים זה מזה יהיה קצב האחד מן השני חלקים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כאלו היית רוצה לדעת מספר ז' מן מ' אתה אומר שחלקו ממנו שבעה חלקים מארבעים חלק באחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| זהו דרך בעלי חשבון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ויש מהם המדקדק והוא לוקח חלק אחד מהמספר הרב ומקיש אליו המספר המעט | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והוא בדמיון הזה עישור הארבעים והוא ד' ומקיש אליו השבעה ומוצא בה שנים פחות רביע העשור או חומש פחות שמינית החומש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם הוא מקיש אותו אל שמינית הארבעים שהם חמשה הוא אומר שמינית וב' חמישית שמינית | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכענין הזה הוא הוצאת קצב מנין מן מנין והוא חלוק מן מספר מעט על מספר רב ממנו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וחלוק מספר רב על מספר שהוא המעט ממנו אם יהיה ביניהן חלק שהן שוין בו אתה מחלק חלק הרב על חלק המעט והוא הדין לשני מספרים השלמים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כאלו היית רוצה לחלק מספר מאה על מספר ט"ו אם אתה מוצא לשניהם חלק אחד והוא החומש שהוא כ' ממספר מאה והוא ג' ממספר ט"ו ואם אתה מחלק כ' על ג' יהיה ששה ושני שלישי אחד והוא מספר חלוק ק' על ט"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם אין להם חלק שיהיו שוין בו אתה מחלק שני המספרים בעצמן ולעולם כשאתה חושב החלק בנחלק עליו והוא המספר המעט יצא לך המספר הרב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כאלו היית אומר מספר שחלקתי אותו על ט"ו והיה החלק ו' וב' שלישיים כמה היה המספר הזה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אתה חושב ט"ו על ו' וב' שלישיים ויעלה החשבון למאה והוא מספר אשר חלקת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ומהכללות האלה אתה יודע לחלק מנין על מנין אם רב ממנו אם מעט ממנו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Subtraction |
דרך חסרון מנין ממנין | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואין אתה צריך בחסרון מנין מן מנין לשים לך דרך שתהיה נוהג עליו אלא במעלת החשבון אשר למעלה מאלפי אלפים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון האומר לך איך תפחות אלף וקפ"ה מעשרת אלפי אלפים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אתה לוקח ראשונה אחד מן המעלה והוא אלף אלפים ונשאר לך ט' אלפי אלפים ומהאלף אלפים אשר לקחת תפחות ממנו האלף וקפ"ה ויהיה הנשאר בידך ט' מאות אלף ושמנה ותשעים אלף ושמונה מאות וחמשה עשר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכענין הזה אתה מוסיף מנין על מנין ומשלים מנין במנין | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואין אתה צריך להוספת פירוש אחר כי הענינים האלה קלים במנין השלם וכל אדם יכול להוציאם מלבו מכח הכללות אשר למעלה ואנו באים להורות על אלו הענינים בחלק האחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Multiplication of Fractions |
דרך חשבון חלקי האחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הוי יודע כי חשבון המספר השלם בחלקים הוא מענין קצב מנין מן מנין | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי האומר חשוב י"ז בשליש או חשוב שליש בי"ז דומה למי שאומר כמה הוא שליש מי"ז | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואין בין הענינים שום הפרש בעולם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ומפני זה אתה אומר חשבון שליש באחד הוא שליש וחשבון שליש בשנים הוא שני שלישי האחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תבא לחשבון החלקים בחלקים יהיה בענין הזה הוצאה חלקי החלקים ויהיה החשבון שליש בשליש הוא שליש השליש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובעלי החשבון הקימו לענין החלקים בכל דרכי החשבון כלם מספר שיהיה דיין ומוכיח ועל פיו יצא דיני החלקים בכל דרכי החשבון בענין הזה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אם יאמר לך חשבו שני שלישים בשני שלישים כמה הם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הוה יודע כי שם השלישות הוא שלשה ומן המספר הזה הוא שם השליש חצוב ובא וחשוב השלשה על השלשה כשם החלק השני ויהיו ט' ואתה משים המספר הזה למוכיח | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואלו הדמיונים מסורים לך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חשבון ב' שלישיים על ב' חמישיים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תחשוב אתה ג' על ה' שהן שמות החלקים ויהיה לך המספר המוכיח ט"ו ואליו תקיש הד' שהוא חשבון החלקים ותאמר כקצב ד' מט"ו כן קצב החשבון הזה מן האחד והוא חמישית ושליש חמישית | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואלו היו אומרים לך חשוב שני חלקים מי"א באחד בב' חלקים מי"ג באחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תחשוב שמות החלקים והם י"א על י"ג ויהיה קמ"ג ותדע כי קצב ד' מקמ"ג הוא קצבם מן האחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם יאמר לך חשוב ב' חלקים מה' בעשירית האחד בב' שלישי האחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תדע אתה כי שם האחד הוא חמישים כמנין חמשה בעשרה ותמנה אלו החמישים בשלשה שהוא שם החלק השני ויהיה הכל ק"נ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן אם יאמר חשוב בב' חלקים מחמשה בעשירית האחד בב' חלקים משמנה בשלישית האחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אתה נזקק לדעת שמות החלקים ותחשוב ה' בי' ויהיה נ' והם שם החלק האחד ותחשוב ח' בג' ויהיה כ"ד והוא שם החלק השני | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ומהדמיונות האלה תוכל להבין דרך חשבון החלקים וחלקי החלקים במספר השלם ובחלקים ובחלקי החלקים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Division of Fractions |
דרך חלוק החלקים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אתה מקים ראשונה מספר שיהיה מוכיח ואליו תקיש כל חשבונך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
כגון האומר לך חלק ג' שמיניות על ב' חמישיות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
אתה חושב ראשונה שמות החלקים והם ח' על ה' והנה המספר המוכיח מ' וקח ג' שמיניות מ' והם ט"ו וב' חמישיותיו והם י"ו ונחלק ט"ו על י"ו הוא חלק ג' שמיניות על ב' חמישיות והוא אחד חסר חצי שמינית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ועל הדרך הזה אתה יכול להוציא קצב חלק מחלק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
כגון האומר כמה הם ג' שמיניות מב' חמישיות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
אתה מקים המספר המוכיח מ' וב' חמישיות הם י"ו וג' שמיניות י"ו הוא ו' וכקצב ו' מן מ' כן קצב ג' שמיניות מב' חמישיות מן האחד והוא שמינית וחומש שמינית וכן כל כדומה לזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Subtraction of Fractions |
דרך חסרון חלק מחלק | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן לפחות חלק מחלק יצטרך למספר המוכיח ועל פיו יצא מספר החשבון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
כגון האומר השלך ג' שביעיות מב' שלישיות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ואתה מקים מספר המוכיח במקום הזה כ"א ותקח ב' שלישיות והם י"ד ותשליך מהם ג' שביעיות והם ט' ונשאר לך ה' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Addition of Fractions |
דרך תוספת חלק על חלק | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן נצטרך אל המספר המוכיח | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
כגון האומר הוסף ג' שמיניות על ז' עשיריות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
תקים אתה בכאן לעמת המספר המוכיח והוא פ' תצרף ג' שמיניותיו והם ל' אל ז' עשיריותיו והם נ"ו שהם ז' על ח' ויהיו פ"ו והוא הנכלל מב' חלקים בהצטרפם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Converting of Fractions |
דרך חזרת החלקים אחד אל אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והענין הזה נוהג בחלקים ואינו נוהג במספר השלם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
כגון האומר ג' שמיניות כמה עשיריות יהיו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ואתה מקים המוכיח בכאן פ' ותקח ג' שמיניות והם ל' ותחלוק אותן על עשיריותיו והוא ח' ויהיה החלק ד' פחות רביע מן האחד וכן כל הדומה לענין הזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Completion of Fractions |
דרך תשלומי החלקים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכמו כן הענין הזה אינו נוהג במספר השלם כי אם על דרך שאזכיר לך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואני מתחיל ראשונה בתשלומי החלקים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
אם יאמר לך אדם איך תעשה ג' שמינית האחד עד שיהיה אחד שלם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
אתה יודע כי שם השמיני חצוב משמנה כאשר זכרנו למעלה ומספר הפעמים אשר הם שלשה מונים את השמנה הם ג' פעמים פחות שליש ובמספר הזה אתה חושב את שלשת השמיניות ויהיו אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כי כמנין הפעמים אשר מספר אחד מונה את המוכיח כמו כן החלק מונה את האחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
כגון האומר איך תשלים ב' חמישיות ועשירית החומש עד שיהיו אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
אתה יודע כי המספר המוכיח בענין הזה הוא נ' כמו שנתפרש לך מהדמיונות אשר למעלה וב' חמישי המספר הזה כ' ועשירית חמישיתו הוא א' הנה בין הכל הוא כ"א | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ומנה התשלומין במספר השלם הוא כמו כן על הענין הזה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
כגון האומר איך תשלים את השבעה עד שיהיו י"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
אתה יודע כי הז' מונה את י"ו ב' פעמים וב' שביעי פעם ובהם יהיו תשלומין | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכל הענינים האלה הם דרכי החשבון המונה את כל עסקי העולם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והמבין אותם יכול להוציא מהם דרך חשבוני בני אדם במקחם ובממכרם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולפי שרצוני להקל על המעיין בחבור הזה אני מפרש מחשבוני המקח והממכר כללות שיוכל אדם להקיש אליו כל דבר ולהוציא מהם על חשבוני עסקיו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Business Arithmetic |
פתח חשבוני המקח והממכר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הוי יודע כי כל ד' מספרים שיהיו בב' סדרי ההקש השוה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והוא שיהיה חלק האחד או חלקיו מן השני הן הן חלק השלישי או חלקיו מן הרביעי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
כי המספרים האלה אם אתה חושב הראשון ברביעי יהיה מספר חשבונו כמו חשבון השני בשלישי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והדמיון לזה הם שני מספרים ד' וט"ו עם מספרי י"ב ומ"ה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והראשון שהוא ד' הוא חלקים ממספר ט"ו אשר הוא השני כמו חלקי י"ב אשר הוא שלישי מן מספר מ"ה והוא הרביעי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ואם אתה חושב ד' והוא הראשון במספר מ"ה והוא הרביעי יהיה מספרו כמספר ט"ו והוא השני במספר י"ב השלישי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ועוד המספר הראשון והוא ד' אם תקיש אותו אל י"ב השלישי יהיה דומה להקשתך ט"ו אל מ"ה הרביעי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואתה מוצא מספר ד' והוא הראשון נקוש אל שני מספרים אל השני ואל השלישי ואינו נקוש אל הרביעי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכן השני נקוש אל הראשון ואל הרביעי ואינו נקוש אל השלישי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והמספרים הנקושים זה לזה נקראים חברים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ושאינן נקושים נקראים נכריים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ומן כאן אתה למד שכל ד' מספרים שהם שוים בהקשה אם אתה חושב האחד מן סדרי ההקשה עם הנכרי לו מסדר ההקשה השנית יהיה שוה לחשבון חברו בהקשה באשר הוא נכרי לו מן ההקשה השנית כאשר הראיתיך בדמיון זה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואתה צריך לתת לבך בענין הזה ולהבין אותו עד אשר תוציא בו כל חשבון נסתר מן החשבון הגלוי בכל עניני המקח והממכר והשכירות ואמידת המעשים ושיעור שכרם וכל עסק ושכר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Word problems | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Trade | דרך חשבוני המקח והממכר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| all human affairs associated with commerce, employment of workers, and exchange are based on two orders of the equivalence ratio = [the "Rule of Four"] | תדע כי כל עסקי בני אדם בחשבוני מקחם וממכרם ושכירות מעשיהם ושיעור כל חלופיהם הם עומדים בין ד' מספרים בב' סדרי ההקשה שוה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
the first order:
|
הסדר האחד הוא העסקא והמעשים והשני השער המסור לו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
the second order:
|
והסדר השני הנלקח או הנמכר או הנשכר והשני הדמים החייבים לו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והעסק נקוש אל השער כאשר המכר נקוש אל הדמים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועוד נקוש העסק אל המכר כאשר נקוש השער אל הדמים ואלו הם החברים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותמצא לעולם העסק נכרי לדמים והמכר נכרי לשער | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ומפני זה אם אתה חושב העסק בדמים יהיה בחשבון המכר בשער וכן בחלוף | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| in all human affairs three of these values are known and the fourth is unknown but can be deduced from the three that are known: | ובכל עסקי בני האדם שלשה מאלו הארבעה הם ידועים לעולם והרביעי נסתר ואנו נוציא אותו מכח הידועים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם אתה חושב אחד מהשלשה הידועים בנכרי לו מהם ותדע המספר הנכלל בחשבון ותחלק על השלישי הידוע אתה מוצא הרביעי הנסתר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Pricing problems | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כגון האומר י' כורי חטה בו' דינרין כמה כורין אוכל ליקח בד' דינרין | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והמסחר הוא י' כורין | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והשער המסור לו ו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואלו הב' עומדים בהקשה אחת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואתה יודע מן ההקשה השנית ד' דינרין והם הדמים הנכרים לגבי המסחר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואתה מבקש לדעת המכר הנסתר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובענין הזה ב' הנכריים אשר בב' הידועים הם הדמים והמסחר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וחשוב אתה מפני זה י' בד' ויהיה מ' ותחלק אותם על השער ידוע והוא ו' יהיה המכר ו' כורין וב' שלישי כור והוא המספר הנסתר אשר אתה מבקש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| in the above example a3 = the sold merchandise = unknown | ובכאן היה המספר השלישי נסתר והוא המכר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה הכלל יהיה בידך כי כפל הקצות ככפל האמצעיים והנה אם לא ידעת האמצעי האחת ותכפול הקצות זה על זה ותחלק על האמצעי אשר לך ותמצא האמצעי הנעלם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וככה אם לא ידעת אחת הקצות ערוך האמצעי האחד על חברו וחלק על אחת הקצות הנודעות וכמוהו יהיה הקצה הנסתר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה יודע בכפול מה שיצא בחלוק עם המחולק עליו כאשר אמרנו ובין תדע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| in the following example a4 = the money [paid] = unknown: | ואילו היה המספר הרביעי נסתר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כגון האומר י' כורי חטין בו' דינרין כמה הם דמי ד' כורין | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ובכאן הוא דמי המכר נסתר והוא המספר הרביעי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ואם אתה רוצה לגלותו חשוב השער שהוא ו' במכר שהוא ד' ויהיה כ"ד חלקהו על המסחר והוא י' ויצא לך דמי המכר הנסתר והוא ב' דינרין וב' חמישי דינר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| if a2 = the price = unknown: | וכן אילו היה השער נסתר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כגון האומר קניתי ג' עמרים בד' דינרין בכמה הייתי קונה את האיפה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אתה יודע בכאן המכר ודמיו והם ג' עמרים וד' דינרין | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן אתה יודע המסחר י' עמרים האיפה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונסתר ממך שער האיפה ותרצה לגלותו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ואתה חשוב עמרי האיפה בד' שהם דמי המכר ויהיה מ' נחלק אותו על ג' והם המכר ויצא לך השער הנסתר והוא י"ג דינרין ושליש דינר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| if a1 = the [amount of goods offered in the] business = unknown: | וכן אלו היה המסחר נסתר ותדע השלשה והם השער והמכר ודמיו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כגון האומר לקחתי ו' כורין בד' דינרין כמה כורין אוכל לקנות בז' דינרין | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואתה יודע כאן המכר ודמיו והם ו' כורין וד' דינרין והם הקשה אחת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וגם אתה יודע מן ההקשה ראשונה את השער והוא ז' נכרי למכר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ומפני זה אתה חושב אותו בו' אשר הוא המכר ויהיה מ"ב וחלק אותו על ד' והם הדמים ויצא לך המסחר שהיית מבקש והם י' כורין וחצי כור | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואתה רואה מכאן דרך הוצאת המספר הנסתר מתוך המספרים הארבעה שעליהם סובל כל עסקי העולם וכל מקח וממכר וכל הדומה לו ותוכל לדעת לעולם הרביעי הנסתר מן הג' הגלויים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Payment problems - employment of workers | וכן לענין השכירות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כגון האומר שכרתי פועל לשלשים יום בי' זוזים ועשה עמי ח' ימים כמה הוא שכרו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאן אתה מדמה ל' ימי השכירות למסחר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והי' זוזים לשער המסחר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וח' ימים שעבד למכר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויהיה המספר הנסתר ממך דמי המכר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה דומה למי שאומר י' כורין בו' דינרין כמה הם דמי ד' כורין אשר שמתי לך למעלה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ואתה בא ועשה כאשר עשית למעלה וחשוב המכר עם הנכרי לו וחשוב ח' ימים אשר העמדת אותם במקום המכר בי' שהם השער והוא הנכרי למכר ויהיה פ' חלק אותו על המסחר והוא ל' יום ויהיו ג' פחות שליש והוא השכר שחייב לו בעבודתו והוא ג' זוזין פחות שליש הזוז | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ועל הדרך הזה אתה מדמה כל ענין שיבא לידך לאלה ד' דמיונות ששמתי לך בשער הזה ותוציא הנסתר בחשבונות הן במקח ובממכר הן בשכירות ומלאכה וכל מיני חלופין הנוהגין בבני אדם הנזקקים אל החשבון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והבאתי לך כל המשלים והדמיונות מחשבונים קלים שלא להטריח הלמד והמשכיל יוכל להוציא מאלו הדמיונות כל חשבון חמור | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובכאן חתמתי לך העמוד הראשון במה שיראה לי הכרחי בידיעת אריתמיתיקא כמו שידענו אמנם הערכים והשרשים מפורשים ברובתא אחרינא ואתחיל לפרש העמוד השני מן היסוד בעזרת האל |
Section Two – Geometry |
העמוד השני מפרש חכמת השיעור |
|---|---|
Introduction |
|
| והחכמה הזאת קורין לה בלשון ישמעאל הנדסה ובלשון יון גיאומיטריאה | |
| geometry leans on numbers and therefore on arithmetic | והחכמה הזאת תלוייה לחכמת המנין |
| כי המקרה הנמצא בעולם תחלה הוא המנין | |
| כי כל הנמצא מעניני העולם הוא אחד או שנים או יותר והאחד או שנים הן מחכמת המנין | |
| וכל אחד בעולם הוא מתחלק לחלקים או לאברים או לגזרים והענינים האלה הם מחכמת השיעור וחכמת המנין | |
| ועוד כי כל נמצא בעולם אשר אנו שואלים עליו בכמה השאלה באה על דמות נפרדת או על דמות נמשכת | |
| וכל דמות נמשכת צריכה למדירה ואין המדירה יכולה להיות בלא מנין | |
| ומפני כל הענינים האלה היתה חכמת המנין תחלת כל החכמות והחכמה הסמוכה לה חכמת השיעור | |
| והחכמה הזאת מתחלקת בחכמות לחלקים רבים בחכמות אשר יוצאות מכחה | |
| ואנו מחלקים עניניה בשני חלקים בערך החבור הזה | |
Part One – Theoretical Geometry |
החלק הראשון בגדר חכמת השיעור וגדר כל הענינים אשר היא מעיינת בהם ופירושם בדרך קצרה |
| Initial definitions: | |
| geometry | חכמת השיעור היא חכמת מפרשת את הגידולים ומודיעה ערכם ויצירתם ומיניהם וסימניהם |
| measure | והגידולים הם הערכים בלשון אחת הוא כל דבר שיש לו מרחק |
| dimensions: length, breadth and depth | והמרחקים הם ג' אורך ורוחב ועומק או רום |
| כי המרחק השלישי הוא נקרא בשני שמות רום ועומק כפי שני הדרכים שהוא נערך אליהם | |
| והערכים שיש להם המרחקים הם שלשה | |
|
הראשון נקרא גולם ויש לו שלשה מרחקים |
|
והשני נקרא פרוש וקראו לו בשם הזה מפני שהוא פרוש על הגולם כאלו היה חוצה ממנו וזה הפרוש יש לו אורך ורוחב בלבד |
|
והשלישי נקרא קו ויש לו מרחק אחד והוא אורך בלבד |
| ואין לך מרחקים יותר מהשלשה אשר לגולם ולהם תמצא ששה צדדין אשר הם תכלית כל גולם קטון וגדול אפיה כל העולם כלו תמצא לו ששה צדדין | |
| מהם באורך ב' צדדין והן ימין ושמאל או מזרח ומערב | |
| ומהן ברוחב ב' צדדין והם פנים ואחור או צפון ודרום | |
| ומהם בעומק או ברום שני צדדין והם ראש וסוף או מטה ומעלה | |
| ואם אתה מתחיל מן הראש והולך אל הסוף או מלמעלה ויורד אל מטה אתה קורא זה המרחק עומק | |
| ואם אתה מתחיל מן הסוף והולך אל הראש ומלמטה ועולה למעלה אתה קורא זה המרחק רום | |
| ובדרך קצרה אתה אומר לכל גולם אשר הוא תחת הקרקע יש לו עומק | |
| ולכל גולם שהוא למעלה יש לו רום | |
| תמצא הגולם כלה עם רקיע גולמי ויהיה תכלית הגולם פרושים ויהיה להם ב' מרחקים אורך ורוחב וד' צדדין והן ימין ושמאל וצפון ודרום | |
| ואי אתה מוצא להם מעלה ומטה מפני שאין להם עומק | |
| ויהיו כמו כן תכליתי הפרוש פוחתים מרחק אחד ויהיה תכליתם הקו ולו אורך בלבד | |
| ותכליתי הקו הוא הנקודה ואין אתה יכול לשום לה מרחק | |
| ומפני זה אמרו הנקודה הוא דבר שאין לו ערך ולא מרחק כלל והוא תכלית דבר שאין לו אלא מרחק אחד | |
| והגולם נמצא בלב ובעין ובכל חושי הגוף והוא נמצא עומד בעצמו | |
| והפרוש אינו נמצא ואינו נראה אלא מדרך עמידתו בגולם ואינו נפשט מהגולם אבל הדעת פושט אותו מן הגוף ומעמידו לבדו בתוך הלב ומפרש ענינו | |
| והקו אינו נמצא אלא בפרוש ואינו נפשט ממנו אבל הדעת פושטו והוא מעמידו בלב ומעיין בו | |
|
והנקודה מציאותה בתוך הקו מפני שהיא תכליתו והדעת פושט אותה ומעמידה בתוך הלב |
| והחכמה הזאת מעיינת בכל הערכים האלה השלשה ומגידה את יצירתם ומיניהם | |
| ואנו מתחילים לפרש עתה חלקי הקו | |
| Classification of lines | מיני הקו הראשונים שנים מתפרד ומתרכב |
|
ומיני הקו המתפרד ג' קו מיושר וקו עגול וקו עקום |
|
והקו המיושר הוא ההולך לנוכח שתי הנקודות אשר תכליתיו |
|
והקו העגול הוא כל אשר אי אתה יכול למצוא ג' נקודות על נוכח וימצא בתוכו נקודה שיהיה מרחקה מכל נקודות העגול מרחק אחד |
|
והקו העקום כל קו שאי אתה מוצא שלשה נקודות על נוכח אחד ואף נקודה שיהיה מרחקה מנקודות העקום מרחק אחד אי אתה מוצא בו |
|
והקו המורכב הוא המתחבר משני קוים או יותר יכול יהיו הקוים האלה ממין אחד או יותר ממין אחד |
| והקוים המתחברים הם נצמדים בנקודה אחד ונפרדים עליה ואנו קורין לפירוד הבא על זאת הנקודה זוית | |
| Classification of angles | מיני הזויות |
| והזויות נחלקים ראשונה לשתים | |
| זוית שטוחה וזוית גלומה | |
|
והזוית השטוחה היא פירוד שני קוים הנצמדים יחד בנקודה אחת ונפרדים עליה על שטח אחד |
|
והזוית הגלומה הוא פירוד שלשה קוים הנצמדים יחד בנקודה אחת ונפרדים מעליה על שני שטחים |
| ועוד נחלקים על דרך אחרת לקוים ישרים ולשאינן ישרים ושהאחד מהם ישר והשני אינו ישר אבל עגול או עקום הן בזוית שטוחה או גלומה | |
|
ואנו מניחים פירוש הזוית אשר אין קויהם ישרים ומדברים על הזוית הישרה |
| מיני הזויות הישרות שלושה | |
| זוית נצבת וזוית נרוחת וזוית חדה | |
|
והזוית נצבת היא אחת משני זויות אשר על צדי קו העומד על קו אחד וכל אחד מהם שוה בערך לחברתה |
|
והזוית הנרוחת היא המוסיפה בערכה על הנצבת |
|
והזוית החדה המחסרת בערכה מן הנצבת |
| Relations of lines | סדר הקוים בישובם |
| והקוים מדרך ישובם הם על שלשה מינים | |
|
מהם אשר ישובם אחד לנכח השני וערך המרחק אשר ביניהם עומד לעולם על דרך אחת ואינו לא מוסיף ולא גורע |
|
ומהם אשר אין ישובם נכוחים וערך המרחק אשר ביניהן נוסף מצד אחד ונגרע מצד אחד וגם המינים האלה נמצאים בקוים ישרים ובשאינם ישרים |
|
והמין השלישי הוא הקוים הנמשכים אשר האחד מושש את השני על נקודה ונפרד ממנו ואינו מחלק אותו ולא עובר עליו |
| ואין הענין הזה בין שני קוים ישרים אבל הוא נמצא בין שני עגולים או עקומים או בין שני מינין ממיני הקוים כגון קו ישר וקו עגול או עקום | |
| וזה הענין מספיק בפירוש מחלקי הקו | |
| Classification of surfaces | באור חלקי הפרוש |
| והפרוש הוא המוקף מכל סביבותיו בקוים הן ישרים הן שאינן ישרים או מעורבים מן ישר ומן שאינו ישר | |
| מיני הפרוש מדרך משיכתו בקרקע הגולם הם שלשה מינין | |
| האחד ישר והשני קבוב והשלישי עקמומי | |
|
והשטח הישר הוא הנמשך על יושר הקוים המקיפים אותו ועל נכחם |
| וכל קו אשר תשים אותו על גב השטח תמצאנו מכוון כנגד קוי תכליתו ואינו עולה מהם ולא יורד | |
| וזהו הנקרא לבדו שטח בחכמת השיעור | |
|
והפרוש הקבוב הוא הרקיע המקיף את קו הקובה מלמעלה והרקיע הזה יהיה עגול ויהיה עקום |
|
והפרוש העקמומי הוא הרקיע המקיף את גב הקובה מלמטה ויהיה כמו כן עגול או עקום |
| Classification of plane surfaces | עניני השטח הישר |
| והשטח הישר הוא נחלק על ג' מינים גדולים | |
|
האחד הוא אשר יקיף אותו קו אחד מכל סביביו ויהיה הקו הזה עגול או עקום ולא יתכן להיות קו ישר |
|
והשטח אשר קו האחד המקיפו הוא עגול אנו קורין לשטח עגולה ישרה אם הוא בשטח ישר |
|
ואם תמצא בכדור או בעגול הרקיע אנו קוראים לה אופן |
|
ואם יהיה הקו המקיף אותו עקום אנו קורין לה עגולה עקומה |
|
והמין השני הוא המקיף אותו שני קוים ולא יתכן גם בזה להיות הקוים שניהם ישרים אבל יכול יהיה האחד מהן ישר והשני אינו ישר או שניהם עגולים או עקומים או מתחברים מעגול ועקום |
| ואין אנו משגיחין לפרש המין הזה בכאן | |
|
והמין השלישי אשר הקוים המקיפים אותו יתר משני קוים הנה כלם ישרים או אינם ישרים או מתחברים מן הישרים ושאינן ישרים |
| סימן המין הראשון אשר יקיף אותו קו אחד והוא הנחלק לעגול ועקום | |
| השטח העגול הוא הנמצא באמצעיתו נקודה אחת אשר כל קו שתוציא ממנה אל הקו המקיף יהיו שוים בערכם זה לזה | |
| והנקודה הזאת נקראת ציר העגול אשר הוא סובב עליו | |
| וכל קו אשר הוא עובר על ציר העגול ומגיע מב' פנותיו אל הקו המקיף הוא נקרא אלכסון העגול | |
| והשטח העקום אין מרחק הנקודה אשר באמצעיתה מהקו המקיף לו מרחק אחד ויש לו שני אלכסונים האחד עודף על השני ואין אנו צריכין לפרש סימני השני מהמינין מפני שאינו מותיר בחבור הזה | |
| Plane surfaces surrounded by straight lines | סימני המין השלישי והוא השטח המוקף בקוים ישרים |
| ומיני השטח אשר כל קויו ישרים הם שלשה מינים גדולים | |
|
הראשון מהם הוא המשלש והוא המקיף אותו ג' קוים ישרים |
|
והשני הוא המרובע והוא אשר יקיף אותו ד' קוים ישרים |
|
והשלישי הוא המרבה ד' פנות אשר הקוים המקיפים אותו הן עודפים על ד' |
| כגון המחומש אשר יקיפו אותו ה' קוים וכן ממנו ולמעלה עד אין סוף | |
| ואנו קורין לקוי המקיפים את השטח צלעי השטח | |
| Classification of triangles | פירוש עניני השטח אשר לו שלשה צלעים ונקרא משלש |
| סימני השטח כי כל שני צלעים מצלעיו המקיפות אותו הן עודפות באורך על הצלע השלישית מהן לעולם | |
| ומסימניו כי כל זויותיו השלש ערכם כערך שתי זויות נצבות לא פחות ולא יותר | |
| והמשלש נחלק מצד צלעיו המקיפות אותו לשלשה מינין | |
|
האחד הוא אשר כל זוית מזויותיו זוית חדה והוא הנקרא מחודד הזוית |
| והמין הזה תמצא בו שלשה מיני צלעים | |
| יכול יהיה בכל צלעיו שוות ויכול יהיה שני מצלעיו שוות ויכול שלא תהיה אחת מהן שוה לחברתם | |
|
והמין השני הוא אשר יש לו זוית אחת נצבת ושתים חדות והוא נקרא משלש נצב הזוית |
| ולא יתכן להיות ג' צלעות המשלש הזה שוות יחד אבל יכול להמצא ב' מהן שוות יחד | |
|
והמין השלישי הוא אשר יש לו זוית אחת נרוחת והוא נקרא מרווח הזוית |
| ולא יתכן להיות שלש צלעותיו שוות כאשר לא נכון בנצב הזויות | |
| וסימן המשלש מחדד הזויות אם אתה מרבע איזה צלע שתרצה מצלעיו תמצא רבועו חסר מרובע ב' הצלעות הנשארות | |
| וסימן המשלש אשר לו זוית נצבת אם אתה מרבע את צלעו העומדת נכח הזוית הנצבה יהיה רבועה שוה לרבוע צלעות הנשארות העומדות על קרן הזוית הנצבה לא פחות ולא יותר | |
| וסימן המשלש מרווח הזוית אם אתה מרבע צלעו העומדת נכח הזוית המרויחה יהיה רבועה עודף על רבוע שני צלעות הנשארות העומדות על קרן זוית המרויחה | |
| Classification of quadrilaterals | פירוש עניני השטח המרובע |
| השטח המרובע הוא אשר יש לו ד' צלעות מקיפות אותו מארבע פנותיו | |
| ואתה יכול לחלקו לשני משלשים בקו האלכסון החולק אותו | |
| והמרובע יש לו ד' זויות והם שוות לעולם בערכם לד' זויות נצבות לא פחות ולא יותר | |
| והוא מתחלק מדרך צלעיו מן זויותיו לה' חלקים | |
|
החלק הראשון הוא אשר ארבע צלעיו כלם שוים בערכם אחת אל אחת וכן זויות ד' כל אחת מהן זוית נצבה וזה נקרא רבוע |
|
והשני הוא אשר שני מצלעיו הם נכוחיות ושוות וכן צלעותיו אחרות שוות כמו כן וד' זויותיו כלם (נצבות?) ולה (וזה) נקרא מרובע ארוך |
|
והשלישי דומה לראשון בצלעיו שהן שוות אלא שזויותיו אינם נצבות וזה נקרא מעויין |
|
והרביעי דומה לשני שכל שני מצלעותיו העומדות זו כנגד זו נכחיות ושוות אלא שזויותיו אינן נצבות וזה נקרא דומה למעויין |
| ואלו הד' מינין מן המרובעות הם המינים אשר החכמה הזאת מעיינת בהן מן המרובעות וחוקרת על עניניהם והחקירה בהם מועלת בחכמות אשר אחריה מפני שאלו הארבעה יש להם איזון בהקשת צלעותם אחת אל אחת | |
|
והמין החמישי הוא כל מרובע שאתה אין מוצא בו אחד מעניני הד' מינין שלפניו והמין הזה נקרא מרובע נפתל |
| ואם אתה מחלק המין הזה לכל צורות המרובעים הנפרדים ממנו יגיע מספר חלקיו אל שמנה עשרה צורה | |
| Classification of polygons | פירוש עניני השטח המרבה צלעות |
| הוא כל שטח אשר צלעותיו עודפות על ארבע כגון המחומש והמשושש | |
| וכל אחד מהם נחלק לשלשה חלקים | |
|
האחד הוא אשר כל צלעותיו וזויותיו שוות בערכם זו לזו ובארכן |
|
והשני הוא כל אשר [צלעותיו] שוות בארך זו לזו ואין זויותיו שוות בערכם |
|
והשלישי הוא כל אשר אין צלעותיו שוות ולא זויותיו |
| וכל שטח אשר תהיינה צלעותיו וזויותיו שוות אתה יכול לעגל בתוכו עגולה ויהיה כל צלע מצלעות השטח מושש לעגול מבחוץ | |
| וכן אתה יכול לעגל עליו עגולה ויהיה כל קרן מקרנות השטח מושש לעגולה מבפנים | |
| וכל שטח אשר צלעיו מרבות על המשלש הוא נחלק למשלשות | |
| ומנין המשלשות אשר הוא נחלק אליהם פוחת ממספר צלעותיו שנים | |
| כגון המרובע אשר לו ארבע צלעות והוא נחלק לשני משלשים והם חסרות ממספר צלעותיו שנים | |
| ואתה למד מן הענין הזה כי ערך זויותיו בזוית הנצבה כפל מנין המשלשות אשר הוא נחלק אליהם | |
| כי כבר למדת שזוית המשלש שוות לשני זויות נצבות | |
| ובמחומש ערך זויותיו החמש כערך שש זויות נצבות | |
| והמשושש ערך שש זויות כערך ח' זויות נצבות | |
| ועל הענין הזה בין והבן ערך זוית כל שטח ומספר המשלשות שהוא נחלק אליהן | |
| Classification of solids | פירוש חלקי הגולם |
| והגולם הוא כאשר למדת למעלה כל ערך אשר יש לו ג' מרחקים ותכליותיו פרושים | |
| ומיני הגולם הראשונים הגדולים שנים | |
| האחד מקיפין לו פרושים שהם שטוחים | |
| והשני מקיפין לו פרושים שאינן משוטחים אבל עגולים או עקומים או מעורבים | |
|
והגולם המוקף בשטחים מתחלק לשני מינים |
|
האחד גולמים שהכדור יכול להקיפן מלמעלה ויהיה מושש לכל אחד מקרנותיו |
|
והשני הגולמים שאין הכדור יכול להקיפן כענין הזה |
| והגולמים שהכדור יכול להקיף הם ה' מינין שוין בשטחים | |
| הראשון גולם אשר לו ד' קרנות חדות וד' צדים ומקיפים מד' צדיו ד' משלשות שוות בצלעותן | |
| והשני אשר לו ח' קרנות וו' צדים ויקיפו מו' צדיו ו' רבועות שוות | |
| והשלישי גולם שיש לו שש קרנות וח' צדים ומקיפים אותו מצדדיו ח' מושבות משלשות שוות בצלעותן | |
| והרביעי גולם שיש לו כ' קרן וי"ב צדדין ומקיפים לו מכל צדדיו י"ב מושבות מחומשות שוות בזויותם וצלעותם | |
| והחמישי שיש לו י"ב קרנות וכ' צדין כמו הן מקיפים מכל צדיו כ' מושבות משלש שוה בצלעותיו | |
| ולא יתכן להיות הכדור מקיף לגולם שוה בצלעותן וזויותיו כי אם לחמשה האלה | |
| ויש גולמים שאין מושבותיהן שוות והכדור מקיף להם ואין החבור הזה מכיל פירושם | |
| והגולם אשר הוא מוקף בשטחים ואין הכדור יכול להקיפו על קרנותיו נחלק על חלקים רבים ומינים עד אין סוף אלא שאנשי חכמת השיעור הכניסום בג' מינים | |
| האחד אשר שטחיו משולשות שאין שוות | |
| והשני שטחיו מרובעות שאין זויותיו נצבות | |
| והשלישי מורכב ממשולשות ומרובעות שאינן שוות ומשאר מיני השטחים | |
|
פירוש עניני הגולם המוקף בפרושים שאינם שטוחים |
| ומיני הגולם הזה הגדולים הם שני מינים | |
|
האחד גולם אשר יקיף אותו פרוש אחד עגול או עקום |
| והשני אשר יקיפו אותו שני פרושים או יותר מהם | |
|
והגולם אשר יקיף אותו פרוש אחד עגול הוא הנקרא כדור |
|
ואשר יקיף אותו פרוש אחד עקום נקרא גולם ביצני או גולם דומה לביצה |
| וסימני הגולם הנקרא כדור | |
| הוא אשר יקיפו פרוש אחד מכל סביביו ובאמצעיתו נקודה אחת וכל הקוים היוצאים ממנה אל פרוש הכדור שוים זה לזה | |
| והנקודה הזאת נקראת ציר הכדור | |
| וכל קו העובר על ציר הכדור והוא מגיע בשני צדיו אל הפרוש נקרא אלכסון הכדור | |
| ואם יהיה הכדור סובב על האלכסון הזה אנו קורין לו בעת ההיא בריח הכדור | |
| וב' הנקודות אשר הם תכליתי הבריח נקראים ראשי הבריח וקוראים להם בלשון ישמעאל קטבי הבריח | |
| וסימני הגולם הדומה לביצה | |
| ומסימני הגולם הזה שהנקודה האמצעית אשר בתוכו אין מרחקה מכל צדי הפרוש הסובב לה מרחק אחד | |
| ואתה מוצא על הנקודה הזאת קו עובר עליה ומגיע בשתי קצותיו אל פרוש הביצה והקו הזה ארוך מכל קו ישר אשר ימצא בגוף הביצה והקו הזה נקרא אלכסון | |
| וזאת הנקודה נקראת צירה הביצה | |
| וזה הגולם הביצני יש לו צורות רבות שאין אנו נזקקין להאריך בפירושן | |
|
פירוש עניני הגולם המקיפים אותו שני פרושים או יותר מהם |
| והגולמים המקיפים אותם פרושים שאינן שטוחים אבל יש מהן שטוח ויש מהן שאינו שטוח נכללים בם מינין | |
| מהם גולמי המצבות וגולמי החרוטות | |
| ומהן שברי הכדור ושברי המצבות ושברי החרוטות | |
|
והמצבה הזאת הנזכרת בחכמה הזאת הוא גולם אשר תכלית ראשו וסופו עגולה |
| והוא עולה בתבניתו עגול על ב' העגולות האלה | |
| והמצבה נוצרת בתוך הלב וגם בענין המעשה אם אתה מעמיד בתוך החרט צלע אחת מצלעי המרובע ותסובב אותו על צלע המעמד בחרט מסבה אחת עד אשר יחזור אל מקומו אשר התחיל לסבוב ממנו ותעמיד הצורה הזאת בתוך לבך ותבין ממנה תבנית המצבה | |
|
והגולם החרוט הוא לדומה לפרי האלון |
| והגולם הזה נוצר ואם אתה מעמיד בתוך החרט צלע אחת מצלעי משלש שהן נפרדות בו על זוית נצבה ותסוב את המשלש על הצלע הזאת עד שיחזור למקומו אשר התחיל לסבוב ממנו ומהצורה הזאת תבין תבנית הגולם האלוני | |
|
ושברי הכדור ג' מינים |
| מהן חצי כדור | |
| ומהן יותר מחציו | |
| ומהן פחות מחציו | |
|
ושברי המצבה הם שבריה אשר תחלק אליהם בהפרידך אותה בשטח מרובע שיהיה עובר על ראשה ומבתר את שני עגולותיה אשר על ראשה ועל סופה |
|
ושברי האלון הם שבריו אשר יחלק אליהן אם אתה מפרידו בשטח שיהיה מפרידו על נקודת ראשו או על צדי הנקודה הזאת והעובר על ראש האלוני הוא מפרידו בנתים והעובר על שני צדי הנקודה הזאת הוא מחלק את האלוני לשברים אחד גדול ואחד קטון |
| References for further study | והחכמה הזאת חוקרת על כל הענינים האלה ובוחנת על צורתם ותבניתם ועל ערכם בשוים ועודפם וחסרונם וענינם וישובם ונותנת בכל ענין וענין מהם מופתים ואותות נאמנים שאין בהם שום ספק |
| והיא נחלקת בעיונה בערכים האלה על שני חלקים | |
| החלק האחד מעיין בקוים ובפרושים ובדומה להם והוא נחלק במחקרו אליהם לחלקים רבים | |
| ממנו חוקר על הקוים אשר בשטח ועל השטחים ועל הגלמים המקיפים בשטחים ועל כל עניניהם המפורשים בספר השרשים לאיקלידש ובדומה לזה הספר מחבורי אקלידש הנזכר וחבור שאר החכמים המעיינים בשיעור על דרכו הנבונה | |
| וממנו מעיין בקוים ובפרושים אשר בכדור ובכל עניניהם הנראין מהם בעמידתן כגון ספרי הכדורות לתאודוסיס ומיליאוס וחבריהם | |
| וגם הוא מעיין בהם בסביבתם ובהחלופם את מקומם כאשר הוא מפורש בספרי תנופי הכדורות לטליקוס ולשאר חכמי השעור | |
| וממנו מעיין בקוים ובפרושים העמוקים ובכל עניניהם ובכל הטעמים הנמצאים בהם כאשר הוא מפורש בספר הצורות האלוניות לאבלניוס וספר הכדור והמצבה לאריסמידש | |
| והחלק השני מעיין בגולמים על רוב מיניהם ובכל עניניהם ובצדי מעשיהן ובכל המלאכות אשר הן פארות משרשי החכמה הזאת בספרי הצדדין לאיטימיש וחבריו | |
| וכמו ספרי המשקל והכימת והמשא והכבד לאירן ודימומס וחבריהם | |
| ומן החלקים האלה יצמחו חכמות רבות ותקון מלאכות שהן מועילות לבני העולם | |
| ואין החבור הזה יכול לסבול פירושם ועל כן אנו מפרשין עניני חכמה אחת לתת ממנה דמיון לחברותיה בעזרת האל | |
Part Two – Optics |
החלק השני מהעמוד השני מפרש עניני חכמת המראה |
| That by which the eye can see all the things it reaches, that deserve to be seen due to the faculty of the living being. | והוא אשר העין יכול לראות בו את כל הדברים אשר היא מגעת אליהם והם ראויים להראות מכח הגוף החי |
| We find that the sages who investigate the external sciences study this issue in two aspects: | מצינו החכמים המעיינים בחכמות החצונות חוקרים על הענין הזה על שני דרכים |
|
האחד הוא מחקר החכמה החוקרת על תמונת המראה או הראות ועל ערכו ועל שעור מרחקו מן הנראה בתמונתו ואיך יהיה הדבר מדבר מעמדו מן העין נראה בתמונתו |
|
והדרך השנית היא מחקר חכמת היצורית חוקרת על הענינים אשר הם נראים בעין איך הם נראים ועל איזה ענין הכח פושטת עליהם ונוגעת עליהם |
| This matter cannot be separated from two aspects: | ואין זה הדבר נפרד משני הדרכים |
|
יכול יהיה האור יוצא מהעין והולך ופושט באויר העולם עד שהוא מגיע אל הנראה וכשהוא נוגע אל הנראה הוא מתבונן בצורתו ומודיע את ערכם אל הנפש ההוגה |
|
או יכול יהיה שיהיה אור העולם הנפשט בתוך האויר נושא את צורת הדבר הנראה ומקריב אותה אל שטח העין ואל הלוחות הנזהרות אשר בעין עד שתהיה הצורה נרשמת בשטח העין ונטבעת באור הזהיר אשר בתוך העין |
| The soul knows the seen thing from this figure that is embedded inside the eye. | והנפש יודעת את הדבר הנראה מהצורה הזאת הטבועה בתוך העין |
| It one sees, then, that this disagreement is only in the increase of the distance between the eye and the seen thing, whether it starts from the eye and goes to the seen thing, or starts from the seen and goes to the eye. | ואתה רואה כי המחלוקת הזאת אינה כי אם בצמיחת המרחק בין העין ובין הדבר הנראה אם הוא מתחיל מהעין והולך אל הנראה או הוא מתחיל מהנראה והולך אל העין |
| Whoever wants to measure and estimate this distance, should not worry whether it starts from the eye or starts from the seen, because this difference does not affect his measuring, since the measure is one, whether it starts from here, or starts from there. | והרוצה למדוד המרחק הזה ולשערו אינו חושש אם הוא מתחיל מן העין או מתחיל מהנראה כי אין החלוק הזה מזיק לו בשעורו כי השעור אחד הוא אם מתחיל מכאן או מתחיל מהלן |
| Because of this, the geometricians were not worried about it, and did not examine which is the primary. | ומפני זה לא חשו לו חכמי השעור ולא חקרו עליו איזה הוא העקר |
| But, they relied on the one matter that seemed easier for them to calculate and measure - which is the starting from the eye. | אבל סמכו על הענין האחד אשר הוא קל בעיניהם לחשבון ולשיעור והוא המתחיל מהעין |
| Since, this is a thing that is fixed in its place, while the seen gets closer to it or moves away. | מפני שהוא דבר עומד במקומו והנראה הוא מתקרב אליו ומתרחק |
| Not because they found it more appropriate than the other matter, but because it was for them more precise in the method of their research. | לא מפני שראו אותו נכון יותר מהענין השני אלא מפני שהיה מתוקן להם בדרך מחקרם |
| For this reason, it was said at the beginning of this science: the light comes out of the eye in straight lines and goes in the direction of the seen. | ועל הטעם הזה התחילו בתחלת החכמה הזאת ואמרו האור היוצא מהעין על קוים ישרים והולך אל נוכח הנראה |
| For each of these lines there is a parallel to it in the seen and as the number of the lines so is the number of the parallels to them. | וכל קו וקו מהם יש נוכח כנגדו מן הנראה וכרוב הקוים כן רוב הנכוחיים אשר כנגדם |
| The lines go out from a single point of the eye, and when they are going away they separate from it at a plane angle. | והקוים האלה יוצאים מנקודה אחת מן העין ובצאתם הם מתפרדים ממנה על זוית שטוחה |
| These lines are summed together to a solid angle. | ויתקבץ מן הקוים האלה בהתחברם יחד זוית גלומה |
| When they reach the seen, these lines are as a cone body whose vertex is in the eye, and the circular base is the surface of the seen. | ויהיו הקוים האלה בהגיעם אל הנראה כתמונת גולם אלוני ראשו מצד העין ועגולת מושבו הוא עם שטח הנראה |
| Because of this, we see the quadrangular shapes, when they are getting far from the eye, as circles. | ומפני זה אנו רואים את התמונות המרובעות כשהם מתרחקים מן העין עגולות |
| Anything that the luminous lines reach is visible, and that they do not reach is invisible. | וכל דבר שהקוים המאירים נוגעים אליו הוא נראה ואשר אין נוגעים אליו ואינו נראה |
| Anything that is seen by the eye in a known angle has a known limit and an end in which, once reached, it is hidden from the eye and invisible. | וכל דבר שהוא נראה בעין על זוית ידועה יש לו תכלית ידועה וסוף כשהוא מגיע אליו הוא נסתר מן העין ואינו נראה |
| All that is close to eye is seen in one measure; if it moves away from the eye, its size decreases in the vision, so when its distance increases its measure decreases also, until it becomes hidden from the eye and the faculty of sight does not reach it. | וכל הקרוב אל העין יראה אל שעור אחד ואם יתרחק מהעין יתמעט שעורו בראיה וכשהוא מוסיף הרחוק יהיה שעורו מתמעט כמו כן עד שיהיה נסתר מהעין ואין כח הראות מגעת אליו |
| All that is seen in a large angle seems great, and the seen in a small angle, seems small. | וכל הנראה על זוית גדולה נראה גדול והנראה על זוית קטנה נראה קטן |
| The matters that the eye reaches, which are known through its faculty, are the colors, the shapes, the body, the proportion, the position, the movement, and the rest. | והענינים אשר העין מגעת אליהם והם ידועים מכחה הם הצבעונים והתמונות והגולם והערך והיישוב והתנועה והעמידה |
| The eye does not perceive any of these matters, but through two things: light and thickness. | ואין העין מכרת אחד מהענינים האלה אלא על ידי שני דברים והם אור ועובי |
| Anything that the light does not penetrate and has no thickness that prevents the light from passing through it, is invisible. | וכל דבר שאין האור נופל עליו ואין לו עובי שיהיה מעמיד את האור מלעבור עליו אינו נראה |
| Because of this, the eye does not see any faint thing, through which the light passes. | מפני זה אין העין רואה כל דבר רקיק שהאור עובר עליו |
| Among the seen by the eye, there is that which is seen first without another thing and that which is seen through another thing on which it depends. | וכל הנראה בעין יש ממנו נראה ראשונה שלא על ידי דבר אחר ויש ממנו נראה על ידי דבר אחר שהוא תלוי בו ותובע לו |
| The seen, in another way, is divided into two categories: | והנראה נחלק על דרך אחר לשני חלקים |
| Some, in their shape and structure, and some not in their shape, but are as the image of the eye or as image of the thing that misleads the eye. | יש מהם בתמונתו ותבניתו ויש ממנו שלא בתמונתו אבל הוא כדמות העין או כדמות הדבר המטעה את העין |
| The seen first is the thing to which the eye reaches and rests first, that is, the body of the seen and its color. | והנראה ראשונה הוא הדבר אשר העין נוגעת אליו ראשונה ונופלת עליו תחלה והוא גוף הנראה וצבעונו |
| Because, any thing whose color is invisible is invisible, despite having thickness in the construction of its body, the light that falls on it is invisible until it has color. | כי כל דבר שאין צבעונו נראה אינו נראה ואפ"י יש לו עובי בארג גופו ויהיה האור נופל עליו אינו נראה עד שיהיה לו צבעון |
| All that is colored by color is seen only through the light and the thickness and strength of the construction of the body that prevents the light from passing through it. | וכל המצטבע בצבעון אינו נראה אלא עם האור ועובי אורג הגוף וחזוקו כדי שיהיה מונע את האור מעבור עליו |
| One finds that the eye needs three things: | ואתה מוצא את העין צריכה לשלשה דברים |
|
והוא אור שיהיה נופל על דבר נוגה שיש לו צבעון |
|
והצבעון הוא הנראה ושני הענינים האחרים משמשים לו ועוזרין אותו עד הראות |
| Anything that is in darkness is invisible. | וכל דבר שהוא בחשך אינו נראה |
| Furthermore, the darkness is invisible, but it is known. | וכן החשך אינו נראה אבל הוא נודע |
| Because, no one sees darkness, but he recognizes it through his intelligence and wisdom, since it is the lack of light. | כי אין אדם רואה את החשך אבל הוא מכיר את החשך בדעתו ותבונתו מפני שהוא העדר האור |
| Similarly, the sound and the silence: since the sound is heard by the ear, and one recognizes the silence not because he hears it, but since he does not hear the sound. | והדומה לזה הקול והשתיקה כי הקול הוא נשמע באזנים ואתה מכיר את השתיקה לא מפני שאתה שומעה אבל מפני שאי אתה שומע קול |
| Likewise, everyone who recognizes the thing must recognize its opposite. | וכמו כן כל המכיר את הדבר הוא ראוי להכיר את חלופו |
| Because of this, it has been said that darkness is recognizable but invisible. | ומפני זה אמרו על החשך שהוא נכר ואינו נראה |
| One finds that the seen first is the color. | ותמצא הנראה תחלה הוא הצבעון |
| All that are seen with the color, are seen through the color and depend on it - for example, the body, the shape and the proportion - one sees them only through the color. | וכל הנראים עם הצבעון הם נראים על ידי הצבעון ותלויים בו כגון הגולם והתמונה והערך אין אתה רואה אותם אלא על ידי הצבעון |
| For all are recognized and understood by the faculty only through the surface of the colored body, on which the light falls. | כי כלם אין הכח מכיר אותם ומבין את תבניתם אלא בשטח הגולם הצבוע אשר האור נופל עליו |
| One finds that there is no thing that is seen first except for the color alone, which is the thing that is seen by the sight of the eye, and there is no other bodily sense that can recognize it and control it. | ומצינו כי אין דבר נראה ראשית אלא הצבעון בלבד והוא הדבר הנראה לראות העין ואין חוש אחר מכל חושי הגוף יכול להכירו ולשלוט בו |
| All the matters that are seen through the color are recognized also by another sense of the bodily senses, therefore it is said that they are seen secondly and mediated by a thing on which they depend, such as the structure of the body, the number, the movement, and the rest, which can be recognized by touch, as they are recognized by the sight of the eye. | וכל הענינים הנראים עם הצבעון הם נכרים כמו כן בחוש אחר מחושי הגוף ומפני זה אמרו עליהם שהם נראים שנית ועל ידי דבר שהן תלויין בו כגוף התבנית והמספר והתנועה והעמידה אשר אתה יכול להכיר אותם במשישה כאשר אתה מכיר אותם בראיית העין |
| For, one can say about this body that it is a square or that it is moving, when touching it by the hands, as one recognizes it by the sight of the eye. | והרי אתה יכול לומר על הגולם הזה שהוא מרבע או שהוא מתנענע כשאתה מושש בידך כדרך שאתה מכיר אותו בראיית העין |
| But, it is not so with color, since no bodily sense can recognize it except for the eye, as it is granted to the eye and all that are seen by the eye are seen through it. | ואין הצבעון כך שאין אחד מחושי הגוף יכול להכירו בלתי העין בלבד לפי שהוא המסור לעין וכל הנראין בעין נראין על ידו |
| It is clear then what is the thing that is seen firstly, which shows its essence and structure and what is the thing that is seen secondly, through another thing. | ונתברר לך מה הוא הדבר הנראה ראשונה אשר הוא מראה את עצמו ואת תבניתו ומה הוא הדבר הנראה שנית ועל ידי דבר אחר |
| It should be explained in what way the thing is seen in its construction and how it is seen not in its construction. | ואנו ראויים לפרש על אי זה דרך יראה הדבר בתבניתו ואיך יראה שלא בתבניתו |
| It is said that the eye does not recognize the seen until it shines in the light of the air and colored with the color of the seen thing and the shape the seen is embedded and drawn in the eye. | ואנו אומרים כי אין העין מכיר את הנראה עד שתהיה נזהרת באור האויר ומצטבעת בצבעון הדבר הנראה ותהיה צורת הנראה נטבעת בעין ומצטיירת בעין |
| Because of this, the eye should not have any color, but should be separate from any light and color, and designated to receive the light and the color that arrive to it or which it reaches. | ומפני זה העין צריכה שלא תהיה לה צבעון אבל תהיה חלוקה מכל אורות ומכל צבעון ומזומנת לקבל את האור ואת הצבעון הבאים אליה או אשר היא נוגעת אליהם |
| From this matter it is seen that the eye recognizes the red because it becomes red, and the white, because it turns white; and all the matters that are seen by the color are seen to it as depending on the color with which it is colored. | ויראה לך מהענין הזה כי העין מכירה את האדום מפני שהיא מתאדמת ואת הלבן מפני שהיא מתלבנת וכל הענינים הנראים עם הצבעון נראים לה תלויים בצבעון אשר היא מצטבעת בו |
| If the eye was red or green before the sight, any thing at which it looks would seem to it as red or green or as one of the colors that it had in it, and this is one matter of error of the eye, when it sees the seen not as its image. | ואם תהיה העין קודם הראייה אדמדמת או ירקרקת יראה לה כל דבר שהיא מביטה אליו ירקרק או אדמדם או על צבעון אחד מעין הצבעונים אשר בתוכה וזהו ענין אחד מטעות העין כשהוא רואה את הנראה שלא כדמותו |
| The eye also makes another error concerning the proportion of the seen and its measure, by its closeness and its remoteness from the eye. | וגם העין טועה טעות אחר בערך הנראה ושעורו מדרך קרובו אל העין ורחקו ממנה |
| Likewise the figures, the shapes and the images change in the sight of the eye until one sees the long as short, and the short as long; the wide as narrow, and the narrow as wide; the circular as square, and the square as circular; and so on for the rest of the images. | וגם הדמויות והצורות והתמונות מתחלפות בראות העין עד שתהיה רואה את הארוך קצר ואת הקצר ארוך ואת הרחב צר ואת הצר רחב ואת העגול רבוע ואת הרבוע עגול וכן בשאר התמונות |
| It also makes error concerning the the position of the seen and its arrangement, seeing the left as right, and the right as left; the prior as late, and the late as prior; the ordered one by the other as unordered; and the given on the one surface as if the one is going up and other is going down. | וכן היא טועה בישוב הנראה ובסדרו עד שתהיה רואה את השמאל ימין ואת הימין שמאל ואת המוקדם מאוחר ואת המאוחר מוקדם ואת הסדורים אחד כנגד אחד כשאינם סדורים ואת הנתונים בשטח אחד כאלו האחד עולה והאחד יורד |
| However, by this science, one can separate these sciences from the errors concerning the seen as it is and the seen not as it is. | ובחכמה הזאת יכול אדם להפריש בין החכמות האלה הטעיות בנראה כדרכו ובנראה שלא כדרכו |
| It offers proofs and evidences about all these matters, investigates their causes, and gives ways and conditions to be saved from all these errors, so that one can know the proportion of the seen, its measure, its shape, and all the matters relating to its sight, correctly and truly, without any error, approximation, or doubt, so that any doubt that comes in the sight will fade away. | והיא נותנת אותות ומופתים על כל אלה הענינים וחוקרת על עלתם ונותנת צדדים ותנאים להשמר מכל אלה הטעיות עד שיהיה אדם יודע את ערך הנראה ושעורו ותמונתו וכל הענינים הנתלים בראותו על תקונם וישרם בלא שום טעות ולא קירוב ולא ספקא ויסור מעליו כל ספקא שהיא באה בראייה |
| Through this science, one knows by the sight of his eye the measure of any thing that cannot be measured or brought closer to him. | ומתוך החכמה הזאת יהיה האדם יודע בראות עינו שעור כל דבר שאינו יכול למדוד אותו ולא לקרב אליו |
| One knows the distance between him and any thing that is far from him, as well as the distance between things that are granted to the sight of the eye, even if he does not reach them. | וידע שעור המרחק בינו ובין כל דבר שהוא רחוק ממנו וגם המרחק אשר הוא בין דברים שהם נמסרים למראית העין וגם אינו מגיע אליהן |
| One also knows the height of trees, towers and mountains, only through sight of his eye; the width of the seas and rivers whose shores he sees; the depth of wells and waterholes, while standing by the river or the lake, or by the side of the well or dugout. | וכן ידע אורך האילנות והמגדלים וההרים במראית עינו בלבד וגם רוחב הימים והנהרות אשר הוא רואה את שפתם וכן עומק הבורות והגבים בעמידתו על שפת הנהר והאגם או על פי הבאר והשוחה |
| One can know the distance of the clouds from the earth, and say on which spot they are standing; concerning the distance of the stars from the earth, their size, and their measure, [one can say] which of them is greater than the earth or which is greater than the other. | ובה יכול לדעת את רוחק העבים מן הארץ ולאמר על איזה מקום הם עומדים ועל מרחק הכוכבים מהארץ ועל מדתם ועל שעורם ואיזה מהם גדול מן הארץ ואיזה מהם גדול מחברו |
| One recognizes all these matters by looking on the star or the clouds. | והוא מכיר את כל הענינים האלה בהביטו אל הכוכב או על העבים |
| When observing them, there are matters for which he needs precise instruments to lead the light of the eye along the straight path, by looking on the seen through these instruments. | ובראותו אותם יש מהם ענינים שהוא מצטרך בהם אל כלים מתוקנים להנהיג אור העין על דרך ישר כשהוא מסתכל אל הנראה על הכלים האלה |
| There are matters for which an instrument is not needed. | ויש ענינים שאין צריך בהם אל כלי |
| All the seen things are seen, as we noted above, through the light spread through the air or through a bright body in the air, until it reaches the seen. | וכל הדברים הנראים הם נראים כאשר זכרנו למעלה על ידי אור הנפרש באויר או בגולם זהיר באויר עד שיגיע אל הנראה |
| This light exists in lines that go to the eye or leave the eye. | והאור הזה נמצא בקוים ההולכים אל העין או היוצאים מהעין |
|
ואלו הקוים יש מהם על יושר דרכו עד שהוא מגיע אל הנראה או עד שיכלה כחו ויסוף אורו ואלו נקראים אורות ישרים |
|
ויש מהם קוים אשר יקרה אותם בדרכם קודם הגעתם אל הנראה מונעות וכלים נזהרים שיהיו מונעים את הקוים מלעבור אל הנראה והם משיבים אותם מדרכם אחורנית |
|
והקוים האלה שונים מן המקרה הזה הקרה אותם על ג' ענינים |
|
יש מהם חוזרות אחורנית על דרך עצמן ועל הדרך שיצאו בה והם נקראים אור נשבר |
|
והאדם רואה בענין הזה צורת עצמו כשהוא מביט בדבר הזהיר השובר את האור ומשיבו לאחור |
|
ויש מהם שהולכים כנגד הדבר המונע כגון הצורה הזאת |
|
והאור הזה נקרא אור פושט והשם הזה חצוב מן ופשטת על העיר[note 35] |
|
ואתה הבן ממנו שהאור פושט לפניו והולך כנגדו ואינו שב לאחוריו ורואה באור הזה דברים שהם רחוקים ואין העין עומדת כנגדם ומביטה אליהן |
|
ויש מהן קוים שהן חוזרין אל נוכח העין ולא על נכחה ממש אלא על ימין או על שמאל כגון הצורה הזאת |
|
ואלו הקוים נקראים אור נזור |
|
ואדם רואה בענין הזה דבר אשר הוא עומד על ימינו או על שמאלו או למעלה ממנו או לאחוריו ואם אינו מביט אליו או מסתכל בו |
|
והקוים החוזרים אם יהיה המחזירם זוהר שטוח הם חוזרות על זויות שוות לזויות אשר הגיע בהם אל השטח הזהיר |
|
ואם יהיו נופלות על זוית נצבה הם חוזרות על עצמן והיא הזוית הנצבה היא שוה משני צדי הקו |
|
ואם הם נופלים על זוית חדה מצד נפילתן הן חוזרין על זויות שוות להן מהצד אשר כנגדן |
|
ואם לא יהיה הזוהר המשיב את האור שטוח אבל יהיה עגול או עקום יהיה האור הנזור ממנו חוזר על זוית דומה לזוית אשר הוא נופל בה אלו היה ביניהן שטח וזה המזהיר החוצץ בין העין ובין הדבר הנראה יהיה אויר עבה או זכוכית או מים או דבר מלוטש |
| Optics studies the path of sight through all these four lines: the straight lines, the fractured lines, the spreading lines and the reflecting lines; and it explains all the events that take place in these pathes of sight. | וחכמת המראה חוקרת על דרך הראייה בכל הקוים הארבעה האלו והם הקוים הישרים והקוים הנשברים והקוים הפושטים והקוים הנזורים ומפרשת כל מאורעות שהן קורות בדרכי הראייה האלה |
|
והחקירה על דרך המראה בקוים הישרים נקראת חכמת המראות הישרה |
|
ואותה החוקרת על דרך הראיה הנשברת והנזורה והפושטה נקראה חכמת המראות המעוקלות |
| This whole science is one of the effects of the Geometry science that is called in Arabic al-handasa. | וכל החכמה הזאת היא תולדה אחת מתולדות חכמת השעור הנקראת אלהנדסה בערבית |
| Whoever delves into this science completely is called mathematician, since all his wisdom and intelligence dealt only with this science all his life. | והמעמיק בחכמה הזאת עד סופה הוא נקרא חכם מוסרי או חכם סורי מפני שכל חכמתו ובינת לבו עסק בה כל ימיו בחכמה הזאת בלבד |
| Those who delve into the other sciences, such as astronomy, physics, and theology, that is called metaphysics, or according to the words of our Rabbis, "Work of Creation" and "Merkabah Mysticism" - those are called metaphysical philosophers. | והמעמיקים בשאר החכמות כמו חכמת התכונה וחכמת הטבע וחכמת האלקות שהוא מה שאחר הטבע ובלשון רז"ל מעשה בראשית ומעשה מרכבה והמעמיקים בה הם הנקראים פלוסופים אלקיים |
| They do not praise the one who spends his life studying only this science | ואינם משבחים את האדם המכלה כל ימיו בלמוד החכמה הזאת בלבד |
| Although it is a great science, very useful, that leads the one's heart and intelligence towards the wisdom, it is not praiseworthy to lose all his life in its study until reaching its depth. | ואע"פ שהיא חכמה גדולה ומועילה ומוסרת לבו של אדם ודעתו אל הבינה אין נאה להאביד כל ימיו בלמודה עד שיהיה מגיע אל עמקה |
| Some of it is enough to lead the heart toward understanding the other sciences that follow it. | אבל ספק לו ממנה מקצתה כדי שינהיג בה את לבו להבין שאר החכמות שאחריה |
| Since, one cannot understand most of the sciences that follow it, if he does not use this science. | כי אין אדם יכול להבין רוב החכמות אשר אחריה אם לא ישתמש בחכמה הזאת |
| Therefore, it is said that its study is a necessity, an obligation, and a pleasure for the study of the other sciences, and a part of it is enough for this [purpose]. | ומכאן אמרו שלמודה צורך וחובה וחמדה ללמוד שאר החכמות ומקצתה מספיק בזה |
| If one delves into it, he should not use it all his life, but lead his heart from its study towards the study of the other following sciences. | ואם יהיה אדם מעמיק בה אל ישתמש בה כל ימיו אבל יהיה מנהיג את לבו מלמודה אל למוד שאר החכמות שאחריה |
Conclusion of Section Two |
כותרת העמוד השני |
| This science [of geometria] came into the world through Bezalel, while in the preceding science - arithmetic - it was very proficient Oholiab, son of Ahisamach, which is said to be a craftsman, and an arithmetician [Exodus 38, 23]. | והחכמה הזאת יצאה לעולם על ידי בצלאל והחכמה הזאת אשר לפניה מחכמת המנין היה מחכים בה אהליאב בן אחיסמך אשר נאמר עליו חורש וחושב[note 36] |
| The meaning of arithmetician is wise in the science of calculation and in all arts that require calculation, such as the work of an embroiderer and a weaver. | ויהיה פירוש חושב חכם בחכמת החשבון ובכל מלאכות שהן צריכות לחשבון כגון רוקם ואורג |
| As for Bezalel, he was wise in all the sciences that exist in the world, for it is said: and I have imbued him with the spirit of God [Exodus 31, 3] | והיה מן הענין הזה בצלאל חכם בכל החכמות הנמצאות בעולם כי כן כתוב בו ואמלא אותו רוח אלהים וגו'[note 37] |
| The four virtues with which God imbued Bezalel correspond to the four foundations of science in the world. | ויהיה אלו ארבע מדות טובות אשר מלא הב"ה בצלאל כנגד ארבע יסודות החכמה אשר בעולם |
| The exegesis of this verse is as follows: | ויהיה מדרש הפסוק הזה כך |
|
ואמלא אותו רוח אלהים[note 38] זו חכמת אלהית ותלמוד תורה שהוא היסוד הרביעי אשר הוא ממלא האדם וגומר את תמימותיו |
|
והרוח הזה מסרו הב"ה מחובר בג' ענינים טובים |
|
בחכמה זו חכמת המספר וחכמת המספר הוא היסוד הראשון המעיין בראש החכמות ותחלתן שהן מתקנות את הלב ומקבילות אותו כלפי בינה |
|
ובתבונה היא חכמת היצורים המעיינת בעניני היצירה ותבנית כל הנבראים והיא היסוד השני אשר אין האדם יכול ללומדו עד שיתגבר בחכמה |
|
וקרא אותה תבונה לפי שהיא עודפת על החכמה כמו שאמר הפסוק מי חכם ויבן אלה נבון וידעם [note 39] נקרא תחלה חכם אח"כ נבון |
|
ובדעת זו חכמה אנושית אשר היא יסוד שלישי כי דרך העולם לקרוא למי שהוא מכוון בכל דבריו וזריז בדרך ארץ ולתת תושיה ועצה לבני עמו הוא דעתן ובעל דעת |
|
ויהיה שם מלאכה[note 40] אמור על כל אומניות אשר בעולם ונמצא בצלאל חכם ומבין בכל חכמה שכליית ועמלנית |
| We find that the foundations of science related to Bezalel are in an inverse order in the first verse with which we opened this book | ומצינו יסודי החכמה סדורים בבצלאל חלוף סדורן בפסוק הראשון אשר פתחנו בו את הספר הזה |
| Because, the [verse related] to Bezalel mentions the divine science [theology] first, and in the first verse it is mentioned last. | כי בבצלאל זכר החכמה האלהית תחלה ובפסוק הראשון זכר אותה באחרונה |
| This difference [in the order of the sciences] comes since in the Bezalel's [verse] they are ordered according to the way that man should acquire them, which is the way they were given to Bezalel: | וזו החלוף בא מפני בצלאל וסדר אותם על הדרך שאדם ראוי לקנותן ועל הדרך שמסר אותן בבצלאל |
|
והתחיל ראשונה ברוח אלהים והוא תלמוד תורה ויראת השם אשר האדם חייב להקדימם וללמד קודם כל חכמה |
|
ואחר סדר בו שאר החכמות על דרך למודם ועל סדרם הקל תחלה ואחריו החמור ממנו עד שהשלים יסודי החכמות הד' |
| In the other verse, they are ordered by the order of their virtue and the virtues of the matters they investigate: | ובפסוק האחר סדר אותם על סדר מעלתם ומעלות הענינים אשר היא חוקרת עליהם |
|
מפני זה התחיל בחכמת המוסר שהיא חוקרת עליהם על תכלית הנמצאות וחתם בחכמת השכל והיא חכמת האלהית המעיינת בפלאי פלאות החכמה |
|
ומצינו חכמת המוסר קרואה בשני הפסוקים האלו חכמה מפני שהיא קלה בלמודה וקרובה היא במעלתה |
|
וקרא לחכמה היצורית בפסוק אחד גבורה מפני שהיא מעיינת בחכמת הבורא וחוקרת על הנמצאות ועקרם ולא יכול אדם לירד לעומק החכמה הזאת עד שיתגבר בבינה |
|
וקרא לה הפסוק השני תבונה והתבונה מוסיפה על החכמה ועודפת עליה כמו שזכרנו למעלה |
| וקרא לחכמה האנושית בפסוק האחד עושר מפני שהיא מעיינת בדרך מנהג האדם בעולם | |
| וקרא לה בפסוק השני דעת מפני שהאדם צריך בשימושו עם בני העולם אל הדעת | |
| וכן קרא לחכמה האלהית בפסוק האחד השכל מפני שהענינים שהיא חוקרת עליהם הם עומדים בהשכל ומצויירים בו ואין להם צורה ודמות חוץ מהלב ואין לאחד מחושי הגוף כוח להגיע אליהם | |
| וקרא לה בפסוק השני רוח מפני שאין אדם יכול להבין אותה על דרכה כי אם ברוח אלהים מרוב פליאותה | |
| ותמצא כל החכמות קרואות בשני הפסוקים בשמות נמנות ונכונות על שני המנהגים | |
| האחד על דרך בינת האדם להם וסדר חיובם בלמוד | |
| והמנהג השני על דרך מעלתם ודקדוק הענינים אשר היא חוקרת עליהם | |
| At the end of the chapter dealing with optics, which concludes the section on geometry, appears a sentence that apparently was supposed to open the section devoted to metaphysics now lost or eventually not written. The author presents this expected section on metaphysics as dealing with sacred matters that might purify him from engaging with the previous secular affairs | ובאתי בכאן לבאר כל הענין הזה ואם אינו מדרך החבור מפני שעסקתי לפנים בדברי חול מדרך ארץ והבאתי הענין הזה אולי אטהר דברי חול בדברי קודש |
| ואני חותם במקום הזה העמוד השני ומתחיל לפרש העמוד השלישי | |
| והבורא ברחמיו וברוב חסדיו יישירנו ללכת בדרכיו כי הכל בידיו | |
Section Three – Music |
העמוד השלישי מפרש חכמת הנגון, והחכמה הזאת נקראת בלשון יון מושיקא |
Notes |
||
|
||
Apparatus |
||
Appendix: Bibliography
Abraham bar Ḥiyya ha-Nasi (known as Abraham Judaeus or Savasorda)
b. 1065 – d. 1136 or 1145, worked in Barcelona, Spain
Yesodei ha-Tevunah u-Migdal ha-Emunah (The Foundations of Understanding and Tower of Faith)
Manuscripts:
- 1) Berlin, Staatsbibliothek (Preußischer Kulturbesitz) Or. Oct. 244/15 (IMHM: f 1996), ff. 121r-136v (15th-16th century)
- 2) Madrid, Biblioteca Nacional de España 5474/8 (IMHM: f 7233), ff. 340v-342v (14th-15th century)
- 3) Moscow, Russian State Library, Ms. Guenzburg 698/1 (IMHM: f 47914), ff. 2r-9v (14th century)
- 4) München, Bayerische Staatsbibliothek, Cod. hebr. 36/19 (IMHM: f 1166), ff. 203v-209r (1485)
- 5) Oxford, Bodleian Library MS Mich. 536/8 (IMHM: f 22082), ff. 118-125 (cat. Neub. 1268, 8) (1518-1520)
- 6) Parma, Biblioteca Palatina Cod. Parm. 2635/1 (IMHM: f 13551), ff. 1r-6r (Lecce, 1437)
- 7) Vatican, Biblioteca Apostolica ebr. 400/6 (IMHM: f 478), ff. 66r-75r (14th-15th century)
Edition:
- La obra enciclopedica Yesode ha-Tebuna u-Migdal ha-Emuna de R. Abraham Bar Hiyya Ha-Bargeloni. edición critica con traducción, prólogo y notas por Jose M. Millás Vallicrosa. Madrid-Barcelona: Casa Provincial de Caridad de Barcelona, 1952.
Bibliography:
- Adler, Israel. 1975. Hebrew Writings Concerning Music: In Manuscripts and Printed Books from Geonic Times up to 1800. München: G. Henle Verlag, pp. 6-7.
- Efros, Israel. 1926-7. Studies in Pre-Tibbonian Philosophical Terminology: I. Abraham Bar Hiyya, the Prince, The Jewish Quarterly Review, New Series, vol. 17, no. 2 (Oct., 1926), pp. 129-164; vol. 17, no. 3 (Jan., 1927), pp. 323-368.
- Freudenthal, Gad and Mauro Zonta. 2009. Nicomachus of Gerasa in Spain, Circa 1100: Abraham bar Ḥiyya’s Testimony, Aleph 9.2, pp. 189-224.
- Levey, Martin. 1952. The Encyclopedia of Abraham Savasorda: A Departure in Mathematical Methodology, Isis, Vol. 43, No. 3 (Sep., 1952), pp. 257-264.
- ———.1954. Abraham Savasorda and His Algorism: A Study in Early European Logistic, Osiris, Vol. 11, pp. 50-64.
- Rubio, Mercedes. 2000. The First Hebrew Encyclopedia of Science: Abraham bar Ḥiyya’s Yesodei ha-Tevunah u-Migdal ha-Emunah. In: Steven Harvey ed. The Medieval Hebrew Encyclopedias of Science and Philosophy. Dordrecht, Boston, London: Kluwer Academic Publisher, pp. 140–53
- Sarfatti, Gad ben ‛Ami. 1968. Mathematical Terminology in Hebrew Scientific Literature of the Middle Ages. Jerusalem: Magnes Press, pp. 61-129.
- Steinschneider, Moritz. 1893-1901. Mathematik bei den Juden. Berlin-Leipzig-Frankfurt: Kaufmann, pp. 83-87 (d34-d38); repr. Hildesheim: G. Olms, 1964 and 2001.
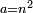
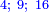
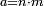
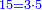
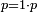
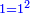

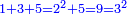
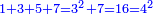
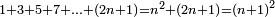


![\scriptstyle x_1=a_3-\left[a_2+\left(a_2-a_1\right)\right]{\color{blue}{=9-\left[6+\left(6-4\right)\right]=1}}](/mediawiki/images/math/1/6/4/1649bb86dbe1e6c0d1ff4dcf2950fb76.png)
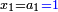
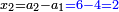
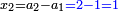
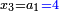
![\scriptstyle x_3=a_3-\left[a_2+\left(a_2-a_1\right)\right]{\color{blue}{=4-\left[2+\left(2-1\right)\right]=1}}](/mediawiki/images/math/8/2/f/82f4a8248c1e2a954670da875f6348cd.png)
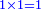
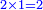
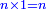
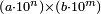
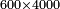
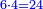
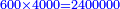
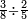
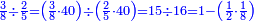
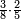
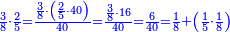
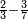
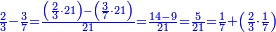
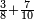
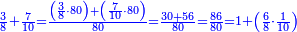
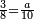
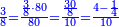
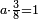
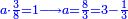
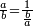
![\scriptstyle a\sdot\left[\frac{2}{5}+\left(\frac{1}{10}\sdot\frac{1}{5}\right)\right]=1](/mediawiki/images/math/3/7/7/3778176acc4bf275d05b23058a9d3c17.png)
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle a\sdot\left[\frac{2}{5}+\left(\frac{1}{10}\sdot\frac{1}{5}\right)\right]=1\\&\scriptstyle\longrightarrow a=\frac{50}{\left[\frac{2}{5}+\left(\frac{1}{10}\sdot\frac{1}{5}\right)\right]\sdot50}=\frac{50}{21}=2+\frac{1}{3}+\left(\frac{1}{7}\sdot\frac{1}{3}\right)\\\end{align}}}](/mediawiki/images/math/2/e/8/2e83d9632e9f82af8480b6472d23dab8.png)
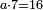
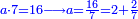
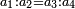
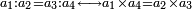
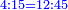
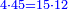
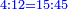
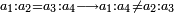
![\scriptstyle\frac{\left[amount\ of\ goods\ offered\ in\right]\ business}{price}=\frac{sold\ \left[amount\ of\ goods\right]}{money\ \left[paid\right]}](/mediawiki/images/math/f/9/5/f955baa1cc41bb6ac559907a3ec3bfab.png)