Barter Problems
|
|
|
|
261) שאלה שנים מחליפים צמר ופשתים יחדו בעל הבגד שוה הקנה במעות ה' ובחלוף משים ו' בחלוף ושואל החצי במעות ובעל הצמר מכר צמרו ק"ס בחלוף עם בעל הבגד ח' יותר ממה שהיה שוה במעות כדי להרויח כמוהו אשאל כמה היה שווי הצמר בראשנה
|
|
|
עשה כך הסר חצי ו' מו' יען כי שואל החצי בממון וישאר ג' גם תסירם מה' ונשאר ב' ולכן תאמר אני מרויח א' עם ב' מה ארויח עם ח' ותמצא כי ישובו י"ו וכך היה שווי הצמר בראשנה ובחלוף משים אותו כ"ד
|
|
|
262) שאלה שנים מחליפים בגד עם צמר הבגד שוה ח' במעות ובחלוף משים אותה ט' ורוצה השליש במעות ומאה מהצמר שוה במעות ל' דוקט' ובחלוף שם אותה פרחים עשרה אשאל כמה שווי הפרח
|
|
|
עשה כך הסר שליש ט' שהם ג' ונשארו ו' גם תסירם מח' ונשאר ה' ותאמר [א]ם ה' שוים ו' כמה שוים ל' ותמצא כי שוים ל"ו חלק ל"ו על עשרה ותמצא ג' וג' חמישיות וכך שוה הפרח
|
|
|
263) שאלה שנים מחליפים בגד עם צמר והנה קנה הבגד שם אותה בחלוף ח' ושואל שליש במעות ומאה מהצמר במעות שוה ל' ובחלוף משים אותה מ' והרויחו זה לזה אשאל כמה שווי הקנה במעות
|
|
|
קח שליש ח' שהוא ב' וב' שלישיות הנשאר ה' ושליש ולכן תאמר כי היה שוה במעות
|
|
|
ולבחון אותו תאמ' אם מ' באו מל' מאיזה דבר באו ה' ושליש ותמצא ד' וכך היה שווי הקנה כדי לנכות השליש שהיה שואל במעות תוסיף ב' וב' שלישיות על ד' והם ו' וב' שלישיות וזהו שווי הקנה
|
|
|
264) שאלה שנים מחליפים ברזל ועופרת הברזל שוה במעות כ"ח ובחלוף ל"ו ובעל הברזל האלף שוה כ"א בממון אשאל אם בעל העופרת יתן לבעל הברזל הרביע בממון כמה ראוי שישים העופרת בחלוף
|
|
|
עשה כן הסר רביעית ל"ו והם ט' הסירם מל"ו נשאר כ"ז גם תסירם מכ"ח ונשאר י"ט ולכן אם י"ט שבו כ"ח כמה ישובו כ"א ויצא לך כ"ט וי"ו חלקי' מי"ט וכך ראוי לשים העופרת
|
|
|
265) שאלה שנים מחליפי' צוקרו ובאנבאגיני המאה מהצוקרו שוה במעות תשעה ובחלוף משים אותו י"ב ורוצה השליש במעות והק' מהבנבגיני שואל במעות ה' ורוצה וחצי אשאל אם יתן הרביעית במעות לבעל הצוקארו כמה ישים אותו בחלוף
|
|
|
כך תעשה הסר הרביעית שמבקש בעל הבאנבאגיני מהשליש שמבקש בעל הצוקארו וישאר א' חלק מי"ב אח"כ תאמר כי בעל הצוקארו מבקש מחבירו חלק א' מי"ב והאחר אינו מבקש כלום הסר חלק אחד מי"ב מי"ב שהוא אחד ונשאר י"א הנה הקרן יהיה ח' ובחלוף י"א ולכן תאמר אם ח' שם י"א כמה ישים ה' וחצי ויצא לך המבוקש
|
|
|
266) שאלה שנים מחליפים לאחד יש לו מוך ולאחר זנגביל המוך שוה המאה ט' במעות ובחלוף י"ב ורוצה לתת החצי במעות ולאחר יש לו זנגביל אשר המאה במעות שוה ט"ו דוקטי בחלוף כמה ישים אותו ובעד ז' מאות וס"ח ליט' של זנגביל כמה מוך יקבל
|
|
|
דע כי כי כשאיש רוצה לתת חלק מה במעות ראוי להוסיף חלק על החלוף ובקרן ג"כ וכן בהפך כשהוא שואל מחבירו חלק מה ראוי לחסר כנז' לעיל על כן קח חצי י"ב והם ו' תוסיפם על י"ב ויהיו י"ח גם תוסיפם על ט' ויהיו ט"ו ועל כן תאמר אם ט"ו שבו י"ח כמה ישוה ט"ו ויצא י"ח ולדעת כמה מוך יקח בעד ז' מאות וס"ח ליט' כפול שתי וערב ק' של מוך נגד י"ח של זנגביל ויצא א' וח' מאות עו' כפול ק' של זנגביל נגד י"ח של זנגביל דרך שתי וערב והוא ג"כ אלף וח' מאות ותאמר כי אלף וח' מאות של זנגביל וכך יתן ג"כ המוך כי הדבר יצא שוה כי כך יצא ערך המוך כמו הזנגביל
|
|
|
267) שאלה שנים מחליפים בגד עם צמר בעל הבגד מוכר הקנה ח' ובחלוף ט' ורוצה השליש במעות והק' מהצמר שוה ל' ובחלוף משים אותו באופן כי בעל הבגד מרויח ה' בעד ק'
|
|
|
כך תאמר אם ה' במעות שוות ו' בחלוף ק' בממון כמה ישוו ויצא ק"כ וכך שוה המאה מבעל הבגד ויען כי אמר כי מרויח ה' בעד ק' הסר ה' מק"כ ונשאר קט"ו ותאמר אם קסא ק' במנויים שבו קט"ו כמה ישובו ל' ותמצא כי ישובו ל"ד וחצי וכך הוא שווי מהצמר בחלוף
|
|
|
268) שאלה שנים מחליפי' צמר עם בגד בעל הבגד מוכר הקנה במחושבים ז' ובחלוף ח' ושואל השליש בממון ובעל הצמר מוכר הק' ל' דוקט' בממון ובחלוף משים אותה באופן כי בעל הבגד מפסיד ה' בעד ק' כמה מכר בעל הצמר המאה
|
|
|
כך תעשה הסר השליש מח' הנשאר ד' ושליש והוא הקפיטאל ובחלוף ה' ושליש ויען כי הפסיד ה' בעד ק' תאמ' אם ד' ושליש שבו ה' ושליש כמה ישובו ק' ותמצא כי ישובו קכ"ג וחלק א' מי"ג תוסיף בם הה' מהפסד והנם קכ"ח וחלק מי"ג ותאמר אם ק' במנויים שבו קכ"ח וחלק מי"ג כמה ישובו ל' ותמצא ל"ח וי"א חלקים מקכ"ו וזהו שווי הק' מהצמר בחלוף ותבחון אותו
|
|
|
269) שאלה שנים מחליפים בגד עם צמר בעל הבגד מוכר הקנה ז' ובחלוף משים אותו ח' ושואל רביעית בממון ובעל הצמר מוכר הק' עשרי' ובחלוף משים אותו באופן כי בעל הצמר מרויח י' בעד ק' אשאל כמה שווי הק' מהצמר
|
|
|
עשה כך הסר הרובע מז' ומח' וישאר ו'ה' ותאמר אם ה' שבו ו' כמה ישובו ק' ויצא ק"כ וכך שוה בחלוף ויען כי בעל הצמר מרויח י' בעד ק' תוסיף י' על ק"כ ויצא ק"ל ותאמר אם ק' מבגד שבו ק"ל כמה ישובו עשרי' ויצא כ"ו וכך שווי הק' מהצמר
|
|
|
270) שאלה שנים מחליפי' צמר ופשתים יחדו קנה הבגד שוה ח' במעות מנוים ובחלוף משים אותה ט' ובעל הצמר הק' שוה ל' ו' ובחלוף משים אותה באופן כי בעל הצמר יפסיד י' בעד ק'
|
|
|
עשה כן בעל הבגד שואל השליש במעות הסר השליש ונשאר ו'ה' ותאמר אם ה' ישובו ו' כמה ישובו ק' ויצא לך ק"כ ויען כי בעל הצמר מפסיד י' בעד ק' הסירם מק"כ וישאר ק"י אח"כ תאמ' אם ק' במעות שבו ק"י כמה ישובו ל' ויצא ל"ג וכך שוה הצמר בחלוף
|
|
|
271) שאלה שנים מחליפים צמר ופשתים יחדו קנה הבגד שוה ח' ובחלוף משים אותו ט' ורוצה השליש במעות וק' מהצמר בחלוף משים אותו ל"ו אשאל כמה שוה בממון
|
|
|
עשה כך באופן כי בעל הבגד ירויח י' הסר השליש מט' וישאר ו'ה' ותאמ' אם ה' שבו ו' כמה ישובו ק' ונמצא ק"כ ויען כי אמר כי בעל הבגד הרויח י' הסר י' מק"כ וישאר ק"י ותאמר אם ק"י מחלוף שבו ק' מממון כמה יתן ל"ו ויצא ל"ב וח' חלקים מי"א וכך שווי בממון
|
|
|
272) שאלה איש מחליף עם חבירו צמר ופשתים קנה הבגד שוה ז' ורוצה השליש בממון וק' מהצמר שוה ל' ומשים אותה ל"ו ובעל הבגד הפסיד י' בעד ק' אשאל בעל הבגד כמה מכר אותה בחלוף
|
|
|
ראשנה הסר השליש שהוא ב' ושליש וישאר ד' וב' שלישיות אח"כ כפול ל"ו מהצמר בבגד ק' וחלק על ל' ויצא ק"כ וכך הוא בחלוף ומצד כי בעל הבגד הפסיד י' בעד ק' הסר י' מק"כ וישאר ק"י ותאמר אם ק"י מחלוף שבו ק' בממון מאי זה יבואו ד' וב' שלישיות ותמצא כי יבא מד' וי"ח חלקים מל"ג ואח"כ תוסיף בם ב' ושליש אשר חסרת ויעלה ו' וי"ט חלקי' מל"ג וזהו שווי הבגד בממון
|
|
|
273) השאלה איש מחליף צמר ופשתים הבגד שוה ב' בממון ובחלוף משים אותו ב' פיוריני וחצי יותר ומבקש השליש בממון והק' מהצמר בממון שוה עשרים ובחלוף משים אותו כ"ה ומרויח י' בעד ק' אשאל כמה שווי הפרח
|
|
|
כך תעשה הסר השליש מב' פרחים וחצי היינו ה' שישיות נשאר א' פרח וב' חמישיות מחלוף א"כ ק' מהצמר כפול כ"ה כנגד ק' והעולה חלק על כ' שהיה שוה בממון ויצא קכ"ה וכך שוה בחלוף
|
|
|
ויען כי אמר כי בעל הצמר מרויח י' בעד ק' הסר י' מקכ"ה ונשאר הנשאר קט"ו אח"כ תאמר אם קט"ו מחלוף כ"א מק' בממון מאי קסב זה דבר ב' שלישיות ויצא לך א' ול"א חלקים מס"ג פרחים וכך שווי הקנה בממון ותוסיף בם ה' שישיות שהוא שליש ב' וחצי ויעלה ב' וי"ג חלקים ממ"ו ויצא ג' וכ"ג חלקים מק"ה וכך שוה הפרח
|
|
|
274) שאלה שנים מחליפים לא' יש לו זינזיברו אשר הק' שוה י"ח דוקטי ולחברו יש לו סוקרו אשר הק' שוים עשרים דוקט' גם יש לו קנילא אשר המאה שוה י"ו דוקט' ומאסיש אשר המאה שוה י"ב דוקט' ובעל הפלפל יש לו כ"ב פלפל שעולה תתפ"ו דוקט' ומבקש מואותם הסחורות כ"כ מזה כמו מזה אשאל כמה יקח מכל א' וא'
|
|
|
קח איזה סכום ונניח כי יש לו מאה מכל א' וא' והנה המאה מהסוקרו שוה כ' ומאה מהמאסיש י"ב ומאה מקנילא י"ו ובין הכל עולה מ"ח מאה מכל א' וא' ומבקש תתפ"ו ולכן תאמר אם מ"ח יהיו תתפ"ו כמה יהיו כ' וכמה יהיו י"ו וכמה יהיו י"ב
והנה הסוקרו יעלה שס"ט ושישית וכך יקח מהסוקרו וכן תעשה מהאחרים
|
|
|
275) שאלה שנים מחליפים לאחד יש לו צמר ולאחר יש לו אשטמי ופלפל והק' מהצמר שוה ל' בממון אמנם בחלוף לא ידעתי ורוצה השליש בממון והשליש באשטמי והשליש מפלפל והק' מהאשטמי שוה ל' בממון ובחלוף שוה ל"ו והמאה מהפלפל שוה מ' בממון ובחלוף שוה מ"ה אשאל כמה ישוה המאה מהצמר בחלוף למען יצא מספר שוה לכלם
|
|
|
כך תעשה אם מה ששוה ל' בממון הוא שוה ל"ו בחלוף כמה ישוה מ' בממון ובחלוף ותמצא כי ראוי שישוה מ"ח ותוסיפם על מ"ה ויעלה צ"ג גם תוסיפם על המ' מהאשטמי ויעלה פ' גם על הארבעים מהפלפל ויעלה פ' ויען כי אמר כי בעל הצמר מבקש השליש בממון ושליש באשטמי ושליש בפלפל עשה כך שים כי הק' מהצמר שוה קוסא הסר מהם השליש ויצא ל' פחות שליש דבר ובחלוף ב' שלישיות קוסא עתה כפול ל' פחות שליש נגד צ"ג ויצא לך אלפים וז' מאות וצ' פחות ל"א קוסי אח"כ כפול ב' שלישיות קוסא שהוא החלוף כנגד פ' ויצא לך נ"ג ושליש קוסא וזהו שוה אל אלפים וז' מאות וצ' פחות ל"א קוסא ותמצא כי הקוסא שוה ל"ג וכ"א חלקים מרנ"ג וכך ישוה המאה מהצמר בחלוף
|
|
|
276) שאלה שנים מחליפים לא' יש לו צמר אשר בממון שוה כ' ובחלוף כ"א ומבקש הרביע בממון ולאחר יש לו ב' מיני בגד הא' שוה ד' ומשים אותו בחלוף ה' והאחר שוה י"ב אשאל כמה ראוי לשים בחלוף אותו של י"ב אם יתן מזה כמו מזה
|
|
|
כך תעשה ראשנה הסר הרביע מכ' ומכ"ה וישאר י"ג וג' רביעיות וי"ח וג' רביעיות אח"כ קח שווי הב' מיני בגד היינו ה' וי"ב ויעלה י"ז ותעשה חשבון כי אלו הב' מיני בגד אינו כי אם מין אחד ותאמר אם י"ג וג' רביעיות שוה י"ח וג' רביעיות כמה ישובו י"ז ויצא כ"ג וב' חלקים מי"א ואלו הם שווי הב' מיני בגד והנך רואה כי מן אחד שוה ה' לכן הסר ה' מכ"ג וישאר י"ח וב' חלקים מי"א וכך ראוי שישוה הקנה מאותו של י"ב
|
|
|
277) שאלה שנים מחליפים לא' יש לו פלפל בממון שוה הק' ל' ובחלוף משים ל"ה והק' מהננגיברי בשוה בממון כ"ז ובחלוף ל"ג ולאחר יש לו צמר וק' מהצמר שוה עשרה אשאל כמה ישים אותה בחלוף והוא מבקש החצי מפלפל והחצי מזנגביל ורוצה להחליף י' בעד ק'
|
|
|
ראשנה תאמר אם ק' שוים ק"י כמה שוים י' ותמצא י"א ותאמר כי הק' מהצמר שוה י"א ויעקב שואל מזה כמו מזה ר"ל אם יקבל ק' מפלפל כן יקבל ק' מזנגביל לכן חלק י"א על ב' ויצא ה' וחצי ונתחיל עם הפלפל ונאמר אם ל' אתה משים ל"ה כמה אשים ה' וחצי ויצא לך ו' וה' חלקים מי"ב וכן ישוה חצי ק' מצמר מצד הפלפל עוד מצד הזנגביל תאמר אם כ"ז שוה ל"ג כמה ישוה ה' וחצי ויצא לך ו' וה' חלקים מי"ב וכך ישוה חצי הק' מצמר מצד הפלפל קסג עו' מצד הזנגביל תאמר אם כ"ז שוה ל"ג כמה ישוה ה' וחצי ויצא לך ו' מ"ג חלקים מנ"ד וכך ישוה החצי האחר מהצמר מצד הזנגביל ועתה אנו יודעים כמה ישוה חצי ק' מצד הפלפל ומצד הזנגביל עתה תחבר ו' וה' חלקים מי"ב וו' ומ"ג חלקים מנ"ד וישוה י"ג ונ"ג חלקים מק"ה וכן ישוה הק' מהצמר בחלוף עתה תחבר שווי הפלפל ושווי הזנגביל בממון היינו כ"ז ול' ויעלה נ"ז חלקם על ב' ויצא כ"ח וחצי גם תחבר ל"ה עם ל"ג שהוא שווים בחלוף והעולה חלק על ב' ויצא ל"ד ואח"כ תאמר אם כ"ח וחצי שוים ל"ד כמה ישוה י"א שהוא הצמר ויצא לך י"ג וז' חלקים מנ"ז ובזה האופן בעל הצמר ירויח י' בעד ק'
|
|
|
278) שאלה שנים מחליפים לא' יש לו מג' מיני תבלין היינו פלפל והק' שוה כ"ד ובחלוף משים אותו כ"ח וקאנילא שוה מ"ה ובחלוף משים אותה נ"ג וגארופאנו שוה ל"ד ובחלוף משים אותו מ' והק' מהצמר שוה י"ב אשאל אם רוצה חציו פלפל והשליש קאנילא והרובע גארופאני כמה ישים אותו בחלוף כדי שהמסחר יצא שוה
|
|
|
כך תעשה תראה שווי הצמר היינו תחלק לחצי ושליש ורביע חציו ו' ושלישיתו ד' ורביעיתו ג' ובין הכל י"ג ועל כן תאמר אם י"ג היה י"ב כמה יהיה ו' וג' וד' והנה החצי יהיה ה' וז' חלקים מי"ג והשליש יהיה ג' וט' חלקים מי"ג והרובע יהיה ב' וי' חלקי' מי"ג ותמצא ו' וי"ט חלקים מל"ט והוא שווי הפלפל וכן תעשה מהקאנילא אתה משים אותה נ"ג כמה אשים אותה ג' וט' חלקים מי"ג ויצא לך ד' וס"ח חלקים מקצ"ה וכן מהגרופלי אם ל"ד שוים מ' כמה ישוה ב' וי' חלקים מי"ג ויצא לך ג' ונ"ז חלקים מרכ"ה וכל זה תחבר ויעלה י"ד וד' אלפים ומ"ג חלקי' ממ"ג אלפים וצ"ה וכן ישוה המאה מהצמר בחלוף
|
|
|
279) שאלה שנים מחליפים לא' יש לו בגד ומוכר אותו א' פרח יותר ולאחר יש לו צמר והק' שוה י' בממון ומשים אותו י' בממון ובחלוף משים אותו י"ב ואותו מהבגד נמצא שהרויח פעם וחצי ממון בגד אשאל כמה היה שווי הבגד בממון
|
|
|
נניח איזה מספר שתרצה ונניח כי היה לו ד' פרחים א"כ מכרו ה' ונניח כי היה לו לאחד כ"ה קנים ושווים ק' פרחים והוא מבקש כ"כ צמר שישוה קכ"ה פרחים חלק קכ"ה על ערך הצמר בחלוף שהוא י"ב וישוה אלף ומ"א וב' שלישיות וראה כמה שוים אלו האלף ומ"א וב' שלישיות במנוים ויצא לך ק"ד ושישית והקנה שוה ד' והנחנו ה' וראוי להניחה ו' למען ישוב ממונו כמוהו וכמו מחציתו ויחסר לי א' וה' שישיות וזה תניח כמו שעושים ההנחות כוזבות
|
|
|
עו' שוב לעשות הנחה אחרת ונניח כי הקנה שוה ה' ומשים ו' בחלוף גם הק' מהצמר שוים י' בממון י"ב בחלוף ונניח כי היו לו עשרים קנים ושווים בחלוף ק"כ וחלק ק"כ על י"ב שהוא שווי הצמר בחלוף ויצא י' ובממון משים ק' והנך רואה כי אינו מרויח ואינו מפסיד ואני מבקש כי בעל הצמר ירויח ז' וחצי כדי שישוב ממונו כמוהו וכמו חציו ותאמר כי מזאת ההנחה יחסר ז' וחצי ומצד האחרת היה לך פחות א' וה' שישיות ועשה כמו שידעת ותמצא כי הקנה שוה ג' פרחים וכ"ג חלקים מל"ד ושם אותה ד' וכ"ג חלקים מל"ד ושב ממונו כמוהו וכמו חציו
|
|
|
280) שאלה שנים מחליפים בגד וצמר בעל הבגד הקנה שוה בממון ד' ובחלוף ה' ובעל הצמר הק' שוה י' בממון ובחלוף י"ג אשאל מי מרויח יותר מאלו
|
|
|
ראשנה תעשה כך אם ד' שבו ה' כמה ישובו י"ב ותמצא כי ישובו י"ב וחצי הנה בעל הצמר מרויח חצי כי מן הדין אינו ראוי למכרה כי אם י"ב וחצי ולראות כמה ראוי לקבל בעל הבגד בממון להיות שוה לחבירו ראה כמה הפרשים מד' לה' והיינו א' עתה תחלק ה' על א' ויצא ה' כן תעשה מהצמר וראה ההפרש שיש מי' לי"ג והוא ג' עתה תחלק י"ג על היתרון שיש מי' לי"ג והוא ד' ושליש ואתה רואה כי חלק הוא ה' ומהצמר הוא ד' ושליש עתה תחלק ד' וחצי על ה' ויצא י"ג קסד חלקים מט"ו וזה החלק הוא בצמר ראוי לקבל בעד הבגד והנשאר עד תשלום א' היינו ב' חלקים מט"ו ראוי לקבל במעות והדבר יצא שוה
|
|
|
281) שאלה שנים מחליפים צמר ופשתים יחדו קנה הבגד שוה ח' ובחלוף משים אותו י"א ורוצה השליש בממון והק' מהצמר שוה י"ד ובחלוף שוה י"ו אשאל כמה יתן בממון בעל הצמר לבעל הבגד
|
|
|
ראשנה תסיר השליש שהוא ג' וב' שלישיות וישאר א ד' ושליש וז' ושליש ותאמר אם שוה הקנה ד' ושליש ובחלוף ז' ושליש ובאחד יש צמר שוה י"ד ובחלוף י"ו מי ראוי לתת לחבירו נניח כי בעל הבגד שואל קוסא אחת תסיר זה מי"ו וישאר י"ו פחות קוסא אחת גם תסירהו מי"ד וישאר י"ד פחות קוסא אחת ותאמר אם י"ד פחות קושא אחת שוה י"ו פחות דבר כמה ישוה ד' ושליש ותמצא כי ישוה ס"ט ושליש פחות ד' ושליש קוסא חלק על י"ד פחות קוסא אחת ויצא ז' ושליש א"כ הקוסא ישוה י"א ותשיעית תחלק זה על י"ו ששוה הצמר בחלוף ויצא כ"ה חלקים מל"ו וכן יהיה החלק אשר ראוי שישוב לו במעות י"א חלקים מל"ו בבגד ויצא החלוף שוה
|
|
|
282) שאלה שנים מחליפים בעל הבגד שוה ד' ובחלוף משים ה' ובעל הצמר שוה כ' ובחלוף כ"ד אשאל מי ראוי לבקש מחבירו איזה קצת חלק בממון ואיזה חלק יבקש
|
|
|
תאמר ד' פעמים [כ]ד' הם צ"ו וה' פעמים כ' הם ק' הסר מהם צ"ו הנשאר ד' וזה תחלק על יתרון הבגד מהממון בחלוף שהוא א' ויצא ד' וחלקם על כ"ד ויצא שישית אחד כי כן שוה הצמר בחלוף וכן ראוי לו לקבל מבעל הצמר בממון
|
|
|
283) שאלה שנים מחליפים צמר ופשתים קנה הבגד שוה ה' ובחלוף ח' ורוצה הרביעית בממון וק' הצמר שוה י"ג ומשים בחלוף ט"ו ובעל הצמר הרויח ה' בעד מאה אשאל איזה חלק יבקש מחבירו למען יצא המספר שוה
|
|
|
ראשנה הסר הרביע מח' והנה רביע ח' הם ב' הסירם מה' ומח' ונשאר ו' ג' ויען כי אמר כי בעל הצמר מרויח ה' בעד ק' כפול ו' על ק' ויצא ו' מאות וחלקם על ג' ויצא ב' מאות ותוסיף ה' מריוח ויהיו ר"ה ותאמר כי בעד כל ק' בממון בחלוף משים אותו ר"ה ויען כי אמ' איזה חלק ראוי לתת לו למען יצא המספר שוה נניח כי ראוי לתת לו א' קוסא בממון הסירהו מט"ו נשאר ששוה בחלוף ט"ו פחות קוסא אחת גם גם תסירהו מי"ג ששוה בממון ונשאר י"ג פחות א' קוסא וכפול י"ג פחות א' קוסא כנגד ר"ה ויצא ב' אלפים וו' מאות וס"ה פחות ר"ה קוסי גם כפול ט"ו פחות קוסא א' כנגד ק' ויצא אלף וה' מאות פחות ק' קוסי הסירם מב' אלפים וו' מאות וס"ה ונשאר אלף וקס"ה דבר ותמצא כי הקוסא ישוה י"א וב' חלקים מכ"א וחלק זה על ט"ו ששוה הצמר בחלוף ויצא לך רל"ז חלקים משט"ו וזה החלק ראוי שיתן בעל הצמר לבעל הבגד ויצא החלוף שוה
|
|
|
284) שאלה שנים מחליפים בגד וצמר קנה הבגד משים אותו בחלוף א' דוקטו יותר ממה ששוה בממון וק' מהצמר בממון שוה כ' ובחלוף משים אותו כ"א והפסיד י' בעד ק' אשאל כמה שוה קנה הבגד בממון
|
|
|
נניח כי הקנה שוה א' קוסא א"כ בחלוף שוה קוסא יותר ויען כי בעל הצמר הפסיד י' בעד ק' נאמר כי הק' שבו צ' ולכן תאמר אם ק' שבו צ' כמה ישובו עשרים וישובו י"ח וכן תאמר כי שוה הצמר בממון ותאמר אם י"ח שבו כ"א כמה ראוי שנשים א' קוסא תכפול כ"א על א' קוסא ויצא לך כ"א קוסא ותחלקהו על י"ח ויצא לך א' ושישית והוא שוה אל א' קוסא יותר אחד ותעשה בדרך ויצא לך ו' וכך היה הקנה ובחלוף שם אותו ז' והוא נכון
|
|
|
285) הבן כי אם תאמר איש רוצה רביעית הממון הוא שוה כאלו תאמר איש רוצה שינתן לו רביעית בממון
|
|
|
המשל איש מחליף בגד ששוה עשרים ובחלוף משים אותו כ"ג וט' חלקים מי"ז ורוצה רביעית בממון ולאחר יש לו צמר ששוה הק' בממון י"ב אשאל כמה ישימנה בחלוף למען לא יהיה מרומה
|
|
|
ראשנה קח רביעית כ"ג וט' חלקים מי"ז שהם ה' וט"ו חלקים מי"ז ותסיר זה מערכו בממון ומערכו בחלוף וישאר י"ד וב' חלקים מי"ז וי' וי"א חלקי' מי"ז ותאמר אם י"ד והחלקים שבו י"ז והחלקים כמה יעלה י"ב ויצא לך ט"ו
|
|
|
ובדרך אחר נניח כי א' מהם רוצה לתת לחבירו קסה רביעית בממון וכבר ידעת כי כשרוצה לתת איזה דבר ראוי להוסיף וכששואל ראוי לחסר כי אם רוצה לתת חצי ראוי להוסיף כמוהו ואם שואל שליש ראוי להוסיף חצי ממונו ובעד הרביע ראוי להוסיף שליש וכן ראוי לעשות ולכן אם הערך עשרים ושואל שליש ראוי להוסיף חצי שהוא י' ויהיו ל' ולכן תאמ' כי מה ששוה י"ב ראוי שישים אותה ט"ו שהם ה' ותוסיפם לשניהם ר"ל לי"ב ולט"ו ויעלה י"ז וכ' מה יעשה חבירו מעשרים ויצא כ"ג וט' חלקים מי"ז וכמו שראית למעלה
|
|
|
286) שאלה שנים מחליפים צמר ופשתים יחדו הקנה מהבגד שוה כ"ה ובחלוף שוה ל' ורוצה הרביעית בממון והק' מהצמר שוה ארבעים ורוצה העשור ממה שמשים אותה בחלוף והחלוף יצא שוה אשאל כמה שוה הק' מהצמר בחלוף
|
|
|
והדרך נודע מצד השאלות שקדמו
|
|
|
287) שאלה שנים מחליפים צמר ופשתים הבגד שוה ה' ובחלוף משים אותו ח' והק' מצמר במעות שוה חמישים ובחלוף משים אותה בדרך כי בעל הצמר מרויח יותר מבעל הבגד ל"ו וב' שלישיות בעד כל ק' אשאל כמה הצמר בחלוף
|
|
|
ראוי לך לדעת הקדמה כי אם תעשה חלוף והרויח י' בעד ק' אתה מרויח העשור וחבירו מפסיד חלק מי"א ר"ל כי מפסיד ט' וחלק מי"א בעד ק' כי המרויח הק' שוים ק"י
|
|
|
ודע כי המחליף עם חברו לדעת כמה מרויח וכמה מפסיד חבירו קח החלק המבטא שהרויח ותוסיף אותו על החלק שמרויח
|
|
|
288) המשל מי שמרויח עם חברו עשרה בעד ק'
|
|
|
שים עשרה על עשור ק' שהוא חלק מי' ויהיו י"א וזה יהיה החלק שמפסיד המפסיד ושימם ככה א"כ אתה מפסיד י"א ר"ל כי אתה תתן לי מה ששוה ק"י בעד ק' או תאמר כי אתה תתן לי יא בעד י'
|
|
|
והאומר פלוני הפסיד עם חברו עשרים בעד ק'
|
|
|
כבר ידעת כי עשרים חומש ק' תוסיף על חמש א' ויהיו ו' א"כ תאמ' כי הפסיד שישית ממונו בעד ק'
|
|
|
289) שאלה שנים מחליפים לא' יש לו ברזל ושוה ו' פרחים המאה ובחלוף משים אותו ז' ורוצה לתת לחברו זמן ד' חדשים וחברו יש לו עורות אלים מאדמים ושוה העור במעות ח' גרושי ובחלוף משים אותו ט' אשאל כמה זמן ראוי שימתין בעל העור לבעל הברזל
|
|
|
כך תעשה למען יהיה המסחר שוה לזה כמו לזה הלא מן הדין אם בעל הברזל מעלה מו' לז' ראוי לבעל העור שיעלהו מח' לט' ושליש ולכן כפול ז' על ח' ויעלה נ"ו וחלק על ו' ויצא ט' ושליש והנה התוספת מח' עד ט' ושליש הוא א' ושליש וחלק ד' שהם החדשים עליהם ויצא ג' שלמים וכן ראוי שימתין בעל העור לבעל הברזל להיות חלופם שוה
|
|
|
290) שאלה שנים מחליפים בגד ופשתים קנה הבגד שוה י' ובחלוף י"א וממתין לו שנה תמימה וחברו מוכר ק' מהצמר ל"ו ארצה לדעת כמה ימכרנה באופן לחברו ח' חדשים
|
|
|
כך תעשה הנך רואה כי בעל הב' מרויח עם י' א' בשנה תמימה והוא עשור ממונו בי"ב חדשים א"כ ירויח בכל חדש חלק מק"כ ותאמר אם י' מרויח חלק מק"כ כמה ירויחו ל"ו ויצא לך ג' עשיריות כפול ג' עשיריות על ח' ויצא לך ב' וב' חמישיות תוסיפם על ל"ו ויהיו ל"ח וב' חמישיות וכן ראוי שישים הצמר בחלוף כדי לעשות לחברו המתנה ח' חדשים
|
|
|
291) שאלה שנים מחליפים צמר ופשתים הבגד שוה ד' וחצי בממון ובחלוף משים אותו ו' ונותן לחבירו המתנה ח' חדשים והצמר היה שוה בחלוף ט"ו ונתן לחברו המתנה י' חדשים אשאל כמה שוה הצמר בממון
|
|
|
ראשנה ראה הפרש הזמן מהבגד והצמר והוא ב' חדשים לכן תסיר ההפרש ר"ל הקטן מהגדול הנשאר ב' וראה איזה חלק הוא ב' מח' והוא רביעיתו ושמור עתה קח ממון הבגד בממון שהוא ד' וחצי ואתה רואה כי ההפרש מממון ומחלוף הוא א' וחצי ומזה תקח ומזה תקח רביעיתו ויצא לך ג' רביעיות ותוסיפם על ו' ויצא קסו לך ו' וג' רביעיות וכן ראוי שישוה קנה הבגד בחלוף ותאמר כי ו' וג' רביעיות בא מקנה ששוה בממון ד' וחצי מה יתן לי ט"ו ויצא י' וי' חלקים מי"ז וכך שוה הק' בממון להיות המסחר שוה
|
|
|
292) שאלה שנים מחליפים בגד עם צמר קנה הבגד שוה ג' ובחלוף ד' ונותן לו זמן י"ב חדשים והצמר שוה ט"ו ונתן לו זמן ו' חדשים אשאל כמה שוה מאה מהצמר בממון
|
|
|
הסר זמן הצמר מזמן הבגד הנשאר ו' וראה איזה חלק הוא ו' מי"ב והנה הוא חציו וכן תסיר החצי מד' הנשאר ג' וחצי וכן תאמר ששוה הבגד בחלוף ותאמר אם ג' וחצי בחלוף יצא מג' בממון מאיזה מספר יצא ט"ו ויצא לך י"ב וב' חלקי' מז' וכך שוה הק' מהצמר בממון
|
|
|
293) שאלה שנים מחליפי' צמר ופשתים יחדו קנה הבגד שוה י' ובחלוף משים אותו י"ג ונותן זמן י"ב חדש ובעל הצמר הק' שוה בחלוף חמישים ונתן לו זמן ט"ו חדשים אשאל כמה שוה הצמר בממון
|
|
|
ראשנה ראה כמה מרויח הליט' לחדש מבעל ה' הבגד והנה תמצא פיצולי ו' אח"כ ראה בעל הצמר שהם נ' בט"ו חדשים ויצא לך צ' פיצולי שהם גרושי ז' ופיצולי ו' היינו ג' שמיניות ליט' ולכן תאמ' אם א' ליט' מרויח ג' שמיניות והוא משים אותו בחלוף א וג' שמיניות ולכן תאמ' אם א' וג' שמיניות בא ממה ששוה במחושב א' ליט' מאיזה דבר יצא חמישים ליט' ויצא לך כי הק' מהצמר בממון שוה י"ו וד' חלקים מי"א
|
|
|
294) שאלה שנים מחליפי' צמר ופשתים המאה מהצמר שוה בממון כ' ומשים אותו ל' ורוצה החצי בממון ונותן לו זמן י"ו חדשים ולחברו יש לו בגד שוה הקנה ח' ובחלוף י' והיה המסחר שוה אשאל כמה זמן המתין בעל הצמר חברו
|
|
|
כך תעשה נניח כי בעל הצמר היו לו ג' מאות ושוה צ' ומזה מבקש חצי הממון שהם מ"ה ומזה נותן זמן י"ו חדשי' והחצי האחר מבקש בגד והנה הבגד בחלוף י' חלק מ"ה על י' ויצא ד' וחצי והנה ד' וחצי בממון שוים ל"ו
|
|
|
עתה ראה ג' מאות מצמר בממון שוה ס' כך היה ראוי שיתן בעל הבגד לבעל הצמר להיות החלוף שוה אמנם לא נותן לו כי אם ד' קנים וחצי היינו ל"ו ויחסר עד ס' כ"ד וכך היה ראוי שיפרע בעל הבגד להיות החלוף שוה והוא פרע מ"ה א"כ ראוי שנאמ' כי כ"ד מרויחים מ"ה בי"ו חדשים
|
|
|
ולדעת כמה עמד הבגד בהמתנה אתה יודע כי כ"ד שוים מ"ה א"כ כ"ד ירויחו כ"א חלק כ"א על כ"ד ויצא ז' שמיניות וכך מרויח הקנה בי"ו חדשים שמגיע לכל חדש ז' חלקים מקכ"ח בעד י"ג קנים ושמין
|
|
|
295) שאלה שנים מחליפים הקנה מהבגד שוה ד' ובחלוף ה' והצמר שוה המאה י' ובחלוף י"ג ואמר בעל הצמר לחבירו אני רוצה שתמתין לי שנה וארצה לתת לך חלק מה בממון באופן כי תרויח י' בעד ק' אשאל איזה חלק נתן בעל הצמר לחברו בסוף שנה באופן כי ירויח י' בעד ק'
|
|
|
כך תעשה תאמר אם ק' שוים ק"י כמה ישוב ד' ותמצא כי ישוב ד' וב' חמישיות וכך שוה הקנה בממון ובחלוף ה' והצמר שוה י' ובחלוף י"ג עתה ראה ההפרש מי' אל י"ג והוא ג' חלק י"ג בג' ויצא ד' ושליש עתה חלק ד' ושליש על ח' ושליש ויצא לך י"ג חלקים מכ"ה וכן ראוי שיקבל מצמר והנשאר שהוא י"ב חלקים מכ"ה יקבל בממון בסוף השנה והדבר יצא שוה
|
|
|
ולבחון תאמר ב' מחליפים צמר ופשתים קנה הבגד שוה ד' ובחלוף ה' ורוצה י"ב חלקים מכ"ה בממון וי"ג חלקים מכ"ה בצמר והצמר שוה י' ובחלוף י"ג אשאל מי מרויח וכמה מרויח בעד כל ק' כך תעשה נניח כי מחליפים כ"ה קנים ששוים קכ"ה בחלוף ומזה מבקש י"ב חלקים בממון שהם ס' בממון והנשאר שהם ס"ה בחלוף והנה הצמר מקבל לחשבון י"ג המאה בעד ס"ה תקבל ה' מאות וראה כמה שוה בממון ה' מאות מצמר שהם חמישים ועולה ק"י ובעד ק"י נתן כ"ה קנים ששוים בממון ק' א"כ מרויח שלחנות א"כ מרויח י' שהם ק"י
|
|
|
296) שאלה הבולונייני שוה בפלורינצא קסז כ"ו פיצולי ובפירושא שוה ל' אשאל אם איש יש לו לקבל ג' מאות בולונייני בפיורינצא כמה שוים בפירושא
|
|
|
תאמר אם כ"ו שוים ל' ג' מאות כמה שוים ויצא לך שמ"ו וד' חלקים מכ"ו
|
|
|
297) שאלה איש אחד יש לו לקבל בפיורינצא ר"נ פרחים וסולדי עשרה ופיצולי ח' והם שוים בפירושא רנ"ט פרחים וט"ו סולדי אשאל אם ארצה לקבל בפירושא ס' פרחים וי"ב סולדי וו' פיצולי כמה ראוי לקבל
|
|
|
כך תעשה כבר ידעת כי עשרים סולדי הם פרח א' והנה תמצא כי רנ"ו פרחים וי' סולדי וח' פיצולי הם ר"נ פרחים וח' חלקים מט"ו והרנ"ט וט"ו סולדי הם רנ"ט וג' רביעיות פרחים וי"ב סולדי וו' פיצולי הם ס' פרחים וה' שמיניות לכן תאמר אם רנ"ט וג' רביעיות שבו ר"נ וח' חלקים מט"ו כמה ישובו ס' פרחים וה' שמיניות ויצא לך נ"ח פרחים וט' סולדי ואלף ושכ"ז חלקים מג' אלפים וקי"ז
|
|
|
298) שאלה איש נדר לתת לאיש אחר ג' מאות מטבעי' פיורינטיני ונתן לו ב' מיני מטבעים היינו בולונייני וגרושוני בולונייני שוה בפיורינצא ה' וחצי ובפירושא שוה ו' ורביע אשאל איזה יותר נכון לו לפרעו בבולונייני או בגרושוני
|
|
|
יש לך לדעת כי יש דבר מה שוה בפיורינצא כ"ו ובפירושא שוה ל' כן כל מטבע ששוה בפיורינצא כ"ו שוה בפירושא ל' כי יחס הבולונייני אל הכ"ו הבולונייני כיחס הגרושוני אל הגרושוני וכן מכל מטבע ונניח כי יפרענו במטבע בולונייני ותאמר אם כ"ו מן פיורינצא שוה בפירושא ל' כמה ישוה ג' מאות ויצא לך שמ"ו וחלקים ושמרם וכן תאמר מהגרושוני ותאמר אם ה' וחצי שוה בפירושא ו' ורביע כמה ישוו ג' מאות ויצא לך ש"מ וחלקים א"כ אתה רואה כי יותר טוב לפרעו בגרושוני יותר מבולונייני כי הגרושוני צריך לתת לו ש"מ ומבולונייני צריך לתת לו שמ"ו
|
|
|
299) שאלה לאיש יש לו מב' מיני מטבעים מתחלפים כאלו תאמ' ארמיליני מז' טורניסי ומי' טורניסי ובין הכל יש לו מאתים ורוצה להחליפם שיתן לו החלפני מהם קרליני והחליפם ונתן לו צ"ב קרלי' וחצי אשאל כמה ארמיליני מז' וכמה ארמיליני מי' היו בסכום
|
|
|
כך תעשה ראה כמה ישוו המאתים אלו היו כלם מז' טורניסי והנה ישוו ע' קרלי' וראה ההפרש שיש מע' אל צ"ב וחצי וההפרש הוא כ"ב וחצי וראה אלו היו כל המאתים מי' טורניסי היו שוות ק' קרלי' וההפרש מצ"ב וחצי עד ק' הוא ז' וחצי חלק כ"ב וחצי על ז' וחצי ויצא ג' קח ג' חלקים ממאתים והם ק"נ וכך יקח מהארמיליני מי' ונ' יקח מאותן ששוות ז' טורניס
|
Section Three: Geometry
|
החלק השלישי ידבר על ענין המדות ר"ל גיבמאטריאה או ההנדסה
|
|
|
300) אם יש לך מרובע רבוע י' על י' ויש לך מרובע אחר ב' על ב' לדעת כמה תשבורת הגדול הנקרא רֵיאַה עודף על תשבורת הקטן
|
|
|
כך תעשה תרבע י' על י' והם ק' גם תרבע ב' על ב' והם ד' חלק ק' על ד' ויצא כ"ה וכך פעמים גדול הגדול על הקטן
|
|
|
301) שאלה אם תדע ממרובע אורך הקוים ותרצה לדעת ארך האלכסון
|
|
|
תוכל למצא אורך האלכסון כאלו תאמר הקו האחת מהמרובע ו' והאחר ח' כפול ח' על ו' ויצא מ"ח ו' על ו' ויצאו ל"ו וח' על ח' והם ס"ד ושניהם מחוברים הם ק' ושרשם י' וכך הוא האלכסון
|
|
|
ואם תדע האלכסון עם ארך אחד מהקוים לדעת הקו האחר כמה
|
|
|
כאלו תאמ' שהאלכסון י' והקו הנודע ו' תרבע [י'] על [ו'] והם והם ק' גם תרבע ו' על ו' והם ל"ו תסיר ל"ו מק' הנשאר ס"ד וקח שרשם והם ח' קסח והוא הקו האחר
|
|
|
ואם תדע קו ח' והאלכסון ולא תדע קו ו' למצא אותו תרבע האלכסון והוא ק' גם תרבע ח' על ח' והם ל"ו ס"ד תוציאם מק' ונשאר ל"ו ושרשם ו' והוא הקו האחר
|
|
|
302) שאלה אם יש לך משולש שוה הצלעו' ותרצה לדעת ארך העמוד כגון משולש כל צלע עשרה ותרצה לדעת העמוד
|
|
|
כפול עשרה על עצמם והם ק' הוצא מהם רביעיתם והם כ"ה הנשאר ע"ה וקח שרשם והם ח' וי"א חלקים מי"ו והוא אורך העמוד
|
|
|
303) שאלה אם יש לך מרובע רבוע כל קו עשרה לדעת האלכסון
|
|
|
כפול עשרה על עצמם והם ק' וכפלם על ב' ויהיו מאתים וקח שרשם והם י"ד ושביעית אחד והוא האלכסון
|
|
|
304) שאלה איך נדע מופת כל משולש הן שוה הצלעות או שוה השוקים או מתחלף הצלעות אחר שידעת העמוד
|
|
|
תעשה מרובע אורך הב' קוים הנכוחיים הארוכים יהיו כמו התושבת ואורך הב' קוים הקצרים יהיו כמו העמוד ר"ל חציו וכמו שיעלה תשבורת המרובע כי הוא תשבורת המשולש כמו זה מזה המשולש לא תוכל לדעת העמוד יען כי התושבת מרובעו עולה יותר ממרובע שתי ו' הצלעות מחוברים יחדו כי הצלעות אינם כי אם י"ב כל אחד ושני רבועיהם עולה רפ"ח אמנם מרובע התושבת שהוא כ"ו עולה תרע"ו על כן צריך למדוד העמוד ותכפול העמוד על חצי התושבת או התושבת על חצי העמוד והוא תשברתו
|
|
|
305) שאלה אם יש לך משולש מתחלף הצלעות כמו אם הצלע האחד ט"ו והא' י"ד והא' י"ג הנה תשברתו הוא פ"ד יען כי עמודו הנקרא קַאטְיט הוא י"ב
|
|
|
ואם תרצה לדעת המופת על זה תעשה מרובע ויהיה התושבת אורך הצלעות הב' הארוכים וחצי העמוד שהוא ו' יהיו ב' צלעות המרובע הקצרים כפול י"ד שהוא התושבת על ו' ויהיו פ"ד
|
|
|
306) שאלה אם יש לך משולש שוה השוקים כגון משולש ארך כל קו עשרה והתושבת י"ב
|
|
|
לדעת העמוד תרבע הצלע שהוא י' והם ק' וקח חצי התושבת שהוא ו' ותרבעהו והם ל"ו תסירם מק' ונשארו ס"ד ושרשם ח' וכך הוא העמוד
|
|
|
והתשבורת תרבע חצי התושבת שהוא ו' על כל העמוד או חצי העמוד על כל התושבת ויעלו מ"ח וכך הוא התשבורת
|
|
|
והאות המעיד על זה תעשה מרובע על המשולש כזה
|
|
|
והנך רואה כי זה המרובע הוא מרובע ארוך אורך הב' קוים הקצרים הם ו' ואורך הב' הארוכי' הם ח' ותשברתו מ"ח ואתה רואה כי כך תשבורת המרובע כמשולש
|
|
|
307) דרך למדוד משולש בג' מינים הדרך הראשון הוא ככה כגון משולש מתחלף הצלעות אשר אורך הקו האחד ט"ו והאחר י"ד והאחר י"ג
|
|
|
כפול הצלע הקצר והוא י"ג קסט ומרובעו קס"ט גם כפול התושבת שהוא י"ד ומרובעו קצ"ו ותחברם עם קס"ט ויעלה שנ"ב ומזה תסיר כפל הצלע הארוך והוא רכ"ה הנשאר ק"מ חלקם על כפל התושבת שהוא כ"ח ויצא ה' והוא מקום שנפל בו העמוד או חלק ק"מ על ב' והם ע' וחלקם על י"ד ויצא ג"כ ה' הסר ה' מי"ד הנשאר ט' והוא אורך העמוד מהתושבת רחוק מקצה אחד ה' ומהאחר ט'
|
|
|
או אם תרצה כפול הצלע הארוך והוא רכ"ה על התושבת שהוא קצ"ו וחברם ויעלה תכ"א תסיר מהם הכפל מהצלע הקצור שהוא קס"ט וישאר רנ"ב חלקם על ב' ויהיו קכ"ו חלקם על התושבת ויצא ט' ואתה רואה כי מצאת נפילת העמוד בקצה האחר
|
|
|
דרך שני חבר שני הצלעות שהם י"ג וט"ו והם כ"ח וחלקם על ב' ויצא י"ד וחלקם על ההפרש שיש מי"ג שהוא אחד הצלעות אל י"ד שעלה בחלוק ויצא י"ד או חלק י"ד אל ההפרש יש בין י"ד שעלה בחלוק אל ט"ו שהוא הצלע אחד ויצא י"ד וחלק אלו הי"ד על חצי התושבת שהוא ז' ויהיו ב' תסירם מחצי התושבת שהם ז' וישארו ה' והנה ט' הוא המעמד ארוך וה' הוא המעמד קצור
|
|
|
דרך שלישי הסר מרובע הצלע הקצור מן מרובע הצלע הארוך היינו מרכ"ה הסר קס"ט הנשאר נ"ו חלקם על י"ד ויצא לך ד' תוסיפם על התושבת ויהיו י"ח חלקם ויהיו ט' ולמצא המעמד קצור הסר ד' מי"ד נשאר י' חלקם על ב' ויצא ה' והוא המעמד הקצור
|
|
|
אח"כ למצא הקטיטו תרבע הצלע הארוך שהוא רכ"ה הסר ממנו מרובע המעמד הארוך שהוא פ"א ונשאר קמ"ד ושרשם י"ב והוא אורך הקאטיטו או פינדוקולארי או תרבע הצלע י"ג שהוא קס"ט תסיר ממנו מרובע מעמד קצור שהוא כ"ה נשאר ג"כ קמ"ד
|
|
|
308) שאלה איך נמדוד משולש בלי עמוד כגון אותו הנזכר חבר הג' צלעות והם מ"ב וחלקם על ב' והם כ"א הסר מהם ט"ו ונשארו ו' הסר מהם י"ד ונשארו ז' כפול ז' על ו' והם מ"ב הסר מכ"א י"ג נשאר ח' כפול ז' על מ"ב ויעלו של"ו כפול של"ו על כ"א ויעלה ז' אלפים ונ"ו וקח שרשם והם פ"ד והוא תשבורת המרובע
|
|
|
309) שאלה אם יש לך זוית נצב ותרצה לעשות עליו משולש אם תרצה לדעת ארך הצלע המשלים המשולש כמה הוא
כמו אם יש לך זוית נצב כזה ארך כל קו עשרה
|
|
|
כפול כל קו על עצמו וחברם ויהיו מאתים וקח שרשם והם י"ד ושביעית וכך היא הצלע אשר הוספת על זוית נצב ולמדוד אותו אין צריך עמוד כי הצלע האחד הוא העמוד על כן כפול י' על חצי הצלע האחר שהוא י' וחציו ה' והם נ' וכך הוא תשברתו
|
|
|
310) שאלה אם תרצה לדעת מתוך ידיעת זה המשולש הקטן אשר א' מהקוים ג' והאחר ד' והאחרת ה' אשר תשברתו הוא ו' מתוך ידיעת זה המשולש הקטן תוכל לדעת תשבורת המשולש הגדול אשר אחד מהקוים הם עשרים והאחרת י"ו והאחר י"ב כי כל צלע מהגדול הוא ד' פעמים צלעי הקטן וידוע כי יחס משולש אל משולש כיחס מרובע אל מרובע
|
|
|
ואם כל קו הגדול היה ב' פעמי' כצלעי הקטן היה תשברתו ד' פעמים כמוהו ועכשו שהוא ד' יהיה תשברתו י"ו פעמים כמוהו
|
|
|
311) שאלה איך נוכל למדוד משולש בלי צלעות שהוא שוה קע הצלעות תרבע אחד מהצלעות ומהעולה קח י"ג חלקים מל' וכך יעלה תשברתו
|
|
|
המשל משולש בכל צלע הוא י'
|
|
|
כפול י' על י' ויהיו ק' וקח י"ג חלקי' מל' ויעלה מ"ג ושליש וכך הוא תשברתו
|
|
|
312) שאלה לדעת מרובע הרבוע שחשב אדם בלבו כמה אורך כל קו
|
|
|
תאמר לו שיקח תשבורת המרובע ויוסיף עליו ארך הד' קוים ותאמ' לו כמה עולה ותוסיף על זה ד' וקח שרשם ומזה תסיר ב' והנשאר הוא צלע המרובע
|
|
|
דמיון אדם חשב מרובע ארך כל צלע ה' והנה תשברתו כ"ה תוסיף בם ד' צלעי המרובע שהם עשרים והם מ"ה תוסיף בם ד' והם מ"ט וקח שרשם והם ז' תסיר ב' והם ה'
|
|
|
313) שאלה לדעת אורך צלעי המרובע מתוך ידיעת אלכסונו
|
|
|
כפול האלכסון על עצמו וחלקהו על ב' ומהיוצא קח שרשו והוא המבוקש
|
|
|
המשל האלכסון הוא י"ד ומרובעו קצ"ו חלקהו על ב' ויצא מ"ט ושרשו ז' והוא ארך כל צלע
|
|
|
314) שאלה אם תדע רבוע האלכסון עם רבוע הצלע כאלו עולה בין שניהם ג' מאות חלקם על ג' והם מאה וקח שרשם והם י' והוא ארך כל צלע ושרש מאתים הוא האלכסון
|
|
|
315) שאלה אם חברת על תשבורת מרובע רבוע ד' צלעיו ואח"כ תוסיף על אותו הסכום ד' ומהעולה תקח השרש והוא יהיה אורך כל צלע פחות ב'
|
|
|
316) שאלה ממרובע לקחתי ארך הד' קוים ונשאר בידי כ"א כמה ארך כל קו מהמרובע
|
|
|
תוסיף על כ"א ד' והנם כ"ה וקח שרשם והם ה' ותוסיף בם ב' והם ז' והוא ארך כל צלע
|
|
|
317) שאלה אם ידעת צלע המרובע עם האלכסון ועולה מרובע הצלע בעצמו עם מרובע האלכסון בעצמו ושניהם מחוברים כפולים זה על זה עולה ה' אלפים כמה הצלע וכמה האלכסון
|
|
|
חלקם על ב' ויהיו ב' אלפים וה' מאות וקח שרשם והם נ' וקח שרשם והם ז' והוא ארך הצלע וכפול חמישים על ב' והם ק' ושרשם י' והוא ארך האלכסון
|
|
|
318) שאלה כשחברנו הצלע עם המרובע * עולה האלכסון י"ז כמה ארך הצלע וכמה ארך האלכסון
|
|
|
עשה מי"ז ב' חלקים שהחלק הגדול כפול בעצמו יהיה ב' פעמים מהחלק הקטן כפול בעצמו נניח ונקח משל ונאמ' ב' כפלם ויהיו ד' ואם תחלק הקטן כפול בעצמו יצטרך כי החלק הגדול כפול בעצמו יעלה ח' כי הוא ב' פעמים כמוהו וקח שרשם והם ב' וה' שישיות קבצם עם ב' ויהיו ד' וה' שישיות ותאמר אם ד' וה' שישיות יתן לי ב' כמו החלק הקטן כמה יתן לי י"ז ויצא לך ז' והוא החלק הקטן והחלק האחר י' ושניהם מקובצים הם י"ז
|
|
|
319) שאלה מרובע ארוך ארך השני קוים הנכוחיים הקצרים (ו') והב' קוים האחרים ח' אשאל כמה האלכסון
|
|
|
כפול ו' על ו' ויהיו ל"ו עו' כפול ח' על ח' ויהיו ס"ד וחברם ויהיו ק' וקח שרשם ויהיו י' וכך הוא האלכסון
|
|
|
320) שאלה בכאן מרובע ארוך תשברתו מ"ח והנה חברנו ארך הקו הארוך עם הקו הקצור ויעלה י"ד ארצה לדעת ארך הקו הארוך והקצור
|
|
|
קח חצי י"ד והם ז' ומרובעם מ"ט הוצא מהם מ"ח ונשאר א' ושרשו א' הוסיפהו על ז' והם ח' תוציאהו מ[י"ד] ונשאר ו' והוא הקצור
|
|
|
321) שאלה בכאן מרובע ארוך אלכסונו י' ומרובעו ק' ותשבורת המרובע מ"ח ארצה לדעת כמה ארך כל צלע מהמרובע
|
|
|
כפול מ"ח על ב' ויעלה צ"ו ותוסיפם על ק' ויהיו קצ"ו וקח שרשם והם י"ד ואתה ידעת כי בין השני קוים ארכם י"ד ולדעת ארך כל צלע חלק י"ד והם ז' ומרובעם מ"ט הוצא מהם מ"ח והוא תשבורת המרובע המרובע נשאר א' ושרשו א' תוסיפהו על ז' והם ח' והוא הארוך קעא תוציאהו ממנו והוא הקצור
|
|
|
322) שאלה בכאן מרובע ארוך אורך אלכסונו י' ובין שני הקוים ארוך וקצר עולה י"ד אשאל כמה כל צלע מהמרובע
|
|
|
תרבע י"ד והם קצ"ו הוצא מהם מרובע האלכסון והוא צ"ו חלקם על ב' והוא תשבורת המרובע ולדעת ארך כל צלע נאמ' הנה תשבורת אלכסון המרובע הוא ק' ועשה כאמור ותמצא האחת ח' והאחר ו'
|
|
|
323) שאלה בכאן מרובע ארוך ארך הקו הקצור עם האלכסון עולה י"ו והצלע הארוך הוא ח' ארצה לדעת כמה הוא ארך הצלע הקצור והאלכסון
|
|
|
כך תעשה כפול י"ו ועלה רנ"ו והוצא מהם מרובע הצלע הידוע שהוא ח' היינו ס"ד ונשאר קצ"ו וחלקם על כפל י"ו שהוא ל"ב ויצא ו' והוא הצלע הקצור ומו' עד י"ו הוא י' והוא ארך האלכסון
|
|
|
324) שאלה בכאן מרובע ארוך ארך אלכסונו מוסיף על הצלע הקצור ד' והצלע האחר ח' אשאל כמה ארך הצלע הקצור עם האלכסון
|
|
|
כך תעשה תרבע ח' והם ס"ד תוסיף בם מרובע ד' ויהיו פ' חלקם על כפל ד' שהם ח' ויצא י' והוא האלכסון הוצא מי"ו י' הנשאר ו' והוא הצלע הקצור
|
|
|
325) שאלה בכאן מרובע ארוך אשר כפלתי ארך הקו הארוך עם תשבורת המרובע ועלה שפ"ד והצלע הקצור ו' אשאל כמה ארך הצלע הארוך
|
|
|
חלק שפ"ד על ו' ו' ויצא ס"ד ושרשם ח' והוא ארך הצלע הארוך
|
|
|
326) שאלה מרובע ארוך תשברתו מ"ח חלקנו הצלע הארוך על הצלע הקצור עולה א' ושליש אשאל כמה ארך הצלעות
נניח כי הצלע הארוך היה ד'
|
|
|
בעבור כי אמ' א' ושליש והקצור ג' ונראה היחס שיש מד' אל ג' והנה כפול ג' על ד' ויצא י"ב חלק עליהם מ"ח ויצא ד' ושרשם ב' וכפול ב' על ג' ועל ד' והנה החלק האחד ו' והאחר ח' א"כ הצלע הארוך ח' והקצור
|
|
|
או עשה כך כפול ג' על מ"ח והעולה חלק על ד' והוא ל"ו ושרשם ו' והוא הצלע הקצור
|
|
|
ולדעת הצלע הארוך כפול מ"ח על ד' והעולה חלק על ג' והוא ס"ד ושרשם ח' והוא הצלע הארוך
|
|
|
327) שאלה ממרובע ארוך מחובר הצלע הקצור עם האלכסו' עולה י"ו והצלע הארוך מוסיף על הצלע הקצור ב' אשאל כמה הצלע הקצור והאלכסון
|
|
|
כך תעשה תאמר אם תחבר הצלע הארוך עם האלכסון יהיה י"ח כפי מה שאמר כי הארוך מוסיף ב' על הקצור והקצור עם האלכסון הם י"ו על כן כפול י"ו על עצמם וי"ח על עצמם והעולה רנ"ו ושכ"ד וחברם יחד והעולה תק"פ והוצא מהם כפל ב' שהם ד' וישארו תקע"ו ושרשם כ"ד הוצא מהם י"ו ונשאר ח' והוא הצלע הארוך גם הוצא מהם י"ח ונשאר ו' והוא הצלע הקצור ולדעת האלכסון הוצא מי"ו ו' הנשאר י' והוא האלכסון או הוצא מי"ח ח' ונשאר ג"כ י' או מי"ו ו' ונשאר י' והוא האלכסון
|
|
|
328) שאלה מרובע ארוך אשר תשברתו הנקרא רֵיאַה מחובר עם אורך ב' צלעותיו עולה ס"ב אשאל כמה ארך כל צלע מהמרובע
|
|
|
עשה כך הוצא ב' מס"ב ונשאר ס' אח"כ כפול ב' ויהיו ד' והוסיפם על ס' ויהיו ס"ד ושרשם ח' והוא הצלע הארוך ואם תרצה לדעת הצלע הקצור הוצא ב' מח' ונשאר ו' והוא הצלע הקצור
|
|
|
329) שאלה מרובע ארוך כפלתי ארך הצלע הארוך כנגד האלכסון ועלה פ"א והצלע הקצור הוא ו' אשאל כמה הוא הצלע הארוך גם האלכסון
|
|
|
כך תעשה כפול פ' על עצמם ויעלו ו' אלפים וד' מאות גם כפול ו' ויעלו ל"ו וקח חצי ל"ו והם י"ח ומרובעו הוא שכ"ד ותחברם עם ו' אלפים וד' מאות ויהיו ו' אלפים ותשכ"ד ו' ושרשם פ"ב כי עם חצי ל"ו שהם י"ח הם ק' ושרשם י' והוא אלכסון אח"כ חלק פ' על י' ויצא ח' והוא הצלע הארוך או אם תרצה מפ"ב הוצא י"ח הנשאר ס"ד ושרשם ח' והוא הצלע הארוך
|
|
|
330) שאלה בכאן מרובע ארוך אשר הוצאתי מתשברתו הצלע הארוך ונשאר מ' והצלע הארוך עודף על הקצור שנים קעב אשאל כמה ארך כל צלע וצלע
|
|
|
תאמר אחר שהוצאתי הצלע הארוך מתשברתו נשאר מ' אם הוצאתי הצלע הקצור מתשברתו הנשאר מ"ב ועל כן עשה כנזכר לעיל בשאלות הקודמות ותמצא כי הצלע הארוך ח' והקצור ו'
|
|
|
331) שאלה בכאן מרובע ארוך כי כשתחבר הב' קוים הארוך והקצור עם האלכסון עולה כ"ד והצלע הארוך עודף על הקצור ב' אשאל כמה ארך כל צלע והאלכסון
|
|
|
כך תעשה כפול כ"ד והם תקע"ו וכפלם עלה אלף וקנ"ב תוסיף בם כפל היתרון שיש מהצלע הארוך על הקצור והם אלף וקנ"ו ושרשם ל"ד הוצא מהם כ"ד הנשאר י' והוא האלכסון ומכ"ד עד עשרה הנשאר י"ד והוא ארך שתי הצלעות הוצא מהם ב' הנשאר י"ב וחצים ו' והוא הצלע הקצור וח' הוא הצלע הארוך
|
|
|
332) שאלה בכאן מרובע ארוך אשר ארך אלכסונו הוא עודף ב' על הצלע הקצור אשאל כמה ארך כל צלע
|
|
|
לעולם כשהעודף שוה ר"ל כי האלכסון עודף ב' על הצלע הארוך והקו ארוך עודף ב' על הקצור כי הוא שוה כפול היתרון היינו ב' על ה' ויהיו י' וזה יהיה האלכסון עוד כפול ב' עד ד' ויהיו ח' והוא הקו הארוך עוד כפול ב' על ג' והוא הקו הקצור
|
|
|
333) שאלה בכאן מרובע מעויין אשר אם תחבר ב' אלכסוניו עולה ל"ד כמה ארך כל אלכסון והגדול מוסיף על הקטן י"ד כמה ארך כל אלכסון וכמה תשברתו
|
|
|
הוצא י"ד מל"ד הנשאר כ' וחצים עשרה והוא הקצור והארוך כ"ד עתה כפול א' מן אלכסוניו על כל האחר ויעלה ק"כ והוא התשבורת
|
|
|
334) שאלה בכאן מרובע מעויין אשר ארך אחד מאלכסוניו עם תשברתו עולה קנ"ד כמה ארך כל אלכסון ותשברתו
|
|
|
והגדול מוסיף י"ד על הקטן בהיות כי הב' אלכסונים שוים אל הד' צלעות כנז' לעיל
|
|
|
335) שאלה בכאן מרובע מעויין אם תחבר מרובע ב' אלכסוניו עולה תרע"ו ומרובעו כ"ה אשאל כמה כל א' מאלכסוניו
|
|
|
כך תעשה קח רביע תרע"ו והוא קס"ט וקח שרשם והם י"ג והוא אחד מאלכסוניו ואם תבין כל הדרכי' האמורים לעיל תוכל לשער א"כ האלכסון הארוך עודף על הקטן י"ד והוא כ"ד והאחר י'
|
|
|
336) שאלה אם תרצה לדעת מתוך אלכסון העגלה כמה הקפה
|
|
|
כפול האלכסון על ג' ושביעית וכך יהיה הקפו כאלו אלכסון העגול י"ד כפול ג' פעמים י"ד ושביעית ויעלה מ"ד וכך ההקף
|
|
|
או כפול האלכסון על כ"ב וחלקהו על ז'
|
|
|
ואם אמר הקף העגולה מ"ד כמה האלכסון חלק מ"ד על ג' ושביעית ויצא י"ד והוא האלכסון או כפול מ"ד על ז' וחלק על כ"ב
|
|
|
ואם תרצה לדעת העגול אשר אלכסונו הוא י"ד והקפו מ"ד כמה תשברתו קח חצי האלכסון שהוא ג' וחצי וכפול אותו על חצי הקפו שהוא כ"ב ויעלה קנ"ד וכך הוא תשברתו
|
|
|
או אם תכפול כל האלכסון שהוא י"ד על חצי הקפו שהוא כ"ב ויעלה ש"ח והעולה חלק על ב' ויצא קנ"ד
|
|
|
או תחלק חצי האלכסון שהוא ג' וחצי על כל ההקף שהוא מ"ד ויהיו ש"ח וחלקם על ב' והוא קנ"ד
|
|
|
או כפול כל האלכסון על כל ההקף והעולה חלק על י"ד ויצא קנ"ד
|
|
|
או כפול כל האלכסון על עצמו ומהעולה קח י"א חלקים מי"ד ויעלה קנ"ד
|
|
|
או קח רביעית ההקף שהוא י"א וכפלם על עצמם ויהיו קכ"א וזה כפול על האלכסון שהוא י"ד ויהיו אלף תרס"ד וחלקם על י"א ויהיו קנ"ד
|
|
|
או כפול הקפו על עצמו וחלק על י"ב וד' שביעיות כאלו תאמר כפול מ"ד על עצמם ויהיו אלף תתקצ"ו עוד כפול זה על ז' וחלקם על פ"ח היינו על ז' גם על י"א ויצא לך קנ"ד
|
|
|
337) שאלה אם תרצה למדוד חצי עגול אשר האלכסון הוא כ"ד אם תרצה לדעת קשת
|
|
|
קח חצי ג' ושביעית שהוא א' וד' קעג שביעיות כפול א' וד' שביעיות על כ"ד ויהיו ל"ז ושביעית וקח חציו שהם י"ח וד' שביעיות וכפלם על י"ב שהוא חצי כ"ד ויצא לך רכ"ו וד' שביעיות וככה תשבורת חצי זה העגול
|
|
|
338) שאלה דע כי העגול מוסיף על המרובע שהוא בתוכו ג' חלקים מי"ד
|
|
|
כגון עגול אלכסונו ז' הנה תשברתו הוא ל"ח וחצי
|
|
|
והמרובע שהוא בתוך העגול תשברתו הוא כ"ד וחצי הנה ל"ח וחצי מוסיף על כ"ד וחצי ג' חלקים מי"ד
|
|
|
339) שאלה עשה עגול תוך מרובע המרובע מוסיף על העגול ד' חלקים מי"א
|
|
|
כגון מרובע אשר כל צלעיו ה' הנה תשברתו כ"ה ואם תעשה עגול בתוכו לא יהיה כי אם י"ט ורביע ד' חלקים מי"א
|
|
|
340) שאלה בכאן תיבה ארכה ג' אמות וגבהה א' וחצי ורחבו ג' רביעיות אשאל כמה תכיל מחטה באופן כי תכיל כל אמה מרובעת ט' סטארי בתחלה
|
|
|
כפול ג' על א' וחצי והעולה כפול על ג' רביעיות ויצא לך ג' וג' שמיניות ותאמר אם א' שוה ט' ג' וג' רביעיות כמה ישוה ויצא לך המבוקש
|
|
|
341) שאלה בכאן כרי של חטה עגול אשר סביבו הוא כ"ב וגבהו ג' אשאל כמה חטה תכיל הכרי באופן תכיל כל אמה מרובעת ט' סיטארי
|
|
|
כפול כ"ב על עצמם וחלק העולה על י"ב ויצא ל"ח וחצי וכך אמות מרובעות יש בכרי כפול זה על ט' ויעלו שמ"ו אשטארי וחצי
|
|
|
342) שאלה בכאן עגול אשר אלכסונו הוא ז' נרצה לעשות בתוכו מרובע ימשש בכל ד' זויותיו העגול כמו זה כמה כל צלע מהמרובע
|
|
|
אתה רואה כי אלכסון המרובע הוא כמו אלכסון העגול כי הוא ז' כפול ז' על עצמם ויהיו מ"ט חלקם על ב' ויצא כ"ד וחצי ושרשם שהוא קרוב לה' הוא צלע המרובע
|
|
|
343) שאלה בכאן מרובע ארך כל צלע ז' ונרצה לעשות עגול ימשש המרובע כמה הוא אלכסונו
|
|
|
אתה רואה כי ארך אלכסון העגול כמו צלע המרובע ממש היינו ז'
|
|
|
344) שאלה בכאן משולש שוה הצלעות ארך כל צלע י' ונרצה לעשות בתוכו עגול היותר גדול שאפשר שימשש המשולש כמה ארך אלכסון העגול כזה
|
|
|
אתה רואה כי אלכסון העגול הוא ב' שלישיות מעמוד המשולש והנה עמוד המשולש הוא שרש מע"ה שהוא ח' וי"א חלקים מי"ו קח שתי שלישיות מח' וי"א חלקי' מי"ו והוא ארך אלכסון העגול כזה שהוא ה' וז' תשיעיות
|
|
|
345) שאלה אם תרצה לדעת מתוך אלכסון העגול שהוא תוך המשולש כמה עמוד המשולש
|
|
|
קח שליש ז' וז' תשיעיות ותוסיף אותו על ה' וז' תשיעיות ויעלה ח' ושליש וכך הוא עמוד המשולש שהוא חוץ לעמוד
|
|
|
ולדעת ארך צלע המשולש כפול ח' ושליש על עצמם ויהיו ע"ה תמצא מספר ע"ה יהיו ג' רביעיות ותמצא ק' וקח שרשם והוא י' והוא ארך כל צלע מהמרובע
|
|
|
346) שאלה בכאן עגול אשר אלכסונו הוא ח' נרצה לעשו' מרובע על רביעית העגול כמה צלעי המרובע כמו זה
|
|
|
אתה רואה כי אלכסון המרובע כמו חצי אלכסון העגול ואם אלכסון העגול ח' אלכסון המרובע ד' ולדעת הצלע כפול ד' על ד' והם י"ו חלקם על ב' והם ח' וקח שרשם והוא ארך כל צלע המרובע
|
|
|
347) שאלה בכאן ביבר ארוך ח' רוחבו ו' גבהו ד' והוא מלא מים הושלך תוכו קע"ד אבן ארכה ג' ורחבה ג' וגבהה ג' על כל אמה מרובעת שתשליך תוך הביבר ה' בארילי אשאל אם תשליך זאת האבן כמה יצא
|
|
|
כפול ג' על ג' והם ט' וזה על ג' והם כ"ז א"כ תשבורת האבן כ"ז כפול כ"ז על ה' ויצא קל"ה וכך ברילי ממים יצאו חוץ אם תשליך שם האבן
|
|
|
348) שאלה בכאן ביבר ארכו ח' ורחבו ו' וגבהו ו' והמים גבוהים ד' אמות אם נשליך אבן ארכה ג' וגבהה ג' ורחבה ג' כמה יעלו המים תוך הויוארו
|
|
|
קח תשבורת האבן שהוא כ"ז וקח תשבורת הויוארו ארכו עם רחבו שהם מ"ח חלק כ"ז על מ"ח ויצא לך ט' חלקים מי"ו וכך יגברו המים
|
|
|
349) שאלה בכאן אבן עגולה אשר אלכסונה הוא ב' אשאל כמה משקלה באופן תשקול כל אמה מרובעת אלף וו' מאות ליט'
|
|
|
כך תעשה כפול ב' על ב' והם ד' גם זה על ב' והם ח' ומזה תסיר י"א חלקים מכ"א ויצא לך ד' וד' חלקים מכ"א כפלם על אלף וו' מאות ליט' וכך תשקול האבן
|
|
|
350) שאלה אם יש לך עגול ותרצה לעשות עגול אחר יהיה ב' פעמים כראשון
|
|
|
כך תעשה עשה עגול וחוץ לעגול עשה מרובע ימשש לעגול וחוץ לאותו מרובע עשה עגול אחר ותמצא כי העגול החצון הוא ב' פעמים מהפנימי
|
|
|
351) שאלה אם תרצה לעשות מרובע יהיה ב' פעמים כמו המרובע האחר
|
|
|
עשה מרובע וחוץ למרובע עשה עגול ימשש וחוץ לעגול עגול ותמצא ותמצא כי המרובע החצון יהיה ב' פעמים מהפנימי
|
|
|
352) שאלה בכאן מגן אחד עשוי ככה ארך העמוד י"ב והתושבת (ח') ונרצה לדעת כמה תשברתו
|
|
|
תחבר התושבת עם העמוד ויעלה כ' וקח שלישיתם ר"ל ב' שלישיות שהם י"ג ושליש ומהעולה קח י"א חלקים מי"ד ויצא ס"ט וחלקים וככה התשבורת
|
|
|
353) שאלה אם תרצה למדוד צורה כזאת אשר ארך האלכסון ו' והתושבת ד'
|
|
|
תחבר התושבת עם האלכסון והם י' וקח מחציתם והם ה' ותרבעם והם כ"ה וקח מהם י"א חלקים מי"ד ונשאר י"ט וט' חלקים מי"ד וכך הוא תשברתה
|
|
|
354) שאלה איש אחד רוצה לעשות סרבל שיהיה ארוך ב' אמות ורוצה לעשות אותו מבגד רחבו אמה וחצי ארצה לדעת כמה אמות יצטרך לעשות אותו הסרבל
|
|
|
כך תעשה ידוע הוא כי הסרבל הדיאמטרו הוא ב' פעמים כמו האורך ואם האורך הוא ב' אמות הרוחב הוא ד' על כן תאמר בכאן עגול אשר אלכסונו הוא ד' כמה תשברתו כפול ד' על עצמם ויהיו י"ד וקח מהם י"א חלקים מי"ד הנשאר י"ב וד' חמישיות וכך הוא תשברתו מאמות מרובעות ואנו אמרנו כי הבגד רחב אמה וחצי על כן חלק י"ב וד' שביעיות על א' וחצי ויצא לך ח' וח' חלקים מכ"א וכך בגד יצטרך לעשות הסרבל
|
|
|
355) שאלה אדם רוצה לעשות מלבוש מבגד רחב אמה וב' שלישיות ויצטרך מאותו בגד ט' אמות ואח"כ נמלך ורוצה לעשותו מבגד רחב אמה וחצי כמה בגד יצטרך
|
|
|
כפול ט' על א' וב' שלישיות חלקם על א' וחצי ויצא י' וכך אמות יצטרך מאותו בגד השני
שאלה בכאן מרובע בלתי מתיחס כזה
|
|
|
חלק ב' קוים נכוחיים היינו ד' וי' וחצי י' הם ה' וחצי ד' הם ב' הסר ב' מה' הנשאר ג' וכפלם והם ט' אח"כ חבר י"ב וי"ו ויהיו כ"ח וחלקם על ב' ויהיו י"ד ומרובעם קצ"ו הסר מהם הט' וישארו קפ"ז הסר מהם שרשם והם י"ג וט' חלקים מי"ג אח"כ חבר ד' עם י' והם י"ד וחלקם על ב' קעה והם ז' כפול ז' על י"ג וט' חלקים מי"ג ויצא לך צ"א וב' שלישיו'
|
|
|
וכן תעשה מכל תמונה מתחלפת הצלעות
|
|
|
356) שאלה אם תרצה למדוד מרובע שהוא מתחלף הצלעות כזה
|
|
|
כך תעשה כפול ג' על ה' והם ט"ו וכפול ז' על ג' והם כ"א וכפול כ"א על ט"ו והם שט"ו וקח שרשם והם י"ז וכ"ו חלקים מל"ד וכך הוא התשבורת
|
|
|
וכן תוכל לעשות מכל מרובע בין שיהיה ארוך או רבוע או נפתל או מתחלף הצלעות כי כל ד' קוים מתחלפים כשתכפול זה על זה ר"ל ב' מהם איך שיזדמן וכן הב' האחרים זה על זה והסך העולה תכפול זה על זה תמצא תשברתו ולעולם יצא שוה
|
|
|
357) שאלה אם ד' בראצי מקורדי מספיקות לקשור י' זמורות ק' בראצי כמה זמורות יקשרו
|
|
|
כפול ד' על ד' והם י"ו גם כפול י' על י' ויהיו ק' ותאמר אם י"ו יקשרו ק' כמה יקשרו ק' ויצא לך תרכ"ה א"כ ק' בראצי יקשרו תרכ"ה זמורות
|
|
|
ואם אמר ד' בראצי קושרים ק' זמורות עשרה בראצי כמה קורדי יצטרך לקשור תרכ"ה
|
|
|
כפול תרכ"ה על י"ו והעולה תחלק על ק' ויצא לך שרש ק' שהוא י' והוא הדרוש
|
|
|
358) שאלה אם פיורינצא מקפת ה' מילין והנה החומה עביה ג' אמות וחצי והפושי אשר היא ברגל החומה עביה י"ד אשאל כמה תקיף פיורינצא חוץ לחומה
|
|
|
ידוע כי החומה עביה ג' אמות וחצי מכל צד וחברם עם י' והם י"ד והם י"ז וחצי וכפלם ויהיו ל"ה כפלם על ג' ושביעית ויצא ק"י א"כ פיורינצא מקפת ה' מילין וק' אמות
|
|
|
359) שאלה פיורינצא היא עגולה ומקפת ז' מילין ופאדואה היא עגולה ומקפת ב' מילין אשאל כמה פעמי' יותר גדולה פיורינצא מפאדואה
|
|
|
כפול ב' על ב' והם ד' גם כפול ז' על ז' והם מ"ט חלק מ"ט על ד' ויצא י"ב ורביע וכך פעמים יותר גדולה פיורינצא מפאדואה
|
|
|
360) שאלה רומא היא עגולה ומקפת ל"ג מילין וקושטאנטינופלי היא בדמות משולש ומקפת מ"ב מילין צלע אחד ט"ו ואחר י"ג ואחר י"ד איזו גדולה מחברתה
|
|
|
קח תשבורת רומא היינו חצי ההקף שהוא י"ו וחצי וכפלהו על חצי האלכסון ויצא פ"ו וה' שמיניות וזה הקף רומא קח תשבורת המשולש מקושטאנטינופולי ויצא פ"ד א"כ רומא יותר גדולה
|
|
|
361) שאלה איש רוצה לחפור בור ולקבל ד' דוקטי וחפרו באופן כי קבל ד' דוקטי אשאל כמה חפר
|
|
|
תאמר כי בעד י' ראוי לעשות נ"ה יגיעות כמו שהוא מחובר מא' עד י' בעד ד' כמה יגיעות ראוי שיעשה ויצא לך כ"ב יגיעות וכבר ידעת כי מא' עד ו' הם כ"א ואחר ו' הוא ז' ושים אותו העודף מכ"א עד כ"ב ושימהו על ז' ויהיה שביעית אחד א"כ בו' אמות ושביעית אמה ראוי שיקבל ד' דוקטי
|
|
|
362) שאלה לאיש אחד יש לו ב' שקים אחד מכיל ו' אשטרי ואחד מכיל כ"ד ורוצה לעשות משניהם שק אחד ולחברם אשאל כמה יכיל השק
|
|
|
כך תעשה חבר ו' עם כ"ד ויהיו ל' אח"כ כפול ו' על כ"ד ויהיו קמ"ד וקח שרשם ויהיו י"ב וכפלם ויהיו כ"ד וחברם ויהיו נ"ד וכך אשטארי יכיל השק
|
|
|
363) שאלה בכאן צורה עשויה כדמות כסוי מאלביקו הנקרא פיראמידא גבהה ו' אמות ונרצה לחלקה לשני חלקים שוים במשקל לא במדה באיזה מקום ראוי לחתוך אותה
|
|
|
כך תעשה כפול ו' על ו' ויהיו ל"ו גם כפול ל"ו על ו' ויהיו רי"ו וחלקם על ב' ויהיו ק"ח וקח ו' שרשו המעוקב וזה יהיה גובה החלק האחד והנשאר עד ו' קעו הוא החלק האחר
|
|
|
364) שאלה אם יש לפניך צורה כזאת שהיא קטומת הראש אשר שני צלעיו י"ג והראש ח' והתושבת י"ח
|
|
|
לדעת מרובעה תחבר הראש עם התושבת ויהיו כ"ו וקח מחציתם והם י"ג וכפול אותם כנגד העמוד שהוא י"ב ויהיו קנ"ו וכך הוא תשברתה
|
|
|
ואם תרצה להשלים הצורה כדמות משולש ותרצה לדעת כמה יצטרך להשלימה עד שיהיה כדמות משולש
|
|
|
כפול ח' שהוא הראש על י"ג ויעלה ק"ח וחלק ק"ח על היתרון שיש לתושבת אל הראש שהוא י' ויצא י' וב' חמישיות
|
|
|
גם תוכל לדעתו באופן אחר והוא תדע ערך הראש אצל מה שעודף התושבת והנה העודף הוא י' חלק ח' על י' והם ד' חומשים קח ד' חומשים מי"ג והם י' וד' חומשים
|
|
|
והמופת תאמר אם י"ג שהם הקוים הרחיבו י' שהוא יתרון התושבת אל הראש כמה יתנו י' וד' חומשים ויצא לך ח' א"כ יצטרך שהראש העומד על נקדה עד שירחיב ח' יצטרך י' וד' חומשים
|
|
|
365) שאלה אם תרצה לחלק משלש שוה הצלעות לב' חלקים שוים
|
|
|
חלק התושבת על חציו ותוציא עמוד מראש המשלש עד חצי התושבת והוא נחלק לב' חלקים שוים כזה
|
|
|
366) שאלה אם תרצה למדוד איזה דבר מעוקב ר"ל שיש לו ג' רחקים
|
|
|
כגון אם תרצה לדעת מגדל ארוך י' ורחבו י' וגבהו י'
|
|
|
כפול י' על י' והם ק' וכפול זה על י' והם אלף וכך הוא התשבורת כל חלק אמה על אמה ברום אמה
|
|
|
ואם הארך והרוחב אינו שוה
|
|
|
כגון שיהיה ארכו ו' ורחבו ו' וגבהו עשרה
|
|
|
כפול ו' על ו' והם ל"ו וכפלם על י' והם ש"ס וכך הוא תשברתו
|
|
|
ואם הם מתחלפים הארך והרחב והגבה
|
|
|
כגון אם הארך ו' והרחב ה' והגובה עשרה
|
|
|
כפול ו' על ה' ויהיו ל' וכפלם על י' והם ש'
|
|
|
367) שאלה יש לנו משלש ארך הקו האחד ט"ו והשנית י"ד והאחרת לא ידענו אמנם תשבורת המשלש פ"ד אשאל כמה הצלע
|
|
|
כבר ידעת כי כשתכפול חצי העמוד על חצי התושבת הוא תשבורת המשלש ונניח כי הוא י"ד א"כ כשנחלק פ"ד על י"ד יצא חצי העמוד יצא ו' ואם חציו ו' כלו י"ב
|
|
|
ועכשו שמצאת העמוד תמצא באיזה מקום רחוק מקו ט"ו נופל העמוד
|
|
|
והנה תעשה כך כפול י"ב על עצמם וט"ו על עצמם ויצא קמ"ד ורכ"ה הוצא מרכ"ה קמ"ד וישאר פ"א וקח שרשם והם ט' א"כ העמוד נופל ט' רחוק מצלע ט"ו א"כ החלק האחר הוא ה' בהכרח כי ט' וה' הם י"ד
|
|
|
ולדעת כמה ארך הצלע
|
|
|
כפול ה' על עצמם וי"ב על עצמם וחברם ויהיו קס"ט ושרשם י"ג והוא הצלע הנעלם
|
|
|
368) שאלה בכאן ג' עגולים משעוה הקף הא' ב' והא' ג' והאחר ו' ונרצה להתיכם ולעשות מהם א' עגול כמה יהיה הקפו
|
|
|
כפול ב' על ב' והם ד' וג' על ג' והם ט' וו' על ו' והם ל"ו וחברם והם מ"ט וקח שרשם והם ז' וכך יהיה הקפו
|
|
|
369) שאלה כל ח' מספרים או ו' או ד' והוא שיהיו זוגות ומוכפלים ב' מהם איך שיזדמן זה על זה והב' הנשארים ג"כ כפולים זה על זה והעולה מהב' הכפלו' כפול זה על זה וכן מהאחרים הנה באיזה דרך שתכפלם לעולם המספר יצא שוה
|
|
|
המשל מו' מספרים א'ב'ג'ד'ה'ו'
|
|
|
כפול א' על ב' והם ב' וכפול ג' על ד' והם י"ב כפול י"ב על ב' השמורים והם כ"ד עו' כפול ה' על ו' ויעלה ל' כפלם על כ"ד והם ש"כ ושמרם
|
|
|
עוד תעשה ההפוך ב' באופן אחר והנה נכפול א' על ג' ד' והם ד' וב' על ג' והם ו' קעז כפלם על ד' והם כ"ד והם ג"כ ש"כ
|
|
|
עוד תהפכם באופן אחר כפול א' על ד' והם ד' וב' על ג' והם ו' כפלם על ד' והם כ"ד וכפול ה' על ו' והם ל' וכפלם על כ"ד והם ש"כ
|
|
|
וכן תעשה מכל ההפוכים איך שתרצה לעולם יצא שוה וכן תוכל לעשות מכל המספרים כשהם זוג
|
|
|
370) שאלה כל דבר מרובע וכל להיות בשני מינים או שלם או חצי כדור או פחות מחצי כדור או יותר מחצי כדור
|
|
|
ולדעת כשהוא חצי כשהחץ הוא חצי המתר הוא חצי עגול וכשהחץ יותר מחצי המתר הוא יותר מחצי עגול וכשהחץ פחות מחצי המתר הוא פחות מחצי עגול
|
|
|
ולמדוד כשהוא חצי עגול כאלו תאמר קשת שמתרו ח' וחצו ד' הוא חצי עגול כפול חצי המתר שהוא ד' על ג' ושביעית והנה יצא י"ב וד' שביעיות והוא ארך הקשת קח חצי י"ב וד' שביעיות וכפול אותם בד' שהוא חצי המתר ויצא לך כ"ה וזהו תשבורת חצי עגול
|
|
|
ותוכל לדעת תשברתו בדרך אחר והוא שתרבע המתר שהוא ח' והם ס"ד ותקח מזה השביעית ומחצית השביעית שהם י"ג וה' שביעיות הנשאר נ' וב' שביעיות חלקם על ב' והם כ"ה ושביעית והוא התשבורת כמו שאמרנו
|
|
|
משל לאותו שהוא פחות מחצי עגול כגון קשת אשר מתרו ח' וחצי ב' הוא פחות מחצי עגול
|
|
|
אם תרצה לדעת קוטר העגולה תרבע חצי המתר והוא שהוא ד' ויהיו י"ו חלק י"ו על החץ שהוא ב' ויצא ח' תוסיף על זה ארך החץ שהוא ב' ויהיו י' והוא קוטר העגולה
|
|
|
371) שאלה אם יש לך תמונה הולכת ומקצרת
|
|
|
כגון גוף משולש אשר למטה כל צלע מהמשלש ח' אמות וראשו כל צלע מן המשולש ד' אמות וגבהו ד' אמות
|
|
|
אתה ידעת כי תשבורת התושבת כ"ח אמות פחות שני שביעיות ותשבורת הראש ז' פחות חלק אחד מי"ד וחברם ויהיו ל"ד וט' חלקים מי"ד ואתה ידעת כי גדר תשבורת התושבת מלמטה שהיה כ"ח וב' שביעיות גדרו ה' וב' שביעיות גם שרש או גדר הראש שהיה תשברתו ז' וגדר וחלק אחד מי"ד גדרו ב' וד' שביעיות וחצי שביעית היינו חלק אחד מי"ד כפול ד' וב' שביעיות וחצי שביעית שהוא גדר הראש עם גדר התושבת מלמטה שהיה ה' ושתי שביעיות ועלה י"ד פחות ב' שביעיות ותוסיפם על ל"ד שהיה לך ותשעה חלקים מי"ד ויעלה הכל מ"ח וחצי כפלם על שליש הגובה שהוא ב' ויעלה הכל צ"ז והוא תשבורת גוף המשלש הזה
|
|
|
372) שאלה תמונה מרובעת אשר ארכה עשרה וארחבה עשרה וגבהה עשרה כמה תשברתה
|
|
|
כפול י' על י' והם ק' וק' על י' והם אלף וכך תשברתה
|
|
|
ואם הארך שוה לרוחב והגובה מתחלף
|
|
|
כגון אם הארך ו' והרחב ו' והגבה י'
|
|
|
כפול ו' על ו' והם ל"ו וכפלם על י' והם ש"ס
|
|
|
ואם כל רחקיו מתחלפים
|
|
|
כגון הארך ו' והרוחב ה' והגובה ד'
|
|
|
כפול ו' על ה' והם ל' וד' על ל' והם ק"כ
|
|
|
ואם יש לך תמונה משולשת אשר א' מצלעיו ג' והאחר ד' והאחר ו'
|
|
|
אתה ידעת כי זה המשלש הוא ו' ואם תכפול ו' על הגובה ונניח כי הגובה י' והם ס' וכך הוא תשבורת הצורה הזאת
|
|
|
והרוצה לדעת גובה ממגדל עגול
|
|
|
כגון שיהיה קוטרו י' אמות וגבהו י"ד
|
|
|
כך תעשה כפול הקוטר על עצמם והם ק' וכפלם על הגובה שהוא י"ד והם אלף וד' מאות קח מהם ג' חלקים מי"ד שהם ג' מאות ונשארו אלף ומאה וכך ממש תעשה קעח אם תוציא מק' שהוא מרובע הקוטר ג' חלקים מי"ד והנשאר כפול על הגובה
|
|
|
ואם התמונה עולה בשפוע כגון תמונה אשר ארכה ד' ורחבה ד' וגבהה עשרה ועולה ומקצרת כפול ד' על ד' והם י"ו
|
|
|
וכפלם בשלישית הגובה שהוא ג' ושליש ויעלה נ"ג ושליש והוא תשבורת התמונה הזאת
|
|
|
וזה יצדק בכל התמונות מתחלפי הצורות מרובעת או משולשת או מעוגלת כשתדע השטח כפול ב' בשלישית הגובה
|
|
|
ואם התמונה הולכת ומקצרת אמנם אינה עומדת על נקדה והיא רחבה למעלה ד'
|
|
|
כגון שהיא למטה ו' בארך וברחב והגובה י' והראש ד' בארך וד' ברוחב
|
|
|
כפול הראש שהוא ד' עם התושבת ויהיו כ"ד וכפול ו' על ו' והם ל"ו וכפול ד' על ד' והם ע"ו בין הכל וכפלם על ג' ושליש שהוא שליש הגובה ויעלה רנ"ג
|
|
|
והוא תשבורתה באיזה דמות שתהיה מרובעת או משלשת אמנם היא עגולה והולכת ומקצרת
|
|
|
כגון מגדל עגול גבהו י"ב וקוטרה למטה ד' אמות וקוטרה למעלה ב' אמות
|
|
|
קח מרובע ד' והם י"ו ו' ומרובע ב' והם ד' ומרובע ב' בד' הם ח' הוצא ממנו שביעיתו ו' ומחצית שביעיתו הנשאר כ"ב כפלם בד' שהוא שליש הגובה ויעלה פ"ח והוא תשבורת המגדל
|
|
|
373) אם תרצה למדוד גוף עגול כמו כדור או דבר אחר
|
|
|
כגון כדור אשר קוטרו ז'
|
|
|
תרבע הקטר שהוא מ"ט ותכפלם על ג' ושביעית ויעלה קנ"ד והם אמות שטח הכדור כפלם בשתות הקוטר כי שתות ז' הוא א' וא' שתות ויעלה הכל ק"פ פחות שליש והוא תשבורת הכדור
|
|
|
וכפי זה הדרך תוכל לדעת תשבורת שברי הכדור
|
|
|
כאלו אמ' ספל מלא מים אשר גופו מבפנים מעוגל ופיה עמוק ומעוגל והוא ברחבו ז' אמות והוא עמוק ג' אמות וחצי תוכל לשער כי הוא חצי כדור כפול עמקו ברוחב פיו אשר הוא קוטר הכדור וקבץ הכל וכפלהו ג' ושביעית כמו שעשית בכדור ויעלה בידך ע"ז והוא תשבורת שטח הספל כפלהו על שישית קוטרו שהיה ז' והוא א' ושתות ויעלה הכל צ' פחות שתות והוא תשבורת הספל
|
|
|
ואם הספל פחות ממחצית רוחב פיה אם תוציא את קוטרה כמו שהראיתיך למעלה בשטחים מעוגלים תמצא כי הוא ז' לכן כפול ז' אשר הוא פיה בב' אשר הוא העומק ויעלה כפול אותם בג' ושביעית והעולה כפול בשתות הקוטר ויעלה נ"א ושליש והוא תשבורת גוף הספל הזה
|
|
|
ואם עומק הספל הוא ה' וקוטר שפתו הוא ז' פחות ב' שלישיות ר"ל שרש מ' שהוא ו' ושליש היתה מוצא קוטרה ז' ואם תכפול העומק בקוטר יהיה ל"ה כפלהו על ג' ושביעית ויעלה ק"י והוא תשבורת שטח הספל כפלהו על שישית הקוטר שהוא א' ושישית ויעלה הכל קכ"ח ושליש והוא תשבורת הספל הזה העודף על המחצית
|
|
|
374) שאלה אם יש לך רביעית כדור כזה אשר ארך הב' קוים ישרים ד' אמה כמה תשברתה
|
|
|
כפול ד' על ד' והם י"ו וקח מהם ג' חלקים מי"ד שהם ג' וו' חלקים מי"ד נשארו י"ב וח' חלקים מי"ד וככה תשברתה
|
|
|
375) שאלה למודוד ק' כדור אשר קוטרו ז'
|
|
|
תרבע ז' על ז' והם מ"ט וכפלם על ג' ושביעית והם קנ"ד כנז' לעיל וכפלם בשתות הקוטר ויעלה ק"פ פחות שליש
|
|
|
או קח מעוקב ז' שהוא שמ"ג ומזה קח י"א חלקים מכ"א ויעלה ק"פ פחות שליש
|
|
|
הטעם למה לוקחים י"א חלקים מכ"א כי אם תרצה
|
|
|
לעשות מקוביה שהיא מרובעת לעגלה הוא י"א חלקים מכ"א והפסולת הוא י' חלקים מכ"א כמו שעשה הנסיון פראלוקא
|
|
|
376) דרך לחבר בשרשים כמו אם תרצה לחבר שרש י"ו עם
|
|
|
שרש י"ו בהיות כי שני המספרים שוים על כן קח אחד משניהם ו' וכפול אותו על שרש האחר והנה נקח י"ו וכפול אותו על שרש י"ו שהם ד' ויעלה ס"ד וקח שרשם והם ח' וכך עולה כפל חבור שרש י"ו עם חבור שרש י"ו
|
|
|
ואם המספרים בלתי שוים כמו לחבר שרש י"ו עם קעט שרש ט'
|
|
|
חבר ט' עם י"ו והם כ"ה אח"כ כפול ט' על י"ו והם קמ"ד וקח שרשם והם י"ב וכפלם והם כ"ד חבר אותם עם כ"ה והם מ"ט וקח שרשם והם ז' והוא המבוקש
|
|
|
וכן תוכל לעשות מב' מספרים שאין להם שרש אמיתי כמו לחבר שרש י' עם שרש מ'
|
|
|
עשה כנז' ויצא לך שרש צ'
|
|
|
לחבר שרש משרש עשרי' עם שרש משרש עשרים
|
|
|
קח השרש שעבר מעשרים שהם ד' וכפלם והם י"ו וכפול י"ו על עשרים והם ש"כ וקח שרש משרש ש"כ וכך הוא שרש משרש עשרים מחובר עם שרש משרש עשרים
|
|
|
נרצה לחבר שרש משרש פ"א עם שרש משרש פ"א
|
|
|
קח ד' וכפול אותם והם י"ו וכפלם על פ"א ויעלה אלף ורצ"ו וקח שרשם והם ל"ו ומל"ו קח שרשם והם ו' והוא המבוקש
|
|
|
נרצה לחבר שרש משרש ש"כ עם שרש משרש עשרים
|
|
|
חלק ש"כ על עשרים ויצא י"ו וקח שרש משרש י"ו והם ב' תוסיף בם אחד והם ג' וקח מרובע מרובעם והם פ"א ואלו הפ"א כפלם על עשרים והם אלף ותר"כ ושרש משרש זה הוא המבוקש
|
|
|
נרצה לכפול שרשי המעוקבי' כמו לחבר שרש כ"ז עם שרש כ"ז
|
|
|
קח המעוקב שעבר שהוא ח' וכפול אותם עם כ"ז והם רי"ו וקח שרשם ה' המעוקב והם ו' וכן הוא המחובר משרש כ"ז עם שרש כ"ז
|
|
|
נרצה לכפול שרש מ' עם שרש מ' שאין להם מעוקב
|
|
|
חלק מ' על ח' ויצא ה' וקח שרש ח' והם ב' חבר בם א' והם ג' וקח מעוקבם והם כ"ז כפול אותם על המספר הקטן שהיה ה' ויעלה קל"ה וקח מעוקבם כן הוא חבור שרש מעוקב מ' עם שרש מעוקב ה'
|
|
|
377) שאלה אילן גבוה ז' אמות ואדם רוצה לחתכו ובכל הכאה כופף אותו אמה אחת מתי יגיע ראשו בארץ
|
|
|
כפול ז' על ג' ושביעית והם כ"ב וקח חצים והם י"א א"כ בי"א הכאות יגע ראשו בארץ והטעם הוא כי העץ בהיותו נעוץ הז' אמות מהגובה הם כמו קוטר העגולה שקוטרה ז' והקו הסובב כ"ב ועל כן כשהאילן נופל הוא עושה תנועה סבובית שקוטרה י"א ועל כן בי"א הכאות יפול לארץ ודעהו
|
|
|
378) אם תרצה לחבר שרש מרובע מי"ו עם שרש מעוקב מח'
|
|
|
כפול ח' ויהיו ס"ד גם קח מעוקב מי"ו שהם ד' אלפים וצ"ו חלקם על ס"ד ויצא ס"ד וקח שרשם שהם ח' וקח שרשם המעוקב שהם ב' תוסיף בם א' ויהיו ג' וקח מעוקבם והם כ"ז ותרבעם ויהיו תשכ"ט ותכפלם על ס"ד ויעלה מ"ו אלפים ותרנ"ו וקח שרשם
|
|
|
המרובע שהם רי"ו וקח שרשם המעוקב שהם ו' וכך הוא חבור שרש מרובע מי"ו מחובר עם שרש מעוקב מח'
|
|
|
379) נרצה לגרוע בשרשים הסר משרש ה' שרש ג'
|
|
|
יען כי אין שרש לשום אחד מהם תאמר כי הנשאר הוא שרש ה' פחות שרש ג'
|
|
|
נרצה להסיר משרש מ' שרש י'
|
|
|
חבר י' עם מ' והם נ' גם כפול מ' על י' והם ת' וקח שרשם והם עשרים כפלם והם מ' הסירם מנ' הנשאר י' אם נשאר עדין שרש י'
|
|
|
נרצה להסיר שרש משרש עשרים משרש שרש חמשת אלפים וק"נ
|
|
|
חלק ה' אלפים וק"נ על עשרים ויצא רנ"ו והסר שרש השרש שהם ד' הסר מהם א' נשאר ג' וקח מרובע מרובעם שהם פ"א וכפלם על עשרי' ויעלה אלף ותר"כ א"כ הנשאר הוא שרש משרש אלף ותר"פ
|
|
|
נרצה להסיר משרש שרש פ"א שרש משרש י"ו
|
|
|
חלק פ"א על י"ו ויצא ה' וחלק מי"ו תעשה מהם חלקים מי"ו והם פ"א וקח שרש משרש פ"א שהוא ג' גם קח שרש משרש י"ו שהוא ב' חלק ג' על ב' ויצא א' וחצי הסר אחד מא' וחצי הנשאר חצי וקח מרובע מרובעו ויצא חלק אחד מי"ו וכפלהו על י"ו ויצא אחד שלם וכך הוא הנשאר
|
|
|
נרצה להסיר משרש מעוקב של רי"ו שרש מעוקב שמונה כמה הנשאר
|
|
|
חלק רי"ו על ח' ונשאר כ"ז וקח שרשם המעוקב שהם ג' הסר מהם אחד ונשאר ב' וקח מעוקבם והם ח' וכפלם על ח' שהוא ק"פ א' מב' מספרים והם ס"ד וקח שרשם מעוקב שהם ד' וכן הוא הנשאר
|
|
|
נרצה להסיר משרש ק"ח שרש ד' ר"ל שרשם המעוקב כמה הנשאר
|
|
|
חלק ק"ח על ד' ויצא כ"ז וקח שרשם המעוקב שהם ג' הסר מהם אחד הנשאר ב' וקח מעוקבם והם ח' כפלם על ד' שהוא אחד מהב' מספרים ויעלה ל"ב א"כ הנשאר הוא שרש מעוקב מל"ב
|
|
|
נרצה להסיר משרש כ"ז שרש ח' ר"ל שרשם מעוקב
|
|
|
חלק כ"ז על ח' ויצא לך ג' וג' שמיניות היינו כ"ז חלקים מח' קח שרש כ"ז שהם ג' גם שרש ח' שהם ב' וחלק ג' על ב' ויצא א' וחצי ומזה תסיר א' הנשאר חצי וקח מעוקבו שהוא שמינית ותכפלהו על א' מן המספרים היינו על ח' ויצא (א') שלם והוא הנשאר
|
|
|
נרצה להסיר משרש מרובע מי"ו שרש מעוקב מח' כמה הנשאר
|
|
|
קח מעוקב י"ו והם ד' אלפים וצ"ו וקח מרובע ח' שהוא ס"ד חלק ד' אלפים וצ"ו על ס"ד ויצא ס"ד וקח שרשם המרובע שהם ח' ומהם קח שרשם המעוקב שהם ב'
|
|
|
הסר מהם אחד הנשאר אחד וקח מעוקבו שהוא אחד וכפלהו על ס"ד ויהיו ס"ד וקח שרשם והם ח' וקח שרשם המעוקב שהוא ב' והוא הנשאר
|
|
|
380) נרצה לכפול שרש מ' על שרש י'
|
|
|
כפול י' על מ' והם ת' וקח שרשם והוא כ' והוא המבוקש כפול שרש מעוקב שמונה על שרש מעוקב ח' כפול ח' על ח' והם ס"ד קח שרשם המעוקב והם ד' והוא המבוקש
|
|
|
כמה יעלה כפל שרש מעוקב מח'
|
|
|
כפול על שרש מעוקב כ"ז כפול ח' על כ"ז ויעלו רי"ו וקח שרשם המעוקב שהם ו' והוא המבוקש
|
|
|
נרצה לכפול שרש מעוקב ט' על שרש מעוקב כ"ח
|
|
|
כפול ט' על כ"ח ויעלה רנ"ו וקח שרשם המעוקב והוא המבוקש
|
|
|
נרצה לכפול שרש מרובע ד' על שרש מעוקב ח'
|
|
|
קח מעוקב ד' והם ס"ד וקח מרובע ח' שהם ס"ד אח"כ כפול זה על זה היינו ס"ד על ס"ד ויעלה ד' אלפים וצ"ו וקח שרשם המרובע שהוא ס"ד ומס"ד קח שרשם המעוקב שהם ד' והוא המבוקש
|
|
|
נרצה לדעת כמה יעלה ה' על שרש מרובע ח' קח מ[עו]קב ה' ויהיו קכ"ה וכפלם על ח' ויעלה אלף וקח שרשם המעוקב ויעלה י'
|
|
|
נרצה לדעת מהו שרש משרש י"ו
|
|
|
כפול על שרש מעוקב מח' כך תעשה קח מעוקב י"ו והם ד' אלפים וצ"ו כן תעשה מח' תרבעם והם ס"ד עוד כפלם על עצמם והם ד' אלפים וצ"ו כפול ד' אלפים וצ"ד על ד' אלפים וצ"ו ויצא 177716 ושרשם ד' אלפים וצ"ו ומזה המספר הוצא שרש משרש המעוקב וקח מס"ד שרשם המעוקב שהם ד' וכך הם הכפל
|
|
|
נרצה לכפול שרש משרש ג' על שרש מב' שרש המעוקב
|
|
|
קח מעוקב ג' שהם כ"ז וקח מרובע ממרובע ב' שהם י"ו כפול כ"ז על י"ו ויעלו ד' מאות ול"ב ויען כי אין לו שרש אמיתי תאמ' תחלק לי עשרים על שרש חמשה תרבע עשרים והם ד' מאות חלקם על ה' ויצא פ' והנה שרש שמונים הוא המבוקש
|
|
|
381) נרצה לחלק שרש מאה על עשרים
|
|
|
כפול שרש מאה על ב' והם מאתים וכפלם והם ד' מאות חלק ק' מאות על ד' מאות ויצא ד'
|
|
|
נרצה לחלק שרש מרובע י"ו על שרש מרובע ד' עשה כך חלק י"ו על ד' ויצא ד' וקח שרשם והם ב' והוא המבוקש
|
|
|
נרצה לחלק שרש מרובע ז' על שרש מרובע ג' חלק ז' על ג' ויצא ב' ושליש ושרש ב' הם א' ושליש והוא היוצא
|
|
|
382) נרצה למצא שרשי המרובעי' שאין להם שרש
|
|
|
כגון אם תרצה לדעת שרש מעוקב מז'
|
|
|
כבר ידעת כי א' היה השרש שעבר ומעוקבו א' הסר א' מז' ונשאר ו' גם הסר א' מח' ונשאר ז' ושים ו' על ז' א"כ תאמ' כי שרש מעוקב מז' הוא א' וו' שביעיות
|
|
|
נרצה למצא שרש כ"ו הנה השרש שעבר היה ח' הסירם מכ"ו ונשאר קפא י"ח אח"כ הסר ח' מכ"ז הנשאר י"ט תשים י"ח על י"ט א"כ שרשו הקרוב הוא ב' וי"ח חלקים מי"ט
|
|
|
תרצה למצא שרש המרובעים שאין להם שרש אמיתי או יש להם והם שלמים עם שברים
|
|
|
כאלו תרצה לדעת שרש י"ב ורביע
|
|
|
קח השרש שעבר מט' שהוא ג' וכפלם והם ו' והנה מט' עד י"ב הם ג' ורביע כפול^ ג' על ו' ויצא חצי וקח מרובעו שהוא חלק רביע ותסירהו מהרביע והוא שרשו ג' וחצי
|
|
|
תרצה למצא שרש י"ד וחצי קח המרובע שעבר שהוא ט' ושרשו ג' הנשאר ה' כפול ג' והם ו' חלק ה' וחצי על ו' ויצא י"א חלקים מי"ב ושרשם ג' וי"א חלקים מי"ב
|
|
|
דרך אחר למצא שרש ממספר קטן בקרוב גדול תוסיף בם ב' זירי וקח שרשם ואח"כ חלק היוצא על י'
|
|
|
דמיון נרצה לדעת שרש ב' מ' תוסיף ב' זירי והם ב' מאות וקח שרשם והם י"ד ושביעית חלקם על י' ויצא א' וכ"ט חלקים מע' והוא קרוב מאד
|
|
|
כן תוכל לעשות מהמעוקבים אם תוסיף בם ג' זירי וקח שרשם וחלק היוצא על י' והוא הדרוש
|
|
|
דמיון נרצה לדעת שרש ח' שים ג' זירי ויהיו ח' אלפים ושרשם עשרים תסיר מהם א' זירא וישאר ב' והוא שרש ח'
|
|
|
383) אם תרצה לדעת תשבורת קטומה כזאת
|
|
|
כך תעשה תרבע הצלע הקצור אשר הוא י"ג ויעלה קס"ט גם תרבע הצלע האחר שהוא ט"ו ויעלה רכ"ה תסיר מהם קס"ט הנשאר נ"ו תחלקם על ב' וישארו כ"ח חלק כ"ח על מה שעודף התושבת על הראש שהוא י"ד ויצא ב' ואלו הב' תוסיפם על מה שעודף מחצית התושבת על הראש שהוא ז' כי התושבת עודף על הראש י"ד ומחציתם ז' ויצא ט' וכך הוא רחוק העמוד מהצלע ארוך ואם תסיר מז' ב' ישאר ה' והוא מעמד העמוד מהקצור ולדעת תשברתה תחבר התושבת עם הראש והם ל' וחצים ט"ו כפלם על העמוד שהוא י"ב ויצא לך ק"פ והוא תשברתו
|
|
|
384) ידוע הוא כי אם תעשה מרובע חוץ לעגול ימשש לעגול כי מוסיף על העגול ג' חלקים מי"ד
|
|
|
המשל יש לנו עגול אלכסונו ז' הנה הקו הסובב יהיו כ"ב כי ראוי לכפול האלכסון על ג' ושביעית ואם תעשה מרובע חוץ לאותו עגול כל צלע יהיה ז' שוה לאלכסון העגול ותשבורת המרובע יהיה מ"ט שהוא כפל ז' על ז' על כן אם תכפול האלכסון שהוא ז' על ג' ושביעית יעלה כ"ב והוא הקו הסובב וד' צלעות המרובע הם כ"ח כי ד' על ז' הם כ"ח וידוע הוא כי כ"ב הם י"א חלקים מכ"ח ולכן ראוי לכפול האלכסון על ג' ושביעית כי אם תחלק ד' צלעות ותקח י"א חלקים מי"ד יעלה ג' ושביעית וכדי למצא הקו הסובב ראוי לכפול האלכסון על ג' ושביעית כי כך עולה י"א חלקים מי"ד מד' שלמים ר"ל אם תכפול ד' על י"א חלקים מי"ד יצא ג' ושביעית
|
|
|
385) לדעת תשבורת תמונה כזאת
|
|
|
והדרך לדעת מרובע זו כפול מה שעודף התושבת על הראש קפב שהוא ז' והם מ"ט כפול ג"כ הצלע הקצור שהוא ט"ו על עצמם ויעלו רכ"ה תוסיף בם מ"ט ויעלה רע"ד תוציאם מת' שהוא כפל הצלע הארוך על עצמו וישאר קכ"ו חלקם על ב' והם ס"ג חלקם על מה שמוסיף התושבת על הראש שהוא ז' ויצא מ"ט וחברם עם ז' שהוא מה שעודף התושבת על הראש ויעלה י"ו ובאותה נקודה יפול העמוד ר"ל כי העמוד רחוק מן הצלע הארוך י"ו ואלו הי"ו שיצאו מהחלוקה הוא גבול מעמד העמוד החצוני כי זאת התמונה יש לה ג' עמודים ב' תכונים וא' חצוני כמו שהוא נרשם לעיל
|
|
|
ואם תרצה לדעת ארך העמוד כפול י"ו על עצמם ויעלו רנ"ו תסירם מכ' שהוא הצלע הארוך ומרובעו ת' הנשאר קמ"ד וגדרו י"ב והוא ארך העמוד וכן העמוד האחר החצוני תדענו בזה הדרך תרבע הצלע הקצור שהוא ט"ו ומרובעו רכ"ה הסר ממנו פ"א שהוא מרובע ט' שהוא המרחק מהעמוד אצל הצלע הקצור הנשאר ג"כ קמ"ד תשרשם י"ב ג"כ ואם תרצה לדעת תשבורת זאת הקטומה נקראת בלשונינו ר"ל חתוכה תחבר י"ד שהוא הראש עם כ"א שהוא התושבת ויעלה ל"ה חלקם על ב' ויעלה י"ז וחצי וכפלם על י"ב שהוא העמוד ויעלה ר"י וכך היא תשברתה
|
|
|
ואם תרצה לדעת אלכסון העגולה תחבר ט' שהוא גבול מעמד העמוד החצוני עם התושבת שהוא כ"א ויעלה ל' ומרובעו ט' מאות תוסיף בם מרובע העמוד שהוא קמ"ד ויעלה הכל אלף ומ"ד שרשם הוא ארך העמוד כמו שהוא בכאן
|
|
|
386) אם תרצה לדעת שרש מאיזה מספר שרש מעוקבו כפול השרש הראשון על עצמו ואח"כ כפלהו על ג' גם כפול השרש היוצא על ג' ושים בקו אחר ומה שנשאר חלק עליו
|
|
|
דמיון נרצה לדעת מעוקב י"ו
|
|
|
המעוקב שעבר היה ח' תפילם מי"ו הנשאר ח' ושרש מעוקב ח' הוא ב' כפלם על עצמם והם ד' כפלם ג' פעמים והם י"ב ושימם למשמרת עוד כפול ב' שהוא השרש על ג' ויהיו ו' ושימם
|
|
|
במקום אחר אח"כ חלק הח' שנשארו על י"ב ולא נתן לו כי אם חצי כי אם נתן חלק יותר גדול לא יספיק כפול י"ב על חצי והם ו' ועד ח' נשארו ב' כפול חצי על עצמו והם רביע אחד כפול רביע אחד על ו' השמורים ויהיו א' וחצי תגרעם מב' הנשאר חצי תגרע ממנו א' שמינית שהוא מעוקב חצי וישאר ג' שמיניות תפילם מכל הסך שהיו י"ו ונשאר ט"ו וה' שמיניות והוא מעוקב מב' וחצי ודוק ותשכח
|
|
|
387) אם תרצה לדעת משני מספרים כפול כל אחד על עצמו ואח"כ תכפול הכפלת שני המספרים זו על זו ומהסך העולה תרצה למצא אותם המספרים כך תעשה קח שרש אותו הסכום וראה מאיזה מספר הוא מורכב והם המספרים המבוקשים
|
|
|
דמיון זה כפלנו שני מספרים כל אחד על עצמו ואח"כ כפלנו הב' הכפלותיהם זו על זו ועלה אלפים וכ"ה מי הם המספרים אשר זה המספר מורכב מהם קח שרשם והם מ"ה ומ"ה מאיזה מספר הוא מורכב מה' וט' על כן כפול ה' על עצמו וט' על עצמו וכפול כ"ה על פ"א ויעלה ב' אלפים וכ"ה גם אלפים וכ"ה (מ"ה) הוא מורכב מג' וט"ו על כן כפול ג' על עצמם והם ט' וט"ו על עצמם ויעלו רכ"ה וכפול ט' על רכ"ה ויהיו ג"כ ב' אלפים וכ"ה ודוק ותשכח כי שפתי ברור מללו
|
Fra Luca Bartolomeo de Pacioli (Tuscany b. ca.1445 – d. 1514/1517)
– Hebrew translation –
by Gad Astruk? (Venice, ca. 1503)
![\scriptstyle{\color{blue}{2\sdot\left[\left[2\sdot\left(1+2\right)\right]\sdot\left(1\sdot2\right)\right]=2\sdot\left[\left(2\sdot3\right)\sdot2\right]=2\sdot\left(6\sdot2\right)=2\sdot12=24}}](/mediawiki/images/math/0/3/f/03fb1c4d938211577965d2fa10b41347.png)
![\scriptstyle{\color{blue}{2\sdot\left[\left[2\sdot\left(2+3\right)\right]\sdot\left(2\sdot3\right)\right]=2\sdot\left[\left(2\sdot5\right)\sdot6\right]=2\sdot\left(10\sdot6\right)=2\sdot60=120}}](/mediawiki/images/math/f/f/c/ffc2b198cef408bd54c50be990d61a5b.png)
![\scriptstyle{\color{blue}{2\sdot\left[\left[2\sdot\left(3+4\right)\right]\sdot\left(3\sdot4\right)\right]=2\sdot\left[\left(2\sdot7\right)\sdot12\right]=2\sdot\left(14\sdot12\right)=2\sdot168=336}}](/mediawiki/images/math/e/4/1/e411bee01f04a5ce448280abb3408cdd.png)
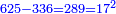
![\scriptstyle{\color{blue}{2\sdot\left[\left[2\sdot\left(4+5\right)\right]\sdot\left(4\sdot5\right)\right]=2\sdot\left[\left(2\sdot9\right)\sdot20\right]=2\sdot\left(18\sdot20\right)=2\sdot360=720}}](/mediawiki/images/math/9/2/9/9293bea2165238f0b59a91ce5200d50c.png)
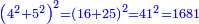
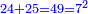
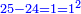
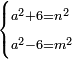
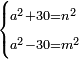
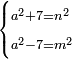
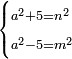
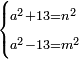
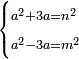
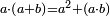
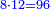
![\scriptstyle a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]=\left(a+b\right)^2](/mediawiki/images/math/8/2/e/82e411d047c5fc9961bdf7306ae1b255.png)
![\scriptstyle{\color{blue}{8^2+4^2+\left[2\sdot\left(8\sdot4\right)\right]=64+16+\left(2\sdot32\right)=64+16+64=144=12^2}}](/mediawiki/images/math/0/7/6/0763075873a48f89d2da9ccfcb00cafe.png)
![\scriptstyle\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2=\left(a\sdot b\right)+\left[a-\left[\frac{1}{2}\sdot\left(a+b\right)\right]\right]^2](/mediawiki/images/math/6/1/1/611e6ae1884ec0303bcfce33a731758d.png)