ספר המספר / אברהם אבן עזרא
Contents
- 1 Prologue
- 2 Chapter One – [Multiplication]
- 3 Chapter Two – Division
- 4 Chapter Three – Addition
- 5 Chapter Four – Subtraction
- 6 Chapter Five - Fractions
- 7 Chapter Six - Proportions
- 8 Chapter Seven - Extraction of Roots
- 9 Additional Excerpt
- 10 Notes
- 11 Apparatus
- 12 Appendix I: Glossary of Terms
- 13 Appendix II: Bibliography
| ראה ספר מחוקק באמונה[1] | |
| ותמצא בו[2] לכל מספר תכונה | |
| אשר חבר בנו מאיר למאיר | |
| קטן שנים וחכם בתבונה[3] | |
| ספר המספר[4] | |
|---|---|
Prologue |
|
Numeration |
|
| Since the sublime God alone has created in the upper world nine large heavenly spheres revolving around the earth, which is the lower world. | בעבור[5] כי השם הנשגב[6] לבדו[7] ברא בעולם[8] העליון[9] תשע עגולות גדולות[10] סובבות את[11] הארץ שהוא[12] העולם[13] השפל |
| Reference to the triple repetition of the word sefer in Sefer Yezira [the Book of Creation] – interpretation of one of them as representing the concept of the nine numbers: | |
| And the author of the Sefer Yezira has said that the paths of the wisdom are by Sefar and Sefer and Sipur and the Sefar is nine numbers. | ובעל ספר[14] יצירה[15] אמר[16] כי נתיבות החכמה[17] הם בִּסְפָר[note 1] וְסֵפֶר[18] וְסִפּוּר[19][note 2] |
|
|
|
כי תשעה[22] סוף כל חשבון[23] ואלה[24] יקראו[25] האחדים[26] שהם במעלה הראשונה[27] |
|
|
|
כי עשרה[28] דומה לאחד |
|
|
|
והיה[32] ראוי שיקראוהו[33] עֶשְׂרַיִם[34] כאשר יקראו[35] ממאה[36] מאתים ומאלף[37] אַלְפַּים רק בעבור[38] חבריו הבאים אחריו[39] שהם[40] שלשים[41] עד תשעים נהגו[42] כמנהגם[43] |
|
והנה שלשים[44] מגזרת שלש[45] וככה כלם[46] |
|
והנה מאה[47] דומה[48] לאחד גם[49] לעשרה[50] |
|
וככה אלף ורבבה שהם ראשי[54] כללים למספרים[55] הבאים אחריהם[56] שהם[57] א'י'ק' ב'כ'ר'[58][note 3] |
|
|
|
והאות על זה[59][note 4] כשתעשה[60] עגול[61][note 5] ותכתוב סביבו[62] תשעה מספרים |
|
ותכפול תשעה[63] על[64] עצמו והטעם[65] להיותו[66] מרובע ארכו כרחבו תראה זה[67] וככה הוא[68] |
|
והנה המרובע[69] אחד ושמונים[70] והנה[71] האחד[72] לשמאלו של[73] תשעה[74] שהוא ראש האחדים[75] וח' שהוא[76] כנגד שמונים[77] בכלל לימין תשעה |
|
ואם תכפול ט' על ח' יהיה המחובר[78] ע"ב והנה ב'[79] לשמאלו[80] וז' שהוא[81] כנגד[82] ע'[83] לימינו |
|
ואם תכפול[84] ט' על[85] ז'[86] יהיה המחובר[87] ס"ג והנה[88] ג'[89] לשמאלו וו'[90] לימינו שהוא כנגד ס'[91] |
|
ואם תכפול ט' על ו' יהיה המחובר[92] נ"ד והנה[93] ד' לשמאלו[94] וה'[95] שהוא[96] כנגד נ'[97] לימינו[98] |
|
ובעבור כי חשבון[99] חמשה[100] הוא אמצעי בט' מספרים[101] על[102] כן[103] נקרא חשבון עגול[note 6] כי הוא מתגלגל[104] על עצמו כי מרובעו[105] יש בו חמשה[106] |
|
וכאשר תכפול[107] ט' על ה'[108] יתגלגל הדבר בעגול[109] כי[110] האחדים יהיו[111] לימין ט'[112] והכללים[113] לשמאלו כי המחובר[114] הוא[115] מ"ה והנה הה'[116] מפאת ימין ט'[117] והכללים[118]לשמאלו שהוא[119] ד'[120] במקום המ'[121] |
|
וכאשר תכפול ט' על ד'[122] יהיה המחובר ל"ו והנה ג'[123] כנגד שלשים[124] |
|
וכאשר תכפול ט'[125] על ג'[126] יהיה המחובר כ"ז והנה[127] ב'[128] כנגד עשרים[129] |
|
וכאשר תכפול ט'[130] על ב'[131] יהיה המחובר י"ח והנה[132] א' כנגד עשרה[133] |
| Hence the checking scales are based on modulo 9 | |
| Therefore, the scales of a number that is multiplied by itself or by another is 9. | על[134] כן[135] מאזני מספר[136] שהוא כפול[137] על עצמו או על אחר[138] הם[139] ט'[140] |
The Positional Decimal System |
|
|
|
|
[141]על כן[142] עשו[143] חכמי הודו כל מספרם[144] על תשעה[145] ועשו צורות לט' מספרים[146] |
|
|
|
והנה לעולם אם[149] יש בידך[150] מספר[151] אחדים[152] ותחלת[153] הכללים[154] שהם עשרות[155] יכתוב בתחלה[156] מספר[157] האחדים[158] ואחר כך מספר הכלל[159] |
|
|
|
ואם אין[160] לו[161] מספר האחדים[162] ויש לו מספר[163] במעלה השנית שהם[164] העשרות[165] ישים[166] כדמות גלגל[167][note 7] בראשונה[168] להורות[169] כי אין[170] במעלה הראשונה[171] מספר[172] ויכתוב[173] המספר[174] שיש לו בעשרות[175] אחריו[176] |
|
|
|
ואם הכלל שלו[177] מהמאות[178] ומהעשרות[179] יכתוב גלגל[180] בראשונה ואחר כך[181] מספר העשרות[182] בשנית ומספר[183] המאות בשלישית[184] |
|
|
|
ואם[185] יש לו מספר[186] אלפים ברביעית[187] ומספר עשרת[188] אלפים בחמישית ומספר מאות[189] אלפים[190] בששית[191] |
|
|
|
כי א'י'ק'[192] יחזור[193] ברביעית לאלפים[194][note 8] ובשביעית[195] לאלף[196] אלפים ובעשירית לאלף[197] אלפי אלפים[198] וככה[199] עד אין קץ[200] |
|
|
|
ואם יש[201] לו מספר אחדים ומאות ואין לו עשרות[202][note 9] יכתוב[203] מספר[204] האחדים[205] בראשונה וגלגל בשנית ומספר המאה[206] בשלישית |
|
|
|
ועל זה הדרך[207] ישים[208] שנים[209] גלגלים בראשונה[210] או כפי מה שיצטרך עד אין חקר[211] או באמצע[212] |
Table of Contents |
|
| ואחר שהזכרתי זה אזכיר[213] שערי זה[214] הספר[215] ונאמר[216] שהם[217] שבעה[218] | |
|
השער הא'[219][note 10] לכפול[220] חשבון על עצמו[221][note 11] או על[222] אחר[note 12] או כפל[223] חשבון אחד[224] על שנים[225] חשבונות[226][note 13] או יותר[227] או כפל[228] חשבונות[229] רבים על רבים[230][note 14] |
|
השער הב'[231][note 15] לחלק[232] חשבון כלל[233] על פרט[234] או שנים[235] כללים[236] על פרט אחד[237] או כללים גבוהים על כללים[238] שפלים או[239] כללים ופרטים[240] על פרטים[241] גם אדבר על המאזנים[242][note 16] של[243] שער[244] הכפל[245] והחלוק[246] |
|
השער הג'[247][note 17] בחבור[248] מספר על[249] מספר[250][note 18] פרט[251] עם[252] כלל[253] או כלל עם[254] כלל[255] |
|
השער הד'[256][note 19] לחסר[257] מספר[258] ממספר[note 20] פרט[259] מכלל[260] או כלל מכלל גם אדבר[261] על מאזני שער[262] החבור[263] והמגרעת[264] |
| השער הה'[265] על השברים[266] והם על[267] דרכים[268] רבים שלמים על[269] שלמים[270] ונשברים[271] עמהם או שלמים ונשברים[272] עם[273] שלמים[274] ונשברים[275] למיניהם[276] או שברים עם[277] שברים או שברים[278] על[279] שברי[280] שברים[281] או שברי שברים[282] על[283] שברי[284] שברים[285] בין לכפול בין לחלק בין לחבר[286] בין לגרוע[287] ומאזניהם[288] | |
| השער הו'[289] בערכים[290] והוא שער נכבד מאד[291] כי ממנו יוכל[292] להוציא[293] רובי[294] השאלות הקשות ורוב[295] הראיות[296] מחכמת[297] המזלות יצאו מזה[298] הערך[299] | |
| השער הז'[300] על שרשי[301] המרובעים והמאזנים[302] שלהם כי הם רבים[303] וחכמת המדות תלויה[304] בשער הזה[305] וזה[306] השער[307] חמור[308] מכל השערים[309] ואין[310] כח במשכיל[311] לדעת קדרות[312] המאורות אם לא ילמד[313] זה[314] השער[315] ויתרי[316] קשתי[317] העגול[318] יצאו[319] מהשער הזה[320] |
Chapter One – [Multiplication] |
השער הראשון |
|---|---|
Shortcuts |
|
|
|
|
|
כבר הזכרתי איך הם[I 1] מעלות המספר[I 2] והנה[I 3] כשיבואו[I 4] לך שנים[I 5] מספרים לכפול[I 6] כלל על[I 7] כלל בין שיהיה[I 8] על עצמו[I 9] |
| I will discuss the meaning of the foundation in my discussion about the secret of the one, with the help of God. | ועוד אדבר על טעם[I 33] המוסד[I 34] בדברי על סוד האחד[I 35] בע"ה[I 36] |
|
דמיון רצינו[I 37] לכפול שלשים על מאתים |
|
והנה[I 38] דמיון שלשים[I 39] שלשה[I 40] ודמיון[I 41] מאתים שנים[I 42] כפלנו ב'[I 43] על ג' והנה[I 44] עלו[I 45] ששה וזהו[I 46] החשבון השמור[I 47] |
|
דמיון[I 71] אחר[I 72] בקשנו[I 73] לכפול מאתים על שבע מאות |
|
והנה כפלנו שנים על שבעה[I 74] והנה[I 75] י"ד והוא[I 76] השמור והנה מאתים[I 77] מהמעלה השלישית וז' מאות גם כן[I 78] מהמעלה השלישית[I 79] נקח[I 80] להם[I 81] ששה ונחסר[I 82] אחד[I 83] הנה[I 84] חמשה |
|
ועל[I 100] זה הסדר[I 101] תוכל לעשות עד אין קץ[I 102] |
|
|
|
|
ואם היו שנים[I 103] מספרים מרחקם[I 104] מחשבון[I 105] כלל כמרחק שנים[I 106] מספרים[I 107] אחרים[I 108] רק[I 109] האחד במגרעת והשני בתוספת[I 110] דע כמה[I 111] מרובע[I 112] מספר[I 113] הכלל[I 114] וגרע ממנו לעולם מרובע החשבון היתר והחסר[I 115] והנשאר הוא[I 116] החשבון[I 117] המבוקש |
|
דמיון רצינו לכפול כ"ט על ל"א[I 118] |
|
והנה חשבון[I 119] הכלל הוא[I 120] שלשים ומרובעו[I 121] ט' מאות כי שלשה על שלשה[I 122] הם[I 123] תשעה [I 124]והיתרון והחסרון[I 125] הוא[I 126] אחד[I 127] ומרובעו אחד[I 128] חסרנום[I 129] ממרובע[I 130] הכלל[I 131] והנשאר הוא המבוקש והוא[I 132] תתצ"ט[I 133] |
|
דמיון אחר רצינו לכפול ס"ו על נ"ד[I 134] |
|
והנה חשבון[I 135] הכלל ס'[I 136] והחסרון והיתרון[I 137] הוא[I 138] ששה והנה מרובע הכלל[I 139] ג' אלפים ות"ר נחסר ממנו ל"ו שהוא מרובע[I 140] החסרון והיתרון[I 141] והנשאר[I 142] הוא המבוקש[I 143] |
|
[I 144]דמיון אחר[I 145] המספר האחד ר"נ והמספר האחר[I 146] ש"נ |
|
והנה הכלל[I 147] הוא[I 148] ש' ומרובעו[I 149] צ'[I 150] אלף נחסר ממנו מרובע[I 151] נ' שהוא[I 152] החסרון והיתרון[I 153] ומספרו[I 154] אלפים ות"ק והנשאר הוא המבוקש[I 155] |
|
ועל זה הסדר[I 156] נוכל[I 157] לעשות שאר[I 158] המספרים[I 159] הדומים לאלה[I 160] שהחסרון[I 161] כמו היתרון[I 162] |
|
|
|
|
[note 21]דרך אחרת נכבדת[I 163] שהוצאתי[I 164] בדרך[I 165] השלישית[I 166] שנקח[I 167] שלישית החשבון[I 168] ונדע כמה מרובעו ונקח כמוהו בכלל הגבוה ממנו ונחסר מרובע השלישית ממנו[I 169] והנשאר הוא המבוקש |
|
[I 170]דמיון בקשנו[I 171] לדעת כמה מספר מרובע[I 172] ג' |
|
נקח[I 173] שלישיתו[I 174] שהוא[I 175] אחד ומרובעו[I 176] אחד[I 177] ועשרה[I 178] שהוא הכלל[I 179] הקרוב אליו נחסר ממנו[I 180] מרובע אחד שהוא[I 181] השלישית[I 182] וישאר[I 183] ט' והוא[I 184] המבוקש |
|
דמיון אחר[I 185] בקשנו לדעת מרובע ט"ו |
|
ושלישיתו ה' ומרובעו כ"ה והדומה[I 186] בכלל הקרוב אליו[I 187] ר"נ[I 188] חסר[I 189] ממנו מרובע ה' שהוא השלישית[I 190] ישאר[I 191] רכ"ה[I 192] |
|
[I 193]דמיון אחר[I 194] בקשנו לדעת כמה[I 195] מרובע כ"ד |
|
הנה[I 196] שלישיתו[I 197] ח' ומרובעו ס"ד ודמיונו[I 198] במעלה הגבוהה[I 199] ממנו תר"מ[I 200] נחסר ממנו[I 201] מרובע[I 202] השלישית שהוא ס"ד ישאר[I 203] תקע"ו והוא המבוקש |
|
|
|
|
ואם לא היה[I 204] למספר שלישית שלמה ויהיה בו[I 205] תוספת אחד[I 206] חסר[I 207] האחד[I 208] מהמספר[I 209] והוצא[I 210] המספר[I 211] המבוקש כמשפט[I 212] שהראיתיך ומה שיעלה[I 213] הוסף[I 214] עליו המספר שיש לו[I 215] שלישית[I 216] והמספר בעצמו והמחובר הוא המבוקש |
|
דמיון בקשנו לדעת מרובע ז' |
|
והנה אין[I 217] לו[I 218] שלישית חסרנו[I 219] ממנו[I 220] אחד שהוא נוסף[I 221] והנה שלישית[I 222] הנשאר[I 223] שנים ומרובעו ארבעה והנה[I 224] בכלל הקרוב הדומה[I 225] אליו מ'[I 226] נחסר[I 227] ממנו[I 228] ד' שהוא מרובע השלישית[I 229] וישאר[I 230] ל"ו שהוא[I 231] מרובע ו' נחבר אליו[I 232] הו' שיש לו שלישית[I 233] והז' שהיה[I 234] מספרנו בראשונה ושניהם י"ג יהיה המחובר[I 235] מ"ט והוא מרובע ז' |
|
דמיון אחר[I 236] רצינו[I 237] לדעת[I 238] כמה[I 239] מרובע כ"ב |
|
והנה[I 240] חסרנו אחד ונשאר[I 241] כ"א ושלישיתו[I 242] ז' ומרובעו[I 243] מ"ט והנה[I 244] בכלל[I 245] הקרוב[I 246] אליו[I 247] ת"צ[I 248] נחסר ממנו[I 249] מ"ט שהוא מרובע השלישית[I 250] נשארו[I 251] תמ"א שהוא מרובע כ"א נוסיף כ"א גם[I 252] כ"ב מחוברים[I 253] שהם[I 254] מ"ג[I 255] יעלה[I 256] המחובר[I 257] תפ"ד וזהו[I 258] מרובע כ"ב |
|
|
|
|
ואם היו[I 259] שנים[I 260] בין המספר[I 261] שלנו[I 262] ובין[I 263] המספר[I 264] שיש לו שלישית[I 265] נעשה להפך שנוסיף[I 266] על המספר שלנו[I 267] אחד ונדע כמה מרובע[I 268] מספר[I 269] שיש לו שלישית[I 270] ונחסר[I 271] ממנו כמספר[I 272] שיש לו שלישית[I 273] וכמספר[I 274] שהיה לנו והנשאר הוא המבוקש |
|
דמיון בקשנו לדעת כמה מרובע[I 275] כ"ג |
|
והנה בעבור שאין לו[I 276] שלישית שלמה[I 277] נוסיף אחד יהיו[I 278] כ"ד ושלישיתו[I 279] ח' ומרובעו ס"ד והדומה לו[I 280] תר"מ נחסר ממנו ס"ד שהוא מרובע השלישית ישאר[I 281] תקע"ו והוא מרובע כ"ד גם[I 282] נחסר[I 283] מזה המספר[I 284] מ"ז שהוא כ"ד עם כ"ג מחוברים[I 285] ויהיה הנשאר[I 286] תקכ"ט והוא המבוקש |
| The number of steps required for receiving the product: | |
|
|
|
ודע כי אם יהיו[I 287] שנים[I 288] מספרים לכפול זה על זה יספיק לך פעם אחת |
|
|
|
ואם היה[I 289] מספר אחד[I 290] על[I 291] שנים[I 292] מספרים[I 293] אתה צריך לעשות זה פעמים[I 294] |
|
|
|
ואם על שלשה שלשה[I 295] |
| And so on according to this rule. | ועל[I 296] זה המשפט הכל |
|
|
|
ואם הם שני[I 297] מספרים על שני[I 298] מספרים[I 299] אתה צריך[I 300] לעשות[I 301] זה[I 302] ד' פעמים |
|
דמיון רצינו לכפול י"ג על כ"ח |
|
והנה[I 303] כפלנו י' על כ' שהוא כלל[I 304] גם י'[I 305] על[I 306] ח'[I 307] עלו[I 308] ר"פ[I 309] ואחר[I 310] כפלנו ג' על כ' גם[I 311] על[I 312] ח' עלו[I 313] פ"ד[I 314] והנה[I 315] הכל[I 316] שס"ד |
|
|
|
ואם היה כלל אחד כולל[I 317] שני[I 318] המספרים[I 319] די לך[I 320] בג' פעמים |
|
דמיון בקשנו[I 321] לכפול[I 322] י"ג על י"ו |
|
והנה[I 323] י' כולל שני[I 324] המספרים[I 325] והנה נחבר[I 326] ג' עם[I 327] ו'[I 328] עם[I 329] י'[I 330] והנה יהיה[I 331] מספרינו י"ט נכפול[I 332] אותו[I 333] בעשרה עלו[I 334] ק"צ[I 335] נכפול[I 336] שני[I 337] המספרים הקטנים[I 338] שהם[I 339] ג' על ו' יעלו[I 340] י"ח והנה הכל[I 341] ר"ח[I 342] |
|
ויש[I 343] שיספיק לך שני[I 344] פעמים לבדם |
|
דמיון[I 345] בקשנו לכפול[I 346] כ"ד[I 347] על כ"ו[I 348] |
|
הנה[I 349] כ'[I 350] כולל שני[I 351] המספרים חברנו ד' עם[I 352] כ"ו שהוא הגדול[I 353] עלה[I 354] המספר ל' כפלנו כ' על ל' עלו[I 355] ת"ר וכפלנו[I 356] הקטנים זה על זה עלו[I 357] כ"ד[I 358] והנה[I 359] המבוקש[I 360] תרכ"ד[I 361] |
|
|
|
ואם[I 362] תכפול ג' מספרים על ג'[I 363] אתה צריך לעשות זה ט' פעמים |
| According to this procedure for every number. | ועל זה הסדר[I 364] כל החשבון[I 365] |
| See, whether the number consists of one or many [digits]. | וראה[I 366] אם המספר אחד[I 367] או רבים[I 368] |
| Multiplication of evens and odds | |
|
אם[I 369] הוא[I 370] מספר זוג גם המחובר יהיה זוג[I 371] |
|
|
|
וטעם הזוג[I 372] הוא באחדים |
|
כי כל כלל הוא זוג[I 373] |
|
ואם[I 374] המספר האחד[I 375] זוג[I 376] והשני נפרד[I 377] והטעם[I 378] שאינו[I 379] זוג[I 380] איזה מהם[I 381] שיהיה גם המחובר יהיה זוג |
|
ואם המספר[I 382] האחד[I 383] נפרד[I 384] וגם[I 385] כן[I 386] האחר[I 387] גם[I 388] המחובר[I 389] יהיה נפרד[I 390] |
Written calculations |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Know that if the numbers to be multiplied by each other are many, you have to multiply them by writing the 9 characters that I have showed you. | ודע כי אם היו[I 391] המספרים[I 392] הנכפלים[I 393] אלה[I 394] על אלה רבים אתה צריך לכפול[I 395] אותם[I 396] במכתב[I 397] ט' אותיות שהראיתיך[I 398] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והדרך הסלולה[I 399] שתשים טורי המספר המעט[I 400] עליונים[I 401] ופירוש[I 402] המעט[I 403] בחשבון הכלל ולא[I 404] תחוש מן[I 405] הפרטים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותשים בטור אחר שפל למטה החשבון שהוא כללו גדול | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם[I 406] החשבון שכללו קטן[I 407] הם[I 408] יותר מספרים מחשבון שכללו גדול[I 409] שים אותם[I 410] עליונים ולא תחוש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If you would do the other way around, it does no harm, just confuses the student a little. | ואלו[I 411] היית[I 412] עושה להפך לא יזיק[I 413] רק יתבלבל מעט[I 414] על התלמיד[I 415] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר שתשים המספרים כמה שיהיו בטור העליון[I 416] והאחרים[I 417] בטור השפל כפול הראשון[I 418] של[I 419] הטור[I 420] העליון על הראשון[I 421] שבטור[I 422] השפל[I 423] והעולה כתוב[I 424] אותו כנגד הטור[I 425] הראשון[I 426] העליון[I 427] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר כן[I 428] כפול המספר[I 429] הראשון[I 430] העליון על המספר[I 431] השני השפל וכתוב בטור השלישי[I 432] כנגד המספר[I 433] השני העליון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וככה לכל המספרים השפלים עם המספר העליון הראשון[I 434] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם כאשר תכפול הראשון העליון[I 435] על שכנגדו בשפל ויתחבר[I 436] במספר כלל ופרט תכתוב הפרט במקום הראוי לו והכלל[I 437] במספרו[I 438] תכתבנו בחשבון שהוא אחריו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר שתשלים[I 439] לכפול החשבון הראשון של הטור[I 440] העליון על כל מספרי[I 441] הטור[I 442] השפל תחל לכפול[I 443] המספר[I 444] השני של הטור[I 445] העליון על מספר[I 446] הראשון של הטור[I 447] השפל והעולה כתבהו[I 448] בטור השלישי כנגד השני העליון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר[I 449] כן תכפול השני[I 450] העליון על שני[I 451] שבטור השפל ותכתבהו[I 452] בטור השלישי[I 453] במספר השלישי[I 454][note 22] שהוא שני[I 455] למספר[I 456] שהחלות[I 457] עתה ממנו[I 458] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר[I 459] כן תחל במספר השלישי העליון[I 460] לכפול אותו[I 461] על הראשון שבטור השפל והעולה תכתבהו[I 462] כנגד טור[I 463] השלישי שהחילות[I 464] ממנו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This is the procedure for all endlessly with the rule that the units are into the lower rank and the decade following it in the next rank. | וככה[I 465] המשפט[I 466] לכלם[I 467] עד[I 468] אין קץ עם משפט[I 469] הפרט[I 470] להיות התחתון[I 471] והכלל[I 472] שיבא[I 473] אחריו בטור[I 474] השני לו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If there is zero, whether in the top row or in the bottom row, the rule is to write it in its appropriate position, as is the rule for all numbers next to it. | ואם היה[I 475] גלגל בין בטור[I 476] העליון בין[I 477] בטור[I 478] השפל משפטו[I 479] לכתבו במקום[I 480] הראוי לו[note 23] כמשפט כל המספרים שעליו[I 481] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר כן תחל[I 482] לחבר[I 483] מה שעלה[I 484] בטור[I 485] העליון עם השפל[note 24] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אם[I 486] אין בו[I 487] עשרות[I 488] תכתוב מה שהוא בחבור[I 489] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם יש בו עשרה כתוב אחד אחריו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם יש בו[I 490] יותר כתוב[I 491] היותר[I 492] מבחוץ[I 493] בחבור[I 494] שיש לך[I 495] ובמקום העשרה כתוב אחד שני[I 496] לו[I 497] נוסף | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן תעשה[I 498] לכל היוצאים[I 499] מהטור[I 500] העליון[I 501] והשפל[I 502] והוצא[I 503] הנותר[I 504] מעשרות[I 505] מבחוץ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר שידעת כמה הוא[I 506] המחובר בטור השלישי ספור מעלותיו וראה אם היו[I 507] כמספר מעלות השנים[I 508] טורים העליונים[I 509] ממנו בחסרון אחד[I 510] תדע[I 511] כי חשבונך אמת[note 25] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם המספר[I 512] האחרון[I 513] בטור העליון הנכפל במספר האחרון[I 514] בטור השפל ממנו[I 515] יוצא אל כלל[I 516][note 26] יהיה[I 517] מספר[I 518] מעלות הטור[I 519] השלישי[I 520] כמספר שני טורים[I 521] העליונים[I 522] בלי[I 523] מגרעת אחד[I 524] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Check: casting out by 9 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Finally, check it through the scales. | [I 525]ובחן[I 526] באחרונה במאזנים[I 527] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| You proceed as follows: | וככה[I 528] תעשה[I 529] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Consider every digit in the top row in any rank as if it were units, sum them and cast out the nines from the sum if it is more than 9, or less than it write alone, and this is the scale of the top row. | חשוב[I 530] כל חשבון[I 531] שתמצא בטור העליון באיזו[I 532] מעלה שיהיה[I 533] כאילו הם אחדים וחברם והוצא המחובר[I 534] ט' ט' אם[I 535] יותר[I 536] ט'[I 537] או[I 538] פחות ממנו כתוב אותו לבדו[I 539] והוא[I 540] מאזני הטור העליון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Do the same with the scale of the bottom row until you know how much its scale is. | ככה[I 541] תעשה למאזני הטור[I 542] השפל עד שתדע כמה המאזנים[I 543] שלו[I 544] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Multiply the scale of the top row by the scale of the other row, then cast out the nines from the product and keep the remainder with you. | וכפול מאזני הטור העליון[I 545] על מאזני הטור השני[I 546] והנכפל[I 547] הוציאהו[I 548] ט' ט' והנשאר[I 549] יהיה[I 550] עמך[I 551] שמור | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If the scale of one of the rows is 9, do not weary yourself to find the scale of the other row, because it will always be casted out by 9. | ואם מאזני אחד מהטורים[I 552] יהיה ט' אל תיגע עצמך לבקש מאזני הטור האחר כי ט' יצא לעולם[I 553] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Then, examine the scale of the third row and see: if it is the same as the reserved, then your calculation is true, but if not, you were wrong. | ואחר[I 554] בדוק מאזני[I 555] הטור השלישי וראה אם[I 556] היה שוה[I 557] לשמור חשבונך[I 558] אמת ואם לאו[I 559] הנה[I 560] טעית[I 561] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
[I 562]דמיון זה[I 563] רצינו לכפול קכ"ז על שנ"ה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכתבנו[I 564] קכ"ז בטור העליון[I 565] כזה[I 566] ומספר[I 567] שנ"ה תחתיו אות אות[I 568] במקומו[I 569] כזה[I 570] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כפלנו[I 571] ז' על ה' עלו[I 572] ל"ה כתבנו[I 573] ה' במעלה הראשונה וג' שהוא ל'[I 574] במעלה השניה[I 575] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עוד כפלנו[I 576] ז' על ה' השני התחתון[I 577] עלו[I 578] ל"ה[I 579] כתבנו[I 580] ה'[I 581] במעלה השנית[I 582] תחת ג'[I 583] וג' בשלישית[I 584] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עוד כפלנו[I 585] ז' הראשון[I 586] על ג' התחתון[I 587] עלו[I 588] כ"א כתבנו[I 589] א'[I 590] בשלישית תחת ג'[I 591] וב' ברביעית[I 592] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עוד[I 593] כפלנו[I 594] ב' האמצעי העליון[I 595] על ה' הראשון[I 596] מן[I 597] התחתון[I 598] עלו[I 599] י' כתבנו[I 600] א' בשלישית[I 601] תחת הא'[I 602] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עוד כפלנו[I 603] ב'[I 604] העליון[I 605] על ה'[I 606] השנית[I 607] התחתון[I 608] היו[I 609] גם כן[I 610] י' כתבנו[I 611] א'[I 612] תחת ב'[I 613] ברביעית[I 614] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עוד כפלנו[I 615] ב'[I 616] העליון[I 617] על ג'[I 618] התחתון[I 619] והיו[I 620] ו' כתבנו אותו[I 621] תחת א'[I 622] ברביעית[I 623] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עוד כפלנו[I 624] א' העליון האחרון[I 625] על ה'[I 626] הראשון התחתון[I 627] עלו[I 628] ה'[I 629] כתבנוהו[I 630] בשלישית[I 631] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עוד כפלנו[I 632] א'[I 633] על ה'[I 634] השני[I 635] התחתון[I 636] עלו[I 637] ה'[I 638] כתבנוהו[I 639] ברביעית[I 640] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עוד כפלנו[I 641] א'[I 642] העליון על ג' התחתון[I 643] היו[I 644] ג' כתבנוהו[I 645] בחמישית[I 646] אחר ב'[I 647] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה נשלם הכפל[I 648] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חברנו[I 649] כל אלו[I 650] המספרים כל[I 651] מה שהוא ממעלה[I 652] אחת יחד[I 653] הכל ומה שיעלה יותר מעשרה או עשרה[I 654] כתבהו[I 655] אחר המעלה ההיא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויעלה[I 656] המחובר מ"ה אלפים ופ"ה[I 657] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| P1050 marg. another method | דרך אחרת יותר קצרה עשויה בשליבה נק' בלשונ' ביריקוקלי ונעשית בזה הדרך שאין כותבי' רק האחדי' שבידך ושומרי' העשרו' לקבצם עם העשרו' מהמספר הבא אחריו וכן ממדרגה למדרגה עושין כן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמ' תרצה לכפול קכ"ז על שנ"ה תכפול ז' על ה' עלה ל"ה כתו' ה' במדרגת האחדי' ושמור בפיך ובלבבך ל' שהם ג' במדרג' השנית וכפול ז' על ה' עלו ל"ה וג' עשרו' וג' עשרו' היו בידך בין הכל עלו ל"ח כתו' ח' במדרגה השנית ושמור ג' מאות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עו' תשוב תכפול ב' עם ה' עלו י' והיה ראוי לכותבו תחת העשרות בשורה אחרת תחת הראשונה ולפי שהו' ר"ל י' עשרות שהם מאה כתו' עגול במדרגת העשרו' ושמור אחד שהוא מאה וכפול ב' על ה' השני עלו י' וא' שהיה שמור הנה י"א כתו' א' במדרגת המאות ובידך שמור א' שהוא אלף | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד כפול א' על וא' על ה' השני וכתו' במדרגת האלפי' ה' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואח"כ קבץ הכל בדרך קבוץ וכתו' למטה כאשר אתה רואה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Chapter Two – Division |
השער השני | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Introduction - Preliminary definitions |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Definition of a number:Know that that every number is a sum of units. | דע כי[II 1] כל חשבון הוא חברת האחדים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| One | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| One alone does not assume any change, no increase and no division. | והאחד[II 2] לבדו לא יקבל שנוי[II 3] ולא[II 4] רבוי ולא חלוק | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| It is the cause of every increase, change and division. | והוא סבת כל[II 5] רבוי ושנוי[II 6] וחלוק | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| One is eternal and every number created through it. | והאחד קדמון לבדו וכל חשבון מתחדש בעבורו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והוא יעשה[II 7] בפאה אחת[II 8] מה שיעשה כל חשבון בשתי פאותיו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כי שנים[II 9] לחשבון שלשה[II 10] הפאה[II 11] האחת שהיא לפניו וארבעה הפאה[II 12] האחרת שהיא אחריו ושתי[II 13] הפאות המחוברות[II 14] ששה שהם[II 15] כפל שלשה וככה כל מספר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה האחד[II 16] אין לפניו[II 17] פאה ואחריו[II 18] פאה אחת שהיא שנים[II 19] והם כפל האחד[II 20] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Now I shall talk about every number that has whole integers without fractions. | ועתה אדבר על כל חשבון שיש לו אחדים שלמים בלי[II 21] שבר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Sexagesimal Fractions | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12 zodiac signs: Know that the astrologers have divided the celestial sphere into twelve parts. | ודע כי חכמי המזלות חלקו את[II 22] הגלגל על שנים עשר[II 23] חלקים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועשו זה בעבור ששנת השמש י"ב[II 24] חדשי[II 25] הלבנה[II 26] ואין חשבון[II 27] קטן מי"ב שיש לו חלקים רבים[II 28] כמוהו כי יש לו אחדים[II 29] שלמים[II 30] בחציו ושלישיתו[II 31] ורביעיתו[II 32] וששיתו וחצי ששיתו[II 33][note 27] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| degrees: They divided each sign to thirty degrees. | וחלקו המזל לשלשים[II 34] מעלות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כי זה המספר יש לו אחדים שלמים יותר מי"ב כי יש לו חצי ושלישית וחמישית וששית[II 35] ועשירית[note 28] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה עלה מספר[II 36] מעלות[II 37] הגלגל[II 38] ש"ס[II 39] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה המספר[II 40] יש[II 41] לו חצי ושלישית[II 42] ורביעית[II 43] וחמישית[II 44] וששית ושמינית ותשיעית ועשירית[II 45] והנה לא[II 46] יחסר לו רק[II 47] השביעית[note 29] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר תכפול זה המספר[II 48] על ז' יהיה העולה אלפים ותק"כ וזה החשבון כולל כל החלקים עד עשרה[II 49] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה חכמי המזלות כאשר יכפלו מעלות[II 50] על מעלות יהיה המחובר מעלות שהם[II 51] אחדים[II 52] שלמים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וככה כאשר יחלקו[II 53] מעלות על מעלות יהיה העולה בחלוק[II 54] מעלות שהם אחדים שלמים[II 55] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Written calculations |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Now I shall give you a rule how to divide every number, whether it consists of one, two or many digits: | ועתה אתן לך כלל[II 56] איך תחלק[II 57] כל חשבון בין שיהיה אחד או שנים או מספרים רבים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Write them in one row, each according to its rank, then write the number by which you divide in another row, whether it consists of one or many digits, each according to its rank corresponding to each digit according to its rank in the top row, and leave a space between the upper row and the bottom row so that you can write a middle row in between them; whether the quotient consists of one or many digits, you place each one according to its rank. | כתוב אותם[II 58] בטור אחד כל אחד כפי[II 59] מעלתו ואחר כך[II 60] כתוב[II 61] החשבון שתחלק עליו בטור[II 62] אחר[II 63] בין שיהיה[II 64] מספר אחד או רבים כל אחד כפי מעלתו[II 65] ויהיה כל חשבון[II 66] לפי מעלתו[II 67] כנגד כל[II 68] חשבון[II 69] כפי מעלתו בטור העליון וריוח תשים בין הטור[II 70] העליון והטור[II 71] השפל כדי שתוכל לכתוב טור אמצעי[II 72] ביניהם[II 73] בין שיהיה העולה מספר אחד או מספרים רבים כל אחד תשים כפי מעלתו[II 74] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The number by which you divide should be less than the number that you divide by it. | וראוי להיות המספר שתחלק עליו פחות מהמספר המחולק ממנו[II 75] וזה הדבר הוא בחלוק השלמים[II 76] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| But this is only for the division of integers, not for fractions, as I will explain with the help of God. | ולא[II 77] כן בשברים כאשר אפרש בעזרת האל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| When you set up the rows, as I said, you start dividing by the last digit in the top row. | ובתקנך הטורים כאשר אמרתי תחל[II 78] לחלק מהמספר האחרון שהוא בטור[II 79] העליון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Divide it by the last number in the bottom row. | ותחלק אותו על המספר האחרון שהוא בטור[II 80] השפל[II 81] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Consider the two numbers, even though they are decades, consider them as units. | וחשוב שנים[II 82] המספרים[II 83] אע"פ שהם כללים חשוב[II 84] אותם[II 85] כמו אחדים[note 30] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The quotient: see how far the last digit of the bottom row is from the first digit, whether it is units or a zero, and as the number of the distance, return back and write the quotient there above the bottom row, which is beneath the top row. | והעולה בחלוק ראה כמה מרחק המספר[II 86] האחרון מהטור השפל[II 87] מהמספר הראשון בין שיהיו[II 88] בו אחדים או גלגל וכפי מספר המרחק תשיב[II 89] אחורנית[note 31] ושם תכתוב העולה בחלוק למעלה מהטור השפל שהוא למטה מהטור העליון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If a number that cannot be divided remains from the last digit, and [the division] has not yet reached the ranks of the units, return the remaining number back to the preceding rank, which is lower than it and consider each unit as ten. | ואם ישאר במספר האחרון[II 90] חשבון שלא נתחלק ולא הגיע למעלת האחדים[II 91] השב אחורנית המספר הנשאר למעלה[II 92] הראשונה שהיא פחותה ממנו וחשוב כל[II 93] אחד עשרה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Then, divide by the number by which you divide, and write the quotient back from the first rank you wrote, before the first quotient. | ואחר כך חלק על המספר[II 94] שחלקת עליו והעולה בחלוק תכתוב אותו[II 95] אחורנית מהמעלה הראשונה שכתבת לפני[II 96] מה שעלה בחלוק בראשונה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Proceed always like this until you reach a number that is smaller than the divisor and write the remainder above the top row according to its rank. In the fifth chapter I will explain what you should do with it. | ככה תעשה תמיד עד שתגיע[II 97] אל המספר[II 98] שהוא פחות מהמחולק עליו[II 99] ואותו הנשאר תכתבנו[II 100] למעלה מהטור[II 101] העליון כפי מעלתו ובשער החמישי[II 102] אפרש לך מה שתעשה[II 103] ממנו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון[II 104] בקשנו לחלק ט' אלפים על ע' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
בזאת הצורה[II 105] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
- [Illustration of the procedure:]


0 
00 2 26 264 9000 9000 9000 9000 1 12 128 70 70 70 70
|
הנה נשים ע'[II 106] בטור השפל[II 107] כפי מעלתו ונחשוב כי הכל אחדים והנה[II 108] נתן לו[II 109] א' ונכתבנו[II 110] במעלה השנית[II 111] אחורנית מהמספר[II 112] האחרון שהוא בטור הראשון[II 113] כי ע' הוא שני לטור השפל[note 32] ונכתבנו[II 114] באמצע ונשארו לנו[II 115] שנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נשיבם אחורנית והם עשרים נחלק[II 116] על ז' והנה נתן[II 117] לו[II 118] ב' ונכתוב אותו אחורנית לפני הנכתב בראשונה[note 33] ונשארו לנו ו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נשיבהו[II 119] אחורנית יהיו[II 120] ששים נחלקנו[II 121] על ז' נתן לו[II 122] ח' תכתבהו[II 123] אחורנית[note 34] | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונשארו לנו ד'[II 124] והם במעלה השנית והם מ'[II 125] והמספר המחולק עליו[II 126] גדול ממנו[II 127] | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| If the divisor as units is greater than the last digit in the top row, return it back and calculate from this position, according to the distance of the divisor, return it back and proceed according to the rule. | ואם היה המספר באחדים[II 128] המחולק עליו גדול מהמספר האחרון בטור העליון תשיבהו אחורנית ותחשוב[II 129] מאותו מקום[II 130] וכפי מרחק[II 131] המספר המחולק עליו תשיב[II 132] אחורנית[II 133] ועשה[II 134] כמשפט | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון בקשנו[II 135] לחלק כ' אלף על צ' | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
בזאת הצורה[II 136] | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
- [Illustration of the procedure:]


0 
00 02 022 0222 20000 20000 20000 20000 2 22 222 90 90 90 90
|
והנה[II 137] בעבור כי מספר[II 138] ט' גדול מב' נשיבהו[II 139] אחורנית[II 140] והם[II 141] כ' נחלקם[II 142] על ט' והנה[II 143] ב' נכתבנו[II 144] במעלה השלישית אחורנית שהיא שנית לחשבון שחלקנו ממנו[II 145] ונשארו ב'[II 146] | ||||||||||||||||||||||||||||||||||||||||||
|
נשיבם[II 147] אחורנית במעלה השלישית[II 148] והם[II 149] כ' נחלקם[II 150] על ט'[II 151] והנה[II 152] ב' ונשארו[II 153] ב'[II 154] | ||||||||||||||||||||||||||||||||||||||||||
|
נשיבם אחורנית במעלה השנית[II 155] והם עשרים נחלק על ט'[II 156] והנם[II 157] ב'[II 158] ונשארו[II 159] ב' שהם עשרים כי הם[II 160] במעלה השנית בטור העליון[II 161] וזה המספר[II 162] פחות ממספרנו[II 163] על[II 164] כן נכתוב גלגל אחורנית כי לא עלו אחדים[II 165] כי לא יצא לחוץ | ||||||||||||||||||||||||||||||||||||||||||
| If there is a zero in one of the positions and you cannot divide by the divisor, return it back from the higher [rank]. | ואם היה גלגל[II 166] באחד המקומות[II 167] ולא[II 168] תוכל[II 169] לחלק על המספר המחולק[II 170] השב אחורנית מהגבוה[II 171] ממנו | ||||||||||||||||||||||||||||||||||||||||||
|
דמיון בקשנו[II 172] לחלק[II 173] ד' אלפים ול"ב על שלשים[II 174] | ||||||||||||||||||||||||||||||||||||||||||
|
|
- [Illustration of the procedure:]


0 
00 1 11 111 4032 4032 4032 4032 1 13 134 30 30 30 30
|
חלקנו ד' על ג'[II 175] ועלה בידינו א'[II 176] וכתבנוהו אחורנית במעלת[II 177] המאות כי הוא שני לו[II 178] נשאר[II 179] לנו[II 180] עוד[II 181] א'[note 35] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נשיבהו[II 182] אחורנית במעלת[II 183] המאות[note 36] והיו[II 184] י'[II 185] נחלקנו[II 186] על ג' ועלה בחלוק[II 187] ג' נשאר[II 188] לנו א'[II 189] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
השבנוהו[II 190] אחורנית במעלת העשרות ויהיו[II 191] י' חברנו אותו עם הכתוב במעלה[II 192] השנית[II 193] היו[II 194] י"ג[II 195] חלקנו אותו[II 196] על ג' ונתנו[II 197] לו[II 198] ד'[II 199] נשאר[II 200] לנו[II 201] א'[II 202] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
השיבונוהו[II 203] אחורנית[II 204] במעלה הראשונה[II 205] היו[II 206] י"ב[II 207] שלא[II 208] יתחלקו כי הנשאר[II 209] פחות מאותו[II 210] המחולק[II 211] עליו וכבר[II 212] יצא לחוץ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If we want to divide one digit or two digits or many digits by one digit or two digits or three or many, provided that they are less than the digits in the top row, you proceed as follows: | וכאשר נרצה לחלק מספר אחד או שני[II 213] מספרים או מספרים[II 214] רבים על מספר אחד או על שני[II 215] מספרים[II 216] או על[II 217] שלשה או על[II 218] רבים על מנת שיהיו פחותים ממספרי הטור העליון ככה תעשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Give the last in the bottom row of the top row, as much as you can give it from the last digit in the top row, and give the preceding in the bottom row, which is first to the last, as much as the product of the number you gave the last multiplied by the digit in the bottom row that precedes the last digit. | תן לאחרון שבטור השפל מן הטור[II 219] העליון מה שתוכל לתת לו מהמספר[II 220] האחרון שבטור העליון ותן[II 221] לראשון מן הטור[II 222] השפל שהוא ראשון לאחרון[note 37] ככפל המספר שנתת לאחרון על מספר[II 223] הטור השפל שהוא לפני האחרון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If you cannot do this, reduce the number that you gave it first. | ואם לא תוכל לעשות[II 224] ככה שוב וגרע ממספרך[II 225] שנתת לו בתחלה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| When you have to take any digit from the digit that precedes the last, return it back as tens. | וכשאתה צריך לקחת מהטור[II 226] שהוא לפני האחרון שום מספר השיבהו אחורנית לעשרות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This is how you proceed with all the ranks. | ככה תעשה לכל המעלות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If there is a zero in one of the ranks of the upper row, return back from the higher rank next to it as tens and take from them as much as is necessary. | ואם[II 227] היה באחת ממעלות[II 228] הטור העליון גלגל השב מן הגבוה[II 229] ממנו אחורנית[II 230] בעשרות וקח ממנו[II 231] מה שצריך לו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If there are two zeros in the ranks of the upper row and in the ranks of the lower row there are numbers, you return back the higher [number] that corresponds to the digit that follows the last zero and take what you need from it. Then you return the remainder back as tens, and take what you need for the multiple of the number that is in the bottom row from the rank from which it should be taken. | ואם היו שני[II 232] גלגלים במעלות[II 233] הטור העליון ובמעלות[II 234] הטור השפל מספרים[II 235] תשיב[II 236] אחורנית הגבוה שהוא כנגד החשבון שהוא אחר[II 237] הגלגל האחרון[II 238] ותקח מהם[II 239] מה שתצטרך[II 240] ומהנשאר[II 241] תשיב אחורנית בעשרות ותקח ממנו מה שתצטרך[II 242] בכפל[II 243] המספר שהוא[II 244] בטור השפל מן המעלה[II 245] שהיא ראויה לקחת ממנה[II 246] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון זה[II 247] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
- [Illustration of the procedure:]

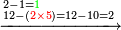
1 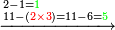
1 2 2 215 8213 8213 8213 8213 2 2 2 353 353 353 353
|
ד'ט'[II 248] שכתבנו הוא[II 249] הנשאר[II 250] מן החשבון[II 251] [II 252]שלא יתחלק[II 253] |
|
והנה[II 254] כאשר[II 255] חלקנו ח' שהוא[II 256] אחרון בטור העליון על[II 257] ג' שהוא אחרון[II 258] בטור השפל והנה נתנו[II 259] לו שנים ובעבור שהיה[II 260] הג'[II 261] שבטור השפל שלישי[II 262] החזרנו[II 263] לשלישי[II 264] ממנו אחורנית והגיע למעלת[II 265] העשרות ונשאר לנו במספר הח'[II 266] שנים |
|
והנה הנחנו שם אחד[II 267] כי אחד יספיק לנו והחזרנו האחד[II 268] אצל השנים והיו[II 269] י"ב וחסרנו[II 270] ממנו י' שהוא כפל חמשה האמצעי שבטור השפל והנה נשארו ב' על הב'[II 271] |
|
נניח שם אחד ונחזיר אחד אחורנית על אחד שהוא שלישי ויהיו[II 272] י"א נסיר ממנו ו'[II 273] לג' שהוא ראשון שבטור[II 274] השפל[II 275] נשארו ה'[II 276] |
|
והנה[II 277] לכל הג' השפלים מה שראוי להם |
|
נשוב[II 278] לחלק כי נשאר[II 279] לנו א' על ח' וא' על ב' וה' על א' |
- [Illustration of the procedure:]

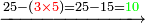
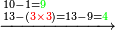
0 0 01 019 12 120 120 215 215 2154 8213 8213 8213 23 23 23 353 353 353
|
נשיב הא' שהוא[II 280] על הח'[II 281] אחורנית על א' אשר על הב'[II 282] יהיו[II 283] י"א נחלק אותם על ג' שהוא[II 284] בטור[II 285] השפל יהיו ג'[II 286] ונכתבנו[II 287] כנגד הטור הראשון שהוא לפני השנים[II 288] ונשארו[II 289] לנו ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נשיבם על הה'[II 290] אחורנית[II 291] יהיו כ"ה נתן לחמשה האמצעי[II 292] שבטור השפל[II 293] ט"ו ונשארו[II 294] עשרה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נשיב אחד אחורנית על הג'[II 295][note 38] וישארו ט' והא' עם הג'[II 296] י"ג[II 297] ונקח[II 298] מהם[II 299] ט'[II 300] וישארו[II 301] ד'[II 302] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וט' על הה'[II 303] כי לא יכולנו[II 304] לקחת בראשונה[II 305] הג' מהי'[II 306] אע"פ שיספיק לו[II 307] כי אינו מעלתו עכשיו[II 308] אע"פ שלקח ממנו בראשונה[II 309] כי בראשונה[II 310] היה[II 311] שלישי[II 312] לו כי האחרון שבטור השפל לקח מן הח' אבל עתה לקח מן[II 313] הב'[II 314] א'[II 315] ואחר שהוא שלישי צריך הוא[II 316] שיקח[II 317] ממעלתו[II 318] השלישית[II 319][II 320] והנה[II 321] הנשאר[II 322] ד' ט'[II 323] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון אחר[II 324] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
- [Illustration of the procedure:]

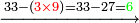
0 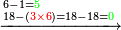
05 3 36 360 9381 9381 9381 9381 3 3 3 296 296 296 296
|
באנו[II 325] לחלק[II 326] ט'[II 327] על שנים[II 328] והנה לא יכולנו[II 329] לתת לו ד' כי לא ישאר[II 330] אלא א' וכאשר תשיבהו[II 331] אחורנית הנה[II 332] עם הג'[II 333] י"ג וט' ד' פעמים ל"ו[II 334] על כן[II 335] נתן לו ג' נשארו[II 336] ג' |
|
נשיבם כלם[II 337] אחורנית לשני לו שהוא ג' ויהיו[II 338] שם[II 339] ל"ג נתן לט'[II 340] ג' יהיו[II 341] כ"ז נשארו[II 342] ו' על הג'[II 343] |
|
נקח[II 344] מהם א'[II 345] ונניח ה' נשיבהו[II 346] על הח' שהוא שלישי[II 347] לאחרון[II 348] שבטור העליון ועם הח' יהיו[II 349] י"ח נתן[II 350] אותם[II 351] כלם לו' שהוא שלישי שבטור השפל נכתוב[II 352] על הח' גלגל לפי שלא נשאר[II 353] על הח'[II 354] מאומה |
- [Illustration of the procedure:]

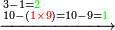
2 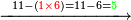
2 3 3 30 05 051 051 360 360 3605 9381 9381 9381 31 31 31 296 296 296
|
נשוב לחלק שעדין[II 355] לא יצא לחוץ נקח מן הה' שהנחנו על הג' שהוא שני בטור העליון שנים שהוא[II 356] אחד נכתוב[II 357] זה האחד[II 358] על הו' אחרי הג' ששמנו על הט'[II 359] בחלוק הראשון[II 360] והוא שלישי[II 361] בטור השפל וכבר יצא לחוץ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נקח מן הג'[II 362] שעל הג' אחד וישארו שנים נתן האחד על הגלגל והם י' נתן לט' שבטור[II 363] השפל ט' נשאר על הגלגל א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נשיבהו אחורנית על הא' שהוא רביעי וראשון[II 364] בטור העליון והם י"א נתן לו ו' נשארו[II 365] ה' על הא' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה[II 366] הנשארים[II 367] על הטור העליון ה' וגלגל וב' שהם ר"ה[II 368] ולא יתחלקו יותר[II 369] שהג' שבטור[II 370] השפל הם רצ"ו[II 371] והנלקח לכל אחד ל"א | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון אחר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
- [Illustration of the procedure:]
 |
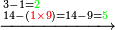 |
2 | 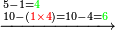 |
24 | 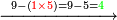 |
24 | ||
| 3 | 35 | 356 | 3564 | |||||
| 54093 | 54093 | 54093 | 54093 | 54093 | ||||
| 1 | 1 | 1 | 1 | |||||
| 2945 | 2945 | 2945 | 2945 | 2945 |
|
בקשנו לחלק הטור העליון על הטור השפל[II 372] לתת לו[note 39] ב'[II 373] לא[II 374] נוכל[II 375] שלא[II 376] ישאר כי אם[II 377] א' וד'[II 378] והם[II 379] י"ד[II 380] ויש לנו[II 381] לחלק על ט'[note 40] ב' פעמים[II 382] אך נתן[II 383] לו[II 384] א' ונשים אותו[II 385] כנגד ט'[II 386] שהם[II 387] בטור העליון שהוא רביעי לה' אחורנית כשנים[II 388] בטור[II 389] השפל[II 390] שהוא[II 391] רביעי לה' ראש[II 392] שבטור[II 393] השפל נשארו ג' על[II 394] הה'[II 395] |
|
נקח מהם אחד[II 396] ישארו[II 397] ב' על הה'[II 398] נשיבהו[II 399] אחורנית על הד' יהיו י"ד[II 400] יקח[II 401] ט'[II 402] ישארו ה' |
|
יש[II 403] לד'[II 404] שבטור[II 405] השפל לקחת מן השלישי שבטור העליון למען כי שלישי הוא[II 406] ולא נוכל כי השלישי[II 407] שבטור העליון גלגל הוא[II 408] נשיב[II 409] מן הה' שהנחנו על הד' אחד על הגלגל[II 410] יהיו י' יקח[II 411] ד' ישארו[II 412] ו' על הגלגל |
|
יקח הה'[II 413] שהוא ראש בטור השפל והוא רביעי[II 414] יקח[II 415] מהרביעי שבטור[II 416] העליון שהוא ט' ישארו[II 417] על ט'[II 418] ד' |
|
נשוב[II 419] לחלק כי עדין לא יצא[II 420] והנשארים ג' מן הטור[II 421] העליון שהוא ראשון וחמישי[II 422] ועל הט' ד'[II 423] ועל הגלגל ו' ועל הד' ד' ועל הה' ב'[321] |
- [Illustration of the procedure:]
 |
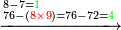 |
1 | 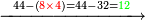 |
1 | 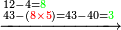 |
10 | ||
| 08 | 08 | 081 | 0818 | |||||
| 24 | 244 | 2442 | 2442 | |||||
| 3516 | 3516 | 3516 | 3516 | |||||
| 54093 | 54093 | 54093 | 54093 | |||||
| 18 | 18 | 18 | 18 | |||||
| 2945 | 2945 | 2945 | 2945 |
|
נשיב[II 424] הב' על הד' והם כ"ד נתן[II 425] לב' שהוא רביעי שבטור[II 426] השפל ח'[II 427] נשארו[II 428] ח' על הד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נשיב[II 429] מהם ז' על הו'[II 430] אחורנית[II 431] וא' נשאר על הד' ויהיו[II 432] ע"ו נקח[II 433] לט'[II 434] ע"ב נשארו[II 435] ד' במקום הו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אם[II 436] נשיב מהם ג'[II 437] ואמת[II 438] כי הד' שבטור[II 439] השפל יוכלו לקחת[II 440] מהג'[II 441] עם הד' שאחריהם[II 442] שהם ל"ד אך לא ישאר כי אם שנים וכשנשיב[II 443] אותו על הג'[II 444] יהיו כ"ג לבד[II 445] ויש לה'[II 446] שיקחו[II 447] מ'[II 448] | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
לפיכך נשיב כל הד' אחורנית על הד' ונכתוב גלגל במקום הו' כנגד הגלגל[II 449] שבטור העליון והם מ"ד יקחו[II 450] הד' ל"ב[II 451] נשארו[II 452] י"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נקח מהם ד'[II 453] כי לא יהיה די[II 454] לנו[II 455] בפחות וישארו ח' על הד' שהם על הט' ועם[II 456] הג'[II 457] הם[II 458] מ"ג[II 459] יקחו[II 460] הה' מ'[II 461] | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ישארו[II 462] ג' על[II 463] הג' וח' על הט'[II 464] שהם פ' וגלגל להוציאו ממאות ולהכניסו לאלפים[II 465] וא' על[II 466] הרביעי שהוא על הד'[II 467] שהוא אלף[II 468] ואלה לא יתחלקו כי המחולק גדול מזה שהוא אלפים וט' מאות ומ"ה[II 469] | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון אחר בקשנו לחלק ס"ח אלפים[II 470] וט' מאות וכ"א[II 471] על ז' אלפים ונ"ג[II 472] | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וזהו הדמיון[II 473] | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
- [Illustration of the procedure:]

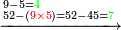
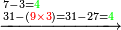
4 05 0547 05474 68921 68921 68921 68921 9 9 9 7053 7053 7053 7053
|
ז'[II 474] שהוא רביעי[II 475] בטור השפל לא יוכל[II 476] לקחת מו'[II 477] שהוא חמישי בטור העליון ומאחר[II 478] שלא נוכל[II 479] לתת לז' כל[II 480] הצורך[II 481] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נשיב אותו[II 482] כלו[II 483] אחורנית[II 484] על הח' ויהיו[II 485] ס"ח הנה[II 486] חלקנו מן הח'[II 487] שהוא רביעי לטור העליון[II 488] נתן לז'[II 489] ט'[II 490] נוציאנו[II 491] לחוץ[II 492] על הג'[II 493] שהוא רביעי בטור[II 494] השפל נשארו[II 495] ה' על הח'[II 496] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה[II 497] השני לז' לא יקח מאומה[II 498] כי הוא גלגל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
יש לה'[II 499] שיקח[II 500] מן ב'[II 501] הרביעי[II 502] בטור העליון שהוא שלישי לחלוק[II 503] לא[II 504] יוכל[II 505] לקחת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נקח[II 506] מן הט' שאחריו ה' נשיבם[II 507] על הב'[II 508] יהיו[II 509] נ"ב[II 510] וד' נשאר[II 511] על הט' והה' מנ"ב[II 512] יקחו מ"ה[II 513] ישארו[II 514] ז' על הב'[II 515] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
מן[II 516] הז' נקח ג' ונשיבם[II 517] אחורנית על א'[II 518] והם[II 519] ל"א יקחו ג' כ"ז[II 520] נשאר[II 521] ד' על א'[II 522] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון אחר[II 523] נרצה[II 524] לחלק תר"פ אלפים ות"ב על אלפים וט'[II 525] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
מספרים על מספרים[II 526] שיהיה[II 527] בטור העליון[II 528] ב'[II 529] גלגלים וכן בטור השפל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נתן[II 530] לב' הרביעי בטור[II 531] השפל ג' מהו' הששי[II 532] בטור[II 533] העליון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה[II 534] הגלגל שני[II 535] בטור השפל יש לו שיקח[II 536] מן הח' ולא יקח כלום | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והגלגל השלישי שבטור השפל יש לו שיקח[II 537] מן הגלגל[II 538] השלישי בטור[II 539] העליון ולא יוכל[II 540] לקחת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
יש[II 541] לט' הראשון[II 542] בטור השפל לקחת[II 543] מד' שבטור העליון לא[II 544] יוכל[II 545] צריכין[II 546] אנו שנשיב מן הח' השני בטור העליון מה שיספיק לו[II 547] נשיב א' אחורנית כי די לנו בא' ונכתוב[II 548] על הח' ז' והא' שהשיבונו[II 549] אחורנית על הגלגל יצא לנו בעשרות ועוד[II 550] לא יספיק נקח מהם ג' ונשיבם אחורנית ונשארו ז' על הגלגל והג'[II 551] הם ל'[II 552] על הד'[II 553] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נשארו[II 554] ז' במקום ד'[II 555] וגלגל ושנים הראשונים[II 556] שבטור[II 557] העליון וז' שעל הגלגל וז'[II 558] שעל הח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עוד נשוב[II 559] לחלק שהרי לא[II 560] יצא[II 561] נקח[II 562] לו[II 563] ג' מן הז' שעל הח' ונשימהו[II 564] תחת הגלגל הראשון שהוא רביעי לח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונשאר א' על הח'[II 565] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
יש לגלגל שיקח מן הגלגל[II 566] לא יוכל[II 567] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויש לגלגל[II 568] שאחריו[II 569] שיקח[II 570] ממעלתו שהיא[II 571] הז' שעל[II 572] הד' לא[II 573] יוכל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
יש לט'[II 574] שיקח[II 575] מן הגלגל[II 576] שהוא מעלתו לפי שהוא רביעי[II 577] לחלוק ולא יוכל לפי שאין על הגלגל כלום וגם לא[II 578] יוכל להשיב אותו אחורנית על השנים כי השנים אינם[II 579] מעלתו נשיב מן הז' שעל[II 580] הד' שלפניו ג' נשימם על הגלגל והם ל' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נשארו ג' על הגלגל וד' על הד'[II 581] לפניו[II 582] וז' על הגלגל שהוא לפני הח'[II 583] וא'[II 584] על הח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נשוב[II 585] לחלק שעדין[II 586] לא יצא לחוץ הנה[II 587] מן הא' לא יוכל לקחת[II 588] האחרון שבטור השפל נשיב אותו אחורנית על הז' שהוא על הגלגל והם[II 589] י"ז נתן לו ח'[II 590] נוציאם לחוץ אחרי[II 591] הג' כי הוא[II 592] רביעי לחלוק כי מן הז' שעל הגלגל חלקנו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ושם נשאר[II 593] א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה[II 594] יש[II 595] לגלגל שיקח[II 596] מן הד' ולא יקח | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
גם[II 597] יש לגלגל האחר שיקח מן הג'[II 598] שעל הגלגל שבטור[II 599] העליון ולא יקח[II 600] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויש לט' שיקח[II 601] מן הב'[II 602] ולא יוכל נשיב אחורנית אם נאמר לג' שעל הגלגל שיתן[II 603] לב' הראשון לגלגל[II 604] אין לו מה שיספיק לו[II 605] כי אין לו אלא[II 606] ג' נקח מן הד' שבמקום הד' אחד ויהיה על הגלגל[II 607] עם הג' י"ג נקח מהם ז' ונשיבם על הב' והם ע"ב יצאו הכל[II 608] בט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב[II 609] גלגל על הב' שלא נשאר עליו כלום[II 610] ועל הגלגל שהוא שני לב'[II 611] נשארו ו' וג'[II 612] על ד'[II 613] וא'[II 614] על הגלגל שהוא[II 615] שני[II 616] לח' ואלה נשארו[II 617] שלא יתחלקו כי המחולק גדול מזה כי המספר הנשאר אלף[II 618] וג' מאות וס'[II 619] והמחולק עליו הוא אלפים וט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון אחר נכבד וקשה מכל החשבונים שתחתיו[II 620] מאין[II 621] גלגל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| First, I shall explain that whenever a digit is separated from a digit, meaning that a zero is written in between, as for example, 203, we do not say: we return the 2 or, as much is needed according to the digit in the lower row, back to the 3, because the zero is in the middle, so we return the 2 or the one back to the zero and then divide according to the rule. | ובראשונה אפרש[II 622] כי לעולם כשיתרחק[II 623] חשבון מחשבון והטעם שיכתב[II 624] גלגל באמצע כדמיון זה[II 625] ג0ב[II 626] [II 627]לא נאמר נשיב הב'[II 628] אל הג'[II 629] או כמה[II 630] שיצטרך[II 631] לפי החשבון[II 632] שבטור השפל לפי שגלגל באמצע אך נשיב הב'[II 633] או האחד[II 634] אל[II 635] הגלגל ואז נחלק כמשפט[II 636] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| I shall tell you one rule for all the numbers you divide, whether they are many or a few: You always have to divide the upper number by the lower one, until the end of the digits when it has come to its end. If there is a zero above, it can no longer be divided. | ואומר לך כלל אחד מכל החשבונות שתחלק בין רבים בין מעטים לעולם יש לך לחלק חשבון העליון על התחתון עד שיצא לסוף החשבונות בא על סופו אם יש גלגל עליו לא יתחלק עוד[II 637] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו זה וזה צורת הנכבד והקשה[II 638] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון בקשנו לחלק חשבון[II 639] ט' שביעיות[II 640] על ד' תשיעיות[II 641] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה ראש כל דבר אוֹרְךָ[II 642] איכה[II 643] תחלק[II 644] אחר שתראה שהז' פחות מהט'[II 645] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| First version | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
תצטרך להשיבו אחורנית וזהו הדמיון[II 646] ותחלה כשתחל[II 647] לחלק תתן לט'[II 648] ז' ותכתבנה אחורנית[II 649] במעלת[II 650] הד' שתחלק[II 651] ממנו שהוא שני לט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנשאר י"ד וכן תעשה עד שישאר במעלת א' לחלוק ז' וכן בשני לחלוק ז'[II 652] ובשלישי[II 653] לחלוק ח' וברביעי לחלוק ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נשוב לחלק נשיב[II 654] הז'[II 655] שהוא בשני אל השלישי אחורנית[II 656] ונחלק[II 657] ממנו[II 658] ונכתוב ז' תחת ז' ששי[II 659] שהוא ד' לחלוק והנשאר י"ד וכן תעשה עד שישאר ז'[II 660] ואחריו נכתוב ח' ואחריו ה'[II 661] ואחריו ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נשוב[II 662] לחלק נשיב ז'[II 663] על הח'[II 664] ונשים אותה במערכת ד' והנותר ט"ו ומה[II 665] שתשאיר[II 666] ח' ואחריו ה' ואחריו ה' ואחריו ד' ותכתוב ז' תחת השלישי שהוא הרביעי[II 667] לחלוק[II 668] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נשוב לחלק נשיב[II 669] ח' על ה' ונתן ח'[II 670] תחת השמיני[II 671] שהוא ז'[II 672] רביעי[II 673] לחלוק ישאר ה' על ה'[II 674] ואחריו[II 675] ה' ואחריו ה'[II 676] ואחריו ה'[II 677] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נשוב לחלק נתן ה' על ה' אחורנית[II 678] ונתן ה' תחת ז' התשיעי והוא רביעי לחלוק והנשאר י' ומה שתשאיר[II 679] ה' ואחריו ה' ואחריו ו'[II 680] ואחריו ב'[II 681] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועוד לא יתחלק כי כבר יצא[II 682] לחוץ בה' וכי הנותר הוא ה' אלפים וה' מאות וס"ב[II 683] והמחולק עליו ט' אלפים וט' מאות וצ"ט[II 684] והמקובל[II 685] ע"ז אלף[II 686] וז' מאות ופ"ה[II 687] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכלל חלוק החשבון ג'[II 688] זיינין וג'[II 689] חיתין וג'[II 690] דלתין[II 691] וט' ההין וו' אחת וב' אחת[II 692] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והכלל כי עם[II 693] כל[II 694] החלוקים ד' חוץ[II 695] מן האחרון שנתמעט עד ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Second version | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| לכן שימהו לאחור לז' ויהיו ע"ז וחלקם על ט' ולא תוכל ליתן[II 696] לו יותר מז' לצורך שאר המספר וישארו י"ד תניח מהם ז' לחלוק השני וז' תשימהו לאחור על הז' השלישי ויהיו ע"ז וחלקם על ט' השני וישארו י"ד תניח מהם ז'[II 697] לחלוק שני[II 698] והז' תשימהו לאחור אל הרביעי יהיו ע"ז וחלקם על[II 699] הט' השלישי וישארו י"ד תניח מהם ח' לחלוק שני והו' תשימהו לאחור אל הז' החמישי ויהיו ס"ז וחלקם על הט' הרביעי וישארו ד' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נמצא שנשארו[II 700] לחלוק השני ז' ז' ז' ז' ז' ח' ז' ז'[II 701] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| החלוק השני תשלח ז' לאחור ויהיו ע"ז וחלקם על הט' הראשון וישארו י"ד תניח מהם ז' לחלוק שלישי והז' שלחהו לח' שלפניו ויהיו ע"ח וחלקם על הט' השני ותן[II 702] לו ז' כמו כן וישארו ט"ו תניח מהם ח' לחלוק שלישי וז' תשלחהו לאחור אל הד' ויהיו ע"ד וחלקם על הט' השלישי וישארו י"א תניח מהם ה' לחלוק שלישי והו' שלחהו אל הז' ויהיו ס"ז וחלקם על הט' הרביעי וישארו ד' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נמצא שנשארו לחלוק שלישי ז' ז' ז' ד' ה' ח' ז'[II 703] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| החלוק השלישי[II 704] תשיב[II 705] ז' לאחור ויהיו ע"ח חלקם על ט' הראשון ותוכל לתת לו ז' ולא[II 706] יותר וישארו ט"ו תניח מהם ח' לחלוק הרביעי והז'[II 707] שימהו לאחור אל הה'[II 708] ויהיו ע"ה וחלקם על ט' השני ותן לו ז' כמו כן וישארו י"ב תניח מהם ה' לחלוק רביעי והז' שימהו[II 709] לאחור אל ד'[II 710] ויהיו ע"ד וחלקם[II 711] על ט' שלישי וישארו י"א תניח מהם ה' לחלוק הרביעי[II 712] והו' שימהו אחורנית אל הז' ויהיו ס"ז וחלקם על הט' הרביעי וישארו ד' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונמצא שנשארו לחלוק רביעי ז' ז' ד' ה' ה' ח' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חלוק הרביעי[II 713] שים ח'[II 714] אחורנית[II 715] על הה' ויהיו פ"ה תוכל לחלקם על הט' הראשון וליתן לו ח' וישארו י"ג תניח מהם ה' לחלוק חמישי[II 716] והח'[II 717] שלחהו אחורנית אל הה' ויהיו פ"ה וחלקם[II 718] על הט'[II 719] השני וישארו י"ג תניח מהם ה' לחלוק חמישי[II 720] והח'[II 721] שלחהו אחורנית אל הד' ויהיו פ"ד וחלקם על הט' השלישי ח' כמו כן וישארו י"ב תניח מהם ה' לחלוק חמישי והז' שלחהו לאחור אל הז'[II 722] ויהיו ע"ז וחלקם על הט' הרביעי וישארו ה' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונמצא הנשאר לחלוק חמישי ז' ה' ה' ה' ה' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חלוק חמישי שים ה' אחורנית ויהיו נ"ה תן מהם ה' על הט' הראשון[II 723] וישארו י' תניח מהם ה' בלתי מחולקים והה'[II 724] תשלח אחורנית אל הה' השלישי[II 725] ויהיו נ"ה ותן על הט' השני ה' כמו כן וישארו י' תניח מהם ה' בלתי מחולקים והה'[II 726] שלחהו[II 727] אל ה'[II 728] הרביעי ויהיו נ"ה ותן על הט' השלישי ה' כמו כן[II 729] וישארו י' תניח מהם ו' בלתי מחולקים והד' שלחהו[II 730] אל הז' ויהיו מ"ז וחלקם על הט' הרביעי ה' כמו כן | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וישארו בלתי מחולקים ב' ו' ה' ה'[II 731] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Check | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| We complete by knowing the test for whether you divided correctly. | והנה נשלים[II 732] לדעת המאזנים אם חלקת נכונה[II 733] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דע מאזני המספר[II 734] שחלקת עליו בין שיהיה[II 735] אחד או רבים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
גם[II 736] דע מאזני המספר[II 737] שעלה בחלוק שכתבת[II 738] בין שני הטורים בין שיהיה אחד או רבים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכפול זה[II 739] על זה האמצעי[II 740] על התחתון ודע כמה נשאר[II 741] על ט' ט'[II 742] והוא השמור אם[II 743] לא נשאר לך מספר שנשאר[II 744] שהוא פחות מהמספר[II 745] שחלקת עליו[II 746] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כי[II 747] אם[II 748] נשאר קח[II 749] המאזנים שלו וחבר[II 750] אותו עם השמור שהיה לך והמחובר הוא השמור באמת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וראה מאזני המספר הגדול שחלקת אותו שהיה[II 751] בטור העליון אם[II 752] היה[II 753] שוה למאזני[II 754] השמור תדע כי חשבונך אמת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תכפול מה[II 755] שיעלה[II 756] בחלוק על[II 757] המספר שחלקת עליו אחר שתחבר אליהם מה שנשאר לחלק[II 758] אז יהיה המחובר שוה למספרי[II 759] הטור העליון וחלוק נכון[II 760] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Additional excerpts[II 761] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The rule of Division | כלל החלוק | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If the number you by which you divide [= the divisor] is two digits or more, divide the last of the top row by the last of the bottom row, if the digit of the top row is greater than that of the bottom [row]. | אם המספר שתחלק עליו שני מספרים או יותר חלק סוף הטור העליון[II 762] על סוף הטור השפל אם מספר העליון גדול מהשפל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| But if the lower one is greater than the upper one, return the last of the upper one back as tens to the preceding rank and add it to what is written there. | ואם השפל גדול מהעליון השב סוף העליון לעשרות אחורנית על המעלה הקודמת לה ותצרפם עם הנכתב בה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If there is a zero in the preceding rank, count the tens. | ואם במעלה הקודמת לה גלגל ספור העשרות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Take from there what you can give the last lower digit. Write down what you can give to all the other bottom digits, as what you give to the last, and write the quotient in the middle between the two rows, far from the rank you divided as the distance from the last bottom digit from the starting digit. | וקח ממנו מה שתוכל לתת למספר השפל האחרון וכתוב מה[II 763] שתוכל לתת לכל מספרי השפל האחרים מה שתתן לאחרון והיוצא כתבהו באמצע שני הטורים רחוק מן המעלה שחלקת ממנה כמרחק סוף השפל מראשו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Proceed like this for all the divisions, doing the same for them as for this division: count from the rank which you divided as the distance of the last bottom digit from its starting digit, and write the quotient there. Then, from the digit that is second to the last bottom digit take the digit that is next to the rank from which you divided, as much times as the number that is written between the rows. | וכן תעשה לכל החלוקים שתשוב עליהם בזה החלוק שתמנה מן המעלה שחלקת ממנה כמספר סוף השפל מראשו ושם תכתוב היוצא בחלוק ומהמספר[II 764] השני לסוף השפל תקחנו מן הסמוך למעלה שחלקת ממנו כמספר הכתוב באמצע הטורים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If it is not enough for you, return what is left of the rank that you first divided back to the preceding rank and add it to what is written in it, then take your number from it. Do this with all. | ואם לא יספיק לך תשיב[II 765] מה שנשאר מן המעלה שחלקת תחלה אחורנית אל המעלה הקודמת לה ותצרף[II 766] עם מה שנכתב בה וקח ממנה מספרך וכן תעשה לכלם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון רצינו לחלק פ"ג אלפים ותקכ"א על תתק"ג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה הט' שבטור השפל יותר[II 767] מח' שהוא סוף העליון על כן תשיב[II 768] הח' אחורנית על הג' יהיו פ"ג ונתן לט' מהפ"ג ט' יהיו פ"א ונשארו ב' על הג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והגלגל לא יוכל לקחת מן הה' העליון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והג' התחתון לא יוכל לקחת מן הה' העליון[II 769] כי[II 770] אינו מעלתו לכן השיב מן הה' שלשה על הב' יהיו ל"ב נסיר מהם כ"ז שהם ט' פעמים ג' שהוא ראשון השפל ונשארו ה' על הב' וב' על הה' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ובעבור שהט' התחתון הוא במעלה השלישית וכבר יצא בחלוק ט' נכתבנו[II 771] במעלה השנית שהוא שלישי לג' העליון שחלקת ממנו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נשוב לחלק ונשיב ב' אשר על הג' אל הב' אשר על[II 772] הה' יהיו כ"ב נסיר מהם ב' פעמים ט' כי ט'[II 773] הוא השפל ונשארו ד' על הה' ונכתוב ב' במעלה הראשונה שהיא שלישית לה' העליון שחלקת ממנו בזה החלוק | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה הגלגל לא יוכל לקחת מאומה מן הה' אשר על[II 774] הב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והג' השפל לא יוכל לקחת מן הא' העליון ב' כי אין בו רק אחד על כן נשיב אחד מן הה' שעל הב' אל הא' יהיו י"א ונקח מהם לג' התחתון ו' שהם ב' פעמים ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונשארו ד' על הה' וד' על הב' וה' על א' שלא יתחלקו[II 775] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון אחר רצינו לחלק י"א אלף וש"נ[II 776] על ק"י | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
לקחנו א'[II 777] מן הא' האחרון העליון[II 778] וכתבנוהו[II 779] במעלה השלישית תחת הג' העליון לפי שא' האחרון השפל הוא במעלה השלישית וככה נרחיק היוצא מסוף המספר[II 780] שהחלות לחלק ממנו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן קח מא' הרביעי העליון א' השני התחתון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ובעבור שלא נשאר במעלה הרביעית מאומה ונצטרך לשוב לחלק מהג' העליון נקח מהם ג' לא' האחרון מהשפל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב ג' במעלה הראשונה שהיא שלישית לג' העליון שהחלנו עתה לחלק ממנו ולכן שמנו גלגל במעלה השנית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה כי בחלוק הראשון החלונו מסוף העליון ולכן כתבנו היוצא בחלוק ברחוק ג' מעלות ממנו אחורנית כמספר מעלות סוף השפל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אבל בחלוק השני הזה החלונו לחלק מהג' העליון ולכן נכתוב היוצא רחוק ג' מעלות אחורנית והגיע זה אל המעלה הראשונה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וא' השני בטור השפל נקח מה' העליון ישארו ב' על הה'[II 781] והם עשרים שלא יתחלקו[II 782] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה היוצא בחלוק ק"ג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| from here proceeds to the check |
Chapter Three – Addition |
השער השלישי[III 1] |
|---|---|
Sums |
|
| It is written in the books of the arithmeticians that he who wants to know how much is the sum of the numbers that proceed successively up to a known number, multiplies it by its half plus one half and the result is the sum.
|
כתוב בספרי[III 2] חכמי החשבון כי[III 3] הרוצה לדעת כמה המחובר מן המספרים[III 4] שיעברו[III 5] על הסדר עד סוף מספר ידוע יכפול[III 6] אותו על חציו[III 7] בתוספת[III 8] חצי אחד והעולה הוא המחובר |
|
דמיון רצינו לדעת כמה הם[III 9] המספרים[III 10] המחוברים[III 11] מא' עד סוף[III 12] י"א |
|
הנה ידענו[III 13] כי חצי י"א ה' וחצי נוסיף חצי אחד הנה[III 14] יהיו[III 15] ו' והנה[III 16] נכפול י"א על ו' יעלו[III 17] ס"ו והוא המחובר[III 18] |
|
דמיון אחר בזוגות כמה[III 19] המחובר עד סוף[III 20] י"ח |
|
והנה[III 21] לקחנו חציו והוא[III 22] ט' כפלנו[III 23] י"ח עליו ועלו[III 24] קס"ב ועוד[III 25] יש[III 26] לכפול חשבון[III 27] י"ח על חצי אחד יעלו[III 28] ט' חבר אותו[III 29] עם[III 30] קס"ב יעלו קע"א והוא המחובר |
| Every number is in accordance with these two ways. | ועל אלו שני[III 31] הדרכים[III 32] הולך[III 33] כל חשבון[III 34] |
| Another way: add one to the last number, multiply by half the number and the result is the sum.
|
דרך אחרת הוסף על סוף המספר אחד שלם וכפול על החצי מהמספר והעולה הוא המחובר |
|
דמיון בנפרדים כמה המחובר עד סוף י"א |
|
הוספנו אחד והיו י"ב והנה חצי י"א ה' וחצי כפלנו י"ב על ה' וחצי עלו ס"ו וככה המחובר |
|
ובזוגות עד סוף י"ח |
|
הנה חציו הוא ט' הוספנו אחד על י"ח היו י"ט כפלנו י"ט על ט' עלו קע"א[III 35] |
| Abraham the author said: | אמר אברהם[III 36] המחבר |
| I have found another way: add to the square of the last number the root that is the last number itself, then see how much is the sum and half the sum is the required.
|
מצאתי דרך אחרת תוסיף[III 37] על מרובע[III 38] סוף החשבון השרש שהוא[III 39] בעצמו[III 40] וראה כמה[III 41] המחובר[III 42] וחצי המחובר הוא המבוקש |
|
דמיון ידענו כי מרובע י"א קכ"א ואחר[III 43] נוסיף על[III 44] י"א שהוא השרש[III 45] והוא סוף החשבון יעלו קל"ב וחציו ס"ו |
| From this way you can derive all the questions that are concerning this matter. | ומזה הדרך[III 46] תוכל להוציא כל השאלות שהם בענין הזה[III 47] |
|
דמיון שאל שואל חברתי[III 48] מספרים[III 49] עד שהגיעו[III 50] למספר ידוע ועלה המחובר תס"ה כמה הוא סוף החשבון |
| Always double the sum, then take the root of the preceding square and check it: if between the square and the double remains the root no more and no less, know that the calculation is correct and the [last] number is itself the root.
|
כפול לעולם החשבון[III 51] המחובר וקח שרש הנכפל שעבר ובחון[III 52] אותו כי אם נשאר בין המרובע ובין הנכפל כמו השרש בלי תוספת ומגרעת תדע כי החשבון נכון והחשבון בעצמו השרש[III 53] |
|
והנה כפלנו[III 54] תס"ה ועלה[III 55] תתק"ל וידוע[III 56] כי המרובע שעבר היה[III 57] תת"ק ושרשו ל' והוא סוף המספרים המחוברים והנה אין בין המרובע והנכפל כי אם ל' והוא סוף[III 58] החשבון |
| Another general way for an even and an odd number [of terms]: double the square of half the [last] number, then add to it the root of this square, which is half the number and the result is the required.
|
דרך אחרת כוללת לזוגות ולנפרדים תכפול מרובע חצי המספר ותוסיף עליו שורש זה המרובע שהוא חצי החשבון והעולה הוא המבוקש |
|
דמיון רצינו לדעת כמה המחברים עד י"ב |
|
והנה חצי המספר ו' והמרובע ל"ו כפלהו יהיו ע"ב הוסיף על זה ו' שהוא השורש עלו ע"ח והוא המבוקש[III 59] |
| Another question: we sum the squares up to a known number, how much is the sum?
|
שאלה אחרת חברנו כל המרובעים[III 60] שהם עד סוף החשבון[III 61] שהוא[III 62] ידוע כמה המחובר |
| You should know the sum of the numbers preceding the [last] mentioned number including [the last number] and we name it and call it a sum, then we take two thirds of the [last] mentioned number plus one third, multiply it by the sum and the result is the required, which is the sum of the squares up to the mentioned number.
|
יש לך לדעת אותו החשבון שהזכיר כמה יעלה המחובר מהמספרים שלפניו ועמו נשים[III 63] שם[III 64] לאותו המספר[III 65] הידוע ונקראנו[III 66] סכום והנה נקח שתי שלישיות המספר שהזכיר עם תוספת שלישית אחד[III 67] ונכפול[III 68] זה המחובר[III 69] על סכום המספר והעולה הוא המבוקש והוא המחובר מהמרובעים עד סוף המספר הנזכר |
|
דמיון רצינו לדעת כמה המרובעים שהם[III 70] עד סוף שבעה[III 71] |
|
וכבר[III 72] ידענו שהמחובר[III 73] כ"ח ונשוב[III 74] לדעת כמה שתי שלישיות שבעה[III 75] עם תוספת שלישית אחד[III 76] והם חמשה כי שתי שלישיות ששה הם[III 77] ארבעה ויש[III 78] לנו עוד שתי שלישיות ועם תוספת שלישית אחד[III 79] והנה נכפול[III 80] על הסכום ה' ועלו ק"מ והוא המבוקש |
|
דמיון אחר כמה המחובר[III 81] מהמרובעים שהם[III 82] עד סוף[III 83] י"ב[III 84] |
|
וידוע[III 85] כי הסכום שלו ע"ח ושתי שלישיותיו ח' נכפלנו על ע"ח יעלו[III 86] תרכ"ד נחבר[III 87] אליו שלישית הסכום שהוא כ"ו יעלו תר"נ והוא המבוקש |
| From this way you can derive all the questions that are concerning this matter. | ועל זה הדרך תוכל להוציא כל השאלות שהם[III 88] מזה הענין |
| Additional excerpts | |
| I have found an easy way to sum the cubes: | ואני[III 89] מצאתי דרך נקלה לחבור[III 90] המעוקבים |
| If you want to know the [sum of the] cubes up to a known number, know the sum of the numbers up to that last number and take its square - it is the sum of the cubes up to the last number.
|
שאם תרצה לידע המעוקבים שהם עד מספר ידוע דע[III 91] המספר המחובר עד סוף המספר ההוא וקח מרובעו והוא יהיה חבור המעוקבים עד סוף החשבון ההוא[III 92] |
|
דמיון רצינו לידע כמה מספר המעוקבים המחוברים עד ה' |
|
והנה מספר המחובר עד סוף ה' הוא ט"ו קח מרובעו יהיו רכ"ה והוא יהיה מספר המעוקבים עד ה'[III 93] |
| Another matter: to know the sum of all the doubles.
|
[III 94]ענין אחר לדעת כמה המחובר מכל הנכפל |
| It is [equal to] double the last minus the first.
|
והוא כפל האחרון במגרעת הראשון |
|
דמיון כי המחובר מן ג' ו' י"ב |
|
הם כ"ד בחסרון ג' הרי כ"א והוא המחובר |
|
דמיון אחר א' ב' ד' |
|
הם ח' במגרע א' הרי ז' והוא המחובר |
| Likewise, if one says only the last number. | וכן אם לא יגיד כי אם סכום אחרון |
|
כמו אם ישאל כמה הם הכפולים זה על זה עד ל"ב |
|
כפול ל"ב יהיה ס"ד תחסר אחד שהוא ראשון ישאר ס"ג והוא המבוקש |
| תמצא חבורו מראשו כמ' שהראיתיך עתה ויהיו כ"ח ושמרהו ועוד תקח מן הז' שני שלישיתיו ושליש והם ה' וכפול ה' בכ"ח ששמרת ויעלו | |
| אז תדע חבורו מראשו ועד י"ב והם כמ' שידעת ע"ח ושמרהו וחזור ותקח שני שלישי י"ב והם ח' ותכפלם על ע"ח יהיו תרכ"ד ועוד חבר לאלו שליש ע"ח והם | |
| ודע כי החבור הוא שתחל לחבר האחדים תחלה ואחר כן העשרות וכן בסדר וזה הפך החלוק שהוא יעשה אחורנית | |
| דרך אחרת קח המחובר מן י"ב והם ע"ח ותקח שני שלישי י"ג והם ח' וב' שלישים והסר מהם שליש אחד וישארו ח' ושליש ותכפלם על ע"ח תדע כי הם יעלו כמו כן תר"נ | |
|
ואם יאמר כמה המחובר מהמרובעים עד ח' |
| קח חבורו של ח' והם ל"ו ובקש שני שלישי ט' והם ו' ותכפלם בל"ו ויעלו רי"ו הסר מהם שליש ל"ו והם י"ב וישאר ר"ד והוא המבוקש | |
|
שאלה כמה הוא המחובר מד' עד ט' |
| אז תעשה כמ' שלמדתיך למטה לכפול ה' בט' ויעלו מ"ה והסר מהם ב' פעמים ג' והם ו' וישארו ל"ט והוא המבוקש | |
|
|
ואם עוד ישאל כמה היא המחובר מהמרובעים כסדר מד' ועד ט' |
| אז תעשה כמ' שצויתיך למעלה למצוא מחוברם מראשם והם מ"ה ושמרם וקח שני שלישי ט' והם ו' וכפלם במ"ה ויעלו ר"ע ועוד שליש מ"ה והם ט"ו ויעלו רפ"ה ותסיר מזה מרובע א' ב' ג' והם י"ד וישארו רע"א והוא המבוקש | |
| ועל הדרך הזה[III 95] תוכל להוציא כל השאלות מזה הענין[III 96] | |
| There is no need to mention all of this, but I shall only mention the method of the scales. | ואין צורך להזכיר כל[III 97] זה[III 98] רק אזכיר דרך המאזנים |
Written calculations |
|
| When you add a number to a number, even if they [consist of] many [digits], put one number in the upper row according to its ranks, put also the other number according to its ranks in the lower row. | כשתחבר[III 99] מספר אל מספר בין שיהיו[III 100] רבים אלו ואלו[III 101] שים המספר האחד[III 102] בטור העליון[III 103] כפי מעלותיו[III 104] גם[III 105] שים המספר[III 106] השני כפי מעלותיו[III 107] בטור השפל |
| Then add each [digit] in its rank and write the sum in a third row. | אחר כן חבר כל אחד אל מעלתו והמחובר כתוב אותו בטור שלישי |
| Then add the scale of the top row to the scale of the bottom row. | אחר כן חבר מאזני הטור העליון אל[III 108] מאזני הטור התחתון[III 109] |
| If the sum of the two is equal to the scale of the third row, know that your calculation is correct. | ואם היה העולה בין שניהם כמאזני הטור השלישי[III 110] אז תדע כי חשבונך אמת |
| Now I shall explain how to approach the tables of astrology and how to take add seconds to minutes and minutes to degrees and degrees to signs. | ועתה אפרש היאך יכנס בלוחות חכמת המזלות והיאך יצרף שניים לראשונים וראשונים למעלות ומעלות למזלות[III 111] |
Addition of Sexagesimal Fractions |
|
| Now I shall give you a general method of astrology. | ועתה אתן לך דרך כוללת בחכמת המזלות |
| The celestial sphere was divided into 12 signs and the sign into 30 degrees. | חלקו הגלגל על י"ב מזלות והמזל על ל' מעלות |
| The degrees are as units in the number; each degree is divided into sixtieths, which are called minutes. | והמעלות הם כמו אחדים במספר וכל מעלה מתחלקת על ששים יקראו ראשונים |
| Each minute is also divided into sixtieths, which are called seconds. | גם כל[III 112] ראשון יתחלק לששים עוד[III 113] ויקראו שניים |
| There are no more fractions than these in the tables of the planets. | ואין בלוחות המשרתים שברים יותר מאלה |
| Know that the tables of the planets of the mean motion are according to two ways: | ודע כי לוחות המשרתים במהלך האמצעי על שני דרכים |
|
האחד על שנות השמש והם שנות הכלל מחוברים עשרים עשרים[III 114] |
|
והדרך השנית על שנות הלבנה ושנות הכלל מחוברים שלשים שלשים |
| I will explain this in the book | ובספר[III 115] טעמי הלוחות אפרש זה |
| When they want to know the position of any planet required at any hour required, they approach the years of the decades that have passed and write down the number of the signs they find written there, and they write this at the beginning of a row. | והנה ברצותם לדעת[III 116] מקום איזה משרת שיבקשו[III 117] באיזו שעה שירצו יכנסו בשנות הכלל שעברו ויכתבו מה שימצאו כתוב שם ממספר המזלות ויכתבו זה[III 118] בתחלת הטור |
| Then, they write the degrees they find, after the first number in the same row and they do a long dividing line between the two numbers. | ואחר יכתבו מה שימצאו במעלות [322]אחרי המספר הראשון באותו הטור בעצמו וישימו הפרש בין שני המספרים בקו ארוך |
| Then, they write the minutes they want find after the degrees and the signs and make a separation between the two numbers with a long line in the same row. | אחר כן יכתבו מה שימצאו מן הראשונים[III 119] אחרי המעלות והמזלות וישימו הפרש בין שני המספרים בקו ארוך באותו[III 120] הטור בעצמו |
| Then, they write the seconds after the minutes in the same row and separate between them with a long line. | אחר כן ישימו השניים אחרי הראשונים באותו הטור בעצמו ויפרישו ביניהם בקו ארוך |
| Then, they approach the single years that have passed and write what they find, the signs under the signs, the degrees under the degrees, the minutes under the minutes and the seconds under the seconds. | ואחר כן יכנסו בשנות הפרט שעברו ויכתבו מה שימצאו[III 121] במזלות תחת המזלות והמעלות תחת המעלות והראשונים תחת הראשונים והשניים תחת השניים |
| Then, they approach the months that have passed and write everything they find there, each type under its type. | ואחר כן יכנסו כנגד החדשים שעברו ויכתבו כל מה שימצאו שם כל מין תחת מינו |
| Then, they approach the days of the month that have passed of a month that has not been completed and write everything they find there each type under its type. | ואחר כן יכנסו בימות החדש שעברו אל החדש שלא נשלם ויכתבו כל מה שימצאו כנגדם כל מין תחת מינו |
| The same is done with the whole hours that have passed after the middle of the day and the same with the parts of an hour that has not been completed. | וככה יעשו בשעות השלמות שעברו אחר חצי היום וככה בחלקי השעה שלא נשלמה |
| Then, one starts to add up all the sixtieths: takes one minute for every sixty seconds and write how many minutes come out of the seconds with the minutes that precede the seconds, and write the remainder of the seconds that are less than sixty alone in another place. | ואחר כן יחל לחבר כל הששים ויקח לכל ששים שניים חלק ראשון ויכתוב כמה ראשונים יעלו מן השניים עם הראשונים שהם לפני השניים והנשאר מן השניים שהם פחותים מן הששים[III 122] יכתבם לבדד במקום[III 123] אחר |
| Then, one adds again all the minutes: takes one degree for every sixty minutes and write the degrees that are summed with the degrees that precede the minutes and the remaining minutes that are less than sixty, write them in the row where you wrote the seconds, only that they are written before the seconds. | ואחר כן ישוב לחבר כל הראשונים ויקח לכל ששים ראשונים מעלה אחת ומה שיתחבר מן המעלות[III 124] כתוב אותם עם המעלות שהיו לפני הראשונים והראשונים הנשארים שהם פחותים מששים כתוב אותם בטור שכתבת[III 125] שם השניים רק יהיו נכתבים לפני השניים |
| Then, add again the degrees: take one sign for every thirty degrees and write the [signs] that come out with all the [signs] that you had and what remains of the degrees that are less than thirty, write them alone before the minutes that you wrote before the seconds. | ואחר כן שוב לחבר המעלות וקח לכל שלשים מעלות מזל אחד וכתוב המעלות[III 126] העולים עם כל המעלות[III 127] שהיו לך ומה שישארו מן המעלות[III 128] שהם פחותים משלשים כתוב אותם לפני הראשונים שכתבת לפני השניים לבדד |
| Then, take out every twelve signs you find, and write the remainder alone before the degrees you wrote before the minutes preceding the seconds. | ואחר כן הוצא כל שנים עשר מזלות[III 129] שתמצא והנשאר כתוב אותם לפני המעלות שכתבת לפני הראשונים שכתבת לפני השניים לבדד |
| So, you have the position of the planet on the celestial sphere along with its degrees, minutes and seconds. | אז[III 130] יהיה לך מקום המשרת בגלגל המזלות עם מעלותיו וחלקיו ושנייו |
| You always start to count the signs from the sign of Aries. | ולעולם תחל לספור המזלות מראש מזל טלה |
| If the number of signs is twelve, write a zero in the place where the signs must be written to indicate that the planet is still in the sign of Aries, for this is not yet complete, but that it has only moved away from the sign in accordance with the degrees that have been written there and the minutes belong to the following degree. | ואם היה מספר המזלות שנים עשר כתוב אותם במקום הראוי להכתב שם[III 131] מזלות גלגל להודיע כי המשרת עודנו במזל טלה כי לא נשלם רק עבר מן המזל כפי המעלות שתמצא כתובות ויהיו הראשונים מן המעלה[III 132] הבאה |
|
כי אם[III 133] היו המעלות י"ז יהיו הראשונים הם שעברו ממעלת[III 134] י"ח ונחשוב כי הראשונים השלמים היו ט"ו שלמים ונאמר כי השניים היו מ"ה והנה הם שלש רביעיות החלק הראשון של ששה עשר ראשונים |
Chapter Four – Subtraction |
השער הרביעי |
|---|---|
Written calculations |
|
| Subtracting one number from the another is easy. | לגרוע חשבון אחד מחשבון אחר קל הוא |
| I shall give you only a general method of subtracting many digits from many digits, using the method of the arithmeticians as well as the method of the astrologers, for they have a different method. | רק אתן לך דרך כוללת לגרוע חשבונים רבים מחשבונים רבים[IV 1] על דרך חכמי החשבון גם על דרך חכמי המזלות כי דרך אחרת[IV 2] יש להם |
| Do as follows: | וככה תעשה |
| Write the number from which you want to subtract [= the minuend] in the upper row and write the digits you want to subtract [= the subtrahend] in the lower row. | כתוב החשבון[IV 3] שתרצה לגרוע ממנו בטור העליון וכתוב המספרים שתחפוץ[IV 4] לגרעם[IV 5] בטור השפל |
| The last digit in the top row must always be greater than the last digit in the bottom row. Do not consider the other digits. | ולעולם יהיה המספר האחרון בטור העליון גדול מהמספר האחרון שהוא בטור השפל ואל תחוש מן המספרים האחרים |
| If you find in one of the ranks that the digit in the lower row is greater than the corresponding digit in the upper row, return one alone from the digit that follows, for that is enough for you and consider it as ten, as the way we do in the division. | והנה[IV 6] אם מצאת באחת[IV 7] מן[IV 8] המעלות מספר הטור השפל גדול מהמספר[IV 9] שבטור[IV 10] העליון שהוא כנגדו השב אחורנית מהמספר שאחריו[IV 11] אחד[IV 12] לבדו כי יספיק לך וחשוב אותו עשרה על הדרך שאנו עושין בחלוק |
|
דמיון הטור העליון ב'ג'ד'ה' והטור השפל ט'ז'ג'ב' |
|
וראוי לגרוע כל אחד מהשפלים מן העליונים[IV 13] כל אחד ממעלתו[IV 14] ב' מה' וג' מד' |
|
ולא נוכל לחסר ז' מג' ולא ט' מב'[IV 15] |
| We always start to subtract backwards, as with the way of division, and write the remainder in the third row corresponding to the same rank in the lower row. | ולעולם[IV 16] נחל לחסר[IV 17] אחורנית[323] כדרך החלוק והנשאר נכתבנו[IV 18] בטור השלישי כנגד אותה המעלה שבטור השפל |
|
והנה גרענו ב' מה' נשאר לנו ג' כתבנו אותו[IV 19] תחת מעלה הרביעית[IV 20] |
|
חסרנו ג' מד' נשאר לנו אחד ולא כתבנוהו רק שמנו גלגל במקומו[IV 21] כי הוצרכנו להשיב אחד[IV 22] אחורנית כי המספר שבטור השפל לפניו[IV 23] גדול משכנגדו העליון והנה היו י"ג חסרנו ממנו ז' ונשארו[IV 24] ו' רק בעבור כי[IV 25] החשבון הראשון שבטור השפל[IV 26] גדול מן[IV 27] העליון שבטור[IV 28] העליון על כן הוצרכנו להשיב אחורנית אחד ונכתוב[IV 29] ה' בטור השלישי והנה היו[IV 30] למעלה י"ב נחסר ט'[IV 31] ונשארו[IV 32] ג' |
|
וזו היא הצורה[IV 33] |
| When you want to know the scales: | וכאשר תרצה[IV 34] לדעת המאזנים |
| Subtract the scale of the lower row from the scales of the upper row and keep the remainder. | תגרע[IV 35] מאזני הטור השפל ממאזני הטור העליון ותשמור[IV 36] הנשאר |
| See: if the scale of the third row is the same, then you know that your calculation is correct. | ותראה[IV 37] אם היו[IV 38] מאזני הטור השלישי כמוהו דע[IV 39] כי חשבונך[IV 40] אמת |
| If the scale of the bottom row is greater than the scale of the top row, always add 9 to the scale of the top, subtract the scale of the bottom from the sum and proceed according to the instructions. | ואם היו[IV 41] מאזני הטור השפל גדול ממאזני הטור[IV 42] העליון הוסף[IV 43] לעולם על מאזני העליון ט' וגרע מהמחובר מאזני השפל ותעשה[IV 44] כמשפט[IV 45] |
| Example. We subtract 1 from 2; 1 remains. We return it back to the zero; they are 10. We subtract 7; 3 remain. | דמיון החסרנו[IV 46] א' מב' נשאר א' השיבונו[IV 47] אחורנית על הגלגל והיו י' חסרנו ז'[IV 48] נשארו ג' |
| The scale of the lower [row] is 8 and the scale of the upper [row] is 2. We add 9 to it; they are 11. We subtract 8; 3 remain and so is the bottom scale. | והנה מאזני השפל ח' ומאזני העליון ב' הוספנו עליו ט' והיו[IV 49] י"א החסרנו[IV 50] ח' נשארו ג' וככה מאזני השפל |
| Now, we shall speak about the method of the astrologers, because they need this chapter more than the arithmeticians. | עתה נדבר על דרך חכמי[324] המזלות כי יותר צורך יש[IV 51] להם לשער הזה מחכמי החשבון |
| We already mentioned that you should set up the signs in the first rank, degrees in the second, the minutes in the third and seconds in the fourth. | וכבר הזכרנו כי כן תכון[IV 52] המזלות במעלה הראשונה והמעלות בשנית והראשונים[IV 53] בשלישית[325] והשניים ברביעית |
| One always starts to subtract backwards: the seconds in the bottom row from the seconds in the top row. The remainder is written in the third row corresponding to the upper seconds. | ולעולם יחלו לגרוע אחורנית השניים[IV 54] בטור השפל[IV 55] מהשניים[IV 56] בטור העליון והנשאר יכתבהו[IV 57] בטור השלישי כנגד השניים העליונים |
| If the lower seconds are more than the upper ones, he takes one from the upper minutes, considers it as 60 seconds, adds to them the seconds that are in the upper row, and then subtracts the lower seconds according to the instructions. | ואם היו השניים השפלים רבים מהעליונים יקח מהראשונים העליונים[IV 58] אחד יחשבהו[IV 59] ס' שניים ויחבר אליהם השניים הנמצאים בטור העליון ואחר כן יגרע השניים השפלים כמשפט |
| If he has taken one from the upper [minutes], he subtracts it from the number of minutes that are there. | ואם לקח אחד מהעליונים יגרענו מהמספרים הראשונים שהיו שם |
| Then, he subtracts the lower minutes from the upper minutes that are there and writes the remainder corresponding to them in the third row. | ואחר כן יחסר הראשונים השפלים מהראשונים העליונים הנמצאים שם ויכתוב הנשארים כנגדם בטור השלישי |
| Then, he subtracts the degrees from the degrees and write the [remainder] corresponding to them in the third row. | ואחר כן יחסר מעלות ממעלות והנשארים יכתבם בטור השלישי כנגדם |
| If the degrees in the lower row are more than the degrees in the upper row, he takes one from the signs, considers it as 30, adds them to the degrees that are written there, then subtracts, but makes sure that he subtracts one from the number of the signs that are written in the first [rank]. | ואם היו המעלות בטור השפל רבות ממעלות הטור העליון יקח מהמזלות[IV 60] אחד[IV 61] ויחשבנו[IV 62] ל'[IV 63] ויחברם אל המעלות הכתובות שם ואחר כך יגרע וישמר שיגרע אחד ממספר המזלות הכתובים בראשונה |
| Then, he subtracts the signs from the signs and write the remainder in the third row corresponding to them. | ואחר כך יגרע[IV 64] מזלות ממזלות ויכתוב הנשארים בטור השלישי כנגדם |
| If the lower signs are more than the upper ones, he always adds 12 to the upper ones, then subtracts and proceeds according to the instructions. | ואם היו המזלות השפלים גדולים[IV 65] מהעליונים יוסיף[IV 66] לעולם[IV 67] על העליונים י"ב ואחר כן יגרע ויעשה כמשפט |
| To know the scales: | לדעת המאזנים |
| One starts with the seconds, subtracts the scale of the lower seconds from the scale of the upper ones, keeps the remainder and see if the scale of seconds in the third row is just as much, then his calculation is correct. | יחל מהשניים ויגרע מאזני השניים השפלים ממאזני[IV 68] השניים העליונים וישמור הנשאר ויראה אם היה כמוהו מאזני השניים בטור השלישי חשבונו אמת |
| If he sees that he has taken one minute from the minutes and added to the seconds, he adds 6 to the scale of the upper seconds and then subtracts according to the instructions. | ואם ראה שלקח ראשון אחד מן הראשונים ושם עם השניים יוסיף על מאזני השניים העליונים ו' ואחר כך יגרע כמשפט[IV 69] |
| He does with the scales of the minutes as he has done with the seconds. | ויעשה[IV 70] למאזני הראשונים כאשר עשה לשניים |
| If he had to take a degree and convert it to 60 minutes to add them to those that are written there, add 6 to the scale of the minutes that are there, then subtract and proceed according to the instructions. | ואם הוצרך לקחת מעלה והשיבה[IV 71] לס' ראשונים לחברם[IV 72] עם הכתובים שם הוסף על מאזני הראשונים שהיו שם ו' ואחר כך תגרע ותעשה כמשפט |
| Do with the scales of the degrees the same as with the minutes and seconds. | גם כן תעשה במאזני המעלות כמשפט הראשונים והשניים |
| If you have taken from the signs one that you have set with the degrees, add 3 to the scale of the degrees that are written, then subtract and proceed according to the instructions. | ואם לקחת מן המזלות[IV 73] אחד ששמת אותו עם המעלות הוסף על מאזני המעלות[IV 74] הכתובים בראשונה ג' ואחר כן תגרע ותעשה כמשפט |
| Do with the scales of signs the same as you did with all of them. | ועשה במאזני המזלות[IV 75] כמשפט שעשית בכל אלה |
| If you added 12 to the original signs, add 3 to the scale of the signs that were first written, then subtract and proceed according to the instructions. | ואם הוספת על המזלות הראשונים י"ב הוסף על מאזני המזלות הכתובים בראשונה ג' ואחר כך תגרע ותעשה כמשפט |
| I shall tell you a rule, one thing that is necessary when subtracting: | כלל אומר לך[IV 76] דבר שהוא צורך[IV 77] למגרעת |
| The last [digit] at the end of the upper row must always be greater than the last [digit] in the lower row, when the rows are the same, the upper [has] the same [number of ranks] as the lower one. | לעולם האחרון[IV 78] שבסוף[IV 79] הטור העליון יהיה גדול מהאחרון[IV 80] שבטור[IV 81] השפל כשהטורים שוים שהעליון כמו התחתון |
| If the rows are not the same, as the upper one is greater than the lower one in respect of the number of digits, as here [igure is missing], return one back and that is enough. | ואם אין הטורים שוים שהעליון[IV 82] גדול מן התחתון[IV 83] במספר אותיות[IV 84] כזה ישיב האחד אחורנית ודי לו[IV 85] |
| [IV 86]דרך אחרת לגרוע חשבון מחשבון בהפך שכתוב למעלה שיחל לגרוע מן האחדים | |
| דמיון רצינו לגרוע ט' מב' והנו כזו הצורה | |
| נקח מג' שלפניו ויחזירנה לאחור ויהיו י"ב נשארו ג' ויכתבם בטור השלישי | |
| ועתה נרצה לגרוע ז' מג' ולא נוכל כי לא נשאר במקום הג' כי אם ב' נקח מן הד' א' ונחזירהו לאחור על הג' שהוא ב' ויהיו י"ב גרע מהם ז' וישארו ה' ונכתבנו בטור השלישי כנגד הז' | |
| ואחר כן נגרע ג' מד' שהוא ג' שכבר חסרנו ממנו א' ויצא זה כנגד זה לכן נכתוב גלגל בטור השלישי תחת הג' | |
| ואחר כן נגרע מה' וישארו ג' ונכתבנה בטור השלישי תחת הב' |
Chapter Five - Fractions |
השער הה' הוא שער השברים |
|---|---|
| It is known that the one is as a point in a circle; therefore one cannot be a fraction. Just because the whole is named with one name, as the shape that represents the entire body, while the body is composed of surfaces, therefore man considers the one as fractions and fraction of fractions in thought. | ידוע כי האחד כמו נקודה בתוך עגולה על כן לא יתכן להיות האחד נשבר רק בעבור שיקרא הכלל בשם אחד כמו הצורה שהיא כוללת כל הגוף והגוף מורכב משטחים ובעבור זה יעשה האדם מן האחד שברים במחשבה ושברי שברים |
| The arithmeticians take all their fractions from a great number so that its fractions are whole units, thus they take the half from two, the third from three and so on to the end of the first rank of the number. | וחכמי החשבון יקחו כל שבריהם מחשבון גדול שיהיו שבריו אחדים שלמים על כן יוציאו החצי משנים והשליש משלשה וככה עד סוף המערכת הראשונה בחשבון |
| The analogous number from which they derive is called the "denominator"; for the product is divided by its square. The remainder that cannot be divided is one part of it or a number of parts that can be named by the name of the units, such as one-quarter, one-third and their similar. | והדמיון שיקחו ממנו יקראוהו המורה כי על מרובעו יחלקו העולה בחשבון והנשאר שלא יתחלק יהיה חלק ממנו או חלקים שיוכל להזכירו בשם האחדים כמו רביעית שלישית והדומה להם |
| Sometimes the denominator is a number that has no parts that man can express, because it is a prime number that is not composed, such as 11 or 13, and their like. | ויש פעמים שיהיה המורה חשבון שאין לו חלקים שיוכל האדם לבטא בהם כי הוא חשבון ראשון איננו מורכב כמו י"א או י"ג והדומים להם |
| I have already mentioned that the first rank consists of 9 numbers. | וכבר הזכרתי כי המערכת הראשונה ט' מספרים |
| The one, on the one hand, is not a number, and on the other hand, it is a number. | והנה האחד מפאה אחד איננו מספר ומפאה אחרת הוא מספר |
| It is similar to an odd number, because when you sum all the odd numbers together successively the squares are generated. | והוא דומה לנפרד כי בחברך כל הנפרדים זה על זה על הסדר יולדו המרובעים |
| As well as many other matters, which there is no need to mention. | ודברים רבים אין צורך להזכירם |
| So, eight numbers remain in the first rank, half of which are prime numbers, and the other half are composite numbers. | והנה נשארו במערכת הראשונה שמנה מספרים והנה חציים ראשונים וחציים מורכבים |
|
הראשונים הם שנים שלשה חמשה ושבעה |
|
והמורכבים ארבעה ששה שמנה ותשעה |
| When there is a need for two fractions that are not of one kind, which are not similar to each other, one looks for each of the fractions: from which number each of them is derived and multiplies one number by the other; the product is the denominator. | וכאשר יצטרכו לשנים שברים שאינם ממין אחד שלם שלא ידמה זה לזה יבקשו כל אחד מהשברים מאיזה חשבון יצא כל אחד מהם ויכפלו חשבון האחד על האחר והעולה בחבור הוא המורה |
| If there are 3 types, one multiplies the number from which the [first] fraction is derived by the second number from which the second fraction is derived and multiply the product by the number from which the third fraction is derived. | ואם היה ג' מינים יכפול החשבון שיצאו ממנו השברים על החשבון השני שיצאו ממנו שברי השני והמחובר יכפלהו על המספר שיצאו ממנו שברי השלישי |
| The same is done if there are 4 types or more: one looks for a common denominator for all. | וככה יעשה אם היו ד' מינים או יותר כי יבקשו מורה אחד לכלם |
| It is called by this name [moreh, lit. indicator], because it indicates the straight path; if you want, name it by a different name, it does no harm. | ונקרא בשם הזה בעבור כי הוא יורה הדרך הישר ואם תרצה קרא לו שם אחר כי לא יזיק |
| After I have told you the methods of the denominator, I will tell you how you can calculate two fractions of two denominators, for it is in a shorter way. | ואחר שאומר לך דרכי זה המורה אומר לך איך תוכל להוציא שני שברים משני מורים כי הם יותר דרך קצרה |
| After I will finish talking about the fractions in the method of the arithmeticians and their argumentations, I will explain you the fractions of the astrologers, for they have a different method. | ואחר שאשלים לדבר על שברי דרך חכמי החשבון ומחלוקותיהם אפרש לך שברי חכמי המזלות כי דרך אחרת להם |
| I will start giving you examples from the easy ones, then I will mention the difficult ones. | ואחל לתת לך דמיונות מן הקלים ואח"כ אזכיר הכבדים |
| First, I shall tell you a rule: that the multiplication of fractions is opposite to the multiplication of integers. | ואומר לך כלל בתחלה כי כפלי השברים הפך כפלי השלמים |
| Because when it is said: multiply one-half by one-half it is as if it is said: take one-half of one-half; the result is one-quarter. | כי האומר כפול חצי על חצי כאלו אומר קח חצי החצי והנה העולה רביעית אחד |
| We know that the half is derived from two; its half is 1 and the other half is also one; one multiplied by one is one; the square of the denominator is 4, so this one is one-quarter, that is the half of one-half. | ידענו כי החצי יצא משנים והנה חציו אחד וחצי האחר גם הוא אחד והנה אחד על אחד אחד והנה מרובע המורה ד' והנה זה האחד הוא רביעי והוא חצי החצי |
| We proceed oppositely to our practice with the integers, because we are always looking for the ratio of the product to the square of the denominator. | והנה נעשה להפך מנהגנו בשלמים כי נבקש לעולם מהו ערך הנכפל ממרובע המורה |
|
וכפל שלישית על שלישית יהיה העולה תשיעית |
|
וכפל רביעית על רביעית יהיה העולה י"ו והנכפל אחד והנה הוא חצי שמינית |
| In this way up to ten and beyond. | ועל זה הדרך עד עשרה וככה למעלה ממנו |
|
כמו חלק אחד מי"א כפול על חלק אחד מי"א והנה חלק אחד מקכ"א שהוא המרובע |
| In this way you multiply fractions of one type by fractions of the same type, whether they are the equal or one of them is greater than the other, then you divide the product by the square of the denominator. | ועל זה הדרך תכפול שברי מין האחד על שברי המין בעצמו בין שיהיו שוים או שיהיה אחד מהם גדול מהאחר ואח"כ תחלק על מרובע המורה הנכפל |
|
דמיון רצינו לכפול ג' רביעיות על ג' רביעיות |
|
והנה המורה ד' |
|
לקחנו לכל אחד מג' רביעיות ג' והנה הנכפל ט' |
|
חלקנו אותם על י"ו שהוא מרובע המורה הנה הוא חציו וחצי שמיניתו |
|
ואם תרצה חלק ט' על ד' והדבר יצא שוה כי רביעית הרביעית חצי השמינית |
|
דמיון בקשנו לכפול ג' חמישיות על ד' חמישיות |
|
והנה המורה ה' |
|
לקחנו בעבור הג' חמישיות ג' ובעבור הד' חמישיות ד' כפלנו ד' על ג' עלו י"ב והוא הנכפל |
|
והנה ב' חמישיות המרובע וב' חמישיות חמישית |
| If one says fractions of two kinds: | ואם אמר שברים מב' מינים |
|
שיאמר כפול לי ב' שלישיות אחד על ג' רביעיותיו |
|
נבקש המורה לשניהם ונכפול ג' על ד' והוא המורה |
|
והנה נקח בעבור ב' השלישיות ח' וג' רביעיות ט' נכפול ח' על ט' יעלו ע"ב והוא חצי קמ"ד שהוא מרובע המורה |
|
ועלה בחשבון מחצית אחד שוה |
|
ואם תכפול ב' על ג' יהיה כמו כן מחצית המורה שהוא י"ב |
| If you do it with 2 denominators it is easier and there is no need for the square of the denominator, you only look at the product that resulted by multiplying one denominator by the other, consider it as the square, and divide by it. | ואם עשית זה מב' מורים יהיה הדבר יותר קל ואין צורך למרובע המורה רק הסתכל לעולם אל הנכפל העולה מכפל המורה האחד על האחר וחשבהו כמו המרובע ועליו תחלק |
|
דמיון לקחנו המורה האחד ג' בעבור כי אמר שלישיות והמורה האחר ד' בעבור כי אמר רביעיות נכפול המורה האחד שהוא ג' על המורה האחר שהוא ד' ועלו י"ב והוא המבוקש כי העולה נקח ערכו אליו ונקח בעבור הב' שלישיות שנים כי מג' לקחנוהו ומג' רביעיות שלשה כי מד' לקחנוהו ונכפול ב' על ג' עלו ו' והוא חצי מספר הנכפל מהמורים |
|
שאלה כמה ד' שביעיות כפולים על ז' תשיעיות |
|
נבקש מורה אחד לשניהם והנו ס"ג בכפל ז' על ט' |
|
וד' שביעיותיו הם ל"ו כי השביעית ט' וז' תשיעיות מ"ט כי התשיעית ז' ונכפול ל"ו על מ"ט עלו אלף ותשס"ד |
|
ומרובע המורה ג' אלפים וט' מאות וס"ט |
|
וכאשר חלקנו חשבוננו הראשון על ס"ג עלו כ"ח שהם ד' על ז' והם מן ס"ג ד' תשיעיות שלמות או אם תרצה לומר שהם ג' שביעיות ותשיעית שביעית |
|
ואם לקחנו בב' מורים יהיה הנכפל ס"ג והעולה בידנו בכפל כ"ח והנה הדבר שוה |
| If there are fractions of three types: | ואם היו שברים מג' מינים |
|
כמו ב' שלישיות וה' ששיות וד' שביעיות |
|
קח להם מורה אחד והוא שנכפול ג' על ו' עלו י"ח עוד נכפול י"ח על ז' עלה קכ"ו והוא המורה |
|
הנה ב' שלישיות קכ"ו פ"ד |
|
וה' ששיות ק"ה |
|
וד' שביעיות ע"ב |
|
כפלנו פ"ד על ק"ה והמחובר על ע"ב והעולה מהם בחלוק הוא חלק ממרובע קכ"ו והחלוק יהיה מ' |
| If we take 3 denominators for them, since they are three types, you do not need the square of the denominator, but take the denominator and divide the product of the numbers by it. | ואם נקח להם ג' מורים מפני היותם ג' מינים לא תצטרך למרובע המורה אבל תקח המורה עליו תחלק הנכפל מהמספרים |
|
דמיון כפלנו ב' על ה' עלו י' כפלנו י' על ד' עלו מ' והוא חלק מקכ"ו שהם ב' שביעיות וב' תשיעיות השביעית |
|
או תעשה כן כפול ג' על ו' והוא י"ח והוא המורה וכפול ב' על ה' יהיו י' נקח ד' שביעיות מי' יהיו ב' שביעיות וב' תשיעיות השביעית |
|
או כפול ו' על ז' והיו מ"ב והוא המורה וכפול ה' על ד' יהיו כ' נקח ב' שלישיות מכ' יהיו ב' שביעיות וב' תשיעיות השביעית |
|
או כפול ג' על ז' עלו כ"א והוא המורה ואח"כ כפלנו ב' על ד' עלו ח' לקחנו ה' ששיות והעולה הוא חלק מכ"א |
| If we have integers together with a number that contains no integer but only fractions: | ואם היה לנו שלמים עם מספר שאין שם שלמים כי אם שברים |
| We take the fractions from the denominator and give the whole denominator for each integer according to the number of the whole denominator and finally divide by the denominator. | נקח השברים מהמורה ולכל שלם נתן לו מורה שלם כמספר המורה השלם ונחלק באחרונה על המורה |
|
דמיון רצינו לכפול ד' שלמים על ג' חמישיות אחד |
|
והמורה ה' |
|
ובעבור שיש לנו ד' שלמים נקח להם כ' ונכפול ד' על ג' ונחלק בה' יעלו ב' שלמים וב' חמישיות |
| If we want to multiply integers and fractions by integers and fractions that are of the same kind. | ואם רצינו לכפול שלמים ושברים על שלמים ושברים שהם ממין אחד |
| We first multiply the integers by the integers, then the fractions by the integers of the one number, likewise the integers of the other number by the fractions of the one number and then the fractions by the fractions. | נכפול בתחלה השלמים על השלמים ואח"כ הנשברים על השלמים של חשבון האחד גם השלמים של חשבון האחר על הנשברים של החשבון האחד ואח"כ הנשברים על הנשברים |
| Or we convert all into fractions and multiply these by those and divide the product by the square of the denominator. | או נשיב הכל נשברים ונכפול אלה על אלה והעולה נחלקנו על מרובע המורה |
|
דמיון רצינו לכפול ד' שלמים וב' חמישיות על ה' שלמים וג' חמישיות |
|
כזה |
|
נכפול תחלה השלמים על השלמים עלו כ' |
|
אח"כ נכפול ד' על ג' יהיו י"ב חמישיות שברים |
|
גם ב' על ה' יהיו י' שברים במיניהם |
|
והנה כ"ב שברים |
|
ואח"כ נכפול השברים על השברים ב' על ג' יעלו ו' והם שברי שברים במעלה השלישית השלמים נחלקם על ה' שהוא המורה עלה שבר אחד ונשאר לנו במעלה השלישית אחד שהוא שבר השבר והשבר שעלה בידנו נחברנו אל כ"ב שהיה לנו הנה כ"ג נחלקם על ה' עלו ד' שלמים ונשארו ג' והנה השלמים כ"ד והשברים ג' שהם ג' חמישיות שהם ט"ו מכ"ה שהוא המרובע ושבר השבר שהוא חומש החומש שהוא והם י"ו מכ"ה |
|
והדרך האחרת |
|
לקחנו לד' השלמים כ' הוספנו עליו ב' שהם השברים עלו כ"ב חומשין והוא החשבון האחד |
|
גם השני על הדרך הזאת כ"ח |
|
נכפול זה על זה ונחלק העולה על המרובע שהוא כ"ה יעלו כ"ד וישארו י"ו שלא יתחלקו |
|
דמיון אחר רצינו לכפול ג' שלמים וד' חומשין על ב' שלמים וג' חומשין |
|
כזה |
|
נכפול תחלה שלמים על שלמים והם ו' |
|
ואח"כ נכפול שלמים על שברים האלכסונין |
|
ג' על ג' והם ט' |
|
וב' על ד' והם ח' |
|
ובין הכל י"ז שברים ממעלה העליונה |
|
ונכפול שברים על שברים ד' על ג' והם י"ב שברי שברים מהמעלה השנית |
|
נחלקם על ה' עלו בידנו ב' שברים והנשאר ב' שברי שברים שלא עלה בחלוק נחבר מה שעלה בחלוק עם השברים שהוא י"ז והם י"ט נחלק על ה' עלו ג' שלמים נחברם אל השלמים שהיו ו' והם ט' נשארו ד' שהם כ' שברי שברים ועם שנים שהיו לנו הם כ"ב |
|
והנה סך הכל ט' שלמים וכ"ב שברים מכ"ה השלם |
| Example. We want to multiply integers and fractions by integers and fractions where the fractions are not of the same kind. | דמיון רצינו לכפול שלמים ושברים על שלמים ושברים שאין השברים ממין אחד |
|
הנה על הדרך הזה האחד ג' שלמים וד' חמישיות והשני ו' שלמים וז' שמיניות |
|
כזה |
| Multiply the units by the units that are in the first number. | כפול האחדים על האחדים שהם במספר הראשון |
| Multiply also the fractions by the fractions according to the rule, because the product of the fractions by the fractions is parts of the denominator. | גם כפול השברים על השברים כמשפט כי כפל השברים על השברים הם חלקי המורה |
| But, when multiplying the integers by the fractions, we have to remember that their parts are not the same. | רק יש לנו לשמור כשנכפול השלמים על השברים כי אין מחלקותם שוה |
|
והנה נכפול שלמים על שלמים ג' על ו' עלו י"ח |
|
ונכפול עוד אלו ג' על שברי החשבון שהם ז' יעלו כ"א נחלקם על ח' כי שמיניות הם יעלו ב' שלמים והנה ב' שלמים ונשארו ה' שמיניות ידענו כי המורה הוא מ' כי תכפול ה' על ח' ואלה הה' שמיניות כ"ה חלקים כי תכפול ה' על חמישיות שהם ה' |
|
ונשוב לכפול הו' על ד' חמישיות יעלו כ"ד נחלקם על ה' יעלו ד' שלמים והנה יהיו השלמים כ"ד וישארו ד' חמישיות והם ל"ב חלקים כשתכפול ד' על ח' נחבר אליהם הכ"ה חלקים שהיו לנו יעלו נ"ז חלקים נעשה מהם אחד שלם מארבעים ויהיו כ"ה שלמים ונשארו י"ז אח"כ נכפול ד' על ז' יעלו כ"ח חלקים נחבר אליהם י"ז יהיו מ"ה והנה נתן אחד שלם ממ' ויהיו השלמים כ"ו והנשאר ה' חלקים שהם שמינית אחד |
| The method of the arithmeticians is that they look for one common denominator for fractions that are not of one kind and the number of the denominator is one integer. | ודרך חכמי החשבון שיבקשו לשברים שאינם ממין אחד מורה אחד כולל שניהם ומספר המורה הוא אחד שלם |
|
ובעבור כי השברים הם חמישיות ושמיניות יהיה המורה ארבעים והנה נקח לחשבון שהוא ג' ק"כ ולד' חמישיות ל"ב הנה המספר קנ"ב וזה צורת האותיות ונקח לו' השלמים ר"מ ונחבר אליהם ל"ה שהם ז' שמיניות יהיה המספר השני רע"ה והנה נכפול זה על זה והנה עלה מ"א אלף וח' מאות וז' הצורה |
|
חלקנום על אלף ושש מאות שהוא מרובע המורה עלו כ"ו שלמים נשארו ר' שלא עלו בחשבון |
|
ובקש מהו ר' מן המרובע שהוא אלף ושש מאות והנה הוא שמיניתו |
| We can know the remainder in another way: | ונוכל לדעת זה הנשאר בדרך אחרת |
| We always divide the remainder of the square by the denominator itself, so the quotient is parts of it. | שנחלק לעולם הנשאר מהמרובע על המורה בעצמו והעולה הם חלקים ממנו |
|
והנה נחלק ר' על מ' עלו ה' שהוא שמיניתו |
| Another method with 2 denominators: | דרך אחרת מב' מורים |
|
הנה נשים החשבון האחד שהוא ג' ט"ו ונחבר אליהם ד' יהיה החשבון הראשון י"ט נקח לששה מ"ח נחבר אליהם ז' יעלו נ"ה והוא החשבון השני נכפול זה על זה יעלו אלף ומ"ה נחלק אותו על הנכפל שהוא כפל ה' על ח' והוא מ' ויעלו כ"ו שלמים נשארו ה' שהוא שמינית |
| Now, we should speak of integers and fractions that man cannot express. | ועתה יש לנו לדבר על שלמים ונשברים שלא יוכל האדם לבטא בהם |
| If one of the fractions is one that can be expressed and the other is one that cannot be expressed, then proceed as follows: | והנה אם היה אחד מהשברים שיוכל לבטא בהם והאחרים שלא יוכל לבטא בהם יעשה ככה |
|
דמיון כמה שלש שביעיות אחד על ה' חלקים מי"א כי הוא השלם ולא יוכל אדם לבטא בו |
|
והנה נכפול השברים על השברים והנה יהיה המורה ע"ז |
|
והנה יש לנו להשמר כי השברים יהיו להפך כי כל אחד מהז' יהיו י"א וכל אחד מהי"א יהיו ז' |
|
והנה נקח בעבור ג' שביעיות ל"ג ובעבור ה' חלקים מי"א נקח ל"ה והנה נכפול אלה על אלה עלו אלף קנ"ה נחלקם על ע"ז עד שנדע כמה הם השברים העולים מזה הכפל אל ערך ע"ז שהוא השלם והם ט"ו והנה מן ע"ז פחות מעט מחמישית אחד |
|
ועל דרך דקדוק יפה נחלק אלה ט"ו על י"א שהוא השביעית יעלה שביעית אחד שלם וד' חלקים מי"א |
|
ואם נחלק על ז' יעלו ב' חלקים מי"א ושביעית חלק |
|
דמיון אחר לב' שברים שלא יוכל האדם לבטא בהם |
|
נשים החשבון האחד י"ג והשני י"ט |
|
והנה בקשנו לכפול ט' חלקים מי"ג על י"ז חלקים מי"ט |
|
נבקש בתחלה המורה בזה הדרך שנכפול י"ג על י"ט ועלה המספר רמ"ז והוא המורה |
|
אח"כ כפלנו ט' בי"ט ועלה קע"א |
|
וכפלנו י"ז בי"ג ועלה רכ"א |
|
והנה כפלנו זה על זה והיה העולה ל"ז אלפים ותשצ"א |
|
חלקנום על רמ"ז והיה קנ"ג והנה העולה מכפלנו ט' בי"ז הוא ג"כ קנ"ג וערך זה אל רמ"ז כערך המספר הראשון אל המרובע רמ"ז והוא המבוקש |
|
ואם תרצה לדקדקנו חלק קנ"ג על י"ט ויהיו ח' חלקי' מי"ג וחלק אחד מי"ט בי"ג |
|
או אם תרצה חלקהו על י"ג ויהיו י"א חלקי' מי"ט וי' חלקים מי"ג בי"ט |
| If you have integers and fractions that are like this, proceed in the way that I have shown you when you have integers and fractions that you can express. | ואם היו לך שלמים עם שברים שהם בדרך זה עשה כדרך שהראיתיך כשיהיו לך שלמים עם שברים שתוכל לבטא בהם |
| I mentioned this method because it is very necessary for most problems and for the matters of the square numbers to know their roots, when they are fractions that man cannot express, as I will explain in chapter seven. | והזכרתי זה הדרך כי צורך גדול יש אליו ברובי השאלות ובדברי המרובעים לדעת שרשיהם כשהם נשברים ולא יוכל האדם לבטא בהם כמו שאפרש בשער השביעי |
| I shall tell you a general method for a fraction of fractions of fractions and give you one example that is enough for you, because it is not needed for proportions, neither for roots, nor for problems. | ואומר לך דרך כוללת לשבר שברי הנשברים ואתן דמיון אחד ויספיק לך כי אין צורך לדבר הזה בערכים ולא בשרשים ולא בשאלות |
|
דמיון כפלנו ב' שלישיות רביעית חמישית על שש (ד') שביעיות שמינית |
|
והנה השברים רבים אך אלמד לך דרך קצרה איך תעשה |
|
דע כי מאחר שיש לך ששיות ושמינית אין צורך לשלישית ורביעית והנה נבקש חשבון שיש לו חמישית וששית ושביעית ושמינית |
|
נכפול ה' על ו' יעלו ל' גם ל' על ז' יהיו ר"י גם ר"י על ח' יעלו אלף ו' מאות ופ' |
|
והנה נבקש המספר הראשון והנה חמישית המורה של"ו ורביעיתו פ"ד וב' שלישיותיו נ"ו וזהו החשבון האחד |
|
וכבר ידענו כי השמינית ר"י ושביעיתו ל' ובעבור שהם ד' שביעיות יהיה המספר השני ק"כ |
|
נכפול זה על זה יהיה המספר י' (ו') אלפים ופ' (תש"כ) חלקנו זה על אלף ו' מאות ופ' עלו ו' (ד') ואלה הו' (ד') הם חמישית שמינית (חצי ששית) השביעית שהשביעית ר"מ והשמינית ל' והחמישית ו' |
| Now we talk again about the division of the fractions. Do as I have shown you, by turning the fractions into whole units. | ועתה נשוב לדבר על חלוק השברים עשה כדרך שהראיתיך שתשיב הנשברים אחדים שלמי' |
| If there are integers with the fractions, proceed according to the instructions. | ואם היו שלמים עם השברי' עשה כמשפט |
|
דמיון בקשנו לחלק ג' שלמים ושתי חמישיות על ב' שלמי' וד' שביעיות אחד |
|
והנה המורה ל"ה |
|
והג' שלמים ק"ה וב' חמישיות י"ד והנה החשבון קי"ט ונשיב הב' השלמים האחדים ע' והד' שביעיות כ' הנה צ' חלקנו קי"ט עליו עלה אחד שלם ונשארו כ"ט שהם שתי תשיעיות ועשירית אחד |
|
דמיון לנשברים לבדם חלק ז' תשיעיות על ב' שביעיות |
|
והנה המורה ס"ג |
|
ושבע תשיעיותיו מ"ט |
|
וב' שביעיותיו י"ח |
|
חלקנו זה על זה עלו ב' וו' תשיעיות וחצי תשיעית |
| You proceed in this way, because there is no great need to divide fractions. | ועל זה הדרך תעשה כי אין צורך גדול לחלק הנשברים |
| We talk again about their addition. | ונשוב לדבר על חבורם |
|
חברנו ב' חמישיות אחד על ה' שביעיות אחד כמה העולה |
|
הנה המורה ל"ה |
|
וב' חמישיותיו י"ד |
|
וה' שביעיותיו כ"ה |
|
נחברם והנה ל"ט |
|
נקח בעבור ל"ה אחד שלם ונשארו ד' שהם ד' חמישיות מהשביעית שהם אחד מל"ה |
| How Much Problem - Money | |
|
שאלה חברנו אל ממון תשיעיתו ועשירתו והיו נ' |
|
נשים המורה צ' |
|
וידוע כי תשיעיתו ועשיריתו י"ט נוסיפם על צ' יהיו ק"ט |
|
והנה גם נשיב הנ' מערך התשיעית יהיו ד' מאות ונ' נשיב הד' מאות ונ' מערך העשירית יהיו ד' אלפים ות"ק |
|
נחלק זה על ק"ט ויעלו מ"א שלמים גם ל"א חלקים מזה שחלקנו עליו |
|
והנה נבחן אם זה אמת |
|
ידענו כי עשירית מ' ד' שלמים |
|
ונקח לאחד שנשאר ק"ט נחבר אליו ל"א שהם יתרים על השלמים הנה ק"מ ועשיריתם י"ד ואלה הם חלקי העשירית הנוספים על השלמים |
|
ונשוב לקחת התשיעית והנה מל"ו ד' שלמים |
|
ונשארו ה' שלמים נשים כל אחד ק"ט יהיו תקמ"ה נחבר אליהם ל"א היתרים על השלמים יהיו תקע"ו ותשיעיתם ס"ד |
|
נחבר אליהם י"ד שעלו מן העשירית יהיו ע"ח |
|
גם נחבר אליהם ל"א היתרים יהיו ק"ט והנה אחד שלם |
|
והנה הכל נ' שלמים |
|
שאלה אחרת לקחנו חמישית ממון גם שביעיתו ותשיעיתו כמה הוא מערך הממון |
|
תוכל להוציא שאלה זו על שני דרכים |
|
האחד שהתשיעית פחותה משאר השברים האחרים הנה נחשוב כי הם ג' תשיעיות והיתרון שיש בין החמישית והתשיעית ד' והיתרון שיש בין החמישית והשביעית ב' נכפול ב' על ד' יעלו ח' נעשה מן הז' תשיעית אחת יהיו ד' תשיעיות שלמות ונשאר אחד והיתרון בין השביעית (?) והתשיעית (?) ב' והנה הממון הוא ד' תשיעיות וג' חלקים שהם ג' חמישיות שביעית תשיעית |
|
והדרך האחרת שנבקש מורה שנכפול ה' על ז' יהיו ל"ה גם נכפול זה על ט' יעלו שט"ו והוא המורה |
|
ואח"כ נחבר חמישית זה המורה ושביעיתו ותשיעיתו יהיו קמ"ג נחלקם על ל"ה והנה הם ד' תשיעיות ונשארו ג' חלקים מל"ה כי ל"ה הוא התשיעית וה' הוא שביעית התשיעית ולכן ג' חלקים הם ג' חמישיות שביעית התשיעית |
|
שאלה אחרת ממון הוספנו עליו מחציתו ושלישיתו וחמישיתו וששיתו ובין הכל היו מ' כמה היה הממון |
|
ידענו כי החצי והשלישית והששית הוא אחד שלם |
|
ונחשוב כי היה לו אחד והנה שנים ויש לנו תוספת החמישית |
|
הנה יש לנו לחלק מ' על ב' וחמישית והעולה הוא הממון והנה נקח לכל אחד מהשלמים ה' ונשים עמהם א' שהוא החמישית יהיו י"א גם נכפול מ' על ה' עד שיהיו דרך אחד יהיו ר' נחלקם על י"א יעלו י"ח שלמים ועוד ב' חלקים מי"א |
|
נבחן זה |
|
נקח חציו שהוא ט' שלמים וחלק אחד מי"א |
|
והנה יהיה לנו כ"ז שלמים וג' חלקים מי"א |
|
והשלישית ו' שלמים וב' שלישיות אחד |
|
והנה יהיו לנו ל"ג וג' חלקים וב' שלישיות |
|
והחמישית מט"ו נקח ג' שלמים |
|
היו לנו ל"ו שלמים |
|
ונשאר לנו לקחת חמישית ג' שלמים והנה נקח לכל אחד י"א ונחבר אליהם הב' חלקים היתרים יהיו ל"ה וחמישיתם ז' |
|
נחבר אליהם הג' חלקים שהיו לנו וב' שלישיות |
|
ונקח ששית י"ח יהיו ג' שלמים |
|
נחברם אל ל"ו יהיו ל"ט שלמים |
|
ושתי ששיות הם שליש אחד |
|
נחברנו אל י' חלקים וב' שלישיות חלק שהיו לנו יהיו י"א חלקים והוא אחד שלם |
|
והכל מ' |
| How Many Problem - Group of People | |
| A man passed by a group of people. He said to them: hello one hundred people. They answered him: we are not one hundred people, but all of us, and other like us, and half of us, and a quarter of us together with you would be one hundred.
|
שאלה אדם עבר על אנשים אמר להם שלום עליכם מאה איש ענו לו אין אנחנו מאה רק אנחנו ואחרים כמונו ומחציתנו ורביעיתנו ועמך נהיה מאה |
|
והנה נקח למספרם אחד ואחד כמוהו הנה שנים וחצינו חצי אחד הנה שנים וחצי נוסיף רביעיתנו הנה יהיו שנים וג' רביעית ובעבור שיש לנו רביעיות נקח לכל אחד שלם ד' יהיו ח' ונחבר אליהם הג' רביעים יהיו י"א |
|
ובעבור שאמרו כי עמו יהיו מאה יהיה מספרם עם התוספת (ת)צ"ט נשיבם מדרך הד' יהיו שצ"ו נחלקם על י"א יהיו ל"ו וככה מספרם |
| Buy and Sell Problem | |
|
שאלה אדם קנה בק' זהובים ק' ליט' ואח"כ מכר הנ' ליט' ורביע בזהוב והנ' האחרים מכר ליט' פחות רביע בזהוב נבקש לדעת אם הרויח או הפסיד |
|
נשיב הנ' ראשונים ר' כי רביעיים הם נחלקם על ה' כי ליט' ורבי' ליט' מכר בזהוב ויהיו מ' זהובים גם נכפול הנ' האחרי' על ד' יהיו ר' נחלקם על ג' כי ג' רביעיי' מכר בזהוב והנה יהיו ס"ו זהובים ושתי שלישיות זהוב נחבר אליהם המ' יהיה הריוח ו' זהובים ושתי שלישיות |
|
שאלה אחרת אדם קנה ג' חמישיות ליט' בפשוט ומכר ד' שביעיות ליט' בפשוט והרויח פשוט כמה היה ממונו |
|
בקש המורה והוא ל"ה שהוא כפל ה' על ז' |
|
והנה ג' חמישיותיו כ"א |
|
וד' שביעיותיו כ' |
|
והממון היה כ' והליט' י"ב |
|
שאלה אדם קנה ד' שביעיות ליט' בפשוט ומכר אותם ה' תשיעיות ליט' בפשוט והרויח פשוט כמה היה הממון |
|
ידוע כי ד' שביעיות אחד יותר מה' תשיעיות אחד |
|
והנה המורה ס"ג |
|
וה' תשיעיותיו ל"ה |
|
וד' שביעיותיו ל"ו |
|
ותוכל לבחון זה כי אחר שקנה ד' שביעיות ליט' בפשוט וממונו ל"ה הנה יש לו כ' ליט' עשה מהם תשיעיות יהיו ק"פ חלק זה המספר על ה' כי ה' תשיעיות מכר בפשוט יעלה בידך ל"ו |
|
ואלו אמר כי הרויח ב' פשוטים |
|
כפלם על ל"ה יהיו ע' |
|
ואם אמר ג' פשוטים |
|
יכפול על ל"ה ג' פעמים |
| And so on to the end of all numbers | וככה עד סוף החשבון |
|
שאלה אדם קנה ט' חלקים מי"ז חלקי ליט' בפשוט ומכרם י' חלקים מי"ט חלקי ליט' בפשוט והרויח פשוט כמה היה הממון |
|
בקש המורה והוא שכ"ג |
|
ידוע כי ט' חלקים מי"ז הם קע"א |
|
וי' חלקים מי"ט הם ק"ע וכך היה הממון |
|
והליט' צ' |
| The following reason of subtraction is easy: | וזה דבר המגרעת קל הוא |
| For you set one denominator for two fractions, then consider the denominator as one integer. | כי תשים מורה אחד לב' שברים והמורה תשימנו אחד שלם |
|
דמיון רצינו לגרוע ד' תשיעיות מה' שביעיות |
|
המורה ס"ג |
|
וה' שביעיותיו מ"ה |
|
וד' תשיעיותיו כ"ח |
|
חסרנו כ"ח ממ"ה ישארו י"ז |
| Now, we shall discuss the method of astrology again | עתה נשוב לדבר על דרך חכמת המזלות |
| Make sure you understand their ways; because Ptolemy and his colleagues found the way to the roots of square numbers only according to them. | ושים לבך להבין דרכיהם כי תלמי וחביריו לא מצאו דרך שרשי המרובעים אלא על פיהם |
| Know that man can divide every circle and what is non-circular into as many parts as he wants, depending on his need and desire. | ודע כי כל עגול ומה שאיננו עגול יכול האדם לחלקו על כמה חלקים שירצה כפי חפצו וצרכו |
| The arithmeticians found no smaller number that has many parts that are integers, only 12, because it has a half, a third, a quarter, a sixth and a half of a sixth. | והנה חכמי החשבון לא מצאו חשבון קטן שיש לו חלקים רבים שהם אחדים שלמים רק י"ב כי יש לו חצי ושלישית ורביעית וששית וחצי ששית |
| This is because there is no number smaller than it, whose factors add up to more than itself, only it alone, because its factors exceeds by one-third over itself. | והיה כן בעבור שאין חשבון פחות ממנו שיהיו חלקיו רבים ממנו רק הוא לבדו כי חלקיו יוסיפו עליו שלישית |
| 120 is its analogous number in the tens; therefore, its factors are twice the number, no more nor less. | וק"כ דומה לו בעשרות על כן חלקיו כפל המספר בלי תוספת ומגרעת |
| That is why the astrologers divided the sphere into 12 parts. | ע"כ חלקו חכמי המזלות הגלגל לי"ב |
| They named each sign after the shape of the constellation of the highest stars, which are close to the line of the celestial circle. | וקראו כל מזל בשם צורת הכוכבים העליונים שהם קרובים לקו גלגל המזלות |
| Also because they found that in the solar year the moon reappears 12 times. | ועוד כי מצאו בשנת השמש שתתחדש הלבנה י"ב פעמים |
| They divided the celestial sphere into 360 degrees, because this number is close to the number of the days of the solar year. | וחלקו הגלגל על ש"ס מעלות שזה המספר קרוב למספר ימי שנת החמה |
| There is no number smaller than it that has all the parts that man can express except the seventh. | ואין מספר פחות ממנו שכל החלקים שיבטא אדם בהם יש לו חוץ מהשביעית |
| Therefore, when this number is multiplied by 7, the result is 2520 and this is the number that has all parts. | ע"כ כשיכפול זה החשבון על ז' יעלה אלפַים וה' מאות וכ' וזהו המספר שיש לו כל החלקים |
| Often the arithmeticians need it. | ופעמים רבות שיצטרכו בעלי החשבון אליו |
| As saying: A number, We have added to it all of its parts from half to tenth; what is the ratio of the sum to it? | כאומר חשבון חברנו אליו כל החלקים מחצי עד עשירית מה ערך המספר אליו |
| This whole number is considered as one integer. | כי יחשוב זה החשבון הכולל כי הוא אחד שלם |
| When we divide the celestial sphere into 12 parts, each sign has 30 degrees and there is no number smaller than it that has so many parts as it, because it has a half, a third, a fifth, a sixth and a tenth. | וכאשר חלקנו הגלגל על י"ב עלה לכל מזל ל' מעלות ואין מספר פחות ממנו שיש לו חלקים רבים כמוהו כי יש לו חצי שלישית חמישית ששית ועשירית |
| Since it does not have a quarter, this number has been doubled, so it become 60. | ובעבור שאין לו רביעית כפלו זה החשבון והיה ס' |
| Therefore, they divide each degree by it, which is as a sixtieth, and they called them "primes". | על כן חלקו כל מעלה ממנו שהיא כמו אחד על ששים חלקים וקראו אותם חלקים ראשונים |
| They divided each prime to 60 and called them "seconds". | וחלקו כל ראשון לששים וקראום שניים |
| Likewise, they divide each second into 60 and called the result "thirds". | גם ככה עשו על כל שני על ששים והעולה יקראו שלישיים |
| They proceed so to ten, each [is divided] in sixtieths, and even further if necessary. | וככה יעשו עד עשרה כל אחד לששים ויותר אם יצטרכו |
| Now, it should be discussed about how they are multiplied one by the other. | ועתה יש לדבר איך יכפלו זה על זה |
| Always consider the degrees as if they are units of integers. | ולעולם חשוב כי המעלות הם כמו אחדים שלמים |
| So, if you multiply degrees by degrees, the product is degrees. The product of degrees by minutes is minutes, and by seconds is seconds. | והנה אם כפלת מעלות על מעלות יהיה הנכפל מעלות וכפל מעלות על ראשונים ראשונים ועל שניים שניים |
| The rule: the product of degrees by any type is the same type itself. | והכלל כפל מעלות על איזה מין שיהיה יעמוד אותו המין בעצמו |
| The product of minutes multiplied by minutes is seconds, and the product of minutes by seconds is thirds and in this way for all types. | וכפל ראשונים על ראשונים יהיה העולה שניים וראשונים על שניים יהיה העולה שלישיים ועל זה הדרך כל המינין |
| The product of seconds multiplied by seconds is fourths, and by thirds is fifths. | וכפל שניים על שניים יהיה הנכפל רביעיים ועל שלישיים חמישיים |
| The product of thirds by thirds is sixths, and so is the product of thirds by fourths sevenths. | וכפל שלישיים על ששיים ששיים עד שיהיה כפל שלישיים על רביעיים שביעיים |
| Fifths by fifths or thirds by sevenths is tenths. | וחמישיים על חמישיים או שלישיים על שביעיים עשיריים |
| Now I shall give you two correct methods: | והנה אתן לך שנים דרכים נכונים |
| The first method by writing: | הדרך האחד במכתב |
| Set the degrees in the first rank, the minutes in the second rank and so on, all fractions successively. | שתשים המעלות במעלה הראשונה והראשונים במעלה השנית וככה כל השברים זה אחר זה |
| This writing is opposite to what we do in the multiplication of integers, because the smallest number is in the first [rank]. | וזה המכתב בהפך מה שאנו עושים בכפל השלמים כי החשבון המעט הוא בראשונה |
| If you have no degrees, write a zero in the first [rank]; if you have no minutes, write a zero in its place, and so you do it at the place of each fraction, if there is a smaller fraction after it. | ואם אין לך מעלות כתוב גלגל בראשונה ואם אין לך ראשונים כתוב גלגל במקומו וככה תעשה במקום כל שבר אם יש שבר אחריו פחות ממנו |
| With this method you can know in which rank of the fractions any fraction will stand. | ובזה הדרך תוכל לדעת באיזו מעלה מן השברים יעמד איזה שבר שתרצה |
| Proceed as with integers, but you have to make sure that you put a vertical line between all types of fractions. | ועשה כדרך השלמי' רק יש לך להשמר שתשים קו באורך בין מיני השברים כלם |
| If there are 2 digits of whichever type of fractions, such as 22, when you write them down, you have to do like this: set them breadthwise between the two lines according to their rank, as you do it with integers. | ואם היו ב' חשבונים באיזה מין שיהיה מן השברים כגון כ"ב יש לך לעשות כשתכתבם שים אותם ברוחב שבין שני הקוים במעלתם על הדרך שאתה עושה בשלמים כזה |
| We have already drawn lines between the fractions and arrived to thirds for the upper rows and also for the lower rows. | הנה כבר שמנו קוים בין השברים והגענום עד שלישיים ככה הטורים העליונים וככה השפלים |
| When we multiply the upper rows by the lower rows, their product is the number that is written in the bottom. | וכאשר כפלנו הטורים העליונים על השפלים עלה מספרם המספר הכתוב למטה |
| We divide each rank by 60, then add the quotient to what is in the preceding rank, and write the remainder alone. We do this with each rank until we arrived to the degrees that are as the integers. | חלקנו כל מעלה על ששים וחברנו העולה על ההוה במעלה הראשונה והנשאר כתבנו לבדד וככה עשינו מכל מעלה ומעלה עד שהגענו למעלות שהם כמו השלמים |
| So, of sixths remain 33, of the fifths 56, of the fourths 31, of the thirds 24, of the seconds 30, of the minutes 7 and of the degrees also 7. | והנה נשארו מן הששיים ג'ג' ומן החמישיים ו'ה' ומהרביעיים א'ג' ומהשלישיים ד'ב' ומהשניים 0ג' ומהראשונים ז' ומהמעלות גם כן ז' |
| The second method is by expression: | והדרך השנית במבטא |
| You sum the two fractions by adding the ranks of the fractions. | שתחבר השנים השברים ובמחברתם מעלות השברים |
| When we do according to the method of the arithmeticians that we convert the upper rows into thirds, the resulting number is: 464643. | וכאשר עשינו על דרך חכמי החשבון שהשיבונו הטורים העליונים אל שלישיים עלה החשבון כך ג' ד' ו' ד' ו' ד' |
| Likewise, we do it with the lower [rows], the resulting number is: 715451. | ככה עשינו בשפלים עלה החשבון כך א' ה' ד' ה' א' ז' |
| We multiply one by the other, the resulting number is: 332429298993; it has 12 rows. | והנה כפלנו זה על זה ועלה המספר כזה ג'ט' ט'ח' ט'ב' ט'ב' ד'ב' ג'ג' והם י"ב טורים |
| All these are sixths; we divide them by 60 and the result are fifths: 5540488316, and 35 sixths remain in the first number. | והנה כל אלה ששיים חלקנום על ס' ועלו חמישיים כזה ו' א' ג' ח'ח' ד'0 ד'ה'ה' ונשארו ל"ה ששיים במספר הראשון |
| We proceed so successively; the number resulting last and what is left of each rant will be as the number in the first method. | וככה עשינו על זה הסדר והיה המספר שעלה באחרונה גם הנשאר מכל מעלה ומעלה כמספר הדרך הראשונה |
| I had to show the method of these parts, which are minutes to thirds, because with this method King Ptolemy calculated the chords of the arcs until reaching to fifths, which are by multiplying tenths. | והוצרכתי להראות דרך אלה החלקים שהם הראשוני' עד שלישיים כי על זה הדרך הוציא תלמי המלך יתרי הקשתות עד שהגיעם אל חמישיים והם בכפל עשיריים |
| He also did all of this to extract the roots of the square numbers that do not have a real root truly, but it is only approximated to the truth, because there are no minutes or seconds left in dividing the product, not even thirds, as I will explain in the seventh chapter. | וכל זה עשה להוציא שרשי המרובעים שאין להם שורש נכון באמת רק יוציאוהו קרוב אל האמת כי לא ישארו בחלוק הכפל ראשונים ולא שניים ואפילו שלישיים כאשר אפרש בשער השביעי |
| Know that in every science there are things that are hidden from the eyes of all the ancient sages and also those that follow them. | ודע כי יש בכל חכמה דברים נעלמו מעיני כל החכמים הקדמונים וגם מכל הבאים אחריהם |
| Such as: the roots of the numbers that are not square numbers, in arithmetic. | כמו שרשי המספרים שאינם מרובעים בחכמת החשבון |
| As well as in geometry, to know the the perimeter from a known diameter. | וככה בחכמת המדות לדעת הקו הסובב מאלכסון ידוע |
| Archimedes the wise could not approximate it to the truth, but only gave evidences from geometry that the perimeter should be three times the diameter plus an excess of 10 parts of 70 of the first rank, and he brought evidences that they had to be less than one part of the seconds, but did not know how many they are, only proved that the excess had to be more than 10 parts of 70 parts and one-half of the part. | ולא יכול ארישמדס החכם לקרבו אל האמת רק שנתן ראיות מחכמת המדות כי הקו הסובב ראוי להיותו שלשה מהאלכסון ותוספת י' חלקים מע' במעלה אחת והביא ראיות שיפחתו מחלק אחד מאלו החלקים שניים ולא ידע כמה הם רק הביא ראיה כי התוספת ראויה להיות יותר י' חלקים מע' חלקים וחצי חלק |
| King Ptolemy took the middle path and therefore said that the excess is 8 parts of 63, and 30 seconds. We shall discuss it at the end of the seventh chapter. | ותלמי המלך תפס הדרך האמצעית על כן אמר כי התוספת היא ח' חלקים מס"ג גם ל' שניים ובסוף השער השביעי נדבר על זה |
| So also in astrology sages found, by experiment on herbs, stones and the joints of the human body that are true, but none of them knows why this is so, only the sublime God alone. | וככה בחכמת התולדת מצאו חכמים בדרך נסיון בעשבים ובאבנים ובבתי אברי הגוף האדם והם אמת ואין אחד מהם יודע למה היה ככה רק השם ית' הנשגב לבדו |
Chapter Six - Proportions |
השער הו' הוא שער הערך |
|---|---|
| The types of the proportions are according to three ways: | מיני הערכי' על ג' דרכים |
|
האחד ערכי החשבון והם על הסדר |
|
כמו א' ב' ג' |
|
כי לא יתכן להיות הערך פחות מג' מספרים |
|
או ב' ד' ו' |
|
או ג' ו' ט' |
|
והטעם כי הערך בכלם שוה |
|
פי' כי כיתרון ד' על ב' כן יתרון ו' על ד' |
|
והערך השני ערכי המדות |
|
כמו ד' ו' ט' |
|
כי ערך ד' אל ו' כמו ערך ו' אל ט' |
|
כן כפל הקטן אל הגדול ככפל התיכון על עצמו שהוא מרובעו |
|
ודע כי אלה הג' מספרים הם כמו ד' כי האמצעי יחשב כאלו הוא מספר אחד |
|
על כן כל ד' מספרי' שערך הראשון אל השני כערך השלישי אל הרביעי אם תחבר מרובעי ארבעתן ותדע כמה יעלה ותחבר הראשון עם הרביעי ותקח מרובע המחובר ותוסיף עליו מרובע היתרון שיש בין השני ובין השלישי יהיה שוה כעולה בראשונה |
| Likewise, if you sum the second and third, take the square of the sum and add to it the square of the difference between the first and fourth, the result is the same as the first [result]. | וככה אם תחבר השני והשלישי ותקח מרובע המחובר ותוסיף עליו מרובע היתרון שיש בין הראשון ובין הרביעי ימצא העולה שוה לראשון |
|
דמיון ערך ד' על ו' כערך ח' אל י"ב |
|
והנה מרובעיהם ר"ס והמחובר מן הראשון והרביעי י"ו ומרובעו רנ"ו והיתרון בין ו' וח' הוא ב' ומרובעו ד' והנה המספר שוה |
|
וככה המחובר מן השני והשלישי י"ד ומרובעו קצ"ו והיתרון בין הראשון והרביעי ח' ומרובעו ס"ד והנה המספר שוה |
|
ודע כי רוב חכמת המזלות ותקוני מקום המשרתים תלויים בחכמת ערכי המדות וככה רובי דיני השאלות בחשבון |
|
והדרך השלישי ערכי חכמת הנגינות |
|
והיא חכמה מפוארת מאד כי ערכיה מורכבים מערכי החשבון וערכי המדות |
|
כי לעולם יהיה הערך שבין הראשון לתיכון אל ערך שיהיה בין התיכון [326]לאחרון כערך המספר הראשון למספר האחרון |
|
דמיון ב' ג' ו' |
|
ידענו כי הערך שבין ב' וג' אחד והערך שבין ג' ובין ו' שלשה וככה ערך ב' אל ו' |
|
דמיון אחר ג' ד' ו' או אם תרצה כ' ל' ס' |
|
והנה הערך שבין ג' וד' אחד והערך שבין ד' וו' שנים והנה הוא כפלו וככה ו' אל ג' |
| If you know two numbers, you can extract the third. | והנה אם ידעת השנים מספרי' תוכל להוציא השלישי |
|
כי אם ידעת הראשון והשני ולא תדע השלישי כפול הראשון על השני והעולה חלקנו על הראשון אחר שתגרע ממנו פי' מהראשון היתרון שיש בינו ובין השני |
|
דמיון הראשון כפלנו ב' על ג' וחלקנו העולה על הראשון אחר שגרענו ממנו היתרון שבין הראשון והשני והוא אחד והנה היו ו' והוא השלישי |
|
ובדמיון השני כפל ג' על ד' היו י"ב והיתרון בין ג' וד' אחד גרענוהו מג' שהוא הראשון ונשארו ב' |
|
ונאמ' כי אם ידענו השני והשלישי ולא ידענו הראשון נכפול אלה הידועי' שהם השני והשלישי ונחלק העולה על המחובר מהמספר השלישי עם היתרון שיש בין השני והשלישי והעולה הוא הראשון |
|
והנה בדמיון הראשון כפלנו ג' על ו' והעולה י"ח והיתרון שבין השני והשלישי שלשה חברנום אל ו' והיו ט' חלקנו י"ח עליו עלו ב' והוא הראשון |
|
ובדמיון השני כפלנו ד' על ו' והיו כ"ד חלקנום על ח' שהוא כמספר החשבון השלישי עם היתרון שיש בין השני והשלישי עלו ג' והוא הראשון |
|
ואם לא ידענו האמצעי ונבקש לדעתו נכפול הראשון על השלישי ונחלק העולה על המחובר מן השנים מספרים והעולה בחלוק נכפלנו והוא המספר האמצעי |
|
דמיון הראשון כפלנו ב' על ו' עלו י"ב חלקנו על ח' שהוא המחובר משניהם עלה א' וחצי |
|
ובדמיון האחר כפלנו ג' על ו' עלו י"ח חלקנו על ט' שהוא המחובר משניהם עלו ב' |
|
וככה בערכי המדות אם לא ידענו האחד מן הד' נוכל להוציאו מן הג' |
|
ולעולם נשים שתי הקצוות שהם הראשון והרביעי חברים והשנים האמצעיי' שהם השני והשלישי חברים |
|
והנה אם לא ידענו אחד מן הקצוות איזה מהם שיהיה נכפול האמצעי על חבירו והעולה נחלקנו על אחד מהקצוות שהוא נודע והעולה הוא המבוקש |
|
ואם לא ידענו אחד מהאמצעיים נכפול אחד מהקצוות על חברו ונחלק העולה על האמצעי הנודע אז ימצא המבוקש |
| ועל זה הדרך תעשה בכל השאלות ויש לך להשמר באיזה מקום תשים הגלגל |
Word Problems |
|||||||||||||
| Now I shall write a lot of problem for you to practice | ועתה אכתוב לך שאלות רבות כדי להרגילך | ||||||||||||
| How Much Problem - Money | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Question: a fifth, a sixth, and a seventh of an amount of money make 10, how much is the money?
|
שאלה ממון חברנו חמישיתו וששיתו ושביעיתו והיו עשרה כמה הממון | ||||||||||||
|
בקשנו המורה שכפלנו ה' על ו' עלו ל' גם[327] זה על ז' והיו ר"י והוא המורה | ||||||||||||
|
וחמישיתו מ"ב וששיתו ל"ה ושביעיתו ל' והנה שלשתם ק"ז | ||||||||||||
|
הנה ערך הממון שהוא עשרה המחובר מהם אל כל הממון שאינו נודע כערך ק"ז אל ר"י פי' שהוא המורה | ||||||||||||
|
ונעשה הדמיון כך | ||||||||||||
|
| ||||||||||||
|
כפלנו הקצוות שהם י' על ר"י והיו אלפי' וק' חלקנום על האמצעי שהוא ק"ז עלו י"ט שלמים ונשארו ס"ז חלקי' מן ק"ז והוא כל הממון | ||||||||||||
|
ואלו היינו עושים להפך היה הדבר שוה כזה | ||||||||||||
|
| ||||||||||||
|
ונבחן זה | ||||||||||||
|
כי ג' שלמים חמישית ט"ו ונשארו ד' שלמי' שלא לקחנו חמישיתם נעשה מן כל אחד ק"ז ונחבר אל המחובר ס"ז יהיה הכל תצ"ה וחמישיתם צ"ט | ||||||||||||
|
| |||||||||||||
|
וששית י"ח ג' ונקח לא' הנשאר ק"ז נחבר אליו ס"ז יהיו קע"ד וששיתו כ"ט | ||||||||||||
|
| |||||||||||||
|
גם השביעית שנים שלמי' נשארו ה' שאין להם שביעית נקח לכל אחד ק"ז יהיו תקל"ה | ||||||||||||
|
| |||||||||||||
|
נחבר החלקים יהיו שנים שלמים נחברם אל השלמים והיו י' | ||||||||||||
|
| |||||||||||||
| Another example: We took its seventh and its ninth; they are 7.
|
דמיון אחר לקחנו שביעיתו ותשיעיתו והיו ז' | ||||||||||||
|
המורה ס"ג | ||||||||||||
|
והשביעית והתשיעית י"ו וככה הצורה | ||||||||||||
|
| ||||||||||||
|
הנה החשבון כ"ז שלמים וט' חלקי' מי"ו | ||||||||||||
| First from Last Problem - Money | |||||||||||||
| If one reversed the saying and says: We have subtracted from an amount of money its seventh and its ninth and 7 remain.
|
ואם הפך הדבר ואמר חסרנו מהממון שביעיתו ותשיעיתו נשארו ז' | ||||||||||||
|
גם אנו נעשה המורה להפך כי המורה הוא אחד רק נחסר י"ו שהוא השביעית והתשיעית מהמורה ונשארו מ"ז ונכתבהו ככה | ||||||||||||
|
| ||||||||||||
|
כפלנו ז' על ס"ג והיו תמ"א חלקנו על מ"ז עלו ט' וי"ח חלקי' ממ"ז ועתה הוא | ||||||||||||
|
ושביעיתם כדרך שהראיתיך עלה אחד שלם גם י"ו חלקי' | ||||||||||||
|
לקחנו תשיעיתו והוא אחד שלם וב' חלקי' | ||||||||||||
|
ונשארו ז' שלמים | ||||||||||||
| Partnership Problem - For the Same Time | |||||||||||||
| Question: 4 people - one of them have 11 dinar, the second have 13 dinar, the third have 15 dinar, and the fourth have 17 dinar. They earned 19 dinar. How much does each get? | שאלה ד' אנשים יש לאחד מהם י"א דינ' ולשני י"ג דינ' ולשלישי ט"ו דינ' ולרביעי י"ז דינ' והרויחו י"ט דינ' כמה יקח כל אחד ואחד | ||||||||||||
|
נבחר ראשי כל ממונם והיו נ"ו | ||||||||||||
|
וכערך כל אחד אל נ"ו ככה יקח מי"ט ונעשה כך | ||||||||||||
|
| ||||||||||||
|
נכפול י"א על י"ט יעלו ר"ט נחלק על נ"ו עלו ג' שלמי' ונשארו מ"א חלקי' | ||||||||||||
|
עשינו כן בי"ג | ||||||||||||
|
| ||||||||||||
|
עלו רמ"ז חלקנום על נ"ו עלו ד' שלמי' וכ"ג חלקי' | ||||||||||||
|
עשינו כך בט"ו | ||||||||||||
|
| ||||||||||||
|
ועלו רפ"ה חלקנום על נ"ו עלו ה' שלמי' וה' חלקי' | ||||||||||||
|
עשינו כך בי"ז | ||||||||||||
|
| ||||||||||||
|
עלו שכ"ג חלקנום על נ"ו עלו ה' שלמים ומ"ג חלקים | ||||||||||||
|
חברנו השלמי' ואלה החלקי' ועלו י"ט שלמי' כי אלה החלקי' חלקי נ"ו הם | ||||||||||||
|
דרך אחרת השיבונו הריוח כלו פשוטים | ||||||||||||
|
שכפלנו הי"ט דינ' בי"ב עלו רכ"ח חלקנום על נ"ו עלו ד' פשוטי' גם ד' חלקי' מנ"ו | ||||||||||||
|
והנה כפלנו י"א על ד' עלו מ"ד פשוטי' שהם ג' דינ' ח' פשוטי' ומ"ד חלקי פשוט | ||||||||||||
|
גם כפלנו י"ג על הד' והיו נ"ב שהם ד' דינ' וד' פשוטי' ונ"ב חלקי' | ||||||||||||
|
גם כפלנו ט"ו על ד' והיו ס' פשוטי' שהם ה' דינ' וס' חלקי' חברנו פשוט מנ"ו ושארו ד' חלקים | ||||||||||||
|
גם כפלנו י"ז על הד' והיו ס"ח פשו' שהם ה' דינ' וח' פשו' וס"ח חלקי' נחבר מהם פשוט ישארו י"ב חלקים | ||||||||||||
|
| |||||||||||||
|
נחבר החלקים כלם יהיו ג' פשו' ונחבר הפשוטי' יהיו ב' דינ' נחברם אל החלק הגדול יהיו בין הכל י"ט דינ' | ||||||||||||
|
| |||||||||||||
| Purchase Problem – Moneychanger | |||||||||||||
| Question: the moneychanger has three [kinds of] coins. One zahuv is worth three dinar of the first [kind of] coins; or four of the second [kind]; or six of the third [kind]. A man came and asked the moneychanger to give him from the three [kinds of] coins for one zahuv equally, so that the amount of the expensive will be equal to the amount of the inexpensive.
|
שאלה יש אצל המחליף שלשה המטבעים שוה הזהוב ממטבע האחד ג' דינ' וממטבע השני ד' דינ' וממטבע השלישי' ו' דינ' ובא אדם אחד ובקש למחליף שיתן לו מג' המטבעי' בזהוב ויהיה המספר בשוה מן היקרים כמו משאינם יקרים | ||||||||||||
|
בקש חשבון שיש לו שלישית ורביעית וששית והוא י"ב והוא המורה וכל החלקים הנזכרים הם ט' והוא דינר | ||||||||||||
|
|
ונבקש מה ערך י"ב אל ט' והנה הוא כמוהו ושלישיתו | ||||||||||||
|
|
והנה נוסיף על י"ב פשו' שהוא דינר ד' פשו' שהוא שלישיתו ועלו י"ו פשו' וככה לקח מכל מטבע | ||||||||||||
|
ולבחון דבר זה קל הוא כי הערכי' נמצאים במהרה | ||||||||||||
| והנה נשים המטבע של שלשה עקר | |||||||||||||
|
וידענו כי הי"ו ממטבע ו' הם ח' פשו' ממטבע ג' כי ו' כפל ג' | ||||||||||||
|
והנה בין שניהם כ"ד | ||||||||||||
|
|
וידוע כי ערך ג' אל ד' ג' רביעיות | ||||||||||||
|
על כן יהיה חילוף י"ו פשו' ממטבע ד' הם י"ב פשו' ממטבע ג' והנו דינר אחד | ||||||||||||
|
וג' דינ' ממטבע האחד | ||||||||||||
| וככה תוכל להשיב חלוף מה שלקח לאיזה מטבע שתרצה ואין צורך להאריך | |||||||||||||
| Another example, which is difficult because it has difficult ratios: | דמיון אחר קשה כי אין לו ערכים כי אם בקושי | ||||||||||||
| The moneychanger has three [kinds of] coins. One zahuv is worth five dinar of the first [kind of coins]; or seven of the second [kind]; or nine of the third [kind]. [A man] brings one zahuv and wants to take from all [kinds of coins] for one zahuv equally.
|
וזהו מחליף יש לו ג' מטבעים האחד ה' דינ' בזהוב והשני ז' והשלישי ט' והביא זהוב ורצה לקחת בשוה מספר שוה מכלם בזהוב אחד | ||||||||||||
|
עשה כמשפט וכפול ה' בז' והעולה ל"ה וכפול זה על ט' יהיו שט"ו והוא המורה | ||||||||||||
|
וחמישיתו ס"ג ושביעיתו מ"ה ותשיעיתו ל"ה והנה כשנחבר אלה שלשתם יהיו קמ"ג והוא הדינ' | ||||||||||||
|
נחלק המורה על זה המספר יהיו ב' דינ' וישארו כ"ט חלקים מן קמ"ג וככה יקח מכל מטבע | ||||||||||||
|
ולבחון זה קשה הוא כי אם על הדרך שאומר לך בעבור החלקים | ||||||||||||
|
והנה נחל לבחון להשיב המספר הנזכר ממנו ממטבע ז' וממטבע ט' אל מטבע ה' וככה נעשה | ||||||||||||
|
נשיב הדינ' חלקי' מקמ"ג ונשים עמהן החלקים שהם שט"ו והוא המורה | ||||||||||||
|
ונבקש להחליף מטבע ז' אל ה' ונכפול שט"ו על ה' ויהיו אלף תקע"ה נחלקם על ז' יהיו רכ"ה חלקים ממטבע ה' | ||||||||||||
|
גם אלף תקע"ה על ט' לדעת כמה יהיו מהמטבע השני והנה קע"ה | ||||||||||||
|
וכאשר תחבר אלה ג' מספרים שהם ממטבע אחד שט"ו גם רכ"ה גם קע"ה והנה הכל תשט"ו חלקנום על קמ"ג שהוא הדינ' [328]עלו ה' דינ' שוים | ||||||||||||
|
או אם תרצה חשוב ככה כבר היו ממטבע ה' ב' דינ' וכ"ט חלקים | ||||||||||||
|
וכאשר החלפנו זה המספר ממטבע ז' יהיו רכ"ה חלקים שהם דינ' אחד ופ"ב חלקים | ||||||||||||
|
ואם ממטבע ט' יהיו קע"ה שהם דינ' אחד ול"ב חלקים | ||||||||||||
|
חברנו כל החלקים יהיו קמ"ג שהם דינ' אחד והנה המספר אחד | ||||||||||||
|
ועוד נשיב הכל למטבע ז' והנה כבר היו לנו שט"ו חלקים שהוא המורה | ||||||||||||
|
ונרצה לדעת כמה חלקי' יהיו ממטבע ה' והנה נכפול שט"ו על ז' יעלו אלפים ור"ה נחלק על ה' יעלו תמ"א | ||||||||||||
|
גם נחלק עוד זה המספר על ט' יהיה העולה רמ"ה | ||||||||||||
|
נחבר כל אלה החלקים ונחלק המחובר על קמ"ג יהיו ז' דינ' | ||||||||||||
|
ועוד נשיב הכל למטבע ט' והנה יש לו מהמטבע שלו שט"ו חלקים שהוא המורה שהם ב' דינ' גם כ"ט חלקי' | ||||||||||||
|
ונשוב לכפול שט"ו על ט' יהיו אלפים ותתל"ה נחלק זה המספר על ה' יהיו תקס"ז | ||||||||||||
|
גם נחלק זה על ז' שהוא המטבע האחר יהיו ת"ה | ||||||||||||
|
וכאשר נחבר אלה החלקים של ג' מטבעים יהיו אלף רפ"ז וכאשר נחלק זה על קמ"ג יהיו ט' דינ' שלמים | ||||||||||||
| Do the same if there are [4 types] of coins or more. | וככה תעשה אם היו מטבעים או יותר | ||||||||||||
| explanation - the position of the zero [= representing the unknown] | |||||||||||||
| Now I want to explain to you where to put the wheel. So we shall give an example: | עתה ארצה לבאר לך באיזה מקום תשים הגלגל והנה נעשה דמיון | ||||||||||||
| Payment Problem | |||||||||||||
| Question: Reuven hired Shimon to work with him for 17 days and he will pay him 11 pešuṭim, but he worked 9 days.
|
שאלה ראובן שכר שמעון שיעבוד עמו י"ז ימים ויתן לו י"א פשו' והנה עבד ט' ימים | ||||||||||||
|
והוא אין ספק כי כערך הימים שעבד אל כל הימים שהיה התנאי שאותו הערך בעצמו יקח מי"א שהם הפשוטים | ||||||||||||
|
והנה נשים הגלגל הראשון והשני י"א והשלישי ט' והרביעי י"ז ככה | ||||||||||||
|
| ||||||||||||
|
ואם נרצה נשים הגלגל שני ומספר הרביעי ט' שנעשה ככה | ||||||||||||
|
| ||||||||||||
|
כי כאשר שמנו המספר הגדול בראשונה של פשוטים ככה נשים במספר השני המספר הגדול של ימי העבודה שלישי ראשון לשנים האחרונים | ||||||||||||
|
ונוכל לשום הגלגל שלישי כזה | ||||||||||||
|
| ||||||||||||
|
ונוכל לשום הגלגל רביעי ככה | ||||||||||||
|
| ||||||||||||
|
והכל שוה | ||||||||||||
| Payment Problem - Carrying Wheat | |||||||||||||
| Question: Reuven hired Shimon to carry for him 13 measures of wheat on his beast a path of 17 miles and his payment will be 19 pešiṭim, but he carried 7 measures for a distance of 11 miles. How much should be his wages?
|
שאלה ראובן שכר שמעון שיוליך לו על בהמתו י"ג מדות חטה מהלך י"ז מילין ויהיה שכרו י"ט פשוטים והוא הוליך שבע מדות מהלך י"א מילין כמה שכרו | ||||||||||||
|
ככה תעשה צריך אתה לעשות הערכים פעמים כי אין דרך אחרת להוציאם | ||||||||||||
|
וחשוב כי הז' מדות הוליך אותם כל התנאי שהם י"ז והנה תעשה ככה הדמיון | ||||||||||||
|
| ||||||||||||
|
הנה נכפול הקצוות שהם ז' וי"ט יהיו קל"ג נחלקם על י"ג יעלו י' שלמים ונשארו ג' חלקים מי"ג בפשוט אחד | ||||||||||||
|
ובעבור שלא הוליך אלא ז' מדות רק י"א מילין אנחנו צריכים לעשות ערך אחר ודמיון אחר ונעשה ככה י"א י"ז גלגל י' גם ג' חלקים מי"ג וזה דמיונו | ||||||||||||
|
| ||||||||||||
|
ובעבור שאנו צריכין לכפול הקצוות ולחלק העולה על י"ז ויש לנו ברביעי ג' חלקים מי"ג צריכין אנו לבקש מורה אחד לשניהם וככה נמצאנו | ||||||||||||
|
שנכפול י"ג על י"ז יעלו רכ"א והוא המורה והוא אחד שלם | ||||||||||||
|
והנה ג' חלקים מי"ג יהיו נ"א מרכ"א | ||||||||||||
|
ונשוב לכפול י"א על י' יהיו ק"י גם נכפול י"א שהם שלמים על נ"א שהם חלקים ויעלו תקס"א | ||||||||||||
|
| |||||||||||||
| Payment Problem - Digging a Hole | |||||||||||||
| Question: Reuven hired Shimon to dig for him in the ground 10 in length, 10 in width, for which he would pay him 17 pešuṭim, but Shimon dug 5 in length and 5 in width | שאלה ראובן שכר שמעון שיחפור לו בקרקע י' באורך וי' ברוחב ויתן לו י"ז פשו' ושמעון חפר ה' באורך וה' ברוחב | ||||||||||||
|
אין ספק כי הרביעית יקח כי כפל חצי על חצי רביעי אחד שלם | ||||||||||||
|
כי אלו היה כופל חצי האורך על כל הרוחב או חצי הרוחב על כל האורך אז היה לוקח חצי הממון | ||||||||||||
| If he said that he agreed with him that he should dig 7 in length, 6 in width, 5 in depth, and for this he would pay him 11 pešiṭim, but he dug 6 in length, 5 in width, 4 in depth. How much should be his payment?
|
רק אם אמר שהסכים עמו שיחפור ז' באורך וו' ברוחב וה' בעומק ויתן לו י"א פשו' והוא חפר ו' באורך וה' ברוחב וד' בעומק כמה שכרו | ||||||||||||
|
הנה אנחנו צריכים לערכים | ||||||||||||
|
ונכפול המספר הראשון שהוא ז' על ו' הרי מ"ב כפלה על ה' שהוא העומק ויהיו ר"י | ||||||||||||
|
גם נכפול המספר השני שהוא ו' על ה' והם ל' גם נכפול זה על ד' שהוא העומק יהיו ק"כ | ||||||||||||
|
ועתה נעשה דמיון הערכים כזה | ||||||||||||
|
| ||||||||||||
|
כפלנו האמצעיים הידועים והיו אלף וש"כ חלקנום על ר"י עלו ו' שלמים ונשארו ס' שהם שתי שביעיות פשוט | ||||||||||||
| Pricing Problem - Find the Amount | |||||||||||||
| Question: a man sells 13 measures of wheat for 23 pešuṭim. How many measures will he sell for 7 [pešuṭim]?
|
שאלה אדם מוכר חטה י"ג מדות בכ"ג פשו' כמה מדות יתן בז' פשו' | ||||||||||||
|
נעשה דמיון הערך כמשפט הזה | ||||||||||||
|
| ||||||||||||
|
הנה כפול הקצוות שהם נודעים יהיו צ"א נחלקם על כ"ג יהיו ג' מדות וכ"ב חלקים מכ"ג במדה אחת | ||||||||||||
| Pricing Problem - Find the Price | |||||||||||||
| We reverse the question, by that we want to know how much will he get for 7 measures?
|
ועוד נהפוך הענין שנבקש לדעת בכמה יתן ז' מדות | ||||||||||||
|
והנה נעשה הדמיון כזה | ||||||||||||
|
| ||||||||||||
|
נכפול הקצוות יהיו קס"א נחלקם על י"ג יהיו י"ב פשו' וה' חלקים מי"ג בפשו' אחד | ||||||||||||
| Motion Problem – Pursuit | |||||||||||||
| Question: a man sends a messenger to walk 29 miles a day. After 10 days, he sends another messenger to walk after him 37 miles a day. When will he catch up with him?
|
שאלה אדם שלח רץ שילך בכל יום כ"ט מלין ואחר עשרה ימים שלח רץ אחר אחריו שילך בכל יום יום ל"ז מילין מתי ישיגנו | ||||||||||||
|
נכפול המילין שהלך בי' ימים יהיו ר"צ נחלקם על היתרון שבין שני המהלכים שהוא ח' והנו ל"ו ימים ורביעית יום | ||||||||||||
| Give and Take Problem | |||||||||||||
| Question: a man left his city and arrived to another country. He took an oath that if God will double his money he will donate two pešuṭim each day. After two days he ran out of money. How much did he bring?
|
שאלה אדם יצא מעירו ונכנס במדינה אחרת נדר אם יכפול המקום ממונו יתן בכל יום ב' פשו' לסוף ד' ימים הלך ממונו כמה הביא | ||||||||||||
|
האמת כי היה לו ב' פשוטים פחות שמינית פשוט | ||||||||||||
| Motion Problem – Encounter | |||||||||||||
| Question: Reuven left his city on the morning of the first day of the month, to meet his brother Shimon in his city. On that same day Shimon left his city, to meet his brother Reuven in his city. The distance between the two cities is 100 miles. Reuven walks 19 miles a day and Shimon walks 17 miles a day. We ask: when will they meet? | שאלה ראובן יצא מעירו ללכת לקראת שמעון אחיו לעירו בקר יום ראשון של ראש החדש ובעצם היום הזה יצא גם שמעון מעירו ללכת לקראת ראובן אחיו לעירו והמרחק בין שני הערים ק' מילין ומהלך ראובן ביום אחד י"ט מילין ומהלך שמעון ביום אחד י"ז מילין נשאל מתי יתחברו | ||||||||||||
|
ככה תעשה חבר שני המהלכים והם ל"ו חלק עליו המאה מילין יהיה שני ימים ישארו כ"ח חלקים מל"ו ביום אחד שהם ז' תשיעיות יום | ||||||||||||
|
ותוכל להושיבם לשעות היום בדרך הערכין | ||||||||||||
|
| ||||||||||||
|
וככה תעשה[329] כפלנו ז' על י"ב עלו פ"ד חלקנו על ט' עלו ט' והם שעות נשארו ג' שהם שלישית שעה | ||||||||||||
|
ועל דרך אחרת ידענו כי ערך י"ב אל ט' כמוהו ושלישיתו | ||||||||||||
|
כי תשיעיות היו לנו והנה נקח לז' תשיעיות ז' שלישיות נחלקם על ג' יהיו ב' שעות ושלישית שעה | ||||||||||||
|
ואם בקשנו לדעת כמה מילין הלך ראובן | ||||||||||||
|
כבר ידענו כי בשני ימים הלך ל"ח מילין | ||||||||||||
|
וכבר אמרנו כי ז' תשיעיות היום הלך והנה נעשה הערך כך | ||||||||||||
|
| ||||||||||||
|
כפלנו ז' על י"ט עלו קל"ג חלקנום על ט' עלו י"ד ושבע תשיעיות | ||||||||||||
|
והנה הכל נ"ב מילין וז' תשיעיות | ||||||||||||
| Payment Problem - three workers, three different daily wages, the same actual payment | |||||||||||||
| Question: A man hired three brothers – Reuven, Shimon, and Levi – to do his work for 20 days from morning until evening, any one of them in turns so that the work will not cease. If Reuven works all the days he will pay him 5 zehuvim; if Shimon – 4, if Levi – 3. They worked together for the 20 days and there was a a supervisor sitting with them, who wrote down how many hours and parts of hours each of them worked a day. Finally, he paid each of them an equal share. We wish to know: how much is the share of each of them?
|
שאלה אדם שכר ג' אחים ראובן שמעון ולוי שיעשו עבודתו כ' ימים מן הבקר עד הערב מאיזה מהם שתהיה ולא תשבות המלאכה והנה אם עבד ראובן כל הימים יתן לו ה' זהובים | ||||||||||||
|
דע כי ראובן ישמש ד' ימים בזהוב אחד ושמעון ה' ימים ולוי ו' ימים וב' שלישיות יום והנה הכל ט"ו שלמים וב' שלישיות יום אחד | ||||||||||||
|
נחלק כ' על זה המספר ועלה אחד שלם ונשארו ד' שלמים ושלישית אחד והנה בעבור השלישית נשיב הכל שלישיות והנה נשיב הכ' יום ס' שלישיות והט"ו וב' שלישיות מ"ז שלישיות והד' ושלישית יום י"ג | ||||||||||||
|
ועתה נבקש כמה חיוב כל אחד שיעבוד עד שישלימו הכ' יום | ||||||||||||
|
והנה נחל מלוי שהוא חייב לשמש בזהוב שלקח ו' ימים וב' שלישיות יום ונעשה מאלה שלישיות ויהיו כ' | ||||||||||||
|
ונבקש לדעת כמה יש לו לעבוד בעבור י"ג פשו' שלקח ונעשה הערך כך | ||||||||||||
|
| ||||||||||||
|
כפלנו י"ג על כ' והיו ר"ס חלקנום על מ"ז עלו ה' ונשארו כ"ה חלקים | ||||||||||||
|
| |||||||||||||
|
ונבקש לדעת כמה עבד שמעון | ||||||||||||
|
והנה חייב לעבוד בעבור הזהוב ה' ימים שהם ט"ו שלישיות | ||||||||||||
|
ונבקש לדעת כמה יעבוד בעבור י"ג פשו' שלקח והנה נעשה הערך כך | ||||||||||||
|
| ||||||||||||
|
נכפול ט"ו על י"ג יעלו קצ"ה נחלקם על מ"ז עלו ד' ונשארו ז' חלקים | ||||||||||||
|
| |||||||||||||
|
ונבקש לדעת כמה עבד ראובן | ||||||||||||
|
והנה עבד בשביל הזהוב ד' ימים שהם י"ב שלישיות | ||||||||||||
|
ונעשה בעבור הי"ג פשוטים שלקח הערך כך | ||||||||||||
|
| ||||||||||||
|
נכפול י"ג על י"ב יעלו קנ"ו נחלקם על מ"ז עלו ג' ונשארו ט"ו חלקים | ||||||||||||
|
| |||||||||||||
|
וכאשר תחבר אלה החלקים יתחבר מהם שעה אחת בלי תוספת ומגרעת | ||||||||||||
|
וכאשר תחבר זאת השעה אל השעות הנזכרות יהיו י"ב שעות שהוא יום אחד | ||||||||||||
|
וכאשר תחבר היום לימים הנזכרים יהיו עשרים יום בלי תוספת ומגרעת | ||||||||||||
| Boiling Problem | |||||||||||||
| Question: A man had 10 measures of must and he wants to cook them so that only one-third remains. He starts to cook [them] until eight measures are left of them. Then, two measures overflow. Now he wants to cook [the remaining 6 measures] until it is reduced [as he planned] at first.
|
שאלה אדם היו לו י' מדות מתירוש ורצה לבשלם עד שלא ישאר מהם כי אם השלישית והנה החל לבשל עד שנשארו מהם ח' מדות ונשפך ב' מדות והנה ירצה לבשלם עד שיהיו כמשפט הראשון | ||||||||||||
|
והנה יש לך ג' מספרים ידועים הא' כמה שלישית י' ידוע כי הוא ג' ושליש וידוע כי שמנה יהיו המדות שיתבשלו וידוע כי ששה נשארו | ||||||||||||
|
והנה תעשה הדמיון ככה | ||||||||||||
|
| ||||||||||||
|
והנה נכפול ו' על ג' ושליש יהיו כ' נחלקם על ח' יהיו שנים וחצי | ||||||||||||
| Another example: We have 9 measures of must, and he wants them to be cooked until the third part of it remains. It was now cooked until 6 measures were left. Then 4 measures were overflow, and 2 measures remain. | דמיון אחר היו לנו ט' מדות תירוש וירצה שיתבשלו עד שישאר השליש והוא נתבשל עד שנשארו ו' מדות ונשפכו ד' וב' נשארו | ||||||||||||
|
וככה הערך | ||||||||||||
|
| ||||||||||||
|
כפול ב' על ג' עלו ו' יהיה אחד והנה המשפט להיות המבושל מדה אחת | ||||||||||||
| How Much Problem - Money | |||||||||||||
| Question: an amount of money, we sum its fifth, its seventh, and its ninth and they are 10, how much is the money?
|
שאלה ממון חברנו חמישיתו ושביעיתו ותשיעיתו והיו עשרה כמה הממון | ||||||||||||
|
נבקש המורה והוא שט"ו | ||||||||||||
|
והחלקים הנזכרים הם קמ"ג | ||||||||||||
|
כאשר תחלק שט"ו על ה' יעלו ס"ג | ||||||||||||
|
וכשתחלק על ז' יעלו מ"ה | ||||||||||||
|
ועל ט' יעלו ל"ה | ||||||||||||
|
חברם יחד יעלו קמ"ג | ||||||||||||
|
ונעשה הערך כך | ||||||||||||
|
| ||||||||||||
|
נכפול שט"ו על י' יעלו ג' אלפים וק"נ נחלקם על קמ"ג עלו כ"ב שלמים וד' חלקים מקמ"ג | ||||||||||||
| First from Last Problem - Money | |||||||||||||
| We do the opposite: An amount of money - we have subtracted from it its fifth, its seventh and its ninth and 10 remain.
|
נעשה להפך ממון חסרנו ממנו חמישיתו שביעיתו ותשיעיתו ונשארו י' | ||||||||||||
|
נחסר קמ"ג שהם השברים מן שט"ו שהוא המורה ישארו קע"ב | ||||||||||||
|
ונעשה הערך כך | ||||||||||||
|
| ||||||||||||
|
כפלנו י' על שט"ו עלו ג' אלפים וק"נ חלקנום על קע"ב עלו י"ח שלמים ונ"ד חלקים מקע"ב | ||||||||||||
|
לקחנו חמישית ושביעית ותשיעית זה המספר ישארו לנו י' שלמים | ||||||||||||
|
ועל זה הדרך | ||||||||||||
| Find a Quantity Problem - Whole from Parts - Tree | |||||||||||||
| Question: A tree, a third of it is in the water, a quarter of it is [ingrained] in the soil, and 10 cubits of it are up above the water, how much is the length of the whole tree? |
שאלת האילן ששלישיתו במים ורביעיתו בעפר ולמעלה מן המים י' אמות כמה גבהות כל האילן | ||||||||||||
|
Common Denominator: We seek for a number that has a third and a quarter; it is 12. |
נבקש מנין שיש לו שלישית ורביעית והוא י"ב | ||||||||||||
|
ושלישיתו ורביעיתו מחוברים ז' נחסרם מי"ב ישארו ה' | ||||||||||||
|
נעשה הערך כך | ||||||||||||
|
| ||||||||||||
|
הנה כפלנו הקצוות עלו ק"כ חלקנום על ה' עלו כ"ד וזהו גבהות כל האילן | ||||||||||||
|
כי שלישיתו שמנה ורביעיתו ששה והמחוברים י"ד נחסרם מכ"ד ישארו י' שלמים לא פחות ולא יותר | ||||||||||||
| Another example: A tree, a seventh of it is in the water, a ninth of it is [ingrained] in the soil, and 8 [cubits] of it are up above the water.
|
דמיון אחר אילן שביעיתו במים ותשיעיתו בעפר ולמעלה מן המים ח' | ||||||||||||
|
והנה המורה ס"ג | ||||||||||||
|
נחסר ממנו י"ו שהוא השביעית והתשיעית נשארו מ"ז | ||||||||||||
|
ונעשה הערך כך | ||||||||||||
|
| ||||||||||||
|
הנה כפלנו הקצוות והיו תק"ד חלקנום על מ"ז עלו י' שלמים גם ל"ד חלקים | ||||||||||||
|
ושביעית זה המספר אחד שלם וכ"ה חלקים | ||||||||||||
|
ותשיעיתו אחד שלם וט' חלקים | ||||||||||||
|
חברנו החלקים הנזכרים והם ל"ד והשלמים ב' | ||||||||||||
|
חסרנום מהמספר הנזכר נשארו ח' | ||||||||||||
| Divide a Quantity Problem - Proportional Division – Inheritance | |||||||||||||
| Question: Jacob died. His son Reuven issued a deed with two credible witnesses, according to which his father Jacob has given him alone all the property he had and instructed so in case of death. His son Shimon issued a deed as well, according to which his father instructed that half of his property should be granted to him. Levi also issued a deed, according to which his father instructed that one-third of his property should be given to him. Yehudah too issued a deed, according to which one-quarter of his property should be granted to him. All of them wrote this in Jerusalem in the same day, the same time, the same hour | שאלה יעקב מת והוציא ראובן בנו שטר בשני עדים כשרים שנתן לו לבדו יעקב אביו כל הממון שהיה לו וצוה כן מחמת מיתה ביום מותו גם הוציא שמעון בנו שטר שאביו צוה מחמת מיתה שינתן לו חצי ממונו | ||||||||||||
| Three methods to divide the property between the four sons each according to his relative portion: | |||||||||||||
|
והנה חכמי ישראל מחלקים אותו על דרך בקשת כל אחד | ||||||||||||
|
וחכמי הגוים על דרך ערך הממון שלכל אחד | ||||||||||||
|
וחכמי החשבון יחשבו כי הממון היה אחד | ||||||||||||
|
וכאשר תחבר אליו חציו ושלישיתו ורביעיתו יהיה הכל שנים וחצי ששית | ||||||||||||
|
והנה נשים האחד שלם ששים שיש לו כל החלקים הנזכרים והנה יהיה בין הכל קכ"ה | ||||||||||||
|
או נשים האחד שלם י"ב והשברים הנזכרים י"ג | ||||||||||||
|
ושוה יצא המספר באחרונה איזה מהם שתקח | ||||||||||||
|
והנה נבקש כמה יקח ראובן כפי ערך ממונו ונעשה הערך ככה על דרך ששים כי הוא מבקש כל הממון ונאמר כי הממון עשרה דינרים שהם ק"כ פשוטים | ||||||||||||
|
וזה תורת ערך הממון שיקח ראובן | ||||||||||||
|
| ||||||||||||
|
כפלנו הקצוות ועלו ז' אלפים ור' חלקנום על קכ"ה עלו נ"ז פשו' וע"ה חלקים וזה חלק ראובן | ||||||||||||
|
וזו צורת ערך שמעון | ||||||||||||
|
| ||||||||||||
|
נכפול הקצוות ונחלק כמשפט | ||||||||||||
|
וזו צורת חלק לוי | ||||||||||||
|
| ||||||||||||
|
נכפול ונחלק כמשפט | ||||||||||||
|
וזו צורת חלק יהודה | ||||||||||||
|
|||||||||||||
| Another method in a shorter way [according to the Gentile sages]: | ענין אחר בדרך קצרה | ||||||||||||
|
יקח שמעון חצי חלק ראובן | ||||||||||||
|
גם יקח לוי שליש חלק ראובן | ||||||||||||
|
גם יקח יהודה רביעית חלק ראובן | ||||||||||||
|
וכאשר תחבר כל אלה החלקים והשלמים יהיו ק"כ פשו' שהם י' דינ' | ||||||||||||
| According to the procedure of the sages of Israel: | ועל דרך חכמי ישראל | ||||||||||||
|
יאמרו הג' אחים הגדולים ליהודה אחיהם אין אתה מערער רק על ל' פשוטים וערעור כל אחד ממנו שוה בהם קח ז' וחצי שהוא הרביעית ולך מעמנו וכמו כן יקח כל אחד מהג' אחים | ||||||||||||
|
ועוד יאמר ראובן ללוי אין אתה מערער רק על מ' פשו' וכבר לקחת חלקך מהל' שארבעתנו ערערנו עליהם קח אתה שלישית י' שהוא רביעית מ' ולך מעמנו | ||||||||||||
|
| |||||||||||||
|
גם יאמר ראובן לשמעון אין אתה מערער אלא על חצי הממון שהוא ס' והחצי האחר הוא כלו שלי וכבר לקחת חלקך מהמ' והנה נשאר ביני ובינך הערעור בעשרים קח חציים ולך מעלי | ||||||||||||
|
וחלק ראובן שמונים גם חמש ששיות פשו' אחד | ||||||||||||
|
| |||||||||||||
|
וכאשר תחבר אלו החלקים יהיו עשרה דינ' | ||||||||||||
Rule of Four in Astronomical Tables |
|||||||||
| Now, I shall explain the method of the astrologers in the tables of the determination of the planets. | ועתה אפרש דרך חכמי המזלות בספרי הלוחות בתקון המשרתים | ||||||||
| When determining the moon and also when determining 5 planets, there is a row that is called the row of ratio and this ratio is to 60. | כי בתקון הלבנה גם בתקון ה' המשרתים טור יקרא טור הערך וזה הערך הוא אל ס' | ||||||||
| For, if 60 is written in the row of the ratio, | כי אם היה כתוב בטור הערך ס' יהיה בטור אחריו שיקרא הטור החמשי או הכתוב בטור השביעי מה שיהיה כתוב באחד מהם ראשונים לבדם או ראשונים ומעלות הכל יקח | ||||||||
| So it is when determining the position of the moon. | וככה בתקון מקום הלבנה | ||||||||
| If it is less than 60, one should take the ratio from the parts that are written in the fifth or seventh row. | ואם היתה פחותה מס' יקח כפי הערך מהחלקים הכתובים בטור החמישי או השביעי | ||||||||
|
דמיון יש חלקים יתרים על המעלות מ' ובטור הערך ט"ו | ||||||||
|
ואתה צריך לכפול ט"ו על מ' והעולה תחלקנו על ס' והוא המבוקש ועשה דמיון הערך כזה | ||||||||
|
| ||||||||
|
כפול ט"ו על מ' עלו ו' מאות חלקם על ס' יעלו י' חלקים | ||||||||
|
ויותר קרוב מזה שתבקש מה ערך מ' אל ס' והם ב' שלישיות גם זה הערך קח מט"ו והנו י' | ||||||||
|
או בקש מה ערך ט"ו אל ס' והנו רביעית ס' קח רביעית מ' והוא י' | ||||||||
|
דמיון אחר המספר האחד ל' והשני מ"ה | ||||||||
|
והנה ערך מ"ה אל ס' ג' רביעיות נקח שלש רביעיות ל' והם כ"ב וחצי שהם ל' שניים | ||||||||
|
או נקח הערך מן הל' שהוא חצי ס' ג"כ נקח חצי מ"ה והנו כ"ב וחצי | ||||||||
|
דמיון לב' מספרי' שהאחד יש לו ערך והשני אין לו ערך כמו המספר האחד כ' והשני ל"ג | ||||||||
|
והנה ערך כ' אל ס' שלישית והנה נקח שלישית ל"ג והם י"א ראשונים | ||||||||
|
וככה יבא בדרך הכפל כאשר תכפול כ' על ל"ג ותחלק העולה על ס' והעולה בחלוק יהיה י"א | ||||||||
|
ובעבור כי ל"ג קרוב מחצי ס' נקח גם הערך ממנו והנו י' ראשונים שהוא חצי כ' ובעבור שיש לנו תוספת ג' על החצי נכפול ג' על כ' יהיו ס' ואין ספק כי הם שניים כי כפל ראשונים על ראשונים יעלו שניים כי אחד על אחד שנים והם ס' שניים והם חלק ראשון נחברם על י' והוא י"א | ||||||||
|
דמיון אחר המספר האחד כ' והשני כ"ח | ||||||||
|
והנה ערך כ' אל ס' שלישית ושלישית כ"ח ט' ראשונים וב' שניים | ||||||||
|
ועוד נחשוב כי כ"ח חצי ס' כי הוא קרוב ממנו והנה חצי כ' י' ובעבור כי ב' יחסרו מהחצי נכפול ב' על כ' יהיו מ' שניים נחסרם מהראשון אחד יהיו הנשארים ט' ראשונים וכ' שניים | ||||||||
|
דמיון לחסר הערך שחשבונו האחד י"ד והשני כ"ט | ||||||||
|
והנה נקח הערך מכ"ט ונחשוב כי הוא חצי ס' נקח חצי י"ד והם ז' ראשונים ובעבור כי אחד יחסר מהחצי נכפלנו על י"ד יהיו י"ד שניים נחסרם מחלק ראשון ישארו ו' ראשונים ומ"ו שניים | ||||||||
|
דמיון אחר המספר האחד לחסר והשני להוסיף והנה נשים האחד י"ח והשני מ"ב | ||||||||
|
והנה נקח הערך ממ"ב ונחשוב כי הוא שתי שלישיות נקח שתי שלישיות י"ח והנה י"ב ובעבור שיש לנו תוספת ב' נכפלם על י"ח יהיו ל"ו שניים וככה יהיה העולה בדרך הכפל | ||||||||
|
וגם נקח הערך מי"ח ונחשוב כי הוא שלישית והנה שלישית מ"ב י"ד ובעבור שהוספנו ב' נכפלם על מ"ב והיו פ"ד שניים שהם חלק ראשון וכ"ד שניים נחסרם מי"ד ישאר כמספר הראשון שהוא י"ב גם ל"ו שניים | ||||||||
|
ונוכל לקחת עוד הערך בתוספת משניהם שנחשוב י"ח שהוא רביעית ס' והנה נקח רביעית מ"ב יהיו י' ראשונים ול' שניים ובעבור שיש לנו תוספת ג' נכפול מ"ב על ג' יהיו קכ"ו שניים שהם ב' ראשונים וו' שניים נוסיף זה על המספר הנזכר יהיו י"ב ראשונים ל"ו שניים | ||||||||
|
ואילו היינו חושבים כי מ"ב הם ג' רביעיות היה הדבר יוצא נכון | ||||||||
|
ונוכל לעשות הערך מי"ד שנחשוב כי הוא רביעית ס' נקח רביעית כ"ט והם ז' ורביעית שהם שניים ובעבור כי החסרון מרביעית הוא חלק ראשון נכפול כ"ט על כ"ט יהיו כ"ט שניים נחסרנו מן המספר הנזכר ישארו ו' ראשונים | ||||||||
| I shall tell you the rule: if the parts in the row of the ratio do not share a ratio [to 60], proceed in the way of the multiplication, as I have mentioned for the fraction. | וכלל אומר לך כי אם לא היה ערך לחלקים הנמצאים בטור הערך שוב לעשות על דרך הכפל כאשר הזכרתי בשברים | ||||||||
| Always see: if there are any fractions added to the degrees of the determined center that are less than 30, leave them out and take the minutes that are written in the row of the ratio corresponding to the preceding degrees. | ולעולם ראה אם היו חלקים נוספים על מעלות המוצק המתוקן והם פחותים מל' הניחם וקח הראשונים הכתובים בטור הערך כנגד המעלות שעברו | ||||||||
| If the fractions that are with the determined center are more than 30, add one degree to the preceding degrees and take the fractions you find corresponding to it in the row of the ratio, whether it is after the whole degree or higher. | ואם החלקים שהם עם המוצק המתוקן יותר מל' הוסף מעלה אחת על המעלות שעברו וקח מה שתמצא כנגדה בחלקי טור הערך בין שתהיה אחר המעלה השלמה או למעלה ממנה | ||||||||
| If you find the determined quotient between 4 constellations to 8 constellations and you find that there is a difference between the fractions of the row of the ratio corresponding to the preceding degree and the fractions of the row of the ratio corresponding to the added degree - the difference between them will always be only one minute at most - proceed in the way of the multiplication, that you give the fractions added to the preceding degree the seconds they deserve. | ואם מצאת המנה המתוקנת שהיא בין ד' מזלות עד ח' מזלות ומצאת כי יש הפרש בין חלקי טור הערך שהם כנגד המעלה שעברה ובין חלקי טור הערך שכנגד המעלה הנוספת ולא יהיה לעולם ביניהם רק חלק ראשון עשה כדרך הכפל שתתן לחלקים הנוספים על המעלה שעברה מה שראוי מהשניים | ||||||||
| You need this method when determining the position of Mars or Mercury, however you do not need it for the determination of the position of Saturn and Jupiter, because in the fifth row and the seventh row there are no degrees, only minutes. | וזה המעשה יש לך צורך בתקון מאדים או כוכב חמה רק בתקון שבתי וצדק אין לך צורך כי אם בטור החמישי גם בטור הז' אין מעלות כי אם ראשונים לבדם |
Chapter Seven - Extraction of Roots |
השער הז' בהוצאת השרשים |
| All the numbers are according to three ways: | כל המספרים הם על שלשה דרכים |
|
האחד שרשים והשני מרובעים והשלישי לא שרשים ולא מרובעים |
|
והנה המרובע הוא המחובר מכפל שורש על עצמו |
|
כמו ט' כי הוא מרובע ארכו כרחבו ושרשו ג' |
| There are numbers that have no true [rational] root at all, and they are the majority. | ויש חשבון שאין לו שורש אמת כלל והוא הרוב |
|
כמו ב' במעלה הראשונה גם ג' וה' וו' וז' וח' |
| The square of an integer is always greater than the root. | ולעולם מרובע השלמים גדול מהשורש |
| Vice versa for the squares of fractions. | והפך הדבר במרובעי' הנשברי' |
| This is because when multiplying a fraction by a fraction, the product is less than the multiplied fraction. | והיה כן בעבור כי כפל שבר על שבר יהיה המחובר פחות מהשבר הנכפל |
| The one alone is both root and square; because it is between the fractions and the integers. | והיה האחד לבדו שורש ומרובע כי הוא בין השברי' והשלמי' |
Integers |
||
| First, we shall give test methods: | והנה נתן בתחלה מאזנים | |
Observe:
|
הסתכל אם לא היו מאזני המרובע ככפל מאזני השרש על עצמו אין המספר מרובע | |
|
ואם היה כמוהו יתכן להיות מרובע | |
|
דמיון המרובע קמ"ד | |
|
והמאזנים ט' והשרש י"ב ומאזניו ג' וכפל על עצמו הוא ט' | |
| והוא מאזני השרש ת' | ||
| Another test: | מאזנים אחרים | |
|
אם מאזני המספר ב' או ג' או ה' או ו' או ח' איננו מרובע | |
|
ואם היו המאזנים אחד מהמרובעים שהם במעלה הראשונה שהם א' או ד' או ט' גם ז' עמהם יתכן להיות מרובע | |
| Another test: | מאזנים אחרים | |
|
אם היה במספר המבוקש ממספרי המעלה הראשונה ב' או ג' או ז' או ח' אין המספר מרובע | |
|
ואם היה אחד מן המרובעים א' או ד' או ט' או מן המתגלגלים שהם ה' ו' יתכן שיהיה המספר מרובע | |
| Another test that is reliable: | מאזנים אחרים שהם מאזני צדק | |
|
אם מצאת במספר המבוקש מן המעלה הראשונה אחד דע שיש בשורש אחד או ט' | |
|
ואם היה במספר ד' דע שיש בשורש ב' או ח' | |
|
ואם היה במספר ו' דע שיש בשרש ד' או ו' | |
|
ואם במספר ט' דע כי יש בשרש ג' או ז' | |
|
ואם במרובע ה' דע שיש בשרש ה' | |
| Now I shall give you a way by which you can know which of the two mentioned [digits] is in the root. | ועתה אתן לך דרך שתוכל לדעת איזה מן השנים הנזכרים יהיה בשרש | |
| Now, note that the square numbers that are in the first rank are 3, which are 1, 4 9, | ועתה שים לבך כי המרובעים במעלה הראשונה הם ג' והם א' ד' ט' | |
| In the second rank they are 6, which are 16, 25, 36, 49, 64, 81. | ובמעלה השנית ו' והם י"ו כ"ה ל"ו מ"ט ס"ד פ"א | |
| All the ranks that follow these two have the same method: | וכל המעלות שהם אחר אלה השתים דרך אחת להן | |
|
כי כל מעלה שאיננה זוג הולכת על דרך המעלה הראשונה | |
|
וכל מעלה שהיא זוג הולכת על דרך המעלה השנית | |
| The square numbers that are analogous to the square numbers, which are in the first rank, are always one digit, and those that are in the second rank as well as every even [rank] are two digits and so are all the analogous. | ולעולם יהיו המרובעי' הנמשלים למרובעים שהם במעלה הראשונה מספר אחד ואשר הם במעלה השנית וכל זוג הם שני מספרים גם כל הנמשלים | |
| From the analogous squares you can know all the square numbers that precede them or succeed them. | ומהנמשלים תוכל לדעת כל המרובעים שהם לפניהם או לאחריהם | |
| When you know the root of the first rank or the second and you wish to find the root of the analogous number in whichever rank, proceed as follows: | וכאשר תדע שרש המעלה הראשונה או השנית ותרצה לדעת שרש הנמשל באיזו מעלה שיהיה ככה תעשה | |
| Know that the units that are in the first rank, are tens in the third rank, hundreds in the fifth, thousands in the seventh, tens of thousands in the ninth, hundreds of thousands in the eleventh, and so on by skipping endlessly. | דע כי ההוה במעלה הראשונה מהאחדים הם במעלה השלישית עשרות ובחמישית מאות ובשביעית אלפים ובתשיעית עשרת אלפים ובאחד עשר מאת אלף וככה עד אין קץ בדלוג | |
| Because, the skipping is from an odd number to an odd number. | כי ידלג ממספר שאיננו זוג אל מספר שאיננו זוג | |
| The units that are in the second rank of the roots are tens for the fourth rank, hundreds for the sixth, thousand for the eighth, tens of thousands for the tenth and hundreds of thousands for the twelfth. | והאחדים שהם במעלה השנית בשרשים הם מעלה הרביעית עשרות ובששית מאות ובשמינית אלפים ובעשירית עשרת אלפים ובשנים עשר מאה אלף | |
| Because, the skipping is always from an even number to an even number. | כי לעולם ידלג מזוג אל זוג | |
| Now I will tell you how to proceed if you know the analogous square and you know its root: | ועתה אומר לך איך תעשה כאשר תדע המרובע הנמשל ותדע שרשו | |
Subtract the square from the sought number, after making sure that you take only the preceding square, which is the closest to the number, see the difference between the square [and the sought number] and divide it by double the root of the preceding square. Make it so that you do not give everything you can for it, but leave a little bit of it so that you can still take the square of the quotient of it. When you see that the difference between the preceding square [and the sought number] is as much as the quotient, then you know that the square number is true.
|
חסר המרובע מהמספר המבוקש אחר שתשמור שלא תקח לעולם כי אם המרבע שעבר שהוא קרוב אל מספר וראה המרחק שבין המרבע וחלקהו על כפל שרש המרבע שעבר וככה עשה שלא תתן לו כל מה שתוכל רק הנח ממנו שתוכל לקחת מרבע מה שעלה בחלוק וכאשר תראה שיהיה המרחק בין המרובע שעבר כמספר מה שעלה בחלוק אז תדע שהמרבע אמת | |
If the sought number is less than the analogous square number, see how much the difference between your number and the succeeding square number is. Since you have to give it a little bit more than you can because your number precedes the analogous squares, as I will explain later, do not add the square of the quotient to your number. See if the number is as much as double the root multiplied, then you know that your number is true.
|
ואם היה המספר המבוקש פחות מהמרבע הנמשל ראה כמה מרחק בין מספרך ובין המרבע הבא לפי שאתה צריך לתן לו מעט יותר ממה שתוכל בעבור היות מספרך לפני המרבע הנמשל כאשר אפרש ואל תכניס במספרך מרובע החלוק | |
| If it is 1, subtract one from tens, then 9 remain. | כי אם היה אחד חסר מן העשרות אחד וישארו ט' | |
| In this way you can know: if you find 1 or 9 in the square, then it must be in the root, as you will see from the examples. | ובדרך הזה תוכל לדעת כשתמצא א' במרבע או ט' ראוי להיות בשרש כאשר תראה בדמיונות | |
|
דמיון בקשנו לדעת מרובע שעבר קרוב אל מאתים | |
|
והנה זה מהמעלה השלישית שאיננה זוג ונבקש זה מהמעלה הראשונה וכבר אמרנו כי המרבעי' שיש בה א' ד' ט' והנמשלי' אליהם מאה וד' מאות וט' מאות | |
|
והנה נתן לו ד' כפולים על כ' הם פ' נשארו כ' נחסר ממנו י"ו שהוא מרובע מה שעלה בחלוק ישאר ד' נחסרנו מהמאתים ישארו קצ"ו וזהו המרבע הקרוב אל מאתים | |
|
ונוסיף ד' שעלה בחלוק על השרש הראשון שהיה י' יהיו י"ד וזהו שרש המרבע באמת | |
|
והנה נבחן אותו במאזנים כמשפט ידוע כי מאזני י"ד ה' וכפלו על עצמו כ"ה והנה המאזני' ז' וככה בדרך קצ"ו | |
|
ובמאזני' אחרי' בעבור שיש שם חשבון מתגלגל נכון להיותו מרבע | |
|
ובמאזני' אחרי' בעבור שיש במרובעו ו' ראוי להיות בשרש ד' או ו' | |
|
והנה המרחק מהמרבע הנמשל ק' וכפל [שורש] מרובע הנמשל כ' כפלנוהו על ד' עלו פ' | |
|
דמיון אחר במעלה הזאת בקשנו לדעת מרבע הקרוב אל ג' מאות | |
|
וג' מאות יותר קרובי' אל ד' מאות שהוא מרבע הנמשל במעלה הזאת ממרובע הראשון שהוא ק' | |
|
והנה נסתכל המרחק מהמרבע הבא והוא ק' וידענו כי שרש ד' מאות הוא כ' וכפלו מ' נחלוק ק' עליו ונתן לו מעט יותר ממה שנוכל בעבור היות המספר לפני המרובע | |
|
וכאשר נכפול ג' על מ' שהוא כפל השרש יהיו ק"כ נחסר זה המספר מת' יהיו ר"פ | |
|
והנה נחסר הג' מכ' שהוא שרש המרובע הנמשל וישארו י"ז והוא שרש זה המרובע | |
|
ובעבור כי יש במרובעו ט' הנה התבאר שראוי שיהיה בשרש ז' ולא ג' כי לא יתכן להיות ג' במרובע רק אם היה קרוב אל המרובע הנמשל שעבר | |
| In this way you can know if there is 1 or 9 in the square according to the distance from the preceding and succeeding analogous squares. | ועל זה הדרך תוכל לדעת במרובע ששם א' או ט' כפי המרחק מהמרובע שעבר ומהמרובע הנמשל העתיד | |
| Similarly, you can deduce if you find 4 in the square, whether there is 2 or 8 in the square root. | ובזה תוכל להפריש אם מצאת במרובע ד' אם יש בשרש ב' או ח' | |
| likewise, if there is 6 in the square, you can know whether there must be 4 or 6 in the root. | וככה אם יש במרובע ו' תדע אם ראוי להיות בשרש ד' או ו' | |
| Now I shall reveal to you the secret why this is so. | והנה אגלה לך קצת זה הסוד למה היה כך | |
| Know that the two major orbits, one goes east and the other goes west, and that the upper force is one in both. | דע כי השתים המסיבות הגדולות אחת הולכת למזרח ואחת הולכת למערב וכח עליון הוא אחד בשתיהם | |
| So, one is the square of one, and there is one in the square of 9. | והנה אחד מרובע אחד יש במרובע ט' אחד | |
| As the number 2 is second to the one, so the number 8 is second to the 9 backwards, since the course of this is opposite to the course of the other. | וכאשר הוא חשבון ב' שני לאחד ככה חשבון ח' שני לט' אחרונית כי מהלך זה הפך מהלך זה | |
| The square of 2 is 4 and there is 4 in the square of 8. | ומרובע ב' ד' וככה יש במרובע ח' ד' | |
| The same applies to 3 and 7; 4 and 6. | וכן דרך ג' אל ז' וד' עם ו' | |
| Thus, the number 5 is left as a mean, therefore it is recurring around itself. | והנה נשאר חשבון ה' אמצעי וע"כ הוא מתגלגל על עצמו | |
|
ותוכל להוציא המרובע הנז' על הדרך הראשונה שהזכרתי במרובע קצ"ו שתחסר המרובע שהוא ק' מהמספר הנתון שהוא ש' יהיה המספר ר' וידוע כי שרש ק' י' וכפלו כ' והנה לא נוכל לתת לו י' כי לא ישאר מספר שנוכל לחסר ממנו מרובע מה שיעלה בחלוק | |
|
ונכפול ז' על כ' שהוא כפל השרש יהיו ק"מ נוסיף עליהם הק' שהוא המרובע יהיו ר"מ | |
|
גם נוסיף שעלה בחלוק על י' שהיה השרש והנה יהיה שרש זה המרובע י"ז | |
|
דמיון במעלה הרביעית בקשנו לדעת המרובע הקרוב אל אלף ור' | |
|
והנה בעבור שהוא מספר זוג נבקש במעלה השנית מספר דומה לזה והוא י"ב ומרובע שעבר הוא ט' וככה ט' מאות וכאשר שרש ט' ג' ככה שרש ט' מאות ל' | |
|
נכפול ס' על ד' יהיו ר"מ נחברם אל המרובע הנמשל שעבר יהיה אלף וק"מ | |
|
ובעבור שעלה בחלוק ד' נוסיפנו על שרש המרובע הנמשל שעבר שהיה ל' יהיה שרש זה המרובע ל"ד | |
|
והוא אמת בכל המאזנים | |
|
דמיון אחר במעלה הזאת נבקש המרבע הקרוב לז' אלפים ת"ק | |
|
והנה זה המספר דומה לע"ה כי הוא מן הזוגות ובעבור שהוא קרוב אל פ"א יותר מס"ד וידענו כי שרש פ"א ט' וככה יהיה שרש ח' אלפי' וק' צ' וכפלו ק"פ והנה המרחק ו' מאות נתן לו ד' אע"פ שאינו שלם בעבור שהחשבון הנתון הוא לפני המרובע הנמשל | |
|
וכאשר נכפול כפל השרש על ד' יעלו תש"כ נחסר זה המספר מהמרובע הנמשל יהיה הנשאר ז' אלפים ש"פ | |
|
ושרשו פ"ו כי נחסר ד' וזהו המרובע באמת | |
|
וגם אם עשינו בדרך האחרת שהזכרתי בדמיונים שעברו יהיה הדבר שוה | |
|
דמיון במעלה החמישית נבקש המרובע הקרוב אל כ"ג אלף | |
|
והנה זה דומה למעלה הראשונה כי איננו זוג והנה י' אלפים כמו אחד וכבר אמרנו מה שהוא במעלה הראשונה אחד יהיה במעלה החמישית מאה והנה המרובע [330]שעבר י' אלפים | |
|
נוסיפנו על השרש שעבר יהיה ק"נ ונשאר לנו עוד ג' אלפים נחסר ממנו אלפים ת"ק שהוא מרובע מה שעלה בחלוק ישארו ת"ק | |
|
ויהיה המרובע כ"ב אלף ותת"א והשרש קנ"א | |
|
כאשר יכפול המספר אם יעלה לעשרות חבר עשרות עם עשרות לפי המעלות ואם יש שם אחדים שים במקום האחדים אשר כפלת | |
|
דמיון אחר במעלה הזאת נבקש המרובע הקרוב אל פ"ה אלפים | |
|
והנה הוא קרוב אל המרובע הנמשל שהוא צ' אלף ושרשו ש' והנה המרחק ה' אלפים נחלקנו על כפל השרש שהוא ת"ר ונתן לו ט' הקרוב יותר ממה שנוכל | |
|
והנה יש לו תוספת ת' נחסרם מהמספר הנתון ישארו פ"ד אלפים ות"ר ועם תוספת פ"א שהוא מרובע מה שעלה בחלוק יהיה פ"ד אלף תרפ"א וזה הוא המרובע באמת | |
|
ושרשו רצ"א | |
|
דמיון במעלה הששית בקשנו לדעת המרובע הקרוב אל ר' אלף | |
|
ובעבור שזאת המעלה מן הזוגות היא דומה לעשרים והמרובע שעבר הוא י"ו וכבר אמרנו כי מה שהוא במעלה השנית אחדים יהיו במעלה הששית מאות והנה השרש ת' והמרובע שעבר ק"ס אלפים והנה המרחק מ' אלף נחלקנו על כפל השרש שהוא ת"ת והנה לא נוכל לתת לו ה' בעבור מרובע החלוק נתן לו ד' שהם מ' | |
|
ונכפול זה המספר על ת"ת יעלו ל"ב אלף ונשארו ח' אלף נסיר מהם אלף וו' מאות שהוא מרובע מ' ישארו ו' אלף וד' מאות | |
|
נחסר עוד מרובע ז' נשאר קצ"א נחסר זה המספר מהמספר הנתון ישארו קצ"ט אלף ותת"ט וזהו המרובע | |
|
והשרש תמ"ז | |
|
דמיון אחר במעלה הזאת לדעת מרובע הקרוב אל ו' מאות אלף | |
|
בעבור כי המרובע הנמשל הוא אחרי החשבון נקח המרחק שהוא מ' כי ו' מאות אלף הם כמו ס' וכאשר חלקנום על אלף וו' מאות נתננו לו כל מה שיכולנו ואם יחסר מעט מהאמת | |
|
חסרנו זה משרש המרובע הנמשל שהוא ח' מאות ושהם דומים לח' והנה השרש תשע"ד וכבר היה לנו מ"א אלף ות"ר והיה לנו מ' אלף שהוא המרחק והנה אין לנו לחסר כי אם אלף וו' מאות מהמספר הנתון ויש לנו להוסיף עליו מרובע כ"ו שעלה בחלוק שהוא תרע"ו | |
|
דמיון במעלה השביעית בקשנו לדעת המרובע הקרוב אל ה' אלפי אלפים | |
|
ונאריך לבאר זה הדמיון כהוגן עד שיהיה עקר להוציא המרובעים שהם במעלות אחרות עד אין קץ אע"פ שאין צורך להם בדברי החכמות | |
|
והנה המעלה הזאת דומה לראשונה והחשבון המבוקש כמו ה' והנה נסיר המרובע שהוא ד' ישאר לנו אלף אלפים והשרש שלנו שעבר אלפים וכפלו ד' אלפים נחלק עליו המספר הנשאר | |
|
יעלו ת"ת אלף ונשאר לנו ר' אלף נחסר ממנו מרובע מה שעלה בחלוק שהוא מ' אלף נשאר לנו ק"ס אלף | |
|
ישאר לנו כ"ח אלף נסיר ממנו מרובע מה שעלה בחלוק זה שהוא ל' והם תת"ק נשאר כ"ז אלף וק' | |
|
נשאר לנו ש"מ נחסר ממנו ל"ו שהוא מרובע ו' ישאר ש"ד | |
| Test this with all the testing methods and you will find it correct. | ותבחן זה בכל המאזנים ותמצאנו נכון | |
|
וככה בדרך כפל השרש על עצמו | |
|
כי כפל אלפים על אלפים יהיו שנים על שנים במעלה השביעית שהם ד' אלפי אלפים ונשאר לנו המספר הנז' | |
|
והנה נכפול אלפים במאתים פעמים יהיה ת"ת אלף ונשארו קצ"ט אלפים גם תרצ"ו | |
|
נשוב לכפול אלפים על ל' פעמים יעלו ק"כ אלף | |
|
נסירם מהמספר הנשאר ישארו ע"ט אלף וגם תרצ"ו | |
|
נשוב לכפול אלפים על ו' פעמים[331] יעלו כ"ד אלף | |
|
נסירם מהמספר הנשאר וישארו נ"ה אלפים גם תרצ"ו | |
|
וכבר כפלנו האלפים על כל המספרים | |
|
עתה נחל לכפול מאתים על עצמו ועל האחרים שהם אחריו | |
|
והנה כפלו על עצמו מ' אלפים | |
|
חסרנום מהמספר הנשאר ישארו ט"ו אלפים תרצ"ו | |
|
גם נכפול ר' על ל' פעמ' יעלו י"ב אלף | |
|
נחסרנו מהמספר הנשאר ישארו ג' אלפים תרצ"ו | |
|
ועוד נכפול ר' על ו' פעמ' יעלו אלפים ות' | |
|
נסירם מהמספר הנשאר ישארו אלף ורצ"ו | |
|
וכבר השלמנו לכפול ר' על כל המספרים שהם אחריו | |
|
נחל מן ל' | |
|
והנה כפלו על עצמו תת"ק | |
|
נחסרנו מהמספר הנשאר ישארו שצ"ו | |
|
נכפול עוד ל' על ו' פעמים יהיו ש"ס ונשארו ל"ו שהוא מרובע ו' והנה החשבון נכון | |
| Before I will discuss the numbers that have no root, I shall show you a method how you can know many square numbers from one square number and many roots from one root: | וקודם שאדבר על המספרים שאין להם שרש אראה לך דרך איך תוכל לדעת מרובעים רבים ממרובע אחד גם שרשים רבים משרש אחד | |
| Know that the product of a square by a square is always a square and its root is the product of the root of one of the squares by the root of the other square.
|
ודע כי כפל מרובע על מרובע לעולם יהיה מרובע והשורש יהיה כמו העולה מכפל שרש אחד מהמרובעים על שרש מרובע האחר | |
|
דמיון כפלנו מרובע ה' על מרובע ט' ועלה אלפים וכ"ה וזה החשבון מרובע בקשנו לדעת כמה שרשו כפלנו ה' על ט' ועלו מ"ה והוא השרש באמת | |
| The ratio of a square to a square is also a square. | וערך מרובע אל מרובע גם הוא מרובע | |
| If you divide the larger one by the smaller one, you will find its root. | ואם חלקת הגדול על הקטן תמצא שרשו | |
|
דמיון מה ערך מ"ט אל ק' | |
|
הנה הוא כפלו וב' שביעיות שביעית | |
|
בקשנו לדעת שרש זה המרובע | |
|
חלקנו י' על ז' עלה אחד וג' שביעיות וזהו השרש | |
|
כי אחד על אחד אחד | |
|
וכפל אחד על ג' שביעיות פעמי' ו' שביעיות | |
|
וכפל ג' שביעיות על ג' שביעיות ט' שביעיות שביעית | |
|
והנה נעשה מן הז' שביעיות שביעית אחת ונחברנה אל הו' שביעיות שהיו לנו יעלו אחד שלם | |
|
והנה יש לנו שנים שלמים וב' שביעיות שביעית | |
| We wish to know the square of a known number from a known square of a known number: we divide the greater known number by the smaller known number, whose square we know; we take the square of [the quotient] and multiply it by the known square; the result is the square of the greater number that we knew.
|
בקשנו לדעת מרובע מספר ידוע ממרובע ידוע למספר ידוע חלקנו המספר הידוע הגדול על מספר הידוע הקטן שידענו מרובעו ונקח מרובעו ונכפלנו על המרובע הידוע והעולה הוא מרובע המספר הגדול שידענו | |
|
דמיון בקשנו לדעת מרובע י"ט ממרובע ז' שהוא מ"ט | |
|
חלקנו י"ט על ז' עלו ב' וה' שביעיות | |
|
כפלנו מרובע זה והנה ב' על ב' ד' שלמי' | |
|
וב' על ה' שביעיות פעמי' הם כ' שביעיו' | |
|
וה' על ה' הם כ"ה שביעיות שביעית | |
|
נעשה מהם ג' שביעיות נשאר לנו ד' שביעיות שביעית נחבר הג' שביעיות שהיו לנו על הכ' יהיו כ"ג | |
|
והנה המרובע ז' שלמים וב' שביעיות וד' שביעיות שביעית | |
|
והנה נכפול מ"ט על ז' יעלו שמ"ג נחבר אליהם י"ד שהם ב' שביעיות מ"ט יהיו שנ"ז | |
| If we sum 2 squares, whether they are successive or far apart from each other, we double the sum, then subtract from this double the square of the difference between their two roots. The remainder is always a square, and the sum of the two roots is [its] root. | ואם חברנו ב' מרובעים בין שיהיו על הסדר או שיהיו מרוחקי' זה מזה נכפול המחובר ונחסר מזה הכפל מרובע היתרון שיש בין שני המספרי' שהם השרשים יהיה הנשאר לעולם מרובע והמחובר מהב' שרשים הוא השרש | |
|
דמיון חברנו פ"א שהוא מרובע ט' עם תשכ"ט שהוא מרובע כ"ז יהיו תת"י וכפלו אלף ותר"כ וידענו כי שרש המרובע הקטן ט' ושרש המרובע הגדול כ"ז והיתרון ביניהם י"ח ומרובעו שכ"ד חסרנום מהכפול נשאר אלף ורצ"ו והוא מרובעו ושרשו ל"ו שהוא מחובר מט' עם כ"ז | |
| If we sum 3 squares, we triple them, then subtract from the product the [sum of] squares of the 3 differences that are between the roots of the 3 numbers. The remainder is also a square. If you sum the 3 roots, the sum is the root of the remainder. | ואם חברנו ג' מרובעי' ונכפלם ג' פעמים ונחסר מהעולה באחרונה מרובעי הג' יתרונים שיש בין שרשי הג' מספרים והעולה באחרונה יהיה גם הנשאר מרובע וכאשר תחבר הג' שרשים יהיה המחובר שרש הנשאר | |
|
דמיון חברנו ל"ו שהוא מרובע ו' עם ס"ד שהוא מרובע ח' ועם ד' מאות שהוא מרובע כ' והנה המחובר מג' מרובעי' הוא ת"ק כפלנוהו ג' פעמים עלו אלף ות"ק שמרנו זה החשבון | |
|
והמחובר מן הג' שרשים הוא ל"ד והוא שרש מרובע הנשאר | |
| Likewise, if you sum 4 or 5 numbers and multiply them a certain number of times. | ועל זה הדרך אם חברת ד' מספרים או ה' ותכפלם כך פעמ' | |
| The rule is that you multiply by the number of squares that you sum, then always subtract the squares of the differences, as many as they are, from the sum; the remainder is a square. You just have to be sure to know the differences. | והכלל שתכפול כפי מספר המרובעי' שחברת ותחסר לעולם מרובעי היתרוני' כמה שיהיו מהמחובר יהיה הנשאר מרובע ויש לך להישמר לדעת היתרונים | |
| I will tell you [a rule] according to which you can know how much the number of differences is: always subtract one from the number of squares and know how much is the sum of all numbers that precede this number, as I showed you and as the sum so is the number of differences. | ואומר לך שתוכל לדעת ממנו כמה מספר היתרונים חסר לעולם אחד ממספר המרובעי' ודע כמה מספר המחובר שלפני אותו המספר כאשר הראיתיך וכמספר המחובר יהיה המספר היתרונים | |
|
דמיון חברנו ו' מרובעי' ונרצה לדעת מספרי היתרוני' | |
|
נחסר אחד כאשר דברנו ישארו ה' והמספרי' שהם לפניו יהיו ט"ו וככה יהיו מספרי היתרוני' |
Fractions |
|
| Now we start to discuss the square fractions that have a true root: | עתה נחל לדבר על הנשברי' המרובעי' שיש להם שרש אמת |
| We say a general statement about the square fractions that are alone or combined with integers: | ונאמ' דבר כולל לנשברי' המרובעי' שהם לבדם או שהם עם שלמי' |
| See if the fraction is one-half, third, fifth, sixth, seventh, or eighth, it is not a square. | הסתכל אם היה הנשבר חצי או שלישית או חמישית או ששית או שביעית או שמינית אינו מרובע |
| This is because these numbers as integers are not squares. | והיה כן בעבור כי אלה המספרי' בשלמי' אינם מרובעי' |
| Only if there is one-quarter, or one-fifth of one-fifth, one-sixth of one-sixth, one-seventh of one-seventh; or one-eighth of one-eighth, or one-half of one-eighth, for it is one-sixteenth. | רק אם היה בו רביעית או חמישית חמישית או ששית ששית או שביעית שביעית או שמינית שמינית או חצי שמינית כי הוא חלק מי"ו |
| Observe: if there is one-quarter in square, know that there is one-half in the root; if there is one-ninth there, know that there is one-third in the root; if there is one-half of one-eighth there, know that there is one-quarter in the root. | והנה הסתכל אם היה במרובע רביעית דע כי בשרש חצי ואם שם תשיעית דע כי יש בשרש שלישית |
| We begin to discuss the square fractions that are alone without integers: | ונחל לדבר על המרובעי' נשברי' לבדם שאין עמהם שלמי' |
| We have already said that the fractions are reversed to the integers. | וכבר אמרנו כי הנשברי' הפך השלמי' |
| When you multiply an integer by and integer whether by itself or by another, the product is greater than the [multiplied] numbers; the reverse is with fractions. | וכאשר תכפול חשבון שלם על חשבון שלם בין יהיה על עצמו או על אחר יהיה העולה גדול מהמספרי' והפך זה בנשברי' |
| Also, while the squares of the integers are greater than their roots, the opposite is for the square fractions: their roots are greater than their squares. | וכאשר המרובעי' השלמי' גדולי' משרשיהם יהיו המרובעי' הנשברי' להפך בי' שרשיהם גדולים ממרובעיהם |
| Extracting the squares from their roots is easy: for, the product of one-half by one-half is one-quarter and this is the square; likewise one-third by one-third is one-ninth; 2 thirds by 2 thirds are one-third; one-third of one-third is one-ninth; 4 fifths by 4 fifths are 3 fifths and one-fifth of one-fifth and this is the square. | ולהוציא המרובעי' משרשיהם דבר קל כי כפל חצי על חצי הוא רביעית אחד והוא המרובע וככה שלישית על שלישית תשיעית אחת |
| In this way for all. | ועל זה הדרך הכל |
| But, it is difficult to extract the root from the square. | רק הקשה להוציא השרש מהמרובע |
| I shall give you a general way in the way of the astrologers that extract all their numbers from the number 60. | ואתן לך דרך כוללת על דרך חכמי המזלות שיוציאו כל חשבונם מחשבון ס' |
|
אם ישאל אדם כמה הם ב' שלישיות כפולות על ב' שלישיות |
|
תכפול מ' על מ' יהיו אלף ות"ר חלקם על ס' יהיו כ"ו חלקי' ראשוני' ונשארו מ' שניים והכל ד' תשיעיות |
|
כי תשיעית ו' ראשוני' גם מ' שניים שהם שתי שלישיות ראשון ואם עשינו מזה המספר שלישיות יהיו כ' גם נכפול ס' על ג' יהיו ק"פ והכל יהיו ממתכונת אחת וכאשר נחלק זה המספר על כ' עלו ט' שהוא תשיעית אחת |
|
ואם הפך השואל השאלה ואמר כי המרובע ד' תשיעיות אחד כמה השרש |
|
הפוך גם אתה הדבר שתדע כמה הם ד' תשיעיות ס' וכבר אמרנו שהם כ"ו ראשוני' ומ' שניי' עשה מן הראשוני' שני' ושים השניי' עמהם יהיו הכל אלף ת"ר וזה המספר בזוגות דומה לי"ו וחשוב שהם שלמי' והנה השרש מ' שוב וחשוב כי הם ראשוני' וככה הוא השרש |
|
דמיון בחשבון שלא יתחלק על ס' כפלנו ד' שביעיות על ד' שביעיות |
|
והוא על דרך חכמי החשבון נכפול ד' על ד' יהיו י"ו |
|
ועל דרך הדומה לחכמי המזלות יהיו חלקיו ע' והנה ד' שביעיות הם מ' נכפול מ' על מ' יהיו אלף ות"ר |
|
ואם השואל יהפוך השאלה ויאמר כמה שרש זה המרובע שהוא ככה |
|
גם אנחנו נהפוך הכ"ב ראשוני' ונעשה מהם שניי' ונוסיף עליהם הס' שניים שהיו לנו יהיו אלף ות"ר נחשוב כי הם שלמי' ושרשם מ' ונחשוב כי הם ראשוני' וזהו השרש באמת |
|
ואם רצינו להשיב ממתכונת ע' אל מתכונת ס' |
|
נכפול מ' על ס' ונחלק העולה על ע' יעלו ל"ד וישארו כ' נכפלם פעם אחרת על ס' ונחלק העולה על ע' יעלו י"ז וישאר לנו זה שאמר שהוא אחד הוא עשרה לכן החשבון אינו מדקדק נעשה ממנו ס' ובעבור כי ע' גדול מס' נכפלנו עוד ויהיו ג' אלפים ות"ר |
|
דמיון אחר כפלנו שלישית על שלישית |
|
עלה תשיעית אחד והוא המרובע ונעשה חלקיו צ' ושלישיתו ל' |
|
והפך זה בקשנו לדעת השרש מזה המרובע |
|
עשינו מהי' חלקים שניים והם תת"ק חשבנו שהם שלמי' וכמספר הזה יהיו ראשוני' והוא השרש |
| All of this is true if there is a real square number and a real root, but not if it is said about fractions that have no real root, whether divisible by 60, or not. | וכל זה נכון אם יש מרובע אמת ושרש אמת רק אם אמר חשבון חלקים שאין להם שרש אמת בין שיהיה להם ערך אל ס' או לא יהיה |
|
כי אם אמר י"ב חלקים הוא המרובע כמה השרש |
|
ידענו כי י"ב הוא חמישית ס' וכבר אמרנו כי לא יתכן להיות במרובע חמישית |
|
וככה אם אמר כי המרובע י' חלקים שהוא ששית אחת לא יתכן להיות |
|
רק אם אמר כי המרובע חלק אחד ומ' שניים שהוא ששית הששית הוא הנכון |
| As for the numbers that are divisible by 60, most of them are not squares. | והנה במספר שיש לו ערך אל ס' לא יתכן להיות רובי המספרים מרובעים |
| All the more so the numbers that are not divisible at all, such as 11, 13, (15), 17, 19 and many others that have no divisor. | אף כי המספרים שאין להם ערך כלל כמו י"א י"ג ט"ו י"ז י"ט ואחרים רבים שאין להם ערך |
| [Latter], I will give you a method by which you will be able to extract for every square fraction its root by approximation to the truth. | ועוד אתן לך דרך שתוכל להוציא לכל מרבע נשבר שרשו בדרך שהיא קרובה אל האמת |
Integers and Fractions |
|
| Now, I shall discuss the integers with fractions that are squares. | ועתה אדבר על השלמים שיש בהם נשברים והם מרובעים |
|
דמיון אמר אומר מרובע שהוא י"א ותשיעית כמה השרש |
|
אחר שאמר שיש בו תשיעית נכון הוא להיותו מרובע ובשרשו שלישית נכח התשיעית חסר ממנו התשיעית שהוא מרובע שבר השבר נשארו י"א שלמים |
|
דמיון אחר המרובע שהוא ז' שלמים ונ' חלקים ראשונים וכ"ד שניים |
|
הנה בעבור ששם כ"ד שניים ידענו שיש בחשבון חומש החומש שהוא ב' חלקים וכ"ד שניים נחסר זה מרובע השבר מהמספר הנתון ישאר ז' שלמים ומ"ח ראשונים והנה המרחק מהמרובע שהוא אחריו אחד שלם וי"ב חלקים שהם ע"ב ראשונים |
|
והנה נבחן זה בכפל כי הנה ב' על ב' ד' שלמים וידענו כי ב' על מ"ח פעמים יהיו קצ"ב ומ"ח הם ד' חמישיות יהיו י"ו חמישיות נעשה מהם ג' שלמים וישאר חמישית אחת |
|
דמיון מרובע שהוא מ"ד וד' תשיעיות |
|
ידענו כי התשיעיות מן השלישיות יצאו |
|
והנה נסיר זה המרובע שהוא לשברי שברים ונבקש כמה מרחק השלמים מן המרובע שעבר והנה ח' נשיבם ראשונים יהיו ת"פ |
|
ובדרך חכמי המזלות נכפול ו' על ו' והם ל"ו ונכפול ו' על מ' ומ' על ו' והם ת"פ ראשונים נחלקם על ס' ועלו ח' שלמים |
| After I have mentioned these examples, proceed in this way with all the ranks. | ואחר שהזכרתי אלה הדמיונים תעשה כדרך הזה בכל המעלות |
Approximations |
|
| Now I will tell you a general way for all the numbers that have a root or do not have [a root]: | ועתה אומר לך דרך כלל לכל המספרים שיש להם שרש אמת או אין להם |
| Know that between two successive [square] numbers there are always [numbers] as the number of the roots of both. | דע כי לעולם יהיה בין ב' מספרים שהם על הסדר כמספר השנים שרשים |
Look at the number you want: how much is its distance from the preceding square? If the difference between your number and the preceding square is as the root of the preceding square, it is the mean number. 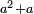
|
והנה הסתכל במספר שתרצה כמה מרחקו מהמרבע שעבר אם היה המרחק בין מספרך ובין המרובע שעבר כשרש המרובע שעבר הוא מספר האמצעי |
Extract any number that is less than the mean from the preceding square number 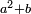
|
וכל מספר שיהיה פחות מהאמצעי הוציאהו מהמספר המרובע שעבר |
If it is greater than the root of the preceding [square], extract it backwards from the succeeding square. 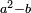
|
ואם היה יותר מהשרש שעבר הוציאהו אחורנית מהמרובע שלפניו |
|
דמיון המספר עשרים |
|
והנה מרחקו מן המרובע שעבר ד' ואם תשיבם ראשונים ותחלקם על ח' שהוא כפל השרש יהיו ל' שהוא חצי ס' |
|
ואם לקחנו מרחק הכ' מהמרובע הבא יהיה כמספר השרש נשיבם ראשונים ונחלקם על י' שהוא כפל השרש יהיו ל' |
|
על כן אמרתי כי כ' הוא חשבון אמצעי |
| Now, note: if your number is close to the preceding square, look at the difference between them, convert it to minutes. | ועתה שים לבך אם היה מספרך קרוב אל המרובע שעבר ראה המרחק שיש ביניהם ועשה ממנו ראשונים |
| If there are minutes in your number, add them to the minutes you got. | ואם יש בחשבונך ראשונים הוסיפם על הראשונים שעשית |
| If you also have seconds, convert all to seconds. | ואם יש עמך שניים השב הכל במערכת השניים |
| Or choose the following shorter way: if the seconds are less than 30, leave them out; if they are more, add one minute instead of them. | או קח דרך קצרה אם היו השנים פחותים מל' הניחם ואם יותר הוסף ראשון אחד עליהם |
| When you know of how many minutes the difference is, divide it by twice the preceding root and add the quotient to the preceding root. The sum is called "the first root". | וכאשר תדע כמה הראשונים של המרחק חלקם על כפל השרש שעבר וההוה הוסיפנו על השרש שעבר והמחובר יקרא שרש ראשון |
| If your number is in hundreds or thousands, this root is enough for you in geometry, because it does no harm. | ואם חשבונך היה במאות ואלפים זה השרש יספיק לך במדות כי לא יזיק |
| However, if the number is small, you still need a second root, which is more precise. | רק אם המספר היה קטן אתה צריך לשרש שני שהוא יותר מדוייק |
| To calculate chords and arches, you need a third root, which is even more precise. | ולהוציא היתרים והקשתות אתה צריך לשרש שלישי שמדוייק יותר |
| This is how the approximation is applied: when you have the minutes of the difference, know how much is their square, divide it by twice the first root, then know how much the quotient is, and in what rank it is, whether in minutes or in seconds, as I have shown you in the chapter of the fractions and subtract it from the first root; the remainder is the second root. | וככה יהיה הדקדוק כשיהיו לך הראשונים של המרחק דע כמה מרובעם וחלקהו על כפל השרש הראשון ודע העולה כמה הם ובאיזה מעלה הם בראשונים או בשניים כאשר הראיתיך בשער השברים וההוה חסרהו מן השרש הראשון והנשאר הוא השרש השני |
| If you want to calculate it more precisely, take the square of the quotient and divide it by double the second root. | ואם תרצה לדקדקו עוד קח מרובע זה שעלה בחלוק וחלקהו על כפל השרש השני |
| Now I shall give you examples according to way of the arithmeticians with approximate calculation. | ועתה אתן לך דמיון על דרך חכמי החשבון בדרך קרוב |
|
בקשנו לדעת שרש מאתים |
|
והנה המרובע שעבר קצ"ו והמרחק ד' שלמים כשתחלקם על כ"ח שהוא כפל השרש תעלה שביעית אחת והנה השרש י"ד ושביעית אחת |
|
ואם רצית לדעת שרש עשרים אלף |
|
כפול זה השרש על י' יעלה קמ"א וג' שביעיות |
|
ואם בקשנו לדעת כמה שרש שנים משרש מאתים שהוא י"ד ושביעית |
|
נקח עשיריתו והנה מי' נקח אחד שלם ועשירית ד' והם ד' עשיריות וידענו כי ד' עשיריות הם ב' חמישיות שהם כ"ד ראשונים |
|
נשוב להוציא זה השרש מכ' אלף |
|
וידענו כי זה החשבון הוא דומה לאחדים וי' אלפים כמו אחד והוא המרובע הנמשל |
|
והנה נחסר י' הפירוש שתקח הראשונים של המרחק אחר שלקחת אותם על כפל השרש שעבר והם הראשונים אשר עלו לך בשרש |
| Or if you wish, say that you take the first root, square it and see how close it is. Then, divide its excess over your first number by double the first root, subtract the quotient from the first root and the remainder is the second root. | או אם תרצה אמור שתקח השרש הראשון ותרבעהו ותראה כמה יהיה הקרוב והתוספת אשר בו על מספרך הראשון והתוספת ההוא תחלק על כפל השרש הראשון והיוצא בחלוקה תחסר מהשרש הראשון והנשאר הוא השורש השני |
|
ת"ו אלפים ממספרנו ישארו י' אלפים נחלקם על כפל השרש שהוא ר' ולא נתן לו כל מה שנוכל אך נניח כפי מרובע החלוק והנה נתן לו מ' וישארו לנו אלפים נסיר מהם אלף ות"ר שהוא מרובע החלוק נשאר ת' והשרש שלנו ק"מ וכפלו ר"פ נחלק הנשאר עליו נתן לו אחד נשארו ק"כ נחסר ממנו א' שהוא מרובע א' נשאר קי"ט והשרש שלנו קמ"א נעשה מהנשארים ראשונים יהיו ז' אלף וק"מ נחלקם על רפ"ב שהוא כפל השרש שלנו עלו כ"ה חלקים ראשונים וי"ט שניים נחלק כל מה שאמרנו מן השלמים והשניים על ק' יהיה העולה אחד שלם כ"ד נ"א י"א וזהו מדוקדק יותר מן הראשון שהזכרנו |
| If you take any number that is twice a square number and multiply the root of this square number by this root, you will get the root of the number exactly. | ואם תקח כל חשבון שהוא כפל מרובע ותכפול שרש המרובע על זה השרש יצא לך שרש החשבון מדוקדק |
|
דמיון רצינו לדעת כמה שרש י"ח |
|
והנה כפלנו שרש המרובע שזה המספר כפלו ועלה ד' שלמים י"ד ראשונים ל"ג שניים ל"ג שלישיים |
|
ואם כפלנו זה המספר יהיה שרש ע"ב שהוא כפל כפל י"ח |
|
ואם לקחנו חצי זה שרש יהיה שרש ד' וחצי שהוא רביעית י"ח |
|
ואם נקח מרובע ז' אלפים ור' שהוא כפל מרובע ס' יהיה השרש פ"ד שלמים נ"א ראשונים י"א שניים וזהו שרש שנים בעצמו כי השיבונום בדרך ראשונים והנה חשוב אלה פ"ד שהיו שלמים חשבם ראשונים והראשונים שניים והשניים שלישיים |
|
ואם תכפול זה המספר על עצמו אחר שתשיבם שלישיים ותחלקם במשפט שתשיבם אל המעלה הראשונה לא ישאר לך שני אחד ואף כי ראשון |
|
נשוב להוציא שרש שנים להיותו דמיון לאחדים הנה המרובע שעבר הוא אחד והמרחק בין חשבוננו ובינו הוא אחד נשיבנו ראשונים יהיו ס' נחלקם על כפל השרש שהוא שנים יהיו ל' ראשונים והנה השרש הראשון א' ול' ראשונים |
|
ואינו נכון בעבור שהוא בחשבון קטן כי הנה כאשר הוציאנו אותו מחשבון ר' היה קרוב אל האמת ומהחשבון כ' אלף יותר מדוקדק ויספיק לנו השרש הראשון |
|
והנה עלה לנו בחלוק ל' חלקים ראשונים ומרובעו ט"ו ראשונים כי כפל ראשונים על ראשונים שניים והם ט' מאות נחלקם על ס' יהיו ט"ו ראשונים נחלקם על כפל השרש שהיה לנו הוא ג' יעלו ה' |
|
נשוב ונקח מרובע החלוק שהוא כ"ה והם שניים והשרש השני שהיה לנו שהיה אחד שלם וכ"ה ראשונים יהיה כפלו ב' שלמים נ' ראשונים נחלק השניים על זה ובעבור שיש לנו ה' ששיות נשיב הכל מערך ו' והנה נכפול כ"ה על ו' יהיו ק"נ נחלקם על י"ז נתן לו ח' ונשארו י"ד נשיבם ממערכת ס' יהיו תת"מ נחלקם על י"ז עלו מ"ט והם שלישיים ונשארו ז' מי"ז נשליכם כי אין צורך אליהם כי יש לנו עוד לחסר מרובע שעלה בחלוק עתה והנה כאשר נחסר ח' שניים גם מ"ט שלישיים מהשרש השני יהיה הנשאר אחד שלם כ"ד ראשונים נ"א שניים י"א שלישיים |
|
ואילו עשינו על דרך חכמי המזלות יהיה הדבר שוה |
|
ואם היינו מדקדקים עוד מדרך מרובע ח' שניים מ"ט שלישיים שאמרנו היה יוצא השרש מדוייק שאין דיוק כמוהו א' כ"ד ראשונים נ"א שניים י"ז שלישיים נ"ד רביעיים |
|
בקשנו להוציא שרש י' |
|
והנה המרחק מהמרובע שעבר אחד נשיבנו ראשונים יהיו ס' |
|
נשוב לדקדקו והנה נקח הק' שהוא מרובע החלוק ונחלקנו על ו' ושלישית שהוא כפל השרש הראשון ונשיב הכל מערך ג' |
|
ואם נדקדקנו יותר יהיה ג' שלמים ט' ראשונים מ"ד שניים י"ב שלישיים |
|
וכשנכפול זה החשבון על י' יהיה העולה ל"א שלמים ל"ז ראשונים כ"ב שניים וזהו שרש אלף |
|
ואם נכפלנו על אלף נמצא שרש עשרת אלפי אלפים |
|
שאלה חלקנו שרש י"ח על שרש ח' כמה יעלה בחלוק |
|
ידענו כי אין לי"ח שרש ג"כ לח' והנה נעשה דרך אחרת שנחלק י"ח על ח' ויעלה בחלוק ב' ורביע וזה החשבון מרובע ושרשו אחד וחצי והנה כאשר נוסיף על כפל שרש ב' חציו תמצא שרש י"ח מדוקדק |
|
שאלה הצבנו סולם אל קיר י' אמות גבהותו וככה גבהות הסולם הורדנו ראש הסולם מלמעלה ב' אמות נבקש לדעת כמה יהיה מרחק הסולם מיסוד הקיר |
| I will give you a rule concerning this matter: the square of the remainder from the top of the ladder plus the square of the distance of the foot from the base are always equal to the square of the ladder. | אתן לך כלל בדבר זה לעולם יהיה מרובע הנשאר מראש הסולם עם מרובע מרחק הרגל מן היסוד שוים אל מרובע הסולם |
|
והנה חסרנו ב' אמות שירד הראש מתחלת הקיר נשארו ח' ומרובעו ס"ד נחסרנו מק' שהוא מרובע הסולם ישארו ל"ו ושרשו ו' וככה הוא מרחק הסולם למטה מן היסוד |
|
דמיון אחר הורדנו הראש אמה כמה המרחק מן היסוד |
|
חסרנו א' מי' ונשארו ט' ומרובעו פ"א נחסרנו מק' ישארו י"ט וזהו מרובע המרחק וככה נוציא שרשו |
The Circle |
|||||||||
| Now we shall start talking about the circle as it depends on the root: | ועתה נחל לדבר בעגול יען שהוא תלוי בשרש | ||||||||
| Know that there are many matters in the circle: one is the perimeter, the second is the diameter, the third is the multiplier [= pi], the fourth is the chord, the fifth is the versed sine, the sixth is the area. | דע כי יש בעגול דברים רבים האחד קו העגול והשני האלכסון והשלישי הכפל והרביעי היתר והחמישי החץ והששי השברים | ||||||||
| You can extract each of them that is unknown from two that are known and there are those among them of which one that is unknown can be known from another, as I will explain and give an example for each. | ותוכל להוציא אחד מהם שאינו ידוע מב' שהם ידועים ויש מהם שיוכל לדעת אחד מהם שאינו ידוע מאחר כאשר אפרש ואתן דמיון לכל אחד ואחד | ||||||||
|
נחשוב עגול אלכסונו י' וחצי היתר ד' והחץ ב' כמה האלכסון | ||||||||
|
חלקנו מרובע חצי היתר על החץ והוספנו החץ בעצמו על מה שעלה בחלוק והמחובר הוא האלכסון | ||||||||
|
דמיון אחר באלכסון י' והחץ ג' ומרובע חצי היתר כ"א | ||||||||
|
חלקנוהו על החץ עלה ז' והוספנו עליו ג' והנה הוא האלכסון | ||||||||
| A way to extract the chord from the versed sine and the diameter: | דרך להוציא היתר מן החץ ומן האלכסון | ||||||||
|
הנה חצי האלכסון ה' והחץ אחד נחסרנו מה' ישאר ד' אל הנקודה ומרובעו י"ו | ||||||||
|
והנה כל היתר ו' | ||||||||
| This matter should be a foundation for you, as the square of what remains from the versed sine to the midpoint plus the square of half the chord are equal the the square of half the diameter. | וזה הדבר יהיה לך יסוד כי לעולם מרובע מה שנשאר מן החץ אל הנקודה עם מרובע חצי היתר יהיו שוים אל מרובע חצי האלכסון | ||||||||
| Another way to extract the chord: multiply the versed sine by the remainder from the diameter; the product is the square of half the chord. Extract its root and double it; then you will find the whole chord. | דרך אחרת להוציא היתר כפול החץ על כל הנשאר מן האלכסון והעולה הוא מרובע חצי היתר קח שרשו וכפלהו ותמצא כל היתר | ||||||||
| Another method: See how much the ratio of the versed sine to the whole diameter is; take the same from the square of the diameter and this is the sum of the square of the versed sine and the square of half the chord. The ratio of the square of the versed sine to the [sum of] the square of the versed sine and the square of half the chord is as the ratio of the versed sine to the entire diameter. | דרך אחרת ראה כמה ערך החץ אל כל האלכסון וככה תקח ממרובע האלכסון והוא המחובר ממרובע החץ וממרובע חצי היתר וערך מרובע החץ אל מרובע החץ ומרובע חצי היתר כערך החץ אל כל האלכסון | ||||||||
|
דמיון בעגול הנזכר החץ ב' והנה ערכו אל כל האלכסון החמישית והנה חמישית ק' שהוא מרובע כל האלכסון כ' וזה המספר כולל מרובע החץ ומרובע חצי היתר וראוי להיות מרובע החץ חמישית כ' שהוא ד' נחסרם מהכ' ישארו י"ו והוא מרובע חצי היתר | ||||||||
|
דמיון אחר בחשבון שיש לו חלקים ונאמר כי החץ ג' שלמים וכ' חלקים | ||||||||
|
וזה ערכו אל י' שלישית הנה נקח שלישית ק' שהוא מרובע האלכסון והוא ל"ג שלמים וו' ראשונים ומ' חלקים שניים והוא מרובע החץ נחסרם מל"ג וישארו כ"ב י"ג כ' והוא מרובע חצי היתר | ||||||||
| I shall give you a general way for the concepts of circle: | ואתן לך דרך כלל בדברי העגול | ||||||||
| We know that 2 equal diameters are cutting the circle. | ידענו כי ב' אלכסונים שוים מחלקים העגול | ||||||||
| If the versed sine is one-third of the diameter, the square of half the chord is its double; together they are three [times]. | ואם החץ שלישית האלכסון יהיה מרובע חצי היתר כפלו בין שניהם הם ג' | ||||||||
| If the versed sine is one-quarter of the diameter, the square of half the chord is triple the square of the versed sine. | ואם החץ רביעית האלכסון יהיה מרובע חצי היתר ג' כפל מרובע החץ | ||||||||
| In this way for every number. | ועל זה הדרך כל החשבון | ||||||||
|
שאלה אם אמר החץ כ' חלקים | ||||||||
|
זה הערך תוכל לקחתו על שני דרכים | ||||||||
|
האחד שתשיב האלכסון כלו ראשונים יהיו ת"ר ותעשה הערך כך | ||||||||
|
| ||||||||
|
והנה נכפול ב' בק' מרובע האלכסון יהיו אלפים נחלקם על ת"ר יהיו ג' שלמים ושלישית אחד שהם ב' חלקים | ||||||||
|
ואם שבנו עוד להפריד מרובע החץ ממרובע חצי היתר נקח מג' כ' ערך ג' כ' אל ק' והיה ו' מ' והוא מרובע החץ | ||||||||
|
וישאר מרובע היתר ג' י"ג ב' | ||||||||
|
ובדרך אחרת ידענו כי כ' חלקים מי' שלמים הוא שליש העשירית נקח מק' שהוא מרובע האלכסון שליש העשירית יהיה ג' שלמים וכ' חלקים | ||||||||
| A way to extract the versed sine from the chord: | דרך להוציא החץ מהיתר | ||||||||
| Subtract the square of half the chord from the square of half the diameter, take the root of the remainder and subtract it from half the diameter; the remainder is the versed sine. | גרע מרבע חצי היתר ממרובע חצי האלכסון וקח שרש הנשאר וגרעהו מחצי האלכסון והנשאר הוא החץ | ||||||||
|
דמיון אמר כי היתר ו' | ||||||||
|
נקח מרובע חציו שהוא ט' נחסרנו מכ"ה שהוא מרובע חצי האלכסון וישארו י"ו ושרשו ד' | ||||||||
| To extract the perimeter from the diameter | להוציא קו העגול מן קו האלכסון | ||||||||
|
חכמי המדות אמרו כי הקו הסובב הוא ג' מהאלכסון ויותר שביעית והנה הוא בחשבון ז' אל כ"ב | ||||||||
|
ואם כפלת האלכסון על ג' ושביעית יהיה העולה הקו הסובב | ||||||||
|
או אם תכפול האלכסון שתרצה על כ"ב ותחלק העולה על ז' תמצא הקו הסובב | ||||||||
|
והפך זה אם ידעת הקו הסובב ותרצה לדעת האלכסון | ||||||||
|
כפול הקו על ז' וחלק העולה על כ"ב תמצא האלכסון | ||||||||
|
והנה על דעת אלה אם היה האלכסון אחד יהיה הקו הסובב ג' שלמים ח' הראשונים ל"ד שניים י"ז שלישיים | ||||||||
|
וארישמדס החכם נתן ראיה כי הוא פחות מזה המספר כי אמר שהנוסף פחות מי' חלקים מע' | ||||||||
|
גם הביא ראיה כי הנוסף יותר מי' חלקים מע' וחצי והנה הנוסף על השלשה שלמים ח' ראשונים כ"ד שניים ל"ה שלישיים | ||||||||
|
ונתן ראיה כי ראוי להיות יותר מזה המספר | ||||||||
|
ותלמי עשה חשבונו אמצעי כי התוספת ח' ראשונים ל' שניים | ||||||||
|
וחכמי הודו אמרו כי אם היה כ' אלף יהיה הקו הסובב ס"ב אלף ותתל"ח | ||||||||
| When you look closely, you will find it closer than Ptolemy's saying; between them only 3 thirds. | וכאשר תסתכל זה תמצאנו קרוב מדברי תלמי ואין ביניהם כי אם ג' שלישיים | ||||||||
| Since 10 is similar to one and the circle is surrounded by one line, if we set the diameter as 10, the square of the chord is as one-third of the diameter by the perimeter, no more nor less. | ובעבור כי י' דומה לאחד והעגול יסובבהו קו אחד הנה אם שמנו האלכסון י' יהיה מרובע היתר כשלישית האלכסון במספר הקו בלי תוספת ומגרעת | ||||||||
| Likewise, if you make the square between the upper third and the lower third, its area is as the perimeter. | וככה אם עשית מרובע בשלישית העליונה ובשלישית השפלה יהיו שבריו במספר הקו | ||||||||
| We can only know the square of it, which is 987, 5 ninths and 4 eighths of one-ninth that are 53 parts of 81. | רק המרובע נוכל לדעת שהוא תת"ק פ"ז וה' תשיעיות וד' שמיניות תשיעית שהם נ"ג חלקים מן פ"א | ||||||||
| If we set the diameter as 10, we extract the chord from its one-third and construct an [isosceles] triangle on it, so that the area of the triangle is as to the perimeter. | והנה אם שמנו האלכסון י' ונוציא יתר בשלישית ונעשה עליו משולש יהיה רבוע המשלש כקו הסובב | ||||||||
| For every number preceding 10, the ratio of the triangle on the third [of the diameter] to the perimeter is as the ratio [of the number] to 10. | וכל מספר שהוא לפני י' יהיה ערך המשלש בשלישית אל הקו המקיף בערכו אל י' | ||||||||
| If it is greater than 10, the ratio of the perimeter to the triangle on the third is as the ratio of 10 to the diameter. | ואם הוא יותר מעשרה יהיה ערך הקו המקיף אל המשלש בשלישית כערך י' אל הקו | ||||||||
| When we look for the perimeter - how much is it if the diameter is one: | וכאשר נחפש הקו הסובב כמה יהיה אם היה האלכסון אחד | ||||||||
| The perimeter is 3 integers, 8 primes, 33 seconds, 42 thirds and 30 fourths. | יהיה הקו הסובב ג' שלמים ח' ראשונים ל"ג שניים מ"ב שלישים גם ל' רביעיים | ||||||||
| Therefore, the area of the circle, whose diameter is 15, is the root of 5 thousand, no more nor less. | על כן שברי עגול שאלכסונו ט"ו שרש חמשת אלפים בלי תוספת ומגרעת | ||||||||
| In geometry and astrology there is no need to make it accurate. | ובמדות ובחכמת המזלות אין צריך לדקדק זה | ||||||||
|
והנה הוא כאשר אמר ארישמדס שהוא יותר מי' חלקים מע' וחצי וקרוב מאד לדברי חכמי הודו שאין ביניהם רק דבר שאין בו ממש | ||||||||
|
ולדעת הקשתות והמיתרים על דעת חכמי המזלות | ||||||||
|
אדבר עליהם בספר טעמי הלוחות | ||||||||
|
כי הם מבקשים למוד הקו הסובב מהיתרים | ||||||||
|
וחכמי המדות מבקשים לדעת כמה שברים יכילו בעגול | ||||||||
|
ולפי דעתם אם ידעת האלכסון כפול מרובעו על י"א וחלק העולה על י"ד אז תמצא שברי העגול | ||||||||
|
והפך זה אם ידעת כמה שברי העגול ותרצה לדעת כמה האלכסון | ||||||||
| Multiply the area by 14 and divide the product by 11; the quotient is the square of the diameter and its root is the diameter. | כפול השברים על י"ד וחלק העולה על י"א והעולה בחלוק הוא מרובע האלכסון ושרשו הוא האלכסון | ||||||||
| Now I shall talk again about why the arithmeticians subtract one for the foundation. | ועתה אשוב לדבר למה יחסרו חכמי החשבון אחד ליסוד | ||||||||
| Know that one to 9 are the real numbers that correspond to the 9 spheres and all numbers that follow them are similar to them. The similar numbers should be given their ranks from them: 10 in first rank, 100 in the second rank, one-thousand in the third, 10 thousand in the fourth, 100 thousands in the fifth and one-thousand of thousands in the sixth, and so on endlessly. | דע כי אחד עד ט' הם המספרים באמת שהם כנגד ט' עגולות וכל המספרים אחריהם הם נמשלים להם והנה הנמשלים הם ראויים לקחת המעלות מהם והי' ראוים אל מעלה ראשונה והק' בשנית והאלף בשלישית והי' אלף ברביעית וק' אלף בחמישית ואלף אלפים בששית וככה עד אין קץ | ||||||||
| The arithmeticians set the first numbers in the ranks, therefore they had to subtract one to the foundation and this is clear. | וחכמי החשבון שמו המספרים הראשונים במעלות על כן הוצרכו לגרוע אחד ליסוד וברור זה | ||||||||
|
ותראה בדמיון בקשנו לכפול ר' על ש' | ||||||||
|
והנה הנמשלים ב' וג' כפלנו זה על זה והיו ו' והמעלות גם כן הם ו' | ||||||||
| I have already mentioned that in the true calculation the beginning of the fourth rank is 10 thousand and this is the same thing. | וכבר הזכרתי כי בחשבון האמת תחלת הארבעה לי' אלפים הוא והנה הדבר שוה | ||||||||
| They only did so to make it easier for the students. | אך עשו כן כדי להקל על התלמידים | ||||||||
| תם ונשלם תהלה לאל עולם סלה |
ראה ספר כליל שפר יסוד מספר שמו נקרא לאברהם בנו מאיר ספרדי אבן עזרא
Additional Excerpt
F14649 ל"ז1
| שאלה ג' אנשים רצו לקנות דג במחיר י"ז פשיטים אמר אחד מהם אני אתן כל מה שיש בידי ואתם תנו חצי מה שיש בידכם | |
| תשובה נבקש מאמר שנוכל להוסיף עליו עד שיהיה המספר ההוא אחר התוספת חציו ושני שלישיותיו ושלש רביעיותיו והוא המורה ובעבור כי מחיר הדג י"ז פשוטים והנה יותר מי"ב | |
| והנה המספר המבוקש פחות מי"ב וכאשר חברנוהו י"ב והוא המורה עם מחיר הדג שהם י"ז יעלו כ"ט | |
| תסיר מהם הי"ז ישארו י"ב נמצאו ביד שנים מהם י"ב פשוטים | |
| וכאשר נוסיף על י"ב חצי הכפל הנשאר שהם ה' מי"ב ועד י"ז וכפלם כ"ה וחציו י"ב וחצי יהיו כ"ד וחצי ויש לך עוד כ"ט ה' וככה ממון ראשונים | |
| וכאשר הוספת על י"ב ו' שיהיה י"ב שתי שלישיותיו היו י"ח הנה יש להשלים עד כ"ט י"ח והוא הממון השני | |
| וכאשר הוספנו על י"ב ד' בלבד עד שיהיו י"ב ג' רביעיותיו והנה היו י"ו וממנו עד כ"ט י"ג והוא הממון השלישי | |
| דבר אחר ממה שיצטרך ידיעתו בחכמה הזאת הוא שהבדל גדול יש בין אמרנו ערך מספר קטן אל הגדול ובין אמרנו ערך מספר גדול אל הקטן | |
| והוא המוזכר אחרון בערך יהיה הראשון הנזכר חלק ממנו ולא יתהפך זה עד שיהיה האחרון חלק מן הראשון וזה יתברר בשני מספרים שאין חלקיהם שוים | |
| המשל בזה כי כאשר אמרנו ערך ג' אל ה' הרצון בו שג' הוא שלשה חלקי הה' ר"ל ג' חמישיותיו | |
| והפך זה אמרנו ערך ה' אל ג' הרצון בו שהחמשה יש בו פעם אחת ג' ושני שלישיותיו | |
| וככה ערך י' אל י"ו הכונה בו שהוא חמש שמיניות של י"ו אבל אמרנו ערך י"ו אל י' הכונה בו שהוא פעם אחת מספר י' וג' חמישיותיו של י' | |
| דבר אחר דע כי כפל מניין על מניין הוא כפל האורך על הרוחב אם שיהיה מרובע רבוע שא' שארכו כרחבו כאמרנו ד' על ד' הם י"ו וגם שיהיה ארכו יותר מרחבו כאמרנו י"ו שהם אמות אומדות שארכם כרחבם כזה או מרובע ארוך כזה | |
| על כן כפל המספר שלמים על שלמים יוסיפו ובו תדע תשבורת הכל אבל כפל שברים על שברים יהיה היוצא ממין השברים | |
| וכשתכפול השברים על השלמים כאמרנו כפול ד' על חצי הוא כאמרנו כפול ד' על חצאים כלומ' שיהיה ארכו ד' אמות ורחבו חצי אמה כזה | |
| כפול שברים על שברים כאמרנו חצי על חצי ויהיה רביעית כלומ' יהיה חצי אמה אורך וחצי אמה רוחב ושברו הוא רביעית | |
| וכאשר נכפול שלמים על שלמים כאמרנו כפול ד' על ד' יהיה מרובעו י"ו מרובעות וכאשר תכפול ב' על ב' יהיה מרובעו ד' | |
| ככה הענין בשברים על כן שלישית על שלישית יהיה תשיעית וכן כל השאר | |
| אבל החלוק הוא שתחלק האורך על הרחב כי לעולם הגדול נחלק על הקטן כי אם חלקנו הקטן על הגדול אותו יקרא ערך ואינו חילוק כי הוא כאמרנו ערך מספר קטן אל מספר גדול | |
| ועל כן כשנחלק שלמים על שלמים יצא בחלוק שלמים כמו שאמרנו | |
| דמיון חלקנו י"ו על ב' עלה ח' הוא שתשבורת הכל השיבונו על קו שיהיה רחבו ב' אם כן יהיה ארכו ח' | |
| ואם חלקנו שלמים על שברים כאמרנו חלקנו י"ו על חצי אחד הנה יהיה ארכו ל"ב ורחבו חצי אחד | |
| ועל כן נחלקנו שברים על שברים ממינם יהיו שלמים | |
| כאמרנו חלקנו ג' רביעיות על ב' רביעיות הוא שנעשה קו ארכו אחד וחצי ורחבו ב' רביעיות כי מה שהיה תשברתו שלשה ו' רביעיות באורך וברוחב חלקנו על הרחב ושמנו רחבו חצי אמה וארכו אמה וחצי | |
| על כן כשנחלק מעלות על מעלות או על ראשונים או על שניים או על איזה חלקים שנרצה יצא בחלוק מעלות שהשיבונו התשבורת כולו אל האורך וקצרנו ברחב | |
| ואם חלקנו ראשונים על שניים יצא בחלוק מעלות גם כן | |
| כי נשיב הראשונים אל השניים ויהיו דומים וישובו מעלות באורך ושניים ברחב ומה שיהיה ישובו מעלות | |
| ואם תחלק הקטן על הגדול ישוב היוצא אל מין אחד גבוה על הקטן והקטן מן הגדול ומזה תבין כל מיני החלוק | |
| שאלה שלשה אנשים באו לקנות דג שמחירו י"ב פשיטי' ומחצה הראשון יתן כל מה שבידו והשני רביעיות והאחרים רביעיתם או השלישי כל מה שבידו והאחרים חמישיתם נרצה לדעת כמה ביד כל אחד | |
| תשובה שמחיר הדג למעלה מי"ב הנה י"ב הוא מספר מכוון שיהיה לנו אחר התוספת שלישית והוא י"ח ורביעית והוא י"ו וחמישית והוא ט"ו הנה כאשר חברנו י"ב על מחיר הדג יהיה כ"ד פשוטים ומחצה | |
| הנה מי"ח עד כ"ד ומחצה הוא ו' מחצה וככה ממון הראשון | |
| ומי"ו עד כ"ד ומחצה ח' ומחצה והוא ממון השני | |
| ומט"ו עד כ"ד ומחצה ט' ומחצה והוא ממון השלישי | |
| ולהוציא אל השאלות והדומות אליהן דע כי חלקי האנשים הן כפי חלקי המורה מחובר עם המחיר | |
| וכאשר רצינו לחדש שאלה דומה לזו הוא שיקח המורה מחובר עם המחיר | |
| ולכן כשנרצה להוסיף עליהם החלקים שנוכל להוסיף עליו ונחבר כל החלקים עמו ונראה כמה עולה עם החלקים וגם החלקים לבד נקח כל העולה והעולה הוא מחיר הדג או מחיר דבר קנוי | |
| דמיון לחלקים כשהם ב' אנשים לבד | |
| נקח ד' על דרך משל המורה וכאשר נכפלהו היו ח' וכאשר נוסיף על ד' שלישית מלבד יהיו ו' הנה הוספנו על זה האחרון ב' על ד' | |
| וכאשר נחבר ב' על ח' עלו י' והוא מחיר הדג | |
| והנה המורה ד' כמו שאמרנו נחברהו על המחיר שהוא י' ויהיו י"ד והנה הראשון שכפל המורה והיו ח' הנה מח' עד י"ד הם ו' והוא ממון הראשון | |
| והב' שליש וד' יהיו ו' והנה מו' עד י"ד ח' וככה ממון השני | |
| הנה בזה אמ' הראשון לשני אני אתן מה שבידי ואתה שליש מה שבידך | |
| וכן תעשה לעולם על הדרך הזה בשני אנשים | |
| ודמיון לשלשה ככה שתקח חצי העולה מן המורה כל החלקים השלשה ותדע להם המחיר והוא שתקח למשל השאלה הראשונה י"ב והוא המורה | |
| וכאשר חברנו אליו כפלו ושלישיתו מלבד שהוא חציו מלגיו והוא ו' ורביעיתו מלבד והוא שלישיתו מלגיו והם ד' וחמישיתו מלבד שהוא רביעיתו מלגיו והם ג' יעלו הכל כ"ה וחצאים י"ב וחצי וככה מחיר הדג | |
| אחר כן תוסיף חלק כל אחד מהם כפי מה שהראיתיך למעלה | |
| וכאשר רצינו לעשות כזה לד' אנשים נקח המורה שנרצה ונחבר אליו כל הד' שנרצה להוסיף עליו ומן המחובר קח השלישית והוא המחיר | |
| וכאשר תרצה לעשות זה בה' אנשים קח הרביעית ולו' קח החמישית וכן עד אין קץ | |
| שאלה שלשה אנשים רצו לקנות דג ואמרו שיתן כל אחד כמה שיש לו . אם כן כמה היה מחירו . וכמה היה לכל אחד ואחד | |
| תשובה דע כי דמי הדג דמי הדג היו י"ז פשוטים והיו לראשון ה' ולשני י"א ולשלישי י"ג | |
| וכיצד הוצאת החשבון נבקש תחלה המורה וככה תעשה תחשוב איזהו חשבון שאם תטול ממנו רביעיתו ישאר ג' מניין האנשים והנה הוא ד' | |
| אחר כן תחשוב מספר אשר תטול ממנו שלישיתו וישאר ג' תמצא שהוא ד' ומחצה | |
| אחר כך תחשוב מספר אשר תטול ממנו חציו וישאר ג' תמצא שהוא ו' | |
| וכדי שלא יהיה שברים בחשבון תכפלם ויהיה המספר הראשון ח' והשני ט' והשלישי י"ב ונמצא שעולין כ"ט | |
| עתה קח מספר האנשים שהוא ג' וחסר ממנו אחד ישארו ב' כפול הי"ב באלו הב' יעלו כ"ד תוציאם מכ"ט וישארו ה' וזהו ממון הראשון | |
| עתה כפול הט' בב' הנזכרים ויעלו י"ח תוציאם מכ"ט וישארו י"א והוא ממון השני | |
| עתה תכפול הח' בב' הנזכרים ויעלו י"ו תסירם מכ"ט ישארו י"ג והוא ממון השלישי | |
| וכולם על זה הדרך | |
| חשבון האצבעות הנקרא בערבי אל גבאר | |
| אלה שמות האצבעות גודל אצבע אמה קמיצה זרת | |
| פרק אמצעי של זרת קרוי א' | |
| אמצעי של קמיצה קרוי ב' | |
| אמצעי של אמה עמהם קרוי ג' | |
| כשתסיר הזרת קרוי ד' | |
| כשתסיר הקמיצה קרוי ה' | |
| כשתסיר האמה ותשפיל הקמיצה לבד קרוי ו' | |
| זרת שוכב קרוי ז' | |
| קמיצה עמו קרוי ח' | |
| אמה עמהם קרוי ט' | |
| הרי באלו הג' אצבעות משתמש האדם מא' ועד ט' | |
| גודל ואצבע משתמשין מי' ועד ק' | |
| כיצד יסודו של אצבע בסוף פרק אמצעי של גודל קרוי י' | |
| גודל ואצבע מחוברין זה עם זה קרוי כ' בשרשיהם זה עם זה קרוי ל' | |
| גודל על אצבע מ' | |
| גודל על הכף קרוי נ' | |
| פרק אמצעי של אצבע על פרק ראשון של גודל קרוי ס' | |
| גודל פשוט ופרק אמצעי של אצבע כנגד חודו קרוי ע' | |
| פרק אמצעי של אצבע על פרק ראשון של גודל קרוי פ' | |
| אצבע בתוך וגודל סביבו קרוי צ' | |
| עד כאן ביד ימין | |
| וביד שמאל משתמשין מאות ממאה ועד מאה אלף | |
| כיצד חודו של אצבע בסוף פרק אמצעי של גודל קרוי ק' | |
| גודל ואצבע מחוברין זה עם זה קרוי ר' | |
| שרשיהם מנשקים זה עם זה קרוי ש' | |
| גודל על אצבע קרוי ת' | |
| גודל כפוף ביד שמאל קרוי רבבה שהם י' אל אלפים | |
| כמו שחשבנו ביד ימין לאחדים כן נחשוב ביד שמאל למאות וסימניך יפול מצדך אלף ורבבה מימנך | |
| והמשכילים יזהירו כזוהר הרקיע | |
| שאלה חלק ס' על ג' בני אדם לאחד השליש ולאחד הרביע ולאחד החומש ולא ישאר מהס' | |
| תשובה נשים המורה והוא שנחבר השליש והרביע והחומש מס' הנה שליש ס' הם כ' ורביעיתם ט"ו וחמישיתם י"ב נחברם ויעלו מ"ז והוא המורה | |
| עתה כפול המספר הראשון המתחלק שהוא ס' על כל אחד מהשלשה חלקים שהם השלישית והרביעית והחמישית והעולה בכפל תחלקהו על המורה והיוצא מהחלוק הוא חלק כל אחד מהשלשה כפי החלק שיש לו לקחת | |
| וככה תעשה כפול ס' על כ' יעלו ת"ר תחלקם על מ"ז שהוא המורה ויעלו י"ג בקרוב כי הנה בדקדוק הם י"ב שלמים ול"ו שברים וזה חלק בעל השליש | |
| עתה נכפול ס' על ט"ו יעלו תת"ק נחלקם על מ"ז ויצא מן החלוק י"ט והוא חלק בעל הרביע | |
| עתה נחזור לכפול ס' על י"ב יעלו תש"כ תחלקם על מ"ז יצא בחילוק י"ח והוא חלק בעל החומש | |
| והבחינה בזה שתחבר הכל יחד ויעלו ס' | |
| וכן כל כיוצא בזה | |
| ושאלה זו יוצאה משאלת ד' אנשים שהרויחו י"ט דינרי' שהוא שאלה שנייה משער ו' | |
| שאלה ממון לקחנו ממנו שלישיתו ורביעיתו ועוד ב' ונש' ונשארו עשרה כמה הוא הממון | |
| תשובה נאמר כי השאלה היא כ"ד | |
| נקח ממנו שלישיתו ורביעיתו שהוא השליש ח' והרביע ו' עלו י"ד ונשארו י' | |
| נסיר ב' מי' ונשארו ח' ועדיין לא יצא אמתי | |
| אם כן נעשה הרביע ובתחלה נעשה המורה והוא שנכפול ג' בד' ויעלו י"ב והוא המורה | |
| נסיר מהם שלישיתו ורביעיתו שהם ז' וישארו ה' והנה יש לנו שלשה מספרים ידועים והם המורה שהוא י"ב | |
| מעתה נשים האמצעיים חברים שהם הי"ב והי"ב ונכפול זה על זה ויעלו קמ"ד נחלקם ה' ויצא בחילוק כ"ד שלמים וד' חומשים | |
| ואם תבדוק תמצאנו אמתי | |
| שאלה היו לשר אחד עשרים משרתים בין זכרים בין נקבות ונתן להם עשרים ככרי לחם ואמר להם מאלו עשרים ככרות תקחו כל א' זכר בכם ב' ככרות וכל נקבה חצי ככר כדי שיבא ככר אחד לשתי נקבות ותשאירו לי ככר לחם אחד יש לשאול כמה היו הזכרים וכמה היו הנקבות | |
| תשובה האנשים היו ששה והנשים י"ד לקחו האנשים הששה י"ב ככרות והנשי' הי"ד לקחו ז' ככרות הרי י"ט ככרות נשאר אחד לאכילת השר | |
| שאלה היו לשר אחד עשרים בהמות בין סוסים ופרדים וחמורים ונתן לעבדו עשרים עמרים של שעורים וצוה לו שיתן לכל סוס מהם ב' עמרים ולכל פרד עמר אחד ולכל חמור חצי עמר כמה בהמות היו לו מכל מין | |
| תשובה הסוסים היו ד' והפרדים היו ח' והחמורים היו ח' ונתן לד' הסוסים ב' עמרים לכל אחד הנה ח' עמרים נתן לח' פרדים עמר לפרד הנה ח' עמרים | |
|
שאלה תגר אחד אמר למשרתו הנני נותן לך ק' פשיטים קנה לי בהם ק' עופות שיהיו מג' מינים תרנוגלין ואווזים וצפרים והיה שוה האווז ה' פשיטים והתרנגול ג' פשיטים והצפרים עשרים מהם בפשוט כמה לקח מכל מין |
| תשובה מן האווזים לקח י"ח ומן התרנוגלין ב' ומן הצפרים פ' נתן בי"ח אווזים צ' פשיטים ונתן בב' תרנוגלין ו' פשיטים הנה צ"ו פשיטים וכ' עופות נתן עוד ד' פשיטים בפ' צפרים הרי ק' עופות וק' פשיטים | |
| שאלה אדם אחד אהב אשה ואמרה לו אם תתן לי תפוח אחד מגנת המלך אהיה נכבשת לך ואם לאו לא אכבש לך והלך לשוער הגן ושאל לו תפוח | |
| תשובה מאשר שאלו כל אחד מחצית שבידו וחצי תפוח יותר ושלא יתחלק שום תפוח מזה ידענו שליקט נפרדים | |
| ועתה נוציא מספרים הוא הוציא לחוץ תפוח אחד והוסיף לשוער הראשון חצי תפוח ממה שהיה בידו אם כן תפוח וחצי היה מחצית מה שנשאר לו מן השוער השני | |
| נכפלם ועולים ג' וחצי תפוח שהוסיף לשני הרי ג' וחצי וזהו החצי שנשאר לו מן השוער הפנימי | |
| נכפלם ויהיו ז' וחצי תפוח שהוסיף לשוער הפנימי הרי ז' וחצי וזהו חצי מה שליקט | |
| [נכפלם] ועולים ט"ו עתה נ | |
| כלל אם תרצה לידע תשבורת העגולה | |
| קח רביע הקו המקיף וכפול אותו על הקוטר ומה שיצא הוא תשבורת העגולה | |
| דמיון הקו המקיף שיעורו כ"ב מעלות הנה הקוטר ז' | |
| כפול ז' על ה' וחצי והנה המבוקש ל"ח וחצי והוא התשבורת | |
| וכל זה בעגולה השטחית | |
| אבל בכדור יצטרך לכפול כל הקוטר על כל הקו המקיף ואז ידע תשבורת כל הקף הכדור | |
| דמיון נכפול ז' שהוא הקוטר על כ"ב שהוא הקו המקיף ויעלה קנ"ד והוא תשבורת הכדור | |
| ולדעת שטח כל הכדור נכפול כל התשבורת בששית הקוטר ונשיג המבוקש | |
| כלל כשתרצה להוציא שורש מספר אחד ממספר אחר | |
| קח כפלו וכפל כפלו ותקח שרש העולה וחצי השורש ההוא הוא שרש מבוקשך | |
| דמיון תרצה למצוא שורש ט' | |
| קח כפלו והוא י"ח וכפל י"ח שהוא כפלו של ט' ויעלו ל"ו, תקח שרשם והוא ו' וחציו ג' וזהו שרש ט' | |
| דמיון אחר רצינו למצוא שרש י"ו | |
| קח כפלו והוא ל"ב וכפלם ועלו ס"ד ושרשם ח' וחציו ד' והוא שרש י"ו | |
| שאלה ראובן לקח משמעון בהלואה תיבה אחת מלאה חטה והיתה מכילה ח' מדות בחשבון מעוקב רוצה לומ' ח' מדות מדות באורך וח' ברוחב וח' בגובה ולקץ שנה רצה לפרוע והביא תיבה אחרת שהיתה מכילה ד' על ד' באורך וברחב ובגובה עתה נדע כמה השיב לו אם חצי החצ החטה או שלישית או רביעית | |
| ונעשה החשבון ככה נכפול ח' על ח' עלו ס"ד ונכפול ח' על ס"ד למצוא המעוקב ועלו תקי"ב והוא מה שלקח שמעון בהלואה | |
| עתה נמנה מה שהשיב לו כמה הוא נכפול ד' על ד' עלו י"ו ונכפול ד' על י"ו עלו ס"ד וזהו מה שהשיב לו | |
| עתה ניחס אותו לדעת אלו הס"ד כמה חלקים הם מתקי"ב מצאנו שהם שמיניתם ואם כן השיב לו שמינית החטה והשאר במעות | |
| ז'ל'ל ש'ל'ע' |
Notes |
||
|
||
Apparatus |
||
| ||
| Chapter One | ||
|---|---|---|
| ||
| Chapter Two | ||
| ||
| Chapter Three | ||
| ||
| Chapter Four | ||
|
Appendix I: Glossary of Terms
| to add | חבר (אל, עם, על), הוסיף (על) |
| addition | חבור |
| sum | סכום, מחובר |
| to divide | חלק (על) |
| division | חלוק |
| dividend | (מספר) המחולק |
| divisor | (מספר) המחולק עליו |
| quotient | היוצא בחלוק |
| to double | כפל |
| double | כפל |
| to multiply | כפל (על) |
| multiplication | כפל |
| to subtract | חסר (מן), גרע (מן) |
| subtraction | חסור, מגרעת |
| arithmetic | חכמת המספר, חכמת החשבון |
| arithmetician | חכמי המספר, חכמי החשבון |
| astronomer | חכמי המזלות |
| astronomy | חכמת המזלות |
| music | חכמת הנגינות |
| geometry | חכמת המדות |
| question | שאלה |
| to calculate | הוציא |
| to extract | הוציא |
| example | דמיון |
| decade | מספר) כלל) |
| difference | מרחק (מן) |
| integer | שלם |
| fraction | שבר |
| fraction of fraction | שבר השבר |
| units | פרטים, אחדים |
| even number | מספר זוג |
| odd number | מספר נפרד |
| odd | נפרד |
| required | מבוקש |
| equal | שוה |
| double | כפל |
| point | נקודה |
| midpoint | נקודה |
| arc | קשתות |
| chord | יתר, יתרים |
| perimeter | הקו הסובב, קו העגול |
| versed sine | חץ |
| circle | עגול, עגולה |
| triangle | משולש |
| diameter | אלכסון |
| figure, shape | צורה |
| area | שברים, (תשבורת additional) |
| rank | מעלה |
| to result | עלה, יצא |
| million | אלף אלפים |
| denominator | מורה |
| zero | סיפרא, גלגל |
| prime number | מספר ראשון |
| proof | מאזנים |
| product | המחובר |
| proportion | ערך |
| square | מרובע |
| square root | שרש מרובע |
| to calculate | חשב |
| calculation | חשבון |
| remainder | הנשאר |
| result | העולה, היוצא |
| diagram | דמיון |
| aspect | פאה |
| degree | מעלה |
| minutes | ראשונים |
| seconds | שניים |
| thirds | שלישיים |
| fourths | רביעיים |
| fifths | חמישיים |
| sixths | ששיים |
| sevenths | שביעיים |
| eighths | שמיניים |
| tenths | עשיריים |
| part | חלק |
| excess | תוספת, יתרון |
| addition | נוסף |
| proportion | ערך |
| arithmetic proportion | ערכי החשבון |
| geometric proportion | ערכי המדות |
| harmonic proportion | ערכי הנגינות |
| square | מרובע |
| root | שרש |
| number | חשבון, מספר |
| digit | אות, חשבון, מספר |
| composite number | מספר מורכב |
Appendix II: Bibliography
Abraham ben Meir Ibn ‛Ezra
b. 1089, Tudela, Spain – d. 1167
Sefer ha-Mispar (The Book of Number)
Lucca, Italy, between 1142 and 1145
Manuscripts:
- 1) Berlin, Staatsbibliothek (Preußischer Kulturbesitz) Or. Oct. 244/13 (IMHM: f 1996), ff. 60r-112r (15th-16th century)
- [B244]
- 2) Cambridge, University Library Add. 670, 2 (IMHM: f 16999) (15th-16th century)
- 3) Cambridge, University Library Add. 1015, 2 (IMHM: f 15886; f 17024), f. 92v (14th-15th century)
- 4) Cambridge, University Library Add. 1527, 2 (IMHM: f 17464) (15th century)
- 5) Firenze, Biblioteca Medicea Laurenziana Or. 489/5 (IMHM: f 19164), ff. 137r-147v (1443)
- 6) Firenze, Biblioteca Medicea Laurenziana Plut.88.28/1 (IMHM: f 17849), ff. 1r-48v (14th-15th century)
- [F88.28]
- 7) Firenze, Biblioteca Medicea Laurenziana Plut.88.46/1 (IMHM: f 17970), ff. 1r-45v (14th century)
- [F88.46]
- 8) Halle, Universitätsbibliothek Yb Qu. 5/1 (IMHM: f 71790), ff. 88r-92v (15th century)
- 9) Jerusalem, Museum of Italian Jewish Art 30 (IMHM: f 5069; f 45045) (16th century)
- 10) Leeuwarden, Tresoar, the Frisian Historical and Literary Centre B.A. Fr. 21/1 (IMHM: f 3481), ff. 1r-51r (14th-15th century)
- 11) London, British Library Add. 27153/7 (IMHM: f 5826), ff. 13v-37r (cat. Margo. 1085, 7) (Siena, 1431)
- [Lo27153]
- 12) London, British Library Or. 10785 (IMHM: f 8100) (Verona, 1647)
- [Lo10785]
- 13) London, Montefiore Library 419 (IMHM: f 5352) (15th century)
- 14) Moscow, Russian State Library, Ms. Guenzburg 30/1 (IMHM: f 6711), ff. 2r-38r (1503)
- [Mo30]
- 15) Moscow, Russian State Library, Ms. Guenzburg 1383 (IMHM: f 48474) (Paris, 18th-19th century)
- 16) München, Bayerische Staatsbibliothek, Cod. Hebr. 43/8 (IMHM: f 1150), ff. 103v-146r (16th century)
- [Mu43]
- 17) München, Bayerische Staatsbibliothek, Cod. Hebr. 150/5 (IMHM: f 1168), ff. 83v-108v (15th century)
- [Mu150]
- 18) New York, Columbia University X 893 Sh 4 (IMHM: f 16483) (16th-17th century)
- 19) New York, Jewish Theological Seminary Ms. 2561, (IMHM: f 28814) (17th century)
- short excerpt from Chapter VI - Proportions
- [N2561]
- 20) New York, Jewish Theological Seminary Ms. 2624/1 (IMHM: f 28877), ff. 1r-10v (16th century)
- partial: mid. Chapter I - mid. Chapter IV
- [N2624]
- 21) New York, Jewish Theological Seminary Ms. 2627/1 (IMHM: f 28880), ff. 1r-48v (17th century)
- [N2627]
- 22) Oxford, Bodleian Library MS Mich. 213/1 (IMHM: f 19304), ff. 1r-9v (cat. Neub. 2019, 1) (15th century)
- 23) Oxford, Bodleian Library MS Mich. 213/2 (IMHM: f 19304), ff. 14r-66r (cat. Neub. 2019, 2) (16th century)
- 24) Oxford, Bodleian Library MS Mich. 319/1 (IMHM: f 19303), ff. 1r-64v (cat. Neub. 2018, 1) (14th century)
- 25) Oxford, Bodleian Library MS Opp. 697/9 (IMHM: f 19364), ff. 46v-52v (cat. Neub. 2079, 9) (1428)
- 26) Oxford, Bodleian Library MS Poc. 187/2 (IMHM: f 19350), ff. 49r-86r (cat. Neub. 2065, 2) (1503)
- [O187]
- 27) Paris, Bibliothèque Nationale de France heb. 1029/3 (IMHM: f 15721), ff. 45r-71v (15th-16th century)
- [P1029]
- 28) Paris, Bibliothèque Nationale de France heb. 1049/1 (IMHM: f 27767), ff. 1r-34v (14th century)
- starts from Chapter IV - Subtraction
- [P1049]
- 29) Paris, Bibliothèque Nationale de France heb. 1050/2 (IMHM: f 14646), ff. 1v-29v (15th century)
- [P1050]
- 30) Paris, Bibliothèque Nationale de France heb. 1051/2 (IMHM: f 14656), ff. 2r-40v (1482)
- [P1051]
- 31) Paris, Bibliothèque Nationale de France heb. 1052/1 (IMHM: f 14649), ff. 1r-41v (15th century)
- [P1052-1]
- 32) Paris, Bibliothèque Nationale de France heb. 1052/4 (IMHM: f 14649), ff. 55r-58r (15th century)
- [P1052-4]
- 33) St. Petersburg, Inst. Of Oriental Studies of the Russian Academy B 13/5 (IMHM: f 52914), ff. 155r-163r (18th-19th century)
- 34) St. Petersburg, Inst. Of Oriental Studies of the Russian Academy B 454 (IMHM: f 53740) (17th -18th century)
- 35) St. Petersburg, Russian National Library Evr. I 374/1 (IMHM: f 50951), ff. 1r-2v (18th century)
- two short excerpts: (1) from Chapters III-IV; (2) from Chapter II
- [St.P374]
- 36) St. Petersburg, Russian National Library Evr. II A 569 (IMHM: f 70777) (14th-15th century)
- two short excerpts: (1) from Chapters II-IV (ff. 10, 2-9, 1v); (2) from Chapter II (f. 11r-v)
- [St. Petersburg569]
- 37) St. Petersburg, Russian National Library Evr. II A 1385 (IMHM: f 66722) (17th century)
- short excerpt from Chapter VI - Proportions
- [St.P1385]
- 38) Vatican, Biblioteca Apostolica ebr. 171/18 (IMHM: f 8630), ff. 98r-101r (Canea, 1493)
- [V171]
- 39) Vatican, Biblioteca Apostolica ebr. 386/3 (IMHM: f 468), ff. 137v-206v (14th century)
- [V386]
- 40) Vatican, Biblioteca Apostolica ebr. 397/2 (IMHM: f 475), ff. 3r-49r (Murcia, 1384/1385)
- [V397]
- 41) Vatican, Biblioteca Apostolica ebr. 398/1 (IMHM: f 476), ff. 1r-2v; 9r-30v; 118r-123v (14th century)
- [V398]
- 42) Vatican, Biblioteca Apostolica ebr. 530/11 (IMHM: f 2707; f 18511), ff. 101r-v (26.fs.0000) (14th century)
- short excerpt from Chapter VII - Square Roots
- [V530]
- 43) Warszaw, Żydowski Instytut Historyczny 288/2 (IMHM: f 12013), ff. 24r-64v (15th century)
- 44) Wien, Öesterreichische Nationalbibliothek Cod hebr. 152/2 (IMHM: f 1422), ff. 4r-34v (18th-19th century)
- [W152]
- 45) Wien, Öesterreichische Nationalbibliothek Cod hebr. 194/7 (IMHM: f 1456), ff. 90v-99v (16th century)
- [W194]
Edition:
- Ibn ‛Ezra, Abraham. Sefer ha-Mispar, Das Buch der Zahl: ein hebräisch-arithmetisches Werk. Ed. Moritz Silberberg. Frankfurt a. M.: J. Kauffmann, 1895.
Bibliography:
- Langermann, Tzvi and Shai Simonson. 2000. The Hebrew Mathematical Tradition. In: Helaine Seline ed. Mathematics Across Cultures. Dordrecht: Kluwer, pp. 167–188.
- Sarfatti, Gad ben ‛Ami. 1968. Mathematical Terminology in Hebrew Scientific Literature of the Middle Ages. Jerusalem: Magnes Press, pp. 130-155.
- Sela, Shlomo. 2000. Encyclopedic Aspects of Abraham Ibn Ezra’s Scientific Corpus. In: Steven Harvey ed. The Medieval Hebrew Encyclopedias of Science and Philosophy. Dordrecht, Boston, London: Kluwer Academic Publisher, pp.154-170
- Sela, Shlomo, and Gad Freudenthal. 2006. Abraham Ibn Ezra’s scholarly writings: a chronological listing, Aleph 6, pp. 13-55.
- Steinschneider, Moritz. 1893-1901. Mathematik bei den Juden. Berlin-Leipzig-Frankfurt: Kaufmann, pp. 87-91 (d38-d42); repr. Hildesheim: G. Olms, 1964 and 2001.
– Commentary on Sefer ha-Mispar–
Anonymous
Manuscript:
- Genève, Bibliothèque de Genève, MS héb. 10/2 (IMHM: f 2320), ff. 39r-65r (14th-15th century)

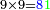
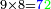
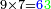
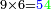
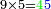
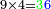
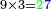
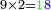
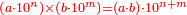
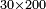
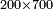
![\scriptstyle{\color{red}{\left[\left(a\sdot10^n\right)-b\right]\times\left[\left(a\sdot10^n\right)+b\right]=\left(a\sdot10^n\right)^2-b^2}}](/mediawiki/images/math/4/4/5/445f0b6ba2c046e985fc7285911c7ae4.png)
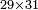
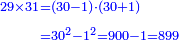
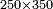
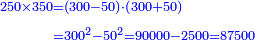
![\scriptstyle{\color{red}{a^2=\left[10\sdot\left(\frac{1}{3}a\right)^2\right]-\left(\frac{1}{3}a\right)^2}}](/mediawiki/images/math/e/5/7/e577c61600f6b12e71ad3564488516ee.png)
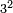
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle3^2&\scriptstyle=\left[10\sdot\left(\frac{1}{3}\sdot3\right)^2\right]-\left(\frac{1}{3}\sdot3\right)^2=\left(10\sdot1^2\right)-1^2\\&\scriptstyle=\left(10\sdot1\right)-1=10-1=9\\\end{align}}}](/mediawiki/images/math/7/1/6/71627f17819b958210714713ec0ebcae.png)
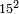
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle15^2&\scriptstyle=\left[10\sdot\left(\frac{1}{3}\sdot15\right)^2\right]-\left(\frac{1}{3}\sdot15\right)^2=\left(10\sdot5^2\right)-5^2\\&\scriptstyle=\left(10\sdot25\right)-25=250-25=225\\\end{align}}}](/mediawiki/images/math/4/3/3/4336c02cd7e1b2892fed517a67a26cab.png)
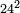
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle24^2&\scriptstyle=\left[10\sdot\left(\frac{1}{3}\sdot24\right)^2\right]-\left(\frac{1}{3}\sdot24\right)^2=\left(10\sdot8^2\right)-8^2\\&\scriptstyle=\left(10\sdot64\right)-64=640-64=576\\\end{align}}}](/mediawiki/images/math/e/6/c/e6ca108d11ec4cfb5a8e03f8aebb9c74.png)
![\scriptstyle{\color{red}{a^2=\left[10\sdot\left[\frac{1}{3}\sdot\left(a-1\right)\right]^2\right]-\left[\frac{1}{3}\sdot\left(a-1\right)\right]^2+\left[a+\left(a-1\right)\right]}}](/mediawiki/images/math/4/0/a/40a23cef85a31ebfa9d3cfa7fa138efe.png)
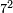
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle7^2&\scriptstyle=\left[10\sdot\left[\frac{1}{3}\sdot\left(7-1\right)\right]^2\right]-\left[\frac{1}{3}\sdot\left(7-1\right)\right]^2+\left[7+\left(7-1\right)\right]\\&\scriptstyle=\left[10\sdot\left(\frac{1}{3}\sdot6\right)^2\right]-\left(\frac{1}{3}\sdot6\right)^2+\left(7+6\right)\\&\scriptstyle=\left(10\sdot2^2\right)-2^2+13=\left(10\sdot4\right)-4+13\\&\scriptstyle=40-4+13=36+13=49\\\end{align}}}](/mediawiki/images/math/b/b/4/bb494ac822e69cc72a12d9f402a6f278.png)
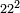
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle22^2&\scriptstyle=\left[10\sdot\left[\frac{1}{3}\sdot\left(22-1\right)\right]^2\right]-\left[\frac{1}{3}\sdot\left(22-1\right)\right]^2+\left[22+\left(22-1\right)\right]\\&\scriptstyle=\left[10\sdot\left(\frac{1}{3}\sdot21\right)^2\right]-\left(\frac{1}{3}\sdot21\right)^2+\left(22+21\right)\\&\scriptstyle=\left(10\sdot7^2\right)-7^2+43=\left(10\sdot49\right)-49+43\\&\scriptstyle=490-49+43=441+43=484\\\end{align}}}](/mediawiki/images/math/f/9/1/f9148c9db3895b7621089f8bdf8ab194.png)
![\scriptstyle{\color{red}{a^2=\left[10\sdot\left[\frac{1}{3}\sdot\left(a+1\right)\right]^2\right]-\left[\frac{1}{3}\sdot\left(a+1\right)\right]^2-\left[a+\left(a+1\right)\right]}}](/mediawiki/images/math/a/b/8/ab8f8040fba5408eedb7629cf7320b33.png)
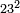
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle23^2&\scriptstyle=\left[10\sdot\left[\frac{1}{3}\sdot\left(23+1\right)\right]^2\right]-\left[\frac{1}{3}\sdot\left(23+1\right)\right]^2-\left[23+\left(23+1\right)\right]\\&\scriptstyle=\left[10\sdot\left(\frac{1}{3}\sdot24\right)^2\right]-\left(\frac{1}{3}\sdot24\right)^2-\left(23+24\right)\\&\scriptstyle=\left(10\sdot8^2\right)-8^2-47=\left(10\sdot64\right)-64-47\\&\scriptstyle=640-64-47=576-47=529\\\end{align}}}](/mediawiki/images/math/9/d/c/9dcf5ef101472d9e434643f0ca31067f.png)
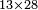
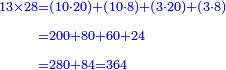
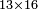
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle13\times16&\scriptstyle=\left[10\sdot\left(3+16\right)\right]+\left(3\sdot6\right)\\&\scriptstyle=\left(10\sdot19\right)+18\\&\scriptstyle=190+18=208\\\end{align}}}](/mediawiki/images/math/b/2/5/b251f01fbbdc0a952db9d2690ddc0faf.png)
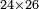
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle24\times26&\scriptstyle=\left[20\sdot\left(4+26\right)\right]+\left(4\sdot6\right)\\&\scriptstyle=\left(20\sdot30\right)+24\\&\scriptstyle=600+24=624\\\end{align}}}](/mediawiki/images/math/0/8/1/08156f90b58307b7f096c618bc1194dc.png)
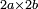
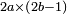
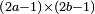
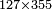
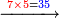
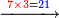
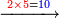
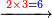
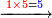
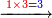
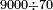

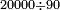

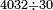

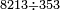

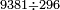

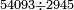

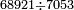
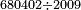
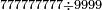
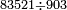
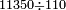
![\scriptstyle\sum_{i=1}^{n} i=n\sdot\left[\left(\frac{1}{2}\sdot n\right)+\frac{1}{2}\right]](/mediawiki/images/math/3/5/2/352391748eb2e7ace44f90cd627ef185.png)
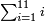
![\scriptstyle{\color{blue}{\sum_{i=1}^{11} i=11\sdot\left[\left(\frac{1}{2}\sdot11\right)+\frac{1}{2}\right]=11\sdot\left[\left(5+\frac{1}{2}\right)+\frac{1}{2}\right]=11\sdot6=6}}](/mediawiki/images/math/2/2/d/22de77a228550c8df906f2b1e8c65725.png)
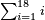
![\scriptstyle{\color{blue}{\sum_{i=1}^{18} i=\left[18\sdot\left(\frac{1}{2}\sdot18\right)\right]+\left(\frac{1}{2}\sdot18\right)=\left(18\sdot9\right)+9=162+9=171}}](/mediawiki/images/math/8/7/4/874803a8411918954e47b3f65a1fc030.png)
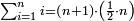
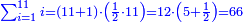
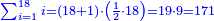
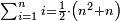
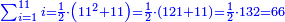
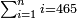
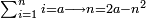
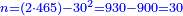
![\scriptstyle\sum_{i=1}^{n} i=\left[2\sdot\left(\frac{1}{2}\sdot n\right)^2\right]+\left(\frac{1}{2}\sdot n\right)](/mediawiki/images/math/2/6/7/2671e4a0d340332685868b16542fefd5.png)
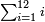
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\sum_{i=1}^{12} i&\scriptstyle=\left[2\sdot\left(\frac{1}{2}\sdot12\right)^2\right]+\left(\frac{1}{2}\sdot12\right)\\&\scriptstyle=\left(2\sdot6^2\right)+6\\&\scriptstyle=\left(2\sdot36\right)+6=72+6=78\\\end{align}}}](/mediawiki/images/math/5/3/8/5386d11a4a2f69552f5c608d501c4696.png)
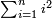
![\scriptstyle\sum_{i=1}^{n} i^2=\left(\sum_{i=1}^{n} i\right)\sdot\left[\left(\frac{2}{3}\sdot n\right)+\frac{1}{3}\right]](/mediawiki/images/math/f/3/8/f383bed5b67ee7c245135a7fb57622d9.png)
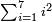
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\sum_{i=1}^{7} i^2&\scriptstyle=\left(\sum_{i=1}^{7} i\right)\sdot\left[\left(\frac{2}{3}\sdot7\right)+\frac{1}{3}\right]\\&\scriptstyle=28\sdot\left[\left(\frac{2}{3}\sdot6\right)+\frac{2}{3}+\frac{1}{3}\right]\\&\scriptstyle=28\sdot\left(4+1\right)\\&\scriptstyle=28\sdot5=140\\\end{align}}}](/mediawiki/images/math/2/6/9/26955345db1f1607798af84338e4bc4f.png)
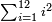
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\sum_{i=1}^{12} i^2&\scriptstyle=\left(\sum_{i=1}^{12} i\right)\sdot\left[\left(\frac{2}{3}\sdot12\right)+\frac{1}{3}\right]\\&\scriptstyle=78\sdot\left(8+\frac{1}{3}\right)\\&\scriptstyle=\left(78\sdot8\right)+\left(\frac{1}{3}\sdot78\right)=624+26=650\\\end{align}}}](/mediawiki/images/math/5/5/7/557f6b860059c88e384ab692f9fd9cc7.png)
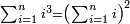
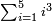
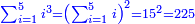
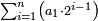
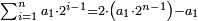
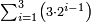
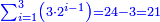
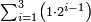
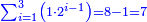
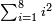
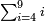
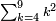
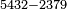
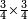
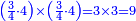
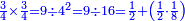
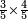
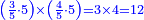
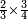

![\scriptstyle{\color{blue}{\left[\frac{2}{3}\sdot\left(3\times4\right)\right]\times\left[\frac{3}{4}\sdot\left(3\times4\right)\right]=8\times9=72=\frac{1}{2}\sdot144=\frac{1}{2}\sdot\left(3\times4\right)^2}}](/mediawiki/images/math/2/1/5/215d2c7b0742cce91ae400beb3c3806b.png)
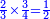
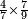
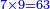
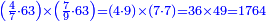
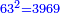
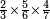
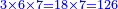
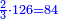
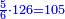
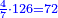
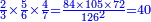
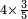
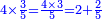
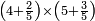
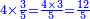
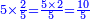
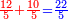
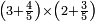
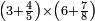
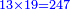

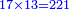
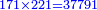
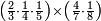
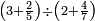
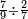
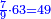
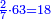
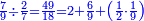
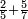
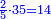
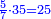

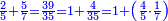
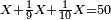
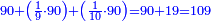

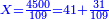
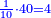
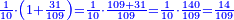

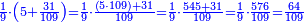
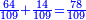
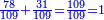
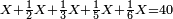
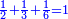
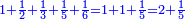
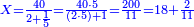
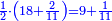
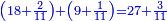
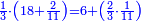
![\scriptstyle{\color{blue}{\left(27+\frac{3}{11}\right)+\left[6+\left(\frac{2}{3}\sdot\frac{1}{11}\right)\right]=33+\frac{3}{11}+\left(\frac{2}{3}\sdot\frac{1}{11}\right)}}](/mediawiki/images/math/d/2/b/d2bfd3f54a1426769648b9ae7c4c1ffb.png)
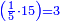
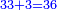
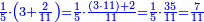
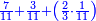
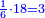
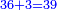
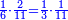
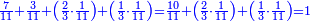
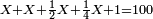
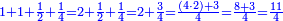
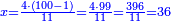
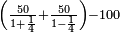
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left(\frac{50}{1+\frac{1}{4}}+\frac{50}{1-\frac{1}{4}}\right)-100&\scriptstyle=\left(\frac{4\sdot50}{5}+\frac{4\sdot50}{3}\right)-100\\&\scriptstyle=\left(\frac{200}{5}+\frac{200}{3}\right)-100\\&\scriptstyle=\left[40+\left(66+\frac{2}{3}\right)\right]-100\\&\scriptstyle=6+\frac{2}{3}\\\end{align}}}](/mediawiki/images/math/f/f/e/ffec10b7402d6c289bc7ae654748b4d6.png)
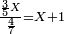
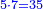
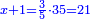
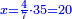
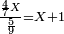
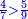


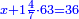
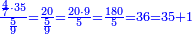
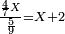

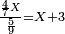

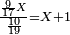

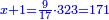
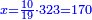
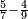
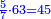
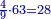

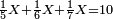

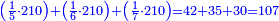
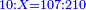
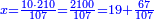
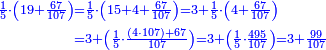
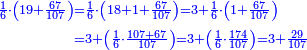
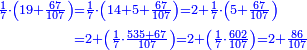
![\scriptstyle{\color{blue}{\begin{align}&\scriptstyle\left[\frac{1}{5}\sdot\left(19+\frac{67}{107}\right)\right]+\left[\frac{1}{6}\sdot\left(19+\frac{67}{107}\right)\right]+\left[\frac{1}{7}\sdot\left(19+\frac{67}{107}\right)\right]\\&\scriptstyle=\left(3+\frac{99}{107}\right)+\left(3+\frac{29}{107}\right)+\left(2+\frac{86}{107}\right)=3+3+2+2=10\\\end{align}}}](/mediawiki/images/math/b/4/8/b4826ea35cb4dcb01a63849b0817a056.png)
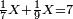
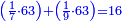
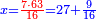
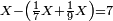
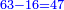
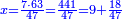
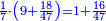
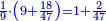
![\scriptstyle{\color{blue}{\left(9+\frac{18}{47}\right)-\left[\left(1+\frac{16}{47}\right)-\left(1+\frac{2}{47}\right)\right]=7}}](/mediawiki/images/math/2/a/5/2a59a0d2d2706fec62409829e96956f4.png)
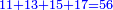

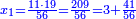
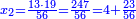
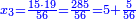
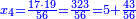
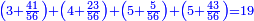
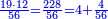
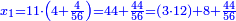
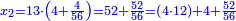
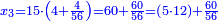
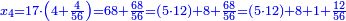
![\scriptstyle{\color{blue}{\left[\left(3\sdot12\right)+8+\frac{44}{56}\right]+\left[\left(4\sdot12\right)+4+\frac{52}{56}\right]+\left[\left(5\sdot12\right)+\frac{60}{56}\right]+\left[\left(5\sdot12\right)+8+1+\frac{12}{56}\right]=19\sdot12}}](/mediawiki/images/math/0/2/2/0229f56668a3c70d6b4891ada0ff0c48.png)
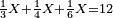
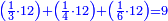
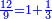
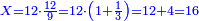
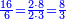
 [which are two dinar]
[which are two dinar]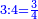

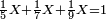
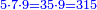
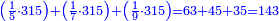
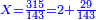
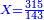
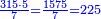
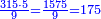

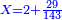
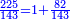
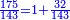
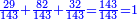
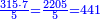
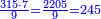
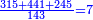
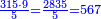
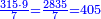

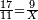
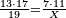
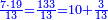
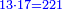
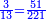
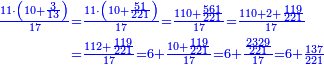
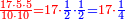
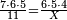


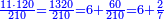
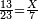
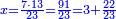
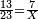
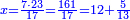
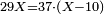
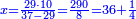
![\scriptstyle2\sdot\left[2\sdot\left[2\sdot\left(2X-2\right)-2\right]-2\right]=2](/mediawiki/images/math/a/c/0/ac095356b36a77f4fb4a1ac6de9f4dd9.png)
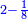
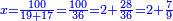
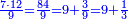
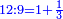
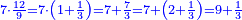
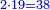
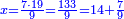
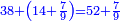
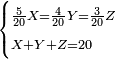
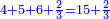
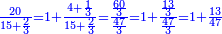
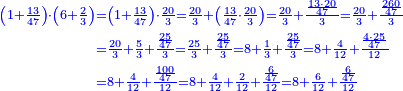
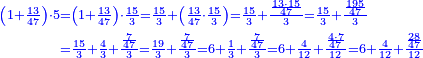
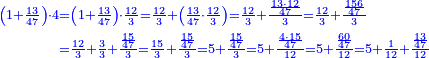
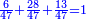
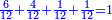
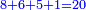
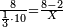
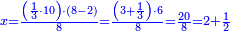
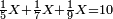

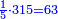
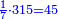
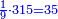
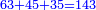
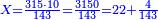
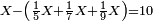
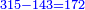
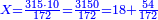
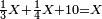
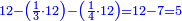
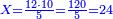
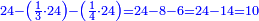
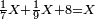
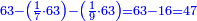
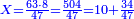
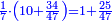
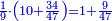
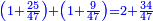
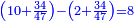
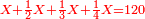
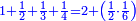
![\scriptstyle{\color{blue}{\left[2+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\sdot60=125}}](/mediawiki/images/math/f/e/e/feee1688775c37c50f8c73a0ca686bf5.png)
![\scriptstyle{\color{blue}{\left[2+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\sdot12=12+13}}](/mediawiki/images/math/c/8/4/c84d44d55e4f0aecc61dd6b809638c69.png)
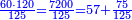
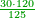
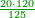
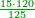
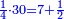
![\scriptstyle{\color{blue}{\left(\frac{1}{4}\sdot30\right)+\left[\frac{1}{3}\sdot\left(\frac{1}{4}\sdot40\right)\right]=\left(7+\frac{1}{2}\right)+\left(\frac{1}{3}\sdot10\right)=\left(7+\frac{3}{6}\right)+\left(3+\frac{2}{6}\right)=10+\frac{5}{6}}}](/mediawiki/images/math/8/0/2/8025548d7ffea180aaf74b2aa258a187.png)
![\scriptstyle{\color{blue}{\left(\frac{1}{4}\sdot30\right)+\left[\frac{1}{3}\sdot\left(\frac{1}{4}\sdot40\right)\right]+\left[\frac{1}{2}\sdot\left(\frac{1}{3}\sdot60\right)\right]=20+\frac{5}{6}}}](/mediawiki/images/math/6/3/9/639c2256db341185f9c23923c2b05f10.png)
![\scriptstyle{\color{red}{\left(\frac{1}{4}\sdot30\right)+\left[\frac{1}{3}\sdot\left(\frac{1}{4}\sdot40\right)\right]+\left[\frac{1}{2}\sdot\left(\frac{1}{3}\sdot60\right)\right]+\left(\frac{1}{2}\sdot120\right)=80+\frac{5}{6}}}](/mediawiki/images/math/2/6/5/265522ddfc53b15a08af105f276818cf.png)
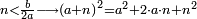
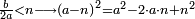
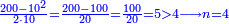
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle14^2=\left(10+4\right)&\scriptstyle={\color{red}{200-\left[200-\left(10+4\right)^2\right]}}\\&\scriptstyle=200-\left[100-\left(2\sdot10\sdot4\right)-4^2\right]\\&\scriptstyle=200-\left[100-\left(20\sdot4\right)-4^2\right]\\&\scriptstyle=200-\left(100-80-16\right)\\&\scriptstyle=200-\left(20-16\right)=200-4=196\\\end{align}}}](/mediawiki/images/math/b/7/2/b7259e2f5d0b1f0f11412fa84adf0e32.png)
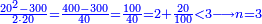
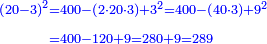
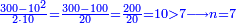
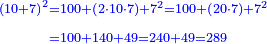
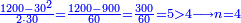
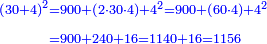

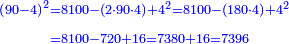
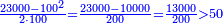
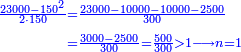
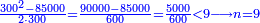
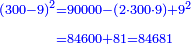
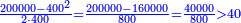
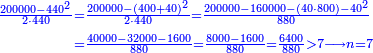
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle447^2=\left(440+7\right)^2&\scriptstyle={\color{red}{200000-\left[200000-\left(440+7\right)^2\right]}}\\&\scriptstyle{\color{red}{=200000-\left[200000-440^2-\left(2\sdot440\sdot7\right)-7^2\right]}}\\&\scriptstyle=200000-\left[6400-\left(2\sdot440\sdot7\right)-7^2\right]\\&\scriptstyle=200000-\left(240-7^2\right)=200000-191=199809\\\end{align}}}](/mediawiki/images/math/6/1/c/61c58bb30da58573d3a27dd1384840c1.png)

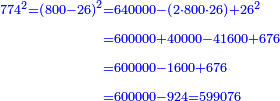
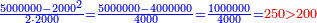
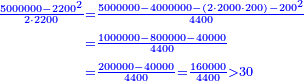

![\scriptstyle{\color{blue}{\begin{align}\scriptstyle2236^2=\left(2230+6\right)^2&\scriptstyle={\color{red}{5000000-\left[5000000-\left(2230+6\right)^2\right]}}\\&\scriptstyle{\color{red}{=5000000-\left[5000000-2230^2-\left(2\sdot2230\sdot6\right)-6^2\right]}}\\&\scriptstyle=5000000-\left[27100-\left(2\sdot2230\sdot6\right)-6^2\right]\\&\scriptstyle=5000000-\left(340-36\right)=5000000-304=4999696\\\end{align}}}](/mediawiki/images/math/2/a/6/2a64d5bea114f5b6c43277e25c9b5644.png)
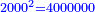




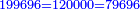


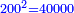




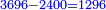
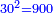

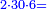

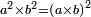
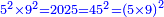
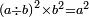
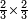
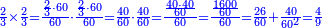
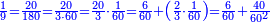
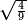
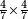
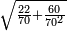
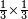
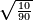
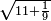
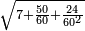
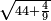
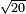
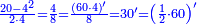
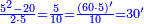
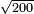
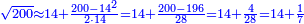
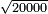
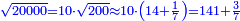
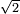
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\sqrt{2}=\frac{1}{10}\sdot\sqrt{200}&\scriptstyle\approx\frac{1}{10}\sdot\left(14+\frac{1}{7}\right)\\&\scriptstyle=\left(\frac{1}{10}\sdot10\right)+\left(\frac{1}{10}\sdot4\right)+\left(\frac{1}{10}\sdot\frac{1}{7}\right)\\&\scriptstyle=1+\frac{4}{10}+\left[\frac{1}{10}\sdot\left(8^\prime+34^{\prime\prime}\right)\right]\\&\scriptstyle=1+\frac{2}{5}+\left(\frac{1}{10}\sdot514^{\prime\prime}\right)\approx1+24^\prime+52^{\prime\prime}\\\end{align}}}](/mediawiki/images/math/8/9/0/8901182bd27b3df60b59121aca28e18c.png)
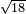
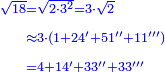
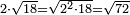
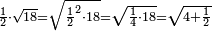
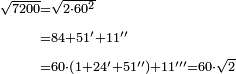
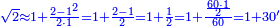
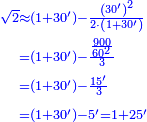
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\sqrt{2}&\scriptstyle\approx\left(1+25^\prime\right)-\frac{\left(5^\prime\right)^2}{2\sdot\left(1+25^\prime\right)}\\&\scriptstyle=\left(1+25^\prime\right)-\frac{25^{\prime\prime}}{2+50^\prime}\\&\scriptstyle=\left(1+25^\prime\right)-\frac{25^{\prime\prime}}{2+\frac{5}{6}}\\&\scriptstyle=\left(1+25^\prime\right)-\left(\frac{6\sdot25}{17}\right)^{\prime\prime}\\&\scriptstyle=\left(1+25^\prime\right)-\left(\frac{150}{17}\right)^{\prime\prime}\\&\scriptstyle=\left(1+25^\prime\right)-\left(8+\frac{14}{17}\right)^{\prime\prime}\\&\scriptstyle=\left(1+25^\prime\right)-\left[8^{\prime\prime}+\left(\frac{60\sdot14}{17}\right)^{\prime\prime\prime}\right]\\&\scriptstyle=\left(1+25^\prime\right)-\left[8^{\prime\prime}+\left(\frac{840}{17}\right)^{\prime\prime\prime}\right]\\&\scriptstyle=\left(1+25^\prime\right)-\left[8^{\prime\prime}+\left(49+\frac{7}{17}\right)^{\prime\prime\prime}\right]\\&\scriptstyle\approx\left(1+25^\prime\right)-\left(8^{\prime\prime}+49^{\prime\prime\prime}\right)=1+24^\prime+51^{\prime\prime}+11^{\prime\prime\prime}\\\end{align}}}](/mediawiki/images/math/9/1/7/9170ee4ca78c56740eea9ea949551c83.png)
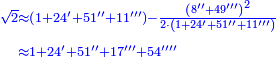
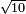
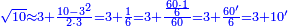
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\sqrt{10}&\scriptstyle\approx\left(3+10^\prime\right)-\frac{\left(10^\prime\right)^2}{2\sdot\left(3+10^\prime\right)}\\&\scriptstyle=\left(3+10^\prime\right)-\frac{100^{\prime\prime}}{6+\frac{1}{3}}\\&\scriptstyle=\left(3+10^\prime\right)-\frac{3\sdot100^{\prime\prime}}{19}\\&\scriptstyle=\left(3+\frac{10}{60}\right)-\left(\frac{300}{19}\right)^{\prime\prime}\\&\scriptstyle=\left(3+10^\prime\right)-\left(15+\frac{15}{19}\right)^{\prime\prime}\\&\scriptstyle=\left(3+10^\prime\right)-\left[15^{\prime\prime}+\left(\frac{60\sdot15}{19}\right)^{\prime\prime\prime}\right]\\&\scriptstyle=\left(3+10^\prime\right)-\left[15^{\prime\prime}+\left(\frac{900}{19}\right)^{\prime\prime\prime}\right]\\&\scriptstyle=\left(3+10^\prime\right)-\left[15^{\prime\prime}+\left(47+\frac{7}{19}\right)^{\prime\prime\prime}\right]\\&\scriptstyle\approx\left(3+10^\prime\right)-\left(15^{\prime\prime}+47^{\prime\prime\prime}\right)=3+9^\prime+44^{\prime\prime}+{\color{red}{13}}^{\prime\prime\prime}\\\end{align}}}](/mediawiki/images/math/9/8/3/98331d1b1b88798e850fe18745d1155b.png)
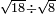
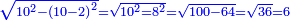
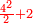
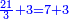
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\sqrt{\left(\frac{1}{2}\sdot10\right)^2-\left[\left(\frac{1}{2}\sdot10\right)-1\right]^2}&\scriptstyle=\sqrt{5^2-\left(5-1\right)^2}\\&\scriptstyle=\sqrt{25-4^2}=\sqrt{25-16}=\sqrt{9}=3\\\end{align}}}](/mediawiki/images/math/8/d/6/8d69320b4b1636373c78f7298f28da0c.png)