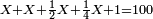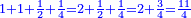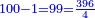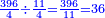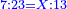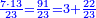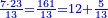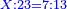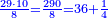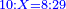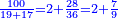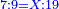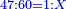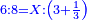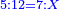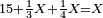Excerpts Attributed to Immanuel Bonfils
Contents
[hide]- 1 Introduction - Decimal Fractions
- 2 Table – multiplication of sexagesimal fractions (Firenze)
- 3 Table – multiplication of sexagesimal fractions (Firenze)
- 4 Multiplication of integers (Firenze)
- 5 Division of integers
- 6 Extracting roots
- 7 Squares
- 8 Division of sexagesimal fractions
- 9 Extracting roots of sexagesimal fractions
- 10 Multiplication of sexagesimal fractions
- 11 Chapter on Summation [MS London]
- 12 Word Problems [MS London]
- 13 Glosses on Abraham Ibn Ezra’s Book of the number (P1026; London)
- 14 Notes
- 15 Appendix: Bibliography
Introduction - Decimal Fractions |
||||||||||||||||||||||||||||||||||||||||||||||||||
| The division method of R. Immanuel | [1]דרך חלוק לר' עמנואל וע'א' | |||||||||||||||||||||||||||||||||||||||||||||||||
| Introduction | הקדמה | |||||||||||||||||||||||||||||||||||||||||||||||||
| Know that the one is divided into ten parts called primes; each prime is divided into ten parts calles seconds and so on endlessly. | דע כי האחד נחלק לעשרה חלקים יקראו ראשונים וכן כל ראשון נחלק לעשרה חלקים יקראו שניים וכן לאין תכלית | |||||||||||||||||||||||||||||||||||||||||||||||||
| Similarly I want to remind you that I call the rank of tens of integers "primes"; the hundreds of integers "seconds" and so on endlessly. | וכן אמרתי להזכירך כי הנני קורא למעלת העשרות שלימים ראאשונים ולמאות שלמים שניים וכן לאין תכלית | |||||||||||||||||||||||||||||||||||||||||||||||||
| I call the rank of units by their name "units", since it is mean between the integers and the fractions, therefore, when the units are multiplied by units the result is units. | אמנם מעלת האחדים אני קורא אותם בשמם אחדים לפי שהוא אמצעי בין השלמים והשברים ולזה כשיכפל אחדים באחדים יצאו אחדים | |||||||||||||||||||||||||||||||||||||||||||||||||
| I call the ranks whose name is greater "having a greater name", meaning I call the thirds "having a greater name than" the seconds, since the [name of] the thirds is derived from three and [the name of] the seconds [is derived] from two; likewise the fourths "having a greater name than" the thirds, and so the fifths ["having a greater name than"] the fourths. This is for the integers as well as for the fractions. | וכן אני קורא המעלות שהם גדולות השם גדול השם רצוני בזה שלישיים אני קורא יותר גדול השם משניים לפני ששלישיים נגזר משלשה ושניים משנים וכן רביעיים יותר גדול השם משלישיים וכן חמשיים מרביעיים וזה הוא בשלמים ובשברים | |||||||||||||||||||||||||||||||||||||||||||||||||
| When I say: add the name of this to the name of this, or subtract the name of this from the name of this: | וכן כשאומר חבר שם זה עם שם זה או גרע שם זה משם זה | |||||||||||||||||||||||||||||||||||||||||||||||||
| I mean add the name of the seconds to the name of the thirds and they are fifths.
|
רצוני בזה חבר שם שניים עם שם שלישיים ויהיו חמשיים | |||||||||||||||||||||||||||||||||||||||||||||||||
| If the name of the seconds to the name of the seconds, they are fourths.
|
ואם שם שניים עם שם שניים יהיו רביעיים | |||||||||||||||||||||||||||||||||||||||||||||||||
| Also, subtract the name of the seconds from the name of the thirds; primes remain.
|
וכן גרע שם שניים משם שלישיים וישאר ראשונים | |||||||||||||||||||||||||||||||||||||||||||||||||
| If the name of the seconds from the name of the seconds, nothing remains, so they are in the rank of the units.
|
ואם שם שניים משם שניים לא ישאר דבר ויפול במעלת האחדים | |||||||||||||||||||||||||||||||||||||||||||||||||
| This is for integers as well as for fractions. | וזה בשלמים ובשברים | |||||||||||||||||||||||||||||||||||||||||||||||||
| When you subtract a greater name from a smaller name, as if we say: we subtract fourths from seconds, whether fractions, or integers; the result is in the rank of seconds of the other type. | וכאשר תגרע שם גדול משם קטן כאמרנו נגרע רביעיים משניים הן בשברים [הן בשלמים][2] יביא במעלת השניים לצד האחר | |||||||||||||||||||||||||||||||||||||||||||||||||
| As if we say: we subtract the name of the fourths that are fractions from the name of the seconds that are fractions; the result is in the rank of seconds that are integers.
|
כאמרנו נגרע שם רביעיים בשברים משם שניים גם כן בשברים יפול במעלת שלמים שניים | |||||||||||||||||||||||||||||||||||||||||||||||||
| When we say this for integers, i.e. we wish to subtract the name of the fourths that are integers from the name of the seconds that are integers, the result is of the seconds that are fractions.
|
וכן באמרנו זה בשלמים ר"ל שנרצה לגרוע שם רביעיים שלמים משם שניים שלמים יפול בשברים שניים | |||||||||||||||||||||||||||||||||||||||||||||||||
| When you multiply a number by a number and they are both integers or both fractions: | כשתכפול מספר על מספר ושניהם שלמים או שניהם שברים | |||||||||||||||||||||||||||||||||||||||||||||||||
| Add the names of the ranks [one to the other] and the product is [in the rank whose name is their sum], of the integers, if both are integers, or of the fractions, if both are fractions.
|
חבר שם המדרגות האחד ושם היא הנכפל בשלמים אם שניהם שלמים ובשברים אם שניהם שברים | |||||||||||||||||||||||||||||||||||||||||||||||||
| If [one is] integer and the other fraction: | ואם שלמים והאחר שברים | |||||||||||||||||||||||||||||||||||||||||||||||||
| If their names are the same, the product is in the rank of units.
|
אם הם שוים בשם הנה יכפול הנכפל במעלת האחדים | |||||||||||||||||||||||||||||||||||||||||||||||||
| If the name of one is greater than the other, subtract the smaller from the greater and the product is as the name that remains: integers, if the [name of] the integers is greater, or fractions, if the [name of] the fractions is greater.
|
ואם שם האחד רב על האחר גרע הקטן מהגדול וכמספר השם שישאר שם יפול הנכפל בשלמים אם הם שלמים היותר גדול או בשברים אם שם השברים הוא יותר גדול | |||||||||||||||||||||||||||||||||||||||||||||||||
| When you divide a number by a number and they are both integers or both fractions: | כשתחלק מספר על מספר ושניהם שלמים או שניהם שברים | |||||||||||||||||||||||||||||||||||||||||||||||||
| If the names of their ranks are the same, the quotient is in the rank of units. Because, when you subtract this name from this name, nothing remains, so it is in the rank of units.
|
ושם מדרגותיהם שוה הנה יפול החלוקה במעלת האחדים לפי שכאשר תגרע שם זה משם זה לא ישאר דבר ויפול במעלת האחדים | |||||||||||||||||||||||||||||||||||||||||||||||||
| If [the name of] the upper is greater than the name of the lower, subtract the name of the lower from the name of the upper and the quotient is as the name that remains of the same type, i.e. integers, if [both are] integers, or fractions, if [both are] fractions.
|
ואם העליון יותר גדול השם מתחתון גרע שם התחתון משם העליון וכמספר שֵם הנשאר יפול החלוקה בצד ההוא ר"ל בשלמים אם הי | |||||||||||||||||||||||||||||||||||||||||||||||||
| If [the name of] the lower is greater, subtract the name of the greater from the name of the lower and the quotient is as the name that remains of the opposite type: fractions, if both are integers, or integers, if both are fractions.
|
ואם התחתון יותר גדול גרע שם העליון משם התחתון וכמספר שם הנשאר יפול החלוקה בהפך הצד ר"ל בשברים אם היו שניהם שלמים או בשלמים אם היו שניהם שברים | |||||||||||||||||||||||||||||||||||||||||||||||||
| If one is integer and the other is fraction and the names of their ranks are the same, or not the same, add the names of their ranks and the quotient is as the name of the sum: fraction, if the upper is a fraction, or integer, if the upper if integer.
|
ואם האחד שלמים והשני שברים ושם מדרגותיהם שוה או בלתי שוה חבר שם המדרגות וכמספר שם העולה בשברים אם העליון שברים או בשלמים אם העליון שלמים שם יפול החלוקה | |||||||||||||||||||||||||||||||||||||||||||||||||
| Another Version - MS Paris 903 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| דע כי האחד נחלק לי' חלקים יקראו שלמי'שברי' ראשוני' וכל אחד מהראשוני' לי' חלקי' יקראו שלמי' שברי' שניים וכל שניי' לי' שלישיי' וכל שלישיי' לי' רביעיי' וכן עד אין קץ | ||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן אני קורא מעלת העשרו' שלמים ראשונים ולמאות שלמי' שניי' ולאלפי' שלמי' שלשיי' ולרבואות שלמים רביעיי' ולרבבות חמשיי' וכן עד אין קץ | ||||||||||||||||||||||||||||||||||||||||||||||||||
| אך האחדי' אני קור' בשמם אחדי' כי הם כאמצעיים בין השלמי' והשברי' על כן בכפל אחדי' באחדי' יצאו אחדי' מש"כ בשום מעל' אחרת | ||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן אני קורא לשניי' גדולי השם מראשוני' וכן שלישיים משניי' וכן כלם בי' בשלמי' בי' בשברי' וכן באמ' חבר שם שניי' עם שם שלישיי' יצא חמשיי' וכן כלם | ||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן באמ' גרע שם ראשוני' משם שניים ישאר ראשוני' | ||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם משם ראשונים לא ישאר דבר ויכפול במעל' האחדי' בי' בשלמי' בי' בשברי' | ||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם הנגרע גדול השם מאשר גרעון ממנו כגון שתגרע רביעיי' משניי' אם הם בשברי' יצאו שניי' שלמי' | ||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם הם בשלמי' יצאו שברי' שניים וכשתכפל שלמי' בשלמי' או שברי' בשברי' חבר שם המדרגו' ושם יפול הנכפל וכשתכפל שלמי' בשברי' אם הם שוים בשם יפול הנכפל באחדי' | ||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם לאו גרע שם הקטן מן שם הגדול ושם יפול הנכפל [..] בצד הגדול בשם הנשאר אחר הגרעון | ||||||||||||||||||||||||||||||||||||||||||||||||||
| כאלו תכפול ג' שלמי' שניי' בב' שברי' שביעיי' תגרע ב' מז' וישאר ה נמצ' יעלה הכפל ו' שברי' חמשיים | ||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם ג' שברי' שניי' בב' שלמי' שביעיי' יהיה הנכפל ו' שלמי' חמשיים | ||||||||||||||||||||||||||||||||||||||||||||||||||
| וזו לך צורה לזה כשתחלק מספר על מספר ושניהם שלמי' או שניה' שברי' אם שם מדרגותיה' שוה תפול החלוק באחדי' לעולם | ||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם שם העליון גדול מהתחתון גרע שם התחתון ממנו וכמספר הנשאר תפול החלוקה בצד ההו' ר"ל אם הם שלמי' שלמי' ואם שברי' שברי' | ||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם שם התחתון גדול גרע העליון ממנו וכמספר הנשאר תפול החלוק בהפך הצד ר"ל בשברי' אם החולק והנחלק שלמי' ובשלמי' אם הם שברים | ||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם האחד שלם והשני שברי' יהיה שם מדרגותיהם שוה או בלתי שוה חבר שמות המדרגו' יחד וכמספר המחובר יהיה שם הנופל בחלוק לצד שבו היה המספר העליון ר"ל המתחלק אם שלמי' בשלמי' ושברי' בשברי' | ||||||||||||||||||||||||||||||||||||||||||||||||||
Table – multiplication of sexagesimal fractions (Firenze) |
לוח כפילת המעלות ושבריהם | |||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
Table – multiplication of sexagesimal fractions (Firenze) |
לוח חילוק השברים האחד על השני | |||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||
Multiplication of integers (Firenze) |
|||||||||||||||||||||||||||||||
|
דמיון על דרכי הכפל רצינו לכפול קכ"ז על שנ"ה | ||||||||||||||||||||||||||||||
|
וכתבנו בטור העליון קכ"ז ובשני השפל שנ"ה וזה צורתו | ||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||
|
כפלנו ז' על ה' והוא ל"ה | ||||||||||||||||||||||||||||||
|
כתבנו ה' במעלה הראשונה כנגד ז' ושמרנו הג' כדי לצרף אותה אל המעלה השנייה | ||||||||||||||||||||||||||||||
|
עוד כפלנו ז' על ה' השני התחתון עלו ל"ה | ||||||||||||||||||||||||||||||
|
חברנו הה' עם הג' ששמרנו ועלו ח' | ||||||||||||||||||||||||||||||
|
ושמנו ח' במעלה השנית תחת ב' מטור העליון והג' שמנו במעלה השלישית תחת הא' מטור העליון עם היוצא מכפל אותה המעלה | ||||||||||||||||||||||||||||||
|
עוד כפלנו ז' הראשון על הג' התחתון עלו כ"א | ||||||||||||||||||||||||||||||
|
חברנו א' עם הג' ששמרנו והיו ד' | ||||||||||||||||||||||||||||||
|
וכתבנו ד' תחת הא' במעלה השלישית וב' במעלה רביעית | ||||||||||||||||||||||||||||||
|
עוד כפלנו ב' האמצעי העליון על ה' הראשון מן הטור השפל עלו עשר | ||||||||||||||||||||||||||||||
|
כתבנו ציפרא בשינית וא' בשלישית תחת הג' שבטור השפל | ||||||||||||||||||||||||||||||
|
עוד כפלנו ב' העליון על הה' השני התחתון עלו עשר | ||||||||||||||||||||||||||||||
|
חברנו י' עם הא' ששמרנו והיא י"א | ||||||||||||||||||||||||||||||
|
שמנו א' בשלישית וא' שמרנו ברביעית | ||||||||||||||||||||||||||||||
|
עוד כפלנו ב' על ג' והיו ששה | ||||||||||||||||||||||||||||||
|
חברנו הו' עם הא' והיו ז' וכתבנוהו ברביעית | ||||||||||||||||||||||||||||||
|
עוד כפלנו א' על ה' הראשונ שבטור השפל וכתבנו ה' בשלישית עוד כפלנו א' על ה' הראשון שבטור השפל וכתבנו ה' בשלישית | ||||||||||||||||||||||||||||||
|
עוד כפלנו א' על ה' השני וכתבנו ה' ברביעית | ||||||||||||||||||||||||||||||
|
עוד כפלנו א' על ג' וכתבנו ג' במעלה החמישית | ||||||||||||||||||||||||||||||
|
נשלם כפל החבור | ||||||||||||||||||||||||||||||
| נבוא לחבר היוצא מכפל שני הטורים ונכתוב ה' לכח במעלה הראשונה וח' בשנית וד' וא' וה' עולים עשרה נעשה 0' בשלישית ונשים נקודה ברביעית להיות לזיכר בעבו' העשרה | |||||||||||||||||||||||||||||||
| ואחר נחבר ב'ז'ה' והם י"ד ואחר השמור הרי ט"ו נשים ה' במעלה הרביעית ונקודה בחמישית | |||||||||||||||||||||||||||||||
| נחבר אחד עם הג' ויהיו ד' ונכתוב ד' במעלה החמשית נשלם החבור | |||||||||||||||||||||||||||||||
| המאזניים מן הכפל על חש' ט' ט' | |||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| הנה חשבנו חשבון הטור העליון כאילו הם אחדים והיו עשרה כזה הדרך השלכנו התשעה ונשאר א' וכתבנוהו בצד הטור העליון | |||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||
| אחר כן חשבנו הטור השפל ומצאנוהו עולה י"ג הפלנו הט' ונשארו ד' וכתבנום בצדו אחד | |||||||||||||||||||||||||||||||
| ואחר כפלנו א' על ד' והיה ד' ושמרנום | |||||||||||||||||||||||||||||||
| ואחר חשבנו המחובר והיה זה ה ח 0 ה ד ועלה כ"ב השלכנו י"ח שהולך לתשיעיות ונשארו ד' והוא שווה לכפל מאזני שני הטורים ואז ידענו שחשבונינו אמתי | |||||||||||||||||||||||||||||||
| והכלל הוא כי כשאחד ממדרגות הכפל הולך לתשיעיות הן העליון הן השפל היוצא מחבור הכפל ראוי ללכת בתשיעיות ואם לאו אינו צורך | |||||||||||||||||||||||||||||||
| ואם אינו הולך לתשיעיות כל אחד משניהם תכפול העודף משני טורי הכפל זה על זה וראה מה שיעדיף על תשיעיות אם ה' אם ו' אם ז' | |||||||||||||||||||||||||||||||
| ר"ל תראה מה שיעלה הטור העליון ותכפלהו על מה שיעלה הטור השפל כאלו יהיה בעליון ד' ג' שעולה ז' ובתחתון ג' ב' שעולה ה' תכפול ז' על ה' עולה ל"ה נשאר על תשיעיות שהשלכת ח' וכן יהיה בחבור בלי פחות ויתר כאשר תעיין כמה חבור הכפל וכמה יעדיף על תשעה | |||||||||||||||||||||||||||||||
| ואם בין הטור העליון והשפל לא יעלה הכל ט' תפיל העליון על השפל וראה מה שיעדיף על תשיעיות וככה יהיה החבור אם הכפל יצדק ואם לא יצדק תם |
Division of integers |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [3]עשאו שין בונפייל נ"ע[4] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כשתרצה לחלק מספרים רבים על מספרים רבים כמה שיהיו[5] תשים המספר שתרצה לחלקו והוא ביותר גדול בטור כל אחד ואחד כפי מעלתו וקרא טור עליון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והמספר השני שתרצה לחלק עליו והוא היותר קטן תשים בטור[6] אחד תחת הטור[7] העליון כל מין תחת מינו ר"ל אחדים תחת אחדים עשרות תחת עשרות וכו'[8] שהטור[9] יקרא הטור השפל[10] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וריוח תשים בין שני הטורים שהזכרנו כדי שתוכל לכתוב ביניהם העולה בחלוק וזה הטור[11] יקרא טור אמצעי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכאשר תחל לחלק חשבונך ותחשוב כל המספרי' כאלו [הם][12] אחדים תראה כמה פעמים יהיה המספר האחרון שבטור השפל כמספר אחרון שבטור עליון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובאופן שיהיה מספר הפעמים ההם השני לאחרון שבטור השפל[13] ר"ל לפניו השני לאחרון שבטור העליון לפניו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן השלשי לאחרון שבטור | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואותו המספר אשר יעלה לך עם האופן הקודם ר"ל מספר[15] הפעמים[16] אשר[17] יהיה המספר האחרון שבטור השפל כמספר האחרון שבטור העליון תכתוב בטור האמצעי[18] ר"ל בין הטור העליון והשפל ותכתוב כמספר ההוא[19] רחוק מהמספר האחרון שבטור העליון אשר תקח[20] ממנו החלק כמו מדרגות אשר רחק כמספר האחרון שבטור[21] השפל ממדרגת[22] האחדים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ודע לך[23] שאם לא[24] תוכל לקחת[25] שום פעם[26] המספר[27] האחרון שבטור השפל כמספר האחרון[28] שבטור[29] העליון כאלו נאמר דרך משל | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שהאחרון שבטור השפל הוא[30] א' והאחרון שבטור העליון[31] הוא[32] ח' או פחות כמו בדמיונו זה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אז תשוב כל המספר ההוא אחורנית ר"ל[33] מספר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אחר כן[52] תשים קו תחת הטור השפל וכפול[53] זאת [האות][54] שיצא לך[55] בחלוק ר"ל ט' עם כל הטור השפל כאשר ידעת דרך הכפל[56] והיוצא מהכפל גרע מהטור[57] העליון כל מין ממינו ונתחיל מן המדרגה הקרובה אל האחדים או מן האחדים[58] אם יש שם אחדים והנשאר אחר[59] הגרעון[60] כתוב על הטור[61] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אחר זה שוב[62] לחלק הנשאר על הטור העליון על הטור השפל על הדרך שביארנו ואחר כפול האות היוצא בחלוק על כל הטור השפל[63] כאשר בתחלה ואחר גרע העולה מהכפל[64] מן הנשאר[65] בטור העליון וישאר הנשאר עליו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואחר[66] תשוב לחלק עוד אם יש בה לחלק ולכפול[67] ולגרוע כדבר האמור | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והסימן לזה הדרך[68] ח'כ'ם' ר"ל חלוק כפל ומגרעת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תעשה תמיד עד שישאר בטור[69] עליון פחות ממה שבטור[70] השפל | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכאשר עשית[71] זה ונשאר בטור העליון[72] פחות ממה שבטור[73] השפל ותרצה לבחון אם נעשית מלאכתך[74] בזולת[75] נפילת בה[76] שום טעות תחבר[77] כל טורי הכפל אשר [יצאו][78] לך כל[79] מין עם מינו וגם[80] הנשאר לך בטור עליון ותנהוג מנהג[81] החבור אשר ידעת מנהגו[82] ואם המחובר יהיה שוה למספר שיהיה לך ראשונה בטור העליון[83] הנה[84] החשבון[85] אמיתי ואם תמצא שום התחלפות[86] ביניהם הנה[87] טעות ודוק ותשכח | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Table in MS Firenze 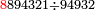
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| MS Firenze margin | שלא מן המאמ' והוא תוס' ביאור ואם תרצה לחלק עוד הנשאר לחלק בזה הדרך שעשינו שבר הנשאר למעלה ולמדרגה שלפניה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Extracting roots |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| After I have explained to you the method of division in the easiest possible way, in addition to mentioning most of the number operations such as division, multiplication and subtraction, as well as addition and checking, I intend to clarify and inform an easy way to find the square roots of the numbers that have a real root, or the closest to the numbers that do not have a real root, whether they are integers alone, integers with fractions, or fractions alone; their rules and approximations, while mentioning the other methods of calculation also. | [88]אחר שביארתי לך[89] דרך החלוק על הדרך היותר קל שאיפשר מצורף מה שיש בו[90] מן ההזכרה[91] מרוב דרכי המספר כמו חלוק כפל ומגרעת גם החיבור בבחינה אמרתי לבאר ולהודיע דרך קל למצא שרשי המרובעים מהמספרים שיש להם שורש אמיתי או היותר[92] קרוב להם[93] מהמספרים אשר אין[94] להם שורש אמיתי שלמי' לבדם הן מהמספרים שיש שלמים[95] עם נשברים[96] או[97] מנשברים לבדם[98] הן וכלליהם ודקדוקהם ויהיה גם זה מן ההזכרה[99] בשאר דרכי החשבון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| From now on I will start and say: | ומעתה[100] אתחיל ואומר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Know that in the rank of units there are three square numbers, i.e. whose roots are known integers and they are: one, whose root is one; four, whose root is two; and nine, whose root is three. | דע כי במעלת[101] האחדים יש בה[102] שלשה מספרים מרובעים ר"ל ששרשיהם שלמים וידועים והם אחד ששרשו אחד וארבעה[103] ששרשו שנים ותשעה ששרשו שלשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The second rank, which is the rank of tens, does not have a square number at all, only together with units, because ten is not a square number, nor twenty, nor 30, nor 40, nor 50, 60, 70, 80, 90. Yet with the addition of units, it has six squares, i.e. we add to the number of tens some units: like 16, whose root is 4; 25, whose root is 5; 36, whose root is 6; 49, whose root is 7; 64 whose root is 8; 81, whose root is 9. | ובמעלה[104] השנית[105] שהיא מעלת עשרות[106] אין בה[107] מספר מרובע כלל[108] רק עם[109] חבור אחדים כי עשרה אינו מספר מרובע ולא[110] עשרים ולא ל' ולא מ' ולא נ' ס' ע' פ' צ'[111] אמנם[112] עם חבור אחדים[113] יש בה[114] ששה מרובעים ר"ל[115] שנוסיף על מספר[116] העשרות אחדים מה[117] כמו י"ו שרשו[118] ד' כ"ה שרשו[119] ה' ל"ו שרשו[120] ו' מ"ט שרשו[121] ז' ס"ד שרשו[122] ח' פ"א שרשו ט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Every rank of a number, whose numerical position is odd, such as third, fifth, seventh, ninth, and the like endlessly, is analogous to the rank of units. | וכל מעלת[123] המספר שמספר מדרגתה נפרד כמו שלישית חמישית שביעית תשיעית ודומיהן[124] לאין תכלית דומה למעלה[125] האחדים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| As, if you say, for example, the rank of hundreds, which is the third rank, also has three squares: | כאלו תאמר דרך משל במעלת[126] המאיות[127] שהיא מדרגת[128] שלישית יש בה גם כן[129] שלשה מרובעים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והוא מאה [שדומה][130] לאחד שרשו עשרה שדומה לאחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וארבע[131] מאות שדומה לארבע אחדים[132] שרשו עשרים שדומה לשנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וט'[133] מאות שדומה לט' אחדים[134] שרשו שלשים שדומה לשלש[135] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Likewise every rank whose numerical position is even, like fourth, sixth, eighth, tenth, and so on endlessly, which is called an even rank, is analogous to the rank of tens, which has six squares by adding units to it as we have explained. So, the rank of thousands has six squares by adding hundreds, i.e. we shift each thousand backward as ten hundreds and add them to what is in the hundreds: | וכן כל[136] מעלה שמספר[137] מדרגתה זוג כמו רביעית ששית שמינית עשירית וכן לאין תכלית והיא[138] אשר תקרא מעלה [139] זוגיית[140] דומה למעלה העשרות שיש בה ששה מרובעים עם חבור אחדים בה כמו שבארנו כן במעלת האלפים יש בה[141] ששה מרובעים עם חבור המאיות[142] ר"ל שנשים[143] כל אלף ואלף[144] אחורנית לעשרה מאיות ותחבר[145] עם[146] מה שנמצא במאיות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו אלף ושש מאות הדומה לשש [147]עשרה[148] שרשו ארבעים הדומה לארבעה[149] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואלפים ות"ק הדומה לכ"ה שרשו חמשים הדומה לחמשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ושלשת אלפים ושש מאות הדומה אל ל"ו[150] שרשו ששים הדומה[151] לששה[152] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וארבעה אלפים ותשע מאות שדומה למ"ט שרשו שבעים שדומה לשבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וששת אלפים ארבע מאות הדומה לס"ד שרשו שמנים הדומה לשמנה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ושמנה אלפים ומאה[153] הדומה לפ"א שרשו תשעים הדומה לתשעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| And so on every rank whose numerical position is even, like fourth, sixth, eighth, to infinity. | וכן[154] כל מעלה שמספר מדרגתה זוג כמו רביעית ששית שמינית[155] לאין תכלית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| You should know that the result of any number falls in the middle rank of the ranks of that number. | ולך לדעת כי היוצא מכלל איזה מספר שיהיה יפול במעלת [156] האמצעית[157] שבמספר המדרגות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כאלו תאמר דרך משל יש לנו מספר[158] ד' במעלה השביעית שהוא מעלה נפרדת כמו הענין[159] בזאת הצורה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ושרשו[160] [ב'][161] כמו שביארנו שראוי לכתוב ב' במעלה הרביעית[162] שהיא מעלה[163] האמצעית שיש לפניה ג' מדרגות וכהנה לאחריה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Understand it for the other odd ranks. | ובין תבין בשאר המעלות הנפרדות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The same for the even rank: as we explained, there is no square in it, unless we return the last digit in the even rank backward, so each unit becomes a ten and we add everything to what is in the preceding rank. Then, the root should be extracted. The number of the ranks becomes odd, and every odd rank has a middle rank. | וגם במעלה הזוגיית כמו שבארנו[164] אין בה שום מרובע אם לא בהשיב כל אחד[165] מהמספר האחרון שבמעלה הזוגיית אחורנית ולעשות מכל אחד עשרה ולחבר הכל עם מה שבמעלה[166] שלפניה ואז ראוי לקחת השרש ואז[167] ישובו[168] מספרי המעלות נפרד וכל נפרד יש לה מעלה אמצעית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וראוי לכתוב השרש היוצא במדרגת האמצעית ר"ל רחוק ממדרגה האחרונה[169] אשר ילקח[170] מהם כאשר מרחקו מן האחדים מפני שהאחדים עומדים בעצמם ובמקומם והוא שרש האחדים בטור[171] האחדים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והענין אחר שהשרש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואחר שהקדמתי לך זה[175] אזהירך[176] להזכירך[177] מסורת המרובעים אשר במדרגת[178] האחדים שהיא הראשונה שהם א'[179] ד'[180] ט' ושרשם א' ב' ג' ובמדרגות העשרות יש ששה מרובעים והם י"ו כ"ה ל"ו מ"ט ס"ד פ"א[181] ושרשם ד' ה' ו' ז' ח' ט' ויהיה זה ידוע אצלך וכבר הודעתיך כי המעלה הנפרדת הנה[182] דינה כדין האחדים והזוגית דינה כדין העשרות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ועתה אורה לך[183] דרך זו תלך בידיעת[184] שורש[185] כל[186] מספר שתרצה אם יש להם שורש אמתי או היותר קרוב לפניו אם אין להם[187] שורש הנה תכתוב המספר אשר תרצה[188] לדעת שרשו בטור אחד איזה[189] מדרגות שתהיינה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונאמר תחלה שתהיינה ה' מדרגות דרך משל א'ב'ג'ד'ה'[190] הנה המעלה האחרונה היא נפרדת ודינה כדין האחדים כזה[191] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| לכן נדמה מספר ה'[192] האחרון כאלו הם[193] ה'[194] אחדים הנה שרשו היותר קרוב לו[195] לפניו הוא ב' שהוא שורש[196] ד' ולכן[197] נכתוב ב' באמצע שהוא שורש[198] תחת אות הג'[199] ונרשום[200] קו תחת הב' עם מעט ריוח[201] כדי שנוכל לכפול אותיות השורש[202] היוצאות מן האחדים ולכן ראוי לכתוב גלגלים כמספר המדרגות לפניה[203] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונכפול אות הב' שהוא השורש בעצמה[204] והנה ראוי לכתוב הכפלה רחוק ממנה[205] לאחריה כאשר היא רחוקה מן האחדים ולכתוב ראוי לכתוב הגלגלים כמספר המדרגות אשר לפניה והתחלתם כנגד הב' ביושר ובמדרגתה כאשר נאמר עתה כנגד ב' נתחיל ב' גלגלים כאשר אות הג' רחוקה מן האחדים[206] ב'[207] מדרגות[208] ואחר השתי גלגלים נכפול הב' בעצמה ויהיה ד' ובין תבין בכל התחלת[209] הכפילה וזכור לך זה ואחר גרע העולה מהכפל מהמספר[210] הראשון מין עם מינו[211] כאשר ידעת[212] דרך המגרעת והנשאר ישאר[213] על הטור העליון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אחר זה[214] תכפול השורש בשנים ר"ל שאם היה ג'[215] תכתוב[216] תחתיה[217] ה' ואם[218] היה[219] ד' ח' ובדמיוננו זה שהיא[220] ב' תכתוב תחתיה[221] ד' והוא השורש הכפול[222] השנים[223] תחלק הנשאר מהמספר האחרון[224] על זאת[225] הד' ותקח ממנו[226] כל מה שתוכל לקחת מרובע המספר היוצא[227] מן החלוקה[228] כאלו תאמר[229] בדמיוננו זה הנה נשיב הא' אחורנית כי לא נוכל לקחת ד' ממנו והשיבו[230] אחורנית עם הד' שלפניה ויהיה י"ד ונאמר כמה פעמי' ד'[231] בי"ד[232] הנה נקח ג' כי מהנשאר לפניו נוכל[233] לקחת ג' פעמים ג' שהוא מרובע המספר[234] היוצא מן החלוקה ונכתוב ג' לפני השורש הראשון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונכפול זה הג'[235] על עצמה ראשונה ואחר על[236] השורש הכפול כמשפט הכפל[237] ונתחיל[238] לכתוב זאת האות הנופלת[239] כנגדה ותעשה ראשונה גלגלים כאשר אות הג' רחוקה מן האחדים והוא גלגל אחד ראשונה כנגד הג' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואחר נאמר ג' פעמים ג' הם ט' ונכתוב ט'[240] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואחר נאמר ג' פעמים ד' הם ב'א' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואחר נגרע זה הטור הנכפל מן הנשאר[241] למעלה מין ממינו[242] כמשפט המגרעת והנשאר ישאר למעלה בטור העליון[243] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אחר זה[244] תכפול זאת[245] האות השינית[246] מן השורש[247] שהיא[248] ג' בשנים ונכתוב ו' תחתיה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונשוב לחלק כל הנשאר למעלה על כל השורש הנכפל שהוא הכפל[249] ו'ד' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונקח כל מה שנוכל באופן שנוכל[250] לקחת באחרונה מרובע המספר[251] היוצא מן החלוקה[252] כאלו תאמר בדמיוננו זה הנה נשיב הא' אחורנית כי לא נוכל לקחת ד' ממנו ויהיה י"ד ונאמר כמה פעמי' ד' בי"ד ונקח ג' כי מהנשאר נוכל לקחת ג' פעמי' ו' ומהנשאר אחר זה נוכל לקחת[253] ג' פעמים ג' ונכתוב ג' לפני הו' והיא[254] במעלת האחדים ונכפול זאת הג' ראשונה על עצמה והיא ט' ונכתבנה כנגדה שאות הג' היא במדרגת האחדים[255] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אחר נכפול ג' על ו' ואחר ג' על ד' ואחר נגרע העולה מהכפל מהנשאר למעלה והנשאר ישאר למעלה וישאר למעלה[256] ל"ב והשורש ג'ג'ב' ונשלם ביאורו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אך אמנם[257] אתן לך כללים מתחלפים יש צורך בידיעתם במעשה השרשים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הכלל הראשון כאשר לקחת השורש הראשון מהמספר האחרון אשר בידך אם היא מדרגה נפרדת או מהקודם לאחרון אם היא מדרגה זוגית ראוי לכתוב השורש ההוא במדרגה האמצעית כאשר הראיתיך ותקח כל מה שתוכל ואם לא תוכל לקחת דבר מהמקום ההוא האחרון[258] הנשאר לקחת[259] מהשני לו גם כן[260] תכתבנו רחוק מהמקום אשר תקח[261] ממנו החלוק כאשר השורש[262] הראשון רחוק מן האחדים[263] ולכן ראוי לכתוב גלגל במקום אשר לפני[264] השורש הראשון וקודם לזה הגלגל תכתוב היוצא מן החלוקה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הכלל השני כאשר תשוב[265] לחלק הנשאר מהמספר אשר בידך על כפל[266] השורש לא תקח המספר האחרון אשר לקחת[267] ממנו[268] ראשונה ואף כי מהמספרים[269] אשר אחריו[270] ואף כי תראה כי[271] האפשר לקחת בו מפני שכאשר לוקח ממנו השורש[272] ראשונה כבר לוקח ממנו כל[273] הראוי כמו שתראה[274] בדמיוננו זה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| רצינו לדעת השורש הקרוב אל ט'ט'ג'[275] והנה לקחנו השורש הקרוב והוא א' וכתבנוהו במדרגה האמצעית שהיא[276] תחת הט' השניה וגרענו א' מהמספר[277] האחרון שהוא ג' והנה נשאר[278] ב' על הג' ונכפול אות הא' והיא[279] ב' ולא נאמר לראות כמה פעמים יהיה ב' שהוא כפל השורש במספר הנשאר[280] במספר הראשון והוא ב' מאשר נוכל לקחת פעם אחת ב' מב' וגם נוכל לקחת מרובע א' מהנשאר[281] זה אין ראוי לעשות מפני כי[282] יהיה[283] מהראוי לכתוב זה הא' היוצא רחוק מהמספר אשר לקחנו[284] ממנו החלוק כאשר אות הא'[285] הנכתב ראשונה[286] נכתב[287] כמשפט[288] הזה וכבר לקחנו כל המצטרך במדרגה ההיא ולכן נשיב הב' אחורנית על הט' אשר לפניה[289] ויהיה כ"ט ונאמר כמה פעמים יהיה ב' שהוא כפל השורש במספר כ"ט[290] באופן שנוכל לקחת מהמדרגה אשר לפניה[291] מרובע המספר היוצא מהחלוקה ודי בזה מזה[292] הכלל והוא נמשך עם הכלל השלישי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הכלל השלישי כאשר שבת לחלק המספר[293] הנשאר על השורש הכפול לא תטרח בעצמך לראות אם תוכל לקחת עשרה פעמים המספר[294] המחלק במחולק[295] כמו שנאמר בדמיוננו שלמעלה מזה וראה[296] כמה פעמים יהיה[297] ב' במספר כ"ט ונאמר שיהיה בו עשר[298] פעמי'[299] כי[300] זה אי אפשר ואף כי יותר מהעשרה[301] כי לא נוכל[302] לקחת מהמדרגה שלפניו עשר[303] פעמים עשרה ואין ראוי לטרוח בזה וכן זה[304] הדין בענין החלוק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הכלל הרביעי מאשר אמרנו בכלל השני כי כאשר נשוב[305] לחלק הנשאר על כפל השורש שלא נשוב לקחת מן המדרגה[306] אשר לקחנו ראשונה זהו כאשר היה שכפלנו[307] השורש לא הוספנו[308] עליו מדרגה כמו אם כפלנו ב' היה ד' באותה מדרגה וכן ג' וכן ד' אמנם אם היה השורש ה' או ו' או ז' או ח' או ט' והנה[309] כשכפלנו זה השורש כבר[310] נתוספה בשורש מדרגה אחת כאלו תאמר היה השורש ו' עשרות הנה כפל השורש ב' עשרות ומאה הנה נתוספה[311] בשורש[312] מדרגה אחת ולפי זה כאשר תשוב לחלק[313] תקח מהמדרגה אשר לקחת ממנו ראשונה ותכתבנה גם כן[314] רחוקה מהמספר האחרון כאשר ראש השורש הכפול[315] רחוק מן האחדים[316] וזה מה שרצינו לבאר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Another Version - MS Paris 903 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [317]
הדרך להוציא שרשי המרובעי' ממספר בעל שרש אמתי או שרש המרוב' הקרוב מאשר אי' להן שרש אמתי הן משלמי' לבד או נשברי' לבד הן ממספר שלמי' ונשברי' יחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דע כי במעלת האחדי' יש בה ג' מספרי' מרובעי' ר"ל ששרשם שלמי' וידועי' והם א' וד' וט' ששרשם א' ב' ג' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובמעלה השנית שהי' עשרות [אין בה] מספר מרובע כלל רק עם חבור אחדי' כי י'כ'ל'מ'נ'ס'ע'פ'צ' אי גם אחד מהם מרובע אך עם חבור אחדי' יש בה ו' מרובעי' כמו י"ו שרשו ד' כ"ה שרשו ה' ל"ו שרשו ו' מ"ט שרשו ז' ס"ד שרשו ח' פ"א שרשו ט' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכל מעלה נפרד' כגו' המאו' שהי' השלישי' או הרבואו' שהם חמישית ושביעי' ותשיעי' וכן כלם דומי' דומי' למעל' האחדי' בשיש בם ג"כ ג' מרובעי' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגו' במאו' יש ק' ושרשו י' ת' ושרשו כ' ת'ת'ק' ושרשו ל' וכן כלם ולעול' א'ד'ט' מרבעי' במעלו' נפרדו' ושרשם א'ב'ג' מהמעלה שלפניה וימינה הקרובה לה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן כל מעלה זוגית דומ' לעשרו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגו' האלפי' יש בה ו' מרובעי' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכמו שבעשרו' המרובעי' עם חבור אחדי' מה שהיא המעל' הקרובה לימינ לפניה כן תחבר לעולם עם המעל' הזוגיי' אחדי' מהמעלה שלפניה במספר שתצטרך להוסיף אחדי' ע' העשרו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגו' באלפי' יש אלף ות"ר הדומ' לי"ו ושרשו ת'מ' והו' דומ' לד' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אלפים ות"ק הדומ' לכ"ה ושרשו נ' הדומ' לה' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ג' אלפי' ות"ר הדומ' לל"ו ושרשו ס' הדומ' לו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וד' אלפים תת"ק הדומ' למ"ט ושרשו ע' הדומ' לז' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וו' אלפי' ות' הדומ' לס"ד ושרשו פ' הדומ' לח' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וח' אלפי' ק' הדומ' לפ"א ושרשו צ' הדומ' לט' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן כל מעל' זוגיית | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה הכלל כל מרובע של מעלה נפרדת הו' א' ד' ט' ושרשם א' ב' ג' וכל מעל' זוגיי' שרש מרובעיה ו"א ה"ב ו"ג ט"ד ד"ו א"ח ושרשם ד' ה' ו' ז' ח' ט' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואבל אי' מעלת השרשי' לעול' הסמוכה לה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכה תדע מעלת מקו' השרש לעולם ראה במספרי' מעל' נפרדת להשיב השרש רחוק מהמרובע אחורני' מספר מעלו' כמספר מעלו' שירחק מהאחדי' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והמשל מצאנו ד' במעל' תשיעי' כזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה ידענו כי זה המספר מרובע כי הו' מעלה נפרד' ודומ' לאחדי' ובאחדי' ד' הו' מרובע ושרשו הו' ב' א"כ גם זה שרשו ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומקומה של הב' ראויה להיות ממוצעת בין מעלת האחדי' ומעלת המרובע והיינו בחמשית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן מספרי' הזוגו' מאחר שצריך לך לעול' לחבר עם המרובע אחדי' מהמעלה שלפניו וצריך להשיב מעלת הזוג אחורנית לחשבה בעשרו' ויהיו שם במעלה נפרדת עשה ג"כ כנ"ל ושים השרש באמצע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כאלו תאמ' מצאנו ו'ג' במעל' ח' והי' זוגיי' ודומה לל"ו שבעשרו' שהו' מרובע ושרשו ו' א"כ גם זה שרשו ו' וצרי' להשים הו' בין תחלת המספר המרובע ובין האחדי' באמצע דהיינו במעל' ד' שהו' רחוק מהאחדי' ג' מעלו' וכן הו' רחוק מהמעל' הה' אשר שם החל מספר המרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והילך מעשה ידיע' השרש הקדו' או האמתי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כתו' המספר הדרוש שרשו בטור אחד כפי מעלותיו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל בזה שמטהו ה' מעלו' כזה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה ידעת מהנ"ל שזה המספר נפרד ודומ' לאחדי' ר"ל הה' ושרש היותר קרו' בה הו' ב' שהו' שרש ד' הקרוב לה לפניו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומקו' הב' כנ"ל הו' במעל' ג' תחת הג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ראה מעתה כמה מעלו' עברו מהאחדי' עד מקו' הב' שהי' שרשך ושם החל לכתו' גלגלי' כמספר המעלו' ההם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כאלו תאמ' מהאחדי' עד הב' יש ב' מעלו' לכן נכתו' תחת הקו ב' גלגלי' מתחילי' תחת הב' בעצמ' והולכי' לשמאל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אח"כ נכתו' העול' מכפל ב' על ב' שם והו' ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אח"כ גרע הד' מהה' של מספר הדרוש וישאר א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן כתו' א' ממעל לה' והעבר קו סביב הה' כי אי' בה צורך עוד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומעתה נשאר לדעת השרש היותר קרוב מהב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה יצטרך לקחת לכל מה מספר שתוסיף על השרש כפל אותו מספר על פעמים זה השרש שהו' הב' במשלינו במעל' המאות וגם כפל המספר ההו' על עצמו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומופת זה כי אנחנו הנחנו מספר מרובע של ד' רבואו' א"כ שרשו ב' מאו' כמ' שראית ושרשו הוא מספר הצלע האחת מהמרובע בעצמ' כי ב' מאו' אמ' ארך על ב' מאו' אמ' רחב ימצא בם ד' רבואו' אמו' של אמה על אמ' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונניח שנוסיף על שרש זה המרובע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נמצא שתשים ל' רצועו' כל אחת של מאתים אמ' ארך וא' אמ' רחב דהיינו רצועה אחת של מאתים על ל' ותחברנה בצלע אחד מהמרובע כאלו תאמ' למזרחו ויהיה המרובע אז ארכו יתר על רחבו ארכו ר"ל ורחבו ר' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אח"כ הוספת עוד רצוע' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וא"כ כבר הוספת על זה השרש כפל ל' על ר' פעמי' פעם א' המזרח ופעם א' הדרום | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועדיין חסרה קרן זוית בזה המרובע והי' הקרן דרומי' מזרחי' אשר לא תתמלא רק אחר שומך שם מרובע ל' על ל' ואז ישוב מרובע שוה הצלעו' שרשו ר"ל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [...] והיוצא מזה [...] שתכפול מה שתרצה להוסיף עליו על עצמו אח"כ על ב' פעמי [...] לעשו' שיהא בא צריך להוסיף עליו כפל ד' על עצמו שהו' י"ו [...] פעמי [...] גם כפל ד' ל"ד שהו' ב' פעמי' י"ז | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונשוב לכונתינו ונאמ' אחרי שמצאת [...] וכתבתם [..] על מקומ' גם חסרונ' מרובעה של הב' מה"ה ונשאר א' שוב מעתה הוסיף על השרש מהמספר הנשאר והו' א' ב' ג' ד' א' ככל מה שתוכל וזה הדרך תלך בו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קח השרש שמצאת ב' פעמים ר"ל כפול אותו עם ב' אם הו' ג' כתו' ו' ואם ח' ו'א' ובדמיוננו הו' ב' לכן כת'[...] במעלתו ד' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וחלק מעתה המספר העליון על הד' וראה כמ' פעמי' ימצא ד' בא' האחרונ' עם הד' שלפניה כשתשיבנה אחורני' ויהיו י"ד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הוי או' ג' פעמי' ימצא וצריך לראו' אם ימצא ג"כ למלאת הקרן זוי' והו' ט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כי אם לא היה אפשר לא הייתי לוקח רק ב' והנה בדמיוננו נוכל לקח[ת] ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתו' מעת' ג' קדם הב' לימינ' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ראה כמ' מעלו' מהאחדי' עד הג' והנה הי' אחת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
לכן כתו' תחת הקו במעלה ב' דהיינו תחת הג' ההי' גלגל אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אח"כ כפול ג' על עצמו ויצא ט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כתבהו במקומו תחת הקו לשמאל הגלגל היחיד שעשית תחת הג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
שוב כפול הג' על | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכתבם במקומ' אחרי הט' תחת הקו כי הג' הי' ממעל' העשרו' והד' מהמאו' וכפל עשרו' במאו' יעלו אלפי' לכן תחל לכתו' הב' תחת מעלת האלפי' והא' תחת הרבואו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אח"כ גרע זה מהמספר העליון כל מין ממינו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דהיינו הא' מן הא' ולא ישאר דבר והב' מהד' ישאר ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ולפי שלא נוכל לקחת אז הט' מהג' לכן נשיב א' אחורני' ונכתו' א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונקח הט' מהא' המושבת אחורני' על הג' שהם י"ג וישארו ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן נכתו' ד' ונכתו' זה למעלה מהטור העליון איש איש על מעלתו כמו שתראה בדמיונינו זה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והעבר קו על ג"ד ועל א' כי אי' בם צרך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה מצאת שרש הקרו' ר"ל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עו' תרצה להגדיל המרובע והשרש כי יש עוד מספר רב מן המספר הראשון הדרוש כי נשאר לך עדיין א' ב' ד' א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ושוב מעתה לכפול גם הג' בב' ויהיה ו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כתבה תחת הג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומעתה חלק המספר הנותר מהדרוש על כפל כל השרש והו' ו'ד' דהיינו ת"ס כי השרש הו' ר"ל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וראה כמה פעמי' ימצא ד' בי"ד והנהו ג' פעמי' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כתו' ג' לפני הג'ב' של השרש ותחת הא' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכפול מעתה ג' על עצמו ויהיה ט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כתבה תחת הקו ותחת הג' האחדית [ויהיה למלא הקרן זוית] ולפי שהג' אינ' רחוקה דבר ממעלת האחדי' ע"כ אין צרי' לשים שום גלגל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עוד כפול הג' בשרש ב' פעמי' שהם ו'ד' ותמצא ח'ג'א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כתבם על מקומ' דהיינו שתתחיל אצל הט' למטה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויהיה המספר היוצא מכפל ג' על עצמו ועל השרש פעמים ט ח ג א | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה המספר גרע מאשר נשאר לך מהמספר הדרוש והו' א ב ד א | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה חסר א' מא' לא ישאר כלום | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עוד חסר ג' מד' ישאר א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ולפי שלא נוכל לקחת ח' מב' צריך להשיב זו הא' אחורנית ולא ישאר כלו' בזאת המעל' ג"כ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חסר ח' מב'א' ר"ל מי"ב ישאר ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועו' צרי' להשי' אחורני' א' מהד' נשאר ג' וכן תכתו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עו' חסר ט' מא"א והו' י"א וישאר ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכתבה במקומ' והעבר קו על א"ב ד"א כי אי' בם צורך עוד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ויהיה השרש הקרוב למספר אבגדה בדרוש גגב ויהיה המרוב כמספר כל המרובעי' שהוצאת מהשרשי' מגגב אחרי התחברם והו' טחבדה והנשאר מהמספר הו ב"ג ואם תשוב לחבר ב"ג על המרובע יצא לך המספר הדרוש ויהיה השרש הקרוב למספר א ב ג ד ה הדרוש . ג' ג' ב' . ויהיה המרובע כמספר כל המ[רובעי'] שהוצאת מהשרשי' מגג"ב אחרי התחברם והו' ט ח ב ד ה . והנשאר מהמספר הו' ב"ג | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תשוב לחבר ב"ג על המרובע יצא לך המספר הדרוש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אך אמנם אתן לך כללי' מתחלפי' יש צורך בידיעתם במעשה השרשים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הכלל הא' כשלקחת השרש הראשון מהמספר האחרון שבידי אם הו' מעלה נפרדת או מהקודם לאחרון אם היא מעלה זוגיית ראוי לכתו' השרש ההו' במדרגה האמצעי' כהראיתיך ותקח כל מה שתוכל ואם לא תוכל לקחת דבר מהמקו' ההוא הראשון ולקחת מהשני לו גם כן תכתבהו רחוק מהמקו' שתקח ממנו ראש החלוק כאש[ר] השרש הראשון רחוק מהאחדי' ולכן ראוי לכתו' גלגל במקו' שלפני השרש הראשו' וק[ודם] לזה הגלגל תכתו' היוצא מהחלוק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הכלל הב' כשתשוב לחלק הנשאר מהמספר שבידך על כפל השרש לא תקח המספר האחרון שלקחת ממנו ראשונה ואף כי מהמספר [שאחריו] ואף כי תראה כי האפשר לקחת בו מפני שכשלוקח ממנו השרש ראשונה כבר לו[קח ממנו כל הראוי |
Squares |
כלל בבחינת המרובעים |
|---|---|
| הנה כאשר יהיה בידך מספר ותרצה לבחון אותו אם הוא מרובע תוכל לבחון אותו עם המרובע הקודם לו לפניו ועם המרובע הקודם לו לאחריו ראשונה עם המרובע הקודם לו לפניו תחשוב המרחק שבין המרובע שעבר ובין המרובע אשר בידך חלק המרחק ההוא על כפל שורש המרובע שעבר פחות מן האיפשר על המעט שתוכל גרע מהמרחק ההוא היוצא ואם היוצא לך מחלוק המרחק על כפל השורש שעבר עם מרובע המספר היוצא מן החלוקה שוה אל המרחק אשר בידך לא פחות ולא יתר הנה המספר מרובע ואם לא הנה טעית | |
| ותוכל לבחון גם כן עם המרובע הקודם לו לאחריו תחשוב המרחק שבין מספרך ובין המרובע העתיד חלק המרחק ההוא על כפל שורש המרובע העתיד ותתן אלו יותר על האיפשר על המעט שנוכל נדע המרחק ומרובע המספר היוצא מהחלוקה בחלוק | |
| ואם העולה מהחלוק עם מרובע המספר היוצא שוה למרחק עם מרובע המספר היוצא הנה המספר מרובע ואם לא הנה טעית | |
Division of sexagesimal fractions |
|
| [318]כאשר תרצה לחלק חשבון מעלות ודקים ושניים על חשבון אחר יותר קטן או יותר גדול | |
| תקח חשבון הטור התחתון והוא החשבון אשר עליו מחלק חשבון הטור העליון ותשבר הכל אל מין השבר היותר קטן אשר בו ר"ל שאם השבר היותר קטן אשר בו הוא שניים תעשה מהכל שניים ואם שלשיים תעשה מה מהכל שלשיים וכן על זה הדרך | |
| ואחר כן קח חשבון הטור העליון והוא החשבון אשר יחולק על חשבון הטור התחתון וישבר אותו אל מן השברים שיהיה רחוק ממין השברים ששברת בו התחתון כמו שיהיה מרחק המין שתרצה שיצא לך בחלוקה מן המעלות ר"ל שאם שברת חשבון הטור התחתון מן השניים ותרצה שיצא לך בחלוקה שלשיים הנה תשבר חשבון הטור העליון למין חמשיים שהוא רחוק מן השניים שלשה מדרגות כמו מרחק השלשיים מגדר המעלות וזה יצא בחלוקה שלשיים | |
| ואם תרצה לדקדק עוד שיצא בחלוקה רבעיים תשבר הטור העליון לששיים שהוא רחוק מהשניים ארבע מדרגות כמו מרחק הרבעיים מגדר המעלות ואז יצא לך בחלוקה רבעיים וכן על זה הדרך | |
| וכן אם שברת הטור התחתון לשלשיים ותרצה לדקדק עד שיצא לך בחלוקה רבעיים תשבר חשבון הטור העליון לשבעים שהוא רחוק משברי הטור התחתון ארבע מדרגות כמו מרחק הרביעיים מגדר המעלות ויצא לך בחלוק רביעיים | |
| ואם תרצה לדקדק עד שיצא לך בחלוקה חמשיים תשבר חשבון הטור העליון לשמניים שהוא רחוק משברי הטור התחתון חמש מדרגות כמו מרחק החמשיים מגדר המעלות ויצא לידך בחלוקה חמשיים וכן על זה הדרך ודי לך בזה | |
Extracting roots of sexagesimal fractions |
|
| וכן אם תרצה למצוא שרש אי זה חשבון שיהיה בידך ממעלות הראשונים ושניים כפי מה שיהיה | |
| דע לך עד כמה שברים תרצה לדקדק שיצא בשרש ר"ל אם רבעיים או חמשיים או ששיים או אי זה מן שברים אשר תרצה לדקדק שיצא בשרש תקראהו מין השרש ואחר זה תתיך כל החשבון אשר בידך אל מין השברים שיהיה רחוק ממין השרש כמו מרחק מן השרש מהמעלות שאם מין השרש רביעיים תתיך חשבון לשמוניים ומה שיצא השרש יהיה רביעיים ואם מין השרש חמישיים תתיך החשבון לרביעיים ומה שיצא בשרש זה יהיה חמשיים וכן על זה הדרך | |
| והכלל בזה הדרך שתכפול מן השרש בשלו המראה לו כפלה פשוטה שאם יהיה שניים תתיך לרביעיים ואם יהיה שלשיים תתיך לששיים ואם יהיה רביעיים תתיך לשמוניים ואם הוא חמישיים תתיך לעשריים | |
Multiplication of sexagesimal fractions |
|
| אמנם בכפילת חשבון עם חשבון | |
| תתיך הטור העליון אל מין השבר היותר קטון אשר בו וכן הטור התחתון תתיך אל מין השבר היותר קטון אשר בו והיוצא בכפילה יהיה מין השבר יקרא בשם המחובר המחובר משום הטורים ר"ל שאם תכפול שניים על שניים יהיה היוצא רביעיי [319]ואם שניים על שלשיים יהיה היוצא חמישיים
כאשר יהיה בידך מספר ותרצה לבחון אותו אם הוא מרובע תוכל לבחון אותו עם המרובע הקודם לו לפניו ועם המרובע הקודם לו לאחריו ראשונה עם המרובע הקודם לו לפניו תחשוב המרחק שבין המרובע שעבר ובין המספר אשר בידך חלק המרחק ההוא על כפל שרש המרובע שעבר פחת מן האפשר על המעט שתוכל גרע מהמרחק ההוא היוצא מחלוקה וזה מרובע המספר היוצא מחלוקה ואם היוצא לך מחלק המרחק על כפל השרש שנים עם מרובע המספר היוצא מחלוקה שוה אל המרחק אשר בידך לא פחות ולא יתר הנה המספר מרובע ואם לא הנה טעות תוכל לבחון גם כן עם המרובע הקודם לו לאחריו תחשוב המרחק שבין מספר ובין המרובע העתיד חלק המרחק ההוא על כפל שרש המרובע העתיד ונכון לו יותר על האפשר על המעט שנוכל גרע המרחק ומרובע המספר היוצא מחלוקה מהעולה בחלוק ואם העולה מהחלוקה עם מרובע המספר היוצא מחלוקה שוה למרחק הנה המספר מרובע ואם לא הנה טעות תם ונשלם תהלה לאל עולם | |
| כאשר יהיה המרובע הנמשל פחות מהמספר המבוקש צריך שנקח החלוק מספר היותר גדול שנוכל שיעלה בחלוקה המרחק כאשר יחוסר ממנו מרובע מה שיעלה בחלוק | |
| וכאשר תוסיף על המרובע הנמשל כמו הכפל עם מרובע מה שיעלה בחלוק הוא המרובע היותר קרוב על המספר המבוקש
וכאשר תוסיף על שורש המרובע הנמשל מספר מה שיעלה בחלק הוא שרשו | |
| וכאשר היה המספר המבוקש פחות מהמרובע הנמשל צריך שנקח החלוק מספר היותר קטן שנוכל שיעלה כמו המרחק מחובר עם מרובע מה שיעלה בחלוק | |
| וכאשר תגרע מהמרובע הנמשל כמו הכפל כאשר יחובר ממנו מרובע מה שיעלה בחלוק הוא המרובע היותר קרוב אל המספר המבוקש | |
| וכאשר תגרע משרש הנמשל מספר מה שיעלה בחלוק הוא שרשו | |
| המרחק הוא המרחק שבין המרובע הנמשל ובין המספר המבוקש | |
| הנכפל הוא מה שיעלה מכפלת מספר מה שיעלה בחלוק עם כפל שורש המרובע הנמשל כי יהיו שני מרובעים מתחלפים יחס המחובר מכפלת אחד מן השרשים על האחר אל המרובע הראשון כיחס המרובע השני אל המחובר |
אמר עמנואל בן יעקב לפי שמעשה החלוק יותר קשה למתלמדים ממעשה הכפל והיא הדרך לשאר החשבנים החכמים להוציא המספר האחד הנעלם איזה שיהיה מתוך ידיעת החמשה מספרים הנשארים ויעשה בזה שני כפלים ושני חלקים בדרכים שונים ראינו לבאר להוציא הנעלם מתוך ידיעת החמשה הנשארים ויעשה בזה שלשה כפלים וחלוק אחד ואומר ראשונה לתת קצת אותות אל זה המעשה הנה יחס א' אל ב' מחובר מיחס ג' אל ד' ומיחס ה' אל ו' וכבר התבאר מתמונת כ"ג מששי אקלידיס שיחס השטח ההווה מן ג' בה' אל השטח ההוה מן ד' בו' מחובר מיחס צלע ג' אל צלע ד' ומיחס צלע ה' אל צלע ו' אם כן יחס ו' אל ב' כיחס השטח ההווה מן ג' בה' אל השטח ההווה מן ד' בו' ויהיה שטח ג' בה' מספר ז' ושטח ד' בו' מספר ט' אם כן יחס א' אל ב' כיחס ז' אל ט' אם כן נכפול הקצות שהם א' בט' ויהיה ל' ונחלק ל' על האמצעי והוא ב' ויעלה הז' שהוא האמצעי האחר או נחלק ל' על האמצעי והוא ז' ויעלה ב' והוא האמצע האחר או נכפול האמצעיים שהם ב' בט' ויהיה ל' ונחלק על הקצה
ברוחב הנה [......] הזאת פחותה מחצי הכדור כגון עגולת [....] שעמקה שתי אמות ורוחב עגולת [....] שורש מ' והוא [....] ושליש [.......] ואתה יודע ש[.......................................] מפני שעמקה פח[ות] ממחצית רוח[.....] ואם אתה מוציא [..............] כאשר למדת תמצא [....] כפול שנים שהם עומק הבריכה שהוא [....] בז' שהוא קוטר הכדור יהי[ה] י"ד כפול [.....] פעמים ושביעית פעם יהיו מ"ה והוא משיח[ת] שטח הבריכה כפ[.]ל[................] והוא אחד ושתות [.....] בז' ושליש והוא תשבורת [....] הבריכה ואם היה עמק הבריכה ה' אמות ורחב[......] גדר ארבעים [....] [........] ואם אתה כופל העומק בקוטר יהיה ל"ה נכפילה בג' ושביעית יהיה ק"י והוא משיחת שטח הבריכה כפולה בש[....] הקוטר יהיה קכ"ח ושליש והוא תשבורת רבוע [....]
אמר טעם החלוק הם שניים א שנכפול בדרך הכפל מה שיצא בחלוק על הטור השפל שמחלקים עליו תחבר עם העולה מה שנשאר לחלק [.....] דבר ואם המחובר שוה למספר הטור המחולק עשינו נכונה הב' שנכפול מאזני מה שעלה בחלוק עם [.....] הטור השפל ונקח ממנו העולה ואם נשאר דבר לחלק נחבריהו עמו ואם הוא שוה למאזני הטור העליון חשבונינו אמת והטעם למאזנים הראשונים כי בחשבון המחולק [....] החשבון שמחלקים עליו כשיעור אחד מה שיעלה בחלוק הוא מספר מה שימנה המספר שמחלקים עליו למספר גדול המחולק לזה הכה זה על זה ויצא המחולק
Chapter on Summation [MS London] |
שער המחברת |
| To know how much is the sum of numbers from a known number to the last number. | לדעת כמה המחובר מהמספרי' ממספר ידוע עד סוף מספר |
|
כאלו תאמר רצינו לדעת המחוברים מאחד עד עשרה כמו א' עם ב' הם ג' ג' עם ד' הם ז' ותרצה לדעת בקצור |
|
אם הם זוג כמו עשרה ונוסיף עליו א' ותקח חצי העשר שהם חמשה וכפול החמשה על הי"א והוא המספר האחרון |
|
ואם נפרד כמו מאחד עד שבע תוסיף על ז' אחד ויהיו ח' ותקח חצי המספר והם ד' וכפול הד' על הז' והוא המכוון |
| Do this with any number, small of large, even or odd. | וכן תעשה בכל מספר קטן או גדול זוג א[ו] נפרד |
| אם תרצה לדעת ערך נעלם כמו שתאמר ערך ד' אל ו' כערך ח' אל הנעלם ותרצה לדעת האמצעיים ו' על ח' יהיו מ"ח ותחלק המספר הראשון שהוא ד' על המ"ח ויעלה לך חלק מ"ח והוא הנעלם | |
| אמר אברהם מצאתי דרך אחר שהמוסיף על מרובע סוף החשבון שרשו ולוקח חצי בעולה שם ימצא המחובר והדרך הזה יורה להבין הפך השאלה | |
| דמיון שאל שואל חברתי מספרים עלו תס"ה כמה יהיה סוף החשבון כלל זה תקח בידך היוצא מחודך כפול לעולם החשבון המחובר והשורש תקח מן המרובע כלו' [..] הנכפל שעבר ובחן אותו כ"א נשאר בין המרובע ובין הנכפל כמו שורש בלי תוספת ומגרעת תדע כי החשבון והשורש הוא המבוקש והנה כפלנו תס"ה על(ה) תתק"ל ידענו כי מרובע שעבר הוא ט מאות ושרשו ל' שהם המספרי' המרובעי' ואין בין המרובע והנכפל כ"א ל' ועל כן תבין כי נכון מה שחשב והמבוקש ל' | |
Word Problems [MS London] |
|
| "How Many" Problem | |
|---|---|
|
שאלה אדם עבר על |
|
נקח להם אחד נוסיף להם עוד אחד הנה נוסיף להם מחציתו הנה שנים וחצי נוסיף רביעיתו יהיה ג רביעי' ובעבור שהם רביעיות נוספות על השלמי' נשים גם השלמי' לרביעיות ויהיו ה וג' רביעיות הנה י"א |
|
ובעבו' כי אמר שיהיו יהיה מספרם עם התוספת ט"ט לבד אותו שדבר עמהם |
|
נחלק הט"ט שברים לרביעי' ויהיו שצ"ו |
|
נחלקם על י"א יהיו ל"ו וככה מספרם |
| "If You Give Me" Problem | |
|
שאלה ארבעה קונים חפץ אחד אחד אמר לחבירו כל אחד יתן החצי אשר בכיסו ואני אתן כל מה שיש בכיסי ואקנה החפץ |
|
ערך החפץ מ"ו דינרי' |
|
לראשון ט"ו פשוטי' |
|
ולשיני כ"ג דינרי' וט' פשיטי' |
|
לשלישי ל"א דינרי' ג פשיטי' |
|
לרביעי ל"ה דינרי' |
|
ע"א להגיע עד חצי שליש ורביע החפץ י"ז פשיטי' לאחד ה' לשנים י"א לשלישי י"ג |
| "Find the Amount" Problem | |
|
שאלה אדם מכר י"ג מדות בכ"ג פשי' כמה מדות יתן בז' פש' |
|
ערך ז' אל כ"ג כן ערך הנעלם אל י"ג |
|
נכפול הקצוות שהם נודעים יהיו צ"א |
|
נחלקם על כ"ג יעלו ג' מדות וכ"ב חלקי' מכ"ג במדה |
| "Find the Price" Problem | |
|
ועוד נהפך הענין שנרצה לדעת בכמה יתן לו ז' מדות |
|
והנה נעשה הדמיון הזה נכפול הקצוות יהיו קס"א |
|
נחלקם על י"א והיו י"ב פשיטי' וה' חלקי' מי"ג בפשיט |
|
אם שאל בכמה יתן ז' מדות יהיה ערך הנעלם בכ"ג אל כ"ג כערך ז' אל י"ג |
| Pursuit Problem | |
|
שאלה אדם הולך בכל יום כ"ט מילין אחר י' ימים נסע השני ההולך בכל יום ל"ז מילין |
|
כפול המילין שהולך בי' ימים יהיו ר"צ |
|
נחלקם על היתרון שיש בין שני המהלכים שהוא ח' והנה ל"ו ימים ורבע יום |
|
הנה כערך י' ימים אל הנעלם כן ערך היתרון שהוא ח' אל כ"ט |
| Encounter Problem | |
|
שאלה בכמה ימים יכלה מהלך ק' על ידי שני מהלכים של י"ט ושל י"ז זה לקראת זה |
|
וקל לדעת כי הוא כערך מחובר שניהם אל קו וחלקם עליו יהיה ב' וכ"ח מל"ו כמו כן בב' ימים וכ"ח מל"ו ביום יכל ישהו לכלות וכ"ח מל"ו הם ז' תשיעיות היום |
|
ואם תרצה לדעת כמה שעות הם ידוע הוא כי שעות היום י"ב |
|
והנה ז' אל ט' כן ערך הנעלם אל י"ט |
| שאלה אדם עם ג' שיתן לראשון ה' זהובים ויעבוד לו כ' ימי' ולא רצה לגמור כל העבודה ואמר לשיני שיתן לו ד' ולא רצה לגמור | |
| הנה זה דומה לשאלת המחליף אך נשים הזהובים המחולקי' לפועלי' במטבעות והעבודה הנשכרת היא הזהוב והמורה הוא ס' ומחובר החלקי' מ"ז | |
|
והנה כערך מ"ז אל ס' כן ערך הזהוב אל הנעלם |
| והנה החלק השוה זהו' אחד וי"ג ממ"ז בזהוב אחר נבקש ערך כל אחד ב' | |
| והנה בעל הג' הם ו' ימי' וב' שלישיות היום | |
| ובעל הד' בזהו' אחד ה' ימים | |
| ובעל הה' בזהוב אחר ד' ימי' | |
| והנה של ג' עובד בשביל ח חלק העולה לו במ"ז כערך י"ג אל מ"ז כן ערך הנעלם אל כ' שהוא מספר שעות עבודתו בזהו' אחד | |
| ושל ד' כערך י"ג אל מ"ז כן ערך הנעלם אל מ"ח | |
| ואם תחבר כל העולה בזה יעלה המחובר כ ימים | |
| שאלה אדם אמר לבשל עשרה מדות מתירוש עד השאיר שליש לאחר שנתמעטו ב והיו ח נשפך ב והיו ו ושאל השואל כמה יהיה ראוי לישאר מן העומד לכ' לפנינו אם יבא לבשלו עד שיהיה כמשפט הראשון לפי מה שהתחיל כי ידוע שנתמעטו מג' ושליש | |
|
והנה כערך ו' אל ח' כן ערך הנעלם אל ג' ושליש |
| שאלה רומח מחציתו שלישיתו במים רביעיתו בעפר וגלוי ז אמות כמה גבהות כלו | |
| הנה המורה י"ב נכסה ממנו חלקיו אלה יהיה הגלוי ה | |
|
והנה כערך ה' אל י"ב כן ערך ז' אל הנעלם |
| שאלה אדם צוה לתת כ פשוט לכ בני אדם אנשים ונשים ובנים לאיש נתן ב פשיט ולאישה מחצה ולבנים [...] כמה לאיש | |
| לח' אנשי' יו פשיטי' לח בני' ב פשיטי' לד נשי' ב פשי' | |
| שאלה אדם אמר לעבדו קח ל פשיטי' וקנה לי ל עופות אווז ב פשיטי' שליו מחצה פרגיות פשיט כמה יהיו מכל מין | |
| ו פרגיות ח אווזות יו שלוים | |
|
שאלה דג יש לו טו אצבעות בגודל גופו לבד ראשו וזנבו וראשו מחזיק שלישית כל הדג והזנב מחזיק רביעיתו כמה מחזיק כלו עם הראש והזנב |
|
ל"ו אצבעות שלישיתו י"ב והרביעית ט |
| כפל החשבון שלישי' ורביעי' ותמצא כך | |
| שאלה גנב הולך סכום אחד והרודף יום ראשון א ויום שיני ב וכן ויוסיף כל הימי' ב' כאשר יגדלו הסכום כפל הגנב ובתוך כך תפל אחד ובתוך כך סכום ימים ישיג הגנב בכל סכום שילך כמה בכל יום | |
| שאלה שמעון הרויח שביעית ממנו היום ולמחר הרויח מן הכל חמישית ויום שלישי מן הכל שלישית והתחבר י' דינרי' ונשאל כמה הממון המורה [..] | |
| שאלה לשקול ביא אבני' ס' [..] גם בי"ח טבעות לשכירות לד שנים וב חדשי' יצא בכפל למשקל וכן תעשה בטבעות א ב ד ח י"ו וכפול עד שיעלה החשבון ובאבנים יצא בשלישות א ג ט כז |
Glosses on Abraham Ibn Ezra’s Book of the number (P1026; London) |
|
| ובעל ספר יצירה | |
| פי' בעל כוונת ספר יצירה להודיע איך נברא האדם בתחבולה אחת מין הנבראים | |
| ואמ' שיצטרכו בו ג' עניני' | |
| הספר הוא הכתיבה כי בכחות האותיות יורו בו באותיות יעשה היצירה | |
| וספר הוא המנין כי ההרכבה והמזגה לא תעשה רק במספר שבאחד מהם יהיה בו מיסוד האחד כפל האחר | |
| וספור כי חכמי חכמה זו הניחו שהם יורידו כח אשר נתן כח בהרכבה ההיא עד שיעשה פעל הכח בלתי מדבר אבל לא מדבר כי זה לא יתכן אלא לאל ית' | |
| בעבור | |
| מלת בעבור נמשכת עד אמרו למטה על כן כל מאזני כל מספר | |
| ספר הוא המרוכב | |
| וספר הוא המספר כמו אחר הספר אשר ספרם | |
| וספור הוא הדבור באחדים | |
| בכלל הגבוה | |
| פי' הקרוב לו לפניו | |
| והנשאר הוא המבוקש | |
| פי' שהשלישית הנכפל על השלישית יצא תשיעית אם כן בכפלנו שליש המספר על שלישו יצא לנו תשיעית מרובע הדרוש וכאשר לקחנו כמוהו בכלל הגבוה ממנו יצא לנו עשרה דמיוני תשיעית המרובע | |
| והמחובר הוא הדרוש | |
| פי' אעפ"י שלא זכר המחבר דרך זו רק בהוצאת המרובעים יתכן זה בכפל כל שני מספרים בעלי שליש כמו י"ב וי"ח | |
| אנו נכפול שליש האחד והוא ד' בשליש השני והוא ו' ויעלה כ"ד נגביההו מעלה אחת ויהיה ר"מ הסיר כפל השני שלישיות שהוא כ"ד ישארו רי"ו והוא כפל י"ח על י"ב | |
| ואם שהם נעדרי השליש ומוסיפין אחד כמו י"ג י"ט נעש[ה] כן נוציא סך החשבון לי"ב וי"ח ויעלה רי"ו ולפי שכל אחד מהמספרים מוסיף אחד על השליש נוסיף י"ב וי"ח ואחד ועלה רמ"ז וזהו כפל י"ג בי"ט | |
| ואם היו שני המספרים חסרין אחד בי"א וי"ז נעשה החשבון בי"ב וי"ח ויעלה רי"ו ובעד חסרון האחד נגרע י"א וי"ז ואחד מן רי"ו וישאר קפ"ז והוא כפל י"א בי"ז | |
| ואם האחד מוסיף אחד והשני חוסר אחד בי"א וי"ט או י"ג וי"ז נעשה החשבון בי"ב וי"ח ויעלה רי"ו הנה אם היו י"א וי"ט התוספת הוא י"א והחסרון הוא י"ח אם כן החסרון רב על התוספת ז' חסרם מן רי"ו וישאר ר"ט והוא הדרוש | |
| ואם היו י"ג וי"ז הנה התוספת הוא י"ז והחסרון י"ג אם כן התוספת רב ה' נוסיפם על רי"ו והיה רכ"א והוא הדרוש | |
| ואם הן כמו י"ח וי"ג נוסיף על רי"ו י"ח והיה רל"ב והוא הדרוש ואם הן י"ח וי"א נגרע י"ח מן רי"ו וישאר קצ"ח | |
| דמיון רצינו לכפול כ"ט על ל"א | |
| פי' דמיון אחר ברצותנו לכפול כמשל ח' על י"ב שמרחקם מי שהוא כלל מספר שוה והוא ב' נכפול י' על עצמו והיה ק' נחסר ממנו ד' שהוא מרובע ב' | |
| ובאור זה שכפל ח' על י"ב הוא כפל ח' על י' ועל ב' וכפל י' על י' הוא כולל כפל י' על ח' ועל ב' וכפל י' על ב' הוא כולל כפל ח' על ב' וב' על ב' נמצא יתרון י' על י' מן ח' על י"ב הוא ב' על ב' | |
| ומזה תבין לכל המשלים האחרים וזה מתמונת ו' ממאמר ב' לאיקלידיס | |
| וכן ההנהגה בכל שני מספרים מתחלפים אך כי לא יהיו כללים שנוסיף על המספר היותר קטן חצי יתרון שבין שני המספרים ונרבעהו ונחסר מהמרובע מרובע חצי היתרון והנשאר ישוה להכאת אחד משני המספרים באחר | |
| אך זה החכם בא להקל ולא להחמיר ולזה לא באר במספרים שמרחקן מחשבון כלל מספר שוה | |
| ודע כי אם יהיו שני מספרים לכפול | |
| פי' כי אם תרצה להכות ב' על מ' אין כאן הכאה רק ממדרגה האחת על האחרת אך אם יהיה לנו מספר על שני מספרים או שנים על שנים אז צריך לכפול המעלות זו על זו כפי מנין המספרים | |
| אתה צריך | |
| פי' אמ' זה בשלוח אעפי שלפעמים יתכן בפחות מזה כי כן אמר למעלה ואם הם שנים על שנים צריך לעשות זה ד' פעמים ואחר כן באר שאפשר בפחות וגם בזה אפשר בפחות ובין | |
| כאלו הם אחדים | |
| פי' וסבת זה כי כל כלל יוסיף אחד על תשיעיות וכן שנים | |
| לא יקבל שנוי | |
| פי' כי השנוי יבא מצד ההרכבה והאחד פשוט כי מהיותו אחד | |
| לא יקבל רבוי כי א' על א' הוא א' | |
| ולא חלוק כי אם תחלקהו יהיו שנים | |
| והוא סבת כל שנוי כי בהרכבת שני ענינים יבא השנוי וכן במספר | |
| כפי מעלתו | |
| פי' אחדים כנגד אחדים ועשרות כנגד עשרות | |
| ופחות מהמספר | |
| פי' שהמספר המחולק ראוי להיות יותר גדול מהמספר המחלק כי זה כמו המדה עם הנמדד | |
| וזה ביותר נכון לא מחויב כמו שיתבאר בחלוק השברים שנחלק חמש תשיעיות על שלם | |
| ולא הגיע למעלת האחדים | |
| פי' שהיוצא בחלוק לא הגיע למעלת האחדים שאם היה כן כבר יצא לחוץ ולא יקבל עוד החלוקה שכבר נתך המחולק אל מספר יותר קטן מהמחולק עליו | |
| ובאמרנו לא יקבל החלוקה ר"ל בשלמים אך בשברים יקבל החלוק ובין | |
| כי לא יצא לחוץ | |
| פי' התכת המחולק עד שיגיע למספר יותר קטן מהמחולק עליו יקרא יציאה לחוץ | |
| שאם נחלק [..]יצא לחוץ ממעלת האחדים ויהיו שברים אשר העשרה מהם הוא אחד שלם יקראו ראשוניים וכן כל ראשון יחלק לי' שניים והוא לא כיון רק בחלוק שלמים על שלמים | |
| ולעולם נחזור אחורנית | |
| צ"ע מה הביאו לזה כי יותר נכון ונקל לחסר ביושר | |
| האחד כנקדה | |
| פי' כי הנקדה כיסוד לעגול כי המקוה לעגול טרם הקוותו יניח מוצק עליה יכונן רחב העגול וכן האחד הוא יסוד המספר ולכן לא יתכן לחלק כמו הנקדה מצד שהוא אחד ואולם מצד ההוה כל כלל בשם אחד עם היותו מורכב מאישים רבים כמו הגוף המורכב מד' ליחות ומשאר אברים מתדמי החלקים ומהיד והזרוע ושאר אברים הכליים והנה הוא בלי ספק יתכן בו התפרקו לחלקו חוץ לשכל יתחדש בו הדבור בעבור זה החליטו החלוק הפשוט להעשותו בו בשכל כי חוץ לשכל אי אפשר בשום פנים | |
| עוד פי' כל זה הצעה לחלוקת האחד לשברים וכמו שהנקדה היא דבר בלתי מתחלק וכל הקוים יוצאים ממנה כן האחד ולזה לא היה ראוי לחלק | |
| מורכב משטחים | |
| פי' אין כונתו שהגוף הרכבה מזגיית משטחים ולא מקוים ונקדות כמבואר בספרי הטבע אך כונתו באמרו שטחים התכליות המקיפות ורבים בגוף האדם כמו הגלגלת יקיפהו שטח אחד וכן אברים רבים והגוף יקרא אחד | |
| והוא דומה לנפרד | |
| פי' שכשתחבר הנפרדים על הסדר יולידו מרובעי מספר הנפרדים כי א' הוא מרובע א' וא' עם הוא מרובע ב' וא' עם ג' וה' הוא מרובע ג' וזה אחד מסגלת המספר | |
| הוא חצי שמינית | |
| אם תחלק הנכפל על מרובע המורה יהיה היוצא מהחלוקה שלמים | |
| ואם לא יתחלק ר"ל שיהיה מרובע המורה יותר גדול מהנכפל או יתחלק וישאר שלא יתחלק יהיו שברים נקראין בשם המרובע ואם תחלק הנכפל על המורה יהיה היוצא שברים נקראין בשם המורה ומה שלא יתחלק יהיו שברי שברים נקראין בשם המורה ובין | |
| ויהיה כלל זה מסור בידך אחר שתדע המורה ומרובעו והנכפל תחלק המרובע על הנכפל או תחלק הנכפל על המורה | |
| רק אלמד דרך קצרה | |
| פי' כי לפי מה שאמרנו למעלה היה צריך לעשות מורה אחד לכלן בכפל האחד על האחר כי הסבה מענין המורה הוא למצא מספר שיהיו בו כל חלקים אלו | |
| עוד באמת לא היה צריך לקחת ששיים כי די לו בשלישיות וזה נכפול על ה' יהיו ט"ו עוד נכפול זה על ז' יהיו ק"ה עו' נכפול זה בח' יהיו תק"מ והוא המורה נבקש המספר ראשון שהוא ב' שלישית רביעית החמשית יהיו ר"ח כי החמשית הוא קס"ח ורביעיתו מ"ב ושתי שלישיותיו כ"ח וזהו החשבון הראשון וידענו ששמיניתו ק"ה ושביעיתו ט"ו והשש שביעיות הם צ' נכפול כ"ח על צ' יעלה אלפים ת"ק חלקנום על תת"מ שהוא המורה ויעלה ג' שהן חלקים מהתת"מ שלמים והן חמשית שביעית השמינית שהשמינית ק"ה ושביעיתו ט"ו וחמישיתו ג' והוא הדרוש | |
| וצ"ע בדמיון שלקח החכם כי יותר ראוי לקחת הדמיון בקטן המספר שאפשר | |
| גם צ"ע למה הוצרך לבאר שאחר שיש לנו ששיות אין צריך לשלישית כאלו היה צריך לחלק ששית | |
| החמשית והתשיעית ארבע | |
| צ"ע איך לקח דרך זה הראשון כי לא ימשך בכל המספרים וזה שנאמר לקחנו שלישית הממון וחמשיתו ושביעיתו כמה הוא מערך הממון ולפי דרכו יהיה כן נחשב כאלו הן ג' שביעיות שהוא השבר היותר פחות אחר נכפול מה שבין השביעית והשלישית שהוא ד' על מה שבין החמישית והשלישית שהוא ב' ויעלה הכפל ח' ונעשה מהחמשה שביעית אחת ויהיו ד' שביעיות וישאר ג' ונחברם עם ב' שהוא היתרון שבין שלישית לחמישית והיה ה' ולפי זה יהיה הערך ה' שביעיות ויעלה ע"ה לפי שהמורה ק"ה ולפי הדרך שני שהוא האמתי יהיו ע"ה חלקים מן ה' | |
| עו' צ"ע איך אמ' בדמיונו שהשלשה היו ג' חמשיות שביעית התשיעית והוא אמר תחלה נעשה מן הו' תשיעית אחת | |
| ויש בזה דרך אחרת נכונה רק שיהיה הדלוג בשברים שוה כמו ד'ה'ו' ה'ז'ט' והוא לקחת מקום הג' מינין ג' שברים ממין האמצעי ואחר יוכפל מרחק הקצוות כמרחק הדלוגים והמחובר הוא הדרוש | |
| דמיון ערך ד' וה' | |
| פי' וזה יתבאר כי מרובע הקו כלו שהוא י"ו שוה לשני מרובעי י"ב וד' בתמונת ד' מ"ב לאקלידיס ושטח ו' בח' שוה לשטח שיקיפו בו י"ב וד' לפי שיחס ד' אל ו' כיחס ח' אל י"ב אם כן מרובע י"ו שוה לשני מרובעי י"ב וד' ולכפל השטח שיקיפו בו ו' וח' אבל שני מרובעי ו' ח' שוין לכפל השטח שיקיפו בו ו' ח' עם מרובע מה שבין ו' ח' כמבואר בה' מ"ב אם כן מרובע י"ו עם מרובע היתרון שבין ו' לח' שוה לד' מרובעי ד' ו' ח' י"ב ובזה יתבאר מהשני והשלישי | |
| כי ערכיה מורכבין | |
| פי' ערכי הנגונים הן מורכבים ערכי המדות וערכי המספר כי יעשה בחלק היתרון האחד על האחר וכיחס המספר האחד אל המספר האחר | |
| כי לעולם יהיה הערך | |
| כי לעולם יהיה היחס מה שבין הראשון והאמצעי אל מה שבין האמצעי והאחרון כיחס המספר הראשון אל האחרון | |
| שאלה ראובן שכר שמעון | |
| הכלל בכל דרכים אלו שנכפול י"א על ט' ויהיו צ"ט וחלקם על י"ו ועלה ה' פשו' וי"ד חלקים מי"ו בפשו' | |
| כלל זה יהיה בידך בערכין שאותו המספר שיהיה גיל הנעלם שהוא מקום הגלגל מן המורה שאם היה הגלגל אחד מהקצוות הקצה האחד הוא המורה ואם הגלגל הוא אחד מהאמצעיים האמצעי האחר הוא המורה | |
| ולא תדע השלישי כפול הראשון על השני | |
| זה יתבאר מי"ט מה' באמת כאשר היה המחובר אל המחובר כיחס הכל אל הכל הנה יחס הנשאר אל הנשאר כיחס הכל אל הכל | |
| ולכן בדמיונו השני לפי שיחס היתרון שבין ג' וד' הידוע אל היתרון שבין ד' והמספר הנעלם כיחס ג' הידוע אל ו' הנעלם והנה הנעלם גדול מיתרונו על ד' הנה אם כן ג' גדול יותר מהיתרון שבין ג' לד' מי"ד מה' אקלידיס | |
| והיתרון שבין ג' לד' ידוע אם כן כשחסרנוהו מג' יהיה הנשאר ידוע והוא ב' וגם כן ידענו שד' הוא הנשאר כשחסרנו מו' היתרון שנוסף על ו' | |
| ועתה יש לנו ג' מספרים ידועין האחד ב' והוא הנשאר מג' כשחוסר ממנו היתרון שבין ג' לד' השני ג' שהוא הכל ידוע השלישי ד' שהוא הנשאר מהנעלם כשחוסר ממנו היתרון שהוא נוסף על ד' וידענו שיחס המחוסר מג' אל המחוסר מהנעלם כיחס ג' שהוא הכל אל הנעלם אם כן יחס ב' הנשאר אל ד' הנשאר כיחס ג' אל הנעלם ולכן נכפול האמצעיים שהן ד' וג' והיו י"ב ונחלק י"ב על ב' והיה ו' וכו' | |
| וכן תבין האחרים מי"ח מה' אקלידיס | |
| צורת הי"ו מוציאין אותה בדרך זו לוקחין הראשונה והשביעית והן יתדות ומוציאין משתיהן צורה אחת ומהרביעית והעשירית והן יתדות מוציאין צורה אחרת ומשתיהן מוציאין צורה אחת והיא נקראת הי"ו והיא חזקה מכלן | |
| ומצאתי בע"ה צורת הי"ו נקח הצורה הראשונה והשביעית ועושין משתיהן צורה אחת ונקח צורת הט"ו ומשתים אלו נעשה צורה אחרת והיא הי"ו וזה סוד | |
| שאלה שלשה הלכו לקנות דג בשוק ערכו ה' פשו' אמר אחד אני אתן כל מה שבכיסי ואתם לא תתנו רק החצי שבכיסכם | |
| נבקש המורה והוא י"ב כ"ט כי ממנו נוכל לעשות ג' מספרים שישתוו שלשתן למספר אחד והן ה' י"א י"ג בעל ה' ישאל החצי בעל י"א ישאל השליש בעל י"ג ישאל הרביע | |
| שאלה ראובן שמעון לוי ויהודה אמ' ראובן לשמעון כל מה שבכיסי עם חצי שבכיסך הוא ה' די' | |
| תשובה ראובן ל"ז פשו' צ"ז חלקי' מקי"ו בפשו' שמעון מ"ד פשי' מ"ד חלקים | |
| ובזה נמצא כל ראובן עם חצי שמעון ה' וכן שמעון עם שליש לוי | |
| נסיר חצי שמעון המשותף וישאר ראובן שוה לחצי שמעון עם שליש לוי ושמעון שוה לשני שלישי לוי עם רביע יהודה | |
| אם כן ראובן שוה לשני שלישי לוי עם שמינית יהודה אם כן לוי שוה לג' רבעי יהודה עם חומש ראובן | |
| א'פ'ד' ראובן ע"ה שמעון פ"ח לוי צ"ג יהודה ק"ד | |
| או ראובן ל"ז וחצי שמעון מ"ד לוי מ"ו וחצי יהודה נ"ב וכן לחציין וכן וכן | |
| שאלה אדם נכנס [בע]יר ונודר שאם יכפול ממונו בכל יום יוציא ממנו בכל יום סך מוגבל ולימים לא נשאר בידו מאומה כמה הוא הממון שבידו | |
| הדרך בזה שנבקש מספר שבהכפלו פעמים כמספר הימים על יחס הכפל שאחריהם לא נשאר לו מאומה יעלה לסך שיוציא מהם בכל יום והמספר ההוא המבוקש נגרע מהסך שיוציא בכל יום והנשאר הוא הממון שבידו | |
| המשל שיוציא בכל יום מ"ח פשי' ולסוף ג' ימים לא נשאר לו מאומה הנה המספר שבהכפלו על יחס הכפל כמספר הימים שהם ג' יעלה מ"ח הוא ו' כי כשנכפול ו' יעלה י"ב וכשנכפול י"ב עלה כ"ד וכשנכפול כ"ד עלה מ"ח נגרע מספר ו' ממ"ח וישאר מ"ב והם המעות שבידו | |
| או שיוציא בכל יום י"ח פשי' ולסוף ה' ימים לא נשאר לו מאומה הנה המספר שבהכפלו על יחס הכפל פעמים כמספר הימים שהוא ה' יעלה י"ח הוא חצי וחלק אחד מי"ו שהן ט' חלקים מי"ו כי כשנכפול חצי וחלק אחד מי"ו יעלה א' ושמינית וכשנכפול א' ושמינית יעלה ב' ורביע וכשנכפול ב' ורביע יעלה ד' וחצי וכשנכפול ד' וחצי יעלה ט' וכשנכפול חמשית ט' יעלה י"ח נגרע מספר חצי וחלק אחד מי"ו יעלה י"ז וז' חלקים מי"ו והם המעות שבידו | |
| טעם למה יוציא השרש אל אמצע המדרגות בין שיהיו המדרגות נפרדים כמו זה או זוגות שנשים המדרגה הזוגיית למעלה מהמדרגה שלפניה שנחבר הכל כמו שנשים [ז'] למעלה מט' ויהיה שבעים | |
| לפי שלעולם בכל כפל המדרגות כפולות אחד שנעשה מהם מרובע מהכאתם עולה לששה מדרגות אם יש ליוצא מההכאה זוגות כמו זה שח' על ח' עולה לס"ד ולכן ס"ד הוא תחת המדרגה הששית | |
| ואם המספר נפרד לא נקח שרש כי אם מה |
Notes
- Jump up ↑ P1054 31r
- Jump up ↑ P1054 om.
- Jump up ↑ Guenzburg 193v
- Jump up ↑ MS Firenze: ביאור החלוק עשאו ה'ה'ר' עמנואל בן יעקב ע"ב בעל הכנפיים; MS London: כלל שעשה החכם הגדול ר עמנואל בן יעקב למצוא דרך קל לכל חשבון קראו חכם אמר; MS P1081 אמר עמנואל בן יעקב
- Jump up ↑ על מספרים רבים כמה שיהיו: MS P1081 om.
- Jump up ↑ בטור: MS L om.
- Jump up ↑ הטור: MS L om.
- Jump up ↑ וכו': Lומאיות תחת מאיות
- Jump up ↑ שהטור: MS L וזה
- Jump up ↑ הטור השפל: MS L טור שפל
- Jump up ↑ הטור: MS L om.
- Jump up ↑ Guenzburg: קח
- Jump up ↑ כמספר אחרון שבטור... לאחרון שבטור השפל: MS P1081 om.
- Jump up ↑ כשלשי לאחרון שבטור העליון לפניו: MS L om.
- Jump up ↑ מספר: MS L כמה
- Jump up ↑ הפעמים: MS L פעמים
- Jump up ↑ אשר: MS L om.
- Jump up ↑ האמצעי: MS L אמצע
- Jump up ↑ ותכתוב כמספר ההוא: MS L ותכתבינו
- Jump up ↑ תקח: MS L יקח
- Jump up ↑ שבטור: MS L om.
- Jump up ↑ ממדרגת: MS L שבמדרגת
- Jump up ↑ לך: MS L om.
- Jump up ↑ לא: MS L om.
- Jump up ↑ לקחת: MS L לדעת
- Jump up ↑ פעם: MS L om.
- Jump up ↑ המספר: MS L מספר
- Jump up ↑ האחרון: MS P1081 אחרון
- Jump up ↑ שבטור: MS P1081 שבטור שבטור
- Jump up ↑ הוא: MS L om.
- Jump up ↑ הוא א' ... העליון: MS P1081 om.
- Jump up ↑ הוא: MS L om.
- Jump up ↑ כל המספר ... ר"ל: MS L om.
- Jump up ↑ הח': MS L ח'
- Jump up ↑ יהיו: MS L יהיה
- Jump up ↑ ותראה: MS L וראה
- Jump up ↑ יהיה: MS P1081 הוא
- Jump up ↑ Guenzburg: בפניו
- Jump up ↑ בעצמך: MS L כל כך
- Jump up ↑ המספר: MS L מספרו
- Jump up ↑ Guenzburg om.
- Jump up ↑ שבטור העליון: MS L שבטור הח'
- Jump up ↑ ט': MS L om.
- Jump up ↑ ועם: MS L
חסרינועם - Jump up ↑ הנה: MS L om.
- Jump up ↑ כן: MS L om.
- Jump up ↑ ד' במספר פ"ד: MS L om.
- Jump up ↑ ט': MS L ד' ט'
- Jump up ↑ ממדרגתו: MS L ממדרגות
- Jump up ↑ בט': MS P1081 הד'
- Jump up ↑ במדרגת: MS L במדרגות
- Jump up ↑ כן: MS L om.
- Jump up ↑ וכפול: MS L אחר זה כפול
- Jump up ↑ Guenzburg om.
- Jump up ↑ זאת האות שיצא לך: MS L אשר יצא
- Jump up ↑ L: הכפל ר"ל ט' על ב' על ג' על ד' על ט'
- Jump up ↑ מהטור: MS L מטור
- Jump up ↑ או מן האחדים: MS L om.
- Jump up ↑ אחר: MS L מן
- Jump up ↑ Guenzburg 194r
- Jump up ↑ הטור: MS L טור
- Jump up ↑ שוב: MS L ישוב
- Jump up ↑ על הדרך ... הטור השפל: MS L om.
- Jump up ↑ מהכפל: MS L om.
- Jump up ↑ מן הנשאר: MS L מהנשאר
- Jump up ↑ ואחר: MS L אחר כן
- Jump up ↑ ולכפול: MS L לכפול
- Jump up ↑ לזה הדרך: MS L om.
- Jump up ↑ בטור: MS P1081 הטור
- Jump up ↑ שבטור: MS L שהוא בטור
- Jump up ↑ עשית: MS L עשיתה
- Jump up ↑ העליון: MS P1081 עליון
- Jump up ↑ שבטור: MS L שנשמר בטור
- Jump up ↑ נעשית מלאכתך: MS L מלאכתך נעשית
- Jump up ↑ בזולת: MS L מבלי
- Jump up ↑ בה: MS L om.
- Jump up ↑ תחבר: MS P1081 תסדר
- Jump up ↑ Guenzburg: שאו
- Jump up ↑ כל: MS L om.
- Jump up ↑ וגם: MS L גם
- Jump up ↑ מנהג: MS L om.
- Jump up ↑ ידעת מנהגו: MS L om.
- Jump up ↑ העליון: MS P1081 עליון
- Jump up ↑ הנה: MS L om.
- Jump up ↑ החשבון: MS L חשבונך
- Jump up ↑ שום התחלפות: MS L om.
- Jump up ↑ הנה: MS L om.
- Jump up ↑ L: אמר החכם הנז'
- Jump up ↑ לך: L om.
- Jump up ↑ מה שיש בו: L om.
- Jump up ↑ מן ההזכרה: L מההזכרה
- Jump up ↑ היותר: P1081 margin
- Jump up ↑ להם: MS L om.
- Jump up ↑ אשר אין: MS L שאין
- Jump up ↑ שלמים: MS L שברים
- Jump up ↑ נשברים: MS L השברים
- Jump up ↑ או: MS L הן
- Jump up ↑ לבדם: MS L om.
- Jump up ↑ מן ההזכרה: MS L מהזכרה
- Jump up ↑ ומעתה: MS L ומזה
- Jump up ↑ במעלת: MS L במעלות
- Jump up ↑ בה: MS P1081 בו
- Jump up ↑ וארבעה: MS L ארבעה
- Jump up ↑ ובמעלה: MS P1081 והמעלה
- Jump up ↑ השנית: MS L שינית
- Jump up ↑ שהיא מעלת עשרות: MS L om.
- Jump up ↑ בה: MS L בו
- Jump up ↑ כלל: MS L om.
- Jump up ↑ עם: MS L om.
- Jump up ↑ ולא: MS L לא
- Jump up ↑ MS L: אין בהם שום מספר מרובע
- Jump up ↑ אמנם: MS L רק
- Jump up ↑ אחדים: MS L האחדים
- Jump up ↑ בה: MS L בו
- Jump up ↑ Guenzburg: ול"י
- Jump up ↑ שנוסיף על מספר: MS L שנשיב אחור
- Jump up ↑ אחדים מה: MS L ונחברם עם אחדים
- Jump up ↑ שרשו: MS L ששורשו
- Jump up ↑ שרשו: MS L ששורשו
- Jump up ↑ שרשו: MS L ששורשו
- Jump up ↑ שרשו: MS L ששורשו
- Jump up ↑ שרשו: MS L ששורשו
- Jump up ↑ P1081: מעלות; L: מעלה ממעלות
- Jump up ↑ ודומיהן: MS L וכן
- Jump up ↑ MS L למעלו'
- Jump up ↑ במעלת: MS L במעלות
- Jump up ↑ המאיות: MS L
האחדי'המאיות - Jump up ↑ מדרגת: MS L om.
- Jump up ↑ גם כן: MS L om.
- Jump up ↑ Guenzburg: ששרשו
- Jump up ↑ MS L ד'
- Jump up ↑ אחדים: MS L om.
- Jump up ↑ וט': MS L ט'
- Jump up ↑ אחדים: MS L om.
- Jump up ↑ Guenzburg: לשלש הם; MS L: וכן כל מעלה שמספר מדרגתה נפרד כמו חמישי' ושביעי' ותשיעי' וכן לאין קץ
- Jump up ↑ וכן כל: MS L וכל
- Jump up ↑ שמספר: MS L om.
- Jump up ↑ והיא: MS P1081 והוא
- Jump up ↑ מעלה: MS L מעלת
- Jump up ↑ MS L זוגות
- Jump up ↑ בה מרובעים ... יש בה: MS L om.
- Jump up ↑ המאיות: MS L
עשרותמאיות - Jump up ↑ MS L שנשיב
- Jump up ↑ ואלף: MS L אלף
- Jump up ↑ ותחבר: MS L ונסדר
- Jump up ↑ עם: MS L כל
- Jump up ↑ Guenzburg 194v
- Jump up ↑ עשרה: MS L עשר
- Jump up ↑ לארבעה: MS L לארבע
- Jump up ↑ לל"ו: MS P1081 ל"ו
- Jump up ↑ ששים הדומה: MS L om.
- Jump up ↑ לששה: MS L ו'
- Jump up ↑ וח' אלפים ומאה: MS P1081 ומאה אלפים ושמנה
- Jump up ↑ Guenzburg: וכל
- Jump up ↑ Guenzburg: שמנים
- Jump up ↑ Guenzburg במעלת במעלת; MS P1081 המעלה
- Jump up ↑ האמצעית: MS P1081 הממוצעת
- Jump up ↑ מספר: MS L om.
- Jump up ↑ הענין: MS L om.
- Jump up ↑ ושרשו: MS L שרשו
- Jump up ↑ Guenzburg om.
- Jump up ↑ הרביעית: MS L רביעית כמו העניין בצורה; Guenzburg om.
- Jump up ↑ המעלה: MS L למעלה
- Jump up ↑ כמו שבארנו: MS P1081 om.
- Jump up ↑ אחד: MS P1081 om.
- Jump up ↑ Guenzburg
שמשבמעלה - Jump up ↑ ואז: MS P1081 ואם
- Jump up ↑ ישובו: MS P1081 יש בו
- Jump up ↑ האחרונה: MS L
הראשונההאחרונה - Jump up ↑ אשר ילקח: MS L שילקח
- Jump up ↑ בטור: MS P1081 ביאור
- Jump up ↑ אשר לוקח: MS L שלוקח
- Jump up ↑ ר"ל שזה וזה: MS L נ'
- Jump up ↑ מן האחדים: MS L מהאחדים
- Jump up ↑ זה: MS L om.
- Jump up ↑ אזהירך: MS L אזכירך
- Jump up ↑ להזכירך: MS L להזהירך
- Jump up ↑ MS P1081 במדרגות
- Jump up ↑ א': MS L ב'
- Jump up ↑ ד': MS P1081 א'
- Jump up ↑ פ"א: MS P1081 פ"א פ"א
- Jump up ↑ כי המעלה הנפרדת הנה: MS L om.
- Jump up ↑ לך: MS P1081 אותך
- Jump up ↑ בידיעת: MS P1081 וידיעת
- Jump up ↑ שורש: MS P1081 השורש
- Jump up ↑ כל: MS P1081 איזה
- Jump up ↑ להם: MS L לו
- Jump up ↑ אשר תרצה: MS L שתרצה
- Jump up ↑ איזה: MS L איזו
- Jump up ↑ א' ... ה': MS L om.
- Jump up ↑ כזה: MS P1081 om.
- Jump up ↑ ה': MS L om.
- Jump up ↑ הם: MS L om.
- Jump up ↑ ה': MS P1081 om.
- Jump up ↑ לו: MS L om.
- Jump up ↑ שורש: MS L om.
- Jump up ↑ ולכן: MS L לכן
- Jump up ↑ שורש: MS P1081 om.
- Jump up ↑ הג': MS L ג'
- Jump up ↑ ונרשום: MS L וירשום
- Jump up ↑ ריוח: MS L om.
- Jump up ↑ אותיות השורש: MS L האותיות
- Jump up ↑ מן האחדים ... לפניה: MS P1081 om.
- Jump up ↑ בעצמה: MS P1081 בעצמו
- Jump up ↑ ממנה: MS L om.
- Jump up ↑ ולכתוב ... מן האחדים: MS L om.
- Jump up ↑ ב': MS P1081 שבו
- Jump up ↑ מדרגות: MS L המדרגות
- Jump up ↑ התחלת: MS L התחלה
- Jump up ↑ מהמספר: MS L המספר
- Jump up ↑ עם מינו: MS P10181 ממינו
- Jump up ↑ ידעת: MS P10181 נודע
- Jump up ↑ ישאר: MS L יהיה
- Jump up ↑ זה: MS P10181 om.
- Jump up ↑ ג': MS P10181 om.
- Jump up ↑ תכתוב: MS L תכפול
- Jump up ↑ תחתיה: MS L תחתיו
- Jump up ↑ ואם: MS L
והאםואם - Jump up ↑ היה: MS P10181 om.
- Jump up ↑ שהיא: MS L שאם היה
- Jump up ↑ תחתיה: MS P10181 om.
- Jump up ↑ השורש הכפול: MS L שורש הכפל
- Jump up ↑ השנים: MS L om.
- Jump up ↑ מהמספר האחרון: MS L om.
- Jump up ↑ זאת: MS L אות
- Jump up ↑ ממנו: MS P10181 om.
- Jump up ↑ היוצא: MS P1081 אשר יצא
- Jump up ↑ מן החלוקה: MS P1081 מהחלוקה
- Jump up ↑ תאמר: MS P1081 אומר
- Jump up ↑ והשיבו: MS L והשיבו ה
עם הד' - Jump up ↑ ד' ממנו ... פעמי' ד': MS P10181 om.
- Jump up ↑ בי"ד: MS P1081 מן י"ד
- Jump up ↑ נוכל: MS L תוכל
- Jump up ↑ המספר: MS L om.
- Jump up ↑ זה הג': MS L ג'
- Jump up ↑ ואחר על: MS L ועל
- Jump up ↑ כמשפט הכפל: MS P10181 om.
- Jump up ↑ ונתחיל: MS L ותתחיל
- Jump up ↑ הנופלת: MS P1081 הכופלת
- Jump up ↑ ונכתוב ט': MS L om.
- Jump up ↑ מן הנשאר: MS L מהנשאר
- Jump up ↑ ממינו: MS L מן מינו
- Jump up ↑ העליון: MS P1081 עליון
- Jump up ↑ זה: MS L om.
- Jump up ↑ זאת: MS P1081 זה
- Jump up ↑ השינית: MS P1081 השני
- Jump up ↑ מן השורש: MS L מהשורש
- Jump up ↑ שהיא: MS L שהוא
- Jump up ↑ הכפל: MS P1081 om.
- Jump up ↑ באופן שנוכל: MS P1081 om.
- Jump up ↑ המספר: MS L om.
- Jump up ↑ מן החלוקה: MS L מהחלוקה
- Jump up ↑ ד' ממנו ... ומהנשאר אחר זה נוכל לקחת: MS P1081 om.
- Jump up ↑ והיא: MS P1081 והוא
- Jump up ↑ ונכפול זאת הג' ... היא במדרגת האחדים: MS P1081 om.
- Jump up ↑ למעלה: MS L om.
- Jump up ↑ אמנם: MS L om.
- Jump up ↑ האחרון: MS L הראשון
- Jump up ↑ הנשאר לקחת: MS L ולקחת
- Jump up ↑ גם כן: MS L ג"כ
- Jump up ↑ אשר תקח: MS L שתקח
- Jump up ↑ השורש: MS L ראש השורש
- Jump up ↑ מן האחדים: MS P1081 מהאחדים
- Jump up ↑ אשר לפני: MS L שלפני
- Jump up ↑ תשוב: MS P1081 תשיב
- Jump up ↑ כפל: MS L כפלו
- Jump up ↑ אשר לקחת: MS L שלקחת
- Jump up ↑ ממנו: MS P1081 om.
- Jump up ↑ מהמספרים: MS L ממספר
- Jump up ↑ אשר אחריו: MS L שאחריו
- Jump up ↑ תראה כי: MS L om.
- Jump up ↑ השורש: MS L השורש
הקרוב והואא - Jump up ↑ כל: MS L om.
- Jump up ↑ כמו שתראה: MS L om.
- Jump up ↑ רצינו ... ט'ט'ג': MS L om.
- Jump up ↑ שהיא: MS P1081 שהוא
- Jump up ↑ מהמספר: MS L ממספר
- Jump up ↑ והנה נשאר: MS P1081 ונשאר
- Jump up ↑ והיא: MS L והוא
- Jump up ↑ הנשאר: MS L ב' הנשאר
- Jump up ↑ מהנשאר: MS P1081 מהראשון מהנשאר
- Jump up ↑ מפני כי: MS L ומפני זה
- Jump up ↑ יהיה: MS L om.
- Jump up ↑ אשר לקחנו: MS L שלקחנו
- Jump up ↑ הא': MS L הג'
- Jump up ↑ ראשונה: MS L ראשון
- Jump up ↑ נכתב: MS P1081 ב' נכתב
- Jump up ↑ כמשפט: MS L כמספר
- Jump up ↑ אשר לפניה: MS L שלפניה
- Jump up ↑ כ"ט: MS L om.
- Jump up ↑ לפניה: MS L שלפניה
- Jump up ↑ מזה: MS P1081 om.
- Jump up ↑ המספר: MS L מספר
- Jump up ↑ המספר: MS P1081 om.
- Jump up ↑ במחולק: MS P1081 במחלק
- Jump up ↑ וראה: MS P1081 נראה
- Jump up ↑ יהיה: MS P1081 נקוה
- Jump up ↑ עשר: MS P1081 עשרה
- Jump up ↑ פעמי': MS P1081 om.
- Jump up ↑ כי: MS L om.
- Jump up ↑ ואף כי יותר מהעשרה: MS L om.
- Jump up ↑ נוכל: MS P1081 תוכל
- Jump up ↑ עשר: MS P1081 עשרה
- Jump up ↑ זה: MS L om.
- Jump up ↑ נשוב: MS P1081 נשאר
- Jump up ↑ מן המדרגה: MS P1081 מהמדרגה
- Jump up ↑ שכפלנו: MS P1081 השפלנו
- Jump up ↑ הוספנו: MS L נוסף
- Jump up ↑ והנה: MS L הנה
- Jump up ↑ כבר: MS L om.
- Jump up ↑ נתוספה: MS P1081 נוספה
- Jump up ↑ בשורש: MS L השורש
- Jump up ↑ לחלק: MS L om.
- Jump up ↑ גם כן: MS L ג"כ
- Jump up ↑ הכפול: MS L כפול
- Jump up ↑ מן האחדים: MS L מהאחדים
- Jump up ↑ P903 138v
- Jump up ↑ Guenzburg 196r
- Jump up ↑ Guenzburg 196v
Appendix: Bibliography
Immanuel ben Jacob Tov-Elem / Immanuel Bonfils / Immanuel of Trascon (flourished c. 1340-1377)
Manuscripts:
- 1) Firenze, Biblioteca Medicea Laurenziana Plut. 88.30/2 (IMHM: f 17853), ff. 37r-38r (15th century)
- Plut. 88.30/2
- 2) London, British Library Or. 10878 (IMHM: f 8193), ff. 6r-7v (15th century)
- Or. 10878
- 3) Moscow, Russian State Library, Ms. Guenzburg 365/11 (IMHM: f 43035), ff. 193v-196v (15th-16th century)
- Guenzburg 365
- 4) Paris, Bibliothèque Nationale de France heb. 903/7 (IMHM: f 26859), ff. 138r-140r (15th century)
- heb. 903/7
- 5) Paris, Bibliothèque Nationale de France heb. 1026/6 (IMHM: f 15025), ff. 72r-80v (16th century)
- heb. 1026/6
- 6) Paris, Bibliothèque Nationale de France heb. 1054/8 (IMHM: f 33997), ff. 31r-v (15th century)
- heb. 1054/8
- 7) Paris, Bibliothèque Nationale de France heb. 1081/3 (IMHM: f 15037), ff. 4r-15v (16th-17th century)
- heb. 1081/3
Bibliography:
- Gandz, Solomon. 1936. The Invention of the Decimal Fractions and the Application of the Exponential Calculus by Immanuel Bonfils of Tarascon (c. 1350), Isis XXIV, pp. 16–45.
- Lévy, Tony. 2003. Immanuel ben Jacob de Tarascon (XIVe s.): fractions décimales, puissances de 10 et opérations arithmétiques, Centaurus 45, pp. 284-304.
- ———. 2012. Immanuel ben Jacob of Tarascon (Fourteenth Century) and Archimedean Geometry: An Alternative Proof for the Area of a Circle, Aleph. 12.1, pp. 135-159.
- Rabinovitch, Nahum. 1974. An Archimedean Tract of Immanuel Tov-Elem (14th Cent.), Historia Mathematica 1, pp. 13–27.
- Rashed, Roshdi. 1994. The development of Arabic mathematics: between arithmetic and algebra. Translated by A.F.W. Armstrong. Dordrecht, Boston, London: Kluwer Academic Publishers, pp. 85-146.
- Sarton, George. 1934. Simon Stevin of Bruges (1548-1620), Isis, vol. 21, no. 2 (Jul., 1934), pp. 241-303.
- ———.1935. The First Explanation of Decimal Fractions and Measures (1585). Together with a History of the Decimal Idea and a Facsimile (No. XVII) of Stevin's Disme, Isis, vol. 23, no. 1 (Jun., 1935), pp. 153-244.
- Steinschneider, Moritz. 1893-1901. Mathematik bei den Juden. Berlin-Leipzig-Frankfurt: Kaufmann, pp. 155-163 (f79-f87); repr. Hildesheim: G. Olms, 1964 and 2001.
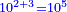
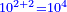
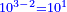
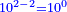
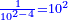
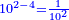
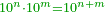

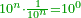
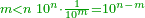

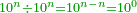
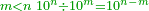
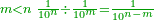
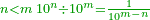
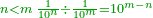
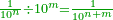

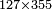
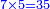
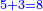


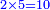
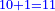

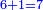
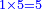

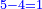
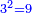
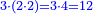
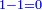

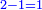
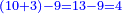

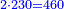
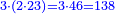
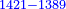


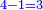
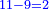
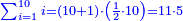
![\scriptstyle{\color{blue}{\sum_{i=1}^7 i=\left[\frac{1}{2}\sdot\left(7+1\right)\right]\sdot7=\left(\frac{1}{2}\sdot8\right)\sdot7=4\sdot7}}](/mediawiki/images/math/2/f/9/2f9d158f8016c8cb4b4682a2f2ba2880.png)