Royslist

Category	Category	Comment	Link	Annotated text
plane number/heteromecic number	זולת	term	האריתמטיקה_של_ניקומכוס#qOjh	הזולת
plane number/heteromecic number	זולת/זולתי האורך	term	האריתמטיקה_של_ניקומכוס#l7zm	זולתיות האורך
plane number/heteromecic number	זולת/זולתי	term	האריתמטיקה_של_ניקומכוס#kY9X	המספרים הזולתיים
plane number/heteromecic number	זולת	term	האריתמטיקה_של_ניקומכוס#xyKW	זולתיים
plane number/heteromecic number	זולת/זולתי האורך	term	האריתמטיקה_של_ניקומכוס#Rs4e	המספר הזולתי האורך
plane number/heteromecic number	זולת	term	האריתמטיקה_של_ניקומכוס#kdOx	זולתיי
plane number/heteromecic number	זולת	term	האנציקלופדיה_של_אבו_אלצלת#jTnG	זולתיות
plane number/heteromecic number	זולת/זולתי האורך	term	האנציקלופדיה_של_אבו_אלצלת#DBjI	הזולתיים
plane number/heteromecic number	זולת/זולתי	definition	ספר_המספר_/_אליהו_מזרחי#R9lF	It has already been clarified in the second section of the Book on Arithmetic by Nicomachus of Gerasa that the heteromecic numbers, which are those whose one side exceeds over the other by one, such as 1 and 2; 2 and 3; 3 and 4; 4 and 5; and so on; are generated by the increment of the natural even numbers. :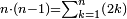$\scriptstyle n\sdot\left(n-1\right)=\sum_{k=1}^{n} \left(2k\right)$ והוא שכבר התבאר בספר הארתמטיקא לניקומכוש הגהרשיני במאמר השני שהמספרים הזולתיים שהם אשר יהיו צלעותיו נוסף אחד מהם על האחר בתוספת האחד כמו א"ב וב"ג וג"ד וד"ה וכן תמיד הנה צמיחתם תהיה בתוספת הזוגות הטבעיים קצתם על קצת
plane number/heteromecic number	זולת/זולתי	term	ספר_המספר_/_אליהו_מזרחי#QNd6	זולתיי
plane number/heteromecic number	זולת/זולתי	term	ספר_המספר_/_אליהו_מזרחי#v4QK	המספר הזולתיי
plane number/heteromecic number	זולת/זולתי האורך	term	האנציקלופדיה_של_אבו_אלצלת#HRNQ	המספרים הזולתיים הארך
plane number/heteromecic number	זולת	term	האריתמטיקה_של_ניקומכוס#Gk5s	זולתיות
plane number/heteromecic number	זולת/זולתי האורך	term	האנציקלופדיה_של_אבו_אלצלת#XsrB	זולתיי הארך