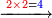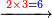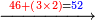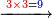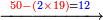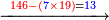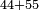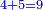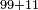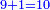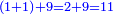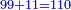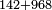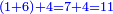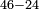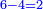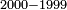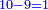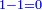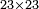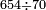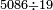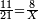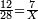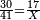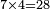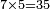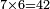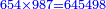ספר אגריס

	אתחיל לכתוב ספר חשבונות
	שקורין צאיפור
	בשם הדר במעונות
Sefer Agris was prepared according to the script [= perhaps an indication that the work relies on another book]	ספר אגריס אשר נעשה על פי הכתב
	ויש בו שערים אשר בהכנתם תוחלת רב
The treatise apparently consisted of nine chapters	ומיניינם אשר החילותי לפרשם הם ט‫'
	ושאריתם לא מצאתי מפרש

Introduction: The Positional Decimal System
The numerals
The nine numerals - the nine first Hebrew letters	ומהנה אתחיל ואומר האותיות היוצאות במילת אגריס לפועל הם ט' כמספרם ואילו הם
1 2 3 4 5 6 7 8 9	ט ח ז ו ה ד ג ב א
Every number is written with these nine numerals	ובהם כתוב כל מספר
The written ranks [= decimal places]
Units	ודע כל מניין שתחפוץ לכתוב מא' עד ט'
written with one letter only	תוכל לכתוב באות אחת כגון אחת א' או שתים ב' כו' עד ט‫'
Ten cannot be indicated by the nine numerals	אך עשרה לא תמצא באותיות האילו הנרמזים אך תכתוב 0"א פי' עשרה עמוד גלגל ואחר תכתוב הא‫'
Zero: 10 - the zero indicates that 1 is in the second rank; 1 without a zero is one	והגלגל יורה שהא' במעלה שנייה והיא עשרה והא' בלא גלגל אחד
Tens	וכן כל האותיות עד ט‫'
0 before any numeral indicates tens	ואולם כשיש גלגל לפני האות מורה על העשיריות
20	וכדרך זה תכתוב אם דעתך לכתוב עשרים תכתוב 0"ב
30	שלשים 0"ג
40	ארבעים 0"ד
	ועל דרך זה תוכל להבין כל אות שהיא במעלה שנייה שהיא עשירית
90	וכדרך זה תכתוב עד תשעים והוא 0"ט
Hundreds
100	אך מאה היאך תרצה לכתוב תכתוב א' במעלה השלישית כזה 00"א
200	ב' מאות כזה 00"ב
300	ג' מאות 00"ג
400	ד' מאות 00"ד
900	וכן תעשה עד ט' מאות כזה 00"ט
Thousands
1000	רק אלף היאך תרצה לכתוב תכתוב במעלה רביעית כזה 000"א
2000	אלפים כזה 000"ב
3000	ג' אלפים כזה 000"ג
4000	ד' אלפים 000"ד
9000	וכו' עד ט' אלפים כזה 000"ט
Tens of thousands
10000	ועשרת אלפים תכתוב כזה 0000"א והא' עומד במעלה החמישית
20000	עשרים אלפים 0000"ב
30000	שלשים אלפים 0000"ג
40000	ארבעים אלפים כזה 0000"ד
90000	וכו' עד תשעים אלפים כזה 0000"ט
Hundreds of thousands
100000, etc.	מאה אלפי' תכתוב הא' במעלה שישית כזה 00000"א וכו‫'
Every rank is ten times the preceding rank	ועתה תבין ותדע שהא' במעלה ראשונה עשיר' היא שהיא במעלה השנייה והשנייה עשרי' השלישי' והשלישי' עשירי' הרביעי' וכן לעולם כל אשר יתרבו המעלות כן יתרבו המניין ותבין בו כי הוא דרך אמת
	ומכאן אפרש לך שער המועל סכום לסכום

Addition	שער החיבור
To let you know how to sum two numbers together.	להודיעך איך תתחבר שני חשבונות יחד
Write one number in a line and beneath is the second number: units corresponding to units and tens corresponding to tens, meaning write the digit [lit. letter] that is in the first rank beneath the digit that is also in the first rank, then the second beneath the second in rank and so on.	תכתוב חשבון אחד בשורה ותחתיו חשבון השני פרט נגד פרט וכלל נגד כלל פי' האות שהיא במעלה הראשונה כתוב האות תחת אות שהיא ג"כ למעלה ראשונה והשנייה תחת השנייה במעלה וכן כולם
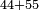
Example: you wish to add 44 to 55. $\scriptstyle44+55$	דומיון רצונך לחבר ד' וארבעים לה' וחמשים
Write as follows:	תכתוב כך
4 4 5 5	ד ד ה ה
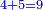
Sum 4 with 5 in the bottom [row], it is 9. $\scriptstyle{\color{blue}{4+5=9}}$	חבר ד' עם ה' שבתחתון והיא ט‫'
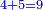
Sum the second 4 with the second 5, it is 9. $\scriptstyle{\color{blue}{4+5=9}}$	חביר ד' שנייה ה' שנייה והוא ט‫'
Thus, we found that their sum is 99, which is ninty-nine. $\scriptstyle{\color{blue}{44+55=99}}$	א"כ מצאנו צירופם ט"ט והם תשעה ותשעים
Sum all the digits according to this way.	ובזה הדרך חבר כל האותיות
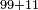
Another example: $\scriptstyle99+11$	דומיון אחר
9 9 1 1	ט ט א א
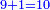
Add 9 to 1 that is on the bottom [row], which is 11, [it is] ten. $\scriptstyle{\color{blue}{9+1=10}}$	חבר ט' על א' שבתחתה והיא א"א עשרה
Write 0 and you are left with 1, which is in the second rank.	כתוב 0' ישאר לך א' והיא א' שנייה במעלה
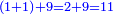
Add it to the second 1 that is also in the [second] rank, it is 2. Add the 2 to the 9 in the second rank, it is 11. $\scriptstyle{\color{blue}{\left(1+1\right)+9=2+9=11}}$	צרוף אותה במעלה לא' השנייה גם כן במעלה ויהיה ב' צרוף הב' על הט' במעלה שנייה ויהיה א"א
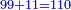
And 0 first, it is 110. $\scriptstyle{\color{blue}{99+11=110}}$	ובתחילה 0' ויהיה 0'א'א‫'
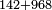
Another example: $\scriptstyle142+968$	דומיון אחר
1 4 2 9 6 8	א ד ב ט ו ח
Add 2 to 8, it is ten. $\scriptstyle{\color{blue}{2+8=10}}$	חבר ב' על ח' זה עשרה
Write 0.	כתוב 0‫'
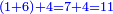
Sum the remaining 1 with 6, it is 7. Add it to 4, it is 11. $\scriptstyle{\color{blue}{\left(1+6\right)+4=7+4=11}}$	והא' הנותרת חבר עם הו' ויהיה ז' חברה על הד' ויהיה א"א
Write 1 in the second rank.	כתוב א' במעלה שנייה
Add 1 in the third rank to 9 and 1, it is 11. $\scriptstyle{\color{blue}{1+9+1=11}}$	והא' השלישי' במעלה חברה על הט' ועל הא' זהו א"א
So it is 1110. $\scriptstyle{\color{blue}{142+968=1110}}$	אז הוא 0אא"א

Subtraction	שער החסור
If you know a number and you wish to subtract [from it] a certain amount and know what remains from the first number after subtracting the amount from it, I will teach you this:	אם ידעת חשבון ורצונך לחסר מי"ט סך אחד וחפצתה לידע מה יסיר מן החשבון הראשון אחר סלוק הסך הן אשכילך
Write your greater number on a row and write the smaller [number] beneath it on a bottom row.	כתוב מיניינך המרובה בטור ותחתיו בטור שפלה כתוב המועט
Subtract units from units, tens from tens and so on.	והוציא אחדי' מן אחדים ועשיריות מן העשיריות וכו‫'
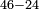
Example: to subtract 24 from 46. $\scriptstyle46-24$	דומיון להסיר כ"ד מן מ"ו
Write as follows:	כתוב כך
4 6 2 4	ד ו ב ד
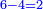
Subtract 4 from 6, 2 remains. $\scriptstyle{\color{blue}{6-4=2}}$	הסר ד' מן ו' וישאר ב‫'
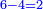
Subtract 2 from 4, 2 remains, which is in the second rank. $\scriptstyle{\color{blue}{6-4=2}}$	הסר ב' מן ד' וישאר ב' והיא במעלה שנייה
It is 22. $\scriptstyle{\color{blue}{46-24=22}}$	ויהיה ב"ב
[Borrowing one for the preceding rank:] Always follow this way: when you know that the [upper] digit [of the minuend] is greater than its corresponding the bottom digit [of the subtrahend], not considering the measure of the others - always add ten to the upper digit, from which you cannot subtract the [corresponding] bottom [digit].	לעולם כדרך זה תלך אחר שתדע שבמעלה האחרונה שהאות גדולה מחבירת' התחתונ' אז לא תחוש בגדול האחרים צרוף לעולם עשר אל כל אות עליונ' שלא תוכל ליקח ממנו תחתונות
The beginning [of the procedure] is from the first digit [= the units].	ויהיה התחלתך באות ראשונה
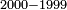
Example: $\scriptstyle2000-1999$	דומיון
2 ‫0 ‫0 ‫0 1 9 9 9	ב ‫0 ‫0 ‫0 א ט ט ט
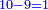
Subtract 9 from 10, one remains. $\scriptstyle{\color{blue}{10-9=1}}$	הסר ט' מי' ונשאר אחד
Subtract 9 from 9, since we have shifted one for our matter, 0 remains. $\scriptstyle{\color{blue}{9-9=0}}$	הסר ט' מט' כי דחינו אחד לעניינו וישאר 0‫'
Subtract 9 from the third 9, 0 remains. $\scriptstyle{\color{blue}{9-9=0}}$	הסר ט' שלישי' מט' וישאר 0‫'
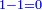
Subtract 1 from 1, 0 remains. $\scriptstyle{\color{blue}{1-1=0}}$	הסר א' מא' וישאר 0‫'
	ואעפ"י שיש מאותו אחד נולד לנו כל העשיריות שעשינו כי דחינו הא' אל הט' שלפניה והיא 0' לקחת ממנה ט' נותר א' הא' הזאת דחינו אל ה0' שלפניה כדי ליקח ממנו ט' וכל מ"י ונשאר א' אותה א' דחינו אל ה0' הראשונה ויהיה י' הסר מן הי' ט' הראשונה וישאר א"ב על והוא אחד ועל דרך זה תוכל להבין כל מניין כזה וזולתו

Multiplication	שער הכפל
	לידע כפל חשבון על חשבון כתוב מניין אחד בטור העליון ובטור שפל מניין אחד וככה תכתבם כתוב אות ראשון של התחתון תחת אות אחרונה של העליון
The interim product	אם תכפול אות אחרונה שלמטה על אות אחרונה של מעלה וה[עול]ה כתוב על אות אחרונה של מטה
If the interim product is of the units	אם יעלה הכפל פחות מ"ט כתוב הפרט על אות אחרונה של מטה והכלל תרחיק מעלה ממנו
If the interim product is of the tens	ואם אין פרט רק כלל כתוב 0' על אות אחרונה של מטה והכלל תרחיק וה0' תשי' למעלה
The procedure: multiplying and shifting	ואחריו כפול האות שלפני האות אחרונה שלמטה ג"כ על אות אחרונה שבטור העליון והעולה כתוב אל אותה אות שלמטה שכפלת אות' וכן עשה לכל האותיות כיפלם על אות אחרונה ולאחר שתכפלם כל טור שלמטה על אות אחרונה שלמעלה תשיב אחורני' אילו אילו האותיות של טור השפל וכפול אותי' אחרוני' שלמטה על אות שלפני הראשוני' שכנגד העליון וכן האות שלמטה שלאחר האחרונה על אותה שכפלת האחרונה וכן כולם על אותה
If the upper multiplier consists of more than two ranks	ואם יש יותר מב' מעלות בטור עליון תשיב אותה אחורנית עוד כאשר פירשתי לך
$\scriptstyle23\times23$	דומיון על כפול כ"ג על כ"ג

23	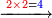$\scriptstyle\xrightarrow{{\color{red}{2\times2}}={\color{blue}{4}}}$	423	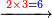$\scriptstyle\xrightarrow{{\color{red}{2\times3}}={\color{blue}{6}}}$	463	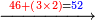$\scriptstyle\xrightarrow{{\color{red}{46+\left(3\times2\right)}}={\color{blue}{52}}}$	523	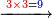$\scriptstyle\xrightarrow{{\color{red}{3\times3}}={\color{blue}{9}}}$	529
23		23		23		23

	לדע כמה עולה כתוב כגון זה
2 3 2 3	ב ג ב ג
	כפול הב' שלמטה על הב' של מעלה ויהי' ד' אותה הד' כתוב במעלה השלישית אחר ב' העליונה כגון זה
4 2 3 2 3	ד ב ג ב ג
	כפול הג' ג"כ על הב' שעליה ויהיה ו' מחק הב' העליונה וכתוב הו' במקומה והדומיון
4 6 3 2 3	ד ו ג ב ג
	כתוב הג"ב האחרונים תחת הג' השנייה ויהיה
4 6 3   2 3	ד ו ג   ב ג
	כפול הב' על הג' ויהיה י"ב מחק הו' וכתוב ב' במקומה והא' שהיא שלישי' במעלה צרוף אותה אל הד' ויהיה ה' הדומיון כך
5 2 3   2 3	ה ב ג   ב ג
	כפול הג' אל הג' ויהיה ט' זה ג"כ על ג"ב הוא
5 2 9	ה ב ט
	ועל דרך זה תוכל לידע כל הכפל דבר לכפול דבר
Multiplying a number that consists of three ranks by a number that consists of three ranks	לכפול ג' אותיות על ג' אותיות כפול התחתון על השניות במעלה תשיב אחורנית וכפול אותם ג"כ במעלה ראשונה וכפול אותם על אות התחתונה שתכפול ומה של מעלה תמחוק

Division	שער החלוק
	אם ישאלך אדם כמה פעמים סך הקטון בסך הגדול כתוב החשבון הגדול בטור אחד לפי מעלות ותחתיו כתוב בטור שפל סך הקטון ואות אחרונה של השפל כתוב אותה תחת אות אחרונה של העליון וראה כמה פעמים התחתון בעליון והעולה תכתוב אותה בטור שלישי תחת אות ראשונה שבטור שניה וכל כך פעמים שתקח אות אחרונה מן האחרונה כל פעמים קח האותיו' האחריות מן הסך העליון
$\scriptstyle654\div70$	והא לך דומיון ביקשנו לדע כמה פעמים ע' בתוך תרנ"ד
	תכתוב תרנ"ד בטור זה
	ואחר כתוב ע' בטור שפל כזה
6 5 4   7 0	ו ה ד   ז ‫0
	אומנם אם נכתב ז' אחרונה תחת הו' שהיא גם כן אחרונה לא נוכל למצוא ז' בו לכן אנו צריכין לכתוב הז' כנגד הה' של דה"ו [...] אמור כמה פעמים ז' בס"ה נאמר ט' פעמים אות' ט' כתוב בטור שלישי' תחת ה0' וישאר ב' במקו' ה' של דה"ו והד' שלפני דה"ו בב' שלא חלקנו עדיין בז' א"כ מצאנו ע' בתוך תרנ"ד ט' פעמים וישאר כ"ד
$\scriptstyle5086\div19$	דומיון אחר בקשנו לידע כמה פעמים י"ט בתוך שמנים ושש וחמש אלפים

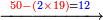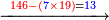5086	$\scriptstyle\xrightarrow{{\color{red}{50-\left({\color{blue}{2}}\times19\right)}}={\color{blue}{12}}}$	1286	$\scriptstyle\xrightarrow{{\color{red}{128-\left({\color{blue}{6}}\times19\right)}}={\color{blue}{14}}}$	146	$\scriptstyle\xrightarrow{{\color{red}{146-\left({\color{blue}{7}}\times19\right)}}={\color{blue}{13}}}$	13
19		19		19		19
		2		26		267

	כתוב מניין הגדול על פי אגורימא וכתוב תחתיו הי"ט כזה
5 0 8 6 1 9	ה 0 ח ו א ט
	אמור כמה פעמים א' שפלה בתוך ה' של מעלה אם תיקח ה' פעמים ואז ממה תקח הט' ה' פעמים ואם ד' פעמים ותאמר א' שהיא עשר במקום ה0' שלפניה לא תוכל ליקח ט' ד' פעמים מעשר' ואם תקח א' ג' פעמים וישאר ב' במקום הב' שהם עשרים במקום ה0' הן לא תוכל ליקח הט' ג' פעמי' מעשרים אכן קח הא' ב' פעמים וישאר במקום הה' ג' קח ב' מהג' והשב אחורנית מקום ה0' ויהיה עשרים וקח ט' ב' פעמים מעשרים וישאר ב' במקום ה0' וא' במקום הה' כתוב ב' שכל סך פעמ' מצאת י"ט בתוך מעלה אותה ב' כתוב תחת הט' ויהיה דמיונ' כך
1 2 8 6 1 9       2	א ב ח ו א ט       ב
	והנה לא תוכל למצוא ט"א בב"א אכן השם ט"א אחרונית כזה
1 2 8 6   1 9     2	א ב ח ו   א ט     ב
	ואמור כמה פעמים א' בב"א וקח אותה כל כך מעט כדי שתוכל ליקח הט' גם כל כך ז' פעמים לא תוכל ליקח הט' מן הנשאר ז' פעמים כי מן הב"א ישאר ו"ח שעל הט' זהו ח"ה לא תשיג ליקח ממנו ז' פעמים ט' כי הוא עולה יותר אכן קח מן מ"ו פעמים מן הי"ב שעליה וישאר ו' במקו' הב' כזה
6 8 6	ו ח ו
	השב הט' אחורנית תחת הו' העליונה קח ו' פעמי' ט' מח"ו וישאר במקום הח' ד' ובמקום הו' א' כזה
1 4 6 1 9   2	א ד ו א ט   ב
	ומונת עתה ו' פעמים ט"א במעלה שנייה כתוב ו' תחת הט' כזה
1 4 6 1 9   2 6	א ד ו א ט   ב ו
	השב הט' אחורנית תחת הו' עליונה כזה
1 4 6   1 9 2 6	א ד ו   א ט ב ו
	קח א' שפלה מד"א ז"פ וישאר במקום ז' במקום הד' ויהיה הדומיון כזה
7 6   1 9 2 6	ז ו   א ט ב ו
	קח הט' גם כן ז' פעמים מו"ז וישאר ג' במקום הו' וא' במקום הז' יכתוב הז' שמצאת' תחת הט' ויהיה הדומיון כך
1 3   1 9 2 6 7	א ג   א ט ב ו ז
	וזה יורה לך שמצאת ט"א בתוך וח0"ה במעלה השלישית שהם מאות ו' במעלה השנייה שהם עשיריו' וז' במעלה ראשונה שהם אחדים וישארו ג"א שלא באו לחלק א"כ הן כמניין הגדול וז' פעמי' וג"א חלקים בשלימות ועל דרך זה תחלוק

Proportions	שער הערוך
	הוא מועיל לידע מתוך חשבון ידוע חשבון נסתר
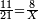
When one asks: you know that 11 roosters are sold for 21 pešiṭim. Now, you ask: what is the price of 8 roosters? $\scriptstyle\frac{11}{21}=\frac{8}{X}$	כאשר ישאל השואל הנה ידוע לך שי"א תרנגולים נמכרים בכ"א פ' ועתה תשאל היאך ערך ח' תרנגולים
	והנה אתן לך דרך אשר ממנו תדע הדרך כתוב י"א תרנגולים בטור ואחריו באותו טור כתוב הכ"א ובטור שנייה תחת הי"א כתוב כזה
21 11   8	אב אא   ח
	ואמור כערך א"א על א"ב כן ערך א' על הנסתר
	כפול ח' על הנסתר א"ב ויעלה חו"א
	חלקיהא בא"א ותמצא כ"ו ט"ו פעמים א"א בתוך חו"א וישאר ג' שלא תוכל לחלוק
	א"כ ח' תרנגולים ימכרו עבור ט"ו וג' שברים מן א"א כשלמין
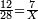
Example: I bought 12 cubits of cloth for 28 dinar. You wish to know: what is the price of 7 cubits? $\scriptstyle\frac{12}{28}=\frac{7}{X}$	דומיון הנה קניתי י"ב אמות בגד בכ"ח דינ' וביקשת לידע כמה ערך של ז' אמות
	כתוב י"ב והם האמות בטור ואחריו כתוב כ"ח והם דמים בטור שנייה כתוב הז' והם אמות אשר לא יתנם עד כ"ח וכותבם תחת הי"ב כזה
28 12   8	חב בא   ח
	ויאמר כערך י"ב על ט"ו כן ערך הנסתר אל ז'
	וככה תעשה כפל ח"ב בז' ויעלה וט"א
	חלקם בב"א ויעלה ו"א וד' מי"ב בשלימים
	א"כ ערך הז' אמות י"ז דינר וד' מי"ב בשלימי‫'
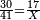
Example: you hired a worker for 30 days for 41 dinar, but he worked with you only 17 days. You wish to know: how much should his payment for these days be? $\scriptstyle\frac{30}{41}=\frac{17}{X}$	דומיון הנה שכרתה שכיר ל' ימים במ"א דינר ולא עבד אתך אלא י"ז ימים ובקשת לידע כמה שכרו לאותו הימים
	כתוב ל' והם הדמים אשר היה לו לעבוד בטור העליון ואחריו מ"א באותו הטור והם דמי השכיר אם עבד עמך כל הימים וכתוב בטור שנייה תחתיו הל' י"ז והם אשר עבד
Written according to agorima as follows	יכתוב אותם על פי אגורימא כזה
41 30   17	אד ‫0ג   זא
	ואמר כערך ז"א אל א"ד כך ערך 0"ג אל הנסתר
	כפול ז"א על א"ד והם זט"ו
	חלקם ב0"ג ויעלה ג"ב וז' חלקים מ0"ג בשלמי'
	א"כ אתה חייב לו מן העבודה אשר עבד אתך הי"ז ימים כ"ג דינר וז' פרוטות מל' בדינר
	סליק שער הערוך
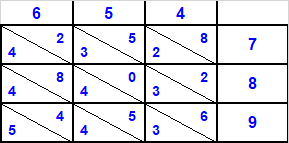
Gelosia
	פי' זה הלוח
	עשה עמו כפל בלי מחק כאשר רמזתי תקן
$\scriptstyle654\times987$	ותאמר אם תרצה לידע כמה עולה ד'ה'ו' אז תכתוב כמו שכתבתי ז'ח'ט'
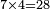
$\scriptstyle7\times4=28$	ותאמר ז' פעמי' ד' הרי כ"ח
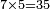
$\scriptstyle7\times5=35$	ז' פעמי' ה' הרי ל"ה
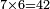
$\scriptstyle7\times6=42$	ז' פעמים ו' הרי מ"ב
	וכן תעשה לכולם
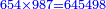
the result: $\scriptstyle{\color{blue}{654\times987=645498}}$	ח'ט'ד'ה'ד'ו' זה עולה
	פי' זה הלוח לידע כמה הוה ב"פ ב' ג"פ ג' ד"פ ד' ה"פ ה' וכן כולם
	סליק ספר צאיפור

Appendix: Bibliography

Anonymous
Sefer Agris / Agrima / Sefer Ṣaifur / Ṣifur

Manuscripts:

1) Darmstadt, Hessisches Landes-und Hochschulbibliothek Cod. Or. 25/39 (IMHM: f 12695), ff. 71v-73r (14th century)

Or. 25/39

2) Oxford, Bodleian Library MS Opp. 757/17 (IMHM: f 20981), ff. 322v-326v (cat. Neub. 2289,17); (16th century)

3) Warszaw, Żydowski Instytut Historyczny 288/2 (IMHM: f 12013), ff. 6r-22r (15th century)

Bibliography:

• Steinschneider, Moritz. 1906. Mathematik bei den Juden, Band II: 1551-1840. Monatsschrift für die Geschichte und Wissenschaft des Judenthums 50, p. 213. repr.: ed. Gad Freudenthal, Hildesheim, Zürich, New York: Olms, 2014, p. 136.