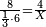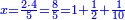ספר החשבון והמדות
Contents
[hide]
Introduction |
|
| אמר מרדכי בכ"ר אליעזר כומטיינו יעמ"ש הקושטנדיני | |
| להיות שההתחלה הראשונה לכל הושפעו ממנה שאר הנמצאות במדרגה ובסדר מדרגה אחר מדרגה ובזה נמצא כל אחד לפי שלמותו הראוי לו עד תכליתו ונמצא לכל דבר חקו | |
| והשלמות הזה רודף לבעליו על התמידות בלתי סר ממנו וזה בדברים אשר אין מציאותם בפעולותינו | |
| והדברים אם מציאותם בפעולותנו כאשר רצינו להיותם שלמים נמשילם אל הדברים אשר אין מציאותם בפעולותינו כפי היכולת ראוי לנו ג"כ אם רצינו השלימות והסדור לדמות הדברים אשר מציאותם בפעולותינו | |
| והדברים אשר מציאותם בפעולותנו יחלקו לשני סוגים | |
| האחד הדברים שבין האדם לעצמו | |
| והשני הדברים שבין האדם לזולתו | |
| והסוג הראשון בלתי נכנס בזה החבור ואף על פי שגם בזה חברו הפילוסופים ספרים הרבה | |
| כי כונת זה החבור הוא במה שיפול ממנו אל זולתו | |
| ואם השלמות הנופלת בדברים אשר אין מציאותם בפעולותינו מהעצם האחד לזולתו בלתי חוזרת אליו אבל הולכת על יושר | |
| והשלמות אשר תפול בדברים אשר מציאותם בפעולותינו תלך על דרך הסבוב | |
| הדמיון יהיה במה שממנו לאליו מצד מה שהוא ממנו ואליו וזה הסוג יחלק לשלשה חלקים | |
| האחד הדברים אשר יגיעו מהאיש לזולתו על דרך החמלה והחנינה | |
| והשני הדברים אשר יגיעו לו על צד הצדק והיושר | |
| והשלישי הוא מהדברים אשר יגיעו מהאדם לזולתו על צד העול והחמס | |
| והחלק הראשון הוא הדבר המוסיף על השווי | |
| והחלק השלישי הוא דבר גורע מהשווי | |
| והשני הוא השווי בעצמו | |
| אם כן יהיה החלק השני שרש ויסוד לשאר החלקים ולכן ראוי שתהיה החקירה בו | |
| ובראותי שזה החלק משתמש לשני סוגים | |
| הסוג האחד במקח וממכר וזהו הנקרא בלשון חכמינו זכרונם לברכה אונאה | |
| אם היה שם שתות הפרש בין הצדק ובין המכר וזה הדבר הוא בלתי מוגבל ולכן לא תקיף בו ידיעה כי ישתנו מחירי הדברים בכל זמן מפני זה לא נדבר בו | |
| והסוג השני הוא בחשבון ובמדות כי אחר שנתפשרו שני הצדדים בקנין א' כלל אחד בכך וכך מחיר בחלקו המונה אותו אחר כשיבואו לכפול המחיר כמנין החלקים אשר נמנה בהם הכלל ולא יצא החשבון שוה להעדר ידיעתם בחשבון או במדידת הקרקעות יהיה מזה עול וחמס ויוסר הצדק משם ותחת אשר נרצה להדמות אל הדברים אשר אין מציאותם בפעולותינו נתרחק מהם הרבה ואוי על הקנין הרע הזה אשר נקנה לנפשנו | |
| לכן ראיתי לחבר זה הספר כדי שאסיר העול מבני אדם ויהיה הצדק נמצא ביניהם | |
| וחלקתי אותו אל שני ספרים | |
| הספר הראשון מדבר בעניני החשבון | |
| והספר השני מדבר בעניני המדות | |
| והקדמתי ספר החשבון לספר המדות כי חכמת החשבון קודמת בטבע לשאר מיני ההרגליות השלש כאשר ביאר זה
ניקומאכוש הגהרשני בהצעת מאמרו מספר האירתימיטיקא | |
| והספר הראשון חלקתי אותו אל ארבעה חלקים | |
| הראשון לקבץ מספר עם מספר ולחסר מספר ממספר | |
| והשני לכפול מספר על מספר | |
| והשלישי לחלק מספר על מספר ולהוסיף מספר על מספר | |
| והרביעי לערך מספר על מספר | |
| עוד שמתי חלק אחד אחריהם לדבר על הנשברים | |
| ודרכתי בזה הדרך דרך הנוצרים לדבר בקיצור כדי שלא יתבלבל התלמיד | |
| עוד הספר השני חלקתי אותו לארבעה חלקים | |
| האחד במדידת התמונות השטחיות כגון העגולות והמשולשים והמרובעים וזולתם | |
| והשני בחלוקתם | |
| והשלישי במדידת התמונות הגופניות | |
| והרביעי בחלוקתם | |
| ומהנה אתחיל בעזרת המלמד לאדם דעת |
Part One: Addition & Subtraction |
|
Chapter One: Introduction |
הפרק הראשון מהחלק הראשון מהספר הראשון |
|---|---|
| ראוי שנודיע למה הקדמנו קבוץ מספר על מספר משאר החלקים | |
| ואומר לפי שהוא יותר פשוט מהם וקודם בטבע מהם עם היותו יותר פשוט מהם להיות שכל אחד מהם מורכב מזה ומהענין המיוחד לו | |
| והדבר אשר יורכב מדבר הדבר אשר יורכב ממנו הוא יותר פשוט מהמורכב ההוא | |
| ואומר שכל אחד מהם מורכב מזה ארצה מאחד משני חלקיו או משניהם יחד | |
| כי זה יחלק לשני מינים | |
| אם שיהיה הקבוץ הזה בלתי משתנה ממדרגת נקבציו וזה באחד עד תשעה פעמים ובשנים עד ארבעה פעמים ובשלשה עד שלשה פעמים | |
| ואם יורכב מאלה יהיה לפי חשבונו המיוחד לו או שיהיה הקבוץ הזה משתנה ממדרגת נקבציו וזה יחלק לשני חלקים | |
| אם שישתנה ממדרגת נקבציו ולא יהיה שם רושם כלל מהמדרגה ההיא | |
| או שישתנה וישאר גם רושם מדרגת נקבציו שם ולכן הוא קודם מהמורכבים ממנו | |
| ואין לאומר שיאמר כי להיותו פשוט ראוי לאחרו מן המורכב ממה שביאר אריסטו בתחלת ספר השמע שראוי להקדים הכולל מהמיוחד לשלש סבות | |
| האחת שהכולל יותר ידוע מהמיוחד וראוי ללכת מהיותר ידוע אל היותר מוסכל | |
| והשנית שלא נשיב המאמר האחד פעמים הרבה | |
| והשלישית שתהיינה ההקדמות מיוחדות כי יצדק הכולל שגדרו נשוא על המיוחד כאשר ינשא גדר המין על אישיו וכן המספר נשוא על חלקיו | |
| אולם גדר העשרה מצד מה שהם עשרה לא ינשאו על מספר אחר לא על תשעה ולא על זולתו | |
| ולכן בכזה ראוי להקדים המיוחד על הכולל כי מקבוצו יודע הכולל | |
| ואם היותו קודם בטבע מהם מפני שכאשר נעלה הוא יעלו גם הם ולא יתהפך וכשימצאו הם ימצא גם הוא ומפני אלו הסבות היה ראוי להקדימו מהם | |
| וראוי שנקדים להזכיר קודם שכל המספרים נכללים בתשעה | |
| כי מאחד עד תשעה ישלמו האחדים ובהגיעך אל העשרה הגעת אל עשירית אחת עד שתשלים כל העשרות עד תשעים | |
| עוד ממאה התחלת באחד ובהגיעך אל תשע מאות השלמת כל המאות עד שתתחיל עוד מאלף אחד וכן ללא תכלית | |
| ולהיות זה בטבע כאשר חשבו רבים או בבחירה כאשר נחשב אנחנו אין עת להכריע עתה בזה כי אינו מכונתינו | |
| ולכן תקנו אנשי הודו תשעה אותיות להיותן מורין על תשעה מספרים והתחלפות מדרגותם יורו על התחלפות מדרגות התשיעיות כאשר נבאר וזה צורתם | |
| 1 2 3 4 5 6 7 8 9 | |
| ולא הסתפקו באותיות האלפבית כי לכל אחד מהם צורה מיוחדת הנחיית מה שאין כן לאלו האותיות כי הן מופשטות מכל הנחה ומשותפות לכל צורה שתחול עליהן והן כדמות ההיולי הראשון | |
| ומדרגת הנחתן הוא כמו הצורה להן | |
| וכן יוכל כל אדם לחדש אותיות אחרות זולת אלה | |
| ואמרי אותיות לא ארצה מן אותיות האלפביתא אבל סימנים מופשטים מכל חשבון כאלה | |
| אבל כבר נהגו כל בעלי החשבון להשתמש באלה | |
Chapter Two: Addition |
הפרק השני |
| ראוי להודיע כי המספרים אשר הם מאחד ועד תשעה יקראו פרטים | |
| ומן העשרות ומעלה יקראו כללים ר"ל העשרות והמאות והאלפים והרבבות והשאר | |
| ואע"פ שיקראו בשם הכלל אבל אין מדרגתם אחת רק יש כלל כולל כלל אחד וכן זה אחד עד שיגיע אל האחדות | |
| לכן ראוי לבעלי החשבון לכתוב מדרגות חשבונם כסדר שיכתבו הכלל היותר כולל ראשונה ואחריו הכלל השפל ממנו וכן על הסדר עד שיגיעו אל האחדים | |
| עוד כשיבואו לכתוב מספר אחר תחת אלה שישמרו הסדר הזה ויכתבו כל כלל תחת הדומה לו ר"ל הרבבה תחת הרבבה והאלף תחת האלפים והמאה תחת המאות והאחדים תחת האחדים | |
| ונקרא א"כ האחדים מדרגה ראשונה והעשרות מדרגה שניה והמאות מדרגה שלישית והאלפים מדרגה רביעית וכן ללא תכלית | |
| ואם יהיה בידך מספר שאינו מסודר בכל מדרגותיו כגון שהיו בידך אלפים ועשרות ואחדים והנה המאות הם חסרים משם השמר לך שלא תכתוב העשרות בצד האלפים אבל תכתוב האלפים ובמקום המאות תכתוב גלגל אחד 0 הנקרא בלשון ישמעאל סיפרא ובלשון יון אודין ובלשון לעז נולא | |
| כלומר כי בכאן הוא מקום המאות ואין שם דבר | |
| ואחר הגלגל תכתוב העשרות במקומו ובזה יהיו המדרגות כל אחת עם חברתה על קו ישר | |
| וכשתרצה לקבץ כל הטורים לעשות אותם סך אחד תעשה ותתחיל מן האחדים לעולם ותרד על קו ישר באחדים אשר תחתיהם בכל הטורים | |
| ואם לא יעלו עד עשר כתוב מה שתמצא תחת הכל כנגד האחדים למטה | |
| ואם יעלו יותר מעשר בכל עשירית ועשירית כתוב נקדה אחת בעשרות ר"ל כמספר העשרות יהיו הנקודות שתכתוב והנשארים אשר לא הגיעו לכלל עשר כתוב אותם תחת האחדים | |
| עוד תרד במדרגת העשרות ועם הנקודות שכתבת וקבצם ותעשה כמשפט הזה כי אם לא תגיע לעשר כתוב מה שתמצא תחת העשרות ואם הגעת לעשרות בכמות העשרות שעלו תעשה נקודות במאות והשאר אשר לא הגיעו לעשרות כתבם תחת מדרגת העשרות וכן אל בלתי תכלית | |
| ואם כן יהיה הסך למטה בכל אחת מהמדרגות פחות מעשר והנמצאים בסך במדרגת האחדים הם אחדים ובמדרגות העשרות הם עשרות וכן בכל מדרגה כפי מדרגתה | |
| ואם היו הטורים אשר רצית לעשות אותם סך הרבה מאד תחלקם לשלשה חלקים או לארבעה או לפחות או ליתר לפי רוב הטורים ומיעוטם ותעשה סך לכל חלק וחלק בפני עצמו כאשר הראית אחר כן תחבר שני החלקים ותעשה אותם סך כזה המשפט בעצמו והמקובץ יהיה סך כל החלקים יחד | |
| וזאת צורת הקבוץ הנקרא סך | |
| רצינו לקבץ אלף ומאתים וחמש עשרה ואלפים ושלש מאות ועשרים ושנים | |
| כתבנו אותם סך כך | |
| אחר חברנו אותם והיה קבוצם למטה שבע אחדים ושלש עשרות וחמש מאות ושלשת אלפים וידענו שהם שלשת אלפים וחמש מאות ושלשים ושבעה | |
| ואלה המספרים בסכום היורד לא הגיעו לכלל עשר בשום מדרגה | |
| ונצייר עוד צורה אחרת המגעת במדרגותיה לכלל העשרות והיא שנחבר עוד תחת אלה השני טורים שני טורים אחרים האחד תשעת אלפי' ושש מאות וחמשים ושבעה והשנית שמנת אלפים וחמש מאות וששים ושלש וזאת היא הצורה | |
| קבצנו אותם ויצא הסך למטה שבעה אחדים וחמש עשרות ושבע מאות ואלף אחת ושתי רבבות | |
| והנה קבוץ האחדים כאשר תרד במדרגותם על קו היושר תמצאם שבעה עשר הוצאנו העשרה מהם וכתבנו נקודה אחת במדרגת העשרות ונשארו שבעה וכתבנו אותם תחת האחדים | |
| עוד כאשר קבצנו מדרגת העשרות על קו היורד ביושר יחד עם הנקודה שכתבנו שם כנגד העשירית שהוצאנו מהאחדים מצאנום חמש עשרה הוצאנו עוד העשרה מהם וכתבנו נקדה בעבורם במדרגת המאות והחמשה הנשארים כתבנום למטה במדרגת העשרות וכן כשקבצנו המאות בירידתנו על קו היושר יחד עם הנקדה שכתבנו כנגד העשירית שהוצאנו מהעשרות מצאנום שבעה עשר הוצאנו מהם העשרה וכתבנו בעדם נקדה במדרגת האלפים והשבעה הנשארים כתבנו אותם במדרגת המאות | |
| וכן כשקבצנו את האלפים בירידתנו על קו היושר עם הנקדה שכתבנו עמם בעד העשירית שהוצאנו מהמאות מצאנו אותם עשרים ואחד הוצאנו העשרים שהם ב' עשרות וכתבנו בעבורם שתי נקודות במדרגת הרבבות והאחד הנשאר כתבנוהו תחת האלפים וידענו מזה שהם שתי רבבות ואלף אחד ושבע מאות וחמשים ושבעה | |
| מאזנים לדעת אם הסכום שלך אפשר להיותו אמת על דרך התשעה תחשוב כל המדרגות כאילו הם אחדים ותקבצם ותשליכם תשעה תשעה ומה שישאר שמרהו ואם לא ישאר דבר תחשוב בליבך סיפרא | |
| עוד קבץ מדרגות הסך גם הוא כאילו הם אחדים והשליכם ט' ט' ואם ישארו בידך כהשארות הראשון אפשר שחשבונך יהיה אמת ואם לא ישארו כראשונים דע בודאי שטעית ותחזור ותחשוב בטוב | |
| מאזנים אחרים על דרך השבעה תחשוב כל המדרגות כאשר הם ר"ל האלפים אלפים והמאות מאות והעשרות עשרות והאחדים אחדים לא שתחשבם כאילו הם אחדים הכל כאשר עשית בדרך התשעה ואחר שתחשבם השליכם ז' ז' והשאר שמרהו ואם לא ישאר דבר שמור בלבך סיפרא | |
| אחר תבוא אל מדרגות הסך ותתחיל מהכלל היותר גדול עם מה שבצדו ותחשוב כאילו הכלל הם עשרות ומה שבצדו אחדים והשליכם ז' ז' ומה שישאר תחשבהו עשרות וחברהו עם מה שבצדו ותחשוב מה שבצדו לאחדים והשליכם ז' ז' וכן תעשה עד שתגיע אל האחדים וכשתגיע אליהם והשלכתם ז' ז' ראה הנותר ואם הוא שוה עם מה ששמרת אפשר שחשבונך יהיה אמתי ואם הוא בלתי שוה דע בודאי שטעית ותחזור ותחשוב בטוב | |
| וכן אם חלקת הטורים לחלקים מצד ריבויים כאשר הזכרתי ועשית הסך חלקים חלקים תעשה גם המאזנים שלהם ככה אחר חבר גם המאזנים כמו שתחבר הסכום על הדרך אשר ידעת | |
Chapter Three: Subtraction |
הפרק השלישי |
| אם רצית לחסר מספר ממספר ראוי שיהיה כלל המספר אשר תחסר ממנו יותר גדול מהמספר אשר תחסרנו וזה בשלמים אך לא בשברים ובשאר המדרגות אין צורך | |
| ולעולם תכתוב המספר אשר תחסר ממנו ראשונה אחר תכתוב תחתיו המספר אשר תחסר כל מדרגה תחת הדומה לה | |
| ואם יש לשם חסרון מדרגה תכתוב סיפרא במקומה והזהר לעולם אל הסיפרא שלא תשכחנה אך בכל מקום שתחסר מדרגה תשימנה אחר כן תתחיל לחסר מהאחדים | |
| ואם האחדים אשר תחסר מהם הם יותר מאלה אשר תחסר חסרם מהם והנשאר תכתוב למטה במדרגת האחדים | |
| ואם הם פחותים מהם תחזור אל העשרות אשר בצדם וקח עשירית אחת וחסרה מן העשרות וחברה עם האחדים אחר גרע מהם מה שתגרע והשאר תכתבם למטה במדרגת האחדים | |
| עוד תבוא לחסר העשרות מהעשרות ואם הם יותר העשרות אשר תחסר מהם חסר מהם והשאר כתבם תחת העשרות | |
| ואם הם מעטים שוב אל המאות ועשה כמשפט עד שתגיע אל הכלל היותר גדול | |
| אמנם אם יש לשם סיפרא ותרצה לחסר ממנה מה שלמטה ממנה מהפרטים תקח מהכלל אשר למעלה ממנה ותשיבהו אל הספרא אחר תקח אחד מהמספ' ותשיבהו אל מה שלמטה ממנה ולא תשיב מהכלל אשר למעלה ממנה אל מה שלמטה ממנה כי זה הוא טעות גדולה | |
| וזאת היא הצורה נרצה לחסר ד' אלפים ומאתים ועשרים וחמשה מה' אלפים ומאה וארבעה עשר | |
| הוצאנו החמשה מן הארבעה ומפני שהארבעה פחותים מהם חזרנו אל העשרות אשר למעלה מהם ומצאנו עשירית אחת ולקחנוה ועשינוה עשרה וחברנוה עם הארבעה ונהיו ארבעה עשר הוצאנו מהם החמשה ונשארו תשעה וכתבנום במדרגת האחדים | |
| עוד רצינו לגרוע העשרים מן הסיפרא כי לא נשאר דבר מהעשרות וחזרנו אל המאות והיה מאה אחת ולקחנוה והחזרנוה אל עשר עשרות והוצאנו ממנה העשרים ונשארו שמנים וכתבנום למטה | |
| עוד רצינו לגרוע המאתים מהסיפרא כי לא נשאר לנו במאות דבר וחזרנו אל האלפים ולקחנו אלף אחת מן האלפים ונשארו האלפים ד' והאלף אשר לקחנו החזרנוה עשר מאות וגרענו מהם המאתים ונשארו שמנה מאות וכתבנום במדרגת המאות | |
| עוד גרענו הד' אלפים מד' אלפים ונשאר 0' | |
| אם כן ידענו שכשחסרנו ד' אלפים ורכ"ה מה' אלפים וקי"ד נשארו סך סיפרא אלפים ושמנה מאות ושמנים ותשעה | |
| מאזנים על דרך התשעה תחשוב כל מדרגות המספרי' אשר גרעת מהם כאילו הם אחדים והשליכם ט' ט' ומה שישאר שמרהו ויקרא השמור הראשון | |
| וכן תעשה במספרים אשר גרעת אותם שתשמור מהם הנשאר מהט' ט' וזה יקרא השמור השני | |
| אחר תגרע השמור השני מהשמור הראשון ומה שישאר שמרהו וזה יקרא השמור השלישי | |
| עוד תעיין אל הסך שנשאר אחר שגרעת המספרים מהמספרים ותחשבם כאילו הם אחדים והשליכם ט' ט' והנשאר אם יהיה שוה לשמור השלישי אפשר שחשבונך יהיה אמת ואם אינו שוה דע בודאי שטעית | |
| ואם השמור הראשון פחות מהשמור השני תוסיף עליו ט' אחר תגרע השמור השני ממנו ותעשה כמשפט | |
| מאזנים אחרים על דרך השבעה תחשוב כללי המספרים אשר גרעת מהם עשרות ואשר בצדם אחדים והשליכם ז' ז' ומה שישאר תחשבהו עשרות והמספר הבא אחריו אחדים והשליכם ז' ז' ועו' כמה שישאר חשב ככה עד שתגיע אל האחדים והשליכם ז' ז' ומה שישאר שמרהו וזה יקרא השמור הראשון | |
| עוד תעשה ככה במספרים אשר גרעת אותם והנשאר שמרהו ויקרא השמור השני | |
| גרע השמור השני מהשמור הראשון ואשר ישאר יקרא השמור השלישי | |
| אחר כן תעיין אל המספרים אשר נשארו כשגרעת המספרים מהמספרים וחשבם ככה כאשר אמרנו בטורים הראשונים כלומר כשתחשוב הכללים עשרות ואשר בצדם אחדים והשליכם ז' ז' והנשאר תחשבהו עשרות ואשר בצידו לאחדים עוד ותשליכם ז' ז' עד שתגיע אל האחדים ואחר שהשלכתם ז' ז' עיין בנשארים ואם הם שוים לשמור השלישי אפשר שחשבונך יהיה אמת ואם לאו דע כי בודאי טעית | |
| מאזנים אחרים על דרך הקבוץ והם מאזני צדק | |
| חבר המספרים שגרעת אותם עם המספרים שנשארו אחר הגרעון וראה ואם יהיו שוים עם המספרים אשר גרעת מהם תדע בודאי כי חשבונך אמת ואם לאו בודאי טעית | |
| תם החלק הראשון |
Part Two: Multiplication |
החלק השני מהספר הראשון |
|---|---|
| הפרק הראשון לכפול מספר על מספר | |
| הרוצה לכפול מספר על מספר ראוי שיהיה הלוח הזה שגור בפיו כי בזה יהיה זריז לכפול מספר פלוני על מספר פלוני מא' עד ט' | |
| ואם יהיה המספר אשר ירצה לכפול על מספר אחר כל אחד ממדרגה אחת או מאיזו מדרגה שיורה יקח דמיון לכל אחד ממדרגת האחדים ויכפול זה על זה כאלו הם אחדים ויראה העולה ואח"כ יקח לכל האחד מספר במדרגתו שאם היה האחד עשרות והאחר מאות נקח בעד העשרות שנים ובעד המאות שלשה ונחברם ויהיו חמשה אח"כ נשליך לעולם אחד והשאר יורה לנו העולה מאיזה מדרגה הוא | |
| דמיון זה רצינו לכפול שמנים על חמש מאות | |
| לקחנו דמיונם מהאחדים בעד השמני' שמנה ובעד החמש מאות חמשה וכפלנו חמשה על שמנה ויצא לנו הסכום ארבעים | |
| עוד לקחנו בעד המאות שלשה ובעד השמנים שנים כי הם מהמדרגה השנית חברנום ונהיו חמשה השלכנו אחד ונשארו ארבעה ואלה הארבעה הם מדרגת האלפים | |
| וידענו מזה שהארבעים אשר יצאו כשכפלנו השמנים על החמש מאות הם ארבעים אלף | |
| אולם כשתרצה לכפול שני מספרים על שני מספרים צריך שנכתוב אותן כל אחד במדרגתו ושנכפול אותן ארבעה פעמים כל אחד מהטור שלמטה עם כל אחד מהטור שלמעלה ונכתוב המספר המונח בטור הראשון והמספר אשר נרצה לכפול עליו בטור התחתון ונתחיל לכפול אחדי התחתון על אחדי העליון וההוה נכתוב אותו למטה במדרגת האחדים וזה אם לא הגיע לעשרות | |
| אבל אם הגיע לעשרות נוציא העשרות מהם ונשמרם והנשארים אשר לא הגיעו לכלל העשרה נכתוב במדרגת האחדים | |
| עוד נכפול האחדים שלמטה עם מדרגת העשרות שלמעלה ואשר יהיה נחבר גם מספר העשרות ששמרנו עם אחדי זה הכפל כי אע"פ שהם עשרות אבל מה שיצא מהם יהיה כאלו הם עשרות ואחדים כי על דמיון האחדים אנו כופלים הכל והאחדים אשר יתקבצו מזה הכפל נכתבם במדרגת העשרות והעשרות אם יהיו נכתבם במדרגה השלישית | |
| אחר נראה העולה והוא חשבון כפל המספר ההוא | |
| דמיון רצינו לכפול עשרים וחמשה על ארבעים ושלשה כזה | |
| כפלנו הה' על הג' ונהיו ט"ו גרענו העשירית ושמרנוה נשארו ה' וכתבנום במדרגת האחדים | |
| עוד כפלנו הה' על הד' ונהיו עשרים ומפני שלא יצאו מזה אחדים כתבנו העשירית האחת לבד ששמרנו במקום העשרות והעשרים כתבנום במדרגה השלישית | |
| עוד כפלנו הב' על הג' ונהיו ששה ומפני שלא יצאו גם בכאן אחדים כתבנו במקום האחדים סיפרא והששה כתבנום במקום העשרות | |
| עוד כפלנו העשרים על הארבעי' ונהיו שמנה מאות וכתבנום במדרגה השלישית כי כל אחד מהכפולים היו ממדרגה שנית ובהשלכת האחד נשארו שלשה | |
| אחר כן קבצנום ונהיו אלף ושבעים וחמשה | |
| ואם נרצה לכפול שלשה מספרים על שלשה מספרים אז ראוי שנכפלם תשעה פעמים בזה הסדר | |
| דמיון רצינו לכפול שלש מאות וארבעים ושמנה על מאתים ושלשים וחמשה | |
| כתבנו אותם בצורה הזאת | |
| כפלנו הח' על הה' ונהיו ארבעים ומפני שאין כאן אחדים כתבנו סיפרא במדרגת האחדים ושמרנו העשרות הארבעה | |
| עוד כפלנו הג' על הח' ונהיו כ"ד שמרנו שתי עשרות ועם הארבעה שהם אחדיו חברנו הארבעה אשר שמרנו ונהיו שמנה וכתבנום במדרגת העשרות | |
| עוד כפלנו הב' על הח' ונהיו י"ו שמרנו העשירית האחת וחברנו עם אחדיו שהם הששה את השתי עשרות שהיו שמורות לנו ונהיו ח' וכתבנום במדרגת המאות והעשירית האחת אשר שמרנו עתה כתבנוה במדרגת האלפים | |
| הנה כבר כפלנו הח' על כל אחד ואחד מהמספרים שבטור הראשון השלשה | |
| עוד שבנו לכפול הד' עם כל אחד ואחד מהם וכפלנוה תחלה עם הה' ונהיו עשרים ומפני שלא יצאו אחדים כתבנו ספרא במדרגת העשרות שהיא מדרגת אחדיו כי המספרים שכפלנו הם ממדרגה הראשונה והשנית והעשרים שהם שני עשרות שמרנום | |
| עוד כפלנו הד' עם הג' ונהיו י"ב שמרנו העשירית האחת וחברנו עם השנים שהם אחדיו השני עשרות שהיו שמורות לנו ונהיו ד' כתבנום במדרגת המאות לפי שהמספרים שכפלנו הם במדרגה השניה | |
| עוד כפלנו הארבעה עם הב' ונהיו ח' חברנו גם העשירית השמורה לנו עמם ונהיו ט' כתבנום במדרגת האלפים לפי שהמספרים אשר כפלנו היו ממדרגה השנית והשלישית | |
| הנה כבר כפלנו גם הד' שבטור השפל עם כל אחד ואחד מהשלש מספרים שבטור העליון | |
| עוד נשוב לכפול הג' עם כל אחד ואחד מן שלשת המספרים העליונים כפלנו אותו עם ה' והיה ט"ו הוצאנו העשירית ושמרנוה והה' כתבנום למטה במדרגת המאות כי שני המספרים האלה מדרגותם הם הראשונה והשלישית | |
| עוד כפלנו אותם עם ג' ונהיו ט' חברנו גם העשירית השמורה ונהיו י' ולא היו לשם אחדים ולכן כתבנו במדרגת האלפים ספרא והעשירית אנו שומרים אותה | |
| עוד הכינו אותם עם שנים ונהיו ו' חברנו גם העשירית השמורה עמם ונהיו ז' וכתבנום במדרגת הרבבות כי שני המספרים האלה הם במדרגה השלישית | |
| אחרי כן קבצנו שלשה הסכום כמשפט ונהיו פ"א אלף ושבע מאות ושמנים | |
| דמיון אחר במספר שיש לו ספרא רצינו לכפול מאה וחמשה על מאתים ועשרים וארבעה | |
| כתבנו אותם ככה בזאת הצורה | |
| כפלנו הה' על הד' ונהיו כ' ומפני שאין שם אחדים כתבנו סיפרא במדרגת האחדים והשתי עשרות שמרנום | |
| עוד כפלנו הה' עם הב' ונהיו י' ומפני שאין שם אחדים כתבנו הב' עשרות השמורות במדרגת העשרות וזאת העשירית שמרנוה | |
| עוד כפלנו הה' עם ב הב' ונהיו י' ומפני שאין שם אחדים כתבנו למטה העשירית אשר שמרנו במדרגת המאות וזאת העשירית במדרגת האלפים | |
| עוד שבנו להכות כל אחד משלשה המספרים העליונים עם הסיפרא וכתבנו סיפרא במדרגת העשרות וכן במדרגת המאות וכן במדרגת האלפים | |
| עוד שבנו לכפול הא' עם הד' ונהיה ד' וכתבנוהו במדרגת המאות כי שני המספרים הנכפלים היו מהמדרגה הראשונה והשלישית | |
| עוד כפלנו הא' עם הב' ונהיו ב' וכתבנום במדרגת האלפים כי שני המספרים הכפולים היה האחד מהמדרגה השנית והאחר מהמדרגה השלישית | |
| עוד כפלנו הא' עם השנים ונהיו ב' וכתבנום במדרגת הרבבות כי שני המספרים הכפולים היה כל אחד מהמדרגה השלישית | |
| אחר כן קבצנו העולה מהם והם כ"ג אלף וחמש מאות ועשרים | |
| אמר מרדכי ראיתי להודיעך הכפל הזה בדרך אחרת נקלה מצאתיה אצל חכמי הישמעלים והוא שתעשה כל סך הנכפלים בשטה אחת מבלתי שתצטרך אל יותר מזה | |
| וככה תעשה תשים המספר אשר תרצה לכפול עליו בשטה העליונה כמנהג | |
| עוד שים המספר אשר תרצה לכפול אותו עליו בשטה השפלה כל מדרגה כנגד הדומה לה | |
| ואחר כן החל לכפול האחדים על האחדים ותכתוב העולה למטה | |
| ואם יעלו עשרות תפוש אותם בלבך ותכתוב האחדים לבדם למטה | |
| עוד תכפול האחדים שבשטה השפלה עם העשרות שבשטה העליונה כאלו הם אחדים על אחדים והעשרות אשר תפשת בלבך מהחשבון הראשון חשוב אותם אחדים וחברם עם אלה | |
| גם תכפול האחדים שהם בשטה העליונה עם העשרות שהם בשטה השניה וחבר הכל ותכתוב העולה למטה | |
| ואם עלו עשרות והטעם מדרגה עליונה מזאת תפוס בלבך | |
| גם תכפול האחדים שבשטה השפלה עם המאות שבשטה העליונה | |
| וכן האחדים שבשטה העליונה עם המאות שבשטה השפלה | |
| גם העשרות שבשטה השפלה עם העשרות שבשטה העליונה | |
| והכלל המדרגות אשר בקבוצן תהיינה שוות הסך | |
| כי הראשונה עם השלשה יעשו ד' וככה השלישית עם הראשונה והשנית עם השנית | |
| גם הראשונה עם הרביעית יעשו חמשה וככה השנית עם השלישית | |
| וככה תעשה עד אין קץ ואשר יהיה תחבר המספר שהיה במדרגה שחשבנוה עשרות שתפשת בלבך עמם וכתבם למטה והוא הסך המבוקש | |
| דמיון רצינו לכפול שלש מאות וארבעים ושמנה על מאתים ושלשים וחמשה כזה | |
| כפלנו הח' על הה' ונהיו מ' ובעבור שלא נשארו אחדים כתבנו גלגל במדרגה הראשונה והמ' תפשנום בלבנו ארבע | |
| עוד כפלנו ח' עם ג' והיו כ"ד גם ד' עם ה' כי הם שוה המדרגות והיו כ' חברנום עם הכ"ד והיו מ"ד גם חברנו עמהם הד' שתפשנו בלבנו היו מ"ח וכתבנו למטה במדרגת העשרות ח' והמ' תפשנו בלבנו ד' | |
| עוד כפלנו ח' עם ב' והיו י"ו גם ג' עם ה' והיו ט"ו גם ד' עם ג' והיו י"ב כי כל אלה שוה המדרגות והם מ"ג חברנו עמהם הד' שתפשנו בלבנו והם מ"ז כתבנו הז' במדרגת המאות והד' שהם המ' תפשנו בלבנו | |
| עוד כפלנו ד' עם ב' והיו ח' גם כפלנו ג' עם ג' והיו ט' גם חברנו הד' שתפשנו בלבנו עמם והיו כ"א כתבנו הא' במדרגת האלפים והכ' תפשנו אותם בלבנו שנים | |
| עוד כפלנו ג' עם ב' והיו ו' חברנו עמהם הב' שתפשנו בלבנו והיו ח' כתבנו הח' במדרגת הרבבות | |
| וידענו מזה שהסך העולה מכפל השטה השפלה על השטה העליונה הם שמנים ואחת אלפים ושבע מאות ושמנים | |
| וכבר נהגו בעלי החשבון לכפול בדרך שלישית | |
| והוא שתקח שלישית המספר ותכפלהו על עצמו וההוה הוא מרובעו ותקח כדומה לו ממדרגה הבאה אשר היא יותר עליונה ממנה ותוציא מזאת המדרגה מרובע השלישית והנשאר הוא המבוקש | |
| דמיון רצינו לדעת מרובע ט' ולקחנו שלישיתו וכפלנו אותו על עצמו ונהיה ט' לקחנו דמיונו ממדרגה הבאה העליונה ממנה והיה צ' הוצאנו ממנו הט' שהוא מרובע השלישית ונשארו פ"א והוא המבוקש | |
| ואם רצית לכפול מספר שאין לו שלישית אתה לוקח שלישית המספר היותר קרוב אליו ותרבע אותו ותעשה כמשפט אחר תעיין ואם המספר אשר לקחת שלישיתו הוא יותר פחות מהמספר המבוקש קבץ שני המספרים והוסיפם על הסך וההוה הוא המבוקש | |
| דמיון רצינו לדעת מרובע עשרה וזה אין לו שלישית והמספר הקרוב אליו אשר יש לו השלישית הוא התשעה והוא פחות ממנו לקחנו מרובע שלישיתם והוא ט' ולקחנו דמיונם מהמדרגה הבאה והוא צ' גרענו ממנו הט' ונשארו פ"א ומפני שהמספר אשר לקחנו השלישית ממנו הוא פחות מהמספר המבוקש קבצנו שני המספרים הט' עם הי' ונהיו י"ט הוספנום על הפ"א ונהיו ק' והוא מרובע העשרה | |
| אבל אם היה המספר אשר לקחנו השלישית ממנו יותר מהמספר המבוקש אנו מקבצים שני המספרים וגורעים אותם מהסך והנשאר הוא המבוקש | |
| דמיון רצינו לדעת מרובע י"א ומפני שאין לו שלישית והמספר הקרוב אליו שיש לו שלישית הוא הי"ב והוא יותר ממנו לקחנו שלישיתו וכפלנוהו במספר המרובע ולקחנו דמיונו במדרגה הבאה והוא ק"ס גרענו ממנו הי"ו שהוא מרובע השלישית ונשארו קמ"ד ומפני שהמספר אשר לקחנו השלישית ממנו שהוא י"ב הוא יותר מהמספר המבוקש מרובעו שהוא י"א קבצנו שתיהן ונהיו כ"ג וגרענו אותם מן קמ"ד ונשארו קכ"א וזהו המבוקש שהוא מרובע י"א | |
| אמר מרדכי מצאתי דרך נכבד בענין הכפל בדרך החמישיות והוא כי כאשר תרצה לכפול מספר על עצמו תקח חמישיתו ותכפלהו על עצמו ותעלהו במעלה הבאה הסמוכה לה אחר תכפול אותה על שנים וחצי והוא המבוקש | |
| דמיון רצינו לכפול ששים על ששים וחמישיתו י"ב כפלנום על עצמם נהיו קמ"ד העלנו אותם במדרגה הבאה הסמוכה להם ונהיו אלף וארבע מאות וארבעים כפלנום על ב' וחצי ונהיו ג' אלפים ת"ר וזהו המבוקש | |
| דמיון אחר רצינו לכפול חמשים על חמשים וחמישיתו עשרה כפלנוהו על עצמו ונהיה מאה העלינוהו אל המדרגה הסמוכה לה ונהיו אלף כפלנום על ב' וחצי ונהיו ב' אלפים וחצי וזהו המבוקש | |
| ואם רצית לכפול מספר על עצמו ואין לו חמישית תעיין המספר הקרוב אליו שיש לו חמישית אם מלפניו אם מלאחריו ולא יעבור ההפרש לעולם על שנים | |
| ואם היה המספר אשר יש לו חמישית הקרוב אל מספרך קודם ממספרך באחד תחשבהו בדרך שהזכרתי ראשונה על המספר שיש לו חמישית אחר תחבר מספרך עם המספר שיש לו החמשית ותוסיפהו על הסך והוא המבוקש | |
| ואם היה ההפרש שנים תכפול מספרך אחר שתחברהו עם המספר שיש לו חמישית עם שנים ואחר תוסיפנו על הסך והוא המבוקש | |
| אמנם אם המספר שיש לו החמשית הוא אחר מספרך תחשוב חשבונך על המספר שיש לו החמישית אחר תחבר מספרך עם המספר פעם אחת אם ההפרש אחד או תכפול אותו עם ב' אחר שחברתו אם ההפרש שנים ותגרעהו מהסך והנשאר הוא המבוקש | |
| דמיון רצינו לכפול י"א על י"א והנה זה המספר אין לו חמשית והמספר הקרוב אליו אשר יש לו חמישית הוא העשרה וכפלנו אותו בדרך החמישיות ועלו ק' אחר חברנו הי' שיש לו החמישית עם הי"א שהוא מספרינו פעם אחת מפני שההפרש בין שמספרנו ובין י' הוא אחד ונהיו כ"א חברנו עם הק' ונהיו קכ"א וזהו המבוקש | |
| דמיון אחר במספר שההפרש שנים רצינו לכפול י"ב על י"ב והנה זה המספר אין לו חמישית והמספר הקרוב לו בעל החמשית הוא העשירי' כפלנוהו בדרך החמישיות ונהיו ק' אחר חברנו הי' שיש לו החמישית עם הי"ב שהוא מספרנו ונהיו כ"ב ומפני שההפרש שנים כפלנום ב' פעמים ונהיו מ"ד וחברנום עם הק' והיו קמ"ד וזהו המבוקש | |
| דמיון אחר במספרים אשר המספר שיש לו חמשית הקרוב אליו הוא אחריהם כי הדמיונים אשר עשינו היה בהיותו לפניהם | |
| רצינו לכפול י"ד על י"ד והנה זה המספר אין לו חמישית ראינו המספר אשר יש לו חמישית הקרוב אליו והוא ט"ו כפלנום בדרך החמישיות ועלה רכ"ה אחר חברנו את המספר הזה שיש לו חמישית עם מספרינו שהוא י"ד פעם אחת מפני שההפרש אחד והיה כ"ט גרענום מן הסך מפני כי המספר אשר יש לו החמישית היה אחרי מספרנו ונשארו קצ"ו וזהו המבוקש | |
| דמיון במספר כזה שההפרש אשר בינו ובין אשר יש לו החמישית שנים | |
| רצינו לכפול י"ג על י"ג וזה המספר אין לו חמישית והמספר הקרוב אליו שיש לו החמישית הוא החמשה עשר כפלנוהו בדרך החמישיות והיה רכ"ה אחר חברנו זה המספר שיש לו החמישית עם י"ג שהוא מספרנו ונהיו כ"ח כפלנום על ב' מפני שההפרש אשר בין שני המספרים ב' ונהיו נ"ו גרענום מן רכ"ה מפני שהמספר שיש לו החמישית הוא אחרי מספרנו ונשארו קס"ט וזהו המבוקש | |
| ואם תרצה לכפול מספר על מספר שהם רחוקים מהכלל בשווי האחד חסר ממנו והאחר מוסיף עליו אתה יכול לכפול הכלל על עצמו אחר תרבע המספר היתר והחסר ותגרעהו מחשבון הכלל וההוה הוא המבוקש | |
| דמיון רצינו לכפול כ"ה על ל"ה והכלל ל' והה' בתוספת וחסרון כפלנו הכלל ונהיו תת"ק אחר כפלנו הה' ונהיה כ"ה גרענום מהתת"ק ונשארו תתע"ה והוא המבוקש | |
| אמר מרדכי עם היות שאמרנו שאם היו המספרים שתים על שתים אתה צריך לכפלם ארבעה על ארבעה ר"ל ארבעה פעמים צריך אתה לדעת שאם היה כללם אחד יספיק לכפלם שלש פעמים | |
| כגון הרוצה לכפול י"ג על י"ד והנה כלל שניהם עשרה תחבר שני הפרטים ויהיו ז' ותכפול ז' פעמים י' נהיו ע' וי' פעמים י' הרי ק' וג' פעמים ד' הרי י"ב והעולה קפ"ב וזהו המבוקש | |
| מאזנים על הכפל בדרך הט' | |
| תחשוב הטור העליון כולו כאלו הם אחדים והשליכם ט' ט' והשאר שמרהו וזה יקרא השמור הראשון | |
| עוד תעשה כן בטור השפל והשאר יקרא השמור השני | |
| תכפול השמור הראשון על השמור השני ואשר יהיה השליכהו ט' ט' והשאר שמרהו וזה יקרא השמור השלישי | |
| אחר תעיין הטור השלישי השפל אשר יקרא הסך ותחשבהו כאלו הם אחדים והשליכם ט' ט' והשאר עיין ואם הוא שוה לשמור השלישי אפשר שחשבונך יהיה אמת ואם לאו דע בודאי שטעית | |
| מאזנים בדרך השבעה | |
| עיין מספרי הטור הראשון ותתחיל מהיותר כולל ותחשבהו עשרות ואשר בצדו אחדים והשליכם ז' ז' ואשר ישאר חשבהו עשרות ואשר בצדו אחדים והשליכם עוד ז' ז' ואשר ישאר עוד חשבהו עשרות ואשר בצדו אחדים והשליכם עוד ז' ז' ואשר ישאר עוד חשבהו עשרות ואשר בצדו אחדים והשליכם ז' ז' וכן תעשה עד שתגיע למעלת האחדים ואשר ישאר שמרהו וזה יקרא השמור הראשון | |
| עוד תקח מספרי הטור השני ועשה כמשפט הזה ואשר ישאר יקרא השמור השני | |
| אחר תכפול השמור השני על השמור הראשון ואשר יהיה השליכהו ז' ז' והשאר יקרא השמור השלישי | |
| אחר כן תעיין מספרי הטור השפל השלישי אשר יקרא הסך ועשהו כמשפטי הטורים העליונים ועיין הנשאר ואם הוא שוה לשמור השלישי אפשר שחשבונך יהיה אמת ואם לאו דע בודאי שטעית | |
Euclidean Propositions |
|
| אמר מרדכי ראיתי לכתוב לך דברים מעניני המספר להרגילך בהם כדי שתהיה זרִיז בענינים אלו | |
| Euclid, Elements, Book II, propositions 1-2: If you divide any number into parts as you wish, [the sum of] the products of each of the parts by the whole number is equal to the square of the whole number
|
ואומר כל מספר שחלקת אותו לחלקים איך שרצית הנה כפל כל אחד מהחלקים על כל המספר מקובץ שוה למרובע כל המספר |
|
|
דמיון המספר י"ב וחלקנוהו על שלשה וארבעה וחמשה כפלנו הג' על הי"ב והיו ל"ו עוד כפלנו הד' על הי"ב והיו מ"ח עוד כפלנו הה' על הי"ב והיו ס' חברנו אותם והיו הכל קמ"ד והם שוים למרובע י"ב |
| Euclid, Elements, Book II, proposition 2: |
עוד כל מספר שחלקת אותו לשני חלקים איך שקרה הנה כפל כל אחד משני החלקים על כל המספר מקובץ שוה למרובע כל המספר |
|
|
דמיון המספר עשרה וחלקנוהו על ז' וג' כפלנו הז' על הי' והיו שבעים גם ככה כפלנו החלק האחר שהם השלשה עליו והיו ל' ושניהם ק' והוא מרובע העשרה |
| Euclid, Elements, Book II, proposition 3: For any number divided into two parts as you wish, the product of the whole number by any of its two parts is equal to the product of the one part by the other plus the square of the part by which you multiplied the whole number
|
עוד כל מספר שחלקת אותו לשני חלקים איך שקרה הנה כפל המספר כולו על אחד משני חלקיו איזה שיהיה שוה לכפל החלק האחד על השני ולמרובע החלק משניהם אשר כפלת על כל המספר |
|
|
דמיון המספר עשרה חלקנוהו לשני חלקים על שלשה ושבעה כפלנו השלשה עמו והיו ל' וזה שוה לכפל הג' על השבעה שהם כ"א ולמרובע הג' שהם ט' שהוא החלק אשר כפלנו |
|
|
גם ככה אם היינו כופלים הז' שהוא החלק האחד על העשרה היו שבעים וזה שוה לכפל הג' על הז' שהם כ"א ולמרובע הז' שהם מ"ט שהוא החלק אשר כפלנו ושניהם שבעים |
| Euclid, Elements, Book II, proposition 4: For any number divided into two parts as you wish, the square of the whole number is equal to [the sum of] the squares of the two parts and twice the product of the one part by the other
|
עוד כל מספר שחלקת אותו לשני חלקים איך שקרה הנה מרובע כל המספר שוה לשני המרובעים ההוים משני החלקים ולכפל החלק האחד על חברו פעמים |
|
|
דמיון המספר עשרה חלקנוהו על שלשה ושבעה ומרובע הג' ט' ומרובע הז' מ"ט וכפל הג' על הז' כ"א וחשבהו פעמים הם מ"ב והכל ק' וזה שוה למרובע העשרה |
| Euclid, Elements, Book II, proposition 5: For any number divided into two equal parts and into two unequal parts, [the sum of] the product of one of the unequal parts by the other and the square of the difference between the two parts, i.e. between the equal part [= the half of the whole number] and the unequal [part] is equal to the square of half the [whole] number
|
עוד כל מספר כאשר תחלקהו לשני חלקים שוים ולשני חלקים בלתי שוים הנה כפל החלק האחד אל חברו מהחלקים הבלתי שוים ומרובע מה שבין שני החלקים ר"ל בין החלק השוה ובלתי שוה שוה למרובע חצי המספר |
|
|
דמיון המספר עשרה חלקנוהו לחמשה וחמשה שהם חלקים שוים גם חלקנוהו לז' וג' שהם חלקים בלתי שוים כפלנו הג' על הז' והיו כ"א עוד לקחנו מרובע השנים שהם בין הה' שהם החלק השוה לשלשה או לז' שהם החלק הבלתי שוה והיו ד' והכל כ"ה והם שוים למרובע ה' שהוא מרובע חצי המספר |
| Euclid, Elements, Book II, proposition 6: If you divide any number into half and add to it another number, [the sum of] the product of the whole number plus the additional [number] by the additional [number] and the square of half the number is equal to the square of half the number and the additional [number] together
|
עוד כל מספר כאשר חלקת אותו לחצאים והוספת עליו מספר אחר הנה כפל המספר כלו מקובץ עם התוספת בתוספת והמרובע ההוה מחצי המספר שוה למרובע חצי המספר והתוספת ביחד |
|
|
דמיון המספר עשרה וחלקנוהו לשני חצאים שהם כל חצי חמשה הוספנו על העשרה שנים והיו י"ב כפלנו כל הי"ב שהוא המספר עם התוספת ביחד עם השנים שהם התוספת והיו כ"ד חברנו עמהם כ"ה שהם מרובע ה' שהוא חצי המספר והיו מ"ט וזה שוה למרובע ז' שהוא חצי המספר עם התוספת ביחד |
| Euclid, Elements, Book II, proposition 7: For any number divided into two parts, the sum of the square of the whole number and the square of one of the parts is equal to twice the product of this part by the whole number plus the product of the other part by itself
|
עוד כל מספר כאשר תחלקהו בשני חלקים איך שיקרה הנה המרובע ההוה מן המספר כלו והמרובע ההוה מאחד משני חלקים כאשר התקבצו שוים לכפל המספר כלו עם החלק הנזכר פעמים והמרובע ההוה מן החלק השני |
|
|
דמיון המספר עשרה וחלקנוהו איך שקרה על שבעה ועל שלשה והמרובע ההוה מעשרה הם ק' וההוה מז' הם מ"ט ומקובצים קמ"ט והם שוים לכפל העשרה על ז' פעמים שהם מאה וארבעים ולמרובע ג' שהם ט' שהוא החלק השני והכל קמ"ט |
| Euclid, Elements, Book II, proposition 8: For any number divided into two parts as you wish, if you multiply the whole number by one of the parts four times, the sum of the product with the square of the other part is equal to the [square] of the whole number plus the one part
|
עוד כל מספר כאשר חלקת אותו בשני חלקים איך שיקרה וכפלת המספר כלו עם אחד משני חלקיו ארבעה פעמים ועם מרובע החלק הנשאר שוה למרובע ההוה מן המספר כלו והחלק הנזכר כאשר תחברם ביחד ותקח מרובעם |
|
|
דמיון יש לנו מספר מניינו העשרה וחלקנוהו איך שהזדמן על ג' ועל ז' הנה כאשר כפלנו הז' עם הי' ד' פעמי' היו ר"פ וכאשר חברנו עמהם מרובע הג' שהוא ט' והוא החלק השני נהיו רפ"ט והם שוים למרובע י"ז שהוא המספר כלו יחד עם החלק אשר כפלנוהו עם המספר כולו והם גם אלה רפ"ט |
| Euclid, Elements, Book II, proposition 9: For any number divided into two equal parts and into two unequal parts, [the sum of] the squares of the unequal parts is equal to twice [the sum of] the square of half the [whole] number and the square of the difference between the large part and the half [of the whole number]
|
עוד כל מספר שחלקת אותו לשני חלקים שוים ושני חלקים בלתי שוים הנה שני המרובעים אשר יהיו מהחלקים הבלתי שוים הם כפל שני המרובעים אשר יהיו מחצי המספר ומהתוספת אשר לחלק הגדול על המחצית |
|
|
דמיון יש לנו מספר מנינו עשרה וחלקנוהו לשני חלקים שוים על ה' ושני חלקים בלתי שוים על ג' וז' הנה מרובע ג' שהוא ט' ומרובע ז' שהוא מ"ט שניהם נ"ח הם כפל מרובע ה' שהוא כ"ה והוא מחצית המספר וכפל מרובע ב' שהוא
ד' ושניהם כ"ט שהוא התוספת שיש לז' שהוא החלק הגדול על הה' שהוא המחצית |
| Euclid, Elements, Book II, proposition 10: If you divide any number into half and add to it another number, [the sum of] the square of the whole number plus the additional [number] and the square of the additional [number] is equal to twice [the sum of] the square of half the number and the square of half the number plus the additional [number] together
|
עוד כל מספר שחלקת אותו לשני חציים והוספת עליו מספר אחר הנה מרובע המספר עם התוספת יחד ומרובע התוספת בעצמו הם כפל שני המרובעים שהם מרובע חצי המספר ומרובע חצי המספר עם התוספת יחד כאשר יחוברו |
|
|
דמיון יש לנו מספר מניינו עשרה וחלקנוהו לשני חצאים על הה' והוספנו עליו מספר אחר ב' ונהיה י"ב הנה מרובע י"ב שהוא המספר עם התוספת יחד קמ"ד ומרובע ב' שהוא התוספת ד' ושניהם קמ"ח והוא כפל מרובע ה' שהוא כ"ה ומרובע ז' שהוא מ"ט ושניהם ע"ד אשר הוא מרובע חצי המספר והתוספת ביחד |
| הנה הודעתיך דרכים נאותים במספרים מועילים כי כאשר יהיו דרכים מתחלפים מוציאים אל חשבון אחד כאשר יטעה מהדרך האחד יתיישר מהדרך האחר ותרגיל עצמך בהם |
Part Three: Division & Sum |
החלק השלישי לחלק מספר על מספר ולהוסיף מספר על מספר |
|---|---|
Chapter One: Division |
הפרק האחד |
| אמר מרדכי הקדמנו זה השער
משאר הערכי' להיותו קודם בטבע מן הערכי' ופשוט ממנו אם קודם בטבע כי לא נוכל למצוא בערכים הגבול האחד מהשנים או מהשלשה אם לא בדרך הכפל והחלוקה כאשר יתבאר בשער אשר נזכירם .. ואם פשוט ממנו להיות השער ההוא מורכב מזה ומהמיוחד לו וזה השער מיוחד בזה משניהם והנה החלוקה הזאת עושים אותה בעלי החשבון על שני דרכים הדרך האחת כאשר הזכירה החכם ר' אברהם ן' ע' עז' ז"ל . והדרך השנית היא אשר קורים אותה הלועזים גליאה בלשונם ופירושו דוגית . ואני אזכיר הנה גם שתי הדרכים : הדרך הראשונה היא כאשר תרצה לחלק מספר על מספר בין שיהיה אחד על רבים או רבים על אחד או רבים על רבים כתוב המספר אשר רצית לחלקו ראשונה וראוי שיהיה לעולם המספר המתחלק יותר מהמחולק עליו בשלימים אחר תכתוב המספר אשר תרצה לחלק עליו בטור השפל וריוח תשים בין העליון והשפל כדי שתשים ביניהם העולה בחלוק והשמר שתכתוב המספר השפל במדרגותיו כנגד מדרגות הטור העליון כל אחד כנגד הנכחי לו אחר תתחיל לחלק מהכלל היותר גדול ותחשבהו כאלו הם אחדי' ותחלקהו על הכלל היותר גדול שבטור השפל ואם הכלל היותר גדול שבטור העליון כשתחשבהו במספר אחדים יהיה יותר מעט מהטור מהכלל שבטור השפל החזירהו אחורנית ואז יהיה יותר גדול מהכלל שבטור השפל ותחלק עליו וראה ואם המספר אשר תחלק עליו הוא מהמדרגה הראשונה כתו' העולה בחלוק במדרגה האחרונה ואם הוא במדרגה השנית כתוב העולה בחלוק במדרגה השנית אח אחורנית ר"ל השנית לאחרונה וכן על זה הסדר . ואם ישאר שום מספר אשר בכללי הטור הראשון אשר לא יכול להתחלק במדרגתו השיבהו אחורנית וחשבהו עשרה ר"ל כל אחד מהנשארי' אשר לא יכול להתחלק וחברהו עם המדרגה הקרובה לו השפלה ממנו וחלקהו וכן אם ישאר גם מזאת המדרגה ככה תעשה עד שתגיע למדרגת האחדים . וכן ראוי שתדע שאם היו המספרים אשר תחלק עליהם רבים וכשחלקת הכלל שבטור הראשון על הכלל שבטור השני לא נשאר דבר אין ראוי שתתן לו כל החלקים אבל תשאיר חלק אחד כדי שתשיבהו אחורנית ותחלקהו גם על שאר המספרים שבטור השפל וכן בכל מדרגה ומדרגה . דמיון רצינו לחלק ד' אלפים ורט"ו על י"ד כזו הצורה 5 1 2 4 חלקנו הד' שבטור העליון שהוא במדרגת האלפים על האחד שבטור השפל שהוא במדרגת 1 0 3 העשרות ונתננו לו ג' כדי שנוכל לחלק גם על הד' האחדים ואלה הג' כתבנום במדרגה השנית 4 אחורנית תחלתה מהכללים לפי שהאחד אשר חלקנו עליו היה במדרגה השנית מהאחדים . עוד הא' הנשאר השיבונוהו אחורנית לעשרה וחברנוהו עם הב' אשר במדרגת המאות ונהיו י"ב חסרנו מהם הד' אחדים ג' פעמים ולא נשאר דבר ומפני שלא נשאר דבר להיותו מקושר וכן עדיין לא יצא בחוץ כתבנו ספרא אחרי הג' במדרגת העשרות עוד שבנו לחלק הט"ו שבטור העליון על הי"ד שבטור השפל ונתננו לו אחד וכתבנוהו במדרגה הראשונה ממדרגת האחדים מפני שגם המחולקים הם במדרגה הד' ממדרגת האלפי' ונשאר אחד בלתי מתחלק ומזה ידענו שהחלק הוא ג' מאות וא' ונשאר גם חלק אחד אשר לא נחלק .. דמיון אחר רצינו לחלק ק' אלפי' וסיפ' וד' אלפי' וסיפ' ול' וד' על קי"ד כזה 4 3 0 4 0 1 השיבונו האחד שבטור העליון שהוא במדרגת העשר רבבות אל י' אחורנית 2 1 9 במדרגת הרבבות ונתננו לחלק ט' הוצאנו ט' פעמי' אחד ממנו נשאר אחד ואלף 4 1 1 הט' כתבנום במדרגה הג' אחורנית מן הכלל המתחלק כי חלקנום על אחד שהוא ב במדרגה השלישית מן האחדים והאחד אשר נשאר במדרגת הרבבות השיבונוהו נ אחורנית י' במדרגת האלפים וחברנוהו עם הד' אשר שם ונהיו י"ד גרענו עוד מהם ט' פעמי' אחד שהוא במדרגת העשרו' ונשארו ה' במדרגת האלפי' . עוד גרענו מהם ד' פעמי' ט' שהם האחדים שבטור השפל והם ל"ו ולא הספיקו השיבונו הד' אחורנית לעשרות במדרגת המאות ונהיו מ' גרענו מהם הל"ו נשארו ד' במדרגת המאות וא' במדרגת האלפי' . עוד שבנו לחלק הא' שבמדרגת האלפים והד' שבמדרגת המאות על הקי"ד שבטור השפל ונתננו אחד לחלק וכתבנוהו במדרגה השנית אחרי הט' . גרענו א' מהא' אשר במדרגת האלפי' ולא נשאר דבר במדרגת האלפים . עוד גרענו הא' אשר במדרגת העשרות מהד' אשר במדרגת המאות נשארו ג' במדרגת המאות עוד גרענו הד' האחדים שבטור השפל מהג' שבמדרגת המאות ולא הספיקו ולכן [החזר]נו הא' אחורנית לעשרה וחברנום עם הג' הג' א אשר במדרגת העשרות ונהיו י"ג ובמדרגת המאות נשארו ב' גרענו הד' מהי"ג נשארו ט' במדרגת העשרות עוד שבנו לחלק הב' אשר נשארו במדרגת המאות והט' אשר נשארו במדרגת העשרות על הקי"ד ונתננו ב' לחלק וכתבנוהו במעלת האחדים והוצאנו ב' פעמי' א' מהט' מהט' ונשארו במדרגת העשרות ז' עוד הוצאנו ב' פעמי' ד' מהד' שבטור העליון ולא הספיק ולכן החזרנו א' מהז' שהיו על מדרגת העשרות אחורנית לעשר וחברנום עם הד' שבטור העליון ונהיו י"ד וגרענו מהם הח' ונשארו במדרגת האחדים ו' וו' במדרגת העשרות וידענו מזה שנחלק מספרינו לתשע מאות וי"ב חלקים ונשארו גם [..] [.] ס"ו אשר לא נחלקו . וראוי לך לדעת שכאשר תחלק המספרים שבטור העליון על כל המספרים שבטור השפל וקודם שתצא לחוץ הותרו ולא היה לשם השארות שיקשרו עם הבאים אחריהם אז ראוי לך להשים בצד החלקים שחלקת סיפ' ואחר כשתתחיל לחלק הבאים תכתבם בצד הסיפ' כאשר עשינו בדמיון הראשון אשר למעלה מזה דמיון אחר רצינו לחלק ה' אלפי' וד ור"ד ורי"ד על ק' וסיפ' וח' כזה 4 1 2 5 נתננו לחלק ד' כדי שיספיק וכתבנוהו במדרגה השלישית אחורנית כי האחד אשר 8 4 חלקנום עליו היה במדרגה השלישית ממדרגת האחדים גרענו ד' פעמים אחד ממנו 8 0 1 ונשאר א' במדרגת האלפים עוד גרענו ד' פעמים ח' שהם ל"ב מהא' ולא הספיק והשיבונו אחורנית לעשרות ונהיו י"ב כי חברנום עם הב' שבמדרגת המאות ועדיין אינו מספיק להוציא מהם ל"ב השיבונו אחורנית הד' מהי"ב לעשרות וחברנום עם הא' אשר במדרגת העשרות ונהיו מ"א ונשארו במדרגת המאות ח' וגרענו הל"ב ממ"א ונשארו ט' במדרגת העשרות עוד שבנו לחלק הח הח' על הא' ונתננו לו ח' וכתבנום במדרגה הראשונה מהאחדי' גרענו ח' מהח' עוד נשארו ח' גרענו ח' פעמי' ח' שהם ס"ד מהט' שהם במדרגת העשרות ולא הספיקו ולכן השיבונו אחורנית הו' אל האחדים ונהיו ס' ונהיו וחברנום עם הד' שבטור העליון ונהיו ס"ד וגרענו מהם הס"ד ונשארו ג' במדרגת העשרות וידענו מזה שהחלק הוא מ"ח ונשארו גם ס' אשר לא חלקנום . זאת היא הדרך האחת מהשתי דרכים מדרכי החלוקה .. והדרך השנית והיא אשר תקרא בלשנם גליאה היא דרך שרוב הסוחרים משתמשים בה והיא שתכתו' המספרי' אשר תרצה לחלק אותם בטור העליון . והמספרים אשר תרצה לחלק עליהם בטור השפל ולא תכתבם במדרגתם כנגד העליונים אבל אי זו מדרגה שיהיו כתוב הכולל שלהם תחת הכולל שבטור הראשון והמספר הבא אחריו כנגד המספר אשר בצד הכולל אחר תתחיל לחלק הכולל שבטור העליון על הכולל שבטור השפל ולא תתן לו מה שתמצא ואם אין המספרים אשר בצדו מספיקים לחלקם על המספרים אשר תחלק עליהם תשאיר אחד או יותר לפי מה שתצטרך ותעיין כמה פעמי' הוא נכנס בו ר"ל הכולל בכולל או הכולל בכולל אחר שהשארת ממנו אם השארת וכמספר הפעמי' אשר יכנס בו כתוב במקום מיוחד המספר ההוא ותכה עם המספר הזה הכתוב במקום המיוחד את הכולל מהמספרים אשר תחלק עליהם ותגרעהו מכולל המספר הנחלק והנשאר אם ישאר כתו' אותו למעלה ממנו ותמחוק האחר עוד תכה עם המספר הכתו' במקום המיוחד את המספר הבא אחר הכולל מהמספר אשר תחלק עליו ותגרעהו מהמספר הבא אחדר הכולל מהמספרים הנחלקים ותעשה כמשפט וכן תעשה עד שתחלק על כל המספרי' אשר תחלק עליהם ואם לא הספיק המספר הנחלק לגרוע ממנו תחזיר את האחד הנשאר או היותר אם היו אחורנית לעשרות ותחלקם על המספר אשר תחלק עליהם וכן תעשה עד שתוציא כל המספרי' הנחלק עליהם בחלוקה עוד תשוב לכתו' המס' -פרים אשר תחלק עליהם ותרד מדרגה אחת ותתחיל משם ותכתוב כסדר ותראה כמה פעמי' הוא נכנס הכולל מהמספרי' אשר תחלק עליהם במספר השני הבא אחר הכולל במספרי' הנחלקי' והמספר ההוא ר"ל כמות הפעמי' כתבהו בצד המספר אשר כתבת במקום המיוחד והכה עמו כל המספרי' אשר תחלק עליהם ועשה כמשפט ותוציא הנכפל מהמספרי' אשר תחלק עליהם מהראשון שבמספרי' המוחלקי' הנשארים ותמחוק המספר הכתו' ואשר ישאר כתבהו עליו וכן תעשה עד שתצא בחוץ ואם בתוך המספר קודם שתצא בחוץ הוצאת כל המספרי' אשר חלקת עליהם מהמספרי' ההם ולא נשאר דבר כתו' סיפ' בחוץ לשם שאתה כותב החלקים בצד החלק אשר אתה בו עוד תשוב לחלק המספרי' הבאים עד שתצא בחוץ וה והחלקי' כתבם בצד הסיפ' . דמיון רצינו לחלק ד' אלפי' ורט"ו על י"ד כזאת הצורה 1 0 3 כתבנו אותם בטור העליון והי"ד בטור השפל והתחלנו מהמדרגה היותר כוללת 4 1 ושמנו גם קו אחד יורד בצד המספרים וראינו כמה פעמי' נכנס א' בד' ומצאנו שנכנס ד' פעמי' ולא נתננו לו כל הד' אבל נתננו לו ג' כדי שיספיק לחלק גם על השאר והג' כתבנום בחוץ בצד הקו היורד וגרענו הא' ג' פעמי' מהד' ונשאר אחד ומחקנו הד' וכתבנו למעלה במדרגתו אחד עוד מצאנו הוצאנו הד' ג' פעמי' שהם י"ב מזה האחד הנותר אחר שהשיבונוהו אחורנית לי' וחברנוהו עם הב' ונהיו י"ב ולא נשאר דבר ומפני שלא נשאר דבר קודם שנצא בחוץ כתבנו בצד הג' סיפ' עוד שבנו לחלק הט"ו שלמעלה על הי"ד ומחקנו הי"ד ממקומם וכתבנום תחת הט"ו ^ כי הותרו הי"א ואינם קשורים אחר שיצאנו בצמצום ונתננו חלק אחד לאחד וכתבנוהו בצד הסיפ' ונשאר חלק אחד בלתי מתחלק כי הוצאנו האחד מן האחר ומחקנו את שתיהם והוצאנו הד' מן הה' ונשאר א' ומחקנו את שתיהם וכתבנו האחד למעלה וידענו מזה שנחלק לש' וסיפ' וא' חלק ונשאר גם אחד בלתי מתחלק .. דמיון אחר רצינו לחלק ק' אלף וסיפ' וד' אלפי' וסיפ' ול"ד על קי"ד כזה .. 6 2 השיבונו הא' שבמספרי הטור העליון הכולל לעשרות וכתבנוהו 7 3 1 במדרגת העשרות הרבבות ולכן כתבנו הקי"ד ממנו כי הוא לא הספיק 8 9 4 7 1 וראינו שהמספר אשר נחלק עליו נכנס בו ט' פעמי' וכתבנו הט' בחוץ בצד הקו היורד בחוץ כפלנו הא' עם הט' ונהיו ט' גרענום מן הי' שבמדרגת הרבבות נשאר א' במדרגת הרבבות ומחקנו הא' שבטור השפל עו' כפלנו הט' עם הא' השני שבטור השפל ונהיו ט' החזרנו אחורנית את הא' שבמדרגת הרבבות לי' וחברנוהו עם הד' שיש שם במדרגת האלפי' ונהיו י"ד גרענו מהם הט' ונשארו ה' במדרגת האלפי' עוד כפלנו הד' שבטור השפל על הט' ונהיו ל"ו והחזרנו הד' מהה' שבמדרגת האלפי' לעשרות על מדרגת המאות ונשאר אחד במדרגת האלפי' ומחקנו הה' וכתבנו במקומו א' והנשאר והד' אשר החזרנו נהיו מ' וגרענו מהם הל"ו ונשארו ד' במדרגת המאות וכתבנום ומחקנו גם הד' שבטור השפל ומפני שהחשבון לא יצא בחוץ עדין שבנו עוד וכתבנו הקי"ד כל אחד מהם קודם מדרגה אחת ממה שכתבנום בפעם הראשונה ורצינו לחלק האחד אשר בטור העליון במדרגת האלפי' עם המספרי' אשר בצדו עליהם וראינו שהם נכנסי' בו פעם אחת וכתבנו אחד בחוץ בצד המספר אשר בצד הקו היורד בחוץ כפלנוהו עם הא' שבטור השפל ונהיה א' גרענוהו מן האחד שבמדרגת האלפי' ומחקנוהו וגם מחקנו גם זה האחד עוד כפלנו הא' שבחוץ עם האחד השני שבטור השפל וגרענוהו מהד' שבמדרגת המאות ונשארו ג' ומחקנו הד' וכתבנו במקומם ג' וכן מחקנו גם האחד . עוד כפלנו האחד שבחוץ עם הד' שבטור השפל ונהיו ד' רצינו לגרעם מן הג' הכתובי' במדרגת העשרות ולא הספיקו ולכן השיבו נו מן הג' שבמדרגת המאות אחד אחור אחורנית לעשרות ומחקנום וכתבנו במקומם ב' והי' חברנום עם הג' שבמדרגת העשרות ונהיו י"ג גרענו מהם הד' נשארו ט' במדרגת העשרות ומחקנו הג' וכתבנו ט' במקומם וכן מחקנו גם הד' שבטור השפל עוד מפני שעדיין לא יצא החשבון בחוץ שבנו וכתבנו הקי"ד מדרגה אחת קודם המדרגה שכתבנום בפעם השניה וראינו כמה פעמי' הם נכנסי' בחשבון הנשאר אשר לא נתחלק עדין ומצאנו שנכנסי' ב' פעמי' ולכן כתבנו בחוץ בצדי צד הקו היורד מחוץ ב' כפלנו אותם עם הא' שבטור השפל ונהיו ב' גרענום מהב' אשר במדרגת האלפי' ולא נשאר דבר ומחקנו אותם וגם הא' שבטור השפל . עוד כפלנו הב' עם הא' השני שבטור השפל ונהיו ב' גרענום מהט' שבטור העליון הכתו' במדרגת העשרות ונשארו ז' מחקנו הט' וכתבנו ז' במקומם וכן מחקנו גם הא' השני שבטור השפל עוד כפלנו הב' עם הד' שבטור השפל ונהיו ח' ומפני שלא הספיקו לגרעם מן הד' שבטור העליון במדרגת האחדים השיבונו מן הז' אחד אחורנית לי' ומחקנו הז' וכתבנו במקומם ו' והי' חברנום עם הד' ונהיו י"ד וגרענו מהם ח' ונשארו ו' ומחקנו את הד' וכתבנו במקומם ו' וכן מחקנו גם הד' שבטור השפל ומזה ידענו שנחלקו לתתקי"ב חלק ונשארו גם ס"ו אשר לא נתחלקו .. מאזנים על דרך הט' תכפול מאזני המספר אשר חלקת עליו עם מאזני החלקי' אשר כתבת אותם באמצע לפי הדרך הראשון ולפי הדרך השנית הם אשר כתבת אותם בצד הקו היורד בחוץ ואחר שתכפלם השליכם ט' ט' ואשר שישאר תשמור אותו . וזה אם לא נשאר מהמספר אשר חלקת אותו שום דבר אשר לא נתחלק אבל אם נשאר קח גם המאזנים שלו וחבר אותם עם ה[מספר] אשר שמרת ואם יעדיפו מהט' תשליך הט' והנשאר הוא השמור האמתי אחר תעיין גם אל מאזני המס[פרים] שחלקת אותם ואם הם שוים עם השמור אפשר שחשבונך אמת . ואם לאו דע בודאי שטעית .. מאזנ[ים] אחרי' ע"ד הז' תחשב כללי המספר אשר חלקת עליהם עם אשר בצדם כאלו הם עשרות ואחדים והשליכם ז' ז' ואשר נשאר תחשבהו עוד לעשרות והמספר הבא אשר בצדו לאחדי' והשליכם ז' ז' עד שתגיע למדרגת האחדים ואשר ישאר יקרא מאזני המספר אשר חלקת עליו עוד כן תעשה במאזני החלקים והם אשר כתבתם באמצע בדרך הראשונה ובחוץ בצד הקו היורד בדרך השנית והשליכם ז' ז' ואשר ישאר יקרא מאזני החלקים אחר תכפול מאזני המספר אשר חלקת עליו על מאזני החלקים ואשר יהיה השליכהו ז' ז' ואשר ישאר שמרהו ויקרא השמור וזה אם לא נשאר במספרי' אשר חלקת אותם מספר אשר לא נתחלק אכן אם נשאר מספר אשר לא נתחלק קח גם מאזני המספר ההוא אשר לא נתחלק בכזה הדרך והשליכהו ז' ז' והנשאר חברהו עם השמור ואז יקרא השמור באמת אחר תעיין אל מאזני המספרי' אשר חלקת אותם וזה כשתוציאם בכזה הדרך ותשליכם ז' ז' ואשר ישאר אם הוא שוה לשמור באמת אפשר שחשבונך יהיה אמת ואם לאו דע בודאי שטעית .. מאזנים אחרי' שהם מאזני צדק תכפול החלקי' אשר באמצע בדרך הראשונה או בצד הקו היורד בחוץ בדרך השנית עם המספר אשר חלקת עליו ואשר יהיה אם הוא שוה עם המספרי' אשר חלקת אותם אם נחלקו הכל או אם לא נחלקו הכל אם הוא שוה להם אחר אשר תגרע מהם המספרים אשר לא נחלקו אז תדע בודאי כי חשבונך אמת ואם אין דע בודאי שטעית |
Chapter Two: Progression |
הפרק השני להוסיף מספר על מספר כסדרו או על סדר אחר |
|---|---|
| הרוצה להוסיף מספר על מספר
כסדרו יכפל אותו על חציו בתוספת חצי אחר והעולה הוא המבוקש .. דמיון רצינו להוסיף המספרי' שהם מא' עד י' זה על זה כפלנו הי' בה' ונהיו נ' עוד הוספנו ה' שהוא חצי הי' ונהיו נ"ה וזהו המבוקש .. דמיון אחר לנפרדי' רצינו לדעת כמה תוספת המספרי' זה על זה מא' עד ט' והנה חציו ד' וחצי הוספנו על זה עוד חצי האחר ונהיו ה' כפלנו הט' בה' ונהיו מ"ה וזהו המבוקש ועל אלו שתי הדמיונים כל המספרי' .. ואם תרבע כל המספר ותוסיף עליו שרשו וקח מחציתו והוא המבוקש . דמיון כפלנו הי' על עצמו ונהיו ק' הוספנו עליו השרש שהוא י' ונהיה ק"י וחצים נ"ה וזהו המבוקש .. אמר מרדכי מצאתי דרך אחרת נכבדת מאד והוא שתכה תכלית המספר המבוקש עם המספר הבא אחריו וחצי ההווה הוא המבוקש דמיון רצינו לדעת כמה תוספת המספרי' שהם מא' עד י' הכינו הי' עם הי"א שהוא המספר הבא אחריו ונהיו ק"י וחציו נ"ה והוא המבוקש .. שאלה אם ישאלך אדם חברתי מספרי' והיו נ"ה כמה היו המספרי' . תשובה כפול הנ"ה על ב' וקח השרש המרובע שעבר וראה ואם הוא שוה למספר הנשאר מהמרובע שעבר כמו הם היו מספרי' . המשל כפלנו הנ"ה והיו ק"י והמרובע שעבר ק' ושרשו י' והמספר הנשאר מהמרובע שעבר שהוא ק' עוד כפל הנ"ה שהם ק"י י' וא"כ המספרי' שחברת והיו נ"ה הם י' .. שאלה חברתי מד' עד י' כמה יהיו . תשובה תעשה כמשפט הראשון ותמצא נ"ה אחר תחבר מא' עד ג' ותמצא ו' גרע אותם מנ"ה ונשארו מ"ט וזהו המבוקש .. ואם ישאלך אדם כמה הם מרובעי המספרים עד מספר פלו' על הסדר . תשיב שימצאם חבורם בפשוטיהם ואחר יכה אותה בשני שלישי תכלית המספר המבוקש עם תוספת שליש אחד ואשר יהיה הוא המבוקש .. דמיון כמה הם המרובעים המחוב' -רים מא' עד ד' כפלנו אותם בחציים עם תוספת חצי אחר ונהיו י' עוד לקחנו ב' שלישי ד' עם תוספת שליש אחר והם ג' הכינו אותם עם הי' ונהיו ל' וזהו המבוקש |
Part Four: Proportions & Fractions |
החלק הד' לערך מספר על מספר |
|---|---|
| זה השער נדבר בו על השלימי' כי לנשברי' יש דרך אחרת נבאר אותה בפרק הבא ונאמר שעם
היות שהאמצעיים הם י' אבל הקדמוני' לא בחרו רק ג' מיני הערכים והם ערכי החשבון וערכי המדות וערכי הנגוני' . ואנחנו לא נזכיר הנה רק ערכי המדות כי הם צורך לרוב השאלות הנעשות בחשבון .. וכבר התבאר בחכמת השיעור כי ההתיחסות לא תתכן בפחות מג' גבולים ואם הגבול האמצעי הוא בעד שני גבולין ולכן ההתיחסות תפול בד גבולי' מפני זה כל מספרי' ארבעה אשר יחס הראשון אל השני כיחס הג' אל הד' אם תחבר מרובע ארבעתם יהיה שוה למרובע הראשון והד' מחוברי' ומרובע ההפרש שיש בין השני והשלישי . וכן אם תחבר מרובע השני והשלישי יחד עם מרובע ההפרש שיש בין הראשון לרביעי יהיה שוה בחשבון וכן כאשר הומרו היו מתיחסי' כיחס הב' אל הג' יהיה כיחס הב' אל הד' ומפני זה מהג' הידועים נדע הרביעי המוסכל וכבר נהגו בעלי החשבון לכתו' המוסכל בקצה האחרון לעולם בין שיהיה מהאמצעיים ובין שיהיה הקצה הראשון ובלבד שידע איך יסדר האחדים . דמיון שאם שאל שואל שאם הח' ירויחו ד' הו' מה ירויחו ובשאלת המה ישים הגלגל כזה 8 4 6 0 . הנה נקראו האמצעיים הד' והו' ושתי הקצוות הח' והגלגל . כפלנו ב' האמצעיים ונהיו כ"ד חלקנום על הקצה הידוע שהם ח' ונהיה החלק ג' ומזה ידענו שבמקום הגלגל צריך ג' והוא המבוקש . וכן אם הפך הסדר ושאל אם הד' הרויחו אותם הח' . מהו שירויחו הו' ועתה נהיו הב' אמצעיים הח' והגלגל כזה 4 8 0 6 והנה כשנפל שני הקצוות ונחלקהו על האמצעי הידוע נמצא האמצעי המוסכל כפלנו ד' על הו' ונהיו כ"ד חלקנום על ח' ונהיה החלק ג' וזהו המבוקש . וכן אם הפך השאלה ושם הגלגל ראשונה ואמר מה ירויחו הו' אם הח' ירויחו ד' כזה 0 6 8 4 . נכפול הקצה הידוע עם האמצעי אשר בצד המוסכל ונחלקהו על האמצעי אשר בצד הקצה הידוע ונמצא המוסכל . ואע"פ שכל אלה הם דרך נכונה אבל לעולם בעלי החשבון יהפכו הגלגל אל הקצה האחרון בלבד שישמרו הסדר עד שיהיו המרויחים במקומם והריוח במקומו וכן אם היו מדות ודינרים שיהיו המדות במקומם והדינרי' במקומם ויזהר שלא יחליף ויטעה . דמיון אם שאל שואל שאדם אחד מוכר חטה ז' מדות בי"ב פשוטי' כמה מדות יתן בי"ד פשוטי' ראוי להפך השטה לבד שישמר הסדר ושיכתוב הסדר כך אם י"ב פשוטי' נתנו ז' מדות הי"ד פשוטים מה יתנו ואז נ נופל הגלגל בתכלית האחד ולעולם כזה הסדר 1 2 7 1 4 0 הוא כופל האמצעיים ומחלק אותם על הקצה הראשון ולומד הקצה האחרון וכאשר תחלק הכפול על הנחלק עליו ולא יצא בצמצום אבל נשאר חשבון אשר לא נתחלק תעיין ואם זה החשבון אשר לא נתחלק הוא תחת כפלי החשבון אשר נתחלק עליו דע כי הוא חלק ממנו לפי הפעמי' אשר ישערהו כי אם ישערוהו ב פעמים הוא מחציתו ואם בג' פעמי' הוא שלישיתו וכיוצא בם ואם לא יהיה תחת כפליו אם תרצה תוציא ממנו חלק אשר יהיה תחת כפליו והשאר השיבהו אל הפרטי' או אם תרצה השב הכל אל פרטים וחלקהו ואם ישאר עוד השיבהו אל פרטי פרטים עד שיצא בצמצום או עד שיצא דבר שאין חשש בו . דמיון שאלנו אם הי"ב דינרי' נתנו ז' דינ' ריוח הי"ד דינ' כמה יתנו . וכתבנוהו כך 1 2 7 1 4 0 כפלנו האמצעיים ונהיו צח צ"ח חלקנום על הקצה האחד שהם י"ב ונהיה החלק האחד ח' ונשארו גם ב' אשר לא נתחלקו ומפני שאלה הב' הם תחת כפלי הי"ב וישערום בו' פעמי' ידענו מזה שהמבוקש הוא ח' וששית . אבל אם שאל אם הי"א דינ' נתנו ז' דינ' ריוח הי"ד מה יתנו כתבנוהו כך 1 1 7 1 4 0 כפלנו האמצעיים ונהיו צ"ח חלקנום על הי"א ונהיה החלק ח' ונשארו גם י' אשר לא נתחלקו השיבונו אותם אל פרטי' שהם י"ב בדינר ונהיו ק"כ חלקנום על י"א ונהיה החלק י' י' פשוטי' ונשארו עוד י' בלתי מתחלקים השיבונום אל פרטי פרטים שהם גם הם י"ב בפרוטה ונהיו ק"כ חלקנום על י"א ונהיה החלק האחד י' ונשארו הי' בלתי מתחלקי' ומפני שאין בם חששא הנחנום וידענו מזה שהחלק הא' הוא ח' דינ' וי' פרוטו' מי"ב בדינ' וי' פרטי פרוטו' מי"ב בפרוטה ודבר שאין בו חששא וזהו הריוח אשר יתנו הי"ד דינ' ואלה הם אשר יקראו אותם בעלי ג' הצורות . אולם יש שאלות אחרות אשר יקראו אותם בעלי ה' צורות והם אשר ישתף השואל דבר אחד עם כל אחד מהיחסי' כגון זמן וכיוצא ואז הם נכתבי' ככה .. דמיון אם אדם שכר ו' אנשי' לעבוד עמו ג' ימי' בח' דינ' ועבדו עמו הד' בשני ימי' כמה יקחו . אע"פ שאין ספק שזה מחובר מב' ערכים אל ג' צורות אבל בעלי החשבון נתנו דרך למצוא הכל בתשובה אחת להקל על המחשב כאלו הוא ערך אחד וקראו אותו בעלי ה' צורות ונעשה ככה 6 3 8 4 2 0 אנו כופלי' את הקצה הראשון עם הימים אשר בצדו ומה שיהיה הוא היסוד אשר אנו חולקי' עליו את השאר כאשר נראה כפלנו הו' בג' ונהיו י"ח והוא היסוד אחר כפלנו הח' בד' ונהיו ל"ב עוד הל"ב בב' ונהיו ס"ד חלקנו הס"ד על הי"ח ונהיה החלק האחד ג' ונשארו גם י' בלתי מתחלקי' השיבונו הי' אל הפרוטות אשר הם י"ב באחד ונהיו ק"כ חלקנום על הי"ח ונהיה החלק האחד ו' פרוטות ונשארו גם י"ב בלתי מתחלקי' השיבונו הי"ב אל פרוטי פרוטות אשר הם י"ב באחד ונהיו קמ"ד חלקנום אל הי"ח ונהיה החלק באחד ח' וידענו מזה שהד' האנשי' בב' הימי' אשר עברו יקחו ג' דינ' וו' פרוטות וח' פרוטי פרוטות לפי חשבון התנאי אשר התנה לעבד עמו הו' אנשים בג' ימים ולקחת ח' דינ' | |
| החלק הנפרד המדבר על הנשברי' | |
| אמר מרדכי להיות שהחשבון הוא מהכמה
המתחלק והשברי' הם שברי הכמה המתדבק . והמתחלק עם המתדבק הם ב' הפכי' כי זה יקבל התוספת אל בלתי תכלית ולא יקבל החלוקה אל בלתי תכלית כי יעמוד באחד וזה יקבל החלוקה אל בלתי תכלית כי אי אפשר להיות הגודל מחובר מחלקי' אשר לא יתחלקו לכן היה משפט השברי' הפך משפט השלימי' כי כפל השלימי' הוא יותר מהמספרי' אשר יכפלו וכפל השברי' הוא פחות מהממספרי' אשר יכפלו ומפני שהאחד הוא אמצעי בין השלימי' ובין השברי' לכן היה כפלו כמוהו כי ימשך אל שתי צדדיו בשווי . ומפני שהשברים בגודל יסכימו עם החלקים שהם בכלל אחד מקובץ לקחו השם מהם כי השם החצי נגזר משנים והשלישית משלשה והרביעית מארבעה ולכן יהיה המורה מהם כאשר נבאר אחר יחלקו על מרובע [המורה] ויצא המבוקש . דמיון שאל השואל כפל שלישית על שלישית כמה יהיה והנה המורה ט' כי כפלנו ג' על ג' . ומרובעו פ"א חלקנו המורה על מרובעו ועלה תשיעית אחת ומזה ידענו שכפל שלישית על שלישית יהיה תשיעית . וכן אם היו ב' שלישיות על ב' שלישיות המורה ט' כי כפל שלישית על שלישית המורה שלו ט' ומרובעו פ"א ומפני שהשלישיות היו ב' על ב' לקחנו בעד הב' שלישיות ו' וכן ו' בעד הב' שלישיות האחרי' כפלנו ו' על ו' ונהיו ל"ו חלקנום על פ"א ונהיה החלק האחד שלישית ותשיעית וזהו המבוקש . דמיון אחר שאל שואל כמה ג' רביעיות הכפולות על ד' תשיעיות הנה המורה ל"ו כי כפל ד' על ט' ככה ומרובעו אלף רצ"ו ומפני ש שהרביעיות היו ג' לקחנו י"ב בעדם כי ג' פעמי' ד' הם י"ב ומפני שהתשיעיות הם ד' לקחנו ל"ו בעדם הכינו הי"ב עם הל"ו ונהיו תל"ב חלקנום על מרובע המורה שהם אלף רצ"ו ונהיה החלק האחד שלישית אחד ומזה ידענו שהמבוקש הוא שלישית אחד . אבל בעלי החשבון לוקחי' החשבון המורה באופן יותר נקל כי זה המורה הוא רב החשבון ועושי' ככה כשישאלו על כפל שלישית אחד על שלישית אחד כותבי' האחד למעלה ואחר הם מתויכים עם קו וכותבי' השלישית למטה וככה יעשו בשלישית האחרת כזו הצורה 1 1 וכופלים האחד על האחד ונהיה אחד אח"כ יכפלו הג' על הג' ונהיו ט' 3 3 אחר רואים מה ערך האחד אל הט' והוא המבוקש .. דמיון אחר כמה ב' שלישיות הכפולות על ד' רביעיות כתבנו הב' למעלה והשלישיות למטה והתיכנו עם קו אחד וכן עשינו בד' רביעיות כזה 2 4 כפלנו הב' עם הד' ונהיו ח' עוד כפלנו הג' שלמטה עם הי הד' אשר למטה ונהיו י"ב אחר 3 4 עייננו מה ערך הח' אל הי"ב והם שני שלישיים וידענו מזה שהמבוקש הם שני שלישיות אחד .. ואם רצינו לכפול שלימי' ונשברי' עם שלימי' ונשברי' אנו כותבים אותם ככה השלימי' ובצדם הנשברים וכן אם נרצה לכפול עליהם אחר אנו משברי' השלימי' בכזה האופן . אנו מכים חלקי המתדבק עם השלימי' כמו שאם היו גם הם שלימי' ואנו מחברי' גם מספר החלקי' עמהם ואז שבו כלם נשברים כזה כמה הם ה' שלימי' וג' רביעיות הכפולי' על ד' שלימי' וב' שלשיות והנה הצורה 5 3 הכינו הד' שהם חלקי מורה המתדבק עם הה' שלימי' ושבו כ' חברנו גם הג' שהם מספר 4 הרביעיות ונהיו כ' וג' רביעיות עוד הכינו הג' שהם מורה חלקי המתדבק עם הד' השלימי' 4 ונהיו י"ב חברנו גם הב' עמהם ונהיו י"ד שלישיות והנה הראשוני' כ"ג רביעיות ואלה י"ד שלישיות הכינו אלה עם אלה והיו שכ"ב עוד הכינו הד' עם הג' שהם מורה השלישיות והרביעיות ונהיו י"ב ראינו מה ערך השכ"ב אל הי"ב והם כ"ז פחות ששית וידענו מזה שכפל ה' שלימי' וג' רביעיות על ד' שלימי' וב' שלישיות הם כ"ז פחות ששית . זאת היא הדרך אשר נהגו בעלי החשבון להתנהג בהיות שם שברי' עם שלימי' בין שהיו שלימי' לבד עם שלימים ושברי' ובין שהיו שלימי' ושברי' עם שלימי' ושברי' ובין שהיו שלימי' לבד עם שברי' לבד . אמנם בהיות שלימים לבד עם שברי' לבד יש ג"כ דרך אחרת והיא שנקח בעבור השלימי' מורה במספרי' ונכה אותו עם מספר חלקי השברי' ונחלקהו על המורה שנקח מהשברי' והעולה הוא המבוקש . דמיון כמה ב' שלימי' הכפולים על ג' רביעיות לקחנו בעד הב' שלימי' ב' והוא המורה שלהם כפלנום עם ג' שהוא מספר חלקי השברי' נהיו ו' חלקנום על ד' שהוא המורה שלקחנו מהשברי' ונהיו אחד וחצי וזהו המבוקש . ואם רצית לערך שברי' על שברי' בין שיהיו שלימי' עם כל אחד מהם או עם האחד לבד ראוי בתחלה לשבור השלימי' ולעשותם שברי' כפי המין אשר היו השברי' הדביקים עמהם וככה תכתבם 2 2 3 4 4 3 תכה בתחלה הב' שלימי' עם הג' שהוא מורה השלישיות ונהיו ו' 3 4 6 0 אחר תחבר גם הב' עמהם שהוא מספר השלישיות ונהיו ח ח' שלישיות עוד הכינו הג' שלימי' עם הה' שהוא מורה החמשיות ונהיו ט"ו חברנו גם הד' עמהם שהם מספר החמשיות ונהיו י"ט חמשיות עוד הכינו הד' שלימי' עם הו' שהם מורה הששיות ונהיו כ"ד חברנו גם הג' שהם מספר הששיות עמהם ונהיו כ"ז ששיות כי השאלה היתה אם הב' מדות וב' שלישיות יתנו לנו ג' דינרי' וד' חמשיות הד' מדות וג' ששיות כמה יתנו ושבה השאלה עתה אם הח' שלישיות יתנו לנו י"ט חמשיות הכ"ז ששיות כמה יתנו ואחר שהשיבונו השאלה אל השברי' אנו כותבי' אותם כך 5 7 אלף תקל"ט אחר אנו מכים אותם כדמות מספריי' ואנו מכי' הח' עם הה' ונהיו 1 9 מ' ואנו כותבי' אותם תחת הה' עוד אנו מכי' המ' עם הו' ונהיו ר"ם 8 2 7 ואנו כותבי' תחת הו' וזהו המספר אשר נחלוק עליו עוד אנו מתחילי' 3 5 6 להכות הג' עם הי"ט ונהיו נ"ז ואנו כותבי' אותם על הי"ט עוד אנו מכים 0 4 0 4 2 הנ"ז עם הכ"ז ונהיו אלף תקל"ט אח"כ אנו מחלקי' אותם על הר"מ ונהיו ו' שלימי' וב' חמשיות וחלק אחד מפ' וזהו המבוקש אשר יתן לנו החשבון הדרוש . אבל אם החשבון יהיה בעל חמש צורות כגון שישתף השואל דבר אחר עם שאלתו כגון זמן וכדומה לו כאשר בארנו בשלימי' אז נכתו' אותו ככה .. דמיון שאל השואל אם ב' רביעיות דינר בד' שמיניות היום שהם י"ב שעות כי שמינית היום ג' שעות הרויחו ג' רביעיות דינר הד' רביעיות בד' שמיניות היום כמה ירויחו . וזה צורתו 8 9 6 3 8 4 || 1 5 3 6 אז נכפול הב' עם הד' שהם בטור העליון והם מספר 2 4 3 4 || 4 0 הרביעיות והשמיניות ונהיו ח' אחר הכינו הח' עם הד' 4 8 4 4 || 8 שבטור השפל שהוא תחת הג' ונהיו ל"ב וכתבנום תחתיהם 3 2 3 4 1 2 8 || 1 0 2 4 עוד הכינו הל"ב עם הד' אשר בצדם שהם תחת הד' שבטור העליון ונהיו קכ"ח וכתבנום תחתיהם עוד הכינו הקכ"ח עם הח' אשר בצדם ונהיו אלף כ"ד וכתבנום תחתיהם ואלה הם היסוד אשר נחלוק עליהם עוד אנו מכים הד' עם הח' שבטור השפל ונהיו ל"ב ואנו כותבים אותם תחתיהם עוד אנו מכים הד' הל"ב עם הג' שבטור העליון ונהיו צ"ו ואנו כותבים אותם תחתיהם עליהם עוד אנו מכים (...) השפ"ד עם הד' אשר בצדם ונהיו אלף תקל"ו ואנו כותבי' אותם עליהם אח"כ אנו מחלקי' אותם על האלף וכ"ד ויצא החלק אחד וחצי וידענו מזה שזהו החשבון המבוקש אשר ירויחו הד' רביעיות בד' שמיניות היום כי ירויחו דינר אחד וחצי . דמיון אחר לזה רצינו לדעת אם הב' שלישיות דינר בד' חמשיות היום ירויחו ו' שביעיו' הח' תשיעיות בז' עשיריות כמה יתנו וכתבנום ככה 4 9 0 || 7 2 0 7 8 0 כפלנו הב' עם הד' שבטור העליון ונהיו ח' וכתבנום 2 4 5 || 8 0 1 עליהם עוד הכינו הח' עם הז' שהוא שלישי לטור השפל 3 5 7 || 9 0 1 0 ונהיו נ"ו וכתבנום תחת הז' שבטור השפל עוד הכנו הכינו 5 6 || 5 0 4 5 0 4 0 הנ"ו עם הט' ונהיו תק"ד וכתבנום תחת הט' . עוד הכינו התק"ד עם הי' ונהיו ה' אלפי' ומ' וכתבנום תחת הי' ואלה הם היסוד אשר נחלוק עליהם עוד חזרנו והכינו את הג' עם הה' שבטור השפל ונהיו ט"ו וכתבנום למטה תחת הה' אחר הכינו את הט"ו עם הו' שבטור העליון שהוא השלישי ונהיו צ' וכתבנום על הו' עוד הכינו הצ' עם הח' ונהיו תש"כ וכתבנום על הח' עוד הכינו התש"כ עם הי' ונהיו ז' אלפי' ור' חלקנו אותם על היסוד שהם ה' אלפי' מ' ונהיה ח החלק אחד ושליש וחלק אחד מי' וידענו שזהו אשר ירויחו הח' תשיעיות דינר בז' עשיריות היום אם הב' שלישיות דינר הרויחו ו' שביעיות בד' חמשיות היום. זו הדרך אשר ישתמשו בה הסוחרי' וכל בעלי החשבון באלה שתי מיני הצורות לשברים . ר"ל בבעלי הג' צורות ובעלי הה' מיני צורות לשברי' הה' צורות . אולם יש דרך אחרת גם היא נכונה אבל יצטרך לחלק ג' פעמי' והיא זאת . דמיון בבעלת הג' צורות הראשונה שהשאלה היא אם הח' שלישיות יתנו לנו י"ט חמשיות הכ"ז ששיות כמה יתנו אנו כותבים אותם כמשפט הראשון עם הקו המתויך כך 8 1 9 2 7 אחר אנו מכים מספר החלקים שבטור העליון השני עם השלישי ואנו מחלקים 3 5 6 0 אותם על הראשון וכן נעשה גם בטור השפל אחר כן אנו מחלקי' מה שיצא מן החלק בטור העליון על מה שיצא מן החלק בטור השפל והיוצא הוא המבוקש . דמיון הכינו הכ"ט הי"ט עם הכ"ז ונהיו תקי"ג חלקנו אותם על הח' ונהיה החלק האחד ס"ד ושמינית ושמרנום עוד הכינו הה' עם הו' שבטור השפל ונהיו ל' חלקנו אותם על הג' ונהיה החלק האחד י' אחר כן חלקנו הס"ד ושמינית השמורים על הי' ונהיה החלק האחד ו' שלימי' וב' חמשיות וחלק אחד מפ' . דמיון אחר על בעלת ה' צורות הראשונה שהשאלה היא אם ב' רביעיות דינר בד' שמיניות היום הרויחו ג' רביעיות דינר הד' רביעיות בד' שמיניות היום כמה ירויחו וכתבנום כמשפט הראשון ככה כפלנו הב' על הד' שבטור העליון ונהיו ח' 2 4 3 4 4 ושמרנום כי על אלה הח' נחלוק כפל המספרי' הנשארים אשר בטור העליון 9 8 4 4 4 0 אח"כ כפלנו הג' שבטור העליון על הד' שבטור העליון אשר בצדו ונהיו י"ב עוד כפלנו הי"ב עם הד' אשר בצדם ונהיו מ"ח חלקנו אותם על הח' השמורים ונהיה החלק האחד ו' ושמרנום עוד כפלנו הד' על הח' שבטור השפל ונהיו ל"ב ושמרנום כי על אלה הל"ב נחלוק כפל המספרים הנשארים אשר בטור השפל אח"כ כפלנו הד' על הד' אשר בטור השפל בצדם ונהיו י"ו עוד כפלנו הי"ו עם הח' אשר בצדם ונהיו קכ"ח ח' חלקנו אותם על הל"ב השמורים ונהיה החלק האחד ד' אח"כ חלקנו הו' אשר שמרנום על אלה הד' ונהיה החלק אחד וחצי ומזה ידענו שהריוח אשר ירויחו הד' רביעיות דינר בד' שמניות היום הוא אחד וחצי דינר גם הב' רביעיות בד' שמיניות הרויחו ג' רביעיות דינר .. ואם רצית לקבץ שברים עם עם שברים אתה צריך לעשות מורה מהם ולהביט השברים ההם על אותו המורה ולערך אותם על המורה ואז תדע כמה יהיה הסך . דמיון אם שאל שואל קבצנו ב' שלישיות עם ג' רביעיות כמה יהיו הכינו הג' עם הד' ונהיו י"ב והוא המורה וב' שלישיותיו ח' וג' רביעיותיו ט' ושניהם מקובצים י"ז תערכם אל הי"ב שהוא האחד השלם יהיו אחד שלם ושליש וחלק אחד מי"ב . וכן אם היו מיני השברי' יותר ככה תעשה .. דמיון קבצנו ב' שלישיות וג' רביעיות וד' חמשיות כמה יהיה המקובץ כפלנו ג' על ד' ונהיו י"ב עוד כפלנו הי"ב על הה' ונהיו ס' והוא המורה וב' שלישיותיו מ' וג' רביעיותיו מ"ה וד' חמשיותיו מ"ח והכל מקובצי' קל"ג ערכנו אותם על ס' שהוא המורה והוא האחד השלם ונהיו שנים שלימי' וחמשית אחת וחלק אחד מס' וכן אם תרצה לקבץ יותר מאלה כך תעשה כמשפט הזה . ואם תרצה לחלק נשברי' על נשברים בקש מורה אחד לשניהם וקח ממנו כמספר החלקים הדרושים וחלק זה על זה והעולה הוא המבוקש . דמיון רצינו לחלק ד' תשיעיות על ה' שביעיות והמורה הוא ס"ג כי ט' פעמי' ז' הם ס"ג וד' תשיעיות הם כ"ח וה' שביעיותיו הם מ"ה חלקנו הכ"ח על המ"ה ונהיו חצי אחד ותשיעית אחד וחלק א' מס' וזהו המבוקש . ואם היו שלימי' שם עם שברי' תעשה ככה בקש השלם המורה והוא האחד השלם ועליו תביט את מספר החלקים ותכפלם כמספרו ותחבר גם השברים עמהם וכן תעשה גם במספר אשר תחלוק עליו אח"כ חלק זה על זה והעולה הוא המבוקש . דמיון רצינו לחלק ג' שלימי' וב' חמשיות על ב' שלימי' וד' שביעיות אחד והמורה ל"ה כי ה' פעמי' ל"ה הם ז' הם ל"ה והוא האחד השלם והג' שלימי' הם ק"ה כי ג' פעמי' ל"ה הם ק"ה והב' חמשיות הם י"ד כי חמשית הל"ה הם ז' חברנום עם הק"ה ונהיו קי"ט עוד שמנו הב' שלימי' האחרי' ע' והד' שביעיות כ' כי שביעית הל"ה הם ה' חברנום עם הע' ונהיו צ' חלקנו עליהם הקי"ט ונהיה אחד שלם ונשארו כ"ט חלקי' שהם ב' תשיעיות מן הצ' ועשירית אחד . וכן אם רצית לחסר שברי' משברי' ככה תעשה בקש המורה בתחלה וראה חלקיו וחסר אלה מאלה . דמיון רצינו לחסר ב' שביעיות מד' תשיעיות והמורה הוא ס"ג . (וב' שביעיותיו י"ח) וד' תשיעיותיו כ"ח תחסר י"ח מכ"ח ונשארו י' שהם פחות מששית מעט | |
| ועתה ארגילך בענין השאלות כדי שתהיה זריז בחשבונך | |
| מקום השאלות | |
| א כמה ט' פעמי' מי"ג הכפולים על י"ז חלקי' מי"ט | |
| כי אלה אין להם ערך מדובר לכן ראוי שתדע איך תכפול ומה תעשה | |
| ראוי שנדע בתחלה המורה והנה נכפל י"ג על י"ט יהיו רמ"ז והוא המורה אח"כ נקח לכל אחד מט' חלקים י"ט נהיו קע"א והוא המספר האחד | |
| ואם תרצה לדקדקו חלק קנ"ג על י"ט יהיה החלק ח' חלקי' מי"ג וישאר שבר א' שהוא שבר אלפי' תשצ"א חלק מי"ט | |
| או אם תרצה חלקנו זה קנ"ג על י"ג ויהיו י"א חלקי' שלימי' מי"ט וי' נשברי' שי"ג מהם עושה חלק אחד מי"ט | |
| ב שאלה דרך חברנו אליה רביעיתה וחמשיתה והיתה י' מילין כמה היתה הדרך | |
| נשים המורה כ' כי ד' פעמי' ה' הם כ' ורביעיתו וחמשיתו הם ט' נחברם עם המורה נהיו כ"ט | |
| ג שאלה לקחנו תשיעית ממון ועשיריתו וחלק אחד מי"א ממנו כמה הוא כל זה מערך הממון | |
| והנה זה נקל הוא מי שידע לחבר השברים כאשר כתבנו בחבורם וכן נעשה נבקש מורה והוא שנכפול ט' על י' ונהיו צ' עוד צ' על י"א ונהיו תתק"ץ וזהו המורה | |
| ד שאלה ממון הוספנו עליו מחציתו שלישיתו חמשיתו וששיתו ובין הכל היו ס' כמה היה הממון | |
| ידענו שהחצי והשלישית והששית הוא אחד שלם ונחשב שהיה לו אחד והיה לו עתה שנים וחמשית נחלק הס' על הב' וחמשית וכך היה הממון | |
| ה שאלה אדם רוכב ראה איש מושך סוסים וא"ל אנה אתה מוליך אלה הק' סוסים והשיב לו אלה ואחרים כמותם ומחציתם ורביעיתם ועם הסוס שאתה רוכב הם ק' כמה היו הסוסים | |
| הנה נוציא הסוס שרוכב זה ונשארו צ"ט יש לנו שנים ומחצית ורביעית ומפני שיש לנו רביעית נשיב הכל לרביעיות והנה הב' שלימי' הם ח' רביעיות והמחצית ב' הרי י' נחבר גם הרביעיות שיש לנו עמם נהיו י"א רביעיות | |
| ו שאלה אדם קנה כ"ד ליט' בכ"ד דינ' ומכר הי"ב ליט' ורביע ליט' בדינר והי"ב ליט' מכר ליט' פחות רביע ליט' בדינר נבקש לדעת אם הרויח או הפסיד | |
| נשיב הי"ב ליט' הראשוני' לרביעיות ונהיו מ"ח נחלקם על ה' כי ה' רביעיות מכר בדינר ונהיו ט' וחצי ועשירית ואלה הם הדינ' שלקח מהי"ב ליט' הראשונים | |
| ז שאלה אדם קנה ג' חמשיות ליט' בפשוט ומכר ד' שביעיות ליט' בפשוט והרויח פשוט כמה היה ממונו | |
| נבקש המורה והוא ל"ה וג' חמשיותיו כ"א וד' שביעיותיו כ' והממון היה כ' פשוטי' כי בכל פשוט ירויח חלק אחד מכ' בפשוט וכשימכור של כ' פשוטי' ירויח פשוט אחד | |
| שאלה אדם קנה ט' חלקים מי"ז חלקי' ליטר' בפשוט ומכר י' חלקי' מי"ט בפשוט והרויח פשוט כמה היה הממון | |
| נבקש המורה והוא שנכפול י"ז על י"ט ונהיו שכ"ג וידוע כי ט' חלקי' מי"ז הם קע"א וככה היה הממון וי' חלקי' מי"ט הם ק"ע והנה הרויח הפשוט | |
| ח שאלה ממון חברנו שלישיתו רביעיתו חמשיתו והיו ל' כמה הוא כל הממון | |
| נבקש המורה והוא ס' ושלישיתו כ' ורביעיתו ט"ו וחמשיתו י"ב וכלם מ"ז הנה כערך מ"ז אל ס' כן ערך ל' אל כל הממון | |
| ט שאלה אם אנשים ה' נתן האחד ו' דינ' והשני ז' דינ' והשלישי ח' והרביעי ט' דינ' והחמשי י' דינ' והרויחו בין הכל י"א דינ' כמה יקח כל אחד מהם | |
| הנה אלה הי"א דינ' הרויחו אותם כל הדינ' מקובצי' ונראה אותם כמה הם אח"כ נשיב אותם אל הערך של כל אחד ואחד וכפי ערך ממונו ככה יקח | |
| ונכתו' הערך של הראשון ככה אם המ' דינ' הרויחו י"א הו' כמה ירויחו | |
| עוד נכתו' הערך של השני ככה אם המ' דינ' הרויחו י"א הז' דינ' כמה ירויחו | |
| עוד נכתו' הערך של השלישי ככה אם המ' דינ' הרויחו י"א דינ' הח' דינ' כמה ירויחו | |
| עוד נכתו' הערך של החמשי ככה אם (המ') דינ' הרויחו י"א הי' כמה ירויחו | |
| וכשתקבץ כל החלקי' שיקחו הכל תמצאם י"א לא פחות ולא יתר | |
| דרך אחרת למצוא זה תעשה הי"א דינ' שהם הריוח כלם פשוטי' ותחלקם על מ' ותראה כמה ריוח יגיע לכל דינר מהמ' | |
| והריוח ההוא תכפול אותו עם הו' ואשר יהיה ככה יגיע לבעל הו' | |
| עוד תכפול אותו עם הז' ואשר יהיה ככה יגיע לבעל הז' | |
| וכן תעשה עם הח' והט' והי' | |
| י שאלה יש אצל הקונה שלשה מטבעים והלך אצל המוכר לקנות ליט' אחת משי והמטבע האחת היתה שווה ג' דינ' והמטבע השנית היתה שוה ד' דינ' והמטבע השלישי' היתה שוה ו' דינ' ואמ' הקונה תן לי ליט' משי וקח מג' מטבעותי בשווי עד שתקח מה ששוה הליט' כמה יקח מכל מטבע ומטבע | |
| נבקש המורה והוא ע"ב כי כפל ג' על ד' י"ב וכפל י"ב על ו' ע"ב ושלישיתו כ"ד ורביעיתו י"ח וששיתו י"ב והכל נ"ד וזהו הדינ' | |
| ואם תרצה לדעת איך הוא כך כך תחשוב שרוצה לקחת ל"ו פרוטות ממטבע ששוה ג' דינ' ולקח ממנו י"ו פרוטות וכשלקח עוד י"ו פרוטות ממטבע ששוה ד' דינ' כאלו לקח י"ב פרוטו' ממטבע ששוה ג' דינ' כערך הד' אל הג' נחבר הי"ב עם הי"ו ונהיו כ"ח | |
| יא שאלה אדם התנה עם אומן לבנות לו אצטבא ו' באורך ו' וו' ברוחב ויתן לו ח' דינ' והוא בנה לו ג' בארך וג' ברחב כמה יתן לו | |
| אין ספק כי יתן לו הרביעית שהוא ב' דינ' כי
כפל חצי על חצי הוא רביעית אחד שאלו היה בונה כל האורך עם חצי הרוחב או ההפך היה נותן לו המחצית אבל אם התנה עמו שיבנה לו ה' בארך ו' ברוחב ז' בגובה ויתן לו ח' דינ' והוא בנה ד' בארך וה' ברחב וו' בגובה כמה יתן לו אז ראוי שנחבר כל מספרי התנאי ונשיבם אל הערכים וכן מספרי הבניין חברנו תחלה מספרי התנאי ונהיו י"ח עוד חברנו מספרי הבניין ונהיו ט"ו ועשינו הערך ככה אם אם הי"ח יתנו ח' דינ' הט"ו כמה יתנו 1 0 8 1 5 0 כפלנו האמצעיים ונהיו ק"כ חלקנום על הי"ח שהוא הקצה ונהיה החלק ו' וב' שלישיות וככה יקח | |
| יב שאלה אדם אחד שכר ג' אחים ראובן שמעון לוי לעבוד אחד מהם עמו ב' ימי' ואם יעבוד ראובן עמו כל הב' ימי' יתן לו ו' דינ' ואם יעבוד שמעון לבדו יתן לו ד' דינ' ואם יעבוד לוי לבדו יתן לו ג' דינ' עתה בין הכל עבדו ב' ימי' ובאחרונה פרע לכל חלק שוה כמה פרע כל אחד ואחד וכמה שעות עבד כל אחד ואחד | |
| נבקש המורה והוא
ע"ב כי כפל ו' על ד' הם כ"ד ואלה על ג' הם ע"ב וששיתו ושלישיתו ורביעיתו הם נ"ד הנה כערך ע"ב אל נ"ד ככה יקח מהדינרי' וערך ע"ב אל נ"ד הוא אחד ושליש וככה יקח כל אחד ואחד נבקש לדעת כמה שעות עבד כל אחד ואחד ונשיבהו אל הערכים ונשיב הדינ' שלישיות מפני השליש שעודף על הדינר והיום י"ב שעות ונעשה ערך ראובן כך אם הי"ח שלישיות כ"ד שעות הד' שלישיות כמה יתנו 1 8 2 4 4 0 נכפול האמצעיים ונהיו צ"ו נחלקם על י"ח ונהיה החלק ה' שעות ושליש וככה עבד ראובן .. ונעשה ערך שמעון כך אם הי"ב שלישיות כ"ד שעות הד' שלישיות כמה יתנו 1 2 2 4 4 0 כפלנו האמצעיים והם צ"ו חלקנום על י"ב ונהיה החלק ח' שעות וככה עבד ראובן שמעון .. ונעשה ערך לוי כך אם הי"ו שלישיות יתנו [..] כ"ד שעות הד' שלישיות כמה יתנו כפלנו האמצעים ונהיו צ"ו 6 2 4 4 חלקנום על ט"ו ונהיה החלק י' שעות וב' שלישיים וככה עבד לוי חבר כל השעות שעבדו שלשתם ותמצאם כ"ד שעות שהם ב' ימים .. הזה בסוף השאלה הט' עיין הטב | |
| Boiling Problem | |
|
יג שאלה אדם אחד היה מבשל משקה ו' מדות ורצה שישאר השליש ונחסרה המדה האחת בבשול אחד נשפכה מדה אחת ונשארו הד' מדות ורוצה להשיבם להשאירם כמשפט הראשון |
| נשיבם אל הערכים ככה אם הה' מדות יתנו ב' הד' כמה יתנו 5 2 4 0 | |
|
|
נכפל האמצעיים ונהיו ח' נחלקם על הקצה שהוא הה' ונהיה החלק אחד וחצי ועשירית וככה ראוי שישאר |
| יד שאלה יריעה ק' אמות והתחיל למנותה ראובן מן הקצה האחד ושמעון מן הקצה האחד וראובן מונה י' אמות בשעה ושמעון י"ב מתי יפגשו | |
| נחבר שני המניינים אשר הם כ"ב אמות בשעה ונחלק הק' אמות עליהם ונהיה
החלק ד' וחצי וחלק אחד מכ"ב מכ"ב וידענו שבד' שעות וחצי וחלק מכ"ב בשעה יפגשו שניהם על המניין ואם תרצה לדעת כמה אמות מנה ראובן תכפול י' בד' וחצי וחלק א' מכ"ב ואשר יעלה כן מספר האמות אשר מנה ראובן . וכן אם תרצה לדעת כמה מנה שמעון תכפול תכפול הד' שעות וחצי וחלק מכ"ב על י"ב ואשר יעלה כך מספר האמות אשר מנה שמעון | |
| טו שאלה חבית מליאה יש בה ג' נקבים אם תפתח הא' יכלה החבית בחצי היום ואם תפתח השנית יכלה בשלישית יום ואם תפתח השלישית יכלה ברביעית יום ואם פתחת גם הג' ביחד בכמה שעות יכלה החבית אתה צריך לדעת בכמה שעות יכלה החבית | |
| אתה צריך לדעת כי היום י"ב שעות וכן החבית כמה
מדות מכילה ונניח שמכילה מ"ח מדות והנה בפתיחת הנקב האחד יכלה בו' שעות שהם ח' מדות בשעה ובפתיחת הנקב השני יכלה בד' שעות שהם י"ב מדות בשעה . ובפתיחת הנקב הג' יכלה בג' שעות שהם י"ו מדות בשעה תחבר כל המדות אשר יכלו בשעה אחת והם ל"ו תחלק המ"ח ע על הל"ו יהיה אחד ושליש והנה בשעה אחת ושליש תכלה הכל . ונעשה הערכים ככה אם הל"ו שעה אחת המ"ח על כמה יהיה 3 6 1 4 8 0 נכפול האמצעיים והם מ"ח נחלקם על הקצה שהם ל"ו ונהיה החלק אחד ושלישית | |
| טז שאלה רומח חציו במים שלישיתו בעפר ולמעלה ו' אמות כמה גבהות כל הרומח | |
| נבקש המורה והוא ו' וחציו ושלישיתו ה' ה' נגרעם מן הו' ונשארו
א' נכפול הו' עם הו' שהם האמצעיים ונחלקם על הא' שהוא הקצה נהיה ל"ו וככה גובה הרומח .. וחציו י"ח ושלישיתו י"ב הרי ל' ולמעלה ו' ונעשה הערך כך אם הא' יתנו ו' הו' כמה יתנו .. 1 6 6 0 | |
| יז שאלה אילן חמשיתו בעפר וששיתו במים ולמעלה מהמים ז' אמות כמה גבהות כל האילן | |
| הנה המורה ל' וחמשיתו וששיתו י"א נגרעם מל' שהוא המורה נשארו י"ט נכפול האמצעיים שהם הז'
בל' נהיו ר"י נחלקם על י"ט ונהיו י"א חלקים וחלק אחד מי"ט וככה גבהות האילן ונעשה הערך כך 1 9 3 0 1 0 | |
| יח שאלה אם היו שני מגדלים גובה הא' ס' אמה וגובה השני מ' אמה והמרחק שביניהם נ' אמה ובראש כל מגדל צפור יושב ובין המגדלים בריכת מים ועפים הצפרים בהתעופפות שוה ויורדים ושותים בזמן שוה ועולים בזמן שוה כמה מרחק הבריכה מיסוד כל מגדל | |
| נחבר מרובע מ' שהוא אלף ת"ר עם מרובע נ' שהוא אלפים ות"ק נהיו ד' אלפי' ק' אח"כ נקח
מרובע ס' שהוא ג' אלפי' ות"ר ונגרעם משתי המרובעים הנזכרים שהם ד' ק' ונשארו ת"ק והוא המורה נכפול גם מרחק שני המגדלים שהוא נ' על ב' ונהיו ק' נחלקם המורה עליהם ונהיו ה' וככה מרחק הבריכה מן המגדל שגובהו ס' אמו' ומהמגדל האחר המ"ה אמות הנשארות | |
| יט שאלה ג' אנשים אשר הלכו בשוק לקנות דג אחד האחד אמר אני אתן כל מה שיש לי ואתם תנו החצי ממה שיש לכם ונקנה הדג . אמר השני אני אתן כל מה שיש לי ואתם תנו שליש ממה שיש לכם ונקנה הדג .. אמר הג' אני אתן כל מה שיש ואתם תנו הרביע ממה שיש לכם ונקנה הדג | |
| כתוב דבר הקונים החצי
והרביע כזה 2 3 4 אח"כ תאמר מהו כאשר תקח חציו ממנו ישאר ג' כמספר הקונים והנה הוא ו' כתוב 6 4 4 אותו תחת הב' . עוד תאמר מהו כאשר תקח שלישיתו ממנו ישאר ג' כמספר הקונים והנה הוא ד' וחצי כתוב אותו תחת הג' עוד תאמר מהו כאשר תקח רביעיתו ממנו ישאר ג' כמספר הקונים והנה הוא ד' ת . כתבהו תחת הד' . כפול הכל עם הב' ותאמר ב' פעמי' ו' הם י"ב עוד ב' פעמי' ד' וחצי הם ט' עוד ב' פעמי' ד' הם ח' חבר הכל הם כ"ט וזהו המורה כפול הראשון שהוא י"ב עם ב' וחסרהו מן המורה נשארו ה' וכך יש לראשון בכיסו . כפול השני שהוא ט' עם הב' וחסרהו מן המורה נשארו י"א וכך יש לשני בכסו . כפול השלישי שהוא ח' עם ב' וחסרהו מן המורה ונשארו י"ג וכך יש לשלישי בכסו נמצא שקנו הדג בי"ז . ואם תרצה לבחון זה תביט כי הראשון נתן כל מה שיש לו והיו ה' והם נתנו החצי שיש להם ומה שיש להם הם כ"ד כי השני יש לו י"א והג' י"ג והחצי י"ב תחברם עם הה' והוא י"ז והוא מחיר הדג . עוד השני נתן כל אשר לו והם י"ח והראשון והשלישי נתנו השליש ממה שיש להם והם ו' כי לשניהם י"ח לראשון ה' ולשלישי י"ג חבר הי"א עם הו' ונהיו י"ז והוא מחיר הדג . עוד השלישי נתן כל אשר לו והם הי"ג והראשון עם השני נתנו ד' שהוא הרביע ממה שיש להם כי לראשון ה' ולשני י"א והם י"ו והוא מחיר הדג | |
| כ שאלה אדם אחד הוציאו עליו שטר חוב ד' אנשים הראשון שאם יעבוד עמו חדש ימי' יתן לו י' זהובי' והשני שאם יעבוד עמו חדש ימים יתן לו ה' זהובים שהם מחציתם והשלישי שאם יעבוד עמו חדש ימים יתן לו ג' זהובים ושליש שהם שלישיתם .. והד' שאם יעבוד עמו חדש ימים יתן לו ב' זהובים וחצי שהוא רביעיתם ועבדו כלם החדש בשלימות ולא פרע לשום אחד ומת ולא נמצא לו יותר מי' זהובים בכל אשר היה לו | |
| הנה חכמי החשבון יתנו לכל אחד כפי ערך ממונו . והנה המורה כ"ד כי תכפול הב' על הג' והם ו' .
עוד הו' על הד' הם כ"ד ובזה ימצאו כל החלקי' הנשארי' ונשים האחד השלם כ"ד כי הוא המורה וכשתחבר אליו חציו ושלישיתו ורביעיתו יהיה בין הכל נ' ונעשה הי' זהובים ק"כ פשוטי' מי"ב פשוטי' בזהוב ונעשה ערך הראשון כך אם הנ' יתנו לו כ"ד כ"ד הק"כ מה יתנו לנו 5 0 2 4 1 2 0 0 נכפול האמצעיים ונהיו ב' אלפים תת"פ נחלקם על הנ' שהוא הקצה נהיה החלק נ"ז פשוטים וחצי פשוט ועשירית פשוט וזהו חלק הראשון בעל הי' זהובים . ונעשה ערך השני כך אם הנ' יתנו לנו י"ב הק"כ מה יתנו לנו 5 0 1 2 9 2 0 0 נכפול האמצעיים ונהיו אלף ת"מ נחלקם על הנ' שהוא הקצה ועלו כ"ח פשוטי' וחצי פשוט וחמשית פשוט ועשרית פשוט וזהו החלק השני בעל הה' זהובים ונעשה ערך השלישי ככה אם הנ' יתנו ח' הק"כ כמה יתנו 5 0 8 1 2 0 0 נכפול האמצעיים ונהיו תתק"ס נחלקם על הנ' שהוא הקצה יהיו י"ט פשוטי' וחמשית פשוט וזהו חלק השלישי בעל ג' זהובים ושליש ונעשה ערך הרביעי ככה אם הנ' יתנו ו' הק"כ כמה יתנו 5 0 6 1 2 0 0 נכפול האמצעיים ונהיו תש"כ נחלקם על הנ' שהוא הקצה ונהיו י"ד פשוטי' וב' חמשיות פשוט וזהו חלק הרביעי בעל הב' זהובי' וחצי וכשתחבר כל כל אלה החלקים יעלו ק"כ פשוטי' שהם י' זהובי' . ואם לא תרצה להשיב הכל אל הערכים מפני הטורח תעשה כך אחר שידעת חלק הראשון מן הערכי' תן מחציתו לשני ושלישיתו לשלישי ורביעיתו לרביעי . ושוה יהיה זה וזה | |
| וכן תוכל אתה לעשות שאלות אחרות עד אין קץ ותוכל להשיב
עליהם אם תדע ואם תדע הכללים שהקפנו בהם בזה החבור ולא הזכרתי דרך מציאות שרשי המרובעי' הנה כי אינם צורך בזה החבור ואחרתים עד מקומם ושם אבארם אם יחפוץ הנותן ליעף כח | |
| תם ונשלם שבח לבורא עולם .. אבגדה גם |
Appendix: Bibliography
Mordecai ben Eliezer Comṭino
Constantinople & Adrianople c. 1402-1482
Sefer ha-Ḥeshbon we ha-Middot
Manuscripts:
- 1) Berlin, Staatsbibliothek (Preußischer Kulturbesitz) Or. Qu. 308 (IMHM: f 1734), (15th-16th century)
- 2) London, British Library Add. 27107/6 (IMHM: f 5782), ff. 44r-80v (cat. Margo. 1016, 6); (15th-16th century) (Book 2)
- 3) New York, Jewish Theological Seminary Ms. 2616 (IMHM: f 28869), (19th century) (Book 2)
- [NY2616]
- 4) New York, Jewish Theological Seminary Ms. 2632 (IMHM: f 28885), (19th-20th century)
- [NY2632]
- 5) New York, Jewish Theological Seminary Ms. 2633 (IMHM: f 28886), (16th century)
- [NY2633]
- 6) New York, Jewish Theological Seminary Ms. 2639 (IMHM: f 28892), (1478)
- [NY2639]
- 7) Oxford, Bodleian Library MS Heb. d. 5/1 (IMHM: f 22729), ff. 1r-17r (Cat. Neub. 2774, 1); (1522)
- 8) Paris, Bibliothèque Nationale de France heb. 1031/3 (IMHM: f 15723), ff. 26r-64v (15th-16th century)
- 9) St. Petersburg, Russian National Library Evr. I 320b (IMHM: f 50984) (1495)
- 10) St. Petersburg, Russian National Library Evr. I 343-344 (IMHM: f 50961, f 41596, f 41597) (Istanbul, 1485)
Bibliography:
- Schub, Pincus. 1932. A Mathematical Text by Mordecai Comtino, Isis vol. XVII, no. 1, (1932), pp. 54–70.
- Silberberg, Moritz. 1905–1906. Ein handschriftliches hebräisch-mathematisches Werk des Mordecai Comtino, Jahrbuch der Jüdisch-Literarischen Gesellschaft III, pp. 277–292.
- Steinschneider, Moritz. 1893–1901. Mathematik bei den Juden. Berlin-Leipzig-Frankfurt: Kaufmann, pp. 197-198 (h63-h64); repr. Hildesheim: G. Olms, 1964 and 2001.
![\scriptstyle\sum_{k=1}^n \left[\left(\sum_{i=1}^n a_i\right)\sdot a_k\right]=\left(\sum_{i=1}^n a_i\right)^2](/mediawiki/images/math/2/a/1/2a190390030d9c138d548197fab10837.png)
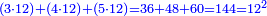
![\scriptstyle\left[\left(a+b\right)\sdot a\right]+\left[\left(a+b\right)\sdot b\right]=\left(a+b\right)^2](/mediawiki/images/math/9/c/9/9c9305cbc3ba9b0e4edc1ee228e83fa9.png)

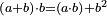
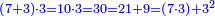
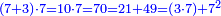
![\scriptstyle\left(a+b\right)^2=a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]](/mediawiki/images/math/7/2/7/727b0c35fd93a7a347bed8413905049f.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle
3^2+7^2+\left[2\sdot\left(3\sdot7\right)\right]&\scriptstyle=9+49+\left(2\sdot21\right)=9+49+42\\&\scriptstyle=100=10^2\\&\scriptstyle=\left(3+7\right)^2\\\end{align}}}](/mediawiki/images/math/8/4/8/8485bf1fc7542ef51ab16602c07e9c8b.png)
![\scriptstyle\left(a\sdot b\right)+\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]^2=\left(a\sdot b\right)+\left[b-\left[\frac{1}{2}\sdot\left(a+b\right)\right]\right]^2=\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2](/mediawiki/images/math/c/e/d/ceda777c2ea9424440ecf784d4535ff0.png)
![\scriptstyle{\color{blue}{\scriptstyle\left(3\sdot7\right)+\left[\left(\frac{1}{2}\sdot10\right)-3\right]^2=\left(3\sdot7\right)+\left(5-3\right)^2}}](/mediawiki/images/math/0/3/d/03dfdce3ec288d58b8f094e10b1397f2.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left(3\sdot7\right)+\left[7-\left(\frac{1}{2}\sdot10\right)\right]^2&\scriptstyle=\left(3\sdot7\right)+\left(7-5\right)^2\\&\scriptstyle=\left(3\sdot7\right)+2^2\\&\scriptstyle=21+4=25=5^2=\left(\frac{1}{2}\sdot10\right)^2\\\end{align}}}](/mediawiki/images/math/3/9/8/398cace15239fa9433c0a2f9fcf38677.png)
![\scriptstyle\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2](/mediawiki/images/math/a/0/b/a0b403dd8b7c15a5cb1dc47a5f8ca5bb.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left[2\sdot\left(10+2\right)\right]+\left(\frac{1}{2}\sdot10\right)^2&\scriptstyle=\left(2\sdot12\right)+5^2\\&\scriptstyle=24+25\\&\scriptstyle=49=7^2=\left(5+2\right)^2\\&\scriptstyle=\left[\left(\frac{1}{2}\sdot10\right)+2\right]^2\\\end{align}}}](/mediawiki/images/math/6/0/9/6096e9f7553e21c7650a3ee7d05439b9.png)
![\scriptstyle\left(a+b\right)^2+a^2=2\sdot\left[\left(a+b\right)\sdot a\right]+b^2](/mediawiki/images/math/5/e/f/5ef738b800e1b84fc257df70a83fb86b.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle10^2+7^2&\scriptstyle=100+49=149\\&\scriptstyle=140+9\\&\scriptstyle=\left[2\sdot\left(7\sdot10\right)\right]+3^2\\\end{align}}}](/mediawiki/images/math/5/a/0/5a0e68f34ec6e37d68c92ab618338648.png)
![\scriptstyle4\sdot\left[\left(a+b\right)\sdot a\right]+b^2=\left[\left(a+b\right)+a\right]^2](/mediawiki/images/math/f/6/2/f62f5f20431f619df80a01a1d97e57cf.png)
![\scriptstyle{\color{blue}{\scriptstyle\left[4\sdot\left(10\sdot7\right)\right]+3^2=280+9=289=17^2=\left(10+7\right)^2}}](/mediawiki/images/math/2/d/9/2d930b3cf54ef8cfc52718dc74fc4c81.png)
![\scriptstyle a^2+b^2=2\sdot\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2+\left[a-\left[\frac{1}{2}\sdot\left(a+b\right)\right]\right]^2\right]](/mediawiki/images/math/5/e/8/5e87deb6f6b5cec598e43b4b3374a25c.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle7^2+3^2&\scriptstyle=58=2\sdot\left(25+4\right)=2\sdot\left(5^2+2^2\right)\\&\scriptstyle=2\sdot\left[5^2+\left(7-5\right)^2\right]\\&\scriptstyle=2\sdot\left[\left(\frac{1}{2}\sdot10\right)^2+\left[7-\left(\frac{1}{2}\sdot10\right)\right]^2\right]\\\end{align}}}](/mediawiki/images/math/6/0/e/60e2c8e906170cf2be7705524d6f41d4.png)
![\scriptstyle\left(a+b\right)^2+b^2=2\sdot\left[\left(\frac{1}{2}\sdot a\right)^2+\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2\right]](/mediawiki/images/math/b/7/d/b7dd112f5309b8cd4f778bd6269c21f3.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left(10+2\right)^2+2^2&\scriptstyle=12^2+2^2\\&\scriptstyle=144+4=148=2\sdot74=2\sdot\left(25+49\right)\\&\scriptstyle=2\sdot\left(5^2+7^2\right)=2\sdot\left[5^2+\left(5+2\right)^2\right]\\&\scriptstyle=2\sdot\left[\left(\frac{1}{2}\sdot10\right)+\left[\left(\frac{1}{2}\sdot10\right)+2\right]^2\right]\\\end{align}}}](/mediawiki/images/math/0/3/e/03e712da00104b0b92112fed9e8e4c88.png)