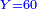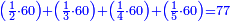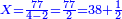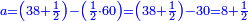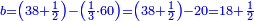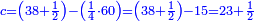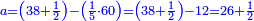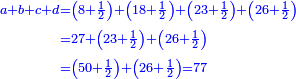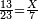Chapter Three: Multiplication
|
השער השלישי ידבר על הכפל בכל האופנים שאפשר להמצא בשלמי'
|
|
|
דע כי הרוצה לכפול שום מספר על מספר אחר יש לו לשים המספר הגדול למעלה והקטן למטה ויש לו להתחיל מן האחדים לכפול ר"ל האות הראשנה אשר למטה שהם האחדים יש לו לכפול על מדרגת האחדים אשר למעלה אח"כ על מדרגת העשרו' ואח"כ על מדרגת המאות וכן תמיד עד תומם ואחר שעשית כל ההכאו' הראויות לעשות עם האות הראשנה יעשה כן מהשניה וכן מהג' אם המספר כל כך גדול ואח"כ יחבר הכל מין עם מינו ר"ל אחדים עם אחדי' עשרות עם עשרות מאיות עם מאיות והעולה הוא המבוקש
|
|
|
ודע כי מיני הכפל הם רבים ואנו נעשה ההכפלה על ג' דרכים אם יסכים השם בחיים גם נדבר מעט על הכפל הרביעי הנקרא בלשונם אשקקי או קואדרו
|
Type one
|
ונדבר בתחלה על הכפל הנהוג אצל רוב הסוחרים ואח"כ נדבר בדרכים האחרים
|
|
|
דמיון זה נרצה לכפול כ"ג על כ"ג (כ"ד)
|
|
|
הנה נשים הכ"ג למעלה והד' (כ"ד) למטה ואם תהפכם לא יזיק כי הכל הולך אל מקום אחד ודרך אחד לכלם והנה בתחלה נכפול הד' אשר הם למעלה (למטה) עם הג' אשר הם למטה (למעלה) שהם במדרגת האחדים ונאמ' ד' פעמים ג' הם י"ב והנה נשים הב' למטה בקו שלישי ונעכב העשרה אח"כ נכפול הד' אשר הם למטה במקום האחדים עם הב' אשר הם למעלה במקום העשרות ויהיו ח' ותחבר אליהם העשרה שיש לך מן האחדים ויהיו ט' ושימם במקום העשרות אח"כ תוציא לחוץ האות הראשנה ר"ל שלא תעשה שום הכאה עוד עם הד' אשר הם למטה במקו' האחדים מאחר שהכינו אותה עם כל המדרגות העליונות אח"כ תכה המדרגה השנית אשר למטה עם כל המדרגות אשר הם למעלה ותכה אותה תחלה עם ג' ר"ל הב' אשר הם למטה במקום העשרות עם הג' אשר הם למעלה במקום האחדים ויהיו ו' ושים אלו הו' בקו אחרת ונקראנו קו רביעי ושים אותם במקום העשרות אח"כ תכפול הב' אשר הם למטה עם הב' אשר הם למעלה ותאמר ב' פעמים ב' הם ד' ושים ד' אל המדרגה הבאה אחר העשרות ר"ל במקום המאיות אח"כ תחבר הכל ויהיה העולה תקנ"ב וזהו צורתם
|
|
|
ודע כי אם תרצה לכפול ג' מספרים על אחד יצטרך לעשו' ג' הכאות ולא יותר
|
|
|
ואם תרצה לכפול ג' אותיות על ב' אותיות אתה צריך לעשות ו' הכאות
|
|
|
ואם תכפול ג' אותיות על ג' אותיות תצטרך לעשות ט' הכאות
|
|
|
דמיון נרצה לכפול רל"ד על כ"ד
|
|
|
הנה יש לך לכפול תחלה הד' אשר הם למטה במקום האחדי' עם הד' אשר הם ג"כ למעלה במקום האחדים ויהיו י"ו ושים ו' במקום האחדים בקו שלישי והי' תקים עמך עוד תשוב ותכפול הד' אשר הם במקו' האחדים למטה על הג' אשר למעלה במקום העשרות ויעלו י"ב ותחבר אליהם אותה העשרה שיש לך ויהיו י"ג ושים ג' במקום העשרות בקו שלישי והעשרה תחזיק עמך עוד תשוב ותכפול הד' התחתונים נגד הב' אשר הם למעלה במקום המאיות ויהיו ח' ותחבר אליהם העשרה ויהיו ט' הנה כבר נשלם הכפל מהאות הראשנה אשר למטה ועתה נשוב לכפול האות השניה אשר במדרגת העשרות עם כל האותיות העליונות ונכפול הב' אשר הם למטה במדרגת העשרות עם הד' אשר למעלה במדרגת האחדים ויהיו ח' ושים אותם הח' בשטה רביעית נגד העשרות אחר כן תכפול עוד הב' אשר הם למטה נגד הג' אשר הם למעלה במקום העשרות ויהיו ו' ושים אותם בשטה רביעית במקום המאיות אח"כ תשוב ותכפול הב' אשר הם למטה עם הב' אשר הם למעלה במדרגת המאיות ויהיו ד' ושים אותם הד' בשטה רביעית במקום האלפים אח"כ תחבר כל אלו ההכאות ויהיה העולה ה' אלפים ותרי"ו על זאת הצורה
|
|
|
ואם תרצה לכפול ג' אותיות על ג' אותיות ראוי לעשות ככה
|
|
|
דמיון זה נרצה לכפול רכ"ב על של"ג
|
|
|
הורידם בשתי שטות ותתחיל לכפול הב' אשר הם למטה במקום האחדים נגד הג' אשר הם למעלה במקום האחדים גם כן ויעלו ו' ושים אותם בקו שלישי במקום האחדים עוד תכפול אותם הב' ממש ר"ל אותם אשר הם למטה במדרגת האחדים נגד העשרות אשר הם למעלה ויהיו ו' ושים אותם בקו שלישי במקום העשרות עוד תכפול אותם הב' אשר (הם למטה) על הג' אשר למעלה במקום המאות ויהיו ו' ג"כ ותקים אותם במקום המאות והנה עשינו עם האות הראשנה התחתונה כל ההכאות
|
|
|
ועתה נרצה להכות האות השנית שהיא ב' במקום העשרות עם כל האותיות העליונות ותכפול הב' בתחלה על הג' אשר הם למעלה במקום האחדים ויהיו ו' ושים אותם בקו רביעי במקום העשרות עוד תשוב ותכפול הב' אשר (הם למטה) על הג' אשר למעלה במקום העשרות ויהיו ו' ושים אותם בקו רביעי במקום המאיות עוד שוב וכפול אותם הב' עצמם על הג' אשר למעלה במקום המאיות ויהיו ו' ושים אותם בקו רביעי במקום האלפים
הנה עשינו כל הכפל וההכאה מהאות השניה אשר למטה עם כל האותיות העליונות אח"כ שוב והכה המדרגה הג' ר"ל האות הג' אשר למטה עם כל האותיות העליונות ותכה תחלה הב' אשר למטה עם הג' אשר למעלה במקום האחדים ויהיו ו' ושים אותם בקו חמישי במקום המאיות אח"כ תשוב ותכפול הב' על הג' אשר למעלה במקום העשרות ויהיו ו' ושים אותם בקו חמישי במקום האלפים אח"כ תשוב ותכפול הב' אשר למטה על הג' אשר למעלה במקום המאיות ויהיו ו' ושים אותם בקו חמישי במקום עשרת אלפים והנה נשלמו כל הט' הכאות אח"כ תחבר כל אלו ההכאות מין עם מינו ויהיה העולה ע"ג אלפים ותתקכ"ו על זאת הצורה
|
|
|
ואם תרצה לכפול איזה דבר שיהיה על האחר ויהיה באחד משניהם ציפרא ראוי למנות הציפרא ולעשות ההכאה עמה כאלו היתה אות באיזה מקום שתמצאנו או למעלה או למטה
|
|
|
דמיון זה נרצה לכפול מספר ר"ל על מספר שכ"ד
|
|
|
הנה יש לך לכפול בתחלה הד' אשר הם למטה במדרגת האחדים על הציפרא אשר למעלה במדרגת האחדים ג"כ ותאמר ד' פעמים ציפרא היא ציפרא ולכן תשים ציפרא במקום האחדים אח"כ תשוב ותכפול אותם הד' מלמטה על הג' אשר הם למעלה במקום העשרות ויעלה י"ב ותשים ב' במקום העשרות ותעכב העשרה עמך אח"כ תשוב ותכפול אותם הד' נגד הב' אשר למעלה במקו' המאיות ויעלה ח' ותחבר אליהם אותה העשרה שהיה לך כבר ויעלה ט' ושים אותם הט' במדרגת המאות בקו שלישי אח"כ תחבר הב' אשר הם למטה במקום העשרות כי כבר השלמנו הכפל מהאות הראשנה התחתונה עם כל האותיות העליונות ותכפול אותם הב' על הציפרא אשר היא למעלה במקו' האחדים ויעלה בידך ציפרא ולכן תשים ציפרא בקו רביעי במקום העשרות אח"כ תכפול אותם הב' ג"כ השפלים נגד הו' (הג') אשר הם למעלה במקום העשרות ויעלו ו' ושים אותם נגד המאות בקו רביעי אח"כ תשוב ותכפול אותם הב' ג"כ העליונים על הב' אשר הם במקום המאות ויעלו ד' ושים אותם בקו ד' במקום האלפים והנה נשלם הכפל מהאות הב' שלמטה אח"כ תכפול האות הג' שלמטה עם כל האותיות העליונות ותכפול אותה עם הציפרא תחלה ויעלה ציפרא ולכן שים ציפרא בקו ה' במקום המאות עוד תכפול הג' ג"כ שלמטה נגד הג' אשר הם למעלה במדרגה הב' ויהיו ט' ושים אלו הט' במדרגת האלפים בקו ה' אח"כ תכפול הג' פעם ג' על הב' אשר הם למעלה במקום המאות ויהיו ו' ושים אותם במקום עשרת אלפים בקו ה' ונשלם הכפל מכל הג' אותיות אח"כ תחבר הכל זה על זה ויהיה סך העולה ע"ד אלפים תק"כ וזאת צורתם
|
|
|
ואם תרצה לכפול ב' סכומות ויהיה בכל אחד מהם ציפרא יש לך לכפול הציפרא על כל האותיות אשר תמצא ותחבר הכל מין עם מינו והעולה הוא המבוקש
|
|
|
דמיון נרצה לכפול ר"ם על שס"ח
|
|
|
הנה תכפול תחלה הח' אשר הם למטה על הציפרא אשר היא למעלה במקום האחדים ויעלה לך ציפרא עוד תשוב ותכפול הח' התחתונים שהם במדרגת האחדים על הד' אשר במדרגת העשרות ויהיו ל"ב ותשים הב' במקום העשרות ותקיים בידך הל' אח"כ תכפול הח' על הב' אשר הם למעלה במדרגת המאות ויהיו י"ו ותחבר אליהם הג' ויהיו י"ט ושים אותם בקו ג' הנה עשינו כל ההכאות עם הח' אשר הם למטה במקום האחדים אח"כ תכפול העשרות העומדות למטה שהם ו' ותכפול אותם בתחלה על הציפרא העומדת למעלה ויעלה בידך ציפרא ושים ציפרא בקו רביעי במקום העשרות אח"כ תכפול העשרות ג"כ התחתונות על המ' אשר למעלה ויעלה בידך כ"ד והנה תשים הד' במקום המאות והב' תעכב עמך אח"כ תכפול הו' אשר למטה על הב' אשר הם למעלה ויעלה י"ב תחבר אליהם הב' ויהיו י"ד אח"כ נכפול המאיות אשר הם למטה על כל האותיות שהם למעלה והנה נכפול בתחלה על הציפרא אשר היא למעלה במקום האחדים ויהיה ציפרא אח"כ נכפול אותו על הד' אשר הם למעלה במדרגת העשרות ויהיו י"ב ושים הב' במקום האלפים אח"כ תכפול אותם על המאות אשר למעלה ויעלו ו' ותחבר אליהם האחד והיו ז' הנה א"כ היוצא מכפל זה על זה הוא פ"ח אלפים וש"כ על זאת הצורה
|
|
|
ואם תרצה לכפול איזה מספר יהיה בו ב' ציפרי או יותר יש לך לחשוב כל א' מאלו כאלו היה מספר ועשות ההכאה עם כל א' וא'
|
|
|
דמיון נרצה לכפול מספר ת"ג על מספר ר"ל
|
|
|
הנה יש לך לכפול בתחלה הציפרא אשר למטה במדרגת האחדים על הג' אשר הם למעלה במדרגת האחדים ג"כ ויהיה העולה ציפרא ושים אותם למטה במדרגת האחדים בקו ג' עוד תכפול הציפרא על הציפרא אשר היא למעלה ויהיה העולה ציפרא ושים אותה בקו ג' במדרגת העשרות עוד כפול הציפרא על הד' העליונים אשר הם במקום המאיות ויעלה בידך ציפרא ושים ציפרא בקו ג' במדרגת המאות והנה כבר עשינו כל ההכאות מהציפרא אשר היא בשטה התחתונה עם כל המדרגות העליונות אח"כ נכה הג' אשר למטה במדרגת העשרות עם כל המדרגות העליונות ונכה אותה תחלה עם הג' אשר היא למעלה במדרגת האחדים ויהיה העולה תשעה ושים אותם בקו רביעי במדרגת העשרות עוד תכה אותם הג' של מטה עם הציפרא אשר היא למעלה במקום העשרו' ויהיה היוצא ציפרא ושים אותה במדרגת המאות עוד תשוב ותכפול אותם הג' של מטה על הד' העליונים אשר הם במקום המאיות ויעלה י"ב ושים הי' במדרגת העשרות אלפים והב' במקום אחדי האלפים והנה השלמנו ההכאה מהג' אשר הם למטה במקום העשרות עם כל המדרגות העליונות ועתה נכה הב' אשר הם למטה במקום המאיות עם כל המדרגות העליונות ונכה תחלה הב' עם הג' אשר הם למעלה במקום האחדים ויעלו ו' נשים אותם בקו הה' במקום המאיות אח"כ תכה הב' נגד הציפרא אשר היא למעלה במקום העשרות ויעלה בידך ציפרא ושים אותה הציפרא במ[דרגת ה]אלפים אח"כ תכה הב' פעם ג' עם הד' אשר הם למעלה במקום המ[או]ת [ויעלה] ח' ושים אלו הח' למטה בקו ה' במקום עשרת אלפים והנה השלמנו כל הט' הכאות ואח"כ נחבר הכל ויהיה העולה צ"ב אלפים ותר"צ וזאת היא צורתם
|
|
|
ואם תכפול ד' אותיות על ד' אותיות ראוי לעשות י"ו הכאות
|
|
|
וה' על ה' ראוי לעשות כ"ה וכן עד אין קץ ואין צורך להאריך
|
Type two
|
ועתה נרצה לדבר על הכפל הנקרא בלשונם קרוציטא
|
|
|
והנה נעשה ככה כי נצטרך להניח המספר הגדול למעלה והקטן למטה האמנם אם תעשה ההפך לא יזיק אך להקל ההכאות מוטב להניח הגדול למעלה והקטן למטה ותתחיל להכות מהאות הראשנה של מטה עם האות הראשנה של מעלה ומה שיעדיף על העשרות שים בקו ג' ותעכב העשרות עוד תשוב ותכפול האחדים של מטה עם העשרות שלמעלה ותחבר על העולה העשרות שיש לך מן האחדים ומה שיעלה על העשרות ר"ל מהסך שיש לך עתה אל תשים מאומה אלא תשוב לחבר העשרות של מטה עם האחדים שלמעלה ותחבר העולה על מה שיש לך מן העשרות ומה שישאר על העשרות תשים במקום העשרות ותעכב העשרות בידך אח"כ תשוב לכפול העשרות של מטה עם העשרות של מעלה ותחבר על העולה סך העשרות שיש לך ויצא לך המבוקש
|
|
|
דמיון זה נרצה לכפול כ"ד על כ"ה
|
|
|
תשימם בב' שטות ותתחיל לכפול הד' אשר הם למטה במקום האחדים עם הה' אשר הם למעלה במקום האחדים ג"כ ויהיו עשרים ותשים ציפרא במקום האחדים כי לא נשאר לך על העשרות מאומה עוד תשוב לכפול הד' אשר הם למטה במקום האחדים נגד הב' אשר הם למעלה במקום העשרות ויהיו ח' ותחבר אליהם ב' עשרות שיש לך ויהיו י' ואל תניח מאומה אלא שוב וכפול הב' אשר הם למטה במקום העשרות נגד הה' אשר הם למעלה במקום האחדים ויעלו עשרה ותחבר אליהם הי' אחדים ויהיו כ' והנה בעבור כי לא נשאר לך מאומה על העשרות לכן נשים גלגל למטה במקום העשרות ונעכב אותם הב' עוד נשוב לכפול הב' אשר הם למטה במדרגת העשרות על הב' אשר הם למעלה במדרגת העשרות ויהיו ד' ותחבר אליהם אותם הב' שיש לך ויהיו ו' ושים אותם במקום המאות ויהיה א"כ היוצא ו' מאות כמו זאת הצורה
|
|
|
ואם תרצה לכפול ג' מספרים על ג' מספרים תצטרך לעשות ט' הכאות על זה האופן
|
|
|
דמיון זה נרצה לכפול קכ"ג על תנ"ו
|
|
|
הנה נכפול בתחלה הו' אשר למטה במדרגת האחדים על הג' אשר הם למעלה במדרגת האחדים ג"כ ויהיו י"ח נשים ח' למטה בקו שלישי והאחד תקים עמך אח"כ תכפול עוד הו' אשר למטה במקום האחדים נגד הב' אשר הם למעלה במקום העשרות ויהיו י"ב ותחבר אליהם האחד ויהיו י"ג ולא תשים מאומה עוד תכפול הג' אשר הם למעלה במדרגת האחדים עם הה' אשר למטה במדרגת העשרות ויהיו ט"ו ותחבר אליהם הי"ג ויהיו כ"ח ושים הח' למטה במקום העשרות ותעכב הב' עוד תשוב ותכפול הו' אשר הם למטה במקום האחדים על האחד אשר הוא למעלה במקום המאות ויהיו ו' ותחבר אליהם הב' שעכבנו בידינו ויהיו ח' עוד תשוב לכפול הה' אשר למטה במדרגת העשרות עם הב' אשר הם למעלה במדרגת העשרות ג"כ ויהיו עשרה ותחבר אליהם הח' ויהיו י"ח עוד תשוב לכפול הד' אשר הם למטה במקום המאות עם הג' אשר הם למעלה במקום האחדים ויהיו י"ב ותחבר אותם אל הי"ח ויהיו ל' אח"כ תשים ציפרא למטה במקום ה' המאות עוד תשוב לכפול הד' אשר הם למטה במקום המאות עם הב' אשר הם למעלה במקום העשרות ויהיו ח' ותחבר אליהם הל' ששוים ג' ויהיו י"א עוד תשוב לכפול הה' אשר הם למטה במקום העשרות עם הא' אשר הוא למעלה במקום המאיות ויהיו ה' ותחבר אל הי"א ויהיו י"ו ושים ו' במקו' האלפי' אח"כ תכפול הד' אשר הם למטה במקום המאיות על הא' אשר הוא למעלה במקום המאיות ג"כ ויהיו ד' ותחבר אליהם האחד שיש לך ויהיו ה' ושים אותם במקום עשרת אלפים ויהיה העולה א"כ נ"ו אלפים ופ"ח כמו זאת הצורה
|
|
|
ואם תרצה לכפול איזה מספר יהיה בו ציפרא יצטרך ג"כ לעשות ההכאה מהציפרא עם כל האותיות אע"פ שלא יצא לעולם כי אם ציפרא
|
|
|
דמיון זה נרצה לכפול רמ"ו על ק"מ
|
|
|
הנה תכפול תחלה הציפרא אשר היא למעלה (למטה) במקום האחדים על הו' אשר הם למעלה במקום האחדים והנם ציפרא ושים ציפרא במקום האחדים אח"כ תכפול הציפרא ג"כ על הד' אשר הם למעלה במקום העשרות ויהיו ציפרא עוד תשוב ותכפול הד' אשר הם למטה במקום העשרות על הו' אשר הם למעלה במקום האחדים ויהיו כ"ד ושים הד' למטה במקום העשרות והב' תעכב עמך עוד תשוב ותכפול הציפרא על הב' אשר הם למעלה במקום המאיות ויהיו ציפרא ועם ב' שיש לך ויהיו ב' עוד תשוב ותכפול הד' אשר הם למטה במדרגת העשרות עם הד' אשר הם למעלה ג"כ במדרגת העשרות ויהיו י"ו ועם הב' יהיו י"ח עוד תשוב ותכפול האחד אשר הוא למטה במדרגת המאות נגד הו' אשר הם למעלה במדרגת האלפים ויהיו ו' ועם הי"ח יהיו כ"ד ושים הד' במקום המאיות וקיים עמך הב' עוד תשוב ותכפול האחד אשר הוא למטה במדרגת המאות נגד הד' אשר הם למעלה במקום העשרות ויהיו ד' תחבר אליהם ב' ויהיו ו' עוד תשוב לכפול הב' אשר הם לעיל במדרגת המאות עם הד' השפלים אשר במדרגת העשרות ויהיו ח' ועם הו' והנם י"ד ושים הד' למטה במדרגת האלפים והאחד תקים עמך עוד תכפול האחד אשר למטה במדרגת המאיות על הב' אשר למעלה במדרגת המאיות ג"כ ויהיו ב' תחבר אליהם הא' ויהיו ג' ושים אותם במקום עשרת אלפים ויהיה א"כ היוצא ל"ד אלפים ות"מ על זאת הצורה
|
|
|
וזה יספיק לך בידיעת זה הכפל אם תקיש על זה
|
Type three
|
ואולם המין הג' מהכפל
|
|
|
הוא בהפך אלו השנים כי בב' אשר עברו היינו מתחילים ההכאו' מן האחדים ואח"כ העשרות ואח"כ המאות וכן תמיד היינו עולים למעלה מעלה ובזה ראוי לעשות ההפך כונתי לרדת מטה מטה ר"ל שתתחיל ההכאה מהמאיות או מהאלפים אם הוא כל כך גדול ואח"כ תבא אל העשרות וכן עד שתגיע אל האחדים
|
|
|
ונניח לזה דמיונות למען תהיה בקי בכל ההכפלות בכל האופנים שאפשר להמצא
|
|
|
דמיון זה נרצה לכפול כ"ג על י"ז
|
|
|
הנה נכפול בתחלה הא' אשר למטה במקום העשרות על הב' אשר למעלה במקום העשרות ג"כ ויהיו ב' ודע כי אלו הב' היוצאים הם מאות והכלל על זה כי עשרות על עשרות הם מאות ומאות על מאות הם עשרות אלפים ו(עשרות) אלפים על מאות הם מאות אלפים הנה א"כ אלו הב' שיצאו לנו הם ב' מאות ונניחם בשטה אחת למטה תחת ב' שטות מהכפל במקום הראוי ר"ל במקום המאיות אח"כ נכפול האחד העומד למטה במקום העשרות על השלשה אשר הם למעלה במקום האחדים ויהיו ג' והם עשרות כי אחדים על עשרות הם עשרות וא"כ יהיו ג' עשרות אח"כ תכפול השבעה אשר הם למטה במקום האחדים על הב' אשר הם למעלה במקום העשרות ויהיו י"ד ויהיו עשרות ותחבר אליהם הג' עשרות שהם י"ד ויהיו י"ז עשרות שהם מאה ושבעים ותשימם במקום אחר כן תחבר (תכפול) האחדים עם האחדים והם ז' עם ג' ויהיו כ"א אח"כ חבר הכל מין עם מינו ויהיה העולה ג' מאות וצ"א על זאת הצורה
| 2 3
|
| 1 7
|
| 2 0 0
|
| 1 4 0
|
| 3 0
|
| 2 1
|
| 3 9 1
|
|
|
|
|
ואם תרצה לכפול ג' מדרגות על ג' מדרגות תצטרך לעשות ט' שורות
|
|
|
דמיון זה נרצה לכפול רמ"ב על קמ"ד
|
|
|
והנה נכפול בתחלה הא' אשר היא למטה במדרגת המאות על הב' אשר היא למעלה במדרגת המאות ויהיו ב' וכבר אמרנו כי מאיות על מאיות הם עשרות אלפים ונניחם במקום אחד עוד נכפול הא' אשר היא למטה במדרגת המאות נגד הד' אשר הם למעלה במדרגת העשרות ויהיו ד' ושים אותם במקום האלפים כי כן אמרנו כי מאיות על מאיות (עשרות) הם אלפים עוד נשוב ונכפול הא' מלמטה אשר במדרגת המאות עם הב' אשר הם למעלה במדרגת האחדים ויהיו שנים ושים אותם במקום המאות הנה כבר עשינו כל ההכאות מהמאות שלמטה עם כל המדרגות של מעלה אח"כ נכפול הד' שהם עשרות העומדות למטה על הב' אשר היא למעלה במקום המאיות ויהיו שמונה והם אלפים ותניחם במקום האלפים אח"כ תשוב ותכפול אותם הד' עוד עם הד' אשר הם למעלה במקום העשרות ויהיו אלף ות"ר ותניחם במקומם עוד תשוב וכפול אותם הד' פעם שלישית עם הב' אשר למעלה במקום האחדים עם הב' אשר הם למעלה במקום המאות ויהיו שמונה ושים אותם במקום המאות עו' תכפול אותם הד' פעם שנית עם הד' העומדים למעלה במקום העשרות ויהיו י"ו שהם ק"ס ותניחם במקומם עוד תשוב ותכפול הד' פעם ג' על הב' אשר הם למעלה במקום האחדים ויהיו ח' ושימם במקום האחדים ותחברם כלם ויהיו ל"ד אלפים תתמח על זאת הצורה
| 2 4 2
|
| 1 4 4
|
| 2 0 0 0 0
|
| 4 0 0 0
|
| 2 0 0
|
| 8 0 0 0
|
| 1 6 0 0
|
| 8 0
|
| 8 0 0
|
| 1 6 0
|
| 8
|
| 3 4 8 4 8
|
|
|
|
|
ואם תרצה לכפול איזה מספר יהיה בם ציפרא צריך שתמנה הציפרא כמו האותיות האחרות ותעשה ההכאה עם הציפרא אע"פ שלא יצא לעולם מן המחובר כי אם ציפרא
|
|
|
דמיון זה נרצה לכפול ר"ם על ק"ע
|
|
|
הנה תכפול תחלה הא' אשר הוא למטה במקום המאיות על הב' אשר הם למעלה במקו' המאות ג"כ ויהיו ב' ושים אותם במקו' עשרות האלפים כמו שביארנו עוד תכפול פעם שנית הא' אשר הוא למטה נגד הד' אשר הם למעלה במקו' העשרו' ויהיו ד' אלפים עוד תכפול פעם ג' הא' אשר למטה על הציפרא אשר למעלה במקו' האחדים אח"כ תכפול הז' אשר למטה במדרגת העשרות על הב' אשר הם למעלה במדרגת המאות ויהיו י"ד אלפים עוד תכפול פעם ב' אותם הז' על הד' אשר למעלה במדרגת העשרות ויהיו ב' אלפים וח' מאות עו' כפול הז' פעם ג' נגד הציפרא אשר למעלה ולא יעלה בידך מאומה ומהציפרא הבאה ר"ל הציפרא אשר היא למטה במקום האחדים אין צורך לעשות עמה שום הכאה הנה א"כ היוצא הוא מ' אלפים וח' מאות על זאת הצורה
| 2 4 0
|
| 1 7 0
|
| 2 0 0 0 0
|
| 4 0 0 0
|
| 1 4 0 0 0
|
| 2 8 0 0
|
| 4 0 8 0 0
|
|
|
Type four
|
ואולם המין הד' מהכפל
|
|
|
הוא הפך הכפל אשר כתבנו בתחלה והוא כי יש לנו להתחיל מן האלפים או יותר מכן אם הוא כל כך גדול עד אשר תגיע לאחדים ראוי לך לשוב אחורנית
|
|
|
דמיון זה נרצה לכפול קכ"ב על רל"ב
|
|
|
הורידם בב' שטות אח"כ תתחיל לכפול מן המאיות ותכפול הא' אשר היא למטה במקום המאיות על ב' אשר היא למעלה במקום המאיות ג"כ ויהיו ב' ולא תשים מאומה אלא תחזיקם ואם תרצה לשים אותם לא תכתוב שום ציפרא כמו שיהיה ראוי לכתוב כי מאה על ב' מאות הוא עשרים אלף ולא תוכל לכתוב עשרים אלף בזולת הציפראות המצטרכות אבל בכאן אין ראוי לכתוב מפני כי עדין לא עשית כל ההכאות מהאותיות העליונות עם זה האחד אשר התחלת עמה לעשות הכאתו אבל כשתסיים כל ההכאות מהאותיות של מעלה עם זה האחד יש לך לראות המרחק אשר יש מזה האחד עד האות הראשנה של מטה ר"ל כי זה הא' הוא למטה במדרגת המאיות והנה עד המדרגה הראשנה שהיא מדרגת האחדים יצטרך עדין ב' מדרגות ולכן ראוי שתשים ב' ציפראות אחר שסיימת הכאת זאת המדרגה מה' מהמאיות אשר היא למטה עם כל המדרגות העליונות ושמור זה הסוד מאד כי זה יישירך שלא תטעה בשום צד שבעולם ונחזור לראשנות והנה נכפול הא' אשר היא למטה במדרגת המאות עם הב' אשר הם למעלה במדרגת המאות ויהיו שנים ושימם לבדם בלי שום ציפרא אלא שימם כאלו הם אחדים בידך עוד כפול אותו הא' אשר הוא למטה במדרגת המאות עם הג' אשר הם למעלה במדרגת העשרות ויהיו ג' וכתוב אותם אצל הב' שכבר כתבת אחורנית אח"כ כפול זה הא' פעם ג' עם הב' אשר הם למעלה במקום האחדים וכתוב אותם אחורנית אצל הג' כמו שעשית ג"כ מהג' והנה עתה השלמת הכאת המאות אשר למטה עם כל האותיות העליונות ולכן תכתוב ב' ציפרי אחורנית אצל היוצא מההכאה שעשית עם המאיות אח"כ תכפול העשרות של מטה שהם ב' על הב' אשר הם למעלה ויהיו ד' עוד תכפול פעם שנית העשרות מלמעלה (מלמטה) עם הג' של מעלה שהם במקום העשרות ויהיו ו' וכתוב אלו הו' אחורנית אצל הד' עוד תכתוב פעם ג' העשרות של מטה עם הב' של מעלה שהם במקום האחדים ויהיו ד' וכתוב אותם אצל הו' אחורנית ודע כי זה הכפל שעשית עתה היה מהעשרות של מטה עם כל האותיות העליונות ולכן יש לך לראות כמה ציפרי יצטרך מא' עד י' ותמצא א' על כן תכתוב ציפרא אחורנית אצל היוצא מההכאה מהעשרות השפלות ר"ל מהשטה התחתונה עוד תשוב ותכפול הב' אשר הם למטה במקו' האחדים על הב' אשר הם למעלה במקום המאיות ויהיו ד' וכתוב אותם אח"כ שוב וכפול אלו הב' פעם ב' על הג' אשר הם למעלה במדרגת העשרות ויהיו ו' וכתוב אותם אחורנית אצל הד' שכבר כתבת עוד שוב פעם ג' אלו הב' על ב' אשר הם למעלה במקום האחדים ויהיו ד' אח"כ תצרף הכל מין עם מינו ויעלה הכל כ"ח אלפים וג' מאות וד' וזאת היא צורתם
| 2 3 2
|
| 1 2 2
|
| 2 3 2 0 0
|
| 4 6 4 0
|
| 4 6 4
|
| 2 8 3 0 4
|
|
|
|
|
ואם תרצה לכפול מספר יהיה בו ציפרא תעשה על אופן שעשינו
|
|
|
דמיון זה נרצה לכפול ת"ע על תק"פ
|
|
|
הנה נכפול בתחלה הג' (הה') אשר הם למטה במקום המאיות על הד' אשר הם למעלה במקום המאות ויהיו עשרים ושים אותם הכ' ר"ל שנים עם ציפרא אחת ויהיו כ' אח"כ תכפול הה' שלמטה פעם שנית עם הז' אשר הם למעלה ויהיו ל"ה ושים ל' על הציפרא אשר כתבת עם העשרים ושים תחת הציפרא ג' שהם ל' והה' הבאים תכתוב לאחור והנה נצטרך לעשות על זה ג' ציפרי ב' בעד המספר התחתון וא' שעומדת למעלה במקום האחדים עוד נכפול הח' אשר הם למטה במקום העשרות אצל הד' אשר הם למעלה במקום המאיות ויהיו ל"ב ושים ל"ב בקו אחד תחת הל"ה אשר למעלה עוד תכפול ח' על ז' שהם למעלה במדרגת העשרות ויהיו נ"ו ותכתוב הנ' תחת הב' מהל"ב והו' תכתוב אחורנית אח"כ תחברם ויהיו רע"ב אלפים ות"ר וזאת צורתם
| 4 7 0
|
| 5 8 0
|
| 2 0 0 0 0 0
|
| 3 5 0 0 0
|
| 3 2 0 0 0
|
| 5 6 0 0
|
| 2 7 2 6 0 0
|
|
|
Type five
|
ואולם המין הה' מהכפל הוא אשר כתבנו הנקרא בלשונם קרוציטא
|
|
|
ונעשה אותו בזה האופן והוא שנחזיק לעולם המספר ממה שיעלה מהאות הראשנה עד שנראה מה יצא מהשניה כדי שלא נצטרך למחוק אותה האות ולרשום אחרת תעמוד תחתיה וזה תבין בבירור בלי שום ספק אחר שנעיין בעין פתוחה בדמיונות
|
|
|
דמיון זה נרצה לכפול כ"ז על ל"ב
|
|
|
הנה נכפול תחלה הג' אשר במדרגה השנית על הב' אשר הם למעלה ב' במדרגה השנית ג"כ ר"ל במדרגת העשרות ויעשה בידך י' (ו') ולא נניח אותם כמו שקדם שמא יעלה לנו משאר ההכאות שאנו עתידין להכות עם שאר האותיות עוד נכפול אותם הג' על הז' אשר הם לעיל במדרגת האחדים ויהיו כ"א עוד נכפול הב' אשר הם למטה במדרגת האחדים עם הב' אשר הם למעלה במדרגת העשרות ויהיו ד' נחברם אל הכ"א ויהיו כ"ה ונעשה מהכ' ב' עשרות ב' שלמים ר"ל שאותם הכ' שהם ב' עשרות ישוו ב' מאות ונחבר אלו הב' אצל הו' ויהיו ח' ותניח ח' במקום המאות וישארו בידך ה' עוד תכפול הב' אשר הם למטה על הז' אשר הם למעלה במדרגת האחדים ויהיו י"ד ונעשה מהעשרה אחד ונחבר זה הא' אצל הה' שיש לנו ויהיו ו' נשים אותם אצל העשרות והד' הנשארים תשיבם אחורנית אצל הנשארים ויהיו ד' הנה א"כ היוצא הוא תתס"ד על זאת הצורה
|
|
|
דמיון אחר נרצה לכפול רל"א על שמ"ב
|
|
|
והנה נתחיל לכפול הג' אשר הם למטה במקום המאיות על הב' אשר הם למעלה במקום המאיות ויהיו ו' ולא תניחם אח"כ נשוב לכפול הג' אשר הם למטה במקום המאיות על הג' אשר הם למעלה במקום העשרות ויהיו ה' ט' ושמור אותם עוד כפול הב' אשר הם למעלה במקום המאיות על הד' אשר הם למטה במקו' העשרות ויהיו ח' ותחברם אל הט' ויהיו י"ז ותעשה מהעשרה אחד ותחבר זה הא' עם הו' שהיו לנו ושים אותם למטה בקו שלישי והז' יהיו לאחדים בידך אח"כ תשוב לכפול הג' אשר הם למטה במדרגת המאיות אצל הא' אשר היא למעלה במדרגת האחדים ויהיו ג' ושמור אותם עוד שוב וכפול הב' אשר הם למעלה במדרגת המאות אצל הב' אשר הם למטה במדרגת האחדים ויהיו ד' ותחברם אל הג' השמורים ויהיו ז' עוד כפול הד' אשר הם למטה במדרגת העשרות עם הג' אשר הם למעלה במדרגת העשרות ויהיו י"ב ותחברם אל הז' השמורים ויהיו י"ט תעשה מהי' אחד ושים זה האחד עם הז' השמורים הראשנים ויהיו ח' ושים אלו הח' אצל הז' אשר הם בקו ג' ונשארו בידך עדין ט' אח"כ תשוב לכפול הד' אשר הם למטה במדרגת העשרות עם הא' אשר הוא למעלה במדרגת האחדים ויהיו ד' עו' תכפול הג' אשר הם למעלה במדרגת העשרות אצל הב' אשר הם למטה במדרגת האחדים ויהיו ו' ושים אותם על הד' ויהיו י' ותעשה מהם א' ותחבר זה הא' עם הט' ויהיו י' ואלו הי' ישוו ג"כ א' אצל הח' המונחים בקו ג' ויהיו עתה ח' תחת הט' ותעשה ב' ציפרי א' מצד כי עלה בידך י' מצומצמים מהמספר האחרון והשניה כי היו בידך ט' ובא זה והשלים המנין באופן שהיו עשרה כי אין מנין פחות מעשרה אח"כ תכפול הב' אשר הם למטה אצל האחדים עם הא' אשר הוא למעלה ויהיו ב' הנה א"כ העולה הוא ע"ח (ע"ט) אלפים וב' על זאת הצורה
|
|
|
ואם יצטרך לך לע[שו]ת הכפל עם ציפרי תעשה כנז' בכמה מקומות מזה החבור ולא תחטיא אם תקיש זה לזה
|
Type six: Gelosia
|
ואולם המין הו' מהכפל
|
|
|
הוא הפך הכפל הג' אשר כתבנו בכאן כי הכפל הג' צריך להתחיל ההכאות מן המדרגה היותר גדולה ר"ל מן האלפים אם המספר הוא כל כך גדול וזה צריך לעשות הכפל ולהתחיל מן המספר היותר קטן להתחיל מן האחדים ואל תחשוב כי זה הכפל הוא כמו הכפל הראשון כי הפרש בין זה לזה וזה הכפל נקרא בלשונם מולטיפליקארי פיראושקאקי
|
|
|
ודע כי צריך לעשות מרובע אחד כפי האותיות שתרצה לכפול ר"ל שאם תרצה לכפול ב' אותיות על ב' אותיות תצטרך לעשות ג' קוים באורך וג' ברוחב וג' באלכסון הא' והג' קצרות והאמצעית ארוכה וצריך שתשים היוצא בין הקוים ואחר כן תחבר הכל מין עם מינו ודע כי בזה המרובע תמצא כמו בתים
|
|
|
ודע כי אם תמצא בבית הראשון ציפרא זה יורה כי אין במדרגת האחדים דבר כי אם ציפרא וכן תעשה מהבתים האחרים ותחבר הבתים המכוונים זה מזה והשמר לך ושמור נפשך שלא תטעה בחבור ר"ל שתחבר הבית הב' עם הב' והג' עם הג' והד' עם הד' וכן תמיד
|
|
|
דמיון זה נרצה לכפול כ"ה על כ"ה
|
|
|
הנה בתחלה תצטרך לעשות מרובע מג' קוים באורך וג' ברוחב וג' באלכסון מצד כי המדרגות אינם כי אם ב' כמו זאת הצורה
|
|
|
|
|
|
ותתחיל לכפול בתחלה הה' אשר למטה במדרגת האחדים על הה' אשר למעלה במדרגת האחדים ג"כ ויהיו כ"ה ושים הה' בבית הראשון והב' עשרות תעכב עמך אח"כ תכפול הה' אשר למטה פעם שניה על הב' למעלה במדרגה הב' ויהיו י' ותחבר אליהם הב' ויהיו י"ב ושים הב' בבית השני והאחד בבית הג' עוד תשוב ותכפול הב' אשר הם למטה במדרגת העשרות עם הה' אשר הם למעלה במדרגת האחדי' ויהיו י'
|
|
|
ודע כי כל אלו האותיות אשר שמנו עד עתה היו בבתים העליונים ר"ל באותם הבתים אשר בין הקו הא' והב' שהולכים ברוחב אבל מה שיצא עתה נשים בבתים אשר בין הקו הב' והג' והנה נשים זה הגלגל בבית הב' אח"כ נשוב ונכפול הב' אשר הם למטה במקום העשרות על הב' אשר הם למעלה במקום העשרות ג"כ ויהיו ד' ונחבר אליהם זה הא' שעלה בידינו ויהיו ה' ושים אותם בבית הג' אח"כ נחבר הכל והנה תמצא למעלה בבית הראשון ה' וזה מורה שהם אחדים גם תמצא בבית הב' ב' וזה מורה כי הם עשרות גם תמצא בבית העליון ר"ל בבית השלישי א' ג"כ למטה בבית הג' וה' עם א' ויהיו ו' ומאחר שמצאנו אלו הו' בבתים השלישיים יורה על המאיות ויהיה היוצא ו' מאות וכ"ה כמו זאת הצורה
|
|
|
ולמען תהיה בקי לעשות זה הכפל נכתוב דמיון אחר ויהיה מג' מדרגות
|
|
|
דמיון זה נרצה לכפול רי"ב על קל"ב
|
|
|
הנה נצטרך לעשות מרובע מג' (ד') קוים ברוחב וד' באורך וד' באלכסון מאחר שהאותיות הם ג' וראה ועשה כתבניתו אשר אתה מראה בכאן
|
|
|
|
|
|
והנה תתחיל לכפול הב' אשר הם למטה במקום האחדים על הב' אשר הם למעלה במקום האחדים ג"כ ויהיו ד' נשים אותם לעיל בבית הא' אח"כ נכפול הב' אשר הם למטה במקו' האחדים על הג' אשר הם למעלה במקום העשרות ויהיו ו' וכתו' אותם לעיל בבית הב' אח"כ תשוב לכפול פעם ג' הב' מלמטה נגד הא' אשר הוא למעלה במקום המאיות ויהיו ב' ושים אותם למעלה בבית הג' אח"כ תכפול הא' אשר הוא למטה במדרגת העשרות נגד הב' אשר הוא לעיל במדרגת האחדים ויהיו ב' ושים אותם באמצע הבתים ר"ל בין הבתים אשר הם בין הקו הב' והג' ושים אותם הב' בבית הב' אח"כ שוב וכפול אותו הא' פעם ב' עם הג' אשר הם למעלה במדרגת העשרות ויהיו ג' ושים אותם בבית הג' אח"כ שוב וכפול אותו הא' פעם ג' עם הא' אשר הוא למעלה במדרגת המאות ויעלה א' ושים אותו בבית הד' אח"כ תשוב לכפול השנים אשר הם למטה במדרגת המאות עם הב' העליונים אשר הם במדרגת האחדים ויעלו ד' ושים אותם למטה בין הבתים אשר הם בין הקו הג' והד' ושים אלו הד' בבית הג' עוד שוב וכפול אלו הב' פעם ב' עם הג' אשר הם למעלה במדרגת העשרות ויהיו ו' ושימם בבית הד' עוד כפול אלו הב' פעם ג' עם הא' אשר הוא לעיל במדרגת המאות ויעלה ב' ושים אותם בבית הה' אח"כ תחברם זה עם זה ולא תטעה בחבור ויצא לך כ"ז אלפים תתקפ"ד על זאת הצורה
|
Type seven: multiplying by tens
|
ואולם המין הז' מהכפל
|
|
|
נעשה על זה האופן והוא שאם תרצה לכפול איזה מספר על כלל אחד ר"ל כי הכלל נקרא כמו י' או ק' או אלף או י' אלפים אבל אלפים אינו נקרא כלל וזה הכלל יהיה בידיך כי כשתמצא יותר מאות א' אינו נקרא כלל
|
|
|
וכשתרצה לדעת זה הכפל אם תרצה לכפול על עשרה תשים ציפרא למעלה על המספר המונח ומה שיעלה הוא המבוקש
|
|
|
ואם תרצה לכפול אותו על ק' תוסיף בו ב' ציפרי על המספר העליון
|
|
|
ואם תרצה על אלף תוסיף ג' ציפרי
|
|
|
דמיון זה נרצה לכפול ל"ג על י'
|
|
|
הנה יש לך לשים למעלה על הל"ג ציפרא א' הנה ישוו עתה הל"ג ש"ל והוא המבוקש
|
|
|
ואם תרצה לכפול אותם על מאה
|
|
|
ראוי להוסיף על ל"ג ב' ציפרי ויגיעו למדרגת האלפים ויהיה העולה ג' אלפי' וש'
|
|
|
ואם תרצה לכפול אותם על אלף
|
|
|
יש לך להוסיף על הל"ג ג' ציפרי ויגיעו לעשרות אלפים ויעלה ל"ג אלפים
|
|
|
ואולם אם תרצה לכפול המספר המונח על עשרים
|
|
|
הנה יש לך לכפול המספר המונח על ב' ואח"כ תוסיף על הסך ציפרא א' ומה שיעלה הוא המבוקש
|
|
|
דמיון זה נרצה לכפול מ"ה על עשרים
|
|
|
הנה יש לך לכפול מ"ה על ב' והטעם למה אנו כופלי' אותו ב' פעמים מצד כי עשרים הם כפל עשרה והנה ב' פעמים מ"ה הם צ' ועתה יש לך להוסיף על הצ' ציפרא אחת ויעלה ט' מאות והוא המבוקש
|
|
|
ואם תרצה לכפול המספר המונח שהוא מ"ה על מאתים
|
|
|
יש לך ג"כ לכפול מ"ה על ב' ותוסיף עליו ב' ציפראות ויהיו ט' אלפים
|
|
|
ואם תרצה לכפול אותו על אלפים יש לך לכפול המספר כאשר אמרנו ותוסיף עליו ג' ציפרי ויעלה צ' אלפים והוא המבוקש וכן כל כיוצא בזה
|
|
|
אבל אם תרצה לכפול המספר המונח על ד' יש לך לכפול המספר המונח ד' פעמים ולהוסיף עליו כפי הציפרי ר"ל אם הם ד' אלפי' תוסיף עליו ג' ציפראות
|
|
|
ואם ד' מאות תוסיף עליו ב' ציפרי
|
|
|
ואם הם ד' עשרו' תוסיף ציפרא והעולה הוא המבוקש
|
|
|
דמיון זה נרצה לדעת כפל ט"ו על מ'
|
|
|
הנה יש לך לכפול ט"ו ד' פעמים ויעלו ס' ואח"כ ראוי להוסיף על הס' ציפרא א' ויהיו ו' מאות והוא המבוקש וכן על ד' אלפים תוסיף ג' ציפרי ויעלה ס' אלפים ותקיש על זה
|
Type eight: subtraction and multiplication
|
ואולם המין הח' מהכפל הוא מעורב ממגרעת ומכפל
|
|
|
במקום אחד עומד הכפל ובמקום אחד הגרעון מהמספר הא' וכך ראוי לעשות מהמספר הב' ר"ל שהכפל עומד בזוית זו והגרעון בזוית זו והנה יש לך להתחיל ההכפלה מגרעון המספר הראשון עם תוספת המספר השני ושמור העולה ואח"כ יש לך לכפול גרעון המספר השני על תוספת המספר הראשון (ואח"כ יש לך לכפול גרעון המספר הראשון עם תוספת המספר השני) ושמור העולה מאלו הב' הכפלות אח"כ תכפול תוספת המספר הראשון על תוספת המספר השני ושמור העולה ועוד יש לך לכפול שני החסרונות ר"ל חסרון המספר הא' על חסרון המספר הב' ותחבר העולה עם התוספת ממה שעלה ב' המספרים ותגרע מזה מה שיש לך מהתוספת והחסרון והנשאר הוא המבוקש
|
|
|
דמיון זה נרצה לכפול ד' פחות שנים עם ח' פחות ג' הורידם בב' שטות כמו זאת הצורה
|
|
|
| תוספת |
תוספת
|
| 4 |
8
|
| 2 |
3
|
| חסרון |
חסרון
|
|
|
|
|
והנה יש לך להתחיל ההכפלה בזה האופן והוא שתכפול הב' אשר הם תחת הד' על הח' אשר הם על הג' 3 2 ויעלה בידך י"ו אח"כ כפול עוד הג' אשר הם תחת חסרון חסרון הח' נגד הד' אשר הם על הב' ויהיו י"ב אח"כ תחבר י"ב עם י"ו ויהיו כ"ח עוד כפול הד' אשר הם על הב' נגד הח' אשר הם על הג' ויהיו ל"ב עוד תכפול הב' אשר הם תחת הד' על הג' אשר הם תחת הח' ויעלו ו' ותחברם אל ל"ב ויהיו ל"ח הסר משם כ"ח נשארו עשרה והוא המבוקש
|
|
|
דמיון אחר נרצה לכפול ז' פחות ב' על ח' פחות ד' הורידם בזאת הצורה
|
|
|
| תוספת |
תוספת
|
| 7 |
8
|
| 2 |
4
|
| חסרון |
חסרון
|
|
|
|
|
והנה בתחלה יש לך לכפול הב' אשר הם תחת הז' על הח' אשר הם על הד' ויהיו י"ו ושמור אותם אח"כ תכפול הד' אשר הם תחת הח' על הז' אשר הם על הב' ויהיו כ"ח ותחברם אל הי"ו ויהיו מ"ד אח"כ תכפול הז' אשר הם על הב' על הח' אשר הם על הד' ויהיו נ"ו עוד תכפול הד' אשר הם תחת הח' על הב' אשר הם תחת הז' ויהיו ח' ותחברם עם נ"ו ויהיו ס"ד גרע מהם מ"ד הנשאר עשרים והוא המבוקש ותקיש על זה
|
|
|
ובכאן נשלם השער הג'
|
Chapter Twelve: Word Problems
|
השער הי"ב ידבר על שאלות אשר קצתן הן מהערכין וקצתן מהחבורות ומהן מקשירת הכסף ומהם מחלופים ומהם משרשים וכן כל כיוצא בזה
|
[currency:
- 1 ducato/minyan/magen/peraḥim = 10 carlini = 120 cavalli
|
|
- 1) Question: a man wants to buy a qaneh [=six cubits] from four kinds of clothes, one qaneh from each types - red, green, black and white, and the total amount is 17 peraḥim
- He said that
|
א) שאלה אדם רוצה לקנות קנה אחד מד' מיני בגד א' קנה מכל מין ומין אדום וירוק ושחור ולבן וסך הכל עולה י"ז פרחים
ואמר כי הקנה מהשחור שוה יותר מהלבן י"ב קרליני וב' חלקים מט"ו
והקנה מהירוק שוה יותר מקנה השחור ט"ו קרליני וב' חלקים מז'
ואמר שהקנה מהאדום שוה יותר מהירוק כ"ג קרליני וב' חמישיות
נרצה לדעת כמה ערך כל א' וא' באופן שכשנחבר ערך כלם יעלו י"ז פרחים
|
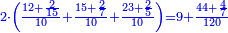
|
תשובה תקח י"ב וב' חלקים מט"ו ותחבר אותם עם ט"ו וב' שלישיות שביעיות ועם כ"ג וב' חמישיות עוד שוב לחבר פעם שניה י"ב וב' חלקים מט"ו וט"ו וב' שביעיות וכ"ג וב' חמישיות ויעלה ט' פרחים ומ"ד קאוואלי וד' חמישיות תסיר כל זה מי"ז פרחים וישארו ז' פרחים וט' קרליני וע"ה קאוואלי וג' שביעיות ותחלקם לד' חלקים ויצא לך י"ז קרליני וק"ב קאוואלי וו' שביעיות וזה יהיה ערך הבגד הלבן שהיה יותר גרוע
|
|
|
אח"כ תוסיף על זה י"ב קרליני וב' חלקים מט"ו ויצא לך ל"א קרליני וקי"ח קאוולי ג' ו' שביעיות וזה היה ערך השחור עוד תוסיף על סך השחור ט"ו קאוואלי וב' שביעיות ויצא לך מ"ז קרליני ול"ט קאוואלי ושביעית אחד וזה יהיה חלק הירוק עוד תוסיף על סך הירוק כ"ג קרליני וב' חמישיות ויעלה הכל ע' קרליני וב' קואלי ושביעית וזה נשים ערך האדום
|
|
|
וכשנחבר הכל יעלה י"ז פרחים בלי פחות ויתר
|
- 2) Question: two men formed a partnership.
- One contributed 100 minyanim, stayed in the partnership for 6 months, and earned 40 minyanim.
- The other contributed unknown amount of money, stayed in the partnership for 7 months, and earned 90 minyanim.
- How much was his money?
|
ב) שאלה ב' אנשים עושים שותפות
הא' שם ק' מנינים ועמדו בשותפות ו' חדשים והרויחו מ' מנינים
והאחר שם ממון נעלם ועמדו בשותפות ז' חדשים והרויחו צ' מנינים
כמה היה ממונו
|
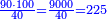
|
התשובה הנה ראוי לך לכפול הממון שעשה השני שהוא צ' ולכפול על ק' ויעלה ט' אלפים ותחלקם על ריוח הראשון שהוא מ' ויעלה רכ"ה הנה א"כ השני היה ממונו רכ"ה לערך ו' חדשים ועמדו בשותפות ז' חדשים
|

|
ונאמר אם ז' שוים רכ"ה ו' כמה שוים
|

|
ויצא לך קצ"ב וו' שביעיות והוא ממון השני
|
|
|
ג) שאלה אדם הרויח עם ד' מנינים בג' חדשים ג' פשוטים ו' מנינים בכמה חדשים ירויחו ז'
|
|
|
התשובה כפול ג' על ד' ויהיו י"ב אח"כ תחלק י"ב על ו' ויצאו שנים הנה א"כ ו' מנינים בב' חדשים הרויחו ה והריוח שלנו היה ז' ולכן נעשה כך ונאמר אם ה' מנינים שוים ב' חדשים ז' מניני' כמה חדשים שוים כפול שנים על ז' ויצאו י"ד ותחלק י"ד על ה' ויצא ב' חדשים וד' חומשי חדש הנה א"כ בב' חדשים וד' חומשי חדש ירויחו ז' מנינים
|
Find a Quantity
|
|
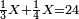
|
ד) שאלה על סך ממון בלתי נודע קבצנו השליש והרובע ועלה כ"ד כמה הממון
|
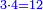
- False Position:
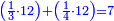
- Rule of Four:
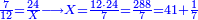
|
התשובה תקח המורה שהוא י"ב מכפל ג' על ד'
אח"כ קח מהם השליש והרובע והם ז'
הנה א"כ ערך אלו הז' אל י"ב כערך כ"ד אל מספרינו הנעלם לכן נכפול י"ב על כ"ד ויעלה רפ"ח נחלקם על ז' ויצא לך מ"א ושביעית והוא סכום כל הממון
|
|
|
ותוכל לבחון אותו והוא שתקח שליש מ"א ושביעית ויהיו י"ג שלמים וה' שביעיות עוד קח הרביעית ממ"א ושביעית ויצא לך י' וב' שביעיות ותחברם אל י"ג ויהיו כ"ד בלי תוספת ומגרעת
|
![\scriptstyle\left(\frac{1}{3}X+\frac{1}{5}X\right)+\left[\frac{1}{3}\sdot\left(X-\frac{1}{3}X-\frac{1}{5}X\right)\right]=12](/mediawiki/images/math/0/b/d/0bdc270c3b686caf42ecf09c9a1d5798.png)
|
ה) שאלה מסך ממון לקחנו שלישיתו וחמישיתו ושליש מהנשאר והיו י"ב כמה היה כל הממון
|
- False Position:
![\scriptstyle{\color{blue}{\left(\frac{1}{3}+\frac{1}{5}\right)+\left[\frac{1}{3}\sdot\left(1-\frac{1}{3}-\frac{1}{5}\right)\right]=\frac{8}{15}+\left(\frac{1}{3}\sdot\frac{7}{15}\right)=\frac{62}{90}}}](/mediawiki/images/math/8/1/e/81e89f769e5c3da454c012bb1ed4a1f9.png)
- Rule of Four:
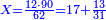
|
התשובה תקח המשל על א' ותוציא ממנו השליש והחומש ויהיו ח' חלקים מט"ו עוד תקח חצי שליש מהנשאר רצוני (?) שליש ז' חלקים מט"ו ותחבר הכל עליהם הח' חלקים מט"ו ויעלה הכל צ"ב (ס"ב?) חלקים מצ'
אח"כ יש לך לכפול י"ב על ס"ב (צ?) ותחלק העולה על צ' (ס"ב?) ויצא לך י"ז שלמים וג' (י"ג?) חלקים מל"א וככה היה כל הממון
|
|
|
ולבחון אותו קח שליש זה המספר ויהיו ה' שלמים וכ"ה חלקים מל"ז (ל"א) עוד תקח חומש המספר ויהיו ג' שלמים וט"ו חלקים מל"א אחר כן תחברם יחד ויעלו ט' שלמים וט' חלקים מל"א ותוציא זה המספר מי"ז שלמים וי"ג חלקים מל"א הנשאר ח' שלמים וד' חלקים מל"א ותחלקם על ג' ותחבר היוצא עם ט' שלמים וט' חלקים מל"א ויעלה בין הכל י"ב
|
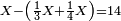
|
ו) שאלה אם יאמ' לך אדם מסך ממון לקחנו שלישיתו ורביעיתו ונשאר עדין י"ד כמה היה כל הממון
|
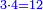
- False Position:
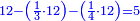
- Rule of Four:
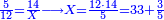
|
התשובה ראוי לכפול ג' על ד' ויהיו י"ב
אח"כ תוציא מהם השליש והרביעית ונשאר עדין ה'
הנה אלו הה' ערכם אל י"ב כערך י"ד אל כל הממון ונעשה הערך כך אם ה' שוים י"ב י"ד כמה שוים ויצא לך ל"ג ושלש חומשים
|
|
|
ולבחון אותו תקח שליש ל"ג ושלש חומשים והנם י"א וחומש אחד אח"כ נקח רביעית ל"ג וג' חומשים ויהיו ח' וב' חומשים חברם אל י"א וחומש ויהיו י"ט ושלשה חומשים הפילם מהל"ג ושלש חומשים וישארו י"ד בלי תוספת ומגרעת
|
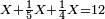
|
ז) שאלה על סך ממון הוספנו שלישיתו רביעיתו וחמישיתו והיו י"ב כמה היה הממון בתחלה
|
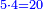
- False Position:

- Rule of Four:
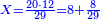
|
התשובה תבקש המורה שהוא כף שהוא מכפל שלישיתו חמישיתו על רביעיתו
וקח רביעיתו שהוא ה' וחמישיתו שהוא ד' ותוסיפם על המורה שהוא (כ') ויהיו כ"ט
אח"כ קח המורה שהוא כ וכפול אותו על י"ב והעולה חלק על כ"ד (כ"ט) ויצא לך ח' וח' חלקי' וכך היה הממון בתחלה
|
|
|
ולבחון אותו קח רביעית הממון שהם ח' שלמים ויעלו ב' שלמים גם ב' חלקים מכ"ט אח"כ קח חומש הממון ויעלה א' שלם וישארו ג' נעשה מכל אחד מהם כ"ט חלקים וחבר אליהם הח' חלקים ויהיו צ"ה חלקם על ה' ויהיו י"ט אח"כ חבר כל המספרים ויהיו י"ב
|
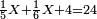
|
ח) שאלה אם יאמר לך אדם ממון לוקח חמישיתו ושישיתו וד' פשוטים ועלה כ"ד כמה הממון
|
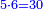
- False Position:
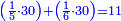
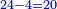
- Rule of Four:
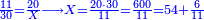
|
התשובה כפול ה' על ו' ויהיו ל'
ותוציא מהם החומש והשישית וחברם ויהיו י"א
אח"כ תוציא מכ"ד הד' אשר הם מתוספת ונשאר עשרים
הנה ערך אלו הי"א אל הל' כערך עשרים אל כל הממון וכפול כ' על ל' ויעלה ת"ר תחלקם על י"א ויעלו נ"ד שלמים וו' חלקים מי"א
|
|
|
ולבחון אותו תקח החומש מן נ"ד והם עשרה שלמים גם עשרה חלקים מי"א אח"כ קח שישית נ"ד והם ט' שלמים וחלק א' מי"א ותחברם ויהיו עשרים [של]מים תוסיף עליהם ד' ויהיו כ"ד שלמים
|
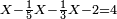
|
ט) שאלה חסרנו ממון שלישיתו וחמישיתו וממה שנשאר נקח ג"כ שנים ונשאר ד'
|
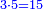
- False Position:
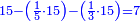

- Rule of Four:

|
התשובה תבקש המורה והוא שתכפול ג' על ה' ויהיו ט"ו
אח"כ נקח השליש והחומש הנשאר ז'
והנה מצד כי אמר אחר שנלקח מסך המעות השליש והחומש לקח עוד מסך הנשאר ב' נוסיפם על ד' ויהיו ו'
והנה נקח הז' שנשארו מהט"ו אחר לקיחת השליש והחומש ונאמר אם ז' שוים ט"ו ו' כמה שוים יצא לך י"ב וב' (ו') שביעיות
|
|
|
ולבחון אותו והוא שתקח שליש י"ב שהם ד' וב' שביעיות וקח ו' (?) חומשי ב' (יב) וו' שביעיות ויהיו ב' וד' שביעיות תסיר כל זה מי"ב וו' שביעיות הנשאר ו' תסיר מאלו הו' ד' נשאר ב' (?) ד'
|
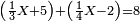
|
י) שאלה מממון חסרנו (חברנו) שלישיתו וחמשה פשוטי' ורביעיתו פחות ב' פשוטים ועולה ח' פשוטים
|
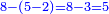
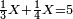
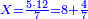
|
התשובה ראוי לך לדעת כי ה' הם מתוספת וב' הם של גרעון ועל כן יש לך לקחת ב' מה' נשארו ג' כפול (?) אלו הג' מח' פשוטים
ויהיה כאלו אמר מממון חסרנו (חברנו) שלישיתו ורביעיתו ועולה ה' פשוטים
והנה יש לך לכפול ה' על י"ב ולחלקנו על ז' ויעלה ח' שלמים וד' שביעיות
|
|
|
ותוכל לבחון אותו והוא שתקח שלישית ח' ויהיו ב' וב' (ו') שביעיות עוד תוסיף על זה ה' מצד כי אמר שלישיתו עם תוספת ה' ויהיו ז' שלמים וו' שביעיות עוד תקח רביעית סך הממון שהוא ז' (ח') וד' שביעיות ויעלו ב' שלמים וחלק א' מז' תסיר מהם ב' כי אמר אל רביעיתו פחות שנים וישאר שביעית אחד תוסיף אותו אל ז' שלמים וו' שביעיות ויהיו ח' שלמים בלי תוספת ומגרעת
|
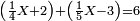
|
יא) שאלה אם אמור יאמר השואל חברנו רביעית מספר מה עם תוספת שנים לחמישיתו פחות ג' ועולה ו'
|
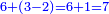
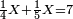
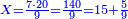
|
התשובה כבר ידעת כי התוספת הוא ב' והחסרון הוא ג' והוא הפך השאלה הקודמת ולכן נעשה בהפך והוא שבמקום הגרעון נוסיף והנה נקח [ב' מג' ו]נשאר א' נוסיף זה הא' אל ו' ויהיו ז'
והוא כאלו אמר מסך ממון לקחנו רביעיתו וחמישיתו ועלה ז' כמה הממון
נעשה הערך ככה והוא שנכפול ז' על כ' ויהיו ק"מ נחלקם על ז' (ט) ויצא לנו ט"ו שלמים וה' חלקים מט' וכן היה סך הממון
|
|
|
ותוכל לדעת זה והוא שתקח רביעית ט"ו ויהיו ג' שלמים וח' חלקים מט' וכן היה סך הממון ותוכל לדעת זה אח"כ העמד החומש מט"ו והם ג' וחלק א' מט' תוסיף על זה ב' ותגרע עמהם ג' וישארו ו'
|
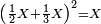
|
יב) שאלה לקחנו מסך ממון מחציתו (ו)שלישיתו ומהעולה לקחנו מרובעו ושב כמו שהיה בתחלה כמה היה הממון
|

- False Position:
![\scriptstyle{\color{blue}{\left[\left(\frac{1}{2}\sdot6\right)+\left(\frac{1}{3}\sdot6\right)\right]^2=5^2=25}}](/mediawiki/images/math/9/b/7/9b7c81bb4ccb8defbc0ffdc19ed0ebd5.png)

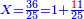
|
התשובה העמד החצי והשליש מו'
אולם אמרו מו' כי בו נמצא חצי ושליש והנם ה' וקח מרובעם ויהיו כ"ה
אח"כ תקח מרובע המורה ג"כ שהוא ו' ויהיו ל"ו
תחלק ל"ו על כ"ה ויצא לך א' שלם וכ"א חלקים מכ"ה וכן היה הממון
|
|
|
ותבחון אותו (ו)קח חצי א' וי"א חלקי' מכ"ה ויהיו י"ח חלקים מכ"ה אח"כ קח שליש א' וי"א חלקים מכ"ה ויהיו י"ב ותחברם אל י"ח ויהיה א' וחומש וקח מרובעם ויצא א' שלם וי"א חלקים מכ"ה ושב כאשר בתחלה
|
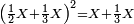
|
יג) שאלה מממון לקחנו מחציתו (ו)שלישיתו ולקחנו מרובע מהעולה ושב כמו הממון וכמו שלישיתו
|

- False Position:
![\scriptstyle{\color{blue}{\left[\left(\frac{1}{2}\sdot6\right)+\left(\frac{1}{3}\sdot6\right)\right]^2=5^2=25}}](/mediawiki/images/math/9/b/7/9b7c81bb4ccb8defbc0ffdc19ed0ebd5.png)
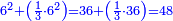
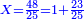
|
התשובה תעשה ככה תקח המורה ר"ל המספר הכולל החצי והשליש והוא ו'
אח"כ קח החצי והשליש והנם ה' וקח מרובעם שהם כ"ה
אח"כ קח מרובע המורה שהוא ל"ו ותחבר אליהם שלישיתם ויהיו מ"ח
אח"כ תחלק מ"ח על כ"ה ויצא לך א' וכ"ג חלקים מכ"ה וכך הוא הממון
|
|
|
ולבחון אותו תקח מחצית זה המספר שהם כ"ד חלקים מכ"ה ואח"כ קח שלישיתם שהם י"ו ותחברם ויהיו א וג' חומשים ותקח מרובעם ויהיו ב' שלמים וי"ד חלקים מכ"ה שהם כמו סך הממון עם תוספת שלישיתו
|
![\scriptstyle\left[\frac{1}{4}\sdot\left(\frac{1}{2}X+\frac{1}{3}X\right)\right]+\left[\frac{1}{5}\sdot\left[X-\left(\frac{1}{2}X+\frac{1}{3}X\right)\right]\right]=12](/mediawiki/images/math/9/f/b/9fb42766182ab84ca76f0ac2ea220a12.png)
|
יד) שאלה מסך ממון לקחנו שלישיתו ומחציתו ומהמרובע ר"ל ממה שיעלה השליש והחצי לקחנו רביעיתו וחומש מה שנשאר מסך כל אחר שילקח החצי והשליש ושוה י"ב כמה כל הממון
|
|
|
התשובה תמצא מספר יהיה לו חצי ושליש ורביעית וחומש יהיה זה ס' והנה נקח מס' שלישיתו ומחציתו ויהיו נ' ונשארו עדין י' אח"כ נקח חומש אלו הי' הנשארים ויהיו ב' שלמים אח"כ נקח רביעית חמישים והנם י"ב וחצי נחברם אל הב' שהיו לנו ויהיו י"ד וחצי אח"כ נכפול י"ב אשר הוא המספר הנודע על המורה אשר הוא ס' ויעלה תש"כ וחלקם על ד' (י"ד) וחצי ויצא לך מ"ט וי"ט חלקים מכ"ט
|
|
|
ולבחון אותו תקח מחצית מ"ט שלמים ומחלקהם ויצא לך כ"ד וכ"ד חלקים מכ"ט אח"כ קח שליש מ"ט ומחלקיהם ויצא לך י"ו וי"ו חלקים מכ"ט וחברם ויהיו מ"א וי"א חלקים מכ"ט אח"כ תקח רביעית זה המספר מצד כי אמר ורביעית מהמחובר מהחצי והשלישית ויהיו י' שלמים גם י' חלקים מכ"ט אח"כ נסיר מ"א שלמים וי"א חלקים שהם החצי והשליש מסך הממון שהוא מ"ט שלמים וי"ט חלקי' מכ"ט הנשאר ט' (ח') וח' חלקים מכ"ט קח מהם החומש מצד שאמר עם חומש הנשאר ויהיה א' שלם עם י"ט חלקים מכ"ט וחברם אל הי' שלמים עם הי' חלקים מכ"ט ויהיו י"ב
|
![\scriptstyle\frac{1}{2}X+\left[\frac{1}{3}\sdot\left(X-\frac{1}{2}X\right)\right]+\left[\frac{1}{4}\sdot\left[X-\left[\frac{1}{2}X+\left[\frac{1}{3}\sdot\left(X-\frac{1}{2}X\right)\right]\right]\right]\right]=14](/mediawiki/images/math/6/f/9/6f9ff55e47632097b32644bf2a91f9fe.png)
|
טו) שאלה מממון חברנו מחציתו ושליש מה שנשאר ורביעית מה שנשאר אחר שנלקח השלישית ושוה הכל י"ד כמה הממון
|
|
|
התשובה ראוי למצא מספר יכלול חצי ושליש ורביע ותמצא י"ב הוצא ממנו החצי שהם ו' הנשאר ו' וקח מהו' הנשארים שלישיתם שהם ב' הנשאר עדין ד' וקח רביעית הד' שהוא א' הנשאר עדין ג' והנה כל חלקי המספרי' הם ט' אח"כ תכפול י"ד שהוא סך הידוע על המורה שהוא י"ב ותחלק העולה על ט' ויצא לך י"ח וב' שלישיות שהם ט' ושליש וקח שליש הנשאר והם ג' ותשיעית וקח רביעית הנשאר שהם א וה' תשיעיות
|
|
|
ותחבר הכל ויהיו י"ד שלמים
|
|
|
יו) שאלה חברנו שני סכומות של ממון מתחלפים זה מזה רביעית א' מן הסכומות וחומש הסכום האחד והיו ח' כמה סך כל א' וא'
|
|
|
התשובה תוכל להשיבה בפנים מתחלפים והוא כי תשים איזה מספר שיהיה רביעית הסך הראשון ואותו המספר תפיל מח' ומה שישאר מהח' תשים אותו חומש הסכום השני ועל זה האופן תמצאנו
|
|
|
והנה נניח דרך משל כי ג' היה (רביע) הסכום הראשון א"כ הסכום השני (הראשון) היה י"ב כי ג' הוא רביעית י"ב תפיל ג' מח' הנשאר ה' ושים אלו הה' חומש המספר השני א"כ הסכום הב' היה כ"ה או אם תרצה שים ב' סכום רביע הסך הראשון א"כ הסך הראשון הוא ח' ותפיל ב' מח' הנשאר ו' ושים אלו הו' חומש הסכום הב' א"כ הסך השני יהיה ל' או אם תרצה שים ד' רביע המספר הראשון א"כ המספר הא' היה י"ו תפיל ד' מח' הנשאר ד' ושים אותם חומש המספר הב' א"כ המספר הב' היה כ' וכן עד אין קץ שתשים איזה מספר שתרצה רביע הסכום הראשון ותפיל זה מהח' ומה שישאר תשים חומש המספר הב'
|
Sums
|
|
|
|
יז) שאלה אם תרצה לקבץ מא' עד י"ד ר"ל א' עם ב' ועם ג' וכן עד י"ד
|
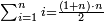
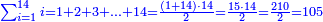
|
ראוי להוסיף א' על י"ד ויהיו ט"ו אח"כ כפול ט"ו על י"ד והם ר"י תחלקם על ב' ויצא לך ק"ה והוא המבוקש
|
![\scriptstyle\sum_{i=1}^{2m} i=\left[\left(\frac{1}{2}\sdot2m\right)\sdot2m\right]+\left(\frac{1}{2}\sdot2m\right)](/mediawiki/images/math/1/8/b/18bd1a03b4210da19a2a238a1343388b.png)
|
יח) שאלה הנה תוכל לעשותה באופן אחר והוא אם המספר הוא זוג ראוי לקחת מחצית אותו המספר ולכפול אותו על כל המספר ולחבר על סך העולה מחצית המספר
|
|
|
דמיון זה נרצה לדעת מא' עד י"ו
|
![\scriptstyle{\color{blue}{\sum_{i=1}^{16} i=1+\ldots+16=\left[\left(\frac{1}{2}\sdot16\right)\sdot16\right]+\left(\frac{1}{2}\sdot16\right)=\left(8\sdot16\right)+8=128+8=136}}](/mediawiki/images/math/1/2/3/123611d802c3533eedae98767a2ea39c.png)
|
ראוי לקחת מחצית י"ו שהם ח' ותכפלם על י"ו ויהיה העולה קכ"ח עו' תוסיף על זה מחצית י"ו שהם ח' ויהיו קל"ו והוא המבוקש
|
|
|
יט) שאלה אולם אם הוא נפרד ראוי לקחת החלק היותר גדול ולכפול אותו על כל המספר והעולה הוא המבוקש
|
|
|
דמיון זה נרצה לדעת המחובר מא' עד כ"ה
|
|
|
הנה ראוי לקחת מכ"ה החלק היותר גדול שהוא י"ג ותכפול י"ג על כ"ה והעולה הוא שכ"ה והוא המבוקש
|
|
|
או אם תרצה תחלק כ"ה על ב' ויהיו י"ב וחצי וכפול אותם על כ"ה ויהיו ג' מאות וי"ב וחצי אח"כ תוסיף על זה מחצית כ"ה שהם י"ב וחצי ויהיו שכ"ה
|
|
|
כ) שאלה קבץ מא' עד י' ולא יהיו הג' בכלל
|
|
|
הנה ראוי לקבץ מא' עד י' שהם נ"ה כאשר ידעת אח"כ קבץ מא' עד ג' שהם ו' ותפיל ו' מנ"ה הנשאר מ"ט והוא המבוקש
|
|
|
כא) שאלה חברנו כל המספרים עד מספר נעלם ועלה המחובר ק"כ
|
|
|
ראוי לחלק זה המספר על ב' ויהיו ס' ולכפול אותו על ד' ויהיו ר"מ והנה יש לך עתה לקחת השרש שעבר ר"ל שהוא קרוב אל ר"מ ותמצא ט"ו והוא המבוקש ר"ל כי כשתקבץ מא' עד ט"ו יעלה ק"כ
|
|
|
כב) שאלה קבץ מא' עד ט' כל הנפרדים
|
|
|
הנה ראוי לשים א' על אותו המספר שהזכיר ולחלק סך העולה על ב' אח"כ ראוי לקחת מרובע העולה מהחלוקה והוא המבוקש והנה נשים על ט' א ויהיו י' אח"כ נחלק אותו על ב' ויהיו ה' נקח מרובעו והוא כ"ה והוא חבור כל נפרדים מא' עד ט'
|
|
|
כג) שאלה אם תרצה לדעת חבור כל הזוגות אשר הם מב' עד י"ב
|
|
|
הנה ראוי לקחת מחצית י"ב [והוא ו'] ולקחת מרובעם שהם ל"ו ויהיו מ"ב
|
|
|
כד) שאלה חברנו כל הנפרדים על מספר נעלם ועלה כ"ה
|
|
|
ראוי לקחת שרש כ"ה ואח"כ כפול אותו על י"ב ותפיל א מהמקובץ והנה שרש כ"ה הוא ה' וכפול אותו והוא י' ותפיל ממנו א ונשאר ט' והוא המבוקש
|
|
|
כה) שאלה חברנו כל הזוגות מא' עד מספר בלתי ידוע ועלה המחובר מ"ב
|
|
|
הנה ראוי לקחת השרש שעבר וידוע כי השרש שעבר היה ו' כפול אותו על ב' ויהיו י"ב והוא המבוקש
|
|
|
כו) שאלה אם תרצה לחבר כל המרובעים אשר הם מא' ועד ד'
|
|
|
הנה ראוי לחבר כל המספרים אשר מא' עד ד' שהם עשרה אח"כ קח ב' שלישיות ד' עם תוספת שליש שהם ג' כפול ג' על י' ויהיו ל
|
|
|
כז) שאלה אם תרצה לחבר כל המרובעים אשר הם מא' עד כ"ה
|
|
|
תחבר כל המספרי' והנם ט"ו וקח ב' שלישיות ה' עם תוספת שלישית ויהיו ג' וב' שלישיות וכפול אותם על ט"ו ויעלה נ"ה
|
|
|
כח) שאלה ואלו אמר קבץ ממרובע ג' עד מרובע ח'
|
|
|
ראוי לקבץ כל המרובעים אשר הם מא' עד ח' שהם ר"ד אח"כ תקבץ המרובעים מא עד ד' ותפיל י"ד מן ר"ד הנשאר ק"ץ והוא המבוקש
|
|
|
כט) שאלה אם תרצה לקבץ כל המרובעים אשר הם מב' עד ח' על המשך הזוגות
|
|
|
הנה ראוי לחבר כל הזוגות אשר הם מב' עד ח' שהם עשרים אח"כ קח שני שלישי ח' עם תוספת ב' שלישיות א ויהיו ו' שלמים כפול אותם על כ' ויהיו ק"כ והוא המבוקש
|
|
|
ל) שאלה קבץ ממרובע א עד מרובע ז' על המשך הנפרדים
|
|
|
תחבר כל הנפרדים אשר הם עד ז' והנם י"ו אח"כ כפול שלישית י"ו עם תוספת ב' חלקים מי"ב או תפיל מט"ו שלישיתם וישאר עד י"ו אח"כ תפיל מזה הא' מחציתו וחבר אותו עם ב' שלישיות ט"ו ויהיו י' וחצי אח"כ תוסיף א על ז' ויהיו ח' והכם בי' וחצי ויצא לך פ"ד
|
|
|
לא) שאלה קבץ לי ממעוקב א עד מעוקב ז'
|
|
|
ודע כי מעוקב ר"ל א' פעם א' א' פעם ב' א' פעם ג' א' פעם ד' וכן עד ז' ואח"כ תקח הב' ותכה אותו עם כל המספרים מא' עד ז' ואח"כ תכה הג' מא' עד ז' וכן הד' וכן עד כלות כל המספרים אם תרצה לדעת סך העולה ראוי לחבר כל הנפרדים אשר הם מא' עד ז' והם כ"ח אח"כ קח מרובע כ"ח שהם תשפ"ד וכן הוא חבור כל המעוקבים מא' עד ז'
|
|
|
לב) שאלה קבץ לי ממעוקב ה' עד מעוקב י"ב
|
|
|
תקבץ כל המעוקבים מא' עד י"ב שהם ו' אלפים ופ"ד אח"כ תקבץ כל המעוקבים אשר הם מא' עד ד' שהם ק' תפילם מו' אלפים ופ"ד הנשאר ה' אלפים וט' מאות ופ"ד והוא המבוקש
|
|
|
לג) שאלה אם אמר קבצנו כל המעוקבים מא עד מספר נעלם ועלה המחובר רכ"ה כמה הוא המספר הנעלם
|
|
|
ראוי הוא לקחת שרש סך החשבון ר"ל שרש רכ"ה והכה שרשו ט"ו אח"כ תקיש זאת השאלה אל קבוץ המספרים ולומר קבצנו כל המספרים אשר הם מא' עד מספר נעלם ועלה המחובר ט"ו יצא לך ה' והוא המבוקש
|
|
|
ודע שאם לא תמצא שרש שלם כמספר שהזכיר דע כי טעית בחשבון
|
|
|
לד) שאלה אם נשאל לך קבץ לי ממעוקב א' עד מעוקב י"ג כדרך הנפרדים
|
|
|
ראוי לחבר כל הנפרדים מא' עד י"ג ויהיו מ"ט וראוי לקחת מרובע מ"ט ויהיו ב' אלפים וד' מאות וא' והוא המבוקש
|
|
|
לה) שאלה אם ישאל לך אדם קבץ לי ממעוקב ה' עד מעוקב ט' על המשך הנפרדים
|
|
|
ראוי לך לקבץ כל המספרים הנפרדים שהם מא' עד ט' והנם כ"א וקח מרובעם ויעלה תמ"א
|
|
|
לו) שאלה קבצנו כל המעוקבים מא' עד מספר נעלם על דרך הנפרדים ועלה רנ"ו
|
|
|
לקחת שרש רנ"ו ויעלו י"ו אח"כ ראוי להקיש ולומ' חברנו כל הנפרדים מא' עד מספר נעלם ועלה י"ו הנה הדרך שתכפול י"ו ד' פעמים ויהיו ס"ד וקח שרשם והנם ח' תגרע ממנו אחד הנשאר ז' והוא המבוקש
|
|
|
לז) שאלה קבץ ממעוקב ב' עד מעוקב י"ב על המשך הזוגות
|
|
|
והנה יש לך לחבר כל המספרים מב' עד י"ב ויהיו מ"ב אח"כ תקח מרובעם שהם אלף תשס"ד
|
|
|
לח) שאלה קבץ ממעוקב ד' עד מעוקב י"ב על המשך הזוגות
|
|
|
ראוי לקבץ כל המספרים מהזוגות שהם מד' עד י"ב שהם מ' וקח מרובע מ' שהוא אלף ות"ר והוא המבוקש
|
|
|
לט) שאלה אם יאמר לך קבצנו כל המעוקבים מב' עד מספר נעלם על דרך הזוגות ועלה המחובר ד' מאות
|
|
|
הנה הדרך בזה שתקח שרש ד' מאות והוא עשרים ואח"כ תאמר [ז]כרנו כל הזוגות שהם מב' עד מספר נעלם ועלה המחובר עשרי' כמה הוא המספר הנעלם ראוי לכפול עשרים על ד' ולהוסיף על המחובר א ויהיה בין הכל פא וקח שרשו והוא ט' ולעולם תפיל מן השרש א' וישאר ח'
|
|
|
מ) שאלה אם תרצה לדעת המחובר מא עד ב' עם ד' עם ח' ועם י"ו וכן לעולם מוסיף המספר הבא על המספר העבר ב' פעמים כמוהו והמספר האחרון עולה קכ"ח
|
|
|
ראוי לכפול קכ"ח על ב' ויעלה רנ"ו ותגרע ממנו לעולם א' והנשאר רנ"ה והוא המבוקש
|
|
|
ואם תרצה לחבר א' עם ב' ועם ד' ועם ח' וכן תמיד עד י"ב
|
|
|
ראוי לחבר עד ד' ר"ל א עם ב' ועם ד' ועם ח' והנם ט"ו תוסיף א ויהיו (ו)י"ו אח"כ כפול ט"ו על עצמם ויהיו רנ"ו אח"כ כפול י"ו על רנ"ו ויצא ד' אלפים וצ"ו והוא מה שבכל הבתים עד י"ב ותגרע א' לעולם וישארו ד' אלפים וצ"ה
|
|
|
וכן תוכל לדעת לעולם אם תכפול מה שיצא לך על י"ו שהוא ד' אלפים וצ"ו עלה פ'ה (ס"ה) אלפים ותקל"ו תגרע מהם א' וישארו ס"ה האלפים ותקל"ה והוא מה שבבית הי"ו
|
|
|
ואם תרצה לדעת מכל ב' בתים תכפול מה שיצא לך על ד' ויצא לך מה שבבית השני
|
|
|
דמיון עתה שידעת מה שבבית הי"ו שהוא ס"ה אלפים ותקל"ו עם תוספת א' תכפול אותו המספר על ד' ויצא לך רס"ב אלפים וקמ"ד והוא מה שבבית הי"ח
|
|
|
וכן תמיד גם מה שבבית הג' תוכל לדעת אם תכפול המספר על ח' ואם תכפול המספר על י"ב יצא לך מה שבבית הה' ר"ל שאם תכפול רס"ב אלפים וקמ"ד על שהוא מה שבבית הי"ח על ל"ב יצא ח' אלפי אלפים וג' מאות ופ"ח אלף וו' מאות וח' והוא מה שבבית הכ"ג מאחר שתוסיף על הבית הי"ח ה' ותגרע א לעולם מן הסך העולה ועל זה הדרך תוכל לדעת בתי האשקאקי שהם ס"ד
|
|
|
מב) שאלה ג' אנשים רצו לקנות דג אחד במחיר י"ז פשוטים אמ' הא' אני אתן כל מה שבידי ואתם תנו חצי מה שבידכם אמר השני אני אתן כל מה שבידי ואתם תנו שליש שלכם אמר השלישי אני אתן את שלי ואתם תנו רביעית ממונכם אשאל כמה היה לכל א' וא'
|
|
|
התשובה נבקש מספר שנוכל להוסיף עליו עד שיהיה המספר ההוא אחר התוספת חציו ושני שלישיותיו וג' רביעיותיו והוא המורה ובעבור שמחיר הדג י"ז פשוטים והוא יותר מי"ב הנה המספר המבוקש פחות מי"ב וכאשר חברנו י"ב והוא המורה עם מחיר הדג והוא י"ז יעלו כ"ט והוא ממון כלם וכאשר נקנה הדג הנה ביד שנים מהם י"ב פשוטים ר"ל אחר שתסיר י"ז פשוטים מכ"ט וכאשר נוסיף על י"ב חצי הכפל הנשאר בידו יהיו כ"ד ויש להשלים עד כ"ט ה' וככה ממון הראשון
|
|
|
וכאשר הוספנו על י"ב ו' (ויהיו י"ב) ויהיו י"ב שתי שלישיותיו ויהיו י"ח הנה יש להשלים עד כ"ט י"א והוא ממון השני
|
|
|
וכאשר הוספנו (על) על י"ב ד' (בלבד) בלבד ויהיו י"ו עד שיהיו שלש רביעיותיו ממונו עד כ"ט יג והוא ממון השלישי
|
|
|
מג) שאלה תמצא לי מספר אשר כשתכפול על ג' ותחלק על ד' ומה שישאר יהיה יחסו אל ד' כיחס ד אל ו'
|
|
|
התשובה נבקש איזה מספר שתרצה והנה נבקש מספר ד' נכפול אותו (ו) על ג' ויהיו י"ח ותחלק י"ח על ד' ויצאו ד' וחצי וידוע כי יחס ד' אל ו' ב' שלישיות ואנו מבקשים מספר שיהיה ב' שלישיותיו מד' והנה נאמר ככה אם בעד ו' ששמנו המספר שנתן לנו ד' וחצי איזה מספר (יתן לי באופן) יתן לי באופן שיבא ב' וב' שלישיות שהם ב' שלישיות ד' כפול ב' פעמים ב' וב' שלישיות על ו' ויעלו ו' והעולה תחלק על ד' וחצי הנה א"כ העולה ג' וה' חלקים מט' הנה א"כ כשתכפול ג' פעמים ג' וה' חלקים מט' והעולה תחלק על ד' יצא לך ב' וב' שלישיות ויחסו אל ד' כיחס ד' אל ו'
|
|
|
מד) שאלה ג' אנשים רוצים לקנות דג אחד כ' מנינים אמר הא' אני אתן כל ממוני ותנו אתם חצי כל אשר לכם אמר השני אני אתן כל ממוני ותנו אתם שליש ממונכם אמר הג' אני אתן כל ממוני ותנו אתם רביעית ממונכם כמה לכל א' וא'
|
|
|
התשובה ראוי לדמות זאת השאלה לאותה שלמעלה אבל אותה שלמעלה הנה הערך [י"ז] וזאת הוא כ' לכן נאמר אם י"ז יתנו לו ה' שהוא סך מאותו שיבקש שיתנו חביריו חצי ממונם כמה ישוו עשרים ויצא לך ה' שלמים וט"ו חלקים מי"ז (אח"כ תאמר) א"כ תאמר אם י"ז יתנו יא וזה הוא חלק מאותו שרוצה שיתנו חביריו שליש ממונם כמה ישוו עשרים ויצא לך י"ב וי"ו חלקים מי"ז והוא ממון השלישי ותבחון אותו ותמצאהו נכון
|
Motion Problems
|
מה) שאלה אדם שלח רץ ג' שילכו מהלך ג' מאות מילין ואח"כ ישובו לאחור וכשיגיעו לאדניהם ילכו גם כן לדרכם וכן תמיד הלוך ושוב ומקצה ועד קצה הם ש' מילין ושלחם ביום אחד בשעה אחת וברגע ומהלך א מהם הוא כ' מילין והשני כ"ה והשלישי ל"ב נרצה לדעת מתי ישיגו זה את זה
|
|
|
התשובה יש לנו לחלק אלו הג' מאות על כ' שהוא מהלך הראשון ויצא ט"ו א"כ בט"ו ימים ילך ג' מאות מילין עוד נחלק ש' על כ"ה ויצא י"ב א"כ בי"ב ימים ילך וכפול י"ב על ט"ו ויעלו ק"פ א"כ בק"פ ימים יהיו אלו הב' זה אצל זה והנה ראוי למצא חשבון שכשתחלקהו על ל"ב יהיו מצומצם (ר"ל שיש לנו למצא מספר ולכפלו נגד ג' מאות ולחלק על ל"ב יהיה מצומצם) ר"ל שיש לנו למצא מספר ולכפלו נגד ג' מאות ולחלק העולה על ל"ב ויצא מצומצם על כן נכפול ק"פ על ג' מאות ויעלה נ"ד אלפים על כ' שהוא מהלך הראשון ותחלק העולה על ש' ויצא בצימצום עוד תכפול נ"ד אלפים נגד כ"ה ותחלק העולה על ש' ויצא בצימצום ג"כ עוד כפול נ"ד אלפים על ל"ב וחלק העולה על ש' ויצא ג"כ שוה
|
|
|
שאלות מר'ל[וי] בן גרשו[ם]
|
|
|
מו) שאלה ג' שביעיות וד' חמישיות המספר הנעלם מוסיפים על ב' חמישיות (שלישיות?) ורביעית המספר הנעלם חמישים (עשרים?) רצינו לדעת כמה המספר הנעלם
|
|
|
התשובה הנה המורה הוא ת"ק (ת"ך?) וג' שביעיותיו עם ד' חמישיותיו הוא תקי"ו וב' שלישיותיו הוא ת"ק ורביעיתו הוא שפ"ה הנה החלקים הראשנים מוסיפים על השניים מספר קלה ערכנו המורה על עשרים וחלקנו העולה על קל"ה ועלה ס"ד שלמים וי"ו חלקי' מקלא והוא המבוקש
|
|
|
מז) שאלה המתנועע מתנועע בי"ג ימים י"ז (ז?) שעורים מן הדרך ול"ו ראשנים ונ"ז שניים ורצינו לדעת כמה מן הדרך ילך בכ"ג (בג'?) ימים וי"ז שעורים ונ"ב ראשנים וי"ו שניים
|
|
|
התשובה הנה נשיב הימים שעות ויהיה הזמן הראשון שי"ב והשמן (זמן) השני בפ"ט ונ"ב ראשנים וי"ו שניים ערכנו ז' ראשנים (שלמים) ל"ו ראשנים נ"ז שניים על פ"ט שלמים נ"ב ראשנים י"ו {והעולה חלקנו...} והוא (זמן) השעורים שהלך מן הדרך בזמן המונח השני
|
|
|
מח) שאלה המתנועע הולך ז' שעורים מן הדרך ול"ו ראשנים נ"ז שניים בכ"ג (י"ג?) ימים ורצינו לדעת בכמה מן הזמן ילך ג' שעורים מן הדרך
|
|
|
ערכנו ג' שעורים על שי"ב שלמים וחלקנו העולה על ז' שלמים ול"ו ראשנים ונ"ז שניים ועלה קכ"ב שעות ונ"ד ראשנים וי"ו שניים והוא המבוקש ר"ל הזמן הנעלם
|
|
|
מט) שאלה אדם מהיר בשעה א' ב' שעורים ול"ז שניים ויהיה מהלך המתוני לשעה א' ל' ראשנים כ"ד ראשנים (שניים) והיה מרחק המתוני מהמהיר לפניו כ"ט שעורים ומ"ט ראשנים והיה יתרון מהלך המהיר על מהלך המהיר (המתוני) לשעה הוא שעור א' ול' ראשנים וי"ג חלקנו עליו המרחק המונח ועלה י"ט שעות מ"ז ראשנים מ"ט שניים והוא המבוקש
|
Purchase Problems
|
נ) שאלה הסוחר מוכר מד' סמים ערך הסם הראשון ז' פשוטים הליט' וערך הסם השני ח' פשוטים הליט' וערך הסם השני (השלישי) י' פשוטים הליט וערך הסם הרביעי ט"ו פשוטים הליט' ובא הקונה לקנות בג' דינרין משקל שוה מכל א' מהסמים והנה בג' דינרין וד' פשוטים יקח ליט' מכל א' והנה יחס ג' דינרין אל ג' דינרין וד' פשוטי' הוא ט' שעיריות (עשיריות) וככה יקח מכל סם וסם ר"ל ט' עשיריות ליט' ויהיה ערך הכל ג' דינרין ותוכל לבחון אותו
|
|
|
נא) שאלה הסוחר מוכר מד' סמים ערך הא' ב' דינרין הליט' וערך האחר ב' דינרין ומהאחר י"ב דינרין הליט' והאחרת כ' דינרין הליט' ורצינו לדעת כמה מן הליט' יילקח מאחד אחד מהסמים ויהיה ערך מה שילקח מזה כמו ערך מה שילקח מזה
|
|
|
והנה תכתו' בטור א' ערכי הליט' והוא אבגב (אבגד) ובטור תחתיו תמיד הענין על זה הסדור הנז' רצוני שתכתוב בג' ותחת ג' ב' וגם כן הנה תכתוב תחת י"ב ב' ותחת ב' י"ב ואחר תקח קטני המספרים המתיחסים בכמה זה היחס ר"ל מיחס ב' אל ג' ומיחס י"ב אל ג' ומיחס כ' אל י"ב וזה שיחס כ' אל ל כיחס ג' אל ב' ויחס ה' אל ה' כיחס י"ב אל ג' ויחס ה' אל ג' כיחס כ' אל י"ב ולזה תקח מן הסם אשר ערכו ב' דינרין ל' ליט' והוא המספר הנכחי לו ומהסם אשר ערכו ג' דינרין הליט' תקח ה' ליט' ומהסם אשר ערכו כ' דינרין תקח ג' ליט' ויהיה ערך מה שתקח מכל א' מהם שוה וראוי שתשמור בזה הדרך הנזכר אם היה ערך אחד הסמים מספר הפשוטים שתשיב ערך הסמים הנשארים לפשוטים
|
|
|
נב) שאלה הסוחר מוכר מג' סמים ערך הא' ז' פשוטים הליט' וערך הב' י' פשוטים הליט' וערך הג' כ' פשוטים הליט' ובא הקונה לקנות ליט' מכלם ויהיה ערך מה שיקח מא' מהם כמו ערך מה שיקח מכל א' מהאחרים
|
|
|
והנה קטני המספרים שילקחו מאחד אחד מהם ויהיה הערך שוה הם מספרי כ' י"ד ז' והנה מקובצם הוא מ"א והם חלקי הליט' וילקחו מאלו החלקים מהם [ב]אשר ערכו ז' פשוטים הליט' כ' חלקים ומהסם אשר ערך הליט' ממנו י' פשוטים ילקחו י"ד חלקים ומהסם אשר (אשר) ערך הליט' ממנו ב' פשוטים ילקחו ז' חלקים והנה הכל מ"א חלקים שהוא ה' ליט' ואולם ערך הליט' הנה תקח ערך מספרי כ' י"ד ז' כל אחד מהנכחי לו ותקבץ הכל והנה הכל ל"ה דינרין חלק ל"ה על מ"א ועלה י' פשוטים וי' חלקים ממ"א בפשוט והוא המבוקש
|
|
|
נג) שאלה הסוחר מוכר משני סמים ערך הסם הא' י"ז פשוטים וערך האחר כ"ד פשוטים הליט' ובא הקונה לקנות מדה משניהם ויהיה ערכה י"ט פשוטים
|
|
|
והנה יתרון המוסיף על המחסיר הוא ז' והם חלקי המדה והנה חסרון המחסיר מי"ט הוא שנים והם החלקים מחלקי המדה שיקח מהסם אשר ערכו מוסיף והנה יתרון המוסיף הוא ה' והם חלקים שיקח מהסם אשר ערכו מחסיר ויהיה ערך המדה י"ט פשוטים
|
|
|
נד) שאלה הסוחר מוכר מז' סמים ערך הא' ג' פשוטים הליט' וערך הב' ה' פשוטים וערך הג' ח' פשוטים וערך הד' י"א וערך הה' ט"ו וערך הו' י"ט פשוטים וערך הז' כ"ח פשוטים ורצה אדם לקנות ליט' א' מכלם בט"ו פשוטים
|
|
|
והנה המוסיפים הם ב' הסם אשר ערכו י"ב והסם אשר ערכו כ"ד פשוטים והמחסירים הם ד' אותה אשר ערכה ג' ואשר ערכה ה' ואשר ערכה ח' ואשר ערכה יא הנה נשים ג' פשוטים נלוו לי"ט פשוטים וה' פשוטים נלוו לכ"ח ומפני שנשארו עו' סמים במחסירים ולא נשארו מהמוסיפים נקח מהמוסיפים היותר קרוב אל ט"ו שהוא הערך המבוקש והוא י"ט ונזווג י"ט עם כל א' הנשארים מהמחסירים כמו שתראה בזאת הצורה
|
|
|
וכבר ידענו דרך נקח ליט' מכל זוג מאלו יהיה ערכה ט"ו פשוטים ולזה נקח מסם ג' ד' חלקים מי"ו בליט' ומסם י"ט ב' חלקים מי"ו בליט' ונקח ג"כ מסם ה' י"ג חלקים מכ"ג בליט' ומסם כ"ח י' חלקים מכ"ג בליט' ונקח ג"כ (ונקח ג"כ) מסם ח' ד' חלקים בליט' ומסם י"ט ז' חלקים מי"א בליט' ונקח ג"כ מסם י"א ד' חלקים מכ"ח בליט' ומסם ד י"ט חלקים בליט' והנה מספר כל אלו החלקים הוא נ"ח ונוסיף שני חלקים בעבור ט"ו שאין לו גלוי והנם ס' והם חלקי הליט' נקח מהם מסם ג' פשוטים ד' חלקים ומסם ה' י"ג חלקים ומסם ח' ד' חלקים ומסם יא ד' חלקים ומסם ט"ו ב חלקים ומסם ט"ו כ"ג חלקים ומסם י"ח י' חלקים ויהיה ערך הליט' ט"ו פשוטים והוא המבוקש
|
|
|
נה) שאלה ראובן שכר שמעון י' ליט' שיעשה מלאכתו ט' ימים ובזאת המלאכה ישכור לו בכל יום י"ג מן האנשים ינהוג כל אחד מהם ז' בהמות תשא כל בהמה ט"ו מדות ותלך ו' פרסאות והוא שכר לו ח' ימים (י)ז' מן האנשים והנהיג כל אחד מהם ו' מדות ונשאה כל א' מהם י"א מדות והלכה ז' פרסאות
|
|
|
והנה המספר המורכב מהמספרים שהתנה הם ט' י"ג ז' ט"ו ו' והוא ע"ג אלפים ותשי' והוא השמור והמספר המורכב מהמספרים שהשלים ח' י"ז ו' י"א ז' והוא תתל"ב * אלפים והנה וס'ב' יחס י' ליט' אל מה שהוא חייב לו כיחס השמור אל ס"ב אלפים ותתל"ב ואם תערוך י' לט ד' שהוא הא' על הד' שהוא ס"ב אלפים ותתל"ב והעולה תחלק על השמור יצא לך ח' ליט' וחצי ואלף (ואלף) וז' מאות ופ"ה חלקים מס"ב אלפים ותתל"ב הליט' שהם ה' פשוטים וכ"ה אלפים תת"נ מע"ג אלפים תש"י בפשוט
|
|
|
נו) שאלה ראובן קנה ב' חמישיות המדה וג' שביעיות ב' דינרין ומכר ד' תשיעיותיה ה' דינרין והרויח ק' דינרין נרצה לדעת כמה הממון
|
|
|
הדרך בזה שתקח המורה לכל אלו החלקים הן מהמדה הן מהדינרין ואם קרה שיהיו בהם חלקים והנה המורה לכל אלו החלקים כמשלינו הוא שנית והוא המדה קח ממנו ב' חמישיותיו וג' שביעיותיו ויעלה רי"ו הנה א"כ בדינר יקנה מאלו החלקים ק"ח גם קח ממנו ד' תשיעיות ויעלה ק"מ הנה א"כ בדינר יתן ע' מאלו החלקים ולזה ירויח בדינר ל"ג חלקים וכבר היה הריוח ק' דינרין שהוא ז' אלפים מאלו החלקים הנה ראוי שנקח מספר יהיה יחסו אל ק"ח כיחס ז' אלפים מאלו החלקים הנה ראוי שנקח מספר יהיה יחסו אל ק"כ כיחס ז' אלפים אל ל"ח אלפים וכבר התבאר דרך לקיחתו
|
|
|
ואם חלקת העולה על ע' הנה תמצא מספר הממון עם מה שהרויח יחד ואם חלקת העולה על ק"ח שהוא סך ערכי הדינר לפי מה שקנה תמצא מספר הממון וזה מבואר
|
|
|
ואם היתה השאלה בהפך ר"ל שהפסיד ק' דינרין כשקנה ד' תשיעיות המדה כ' דינרין ומכר ב' חמישיותיה עם ג' שביעיותיה ב דינרין
|
|
|
הדרך אחר אלא שכאשר תחלק העולה על ע' יהיה לך מספר הממון ואם תחלקהו על ק"ח יהיה לך הנשאר לו אחר ההפסד
ואם שאל כמה המקח חלק העולה על שפה והם חלקי המדה והנה מדות המקח
|
|
|
נז) שאלה איש אחד מחליף מסחר מה במסחר אחר וערך חלקים מה מן המדה ממה שנתן ככה וערך חלקים ממה שקבל ככה ונתן מספר ככה מן המדות כמה ראוי שיקבל
|
|
|
והמשל שהמסחר שנתן ישוו ג' חמישיות המדה עם ב' תשיעיותיה ב' דינרין והמסחר שקבל ישוו ג' דינרין מי"א במדה עם ב' שביעיותיה ג' דינרין ונתן לו ב' מדות ורצינו לדעת כמה ראוי שיקבל
|
|
|
הדרך בזה שתקח המורה לכל אלו החלקים הן מהמדה הן מהדינרין אם קרה שיהיו שם חלקים וממנו תקח החלקים שילקחו בדינר לכל א' מאלו הערכין וכמו ערכי הדינר ממה שנתן אל חלקי הדינר ממה שקבל כן יחס מה שנתן אל מה שקבל והנה המורה לכל אלו החלקים הם ג' אלפים ותס"ה לקחנו ג' שביעיותיו וב' תשיעיותיו והם אלפים תס"ד ולזה יהיו החלקים שילקחו בדינר ממה שנתן אלף רל"ב לקחנו ב' שביעיותיו וג' חלקים מי"א במדה [.] יעלה אלף תתקל"ה ולזה יהיו החלקים שילקחו בדינר ממה שקבל תרמ"ה והנה כיחס אלף רל"ה אל תרמ"ה כן יחס מה שקבל אל ב' מדות
|
|
|
וכבר ידעת דרך לקיחת זה המספר הנעלם ומה התבאר אם התנה ראובן עם שמעון לעשות מלאכתו ויתן לו בשכירותו כ"ט ימים וחומש יום ב' דינרין ושמעון יתן לראובן בכל יום שיבטל ד' חלקים מי"א בדינר ועשה שמעון ב' ימים וג' שביעיות יום ובטל ויצא שכרו בהפסדו רצינו לדעת כמה בטל לקחנו המורה לכל אלו החלקים בכללם ועלה שפ"ה והוא חלקי היום
|
|
|
הנה נראה בכמה חלקים מאלו ירויח דינר ובכמה חלקים מאלו יפסידהו וכיחס מספר הריוח אל יחס ההפסד כן יחס ג' ימים וג' חמישיות אל הזמן שבטל והנה בקלה חלקי' וי"ב חלקים מעשרים בחלק ירויח דינר ובאלף וי"ח חלקים וכ"ג מד' בחלק יפסיד דינר וככה יחס ב' ימים וג' חמישיות אל הזמן שבטל
|
|
|
נח) שאלה שיהיה מספר ראשון כשחובר אל מספר שני היה יחסו אל הג' ג' שלמים וב' חמישיות ושביעיות וכשחובר הראשון אל הג' היה יחסו הראשון ז' שלמים וב' שלישיות ורביעיות והמספר הב' ל' רצינו לדעת כמה כל א' מהנשארים
|
|
|
הנה תוציא תחלה ג' מספרים יונהגו זה המנהג על הדרך שהתבאר במאמר הראשון מספרינו ולזה תדע משטח מג' שלמים וב' חמישיות ושביעית ויהיו בידך ד' שלמים וב' חמישיות ושביעית והוא המספר השני גם תוסיף א על ז' שלמים וב' שלישיות ורביעית והעולה בידך הוא המספר השלישי והוא ח' שלמים וב' שלישיות ורביעית וכבר ידעת שהמספר הגלוי לשניים הוא ל ולזה יהיה המספר הגלוי לראשון ראשון שני שלישי כא שלמים ושלישית שביעית ד שלמים וב חמישיות ושביעית ח שלמים וב' השלישיות ורביעית שלשים שלישיות קע"ח שלמים וצ"ח חלקים נ"ח שלמים רפ"א חלקים מקט"ו באחד משי"א באחד קע"ח שלמים וצ"ח שלמים ק' חלקים מקנ"ז באחד והמספר השלישי נ"ח שלמים ורפא חלקים משי"א באחד ואלו המספרים הם המבוקשים ואלו תחקור תמצא
|
|
|
נט) שאלה יהיה יחס הראשון עם השני מקובצים אל השלישי ג' חמישיות ושישית ויחס הראשון והג' מקובצים אל השני ב' שלמים ושלישית והמספר הראשון עשרים נרצה לדעת כמה כל א מהמספרים הנשארים
|
|
|
הנה לפי מה שהתבאר נוציא המספרים אשר מנהגם זה המנהג ויהיה המספר הראשון לפי מה שקדם ב' חמישיות ושלישית ושליש שישית ויהיה השני אחד ול' שלם וג' חמישיות ושישית ולפי שהיה המספר הגלוי לראשון עשרים יהיה המספר הגלוי לשני מ"ד שלמים וכ"ו חלקים מע"א בא' שלם והמספר הגלוי לשלישי פ"ד שלמים ול"ו חלקים מע"א בא' שלם והם המספרים המבוקשים
|
|
|
ס) שאלה שיהיה יחס הב' אל הנשאר מהג' כשחוסר ממנו הא' ג' שלמים ושליש ויחס הג' אל הנשאר מהב' כשחוסר ממנו הא' מספר ו'
|
|
|
והנה נוציא ג' מספרים על הדרך הקודמת באלו היחסים הנזכרים הנה ר"ל שיהיה יחס מקובץ הראשון והשני אל השלישי ג' שלמים ושליש ויחס מקובץ הראשון והג' מקובצים אל הב' ו' שלמים והנה הראשון י"ט והשני ד' ושליש והג' ז' ולזה יהיה הראשון י"ט ותחבר עם השני יט ויהיו כ"ג שלמים ושליש והוא המספר השני ותחבר עם השלישי י"ט ויהיו כ"ו והוא המספר השלישי ותקיש על זה
|
|
|
סא) שאלה שיהיה יחס הראשון והשני מקובצים אל הנשאר מהג' כשחוסר ממנו הראשון ד' שלמים וחצי ויחס הראשון והג' מקובצים אל הנשאר מהב' כשחוסר ממנו הראשון הוא ה' שלמים ונרצה לדעת כמה כל המספרים שינהגו זה המנהג
|
|
|
הנה נוציא המספרים הג' על הדרך הקודמת לפי אלו היחסים רצוני שיהיה יחס הראשון והשני מקובצים אל הג' ד' וחצי ויהיה יחס הא' והג' מקובצים אל הב' מספר ה' ולזה יהיה הראשון נ"א וחצי והשני ו' וחצי והג' ו' והנה חצי הא' הוא י' וג' שביעיות והוא הראשון הנה חברנו י' וג' שביעיות אל השני ועלה י"ו ורביע והוא השני הנה חברנו י' וג' שביעיות עם השלישי ועלה י"ו וג' רביעיות והוא הג'
|
|
|
סב) שאלה שיהיה הראשון עם רביעית הנשארים שוה אל השני עם שישית הנשארי' והוא ג"כ שוה אל השלישי עם תשיעית הנשארים
|
|
|
כבר התבאר לך במאמ' הראשון מזה הספר שסדור אלו המספרים הג' הוא על זה הסדר אשר סדרוה רצוני שהראשון הוא אשר יתחבר המתחלק יותר גדול מן הנשארים והל' הוא אשר יתחבר עמו יותר קטן והנשארים והזכרתי זה לך למען לא תבלבל בביאורים והנה יהיה המספר השני מהם כ' ורצינו לדעת כמה כל א' מהנשארים
|
|
|
וכבר ידענו שהמספרים שינהגו כמו זה המנהג הראשון מהם קי"ט והשני קנ"א והג' קס"ט מזה הגליים ונוציא שאר הגליים על היחס ולזה יהיה הגליים לראשון ט"ו שלמים וקט"ו חלקים מק"א בא' שלם והוא הראשון הנה ויהיה הגליי לג' כ"ב שלמים ונ"ח חלקים מקנ"א בא' והוא השלישי הנה והם המספרים המבוקשי' ואם תרצה תוכל לבחון אותו
|
- 63) Question: three men formed a partnership.
- The money of all three together is 25 minyanim.
- The share owed to the first from the profit they earned is 16 minyanim.
- The share owed to the second from the profit is equal to the root of the money earned by the first.
- The share owed to the third from the profit is equal to the root of the money [earned by] the second.
- How much did each contribute to the partnership?
|
סג) שאלה ג' אנשים עושים שותפות
והנה ממון שלשתן עולה כ"ה מניינים
והנה לראשון מגיע לחלקו מהריוח שעשו י"ו מנינים
ולשני מגיע לחלקו מהריוח הממון שרש ריוח ממון הראשון
והשלישי ראוי לו ליקח מהריוח כמו שרש ממון השני
כמה שם כל אחד ואחד בשותפות
|
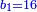
|
התשובה כבר ידעת כי ריוח ממון הראשון הוא י"ו
|
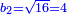
|
על כן יש לך לקחת שרש י"ו והם ד' וזה יהיה ריוח ממון מהשני
|

|
עוד יש לך לקחת שרש ד' והם ב' וזה סך ריוח ממון השלישי
|
- Three formed a partnership - one contributed 2 minyanim, the second [contributed] 4 [minyanim], and the third [contributed] 25 [minyanim]. They earned 25. How much should each have?
|
ונעשה ככה בכאן ג' עושים שותפות הא' שם ב' מנינים והב' ד' והג' י"ו והרויחו כ"ה כמה היה לכל אחד ואחד
|
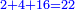
|
תחבר ממון שלשתן והם כ"ב
|
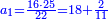
|
וכפול חלק הראשון שהוא י"ו על כ"ה ותחלק מה שיעלה על כ"ב ויצא לך י"ח וב' חלקים מי"א והוא סך ממון מה ששם הראשון בחבורה שהגיע לחלקו מהריוח י"ו מנינים
|
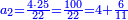
|
עוד תכפול ד' על כ"ה ויצא לך ק' וחלקם על כ"ב ויצא לך ד' וו' חלקים מי"א והוא חלק השני
|
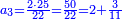
|
עוד כפול ב' על כ"ה ויצא לך נ' וחלקם על כ"ב ויצא לך ב' שלמים וג' חלקים מי"א והוא חלק הג' ר"ל מה ששם בחבורה מי שהגיע לו מריוח הממון ב' ותקיש על זה
|
|
|
סד) שאלה יש כאן אנשים ידועים לכל א' יש סכום מטבעים מתחלפי' מהסכום גם מהמטבעים ונרצה לדעת איזה מטבע יש לכל א' וכמה מטבעים יש לו ומי הם ד' בעלי המטבעים ר"ל מחזיקי המטבעים
|
|
|
התשובה ראוי לכפול בעל המטבע הגדול ולהוסיף על זה ו' ולכפול העולה על ה' ולהוסיף על הסכום בעל המטבע הב' שהוא המטבע התיכונה ולכפול העולה על ה' ולחסר מהסך ק"נ ולכפול הנשאר על ב' ולהוסיף על זה בעל מטבע הג' ולכפול אותו על ה' והעולה יכפול ג"כ על ב' ולהוסיף על זה בעל מטבע הד' ועתה תוכל לדעת מי הוא מחזיק מטבע הזהב על דרך משל שהוא שהוא היותר גדול ומי הוא מחזיק הכסף הבא אחריו ומי מחזיק הנחושת ומי מחזיק הברזל אך לא תדע סכום המטבעים המחזיקים כל א' ודע כי האלפים הוא מספר הזהב והמאיות מספר הכסף והעשרות הנחושת והאחדים הברזל ועתה תשוב לעשות המספר הנז' פעם אחרת ותוכל לדעת סכום המטבעים המחזיק כל א וא' כי האלפים סכום הזהב והמאיות סכום הכסף והעשרות הנחושת והאחדים הברזל
|
|
|
ואתן לך דמיון : דמיון נתתי ג' מניני זהב לאיש רביעי וה' קרליני מכסף לאיש ו' וז' קאוואלי מנחושת לאיש ח' וט' פיצולי מברזל לאיש ט' ותרצה לדעת למי הם מטבעי הזהב וכמה הם
|
|
|
תאמר לו שיכפול האיש מחזיק הזהב ויהיו ח' ותוסיף עליו ו' ויהיו י"ד כפול אותם על ה' ויהיו ע' תוסיף על זה בעל מטבע הכסף שהוא הו' ויהיו ע"ו תכפלם על ה' ויהיו ש"פ תסיר מהם ק"נ נשארו ר"ל תכפלם על ב' ויהיו ת"ס תוסיף על זה בעל מטבע הנחושת שהוא הח' ויהיו תס"ח תכפלם על ה' ויהיו ב' אלפים וג' מאות ומ' וכפול זה על ב' ויהיו ד' (אלפים) וו מאות ופ' ותוסיף על זה בעל מטבע הברזל ויהיו ד' אלפים וו' מאות ופ"ט הנה ד' אלפים הם ד' אנשים ר"ל איש רביעי והוא מחזיק הזהב אך לא תדע סך המטבעים עדין ו' מאות הם איש ו' מחזיק הכסף ופ' איש ח' בעל הנחושת וט' איש ט' בעל מטבע הברזל ועדין לא תדע כי אם האנשים ר"ל מי מחזיק הזהב וכן הכסף אך לא תדע סך מנינם
|
|
|
ואם תרצה לדעת סך כל מטבע ומטבע תאמר לו שיכפול הג' מניני' ויהיו ו' תוסיף עליו ו' ויהיו י"ב תכפלם על ה' ויהיו (ס' תוסיף על זה ה' שהוא סך מטבעי הכסף ויהיה ס"ה כפול על ה' ויהיה) שכ"ה תסיר מהם ק"נ נשארו קע"ה תכפלם על ב' ויהיו ש"נ תוסיף על זה ז' שהוא סך מטבעי הנחושת ויהיו שנ"ז תכפלם על ה' ויהיו אלף ותשפ"ה ותכפלם על ב' ויהיו ג' אלפים ותק"ע ותוסיף על זה סכום מטבעי הברזל שהם ט' ויעלה הכל ג' אלפים ותקע"ט הנה א"כ הג' אלפים הם ג' מטבעי זהב והה' מאות הם ה' מטבעי כסף והע' הם ז' מטבעי נחושת והט' הם ט' מטבעי ברזל הנה א"כ האיש הד' מחזיק ג' מניני זהב והאיש הו' מחזיק ה' מטבעי כסף והאיש הח' מחזיק ז' מטבעי נחושת והאיש הט' מחזיק ט' מטבעי ברזל שהם פיצולי
|
|
|
סה) שאלה אם מספר ד' הוא שליש מספר ט"ו מהו חומש כ"ה
|
|
|
התשובה היא על ב' פנים הא' ראוי להעמיד שליש ט"ו שהוא ה' ותאמר אם ה' שבו ד' מצד כי אמר כי ד' הם שליש ט"ו מספר ה' שהוא חומש כ"ה כמה שוים תכפול ד' על ה' וחלק על ה' ויצא לך ד' והוא המבוקש
|
|
|
והדרך הב' הוא כן והוא כי יש לנו לכפול מספר ד' על ג' ויעלו י"ב א"כ מספר ד' הוא שליש י"ב ונרצה שיהיה שליש ממספר ט"ו ויש לך לעשות הערך כך ולומ' אם ט"ו שבו י"ב כ"ה כמה ישוו כפול כ"ה על י"ב וחלקם על ט"ו ויצא לך עשרים תקח חמישיתם ויצא ד'
|
|
|
סו) שאלה אם תרצה לדעת מה שחשב אדם בלבו תאמר לו שיחלקהו על ב' אח"כ שאל לו אם יש בחלוקה חצי ותעשהו שלם ותקח אתה בעד החצי א' אח"כ תאמר לו שיוסיף מחצית המספר על המספר כלו ואח"כ תאמר לו שיחלק העולה על ב' ואם יש בו חצי ג"כ תקח שנים בעבור החצי הב' ותאמ' לו שיעשהו שלם ותאמ' לו שיוסיף זה על מה שהיה לו קודם החלוקה השניה ותשאל לו כמה תשיעיות יש בו וקח בעד כל ט' ד' ותוסיף העולה על מה שיש לך מהב' חלוקות והיוצא הוא המבוקש
|
|
|
דמיון אדם חשב מספר ל"ג תאמר לו שיחלקהו על ב' ויצא לך י"ו וחצי ותאמ' לו שיעשהו שלם ויהיו י"ז ותקח א' אח"כ תוסיף אלו הי"ז על ל"ג ויהיו נ' ותחלקם על ב' ויצא לך כ"ה תוסיף אלו הכ"ה על נ' ויעלה ע"ה תקח בעד כל ט ד' ויעלו ל"ב כי ח' תשיעיות שלמות יש בו ותוסיף עליו א' שהיה מן החלוקה הראשנה ויהיו ל"ג וסימניך אבג"ד ר"ל תקח א בעד החלוקה הראשנה אם יש בו חצי ותקח ב' בעד החלוקה השניה אם יש בו חצי ותקח ג' אם יש חצי בראשנה גם בשניה ותקח ד' בעד כל ט'
|
|
|
סז) שאלה אם תרצה לדעת כמה מדות קטנות יכיל כלי גדול דע כמה אצבעות מבוהן היד יש בארכו מבפנים ובעמקו באמצע ג"כ בעומק ראשו מפני שהוא צנה וקח שעור חצי האצבעות שמצאת בעמקו באמצעו ובראשו ותכפלם בעצמם והעולה תכפלם ג"כ בשעור מספר האורך והעולה תחלקהו על קמ"ד והיוצא הוא המדות שיכיל הכלי
|
|
|
דמיון זה רצינו לדעת כמה יכיל כלי שהיה בארכו מבפנים נ' אצבעות באצבע הגודל שלי שהוא בזה השעור ויש בעמקו באמצע נ"ח (מ"ח) אצבעות ובעומק הראש שהוא יותר צרה ב' קח מחציתם שהם כ"ד ותכפלם על עצמם ויעלו ב' מאות (ת"ק) וע"ו תכפלם ג"כ על שעור האורך שהם נ' ויעלו כ"ח אלפים וח' מאות חלקם על קמ"ד ויצאו מאתים ואלו הם המדות ש[יכי]ל הכלי במדה שנוהגים עכשו למדוד היין פה עיר קורוניאה
|
|
|
סח) שאלה אם תרצה לדעת מכלי שיש בו יין ואינו מלא ותרצה לדעת כמה יכיל החסרון דע שעור האצבעות שיש בעומק הכלי באמצעו וקח מחציתם ותכפלהו בעצמו וחלק עליו חצי המדות שיכיל הכלי בהיותו מלא והיוצא הם המדות שיחסר מהכלי ובאצבע הראשון ובשנית כמות הראשון ובכפלו ובשלישית כמות השנית וכפל הראשון וברביעית כמות השלישי וכפל הראשון וכן כלם בין רב למעט
|
|
|
ולדעת כמה מדות יכיל בחסרון כלי תכפול החסרון כלי בעצמו ותכפלהו בראשון והעולה הם המדות שיש בחסרון
|
|
|
דמיון יש לנו כלי שיכיל ד' מדות קטנות ויש בעמקו באמצע כ"ח אצבעות קח חצים שהם י"ד ותכפלם בעצמם ויעלו קצ"ו חלק עליהם חצי מאתים מדות שיכיל הכלי שהם ק' ויצא לך חצי יותר מעט ואין לחוש על השאר והוא מה שיחסר בשעור האצבע הראשנה ואם יחסר ו' אצבעות תכפלם בעצמם ויהיו ל"ו תכפלם על החצי ויעלו לי"ח והם המדות שיכיל שעור הו' אצבעות שיחסר הכלי
|
|
|
סט) שאלה אם תרצה לעשות כלי שיכיל מדה ידועה לא פחות לא יתר דע תחלה אורך הלוחות שתרצה לעשותו והוצא מהם הנצרך לשייר לעשות מקום לישיבת תחתיות הכלי וקח הנשאר מאורך הלוח ושמרהו וחלק עליהם שעור המדות שרצונך שיכיל הכלי מוכפלים על קמ"ד ומהיוצא קח שרשו והוא השעור שצריך להיות בעומק הכלי ברביעיתו שהוא בין האמצע ובין הראש
|
|
|
דמיון רצינו לעשות כלי שיכיל מאתים מדות ויש לנו לעשותן מלוחות שיש בארכן נ"ד אצבעות חסר מהם ד' למושב תחתית הכלי וישארו נ' תכפול מאתים על קמ"ד ויעלו 0 0 8 4 1 חלקם על נ' שבאורך ויצא לך 6 7 5 קח גדרם שהוא כ"ד וזה השעור צריך להיות בעומק שבין האמצע ובין הראש שהוא ברביעית אורך הלוח מפני שצריך להיות עומק האמצע גדול מעומק הראש
|
|
|
או אם תרצה עשה הלוחות כתקנן באופן שלא ישאר לגמר מלא כל הכלי אלא חבורם ותעשה בענין שיהיה רוחב כלם ברביעיתן הגדר מוכפל על ג' ושביעית
|
|
|
דמיון זה יצא בגדר כ"ד תכפלהו בג' ושביעית ויהיו ע"ה וג' שביעיות תעשה רוחב כל הלוחות ברביעית אורך הלוח שתהיו שוות לע"ה וג' שביעיות הנז' ותעשה כלי כרצונך
|
|
|
ע) שאלה ד' אנשים אמר הא' לב' אם תתן לי חצי ממונך עם שלי יעלה עשרה אמר הב' לג' אם תתן לי שליש ממונך עם חצי הממון שהיה לי קודם שנתתי לחבירי מחציתו יעלה עשרה ר"ל עם מה שנשאר לי השיב הג' לד' אם תתן לי רביעית ממונך עם מה שנשאר לי אחר נתינת השליש יעלה עשרה גם נשארו לך עשרה כמה היה הממון
|
|
|
הנה תקח המורה על ממון האחרון רצוני הד' כי ידוע הוא כי אחר שנתן רביעית הממון נשארו י' א"כ נאמר עשרה מאיזה מספר הוא ג' רביעיותיו תמצא י"ג ושליש א"כ ממון האחרון היה י"ג ושליש ונתן הרובע ונשארו לו י' א"כ אלו הג' ושליש נתן לג' כדי שישלים לו מנין עשרה א"כ היה לו ו' וב' שלישיות אחר שנתן שליש ממונו לשני ונאמר ו' וב' שלישיות מאיזה מספר הוא ב' שלישיות תמצא י' א"כ לג' היה לו י' ונתן מהם ג' ושליש שהם שלישיתם וקבל ג"כ ג' ושליש ויצא שכרו בהפסדו הנה א"כ היה לו עשרה כי מה שחסר זה מלא זה וא"כ נשוב לשני וידוע כי ממון שנשאר לו אחר שנתן החצי לחבירו הוא ו' וב' שלישיות בעבור כי יש לו לקבל ג' ושליש ויעלה י' א"כ נאמר ו' וב' שלישיות מאיזה מספר הוא חציו נמצא י"ג ושליש א"כ ממונו היה י"ג ושליש ונתן מהם מחציתם שהם ו' וב' שלישיות וככה נשאר לו וקבל ג' ושליש וממונו ג"כ עשרה א"כ נשוב אל הא' וכבר ידענו כי קבל מחבירו ו' וב' שלישיות א"כ יחסר לו להשלים המנין ג' ושליש א"כ ממונו היה ג' ושליש וממון הב' ג' ושליש קודם שיתן מאומה וממון הג' י' קודם שנתן דבר וממון הד' י"ג ורביע
|
|
|
ואם אמר הראשון לשני תן לי חצי ממונך ועם שלי ויעלה י' והב' אמר לג' תן לי שליש ממונך עם מה שנשאר לו יעלה י"ב והג' אמר לד' תן לי רביעית ממונך עם מה שיש לי ויהיו ט"ו וישארו עדין עשרים הדרך הוא ממש כנז' לעיל וסבת זה מבוארת
|
|
|
עא) שאלה הנה ג' אנשים רוצים לקנות קנין בערך ק' מנינים אמ' הא' לב' ולג' אם תתנו לי שליש ממונכם עם כל ממוני יעלה ק' השיב הב' לג' ולא' אם תתנו לי רביעית ממונכם עם כל ממוני יעלו ק' אמר הג' לא' ולב' אם תתנו לי חומש ממונכם עם כל ממוני יעלה ק' כמה לכל א' וא'
|
|
|
התשובה עשה כך והוא שתקח איזה מספר יהיה לו שליש ורביע וחומש והוא ס' אח"כ תאמר ס' מאיזה דבר הוא ב' שלישיות תמצא צ' עוד תאמר ס' מאיזה דבר הוא ג' רביעיות תמצא פ' עו' תאמר ס' מאיזה מספר ד' חומשים תמצא ע"ה אח"כ תחבר אלו הג' מספרים ויעלו רמ"ה תחלקם על ב' מצד כי לעולם הם ב' מחוברים ר"ל כי הא' אומ' לב' הנשארים שיתנו לו שליש וכן כלם ויצא לך קכ"ב וחצי הוצא מהם צ' כי הוא חלק הראשון נשארו ל"ב וחצי והוא חלק הא' עו' הוצא מקכ"ב וחצי פ' ישארו מ"ב וחצי והוא חלק השני עוד הוצא מקכ"ב וחצי ע"ה נשארו מ"ז וחצי והוא חלק הג' אח"כ קח שליש ממ"ב וחצי לבחון השאלה וממ"ז וחצי ותחברם אל ל"ב וחצי ויעלה ס"ב וחצי עו' קח רביעית מ"ז וחצי ול"ב וחצי ותחברם אל מ"ב וחצי ויהיו ס"ב וחצי אח"כ קח חומש ל"ב וחצי וממ"ב וחצי וחברם אל מ"ז וחצי ויהיו ג"כ ס"ב וחצי הנה א"כ אלו היה ערך הקנין ס"ב וחצי כבר עשינו השאלה כי ממון הא' היה ל"ב וחצי וממון הב' מ"ב וחצי וממון הג' ל"א וחצי הנה ערך הקנין הוא ק' על כן נעשה הערך כך ונאמר אלו ס"ב וחצי שוים ל"ב וחצי ק' כמה שוים יצא לך נ"ב והוא חלק הא' עוד תאמר אלו ס"ב וחצי שוים כמה שוים ויצא לך ס"ח והוא החלק מהב' עו' תאמר אלו ס"ב וחצי שוים מ"א ק' כמה שוים ויצא לך ע"ו והוא החלק מהג' וכו' ואלו היו ד' אנשים תעשה כנז' אך ראוי לחלק העולה על ג' מצד כי הם קשורים לעולם ביחד כמו שחלקנו אותם שלמעלה על ב' כי הם קשורים ביחד והבן זה מאד כדי שלא תטעה בחשבונך וסבת זה מבוארת ואתן לך דמיון מד'
|
|
|
עב) שאלה בכאן ד' אמר א' אני אתן כל ממוני ותנו אתם חצי ממונכם ויהיו ק' השיב הב' לג' אני אתן כל ממוני ותנו אתם שליש ממונכם ויעלה ק' השיב הג' לג' הנשארים אני אתן כל ממוני ותנו אתם רביעית ממונכם ויעלה ק' אמר הד' תנו חומש ממונכם עם כל ממוני ויעלה ק' כמה לכל א' וא'
|
|
|
הנה יש לך למצא חשבון יכלול חצי ושליש ורביע וחומש ותמצא ס' ותאמר ס' מאיזה דבר הוא מחציתו תמצא ק"כ עו' תאמ' ס' מאיזה מספר הוא ב' שלישיותיו תמצא צ' עוד תאמר ס' מאיזה מספר הוא ג' רביעיותיו תמצא פ' ומאיזה דבר ד' חמישיותיו תמצא ע"ה אח"כ חברם ויהיו שס"ה חלקם על ג' כי לעולם הם דבוקי ביחד בבקשת שליש הממון וחצי ורביעית וחומש יצא לך קכ"א וב' שלישיות והוא ממון ארבעתן אח"כ תוציא מקכ"א וב' שלישיות ק"כ נשאר א וב' שלישיות והוא חלק הא' עוד תוציא ממנו צ' ונשארו ל"א וב' שלישיות והוא ממון הב' עוד תוציא ממנו פ' וישארו מ"א וב' שלישיות והוא ממון הג' עוד תוציא ממנו ע"ה ונשארו ממנו מ"ו וב' שלישיות והוא ממון הד' ואמר בעל הא' לג' הנשארים שיתנו לו חצי ממונם ויעלה ק' והנה כשתחבר כל ממונם ותחלקהו על ב' לא יצא כי אם ס' וב' שלישיות על כן נאמר אם ס' וב' שלישיות יתנו לי א וב' שלישיות מה יתן לך ומה יוסיף לך ק' ותעשה כנז' והטעם מבואר ואין צריך לפנים
|
|
|
עג) שאלה אם תרצה לדעת מרובע משטרות איזה מהם נגע חבירך תשים ה' באורך וה' ברוחב ואמור לה' בני אדם שכל א יגע א' בשורה א' ר"ל שבשורה שיגע הא' לא יגע הב' ותקחם בידך אא' בצד ימין ותלך בצד שמאל ומצד שמאל לצד ימין ומן ימין לשמאל וכן עד כלות כל הה' שורות אח"כ הניחם על השלחן אחת אחת ממעלה למטה וממטה למעלה וכן עד שהנחת כל הה' שורות על השלחן ואח"כ שאל להם באיזו שורה השטר שנגע וכן לכל א' וא'
|
|
|
ותמצא שהראשון שנגע בראשנה היא השטר שלפניך באותה שורה שאמ' לך והשניה ר"ל אותה שנגע השני היא השניה דרך ירידה ואותה שנגע הג' היא הג' דרך ירידה וכן לעולם וכן תוכל לעשות מו' או מז' אם תעשה מרובע מו' או מז'
|
|
|
עד) שאלה אם תרצה לדעת איזה שטר לקח חבירך מצחוק שלם משטרות יש לך לעשות ככה ידוע תדע כי כל הנקדות מצחוק שלם משטרות עולים שיב וכל כך שישוה הפרש עשרה ורוכב הסוס י"א והמלך י"ב ותמנה כל הנקדות ויחסר לך עד תשלום שי"ב רמ'ה' תשוב להפך השטרות פעם שניה ותמנה הה' החסרים מאיזה מין הוא ר"ל אם מסוסים או מכוסות או ממקלות או מסייפים ותשיג המבוקש
|
|
|
עה) שאלה ג' בני אדם רוצים לקנות ג' סוסים ערך הא' ס' מנינים והב' פ' והג' ק' ואמר הא' לב' תן לי חצי ממונך עם כל ממוני ונקנה סוס הס' אמר הב' לג' אם תתן לי שליש ממונך עם כל שלי נקנה סוס הפ' אמר הג' לא' אם תתן לי רביעית ממונך עם תוספת עשרים ועם כל ממוני נקנה הסוס השוה ק' כמה היה לכל א' וא'
|
|
|
התשובה היא ככה נניח שלראשון היה לו מ"ח מנינים ויחסר עד ס' כ"ד (י"ב) מנינים א"כ לשני היה לו כ"ד ונתן לו י"ב והם ס' ולשני (ולשלישי) היה לו קס"ח כי שליש ממונו הוא נ"ח (נ"ו) ועם כ"ד הם פ' אח"כ אמר הג' לא' שיתן לו רביעית ממונו עם תוספת עשרים ויתן לו ל"ב ועם קס"ו (קס"ח) ויהיו מאתים ואין אנו מבקשים כי אם ק' כדי לקנות הסוס א"כ יותירו מאה ושמרם ותאמר בעד מ"ח נשארו מאה
|
|
|
אח"כ נעשה ערך ב' ונניח שלראשון היו לו מ' מנינים א"כ יצטרך שיהיה לשני מ' ג"כ גכ יצטרך שיהיה לג' ק"כ ועם שואל לראשון רביעית ממונו עם תוספת עשרים שהם ל' ויהיו ק"נ אח"כ תאמר בעד מ' נשארו נ' אח"כ הוצא מנ' (מק"נ) ק' נשארו נ' אח"כ כפול מ"ח על נ' ויהיו אלפים וד' מאות אח"כ כפול ק' על נ' ויהיו ד' אלפים הוצא מד' אלפים (אלפים) וד' מאות הנשאר אלף ת"ר וחלקם על תוספת ערך האחד על תוספת ערך האחד שהוא ג' ויעלו ל"ב וכן היה לראשון
|
|
|
עו) שאלה ג' אנשים קונים דבר ערך י"א מנינים וחצי א' שואל לב' הנשארים מחצית ממונם פחות ב' והאחר שואל שליש ממונם פחות ג' והאחר שואל רביעית ממונם פחות ד' כמה לכל א' וא'
|
|
|
התשובה תמצא מספר יכלול חצי ושליש ורביע והוא י"ב וי"ב הוא מחצית כ"ד וב' שלישיות י"ח וג' רביעיות י"ו קח מכ"ד ב' ישארו כ"ב קח מי"ח ג' ישארו ט"ו קח מי"ו ד' ישארו י"ב ותחברם ויעלו מ"ט ותחלקם על ב' ויעלו כ"ד וחצי הסר מהם כ"ב ישארו ב' וחצי והוא חלק משואל לחבירו מחצית הממון גם הסר ט"ו ישארו ט' וחצי והוא חלק משואל שליש ממון חבירו פחות ג' קח י"ב מכ"ד (וחצי) ישארו י"ב וחצי והוא חלק משואל רביעית הממון פחות ד' והכלל בזה כי אם תוסיף לשואל חצי ממון חביריו ב' יצטרך שתוסיף לשואל השליש ג' ולשואל הרובע ד' ואם בעל החצי אמר פחות שנים צריך שבעל השליש יאמר פחות ג' ובעל הרובע יאמר פחות ד' ודוק ותשכח
|
|
|
עז) שאלה ג' אנשים רוצים לקנות קנין כ"ב מנינים וחצי אמר הא' לב' אם תתנו לי חצי ממונכם עם תוספת שנים ועם שלי יהיו כ"ב וחצי אמר הב' לא' ולג' אם תתנו שליש ממונכם עם תוספת ג' ועם שלי יהיו כ"ב וחצי אמר הג' לב' ולא' אם תתנו רביעית ממונכם עם תוספת ד' ועם שלי יהיו כ"ב וחצי כמה לכל א' וא'
|
|
|
התשובה בקש מספר יכלול חצי ושליש ורביע והוא י"ב ותאמר י"ב מאיזה מספר חציו תמצא כ"ד עוד תאמר י"ב מאיזה דבר ב' שלישיות תמצא י"ח עוד תאמר י"ב מאיזה דבר ג' רביעיות תמצא י"ו אח"כ תוסיף לכל א' מה ששואל מהתוספת ר"ל שתוסיף על כ"ד ב' ויהיו כ"ו ועל י"ח (ג') ויהיו כ"א ועל י"ו ד' ויהיו כ' ותחבר הכל ויעלה ס"ז ותחלקם על ב' ויצא לך ל"ג וחצי תסיר מהם כ"ז (כ"ו) וישארו ז' (וחצי) והוא חלק משואל חצי ממון חביריו עם תוספת ב' עוד תסיר מהם כא וישארו י"ב וחצי והוא ממון שואל לחביריו שליש ממונם עם תוספת ג' עוד תסיר מהם כ' וישארו י"ג וחצי והוא ממון משואל לחביריו רביעית ממונם עם תוספת ד'
|
|
|
ודע כי אם תוסיף על שואל חצי ממון חביריו ב' יצטרך שתוסיף לשואל שליש ממון חביריו ג' ולשואל רביעית ממון ד'
|
|
|
ואם תוסיף ד' לשואל חצי הממון תוסיף לשואל שליש ממון ו' ולשואל הרביעית ח' וכן תמיד
|
|
|
עח) שאלה הנה בכאן חומה אחת גבוהה חמישים אמות וברגל החומה יש גומה רחבה ל' נשאל אם נרצה להוריד חבל אחד מראש החומה עד סוף הגומא הרחוקה מרגל החומה ל' אמות כמה יהיה ארכה
|
|
|
התשובה יש לנו לכפול החומה שהוא נ' על עצמם ויהיו אלפים וה' מאות אח"כ נכפול רוחב הגומה על עצמם שהם ל' ויהיו ט' מאות ונחברם עם אלפים וה' מאות ויהיו ג' אלפים וד' מאות וקח שרשם ויהיו נ"ח וכ"ו חלקים מקי"ו והוא אורך החבל
|
|
|
עט) שאלה אם משולש כזה אם אורך הקו השוה המחברת דרך ירידה השנים קוים האלכסוניים ארכה ל כמה אורך כל קו וקו מהמשולש
|
|
|
התשובה יש לך לכפול אורך הקו על עצמו שהוא ל' על ל' ויהיו ט' מאות וקח שלישיתם שהם ג' מאות ותוסיפם על ט' מאות ויהיו י"ב מאות וקח שרשם שהוא ל"ד וע' חלקים מע"ה וזה יהיה אורך כל קו מהמשולש
|
|
|
פ) שאלה בכאן שני מגדלים אורך האחד נ' אמות והאחרת ל' אמות ומרחק שבין שניהם עשרים אמות ונרצה לעשות גשר מראש המגדל האחד על האחר כמה יהיה ארכו
|
|
|
התשובה יש לנו לכפול המרחק שבין שני המגדלים שהוא כ' על עצמם ויעלו ד' מאות אח"כ ראוי לכפול ד' מאות על ב' ויהיו ח' מאות כ אמות ונקח שרשם ויהיו כ"ח שלמים וי"ו חלקים מנ"ו וכן יצטרך שיהיה אורך הגשר ודוק ותשכח
|
|
|
פא) שאלה בכאן מגדל מרובע כזה שכל הקפו ר"ל עביו נ' אמות מבחוץ והעובי מהקיר מכל ד' זויותיו ב' אמות ורביע נרצה כמה הקף המגדל
|
|
|
התשובה הנה יש לך לכפול ד' מצד כי הם ד' קירות על ב' ורביע ויעלו ט' וכפול אותם על ב' ויהיו י"ח ותחסרם מנ' וישארו ל"ב וכן יהיה הקף המגדל מבפנים
|
|
|
פב) שאלה הנה בכאן מרובע כזה שהקו שהוא מבפנים ארכה עשרה אמות ר"ל הקו ההולך באלכסון כמה אורך כל קו וקו מהמרובע
|
|
|
התשובה יש לך לכפול עשרה על עצמם ויהיו מאה וחלקם על ב' ויצאו חמישים וקח שרשם והוא ז' וחלק מי"ד והוא יהיה אורך כל קו וקו מהמרובע
|
|
|
פג) שאלה אם תרצה לדעת ממרובע שכל ד' קוים ארכם עשרה נרצה לדעת כמה אורך הקו ההולכת באלכסון
|
|
|
יש לכפול עשרה על עצמם ויהיו מאה וכפול אותם על ב' ויהיו ב' מאות וקח שרשם ויהיו י"ד וד' חלקים מכ"ח וזה יהיה אורך האלכסון
|
|
|
פד) שאלה הנה בכאן אילן גבוה עשרים וברגל האילן יש נהר רחבו עשרה אמות ונשבר האילן ונגע הראש בסוף רוחב הנהר ר"ל רחוק מרגל האילן עשרה אמות נשאל באיזה מקום נשבר האילן
|
|
|
התשובה הנה יש לך לכפול אורך האילן על עצמם ר"ל כ' על כ' ויהיו ד מאות אח"כ כפול רוחב הנהר על עצמם ר"ל עשרה על עשרה ויהיו ק' תוציאם מד' מאות וישארו ג' מאות ותחלקם על ב' ויהיו ק"נ אח"כ תחלק ק"נ על כ' ויהיו ז' וחצי והוא הקיים מהאילן והנשבר י"ב וחצי
|
|
|
פה) שאלה הנה בכאן מרובע ונרצה לעשות משולש בתוכו שכל א' מג' קוים ארכה עשרים כמה יקיף כל המרובע וזה הוא צורתו
|
|
|
קח חצי אורך המשולש שהוא עשרה וכפול אותם על עשרים ויהיו ב' מאות וככה יקיף כל המרובע
|
|
|
פו) שאלה הנה בכאן משולש כל א' מהג' קוים ארכה ל"ה ארכה ל"ה כמה אורך הקו הנמשכת כזה
|
|
|
הנה יש לך לכפול אורך כל קו על עצמם שהם ל"ה ויעלו אלף ורכ"ה ותחלק העולה על ד' ויצא לך ג' מאות ורביע ותחסר זה מכל הסך ר"ל מאלף ורכ"ה וישאר עדין ט' מאות וח' וג' רביעיות וקח שרשם שהוא ל' שלמים וי"ח חלקים מס' וחלק מי"ו וככה יהיה אורך הקו הנמשכת
|
|
|
פז) שאלה אם תרצה לעשות ממרובע א' עגול א כזה
|
|
|
הנה יש לך לדעת אורך מקוי אחד המרובע ותכפול העולה על ג' ושביעית אחד וכן יהיה הקף כל העגול
|
|
|
פח) שאלה הנה בכאן שני קוים מחוברים אורך הא' ל ואורך הב' מ' אם נרצה לעשות מאלו הב' קוים משולש כמה אורך הקו הג'
|
|
|
הנה יש לך לכפול כל קו על עצמו ר"ל ל' על ל' ויהיו ט' מאות גם כפול מ' על מ' ויהיו אלף וו' מאות ותחבר אלף וו' מאות עם ט' מאות ויעלו אלפים וה מאות וקח שרשם שהוא נ' וזה יהיה אורך הקו הנ' כדי להשלים המשולש וזאת היא צורתו
|
|
|
פט) שאלה אדם נוסע מנפולי ללכת עד רומא בה' ימים ובאותו יום ובאותה שעה נוסע איש אחר מרומא ללכת בנאפולי בז' ימים נרצה לדעת בכמה ימים יפגעו זה את זה
|
|
|
יש לך לחבר מהלך האחד עם האחר ויהיו י"ב אח"כ כפול ב' (ה') על ז' ויהיו ל"ה ותחלקם על י"ב ויעלה ב' שלמים וי"א חלקים מי"ב
|
|
|
צ) שאלה חבית א' מעשרים קרשים מכילה עשרים מדות מים אם נחסר ב' קרשים כמה יכיל
|
|
|
תכפול כ' על עצמם ויהיו ד' מאות אח"כ כפול הקרשים ר"ל י"ח על י"ח ויהיו ג' מאות וכ"ד תכפול ג' מאות וכ"ד על כ' ויעלה ו' אלפים וד' מאות ופ' ותחלקם על ד' מאות ויצא לך י"ו ופ' חלקים מד' מאות וכך יכיל החבית מי"ח קרשים
|
- 91) Question: three men found a purse with some dinar.
- The first said to the two: if you give me the purse I will have as much dinar as both of you.
- The second answered: if you give me the purse I will have two times as much dinar as both of you.
- The third said: if you give it to me I will have three times as much money as both of you.
- How much money was in the purse and how much did each have?
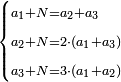
|
צא) שאלה ג' אנשים מצאו כיס אחד עם סך דינרין
אמר הראשון נגד הב' אם תתנו לי הכיס יהיה לי דינרין כל כך כמו שיש בין שניכם
השיב השני אם תתנו לי הכיס יהיה לי דינרין ב' פעמים כמו שיש לכם
אמר הג' אם תתנו אותה יהיה לי מעות ג' פעמים כמו בין שניכם
כמה ממון היה בכיס וכמה דינרין היה לכל א וא'
|
- Money in the purse:
![\scriptstyle{\color{blue}{N=\left[\left(\frac{1}{2}\sdot12\right)+\left(\frac{2}{3}\sdot12\right)+\left(\frac{3}{4}\sdot12\right)\right]-12=\left(6+8+9\right)-12=23-12=11}}](/mediawiki/images/math/f/0/3/f03e46121cbbf95d6e3b2685d2d09227.png)
|
התשובה תבקש מספר יהיה לו חצי ושליש והוא י"ב ותקח בעד הראשון ו' שהוא חצי י"ב ובעד השני ח' שהוא ב' שלישיות י"ב ובעד השלישי ט' שהוא ג' רביעיות י"ב ותחברם ויהיו כ"ג ותחסר מהם י"ב ישארו י"א והוא סך דינרי הכיס
|
- The first had:
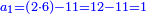
|
ולדעת כמה דינרין היה לראשון כפול ב' פעמים ו' ויהיו י"ב תוציא מהם י"א וישאר א' וכן היה לו
|
- The second had:
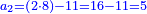
|
ולדעת מה שיש לשני כפול ח' על ב' ויהיו י"ו תחסר מהם י"א ונשארו ה' והוא מה שיש לשני
|
- The third had:
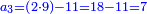
|
ולדעת מה שיש לג' כפול ט' על ב' ויהיו י"ח תוציא מהם י"א וישארו ז' והוא המבוקש
|
- 92) Question: two men want to buy a horse whose price is unknown.
- The first said to the second: if you give me a third and a quarter of your money, with my money I will buy the horse.
- The second said to the first: if you give me a quarter and a fifth of your money, with my money I will buy the horse.
- I ask: how much did each have and how much is the price of the horse?
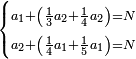
|
צב) שאלה ב' בני אדם רוצים לקנות סוס אחד ערכו נעלם
אמר הא' לב' אם תתן לי שליש ממונך ורביעיתו עם כל ממוני אקנה הסוס
אמר הב' לא' אם תתן לי רביעית ממונך וחמישיתו עם כל ממוני אקנה הסוס
אשאל כמה היה לכל א' וא' וכמה ערך הסוס
|
![\scriptstyle{\color{blue}{12-\left[\left(\frac{1}{3}\sdot12\right)+\left(\frac{1}{4}\sdot12\right)\right]=12-7=5}}](/mediawiki/images/math/9/9/4/994410b776b40d19b554ba92d759d4ae.png)
|
התשובה תמצא מספר יהיה לו שלישית ורביעית בעד הראשון ותמצא י"ב תחסר מהם השליש והרביעית וישארו ה' ושלישיתו ורביעיתו הוא ז'
|
![\scriptstyle{\color{blue}{20-\left[\left(\frac{1}{4}\sdot20\right)+\left(\frac{1}{5}\sdot20\right)\right]=20-9=11}}](/mediawiki/images/math/f/f/8/ff8cbb7d14317cac82e03ace86d629d4.png)
|
אח"כ תבקש מספר יהיה לו רביעית וחומש בעד השני ותמצא כ' תחסר הרביעית והחומש וישארו י"א והרביעית והחומש הם ט'
|
- The first had:
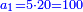
|
אח"כ כפול הה' שנשארו מי"ב על הכ' ויהיו מאה והוא סך הממון מהראשון ר"ל ממבקש השליש והרביעית
|
- The second had:
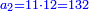
|
אח"כ תכפול הי"א שנשארו מהכ' על י"ב ויהיו קל"ב והוא חלק מהשואל הרביעית והחומש
|
- The price of the horse:
![\scriptstyle{\color{blue}{N=132+\left[\left(\frac{1}{4}\sdot100\right)+\left(\frac{1}{5}\sdot100\right)\right]=132+45=177}}](/mediawiki/images/math/0/c/7/0c7db4cfa0209cf9b9f5ad813aa9161a.png)
|
ואם תרצה לדעת ערך הסוס הוצא הרביעית והחומש ממאה שהם מ"ה ותוסיפם על קל"ב ויעלו קע"ז
|
![\scriptstyle{\color{blue}{N=100+\left[\left(\frac{1}{3}\sdot132\right)+\left(\frac{1}{4}\sdot132\right)\right]=100+77=177}}](/mediawiki/images/math/2/c/d/2cd0cf9d142ec7df7fa2ad8a2c868d00.png)
|
או תקח הרביעית והשלישית מקל"ב שהם ע"ז ותוסיפם על ק' ויהיו קע"ז
|
|
|
צג) שאלה הנה בכאן עיר שהחומות הסובבות כל העיר ג' מילין נרצה לדעת עיר שחומותיה עשרה כמה היא יותר גדולה מהאחרת
|
|
|
ראוי לכפול ג' על עצמם ויהיו ט' אח"כ כפול עשרה על עצמם ויהיו מאה תחלק מאה על ט' ויצא לך י"א ותשיעית והוא סך הפעמים שהיא יותר גדולה אותה של עשרה מאותה של ג'
|
|
|
צד) שאלה הנה בכאן עגול אחד כזה שהבריח האלכסונית הוא ז' ושביעית נרצה לדעת כמה אורך כל קו וקו מהמרובע
|
|
|
יש לך לכפול ז' ושביעית על עצמם ויעלה נ' חלקם על ב' ויהיו כ"ה וקח שרשם שהוא ה' וכן יהיה אורך כל קו מהמרובע
|
|
|
צה) שאלה בכאן עגול שהבריח האלכסונית י"ו אם תרצה לעשות משולש בתוכו כמה יהיה הקפו וכמה יהיה אורך כל קו וקו מהמשולש
|
|
|
תעשה ככה תעשה תסיר רביעית י"ו שהוא ד' וישארו י"ב כפול י"ב על עצמם שהם קמ"ד אח"כ תוסיף בו שליש קמ"ד ויהיו קצ"ב וקח שרשם שהם י"ג וכ"ג חלקים מכ"ו
|
|
|
צו) שאלה אם תרצה לדעת מעגול שמקיפו ל כמה אורך הבריח המחלקת
|
|
|
קח שליש ל שהם עשרה וכן יהיה אורך הבריח ובכל דבר עגול תוכל לדעת בזה האופן
|
|
|
צז) שאלה בכאן מרובע אורך השני קוים הארוכים מ' ורוחב השני קוים הקצרים ל' נרצה לדעת כמה אורך הבריח האלכסונית וריקות כל המרובע
|
|
|
תכפול הבריח הרחבה שהוא ל על הבריח הארוכה שהוא מ' ויעלה אלף וב' מאות וכן הוא שעור הריקות
|
|
|
ואם תרצה לדעת אורך הבריח האלכסונית כפול ל על ל שהם ט' מאות וכפול מ על מ' שהם אלף וו' מאות ותחברם ויהיו אלפים וה' מאות וקח שרשם שהם נ' וכן אורך הקו
|
|
|
צח) שאלה הנה בכאן עיר שחומותיה גובה נעלם אם תרצה לדעת גבהם
|
|
|
קח מקל וזקוף אותו ר"ל שיהיה ארכו מהארץ ר"ל מרגליך עד שיגיע ראשו בין עיניך ותשכב על פניך למעלה ר"ל פשוט ידים ורגלים ותאמר לחבירך שישים המקל זקוף בין כפות רגליך וראה אם לפי ראות עיניך ראש המקל הוא כל כך גבוה כמו החומה שוה בשוה ואם אינו שוה התרחק או התקרב בעודך שוכב בארץ עד שיהיה נראה לך שהוא שוה ואח"כ תמדוד ממקום המקום עד רגל החומה (עד רגל החומה) כמה הוא וכן יהיה גובה החומה
|
|
|
צט) שאלה יש בכאן חבית מלאה שמן שהיא רחבה מהרגל שלמטה ז' אמות והולכת ומקצרת עד שהראש העליון עומד על אמה ושוה ח' מנינים כמה ישוה חבית שרחבה למטה ז' אמות גם הראש העליון רחבו ז' אמות
|
|
|
הנה יש לך לחבר כל המספרים שהם מא' עד ז' מצד כי הולכת ומקצרת ויעלו כ"ח אח"כ כפול ז' על ז' מצד כי כל שני ראשיה הם ז' ויהיו מ"ט ותאמר אם כ"ח שוים ח' מנינים כמה ישוו מ"ט וכו'
|
|
|
ק) שאלה יש לנו שני כותלים שווים רחוקים זה מזה מספר נעלם וידענו הכאת הא' בגילו ר"ל הכאת הכותל במרחק שבין הכותלים והוא מ"ח והנה המרחק עם גובה א' הכותלים הוא י"א כמה הוא גובה הכותל וכמה מרחק זה מזה
|
|
|
קח חציו והוא ז' ומרובעו מ"ט תחסר מ"ח ישאר א' ושרשו א' נוסיפהו על ז' שהוא חצי י"ד והוא גובה המגדל נחסרנו ממנו וישאר המרחק שביניהם וכן כל כיוצא בזה
|
|
|
קא) שאלה יש לנו שני כותלים שוים שהאחד הוא עד"מ קו א"ב והשני הוא קו ג"ד וגבהם אחד וידענו שהאלכסון הוא א"ד י' אמות וידענו שגובה הכותל הוא מוסיף על המרחק שיש בין שני הכותלים ב' אמות ונרצה לדעת כמה הוא גובה כל א' מהכותלים וכמה מרחקם
|
|
|
דרך זה הוא כך נרבע האלכסון שהוא י' והנה הוא ק' נחסר ממנו מרובע ב' שהוא ד' שבו יעדיף הגובה על המרחק וישאר צ"ו וקח חציו והוא מ"ח נוסיף עליו מרובע חצי העודף שהוא א ויהיו מ"ט וקח גדרו והוא ז' וככה הוא הגובה ר"ל גובה כל א' מהכותלים נחסר ממנו ב' והנשאר ה' והוא המרחק שביניהם מכותל לכותל
|
|
|
קב) שאלה יש לנו אילן גבוה חמישים אמה ונשבר ונגע הראש בקרקע וידענו שמרחק שבין שני קצותיו שהם על דרך משל כ"ה נשאלה בכמה נשבר
|
|
|
דרך זה נקח רביעית כ"ה ונחסרנו ממנו ונשאר י"ח וג' רביעיות ובזה המספר נשבר האילן נוסיף עליו רביעו ויצא ל"א ורביע והוא החלק הנופל בארץ
|
|
|
קג) שאלה אדם נתן תפוחים לג' בניו לא' נתן י' ולאחר נתן ל ולאחר נתן נ' ואמר כל כך ישא לי ממון הא' כמו האחר לא פחות ולא יתר ובערך שימכור הא' ימכרו האחרים באיזה ערך מכרו
|
|
|
ראוי לך לדעת כי בעל הי' מכר ז' לפשוט ונשארו עד ג' ומכר כל א' מהם ג' דינרין נמצא ששוים ט' ועם א' הם י' ובעל הל' מכר ג"כ ככה כי הכ"ח מכר ד' פשוטים והב' הנשארים מכר ו' ויהיו י' ובעל הג' מכר מ"ט ז' וא' מכר ג' והם י' ג"כ
|
|
|
קד) שאלה הנה בכאן חבית מכילה ק' קבין חציה מים וחציה יין ונוציא קב אחד ואח"כ נשים בו קב מים עוד נוציא קו (קב) פעם שניה ונמלאנה מים עוד נוציא קב פעם ג' ונמלאנה מים עוד נוציא קב פעם ד' ונמלאנה מים נרצה לדעת כמה קבים של יין נשארו בחבית אחר הפעם הד'
|
|
|
הדרך הוא כך ידוע הוא כי ה' קבין יין וה' של מים הם בחבית ונוציא קב וישארו ד' וחצי מים וד' וחצי יין ונשים קב של מים בחבית ויהיו ה' וחצי מים וד' וחצי יין ומאלו הד' וחצי נקח ט' עשיריות וישארו ד' וא' חלק מעשרים והוא היין שנשאר בחבית בפעם הב' עוד נקח מזה ט' עשיריות וישארו ג' וקכ"ט חלקים ממאתים והוא מה שנשאר בפעם הג' עו' נקח מזה ט' עשיריות וישארו ג' ותקס"א חלקים מב' אלפים והוא מה שנשאר בפעם הד' ואם תקח מג' ותקס"א חלקים מב' אלפים ט' עשיריות מה שישאר הוא הפעם הה' וכן תמיד
|
|
|
קה) שאלה בכאן מגדל גדול גבוה ולא ידענו כמה וצלו ק' אמות וצלו מגיע אצל מגדל אחר קטן גבהו עשרה אמות וגבהו כ"ה נרצה לדעת כמה גובה המגדל הנעלם
|
|
|
תאמר אם כ"ה נתנו לי עשרה ק' כמה יתנו כפול עשרה על ק' ויעלו אלף וחלקם על כ"ה ויצאו מ' והוא גובה המגדל הגדול כמו זאת הצורה
|
|
|
קו) שאלה הנה בכאן חומה גבוהה והגובה נעלם והורדנו חבל חבל מראש החומה עד הארץ וראש החבל רחוק מרגל החומה ב' אמות ואורך החבל הוא ק"ב אמות נרצה לדעת כמה גובה החומה
|
|
|
הנה נמדוד עשרה אמות מראש החבל התחתון ונבריח מ' בריח כנגדו יגיע אל החומה ונמדוד כמה אמות נבלעו מהחומה באותם הי' אמות של חבל ונניח כי באותם הי' מדות מהחבל נכנסו ח' מהחומה ונחלק אורך החבל שהוא ק"ב על י' ויצאו י"ב ונכפול י"ב על ח' ויהיו צ"ו והוא גובה החומה כמו זאת הצורה
|
Guess
|
|
|
|
קכג) שאלה אם תרצה לדעת לאיזה אדם נתן חבירך הטבעת ובאיזה אצבע ובאיזה פרק
|
|
|
תחלה תאמר לו שיכפול אותו ואחר שישים עליו ו' ואחר שיכפול כל זה ה' פעמים ואחר שיוסיף על זה המספר האצבעות ואח"כ שיכפול כל זה ה' פעמים ואחר שיסיר מזה ק"נ ואח"כ יכפול על שנים מה שנשאר ואחר זה יוסיף על זה מספר הפרקים והנה המאיות הם האנשים והעשרות האצבעות והאחדים הפרקים
|
|
|
דמיון נתתי הטבעת לאיש רביעי באצבע הג' ובפרק ב' תאמר לו שיכפול ד' ויהיו ח' ואמור שיוסיף על זה ו' ויהיו י"ד וכפול אותו על ה' ויהיו ע' תוסיף על זה ג' שהוא מספר האצבעות ויהיו ע"ג כפול אותם על ה' ויהיו שסא (שסה) תסיר מהם ק"נ הנשאר רט"ו כפול אותם על ב' ויהיו ד' מאות ול' תוסיף על זה ב' שהם הפרקים ויהיו תל"ב הנה הד' מאות יהיו ד' אנשים והג' עשרות יהיו ג' אצבעות והב' יהיו ב' פרקים
|
|
|
קכד) שאלה אם תרצה לדעת מה שחשב אדם בלבו תאמר לו אם הולך ג"ג ואם הולך לא תקח כלום ואם אינו הולך קח בעד כל א' שישאר ע' ומן החמישיות יש לך לקחת כ"א ומהשביעיות ט' אח"כ תחבר כל זה ותסיר כל המאות ובעד כל מאה תסיר ה' ומה שישאר הוא המבוקש
|
|
|
דמיון הנה לקחתי מספר ד' הנה ישאר על השלישיות א' וקח ע' ועל ה' ישאר ד' וקח ד' פעמים כ"א ויהיו פ"ד וקח בעד השביעיות ס' כי ישאר ד' וד' פעמים ט"ו הם ס' אח"כ חבר הכל ויהיו רי"ד תסיר מזה המאות וישאר י"ד ותסיר בעד הב' מאות עשרה וישאר ד' והוא המבוקש
|
|
|
קכה) שאלה ואם תרצה לדעת באופן אחר מה שחשב אדם בלבו תאמר לו שיכפלהו ואח"כ תאמר לו שיכפלהו פעם ב' ואח"כ תאמר לו שיקח ממנו ד' וזה לך הכלל כי בעד כל ד' שתסיר מהסך תקח א' והוא המבוקש
|
|
|
קכו) שאלה אם תרצה לדעתו באופן אחר תאמר לו שיכפלהו ואחכ יוסיף עליו ה' ואחר יכפול אותו ה' פעמי' ואחר יוסיף בו עשרה ותחסר ממה שיעלה כל זה ל"ה וקח בעד כל עשרה הנשאר א' והוא המבוקש
|
|
|
קכז) שאלה ואם תרצה לדעת המספר והוא כי פעם א' היו הולכים בספינה יהודים וישמעאלים ובא סער בספינה אמר יהודי אחד בואו כלכם בכאן והושיבם היהודים וההגרים באופן כי כשהיה מונה אותם לעולם היה כלה כל התשיעיות אל ההגרים והוכיח כי בעבורם בא הצער בים ובזה האופן השליך ט"ו הגרים בים והיהודים נשארו וזהו אופן עשייתו בם הגרים כל ט' אשפוך גורל אפיל אטיל בים בגאון גליו אשליכמו בתחבולות בדרוש אים אכן ראוי להתחיל מהיהודים ותתקנם בראשי תיבות
|
|
|
קכח) שאלה אם תרצה לדעת איזה אבן נגע חבירך קח י"ו אבנים ועשה ב' שורות מח' אבנים ותאמר לאיש שיגע אבן אחת מאלו השורות אח"כ שאל לו באיזו שורה היא האבן ואם היא בשמאל תהפך כל השורות בשמאל ואם בימין כן תעשה אח"כ שאל באיזו שורה וכן תהפך ג' פעמים ואחר ההפוך הג' תשאל לו באיזו שורה היא וזה הכלל יהיה בידך כי לעולם האות הג' היא אותה שאתה מבקש
|
|
|
קכט) שאלה איש מוכר קופה של ביצות וכאשר מכר אותם הביט בידו ואמר לא עשיתי בטוב כי אלו הייתי נותן א פחות בדינר היה לי ד' פעמים יותר ממעות תאמ' לו כמה היו הביצות הנמכרות וכמה הוא הממון שיצאו מהביצות
|
|
|
תשובה תעשה ככה לפי שאמר שהיו לו ד' פעמים ממעות יותר לכן תכפול ד' לעצמו ויעלו י"ו תחסר ממנו א' וישארו ט"ו ואח"כ תחסר מהד' א' וישארו ג' ותכפול אותם על ט"ו הנזכרים ויעלו מ"ה וככה דינרין יצאו מן הביצות
|
|
|
ולדעת כמה היו הביצות כפול ט"ו על ד' ויעלו ס' וס' ביצות היו הביצות הנמכרות
|
|
|
קל) שאלה אחד היו לו מעות ואינו יודע כמה הם ונתן אותם קל לאנשים רבים ואינו יודע כמה אבל ידע שאם נתן י"ב לכל איש יהיו יותר מהכ' ואם יתן י"ו לאיש יחסר מס' הנה היתי רוצה לדעת כמה ממון היה לזה וכמה אנשים היו
|
|
|
התשובה ראוי לחבר המעות שהיו חסרים עם המעות שהיו יתרים ר"ל נ"ב עם ס' ויעלו קי"ב וראוי לחלק אותם עם ההפרש מהמעות החסרים עם היתרים ר"ל עם ההפרש שיש מנ"ב לס' שהוא ח' אשר אם תעשהו יצא כ"ח והאנשים היו כ"ח
|
|
|
ואחר זה כדי שתדע כמה היו המעות ואחר שתחזיק כמה שתרצה אם אל י"ב ואם אל י"ו אם אל י"ב ראוי שתכפול י"ב פעמים כ"ח ויעלו של"ו ובאלו ראוי שתוסיף מה שיתוסף נ"ב ובאלו יעלו שפ"ח ואם אתה כפלת י"ח פעמים י"ו יעלו שמ"ח ומאלו ראוי שתחסר מה שחסר ר"ל פ' וישארו שפ"ח כאשר נאמר ובזה הדרך תוכל לעשות הדומות לזו
|
|
|
קלא) שאלה הנה בכאן ג' אנשים שיש להם מעות אשר הב' מבלי הא' יש להם י"ט והב' מבלי הב' יש להם כ"ג והב' מבלי הג' יש להם ל' נאמר כמה ממון יש לכל א' וא'
|
|
|
ראוי לך לחבר ממון שלשתן ולחלק העולה על ב' ומה שיעלה הוא ממון שלשתן והדרך הוא נודע
|
|
|
קלב) שאלה הנה במקרה ראובן הגיע אל המות ועשה צוואה בזה האופן ממאה דוקטי שאניח אם אשתי אשר היא הרה תלד זכר תהיה לה השליש והשאר תהיה לבנה ואם נקבה תלד שהשליש מבתה והשאר ממנה וכאשר מת ילדה אשתו תאומים זכר ונקבה
|
|
|
תשובה הנה יראה שהבן ראוי לו כפל מהאם והאם הכפל מהבת ולכן ראוי לנו לעשות ככה שהבת שהיא הפחותה שם א' והאם ב' והבן ד' ותעשה ככה הנה בכאן ג' הא' שם א' והב' ב' והג' ד' והרויחו ק' כמה יגיע לכל א' וזה מבואר
|
Find a Number Problems
|
|
- 133) Question: find me a number such that if you multiply it by 7 and divide by 9 your result will be 45
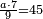
|
קלג)[5] שאלה תמצא לי מספר אשר אם תכה אותו בז' ותחלק אותו על ט' שיצא לך מ"ה
|
- False Position:
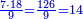
|
תעשה ככה תסכים שאותו המספר יהיה מה שתרצה ולהקל מעליך עשה שבאותו מספר לא יהיה בו שבר ונניח שאותו המספר יהיה י"ח א"כ כאשר תכה ז' פעמים י"ח יעלו קכ"ו ואם תחלקהו בט' יצא י"ד
|
- Rule of Four:
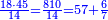
|
וכבר אמרנו שיצא מ"ה לכן ראוי לעשות ככה שתכה המספר אשר שמת אותו כבר שתכפול י"ח על מ"ה אשר יצא תת"י וזה תחלק עם אותו שיצא עם י"ד ויצא נ"ז וו' שביעיות והוא הנשאל
|
Check: 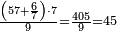
|
ולבחון אותו ראוי שתכה נ"ז וו' שביעיות עם ז' ויצא ת"ה ותחלק עם ט' ויצא מ"ה
|
- 134) Question: find a number such that if you divide it by 5 and multiply by 8 the result will be 23
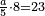
|
קלד)[6] שאלה תמצא מספר אשר אם תחלק אותו עם ה' ותכה אותו עם ח' יעלה כ"ג
|
- False Position:
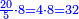
|
שים שאותו המספר יהיה עשרים ונחלק אותו עם ה' ויצא ד' ותכה אותו עם ח' ויצא ל"ב
|
- Rule of Four:
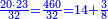
|
ואנו מבקשים כ"ג ראוי שתכה לפי הדרך הנאמר עשרים פעמים כ"ג ויצא לך ת"ס תחלק עם ל"ב ויצא י"ד וג' שמיניות והוא המבוקש
|
- 135) Question: find me a number such that if you subtract its third and its quarter from it the remainder is 29
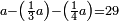
|
קלה)[7] שאלה תמצא לי מספר אשר אם תוציא ממנו שלישיתו ורביעיתו הנשאר כ"ט
|
- False Position:
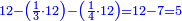
|
תשמור הדרך ותאמר ככה נניח שאותו המספר הוא י"ב תוציא ממנו שלישיתו ורביעיתו שהם ז' וישאר ה'
|
- Rule of Four:
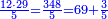
|
ואנו מבקשים כ"ט א"כ תכה י"ב פעמים כ"ט ויצא שמ"ח וחלק אותו על ה' ויצא ס"ט וג' חמישיות
|
- 136) Question: find me a number such that if you add to it its third and its two fifths it makes 18
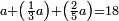
|
קלו)[8] שאלה תמצא לי מספר אשר אם תוסיף עליו שלישיתו ושני חמישיותיו יעשה י"ח
|
- False Position:
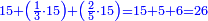
|
תשמור הדרך נניח שאותו המספר יהיה ט"ו והשליש מט"ו הוא ה' ושני חמישיותיו הם ו' שים אותם על ט"ו ויעלו כ"ו
|
- Rule of Four:

|
ואנו נרצה י"ח א"כ נאמר אם ט"ו יתנו לי כ"ו מה יתן לנו י"ח
|
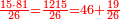
|
ולכן ראוי שתשמור הדרך שתכה הו' ששמת עם י"ח ויצא לך אלף ומאתים וט"ו וזה תחלק על מה שייצא עם כ"ו ויצא מ"ו וי"ט חלקים מכ"ו
|
- 137) Question: if you want to divide 30 into two parts such that if you multiply the one by 4 it becomes the same as the other part if you multiply it by 3
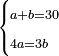
|
קלז)[9] שאלה אם תרצה לעשות מל' ב' חלקים אשר אם תכה הא' בד' יעשה כמו החלק האחר אם תכה אותו בג'
|
- False Position:
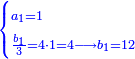
|
תעשה ככה תשים שאותו החלק יהיה אחד ואם תכה אותו בד' יהיה ד' והחלק השני תעשה שיהיה מספר שאם תחלק אותו בג' יצא ד' והוא מספר י"ב
|
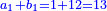
|
הנה כבר היינו יכולין לומ' שנעשינו הדרך אבל אינו אמת כי אנחנו לא חלקנו ל'
אבל היה החלק הראשון א' והשנית י"ב אשר יעלה הכל י"ג אשר כדי להביא החשבון אל מקומו מהאחר אשר שם בא לנו י"ג ואנו מבקשים ל'
|
- Rule of Four:
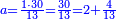
|
לכן ראוי שתכה א' עם ל' ויצא ל' וזה תחלק ויצא ב וד' חלקים מי"ג וככה ראוי להיות החלק הא'
|
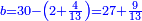
|
א"כ בהכרח החלק השני ראוי להיות עד הל' אשר יהיה כ"ז וט' חלקים מי"ג
|
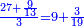
|
אשר תחלק כ"ז וט' חלקים מי"ג עם ג' ויצא לך ט' וג' חלקים מי"ג א"כ עשינו השאלה
|
|
|
קלח) שאלה אם תרצה לעשות מי"ח ג' חלקים בזה האופן אשר אחר שהוצאת החומש מהחלק הראשון וחברת אל השני שלישיתו והג' מוכה עם ב' וחצי כל א' יהיה שוה
|
|
|
תשים שהחלק הא' יהיה ה' ואם תוציא ממנו החומש שהוא א' ישאר ד' ועתה ראוי לראות אל החלק השני כמה ראוי להיות כדי שאם תוסיף עליו שלישיתו יהיה ד' ויהיה ג' עוד ראוי לראות כמה ראוי להיות החלק הג' אשר כאשר תכה אותו בב' וחצי ראוי להיות א' ושני חומשים א"כ עתה ראוי לך להוסיף החלק הראשון שהוא ה' והשני שהוא ג' והשלישי שהוא א' ושני חומשים ויעלו כלם ט' וב' חומשים ואנו נרצה שיהיו י"ח והנה נאמר אם בעד ה' ששם אלו יצא ט' וג' חומשים ממה יצא לי י"ח שהיינו רוצים לחלוק ראוי שתכה כפי הדרך ה' ששמנו כנגד י"ח שרצינו ויצא צ' וזה ראוי לחלק עם ט' וג' חומשים ויצא ט' וג' שמיניות וככה היה החלק הראשון
|
|
|
ותאמר ככה בעד השנית נתן לי ט' וג' של חמישיות ובא אלי ג' מה שיצא אלי מיח ראוי שתכה ג' עם י"ח ויעלה נ"ד ותחלק אותם על ט' וג' חמישיות ויצא ה' וה' שמיניות וכך היה החלק השני
|
|
|
ובעד הג' ראוי שתאמר אם מט' (ו)ג' חמישיות שהיה לנו א וג' חמישיות מה יצא לנו מי"ח ראוי שתכה א' וג' חמישיות עם י"ח ויעלו כ"ח וד' חמישיות ותחלק על ט' וג' חמישיות ויצא לנו ג' וכך היה החלק הג'
|
|
|
וכדי לאמת זה תוציא החומש מהראשון שהוא ט' וג' שמיניות וישארו ז' וחצי ובעד הב' תקח השנית מה' (ו)ה' שמיניות שהוא א' וה' שמיניות וזה תוסיף עליו ויעלה ז' וחצי וכדי לאמת הג' תכה ג' על ב' וחצי ויעלה ז' וחצי
|
|
|
קלט) שאלה אם תרצה לעשות מכ' ב' חלקים שהחלק הא' יהיה ד' פעמים מהחלק האחר
|
|
|
כך תעשה תשים שהחלק הא' היה א' א"כ החלק הב' ראוי שיהיה ד' והנה א' עם ד' הם ה' ואנו נרצה כ' לכן תאמר אם ה' נתנו א' כ' מה יתנו ויצא י"ו
|
|
|
קמ) שאלה אם תרצה לעשות מי' ב' חלקים אשר אם תחלק החלק יותר גדול על הקטן יצאו מאה
|
|
|
תעשה ככה תשים שהחלק הראשון יהיה א' כמה ראוי שתהיה השנית ראוי שיהיה מאה והנה א וק' הם ק"א ואנו רוצים י' א"כ תאמ' אם ק"א נתן לי א' מה יתן לי עשרה ויצא לך עשרה חלקים מק"א וזה מבואר
|
|
|
קמא) שאלה הנה בכאן אנשים שלקחו לעשות בגד א' הא' לקחו לעשות בג' שביעיות והב' בד' שביעיות ואם שניהם יעשו מלאכתם בכמה זמן יעשוהו
|
|
|
תעשה ככה נניח שבי"ב שביעית יעשוהו וכבר אמרנו שהא' יעשהו בג' שביעיות א"כ מעצמו היה עושה ד' מלאכות והשני יעשהו בג' שביעיות א"כ עושים ז' מלאכות ואנו מבקשים מלאכה א א"כ ראוי שתאמ' אם י"ב יתנו ז' מה יתן לי א' תחלק י"ב על ז' ויצא א' וה' חלקים מי"ב מז'
|
|
|
קמב) שאלה אם תרצה לעשות מל' ג' חלקים שאם תכה הא' בז' ותחלק הב' בה' והג' בי' והחלקים וההכאות יהיו מאותו הכמות עצמו
|
|
|
ואם תרצה לעשות זה נניח שהחלק הא' היה א' ואם תכפול אותו בז' יעשה ז' ולדעת הב' ראוי שתמצא מספר שאם נחלק אותו בה' יצא ז' ראוי שאותו המספר יהיה ל"ה והג' ראוי שיהיה ע' א"כ החלק הא' הוא א' והב' ל"ה והג' ע' אשר הם ק"ו ואנו מבקשים ל' ראוי שתאמר אל הא' אם מן ו' יבא א' מה יבא מל' וכו'
|
|
|
קמג) שאלה אם תרצה לעשות מי"א ב' חלקים אשר החצי והרובע מהחלק הא' יהיה כמו השליש והחומש מהחלק האחר
|
|
|
תעשה ככה תשים שהחלק הא' יהיה ד' והחצי הוא ב' והרובע הוא א ויהיו ג' וגם ראוי למצא מהב' מספר שאם תחסר ממנו השליש והחומש שיהיה ג' תשים שאותו המספר יהיה ט"ו והשליש והחומש מט"ו הוא ח' ואנו רוצים ג' א"כ נכה ג' על ט"ו ויעלו מ"ה ותחלק אותו בה' ויצא ה' וה' שמיניות וככה היה המספר השני א"כ נאמר ככה החלק ראשון היה ד' והב' היה ה' וה' שמיניות אשר יעלו ט' וה' שמיניות ואנו מבקשים י"א א"כ ראוי שתאמר אם ט' וה' שמיניות נותן לנו החלק הראשון ד' מה יתן לנו י"א וכן תעשה מהשנית ובחלק הא' יבא ד' מד' חלקים מע"ז והב' יהיה ג' ול"ג חלקים מע"ז
|
|
|
קמד) שאלה אם תרצה לחלק מספר עם שרש או שרש עם מספר ראשנה תביא המספר אל מרובעו
|
|
|
ר"ל אם תחלק י"ב עם שרש ד' תביא י"ב למרובעו שהוא קמ"ד ואח"כ תחלק שרש מקמ"ד עם שרש ד' ויבא לך שרש מל"ו
|
|
|
קמה) שאלה אם תרצה להוסיף שרש מט' עם מד'
|
|
|
תחבר תחלה ט' עם ד' ויצא לך י"ג א"כ תכפול ט' פעמים ד' ויעלו ל"ו אח"כ תכפול הל"ו הנז' עם ד' ויעלו קמ"ד וקח שרש מזה המספר שהם י"ב ותחבר עם י"ג הראשנים ויהיו כ"ה וקח השרש מכ"ה והם ה'
|
|
|
קמו) שאלה דרך אחרת תחבר ט' עם ד' ויעלו י"ו אח"כ תכפול ט' על ד' ויעלו ל"ו וקח השרש שהם ו' ותכפול אותם והם י"ב ותחברם עם י"ג ויהיו כ"ה וקח השרש והם חמשה
|
|
|
קמז) שאלה אם תרצה להוציא שרש ט' משרש י"ו
|
|
|
ראשנה תחבר ט' עם י"ו ויהיו כ"ה אח"כ כפול ט' על י"ו ויעלו קמ"ד אשר אלו תכפול ד' יעלו תקע"ו ומהם תוציא השרש והם כ"ד אח"כ תחסר הכ"ד מהכ"ה הנשאר א' א"כ אם תחסר משרש י"ו שרש ט' ישאר א'
|
|
|
קמח) שאלה דרך אחרת כפול ט' על י"ו ויעלו קמ"ד ומזה תוציא השרש שהוא י"ב וכפלם ויהיו כ"ד אח"כ תוציא כ"ד מהכ"ה הנז' וישאר השרש מא ותקיש על זה
|
|
|
קמט) שאלה אם תרצה למצא מספר מרובע אשר אם תשים עליו י"ט יהיה מרובע
|
|
|
תעשה ככה תוציא א' מי"ט וישאר י"ח וקח חצי מזה המספר וישארו ט' ותכפלם על עצמם ויהיו פ"א ותוסיף עליו י"ט והוא מרובע כאשר אמרנו
|
|
|
קנ) שאלה אם תרצה למצא מרובע שאם תוציא ממנו ט"ו ישאר מרובע
|
|
|
תעשה ככה תוסיף א' על ט"ו ויהיו י"ו תקח החצי מי"ו שהם ח' ותכפול אותם על עצמם ויהיו ס"ד וזהו המספר ואם תוציא ט"ו מס"ד ישאר מרובע והוא מ"ט
|
|
|
קנא) שאלה אם תרצה למצא מספר אשר אם תוסיף עליו ד' יהיה מרובע ואם תחסר ג"כ יהיה מרובע
|
|
|
תעשה ככה תחבר ד' עם ד' ויהיו ח' אח"כ תאמר תמצא לי מספר מרובע אשר אם תוסיף עליו ח' יהיה מרובע לכן תעשה כנז' תוציא א' מח' ישארו ז' וקח מהם חציים והם ג' וחצי ותכפלם על עצמם ויעלו י"ב ורביע תוסיף עליהם ד' יהיו י"ו ורביע וזהו המספר
|
|
|
קנב) שאלה עוד תוכל למצא אותה יותר מהרה תקח החצי מד' שהם ב' ותכפול אותם על עצמם ויהיו ד' תוסיף א על ד' ויהיו ה' וזה המספר ג"כ הוא כמו המספר הט' לעיל
|
|
|
קנג) שאלה לכפול בשרשים אם תרצה למצא שרש ז' על שרש מח' ראוי שתכפול ז' עם ח' ויהיו נ"ו והשרש מט' הוא מה שיעלה השרש מז' עם מח'
|
|
|
קנד) שאלה אם תרצה לכפול השרש מ' מכפילת ז' עם ח' בראשנה ראוי להביא ח' אל מרובעו שהם ס"ד אח"כ שרש ז' עם שרש ס"ד כאשר נאמר למעלה ויעלה שרש ד' מאות ומ"ח ודע שאם תכפול שרש מז' עם שרש מז' ויעשה ז'
|
|
|
קנה) שאלה אם תרצה למצא מספר אשר אם תחלק ג' מאותו המספר יבא ה' וישאר
|
|
|
תדע תחלה שאם ישאר ז' מהמחלק היה יותר גדול מז' א"כ תשים מז' ולמעלה ואח"כ ראוי לנו למצא מספר שיהיה מז' ומעלה אשר אם תכפלהו עם ה' מה יצא וכשנוסיף עליו ז' מה יתוסף ושיתחלק בג' חלקים שלמים מבלי שברים א"כ בתחלה תשים שאותו המספר היה ח' ואם תכפלהו בה' יעלו מ' יתוסף עליו ז' ויעלו מ"ז תחלקם בג' ולא תוכל א"כ תוסיף עליו א יותר ויהיו ט' תכפלהו על ה' ויעלו מ"ה תוסיף עליו ז' יעלו נ"ב תחלקם על ג' ולא תוכל א"כ תוסיף עליו א' יותר ויהיו עשרה ותכפלם בה' ויעלו נ' תוסיף עליו ז' ויעלו נ"ז ותחלקם בג' ויעלו י"ט מבלי שום שבר א"כ בזה המספר תמצא הנאמר ולעולם תוסיף א' יותר אח"כ תחלק העשרה אשר מצאת עם שליש מנ"ז שהוא י"ט ויצא לך עשרה חלקים מי"ט וזהו המספר הנשאל אשר אם תחלק ג' עם המספר הנאמר יצא ה' וישאר ז' וככה יעשו השאלות הדומות לזו
|
|
|
קנו) שאלה ואם תרצה למצא מספר אשר אם תוציא ממנו השרש ותחבר אותו עם השרש מהנשאר יעשה ג'
|
|
|
תעשה ככה תכפול ב' פעמים ג' ויעלו ו' תוציא ממנו לעולם א וישארו ה' וזה יהיה לך המחלק אח"כ תכפול אותו המספר אשר תרצה שיבא לך ר"ל ג' על עצמו ויהיו ט' ואותו תחלק על ה' ויעלה א וד' חומשים אשר זה המספר הוא השרש מהמספר הנשאל אשר ראוי להוציא ממנו שרש ולהוסיף עם השרש מהשאר ויעשה ג' א"כ לדעת המספר ראוי לכפול א וד' חמישיות בעצמו ויעלה ג' שלמים וו' חלקים מכ"ה וזהו המספר הנאמר ולאמתה תקח שרש מג' וו' חלקים מכ"ה אשר נאמר שהוא א' וד' חמישיות ומהנשאר עד ג' וו' חלקים מכ"ה ושרש מהמרובע הוא (ו)א' וחמישית ואם תוסיף אותו עם א וד' חמישיות יהיו ג' והוא שרש ג' וו' חלקים מכ"ה שהוא המספר השאל ועשה ג' כאשר נאמר
|
|
|
ובזה האופן תוכל לעשות הדומות לאלו ומאיזה מספר שיהיה לך לעולם שתכפול המספר שתרצה שיבא עם ב' וממנו יבא להוציא אחד כאשר כבר עשינו אח"כ יש לך לעשות כאשר נאמר למעלה ואם המספר השאל היה פחות מב' אז זאת הדרך לא יהיה נאותה ומסכמת ואז ראוי שיעשה על דרך הפוזיציאוני דלאלזיברא המספר [..] הנאמר פרוביקו בלשונם הוא כאלו תאמר ט' פעמי' ט' הם פא ואח"כ תקח שרש ט' שהוא ג' ותוסיף אותו על פא ויעלו פד ומספר פרוביקו מפ"ד הוא ט' המספר הרולטו בלשונם הוא כאלו תאמר ט פעמים ט יעלו פ"א אח"כ תקח השרש מט' שהם ג' ותכפלם על פ"א ויעלו רמ"ג א"כ מספר רמ"ג הוא מספר אשר שרשו הרולטו הוא ט'
|
|
|
קנז) שאלה אם תרצה לעשות לי מכ"ז ג' חלקם שכל חלק ממנו יהיה לו שרש מעוקב
|
|
|
דרך הוא שיש לך למצא ג' מספרים מקובצים יחד יעשו מעוקב וכל א שיחולקו במספר אחד מעוקב קטן מכלם וכאשר יחולק הסכום מאותם המספרים הנז' עם אותו המספר הקטן יעשה מהם מספר כ"ז כנז' ובזה המספר הא' הוא כ"ז והב' ס"ד והג' קכ"ה וכאשר יקובצו יחד הם רי"ו והוא מספר מעוקב וכשיקובצו שלשתן בשמונה שהוא מעוקב קטן מכל א' מהג' יבא כ"ז ולכן החלק הא' יהיה אם תחלק כ"ז בשמונה ג' וג' שמיניות והב' אם תחלק ס"ד בח' שיבא ח' והג' אם תחלק קכ"ה בח' שיבא ט"ו וה' שמיניות אשר שלשתן יחד מקובצים יעלה כ"ז ותדע כי לא בכל מספר יצדק זה
|
|
|
קנח) שאלה אם תרצה לדעת מספר אחד מרובע אשר אם תוציא אותו מה' שרשיו וישאר מרובע ואם תוסיף עליו שבעה שורשיו יהיה מרובע
|
|
|
הנה המספר הזה הוא י"ח כי חמשה שרשיו הם נ"ד תוציא ממנו י"ח ישארו ל"ו והוא מספר מרובע ושבעה שרשיו הם ס"ג ותחברם עם י"ח יעשה פ"א והוא מספר מרובע
|
|
|
קנט) שאלה אם תרצה למצא מספר אשר ב' חמישיות שלו יהיה שרשו
|
|
|
תעשה ככה תהפך השאלה זאת לדעת תשים ה' למעלה וב' למטה ככה ותכפול אותו ויעשה וזהו המספר אשר תשאל
|
|
|
ואם תרצה לבחון אותו תקח שני חמישיות מ שהם א"כ והוא השרש וכן יעשה
|
|
|
קס) שאלה ג' נמצאו באכסניא א' פרש והב' סוחר והג' אורח הפרש אמר שרוצה לפרוע ב' פעמים יותר מהסוחר ויותר דינר א' והסוחר אמר שרוצה לפרוע ג' רביעיות יותר מהאורח ויותר ב' דינרין ועולה [.....] מאכלם י"א פשוטים כמה ראוי לפרוע לכל א' מהם
|
|
|
תשובה תקח א' בעד [.] האורח שהוא הפחות מכלם וא' וג' רביעיות בעד הסוחר עם תוספת שנים ויהיה א"כ חלק הסוחר ג' וג' רביעיות ונכפול זה ויעלה ז' וחצי ועם תוספת א ויהיו ח' וחצי וזה יהיה חלק הפרש א"כ תקח א' בעד האורח ומעות הסוחר והפרש ובין הכל הם י"ג ורביע אח"כ תקח א' בעד העני וא' וג' רביעיות בעד הסוחר בזולת השנים וג' וחצי בעד הפרש שהוא כפל ממון הסוחר ויעלה הכל ו' ורביע ומספרינו הראשון היה י"ג ורביע נסיר הקטון מהגדול וישארו ז' הנה נסיר עתה ז' מסך המעות ר"ל מיא שיש לפרוע וישארו ד' ויש לך עתה לקחת חלק העני שהוא א' וכפול אותו על ד' ויהיו ד' חלקם על ו' ורביע ויצא לך י"ו חלקים מכ"ה וזה חלק העני אח"כ כפול א וג' רביעיות שהוא ממון הסוחר על ד' ויהיו ז' חלקם על ו' ורביע ויצא לך א וג' חלקים מכ"ה והוא ממון הסוחר
|
|
|
תוסיף עליו ב' ויהיו ג' וג' חלקים מכ"ה אח"כ כפול ג' וחצי שהוא ממון הפרש על ד' ויעלה י"ד חלקם על ו' ורביע ויצא לך ב' וו' חלקים מכ"ה ותוסיף על זה ד' שהוא כפל ב' שנותן הסוחר על העני ותוסיף עליו א' ויהיה חלקו של פרש ז' שלמים וו' חלקים מכ"ה וכן כלם
|
|
|
קסא) שאלה אם תרצה לחלק מספר לב' חלקים אשר החלק או החלקים מהאחד מקובץ עם החלק או החלקים מהאחר ישוה (יהיה) שוה לאחד
|
|
|
המשל תחלק כ"ד לב' חלקים אשר ב' שלישיות מהחלק הראשון וגם ג' רביעיות מהשני מקובצים יחד יהיו שוים אל החלק הראשון דרך בו התשלום מהחלק הראשון אם יהיה א' שליש אשר יהיה שוה אל ג' רביעיות מהשני אם כן תוכל לומר אם שליש מהראשון הם ג' רביעיות מהב' ג' שלישיות מן הראשון זה לדעת הכל כמה רביעיות יהיו מהשני אשר אם תעשה יצא לך ט' רביעיות וכל השני הוא אשר יהיו וכל שני החלקים אשר הם כ"ד במספר א"כ לדעת החלק הראשון מהשנים ראוי שתאמר אם ראוי שיהיה כ"ד מה ראוי להיות אשר הוא הראשון ויתן לך י"ו והשנית יתן לך הנשאר שהם הבחינה מהראשון אשר הם י"ו הם יא וג' רביעי מן השנית אשר הם ז' הם ה אשר הם בכלל י"ו אשר הם החלק הראשון
|
|
|
קסב) שאלה הנה בכאן ב' רוצים ללכת מרחק הא' הולך בכל יום ל' מילין והאחר הולך מיל ביום הא' ובב' ב' ובג' ג' מילים וכן בכל יום מוסיף מיל א' א"כ בכמה ימים יגיע אל הראשון כדי שיגיעו שניהם יחד במקום אחד
|
|
|
הדרך ראוי לך לכפול המילין מאותו שמתמיד ללכת מהלך שוה ר"ל אותו מהל' מילין ויהיו ס' ומאלו תגרע א וישארו נ"ט א"כ בנ"ט ימים ישיגנו
|
|
|
קסג) שאלה איש הולך ל' מילין והאחר ביום א י"ד מילין ובכל יום מוסיף מיל מתי ישיג הראשון
|
|
|
ראוי לדעת כי מכפילת המילים מהיום הראשון ראוי לך לגרוע לעולם המילים מהיום הראשון ר"ל מס' נקח י"ד וישארו מ"ו ובמ"ו ימים ישיגנו
|
|
|
קסד) שאלה ואם אמר לך היום הא' הולך ב' והב' הולך ד' והג' ו' וכן בכל יום מוסיף ב' מילין
|
|
|
ראוי לחסר מיל א' בכל יום מאותו ההולך תחלה ואותו הנשאר בכמה ימים יגיעו הא' לאחר
|
- 165) Question: courier one is in Avignon and he wants to walk to Milan within 8 days.
- Another courier is in Milan and he wants to walk to Avignon within 5 days.
- Both of them will start moving together at the same time.
- Within how many days will they meet?
|
קסה) שאלה רץ א' הוא באוינייון ורוצה ללכת במילנו בח' ימים ורץ אחר הוא במילנו ורוצה ללכת באוינייון בה' ימים ושניהם יחד בעת א יתחילו להתנועע בכמה ימים יפגעו זה את זה
|
|
|
ראוי לך שתחסר הימים הראוים לכל א' במהלכם ר"ל ה' עם ח' והנם י"ג וזהו המחלק אח"כ תכה הימים מהא' עם הימים מהאחר ר"ל ה' עם ח' ויהיו מ' וזהו הנחלק ומה שיצא הוא בכמה ימים יתנועעו בדרך אח"כ תחלק מ' על י"ג ויעלו ג' ושליש ובאלו הג' ימים ושליש יגיעו הא' לאחר
|
|
|
קסו) שאלה שני מגדלים גבהם שוה והמרחק שבין שניהם ג"כ הוא שוה לכל אחד מהם והנה ידענו שאדם חסר מהכאת האחת בחבירו כפל מקובץ שני הצלעים אשאל כמה היה גובה כל א' מהם
|
|
|
התשובה נניח שהנשאר על דמ' הוא כ"א ר"ל הנשאר מהכאת גובה המגדל הא' בחבירו כשחוסר ממנו כפל מקובץ שני המגדלים שהם שנים
|
|
|
ונרצה לדעת כמה היה גבהות המגדלים הנה ידענו שהמגדלים הם ב' ולזה ב' בעצמו יעלו ד' ונוסיפם על כ"א ויעלו כ"ה ושרשם ה' והנה נוסיף עליו ב' שהוא מנין המגדלים העולה שהוא ז' הוא גבהות כל א' מהמגדלים
|
|
|
ומופת זה נתבאר במאמר הראשון מאבו בכר
|
|
|
קסז) שאלה הנה בידינו ב' כיסים ולא ידענו כמה מעות היו בהם רק ידענו שבכיס הגדול היה החצי והשליש ממה שהיה בב' הכיסים מקובצים ובכיס הקטנה היה י"ג אשאל כמה ממון היו בב' הכיסים
|
|
|
תשובה קח המורה שהוא ו' ושלישיתו ומחציתו הם ה' והנה עד ו' יחסר א' ועליו תחלק ו' כפול על י"ג הם ע"ח חלק על א' והוא ע"ח וכך מעות היו בכל כיס והוא המבוקש
|
|
|
קסח) שאלה בקש לי מספר שאם תחלקהו על ג' ועל ה ועל ז' ישאר א'
|
|
|
תשובה קח א' שנשאר על הג' בחלקנו אותו על הג' קח ע' ועל א' שנשאר בחלקנו על ה' קח כ"א ועל א' שנשאר בחלקנו על ו' קח ט"ו וקבצם ויהיו ק"ה תוסיף אחד ויהיו ק"ו וכן תעשה
|
|
|
קסט) שאלה ואם אמר לך שנשאר בהשליכך ג"ג ב' או ג'
|
|
|
עשה בדרך הזה עד"מ ואם אמר כשנחלקהו על ג' ישאר ב' ואם יחולק על ה' ישאר ד' ואם יחולק על ז' ישאר ו' קח על כל א' מהב' והנשאר ע' וכפול ע' על ב' ויהיו ק"מ אח"כ כפול ד' על כ"א ויהיו פ"ד אח"כ כפול ו' על ט"ו ויהיו צ' קבצם ויהיו שי"ד והוא המבוקש
|
|
|
קע) שאלה אדם מצא ג' כיסות וידע שבכיס הראשון יש בו מספר נעלם ובכיס הב' יש בו ב' כפלים מהא' ובג' יש בו כמו שיש בשנים ובין כלם ק' מנינים נשאל כמה לכל א' וא'
|
|
|
תשובה נניח שבכיס הא' היה שם דינר א' ובב' ב' ובג' ג' ובין כלם ו' וחלק ק' על ו' ויצא לך י"ו וב' שלישיות והוא מה שבכיס הקטן
|
|
|
קעא) שאלה ב' רוצים לקנות סוס אחד אמר הראשון לשני אם תתן לי החצי ושליש ממעותיך עם מה שיש לי נקנה הסוס אמר הב' אם תתן לי שלישית ורביעית ממעותיך עם מה שיש לי נקנה הסוס אשאל כמה לכל א וכמה שוה הסוס
|
|
|
תשובה בקש המורה הוא י"ב וקח החצי והשליש והוא י' נחסרם מי"ב נשארו ב' א"כ הראשון היה לו ב' אח"כ קח שליש ורביעית המורה שהוא ז' חסר ז' מי"ב הנשאר ה' וכך היה לשני
|
|
|
ואם תרצה לדעת ערך הסוס קח חצי ושליש ה' יהיו ב' ושתות ושים בו ב' שהוא ו' מעות והוא המבוקש ר"ל ח' ושתות
|
|
|
קעב) שאלה יש לנו אילן גבהותו נעלם רק ידענו שאם נקח ד' פעמים כמוהו ונוסיפנו על מרובעינו יצא לנו מספר מונח כמה גבהות האילן
|
|
|
תשובה נניח שעלה בידינו אחר שהוספנו על מרובע האילן ד' פעמים כמוהו קכ"ח ורביע א' שלם
|
|
|
ונרצה לדעת גבהות האילן
|
|
|
הנה תעשה כן הוסף לעולם על המספר העולה ד' שלמים ויהיה העולה במשלינו קל"ב ורביע ונוציא שרשו הרביעי והוא י"א וחצי נחסר ממנו לעולם ב' שלמים והנשאר הוא ט' ורביע והוא גבהות האילן וכן כל היוצא בזה
|
|
|
קעד) שאלה אדם בנה ביתו ובא לתת שכר לפועלים ואמ' להם אני יש לי מעות שאם אתן ג' דינרין לכל א' ישאר בידי ט"ו דינרין ואם אתן ג' דינרין וחצי לכל אחד יחסר לי עשרה דינרין אשאל כמה היו הפועלים וכמה הם מעותיו
|
|
|
תשובה חסר ג' דינרין מג' וחצי וישאר חצי דינר ועליו תחלק חבר ט"ו דינרין עם י' דינרין ויהיו כ"ה חלקם על חצי ויהיו נ' וככה היו הפועלים ואם תרצה לדעת המעות כפול נ' בנ' ויהיו ק"נ הוסף עליהם ט"ו ויהיו קס"ה והוא המעות ואם תכפול נ' בנ' וחצי יהיה העולה קע"ה ויפסיד י' דינרין
|
|
|
קעה) שאלה ג' אנשים יש להם ממון ולא ידענו כמה רק הראשון יש לו חצי השני והב' יש לו חצי הג' ובין כלם י"ב נשאל כמה לכל א' וא
|
|
|
תשובה הא' היה לו פשוט א' והב' היו לו ב' פשוטים והג' ד' קבצם והם ז' פשוטים וחלק י"ב על ז' ויצא לך א וה' שביעיות והוא סך הראשון וכפל זה היה לשני וכפל השני לג'
|
|
|
קעו) שאלה אדם שכר חבירו לבנות לו בית כל יום והתנה עמו שיתן לו בכל יום ה דינרין ובכל יום שלא יעשה מלאכה יתן הנשכר אל בעל הבית ט' דינרין והוא עבד ימים ידועים ולבסוף הבעל הבית נתן לו דינר א' נרצה לדעת כמה ימים עבד
|
|
|
הנה יש לך לחבר ה' עם ט' ויהיו י"ד אח"כ נכפול ט' על ל ויהיו ר"ע נוסיף עליו א' ויהיו רעא נחלקם על י"ד ויצא לך י"ט וה' חלקים מי"ד אח"כ נכפול ל' על ה' ויהיו ק"נ נסיר מהם א' ויהיו קמ"ט נחלקם על י"ד יצא לך עשרה וט' חלקים מי"ד הנה א"כ הוא עבד י"ט ימים וה' חלקים מי"ד ושבת מכל מלאכתו י' ימים וט' חלקים מי"ד
|
|
|
קעז) שאלה אדם הולך לסחורה נדר אם המקום יכפול ממונו בכל יום יתן ג דינרין לצדקה ובתוך ג' ימים הלך ממונו
|
|
|
יש לך לעשות ככה והוא שכבר ידעת כי ביום ג' הלך כל ממונו אחר שנתן ג' דינרין א"כ מה שהיה לו ביום הג' היה ג' תחלקהו על ב' יצא לך א וחצי תוסיף על זה ג' ויהיו ד' וחצי והוא מה שהיה לו ביום השני קודם נתינת ממונו
|
|
|
וחלק זה על ב' ויצא לך ב' ורביע תוסיף על זה ג' ויהיו ה' ורביע וזה היה לו ביום הראשון קודם נתינת הממון
|
|
|
ואם תרצה לחלק זה על ב' יצא לך ב' וה' שמיניות והוא המעות ותקיש על זה
|
|
|
קעח) שאלה אדם יש לו מעות ואמר אם השם יוסיף על ממונו ב' דינרין בכל יום יתן ג' דינרין בכל יום ובסוף ד' ימים הלך כל ממונו נשאל כמה ממון היה לו ביום הראשון
|
|
|
נעשה זאת השאלה על זה הדרך והוא כי כבר ידעת כי מה שנתן ביום הד' היה ג' ולא נשאר מאומה בידו והריוח שהיה עושה בכל יום היה ב' נסיר מג' ב' שהם הריוח ישאר א' והוא מה שהיה לו ביום הרביעי קודם הריוח שעשה באותו יום אח"כ נוסיף על א' ג' ויהיו ד' נסיר מהם הב' מהריוח וישארו ב' וזה היה לו ביום הג' קודם הריוח אח"כ נשים על זה ג' ויהיו ה' נסיר מהם הריוח שהוא ב' הנשאר ג' וזה היה לו ביום השני קודם הריוח א"כ נוסיף על זה ג' ויהיו ו' נסיר מהם ב' בעד הריוח הנשאר ד' וזה היה לו ביום הראשון קודם שהרויח מאומה והוא סך הממון הנמצא עמו בתחלה
|
|
|
קעט) שאלה אנשים ונשים וטף הולכין לאושפיזה לאכול האנשים נותנים ב' פשוטי' והנשים חצי פשוט והטף רביעית ופרעו י"ב פשוטים ובין כלם י"ב ג"כ כמה הם האנשים והנשים והטף
|
|
|
תשובה תשים האנשים כפי מה שתרצה וכן הנשים והטף ונניח שהאנשים היו ד' ששוים ח' פשוטים וד' נשים מב' פשוטים והנה מספרם ח' ומספר המעות י' והנערים ד' והנם י"ב והמעות י"א ויחסר א' עד י"ב לכן יש לנו למצא מספר שיעלה אחד ונעשה ג' מהד' אנשים ויהיו ו' נשים ומהאנשים נעשה מהם ב' נערים והמספר יצא שוה
|
|
|
והתשובה היא ה' אנשים ואשה אחת ובו' נערים ובין כלם י"ב גם כל הממון עולה י"ב
|
|
|
קפ) שאלה אדם נוסע מנפולי עם דינרין ידועים ורוצה ללכת עד רומא ובעד כל דינר ירויח א רצוני א' ישוב ב' ופזר לשם ד' מנינים ואח"כ הולך מרומא עד פלורינצא וכל עוד שיש לו ב' דינרין ישובו ג' ופזר לשם ו' דינרין אח"כ הולך מפלורינציאה עד וינישיאה וכל עוד שיש לו דינר א ישוב ג' ופזר ו' בויניציאה י"ד מנינים ואחר הפזור נמצא בידו ד' מאות מנינים נרצה לדעת כשנסע מנאפולי כמה דינרין היה לו
|
|
|
ראוי לעשות ככה תהפך כל המספר וידוע כי ד' מאות וי"ד היו לו בוינישיאה עם הי"ד שפזר ויש לך לומר ככה אם ג' שוים א' ד' מאות וי"ד כמה שוים יצא לך קל"ח וזה המעות היה לו בפלורינציאה ותוסיף עליו מה שפזר שהוא ו' יהיו קמ"ד ותאמר אם ג' שוים ב' קמ"ד מה ישוו ויצא לך צ"ו והוא סך הדינרין שהיו לו ברומא יהיו מאה ותאמר אם ב' שוים א' ק' כמה שוים תמצא נ' והוא מה שהיה לו כשנסע מנפולי ובהגיעו בוינישיאה נמצא בידו י"ד ד' מאות מנינים זולת י"ד שפזר בדרך
|
|
|
קפא) שאלה אדם קנה בפלורינציאה קנה א' ממשי ג' מנינים וחצי ממטבע של פלורינצא והקנה ג"כ הוא קנה של פלורינצא ופזר בדרך בלכתו בנאפולי ב' שלישיות ממון של פלורינצא באיזה אופן ימכור לנאפולי באופן שירויח כ"ה מנינים בעד כל מאה ומאה ויש לנו ב' הפרשות מפלורינצא לנאפולי כי הח' קנים מפלורינצא הם ט' קנים של נאפולי והק' מנינים של פלורינציני הם קי"א מנאפוליטאני
|
|
|
וראוי לעשות ככה שתוסיף הב' שלישיות שפזר על ג' וחצי ויהיו ד' ושתות והם מנינים של פלורינציאה ותאמר אם ק' שוים קי"א הד' ושתות מה ישוו תמצא ד' וד' חומשים הנה א"כ הקנה של פלורינצא שוה בנפולי ד' מנינים וד' חומשים ממטבע של נאפולי אם ח' קנים שוות הט' א כמה יצא לך א' ושמין הנה הקנה של פלורינצא שוה של נאפולי א' ושמין וא ושמין מקנה של נאפולי שוה ד' וד' חומשים מה ישוה הא' תמצא ששוה ד' מנינים וד' חלקים מט"ו הנה א"כ כל עוד שהקנה של פלורינצא שוה ד' מנינים ושתות משל פלורינצא הקנה מנאפולי שוה ד' מנינים וד' חלקים מט"ו ממניני נאפולי נאמר שרוצה להרויח בעד כל קכ"ה ותאמר ככה אם מאה שוים ד' וד' חלקים מט"ו קכ"ה כמה שוים יצא לך ה' מנינים וכ"ג חלקים מק' והוא שווי הקנה הנה ראוי למכור הקנה ה' מנינים וכ"ג חלקים מק' ובזה האופן ירויח כ"ה בעד כל מאה מנינים ודוק ותשכח
|
|
|
קפב) שאלה אדם יש לו י"ז אוק' מכסף שוה כל אוק' ז' קרליני לכלול בו עופרת באופן לא ישוה כל אוק' כי אם ה' קרליני וחצי כמה עופרת יכלול באלו הי"ז אוק'
|
|
|
הנה ראוי לחלק ז' על ה' וחצי ויצא אחד וג' חלקים מי"א הנה יש לו לשים בכל אוק' ג' חלקים מי"א מעופרת ובין כל הי"ז אוק' יש לו לשים ד' אוק' וז' חלקים מי"א מעופרת
|
|
|
ואם תרצה לבחון אותו כפול י"ז על ז' יהיה קי"ט ושמור אותם ועתה כפול ז' וחצי על כ"א וז' חלקים מי"א כי בראשנה היו י"ז אוק' ויש לנו להוסיף הד' אוק' וז' חלקי' מי"א על אותו הסך ויהיה כ"א וז' חלקים מי"א ויעלה קי"ט בלי תוספת ומגרעת
|
|
|
קפג) שאלה יש לו לאדם ג' ליט' וג' אוק' וג' רביעיות מכסף שמכיל רכ"ב איצטרליני מטוב לליט' ושוה ח' מנינים א ליט' וא אוק' וז' שמיניות אוק' מכסף שאינו מכיל הליט' כי אם קי"א איצטרליני כמה שוה
|
|
|
הנה ראוי לעשות מהליט' אוק' והמספר הראשון הוא ב' ליט' וג' אוק' וג' רביעיות יהיה י"ז אוק' וג' רביעיות כפול אותם על רכ"ב יעלה ק אלפים וק"ס וחצי אח"כ קח המספר השני שהוא א' אוק וא' ליט' וז' שמיניות ותעשה מהליט' אוק ועם האוק' יהיו י"ג וז' שמיניות כפול אותם על מה שמכיל רצוני שתכפול י"ג וז' שמניות על קי"א שהוא מה שמכיל כל ליט' ועלה אלף וה' מאות ומ' ושמין א' וזה יהיה המספר השני ותאמר אם ו' אלפים וק"ס וחצי שוה ח' מנינים המספר השני שהוא אלף וה מאות ומ' ושמין כמה שוה הנה יהיה שווי שנים שלמים בלי תוספת ומגרעת
|
|
|
קפד) שאלה יש בכאן אנשים שעומדי שעומדים עם אדון והאדון נותן לכל א' וא' בעד שנה תמימה עשרים מנינים ויש מהם שעבדו ו' חדשים ויש ו' וחצי ויש ז' חדשים וכו' הנה תמצא שכל מה שהרויחו בין כלם לפי יחס הזמן שעבדו עולה ק"ט מנינים וז' פשוטים והאדון רוצה לפרוע אותם ואין לו כי אם ק' מנינים נרצה לדעת כמה יקח כל א' וא'
|
|
|
הנה ראוי לחלק ק' על ק"ט מנינים וז' פשוטים וידוע כי הפשוט עשור המנ(י)ן על כן ראוי לעשות מכל הב' מספרים עשיריות הא' אלף והאחר אלף וצ"א חלק אלף על אלף וצ"א ויצא לך אלף חלקים מאלף וצ"א
|
|
|
קפה) שאלה אדם שכר בית לחבירו בעד ג' שנים לערך מ' מנינים לשנה ובכניסתו לבית נותן לו חצי השכר מאותה השנה ובסוף השנה נותן לו מ' מנינים עשרים בעד תשלום פרעון אותה שנה ועשרים בעד תשלום השנה האחרת וכן עד כלות הג' שנים והנה הבעל הבית אמר לאותו ששוכר הבית בבקשה ממך תפרע לי עתה מכל הג' שנים ואתן לך עשרים מריוח על כל מאה לשנה תמימה וכן עשה נתן לו כל הממון נרצה לדעת כמה ממון מחוייב לתת לו באופן שיבא עשרים על כל מאה מריוח
|
|
|
התשובה תאמר אם מאה ועשרים שוים ק"כ כמה שוים והם העשרים שהוא מחוייב לו לתת בסוף השנה ותמצא י"ו וב' שלישיות תוסיף עליו העשרים שהוא מחוייב לתת לו עתה בכניסתו בבית יהיו ל"ו וב' שלישיות וזה יהיה בעד שנה ראשנה עוד תאמר ק"כ שוים ק' ל"ו וב' שלישיות כמה שוה יצא לך ל' וה' חלקים מט' וזה בעד שכירת שנה שניה עוד תוסיף ותאמר אם ק"כ שוים ק' ל' וה' חלקים מט' כמה שוה יצא לך כ"ה וכ"ה חלקים מנ"ד וזה הוא בעד שכירות שנה שניה אח"כ תחבר כל אלו הג' מספרים רצוני ל"ו וב' שלישיות ול' וה' חלקים מט' וכ"ה וכ"ה חלקים מנ"ד ויעלה בין הכל צ"ב ול"ז חלקים מנ"ד וכן ראוי לתת לו בבת אחת בלי תוספת ומגרעת
|
|
|
קפו) שאלה באיזה אופן באיזה אופן נשקול עם ד' אבנים מ' ליט' או אוק'
|
|
|
הנה יש לך לקחת א' כפול אותם על ג' ויהיו ג' כפול ג' על ג' ויהיו ט' כי כיחס א' א' ג' כן יחס ג' אל ט' והוא השלישית כפול ט' על ג' ויהיו כ"ז כי יחס ט' אל כ"ז כיחס ג' אל ט' והוא הד' הנה ראשנה ישקול ליט' אחת והשניה ג' ליט' והשלישית ט' והרביעית כ"ז ובין הכל מ'
|
|
|
ואם תרצה לשקול ה' הנה תשים אותה של ג' ליטראות ואותה של א' בכף אחת אח"כ תשים בכף שניה אותה של ט' אח"כ תשים בכף ראשנה ששם הב' אבנים ששוקלות ד' ושים ה' שתרצה לשקול ויהיו ט' בכף ראשנה גם בשניה
|
|
|
ואם תרצה לשקול ח' הנה תשים בכף הראשנה האבן ששוקלת א' ועם הח' יהיו ט' אח"כ תשים בשניה השוקלת ט' ויהיה שוה בשוה וזה המספר נקרא מספר יחסיי וכו'
|
|
|
קפו) שאלה אדם הולך לאושפיזא ועמד לשם ל"א יום ונושא ה' גביעים של כסף ששוקלים בין כלם ל"א אוק' והתנו שיתן לאושפיז בכל יום אוק' של כסף באיזה אופן יפרענו בכל לילה ולילה שלא יתן הגביעים ויתן לו אוק' שלימה בכל יום
|
|
|
הנה ראוי לקחת א' ואח"כ לכפול אותו ויהיו ב' ואח"כ כפול על ב' ויהיו ד' כי יחס א' אל ב' כיחס ב' אל ד' אח"כ כפול ד' על ב' ויהיו ח' כי יחס ד' אל ח' כיחס ב' אל ד' אח"כ כפול ח' על ב' ויהיו י"ו כי יחס ד' אל ח' כיחס ח' אל י"ו א"כ הנה הא' שוקל אוק' והב' ב' והג' ד' והד' ח' והה' י"ו וכן עולה ל"א עם ב' כוסות תוכל לפרעו עד ס"ג והוא שתכפול י"ו על ב' ויהיו ל"ב והוא הגביע הו' ועם הל"א הם ס"ג ועם ז' כוסות תוכל לפרעו עד קכ"ז ימים והוא שתכפול ל"ב על שנים ויהיו ס"ד ועם ס"ג והם קכ"ז וכן עד אין קץ
|
|
|
קפז) שאלה אדם מוכר מג' מיני צמר הראשנה מוכרה ככר שהם ק' ליט' עשרה מנינים והב' מוכר הככר עשרה מנינים וחצי והג' מוכר הככר י"ב מנינים ושליש והנה כשתרחץ הראשנה הנה הככר ישוב פ' ליט' מצמר נקי וכשתרחץ השניה ישוב הככר צ' ליט' מצמר נקי וכשתרחץ השלישית ישוב הככר צ"ט ליט' מצמר נקי נרצה לדעת איזה מהם יותר טוב לקחת משלשתן
|
|
|
ידוע כי הראשנה הפ' ליט' שוות י' מנינים וידוע כי השניה הצ' ליט' שוות עשרה מנינים וחצי וידוע כי השלישית הצ"ט ליט' שוות י"ב מנינים ושליש ונעשה הערך ככה אם הפ' שוה עשרה א' כמה שוה הנה יצא לך שמין א' והוא שווי הליט' מהראשנה עוד שוב אל הב' ותאמר אם צ' שוות עשרה וחצי א' כמה שוה יצא לך שמין א' וד' שביעיות השמין הנה הנה זאת יותר טובה מהראשנה ונעשה כן מהג' ונאמר אלו צ' שוות י"ב ושליש א' כמה שוה יצא לך פחות משמין ואין ראוי לקחת ממנה כי היא יותר גרועה מהאחרות
|
|
|
קפח) שאלה הנה בכמה עומדים י"ב גלחים והנה אם יעבוד א' מהם שנה תמימה ראוי לקחת אוק א' וב' טריניריש אחר שעבד שנה רצופה בצימצום ושואל אוק' וב' טריני והב' עבד יותר מעט עד ששואל אוק' א' וג' טריני והג' עבד יותר עד ששואל אוק' א' וא טרי והרביעי שואל אוק אחת וד' טריני והה' שואל אוק' וו' טריני והו' ב' אוק' וד' טרי והח' אוק' אחת והעשירי אוק' א' וט' טריני והוא אוק' א' וי"ט טריני והי"ב אוק' א וכ"ב טריני והנה האדון העושה הפרעון אין לו כי אם י' אוק' וה' טריני ומזה הממון רוצה לחלק לגלחים כפי עבודתו כמה ראוי שיתן לכל א' וא'
|
|
|
הנה ראוי לחבר כל הסך מאלו הי"ב גלחים ותמצא שעולה ט"ו אוק' וי"ח טרי והנה ראוי לחלק העשרה אוק' על ט"ו אוק' וי"ח טרי והנה ראוי לעשות מהי' אוק' טרי ולחבר עמהם הה' טרי ויעלה ש"ה עוד תעשה מהט"ו אוק וי"ח טרי טרי ויעלה ד' מאות וס"ח עוד שוב וכפול ש"ה על ל' ויעלה ק"נ וחלקם על ד' מאות ויצא לך טרי והם י"ט וט"ו נרות וב' דינרין וככה יקח בעד כל אוק' ואוק'
|
|
|
ואם תרצה לדעת כמה יקח בעד כל טרי הנה כבר ידעת כי בעד אוק ראוי לקחת י"ח וט"ו נרות וב דינרין כפול י"ט על ב' רצוני שתעשה מהי"ט טרי נרות והעולה חלק על ל' בעבור כי הל' טרי שוים אוק' ויצא לך המבוקש וכן תוכל לעשו' מכל מטבע
|
|
|
קפט) שאלה אדם נתן ליט' של כסף לחבירו לחלופי' והתנה עמו שיתן לו מהג' ליט' עשרה מבגד וב' קנים מהבגד שוה ג' חביות של יין וב' חביות מיין שוה ח' דינרין נרצה לדעת כמה היו שוות הד' ליט' של כסף לפי זה היחס גם כמה שוות הה' קנים מהבגד
|
|
|
התשובה ראוי לך לדעת כי הב' חביות הם שוות ח' דינרין ותאמר אם ב' שוות ח' ג' כמה שוות ויצא לך י"ב הנה הג' חביות של (יין) שוות י"ב דינרין וידוע הוא כי ב' קנים היו שוות אלו הג' חביות הנה יש לך לעשות ככה והוא שתאמר אלו ב' קנים שוות י"ב דינרין הי' קנים כמה שווים ויצא לך ס' וידוע כי הי' קנים היה שווי ג' ליט' של כסף ותאמר אלו ג' שוות ס ד' כמה שוות ויצא לך פ' בלי תוספת ומגרעת
|
|
|
קצ) שאלה אדם אמר לחבירו אם תרצה לשאת על ספינתך כל החטה שלי אתן לך החצי בא שני ואמר לו אם תשא את שלי אתן לך השליש בא אחר ואמר אם תשא את שלי אתן לך רביעית עוד זה מדבר וזה בא ויאמר אם תשא את שלי אתן לך החומש ואח"כ נמצא בידו ש' מדות אשאל כמה מדות נשא
|
|
|
תשובה בקש מספר יהיה לו חצי ושליש ורביעית וחומש ותמצא ס' קח חציו והוא ל' ושלישיתו והוא כ' ורביעיתו והוא ט"ו והחומש והוא י"ב ובין הכל ע"ז ותאמר אם ע"ז שוים ס' ג' מאות כמה ישוו כפול ס' על ג' מאות וחלקם על ע"ז ויצא לך ב מאות ול"ג ונ"ט חלק מע"ז והוא סך מה שנשא לכל א' וא'
|
|
|
ואם תרצה לבחון אותו קח חצי זה הסכום גם שלישיתו ורביעיתו וחמישיתו יוסף עליו ויעלה ג' מאות
|
|
|
קצא) שאלה בכאן אדם שיש לו ו' ליט' של כסף ובכל ליט' יש ז' אוק' מכסף מזוקק עוד יש לו ה' ליט' מכסף שיש לו בכל ליט' ו' אוק' מכסף טוב ועוד יש לו ליט' בלתי נודעות שבכל ליט' יש כסף י"א אוק' ורוצה לשרוף כל זה ולעשות ממנו גביעים שיכיל כל ליט' א' אוק' מכסף מזוקק ונרצה לדעת כמה ליט' יקח מהכסף המכיל י"א אוק' הליט'
|
|
|
תשובה ראוי שתדע כמה אוק' יכיל המספר הראשון שהוא ו' ליט' המכיל ז' אוק' לליט' יהיו מ"ב והוא מספר אוקי' הטובות ועוד קח המספר השני שהוא ה' ליט' המכיל ו' אוק' לליט' ויהיו ל' והוא מספר אוק' הטובות וחבר אלו הל' אל מ"ב ויהיו ע"ב אח"כ חבר הליט' שהם הו' ויהיו י"א א"כ י"א ליט' יכיל ע"ב אוק' מכסף טוב אח"כ כפול ט' שהוא הסך שתרצה לעשות על הליט' שהם י"א יהיה זה צ"ט הוצא ע"ב מצ"ט הנשאר כ"ז וחלק אלו הכ"ז על היתרון שיש בין ט' לי"א ותמצא ב' חלק כ"ז על ב' ותמצא י"ג וחצי שהם ליט' וככה יקח מן הכסף המכיל י"א
|
|
|
ואם תרצה לבחון אותו חבר כל הליט' שהם י"ג וחצי וו' וה' ויהיו כ"ד וחצי וכפול כל אחד על מה שמכיל ויעלה ר"כ וחצי והוא השמור אח"כ כפול ט' על כ"ד וחצי ויעלו ר"כ ג"כ
|
|
|
קצב) שאלה יש כאן ג' בני אדם כי הרויחו י"ב מנינים הא שואל חצי הממון עם תוספת ב' והאחר שואל שלישית הממון עם תוספת ג' והאחר שואל רביעית הממון עם תוספת ד' נשאל כמה יקח כל א' וא'
|
|
|
תשובה ראוי לחבר כל מה ששואלים מתוספת והם בגד והם ט' תחסרם מי"ב ישארו ג' אח"כ קח חצי י"ב יהיו ו' והשליש ד' והרביעית ג' וכלם י"ג אח"כ כפול חצי המספר על ג' והנם י"ח חלקם על י"ג ועלה א וה' חלקים מי"ג וזה חלק משואל חצי הממון ובעבור שאמר יותר ב' וקח ג' וה' חלקים מי"ג אח"כ קח השליש וכפול אותם על ג' ויעלו י"ב וחלקם על י"ג ויעלו י"ב חלקים מי"ג וזה חלק ממבקש שליש הממון ובעבור שאמר ג' מתוספת וקח ג' וי"ב חלקים מי"ג אח"כ קח רביעית המספר וכפול אותם על ג' ויעלו ט' וחלקם על (י)"ג ויעלו ט' חלקים מי"ג ובעבור שאמר עם תוספת ד' וקח ד' וט' חלקים מי"ג ותחבר הכל ויעלה י"ב שלמים
|
|
|
קצג) שאלה ג' אנשים רוצים לחלק י"ו מנינים הא' שואל חצי הממון פחות ג' והאחר שואל הרביעית עם תוספת ד' והאחר שואל החומש עם תוספת ה' נרצה לדעת כמה יקח כל א' וא'
|
|
|
תשובה ראשנה תחבר התוספת ששואלים הב' מהם והוא ט' חסר מהט' ג' כי א' מהם אמר פחות ג' וישארו ו' הסר מסך הממון ו' הנשאר י' אח"כ קח חצי הממון שהוא ח' אח"כ קח חמישיתו שהוא ג וחומש ורביעיתו שהוא ד' ותחבר הכל ויעלו ט"ו וחומש אח"כ כפול מחציתו שהם ח' על הי' שנשארו אחר לקיחת התוספת של כל אחד והיו פ' חלקם על ט"ו וחומש ויעלו ה' הסר מהם ג' מצד שאמר פחות ג' יהיה חלקו ב' שלמים וב' חלקים מט"ו עוד קח רביעית הממון וכפול אותם על י' והעולה תחלק ויצא לך ב' שלמים ומ"ח חלקים מע"ו וזה יהיה חלקו משואל רביעית הממון ונתן לו ד' מצד שאמר ד' מתוספת אח"כ קח חומש המספר וכפול אותם על עשרה וחלק העולה על ט"ו וחומש ויצא לך שנים שלמים וח' חלקים מע"ו ובעבור שאמ' ה' מתוספת יקח ז' שלמים וח' חלקים מע"ו ובין שלשתן י"ו שלמים
|
|
|
קצד) שאלה יש כאן ב' שרוצים לחלק עשרים מנינים הא' שואל השליש פחות ד' והאחר שואל החומש פחות ג'
|
|
|
הנה ראשנה ראוי לחבר ג וד' והנם ז' תוסיפם על הממון שהוא כ' יהיו כ"ז אח"כ קח שלישית כ' יהיו ו' וב' שלישיות אח"כ קח החומש יהיה זה ד' חברם יחד יהיו עשרה אח"כ כפול ו' וב' שלישיות על כ"ז יהיה זה ק"פ חלקם על ו' וב' שלישיות ויהיה העולה י"ו וכ"ח חלקים מל"ב ובעבור שאמר פחות ד' נחסר ד' וישאר י"ב וכ"ח חלקים מל"ב וזה חלק השואל שלישית הממון עוד נכפול ד' על כ"ז יהיה זה מאה וח' חלקם על עשרה וב' שלישיות יעלו עשרה וד' חלקים מל"ב ומצד שאמר פחות שלשה נקח מעשרה ג' הנשאר ז' וד' חלקים מל"ב
|
|
|
קצה) שאלה ג' אנשים מצחקים בקוביא הב' משימים כל ממונם נגד הג' והג' המצחק הפסיד ופרע לכל א' סך כל ממונם נגדו והוא הפסיד ופרע לכל א' ממונו עתה מצחק הג' והב' הנשארים שמו כל ממונם והוא הפסיד ופרע לכל א וא' ונמצא עתה ביד כל א' וא' ק' מנינים כשהתחילו לצחק כמה לכל א' וא'
|
|
|
תשובה תקח סך האנשים שהם ג' תוסיף עליו א' בעבור הכפל הראשון ויהיו ד' עוד כפול ג' ויהיו ו' תוסיף עליו א' ויהיו ז' עוד כפול ז' ויהיו י"ד תסיר ממנו א' ויהיו י"ג וידוע כי הממון היה ג' מאות על כן נעשה ככה ונאמ' בכאן ג' אנשים הא' נשא י"ג דינרין והאחר ז' והאחר ד' והרויחו ג' מאות כמה יקח כל א' וא' תחבר כל ממונם שהם ד' ז' וי"ג הנם כ"ד כפול י"ג על ג' מאות יהיה זה ג' אלפים וט' מאות וחלקם על השמור שהוא כ"ד ויצא לך קס"ב וחצי והוא ממון הראשון
|
|
|
עוד כפול ז' שהוא ממון השני עם ג' מאות ויעלו ב' אלפים ומאה וחלקם על כ"ד ויצא לך פ"ז וחצי והוא ממון השני
|
|
|
עוד יש לך לכפול ממון השלישי שהוא ד' על ג' ויעלו י"ב מאות וחלקם על כ"ד ויצא לך חמישים שלמים והוא ממון הג'
|
|
|
ובין הכל ג' מאות
|
|
|
קצו) שאלה יש כאן חבית שיש לה ג' פתחים מהפתח הראשון יצא כל היין בד' שעות ומהפתח השני בלתי הראשון יצא כל היין בג' שעות ומהפתח הג' זולת האחרים יצא כל היין בב' שעות ואם נפתחם שלשתם בכמה יצא כל היין
|
|
|
תשובה תוכל לעשותה בב' פנים א והוא שתקח החשבון היותר גדול מכלם שהוא ד' ותחלק אותו על עצמו גם על האחרים ראשנה תחלקהו על עצמו יצא א' אח"כ חלק ד' על ג' ויצא לך א' ושליש אח"כ חלק ד' על ב' ויצא לך ב' חברם כלם ויהיו ד' ושליש חלק ד' עליהם ויצא לך י"ב חלקים מי"ג והוא השעור מיציאת היין
|
|
|
ואם תרצה לבחון אותו תעשה ככה נניח שהיו י"ב לוגים יין בחבית ונאמ' אלו הד' שעות יצאו י"ב לוגים כמה יצאו בי"ב חלקים מי"ג תמצא שיצאו ב' לוגים ועשרה חלקים מי"ג עוד נשוב ונאמר אלו בב' שעות יוצאים י"ב כמה יצאו בי"ב חלקים מי"ג (חלקים מי"ג) תמצא שיצא ה' לוגים וח' (ז) חלקים מי"ג עוד נשוב ונכפול אלו הג' שעות יצאו י"ב כמה יצא בי"ב חלקים מי"ג תמצא ג' וט' חלקים מי"ג חבר הכל ותמצא שהם י"ב שלמים
|
|
|
והדרך האחר הוא שנבקש המורה יהיו בו כל החלקים הנז' רצוני שלישית בעבור שאמר ג' שעות ורביעית בעבור ד' שעות ומחצית בעבו' ב' שעות תמצא י"ב ומחציתו ו' ורביעיתו ג' ושלישיתו ד' חבר הכל יהיו י"ג חלק המורה שהוא י"ב על י"ג יהיו י"ב חלקים מי"ג והכל הולך אל מקום אחד
|
|
|
קצז) שאלה ג' בני אדם רוצים להחליף סחורה זה עם זה הא' מוכר בגד והאחר מוכר צמר מי שמוכר הבגד מוכר אותה הקנה שוה ג' מנינים במעות מנויים ומצד שהוא רוצה להחליף העלה אותו מנין א' לקנה ושם אותו ה' מנינים ומזה רוצה שינתן לו ב' חמישיות במעות מנויים והב' חמישיות רוצה שיתן לו האחר מצמר והבגד מן הצמר שוה ג' מנינים הבגד נרצה לדעת כמה יעלה לו סך הצמר כאשר העלה לו סך הבגד
|
|
|
ראוי לעשות ככה והוא שתקח ב' חמישיות מהממון שהוא שואל רצוני מהה' מנינים ישארו ה' אח"כ קח ב' מהד' שהיה שווי הקנה במעות מנויים ישאר ב' אח"כ תאמר אם ב' שוים ג' כמה שוים ז' יצא לך י' וחצי וככה ישים הצמר
|
|
|
ואם תרצה לבחון נניח שקנה ב' קנה שהיו שוות פ' מנינים במעות מנויים ועתה שוות ק' נחליף שעושים ומהק' הוא שואל ב' חמישיות במעות מנויים שהם מ' מנינים הסר מפ' מ' הנשאר מ' ומאלו המ' העלה אותם עד ס' כמה יקח מהצמר ראוי לחלק מ' על ז' שהוא שווי הצמר התחלה יעלה לך ה' וה' שביעיות ואמר אלו הה' וה' שביעיות כמה שוים לערך עשרה מנינים וחצי תמצא שישוו ס' מנינים כי העלה אותם ממ' עד ס'
|
- 198) Question: there are four [men] who formed a partnership.
- Three of them, without the fourth, contributed 600 minyanim.
- Three of them, without the third, contributed 700 minyanim.
- Three of them, without the first, contributed 800 minyanim.
- Three of them, without the second, contributed 900 minyanim.
- We wish to know how much did each contribute?
|
קצח)[10] שאלה יש כאן ד' עושים שותפות
הג' בלתי הרביעי שמו ו' מאות מנינים
והג' האחרים בלתי הג' שמו ז' מאות
והג' בלתי הא' שמו ח' מאות
והג' בלתי השני שמו ט' מאות
נרצה לדעת כמה שם כל א
|

|
ראוי לעשות כן תחבר כל ממונם יהיה זה אלף אחר שנחלקם על ג' והוא כל הממון ששמו בין כלם
|

|
ונסיר מזה ת"ר ישאר ת' והוא חלק הרביעי
|

|
עו' נסיר מזה ז' מאות וישארו ג' מאות והוא מה ששם השלישי
|

|
עוד נסיר מזה ח' מאות ישארו ב' מאות והוא מה ששם השני
|
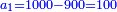
|
עוד נסיר מזה ט' מאות ישארו מאה והוא מה ששם הראשון
|

|
ובין כלם אלף
|
- [L] Question: there are four [men] who formed a partnership.
- Three of them, without the first, contributed 18 [minyanim].
- Three of them, without the [second], contributed 20 minyanim.
- Three of them, without the [third], contributed 22 [minyanim].
- Three of them, without the fourth, contributed 24 [minyanim].
- We wish to know how much did each contribute?
|
קצו)[11] שאלה ד' עושים שותפות
הג' בלתי הראשון שמו י"ח
והג' מהם בלתי האחד שמו כ' מנינים
והג' האחרים זולת האחר שמו כ"ב
והג' בלתי הרביעי שמו כ"ד
כמה שם כל אחד ואחד
|

|
תחבר כל ממונם ויעלה פ"ד תחלקם על ג' ויצא לך כ"ח וכן כל ממונם
|
|
|
והנה חלקנו פ"ד על ג' כי לעולם הם מחוברים
|
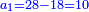
|
ונסיר מהם י"ח ששמו הג' הראשנים וישארו עשרה והוא חלק הראשון
|

|
עוד נסיר כ' וישארו ח' והוא חלק השני
|
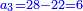
|
עוד נסיר כ"ב וישארו ו' והוא חלק השלישי
|
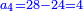
|
עוד נסיר כ"ד ונשאר ד' והוא חלק הרביעי
|
- [L] Question: there are five - four of them contributed 22, four of them contributed 24, four of them contributed 26, four of them contributed 28, and four of them contributed 30
- How much did each have?
|
קצז)[12] שאלה בכאן חמשה שד' שמו כ"ב וד' מהם שמו כ"ד וד' מהם שמו כ"ו וד' מהם שמו כ"ח וד' מהם שמו ל'
כמה לכל אחד ואחד
|

|
תחבר כל ממונם ויעלה ק"ל חלקם על ד' שהם קשורים לעולם ויצא לך ל"ב וחצי והוא כל ממונם
|
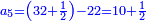
|
תסיר מהם כ"ב הנשאר עשרה וחצי והוא ממון החמישי
|
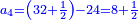
|
תסיר מהם כ"ד הנשאר ח' וחצי והוא ממון הרביעי
|
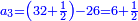
|
תסיר מהם כ"ו וישארו ו' וחצי והוא ממון השלישי
|
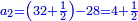
|
תסיר מהם כ"ח וישארו ד' וחצי והוא ממון השני
|
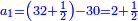
|
תסיר מהם ל' וישארו ב' וחצי הוא ממון הראשון
|
|
|
קצט) שאלה יש כאן אדם שמוכר מדת החטה י' מנינים ויש לו חטה אחרת יותר טובה שמוכר המדה י"ו מנינים ובא אדם ואמר לו מכור לי מ[ב'] מיני חטה לערך י"ד מנינים ואקנה כ' מדות כמה יתן לו מכל חטה וחטה באופן שיבא י"ד מנינים החטה
|
|
|
תשובה כך תעשה ראה איזה הפרש יש בין י"ד לי' תמצא ד' ותשימם על י"ו שהוא הפכו עוד תראה איזה תוספת יש בין י"ד לי"ו שהוא הערך השני תמצא ב' ותשים אותם על י' אח"כ חבר ב' וד' שהם הנוספים ויהיו ו' ושמרם אח"כ קח הד' וכפול אותם על הסך שהוא רוצה לקחת שהם כ' מדות יעלה פ' חלקם על ו' יעלה לך י"ג שלמים ושליש ושים אותם אצל המדות ששוות י"ו מנינים אח"כ כפול הב' שהוא המספר השני על כ' שהוא סך המדות יעלה מ' חלקם על ו' יצא לך ו' שלמים וב' שלישיות וככה יקח מהחטה ששוה י' מנינים המדה הנה א"כ יש לו לקחת מהחטה ששוה י"ו מנינים י"ג מדות ושליש ומהחטה ששוה י' יקח ו' וב' שלישיות ובין הכל כ' מדות
|
|
|
ואם תרצה לבחון אותו ידוע הוא כי הוא שאל כ' מדות לערך י"ד מנינים במדה כפול י"ד על כ' יצא לך ר"פ הנה א"כ הכ' מדות שוות ר"פ מנינים ואתה אמרת שראוי לקחת י"ג מדות ושליש מאותו ששוה י"ו מנינים כפול י"ו על י"ג ושליש ויצא לך רי"ג ושליש ושמור אותם אח"כ שוב אל החטה ששוה י' מנינים המדה ואתה אמרת שראוי לקחת ממנה ו' מדות וב' שלישיות כפול ו' וב' שלישיות על עשרה יצא לך צ"ו (ס"ו) וב' שלישיות חבר ס"ו וב' שלישיות אל רי"ג ושליש ויצא לך ר"פ שלמים והוא שוה אל הר"פ השמורים
|
|
|
ר) שאלה יש כאן א שיש לו מגן א' ורוצה שינתן לו בעד זה מגן קרליני וגרני וטורנישי ודינר וקאוואלי שוה בשוה שיקח מהא' כמו מהנשארים
|
|
|
ראוי לעשות ככה והוא שתדע כמה קאוואלי יש במגן תמצא י"ב מאות אח"כ תאמר כמה דינרין יש במגן תמצא ו' מאות אח"כ תאמ' כמה טורני יש במגן תמצא ב' מאות וק' נרות וי' קרליני קח המספר הגדול שבכלם והוא י"ב מאות וחלקהו על עצמו יצא א' ועל הדינרין יצא ב' ועל הטורני ו' ועל הנרות י"ב ועל הקרליני ק"כ חברם כלם ויהיו קמ"א חלק י"ב עליהם ויהיו ח' וע"ב חלקים קמ"א וכך יקח מכל מטבע
|
|
|
ואם תרצה לבחון השב כל המטבעים אל המטבע היותר דקה שהם קאוואלי וגם החלקים ויעלה י"ב מאות
|
|
|
רא) שאלה יש כאן מי שיש לו שורים ואמר לרועה אלו ירעה שוריו ה' שנים יתן לו חצי כל הריוח וגם חצי השורים אחר תשלום הה' שנים והרועה מת לסוף ל"א חדשים וחצי והשורים הם ג' מאות ונ' נרצה לדעת כמה יקח הרועה שאלו לא מת עד סוף ה' שנים לקח חצי השורים
|
|
|
ראוי לעשות ככה והוא שתשיב ה' שנים חדשים ויהיו ס' ותאמר אם ס' שוים ש"נ לא וחצי כמה שוים ומה שיבא הוא קפ"ג ומה חלקים מס'
|
|
|
רב) שאלה אדם רוצה לעשות מלחמה ועשה ב' מאות אנשים רוכבים על סוסים וד' מאות רגליים אמר להם כל מה שיבוזו יהיה שלהם והתנו ביניהם כי רוכב הסוס יקח כל א' ה' מנינים והרגליים ג' מנינים והשלל הוא אלף מנינים נרצה לדעת כמה יקחו רוכבי על סוסים וכמה יקחו הרוגליים
|
|
|
ראוי לעשות ככה והוא שתכפול המנינים הראוים לקחת הרגליים על ד' מאות מצד כי הם ד' מאות תכפלם על ג' ויצא לך י"ב מאות עוד כפול ה' שהוא מה שראוי לקחת רוכבי הסוסים על ב' מאות מצד שהם ב' מאות ויצא אלף אח"כ חבר אלף עם י"ב מאות ויהיו כ"ב מאות אח"כ קח א' מהמספרים רצוני או אלף או י"ב מאות ותכפלם על אלף שהוא הכזה ותחלקם על ב' אלפים וב' מאות ויצא לך חלק כל א וא' אח"כ כפול אלף על אלף וחלקם על כ"ב מאות יצא לך תנ"ד וו' חלקים מי"א אח"כ כפול י"ב מאות על אלף וחלקם על כ"ב מאות ויצא לך תקמ"ה וה' חלקים מי"א והוא חלק הרגליים
|
|
|
רג) שאלה יש כאן ג' טוחנות הא' טוחנת י"ב מדות ביום והב' ט' והג' ו' ובא א' עם ק' ורוצה לטחנם מהרה ורוצה שיחלקו המדה לג' טוחנות ויהיה עשוי הכל בבת אחת כמה מדות נשים בכל א' וא'
|
|
|
הנה ראוי לחבר מספר כלם רצוני י"ב וט' וו' יעלה כ"ז אח"כ כפול ק' וחלקם על כ"ז יצא לך מ"ד וכ"ב חלקים מכ"ז והוא המדות שנתן לו עוד נכפול ט' על ק' וחלק על כ"ז ויצא לג וט' חלקים מכ"ז עוד כפול ו' על ק וחלק על כ"ז ויצא כב וו' חלקים מכ"ז ובין הכל מ'
|
|
|
ולדעת כמה זמן תעמוד החטה על הטוחנת תאמר אלו י"ב מדות נעשות י"ב שעות בכמה שעות אעשה מ"ד מדות וי"ב חלקים מכ"ז וזה נודע
|
|
|
רד) שאלה אשה נושאת ביצות והפילם אדם ואמרה שיפרעם ואמרה כשמניתים בב נשאר א גג' א' דד' א' הה' א' וו' א' זז' שוה כמה היו
|
|
|
בקש מספר אשר לו חצי ושליש ורביעית וחומש ושתות ותמצא ס' תוסיף א' בעבור התוספת על בב' גג' וכו' יהיו ס"א אח"כ כפול ה' על ס"א ויעלה ש' תוסיף בו א' ויהיו ש"א
|
|
|
שאלה אדם נושא ביצות ואחר הפילם ואמר שיפרעם ואמר כשמניתים א' בב' נשאר א גג' ב' הה' ד' וו' ה' זז' שוה כמה היו
|
|
|
בקש מספר לו שליש ורביע וחומש ושתות והוא ס' תסיר א' נשאר נ"ט תוסיף ס' ויהיו קי"ט והוא המבוקש
|
|
|
רה) שאלה אדם יש לו ליט' מב' מיני כספים שא' מהם יש לליט' ז' אוק' מכסף טוב ובאחר אוק' ורוצה להתיך מהב' כספים ולהשיבם שיכיל כל ליט' ט' אוק' מכסף טוב נשאל כמה יקח מכל א' וא'
|
|
|
ראה איזה הפרש מט' לז' תמצא ב' ושימם על י"א ואח"כ ראה ההפרש מט' לי"א והוא ב' ושימם על ז' הנה ראוי לקחת מזה כמו מזה
|
|
|
רז) שאלה לאדם מג' מיני כסף בא' ה' אוק' לליט' מטוב ובאחר ז' ובאחר י"א ורוצה לקחת משלשתן באופן שיכיל לליט' ח' אוק'
|
|
|
כך תעשה ראה איזה הפרש יש בין ז' לח' תמצא א' ושים אותו על ה' עוד תאמר איזה הפרש מה' לח' תמצא ג' ושימם על ז' אח"כ כפול א' על ה' ויצא ה' עוד כפול ז' על ג' ויצא כ"א חברם אל ה' ויהיו כ"ו אח"כ קח הליט' שהם א' וג' יהיו ד' וכפלם על ח' ויהיו ל"ב הוצא מל"ב כ"ו נשארו ו' ושמרם אח"כ חלק אלו הו' בין ההפרש שיש בין ח' לי"א תמצא ג' חלק ו' על ג' יצא ב' הנה א"כ ראוי לקחת א ליט' מכסף ה' וג' מכסף ז' וב' מכסף י"א
|
|
|
ואם תרצה לבחון אותו חבר כל הליט' וקח שוויים מהג' כספים ממה שמכיל ויעלו מ"ח עוד כפול סך הליט' שהם ו' על ח' ויעלו מ"ח והם שוים
|
|
|
רח) שאלה אם יש לך ג' ליט' מכסף שמכיל ז' אוק' מטוב בכל ליט' ותרצה להשיב באופן שיכיל ט' אוק' כל ליט'
|
|
|
ראוי לחלק ז' על ט' יצא ז' תשיעיות אח"כ כפול הז' תשיעיות על ג' ויצא כ"א וחלקם על ט' יצא ב' ושליש
|
|
|
ותבחון אותו ותמצאנו נכון כי הג' ליט' מז' שוות כ"א והב' ושליש מט' שוות כ"א
|
|
|
רט) שאלה לאדם ו' ליט' מכסף שמכיל ח' מטוב ונרצה להשיבם באופן שלא יכילו כי אם ד אוק' מטוב לליט
|
|
|
חלק ח' על ד' יצא ב' כפול ב' על ו' ויצאו י"ב הנה הו' ליט' המכילות ח' יעשו י"ב מכילות ד'
|
| 210) How Many Problem - Group of People
|
|
A man passed by a group of people. He said to them: hello one hundred people. They answered him: we are not one hundred people, but all of us, and other like us, and half of us, and a quarter of us plus one will make 100
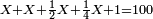
|
רי) שאלה אדם עבר על אנשים אמר שלום עליכם מאה איש אמרו אין אנחנו ק' רק אנו ואחרים כמונו ומחציתנו ורביעתנו ועמך נהיה מאה שאל שואל כמה היו אל
|
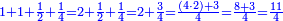
|
הנה נקח למספרם א' וא' כמוהו והם ב' וחצי ורביע הם ג' רבעיו' ונעשה מב' ג' רביעיות ויהיו י"א
|
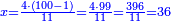
|
ויען כי אמרנו עמו היו מאה מספרם צ"ט כפלם על ד' וחלק על י"א ויצאו ל"ו
|
| 211) Buy and Sell Problem
|
|
A man bought 100 liṭra for 100 zehuvim. He sold 50 [of them] at 1¼ liṭra for one zahuv, and the other 50 at ¾ liṭra for one zahuv. We want to know: did he earn or lose?
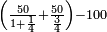
|
ריא) שאלה אדם קנה בק' זהובים ק' ליטרי' ומכר החמישים ראשנים ליט' ורביעית ליט' בזהוב והנ' אחרונים ג' רביעיות בזהוב נשאל אם הרויח או הפסיד
|
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left(\frac{50}{1+\frac{1}{4}}+\frac{50}{1-\frac{1}{4}}\right)-100&\scriptstyle=\left(\frac{4\sdot50}{5}+\frac{4\sdot50}{3}\right)-100\\&\scriptstyle=\left(\frac{200}{5}+\frac{200}{3}\right)-100\\&\scriptstyle=\left[40+\left(66+\frac{2}{3}\right)\right]-100\\&\scriptstyle=6+\frac{2}{3}\\\end{align}}}](/mediawiki/images/math/f/f/e/ffec10b7402d6c289bc7ae654748b4d6.png)
|
נשיב הנ' ראשנים ר' נחלקם על ה' בעבור ה' רביעיות שנתן בפשוט יעלה מ' גם נשיב הנ' אחרונים מאתים נחלקם על ג' ויעלו ס"ו וב' שלישיות חברם אל מ' ויהיו ק"ו וב' שלישיות הנה הרויח ו' וב' שלישיות
|
|
|
ריב) שאלה אדם קנה ג' חמישיות ליט' בפשוט ומכר ד' שביעיות בפשוט והרויח פשוט כמה ממונו
|
|
|
בקש המורה שהוא ל"ה שהוא כפל ז' על ה' והנה ג' חמישיות כ"א וד' שביעיות כ' והממון היה כ' ושב כ"א והרויח פשוט ומהכ' דינרין קנה י"ב ליט'
|
|
|
ריג) שאלה אדם קנה ד' שביעיות בפשוט ומכר ה' תשיעיות בפשוט והרויח פשוט
|
|
|
הדרך נודע
|
| 214) Purchase Problem – Moneychanger
|
|
The moneychanger has three [kinds of] coins. One zahuv is worth three dinar of the first [kind of] coins; or four of the second [kind]; or six of the third [kind]. A man came and asked the moneychanger to give him from the three [kinds of] coins for one zahuv equally, so that the amount of the expensive will be equal to the amount of the inexpensive
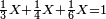
|
ריד) שאלה יש אצל המחליף מג' מטבעים שוה בזהוב מהא' ג' בזהוב ומהאחרת ד' ומהאחרת ו' ובא אדם אמר למחליף יחליף לו זהוב יתן לו מג' המטבעי' מספר שוה
|
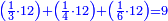
|
בקש מספר לו שליש ורביע ושישית תמצא י"ב וכל החלקים הם ט' והוא דינר
|
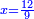
|
ונבקש מה ערך י"ב אל ט' והוא א ושליש וככה יקח מכל מטבע
|
|
|
רטו) שאלה ראובן שכר שמעון שיחפור לו בקרקעו ז' באורך ובאורך (ו' ברוחב) וה' בעומק ויתן לו י"א והוא חפר ו' באורך וה' בעומק וד' ברוחב כמה ראוי שיקח
|
|
|
זאת השאלה הוא מערכים כפולים נקר' ריגולא דיטרי דנפיצה ויצא לך ו' וב' שביעיות וכך ראוי שיקח
|
| 216) Motion Problem – Pursuit
|
|
A man sent a messenger to walk 29 miles a day. After 10 days of walking, he sent another messenger to walk after him 37 miles a day. When will he catch up with him?
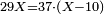
|
ריו) שאלה איש שלח רץ ילך בכל יום כ"ט מילין ובסוף י' ימים שלח אחר ילך בכל יום ל"ז מתי ישיגנו
|
Rule of Four: 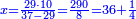
|
נכפול המילין שהלך הראשון בי' ימים והם רץ נחלקם על היתרון שהוא בין ב' המהלכים שהוא ח' ויצא לך ל"ו ורביעית יום
|
| 217) Boiling Problem
|
|
A man had 10 measures of must and he wanted to boil them so that only one third will remain. He started to cook [them] until eight measures remained of them. Then two measures overflow. Now he wants to boil [the remainder] until it will be reduced [as planned for] the original [amount] of must
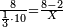
|
ריז) שאלה אדם היו לו י' מדות מתירוש ורצה לבשלם עד לא ישאר כי אם שליש והחל לבשל עד שנשארו ח' ונשפכו ב' ורוצה לבשלם כמשפט הראשון
|
Rule of Four: 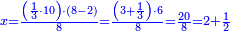
|
יש לך ג' מספרים ידועים א כמה שליש עשרה והוא ג' ושליש וידוע כי ח' היו המדות שנתבשלו וידוע כי ו' נשארו ונעשה כך נכפול ו' על ג' וחלק על ב' ויצא ב' וחצי
|
|
|
אדם יש לו ט' מדות ורצה לבשלם עד ישובו לשליש ונתבשל עד נשארו ו' ריח מדות ונשפך ד' נשארו ב' כמה ראוי לבשל
|
|
|
כפול ב על ג' יעלו ו' חלקם על ו' יעלה א' והוא הנדרש
|
|
|
ריט) שאלה אילן שביעיתו במים ותשיעיתו בעפר ולמעלה ה' כמה ארכו
|
|
|
המורה הוא ס"ג נחסר ממנו י"ו שהוא השביעית והתשיעית ישארו מ"ז ונעשה הערך כפלנו ח' על ס"ג עלו תק"ד חלקנום על מ"ז עלו י' שלמים גם ל"ד חלקים ממ"ז ושביעית זה המספר א' שלם גם כ"ה חלקים ממ"ז ותשיעיתו א שלם גם ט' חלקים חברנו כל החלקים והם ל"ד והשלמים ב' חסרנו זה מן עשרה נשארו ח'
|
|
|
רכ) שאלה הצבנו סולם אל קיר עשר אמות גבהותו וככה גובה הסולם הורדנו ראש הסולם מלמעלה ב' אמות נרצה לדעת כמה רחוק ראש הסולם מיסוד הקיר
|
|
|
אתן לך כלל בדבר זה לעולם יהיה מרובע הנשאר מראש הסולם אל היסוד עם מרובע מרחק הרגל מן היסוד שוים למרובע הסולם והנה חסרנו ב' אמות שירד הראש מתחלת הקיר נשארו ח' ויהיה מרובעו ס"ד נחסרם מק' שהוא מרובע הסולם ישארו ל"ו ושרשו ו' וככה מרחק הסולם למטה מן היסוד
|
|
|
רכא) שאלה באר ארבע עשרה ורחבו ח' גבהו ה' יכיל אלף ליט' מים ונשפכו כמה חסרו המים
ערוך המאה על הגובה והעולה חלק על אלף והוא חצי א' וחצי אמה [....]
|
|
|
רכב) שאלה ראובן שכר שמעון בי' כספים לל' יום ונתנ[.]לו ושמעון חלה והשכיר אחר במקומו י"ב כספים ביום ועשה השכיר ימים ידועים והאחר כמו כן ונתן לו עשרה כספים
|
|
|
ידוע כי לל' יום היה שכרו י"ב כספים ונאמר אלו י"ב שוים ל' י' כמה שוים כפול ל על י' ועלה רק חלקם על י"ב יעלו כ"ה
|
|
|
רכג) שאלה אם הלויתי לך ק"נ מנינים בעד ו' חדשים ואח"כ אני מצטרך ואמר לי הלוה לי מעות בעד ב חדשים שיהיה שוה לק"נ שהלויתי לך בעד ו' חדשים
|
|
|
ראוי לכפול ו' על ק"נ ויעלו ט' מאות חלקם על ב' ויצא ד' מאות ונ' וכן ילוה לו בעד ב' חדשים
|
|
|
רכד) שאלה אצל המחליף מד' מטבעים הא' ו' שוות זהוב והב' ד' והאחר ג' ואחר ב' ורוצה שיתן לו מכל א' רביעית זהוב כמה יקח מכל אחת
|
|
|
ראוי לחלק המטבע הא' שהוא ו' על ד' ויצא א וחצי וכן יקח ממנה עוד חלק ד' על ד' ויצא א וכן יקח עוד חלק על ג' ויצא ג' רביעיות עוד חלק ב' על ד' ויצא חצי וכן יקח ממנה
|
|
|
רכה) שאלה אדם עזב ממון לבניו בלתי נודע ואמר לראשון אתה תקח מממוני ז' דינרין ועשור הנשאר ואמ' לאחר ואתה קח לך י"ד מהנשאר והעשור ואמ' לאחר אתה תקח כ"א ועשור הנשאר וכן כלם לעולם מוסיף לו ז' ואחר העשות זה נמצא לכלם חלק שוה נרצה לדעת כמה בנים היו לו וכמה חלק כל א' וא' וכמה בנים היו לו
|
|
|
ראוי לקחת המספר השוה והוא העשור כי לכלם אמר עשור חסר א' ישארו ט' כפול ט' על זה שהוא חלק הראשון זולת העשור יעלה ס"ג א"כ הבנים היו ט' וממונו היה ס"ג ועתה כפול ס"ג על ט' ויעלה תקס"ז והוא כל הממון ודוק ותשכח
|
|
|
רכו) שאלה יש כאן ג' שרוצים לחלק ק"כ מנינים ויהי ריב וה[.]לו ממונם וכל א' וא' לקח מה שיכול לקחת ויתקוטטו ביניהם בא אדם ואמ' אל תרגזו ואמר לא' תן לי חצי ממונך ולאחר שליש ולאחר רביעית וחלק זה הממון לג' חלקים שווים ונמצא ביד כל אחד מ' מנינים נבקש לדעת כמה לקח כל א' וא'
|
|
|
בקש מספר לו חצי ושליש ורביע תמצא י"ב ותאמר י"ב מאיזה מספר חציו תמצא כ"ד אח"כ תאמר י"ב מאיזה מספר הוא ב' שלישיות בעבור שעכב לעצמו ב' שלישיות תמצא י"ח עוד תאמר י"ב מאיזה מספר ג' רביעיות תמצא י"ו קבץ הכל ויהיו נ"ח ושמרם אח"כ כפול המספר הראשון שהוא כ"ד על ק"כ והעולה חלק על נ"ח ויצא מ"ט ול"ח חלקים מנ"ח עוד כפול י"ח על ק"כ וחלק על נ"ח יצא לז וי"ד חלקים מנ"ח עוד כפול י"ו על ק"כ וחלק על נ"ח ויצא ל"ג וו' חלקים מנ"ח
|
|
|
ולבחון אותו קח חצי הראשון ושליש השני ורביעית הג' ועשה ג' חלקים שוים ותן לכל א חלק א' ויעלה מ' לכל א'
|
|
|
רכז) שאלה יש כאן ב' קנו ה' לחמים א קנה ב ב פשוטים ואחר ג ג פשוטים בא א ואמר אם תרצו שאוכל עמכם אפרע כלם שווים ואכלו ביחד ונתן לבעל הג' ד' ובעל הב' א' אשאל לדעת מה זה ועל מה זה
|
|
|
ראוי לחלק ה' לג' יעלה א וב' שלישיות וכך אכל כל א וא א"כ הראשון אכל כל לחמו פחות שליש לכן נתן לו א' והאחר אכל כל לחמו פחות ד' רביעיות לכן נתן לו ד'
|
|
|
רכח) שאלה אדם הולך לגן ללקוט שושנים ובבואו יש לו לעבור בג' פתחים ראשון יש לו לתת חצים עם תוספת ג' ובב' יש לתת השליש מהנשאר עם תוספת ב' ובג' יש לתת רביעית עם תוספת א' ונשארו לו ב' כמה לקט
|
|
|
שים על ב' א' בעבור א מתוספת ויהיו ג' וידוע כי ג' הם ג' רביעיות והשלם הוא ד' עוד תוסיף על ד' ב' נשארו ו' וידוע הוא כי ו' ב' שלישיות והשלם ט' ושים עליו ג' והנם י"ב והוא חצי המספר ויהיו כ"ד וכך לקט
|
|
|
רכט) שאלה אדם מלוה לחבירו אלף מנינים בעד שנה ומחוייב לתת לו על כל ק' כ"ה ובסוף ו' בעל הממון נצטרך למעות ואמר למחוייב לו תן לי ק' מנינים וכן עשה ובסוף ד' חדשים נתן לו ד' מאות עוד לסוף ו' נתן לו ב' מאות נרצה לדעת כמה ראוי שיקבל בעל הממון לסוף השנה וכמה הוא הרבית
|
|
|
כך תעשה תאמר אם ק' מרויחים כ"ה אלף כמה ירויחו תמצא רכ"ה אח"כ תאמר הפרעון הראשון שהוא ק' בסוף ו' כפול ק' על ו' ויהיו ת"ר ותאמר אם ק' מנינים בי"ב מרויחים כ"ה ק' בו' חדשים מה ירויחו תמצא י"ב וחצי עוד קח הפרעון הב' שהוא ת' לסוף ד' וכפול על החדשים ויעלו אלף ות"ר ותאמר אם ק' בי"ב מרויחים כ"ה ת' בד' יתנו לך ל"ג ושליש עוד קח הפרעון הג' שהוא ד' בתוך ג' ותאמר אם ק בי"ב יתנו כ"ה ב' מאות בג' מה יתנו ויצא י"ב וחצי אח"כ חבר (י"ב) וחצי עם ל"ג ושליש ועם י"ב וחצי ותוציאם מר"נ וישאר קמ"א (קצ"א ?) וב' שלישיות והוא הרבית שראוי שיקבל בסוף השנה ויש לו לקבל מהקרן ג' מאות ויעלה עם הקרן והריוח תמ"א וב' שלישיות
|
|
|
רל) שאלה אדם קנה ה' חביות שמן וי' חביות יין ובין הכל שוה ק' מנינים אח"כ קנה ט' חביות שמן וב' חביות יין ק' מנינים ובאותו ערך שקנה בראשנה קנה בשניה אבקש לדעת כמה קנה השמן וכמה קנה היין
|
|
|
כך תעשה קח איזה מספר שתרצה ושימהו ערך השמן או היין ונשים ערך השמן ח' מנינים הנה הה' שוות מ' מנינים ונשארו ס' א"כ ערך החבית ישווה ו' מנינים ונשוב אל השני ונאמר שהט' חביות שוות ע"ב והב' שוות י"ב ויעלה פ"ד ויחסר עד ק' י"ו ותאמר בעד הערך שהוא ח' יחסר י"ו אח"כ בקש מספר אחר ונאמר כי חבית השמן שוה ט' והה' שוות מ"ה וחבית היין ה' וחצי ויהיו ק' שוב אל הב' והט' חביות שוות פ"א והב' יין י"א ויהיו צ"ב ויחסר ח' עד ק' הוצא ח' מי"ו נשארו ח' אח"כ כפול ט' שהוא הערך על י"ו שהוא השיור מהערך הא' ויהיו קמ"ד אח"כ כפול ח' שהוא הערך הראשון על ח' יעלה ס"ד הוצא ס"ד מקנ"ד נשארו פ' חלקם על ח' ויצא י' וכן קנה
|
|
|
רלא) שאלה בכאן כלב וארנבת והארנבת רחוקה מהכלב ק' פסיעות וכל פסיעה מהכלב שוה ה' מהארנבת וכך יפסיע הא' כמו זה אתאב לדעת בכמה פסיעות ישיגנו
|
|
|
הדרך ראוי לחלק ק' על היתרון שהוא מא' עד ה' שהוא ד' ויעלה כ"ה והוא המבוקש
|
|
|
רלב) שאלה תעשה לי מל' ד' חלקים שיהיה יחס הד' אל הג' כג' לב' וכב' לא'
|
|
|
נניח שהא' א' והב' ב' והג' ד' והד' ח' ובין כלם ט"ו לכן כפול א' על (ל) וחלק על ט"ו ויצא ב' והוא הראשון עוד כפול ב' על ל וחלק על ט"ו ויצא ד' והוא הב' וכן מהג' ויצא ח' וכן מהד' ויצא י"ו וכלם מתיחסים
|
|
|
רלג) שאלה אדם שואל לחבירו כמה שעות הקישו השיב הב' שלישיות מהמוקשות שוות לג' שרביעיות לאותם שראוי להקיש נשאל כמה שעות הקישו
|
|
|
כבר ידעת כי שעות היום הם כ"ד ונניח כי הקישו ג' וידוע כי ב' שלישיותיו הם ב' ונבקש מספר אשר ב' יהיו ג' רביעיותיו ונמצא ב' וב' שלישיות ובין הכל עולה ה' וב' שלישיות לכן נכפול ג' על כ"ד וחלק על ה' וב' שלישיות ויצא י"ב וי"ב חלקים מי"ז והם השעות שהקישו והנשאר עד כ"ד שהם י"א וה' חלקים מי"ז
|
|
|
ראוי להקיש ולבחון אותו קח ב' שלישיות מי"ב ומי"ב חלקים מי"ז ויעלה ח' וח' חלקים מי"ז עוד קח ג' רביעיות י"א וה' חלקים מי"ז ויעלה גכ ח' וח' חלקים מי"ז
|
|
|
רלד) שאלה אדם נותן ביצות לז' בניו למכור ונותן לא' מחצית השני ר"ל שאם יתן א לראשון יתן ב' לשני וג' לג' וד' לד' וה' לה' וו' לו' וז' לז' ובאופן שימכור הא ימכרו כלם וכל כך ממון ישא הא' כמו האחר ארצה לדעת כמה ממון נתן לכל א' וא' ובאיזה אופן מכרו
|
|
|
הדרך בזה שתכפול ז' על ב' הנם י"ד תוסיף א' ויהיו ט"ו והוא סך הביצות מהראשון שים בו ט"ו ויהיו ל' והוא חלק הב' שים בו ט"ו והוא מ"ה והוא חלק הג' שים בו ט"ו ויהיו ס' והוא חלק הד' והאחר ע"ה והאחר צ' והאחר ק"ה
|
|
|
ולדעת איך מכרו תחסר החלק היותר גדול מט"ו שהוא ח' נשאר ז' וכן נתן בפשוט ר"ל ח' והז' הנשארים מכר ב' פשוטים כל א' וא' וכך מעות נשא הא' כמו האחר
|
|
|
רלה) שאלה ואלו אמר כי הבנים ג' ונתן לכל א מספר מונח ולב' אותו המספר מונח וג' פעמים כמוהו ולג' המספר המונח וו' פעמים מספר מונח ובאופן שמכר הא' ימכור האחר כמה לכל א ובאיזה אופן מכרו
|
|
|
ראוי לכפול מה שמוסיף הב' על הא' על סך הבנים וידוע כי הבנים ג' והשני מוסיף במספר עם הראשון ג' ועם המספר המונח הם ד' כפול ג' על ד' ויהיו י"ב תוסיף בו א ויהיו י"ג תחסר מי"ג סכום הבנים וישאר י' כי לעולם ראוי לחסר מהמקובץ סכום הבנים הנה י' נתן בפשוט
|
|
|
ואם תרצה לדעת באיזה ערך מכר הג' שנשארו כבר ידעת כי השני מוסיף על הראשון ד' פעמים כמוהו ועם המספר המונח הנה א"כ כל א מהג' מכר ד' פשוטים
|
|
|
ואם היה מוסיף השני על הראשון ה פעמים כמוהו היה מוכר כל א' ה' פשוטי' ואם ו' ו'
|
|
|
רלו) שאלה אדם רוצה לעשות סרבל מבגד שרחבו ה' זרתות ונכנס בו י"ד זרתות ורוצה לעשות סרבל אחר מבגד שרחבו ד' זרתות כמה זרתות ישים בו
|
|
|
תוציא ד' מה' נשאר א' תחלק י"ד על ד' ויהיו ג' וחצי תוסיפם על י"ד ויהיו י"ז וחצי הנה א"כ ראוי לקחת מבגד אחד י"ז זרתות וחצי ולבחון אותו כפול י"ד על ה' ויהיו ע' עוד כפול ד' על י"ז וחצי ויהיו ע'
|
|
|
רלז) שאלה איש מחוייב לחבירו ד' מאות מנינים וכל מגן שוה ל"ג גרושי וי"ב גרושי שוים פרח א' ובעל הממון שואל ד' מאות מניניו והשיב כי אין לו כי אם פרחים אתאב לדעת כמה פרחים יקבל
|
|
|
הנה הדרך שתכפול ד' מאות על ל"ג ויהיו י"ג אלפים וב' מאות וחלקם על י"ב ויצא לך אלף ומאה והוא סך הפרחים שראוי שיקבל
|
|
|
רלח) שאלה מספר אנשים הולכים בדרך וימצאו כיס א' עם ק' מנינים הא שואל ד' עם שתות הנשאר והאחר ח' עם שתות הנשאר והאחר י"ב עם שישית וכן עד תומם נרצה לדעת כמה הם הבנים באופן שיגיע לכל א מספר שוה
|
|
|
ראוי לחלק ק על ד' ויצא כ"ה וקח שרשם והם ה' כפלם על ד' ויצא כ' והוא המגיע לכל א' וא'
|
|
|
ולדעת סכום הבנים חלק ק' על כ' ויצא לך ה'
|
|
|
דרך אחרת חסר מהסך השוה לכלם שהוא השתות א וישאר ה' והוא סכום הבנים
|
|
|
ולדעת ממון כל א' כפול ד' על ה' שהוא מה שיקח הראשון זולת השתות ויעלה כ' והוא הממון
|
|
|
רלט) שאלה ב' בני אדם כל א מצא כיס אמ' הראשון אם תתן לי שליש ממון כיסך אני אתן לך רביעית ממון כיסי וכן עשו ונמצא לכל א י"ב נשאל כמה בכל כיס
|
|
|
נניח מנותן שליש ממון כיסו היה לו ט"ו חסר ה' שהוא שלישיתו וישארו י' א"כ יצטרך בכיס השני יהיה ח' באופן כשיתן מח' רביעיתם שהם ב' ישלימו י"ב עם י' שיש לחבירו וידוע כי קבל ה' עם ו' הנם י"א ויחסר עד י"ב א' ותאמר בעד ט"ו חסר א' עוד בקש מספר אחר נניח כי בכיס נותן שליש היה י"ו חסר שלישיתם שהוא ה' ושליש ישארו י' וב' שלישיות ויחסר עד י"ב א' ושליש א"כ ממון השני הוא ה ושליש חסר הרביעית שהוא א' ושליש ישארו ד' שלמים והוא קבל ה' (ושליש) א"כ יש לו ט' ושליש ויחסר עד י"ב ב' וב' שלישיות ותאמר בעד י"ו ששמנו חסר ב' וב' שלישיות א"כ הוצא א שהוא חסרון הערך הא' מב' וב' שלישיות הנשאר א וב' שלישיות אח"כ כפול י"ו שהוא הערך הב' על א שהוא חסרון הערך הא' ויהיו י"ו עוד כפול ט"ו שהוא הערך הא' על ב' וב' שלישיות שהוא חסרון הערך הב' ויעלו מ' הוצא י"ו ממ' נשאר כ"ד חלק כ"ד על א וב' שלישיות יצא י"ד וב' חמישיות והוא מה שבכיס מנותן השליש וט' וג' חמישיות יש בכיס נותן רביעית ותבחון אותו כי הוא צודק
|
|
|
רמ) שאלה בכאן מקל זקוף וברגל המקל התחתון יש בו נמלה ורוצה לעלות והולכת ד' אמות וחומש המקל בשעה אחת ובראש המקל העליון נמלה יורדת והנה תרד בשעה אחת ו' אמות ורביעית המקל ואורך המקל ק' אמות אשאל מתי ישיגו זה את זה
חלק ק' על ה' ויצא עשרים תוסיף עליהם ד' ויהיו ק"ד אח"כ תחלק ק' על ד' ויצא כ"ד תוסיף בם ו' ויהיו ל תחבר ל' עם כ"ד ויהיו נ"ד חלק ק' על נ"ד ויצא א וכ"ג חלקים מכ"ז והוא הזמן שישיגו זה את זה
|
|
|
ותוכל לבחון אותו ואמור אם א שוה ל א וכ"ג חלקים מכ"ז כמה ישוה ויצא לך נ"ה וט חלקים מכ"ז והוא מהלך מהולך ו' אמות ורביעית המקל עו' תאמ' אם א שוה כ"ד א' (ו)כ"ג חלקי' מכ"ז כמה שוים ויצא לך מ"ד וי"ב חלקים מכ"ז ובין הכל ק'
|
|
|
רמא) שאלה לאדם יש לו ד' בנים ואמ' שהא' יקח מממונו החומש ועשרים מנינים יותר והשני החומש מהנשאר ומ' יותר והג' חומש הנשאר וס' יותר והד' חומש הנשאר ופ' יותר נשאל כמה ממון אביהם וכמה חלק כל א וא'
|
|
|
תקח תוספת האחרון שהוא פ' ותכפלם על ה' מצד כי כל א' שואל החומש ויהיו ד' מאות והבנים ד' א"כ הגיע לכל א' ק' מנינים
|
|
|
ותוכל לבחון אותו וכן לו ב' נשארו פ' חומש הנשאר ד' מאות וחלקו ק' וכן לכל א' וא'
|
Partnership Problems
|
|
|
|
רסב) שאלה ה' בני אדם עשו ספינה והתנו ביניהם כי ממה שירויחו הא' יקח עבור כל מאה ג' (ב') והאחר ב' (ג') והאחר ד' והאחר ה' והאחר ו' ופזרו לתקן האניה ל' כמה יפרע כל א' לפי יחס הריוח המגיע לכל א' וא'
|
|
|
תחבר כל ממונם ויהיו כ' אח"כ תכפול הראשון על ל' ותחלק לכ' ויגיע לחלקו לפרוע ג' וכן תעשה מהב' ויפרע ד' וחצי והג' ו' והד' ז' וחצי והה' ט'
|
|
|
רסג) שאלה ג' בני אדם עושים שותפות הא' שם ג' מנינים ועמדו בשותפות ב' חדשים והאחר שם ד' מנינים ועומדו בשותפות ה' חדשים והאחר שם ב' מנינים ועמד בשותפות ט' חדשים והרויחו כ"ה מנינים כמה יגיע לכל א'
|
|
|
ראוי לכפול ממון כל א' על החדשים והנה נכפול ב' על ג' ויהיו ו' והוא הראשון כן תעשה מהב' ויהיו כ' וכן מהג' ויהיו י"ח ובין הכל מ"ד אח"כ כפול ו' על כ"ה והעולה חלק על מ"ד ויצא ג' וי"ח חלקים ממ"ד והוא חלק הראשון כן תעשה מהב' ויגיע לו י"א וי"ו חלקים (מ)מ"ד וכן תעשה מהג' ויצא י' וי' חלקים ממ"ד והוא חלק הג'
|
|
|
רסד) שאלה ג' עושים שותפות ושמו בין שלשתן כ' מנינים והרויחו ל' ולראשון מגיע מהריוח ד' מנינים ולשני ו' כמה יגיע לג' וכמה היה ממון כל א' וא' הנה ראוי לחבר ד' עם ו' ויהיו י' תחסרם מל' וישארו כ' והוא החלק מה שמגיע לחלקו ריוח הג' ולדעת כמה שם כל א' וא'
|
|
|
תעשה כן תאמ' אם כל הל' מנינים שהוא ריוח שלשתן נתן לי כ' שהוא ממון שלשתן מה יתן לי ד' שהוא ריוח הראשון כפול ד' על כ' וחלק על ל' ויצא ב' וב' שלישיות והוא מה ששם הא' וממון הב' היה ד' וממון הג' היה י"ג ושליש וחברם ויהיו כ' והוא סך הממון ששמו בין שלשתן
|
|
|
רסה) שאלה ג' עושים שותפות הא' שם קי"ז מנינים והב' שם פ"ג והג' לא ידעתי כמה והרויחו שי"ט וחלק הג' הוא קכ"ד מניני' אשאל כמה שם בשותפות
|
|
|
הנה יש לך להוציא ריוח השלישי מסך כל הריוח וישארו עדין קצ"ה א"כ בין הב' לא הרויחו כי אם קצ"ה מנינים ועתה תחבר מה ששם הא עם מה ששם הב' ויהיו ר' אח"כ תאמר אם כדי להרויח קצ"ה מנינים הוצרך להיות מאתים כמה יצטרך להיות הקרן כדי להרויח קכ"ד כפול קכ"ד על מאתים והעולה תחלק על קצ"ה ויצא לך קכ"ז שלמים ול"ה חלקים מקצ"ה והוא חלק השלישי
|
|
|
רסו) שאלה ג' עושים שותפות הראשון שם נ"ו מנינים ועמדו בשותפות ה' חדשים והשני שם סך נעלם ועמד בשותפות ח' חדשים והג' שם מרגלית אחת ועמדה בשותפות עשרה חדשים והרויחו בין כלם פ"ו מנינים והראשון מגיע לחלקו כ' ולשני י"ב ולג' נ"ד אשאל כמה שם השני וכמה סך מרגלית הג'
|
|
|
הנה ראוי לכפול ממון הראשון על החדשים ואחר כן תאמר אם כ' שהוא ריוח ממון הא' שבו ר"פ כמה ישובו י"ב שהוא ריוח הב' ויצא לך קס"ח אח"כ חלק קס"ח על החדשים שעמד ממון הראשון (השני) שהוא ח' ויצא כ"א וזהו ממון השני ולדעת כמה סך מרגלית הג' כפול נ"ד על ר"פ וחלק על כ' ויצא לך ז' מאות נ"ו וחלק זה על החדשים ויצא לך ע"ה וו' חלקים מי' והוא סך המרגלית
|
|
|
רסז) שאלה ג' עושים שותפות הא' שם קלה מטבעים והב' צ"ז והג' מ"ג והרויחו תשל"ד מטבעים ולג' רצ"ד מטבעים ארצה לדעת כמה שווה המגן
|
|
|
הוצא ריוח הג' שהוא רצ"ד מתשל"ד הנשאר ת"מ אח"כ תחבר ממון הא' והב' ויעלה ר"מ (רל"ב) א"כ אלו הב' הרויחו ת"מ מטבעים ולכן תאמר אם רצ"ד שבו מ"ג ת"מ כמה ישובו ויצא לך ס"ד וק"ד חלקים מרצ"ד א"כ רל"ב מטבעים שיש בין הא' והב' שוים ס"ד מטבעים ולדעת כמה מטבעים שוה כל מגן תאמ' אם ס"ד וק"ד חלקים מרצ"ד שוים רל"ב א' כמה שוה ויצא לך ג' וחלקים מה
|
- 268) Question: three formed a partnership.
- The first contributed 2 minyanim at the first of the month of Tishri [= first month in Heb. year] and withdrew one magen at the first of the month of Marheshvan [= 2nd month in Heb. year].
- The second contributed 3 minyanim at the first of the month of Kislev [= 3rd month in Heb. year] and withdrew one magen at the first of the month of Teveth [= 4th month in Heb. year].
- The third contributed 4 minyanim at the first of the month of Shevat [= 5th month in Heb. year] and withdrew 2 minyanim at the first of the month of Adar [= 6th month in Heb. year].
- What remained for each was kept [in the prartnership] until the [next] first of the month of Tishri
- They earned 20 minyanim.
- I ask how much did each earn?
|
רסח) שאלה ג עושים שותפות
הא' שם ב' מנינים ר"ח תשרי והוציא ר"ח מרחשון א' מגן
והאחר שם ג' מנינים ר"ח כסלו והוציא ר"ח טבת א' מגן
והאחר שם ד' מנינים ר"ח שבט והוציא ר"ח אדר ב' מנינים
ומה שנשאר לכל א' עמד ביחד עד ר"ח תשרי
והרויחו כ' מנינים
אשאל כמה הרויח כל א'
|
- the share of the first:
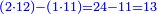
|
הנה ראשו' ראוי שתכפול ב' מנינים מהראשון ששם אותו בר"ח תשרי עד ר"ח תשרי הבא שהם י"ב חדשים ויהיו כ"ד א"כ כפול א' שהוציא מהשותפות בר"ח מרחשון והנה מר"ח מרחשון עד ר"ח תשרי י"א הוצא מכ"ד י"א הנשאר י"ג והוא עבור הא'
|
- the share of the second:
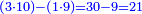
|
וכן כפול ממון הב' על החדשים ויהיו ל' כי החדשים הם י' והממון ג' גם כפול א' מגן שהוציא על החדשים שהם ט' הוצא מל' ט' וישארו כ"א
|
- the share of the third:
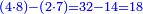
|
גם כפול ממון הג' על החדשים ויעלו ל"ב כי הממון ד' והחדשים ח' גם כפול מה שהוציא על החדשים ויהיו י"ד והוציאם מל"ב וישארו י"ח והוא ממון הג'
|
- Three formed partnership: one contributed 13, another 21, and another 18. They earned 20. How much should each take?
|
א"כ תאמ' ג' עושים שותפות הא' שם י"ג והאחר כ"א והאחר י"ח והרויחו כ' כמה יקח כל א וא' וכבר ידעת הדרך
|
- 269) Question: three formed a partnership.
- The first contributed 4 minyanim at the first of the month of Tishri [= first month in Heb. year] and added 2 minyanim at the first of the month of Marheshvan [= 2nd month in Heb. year].
- The second contributed 5 minyanim at the first of the month of Marheshvan and added 4 minyanim at the first of the month of Kislev [= 3rd month in Heb. year].
- The third contributed 3 minyanim at the first of the month of Teveth [= 4th month in Heb. year] and withdrew 2 minyanim at the first of the month of Adar [= 6th month in Heb. year].
- They stayed in the partnership from the first of the month of Tishri until the next first of the month of Tishri, i.e. a whole year, and earned 30 minyanim.
- How much should each take?
|
רסט)[18] שאלה ג' עושים שותפות
הא' שם ד' מנינים ר"ח תשרי והוסיף ר"ח מרחשון ב' מנינים
והב' שם ה' מנינים ר"ח מרחשון והוסיף ד' מנינים ר"ח כסלו
והאחר שם ג' מנינים ר"ח טבת והוציא ב' מנינים ר"ח אדר
ועמדו בשותפות מר"ח תשרי עד ר"ח תשרי הבא ר"ל שנה תמימה והרויחו ל' מנינים
כמה יקח כל א' וא'
|
- the share of the first:
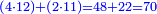
|
ראוי לכפול ממון הא' על החדשים והנה שם בראשנה ד' מנינים ועמדו י"ב חדשים וכפלם ויהיו מ"ח גם ראוי לכפול מה שהוסיף על החדשים והנה הוסיף בר"ח מרחשון ב' מנינים ולכן כפלם על החדשים שהם עד תשרי והנם י"א וכפלם על ב' ויהיו כ"ב הוסיפם על מ"ח ויהיו ע' והוא ממון הא'
|
- the share of the second:
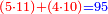
|
וכן תעשה מהב' ויהיו צ"ה
|
- the share of the third:
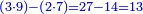
|
ומהג' כפול ממונו על החדשים ויהיו כ"ז כי ממונו ג' והחדשים ט' גם כפול מה שהוציא שהם ב' על החדשים שהם ז' ויהיו י"ד הוציאם מכ"ז וישארו י"ג והוא הג'
|
- Three formed partnership: one contributed 70, another 95, and another 13. They earned 30. How much should each take?
|
אח"כ תאמ' ג' עושים שותפות הא' שם ע' והאחר צ"ה והאחר י"ג והרויחו ל' כמה יקח כל א' וא' והדרך נודע
|
- 270) Question: three formed a partnership - one contributed 65 minyanim, another 53, and another 38.
- They agreed to keep the partnership for 5 years and after the 5 years to divide the fund and the profit into three equal parts, so that each will take one part.
- They kept the partnership only 3 years and earned 123 minyanim.
- I ask how much should each take?
|
רע)[19] שאלה ג' עושים שותפות הא' שם ס"ה מנינים והאחר נ"ג והאחר ל"ח
והסכימו לעשות שותפות ה' שנים ואחר הה' שנים רוצים לחלק הקרן עם הריוח לג' חלקים שוים וכל א' וא' יטול חלק אחד
והם לא עשו השותפות כי אם ג' שנים והרויחו קכ"ג מניני'
אשאל כמה יקח כל אחד ואחד
|
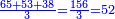
|
ראוי לעשות ככה כבר ידעת כי אלו עמדו בשותפות ולא הרויחו ולא הפסידו בה' שנים היה ראוי לחלק ממונם לג' חלקים שוים לכן נחבר ממון שלשתן ויהיו קנ"ו נחלקם על ג' ויצא לך נ"ב לכל אחד ואחד
|

|
ובזה האופן הראשון ששם בשותפות ס"ה יפסיד י"ג
|
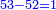
|
והב' שם נ"ג יפסיד א'
|

|
והאחר ששם ל"ח ירויח י"ד
|
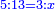
|
ועתה ראוי שתאמר בעבור הראשון אם ה' שנים היו ג כמה שהפסיד הראשון י"ג כמה יפסיד בעבור ג' שנים
|
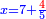
|
ויצא ז' וב' חמישיות
|
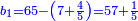
|
ותוציאם מס"ה שהיה ממונו ונשארו נ"ז וחומש
|
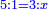
|
ובעבור הב' תאמר אם ה' הפסידו א' ג' כמה יפסיד
|
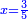
|
ויצא ג' חמישיות
|
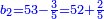
|
תוציאם מממון הב' וישאר נ"ב וב' חמישיות
|
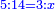
|
ובעבור הג' תאמר אם ה' הרויחו י"ד כמה ירויחו ג'
|
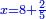
|
ויצא לך ח' וב' חמישיות
|
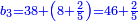
|
תוסיפם על ממון הג' ויצא מ"ו וב' חמישיות
|
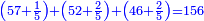
|
ועתה תחבר מה שנשאר לא' ולב' ולג' ויעלה קנ"ו ועליהם תחלק
|
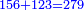
|
ולדעת כמה יגיע לכל אחד ואחד תחבר הריוח שעשו שהוא קכ"ג עם מה שנשאר עדין ויהיו רע"ט
|
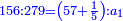
|
עתה תאמר אם קנ"ו שהוא הקרן שמשלשתן נתן לי רע"ט שהוא עם הקרן והריוח מה יתן לי נ"ז וחומש בעבור הראשון
|
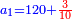
|
ויצא לך ק"ב דוקט' וחלקים והוא מה שראוי לקחת הראשון עם הקרן והריוח
|
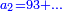
|
וכן תעשה מהב' ויצא לך צ"ג וחלקים בין הקרן והריוח
|

|
כן תעשה מהג' ויצא לך פ"א וחלקים בין הקרן והריוח
|
- 271) Question: two men formed a partnership - one contributed 80 minyanim and the other 20.
- They agreed that the owner of the 80 will take two thirds of the profit and the owner of the 20 [will take] a third of the profit.
- A third man came and said: if you want that I will join the partnership with you, I will contribute 120 minyanim and keep the ratio agreed by both of you.
- Eventually they earned 120 minyanim.
- I ask: how much will each take?
|
רעא)[20] שאלה שני בני אדם עושים שותפות הא' שם פ' מנינים והאחר כ'
והסכימו ביניהם שבעל הפ' יקח ב' שלישיות מן הריוח ובעל הכ' שליש הריוח
נזדמן שלישי ואמר אם תרצו כי אעשה שותפות עמכם אשים ק"כ מנינים ואעמוד כפי היחס המוסכם ביניכם
ולבסוף הרויחו ק"כ מנינים
אשאל כמה יקח כל א' וא'
|
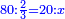
|
הדרך הוא כך כבר ידעת כי ממון הראשון היה פ' והיה ראוי לקחת ב' שלישיות הריוח ולכן תאמר אם פ' נתן לי ב' שלישיות כ' שהוא ממון השני כמה ישוו
|
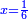
|
ויצא לך שישית אחד וזה תשים בעד השני
|
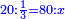
|
גם תאמר אם כ' נתן לי שליש שהיה ראוי לקחת מה יתן לי פ'
|
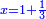
|
ויצא לך א' ושליש וזה תשים חלק הראשון
|
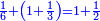
|
עתה תחבר א' ושליש עם שישית ויהיו א' וחצי
|

|
גם תחבר פ' עם כ' ויהיו ק'
|
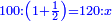
|
אח"כ תאמר אם ק' נתן לי א' וחצי מה יתן לי ק"כ
|
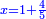
|
ויצא לך א' וד' חומשים וזה תשים עבור השלישי
|

|
אח"כ בקש מספר יהיה לו שלישית ושישית וחומש ויצא צ' אח"כ קח ד' שלישיות מצ' עבור הראשון ויצא לך ק"כ וזה תשים עבור הראשון
|
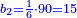
|
גם קח שישית צ' ויצא ט"ו וזה תשים עבור השני
|

|
גם תקח ט' חמישיות מצ' ויצא לך קס"ב וזה תשים חלק השלישי
|

|
אח"כ תחבר אלו הג' מספרים ויהיו רצ"ז ועליהם תחלק
|
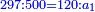
|
ולדעת כמה יגיע לכל אחד ואחד תאמר אם רצ"ז נתן לי ה' מאות שהוא סך הריוח מה יתן לי ק"כ עבור הראשון
|

|
ויצא לך ק"ב וחלקים
|
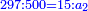
|
ובעבור השני תאמר אם רצ"ז נתן לי ה' מאות מה יתן לי ט"ו
|
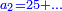
|
ויצא לך כ"ה וחלקים
|
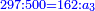
|
ובעבור הג' תאמר אם רצ"ז נתן לי ה' מאות מה יתן לי קס"ב
|

|
ויצא לך רע"ב וחלקים ודוק ותשכח
|
- 272) Question: three formed a partnership and earned a thousand golden coins - the first takes two thirds, the other takes four fifths, and the other takes five eighths.
- I ask: how much should each one have?
|
רעב)[21] שאלה ג' עושים שותפות והרויחו אלף זהובים הא' שואל ב' שלישיות והאחר שואל ד' חומשים והאחר שואל ה' שמיניות
אשאל כמה יגיע לכל אחד ואחד
|
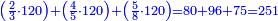
|
הדרך הוא כך ראוי לבקש מספר ימצאו בו שליש וחומש ושמינית ותמצא ק"כ
אח"כ קח ב' שלישיות עבור הראשון שהוא פ' וד' חמישיות שהוא צ"ו וה' שמיניות שהוא ע"ה וחברם ויעלו רנ"א
|
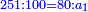
|
אח"כ תאמר אם רנ"א נתן לי אלף פ' מה יתן בעד השני
|
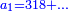
|
ויצא לך שי"ח וחלקים
|
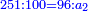
|
גם תאמר אם רנ"א נתן לי אלף מה יתן לי צ"ו
|

|
ויצא לך שפ"ב והוא חלק השני
|
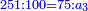
|
גם תאמר אם רנ"א נתן אלף מה יתן לי ע"ה
|
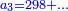
|
ויצא לך רצ"ח וחלקים והוא חלק הג'
|
- 273) Question: three formed a partnership.
- The first contributed 100 minyanim at the first of the month of Tishri [= first month in Heb. year].
- The second contributed 322 minyanim at the first of the month of Marheshvan [= 2nd month in Heb. year] and the share owed to him in the profit is the same as the first.
- The third contributed 22 minyanim at the first of the month of Kislev [= 3rd month in Heb. year] and the share owed to him in the profit is the same as the first.
- I wish to know how much did the second and the third contributed?
- They kept the partnership for a whole year and earned 600
|
רעג)[22] שאלה ג' עושים שותפות
הראשון שם ק' מנינים ר"ח תשרי
והאחר שם שכ"ב ממון ר"ח מרחשון שמגיע לחלקו מהריוח כמו לראשון
והשלישי שם כ"ב ממון ר"ח כסלו שמגיע לחלקו מהריוח כמו לראשון ג"כ
ארצה לדעת כמה שם הב' והג'
ועשו השותפות שנה תמימה והרויחו ו' מאות
|
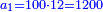
|
הדרך הוא כך כבר ידעת כי ממון הראשון היה ק' ועמדו בשותפות שנה תמימה ולכן כפול ק' על החדשים והם י"ב ויהיו י"ב מאות
|
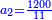
|
גם ידעת כי ממון השני עמד בשותפות י"א חדשים לכן חלק י"ב מאות על י"א והיוצא יהיה ממון השני
|
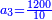
|
גם ידעת כי ממון השלישי עמד בשותפות י' חדשי' לכן תחלק י"ב מאות על י' ויצא לך ממון השלישי
|
Check: Three formed a partnership.
- The first contributed 100 minyanim at the first of the month of Tishri
- The second contributed as owed to the second at the first of the month of Marheshvan.
- The third contributed as owed to the third at the first of the month of Kislev.
- They earned 600.
- How much should each take?
|
ולבחון אותו אם הוא אמת תאמר ג' עושים שותפות
הא' שם ק' מנינים ר"ח תשרי
והאחר מה שמגיע לשני ר"ח מרחשון
והאחר מה שמגיע לג' ר"ח כסלו
והרויחו ו' מאות
כמה יקח כל א' וא'
|
- Answer: 200 each
|
ותמצא כי לכל א וא' יגיע ב' מאות
|
- 274) Question: three formed a partnership - one contributed 25, the other 17, and the [contribution] of the other is unknown, but the share owed to him is a third of what they earned.
- They earned 60 minyanim.
- We wish to know how much did the third contribute to the partnership?
|
רעד)[23] שאלה ג' עושים שותפות הא' שם כ"ה דוקטי והאחר י"ז והאחר לא ידענו אך מגיע לחלקו שליש ממה שהרויחו
והרויחו ס' מנינים
נרצה לדעת כמה שם השלישי בשותפות
|
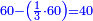
|
הדרך הוא כך הוצא השליש מס' שהוא חלק השלישי הנשאר מ'
|
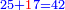
|
אח"כ תחבר כ"ה עם כ"ז ויהיו מ"ב א"כ מ"ב הרויחו מ'
|
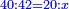
|
א"כ תאמר אם כדי להרויח מ' הוכרח להיות הקרן מ"ב כמה ראוי להיות הקרן כדי להרויח כ'
|
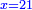
|
ויצא לך כ"א והוא מה ששם השלישי
|
Check: Three formed a partnership - the first contributed 25, the second [contributed] 17, the third [contributed] 21, and they earned 60
- How much should the third have?
|
ולבחון אותו תאמר ג' עושים שותפות הא' שם כ"ה והב' י"ז והג' כ"א והרויחו ס'
כמה יגיע לשלישי
|
- Answer: 20
|
ויצא לך כ' שלמים
|
- 275) Question: three formed a partnership for a whole year.
- The first contributed 14 minyanim at the first of the month of March.
- The second contributed some money at the first of the month of June, so that the share owed to him is a third of what owed to the first.
- The third contributed some money at the first of the month of August, so that the share owed to him is a quarter of what owed to the first.
- I wish to know how much did the second and the third contributed?
|
רעה)[24] שאלה ג' עושים שותפות עבור שנה תמימה
הראשון שם י"ד מנינים קליני ר"ח מרסו
והאחר שם ממון ר"ח יונייו כ"כ שמגיע לחלקו שליש מה שמגיע לראשון
והאחר שם ממון ר"ח אגוסטו שמגיע לחלקו כמו רביעית מה שמגיע לראשון
ארצה לדעת כמה שם הב' והג'
|
- the share of the first:

|
כבר ידעת כי ממון הראשון היו י"ד ועמדו י"ב חדשים לכן כפול י"ד על י"ב ויהיו קס"ח
|
- the share of the second:
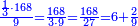
|
וכבר ידעת כי ממון הראשון עמדו בשותפות ט' חדשים תעשה מהם שלישיות ויהיו כ"ז אח"כ תחלק קסח על כ"ז ויצא ו' שלמים וב' תשיעיות והוא ממון השני
|
- the share of the third:
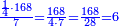
|
ולדעת מה ששם הג' הנה כבר ידעת כי ממונו עמד ז' חדשים תעשה מהם רביעיות מצד כי היה רביעית ריוח הראשון ויהיו כ"ח תחלק קס"ח על כ"ח ויצא ו' שלמים והוא מה ששם הג'
|
|
|
ולבחון אותו תאמר ג' עושים שותפות הא' שם י"ד ועמד בשותפות שנה והאחר שם ו' וב' תשיעיות ועמד בשותפות ט' חדשים והאחר שם ו' ועמד בשותפות ז' ונניח כי הרויחו ק' ותמצא כי מה שמגיע לשני אינו כי אם שליש ממה שמגיע לראשון ומה שמגיע לשלישי אינו כי אם רביעית ממה שמגיע לראשון
|
|
|
רעו) שאלה ג' עושים שותפות הא שואל עבור כל מאה ששם בשותפות י"ב מריוח והשני עבור כל ק' י"ח והג' עבור כל מאה ל' והרויחו אלף וח' מאות אשאל כמה ראוי שיקח כל א' א' וכמה שם כל א' וא' בשותפות
|
|
|
הנה ראוי לקבץ י"ב וי"ח ול' ויהיו ס' אח"כ תקח עבור י"ב ק' ועבור י"ח ק' ועבור ל' ק' ויהיו ג' מאות א"כ ראוי שתאמר כי עם ג' מאות הרויחו ס' א"כ תאמר אם כדי להרויח ס' נצטרך לג' מאות כמה נצטרך להרויח אלף וח' מאות ויצא ט' אלפי' חלקם על ג' ויצא לך ג' אלפים והוא מה שהיה לכל א וא'
|
|
|
ולדעת כמה הרויח כל א' וא' תאמר אם ק' הרויחו י"ב ג' אלפים כמה ירויחו יצא לך ג' מאות וס' והוא מה שהרויח הראשון
|
|
|
ולדעת כמה הרויח השני תאמר אם ק' הרויחו י"ח כמה ירויחו ג' אלפים ויצא לך תק"מ והוא מה שהרויח הב'
|
|
|
ולדעת כמה הרויח הג' תאמר אם ק' הרויחו ל' כמה ירויחו ל' ג' אלפים ויצא לך ט' מאות ובין הכל אלף וח' מאות
|
|
|
רעז) שאלה ב' עושים שותפות הראשון שם פ' מנינים ומרויח עבור כל מאה כ"ה והב' שם ס' ומרויח עבור כל מאה כ' והרויחו ל"ו אשאל כמה ראוי שיקח כל א' וא'
|
|
|
כך תעשה תואמר אם ק' הרויחו כ"ה פ' כמה ירויחו ויצא לך כ' והוא עבור הראשון ועבור השני תאמר אם ק' שבו כ' ס' כמה ישובו ויצא לך י"ב * וחצי והוא מה שהרויח הראשון עוד תאמר אם ל"ב הרויחו ל"ו ויצא *[ה]נה תחבר כ' וי"ב לך י"ג וחצי והוא מה שמגיע מהריוח לשני
|
|
|
ולבחון אותו תחבר כ"ב וחצי וי"ג [י]היו ל"ב אח"כ תאמ' וחצי ויהיו ל"ו
|
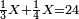
![\scriptstyle\left(\frac{1}{3}X+\frac{1}{5}X\right)+\left[\frac{1}{3}\sdot\left(X-\frac{1}{3}X-\frac{1}{5}X\right)\right]=12](/mediawiki/images/math/0/b/d/0bdc270c3b686caf42ecf09c9a1d5798.png)
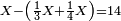
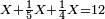
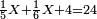
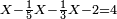
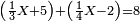
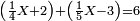
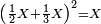
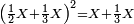
![\scriptstyle\left[\frac{1}{4}\sdot\left(\frac{1}{2}X+\frac{1}{3}X\right)\right]+\left[\frac{1}{5}\sdot\left[X-\left(\frac{1}{2}X+\frac{1}{3}X\right)\right]\right]=12](/mediawiki/images/math/9/f/b/9fb42766182ab84ca76f0ac2ea220a12.png)
![\scriptstyle\frac{1}{2}X+\left[\frac{1}{3}\sdot\left(X-\frac{1}{2}X\right)\right]+\left[\frac{1}{4}\sdot\left[X-\left[\frac{1}{2}X+\left[\frac{1}{3}\sdot\left(X-\frac{1}{2}X\right)\right]\right]\right]\right]=14](/mediawiki/images/math/6/f/9/6f9ff55e47632097b32644bf2a91f9fe.png)
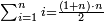
![\scriptstyle\sum_{i=1}^{2m} i=\left[\left(\frac{1}{2}\sdot2m\right)\sdot2m\right]+\left(\frac{1}{2}\sdot2m\right)](/mediawiki/images/math/1/8/b/18bd1a03b4210da19a2a238a1343388b.png)
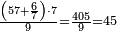
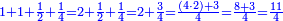
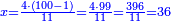
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left(\frac{50}{1+\frac{1}{4}}+\frac{50}{1-\frac{1}{4}}\right)-100&\scriptstyle=\left(\frac{4\sdot50}{5}+\frac{4\sdot50}{3}\right)-100\\&\scriptstyle=\left(\frac{200}{5}+\frac{200}{3}\right)-100\\&\scriptstyle=\left[40+\left(66+\frac{2}{3}\right)\right]-100\\&\scriptstyle=6+\frac{2}{3}\\\end{align}}}](/mediawiki/images/math/f/f/e/ffec10b7402d6c289bc7ae654748b4d6.png)
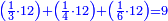
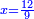
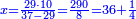
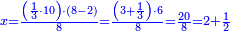
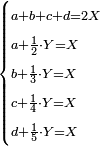
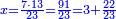
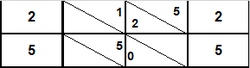
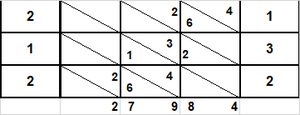
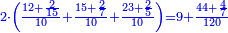
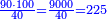


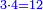
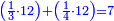
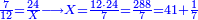
![\scriptstyle{\color{blue}{\left(\frac{1}{3}+\frac{1}{5}\right)+\left[\frac{1}{3}\sdot\left(1-\frac{1}{3}-\frac{1}{5}\right)\right]=\frac{8}{15}+\left(\frac{1}{3}\sdot\frac{7}{15}\right)=\frac{62}{90}}}](/mediawiki/images/math/8/1/e/81e89f769e5c3da454c012bb1ed4a1f9.png)
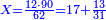
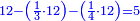
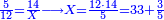
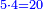

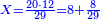
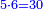
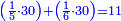
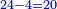
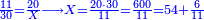
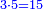
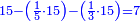


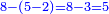
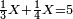
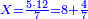
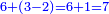
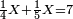
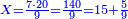

![\scriptstyle{\color{blue}{\left[\left(\frac{1}{2}\sdot6\right)+\left(\frac{1}{3}\sdot6\right)\right]^2=5^2=25}}](/mediawiki/images/math/9/b/7/9b7c81bb4ccb8defbc0ffdc19ed0ebd5.png)

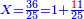
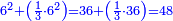
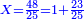
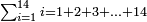
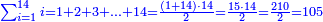
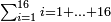
![\scriptstyle{\color{blue}{\sum_{i=1}^{16} i=1+\ldots+16=\left[\left(\frac{1}{2}\sdot16\right)\sdot16\right]+\left(\frac{1}{2}\sdot16\right)=\left(8\sdot16\right)+8=128+8=136}}](/mediawiki/images/math/1/2/3/123611d802c3533eedae98767a2ea39c.png)
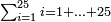
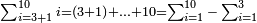
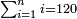
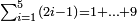
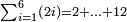
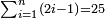
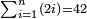
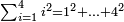
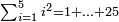
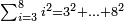
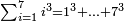
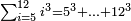
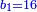
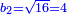

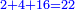
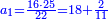
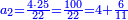
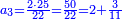
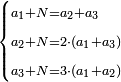
![\scriptstyle{\color{blue}{N=\left[\left(\frac{1}{2}\sdot12\right)+\left(\frac{2}{3}\sdot12\right)+\left(\frac{3}{4}\sdot12\right)\right]-12=\left(6+8+9\right)-12=23-12=11}}](/mediawiki/images/math/f/0/3/f03e46121cbbf95d6e3b2685d2d09227.png)
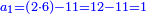
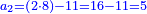
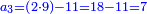
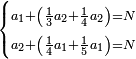
![\scriptstyle{\color{blue}{12-\left[\left(\frac{1}{3}\sdot12\right)+\left(\frac{1}{4}\sdot12\right)\right]=12-7=5}}](/mediawiki/images/math/9/9/4/994410b776b40d19b554ba92d759d4ae.png)
![\scriptstyle{\color{blue}{20-\left[\left(\frac{1}{4}\sdot20\right)+\left(\frac{1}{5}\sdot20\right)\right]=20-9=11}}](/mediawiki/images/math/f/f/8/ff8cbb7d14317cac82e03ace86d629d4.png)
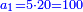
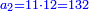
![\scriptstyle{\color{blue}{N=132+\left[\left(\frac{1}{4}\sdot100\right)+\left(\frac{1}{5}\sdot100\right)\right]=132+45=177}}](/mediawiki/images/math/0/c/7/0c7db4cfa0209cf9b9f5ad813aa9161a.png)
![\scriptstyle{\color{blue}{N=100+\left[\left(\frac{1}{3}\sdot132\right)+\left(\frac{1}{4}\sdot132\right)\right]=100+77=177}}](/mediawiki/images/math/2/c/d/2cd0cf9d142ec7df7fa2ad8a2c868d00.png)
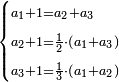
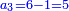
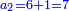
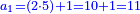
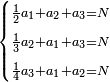
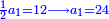
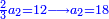
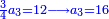
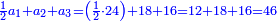
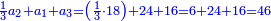
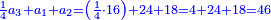
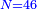
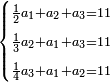
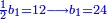
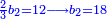
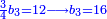
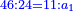
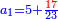
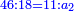
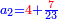
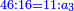
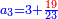
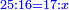

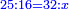

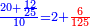
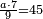
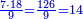
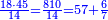
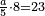
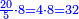
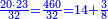
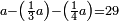
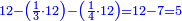
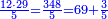
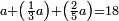
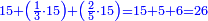

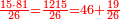
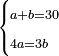
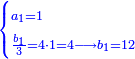
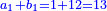
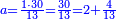
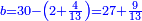
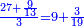




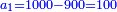


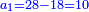

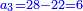
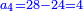

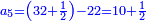
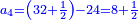
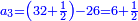
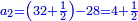
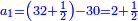
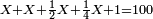
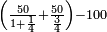
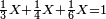
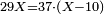
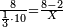
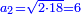
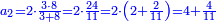
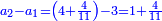
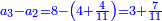
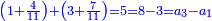
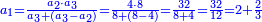
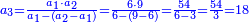
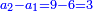
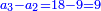
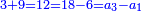
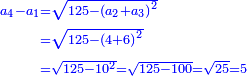
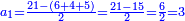
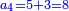
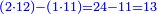
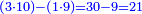
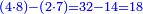
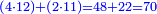
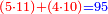
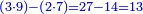
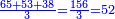

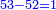

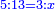
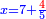
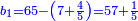
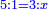
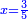
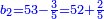
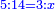
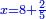
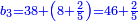
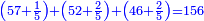
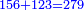
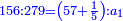
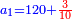
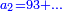

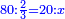
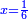
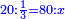
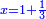
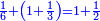

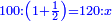
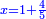

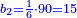


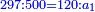

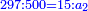
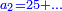
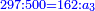

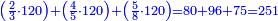
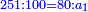
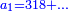
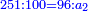

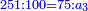
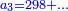
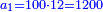
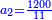
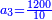
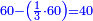
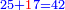
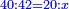
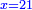

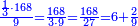
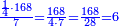

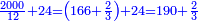
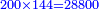

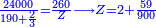
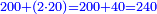
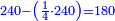








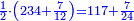
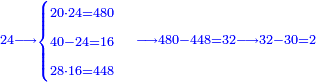
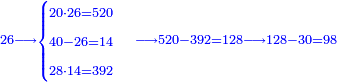
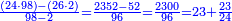
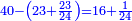
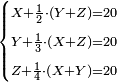
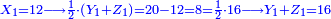
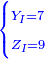
![\scriptstyle{\color{blue}{Y_I+\frac{1}{3}\sdot\left(X_1+Z_I\right)=7+\left[\frac{1}{3}\sdot\left(12+9\right)\right]=7+\left(\frac{1}{3}\sdot21\right)=7+7=14}}](/mediawiki/images/math/a/3/8/a385ddbda665dd4ff41baa5ce7fb2d21.png)
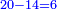
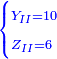
![\scriptstyle{\color{blue}{Y_{II}+\frac{1}{3}\sdot\left(X_1+Z_{II}\right)=10+\left[\frac{1}{3}\sdot\left(12+6\right)\right]=10+\left(\frac{1}{3}\sdot18\right)=10+6=16}}](/mediawiki/images/math/6/4/b/64b362bcd1beaa81a248361e5f6ed9ef.png)
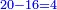
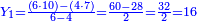
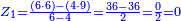
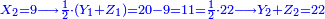
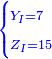
![\scriptstyle{\color{blue}{Y_I+\frac{1}{3}\sdot\left(X_1+Z_I\right)=7+\left[\frac{1}{3}\sdot\left(9+15\right)\right]=7+\left(\frac{1}{3}\sdot24\right)=7+8=15}}](/mediawiki/images/math/8/1/b/81b76c30e21100d5997ebd09dc4a9d27.png)
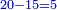
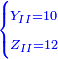
![\scriptstyle{\color{blue}{Y_{II}+\frac{1}{3}\sdot\left(X_1+Z_{II}\right)=10+\left[\frac{1}{3}\sdot\left(9+12\right)\right]=10+\left(\frac{1}{3}\sdot21\right)=10+7=17}}](/mediawiki/images/math/0/7/c/07c99984dad1c99febedac0f17516ae7.png)
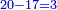
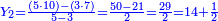
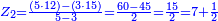
![\scriptstyle{\color{blue}{X_1+\frac{1}{2}\sdot\left(Y_1+Z_1\right)=12+\left[\frac{1}{2}\sdot\left(16+0\right)\right]=12+\left(\frac{1}{2}\sdot16\right)=12+8=20}}](/mediawiki/images/math/6/d/6/6d66fa8623f2c5c8cb8cf321dfe7dfd5.png)
![\scriptstyle{\color{blue}{Y_1+\frac{1}{3}\sdot\left(X_1+Z_1\right)=16+\left[\frac{1}{3}\sdot\left(12+0\right)\right]=16+\left(\frac{1}{3}\sdot12\right)=16+4=20}}](/mediawiki/images/math/0/d/8/0d8dd6c8d5d3b611025a659c200c1d6b.png)
![\scriptstyle{\color{blue}{Z_1+\frac{1}{4}\sdot\left(X_1+Y_1\right)=0+\left[\frac{1}{4}\sdot\left(12+16\right)\right]=0+\left(\frac{1}{4}\sdot28\right)=0+7=7}}](/mediawiki/images/math/1/5/8/1588802d6f84f539655ed605ea091267.png)
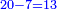
![\scriptstyle{\color{blue}{X_2+\frac{1}{2}\sdot\left(Y_2+Z_2\right)=9+\left[\frac{1}{2}\sdot\left[\left(14+\frac{1}{2}\right)+\left(7+\frac{1}{2}\right)\right]\right]=9+11=20}}](/mediawiki/images/math/9/d/a/9da4c8767d5abb357e66a66cdfc07b61.png)
![\scriptstyle{\color{blue}{\scriptstyle\begin{align}\scriptstyle Y_2+\frac{1}{3}\sdot\left(X_2+Z_2\right)&\scriptstyle=\left(14+\frac{1}{2}\right)+\left[\frac{1}{3}\sdot\left[9+\left(7+\frac{1}{2}\right)\right]\right]\\&\scriptstyle=\left(14+\frac{1}{2}\right)+\left[\frac{1}{3}\sdot\left(16+\frac{1}{2}\right)\right]\\&\scriptstyle=\left(14+\frac{1}{2}\right)+\left(5+\frac{1}{2}\right)=20\\\end{align}}}](/mediawiki/images/math/2/e/f/2ef645338f3a361a27a20c7252890003.png)
![\scriptstyle{\color{blue}{\scriptstyle\begin{align}\scriptstyle Z_2+\frac{1}{4}\sdot\left(X_2+Y_2\right)&\scriptstyle=\left(7+\frac{1}{2}\right)+\left[\frac{1}{4}\sdot\left[9+\left(14+\frac{1}{2}\right)\right]\right]\\&\scriptstyle=\left(7+\frac{1}{2}\right)+\left(5+\frac{7}{8}\right)=13+\frac{3}{8}\\\end{align}}}](/mediawiki/images/math/6/e/c/6ecd2e03a7a1dbfc571cb74094ef8ca8.png)
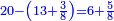
![\scriptstyle{\color{blue}{X=\frac{\left(13\sdot9\right)-\left[12\sdot\left(6+\frac{5}{8}\right)\right]}{13-\left(6+\frac{5}{8}\right)}=\frac{117-\left(79+\frac{1}{2}\right)}{6+\frac{3}{8}}=\frac{37+\frac{1}{2}}{6+\frac{3}{8}}=5+\frac{15}{17}}}](/mediawiki/images/math/f/2/4/f24da28bae5059ba127505c04aaf67cb.png)
![\scriptstyle{\color{blue}{Y=\frac{\left[13\sdot\left(14+\frac{1}{2}\right)\right]-\left[16\sdot\left(6+\frac{5}{8}\right)\right]}{13-\left(6+\frac{5}{8}\right)}=\frac{\left(188+\frac{1}{2}\right)-106}{6+\frac{3}{8}}=\frac{82+\frac{1}{2}}{6+\frac{3}{8}}=12+\frac{16}{17}}}](/mediawiki/images/math/f/a/c/fac9581332c4f05b4f0022d7956778c1.png)
![\scriptstyle{\color{blue}{Z=\frac{\left[13\sdot\left(7+\frac{1}{2}\right)\right]-\left[0\sdot\left(6+\frac{5}{8}\right)\right]}{13-\left(6+\frac{5}{8}\right)}=\frac{\left(97+\frac{1}{2}\right)-0}{6+\frac{3}{8}}=\frac{97+\frac{1}{2}}{6+\frac{3}{8}}=15+\frac{5}{17}}}](/mediawiki/images/math/4/2/3/4231a616d7dff2262b5c61ed9d23e522.png)