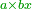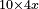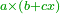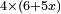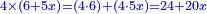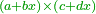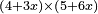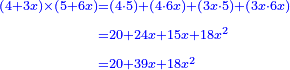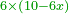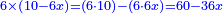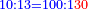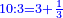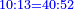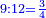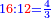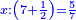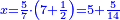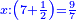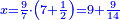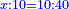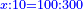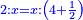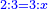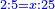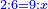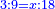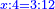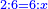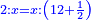Difference between revisions of "Kaufmann A506/2 – Discussion on Numbers"

From mispar
Jump to: navigation, search
(→‎The Third Introduction)
(→‎Chapter on the Multiplication of Numbers by Numbers, Some of which are Knowns and Some are Unknown)
Line 142: Line 142:
 
|-
 
|-
 
|
 
|
−
:*As our saying: multiply 4 numbers and 3 things by 5 numbers and 6 things.
+
:*Multiply 4 numbers and 3 things by 5 numbers and 6 things.
 
::<math>\scriptstyle\left(4+3x\right)\times\left(5+6x\right)</math>
 
::<math>\scriptstyle\left(4+3x\right)\times\left(5+6x\right)</math>
 
|style="text-align:right;"|כפול ד' מספרי' וג' דברים בה' מספרי' וו' דברים
 
|style="text-align:right;"|כפול ד' מספרי' וג' דברים בה' מספרי' וו' דברים
Line 303: Line 303:
 
|-
 
|-
 
|
 
|
 +
 +
=== Chapter on the Finding a Number from a Number by Knowing Their Ratio ===
 +
 
|style="text-align:right;"|&#x202B;<ref>116</ref>הפרק בהוצאת מספר ממספר מתוך ידיעת יחסו
 
|style="text-align:right;"|&#x202B;<ref>116</ref>הפרק בהוצאת מספר ממספר מתוך ידיעת יחסו
 
|-
 
|-
Line 318: Line 321:
 
|-
 
|-
 
|
 
|
 +
:*For example: the ratio of ten to 13 is the same as the ratio of 100 to 1[30].
 +
::<math>\scriptstyle{\color{blue}{10:13=100:1{\color{red}{30}}}}</math>
 
|style="text-align:right;"|דמיונו שיחס עשרה לי"ג כיחס ק' לק"ג
 
|style="text-align:right;"|דמיונו שיחס עשרה לי"ג כיחס ק' לק"ג
 
|-
 
|-
Line 324: Line 329:
 
|-
 
|-
 
|
 
|
 +
:*As our saying: the ratio of 3 to ten is the ratio of 3 times and a third
 +
::<math>\scriptstyle{\color{blue}{10:3=3+\frac{1}{3}}}</math>
 
|style="text-align:right;"|כאמרנו יחס ג' לעשרה כיחס ג' דמיונים ושליש
 
|style="text-align:right;"|כאמרנו יחס ג' לעשרה כיחס ג' דמיונים ושליש
 
|-
 
|-
Line 330: Line 337:
 
|-
 
|-
 
|
 
|
 +
:*For example: the ratio of ten to 13 is the same as the ratio of 40 to 52.
 +
::<math>\scriptstyle{\color{blue}{10:13=40:52}}</math>
 
|style="text-align:right;"|דמיונו יחס עשרה לי"ג כיחס מ' לנ"ב
 
|style="text-align:right;"|דמיונו יחס עשרה לי"ג כיחס מ' לנ"ב
 
|-
 
|-
Line 345: Line 354:
 
|-
 
|-
 
|
 
|
−
|style="text-align:right;"|כאלו תאמר יחס י"ג לי"ב הוא ג' רביעיות
+
:*As if you say: the ratio of 9 to 12 is 3-quarters
 +
::<math>\scriptstyle{\color{blue}{9:12=\frac{3}{4}}}</math>
 +
|style="text-align:right;"|כאלו תאמר יחס ט' לי"ב הוא ג' רביעיות
 
|-
 
|-
 
|
 
|
 +
:*Also the ratio of 1[6] to 1[2] is 4-thirds
 +
::<math>\scriptstyle{\color{blue}{1{\color{red}{6}}:1{\color{red}{2}}=\frac{4}{3}}}</math>
 
|style="text-align:right;"|ויחס י"ב לי"ו הוא ד' שלישיות
 
|style="text-align:right;"|ויחס י"ב לי"ו הוא ד' שלישיות
 
|-
 
|-
Line 357: Line 370:
 
|-
 
|-
 
|
 
|
 +
:*For example: one of the terms is 7 and a half and the ratio of the other to it is 5-sevenths.
 +
::<math>\scriptstyle{\color{blue}{x:\left(7+\frac{1}{2}\right)=\frac{5}{7}}}</math>
 
|style="text-align:right;"|דמיונו שאחד השעורים ז' וחצי והאחר יחסו לו שהוא ה' שביעיות
 
|style="text-align:right;"|דמיונו שאחד השעורים ז' וחצי והאחר יחסו לו שהוא ה' שביעיות
 
|-
 
|-
 
|
 
|
 +
::We multiply 5-sevenths by 7 and a half; it is 5 and 5 parts of 14.
 +
::<math>\scriptstyle{\color{blue}{x=\frac{5}{7}\sdot\left(7+\frac{1}{2}\right)=5+\frac{5}{14}}}</math>
 
|style="text-align:right;"|הנה נכפול ה' שביעיות בז' וחצי יהיה ה' וה' חלקים מן י"ד
 
|style="text-align:right;"|הנה נכפול ה' שביעיות בז' וחצי יהיה ה' וה' חלקים מן י"ד
 
|-
 
|-
 
|
 
|
−
|style="text-align:right;"|ואם היה ט' שביעיות יהיה תשעה וט' חלקים מי"ד
+
:*If [the ratio] is 9-sevenths.
 +
::<math>\scriptstyle{\color{blue}{x:\left(7+\frac{1}{2}\right)=\frac{9}{7}}}</math>
 +
|style="text-align:right;"|ואם היה ט' שביעיות
 +
|-
 +
|
 +
::It is 9 and 9 parts of 14.
 +
::<math>\scriptstyle{\color{blue}{x=\frac{9}{7}\sdot\left(7+\frac{1}{2}\right)=9+\frac{9}{14}}}</math>
 +
|style="text-align:right;"|יהיה תשעה וט' חלקים מי"ד
 
|-
 
|-
 
|
 
|
Line 372: Line 396:
 
|-
 
|-
 
|
 
|
 +
:*As if you say: the ratio of an unknown term to ten is the same as the ratio of ten to forty.
 +
::<math>\scriptstyle{\color{blue}{x:10=10:40}}</math>
 
|style="text-align:right;"|כאלו תאמר יחס שעור נעלם אל עשרה כיחס עשרה לארבעים
 
|style="text-align:right;"|כאלו תאמר יחס שעור נעלם אל עשרה כיחס עשרה לארבעים
 
|-
 
|-
Line 387: Line 413:
 
|-
 
|-
 
|
 
|
−
|style="text-align:right;"|ואם שיהיה בין ד' שעורים כאלו תאמר יחס הנעלם לעשרה כיחס ק' לג' מאות
+
|style="text-align:right;"|ואם שיהיה בין ד' שעורים
 +
|-
 +
|
 +
:*As if you say: the ratio of the unknown to ten is the same as the ratio of 100 to 3 hundred.
 +
::<math>\scriptstyle{\color{blue}{x:10=100:300}}</math>
 +
|style="text-align:right;"|כאלו תאמר יחס הנעלם לעשרה כיחס ק' לג' מאות
 
|-
 
|-
 
|
 
|
Line 405: Line 436:
 
|-
 
|-
 
|
 
|
−
|style="text-align:right;"|וזה בג' מספרים כאמרך יחס שנים לנעלם כיחס הנעלם לד' וחצי
+
|style="text-align:right;"|וזה בג' מספרים
 +
|-
 +
|
 +
:*As your saying: the ratio of two to the unknown is the same as the ratio of the unknown to 4 and a half.
 +
::<math>\scriptstyle{\color{blue}{2:x=x:\left(4+\frac{1}{2}\right)}}</math>
 +
|style="text-align:right;"|כאמרך יחס שנים לנעלם כיחס הנעלם לד' וחצי
 
|-
 
|-
 
|
 
|
Line 414: Line 450:
 
|-
 
|-
 
|
 
|
−
|style="text-align:right;"|דמיונו שיחס ב' לג' כיחס ג' לנעלם נכפול ג' על עצמו ונחלק העולה על ב' ויצא ד' וחצי וכן הנעלם
+
:*For example: the ratio of 2 to 3 is the same as the ratio of 3 to the unknown.
 +
::<math>\scriptstyle{\color{blue}{2:3=3:x}}</math>
 +
|style="text-align:right;"|דמיונו שיחס ב' לג' כיחס ג' לנעלם
 +
|-
 +
|
 +
|style="text-align:right;"|נכפול ג' על עצמו ונחלק העולה על ב' ויצא ד' וחצי וכן הנעלם
 
|-
 
|-
 
|
 
|
Line 420: Line 461:
 
|-
 
|-
 
|
 
|
 +
:*For example: the ratio of 2 to 5 is the same as the ratio of the unknown to 25.
 +
::<math>\scriptstyle{\color{blue}{2:5=x:25}}</math>
 
|style="text-align:right;"|דמיונו יחס <s>ה' לב'</s> ב' לה' כיחס הנעלם לכ"ה
 
|style="text-align:right;"|דמיונו יחס <s>ה' לב'</s> ב' לה' כיחס הנעלם לכ"ה
 
|-
 
|-
Line 432: Line 475:
 
|-
 
|-
 
|
 
|
 +
:*For example: the ratio of 2 to 6 is the same as the ratio of 9 to the unknown.
 +
::<math>\scriptstyle{\color{blue}{2:6=9:x}}</math>
 
|style="text-align:right;"|דמיונו יחס ב' לו' כיחס ט' לנעלם
 
|style="text-align:right;"|דמיונו יחס ב' לו' כיחס ט' לנעלם
 
|-
 
|-
Line 447: Line 492:
 
|-
 
|-
 
|
 
|
−
|style="text-align:right;"|דמיונו יחס ג' לט' כיחס הנעלם לי"ח הנה נחלק ט' על ג' עלה שליש כפלנו שליש בי"ח יעלו ו' וכן האמצעי הנעלם
+
:*For example: the ratio of 3 to 9 is the same as the ratio of the unknown to 18.
 +
::<math>\scriptstyle{\color{blue}{3:9=x:18}}</math>
 +
|style="text-align:right;"|דמיונו יחס ג' לט' כיחס הנעלם לי"ח
 +
|-
 +
|
 +
|style="text-align:right;"|הנה נחלק ט' על ג' עלה שליש כפלנו שליש בי"ח יעלו ו' וכן האמצעי הנעלם
 
|-
 
|-
 
|
 
|
Line 453: Line 503:
 
|-
 
|-
 
|
 
|
 +
:*As our saying: the ratio of the unknown to 4 is the same as the ratio of 3 to 12.
 +
::<math>\scriptstyle{\color{blue}{x:4=3:12}}</math>
 
|style="text-align:right;"|כאמרנו יחס הנעלם לד' כיחס ג' לי"ב
 
|style="text-align:right;"|כאמרנו יחס הנעלם לד' כיחס ג' לי"ב
 
|-
 
|-
Line 462: Line 514:
 
|-
 
|-
 
|
 
|
 +
:*As our saying: the ratio of 2 to 6 is the same as the ratio of 6 to the unknown.
 +
::<math>\scriptstyle{\color{blue}{2:6=6:x}}</math>
 
|style="text-align:right;"|כאמרנו יחס ב' לו' כיחס ו' לנעלם
 
|style="text-align:right;"|כאמרנו יחס ב' לו' כיחס ו' לנעלם
 
|-
 
|-
Line 474: Line 528:
 
|-
 
|-
 
|
 
|
−
|style="text-align:right;"|דמיונו יחס ב' לנעלם כיחס הנעלם לי"ב וחצי כפלנו ב' בי"ב וחצי עלה כ"ה לקחנו שורשו והוא ה' וכן הוא האמצעי
+
:*For example: the ratio of 2 to the unknown is the same as the ratio of the unknown to 12 and a half.
 +
::<math>\scriptstyle{\color{blue}{2:x=x:\left(12+\frac{1}{2}\right)}}</math>
 +
|style="text-align:right;"|דמיונו יחס ב' לנעלם כיחס הנעלם לי"ב וחצי
 +
|-
 +
|
 +
|style="text-align:right;"|כפלנו ב' בי"ב וחצי עלה כ"ה לקחנו שורשו והוא ה' וכן הוא האמצעי
 
|-
 
|-
 
|
 
|

Revision as of 05:29, 28 May 2024

Discussion about Numbers Divided into Chapters

 ‫[1]המאמר במספרים נחלק לפרקי‫'

The First Method in the Introduction to the Discussion

 הדרך הא' בהצעת המאמר
המספר הנעלם דרוש הידיעה יודע אם מפני מספר או מספרי' אחדים או מפני יחסו או סדורו
אולם מפני מספר אחר ידוע הנה או שזה שוה לו והוא פשוט או שזה יותר גדול ממנו וידיעת השעור שהוא יותר גדול ממנו ויקרא זה חבור או שהוא יותר קטן ויודע בכמה יותר קטן ויקרא מגרעת
אולם מפני מספרי' אחרי' שיוכפלו יחד ויקרא זה הכפלה אולם מפני יחסו ויקרא ערך או סדרו ויקרא המספר המסודר ביחס

The Second Introduction

 הצעה שנית
המספרים שיעיין בם בעל חכמת החשבון הם מחוברי' מאחדי' שלמים ויקרא לאחר החלוקה בבחינת נושאו שהוא המתדבק
ויעיין בו הלמודי ג"כ כשיצייר נושא האחד נחלק לחלקי' אם לחצי או לשלישי או לרביע וזולתם ויקרא שם לשברי' נגזר מהשלמי' יקרא השליש נגזר משלש למה שהגדול ג' דמיוני הקטן
הקטן חלק משלשה בו
והרביע נגזר מהארבעה וכן זולתם

The Third Introduction

 הצעה ג‫'
המספרי' החשבוניי' מסודרי' בהדרגה ועל יחס האחד לעשר על שיחס כל אחדי המעלה הא' לאחדי המעלה הב' כיחס אחדי השנית אל אחדי השלישית וכיחס אחדי העשירית לאחדי האחד עשר
דמיונו שכמו ששנים במעלה השנית הם עשרה פעמי' שנים במעלה הא' כך שניים במעלה החמישית הם עשרה דמיוני לשנים במעלה רביעית
וכן מדרגות שברי חכמי התכונה אלו שאותם הם יחס הגרעון ואלו יחס התוספת
ואותם יחס אחר ששים לאחר ואלו יחס אחד מששים
ועם זה יחס ג' דקי' לג' שניים כיחס ג' שביעיים לג' שמיניים
ולזה יפול בכל אחד מהמספרי' בחינה בבחינות המספר ומה שבו מהאחדים ובחינה במדרגתו

Chapter on the Multiplication of Numbers by Numbers, Some of which are Knowns and Some are Unknown

 הפרק במכפלת מספרי' במספרי' קצתם ידועי' וקצתם נעלמי‫'
ויקרא הנעלם בשם הסוג היותר כולל והוא דבר
אם ינתן לך לכפול מספרי' ידועי המניין והשעור בדברי' ידועי המניין לא השעור כאלו נאמר כפלנו עשרה אחדי' בד' כ דברים והיה מהנעלם [....] אם הדברי' ההם מספרי' או קבוץ מספרים או מרובעים או הדומה לזה
הנה איך אתה השיב תשובה ידועה מצד ונעלמת ונכפול עשרה בארבעה יעלו מ‫'
ואחר בדבר יהיה דבר ולכן תאמר שהעולה מ' דברים כלומר הוא מ' פעמים השעור ש[כינת] אותו אתה בשם דבר מספר היה או מקובץ אחדים
ואלו היה המכוון בדבר עשריים היה מובן השאלה תכפול עשרה אחדי' בארבעה דברים על שכל דבר הוא עשרה מספרי'
ואם היה המכוון בדבר מאה היו מ' מאות וכן בכל מה שרצהו מהכוונות ואז צריך ב' הכפלות
ויתחדשו בזה ו' מינים מההרכבות
  • The first is that you multiply the numbers by things.
\scriptstyle{\color{OliveGreen}{a\times bx}}
 הא' שתכפול המספרי' בדברי‫'
  • As our saying: 10 numbers by 4 things.
\scriptstyle10\times4x
 כאמרנו י' מספרי' בד' דברי‫'
  • The second is that you multiply numbers by numbers and things.
\scriptstyle{\color{OliveGreen}{a\times\left(b+cx\right)}}
 הב' שתכפול מספרי' במספרי' ודברי‫'
  • As our saying: multiply 4 numbers by 6 numbers and 5 things.
\scriptstyle4\times\left(6+5x\right)
 כאמרנו כפול ד' מספרי' בו' מספרי' וה' דברים
Then two products are needed.
 ואז צריך ב' הכפלות
The way is that you multiply 4 numbers by 6 numbers; the result is 24.
 והדרך שתכפול ד' מספרי' בו' מספרי' יעלו כ"ד
Multiply 4 by 5 things; the result are 20 things.
 כפול ד' בה' דברים יעלו כ' דברים
The sum is 24 numbers and 20 things.
\scriptstyle{\color{blue}{4\times\left(6+5x\right)=\left(4\sdot6\right)+\left(4\sdot5x\right)=24+20x}}
 הנה המקובץ כ"ד מספרים וכ' דברים
ºc nº
5 4 6
  • The third is that you multiply numbers and things by numbers and things.
\scriptstyle{\color{OliveGreen}{\left(a+bx\right)\times\left(c+dx\right)}}
 הג' שתכפול מספרים ודברי' במספרי' ודברי‫'
Then four products are needed.
 ואז צריך ד' הכפלות
  • Multiply 4 numbers and 3 things by 5 numbers and 6 things.
\scriptstyle\left(4+3x\right)\times\left(5+6x\right)
 כפול ד' מספרי' וג' דברים בה' מספרי' וו' דברים
We multiply 4 numbers by 5 numbers; the result is 20.
 הנה נכפול הד' מספרים בה' מספרי' עלו כ‫'
4 numbers by 6 things; the result are 24 things.
 וד' מספרי' בו' דברי' עלה כ"ד דברים
We multiply 3 things by 5 numbers; the result are 15 things.
 עוד נשוב ‫[2]נשוב נכפול ג' דברי' בה' מספרים עלו ט"ו דברים
We multiply 3 things by 6 things; the result are 18 things of things, i.e. 18 squares of the given thing.
 נשוב נכפול ג' דברים בו' מספרים דברים עלו י"ח דברים מדברים כלומר י"ח מרובעי הדבר המונח
We sum them, the result is 20 numbers, 39 things, and 18 squares of the things.
 נקבצם עלה כ' מספרים ל"ט דברים וי"ח מרובעי הדברים
\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left(4+3x\right)\times\left(5+6x\right)&\scriptstyle=\left(4\sdot5\right)+\left(4\sdot6x\right)+\left(3x\sdot5\right)+\left(3x\sdot6x\right)\\&\scriptstyle=20+24x+15x+18x^2\\&\scriptstyle=20+39x+18x^2\end{align}}}
  • The fourth is the subtraction method.
 הד' דרך הגרעון
  • If you are told: six numbers by ten numbers minus 6 things.
\scriptstyle{\color{OliveGreen}{6\times\left(10-6x\right)}}
 אם יאמר לך ששה מספרים בעשרה מספרים פחות ו' דברים
You multiply six by ten; the result are 60 numbers.
 הנה תכפול ששה בעשרה עלו ס' מספרים
Multiply 6 numbers also by subtractive six things; they are 36 subtractive things.
 עוד שוב כפול ו' מספרים בששה דברים חסרים יהיו ל"ו דברים חסרים
The sum is 60 minus 36 things.
\scriptstyle{\color{blue}{6\times\left(10-6x\right)=\left(6\sdot10\right)-\left(6\sdot6x\right)=60-36x}}
 הנה המקובץ ששים פחות ל"ו דברים
הה' גרעון ותוספת
אלו אמ' לך כפול ו' מספרים וג' דברים בז' מספרים פחות ה' דברים
הנה תכפול ו' מספרי' בז' מספרים עלו מ"ב
כפול ו' מספרים בה' דברים חסרים עלו ל' דברים חסרים
כפול ג' דברים נוספים בז' מספרים עלו כ"א דברים נוספים
ג' דברים נוספים בה' דברים חסרים עלו ט"ו דברים מדברים חסרים כלומ' ט"ו מרובעי הדברים חס(ר)ים
ונסיר מן השלשים דברים הנגרעים כ"א דברים נוספים נשארו ט‫'
ויהיה כלל המקובץ מההכפלה מ"ב מספרי' ט' דברים חסרים וט"ו דברים מדברים
וראוי שתקדם ותדע שהכפלת כל מספר בכל מספר העולה מספר
ומספר בדבר או מניין מדברים יעלה דבר או דברים כמו העולה מכפל מניין הדברים על המספר
ודבר בדבר או דברים יעלה דבר מדבר כלומ' מרובע המספר ההוא הנעלם או דברים כעולה מכפל מניין הדברים קצתם בקצת
ומספר בדבר נוסף יעלה דבר נוסף
ובדבר גורע יעלה דבר גורע
ודבר גורע בדבר מוסיף או גורע יעלה דבר מדבר גורע
הו' דרך הגרעון בכופל והנכפל
שיאמ' כפול עשרה פחות ג' דברים בח' פחות ה' דברים
הנה זה בד' הכפלות א' להוסיף וג' לגרוע
נכפול י' בח' ויעלו פ‫'
י' בה' דברים גורעים יהיו נ' דברים גורעים
ח' בג' דברים גורעים יהיו כ"ד דברים גורעים
ג' דברים גורעים בה' דברים גורעים הרי ט"ו דברי' מדברי' גורעים
היה כלל המקובץ פ' מספרים פחות ע"ד דברים וט"ו דברים מדברים
הז' גרעון ותוספת
שיאמ' כפול עשרה מספרים ודבר על דבר פחות עשרה מספרים הנה זה בד' הכפלות גם כן
והוא שתכפול הדבר הנוסף על הדבר הנוסף יעלה יעלה דבר מדבר נוסף
הנה העשרה מספרים בי' מספרים הגורעים יהיו ק' מספרים גורעים
תכפול י' בדבר עלו י' דברים נוספים
שוב כפול דבר נוסף בי' מספרי' גורעי' עלו י' דברים גורעים
כפול דבר בדבר נוסף עלה דבר מדבר נוסף
נתן הי' דברים נוספים כנגד הגורעים ועלה כלל החשבון ק' מספרים חסרים ודבר מדבר נוסף הנה העולה דבר מדבר פחות ק' מספרים
וכמו שהמשלנו בשלמי' כן יתכן ביחס בשברים דמיונו כפלנו י' מספרים ושני שלישי דבר על ג' מספרים פחות ו' דברים
הנה נכפול עשרה מספרים על ג' מספרים עלה ל' מספרים
נכה עשרה דברים בששה דברים הגורעים יהיו ס' דברים גורעים
נכה ב' שלישי דבר על ג' מספרים יהיו ב' דברים נוספים
נכה ב' שלישי דבר בו' דברים גורעים יהיו ד' דברים מדברים גורעים
נקבץ הכל אלא שנגרע הב' דברים הנוספים מהששים הגורעים נשארו נ"ח גורעים
ולזה יהיה המקובץ ל' מספרים פחות נ"ח דברים וד' דברי' מדברים גורעים

Chapter on the Finding a Number from a Number by Knowing Their Ratio

 ‫[3]הפרק בהוצאת מספר ממספר מתוך ידיעת יחסו
כשהיה מספר מה נעלם ידוע היחס למספר אחר ותבקש ידיעתו מתוך ידיעת המספר האחר ויחסו לו
הנה ראשונה ראוי שתדע שהיחס ימצא על ג' פנים
אם יחס מספרי והוא הבדל במספרים שלימים ידועי' כאלו תאמר יחס ג' לי' כיחס ג' דמיונים ואחד
ויהיו המספרים מתיחסים כשהיה התוספת בהם שוה
  • For example: the ratio of ten to 13 is the same as the ratio of 100 to 1[30].
\scriptstyle{\color{blue}{10:13=100:1{\color{red}{30}}}}
 דמיונו שיחס עשרה לי"ג כיחס ק' לק"ג
ואם יחס למודי והוא יחס בין ההבדל וכלל המספרים המתיחסים
  • As our saying: the ratio of 3 to ten is the ratio of 3 times and a third
\scriptstyle{\color{blue}{10:3=3+\frac{1}{3}}}
 כאמרנו יחס ג' לעשרה כיחס ג' דמיונים ושליש
ויהיה היחס בין המספרים אחר כשיהיה ההבדל לו יחס אחד למתיחסים
  • For example: the ratio of ten to 13 is the same as the ratio of 40 to 52.
\scriptstyle{\color{blue}{10:13=40:52}}
 דמיונו יחס עשרה לי"ג כיחס מ' לנ"ב
כי ההבדל בין הראשוני' הוא ג' ויחסו לעשרה כיחס כמוהו וחומשו וחצי
וכן יחס מ' לנ"ב
והג' הוא יחס נגוני
אולם היחס למודי יהיה לקוח אם בין שני שעורים לבד
  • As if you say: the ratio of 9 to 12 is 3-quarters
\scriptstyle{\color{blue}{9:12=\frac{3}{4}}}
 כאלו תאמר יחס ט' לי"ב הוא ג' רביעיות
  • Also the ratio of 1[6] to 1[2] is 4-thirds
\scriptstyle{\color{blue}{1{\color{red}{6}}:1{\color{red}{2}}=\frac{4}{3}}}
 ויחס י"ב לי"ו הוא ד' שלישיות
והדרך בזה כשיהיה אחד השעורים ידוע ויחס האחר אליו ידוע
שיכפל היחס בשעור האחד ויצא האחר
  • For example: one of the terms is 7 and a half and the ratio of the other to it is 5-sevenths.
\scriptstyle{\color{blue}{x:\left(7+\frac{1}{2}\right)=\frac{5}{7}}}
 דמיונו שאחד השעורים ז' וחצי והאחר יחסו לו שהוא ה' שביעיות
We multiply 5-sevenths by 7 and a half; it is 5 and 5 parts of 14.
\scriptstyle{\color{blue}{x=\frac{5}{7}\sdot\left(7+\frac{1}{2}\right)=5+\frac{5}{14}}}
 הנה נכפול ה' שביעיות בז' וחצי יהיה ה' וה' חלקים מן י"ד
  • If [the ratio] is 9-sevenths.
\scriptstyle{\color{blue}{x:\left(7+\frac{1}{2}\right)=\frac{9}{7}}}
 ואם היה ט' שביעיות
It is 9 and 9 parts of 14.
\scriptstyle{\color{blue}{x=\frac{9}{7}\sdot\left(7+\frac{1}{2}\right)=9+\frac{9}{14}}}
 יהיה תשעה וט' חלקים מי"ד
ואם יהיה בין ג' שעורים לבד
כאלו תאמר יחס אחד השעורי' והוא הנעלם אל שעור ידוע כיחס הידוע אל ידוע אחר
  • As if you say: the ratio of an unknown term to ten is the same as the ratio of ten to forty.
\scriptstyle{\color{blue}{x:10=10:40}}
 כאלו תאמר יחס שעור נעלם אל עשרה כיחס עשרה לארבעים
והנה זה הנעלם אפשר שיהיה
אם הראשון כמו בהמשלנו
ואפשר שיהיה השני כאמרנו יחס עשרה לנעלם כיחס הנעלם לחמשים
ואם שיהיה בין ג' שעורים לבד כאלו תאמר יחס אחד השעורים והוא הנעלם אל שעור ידוע כיחס הידוע
ואם שיהיה בין ד' שעורים
  • As if you say: the ratio of the unknown to ten is the same as the ratio of 100 to 3 hundred.
\scriptstyle{\color{blue}{x:10=100:300}}
 כאלו תאמר יחס הנעלם לעשרה כיחס ק' לג' מאות
וזה גם כן אם שיהיה הנעלם מהמספרים אשר מהקצוות או מהמספרים האמצעיים
והראשון מאלו כבר המשלנו בו
והשני כאמרנו יחס עשרה לנעלם כיחס ק' לג' מאות
והדרך בזה הוא אחד משני דברים
אם לכפול הקצוות כשהיה הנעלם האמצעי ושורש העולה הוא הנעלם
וזה בג' מספרים
  • As your saying: the ratio of two to the unknown is the same as the ratio of the unknown to 4 and a half.
\scriptstyle{\color{blue}{2:x=x:\left(4+\frac{1}{2}\right)}}
 כאמרך יחס שנים לנעלם כיחס הנעלם לד' וחצי
הנה נכפול הראשון והוא ב' בג' השלישי והוא ד' וחצי והעולה והוא ט' נקח שורשו והוא ג' וכן השני
וכשהיה הנעלם הוא אחד הקצוות נכפול האמצעי בעצמו ונחלק העולה על אחד הקצוות ויצא האחר
  • For example: the ratio of 2 to 3 is the same as the ratio of 3 to the unknown.
\scriptstyle{\color{blue}{2:3=3:x}}
 דמיונו שיחס ב' לג' כיחס ג' לנעלם
נכפול ג' על עצמו ונחלק העולה על ב' ויצא ד' וחצי וכן הנעלם
ואולם בד' מספרים הנה אם היה הנעלם אחד האמצעיים הנה נכפול הקצוות ונחלק העולה על האמצעי הידוע יצא האמצעי האחר
  • For example: the ratio of 2 to 5 is the same as the ratio of the unknown to 25.
\scriptstyle{\color{blue}{2:5=x:25}}
 דמיונו יחס ה' לב' ב' לה' כיחס הנעלם לכ"ה
הנה נכפול ב' בכ"ה עלו נ' נחלקם על ה' יצא עשרה והוא הנעלם השלישי
ואם היה אחד הקצוות הוא הנעלם
הנה נכפול האמצעיים בעצמם ונחלק העולה על אחד הקצוות והוא הידוע יצא האחר
  • For example: the ratio of 2 to 6 is the same as the ratio of 9 to the unknown.
\scriptstyle{\color{blue}{2:6=9:x}}
 דמיונו יחס ב' לו' כיחס ט' לנעלם
הנה נכפול ו' בט' עלה נ"ד נחלקם על ב' עלה כ"ז
וכן הרביעי
והדרך הב' מהמצאתינו שבד' שעורים שנחלק השוים הן הקרובים הידועים
ונכפול העולה על האחר על הקרוב לנעלם
  • For example: the ratio of 3 to 9 is the same as the ratio of the unknown to 18.
\scriptstyle{\color{blue}{3:9=x:18}}
 דמיונו יחס ג' לט' כיחס הנעלם לי"ח
הנה נחלק ט' על ג' עלה שליש כפלנו שליש בי"ח יעלו ו' וכן האמצעי הנעלם
בהיות הנעלם אחד הקצוות
  • As our saying: the ratio of the unknown to 4 is the same as the ratio of 3 to 12.
\scriptstyle{\color{blue}{x:4=3:12}}
 כאמרנו יחס הנעלם לד' כיחס ג' לי"ב
הנה חלקנו י"ב על ג' עלה רביע כפלנוהו על ד' עלה אחד והוא הראשון
ואולם בג' שעורים בהיות הנעלם אחד הקצוות
  • As our saying: the ratio of 2 to 6 is the same as the ratio of 6 to the unknown.
\scriptstyle{\color{blue}{2:6=6:x}}
 כאמרנו יחס ב' לו' כיחס ו' לנעלם
הנה חלקנו ו' על ב' עלה ג' כפלנו ג' בו' עלה י"ח וכן השלישי הנעלם
ואם היה האמצעי נעלם
הנה חלקנו הקצוות האחד על האחר ונקח שורש העולה והוא השני
  • For example: the ratio of 2 to the unknown is the same as the ratio of the unknown to 12 and a half.
\scriptstyle{\color{blue}{2:x=x:\left(12+\frac{1}{2}\right)}}
 דמיונו יחס ב' לנעלם כיחס הנעלם לי"ב וחצי
כפלנו ב' בי"ב וחצי עלה כ"ה לקחנו שורשו והוא ה' וכן הוא האמצעי
9 º 2
12 º
והסבה בכל אלו הדרכים אם לראשון הנה לפי שהיו השעורים המתיחסים שיור העולה מהכאת הראשון בשלישי כהכאת השלישי השני בעצמו בהיות היחס בין ג' שעורים
ובהיותו בין ד' מספרים היה הכאת הראשון באחרון כהכאת השני בשלישי היה יחס הנעלם הנה יצא כהכאת הראשון באחרון כשיהיה הנעלם האמצעי שטח האמצעי בעצמו ידוע להיותו שוה לו
כי הכאת השני בשלישי ידוע כשהיה היחס בין ד' שעורים ‫[4]שעורים והנעלם אחד מהאמצעים
או שטח הראשון באחרון ידוע כשהיה הנעלם אחד הקצוות
וכשהיה שטח מה ידוע ואחד צלעיו ידועים הנה הצלע האחר גם כן ידוע בדרך חלוקה כמו שקדם
הוא כשנחלק שטח האמצעי בעצמו או האמצעים על אחד הקצוות יצא האחר
ואם נחלק שטח הקצוות על אחד האמצעיים יצא האחר בד' שעורים
ובג' כשנמצא של שרשו הוא צלע המרובע השוה לשטח המתחדש מהכפלת הקצוות
ואולם לדרך הב' כי אחר שהיה היחס הנעלם לידוע ידוע כי הוא כיחס הידוע לידוע אחר
יצא היחס בין שני הידועים והוא בעינו כיחס הנעלם לידוע ולזה כשיכפל היחס בידוע יצא הנעלם הידוע
והיחס בין ששה שעורים שתאמר יחס עשרה לעשרים מורכב מיחס ד' לי"ו ומיחס י"ד לז'
עשרה עשרים
ד' י"ד י"ו ז‫'

The Chapter on Knowing the Root from Another Root or Roots

 ‫[5]הפרק בידיעת השורש מפני שורש אחר או שרשים
ויחלק לה' דרושים
הא' מפני קבוץ השרשים
הב' מפני כפלם
הג' מפני חלוקתם
הד' מפני סדרם
הה' מפני יחסם

The First Investigation

 הדרוש הא‫'
בקשנו השורש העולה מחבור ב' שרשי' כאלו תאמר חברנו שורש כ"ה בשורש י"ו ונבקש השורש המקובץ
הנה הדרך בזה שתחבר השני מרובעים יחד ועלה מקובצם מ"א הכה שני המרובעים קצתם בקצת עלה ת' קח שני שרשיו והם מ' תקבצם עם מחובר השני מרובעי' שהוא מ"א עלה פ"א קח שרשו והוא ט' והוא כמו מקובץ שורש י"ו בשורש כ"ה
וכזה כשבקשנו חבור שורש י"ו י' בשורש כ' חברנו עשרה בעשרי' עלו ל' כפלנו י' בכ' עלה מאתים בקש [נקח ‫[6] שרשו והוא י"ד ונעלם כפלנום עלה כ"ח וב' נעלמים קבצנום עם ל' עלה נ"ח וב' נעלמים
ושורשו הוא הדרוש
והסבה בזה שנניח השני שרשי' קוי א"ב ג"ד ומרובע א"ב ד"ט ומרובע ב"ג ה"ג מרובע ב"ג
הנה לפי שמרובע א"ג שוה לשני מרובעי א"ב ב"ג וכפל שטח א"ב בב"ג שהוא כמו כפל שטח כ"ה
ושטח א"ה אמצעי ביחס בין שני מרובעי ה"ט וה"ג היה כפל מרובע ד"ט בה"ג כמו כפל א"ה בעצמו הנה כשכפלנו מרובע ד"ט בה"ג ולקחנו שורש
העולה היה השורש ההוא שוה לשטח א"ה
וכאשר הכפלנוהו על שני שטחי א"ה ה"ב וכאשר קבצנום עם שני מרובעי ד"ט ה"ג הידועים היה כלל מרובע א"ב ידוע שרשו המחובר מן א"ב ב"ג ידוע

The Second Investigation

 הדרוש הב‫'
בקשנו העולה מגרעון שני שרשים האחד מהאחר כאלו תאמר בקשנו לגרוע שורש

Appendix: Bibliography

Manuscript:

  • Budapest, Magyar Tudományos Akadámia, Ms. Kaufmann A 506/2 (IMHM: f 14991), ff. 114-118 (15th century)
Kaufmann A 506/2
  1. ↑ 114
  2. ↑ 115
  3. ↑ 116
  4. ↑ 17
  5. ↑ 18
  6. ↑ marg.
    7. Retrieved from "http://mispar.ethz.ch/mediawiki/index.php?title=Kaufmann_A506/2_–_Discussion_on_Numbers&oldid=62819"