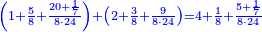The Third Section: Integers and Fractions
|
[138]הש[ער הג']
|
- The first chapter on addition [of integers and fraction]
|
הפרק הראשון בחיבור [שלמים ושברים]
|
- The second chapter on multiplication of integers and fraction
|
הפרק השני בכפל שלמים ושברים
|
- The third chapter on subtraction of integers and fractions
|
הפרק השלשי במגרעת שלמים ושברים
|
- The fourth chapter on division of integers and fractions
|
הפרק הרביעי בחילוק שלמים ושברים
|
The First Chapter on Addition of Integers and Fractions
|
הפרק הראשון בחיבור שלמים ושברים
|
|
|
ואומר כי רצינו לחבר השלם והשבר למיניהם הנה נוכל לעשות זה בשני דרכים
|
|
|
אשר הראשון האחד הוא שתעשה כל השלמים שברים וחלקם על המורה אחר שתשוים אל מורה אחד
|
|
|
והדרך השני הוא שתחבר השלמים ואחר תשויה השברים והעולה מחיבור השברים תחלק על המורה והיוצא בחילוק הם שלמים והנשאר הם חלקי המורה
|
- Example of the first method: we wish to sum 4 integers and two-thirds with 5 integers and 3-quarters.
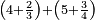
|
והמשל מן הדרך הראשון רצינו לחבר ד' שלמים ושני שלשיים עם ה' שלמים וג' רביעיים
|
- According to this diagram:
|
בזה הצורה
|
|
|
 |
שלמים |
ד'
|
 |
שלמים |
ה'
|
|
|
|
|
בשויה השלמים עם מורה שברים יהיו י"ב וב' שברים יהיו י"ד והם שלישיות גם השני עם מורה שברים יהיו כ"ג רביעיות כשוים כזה הצורה [השנית] יהיו שניהם ס"ט נ"ו [139][...] נחברם [...] יהיו [...] חלקים מי"ב בשלם [...] זה המשל בדרך [...] וה' יהיו ט' נשויה השברים [...] נחלקים על המורה הכללי [שהוא י"ב] [...] שהיו לנו יהיו עשרה ונשארו חמשה י"ב [...]
|
- The second example: we wish to sum integers and fractions with integers and fractions, such as 13 integers and five-ninths with 26 integers and three-fifths and with 236 integers and a half.
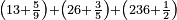
|
משל שני רצינו לחבר שלמים ושברים על עם שלמים ושברים כמו י"ג שלמים וחמשה תשיעיות עם כ"ו שלמים ושלשת חמשיות ועם רל"ו שלמים וחצי
|
- According to this diagram:
|
כזאת הצורה
|
|
|
|
|
|
נחבר השלמים יהיו רע"ה גם נחבר השלמים השברים כמו שעשינו בפרק חיבור שברים יהיו אחד שלם ונ"ט חלקים מצ' כיצד נשויה השברים יהיה האב הכולל צ' והנה ה' תשיעיותיו הם נ' וג' חמשיותיו הם נ"ד וחציו מ"ה ויהיה כזאת הצורה
|
|
|
|
|
|
נחברם כולם יהיו קמ"ט נגרע מהם צ' לשלם אחד ישארו נ"ט והם חלקים מצ' כנזכר והנה עלה לנו מחיבור י"ג שלמים וה' תשיעיות עם כ"ו וג' חמשיות ועם רל"ו וחצי רע"ו שלמים ונ"ט חלקים מצ' בשלם והוא הדרוש
|
- The third example on addition of integers and fractions of two types: such as 22 integers and three-quarters plus 4-fifths with 30 integers and a quarter plus 2-thirds.
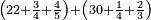
|
משל שלשי בחיבור שלמים ושברים משני מנים עם דומיהם כמו כ"ב שלמים ושלשת רביעיות וד' חמשיות עם ל' שלמים ורביעית וב' שלשיות
|
|
|
[140]
| |
|
כב
|
 |
 |
ל
|
ז
הא |
נ"ד
|
|
|
|
|
[...] השברי' [...] ס' וג' רביעיות [...] ורביעיתו ט"ו וב' שלישיותיו [...] נחלקם על המורה יעלו ב' שלמים ונשארו [...] מס' [בש]לם שאם תקצרם ישובו לז' חלקים מט"ו [בשלם] והנה המחובר מכ"ב שלמים וג' רביעיות וד' חמשיות עם ל' שלמים ורביעית וב' שלישיות יהיה נ"ד שלמים וז' חלקים מט"ו בשלם
|
- The fourth example: we wish to sum integers and fractions of fractions with integers and fractions of fractions, such as 235 integers and a quarter of a fifth with 326 integers and two-thirds of 3-quarters.
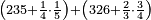
|
משל רביעי רצינו לחבר שלמים ושברי שברים על שלמים ושברי שברים כמו רל"ה שלמים ורביעית חמשית עם שכ"ו שלמים וב' שלשיות מג' רביעיות
|
- According to this diagram:
|
בזאת הצורה
|
|
|
|
|
|
נחבר השלמים יהיו תקס"א נשוה השברים יהיה אחד הקיצור י"א חלקים מכ' שהם חצי שלם וחלק מכ' בשלם
|
|
|
והמעשה אעשה בשני דרכים להרגילך בדרכי המספר
|
|
|
הדרך האחד הוא שתקח כל שבר השבר בפני עצמו וקח חלק כל אחד ואחד תשוה את שניהם והעולה משניהם תחבר וחלקם על המורה והם שלמים וכן נעשה נקח הרביעית חמשית מן החלק הראשון שהוא חלק מכ' ושני שלישיות מג' רביעיות מן השבר השני והוא ו' חלקים מי"ב שהוא חצי ואז היה לנו מן השני שברים חלק מכ' ומן השני [141][...] מורה [...] ד' ורביע[י]ת [...] כנזכר והוא [...] וכן נעשה בשבר השבר [...] רביעיותיו הם ט' ושני שלישיות [...] השבר השני נקצרהו יהיה [...] בצורה המונחת והמורה הכולל מ' ואם נרצה הוא כ' אבל נניח זה והנה חציו הוא כ' מונח על חצי וחלק אחד מכ' הוא ב' והוא עליו נחברם יהיו כ"ב חלקם ממ' בשלם ואן בשבר הזה שלם אבל נקצרם בחצי יהיו י"א חלקים מכ' כנזכר
|
|
|
הדרך השני הוא שנשוה המורים אל אב אחד ויהיה ס' ונסדר השברים בזאת הצורה
|
|
|
|
|
|
ונקח ג' רביעיות ס' והם מ"ה וב' שלישיותיו ל' וזה שבר השבר האחד גם נקח חמשית ס' והוא י"ב ורביעית י"ב הוא ג' וזה שבר השבר האחר נחבר ג' עם ל' יהיו ל"ג וזה המבוקש שהם ל"ג חלקים מ' ס' כזה
|
|
|
|
|
|
נקצרם בשלישית ישובו י"א חלקים מכ' כנזכר והנה יצא לנו מחיבור רל"ה שלמים ורביעית חמשית עם שכ"ו שלמים ושני שלישי ג' רביעיות תקס"א שלמים וחצי וחלק מכ' בשלם
|
|
משל חמשי רצינו לחבר שלמים ושברי שלמים עם שלמים ושברי שלמים כגון ב' שלמים וג' רביעי ד' שלמים עם ה' שלמים ושני [142]שלישי [...] הנה יש בו [...] דרך משל אחד [...] המשל הוא שתכפול ה[...] שבריו וחלק העולה על [...] השלמים ואם יש בידך שלמים [...] חברם אלהם וכן תעשה בחלק השבר ואם [...] והמעשה במשלנו שכפלנו ד' בג' יעלו י"ב רביעיות וחלקם על ד' שהוא המורה יעלו ג' שלמים ונשמור אותם או נחברם עם הב' שלמים יהיו ה' בחלק הראשון גם נכפול ו' על ב' שלישיים יעלו י"ב שלישיים מונח על ב' נחלקם על ג' יעלו ד' שלמים וה' שלמים שהיו בחלקו יהיו ט' וה' שהיו לנו היו י"ד והוא המבוקש
|
|
משל חמשי שרצינו לחבר שלמים ושברי שלמים על דומהם בדרך השני והוא שתכפול כל שלם אשר שברו אתה מבקש על שבריו והעולה מהכפל תתן למעלה על שבריו כמו שעשינו בהשואה ואחר תשוים עם מוריהם וחיבורם תחלק על המורה הכולל והעולה הוא המבוקש
|
|
|
כמו בזה המשל שרצינו לחבר י"ח שלמים וה' שמניות מי"א שלמים עם כ"ה שלמים וז' תשעיות מח' שלימים בזאת הצורה
|
|
|
| מי"א |
 |
י"ח
|
| מח' |
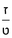 |
כ"ה
|
|
|
|
|
נכפול י"א על ה' יהיו נ"ה שמיניות גם ח' על ז' יהיו נ"ו תשיעיות ויהיו שניהם בזאת הצורה השנית תשוים יהיו האחד תצ"ה והשני [143][...] וחלקם [...] שלמים וז' [...] נ"ה יהיו נ"ו [...] והוא המבוקש והנה [...] תכפול י"א על ה' יעלו נ"ה [...] מורה חברו יעלו שהוא ט' יעלו [...] בח' על ז' יעלו נ"ו גם נ"ו על מורה חברו שהוא ח' יעלו תמ"ח תחבר שניהם יהיו תתקמ"ג חלקים על המורה הכולל יעלה בחילוק י"ג וז' ע"בין כנזכר
|
|
משל שביעי בחיבור שלמים ושברים מדברים מתחלפים מממון ומזמן וממשקל וממדה ואקצר כפי מה שאוכל
|
|
|
ואומר שרצינו לחבר רל"ג לטרי ממון וי"ט דנרין וג' פשיט' ומחצה עם תס"ג לטרי ממון י"ב דנרי' עשרה פשי' ומחצה ועם תש"ט לטרי' י"ד די' י"א פשי' ומחצה נקבץ כל מין עם מינו והיוציא יהיה אלף תכ"ז לטרי ממון ז' די' ופשי' ומחצה ויהיה בצורה הזאת
|
|
|
| לטרי' |
דנרי' |
פשי' |
מחצה
|
| גהב |
טא |
ג |
א
|
| גוד |
דא |
0א |
א
|
| ט0ז |
דא |
אא |
א
|
| זבדא |
ז |
א |
א |
המקובץ
|
|
|
|
וראוי שתדע כי ב' מחצות הרי פשוט וי"ב פשיטי הם דנר וכ' דינרין לטרה גרע מהמחצות פשוט ישאר מחצה ויהיה הפשיטי כ"ה קח מהם ב' די' [144]קח מ[...] דיני' ופשוט [...]
|
|
משל שמני [...] [רנ"ב כיכרין] וג' שקל[...] [כ"ח ליט' ט' אוקיות] וי"ב דראהם עם שע"ח כיכרים [ב' שקלי' כ"ד ליט' י"א] אוקיות ז' דראהם ועם תתקפ"ו כיכרי' [ושקל אחד] וי"ג לטרין ועשרה אוקיות וי"ד דראהם נקבץ כל מין עם מינו והיוציא יהיה אלף תרי"ח כיכרים וז' לטרין וח' אוקיות וא' דראהם ויהיה כזאת הצורה
|
|
|
| כיכרים |
שקלים |
ליטר |
אוקיות |
דרהם
|
| בהב |
ג |
חב |
ט |
בא
|
| חזג |
ב |
דב |
אא |
ז
|
| וחט |
א |
גא |
0א |
דא
|
| חאוא |
0 |
ז |
ח |
א
|
|
|
|
[145]והבחינה עם משל אחר מג' טורים גרע מהעולה מכולם חיבור הב' טורים וישאר הטור השלישי או יותר טורים אם יהיו
|
|
|
[146]והמשל בג' טורים חיברנו ב' ליטרי ממון וג' די' ו' פשוטי' עם ג' לטרי' ד' די' ה' פשי' ועם ד' לטר ה' די' ג' פשי' ויהיה כזאת הצורה
|
|
|
| לט' |
די' |
פש'
|
| ב |
ג |
ז
|
| ג |
ד |
ה
|
| ד |
ה |
ג
|
|
|
|
|
חיברנו שלושתן יעלו ט' לטרי' י"ג די' ב' פשי' וזה כל הממון ושמור אותו
|
|
|
[147]והבחינה חיברנו הב' טורים העליונים יהיו ה' ליטרי' ז' די' י"א פשי' גרענום מכל הממון השמור נשאר הטור השלישי שהוא ד' ליטרי' ה' די' ג' פשי' עוד חיברנו הטור השני והשלישי שהם ז' לטרי' ט' די' א' פשי' גרענום מכל הממון ישאר הטור הראשון שהוא ב' ליטרי ג' די' ו' פשי' עוד נחבר שני טורים הראשונה והשלישית שהם ו' ליטרי ח' די' ט' פשי' גרענום מכל הממון וישאר האמצעי שהוא ג' לטרי ד' די' ב' פשי' ובזה הדרך תעשה [...] טורים או יותר שתקבץ כולם חוץ מאחד [...] תחזור ה[...]
|
|
|
וראוי שתדע כי י"ו דרהם הם אוקיא וי"ב אוקיות הם לטרה ושלושים לטרין הם שקל אחד וד' שקלים הם כיכר
|
|
משל תשיעי ממדה רצינו לחבר רנ"ח כורי חיטה וג' ארובש ד' קוארטאליש ג' אלמודיש עם תכ"ג כורים ב' ארוכה ה' קוארטאליש ב' אלמודיש ועם קס"ז כורי' ב' ארוביש ב' קוארטאל א' אלמוד נחבר הכל יהיה תת"ק כורים וח' קוארטרלי ז' ארובלה ב' אלמודיש ב' אלמודש הכול בזאת הצורה
|
|
|
וראוי שתדע כי ד' אלמודש הם קוארטאל וכ"ד קוארטאלי כאפיז ו' קוארטאליש הם ארובה וד' ארובש הם כאפיז [148][...]
|
- [Example ten] of time: we sum 571 years, 26 days, 18 hours, 55 minutes, 50 seconds, 36 thirds, and 29 fourths, with 257 years, 29 days, 13 hours, 29 minutes, 11 seconds, 50 thirds, 40 fourths, and with 588 years, 16 days, 19 hours, 38 minutes, 52 seconds, 41 thirds, 14 fourths.
|
[משל עשירי] מזמן חיברנו תקע"א שנים כ"ו ימים י"ח שעות נ"ה דקים נ' שניים ל"ו שלישיים כ"ט רביעיים עם רנ"ז שנים כ"ט ימים י"ג שעות כ"ט דקים י"א שניים נ' שלישי' מ' רביעיים ועם תקפ"ח שנים י"ו ימים י"ט שעות ל"ח דקים נ"ב שניים מ"א שלשי י"ד רביעיים
|
- We sum up all; the result is one thousand and 416 years, 73 days, 4 hours, 3 minutes, 55 seconds, 8 thirds, 23 fourths. Like this diagram:
|
נחבר הכל ויהיה היוציא אלף תי"ו שנים ע"ג ימים ד' שעות ג' דקים נ"ה שניים ח' שלישים כ"ג רביעיים ויהיה בצורה הזאת
|
|
|
| שנים |
ימים |
שעות |
דקי' |
שניי' |
שלישי' |
רביעיי'
|
אזה
זהב
חחה |
וב
טב
וא |
חא
גא
טא |
הה
טב
חג |
0ה
אא
בה |
וג
0ה
אד |
טב
0ד
דא
|
| ואדא |
גז |
ד |
ג |
הה |
ח |
גב
|
|
|
|
והנה [יד]עת כי ס' רביעיי' הם שלישי וס' שלישיים הם שני רביעי וס' שניים הם דק וס' דקים שעה וכ"ד שעות יום ושס"ה ימים ושש שעות שנה בהסכמה והרשות בידך לעשות השנה עיבורית או כפי מה שתרצה וכן החדשים ובעבור זה הנחתי הימים ולא עשיתי מהם חדשים
|
|
[149][משל אחד עשר] [...] [מזלות כ"ו מעלות נ"א דקים ל"ב שניים כ"א שלישים כ"ז] רביעיים [נ' חמשיים עם ז' מזלות כ"א מעלות ל"ו דקים] מ"ד שניים נ' שלש[ים נ"ח רביעים י"ו חמשים עם י"א] מזלות כ"ח מעלות נ"ז [דקים מ"ב שניים ל"א שלישים כ'] רביעיים י"ז חמשים וה[יוציא] [...] [מזלות י"ז] מעעלות כ"ה דקים נ"ט שניים מ"ג [שלשים מ"ו רביעים] כ"ג חמשים ויהיה בזה הצורה
|
|
|
| מזלות |
מעלות |
דקים |
שניי' |
שלישי' |
רביעיים |
חמשיים
|
0א
ז
אא |
וב
אב
חב |
אה
וג
זה |
בג
דד
בד |
אב
0ה
אג |
זב
חה
0ב |
כה
וא
זא
|
| ה[.] |
זא |
הב |
טה |
גד |
וד |
גב
|
|
|
|
וכבר ידעת כי המזלות י"ב וכל מזל ל' מעלות וכל מעלה ס' דקים וכל דק ס' שניים וכן לעולם
|
|
|
והבחינה תחבר הב' טורים וגרע [מן הגדול מן הג' טורים שחיברת והנשאר תהיה הטור השלישי שהנחת עוד תחבר ב' טורים ותגרעם מן הגדול ושאר הטור שנחת וכן לעולם כמו שאמרתי בפרק המאזנים ובלטרי ממון ודי' ופשיט']
|
- Example twelve: we wish to sum 4 days, 19 hours, and 925 intercalary parts, which is the excess of seven cycles, with one day, 11 hours, and 590 parts, which is the excess of 50 months.
|
משל שנים עשר רצינו לחבר ד' ימים י"ט שעות תתקכ"ה חלקים עיבוריים שהוא מותר שבעה מחזורים עם יום אחד י"א שעות תק"ץ חלקים שהוא מותר נ' חדשים
|
- The result is 6 days, 7 hours, and 435 parts. As this diagram:
|
יהיה היוציא ו' ימים ז' שעות תל"ה חלקים בצורה הזאת
|
|
|
| ימים |
שעות |
חלקים
|
ד
א |
טא
אא |
הבט
0טה
|
| ו |
ז |
הגד
|
|
|
|
וזה מותר נ"ז מחזורים כי נעשה מאלף מאלף ופ' חלקים שעה אחת ומכ"ד שעות יום אחד ואם יעלה מקיבוץ הימים [150][....] כאן די בזה[151] [...] למיניהם
|
The Second Chapter on Multiplication of Integers and Fractions
|
|
|
|
[...] הרוצה לכפול שלמים [...] השלמים על השברים [...] והיוציא בחילוק הוא המבוקש
|
- For example: we wish to multiply 13 by 3-quarters, or 3-quarters by 13 integers, because it is the same.
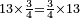
|
[המשל] בזה רצינו לכפול י"ג על ג' רביעיות [או ג' רביעיות על י"ג שלמים כי הכל אחד]
|
- According to this diagram:
|
בזאת הצורה
|
|
|
 |
יג
|
|
|
- Multiply 13 by the numerator 3; the result is 39-quarters, like this:
|
כפול י"ג על ג' שברים יעלו ל"ט רביעיות כזה
|
|
|
|
- Divide them by the denominator, which is 4; the resulting quotient is 9 integers and 3-quarters and this is the required.
|
וחלקם על המורה שהוא ד' יעלו בחילק ט' שלמים וג' רביעיות והוא המבוקש
|
- The second example of integers by fractions of fractions: we wish to multiply 38 integers by 2-thirds and 3-quarters.
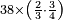
|
משל שני משלמים על שברי שברים כמו שרצינו לכפול ל"ח שלמים על ב' שלישיות מג' רביעיות
|
- According to this diagram:
|
בזאת הצורה
|
|
|
 |
- |
 |
על |
חג
|
|
|
|
|
נשום והנה האב הכולל הוא י"ב וג' רביעיותיו הם ט' וב' שלישיות ט' הם ו' חלקים מי"ב שהם שבר השבר הנרצה לכפול על ל"ח ולחלק היוציא על י"ב אבל אם נרצה נוכל לקצרו ויהיה יותר נקל ויהיה חצי והנה שבה השאלה כאומר כפול [.] ל"ח שלמים על חצי כזאת הצורה
|
|
|
 |
חג
|
|
|
|
|
כפול ל"ח על אחד שהוא השבר יהיו ל"ח חלקים על המורה שהוא ב' יעלה בחילוק י"ט שלמים והוא המבוקש
|
|
|
משל שלישי משלמים ושברים על שלמים ושברים כמו ב' שלמים וב' שלשיות על ג' שלמים וג' רביעיות בזאת הצורה
|
|
|
| ג |
 |
על |
 |
ב
|
|
|
|
|
הנה לעשותה בשני פנים הראשונה הוא שתכפול השלמים על השלמים ואחר תכפול כל שלם [152]בשבר [...] שברים [...] עליו ויהיו [...] ב' שלמים על ג' [...] הב' שלמים על ג' רביעיות [...] השלם האחר על שהוא ג' על ג' שליש[...] גם תכפול השברים ג' רביעיות על ב' שלישיות [...] השיווי ששה חלקים מי"ב שאם תקצרם יהיו חצי ואחר תקבץ תקבץ הכל ששה שלמים וששה שלישיות שהם ב' שלמים יהיו שמונה ואחד וחצי מששה רביעיות יהיו ט' וחצי וחצי שהיה לנו מהשברים יהיו עשרה והוא המבוקש
|
|
|
והפנים השניים אשר בה אעשה כל המשלים הוא שתתן השלמים בשבריהם ואחר כפול שבר על שבר ומורה על מורה והיוצה בחילוק על המורה שהם השלמים כציד במשל המונח שהוא ב' שלמים ושני שלישיות על ג' שלמים וג' רביעיות כפול ב' שלמים במורה שברו שהוא ג' ויהיו ו' תחברם עם שברו שהוא ב' יהיו ח' שלישיות גם כפול ג' על מורה שברו שהם ד' יהיו י"ב ועם ג' יהיו ט"ו והם רביעיות ויהיו שניהם כזאת הצורה
|
|
|
|
|
|
ואחר כפול שבר על שבר ומורה על מורה ויהיו ק"ך חלקים מי"ב חלקם לי"ב יעלו בחילוק עשרה והוא המבוקש שאלת סוחר
|
|
|
משל ששי רביעי בכפל שלמים ושברי שברים על שלמים ושברים כמו נ"ח [153][...] וד' פשיט [...] בשני דרכים [...]
|
|
|
הדרך הראשון הוא [...] ד' הוא שלש וג' רביעיות [...] שהוא שלישית דינר נתן הי"ב דינ' [...] שלשיות וזה סך כור אחד נכפלם על עשרה יהיו שי"ג נחלקם על ג' שהוא המורה יעלו קכ"ג די' ושליש דנר שהוא ד' פשי'
|
|
|
ובדרך השנית נתן הי"ב דנ' בפשיטי' ונוסיף עליהם הפשיט' ונכפול אלה הפשי' על הנשאל והעולה אם נרצה דנר' נחלקם על י"ב ויהיו די'
|
|
|
והמשל הנה הסוחר קנה עשרה כורי [.] חיטה לסך י"ב די' וד' פשיט' נתן הי"ב די' בפשטי' יהיו קמ"ד ועם ד' שהיה לנו יהיו קמ"ח וזה סך כור חיטה אחד נכפול קמ"ח על עשרה יהיו אלף ת"ף פשיט' שהם סך כל החטה
|
|
|
ולעשותם דינ' נחלקם על י"ב יהיו קכ"ג די' וד' פשיט'
|
|
|
ואם תרצה לעשות מקכ"ג די' פרחים תחלקם על סך הפרח ואם לטרי' על כ' ואם דוקאדש על סך הדוקאדו וכן לכל מטבע שתרצה
|
|
|
דרך אחרת כפול שלמים על שלמים והנשברים גם על מה שקנית והכל יהיה שוה
|
|
|
והמשל בזה כפול י"ב על עשרה הם ק"ך גם כפול ד' פשי' על עשרה הם מ' פשי' והם ג' די' וד' פשי' ועם ק"כ יהיו קכ"ג די' וד' פשי' כנז'
|
|
|
שאלה אחרת ראובן קנה ע"ה משאור ע"ה משאות ע"ב פאשטולי לס' ה' לטרין וז' די' וה' פשיט כל משא שאלתי סך הע"ה משאות
|
|
|
תשובה נעשה סך [154]המשא [...] ע"ה והוא [...] תרצה שיהיו די' [...] תרצה לטרי' חלק [...] יהיו ליטרי'
|
|
|
והמשל נעשה [....] ק"ז די' נכפלם על [...] הה' פשוט והם פשטי משא אחת נכפלם על ע"ה יהיו צ"ז אלפים תרע"ה והם פשיטי המכר כולו ונרצה לעשות מהם די' נחלקם על י"ב יהיו ח' אלפים קל"ט די' וי"א פשי' ועתה שהם די' הרשות בידך לעשותם המטבע שתרצה מזהב ועתה נעשה מהם ליטרי' נחלקם על כ' יהיו ת"ו ליטר' י"ט די' ואם כן ע"ה משאות שוים [.] ת"ו לטרי' י"ט די' י"א פשיטי'
|
|
|
ואם כשהם פשיט' תרצה לעשות מהם לטרי' תחלק הפשי' על ר"ע יעלו [.] ת"ו ליטרי' ונשארו רל"ט פשי' לחלק נחלקם על י"ב [.] יעלו י"ט די' ונשארו י"א פשיט'
|
|
|
וכן אם תרצה לעשות מן הפשי' מטבע אחר אם מכסף או מזהב תחלק הפשיט על פשיטי המטבע שתרצה וכן
|
|
|
וכן תעשה בכל השאלות אשר בהם די' ופשי' כי יש בהם שנים דרכים
|
|
|
אשר הדרך הראשון הוא שנעשה הכל פשי' ונכפלם על המכר והיוציא הם פשי' נחלקם על י"ב יהיו די'
|
- Example: Reuven bought 32 loads of grapes
|
והמשל ראובן קנה ל"ב משאות ענבים לס' ח' די וט' פשי' נעשה הדי' פשיטי' בשנכפלם על י"ב יעלו צ"ו ועם הט' פשי' שהיו לנו יהיו ק"ה פשי' והם [.] סך משא אחד נכפלם על ל"ב יעלו ג' אלפים ש"ס פשי' ולעשות מהם די' נחלקם על י"ב ועלו ר"ף די' והם סך הל"ב משאות
|
|
|
הדרך השני ראובן קנה ל"ב משאות ענבים לס' ח' די' [155][...] גם [...] נחלקם על י"ב יעלו [...] שהוא סך הל"ב משאות [...] שלא להאריך אומר [...] והיוציא תחלק על י"ב [...] השברים תלמוד זה בע"ה
|
|
|
אחרת מן הדרך הראשון שתעשה כל מה שתרצה לכפול פשי' ותחבר עמהם הפשי' ואחר תכפול הפשי' על הנרצה והיוציא הם פשי'
|
|
|
ואם תרצה לעשות מהם מטבע כסף תחלקם על סך פשי' המטבע שתרצה
|
|
|
ואם תרצה מטבע זהב עשה הפשי' די' שתחלקם על י"ב וחלק היוציא על די' המטבע שתרצה
|
|
|
והמשל רצינו לכפול ק"ב די' וג' פשי' על י"ד נעשה הדני' פשיט' בשנכפלם על י"ב יעלו אלף רכ"ב פשי' נחבר עליהם הג' יהיו אלף רכ"ז פשי' נכפלם על י"ד יהיו י"ז אלפים קע"ח וכולם פשי' נחלקם על י"ב לעשותם די' יעלו אלף תל"א והם די' [וששה פשי']
|
|
|
ואם תרצה לעשות מהם פרחים תחלקם על סך הפרח ואם לטרי' על כ' וכן לכל מטבע שתרצה
|
|
|
והדרך השני הוא שנכפול הדי' על הנרצה ושמרם כי הם די' וגם נכפול הפשי' על הנרצה ויהיו פשיטי' נחלקם על י"ב ויהיו די' אשר תחברם על הדי' השמורים
|
|
|
והמשל כפלנו ק"ב די' על י"ד יעלו אלף תכ"ח די' ונשמור אותם גם כפלנו ג' פשי' על י"ד יעלו מ"ב פשי' נחלקם על י"ב יעלו ג' די' וששה [פשיטי'] נחברם על אלף תכ"ח יעלו אלף תל"א והם די' ועוד ששה פשי'
|
|
|
[156]משל [...] שלוש[...] חציים יהיו הט' [...] נחלק גם נעשה [...] חציים כמו המחלק יהיו [...] ג' אוקיות וט"ו חלקים מי"ט וזה הראוי לכל [...] חלקים על י"ו שהם חלקי האוקיה נקראים אריאינסיש יעל[...] נחלקם על י"ט ותציא בחילוק י"ב אריאינסוש ונשארו י"ב והם חלקי י"ט באריאינסו והנה עלה לכל פשוט ג' אוקיות י"ב אריאינסוש י"ב יטין מאריאינסו כזה
|
|
|
|
|
|
והבחינה כפול מה שיציא למחצה שהוא אוקייה אחת וי"ד אריאינסוא וששה יטין י"ט פעמים יעלו ל"ו אוקיות שהם ג' ליטרי' כנז'
|
|
|
משל אחר סוחר קנה ב' ליטרי סוקרי וחצי בסך ב' די' שאלתי סך כל ליטרה התשובה נחלק ב' די' על ב' וחצי לא תוכל נתן השלמים בשברהם יהיו הסוקרי ה' חציי ליטרה והב' די' כ"ד פשיט חלק כ"ד על ה' יעלה בחילוק ד' פשי' וד' חומשים לחצי הלטרה
|
|
|
והבחינה נכפול ד' וד' חמשיות על ה' יעלו כ"ד פשי'
|
|
|
אחרת סוחר קנה ד' ליטרין וחצי סוקרי בשני די' וט' פשיט' שאלתי סך הליטרה התשובה תן הכל בשברהם יהיו ט' חציי ליטרה והפשיט ל"ג נחלק ל"ג על ט' יבואו ג' פשיטי' ושני שלישי פשוט וזה ראוי לחצי הליטרה
|
|
|
והבחינה כפול ג' ושני שלשים על ט' יעלו כ"ד פשיטי' וכן כל הדומה לזה
|
|
|
משל בכפל שלמים ושברי שברים על שלמים ושברים כמו נ"ח [157][...]
|
|
|
 |
מ"ד |
על |
[...]
|
|
|
|
|
[...] שברים והוא ל' וקח [...] על ד' חמשיות נקח [...] שהם כ' וזה השבר המבוקש שהוא כ' חל[קים] מל' בשלם ו[אי]ן לנו עסק בד' חמשיות [...] עתה יש לנו לכפול נ"ח שלמים וכ' חלקים מל' על מ"ד שלמים וג' חמשיות נסדרם בזה הצורה השנית
|
|
|
 |
דד |
על |
0ב
0ג |
חה
|
|
|
|
|
ואז ננהיג בו כמשל שלישי שתכפול נ"ח על מורה שבריו שהוא ל' יעלו אלף ותש"ם תוסיף עליהם שבריו שהם כ' יהיו אלף תש"ס ותנם על ל' שהוא מורה שבריו שמור [שנית] וכן נעשה למ"ד על ג' חמשיות שנכפול מ"ד על מורה שבריו שהוא ה' יעלו ר"ך נחבר עליו ג' שבריו יהיו רכ"ג חמשיות ויהיו כזאת הצורה השלשי'
|
|
|
|
|
|
ועתה נכפלם בדרך השברים שברים על שברים ויהיו שצ"ב אלפים ות"ף וגם מורה על מורה ויהיו ק"ן חלק השברים שהם שצ"ב על אלפים ות"ף על המורה שהוא ק"ן יעלה בחילוק ב' אלפים ותרי"ו ונשארו פ' חלקים מק"ן ואם תקצרם יהיו ח' חלקים מט"ו והוא המבוקש
|
|
|
ואם תרצה להקל מעט בזה הכפל מצד הכ' חלקם מל' תוכל לקצרם ויהיו ב' שלישיות ואחר כפול נ"ח בג' [158]שהיה [...] מ"א [...] השני מורים [...]
|
|
|
משל חמשי רצינו לכפול [...] שלמים כמו ז' שלמים [...] ד' שלמים כזה הצורה
|
|
|
| מד' |
 |
על |
ז'
|
|
|
|
|
הנה ראשונה תשויה הד' שלמים בעבור כי מהם נסרו ג' רביעיות והוא שנכפלם במורה השברים שהוא ד' ויעלו י"ו נקח מהם ג' רביעיותם שהם י"ב והם י"ב רביעיות אשר אם תחלקם על ד' יעלו ג' שלמים והנה שבה השאלה לכפול שלמים על שלמים שהם ז' על ג' שיעלו כ"א והוא המבוקש
|
|
|
והנה תוכל למצוא הג' רביעי ד' בדרך אחרת והוא שתכפול השלם על שברו כי ד' על ג' הם י"ב רביעיות חלקם על ד' שהוא המורה יעלו ג' שלמים ועתה כפול שלמים על שלימים עלו ג' על ז' כ"א כנזכר
|
|
|
משל ששי רצינו לכפול שלמים ושברי שלמים על שלמים ושברי שלמים כמו י"ג שלמים וג' חמשיות מי"ב שלמים על כ"ב שלמים ושני שלישיות מט' שלמים כזאת הצורה
|
|
|
| |
|
|
|
|
וג |
|
| מט' |
 |
כב |
על |
מי"ב |
 |
גא
|
|
|
|
|
והמעשה הוא שתעשה ראשונה מן השלמים [159][...] אחד תכפול [...] כפל המורים [...] שבריו שהוא ה' יעלו [...] יהיו ס' נקח מהם ג' חמשיותיו [] השברים שהם ג' על י"ב יעלו ל"ו חמשיות [...] חברם עם ס"ה חמשיות יהיו ק"א חמשיתיות כזה
|
|
|
|
|
|
והוא החלק הראשון הכופל וכן נעשה לכ"ב שלמים וב' שלישיות מט' שלמים כי כפלנו כ"ב בג' שהוא מורה שבריו יהיו ס"ו שלישיות גם כפלנו ט' בג' יהיו כ"ז נקח ב' שלישיות כ"ז שהם י"ח שלישיות נחברם על ס"ו יהיו פ"ד והם שלשיות כזה
|
|
|
|
|
|
והוא הנכפל נכפול ק"א שהיה לנו על פ"ד יהיו ח' אלפים תפ"ד נחלקם על ט"ו שהם כפל ה' בג' שהם המורים יעלה בחילוק תקס"ז שלמים וט' חלקים מט"ו שאם תקצרם יהיו ג' חמשיות כזה 
|
|
|
משל שביעי רצינו לכפול שלמים ושברי שברי שלמים על שלמים ושברי שברי שלמים כמו ב' שלמים וחצי שלישית י"א על עצמו כזאת הצורה
|
|
|
|
|
|
הנה ראשונה נוציא האב הכולל לשברים והוא ששה [...] ונכפול הי"א שלמים על המורה שהוא ששה יהיו ס"ו נקח שלשית ס"ו יהיו כ"ב והם שלישית י"א שלמים וחציו הוא י"א [160]חלק [...] הב' שלמים [...] מחצי שלישית [...] נכפלהו על [...] על ל"ו שהם כפל [...] י"ד שלמים וכ"ה חלקים מל"ו [...]
|
|
|
|
|
|
משל שמני רצינו לכפול שלמים על שלמים כמו ד' שלמים על ה' שלמים וג' רביע[יות]
|
|
|
כזאת הצורה
|
|
|
| גב |
|
|
|
 |
ה |
על |
ד
|
|
|
|
|
נתן השלם בשברו ה' [על] ד' יהיו כ' וג' שברים יהיו כ"ג נכפול הד' שלמים על כ"ג יהיו צ"ב רביעיות חלקם על ד' ש[הם] המורה יציא בחילוק כ"ג שלמים והוא המבוקש
|
The Third Chapter: Subtraction of Integers and Fractions
|
הפרק השלשי במגרעת המורכבים משלמ[ים] ושברים
|
|
|
דע כי יסוד המגרעת וזולתו מן כפל וחיבור וחילוק בשברים או במורכבים הוא ההשואה ואז יהיו שוים ויהיה נקל לעשות מהם כל מה שתרצה כמו שעשינו במה שעבר בשברים ובמורכבים ועתה במגרעת שלמים ושברים ראשונה תשובת השברים ואחר גרעון אילו מאילו ואז השברים ממורים שוים אין צריך השואה כמו שתראה וכמו שעשינו בחיבור וכמו שתראה עתה בזה המשל
|
|
|
משל ראשון רצינו לגרוע אלף ורמ"ז וח'[161] [162][...] ימים כ"א [...] שלישי לו רביעיים [...] ימים ר"ט שעות [...] שלישיים נ"ב רביעיים כ"ח חמשיים [...]
|
|
|
|
|
| שנים |
ימים |
שעות |
דקים |
שניים |
שלשים |
רביעי |
חמשי'
|
| דגב |
בדב |
טא |
0ג |
בד |
חג |
בה |
חב
|
| האב |
גהא |
אב |
גד |
בה |
אד |
וג |
אה
|
| טא |
חח |
בב |
וד |
וד |
זה |
הא |
זג
|
|
|
|
|
וראשונה תדע כי כאשר תעבור אחד [לשמאל] [...] לימין הוא ששה או שישים ואם מימין לשמאל כל שישים הם אחד
|
|
|
כיצד במשל המוטל נגרע נ"א חמשית מכ"ח לא נוכל נעבור רביעי אחד והם ששה עשרות חמישיות ועתה גרע חמשית אחד מח' חמשיות נשארו ז' למטה נ' שהוא ה' מו' שערכנו ומב' שיש בחמשיות נשארו ג' עם ז' ויהיו ל"ז חמשיות עוד נגרע ל"ו רביעיות מנ"ב נשארו ט"ו כי הם נ"א שעברנו אחד עו' נגרע מ"א שלישיות מל"ח ונעבור אחד נשארו נ"ז שלישיים עו' נגרע נ"ב ממ"ב ומאחד שעברנו נשארו מ"ו שניים עוד נגרע מ"ג מל' ומס' שנעבור משעה ישארו מ"ו כי מל' עברנו אחד עוד נגרע כ"א שעות מי"ח שעות נשארו כ"ב שעות עוד נגרע קנ"ג ימים כי עברנו יום אחד מרמ"א כי יום אחד עברנו נשארו פ"ח ימים עוד נגרע רי"ה שנים מרל"ד נשארו י"ט שנים
|
|
|
והבחינה נחבר טור [ה]גורע עם טור הנשאר ותציא הטור אשר ממנו גרענו כי נ"א ול"ז חמשים יעלו רביעי וכ"ח [163]וכן ל"ו [...] ל"ח עם השלישי [...] שניים ודק אחד [...] אחת ועם כ"א יהיו כ"ב [...] שעות ויום אחד ועם קנ"ג [...] וי"ט יהיו רל"ד שנים והכל בדוק כי שב ה[...] ממנו גרענו
|
|
|
משל אחר רצינו לגרוע שלמים ושברים משלמים ושברים כמו י"ד שלמים וח' שברים מי"א בשלם מכ"ד שלמים וט' שברים מי"ג בשלם כזאת הצורה
|
|
|
צט
ט
גא |
כד |
קד
ח
אא |
זא
|
| קמג |
|
המורה |
|
|
|
|
|
נגרע י"ז מכ"ד ישארו ז' שלמים ואחר תשויה השברים יהיו ק"ד לגרוע מצ"ט והמורה קמ"ג והנה בעבור שלא נוכל לגרוע ק"ד מצ"ט ניקח אחד מהז' שלמים ונעשה אותו שברים כסך המורה שהוא קמ"ג נחבר צ"ט עם קמ"ג יהיו רמ"ב וגרע מהם ק"ד נשארו קל"ח והם חלקים מקמ"ג בשלם והנה אחר שגרענו י"ז שלמים וח' חלקים מי"א בשלם מכ"ד שלמים וט' חלקים מי"ג בשלם נשארו ו' שלמים וקל"ח חלקים מקמ"ג בשלם והוא המבוקש
|
|
|
דרך אחרת לאלה השאלות והוא שניתן השלמים בשבריהם יהיו בזה המשל הי"ז שלמים עם שבריהם קצ"ה שברים מי"א בשלם והכ"ד עם שברהם שכ"א מי"ג בשלם כזה הצורה
|
|
|
|
|
|
ואחר נשוים אל מורה אחד ויהיו הראשון ב' אלפים תקל"ה [164][...] המורה שהוא [...] חלקים מקמ"ג [...]
|
|
|
[...] דברים מתחלפים כמו [...] ופשי' וכו' או מזלות מעלות דקים וכו' [או שנים] וחדשים וימים ושעו' וכו'
|
|
|
תן המספרים במעלותם ואם לא יספיק תעבור אחד ויהיה כמספר המעלה אשר תעבור אותו כמו שתראה ואם תעבור אותו מעלות יותר מאחד תניח במעלות שבאמצע המספר היותר גדול שיוכל להיות בכל המעלות האמצעיות
|
|
|
והמשל בזה רצינו לגרוע קס"ה לטרי ממון ועשרה די' וט' פשיט' ומחצה ורביע מרפ"ז לטרי' הנה ניתן הממון הקטן תחת הגדול במעלותם וניתן ספראש במקום השברים כזאת הצורה
|
|
|
| |
|
ו |
|
| ב |
ח |
ז |
לטרי'
|
| א |
ו |
ה |
לטרי'
|
| א |
ב |
א |
|
|
|
|
|
|
|
|
|
ועתה לגרוע רביעית פשיט מספרא לא נוכל [גם] אין מחצה לעבור ולא פשיט ולא די' הנה נקח לטרא אחת מז' ונשארו ו' ונעבור אותה למקום הרביעיות ונאמר שהיא כ' רביעיות ועתה נאמר כי בעבור הלטרה על כל השברים הניח על הדי' י"ט דינרים ועל הפשי' י"א ועל המחצות אחד ועל הרביעיות ב' כי מב' נגרע רביע אחד ונשאר רביע וממחצה נגרע מחצה ונשאר 0' ומי"א [.] נגרע ט' פשיט [165][...] ליטרי' ה' [...] נשאר א' והנה [...] ורביע פשוט
|
|
|
והבחינה תחבר הנשאר עם ה[...]
|
|
|
משל אחר רצינו לגרוע ח' מזלות י"ז מעל[ות] [מ"ב] דקים ל"א שניים כ"א שלישי י"ב רביעיים מי"ב מזלות נסדרם במעלותם וניתן ספרא במקום שאין מספר ויהיו כזה הצורה
|
|
|
| אא |
|
טב |
|
טה |
|
טה |
|
טה |
|
0 |
|
| בא |
מזלו |
0 |
מעלות |
0 |
דקים |
0 |
שניי |
0 |
שלישיי |
0 |
רביעיים
|
| ח |
מזל |
זא |
מעלו |
בד |
דקים |
זג |
שניים |
אב |
שליש |
בא |
רביע
|
| ג |
מזלו |
בא |
מעלו |
זא |
דקי' |
בב |
שניי' |
חג |
שליש |
מח |
רביע
|
|
|
|
|
נגרע י"ב רביעים מספר לא נוכל ולא השברים האחרים אבל נעבור מזל אחד על הרביעיים ונאמר שהוא ס' רביעיים ונגרע ממנו י"ב ונשארו מ"ח רביעיי ועתה תכתוב על ספרא שלישיים נ"ט ועל השניים נ"ט ועל השלישיים נ"ט ועל הדקים נ"ט ועל המעלות כ"ט ועל המזלות י"א ועתה גרע כל מין ממינו ישארו בשלישי' ל"ח ובשניים כ"ב ובדקים י"ז ובמעלות י"ב ובמזלות ג' והוא מה שרצינו
|
|
|
והבחינה תחבר הנשאר והמספר הקטן ותציא הגדול
|
|
|
משל אחר לגרוע מזלות מעלות עד שלישיות או יותר אם תרצה ממזלות לבד תשטח מזל אחד עד השבר שתרצה ובאחרון תן ס' ובאמצעיים נ"ט בכל אחד ובמעלות כ"ט ויהיה כזה הצורה שנגרע מי"א מזלות שנשארו מזלות [166][...] מזלות ה' ונשארו ששה וט' מעלות מכ"ט נשארו עשרים מעלות [...] נשארו י"ח ול"ד שניי מנ"ט נשארו כ"ה [...] מכ"ג נשארו כ' שלישיים
|
|
|
והבחינה תחבר השני טורים התחתונים שהם הקטנים ותציא י"ב מזלות
|
|
|
משל אחר רצינו לגרוע מטבע זהב מאחר ושיהיה דני' ופשיט ואם תרצה מחצות הנה אם קצת מעלות הנשאל לגרוע ממנו הוא קטן הנה הוא קשה מעט אבל קודם שתגרע תעבור סך אחד ממטבע הזהב ותחלקהו על מעלות שבריו ואז תגרע בנקל
|
|
|
המשל בזה רצינו לגרוע מאלף רמ"ה דוקאדוש וי"ו די' וט' פשי' כל אלה מתקצ"ה י"ח די' י"א פשי' ויהיה כזאת הצורה
|
|
|
| ד |
|
אב |
|
בא |
|
| הדבא |
דוקדוש |
וא |
דינ' |
ט |
פשי
|
| הטה |
דוקאדוש |
חא |
דניר |
אא |
פשי
|
| טדו |
דוקדוש |
טא |
דנרי |
0א |
פשי
|
|
|
|
|
הנה בעבור שלא נוכל לגרוע י"א פשי מט' ולא י"ח די' מי"ו נעבור דוקאדו אחד בשבריו ונתן על י"ו די' כ"א ועל ט' פשי' י"ב כי זהו סך הדוקאדו ועתה נגרע י"א פשי' מט' וי"ב שהם כ"א פשי' נשארו עשרה פשי' גם נגרע י"ח די' מי"ו וכ"א שהם ל"ז נשארו י"ט די' גם נגרע תקצ"ה דוקאדי מאלף רמ"ד נשארו תרמ"ט והוא המבוקש
|
|
|
ומשל תראה ממזלות ומלטרי' שהם דומים לזה
|
|
|
[167]משל א[חר] [...] תתקמ"ו [...] בזה השואה אל[...] ותתנהו על מורה התשיעית [...] על ט' וגרע ממנו הח' ישאר א' יהיו [...] תשיעית ואחר גרע שלמים משלמים [...] לנו אחר שגרענו הנז' תצ"ו ותשיעית כזה  והוא המבוקש והוא המבוקש
|
|
|
והבחינה תחבר הב' הקטנים ותציא הגדול
|
|
|
משל אחר שרצינו לגרוע שלמים ושברי שברים משלמים ושברי שברים שלמים כמו קי"א שלמים וששה שביעיות מה' תשיעיות שרצינו לגרוע מקמ"ד שלמים וח' תשיעיות עשרית מד' שלמים כזאת הצורה
|
|
|
| |
|
|
|
|
הג |
|
|
|
|
| מד' |
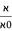 |
מ |
ח
ט |
דדא |
 |
מ |
X |
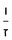 |
אאא
|
| |
|
|
|
|
|
|
גו |
|
|
|
|
|
|
הנה ראשונה נשויה שברי הגורע ונמצא המורה וה' תשיעיותיו הם ל"ה נקח ו' שביעיות ל"ה והם ל' וזה השבר הנרצה שהוא ל' חלקים מס"ג והנה שב הגורע קי"א ול' חלקים מס"ג כזה
|
|
|
|
|
|
ונשמרם עד שנשויה המספר השני וראשונה נוציא השברים והמורה שהוא צ' ואחר נשויה הד' שלמים והוא שנכפול ד' על צ' שהוא המורה הראשון יעלו ש"ס והוא מורה שני ועשיריתו הוא ל"ו וח' תשיעיותיו הם ל"ב חלקים מש"ס בשלם כי תשעית ל"ו הם ד' וח' פעמים ד' הם ל"ב כנז' והוא השבר השני המבוקש והנה שב המספר ושבריהם לגרוע קי"א שלמים ול' חלקים [168][...] בזה הצורה [...] בשאלו [...]רים הם משני מינים [...] תשוים השואה שלישית וזה שנכפול כל שבר על מורה חברו ויעלו לעשרת אלפים [...] ולשני ב' אלפים וי"ו ואז יהיו השברים שוים אשר [נו]כל לגרוע זה מזה אלא שהשברים הגורעים הם יותר משברי המספר השני ולכן נקח אחד שלם ונעשה ממנו חלקים כפי המורה הכולל מש"ס על ס"ג שהוא כ"ב אלפים תר"ף ונחברם עם שברי המספר שרצינו לגרוע ממנו שהם ב' אלפים וי"ו ואז יהיו כ"ד אלפים תרצ"ו ואחר נסדרם לגרוע זה מזה וגם השלמים ויהיו כזאת הצורה
|
|
|
|
|
| שברים
|
| ב |
ד |
ו |
ט |
ו
|
| א |
0 |
ח |
0 |
0
|
| א |
ג |
ח |
ט |
ו
|
|
| השיור
|
|
|
|
גרענו השברים מן השברים נשארו י"ג אלפים תתצ"ו מכ"ד אלפים ותר"ף בשלם גם נגרע קי"א שלמים מקמ"ג ישארו ל"ב כמו שתראה בצורה למטה ואם נקצר השברים ישובו לקצ"ג חלקים משט"ו בשלם כזה
|
|
|
|
|
|
וזה מה שרצינו
|
|
|
ועיין שגם כן תוכל לעשות ההשואה בדרך האחד עם מורה אחד וקח חלקיהם
|
|
|
וגם כן תוכל לעשות מכל השלמים שברים ותגרע אלו מאלו והנשאר תחלק על המורה והיוציא הם שלמים
|
|
|
והכל שוה כי יש בכל מין דרכים רבים אבל די בזה למבין ותן לחכם ויחכם עוד
|
|
|
והנה כל המשלים שנתתי [.] בפרק החיבור תוכל ללמוד מהם בגרעון וגם מה שבגרעון בחיבור ואין צריך להאריך [169]
|
The Fourth Chapter: Division of Integers and Fractions
|
|
|
|
[170][...] שלמים [...] ושברים [...] שתתן השלמים [...] ותחלקם והיוציא בחלוקה [...] נרצה לחלק יהיו שלמים על שברים [...] שברים ממין השבר המחלק והעולה [...]
|
|
|
המשל רצינו לחלק כ"ב לטרין ועשרה דני' וששה פשיט' על ששה ניתן הכל בפשיטי' יהיו ה' אלפים ות"ו כי הכ"ב ליטרי' יהיו ת"מ די' ועוד נכפלם בי"ב יהיו ה' אלפים ר"ף והכל פשי' והעשרה די' עם [..] הששה פשי' יהיו קכ"ו נחברם עם ה' אלפים ור"ף יהיו כולם ה' אלפים ת"ו נחלקם על ששה יעלה בחילוק תתק"א והם פשי'
|
|
|
ואם נרצה נעשה אותם די' ויהיו ע"ה די' ופשוט שהם ג' ליטרי' וט"ו די' ופשוט אחד
|
|
|
והבחנה כפול מה שיצא בחילוק על ששה ויעלו ג' ליטרי וט"ו די' ופשוט
|
|
|
והמשל נכפול הפשוט האחד בששה יעלו ששה פשיט' ונשמרם וששה פעמים ט"ו הם צ' שהם ד' ליטרי' ועשרה די' נשמרם וששה פעמים ג' לטרי' הם י"ח ליטרי' וד' שהיו בידינו יהיו כ"ב ליטרים והנה היו כולם כ"ב ליטרי' ועשרה די' וששה פשיט
|
|
|
משל אחר רצינו לחלק שלמים על שברים כמו כ"ה שלמים על ג' חמשיות כזאת הצורה
|
|
|
| כ"ה |

|
|
|
|
הנה נעשה השלמים חמשיות שנכפלם על מורה השברים ויהיו קכ"ה חמשיות נחלקם על ג' יעלה בחילוק מ"א שלם וב' שלישיות ואל תתמה על היוציא בחלוקה שהוא יותר ממה שהיה לנו כי הוא כאומר חלק חצי לחצי [171][...] כי [...] שיהיה יעלה הראוי ל[...] חצי דבר אחד לכולו תתן [...] בחלוקה הוא ראוי לאחד שלם [...] ותעיין ותבין שאם תחלק תחלק ו' על ב' [...] בחלוקה ט' שלמים והנוסף שהם ג' הוא הגורע לתשלום [...] שלישיות
|
|
|
משל אחר רצינו לחלק ג' שלמים וג' רביעיות על ב' שלישיים תן השלמים בשברו יהיו ד' רביעות ט"ו רביעיו' השוים עם המחלק שהוא ב' שלישי' יהיו כזה הצורה
|
|
|
|
|
|
יהיו מ"ה חלק על ח' יעלו ה' שלמים וה' שמיניות
|
|
|
משל אחר רצינו לחלק מ"ט שלמים וה' ששיות על ג' רביעי ששית מב' חמשיות כזאת הצורה
|
|
|
|
|
|
הנה ראשונה נתן השלמים בשברהם שהם שישיות ונחברם עם שבריו שהם ה' יהיו רצ"ט ותשמרם לחלק על ג' רביעיות משישית מב' חמשיות תשויה זה השברי שברים ויהיה המורה הכולל ק"ך והנה ב' חמשיותיו הם מ"ח והוא עליו ושישית מ"ח הוא ח' וג' רביעיות ח' [.] הם ששה וזה השבר הנרצה אשר עליו נחלק שהוא ו' חלקם מק"ך בשלם והנרצה לחלק הם שישיות ויהיה כזה הצורה
|
|
|
|
|
|
|
|
|
נשוים כל שבר במורה חברו או בדרך האחרת ויהיו החלקים אשר תרצה לחלק ל"ה אלפים תת"ף והחלקם [172][...] הם אלף [...] תקצ"ו וכ"ד חלקי' [...] וכן תמצאם אם תקצרים [...] תתק"ץ ותחלקים על ג' [...] ההשואה תוכל לקצר אם תרצה [...] זה המשל ורבים ביותר נקל כי תוכל [...] עם שתעשה מורה השברים ס' כי ב' חמשיות חמשיות ס' הם כ"ד ושישית כ"ד הוא ד' וג' רביעיות ד' הם ג' וזה שבר השבר הנרצה שהוא ג' חלקים מס' בשלם ואחר תשויה רצ"ט ששיות עם ג' חלקים מס' כזה
|
|
|
|
|
|
יהיו על רצ"ט י"ז אלפים תתק"מ והם לחלק על י"ח שהוא כפל ו' על ג' ויציא בחילוק תתקצ"ו וב' שלישיות מקוצר כנזכ'
|
|
|
ואם תרצה תוכל להקל עוד כאשר היו בידך ג' חלקים מס' תקצרם קודם שתשוים יהיו חלק אחד מב' תשויהו על ו' שהוא מורה החלק השני יהיה ו' גם תשויה רצ"ט עם כ' יהיו יעלו ה' אלפים תתק"ף חלקם על ו' יעלה בחילוק תתקצ"ו כנז'
|
|
|
והרי לך כי כל זמן שתעיין בהשואה אולי תוכל לקצר מספרך והקל מעליך והכל דרך ישר כי מי יוכל לכתוב הכללים כל שכן הפרטים
|
|
|
משל אחר נרצה לחלק שלמים ושברי שלמים על שברי שלמים כמו ק"ח שלמים וד' תשיעיות מי"ח שלמים על ג' שביעיות ח' שלמים כזאת הצורה
|
|
|
| שלמים |
דב |
|
שלמים |
בז |
שלמים
|
| מח |
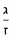 |
על |
יח |
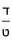 |
קח
|
|
|
|
|
וקח מן הח' שלמים הנשאל והוא שנכפול ח' על ז' שהוא מורה שברו יהיו נ"ו נקח מהם ג' שביעיותיו והוא כ"ד [173]ונשמר[...] שלא תצטרך [...] השברים [...] לכפול ח' על [...] כי אחר שעש[י]ת כל זה [...] פעמים י"ח וכן כדרך זה [...] מי"ח שנכפול י"ח בט' יעלו קי"ו [...] והם ע"ב כי תשיעית קי"ו הוא י"ח וד' פעמים י"ח הם [ע"ב]
|
|
|
ואם תרצה כפול השברים על השלמים אשר תרצה לקחת מהם וה והעולה תתנם עליהם והוא המבוקש ואחר שהיה לנו שברי השלמים שהם ע"ב נחבר אליהם השלמי' שהם ק"ח והוא שנכפלם על מורה אלו השברים שהוא ט' יעלו תתקע"ב והם תשיעיים והשברים אשר נרצה לחלק עליהם שהם כ"ד שביעיים נשויה שניהם כזאת הצורה
|
|
|
|
|
|
ויהיה המספר הנחלק ו' אלפים תת"ד והמספר אשר עליו נחלק רי"ו והיוציא בחילוק ל"א שלמים וק"ח חלקים מרי"ו בשלם ואם נקצרם יהיו חצי שלם ואם כן המחלק ק"ח שלמים וד' שביעיות מי"ח שלמים על ג' שביעיות מח' שלימים יציא בחילוק לא שלם וחצי וכן כל הדומה לזה
|
|
|
משל אחר אם רצינו לחלק מטבעות מתחלפות עם דנר' ופשטי' וכו' או מזלות ודקים ושניי' וכו' או שניי' חדשי' וכו' הנה נחלק הגדול ראשונה ומה שיציא בחילוק שמור אותו בשמו כופלהו בסך שהוא אם פריס בסך הפרח וכן לטרין או לסך המרובע שיהיה
|
|
|
המשל רצינו לחלק רל"ד לטרי ממון וי"ו די' [174][...] רל"ד [...] לכל אחד [...] ונשמרים [...] על כ' שהוא סך הלטרה [...] י"ו די' שלשו יהיו צ"ו די' נחלקם [...] ד' דינ' ונשמור אותם בשמן ונשארו [...] נכפלם בי"ב יעלו מ"ח פשיט' ועם ט' שלמו יהיו נ"ז נחלקם על כ"ג יעלו ב' פשי' ונשארו י"א פשיט נכפלם על ד' יעלו מ"ד רביעיות נחלקם על כ"ג יעלה בחילוק אחד שהוא רביעית פשוט ונשארו כ"א רביעי' והם כ"א מכ"ג ברביע פשוט כזה
|
|
|
|
|
|
ועלה מזה כי המחלק רל"ד לטרי' י"ו די' ט' פשיט' על כ"ג שעלה לכל אחד עשרה לטרי' י"ד די' וב' פשי' ורביע פשוט וכ"א חלקים מכ"ג ברביע פשוט
|
|
|
והבחינה כפול הרביעיות על כ"ג ועם כ"א שנשארו יהיו מ"ד והם י"א פשוט גם כפול ב' פשוט' על כ"ג יהיו מ"ו פשי' וי"א יהיו נ"ז שהם ד' די' וט' פשיט' גם כפול ד' די' על כ"ג יהיו צ"ב ועם ד' יהיו צ"ו די' שהם ד' לטרי' וי"ו די' גם כפול עשרה לטרי' על כ"ג יעלו ר"ל ועם ד' לטר' יהיו רל"ד והנה שב הכל רל"ד לטר' וי"ו די' וט' פשי'
|
|
|
ותוכל לעשות זה בדרך אחרת שתעשה הכל מן השבר היותר קטן ואחר תחלוק ואחר החילוק תעלה הכל לכללים כמו במשלנו שנעשה הכל פשיט כי הם השבר הקטן והם נ"ו אלפים שס"א הכל פשי' ועתה תחלקם על כ"ג שהוא המורה יעלה בחילוק ד' אלפים תרצ"ו [די'] ונשארו ט' פשיט ונשמרם בשמן ועתה נחלק [175] אלו הדי' [...] רל"ד לטרי' [...] לטרי' וי"ו די' [...]
|
Chapter: The Checking Methods for Fractions
|
פרק במ[...] מאזני השברים [...]
|
|
|
[176]פרק במאזני השברים ואומר כי מאזני השברים הם כמאזני השלמים בעבור כי כאשר תחבר או תגרע או תחלק יהיו לעולם השברים שוים מאיזה מין שיהיה ועל כן תנהיג
|
|
|
[177]פרק במאזני השברים
|
|
|
ואומר כי מאזני השברים הם כמאזני השלמים בעבור כי כאשר תחבר או תגרע או תחלק יהיו לעולם השברים שוים מאי זה מין שיהיו ועל כן תנהיג במאזני השברים כמנהג מאזני השלמים ועם כל הדרכים הנתונים בפרק מאזני השלמים
|
|
|
ובעבור שלא תצטרך לעיין ותראה הדרך למין אכתוב כאן משל אחד מכל אחד מבדיקת כל אחד בהפכו חיבור עם גרעון וגרעון עם חיבור כפל עם חילוק וחילוק עם כפל
|
|
|
והמשל בחיבור הנה אחר שנחבר שברי המספר נגרע מן המקובץ השבר הקטן וישאר הגדול או נגרע הגדול וישאר הקטן כיצד הרי שחיברנו ק"א חלקים מר"א בשלם עם ל"ג חלקים מר"א גם כן [178][...]
|
|
|
|
|
|
[...] ל"ג [...] הנה אחר שנכפול שברי המספר נחלק [...] כאשר תראה כזאת הצורה
|
|
|
|
|
|
ויצאו לך שברי המספר כיצד כפלנו ג' רביעיות וד' חמשיות וה' ששיות והנכפל יהיה ס' חלקים מק"ך כזאת הצורה השנית
|
|
|
|
|
|
נחלק כדרך שכפלנו כי כפלנו ג' על ד' והעולה על ה' יהיו ס' ועתה נחלק ס' על ה' יציא בחילוק י"ב נחלק י"ב על ד' ותציא בחילוק ג' והוא הראשון
|
|
|
או נחלק ראשונה ס' על ג' יצא כ' וכ' על ה' יציא ד'
|
|
|
או נחלק ס' על ד' ותציא ט"ו גם ט"ו על ג' ותציא ה' והוא השלישי
|
|
|
ועשיתי אילו החלוקות להרגילך ובזה הדרך תוכל לבדוק שברים רבים
|
|
|
משל אחר במאזני המגרעת אחר שגרענו שברי המספר נחבר השברים הגורעים עם הנשאר מן הגדול ותציא הגדול כיצד נגרע ת"ח מאלף ש"ל יש ישארו תתקכ"ב כזאת הצורה
|
|
|
| הגדול |
א |
ג |
ג |
0
|
| הגורע |
|
ד |
0 |
ח
|
| הנשאר |
|
ט |
ב |
ב
|
|
|
|
|
והמאזנים אם זה אמת נחבר השבר הקטן שהוא הגורע שהוא ת"ח עם הנשאר מן הגדול שהוא תתקכ"ב הנשאר ותציא הגדול שהוא אלף ש"ל
|
- Example for the check of division:
|
משל במאזני החילוק
|
- After we have divided the fractions of a number, we multiply the result of division by the divisor, then we add the remainder of division to the product and the result is the dividend [lit. the greater].
|
הנה אחר שחילקנו שברי המספר נכפול היוציא בחילוק על המחלק ועל היוציא בכפל נוסיף הנשאר לחלק ותציא הגדול
|
- As when we have divided 256 parts of 168, which is derived from 2-thirds and six-sevenths after the equalization, by 63 parts of 168, which is derived from 3-eighths also after the equalization.
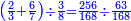
|
כמו שחילקנו רנ"ו חלקים מקס"ח שבא אחר ההשואה מב' שלישיות ומששה שביעיות על ס"ג חלקים מקס"ח גם כן שבא אחר ההשואה מג' שמיניות
|
- They are as this diagram:
|
ויהיו כזאת הצורה
|
-
|
|
|
|
ואם תרצה לבדוק זה אם הוא אמת כפול היוציא [179]בחילוק שהוא ד' [...] עליהם הנשאר שהוא [...]
|
Section Four: Roots
|
השער המורכב [...] בעבור רוב [...]
|
|
|
[...] פרקים
|
|
|
הפרק הראשון הראשון בשרשים
|
|
|
הפרק השני ב[...] מספרים נמשכים
|
|
|
הפרק השלישי
|
The First Chapter
|
הפרק הראשון
|
| I have divided it into four types and an introduction needed for roots at the beginning
|
חלקתי אותו לד' מינים והקדמה בראשונה ראויה לשרשים המין
|
- The first type: extracting the perfect and imperfect square roots
|
המין הראשון בהוצאת בהוצאת השרשים המרובעים השוים והבלתי שוים
|
- The second type: extracting the perfect and imperfect cube roots
|
המין השני בהוצאת השרשים המעוקבים השוים והבלתי שוים
|
- The third type: knowing the root of a number that has no real root
|
המין השלישי לדעת שורש איזה מספר מן המספרים שאין להם שורש אמיתי
|
- The fourth type: knowing the root of fractions
|
המין הרביעי בידיעת שורש השברים
|
Introduction Needed for Roots
|
הקדמה הראויה לשרשים
|
| I say that the square number that is equal in all its sides is the number that is multiplied by itself, which is the root, and the product is the square.
|
ואומר כי המספר המרובע השויה בכל צלעותיו הוא המספר הנכפל על עצמו והוא השורש והנכפל הוא המרובע
|
| The essence of the extraction of the root is that if a number is a product of two different numbers and they generate a rectangle, then the exraction of the root considers it as a square that is equal in all its sides, or a product of two equal numbers and what is left remains.
|
וטבע הוצאת השורש הוא שאם יהיה מספר מה נכפל משני מספרים מתחלפים והם עושים מספר מרובע ארוך הנה הוצאת השורש חוזיר אותו מרובע שויה מכל צלעיו או לכפל שני מספרים שוים או לכפ וישאר מה שנשאר
|
|
|
וזה כגון ב' על ח' [180][...] שורש ד' וזה כי [...] אשר תוכל לשנות צלעותהם [...]חלקיו [...] מורכב מב' ולא יותר ואל ב' תחלקנו [...] צלע ב' ותהיה כזה
|
-
|
|
- If its sides are 2 and 3, like this:
|
ואם צלעותיו ב' וג' כזה
|
-
|
|
- The sides of 8 are 2 and 4.
|
וח' צלעותיו ב' וד'
|
|
|
וכן עשרה
|
- 12 has two combinations: 2 by 6; and 3 by 4.
|
וי"ב יש בו ב' הרכבות ב' על ו' וג' על ד'
|
- 30 has three combinations: 2 by 15; 3 by 10; and 5 by 6.
|
ול' יש בו ג' רכבות ב' על ט"ו וג' על עשרה וה' על ו'
|
- 60 has five combinations: 2 by 30; 3 by 20; 4 by 15; 5 by 12; and 6 by 10.
|
וס' יש לו ה' הרכבות ב' על ל' וג' על כ' וד' על ט"ו וה' על י"ב וו' על עשרה
|
- The root of 60 is 7 and 11 remains.
|
והנה שורש ס' הוא ז' ונשארו י"א
|
|
|
ומאלה הערה לכולם והנה גם כפל מרובע על מרובע יהיה מרובע ואם יהיו כמה שיהיו גם תעין כי כל המדריעות הנפרדים יש להם שורש ואן לזוגות שורש ולכן יהיו המדריעות נחלקים במעשה שנים שנים כמו שתראה
|
|
|
המין הראשון בהוצאת השרשים מן המספר המרובע השוה
|
| The result is a true root.
|
והיוציא יהיה שורש אמתי
|
| This method itself is [also suitable] for an imperfect square, only the perfect square has no remainder and the imperfect square has a remainder.
|
וזה הדרך עצמו הוא למרובע הבלתי שוה אלא כי מן השוה לא ישאר מספר ומהבלתי שוה ישאר מספר
|
| The procedure and arrangement of the ranks to extract the root is as follows: first you divide your number into pairs.
|
והנה תיקון וסדר המדרגות להוציא השורש כך היא שתחלק ראשונה כל מדרגות מספרך שנים שנים וההתחלה ממעלת האחדים ומן המעלה האחרונה או מן השנים אם יהיו שנים באחרונה תתחיל להוציא השורש או מן האחד אם אין שם שנים וממנה תוציא שורש אחד או מן השנים
|
| Because, from each part you have to extract one root, i.e. one part of the root and I called every two ranks one part.
|
כי מכל חלק תצטרך להוציא שורש אחד ר"ל חלק מן השורש וקראתי לכל שתי מעלות חלק אחד
|
| Consider each part as units and tens, except when you extract it with the remainder of the previous part, because then they are thousands and hundreds, as you will see with God's help.
|
ותחשוב כל חלק לאחדים ועשרות זולת כאשר תקחינו עם הנשאר מן החלק הקודם לו כי אז יהיה אלפים ומאות כאשר תראה בע"ה
|
|
|
ואחר קח החלק האחרון ר"ל בשני מעלות מספרים שבו או מה [181]שיש בו ותוציא ממנו [...] ותן אותו תחת החלק אשר [...] תחבר אותו עם מספרי החלק[...] כמו שעשית בחילוק כי הוצאת השורש [...] הנשאר יהיו אלפים ומאות [בעדף ה]חלק הקוד[ם] [...] השורש וכופלהו בשנים וכן [נתן] לפניו מספר מה ומה שיעלה [...] השורש והמספר הנתון כופלהו על המספר הנתון ואם העולה יהיה שוה למה שנשאר בחלק הראשון יהיה החלק [...] ואם הוא גדול גרע מן המספר הנתון [...] עליו אם הוא קטן ועם אחד שתוסיף ואם עם אחד שתוסיף יהיה [גדול] [קח] קח הראשון אפש"י שהוא קטן וכן סיפרא [...] שאם יקרה שתתן אחד לבד לפני השורש הכפול ויהיה העולה יותר ממה שבחלק ו[...] בחלק השני לא תתן מאומה לפני השורש או תתן ספרא בחלק ההוא ויהיה כמו שורש וכך תנהיג בכל המספר ובכל החלקים עד שיהיה תחת כל חלק חלק מן השורש אם שיהיה מספר או ספרא ויהיה אות החלק אשר יציא ראשונה הוא תחת החלק האחרון שהוא המספר היותר גדול כי האחרון הוא תחת החלק הקטן שהוא אחדים ועשרות והאחדים נמשכים אחריו וכולם הם השורש המבוקש
|
|
|
ובמשלים תראה כל זה מבואר בע"ה
|
- Example: we wish to know the root of 29 million, 505 thousand and 124, and if it is a perfect square or not.
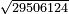
|
המשל בזה רצינו לדעת שורש כ"ט מספרים ותק"ו אלפים וקכ"ד ואם הוא מרובע שוה ואם לא
|
- We arrange the number on this diagram:
|
הנה נסדר המספר בזאת הצורה
|
-
|
|
- I divide the ranks into pairs; they are 4 parts. Now, we know that the number multiplied by itself is 4 ranks by 4 ranks, because each part is one [rank] of the root.
|
והנה חלקתי מעלות המספר שנים שנים ויהיו ד' חלקים ועתה ידענו כי המספר הנכפל על עצמו הוא ד' מעלות על ד' מעלות כי לכל חלק ראוי חלק אחד מהשורש
|
- We start from the last part and say: the greatest square found in 29 is 25 and 4 remains above 9. The root of 25 is 5; we write 5 beneath the fourth part because it is extracted from it.
|
והנה נתחיל מן החלק האחרון ונאמר כי המרובע היותר גדול שיש בכ"ט הוא כ"ה ונשארו ד' על ט' והנה שורש כ"ה הוא ה' נתן ה' תחת החלק הרביעי כי ממנו יציא
|
|
|
וכבר [182][...] והנה לדעת שורש [...] שורש ונכפול אותו בשנים [...] ונאמר שהוא ד' ויהיו אז העשרה [...] נכפול ק"ד על הד'
|
-
|
|
|
|
[...] נגרע תי"ו מת"ן כי הד' שנשארו על הט' [...] בערך לחלק השלישי ונשארו ל"ד בחלק השלשי והם ג' [...] כערך לחלק השני והנה מאחר שהד' הנתון הוא הראוי נכתוב ד' תחת החלק השלישי
|
- If you say that since 34 remains in the third part, the given number is 5, the result exceeds by 75, so we take 4, as mentioned. For with a little investigation you see the number that should be given before doubling the root found.
|
ואם תאמר כי בעבור שנשאר ל"ד בחלק השלשי שיהיה המספר הנתון ה' הנה יעלה יותר מן הראוי ע"ה ובעבור זה לקחנו ד' כנזכר כי עם מעט עיון תראה המספר הראוי לתת לפני כפל השורש הנמצא
|
- To know the root of the second part, do as mentioned, that is, double the two roots found that are 4 and 5, which is 54; it is 108, like this:
|
והנה לדעת שורש החלק השני עשה כנז' והוא שתכפול השני שרשים הנמצאים שהם ד' וה' שהם נ"ד יהיו ק"ח כזה
|
|
|
|
|
|
נתן לפני המספר הזה מספר אחד והראוי הוא ג' ויהיו אז אלף ושמונים ושלושה כזה
|
|
|
|
|
|
כפלנו זה המספר על המספר הנתון שהוא ג' יהיה העולה ג' אלפים ורמ"ט נגרעם מן החלק השני ומהנשאר מן השלישי שהם ג' אלפים ותס"ו ישארו ב' בחלק השלישי וי"ז בשני והם כ"א אלף ות"ש בערך לחלק הראשון והנה מאחר כי ג' הנתון הוא הראוי נכתוב ג' תחת החלק השני
|
|
|
ולדעת שום החלק הראשון עשה כאשר עשית וכפול השרשים הנמצאים בשנים שהם עתה תקמ"ג כזה
|
|
|
|
|
|
ויהיו אלף ושמונים וששה כזה
|
|
|
|
|
|
ויעלה זה המספר מעלה אחד עם המספר שניתן לפניו שהראוי הוא ב' ויהיו אז עשרת אלפים ותתס"ב כזה
|
|
|
|
|
|
כפלנו זה המספר על המספר הנתון שהוא ב' יעלו כ"א אלפים תשכ"ד נגרעם מן החלק הראשון ומן הנשאר מן השני ומן השלישי שהוא כ"א אלפים תשכ"ד לא נשאר כלום וזה יורה שהמספר המונח שהוא כ"ט מספרים ותק"ו אלפים וקנ"ד שהוא מרובע שוה הצלעות וניתן המספר הנתון שהוא ב' תחת החלק הראשון ויהיה אז השורש שלם כי מה שאמרנו ל[.] חלק שורש [183]הוא בדרך ההשאלה [...] תל"ב כזה
|
|
|
|
|
|
[...] דומה על עצמו ואם יציא לך [...]
|
|
|
משל אחר רצינו לדעת שורש [...] ותס"ד ואם הוא שוה הצלעות [...] הצורה
|
|
|
| ה |
ז |
ח |
ד |
ה |
ו |
ד |
ו |
ד
|
| ב |
ד |
0 |
ה |
ו
|
|
|
|
|
והנה [...] וראוי להוציא ה' חלקים כאשר [...] לזה השורש [...] מן הראשון שהוא האחרון אשר בזה ומרובעו הגדול הוא ד' [...] ישאר א' על ה' והנה שורש ד' הוא ב' נתן אותו תחת החלק החמשי כי [...]
|
|
|
ולדעת השורש השני נכפול ב' שהוא השורש הראשון יהיו ד' נתן מספר מה לפניו והנה הראוי הוא ד' ויהיו מ"ד כפלנו מ"ד על ד' הנתון כזה
|
|
|
|
|
|
יעלו קע"ו נגרעם מקע"ח שיש בחלק הרביעי ובנשאר בחמשי ישארו ב' ברביעי והוא ק"ק בערך לחלק השלישי והנה המספר הנתון שהוא ד' הוא תחת החלק הרביעי
|
|
|
ולדעת השורש השלישי נכפול השני שרשים הנמצאים בידינו שהם כ"ד יהיו מ"ח ניתן מספר לפניהם והנה הראוי הוא ספרא לעלות מעלה שאם ניתן א' שהוא המספר היותר קטן יעלה תפ"א לגרוע מרמ"ה ולא נוכל כי רמ"ה קטן מתפ"א ולכן המספר הנתון הוא ספרא ונתן הספרא תחת החלק החמשי השלישי ולא נגרע דבר לא מן החלק השלישי ולא משיור החלק הרביעי ויהיה ב' שהוא החלק החמשי עשרים אלפים כערך החלק השני
|
|
|
ולדעת השורש הרביעי נכפול השלשה שרשים הנמצאים שהם יחד רי"ו יהיו ת"ף נתן לפניהם מספר אחד והראוי הוא ה' ויהיו ד' אלפים תת"ה כפלנום על ה' הנתון יהיו כ"ד אלפים וכ"ה כזה
|
|
|
|
|
|
גרענום ממספרי החלק השני והנשאר מן השלישי ומן הרביעי שהם כ"ד אלפים ותקס"ד ישארו תקל"ט שהם בערך החלק הראשון נ"ג אלפים תתקס"ד והנה המספר הנתון שהוא ה' הוא השורש הרביעי וניתן אותו תחת החלק השני שהוא רביעי [184][...] הד' שרשים שהם [...] אלפים תת"י ניתן לפניהם [...] מ"ח אלפים וק"א כפלנום [...] הכפול הוא בעצמו כי הכופל [...] אינו עולה ולא יורד [] וק"א מנ"ג אלפים ותתקס"ד ישארו ה' אלפים ותתס"ג והנה המספר הנתון שהוא אחד הוא השורש החמש וניתן אותו כזה בחלק החמישי שהוא חלק האחדים והעשרות והנה אם ניתן לפני השורש שנים בעבור שלא ישארו ה' אלפים תתס"ג יעלה הכפל יותר ויותר ממה שנצטרך לזה השיור ואם כן הא' הנתון הוא הראוי והנה השיור שנשאר יורה שהמספר המונח שאינו מרובע שוה הצלעות אבל כל חשבון אשר שרשיו [יציא] כל החשבון יורה שהוא מרובע שוה הצלעות
|
|
|
|
|
|
הבחינה תכפול השורש [.] על עצמו ועל הכפל תוסיף הנשאר ואם יהיה שוה למספר המונח הוא טוב ועוד תעיין שלא יהיה הנשאר אחר הוצאת השורש יותר מכפל השורש שאם הוא יותר מכפל השורש הנה תוכל לתת עוד אחד במספר הנתון שהוא חלק השורש האחרון
|
|
|
המשל הנה נניח כי שורש ד' הוא א' ישארו ג' והוא יותר מכפל השורש כי כפל כפל השורש הוא פעם אם כן נוכל לתת ב' בשורש ולא נשאר דבר
|
|
|
עוד רצינו שורש ט"ו והוא ג' ישארו ששה שהוא כפל השורש בצמצום ואם כן הוא השורש הראוי
|
|
|
וכן כ"ד והשורש ד' ונשארו ח' שהוא כפל השורש בצמצום
|
|
|
עוד נניח כי שורש ל"ו הוא ה' ומרובע חמשה הוא כ"ה נגרע כ"ה מל"ו נשארו י"א והוא יותר מכפל השורש כי השורש שהנחנו הוא חמשה וכופלו עשרה והנשאר יותר מעשרה כי הוא י"א אם כן השורש הראוי הוא ששה
|
|
|
עוד רצינו שורש מאה נניח [185]כי הוא ט' [...] הוא י"ח והנה י"ט הוא [...] בשורש עשרה וכן כולם
|
|
|
דרך קל מאוד אחר שתציירהו [...] פעמים והדרך שתתן מספרך ב[...] שנים שנים וכל חלק תאמר שהוא אחדים [עשרות] [...] זמן שישאר לצד שמאל תאמר תאמר מאות ואלפים ומה שימשך כמו שעשינו ואחר שחילקת מספריך ב'ב' תעשה תחת אחדי כל חלק בתים לחלקי השורש ואחר קח החלק האחרון ותגרע ממנו המרובע היותר גדול שבו וקח שורשו ותתנהו בביתו ואחר קח זה השורש ותכפלהו בשנים ולפני הכפל תבקש מספר ראוי אשר עם זה המספר הנתון לפני כפל השורש תכפול הכל והיוציא תן אחדי המספר תחת אחדי החלק אשר ממנו תבקש השורש השני ואם תתן א' במספר הנתון ויעלה יותר תן ספרא בשורש ולא תגרע דבר ושוב לכפול הספרא וכל השורש כי לעולם הספרא מן השורש ונעשה כנהוג במשל שעבר המשל
|
- Example: we wish [to know] a root of five parts, which is two thousand and 950 million, 771 thousand and 41.
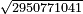
|
המשל רצינו שורש חמשה חלקים אשר הוא שני אלפים ותתק"ן מספרים ותשע"א אלפים ומ"א
|
- As this diagram:
|
כזאת הצורה
|
| |
|
|
|
1 |
0 |
8 |
6 |
4 |
6
|
| |
|
|
2 |
2 |
8 |
1 |
9 |
|
|
| |
|
3 |
4 |
7 |
7 |
|
|
|
|
| |
4 |
5 |
0 |
|
|
|
|
|
|
| 2 |
9 |
5 |
0 |
7 |
7 |
1 |
0 |
4 |
1
|
| |
|
5 |
|
|
|
|
|
|
|
| 2 |
5 |
|
4 |
|
3 |
|
2 |
|
1
|
| |
4 |
1 |
6 |
|
|
|
|
|
|
| |
|
3 |
2 |
7 |
9 |
|
|
|
|
| |
|
|
2 |
1 |
7 |
2 |
4 |
|
|
| |
|
|
|
1 |
0 |
8 |
6 |
4 |
1
|
|
|
| |
|
|
|
א |
0 |
ח |
ו |
ד |
ו
|
| |
|
|
ב |
ב |
ח |
א |
ט |
|
|
| |
|
ג |
ד |
ז |
ז |
|
|
|
|
| |
ד |
ה |
0 |
|
|
|
|
|
|
| ב |
ט |
ה |
0 |
ז |
ז |
א |
0 |
ד |
א
|
| |
|
ה |
|
|
|
|
|
|
|
| ב |
ה |
|
ד |
|
ג |
|
ב |
|
א
|
| |
ד |
א |
ו |
|
|
|
|
|
|
| |
|
ג |
ב |
7 |
9 |
|
|
|
|
| |
|
|
ב |
א |
ז |
ב |
ד |
|
|
| |
|
|
|
א |
0 |
ח |
ו |
ד |
א
|
|
|
|
|
אשר החלק הראשון לצד שמאל אשר ממנו נתחיל הוא כ"ט והשני נ' והשלישי ע"ז והרביעי עשרה והחמשי שהוא הראשון על דרך האמת הוא מ"א
|
|
|
ועתה רצינו שורש כ"ט [186][...] ישארו ד' על ט' [...] חלק שני ויהיו אז החלק [...] שנגרע מרובעו מ[..] [...] שהוא חמשה יהיו עשרה ניתן [...] והוא ארבעה ויהיו כזה ק"ד [...] הנתון כמו שתראה בצורה
|
|
|
|
|
|
יהיו תי"ו [...] במעלותם בדרך שיהיו האחדים שהם ששה תחת אחדי החלק השני שהם סיפרא והם תחת בית השורש נגרע תי"ו מת"ן נשארו ל"ד על החלק השני וד' התחתון הוא השורש השני ונתנהו בביתו תחת אחדיו חלק שני
|
|
|
ועוד רצינו שורש חלק שלישי שהוא ע"ז ועם הנשאר בחלק שני והוא ג' אלפים תע"ז כמו שתראה בצורה נכפול השני שרשים הידועים לנו שהם ד"ה שהם נ"ד על שנים יהיו ק"ח נבקש מספר ראוי לתת לפני ק"ח והוא ג' ויהיו כזה הצורה
|
|
|
|
|
|
אשר כולם יהיו אלף ופ"ג נכפול כל המספר על ג' הנתון והוא השורש יעלו ג' אלפים רמ"ט אשר נגרעם מג' אלפים תמ"ז והוא שניתן אחדי [..] הג' אלפים רמ"ט תחת אחדי החלק השלשי אשר בו ע"ז ואחר תגרעם מג' אלפים תע"ז ישארו כ"ב אלפים תת"י וג' הנתון הוא השורש ונתנהו בביתו תחת אחדי החלק השלישי שהם ז'
|
|
|
עוד להוציא שורש רביעי אשר בו עשרה נכפול השרשים הידועים שהם הד"ג בשנים יהיו אלף פ"ו נתן לפניהם מספר ראוי והוא ב' ויהיו עשרת אלפים תתס"ב נכפלם על המספר הנתון שהוא ב' יהיו כ"א אלפים תשכ"ז כזה הצורה
|
|
|
|
|
|
נגרעים מכ"ב אלפים תת"י אחר אשר ניתן אחדי המספר שהוא ד' תחת אחדי החלק הרביעי אשר בו ספרא ונשארו ק"ח אלפים תרמ"א והנתון שהוא ב' הוא השורש וניתנהו בביתו
|
|
|
עוד להוציא שורש החלק החמשי אשר בו מ"א נכפול השברים הידועים שהם הדג"ב בשנים יעלו עשרת אלפים תתס"ד נבקש מספר ראוי לתת לפני [187]זה המספר [...] ק"ח אלפים תרמ"א [...] הנתון שהוא אחד יעלה כמו [...] ניתן אחדי המספר שהוא אחד תחת [..] גם כן ואחר כל הנמשכים לצד שמאל [...] שהוא גם כן ק"ח אלף תרצ"א לא נשאר דבר ותו[...] שוה הצלעות ודי בזה המשל לאיש שהוא משכיל
|
|
|
והבחינה כפול האחד השורש על עצמו שהוא נ"ד אלפים שכ"א ותציא כל המספר שהוא [..] שני אלפים ותתק"ן מספרים ותשע"א אלפים ומ"א והוא טוב
|
The second type: extracting the perfect and imperfect cube roots
|
המין השני בהוצאת השרשים המעוקבים השוים והבלתי שוים
|
| I say that extracting the cube roots is according to this procedure: first, divide the ranks of the given number into triplets and start from the rank of units.
|
ואומר כי הוצאת שורשי המעוקבים הוא על זה הסדר שתחלק ראשונה מעלות המספר המונח ג' ג' ותתחיל ממעלות האחדים
|
| I called every three ranks a "part", even if the last one is of two ranks, or of one rank.
|
וקראתי לכל ג' מעלות חלק ואם האחרון יהיה מב' מעלות או ממעלה אחת
|
| For each part, you must extract a part of the root, either a number, or a zero, whether the part is of three [ranks], or the last is of two ranks, or of one rank, as you will see and as we did with the square roots.
|
ולכל חלק תצטרך להוציא חלק מן השורש בן יהיה מספר או ספרא בין יהיה החלק מג' בין שיהיה האחרון מב' מעלות או ממעלה אחת כאשר תראה וכאשר עשינו בשורשי המרובעים
|
| Then, subtract the cube from the last part of the ranks you find there; extract the root from the cube; write it beneath the part from which it was subtracted and this is the first part of the root.
|
ואחר תוציא המעוקב מן החלק האחרון מן המעלות אשר תמציא שם ומן המעוקב תיקח השורש ותן אותו תחת החלק אשר יציא משם והוא חלק ראשון מן השורש
|
| To extract the next part of the root, take the found root and write it next to the preceding number.
|
ולהוציא החלק האחר מן השורש קח השורש הנמציא ותן מספר לפניו
|
| Multiply the root and the given number by three times the found root; multiply the result by the given number before the root one more time and keep the result of both multiplications.
|
וכפול השורש והמספר הנתון על ג' כפלי השורש הנמצא והעולה תכפול פעם אחרת על המספר הנתון לפני השורש ושמור העולה מן השני הכיפילות
|
| Then take the cube of the given number and add it to the multiplied number, provided that the tens of this cube correspond to the units of the multiplied number; if there are no tens there but units, write them as units in this number; the rank of units of this number is raised to tens.
|
ואחר קח מעוקב המספר הנתון וחברהו על המספר הנכפל ובלבד שיהיה עשרות זה המעוקב נגד נוגד אחדי המספר הנכפל ואם אין שם עשרות אלא אחדים שתתנים לאחדים בזה המספר ויעלו מעלת האחדים מזה המספר לעשרות
|
| If the result of addition of both is equal to the number of the part whose root you want [...]
|
ואם העולה מחיבור שניהם הוא שוה למספר החלק אשר תרצה שורשו ולשאר מין האחרים מוטב [188][...] ותן המספר [...] מספרך ותן המספר [...] המספר הנתון אחד ותראה אחר [...] העולה הוא גדול לא תכפול דבר [...] בחלקו ויהיה מספרי מעלות חלקו כמו שיור [האחדות] כאשר עשינו בשורשי המרובעות
|
|
|
ובעבור כי זה המעשה המעשה קשה לציירו אניח צורות כפי המשכת המעשה בכל הכפלים וראשונה אכתוב לוח מעוקבי כל אחדי המעלה הראשונה בעבור כי לעולם החלק האחרון הנתון אשר ניקח שורש מעוקבו בראשונה [.] לא יוסיף שורשו מאחדים
|
|
|
ובעבור זה תמצא בטור ראשון מזה הלוח כל אחדי המעלה הראשונה והטור השני מעוקבהם וזה צורת הלוח
|
- Example: we wish to know the approximate cube root of this number, which is 74 thousand and 88, or if it is a perfect cube.
![\scriptstyle\sqrt[3]{74088}](/mediawiki/images/math/d/9/b/d9b99fd447ac159f387c8d18100d998d.png)
|
המשל בזה רצינו לדעת שורש המעוקב הגדול שיוכל להיות בזה המספר שהוא ע"ד אלפים ופ"ח או אם הוא מעוקב בלא שיור
|
|
|
וראשונה אניח מעלות המספר ואחלקים ג' ג' ואתן קו תחת כל חלק ומקום לשרשים ויהיה כזה
|
|
|
|
|
|
ואחר נוציא מעוקב ע"ד והנה המעוקב הגדול שבו הוא ס"ד ושורשו ד' כמו שתראה בלוח
|
| 1 |
1
|
| 8 |
2
|
| 27 |
3
|
| 64 |
4
|
| 125 |
5
|
| 216 |
6
|
| 343 |
7
|
| 512 |
8
|
| 729 |
9
|
|
|
| א |
א
|
| ח |
ב
|
| כז |
ג
|
| סד |
ד
|
| קכה |
ה
|
| ריו |
ו
|
| שמג |
ז
|
| תקיב |
ח
|
| תשכט |
ט
|
|
|
|
|
כי ד' על ד' הוא י"ו וי"ו על ד' הוא ס"ד נגרע ס"ד מע"ד ישארו עשרה שהוא עשרת אלפים כערך אחדי החלק הראשון והשורש שהוא ד' נתן אותו תחת החלק השני כי ממנו יציא והרי לנו שורש אחד מן החלק השני
|
|
|
ולדעת שורש החלק הראשון לקחנו השורש הנמצא והוא ד' וניתן מספר לפניו והנה הראוי הוא ב' ושניהם יעלו מ"ב כזה ב"ד ועתה נכפול מ"ב על י"ב שהוא ג' כפל השורש ויהיה העולה תק"ד [189] כזה ד0ה [...] שהוא י"ב יהיו אלף ושמונה [...] מעוקב ב' שהוא המספר [...] השמור [...] יהיה ח' אחדים ויעלה כל [..] אלפים ושמונים ויהיה כזה נגרע זה המספר [...] מן החלק הראשון ומהנשאר בשני והנה הכל שוה כי גם כן [..] עשרת אלפים ושמונים משמונה [...] ולקחנו המספר הנתון שהוא ב' וניתן אותו תחת החלק הראשון ויהיה אז שורש מעוקב זה המספר המונח מ"ב בשוה והוא שוה בכל צלעותיו
|
|
|
ואם תרצה לבדוק אם זה אמת כפול מ"ב על מ"ב שהוא השורש והיוציא על מ"ב ותציא המספר המונח
|
|
|
משל שני רצינו לדעת שורש המעוקב היותר גדול שהוא כזה המספר המונח שהוא ח' אלפים ותי"ד מספרים ותתקע"ה אלפים ות"ה כזאת הצורה
|
|
|
| ח |
ד |
א |
ד |
ט |
ז |
ה |
ד |
0 |
ה
|
| ב |
|
0 |
|
|
ג |
|
|
ד |
|
|
|
|
|
והוא ד' חלקים נוציא מעוקב החלק האחרון שהוא ח' והוא מעוקב ושורשו ב' נגרע ח' מח' לא נשאר כלום וניתן ב' תחת הח' האחרון
|
|
|
ולדעת שורש החלק השלישי לקחנו השורש הנמצא שהוא ב' וניתן לפניו מספר אחד והנה אם ניתן א' לפני השורש יעלה יותר מן הראוי תתמ"ז ולכן לא נעשה דבר אלא ניתן ספרא כחלק השלישי ולא נגרע ממנו דבר אלא יהיה שיור לחלק השני וניתן ספרא תחת החלק השלשי
|
|
|
ולדעת שורש החלק השני ניקח השני שרשים הנמצאים שהם יחד עשרים וניתן מספר לפניהם והנה הראוי הוא ג' ויעלה המספר הג' כזה ג0ב ונכפול זה המספר בשישים שהוא ג' כפלי השורש יעלו י"ב אלפים וק"ף ועוד כפלנו זה המספר על המספר הנתון שהוא ג' יעלו ל"ו אלפים ותק"מ ונשמרים אחר נקח מעוקב המספר הנתון שהוא ג' ויהיה מעוקבו כ"ז ניתן העשרות ניגד אחדי המספר הנתון ויהיה כזה [190][...] כולם שס"ה [...] תכ"ז נגרע זה [...] החלק [...] בשלישי מ"ט ובשני תקמ"ח [...] ותקמ"ח אלפים ואם ניתן מספר [...] הגדול הנה יעלה יותר מן הראוי ד' [...] אלפים ותרס"ד ואם כן ג' הוא הראוי כנזכר וניתן ג' שהוא המספר הנתון תחת החלק השני
|
|
|
ולדעת השורש הרביעי שהוא תשלום שהוא ת כל השורש ככלל ניתן מספר אחד לפני השרשים הנמצאים שהם ב 0 ג והראוי הוא ד' ויהיה אז מספר השורש עם הנתון ב' אלפים ול"ד כזה
|
|
|
|
|
|
נכפול זה המספר בכלל על תר"ט שהוא ג' כפלי השרשים יעלה מספר אחד ורל"ח אלפים ותש"ו כזה
|
|
|
|
|
|
נכפול זה המספר על המספר הנתון שהוא ד' יעלה ד' מספרים ותתקנ"ד אלפים תתכ"ד ויהיה כזה
|
|
|
|
|
|
ונשמרם ואחר נקח מעוקב המספר הנתון שהוא ס"ד נחברהו עם המספר השמור וניתן עשרות זה המעוקב עם אחדי המספר השמור ויעלו כל מדרגות המספר השמור מעלה אחד ויהיו מ"ט מספרים ותקמ"ח אלפות וש"ד כזה
|
|
|
|
|
|
ניגרעם ממספר החלק הראשון ומן הנשאר מן השני והשלישי שיהיה הכל מ"ט מספרים ותקמ"ח אלפים ות"ה ישארו ק"א והרי כי המספר המונח אינו מעוקב אבל המעוקב היותר גדול שבו הוא ח' אלפים תי"ד מספרים ותתקע"ה ות"ד ונשארו ק"א
|
|
|
ואם תרצה לבדוק אם זה אמת קח השורש וכפלהו על עצמו והיוציא כפול פעם אחרת על השורש ותציא המונח
|
|
|
קיצור המשל אחר שתצייר הכל תחלק מעלות המספר המונח ג'ג' וקח שורש החלק האחרון ותן מספר לפני השורש וכפול המספר הנתון והשורש על ג' כפלי השורש והעולה כפול במספר הנתון ועל הכל תחבר מעוקב הנתון שיהיו עשרות המעוקב ניגד אחדי מספרך
|
The third type: knowing the root of a number that has no real root
|
[191]המין הש[לישי] [...]
|
|
|
[והוא ב' סדרים] מספרים [..] מזה המין רוב המספר [...] ד' וט' שיש להם שורש אמתי [...] ובמעלת העשרות לא תמצא [...] האחרים אין להם שורש ואם תרצה לדעת [...] תחבר על כל מרובע המספרים הנפרדים הנמשכים בסדר ואז תדעם והנשארים הם המספרים שאין להם שורש אמיתי
|
|
|
והמשל בזה האחד הוא מרובע תחבר עליו הנפרד הנמשך לו שהוא ג' יהיו ד' והוא מרובע
|
|
|
תחבר על ד' הנפרד הנמשך אחר ג' שהוא ה' יהיו ט' והוא מרובע
|
|
|
תחבר על ט' ז' יעלו י"ו והוא מרובע
|
|
|
ועל י"ו ט' יהיו כ"ה והוא מרובע
|
|
|
וכן לעולם
|
|
|
והנה כל הנשארים הם מספרים אשר אין להם שורש אמתי אלא בקירוב
|
|
|
ואומנם תמצא קירוב ויותר קירוב כאשר תראה בע"ה
|
|
|
ולכן חלקתי זה המין לשני סדרים
|
|
|
אשר הסדר הראשון הוא לדעת השורש המוסכם
|
|
|
והשני לדעת השורש המדוקדק והיותר מדוקדק אם תרצה
|
|
|
הסדר הראשון הוא לדעת השורש המוסכם ויש בו דרכים רבים אבל בראותי הטורח הגדול והתועלת הקטן לא אאריך אלא הראוי להבנת הענין בלבד
|
|
|
וכבר ידעת כי כל המספרים אשר אין להם שורש אמתי הם בין שני מרובעים אחד גדול ואחד קטן ואילו המספרים האמצעים הם זוגות לעולם
|
|
|
כמו ב"ג בין אל א"ד והוז"ח בין ד"ט בין כל מרובע ומרובע בתוספת שנים
|
|
|
ואחר שכל המספרים אשר בין המרובעים הם זוגות נחלקם בשנים חציים קרובים למרובע הקטן וחציים קרובים למרובע הגדול
|
|
|
כי ב' קרוב א' וג' קרוב ד' וכן כולם
|
|
|
ולזה חילקתי זה הסדר בשני דרכים
|
|
|
הדרך הראשון בקרובי הקטנים ואומר כי הדרך הוא שתקח שורש המרובע הקטן ושומרהו [192][...] על השורש על [...] בין השורש והמספר אשר [...] המספר שום על המורה ואלה [...] הוא השורש
|
|
|
המשל בזה רצינו [...] ושורש ד' הוא ב' ונשמרהו [...] ב' שהוא שורש ד' יהיו ד' וזה מורה השברים וההפרש או המספר אשר בן המרובע ובין ה' הנשאל הוא אחד שום אותו על המורה יהיה כזה 
|
|
|
ויורה שהוא רביע וב' השמור יהיו ב' ורביע והנה שורש ה' הוא ב' ורביע
|
|
|
והבחינה לזה תכפול ב' ורבע על ב' ורביע יעלו ה' וחלק מי"ו כי תשוים כמו שידעת ותציא לך פ"א חלקים מי"ו בשלם חלק פ"א על י"ו תציא לך ה' שלמים וחלק מי"ו וזה כל כך קרוב אל האמת
|
|
|
משל שני רצינו לדעת שורש י"ח והוא קרוב למרובע הקטן שהוא י"ו כי הגדול הוא כ"ה ושורש י"ו הוא ד' ונשמרהו וכפלו ח' והוא מורה השברים וההפרש בין י"ו לי"ח שהם [שה] המרוב[ע] הקטן והנשאל שהוא י"ח הם שנים נתנם על ח' שהוא המורה יהיו ב' שמיניות נקצרם יהיו רביע כזה 
|
|
|
ואם כן שורש י"ח הוא ד' ורביע
|
|
|
הדרך השני בקרובי המרובעים הגדולים ואומר כי הדרך הוא שתקח שורש המרובע הקטן ותשמרהו ואחר כפול שורש המרובע הגדול ויהיה המורה ואחר קח ההפרש שיש מן המספר הנשאל הנשאל למרובע הגדול ותגרעהו מן המורה והנשאר הם שברי חלקי המורה אם תצטרך להוסיף על השורש השמור
|
|
|
המשל בזה רצינו לדעת שורש ח' לקחנו שורש המרובע הקטן שהוא ב' ונשמרהו ואחר נכפול שורש המרובע הגדול שהוא ג' יהיו ו' והם המורה והנה היה לנו השורש השלם שהוא ב' ומורה השברים שהוא ו' ונצטרך השברים והנה המרובע הגדול גדול מהמספר הנשאל מאחד נגרעהו מן המורה שהוא ו' יהיו ה' [193]והם השברים [...]
|
|
|
משל שני רצינו לדעת [...] הוא ה' ונשמרהו והנה [...] י"ב והנה המרובע הגדול גדול מה[...] י"ב ישארו ט' והם והם השברים והמורה [...] יהיו ג' רביעיות והנה עלה בידנו כי שורש ל"ג הוא [...] כזה ה 
|
|
|
ואם נכפול השרשים על עצמם יעלו ל"ג וחלק מי"ו בשלם
|
|
|
הסדר השני הוא לדעת השורש המדוקדק והיותר מדוקדק אם תרצה ואומר כי הרוציא לדקדק השורש המוסכם קח השורש המוסכם כדרך שאמרנו בסדר ראשון ואחר אם השורש ואחר אם השורש שמצאת הוא גדול גרע מן השברים ואם הוא קטן תוסיף על השברים ואם עם שבר אחד יהיה גדול ואם עם אחר הקרוב לו הוא קטן תכפלהו במספר גדול ואחר תוסיף מאילו החלקים הדקים או תגרע כפי הראוי
|
|
|
ואם תרצה לדקדק עוד אחר שעם חלק אחד מן הדקים יוסיף ועם אחר הקרוב לו יגרע כפול עוד במספר גדול ויקטינו השברים
|
|
|
ותוכל לעשות זה עם ג' דרכים
|
|
|
הא' שתכפול השברים והמורה
|
|
|
והשני השברים שתוסיף או תגרע כפי הצורך
|
|
|
והשלישי שתוסיף או תגרע מן המורה
|
|
|
וכל זה יורה השכל
|
|
|
המשל בזה רצינו לדקדק שורש ה' והנה שורשו המוסכם הוא ב' ורביע כזה ב  כאשר אמרנו בסדר ראשון ובעבור שהוא עולה יותר מה' חלק אחד מי"ו נכפול השבר והמורה במאה כי בסדר ראשון כפלנו פ"א חלקים מי"ו נתן ספרא לפני כל אחד יהיו תת"י חלקים מק"ס ובעבור שהוא גדול לא ניקח כולו כי כולו מקוצר ושוב ישוב לרביע אבל ניקח מהמאה שברים צ"ה חלקים ויהיו כזה כאשר אמרנו בסדר ראשון ובעבור שהוא עולה יותר מה' חלק אחד מי"ו נכפול השבר והמורה במאה כי בסדר ראשון כפלנו פ"א חלקים מי"ו נתן ספרא לפני כל אחד יהיו תת"י חלקים מק"ס ובעבור שהוא גדול לא ניקח כולו כי כולו מקוצר ושוב ישוב לרביע אבל ניקח מהמאה שברים צ"ה חלקים ויהיו כזה
|
|
|
|
|
|
ואז יהיה השורש ב' שלמים וצ"ה חלקם מת' ניתן הב' שלמים בשברים יהיו תת תחביר עליהם צ"ה יהיה תתצ"ה כזה
|
|
|
|
|
|
כופלם על עצמם יהיה תת"א אלפים וכ"ה נחלקם [194][...] יהיה מרובעו [...] וכ"ה והם חלקים [...] השיור הזה נגרע עוד [...]
|
|
|
|
|
|
ניתן הב' שלמים בשברם [...] יהיו תתצ"ד כזה
|
|
|
|
|
|
כופלם [...] ומורה על מורה יהיו תשצ"ט [...] חלקם על כפל המורה על עצמו שהוא ק"ס אלפים יעלה בחילוק ה' עם גרעון תשס"ד וזה יותר קרוב מן הראשון שהוא צ"ה שנשארו אלף וכ"ה ובצד וגרעו תשס"ד
|
|
|
ואם תרצה לדקדק עוד כפול כפול השברים והמורה לחשבון יותר ותכפלם כאשר עשיתי ואם הוא גדול גרע עד שאם תגרע יגרעו ואם יגרעו תוסיף או אם יש לך לב כפול המורה ויקטנו השברים או גרע מהמורה ויגדלו השברים
|
|
|
או תעיין באילו המשלים [..] אם תרצה לקצר הראשון בחמשיות והשני בחצים יהיה יותר נקל וכל זה כפי מה שיורה השכל כי אין להאריך עוד כי די בזה
|
The fourth type: knowing the root of fractions
|
[195]המין הרביעי ב[..]
|
|
|
[...] כי השבר ש[...] מונח במספר גדול כי ה[...] תקצרהו כל מה שתוכל ואחר [...] מרובע יחויב שיהיה גם המורה [...]
|
- To know the root of four-ninths, like this:
 . .
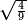
|
לדעת שורש ארבע תשיעיות כזה 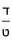
|
- [The root of 4], which is the numerator, is 2; the root of the denominator is 3. So, the root of 4-ninths is 2-thirds, like this:
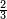 . .
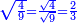
|
הנה [...] שהוא השבר הוא ב' ושורש המורה הוא ג' ואם כן שורש ד' תשיעיות הוא ב' שלשיות כזה 
|
- To see if this is true, multiply it by itself; the result is 4-ninths, like this:
 . .
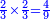
|
ולראות אם זה אמת כופלהו על עצמו ותציא ד' תשיעיות כזה 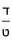
|
- Another example: we wish [to know] the root of 12 parts of 27, like this:
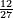 . .
|
משל אחר רצינו שורש י"ב חלקים מכ"ז כזה
|
|
|
|
|
|
ראה אם תוכל לקצר שניהם והנה תוכל לקצרם בשלישית ויהיה ד' תשיעיות ושורש ב' שלישיות כזה 
|
|
|
וחזור למשל שעבר ואם השברים מתחלפים
|
|
|
משל אחר רצינו שורש ק"ף מרמ"ה חלקים כזה
|
|
|
|
|
|
נראה אם נוכל לקצרם והנה יתקצרו בחמשית כי חמשית ק"ף הוא ל"ו וחמשית רמ"ה הוא מ"ט ושניהם מרובעים ורצינו לדעת שורשם ויהיו כזה
|
|
|
|
|
|
והנה שורש ל"ו הוא ו' ושורש מ"ט הוא ז' ויהיו ו' שביעיו' כזה 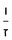
|
|
|
והבחינה ברורה שתכפול ו' שביעיות על עצמו
|
|
|
משל אחר רצינו לדעת שורש קמ"ד חלקים מקס"ט כזה
|
|
|
|
|
|
ובעבור כי הוא ג' מעלות נוציא השורש מכל אחד כמנהג השלמים כאשר תראה במין הראשון בארוכה והוא שנקח בראשונה השבר שהוא קמ"ד ונחלק המעלות בב' מצד ימין כזאת הצורה
|
-
|
|
|
|
ונוציא שורש החלק האחרון והוא א' ניגרע א' מא' לא נשאר כלום וניתן השורש שהוא א' תחת החלק שיציא ממנו כפול זה השורש בשנים ותן לפניו מספר מה והראוי הוא ב' כפלהו עם [..] השורש יהיו כ"ב כפול כ"ב על ב' שהוא הנתון יעלו מ"ד גרע[ם] מ"ד מן החלק הראשון שהוא מ"ד לא נשאר כלום וניתן ב' תחתיו
|
|
|
ואם היו לנו ב' חלקי השורש א"ב שהם י"ב ונאמר כי י"ב הוא שורש קמ"ד שהוא השבר ונעשה כדרך הזה במורה שהוא קס"ט ויעלה בידינו [196][...] שורש קמד חלקים[...] היוציא בזה ומאלה ממשלים [...] שוים ובלתי שוים ומהנשאר מהשרשים [...]
|
The Second Part: Word Problems
|
[203]הכלל [השני] [...]
|
|
|
[השער הראשון בשאלות חיבור חילקתיו] לפרקים
|
|
|
[הפרק הראשון] השער
|
|
|
[הפרק השני בשאלות חיבור] שלמים
|
|
|
[הפרק השלישי בשאלות] חיבור שברים
|
|
|
[הפרק] הרביעי בשאלות חיבור מורכבים
|
|
|
השער השני בשאלות כפל חילקתיו לפרקים
|
|
|
הפרק הראשון בשאלות כפל שלמים
|
|
|
הפרק השנית בשאלות כפל שברים
|
|
|
הפרק השלישי בשאלות כפל מורכבים
|
|
|
השער השלישי בשאלות גרעון חילקתיו לפרקים
|
|
|
הפרק הראשון בשאלות גרעון שלמים
|
|
|
הפרק השני בשאלות גרעון שברים
|
|
|
הפרק השלישי בשאלות גרעון מורכבים
|
|
|
השער הרביעי בשאלות חילוק חלקתיו לפרקים
|
|
|
הפרק הראשון בשאלות חילוק שלמים
|
|
|
הפרק השני בשאלות חילוק שברים
|
|
|
הפרק השלישי בשאלות חילק מורכבים
|
|
|
השער החמשי בשאלות מעורבות עם שתי הנחות כוזבות חלקתי ל פרקים
|
|
|
הפרק הראשון ב[ש]אלות מעורבות מקצת דרכים
|
|
|
הפרק השני בשאלות תחבוליות ואם הם אמיתיות
|
|
|
הפרק השלישי בשאלות מתחלפות
|
|
|
הפרק הרביעי בתערובת המטבעות ובו שלושה סדרים
|
|
|
[204]הערה לדרך [השלשה]
|
| [...] you find 3 categories [...]
|
[...] תמצא ג' [מנהגים] [...]
|
| The [first category]: we assume 3 numbers in it [...]
|
[המנהג הראשון] אשר בו נניח ג' מספרים [...] אבל כולם ישובו לשלושה
|
| The second category: you find in it 4 parts.
|
המנהג השני תמצא בו ד' חלקים [...]
|
| The third category: you find in it 5 parts.
|
המנהג השלישי תמצא בו ה' חלקים [...]
|
- The first example for all cases of the first category: we say: if 2 gives 3, [how much will] 4 [give]?
|
והמשל לכולם אשר לדרך הראשון נאמר אם ב' נתן ג' [כמה יתן] ד'
|
| You will see all this in the examples, whether the first is unknown, or the second, or the third, of the fourth.
|
וכל זה תראה במשלים אם נעלם הראשון או השני או שלישי או הרביעי
|
- Sometimes, four numbers are given in this way.
|
והנה בזה הדרך פעמים יבואו ד' מספר[ים]
|
- As: if 2 dinar yield 4 pešiṭim in 3 days, how much will 5 dinar yield?
|
כמו אם ב' די' בג' ימים הרויחו ד' פשי' ה' די' כמה ירויחו
|
- In this question you multiply the money by the time, 2 by 3; it is 6. Then, the question becomes of three parts.

|
ובזה השאלה תכפול הממון על הזמן ב' על ג' יהיו ו' ואז תשוב השאלה לג' חלקים
|
- Say: if 6 yields 4 pešiṭim, how much will 5 yield?
|
ואמור אם ו' נתן ד' פשיטי' ה' מה יתן
|
- Sometimes, five numbers are given in this way, and they are also transformed into three.
|
גם פעמים יבואו בזה הדרך ה' מספרים מונחים וישובו לג' גם כן
|
- As the one who says: if 4 dinar yield 5 dinar in 3 months, how much will 7 dinar yield in 8 months?
|
כאומר אם ד' דינ' בג' חדשים הרויחו ה' די' ז' די' בח' חדשים מה ירויחו
|
- Now, multiply each amount of money by its [corresponding] time:
|
ועתה כפול כל הממון על זמנו
|
- As 4 by 3; it is 12 and this is the first term.

|
כמו ד' על ב ג' יהיו י"ב וזה חלק ראשון
|
- The 5 dinar are the second term as it is.
|
וה' די' חלק שני כמו שהוא
|
- 7 by 8; it is 56 for the third term.
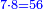
|
וז' על ח' יהיו נ"ו לחלק שלשי
|
- The question is transformed into three terms and we say: if 12 yields 7, what will 56 yield.
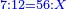
|
וחזר השאלה לג' חלקים ונאמר אם י"ב נתן ז' מה יתן נ"ו
|
- As you will see in the questions of time, measurement and weight, with God's help.
|
כמו שתראה בשאלות בע"ה מזמן ממידה וממשקל
|
- After I give an example or examples for five general ways by which each question should be solved, as you will see with God's help.
|
אחר שאתן משל או משלים מחמשה דרכים כוללים שיש להוציא כל שאלה כמו שתראה בע"ה
|
| In the second category, four necessary numbers should be given.
|
המנהג השני ראוי ל[הני]ח בו ד' מספרים הכריחיים
|
- As: if 3 peraḥim yield 5 dinar in 8 days, I ask: in how much time will 4 peraḥim yield the same?
|
כמו אם ג' פרחים בח' ימים הרויחו ה' די'
שאלתי ד' פרחים באי זה זמן ירויחם
|
- Also: Reuven buys a cloth for 3 peraḥim; 8 cubits are worth 5 dinar.
- I ask: how many cubits of this cloth will 5 dinar give, when the total price of the cloth is 5 peraḥim?
|
וכמו כן גם כן ראובן קנה בגד בסך ג' פרחים והח' אמות שוה ה' די'
שאלתי כמה אמות מזה הבגד יתן ה' די' כאשר סך הבגד הוא ה' פרחים
|
- The same for weights: Reuven buys kor of wheat for 2 dinar and sells 15 ՚oqya of bread for 2 pešiṭim.
- I ask: when he buys the kor for 24, how many ՚oqya will he sell for two pešiṭim?
|
ובמשקל גם כן ראובן קנה כור חיטה בסך ב' די' ונתן ט"ו אוקיות לחם בסך ב' פשיטי'
שאלתי כאשר קנה הכור בסך כ"ד כמה אוקיות יתן בשני פשי'
|
| In the third category [...]
|
המנהג [205][השלישי][...] מיניהם ואומנם [...] ומורכבים
|
- I say: if 3 [peraḥim yield 5 dinar in 8 days], I ask: in how much time will 4 peraḥim yield [7 dinar]?
|
ואומר אם ג' [פרחים בח' ימים ירויחו ה' די'] שאלתי ד' פרחים באי זה זמן ירויחו [ז' די']
|
| 3 peraḥim |
8 days |
5 dinar |
4 peraḥim |
7 dinar
|
|
|
| ז' די' |
ד' פרחים |
ה' די' |
ח' ימים |
[ג פרחים]
|
|
|
- Or, Reuven [buys 12 cubits of cloth]; the price of 3 cubits is 14 dinar.
- I ask: when he buys it at a price of 18 peraḥim, how much cloth will he sell for 16 dinar?
|
או ראובן [קנה י"ב אמות בגד] וסך הג' אמות הוא י"ד די'
שאלתי כאשר קנה [זה] בסך [י"ח] פרחים כמה בגד יקנו בסך י"ו די'
|
- Or, Reuven buys kor of wheat for 12 dinar and sells [13] ՚oqya of bread for [2] pešiṭim.
- I ask: when he buys the kor for 16 dinar, how many ՚oqya will he sell for [2] pešiṭim?
|
או ראובן קנה כור חיטה בסך י"ב די' ונתן לחם [י"ג] אוקיות [ב'] פשי' שאלתי כאשר קנה הכור לסך י"ו די' כמה אוקיות נתן [בב'] פשיטי'
|
| Or when there are three things that are different and compound, as if we assume 5 and 3 are different:
|
או יהיה מג' דברים מתחלפין ומורכבים כמו שנניח ה' וג' שיהיו מתחלפין
|
- As: if 4 pešiṭim of Zaragoza are equal to 5 pešiṭim of Barcelona and 3 pešiṭim of Barcelona are equal to 4 of Lisbon, I ask: how many pešiṭim of Zaragoza are 15 pešiṭim of Lisbon equal to?
|
כמו אם ד' פשיטי סרגוסה שוים לה' פשיטי ברצילונה וג' פשיטי ברצלונה שוים לד' מלשבונה שאלתי ט"ו פשיטין לשבונה כמה מפשיטי סרגוסה יהיו
|
| The examples of the three rules by the "Rule of Three":
|
ויהיו המשלים בזה הצורה משלושת מנהגי דרך השלושה
|
| If |
0 |
4 |
3 |
2 |
|
|
| |
dinar |
days |
profit |
dinar |
|
|
| If |
2 |
32 |
4 |
5 |
0 |
|
|
| |
dinar |
months |
profit |
dinar |
months |
|
| If |
4 |
32 |
5 |
7 |
82 |
0
|
| If |
12 |
5 |
56 |
0
|
|
| |
peraḥim |
days |
dinar |
peraḥim |
days |
|
| If |
3 |
8 |
5 |
4 |
0
|
| |
peraḥim |
cubits |
dinar |
dinar |
peraḥim |
|
| If |
3 |
8 |
5 |
5 |
5
|
| |
dinar |
pešiṭim |
՚oqyot |
pešiṭim |
dinar |
|
| If |
20 |
2 |
15 |
2 |
24
|
|
| |
peraḥim |
days |
dinar |
peraḥim |
dinar
|
| If |
3 |
8 |
5 |
4 |
7
|
| |
cubits |
cubits |
dinar |
peraḥim |
dinar
|
| If |
12 |
3 |
14 |
18 |
16
|
| |
dinar |
՚oqyot |
pešiṭim |
dinar |
pešiṭim
|
| If |
12 |
13 |
2 |
16 |
2
|
| |
pešiṭim |
pešiṭim |
pešiṭim |
pešiṭim |
pešiṭim
|
| If |
4 |
5 |
3 |
4 |
15
|
|
|
| |
|
0 |
ד |
ג |
ב |
אם
|
| |
|
די' |
ריוח |
ימים |
די' |
|
| |
0 |
ה |
ד |
בג |
ב |
אם
|
| |
חדשים |
די' |
ירוי' |
חדשים |
די' |
|
| 0 |
בח |
ז |
ה |
בג |
ד |
אם
|
| 0 |
וה |
ה |
בא |
אם
|
|
| ימים |
פרחי' |
דינ' |
ימים |
פרחי |
|
| 0 |
ד |
ה |
ח |
ג |
אם
|
| פרחי' |
דינרי' |
דינ' |
אמות |
פרחי |
|
| ה |
ה |
ה |
ח |
ג |
אם
|
| דינרי' |
פשיט |
אוקיות |
פשיט |
דיני |
|
| דב |
ב |
הא |
ב |
0ב |
אם
|
|
| דינר' |
פרחים |
דינר' |
ימים |
פרחי' |
|
| ז |
ד |
ה |
ח |
ג |
אם
|
| דינרי |
פרחים |
דינר |
אמות |
פרחי' |
|
| וא |
חא |
דא |
ג |
בא |
אם
|
| פשיטי |
דינרי |
פשיט |
אוקיות |
דינרי |
|
| ב |
וא |
ב |
גא |
בא |
אם
|
| פשיטי' |
פשיט |
פשיט |
פשוט |
פשוט |
|
| הא |
ד |
ג |
ה |
ד |
אם
|
|
|
| The conduct of the "Rule of Three" procedure differs in three ways, as I said:
|
אמנם הנהגת מעשה דרך השלושה יתחלף בג' דרכים כאשר אמרתי
|
- The first is: if 2 is equal to 3, how much will 4 be equal to?
|
אשר הראשון הוא אם ב' שוה ג' ד' מה יהיה שוה
|
- As you see in the first category.
|
כמו שתראה במנהג הראשון
|
- The second way: if 2 liṭra of copper are worth 3 dinar, how much are 4 liṭra of copper worth?
|
הדרך השני אם ב' לטר' נחושת שוה ג' דיני' ד' לטרי נחושת מה יהיה שוה
|
- You should know that the 2 liṭra of copper is the first term of the question; the 3 is the second [term]; and the 4 is the third [term].
|
הנה ראוי שתדע כי ב' ליטרי' נחושת הוא הגבול הראשון מן השאלה וג' השני וד' השלישי
|
- See that the first term is the known [...] and 3 remains, which is the second term [...]
|
והנה תעיין כי הגבול [206]הראשון הוא הידוע [...] ונשאר ג' שהוא הגבול השני [...] הנשאל הוא דמה לו
|
- So, [...] the second by the known, which is the first, [...], which is the third.
|
ואם כן [...] השני על הידוע שהוא הראשון [...] שהוא השלישי
|
- Example: we say: if 2 cubits are worth [6] [peraḥim], how much are [4 cubits] worth?
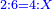
|
המשל בזה נאמר אם ב' אמות [...] אמות מה יהיו שוים
|
- We divide the opposite, which is the mean, which is 6, by the first, which is 2; the result of division is 3.
|
נחלק ההפכי שהוא האמצעי שהוא ו' על הראשון שהוא ב' יעלו בחילוק ג'
|
- We multiply it by the third, which is 4; the result is 12 and this is the required unknown, which is 12 peraḥim and it is proportional to the mean.
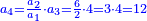
|
נכפול אותו על השלישי שהוא ד' יעלו י"ב והוא הנשאל הנעלם שהוא י"ב פרחים והוא דומה לאמצעי
|
- They are like this: if 2 6 4 12.
|
ויהיו כזה אם ב' ו' ד' ב"א
|
- The check is clear, because, you say: if 2 equals 6, which is 3 times in 6, [4] is also 3 times in [12].

|
והבחינה מבוארת כי תאמר אם ב' שוה ו' שהוא ג' פעמים בו' גם י"ב ג' פעמים בד'
|
- Or, we multiply 4 by the opposite, which is 6; it is 24.
|
או נכפול ד' על ההפכי שהוא ו' יהיו כ"ד
|
- We divide it by 2, which is proportional to the third; the result is 12 and it is the required.
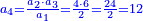
|
נחלקם על ב' שהוא דומה לשלישי יעלו י"ב והוא המבוקש
|
- The third way should be examined: we want to know the [ratio] of the third term to the known, which is the first term and they are proportional. We take the [same ratio] from the opposite, which is the second term.
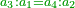
|
הדרך השלישי וצריך לעיין בזה נרצה לדעת שהוא הגבול השלישי אצל הנודע שהוא הגבול הראשון שהם דומים וניקח כמינו מן ההפכי שהוא הגבול השני
|
- Example: if 2 liṭra of copper are worth 3 peraḥim, how much are 4 liṭra of copper worth?
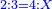
|
והמשל אם ב' ליטרי נחושת שוות ג' פרחים ד' ליטרי נחושת מה יהיה שוה
|
- We examine the ratio of 4 to 2; it is twice. We take double 3, which is 6. So, 4 liṭra of copper are worth 6 peraḥim.

|
הנה נעיין ערך ד' אצל ב' והוא שתי פעמים וכן ניקח כפל ג' שהוא ו' וד' ליטרי נחוש הם ו' פרחים
|
- Check: according to the first way, we multiply 3 by 4; it is 12. We divide it by 2; it is 6.
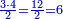
|
והבחינה כדרך הראשון נכפול ג' על ד' יהיו י"ב נחלקם על ב' יהיו ו'
|
The [First] Chapter: The Introductions Needed for this Section
|
הפרק בהקדמות הראויות לזה השער
|
| I say that the particular ways to know every question and solve every mystery are many, but generally they are five, even if there is one that includes another, but not vice versa.
|
ואומר כי הדרכים הפרטיים לדעת כל שאלה ולהוציא ולהוציא לאור כל תעלומה הם רבים אבל על הכלל הם חמשה ואם יש אחת כוללת אחרת אבל לא יתהפך
|
| The arithmeticians called them by different names, because each one used a name as he wished, but the desired is the same.
|
ואומנם חכמי המספר שמו להם שמות מתחלפים כי כל אחד קרא שם כפי רצונו אבל הנרצה אחד
|
| I will arrange each one here by its name.
|
ואני אסדרם כאן כל אחד בשמו
|
- I say that the first is the "Rule of Three".
|
ואומר כי הראשון הוא דרך השלושה
|
- The virtues of this way are that it reveals secrets and deciphers the hidden; it directs to the remaining ways, it is the principal of all and it completes what is asked of them, as you will see with God's help.
|
ואומנם מסגולות זה הדרך שהוא מגלה סתרים ומפענח נעלמים והוא מיישר לדרכים הנשארים והוא ראש לכולם והוא משלים מה שנשאל מהם כמו שתראה בע"ה
|
- I say: you should know that every four [...] the first [...] [the first] and the third are brothers and so are the second [and the fourth] [...] the second is [companion of the first and] the fourth is companion of the third [...] if one of these four numbers is unknown [...] you have three numbers [...] two of them are either fathers or sons and the third is single that has no companion.
|
ואומר שמן הראוי שתדע כי כל ארבעה [207][...] הנה הראשון [...] כמו בנים מאחר [...] הראשון וכן הרביעי מן [...] והשלישי הם אחים וכן השני [...] תראה במקומו והנה השני הוא [...] [ה]רביעי בן זוג השלישי ועם זאת זאת [...] נעלם מספר מה מאלו הד' מספרים [...] לידיעתו הנה [..] כי האחד נעלם ימצאו בידך ג' מספרים [...] השנים מהם הם שוים אם שיהיו אבות אם שיהיה בנים והשלישי הוא נפרד שאין לו בן זוג
|
- To know the unknown, [multiply] whichever of the brothers by the one that does not have a companion, and divide the result by the brother whose companion is with it; the result of division is the companion of the single.
|
והנה [...] לדעת זה הנעלם הנעלם הוא שתקח איזה מן האחים הנמצאים על אשר אין לו בן זוג והיוציא תחלקהו על האח האחד אשר בן זוגו עמו והיוצא בחלוקה הוא בן זוג הנפרד
|
- Be careful not to multiply one by its brother nor by its companion.
|
והשמר לך פן תכפול איש על אחיו ולא על בן זוג
|
- You always find that the product is either a mean by a mean, or the extremes [by each other].
|
ולעולם תמצא כי הכפל יהיה אם אמצעי על אמצעי או הקצוות
|
- I will give you four examples for this:
|
ואתן ארבעה משלים לזה
|
- Example: the four proportional numbers:.
|
והמשל בזה ה[צ]ד אלו הארבע מספרים נערכים
|
-
|
|
- We suppose that the first 2 is unknown. Then, 3 remains alone and 6 and 9 are apart.
|
ונאמר כי ב' הראשון נעלם ונשאר ג' לבדו וו'ט' לבד
|
- They are as this diagram:
|
ויהיו כזאת הצורה
|
-
|
|
- 3 and 9 are brothers.
|
הנה ג'ט' הם אחים
|
- Hence, we cannot multiply 9 by 3, because they are brothers, nor 9 by 6, because it is its companion.
|
ולא נוכל לכפול ט' על ג' כי הם אחים ולא ט' על ו' כי הוא בן זוגו
|
- So, we multiply 6 by 3 that have no relation at all and divide by the brother.
|
אבל נכפול ו' על ג' שאין להם קירבה כלל וחלק על האח
|
- 3 by 6 is 18. Divide it by 9; the result is 2 and it is the unknown.
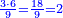
|
כי ג' על ו' הם י"ח תחלקם על ט' יעלו ב' והוא הנעלם
|
- In the "Rule of Three" we say: what will 3 give us, if 6 gives 9?
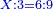
|
ובדרך השלושה נאמר מה יתן לנו ג' אם ו' נתן ט'
|
- This sentence indicates that the first is unknown, because the word "what" indicates the unknown that is first.
|
והנה זה הדיבר יורה כי הראשון נעלם כי מלת מה יורה על הנעלם כי הוא ראשון
|
- We multiply the means: we multiply 3 by 6; the result is 18. We divide it by 9, which is a brother; the result is 2 and this is the first unknown.
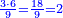
|
ונכפול האמצעיים והנה כפלנו ג' על ו' יעלו י"ח נחלקם על ט' שהוא אח יעלו ב' וזה הנעלם הראשון
|
- Second example: the second is unknown, so 2 is left alone.
|
משל שני נאמר שהשני נעלם ישאר ב' לבד
|
- According to this diagram:
|
כזאת הצורה
|
-
|
|
- In this question: what will 2 give, if 6 gives 9?
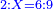
|
בזאת השאלה ב' מה יתן אם ו' נתן ט'
|
- This expression indicates that the second is unknown [...] the extremes, which are 2 by 9 [...] the second unknown 2, 4, 6, 9.
|
והנה זה הדיבור יורה [208]יורה כי השני נעלם כי [...] החיצוניות שהם ב' על ט' [...] הנעלם השני [ב ד ו ט]
|
- Third example: [...] as this:
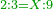
|
משל שלישי [...] כזאת הצורה
|
-
|
|
- This expression indicates that the word "what" is third.
|
[...] והנה זה הדיבור יורה כי מלת מה היא [השלישית]
|
- We multiply the extremes, which are 2 by 9; the result is 14. Divide it by 3; the result is 6 and [it is] the third.
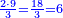
|
[הנה נכפול] החיצוניות שהם ב' על ט' יעלו י"ח וחלקהו על ג' יעלו ו' והוא [...] השלישי
|
- Fourth example: we suppose that the fourth is unknown, so 6 is left alone as this:
|
משל רביעי נאמר כי הרביעי נעלם ישאר ו' לבד [כזאת] הצורה
|
-
|
|
- We suppose that the fourth is unknown and say: if 2 yields 3, what will 6 yield?
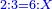
|
הנה נאמר בזה הנעלם רביעי ונאמר אם ב' נתן ג' ו' מה יתן
|
- This expression indicates that the word "what" is fourth.
|
והנה זה ה[דיבור] יורה כי מילת מה היא רביעית
|
- We multiply the means: 6 by the one that does not correspond to it, which is 3; the result is 18. Divide it by its brother, which is 2; the result is 9 and this is the required.
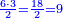
|
ועתה נכפול האמצעים ו' על הבלתי דומה לו שהוא ג' יעלו י"ח נחלקם על אחיו שהוא ב' יעלו ט' והוא המבוקש
|
- I did throughout book as these [four examples], and you can change the questions of all these examples, as long as you are careful not to multiply the corresponding ones, as I said, since the expression indicates the unknown.
|
והנה [בזה] המשל הרביעי נהגתי בכל הספר ואתה תוכל להחליף השאלות בכל אלה המשלים ובלבד שתשמור שלא תכפול דומים כאשר אמרתי כי הדיבור מורה הנעלם כאשר אמרתי
|
- You can see it also in this diagram, from which you learn how to write the three numbers according the "Rule of Three" in order to find the fourth that is unknown:
|
ותראהו גם כן בזה הצורה מה אשר בה תלמוד כיצד תניח הג' מספרים מדרך השלושה לדעת הרביעי הנעלם
|
| what 0 |
yields |
3 |
If |
6 |
yields |
9
|
| 2 |
[yields] |
what 0 |
If |
6 |
yields |
9
|
| If |
2 |
yields |
3 |
what 0 |
yields |
9
|
| If |
2 |
yields |
3 |
6 |
[yields] |
what 0
|
|
|
| ט |
נתן |
ו |
אם |
ג |
יתן |
מה 0
|
| ט |
נתן |
ו |
אם |
מה 0 |
|
ב
|
| ט |
יתן |
מה 0 |
ג |
בא |
ב |
אם
|
| מה 0 |
|
ו |
ג |
נתן |
ב |
אם
|
|
|
- When you have three numbers, they are four in a line, like:
|
והנה זה שאמרתי שיהיו בידך שלושה מספרים כאשר אמרת הנה [..] ולהיות בידך שלושה מספרים שהם בטור ארבעה כמו
|
-
|
|
- Because they are like:
|
כי הם כמו
|
-
|
|
| [Illegible].
|
[209][...] והרי לך [...] ובדדח האמצעיות [...] וכן אם נכפול [...] ח' ואם נחלק על ח' יציא [...] שתכפול ח' על ב' ותחלק [...]
|
| You will understand all this in what follows, with God's help.
|
כי במה שיבא בע"ה תבין כל זה[210]
|
- [The second way] is called "False Position", which is to know an unknown number [...] suppose any number, but they choose to assume a number that has all the required fractions to avoid the trouble, and if we do not do so, it does not matter, except that the calculation will involve fractions. By this method you find what you cannot find by the "Rule of Three", using the "Rule of Three" as you will see.
|
[...] נקרא מונח כוזב והוא לדעת מספר נעלם [...] שתניח מספר מה איך שיזדמן אלא שבחרו להניח מספר שנמצאו בו כל החלקים הנשאלים להסיר הטורח ואם לא נעשה כן אין בכך כלום אלא שיהיו בחשבון שברים והנה עם זה הדרך תמצא מה שלא תמצא עם דרך השלושה אבל עם [..] עזר דרך השלושה כאשר תראה
|
- I will give here one example and say that you assume any number that has all the required fractions, like six, or 12, or whatever number you want:
|
ואתן בכאן משל אחד ואומר שתניח מספר מה שיהיו בו כל החלקים הנשאלים כמו ששה או י"ב או איזה מספר שנרצה
|
- Example: what is the number whose half and third [summed together] are six?
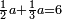
|
המשל בזה מהו המספר אשר חציו ושלשיתו יהיה ששה
|
- Suppose is is six, because it has a whole half and third. We take the half and the third of six; they are five, but we ask for six.
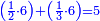
|
נניח ששה כי בו ימציא חצי ושלישי' בשלמות וניקח חצי ושלישית מששה יהיו חמשה ואנחנו שאלנו ששה
|
- We turn to the "Rule of Three", so this will complete our question, and say: if 6 gives us 5, what will give us 6?
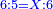
|
נלך אל דרך השלושה והוא ישלים לנו שאלתנו ונאמר אם ו' נתן לנו ה' מי יתן לנו ו'
|
- As this diagram:
|
ויהיה בצורה הזאת
|
-
|
|
- We multiply the extremes that do not share love and brotherhood; it is 36. Divide it by 5; the result of division is 7 and a fifth and this is the unknown.
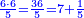
|
נכפול הקצוות שאין להם אהבה ואחוה יהיו ל"ו חלקים על ה' יעלה בחילוק ז' וחמשית והוא הנעלם
|
- You see that in these questions there is no need to write a zero instead of the unknown.
|
ובשאלות תראה שאין צורך לכתיבת הספרא במקום הנעלם
|
- The check: convert 7 into fifths; with the fifth they are 36 fifths.
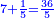
|
והנה הבדיקה היא שתתן ז' בחמשיות יהיו עם החמשית ל"ו חמשיות
|
- A half and a third of 36 are 30 fifths.
|
וחצי ושלישית ל"ו הם ל' חמשיות
|
- Divide them by 5; the result is six integers. So, 7 and a fifth is the number, whose half and third are six.
|
חלקם על ה' יעלו ששה שלמים ואם כן ז' וחמשית הוא המספר אשר חציו ושלישיתו הוא ששה
|
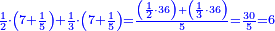
|
- [Illegible].
|
[211]הדרך [...] הכוז[ב] [...] המונח הכוזב וה[...] פעמים שני מספרים אין [...] היותר נאותים וראוים הם שתקח [...] כל החלקים הנשאלים בשלמות [...] כאשר כתבתי במונח הכוזב
|
- The mighty and powerful act [Esther 10, 2] of this way is that you assume a certain number as the first term, then add or subtract the required parts.
|
ומעשה תוקפו וגבורתו[212] בזה הדרך והוא שתקח למונח הראשון מספר מה ואחר תוס[יף] או תגרע החלקים הנשאלים
|
- If, after you perform your operation, [the outcome] is less or exceeds your question, keep the excess or the deficiency.
|
ואם אחר שעשית מלכתך יגר[עו] או יעדיפו תשמור אותו העודף או הגורע משאלתך
|
- Then, assume a second term and do as you have done with the first and keep the excess or the deficiency.
|
ואחר תניח מונח שני ותעשה כמו שעשת לראשון ותשמור המספר העודף או הגורע משאלתך
|
- Now, you relate your question and say: if a term exceeds or deficient by something and so for the second term; then you know that if the two terms exceed or both are deficient, subtract the smaller from the greater and keep the remainder to divide by it, because this is the denominator. If one exceeds and the other is deficient, add them both together and they are the divisor. This is their sign: subtract when they are similar and sum when they are different. As deficient and deficient, or exceeding and exceeding, are similar, so subtract the [smaller from the greater], whereas if one is deficient and the other exceeds, add up both.
|
ועתה תערוך שאלתך ותערוך שאלתך ותאמר אם מונח כך פחות או יותר כך וכן במונח השני ואחר תדע כי כאשר תציא מן המונחים יותר בשניהם או פחות בשניהם גרע הקטן מן הגדול והנשאר תשמרהו לחלק עליו כי הוא המורה ואם יהיה היוציא האחד עודף והשני גורע תחבר שניהם יחד ושניהם יהיו המחלק וסמנם גרע בשוים ובמתחלף חבר כי פחות ופחות ועודף ועודף בשניהם שוים [תגרע הגדול מן הקטן] ופחות באחד ועודיף באחר תחבר שניה'
|
- Then, multiply the first assumption by the result of the second and multiply the second assumption by the result of the first.
|
ואחר תכפול המונח הראשון על היוציא בשני וכן תכפול המונח השני על היוציא בראשון
|
- Subtract the smaller of them by the other, if the results of both exceed the required or less than it, and divide the remainder by the reserved.
|
ותגרע הקטן משניהם מן האחר אם היוציא משניהם יותר מן המבוקש או פחות והנשאר תחלק על השמור הנשאר אשר גרעת זה מזה
|
- Or, add them together, if one of them exceeds and the other deficient, then divide the sum by the reserved that you added one to the other; the result of division is the required.
|
או תחברם יחד אם היוציא משניהם יהיה אחד עודף ואחד גורע והמחובר חלק על השמור אשר חיברת זה עם זה והיוציא בחילוק הוא המבוקש
|
- Example: what is the number whose half and third [summed together] are six?
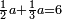
|
המשל בזה מה הוא המספר אשר חציו ושלישיתו יהיה ששה
|
|
|
נניח מונח אחד ויהיה המונח ששה בעבור שימצאו [213][...] חסר [...]
|
| [..] |
minus |
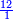 |
5 |
36
|
| X
|
| 12 |
plus |
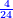
|
|
|
| וג |
ה |
בא |
פחות |
[..]
|
| א
|
| X
|
| ד |
עודף |
יב
|
| דב
|
|
|
|
|
[...] ד' ונאמר עם י"ב עוד ד' ונניחם [...] והנה בעבור שהיו פחות ועודף נחברם יהיו חמשה והוא המורה לחלק עליו ואחר נכפול המונח הראשון שהוא ששה על העודף בשני שהוא ד' ויהיו כ"ד תתנם תחת ד' גם כפול המונח השני שהוא י"ב על הפחות בראשון שהוא אחד יעלו י"ב תתנם על א' ומאחר כי המונח האחר הוא פחות והשני עודף חברנו שניהם י"ב וכ"ד יהיו ל"ו חלקים על השמור שהוא חמשה יעלה בחילוק ז' וחמשית והוא המבוקש
|
|
|
כי חצי ושלישית ז' וחמשית הם ששה
|
|
|
עיין במשל דרך השלושה ועוד תראה זה בע"ה ועיין וראה במה שעשינו עם המונח הכוזב ועם דרך השלושה עשינו עם ב' הנחות כוזבות
|
- The fourth way, which I call the single, since by this way alone you can solve most questions that are solved by the way of "Double False Position", and it does not requires the "Rule of Three":
|
הדרך הרביעי קראתי אותו דרך [יחידי] יהיה בעבור שעם זה הדרך לבד תוכל להוציא רוב השאלות היוצאות עם הדרך השני מונחים הכוזבים וגם שאינו צריך לדרך השלושה
|
- In this way you always assume one for the first unknown and if it is said double the first or a multiple of the first plus so and so, or minus so and so, and the same for the others, subtract the smaller from the greater, whether the additive from the subtractive or the subtractive from the additive. If the remainder remains from the additive, subtract it from the amount you bought, then divide what remains by the sum of the terms, and the result of division is the required [...]. [If the remainder remains from the subtractive, add it] to the amount you bought, [then divide the sum by the sum of the terms, and the result] of division is the required. [...] The sum of the terms is always [...].
|
ולעולם בזה הדרך תניח לשאלתך אחד והוא שתקח אחד לראשון הנעלם ואם אמר כפל או כפלי הראשון בתוספת כך או בפחות כך וכן לאחרים גרע הקטן מן הגדול אם שיהיה העודף מן הפחות או הפחות מן העודף והנשאר אם הוא מן העודף גרעהו מסך מה שקנית והנשאר תחלק על קיבוץ המונחים והיוציא בחילוק הוא [214]הראוי [....] על הסך שקניתי [...] בחילוק הוא הראוי [...] שנפל בחלקו והנשאר הוא [...] כי אין מזה הדרך משל עוד [...] תראה ולעולם קיבוץ המונחים הוא [...] הוא לראשון הנעלם ואחר שתדע הראשון [...]
|
| Multiple quantities problems
|
|
- The first example: three students bought one book for [24 dinar], we do not know how much each one paid for the book, but we know that the second paid twice the first plus 3 dinar and the third paid three times the second minus 7.
- I ask: how much did each one pay for the book and how much time he had it according to what he paid?
|
והמשל הראשון שלשה תלמידים קנו ספר אחד בסך [כ"ד די'] [ולא] ידענו מה שפרע כל אחד בספר אבל ידענו כי השני פרע כפל הראשון ועוד ג' די' והשלישי פרע ג' כפלי השני פחות ז'
שאלתי כמה פרע כל אחד בספר וערך הזמן שיהיה בידו כפי מה שפרע
|
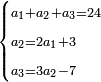
|
|
- Answer: assume one to the first.
|
תשובה תניח אחד לראשון
|
- Since it is said that the second paid double the first plus 3, double the assumption; it is 2. Write 3 elsewhere to indicate "plus 3".
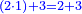
|
והנה בעבור שאמר כי השני נתן כפל הראשון ועוד ג' תכפול המונח יהיו ב' ותכתוב ג' במקום אחר שיורה ועוד ג'
|
- Since it is said that the third [paid] 3 times the second, multiply all parts of the second by 3; it is 6 beneath the assumption and 9 beneath what he said "plus 3", because its product is 9. Write 7 elsewhere and write there "minus".
|
ובעבור שאמר השלישי ג' כפלי השני תכפול כל חלקי השני בג' ויהיו ו' תחת המונח וט' תחת מה שאמר ועוד ג' כי כפלו ט' ותכתוב ז' במקום אחר ותרשום בו פחות
|
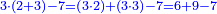
|
- It is according to this diagram:
|
ויהיה בזה הצורה
|
| given terms
|
| minus |
1 |
plus
|
| |
2 |
3
|
| 7 |
6 |
9
|
| denominator |
9 |
|
|
|
|
| המונחים
|
| עוד |
א |
פחות
|
| ג |
ב |
|
| ט |
ו |
ז
|
| |
ט |
המורה
|
|
|
- Sum the assumption; it is 9 and this is the denominator.

|
תחבר המונח יהיו ט' והוא המורה לחלק עליו
|
- Subtract 7, which is the subtractive, from the additive, which is 12; 5 remains and this is the excess.
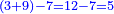
|
תגרע ז' שהוא הפחות מן העודף שהוא י"ב ישארו ה' והם מן העודף
|
- Subtract it from the price, which is 24; 19 remains.
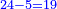
|
תגרעם מן הסך שהוא כ"ד ישארו י"ט
|
- Divide it by 9, which is the denominator; the result of division is 2 and a ninth and this is the money of the first.
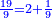
|
תחלקם על ט' שהוא המורה יעלה בחילוק ב' ותשעית וזה ממון הראשון
|
- Double it; it is 4 and 2-ninths plus 3 and this is the money of the second.
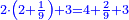
|
תכפלם יהיו ד' וב' תשיעיות ועוד ג' וזה ממון השני
|
- Multiply the money of the second by 3; it is 12 and six-ninths plus 9 minus 7.
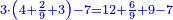
|
תכפול ממון השני בג' יהיו י"ב וששה תשיעיות ועוד ט' ופחות ז'
|
- According to this diagram:
|
ותהיה בזאת הצורה
|
-
|
|
|
|
השנית ואחר גרע הפחות מן השלשי ישאר [...][215][...]
|
|
|
[...] הזמן שיהיה ביד כל אחד כפי הממון שנתן
|
|
|
[...] וו' תשיעיות וזה הוא המבוקש
|
- The result is that the money of the first is 2 dinar and one-ninth of a dinar, and he has the book 2 hours and one-ninth of an hour every day.
|
ויציא מזה כי ממון הראשון ב' די' ותשיעית דנר והנה ב' שעות ותשעית שעה [..] יהיה הספר אצלו בכל יום
|
- The money of the second is 7 dinar and 2-ninths of a dinar, and the book is in his hand 7 hours and 2-ninths of an hour every day.
|
וממון השני הוא ז' די' וב' תשיעי דנר וז' שעות וב' תשעי שעה יהיה הספר בידו בכל יום
|
- The money of the third is 14 dinar and six-ninths of a dinar, which is 2-thirds of a dinar, which are 8 pešiṭim, and the book is in his hand 14 hours and 2-thirds of an hour, which are 40 minutes, every day.
|
והנה ממון השלישי הוא י"ד די' וששה תשיעיות דנר שהם ב' שלישיות דנר שהם ח' פשי' והנה י"ד שעות וב' שלישי שעה שהם מ' דקים יהיה הספר בידו בכל יום
|
- As you can see in the third correct diagram.
|
כמו שתראה בצורה השלישית המתוקנת
|
- The check: sum the ninths; they are one. Add it to 23 integers; they are 24 integers and this is the required.
|
והבחינה שתחבר התשיעיות יהיו אחד תחברהו עם כ"ג שלמים יהיו כ"ד והוא המבוקש
|
- The second example: three goblets, their total value is 85 peraḥim and their weight is 85 ՚oqya. We do not know the value of the first, but we know that the value of the second is 3 times the first plus 5 and the value of the third is 4 times the second minus 7.
|
משל שני ג' גביעים אשר סך כולם פ"ה פרחים וכן משקלם פ"ה אוקיות ולא ידענו סך הראשונה אבל ידענו כי סך השנית הוא ג' כפלי הראשונה ועוד ה' וסך השלישית הוא ד' כפלי השנית פחות ז'
|
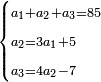
|
|
- The answer: we assume 1 for the first.
|
תשובה נניח א' לראשונה
|
- So, the second, which is 3 times the first, is 3 plus 5.
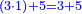
|
ואם כן תהיה השנית שהיא ג' כפלי הראשונה ג' ועוד ה'
|
- The third, which is 4 times the second minus 7, is 12 plus 20 and elsewhere minus 7.
|
והשלישית שהיא ד' כפלי השנית ופחות ז' יהיה י"ב ועוד כ' ובמקום אחר פחות ז'
|
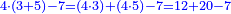
|
- It is according to this diagram:
|
ויהיה כזאת הצורה
|
| given terms
|
| minus |
1 |
plus
|
| |
3 |
5
|
| 7 |
12 |
20
|
| denominator |
16 |
|
|
|
|
| המונחים
|
| עוד |
א |
פחות
|
| ה |
ג |
|
| כ |
יב |
ז
|
| |
יו |
המורה
|
|
|
- We sum the terms together; they are 16 and this is the denominator.
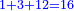
|
נחבר המונחים כולם יהיו י"ו והוא המורה לחלק עליו
|
- We subtract the subtractive, which is 7, from the additive, which is 25; 18 remains.
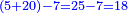
|
נגרע הפחות שהוא ז' מן מן העודף שהוא כ"ה ישארו י"ח
|
|
|
והנשאר יהיו מן העודף נגרעם מסך [216]הכל שהוא [...] ד' וג' חלקים [...] ד' פרחים וג' חלקים [...] מי"ו חלקים באוקיא וסך ה[...] חלקים מי"ו ועוד ה' וי"ב יהיו י"ז [...] השני הוא י"ז פרחים וט' חלקים מי"ו בפרח [...] האוקיא י"ו חלקים
|
|
|
וסך השלישי שהוא ד' כפלי השני [...] מ"ח ול"ו חלקים מי"ו ועוד כ' ופחות ז' נגרע הפחות מן העודף ישארו י"ג ומ"ח שהיו לנו יהיה ס"א ושנים שיצאו מל"ו יהיו ס"ג וד' חלקים [.] מי"ו שהוא רביעית והנה סך הגביע השלישי הוא ס"ג פרחים וד' חלקים אשר הפרח הוא י"ו חלקים והוא רביע פרח ומשקלם הוא י"ז אוקיות וד' חלקים אשר האוקיא הוא י"ו ומקוצר יהיה רביע אוקיא ויהיה כזה הצורה
|
| third example
|
| 3 |
4 |
first
|
| 16 |
|
|
| 9 |
17 |
second
|
| 16 |
|
|
| 4 |
63 |
third
|
| 16 |
|
|
|
|
| משל שלישי
|
| ג |
ד |
לראשונה
|
| יו |
|
|
| ט |
יז |
שנית
|
| יו |
|
|
| ד |
סג |
שלישית
|
| יו |
|
|
|
|
- The check: sum up the fractions of the peraḥ; they are one peraḥ, or one ՚oqya. Sum up the peraḥim; they are 84. With the one; they are 85 peraḥim or ՚oqyot and this is the required.
|
והבחינה חבר שברי הפרח יהיו פרח אחד או אוקיא אחת תחבר הפרחים יהיו פ"ד ועם האחד יהיו פ"ה פרחים או אוקיות והוא המבוקש
|
|
|
משל שלישי שלא יעדיף אלא יפחות
|
- Three bought a mule to go to Jerusalem, for a price of 30 peraḥim, we do not know how much each one paid, but we know that the second paid 3 times the first minus 4 and the third paid 4 times the second minus 5.
- I ask: how much did each one pay and how many parsa will each ride the mule?
|
והוא שג' קנו חמור פרדה ללכת לרושלים בסך ל' פרחים ולא ידענו מה שפרע כל אחד אבל ידענו שהשני נתן ג' כפלי הראשון פחות ד' והשלשי נתן ד' כפלי השני פחות ה'
שאלתי סך כל אחד וכמה פרסאות ירכב כל אחד בפרדה
|
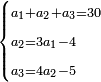
|
|
- Suppose the first gave 1.
|
נניח כי הראשון נתן א'
|
- So, the second gave 3, which is 3 times the first, minus 4.
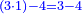
|
ואם כן השני נתן ג' שהוא ג' כפלי הראשון ופחות ד'
|
- The third [gave] 4 times the second minus 5: 4 times the second are 12 and four times the minus of the second are minus 16 with his own minus 5 they are minus 21.
|
והשלישי ד' כפלי השני ופחות ה' והנה ד' כפלי השני הם י"ב גם ד' פעמים פחות השני הם י"ו פחות ולעצמו פחות ה' יהיו [כ"א]
|
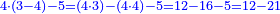
|
- The subtractive is 25 and the sum of the [additive] is 16.
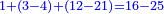
|
הפחות כ"ה וקיבוץ המונחים י"ו לחלק עליו
|
|
|
ויהיה [217][...] יהיו כ"ה [...] הראוי לראשון וג' [...] פחות ד' והשלישי שאמר [...] ופחות י"ו שבא מד' כפלי [...] שתראה בזה הצורה השנית
|
| the first gave |
plus |
 |
minus
|
| the second gave |
9 |
 |
4
|
| the third gave |
36 |
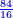 |
16
|
|
|
| פחות |
[..] |
[עוד] |
[הראשון נתן]
|
| ד |
כא |
ט |
השני נתן
|
| |
יו |
|
|
| יו |
פד |
לו |
השלישי נתן
|
| |
יו |
|
|
|
|
- The money [of the first] is 3 peraḥim and 7 parts of 16 of a peraḥ; he rides the mule 3 parsa and 7 parts of 16 of a parsa.
|
והנה הסך הוא ג' פרחים וז' חלקים מי"ו בפרח וג' פרסאות וז' חלקים מי"ו בפרסה ירכב הראשון בפרדה
|
- The money of the second is 9 peraḥim and 21 parts of 16 minus 4.
|
והנה סך השני הוא ט' פרחים וכ"א חלקי י"ו פחות ד'
|
- Subtract 4 from 9; 5 remains; plus the 1 of the fractions they are 6 and 5 parts of 16 of a peraḥ.
|
גרע ד' מט' ישארו ה' וא' מן השברים יהיו ו' וה' חלקים מי"ו בפרח
|
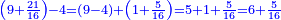
|
- The money of the third is 36 and 84 parts of 16, which are 5 integers and 4 parts of 16; they are 41 and 4 parts of 16.
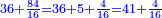
|
וסך השלישי הוא ל"ו ופ"ד חלקים מי"ו אשר הם ה' שלמים וד' חלקים מי"ו יהיו מ"א וד' חלקים מי"ו
|
- Subtract from 41 the subtractive in his share, which is 16 plus 5, which are 21; 20 peraḥim remains and 4 parts of 16 of a peraḥ, which when reduced is a quarter.
|
גרע הפחות אשר בחלקו שהוא י"ו וה' שהם כ"א ממ"א ישארו כ' פרחים וד' חלקים מי"ו בפרח שמקוצר הוא רביע
|
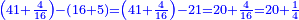
|
- The result is that the money of the first is 3 peraḥim and 7 parts of 16 of a peraḥ; and the first has the mule for 3 parsa and 7 parts of 16 of a parsa.
|
ועלה מזה כי סך הראשון הוא ג' פרחים וז' חלקים מי"ו בפרח וג' פרסאות וז' חלקי פרסה מי"ו בפרסה יהיה הפרדה ביד הראשון
|
- The money of the second is 6 peraḥim and 5 parts of a peraḥ; and the second has the mule for 6 parsa and 5 parts of a parsa.
|
וסך השני ו' פרחים וה' חלקי פרח וו' פרסאות וה' חלקי פרסה יהיה הפרדה ביד השני
|
- The money of the third is 20 peraḥim and 4 parts of 16 of a peraḥ, which is a quarter; and the third has the mule for 20 parsa and a quarter.
|
וסך השלשי הוא כ' פרחים וד' חלקים מי"ו בפרח שהוא רביעית וכ' פרסאות ורביעית יהיה הפרדה ביד השלישי
|
- The same for everything similar to it.
|
וכן כל הדומה לזה
|
- Here you have the diagram of the three:
|
והרי לך צורת שלושתם
|
| the first |
3 |
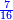
|
| the second |
6 |
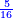
|
| the third |
20 |
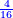
|
|
|
| ז |
ג |
לראשון
|
| יו |
|
|
| ה |
ו |
לשני
|
| יו |
|
|
| ד |
כ |
לשלשי
|
| יו |
|
|
|
|
|
|
והבחינה חבר חלקי שלושתם ואם יהיו ל' מוטב המשל בזה חלק הראשון ג
|
|
|
שאלה ראובן שלי"ס וכו' בשיור
|
- Reuven, Shimon, Levi, Yehuda, and Joseph bought one bull.
- Reuben took a third, Shimon a quarter, Levi a fifth, Yehuda a sixth, and Joseph 5 liṭra.
- I ask [how much] is the weight of the whole bull?
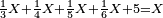
|
[218]שאלה ראובן שמעון לוי יהודה יוסף קנו שור אחד ראובן לקח השלישית ושמעון הרביעית ולוי החמישית ויהודה הששית ויוסף ה' ליטרין שאלתי משקל כל השור
|
- We assume a false position: the liṭra of the bull are 60. A third of 60 is 20; its quarter is 15; its fifth is 12; its sixth is ten. All together they are 57.
|
נניח מונח כוזב כי ליטרי השור הם ס' הנה שליש ס' הוא כ' ורביעיתו ט"ו וחמשיתו י"ב וששיתו עשרה והנה כולם נ"ז
|
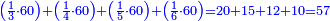
|
- Joseph is left with 3, but we asked 5 for Joseph.
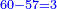
|
ונשארו ג' ליוסף ואנחנו שאלנו ה' ליוסף
|
- Now, we say: if 3 comes from 60, from which number will 5 come?
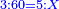
|
עתה נאמר אם ג' בא מס' מאי זה מספר יבא ה'
|
- We multiply 5 by 60; the result is 300.
|
נכפול ה' בס' יעלו ש'
|
- We divide it by 3; the result is 100; so the weight of the bull is a hundred liṭra.
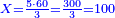
|
נחלקם על ג' יעלו ק' והנה מאה ליטרין משקל השור
|
- The check: the third is 33 liṭra and a third, which is 12 ՚oqya, because 36 ՚oqya are one liṭra in Zaragoza; the quarter is 25; the fifth is 20; and the sixth is 16 and two-thirds, which are 24 ՚oqya. We sum up all; they are 95 liṭra and with the 5 of Joseph they are 100 [and this is] the required, which is the liṭra of the bull.
|
והבחינה הנה השלישית ל"ג ליטרי' ושליש שהם י"ב אוקיות כי ל"ו אוקיות הליטר' [..] בסרקוסה והרביעית כ"ה והחמשית כ' והשישית י"ו ושני שלישיות שהם כ"ד אוקיות
נחברם כולם יהיו צ"ה לטרין ועם ה' מיוסף יהיו ק' [..] המבוקש שהם לטרי השור
|
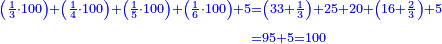
|
|
|
[219]הדרך [החמישי]
|
|
|
[...] הממון תוסיף על ה [...] הדרך לא אזכרנו אלא בכאן [...]
|
|
|
והמשל בזה שהיו בפתח הבית [...] בעל הבית לעבדו שיחלק לכל איש ב' פשיט' ולכל אשה פשוט שאלתי סך האנשים
|
- The answer: assume the [number of] men and the women as you wish and give them as he said, then, if there are any pešiṭim left, add to the men and subtract from the women.
|
והתשובה תניח האנשים והנשים שתרצה וחלק להם כמו שאמר ואחר אם נשארו פשיטי' תוסיף על האנשים ותגרע מן הנשים
|
- We suppose the men are 4 and the women are 18.
|
כיצד נאמר כי האנשים ד' והנשים י"ח
|
- 2 pešiṭim for each man are 8 and one pašuṭ for each woman are 18; plus 8 they are 26.
|
והנה ב' פשיט' לכל אחד איש יהיו ח' ופשוט לכל אשה יהיו י"ח וח' יהיו כ"ו
|
|
|
וגרעו ב' כי אנחנו כ"ד שאלנו גרע מן האנשים ב' יהיו ב' אנשים וכ' נשים והוא יהיה שוה ד' פשי' לב' אנשים וכ' לכ' נשים
|
|
|
משל שני חלק ל' לל' אנשים ונשים ונערים אשר תתן לכל איש ב' פשיט' ולכל אשה פשיט' ולכל נער מחצה הנה האנשים הם ז' והנשים ט' והנערים י"ד
|
|
|
וכן כל הדומה לזה בחומרים שתרצה ועיין בם
|
The Second Chapter - Problems Concerning the Addition of Integers
|
הפרק הש[ני בשאלות חיבור שלמים]
|
- Question one: [What is] the number, such that if you add [to it] its half, its fifth, and its seventh, [the total is 2].
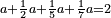
|
[220][...] [שאלה ראשונה] [מהו ה]מספר אשר אם תחבר [עליו] חציו חמשיתו ושביעיתו [יהיה עם הכל שנים]
|
- Answer with a false position: we look for a number that has [a half, a fifth, and a seventh; it is 70]. Because the half indicates 2, the fifth 5, the seventh 7; we multiply them by each other as the rule: 2 by 5 is ten, ten by 7 is 70.
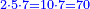
|
תשובה עם מונח כוזב [...] נבקש מספר שימצאו בו [...] [והוא ע'] כי חצי יורה על ב' וחמשית על ה' ושבעית על ז' נכפול זה על זה כמנהג ב' על ה' עשרה ועשרה על ז' ע'
|
- We suppose this is the number. We add to it the mentioned parts: its half, which is 35; its fifth, which is 14; its seventh, which is ten. We add all of them to 70; it is 129.
|
ונניח כי זהו המספר ונחבר עליו החלקים הנז' שהם חציו שהוא ל"ה וחמשיתו שהוא י"ד ושביעיתו שהוא עשרה
נחברם כולם על ע' יהיו קכ"ט
|
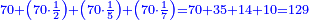
|
- The number we assumed is 70 and it is false, because we ask for 2 and it gives us 129.
|
והנה המספר שהנחנו הוא ע' והוא כוזב כי אנחנו שאלנו ב' והוא נתן לנו קכ"ט
|
- We apply the "Rule of Three" and it gives us the solution. We say: if 70 gives us 129, what will give us 2?

|
נלך אל דרך השלושה והוא יתן לנו שאלתנו ונאמר אם ע' נתן לנו קכ"ט מי יתן לנו ב'
|
- We write this question as this diagram:
|
[221]נניח השאלה כזאת ה[צורה]
|
-
|
|
- We multiply the extremes, which are 2 by 70; the result is 140.
|
נכפול הקצוות שהם ב' על ע' יעלו ק"מ
|
- We divide it by the second number, which is 129; the result of division is 1 and eleven parts of 129 of a units, like this:
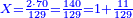
|
חלקם על המספר השני שהוא קכ"ט יעלו בחילוק א' ואחד עשר חלקים מקכ"ט בשלם כזה
|
|
|
|
- This is the number that if you add to it its half, its fifth, and its seventh, the total is two and this is the required.
|
וזה הוא המספר אשר אם תחבר עליו חציו חמשתו ושבעיתו יהיה עם הכל שנים וזה הוא המבוקש
|
- If you want to check if it is true that 1 and 11 parts of 129 is the number to which if you add the mentioned parts the result is two:
|
ואם תרצה לבדוק אם זה אמת כי א' וי"א חלקים מקכ"ט הוא המספר אשר אם תחבר עליו החלקים הנזכרי' שלא יעלו אלא שנים
|
- The procedure is as follows: decompose the integer into fractions; they are 129. With 11, it is 140.
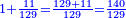
|
הנה מעשה הבחינה כך הוא שתתן השלם בשברו יהיו קכ"ט ועם י"א יהיו ק"מ
|
- Add to 140 its half, which is 70; it is 210.
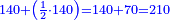
|
תחבר על ק"מ חציו שהוא ע' יהיו ר"י
|
- Add a fifth of 140, which is 28, to 210; it is 238.
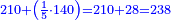
|
חבר על ר"י חמשית ק"מ שהוא כ"ח יהיו רל"ח
|
- Add to it also a seventh of 140, which is 20; it is 258.
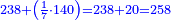
|
עוד חבר עליו שביעית ק"מ שהוא כ' יהיו רנ"ח
|
- Divide it by 129, which is the whole; the result of division is 2 and this is the required.
|
חלקם על קכ"ט שהוא השלם יעלה בחילוק ב' והוא המבוקש
|
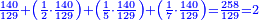
|
- Question two: What is the number, such that if you add to it its third, then to the sum 2-fifths of the sum, then to this sum 3-quarters of the sum, [and after all this the result is 13].
|
שאלה שנית מהו המספר אשר אם תחבר עליו שלישיתו ועל העולה ב' חמשיות מן העולה ועל העולה ג' רביעיות מן [222]העולה [ ועם כל זה יעלה י"ג]
|
![\scriptstyle\left(a+\frac{1}{3}a\right)+\left[\frac{2}{5}\sdot\left(a+\frac{1}{3}a\right)\right]+\left[\frac{3}{4}\sdot\left(a+\frac{1}{3}a\right)+\left[\frac{2}{5}\sdot\left(a+\frac{1}{3}a\right)\right]\right]=13](/mediawiki/images/math/8/3/6/8369d7990f744b9a523db6ca37d54373.png)
|
|
|
[...] כוזב ועם דרך [...] האלו השברים בשלישית [...] ס' ונניח כי זה הוא המספר [...] נחבר על פ' ב' חמשיותיו שהוא [...] רביעיותיו שהם פ"ד יהיו קצ"ו והנה [...] כי קצ"ו נתן לנו ואנחנו לא שאלנו כי אם י"ג
|
|
|
נלך [...] והוא ישלים שאלתנו ונאמר אם ס' נתן לנו קצ"ו מי יתן לנו [י"ג] נניח השאלה בזאת הצורה
|
|
|
|
- Multiply the extremes, which are 13 by 60; the result is 780.
|
ותכפול הקצוות שהם י"ג על ס' יעלה תש"ף
|
- We divide it by the second number, which is 196; the result of division is 3 integers and 192 parts of 196 of a units and if you reduce them, they are 48 parts of 49 of a unit.
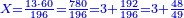
|
נחלקם על המספר השני שהוא קצ"ו יעלה בחילוק ג' שלמים וקצ"ב חלקים מקצ"ו בשלם אשר אם תקצרם יהיו מ"ח חלקים ממ"ט בשלם
|
- This is the number, such that if you add its third to it, then to the sum 2-fifths of the sum, then to this sum 3-quarters of the sum, and after all this the result is 13 and this is what we wanted.
|
וזהו המספר אשר אם תחבר עליו שלישיתו ועל העולה ב' חמשיות מן העולה ועל העולה ג' רביעיות מן העולה ועם כל זה יעלה י"ג וזה מה שרצינו
|
- The checking procedure: decompose the integers to fractions and add to the result the fractions added to the 3 integers, which are 192; they are 780 parts of 196, which is the required number, so if you add to it the mentioned fractions, they are 2548 that are 13 integers.
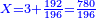
|
מעשה הבחינה כך הוא שתתן השלמים בשברם ועל העולה תחבר השברים העודפים על ג' שלמים שהם קצ"ב יהיו תש"ף חלקים מקצ"ו בשלם שהוא המספר המבוקש אשר אם תחבר עליו החלקים הנזכרים יהיו ב' אלפים תקמ"ח שהם י"ג שלמים
|
- The unknown number we were looking for is 780.
|
כיצד המספר הנעלם אשר בקשנו הוא תש"ף
|
- We add its third to it, which is 260; it is 1040.
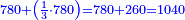
|
חברנו עליו שלישיתו שהוא ר"ס יהיו אלף ומ'
|
- We add 2-fifths of 1040 to it, which is 416; it is 1456.
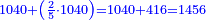
|
חברנו עליו ב' חמשיות אלף ומ' שהם תי"ו יהיו אלף תנ"ו
|
- We add 3-quarters of 1456 to it also, which is 1092; it is 2548.
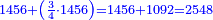
|
עוד חברנו עליו ג' רביעי אלף תנ"ו שהם אלף וצ"ב עליו יהיו ב' אלפים ותקמ"ח
|
- Divide it by the denominator, which is 196; the result of division is 13 integers
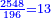
|
חלקם על המורה שהוא קצ"ו יעלה בחילוק י"ג שלמים
|
- Hence, we receive that 3 integers and 192 parts of 196 is the unknown number, such that with the sum of its parts it is 13 as said.
|
ואם כן עלה בידנו כי ג' שלמים וקצ"ב חלקים מקצ"ו הוא המספר הנעלם אשר עם חיבור חלקיו יהיה י"ג כנזכר
|
- Question: What is the unknown number, such that when we add to it half of its half, a third of its third, and a quarter of its quarter, it is exactly 7.
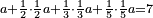
|
[223]שאלה מהו המספר הנעלם אשר חיברנו עליו חצי חציו ושלישית שלישיתו ורביעית רביעיתו ולא יהיה אלא ז'
|
|
|
בזה השאלה תצטרך לכפול כל המורים זה על זה ד' על ד' יהיו י"ו וי"ו על ג' יהיו מ"ח ומ"ח על ג' פעם שנית יהיו קמ"ד וקמ"ד על ב' והיוצא על [ב' תק]ע"ו וזהו המונח נחבר עליו חצי חציו והוא קמ"ד יעלו תש"ך [224]תש"ך נחבר עליו שלישית שלישיתו שהוא ס"ד יהיו תשפ"ד ונחבר על זה רביעית רביעיתו שהוא ל"ו יהיו תת"ך ואנחנו שאלנו ז' נאמר בדרך השלושה אם תקע"ו נתן לנו תת"ך ז' מי יתן לנו ויהיה כזה הצורה
|
|
|
|
- We multiply the extremes; the result is 4032.
|
נכפול קצוות יעלו ד' אלפים ול"ב
|
- We divide it by 820; the result is 3 and 752 parts of 820.
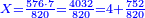
|
נחלקם על תת"ך יעלה ד' תשנ"ב חלקים מתת"ך
|
|
|
וזה המספר אשר אם חיברנו עליו חצי חציו וכו' וכל העולה נחלק על תת"ך יעלו ז' כנשאל
|
|
|
[225]שאלה שלישית מהו המספר הנעלם אשר אם תחבר עליו [226][...] אותו ורביעית [...]
|
|
|
תשובה עם [...] לאלה [...]ת וששית יעלו ק"ך ומה שלא [...] כי חצי נמצא ברבעית ושלשית [...] בפרק קיצור המורים ואם כן נאמר [...] המספר הנשאל אשר עם חבור חלקיו יהיה אחד והנה נקח חצי שלשית רביעית ק"ך יהיה ה' כי רביעית ק"ך הוא ל' ושלשית ל' הוא עשרה וחציו ה' נחבר ה' עם [ק"ך] יהיו קכ"ה עוד נחביר אליו שלישית רביעית חמשית ק"ך שהוא ב' יהיו קכ"ז כי חמשית ק"ך הוא כ"ד ורביעית כ"ד הוא ו' * הוא ב' כנז' עוד נחבר על קכ"ז רביעית חמשית ששית ק"ך שהוא א' יהיו קכ"ח כי השישית הוא כ' וחמשית כ' ד' ורביעית ד' א' ואם כן כאשר תחבר ה' שיצא מן הראשון וב' מן השני וא' מן השלישי עם ק"ך יהיו קכ"ח ואנחנו לא שאלנו כי אם אחד ויצאו קכ"ז יותר ממה ששאלנו
|
|
|
נלך אל דרך השלושה והוא ישלים שאלתנו שהוא כמשל ראשון מדרך השלושה הנה הדרך הוא בזאת הצורה
|
|
|
|
|
|
שתכפול האמצעיות שהם א' על ק"ך יהיו ק"ך חלקם על קכ"ח והנה הוא מחולק והוא ק"ך חלקים מקכ"ח בשלם שאם תקצרם יהיו ה' ששיות כי ערך ק"ך אל קכ"ח כערך ה' אל ו' והנה המספר הנעלם הוא ה' ששיות
|
|
|
מעשה הבחינה כך הוא שתחזור הה' ששיות אל ק"ך חלקים מקכ"ח בעבור כי בו תמצה החלקים הנזכרים ותקח חצי שלישית רביעית ק"ך והוא ה' ושלישית רביעית חמשיתו והוא ב' ורביעית חמשית שישיתו והוא א' תחבר עם ק"ך שהוא המספר הנעלם ה' וב' וא' יהיה קכ"ח תחלקם על המורה שהוא קכ"ח גם כן יעלה בחילוק אחד שלם [227]ואם כן [...] הנעלם [...]
|
| Partnership problems
|
|
- The fourth question: Reuven and Shimon formed a partnership, Reuven contributed 3 dinar and Shimon [contributed] 11 [dinar]; and they earned 3 dinar.
|
שאלה רביעית [ראובן ושמעון עשו חברה ראובן נתן ז' די' ושמעון י"א והרויחו] ג' דינר'
|
|
|
ויהיו כזאת הצורה
|
|
|
|
|
|
ש[אלתי] [...] כל אחד כפי [...] שניהם והוא המורה ועתה אם תרצה הראוי מן הריוח לראובן כפול הריוח על ממונו יעלו כ"א חלקם על י"ח שהוא ממון שניהם יעלה בחילוק אחד ושישית שהוא דניר אחד וששית דניר שהוא ב' פשי' ולדעת חלקי שמעון הוא הנשאר אלא שנעשה אותו בדרך המספר ונאמר שנכפול י"א על ג' יעלו ל"ג נחלקם על י"ח יעלה בחילוק אחד והוא דנר ונשארו ט"ו חלקים מי"ח נקצרם יהיו ה' ששיות והוא הראוי לשמון הנותן בחברה י"א דינר שהוא דנר אחד ועשרה פשי' והנה עם עם דנר וששית שנפל לראובן יהיו ג' די' והוא מה שרצינו
|
|
|
בדיקה אחרת ושמור אותה קח ממונם והריוח וראה אם יחסם שוה ואמור אם י"א הרויחו א' ועשרה פשיט' ז' מה ירויח או תהפוך השאלה כמו שהראתך בדרך השלושה או עשה הדנר פשי' ואמור אם י"א הרויחו כ"ב פשי' ז' מה ירויחו
|
- The fifth question: Reuven, Shimon and Levi formed a partnership, Reuven contributed 29 liṭra to the partnership, Shimon [contributed] 25 [liṭra], and Levi [contributed] 11 [liṭra]; and they earned 13 liṭra.
|
שאלה חמשית ראובן שמעון לוי עשו חברה ראובן נתן בחברה כ"ט לטרין ושמעון כ"ה ולוי י"א והרויחו י"ג לטרין
|
|
|
ויהיו בצורה הזאת
|
|
|
| 0 |
ה |
יג |
כט |
ראובן
|
| |
ה |
כה |
שמעון
|
| ד |
ב |
יא |
לוי
|
| |
|
|
סה |
|
|
|
|
|
שאלתי הראוי לכל אחד
|
|
|
תשובה חבר כל ממונם יהיה ס"ה והוא המורה ואחר כפול ממון ראובן על הריוח שהוא [228][...] שהוא ס"ה [...] נכפלם בסך [...] תחלת השברים ויעלו [...] בחילוק י"ו דנרי' ולא נשאר [...] הוא ה' לטרי' וי"ו דינרי' [...] נכפול ממונו על הריוח יעלו שכ"ה [...] על המורה יעלה בחילוק ה' לטרי' שוים וזה הראוי לשמעון
|
|
|
ולדעת הראוי ללוי הנה הנשאר משניהם הוא חלקו אבל בדרך המספר נכפול י"א שהוא ממונו על י"ג יעלו קמ"ג אשר חלקנום על המורה יעלה בחילוק ב' לטרי' ונשארו י"ג אשר אם כפלנום על סך הלטרה יעלו ר"ס חלקנום על המורה יעלה בחילוק ד' דינ' ולא נשאר כלום והנה הראוי ללוי ב' לטרי' וד' דנרי' ולשמעון ה' לטרי' ולראובן ה' לטרי' וי"ו דנרי' וזה המבוקש
|
|
|
והבחינה נחבר כל הראוי לכולם ואם הוא כסך הריוח מוטב ואם לא שוב לעיין
|
- The sixth question: Reuven and Shimon formed a partnership, Reuven contributed 3 dinar to the partnership on the first day of the year and Shimon contributed 5 [dinar] to the partnership on the first day of Adar [= the sixth month in the Jewish calendar]; they stayed in the partnership until the beginning of the following year and earned 7 dinar.
|
שאלה שישית ראובן ושמעון עשו חברה וראובן נתן בחברה ג' די' ביום ראש השנה ושמעון נתן בחברה ה' דינרים ביום ראשון לחודש אדר ושהו בחברה עד ראש השנה הבאה והרויחו ז' דינרי'
|
|
|
ויהיה כזאת הצורה
|
|
|
די'
ז' |
לו
לה |
ג דינרי'
ה דינרי' |
י"ב חדשים
ז חדשים |
ראובן
שמעון
|
|
|
|
שאלתי הראוי לכל אחד
|
|
|
התשובה שתעשה זמן שניהם דומה בזה השאלה או בכל שאלה אם תוכל שיהיו שניהם כולם שנים או חדשים או ימים או שעות או דקים או לאי זה מין שתוכל כפי צורך כל השאלה כאשר תראה במשלים הבאים ואחר כפול זמן כל אחד על ממונו והיוציא יהיה כמו שהוא הממון שנתן ותעשה כמנהג כיצד [229]בעבור [...] חדשים ויהיו י"ב [...] ל"ו ונאמר בהשאלה כי הממון [...] שמעון בז' חדשיו יהיו ל"ה [...] כמו שתראה בצורה ועשה כמנהג [...] ע"א שהוא קיבוץ שניהם ויעלו לראובן ג' די' [...] ואם תכפלם בי"ב והיוצא תחלק על ע"א יהיו [...] ז' וחלק על ע"א ויהיה העולה ג' די' ול"ב חלקי דינר
|
|
|
והבחינה תקבץ חלקהם ויהיו דנר וששה יהיו ז' בריוח
|
|
|
ודי בזה כי במוקומות אחרים בזה השער תראה שאלות מזה המין יותר קשים
|
|
|
[230]ואם תרצה להקל שאלתך תקצר אותה בחצי ואז תהיה לראובן ו' ולשמו' עשרה ולוי ט"ו והמורה ל"א וכן תעשה תעשה בכל שאלה שתקצרנה בחצי או בשליש או בחלקים שתוכל לקצרה ואחר זאת אחרות בצור'
|
- The seventh question: Reuven, Shimon and Levi formed a partnership together; Reuven contributed 3 dinar and stayed [in the partnership] for 4 months; Shimon [contributed] 4 dinar and stayed [in the partnership] for 5 months; Levi [contributed] 5 dinar and stayed [in the partnership] for 6 months; they earned six dinar. I ask: how should they divide them?
|
שאלה שביעית ראובן שמעון לוי עשו חברה יחד ראובן נתן ג' די' ושהה ד' חדשים ושמעון ד' דינר' ושהה ה' חדשים ולוי ה' די' ושהה ו' חדשים והרויחו ששה די' שאלתי כיצד יחלוקו
|
- The answer: multiply the months of each by his money and the result is the [earned] money of each.
|
תשובה כפול כפול חדשי כל אחד בממונו והיוציא יהיה כמו ממון כל אחד
|
- Hence, Reuven has 12, Shimon has 20, and Levi has 30.
|
ויהיה לראובן י"ב ולשמעון כ' וללוי ל'
|
- We add up the three amounts; it is 62 and this is the denominator to divide by it.

|
חברנו כל השלושה סכום יהיו ס"ב והוא המורה לחלק עליו
|
- The whole question is like this:
|
ויהיה כל השאלה כזאת הצורה
|
| parts of a quartyer |
quarters |
pešuṭim |
dinar |
profit |
money |
months |
dinar |
|
10
62 |
3 |
1 |
1 |
6 |
12 |
4 |
3 |
Reuven
|
58
62 |
0 |
11 |
1 |
20 |
5 |
4 |
Shimon
|
15
62 |
3 |
10 |
2 |
30 |
6 |
5 |
Levi
|
| |
|
|
|
|
62 |
denominator |
|
|
|
| חלקי רביע |
רביעי |
פשיט |
דניר |
ריוח |
ממון |
חדשי |
דנר |
|
י
סב |
ג |
א |
א |
ו |
יב |
ד |
ג |
ראובן
|
נח
סב |
0 |
יא |
א |
כ |
ה |
ד |
שמעון
|
טו
סב |
ג |
י |
ב |
ל |
ו |
ה |
לוי
|
| |
|
|
|
|
סב |
המורה |
|
|
- Now we shall see how much each one deserves according to the money [he contributed] and his staying [in the partnership] by multiplying one by the other:
|
ועתה נראה הראוי לכל אחד כפי ממונו ושהיתו שכפלנו זה על זה
|
| [Illegible].
|
ונעשה[231] [232][...] כל אחד על [...] יהיה חלק [...] תחלקם על המורה [...] הנשאר שהוא י"ו על כ' די' [...] חלקם על המורה יציא ד' די' [...] והנה ג' לטרין ד' די' וע"ד חלקי [...] חלק ראובן
|
- Similarly, multiply 32 by 7 and divide the product by the denominator; the result of division is 3 liṭra and 40 parts of 74 and this is Shimon's share.
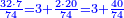
|
ובזה הדרך כפול ל"ב על ז' וחלק היוציא על המורה ותציא בחילוק ג' לטרי' ומ' חלקים מע"ד בשלם וזה חלק שמעון
|
- Multiply also 8 by 7 and divide the product, which is the dividend that is 56 parts, by the denominator, which is 74 of one liṭra: multiply 56 by 20, which is the whole liṭra; the result is 1120. Divide it by the denominator; the result of division is 15 dinar and ten parts of 74 of one dinar and this is Levi's share.
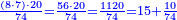
|
עוד כפול ח' על ז' וחלק היוציא על המורה והוא מחולק שהוא נ"ו חלקים מהמורה שהוא ע"ד בליטרה
ותכפול נ"ו על כ' שהוא סך הליטרה יעלו אלף ק"ך
תחלקם על המורה יעלו בחילוק ט"ו דינ' ועשרה חלקים מע"ד בדינ' וזה חלק לוי
|
- We receive that Reuven's share in the profit is 3 liṭra, 4 dinar and 24 parts of 74, which you can reduce to 12 parts of 37.
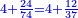
|
והל"ה עלה בידנו שנפל לראובן מן הריוח שהוא ז' ג' ליטרי' וד' דינר' וכ"ד חלקי דינר שתוכל לקצרו שהם י"ב חלקים מל"ז
|
- Shimon's share is 3 liṭra and 40 parts of 74, which are reduced to 20 parts of 37.
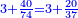
|
וחלק שמעון לג' ליטרי ומ' חלקים מע"ד שהם מקוצרים כ' חלקים מל"ז
|
- Levi's share is 15 dinar and ten parts of 74, which are reduced to 5 parts of 37.
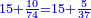
|
וחלק לוי ט"ו די' ועשרה חלקים מע"ד ומקוצרים ה' חלקים מל"ז
|
| And so on for anything like that.
|
וכן כל כיוציא בזה
|
| The check is that you add up the fractions of all three, add the result to the dinar, then convert the dinar to a liṭra or liṭrin, and the result is the profit.
|
והבחינה הוא שתחבר כל שברי שלשתם והיוציא תחבר עם עם הדי' ומהדי' תעשה ליטרה או ליטרין והיוציא יהיה הריוח
|
- In the example: add up their fractions: Reuven has 24, Shimon 40, and Levi ten. Divide them by the denominator; the result is one. With the dinar, which are 19, it is twenty, which is the whole liṭra. With the 3 of Reuven and the 3 of Shimon, they are 7, which is the profit and this is the required.
|
והמשל תחבר שברהם יהיו לראובן כ"ד ולשמע' מ' וללוי עשרה תחלקם על המורה יציא אחד ועם הדי' שהם י"ט יהיו עשרים שהוא לטרה וג' לראובן וג' לשמעו[ן] יהיו ז' שהוא הריוח והוא המבוקש
|
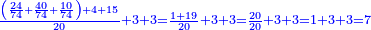
|
- Likewise for the shares of the eighth question: Reuven has 384, Shimon 640, and Levi 160.
|
וכן היו חלקי' השאלה השמינית שהם שפ"ד לראובן תר"מ לשמעון [233]וק"ס ללוי
|
| [Illegible].
|
יהיו [...] המורה שהוא [...] דינר חברהו עם ה[...] הליטרה תחבר אותה [...] והוא הריוח
|
|
|
דרך אחרת לקציר עוד ועיין בה ותשכיל עוד עם דרכים אחרים שאתן תכף זה
|
|
|
ואומר שתקצר הנכפל כל מה שתוכל שוה לכולם
|
|
|
המשל בזה בשאלה התשעית [..] הנה ממון ראובן המשולח הבא מד' קל"ו הוא תקמ"ד וממון שמעון תקי"ב וממון לוי קכ"ח תקצרים בחציים חמשה פעמים ישובו לראובן י"ז ולשמעון י"ו וללוי ד' ולא נוכל עוד לקצר בעבור ממון ראובן שהוא י"ז והנה ש חזרה השאלה כזאת הצורה
|
|
|
|
|
|
ואתן לזה פרק מיוחד ולדרך השלושה
|
|
|
התשובה ידוע הוא כי המבצרים הם ששה וגם מגדלי כל מבצר הם לעיין אבל ידעת כולם בכלל כפי הדרך הראשון שנתתי למספרים הנמשכים בסדר שהוא שתחבר הראשון והאחרון יהיו י"ט תכפלם על חצי המקומות שהם ג' יעלו נ"ז והם כל המגדלים
|
|
|
ועתה לדעת שומרי כל מבצר הנה שומרי מגדלי המבצר הראשון הם ג' לכל מגדל כמו שתראה בצורה שנית כפול ג' [282][...] מגדלי המבצר [...] יעלו ל' כמו שתראה [...] המבצר השלישי שהם ט' על ח' [...] ככפל י"ב על י"א והחמשי ר"י [...] והששי הם ש"ו שומרים ככפל י"ח על [...] בצורת ג' ובכלל הם תשנ"ו
|
|
|
ועתה לדעת [...] כל אחד וכל הפרחים בכלל אומר כי שומרי מגדלי מבצר [רא]שון הם ששה כמו שיורה הצורה השלשית ולכל אחד ז' פרחים כמו שיורה צורה רביעית
|
- Multiply the peraḥim by the guards, 7 by 6; the result is 42 and it is the first in diagram 5.

|
תכפול הפרחים בשומרים ז' על ו' יעלו מ"ב והם ראשונים בצורת ה'
|
- Multiply the 30 guards of the second fortress by the peraḥim of each, which are 6; the result is 180 peraḥim for the guards of the second fortress.
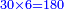
|
גם תכפול ל' שומרים מהמבצר השני על פרחי כל אחד שהם ו' יעלו קף פרחים לשומרי המבצר השני
|
- Multiply the 72 guards of the third fortress by the peraḥim of each, which are 5; the result is 360 peraḥim for the guards of the third fortress.
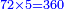
|
עוד תכפול ע"ג שומרי המבצר השלשי על פרחי כל אחד שהם ה' יעלו ש"ס פרחים לשומרי המבצר השלשי
|
- Multiply the 132 guards of the fourth fortress by the 4 peraḥim of each; the result is 528 peraḥim for the guards of the fourth fortress.
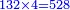
|
גם תכפול קל"ב שומרי המבצר הרביעי על ד' פרחים לכל אחד יעלו תקכ"ח פרחים לשומרי המבצר הרביעי
|
- Multiply the 210 guards of the fifth fortress by 3, which are the peraḥim of each; the result is 630 peraḥim for the guards of the fifth fortress.

|
עוד תכפול ר"י שומרי המבצר החמשי על ג' שהם פרחי כל אחד יעלו תר"ל פרחים לשומרי החמשי
|
- Multiply the 306 guards of the sixth fortress by 2, which are the peraḥim of each; the result is 612 peraḥim for the guards of the sixth fortress.
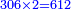
|
עוד תכפול ש"ו שומרי המבצר הששי על ב' שהם פרחי כל אחד יעלו תרי"ב פרחים לשומרי המבצר הששי
|
- You see all of this detailed in diagram 5.
|
וכולם תראה בצורת ה' בפרט
|
- Sum all; they are 2352 peraḥim for each month.

|
תחברם כולם יהיו ב' אלפים שנ"ב פרחים והם לכל חדש
|
- Multiply them by 12; they are 28224 peraḥim for a year.

|
תכפלם על י"ב יהיו כ"ח אלפים רכ"ד פרחים לשנה
|
- If you want to convert them into dinar, multiply them by 14; the result is 395136, which are all the dinars for the guards for a year and this is what I wanted.
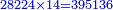
|
ואם תרצה לעשותם דנרי' תכפלם על י"ד יעלו שצ"ה אלפים קל"ו כל זה הדינרים לשומרים לכל שנה וזה מה שרציתי
|
|
|
והנה עלה מזה כי השומרים דרך פרט תראם בצורת ג' ובכלל הם תשנ"ו והפרחים דרך פרט תראם בצורת ה' ובכלל הם ב' אלפים שנ"ב לכל חדש תכפלם על י"ב יעלו כ"ח אלפים רכ"ד הראוי לכל שנה כופלם על י"ד היוציא דינרי' והם שצ"ה אלפים קל"ו כל זה כנזכר
|
- The tenth question: [...]
|
[283][שאלה עשירית] [...] ובכל בד נ"א תפוחים [...] דנרים יעשו כל הפשיט' [...]
|
|
|
תשובה כפלנו ל"ד [...] ב' אלפים תמ"ח ואם [...] יהיה העולה קכ"ד אלפים תתמ"ח והם התפוחים [...] פשיטי' יעלו רמ"ח אלפים תרצ"ו והם הפשוטים תחלקם על [...] כ' אלף תת"ח והם דנרי ואם תחלקם עוד על כ' יהיו ליטירין ואם על י"ד יהיו פרחים וכן כל הדמה לזה כפי סך הפרח שהוא או שיהיה
|
- Question 11: one says: I have one garden which has 77 ruins, in each ruin there are 11 caves, in each cave 8 chicken nests, in each nest 17 eggs, from each of which one chicken emerges and each chicken is worth 3 dinars. I ask: how much is everything in particular and in general?
|
שאלה יא האומר יש לי גן אחד אשר בו ע"ז חורבות בכל חורבה י"א מערות בכל מערה ח' קני תרנ[גול] ובכל קן י"ז בצים אשר מכל ביצה תצא תרנגולת אחד וכל תרנגול היה שוה ג' די'
שאלתי כמה יהיה כל דבר בפרט והרי בכלל
|
- Answer: multiply one by the other, then the product by the second, then the result by the third and so on for all that are given in these questions.
|
תשובה תכפל זה על זה והיוציא על השני והיוציא על השלישי וכן כל מה שיעלו באלה השאלות
|
- The example: multiply 77 by 11 caves; the result are 843 caves.
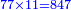
|
והמשל נכפל ע"ז על י"א מערות היוציא יהיה תתמ"ז מערות
|
- We multiply also the caves by 8 nests; the result are 6776 nests.

|
גם כפלנו המערות על ח' קינין יעלו ששה אלף תשע"ו קינין
|
- We multiply also the nests by 17, which are the eggs or the chickens; the result are 115192, which are chickens.
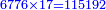
|
גם כפלנו הקינין על י"ז שהם הבצים או התרנגולים יעלו קט"ו אלפים וקצ"ב והם תרנגולים
|
- We multiply also the chickens by 3 dinar, which are the price of each chicken; the result are 345576 dinar.

|
גם כפלנו התרנגולים על ג' דני' שהם שיווי כל תרנגולת יעלו שמ"ה אלפים תקע"ו דנרי'
|
- Likewise for all that is similar.
|
וכן כל הדומה לזה
|
|
|
וכן האומר קניתי תרנגולת בסך מ' פשיטי' ומכרנו הבצים מ' בפשוט ולא ילדה אלא בצה אחד במ' ימים שאלתי בכמה ימים ירויח מ' פשיטי' שהוא סך התרנגולת
|
|
|
התשובה תכפול מ' על מ' יעלו אלף ות"ר והנה באלף ות"ר ימים ירויח סך התרנגולת ומכאן ואילך מה שיוליד ירויח וכן רבים לאין מספר
|
- Question 12: [There was a tax for a king from a spring] that runs [from a mountain; the spring provides water to thirty] provinces; [each province has 40 villages]; in each village [there are 50 people; each person has 4 vineyards]; each vineyard yields 8 [cargos of grapes; each cargo] provides a tax of 20 pešiṭim for the king [each year]. I ask the number of the villages, the number of the people, the number of the vineyards, the number of the cargos [...]
|
[284][...] [שאלה יב] [היה מס למלך ממעיין] אחד יורד [מהר אחד והוא המעיין משקו שלו]שים מדינות [וכל מדינה יש לה מ' מג]רשים ובכל מגרש [נ' אנשים ולכל איש ד' כרמים] וכל כרם נותן ח' [משאות ענבים וכל משא] נותן מס למלך כ' פשיט' [בכל שנה]
שאלתי מספר המגרשים ומספר האנשים [מספר] הכרמים ומספר המשאות ומספר ה[...] ומספר ה[...] והפשי' ומספר [...] אם תרצה לעשותם מטבע אחד [...] אחר שעשית אותם די'
|
- Answer:
- First, we multiply the [fountain] by the provinces; they are thirty.
|
התשובה הנה ראשונה נכפול ה[מעין] על המדינות והם שלושים
|
- Then, we multiply thirty provinces by 40 villages; they are one thousand and two hundred, like this:
|
עוד נכפול שלושים מדינות על מ' כפרים יהיו אלף ומאתים כזה
|
-
|
|
- This is the number of the villages.
|
והוא מספר הכפרים
|
- We multiply the number of the villages by 50 people of each village; the result is 60 thousand, like this:
|
עוד נכפול מספר הכפרים על נ' אנשי כל כפר יעלו ס' אלפים כזה
|
-
|
|
- This is the number of the people.
|
והם מספר האנשים
|
- We multiply the number of the people by 4 vineyards that each has; the result is two hundred and forty thousand vineyards, like this:
|
עוד נכפול מספר האנשים על ד' כרמים אשר לכל אחד יעלו הכרמים מאתים וארבעים אלף כזה
|
-
|
|
- We multiply the [number of the] vineyards by 8 cargos? that are in each vineyard; the result is 1920 thousand cargos?, like this:
|
עוד נכפול הכרמים על ח' משאות אשר בכל כרם יעלו המשאות מספר אחד ותתק"ך אלפים כזה
|
-
|
|
- We multiply the cargos by 2 pešiṭim of the tax; the result is 3840 thousand, like this:
|
עוד נכפול המשאות על ב' פשיטי המס ויעלו ג' מספרים תת"מ כזה
|
-
|
|
- These are the pešiṭim of the tax.
|
והם פשיטי המס
|
|
|
ועתה רצינו לעשות מפשיטי המס די' נחלקם על י"ב יעלו ש"ך אלפים כזה
|
-
|
|
|
|
והם די' המס
|
|
|
ועתה אם נרצה לעשות מהם קאשטיללנו' נחלקים על כ"ח ואם פרחים על י"ו כי עתה הם מזומנים למטבע שנרצה מזהב וכאשר היו פשי' נוכל לעשות מהם המטבע שנרצה מכסף ועתה נעשה מהם [285]לטרין וזה [...] 000וח כזה וזה [...] ומתחלפים [...]
|
The Second Chapter: Problems of Multiplication of Fractions
|
הפרק השני בשאלות כפל שברים
|
|
|
שאלה אם ב' שלישיות שוה ג' חמשיו[ת] שאלתי רביעית מה יהיה שוה
|
|
|
כזאת הצורה
|
-
|
|
|
|
תשובה כפול האמציות שבר על שבר ומורה על מורה יהיו ג' חלקים מעשרים כזה
|
|
|
|
|
תחלקם על ב' שלשיות וראשונה תשוים יהיו כזה
|
| 9 |
|
40
|
 |
X |
|
| 60
|
|
|
|
|
|
הג' חלקים מכ' יהיו ט' עליו והם חלקים מס' וב' שלישיות יהיו מ' חלקים מס' נחלק ט' על [...] מחולק כזה
|
|
|
|
|
והוא הנשאל הנעלם והנה אם ב' שלישיות שוים ג' חמשיות רביעית יהיה שוה ט' חלקים ממ'
|
|
|
והבחינה תשוה כל אב על הט' ב' שלישי' עם ג' חמשיות [...] כמו שתראה בזאת הצורה
|
|
|
| וג |
|
0ד |
ט |
|
0א
|
| ט |
X |
א |
ג |
X |
ב
|
| 0ד |
ד |
ה |
ג
|
|
|
|
|
והנה הראשונים עשרה ותשעה והשניים הם מ' ול"ו תקצר השניים יהיו כראשונים או קח מורה כולל לכולם ותציא שוה גם כן
|
|
|
שאילה אחרת סוחר קנה ב' שלישיות [...] רביעיות בגד לא ידענו אורכו בס' וג' פרחים שאלתי סך כל הבגד ומדת אורכו
|
|
|
תשובה תשוה השברים ויהיו כזאת הצורה
|
|
|
|
[286]
| ט |
|
[.]
|
 |
X |

|
| בא
|
|
|
|
|
[...] סך הבגד השלם שהוא י"ב [...] אם י"ז [...] י"ג י"ב שהוא הבגד השלם כמה [...] פרחים יהיה שוה כפול האמצעיים יעלו [...] חלקם על י"ז יעלה בחילוק ט' שלמים וג' חלקים [..] בשלם והנה עלה בידינו כי הבגד השלם י"ב אמות [...] השברים הוא י"ב וסך כל הבגד הוא ט' פרחים [...] מי"ז חלקים בפרח אחד
|
|
|
והבחינה [...] או אמור אם ט' פרחים [.] וג' חלקים מי"ז יתן לנו י"ב פרחים אמות י"ב פרחים מה יתן לנו וכו'
|
|
|
שאלה אחרת אם ב' חמשיות מג' רביעיות שוה ג' שביעיות מה' שישיות שאלתי ד' חמשיות מה' שמיניות מה יהיה שוה ויהיה כזאת הצורה
|
|
|
|
|
|
התשובה כפול [...] ותקצרם ותהיה יותר נקל ההמשל
|
|
|
כי ב' חמשיות מג' רביעיות יהיו ו' חלקים מעשרים [תקצרם יהיו ג'] חלקים מעשרה כפי שתראה בצורה שנית וזה החלק הראשון
|
|
|
גם כפול החלק השני שהוא ג' שביעיות מה' ששיות יהיו ט"ו חלקים ממ"ב תקצרם יהיו ה' חלקים מי"ד וזה החלק השני
|
|
|
גם כפול החלק השלישי שהוא ד' חמשיות מז' שמיניות יהיו כ"ח חלקים ממ' נקצרם יהיו ז' חלקים מעשרה
|
|
|
ושבה השאלה כמו אם ג' עשיריות שוה ה' חלקים מי"ד שאלתי ז' חלקים מעשרה מה יהיו שוה כזאת הצורה
|
|
|
|
|
|
כפול האמצעיים ה' על ז' יהיו ל"ה גם י"ד על עשרה [287]יהיו [...] על ג' חלקים [...] י"ב ומקוצר יהיה [...]
|
|
|
שאלה אחרת אם ג' [...] שלישית [...] ליטרה כמ' יהיה שוה [ויהיה] כזאת הצורה [...]
|
| הנעלם |
|
מלטרה |
|
מפרח |
|
מלטרה |
|
ה
חזב |
|
 |
מ |
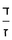 |
|
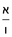 |
מ |
 |
מ |
 |
מ |
 |
|
 |
אם
|
|
|
|
|
[...] מורה יהיו ב' אלפים תק"ך וזה המורה הכללי [...] האמצעיים והנה עלה מן הכפל כ' חלקים מב' אלפים ותק"ך כזה
|
|
|
|
|
|
תקצרם יהיו חלק אחד מקכ"ו כזה
|
|
|
|
|
|
תחלקהו על הג' חמשיו[ת] וראשנה תשים כצורה הזאת
|
|
|
|
|
|
יהיו הג' חמשיות שמ"ח חלקים מתר"ל והמספר הנכפל שתרצה לחלק הוא ה' חלקים מתר"ל חלק ה' על שע"ח והוא מחולק שהוא ה' חלקים משע"ח [...]
|
|
|
|
|
|
ואם תכפול ה' על פשיטי הפרח [...] על סך הלטרה והעולה תחלק על שע"ח היוציא יהיה פשיטי' ואם על רביעי היוציא יהיה רביעי פשי'
|
|
|
והבחינה [...] [הפרק השני]
|
|
|
[288][...] בפני עצמו [...] מפרחים או מימים או [...] משל מקצתם ואתן שני משלים [...] המשל רצינו לדעת כ"ה חלקים [...] נאמר בדרך השלושה אם נ"ב שוה כ"ב [...] יהיה שוה ויהיה כזאת הצורה
|
|
|
|
|
|
נכפל כ"ב על[289]
|
|
|
שאלה רביעית ראובן נשכר אצל שמעון לעשות מלכתו ונתן לו בג' רביעיות שנה חצי מתשיעית מג' שביעיות פרח שאלתי ברביעית מתשיעית שנה מה יתן לו ויהיה כזאת הצורה
|
|
|
| הנעלם |
|
שנה |
|
פרח |
|
שנה
|
| 0 |
|
 |
|
 |
|
 |
- |
 |
- |
 |
|
 |
אם
|
|
|
|
|
תשובה כפול האמצעיים יהיו ג' חלקים מד' אלפים תקל"ו תקצרם יהיו אחד מאלף תקי"ב כזה
|
|
|
|
|
|
תחלקם ג' רביעיות וראשונה תשוים יהיו הג' רביעיות ד' אלפים תקל"ו חלקם והחלק השני יהיה ד' חלקים והמורה הכללי משניהם הוא ו' אלפים מ"ח ויהיה כזאת הצורה
|
|
|
|
|
|
תח תחלק ד' על ד' אלפים תקל"ו והוא מחולק תקצרם יהיו חלק אחד מאלף קל"ד והוא הנעלם ואז עלה בידינו כי חצי תשיעית מג' שביעיות [290]שביעיות הוא [...] חלק אחד מל"ו [...] כי כולם שוים כי ערך ג' על ג' כערך א' על [א'] [...]
|
|
|
|
|
|
[בחינה] אחרת מן המורים תחלק תן כל אב על בניו יהיה [...] האחד ד' חלקים מקכ"ו והשני ל"ו חלקים מאלף קל"ד והנה ערך ד' אל אל קכ"ו כערך ל"ו אל אלף קל"ד
|
|
|
בחינה אחרת תחלק המורים כל בן על אביו ותציא ל"א וחצי מכל אחד
|
|
|
בחינה אחרת חלק בן על בן ואב על אב ותיצא בחילוק ט' מכל אחד
|
|
|
ועיין באלו הבחינות כי בשאלות אקח מתי שבא לידי
|
|
|
שאלה חמשית ממידה אם חצי שתי חמשיות מג' רביעיות אמה מבגד שוה ג' שביעיות מחצי ב' שלישיות פרח שאלתי חצי ושלישית וב' שביעיות מזה הבגד כמה יהיה שוה ויהיה כזאת הצורה
|
|
|
| הנעלם |
אמה |
פרח |
אמה
|
| 0 |
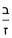   |
 מ מ מ מ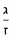 |
 מ מ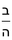 מ מ
|
|
|
|
התשובה כפול האמצעיות ג' על א' והעולה על ב' והעולה על א' והעולה על א' והעולה על ב' והנה כל השברים יעלו י"ב גם כפול המורים זה על זה יעלו אלף ת תשס"ד תקצרם יהיו ו' חלקים מתתפ"ב תקצרם עוד יהיו ג' חלקים מתמ"א תקצרם עוד בשלישית יהיו חלק מקמ"ז חלקם על הראשון שהוא חלקי אמה וראשונה תן השברים בשבר אחד וזה שתוציא המורה הכללי יהיה מ' וג' רביעיות מ' הוא ל' וב' חמשיות ל' הם י"ב וחצי [291][...] ג' חלקים מכ' [...] מחולק [...] והוא [...] והנה אם חצי ב' [...] מאמה מבגד שוה ג' שביעיות מחצי שני [...] פרח חצי שלישית מב' שביעיות אמה מבגד שוה כ' חלקים מקמ"ח בפרח
|
|
|
|
|
|
ואם תרצה לדעת כמה זרתות יהיה הבגד כפול סך זרתות האמה שהם ד' על חלקי השבר והעולה תחלק על המורה וכן תעשה בכל שברי אי מין שיהיה כאשר אמרתי
|
|
|
והבחינה כך היא שתתן כל שברי השבר בשבר אחד בפני עצמו ותקצרם אם תוכל ואחר תשוה כל אב עם בנו ואחר השיוי תן כל בן על אביו ואם יהיו שברים רבים ולא תוכל להכיר הערך חלק האב על הבן והיוציא בחלוקה יהיה שוה לשניהם
|
|
|
המשל בזה תשוה שברי כל אחד בפני עצמו יהיה הראשון אחר הקצור ג' חלקים מכ' כזה
|
|
|
|
|
|
והשנית שביעית כזה 
|
|
|
והשלישית חלק מכ"א כזה
|
|
|
|
|
|
והרביעי שהוא הנעלם כ' חלקים [..] מתמ"א כזה
|
|
|
|
|
|
ויהיו כולם כזאת הצורה
|
|
|
| 0בד |
|
אדד |
0ב |
|
אב
|
| 0ב |
X |
א |
א |
X |
ג
|
| אדד |
אב |
ז |
0ב
|
|
|
|
|
תשוים שנים שנים יהיו ל"ג חלקים מכ' שהוא הראשון כ"א ולחלק השני כ' חלקים ולחלק השלישי תמ"א חלקים ולחלק השלישי ת"ך חלקים ולחלק הרביעי הנעלם ת"ך והנה ערך כ"א אל כ' כערך תמ"א אל ת"ך שאם תחלק כ"א אל כ' יצא [292]א' וחלק [...] אחר הקיצור [...] ואב על אב יעלה מכל [...] כי אני
|
|
|
מספר מהו המספר אשר יהיו ב' שבי[..] שמיניות השני כזאת הצורה
|
|
|
| אב |
|
וא
|
 |
X |
|
|
|
|
|
יהיו י"ו שביעיות כ"א שמיניות והנה שני שביעיות כ"א הם ששה וג' שמיניות י"ו הם ששה גם כן והוא המבוקש
|
|
|
אחרת מהו המספר אשר ו' חלקים מי"א יהיו נ"ה שמניות השני
|
|
|
כזה הצורה
|
|
|
| הה |
|
חד
|
 |
X |
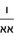
|
|
|
|
|
ששה חלקים מי"א הם שלושים כי כשנחלק נ"ה אל י"א יעלה בחילוק ה' וששה פעמים ה' הם ל' וגם ה' שמיניות י"א הם ל' כי חלקנו מ"ח על ח' יעלה בחילוק ו' וה' פעמים ו' הם ל' כשני וכן לכל שני מספרים איך שיהיו כי לכולם דרך אחד
|
|
|
אחרת רצינו ג' מספרים אשר ב' חמשיות הראשון יהיו כג' שביעיות השני וג' שביעיות השני כד' תשיעיות השלישי
|
|
|
|
|
|
התשובה כפול ה' שהוא מורה הראשון על שברי השנים שהם ג' וד' ועלו ס' על ב' חמשיות גם כפול ז' שהוא המורה השני על שברי האחרים שהם ב' וד' יעלו נ"ו על ג' שביעיות גם כפול ט' שהוא מורה השלישי על שברי האחרים שהם ב' וג' יעלו נ"ד על ד' תשיעיות ועתה ב' חמשיות ס' הוא כ"ד והוא כ"ג שביעיות נ"ו שהוא כ"ד וכן ד' תשיעיות נ"ד הוא כ"ד ואם כן ב' חמשיות הראשון הוא ג' שביעיות השני וג' שביעיות השני הוא ד' תשיעיות השלישי ומש"ל
|
|
|
[293][...]
|
|
|
| חטא |
|
בז |
|
[...] |
|
[...]
|
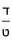 |
|
 |
|
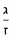 |
|
[...]
|
| חד |
|
חד |
|
חד |
|
חד
|
|
|
|
|
[...] וג' שביעיות השני יהיה כ"ב [...] וב' שלישיות השלישי יהיה כ"ד תשיעיות רביעי או נוכל לאמר כי ב' חמשיות הראשון כג' שביעיות בג' שביעיות השני וכב' שלישיות השלישי וכד' תשיעיות הרביעי וכן לכל אחד שתקח השבר שתרצה
|
|
|
והמשל בזה הצורה הנה נכפול כל מורה על שברי כולם חוץ משבריו ואחר קח מה שיורה כל אחד כמו [...] שנקח ה' שהוא מורה הראשון ונכפלהו על שברי האחרים שהם ג'ב'ד' יהיו כ"ד נכפול כ"ד על המורה שהוא ה' יהיו ק"ך ותתנם על ב' חמשיות ואחר נקח ז' שהוא [...] מורה ג' שביעיות ונכפלם על בב"ד
שהם שברי האחרים יעלו קי"ב תתנם על ג' שביעיות ואחר נכפול ג' על בג"ד יעלו ע"ב נתנם על ב' שלשיות ואחר נכפול ט' על בג"ב יעלו ק"ח נתנם על ד' תשיעיות ועתה נראה כי ב' חמשיות ק"ך הם מ"ח וג' שבעיות קי"ב הם מ"ח וב' שלשיות ע"ב הם מ"ח וד' תשיעיות ק"ח הם מ"ח וכל תנהיג לכל השברים שתרצה
|
|
|
שאלות ממינים אחרים אם נרצה חלק או חלקים מאיזה מטבע שנרצה נכפול סך המטבע על השבר ונחלק על המורה והוא המבוקש
|
|
|
והמשל רצינו ב' שלשיות לטרה כזה 
|
|
|
נכפול סך הלטרה שהוא כ' על השבר שהוא ב' יעלו מ' נחלק מ' על המורה שהוא ג' יעלה בחילוק [294]י"ג די' [...]
|
|
|
והבחינה נחבר [...] ליטרה תחבר [...] המבוקש
|
|
|
משל אחר רצינו לדעת ג' רביעי[ות] [...]
|
|
|

|
| 22
|
|
|
|
נכפול סך הדוקאדו ש[...] השברים שהם ג' יעלו ס"ו נחלקם [על] המורה שהוא ד' יציא בחילוק י"ו די' וב' רביעיות שהם חצי
|
|
|
והבחינה רביעית כ"ב הוא ה' וחצי וג' פעמים ה' וחצי הם י"ו וחצי
|
|
|
משל אחר רצינו לדעת כמה ד' חמשיות פרח כזה
|
|
|
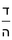
|
| 16
|
|
|
|
הנה סך הפרח הוא י"ו די' נכפול י"ו על המורה שהוא ד' יעלו ס"ד נחלקם על ה' יעלה בחילוק י"ב די' וד' חמשיות דינ' נכפול הד' חמשיות על י"ב שהם פשיטי הדינ' יעלו מ"ח נחלקם על המורה שהוא ה' יעלו ט' פשי' ונשארו ג' פשי' נכפול ג' על ב' שהם מחצית הפשוט ויעלו ששה מחצות נחלקם על ה' יעלה מחצה ונשאר א' שהוא חמשית מחצה
|
|
|
משל אחר רצינו כ"ה חלקים מנ"ב מנ"ב בדוקאדו כזה
|
|
|
|
|
|
הנה נאמר בדרך השלושה אם נ"ב שוה כ"ב די' שהם סך הדוקאדו כ"ה מה יהיה שוה ויהיה
|
|
|
|
|
|
נכפול כ"ב דנרי הדוקדו על כ"ה שהוא השבר הנשאל יעלו תק"ן נחלקם על המורה שהוא נ"ב יעלה בחילוק עשרה די' ונשארו ל' חלקים נכפלם על י"ב יעלו ש"ס נחלק על נ"ב שהוא מורה השברים יעלו ו' פשי' ונשארו מ"ח נכפלם על ד' רביעי הפשוט [295][...] יעלה בחילוק ג' רביעיות [...] ברביעית פשוט כזה
|
|
|
|
|
|
[...] כל מה שעשינו לתשלום [...] יהיו שניהם שוים למורה הדוקדו [...] הנה שאלנו כ"ה חלקים מנ"ב בדוקאדו [...] לתשלום נ"ב כ"ז חלקים מנ"ב שהוא המורה ועתה אמור אם נ"ב שוה כ"ד כ"ז מה יהיה שוה והנה כפלנו כ"ז על כ"ב יעלו תקצ"ד נחלקם על נ"ב ויציא בחילוק י"א י"א די' ונשארו כ"ב כפלנום על י"ב יעלו רצ"ד נחלקם על נ"ב יעלו ה' פשיטי' ונשארו ד' נכפלם על ד' ויהיו י"ו רביעיות ולא נוכל לחלקם על נ"ב ונשארו עליו כזה
|
|
|
|
|
|
והוא מחולק לשברי רביעיות והנה יהיו סבי השאלה עם סבי הבחינה כזאת הצורה
|
|
|
|
|
| רביעיות |
ג |
פשיטי |
ו |
די' |
0א
|
| |
0 |
פשי |
ה |
די' |
אא
|
|
|
|
|
והנה ל"ו חלקים מנ"ב וי"ו חלקים מנ"ב הם רביעית פשוט וג' רביעיות שלנו יהיו פשוט אחד ועם י"א פשיט שבצורה יהיו י"ב שהם די' אחד ועם כ"א די' שבצורה יהיו כ"ב והוא המבוקש ועם זאת הבדיקה תוכל לבדוק כל השאלות מזה המין
|
|
|
משל אחר רצינו לדעת נ"ז חלקים מצ"א חלק ביום כמה שעות ודקים ושניי' וכו' הם
|
|
|
התשובה הנה נאמר בדרך השלושה אם צ"א שוה כ"ד נ"ז מה יהיה שוה ויהיה כזאת הצורה
|
|
|
|
|
|
הנה נכפול כ"ד על נ"ז יעלו אלף שס"ח נחלקם על צ"א יעלה בחילוק ט"ו שעות ונשארו ג' נכפול ג' על ס' [296]ס' יעלו ק"ף [...] נכפלם על ס' יעלו ה' [...] המורה יעלה בחילוק נ"ח [...] יעלו ג' אלפים תש"ך נחלקם על ה[...] ונשארו פ' נכפול פ' על ס' יעלו ד' אלפים [...] יעלו נ"ב רביעיים ונשארו ס"ח נכפלם על ס' יעלו [...] ופ' נחלקם על המורה יעלה בחילוק מ"ד חמשיים ונשארו ע"ו כפלנו ע"ו על ס' יעלו ד' אלפים תק"ס נחלקם על המורה יעלו נ' ששיים ועשרה חלקים מצ"א בשישית כי לא רציתי לעשות שביעיים לדקדק יותר ומי שירצה עוד לדקדק ידקדק לכפול על ס' ולחלק הציוציא על המורה
|
|
|
והבחינה היא שניקח הנשאר מנ"ז חלקים עד צ"א והם ל"ד ונאמר אם צ"א נתן כ"ד שעות ל"ד כמה שעות יתן ודקים וכו' יתן נכפול כ"ד על ל"ד יעלו תתי"ו נחלקם על צ"א שהוא המורה ויעלה ח' שעות ונשארו פ"ח נכפלם בס' יעלו ה' אלפים ר"ף נחלקם על המורה יעלה בחילוק נ"ח דקים ונשארו ב' נכפלם בס' יעלו ק"ך נחלקם על המורה יעלה בחילוק שני אחד ונכפול כ"ט שנשארו על ס' יעלו אלף תש"מ נחלקם על המורה יעלו י"ט שלישיים ונכפול י"א שנשארו על ס' יעלו תר"ס נחלקם על המורה יעלו ז' רביעיות ונשארו כ"ג נכפלם על ס' יעלו אלף ש"ף נחלקם על המורה יעלה בחילוק ט"ו חמישיות ונשארו ט"ו נכפלם בס' יעלו תת"ק נחלקם על המורה יעלו ט' ששיות ונשארו פ"א
|
|
|
ואין צריך לדקדק עוד ומי שירצה לדקדק עוד ידקדק כמו שאמרתי
|
|
|
אבל זה שיור נבחון עם מה שיציא לנו משאלתנו מחוברים אם יהיו כ"ד שעות בכיון שהם יום אחד הוא טוב ויהיו הנשאל
|
|
|
[297]
|
| חלקי ששיות |
0א
אט |
ששי |
חמשי |
[רביעי] |
[שלישי] |
[שני] |
[דקים] |
[שעות]
|
אח
צא |
נ |
מד |
[נב] |
[מ] |
[נח] |
[א] |
[טו]
|
| ט |
טו |
ז |
[יט] |
[א] |
[נח] |
[ט]
|
| |
משברים |
א |
0 |
0 |
0 |
0 |
0 |
0
|
|
|
|
|
חברנו השברים שהם פ"א ועשרה יהיו צ"א ששי ועם נ' וט' ששיות יהיו חמשי אחד ועם מ"ד וט"ו חמשיות יהיו רביעי אחד ועם נ"ב וז' רביעיות יהיו שלישי אחד ועם מ' וי"ט יהיו שני אחד ועם נ"ח וא' יהיו דק אחד ועם א' ונ"ח דקים יהיו שעה אחת ועם ט"ו וט' שעות יהיו כ"ד שעות שהם יום אחד וזה מה שרצינו
|
|
|
גם נוכל לעשות אלו השאלות מכ"ה חלקי הדוקאדו שכפלנו סך המטבע על השבר הנשאל וחלקנו על המורה בצורה הזאת בשאלה שעשינו בדרך השלושה ששאלנו נ"ז חלקים מצ"א ביום
|
|
|
| כ"ד |
שעות היום
|
| נ"ז |
החלקי' הנשאלים
|
| צ"א |
המורה
|
|
|
|
הנה נכפול סך שעות היום שהם עליונים בזאת הצורה שהם כ"ד על החלקים הנשאלים שהם נ"ז אמצעיים בצורה יעלו אלף שס"ח נחלקם על צ"א שהוא המורה ותציא בחילוק ט"ו שעות וז' חלקים מצ"א ומהם עשתי דקים ושניים וכו'
|
|
|
שאלה רש"ל עשו חברה ראובן נתן בחברה חצי שלישית רביעית פרח והפרח שוה י"ו די' ושמעון נתן רביעית ששית דוקאדו והדוקאדו שוה כ"ב די ולוי נתן רביעית חצי שלישית קאשטיללנו והוא שוה כ"ח די' והרויחו ששית רביעית שלישית פאלומיטה והוא שוה כ"ד די' שאלתי [298]שאלתי כיצד [...] פשוטי[...] הם קצ"ב ופשטי הדוקאדו [...] הקאשטיללנו הם של"ו ופשטי הפל[...] חלקו מן הפרח שהם קצ"ב פשי' הרביעית [..] מ"ח הוא י"ו וחצי י"ו הוא ח' פשיטי' וזה חלק ראובן
|
|
|
וחלק שמעון י"א פשי' כי פשיטי הדוקאדו רס"ד ושישית רס"ד הם מ"ד ורביעית מ"ד הם י"א וזה חלק שמעון
|
|
|
והנה חלק לוי הוא י"ד פשיטי' כי פשיטי הקאשטיללש הם של"ו ושלישית של"ו הם קי"ב וחצי קי"ב נ"ו ורביעית נ"ו הוא י"ד פשי' והוא מה שנתן לוי
|
|
|
והנה הריוח הוא ב' פשי' שהם ששית רביעית שלישית חצי פאלומטה כי הפשוט הם רפ"ח וחצי רפ"ח הם קמ"ד ושלישית קמ"ד הם מ"ח ורביעית מ"ח הם י"ב ושישית י"ב הם שנים והוא הריוח ויהיו כזאת הצורה
|
|
|
| ב |
ח |
ראובן
|
| יא |
שמעו
|
| יד |
לוי
|
| |
לג |
המורה
|
|
|
|
|
נכפול ח' על ב' יעלו י"ו נחלקם על ל"ג והוא מחולק י"ו חלקים מל"ג בשלם וזה חלק ראובן וגם לשמעון כ"ב חלקים מל"ג בשלם וגם לחלק לוי כ"ח חלקים מל"ג בשלם
|
|
|
והבחינה תקביץ חלקי שלושתן יהיו ב' פשי' כי י"ו וכ"ב וכ"ח תחלקם על ל"ג יצאו שנים שהוא הריוח [299][...]
|
|
|
דע כי [...] מעלות ומעלות על [...]לות על איזה שבר שיהיה [...] הנכפל ואם נרצה לכפול [...] היוציא רביעיים והדמיון כי שנים [...] ארבעה ואם שניים על שלישיים היוציא חמשיים [...] ושלושה הם חמשה ואם שניים על רביעיים היוציא ששיים וכן כל כפל כי דקים על דקים היוציא דקים ואם דקים על שניים היוציא שניים ואם שני' על שניי' רביעיים ואם שלישי על שלישי ששי ואם רביעיי על רביעי היוציא שמיניי וכן שני בשלישי חמשיי ושני ברביעי ששיי וכן כולם בחיבור שני הנכפלים כי חמשי על חמשי עשיריי
|
|
|
והמשל בזה רצינו לכפול ד' מעלות ו' דקים ח' שניים י"ב שלישיים על ה' מעלות ט"ו דקים עשרה שניים י"ג שלישים
|
|
|
ומעשה הוא שכפלנו ד' על כל הטור התחתון וכן נכפול ו' וכן כולם כל הטור העליון על כל הטור התחתון כמנהג כפל השלמים כמו שתראה בזאת הצורה
|
| מעלות |
דקים |
שני' |
שלישיי |
רביעי' |
חמשיי' |
ששי'
|
ד
ה |
ו
הא |
ח
0א |
בא
גא |
|
|
|
| 0ב |
0ו |
0ד |
בה |
|
|
|
| |
0ג |
0ט |
0ו |
חז |
|
|
| |
|
0ד |
0בא |
0ח |
ד0א |
|
| |
|
|
0ו |
0חא |
0בא |
והא
|
|
|
|
ונאמר כי ד' פעמים ה' הם מעלות הם כ' מעלות גם ד' מעלות על ט"ו דקים הם ס' דקים גם ד' מעלות [300]על עשרה הם [...] נ"ב שלישים והנה ד' [...] כל הטור עם ו' דקים והנה [...] גם ו' על ט"ו יעלו צ' שניים גם ו' [...] גם ו' על י"ג יעלו ע"ח רביעיים והנה [...] עתה נכפול כל הטור על ח' והנה ח' על ה' הם [...] ח' על ט"ו יעלו ק"ך שלישיים גם ח' על עשרה יעלו פ' רביעי[יים] גם ח' שניים על י"ג שלישיים יעלו ק"ד חמשיים והנח ח' כפל כל הטור עתה נכפול י"ב על כל הטור ונאמר י"ב פעמים ה' הם ס' שלישיות גם י"ב שלישיות על ט"ו ראשונים הם ק"ף רביעיים גם י"ב על עשרה יהיו קי"ב חמשיות גם י"ב על י"ג יהיו קנ"ו ששיים והנה עתה חברנו את כולם מין עם מיניו יהיו הששיים קנ"ו והחמשיים רי"ו והרביעיים של"ח והשלישים רצ"ב והשניים ק"ע והדקים צ' והמעלות כ' נחלק השישיות על ס' יעלו ב' חמשיות ונשארו ל"א ששי נחבר הב' חמשיות עם רי"ו חמשיות יהיו רי"ח חמשיות נחלקם על ס' יעלו ג' רביעיות ונשארו נ"ח חמשיות נחבר הג' רביעיות עם של"ח יהיו שמ"א רביעיות נחלקם על ס' יעלו ה' שלישיות ונשארו מ' רביעיות נחבר הה' שלישיות עם רצ"ב יהיו רצ"ז שלישיות נחלקם על ס' יעלו ד' שניים ונשארו נ"ז שלישיות נחבר ד' עם ק"ע שניים יהיו קע"ד נחלקם על ס' יעלו ב' דקים ונשארו נ"ד שניים נחבר הב' דקים עם הדקים שהם צ' יהיו צ"ב נחלקם על ס' יעלו מעלה אחת ונשארו ל"ב דקים נחבר זאת המעלה עם כ' מעלות יהיו כ"א מעלה ואז עלה [301][...] כ"א מעלות ל"ב [...] [ר]ביעיים נ"ח חמשיים ל"א [...] לזה [302]
|
[Chapter Three: Problems of Compound Multiplication]
|
[303][...]בים
|
|
|
[...] ושלשית שוה ד' וחמשית [...] ב' ושישית מה יהיה שוה ויהיה כזאת [הצורה
|
-
|
|
|
|
[...] [תשו]בה [...] בשברו ואחר כפול האמצעיות וחלק על הראשון
|
|
|
והמשל תן ג' בשבורו יהיו ט' וא' יהיו עשרה שלישיות [וגם הד' בשבורו] והד' היו כ"א [..] והב' בשברו יהיו י"ג ששיות ועתה תסדר שאלתך כשלמים כזאת הצורה השנית
|
|
|
|
|
|
ואמור אם עשרה נתן כ"א מה יתן י"ג כפול האמצעיות כ"א על י"ג יעלו רע"ג חלקים מל' חלק רע"ג על הראשון שהוא עשרה יציא בחילוק וראשונה תשוים רע"ג חלקים מל' על עשרה חלקים מג' ויהיו כזה הצורה
|
|
|
|
|
|
לעשרה שלישיות ש' ולאחר תתי"ט עתה תחלק תתי"ט על ש' יעלה בחילוק שנים ורי"ט חלקים מש' אשר אם תקצרם יהיו ב' וע"ג חלקים מק' וזהו הנעלם
|
|
|
והבחינה הוא שתתן האב על הבן עשרה חלקים מכ"א כזה
|
|
|
|
|
|
גם השני על בנו שהוא הנעלם ויהיה אחר שתתן השלם בשברו והאב שהוא י"ג בשברי בנו ויהיה כזה
|
|
|
|
|
|
אשר אם תקצרם על י"ג ישובו לעשרה חלקים מכ"א כנזכר ויהיו שוים
|
|
|
[304]שאלה שנית [...] הרויחו ד' [...] כמה ירויחו והיה כזאת [הצורה]
|
|
|
| |
פרח |
דנר |
פרח |
|
| |
טב |
טא |
ח |
|
| 0 |
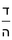 ה ה |
 ד ד |
 ב ב |
אם
|
|
|
|
|
[...] האמצעיות והעולה תשוה עם הראשון ואחר ההשואה תחלק היוצא על הראשון
|
|
|
והמשל תן הב' פרחים בשברו יהיו ח' שלישיות לראשון ולשני כפול ד' על מורה שברו יהיו י"ט רביעיות ולשלישי כפול ה' על ה' שהוא מורה שברו יהיו כ"ט עם שבריו והם חמשיות ויהיו כולם כזאת הצורה השנית
|
|
|
|
|
|
כפול האמצעיות שהם י"ט על כ"ט יעלו תקנ"א חלקים מכ' בשלם תחלקים על ח' שלשיות אחר ההשואה ויהיה בזאת הצורה
|
|
|
|
|
|
יהיו למחלק שהוא הראשון ק"ס ולמחולק שהוא הנכפל אלף תרנ"ג תחלקהו על ק"ס יעלה בחילוק עשרה שלמים שהם עשרה דינרים ונ"ג חלקים מק"ח בדינר כזה
|
|
|
|
|
|
והוא הנעלם והנה עלה בידנו כי כאשר ב' פרחי' וב' שלישיות הרויחו ד' דינרין וג' רביעיות כן ה' פרחים וד' חמשיות ירויחו עשרה דינרין ונ"ג חלקים מק"ס בדניר וזה מה שרצינו
|
|
|
והבחינה היא שתשוים שניים שנים ואחר ההשואה תחלק כל כך על אביו
|
|
|
המשל [305] [...] יהיו לראשון ל"ב [...] רס"ה חלקים [...] שהוא הנעלם תחלק כל בן על אביו יעלה בחילוק א' וכ"ה חלקים מל"ב מכל אחד כיצד חלקנו נ"ז על ל"ב יעלה אחד וכ"ה חלקים מל"ב גם חילקנו ח' אלפים רס"ה על ד' אלפים תר"מ ותצא בחילוק אחד ונשארו ג' אלפים תרכ"ה לחלק על ד' אלפים תר"מ ולדעת אם זה השבר הגדול הוא כ"ה חלקים מל"ב תקצרם על כ"ט ותציא לך כ"ה חלקים מל"ב ואם לא תדע לקצרו על כ"ט חלק כל אחד על כ"ט ותציא מן המתחלק כ"ה ומן המחלק ל"ב וזה המבוקש שיורה שהנעלם [..] הוא אמת
|
|
|
| הובח |
|
0דוד |
|
זה |
|
[בג]
|
גהוא
0וא |
X |
טב
ה |
|
טא
ד |
X |
ח
ג
|
| 00ח |
|
בא
|
|
|
|
|
דרך אחרת לבחון זאת השאלה ואחרות וזה הוא שתחלק אחר ההשואה כל שני חלקים כל שבר על מורה שניהם והיוציא יהיו המונחים הידועים ואם הנעלם יהיה כמו שהוא נמצא בידנו מוטב
|
|
|
והמשל תחלק ל"ב ונ"ז על י"ב והוא מורה שניהם יציא לראשון ב' וב' שלשיות אחר הקיצור ולשני ד' וג' רביעיות וכן תחלק ד' אלפים תר"מ השלישי וח' אלפים רס"ה הרביעי על מורה שניהם שהוא ת"ת ותציא לשלישי ה' וד' חמשית ולרביעי עשרה ונ"ג חלקים מק"ס וכל אלו השברים הם אחר הקיצור
|
|
|
דרך אחרת אחר שיהיו לך החלקים הראשונים קודם שתשום [306]כלל תוציא מורה [...] ואחר תחלקם על ה[...]
|
|
|
המשל בזה הנה המספרים [...] שלשיות והשני י"ט [...] והרביעי אלף תרנ"ג חלקים מק"ס כזה [...] עשה מורה כללי ויהיה ת"ף שהוא כפל ג' [...] צריך לכפול ה' וד' כי בק"ס תמציאך חמשית ורביע[ית] ואם כן המורה הכללי הוא ת"ף נקח ממנו נקח ממנו ב' שלישיותיו שהם אלף ר"ף ונחלקם על המורה ותציא בחילוק ב' וב' שלשיות אחר שתקצר הנשאר וזה לראשון
|
|
|
וכן קח ג' רביעיות המורה כי רביעיתו ק"ך כפלהו על י"ט יעלו ב' אלפים ר"ף תחלקם על המורה יציא ד' וג' רביעיות אחר הקיצור וזה לשני
|
|
|
וכן קח כ"ט חמשיות המורה כי חמשיתו צ"ו כפול צ"ו על כ"ט יעלה ב' אלפים תשפ"ד והם כ"ט חמשיות תחלקם על המורה ותציא ה' וד' חמשיות אחר קיצור הנשאר וזה המספר השלישי
|
|
|
וכן קח חלק מק"ס במורה והוא ג' וזה שתחלק המורה על ק"ס ותציא ג' וזה חלק מק"ס כפול ג' על אלף תרנ"ג יעלו ד' אלפים תתקנ"ט אשר תחלקים על ת"ף ותציא לך עשרה ונ"ה חלקים מק"ס אחר קיצור הנשאר וזה הרביעי הנעלם וכן כל כיוציא בזה
|
|
|
והנה כאשר עלה בידי [.] בחינה חדשה או דבר חידוש בדברי אותו ואתה המעיין קח מה שתרצה
|
|
|
שאלה שלישית מהו המספר שאם כפלנו אותו על ט' וה' שביעיות שתציא ד' וג' חלקים מעשרה כזאת הצורה
|
|
|
ג
0א |
ד |
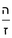 |
ט |
0
|
|
|
|
|
תשובה הנה אעשה זאת השאלה עם [307][...]ים והוא שתחלק הנשאל [...] הראוי לכפול לכפול על הכופל [...] כל שלם במורה שברו וחבר עליו שבריו [...] שביעיות ולשני מ"ג עשריות תשוים בזאת [הצורה]
|
|
|
|
|
|
יהיו לראשון אשר עליו תחלק תר"ף והשני הראוי לחלק ש"א תחלקם על תר"ף והוא מחולק כזה
|
|
|
|
|
|
שהוא ש"א חלקים מתר"ף והוא המספר שאם תכפלהו על ט' וה' שביעיות יעלה ד' וג' עשריות
|
|
|
והבחינה כך היא שתכפול ש"א חלקים מתר"ף על ט' וה' שביעיות וראשונה תתנם בשברו יהיו ס"ח שביעיות כופלם על ש"א חלקים מתר"ף יעלו ב' [עשרים] אלפים תס"ח תחלקם על כפל המורים שהוא ד' אלפים תש"ס ותציא בחילוק ד' שלמים ואלף תכ"ח חלקים מד' אלפים תש"ס תקצרם לחציים שתי פעמים ופעם בשביעית ופעם בי"ז ונשארו ג' עשריות
|
|
|
שאלה אחרת אם שארית חודש אחד הוא יום אחד וי"ב שעות תשצ"ג חלקים שאלתי שארית י"ב חדשים שהם שנה פשוטה כמה ימים ושעות וחלקים יהיה וכן אם שאל מחזור או מחזורים
|
|
|
התשובה תן הכל בחלקים מאלף ופ' בשעה שהוא המורה ואחר אמור אם כך חלקים נתן לנו חדש אחד י"ב חדשים מה יתן לנו או רל"ה חדשים שהם מחזור אחד מה יתן לנו
|
|
|
והמשל בשאלתנו תן היום בשעות יהיו כ"ד וי"ב שהיו לנו יהיו ל"ו כפול ל"ו על אלף ופ' שהם חלקי שעה אחת שהוא המורה יעלו ל"ח אלפים תת"ף תוסיף עליהם תשצ"ג שהיו לנו יהיו ל"ט אלפים תרע"ג וזהו שארית חדש אחד ועתה אמור אם חדש אחד נתן לנו ל"ט אלפים תרע"ג חלקים י"ב חדשים מה יתן לנו ויהיה כזאת
|
|
|
|
|
|
כפול ל"ט אלף תרע"ג על י"ב יעלו תע"ז אלפים וע"ו תחלקם על א' והם מחולקים וזה הראוי לי"ב חדשים והם חלקים אבל נעשה מהם ימים [308]ושעות וחלקים וזה שתחלק [...] ת"מ שעות ונשארו תתע"ו חלקים [...] מהת"מ שעות וזה שנחלקם על כ"ד יעלו [...] ונשמרם ומן הי"ח ימים ניפול י"ד ונשארו ד' [...] שהם ד' ימים ח' שעות תתע"ו חלקים והם מן [...] פשוטה והיודע דרכי העיבור יבין זה
|
|
|
שאלה אם שלישית ורביעית דבר אחד שוה ג' די' כמה יהיה שוה כל הדבר
|
|
|
תשובה תשוים כזה הצורה
|
|
|
| ז
|
 |
X |

|
| בא
|
|
|
|
|
ותמצא ז' חלקים מי"ב כזה
|
|
|
|
|
|
וראה כי הם חלקי השאלה וי"ב הוא השלם ועתה תסדר שאלתך ואמור אם ז' שהם שלישית ורביעית דבר אחד נתן ג' די' כל הדבר שהוא י"ב מה יתן ויהיה כצורה הזאת
|
|
|
|
|
|
כפול האמצעיים שהם ג' על י"ב יעלו ל"ו תחלקם על ז' יעלו ה' שלמים וחלק מ"ז והנה אם שלישית ורביעית דבר אחד שוה ג' די' כל הדבר יהיה שוה ה' די' ושביעית די'
|
|
|
והבחינה עשה כל חלקי השאלה שביעיים יהיה הראשון מ"א והשני כ"א והשלישי פ"ד והרביעי ל"ו כפול האמצעים יהיו אלף תשס"ד וכן יהיו החיצוניים ודי בזה
|
|
|
שאלה אחרת אם שלישית וחמשית דבר אחד שוה ד' די' מה יהיה שוה הנשאר
|
|
|
| ג |
ח |
ה
|
 |
X |

|
| הא
|
|
|
|
|
תשובה תשוים תמצא משני השברים שמונה חלקים מט"ו בשלם כי השברים הם ח' והשלם ט"ו והנה מח' עד ט"ו תמצא ז' הנשאר ועתה תסדר שאלתך ואמור אם ח' שהוא שלישית וחמשית דבר אחד שוה ד' די' הנשאר מח' עד ט"ו שהוא השלם שהוא ז' מה יהיה שוה ויהיה כצורה הזאת
|
|
|
 ג ג |
ז |
ד |
ח |
אם
|
|
|
|
|
כפול האמצעיים ויהיו כ"ח תחלקם על ח' יעלו ג' שלמים וחצי והוא המבוקש והבחנה [309][...]ה חציים בעבור החצי [...] י"ו ח' י"ד ז' וראה כי [...] כפל ז' או בחינה אחרת כפול [...] וכן החיצוניות
|
|
|
[שאלה] אחרת אם ק' די בשליש וחמשית חודש וט"ו שעות הרויחו ז' די' שאלתי כמה ירויחו כל החודש
|
|
|
התשובה הנה שליש החדש הוא כ' ימים וחמשתו הוא ששה וכולם כ"ו ימים וט"ו שעות ועתה אמור אם כ"ו ימים וט"ו שעות נתן לנו ז' די מה יתן ל' ימים שהוא כל החדש ויהיה כזאת הצורה
|
| יתן |
מה |
ימים |
ל |
|
די' |
ז' |
נתן |
שעות |
וט"ו |
ימים |
כ"ו |
אם
|
|
|
|
|
נכפול ז' על ל' יעלו ר"י נחלקם על כ"ו ימים וט"ו שעות וראשונה נשוים שנתן הכל בשעות יהיו הכ"ו ימים והט"ו שעות הכל תרל"ט שעות וגם ר"י על כ"ד יעלו ה' אלפים ומ' שעות נחלקם על תרל"ט יעלה בחילוק ז' די' תקס"ז חלקים מתרל"ט ולעשות מהם פשיטי' נכפול תקס"ז על י"ב יעלו ו' אלפים תת"ד נחלקם על המורה יעלו עשרה פשיטי' ותי"ד מהמורה ואם תרצה מחצות או רביעיות מפשוט תכפלם על ב' למחצות או על ד' לרביעיות ודי בזה
|
|
|
שאלה אחרת אם ק' די' בזמן חמשית וששית וי"ג שעות מחודש אחד מל' ימים הרויחו ט"ו די' שאלתי כמה ירויחו בנשאר מן החדש ויהיה כזאת הצורה
|
|
|
| |
יא |
|
| ה |
|
ו
|
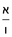 |
X |

|
| ל
|
|
|
|
|
תשוים יהיו י"א חלקים מל' שהם י"א ימים וי"ג שעות ועתה נאמר אם בי"א ימים וי"ג שעות נתן ט"ו די' הנשאר מהחדש שהוא י"ח ימים וי"א שעות מה יתן ועתה נסדר אם י"א ימים וי"ג שעות נתן ט"ו די' י"ח ימים וי"א שעות מה יתן שהם הנשאר מהחדש נכפול ט"ו על י"ח ימים וי"א שעות וראשונה נשוים שנתנם בשעות והנה נכפול י"א ימים על כ"ד יעלו עם הי"ג שעות רע"ז שעות גם נכפול י"ח על כ"ד יעלו עם הי"א שעות תמ"ג ועתה [310]נאמר אם רע"ז נתן [...]
|
|
|
|
|
|
[...] ו' אלפים [...] יעלה בחילוק כ"ג די' ורע"ד חלקי המ[...] המבוקש והבחינה כאחרות
|
|
|
שאלה אחרת רש"ל עשו חברה ראובן נתן בחברה חצי שליש רביעית פרח והפרח שוה י"ו די' ושמעון נתן רביעית שישית דוקאדו והדוקאדו שוה כ"ב די' ולוי נתן רביעית חצי שלישית קאשטיללאנה והוא שוה כ"ח די' והרויחו
|
|
|
שאלה רצינו לכפול שברים על שלמים כפול השלמים על השברים והעולה תחלק על מורה השברים
|
|
|
המשל רצינו לכפול ד' חומשים על ששה שלמים כזה הצורה
|
|
|
|
|
|
נכפול ד' העליום שהם שברים על ו' התחתון שהם השלמים יהיו כ"ד נחלקם על האמצעי שהוא מורה השברים יעלה בחילוק ד' שלמים וד' חמשיות
|
|
|
שאלה אחרת נרצה לכפול י"א חלקים מי"ב בשלם על י"ד שלמים נתנם כזאת הצורה
|
|
|
|
|
|
נכפול העליון על התחתון שהם שברים על שלמים י"א שברים על י"ד שלמים יעלו קנ"ד נחלקם על י"ב [האמצעי] שהוא מורה השברים יעלה בחילוק י"ב שלמים ועשרה חלקים מי"ב שהם מקוצרות ה' ששיות כזה
|
|
|
וכן כל הדומה לזה
|
|
|
וכן נוכל לעשות זה בדרך השלושה עם שיהיה ראשון השאלה האמצעי ואמור אם י"ב נתן י"ד י"א מה יתן נכפול י"ד על י"א יעלו קנ"ד נחלקם על י"ב יעלה י"ב שלמים וה' ששיות כנז'
|
|
|
שאלה אחרת רצינו מספר שאם כפלנו אותו על ג' שלמים וב' חמשיות וגם היוציא כפלנו על ד' שלמים וג' רביעיות [311][...] שלמים [...] יהיו י"ז [...] נשוים עו אל [...] יהיו ס"ח וצ"ה שניהם מחלקי [...] המורה כמו שתראה בצורה שנית
|
|
|
| יט |
יז
|
 ד ד |
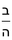 ג ג
|
| 0ב
|
|
|
|
|
|
|
|
[עתה] נניח כי ב' הוא המספר אשר כפלנו אותו על ג' וב' חמשיות והיוציא בכפל נכפול עוד על ד' וג' רביעיות ושיציא מן הכפל ד' שלמים ועתה כפלנו ב' המונח על ס"ח יעלו קל"ו גם כפלנו קל"ו על צ"ה יעלו י"ב אלפים תתק"ך ואנחנו לא שאלנו כי אם ד' הנה נאמר בדרך השלושה אם י"ב אלף ותתק"ך נתן לנו ב' מי יתן לנו ד' כפלנו ד' על ב' יעלו ח' נחלקים על י"ב אלף ותתק"ך והוא מחולק שהוא ח' חלקים מי"ב אלף תתק"ך כזה הצורה והוא הנשאל
|
|
|
|
|
|
והבחינה כפלנו ח' על ס"ח והיציא בצ"ה והעולה נחלק על המורה שהוא י"ב אלף תתק"ך ויעלו ד' שלמים כי כפל ס"ח על ח' תקמ"ד וכפל תקמ"ד על צ"ה יעלו נ"א אלפים תר"ף נחלקם על המורה יציא בחילוק ד' שלמים
|
|
|
או אם תרצה תקצר המספר בשמינית וקח שמינית ח' שהוא אחד ושמינית המורה שהוא אלף תרמ"ו ואחר כפול א' המקוצר משמונה על ס"ח שבא מג' שלמים וב' חמשיות ואחר כפול העולה שהוא ס"ח על צ"ה שבא מד' וג' רביעיות יעלו ו' אלף ות"ס תחלקם על אלף תרמ"ו שהוא המורה מקוצר יעלה בחילוק ד' והוא הנשאל ואם כן המספר שבקשנו הוא חלק אחד מאלף תרמ"ו שאם תכלנו אותו על ג' וב' חמשיות והעולה על ד' וג' רביעיות יהיה העולה ד' שלמים והוא המבוקש
|
|
|
שאלה סוחר קנה י"ז אמות וחצי בגד לסך י"א פרחי וב' שלישיות שאלתי סך ט' אמות
|
|
|
התשובה כפול ט' על י"א וב' שלישיות וחלק על י"ז וחצי ויהיו כזאת הצורה
|
|
|
| ט |
 יא יא |
 יז יז |
אם
|
|
|
|
[312]וראשונה תן הי"א שלמים [...] כפול ט' על ל"ה שלישיות ויהיו [...] י"ז וחצי ויהיו כזאת הצורה
|
|
|
|
|
|
[...] יהיו ל"ה חציים כזה
|
|
|
|
|
|
[...] ל"ה חציים עם שט"ו שלישיות ויהיו תר"ל וכולם [..] תר"ל על השני שהוא ק"ה ששיות כמו שתראה בצורה
|
|
|
| [0גו] |
ה0א
|
| האג |
הג
|
| ג |
ב
|
| ו
|
|
|
|
|
ויעלה בחילוק ששה והם פרחים והנה כאשר י"ז אמות וחצי שוה י"א פרחים וב' שלשיות הנה סך ט' אמות שוה ששה פרחים
|
|
|
והבחינה תן הכל בשברים ממין אחד וכפול האמצעיות והחיצוניות ויהיו שוים
|
|
|
והמשל י"ז וחצי הם ל"ה חציים וי"א ושתי שלשיות הם ל"ה שלישיות ויהיו שניהם כזאת הצורה
|
|
|
|
|
|
תשוים אל מורה אחד יהיה האחד ק"ה ששיות והשני ע' ששיות ועתה תן ט' בשישיות יהיו נ"ד ששיות ובם ו' יהיו ל"ו ששיות ויהיו כולם כזאת הצורה
|
|
|
|
|
|
כפול הקצוות יהיו ס"ג אלפים תש"ף וכן תמצא האמצעיות והכל מבואר
|
|
|
או אם תרצה לבדוק בדרך השלושה ואמור אם ק"ה נתן ע' שאלתי נ"ד מה יתן תכפול האמצעיות וחלק על ק"ה ותיצא ל"ו תחלק ל"ו על המורה שהוא ששה יעלו ששה והוא המבוקש
|
|
|
שאלה סוחר הלך לסחורתו למדינה אחת או לשתים או ליותר ובכל מדינה כפל ממונו והפסיד בכל מדינה מספר מה וכאשר שב לביתו לא נשאר לו כלום מממונו שאלתי הממון שהוציא מביתו
|
|
|
הנה הדרך לכולם הוא שאם הלך למדינה אחד גרע ממנה שהפסיד חציו והנשאר הוא הממון שהוציא מביתו ואם הלך בשתי מדינות וכפל ממונו כנז' גרע ממה שהפסיד רביעיתו והנשאר [313][...] שלושה השמינית וכן בכל [...] שהלך תצטרך לגרוע חצי [...] ולשלושה שמינית ולארבעה חלק [...] המשכת הערך הכפול שהוא כזה הצורה
|
|
|
| א |
א |
א |
א |
א |
א
|
| דו |
בג |
וא |
ח |
ד |
ב
|
|
|
|
|
המשל בזה ראובן הלך למדינה אחד וכפל ממונו והפסיד ד' ולא נשאר לו כלום שאלתי כמה ממון היה לו
|
|
|
התשובה גרע ממה שהפסיד חציו כמו שיורה השבר הראשון ונשארו ב' וזה ממונו
|
|
|
ואם בשתי מדינות גרע רביעית ד' שהוא מה שהפסיד ישארו ג' וזה ממונו שכפלו הוא ו' במדינה ראשונה והפסיד ד' ונשארו ב' לשנית וכופלם יהיו ד' והפסיד ד' ולא נשאר לו כלום
|
|
|
ואם הלך בג' גרע מד' השמינית ישאר ג' וחצי וזה ממונו כי כפלם הוא ז' בראשונה והפסיד ד' נשארו ג' לשנית וכפלם ו' והפסיד ד' נשארו ב' לשלישית וכפלם יהיו ד' והפסיד ד' ולא נשאר לו כלום
|
|
|
ואם בד' מדינות גרע מד' חלק מי"ו ונשארו ג' וי"ב חלקים מי"ו כפול וגרע כמו שעשינו ולא נשאר לו כלום
|
|
|
ולכולם כפי המדינות גרע השבר מלוח הערך הכפול וההפסד שתרצה הוא ההנחה[314]
|
The Fifth Section: Mixed Problems
|
[340][השער החמשי] [בשא]לות מעורבות
|
| I divided it into four chapters:
|
חילקתיו [לארבעה פרקים]
|
- The first chapter on mixed problems with a few [solving] methods.
|
[הפרק הראש]ון בשאלות מעורבות מקצת הדרכים
|
- The second chapter on artificial problems.
|
[הפרק] השני בשאלות תחבוליות
|
- The third chapter on various problems.
|
[ה]פרק השלישי בשאלות מתחלפות
|
- The fourth chapter on mixture of coins, including three methods:
|
[341][הפרק הרביעי בתערובת המטבעות] [342][ובו ג' סדרים
|
- The first method [deals with] adding and subtracting weights and the knowing the pure marci and their fractions.
|
הסדר הראשון בחיבור ובגרעון המשקלים ובידיעת הנקי ממרקוש ושבריו
|
- The second method [deals with] knowing the mixture of different amounts of silver.
|
הסדר השני בידיעת התערובת מסכים מתחלפים מכסף
|
- The third method [deals with] knowing the mixture of gold.
|
הסדר השלישי בידיעת דרכי תערובת הזהב]
|
Introduction on the Method of "Double False Position"
|
הקדמה לשני מונחים
|
| You should know that in every question there is a necessary division, which is that for every [double] false position, either one is less than the required amount and the other exceeds over it, or both are less, or both exceed over it.
|
הנה ראוי שתדע כי בכל שאלה יש חלוקה הכרחית והיא שכל מונח יהיה אם שיגרע האחד מן הסך הנשאל ויעדיף השני או שיגרעו שניהם או שיעדיפו שניהם
|
| If both are less, or exceed, subtract the smaller from the greater and the remainder will be the denominator, by which you divide.
|
[...] או יגרעו שניהם או יעדיפו שניהם גרע הקטן מן הגדול והנשאר הוא המורה לחלק עליו
|
| If one exceeds and the other is less, sum them and it will be the denominator, by which you divide. Keep it.
|
ואם יהיה האחד עודף והשני גורע תחברם והוא ויהיה המורה לחלק עליו ושמור אותו
|
| Then, multiply each false position by the excess of the deficiency of the other.
|
ואחר תכפול כל מונח בעודף או בגרעון השני
|
| Subtract the smaller [product] from the greater [product], if you subtracted the reserved; or sum them, if you added the reserved.
|
וגרע הקטן מן הגדול אם השמור גרעת או תחברם אם השמור חיברתה
|
| Divide the remainder or the sum by the reserved denominator.
|
והנשאר או המחובר תחלק על המורה השמור
|
| You always add twice or subtract twice - the first time in the denominator and the second time in the dividend from which the required amount results.
|
כי לעולם תחבר או תגרע שני פעמים הראשון לחלק עליו והשני הדבר המחולק אשר ממנו יצא הסך הנשאל
|
The First Chapter: Mixed Problems
|
[הפרק הראשון בשאלות מעורבות]
|
- Question: one merchant bought clothes, their number is unknown, but we know that for every 4 clothes he paid [9] peraḥim and that the total clothes and peraḥim were all 92. I ask: how many clothes did he buy and how many peraḥim did he pay?
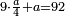
|
שאלה סוחר אחד קנה בגדים נעלמו מספרם אבל ידענו כי בכל ד' בגדים פרע מן פרחים והבגדים והפרחים היו כולם צ"ב
שאלתי כמה בגדים קנה [והפרחים שהוציא]
|
- Answer: you can solve this question with the "Rule of Three", but I will solve this and others by "Double False Position", to train you in it.
|
תשובה הנה זאת השאלה תוכל לעשותה עם דרך השלשה וזה ועוד אחרות אעשה עם השני מונחים כדי שתרגילם
|
- We assume one position and say that 4 clothes are for 9 peraḥim:
|
והנה נניח מונח אחד ונאמר כי ד' בגדים הם בט' פרחים
|
- We add 4 to 9; it is 13.
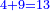
|
נחביר ד' וט' יהיו י"ג
|
- 79 are missing from 13 to 92 for this position.

|
והנה מי"ג עד צ"ב יחסרון ע"ט בזה המונח
|
- We assume the second position is 4 clothes are for 18 peraḥim:
|
עוד נניח המונח השני ד' בגדים והם שוים י"ח פרחים
|
- We add 18 to 8 clothes; it is 26.

|
נחבר [343]י"ח עם ח' בגדים יהיו כ"ו
|
- [66 are missing from 26 to 92 for this position].

|
והנה [...] צ"ב
|
|
|
ונאמר עם ח' בגדים יחסרון ס"ו [...] שהם פחות [...] ישארו י"ג ושמור [...] כי הוא המורה וא[...] מונח על הפחות מן [...] והעולה משניהם גרע הקטן מן הגדול והנשאר תחלק על השמור והיוציא הוא המבוקש
|
- We multiply 4 by 66; the result is 264. [Write it] beneath 66.
|
כיצד כפלנו ד' על ס"ו יעלה רס"ד ות[...] תחת ס"ו
|
- Multiply also 8 by 79; the result is 632.
|
עוד כפול ח' על ע"ט היוציא תרל"ב
|
- Subtract 264 from 632; 268 remains.
|
גרע רס"ד מתר[ל"ב] ישארו רס"ח
|
- Divide it by the reserved 13; the result is 28 and 4 parts of 13.
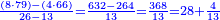
|
תחלקים על י"ג השמור יעלה בחילוק כ"ח וד' חלקים מי"ג
|
- So, he bought 28 clothes and 4 parts of 13 of a cloth and the remainder from the 92, which are 63 and 9 parts of 13 are the peraḥim that he paid.
|
והנה כ"ח בגדים וד' חלקים מי"ג בבגד קנה ונהשאר מהצ"ב שהם ס"ג וט' חלקים מי"ג הם הפרחים שהוציא
|
| |
|
|
632 |
|
| plus |
4 |
minus |
79 |
13
|
| plus |
8 |
minus |
66
|
| |
|
|
264 |
|
|
|
| |
בגו |
|
|
|
| יג |
עט |
פחות |
ד |
עם
|
| סו |
פחות |
ח |
עם
|
| |
דוב |
|
|
|
|
|
- The check is that you say by the "Rule of Three": if 4 clothes yield 9 peraḥim, how much will 28 clothes and 4 parts of 13 of a cloth yield?
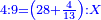
|
והבחינה היא שתאמר עם דרך השלשה אם ד' בגדים נתן ט' פרחים כ"ח בגדים וד' חלקים מי"ג בבגד כמה
|
- They should yield 63 peraḥim and 9 parts of 13, as this diagram:
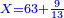
|
והראוי שיתן ס"ג פרחים וט' חלקים מי"ג ויהיה בזאת הצורה
|
|
|
|
|
|
נכפול האמצעיות אחר שתתן כ"ח בי"ג שהם עם הד' שברי' שס"ח חלקים מי"ג עתה נכ[פול] על ט' יהיה העולה ג' אלפים שי"ב נחלקם על ד' אחר שתשוים על י"ג שהם נ"ב יעלו בחילוק ס"ג וישארו ל"ו חלקים מנ"ב שאם תקצרם ברביעית יהיו נ"ו חלקים מי"ג והוא המבוקש כנזכר
|
|
|
והנה כאשר כאשר לקחתי למונח סך הבגדים כך תוכל לקחת למונח הפרחים כי עם מה שתרצה תוכל לעשות המונח
|
- The second question: one merchant bought 3 horses for 200 peraḥim, the price of each by itself is unknown, but it is known [that the price of the second horse is] the double [the price of] the first plus another 4 and the price of the third [is 3 times the price of the second minus 7]. I ask the price of each by himself.
|
שאלה שנית סוחר אחד קנה ג' סוסים בסך ק"ק פרחים נעלם סך כל אחד בפני עצמו אבל הוא יודע [344][כי סך הסוס השני הוא] כפל הראשון ועוד ד' וסך השלשי [הוא ג' פעמים השני פחות ז']
שאלתי סך כל אחד בפני עצמו
|
- The answer: [we assume] the price of the first horse is 5. Its double plus 4 [for the second] are 14. For the third 3 times the second minus [7], [which is 35].
|
[התשובה] [נניח] סך הסוס הראשון הוא ה' וכפלו ועוד ד' [...] יהיו י"ד והנה לשלשי ג' כפלי השני פחות [...]
|
- Sum all; they are 54.
|
תחברם כולם יהיו נ"ד
|
![\scriptstyle{\color{blue}{5+\left[\left(2\sdot5\right)+4\right]+\left[\left[3\sdot\left[\left(2\sdot5\right)+4\right]\right]-7\right]=5+14+35=54}}](/mediawiki/images/math/9/4/b/94b08271bc2cb47bb4420312fce25884.png)
|
- But, we ask for 200. So, the deficiency of the first position is 146.

|
ואנחנו שאלנו ק"ק והנה [...] גרעון קמ"ו במונח הראשון
|
- We assume a second position: [the price of the first horse is 6]. Its double plus 4 for the second are 16. 3 times the second minus 7 [is] 41 for the third.
|
עוד נניח למונח השני [...] והנה כפלו לשני ועוד ד' יהיו י"ו וג' כפלי השני פחות ז' [...] מ"א לשלשי
|
- Sum the three; they are 63.
|
תחבר שלשתם יהיו ס"ג
|
![\scriptstyle{\color{blue}{6+\left[\left(2\sdot6\right)+4\right]+\left[\left[3\sdot\left[\left(2\sdot6\right)+4\right]\right]-7\right]=6+16+41=63}}](/mediawiki/images/math/7/1/8/7187dc5f7380aeb8be727679db6750c3.png)
|
- But, we ask for 200. [So, the deficiency] of this position is 137.

|
ואנחנו שאלנו ק"ק [...] יגרעו מזה המונח קל"ז
|
- The two are according to this diagram:
|
ויהיו שניהם בזאת הצורה
|
|
|
| |
|
תתעו |
|
|
|
| קצא |
ט |
קמו |
פחות |
ה |
עוד
|
| קלז |
פחות |
ו |
עוד
|
| |
|
תרפה |
|
|
|
|
|
- Now, subtract the smaller deficiency from the greater deficiency; 137 from 146; 9 remains and this is the divisor. Keep it.
|
ועתה גרע הפחות הקטן מן הפחות הגדול קל"ז מקמ"ו ישארו ט' והוא המחלק המורה ושמור אותו
|
- Do another subtraction by multiplying each position by the deficiency of the other position:
|
עוד עשה גרעון אחר והוא שתכפול כל מונח בפחות המונח השני
|
- 6 by 146; the result is 876. Write it above 146.
|
ו' על קמ"ו ויעלו תתע"ו ותניחם על קמ"ו
|
- Also 5 by 137; the result is 685. Write it above 137.
|
גם ה' על קל"ז ויעלו תרפ"ה ותניחם על תחת קל"ז
|
- Then, subtract the smaller, which is 685, from the greater, which is 876; 191 remains and this should be divided by 9, which is the reserved divisor.
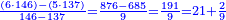
|
ואחר תגרע הקטן שהוא תרפ"ה מן הגדול שהוא תתע"ו ישארו קצ"א והם הראוים לחלק על ט' המורה השמור
|
- The result of division is 21 and 2-ninths, which is the price of the first horse, and from is you know the others.
|
ותציא בחלוקה כ"א וב' תשיעיות והוא סך הסוס הראשון וממנו תדע האחרים
|
|
|
והבחינה היא שאחר שידענו סך הראשון שהוא כ"א פרחים ושני תשיעיות פרח יהיה השני כפל הראשון ועוד ד' יהיו מ"ו פרחים וד' תשיעיות והשלישי שהוא ג' כפלי השני פחות ז' הנה ג' פעמים מ"ו וד' תשיעיות הם קל"ח י"ב תשיעיות גרע ז' ישארו קל"א וי"ב תשיעיות וזה סך השלישי ויהיו שלשה בזאת הצורה תחבר התשיעיות [345]התשיעיות יהיו ב' שלמים ועם [...] כנשאל [...] ואם תרצה [...] השלושה
|
|
|
ב
ט |
כא |
הסוס הראשון
|
ד
ט |
מו |
הסוס השני
|
יב
ט |
קלא |
הסוס השלשי
|
| |
קק |
סך כולם
|
|
|
- The third question: one merchant bought thirty kors of wheat and barley at a price of 400 dinar - the wheat at a rate of 21 dinar and the barley at a rate of 13 dinar. I ask: how many kors of wheat and how many kors of barley did he buy?
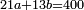
|
שאלה שלישית שאלה סוחר אחד קנה שלושים כורים מחטה ושעורה בס' ת' די' החטה לסך כ"א דינ' והשעורה לסך י"ג דיני'
שאלתי כמה כורי חיטה וכמה כורי שעורה קנה
|
|
|
תשובה תניח כי כורי החטה הם כ' ואם כן יהיו כורי השעורה עשרה והנה סך כ' כורי חיטה ת"ך ועשרה משעורה קל תחברם יהיו תק"ן ואנחנו שאלנו ת' ונשארו ק"ן ונאמר עם מונח כ' יותר ק"ן עוד נניח מונח שני ונאמר שיהיו כורי החטה י"ח ואם כן יהיו כורי השעורה י"ב והנה י"ב כורי שעורה יעלו קנ"ו וי"ח כורי חטה יעלו שע"ח תחברם יהיו תקל"ד ואנחנו שאלנו ת' והנה זה המונח השני נתן קל"ד יותר מהנשאל ונאמר עם מונח י"ח יותר קל"ד ויהיו שני המונחים בזאת הצורה
|
|
|
| |
|
00זב |
|
|
|
| 0ב |
וא |
0הא |
יותר |
0ב |
עם
|
| דגא |
יותר |
חא |
עם
|
| |
|
0חוב |
|
|
|
|
|
|
|
ועתה גרע היותר הקטן מן היותר הגדול שהם קל"ד מק"ן ישארו י"ו והם המורה לחלק עליו ושמור אותו עוד תעשה הגרעון השני אחר שתכפול כל מונח ביתרון המונח השני שהם י"ח על ק"ן וכ' על קל"ד והנה י"ח על ק"ן יעלו ב' אלף ות"ש והשני ב' אלף ותר"ף גרע ב' [346][...] ות"ש ונשארו כ' והם הראוים [...] שהוא י"ו ותציא בחלוק א' ורביע [...] כור אחד ורביע כור קנה מחיטה כי [...] מונח ונשארו לתשלום שלשים כורים כ"ח כורים [...] כור קנה משעורה
|
|
|
[והבחי]נה תכפול כור ורביע מחטה לסך כ"א יעלו כ"ו דנרי' וג' פשי' גם תכפול כ"ח וג' רביעיות בי"ג יעלו הכ"ח כורים שס"ד והג' רביעיות ט' דינ' וט' פשי' תחברם יהיו שע"ג די' וט' פשי' וזה סך השעורה תחברם עם סך החטה שהוא כ"ו די' וג' פשי' יעלו כולם ת' כנשאל
|
|
|
הערה שאם אמר בגדים או ספרים או סוסים קצתם לס' מה לקצתם לסך אחר או דברים אחרים ומספרים אחרים וסכים מתחלפים הנה הכל דרך אחד אלא חילוף החומרים ומה שאומר מהם אקצר
|
- The fourth question: one merchant bought so and so clothes, their number is unknown, but he bought them at 3 clothes for 7 peraḥim and he also knew that the total clothes and peraḥim were all 136.
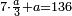
|
שאלה רביעית סוחר אחד קנה כל כך בגדים נעלמו מספרם אבל הוא קנה אותם ג' בגדים בז' פרחים והוא ידע גם כן כי סך הבגדים והפרחים היו כולם קל"ו
|
|
|
[תשובה] נניח שהבגדים יהיו ג' והסך ז' פרחים תחבר הבגדים והסך יהיו עשרה והנה שאלנו קל"ו ויגרעו בזה המונח קכ"ו נניח שיהיו הבגדים ו' והסך יהיה י"ד פרחים נחבר הבגדים והסך יהיו כ' והנה בזה המונח יגרעון קי"ו לתשלום קל"ו נגרע קי"ו מקכ"ו ישארו עשרה לחלק עליו כפול כל מונח על פחות חברו שיעלה לאחד תשנ"ו ולשני שמ"ח
|
|
|
| |
|
תשנו |
|
|
|
| ח0ד |
0א |
קכו |
פחות |
ג |
עם
|
| קיו |
פחות |
ו |
עם
|
| |
|
שמח |
|
|
|
|
|
|
|
[347]נגרע שמ"ח מתשנ"ו ישארו [...] בחילוק מ' וד' חמשיות והנה מ' [...] היה מה שקנה ותשלומו לקל"ו שהם צ"ה [...]
|
|
|
והבחינה הנה כל ג' בגדים שוים ז' פרח[ים] [...] אם ג' נתן ז' מה יתן לנו מ' וד' [...] יתן צ"ה וחמשית או ת[ה]פוך השאלה ואמור אם ז' נתן [...] וחמשית מה יתן והוא יתן מ' וד' חמשיות או תקצר ג' וז' יהיה כל בגד ב' ושליש ואמור אם א' נתן ב' ושליש מ' וד' חמש[..] מה יתן
|
|
|
בחינה אחרת [.] בשברו יהיו ר"ד גם צ"ה בשבר[.] יהיו תע"ו תשוים עם ג' וז' כזה ויצאו שוים ויורה כי כאשר ג' בגדים שוים ז' פרחים מ' וד' חמשיות שוים צ"ה וחמשית
|
|
|
| |
|
א |
ד |
ב |
ח
|
| ג |
X |
|
ב |
0 |
ד
|
| ז |
|
ד |
ז |
ו
|
| |
|
א |
ד |
ב |
ח
|
|
|
|
|
שאלה חמשית ראובן ושמעון עשו חברה ונתחייב ראובן לתן בחרבה ק"ן פרחים ולא נתן אלא ק' ושמעון שנתחייב לתת ק"ק פרחים לא נתן אלה ק"ן והרויח ס' פרחים שאלתי כצד יחלוקו כפי מה שנתנו או שנתחיבו לתת
|
|
|
[348]הנה רוב השאל[ות] שיהיו מזה המין הם על שני דרכים הראשון הוא שנעיין ערך מה שהתנה לתת עם מה שנתן שאם הוא כמו ב' אצל ג' הוא ב' שלישיות וכן כל אחד כמו שתראה מאלו השאלות הדרך השני שאם יהיה מה שהתנו לתת ומה שנתנו מספרים בודדים או אחד מהם שתתן זה על זה ויהיו כמו שברים כמו שתראה בשאלות
|
|
|
התשובה נעיין ערך מה שנתחייב כל אחד או מה שנתן והנה ראובן שנתחייב ק"ן ונתן ק' הנה ערך ק' אל ק"ן הוא ב' שלישיות חמשיות שתקצר ק' על קן וישובו לב' חמשיות כנזכר וערך ק"ק אל ק"ן משמעון הוא ערך ג' רביעיות והנה נאמר כי ממון הראשון הוא ב' שלשי' וממון לוי ג' רביעיות נשוים בזאת הצורה
|
|
|
| ט |
|
8
|
 |
X |

|
|
|
|
|
יהיו לראובן ח' ולשמעון ט' נחבר ממון שניהם יהיו י"ז והוא המורה לחלק עליו [349][...] החברות תכפול ס' על ח' יעלו [ת"ף] תחלקם על י"ז יעלה בחילוק כ"ח פרחים וד' חלקים מי"ז בפרח אם תרצה לכפול ד' על סך הפרח וחלק על י"ז והיוציא יהיו דנרי כמו שידעת לעשות מהנשאר דנרים [...] ולשמעון ל"א פרחים וי"ג יזין
|
|
|
והבחינה תקבץ היזין יהיו אחד שלם ול"א לשמעון וכ"ח לראובן יהיו ס' והוא הרויח
|
|
|
שאלה ששית הנה ב' או ג' סוחרים או יותר נתפשרו לעשות חברה ונתחיבו כל אחד לתת בחברה סך ידוע ולשהות זמן מוגבל והנה לא נתנו מה שנתחייבו מן הממון ולא שהו כפי מה שנתפשרו מן הזמן והרויחו ממון ידוע שאלתי כצד יחלוקו הנה הדרך הוא שתעיין ותדע כמו שאמרתי ערך כל אחד וזמנו כפי מה שראוי לתת ולשהות או כפי מה שנתנו ושהו ואחר תכפול זמן וממון כל אחד ואחד ואחר תשוה שלשתם וכאשר יהיו שוים תחת מורה כללי תכפול הרוח על הממון כל אחד והעולה תחלק על המורה כמנהג
|
|
|
ומשל לשאלתנו ראובן שמעון ולוי נתפשרו לעשות חברה עד ששה שנים ונתחייב ראובן לתת י"ו לטרין ולא נתן אלא י"ב לטרין ולא שהה אלא ה' שנים ושמעון היה לו לתת כ' לטרין ולא נתן אלא ט"ו לטרין ולא שהה אלא ד' שנים ולוי היה לו לתת כ"ד לטרין ולא נתן אלא כ' ולא שהה אלא ג' שנים והרויחו שלשים לטרין שאלתי כיצד יחלוקו כפי מה שנתחייבו לתת או מה שנתנו
|
|
|
תשובה תערוך ממון ראובן י"ו שחייב וי"ב שנתן תקצרם זה על זה יהיו ג' רביעיות כזה 
|
|
|
[350]וערך זמנו הוא ה' ששיות כזה  תכפול ממונו על זמנו יהיו ט"ו טו חלקם מכ"ד ומקוצר יהיו החלקים מח' כזה תכפול ממונו על זמנו יהיו ט"ו טו חלקם מכ"ד ומקוצר יהיו החלקים מח' כזה  וזה ממון ראובן וערך ממון שמעון הוא ג' רביעיות כי ט"ו נתן וכ' חייב לתת נתן ט"ו על כ' כזה וזה ממון ראובן וערך ממון שמעון הוא ג' רביעיות כי ט"ו נתן וכ' חייב לתת נתן ט"ו על כ' כזה
|
|
|
|
|
|
תקצרם יהיו ג' רביעיות כזה  וערך זמנו וערך זמנו
|
|
|
וערך זמנו יהיו ד' ששיות כי ד' שנים שהה מו' שראוי לו לשהות ומקוצר יהיו ב' שלשיות כזה  תכפול ממונו על זמנו יהיו ו' חלקים מי"ב שהוא חצי מקוצר [351]וזה ממון שמעון גם תערוך ממון [...] ששיות כזה תכפול ממונו על זמנו יהיו ו' חלקים מי"ב שהוא חצי מקוצר [351]וזה ממון שמעון גם תערוך ממון [...] ששיות כזה  וערך זמנו חצי כי [...] אל ו' חצי נכפול ה' ששיות על חצי יהיו ה' חלקים [...] תשוים כולם כזאת הצורה וערך זמנו חצי כי [...] אל ו' חצי נכפול ה' ששיות על חצי יהיו ה' חלקים [...] תשוים כולם כזאת הצורה
|
|
|
ו
זג |
יב |
0ג |
טו |
ראובן
|
זב
זג |
ט |
יב |
שמעון
|
ד
זג |
ח |
0א
זג |
שמעון
|
|
|
|
|
ויהיו לראובן ט"ו ולשמעון י"ב וללוי עשרה ותסדרם בדרך החברות בזה הצורה
|
|
|
| [.] |
יב |
טו
|
ה
בא |
 |

|
|
| כד
|
|
|
|
ותחבר ממונם יהיו ל"ז והוא המורה עתה כפול שלשים על ט"ו ועלו ת"ן תחלקם על ל"ז יעלה לראובן י"ב וששה חלקי ל"ז גם תכפול ל' על י"ב יעלו ש"ס תחלקם על ל"ז יעלה לשמעון ט' וכ"ז חלקי ל"ז גם תכפול ל' על עשרה יעלו ש' תחלקם על ל"ז יעלה ללוי ח' וד' חלקי ל"ז
|
|
|
והבחינה תחבר השברים יהיו לטרה אחת והשלמים כ"ט לטרה שיהיו כולם ל' לטרין והוא המבוקש
|
|
|
שאלה שבעית ראובן ושמעון עשו חברה ראובן נתן ל' לטרי ממון ושמעון כ' כורי חטה ונעלם סך החטה והרויחו י"א לטרה ומזה הרויח יתכן למי שנתן החטה ד' לטרי שאלתי סך כורי החטה
|
|
|
תשובה גרע הד' לטרי' מי"א ישארו ז' למי שנתן ל' לטרה ועתה אמור אמור אם ז' לטרה באו לריוח שלשים לטרה ד' לכמה לטרה יבא נכפול ל' על ד' ונחלק על ז' והביא י"ז ושביעית והנה י"ז ושביעית ליטרה יהיה סך החטה
|
|
|
והבחינה נאמר כי ראובן נתן ל' לטרי' ושמעון י"ז לטרין ושביעית ועתה נתן הכל בשביעיות [352][...] [שמ]עון ק"ך והרויחו י"א ליטרין תסדר [...] השאלה כסדר החברות בזה הצורה ותציא לראשון ז' לטרין ולשני ד' ליטרין וזה יורה כי כ' כורי חיטה יהיו שוים י"ז ליטרין ושביעית ליטרה
|
|
|
שאלה אחרת ראובן שמעון לוי ויהודה עשו חברה ראובן נתן בחברה כ"ה לטרי ממון ושמעון בגד נעלם הסך ולוי כ' פרחים נעלמו הסכים ויהודה גביע כסף נעלמה הסך והרויחו י"ד לטרין ונפל לראובן שנתן כ"ה ליטרין ה' ליטרין ולשמעון ד' ליטרין מן הבגד וללוי ג' מכ' פרחים וליהודה ב' מן הגביע
|
|
|
שאלתי סך הבגד וסך הכ' פרחים וסך הגביע
|
|
|
תשובה אחר שהיה לך ידוע ה' ליטרין רוח לראובן שנתן כ"ה לטרי' יהיו לך סך כל אחד ידוע עם דרך השלושה ואמור אם ה' ליטרין באו מכ"ה ד' ליטרין מכמה ליטרן יבוא ואם תרצה לעשות זה יותר כמות תקצר ה' וכ"ה בחמשית ויהיה א' וה' לראובן ואמור אם א' נתן ה' לראובן ד' מה יתן לשמעון והנה נתן כ' ליטרין לשמעון וכ' לטרין היה הבגד שוה עו' אם א' נתן ה' ג' מה יתן והנה נתן ט"ו והנה טו ליטרין היו שוים הכ' פרחים מלוי עוד אמור אם א' נתן ה' ב' מה יתן והנה נתן עשרה ועשרה ליטרין שוה הגביע
|
|
|
והבחינה נניח אלו הסכים לכל אחד והריוח והמורה ויהיה בזאת הצורה
|
|
|
| דא |
הב |
ראובן
|
| 0ב |
שמעו
|
| הא |
לוי
|
| 0א |
יהודה
|
| |
0ז |
המורה
|
|
|
|
|
נכפול ממון כל אחד על הריוח ונחלק על המורה ותציא לראובן ה' ליטרין ולשמעון ד' ליטרין וללוי ג' ליטרין וליהודה ב' ליטרין והם סך מה שנתן כל אחד
|
|
|
שאלה אחרת הנה רצינו לפסוק פסק לאנשים מה לכל אחד [353]כפי מה שיש לו מן הממון הנה [...] החברות שתתן כסדר ממון כל [...] לפסוק להם יהיה כמו ריוח ותחבר כל מה [...] ואחר כפול הממון על כל אחד והעולה תחלק [...] והוא הראוי לו לפרוע וכן תעשה לכל אחד ואין ל[...] כי כבר ידעת סדר החברות וקיצורם
|
|
|
שאלה אחרת ראובן שמעון ולוי עשו חברה ראובן נתן [..] קנ"ב פרחים וי"ג די' ושמעון נתן קכ"ג דוקאדיש וי"ח די' ולוי נתן קל"ב ליטרי ממון וט"ו די'
|
|
|
הנה בזאת השאלה נעשה כל ממונם די' יהיו לראובן ב' אלפים תמ"ה ולשמעון ב' אלפים תשכ"ה ולוי ב' אלפים תרנ"ה והרויחו כ"ד קאשטיללאטוש שהם לסך כ"ח תרע"ה וגמור כסדר הידוע
|
|
|
ואם תרצה שלא לעשות מן הקשטילל[טוש] די' הרשות בידך והעולה מן הקאשטיללטוש והנח לכל אחד עשה אות[ו] די' ויעלו תרנ"ה כנזכר והוא הבחינה
|
- Question: Reuven, Shimon and Levi formed a partnership and agreed that Reuben will contribute 7 peraḥim [florins], Shimon 11 and Levi 13 and that the partnership will last two years. However, Reuven contributed only 5 peraḥim, Shimon contributed only 7 and Levi 11 only. Furthermore, they did not stay [in the partnership]] for the agreed time: Reuven stayed for the whole two years, Shimon stayed for one year and a third and Levi stayed for one year. They earned ten peraḥim. I ask: how would they divide [the shares]?
|
שאלה ראובן שמעון לוי עשו חברה והסכמו שיתן ראובן ז' פרחים ושמעון י"א ולוי י"ג ושיתמשך החברה שתי שנים והנה ראובן לא נתן אלא ה' פרחים גם שמעון לא נתן אלא ז' ולוי לא נתן אל י"א וגם בזמן לא שהו אלא המותנה ביניהם אלא ראובן ששהה כל הזמן ב' שנים ושמעון שהה שנה ושליש ולוי שהה שנה אחת והרויחו עשרה פרחים שאלתי כיצד יחלוקו
|
|
|
הנה כל השאלות מזה המין ניתן מה שנתן על מה שראוי לתת ונתנו שברים מה שנתן ובכמו מורה מה שראוי לתת והוא יהיה ממון כל אחד
|
|
|
והמשל בזה נתן ה' פרחים שנתן על ז' שראוי לתת כזה 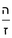 ויהיו ה' שביעיות ויהיו ה' שביעיות
|
|
|
לראובן וז' על י"א כזה
|
|
|
|
|
|
לשמעון וי"א על י"ג כזה
|
|
|
|
|
|
ויהיו בצורה הזאת
|
|
|
| ההכפלה |
זמנם |
ממונם |
|
0בא
דח |
דב
בא |
ה
ז |
ראובן
|
באא
בגא |
וא
בא |
ז
אא |
שמעון
|
בגא
והא |
בא
בא |
אא
גא |
לוי
|
|
|
|
|
והנה זמן ראובן הוא כ"ד חדשים כזה
|
|
|
|
|
|
וזמן שהיות [354][...]
|
|
|
|
|
|
וזמן שהיית לוי י"ב חדשים כזה
|
|
|
|
|
|
[...] אחד בזמנו יהיה לראובן ק"ך [...] קי"ב חלקי קל"ב וללוי קל"ב חלקי קנ"ו ואלה החלקים [...] כל אחד תקבצם כולם והוא המורה לחלק עליו [...] ואחר תקבצם והדרך שתבקש מורה שיכללם ואם לא [...] כפול מורה הראשון על מורה השני והיוציא על מורה השלישי והיוציא הוא המורה כללי כאשר ידעת תחלקיהו על מורה כל אחד והיוציא בחילוק תכפול בשבריו
|
|
|
והמשל נכפול מורה ראובן שהוא פ"ד על מורה שמעון שהוא קל"ב והעולה נכפול על קנו שהוא מורה לוי יהיה על העולה מספר אחד תשכ"ט אלפים תשכ"ח ויהיו כזה
|
|
|
|
|
|
והוא המורה הכללי נחלק אותו על מורה ראובן שהוא פ"ד יעלה בחילוק ב' אלפים תקצ"ב כזה
|
|
|
|
|
|
נכפול זה על שבריו שהם ק"ך יעלו ב' מספרים תע"א אלפים ומ' ויה כזה
|
|
|
|
|
|
וזה חלק ראובן
|
|
|
גם נחלק המורה הכללי על מורה שמעון והעולה נכפלהו בשבריו ויהיו מספר אחד תס"ז אלפים תרמ"ח כזה
|
|
|
|
|
|
וזה חלק שמעון
|
|
|
גם נחלק המורה הכללי על מורה לוי שהוא קנ"ו העולה נכפול בשבריו יעלו מספר אחד תס"ג אלפים תרי"ו כזה
|
|
|
|
|
|
ויהיו שלושתם כזה הצורה
|
|
|
| 0א |
ב |
ד |
ז |
ו |
0 |
ד |
0 |
ראובן
|
| א |
ד |
ו |
ז |
ו |
ד |
ח |
שמעון
|
| א |
ד |
ו |
ג |
ו |
א |
ו |
לוי
|
| |
ה |
ד |
0 |
ב |
ג |
א |
ד |
המורה
|
|
|
|
|
ועתה נכפול חלק ראובן על הריוח ונחלק על המורה הכללי יצא בחילוק ד' שלמים ואלה החלקים שהם ג' מספרים ק"א אלפים קפ"ד ויהיו כזה
|
|
|
|
|
|
כמו שתראה בצורה השנית
|
|
|
| ג |
א |
0 |
א |
א |
ח |
ד |
שלמים |
ד |
ראובן
|
| ג |
ח |
ז |
א |
ח |
ז |
ב |
שלמים |
ב |
שמעו
|
| |
ג |
ח |
ג |
א |
ה |
ה |
שלמים |
ב |
לוי
|
|
|
|
|
ולחלק שמעון ב' שלמים ואלו החלקים
|
|
|
|
|
|
כמו שתראה בצורה שנית
|
|
|
ולחלק לוי ב' שלמים ואלו השברי
|
|
|
|
|
|
כמו שתראה בצורה שנית
|
|
|
[355]והבחינה תקבץ השברים [...] השלמים שהם שמונה יהיו [...] אומנם אם נזדמן שתוכל לקצר שאלתך כזאת [...] לקצר הזמן והמשל בשאלה זאת שתוכל לקצר זמני [...] והנשאר לחציים ויהיו לראובן ששה שלישים כז
|
|
|
|
|
|
ול[שמעון ד'] שלשים כזה
|
|
|
|
|
|
וללוי ג' שלשי' כזה
|
|
|
|
|
|
ועתה נסדר ממונם כזה הצורה
|
|
|
0ג
אב |
ו
יג |
ה
ז |
ראובן
|
חב
גג |
ד
ג |
ז
אא |
שמעון
|
גג
טג |
ג
ג |
אא
גא |
לוי
|
|
|
|
|
נכפול כל ממון בזמנו יהיו לראובן ל' חלקים מכ"א ולשמעון כ"ח חלקים מל"ג וללוי ל"ג חלקים מל"ט כמו שתראה בזה הצורה ועתה תשוים וראשונה נכפול לט על ל"ג והעולה על כ"א ותציא זה
|
|
|
|
|
|
שהוא מורה כללי נחלקהו על מורה כל אחד והיוציא תכפול על שבריו
|
|
|
והמשל חילקנו המורה הכללי על כ"א ותציא אלף רפ"ז נכפלם על ל' ותציא ל"ח אלפים תר"י לראובן
|
|
|
גם חלקנו המורה הכללי על ל"ג יציא תתי"ט נכפלם על כ"ח ויהיו כ"ב אלפים תתקל"ב לשמעון
|
|
|
עוד נחלק המורה הכללי על ל"ט יעלו תרצ"ג ונכפלם על שבריו שהם ל"ג ותציא כ"ב אלפים תתס"ט ויהיו כולם כזאת הצורה
|
|
|
| שברי שלם |
שלמים |
|
| ד |
ח |
ד |
ח |
ד |
ד |
|
0א |
|
ג |
ח |
ו |
א |
0 |
ראובן
|
| ו |
0 |
ה |
א |
ב |
ב |
|
ב |
ב |
ט |
ג |
ב |
שמעון
|
| ה |
ט |
ח |
א |
ב |
ב |
|
ב |
ב |
ח |
ו |
ב |
לוי
|
| |
הריוח |
|
|
|
ח |
ד |
ד |
0 |
ד |
המורה
|
|
|
|
|
נחברם יהיו פ"ד אלפים ת"ד והוא המורה לחלק עליו ועתה נכפול חלק ראובן על הריוח שהוא עשרה והוא שתתן ספרא לפני כל מספר יהיו לראובן שפ"ו אלפים וק' נחלקם על המורה ותציא החילוק ד' שלמים ומ"ח אלפים תפ"ד וזה הראוי לראובן גם נכפול גם נכפול חלק שמעון בעשרה עם ספרא לפניו יהיו רכ"ט אלפים ש"ך נחלקם על המורה ותציא בחילוק [356][...] תקי"ב וזה חלק שמעון גם נכפול [...] רכ"ח אלפים תר"ך נחלקם על המורה ותציא [...] תתי"ב וזה חלק לוי [...] הוא שתמצא ב' שלמים בשברים וח' בשלמים יהיו עשרה
|
|
|
שאלה אחרת ראובן עשה צוואה והנח ק"ך פרחים ושלשה בנים ואמר תנו לגדול חצי הממון ולשני שלשיתו ולשלשי [.] רביעיתו שאלתי סך כל אחד
|
|
|
התשובה נניח י"ב למורה והנה חצי י"ב הם ו' לגדול ושלישית י"ב הוא ד' לשני ורביעית י"ב הוא ג' לשלישי תחבר חלקיהם יהיו יותר מי"ב נלך אל דרך השלושה והוא יתן לנו האמת ואמור אם י"ב נתן [.] ו' לגדול ק"ך מה יתן לו וכן תעשה לכל אחד אומנם בדרך החברות הוא יותר נקל ויהיה כזאת הצורה
|
|
|
| 0בא |
ו |
גדול
|
| ד |
שני
|
| ג |
שלישי
|
|
|
|
|
והמורה יהיה י"ג והממון יהיה כמו הרויח ועתה נכפול ק"ך על ו' יעלו תש"ך נחלקם על י"ג ועלה לגדול נ"ה פרחים וה' חלקים מי"ג בשלם
|
|
|
גם נכפול ק"ך על ד' יעלו ת"ף נחלקם על י"ג יעלו לשני ל"ו פרחים וי"ב חלקי י"ג
|
|
|
גם נכפול ק"ך על ג' יעלו ש"ס נחלקים על י"ג יעלו לשלישי כ"ז פרחים ונ"ו חלקים מי"ג וזה הראוי לכל אחד
|
|
|
והבחינה היא שתחבר השברים יהיו ב' שלמים תחברם עם השלמים יהיו ק"ך כנשאל והנה בזה הסדר תעשה כאשר תרצה לחלק איזה מספר לחצי ולשלש ולרביעית ולחמשי' וכול כל השברים שתרצה שהוא קשה לחלקם
|
|
|
שאלה אחרת שכיב מרע עשה צוואה מרע"ג פרחים ואמר הנה אשתי מעוברת ואני רוציא שתחלקו אלה הרע"ג פרחים בזה הדרך שאם תלד אשתי נקבה שתתנו לאשתי כפל הנקבה ואם תלד זכר שתתנו לזכר כפל אשתי והנה ילדה [357]זכר ונקבה שאלתי כיצד יחלוקו [...] ולהקל נניח א' לבת וב' לשני שהם שהם כפל האם וכללם הם ז' ועתה נאמר [...] רע"ג ויהיה כצורה הזאת
|
|
|
|
|
|
נכפול החיצ[..] רע"ג יעלו רע"ג [...] ז' יעלו בחילוק ל"ט [] והם חלק הבת נכפול ל"ט יעל ע"ח והם חלק האם שהם כפל הבת ונכפול ע"ח יעלו קנ"ו והם חלק הבן שהם כפל האם
|
|
|
והבחינה נקבצם כולם ל"ט וע"ח וקנ"ו ויהיו כולם רע"ג והוא מה שרצינו
|
|
|
הנה נרצה לדעת הנשאר בחלוקת דרך השלושה מאי זה מין הוא כאשר יש בה זמן וממון ואומר שהוא מהמין האמצעי שאין לו דומה כי הנעלם שבקשנו אין לו דומה כמו בדרך משל אם ב' דוקאדיש בג' חדשים הרויחו ד' די' שהוא האמצעי ה' דוקאדיש בב' חדשים כמה די' ירויחו ויהיה כצורה הזאת
|
|
|
|
|
|
נכפול הזמן הזהב ב' דוקאדוש בג' חדשים יהיו ו' וגם ה' דוקאדיש על ב' חדשים יהיו עשרה ואז חזרה השאלה אם ו' נתן ד' עשרה כמה די' יתן והנה ד' די' הוא האמצעי וממנו וממ תהיה התשובה מן המספר הנעלם שנתן ו' די' ונשארו ד' והם די' נעשה מהם פשיט' יהיו מ"ח נחלקם על ו' יעלו ח' פשיט' ועתה נאמר שאם ו' נתן ד' די' עשרה מה יתן והנה נתן ו' די' וח' פשיט' והנה ערך ו' אל ד' די' כערך עשרה אל ו' די' וח' פשי' ולראות זה לעין נעשה כל הדי' פשיט בעבור הח' פשיט יהיו הד' די' מ"ח פשיט והו' די' ע"ב פשיט נחבר עליהם ח' יהיו פ' פשיט והנה תראה כי ערך ו' אל מ"ח כערך עשרה אל פ' כי עשרה בפ' ח' פעמים וכן ו' אל מ"ח ח' פעמים
|
|
|
בחינה אחרת תשוה זה עם זה בצורה הזאת
|
| 480 |
|
480
|
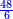 |
X |
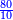
|
|
|
|
|
|
יהיה כל אחד ת"ף
|
|
|
שאלה ה[...] [358][...] עשרה מזהב [...] ח' מכסף וז' מנחושת ולקח מזה [...] משקלה שאלתי כמה יש בה מכל [...]
|
|
|
[תשובה] הנה כל אלו השאלות והדומות הם כמו [...] כי י' מזהב וח' מכסף וז' מנחושת [...] שלושה אנשים וקיבוצם שהוא כ"ה אוקיות הם כמו [...] ומה שלקח הוא כמו הריוח ונשוב לשאלתנו ונאמר כי [...] אוקיות הוא המורה ועתה לדעת הזהב שבחתיכה נכפול החתיכה שהיא ט' אוקיות על עשרה שהוא הזהב שבכולו יעלו צ' תחלקם על כ"ה יעלו ג' אוקיות זהב וט"ו חלקי כ"ה באוקיא וזה הזהב שבחתיכה
|
|
|
עוד לדעת הכסף נכפול ח' על ט' יעלו ע"ב וחלקן על כ"ה יעלו ב' אוקיות כסף וכ"ב חלקים מכ"ה וזה הכסף שבחתיכה
|
|
|
עוד לדעת הנחושת נכפול ז' על ט' יעלו ס"ג נחלקם על כ"ה יעלו ב' אוקיות וי"ג חלקי כ"ה מנחושת שבחתיכה וזה מה שרצינו
|
|
|
והבחינה תחבר השברים יהיו חמשים תחלקם על כ"ה יעלו שנים תחברם לשלמים יהיו כולם ט' כנשאל
|
- Question 12: There are 4 millstones in the miller's house, one of which mills 7 kors of wheat each day, the second 11, the third 13 and the fourth 15. One wants to mill 300 kors of wheat and [use] each of the millstone as needed. I ask how much will he grind each day?
|
שאלה י"ב הנה יש בבית הטוחנים ד' רחים אשר האחד טוחין בכל יום ז' כורי חטה והשנית י"א והשלישית י"ג והרביעית ט"ו ורצה לטחון ש' כורי חטה ולתת לכל אחת מן הרחים די מחסורו שאלתי כמה יטחון בכל יום
|
|
|
תשובה כמו החברות שתקבץ ז' י"א י"ג ט"ו יהיו מ"ו והוא המורה והש' כמו הריוח ועתה תכפול ז' על ש' וחלק על מ"ו והיוציא הוא הראוי למי שטוחן ז' כורים גם כפול י"א על ש' וחלק על מ"ו והיוציא הוא הראוי למי שטוחן י"א כורים גם כפול י"ג על ש' והעולה תחלק על מ"ו והיוציא הוא [359]הראוי למי שטוחן י"ג כורים גם [...] תחלק על מ"ו והיוציא הוא הראוי למי ש[...]
|
|
|
הבחינה כמו החברות
|
- Question 13: Jacob told Joseph his son: I would give [you 500] peraḥim to trade with them for [7 years and at the end of the 7] years you will take the 500 peraḥim and give me the profit that you earned with [the 500] peraḥim. Joseph traded for 3 years, and it turned out that he had earned 300 peraḥim. I asked how much should Joseph get and how much should his father get?
|
שאלה י"ג יעקב אמר ליוסף בנו אני אתן [...] פרחים שתעשה סחורה ז' שנים [...] הז' שנים שתקח הת"ק פרחים ושתתן לי הריוח שתעשה עם [הת"ק] פרחים והנה יוסף סידר סחורתו עד ג' שנים ומצאו שהרויח ש' פרחים שאלתי הראוי ליוסף והראוי לאביו
|
|
|
התשובה נאמר בדרך השלושה אם ז' נתן שנים יתנו ת"ק פרחים ליוסף ג' שנים מה יתנו לו והנה יתנו רי"ד פרחים וב' שביעיות
|
|
|
והבחינה היא שתכפל רי"ד וב' שביע[.] על ב' ושליש כי שליש היא שנה ושנים ששה ויהיה העולה ת"ק כנשאל
|
|
|
שאלה י"ד סחר ברסילונה חייב לסוחר סרקוסטה כ"א לטרין מממון סרקוסטה ורצה לפורעו בממון ברסילונה שאלתי כמה לטרי ברסילונה יתן לו
|
|
|
תשובה הנה באלו השאלות והדומות לאלו קח מטבע משותף לאלה השני מקומות וכן למידה ותאמר אם כך אמות מסרקוסטה שוה כך מידות ברסילונה כך מידות מסרגוסטה וכו' וכן נאמר בשאלתנו ונקח מלך ברסלוניש שהיה שוה י"ו פשיטי' בסרקוס' וי"ח בברסילונה ונאמר אם י"ו שוה י"ח כ"א ליטרין מה יהיה שוה או תקצרהו בחצי והוא הראוי ותאמר אם ח' פשיטי' סרקוסטה שוה ט' פשיטי ברסילונו כ"א לטרי סרקוסטה כמה לטרי ברסילונה יהיה והנה תמצא כי הוא כ"ג לטרין ברסלונה וה' שמיניות לטרה בזאת הצורה
|
|
|
[360]
 כג כג |
כא |
ט |
ח |
אם
|
|
|
|
|
[...] דרך השלושה ותמצא שאלתך וגם תכון כי כאשר י"ו פשיטין מסרקוסטה שוה י"ח מברסילינה כן י"ו לטרין סרגוסאה שוים י"ח לטרין [...] ואם תקצרם יענו האמת גם כן כי ח' לטרי סרקוסטה הם [...] לטרי ברסילונה והקש על זה
|
|
|
[361]ולעולם תחילת השאלה תהיה מהע מהעיר אשר הממון או הלטרין הידועים ממנו כי בכאן אמר כי ליטרי סרגוסה כן נסדר שאלה ונאמר אם ח' פש' סרגוסה שוה ט' פש' בשלושה כ"א לטרי סרגוסה כמה לטרי ברצלונה יהיו
|
|
|
והבחינה היא שתעשה כל הלטרין שמיניות ויהיו הכ"א לטרי קס"ח שמיניות והכ"ג עם שבריו קפ"ט שמיניות ואחר תשוים עם חלקי השאלה ויהיו כזה הצורה
|
|
|
| |
X |
א |
ה |
א |
ב
|
| ט |
|
א |
ח |
ט
|
| ח |
|
א |
ו |
ח
|
| |
א |
ה |
א |
ב
|
|
|
|
|
ואחר השיווי יהיו שניהם שוים אלף תקי"ב
|
|
|
שאלה ט"ו ראובן חייב לשמעון כ"ה כפולות אשר סך הכפולה הוא י"ח דינ' ורצה לפורעו בפרחים אשר סך הפרח הוא י"ד דנרי' שאלתי כמה פרחים יתן ראובן לשמעון שיהיו שוים לכ"ה כפול
|
|
|
תשובה תכפול הכפולות בי"ח יעלו ת"ן דנרי' תחלקים לסך הפרחים שהוא י"ד יעלו ל"ב פרחים ושביעית והנה ל"ב פרחים ושביעית פרח יפרע ראובן לשמעון והראוי וכן אם הפך השאלה
|
|
|
והבחינה הנה יתרון הכפילה על הפרח הוא ד' תחלקם על סך הפרח שהוא י"ד והוא מחולק ד' חלקים מי"ד אשר הם ב' שביעיות תכפלם בכ"ה שהוא מספר הכפולות יעלו חמשים שביעיות תחלקם על ז' יהיו ז' ושביעית תחבר י"ז ושביעית על כ"ה יעלו ל"ב ושביעית כנשאל
|
|
|
שאלה י"ו ראובן קנה ששה אמות מבגד לעשות מלבוש אשר רוחבו שבעה זרתות ורצה לכופלו עם [362]בגד אשר רוחבו ג' זרתות
|
|
|
נצטרך מן הבגד הזה לכפול אורך כל אמה שלנו ד' זרתות והנה [...] הראשון רוחבו ז' זרתות נכפול ז' על האורך [...] זרתות מששה אמות יעלו קס"ח זרתות מרובעות [...] הראשון אחר כן קח אמה אחת מאשר לו ג' [...] מרוחב ותכפול ד' זרתות מאורך על ג' מרוחב יעלו י"ב זרתות מרובעות בזה האמה ואמור אם י"ב זרתות יתן אמה אחת קסח זרתות מה יתן ויהיה כזה הצורה
|
-
|
|
|
|
והנה נתן י"ד אמות והנה י"ד אמות מזה הבגד תצטרך לכפול הששה אמות
|
|
|
והבחינה מבוארת והיא שתכפול י"ד אמות בי"ב זרתות מרובעות שיש בכל אמה ותציא קס"ח
|
|
|
שאלה י"ז אם ב' פרחים בג' חדשים הרויחו ארבעה דינרי' ג' פרחים בה' חדשים כמה ירויחו
|
|
|
[363]בדרך ראשון
|
|
|
תשובה כפול כל ממון בזמנו וישובו החמשה חלקים לשלושה ואחר עשה שאלתך
|
|
|
והמשל כפלנו ב' פרחים בג' חדשיו יעלו ו' והוא הראשון בשאלה גם כפלנו ג' פרחים בה' חדשיו יעלו ט"ו והוא השלישי בשאלה והריוח נשאר קיים ועתה נאמר אם ו' נתן ג' ט"ו מה יתן בזה הצורה
|
-
|
|
|
|
ונכפול ט"ו על ג' יעלו מ"ה תחלקם על ו' יעלה בחילוק ז' וחצי והוא מה שהרויח ג' פרחים בה' חדשים
|
|
|
והבחינה מבוארת מכמה צדדים כי ו' כפל ג' וכן ט"ו כפל הנעלם שהוא ז' וחצי אותן כל אב על בנו או בהפך או תשוים [364][...]מנהג שלישי מדרך השלושה [...]דוש בד' חדשים הרויחו ג' די' ז' אשקודוש [...] [ויהיו] ה' די'
|
|
|
התשובה כפול ה' שתרצה לדעת [...] אשקודוש על ד' חדשים שהם כ"ד ואמור [...] כ"ד הם ק"ח תחלקם על כפל ג' על ז' שהם כ"א יהיה [.]יציא ה' שלמים וט"ו חלקים מכ"א שמקוצרות הם ה' שביעיות והנה בה' חדשים וה' שביעיות חדש הרויחו הז' אשקודוש חמשה די' [ועיין בצורה]
|
|
|
והבחינה תהפוך שאלתך ותאמר אם ז' אשקודוש בחמשה חדשים וט"ו חלקים מכ"א נתן לנו ה' די' מי יתן לנו ג' נכפול ד' חדשים על ו' אשקודוש יעלו כ"ד תשוים עם מותרי שברי החודש יעלו תק"ד לחלק על קס"ח הבא מנתנת החדשים בשברו כי ה' על כ"א ובתוספת ט"ו שברים יהיו קס"ח אשר עליו תחלק תק"ד ותציא ג' די' והוא המבוקש
|
|
|
שאלה אחרת ממדה ממנהג שלשי מדרך השלושה אם בגד אחד שויה ט' דוקאדוש וב' אמות שוים י"ב די שאלתי כאשר עלה הבגד לסך י"ב דוקאדוש כמה בגד יותן בעד ט"ו די' כזא הצורה
|
|
|
התשובה כפול ט"ו על י"ח שבא מכפל ט' דוקאדוש על ב' אמות יעלו ר"ע שתחלקם על כפל י"ב די' על י"ב דוקאדוש שהוא קמ"ד יעלה בחילוק א וקכ"ו חלקים מע"ד שהוא ז' שמניות כזה 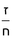
|
|
|
והנה אמה וז' שמניות אמה יותן לנו מזה הבגד בט"ו די'
|
|
|
[365]שאלה ממדה ממנהג שלישי [...] אמות מבגד שוה נ"ב די' וס' [...] סרגוסה שאלתי ה' אמות מבגד זה כמה ליטרין ממטבע סרגוסה יהיו
|
|
|
התשובה כפול ה' אמות שתרצה על כפל ג' ליטרין על נ"ב שהם קנ"ו ותכפול ה' על ותכפול ה על קנ"ו שיעלה תש"ף תחלקם על ר"מ שהם כפל השני דברים הנשארים שהם ס' על ד' יעלה בחילוק ג' ליטרין ורביעית ליטרה ממטבע סרגוסה
|
|
|
שאלה אחרת ממדה סוחר קנה בגד בסך ט"ו די' והג' אמות שוה ז' די' שאלתי אם זה הבגד יוקר וקנה אותו בסך י"ח מה יהיה שוה ה' אמות
|
|
|
התשובה הנה תכפול כל ממון על האמות שלו ותשוב ותשוב השאלה לג' חלקים כי ט"ו על ג' יעלו מ"ה וגם י"ח על ה' יעלו צ' עתה אמור אם אם מ"ה נתן ז' צ' מה יתן והנה נתן י"ד כזה הצורה
|
-
|
|
|
|
והבחינה ברורה כי הראשון כפל השלישי וכן השני כפל הרביעי הנעלם שהוא י"ד
|
|
|
שאלה אחרת ממשקל ראובן קנה כור חיטה בסך י"ח די' ונתן י"ד אוקיות לחםבשני פש' קרא מקרה וקנה הכור בסך כ"ב די' שאלתי י"ז אוקיות לחם כמה פשיטי' יתן ויהיה כזא הצורה
|
|
|
| פשיט |
אוקיות |
די' |
פשיט |
אקיות |
די' |
|
| 0 |
זא |
בב |
ב |
דא |
חא |
אם
|
|
|
|
|
התשובה כפול כל ממון על משקלו יהיה הראשון שכפלנו י"ח על י"ד יעלו רנ"ב והשני כ"ב על י"ז [366][...] פשיטי נשארו קיימים עתה שחזרו חלקי [...] אמור אם רנ"ב נתן ב' שע"ד מה יתן ויהיה [...] תכפול שע"ד על ב' יעלו תשמ"ח תחלקהו על רנ"ב יעלה בחילוק ב' פשטין ורמ"ד חלקים מרנ"ב בפשוט נקצרם יהיו ס"א מס"ג בשלם והנה כאשר קנה ראובן כור חיטה בכ"ב די' הנה י"ז אוקיות שוים ב' פשי' וס"א חלק מס"ג בפשוט
|
-
|
|
|
|
והבחינה תחזור הנעלם בשבריו יהיו תשמ"ח והב' ברנ"ב יהיו תק"ד ואחר תשוים עם רנ"ב ושע"ד כזה הצורה
|
| 188496 |
|
188496
|
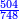 |
X |
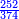
|
|
|
| וטדחחא |
|
וטדחחא
|
ד0ה
חדז |
X |
בהב
דזג
|
|
|
|
|
יהיו שוים כמו שתראה עליהם ויורה על אמיתת השאלה
|
|
|
שאלה אחרת אם י"ח פרחים בה' חדשים הרויחו שני פרחים שאלתי כ"ד פרחים בכמה זמן ירויחם כזאת הצורה
|
|
|
| חדשים |
פרחים |
פרחים |
חדשי' |
פרחי' |
|
| 0 |
כד |
ב |
ה |
יח |
אם
|
|
|
|
|
כפול י"ח פרחים עלו ה' חדשים יעלו צ' תחלקם על כ"ד יעלה בחילוק ג' וג' רביעיות הנה בג' חדשים וג' רביעיות חודש ירויחו כ"ד פרחים ב' פרחים
|
|
|
והבחינה הפוך השאלה ואמור אם כ"ד פרחים נתן ט"ו רביעיות חודש י"ח פרחים מה יתן כפול כ"ד פרחים בט"ו רביעיות חודש יעלו ש"ס תחלקם על י"ח אחר שתשוים עם רביעיות החדשים שיפלו ע"ב ותצא בחילוק ה' חדשים והוא המבוקש
|
|
|
שאלה אחרת ראובן קנה כור חיטה בסך י"ח די' ונתן ט"ו אוקיות מלחם בשני פשיטי שאלתי כאשר קנה כור חיטה בסך כ"ו די' כמה אוקיות יתן בשני פשיט'
|
|
|
ויהיה בצורה הזאת
|
|
|
| פש' |
די' |
פשי' |
אוקיות |
די' |
|
| ב |
כו |
ב |
טו |
יח |
אם
|
|
|
|
|
נכפול י"ח שהוא הממון על ט"ו שהוא המשקל יעלו ר"ע תחלקם [367]על כ"ו יעלה בחילוק עשרה אוקיות וה' חלקי [...] עשרה אוקיות וה' חלקי י"ג באוקיה יתן מלחם בשני [...] עלה כור החיטה [.] לסך כ"ו די'
|
|
|
והבחינה הנה ערך י"ח אצל כ"ו שוה לחלקים הנשארים [...] תחלק כ"ו על י"ח יעלו א' וד' תשיעיות מקוצר גם ט"ו על עשרה אוקיות ועשרה חלקי כ"ו אשר אחר הקיצור הם ה' חלקים מי"ג כיצד נחלק ט"ו על האוקיות וראשונה תשוים ט"ו עם מורה האוקיות יהיו ש"ץ גם האוקיות בשברו יהיו ר"ע נחלק ש"ץ על ר"ע יעלה בחילוק א' וד' תשיעיות כראשון
|
|
|
שאלה אחרת ראובן קנה כור חיטה בסך י"ו די' ונתן י"ז אוקיות לחם בשני פשיט' שאלתי כאשר קנה הכור בסך כ' די' כמה אוקיות יתן בג' פשי' ובזה השאלה תמצא חמשה דברים מונחים והוא מן הסדר השלישי ויהיה כזאת הצורה
|
|
|
התשובה הנה תכפול י"ו די' על י"ז אוקיות ויעלה רע"ב וזה חלק ראשון עוד תכפול הב' פשיטי שנתנו הי"ז אוקיות על כ' די' שהוא סך הכור השני יעלו מ' והוא החלק השני ועתה תכפול הג' פשיטי ששאלת על החלק הראשון שהוא רע"ב יעלו תתי"ו תחלקם על החלק השני שהוא מ' יעלה בחילוק כ' אוקות וב' חמשיות מאוקה מקוצר והנה כ' אוקיות וב' חמשיות אוקיה מלחם יתן בג' פשיט
|
|
|
והבחינה בשאלה שיבא
|
|
|
שאלה ראובן קנה משא ענבים בסך י"ו די' ונתן י"ב אוקיות יין בסך ב' פשי' שאלתי כאשר קנה המשא בסך כ' די' [כמה] אוקיות יין יתן בג' פשי' ויהיה בצורה הזאת
|
|
|
[368]בכאן שאלה כפולה
|
|
|
[369][...] י"ז אל כ"ו שוה לחלקים הנשארים [...] המשל תחלק כ"ו על י"ח יעלו א' וד' תשיעיות [...] על עשרה חלקים אוקיות ועשרה חלקי כ"ו אשר אחר [...] ר"ע גם תן כ"ו בשברי כ"ו יהיו שץ אשר תחלקם [...] יעלה בחילוק א' וד' תשיעיות באחד
|
|
|
[370]הקיצור הם ה' חלקים מי"ג כצד נחלק ט"ו על האוקיות וראשנה נשוה טו עם מורה האוקיות יהיו שץ גם האוקיות בש[..] יהיו ר"ע נחלק שץ על ר"ע יעל[ה] בחילוק א וד תשיעיות כראשון
|
|
|
שאלה כ"ב ראובן קנה כור חטה בסך י"ו די ונתן י"ז אוקיות לחם בשני פשיט' שאלתי כאשר קנה הכור בסך כ' די' כמה אוקיות יתן בג' פשיטי'
|
|
|
ובזה השאלה תמצא חמשה דברים מונחים והוא מן הסדר השלישי ויהיה בזאת הצורה
|
|
|
תשובה הנה תכפול י"ו די' על י"ז אוקיות ויעלה רע"ב וזה חלק ראשון עוד תכפול הב' פשיטי' שנתנו הי"ז אוקיות על כ' דנר' שהוא סך הכור השני יעלו מ' והוא החלק השני ועתה תכפול ג' פשיטי' ששאלת על החלק הראשון שהוא רע"ב יעלו תתי"ו תחלקם על החלק השני שהוא מ' ועלה בחילוק ב' אוקיות וב' חמשיות מקוצר והנה כ' אוקיות וב' חמשי אוקיה מלחם יתן בג' פשיטי'
|
|
|
והבחינה בשאלה שיבוא
|
- Question 23: Reuven buys a cargo of grapes at a price of 16 dinar and sells 12 ՚oqya wine at a price of 2 pešiṭim.
- I ask: when he buys the cargo at a price of 20 dinar, how many ՚oqya wine [he sells] for 3 pešiṭim?
|
שאלה כ"ג ראובן קנה משא ענבים בסך י"ו דינרי' ונתן י"ב אוקיות יין בסך ב' פשיט'
שאלתי כאשר קנה המשא בסך כ' די' כמה אוקיות יין בג' פשיטי'
|
|
|
ויהיה כזאת הצורה
|
|
|
תשובה הנה [371][תכפול] [...] יעלו קצ"ב [...] על ג' [...] תחלקם על כפל [...] דינר שהם מ' יעלה [...] י"ד אוקיות וב' חמשיות [...] מקוצר וזה מה שרצינו
|
|
|
[372]זה כמו שאלה [...]
|
|
|
והבחינה הנה נקח ב' שילשיות י"ד וב' חמשיות אוקיה של יין שהם הראוי לג' פשיטי בעבור שיהיה יותר נקל והיוציא שהוא ט' אוקיות וג' חמשיות הוא הראוי לב' פשיטי' לב' פשיטי' מיין ואחר נשוה ט' אוקיות בחלקיו יעלו קל"ז חמשיות וכפלם על דינרי הכור השני יעלו קצ"ב בחלק הראשון כי ט' על כ' יעלו ק"ף וג' חמשיות על קצ"ב יעלו ס' חמשיות נחלקם על ה' ותציא י"ב ועם ק"ף יהיו קצ"ב ואם תקח הג' פשי' אשר בשאלתנו יהיה הראשון קצ"ב והשני רפ"ח והוא קצ"ב וחצי כמו שג' הוא אחד וחצי מב' וכן [לכולם]
|
|
|
[373]דרך שני
|
-
|
|
- Question 24: if 4 pešiṭim of Zaragoza are equal to 5 pešiṭim of Barcelona and 3 pešiṭim of Barcelona are equal to 4 of Lisbon, I ask: how many pešiṭim of Zaragoza are 15 pešiṭim of Lisbon equal to?
|
שאלה כ"ד אם ד' פשיטי סרקוסטה שוים ה' פשיט' ברסילונה וג' פשיטי ברסילונה הם שוים ד' פשיטי לדידה לשבונה שאלתי ט"ו פשיטי לישבונה כמה פשיטי סרקוס[טה] הם שוים
|
|
|
ויהיו כאזת הצורה
|
- Multiply 15, [whose value] you wish to know, by the product of 4 pešiṭim of Zaragoza by 3 of Barcelona, which is 12; the result is 180.
|
התשובה כפול ט"ו שתרצה לדעת על כפל ד' פשיטי סרקוסטה וג' מברסילונה שהם י"ב יעלו ק"ף
|
- Divide it by [the product of 5 of Barcelona] by 4 of of Lisbon, which is 20 [...]. Hence 15 pešiṭim of Lisbon are equal to 9 of Zaragoza [...].
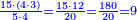
|
תחלקם [374][...][סרגוסא] ד' לשבונה שהם כ' [...] והנה ט"ו פשיטי לשבונה הם ט' מסרקוסא' [...] שאלתי הדומה לזה
|
|
|
[375][...] שאלתך כזאת הצורה [...]כפל ה' על ל"ו שבא מכפל ט' סרגוס' על ד' לשבונה יעלו ק"ף אשר תחלקם על מה שבא מכפול ט"ו לשבו' על ג' ברצלונה ותציא ד' פשיטי סרגוס או תחלק ק"ף על כ' שבא מד' לשבונה על ה' ברצלונה ותציא ץ' אשר הוא שאלתינו וכן כל הדומה לזה
|
Chapter Three on Various Problems
|
הפרק השלישי בשאלות מתחלפות
|
- The first question: Reuben had sons and money and he made a will, but he told some witnesses: write and give one of my sons one and a fifth of the remainder or he said a quarter of the remainder or a third or whichever part he wants and it will be the denominator.
|
שאלה ראשונה ראובן היו לו בנים וממון ועשה צוואה נעלמת אבל אמר לעדים כתבו ותנו לאחד מבני אחד וחמשית הנשאר או אמר רביעית הנשאר או שלישית או איזה חלק שהוא רוצה והוא יהיה המורה
|
- You have to know three things: one is the number of his sons, the second is the amount of money, and the third is the unknown amount of money.
|
והנה יש לך לדעת שלשה דברים האחד סך בניו והשני סך הממון והשלישי הממון הנעלם
|
|
|
והנה [383][...] כשתגרע אחד מן המורה [...] לכל אחד תדעהו כשתכפול המספר [...]ערכת לחלוק הבנים הנודעים והשלישי שהוא [...]דעהו כשתכפול מספר הבנים על מספר הממון
|
- Example: Reuven made a will and wanted an unknown [..] and he said: I have money in a certain house at a certain country [..] also and I want that you will give my oldest son one peraḥ and one-tenth [of the remainder]; to the second 2 peraḥim and one-tenth the remainder; to the third 3 peraḥim and one-tenth of the remainder; and so on by this order successively.
|
והמשל בזה ראובן עשה צוואה ורצה שלא נודע [..] ואמר ממון יש לי בבית פלוני במדנה פלונית [..] גם כן ורציתי ברצון נפשי שתתנו לבני הגדול פרח אחד ועשרית [הנשאר] ולשני ב' פרחים ועשרית הנשאר ולשלישי ג' פרחים [ועש]רית הנשאר וכן כסדר זאת ההמשכה הנערכת
|
- Subtract one from ten, as he said "tenth"; nine remain and these are the sons.
|
גרע אחד [מ]עשרה בעבור שאמר עשירות נשארו תשעה והם הבנים
|
- Now, we wish to know how many peraḥim he gave each: multiply the number of the sons by the number of the successive addition, which is one, because the sequence is 1, 2, 3, 4, 5, etc. We multiply 1 by 9, it is 9 and it is the amount of money given to each.
|
ועתה [נרצה] לדעת כמה פרחים נתן לכל אחד
כפל מספר הבנים [ב]מספר העושה ההמשכה שהוא אחד כי ההמשכה הוא זה [א'ב']ג'ד'ה' כו'
כפלנו א' על ט' יהיו ט' והוא הממון שיתנו לכל [אחד]
|
- Now, we wish to know his unknown [original] amount: we multiply [the number of] his sons by the money of each, 9 by 9 is 81. Thus, we know that the unknown amount of money is 81, the sons are 9 and the share of each of them is 9 peraḥim.
|
ועתה נרצה לדעת ממונו הנעלם
נכפל בניו על הממון [..] לכל אחד ויהיה ט' על ט' יהיו פ"א והנה פ"א פרחים הוא הממון [הנעלם] והנה ידענו כי הממון הנעלם הוא פ"א והבנים [ט'] וחלק כל אחד ט' פרחים
|
- Check:
- We give the oldest one peraḥ and one-tenth of the remainder: we take one from 81; 80 remain. A tenth of 80 is 8. 72 remain and the oldest has 9 peraḥim.
![\scriptstyle{\color{blue}{1+\left[\frac{1}{10}\sdot\left(81-1\right)\right]=1+\left(\frac{1}{10}\sdot80\right)=1+8=9}}](/mediawiki/images/math/7/e/1/7e16e246fab51d35149f72dd0401e6ed.png)
|
בחינה נתן לגדול פרח אחד ועשרית הנשאר נקח מפ"א אחד נשארו פ' ועשירית פ' הוא ח' נשארו ע"ב והנה נפל לגדול ט' פרחים
|
- For the second: 2 from 72; 70 remains; its tenth is 7; with 2 it is 9 for the second and 63 remain.
![\scriptstyle{\color{blue}{2+\left[\frac{1}{10}\sdot\left(72-2\right)\right]=2+\left(\frac{1}{10}\sdot70\right)=2+7=9}}](/mediawiki/images/math/c/f/4/cf41808c6ec759ad834beefcc2d4055d.png)
|
ולשני ב' מע"ב נשארו ע' ועשיריתם ז' וב' יהיה ט' לשני ונשארו ס"ג
|
- We give the third 3 and a tenth of 60, which is 60; 54 remain and the third has 9.
![\scriptstyle{\color{blue}{3+\left[\frac{1}{10}\sdot\left(63-3\right)\right]=3+\left(\frac{1}{10}\sdot60\right)=3+6=9}}](/mediawiki/images/math/7/7/6/776c0ab51c38bdd0b3bbecddee02ae1f.png)
|
נתן לשלישי ג' ועשירית ס' שהוא ו' ישארו נ"ד וט' לשלישי
|
- Likewise for the rest.
|
וכן לכולם
|
- Another [question]: Reuven made a will and said: I have sons and money in a certain country and I want that you will give my smallest son 3 times and a fifth of the remainder; to the second 6 [times] and a fifth of the remainder; to the third 9 [times] and a fifth of the remainder; and so on by this order successively.
|
אחרת ראובן עשה צואה ואמר בנים וממון יש לי במדינה פלונית ורציתי שתתנו לבני הקטן ג' כפילות וחמשית הנשאר ולשני ו' וחמשית הנשאר ולשלישי ט' וחמשית הנשאר וכן כזה ההמשכה הנערכת
|
|
|
נגרע אחד מהמורה [384]שהוא ה' כי חמשית אמר [...] שיתנו לכל אחד נכפול הבנים שהם ד' [...] ההמשכה הנערכת כי הוא ג'ו'ט' כו' יעלו [...] לכל אחד ולדעת הכפולות הנעלמות נכפול [...] והם הכפולות כי כפלנו י"ב הנופל לכל אחד על ד' והנה הבנים ד' והממון מ"ח וחלק כל אחד י"ב
|
- Check:
- We give the first 3 from 48; 45 remains. We take also a fifth of 45, which is 9. With 3 it is 12 for the first and 36 remains.
![\scriptstyle{\color{blue}{3+\left[\frac{1}{5}\sdot\left(48-3\right)\right]=3+\left(\frac{1}{5}\sdot45\right)=3+9=12}}](/mediawiki/images/math/8/f/e/8feda18ef09345637b237d92aef00e30.png)
|
והבחינה נתן לראשון ג' ממ"ח נשארו מ"ה נקח גם [חמשית] מ"ה שהוא ט' ועם ג' יהיו י"ב לראשון ונשארו ל"ו
|
- We give the second 6 from 36; 30 remains. A fifth of 30, which is 6, with 6 it is 12 for the second and 24 remains.
![\scriptstyle{\color{blue}{6+\left[\frac{1}{5}\sdot\left(36-6\right)\right]=6+\left(\frac{1}{5}\sdot30\right)=6+6=12}}](/mediawiki/images/math/8/b/7/8b720e4e9df64a218292b5fba3ccc31e.png)
|
נתן לשני ו' מל"ו נשארו ל' וחמשית ל' שהוא ו' ועם ו' יהיו [י"ב] לשני ונשארו כ"ד
|
- We give the third 9 from 24 and a fifth of the remainder; it is 12 for the third and 24 remains.
![\scriptstyle{\color{blue}{9+\left[\frac{1}{5}\sdot\left(24-9\right)\right]=12}}](/mediawiki/images/math/a/c/8/ac8b361e6878842651863ec8171e62e8.png)
|
נתן לשלשי ט' מכ"ד וחמשית הנשאר יהיו [י"ב] לשלשי
|
- We give the fourth the remaining 12 and all have the same.
|
נתן י"ב הנשארים לרביעי וכולם שוים
|
|
|
וכזה הסדר [..] המשכה נערכת כמו מה שעשינו או ד' ח' י"ו כ' וכו' או ה' י' ט"ו [כ'] או ו' י"ב י"ח כ"ד כולי
|
|
|
דרך להוציא דבר נערך מעיר לעיר ומה שצריך להוציא לפרוע מכס שבכל עיר ואמשל כל זה עם משל [...] ואם כוונתי לקצר יחוייב שאעשה שני שאלות נעלמים ומ[...]
|
- Question: the king's daughter asked his servant: Bring me one apple from the garden.
- He went to the garden and there were two gatekeepers.
- The gatekeeper said to him: Take as many apples, so that you will give me half plus one half [so that they will be whole], and so said the other.
- I asked: How many apples will he take from the garden to give the gatekeepers what they asked for and have an apple left in his hand.
|
שאלה בת מלך אמר לעבדו תוציא לי תפוח אחד מהגן
הלך לגן והיו בו שני שוערים
אמר לו ה[שוער] קח כל כך תפוחים שתתן לי חציים והחצי אחד [ושיהיו שלמים] וכן אמר השני
שאלתי כמה תפוחים יקח מן הגן שיתן לשוערים מה ששאלו ושישאר תפוח בידו
|
- The answer: he takes 7 and gives the second gatekeeper 4, which is half the total plus one half; he is left with 3.
![\scriptstyle{\color{blue}{7-\left[\left(\frac{1}{2}\sdot7\right)+\frac{1}{2}\right]=7-4=3}}](/mediawiki/images/math/b/4/c/b4c9ab73080d1478df2efc91ccbe9abe.png)
|
תשובה יקח ז' ויתן ד' לשוער השני שהם חצי כולם וחצי אחד ונשארו בידו ג'
|
- Then, he gives the first gatekeeper 2 of them, which is a half of 3 plus one half, and he is left with one apple for the king's daughter.
![\scriptstyle{\color{blue}{3-\left[\left(\frac{1}{2}\sdot3\right)+\frac{1}{2}\right]=3-2=1}}](/mediawiki/images/math/d/4/0/d40122d01a3a69e0c380468a9ed7f86c.png)
|
ומהם יתן ב' לשוער הראשון שהם חצי ג' וחצי אחד וישאר בידו תפוח לבת המלך
|
|
|
והנה הדרך הכללי הוא שאם שאל א' והיו ד' שוערים יוציא ט"ו כי ג' לשוער ראשון כופלם עם תוספת אחד יהיו ז' לשני כופלם עם תוספת אחד יהיו ט"ו לשלשי וכן כולם [385][...] עם תוספת אחד ואם שאל ב' תפוחים [...] [תוספת] אחד עד כל השוערים שתרצה [...] כל מה ששאל כמו שתיראה בזה הלוח
|
|
|
[...] אם אמר השועיר או השוערים שיתן [...] עוד ג' הנה הדרך הוא שתקח התפוחים [...] ותכפלם גם תכפול מה שאמר ועוד ג' או מה [ש]אמר ועוד כמו ששאל ב' כופלם יהיו ד' והשומר [..] ועוד ג' כופלם יהיו ו' ועם ד' יהיו עשרה
|
- If there are 2 gatekeepers, double ten plus 3, which is 6; they are 26.
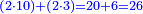
|
ואם [היו ב'] שוערים כפל עשרה והעוד ג' שהם ו' יהיו כ"ו
|
- If there are 3 gatekeepers, double 26 plus the 3; they are 58.
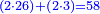
|
ואם [היו] ג' שוערים כפול כ"ו והג' יהיו נ"ח
|
- If there are 4 gatekeepers, double 58 plus the 3; they are 122.
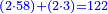
|
ואם ד' שוערים [כפול] נ"ח וג' יהיו קכ"ב
|
- Likewise for as many gatekeepers as you wish.
|
וכן כל מה שתרצה מן השוערים
|
- Question: Shimon went to the garden and asked for two apples for himself.
- He found three gatekeepers and asked the first one for two apples.
- He said to him: Take so many that you will give me half plus a half and two will remain in your hand.
- He went to the second gatekeeper, and he said to him: Take so many apples that you will give me 2-thirds of all of them plus 2-thirds of an apple.
- He went to the third gatekeeper, and he said to him: Take so many apples that you will give me 3-quarters of all of them plus 3-quarters of an apple.
- Despite all this, all the apples will be whole and he will have 2 apples left.
- I asked: How many apples will he take from the garden?
|
שאלה שמעון הלך לגן ושאל לו שני תפוחים ומצא ג' שוערים ושאל מן הראשון ב' [תפו]חים אמר לו קח כל כך שיהיו שתתן לי החצי וחצי [אח]ד ושישאר בידך שנים הלך אצל השוער השני אמר [לו] קח כל כך תפוחים שתתן לי ב' שלשיות כולם וב' שלישיות [תפוח] הלך אצל השוער השלישי אמר לו קח כל כך תפוחים שתתן לי ג' רביעיות כולם וג' רביעיות תפוח ועם כל זה יהיו כל התפוחים שלמים ושישארו לו ב' תפוחים שאלתי כמה תפוחים יקח מן הגן
|
- The way to solve this is that you take the 2 whole [apples] he asks for; multiply them by the last denominator and add its numerator to the product; [multiply] the result by the middle denominatorand add its numerator; then [multiply] the result by the first. The total result is what he should take from the garden.
|
הדרך לעשות זה הוא שתקח הב' שלמים ששאל ותכפלם על מורה האחרון ועל היוציא תוסיף שבריו והיוציא על מורה האמצעי ותוסיף שבריו והיוציא על הראשון והעולה מכולם הוא הראוי לקחת מן הגן
|
- The example: we multiply the 2 requested by the last denominator; the result is 8. Since he said "3-quarters", with the 3 of the 3-quarters, which is its denominator, they are 11.

|
המשל בזה כפלנו ב' הנשאל על מורה אחרון יעלו ח' בעבור שאמר ג' רביעיות וג' מג' רביעיות שהם שבריו יהיו י"א
|
- We also multiply 11 by 3, which is the denominator of 2-thirds; the result is 33. We add 2; [the result is 35].
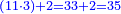
|
גם כפלנו י"א על ג' שהוא מורה ב' [386]שלשיות יעלו ל"ג נוסיף ב' [..]
|
- [We also multiply] 35 by 2, [plus one, which the numerator of a half]; the result is 71.
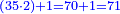
|
[...] ל"ה על ב' וחצי [ואחד מחצי שבריו] יעלו ע"א
|
- [...], since he is left with two.
|
[...] בעבור שישארו לו שנים והנה [...]
|
- We take 3-quarters of 71 for the third gatekeeper [...] the 3-quarters are 53 and a quarter, plus 3-quarters [...]
![\scriptstyle{\color{blue}{71-\left[\left(\frac{3}{4}\sdot71\right)+\frac{3}{4}\right]=71-\left[\left(53+\frac{1}{4}\right)+\frac{3}{4}\right]=17}}](/mediawiki/images/math/7/9/3/793f5dbaea1c9067d5448b0415be62c2.png)
|
[...] כי נקח לשוער השלשי ג' רביעיות ע"א ו[...] הג' רביעיות הם נ"ג ורביע ועוד ג' רביעיות [...]
|
- The second gatekeeper asked for 2-thirds of 17 [plus 2-thirds of an apple] [...] [2]-thirds of 17 and [is 11] and a third, plus 2-thirds [..] it is 5.
![\scriptstyle{\color{blue}{17-\left[\left(\frac{2}{3}\sdot17\right)+\frac{2}{3}\right]=17-\left[\left(11+\frac{1}{3}\right)+\frac{2}{3}\right]=5}}](/mediawiki/images/math/7/9/a/79a87ec3a656d7364329434cb05a5f24.png)
|
השוער השני שאל ב' שלישיות י"ז [וב' שלישי תפוח] והנשאר יהיו [...] שלשיות י"ז הוא [...] ושלישית ועוד ב' שלישיות יהיו [..] ה'
|
- The first asked for its half plus one half, which is 3; he is left with [two].
![\scriptstyle{\color{blue}{5-\left[\left(\frac{1}{2}\sdot5\right)+\frac{1}{2}\right]=5-3=2}}](/mediawiki/images/math/2/0/5/205d885533f39c52333574d6459e71c2.png)
|
והראשון שאל חציים וחצי אחד שהם ג' ונשארו לו [...]
|
- Apply this way when there are many gatekeepers in the garden. As you see:
|
וזה הדרך תעשה אם יהיו בגן שוערים רבים כמו שת[ר]אה כזה
|
- The table of the apples
|
[387]לוח התפוחים
|
| Apples |
Gates |
Gates |
Gates |
Gates |
Gates |
Gates
|
| 1 |
3 |
7 |
15 |
31 |
63 |
127
|
| 2 |
5 |
11 |
23 |
47 |
95 |
191
|
| 3 |
7 |
15 |
31 |
63 |
127 |
255
|
| 4 |
9 |
19 |
39 |
79 |
159 |
319
|
| 5 |
11 |
23 |
47 |
95 |
191 |
383
|
| 6 |
13 |
27 |
55 |
111 |
223 |
447
|
|
| שערי' |
שערי' |
שערי' |
שערי' |
שערי' |
שערים |
תפוחים
|
| קכז |
סג |
לא |
טו |
ז |
ג |
א
|
| קצא |
צה |
מז |
כג |
יא |
ה |
ב
|
| רנה |
קכז |
סג |
לא |
טו |
ז |
ג
|
| שיט |
קנט |
עט |
לט |
יט |
ט |
ד
|
| שפג |
קצא |
צה |
מז |
כג |
יא |
ה
|
| תמז |
רכג |
קיא |
נה |
כז |
יג |
ו
|
|
- Question: 5 people earn 12 with 6 beasts in 8 days.
- I ask: how much will 6 people earn with 8 beasts in ten days?
|
שאלה ה' אנשים עם ו' בהמות בח' ימים ירויחו [יב] [...] שאלתי ו' אנשים עם ח' בהמות בעשרה [ימים] [כמה] ירויחו
|
- The answer: multiply the people by the beasts, then the product by the days.
|
[תשובה] כפול האנשים על הבהמות והעולה על הימים
|
- Do as follows: multiply 5 people by 6 beasts; the result is 30. Then, 30 by 8 days; the result is 240, which is the first known [number].

|
וכן תעשה כפול ה' אנשים על ו' בהמות יעלו ל' גם ל' בח' ימים יעלו ר"מ [...] החלק הראשון הנודע
|
- Multiply 6 people by 8; the result is 48. Multiply 48 by ten; the result is 480, which is the third number.

|
ותניח הדינרי' במקומם וכסדר הנז[..] כפול ו' אנשים על ח' יעלו מ"ח כפול מ"ח על עשרה יעלו ת"ף החשבון השלישי
|
- Rule of Three: Now we say: if 240 gives us 12, how much will 480 give?
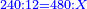
|
ועתה נאמר אם ר"מ נתן לנו י"ב ת"ף מה יתן
|
- It gives 24.
|
ונתן כ"ד
|
- The check is clear: [the product of 240 by 24 is the same as the product of 24 by 480].
|
והבחינה מבואירת כי ר"ם כפל ת"ף וגם כ"ד [...] [ותחלק ר"ם על ...]
|
|
|
|
|
[388][...] כדין של [.] יין מבשל שבו [...] כדין [...] מספר ישוב [...]
|
- Multiply 8 by 3; the result is 24. Divide it by 5; the result is 4 and 4-fifths, like this:
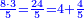
|
כפול ח' על ג' יעלו כ"ד חלקם על ה' יעלו ד' כדין וד' חומשי כד כזה
|
 4 4
|
|
 |
ד
|
|
|
| Likewise for all that is similar to it with the Rule of Three.
|
[וכן] כל הדומה לזה עם דרך השלושה
|
- Check: the product of the means is 600 and so is [the product of] the extremes.
|
הבחינה כפלי האמצעים יהיו ת"ר וגם החיצוניים
|
- Find a Quantity Problem - Whole from Parts - Fish
|
|
- Question: a man bought a fish, its head is one fifth, its body is 3-quarters, and its tail is 5 cubits. I ask: how much is its entire length?
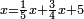
|
שאלה אדם קנה דג או כה שתרצה שראשו חמשית  וגופו ג' רביעיות [וזנבו] ה' אמות וגופו ג' רביעיות [וזנבו] ה' אמות
שאלתי אורך כולו
|
- Match the fractions to one denominator, which is 20; it is according to this diagram:
|
תשובה תשוה השברי אל מורה אחד שהוא כ' ויהיה כזאת הצורה
|
| 4 |
|
15
|
 |
X |

|
| |
20 |
|
|
|
| ד |
|
הא
|
 |
X |

|
| |
20 |
|
|
|
- False Position: We say that 20 cubits is its whole.
|
ונאמר כי כ' אמות [הוא] סך כולו
|
- We take its fifth, which is 4; we take also [¾], which are 15; with the 4 they are 19, which are its body and its head; and only one cubit remains for its tail, but we required [5] cubits for its tail.
|
נקח החמשית שהוא ד' גם נקח ג' אמות שהם ט"ו ועם ד' יהיו י"ט שהם סך גופו [ו]ראשו ולא נשאר רק אמה לזנבו ואנחנו שאלנו אמות לזנבו
|
![\scriptstyle{\color{blue}{20-\left[\left(\frac{1}{5}\sdot20\right)+\left(\frac{3}{4}\sdot20\right)\right]=20-\left(4+15\right)=20-19=1}}](/mediawiki/images/math/4/d/2/4d22c0d307436c88afa3c8befacad96b.png)
|
- Rule of Three: We say: if 20 gives us 1, how much will 5 give us?
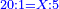
|
ונאמר אם כ' נתן לנו א' מה יתן לנו ה'
|
- We multiply 5 by 20; the result is 100.
|
נכפול ה' בכ' יעלו ק'
|
- Divide it by 1; the result is 100 and it is the measure of the fish.
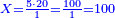
|
חלקם על א' יהיו ק' והוא מדת הדג
|
- For its fifth is 20; its three-quarters are 75; with 20 they are 95 and 5 remain for its tail to complete the 100.
|
כי חמשתו כ' וג' רביעיותיו הם ע"ה וכ' יהיו צ"ה נשארו ה' לזנבו לתשלום ק'
|
![\scriptstyle{\color{blue}{100-\left[\left(\frac{1}{5}\sdot100\right)+\left(\frac{3}{4}\sdot100\right)\right]=100-\left(20+75\right)=100-95=5}}](/mediawiki/images/math/e/5/c/e5c6bfe69df8c01d57472029106120f8.png)
|
| Likewise for all that is similar to it.
|
וכן כל הדומה לזה
|
| The same for a tree whose fifth is in the ground beneath the water, its 3-quarters are in the water, and 5 cubits are above the water.
|
וכזה אילן חמשיתו בקרקע תחת המים וג' רביעיות במים וה' אמות על המים
|
| Also for a lance and all that is similar to it.
|
וכן רומח וכן כל הדומה לזה[389]
|
[Chapter Four]: Mixture of Coins
|
[390][...] תערובת המטבעות
|
The first chapter on addition and subtraction of weights and knowing the pure marci and their fractions
|
הסדר הראשון [בחיבור ובגרעון המשקלים ובידעת הנקי ממרקוש ושברין]
|
| I say that this chapter is proper for money craftsmen.
|
[...] ואומר כי זה הפרק הוא טוב מאוד [...] הוא טוב גם כן לאומני ממון [...]
|
| I will tell you some rules that should be preceded:
|
אומר לך כללים ראויים להקדים
|
|
|
[...] ראשונה דברים אשר קצתם מפורסמים אצל הממון וקצתם נעלמים והנה כזה תמצא שני [...] בהסכמה הראשונה חלוקת המשקלים והשנית חלוקת [...] או הנקי וזה הנקרא הדת
|
| The division of weights: first, they called a certain weight "marco". They divided the marco into eight ounces; the ounce into 24 dinar; each dinar into 24 grani; each grano into 24 polita. This is the division of the weights.
|
אמנם חלוקת המשקלים ראשונה קראו למשקל מה מרקו וחלקו המרקו לשמונה אונסיש והאינסה לכ"ד דינירוש וכל דינירו לכ"ד גראנוש וכל גראנו לכ"ד פוליטאש וזה חלוקת המשקל
|
| The second division is the division of the values: each marco of silver has a value of 12 dinar; each dinar is divided into 24 grani; each grano into 24 polita; and I divide the polita into 24 fractions of a polita.
|
החלוקה השנית שהיא חלוקת הדת הוא כי כל מרקו מכסף הוא י"ב דינירוש מדת וכל דינירו נחלק לכ"ד גראנוש וכל גראנו לכ"ד פוליטאש והפוליטה חילקתי לכ"ד שברי פוליטה
|
| I drew two tables:
|
[...] ציירתי שני לוחות
|
| In the first table I specified the proper value for each of the parts of the weight.
|
הלוח הראשון פרטתי בו הראוי מן הדת לכל חלקי המשקל
|
| The second table is the opposite of the first, which is the appropriate weight for each of the values.
|
והלוח השני הוא הפך הראשון שהוא הראוי מן המשקל לכל חלקי הדת
|
|
|
הלוח הראשון הוא כי החלקים יותר קטנים שהנחתי כאן מן המשקל הם פוליטאש וכתבתי כ"ד פוליטאש ממשקל אשר הראוי לאחד מן הדת שהוא י"ב דיניש [..] כל א' אונסש יש ל"ה שבר וחצי מדת ול"ה פוליטאש ממשקל [..] יש לה ג' שברים עד אשר י"ו פולידאש ממשקל יש להם פוליטה אחת מדת וכ"ד פוליטש שהם גראנו אחד יש להם פוליטה וחצי מדת והוא סוף הטור הראשון מן הלוח הראשון
|
|
|
וראשון הטור השני הוא גראנו אחד ממשקל שהוא פוליטה וחצי מדת וב' גראנוש ג' פוליטאש וי"ו גראנוש גראנו אחד מדת וכ"ד גראנוש שהוא סוף הטור שהוא דינירו אחד יש בו גראנו וחצי מדת והוא [391]הם הטור השלישי וראש הרביעי [...] מדת והנה ראש הלוח הרביעי [...] מדת וה' אונסאש שהוא סוף הטור הרביעי [...] מהם י"ב דיניש מדת וכן בכל מרקו שאם [...] מדת תחלקים על י"ב והיוציא הם מרקיש
|
|
|
והלוח [...] שאם יהיו בידך דיניש או גראנוש או פוליסאש מדת לדעת המשקל הנה כל פוליטה מדת יש לה י"ו פוליט[..] ומכל כ"ד מכל מין תעשה אחד למה של מעלה [...] ב' פוליטי' הם גראנו וח' פוליטי' ממשקל עם כי י"ב פול[..] הם ח' גראנוש ממשקל וכ"ד פליטי' שהם גראנו אחד הם י"ו ג[...] ממשקל והוא ראש הטור השני שהוא גראנו אחד מדת והוא י"ו ג[...] ממשקל והשני דינירו אחד וח' גראנוש וי"ב ח' דיניש [...] סוף הטור השני וראש השלישי הם דינירו אחד מדת וי"ו דיניש ממשקל והנה ראש הטור השלישי הוא דינירו אחד מדת שהוא שוה י"ו דיניש ממשקל וג' דיניש מדת הוא אונסה וח' פשיטי' ממשקל וי"ב דיניש מדת שהם מרקו הם ח' אונסש ממשקל [..] מרקו אחד גם כן והרי לך צורת השני לוחות
|
|
|
ואחר שידענו הסכים נחבר המינים כמו שתראה
|
- We wish to know how much are 16 marco, 5 ounces, 16 dinar, 23 grano and 13 polita, plus 29 marco, 7 ounces, 21 dinar, 17 grano and 5 polita, plus 37 marco, 11 dinar, and 12 polita, according to this diagram:
|
המשל רצינו לדעת כמה יעלה י"ו מרקוש וה' אונסאש וי"ו דיניש וכ"ג גראנוש וי"ג פוליטאש עם כ"ט מרקוש ז' אונסאש כ"א דינירו י"ז גראנוש ה' פוליטאש ועם ל"ז מרקוש וי"א דיניש וי"ב פוליטאש ויהיה [כזאת] הצורה
|
פוליטא
יג
ה
יב |
גראנוש
כג
יז
0 |
דינירוש
יט
כא
יא |
אונסאש
ה
ז
0 |
מרקוש
יו
כט
לז
|
| ו |
יז |
ד |
ו |
פג
|
|
|
|
נחבר[.] הפוליטאש יהיו ל' גרע [...] גראנו אחד ונשארו ו' נחבר הגרנו עם
|
|
|
[392]עם [...] מ"א תן [...] לפשוט אחד יהיו נ"ב [...] גרע מ[..] מ"ח ל"ב אונסאש ד' דיניש [...] הב' אונסאש [..] האונסאש יהיו י"ד גרע מרקו[..] ישארו ו' אונס[..] נחבר גם כן ה[...] יהיו עם האחד שהוספנו פ"ג מרקוש וזה המבוקש מן השלושה חשבונות המונחים והוא הדין אם נרצה לגרוע דומה מדומה
|
|
|
המשל בזה רצינו לגרוע כ"ד מרקוש ד' אונסאש י"ג דיניש כ"ג גראניוש
|
| |
[.] |
|
dinar and grani of weight |
pure grani |
|
grani and polita of weight |
pur polita
|
| [.] |
dinar |
|
|
dinar |
grani |
|
|
grani |
polita |
|
| |
16 |
1 |
|
|
16 |
1 |
|
|
16 |
1
|
| 1 |
8 |
2 |
|
1 |
8 |
2 |
|
1 |
8 |
2
|
| 2 |
0 |
3 |
|
2 |
0 |
3 |
|
2 |
0 |
3
|
| 2 |
16 |
4 |
|
2 |
16 |
4 |
|
2 |
16 |
4
|
| 3 |
8 |
5 |
|
3 |
8 |
5 |
|
3 |
8 |
5
|
| 4 |
0 |
6 |
|
4 |
0 |
6 |
|
4 |
0 |
6
|
| 4 |
16 |
7 |
|
4 |
16 |
7 |
|
4 |
16 |
7
|
| 5 |
8 |
8 |
|
5 |
8 |
8 |
|
5 |
8 |
8
|
| 6 |
0 |
9 |
|
6 |
0 |
9 |
|
6 |
0 |
9
|
| 6 |
16 |
10 |
|
6 |
16 |
10 |
|
6 |
16 |
10
|
| 7 |
8 |
11 |
|
7 |
8 |
11 |
|
7 |
8 |
11
|
| 8 |
0 |
12 |
|
8 |
0 |
12 |
|
8 |
0 |
12
|
| |
|
13 |
|
8 |
16 |
13 |
|
8 |
16 |
13
|
| |
14 |
|
9 |
8 |
14 |
|
9 |
8 |
14
|
| |
10 |
0 |
15 |
|
10 |
0 |
15
|
| |
10 |
16 |
16 |
|
10 |
16 |
16
|
| |
11 |
8 |
17 |
|
11 |
8 |
17
|
| |
12 |
0 |
18 |
|
12 |
0 |
18
|
| |
12 |
16 |
19 |
|
12 |
16 |
19
|
| |
13 |
8 |
20 |
|
13 |
8 |
20
|
| |
14 |
0 |
21 |
|
14 |
0 |
21
|
| |
14 |
16 |
22 |
|
14 |
16 |
22
|
| |
15 |
8 |
23 |
|
15 |
8 |
23
|
| |
16 |
0 |
24 |
|
16 |
0 |
24
|
|
| |
[.] |
|
דיניש וגראנוש ממשקל |
גראנוש דת |
|
גראנוש ופוליטאש ממשקל |
פוליטאש דת
|
| [.] |
דניש |
|
|
דיניש |
גראנוש |
|
|
גראנוש |
פוליטאש |
|
| |
יו |
א |
|
|
יו |
א |
|
|
יו |
א
|
| א |
ח |
ב |
|
א |
ח |
ב |
|
א |
ח |
ב
|
| ב |
0 |
ג |
|
ב |
0 |
ג |
|
ב |
0 |
ג
|
| ב |
יו |
ד |
|
ב |
יו |
ד |
|
ב |
יו |
ד
|
| ג |
ח |
ה |
|
ג |
ח |
ה |
|
ג |
ח |
ה
|
| ד |
0 |
ו |
|
ד |
0 |
ו |
|
ד |
0 |
ו
|
| ד |
יו |
ז |
|
ד |
יו |
ז |
|
ד |
יו |
ז
|
| ה |
ח |
ח |
|
ה |
ח |
ח |
|
ה |
ח |
ח
|
| ו |
0 |
ט |
|
ו |
0 |
ט |
|
ו |
0 |
ט
|
| ו |
יו |
י |
|
ו |
יו |
י |
|
ו |
יו |
י
|
| ז |
ח |
יא |
|
ז |
ח |
יא |
|
ז |
ח |
יא
|
| ח |
0 |
יב |
|
ח |
0 |
יב |
|
ח |
0 |
יב
|
| |
|
יג |
|
ח |
יו |
יג |
|
ח |
יו |
יג
|
| |
יד |
|
ט |
ח |
יד |
|
ט |
ח |
יד
|
| |
י |
0 |
טו |
|
י |
0 |
טו
|
| |
י |
יו |
יו |
|
י |
יו |
יו
|
| |
יא |
ח |
יז |
|
יא |
ח |
יז
|
| |
יב |
0 |
יח |
|
יב |
0 |
יח
|
| |
יב |
יו |
יט |
|
יב |
יו |
יט
|
| |
יג |
ח |
כ |
|
יג |
ח |
כ
|
| |
יד |
0 |
כא |
|
יד |
0 |
כא
|
| |
יד |
יו |
כב |
|
יד |
יו |
כב
|
| |
טו |
ח |
כג |
|
טו |
ח |
כג
|
| |
יו |
0 |
כד |
|
יו |
0 |
כד
|
|
|
|
[393][...] מרקוש ב' אונסאש ג' דיניש ט' [...] כזאת הצורה
|
|
|
| פלוטי |
גראנוש |
[דיניש] |
[אונסאש] |
[מרקוש]
|
| ד |
ט |
ג |
ב |
ל"ה
|
| ז |
כג |
יג |
ד |
כד
|
| כא |
ט |
יג |
ה |
י
|
|
|
|
|
גרענו ז' פוליטאש [...] [ולא] נוכל נעשה מגראנו אחד כ"ד פוליטאש ועם הד' יהיו כ"ח נגרע מהם ז' ישארו כ"א עוד גרענו כ"ג מח' שנשארו נעשה מדינירו אחד כ"ד [ג]ראנוש יהיו ל"ב גרענו מהם כ"ג ישארו ט' גראנוש עוד [גר]ענו מב' דיניש שנשארו י"ג נעשה מאונסה אחד כ"ד פשיטי' [יהיו] כ"ז נגרע מהם י"ג ישארו י"ג עוד נגרע ד' אונסאש מא' [...] נעשה ממרקו אחד ח' אונסאש ועם א' יהיו ט' נגרע [מ]הם ד' ישארו ה' עוד נגרע מל"ד מרקיש שנשארו כ"ד ישארו [עש]רה והנה יצא לנו שנשאר אחר הגרעון עשרה מרקוש ה' [אונס]אש י"ג דיניש ט' גראנוש כ"א פוליטה והוא המבוקש
|
|
|
ואם ואם תרצה לכפול או לחלק משקלים מתחלפים על אחרים תשוים ואחר תכפול או תחלק כאשר עשינו בכפל או בחילוק מורכבים כי לא רציתי להאריך
|
|
|
והנה כאשר יהיה כסף מעורב [...] דע כי לעולם י"ב פשיטי מעורבות אונקיות הם מרקו אחד וכן כל שברי המרקו שלא נקפיד אם הוא נקי או מעורב
|
|
|
ואומנם לדעת הנקי שיש במשקל או במשקלים מתחלפים תדעם עם דרך השלושה בזה הדרך שתקח מרקו אחד ועמו תעשה הערך לאחדים הנשאלים ואם הנקי מהנשאל יהיה פשיטי' עשה [.] מרקו אחד פשיטי' ואם שאל שברים אחרים עשה המרקו אחד ממין הנשאל כמו שתראה ובעבור שלא תצטרך בכל זאת לעשות מהמרקו שברים ממין הנשאל אכתוב כאן [..] אנסאש המרקו והדיניש והגראנוש והפוליטאש ושברי הפוליטאש כי לא קראתי להם שם [394]אלא שברים או שברי פוליטה
|
| |
|
|
|
אונסאש |
ח
|
| |
|
|
דיניש |
|
בטא
|
| |
|
גראנוש |
|
|
ח0וד
|
| |
פוליטאש |
|
|
|
בטה0אא
|
| שברים |
|
|
|
|
ח0ב654ב
|
|
מרקו אחד הוא
|
|
|
|
שאלה ט' מרקוש מכסף ג' אונ[...] זה ממשקל [...] מדת בכל [...] שאלתי [...] נקי [...] בכול [..]
|
|
|
תשובה תן מרקו אחד בדיניש בעבור כי בנשאל תמצא דיניש ויהיו קצ"ב דיניש ובשאלתינו אמר כי יש בכל מרקו ח' דיניש מדת וקצ"ב הם דיניש גם כן ועתה אמור אם קצ"ב נתן לנו ח' ט' מרקוש ג' אונסאש [..] פשיטי כמה נקי יתן לנו תן הנשאל בדיניש כי שבר[...] הוא דיניש ויהיו אלף תתט"ו דיניש כי ט' על מורה האונ[סאש] שהוא ח' יהיו ע"ב וג' אונסאש אשר בשאלה יהיו ע"ה אונסאש כפול ע"ה אונסאש על מורה הדיניש שהוא כ"ד יעלו אלף ות"ת וט"ו שהיו בשאלה יהיו אלף ותתט"ו כנזכר ועתה תסדר השאלה ואמור אם קצ"ב דיניש ממשקל נתן לנו ח' פשיטי דת אלף ותתט"ו דיניש ממשקל מה יתן לנו כזאת הצורה
|
|
|
| |
משקל |
דת |
משקל |
|
| 0 |
האחא |
ח |
קצב |
אם
|
|
|
|
|
כפול האמצעיות יעלו י"ד אלפים תק"ך תחלקם על קצ"ב יעלה בחילוק ע"ה דיניש וק"ך חלקים מקצ"ב תחלק ע"ה דיניש על י"ב שהוא דיניר הדת יעלה בחילוק ו' דינרים ונשארו ג' דיניש והנה ו' דינרים שהם ו' מרקוש מדת וג' דיניש [395][...] אשר אם תקצרם יהיו ה' שמניות [...] תמצא מנקי כ"ט מרקוש ג' אונסאש ט"ו [...] ח' פשיטי מנקי
|
|
|
[והבחי]נה כפול כל אב על הבן הנכרי כמו קצ"ב על הנעלם שהוא ע"ה וחלקיו יהיו י"ד אלפים תק"ך גם [...] תתט"ו על ח' יעלו י"ד אלפים תק"ך כנזכר וזה שתתן ע"ה [..]קצ"ב בעבור שיהיו השני בנים שוים ואחר כפול כל אב על הבן הנכרי כאשר אמרתי
|
|
|
וכבר ראיתה כל הבחינות שעשיתי לדרך השלושה ועתה באלו השאלות שאכתוב אם אביא בחינה אם לא תעיין באחרות כי אכוון לקצר
|
|
|
שאלה ה' מרקוש ו' אנסאש ז' דיניש ח' גראנוש כל זה ממשקל לסך ה' דניש ט' גראנוש מדת בכל מרקו שאלתי כמה נקי יש בכל הנשאל
|
|
|
[תש]ובה תן מארקו אחד בגרנוש יהיו ד' אלפים תר"ח בעבור כי הנקי הוא גראנוש גם תעשה הנשאל גראנוש יהיה הכל כ"ו אלפים תרע"ב גראנוש כל זה ממשקל ושמרם וגם תן ה' דניש מהנקי גראנוש יהיו ק"ך ועם ט' גראנוש שהיה בשאלה יהיו קכ"ט גראנוש מנקי במרקו אחד ואחר ערוך שאלתך ואמור אם בד' אלפים תר"ח גראנוש שהוא מרקו אחד יש בו קכ"ט גראנוש מנקי בכ"ו אלף תרע"ב מה יש בו ויהיה כזה הצורה
|
|
|
| נקי |
משקל |
נקי |
משקל |
|
| 0 |
26672 |
129 |
4608 |
אם
|
|
|
|
|
כפלנו האמצעיות יעלו ג' מספרים ת"מ אלפים תתפ"ח כזה
|
|
|
|
|
|
חלקם על האמצעי הראשון שהוא ד' אלפים תר"ח יציא בחילוק תשמ"ו גראנוש וג' אלף וקי"ב חלקים מד' אלפים תר"ח בשלם שאם תקצרם יהיו ס"ה חלקים [396]מצ"ו כזה
|
|
|
|
|
|
חלק הגראנוש השלמים [...] ונשארו ב' גראנוש חלק ל"א דיניש על [...] ותצא ב' דנרים שהם ב' מרקוש מדת [...] עלה בידנו כי הדת או הנקי אשר בה' מרקוש [...] דיניש ח' גראנוש כל זה ממשקל לסך ה' פשיטי דיניש ט' מדת בכל מרקו שהוא ב' מרקוש וז' דיניש וב' גראנוש [..] חלקים מצ"ו בגראנו
|
The second chapter on the mixture of different amounts
|
הסדר השני בידעת התערובת מסכים מתחלפים
|
| I say that the division of the dinar of the value is that you first know the metal is of a pure type and of a mixed type.
|
ואומר כי חלוקת דינר הדת הוא שתדע תחילה [כי] מתכת שהוא סוג וחלק ממנו נקי וממנו מעורב
|
| The pure is divided into two and each one into two, so they are four [types].
|
והנקי יחלק לשנים וכל אחד לשנים שהם ארבע
|
| The mixed [is divided] into two and each one into three, so they are six [types].
|
והמורכב לשנים וכל אחד לשלוש[ה] שהם ששה
|
| The division of the pure into two: one is pure silver and the other is pure copper.
|
אומנם חלוקת הנקי לשנים האחד כסף נקי והשני נחושת נקי
|
| We can reduce the pure silver with pure copper, or with a mixture.
|
והנה הכסף הנקי נוכל להורידו עם נחושת נקי או עם תערובת
|
| We can improve the pure copper with pure silver, or with a mixture.
|
וחלוקת הנחושת הנקי הוא שנוכל להטבו ע[ם] כסף נקי או עם תערובת
|
| Hence, you have four kinds of pure: two to reduce it and to to improve it.
|
והרי לך ארבע חלקי הנקי שהם שנים להורי[דו] ושנים להטיבו
|
| The mixture has six types: three to improve it and three to reduce it.
|
ואמנם התערובת אשר חלקיו ששה הנה השלושה להטיבו והשלושה להורידו
|
| The three to improve it are: with pure silver, with a better mixture, or by reducing the copper.
|
אומנם השלושה להטיבו הוא עם כסף נקי או עם תערובת יותר טוב או עם שנגרע מן הנחושת
|
| The three to reduce it are: with pure copper, with a poorer mixture, or by reducing the silver.
|
והשלושה להורידו הוא עם נחושת נקי או עם תערובת יותר רע או עם שנגרע מן הכסף
|
| According to this, it is the shape of a tree whose branches are ten.
|
והנה לפי זה הוא צורת אילן אשר ענפיו הם עשרה
|
| I will write one or two questions for each branch, all as appropriate, and from them you will learn others. This is the shape of the tree:
|
והנה אכתוב לכל ענף שאלה אחת או שתים הכל כפי הראוי ומהם תלמוד לאחרים וזה צורת האילן
|
| Reducing pure silver with pure copper
|
|
| I start the chapter on mixture and say that when you have pure silver in your hand, the value of which is 12 dinar, and you want to mix it with pure copper, or other thing, so that it will be of a known pure amount and you will also know [the amount of] the copper [in it]:
|
ואני מתחיל בסדר התערובת ואומר כי כאשר יהיה בידך כסף נקי שהוא מסך י"ב דיניש ותרצה לערבו עם נחושת נקי או עם דבר [397]דבר אחר ותרצה שיהיה בסך ידוע מהנקי ושתדע גם כן הנחושת
|
| You know it by the "Rule of Three" this way: know [the amount of] copper in one marco, according to the value you want, and the [amount of] pure [silver], then say by the "Rule of Three": if this [amount of] pure [silver] yields this [amount of] copper in one marco, how much copper will those marci that I want mix with copper yield?
|
הנה תדענו עם דרך השלושה בזה הדרך שתדע הנחושת אשר במרקו אחד כפי הסך שתרצה גם הנקי ואחר אמור בדרך השלושה אם כך מנקי נתן כך מנחושת במרקו אחד כך מרקוש שאני רוצה לתתנם בנחושת מה יתן מנחושת
|
|
|
וסדר שאלתך ואם הפך השאלה יהיה בהפך
|
- First branch: a moneychanger or a goldsmith has in his hand 7 marci of pure silver and he wants to mix it with copper so that it will be at a value of 8 [dinar] in each marco.
- I ask: how much would he mix with the silver, so that it would be of this value and how much marci would be in this mixture?
|
ענף ראשון הנה יש ביד מחליף או צורף ז' מרקוש מכסף נקי ורצה לערבו עם נחושת ושיהיה לדת ח' פשיטי בכל מרקו
שאלתי כמה יערב עם הכסף ושיהיה לזה הדת וידעת כמה מרקוש יהיה זה התערובת
|
- Since it is asked that the value will be of 8 [dinar], 4 dinar are the complement to 12 dinar, which are the copper we need in each marco.

|
תשובה הנה אחר ששאל שיהיה הדת ח' פשיטי' נשאר לתשלום י"ב דינש ד' דיניש שנצטרך בכל מרקו מנחושת
|
- So, you have three known things: the value of 8 dinar; the 4 dinar of copper; and the 7 marci [...]
|
והנה היה לך שלשה דברים ידועים שהם ח' דיניש [398]הדת וד' דיניש הנחושת וז' מרקוש ש[...]
|
- [Say: if] 8 pure dinar require 4 dinar of copper, how much copper will 84 pure dinar require? It is:

|
ח' דניש נקי צריך ד' דיניש מנחושת פ"ד דיניש נקי כמה נחושת נצטרך ויהיה
|
| |
pure |
copper |
pure |
|
| if |
8 |
4 |
84 |
0
|
|
|
| |
נקי |
נחושת |
נקי |
|
| 0 |
דח |
ד |
ח |
אם
|
|
|
- Multiply the means; the result [is 336]. [Divide it] by 8; the result is 42 dinar.
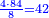
|
כפול האמצעיות יעלו [..] על ח' יעלו מ"ב דניש [...]
|
- We convert them into marci: we divide them by [12]; the result is 3 marci and a half, which is six ounces, all these are of copper.
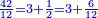
|
נעשה מהם מרקוש נחלקם על ז' תצאו ג' מרקוש וחצי שהם ששה אונסאש כל זה מנחושת
|
- So, we need 3 marci and a half of copper for the 7 marci of pure silver we want to reduce to 8 dinar, and then they are ten marci and a half.
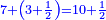
|
ז' מרקיש מכסף נקי שרצינו להורידו לח' דיניש שנצטריך ג' מארקוש וחצי מנחושת ויהיו אז עשרה מרקוש וחצי
|
- The check is that you multiply the extremes by each other and likewise the means; [the products] are equal. Because 8 by 42, which is the unknown, is 336 and so are the means.
|
והבחינה שתכפול הקצוות זה על זה וכן האמצעיות ויהיו שוים כי ח' על מ"ב הנעלם של"ו וכן האמצעיות
|
- If you want to [apply] other checks that I have presented, the permission is granted to you.
|
ואם תרצה עם בחינות אחרות שעשתי הרשות בידך [..]
|
- To train you once more, I do it again, and now I rely on [...]
|
להרגילך פעם אני עושה אחד פעם אחרת פעם אסמוך על [...]
|
- Second question of the first branch, which is compound: a moneychanger has in his hand [...] [2 marci], 3 ounces and 9 dinar of pure silver and he wants to reduce it with pure copper to a value of 7 dinar.
- I ask: how much copper is needed to mix with the silver, so that it will become of a value of 7 dinar?
|
שאלה שנית מענף ראשון והיא מורכבת הנה יש ביד מחליף ב' מ[...] ג' אונסאש ט' דיניש מכסף נקי ורצה להורידו עם נחושת נקי לדת ז' דיניש
שאלתי כמה נחושת הוצרך לערב עם הכסף ושיציא לדת ז' דיניש
|
- The answer: since we know that the value of 7 dinar is asked, you find the complement to 12 is 5 of copper.
|
התשובה הנה אחר שידענו ששאל לסך ז' דיניש מדת הנה לתשלום י"ב תמצא ה' מנחושת
|
- Say: if 7 pure dinar require 5 of copper, how much copper will 2 marci, 3 ounces and 9 dinar of pure [silver] require? It is according to this diagram:
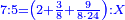
|
ואמור אם ז' דיניש מנקי צריך ה' מנחושת ב' מרקוש ג' אונסאש ט' דיניש כל זה מנקי כמה נחושת הוצרך ויהיה כצורה הזאת
|
| |
dinar |
copper |
marci |
ounces |
dinar |
|
| if |
7 |
5 |
2 |
3 |
9 |
0
|
|
|
| |
דיניש |
אונס |
מרקוש |
נחוש |
דיניש |
|
| 0 |
ט |
ג |
ב |
ה |
ז |
אם
|
|
|
- We convert the integer into the smallest fraction, which is the dinar, multiply the 2 marci by 8, which is an ounce; they are 16 plus the 3 we have, they are 19 ounces.
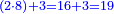
|
נתן השלם בשבר היותר קטן שהוא דיניש תן הב' מרקוש על ח' שהוא אונסאש יהיו י"ו וג' שהיו לנו יהיו י"ט אונסאש
|
- We multiply 19 by 24, which is the denominator of the dinar; they are [456], [plus the 9] we have, they are 465 silver dinar.
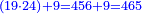
|
נכפול י"ט על כ"ד שהוא מורה הדיניש ויהיו [399][...] שהיו לנו יהיה תס"ה דיניש מכסף
|
- [Say by the "Rule of] Three": if 17 pure dinar require 5 of copper, how much copper is needed for [465 dinar]? According to this diagram:
|
[...] שלושה אם י"ז דיניש מנקי הוצרך ה' מנחושת [...] נחושת הוצרך ויהיה כזה הצורה
|
| |
pure |
copper |
[pure]
|
| if |
17 |
5 |
465 |
0
|
|
|
| |
נקי |
נחוש |
[נקי]
|
| 0 |
הוד |
ה |
זא |
אם
|
|
|
- We multiply the means and divide by 7; the result is 332 dinar and a seventh and this is the required copper.
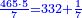
|
נכפול האמצעיו' וחלק על ז' ויעלה של"ב דיניש ושבעית וזה הנשאל מנחושת
|
- If you want, divide them by the denominator of the dinar, which is 24; the result is 13 ounces and 20 dinar remain.
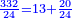
|
ואם תרצה תחלקם על מורה הדיניש שהוא [..] ותציא י"ג אונס' ונשארו כ' דיניש
|
- Divide the 13 by 8; the result is one marco and 5 ounces remain.
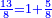
|
עוד תחלק הי"ג על ח' ותציא מרקו אחד וישארו ה' אונסאש
|
- We say that one marco, 5 ounces, 20 dinar and a seventh are needed for the 2 marci, 3 ounces, and 9 dinar.
|
ונאמר כי מארקו אחד וה' אונס' [..] כ' דיניש ושביעית הוצרך לב' מרקוש וג' אונס' וט' דיניש
|
- Sum all; they are 4 marci, 1 ounce, 5 dinar and a seventh of a total value of 7 dinar.
|
תחברם כולם יהיו ד' מרקוש א' אונס ה' דיניש ושביעית כל זה לסך ז' דיניש
|
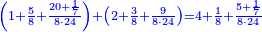
|
- The check is that you multiply each father [= extreme] by the other's son [= mean], provided that you convert all the sons into sevenths for the seventh; or multiply the extremes and the means, or divide them.
|
הבחינה היא שתכפול כל אב על הבן הנכרי ובלבד שתתן כל הבנים [..] בשביעיות בעבור השביעית או תכפול הקצוות והאמצעיות או תחלקם
|
- Third question of the first branch with fractions: a moneychanger or a goldsmith has in his hand 5 ounces, 7 dinar, and 3 grano of pure silver and we want to reduce it to a total value of 9 dinar.
- I ask: how much copper is needed to reduce it to a value of 9 dinar?
|
שאלה שלישית משברים מענף ראשון היה היה ביד מחליף או צורף ה' אונסאש וז' דיניש וג' גראש' מכסף נקי ורצינו להורידו לסך ט' דיניש מדת
שאלתי כמה נחושת הוצרך להורידו לדת ט' דיניש
|
- Answer: convert the 7 dinar into grani and the 5 ounces into dinar [...].
|
תשובה תן ו'ה'ז' דיניש בגראנו [הה' אונס' בדיניש][400]
|
| Reducing pure silver with a mixture
|
|
- [Second branch]: a goldsmith [has in his hand] 12 marci of pure silver and he wants [to reduce it] to a value of 17 dinar. Yet, he does not have copper, but a mixture of [...].
- I ask: how much of this mixture is needed so that it would become of a value of 9 dinar and how much is the weight of all the silver?
|
[401][ענף שני] [הנה יש ביד] צורף י"ב מרקוש מכסף נקי ורצה [...] מדת י"ז דיניש ואין לו נחושת אלא תערובת [...]רקיש
שאלתי כמה מזה התערובת הוצרך עד [...]סף לסך ט' דיניש וסך משקל כל הכסף
|
- Answer: take the three amounts of pure [metal] in all, whether the required is pure or a mixture.
|
[תשוב]ה קח שלושה סכי הנקי שבכולם אם שיהיה הנשאל נקי או תערובת
|
- We take the excess of the mean over the small and this is the first [term] in the "Rule of Three".
|
נקח יתרון האמצעי על הקטן והוא יהיה ראשון בדרך השלושה
|
- The excess of the greater over the mean will be the second [term] in the "Rule of Three" and vice versa when we want the improve.
|
וחסרון האמצעי על הגדול יהיה שני בדרך השלושה ובהפך כאשר רצינו להטיב
|
- The required amount is the third [term] in the "Rule of Three".
|
והסך הנשאל הוא יהיה שלישי מדרך השלושה
|
- The example of this:
|
והמשל בזה
|
- The first amount is 12 dinar, because each marco has value of 12 dinar.
|
הנה הסך הראשון הוא י"ב דיניש כל מרקו הוא י"ב דיניש מדת
|
- The second amount is 9 dinar, because we want to reduce the 12 marci to 9 dinar.
|
והסך השני הוא ט' [ד]יניש כי לט' דיניש רצינו להוריד הי"ב מרקוש
|
- The third [amount] is [7] dinar in the mixture.
|
והסך השלישי הוא [ז'] דיניש אשר בתערובת
|
- The three are: 12, 9, and 7.
|
ושלושתם היו י"ב וט' וז'
|
- The mean is 9; the excess of the mean over 7 is two and this is the first [tern] in the "Rule of Three".

|
והנה האמצעי [הוא] ט' ויתרון האמצעי על ז' הוא שנים והוא ראשון מדרך השלושה
|
- The excess of 12 over 9 is 3 and this is the second [term] in the "Rule of Three".
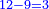
|
[..] חסרון ט' על י"ב הוא ג' והוא שני מדרך השלושה
|
- The required is [12] marci and this is the third [term] in the "Rule of Three".
|
והנשאל שהוא [י"ב] מארקיש הוא שלישי מדרך השלושה
|
- They are according to this diagram:
|
ויהיו כזאת הצורה
|
-
|
|
- Say: if 2 gives us 3, what will 12 give us?
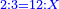
|
ואמור אם ב' נתן לנו ג' י"ב מה יתן לנו
|
- We multiply the means; it is 36.
|
כפול האמצעיים יהיו ל"ו
|
- We divide it by 2; the result is 18.
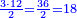
|
נחלקם ב' ותציא י"ח
|
- Thus, 18 marci of this mixture whose value is 7 dinar, are needed to be mixed with the 12 pure marci we have in our hand.
|
והנה י"ח מרקיש מזה התערובת שהוא מדת ז' דיניש הוצרך לערב עם הי"ב מרקיש מהנקי אשר בידינו
|
|
|
ויהיה עם הי"ב מרקיש ל' מרקוש ל"ט ט' דיניש
|
- In 18 marci of the mixture you find 90 dinar of copper and 126 dinar of silver.
|
והבחינה הנה בי"ח מרקוש מהתערובת תמצה צ' דיניש מנחושת וקכ"ו דיניש מכסף
|
- Add to them 144 dinar of silver in our 12 marci; they are 270 dinar of pure silver.
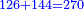
|
תחבר אליהם קמ"ד דיניש מהכסף אשר בי"ב מרקוש שלנו יהיו ר"ע דניש מכסף נקי
|
- Now, say: if 9 of pure silver give us 3 of copper, how much will 270 dinar of pure [silver] give us?

|
ועתה אמור אם ט' מכסף נקי נתן לנו ג' מנחושת ר"ע דיניש מנקי מה יתן לנו
|
- According to this diagram:
|
כזה הצורה
|
| |
dinar |
copper |
dinar |
copper
|
| if |
9 |
3 |
270 |
90
|
|
|
| נחוש |
די' |
נחוש |
די |
|
| 0ט |
0זב |
ג |
ט |
אם
|
|
|
- It yields 90 dinar of copper.
|
ונתן צ' דינש מנחושת
|
- Another check: multiply [...] the result is 270. [...]
|
[402]בחינה אחרת כפול היוציא מן ה[...] יעלו ר"ע והוא חוקי ש[...]
|
- Multiply the 18 marci added by 7 which is [...] add it to the dinar in 12 marci, which are 144; they are [270] [...].
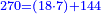
|
כפול הי"ח מרקוש הנוספים על ז' שהוא היה לסך [...] חברם עם דיניש י"ב מרקוש שהם קמ"ד דיניש יהיו [...]
|
- Another check: multiply the 30 marci we received by 3 [..] in each marco; it is 90. Keep it.
|
בחינה אחרת כפול ל' מרקוש שהיצאו לנו על ג' מ[...] אשר בכל מרקו יהיו צ' ושמרהו
|
- Multiply the 18 marci [..] by the 5 of copper in each; they are 90 of copper, as the reserved.

|
ואחר כפול י"ח מרקוש הנו[...] על ה' מנחושת הנודעים אשר בכל אחד יהיו צ' מנחושת בשמור
|
- And so on.
|
וכן כל כיוציא בזה
|
| Improving pure copper with pure silver
|
|
- Third branch: a goldsmith has in his hand 8 marci of copper and he wants to improve it with silver so that it would be of a value of 5 dinar per marco.
- I ask: how much silver is needed so that it would become of this value?
|
ענף שלישי הנה יש ביד צורף ח' מרקוש מנחושת ורצה להטיבו עם כסף ושיהיה לדת ה' דיניש בכל מרקו
שאלתי כמה כסף הוצרך ושתציא זה הסך
|
- Answer: from the 5 dinar asked to 12 there are 7 missing.
|
תשובה הנה מה' דיניש ששאל עד י"ב יחסרון ז'
|
- In each marco there should be 460 of copper.
|
ות"ס הראוים להיות מנחושת בכל מרקו
|
- Now, say: if 7 of copper require 5 of pure [silver], how much silver will 8 marci of copper require?
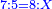
|
ועתה אמור אם ז' מנחושת הוצרך ה' מנקי ח' מרקוש מנחושת כמה כסף הוצרך
|
- Convert the marci into dinar, for there are 12 dinar in each marco, either copper or silver: 8 times 12 are 96 dinar of copper.
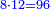
|
עשה המרקוש דיניש כי י"ב דיניש כל מרקו כן נחושת כן כסף ויהיו ח' פעמים י"ב צ"ו דיניש מנחושת
|
- Say: if 7 of copper require 5 of silver, how much silver will 96 dinar of copper require?
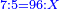
|
ואמור אם ז' מנחושת הוצרך ה' מכסף צ"ו דיניש מנחושת כמה כסף הוצרך ו[..]
|
- According to this diagram:
|
כזאת הצורה
|
| |
copper |
silver |
copper |
|
| if |
7 |
5 |
96 |
0
|
|
|
| |
נחושת |
כסף |
נחושת |
|
| 0 |
וט |
ה |
ז |
אם
|
|
|
- We multiply the means; it is 480.
|
נכפול האמצעיות יהיו ת"ף
|
- Divide it by 7; the result is 68 dinar and 4-sevenths of a dinar.
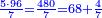
|
תחלקם על ז' ותציא ס"ח דיניש וד' שביעיות דינירו
|
- Divide them by 12; the result is 5 marci and 6 dinar remain.
|
תחלקם על י"ב ותציא ה' מרקוש ונשארו ח' דיניש
|
|
|
והנה ח' מר[קו] מנחושת שרצה לערבם עם כסף ושיהיה לדת ה' דניש הוצרכו ה' מרקוש מכסף וח' דיניש וד' שביעיות דינירו ויהיה כל הכסף המעורב י"ג ח' פשיטי דיניש וד' שביע[י]ות דינירו כולו לסך ה' דיניש
|
|
|
והבחינה אחר שכולם דיניש כפול כל אב על הבן הנכרי אחר שתתן הבנים בשביעית ויהיה ז' על ת"ף וצ"ו על ל"ה ויעלו שניהם ג' אלפים ש"ף
|
| Improving the pure copper with a better mixture
|
|
- [Fourth branch]: a goldsmith has in his hand 15 marci [of] copper and he wants to improve it with silver so that it would be of a value of 5 dinar per marco.
- I ask how much silver is needed so that it would become of this value.
|
[403][ענף רביעי] הנה יש ביד צורף אחד ט"ו מרקוש [...] נחושת ורצה להטבו עד שיהיה לסך עשרה [...] אין לו כסף אלא תערובת שהוא לסך י"א דיניש [...]ה מזה התערובת הוצרך לערב עם זה הנחושת עד [...] עשרה דיניש
|
- Answer: take the three amounts of values.
|
תשובה קח שלושה סכי הדת
|
- Take the excess of the greater over the mean and it will be the first [term] in the "Rule of Three".
|
וקח חסרון האמצעי על הגדול והוא יהיה ראשון מדרך השלושה
|
- Take the excess of the mean over the smaller and it will be the second [term] in the "Rule of Three".
|
ואחר קח יתרון האמצעי על הקטן והוא יהיה שני מדרך השלושה
|
- The required amount, which is 15, will be the third [term] in the "Rule of Three".
|
והסך הנשאל שהוא ט"ו יהיה השלישי מדרך השלושה
|
|
|
המשל בזה הנה לקחנו מרקו אחד מהנשאל והנה אין בו כסף ונתן במקומו ספרה ותורה על הסך הקטן כי אין קטן יותר ממי שאין בו דבר והסך השני עשרה דיניש והסך השלישי י"א דיניש אשר בתערובת ושלושתם היו כזה 0 י' י"א והנה האמצעי הוא עשרה והנה חסרון האמצעי שהוא עשרה על הגדול שהוא י"א הוא אחד והוא ראשון מדרך השלושה גם נקח יתרון האמצעי על הקטן שהוא 0 ויהיה עשרה והוא יהיה שני מדרך השלושה והסך הנשאל שהוא ט"ו יהיה שלישי מדרך השלושה יהיו כזאת הצורה
|
-
|
|
- Multiply the means, which are 15 by ten; the result is 150.
|
כפול האמצעיים שהם ט"ו על עשרה יעלו ק"ן
|
- Divide it by 1; the result is 150.
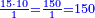
|
תחלקם על א' יעלו ק"ן
|
|
|
וק"ן מרקוש נצטרך מזה התערובת לערב עם ט"ו טו מרקוש מנחושת להטיבו עד שיהיה לסך עשרה דיניש ויהיו כולם קס"ה מרקוש
|
|
|
והבחינה הוא כי הכסף הנמצא בקס"ה מרקוש הוא הנמצא בק"ן מרקוש מן התערובת שבשנ[י]הם תמצא אלף [..] דיניש
|
| Improving a mixture with pure silver
|
|
- Fifth branch: a goldsmith has in his hand 23 marci of mixture whose value is 7 dinar and he wants to improve it and raise it to ten dinar.
- I ask: how much pure silver is needed so that it would rise to ten dinar?
|
ענף חמשי הנה ביד צורף אחד כ"ג מרקוש מתערובת לסך ז' דיניש מדת ורצה להטיבו ולהעלותו לעשרה דיניש
שאלתי כמה כסף נקי הוצרך לעלותו עד עשרה דיניש
|
|
|
[404]תשובה דע הנקי והנחושת [...] תכפול נקי מרקו אחד על כולם על כולם כי ז' על כ"ג הם קס"א וזה הכסף [...] עוד תכפול ה' מנחושת שיש מז' עד י"ב על כ"ג [...] הנחושת אשר בכ"ג מרקוש ואחר סדר שאלתי [...] מרקו אחד מהסך שתרצה שהוא מעשרה דיניש ושני[...] ומאחר כי שאלת כסף תתחיל עם ב' [.] דיניש הנחוש[ת] אשר במרקו אחד ואמור אם ב' דיניש מנחושת נתן לנו עש[רה] מכסף קט"ו מנחושת אשר בכ"ג מרקוש משאלתנו כמה כסף יתן לנו ויהיה כזאת הצורה
|
| |
copper |
silver |
copper |
|
| if |
2 |
10 |
115 |
0
|
|
|
| |
נחושת |
כסף |
נחושת |
|
| 0 |
האא |
0א |
ב |
אם
|
|
|
- Multiply the means; the result is 1150.
|
כפול האמצעיות יעלו אלף ק"ן
|
- Divide it by 2; the result of division is 575 and this is the silver, while there are 115 dinar of copper for a value of ten dinar.
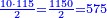
|
תחלקם על ב' ותציא בחילוק תקע"ה וזה הכסף לקט"ו דיניש הנחושת לסך עשרה דיניש מדת
|
|
|
ואמנם בעבור כי יש בתערובת קס"א דניש מנקי נגרעם מתקע"ה ישארו תי"ד וזה הראוי להוסיף על כ"ג מרקוש שאם תעשה אותם מארקוש יהיו ל"ד מרקוש מנקי וחצי תחברם עם התערובת יהיו נ"ז מרקוש וחצי שהם לסך דיניש וחצי
|
|
|
והבחינה היא שתדע הנקי והנחושת מנ"ז מרקוש וחצי ותדעם כאשר תכפול עשרה מנקי על נ"ז וחצי יהיו תקע"ה גם ב' מנחושת על נ"ז וחצי יעלו קט"ו ואחר בדוק בדרך השלושה ואמור אם ב' מנחושת נתן עשרה מכסף קט"ו מנחושת מה יתן מכסף ותציא לך תקע"ה מכסף
|
|
|
או תהפוך השאלה ואמור אם עשרה מכסף נתן ב' מנחושת תקע"ה מכסף מה יתן לנו מנחושת ותציא קט"ו ותורה כי מה שעשינו הוא אמת וכן כל הדומה לזה
|
| Improving a mixture with a better mixture
|
|
- [Sixth branch]: a goldsmith has in his hand 16 marci of a mixture [..] which is 4 dinar, and he wants to improve it. Yet, he does not have pure silver, but he has a [better] mixture [...] dinar.
- I ask: how much of this mixture is needed [...] so that it would become of a value of 7 dinar?
|
[405][ענף ששי] הנה יש ביד צורף י"ח מרקוש מתערוב[ת] [...] שהוא ד' דיניש ורצה להטיבו ולהעלותו [...] שאין לו כסף נקי אבל יש בידו תערובת [...] דיניש
שאלתי כמה מזה התערובת הוצרך להוסיף [...] הראשון שהוא לסך ד' עד שיהיה לסך ז' דיניש
|
|
|
[תש]ובה ידוע כי ג' סכי דיניש תמצא באלו השאלות והדומים להם ולעולם יהיו הסכים זה גדול מזה כמו בזה שהם ד'ו'ט' יקח יתרון הגדול על האמצעי ויהיה [הר]אשון כדרך השלושה שהוא המחלק ועוד קח יתרון האמצעי על הראשון והא המספר השני מדרך השלושה שהוא ראוי לכפול על המרקיש הנשאלות
|
|
|
המשל בזה הנה היותר קטן הוא דיניש התערובת שרצינו להטיב שהוא ד' האמצעי הוא דיניש הסך שרצינו לעלות עד ז' והגדול הוא דיניש התערובת המיטיב שעמו נעלה עד ז' שהוא ט' והנה ט' הוא גדול מז' שנים והוא יהיה ראשון כדרך השלושה אשר עליו נחלק וז' הוא גדול מד' משלושה והוא יהיה שני מדרך השלושה הראוי לכפול על מרקוש ואם כן יתרון האחרון מן השני הוא ראשון ויתרון השני מן הראשון הוא [ה]שני והמרקוש שהם ראשונים הם השלישי ואז נאמר שאם ב' נתן ג' י"ח מרקוש מה יתן לנו כזאת הצורה
|
-
|
|
|
|
נכפול י"ח על ג' יהיו נ"ד
|
|
|
תחלקם על ב' ותציא כ"ז
|
|
|
והנה כ"ז מרקוש נצטרך מן התערובת אשר הוא לסך ט' דיניש המיטיב והעולה הי"ח מרקוש לסך ז' דניש ויהיו כולם מה' מרקוש לדת ז' דיניש כנזכר
|
|
|
והבחינה הוא שתקח הכסף ממ"ה מרקוש הנמצאות [406]ותדעם כאשר תכפול ז' דיניש הנקי על [...] מכסף גם לדעת הנחושת תכפול ה' שנשאר [...] ותציא רכ"ה דיניש נחושת ותשמרם ואחר [...] מי"ח מרקוש ומכ"ז יהיה כנקי מהנמצא שהוא שט"ו [...] הנחושת מי"ח מרקוש ומכ"ז אם יהיה כנחשת הנמצא [...] רכ"ה מוטב כצד הנה [די]ניש הכסף מי"ח מרקוש הם ע"ב [..] כאשר תכפול ד' על י"ח וכן דיניש הכסף שבכ"ז מרקוש הם רמ"[ג] ותמצאם כאשר תכפול כ"ז על ט' ועתה תחבר ע"ב דיניש הנקי מי"ח מרקוש שהוא התערובת הראשון עם רמ"ג דיניש הנקי מכ"ז מרקוש שהוא התערובת השני יהיו שט"ו והם שוים לדיניש התערובת השלישי הנמצא וכן קח נחושת הי"ח מרקוש שהוא קמ"ד דיניש גם נחושת הכ"ז מרקוש שהוא פ"א דיניש ותחברים ויהיו רכ"ה דיניש כנחושת התערובת הנמצא וכל כל כיוצא בזה
|
| Improving a mixture by reducing the copper
|
|
- Seventh branch: a goldsmith has in his hand 13 marci of a mixture whose value is 7 dinar, and he wants to improve it to a value of 8 dinar. Yet, he does not have [pure] silver nor better mixture, but he has to reduce the copper.
- I ask: how should he reduce the copper?
|
ענף שביעי הנה ביד צורף י"ג מארקוש מתערובת לדת ז' דיניש ורצה להטיבו ולהעלות לדת ח' דיניש ואין בידו כסף ולא תערובת יותר טוב אלא שראוי שנחסר מן הנחושת
שאלתי כצד יחסר מן הנחושת
|
|
|
תשובה קח הנקי אשר בי"ג מרקוש יהיו צ"א שהם ז' פעמים י"ג ושומרהו גם תדע הנחושת אשר בי"ג מרקוש והוא ס"ה כי מז' שהוא הנקי עד י"ב הם ה' והוא הנחושת אשר במרקו אחד כפול ה' על י"ג יעלו ס"ה כנז' ושמרם והנה אחר שאתה שואל שיהיה הדת מח' דיניש הנה מח' אל י"ב ד' מנחושת ואמור כדרך השלושה אם ח' מנקי הוצרך ד' מנחושת [.] צ"א מנקי אשר בי"ג מרקיש כמה נחושת הוצרך ויהיה כזאת הצורה
|
| |
silver |
copper |
silver |
|
| if |
8 |
4 |
91 |
0
|
|
|
|
- We multiply the means; the result is 364.
|
נכפול האמצעיות יעלו שס"ד
|
|
|
תחלקים על ח' ותציא מה' וחצי והם הדיניש שהוצרך [407][...] מן הנחושת הנמצא במרקוש שאלתך [...] וחצי הראוי לגרוע מן הנחושת אשר [...] הם מז' דיניש וחבר הנשאר יהיו קל"ו [...] על י"ב ותציא י"א מרקיש ד' דיניש והנה כל זה [...] תערובת מח' דיניש המרקו
|
|
|
הבחינה מבוארת כי צא פשיטי מנקי שהם ז' מרקוש וז' דיניש אם תתנם לח' דניש מדת יהיו י"א מארקיש ד' דיניש וחצי תורידהו לז' דיניש יהיו ג' מרקיש והוא הדין אם תחבר לי"א מרקוש ד' דיניש וחצי מה' שגרענו מהם שהם י"ט דיניש וחצי שישובו לי"ג כבראשונה
|
| Reducing a mixture by pure copper
|
|
- Eighth branch: a goldsmith has in his hand 39 marci of a mixture whose value is ten dinar, and he wants to reduce it to a value of 7 dinar.
- I ask: how much copper is needed to reduce it to a value of 7 dinar?
|
[ענ]ף שמיני הנה יש ביד צור[ף] ל"ט מרקיש מתערובת שהוא לסך עשרה דינריש ורצה להורידו עד שיהיה מדת ז' דיניש
שאלתי כמה נחושת הוצרך להורידו עד שיהיה בסך ז' דיניש
|
|
|
תשובה דע הדיניש מהכסף ומהנחשת אשר בל"ט מרקיש וזה שתכפול דיניש הכסף שהם עשרה על ל"ט יהיו ש"צ דיניש מכסף בל"ט מרקיש גם כפול ב' דיניש הנחושת בל"ט יהיו ע"ח דיניש מנחושת בל"ט מרקיש ואחר קח הנקי והנחושת ממרקו אחד מהמרקו שתרצה להורידו שהוא ז' דיניש מכסף וה' דיניש מנחושת ואמור אם ז' דיניש מנקי נתן ה' דיניש מנחושת ש"צ דיניש מכסף אשר בל"ט מרקיש כמה נחושת יתן לי ויהיה כזאת הצורה
|
|
|
| נחושת |
כסף |
נחושת |
כסף |
|
| 0 |
0טג |
ה |
ז |
אם
|
|
|
- Multiply the means; the result is 1950.
|
כפול האמצעיות יעלו אלף תתק"ן
|
- Divide it by 7; the result of division is 278 dinar of copper and 4-sevenths.
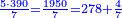
|
תחלקם על ז' ותציא בחילוק רע"ח דיניש מנחושת וד' שביעיות
|
- If you divide them by 12, the result is 23 marci, 2 dianr and 4-sevenths of a dinar.
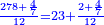
|
שאם תחלקם על י"ב יהיה היוציא כ"ג מרקיש וב' דיניש וד' שביעיות דינרו
|
|
|
וזה הראוי לש"ץ דיניש [408]מכסף אשר בל"ט מרקוש שהם ל"ב [...] מרקוש וב' דיניש וד' שביעיות יהיו כולם [...] שביעיות דינירו וזה שנגרע מרע"ח דיניש וד' שביעיות [..] הנחושת אשר בשאלתנו שהוא ע"ח ישארו ק"ק דיניש וד' [...] מנחושת הראוי להוסיף על התערובת אשר בידנו שהוא נתן ק"ק דיניש וד' שביעיות דינירו במרקוש יהיו י"ו מרקיש וד' שביעיות דינירו תחברם עם ל"ט יהיו נ"ה מרקיש וח' דיניש וד' שביעיות כל זה לסך ז' דיניש [..]
|
|
|
והבחינה קח הנקי והנחושת ממרקו אחד והנקי והנחושת מכולו ואמור אם ז' מכס[ף] נתן ה' מנחושת כך מכסף שבנ"ה מרקוש ח' דיניש ד' שביעי' מה יתן מנחושת או [..] השאלה נאמר אם ה' מנחושת נתן ז' מכסף כך מנחושת שבנ"ה מ[רקוש] וח' דיניש וד' שביעיות מה יתן מכסף וכו'
|
| Reducing a mixture with a poorer mixture
|
|
- Ninth branch: a goldsmith has in his hand 27 marci of a mixture whose value is 11 dinar, and he wants to reduce it to a value of 6 dinar. However, he does not have copper to reduce it, but he has another mixture whose value is 3 dinar.
- I ask: how much of this other mixture is needed [to reduce] it to a value of 6 [dinar]?
|
ענף תשיעי הנה יש ביד צורף אחד כ"ז מרקוש מתערו[בת] מדת י"א דיניש ורצה להורידו לסך ו' דיניש ואין לו נחושת להורידו אבל יש בידי תערובת אחר מסך ג' דיני[ש]
שאלתי כמה מזה התערובת השני הוצרך עד שיהיה לסך ו' [...]
|
|
|
תשובה ידוע הוא כי ג' סכי דיניש תמצא בזאת השאלה שהם י"א מתערובת ראשון וו' מן התערובת הנשאל וג' מן התערובת השני היותר פחות ויהיו שלושתם כזה י"א ו' [ג'] ועתה קח יתרון האמצעי על הקטן והוא יהיה המספר הראשון מדרך השלושה אשר עליו תחלק גם קח יתרון הגדול על האמצעי והוא יהיה המספר השני מדרך השלושה אשר אותו תכפול על הנשאל שהוא כ"ד מרקוש
|
|
|
המשל בזה האמצעי שהוא ו' גדול מן הקטן מג' והנה ג' יהיה הראשון מדרך השלושה ואחר נראה יתרון הגדול [..] שהוא י"א על האמצעי שהוא ו' [409][...] והנה ה' יהיה המספר השני מדרך [...] ג' מרקוש מן התערובת הראשון ראוי ה' מן התערובת השני כ"ז מרקוש מן התערובת הראשון כמה מן השני יהיה ראוי ויהיה [כזאת] הצורה
|
|
|
| |
מרקיש |
מרקיש |
[.]
|
| 0 |
זב |
ה |
[.]
|
|
|
|
|
נכפול ה' על כ"ז יעלו קל"ה תחלקם על ג' [...] מ"ה מרקוש והנה מ"ה מרקוש נצטרך מן התערובת השני [...]ערב עם הכ"ז מרקוש להורדו לששה דיניש נחברם עם [..] הראשונים יהיו ע"ב מרקיש אשר הם מדת ו' דיניש
|
|
|
הבחינה כך היא שתחבר הנקי מכ"ז מרקוש משאלתנו עם הנקי ממ"ה מרקוש הצריכות להוסיף ואם [...] שניהם מחוברים כנקי ע"ב מרקיש שמצאנו מוטב וכן [...]נחשת
|
|
|
המשל הנה הנקי מכ"ז מרקיש שהוא לי"א דיניש הוא מרצ"ז דיניש והנחושת כ"ז והנקי ממ"ה מרקיש הראוים להוסיף הוא קל"ה והנחשת ת"ה והנקי מן התערובת שעשינו הוא תל"ב וכן הנחושת ור ועתה חיברנו רצ"ז עם קל"ה שהם הנקי ממה שבידנו וממה שראוי להוסיף יהיה שניהם תל"ב כנקי התערובת שעשינו וכן נקח נחושת שניהם שהוא כ"ז ות"ה יהיו תל"ב בנחשת התערובת שעשינו וזה תורה שעשינו כהוגן
|
| Reducing a mixture by reducing the silver
|
|
- Tenth branch: a goldsmith has in his hand 17 marci of a mixture whose value is 9 dinar, and he wants to reduce it to a value of 8 dinar. However, he does not have [pure] copper to reduce it, but he has to reduce the silver.
- I ask: how much silver should he reduce from the 17 marci in his hand, so it is reduced to the required value?
|
ענף עשירי הנה יש ביד צורף אחד י"ז מרקיש מתערובת לסך ט' דיניש ורצה להורידו לסך ח' דיניש ואין לו נחושת להורידו אבל יחוייב לגרוע מן הכסף
שאלתי כמה מן הכסף יגרע מהי"ז מרקוש שבידו עד שירידהו לסך הנשאל
|
|
|
תשובה דע הכסף והנחושת אשר בי"ז מרקוש כאשר קדם והנה הכסף הוא קנ"ג דיניש והנחושת נ"א ואחר תסדר שאלתך עם כסף ונחושת ממרקו אחד מהנשאל ואמור אם [410]ד' דיניש נחושת ראוי ח' מנקי נ"א מ[...] כסף הוצרך ויהיה כזאת הצורה
|
|
|
| כסף |
נחוש |
כסף |
נחוש |
|
| 0 |
אה |
ח |
ד |
אם
|
|
|
|
|
כפול ח' על [...] תחלקם על ד' ו[...] מקנ"ג דיניש מכסף [...] מרקוש ישארו נ"א והנה [...] דינירו מכסף קוצרך לגרוע מן הי"ז מרקוש בעבור ש[...] הנשאר לסך ח' דיניש תחבר נ"א מנחושת וק"ב מנקי יהיו קנ"ג דיניש תחלקם על י"ב ותציא י"ב מרקוש וט' דיניש שהם לסך ח'
|
|
|
והבחינה דע הנקי והנחושת מכולו והנה הכסף הוא ק"ב דינ[יש] והנחושת נ"א תסדר השאלה מן האחד ותציא הא[...] מאי זה שתרצה כיצד נאמר אם ח' מכסף נתן ד' מנחושת ק"ב מכסף כמה מנחושת יתן ותציא לך נ"א מנחושת או אמור אם ד' מנחושת ראוי ח' מכסף נ"א מנחושת כמה כסף ראוי ות[ציא] לך ק"ב וכן כל הדומה לזה
|
|
|
בחינה אחרת קח הכסף מ[כולו] ותן תחתיו הכסף ממרקו אחד גם הנחושת כולו ותן תחתיו הנחושת ממרקו אחד ואחר תשוים כאשר ידעת ואם יהיו שוים מוטב כיצד הנקי מכולו ק"ב וממרקו אחד ח' גם הנחושת כולו נ"א וממרקו אחד ד' תתנם זה תחת זה יהיו כזה הצורה
|
|
|
|
|
|
ויהיו כל אחד ת"ח כאשר תשוים
|
|
|
הסדר השלישי בידעת דרכי תערובת הזהב הנקרא דינר הדת וחלוקתו לכ"ד קיראטיש
|
|
|
ואומר כי כמו שכתבתי אילן הכסף במרקוש שלמים כן ראוי לעשות ממורכבים ומשלמים ויהיו שלושה אילנות וכן היה ראוי בזהב אבל בראותי המלאכה מרובה והתועלת מעט קצרתי [411][...] כי לא עשיתי אלא שני דרכים [...] היא שיהיה בידך חתיכה מעורבת ותרצה [...] והדרך השנית היא שיהיה לך [...] ותרצה לתתנו בתערובת
|
|
|
ואומר כי הדרך [...] שאם היה בידך משקל מה מזהב [...] ותרצה לדעת הזהב שבו הנה תדעהו בזה הדרך [ה]יא שתכפול המשקל אשר בידך על הקיראטש שבו והעולה [תח]לק על כ"ד שהוא סך קירטיש הזהב הטהור והיוציא [ב]חילוק הוא הזהב הטהור אשר בזה המשקל שאם המשקלים [מר]קיש היוציא יהיה מרקוש ואם אונסש היוציא יהיה אונסש [ואם] דינירוש דינירוש
|
|
|
המשל הנה היה בידינו י"ב מרקוש [ז]הב מעורב לסך י"ד קירטש
|
|
|
תכפול י"ב על י"ד [י]עלו קס"ח תחלקם על כ"ד יצאו ז' וז' מרקיש מזהב תמצא [בח]תיכת י"ב מרקוש שלנו לסך י"ד קירטיש
|
- Second question: a goldsmith has in his hand a gold goblet weighing 2 marci and 2 ounces of 20 carats and he wants to know the gold in it.
|
שאלה שני הנה היה ביד צורף גביע זהב משקלה ב' מרקוש ב' אונסיש מכ' קיראטיש ורצה לדעת [הז]הב הנה שבה
|
- He should convert all into ounces; they are 18.
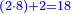
|
[יעשה הכל אנסאש יהיו י"ח]
|
- He multiplies 18 by 20; the product is 360.
|
יכפול י"ח על כ' יעלו ש"ס
|
- Divide it by 24; the result is 15.
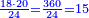
|
תחלקם על כ"ד [י]צאו ט"ו
|
- There are 15 ounces of pure gold in 18 ounces in a goblet whose value is 20 carat, which are one marco and 7 ounces.
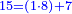
|
וט"ו אונסאש מזהב טהור יש בי"ח אונסאש אשר בגביע [א]שר היא לסך כ' קירטיש והם און מארקו וז' אונסאש
|
- Third question: we have a goblet in our hand, whose value is 16 carat and its weight is 2 marci, 3 ounces, and 4 dinar.
|
שאלה שלישית יש בידנו גביע זהב לסך י"ו קיראטש ומשקלה ב' מרקוש ג' אונסאש ד' דיניש
|
- Convert all into dinar: 2 marci by 8 are 16; plus 3, they are 19 [ounces].
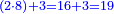
|
[ת]וריד הכל לדיניש ב' מרקוש על ח' יהיו י"ו וג' יהיו י"ט
|
- We convert them into dinar: we multiply them by 24; the result is 456 and with 4 they are 460 dinar.
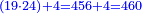
|
נעשה מהם דיניש נכפלם על כ"ד יעלו תנ"ו ועם ד' יהיו ת"ס דיניש
|
- We multiply them by the carat, which is 16; the result is 7360.
|
נכפלם על סך הקירטיש שהם י"ו יעלו ז' אלפים ש"ס
|
- We divide it by 24; the result of division is 306 dinar and 2-thirds of gold.
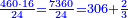
|
נחלקם על כ"ד תצאו בחילוק ש"ו דיניש וב' שלשיות מזהב
|
|
|
נחלק ש"ו ו על כ"ד יעלו י"ב אונסאש על כ"ד יעלו י"ב אונסאש ג' רביעיות ז' תשעיות כי נתין ש"ו [412]בשלשית יעלו תרק"ך נחלקם על ע"[...] בחילוק י"ב אונסאש ז' תשיעיות שהם מרקו וחצי [...]
|
|
|
הדרך השני שיהיה לך זהב טהור [...] בתערובת הנה הדרך בידיעת [...] כי כאשר יהיה בידך זהב טהור שתכפלהו על כ"ד [...] קירטיש הטהור ותחלק העולה על סך הקרטיש שת[..] ותדע משקל הכל כאשר תהיה בתערובת שתרצה
|
|
|
והמשל בזה הנה היה בידינו מרקו אחד וז' אונסיש זהב טהור שהוא ט"ו אונסאש ורצינו לערבו עד שיהיה לסך כ' קואירטיש
|
|
|
נכפול ט"ו אונסאש על כ"ד יעלו [...] נחלקם על הסך שנרצה שהוא כ' קירטיש יעלו י"ח אונס[אש] שהם ב' מרקוש וב' אונסאש מעורבות אשר הם לסך כ' קי[רטיש]
|
|
|
משל שני הנה היה ביד צורף ד' מרקיש א' אונ[סאש] ח' דיניש זהב טהור ורצה לתתנו בסך [..] קיראטיש הנה ראשונה נתן כולם בדיניש יהיו ד' מרקוש [על] ח' יהיו ל"ב אונסאש ועם א' שלנו יהיה ל"ג גם נתן האונס[יש] בדיניש יעלו תשצ"ב וח' שהיה לנו יהיו ת"ת דיניש ועתה נכפול ת"ת על כ"ד קירטיש הטהור יעלו י"ט אלפים וק"ק נחלקם על י"ח שהם הקירטיש הנשאלים יצאו אלף וס"ו וב' שלישיות וזה כולו דיניש והנה ת"ת דיניש מזהב טהור יהיה מעורב לסך י"ח קירטיש אלף וס"ו דינשו וב' שלישיות דינירו אבל נרצא לעשותם אונס' ומרקוש ונחלקם על כ"ד וראשונה נתנם בשלישת בעבור הב' שלישיות יהיו ג' אלפים ק"ק נחלקם על ע"ב שהוא ג' פעמים כ"ד יעלה בחילוק מ"ד אונסאש וד' תשיעיות אונסה גם נתן מ"ד במרקיש יצאו ה' מרקוש וחצי והנה עלה מזה ה' מרקיש וחצי וד' תשיעיות שהם עשרה דיניש ושני שלישיות דינירו על זה לסך י"ח קיר[טיש]
|
|
|
[413][...] לדעת הנחושת שתחבר לזהב גרע [...] התערובת והנשאר הוא הנחושת [...] זהב כמו במשלנו גרע דיניש הזהב [...] מכל התערובת שהוא אלף וס"ו ישארו וב' [של]שיות ישארו קס"ו דיניש וב' שלישיות וזהו הנחושת [שא]תה צריך לערב עם הזהב הטהור ותצא לסך הנשאל
|
- Third example: the goldsmith has 14 ounces of 17-carat gold mixture in his hand and wants to distill it from every dross, until it remains 24 [carat ] pure.
- I ask: [how much is] the remaining gold?
|
משל שלישי הנה יש ביד צורף י"ד אונסאש מתערובת זהב לדת י"ז קיראטיש ורצה לזקוקו מכל סיג עד שישאר זך לדת כ"ד
שאלתי הזהב הנשאר
|
- Answer: he multiplies the weight by the carat in it, then divides by the pure 24.
|
תשובה יכפול המשקל על הקירטיש שבו ויחלוק על כ"ד הנקי
|
- As in this question, he multiplies 14 by 17; the result is 238.
|
כמו בזה השאלה שיכפול י"ד על י"ז יעלה רל"ח
|
- He divides it by 24; the result is 9 ounces and 11 parts of 12 of and ounce.
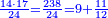
|
ויחלקם על כ"ד ותצא ט' אונסאש וי"א חלקים מי"ב באונסה
|
- So, you find 9 ounces of pure gold and [11] parts of [12] in a mixture of 14 ounces of 7 carat.
|
והנה ט' אונסאש מזהב טהור וט' חלקים מי"א תמצא בי"ד אונסאש מהתערובת שהוא לסך הז' קירטישי
|
- Fourth example: the goldsmith had in his hand an unknown amount of gold weighing 30 for 13 carats and he refined it until it was 24 carats refined and it weighed 15 ounces of pure gold.
- I ask: How much was the weight of the whole unknown amount and the copper in it?
|
משל רבעי הנה היה ביד צורף כל כך זהב נעלם ל' משקלו לסך י"ג קירטיש וזקוקו עד שהיה זך מכ"ד קירטיש והיה משקלו ט"ו אונסאש זהב טהור
שאלתי כמה היה משקל כולו הנעלם והנחושת שבו
|
- Multiply 24 by the 15 ounces of pure gold; the result is 360.
|
תשובה כפול כ"ד על ט"ו אונסאש מזהב טהור הנמצה יעלו ש"ס
|
- Divide it by the 13 carats of the mixture; the result is 27 ounces and 9 parts of 13 and this is the first unknown mixture.
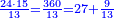
|
תחלקם על י"ג קינטיש שהיה התערובת ותצאו כ"ז אונסאש וט' חלקים מי"ג וזה היה התערובת הנעלם הראשון
|
- Subtract the gold from it, which is 15 ounces; 12 and 9 parts of 13 remain.
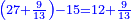
|
גרע ממנו הזהב שהוא [414]ט"ו אונסיש ישארו י"ב וט' חלקים מי"ג
|
- If you want to convert the ounces into marci [...]
|
ואם תרצה לעשות מן האונסאש מרקיש [..]
|
The Fourth Chapter: [Superabundant, Deficient and Perfect Numbers
|
הפרק הד'
|
|
|
[459][...] שהם [...] וגורע והשוה אמצעי בין עודף וגורע [...] החלקים השלמים מאיזה מספר מורכב [...] על כל המספר כמו מספרי זאת הצורה [...] שאם תחבר חלקי כל אחד תמצא שהוא יותר מכולו
|
|
|
והמשל י"ב חציו ו' ושלישיתו ד' ורביעיתו ג' ושישיתו ב' וא' שהוא חלק מכולו תחברם כולם יהיו י"ו והנה חלקיו עודפים מד'
|
|
|
משל שני ס' תמצא בו חצי ושלישית ורביעית וחלקים אחרים רבים עד שתראה שהוא עודף חמשה [..] שרשיו כי חלקיו הם צ"ה וכן כל הדומה לזה
|
|
|
[...] הוא כל זוגי הזוג והנפרד אשר ימצא בו הרכבה אחרת כמו אם תכפול ב' על נפרד והיוציא על [ב' גם] כן ואחר כן אם תמצא במספר הרכבה אחרת המספר עודף ואם לא לא
|
|
|
המשל בזה כפלנו ב' על ג' יהיה [היוציא] ו' גם ו' על ב' יהיה היוציא י"ב והנה בעבור [כי] בזה המספר תמצא הרכבה אחרת שהיא ג' על ד' [.] שהוא עודף
|
|
|
ואם לא תמצא הרכבה אחרת בידוע [שאינו] עודף
|
|
|
כמשל כ"ח כי בא מב' על ז' והיוציא [על] ב' ואין בזה הרכבה אחרת ובעבור זה אינו עודיף [וכן] כל הדומה לזה
|
|
|
ואם לא תוכל לכוון החלקים [הש]למים אשר בו תחלק המספר מתחילתו עד אמצעו [...] כל החלקים אשר עלה בחילוק תמצא בו בשלמות
|
|
|
[ה]משל בזה חלקנו י"ב על אחד יעלו י"ב והנה א' הוא חלק מי"ב נחזור עוד ונחלק י"ב על ב' יעלה בחילוק ו' שהוא חציו כמו שתורה ב' גם נחלקהו על ג' [460]יעלה ד' [...] בחילוק ואין בו חמשית [...] שתורה ו' ואין לחלקו על יותר מחצי [...] הם א' ב' ג' ד' ו' שכללם הוא י"ו ו[...] לא תרצא לטרוח תחלק על המסופקים ודי לך [...] יסופק אם יש בו שביעית תחלק על ז' ואם יסופק [...] על ט' וכן כולם
|
|
|
ואם יהיה המספר גדול שלא תוכל לחלק[ו] אלא בטורח גדול אומר לך דרך כולל שהוא טוב לקצר ואב המורים ועיין בו
|
|
|
הנה כבר ידעת כי חלוקת כל מוגבל הוא אם זוג ואם נפרד ואומר שתעיין במעלת אח[די] המספר ואם תמצא בה מספר זוג או ספרא אז תדע ש[זה] המספר יהיה זוג ויש לו חצי
|
|
|
ואם לא תמצא בו אחדים הנה [יש בו] חצי וחמשית ועשירית ויוכל להיות גם כן חלקים אחרים
|
|
|
במשל נניח ט"ו אלפים ק"ך כזה 0 ב א ה א
|
|
|
נראה [אם] יש בו תשיעית או חלקים אחרים
|
|
|
קח האחרון ותורידהו מעלה אחד וחלקם למה שתרצה והנשאר תורידים עוד ותחלקם וכן תעשה עד הסוף ושמור [..] ואם לא יצא בחילוק תחזור ובקש חלק אחר
|
|
|
כמו שרצינו אם יש במספר המונח תשיעית תוריד המעלה האחרונה ה' ויהיו ט"ו קח תשיעית ט"ו והוא אחד ישארו ו' תוריד[ם] אל א' יהיו ס"א קח תשיעיתו שהם ו' נשארו ז' תורידם אל ב' יהיו ע"ב קח תשיעית ע"ב והיא ח' ולא נשאר כלום ו[...] ספרא והנה יציא זה המספר בתשיעית אלף תר"ף
|
|
|
ות[...] עוד ותראה אם יש בו שמינית תוריד הא' על הה' יהיו ט"ו שמינית ט"ו והוא א' נשארו ז' תורידם על א' יהיו ע"א קח שמיניתם יהיו ח' ונשארו ז' תורידם על ב' יהיו ע"ב קח שמינית [461][...] המספר [..] תציא לך ב' אלפים קס"ב [...] אלפים תק"ך ובחמשית ג' אלפים [...] ובשלישית ה' אלפים ומ' [...]
|
|
|
וכן תנהיג בכל המספרים לכל דבר [...] חלקים ודי בזה במין העודף
|
|
|
[המין] השביעי השני במספר העודף הגורע אשר חלקיו יגרעו ממנו והם מספרי זוג הזוג בפרט [ב'] ד' ח' י"ו וכל מספרי זוג הנפרד כמו אלה י' י"ד כ"ב כ"ו [שחלקי]הם חסרים ממנו
|
|
|
כי ב' יחסר חציו כי אין לו חלקים [אלא] חצי
|
|
|
וד' יחסר רביעיתו כי חלקיו חצי ורביעית [חברם] יהיו ג'
|
|
|
וח' חלקיו חצי ורביעית ושמנית תחברם ויחסר שמיניתו
|
|
|
והנה י"ו חלקיו חצי ורביעית [ושמי]נית וחלק מי"ו תחברים יהיו ט"ו ויחסר חלק מי"ו
|
|
|
[...] זוגי הזוגות שיחסר מכל אחד אחד שהוא חלק מכולו [..] בשם הוראתו שאם הוא ב' יורה על חצי כי מב' יחסר [חציו] ומד' רביעיתו ומח' שמיניתו וכן כולם
|
|
|
והנה זוג [הנפר]ד אין בו חלקים אלא חצי וחלק מכולו
|
|
|
והנה תולדת המספרים ידועים כי זוג הזוג בא מכפל ב' והיוצא ב' וכן לעולם וזוג הנפרד בא מכפל כל נפרד על ב'
|
|
|
[ואם] תכפול זה המין ביותר מפעם אחד אז יולידו העודפים
|
|
|
מג' יצא י"ב שהוא עודיף
|
|
|
המין השמיני השלישי במספר אשר חלקיו השלמים יהיו שוה לכולו ומזה המספר יש מעלות ימציוה ויש מעלות שלא ימצה אומנם במעלה שימצה [462]לא ימצה אלא [...] וכ"ח במעלת העשרות [...] לאלה יהיו חלקהם [...] חלקי ו' הם חצי ושלישית ושישית [...] ששה כאשר אפרש בע"ה [...] ולא מכולם ואם תוסיף על הבודד ה[...] הזוג
|
|
|
והנה תולדת זה המספר תראהו ב[...] בזה הצורה
|
|
|
| |
|
|
א
|
| |
|
|
ב
|
| |
|
|
ד
|
| |
|
|
ח
|
| |
|
א |
ו
|
| |
|
ג |
ב
|
| |
|
ו |
ד
|
| |
א |
ב |
ח
|
| |
ב |
ה |
ו
|
| |
ה |
א |
ב
|
| א |
0 |
ב |
ד
|
| ב |
0 |
ד |
ח
|
|
|
|
והנה ידעת זה הבודד [...] תצא המכוון יהיה בשלשה דרכים
|
|
|
[אחד] הוא שנקח כל מספר מזה הצורה אשר [...] ח' ומספר ח' בכלל וגם כל מספר [...] בסופו ב' ולא מספר ב' בכלל אלא ד' במקום ב' ובדרך כלל כל מספר בסופו ב"ח תקחנו חוץ [...] ראשונה שלא תקח ממנה אלא [...] ואחר שיהיה בידך המספר [...] אחד והנשאר יהיה [...] בודד בלא ספק ותכפול חציו וחצי אחד שהוא [...] הגדול משלמים נכפלהו [...] כולו והיוציא הוא המבוקש
|
|
|
עיון דע שאם עשיתי [דרך] [אחר להוציא הבודדים הנה תדע בכאן כי ד' הוא תחילת הבודדים ואם יש לו שינוי בעבור שהוא במעלת האחדים אבל זה העיון תחילתו מח' ותניח מספר אחד שהוא י"ו כמו שתראה בצורה וקח ל"ב והשלישי בדילוג אחד והוא קכ"ח וכן כולם אלא שתגרע אחד מכל אחד ויהיו מח' ז' ומל"ב ל"א ומקכ"ח קכ"ז ותקי"א וכו' [...] בדרך בדיקת המכוונים]
|
|
|
המשל בזה רצינו לדעת המספר המכוון הראשון במעלת האחדים והנה ב' כפול מא' [אבל] כבר יעדנו כי מב' לא תציא מספר מכוון אלא מכל [..] אשר בסופו ב' ואם כן נניחנו ונקח ד' כי כבר יעדנו שהוא טוב במעלה ראשונה ולא בזולתה והנה נגרע מד' א' [463][...] בשנים שהוא חציו הגדול [...] המבוקש שהוא המכוון במעלת [האחדים]
|
|
|
[משל שני] הנה זוג הזוג של אחר ד' הוא ח' [נגרע אחד] ישאר ז' והוא בודד כפלנו ז' על ד' שהוא [...] יעלה כ"ח והוא המבוקש שהוא המספר המכוון [במעלת] העשרות
|
|
|
משל שלשי אם נקח זוג הזוג הבא אחר ח' [שהוא] י"ו נגרע אחד ישארו ט"ו והוא מורכב נקח הבא [אחריו] שהוא ל"ב נגרע אחד יהיו ל"א כפול ל"א על י"ו שהוא [חציו] הגדול יעלו תצ"ו והוא המכוון במעלה שלישית שהוא [מעל]ת המאות
|
|
|
משל רביעי אם נקח זוג הזוג הבא אחר ל"ב [שהו]א ס"ד נגרע אחד יהיו ס"ג והוא מורכב מט' על ז' [וד'] בסופו ונקח הבא אחריו שהוא קכ"ח נגרע אחד ישארו [קכ"ז] והוא בודד נכפלהו על ס"ד שהוא חציו הגדול יעלה [ח'] אלפים קכ"ח והוא המכוון במעלה רביעית שהיא מעלת [ה]אלפים
|
|
|
משל חמשי אם נקח זוג הזוג הבא אחר קכ"ח והוא [רנ"ו] והנה יש בסופו ו' והנחנו ונקח תקי"ב שיש בסופו [ב'] כי כן יעדנו נגרע אחד ישארו תקי"א והוא בודד [נ]כפלהו על חציו הגדול שהוא רנ"ו יעלה ק"ל אלף תתי"ו והוא מכוון שהוא במעלה השישית שהיא במעלת המאות אלפים
|
|
|
והנה אין במעלת העשרות אלפים מספר מכוון
|
|
|
ויראה מדברי החכם ר' אברהם בן עזרא שסבר שיש בכל מעלה מספר מכוון והמעיין בדבריו יוכל לתרץ שאין כפי כוונתו אלא שאין יותר מאחד בכל מעלה כי כן האמת שאין מספר מכוון בכל מעלה אלא אחד ויש מעלות שלא תמצה מספר מכוון כלל כי במעלה ששית גם במעלת י"א לא תמצה מכוון כלל כמו שתראה בזה הצורה וזה יספיק לדרך הראשון
|
|
|
[464]הדרך השני לדעת [...] מיותר המכוון [...] ותכפלהו על ד' ועל היוציא תוסיף ג'
|
|
|
המשל בזה כפלנו ז' שהוא בודד על [...] תוסיף ג' יהיו ל"א [והוא הבודד המבוקש] תכפלהו על [חציו הגדול] תצ"ו והוא המכוון [השלישי גם קח ל"א שהוא בודד ותכפלהו על ד' יהיו קכ"ד ועם ג' יהיו קכ"ז והוא הבודד תכפלהו על חציו הגדול שהוא ס"ד יעלו ח' אלפים קכ"ח]
|
|
|
[עוד לקחנו קכ"ז ונכפלהו על ד' יהיו תק"ח ועם ג' יהיו תקי"א נכפלה על חציו הגדול שהוא רנ"ו יעלו ק"ל אלפים תתי"ו והוא המכוון החמשי]
|
|
|
[לקחנו תקי"א ונכפלהו על ד' יהיו ב' אלפים ומ"ד ועם ג' יהיו ב' אלפים ומ"ז נכפלהו על חציו הגדול שהוא אלף וכ"ד יעלו ב' מספרים וצ"ו אלפים וקכ"ח והוא המכוון השישי]
|
|
|
וזה הסדר כולל כל הבודדים [חוץ] [...] כי ג' יוציא מן הכלל כאשר מעלת האחדים יוציא מ[...] כל המעלות הכי הכופל מעלות על מעלות יגרע אחד מקיבוץ המעלות כמו שאמרתי במקומו וכמו שהאחד [...] מן האחרים
|
|
|
הדרך השלישי לדעת המספרים המכוונים [..] מוכפלים הנקראים זוג הזוג כפי [..] המספרים המכוונים שתרצה וא' שאינו מוכפל הנחנו [..] ההכפלה מב' כי מב' תצא המכוון הראשון ומד' המכ[וון] השני ומח' השלישי ומי"ו הרביעי וכן כולם כסדר המספרים הכפולים
|
|
|
והדרך להוציאם הוא שתקח המספר [..] וכפלהו על חציו וקח חצי העולה בכפל וכ[פלהו] פעם שנית על כולו בחסרון אחד וזה הדרך לכולם [..] המכוון הראשון שהוא ששה שדרכו דרך אחרת
|
|
|
והמשל רצינו להוציא המכוון הראשון נקח ב' ומרובעו יהיו ששה שהוא המכוון הראשון כי חצי ו' הוא ג' ושליש[יתו] ב' וחלק מכולו א' תחברם יהיו ששה כמוהו ואם יש חילוף בהוצאתו הנה בא מחילוף המעלה הראשונה על שאר המעלות כי כמו שהאחד אינו ממין האחרים כן המעלה הראשונה כי כפל אחד על אחד אחד כן מעלת [465]הכופל מעלות [...] ותציא המבוקש כי שלושים [...] על ב' שהם ששה ושמרם והנה [...] ומאתים ממעלה שלישית תחברם [...] מעלות תגרע אחת ישארו ארבעה ואם כן [...] הם ממעלה רביעית שהיא מאלפים [...] אלף וכן מאי זו מעלה שתכפול על אחרת [ועליך] לגרוע מעלה אחת לעולם ושמור ועיין זה [הדרך]
|
|
|
ועתה להוציא המספר המכוון השני קח המספר השני מן הנערכים בכפל שהוא ד' וכופלהו על חציו [...] ח' גם קח חצי ח' שהוא ד' וכפול אותו על כל המספר [בחסרון] אחד שיהיו ז' יעלו כ"ח והוא המכוון השני
|
|
|
עוד [קח] הכפול השלישי שהוא ח' וכופלהו על חציו יהיו ל"ב כפול [...] חצי ל"ב על ל"א שהוא הכל פחות אחד יעלו תצ"ו והוא המכוון השלישי
|
|
|
עוד נקח הכפול הרביעי שהוא י"ו ונכפול [אותו] על חציו יעלו קכ"ח כפלנו חצי קכ"ח על כולו [ב]חסרון אחד יעלו ח' אלפים אלפים קכ"ח כזה ח ב א ח [ש]הוא המספר המכוון הרביעי
|
|
|
עוד נקח הכפול החמישי שהוא ל"ב ונכפול אותו על חציו יעלו תקי"ב כפלנו חצי תקי"ב על תקי"ב בחסרון אחד יעלו ק"ל אלפים תתי"ו כזה ו א ח 0 ג א שהוא המספר המכוון החמשי
|
|
|
עוד נקח הכפול הששי שהוא ס"ד ונכפלהו על חציו שהוא ל"ב יעלו ב' אלפים ומ"ח כפלנו חצי העולה על כל המספר בחסרון אחד יעלו ב' מספרים וצ"ו אלפים קכ"ח כזה ח ב א ו ט 0 ב והוא המספר המכוון הששי
|
|
|
ויהיו כולם על זה הצורה עד עשרה מספרים מכוונים
|
|
|
[466]
| |
|
|
|
|
|
|
|
|
|
|
ו
|
| |
|
|
|
|
|
|
|
|
|
ב |
ח
|
| |
|
|
|
|
|
|
|
|
ד |
ט |
ו
|
| |
|
|
|
|
|
|
|
ח |
א |
ב |
ח
|
| |
|
|
|
|
|
א |
ג |
0 |
ח |
א |
ו
|
| |
|
|
|
|
ב |
0 |
ט |
ו |
א |
ב |
ח
|
| |
|
|
|
ג |
ג |
ה |
ה |
0 |
ג |
ג |
ו
|
| |
|
|
ה |
ג |
ו |
ח |
ה |
ד |
ה |
ב |
ח
|
| |
|
ח |
ה |
ח |
ט |
ח |
ו |
ט |
0 |
ה |
ו
|
| א |
ג |
ז |
ד |
[ג] |
ח |
ו |
ט |
א |
ג |
ב |
ח
|
|
|
|
שהוא זוג הנפרד ובאחרים אם תוסיף על הנפרד אחד [...] זוג הזוג שתוכל לחלקו עד אחד
|
|
|
והמשל רצינו לכוון חלקי כ"ח כי מששה כבר דברתי חלק כ"ח לחציים [..] י"ד וחצי י"ד ז' וחצי ז' בתוספת אחד ד' וחציו ב' וחציו א' והנה י"ד חציו וז' רביעיתו וד' שביעיתו וב' חלק מי"ד וא' חלק מכולו ויהיה כזאת הצורה
|
|
|
המורה המספר
| ב |
ח |
כולו
|
| א |
ד |
חציו
|
| |
ז |
רביעי'
|
| |
ד |
שביעי'
|
| |
ב |
יד
|
| |
א |
כח
|
|
|
|
משל אחר מתצ"ו שהוא מכוון המאות הנה חציו רמ"ח וחצי רמ"ח קכ"ד וחצי ס"ב וחציו ל"א וחצי ל"א בתוספת אחד י"ו וחציו ח' וחציו ד' וחציו ב' וחציו א' ודע כי רמ"ח הוא חציו בהוראת ב' וקכ"ד הוא רביעיתו בהוראת ד' וס"ב הוא שמיניתו בהוראת ח' ול"א הוא חלק מי"ו בהוראת י"ו וי"ו חלק מל"א בהוראת ל"א כי אז המספר מתגלגיל כי כאשר היה ל"א חלק מי"ו היה י"ו חלק מל"א וכאשר היה ס"ב חלק מח' היה ח' [467]מל"ב ומכאן מתגלגל [...] חלק מרנ"ד ורנ"ה חלק מ[...] וק' חלק מאלף וי"ו וד' חלק מ[...] וס"ד וא' חלק מכולו וכן תנהיג בידיעת [...] כי מספר החלקים יהיו הוראות ומתגלגלים כמו [...]
|
|
|
[468][עוד דרך אחרת נדבקת המכוונים מן ולמעלה והוא גם כן דרך להוציאם הנה הבודד הראשון הוא א' בדרך הזה ועמו נוציא כל הבודדים בזה אחר זה להוליד המכוונם ואחר אשר בידך הבודד כופלהו בשנים ועוד פעם אחר פעם עד שיצא המכוון המשל בזה רצינו המכוון השלישי כי הראשון שהוא ו' והשני שהוא כ"ח ידועים ולהם דרך אחרת והנה תחילת הבודדים בכאן הוא ז' נכפלהו בד' ועל היוציא נוסיף ג' יהיו ל"א והוא בודד ממכוון תצ"ו כי בד' הכפלות שנכפול ל"א תציא תצ"ו וכן יצאו כל המכוונים עם תוספת שתי כפילות על הנמשך אחריו אחריו כי ו' הראשון יציא מכפל ג' ומשתי כפילות ז' יציא כ"ח ומד' כפילות ל"א יצא תצ"ו כי כפל ל"א הוא ס"ב וכפל ס"ב הוא קכ"ד וכפל קכ"ד הוא רמ"ח וכפל רמ"ח הוא תצ"ו והמכוון עוד לבדוק המכוון האחר שהוא ח' אלף קכ"ח נכפול הבודד שעבר שהוא ל"א על ד' יהיו קכ"ד ועם תוספת ג' יהיו קכ"ז נכפלהו ששה פעמים ותציא ח' אלף רכ"ח לבדוק האחר שהוא ק"ל אלף תתי"ו כפול הבודד שעבר שהוא קכ"ז על ד' יעלה תק"ח ועם ג' שהוספנו יהיו תקי"א והוא הבודד נכפלהו [469]שמונה פעמים ותציא ק"ל אלף תתי"ו ולבדוק האחר שהוא ב' מספרים וצ"ו אלפים קכ"ח כפול הבודד שעבר שהוא תקי"א על ד' יעלה ב' אלף ומ"ד תוסיף עליהם ג' יהיו ב' אלפים ומ"ז והוא הבודד נכפלהו עד עשרה פעמים ותציא המכוון שהוא ב' מספרים וצ"ו אלפים וקכ"ח וכן כל הנמשכים]
|
|
|
ואם יש עוד בידי דרכים לכוין חלקי המכוון [...] בכאן זאת החקירה ואכוין לחקירה יותר עמוקה [...] עוד היו שני משיגים לשוה והם שני דרושים עמוקים [...]
|
|
|
הדרוש הראשון הוא שיהיו שני מספרים מסוגלים לאהבה אשר [חלקי] האחד יהיה כמספר השני וחלקי השני כמספר הראשון [...] אלה השני מספרים נאהבים
|
|
|
והדרוש השני הוא שיהיו [...] מרובע מה שוה מכל הטורים בין באורך בין ברוחב בין באלכסון ואמנם יסוגלו שבעה מהם לשבעה כוכבי לכת
|
|
|
ואבאר כל דרוש בפני עצמו אומר כי
|
Amicable Numbers
|
|
| The first postulate is to extract the amicable numbers and I say that [they are] every two numbers, such that [the sum of] the proper divisors of each is as the other number.
|
הדרוש הראשון הוא להוציא המספרים הנאהבים המסוגלים לאהבה ואומר כי כל שני מספרים אשר החלקים השלמים מכל אחד יהיו כמספר חברו
|
|
|
והנה תמצא הראשונים בדרך אחד והאחרונים בדרך אחרת ויסוד שניהם המספרים הכפולים הנקראים זוג הזוג ומהם נוציא הבודידים ומן הבודדים הנאהבים
|
|
|
וראשונה אומר שנסדר מספרם כפולים שהם זוגי הזוגים מתחילין מן האחד כמה שתרצה ואחר קח א"ב יהיו ג' נגד ב' עוד קח שלושה כפולים מא' ועד ד' יהיו ז' נגד הכפול האחרון שלקח[ת] שהוא ד' עוד קח ד' כפולים מא' עד ח' יעלו ט"ו ותתנהו נגד האחרון שהוא ח' עוד קח ה' כפולים מא' עד י"ו ויעלו ל"א נגד י"ו וכן ס"ג נגד ל"ב וכן קכ"ז נגד ס"ד וכן [470][...] הצורה [...] מספר שהוא נגד כל כפול הכפול למעלה ממנו כי א' שהוא למעלה מב' גרענו מג' וישארו ב' בשטה שלישית גם גרענו ב' מז' נשארו ה' גם ד' מט"ו נשארו י"א גם ח' מל"א נשארו כ"ג וי"ו מס"ג ישארו [מ"ז] ול"ב מקכ"ז ישארו צ"ה והוא מורכב מה' על י"ט ומזה שאינו [בודד] לא תציא נאהב אלא תעבור לאחר גם ס"ד מרנ"ה ישארו [קצ"א] וכן עד מה שתרצה ומאלה הבודדים אשר בשיטה שלישית [...] הבודדים נוציא הנאהבים הראשונים מכל זוג כי בודידי [..] [הר]אשון הם ה' וי"א ובודידי הראשון מן הזוג השני הם י"א [..] ובודדי הראשון מן הזוג השלישי כ"ג מ"ז וכן כולם שתניח אחד ותקח אחר וזה לראשונים
|
|
|
| ב |
ג
|
| ה |
ז
|
| יא |
טו
|
| כג |
לא
|
| מז |
סג
|
| צה |
קכז
|
| קצא |
רנה
|
|
|
|
אבל לשניים שיש להם דרך אחרת קח הכפול הבא אחר הכפול שממנו לקחת הנאהב הראשון [ו]תוסיף עליו אחד שהוא ראש זוג הזוג בשלוח ולכפול השני מן השניים תוסיף ב' ולשלישי מן השניים תוסיף ד' וכן כולם ואחר התוספת כפול זה על זה ומן העולה גרע אחד וישאר בודד וכפול אותו על הכפול הקודם לו בטבע והיוציא הוא בן זוגו
|
|
|
והנה אני אתן בזה ששה משלים השלושה לשלושה מספרים הראשונים הנאהבים ושלושה משלים לבן זוגי הראשונים ואם השלושה משלים האחרונים אינם הכריחיים כי בידעת חלקי [471]השלשה המשלים [...] חלקי השלושה השניים תדע [...] תדע המספר הבן זוגו אבל [...] כתבתי משלים למספרם
|
|
|
משל ראשון רצינו לדעת הנאהב הראשון מן [הזוג הראשון]
|
|
|
נקח הנשאר מז' וט"ו כמו שתראה בשיטה [...] מהצורה המונחת שהם ה' י"א והם מספרים בודדים נכפל[ם] זה על זה יעלו נ"ה גם נ"ה נכפול על כפול ד' שממנו [...] יעלו ר"ך וזה נאהב ראשון מן הזוג הראשון והוא הקטן מן [...]
|
|
|
ומזה תדע האחר וזה כי בזה הנאהב תמצא י"א חלקים שהם חצי [מר"ך] ק"י ורביעית נ"ה וחמשית מ"ד ועשירית כ"ב וחלק מי"א כ' וחלק [מכ'] שמתגלגלים חלקיהם י"א וחלק מכ"ב עשרה וחלק ממ"ד ה' וחלק [מנ"ה] ד' וחלק מק"י ב' וחלק מקק"ך א' ויהיו בזה הצורה
|
|
|
| ק"י
|
| נה
|
| מד
|
| כב
|
| כ
|
| יא
|
| י
|
| ה
|
| ד
|
| ב
|
| א
|
|
| חצי
|
| רביעית
|
| חמשית
|
| עשירית
|
| חלק מי"א
|
| חלק מכ'
|
| חלק מכ"ב
|
| חלק ממ"ד
|
| חלק מנ"ה
|
| חלק מק"י
|
| חלק מר'
|
|
| קק"ך נאהב |
היוציא
|
|
|
|
משל שני לדעת הנאהב הר[אשון] מן הזוג השני קח י"א ו[כ"ג] שהם בודדים וכפול זה על זה ותציא רנ"ג ועוד כפול רנ"ג על הכפול שממנו יציא י"א שהוא ח' הכפול הבא אחר ד' שלקחנו ותציא ב' אלפים כ"ד והוא הנאהב הראשון מן הזוג השני כזה
הצורה ד ב 0 ב
|
|
|
משל שלישי לדעת הנאהב הראשון מן הזוג השלשי
|
|
|
קח שני בודדים הנשארים מל"א וס"ג שהם כ"ג ומ"ז תמצאם בשיטה שלישית מהצורה המונחת וכפול זה על זה יעלו אלף ופ"א אשר [472][...] ויעלה י"ז [...] בן הזוג השלישי כזה
|
|
|
|
|
|
[...] הראשונים בדרך הנזכר נוציא השניים [...] זוג הראשונים אמנם יש להם דרך אחרת כנזכר [...] ואומר שתקח הכפולים הבאים אחר הכפולים יצאו הראשונים אשר אם הוא בן זוג הראשון שכבר נודע הראשון שיתכן להיות רפ"ד הנה תכפלהו על עצמו בתוספת [...] בן זוג שני בתוספת שנים ואם הוא בן זוג שלשי בתוספת [...] וכן בתוספת הכפולים וגרע מן העולה בכפל אחד והנשאר [יהיה] בודד כפלהו על הכפול הקודם שלקחת והיוציא יהיה בן זוג שני
|
|
|
[המשל] בזה נרצה להוציא בן זוג הנאהב הראשון אשר בידנו הנה זה הוא הדרך
|
|
|
נקח כפול ח' ונכפלהו על עצמו בתוספת א' שהוא ט' יעלו ע"ב גרע מע"ב אחד ישארו ע"א והוא [בודד] כפול אותו על הכפול הקודם לו בטבע למה שלקחת שהוא ד' עלו קקפ"ד והוא בן זוג הנאהב הראשון והיו שניהם כזה
|
|
|
|
|
|
אמנם החלקים השלמים הם חמשה לא יותר והם חצי ורביעית וחלק מקע"א וחלק מקמ"ב וחלק מרפ"ד ויהיה בזה הצורה
|
|
|
|
|
| חצי
|
| רביעית
|
חלק קעא
|
| חלק קמב
|
| חלק רפד
|
|
| רפד |
היוציא
|
|
|
|
משל שני לתשלום משל שני שעבר ואומר כי להוציא בן זוג השני מן הנאהב אשר במשל שני קח כפול י"ו ותכפלהו על עצמו בתוספת שנים שהוא י"ו על י"ח יעלו רפ"ח נגרע מהם אחד ישארו רפ"ז והוא בודד נכפול אותו על הכפול הקודם לו בטבע שהוא י"ח יעלו ב' אלפים [473]רצ"ו והוא בן [הזוג] [...]
|
|
|
משל שלישי לתשלום [משל שלישי] [...]
|
|
|
ואומר כי להוציא בן זוג [השלישי] [...] קח כפול ל"ב ותכפלהו על עצמו בתוספת על ל"ו יהיה העולה אלף קנ"ב נגרע [מהם] אחד [...] קנ"א והוא בודד כפול אותו על הכפול הקודם לו [...] שהוא י"ו יעלו י"ח אלפים תי"ו והוא בן זוג [...] במשל שלישי ויהיו שניהם כזה
|
|
|
|
|
|
ועם זה די לדרוש הראשון והמשכיל יבין
|
Magic Squares
|
|
| The second postulate is that the numbers of a certain square are equal in all the lines, whether lengthwise, or breadthwise, or in the diagonals.
|
הדרוש השני הוא שיהיו מספרי מרובע מה שוה מכל הטורים בין [באורך] בין ברוחב בין באלכסונים
|
| Seven of them are attributed to the seven planets.
|
ואמנם יסוגלו שבעה מהם לשבעה כוכבי לכת
|
| I say that the shapes of these numbers are endless and one of their properties is that the first seven are attributed to the seven planets.
|
ואומר כי תמונות אלה המספרים הם בלתי בעלי תכלית ומסגולותהם כי השבעה הראשונים הם מסוגלים לשבעה כוכבי לכת
|
|
|
וראשונה אומר כי המספר יחלק [אל] זוג ואל נפרד והזוג יחלק אל זוג הזוג ואל זוג הנפ[רד] ואל זוג הזוג והנפר[ד]
|
|
|
ובמקום אחר[474] תמצא טעם השמות האלה
|
|
|
ואם יש להם חלוקות אחרות אין זה מקומן
|
|
|
כן זה הפרק יחלק לשלושה סדרים
|
|
|
אשר הסדר הראשון ידבר [על] מרובעי הנפרדים
|
|
|
והסדר השני ידבר במרובעי זוג הזוג
|
|
|
והסדר השלישי במרובעי זוג הנפרד וזוג הזוג והנפרד
|
|
|
אם ירצה האל
|
|
|
ואתחיל מספר דרך תולדותם כי לא נמצא אתנו אלא שבעה מרובעים נקראים שבעה מרובעים
|
|
|
[475][...] כוכבי לכת [...] ולדעת [...] דרכים שתראה ואם [...] מהם בארוכה ומהם בקצרה אבל [...] המעיין עד [..] שהאיר השם [...] ומצאתי דרכים אשר בלא עיון יוכל [אדם] להוציא מרובעי [...] השני דרכים שהם [..] הנפרדים וסדר זוג[..] הזוגים אבל סדר [..] הנפרד וזוג הזוג והנפרד אין לו דרך ראוי [...] ועל השנים אני אומר תן לחכם ויחכם
|
|
|
הסדר הראשון המדבר על כל מרובעי הנפרדים
|
|
|
אומר כי הרוציא לדעת המרובעים הנפרדים השוים בכל הטורים באורך ורוחב ובאלכסונות וזה סגולת כל אלה המרובעים יעשה ראשונה לוח בתים מרובעים לתת בכל בית מספר ולפחות יהיו מספרי הבתים שנוכל לכתוב באלכסונו ד' כפלי המרובע הנרצה בנפרדים
|
| Now, to understand and to know the formation of the first square: its foundation are five tables, in which you see by the eye each part as I create it
|
ועתה להבין ולדעת תולדת המרובע הראשון הנחתו חמשה לוחות אשר בם תראה בעין כל חלק כמו שאעשה אותו ומה שלא עשיתי הכל בלוח אחת הוא להצילך מבילבול ואחר שתהיה מורגל תוכל לעשותו על פה ולכל האחרים זולת הראשון אעשה אותו עם ה' לוחות ונשוב למרובע הראשון שאחר שיהיו הה' לוחות מובנות תן בבית העליון מן הלוח הראשון א' וכן כול מרובע שתרצה ואחר אם תרצה מרובע ג' [476]תניח למ[...] ובמרובה ד' [...] תניח ו' בתים ובמרובע [...] כולם כי לעולם יהיו הבתים [...] העליונה לא' התחתונה כסך ה[...] אחד ועיין ותראה
|
|
|
ואחר הנחת השתי[..] תמשוך מן הא' העליונה ד' פעמים המרובע שתרצה [...] הלוח כסדר שיהיו ד' מרובעים שוים בלוח ונשארו [עוד] אלכסונים אחרים רקים בלוח בלוח ועם הא' השנית תמ[..] מהאלכסונים הנשארים מרובע אחד ויהיה נקשר עם ארבעה זויות הארבע מרובעים הנזכ'
|
|
|
ובאמצע מרובע חמישי שהוא מרובע ג' על ג' אשר בכל צלע תמצא ג' ובכל טור תמצא ט"ו וזה המבוקש ועיין שתקח הג' שטין מאמצע הלוח
|
|
|
וזה יורה לך שני דברים
|
|
|
האחד שיהיה חצי המרובע הגדול באמצע הלוח כמו ה' בלוח ג' על ג' וי"ג בלוח ה' על ה'
|
|
|
הדבר השני שיורה לך הוא שיהיו זויות הלוח הכולל במרחק שוה ללוח הקטן
|
- Example: we wish to constract the table of the first square in nature, which is 3 by 3 and it is attributed to Saturn; its diagonal is 15 as the product of the greater mean, which is 5, by the side, which is 3,
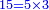 for this is the way of all. for this is the way of all.
|
המשל בזה רצינו לבנות הלוח המרובע הראשון בטבע שהוא ג' על ג' והוא מסוגל משבתי ובלאכסונו הוא ט"ו ככפל האמצעי הגדול שהוא ה' על הצלע שהוא ג' כי זה דרך לכולם
|
|
|
הנה נניח ב' אלכסונין זה למעלה מזה ובאמצע שני בתים רקים כמו שתראה בלוח ראשון ואחר משוך מן הא' העליונה ד' מרובעים מט' בכל מרובע באלכסוני הלוח כמו שתראה בלוח שני גם משוך מרובע אחד מן הא' התחתונה עד ט' באצ' באמצע הלוח כמו שתראה בלוח שלישי ואחר שיהיו השני והשלישי ערוכים לפניך לפניך [477][...] אשר בלוח שלישי באמצע [...] בלוח רביעי ואז תמצא [...] ג' על ג' מסודר בסדר אשר [...] ראשון הוא ט"ו כמו שתראהו [...] לוח חמשי וזה מה שרציתי לבאר והנה כזה [...] תעשה בכל מרובע נפרד עם שתניח הדקים שאמרת כמספר הצלע פחות אחד
|
|
|
שני
| |
|
|
|
|
א |
|
|
|
|
|
| |
|
|
|
ב |
|
ד |
|
|
|
|
| |
|
|
ג |
|
ה |
|
ז |
|
|
|
| |
|
א |
|
ו |
|
ח |
|
א |
|
|
| |
ב |
|
ד |
|
ט |
|
ב |
|
ד |
|
| ג |
|
ה |
|
ז |
|
ג |
|
ה |
|
ז
|
| |
ו |
|
ח |
|
א |
|
ו |
|
ח |
|
| |
|
ט |
|
ב |
|
ד |
|
ט |
|
|
| |
|
|
ג |
|
ה |
|
ז |
|
|
|
| |
|
|
|
ו |
|
ח |
|
|
|
|
| |
|
|
|
|
ט |
|
|
|
|
|
|
|
|
שלישי
|
|
|
רביעי
| |
|
|
|
|
א |
|
|
|
|
|
| |
|
|
|
ב |
|
ד |
|
|
|
|
| |
|
|
ג |
|
ה |
|
ז |
|
|
|
| |
|
א |
|
ו |
א |
ח |
|
א |
|
|
| |
ב |
|
ד |
ב |
ט |
ד |
ב |
|
ד |
|
| ג |
|
ה |
ג |
ז |
ה |
ג |
ז |
ה |
|
ז
|
| |
ו |
|
ח |
ו |
א |
ח |
ו |
|
ח |
|
| |
|
ט |
|
ב |
ט |
ד |
|
ט |
|
|
| |
|
|
ג |
|
ה |
|
ז |
|
|
|
| |
|
|
|
ו |
|
ח |
|
|
|
|
| |
|
|
|
|
ט |
|
|
|
|
|
|
|
|
חמשי
|
|
|
[478]והמשל במרובע [...] עשרה [...] מרובעים מה' על ה' [...] העליון ותניח תחתיו [...] צלעו בחסרון אחד ותכתוב א' אחרת [...]
|
|
|
| |
|
|
|
|
|
|
|
|
א |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
ב |
|
ו |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
ג |
|
ז |
|
יא |
|
|
|
|
|
|
|
| |
|
|
|
|
|
ד |
|
ח |
|
יב |
|
יו |
|
|
|
|
|
|
| |
|
|
|
|
ה |
|
ט |
|
יג |
|
יז |
|
כא |
|
|
|
|
|
| |
|
|
|
א |
|
י |
|
יד |
א |
יח |
|
כב |
|
א |
|
|
|
|
| |
|
|
ב |
|
ו |
|
טו |
ב |
יט |
ו |
כג |
|
ב |
|
ו |
|
|
|
| |
|
ג |
|
ז |
|
יא |
ג |
כ |
ז |
כד |
יא |
ג |
|
ז |
|
יא |
|
|
| |
ד |
|
ח |
|
יב |
ד |
יו |
ח |
כה |
יב |
ד |
יו |
ח |
|
יב |
|
יו |
|
| ה |
|
ט |
|
יג |
ה |
יז |
ט |
כא |
יג |
ה |
יז |
ט |
כא |
יג |
|
יז |
|
כא
|
| |
י |
|
יד |
|
יח |
י |
כב |
יד |
א |
יח |
י |
כב |
יד |
|
יח |
|
כב |
|
| |
|
טו |
|
יט |
|
כג |
טו |
ב |
יט |
ו |
כג |
טו |
|
יט |
|
כג |
|
|
| |
|
|
כ |
|
כד |
|
ג |
כ |
ז |
כד |
יא |
|
כ |
|
כד |
|
|
|
| |
|
|
|
כה |
|
ד |
|
ח |
כה |
יב |
|
יו |
|
כה |
|
|
|
|
| |
|
|
|
|
ה |
|
ט |
|
יג |
|
יז |
|
כא |
|
|
|
|
|
| |
|
|
|
|
|
י |
|
יד |
|
יח |
|
כב |
|
|
|
|
|
|
| |
|
|
|
|
|
|
טו |
|
יט |
|
כג |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
כ |
|
כד |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
כה |
|
|
|
|
|
|
|
|
|
|
|
|
| ג |
כ |
ז |
כד |
יא
|
| יו |
ח |
כה |
יב |
ד
|
| ט |
כא |
יג |
ה |
יז
|
| כב |
יד |
א |
יח |
י
|
| טו |
ב |
יט |
ו |
כג
|
|

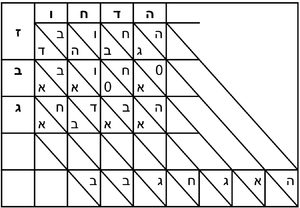
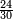 נקצרהו אם נרצה יהיו ד' חמשיות פרח או דרך אחרת נעשה מהפרחים די' יהיו שפ"ד
נקצרהו אם נרצה יהיו ד' חמשיות פרח או דרך אחרת נעשה מהפרחים די' יהיו שפ"ד 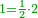 ], every number does in its two closest sides or equally distant sides.
], every number does in its two closest sides or equally distant sides.
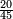 ] שאם תקצרם בחמש יהיו ד' תשיעיות [
] שאם תקצרם בחמש יהיו ד' תשיעיות [ 































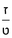

















 והוא המבוקש
והוא המבוקש
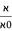

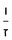

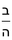
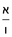


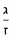
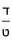

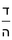

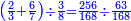



 כאשר אמרנו בסדר ראשון ובעבור שהוא עולה יותר מה' חלק אחד מי"ו נכפול השבר והמורה במאה כי בסדר ראשון כפלנו פ"א חלקים מי"ו נתן ספרא לפני כל אחד יהיו תת"י חלקים מק"ס ובעבור שהוא גדול לא ניקח כולו כי כולו מקוצר ושוב ישוב לרביע אבל ניקח מהמאה שברים צ"ה חלקים ויהיו כזה
כאשר אמרנו בסדר ראשון ובעבור שהוא עולה יותר מה' חלק אחד מי"ו נכפול השבר והמורה במאה כי בסדר ראשון כפלנו פ"א חלקים מי"ו נתן ספרא לפני כל אחד יהיו תת"י חלקים מק"ס ובעבור שהוא גדול לא ניקח כולו כי כולו מקוצר ושוב ישוב לרביע אבל ניקח מהמאה שברים צ"ה חלקים ויהיו כזה
 .
.
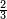 .
.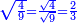

 .
.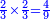
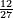 .
.
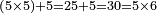

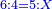

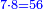
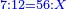
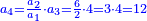

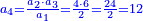

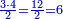
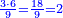
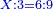
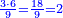
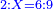
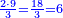
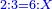
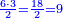
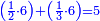
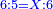
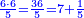
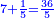
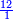
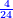
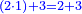

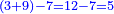
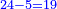
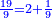
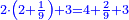
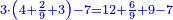




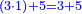
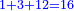
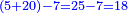
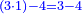
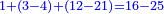
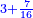
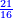
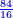
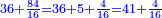
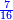
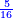
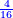
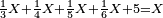
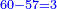
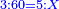
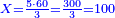
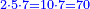

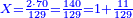
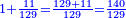
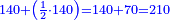
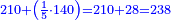
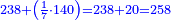
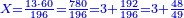
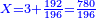
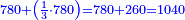
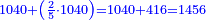
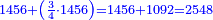
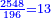
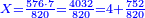

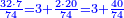
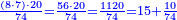
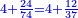
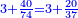
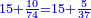
 ח
ח



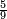

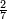
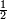
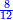
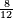

 על ד' יעלו י"ב רביעיות נחלקם על ו' שהם כ"ד רביעיות יעלה בחילוק חצי וזה המספר המבוקש שאם נוסיף עליו חציו יהיו
על ד' יעלו י"ב רביעיות נחלקם על ו' שהם כ"ד רביעיות יעלה בחילוק חצי וזה המספר המבוקש שאם נוסיף עליו חציו יהיו  ג' רביעיות
ג' רביעיות
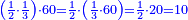
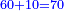
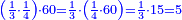
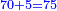
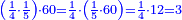
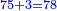
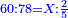


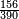
 ]
]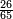
 ]
]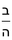
 -
-
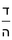 -
-
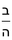 -
-
 -
-
 -
-
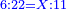
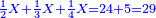
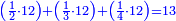
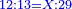
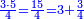
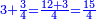 . Convert also its companion into quarters; they are 20
. Convert also its companion into quarters; they are 20 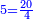 .
.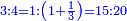
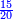

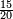

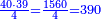
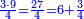
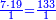
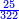
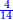







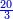


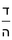



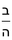

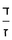
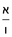










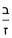


 מ
מ מ
מ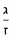
 מ
מ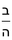 מ
מ
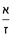
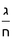
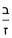

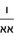
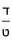
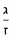
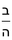
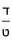

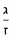


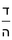
 3
3 4
4 2
2 ב
ב ד
ד ג
ג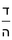 ה
ה ד
ד ב
ב




 ג
ג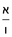

 ד
ד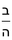 ג
ג
 יא
יא יז
יז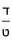
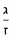

















 וזה סך הספר
וזה סך הספר
 ישאר א' וב' שלישיות וזה ממון ראובן
ישאר א' וב' שלישיות וזה ממון ראובן
 שהוא ממון כולם ישארו ל"א וב' שלישיות וזה ממון שמעון
שהוא ממון כולם ישארו ל"א וב' שלישיות וזה ממון שמעון
 ישארו מ"א וב' שלישיות וזה ממון לוי
ישארו מ"א וב' שלישיות וזה ממון לוי
 ישארו מ"ו וב' שלישיות וזה ממון יהודה
ישארו מ"ו וב' שלישיות וזה ממון יהודה
 שהוא כל הממון
שהוא כל הממון



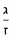






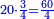
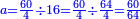
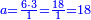

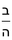

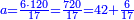
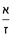
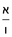


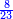
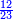
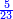
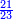
 13
13 11
11 9
9 7
7 5
5
 גא
גא אא
אא ט
ט ז
ז ה
ה






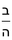
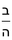

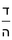 ד
ד
 ו
ו




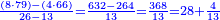
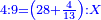
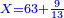


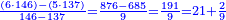



 תכפול ממונו על זמנו יהיו ט"ו טו חלקם מכ"ד ומקוצר יהיו החלקים מח' כזה
תכפול ממונו על זמנו יהיו ט"ו טו חלקם מכ"ד ומקוצר יהיו החלקים מח' כזה  וזה ממון ראובן וערך ממון שמעון הוא ג' רביעיות כי ט"ו נתן וכ' חייב לתת נתן ט"ו על כ' כזה
וזה ממון ראובן וערך ממון שמעון הוא ג' רביעיות כי ט"ו נתן וכ' חייב לתת נתן ט"ו על כ' כזה
 וערך זמנו
וערך זמנו
 תכפול ממונו על זמנו יהיו ו' חלקים מי"ב שהוא חצי מקוצר [351]וזה ממון שמעון גם תערוך ממון [...] ששיות כזה
תכפול ממונו על זמנו יהיו ו' חלקים מי"ב שהוא חצי מקוצר [351]וזה ממון שמעון גם תערוך ממון [...] ששיות כזה  וערך זמנו חצי כי [...] אל ו' חצי נכפול ה' ששיות על חצי יהיו ה' חלקים [...] תשוים כולם כזאת הצורה
וערך זמנו חצי כי [...] אל ו' חצי נכפול ה' ששיות על חצי יהיו ה' חלקים [...] תשוים כולם כזאת הצורה


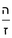 ויהיו ה' שביעיות
ויהיו ה' שביעיות
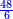
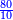
 כג
כג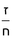
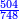
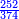
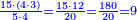

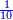
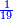
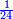
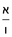
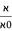
![\scriptstyle{\color{blue}{1+\left[\frac{1}{10}\sdot\left(81-1\right)\right]=1+\left(\frac{1}{10}\sdot80\right)=1+8=9}}](/mediawiki/images/math/7/e/1/7e16e246fab51d35149f72dd0401e6ed.png)
![\scriptstyle{\color{blue}{2+\left[\frac{1}{10}\sdot\left(72-2\right)\right]=2+\left(\frac{1}{10}\sdot70\right)=2+7=9}}](/mediawiki/images/math/c/f/4/cf41808c6ec759ad834beefcc2d4055d.png)
![\scriptstyle{\color{blue}{3+\left[\frac{1}{10}\sdot\left(63-3\right)\right]=3+\left(\frac{1}{10}\sdot60\right)=3+6=9}}](/mediawiki/images/math/7/7/6/776c0ab51c38bdd0b3bbecddee02ae1f.png)
![\scriptstyle{\color{blue}{3+\left[\frac{1}{5}\sdot\left(48-3\right)\right]=3+\left(\frac{1}{5}\sdot45\right)=3+9=12}}](/mediawiki/images/math/8/f/e/8feda18ef09345637b237d92aef00e30.png)
![\scriptstyle{\color{blue}{6+\left[\frac{1}{5}\sdot\left(36-6\right)\right]=6+\left(\frac{1}{5}\sdot30\right)=6+6=12}}](/mediawiki/images/math/8/b/7/8b720e4e9df64a218292b5fba3ccc31e.png)
![\scriptstyle{\color{blue}{9+\left[\frac{1}{5}\sdot\left(24-9\right)\right]=12}}](/mediawiki/images/math/a/c/8/ac8b361e6878842651863ec8171e62e8.png)
![\scriptstyle{\color{blue}{7-\left[\left(\frac{1}{2}\sdot7\right)+\frac{1}{2}\right]=7-4=3}}](/mediawiki/images/math/b/4/c/b4c9ab73080d1478df2efc91ccbe9abe.png)
![\scriptstyle{\color{blue}{3-\left[\left(\frac{1}{2}\sdot3\right)+\frac{1}{2}\right]=3-2=1}}](/mediawiki/images/math/d/4/0/d40122d01a3a69e0c380468a9ed7f86c.png)
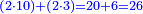
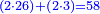
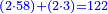

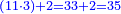
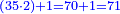
![\scriptstyle{\color{blue}{71-\left[\left(\frac{3}{4}\sdot71\right)+\frac{3}{4}\right]=71-\left[\left(53+\frac{1}{4}\right)+\frac{3}{4}\right]=17}}](/mediawiki/images/math/7/9/3/793f5dbaea1c9067d5448b0415be62c2.png)
![\scriptstyle{\color{blue}{17-\left[\left(\frac{2}{3}\sdot17\right)+\frac{2}{3}\right]=17-\left[\left(11+\frac{1}{3}\right)+\frac{2}{3}\right]=5}}](/mediawiki/images/math/7/9/a/79a87ec3a656d7364329434cb05a5f24.png)
![\scriptstyle{\color{blue}{5-\left[\left(\frac{1}{2}\sdot5\right)+\frac{1}{2}\right]=5-3=2}}](/mediawiki/images/math/2/0/5/205d885533f39c52333574d6459e71c2.png)


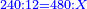
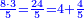
 4
4
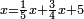
 וגופו ג' רביעיות [וזנבו] ה' אמות
וגופו ג' רביעיות [וזנבו] ה' אמות



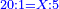
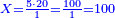


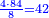
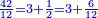
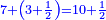
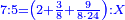
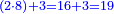
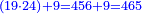
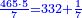
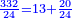
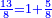

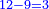
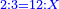
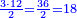
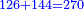

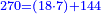

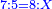
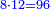
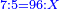
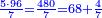
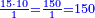
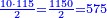
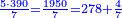
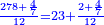
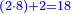
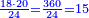
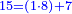
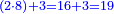
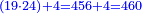
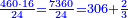
 על כ"ד יעלו י"ב אונסאש
על כ"ד יעלו י"ב אונסאש 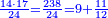
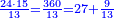
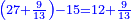










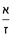
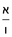













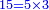 for this is the way of all.
for this is the way of all.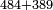
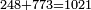
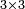

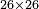

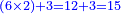
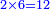
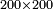
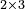

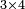
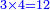
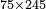
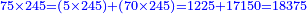
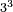
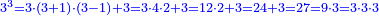
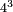
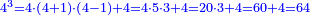

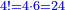




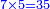
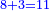
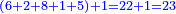
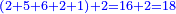
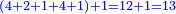
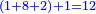
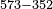

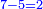


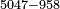

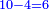
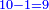
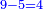
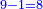


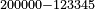
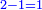
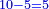
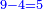

![\scriptstyle{\color{OliveGreen}{n=\frac{1}{2}\sdot\left[\left(n-1\right)+\left(n+1\right)\right]=\frac{1}{2}\sdot\left[\left(n-m\right)+\left(n+m\right)\right]}}](/mediawiki/images/math/0/f/8/0f8e16b2a8156932aac5ef36b1357a46.png)
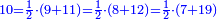 ; and every number up to the end of the first side.
; and every number up to the end of the first side.
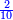
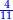
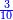
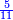
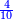



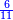
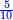


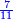
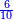


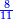
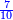




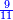
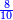





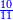
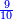



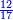
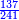
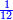
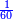
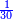
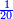

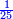
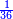
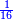
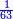

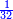
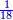
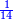






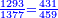






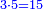
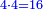
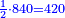
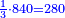
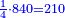
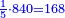
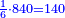
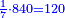
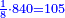
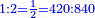

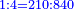



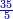
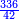
 and 36
and 36  .
.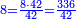
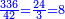
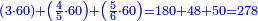
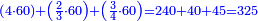
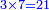 above the 3-fifths.
above the 3-fifths.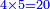 above the 4-sevenths.
above the 4-sevenths.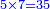 .
.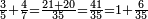
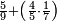
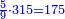 .
.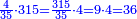
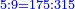 ; and the ratio of 4 to 35 is the same as the ratio of 36 to 315
; and the ratio of 4 to 35 is the same as the ratio of 36 to 315  . Furthermore, 9 to 5 is one time and 4 fifths and 315 to 175 is one and 4-fifths
. Furthermore, 9 to 5 is one time and 4 fifths and 315 to 175 is one and 4-fifths 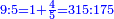 .
.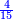
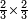
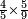
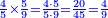
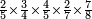
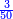

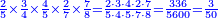
![\scriptstyle\left[\frac{1}{2}+\left(\frac{2}{3}\sdot\frac{1}{4}\right)\right]\times\left[\frac{1}{2}+\frac{1}{3}+\left(\frac{3}{4}\sdot\frac{1}{5}\right)\right]](/mediawiki/images/math/8/4/3/843b73e60173d7c63d915e798bf968b5.png)

![\scriptstyle{\color{blue}{\left[\frac{1}{2}+\left(\frac{2}{3}\sdot\frac{1}{4}\right)\right]\times\left[\frac{1}{2}+\frac{1}{3}+\left(\frac{3}{4}\sdot\frac{1}{5}\right)\right]=\frac{2\sdot3}{2\sdot3\sdot4\sdot2\sdot3\sdot4\sdot5}=\frac{6}{2880}=\frac{1}{480}}}](/mediawiki/images/math/9/5/0/9504ab47631c9e8435f2c15e539b6fd4.png)
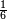 .
.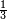 .
.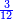
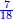
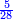
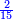
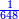
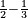
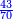
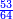
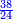
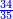
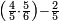
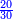
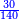
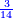
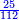


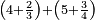
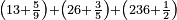
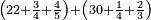
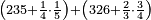
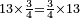
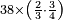
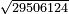
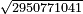
![\scriptstyle\sqrt[3]{74088}](/mediawiki/images/math/d/9/b/d9b99fd447ac159f387c8d18100d998d.png)
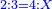
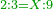
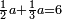
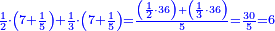
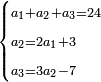
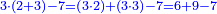
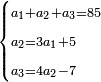
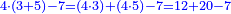
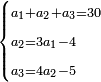
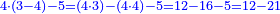
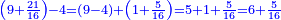
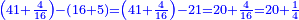
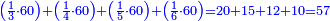
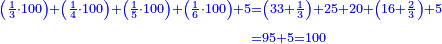
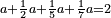
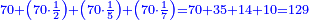
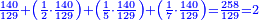
![\scriptstyle\left(a+\frac{1}{3}a\right)+\left[\frac{2}{5}\sdot\left(a+\frac{1}{3}a\right)\right]+\left[\frac{3}{4}\sdot\left(a+\frac{1}{3}a\right)+\left[\frac{2}{5}\sdot\left(a+\frac{1}{3}a\right)\right]\right]=13](/mediawiki/images/math/8/3/6/8369d7990f744b9a523db6ca37d54373.png)
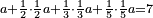
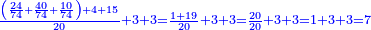
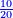
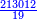

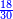
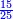
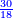
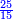
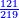
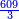

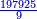
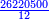

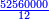

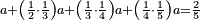
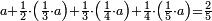
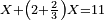
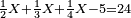
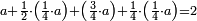
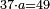
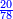
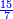
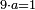
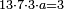

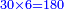
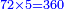
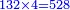

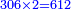


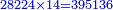
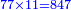

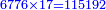

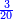
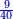
![\scriptstyle\begin{align}&\scriptstyle a-\frac{1}{3}a\\&\scriptstyle-\frac{1}{4}\sdot\left(a-\frac{1}{3}a\right)\\&\scriptstyle-\frac{1}{6}\sdot\left[a-\frac{1}{3}a-\frac{1}{4}\sdot\left(a-\frac{1}{3}a\right)\right]\\&\scriptstyle-\frac{1}{5}\sdot\left[a-\frac{1}{3}a-\frac{1}{4}\sdot\left(a-\frac{1}{3}a\right)-\frac{1}{6}\sdot\left[a-\frac{1}{3}a-\frac{1}{4}\sdot\left(a-\frac{1}{3}a\right)\right]\right]\\&\scriptstyle-\frac{1}{2}\sdot\left[a-\frac{1}{3}a-\frac{1}{4}\sdot\left(a-\frac{1}{3}a\right)-\frac{1}{6}\sdot\left[a-\frac{1}{3}a-\frac{1}{4}\sdot\left(a-\frac{1}{3}a\right)\right]-\frac{1}{5}\sdot\left[a-\frac{1}{3}a-\frac{1}{4}\sdot\left(a-\frac{1}{3}a\right)-\frac{1}{6}\sdot\left[a-\frac{1}{3}a-\frac{1}{4}\sdot\left(a-\frac{1}{3}a\right)\right]\right]\right]\\&\scriptstyle=3\end{align}](/mediawiki/images/math/e/8/0/e806d3163e01f19055b0f5e1693384e9.png)
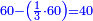
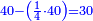
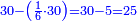
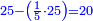
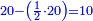
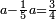
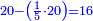
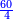
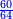
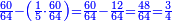
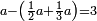
![\scriptstyle{\color{blue}{6-\left[\left(\frac{1}{2}\sdot6\right)+\left(\frac{1}{3}\sdot6\right)\right]=6-\left(3+2\right)=6-5=1}}](/mediawiki/images/math/9/3/f/93f96eb4c7f69fb9f72fee7ca060106b.png)
![\scriptstyle{\color{blue}{18-\left[\left(\frac{1}{2}\sdot18\right)+\left(\frac{1}{3}\sdot18\right)\right]=18-\left(9+6\right)=18-15=3}}](/mediawiki/images/math/1/5/4/1541c2ba2d70c5e671eda419fec51e22.png)
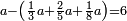
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle120-\left[\left(\frac{1}{8}\sdot120\right)+\left(\frac{2}{5}\sdot120\right)+\left(\frac{1}{3}\sdot120\right)\right]&\scriptstyle=120-\left(15+48+40\right)\\&\scriptstyle=120-103=17\\\end{align}}}](/mediawiki/images/math/9/f/b/9fb63fef9208d6a3a3f324eca83451f0.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\frac{720}{17}-\left[\left(\frac{1}{8}\sdot\frac{720}{17}\right)+\left(\frac{2}{5}\sdot\frac{720}{17}\right)+\left(\frac{1}{3}\sdot\frac{720}{17}\right)\right]&\scriptstyle=\frac{720}{17}-\left(\frac{90}{17}+\frac{288}{17}+\frac{240}{17}\right)\\&\scriptstyle=\frac{720}{17}-\frac{618}{17}=\frac{102}{17}=6\\\end{align}}}](/mediawiki/images/math/4/5/2/452d40b603bf5875721503068d9ec0d7.png)
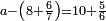
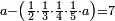
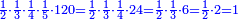
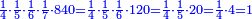
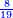



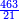
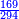
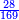
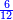
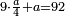
![\scriptstyle{\color{blue}{5+\left[\left(2\sdot5\right)+4\right]+\left[\left[3\sdot\left[\left(2\sdot5\right)+4\right]\right]-7\right]=5+14+35=54}}](/mediawiki/images/math/9/4/b/94b08271bc2cb47bb4420312fce25884.png)
![\scriptstyle{\color{blue}{6+\left[\left(2\sdot6\right)+4\right]+\left[\left[3\sdot\left[\left(2\sdot6\right)+4\right]\right]-7\right]=6+16+41=63}}](/mediawiki/images/math/7/1/8/7187dc5f7380aeb8be727679db6750c3.png)
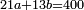
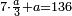
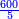
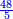
![\scriptstyle{\color{blue}{20-\left[\left(\frac{1}{5}\sdot20\right)+\left(\frac{3}{4}\sdot20\right)\right]=20-\left(4+15\right)=20-19=1}}](/mediawiki/images/math/4/d/2/4d22c0d307436c88afa3c8befacad96b.png)
![\scriptstyle{\color{blue}{100-\left[\left(\frac{1}{5}\sdot100\right)+\left(\frac{3}{4}\sdot100\right)\right]=100-\left(20+75\right)=100-95=5}}](/mediawiki/images/math/e/5/c/e5c6bfe69df8c01d57472029106120f8.png)