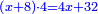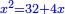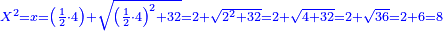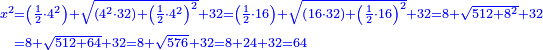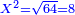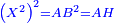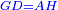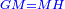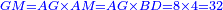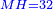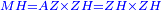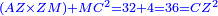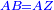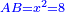Difference between revisions of "תחבולות המספר"
From mispar
(→Subtraction of Roots) |
(→Six Problems Demonstrating the Six Canonical Equations) |
||
| Line 4,709: | Line 4,709: | ||
|- | |- | ||
|I have shown you this problem [to demonstrate] the second of the six categories [of canonical equations], which is the saying: when the squares equal numbers [<math>\scriptstyle{\color{OliveGreen}{ax^2=c}}</math>]. | |I have shown you this problem [to demonstrate] the second of the six categories [of canonical equations], which is the saying: when the squares equal numbers [<math>\scriptstyle{\color{OliveGreen}{ax^2=c}}</math>]. | ||
| − | |style="text-align:right;"|וזאת השאלה הראיתי לך לחלק השני מהששה והוא האומר כאשר המרובעים ישוו אל מספרים | + | |style="text-align:right;"|וזאת השאלה הראיתי לך לחלק השני מהששה ‫<ref>307v</ref>והוא האומר כאשר המרובעים ישוו אל מספרים |
|- | |- | ||
!<span style="color:Green>Geometrical illustration of the problem</span> | !<span style="color:Green>Geometrical illustration of the problem</span> | ||
| Line 4,915: | Line 4,915: | ||
| | | | ||
:*The method that yields the thing: | :*The method that yields the thing: | ||
| − | |style="text-align:right;"|והאופן אשר יראה לך הדבר שהוא החלק הגדול הוא ש{{#annot:term|786|dCUR}}תקח מחצית{{#annotend:dCUR}} הדברים והוא ארבעה וחצי ותכם בעצמם ויהיו עשרים ורביע | + | |style="text-align:right;"|והאופן אשר יראה לך הדבר שהוא החלק הגדול הוא ש{{#annot:term|786|dCUR}}תקח מחצית{{#annotend:dCUR}} ‫<ref>308r</ref>הדברים והוא ארבעה וחצי ותכם בעצמם ויהיו עשרים ורביע |
|- | |- | ||
| | | | ||
| Line 5,086: | Line 5,086: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|תקח שרשם והוא שנים | + | |style="text-align:right;"|תקח שרשם והוא ‫<ref>308v</ref>שנים |
|- | |- | ||
| | | | ||
| Line 5,274: | Line 5,274: | ||
| | | | ||
:Add it to the 512 you kept; the result is 576. | :Add it to the 512 you kept; the result is 576. | ||
| − | |style="text-align:right;"|ותקבצם עם התקי"ב ששמרת ויעלו תקע"ו | + | |style="text-align:right;"|ותקבצם עם התקי"ב ששמרת ‫<ref>309r</ref>ויעלו תקע"ו |
|- | |- | ||
| | | | ||
Revision as of 15:12, 27 June 2022
Contents
[hide]- 1 Introduction
- 2 The Six Canonical Equations
- 3 Chapter: Multiplication of Algebraic Expressions
- 4 Roots
- 5 Six Problems Demonstrating the Six Canonical Equations
- 6 Notes
- 7 Appendix I: Glossary of Terms
- 8 Appendix II: Bibliography
| [1]ספר אבו כאמל בתחבולות המספר | |
Introduction |
|
| The three algebraic species | |
|---|---|
| The beginning of what the reader of this book needs to know are three matters that have already been stated by Muḥammad al-Khwārizmī in his book, which are: roots, squares and numbers. | אמר תחלת מה שצריך לדעת הקורא בזה הספר הוא שלשה ענינים אשר אמרם כבר מהומר אלכוארזמי בספרו והם שרשים מרובעים מספרים |
| Definitions: | |
|
השרש הוא המנין שהוא מוכה על עצמו כאלו תאמר אחד על אחד ושנים על שנים וכן לאין תכלית וכמו כן שברי האחד כאשר הוכו על עצמם כמו חצי על חצי ושלישית על שלישית וכן שברי שבריו עד אין סוף |
|
המרובע הוא המתקבץ מהכאת השרש על עצמו שלם יהיה או נשבר |
|
המספר הוא המנין שלא יובנו בו שיהיה לא שרש ולא מרובע אבל הוא נערך לעצמו במה שבו מן האחדים לבד |
| The six categories of canonical equations | |
| He said: the six categories [of canonical equations] were originated from the combination of these three [species], which are: | אמר וכבר יצאו מהרכבת אלו השלשה ששה חלקי' והם אלו |
|
שרשים שיהיו שוי' למרובעים |
|
ושרשים שישוו למספרים |
|
ומרובעי' שישוו למספרים |
|
ושרשים ומרובעי' שישוו למספרים |
|
ושרשי' ומספרים שישוו למרובעים |
|
ומרובעי' ומספרי' שישוו לשרשים |
| Said Finzi: the author [= Abū Kāmil] did not mention [the instances] in which the three [species] together are equal to one of them, yet it seems that this will be necessary in the categorization. | אמ"פ הנה לא הביא בעל הספר כאשר ישוו שלשתם יחד לאחד מהם והיה נראה שזה יהיה הכרחי בחלוקה |
| As if you say: roots, squares, and numbers are equal to roots, or to squares, or to numbers. | וזה כמו שתאמ' שרשים ומרובעי' ומספרים ישוו לשרשים או ישוו למרובעי' או ישוו למספרים |
The Six Canonical Equations |
|
The Simple Canonical Equations |
|
Squares Equal Roots: bx=ax2 |
|
| He said: when the roots are equal to squares: multiply [the number of] the roots by itself and the result is the square.
|
אמ' כאשר השרשים ישוו למרובעי' תכה השרשי' על עצמם ומה שיתקבץ הוא המרובע |
| Said Finzi: It is the same as saying "the squares are equal to the roots", since the roots should be understood as being equal to the squares that are mentioned with them. | אמ"פ והדבר הוא שוה לאמר המרובעים ישוו לשרשי' מפני כי צריך שיובנו השרשי' שיהיו שוים למרובעים הנזכרים עמהם |
| Moreover, the squares are squares by virtue of the multiplication of the roots by themselves. | וכמו כן המרובעים יהיו מרובעי' מכח הכאת השרשים ההם על עצמם |
|
דמיון זה אם אמרו לך חמשה שרשי' ישוו למרובע אחד כמה הוא המרובע |
|
אמור לו הוא עשרים וחמשה המתקבץ מהכאת חמשה על חמשה |
| It is so, because the root counts the square by the number of times that the one count the root. | והיה זה כן מפני כי המרובע ימנהו השרש במספר הפעמים שימנה האחד לשרש |
| The one counts the root by the number of times by which the root is named. | והאחד ימנה לשרש במספר הפעמים אשר יקרא בו השרש |
|
והנה בזה המשל השרש יקרא בשם חמשה והוא מורכב מחמשה אחדיו כמו שהוא מורכב עשרים וחמשה שהוא המרובע מחמשה דמיוני חמשה שהוא השרש |
| Hence, the square grows and is composed of repetitions of the root by the number that composes the root of repetitions of the unit. | הנה שהמרובע יצמח וישלם מדמיוני השרש במספר מה שישלם השרש מדמיוני האחד |
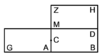
| Geometric illustration | |
|
ולמען הראותך זה לעין נרשום מרובע עליו אבג"ד על משל מרובע עשרים וחמש' |
|
|
|
|
הנה אי זה מצלעיו שיוכה באחד מאחדיו יהיה המתקבץ הוא שרש המרובע |
|
|
|
ונוציא מנקודת ז' קו ז"ח נכחי לקו א"ב |
|
ויצא שטח א"ז והוא שרש זה המרובע |
|
ונחלק מרובע אבג"ד לדמיוני שטח א"ז והם שטחי א"ז ח"ט כ"ל [2]מ"נ ס"ד והם חמשה שרשים למרובע עשרים וחמשה |
|
וכמו כן כל אחד מהם מורכב מחמשה אחדים כמו שרשום |
| This explanation is enough. | ודי בזה באור |
| Normalization: | |
| You must know that if the one who asks increases the squares in his question or reduces them, you should always restore it to a single square. | אמ' וראוי שתדע שאם בא השואל להרבות המרובעי' בשאלתו או לשברם כי אז אתה צריך להשיב השאלה לעולם אל מרובע אחד שלם |
|
דמיון זה אם ישאל חמשה מרובעי' ישוו לעשרים שרשים |
|
ואתה תחלק עשרים על חמשה |
|
ויהיה המרובע האחד ישוה לארבעה שרשים |
|
והמרובע יהיה מספרו ששה עשר |
|
וכן אם יאמ' חצי מרובע ישוה לעשרה שרשים |
|
הנה כל המרובע ישוה לעשרים שרשים |
|
ומספרו ארבע מאות |
Squares Equal Numbers: ax2=c |
|
| He said: when the squares are equal to numbers: the numbers are the squares. | אמ' כאשר המרובעי' ישוו למספרי' הנה המספרים הם המרובעים |
|
כמו אם יאמרו לך המרובע ישוה לששה עשר |
|
הנה ששה עשר הוא המרובע |
|
ושרשו ארבעה |
| Normalization: | |
| Restore the question also to one square. | וכמו כן תשיב השאלה אל מרובע אחד |
|
כי אם אמ' חמשה מרובעי' ישוו לחמשה וארבעי' |
|
הנה המרובע האחד הוא חמישיתם שהוא תשעה |
|
ואם אמ' שלישית המרובע ישוה לשבעה ועשרים |
|
הנה כל המרובע הוא שמנים ואחד |
Roots Equal Numbers: bx=c |
|
| He said: when the roots are equal to numbers: the units of the roots are as the amount of the numbers. | אמ' כאשר השרשים ישוו למספרי' הנה כמנין המספרי' יהיו אחדי השרשי' |
|
כי אם יאמרו לך שרשי המרובע ישוו לארבע' מספרי' |
|
הנה השרש הוא ארבעה |
|
והמרובע ששה עשר |
| Normalization: | |
| Here you should also restore the question to one square. | וכן גם בזה תשיב השאלה למרובע אחד |
|
כמו אם אמ' חמשה שרשים ישוו לשלשים |
|
תחלק שלשים על חמשה |
|
ויהיה השרש האחד ישוה לששה |
|
והמרובע ששה ושלשים |
|
ואם אמ' |
|
יהיה השרש האחד ישוה לעשרים |
|
והמרובע ארבע מאות |
| So far he has been discussing the three first categories [of canonical equations] called the simple. | עד הנה דבר בשלשה החלקים הראשונים אשר יקראו הפשוטים |
The Compound Canonical Equations |
|
Chapter: Squares and Roots Equal Numbers: ax2+bx=c |
פרק |
|
אמ' כאשר יהיו המרובעים והשרשים שוים למספרי' כאלו תאמ' המקובץ ממרובע מהאחד ועשרה משרשיו יחד ישוה לשלשים ותשעה דרהמי |
|
הנה תשובת זאת השאלה יהיה בשני פנים האופן האחד יראך שרש המרובע והשני יראך המרובע |
| First I will explain to you the procedures of these methods and their engagement. | וראשונה אבאר לך דרכי אלו האופני' וההתעסקות בהם |
| Then, I will explain their rules by geometrical demonstrations and figures, which the geometricians who are well versed in Euclid's book [= the Elements] understand . | עוד אחר זה אבאר משפטיהן במופתים ובתמונות גימטריאות יבינום חכמי הגימטריאה אשר ישכילו בספר אקלידס |
| The method that yields the root of the square | |
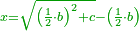
|
|
| He said: the method that reveals the root of the square to you is already stated by Muḥammad al-Khwārizmī in his book. | אמ' האופן אשר יראך שרש המרובע כבר אמרו מהומר אלכוארזמי בספרו |
| It is that you always take half [the number of] the roots, and multiply it by itself, then add the result to the numbers. | והוא שתקח לעולם מחצית השרשים ותכם על עצמם והעולה מההכאה תקבץ עם המספרים |
| You extract the root of the sum and subtract half [the number of] the roots from it; the result is the root of the square. | ותוציא שרש המקובץ ותגרע ממנו מחצית השרשים ומה שישאר הוא שרש המרובע |
|
והנה לקחנו בשאלה הנזכרת מחצית השרשים והוא חמשה |
|
הכינום על עצמם ועלה עשרי' וחמשה |
|
קבצנום עם הל"ט אדרהמי ויצא ששים וארבעה |
|
הוצאנו שרשו והוא שמנה |
|
גרענו [3]ממנו חמשה ונשאר שלשה והוא השרש |
|
| |
|
והמרובע יהיה תשעה |
| The method that yields the root of the square | |
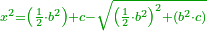
|
|
| He said: the method that reveals the square to you is that you multiply [the number of] the roots by itself, then multiply the product by the numbers and keep the result. | אמ' והאופן אשר יראך המרובע הוא שתכה השרשים על עצמם והעולה תכה על המספרים ומה שיתקבץ שמור |
| Take half the product of [the number of] the roots by itself and multiply this half by itself. | עוד תקח מחצית מה שעלה מהכאת השרשים על עצמם ותכה זה המחצית על עצמו |
| Add the result to the reserved and extract the root of the sum. | ומה שיעלה תקבצהו עם השמור ותוציא שרש המקובץ |
| You subtract it from the sum of half the product of the roots plus the numbers that are equal to the square and its roots; the remainder is the square. | ותגרעהו ממקובץ מחצית הכאת השרשים על עצמם עם המספרי' השוי' למרובע עם שרשיו ונשאר הוא המרובע |
|
והנה בשאלה הנזכרת הכינו עשרה השרשים על עצמם ועלה מאה |
|
והכינו מאה על הל"ט ויצא שלשת אלפים תת"ק ושמרנום |
|
ולקחנו מחצית מאה שהוא חמשים |
|
והכינום על עצמם ויצא אלפים ות"ק |
|
וקבצנום עם השמור והיה המקובץ ששת אלפים ות' |
|
הוצאנו שרש זה המקובץ ויצא שמנים |
|
גרענום ממקובץ חמשים עם ל"ט שהוא פ"ט וישארו תשעה והם המרובע |
|
| |
| Normalization: | |
| He said: if the squares in the question exceed one, or are less than one, you should restore the whole equation to a single square, and restore with it the roots and numbers, exactly by the same way that you restore the square. | אמ' ואם יעדיפו המרובעי' בשאלה על אחד או יחסרו מאחד שלם הנה אז תצטרך להשיב כל השאלה אל מרובע אחד וכן תשיב עמו השרשים והמספרי' בדרך ההוא בעינו שהשיבות המרובע |
|
דמיון זה ששאל שלשה מרובעי' וט"ו שרשי' ישוו לע"ב דרהמי |
|
רצה בזה ששלשה דמיוני מרובע אחד עם ט"ו משרשיו מקובצי' יחד יהיו ע"ב |
|
ובזה אתה צריך לקחת מהמרובעי' אחד מהם והוא שלישיתם וכן תקח מהשרשי' שלישיתם והוא חמשה ומהמספרי' כמו כן שלישיתם והוא כ"ד |
|
ותשוב להיות השאלה כאלו שאל מרובע אחד עם חמשה משרשיו ישוו כ"ד דרהמי |
| I have already shown you the method that reveals the root to you and the method that reveals the square to you. | וכבר הראיתיך האופן שיראך השרש והאופן שיראך המרובע |
|
וכמו כן אם שאל השואל חצי מרובע וחמשה משרשיו ישוו לכ"ח דרהמי |
|
אז תשיב המרובע שלך שלם והוא שתכפלהו ותכפול כמו השרשי' והמספרי' |
|
ותשוב השאלה מרובע ועשרה משרשיו ישוו נ"ו דרהמי |
|
וכבר הראית לדעת מה לעשות לך עמהם |
| Geometric illustration of method that yields the root of the square | |
| He said: now I will show you the reason we use the method that reveals the root of the square. | אמ' ועתה אראך הסבה אשר בעבורה דרכנו באופן שמראה שרש המרובע |
Illustrating the equation: 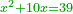
|
|
|
והוא שנניח |
|
ונחבר אליו שטח אבה"ו יהיה על דמיון עשרת השרשים אשר קבצת עם המרובע |
|
והנחנו שכל שטח והד"ג יהיה שלשים ותשעה דרהמי |
|
ורצינו שנודיע שיעור קוי האורך והרחב מזה השטח שהם קוי ה"ג ד"ג |
|
ועם זה יהיה ידוע לנו שיעור קו ב"ג השוה לד"ג שכל אחד מהם הוא שוה לשרש זה המרובע |
|
והוא ידוע כי קו ב"ה עשרה |
|
מפני כי היה צלע ב"א ממרובע אבג"ד כשהוכה באחד מאחדיו יהיה השטח העולה הוא שרש מרובע אבג"ד כמבואר בתמונה הראשונה מזה הספר |
|
וזה השטח כשהוכה בעשרה יהיה העולה עשרה שרשי' ממרובע אבג"ד והוא שטח אבה"ו |
|
הנה כי קו ב"ה עשרה |
|
ונחלק אותו לחצאין על נקודת [5]ח' |
|
ונוסף בארכו קו ב"ג |
|
ולכן יהיה השטח העולה מהכאת קו ה"ג בקו ב"ג עם המרובע ההוה מהכאת ח"ב על עצמו כמו המרובע ההוה מהכאת ח"ג על עצמו כמו שאמר אקלידס במאמ' שני מספרו |
|
אבל הכאת קו ה"ג בקו ב"ג כבר הונחה שלשים ותשעה מפני כי קו ד"ג הוא כמו קו ב"ג |
|
והכאת קו ח"ב על עצמו היא עשרים וחמשה |
|
ומקובצם ששים וארבע' ולכן יהיה הכאת קו ח"ג על עצמו ששים וארבעה |
|
והנה שרשו הוא שמנה ולכן קו ח"ג הוא שמנה |
|
ונבדיל ממנו קו ח"ב הידוע שהוא חמשה וישאר קו ב"ג שלשה והוא שרש המרובע |
|
והמרובע תשעה |
|
ואם תרצה שאראך לעין מה שאמרתי עשה על קו ח"ג מרובע חכנ"ג |
|
ותוציא קו ב"א ביושר עד נקדת ע' |
|
הנה קו ח"ג כמו קו ג"נ |
|
וקו ב"ג כמו קו ד"ג |
|
ישאר קו ב"ח כמו קו מ"כ |
|
ושטח ח"א כמו שטח א"נ |
|
אבל שטח ח"א כמו שטח מ"ה |
|
לכן שטח מ"ה כמו שטח א"נ |
|
ושטחי א"ח א"נ ד"ב השלשה הם שלשים ותשעה |
|
אבל שטח א"כ עשרים וחמשה בעבור כי הוא שוה להכאת ח"ב על עצמו |
|
הנה שטח כ"ג כלו ששים וארבעה |
|
וקו ח"ג שרשיו והוא שמנה |
|
וקו ב"ח היה חמשה |
|
וישאר קו ג"ב שלשה |
|
וזה מש"ל |
| Geometric illustration of method that yields the square | |
| He said: the reason of the method by which we reveal the square: | אמ' והסבה באופן אשר הראנו בו המרובע |
Illustrating the equation: 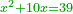
|
|
|
היא שנניח קו אב"ג יהיה שיעורו כמו מקובץ המרובע ועשרה משרשיו שהוא שלשים ותשעה |
|
ויהיה קו א"ב ממנו הוא שיעור המרובע ואנו נרצה שנודיע שיעור א"ב |
|
הנה נעשה על קו ב"ג מרובע ד והוא מרובע דהב"ג והנה הוא כמו מאה פעמים השטח היוצא בהכאת קו א"ב באחד מא[חד]יו |
|
בעבור כי קו ב"ג הוא עשרה שרשים מקו א"ב |
| When ten roots of a thing are multiplied by themselves, the result is as one hundred of that thing.
|
ועשרה שרשים מהדבר כשהוכו על עצמם יהיה המתקבץ כמו מאה דמיוני אותו הדבר |
|
ונשים קו א"מ מקיף עם קו א"ג בזוית נצבה |
|
ונשימהו בשיעור מאה מאשר בם קו א"ג שלשים ותשעה |
|
ונשלים שטח א"נ והנה שעורו ידוע כי הוא שלשת אלפים תת"ק |
|
בעבור כי הוא מהכאת קו א"ג שהוא שלשים ותשעה בקו א"מ שהוא מאה |
|
ונמשיך קו ב"ח נכחי לקו א"מ |
|
והנה יהיה שטח א"ח שוה למרובע ב"ה כי הוא גם כן מאה דמיוני הכאת קו א"ב באחד מאחדיו |
|
בעבור כי אורך קו א"מ מאה |
|
ויהיה מפני זה שטח דהח"נ גם כן שלשת אלפים |
|
כי ג"ה כמו ה"ד |
|
והנה קו ג"נ מאה מפני שהוא שוה לא"מ |
|
ונחלקהו לחציין על נקודת ל' |
|
וכבר נוסף עליו קו נ"ה |
|
ויהיה מפני זה שטח הכאת ה"נ בג"ה ומרובע קו ג"ל יחד שוה למרובע קו ל"ה כמו שביאר אקלידס במאמ' שני מספרו |
|
אבל שטח ה"נ בג"ה ומרובע ג"ל מקובצים הוא ידוע שהם ששת אלפים ות' |
|
כי שטח ה"נ בג"ה הוא שלשת אלפים תת"ק |
|
ומרובע ג"ל הוא אלפים ת"ק |
|
ומפני זה יהיה מרובע קו ל"ה ששת אלפים ות' |
|
וקו ל"ה יהיה שמנים |
|
אבל קו ג"ה כמו מרובע קו ב"ג |
|
הנה כי קוי ב"ג ל"ג מקובצים הם שמנים |
|
וכאשר נגרעם מקוי א"ג ג"ל שהם שמנים ותשעה ישאר קו א"ב שהוא שיעור מרובע תשעה |
|
והוא מש"ל |
| Said Finzi the translator: where do we see and from where did the author [= Abū Kāmil] deduces that ten roots of the thing, multiplied by themselves, generate a surface whose measure is a hundred times the thing? | אמ"פ המעתיק מאי לנו שנתבונן מאין [6]הוציא בעל הספר שעשרה שרשים מהדבר מוכים על עצמם יחדשו שטח שיעורו מאה דמיוני הדבר[7] |
| We say that it is clear from the first geometrical illustration in this book that one root of the thing is of the same length as the side of the thing, and when it is multiplied by itself it is equal to the thing. | ונאמ' כי הוא מבואר מהתמונה הראשונה מזה הספר ששרש אחד מהדבר הוא באורך כמו צלע הדבר וכשהוכה על עצמו הוא שוה לדבר |
| And from the fourth proposition in the second section of Euclid [Euclid, Elements, Book II, proposition 4], when he says: | ומהתמונ' הרביעית ממאמר שני לאקלידס באמרו |
| For every line that is cut into two segments randomly, the square of the whole line equals the two squares of the segments plus double the quadrilateral encompassed by the two segments.
|
כל קו אשר יחלק לשני חלקים איך שהזדמן הנה מרובע הקו כלו שוה לשני מרובעי החלקים ולכפל שטח נצב הזויות שיקיפו בו שני החלקים |
| It is clear from this that when the two segments of the line are equal, the square of the whole line equals four squares of one of the segments.
|
הנה התבא' משם כי כאשר השני חלקים מהקו שוים יהיה מרובע הקו כלו שוה לארבעה מרובעים מחלק אחד מהם |
| The one who understands can easily learn from this that two roots of the thing, multiplied by themselves, generate a square that equals four times the thing.
|
ומזה ישכיל המבין בנקלה כי שני שרשים מהדבר מוכים על עצמם יחדשו מרובע ישוה לארבעה דמיוני הדבר |
| For, when the two roots of the thing are arranged attached on a straight line, they generate a line that is double the two roots of the thing. | כי הנה שני שרשי' מהדבר כאשר סודרו מדובקים על קו ישר יחדשו קו הוא כפל שני שרשים מהדבר כאשר סודרו מדובקים קו צלע מהדבר |
| By this analogy, and from that same illustration, it is possible to explain that as much as the roots of the things are multiplied and gathered together, their square consists of the multiples of the thing by the ratio of the square numbers of multiples of the roots. | והנה על זה ההקש ומהתמונה ההיא בעינה יתכן לבאר כי כל אשר יתרבו השרשים מהדבר להאסף יחד יהיה מרובעם יוסיף להחזיק מדמיוני הדבר על יחס מרובעי מספרי פעמי השרשים |
|
דמיון זה אספנו יחד שלשה שרשים ממרובע מה כאלו תאמ' מאה יהיו שלשים ומרובעם תת"ק |
|
הנה תת"ק הוא תשעה דמיוני מאה כמו שתשעה הוא מרובע שלשה שהוא פעמי השרשים |
| Deduce from this. | והקש על זה |
| This is clear from proposition [1]1 of the eighth of Euclid [Euclid, Elements, Book VIII, proposition 11] | וכבר יתבא' זה אם כן מתמונת א' משמיני לאקלידס |
| Because it is explained there that the ratio of a square to a square is the same as the ratio of the side to the side multiplied by itself.
|
כי הנה התבא' שם כי יחס מרובע אל מרובע כיחס צלעו אל צלעו שנוי בכפל |
| It is clear from what we said at the beginning, that the ratio of the side of the thing to ten of its roots, summed together, is as the ratio of one to ten.
|
והוא מבואר ממה שאמרנו תחלה כי יחס צלע הדבר אל עשרה משרשיו מדובקים יחד הוא כיחס אחד אל עשרה |
|
ויחס אחד אל עשרה שנוי הוא עשירית העשירית שהוא אחד ממאה |
| Therefore, the ratio of the thing, which is the square of the side of the thing, to the square of ten of its roots, is the ratio of one to one hundred.
|
ולכן יהיה יחס הדבר שהוא מרובע צלע הדבר אל מרובע עשרת שרשיו הוא יחס אחד אל מאה |
| So, the square of ten roots of the thing is one hundred times the thing.
|
אם כן יהיה מרובע עשרת שרשי הדבר מאה דמיוני הדבר |
| Q.E.D. | והוא מש"ל |
| This chapter is completed. | ונשלם זה החלק |
Chapter: Squares and Numbers Equal Roots: ax2+c=bx |
פרק |
|
אמ' המרובעי' והמספרי' שישוו לשרשים הוא כאלו תאמ' כאשר תקבץ עם מרובע מה עשרים ואחד דרהמי יהיו שוים לעשרה משרשים מהמרובע |
| We find [the solution] of this category also by the two previous methods, I mean, the method that reveals the root of the square to you and the method that reveals the square to you. | הנה גם כן לזה החלק נמצאם שני האופני' הראשוני' רצו' האופן שיראך שרש המרובע והאופן שיראך המרובע |
| Each [is done] in two ways: one by adding and the other by subtracting. | ולכל אחד משניהם שני צדדים צד אחד לתוספת וצד אחד למגרעת |
| The solution method that yields the root of the square | |
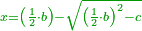
|
|
| He said: the method that reveals the root of the square to you is that you take half [the number of] the roots, and multiply it by itself, then subtract the numbers from the result. | אמ' והאופן אשר יראך שרש המרובע הוא שתקח מחצית השרשים ותכם בעצמם וממה שיתקבץ תגרע המספרים |
| You extract the root of the remainder and subtract it from half [the number of] the roots; the remainder is the root of the square. | ותקח שרש הנשאר ותגרעהו ממחצית השרשים והנשאר הוא שרש המרובע |
|
והנה בדמיון הנזכר לקחנו מחצית השרשים והוא חמשה |
|
והכינו חמשה בעצמו והיה עשרים וחמשה |
|
גרענו מהם מספר האדרהמי ונשארו ארבעה |
|
ושרשם שנים |
|
[8]גרענום מחמשה ונשארו שלשה הוא שרש המרובע |
|
| |
|
והמרובע תשעה |
|
וזה צד המגרעת |
|
ואם תרצה הוסיף השנים על מחצית השרשים ויהיו שבעה והם שרש המרובע |
|
והמרובע יהיה תשעה וארבעים |
| He said: you should know that if the product of half [the number of] the roots by itself is less than the dirham that are with the square, then the problem is false.
|
אמ' וראוי שתדע כי אם יהיה המתקבץ מהכאת מחצית השרשים על עצמו פחות מהאדרהמי אשר עם המרובע כי אז תהיה השאלה כוזבת |
| Yet, sometimes the product is equal to the number of the dirham - then, the root of the square is the same as half [the number of] the roots, no more and no less.
|
אבל פעמים יהיה המתקבץ שוה למספר האדרהמי ואז יהיה שרש המרובע כמו מחצית השרשים בלי תוספת ובלי מגרעת |
| I will explain to you everything we have said with geometric illustrations. | והנני אבאר לך כל אשר אמרנו בגה"ו עם תמונות גימטריות |
| The solution method that yields the square | |
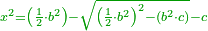
|
|
| He said: the method that reveals the square to you is that we multiply [the number of] the roots by itself, then multiply the product by the numbers. Keep the result. | אמ' והאופן אשר יראה לך המרובע הוא שנכה השרשים על עצמם והעולה נכהו על המספרי' ושמור מה שיתקבץ |
| We take half the product of the roots and multiply it by itself. | עוד נקח מחצית הכאת השרשים ונכהו בעצמו |
| We subtract the reserved from the product. | ומה שיתקבץ נגרע ממנו השמור |
| Extract the root of the remainder. | ותקח שרש הנשאר |
| Subtract it from half the product of the roots. | ותגרעהו ממחצית הכאת השרשים |
| Subtract also the number of the dirham from the remainder; what remains is the square. | עוד תגרע מהנשאר מספר האדרהמי ומה שישאר הוא המרובע |
|
והנה בדמיון הנזכר הכינו השרשים בעצמם ועלה מאה |
|
הכינו מאה בעשרי' ואחד והיו אלפיים ומאה ושמרנום |
|
עוד לקחנו מחצית מאה והכינום בעצמם והתקבץ אלפיים ות"ק |
|
גרענו מהם השמור ונשאר ארבע מאות |
|
ושרשם עשרים |
|
גרענום מחמשי' ונשאר שלשים |
|
וגרענו משלשים מספר האדרהמי ונשאר תשעה והוא המרובע |
|
| |
|
וזה הוא צד המגרעת |
|
ואם תרצה צד התוספת תוסיף העשרים על החמשים ויהיו שבעים |
|
ותגרע מהם מספר האדרהמי וישאר תשעה וארבעי' הוא המרובע |
| Normalization: | |
| He said: if the squares in the question exceed one, or are less than one, always restore them to one square according to the way I have demonstrated to you in the previous chapter. | אמ' וכמו כן אם יעדיפו המרובעים בשאלה על אחד או יגרעו מאחד שלם השיבם לעולם אל מרובע אחד על הדרך שהראיתיך בחלק שעבר |
| The reason for the method that yields the root of the square | |
| He said: now I will show you the reason we use the method that reveals the root of the square. | אמ' ועתה אבוא להראות לך הסבה אשר בעבורה דרכנו באופן שמראה שרש המרובע |
| First, you should know that the reason for the addition and subtraction methods is in accordance with the excess or the deficiency of the square over the number. | וראשונה ראוי שתדע כי סבת צדדי התוספת והמגרעת היא כפי מה שיעדיף המרובע על המספרי' או שיגרע מהם |
For, if [the square] exceeds [the numbers] 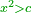 : the addition method is needed. : the addition method is needed.
|
כי אם יעדיף אז הוא צריך צד התוספת |
If [the square] is less than [the numbers] 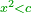 : the subtraction method is needed. : the subtraction method is needed.
|
ואם יגרע אז יצטרך צד המגרעת |
| As I will demonstrate to you in the two illustrations I draw for you now: | כמו שאראה אותך בשתי תמונו' אשר ארשום לך עתה |
Geometric illustration of [the subtraction method]: when the square is less than the numbers 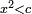
|
|
| First I draw [an illustration for the case] when the square is less than the numbers: | וארשום ראשונה כאשר יגרע המרובע מהמספרי' |
|
|
|
|
והוא שנניח המרובע הוא מרובע אבג"ד |
|
ושטח אבה"ל הדבק אצלו הוא על דמיון העשרים ואחד דרהמי |
|
ומפני כי שטח אבה"ל הנחנוהו גדול מאבג"ד יהיה קו ב"ל גדול מקו ב"ד |
|
ומפני כי כל שטח הלג"ד הנחנוהו עשרה שרשי' ממרובע אבג"ד |
|
יהיה קו ל"ד עשרה כמו שהתבא' למעלה |
|
ואנו מבקשים לדעת שיעור קו ב"ד |
|
הנה נחלק קו ל"ד שהוא עשרה לחצאין על נקודת ח' |
|
וכבר נחלק גם כן לשני חלקים בלתי שוים על נקודת ב' |
|
ויהיה מפני זה הכאת ל"ב בב"ד עם מרובע ח"ב ישוו למרובע ח"ד כמבואר בשני מאקלידס |
|
אבל מרובע ח"ד הוא ידוע [9]שהוא עשרים וחמשה |
|
בעבור כי קו ח"ד חמשה |
|
והכאת ל"ב בב"ד הוא עשרים ואחד |
|
בעבור כי ב"ד הוא שוה לב"א |
|
ולכן ישאר מרובע ח"ב ארבעה |
|
וצלעו שהוא קו ח"ב שנים |
|
גרענום מקו ח"ד שהוא חמשה וישאר קו ב"ד שלשה והוא שרש המרובע |
|
והמרובע תשעה והוא המבוקש |
|
ואם תרצה שאראך לעין מה שאמרתי הנה נשים על קו ח"ד מרובע והוא מרובע כחג"ד |
|
והוא ידוע בשיעוריו עשרים וחמשה |
|
בעבור כי קו ח"ד חמשה |
|
ושטח ח"ג הוא כמו שטח ח"ה |
|
בעבור כי קו ל"ח כמו קו ח"ד |
|
ושטח א"ח כמו שטח א"נ |
|
ולכן כאשר יקובץ שטח א"ח עם שטח ח"ה יהיה שוה למקובץ משטח א"נ עם שטח |
|
אבל מקובץ שטח א"ח עם שטח ח"ה הוא ידוע שהוא עשרים ואחד |
|
ולכן יהיה מקובץ שטח א"נ עם שטח ח"ג גם כן עשרים ואחד |
|
וישאר שטח כ"א ממרובע כהג"ד שיעורו ארבעה |
|
ושטח כ"א מרובע |
|
בעבור כי קו כ"נ כמו קו כ"ח |
|
וקו ח"ס כמו קו נ"מ |
|
וישאר קו כ"ס כמו קו כ"מ |
|
וקו כ"מ שנים והוא שוה לקו ח"ב אם כן קו ח"ב שנים |
|
וישאר קו ב"ד שלשה והוא שרש המרובע |
|
והמרובע תשעה |
| In this illustration, the reason for the method that leads you to know the square of the root is clarified to you by proof and by sight. | הנה כי בזאת התמונה התבאר לך במופת ובעין סבת האופן אשר יובילך אל ידיעת שרש המרובע |
| Moreover, the reason for the subtraction method, when the square is less than the numbers, is also clarified to you from this. | וכן התבא' לך מפניה סבת צד המגרע' כי הוא כאשר המרובע הוא פחות מהמספרים |
|
ולכן הוצרכנו לגרוע קו ח"ב אשר ידענו עם תחבולה מקו ח"ד הנודע בהנחה ויצא לנו שיעור קו ב"ד שהוא שרש המרובע |
Geometric illustration of the addition method: [when the square exceeds the numbers] 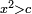
|
|
| Now, the reason of the addition method will be revealed to you from this second illustration as for the previous rule. | ועתה מזאת התמונה השנית יגלה אליך בכמו ההנהגה הקודמת סבת צד התוספת |
|
|
|
|
כי הנחנו בה מרובע אבג"ד גדול משטח אבה"ל |
|
ולכן ימשך בסוף כי כדי לדעת שיעור ב"ד נצטרך להוסיף קו ח"ב על קו ח"ד |
| We do not need to elaborate on that, as it is clear from what we wrote first, for the proof is one [and the same]. | ולא נצטרך להאריך בזה כי הוא מובן מאשר כתבנו ראשונה כי המופת אחד |
| But, in order to illustrate it to your eye, the proof is slightly changed, therefore we will explain it to you: | אבל כדי להראותך זה לעין ישתנה מעט המופת ולכן נבארהו לך |
|
והוא שנשים על קו ח"ד מרובע כחג"ד |
|
ונמשיך קו ח"כ עד ס' וקו ד"נ עד ג' |
|
ונרצה שאראה לך איך שטח אבה"ל כשיתקבץ עם מרובע אמס"כ יהיה שוה למרובע כחג"ד הידוע שהוא עשרים וחמשה |
|
ונאמ' כי הוא ידוע כי שטח ח"ג כמו שטח ה"ח |
|
בעבור כי קו ל"ח כמו קו ח"ד |
|
ושטח מ"ח כמו שטח ס"נ |
|
וישארו שטח אבה"ל ואמס"כ שוים לכחג"ד |
|
אבל אבה"ל הוא עשרים ואחד |
|
ולכן ישאר אמס"כ ארבעה ואמס"כ הוא מרובע |
|
ולכן יהיה קו א"ס שנים והוא שוה לח"ב |
|
הוספנוהו על ח"ד הידוע שהוא חמשה ויצא לנו שיעור קו ב"ד שהוא שבעה והוא המבוקש |
It is clarified from what we have said that [the difference between] the product of half [the number of] the roots by itself [and] the numbers [is] always the measure of the square 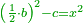 , whether the square is less than the numbers , whether the square is less than the numbers 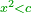 , or exceeds them , or exceeds them 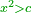 . .
|
אמ' וכבר התבאר ממה שאמרנו כי לעולם תעדיף הכאת מחצית השרשים על עצמם מהמספרים בשיעור מרובע א"כ בין יגרע המרובע מהמספרים או שיעדיף עליהם |
| [The case that] is left for us to explain is when the product of half [the number of] the roots by itself is the same as the numbers.
|
ונשאר עלינו שנבאר כאשר יהיה [10]העולה מהכאת מחצית השרשים על עצמו כמו המספרים |
| In that case, the square is the same as the numbers.
|
שאז יהיה המרובע כמו המספרים |
| And the root of the square is the same as half the roots, no more and no less.
|
ושרש המרובע כמו מחצית השרשים בלי תוספת ובלי מגרעת |
|
דמיון זה שיאמ' מרובע מה ועשרים וחמשה שרשים ישוו לעשרה שרשים מהמרובע |
|
|
|
|
ונניח המרובע שטח מרובע עליו אבג"ד |
|
ונחבר עמו שטח אבה"ו על דמיון העשרים וחמשה דרהמי |
|
ויהיה כל שטח ג"ו עשרה שרשים ממרובע אבג"ד |
|
ולכן יהיה קו ד"ו עשרה |
|
ורצינו שנודיע כמה שיעור קו ב"ד שהוא שרש המרובע |
|
הנה נחלק קו ד"ו לחצאין על נקוד' ח' |
|
ולא ימלט הדבר מאחד משלשה ענינים אם שתפול נקודת ח' למעלה מנקוד' ב' או למטה ממנה או שתפול עליה ממש |
|
ונניח ראשונה שתפול נקודת ח' למעלה מנקודת ב' |
|
אם יתכן זה ויהיה מפני זה קו ד"ו נחלק לחצאין על נקודת ח' ולשני חלקים בלתי שוים על נקודת ב' |
|
ולכן יהיה הכאת ד"ב בב"ו עם מרובע ח"ב על עצמו ישוו להכאת ח"ו על עצמו כמבואר בשני מאקלידס |
|
אבל הכאת ו"ח על עצמו הוא עשרים וחמשה |
|
בעבור כי הנחנוהו חצי ו"ד שהוא עשרה |
|
ולכן יהיה הכאת ד"ב בב"ו עם מרובע ח"ב ישוו עשרים וחמשה |
|
וכבר הנחנו קודם שטח אבה"ו שהוא מהכאת ב"ו בב"א השוה לב"ד עשרים וחמשה מבלעדי מרובע ח"ב |
|
אם כן הרב ישוה למעט זה חלוף לא יתכן |
|
אם כן לא תפול נקודת ח' למעלה מנקודת ב' |
|
וכמו זה יתבאר שלא יתכן |
|
אם כן יצטרך שתהיה נקודת ב' עצמה הוא הנקוד' הנחלק עליה קו ו"ד לחצאי' |
|
ולכן יהיה קו ב"ד שהוא מחצית השרשים הוא שרש המרובע והוא חמשה |
|
ומרובעו חמשה ועשרים |
| The explanation is completed. | ונשלם ביאורו |
| The reason for the method that yields the square | |
| Said Finzi, the translator: the proof of the method that reveals the square to us has been omitted from the book I translated. So, I thought I should explain it, and drew three illustrations for its explanation: | אמ"פ המעתיק הנה נשמט מהספר שהעתקתי ממנו מופת האופן שהראה לנו בו המרובע ולכן ראיתי שאבארהו וארשום בבאורו שלשה תמונות |
| In the first, the addition method is clarified. | הראשונה יתבא' בה צד התוספת |
| In the second, the subtraction method. | ובשנית צד המגרעת |
| In the third, [the case] is shown, where the numbers are equal to the product of half [the number of] the roots by itself - when there is no need for addition or subtraction. | ובשלישית |
Geometric illustration of the addition method: [when the square exceeds the numbers] 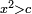
|
|
| We explain it first: | ונקח לבאר זאת הראשונה |
|
|
|
|
והוא שהנחנו קו א"ג המקובץ מהמרובע ועשרי' ואחד דרהמי |
|
וא"ב ממנו הוא שיעור מרובע |
|
וב"ג ממנו הוא שיעור הדרהמי |
|
וא"ב גדול מב"ג כי עם זה יגיע צד התוספת |
|
והנחנו קו א"ג הוא כלו עשרה שרשים מן המרובע כי כן היתה השאלה |
|
ורצינו שנודיע שיעור קו א"ב |
|
נשים על קו א"ג מרובע עליו אגד"ה והנה הוא מאה דמיוני השטח העולה מא"ב מוכה באחד מאחדיו כמו שבארנו למעלה |
|
בעבור כי א"ג עשרה |
| Ten roots of the thing multiplied by themselves are the same as a hundred times the thing.
|
ועשרה שרשים מהדבר מוכים על עצמם כמו מאה דמיוני מהדבר |
|
ונמשיך קו א"ד ביושר עד ו' |
|
ונשימהו מאה ממה שבו קו ב"ג עשרים ואחד |
|
[11]ונוציא קוי בט"ז גה"ח נכחיים לקו א"ו ושוים אליו |
|
ונגיע נקדות ו"ח עם קו וז"ח |
|
הנה שטח אבו"ז שוה למרובע אגד"ה בעבור כי הוא גם כן מאה דמיוני השטח העולה מהכאת קו א"ב באחד מאחדיו |
|
כי צלע א"ו ממנו הוא מאה |
|
ונבדיל שטח א"ט המשותף |
|
וישאר שטח ג"ט שוה לשטח ט"ו |
|
ונבדיל שטח ג"ט משטח בגז"ח וקבצנו עם הנשאר שטח ט"ו השוה לג"ט שהבדלנו ויהיה מפני זה שטח דהו"ח שוה לשטח בגז"ח |
|
ושטח בגו"ח היה ידוע שהוא אלפיי' ומאה |
|
בעבור כי ב"ג הוא עשרים ואחד |
|
וג"ח הוא מאה |
|
ולכן יהיה שטח דהו"ח אלפיים ומאה והוא כמו הכאת ג"ד בה"ח |
|
כי קו ד"ה שוה לקו ג"ה |
|
ונחלק ג"ח לחצאין על נקודת ל' |
|
וכבר נחלק לשני חלקים בלתי שוים על נקודת ה' |
|
ולכן יהיה הכאת קו ג"ל על עצמו שוה להכאת ג"ה בה"ח ולמרובע ה"ל יחד כמו שהוא מבואר בשני לאקלידס |
|
אבל הכאת קו ג"ל על עצמו היא אלפיים ות"ק |
|
ונגרע מהם אלפיים וק' שהם מהכאת ג"ה בה"ח |
|
ושרשם עשרים והם שיעור קו ה"ל |
If the square exceeds the dirham 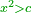 , as is the case in the first illustration: , as is the case in the first illustration:
|
ואם המרובע יעדיף על הדרהמי כמו שהוא הענין בתמונה הראשונה |
|
נוסיף העשרים על קו ג"ל שהוא חמשי' ויהיה קו ג"ה שבעים |
|
וג"א השוה לג"ה יהיה גם כן שבעים |
|
גרענו ממנו קו ב"ג הידוע שהוא עשרים ואחד וישאר קו א"ב תשעה וארבעים והוא המרובע שהוא המבוקש |
Geometric illustration of the subtraction method: when the square is less than the numbers 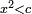
|
|
| ואם המרובע פחות מהדרהמי כמו שהוא הענין בזאת התמונה השנית | |
|
|
|
|
אז נגרע העשרים שהוא שעור קו ה"ל מקו ג"ל שהוא חמשים וישאר קו ג"ה שלשים |
|
וא"ג שוה לג"ה |
|
גרענו ממנו שעור ב"ג הידוע שהוא עשרים ואחד וישאר שעור קו א"ב תשעה והוא המרובע המבוקש |
Geometric illustration of the case in which the product of half the roots by itself equals the dirham 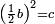 → the square is the same as the dirham → the square is the same as the dirham 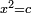
|
|
After explaining the addition and subtraction methods in the two previous figures, when the product of half the roots by itself is greater than the dirham 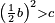 , the method that does not consists of addition or subtraction will be explained in the third figure, which is when the product of half the roots by itself equals the dirham , the method that does not consists of addition or subtraction will be explained in the third figure, which is when the product of half the roots by itself equals the dirham 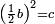 , that is when the square is the same as the dirham , that is when the square is the same as the dirham 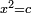
|
ואחר שבארנו בשתי התמונות הקודמות צד התוספת וצד המגרעת הנופלים בזאת השאלה |
|
|
|
|
ונניח קו א"ג מקובץ המרובע עם עשרים וחמשה דרהמי והוא גם כן שוה לעשרה שרשים מהמרובע |
|
ונמשיך המעשה כמעשה הקודם בשתי התמונות הקודמות עד המקום שיתבאר בו ששטח דהו"ח שוה לשטח בגז"ח |
|
והוא שוה גם כן להכאת ג"ה בה"ח |
|
בעבור כי ג"ה כמו ה"ד |
|
אבל שטח ב"ג ז"ח הוא אלפיים ת"ק |
|
כי ב"ג עשרים וחמשה |
|
וג"ח מאה |
|
אם כן הכאת ג"ה בה"ח אלפיים ת"ק |
|
ונחלק קו ג"ח לחצאי' על נקודת ל' |
|
ובהכרח תפול נקודת ל' אז למעלה מנקודת ה' או למט' ממנה או עליה |
| It will be explained that it can only be on H | ונבאר שאי אפש' שתפול כי אם עליה |
|
שאם אפש' נניח שנפלה ממנה |
|
ויהיה אם כן קו ג"ח נחלק לחצאין על נקודת ל' |
|
ולשני חלקים בלתי שוים על נקודת ה' |
|
ויחויב שיהיה הכאת ג"ה בה"ח עם מרובע ה"ל יחד שוים למרובע ג"ל |
|
אבל מרובע ג"ל אלפיים ת"ק |
|
כי ג"ל חמשים |
|
ולכן יהיה הכאת ג"ה בה"ח עם מרובע ה"ל אלפיים ות"ק |
|
וקודם זה התבאר שהכאת ג"ה בה"ח לבדו הוא אלפיים ות"ק מבלעדי מרובע ה"ל |
|
אם כן יהיה הרב שוה למעט זה חלוף לא יתכן |
|
ובכמו זה הביאור יתבא' שאינה נופלת נקדת ל' למטה מנקודת ה' |
|
אם כן תהיה נקוד' ה' בעצמה היא אשר עליה יחצה קו ג"ח |
|
ולכן יהיה קו ג"ה חמשים וא"ג השוה לג"ה יהיה גם כן חמשים |
|
נגרע ממנו ב"ג שהוא עשרים וחמשה וישאר קו א"ב גם כן חמשה ועשרים וככה המרובע המבוקש |
| This chapter is completed. | ונשלם זה החלק |
Chapter: Roots and Numbers Equal Squares: bx+c=ax2 |
פרק |
|
אמ' שרשים ומספרים שישוו למרובע הוא כמו שיאמ' שלשה שרשים וארבעה דרהמי יהיו שוים למרובע |
| This category also has two solution methods: one reveals the root of the square to you the other reveals the square to you. | גם לזה החלק שני האופנים האחד יראך שרש המרובע והשני יראך המרובע |
| I will further illustrate them through geometric figures | ועוד אבארם בתמונות גימטריות |
| The solution method that yields the root of the square | |
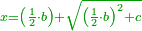
|
|
| He said: the method that reveals the root to you is that you halve [the number of] the roots, and multiply it by itself, then add the result to the numbers. | אמ' והאופן אשר יראך השרש הוא כי תחצה השרשים ותכם על עצמם ותקבץ העולה עם המספרים |
| You extract the root of the sum and add it to half [the number of] the roots; the result is the root. | עוד תקח שרש המקובץ ותקבצהו עם מחצית השרשים ומה שיגיע הוא השרש |
|
והנה לקחנו מחצית שלשה והוא אחד וחצי |
|
הכינוהו על עצמו ועלה ב' ורביע |
|
וקבצנום עם הארבעה והיה ששה ורביע |
|
ושרשם הוא שנים וחצי |
|
וקבצנוהו עם אחד וחצי והגיע ארבעה והוא שרש המרובע |
|
| |
|
והמרובע ששה עשר |
| The solution method that yields the square | |
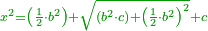
|
|
| He said: the method that reveals the square to you is that you multiply [the number of] the roots by itself, then multiply the product by the numbers and keep the result. | אמ' והאופן אשר יראך המרובע הוא שתכה השרשים על עצמם ומה שיעלה תכהו במספרים והעולה שמור |
| Take half the product of [the number of] the roots by itself and multiply this half by itself. | עוד תקח מחצית הכאת השרשים על עצמם ותכה זה המחצית על עצמו |
| Add the result to the reserved and extract the root of the sum. | והעולה תקבץ עם השמור וקח שרש המקובץ |
| You sum it with half the product of the roots and with the numbers; the total sum is the square. | ותקבצהו יחד עם מחצית הכאת השרשי' ועם המספרים ומה שיתקבץ מהכל הוא המרובע |
|
והנה הכינו השלשה בעצמם ועלה תשעה |
|
הכינו תשעה בארבעה ועלה שלשים ושש ושמרנום |
|
עוד לקחנו מחצית תשעה והוא ארבעה וחצי |
|
והכינום על עצמם והיה עשרים ורביע |
|
קבצנום עם השמור והיה הכל ששה וחמשים ורביע |
|
לקחנו שרשם והוא שבעה וחצי |
|
קבצנום יחד עם הארבעה וחצי ועם הארבעה דרהמי שהיו עם השרשים והתקבץ מהכל ששה עשר והוא המרובע |
|
| |
| Normalization: | |
| Always remember to convert the squares into one square, whether they exceed one, or less than one in the question, as I demonstrated at first. | אמ' וזכור גם כן לעולם להשיב המרובעים אל מרובע אחד אם היה שהונחו מהם בשאלה יותר מאחד או פחות כאשר הראיתי בראשונה |
| Geometric illustration of the solution method that yields the root of the square | |
|
|
|
|
אמ' ולמופת האופן אשר הראנו בו השרש נניח המרובע אבג"ד והוא המחובר משלשה שרשיו וארבעה מספרים |
|
ונניח שיהיה שטח אהג"נ ממנו הוא שלשת השרשים |
|
ושטח ה"ד הנשאר ארבעת המספרים |
|
והוא ידוע ממה שאמרנו בראש הספר כי שלשת השרשים יחזיקו שלשה מספרים מהצלע |
|
ולכן יהיה ידוע שקו א"ה שלשה |
|
ורצוננו להודיע שיעור ה"ב הנשאר |
|
נחלק קו א"ה לחצאי' על נקודת ח' |
|
וכבר נוסף בארכו קו ה"ב |
|
ולכן יהיה הכאת א"ב בב"ה עם מרובע ה"ח ישוו להכאת ח"ב על עצמו כמבואר בשני לאקלידס |
|
אבל שטח הכאת א"ב בב"ה הוא ידוע שהוא ארבעה כי הוא שוה לשטח ה"ד |
|
בעבור כי א"ב שוה לב"ד |
|
ומרובע ה"ח הוא שנים ורביע |
|
ומקובצם ששה ורביע |
|
אם כן הכאת ח"ב על עצמו הוא ששה ורביע |
|
ולכן קו ח"ב שהוא שרשו הוא שנים וחצי |
|
נקבץ עמו קו א"ח שהוא אחד וחצי ויהיה כל קו א"ב ארבעה וככה שרש המרובע |
|
והמרובע ששה עשר |
|
אמ' וכדי לבאר הדבר יותר הנחנו על קו ח"ב שטח מרובע עליו חבע"כ |
|
והוא ידוע שקו מ"ע כמו קו כ"ד |
|
בעבור כי א"ב כמו ב"ד |
|
וב"ח כמו כ"ב |
|
ונשאר כ"ד כמו א"ח |
|
וא"ח שוה לח"ה וח"ה כמו מ"ע |
|
אם כן מ"ע כמו כ"ד |
|
ונשים מ"ט כמו נ"ד |
|
ולכן יהיה שטח ע"ט כמו שטח מ"ד |
|
ונשים שטח ה"כ משותף |
|
ויהיה שני שטחי ע"ט ה"כ שוים לשטח ה"ד כלו שהוא ארבעה |
|
והוא ידוע כי שטח ח"ט מרובע |
|
בעבור כי קו ח"ב כמו קו |
|
ומ"ט כמו ה"ב השוה לנ"ד |
|
וישאר ה"ח כמו ה"ט |
|
וקו ה"ח הנחנוהו אחד וחצי |
|
ולכן שטח ח"ט שנים ורביע |
|
וכל שטח מרובע ח"כ ששה ורביע |
|
וקו ב"ח שנים וחצי |
|
ועם קו א"ח שהוא אחד וחצי יהיה כל קו א"ב ארבעה והוא השרש |
|
והמרובע שש עשרה |
|
|
|
|
אמ' ולמופת זה האופן דרך אחרת והוא שנניח מרובע אבג"ד הוא המקובץ משלשה שרשי' וארבעה דרהמי |
|
ונניח קו א"ח מקו א"ג מחצית השרשים שהוא אחד וחצי |
|
ונוציא קו ח"מ על נכוחות קו א"ב |
|
ויהיה מפני זה שטח א"מ הוא שרש וחצי |
|
וכן נניח קו ע"ד אחד וחצי |
|
ונוציא ע"ט על נכוחות ב"ד |
|
ושטח ע"ב גם כן הוא שרש וחצי |
|
ולכן יהיה שטח א"מ ושטח נ"ד וכמו שטח נ"ב יהיו יחד כמו שלשה שרשים |
|
וישאר שטח ע"ח ארבעה מספרים וכמו שטח נ"ב |
|
אבל שטח נ"ב שנים ורביע |
|
ולכן יהיה שטח |
|
וע"ח מרובע |
|
לכן יהיה ג"ח שנים וחצי |
|
וקו א"ח הנחנוהו אחד וחצי |
|
ולכן קו א"ג כלו ארבעה והוא שרש המרובע |
|
והמרובע ששה עשר |
| Geometric illustration of the solution method that yields the square | |
|
|
|
|
אמר ועלת האופן אשר הראנו בו המרובע הוא שנשים קו א"ב הוא שעור המרובע המקובץ משלשה שרשיו וארבעה דרהמי |
|
וא"ג ממנו הוא שעור השלשה השרשים |
|
וג"ב הנשאר הוא שיעור הארבעה מספרים |
|
ורצוננו להודיע שיעור א"ב כלו במה שבו ג"ב ארבעה |
|
נעשה על קו א"ג מרובע אגד"ה |
|
והוא ידוע ממה שעבר כי הוא כמו תשעה דמיוני השטח העולה מהכאת א"ב באחד |
|
ונשים קו א"נ תשעה במה שבו קו ג"ב ארבעה |
|
ונשלים שטח א"ח והוא ידוע גם כן ממה שעבר שהוא ישוה למרובע א"ה |
|
ונבדיל שטח א"ט המשותף |
|
וישאר שטח ד"ט שוה לשטח ט"ב |
|
אבל שטח ט"ב ידוע שהוא שלשים ושש |
|
כי צלע ג"ב ארבעה |
|
וצלע ב"ח תשעה |
|
ולכן שטח ד"ט גם כן שלשים וששה |
|
וחלקנו קו א"נ לחצאין על נקודת ל' |
|
וכבר נוסף עליו קו נ"ד |
|
ולכן יהיה מרובע קו ל"ד שוה לשטח העולה מהכאת א"ד בד"ג ולמרובע ל"נ |
|
אבל הכאת א"ד בד"נ כמו שטח ד"ט |
|
בעבור כי א"ד כמו ד"ה |
|
אם כן שטח הכאת א"ד בד"נ שלשים וששה |
|
ומרובע ל"נ הוא עשרים ורביע |
|
ומקובצם הוא חמשים ושש ורביע |
|
אבל שרשם שבעה וחצי וככה יהיה קו ל"ד |
|
ונקבץ עמו קו א"ל שהוא ארבעה וחצי ויהיה קו א"ד כלו שנים עשר |
|
וא"ג השוה לא"ד יהיה אם כן שנים עשר |
|
ונקבץ עמו קו ג"ב שהוא ארבעה ויהיה קו א"ב כלו ששה עשר וככה המרובע |
|
והוא מש"ל |
| He said: This section is completed, and with its completion, the explanation we have assigned to the six categories [of canonical equations], their manner of use and their proofs, is completed | אמ' ונשלם זה החלק ובהשלמו נשלם באור הששה חלקים אשר יעדנו באורם באופני השתמשותם והמופתים עליהם |
| Many of the algebraists [lit. the writers of "al-jabber and al-muqabala"] necessarily demonstrated to you some of them. | והרבה מסופרים אלגבר ואלמקאבלא לא יתכן שלא ייראוך קצת מהם |
| For each category of these six categories [of canonical equations] there are questions of restoration [lit. cobramiento] and confrontation [lit. confrontamiento] that the arithmeticians teach you. | ולכל חלק מאלו הששה חלקים שאלות מההפקדה והכוון קובראמיינטו איקונפרונטאמיינטו בלעז אשר יורוך אותם בעלי המספר |
| Linguistic explanation of the Hebrew words chosen as the technical terms: | |
| Said Finzi: I chose hafqadah [restoration], from piqadon [lit. deposit] and kivvun [reduction lit. adjusting, direction], from the words of our Sages of Blessed Memory. | אמ"פ לקחתי הפקדה מלשון פקדון וכוון מלשון כוון חשבון אשר בדברי רז"ל |
| You will understand their meaning from the questions that he presents after he introduces the following explanations now. | ותבין ענינם מתוך השאלות אשר יביא אחר הציעו המצעות האלו אשר יניח עתה |
Chapter: Multiplication of Algebraic Expressions |
פרק |
| He said: I will begin first with the multipliction of things by each other; and things by numbers; and things and numbers by things and numbers; and others than those we have mentioned; and other matters that the one who wishes to read this book cannot avoid knowing. | אמ' וראשונה אתחיל מהכאת הדברים אחד באחר והדברים במספרים והדברי' והמספרים בדברי' ובמספרים ומלבד אלו אשר אמרנו ובענינים אחרי' אשר אינו נמלט מידיעתם הרוצה לקרות בזה הספר |
| I will explain to you how the things that are the roots are multiplied by each other, when they are alone, or with numbers, whether they are subtracted from the numbers or the numbers are subtracted from them; how they are added to each other; and how one is subtracted from the other. | ואבאר לך באי זה צד יוכו הדברי' והם השרשים אחד באחד כאשר יהיו נפרדים או כאשר יהיו עם מספרים בין שיהיו נגרעים מהמספרי' בין שיהיו המספרים נגרעים מהם ובאי זה צד יתקבצו אלו עם אלו וכיצד יגרע האחד מהאחר |
|
אמ' וכאשר יהיו הדברים נוספים על המספרים יהיה החלק הרביעי נוסף והחלק הרביעי אז הוא הכאת הדברים זה עם זה |
| For, when every two numbers are multiplied by two numbers, four multiplications are necessarily applied: each of the first two numbers is multiplied by each of the two other numbers, so there are four multiplications. | כי כל שני מספרים שיוכו בשני מספרים אי אפש' שתהיה מבלעדי בם ההכאה ארבעה פעמים והוא שיוכו כל אחד משני המספרים הראשונים בכל אחד מהשני מספרי' האחרים ולכן תהיה ההכאה ארבעה פעמים |
|
אמ' וכאשר היו הדברים נגרעים מהמספרי' יהיה החלק הרביעי נוסף והוא והוא הכאת הדברים האחד באחר |
|
וכאשר היו האחד נוסף והאחר נגרע היה החלק הרביעי נגרע והוא הכאת הדברים האחד באחר |
|
וכאשר היו המספרי' נגרעים מהדברים יהיה החלק הרביעי נוסף והחלק הרביעי אז הוא הכאת אחד המספרי' באחר |
|
וכאשר יהיו אחד משני המספרים נוסף על הדברי' והאחר נגרע מהדברי' אז יהיה החלק הרביעי נגרע והוא הכאת אחד משני המספרי' באחר |
|
וכאשר היו הדברים נוספים על המספרים והיה מספר אחד נגרע מהדברים יהיה החלק הרביעי נגרע והוא הכאת הדברים הנוספי' במספר הנגרע |
| He said: we have already described what should be done with the fourth [interim product], since I saw that the arithmeticians start the multiplication with it. | אמ' וכבר ספרנו מה הוא הראוי עם החלק הרביעי כפי מה שראיתי שבעלי המספר מתחילי' עמו בהכאה |
The fourth [interim product] can be other than what we have described, yet the general rule is that the product of subtractives one by the other is additive [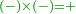 ], subtractive by additive is subtractive [ ], subtractive by additive is subtractive [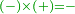 ], and additive by additive is additive [ ], and additive by additive is additive [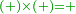 ]. ].
|
ואפשר שיהיה החלק הרביעי זולת אשר ספרנו אלא כי כלל הדבר שהכאת הנשנים האחד באחר הוא תוספת והנשנה בנוסף גורע והנוסף בנוסף יוסיף |
He said: know that the result of multiplication of things by things is a square [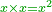 ]; and the result of things by numbers is things, which are roots, i.e. the thing is the root and the root is the thing; they are two names that denote the same meaning. ]; and the result of things by numbers is things, which are roots, i.e. the thing is the root and the root is the thing; they are two names that denote the same meaning.
|
אמ' ודע כי מהכאת הדברים בדברים יגיע מרובע ומהדברי' במספרי' יבאו דברים והם שרשים ר"ל כי הדבר הוא השרש והשרש הוא הדבר והם שני שמות נופלים על ענין אחד |
|
אמ' ואם יאמרו לך כמה יעלה מהכאת דבר אחד בעשרה דרהמי תאמ' עשרה דברי' |
|
ובאור זה שתשים הדבר בדמיון האחד ותכה אחד בעשרה ויהיה עשרה והם עשרה דברים |
|
אמ' ואם יאמרו כמה יבא מהכאת שני דברים בעשרה דרהמי תאמר עשרה דברים |
|
ובאור זה שתשים שני הדברים בדמיון שנים מהמספר ותכה שנים בעשרה ויהיו עשרים דברים |
| For any given amount things, each thing is conceived as one, then the sum of units of the things is multiplied by the number of dirham and the result are things. | וכן כמה שתניח מהדברים תשים לעולם כל דבר בדמיון האחד ותכה כל אחדי הדברי' במספר האדרהמי והעולה יהיה דברים |
| Since, for any number that is multiplied by a certain algebraic species, each unit of the species is conceived as one. | בעבור כי כל מספר מהמספרי' שיוכה במין מה מהמינים יהיה כל אחד מאחדי המין בדמיון האחד |
|
אם היה דבר אחד תשים אחד |
|
ואם היו שנים תשים שנים |
| Also if there are squares, or whichever species one wishes to multiply by numbers - the product is of that same species. | וכן אם היו מרובעים או ענין אחר אי זה שתרצה ותכהו במספרים יהיה העולה הוא מאותו המין |
| Examples: | ואניח לך תמונה על זה לבאר לך לעין מה שאמרתי |
|
אמ' ואם יאמרו לך כמה יהיה העולה מהכאת דבר בדבר תאמ' מרובע |
Conceiving the thing as one, then multiplying it by one, which is one
|
ואופנו שתשי' הדבר בדמיון האחד ותכהו באחד והוא אחד והוא מרובע |
|
ואם יאמרו כמה יעלה מהכאת שני דברים בשני דברי' תאמ' ארבעה מרובעי' כמו שבארתי לך |
|
|
וכן שלשה דברי' בשני דברים |
|
|
תכה שלשה בשנים |
|
|
ויהיו ששה מרובעים |
|
|
וכמו כן חצי דבר בחצי דבר |
|
|
יהיה העולה רביע מרובע |
| For any amount of things added or subtracted, each thing is conceived as a one, then these units are multiplied by the other units, and their product are squares. | וכן כמה שתוסיף מהדברים או תגרע תשים לעולם כל דבר בדמיון האחד ותכה אלו האחדים באחדי' האחרי' והעולה מהם יהיה מרובעים |
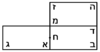
| Geometrical illustration | |
|
אמ' ואשים לך על זה תמונה אשר בה תבין משפט המרובע והדבר |
|
|
ונעמיד זה הענין בהכאת שני דברי' בשני דברים |
|
|
|
|
והוא שנניח קו א"ג שני דברי' |
|
וקו ג"ה שני דברים |
|
והכינו קו א"ג בקו ג"ה והיה שטח א"ה |
Supposition: AH□ = 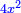
|
ונאמ' ששטח א"ה ארבעה מרובעי' |
| Proof: | מופת זה |
|
שנחלק קו א"ג על מספר מה שבו מהדברים ויהיו חלקיו א"ב ב"ג |
|
עוד נחלק קו ג"ה על מספר מה שבו מהדברי' ויהיו חלקיו ג"ד ד"ה |
|
ונוציא מנקודת ב' קו ישר על ע' על נכוחות קו ג"ה |
|
ונוציא מנקודת ד' קו נכחי לקו א"ג והוא קו ד"ח |
|
והנה נתחדשו עם זה בשטח א"ה ארבעה דברים שוים שטחים והם שטחי ח"ב ב"ד ד"ע ח"ע |
|
וכל אחד מהם מרובע |
|
וכל אחד מקוי א"ב ב"ג ג"ד ד"ה מוכה באחר הוא מרובע |
| This is the "rule of the square and the thing" | וזה הוא משפט המרובע והדבר |
|
ושטח א"ה ארבעה מרובעי' |
| Q.E.D. | והוא מש"ל |
|
אמ' ואם יאמרו לך כמה יעלה מהכאת שלשה דברי' בששה דרהמי |
|
תשים שלשת הדברי' בדמיון שלשה ותכה שלשה בששה ויהיה שמנה עשר והם שמנה עשר דברים |
|
|
|
|
המשל שנניח קו א"ב ששה מהמספרים |
|
וקו ב"ד שלש' דברי' |
|
ונכה קו א"ב בב"ד והוי והיה שטח א"ד ונאמ' ששטח א"ד הוא שמנה עשר דברים |
| Proof | ומופת זה |
|
שנחלק קו א"ב על מה שבו מהאחדים ויצאו ששה חלקים והם א"ג ג"ה ה"ו ו"ז ז"ח ח"ב |
|
ונחלק קו ד"ב על מספר מה שבו מהדברים ויהיו חלקיו ב"ט ט"כ כ"ד |
|
ונוציא מנקוד' גהוז"ח קוים נכחיים לקו ב"ד והם קוי ח"ל ז"ח ו"נ ה"פ ג"ע |
|
נוציא מנקודות ט"כ שני קוים נכחיי' לקו א"ב והם קוי ט"ק כ"ס |
|
ועם זה יצאו בשטח א"ד שמנה עשר שטחים שוים כמו שנגלה בתמונה כל שטח מהם שוה לשטח ח"ט |
|
אבל שטח ח"ט הוא מהכאת קו ב"ט שהוא דבר בקו ב"ח |
|
ולכן יהיה שטח ח"ט דבר |
|
ושטח א"ד כלו יהיה שמנה עשר דברים |
| This is the "rule of the multiplication of the things by numbers" | וזהו משפט הכאת הדברים במספרים |
|
|
אמ' ואם יאמרו לך כמה יהיה מהכאת עשרה דרהמי ודבר בדבר אחד |
|
|
תאמ' שהם עשרה דברים ומרובע |
|
והמעשה בזה שתכה דבר בעשרה אדרהמי ויהיו עשרה דברים |
|
|
עוד תכה דבר בדבר ויהיה מרובע |
|
|
ותקבצם ויהיו עשרה דברים ואלגו ומרובע אחד |
| Geometrical illustration | |
| I will explain this to you by this geometric illustration: | ואבאר לך בזאת התמונה |
|
|
|
|
והוא שנניח קו א"ב עשרה דרהמי |
|
וקו ב"ג דבר אחד |
|
ונשים ג"ד שוה לב"ג |
|
ונכה א"ג בב"ג ויצא שטח א"ד |
Supposition: AD□ = 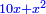
|
ונאמר ששטח א"ד עשרה דברים ומרובע אחד |
| Proof: | מופת זה |
|
שנוציא מנקודת ב' קו ב"ה נכחי לקו ג"ד |
|
ומפני זה יהיה שוה לו וגם לב"ג השוה לג"ד |
|
אבל קו ב"ג דבר אחד |
|
אם כן קו ב"ה דבר אחד |
|
ושטח א"ה יהיה עשרה דברים |
|
מפני כי הוא מהכאת קו א"ב שהוא עשרה דרהמי בקו ב"ה שהוא דבר |
|
ושטח ב"ד הוא מרובע |
|
כי הוא מהכאת ב ב"ג שהוא דבר בעצמו |
|
אם כן שטח א"ד כלו הוא עשרה [ |
| Q.E.D. | והוא מה שרצינו לבאר |
|
|
אמ' ואם יאמרו לך כמה יעלה מהכאת עשרה דרהמי פחות דבר אחד בדבר אחד |
|
|
תאמ' עשרה דברים פחות מרובע אחד |
| The procedure:
|
[12]והמעשה בזה שתכה עשרה דרהמי בדבר ויהיו עשרה דברי' |
|
|
ותכה דבר בדבר ויהיה מרובע |
|
|
תגרעהו מעשרה הדברי' וישאר ארבעה דברים פחות מרובע |
| Geometrical illustration | |
| I will explain this by this geometric illustration: | ואבאר זה בזאת התמונה |
|
|
|
|
והוא שנניח קו א"ג הוא עשרה דרהמי |
|
ונניח קו ב"ג ממנו הוא דבר א' |
|
וישאר קו א"ב עשרה דרהמי פחות דבר |
|
ונשים קו ג"ד שוה לקו ב"ג |
|
ונכה קו א"ג בקו ג"ד ויצא שטח א"ד |
|
ונוציא מנקדת ב' קו ב"ה נכחי לקו ג"ד |
Supposition: AH□ = 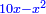
|
ונאמ' כי שטח א"ה הוא עשרה דברי' פחות מרובע |
| Proof: | מופת זה |
|
כי הנה שטח א"ד הוא עשרה דברי' |
|
בעבור כי הוא מהכאת קו א"ג שהוא עשרה בקו ג"ד השוה לב"ג שהוא דבר |
|
ושטח ב"ד הוא מרובע כי הנה הוא מהכאת ב"ג שהוא דבר בקו ג"ד השוה אליו |
|
ולכן ישאר שטח א"ה עשרה דברי' פחות מרובע והוא מהכאת א"ב שהוא עשרה דרהמי פחות דבר בב"ה שהוא דבר |
| Q.E.D. | ומש"ל |
|
|
אמר ואם יאמרו לך כמה יעלה מהכאת עשרה דרהמי ודבר בעשרה דרהמי ודבר |
|
|
תאמ' מאה דרהמי ומרובע ועשרי' דברי' |
| The procedure:
|
והמעשה[13] בזה שנכה עשרה בעשרה ויהיו מאה דרהמי |
|
|
עוד תכה עשרה בדבר ויהיו עשרה דברים |
|
|
ותשוב ותכה דבר בעשרה דרהמי ויהיו עשרה דברים |
|
|
ותכה עוד דבר בדבר ויהיו מרובע |
|
|
ותקבץ הכל יחד ויהיה מאה דרהמי ומרובע ועשרים דברים |
| Geometrical illustration | |
| I will explain this by this geometric illustration: | ואבאר זה בזאת התמונה |
|
|
|
|
והוא שנניח קו א"ב עשרה דרהמי ודבר |
|
וא"ג ממנו עשרה |
|
וג"ב דבר |
|
וכן נניח קו ב"ד עשרה דרהמי ודבר |
|
ב"ה ממנו דבר |
|
וה"ד עשרה |
|
ותכה קו א"ב בקו ב"ד ויצא שטח א"ד |
Supposition: AD□ = 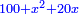
|
ונאמ' כי שטח א"ד מאה דרהמי ומרובע ועשרים דברים |
| Proof: | ומופת זה |
|
שנוציא מנקודת ג' קו נכחי לקו ב"ד והוא קו ג"ח |
|
ונוציא מנקודת ה' קו ה"ז נכחי לקו א"ב |
|
הנה שטח ג"ה מרובע |
|
וז"ח מרובע |
|
ושטח ג"ז כמו שטח ה"ח |
|
כמו שאבאר כל זה באקלידס |
|
אבל שטח ז"ח מאה |
|
כי הוא הוה מהכאת ז"ט השוה לא"ג שהוא עשרה בקו ט"ח השוה לה"ד שהוא גם כן עשרה |
|
ושטח ז"ג עשרה דברים |
|
כי הנה הוא מהכאת ג"ט השוה לב"ה שהוא דבר בקו א"ג שהוא עשרה |
|
ושטח ח"ה גם כן עשרה דברי' |
|
כי הוא מהכאת ט"ה השוה לג"ב שהוא דבר בקו ה"ד שהוא עשרה |
|
ושטח ג"ה הוא מרובע כי הוא מהכאת קו ג"ב שהוא דבר בקו ב"ה שהוא גם כן דבר |
|
ומקובץ הארבעה שטחים הוא שטח א"ד אם כן שטח א"ד הוא מאה דרהמי ומרובע ועשרים דברים |
| Q.E.D. | והוא מש"ל |
|
|
אמ' ואם יאמרו לך כמה יהיה מהכאת עשרה אדרהמי פחות דבר בעשרה אדרהמי פחות דבר |
|
|
תאמ' מאה דרהמי ומרובע פחות עשרים דברים |
| The procedure:
|
ואופן מעשהו שתכה עשרה דרהמי בעשרה דרהמי ויהיה מאה |
|
|
תכה דבר נגרע בעשרה דרהמי ויהיה עשרה דברים נגרעים |
|
|
עוד תשוב להכות עשרה דרהמי בדבר הנגרע ויהיו גם כן עשרה דברים נגרעים |
|
|
ותכה דבר נגרע בדבר נגרע ויהיה מרובע נוסף |
|
|
ותקבץ כל זה ויהיה מאה דרהמי ומרובע פחות עשרים דברים |
| Geometrical illustration | |
| I will explain this by this geometric illustration: | ואבאר זה בזאת התמונה |
|
|
|
|
והוא שנשים קו א"ג עשרה דרהמי |
|
ונפחות ממנו דבר והוא קו ב"ג וישאר א"ב עשרה פחות דבר |
|
וכן נשים קו ג"ד עשרה |
|
וג"ה ממנו הוא דבר |
|
ונכה קו א"ב בקו ה"ד ויעלה מרובע ז"ח |
Supposition: ZC□ = 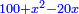
|
ונאמ' שמרובע ז"ח מאה אדרהמי ומרובע פחות עשרים דברים |
| Proof: | מופת זה |
|
שנשלים שטח א"ד |
|
ונוציא מנקוד' ב' קו ב"ח נכחי לקו ב"ד |
|
ונוציא מנקודת ה' קו ה"ז נכחי לקו א"ג |
|
הנה כי שטח א"ד מאה |
|
בעבור כי א"ג עשרה |
|
וג"ד עשרה |
|
ושטח ז"ג עשרה דברים |
|
בעבור כי א"ג עשרה |
|
וג"ה הוא דבר |
|
וכן שטח ב"ד עשרה דברים |
|
בעבור כי ג"ד עשרה |
|
וג"ב הוא דבר |
|
ושטח ב"ה הוא מרובע |
|
כי הוא מהכאת ב"ג שהוא דבר בג"ה שהוא גם כן דבר |
|
וישאר שטח ה"ח עשרה דברים פחות מרובע |
|
ושטח א"ה עשרה דברים |
|
ומקובצם עשרים דברים פחות מרובע |
|
וכשנגרעם שטח א"ה ושטח ה"ח משטח א"ד שהוא מאה ישאר שטח ז"ח מאה דרהמי ומרובע פחות עשרים דברים |
|
|
אמ' ואם יאמרו לך כמה יעלה מהכאת עשרה דרהמי ודבר בעשרה דרהמי פחות דבר |
|
|
תאמ' מאה דרהמי פחות מרובע |
| The procedure:
|
ואופן מעשהו שתכה עשרה בעשרה ויהיו מאה דרהמי |
|
|
ותכה הדבר הנוסף בעשרה ויהיו עשרה דברים נוספי' |
|
|
ותכה הדבר הגורע בעשרה ויהיו עשרה דברים נגרעים |
|
|
ותוציא הנוספים כנגד הנגרעים וישארו מאה דרהמי |
|
|
עוד תכה הדבר הנוסף בדבר הגורע ויהיה מרובע נגרע |
|
|
ותגרעהו מהמאה דרהמי וישארו מאה פחות מרובע |
| Geometrical illustration | |
| I will explain this to you by this geometric illustration: | ואבאר לך זה בזאת התמונה |
|
|
|
|
והוא שנניח קו א"ב עשרה ודבר |
|
א"ג עשרה |
|
וג"ב דבר |
|
ונניח קו ב"ה עשרה פחות דבר |
|
ונדביק עמו קו ה"ד הוא דבר ויהיה קו ב"ד כלו עשרה דרהמי |
|
ונכה קו א"ב שהוא עשרה דרהממי ודבר בקו ב"ה שהוא עשרה פחות דבר ויהיה שטח א"ה |
Supposition: AH□ = 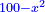
|
ונאמר ששטח א"ה הוא מאה דרהמי פחות מרובע |
| Proof: | ומופת זה |
|
שנשלם שטח א"ד והנה הוא מאה דרהמי ועשרה דברים |
|
בעבור כי שטח א"ח ממנו הוא מאה |
|
כי הנה הוא מהכאת א"ג שהוא עשרה בג"ח שהוא גם כן עשרה כי הוא שוה לב"ד שהנחנוהו עשרה |
|
ושטח ג"ד הנשאר הוא עשרה דברי' |
|
כי הנה הוא מהכאת ג"ד כי שהוא דבר בב"ד שהוא עשרה |
|
הנה כי כל שטח א"ד הוא מאה דרהמי ועשרה דברים |
|
והוא מבואר בנקלה למבין כי שטח ז"ח כמו שטח ח"ב |
|
ונבדיל משטח ז"ח כמו שטח מ"ד המרובע והוא שטח מ"[ב] |
|
ויהיה מפני זה שטח כ"ד שנים מרובעי' |
|
וישאר שטח ז"ט כמו שטח מ"ב |
|
ונשים שטח א"מ משותף |
|
ויהיה שטח א"מ ושטח מ"ב יחד והוא כל שטח א"ה יהיה שוה לשטחי א"מ ז"ט |
|
אבל שני שטחי א"מ ז"ט אתה רואה כי הם מאה דרהמי פחות מרובע |
|
בעבור כי שטח מ"ט הנחסר הוא מרובע |
|
אם כן שטח א"ה יהיה מאה דרהמי פחות מרובע |
| Q.E.D. | והוא מש"ל |
|
|
אמ' ואם יאמרו לך כמה העולה מהכאת עשרה דרהמי ודבר בדבר פחות עשרה דרהמי |
|
|
תאמ' מרובע פחות מאה דרהמי |
| The procedure:
|
ואופן מעשהו הוא שנכה עשרה בדבר הפוחת עשרה ויהיו עשרה דברים נוספים |
|
|
עוד תשוב ותכה עשרה בעשרה הפוחתים ויהיו מאה דרהמי גורעי' |
|
|
ותכה דבר בדבר ויהיה מרובע |
|
|
עוד תכה דבר בעשרה הפוחתים ויהיו עשרה דברי' נגרעים |
|
|
ותשליך העשרה דברי' נוספי' כנגד העשרה הדברים הנגרעים |
|
|
וישאר המקובץ מההכאה מרובע פחות מאה דרהמי |
| Geometrical illustration | |
| I will explain this by this geometric illustration: | ואבאר זה בזאת התמונה |
|
|
|
|
והוא שנשים קו א"ב עשרה דרהמי ודבר |
|
א"ג הוא עשרה |
|
וג"ב דבר |
|
ונניח קו ב"ה דבר פחות עשרה |
|
ונוסיף בו ה"ד שהוא עשרה |
|
ונכה קו א"ב בקו ב"ה ויהיה שטח א"ה |
|
ונאמ' ששטח א"ה הוא מרובע פחות מאה דרהמי |
|
מופת זה שנשלים שטח א"ד ויהיה שטח א"ד עשרה דברים ומרובע בעבור כי הוא מהכאת קו א"ב שהוא עשרה דרהמי ודבר בקו ב"ד שהוא דבר |
|
ונוציא קו ג"ח נכחי לקו ב"ד |
|
והנה יהיה שטח ג"ד מרובע כי הוא מהכאת ג"ב שהוא דבר בב"ד שהוא גם כן דבר |
|
ושטח א"ח כמו שטח ח"ה |
|
בעבור כי קו ח"ג כמו קו ח"ד |
|
וקו א"ג כמו קו ה"ד |
|
ונבדיל שטח ח"ה ממרובע ג"ד ונשתף עמו שטח א"ח השוה לו ויהיה שטח ג"ה הנשאר ממרובע ג"ד ושטח א"ח יחד כמו מרובע ג"ד |
|
ונבדיל מזה שטח כ"ח שהוא מאה דרהמי בעבור כי הוא מהכאת קו כ"ל השוה לא"ג שהוא עשרה בקו ל"ח השוה לה"ד שהוא גם כן עשרה |
|
וישאר שטח א"ה מרובע פחות מאה דרהמי |
|
והוא מש"ל |
|
אמר ואם יאמרו לך כמה יהיה מהכאת עשרה דרהמי ושני שלישי דבר על שלשה דרהמי פחות ששה דברים |
|
|
תאמר שלשים דרהמי פחות ארבעה מרובעים ופחות חמשים ושמנה דברים |
| The procedure:
|
ואופן מעשהו הוא שתכה עשרה דרהמי בשלשה ויהיו שלשים דרהמי |
|
|
ותכה שני שלישי דבר בשלשה דרהמי ויהיו שני דברים נוספים |
|
|
עוד תכה עשרה אדרהמי בששה דברי' הפוחתים ויהיו ששים דברים נגרעים |
|
|
ותכה שני שלישי דבר בששה דברים הפוחתים ויהיו ארבעה דברים נגרעים מרובעים |
|
ונשלמה ההכאה ונבא לקבצם |
|
|
והנה נפיל שני הדברים הנוספים מהששים דברי' הנגרעי' וישארו שמנה וחמשי' |
|
|
ויהיה מקובץ הכל אחר זה שלשים דרהמי פחות ארבעה מרובעי' ופחות שמנה וחמשי' דברים |
| The explanation of the multiplication of things and numbers is enough, and from it one can learn the answer for all the questions presented in this section. | אמ' ודי לך במה שבארתי מכפל הדברים והמספרים וממנו תוכל להתחכם בתשובת כל השאלות אשר יגיעו לפניך מזה השער |
Roots |
|
Chapter: Multiplication of Roots by Numbers |
פרק |
| The doubling of the root of a known number or of an unknown square will be explained in it. | יתבאר בו הכפלת שרש ממספר ידוע או ממרובע בלתי ידוע זה |
| By doubling I mean taking its two roots | ורצוני בהכפלה הנה לקיחת שני שרשיו |
| He said: when you wish to know two roots of a known number or of an unknown square - the root of which number or square are they? | אמ' וכאשר תרצה לדעת שני שרשים ממספר ידוע או ממרובע בלתי ידוע לאי זה מספר אחר או מרובע אחר הם שרש |
| Consider the two roots as two and multiply two by two, then multiply the product by the known number, or by the unknown square; they are a root of the number resulting.
|
תניח השני שרשים בדמיון שנים ותכה שנים על שנים והעולה תכהו במספר הידוע או במרובע הבלתי ידוע והעולה הוא המספר שהם שרש אליו |
| If you want three roots, multiply three by three, then multiply the product by the known number, or by the unknown square; the three roots are a root of the resulting number.
|
ואם תרצה שלשה שרשים תכה שלשה בשלשה והעולה תכה על המספר הידוע או על המרובע בלתי ידוע ויהיו שלשת השרשים שרש למספר העולה |
| Likewise if you wish to halve the root: | וכן אם תרצה לחצות השרש |
| Multiply half by half; it is a quarter. Multiply the quarter by the known or unknown number; half the root is a root of the resulting product.
|
תכה חצי בחצי ויהיה רביע ותכה רביע במרובע הידוע או הבלתי ידוע ויהיה העולה מההכאה הנה חצי השרש הוא שרש לו |
| And so on, as you increase or decrease the roots, do according to the procedure we specified. | וכן כל מה שתוסיף או תגרע מהשרשים תעשה על הדרך שאמרנו |
|
אמ' ונניח דמיון לזה כאשר |
|
תכה שנים בשנים והיו ארבעה |
|
ותכה ארבעה בששה עשר ויהיו ששים וארבע' |
|
ושרשו הוא שמנה והם שני שרשי ששה עשר |
| Geometrical illustration | |
|
ונבאר זה בתמונ' זאת |
|
|
|
|
והוא שנניח שטח מרובע אבג"ד בדמיון ששה עשר דרהמי |
|
וקו ג"ד הוא שרש מרובע אבג"ד |
|
וכאשר נרצה לכפול זה השרש נוציא קו ג"ד על יושר עד ה' |
|
ונשים ג"ה שוה לג"ד |
|
ויהיה קו ה"ד שני שרשים ממרובע א"ד |
|
ואם נרצה לדעת לאי זה מספר הוא שרש |
|
נשים עליו שטח מרובע עליו ה"ז |
|
ונאמר ששטח ה"ז ארבעה דמיוני שטח ג"ב |
| The proof: | מופת זה |
|
שנוציא קו ג"א על יושר עד ח' |
|
ונוציא קו א"ב עד נקודת ט' |
|
ויהיו בשטח ה"ז [14]ארבעה מרובעים שוים והם מרובעי ג"ב ב"ח ח"ט ט"ג |
|
אבל ג"ב הנחנוהו שש עשרה |
|
ולכן יהיה מרובע ה"ז ששים וארבע |
|
ויהיה קו ה"ד שרש לששים וארבע והוא שמנה |
|
והוא מש"ל |
|
אמ' וכאשר נרצה לקחת חצי שרש תשעה |
|
נכה חצי בחצי ויהיה רביע |
|
ונכה רביע בתשעה ויהיה שנים ורביע |
|
נקח שרשו והוא אחד וחצי והוא יהיה חצי שרש תשעה |
|
ואם נרצה לקחת שני שלישי שרש תשעה |
|
נכה שני שלישים בשני שלישים ויהיו ארבע תשיעיות |
|
ותכה ארבעה תשיעיות בתשעה ויהיו ארבעה |
|
ושרשם שהוא שנים הוא יהיה שני שלישי שרש תשעה |
| Geometrical illustration | |
|
ואבאר לך בזאת התמונה |
|
|
|
|
והוא שנניח התשעה שטח מרובע עליו אבג"ד |
|
ויהיה קו ג"ד שרש תשעה |
|
וכאשר תרצה לקחת שני שלישיו |
|
תחלק קו ג"ד לשלשה חלקים שוים והם נ"ז ז"ה ה"ד |
|
ויהיה קו ד"ז שני שלישי קו ג"ד והוא גם כן שני שלישי שרש מרובע ג"ב |
|
וכאשר תרצה לדעת לאי זה שמספר הוא שרש |
|
נעשה על קו ז"ד שטח מרובע עליו כזל"ד |
|
ונאמ' ששטח כזל"ד ארבעה תשיעיות שטח ג"ד והם ארבעה דרהמי |
| The proof: | מופת זה |
|
שנוציא קו ז"כ על יושר עד נקודת ט' |
|
ונוציא מנקודת ה' קו ה"ח נכחי לקו ב"ד |
|
ותוציא מע' קו ע"פ נכחי לקו א"ב |
|
ונוציא קו למ"כ עד ס' |
|
ויהיה עם זה כבר נעשו בשטח ג"ב תשעה שטחים שוים והם |
|
ויהיה שטח ז"ל ארבעה מאלו התשעה שטחים אם כן שטח ז"ל ארבע תשיעיות מרובע ג"ב |
|
וקו ז"ד שרש לארבעה |
|
והוא מש"ל |
| Do the same with all that falls into your hand of this kind. | וכל מה שיפול בידך מזה המין תעשה עמו ככה |
Multiplication of Roots |
|
|
אמ' ואם תרצה לדעת כמה העולה מהכאת שרש תשעה בשרש ארבעה |
|
תכה ארבע' בתשעה ויהיה שלשים ושש |
|
תקח שרשם והוא ששה והוא כמו הכאת שרש תשעה בשרש ארבעה |
| Geometrical illustration | |
|
ואבאר זה בזאת התמונה |
|
|
|
|
והוא שנשים קו א"ב שרש תשעה |
|
וקו ב"ג שרש ארבעה |
|
וכאשר נרצה להכות קו א"ב בקו ב"ג |
|
תשים על קו א"ג שטח מרובע עליו א"ח |
|
ותוציא מנקודת ב' קו נכחי לקוי א"ה ג"ח והוא קו ב"ז |
|
וכל אחד מקוי א"ה ג"ח שרש תשעה ושרש ארבעה |
|
ונשים קו מ"ג שרש תשעה |
|
וישאר קו מ"ח שרש ארבעה |
|
ונוציא מנקודת מ' קו מ"כ נכחי לקוי |
|
ויהיה שטח ע"מ תשעה |
|
וקו ב"ע שרש תשעה |
|
ושטח ע"ח ארבעה |
|
וקו ז"ע שרש ארבעה |
|
כי ז"ע שוה לע"מ וע"מ כמו ב"ג |
|
וע"ב כמו ע"כ |
|
ויחס מ"ע אל ע"כ כיחס ז"ע אל ע"ב |
|
ויחס ז"ע אל ע"ב הוא כיחס שטח ז"כ אל שטח ע"א |
|
ולכן יהיה הכאת המספרים אשר בשטח ז"מ במספרים אשר בשטח ע"א כמו הכאת המספרים אשר בשטח ז"כ בעצמם |
| As Euclid has explained when he said that when there are three proportional numbers, the product of the first number by the third is the same as the product of the second by itself.
|
כמו שבאר זה אקלידס כאשר אמ' כי כאשר היו שלשה מספרים מתיחסים יהיה הכאת המספר הראשון |
|
אבל הכאת מה שבשטח ע"ח [15]מהאחדים שהם ארבעה באחדי שטח ע"א שהם |
|
ולכן שטח ז"כ הוא כמו שרש שלשים ושש והוא ששה והנה שהוא הוה מהכאת שרש תשעה בשרש ארבעה בעבור כי קו |
|
והוא ומש"ל[16] |
|
אמ' ואם יאמרו לך כמה יהיה מהכאת שני שרשי עשרה בחצי שרש חמשה |
|
ראה שני שרשי עשרה לאי זה מספר הם שרש על הדרך שהראיתי לך |
|
ותמצא שהם שרש לארבעי' |
|
וכמו כן ראה חצי שרש חמשה לאי זה מספר הוא שרש |
|
ותמצא שהוא שרש לאחד ורביע |
|
ותשוב השאלה כאלו אמרו כמה יהיה מהכאת שרש ארבעים בשרש אחד ורביע |
|
ולכן תכה ארבעים באחד ורביע ויהיה חמשים |
|
ותאמ' כי שרש חמשים הוא הוא הכאת שני שרשי עשרה בחצי שרש חמשה |
| Geometrical illustration | |
| He said: we give for this procedure a general geometric illustration: | אמ' ונניח לזה המעשה תמונה כוללת |
|
|
|
| We say that for every number multiplied by another number, the root of the product is the same as the product of the root of one of the numbers multiplied by the root of the other number.
|
ונאמ' שכל מספר שיוכה במספר אחר יהיה שרש העולה כמו הכאת שרש מספר אחד מהם לשרש המספר האחר |
|
משל לזה שנניח ב' א' שני מספרים |
|
ושרש ב' הוא ג' |
|
ושרש א' הוא ד' |
|
ונכה ב' בא' ויהיה ז' |
|
ונכה ג' בד' ויהיה ח' |
|
ונאמ' שח' כמו ה' שהוא שרש ז' |
| The proof: | מופת זה |
|
כי ג' הוכה בעצמו והיה ב' |
|
והוכה ב |
|
ולכן יהיה יחס ג' אל ד' כיחס ב' אל ח'[17] |
|
וכמו כן ד' הוכה בעצמו וה |
|
והוכה בג' והיה ח' |
|
ולכן יהיה יחס ג' אל ד' כיחס ח' אל א' |
|
וכבר היה יחס ג' אל ד' כיחס ב' אל ח' |
|
אם כן יהיה יחס ב' אל ח' כיחס ח' אל א' |
|
ויהיה מפני זה הכאת ב' בא' כמו הכאת ח' בעצמו |
|
אבל הכאת ב' בא' הוא ז' |
|
אם כן הכאת ח' בעצמו יהיה כמו ז' |
|
וכבר היה הכאת ה' בעצמו הוא ז' |
|
ולכן יהיה ח' כמו ה' |
|
והוא מש"ל |
| What I have explained of this type is enough. | ובמה שבארתי מזה המין הוא מספיק |
Chapter on Division of Roots |
פרק בחלוק |
| He said: you must also know that when you multiply the divisor by the result of division, the dividend returns.
|
אמ' וגם כן ראוי שתדע כי כאשר תכה המחלק במה שעלה לחלק ישוב המספר שחלקת |
|
משל זה חלקנו עשרה על שנים ויצא לכל חלק חמשה |
|
הנה כאשר הכינו שנים בחמשה יהיה עשרה והוא המספר שנחלק |
| Geometrical illustration | |
| He said: we give for this procedure a general geometric illustration also: | אמ' ונשים לזה המעשה גם כן תמונה כוללת |
|
|
|
| We say that for every number divided by another number, the product of the quotient by the divisor is the same as the dividend.
|
ונאמ' כי כל מספר שיהיה נחלק על מספר אחר יהיה הכאת העולה לכל חלק במספר המחלק כמו המספר הנחלק |
|
משל זה שחלקנו מספר א' על מספר ב' ועלה לכל חלק ג' |
|
ונאמ' שהכאת ב' בג' הוא כמו א' |
| The proof: | מופת זה |
|
כי א' כבר נחלק על ב' והיה ג' ולכן יהיו מדמיוני ג' בא' כמספר מה שבב' מן האחדים |
|
ומפני זה יהיה יחס ג' אל א' כיחס האחד אל ב' |
|
ולכן יהיה מהכאת ב' בג' כמו הכאת האחד בא' אבל הכאת האחד בא' הוא אם כן הכאת ב' בג' הוא גם כן א' |
|
והוא מה שרצינו לבאר |
|
[18]אמ' ואם יאמרו לך תחלק שרש תשעה על שרש ארבעה |
|
הנה תחלק תשעה על ארבעה ויגיע לכל חלק שנים ורביע |
|
תקח שרשו והוא אחד וחצי וככה הוא שרש תשעה מחולק על שרש ארבעה |
|
ואם אמרו תחלק שרש עשרה על שרש שנים |
|
ויגיע לחלק חמשה וקח שרשו |
|
ואם אמר לך תחלק שנים שרשים מעשרים על שרשים שלשה מששה |
|
תחפש שני שרשים מעשרים לאי זה מספר הם שרש |
|
וידענו ממה שבארנו שהם שרש לשמונים |
|
ותחפש כמו כן שלשה שרשים מששה לאי זה מספר הם שרש |
|
והנה הם שרש לחמשים וארבעה |
|
ויהיה כאלו שאל לחלק שרש שמנים על שרש ארבעה וחמשים |
|
והנה נחלק שמנים על ארבעה וחמשים ויעלה אל החלק אחד שלם וארבעה תשיעיות ושלישית התשיעית |
|
ושרש זה הוא העולה אל החלק מחלוקת שני שרשים מעשרים על שלשה שרשים מעשרים על שלשה שרשים מששה |
| Proceed with all that is of this kind as in this procedure. | וכמו כן כל אשר יגיע בידך מזה המין תעשה עמו כמעשה הזה |
| Geometrical illustration | |
| He said: we give for this type also a general geometric illustration: | אמ' ונניח גם כן לזה המין תמונה כוללת |
| We say that for every two numbers, one of which is divided by the other, the root of the quotient is the same as the quotient of the root of the dividend divided by the root of the divisor.
|
ונאמ' כי כל שני מספרים שיחלק אחד מהם על האחר יהיה שרש העולה לחלק כמו העולה מחלוקת שרש המספר הנחלק בשרש המספר המחלק |
|
|
|
|
משל שמספר א' נחלק על |
|
ושרש א' שהוא מספר ח' נחלק על שרש ב' שהוא מספר ד' ועלה לחלק מספר ע' |
|
ונאמ' שע' הוא כמו שרש ג' |
| The Proof: | המופת בזה |
|
שנכה ע' בעצמו והיה מ' |
|
הנה א' נחלק על ב' והיה ג' |
|
ולכן מהכאת ב' בג' ישוב ד' |
|
וכמו כן ד' הוכה בע' והיה ח' |
|
וכבר הוכה ד' בעצמו והיה ב' |
|
ולכן יהיה יחס ד' אל ע' כב' אל ח' |
|
וע' הוכה בעצמו והיה מ' |
|
והוכה בד' והיה ח' |
|
ולכן יהיה יחס ד' אל ע' כיחס ח' אל מ' |
|
וכבר היה יחס ב' אל ח' גם כן כד' אל ע' |
|
ולכן יהיה יחס ב' אל ח' כח' אל מ' |
|
והכאת ב' במ' תהיה כמו הכאת ח' בעצמו |
|
אבל הכאת ח' בעצמו היא א' |
|
ולכן הכאת ב' במ' היא גם כן א' |
|
וכבר הוכה ב' גם כן בג' והיה כמו כן א' |
|
אם כן מ' הוא שוה לג' |
|
אבל ע' היה שרש למ' |
|
ולכן יהיה גם כן ע' שרש לג' |
|
והוא מש"ל |
Chapter on the Addition of the Roots one the the other and Their Subtraction |
פרק בחבור השרשים האחד עם האחר ובגרעונם |
Addition of Roots |
|
| He said: when you wish to add a root of a number to a root of another number so that a root of a certain square is summed from them: | אמ' כאשר תרצה לחבר שרש מספר מהמספרי' עם שרש מספר אחר עד שיקובץ מהם שרש מרובע מה |
| This cannot be done with every number, but it is possible for two [perfect] square numbers, i.e. numbers that have a root; or for two numbers, such that when one [of them] is divided by the other, the quotient has a root, and when one [of them] is multiplied by the other, the product has a root. | הנה לא יהיה נכון לעשות זה בכל מספר אבל יתכן זה בשני מספרי' מרובעי' רצו' שיחזיקו שרש או בשני מספרים שכאשר נחלק האחד על האחר יהיה לאשר עלה אל החלק שרש וכאשר תכה האחד באחר היה אל המקובץ שרש |
| For numbers other than these it is not possible that you sum their two roots to a single root. | ובמספרי' אחרים זולת אלו אי אפש' שתחבר שני שרשיהם עד שתשיבם שרש אחד |
| The same property is found in the subtraction of roots one from the other. | וכמו כן הענין בגרעון השרשים האחד מהאחר |
| This is especially clear when both numbers are [perfect] squares. | ואלו יהיו מאד [19]מבוארים כאשר יהיו שני המספרים מרובעי' |
|
כאלו תאמ' תשעה וארבעה ורצינו לחבר שרשיהם עד שיהיו שרש למספר אחד |
|
תחבר תשעה וארבעה ויהיו שלשה ותשמרם |
|
ותכה תשעה בארבעה ויהיו שלשים ושש |
|
ותקח שני שרשיו והם שתיים עשרה |
|
תחברם עם השמור ויהיו עשרים וחמשה והם כמו שרש תשעה ושרש ארבעה מקובצים |
| Geometrical illustration | |
|
אמ' ואבאר זה בזאת התמונה |
|
|
|
|
והוא שנניח קו א"ב שרש לתשעה |
|
וקו א"ג שרש לארבעה |
|
ונרצה שנדע קו ג"ב שרש לאי זה מספר הוא |
|
נעשה על קו ג"ב שטח מרובע עליו ג"ז |
|
ונעשה על קו א"ב שטח מרובע עליו אבכ"ל |
|
ונוציא קו א"כ על יושר עד נקודת ח' |
|
וכמו כן נוציא קו ל"כ עד נקודת ע' |
|
הנה שטח כ"ב הוא תשעה |
|
בעבור כי היה קו א"ב שרש לתשעה |
|
ושטח ע"ח הוא ארבעה |
|
בעבור כי קו ע"ב שהוא צלעו הוא שוה לא"ג שהנחנוהו שרש לארבעה |
|
ושטח א"ע הוא תשע' |
|
כי הנה הוא מהכאת קו א"ב שהוא כמו שרש תשעה בקו א"ג שהוא שרש לארבעה ולכן הנה הוא ששה ממה שבארנו למעלה בפרק הכאת שרש בשרש |
|
וכמו כן יהיה שטח ל"ח גם כן ששה |
|
ומקובץ כל אלו הארבעה שטחי' הנה הוא עשרים וחמשה והם כל שטח ג"ז |
|
וקו ב"ג שהוא שרשו יהיה חמשה |
|
והוא מש"ל |
Subtraction of Roots |
|
|
אמ' וכאשר תרצה לגרוע שרש ארבעה משרש |
|
תחבר התשעה עם הארבעה ויהיו שלשה עשר ותשמרם |
|
ותכה תשעה וארבעה ויהיו שלשים ושש |
|
ותקח שני שרשיו והם שנים עשר |
|
ותגרעם מהשמור וישאר אחד |
|
ושרש האחד הוא יהיה הנשאר מהשרש תשעה בגרעך ממנו שרש ארבעה והוא אחד |
| Geometrical illustration | |
|
ואבאר לך זה בזאת התמונ' |
|
|
|
|
נניח קו א"ב שרש לתשעה |
|
וקו א"ג שרש לארבעה |
|
וכאשר נגרע קו א"ג מקו א"ב ישאר קו ג"ב |
|
ורצינו לדעת מספר קו ג"ב לאי זה מספר הוא שרש |
|
נשים על קו א"ב שטח מרובע עליו א"ז |
|
ויהיה שטח א"ז תשעה |
|
ונעשה על קו א"ג שטח מרובע עליו א"מ |
|
ויהיה שטח א"מ ארבעה |
|
ותוציא קוי ג"מ וח"מ על יושר עד שתי נקודות נ' וכ' |
|
הנה הוא ידוע כי מרובע מ"ז הוא כמו הכאת קו ג"ב בעצמו |
|
בעבור כי |
|
ושטח ח"כ הוא שנים |
|
בעבור כי היה כל שטח א"כ ששה מפני כי הוא מהכאת קו א"ג שהוא שרש לארבעה בקו א"ה שהוא שרש לתשעה |
|
ושטח א"מ היה ארבעה |
|
ולזה ישאר שטח ח"כ שנים |
|
וכמו כן יהיה שטח מ"ב שנים |
|
הנה כי מקובץ שלשה שטחי ח"כ מ"ב א"מ הוא שמנה |
|
אבל כל שטח א"ז היה תשעה |
|
הנה כי ישאר שטח מ"ז אחד |
|
וקו מ"נ השוה לקו ג"ב הוא שרשו והוא אחד |
|
והוא מש"ל |
|
[20]אמר ואם רצינו לחבר שרש שמנה עשר עם שרש שמנה עד שיהיו שרש למספר אחד |
|
הנה ידענו כי חבורם נכון |
|
בעבור כי כאשר חלקנו שמנה עשר על שמנה יגיע לחלק שנים ורביע והם מחזיקים שרש כי שרשם הוא אחד וחצי |
|
ואם חלקנו שמנה |
|
ואם תכה שמנה עשר בשמנה יהיו קמ"ד ומחזיקים שרש ושרשם שתים עשרה |
| We already noted that for any two numbers that obey this rule, i.e. that have these three properties, we can sum up their two roots so they become a root of a single number. | וכבר אמרנו כי כל שני מספרים יהיה משפטם זה המשפט ר"ל שיסוגלו באלו השלש סגולות הנה אז יהיה נכון לנו לקבץ שני שרשיהם עד שיהיו שרש למספר אחד |
| If one of the three properties is absent, all three properties are absent. | וכאשר יבצר מהם אחת מאלו השלש סגולות יהיו שלשתם נמנעות מהן |
|
וכאשר רצינו לדעת קבוץ השני שרשים אשר אמרנו לאיזה מספר הם שרש תעשה כפי המעשה שאמרנו קודם |
|
והוא שתחבר שמנה עם שמנה עשר ויהיו ששה ועשרים ותשמרם |
|
ותכה שמנה בשמנה עשר ויעלה קמ"ד |
|
ותקח שני שרשיו והוא ארבעה ועשרים |
|
ותחברם עם השמור ויהיו חמשים |
|
ושרשו הוא כמו שרש שמנה ושרש שמנה עשר מקובצים |
|
ואם באנו לגרוע שרש שמנה משרש שמנה עשר |
|
תגרע הארבעה ועשרים מהשמור וישארו שנים ושרש שנים הוא מה שישאר משרש שמנה עשר כאשר יגרע ממנו שרש שמנה |
|
אמ' ואם רצינו לחבר שרש עשרה עם שרש שנים |
|
זה לא יתכן לחברו גם לא יתכן להיות מקובצם שרש למספר אחד |
|
כי הנה כאשר תחלק עשרה על שנים יגיע לחלק חמשה וחמשה אינם מחזיקים שרש |
|
וכאשר תחלק שנים על עשרה יגיע לחלק חומש ואין שרש לחומש |
|
וכאשר תכה שנים בעשרה יהיו עשרים ואין לעשרים שרש |
|
ואם קבצנום על הדרך האמור יהיה השרש משנים שרשים מעשרים מקובצים עם שנים עשר הוא שרש עשרה ושרש שנים מקובצים |
|
ואם גרענו האחד מהאחר על הדרך האמור יצא לנו כי שרש הנשאר משנים עשר כאשר יגרע מהם שנים שרשים מעשרים הוא כמו |
| The question is more proper than the answer. | והשאלה בזה יותר נכונה מהתשובה |
| When you are asked a question of this kind, your answer should be exactly similar to what was introduced to you. | וראוי לך כאשר ישאלו ממך אי זו השאלה מזה הסוג שתהיה תשובתך עליה על דמיון אשר יוציאו לפניך בשוה |
| Because, when it is said "the root of ten and the root of two summed together", it is more proper than saying "the root of twelve plus two roots of twenty". | כי כאשר יאמר שרש עשרה ושרש שנים מקובצי' הוא יותר נכון ממאמ' שרש שנים עשר ושני שרשים מעשרים |
| Also, for subtracting one from the other: it is more proper to say "the root of ten minus the root of two", than to say "the root of twelve minus two roots of twenty, which is the root of eighty". | וכמו כן בגרעון האחד מהאחר יותר נכון הוא לאמר שרש |
| What I have explained about it is sufficient and complete. | ודי במה שבארתי מזה ובו השלמה |
Six Problems Demonstrating the Six Canonical Equations |
[21]פרק |
| He said: I give you a question for each of the six types [of canonical equations] that we noted first, which the algebraists may have already taught you: | אמ' הנני עושה לך שאלה לכל חלק מהששה חלקים אשר הודענו ראשונה ואפש' שכבר יורוך אותם חכמי האלגבר |
|
אמ' והשאלה הראשונה היא כמו אם יאמרו לך תחלק עשרה לשני חלקים באופן שתהיה הכאת החלק הגדול בעצמו כמו פעם וחצי מהעולה מהכאת החלק האחד באחר |
|
והמעשה בזה הוא שנניח החלק הגדול דבר אחד והחלק האחר ישאר עשרה פחות דבר |
|
ונכה דבר בעשרה פחות דבר ויהיה עשרה דברים פחות מרובע |
|
ונכה החלק הגדול והוא דבר בעצמו והוא מרובע |
|
והיה זה המרובע כמו העשרה דברי' פחות מרובע וכמו חצי זה |
|
ונכה עשרה דברים פחות מרובע באחד וחצי ויעלה חמשה עשר דברים פחות מרובע וחצי והם יהיו כמו המרובע |
|
|
|
ותאסוף המרובע וחצי עם הט"ו דברים עד שיהיו חמשה עשר דברים שלמים וכמו כן תקבץ המרובע וחצי עם המרובע |
|
ואז יהיה שנים מרובעים וחצי יהיו שוים לחמשה עשר דברים |
|
|
|
והשיבם אל מרובע אחד ויהיה המרובע ישוה לששה דברים |
|
והדבר ישוה ששה והוא החלק הגדול |
|
וארבעה הנשאר מהעשרה הוא החלק הקטן |
I have shown you this problem [to demonstrate] the first of the six categories [of canonical equations], which is his saying: when the squares equal roots [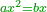 ]. ].
|
וזאת השאלה הראיתיך לחלק הראשון מהששה חלקים והוא אמרו כאשר המרובעים יהיו שוים אל השרשים |
| Geometrical illustration of the problem | |
|
אמ' ואבאר לך זאת השאלה בתמונ' גימטרית |
|
|
|
|
והוא שנניח קו א"ב עשרה |
|
ונחלק בנקודת ג' לשני חלקים בלתי שוים |
|
קו א"ג הוא החלק הגדול |
|
וקו ג"ב החלק הקטן |
|
והכינו קו א"ג בקו ב"ג והיה שטח ג"ד |
|
כי שמנו ב"ד כמו א"ג |
|
והכינו א"ג בעצמו והיה מרובע א"ה |
|
ונניח כי יהיה שטח מרובע א"ה כמו שטח ג"ד וכמו חציו |
|
ולכן יהיה קו ג"א כמו קו ג"ב וכמו חציו |
|
ויהיה קו א"ב כלו כמו קו ג"ב שני פעמים וחצי |
|
אבל קו א"ב הוא עשרה |
|
ונחלק עשרה לשנים וחצי ויעלה לחלק ארבעה ולכן יהיה קו ב"ג הוא ארבע' |
|
וקו א"ג הוא ששה |
|
והוא מש"ל |
|
אמ' והשאלה השנית כמו אם יאמרו לך תחלק עשרה לשני חלקים באופן שיהיה העולה מהכאת עשרה בעצמו כמו הכאת העולה מהכא' אחד החלקי' בעצמו ששה פעמים ורביע |
|
והמעשה בזה שנניח החלק האחד דבר |
|
ונכהו בעצמו והוא מרובע |
|
ונכה העשרה בעצמם והיו מאה |
|
ואלו המאה היו כמו המרובע ששה פעם ורביע הנה תכה המרובע בששה ורביע ויהיה ששה מרובעים ורביע ישוו מאה דרהמי |
|
|
|
והשיבם אל מרובע אחד והוא שתחלק מאה על ששה ורביע שהם כ"ה רביעיות |
|
ויעלה לכל רביע ארבעה ולכל מרובע יעלה שש עשרה ויהיה המרובע שוה ששה עשר דרהמי |
|
ושרשם ארבעה והוא החלק המבוקש |
I have shown you this problem [to demonstrate] the second of the six categories [of canonical equations], which is the saying: when the squares equal numbers [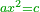 ]. ].
|
וזאת השאלה הראיתי לך לחלק השני מהששה [22]והוא האומר כאשר המרובעים ישוו אל מספרים |
| Geometrical illustration of the problem | |
|
אמ' ואבאר לך זאת השאלה בזאת התמונה |
|
|
|
|
והוא שנניח קו א"ב עשרה |
|
וקו ג"ב ממנו הוא המספר המבוקש |
|
ונכה קו א"ב בעצמו ויצא שטח א"מ והוא מאה |
|
ונכה קו ג"ב בעצמו ויהיה מרובע ג"ד |
|
והנחנו ששטח א"מ שהוא מאה יהיה כמו ששה פעמים ורביע שטח ג"ד |
|
ונחלק מרובע ג"ד לארבעה חלקים שוים כל חלק מהם יהיה כמו שטח ב"ח |
|
הנה מפני שהיה שטח א"מ ששה פעמי' ורביע שטח ג"ד יהיה עשרים וחמשה פעמים כמו שטח ב"ח שהוא רביעיתו שהוא שטח ג"ד |
|
אבל שטח א"מ הוא מאה |
|
ולכן יהיה שטח ב"ח ארבעה |
|
ושטח ג"ד ששה עשר |
|
וקו ג"ב שהוא שרשו יהיה ארבעה והוא החלק המבוקש |
|
והוא מש"ל |
|
אמ' והשאלה השלישית היא כמו אם יאמרו לך תחלק עשרה לשני חלקים באופן שכאשר תחלק החלק הגדול על החלק הקטן יגיע לחלק ארבעה |
|
המעשה בזה הוא שנניח החלק הקטן דבר והגדול עשרה פחות דבר |
|
וחלקנו עשרה פחות דבר על דבר והגיע לחלק ארבעה |
| I have already shown you that when you multiply the quotient by the divisor you get the dividend
|
כבר הראיתיך כי כאשר תכה המגיע לחלק על המחלק שיעלה לידך המספר המחולק |
|
ולכן תכה ארבעה בדבר ויעלה ארבעה דברים וישוו לעשרה פחות דבר |
|
|
|
ותאסוף הדבר עם העשרה עד שיהיו עשרה דרהמי שלמים ותוסיף דבר על הארבעה דברים |
|
ויהיה עשרה דרהמי ישוו חמשה דברים |
|
והדבר יהיה שוה שני דרהמי והוא החלק הקטן והחלק הגדול ישאר שמנה |
I have shown you this problem [to demonstrate] the third of the six categories [of canonical equations], which is the saying: when the things equal numbers [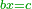 ]. ].
|
וזאת השאלה הוצאתי לך לחלק השלישי מהששה חלקים והוא האומר כאשר הדברים ישוו למספרים |
| Geometrical illustration of the problem | |
|
אמ' ונבאר זאת השאלה בזאת התמונה |
|
|
|
|
והוא שנניח קו א"ב הוא עשרה |
|
וקו ג"ב ממנו הוא החלק הקטן |
|
וקו א"ג החלק הגדול |
|
וכאשר חלקנו קו א"ג על קו ג"ב יעלה לחלק ארבעה |
|
הנה כי קו א"ג ארבעה דמיוני ג"ב |
|
ולכן קו א"ב כלו יהיה חמשה דמיוני ג"ב |
|
וג"ב הוא חמישית א"ב |
|
אבל א"ב הוא עשרה |
|
אם כן ג"ב הוא שנים |
|
והוא מש"ל |
|
אמ' והשאלה הרביעית היא כמו אם יאמרו לך תחלק עשרה לשני חלקים באופן שיהיה העולה מהכאת החלק הגדול בעצמו כמו הכאת החלק הקטן בתשעה |
|
המעשה בזה שנשים החלק הגדול דבר והקטן עשרה פחות דבר |
|
|
והכינו דבר בעצמו והיה מרובע |
|
|
והכינו עשרה פחות דבר בתשעה ועלה תשעי' דרהמי פחות תשעה דברים והיו אלו שוים אל המרובע |
|
תאסוף התשעה דברים עם התשעים דרהמי ותוסיפם על המרובע |
|
|
ויהיה תשעים דרהמי ישוו למרובע ותשעה דברים |
| As shown above, there are two solution methods for this case: one yields the thing and the other yields the square. | וכבר הראיתיך לזה המבוקש שני אופנים האחד |
|
והאופן אשר יראה לך הדבר שהוא החלק הגדול הוא שתקח מחצית [23]הדברים והוא ארבעה וחצי ותכם בעצמם ויהיו עשרים ורביע |
| ותקבצם עם התשעים ויהיו מאה ועשר ורביע | |
| תקח שרש זה והוא עשרה ורביע וחצי | |
| תגרע מהם מחצית השרשים וישאר ששה והוא הדבר והוא החלק הגדול | |
|
| |
|
והאופן אשר יראה לך המרובע הוא שתכה התשעה דברים בעצמם ויהיו שמנים ואחד |
| תכם בתשעים ויהיה שבעת אלפים ומאתים ותשעים ותשמרם | |
| ותקח מחצית שמנים ואחד והוא ארבעים וחצי ותכם בעצמם ויעלה אלף תר"מ ורביע | |
| ותקבצם עם השמור ויהיו שמנת אלפים תתק"ל ורביע | |
| ותקח שרשם והוא צ"ד וחצי | |
| תגרעם ממקובץ הארבעים וחצי שהוא מחצית הכאת השרשים בעצמם עם תשעים שהוא מספר הדרהמי אשר ישוו אל המרובע והשרשים ומקובצם הוא ק"ל וחצי | |
| וישאר ל"ו והם המרובע ושרשם ששה והוא החלק הגדול | |
|
| |
this problem demonstrates the fourth of the six canonical equations: 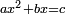
|
וזאת השאלה הוצאתי לך לחלק הרביעי מהששה חלקים והוא האומר כאשר המרובעים ושרשים ישוו למספרים |
| Geometrical illustration of the problem | |
| אמ' ואבארה לך בתמונה הזאת | |
|
|
|
|
והוא שנניח קו א"ב עשרה |
|
וקו א"ג החלק הגדול |
|
וקו ג"ב החלק הקטן |
|
והיה הכאת קו א"ג בעצמו כמו הכאת ג"ב בתשעה |
|
ורצינו להודיע כמה שיעור קו א"ג |
|
הנה אם הכינו א"ג בתשעה וג"ב בתשעה יהיה מקובץ העולה מהכאותיהם תשעים |
|
ובעבור כי היה א"ג בעצמו כמו ג"ב בתשעה |
|
יהיה מפני זה א"ג בתשעה ובעצמו יהיה תשעים |
|
ונניח קו א"ד תשעה |
|
ויהיה העולה מהכאת א"ג בעצמו ובא"ד תשעים והוא כמו הכאת ד"ג בג"א |
|
וקו ד"א תשעה |
|
ונחלק אותו לחצאין על נקודת ה' |
|
ונוסף לארכו קו א"ג |
|
והיה מהכאת ד"ג בג"א תשעים |
|
ונקבץ עמהם הכאת א"ה בעצמו שהוא עשרים ורביע ועלו מאה ועשר ורביע וככה ראוי שתהיה הכאת ה"ג בעצמו |
|
|
ונוציא שרשם והוא עשרה וחצי |
|
וככה קו ה"ג |
|
אבל ה"א הוא ארבעה וחצי |
|
ולכן ישאר א"ג ששה והוא החלק הגדול |
|
וג"ב והוא החלק הקטן |
| Q.E.D. | ומש"ל |
|
אמ' והשאלה החמישית כמו אם יאמרו לך תחלק עשרה לשני חלקים באופן שכאשר נכה החלק האחד באחר יעלה עשרים |
|
המעשה בזה שנניח החלק האחד דבר והחלק האחר יהיה עשרה פחות דבר |
|
|
ונכה דבר בעשרה פחות דבר ויהיה עשרה דברים פחות מרובע ויהיו שוים לעשרים ואחד דרהמי |
|
תאסוף המרובע עם עשרת הדברים פחות מרובע ותוסיפהו על עשרים ואחד |
|
|
ויהיו מרובע ועשרים ואחד דרהמי יהיו שוים לעשרה שרשים |
| It was shown above that there are two solution methods for this case, each method has two aspects. | וכבר הראיתיך למעלה כי לזה הענין שני אופנים ולכל אופן שני צדדים |
|
והאופן אשר יוציא לך השרש הוא שתקח מחצית הדברים והוא חמשה ותכם בעצמם והיה עשרים וחמשה |
| תגרע מהם העשרים ואחד וישאר ארבעה | |
| תקח שרשם והוא [24]שנים | |
| תגרעם מן החמשה וישארו שלשה והם החלק הקטן | |
|
| |
|
|
והחלק הגדול הוא הנשאר מהעשרה והם שבעה |
|
וזה צד המגרעת |
|
ואם תרצה צד התוספת תוסיף השנים על החמשה והיו שבעה והם החלק הגדול |
|
|
והחלק הקטן הוא מה שנשאר מהעשרה והוא שלשה |
|
והאופן אשר יוציא לך המרובע הוא שתכה השרשים בעצמם והיו מאה |
| ותכם בכ"א אשר עם המרובע ויהיו אלפים ומאה ותשמרם | |
| ותקח מחצית המאה שהוא חמשים ותכם בעצמם ויהיו אלפים וחמש מאות | |
| תגרע מהם האלפים ומאה אשר שמרת וישארו ארבע מאות | |
| תקח שרשם והוא עשרים | |
| תגרעם מהחמישים שהם מחצית המאה וישארו שלשים | |
| ותגרע מהם העשרים ואחד וישארו תשעה והם המרובע | |
|
| |
|
וזה צד המגרעת |
|
ומעשה התוספת הוא שתוסיף העשרים על החמשים ויהיו שבעים תגרע מהם העשרים ואחד וישארו תשעה וארבעים והם המרובע |
this problem demonstrates the fifth of the six canonical equations: 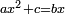
|
וזאת השאלה הוציאתך אל החלק החמשי מהששה חלקים והוא האומר כאשר המרובעי' והמספרים ישוו אל השרשים |
| Geometrical illustration of the problem | |
| אמ' ואבאר זה בזאת התמונה | |
|
|
|
|
והוא שנניח קו א"ב עשרה |
|
ונחלק על ג' |
|
והיה מהכאת א"ג בג"ב עשרים ואחד |
|
ותחלק קו א"ב לחצאי' על ה' |
|
הנה א"ב נחלק לשני חלקים שוים על ה' ולשני חלקים בלתי שוים על ג' |
|
ולכן יהיה העולה מהכאת א"ג בג"ב וה"ג בעצמו כמו העולה מהכאת ה"ב בעצמו |
|
אבל הכאת ה"ב בעצמו עשרים וחמשה |
|
וא"ג בג"ב הוא עשרים ואחד |
|
וישאר ה"ג בעצמו ארבעה |
|
|
ושרשם הוא שנים |
|
ולכן יהיה ה"ג שנים |
|
אבל ה"ב היה חמשה |
|
וישאר ג"כ שלשה |
|
וא"ג יהיה שבעה |
| Q.E.D. | והוא מש"ל |
|
אמ' והשאלה הששית כמו אם יאמרו לך הוספנו על |
|
המעשה בזה הוא שנניח המרובע דבר |
|
וקבצנו עמו שמנה דרהמי והיו דבר ושמנה דרהמי |
|
הכינום בארבעה והיה ארבעה דברים ושנים ושלשים דרהמי |
|
והכינו הדבר בעצמו והוא מרובע וישוה אל ארבעה דברים ול"ב דרהמי |
|
והאופן אשר יוציא לך |
|
ותקבצם עם הל"ב והיו ל"ו |
|
תקח שרשם והוא ששה |
|
תוסיפם על מחצית השרשים ויהיו שמנה וככה הוא המרובע כי הנה הנחנוהו דבר |
|
| |
|
והאופן אשר |
|
ותכם באדרהמי שהם ל"ב ויעלה תקי"ב ותשמרם |
|
ותקח מחצית הששה עשר והוא שמנה ותכם בעצמם והיו ששים וארבע |
|
ותקבצם עם התקי"ב ששמרת [25]ויעלו תקע"ו |
|
תקח שרשם והוא כ"ד |
|
ותקבצם עם השמנה שהם מחצית השש עשרה ועם הל"ב ויעלו |
|
| |
|
ותקח שרשו והוא שמנה והוא המספר המבוקש |
I have shown you this problem [to demonstrate] the sixth of the six categories [of canonical equations], which is the saying: when the numbers and roots equal square[s] [ ]. ].
|
וזאת השאלה הוציאתך אל החלק הששי מהששה חלקים והוא האומר כאשר המספרים והשרשים ישוו אל המרובע |
| Geometrical illustration of the problem | |
|
אמר ואבאר זה בזאת התמונה |
|
|
|
|
והוא שנניח המרובע קו א"ב |
|
והשמנה דרהמי קו א"ג |
|
ונניח קו ב"ד ארבעה |
|
ונכה קו ג"ב בקו ב"ד ויהיה שטח ג"ד |
|
ונכה המרובע שהוא קו א"ב בעצמו והיה שטח א"ה |
|
ויהיה שטח ג"ד בשעור שטח א"ה |
|
ורצינו לידע כמה שיעור קו א"ב |
|
הנה שטח א"ה כמו שטח ג"ד |
|
ונפיל שטח א"ד המשותף |
|
וישאר שטח ג"מ כמו שטח מ"ה |
|
אבל שטח ג"מ שלשים ושנים כי הוא מהכאת א"ג שהוא שמנה בא"מ השוה לב"ד שהוא ארבעה |
|
ולכן שטח מ"ה הוא שלשים ושנים |
|
ושטח מ"ה כמו הכאת א"ז השוה לז"ה בז"ה |
|
וקו א"מ הוא ארבעה |
|
ונחלק אותו לחצאין על נקודת ח' |
|
וכבר נוסף עליו קו ז"מ |
|
ולכן יהיה הכאת א"ז בז"מ שהוא שלשים ושנים עם הכא' מ"ח בעצמו שהוא ארבעה ומקובצם שלשים ושש כמו הכאת ח"ז בעצמו |
|
ומפני זה יהיה קו ח"ז |
|
אבל קו א"ח הוא שנים |
|
ולכן יהיה קו א"ז שמנה |
|
וא"ב הוא שוה לא"ז |
|
אם כן קו א"ב שמנה |
|
והוא מה שרצינו לבאר |
Notes
| |
Appendix I: Glossary of Terms
[Expand]
Appendix II: Bibliography
Kitāb fī al-Jābr wa'l-Muqābala (the first section) / by Abū Kāmil Shujāʽ Ibn Aslam Ibn Muḥammad ibn Shujāʽ (Egypt, ca. 850-930)
– Hebrew translation –
by Mordecai (Angelo) Finzi (Mantua, d. 1475)
Taḥbulot ha-Mispar (Second Hebrew version)
Manuscripts:
- Oxford, Bodleian Library MS Heb. e. 13 (IMHM: f 22714), ff. 64r-72v (cat. Neub. 2747, 2)
- Paris, Bibliothèque Nationale de France heb. 1029/7 (IMHM: f 15721), ff. 296r-309r (15th-16th century)
Bibliography:
- Lévy, Tony. 2007. L’algèbre arabe dans les textes hébraïques (II). Dans l’Italie des XVe et XVIe siècles, sources arabes et sources vernaculaires, Arabic Sciences and Philosophy 17, pp. 81-107.
- Yadegari, Mohammad. 1978. The Use of Mathematical Induction by Abū Kāmil Shujā‘ Ibn Aslam (850-930), Isis, vol. 69, no. 2 (Jun., 1978), pp. 259-262.
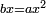
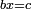
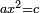
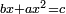
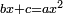
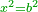
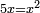
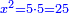
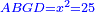
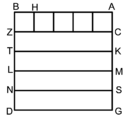
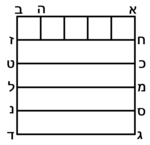
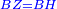
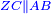

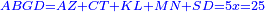
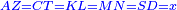
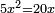
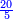

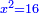
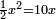
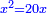
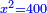
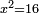
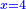
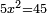
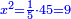
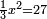
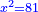
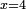
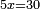
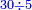
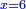
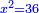
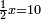
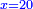


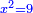
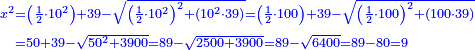
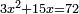
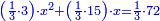
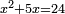
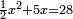
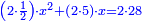
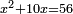

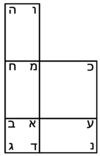
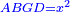
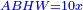
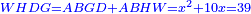

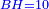

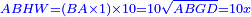
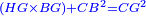

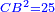
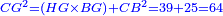
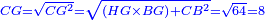
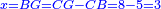

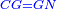

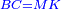
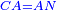
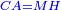
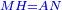
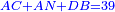
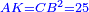
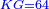
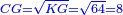


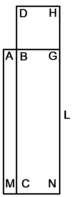
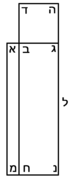
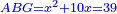
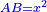
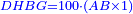
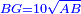
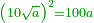
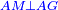
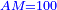
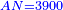

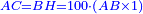


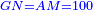
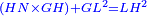
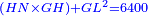

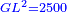
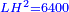
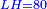
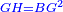
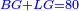
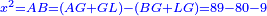
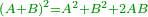
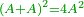
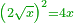
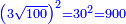

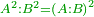
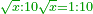
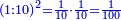
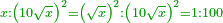
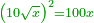


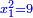
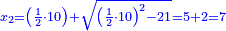
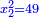
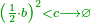

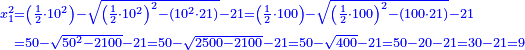
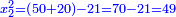

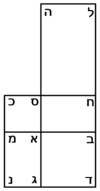

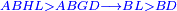
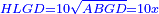
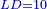
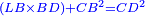
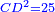


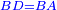
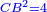

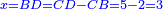
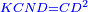

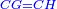
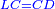
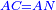



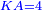
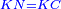
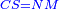
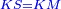


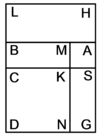
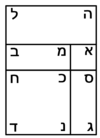

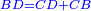
![\scriptstyle{\color{blue}{KC[N]D=CD^2}}](/mediawiki/images/math/8/f/6/8f6b8bf88da3c59c5d8c776997f45470.png)
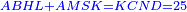
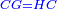
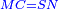
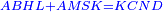

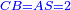
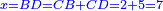
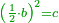
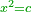
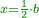
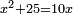
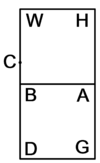
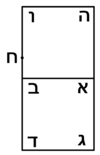


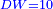

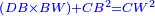
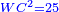
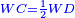
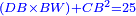
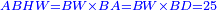
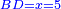
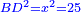


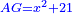
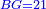


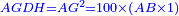
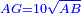
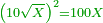
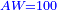
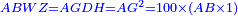
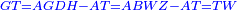


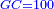

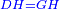
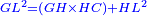
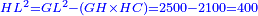
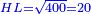
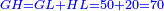

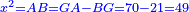




 = AB = AG - BG =
= AB = AG - BG = 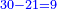
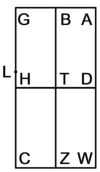
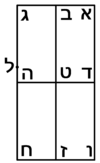
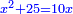


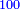



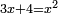
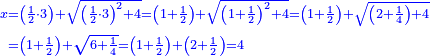
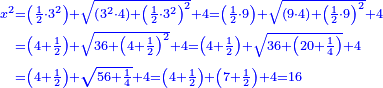

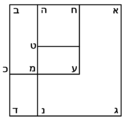
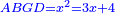
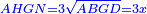


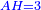

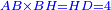

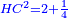
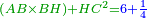
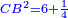
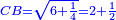
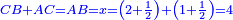
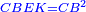
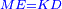
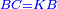
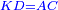
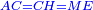

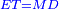

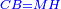


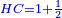
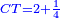
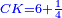
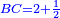
 =
= 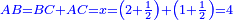

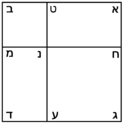
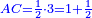
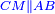

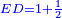
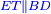
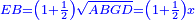
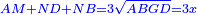
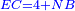
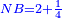
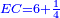
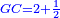
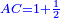
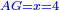
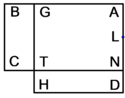
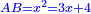


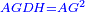

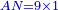
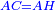
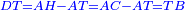
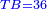

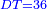
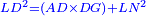
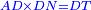

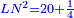
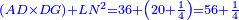
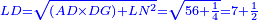
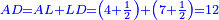

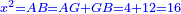
 ].
].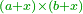
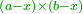
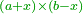
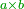 ].
].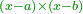
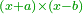
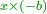 ].
].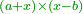
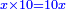
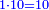

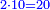
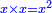
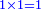 and this is a square
and this is a square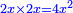
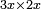

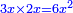
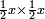
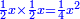
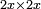

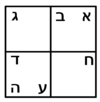

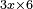
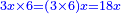

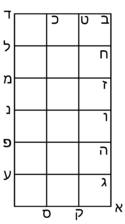

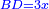



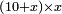
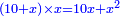
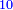
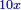

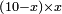
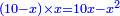
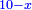
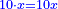
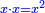
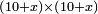
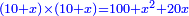
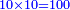
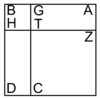
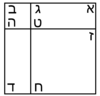
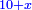
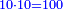
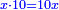
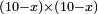
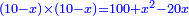
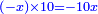
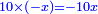
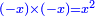
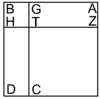
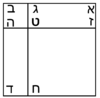

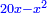
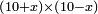
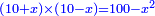

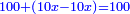
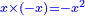
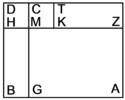
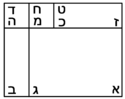
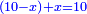
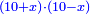

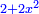
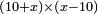
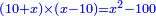
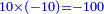
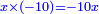
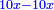

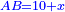
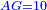

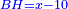
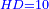
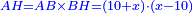

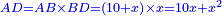
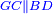
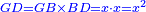
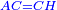
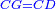

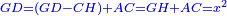
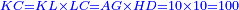
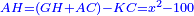
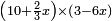
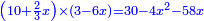

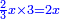
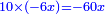
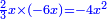

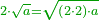
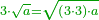
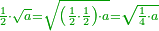
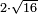
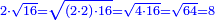

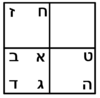
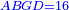
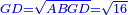

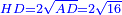
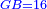
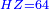
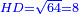
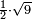
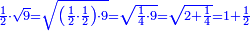
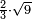
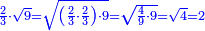


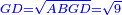
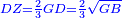

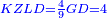
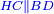
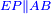
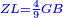
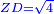
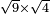
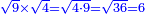
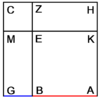
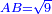
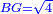

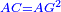
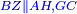
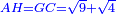
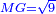
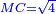
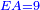
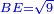

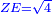

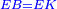
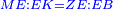
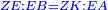
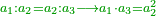
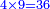
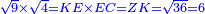
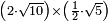
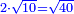
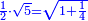
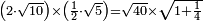
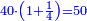
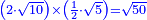
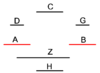
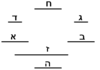
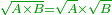
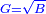
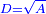


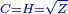
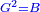

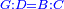
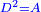

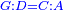
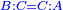
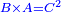
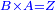
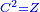
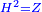
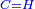
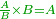

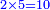
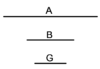
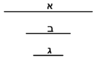
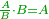


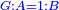
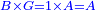
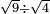
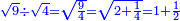
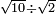

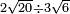
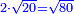

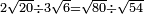
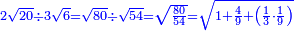
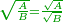
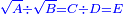
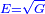
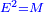

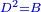


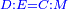

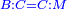
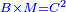
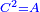

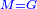
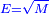
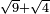
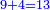
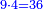
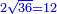
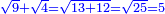
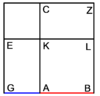
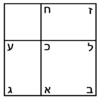
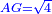
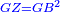
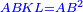

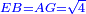

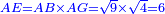

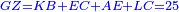
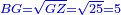
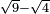
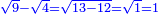
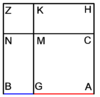
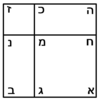
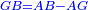
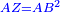

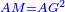

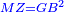
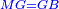

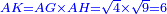


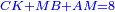


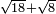
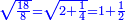
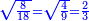

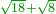
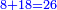
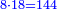
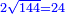
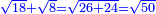
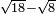

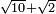
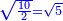
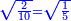
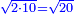
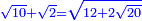
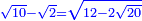
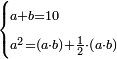
 ] and the other part is ten minus a thing [
] and the other part is ten minus a thing [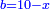 ].
].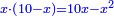
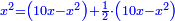
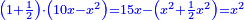
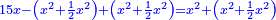
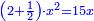
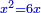

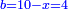
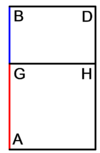
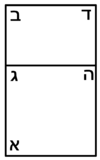
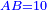

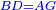
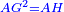
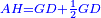
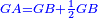
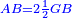
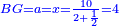
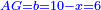
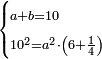
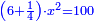
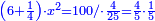
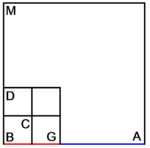
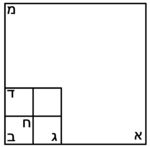
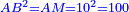
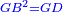
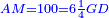
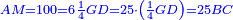

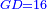

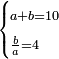
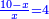
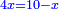
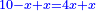
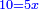
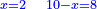
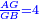
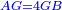
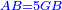
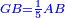

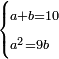
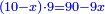

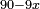 :
: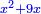
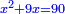
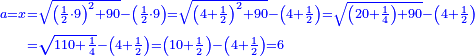
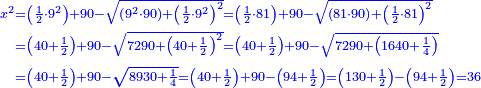


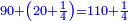
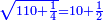
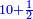
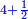
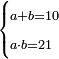

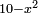 :
:
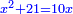

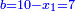
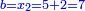
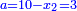
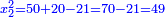
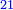

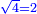




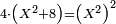
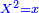 ]
]