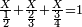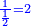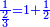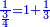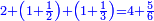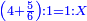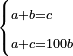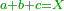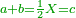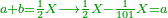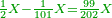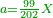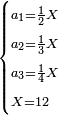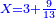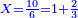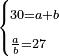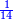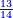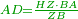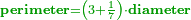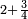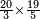Difference between revisions of "מלאכת המספר"
From mispar
(→Supplement (Oxford MS d.5) – operations with fractions) |
(→Chapter Four: The Fourth Type [of Numerical Operations], which is Halving) |
||
| Line 1,045: | Line 1,045: | ||
|- | |- | ||
|The proof of this is doubling: if after it is doubled it becomes equal to the halved, then it is correct, otherwise it is incorrect. | |The proof of this is doubling: if after it is doubled it becomes equal to the halved, then it is correct, otherwise it is incorrect. | ||
| − | |style="text-align:right;"|<big>והמופת</big> על זה הוא הכפול שאם לאחר ש{{#annot:term| | + | |style="text-align:right;"|<big>והמופת</big> על זה הוא הכפול שאם לאחר ש{{#annot:term|785,1564|tZOv}}נכפל{{#annotend:tZOv}} ישוה לנחלק הוא אמיתי ואם לא ישוה אינו אמיתי |
|- | |- | ||
|This is enough for the type of halving. | |This is enough for the type of halving. | ||
Revision as of 08:34, 14 June 2022
Contents
- 1 Introduction
- 2 Book One: Numbers
- 2.1 Section One of the First Book: the definition of arithmetic, the definition of number, the units, a few premises needed and the number of the types of numerical [operations].
- 2.2 Section Two of Book One: [Integers]
- 2.2.1 Chapter One: The First Type of Numerical [Operations], which is Addition
- 2.2.2 Chapter Two: The Second Type [of Numerical Operations], which is Subtraction
- 2.2.3 Chapter Three: The Third Type [of Numerical Operations], which is Doubling, and General Methods for Finding the Perfect Numbers
- 2.2.4 Chapter Four: The Fourth Type [of Numerical Operations], which is Halving
- 2.2.5 Chapter Five: The Fifth Type [of Numerical Operations], which is Multiplication and Some of its Properties
- 2.2.6 Chapter Six: The Sixth Type which is Division
- 2.3 Section Three of Book One: [Fractions]
- 2.3.1 Chapter One: Guiding Methods of the Writing Fractions, their Definition, and their Arrangement
- 2.3.2 Chapter Two: Addition of Fractions
- 2.3.3 Chapter Three: Subtraction of Fractions
- 2.3.4 Chapter Four: Doubling Fractions
- 2.3.5 Chapter Five: Halving Fractions
- 2.3.6 Chapter Six: Multiplication of Fractions
- 2.3.7 Chapter Seven: Multiplication of Fractions in Astrology [= Sexagesimal Fractions]
- 2.3.8 Chapter Eight: Division of Fraction
- 2.4 Section Four of the First Book: [Roots]
- 2.4.1 Chapter One: Giving Guiding Ways for Finding Roots of Square Numbers or Approximate Roots of Non-Square Numbers
- 2.4.2 Chapter Two: Finding the Roots of Fractions Alone or Fractions and Integers Together
- 2.4.3 Chapter Three: Giving one inclusive Method for Finding the Roots of Numbers by Adding Zeros
- 2.4.4 Chapter Four: Giving Guiding Ways for Finding Roots of Cube Numbers or Approximate Roots of Non-Cube Numbers
- 3 Book Two: [Proportions]
- 3.1 Section One: We Talk in It about General Methods and Proportions of This Science
- 3.1.1 Chapter One: Proportions of Integers
- 3.1.2 Chapter Two: Guiding Ways for Finding Proportions of Fractions
- 3.1.3 Chapter Three: Guiding Ways for Finding the Numerator in the Proportions of Fractions
- 3.1.4 Chapter Four: Giving a General Example for all the Teaching Methods of the Denominator and the Numerator in the Context of Knowing the Ratios of Fractions
- 3.1.5 Chapter Five: Knowing the Ratio of the Four Proportional Numbers [= the Rule of Three] in the Two Sciences - Arithmetic and Geometry
- 3.1.6 Chapter Six: [Proportional Triad]
- 3.1.7 Chapter Seven: Knowing the Ratio of the Six Proportional Numbers [= the Proportional Hexad]
- 3.2 The Second Section of the Second Book: We will Discuss in it Some Theoretical and Practical Problems and Guiding Answers of this Science
- 3.2.1 The First Chapter: on the Knowledge of the Exchange of Measurements, Weights, Liquid Measures and Currencies According to the Change of Places
- 3.2.2 The Second Chapter: Knowing the relation of two numbers that have the property that if we subtract one from the greater number and add it to the smaller number, the two numbers become equal; and if we subtract one from the smaller number and add it to the greater, the greater becomes double the smaller, or more if we wish
- 3.2.3 Chapter Three: The relation of two numbers such that if the greater gives one to the smaller, the smaller becomes double the greater; and if the smaller gives one to the greater, the greater becomes three times the smaller
- 3.2.4 Chapter Four: Knowing the whole, whichever it may be, from the sum of its two different parts
- 3.2.5 Chapter Five: Giving general ways for finding any unknown number by the method of double false position
- 3.2.6 Chapter Six: the Teaching of Partnership
- 3.2.7 Chapter Seven: Some Questions and Answers
- 3.1 Section One: We Talk in It about General Methods and Proportions of This Science
- 4 Book Three: We Talk in it about Some Principles of Geometry
- 4.1 Section One: Knowing the Measure of the Line
- 4.2 Section Two of Book Three: Knowing the Measure of the Surface
- 4.2.1 Chapter One: Knowing the Area of the Equilateral Triangle
- 4.2.2 Chapter Two: Knowing the Area of the Isosceles Triangle
- 4.2.3 Chapter Three: Knowing the Area of the Scalene Triangle
- 4.2.4 Chapter Four: Knowing the Area of the Quadrilateral and the Area of the Square
- 4.2.5 Chapter Five: Knowing the Measure of the Circle according to the Opinion of the Sages
- 4.3 Section Three of Book Three: [Solid]
- 5 Supplement (Oxford MS d.5) – operations with fractions
- 6 Notes
- 7 Apparatus
- 8 Appendix I: Glossary of Terms
- 9 Appendix II: Bibliography
Introduction |
|
| The author said: When I saw the lengthiness of the discussions of the ancient scholars, the composers of the books of number, and that the necessary methods and teachings in astronomy, geometry, and the ratios of music are explained in those books merely in great difficulty; likewise the seven types of [operations] with integers as well as with fractions, the roots and the proportions of numbers; and since the teaching that is [based] on brief and comprehensive methods is better chosen for the student as well as for the teacher, for every lengthiness of words and loquacity are exhaustion of the body [Ecclesiastes 12, 12]. | [1]אמר המחבר בראותי אורך דברי החכמים הקדומים מחברי ספרי המספר ושהסדרים והלימודים ההכרחיים בחכמת התכונה וההנדסא ויחסי המושיקא אינם מבוארים בספרים ההם אלא בקושי גדול וכן ג"כ בשבעה מיני השלמים כמו בשברים ובשרשי' וביחסי המספרים ולהיות הלמוד שהוא בדרכים הקצרי' והכוללים יותר נבחר כן ללומד כמו למלמד כי כל אריכות דברים ולהג הרבה יגיעת בשר[note 1] |
| Therefore, I Yiẓḥaq b. R. Moshe ʽEli ha-Sefaradi [= the Spanish] from the city of Oriola of the kingdom of Aragon, at the request of my friends, who studied astronomy and geometry, because they used those methods with a great difficulty and bother, I shook out my lap and wrote this short treatise that encompasses all that is necessary for this science, arithmetic, that is called arishmetika, by the grace of God to me [Psalms 57, 2], and according to the good hand of my God upon me [Nehemiah 2, 8]. | לכן אני יצחק בכ"ר משה עלי נ"ע הספרדי ממדינת אוריאולה ממלכות ארגון נערתי חצני לבקשת קצת אוהבי המעיינים בחכמת התכונה וההנדסא למה שהיו פועלם בקושי וטורח גדול בדרכים ההם וחברתי זה החבור הקצר כולל כל מה שהוא הכרחי בזאת המלאכה ר"ל מלאכת המספר הנקראת אריתמתיקא כפי שחנני השם וכפי יד אלהי הטובה עלי |
| I have written in it comprehensive and short ways in all seven types of [operations] of number, its properties and the existence of the ratios in all that is possible in this science. | וחברתי בו דרכים כוללים וקצרים בכל ז' מיני המספר וסגולותיו ומציאות היחסים בכל מה שהוא אפשרי במלאכה הזאת |
| This is by demonstrative ways that are loved by the intellectuals, in a manner that anyone who endeavors in studying this short book will comprehend all that is necessary for this science, will be saved from the non-useful lengthiness and from the loss of time, and will attain in it whatever his heart desires; since it is for mathematics as the light of dawn shines ever brighter until the perfect [Proverbs 4, 18]. | וזה בדרכים מופתיים ונאהבים למשכילים באופן שכל מי שישתדל לעיין בזה הספר הקצר [2]יקיף בכל מה שהוא הכרחי בזאת המלאכה וינצל מהאריכות הבלתי מועיל ומהפסד הזמן וישיג בו מה שלבו חפץ כי הוא לחכמת הלימודיות כאור נוגה ואור עד נכון[note 2] |
| With the help of God, Blessed is He, I will begin and say: | ובעזר ה' [ב"ה] אתחי' ואומ' |
Table of content |
|
| This work is divided into three books: | הספר הזה יחלק לשלשה מאמרים |
|
במאמר הראשון נדבר בז' מיני המספר |
|
במאמר הב' נדבר בדרכים ויחסים ושאלות ותשובות הצריכות במלאכה הזאת |
|
במאמר הג' נדבר בקצת דרכים והתחלות משותפות למלאכת המספר וההנדסא |
|
המאמר הא' |
|
יחלק לד' כללים |
|
הכלל הראשון בגדר מלאכת המספר וגדר המספר והאחדות וקצת התחלות צריכות אליה ומניין מיני המספר |
|
בכלל הב' נדבר בו' מיני המספר השלמים |
|
בכלל הג' נדבר בז' מיני השברים ואופני רבוע השברים בחכמת התכונה |
|
בכלל הד' נדבר בדרכים מיישירים למצא שרשי המספרים המרובעים והמעוקבים |
|
הכלל הא' מהמאמר הא' בגדר מלאכת המספר וגדר המספר והאחדות וקצת התחלות הצריכות אליה ומניין מיני המספר |
|
הכלל הב' |
|
יחלק לששה פרקים |
|
הפרק הא' נדבר בו מהמין הראשון מהמספר שהוא הקבוץ |
|
הפרק הב' במין הב' שהוא חסור |
|
הפרק הג' מהמין הג' שהוא הכפול ודרכים כוללים בידיעת המספרים השלמים |
|
הפרק הד' במין הד' שהוא חלוק באמצע |
|
הפרק הה' במין הה' שהוא הרבוע וקצת מסגולותיו |
|
הפרק הו' מהמין [3]השישי שהוא בהחלק |
|
הכלל הג' מהמאמר הא' |
|
ויחלק לח' פרקים |
|
הפרק הא' בדרכים מיישירים בענייני הנחת השברים וגדרם וסדורם |
|
הפ' הב' בקבוץ השברים |
|
הפרק הג' בחסור השברים |
|
הפרק הד' בכפול השברים |
|
הפרק הה' מחלוקת השברים באמצע |
|
הפרק השישי מרבוע השברים |
|
הפרק הז' באופני רבוע השברים בחכמת התכונה |
|
הפרק הח' מהחלק השברים |
|
הכלל הד' מהמאמר הא' |
|
ויתחלק לד' פרקים |
|
הפרק הא' בנתינת דרכים מיישירים למציאות שרשי המספרים המרובעים או היותר קרובים למספרים הבלתי מרובעים |
|
הפרק הב' |
|
הפרק הג' בנתינת דרך אחד כולל למצא בו שרשי המספרים על דרך תוספת הסאפרש |
|
הפרק הד' בדרכים מיישירים למציאות שרשי המספרי' המעוקבים או היותר קרובים למספרים הבלתי מעוקבים |
|
המאמר השני[5] |
|
יתחלק בב' כללים |
|
בכלל הראשון נדבר בדרכים ויחסים כוללים בזאת המלאכה |
|
בכלל הב' נדבר בקצת שאלות ותשובות מיישירות בעיון ובמעשה בזאת המלאכה |
|
הכלל הא' מהמאמר הב' |
|
יחלק לז' פרקים |
|
הפרק הראשון ביחסי המספרים מהשלמים |
|
הפרק הב' בדרכים מיישירים במציאות יחסי המספרים השבריים |
|
[6]הפרק הג' בדרכים מיישירים למציאות המחולק ביחסי השברים |
|
הפרק הד' בנתינת משל א' כולל לכל חלקי הלמוד במחלק ובמחולק בידיעת יחסי השברי' |
|
הפרק ה' בידיעת יחסי הד' מספרים המתייחסים בב' המלאכות מלאכת המספר וההנדסא |
|
הפרק הו' בידיעת יחסי כל ג' מספרים המתייחסים |
|
הפרק הז' בידיעת יחס הו' מספרים המתייחסים |
|
הכלל הב' מהמאמר הב' |
|
ויחלק לז' פרקים |
|
הפרק הא' בידיעת חלוף המדות והמשקלים והמשורות והמטבעות לפי חלוף מקומם |
|
הפרק הב' בידיעת התייחסות ב' מספרים שיש להם זאת הסגולה שאם נחסר א' מהמספר [.] הגדול והוספנום על הקטן יהיו שוים ואם בהפך יהיה הגדול כפל הקטן או יותר כפי שנרצה |
|
הפרק הג' ביחס שני מספרים שאם הגדול יתן א' לקטן יהיה הקטן כפל הגדול ואם בהפך יהיה הגדול ג' פעמים יותר |
|
הפרק הד' שבידיעת קבוץ ב' חלקים מתחלפים מאיזה כל או יותר איך נדע הכל |
|
הפרק הה' בנתינת דרכים כוללים לידיעת איזה מספר בלתי ידוע בדרך המתנגדים |
|
הפרק השישי [בלמוד החבורות |
|
הפרק הז'][7] בקצת שאילות ותשובות |
|
המאמר הג' נדבר בו בקצת התחלות מההנדסא |
|
ויתחלק לג' כללי' |
|
הכלל הא' בידיעת השיעור הקויי |
|
הכלל הב' בידיעת השיעור [השטחיי |
|
הכלל השלישי בידיעת השעור][8] הגשמי |
|
הכלל הא' מהמאמר הג' |
|
יתחלק לג' פרקים |
|
הפרק הא' בקצת התחלות ההנדסא [9]וגדר הקו ובידיעת השיעור הקויי בגובה |
|
הפרק הב' בידיעת שיעור הקויי במשור |
|
הפרק הג' בידיעת השיעור |
|
הכלל הב' מהמאמר השלישי בידיעת השיעור השטחי |
|
ויתחלק לה' פרקים |
|
פרק הא' בידיעת שיעור השטח המשולש השוה הזויות |
|
הפרק הב' בידיעת שיעור שטח המשולש שוה הצלעו' |
|
הפרק הג' בידיעת שיעור שטח המשולש מתחלף הצלעות |
|
הפרק הד' בידיעת שיעור שטח המרובע ושטח הרבוע |
|
הפרק הה' בידיעת שיעור שטח העגול לפי סברת החכמים |
|
הכלל הג' מהמאמר הג' ובו פרק א' בידיעת שיעור איזה [גשם][10] שיהיה |
Book One: Numbers |
|
Section One of the First Book: the definition of arithmetic, the definition of number, the units, a few premises needed and the number of the types of numerical [operations]. |
הכלל הא' מהמאמר הא' בגדר מלאכת המספר וגדר המספר והאחדות וקצת התחלות צריכות אליה ומניין מיני המספר |
| Necessary preliminary definitions: | |
|
מלאכת המספר היא מלאכה תורה למנות הרבה אחדים והבדליהם וסגולותם ובנקלה יקויימו בזכירה |
|
אחדות הוא יסוד וחלק ראשון מהמספר וכל מספר יורכב ממנו אבל הוא חוץ לכל מספר |
|
כי ב' או ג' לא יצויירו בלתי הא' |
|
כי הב' אינם אלא |
|
והג' אינם אלא שלש הא' |
|
אבל הא' יצוייר מבלתי שיצויירו ב' או ג' |
|
ולכן יגדר המספר בשהוא קבוץ אחדים |
The Positional Decimal System |
|
| The digits | |
|---|---|
| The first thing that you should know is that the numerals are ten and they are: 1, 2, 3, 4, 5, 6, 7, 8, 9. | והראשון שצריך שתדע שתמונות המספר עשרה והם אלו 9 8 7 6 5 4 3 2 1 [11] |
|
התמונה הראשונה או האות או הסימן כמו שתרצה לקרא לה תורה אחד והשנית תורה [12]שניים והשלישית שלשה וכן כסדר עד ט' |
|
והעשירית תקרא ספרא ואינו שוה דבר בעצמו אבל להורות מקום מקנה יותר כמות לאות הנמשכת אליה |
| The written ranks [= decimal places] and their writing order | |
| These figures should be written by the order as they are here: | ואלו התמונות צריך שיכתבו כמו שהם בכאן כסדר |
|
והאות הראשונה שבטור יקרא תמונה של אחדות בעבור שתרמוז לאחדות בין שתהיה הראשונה מהט' או איזו שתהיה מהן |
|
והאות השני שבטור יקרא תמונה של עשרות |
|
והאות השלישית יקרא תמונה של מאות |
|
והרביעית של אלפי' |
|
והה' של עשרת אלפי' |
|
והו' של מאות אלפי' |
|
והז' של אלף אלפי' |
|
והח' של לעשרות אלף אלפים |
|
והט' של מאות אלף אלפים |
|
והאות העשירי שבטור יקרא תמונה של אלף אלפי אלפי' בעבור שתרמוז אליהם |
|
וכן מעשרה לעשרה |
| Every rank is ten times the preceding rank and so on endlessly as we wish. | [.] כי כל מעלה או מדרגה עלה יותר מהקדומות לה מניין עשרה וכן אל לא תכלית אם נרצה |
| So, the value of the numerals mentioned, i.e. the digits, is according to their decimal place: | א"כ התמונות הנזכרות ר"ל האותיות לפי מקומם כך יהיה שיווים |
|
בדרך זה שהא' במקום האחדות שוה אחד ובמקום העשרות עשרה ובמקום [המאות מאה][13] או במדרגת האלפי' אלף וכן כסדר ממדרגה למדרגה |
|
וכן ב' במקום האחדות שוה שניים ובמקום העשרות עשרים ובמקום המאות מאתיים ובמקום האלפי' אלפיים וכן כסדר בהדרגה ממעלה למעלה |
| Every number necessarily belongs to one of three categories: either it is units, or tens, or consists of both: | וכל מספר לא ימנע מא' מג' דרכים אם שיהיה אחדות או שיהיו עשרות או מורכב משניהם |
|
והאחדות הוא כל מספר שהוא פחות מי' |
|
והעשרות הוא כל מספר ששוה עשרה או עשרות |
|
ומורכב משניהם הוא כל מספר שיש בו אחדות ועשרות יחד |
| List of arithmetical operations | |
| Know that the types [of operations] in arithmetic are seven: addition, subtraction, doubling, halving, multiplication, division, and extracting roots of square and cube numbers. | ודע שמיני [14]מלאכת המספר הם ז' והם קבוץ חסור כפול חלוק באמצע רבוע חלוק מציאות עקרי המספרים המרובעים והמעוקבים |
Section Two of Book One: [Integers] |
הכלל השני מהמאמר הראשון | |||||||||||||||||||||
| It is divided into seven chapters. | ויתחלק לז' פרקים | |||||||||||||||||||||
Chapter One: The First Type of Numerical [Operations], which is Addition |
הפרק הראשון במין הראשון מהמספר והוא הקבוץ | |||||||||||||||||||||
| Definition of the addition operation: Addition is summing two numbers or more to one inclusive number. | קבוץ הוא חבור שני מספרים או יותר במספר אחד כולל לכולם | |||||||||||||||||||||
| Description of the procedure: | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| In this type [of operation] we can write as many lines as we wish. | במין הזה נוכל לכתוב כל הטורים שנרצה | |||||||||||||||||||||
|
וצריך לכתוב האחדות כנגד האחדות ועשרות כנגד עשרות ומאות כנגד מאות וכן כסדר מדרגה כנגד כל מדרגה הדומה לה | |||||||||||||||||||||
|
ואחר כך יקובצו כל אותיות האחדות | |||||||||||||||||||||
| This sum necessarily belongs to one of three categories, as you know: either it is units, or tens, or consists of both. | והקבוץ הזה לא ימנע מלהיות [אחד][15] משלש [דרכים][16] כמו שידעת אם שיהיה מאחדות או מעשרות או מורכב משניהם | |||||||||||||||||||||
|
ואם יהיה מאחדות נכתוב אותו תחת האחדות | |||||||||||||||||||||
|
ואם יהיה מעשרות נכתוב ספרא ונעביר הי' אל המדרגה הראשונה הנמשכת אחריה שהיא מדרגת העשרות | |||||||||||||||||||||
|
ואם יהיו אחדות ועשרות יחד נכתוב האחדות תחת האחדות כאמור והעשרות במדרגת העשרות | |||||||||||||||||||||
| By this order for every rank. | ובסדר הזה בכל מדרגה ומדרגה שיהיה | |||||||||||||||||||||
|
כפי הנראה בצורה הזאת | |||||||||||||||||||||
|
| |||||||||||||||||||||
| Check: casting out by 9 | ||||||||||||||||||||||
| The proof of this is that we cast out the nines from the sum and keep the remainder. We do the same with the addend. If the remainders from both are equal, then the addition we made is correct, otherwise it is not. | והמופת על זה שנשליך [המקובץ][17] ט' ט' והנשאר שמור אותו וכן נעשה בנקבץ[18] ואם הנותר משניהם שוה א"כ הקבוץ שעשינו היה אמיתי [ואם לא אינו אמתי][19] | |||||||||||||||||||||
| This is enough for the first type. | וזה יספיק במין הראשון |
Chapter Two: The Second Type [of Numerical Operations], which is Subtraction |
הפרק הב' במין הב' שהוא חסור | ||||||||||||||||||
| Definition of the subtraction operation: Subtraction is knowing the remainder of any number after a number that is smaller than it was subtracted from it. | חסור הוא ידיעת הנישאר מאיזה מספר שיהיה כשיוסר ממנו מספר א' פחות ממנו | ||||||||||||||||||
| Description of the procedure: | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| It is done in this way: we write the two numbers in two lines, the greater above and the smaller beneath, arranged each rank beneath its similar, until all ranks are complete. | ויעשה [20]בדרך זה נכתוב הב' מספרים בשני טורים הגדול למעלה והקטן למטה מסודרים כל מדרגה תחת מדרגה הדומה לה עד תשלום כל המדרגות שיהיו | ||||||||||||||||||
| In this type three categories should be examined: either the digit of the upper number is equal to the digit of the bottom number, or greater, or smaller. | ובזה המין צריך לעיין בג' דברים או האות האחד מהמספר העליון תהיה שוה לאות האחד מהמספר התחתון או יותר או פחות | ||||||||||||||||||
|
ואם יהיו שוות נכתוב למטה מהם ספרא לאות שלא נשאר שום דבר | ||||||||||||||||||
|
כמו שמחסר ו' מן ו' שלא ישאר [דבר][21] | ||||||||||||||||||
|
ואם האות העליון יהיה יותר נחסר מה שלמטה מהמדרגה שלמעלה ונכתוב הנותר | ||||||||||||||||||
|
כמי שמחסר ה' מן ו' שישאר א' ונכתוב א' למטה | ||||||||||||||||||
|
ואם האות העליון יהיה פחות מאותו שלמטה נעיין האות שלמטה כמה יש עד עשרה ומה שיהיה נחבר אותו עם האות העליון שכנגדו וחבור אלה השניים יקרא מותר ונכתוב אותו למטה תחת האות העליון | ||||||||||||||||||
|
וכשנרצה לחסר האות הנמשכת אליה מהעליונה שכנגדה צריך להוסיף א' על האות התחתונה הנמשכת | ||||||||||||||||||
|
וזה [הפעל][22] הכרחי בעבור שהאות העליונה הקודמת היתה פחותה מהתחתונה וזה התוספת מהאחד שאמרנו הוא כמו שאם חסרנו אחד מהאות הסמוכה לעליונה הפחותה מהתחתונה שכנגדה | ||||||||||||||||||
| We do this way until the whole line ends. | ובזה הדרך נעשה עד שיגמר כל הטור | ||||||||||||||||||
|
כפי הנראה בצורה הזאת | ||||||||||||||||||
|
| ||||||||||||||||||
|
וצריך שתדע כמו שאמרנו שבעבור שהאות העליונה שוה לתחתונה כשיחוסר האחת מהאחרת לא ישאר דבר [23]לכן כתבנו ספרא | ||||||||||||||||||
|
ובמדרגה השנית בעבור שהאות העליונה היא [שוה][24] יותר מהתחתונה נראה כמה יש מהתחתונה עד תשלום העליונה וידענו שהם ה' ולכן כתבנו ה' למטה | ||||||||||||||||||
|
ואחר כך במדרגה השלישית בעבור שהאות התחתונה [שוה][25] יותר מהעליונה נדע כמה יש ממנה ר"ל מהתחתונה עד תשלום עשרה וידענו שהם ו' ונחבר אליהם האות העליונה שהיא ב' ויהיה קבוץ שניהם ח' והוא המותר ונכתוב אותו תחת הד' | ||||||||||||||||||
|
ואחר כך בב' שהיא במדרגה הד' נוסיף א' ויהיו ג' ונחסרם מהד' שהיא האות העליון וישאר למטה א' |
- [Illustration of the procedure:]
4282 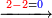
4282 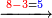
4282 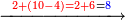
4282 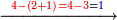
4282 2432 2432 2432 2432 2432 0 50 850 1850
| By this order it should be done, even if the ranks are numerous. | וכסדר הזה צריך לעשות ואם ירבו המדרגות |
| Check: addition | |
|---|---|
| The proof of this is that we add the number we have subtracted from the upper number to the remainder. | והמופת על זה נחבר אותו המספר שחסרנו מהעליון עם המותר |
| If the upper number is as the result of adding of the remainder to the number we subtracted, know that the subtraction we did is correct, otherwise it is not. | ואם יהיה למספר העליון כמו מספר העולה מחבור[26] המותר עם המספר שחסרנו דע כי החסור שעשינו אמיתי ואם לא אינו אמיתי |
| This is enough for the second type. | וזה מספיק במין השני |
Chapter Three: The Third Type [of Numerical Operations], which is Doubling, and General Methods for Finding the Perfect Numbers |
הפרק הג' במין הג' והוא הכפול ודרכים כוללים למצאות המספרים השלמים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Definition of the doubling operation: Doubling is summing any two numbers that are equal. | כפול הוא קבוץ איזה ב' מספרים שיהיו שוים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Description of the procedure: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| In this type we should also start from the units. | וגם בזה המין ראוי שנתחיל מהאחדות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Whichever number we write beneath, by the order, the doubling of each rank is as follows: | ואיזה מספר שיהיה נכתוב למטה כסדר כפל כל מדרגה ומדרגה בזה הדרך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
שאם יהיה הכפל מאיזה מדרגה שתהיה פחות מעשרה נכתוב אותו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם יהיה הכפל עשרה [שלמים][27] נכתוב למטה 0' וישאר בידינו א' להוסיף על כפל האות הנמשכת אליה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם יהיה יותר מעשרה נכתוב מה שיהיה יותר והעשרה נעבירם למדרגה [28]הנמשכת כמו שעשינו במין הקבוץ לא פחות ולא יתר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כפי הנראה בצורה הזאת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Perfect Numbers | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The even-times-even numbers: In this type we can start with 1, whose double is 2; double the 2 is 4; double the 4 is 8. | והמין הזה נוכל להתחיל מהא' שכפלו הב' וכפל הב' ד' וכפול ד' ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| By doubling all the perfect numbers are found. | ובדרך הכפול הזה ימצאו המספרים השלמים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Definition of a perfect number: The definition of a perfect number is any number that is generated from the sum of all its divisors, so that when all its divisors are summed they produce it exactly. | וגדר המספר השלם הוא כל מספר שיבנה מקבוץ כל חלקיו שבשילקח כל אחד מחלקיו ויקובצו יבנו אותו לא פחות ולא יתר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The perfect number is found by that we take the first double of this type and examine if its double minus 1 is a prime number.
|
והמספר השלם ימצא בדרך הזה בשנקח כפל א' מזה המין ונעיין אם כפלו פחות א' יהיה מספר ראשון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If it is a prime number, we multiply the double we took by its double minus 1, and the product is a perfect number.
|
ואם יהיה מספר ראשון אז נכה אותו הכפל שלקחנו עם כפלו פחות א' והעולה מהכאה זו הוא מספר שלם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Definition of a prime number: The definition of a prime number is every number that is not a result of a product of any number. | וגדר המספר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו ז' או ל"א או ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
המשל לקחנו הכפל הראשון מזה המין שהוא ב' ובעבור שכפלו פחות אחד הוא ג' והוא מספר ראשון נכה הכפל הראשון מזה המין שהוא ב' בכפלו פחות אחד והוא שהוא ג' ויצאו ששה [שהוא][30] מספר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Because in every rank there is one perfect number, no more, and it is found by the said procedure. | כי בכל מדרגה יש מספר אחד שלם לא יותר וימצא בדרך האמור | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This is enough for the third type. | וזה המין מספיק במין השלישי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Check: halving | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The proof of this type [of operation] is that we apply the fourth type, which is halving. | והמופת במין הזה הוא בשנעשה המין הרביעי שהוא חלוק באמצע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The sum 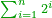
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This type has a property that whoever wants to know the sum of all the even-times-even numbers, doubles the last, then subtracts 1; and it is equal to the sum of all the even-times-even numbers.
|
ולזה המין יש סגולה אחת שמי שירצה לדעת העולה מכל הנכפל יכפול האחרון ויסיר א' ויהיה שוה לכל הנכפל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Here is their diagram: | והנה לך צורתו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Chapter Four: The Fourth Type [of Numerical Operations], which is Halving |
הפרק הרביעי במין הרביעי שהוא חלוק באמצע | ||||||||||||||||||||||||||||||||
| Definition of the halving operation: Halving is dividing any number into two equal parts. | [חלוק באמצע][31] והוא חלוק איזה מספר שיהיה בשני חלקים שוים | ||||||||||||||||||||||||||||||||
| Description of the procedure: | |||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| In this type we start to divide from the highest rank. | [32]ובזה המין נתחיל לחלק מהאות השוה יותר | ||||||||||||||||||||||||||||||||
| We do it this way that if it is an even number, we write its half beneath it. | ונעשה בדרך זה שאם יהיה זוג נשים תחתיו חציה | ||||||||||||||||||||||||||||||||
|
כמו שמשים תחת ח' ד' | ||||||||||||||||||||||||||||||||
| If it is an odd number, we leave one and write half of the remainder. The one that is left becomes ten for the digit that is next to it. | ואם יהיה נפרד נשאיר אחד ונכתוב חצי הנשאר והאחד שנשאר יהיה עשרה לאות הסמוכה לה | ||||||||||||||||||||||||||||||||
| If there are no more digits, we halve it and it is a half of one. | ואם לא יהיו יותר אותיות נחלק אותו ויהיה חציו של אחד | ||||||||||||||||||||||||||||||||
| If in [one of the] middle ranks there is one, we write beneath it 0 and the one becomes ten with the digit that is next to it. | ואם באמצע הטורי' ימצא אחד נשים תחתיו 0' והאחד יחזור עשרה עם האות הסמוכה לה | ||||||||||||||||||||||||||||||||
|
כצורה הזאת[33] | ||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
|
צורה אחרת[34] | ||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||
| Check: doubling | |||||||||||||||||||||||||||||||||
| The proof of this is doubling: if after it is doubled it becomes equal to the halved, then it is correct, otherwise it is incorrect. | והמופת על זה הוא הכפול שאם לאחר שנכפל ישוה לנחלק הוא אמיתי ואם לא ישוה אינו אמיתי | ||||||||||||||||||||||||||||||||
| This is enough for the type of halving. | וזה מספיק בזה המין מחלוק באמצע |
Chapter Five: The Fifth Type [of Numerical Operations], which is Multiplication and Some of its Properties |
פרק ה' במין הה' והוא הרבוע וקצת מסגולותיו |
| Definition of a product: The product is a third number that is necessarily obtained from multiplying any two numbers one by the other so that each of them is found in [the third number] as many times as the units are in the other. | רבוע הוא מספר שלישי מתחייב מהכאת איזה שני מספרי' שיהיו האחד באחר שכל כך פעמים ימצא כל אחד מהם בו כאחדים שבאחר[35] |
| Multiplication table | |
|---|---|
| You should know that whoever wants to be proficient in this type [of operation], must memorize this table that is called the multiplication table. | וצריך שתדע שכל מי שירצה להיות בקי בזה המין צריך שידע זה הלוח על פה ויקרא לוח הרבוע[36] או לוח ההכאות[37] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| What is received from one of these two tables, is received from the other, there is no difference between them, except for the extensiveness versus brevity. | [38]ואלה השתי לוחות מה שיושג באחת יושג באחרת ואין ביניהם הבדל אלא באריכות ובקצור | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Description of the procedure: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| In order that the two numbers we want to multiply will be well distinguished, we call the bottom number "multiplier" and the upper number "multiplied". We write in a line any multiplied number we want and beneath it we write the multiplier. | וכדי שיוכרו בטוב הב' מספרי' שנרצה להכות או לרבע נקרא לתחתון פועל ולעליון פעול ונכתוב מהפעול איזה טור שנרצה ותחתיו נכתוב הפועל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם הפועל יהיה אות אחת נעשה טור א' ונתחיל מהאחדות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם הפועל יהיה מב' אותיות נעשה ב' טורים הטור הראשון יתחיל באחדות והשני בעשרות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם הפועל יהיה מג' אותיות נעשה ג' טורים הראשון יתחיל באחדות והב' בעשרות והג' במאות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| And so on by this order, even if the digits are very many. | וכן כסדר הזה ואם ירבו האותיות מאד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Beneath the rank of the digit of the multiplier, whichever it may be, one should write the beginning of its operation there. This is difference between the lines we said, as you can see in the next diagram, under the lines of the multiplied and the multiplier. | כלומ' שתחת מדרגת אות הפועל איזה שיהיה שם צריך שיכתוב התחלת פעולתו וזהו חלוף הטורים שאמרנו כמו שתראה אותם בצורה הבאה תחת שורות הפעול והפועל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| We do as follows: | ונעשה כן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
שבראשונה נכה אות אחדות הפועל באות אחדות הפעול ומההכאה ההיא או יהיו עשרה או יותר או פחות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם יהיו עשרה נכתוב 0' ונשמור העשרה למדרגה הנמשכת אליה ויהיו שם בשם אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם יהיו יותר מי' נכתוב המותר מהי' ונעביר הי' למדרגה הנמשכת הסמוכה ויהיו שם בשם אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם יהיו פחות מי' נכתוב אותם במקומם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן צריך לעשות מכל אחד מאותיות הפועל עם אותיות הפעול | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וא"כ אם אות הפועל תהיה א' הטור יהיה א' [ואם יהיו שני הטורים יהיו שנים][39] ואם יותר יותר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר נקבץ כל הטורים שעשינו וזו היא ההכאה או הרבוע שבקשנו מהב' מספרים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| As can be seen in each of these diagrams: | כמו שיראה בכל אחת מאלו הצורות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Check: casting out by 9 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The proof of this is that we consider all the digits of the multiplier as units, then cast out the nines and keep the remainder. | והמופת על זה שנמנה כל אותיות הפועל כמו אחדים ונחלקם לתשיעיות ונשמור [40]המותר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Likewise for the multiplied. | וכן מהפעול | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| We multiply the remainder of the multiplier by the remainder of the multiplied, then cast out the nines from the product and keep the remainder. | והמותר מהפועל נכה אותו במותר הפעול והעולה [נשליך ממנו עוד התשיעיו' הנשאר][41] נשמור אותו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| We cast out the nines from the result of the multiplication also and keep the remainder. | והמקובץ מההכאה הראשונה נחלקהו ג"כ בתשיעיות ונשמור הנשאר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If this remainder is equal to the remainder of the product of the remainders of the multiplier and the multiplied, then the multiplication is correct, otherwise it is not. | ואם זה הנשאר או המותר יהיה שוה לעולם [למותר העולה][42] מהכאת מותרי הפועל והפעול ההכאה ההיא אמיתית ואם לא אינה אמיתית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Multiplication with recollection | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| There is another way to multiply. | ויש דרך אחר לרבע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Know that since the multiplier, when multiplied by the multiplied, generates as many lines as the digits in it as we said above, thereafter the sum of its lines indicates the product, if we want to make it easier, instead of making that many lines, we can get from one line what we get from numerous lines, because we already have a method for this and it is this: | דע כי כמו שהפועל בהכאתו בפעול עושה כל כך טורים כאותיות שיש בו כמו שאמרנו למעלה ואחר כך בקבוץ טוריו מורה הרבוע כן גם כן אם נרצה להקל מלעשות הרבה טורים באופן שמה שנשיג בהרבה טורים נוכל להשיג בטור א' כבר יש לנו דרך לזה והיא זאת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Know that the beginning of the multiplier operation is in the multiplication of its units by the units of the multiplied and the position of this product is the position of the units. | דע שהתחלת פעולת הפועל היא בהכאת האחדות שלו באחדות הפעול ומקום ההכאה הזאת היא מקום האחדות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The multiplication, from which the tens are generated, should begin from the position of the tens. | וההכאה שממנה יולדו [העשרות צריך שתתחיל במקום העשרות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The multiplication, from which the hundreds are generated, should begin from the rank of the hundreds. | וההכאה שממנה יולדו][43] המאות צריך שתתחיל במדרגת המאות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The same for the others by the order. | וכן מהאחרות[44] כסדר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This is the way to know the multiplication from which the tens are generated, and the multiplication from which the hundreds are generated, as well as the rest ranks: | ולדעת ההכאה שממנה יולדו העשרו' וההכאה שממנה יולדו המאות וכן מהמדרגות האחרות זו היא הדרך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כבר ידעת שהכאת האחדות באחדו' כתיבתה היא באחדות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וההכאה שממנה יולדו העשרות היא זאת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
שהכאת אחדות הפועל בעשרות הפעול | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וגם כן עשרות הפועל באחדות הפעול | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אלו שתי ההכאות לבד הם העושות עשרות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וההכאות שמהן יולדו המאות הם ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
[הא'][45] מאחדות הפועל במאות הפעול | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והב' עשרות הפועל בעשרות הפעול | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וההכאה הג' היא ממאות הפועל באחדות הפעול | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וקבוץ שלשתם [46]צריך שיכתוב במדרגת המאות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וההכאות שמהם יולדו האלפים הם ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הראשונה היא הכאת אחדות הפועל באלפי הפעול | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ושנית עשרות הפועל במאות הפעול | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ושלישי הכאת מאות הפועל בעשרות הפעול | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ורביעית אלפי הפועל באחדות הפעול | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והעולה מאלו הד' הכאות צריך להכתב במדרגת אות האלפים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| By this order for all the digits of the line: the products are according to their position. | וכסדר הזה בכל אותיות הטור שיהיו כי לפי המקום יהיו ההכאות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ובעבור שמקום האלף הוא מקום רביעי לכן עשינו ד' הכאות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכמו כן בעשרות אלפי' שהוא מקום חמישי צריך ה' הכאות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| So on by this order. | וכסדר הזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If there are many ranks, there are many products. | ואם ירבו המדרגות ירבו ההכאות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Q.E.D. | וזה מה שרצינו הנה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Here is its diagram: | והנה לך צורתו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Since a few special properties are found in this type [of operation], we shall present them here, and they are: | ובעבור שבזה המין ימצאו קצת סגולות מיוחדות נאמר אותם הנה והם אלו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sums |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| First, if we wish to know the sum of many numbers arranged by their order, as counting one, two, three, four, and so on in succession.
|
ראשונה אם נרצה לדעת קבוץ מספרים הרבה מסודרים במדרגותיהם כמו שמונה אחד ושניים ושלשה וארבעה וכן כסדר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If they are many and we wish to know the sum of all of them, we have two way for this: | ואם ירבו מאד ונרצה לדעת קבוץ כולם יש לנו בזה ב' דרכי' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הדרך הראשון [הוא בזה][47] שאמרנו ודרך ידיעתו היא זאת שנעיין המספר האחרון אם הוא זוג או נפרד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם יהיה זוג נקח חציו ונכה אותו על האחרון בתוספת א' ויצא לנו קבוץ כולם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
המשל שנרצה לדעת קבוץ אחד מאחד עד י"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נקח חצי י"ב שהוא ו' ונכהו בי"ג שהוא המספר האחרון עם תוספת א' ויהיו ע"ח וכך הוא הקבוץ מא' עד י"ב[48] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם המספר האחרון יהיה נפרד נקח חציו [49]וחציו של א' יותר ונכה אותו האחרון ויצא לנו קבוץ כולם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
המשל נרצה לדעת המקובץ מאחד עד י"ג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נקח ו' וחצי וחצי יותר שהם ז' ונכה אותם על י"ג ויעלו צ"א וכך הוא המקובץ מכולם |
|
וכסדר הזה ואם המספרי' הרבה מאד |
|
והדרך השנית הוא בזה שאם יהיו המספרי' כלם זוגות כשנתחיל מב' ואחר ד' ואחר ו' וכן אם ירבו מאד כסדר הזה |
|
לדעת המקובץ מכולם נקח חצי הזוג האחרון ונכה אותו על חציו האחר בתוספת אחד ומה שיעלה הוא קבוץ כל הזוגות |
|
המשל בזה שאם הזוג האחרון יהיה י"ב |
|
נקח חציו שהוא ו' ונכהו על ז' שהוא חצי המספר בתוספת א' ויעלה למ"ב וכך הוא הקבוץ של כולם |
|
ואם יהיו המספרים נפרדים כולם כשנתחיל מא' ואחר ג' ואחר ה' ואחר ז' ואם ירבו מאד כסדר הזה |
|
לדעת המקובץ מכולם נקח חצי המספר האחרון וחצי אחד יותר ונכהו בעצמו ומה שיעלה הוא המקובץ מכולם |
|
המשל בזה נרצה לדעת המקובץ מכל הנפרדים מהאחד עד ט"ו |
|
נקח חצי האחרון שהוא ז' וחצי וחצי יותר ויהיו ח' ונכהו בעצמו ויעלו ס"ד וכך הוא המקובץ מכולם |
|
וכסדר הזה תעשה ואם ירבו המספרים הרבה מאד |
Shortcuts |
|
| In this type, i.e. the multiplication, there are other ways to know the product of the numbers by a shortcut. | ובזה המין ר"ל הרבוע יש דרכים אחרים עוד לדעת הכאת המספרים בדרך קצרה |
|
והראשון כשנרצה לדעת הכאת כל שני מספרים שהם תחת העשרה נעשה כך נראה המספר ה[.] היותר גדול כמה הוא [50]פחות מעשרה וכמו שיהיה הגדול פחות מי' כך פעמים נוציא המספר הפחות מעשרתו |
|
המשל שנרצה לדעת קבוץ הכאת ח' בט' |
|
ומצאנו שהמספר היותר גדול שהוא ט' הוא פחות מי' אחד ולכן נחסר ח' פעם אחת מפ' שהוא עשיריתו וישארו ע"ב וזאת היא ההכאה מח' בט' |
|
וכך הוא הסדר באחרים |
|
וכמו שסדרנו פעולתנו על המספר היותר גדול ג"כ נוכל לסדרו על המספר הפחות |
|
המשל כי כמו שאמרנו בהכאת ח' בט' כמה היה הט' פחות מי' כך נעשה כשנעיין כמה היו מח' עד י' שהם פחות ב' ולכן נחסר ב' פעמים ט' מהצ' וישארו ע"ב |
|
והכל פעולה אחת אלא שהוא יותר נקל כשנסדר פעולתינו על המספר הגדול |
|
ואם יהיה במדרגת העשרות כשנרצה להכות איזה מספר שיהיה בעשרה נוסיף עליו 0' |
|
המשל אם נרצה לדעת י' פעמים י"ב כמה הם נוסיף 0' על י"ב ויהיו ק"כ ובדרך המספר יסודרו כן 0בא[51] |
|
ואם יהיה ההכאה על כ' באיזה מספר נכפול המספר המוכה בב' ונוסיף 0' |
|
המשל כ' פעמי' ה' נכפול הה' ויהיו י' ונוסיף 0' ויהיו ק' |
|
וכן מהאחרים |
|
ואם נרצה להכות בשלשים איזה מספר שיהיה נשלש ונוסיף עליו 0' |
|
המשל ל' פעמים כ' נשלש הכ' ויהיו ס' ונוסיף ספרא ויהיו ת"ר וזו היא צורתו בדרך המספר 00ו[52] |
|
וכסדר הזה בכל העשרות |
|
ואם [נרצה][53] להכות במאה איזה מספר נוסיף עליו ב' ספראש ויהיה מוכה במאה |
|
[54]ואם נרצה להכות איזה מספר באלף נוסיף עליו ג' ספרש |
|
וכן כסדר הזה כשנוסיף תמיד בכל מדרגה 0' אחת |
Chapter Six: The Sixth Type which is Division |
פרק שישי במין השישי שהוא החלוק | ||||||||||||||||||||||||||||||||||||
| Definition of the division operation: division is dividing any number into equal parts as the number of units in the divisor. | חלוק הוא חלוקת איזה מספר שיהיה בכך חלקים שוים כמספר האחדים שבמחלק | ||||||||||||||||||||||||||||||||||||
| In this type [of operation] one should start from the highest rank. | ובמין הזה צריך להתחיל באות ששוה יותר | ||||||||||||||||||||||||||||||||||||
| We write the divisor beneath the dividend, leaving an empty space between the divisor and the dividend to write in it the quotient required for each part of the divisor. | ונכתוב המחלק תחת המחולק בשנניח מקום פנוי בין המחלק והמחולק שנכתוב בו החלק המבוקש לכל אחד מחלקי המחלק | ||||||||||||||||||||||||||||||||||||
| Since division is only to know how many times the divisor is found in the dividend, we should examine how many times the digit of the divisor is found in the digit of the dividend and we should write the number of these times in the empty space that we left. | ובעבור שהחלוק אינו אלא לדעת כמה פעמים ימצא המחלק במחולק לכן צריך שנעיין כמה פעמים ימצא אות המחלק באות המחולק ומספר אותם הפעמים צריך שנכתוב במקום הפנוי שהנחנו | ||||||||||||||||||||||||||||||||||||
|
המשל נרצה לחלק קמ"ד על ח' | ||||||||||||||||||||||||||||||||||||
|
תעשה כך כצורה הזאת | ||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||
| You should know that when the digit of the dividend is less than the divisor, as in this example, we take two digits of the dividend and we consider the greater as tens and the other as units. | וצריך שתדע כי כשהאות המחולק תהיה פחות מהמחלק כמו בזה המשל אז נקח ב' אותיות מהמחולק ונקח היותר גדולה בשם עשרה והאחרת בשם אחדות | ||||||||||||||||||||||||||||||||||||
|
כמו שאתה רואה בזאת הצורה | ||||||||||||||||||||||||||||||||||||
|
הא' בשם עשרה והד' בשם ארבעה וקבוצם י"ד ונאמר כמה פעמים ימצא ח' בי"ד וראינו שימצא פעם אחד ונשארו ו' | ||||||||||||||||||||||||||||||||||||
|
והאחד שמנו בשם חלק שהיא א' תחת הד' והו' שנשארו כתבנו על הד' של המחולק | ||||||||||||||||||||||||||||||||||||
|
ובעבור שמהארבעה עשר לא נשארו יותר מו' כתבנו על הא' מהמחולק 0' והו' הנשארים יהיו עשרות להבא | ||||||||||||||||||||||||||||||||||||
|
וא"כ נשארו עדיין לחלק ס"ד ונחלקם בח' ויהיו ח' לחלק | ||||||||||||||||||||||||||||||||||||
|
ונכתוב אותם תחת הד' הראשון של המחולק | ||||||||||||||||||||||||||||||||||||
|
[55]ונאמר ח' פעמים ח' הם ס"ד וכשנחסרם מהמחולק שהם ס"ד לא ישאר דבר | ||||||||||||||||||||||||||||||||||||
|
ולכן כתבנו על ו' ספרא ו0' על הד' |
- [Illustration of the procedure:]

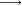

0 06 06 060 144 144 144 144 1 1 18 8 8 8 8
| This way for all the ranks, even if they are very many. | ובדרך הזה צריך בכל המדרגות ואם ירבו מאד | ||||||||||||||||||||||||||||||||||||||||||||||
| All this is when the divisor consists of one digit alone. | וכל זה כשיהיה המחלק מאת אחת בלבד | ||||||||||||||||||||||||||||||||||||||||||||||
| Know that when the digit of the quotient is placed beneath the units, then we know that there is nothing left to divide, and this is clear for the integers. | ודע כי כשאות החלק יבא תחת אחדות המחולק אז נדע שלא נשאר יותר לחלק וזה יובן בשלמים | ||||||||||||||||||||||||||||||||||||||||||||||
| If something remains, relate it to the divisor and as the ratio of the parts to one whole, so is each part to the divisor; or convert each one of the remaining to as many parts as the units that are in the divisor, then we divide them by the divisor. | ואם ישאר דבר תיחסהו למחלק וכאותו היחס מחלקי שלם אחד יהיה לכל חלק מהמחלק או תהפך כל אחד ואחד מהנשארים לכל כך [חלקים][56] כמו האחדים שיש במחלק ואחר נחלקם במחלק | ||||||||||||||||||||||||||||||||||||||||||||||
| Thereafter, there is nothing left to divide. | ואז לא ישאר דבר לחלק | ||||||||||||||||||||||||||||||||||||||||||||||
|
המשל בזה שאם המחלק יהיה ח' והנשאר לחלק היו ג' ניחס הג' לח' ויהיה היחס ג' שמיניות | ||||||||||||||||||||||||||||||||||||||||||||||
|
או נעשה מכל א' מהג' הנשארי' ח' חלקי' ויהיו [כ"ד][57] חלקים ונחלקם על המחלק שהם ח' ויבא לכל חלק ג' שמיניות | ||||||||||||||||||||||||||||||||||||||||||||||
| In this way you proceed whenever anything remains for you to divide. | ובדרך הזה תעשה בכל עת שישאר לך דבר לחלק | ||||||||||||||||||||||||||||||||||||||||||||||
| If the divisor consists of two digits [= units and tens]: we write it beneath the dividend, in the highest rank, leaving a free space, as aforesaid. | ואם יהיה המחלק מב' אותיות נכתוב אותו תחת המחולק במדרגה השוה יותר בהניחנו מקום פנוי כאמו' | ||||||||||||||||||||||||||||||||||||||||||||||
| You should know that if the divisor consists of two digits, we must consider in our procedure the first corresponding digit of the dividend as units and the other as tens. | וצריך שתדע שאם המחלק יהיה מב' אותיות שהאותיות הנגדיות מהמחולק צריך שבפעולתינו נקח האחת כמו אחדות והאחרת כמו עשרות | ||||||||||||||||||||||||||||||||||||||||||||||
| If the divisor consists of three digits, the first corresponding digit of the dividend is [considered] as units, the second as tens, and the third as hundreds. | ואם המחלק יהיה מג' אותיות הנגדיות מהמחולק יהיה האחת כמו אחדות והב' כמו עשרות והג' כמו מאות | ||||||||||||||||||||||||||||||||||||||||||||||
| And so on by this order, if the [digits] are numerous, the [ranks] are numerous. | וכן כסדר הזה ואם ירבו ירבו השמות | ||||||||||||||||||||||||||||||||||||||||||||||
| First, we examine the left digit of the divisor: how many times it is found in the first digit of the dividend. We write [the number of] times that it is found in it as the quotient in the empty space above the digit of the units of the divisor, provided that it will be enough to subtract the product of of the quotient by the right digit of the divisor from the right digit of the dividend with the help of the left digit that is next to it. Because the two digits of the dividend always help each other and this is necessary at all stages of the division. Then, we subtract [the product] from the dividend. | וראשונה נעיין האות השמאלית מהמחלק כמה פעמים ימצא [58]באות הראשון שבמחולק וכל כך פעמים שימצא בו כך נכתבנו בשם חלק במקום הפנוי על אות אחדות המחלק בתנאי זה שהכאת החלק באות הימנית מהמחלק יספיק לחסר אותה מהאות הימנית של המחולק בעזר האות השמאלית [שבצדה][59] למה שהב' אותיות של המחולק נעזרת לעולם וזה הכרחי בכל מדרגות החלוק ואז נחסרם מהמחולק | ||||||||||||||||||||||||||||||||||||||||||||||
| If the two digits of the dividend are smaller than the digits of the divisor, we write zero in the quotient and move to the next [digit]. | ואם הב' אותיות של המחולק היו פחות מאותיות המחלק נכתוב ספרא בשם חלק ונעבור לבאות | ||||||||||||||||||||||||||||||||||||||||||||||
| Then, we should take the two left digits of the dividend for the left digit of the divisor and the other [digit of the dividend] for the right [digit of the divisor]. | ואז צריך שנקח הב' אותיות מהמחולק מצד שמאל בשם אות שמאלית מהמחלק והאחרת בשם אות ימאנית | ||||||||||||||||||||||||||||||||||||||||||||||
| We examine how many times can the left [digit] of the divisor be subtracted from the two left digits of the dividend, so that the right digit of the divisor can be subtracted [the same number of] times from the right [digit] of the dividend. | ומאלו ב' האותיות מהמחולק מצד שמאל נעיין כמה פעמים איפשר לחסר מהן השמאלית מהמחלק ושכל כך פעמים יחסר האות הימנית מהמחלק מהימנית מהמחולק | ||||||||||||||||||||||||||||||||||||||||||||||
| This way until the end of all the digits of the dividend as stated above. | וכדרך זה עד כלות כל האותיות מהמחולק כאמו' למעלה | ||||||||||||||||||||||||||||||||||||||||||||||
| For the meaning of division is nothing but that the digit we put in the quotient is such that as many times that the left [digit] of the divisor is subtracted from the left [digit] of the dividend, the [same number of] times the right [digit] of the divisor is subtracted from the right [digit] of the dividend and [likewise the rest of the digits] if there are more. | כי כונת החלוק אינו אלא שהאות שנשים בשם חלק שכל כך פעמים שיחסר שמאלית המחלק מהשמאלית המחולק כל כך פעמים יחסר ימנית המחלק מימנית המחולק ויותר אם יהיו | ||||||||||||||||||||||||||||||||||||||||||||||
|
כנראה בצורה הזאת | ||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||
|
ונניח שנרצה לחלק ט' אלפי' ותתע"ו בי"ב חלקים | ||||||||||||||||||||||||||||||||||||||||||||||
|
בעבור שהמחלק הוא מב' אותיות נקח הב' אותיות אחרונות מהמחולק שהם ח'ט' הח' בשם אחדות והט' בשם עשרות שהם צ"ח על י"ב | ||||||||||||||||||||||||||||||||||||||||||||||
|
ונעיין כמה פעמים איפשר לחסר האות השמאלית של המחלק שהיא א' מאות השמאלית מהמחולק שהיא ט' ונראה שימצא בה ט' פעמים | ||||||||||||||||||||||||||||||||||||||||||||||
|
האמנם למה [60]שאמרנו שכל כך פעמי' כמו שימצא שמאלית המחלק בשמאלית המחולק כל כך פעמים צריך לחסר ימנית המחולק מהמחולק[61] וזה אינו מספיק לכך כתבנו ח' בשם חלק וחסרנו אותם מהט' וישאר א' על הט' | ||||||||||||||||||||||||||||||||||||||||||||||
|
ונאמ' ח' פעמי' ב' שהם י"ו כשנחסרם מי"ח ישארו ב' על הח' מהמחולק וספרא על הא' מהמחולק | ||||||||||||||||||||||||||||||||||||||||||||||
|
ועתה נחזור ונקח הב' והז' הב' בשם שמאלית והז' בשם שמאלית[62] כאמור ונסדרם כמו שסדרנו בב' האותיות הראשונות כשנאמר כמה פעמי' איפשר לחסר שמאלית המחלק שהיא א' משמאלית המחולק [שהיא][63] ב' ונמצא שאיפשר שיחסר ב' פעמי' | ||||||||||||||||||||||||||||||||||||||||||||||
|
וג"כ נמצא שימנית המחלק שהיא ב' איפשר שיחסר ב' פעמי' מימנית המחולק שהיא ז' | ||||||||||||||||||||||||||||||||||||||||||||||
|
ולכן כתבנו ב' בשם חלק | ||||||||||||||||||||||||||||||||||||||||||||||
|
והכינו הב' מהחלק על הא' שהיא אות שמאלית מהמחלק ויעלו ב' ונחסרם מהב' שהיא שמאלית המחולק וישאר ספרא | ||||||||||||||||||||||||||||||||||||||||||||||
|
עוד נכה הב' שהוא החלק על הב' שהוא ימנית המחולק ויעלו ד' ונחסרם מהז' וישאר ג' על הז' |
- [Illustration of the procedure:]
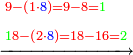
0 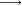
0 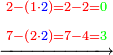
00 12 12 123 9876 9876 9876 9876 8 8 82 12 12 12 12
|
ויהיה ו' ימנית המחולק וג' שמאלית המחולק | |||||||||||
|
ונעיין כמה פעמי' איפשר לחסר א' שהוא שמאלית המחלק מהג' שהיא שמאלית המחולק ומצאנו שג' פעמי' | |||||||||||
|
ובקשנו ג"כ אם ימצא הב' שהוא ימנית המחלק כל כך פעמים בימנית של המחולק ומצאנו שימצא | |||||||||||
|
ולכן כתבנו ג' בשם חלק | |||||||||||
|
והכינו ג' בא' ועלו ג' ונוציאם מהג' של המחולק וישאר 0' | |||||||||||
|
וג"כ נכה הג' של המחלק על ימנית המחלק שהוא ב' ויעלו ו' ונחסרם מהו' שהיא ימנית המחולק וישאר ספרא ונכתוב ספרא על הו' | |||||||||||
|
||||||||||||
|
והנה נחלק הכל ויהיה החלק תתכ"ג[64] | |||||||||||
| Check: multiplication | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| The proof of this is that we multiply the quotient by the divisor and if it is equal to the dividend, it is correct, otherwise we should calculate again. | והמופת [65]על זה הוא שנכה החלק במחלק ואם יהיה שוה למחולק הוא אמת ואם לאו נחזור שנית לחשבונינו | |||||||||||
| Check: casting out by 9 | ||||||||||||
| Another proof is that we cast out the nines from the divisor on one side and from the quotient on the other side, then we multiply the remainders of the two that are less than 9. We cast out the nines from [the product] also and keep what is less than 9. | ומופת אחר שנחסר התשיעיות מהמחלק בצד אחד ומהחלק לצד אחר ונכה הנשאר מהשניים שלא יעלה לט' ונוציא ממנו ג"כ התשיעיות ומה שלא יעלה לט' נשמרהו | |||||||||||
| We cast out the nines from the dividend also and look at the remainder that is less than 9: if it is equal to the remainder of the product, it is correct, otherwise it is not. | ונשליך ג"כ המחולק לתשיעיות ונראה הנשאר שלא הגיע לט' ואם יהיה שוה לנשאר מההכאה הוא אמת ואם לאו אינו אמת | |||||||||||
| If the divisor consists of more than two digits, we do exactly the same way itself: that as many times the left [digit] of the divisor is found in the left [digit] of the dividend, the same [number of] times we subtract the right [digit] of the divisor from the right [digit] of the dividend, and the same [number of] times the third [digit] of the divisor [is subtracted] from the third [digit] of the dividend, and the fourth also, if it consists of four [digits]. | ואם יהיה המחלק יותר מב' אותיות נעשה בדרך זה בעצמו לא פחות ולא יתר שכל כך פעמי' שימצא שמאלית המחלק בשמאלית המחולק כל כך פעמי' נחסר ימנית המחלק מימנית המחולק וכל כך פעמים אות הג' של המחלק מאות הג' של המחולק והד' ג"כ אם יהיה מד' | |||||||||||
| We do this way, even if the digits are very many. | וכן אם ירבו האותיות הרבה מאד נעשה כסדר הזה | |||||||||||
| This is enough for the six types [of operations] with integers. | וזה יספיק בו' מיני השלמים | |||||||||||
| Now, we shall discuss the six types [of operations] with fractions and their properties. | ונדבר עתה מו' מיני השברים ומסגולותיהם |
Section Three of Book One: [Fractions] |
הכלל השלישי מהמאמר הא' | ||
| It is divided into eight chapters | ויתחלק לח' פרקים | ||
Chapter One: Guiding Methods of the Writing Fractions, their Definition, and their Arrangement |
הפרק הראשון בדרכים מיישירים באופני הנחת השברים וגדרם וסדורם | ||
| After we discussed the six types [of operations with] integers, we should now discuss the six types [of operations with] fractions. | [ואחר שדברנו מו' מיני השלמים עתה צריך שנדבר בו' מיני השברים][66] | ||
| You should know that as there are six types [of operations with] integers, there are also six types [of operations with] fractions. | וצריך שתדע כי כמו שיש ו' מיני שלמים כן ג"כ יש ששה מיני שברים | ||
| Before we discuss them, we should say what is a fraction, how it is arranged in writing, and by which number it is fractionalized. | וקודם שנדבר [מהם][67] צריך שנאמר מהו שבר ואיך יסודר בכתיבתו ובאיזה חשבון ישבר | ||
| definition of fraction: A fraction is any part that is taken from the integer. | השבר הוא אי זה חלק שילקח מהשלם | ||
|
כמו חצי או שליש או רביע וכדומה | ||
| How they are arranged in writing: it is since in every fraction two matters are represented - continuous quantity and discontinuous quantity. | ואיך יסודרו בכתיב[ת]ם הוא זה בעבור שבכל שבר ושבר יצויירו שני עניינים ר"ל כמות [68]מתדבק וכמות מתחלק | ||
|
המשל כשנאמ' ב' [שלישיות] או ג' רביעיות | ||
|
הב' והג' הם כמות מתחלק בעבור שמדברים מהמספר כי המספר הוא כמות מתחלק | ||
|
והשלישיות והרביעיות כמות מתדבק בעבור שמדברים מחלק או חלקי' מאיזה כל שיהיה ולכן רומזים לכמות מתדבק | ||
| Since the fractions consist of two types of quantity as stated, each fraction should be written with two digits - one indicates the continuous quantity and the second [indicates] the discontinuous quantity. | ובעבור שהשברים יוכללו בב' מינים מהכמה כאמור לכן צריך שיכתב כל שבר ושבר בשני אותיות הא' ירמוז [על] הכמה המתדבק והב' לכמה המתחלק | ||
| The digit that indicates the discontinuous quantity is written above, and beneath it a line. | והאות הרומזת לכמה המתחלק נכתוב למעלה ותחתיה קו אחד | ||
| The digit that indicates the continuous quantity is written beneath the line. | והאות הרומזת לכמת המתדבק נכתוב תחת הקו | ||
|
המשל אם נרצה לכתוב ב' שלישיות | ||
|
נכתוב ב' ותחת הב' קו אחד ותחת הקו ג' כמו שיראה בצורה הזאת | ||
|
|
| ||
| The upper digit, which is 2, or whichever, indicates the multiplicity of the fractions, as 1, 2, 3, 4, 5, or whichever you want. | והאות העליונה שהיא ב' או מה שיהיה תרמוז לכמות רבוי השברי' כמו א' ב' ג' ד' ה' וכל מה שתרצה | ||
| The bottom digit, which is 3, of whichever, indicates the name of the fraction, as a half, a third, a quarter, a fifth, or whichever parts of the whole. | והאות התחתונה שהיא ג' או מה שיהיה תרמוז לשם החלק כמו חצי או שליש או רביע או | ||
| For the whole is divided into two halves, three thirds, four quarters, five fifths, six sixths, or any parts, into which we wish to divide the whole. | כי השלם יחלק לב' חצאים ולשלשה שלישיות ולד' רביעיות ולה' חמישיות ולו' ששיות וכן כל החלקים שנרצה לחלק בהם השלם | ||
| You should know that as the third is one of three parts of the whole, the whole cannot be divided into thirds that are more than three, nor into quarters that are more than four, nor into fifths that are more than five and so on. | וצריך שתדע כי כמו שהשליש הוא א' משלשה חלקי השלם כך השלם לא יחלק לשלישיות יותר משלש ולא רביעיות יותר מד' ולא בחמישיות יותר מה' וכן כלם כסדר הזה | ||
| The fractions are written in the following arrangement: | והשברי' יכתבו בסדר הזה | ||
|
שאם תרצה לכתוב חצי שלם תכתוב אותו כך | ||
|
|
| ||
|
והשלישיות תכתוב כך | ||
|
|
| ||
|
והרביעיות כך | ||
|
|
| ||
|
ושלשה רביעיות נכתוב [69]כך | ||
|
|
| ||
|
וארבעה חמישיות נכתוב כך | ||
|
|
| ||
| Likewise, whatever you want according to this arrangement. | וכן כל מה שתרצה כסדר הסדר הזה |
Chapter Two: Addition of Fractions |
הפרק השני בקבוץ השברים | ||||||||||
| Definition of the addition of fractions: it is conversion of two types of fractions, or more, to integers, or to one type of fractions, or to integers and one type of fractions together. | והוא השבת שני מיני שברי' או יותר לשלמי' או למין א' מהשברים [או לשלמים ומין אחד מן השברים][70] יחד | ||||||||||
| We do it this way: | ונעשה בדרך זה | ||||||||||
| We write all the fractions that we want. | נכתוב כל השברי' שנרצה | ||||||||||
|
כמו שרוצה לחבר או לדעת [קבוץ][71] חצי ושליש ורביע | ||||||||||
| Or whatever it may be, as is seen in this diagram: | או מה שיהיה כצורה זו | ||||||||||
|
|
| ||||||||||
| Common denominator | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| The first thing that you need to know in this type [of operation] is to find one number in which all these fractions are found. | והראשון שצריך שתדע בזה המין הוא למצא חשבון א' שימצאו בו כל אלו השברי' | ||||||||||
| It is found by that we multiply 2 by 3, then we multiply their product by 4 and so on in this order. We always multiply the product of the preceding digits by the one that follows them, until we complete with all the bottom line, i.e. with all the digits that are beneath the line. | וימצא בדרך זה בשנכה ב' על ג' והעולה משניהם נכה בד' וכן כסדר הזה נכה לעולם כל העולה מהכאת כל האותיות העוברות עם הנמשכת אליהם עד שנשלים כל הטור התחתונה ר"ל כל האותיות שהם תחת הקו | ||||||||||
| The result of all these multiplications is the number in which all the fractions, of whichever type of fractions, are found. | והעולה מכל אלו ההכאות הוא חשבון שימצאו בו כל השברי' באיזה מין שיהיה ממיני השברי' | ||||||||||
|
והחשבון שימצאו בו כל השברי' הכתובי' בזאת הצורה שלמעלה הם כ"ד והוא בדרך זה נכה ב' על ג' ויעלו ו' וכל זה ר"ל הו' על הד' ויעלו כ"ד | ||||||||||
|
ובזה החשבון ימצאו חצי ושליש ורביע ולזה החשבון ר"ל כ"ד יש להם מקום של שלם | ||||||||||
|
כי כמו שמהשלם יקח אדם איזה חלק שירצה כך מזה החשבון של כ"ד שהם במקום השלם נקח איזה חלק שנרצה | ||||||||||
| numerator | |||||||||||
|
ולכן נקח החצי והשליש והרביע בזה הדרך | ||||||||||
|
נתחיל לקחת החצי בזה הדרך שהאות שנמצאת על קו החצי שהיא א' נכה באות ג' שהיא תחת הא' הרומזת לשליש ויהיו ג' ואלו הג' נכם על ד' שהוא [72]תחת אות הרומזת הרביע ויהיו י"ב שהוא חצי של אותו החשבון שאמרנו | ||||||||||
|
ואח"כ נקח השליש בדרך זה שנכה אות השליש שהוא על הקו עם האות של החצי שהוא תחת הקו והוא ב' והיה המוכה ב' ונכה הב' על ד' ויעלה לח' שהוא השליש של זה החשבון | ||||||||||
|
ואח"כ נכה הא' שהוא על ד' על הב' שהוא תחת הקו הרומזת החצי ויהיה ב' ואלו הב' נכה אותם בג' שהם תחת הקו הרומזים השלישי ויעלו לו' שהם רביע זה החשבון ר"ל הכ"ד | ||||||||||
|
א"כ יש לנו ג' חשבונות שהם חצי ושליש ורביע שהם י"ב וח' וו' וקבוץ כולם כ"ו | ||||||||||
|
והשלם שיוחסו אליו אלו הכ"ו הוא כ"ד ולכן נחלק הכ"ו בכ"ד ויצא א' שלם וישארו שנים שלא נחלקו וניחס אותם לחשבון כ"ד ונמצא שהם חלק א' מי"ב של שלם א' וזה העולה מהג' שברי' האמורים למעלה א"כ העולה מהשברים האמורים הוא א' שלם וחלק א' מי"ב חלקי השלם | ||||||||||
| In order that it will be better understood, we give another example: | וכדי שיובן יותר טוב נעשה משל אחר | ||||||||||
|
ונניח שנרצה לקבץ ב' שלישיות וג' רביעיות וד' חמישיות וה' ששיות | ||||||||||
|
שצורתם היא זאת | ||||||||||
|
|
| ||||||||||
| common denominator | |||||||||||
|
הראשון שצריך שנמצא החשבון שהוא במקום השלם ר"ל שימצאו בו כל אלה השברי' ונעשה כך נכה כל האותיות שתחת הקוים בזה הדרך | ||||||||||
|
ראשונה [נכה][73] ג' בד' ויהיו י"ב ואלו הי"ב נכם בה' ויעלו ס' ונכה ס' בו' ויעלו ש"ס וזה המספר שבו ימצאו כל אלו השברי' והוא מקום שלם ויקרא ג"כ מחלק | ||||||||||
| numerator | |||||||||||
|
וצריך שנוציא [ממנו][74] כל השברים ונעשה בדרך זה | ||||||||||
|
ראשונה נוציא השבר | ||||||||||
|
ואח"כ נוציא הג' רביעיות בדרך זה בשנקח הג' שהיא על הד' ונכהו בכל האותיות התחתונות זולת האות שתחתיה שהיא ד' בדרך זה ג' על ג' ויהיו ט' וט' על ה' ויהיו מ"ה ומ"ה על ו' ויעלו ע"ר וזה החשבון שיורה על ג' רביעיות | ||||||||||
|
ואח"כ נוציא הד' חמישיות בדרך זה בשנקח הד' שהוא על ה' ונכהו בכל האותיות התחתונות זולת הה' שהיא תחת הד' בדרך זה נכה ד' בג' ויהיו י"ב וי"ב בד' ויעלו מ"ח ומ"ח בו' ויעלו רפ"ח וזהו החשבון שיורה על ד' חמישיות | ||||||||||
|
ואח"כ נוציא החמשה ששיות בשנקח ה' שהוא על הו' ונכהו בכל התחתונים זולת הו' שתחתיה בדרך זה נכה ה' על ג' ויעלו ט"ו וט"ו על ד' ויעלו ס' וס' בה' ויעלו ש' וזהו החשבון שיורה על ה' ששיות | ||||||||||
|
והנה כבר הוצאנו כל השברים שאמרנו ועתה צריך שנקבץ כל אלה השברי' שאמרנו [ונעשה בדרך זה נקח החשבון הר"מ והר"ע והרפ"ח והש' ונחבר הכל ויהיה קבוצם אלף וצ"ח וזהו קבוץ כל השברים שאמרנו][77] | ||||||||||
|
וכל זה הקבוץ נחלקהו בש"ס שהוא המחלק והוא במקום שלם כמו שאמרנו ויצאו ג' שלמים וחלק א' מכ' חלקים של שלם אחד וזהו קבוץ כל השברים שאמרנו והנה לך צורתו | ||||||||||
| Since we have said that the sum of the whole aforementioned diagram is three integers and one [part] of twenty parts of one whole, we should explain now how we have found this quotient of 20 parts of the whole and how all those that are similar are found. | [78]ובעבור שאמרנו שקבוץ כל הצורה האמורה למעלה עולה לשלש שלמים וא' מעשרי' חלקי' משלם אחד צריך עתה שנבאר איך מצאנו אותו החלוק מכ' חלקי השלם ואיך ימצאו כל הדומים | ||||||||||
| Know that after a number is divided by another number and a certain number remains that cannot be divided as it is less than the divisor, we relate it to the divisor and the ratio between them is its ratio to the whole. | דע כי לאחר שיחלק איזה חשבון שיהיה באחר וישאר איזה חשבון שלא יחלק להיותו פחות מהמחלק אז נייחסהו למחלק והיחס שימצא ביניהם אותו היחס יש לו עם שלם אחד | ||||||||||
|
המשל כבר ראית שבצורה שלמעלה נשארו י"ח שלא נחלקו בעבור שהיו פחות מהמחלק שהוא ש"ס לכן בקשנו היחס שיש בין הי"ח והש"ס ומצאנו שהוא יחס הא' לכ' ולכן אמרנו למעלה | ||||||||||
|
והדרך למצא היחס הוא בנקלה נקח אלו הב' מספרים י"ח למעלה וש"ס למטה ונעיין כמה חלקים איפשר לחלק הי"ח וכל כך חלקים נחלק הש"ס | ||||||||||
|
המשל כי כמו שהי"ח יחלקו בג' חלקים ויהיה החלק ו' כן גם כן נחלק הש"ס בג' חלקים ויצא כ"ק | ||||||||||
|
ונחזור ונחלק הו' בג' חלקי' ויצא ב' ונחלק הק"כ בג' ג"כ ויצאו מ' | ||||||||||
|
עוד נחלק הב' באמצע ויצא א' וגם המ' באמצע ויצאו כ' א"כ יהיה אחד מכ' חלקי השלם | ||||||||||
| In this way we relate any two numbers, so that into as many parts that one is divided, so the other is divided. | ובדרך זה ניחס כל שני מספרים שבכל כך חלקי' שיחלק האחד יחלק השני והנה לך צורתו | ||||||||||
| You should know that in this type [of operation], i.e. the addition, you can sum up many different fractions, which is not so in the other types [of operations]. Because, in every type of them two different fractions are enough, which is not so in this type. | וצריך שתדע שבזה המין ר"ל הקבוץ תוכל לקבץ הרבה חלופים משברי' מה שאינו כן במיני' האחרי' כי בכל מין מהם מספיק חלוף ב' שברי' בלבד מה שאינו כן במין הזה | ||||||||||
| This is enough for this type. | וזה מספיק במין הזה |
Chapter Three: Subtraction of Fractions |
פרק שלישי בחסור השברי' |
| It was already defined for the types [of the operations with] integers and it is in the way that we write two numbers of whichever fractions we want and we write each next to the other. | וכבר נגדר במיני השלמי' והוא בדרך זה שנניח ב' מספרי' של שברי' איזה שנרצה ונכתוב כל א' אצל חבירו |
|
כנראה בזה הצורה [79]שנעשה ונניח שמהשלשה רביעי שלם נרצה לחסר שני שלישי שלם ונרצה לדעת כמה ישארו |
|
ונסדרם כך |
| common denominator | |
|---|---|
| The first this that we should do is the common denominator, which is called also the divisor and the whole. We do it by multiplying the digits that are beneath the lines one by the other. | והראשון שצריך שנעשה הוא המספר המשותף ויקרא ג"כ המאזנים ויקרא המורה ויקרא ג"כ המחלק וג"כ במקום שלם ונעשה בדרך זה שנכה האותיות שהם תחת הקוים האחת בחברתה |
|
המשל מזאת הצורה הד' שהוא מצד א' אחד על הג' שהוא מצד אחר ויעלו לי"ב וזהו המספר שאמרנו שהוא משותף ויקרא משותף כי בו ישתתפו שני המספרי' שתחת הקוים כאמו' |
| numerator | |
|
ועתה צריך שנוציא ג' רביעיות מהמספר המשותף בדרך זה נכה הג' שעל הד' על הג' |
|
ואח"כ נוציא הב' שלישיות בדרך זה נכה הב' שהוא על הג' על הד' שהוא תחת הג' ויעלו ח' ואלו הן שני שלישי המחלק |
| You see that until now we have done three things in this type [of operation]: | והנך רואה שעד עתה עשינו בזה המין שלשה דברי' |
|
ראשונה מצאנו המחלק שהוא במקום שלם |
|
ושנית מצאנו הג' רביעיות ממנו שהם ט' |
|
ושלישית מצאנו שני שלישיות ממנו שהם ח' |
|
ובעבור שכוונתינו היה לחסר שני שלישיות מג' רביעיות לאחר שהם נמצאות אצלינו נוציא הח' שהם ב' שלישיות מהט' שהם ג' רביעיות וישאר אחד |
|
והאחד הזה שנשאר צריך שנדע מה הוא ולדעת זה נחלקהו במחלק או המורה שהוא י"ב ואז נדע מהו ודרך חלוקו הוא זה |
|
א"כ הוא א' מי"ב חלקי מהשלם |
| Check: addition | |
| The proof of this is that we sum up what we have subtracted, which is 2-thirds, and what remained, which is 1 [part] of 12 parts of the whole. If this sum is 3-quarters, then the subtraction that we did is correct, otherwise it is incorrect.
|
והמופת על זה הוא שנחבר מה שהוצאנו שהוא ב' שלישיות ומה שנשאר שהוא א' מי"ב חלקי השלם ואם קבוץ אלו יעלו לג' רביעיות החסור שעשינו הוא אמיתי ואם לאו אינו אמיתי |
| The way to do this in this type [of operation] is by the addition and you already know it. | [81]ודרך עשיית זה במין הוא הקבוץ וכבר ידעתו |
|
וכמו שיראה בזו הצורה |
| common denominator | |
|
והראשון שצריך להוציא המחלק שהוא הכאת הג' בי"ב ויהיו ל"ו |
| numerator | |
|
ומאלו נוציא ב' שלישיות בדרך זה נכה הב' מהצורה שהיא על הג' על הי"ב שהם תחת הא' ויהיו כ"ד ואלו הם ב' שלישיות המחלק |
|
ונוציא גם הא' מי"ב חלקי השלם בדרך זה נכה הא' שעל הי"ב על הג' שתחת הב' ויהיו ג' וזהו א' מי"ב חלקי השלם |
|
ועתה נחבר אלו הג' עם הכ"ד ויהיו כ"ז |
|
ואלו הכ"ז נחלקם במחלק בדרך המין הראשון לא פחות ולא יתר ויהיו כ"ז חלקים מל"ו מהשלם |
|
והחלקים האלו צריך שיהיו ג' רביעיות מהשלם ולדעת זה צריך שתעיין בזאת הצורה |
|
ונעשה כך נכה המספרי' כל א' עם סותרו [ר"ל הד' עם הכ"ז והג' עם הל"ו][82] ואם ההכאות יהיו שוות היא ראיה שאותו המספר שהוא ג' רביעיות מהשלם |
| In this way all the proofs are done, when we want to know the equality of any two numbers we want. | ובדרך זה יעשו כל הראיות כשנרצה לדעת שיווי כל ב' מספרי' שנרצה |
| It is enough for this type. | וזה מספיק במין הזה |
Chapter Four: Doubling Fractions |
הפרק הד' מכפול השברי' |
| You already know its definition. | וכבר ידעת גדרו |
| In this operation one type of fractions is enough. | בזה המין יספיק סוג א' משברי' |
|
המשל נרצה לכפול ב' שלישיות או ה' ששיות או ד' חמישיות או איזה מהשברי' שנרצה |
| We do as follows: we double the digit that is above the line. Then, we divide it by the digit that is beneath the line. The quotient is double the fraction, or fractions that we want. | ונעשה כך נכפול האות שעל הקו ומה שיהיה נחלקהו על האות שהיא תחת הקו ומה שיצא לחלק הוא כפול השבר או השברי' שרצינו |
|
כמי שירצה לכפול זה המספר שהוא ג' רביעיות |
|
נכפול הג' שעל הקו ויעלה |
| Check: halving | |
|---|---|
| The proof of this type [of operation] is the fourth type [of operation], which is halving. | ומופת זה המין הוא המין הד' שהוא חלוק באמצע |
| It is enough for this type. | [וזה מספיק בזה המין][83] |
Chapter Five: Halving Fractions |
הפרק החמישי[84] מחלוק השברי' באמצע |
| We have already stated its definition. | וכבר [85]אמרנו גדרו |
| In this operation you only need to double the digit that is beneath the line and the fraction is the halved. | ובזה המין אינך צריך אלא כפול האות שתחת הקו ויהיה השבר מחולק באמצע |
|
כמי שרוצה לחלק רביע אחד באמצע [שצורתו זאת][86] |
|
נכפול הד' שהיא למטה ויהיה |
| It is enough for this type. | וזה מספיק בזה הצורה |
| Check: doubling | |
|---|---|
| The proof is the doubling. | והמופת הוא הכפול |
Chapter Six: Multiplication of Fractions |
הפרק השישי מרבוע השברי' |
| We have already defined it. | וכבר גדרנוהו |
| It occurs only in one of five categories: | ולא יקרה אלא בא' מה' פנים[87] |
|
הא' |
|
הב' שלם או שלמים ושבר יחד עם שבר |
|
הג' שלם או שלמים ושבר יחד עם שלם או שלמים לבד |
|
הד' שלם או שלמי' ושבר יחד עם שלם ושבר יחד |
|
הה' שבר לבד בשבר לבד |
| First, the first category, which is integer or integers alone by fraction alone. | וראשונה מהאופן הא' שהוא משלם או שלמי' לבד עם שבר לבד |
|---|---|
|
המשל נרצה לרבע ד' שלמים בב' שלישיות |
|
ונעשה כך נניח ב' מספרי' משני צדדין בדרך זה |
|
וראשונה נעשה המחלק בדרך זה שנקח המספר[88] שלמטה מהקו והוא יהיה המחלק והוא ג' בזאת הצורה |
|
אחרי כן נרבע הד' שלמי' בב' שהם על הקו ויהיו ח' |
|
ואלו הח' נחלקם במחלק שאמרנו שהם ג' ויבואו ב' שלמי' וב' שלישיות וזהו הרבוע מד' שלמים האמורי' בשני |
| Example for the second category, which is integer or integers and fraction by fraction alone. | ומשל הפן השני שהוא שלם או שלמי' ושבר יחד עם שבר לבד |
|
כמי שרוצה לרבע ד' וחצי עם שני שלישיות |
|
ראשונה נעשה המחלק בדרך זה שנרבע הב' שהם תחת הא' על הג' שהיא תחת הב' ויעלו ו' ואלה הו' הם המחלק |
|
ואחר כך נרבע הד' שלמי' בב' שהוא בצדו שהוא תחת הא' ויעלה ח' ונחבר אליהם הא' שהוא על הב' ויהיו ט' וזהו המספר של זה הצד ונכה הט' עם הב' של הצד האחר ויעלו י"ח |
|
ואלו הי"ח [89]נחלקם על המחלק שהם ו' ויבא לכל חלק ג' ואלו הג' הם הרבוע העשוי |
| Example for the third category, which is integer or integers and fraction together by integer or integers alone. | ומשל לפן הג' שהוא או שלם או שלמי' ושבר יחד עם שלם או שלמי' לבד |
|
כמי שרוצה לרבע ד' ושליש עם ו' |
|
ובעבור שאין בכאן אלא מין אחד משברי' בלבד לכן יהיה הג' שהוא תחת הא' הוא המחלק |
| Keep this rule that wherever there is only one type of fraction, the number that is beneath the fraction line is the denominator. | ותשמור כלל זה שבכל מקום שלא יהיה אלא מין אחד מהשברים יהיה המספר שהוא תחת הקו השבר המחלק |
|
ואחר שכתבנו דרך המחלק נכה הד' שלמי' שאמרנו על ג' שהוא תחת הא' ויהיו י"ב ונוסיף לו הא' שעל הג' ויהיו י"ג ואלו הי"ג נכם על הו' השלמים שאמרנו ויצאו ע"ח |
|
ואלו הע"ח נחלקם בג' שהוא המחלק שאמרנו ויבאו כ"ו מהחלוקה וזה הוא הרבוע מד' שלמי' ושליש א' על ו' שלמי' |
| Example for the fourth category of integer or integers and fraction together by integer and fraction together. | ומשל הפן הד' משלם או שלמי' ושבר יחד עם שלם ושבר יחד |
|
כמי שרוצה לרבע זה המספר |
| denominator: First of all, we extract the denominator, which is the product of the digits that are beneath the fraction lines as follows: | קודם כל דבר נעשה המחלק כן והוא רבוע האותיות שתחת קוי השברי' |
|
|
|
ואח"כ נכה הד' השלמי' על הד' שהוא תחת הג' שבצדה ויעלה י"ו [ונוסיף עמהם הג' שעל הד' שבצדה ויעלו י"ט ונשמרם][92] |
|
ונעבור לצד האחר ונכה הב' שלמי' בב' שתחת הא' שבצידה ויעלו לד' ונוסיף עמהם הא' שעל הב' שבצדם ויעלו ה' ונשמרם ג"כ |
|
א"כ יש לנו ג' דברי' הראשון המחלק והשני שהשלמי' שמהצד |
|
ועתה נכה הה' עם הי"ט ויעלו צ"ה |
|
ונחלקם על המחלק האמור שהוא ח' ויצא מהחלוקה י"א שלמי' [93]וז' שמיניות וזו היא ההכאה שרצינו |
| Example for the fifth category, which is the multiplication of a fraction by a fraction. | ומשל הפן הה' שהוא רבוע שבר עם שבר |
|
כמי שרוצה לרבע [ב' שלישיו' וד' חמישיו'][94] |
|
נוציא המחלק שהוא הכאת האותיות שתחת הקוים שהם ג' וה' ויעלו ט"ו ונשמור אותו |
|
ואחר נכה האותיות שעל הקוים שהם ב' וד' ויעלו ח' |
|
ואלו הח' נחלקם במחולק שהוא ט"ו ובעבור שהמחלק יותר מהמחולק ניחס המחולק אל המחלק ומצאנו ח' חלקי' מט"ו של שלם [אחד][95] וזהו הרבוע מב' שלישיות וד' חמישיות |
| Check: division | |
| The proof of the multiplication of fractions is that we divide the product that is generated from the two sides by one of the sides and the result is the other side, otherwise it is not correct. | והמופת ממין רבוע השברי' הוא זה שנחלק הרבוע שעשינו מהשני צדדי' על א' מהצדדים ויצא הצד האחר ואם לאו אינו אמיתי |
| Since the proof of the multiplication is by division and we did not speak about the division of fractions yet, we do not elaborate on that until we discuss the division of fractions that follows. | ובעבור שמופת הרבוע הוא בחלוק ועדיין לא דברנו בחלוק השברי' לכן לא הרחבנו בו עד שנדבר מחלוק השברי' הנמשך לזה |
Chapter Seven: Multiplication of Fractions in Astrology [= Sexagesimal Fractions] |
הפרק השביעי באופני רבוע השברי' בחכמת התכונה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| In order to multiply the fractions in astrology [= sexagesimal fractions] you should know that one degree is divided into sixty parts that are called minutes. | האמנם לרבע השברי' שבחכמת התכונה צריך שתדע שהמעלה האחת תתחלק לששים חלקי' ויקראו ראשוני' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Each minute is divided into 60 other parts that are called seconds. | וכל א' מהראשוני' יתחלק לס' חלקי' אחרים ויקראו שניים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Each second is divided into 60 parts that are called thirds. | וכל שני יתחלק לס' חלקי' ויקראו שלישיים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Each third is divided into 60 parts that are called fourths. | וכל א' מהשלישיים יתחלק לס' חלקי' ויקראו רבעיים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| And so on. | וכן כסדר הזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Therefore, when we divide the minutes by sixty, they are degrees, for every degree is 60 minutes as said. | ולכן כשנחלק הראשוני' בשישים יהיו מעלות כי כל מעלה ס' ראשוני' כאמור | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If we divide the seconds by 60, they become minutes. | ואם נחלק השניים בס' ישובו ראשונים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The same for the others, when we divide them by 60 they are converted to the preceding rank. | וכן מהאחרים כשנחלקם לס' ישובו למדרגה הקודמת להם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| You should know that if we multiply degrees by minutes, the result of the multiplication are minutes. | וראוי שתדע שאם נכה מעלות על ראשוני' יהיה כל מה שיצא מההכאה ראשוני' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If we multiply degrees by seconds, the result of the multiplication are seconds. | ואם נכה מעלות על שניים יהיה כל מה שיצא שניים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The same for the others, because as the type of the fraction multiplied by a degree so is always the type of the result of multiplication. | וכן מהאחרי' כי לעולם מהמין שיהיה השבר המוכה עם המעלה מאותו מין יהיה מה [96]שיצא מההכאה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| You should also know that the product of minutes by minutes are seconds; the product of minutes by seconds are thirds; the product of minutes by thirds are fourths; the product of minutes by fourths are fifths and so on. | ועוד צריך שתדע שהכאת ראשוני' על ראשונים שהיוצא מהם הוא שניים והכאת ראשוני' על שניים היוצא הוא שלישיים והכאת ראשוני' על שלישיים הוצא הוא רביעיים והכאת ראשונים על רביעיים היוצא יהיה חמישיים וכן כסדר הזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The product of seconds by seconds are fourths; seconds by thirds are fifths; seconds by fourths are sixths and so on. | והכאת שניים על שניים היוצא רביעיים ושניים על שלישיים עושה חמישיים ושניים על רביעיים עושה ששיים וכן כסדר הזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The rule for knowing all these multiplications easily is by taking the sum of [the ranks of] both multiplied fractions. | והכלל לידיעת כל אלו ההכאות בנקלה הוא בשנקח חבור שני מספרי השברים המוכי' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
המשל שאם נכה שניים עם שלישיים נאמר אות השניים הוא ב' ואות השלישיים הוא ג' והחבור משניהם עולה ה' א"כ היוצא מהכאתם יהיה חמישיות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This rule is enough for all the sexagesimal fractions. | וזה הכלל מספיק לכל שברי התכונה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה לך צורה אחת בקצת זה נניח שרצינו להכות ב' מעלות וכ"ד ראשוניים ומ"ג שניים על ג' מעלות וג' ראשוניים וח' שניים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כנראה בצורה זו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| As seen in this diagram, you should write each type in a cell of its own, beneath every type its amount in a cell of its own, and in two lines one above and the other beneath, degrees corresponding to degrees, minutes corresponding to minutes, seconds corresponding to seconds, thirds corresponding to thirds, and so on. | ולפי הנראה בצורה זו צריך שתכתוב כל מין בבית בפני עצמו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Then, we start from the smallest fraction below and multiply it by all the upper digits. | ואחר נתחיל מהשבר היותר קטן מלמטה ונכהו עם כל האותיות שלמעלה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| For each product of a fraction by a fraction, we examine of which type it is in the mentioned way: if it is more than 60, we write every 60, as many as they are, in the preceding rank. Likewise for all the fractions. | ומכל הכאות שנעשה משבר עם שבר נעיין מאיזה מין הוא בדרך הנזכר ואם יעלה יותר מס' כל ס' וס' כמו שיהיו נכתוב אותם במעלה הקודמת ובשמה וכן בכל השברי' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
המשל אם מההכאה יצאו קכ"ד שניים נכתוב ד' שניים בבית השניים [97]והק"כ שניים שהם ב' פעמי' ששים שהם ב' ראשוני' נכתבם בבית הראשונים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| We keep this order of the multiplication of sexagesimal fractions and multiply all the bottom digits by the upper digits according to this order, until we complete the multiplication of each of the bottom [digits] by all the upper [digits] as written in the preceding diagram. | וזה הסדר נשמור בהכאת שברי התכונה וכסדר הזה נכה כל האותיות שלמטה עם האותיות שלמעלה עד שנשלים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| In order to add a further explanation, I write this second diagram which involves a longer procedure and study. | [וכדי להוסיף לך ביאור כתבתי זאת הצורה השנית שיש בה יותר מלאכה ועיון][98] |
| sixths | fifths | fourths | thirds | seconds | minutes | degrees |
|---|---|---|---|---|---|---|
| 24 | 50 | 24 | 1 | |||
| 24 | 50 | 24 | 1 | |||
| 36 | 9 | 20 | 9 | 0 | 0 | 0 |
| 36 | 24 | 0 | 0 | 0 | ||
| 0 | 0 | 20 | 41 | 20 | 0 | 0 |
| 40 | 50 | 0 | 0 | |||
| 0 | 0 | 36 | 9 | 20 | 9 | 0 |
| 36 | ||||||
| 24 | 50 | 24 | 1 | |||
| 36 | 32 | 32 | 49 | 57 | 35 | 1 |
| ששיים | חמישיים | רביעיים | שלישיים | שניים | ראשונים | מעלות |
|---|---|---|---|---|---|---|
| דב | 0ה | דב | א | |||
| דב | 0ה | דב | א | |||
| וג | ט | 0ב | ט | 0 | 0 | 0 |
| וג | דב | 0 | 0 | 0 | ||
| 0 | 0 | 0ב | אד | 0ב | 0 | 0 |
| 0ד | 0ה | 0 | 0 | |||
| 0 | 0 | וג | ט | 0ב | ט | 0 |
| וג | ||||||
| דב | 0ה | דב | א | |||
| וג | בג | בג | דט | זה | הג | א |
Chapter Eight: Division of Fraction |
הפרק השמיני והוא מהחלק השברי' |
| You already know its definition. | וכבר ידעת גדרו |
| This type [of operation] occurs in eight categories: | והמין הזה יקרה בח' פנים |
|
הא' שבר בשבר |
|
הב' שבר בשלם |
|
הג' שבר בשלם ושבר |
|
הד' שבר ושלם[99] בשבר ושלם |
|
הה' שלם בשבר |
|
הו' שלם ושבר בשבר |
|
הז' שלם ושבר בשלם |
|
הח' שלם בשלם ושבר |
| The first category, which is fraction by fraction | הפן הא' שהוא חלוק שבר בשבר |
|---|---|
|
כמי שרוצה לחלק ג' רביעיות בב' שלישיות |
|
נכתוב כל אחד בצד חבירו בצורה זו |
|
וקודם כל דבר נעשה המחלק כן שנכה ב' שהיא על הג' על הד' שהוא תחת ג' ויעלו ח' וזה הוא המחלק |
|
ואחר צריך שנעשה המחלק בדרך זה שנכה הג' שהוא על ד' בג' שהוא תחת הב' ויעלה ט' וזהו המחולק |
|
אחר כן נחלק המחולק במחלק ויצא שלם א' ושמינית שלם וזהו חלוק ג' רביעיות בב' שלישיות כמו שרצינו |
| The second [category], which is a division of a fractions by an integer | והב' שהוא חלוק שבר בשלם |
| We write each one next to the other, as we did in the first category, as follows: | נכתוב כל א' בצד חבירו כמו שעשינו בפן הראשון בדרך זה |
|
נניח שרצינו לחלק ג' שמיניות בב' שלמי' |
|
בצורה זו |
|
וראשונה נעשה המחלק בדרך זה נכה השלם שהוא ב' על ח' שהוא תחת ג' ויעלו י"ו וזהו המחלק |
|
ואחר כך נעשה המחולק כך שנקח הג' שהוא על הח' והוא המחולק |
|
ונחלק זה המחולק שהוא ג' בי"ו שהוא המחלק ויצאו ג' חלקים מי"ו חלקי שלם א' וזהו מה שרצינו |
| The third [category], which is a fraction by integer and fraction. | והג' שהוא שבר בשלם ושבר |
|
[100]כמי שרוצה לחלק ב' שלישיות בד' שלמי' וחצי |
|
נכתוב כל אחד כצורה זו |
|
ונעשה המחלק בדרך זה שנכה ד' על ב' שהוא תחת הא' ויעלו ח' ונוסיף עליהם הא' שהוא על הב' ויהיו ט' ואלו הט' נכה אותם על ג' שהוא תחת הב' [שבצד הא'] ויעלו כ"ז וזהו המחלק |
|
ונעשה המחולק בדרך זה שנכה הב' שהוא על הג' על הב' שהוא תחת הא' שבצד האחר ויעלו ד' וזהו המחולק |
|
ונחלקהו במחלק שהוא כ"ז ויצא מהחלוקה ד' חלקי' מכ"ז חלקי' של שלם וזהו מה שרצינו |
| The fourth [category], which is integer and fraction by integer and fraction | והד' שהוא שבר ושלם בשבר ושלם |
|
נכתו' כל א' כאמו' למעלה |
|
כמי שרוצה לחלק ט' וחצי בג' וד' חמישיות כזה |
|
ונעשה המחלק בדרך זה שנכה ג' על ה' שהוא תחת הד' ויעלו ט"ו ונוסיף עוד ד' שהוא על הה' על ט"ו ויהיו י"ט ואלו נכם על ב' שהוא תחת א' שבצד האחר ויעלו ל"ח וזהו המחלק ונשמור אותו |
|
ונעשה המחולק בדרך זה שנכה ט' על ב' שתחת א' שבצדה ויעלה י"ח ונוסיף עוד א' שעל הב' שבצדה ויעלו |
|
ואחר כך נחלק המחולק במחלק שאמרנו ויצא מהחלוקה ב' שלמי' וחצי וזהו מה שרצינו |
| The fifth [category], which is integer by fraction | והה' שהוא שלם בשבר |
|
נכתבם כאמור |
|
כמי שרוצה לחלק י"ב בד' תשיעיות כזה |
|
ובזה הפן המחלק הוא לעולם האות שהוא על הקו ולכן המחלק הנה הוא עתה בזה הד' שעל הט' |
|
[והמחולק יהיה מה שיעלה מהכאת הי"ב שלמים על הט' שתחת הד'][102] ואם כן המחולק הוא ק"ח |
|
ונחלקם בד' שהוא המחלק ויהיו כ"ז בחלוקה [103]וזהו מה שרצינו |
| The sixth [category], which is integer and fraction by fraction | והו' שהוא שלם ושבר בשבר |
|
נכתוב כל אחד כאמור |
|
המשל נרצה לחלק ד' ושליש אחד בה' ששיות כזה |
|
ונעשה המחלק כך שנכה ה' שהוא על ו' בג' שתחת הא' שבצדה האחר ויעלה ט"ו וזהו המחלק ונשמור אותו |
|
ואחר נעשה המחולק בדרך זה שנכה ד' על ג' שתחת הא' שבצדה ויעלו י"ב ונוסיף א' שהוא על ג' שבצדה ויהיו י"ג ונכם בו' שתחת הה' שבצד האחר ויעלו ע"ח וזהו המחולק |
|
ונחלקהו במחלק שהוא ט"ו ויצא מהחלוקה ה' שלמי' וא' חמישית וזהו מה שרצינו |
| The seventh [category], which is integer and fraction by integer | והז' שהוא שלם ושבר בשלם |
|
נכתבם כאמור |
|
המשל רצינו לחלק ג' ושלישית בד' כזה |
|
ראשונה נעשה המחלק כך שנכה הד' על הג' שהוא תחת הא' שבצד האחר ויעלה י"ב וזהו המחלק בפן הזה |
|
ונעשה המחולק בדרך זה שנכה הג' שלמי' על הג' שהיא תחת הא' שבצדה ויהיה ט' ונוסיף עליו הא' שעל הג' שבצדה ויעלו עשרה וזהו המחולק |
|
ונחלקהו במחלק שהוא י"ב ויצאו ה' ששיות וזהו מה שרצינו |
| The eighth [category], which is integer by integer and fraction | והח' שהוא שלם בשלם ושבר |
|
נכתוב כל אחד כאמור |
|
המשל שנרצה לחלק נ' בשניים וחצי כזה |
|
וראשונה נעשה המחלק בדרך זה נכה ב' על ב' שתחת הא' שבצדה ויעלו ד' ונוסיף הא' שעל הב' שבצדה ויעלה ה' וזהו המחלק ונשמור אותו |
|
ואחר נעשה המחולק בדרך זה שנכה הנ' על ב' שהוא תחת הא' מהצד האחר ויעלו ק' וזהו המחולק |
|
ונחלקהו במחלק [104]שהוא ה' ויצאו מהחלוקה כ' לכל א' מהשנים השלמים של המחלק |
| Then, we give each fraction its share in relation to what we gave to the whole. | ואחר נתן לכל שבר הראוי לו ביחס מה שנתננו לשלם |
|
המשל במין הזה שחלקנו נ' בב' וחצי ויצא מהחלוקה כ' לשלם |
|
א"כ נאמר אם לכל א' מהשלמי' ראוי כ' לחצי ראוי שיהיו עשרה ובדרך זה נחלק החמישים |
| This is what we wanted. | וזה מה שרצינו[105] |
| Check: multiplication | |
| The proof for all types of division is by that we multiply the divisor by the quotient and if the result is exactly as the dividend, then we know that the quotient is true. | והמופת לכל מיני החלוק הוא שנכה המחלק בחלק ואם יעלה כמו המחולק שוה בשוה אז נדע שהחלק אמיתי |
|
המשל כבר ידעת שהחלק האחרון מזה המין היה כ' והמחלק היה שניים וחצי ולכן אם תכה שניים [וחצי] בכ' יעלו לחמישים |
| This proof is inclusive for all the eight categories of this type of operation, which is division, and this is what we wanted. | וזה המופת כולל לכל ח' פנים שאמרנו בזה המין שהוא חלוק וזה מה שרצינו |
Section Four of the First Book: [Roots] |
הכלל הרביעי מהמאמר הא' | ||||||||||||||||||||||||||||||||||||||||||||
| It is divided into two chapters. | ויתחלק לב' פרקי' | ||||||||||||||||||||||||||||||||||||||||||||
Chapter One: Giving Guiding Ways for Finding Roots of Square Numbers or Approximate Roots of Non-Square Numbers |
הפרק הא' בנתינת דרכי' מיישירי' למציאות שרשי המספרי' המרובעי' או היותר קרובים למספרי' הבלתי מרובעי' | ||||||||||||||||||||||||||||||||||||||||||||
| After we spoke about the six types of arithmetic operations with integers and with fractions that include all that is needed in arithmetic, we should talk now about guiding methods for finding roots of square and cube numbers, since they are necessary and useful in mathematics as well as in other sciences, as used by the mathematicians. | ואחר שדברנו מששת מיני המספר מהשלמי' גם מהשברי' שהם כוללים לכל מה שיצטרך במלאכת המספר עתה צריך שנדבר מדרכי' מיישירי' למציאו' שרשי המספרי' המרובעי' והמעוקבי' בעבור שהם הכרחיי' ומועילים בחכמות הלימודיות וגם בחכמות אחרות כמו שהוא מפורסם אצל בעלי החכמות הלימודיות | ||||||||||||||||||||||||||||||||||||||||||||
| Therefore, we should first say what is the definition of a root of a number. | ולכן ראוי שנאמ' ראשונה מהו גדר שורש המספר | ||||||||||||||||||||||||||||||||||||||||||||
| First of all, you must know that there are two general types of roots of numbers | וקודם כל דבר צריך שתדע שיש ב' מיני שרשי מספר כוללים | ||||||||||||||||||||||||||||||||||||||||||||
|
[106]הראשון שורש המרובע | ||||||||||||||||||||||||||||||||||||||||||||
|
והשני יקרא שרש המעוקב | ||||||||||||||||||||||||||||||||||||||||||||
| First, we shall discuss the root of the square: | וראשונה נדבר מהשרש המרובע | ||||||||||||||||||||||||||||||||||||||||||||
| Definition of a square root: The definition of the root of the square is another number that generates it when it is multiplied by itself. | וא"כ גדר שרש המרובע הוא מספר אחר כשיוכה בעצמו מוליד אותו | ||||||||||||||||||||||||||||||||||||||||||||
|
ולכן ב' הם שרש ד' בעבור כשיוכה בעצמו יוליד ארבעה | ||||||||||||||||||||||||||||||||||||||||||||
| Another definition: or it is a number, such that when it is multiplied by itself it generates a square number. | גדר אחר או הוא מספר אחד כשיוכה בעצמו יוליד מספר | ||||||||||||||||||||||||||||||||||||||||||||
| Hence, every number that is multiplied by itself generates a number that has a root and this number is called a square. | א"כ כל מספר מוכה בעצמו מוליד מספר שיש לו שורש ומספר | ||||||||||||||||||||||||||||||||||||||||||||
|
כמו ב' פעמי' ב' או ה' פעמי' ה' או י' פעמי' י' וכן מהאחרי' | ||||||||||||||||||||||||||||||||||||||||||||
| You should know that every square number that is multiplied by a square number generates a square number.
|
וצריך שתדע שכל מרובע מוכה על איזה מרובע שיהיה יוליד מרובע | ||||||||||||||||||||||||||||||||||||||||||||
|
המשל ד' שיש לו שרש מוכה על ט' שגם כן יש לו שרש יולידו ל"ו ששרשם ו' | ||||||||||||||||||||||||||||||||||||||||||||
| If when the dividend is divided by the divisor, the quotient is a square number, then when the dividend is multiplied by the divisor, the resulting product is a square number. | ואם כשיחולק המחולק במחלק החלק יהיה מרובע אז אם יוכה המחולק במחלק יוליד מההכאה ההוא מרובע | ||||||||||||||||||||||||||||||||||||||||||||
|
המשל י"ח מחולק בח' יצאו והשרש מאלו אחד וחצי | ||||||||||||||||||||||||||||||||||||||||||||
|
א"כ אם נכה י"ח על ח' יצאו קמ"ד[108] ושרש המספר בזה הוא י"ב[109] אע"פ שאין שורש לי"ח ולח' | ||||||||||||||||||||||||||||||||||||||||||||
| Hence, you must know that all the ranks do not have a root, except for those that are formed from the multiplication of other [ranks] by themselves. | ומכאן יתחייב שצריך שתדעהו שכל | ||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||
|
והמדרגה השנית שהוא עשרות אין לו שורש כי לא ימצא שום מספר שבהכאתו בעצמו יוליד אותו | ||||||||||||||||||||||||||||||||||||||||||||
|
והמדרגה הג' שהוא מאות יש לו שורש כי מהכאת עשרה בעצמו יוליד ק' | ||||||||||||||||||||||||||||||||||||||||||||
|
והמדרגה הד' שהוא אלף אין לו שורש כי אין שם מספר שבהכאתו [113]בעצמו יולדהו | ||||||||||||||||||||||||||||||||||||||||||||
|
והטור הה' שהוא עשרת אלפי' יש לו שרש כי המאה מוכה בעצמו יולידהו כי ק' פעמי' ק' יולידו עשרת אלפי' | ||||||||||||||||||||||||||||||||||||||||||||
| The same can be said about the other ranks endlessly that all the ranks that are odd according to the natural succession have a root, such as 1, 3, 5, 7, 9, i.e. the rank of units, the rank of hundreds, the rank of tens of thousand, the rank of thousands of thousands, and the same for all the other ranks that are odd as said. | וכן איפשר לאמר מהטורים האחרים עד בלתי תכלית באופן שכל ההבדלי' שבסדר המספר יהיו נפרדי' ימצא להם שרש כמו א' ג' ה' ז' ט' כלומר במדרגת האחדות או במדרגת הבדל אם תרצה לומ' כן מהמאות ובמדרגת עשרת האלפי' ובהבדל האלף אלפי' וכן מכל המדרגות האחרות שהם נפרדות כאמור | ||||||||||||||||||||||||||||||||||||||||||||
| The ranks that are even do not have a root, such as the second rank that indicates the tens, or the fourth rank the indicates the thousands, or the sixth rank that indicates the hundreds of thousands, and the same for all the other ranks that are even. | וההבדלים או מדרגות שיהיו זוגות אין להם שרש כמו מדרגות הב' הרומזת לעשרות או מדרגת הד' הרומזת לאלפי' או מדרגת הו' הרומזת למאות אלפי' וכן מכל המדרגות האחרות מהזוגות | ||||||||||||||||||||||||||||||||||||||||||||
| In the sexagesimal fractions, or whichever they are, it is vice versa. | ובשברי התכונה או איזו שיהיו הוא בהפך | ||||||||||||||||||||||||||||||||||||||||||||
| For, the first [rank of] sexagesimal fractions do not have a root. | כי השברים התכונים[114] בראשונים אין להם שרש | ||||||||||||||||||||||||||||||||||||||||||||
| But, those that are generated from others have a root. | אבל אותם שיצאו מאחרים יש להם שרש | ||||||||||||||||||||||||||||||||||||||||||||
|
כמו הראשונים שבשברי' בעבור שיש להם מקום ראשון אין להם שרש | ||||||||||||||||||||||||||||||||||||||||||||
|
אבל השניים שיש להם מקום שני בשברים יש להם שרש כי מהכאת הראשונים בעצמם יולדו | ||||||||||||||||||||||||||||||||||||||||||||
|
והשלישיים שבמקום שלישי יעמדו אין להם שרש כי לא יולדו מהכאת אחרים בעצמם | ||||||||||||||||||||||||||||||||||||||||||||
|
והרביעיים שיש להם מקום ההבדל הרביעי יש להם שרש כי מהכאת השניים בעצמם יולדו | ||||||||||||||||||||||||||||||||||||||||||||
| This way for the others. | וכן מהאחרי' בדרך זה | ||||||||||||||||||||||||||||||||||||||||||||
| Likewise for fractions of the other types, i.e. that are not sexagesimal fraction, whether they are of geometry or whichever science. | וכן יעשה בשברי הסוגים האחרים ר"ל שאינם מהתכונה בין שיהיו מההנדסא או מאיזו חכמה שיהיו | ||||||||||||||||||||||||||||||||||||||||||||
|
[115]כמו חציים שלישיי' וחמשיי' וששיי' והדומי' | ||||||||||||||||||||||||||||||||||||||||||||
| Since they are not generated from others, they are called first degree, therefore they do not have a root. | בעבור שלא יולדו מאחרי' יקראו הבדל ראשון או שברי' ראשוני' ולכן אין להם שורש | ||||||||||||||||||||||||||||||||||||||||||||
| But, every [fraction] that is multiplied by itself is called fraction of second degree, therefore it has a root. | אבל כל מספר שיוכה בעצמו יקרא שבירה שנייה לכן יש לו שרש | ||||||||||||||||||||||||||||||||||||||||||||
|
כמו מהכאת חצי בעצמו שיוליד רביעית שיקרא חצי של חצי | ||||||||||||||||||||||||||||||||||||||||||||
|
ומהכאת השלישי' בעצמו שיוליד תשיעית שיקרא שלישית של שלישית | ||||||||||||||||||||||||||||||||||||||||||||
|
ומהכאת החמישית בעצמו שיולד אחד מכ"ה ויקרא חמישית החמישית | ||||||||||||||||||||||||||||||||||||||||||||
|
אבל העשירי' והאחד עשירית ושנים עשירית ושלשה עשירית וארבעה עשירית והדומי' אין להם שורש כי הם שברי' ראשוני' ולא יולדו מהאחרי' | ||||||||||||||||||||||||||||||||||||||||||||
|
אבל העשירי' מעשירי' והאחד עשירית מאחד עשירית ושנים עשירית משנים עשירית ושלשה עשירית משלשה עשירית וארבעה עשירית מארבעה עשירית וחמשה עשירית מחמשה עשירית וכן הדומי' יש להם שורש | ||||||||||||||||||||||||||||||||||||||||||||
| The fractions that are of third degree do not have a root. | האמנם השברי' שמההבדל השלישי שיש להם מקום שלישי אין להם שורש | ||||||||||||||||||||||||||||||||||||||||||||
|
כמו חצי מחצי של חצי או שלשה עשיריות משלשה עשיריות של שלשה עשיריות וכן כל הדומי' | ||||||||||||||||||||||||||||||||||||||||||||
| So, all the fractions that are not generated from the product of others are called fractions of first degree and they do not have a root. | א"כ כל השברי' שלא יולדו מהכאת אחרי' יקראו שברי' של הבדל ראשון ואין להם שורש | ||||||||||||||||||||||||||||||||||||||||||||
| But, all those that are generated from the product of others by themselves are called fractions of second degree and they have a root. | אבל אותם שמהכאת אחרי' בעצמם יולדו יקראו שברי' מהבדל שני ויש להם שורש | ||||||||||||||||||||||||||||||||||||||||||||
| Therefore, it is a clear thing for integers that the ranks that have a root are the odd ranks, but for fractions it is the opposite, the evens have a root and the odds not. | א"כ דבר מבואר הוא בשלמי' שאותם ההבדלי' שיש להם שורש הם אותם שיהיו נפרדי' בטורי' אבל בשברי' הוא בהפך שהזוגות יש להם שורש ולנפרדי' לא | ||||||||||||||||||||||||||||||||||||||||||||
Written calculations |
|||||||||||||||||||||||||||||||||||||||||||||
| After knowing these matters, when we wish to find a root of any number, we arrange it by its ranks, i.e. its decimal positions and its digits. | ואחר ידיעת אלה הענייני' כשנרצה למצוא שורש איזה מספר שיהיה נסדרהו בהבדלותיו ר"ל מדרגותיו כלומר מקומותיו גם אותיותיו | ||||||||||||||||||||||||||||||||||||||||||||
| Since one should always begin from the odd rank, one should see if the [number of] the ranks is even or odd. | ובעבור שלעולם ראוי להתחיל מההבדל הנפרד לכן צריך ראשונה להבחין אם ההבדלי' יהיו זוגות או נפרדי' | ||||||||||||||||||||||||||||||||||||||||||||
|
ואם יהיו נפרדי' תשים תחת ההבדל האחרון מספר אחד שמונה בעצמו יעשה מספר שוה למספר שעליו או פחות היותר קרוב שאפשר [116]שימצא אם לא ימצא שוה | ||||||||||||||||||||||||||||||||||||||||||||
|
ואם ההבדלי' יהיו זוגות יושם תחת האות ר"ל ההבדל שקודם ההבדל ר"ל האחרונה מספר אחד כשיוכה בעצמו יוליד מספר שוה או פחות היותר קרוב שאפשר שימצא למספר שעליו אם לא ימצא שוה לו | ||||||||||||||||||||||||||||||||||||||||||||
| It is subtracted from the one that is above it and from the next to it. | ויחוסר מאותו שעליו ומחברו | ||||||||||||||||||||||||||||||||||||||||||||
|
ואם לא ישאר מאומה נכתו' עליהם סיפרא | ||||||||||||||||||||||||||||||||||||||||||||
|
ואם ישאר יכתב מה שישאר באות הקודמת שהיא הימנית משניהם | ||||||||||||||||||||||||||||||||||||||||||||
| Then, it is doubled and written in the preceding rank. | ואחר יוכפל ויושם בהבדל הנמשך אליו | ||||||||||||||||||||||||||||||||||||||||||||
| In the third rank [from the left] one writes a number, whose product by the double is subtracted from the number that is above the doubled, then its product by itself is subtracted from the number that is above it, so that it is closer than any other number to consume the upper number. | ובהבדל השלישי יושם מספר אחד שמוכה בנכפל ומחוסר מאותו שעל הנכפל ואחר כן מוכה בעצמו ומחוסר מהמספר שעליו יהיה יותר קרוב לבטל המספר שלמעלה משום מספר אחר | ||||||||||||||||||||||||||||||||||||||||||||
|
ואם לא ישאר יותר הבדל אז יהיה המספר הראשון והשלישי שורש המספר שלמעלה | ||||||||||||||||||||||||||||||||||||||||||||
| If there are more digits, i.e. ranks, we double the third of the bottom digits, then shift the first doubled by one rank backwards. We erase the first doubled and write after the second doubled a number, such that when multiplied by the doubles and by itself, will consume all the upper [digits] as said. | ואם יהיה יותר אותיות ר"ל הבדלי' נכפול האות השלישית מהתחתונות ואח"כ נסיע הכפל הראשון אות אחת לפנים ונמחוק הכפלי' הראשוני' ואחר הכפל השני נניח מספר אחד שיוכה בנכפלי' ובעצמו ימחוק כל מה שלמעלה כאמור | ||||||||||||||||||||||||||||||||||||||||||||
| If there are more ranks, i.e. digits, the last [bottom] digit is doubled, then another number is written, such that when multiplied by the doubles, which should be shifted from their place to the preceding rank before the multiplication, and by itself, will consume all the upper [digits] as said. | ואם יהיו יותר הבדלי' ר"ל אותיות יוכפל המספר האחרון ויונח מספר אחר כשיוכה בנכפלי' הצריכי' לסעת ממקומם ללכת מדרגה אחת יותר קודם ההכאה ובעצמו ימחוק כל מה שלמעלה כאמור | ||||||||||||||||||||||||||||||||||||||||||||
| This should be done, until the whole rank is gone, by that the number that is after the doubled is multiplied by the doubles and by itself. | וכן צריך להעשות עד שיגמר כל הטור באופן שלעולם המספר שהוא אחר הנכפל יוכה בנכפלי' ובעצמו | ||||||||||||||||||||||||||||||||||||||||||||
|
המשל שנניח מספר אחד שנרצה לבקש שורשו והוא | ||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||
|
ובעבור שההבדלי' הם זוגות צריך שנתחיל באות שקודם האחרונה שהיא ו' | ||||||||||||||||||||||||||||||||||||||||||||
|
וצריך שנניח מספר א' כשיוכה בעצמו יוליד מספר שוה או פחות היותר קרוב שאפשר שימצא כשלא ימצא מספר שוה לאותו שלמעלה שהוא נ"ו | ||||||||||||||||||||||||||||||||||||||||||||
|
והמספר היותר קרוב לנ"ו הוא ז' כי כשיוכה בעצמו יוליד מ"ט | ||||||||||||||||||||||||||||||||||||||||||||
|
ומ"ט כשיוסרו מהמספר שלמעלה שהוא נ"ו ישארו ז' | ||||||||||||||||||||||||||||||||||||||||||||
|
ואלו הז' שישארו נשימם על הו' שהוא אחת מאותיות נ"ו ועל הה' נשים סיפרא | ||||||||||||||||||||||||||||||||||||||||||||
|
והז' ששמנו למטה לשורש נכפול אותם ויהיו י"ד והעשרה נשים תחת הז' ונמחוק הז' [117]והד' נניחם במקום הנמשך שהוא תחת ב' | ||||||||||||||||||||||||||||||||||||||||||||
|
אחר כך תחת האות האחרת הנמשכת נשים מספר אחד שהוא ה' כשיוכה [בנכפלים ובעצמו][118] ימחוק או יבטל אותו שלמעלה באופן זה | ||||||||||||||||||||||||||||||||||||||||||||
|
בהכות הה' באחד שהוא העשרה מהכפל יוליד ה' כשיוסר מאותו שלמעלה שהוא ז' ישארו ב' על הז' | ||||||||||||||||||||||||||||||||||||||||||||
|
ואחר נכה הה' הנזכרים בד' ויהיו כ' כשיוסרו משלמעלה שהוא כ"ב ישארו ב' | ||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב 0' על ב' העליון שהיה במקום י' לערך הב' הנמשכת | ||||||||||||||||||||||||||||||||||||||||||||
|
אחר כך נכה הה' בעצמו ויהיו לנו כ"ה כשיוסרו משלמעלה שהוא כ"ה לא ישאר כלום | ||||||||||||||||||||||||||||||||||||||||||||
|
ואז יהיה לנו שרש המספר ע"ה כמו שנראה בזו הצורה | ||||||||||||||||||||||||||||||||||||||||||||
|
ובעבור שלא נשאר כלום נכתוב 0'0' על ב' ועל ה' וזה מה שרצינו |
- [Illustration of the procedure:]
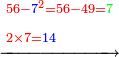
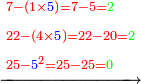
0 2 07 0700 5625 5625 5625 7 74 745 1 1
Chapter Two: Finding the Roots of Fractions Alone or Fractions and Integers Together |
הפרק השני במציאות שרשי המספרים בשברי' לבד או בשברי' ושלמי' יחד |
| You already know that a root can not be found for all fractions, but only for those that are formed from a product of other fractions by themselves. | כבר ידעת שלא ימצא שורש לכל השברי' אלא לאותם שיולדו מהכאת שברי' אחרי' בעצמם |
| Therefore, we examine the fractions, whose root we want to find, whether they are of those that have a root or not. | ולכן נעין בשברי' שנרצה למצא שורשם אם הם [119]מאותם שיש להם שרש אם לא |
| If they are of those that have [a root], we extract the root exactly as with integers. | ואם יהיו מאותם שיש להם נוציא השרש כמו בשלמי' לא פחות ולא יתר |
| You should know that the root you get for fractions is not of the same type of the fractions, whose root you are looking for, but of a different type. | וראוי שתדע שהשרש שיצא לך מהשברי' איננו מסוג אותם השברי' שבקשת שרשם אלא מסוג אחר |
|
המשל אם השברי' שבקשת שרשם יהיו רביעיות השרש שלהם יהיו חציים |
|
ואם יהיו תשיעיות שרשם יהיו שלישיות |
| The roots of the fractions are always of a higher rank than the fractions, of which they are roots. | ולעולם שרשי |
|
כמי שמכה שלישיות בעצמו שיוליד תשיעיות שהוא מספר פחות מהשלישיות שהוא שרשו |
|
ולכן בתכונה ג' ראשוני' לא יהיו שרש לט' ראשונים בעבור שהכאת הראשונים בעצמם עושה שניים שהם מסוג אחר |
| If the fractions, whose root we are looking for, are not of those that have a root, we convert them to other fractions that have roots. | ואם השברי' שבקשנו שרשם לא יהיו מהשברי' שיש להם שרש נחליפם לשברי' אחרי' שיהיו בעלי שרשים |
|
המשל שאם יהיו שלישיים שאין להם שרש אז נחליפם לתשיעיות שהם בעלי שרש |
|
וגם בתכונה אם יהיו ראשוני' ורצינו לבקש שורשם נחליפם לשניים[121] ואז נוציא שרשם |
| If we want to know the root of integers and fractions together, we convert the integers to the same type of the fractions, then we extract their root, if the fractions are of a type that has a root; if not, we convert both the integers and the fractions to a type of fraction that has a root, then extract their root. | ואם נרצה לדעת שורש השלמי' והשברי' יחד נחזיר השלמי' לסוג השברי' ואז נוציא שרשם אם השברי' ממין אותם שיש להם שורש ואם לא נחזיר השלמי' גם השברי' לסוג השברי' שיש להם שרש ואז נוציא שרשם |
Chapter Three: Giving one inclusive Method for Finding the Roots of Numbers by Adding Zeros |
הפרק השלישי בנתינת דרך א' כולל למצא שרשי המספרי' על דרך תוספת הספרש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Know that there is another inclusive method for finding the roots of numbers and it is that we take whichever number we want and add to it six zeros or more, provided that their number is even. | [122]ודע שיש דרך אחר כולל למצא בו שרשי המספרי' והוא זה והוא שנקח איזה מספר שנרצה ונוסיף עליו ו' ספרש או יותר בתנאי שיהיו זוגות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| For, as many zeros you add as easier it will be for you to find the approximate root of numbers if they do not have roots, or the real roots, if they have roots. | כי כל מה שתוסיף בספרש יותר בנקלה תמצא השרשים היותר אמיתיים ר"ל היותר קרובים למספרי' אם לא יהיו בעלי שרשים או אמיתיים אם יהיו בעלי שרשים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| After you add the zeros, extract the root as we said above. | ואחר שתוסיף הספרש תוציא [השרש][123] בדרך שאמרנו למעלה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If something remains after the extraction of the root, know that this number does not have a root, but if nothing remains, then the root is found. | ואם לאחר הוצאת השרש ישאר איזה דבר תדע שאין שרש לאותו מספר ואם לא ישאר דבר הנה שכבר נמצא שרש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Next, examine how many ranks there is in the root you have found. If they are more than half the zeros, take the [exceeding ranks] to the left as integers. | ואחר תעיין כמה הבדלים יש בשרש שמצאת ואם יהיו יותר מחצי הספרש כל מה שיהיו יותר ר"ל מצד שמאל תקחהו בשם שלמי' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
המשל שאם הנחת ו' ספרש ובשרש שמצאת יהיו יותר מג' אותיות שהוא חצי ששה שהוא מניין הספרש כל מה שיהיו יותר תקחם בשם שלמי' כאמור והשאר שהוא ג' הבדלים הכהו בששים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Examine [by] how much [the number of] the ranks of the product [exceeds] the number of half the zeros. The [ranks that exceed the number of] half the zeros are minutes. Multiply the remaining again by sixty. | והעולה מההכאה תעיין כמה הבדלים יש לו מלבד כמות חצי הספרש ומה שיהיה מלבד חצי הספרש יהיו ראשוני' והנשאר נכהו פעם אחרת בששים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Examine in the way stated above by how much [the number of] the digits exceeds the number of half the zeros. All that exceeds are seconds. | ותעיין באופן האמור למעלה ויהיו שניים כמה הוא יותר מחצי הספרש כלומר כמה אותיות הם יותר מחצי הספרש וכל מה שיהיה יותר יהיו שניים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Do like this until only half the zeros that you wrote remain, i.e. in each product what remains from the multiplication is smaller than the preceding [product] by one rank. | וכדרך זה תעשה עד שלא ישאר אלא חצי הספרש שהנחת ר"ל שבכל הכאה ישוה הנותר מההכאה פחות מהקודם לה מדרגה אחת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
שאם ההכאה הקודמת לה היתה ראשונים [124]שתהיה האחרת הנמשכת לה שניים וההכאה האחרת שלישיים וכן כסדר עד שלא ישארו אלא הג' ספרש לבד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
המשל נרצה לדעת השרש היותר קרוב שאיפשר לשנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נניח ב' ונוסיף עליה קודם לה ו' ספרש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונוציא קודם כל דבר השרש בדרך זה שאמרנו בפרק השרשים ונמצא ששורשם באותו הדרך הוא זה [דאדא][125] ומעט יותר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ובעבור שיש בכאן ד' אותיות נקח האות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונקח הב' אותיות האחרונות שהם ב'ד' שהם יותר מחצי הספרש ויהיו ראשונים והתת"מ שנשארו נכם בששים ויצאו [מההכאה 00ד0ה][127] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונקח מה שהוא יותר מחצי הספרש ויהיו נ' ואלו הנ' יהיו שניים והת' הנשארי' נכם בששים ויצאו מההכאה [000דב][128] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונקח הכ"ד שהם יותר מחצי הספרש ויהיו שלישיות וישארו הג' ספרש שהם חצי הספרש הראשונות שהוספנו בלבד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Apply this way on the numbers you want, until only half [the number of] the zeros remains. | ובדרך זה תעשה במספרי' שתרצה עד שלא ישאר אלא חצי הספרש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וא"כ בזה הפועל מצאנו שהשרש היותר קרוב למספר המכוון שהם ב' הוא שלם א' וכ"ד ראשוני' ונ' שניים וכ"ד שלישיים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Know that as you took here the number of the zeros in the multiplications according to the sexagesimal fractions, i.e. minutes, or seconds, or thirds, you can take 20, or 30, or whatever you wish, in similar multiplications, and as we related the fractions here to 60, we can relate them to 20 or 30, according to the number that you take in the multiplications, or according to any number you wish, Q.E.D. | ודע כי כמו שלקחת בכאן בהכאות מניין הספרש והם ראויים למספרי התכונה ר"ל בשם ראשונים או שניים או שלישיים כמו כן תוכל לקחת בהכאות הדומים לאלו מספר כ' או ל' או מה שתרצה וכמו שייחסנו השברי' בכאן למספר הס' כמו כן נוכל ליחס אותם למספר הכ' או לל' כפי המספר שתקח בהכאות או כפי המספר שתרצה וזה מה שרצינו |
Chapter Four: Giving Guiding Ways for Finding Roots of Cube Numbers or Approximate Roots of Non-Cube Numbers |
הפרק הרביעי בנתינת דרכים מיישירים למציאות שרשי המספרי' [129]המעוקבים או היותר קרובים למספרים הבלתי מעוקבים | ||||||||||||||||||||||||||||||||||||||||||||
| The cube root of any number is a number that is multiplied by its square and generates another number that is called a cube number. | ושרש מעקב מאיזה מספר שיהיה הוא מספר אחד שיוכה במרובעו ויוליד מספר אחר ויקרא מספר מעוקב | ||||||||||||||||||||||||||||||||||||||||||||
|
כמו ב' שהם שורש מעוקב של ח' בעבור שהכאת הב' במרובעם שהם ד' יולידו ח' שהוא מספר מעוקב של ב' | ||||||||||||||||||||||||||||||||||||||||||||
|
וכן ג' הם שרש מעוקב של כ"ז בעבור שהכאת ג' במרובעם שהוא ט' יוליד כ"ז שהוא מספר מעוקב של ג' | ||||||||||||||||||||||||||||||||||||||||||||
|
וכן אלף הוא מספר מעוקב של י' כי הוא נולד מהכאת י' במרובעו שהוא ק' וכן מהאחרי' | ||||||||||||||||||||||||||||||||||||||||||||
| Know that the cubic square cannot be found by the technique that will be stated if it is not greater than 9 and all that are less than 10 should necessarily be memorized. | ודע ששורש המעוקב לא ימצאו בזאת התחבולה שנאמ' אם לא שיהיה יותר מט' וכל אותם שהם פחותים מי' צריך שיודעו על פה בהכרח | ||||||||||||||||||||||||||||||||||||||||||||
| Hence, you cannot find the root of a number by the technique if it is not from 1000 and up. | א"כ אתה לא תוכל למצא שרש מספר בתחבולה אם לא שיהיה מאלף ומעלה | ||||||||||||||||||||||||||||||||||||||||||||
| This principle is necessary to know which ranks have a cube root. | ולהבין שהשרש הזה הוא הכרחי לדעת מה הם המדרגות שיש להם שרש מעוקב | ||||||||||||||||||||||||||||||||||||||||||||
| You must know that not all the ranks have a root, but only those that are generated from cubing. | וצריך שתדע שאין לכל המדרגות שורש אלא לאותם שיולדו מהכאה מעוקבת[130] | ||||||||||||||||||||||||||||||||||||||||||||
|
כי המדרגה הראשונה מהמספר שהוא מדרגת האחדות יש לו שרש מעוקב כי האחד מוכה בעצמו באופן מעוקב יוליד אחד שהוא מספר מעוקב | ||||||||||||||||||||||||||||||||||||||||||||
|
והמדרגה הב' שהיא מדרגת העשרות אין לה שרש מעוקב כי לא נמצא שום מספר שמוכה בעצמו באופן מעוקב יוליד עשרה | ||||||||||||||||||||||||||||||||||||||||||||
|
והמדרגה השלישית שהיא מדרגת המאות אין לה שרש מעוקב כי לא ימצא מספר א' שמוכה בעצמו באופן מעוקב יולידהו | ||||||||||||||||||||||||||||||||||||||||||||
|
אבל המדרגה הד' שהיא מדרגת האלפי' יש לה שרש כי יולד מההכאה המעוקבת מהעשרה | ||||||||||||||||||||||||||||||||||||||||||||
|
והמדרגה הה' שהיא עשרת אלפי' אין לה [131]שרש מעוקב לסבה הנזכרת | ||||||||||||||||||||||||||||||||||||||||||||
|
והמדרגה הו' שהיא מאת אלפי' אין לה ג"כ שרש מעוקב לסבה הנזכרת | ||||||||||||||||||||||||||||||||||||||||||||
|
והמדרגה הז' שהיא אלף אלפי' יש לה שרש מעוקב כי יולד מהכאה מעוקבת מהמאה | ||||||||||||||||||||||||||||||||||||||||||||
| The same should be understood for all the other numbers, that a cube root can be found only in the ranks of units and of thousands. | וכן ראוי שיובן בכל המספרי' האחרים והוא שלא ימצא שרש מעוקב אלא במדרגת האחדות והאלפי' | ||||||||||||||||||||||||||||||||||||||||||||
Written calculations |
|||||||||||||||||||||||||||||||||||||||||||||
| After you know all this, if you want to extract a root, we write the number we wish, whether it is a thousand or more and we write the digits starting from the units. | ואחר שידעת כל זה אם תרצה להוציא זה השרש נכתוב המספר שנרצה בין שיהיה אלף או יותר ונרשום האותיות העושות האלפי' בשנתחיל מהאחדות | ||||||||||||||||||||||||||||||||||||||||||||
| Know that the digits that indicate the root are the units, the thousands, the thousands of thousands, the thousands of thousands of thousands and so on by this order, i.e. all the thousands, according to this way: the units, the digit that is fourth to it, counting with it, the seventh digit, the tenth, the 13th, the 16th, the 19th, the 22nd, the 25th and those that are similar, four by four, because all these indicate the [rank] that have a cube root. | ודע שהאותיות המורות השרש הם האחדות והאלפי' והאלף אלפי' והאלף אלפי אלפי' וכן כסדר הזה כלומ' כל האלפי' בדרך זה ר"ל האחדות והאות הרביע לה כשימנה עמה והאות השביעי והעשירי' והי"ג והי"ו והי"ט והכ"ב והכ"ה וכן מהדומות מארבעה ארבעה כי אלו הן המורות על בעלת השרש המעוקב | ||||||||||||||||||||||||||||||||||||||||||||
| After knowing these digits that indicate the thousands, we start to extract the cube root, i.e. to look for a cube root, from the last digit of the hundreds[?] of thousand, by writing a digit beneath it, such that when multiplied by itself cubically, becomes a number that is equal to the one that is above it, or as close as can be found, if the same cannot be found. | ואחר ידיעת אלו האותיות המורות אלפי' נתחיל לעקב ר"ל לבקש השרש המעוקב מהאות האחרונה מהמאות אלפי' בשנכתוב תחתיה אות אחת שכשיוכה בעצמו באופן מעוקב יעשה מספר שוה לאותה שלמעלה המינה או פחות היותר קרוב שאיפשר שימצא אם לא ימצא שוה | ||||||||||||||||||||||||||||||||||||||||||||
| We subtract it from what is above it. | ונחסרהו משלמעלה ממנו | ||||||||||||||||||||||||||||||||||||||||||||
| This digit is called "sub-triple". We triple it, i.e. multiply it three times. | והאות הזה תקרא תחת המשולש' ואחר כך נשלשה ר"ל שנרבה אותה יותר ממה שהיה ג' פעמי' | ||||||||||||||||||||||||||||||||||||||||||||
|
המשל אם יהיו ב' נחזירם ו' | ||||||||||||||||||||||||||||||||||||||||||||
| We write it in the rank that is third to it, i.e. to the right of the sub-triple. We shift the sub-triple one rank backwards and write the original digit. | ונכתוב אותם במקום שלישי אליה ר"ל שלתחת המשולשת לצד הימין והתחת משולשת נסיעה אות אחת לאחור ונרשום הראשונה | ||||||||||||||||||||||||||||||||||||||||||||
| Next to the triple we write another digit called the "present digit", such that when multiplied by the triple, by the sub-triple, and by itself cubically, generates numbers that are equal or as close as possible to the numbers that are above them. | ובמקום הסמוך למשולשת אחריה נכתוב אות אחרת ויקרא אות [132]נמצאת שכשיוכה במשולשת ובתחת | ||||||||||||||||||||||||||||||||||||||||||||
| We subtract them from what is above them. | ונחסרם ממה שלמעלה מהם | ||||||||||||||||||||||||||||||||||||||||||||
| If the line has more digits, we triple the present digit and write its triple in the rank that is third to it in the abovementioned way. | ואם הטור יהיה יותר באותיות נשלש האות הנמצאת והמשולשת שלה נכתוב במקום השלישי לה בדרך הנזכר למעלה | ||||||||||||||||||||||||||||||||||||||||||||
| We shift it, i.e. the present digit, and write it one rank backwards. | והיא ר"ל הנמצאת נרשום אותה ונסיעה אות אחת לאחור | ||||||||||||||||||||||||||||||||||||||||||||
| We shift each of the other triples and sub-triples one rank backwards and write the original digits. | והמשולשות האחרות והתחת משולשות נסיעם כל אחת לאחור אות אחת ונרשום הראשונות | ||||||||||||||||||||||||||||||||||||||||||||
| We look for another digit, such that when multiplied by all the triples, by the sub-triples, and by itself cubically, generates numbers that are equal or as close as possible to the [numbers] that are above them. | ונבקש אות אחרת נמצאת שמוכת בכל המשולשות והתחת משולשות ובעצמה באופן מעוקב יוליד מספר שוה או היותר קרוב שאיפשר לשלמעלה מהם | ||||||||||||||||||||||||||||||||||||||||||||
| We subtract them from them. | ונחסרהו מהם | ||||||||||||||||||||||||||||||||||||||||||||
| We always have this way, even if the digits are numerous. | וזה הדרך יהיה לנו תמיד ואם ירבו מאד האותיות | ||||||||||||||||||||||||||||||||||||||||||||
| You should know that if the triple is two digits, i.e. units and tens, we write the units as stated, i.e. in the place of the units, and we write the tens in the rank that is third to the left of the units, which is the place where the sub-triple is written and so on. | וצריך שתדע שאם המשולשת תהיה ב' אותיות ר"ל אחדות ועשרות האחדות נכתוב כנזכר ר"ל במקום האחדות והעשרות נכתוב במקום השלישי לאחדות מצד שמאל אליה שהוא מקום רשימת התחת משולשת וכן לעולם | ||||||||||||||||||||||||||||||||||||||||||||
| Know that the present digit do its function, then, if there are more digits, it becomes a sub-triple. | ודע שכל אות נמצאת בשתפעול פעולתם ויהיו יותר אותיות תחזור היא תחת משולשת | ||||||||||||||||||||||||||||||||||||||||||||
|
המשל נרצה לדעת השורש המעוקב של י"ב אלף וקס"ז | ||||||||||||||||||||||||||||||||||||||||||||
|
וזו היא צורתו | ||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||
|
ולפי מה שאמרנו למעלה לא ימצא בזה המספר אלא ב' מקומות בעלי שרשים מעוקבי' והם האחדות והאלפי' ונתחיל במקום האלפי' שהוא ב' וא' | ||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב ב' תחתיו בעבור שלא [133]נמצא מספר יותר קרוב לב"א [לי"ב][134] שיקבל הכאה מעוקבת אלא ב' | ||||||||||||||||||||||||||||||||||||||||||||
|
אם כן נכה ב' בעצמם באופן מעוקב ויוליד ח' | ||||||||||||||||||||||||||||||||||||||||||||
|
ונחסרם מי"ב וישארו ד' על ב' ונכתוב ספרא על א' | ||||||||||||||||||||||||||||||||||||||||||||
|
ואחר נשלש הב' ויהיו ו' | ||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב אותה תחת האות השלישית לב' שהיא תחת הו' העליונה | ||||||||||||||||||||||||||||||||||||||||||||
|
ונרשום הב' ונסיעה אות אחת לאחור ונשימה אצל המשולשת ובמקום שהיתה שלישית אליה חזרה שניה אליה מצד שמאל | ||||||||||||||||||||||||||||||||||||||||||||
|
ואחר המשולשת נכתוב ג' שמוכת במשולשת שהיא ו' יוליד י"ח ואלו הי"ח נכם בתחת משולשת שהיא ב' ויהיו ל"ו | ||||||||||||||||||||||||||||||||||||||||||||
|
ונחסרם ממ"א שהם על הב' וישארו ה' על הא' וספרא על הד' | ||||||||||||||||||||||||||||||||||||||||||||
|
ואחר נכה הג' הנזכרת שהיא האות הנמצאת במשולשת שהיא ו' ויוליד י"ח וכל זה נכה בג' ויוליד נ"ד | ||||||||||||||||||||||||||||||||||||||||||||
|
ונחסרם מהמספרי' שהוא נ"ו וישארו ב' על הו' וספרא על הה' | ||||||||||||||||||||||||||||||||||||||||||||
|
ואחר נכה הג' הנזכרת בעצמה באופן מעוקב ויוליד כ"ז | ||||||||||||||||||||||||||||||||||||||||||||
|
ונחסרם ממה שלמעלה מהם [שהם] כ"ז ולא ישאר מאומה | ||||||||||||||||||||||||||||||||||||||||||||
|
ולכן נכתוב ספרא על ב' ועל ז' | ||||||||||||||||||||||||||||||||||||||||||||
|
וא"כ ידענו שהמספר הזה הוא מעוקב ושורשו כ"ג |
- [Illustration of the procedure:]
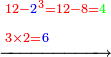
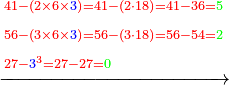
000 04 04520 12167 12167 12167 2 226 2263
|
ומשל אחר אם יקרה באופן אחר נניח שנרצה לדעת השרש המעוקב מת"ק ע"א אלף ותשפ"ז | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וזאת היא צורתו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ובעבור שבזאת הצורה לא ימצא אלא ב' מקומות בעלי שרש נתחיל באחרון שהוא א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב תחתיו מספר אחד שמוכה בעצמו באופן מעוקב יוליד מספר היותר קרוב אליו והוא ח' שאין שם מספר יותר קרוב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
בעבור שמוכה בעצמו באופן מעוקב יעשה תקי"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונחסרם מת"ק ע"א שהם על הח' וישארו נ"ט | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הט' נכתוב [135]על הא' והה' על הז' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונשלש הח' ויהיו כ"ד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב הד' באות השלישית לח' שהיא תחת משולשת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והעשרים הנרמזים בב' נכתוב תחת הח' שכתבנו למטה בראשונה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונרשום אותה ר"ל הח' ונסיעה לאחור מדרגה אחת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויהיו למטה ג' אותיות הב' למטה כנגד הט' העליונה והח' תחת הז' והד' תחת הח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב עוד אחר הד' אות חדשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ודרך ההכאות יהיה זה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נכה הג' שכתבנו באות השוה כ' שהיא ב' ויעלו ו' ואלה הו' נכה במשולשת שהיא ח' ויעלו מ"ח | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואלו המ"ח נחסרם מהאותיות שעל הב' שהם נ"ט וישארו י"א | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונחזור ונכה הג' פעם שנית על הד' שהיא אות האחדות מהשלוש הראשון על הח' ויעלה י"ב ואלו הי"ב נכה על הח' ויעלה צ"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר כך נכה הג' הנזכרת בב' הנזכרת ויעלה ו' ונחזור ונכה אלה הו' על הג' ויהיו י"ח | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואלו הי"ח עם הצ"ו יעלו קי"ד ואלו הקי"ד נחסרם מהג' אותיות העליונות שעל הח' שהם קי"ז וכשנחסר מהם קי"ד ישארו ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
[ונכתוב הג' על הז' ונכתוב סיפרא על כל אחת מהב' אלפים][136] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכה הג' פעם שלישי על הד' שהיא האחדות מהמשולשת ויוליד י"ב ואלו נכה בג' בעצמם ויעלו ל"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונחסרם מהאותיות שעל הד' שהם ל"ח וישארו ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב אותם על הח' [137]העליונה ונכתוב ספרא על הג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ופעם ד' נכה הג' בעצמה באופן מעוקב ויעלה כ"ז | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונחסרם מהאותיות שעל הג' שהם כ"ז ולא ישאר דבר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וא"כ לא נשאר דבר אחר הוצאת השרש הזה יראה המספר הזה הוא מעוקב שלם ושורשו הוא פ"ג |
- [Illustration of the procedure:]
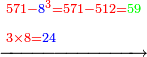
![\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{59-\left(8\times2\times{\color{blue}{3}}\right)=59-\left(8\sdot6\right)=59-48=}}{\color{green}{11}}\\&\scriptstyle{\color{red}{117-\left[\left(8\times4\times{\color{blue}{3}}\right)+\left(3\times2\times{\color{blue}{3}}\right)\right]=}}\\&\scriptstyle{\color{red}{117-\left[\left(8\sdot12\right)+\left(3\sdot6\right)\right]=}}\\&\scriptstyle{\color{red}{117-\left(96+18\right)=117-114=}}{\color{green}{3}}\\&\scriptstyle{\color{red}{38-\left(3\times4\times{\color{blue}{3}}\right)=38-\left(3\sdot12\right)=38-36=}}{\color{green}{2}}\\&\scriptstyle{\color{red}{27-{\color{blue}{3}}^3=27-27=}}{\color{green}{0}}\\\end{align}}](/mediawiki/images/math/2/5/6/25659b3c9703b5f4b750226970caf7e4.png)
00 1100 059 059320 571787 571787 571787 8 884 8843 2 2
|
וכדי להוסיף ביאור נעשה משל אחר והנה לך צורתו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ולפי מה שאמרנו יש במספר הזה שלש מקומות בעלי שרשים מעוקבי' הראשון הוא מקום האחדות והשני מקום האלפי' והשלישי מקום האלף אלפי' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ובעבור שלעולם צריך להתחיל במקום האחרון א"כ נתחיל מהב' שהוא מקום האלף אלפי' ומקום אחרון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב תחתיה ב' כי לא ימצא מספר אחר שמוכה בעצמו באופן מעוקב יהיה יותר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ולכן נכה הב' באופן מעוקב ויוליד ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונחסרם מי"ב וישארו ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב אותם על הב' שבטור העליון שהוא המקום האחרון ונכתוב ספרא על הא' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונשלש הב' ויהיה ו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב אותה תחת האות השלישי של הב' שהיא תחת הא' העליונה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונסיע הב' התחתונה מדרגה אחת לאחור כאמור למעלה ונרשום הב' הראשונה התחתונה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר כך נכתוב אות אחת אצל הו' שהיא האות המשולשת באופן שכשיוכה בו' שהוא המשולשת ובב' שהיא תחת המשולשת ובעצמה באופן מעוקב יוליד מספר שוה לכל האותיות העליונות שעליהן או היותר קרוב שאפשר ובעבור שלא ימצא מספר יותר קרוב מג' נכתוב ג' אצל הו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר כך נעשה ההכאות בדרך זה שנכה הג' באות המשולשת שהיא ו' ויהיו י"ח ואלו הי"ח נכם על הב' שבצדה והיא התחת משולשת ויהיו ל"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונחסרם [139]מהאותיות שעל הב' שהם מ"ח וישארו י"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב ב' על ח' וא' על ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונחזור ונכה הג' על הו' ויהיו י"ח ואלו הי"ח נכם בג' עצמו שהיא האות הנמצאת ויהיו נ"ד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואלו נחסרם מהאותיות שעל הו' שהם קכ"א וישארו ס"ז | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב ז' על א' וו' על ב' ו0' על הא' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונחזור ונכה הג' בעצמו באופן מעוקב ויוליד כ"ז | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונחסרם מהאותיות שעליה וישארו ה' על הב' וד' על הז' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואח' כך נשלש הג' ויהיה ט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונכתוב אותם במקום השלישי אליה שהוא תחת ה0' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והמשולשת שהיא ג' נרשום אותה ונסיעה למקום הסמוך אליה ויעמוד תחת הט' העליונה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וג"כ הו' נרשום אותה ונסיעה אות אחת אצלה ויעמוד תחת הה' העליונה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והב' ג"כ נסיעה למקום הסמוך אליה ויעמוד תחת הד' העליונה |
- [Illustration of the procedure:]
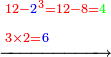

0 164 04 04275 12812904 12812904 12812904 2 226 226339 26
|
ואח"כ נכתוב עוד אות אחת שכשיוכה באותיות הד' התחתונות ובעצמה באופן מעוקב יולידו מספר שוה לכל האותיות שלמעלה או פחות היותר קרוב שאיפשר שימצא ובעבור שלא ימצא מספר יותר קרוב לד' נכתוב ד' | |||||||||
|
ונעשה ההכאות בדרך זה שנכה הד' שהיא האות הנמצאת על הו' שהיא המשולשת הר[א]שונה ויעלה כ"ד ואלו נכם בב' ויעשה מ"ח | |||||||||
|
ואלו נחסרם מהאותיות שעל הב' שהם ס"ד וישארו י"ו | |||||||||
|
ונכתוב ו' על הד' וא' על ו' | |||||||||
|
ופעם שנית נכה הד' הנזכרת במשולשת הראשונה שהיא ו' ויעלה כ"ד ואלו נכם בג' שהיא תחת משולשת השנית שהיא תחת ט' ויהיו ע"ב | |||||||||
|
ופעם שלשית נכה הד' על הט' ויעלה ל"ו ונכם בב' ויהיו ע"ב | |||||||||
|
ואלו עם הע"ב שלמעלה יהיו קמ"ד ונחסרם מהאותיות שהם על הו' [140]שהיא המשולשת הראשונה שהם קס"ה וישארו כ"א | |||||||||
|
והא' נכתוב על הה' והעשרים | |||||||||
|
ופעם ד' נכה הד' על הו' שהיא המשולשת הראשונה ויהיו כ"ד ואלו נכם על ד' עצמם ויהיו צ"ו | |||||||||
|
ופעם חמישית נכה הד' על הט' שהיא המשולשת השנית ויהיו ל"ו ואלו נכם בג' שהיא התחת משולשת השנית ויוליד ק"ח | |||||||||
|
ונחברם עם צ"ו ויהיו ר"ד ונחסרם מהאותיות שהם על הג' שהם רי"ט וישאר ט"ו | |||||||||
|
ופעם | |||||||||
|
ונחסרם מהאותיות שעליו שהם ק"נ וישארו ו' | |||||||||
|
ונכתוב אותם על ה0' ונכתוב 0' על הה' ו0' על הא' | |||||||||
|
ופעם ז' ואחרונה נכה הד' הנזכרת בעצמה באופן מעוקב | |||||||||
|
ונחסרם מהאותיות שעליה שהם ס"ד ולא ישאר דבר | |||||||||
|
ולכן נכתוב ספרא על הד' העליונה ועל הו' העליונה | |||||||||
|
||||||||||
|
ובעבור שלא נשאר שום דבר לכן נקראהו מעוקב ושורשו רל"ד | |||||||||
| Check: cubing | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| The proof of this is that we multiply the root by itself cubically and it yields the original number. Q.E.D. | והמופת לזה שנכה השרש בעצמו באופן מעוקב ויוליד המספר הראשון וזהו מה שרצינו |
Book Two: [Proportions] |
המאמר השני | ||||||||
| It is divided into two sections. | ויחלק לשני כללים | ||||||||
Section One: We Talk in It about General Methods and Proportions of This Science |
הכלל הראשון נדבר בו בדרכי' ויחסים כוללים בזאת המלאכה | ||||||||
| It is divided into seven chapters. | ויחלק לז' פרקי' | ||||||||
Chapter One: Proportions of Integers |
הפרק הא' ביחסי המספרי' השלמי' | ||||||||
| After we discussed the six types of arithmetical operations with integers and the six types of arithmetical operations with fractions that include all that is needed in arithmetic and the guiding ways for finding the roots of square and cube numbers, we shall now talk about proportions, general methods, questions and answers in theory and in practice of this science. | ואחר שדברנו מו' מיני המספר השלמים [142]ומו' מיני השברי' שהם כוללים לכל מה שיצטרך במלאכת המספר ובדרכים מיישירי' למציאות שרשי המספרי' המרובעי' והמעוקבי' עתה נדבר מיחסים ודרכים כוללים ושאילות ותשובות בעיון ובמעשה המלאכה הזאת | ||||||||
| First we will discuss the rule of three [lit. the ways of proportions]: | וראשונה נדבר מדרכי היחסים | ||||||||
| If we wish to know: if so and so are equal so and so, how much such and such are equal?
|
אם נרצה לדעת שאם כך ישוו כך כמה ישוו כך | ||||||||
|
המשל אם ב' שוים ג' כמה ישוו ה' | ||||||||
|
ונסדר אותם כך | ||||||||
|
| ||||||||
| We do it by that we multiply the middle number by the third, then divide the product by the first and the result of division is what the third equals to.
|
ונעשה בדרך זה שנכה המספר האמצעי בשלישי והיוצא נחלקהו בראשון והיוצא לחלק כך הוא השווי השלישי | ||||||||
|
המשל שאם הכינו ג' [שהוא המספר האמצעי בה'][143] שהוא המספר השלישי ויצא ט"ו נחלקם בב' שהוא המספר הראשון ויצאו לחלק ז' וחצי וזהו שיווי המספר השלישי שהוא ה' | ||||||||
| Check | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| The proof: we set three numbers this way and say: if 5 is equal to 7 and a half, how much is 2 equal?
|
והמופת נניח ג' מספרי' בדרך זה ונאמ' אם ה' שוים ז' וחצי כמה שוים ב' | ||||||||
| We arrange them as we have arranged the formers. | ואלו נסדרם כמו שסדרנו הראשוני' | ||||||||
| If the result is the middle number, which is 3 in the original proportion, then the original proportion is correct, otherwise it is incorrect. | ואם יצא המספר האמצעי שהוא ג' ביחס הראשון הראשון היה אמיתי ואם לאו אינו אמיתי | ||||||||
|
המשל אם [הה' ז' וחצי הב' כמה ישוו][144] | ||||||||
|
| ||||||||
|
ועתה נכה ז' וחצי בב' ויעלו ט"ו ונחלקם בה' שהוא הראשון ויבוא מהחלוקה ג' שהם המספר האמצעי ביחס הראשון וא"כ הראשון היה אמיתי | ||||||||
|
ולכן נוכל לאמר אם ב' שוים ג' ה' שוים ז' וחצי וזהו מה שרצינו | ||||||||
| This method is enough for integers alone, but for fractions another method is needed, as will be seen in the chapter that follows. | וזה הדרך מספיק בשלימי' לבד האמנם בשברי' צריך דרך אחר כמו שיראה בפרק הנמשך לזה[145] |
Chapter Two: Guiding Ways for Finding Proportions of Fractions |
הפרק השני בדרכים מיישירי' במציאות יחסי המספרי' [146]השבריי' | ||||||||||||
| Concerning to fractions, there are two things that one should know, which are finding the denominator and finding the numerator. | האמנם בשברי' צריך לדעת ב' דברי' והם מציאות המחלק ומציאות המחולק | ||||||||||||
| Finding the denominator is known by that we examine the first number of the three stated, for it necessarily belongs to one of these five categories: | ומציאות המחלק יודע בדרך זה שנעיין המספר הראשון מהשלשה שאמרנו כי לא ימנע מא' מאלו הה' דרכי' | ||||||||||||
|
הא' אם שיהיה הראשון שבר לבד ובאחרי' או באיזה מהם שיהיה שבר | ||||||||||||
|
השני או הראשון שבר לבד והאחרי' שלימי' | ||||||||||||
|
הג' או הראשון שבר ושלם יחד ובאחרי' או באיזה מהם שבר | ||||||||||||
|
הד' או הראשון שבר ושלם יחד והאחרי' שלימי' | ||||||||||||
|
הה' או הראשון שלם ובאחד מהאחרי' או בשניהם שבר | ||||||||||||
| The first [category] | וראשונה מהראשון הנמשל | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
המשל אם נרצה לדעת אם ב' שלישיות שוים ז' שלימי' וד' תשיעיות כמה שוים ד' וד' שלשה עשיריות | ||||||||||||
|
וזה צורתם | ||||||||||||
|
| ||||||||||||
|
וראשונה נוציא המחלק שנכה הב' שהוא על הג' בט' שהוא תחת הד' ויעלו י"ח וכל זה נכה על י"ג שהוא תחת ד' ויעלה רל"ד וזהו המחלק | ||||||||||||
|
ומשל אחר לזה המין אם שני שלישיות שוות ד' וחצי כמה שוים ו' | ||||||||||||
|
והנה לך צורתם | ||||||||||||
|
| ||||||||||||
|
ונעשה המחלק כך נכה הב' שעל הג' על ב' שהיא תחת א' ויהיה ד' וזהו המחלק | ||||||||||||
| The second category: the first is fraction alone and the others are integers. | הדרך השני או יהיה הראשון שבר לבד והאחרי' שלמי' | ||||||||||||
|
המשל אם ב' שלישיות שוות ח' כמה שווים ט' | ||||||||||||
|
וזה צורתם | ||||||||||||
|
| ||||||||||||
|
וימצא המחלק כך שנקח הב' שהיא על הג' כי הוא לבד המחלק בעבור שלא נצטרך במחלק בזה המין למספרי' אחרי' ר"ל השנים האחרונים אלא כשיהיה באחד מהם או בשניהם שבר או שברי' | ||||||||||||
| The third category: the first is fraction and integer together and the two others are either fraction alone, or fraction and integer together. | הדרך השלישי או יהיה הראשון שבר ושלם יחד [147]ובאחד מהאחרי' מאיזה שיהיה או בשניהם שבר בלבד או שבר ושלם יחד | ||||||||||||
|
המשל אם | ||||||||||||
|
וזה צורתם | ||||||||||||
|
| ||||||||||||
|
ולמצא המחלק נכה ה' על ג' שתחת ב' שבצדה ויעלה ט"ו ונוסיף הב' שעל הג' ויעלו י"ז ואלו נכם בד' שהיא תחת ג' של מספר שני ויעלו ס"ח ואלו נכם בי"ב שהם תחת ה' שהוא המספר השלישי ויעלו תתי"ו וזהו המחלק | ||||||||||||
|
וצריך שתדע שהי"ז שעלו מהכאת ה' בג' מצדה והוספת הב' שעל הג' ואח"כ הכינו אותם בד' שתחת הג' של מספר שני ועלו ס"ח שאם לא היה עוד שבר במספר השלישי זה לבדו ר"ל הס"ח היה המחלק | ||||||||||||
|
וכן הוא הדין אם שבר יהיה במספר השלישי ולא יהיה במספר השני | ||||||||||||
| The fourth category: the first is fraction and integer together and the others are integers. | הדרך הרביעי או הראשון שבר ושלם יחד והאחרי' שלמי' | ||||||||||||
|
המשל אם ה' וב' שביעיות שוות ד' כמה שוים עשרי' | ||||||||||||
|
וזה צורתו | ||||||||||||
|
| ||||||||||||
|
ונמצא המחלק כך נכה הה' בז' שבצדה שהיא תחת הב' ויעלו ל"ה ונוסיף הב' שעל הז' ויהיו ל"ז וזהו המחלק | ||||||||||||
|
ובעבור שהשני מספרי' האחרי' הם שלמי' אינם מצטרפי' במחלק כאמור | ||||||||||||
| The fifth category: the first is integer and the two others are either fraction alone, or integer and fraction. | הדרך הה' או הראשון שלם ובאחד מהאחרי' או בשתיהם שבר לבד או שלם ושבר | ||||||||||||
|
המשל אם כ' שוים ט"ו וה' חלקי' מל"ז כמה שוים ה' וב' שביעיות | ||||||||||||
|
וזה צורתו | ||||||||||||
|
| ||||||||||||
|
ונוציא המחלק כך נכה הראשון שהוא הכ' השלמי' בל"ז שתחת הב' מהמספר השני ויעלו תש"ם ואלו נכם על ז' שתחת ב' של [149]מספר שלישי ויעלה ה' אלפי' וק"ף וזהו המחלק | ||||||||||||
|
ואם לא יהיה שבר אלא באחד מהמספרי' האחרי' נכה הראשון השלם באותו השבר שתחת הקו והוא יהיה המחלק | ||||||||||||
| This is enough with regard to the denominator and now we shall talk about the numerator. | וזה יספיק במה שהוא המחלק ועתה נדבר במחולק |
Chapter Three: Guiding Ways for Finding the Numerator in the Proportions of Fractions |
הפרק השלישי בדרכי' מיישירי' למציאות המחולק ביחסי השברי' | ||||||||||||
| You should know that the numerator is of one of six categories: | וצריך שתדע שהמחולק יקרה באחד מששה דרכי' | ||||||||||||
|
הדרך הא' אם שכל אחד משני המספרי' האחרוני' יהיה שבר לבד | ||||||||||||
|
והשני או השני מספרי' יהיו שלמי' | ||||||||||||
|
והשלישי או שכל אחד משני המספרי' יהיה שלם ושבר ביחד | ||||||||||||
|
והרביעי או אחד מהשני מספרי' יהיה שלם ושבר ביחד והאחר שבר לבד | ||||||||||||
|
והחמישי או אחד מהם שלם ושבר יחד והאחר שלם | ||||||||||||
|
והו' או האחד יהיה שלם והאחר שבר | ||||||||||||
| The first category: | וראשונה מהדרך הראשון | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
המשל אם ב' שלישיות שוות ד' תשיעיות כמה שוים ד' חלקי' מי"ג | ||||||||||||
|
והנה לך צורתו | ||||||||||||
|
|
| ||||||||||||
|
ונבקש המחולק כך בזה המין שנכה המספר שהוא על הקו של האחד מאחרונים על המספר שהוא על קו המספר האחר וזאת ההכאה נשמור אותה ונכה אותו עוד במספר שתחת קו המספר הראשון וזהו המחולק | ||||||||||||
|
ואם המספר הראשון יהיה שלם לבד אז יהיה המחולק מה שעלה מההכאה הראשונה מהשני מספרי' האחרוני' כמו שאמרנו בעניין המחלק כי איננו צריכים שלימי' אלא לשברי' שתחת הקוים [150]של שני המספרי' האחרונים וכן בעניין המחולק איננו צריכי' מהראשון אם יהיה שלם שום הכאה אלא כשיהיה שבר ואז מה שתחת הקו שלו | ||||||||||||
|
ויהיה המחולק בזה המשל מ"ח שכך עולה ד' של אחד מהאחרונים על ד' של אחר שהיא י"ו וי"ו על ג' מהמספר הראשון והם מ"ח כאמור | ||||||||||||
| The second category: the two numbers are integers. | הדרך השני או השני מספרי' יהיו שלימי' | ||||||||||||
|
המשל אם ב' שלישיות שוות ח' כמה שוים תשעה | ||||||||||||
|
והנה לך צורתו | ||||||||||||
|
| ||||||||||||
|
ונמצא המחולק כך שנכה השלם האחד באחר והעולה נכהו בשבר שתחת הקו של המספר הראשון | ||||||||||||
|
המשל נכה ח' על ט' ועלו ע"ב ואלו נכה אותם בג' ועלו רי"ו וזהו המחולק | ||||||||||||
| The third category: each of the two numbers is an integer and fraction together. | הדרך השלישי או שכל מהשני מספרי' יהיה שלם ושבר יחד | ||||||||||||
|
המשל אם ה' וב' שלישיות שוות ו' וג' רביעיות כמה שוים ח' וה' חלקי' מי"ב | ||||||||||||
|
והנה לך צורתו | ||||||||||||
|
| ||||||||||||
|
ונוציא המחולק כך שנכה כל אחד מהשלמי' מהמספרי' האחרוני' במה שתחת הקו שבצדו ונוסיף עוד מה שעל הקו שבצדו ואחר נכה העולה מהשני מספרי' זה על זה ונכה עוד זה ההכאה באות שתחת הקו של מספר ראשון וזהו המחולק | ||||||||||||
|
ואם המספר הראשון יהיה שלם יספיקו למחולק הכאות המספרים האחרונים כמו שאמרנו | ||||||||||||
|
והמשל לזאת הצורה נכה ו' בד' שבצדו ויעלו כ"ד ונוסיף ג' שעל הקו ויעלו כ"ז | ||||||||||||
|
עוד נכה ח' מהמספר האחרון על [151]י"ב שבצדו ויעלו צ"ו ונוסיף ה' שעל הקו ויעלו כולם ק"א | ||||||||||||
|
ועו' נכה ק"א על כ"ז ויעלו אלפים ותשכ"ז ואלו נכם באות שתחת הקו המספר הראשון ויהיו ח' אלפי' וקפ"א וזהו המחולק | ||||||||||||
|
ואם לא יהיה שבר במספר הראשון יהיה המחולק אלפי' ותשכ"ז שהוא הכאת שני המספרי' אחרונים כאמור | ||||||||||||
| The fourth category: one of the two last numbers is an integer and fraction together and the other is a fraction alone. | הדרך הרביעי או אחד מהשני מספרי' האחרונים יהיה שלם ושבר יחד והאחר שבר לבד | ||||||||||||
|
המשל אם אחד שוה ד' חמישיות כמה שוים שנים וחצי | ||||||||||||
|
והנה צורתו | ||||||||||||
|
| ||||||||||||
|
ונוציא המחולק בדרך זה שמהצד שימצא השלם עם השבר נכה השלם בשבר שתחת הקו שבצדו ונוסיף עליו מה שעל הקו שבצדו וכל זה נכהו במספר האחד מהאחרונים שהוא על הקו וזהו המחולק | ||||||||||||
|
ואם היה במספר הראשון שבר היינו מכים עמו כל זאת ההכאה האמורה | ||||||||||||
|
המשל לזאת הצורה נכה ב' שלמי' בב' שהוא שבר שבצדה ויעלה ד' ונוסיף א' שעל [הקו] ויעלו ה' ואלו נכם בד' שהוא על ה' ויעלו כ' וזהו המחולק | ||||||||||||
|
ואם היה שבר במספר הראשון הוצרכנו להכות אלו הכ' באות שתחת הקו של מספר ראשון | ||||||||||||
| The fifth category: one of the last number is an integer and fraction together and the other is an integer alone. | הדרך החמישי או יהיה אחד מהמספרי' האחרוני' שלם ושבר יחד והאחר שלם לבד | ||||||||||||
|
המשל אם ב' שלישיות שוות ד' וחצי מה שוים ששה | ||||||||||||
|
והנה צורתו | ||||||||||||
|
| ||||||||||||
|
ונבקש המחולק ככה שנכה השלם עם המספר שתחת הקו שהוא מצדו ונוסיף מה שלמעלה המנו וכל זה נכה עם השלם היחידי שהוא מהצד האחר וכל זה נכה עוד [152]עם המספר שהוא תחת הקו שבמספר הראשון אם יהיה בו שבר | ||||||||||||
|
ואם לא יהיה בו שבר אלא שלם לבד אינו צריך יותר הכאה | ||||||||||||
|
והמשל לצורה נעשה המחלק בדרך זה שנכה הד' על הב' שהיא תחת הקו שבצדה ויעלה ח' ונוסיף עם זה הא' שהיא על הב' ויעלה ט' וזה נכם על הו' שהוא השלם מהמספר השלישי ויעלה נ"ד וזה היה המחולק אם לא היה במספר הראשון שבר אבל בעבור שיש בו שבר נכה הנ"ד שיש בידינו על האות שהיא תחת הקו של אותו שבר שהוא ג' ויעלה קס"ב ואז יהיה זה המחולק | ||||||||||||
| The sixth category: one of the last numbers is an integer alone and the other is a fraction alone. | הדרך השישי או יהיה אחד מהמספרי' האחרונים שבר לבד והאחר שלם לבד | ||||||||||||
|
המשל אם ט' שוות ב' שלישיות כמה שוים ח' | ||||||||||||
|
והנה צורתו | ||||||||||||
|
| ||||||||||||
|
ונוציא המחולק כך שאי זה שיהיה מהשני מספרי' האחרונים שלם נכה אותו עם המספר שעל הקו שהוא ג"כ מהאחרוני' וזהו המחולק בעבור שאין שום שבר במספר הראשון | ||||||||||||
|
אבל אם יהיה בו שבר בין שיהיה לבדו בין שיהיה עם שלם אז נכה זאת ההכאה עם המספר שהוא תחת הקו וכל זה אז יהיה המחולק | ||||||||||||
|
המשל לצורה זו נעשה המחולק כך שנכה הח' שהיא אחד מהאחרוני' על ב' שהוא על ג' ויעלה [ט"ו] וזהו המחולק | ||||||||||||
|
אבל אם יהיה במספר הראשון שבר נוסיף להכות האמורים | ||||||||||||
| You should know that in this type, i.e. "if so and so are equal so and so, how much such and such are equal?", meaning the type of the said proportions, there are no more categories than those we presented, whether for the denominator or for the numerator. | וצריך שתדע שבזה המין ר"ל אם כך שוים כך כמה שוים כך כלומ' סוג היחסים האמורים לא ימצאו יותר דרכים מאותם שאמרנו בין במחלק בין במחולק | ||||||||||||
| After we have the denominator and the numerator in our hands, we divide the numerator by the denominator and we receive the fourth number, which is what we asked for. | ואחר שיהיו בידינו [153]המחלק והמחולק נחלק המחולק במחלק ויצא לנו מספר רביעי והוא מה שבקשנו | ||||||||||||
| So, we have now four proportional numbers, such that the ratio that is between the first and the second is the same as the ratio that is between the third and the fourth. | וא"כ יש לנו עתה ארבע מספרי' מתיחסים באופן שהיחס שימצא בין הראשון והשני אותו יחס ימצא בין השלישי והרביעי | ||||||||||||
| Check | |||||||||||||
| The proof is that we switch the ratio in the way that we take the three numbers according to this order: we make the third number that we have in our hand a first number, we make the fourth number a second [number], and the first number a third [number]. We arrange them as above and say: if this is equal that, how much is this equal? | והמופת נחליף היחס בדרך זה והוא שנקח הג' מספרים בזה הסדר והוא שנעשה מהמספר השלישי שיש בידינו מספר ראשון והמספר הרביעי נעשה שני והמספר הראשון שלישי ונסדרם כמו שלמעלה ונאמ' אם זה שוה זה [כמה שוה זה] | ||||||||||||
| If we receive that the fourth number in this order is the number that was second in the first order, we know that the fourth number that was received in the first order is correct, otherwise it is not. | ואם יצא לנו המספר הרביעי בסדר זה המספר שהיה שני בסדר הראשון אז נדע שהמספר הרביעי שיצא בסדר הראשון היה אמיתי ואם לאו לא | ||||||||||||
| It is enough for this teaching. | וזה מספיק בזה הלמוד |
Chapter Four: Giving a General Example for all the Teaching Methods of the Denominator and the Numerator in the Context of Knowing the Ratios of Fractions |
הפרק הרביעי בנתינת משל אחד כולל לכל אופני הלמוד במחלק ובמחולק בידיעת יחסי המספרי' [השברי'][154] | ||||||||
| In order to add explanation, we give an example for all part of the teaching together, i.e. the denominator and the numerator and their proof in one of the ways we mentioned. | וכדי להוסיף ביאור נתן משל לכל חלקי הלימוד ביחד ר"ל מהמחלק והמחולק והמופת שלהם וזה באחד מהדרכי' שאמרנו | ||||||||
|
והוא זה אם ב' שלישיות שוים ד' וחצי כמה שוים ששה | ||||||||
|
| ||||||||
|
וראשונה נוציא המחלק כך שנכה הב' שהיא על ג' מהמספר הראשון על ב' שהיא תחת א' של מספר שני ויהיו ד' וזהו המחלק ונשמור אותו | ||||||||
|
ואחר נעשה המחולק כך שנכה ד' מהמספר השני על ב' שהיא תחת הא' שבצדה ויעלה ח' ונוסיף עוד הא' שעל הב' מהמספר השני ויעלה ט' ואלו נכם עוד על ו' שהוא מספר שלישי ויעלה נ"ד עוד נכם על ג' שהוא תחת ב' של מספר ראשון ויעלה קס"ב וזהו המחולק | ||||||||
|
ונחלק אלו במחלק שהוא ד' ויצא מהחלוק מ' וחצי וזהו המספר הד' ששוים ו' [ה]מבוקש | ||||||||
| The ratio of two-thirds to 4 and a half is the same ratio of 6 to 40 and a half.
|
והיחס שיש [155]בין שני שלישיות לד' וחצי אותו היחס יש בין ו' למ' וחצי | ||||||||
| The proof: to know if this is correct we arrange them as follows:
|
והמופת לדעת אם זה אמת נסדרם ככה | ||||||||
|
| ||||||||
|
ונאמ' אם ו' שוים מ' וחצי כמה שוים ב' שלישיות | ||||||||
|
נעשה המחלק כך נכה המספר הראשון על ב' שהוא תחת א' של מספר שני ויהיו י"ב ואלו הי"ב נכם בג' שהיא תחת ב' של מספר שלישי ויעלה ל"ו וזהו המחלק | ||||||||
|
ואחר נעשה המחולק בדרך זה נכה המ' שהוא מהמספר השני על ב' שהיא תחת א' שבצדה ויעלה פ' ונוסיף א' שהוא על ב' של מספר שני ויעלה פ"א ונכם בב' שעל הג' של מספר שלישי ויעלה קס"ב וזהו המח[ו]לק | ||||||||
|
ונחלקהו בל"ו שהוא המחלק ויצא מהחלוק ד' וחצי ואלו הד' וחצי היה המספר השני של סדר ראשון שאמרנו | ||||||||
| This proof indicates that the first order that we applied was correct. | וזה המופת יורה שהסדר הראשון שעשינו היה אמיתי | ||||||||
| So, if two-thirds are equal 4 and a half, the 6 are equal 40 and a half; and this is what we wanted.
|
א"כ אם ב' שלישיות שוות ד' וחצי הו' שוים מ' וחצי וזה מה שרצינו | ||||||||
|
ומשל אחר להוסיף ביאור אם ט' שוים ב' שלישיות כמה שוים ח' | ||||||||
|
| ||||||||
|
ונעשה המחלק בשנכה הט' שהוא המספר הראשון על הג' שתחת ב' מהמספר השני ויעלה כ"ז וזהו המחלק | ||||||||
|
ונעשה המחולק ככה בשנכה הח' שהוא מספר שלישי בב' שעל הג' של מספר שני ויעלה י"ו וזהו המחולק | ||||||||
|
ונחלק [הי"ו על כ"ז שהוא המחלק ויצא מהחלוק] י"ו חלקי' מכ"ז בשלם וזהו המספר הרביעי שרצינו לדעת | ||||||||
|
| ||||||||
|
ולמופת זה נאמ' אם ח' שוים י"ו כמה שוים ט' | ||||||||
|
ונעשה המחלק בשנכה הח' שהוא מספר ראשון מזה הסדר על כ"ז שתחת י"ו של מספר שני ויעלו רי"ו וזהו המחלק ונשמור אותו | ||||||||
|
והמחולק נעשה בשנכה [156]הט' על י"ו שהוא על הקו של מספר שני ויעלו קמ"ד וזהו המחולק | ||||||||
|
ונחלקהו במחלק שהוא רי"ו ויצא מהחלוק קמ"ד חלקי' מרי"ו חלקי' של שלם והנה לך צורתו 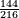
| ||||||||
|
ואם יהיה זה שוה לב' שלישיות של מספר שני של סדר ראשון מה שעשינו הוא אמת | ||||||||
| The proof that it is equal to two-thirds is by that we write 2-thirds this way: | ומופת שהם שוים שני שלישיות הוא זה שנכתוב ב' שלישיות בדרך זה | ||||||||
| We write the number that we want to know if it is 2-thirds opposite to it, as you see:
|
והמספר שרצינו לדעת אם הוא ב' שלישיות נכתוב כנגדו כמו שאתה רואה
| ||||||||
| Then, we multiply each digit by its opposite and if the two products are equal, the fractions are equal as we said, so the order that we have done is correct and this is what we wanted. | ואח"כ נכה כל אות עם סותרו ואם ב' ההכאות יהיו שוות השברי' הם שוים כמו שאמרנו א"כ הסדר שעשינו הוא אמיתי וזהו מה שרצינו | ||||||||
| Know that this proof concerning the fractions is general for every two fractions, when we want to know if they are equal. Q.E.D. | דע שזה המופת מהשברים שעשינו הוא כולל לכל שני השברי' כשנרצה לדעת אם הם שוים וזהו מה שרצינו |
Chapter Five: Knowing the Ratio of the Four Proportional Numbers [= the Rule of Three] in the Two Sciences - Arithmetic and Geometry |
הפרק החמישי בידיעת יחס הד' מספרים המתייחסים בשני המלאכות ר"ל מלאכת המספר ומלאכת ההנדסא |
| After we have discussed in the previous teaching on ratios all the techniques that can be applied concerning them in arithmetic, we shall discuss them now regarding geometry, i.e. as parts of the continuous quantity, although the methods of multiplication and division are the same in both sciences. | ואחר שדברנו בזה הלמוד שעבר מן היחסים בכל הדרכי' שאיפשר שיקרו בהם במה שהיא מלאכת המספר עתה נדבר בהם במה שהם ממלאכת ההנדסא ר"ל במה שהם חלקי הכמה המתדבק ואע"פ שדרך ההכאה והחלוק אחד הוא בשני המלאכות |
| Know that in geometry they are understood in a way that whenever there are four proportional numbers, such that the ratio of the first to the second is as the ratio of the third to the fourth, and the fourth is unknown, if you wish to know it, we multiply the second by the third, then divide the product by the first and we receive the fourth that we asked for.
|
ודע כי במה שהם במלאכת ההנדסא יובנו בדרך זה שבכל זמן שיהיו ד' מספרי' מתיחסים באופן שיהיה יחס הראשון לשני כיחס השלישי לרביעי והרביעי יהיה בלתי ידוע אם תרצה לדעתו נכה השני בשלישי והעולה נחלקהו בראשון ויבא לנו הרביעי שבקשנו |
| All the ratios we mentioned above are according to this way. | [157]ומעין הדרך הזה הם כל היחסים שאמרנו למעלה |
| You should know that this ratio has another quality, which is that as the way that we know the fourth unknown number, if it happens that any of the others is unknown to us and the other three are known, we can know it by the mentioned way. | האמנם צריך שתדע שיש לזה היחס עוד סגלה אחרת והיא שכמו שבדרך הזה ידענו המספר הרביעי הבלתי ידוע אם יקרה שלא יודע לנו אי זה מהאחרים אי זה שיהיה והשלשה האחרי' יודעו נוכל לדעתו בדרך הזה שנאמ' |
|
המשל נניח שהמספר הראשון בלתי ידוע והג' האחרים ידועים ר"ל השני והשלישי והרביעי אז נדע המספר הראשון בדרך זה שנכה השני בשלישי ונחלק העולה ברביעי ויצא לנו הראשון |
|
ואם נסכל השני וידענו האחרי' נכה הרביעי בראשון ונחלק על הג' ויצא לנו השני |
|
ואם נסכל הג' נכה הד' בא' ונחלק העולה בב' ויצא הג' |
| This way the unknown is known through the three knowns and this is what we want. | ובזה הדרך יודע הבלתי ידוע בשלשה הידועים וזה מה שרצינו |
Chapter Six: [Proportional Triad] |
הפרק השישי |
| You should know that there is another way of ratios, which is that if there are three proportional numbers, such that the ratio of the first to the second is as the ratio of the second to the third, and the third is unknown, if we wish to know it, we do as follows: we multiply the second number by itself, then divide it by the first, and the result is the third number that we look for.
|
וצריך שתדע שיש דרך אחר מיחסים והיא זאת שאם יהיו ג' מספרי' מתייחסים באופן שיחס הראשון לשני יהיה כיחס השני לשלישי והשלישי בלתי ידוע אם נרצה לדעתו נעשה כך נכה המספר השני בעצמו ונחלקהו בראשון ויצא המספר השלישי שבקשנו |
|
ואם סכלנו המספר השני נדעהו בדרך זה שנכה הראשון בג' ומזאת ההכאה נקח שורשה וזהו המספר השני שבקשנו |
|
ואם סכלנו המספר הראשון נדעהו בדרך זה בשנכה המספר השני בעצמו ונחלק העולה בג' ויצא לנו המספר הראשון |
| This way the unknown numbers are found through the knowns in this ratio. | ובדרך זה ימצאו המספרי' הבלתי ידועים בידועים בזה היחס |
| This ratio is quite necessary and useful in geometry. | וזה היחס הוא הכרחי מאד [158]ומועיל במלאכת המתייחסים [ההנדסה] |
Chapter Seven: Knowing the Ratio of the Six Proportional Numbers [= the Proportional Hexad] |
הפרק השביעי בידיעת יחס הששה מספרי' המתייחסים | ||||||||||||
| There is another way of ratios, which is that if there are six proportional numbers, such that the ratio of the first to the second is as the ratio of the third to the fourth and the ratio of the fifth to the second is as the ratio of the sixth to the fourth, then the ratio of the sum of the first and the fifth to the second is as the ratio of the sum of the third and the sixth to the fourth. | ועוד יש דרך אחרת מיחסים והיא זאת אם יהיו ו' מספרי' מתייחסים באופן שיהיה יחס הראשון לשני כיחס | ||||||||||||
|
|
|||||||||||||
| This ratio is necessary in geometry to know the height required from two aspects. | וזה היחס הוא הכרחי בהנדסא לדעת אי זה גובה שיהיה הכרחי לדעתו בשתי הבטות | ||||||||||||
|
המשל לששה המספרי' המתייחסי' והם אלו | ||||||||||||
|
| ||||||||||||
|
ובעבור שיחס ב' שהוא מספר ראשון לג' שהוא מספר שני כיחס ד' שהוא מספר שלישי לו' שהוא מספר רביעי ויחס ט' שהוא מספר חמישי לג' שהוא מספר שני כיחס י"ח שהוא מספר ששי לו' שהוא מספר רביעי | ||||||||||||
| Therefore, as long as the six numbers are in this ratio, then the ratio of the sum of the first number and the fifth number to the second number is as the ratio of the sum of the third number and the sixth number to the fourth number.
|
לכן כל זמן שיהיו הששה מספרי' בזה היחס יהיה יחס קבוץ המספר הראשון והחמישי למספר השני כיחס קבוץ המספר השלישי והששי למספר הרביעי | ||||||||||||
|
כמו שהוא נראה באלו הששה מספרי' שיחס י"א שהוא קבוץ המספר הראשון שהוא ב' והחמישי שהוא ט' לג' שהוא המספר השני כיחס כ"ב שהוא קבוץ ד' שהוא מספר שלישי וי"ח שהוא מספר ששי לו' שהוא מספר רביעי | ||||||||||||
|
| ||||||||||||
| Know that for every six numbers of this ratio, the ratio of the sum of the first and the fifth to the second is as the ratio of the sum of the third and the sixth to the fourth. | ודע שלעולם בכל ששה מספרי' מזה היחס יהיה יחס קבוץ הראשון והה' לב' [והחמישי לשני][159] כיחס קבוץ השלישי והששי לרביעי | ||||||||||||
| This way, i.e. by summing, it returns to the ratio of the four numbers [= the rule of three] that is stated in the fifth chapter of this section and this is what we want. | ובזה הדרך ר"ל מהקבוץ ישובו [160]ליחס הארבעה מספרי' הנזכרי' בפרק ה' מזה הכלל וזה מה שרצינו |
The Second Section of the Second Book: We will Discuss in it Some Theoretical and Practical Problems and Guiding Answers of this Science |
הכלל הב' מהמאמר השני נדבר בו בקצת שאלות ותשובות מישרות בעיון ובמעשה בזאת המלאכה | ||||||||||||||||||||
| It is divided into seven chapters: | ויתחלק לז' פרקי' | ||||||||||||||||||||
The First Chapter: on the Knowledge of the Exchange of Measurements, Weights, Liquid Measures and Currencies According to the Change of Places |
הפרק הראשון בידיעת חלוף המדות המשקלים והמשורות והמטבעות לפי חלוף המקומות | ||||||||||||||||||||
| Since in many places an exchange of things mentioned is applied, we must discuss a particular general method by which we can know each exchange that we want of them. | בעבור שבהרבה מקומות יש חלוף באלו הדברי' הנזכרי' צריך שנדבר מאי זה דרך כללי שבו נוכל לדעת כל חלוף מאלה שנרצה | ||||||||||||||||||||
| First we ask: if four measurements or weights or whatever it will be from Constantinople are worth six from Bursa, and nine from Bursa are worth three from Alexandria [= İskenderun], how much are six from Alexandria worth? | וראשונה נשאל אם ד' מדות או משקלים או מה שיהיה מקושטנטינא שוים ו' מברושה וט' מברושה שוים ג' מאלקשדייא ו' מאלקשדיא כמה שוים מאותם של קושטנדינא | ||||||||||||||||||||
|
|
|||||||||||||||||||||
| To know this we arrange all these numbers as follows: | ולדעת זה נסדר כל אלו המספרי' ככה | ||||||||||||||||||||
|
|
| Since our question is how much six from Alexandria are worth in Constantinople, we should know first how much the three from Alexandria are worth in Constantinople. | ובעבור שדרושינו הוא שו' מאלקשדייא כמה שוים מקושטדינא צריך שנדע קודם הג' מאלקשדייא כמה שוים מקושטדינא |
| But, three from Alexandria are worth nine in Bursa, so, when we know how much nine from Bursa are worth in Constantinople, then we will know how much the three from Alexandria are worth in Constantinople. | אבל ג' מאלקשדייא שוים ט' מברושא א"כ כשנדע הט' מברושא כמה שוים מקושטדינא אז נדע הג' מאלקשדייא כמה שוים מקושטדינא אם כן קודם כל דבר צריך שנדע הט' מברושה כמה שוים מקושטדינא |
| We already know that the six from Bursa are worth four from Constantinople, therefore we say: if 6 are equal 4, how much 9 are equal? | וכבר ידענו שהו' מברושה שוים ד' מקושטדינא א"כ נאמר אם ו' שוים ד' כמה שוים ט' |
|
ונסדר הצורה כך |
|
וכשהשלשה [161]מספרי' הם שלמי' הראשון הוא המחלק וא"כ הו' הם המחלק |
|
והכאת המספר השני בשלישי הוא הוא המחולק שהוא ל"ו |
|
ונחלקהו בו' ויבאו ו' מהחלק א"כ ידענו שהט' מברושה שוים ו' מקושטדינא |
|
אבל ג' מאלקשדייא שוים ט' מברושה א"כ הג' מאלקשדייא שוים ו' מקושטדינא |
|
ואחר שידענו ששלשה מאלקשדייא שוים ו' מקושטדינא נסדר דרושינו כך ונאמ' אם ג' מאלקשדייא שוים ו' מקושטדינא כמה שוים ו' מאלקשדייא |
|
וזה צורתו |
|
וכבר ידעת שהמספר הראשון הוא המחלק בשלמי' א"כ ג' הם המחלק |
|
והמחולק הוא הכאת המספר השני בשלישי שהוא הכאת ו' על ו' א"כ הם ל"ו |
|
ונחלקם על ג' ויצאו י"ב מהחלוק א"כ ו' מאלקשדייא שוים י"ב מקושטדיניא וזה מה שרצינו |
The Second Chapter: Knowing the relation of two numbers that have the property that if we subtract one from the greater number and add it to the smaller number, the two numbers become equal; and if we subtract one from the smaller number and add it to the greater, the greater becomes double the smaller, or more if we wish |
הפרק השני בידיעת התייחסות שני מספרי' שיש להם זה הטבע שאם נחסר אחד מהמספר הגדול ונוסיפהו על המספר הקטן יהיו הב' מספרי' שוים ואם נחסר אחד מהמספר הקטן ונוסיפהו בגדול יהיה הגדול כפל הקטן או יותר אם נרצה |
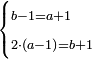
|
|
| We know this by that we first assume the two numbers and we subtract one from each, then we make [the sum of 1+1] a third number, which is 2 and this 2 is the mean by which they are known. | ונדעהו בדרך זה שנניח קודם במחשבה הב' מספרי' ונחסר אחד מכל אחד מהם ונעשהו מספר שלישי ויהיה ב' ואלה הב' יהיו אמצעי לדעת אותם |
|
|
|
| It has the property that if we add it to the smaller number, it will be equal to the greater; and if we add it to the greater number, it will be double the smaller number. | ויש להם זה הטבע שאם נוסיפם על המספר הקטן יהיה שוה לגדול ואם נוסיפם בגדול יהיה כפל הקטן |
|
|
|
| Therefore, we have now three numbers that are the greatest, the smallest, and the mean. | א"כ יש לנו עתה ג' מספרי' שהם הגדול והקטן והאמצעי |
| Suppose that they are all one thing. | ונניח שכולם הם דבר אחד |
| So, they are all one thing and when we add the mean number to the smaller, the two first numbers are equal. Therefore, we have now two equal parts of the whole and since each two equal parts of the whole is a half of the whole, then each of them is half the whole.
|
וא"כ כולם דבר אחד וכשנוסיף המספר האמצעי לקטן יהיו השני [162]מספרי' הראשונים שוים א"כ יש לנו עתה שני חלקים שוים מהכל ובעבור שכל שני חלקים שוים מהכל כל אחד הוא חצי הכל א"כ כל אחד מאלו הוא חצי הכל |
| Therefore, it is visible that when 2, which is the mean number, is added to the smaller, it makes it half the whole; and if we subtract the 2 that we added to the smaller number and add it to the greater number, the greater becomes double the smaller. | א"כ יראה שב' שהוא מספר אמצעי מחובר לקטן עשהו חצי הכל ואם נחסר אלו השנים שהוספנו למספר הקטן ונוסיפם לגדול והגדול ישוב כפל הקטן |
| Hence, it is clear that the greater is two parts of the whole and the smaller is one part, so they are three equal parts of the whole. | א"כ יראה שהגדול יהיה ב' חלקי' מהכל והקטן חלק אחד א"כ הם ג' חלקי' שוים לכל |
| Thus, the smaller number is a third of the whole and the greater is 2-thirds [of the whole]. | וא"כ המספר הקטן יהיה אז שליש הכל והגדול יהיה ב' שלישיות |
|
|
|
| So, we say that if the sum of the mean number with the smaller number is the reason that the smaller number is half the whole and their difference is the reason that it is a third of the whole, then we can deduce from this that the mean number is the difference from the third to the half. But, the difference from the third to the half is a sixth of the whole. To know that this is indeed the difference, we subtract the third from the half; a sixth remains. Hence the mean is a sixth of the whole. | א"כ נאמ' שאם חבור המספר האמצעי למספר הקטן |
| If the mean is a sixth of the whole, and it is 2, then the whole is 12, which is 6 times two. | ואם האמצעי היה ששית הכל והוא היה ב' א"כ הכל יהיה י"ב שהוא ו' פעמי' שנים |
|
|
|
| Since we said above that when we add 1 to the smaller it will become a half of the whole, it is clear that it is a half of the whole minus one, i.e. the smaller; and since the whole is 12, as said, then the smaller is 5. | ובעבור שאמרנו למעלה שכשנוסיף א' לקטן יהיה חצי הכל יראה שהוא חצי הכל פחות אחד ר"ל הקטן ובעבור שהכל י"ב כאמור א"כ המספר הקטן יהיה ה' |
|
|
|
| If the smaller is 5, the greater number is 7 for the said reasons.
|
ואם הקטן יהיה ה' המספר הגדול יהיה ז' לסבות האמורות |
| As one can say: "if we subtract one from the greater and give it to the smaller, it will become equal to the smaller", if we are asked to subtract 2 from the greater and give it to the smaller, we do not need to find these numbers and their similar, but to multiply each of the two current numbers, i.e. 5 and 7. | וכמו שאיפשר לומ' שאם נחסר אחד מהגדול ונתן אותו לקטן יהיה שוה לקטן כן גם כן אם ישאלו לנו שאם נחסר ב' מהגדול ונתנם לקטן לא |
|
|
|
| If the addition or subtraction is by 3, we triple the two numbers. | [ואם] התוספת או החסרון יהיה ג' נשלש השני המספ[רים] |
|
|
|
| If it is by a half, i.e. the addition or subtraction, we take half the two current numbers. | [ו]אם [יהי]ה חצי ר"ל התוספת או החסרון [נ]קח ח[צי ה]שני מספרי' הנמצאי[ם] |
|
|
|
| If the addition or subtraction is by a third, we take a third of the two current numbers that are already known to us, i.e. 5 and 7. | [ואם התוספת או החסרון יהיה שליש נקח שליש השני מספרי' הנמצאים ר"ל][166] הידועים לנו כבר ר"ל [הה' והז'] |
|
|
|
| Because all these questions are established on this and we apply this method in all that is similar, Q.E.D. | כי בזה ייוסדו כל אלה השאלות ובדרך זה נעשה בכל הדומה וזה מה שרצינו |
| In order to elaborate the explanation, we give another example: we assume two numbers, such that if we subtract one from the greater number and add it to the smaller, both numbers become equal; and if we subtract one from the smaller number and add it to the greater, the greater becomes twenty times the smaller. | [ו]כדי לה[וסי]ף ביאור נעשה משל אחר בשנניח ב' מספר[ים] שאם נחסר אחד מהמספר הגדול [ו]נוסיפהו לקטן יהיה [ה]שני מספרי' שוים ואם נחסר אחד מהמספר הקטן ונוסיפהו בגדול יהיה הגדול עשרי' פעמי' בקטן |
|
|
|
| We know them by that we first think of the two numbers and take one from each of the numbers. We make it a third number, which is 2. | ונדעם בדרך זה שנניח קודם במחשבה השני מספרי' ונקח אחד מכל אחד מהשני מספרי' ונעשהו מספר שלישי ויהיה ב' |
|
|
|
| This number has the property that if we add it to the smaller number, it becomes equal to the greater; and if we add it to the greater number, the greater becomes 20 times the smaller number, i.e. twenty times as the smaller.
|
ויש לזה המספר [.] זה הטבע שאם נוס[י]פהו על המספר הקטן יהיה שוה לגדול ואם נוסיפהו על המספר הגדול יהיה הגדול כפל המספר הקטן כ' פעמים ר"ל עשרי' פעמי' כקטן |
| So, we now have three numbers as said above, a great, a small, and a mean. | א"כ יש לנו עתה ג' מספרי' כאמור למעלה גדול וקטן ואמצעי |
| Suppose that they are all one amount. | ונניח שכולם יעשו כלל אחד |
| So, they are all one amount and when we add the mean number to the smaller, the two first numbers are equal. Therefore, we have two equal parts of the whole and since each two equal parts of the whole is a half of the whole, then each of them is half the whole.
|
א"כ כולם כלל אחד וכשנוסיף המספר האמצעי לקטן יהיו הב' מספרי' הראשונים שוים א"כ יש לנו ב' חלקי' שוים לכל ובעבור שכל שני חלקים שוים לכל כל אחד [.] הוא חצי הכל א"כ [כל אחד מאלו הוא חצי הכל |
| Therefore, it is visible that when 2, which is the mean number, is added to the smaller, it makes it half the whole; and if we subtract it from the smaller number and add it to the greater, the greater becomes twenty times as the smaller. | א"כ יראה][167] שב' שהוא מספר [אמצעי][168] מחובר לקטן [עשהו][169] חצי הכל ואם נחסרהו מהמספר הקטן ונוסיפהו בגדול ויהיה הגדול עשרי' פעמי' כמו הקטן |
| Hence, it is clear that the greater is 20 parts of 21 of the whole and the smaller is one part, so they are 21 equal parts of the whole. | יראה שהמספר הגדול יהיה כ' חלקי' מכ"א מהכל והקטן חלק אחד א"כ הם כ"א חלקי' [170]שוים לכל |
| Thus, the smaller number is one part of 21 parts of the whole and the greater is 20 parts of 21 parts of the whole. | א"כ המספר הקטן [י]היה אז חלק אחד מכ"א חלקי' מהכל והמספר [הגדול יהיה] כ' חלקים מכ"א [מהכל |
|
|
|
| So, we say that if the sum of the mean number with the smaller number makes it half the whole and its subtraction makes it one part of 21 parts of the whole, then it can be deduced from this that the mean number is [the difference from] one part of 21 parts of the whole to a half of the whole. But, the difference from one part of 21 parts of the whole to a half of the whole is 19 parts of 42 parts of the whole. So, the mean is 19 parts of 42 parts of the whole. To know that this is indeed the difference, we subtract one part of 21 parts of the whole from a half; 19 parts of 42 parts of the whole remain. | אם כן נאמר] שאם חבור [המספר] האמצעי [למספר הקטן ע]שהו חצי הכל [וחסרנו] עשהו [אחד מכ"א חלקי הכ]ל א"כ יראה מזה [שה]מספר האמצעי הוא [...] שיש [...]לה אחד מכ"א חלקי הכל ובין חצי הכל אבל [ההבדל בין] חלק [אחד מכ]"א חלקי ה[כל] ובין [חצי] הכל י"ט חלקי' ממ"ב חלקי הכל א[ם כן ה]אמצ[עי] הוא י"ט חלקי' ממ"ב של הכל [ול]דעת שזה [ההבדל] נחסר חלק אחד מכ"א חלקי ש[לם מה]חצי וישאר י"ט חלקי' ממ"ב חלקי השלם |
| It is clear that the mean is 19 parts of 42 parts of the whole. But, if it is 19 parts of 42 parts of the whole and it is 2, then the whole is 4 integers and 8 parts of 19 parts of the whole. | [וא"כ] יראה שהאמצעי י"ט חלקי' ממ"ב חלקי השלם ואם האמצעי הוא י"ט חלקי' ממ"ב חלקי השלם והוא היה שנים א"כ הכל היה [ד'] שלמי' וח' חלקי' מי"ט חלקי השלם |
|
|
|
| Check | |
|---|---|
| The proof of this: we say as follows: if 9 is equal to 2, how much is the one that is the required whole equal to? | והמופת על זה נאמר ככה אם [ט'] שוים ב' כמה שוה האחד שהוא הכל הדרוש |
| We know it by one of the methods stated above regarding the ways of proportions. Q.E.D. | וזה נדעהו באחד הדרכי' האמורי' למעלה בדרכי היחסים וזה מה שרצינו |
Chapter Three: The relation of two numbers such that if the greater gives one to the smaller, the smaller becomes double the greater; and if the smaller gives one to the greater, the greater becomes three times the smaller |
הפרק הג' ביחס שני מספרי' שאם הגדול יתן אחד לקטן יהיה הקטן כפל הגדול ואם הקטן יתן אחד לגדול יהיה הגדול שלשה פעמי' יותר מהקטן | ||||||||
|
|
|||||||||
| If we want to know these numbers, we define the mean first of all as above. The mean is always 2 integers in relations like this. | ואם נרצה לדעת אלו המספרי' נעשה קודם כל דבר האמצעי כמו למעלה והאמצעי לעולם הוא ב' שלמי' בכיוצא לאלו היחסים | ||||||||
|
|
|||||||||
| So, we say: if the mean is added to the smaller, it becomes double the greater.
|
א"כ נאמ' אם האמצעי מחובר לקטן יעשה כפל הגדול | ||||||||
| Therefore, it is clear that the smaller plus the mean are two-thirds of the whole.
|
מכאן יראה שהקטן עם האמצעי הם [171]שני שלישי הכל | ||||||||
| And the greater number minus the mean is a third of the whole.
|
ושהמספר הגדול בלתי האמצעי [הוא שליש הכל | ||||||||
| Hence, when we add the mean to the greater, it becomes 3 times the smaller.
|
וא"כ כשנוסיף האמצעי לגדול][172] יהיה ג' פעמי' יותר מהקטן | ||||||||
| Therefore, it is clear that the smaller minus the mean is a quarter of the whole.
|
יראה מכאן שהקטן בלתי האמצעי יהיה רביע אחד מהכל | ||||||||
| We say now: if the whole that we think of consists of three numbers, which are the greater, the smaller, and the mean, then their sum is equal to this whole. | וא"כ נאמ' עתה אם הכל שהנחנו במחשבה הוא מורכב מג' מספרי' שהם גדול וקטן ואמצעי א"כ כמות שלשתם שוה לזה הכל | ||||||||
| But, the greater and the smaller numbers are a third and a quarter of the whole, so the mean number is necessarily their complement to the whole. | אבל כמות המספר הגדול והקטן הם שליש ורביע הכל א"כ מה שיחסר לתשלום הכל הוא המספר האמצעי בהכרח | ||||||||
| Therefore, we sum up a third and a quarter, according to the first type of operations with fractions, which is addition. Their sum is:
|
א"כ נחבר שליש ורביע במין הראשון מהשברי' שהוא הקבוץ ויהיה קבוצם | ||||||||
|
|
| ||||||||
| The complement of the whole is:
|
א"כ לתשלום הכל החסרים | ||||||||
|
|
| ||||||||
| So, the mean is equal to: | וא"כ האמצעי שוה | ||||||||
|
|
| ||||||||
| It is already known the the mean itself is 2 integers and related to the whole it is: | וכבר הוא ידוע שהאמצעי בעצמו הוא ב' שלמי' ומיוחס לכל הוא | ||||||||
|
|
| ||||||||
| We apply the rule of three as follows and say: if 5 parts of twelve of the whole are equal to two integers, how much is the whole equal to? | ולכן נעשה דרך היחסים כך ונאמ' אם ה' חלקי' מי"ב חלקי' מהכל שוים שני שלמי' כמה שוה הכל | ||||||||
| We place one integer for the whole and do the diagram like this: | ובמקום הכל נשים אחד שלם ונעשה הצורה כך | ||||||||
We say: if 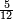 is equal to 2 integers, how much is the one that is instead of the whole equal to? is equal to 2 integers, how much is the one that is instead of the whole equal to?
|
| ||||||||
| We find that the whole that we are looking for is 4 integers and 4-fifths.
|
ונמצא שהכל שבקשנו הוא ד' שלמי' וד' חמישיות | ||||||||
| Now, we should look for the greater and the smaller numbers using it. | ועתה צריך שנבקש המספר הגדול והקטן ממנו | ||||||||
| We find the greater as follows: you already know that the greater number minus the mean is a third of the whole. So, we take a third of this whole, which is: | והגדול נמצאהו כך כבר ידעת שהמספר הגדול בלתי האמצעי היה שליש הכל א"כ נקח מזה הכל השליש שהוא | ||||||||
|
| ||||||||
| We add to it one of the two of the mean; it is: | ונוסיף עליו האחד מהשנים של האמצעי ויהיה | ||||||||
|
| ||||||||
| And this is the greater.
|
וזהו הגדול | ||||||||
| You already know that the smaller minus the mean is a quarter of the whole. So, we take a quarter of the whole, which is: | וכבר ידעת שהקטן בלתי האמצעי הוא רביע הכל ולכן נקח רביע הכל שהוא | ||||||||
|
| ||||||||
| We add to it one of the two of the mean; the smaller number is:
|
ונוסיף עליו האחד מהשנים מהאמצעי ויהיה המספר הקטן | ||||||||
|
| ||||||||
| These are the two numbers that we are looking for. Q.E.D. | ואלו הם השני מספרי' שבקשנו ומה שרצינו | ||||||||
Chapter Four: Knowing the whole, whichever it may be, from the sum of its two different parts |
הפרק הרביעי בידיעת קבוץ שני חלקי' מתחלפי' [173]מאי זה כל שיהיה או יותר איך נדע הכל | ||||
| We do as follows: we take any whole, in which the parts in question are found, and sum them up, then we say: as the ratio of this sum of the parts to the known whole, from which they are taken, so is the ratio of the parts in question to the unknown whole. | ונעשה כך נקח אי זה כל שימצאו בו אותם החלקי' הנשאלים ונעשה קבוץ מהם ונאמ' כיחס זה הקבוץ מהחלקי' אל הכל הידוע שלוקחו ממנו יחס החלקי' הנשאלים לכל הבלתי ידוע | ||||
| We arrange them in the rule of three, and take the parts of the known number as the first number, the whole known number as the second number, the parts of the unknown number as the third number. Then, we complete the rule of three as said in its place. | ונסדרם בדרך הרביעי הד' מספרי' המתיחסים ונקח למספר ראשון חלקי המספר הידוע ולמספר שני המספר הידוע כלו ולמספר שלישי חלקי המספר הבלתי ידוע ונשלים דרך היחסים כפי שנאמ' במקומו | ||||
|
המשל לזה נניח קבוץ אחד משליש ורביע ששוה עשרה וחצי ורצינו לדעת הכל | ||||
|
ולדעת זה נבקש מספר אחד שימצאו בו אלו השברי' ולמציאות אלו השברי' שהנחנו אין שם מספר יותר קרוב מי"ב א"כ נקח קבוץ שלישו ורביעו שהם ז' | ||||
|
ונאמ' אם ז' שוים י"ב כמה שוים י' וחצי | ||||
|
ונשלים זה היחס כמו שכבר נאמ' בלמוד היחסים ונמצא בזה הדרך שהמספר המבוקש הוא י"ח וזה מה שרצינו | ||||
| In this way all that are similar to this proportion are solved by examining all the fractions that may be assumed or asked about. | ובדרך זה יעשו כל הדומים לזה היחס כשיבחנו כל השברי' שאיפשר שיונחו או שישאל עליהם | ||||
|
כמי שישאל על קבוץ רביע וחומש שהם ה' שלימי' ונרצה לדעת הכל כמה הוא | ||||
|
נבקש מספר אחד שימצאו בו אלה השברי' רביע וחומש שהם נמצאים בעשרים א"כ נקח מכ' הרובע והחומש וקבוצם הוא ט' | ||||
|
ונאמ' אם ט' שוים עשרי' כמה שוים ה' | ||||
|
ובדרך היחסים יודע שהכל המבוקש הוא | ||||
|
| ||||
|
וקבוץ רביעיתו וחמישיתו ה' וזה מה שרצינו | ||||
| In this way all that are similar are solved. | ובדרך זה יעשו כל הדומים |
Chapter Five: Giving general ways for finding any unknown number by the method of double false position |
הפרק החמישי בנתינת [174]דרכי' כוללים לדעת אי זה מספר שיהיה בלתי ידוע בדרך המתנגדים |
| It is known in three general ways, in which proportions like these and others whatever they may be are solved. They are called "double false position" [lit. ways of opposites] | וזה יודע בג' דרכי' כוללים בעבור שבהם יעשו כאלה היחסים וזולתם אי זה שיהיו[175] ויקראו דרכי המתנגדות[176] |
| The first way | והראשון הוא זה |
|---|---|
|
נניח שרצינו למצא אי זה כל שקבוץ שלישיתו וחמישיתו יחד הם עשרה |
|
וקודם כל דבר נבקש אי זה מספר שימצאו בו אלו השברי' והוא ט"ו וקבוץ שלישיתו וחמישיתו יחד הוא ח' ואלו הם פחות מהמבוקש שנים |
|
ונקח מספר אחר שהוא ל' ונראה שקבוץ שלישיתו וחמישיתו הוא י"ו וא"כ יהיו יותר מהמבוקש ו' |
|
ועתה נניח כל זה בדרך צורה |
|
והראשון שצריך שנקבץ יחד הם יותר והפחות שהם ב' וו' וזה יהיה המחלק ונשמור אותו |
|
ואחר נעשה המחולק כך שנכה המתנגדים כל אחד עם מנגדו כמו ט"ו עם ו' ויעלה צ' ונכה עוד ל' עם ב' ויעלה ס' ונחבר צ' עם ס' ויהיו ק"נ |
|
ונחלקם במחלק שהוא ח' ויצא מהחלוקה י"ח וג' רביעיות וזהו המספר שקבוץ שלישיתו וחמישיתו יחד י' וזה מה שרצינו בדרך הראשון |
| The second way | הדרך השני |
| In this way, the two numbers, in which we need to find the required fractions, should each be smaller than the sum of the required parts. | והוא שהב' מספרי' שאנו צריכים בדרך זה למצא בהם השברי' המבוקשים צריך שיהיה כל אחד פחות מקבוץ החלקים המבוקשים |
|
המשל רצינו למצא מספר שקבוץ שלישיתו ורביעיתו יהיה כ' |
|
נבקש מספר אחד שימצא בו שליש ורביע והוא י"ב וקבוץ שלישיתו ורביעתו ז' א"כ הוא [177]פחות מקבוץ השברי' י"ג |
|
ונקח עוד מספר אחר שימצא בו שליש ורביע והוא כ"ד וקבוץ שלישיתו ורביעיתו הם י"ד וא"כ הוא פחות מהמבוקש ו' |
|
ואח"כ נאמר י"ב פחות י"ג וכ"ד פחות ו' |
|
וכמו שלמעלה עשינו מחלק מהיותר והפחות בכאן צריך שנעשה מחלק מהפחות ומהפחות והם י"ג וו' |
|
וכמו שלמעלה קבצנו היותר והפחות לעשות המחלק בכאן צריך שנחסר לעשות המחלק |
|
וא"כ נחסר ו' מי"ג וישארו ז' וזהו המחלק ונשמור אותו |
|
ואחר נכה המתנגדים כאמור למעלה והם י"ג עם כ"ד ויעלו שי"ב ונכה עוד ו' עם י"ב ויעלו ע"ב ונחסר ע"ב |
|
ונחלקהו במחלק שהוא ז' ויצא מהחלוקה ל"ד וב' שביעיות [וזה צורתו][178] |
| The third way | הדרך השלישי |
| Each of the two numbers, in which we find the fractions, should be greater [than the sum of the parts]. | והוא שכל אחד משני המספרי' שבהם נבקש השברי' צריך שיהיה יותר |
|
המשל רצינו למצא מספר אחד שרביעיתו ושלישיתו יהיה ו' |
|
נבקש מספר אחד שימצא בו שליש ורביע והוא י"ב וקבוץ שלישיתו ורביעיתו הוא אחד יותר מהמבוקש |
|
ונבקש ג"כ מספר שהוא כ"ד והוא ח' יותר מהמבוקש |
|
ונחסר היותר גדול מהקטן והגדול הוא ח' והקטן הוא אחד ונחסר אחד מח' וישארו ז' וזהו המחלק |
|
ויעשה המחולק כך נכה המתנגדים באופן זה הח' על י"ב ויעלו צ"ו ונכה האחד על כ"ד ויעלו כ"ד ונחסר כ"ד מצ"ו וישארו ע"ב |
|
ונחלקם במחלק שהוא ז' ויצא מהחלוקה ו' וב' שביעיות וזהו המספר [179]ששלישיתו ורביעיתו מקובץ כאחת ששוה ששה |
| Another teaching of proportions | לימוד אחר מיחסים |
|
אם ישאל שואל אם כששוה מדת הקמח י"ב לבני' גזר המלך שיתנו ח' ליטרי' לחם בלבן כששוה כששוה המדה י"א לבני' כמה ראוי שיתנו לפי אותו היחס |
|
נעשה כך שנניח דרושינו זה על שורש התיחסות הג' מספרי' וזה בשנסדר המספר הראשון על השיווי האחרון ר"ל לשיווי הי"א לבני' והמספר השני נסדר על השווי הראשון ר"ל שווי הי"ב והמספר השלישי כמות הלחם |
|
ונאמ' כך אם י"א שוים י"ב כמה שוים ח' |
|
ונשלים הלמוד כמו שהוא כתוב בדרכי היחסים וזה מה שרצינו |
|
שאילה אם כשהפרח שוה מ' לבני' ואדם אחד יש לו ק' פרחי' ורוצה להחליף כל כך פרחי' שהנשארי' יהיו שוים ללבני' ר"ל כמות הפרחי' הנשארי' לו ככמות הלבני' הנשארי' לו |
|
נעשה כן נקח שווי הפרח שהוא מ' לבני' ונוסיף א' ויהיו מ"א ונחלק ק' במ"א ויבואו ב' וי"ח ממ"א של פרח כל כך פרחי' צריך להחליף[180] |
Chapter Six: the Teaching of Partnership |
הפרק השישי בלמוד החברות |
| When we want to know how much is the share of each of the partners in the profit or the loss, in relation to the time and the amount of goods. | והוא כשנרצה לדעת כל אחד מהחבורה כמה יגיע לו מחלק הריוח או ההפסד מיוחס לזמן ולכמות הסחורה |
| Partnership Problem - For the Same Time | |
|---|---|
|
המשל אם יהיו בחבורה ג' אנשים והאחד הכניס לחברה י"ב וחצי והשני ו' והשלישי ז' וחצי ויהיה הריוח נ' |
|
ולדעת זה נקבץ כל המספרי' ויהיה הקבוץ כ"ו וזה הקבוץ יקרא מספר ראשון |
|
והריוח או ההפסד יהיה מספר שני |
|
וכל אחד מהג' מספר [181]שלישי |
|
ונאמ' כך אם כ"ו שוים נ' כמה שוים י"ב וחצי |
|
ונשלים היחס כמו שידעת ומה שיצא הוא [ריוח או הפסד] הראשון שהכניס הי"ב |
|
ואחר נאמ' אם כ"ו שוים נ' כמה שוים ו' |
|
ונשלים היחס ג"כ ומה שיצא הוא הריוח או ההפסד השני שהכניס בחלקו הו' |
|
ואחר נאמ' אם כ"ו שוים נ' כמה שוים ז' וחצי |
|
ונשלים היחס כמו שלמעלה ומה שיצא הוא ריוח [או הפסד][182] השלישי |
| You do the same with all the ratios that could be done in all partnerships. Q.E.D. | ומכדומה לזה תעשה בכל היחסים שאיפשר להעשות בכל החברות [וזה מה שרצינו] |
Chapter Seven: Some Questions and Answers |
הפרק השביעי בקצת שאילו' ותשובות |
| Find a Number Problem - Repeated Subtraction | |
|---|---|
|
שאילה אם מכפלו של אי זה מספר נקח י"ב ומכפל הנשאר נקח ג"כ י"ב אחרי' וכפל הנשאר יהיה י"ב כמה היה המספר הראשון |
|
התשובה נקח המספר הידוע שהוא י"ב ונחבר אליו חציו ויהיו י"ח ומכל זה נקח החצי ויהיה ט' ואלו הט' נחבר עוד י"ב ויהיו כ"א ונקח חצים והם עשרה וחצי וזהו המספר שבקשנו בתחלה |
| Likewise, we can say this for any number, whether integers, or fractions, either few or many. | ובדרך זה נוכל לאמ' בכל מספר שיהיה בין של שלימים בין של שברי' בין מעט או רב |
|
שאילה אם מאי זה כמות ילקח חציו ואחד יותר ומהנשאר חציו ויותר אחד ומהנשאר חציו ויותר אחד ונשאר אחד כמה היה המספר הראשון |
|
התשובה נקח האחד שנשאר באחרונה ויותר אחד ויהיו ב' ונכפול אותם ויהיו ד' ונוסיף יותר אחד ויהיו ה' ונכפול אותם ויהיו עשרה ונוסיף עליהם [183]עוד אחד ויהיו י"א ונכפלם ויהיו כ"ב וזהו המספר הראשון שנשאל עליו |
| Likewise, you can do even if you add each time two, or three, or as much as you wish, instead of the one. | ובדרך זה תוכל לעשות ואף על פי שתוסיף בכל פעם במקום האחד שנים או ג' או מה שתרצה | ||||||||||
| Shared Work Problem - Draining a Vessel - Barrel | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Question: a barrel has three holes. Through one hole it is drained in a half of a day. Through the second hole, it [is drained] in a two thirds of a day. Through the third hole, it [is drained] in a three quarters of a day. When it is drained through the three holes together, how long will it take [the barrel] to be drained?
|
שאילה אם יהיה חבית אחת ויהיו לה ג' נקבים באחד יורק בחצי יום ובנקב השני בב' שלישי יום ובנקב שלישי בג' רביעי יום כשיורק בג' הנקבי' יחד בכמה זמן יורק | ||||||||||
|
התשובה נאמ' כך | ||||||||||
|
באותו נקב שיורק בחצי יום יורקו ב' [חביו'][184] ביום אחד | ||||||||||
|
ובנקב שיורק בב' שלישי יום יורקו ביום אחד א' וחצי | ||||||||||
|
ובנקב שיורק בג' רביעיות יורקו ביום אחד חבית אחת ושליש | ||||||||||
|
ועתה נחבר כל אלה הג' מספרי' ויהיה קבוצם ד' חביות וה' ששיות | ||||||||||
|
ואחר נאמ' כך אם ד' חביות וה' ששיות של חבית שוות יום אחד כמה שוה חבית אחד | ||||||||||
|
ונשלים הדרך וימצא ששוה ו' חלקי' מכ"ט מיום אחד | ||||||||||
|
שאילה אם יהיו ג' מספרי' והראשון והשני יהיו בכמות השלישי והראשון והשלישי כמאה מן השני כמה יהיה כל אחד מהשלשה מספרי' | ||||||||||
|
|
|||||||||||
|
התשובה נניח שאלו הג' מספרי' הם חלקי דבר אחד | ||||||||||
|
ונניח עוד שהמספר הראשון והשני הם חצי אותו הדבר והשלישי הוא חציו האחר | ||||||||||
|
ונאמ' אם הראשון והשלישי הם מאה כשני יראה שהשני הוא אחד ממאה ואחד מחלקי הכל | ||||||||||
|
ואם הראשון עם השני הם חצי הכל א"כ נאמ' שההבדל שיש בין חלק אחד ממאה ואחד מחלקי הכל ובין חצי [185]הכל הוא שיווי המספר הראשון | ||||||||||
|
אבל ההבדל הוא צ"ט חלקים ממאתים ושנים מהכל | ||||||||||
|
א"כ נאמ' שהמספר הראשון הוא צ"ט חלקי' מר"ב מהכל | ||||||||||
|
ואם הכל הוא ר"ב יהיה המספר השני ב' שהוא חלק אחד ממאה ואחד מהכל הנזכר שהוא ר"ב | ||||||||||
|
ובעבור שהמספר השלישי הוא חצי הכל והכל הוא ר"ב א"כ יהיה המספר השלישי מאה ואחד שהוא חצי הכל וזה מה שרצינו | ||||||||||
|
ועתה יש לנו ג' מספרי' הראשון צ"ט והשני ב' והשלישי ק"א | ||||||||||
|
ואם נחבר המספר הראשון עם השני יעלה מאה ואחד שהוא שוה לשלישי | ||||||||||
|
ואם נחבר הראשון והשלישי יעלה ר' שהם מאה כמספר השני | ||||||||||
| We can apply this way with all the proportional numbers of this ratio, whether they are more or less. Q.E.D. | ובדרך הזה נוכל לעשות מכל המספרי' המתיחסים בזה היחס ואם היו יותר או פחות ומ"ש | ||||||||||
|
שאילה אם יהיו ג' אנשים בחברה אחת וחצי הריוח יהיה ראוי לאחד ושלישית הריוח לשני ורביעית הריוח לשלישי והריוח יהיה י"ב כמה יבא לכל אחד מהם | ||||||||||
|
|
|||||||||||
|
התשובה צריך שתדע אם נתן לאחד החצי מזה המספר ר"ל הי"ב ושלישיתו לאחר ורביעיתו לאחר לא יספיקו | ||||||||||
|
ולכן צריך שנעשה בדרך זה שלמי שראוי החצי יקח פחות וכן השני וכן השלישי | ||||||||||
|
ויהיה בדרך זה שנקח אי זה מספר שנרצה שימצאו בו חצי ורביע ושליש כמו י"ב או כ"ד או ל"ו או אי זה שיהיה | ||||||||||
|
ונקח חציו ושלישיתו ורביעיתו ונקבצם יחד וזה הקבוץ יקרא מספר ראשון | ||||||||||
|
והריוח יהיה מספר שני | ||||||||||
|
וכל אחד [186]מחלקי המספר המקובץ יהיה מספר שלישי | ||||||||||
|
וכשיהיו בידינו אלו המספרי' נסדרם בדרך זה ונאמ' אם י"ב שוים י"ג כמה שוים ו' | ||||||||||
|
ונשלים היחס ונמצא ששוה [ה' וז' מי"ג][187] | ||||||||||
|
ואחר נחזור ונאמ' אם כל המקובץ שוה כל הריוח כמה שוה השליש | ||||||||||
|
ובמשלינו זה נאמ' אם י"ג שוים י"ב כמה שוים ד' | ||||||||||
|
ונמצא ששוים [ג' וט' מי"ג][188] | ||||||||||
|
ונחזור עוד ונאמ' אם כל המקובץ שוה כל [הריוח כמה שוה][189] הרובע | ||||||||||
|
ר"ל אם י"ג שוים י"ב כמה שוים ג' וכו' | ||||||||||
|
ונמצא ששוים | ||||||||||
|
| ||||||||||
|
וזה מה שרצינו | ||||||||||
|
שאילה אם יחלקו העשרה בב' חלקי' שהאחד נחלק באחר שיצאו מהחלוקה ה' | ||||||||||
|
|
|||||||||||
| To know this, we should precede two general premises: | ולדעת זה צריך שנקדים שני הקדמות כוללות | ||||||||||
| The first premise: as every dividend divided by the divisor generates the quotient, so when the dividend is divided by the quotient it generates the divisor. | ההקדמה הראשונה היא שכמו שכל מחולק נחלק במחלק יוליד החלק גם כן כשנחלק המחולק על החלק יוליד המחלק | ||||||||||
| The second premise: the quotient and the number [that represents] the ratio of the dividend to the divisor are equal. | ההקדמה השנית היא שמספר החלק ומספר יחס המחולק למחלק שוים | ||||||||||
|
המשל אם נחלק י' על ב' יהיה החלק ה' ומספר יחס המחולק למחלק ה' כי י' הם ה' פעמים שנים וזהו יחס מחולק למחלק וא"כ המחולק ביחס הוא ה' והחלק ה' בלתי היחס וא"כ במה שיש לכל אחד שם של ה' הם שוים וזה מ"ש | ||||||||||
|
ואחר ידיעת זה התשובה היא שנקח במחשבתינו חלק אחד מי' בלתי ידוע ויהיה שמו דבר אחד | ||||||||||
|
ונאמ' כך אם נקח מהעשרה דבר אחד ישארו העשרה עשרה בלתי הדבר אחד והי' בלתי הדבר אחד יהיה המחולק | ||||||||||
|
ולפי ההקדמה [190]השנית יהיה שוה לה' שהוא החלק | ||||||||||
|
וא"כ אם י' בלתי הדבר אחד שוה לה' עם הדבר אחד יהיה יותר מה' דבר אחד | ||||||||||
|
ובעבור שיהיו שוים החלק והמחולק נוסיף דבר אחד על הה' שהוא החלק ויהיו ו' | ||||||||||
|
ואחר שהמחולק והחלק הם שוים נחלק המחולק על החלק ויצא המחלק שבקשנו שהוא | ||||||||||
|
| ||||||||||
|
וזהו הדבר האחד הבלתי ידוע שלקחנו מהעשרה | ||||||||||
|
ומה שנשאר עד תשלום י' שהם | ||||||||||
|
| ||||||||||
|
הם המחולק והם ג"כ העשרה בלתי דבר שהוא ג"כ מספר בלתי ידוע כמו שאמרנו | ||||||||||
|
ועתה אם נחלק | ||||||||||
|
| ||||||||||
|
יבא לחלק ה' ואלו השני מספרי' המחולק והמחלק הם עשרה ומ"ש[191] | ||||||||||
| As we said for ten that the quotient is 5, we can say also for any number we want and for whichever number that we want to keep its ratio to that number, as we did here. | וכמו שאמרנו בעשרה להיות החלק ה' נוכל לאמ' ג"כ איזה מספר שנמצא ועל איזה מספר שנרצה בשנשמור היחסים הראויים לאותו מספר כמו שעשינו בזה | ||||||||||
|
המשל כי כמו שלקחנו לחלק ה' מי' נקח לחלק כ"ז משלשים | ||||||||||
|
|
|||||||||||
|
ונעשה כאמור ותמצא באותו דרך שהמחלק הוא | ||||||||||
|
| ||||||||||
|
והמחולק | ||||||||||
|
| ||||||||||
|
והחלק כ"ז כמו שידעת וזה מה שרצינו[192] |
Book Three: We Talk in it about Some Principles of Geometry |
המאמר השלישי נדבר בו בקצת התחלות מההנדסה |
| It is divided into three sections. | ויתחלק לג' כללי' |
Section One: Knowing the Measure of the Line |
הראשון בידיעת השיעור הקויי |
| It is divided into three chapters. | ויתחלק לג' פרקי' |
Chapter One: Some Principles of Geometry, Definition of a Line, and Knowing the Measure of the Line as a Height |
הפרק הראשון בקצת התחלות ההנדסא וגדר הקו ובידיעת השיעור הקויי בגובה |
| After we discussed the six types of arithmetical operations, the methods of proportions, and some questions and answers, we should start talking now about some principles of geometry, in order that we know the way to use the proportions of numbers in it. | ואחר שדברנו [193]מז' מיני המספר ומדרכי היחסים וקצת שאילות ותשובות צריך שנדבר עתה מקצת התחלות ההנדסא כדי שנדע הדרך איך נשתמש ביחסי המספרי' הצריכים בה |
| You should know that the first geometrical shapes, by which we can know the measure of any solid, or each of its dimensions, or the relation of a solid to a solid, or a surface to a surface, or a line to a line, are three entities that are: | ולכן ראוי שתדע שתמונות ההנדסא הראשונות שבהם נוכל לדעת כמות אי זה גשם שיהיה או כל אחד ממרחקיו או התיחסות גשם לגשם או שטח לשטח או קו לקו הם ג' עצמיות שהם |
|
משולש |
|
ומרובע |
|
ועגולה |
| Since the solid includes three properties that are: | ובעבור שהגשם כולל בג' סגולות שהם |
|
אורך |
|
ורוחב |
|
ועומק |
| We shall talk about the definition of each and its measure: | לכן נדבר בגדר כל אחד ובשיעורו |
| First, we talk about length. | וראשונה נדבר מהאורך |
| Since the length is measured by lines, we determine what is a line: | ובעבור שהאורך ישוער בקוים נאמ' מהו הקו |
| Definition of line: the line is a quantity of length without breadth and depth, whose ends are two points. | והקו הוא כמות אורך בלתי רוחב ועומק וקצותיו הם ב' נקודות |
| The types of the linear measure are three, which are: | ובעבור שמיני השיעור הקויי הם ג' שהם |
|
מישור |
|
וגובה |
|
ועומק |
| We should discuss each of them. | צריך שנדבר מכל אחד מהם |
| First, the height: | וראשונה מהגובה |
| When you want to know the height, whichever it may be, take a pole whose size you know and place it on the surface, standing straight with no inclination | כשתרצה לדעת אי זה גובה שיהיה תקח עמוד אחד שתדע שיעורו ויושם במישור מעומד וביושר בלתי שום נטייה |
| Turn your eyes to the ground while looking at the edge of the height you want in a way that the ray of sight passes through the edge of pole's height in a straight line from your eye to the edge of the height you want. | ותטה עינך בארץ בהיותך מביט לקצה הגובה שתרצה באופן שיעבור ניצוץ הראות על קצה העמוד הגובה בקו ישר מעינך עד קצה הגובה שתרצה |
| Then, estimate [the distance] from the place of inclination of the eye to the bottom of the height you want and this is the third number. | ואחר תשער ממקום נטיית העין עד המקום התחתון מהגובה שאתה מבקש וזה יהיה המספר השלישי |
| The size of the pole is the second number. | ושיעור העמוד יהיה המספר השני |
| The distance between the eye and the pole is the first number. | והרוחק שיש בין העין והעמוד יהיה המספר הראשון |
| Extract the proportion the way you know: if this is equal to that, how much is this equal to? | ואחר תיחס בדרך שידעת אם זה שוה זה כמה שוה [זה][194] |
| Multiply the second by the third, then divide it by the first number; we get the height we want. Q.E.D.
|
בהכותך [195]השני בשלישי ונחלקהו במספר הראשון ויצא לנו הגובה שבקשנו וזה מה שרצינו |
Chapter Two: Knowing the Measure of the Line in the Surface [= Length] |
הפרק השני בידיעת השיעור הקויי במישור |
| When we want to know the length of a surface, a straight pole, whose size we know, is placed on the ground where we want, standing straight with no inclination. | כשנרצה לדעת אורך אי זה מישור שיהיה יושם על הארץ מעומד עמוד אחד ישר שנדע שיעורו ובמקום שנרצה ובלתי שום נטיה |
|
ודרך משל יקרא המישור ב"ה ועמוד הישר א"ב ובעמוד א"ב נשים יתד אחד שיקרא ג"ד על זויות שוות באופן שכשיביט האדם מראש העמוד לקצה המישור יעבור ניצוץ הראות על ראש היתד ביושר עד קצה[196] המישור המבוקש |
|
ואחר תכה כמות ג"ד על א"ב וזה יחלק על א"ג ויצא לנו כמות ב"ה שהוא אורך המישור שבקשנו וזה מה שרצינו |
Chapter Three: Knowing the Measure of the Line as a Depth |
הפרק השלישי בידיעת השיעור הקויי בעומק |
| When we want to know a certain depth: | כשנרצה לדעת אי זה עומק שיהיה |
|
ונניח שיהיה עומק א"ד ונשים עמוד אחד על שפת העומק ויהיה ה"ז ונשים יתד אחד בעמוד בזויות נצבות על שפת העומק ויהיה ז"ב ויעבור עד א' ונקדת המבט יהיה ה' שעל ראש העמוד ויעבור ניצוץ המביט מנקודת ה' ועל קצה היתד לזויות העומק שהוא ד' באלכסון |
|
והנה בעבור שזוית[197] הז"ב הוא שוה לזוית[198] בא"ד הנצבת |
|
וג"כ זוית אב"ד שוה לזוית זב"ה הנגדיים |
|
והזוית הנשארת שמקיף אותו בה"ז שוה לזוית שמקיף [199]אותו אד"ב |
|
א"כ כל זויות משולש אד"ב שוות לכל זויות משולש בה"ז ולכן צלעותיהם מתיחסות |
|
ויהיה יחס ב"ז לז"ה כיחס ב"א לא"ד |
|
ועתה נכה שעור ה"ז על שעור ב"א ונחלקהו על ז"ב ויצא לנו שיעור א"ד וזה מ"ש |
Section Two of Book Three: Knowing the Measure of the Surface |
הכלל השני מהמאמ' הג' בידיעת [השיעור השטחיי |
| It is divided into five chapters. | ויתחלק לה' פרקי' |
Chapter One: Knowing the Area of the Equilateral Triangle |
הא' בידיעת שיעור][200] שטח המשולש השוה הזויות הצלעות |
| After we discussed the size of the line and all its measures, we should now talk about the size of the surface and its measures. | ואחר שדברנו מהכמות הקויי וכל שיעוריו עתה צריך שנדבר מהכמות השטחיי ושיעוריו |
| First, we state its definition: | וראשונה נדבר מגדרו |
| Definition of surface: the surface is a quantity that has length and breadth without depth, whose limits are two lines. | השטח הוא כמות בעל אורך ורוחב בלתי עומק שתכליותיו ב' קוים |
| The primary plane shapes are of three types: either equilateral [lit. having three equal sides], or isosceles [lit. having only two equal sides], or scalene [lit. having three unequal sides]. | והתמונות השטחיות הראשונות הם ג' מינים או יהיה שוה הג' צלעות או שוה השתי צלעות בלבד או מתחלפות ג' הצלעות |
|
ואם תהיה שוות הג' צלעות צורתה זאת |
|
ואם נרצה לדעת כמותה נחלק הצלע האחד בב' חלקי' שוים ומנקודת החלוקה ששם ד' נוציא קו ישר עד הזוית הנגדיי שהוא א' |
|
וזה הקו נדע כמותו באי זה מדה שנרצה ונשמור אותו |
|
וצריך שנדע עוד כמות אחד מהצלעות |
|
ונכה חצי זה הכמות בכמות הקו השמור אצלנו ומה שיעלה הוא כמות כל שטח המשולש וזה מה שרצינו |
Chapter Two: Knowing the Area of the Isosceles Triangle |
הפרק השני בידיעת שיעור שטח המשולש שוה הצלעות |
|
ואם יהיה המשולש שוה שתי הצלעות בלבד צורתו היא זאת |
|
ולדעת כמותה נחלק הצלע הבלתי שוה בשני חלקי' שוים ומנקודת החלוק ששם [201]ד' נוציא קו אחד ישר עד הזוית הנגדיי שהוא א' |
|
ונדע כמות חצי הצלע שחלקנו וכמות הקו הישר שעשינו |
|
ונכה האחד על האחר ומה שיעלה הוא כמות כל שטח המשולש וזה מ"ש |
Chapter Three: Knowing the Area of the Scalene Triangle |
הפרק הג' בידיעת שיעור שטח המשולש מתחלף הצלעות |
|
ואם יהיה המשולש מהג' צלעות מתחלפות צורתו זה |
|
ולדעת כמותו נוציא קו ישר בלתי שום נטייה מהזויות הרחב ששם א' לצלע הנגדיי |
|
ונדע [כמותו][202] ר"ל כמות הצלע הנגדיי ונשמור אותו |
|
ונדע עוד כמות הקו הישר שעשינו |
|
ונכה אותו בכמות הצלע השמור אצלינו וחצי מה שיעלה הכל הוא כמות כל שטח המשולש ומ"ש |
Chapter Four: Knowing the Area of the Quadrilateral and the Area of the Square |
הפרק הרביעי בידיעת שיעור שטח המרובע ושטח הרבוע |
| The types of the quadrilaterals, from which we know the area of any quadrilateral are two: | ומיני המרובע שבהם נדע כמות כל המרובעים שיהיו והם ב' |
|
המין האחד שיהיה שוה האורך והרוחב |
|
והמין השני שהאורך והרוחב בלתי שוים |
|
ולדעת כמות המרובע השוה האורך והרוחב שצורתו זאת |
|
הוא בדרך זה שצריך שנדע כמות הצלע האחד ונכה אותו בעצמו ומה שיעלה הוא כמות כל שטח המרובע וזה מה שרצינו |
|
ואם נרצה לדעת כמות שטח המרובע שאורכו ורוחבו בלתי שוים שזאת היא צורתו |
|
צריך שנדע כמות הצלע הגדול וכמות הצלע הקטן ונכה האחד באחר ומה שיעלה [203]הוא כמות השטח כולו וזה מ"ש |
| Know that there is one rule for all types of quadrilaterals. | שתדע כלל אחד לכל מיני המרובעי' |
Chapter Five: Knowing the Measure of the Circle according to the Opinion of the Sages |
הפרק [החמישי][204] בידיעת שיעור [העגול לפי סברת החכמים |
|
ולדעת כמות][205] שטח העגלה בקרוב שזאת צורתה |
|
צריך שנדע כמות חצי האלכסון ונכהו בחצי הקף העגולה ומה שיעלה הוא כמות השטח |
|
ולדעת כמות העגולה |
|
נשלש האלכסון ונוסיף עוד החלק השביעי ממנו כך הוא כמות כל העגולה |
|
ובעבור שאין יחס בין הקו הישר והבלתי ישר |
|
ובאלו העגולות שאנו עושים נוכל להתקרב לידיעת אמיתתם |
|
ואם יקרה טעות אינו נחשב למיעוטו אבל העגלות הגדולות כ"ש השממיות שיהיה הטעות גדול מאד |
|
ולכן אמ' ארגמידש ואלפרבי שמי שיתן לעגולה כמות שלוש האלכסון ומע' חלקי' ממנו העשרה שהוא נותן יותר מן הראוי ומי שיתן שלוש האלכסון ומע"א חלקי' ממנו העשרה שנותן פחות מן הראוי א"כ הכמות האמיתי הוא בין ע' חלקי' וע"א מהאלכסון |
| This is what we wanted concerning the plane shapes. | וזה מה שרצינו בתמונות השטחיות |
| Having discussed the measure of the surface, we shall talk now about the [measure of] the solid. | ואחר שדברנו מכמות השטחי נדבר עתה מהגשמי |
| First, we should define what is a solid: | ולכן ראוי שנאמ' קודם מה הוא הגשם |
| Definition of solid: The solid is a quantity that has three dimensions, which are length, breadth and depth, whose limits are surfaces. | הגשם הוא כמות שיש לו ג' מרחקי' שהם אורך ורוחב ועומק שתכליותיו הם ב' שטחי' |
Section Three of Book Three: [Solid] |
הכלל הג' מהמאמ' הג' |
Chapter One: Volume |
|
| In it one chapter on knowing the volume of any solid. | ובו פרק א' והוא בידיעת שיעור אי זה גשם שיהיה |
| The first bodily figures are three and they are: | והתמונות |
|
משולש [מחודד] |
|
[207]מרובע [ומוגשם] |
|
ועגולה [כדור] |
| If we wish to know their volume, as if we wish to know the volume of a square, or non-square, or triangular container, how much it contains, we should know first the area of the base in the way we mentioned, then multiply it by its depth, and the result is it volume. | ואם נרצה לדעת כמותם כמו שאם רצינו לדעת כמות כלי אחד מרובע [מעוקב] או בלתי מרובע [מעקב] או משולש [מחודד] כמה יכיל צריך שנדע קודם שטח התושבת בדרך שאמרנו ואחר נכהו בעומקו ומה שיעלה הוא הגשמיות [כמותו הגשמי] |
|
המשל נניח שיש בכאן כלי אחד שהתושבת שלו הוא ג' אמות ועומקו ב' |
|
נכה הב' בג' ומה שיעלה הוא כמותו |
| If the area of the bottom base of the container is greater than the area of its upper base, or vice versa, we know the area of each of them, sum them up, take a half [of the sum] and this is the area that should by multiply by the depth. We multiply them and the result is the volume of any solid container. | ואם שטח תושבת הכלי יותר גדול משטח פיו או בהפך נדע שטח כל אחד מהם ונחברם ונקח החצי וזה יהיה כמות השטח הראוי להכות עם העומק ונכם ומה שיעלה הוא כמות כל גשם הכלי |
| Since there are no other figures that we can know their volume in the way we stated, but these, therefore, if we wish to know the volume of any other figure, we should convert it to one of these triangular or square figures, of whichever type they may be, by cubing the figure we want, or squaring it, Q.E.D. | ובעבור שאין שם תמונות אחרות שנוכל לדעת שיעורם בדרך שאמרנו אלא אלו לכן אם נרצה לדעת שיעור אי זה תמונה אחרת צריך שנהפכנה באחת מאלו התמונות המשולשות או המרובעות מאיזה מין שיהיה מהם וזה בשנשלש התמונה שנרצה או נרבע אותה וזה מה שרצינו |
| Whoever is well versed in these principles can easily study all the books of Euclid and any science that obtains its principles from arithmetic. | וכל מי שיהיה בקי באלה ההתחלות יוכל לעיין בקלות בכל ספרי אוקלידס וכן בכל חכמה שתקנה התחלותיה ממלאכת המספר |
| We have already discussed at length everything that is necessary for our purpose. | וכבר הארכנו בכל מה שצריך לכוונתינו |
Supplement (Oxford MS d.5) – operations with fractions |
|
| Another method shorter than what we wrote in our book on multiplication, division and proportions [of fractions]: | דרך אחרת קצרה יותר ממה שכתבנו בחבורנו בענין ההכאות והחלוק והיחסים |
| First of all, one should know the number of the numerator and the number of the denominator and this is done as follows: | קודם כל דבר צריך לדעת מספר הפועל ומספר הפעול והם נעשים בדרך זה |
|
וראשונה המספר הפעול הוא בכל מה שיכתב תחת הקו |
|
והמספר הפועל הוא בשלש דרכים [שלם לבד] שבר לבדו או שניהם כאחד |
|
ואם יהיה שלם לבד יקרא מספר פועל |
|
ואם יהיה שבר לבד המספר שעל הקו שלו יקרא מספר פועל |
|
המשל אם יהיו בידינו ב' שהם שנים שלמים ושלשה רביעיות |
|
נכה הב' שלמים על ד' ויהיו ח' עוד נוסיף עליהם ג' שעל הקו כאמור ויהיו י"א וזהו המספר הפועל שלהם |
| When we know the numbers of the numerator and the denominator the way we stated and we want to multiply, we multiply the numerator of the first number by the numerator of the second number, then divide this product by the product of the first denominator by the second denominator. | א"כ כשנדע המספר הפועל והפעול בדרך שאמרנו ונרצה לעשות שום הכאה נכה פועל המספר האחד עם פועל המספר השני וזאת ההכאה נחלק בהכאת פעול האחד עם הפעול השני |
| Or if there is one denominator in both numbers, even if there is only one denominator. it is the denominator. | או יהיה פעול לשני המספרים ואם לא יהיה שם אלא פעול אחד הוא יהיה המחלק |
|
המשל נרצה להכות |
|
נעשה המחלק שהוא הכאת הפעולים שהם ה' וג' שעולה ט"ו וזהו המחלק |
|
ואחר נעשה המחולק מהכאת הפועלים שהוא י"ט עם כ' שעולה ש"ף |
|
וזה נחלק בט"ו שהוא המחלק |
| The method of division is that we multiply the numerator of the number that we want it to be the divisor by the denominator of the other, and this is the divisor. | ודרך החלוק הוא זה שהמספר שרצינו שיהיה המחלק הוא שנכה הפועל שלו עם פעול של האחר וזהו המחלק |
| We multiply the numerator of the one that we want it to be the dividend by the denominator of the other and this is the dividend. | ואותו שנרצה שיהיה המחולק נכה הפועל שלו בפעול של האחר וזהו המחולק |
| Then, we divide the one by the other. | ואח"כ נחלק האחד באחר |
|
המשל נרצה לחלק |
|
נעשה הפועלים יותר והראשון הוא ט' והשני י' ונחלק ט' בי' ויהיו ט' עשיריות |
| In the rule of three, the three proportional numbers are given, which are the first, second, and third. | ומדרך היחסים מונחים הג' מספרי היחס שהם ראשון ושני ושלישי |
| We multiply the numerator of the first [number] by the denominator of the second [number] and we multiply the result by the denominator of the third [number], if they have denominators, and if not by whichever denominator found. This product is called the divisor. We keep it. | נבקש הפועל ראשון בפעול שני וכל מה שיעלה נכה בפעול השלישי אם יהיה לו פעול ואם לא באי זה פעול שימצא וזאת ההכאה תקרא המחלק ונשמור אותה |
| Then, we multiply the numerator of the second [number] by the numerator of the third [number] and we multiply this product by the denominator of the first number, if it has a denominator and if the product of the numerators is not enough. This product is called the dividend. | א"כ נכה פועל השני עם פועל השלישי והעולה נכה בפעול המספר הראשון אם לא יהיה לו פעול ואם לא יספיק הכאת הפועלים וזאת ההכאה תקרא המחולק |
| We divide the dividend by the divisor and the result is the wanted ratio. | ואחר נחלק המחולק במחלק ויצא היחס המבוקש |
|
המשל אם כ' שוים ט"ו וה' חלקים מל"ז כמה שוים ה' וב' שביעיות |
|
וזו היא צורתו |
|
ולפי הנאמר פועל הראשון הוא כ' |
|
ופועל המספר הב' תק"ס |
|
ופועל המספר השלישי ל"ז |
|
א"כ נכה הכ' שהם הפועל של המספר הראשון על פעול המספר השני שהם ל"ז ויעלו תש"מ ואלו נכה בפעול המספר השלישי שהם ז' ויעלו ה' אלפים ק"ף וזהו המחלק ונשמור אותם |
|
ואחר כך נכה תק"ס שהוא פועל המספר השני עם ל"ז שהוא פועל המספר השלישי |
|
וזאת ההכאה נחלק במחלק ששמרנו ומה שיצא הוא היחס המבוקש |
| Over and done. | נשלם |
| Praise be to God, may the Lord ascend. | תהלה לאל יתעלה השם |
| This book is complete | ונשלם הספר הזה |
| Colophon | |
|---|---|
| The book of number by ‘Eli in my handwriting, Elijah the son of the honorable rabbi Eliezer may his Rock and Redeemer keep him safe. | ספר המספר לעלי לידי לי אליאו גבה בכ"ר אליעזר יצ"ו |
| In the year help in troubles is present [Psalms 46:2], 25 in Tevet. | בשנת עזרה בצרות נמצא ליצירה בחדש טבת כ"ה בו |
Notes
Apparatus
- ↑ 7v; Opening rhyme: מקור מספר הלא הוא לתכונה - כמפתח במסגרת סגורה - הלא גם למהנדס הוא כצנה - הנחה הוא למושיקא ועזרה - ראות כל איש אשר הוא איש תבונה - נעימותו ותועלתו יקרה - באון שכלו הלא כל איש ידבר - וזה ירחיב וזה ידרוך קצרה - אשר יסד ר' יצחק וחבר - מאד קצר וכולל כל חקירה
- ↑ 7v
- ↑ 8r
- ↑ P1095 בשרשים
- ↑ P1095 הג'
- ↑ 8v
- ↑ P1095 om.
- ↑ P1095 om.
- ↑ 9r
- ↑ P1095 om.
- ↑ marg.: או אלו ט ח ז ו ה ד ג ב א
- ↑ 9v
- ↑ P1095 om.
- ↑ 10r
- ↑ P1095 om.
- ↑ P1095 om.
- ↑ P1095 om.
- ↑ P1095 מהמקובץ
- ↑ P1095 om.
- ↑ 10v
- ↑ P1095 om.
- ↑ P1095 om.
- ↑ 11r
- ↑ P1095 om.
- ↑ P1095 om.
- ↑ P1095 מחובר
- ↑ P1095 om.
- ↑ 11v
- ↑ marg.
- ↑ marg.
- ↑ P1095 om.
- ↑ 12r
- ↑ the following examples do not appear in P1095
- ↑ P1095 om.
- ↑ P1095: שבאחד
- ↑ P1095: רבוע
- ↑ P1095 לוח ההכאה
- ↑ 12v
- ↑ P1095 om.
- ↑ 13r
- ↑ P1095 om.
- ↑ P1095 om.
- ↑ P1095 om.
- ↑ P1095 מהאחדות
- ↑ P1095 om.
- ↑ 13v
- ↑ marg.
- ↑ P1095 marg.: דרך אחרת נכבדת שנכה [תכלית] המספר המבוקש באחד יותר ומה שיתקבץ חציו הוא מה שרצינו ומשלו רצינו לדעת מא' עד י"ב הכינו י"ב עם י"ג שהוא א' יותר ועלו קנ"ו וחציים ע"ח וקבוץ מא' עד י"ב ע"ח א"ב מפי הכר"מ
- ↑ 14r
- ↑ 14v
- ↑ P1095: 120
- ↑ P1095: 600
- ↑ P1095 om.
- ↑ 15r
- ↑ 15v
- ↑ P1095 om.
- ↑ P1095 24
- ↑ 16r
- ↑ P1095 שבצורה
- ↑ 16v
- ↑ P1095 marg.: נ"א מימנית המחולק
- ↑ P1095 marg.: ימנית
- ↑ P1095 om.
- ↑ P1095: 823
- ↑ 17r
- ↑ P1095 om.
- ↑ P1095 om.
- ↑ 17v
- ↑ 18r
- ↑ marg.
- ↑ marg.
- ↑ 18v
- ↑ P1095 om.
- ↑ P1095 om.
- ↑ marg.
- ↑ 19r
- ↑ P1095 om.
- ↑ 19v
- ↑ 20r
- ↑ marg.
- ↑ 20v
- ↑ P1095 om.
- ↑ P1095 om.
- ↑ P1095 השישי marg. הה'
- ↑ 21r
- ↑ P1095 om.
- ↑ P1095 marg.: והסבה אשר בעבורה היו דרכי הרבוע במין השברי' ה' פנים ודרכי החלוק ח' זה יתבאר ממה שאומר וזה כי כשתרבע איזה מספר קטן על איזה מספר גדול סך מה שיצא מהכאת הקטן בגדול יצא גם מהכאת הגדול בקטן א"כ שניהם דרך אחד יחשב המשל אם תאמ' ה' פעמי' ח'
הםיעלו למ' גם אם תאמ' ח' פעמי' ה' יעלו למ' ג"כ כן בשברים כמו בשלמי' אבל בחלוק לא יצדק זה כי אם תחלוק הה' על ח' יבא לחלק אחד ה' שמיניות אבל אם תחלוק הח' בה' יבא לחלק אחד שלם אחד וג' חמישיות ואחר ידיעת כל זה הנה א"כ הג' פנים שברבוע והם רבוע שלם עם שבר ורבוע שלם ושבר יחד עם שבר ורבוע שלם ושבר יחד עם שלם נעשו ששה פנים בחלוק כשיתהפכו והוא חלוק שבר בשלם וחלוק שבר בשבר ושלם וחלוק שלם בשבר ושלם אברהם כהן - ↑ P1095 המחלק
- ↑ 21v
- ↑ marg.
- ↑ marg.
- ↑ marg.
- ↑ 22r
- ↑ marg.
- ↑ marg.
- ↑ 22v
- ↑ 23r
- ↑ P1095 om.:
- ↑ P1095 ושלם שבר
- ↑ 23v
- ↑ marg.
- ↑ P1095 om.
- ↑ 24r
- ↑ 24v
- ↑ P1095 marg.: סבה אחת כוללת לכל מיני החלוק בדרך קצרה והוא כי המחלק יצא מהכאת פועל בפעול אם יהיה ואם לא יהיה פעול מספיק וכן המחולק יצא מהכאת פועל בפעול אם יהיה ואם לא יהיה פעול מספיק והמחלק יצא מאיזה הכמה שתרצה אם מפועל השמאל על פעול הימין ואם מפועל הימין על פעול השמאלי וזה מספיק במין החלוק ולעולם העניין הולך אחרי הפועל אם יהיה פועל הקטן בהכאתו עם פעול הגדול ורצית שיהיה הקטן המחלק הנה הכאת פועל הקטן עם הפעול הגדול הוא המחלק וההפך בהפך זה הכלל הכל הולך אחר הפועל מפי המחבר הספר
- ↑ 25r
- ↑ marg.
- ↑ P1095 144
- ↑ P1095 12
- ↑ marg.
- ↑ marg.
- ↑ marg.
- ↑ 25v
- ↑ P1095 המכונים
- ↑ 26r
- ↑ 26v
- ↑ 27r
- ↑ marg.
- ↑ 27v
- ↑ marg.
- ↑ P1095: לרביעיות
- ↑ 28r
- ↑ P1095 om.
- ↑ 28v
- ↑ P1095 marg. 1414
- ↑ P1095 marg. 04842
- ↑ P1095 marg. 50400
- ↑ P1095 marg. 24000
- ↑ 29r
- ↑ P1095 מהכאת מעוקבת
- ↑ 29v
- ↑ 30r
- ↑ 30v
- ↑ marg.
- ↑ 31r
- ↑ P1095 om.
- ↑ 31v
- ↑ marg.
- ↑ 32r
- ↑ 32v
- ↑ marg.
- ↑ 33r
- ↑ P1095 om.
- ↑ marg.
- ↑ marg.: ואם רצה השואל לעשות ה' צורות ולשתף עמו זמן או מה שירצה לא הזכיר זה החכם דרך למוצאו בתשובה אחת ובעלי החשבון נתנו דרך למוצאו המשל אם ששה פועלים שוים בג' ימים ח' לבנים כמה שוים הד' בשני ימים ונסדרם ככה 6 3 8 4 2 ותחלה ראוי שנוציא המחלק כדרך זה שנכה הו' בג' ויעלו לי"ח אחר נוציא המחלק ככה נכה [..] הח' בד' ומה שיעלה בב' וכל זה נחלקהו במחלק ומה שיצא בחלק הוא מה שרצינו. אברהם כהן
- ↑ 33v
- ↑ 34r
- ↑ marg.
- ↑ 34v
- ↑ 35r
- ↑ 35v
- ↑ 36r
- ↑ 36v
- ↑ marg.
- ↑ 37r
- ↑ 37v
- ↑ 38r
- ↑ 38v
- ↑ marg.
- ↑ 39r
- ↑ 39v
- ↑ 40r
- ↑ marg.
- ↑ marg.
- ↑ 40v
- ↑ marg.
- ↑ marg.
- ↑ marg.
- ↑ marg.
- ↑ 41r
- ↑ 41v
- ↑ marg.
- ↑ 42r
- ↑ 42v
- ↑ marg.: והדרך הראשון [...] יותר נקלה מהג' דרכים שהזכיר החכם הזה וזה משלו רצינו לדעת איזה כל הוא שקבוץ שלישיתו ורביעיתו הוא י"ב ועתה נכה הג' בד' ויעלו לי"ב ואחר נקבץ השליש והרביע של י"ב ומצאנו שהם ז' ונסדרם בדרכי היחסים בשנקח הז' מספר ראשון והי"ב שהוצאנו מהכאת ג' בד' מספר שני והי"ב שהם שליש ורביע לאותו מספר הבלתי ידוע מספר שלישי ועתה נאמר אם ז' שוים י"ב כמה שוים י"ב ומצאנו ששוים כ' וד' שביעיות וזהו המספר שקבוץ שלישיתו ורביעיתו י"ב וזה מש"ל
- ↑ P1095 ההתנגדות
- ↑ 43r
- ↑ marg.
- ↑ 43v
- ↑ marg.: ואחר שאמרנו שהפרחי' המתחלפי' הם ב' וי"ח ממ"א של פרח א"כ השני פרחים הם פ' לבני' והי"ח ממ"א נכה אותם עם מ' ויעלו תש"ך ונחלקם במ"א ויעלו י"ז וכ"ג ממ"א של לבן וא"כ הרי שחלוף הפרחים שהם ב' וי"ח ממ"א הם לבני' צ"ז וכ"ג ממ"א של לבן וכן הפרחים שנשארו צ"ז וכ"ג ממ"א של פרח
- ↑ 44r
- ↑ marg.
- ↑ 44v
- ↑ marg.
- ↑ 45r
- ↑ 45v
- ↑ P1095 om.
- ↑ P1095 om.
- ↑ marg.
- ↑ 46r
- ↑ marg.: פי' כי אחר שנתבאר לפי הקדמה השנית כי כמספר החלק כך יחס המחולק למחלק וכבר ידענו כי החלק ה' לפי שאילתנו אם כן יחס המחולק למחלק ה' א"כ נחלק הי' בו' חלקים ונקח הה' חלקים למחולק והששית למחלק כדי שיהיה המחולק ה' פעמים כמחלק ואז יהיה שוה לחלק שהוא ה' וכאשר נחלק הי' לו' חלקים יבא לכל חלק א' וב' שלישיות והוא המחלק חלק המותר עד י' במחלק והוא ה' לחלק
- ↑ marg.: סוף דבר לעולם אנו מחשבים המחלק לאחד והחלק איך שהם אם הם ה' נחבר עוד אחד בעבור המחלק ואם החלק שלשים נחבר עו' אחד בעבור המחלק שהם ל' וא' וכן על זה הדרך המשל אם נשאל ממנו שנחלק העשרה למחלק ומחולק ויבא בחלק ל' נקח שלשים ואחד בעבור אחד של מחלק כי המחלק נחשב אחד ונחלק י' על ל"א ויבא י' מל"א וזהו המחלק והמותר עד תשלום העשרה הוא המחולק שהוא ט' וכ"א מל"א ונחלקם במחלק ויבא בחלק שלשים והקש על זה
- ↑ 46v
- ↑ P1095 om.
- ↑ 47r
- ↑ P1095 צקה
- ↑ P1095 שזויות
- ↑ P1095 לזויות
- ↑ 47v
- ↑ marg.
- ↑ 48r
- ↑ marg.
- ↑ 48v
- ↑ P1095 השמיני
- ↑ P1095 om.
- ↑ marg.
- ↑ 49r
Appendix I: Glossary of Terms
| arithmetic | ארישמטיקה |
| science | חכמה |
| astrology | חכמת התכונה, התכונה, בתכונה |
| mathematics | חכמות הלמודיות |
| music | מוסיקא |
| arithmetic | מלאכת המספר |
| geometry | הנדסה |
| geometry | מלאכת ההנדסה |
| decimal system | |
|---|---|
| number | מספר (ה), מספרי ה, מספרים |
| number | מנין, מניין ה |
| number | חשבון, חשבונות |
| numeral | תמונה, תמונות המספר |
| numeral, digit, letter | אות (ה), אותיות, האות ה... מה, אותיותיו |
| numeral | סימן |
| zero | סיפרא, סיפרש, סיפראש |
| unity, unit, units | אחדות |
| units | אחדים, אחדות, המספרים האחדים |
| tens | עשרות |
| hundreds | מאות |
| thousands | אלף, אלפים |
| decimal place | מקום (ה / של), מקומם, במקום (ה) |
| rank | מקום, מקומות, מקומותיו |
| rank | מעלה, מעלות |
| rank | מדרגה, מדרגות, מדרגת ה, מדרגותיו, מדרגותיהם |
| rank | הבדל (ה), הבדלים, הבדלותיו |
| decade, none-units rank | כלל, כללים |
| numerical value | בשם |
| numerical value | כמות במספר |
| positional decimal method | בדרך המספר |
| addition | |
| to add | לחבר, נחבר (אותו עם / אליהם / אליו ה / אלו ה... עם ה / ה / עליהם ה / ... עם / הכל / כל אלו ה), נחברם (עם) |
| summing | חבור (ה... ל), החבור משניהם |
| addition | תוספת (ה) |
| to add | להוסיף (על / ... על), הוספנו ל, הוספנוהו על, הוספת ה, נוסיף (אותם עליהם / ה / ל / לו ה / עליהם / עליהם ה / עליו / עליו ה / עמהם ה / ה... ל / ... ל / ... על ה / ... עליה / עוד ה / עוד... על), נוסיפה ל, נוסיפהו (ב / על / על ה), נוסיפם (ב / ל / על ה), תוסיף (ב / ה) |
| to add | יוסיף עוד ה |
| to sum | נעשה קבוץ מהם |
| addition, sum | קבוץ (ה / ה... ל / ה... וה / אלו / ... ל / מה), קבוצם |
| sum | קבוץ כל ה, קיבוץ... יחד, המקובץ מכל ה, המספר המקובץ |
| to sum up | לקבץ, נקבץ (כל ה), נקבצם יחד, קבצנו ה... וה |
| total sum | קבוץ כלם, המקובץ מכלם, הקבוץ של כלם, קבוץ כל ה |
| added | מחובר ל, נקבץ |
| to be summed | יקובצו, מקובץ באחד |
| result of addition, sum | המקובץ, הקבוץ מ...עד |
| division | |
| division | החלוק, חלוק (ה / ... ב), חלוקת, החלק ה, המחלק, בחלוקה, חלוקו, חלק ה |
| to divide (by) | לחלק (ה / ... ב), חלקנו... ב, נחלק (ב / ה / ה... ב / ה... על / ה... על ה / ... ב / ... על / זה ה... ב), נחלקהו (ב / על ה), נחלקם (ב / ל / על / על ה) |
| נחלקהו במחלק, נחלקם במחלק | |
| נחלקם על המחלק | |
| נחלק המחולק במחלק | |
| נחלק המחולק על החלק | |
| נחלק ה... ב... חלקים | |
| נחלק ... בשני חלקים שוים | |
| to be divided (into) | יחולק ה... ב, יחלק (ב / ה / ל / על / ... ב), נחלק (ב / ל), יתחלק ל, תתחלק ל |
| יחלקו ב... חלקים | |
| יחלקו ... ב... חלקים | |
| divisor | מחלק, חלק |
| dividend, divided | מחולק (ב), מתחלק |
| indivisible | בלתי מתחלק, שלא נחלקו, שלא יחלק |
| quotient, result of division | חלק, החלק, מספר החלק, בשם חלק |
| יבא מהחלוקה, יבאו מהחלוקה, יבאו ...מהחלוקה, יבאו ... מהחלק | |
| יבא לחלק | |
| היוצא לחלק | |
| יצא מהחלוק, יצא מהחלוקה, יצאו מהחלוקה, יצאו ... מהחלוק | |
| יצא מחלוקתו | |
| יצא מהחלק | |
| יצאו לחלק | |
| מה שיצא לחלק | |
| halving | |
| halving | חלוק באמצע, חלוק ה... באמצע |
| to halve | לחלק מ, נחלק אותו, לחלק ... באמצע, נחלק ה... באמצע |
| to halve | נקח החצי, נקח חצי ה, נקח מה... חציו |
| ילקח חציו | |
| מחולק באמצע | |
| doubling | |
| doubling | הכפול, כפול ה, כפל ה |
| doubling operation | בדרך הכפול |
| to double | לכפול (כל אחד מ), יכפול, נכפול (אותם / ה), נכפלם |
| double | נכפל, כפל (ה), כפלו של, הכפלים |
| twice | כפול, כפל |
| first double, 2 | הכפל הראשון |
| to be doubled | יוכפל (ה), נכפל, נכפלים |
| sum of doubles | הנכפל |
| sum of doubles | העולה מכל הנכפל |
| multiplication | |
| multiplication | הכאה (על), הכאת (ה / ה... ב / ה... על ה / ה... עם ה / ... ב / ... על), בהכאתו ב, הכאות |
| to multiply | בהכות (ה... ב / ... עם), בהכותך ה... ב, להכות (ב / ה / עם ה / אלו ה... ב / ... על) |
| הכהו ב, הכינו (אותם ב / ... ב), מכים עמו כל, נכה (אותו ב / אותם ב / אותה על ה / אותו על / אותם על / אותו עם ה / אלו ה... על ה / ב / ה / על ה / עליו ה / עם ה / ה... ב / ה... על / ה... עם / זאת ה... עם / ... ב / ... על / ... עם), נכהו (ב / עם כל ה / ... ב), נכם (ב / על / על ה עם ה), תכה (... ב / ... על) | |
| נכה ה... זה על זה | |
| נכה ה... האחת בחברתה | |
| נכה ה... כל אחד עם שכנגדו | |
| נכה האחד על האחר, נכה האחד באחר | |
| to be multiplied by | יוכה (ב / על ה / ה... ב), מוכה (ב / על) |
| multiplied | המספר המוכה, המוכה, המוכה עם ה, המוכים |
| הכאת ... בעצמו, הכאת ... בעצמם | |
| הכאת ה... בעצמו, הכאת ה... בעצמם | |
| הכאתו בעצמו | |
| to multiply by itself | מכה... בעצמו, נכה אותו בעצמו, נכה ה... בעצמה, נכהו בעצמו |
| יוכה בעצמו | |
| מוכה בעצמו | |
| נכה ה... באופן מעוקב | |
| נכה ה... בעצמה באופן מעוקב, נכה ה... בעצמו באופן מעוקב, נכה ... בעצמם באופן מעוקב | |
| יוכה בעצמו באופן מעוקב | |
| מוכה בעצמו באופן מעוקב, מוכה בעצמו באופן מעקב | |
| product, result of multiplication | העולה מהכאה, העולה מהכאת, העולה מההכאה |
| היוצא מהכאתם | |
| product | הכאה, הכאת, הכאות |
| total product | קבוץ הכאת |
| to multiply | לרבע (ה / ... ב / ... עם / זה ה), נרבע (אותה / ה... ב) |
| multiplication | רבוע (ה / מ / מ... ב / ... עם) |
| product, result of multiplication | רבוע |
| product, result of multiplication | העולה, והעולה מ, העולה מהכאת הפועל והפעול |
| product, result of multiplication | המקובץ מההכאה |
| multiplier | פועל (ה), מספר הפועל, הפועלים |
| multiplicand, multiplied | פעול (ה), מספר הפעול |
| מה שיצא מההכאה | |
| יצא מההכאה, יצאו מההכאה | |
| הכאת .. במרובעם, הכאת ה... במרובעם | |
| נולד בהכאת ... במרובעם | |
| הכאה מעוקבת, ההכאה המעוקבת מה, ההכאה המעקבת מה | |
| יולד מההכאה המעקבת, יולד מההכאה המעוקבת, יולדו מהכאת, יולדו מהכאה מעוקבת | |
| ובעצמה באופן מעקב, ובעצמה באופן מעוקב | |
| multiplication table | לוח ההכאות |
| multiplication table | לוח הרבוע |
| to triple, to multiply by three | נשלש (ה), נשלשה, נשלשהו |
| tripled | משולשת, המשולשת, המשולשת ה, המשולשות, המשלשות, משלשת, המשלשת |
| תחת משלשת, תחת המשלשת, התחת משלשת, התחת המשלשת, תחת המשולשת, התחת משלשות, התחת משולשות | |
| subtraction | |
| subtraction | חסור (ה), החסור, חסרונם |
| to subtract | לחסר (אותה מ / ... מ), חסריהו מ, חסרנו (אותם מ), נחסר (... מ / ... מה / ה... מה), נחסרהו (מ / מהם), נחסרם (מ / מה / מהם), מחסר |
| to be subtracted | יחסר, יחוסר, מחוסר (מ / מה), תחוסר |
| to be subtracted | יוסר ממנו, יוסרו (מ / מה / כל אלו ה) |
| subtrahend | המספר שחסרנו, המספר המוסר |
| to subtract | ויסיר |
| to subtract | נוציא, נוציאם מ |
| to cast out by nine | נחסר התשעיות מ, נשליך ה... לתשיעיות |
| to cast out by nine | נשליך ה... ט' ט' |
| to cast out by nines | נחלקם לתשעיות, נחלקהו בתשעיות |
| to cast out by nine | נוציא ג"כ התשיעיות |
| remainder from casting out by nine | הנשאר מהתשיעיות |
| difference | החסרון |
| deficiency | מה שיחסר ל, חסרים |
| ratio | |
| relation, ratio | התיחסות, התיחסות ... ל |
| ratio, relation | יחס (ה... ל), יחסים (ה), יחסי (ה / ה... מ), יחסי המספרים |
| כיחס ... אל, כיחס ה... אל ה | |
| יחס ... ל... כיחס | |
| יחס בין ה... וה | |
| היחס שיש בין ה... וה | |
| היחס שיש בין ... ל | |
| יחס ה... ל... כיחס ה... ל | |
| יחס ה... ל... יהיה כיחס ה... ל | |
| יחס ... ל... כיחס ... ל | |
| מספר יחס ה... ל, מספר היחס ה... ל | |
| היחס שימצא בין ה... וה | |
| אותו יחס ימצא בין ה... וה | |
| ביחס (ה) , ביחסי ה, בזה היחס | |
| לפי אותו היחס | |
| to relate | ליחס אותם ל, ייחסנו ה... ל, ניחס, ניחס אותם ל, ניחסהו ל, תיחס, תיחסהו ל |
| proportional numbers | מספרי היחס |
| המספרי' המתיחסים בזה היחס | |
| דרך היחסים, דרכי היחוסים, בדרכי היחסים | |
| rule of three | בדרך שאם זה שוה זה, בדרך שכך שוה כך כמה שוה כך |
| rule of four, proportion of four numbers | יחס הד' מספרים, יחס הד' מספרים המתיחסים, יחסי הד' מספרים המתיחסים |
| בדרך הד' מספרים המתיחסים | |
| ד' מספרי' מתיחסים, ד' מספרים מתיחסים | |
| rule of three, proportion of three numbers | יחסי כל ג' מספרים המתיחסים, ג' מספרים מתיחסים, התיחסות הג' מספרים |
| rule of six, proportion of six numbers | יחס הששה מספרים המתיחסים, יחס הו' מספרים המתיחסים, ששה המספרים המתיחסים, ו' מספרים מתיחסים |
| proportional | מתיחסות |
| סדר | |
| סדר ראשון, הסדר הראשון | |
| root | |
| root | שרש (ה / מ / ל), שרשים, שרשי (ה), שרשו, שרשם |
| root | עקרי |
| square root | שרש המרובע |
| cube root | שרש המעוקב, השרש המעוקב, שרש מעקב (של), שרשים מעקבים, שרשי המספרים המעוקבים, שרש המספרים המעוקבי' |
| approximate | יותר קרוב (ל), היותר קרוב (ל / אליו), היותר קרובים ל, היותר קרוב שאפשר (ל / ש) |
| בקרוב | |
| to come close | להתקרב ל |
| closest | יותר קרוב ל |
| closer | קרוב מ |
| imperfect square | מספרים הבלתי מרובעים |
| imperfect cube | מספרי' הבלתי מעקבים, מספרים הבלתי מעוקבים |
| square number | מרובע, מרובעים, מספר מרובע, המספרים המרובעים |
| to cube | לעקב |
| cube number | מעוקב (מ), מעוקבים, מספר מעוקב, מספר מעקב (של) |
| מעוקב שלם | |
| מציאות שרשי המספרים | |
| לבקש שרשו, לבקש שרשם, בקשנו שרשם, בקשת שרשם | |
| לבקש השרש המעוקב | |
| למצא שרש, למצא שרש מספר, למצא שרשם | |
| נמצא שרשו, נמצא שרשם, תמצא השרשים | |
| ימצא להם שרש | |
| ימצא שרש ל | |
| ימצא שרש מעקב | |
| הוצאת השרש | |
| להוציא זה השרש, נוציא השרש, נוציא שרשם, ונוציא ... השרש, תוציא השרש | |
| לדעת השרש, לדעת שרש ה, תדע שרש | |
| לדעת השרש המעקב של | |
| לדעת השרש המעוקב מ | |
| יש לה שרש, יש להם שרש, יש לו שרש | |
| בעלי שרש | |
| אין שרש ל, אין להם שרש, אין לו שרש, אין שרש אמתי ל | |
| יש להם שרש מעקב, יש לו שרש מעקב | |
| בעלי שרשי מעוקבים, בעלי שרשים מעקבים | |
| אין לה שרש מעקב | |
| fraction | |
| fraction | שבר, שברים, המספרים השברים |
| to become fraction, to be fractionalized | ישבר |
| fraction line | קו (של), קו השבר ה, קוי השברים |
| numerator | המחולק |
| denominator | מחלק |
| common denominator | מחלק |
| common denominator | משותף, המספר המשותף |
| common denominator | המורה |
| common denominator | במקום שלם, במקום השלם, מקום שלם, מקום של שלם |
| to share a common denominator | ישתתפו שני ה |
| first rank of fractions | שברים ראשונים |
| second rank of fractions | שבירה שנייה |
| conversion, transforming | השבת |
| sexagesimal fraction | שברי התכונה, השברים התכונים, השברים בחכמת התכונה, השברי' שבחכמת התכונה |
| מספרי התכונה | |
| degree | מעלה, מעלות |
| minute | ראשונים, ראשוניים |
| second | שניים |
| third | שלישיים , שלשיים, שליש |
| fourth | רבעיים, רביעיי' |
| fifth | חמשיים |
| to be converted | ישובו (ל) |
| part | חלק (מ / ה... ממנו / ... מ), חלקי (ה), חלקים (מ / ממנו / ... מ), חלקיו |
| part of unit, part of a whole | מחלקי שלם אחד , חלקי השלם, מ... חלקי השלם, חלקים מהשלם |
| אחד מ... חלקי השלם, חלק אחד מ... חלק שלם, חלק אחד מ... חלקים משלם | |
| אחד מהכל, חלק אחד מ... מהכל, חלק אחד מ... חלקים מהכל | |
| אחד מחלקי הכל, חלק אחד מ... חלקי הכל, חלק אחד מ... מחלקי הכל | |
| חלקים מהכל, חלקים מ... חלקי הכל, חלקים מ... של הכל, חלקים מ... מהכל | |
| החלק ... חלקי השלם | |
| חלקים מ... חלקי השלם | |
| חלקים מ... מהשלם, חלקים מ... בשלם | |
| חלקים מ... של שלם אחד | |
| חלקים מ... חלקים של שלם, חלקים מ... חלקים של שלם אחד | |
| name of fraction | שם החלק |
| calculation | |
| calculation | חשבוננו |
| integer | שלם, שלמים, המספרי' השלמים, המספרים השלמים |
| last item, an | האחרון, המספר האחרון |
| even number, even term 2an | זוג, זוגות |
| odd number | נפרד, נפרדים, נפרדות |
| perfect number | מספר השלם, המספר השלם, המספרים השלמים |
| prime number | מספר ראשון, המספר הראשון |
| to count | למנות, מונה, נמנה |
| to be counted | ימנה עמה |
| double false position | בדרך המתנגדים, דרכי המתנגדות |
| false position | המתנגדים |
| geometry | |
| figure | תמונה, תמונות (ה), תמונות ההנדסה |
| shape | צורתה, צורתו |
| measure, measurement | מדה, מדת ה, מדות |
| measure | שעור, שיעורו, שעוריו, שעורם |
| size | שעור (ה), שיעור ה, שעורו, שיעורו |
| area | שיעור ה |
| area | השעור השטחי, שעור שטח ה |
| volume | שעור |
| size | כמות (ה) , כמותה, כמותו |
| area | כמות (ה / כל ה), כמותה, כמות השטח, הכמות השטחי |
| volume | כמות, כמותם, כמותו, כמותו הגשמי |
| container | כלי |
| cubit | אמות |
| pole | עמוד |
| standing | מעומד |
| inclination | נטיה, נטייה, נטיית ה |
| point | נקודת ה, נקדת, נקדות |
| midpoint | נקודת החלוקה, נקודת החלוק |
| line | קו, קוים |
| lined, linear | קווי, קוויי |
| plane | מישור |
| surface | שטח, שטחים |
| area | שטח (ה), כמות שטח ה |
| plane | השטחיי, השטחי, שטחיות |
| straight line | קו ישר, הקו הישר, קו... ישר, בקו ישר מ |
| not straight | הבלתי ישר |
| straight | ביושר, ישר |
| angle | זוית (ה), זויות (ה) |
| right angle | על זויות שוות |
| right angle | זויות נצבות |
| right angle | הנצבת |
| obtuse angle | הזוית הרחב |
| opposite angle | הזוית הנגדיי, נגדיים |
| opposite | הנגדיי |
| distance | רוחק |
| dimension | מרחקים, מרחקיו |
| depth | עמק, עומק, עמקו |
| length | ארך, ארכו, אורך |
| width | רחב, רחבו, רוחב |
| height | גבה, גובה |
| high | הגבה |
| top of | ראש ה |
| on top of | על ראש ה |
| limit | שפת ה |
| limit | תכליותיו |
| end | קצה ה, קצותיו |
| side | צלע (ה), הצלע ה, צלעות, צלעותיהם |
| triangle | משלש, משולש |
| triangular | משלשות |
| equilateral | שוה שלשת הצלעות |
| isosceles | שוה שתי הצלעות בלבד, שוה בשתי צלעות בלבד |
| scalene | מתחלף שלש הצלעות |
| equilateral triangle | המשלש השוה הזויות |
| equilateral triangle | המשלש שוה הצלעות, המשולש שוה הצלעות |
| equilateral triangle | המשולש שוה הזויות |
| scalene triangle | המשלש מתחלף הצלעות |
| quadrilateral | מרבע, מרובע, מרובעים, מרובעות |
| square | רבוע, המרובע השוה האורך והרחב |
| rectangle | המרובע שארכו ורחבו בלתי שוים |
| circle | עגול, עגלה, עגלות |
| diameter | האלכסון |
| diagonally | באלכסון |
| perimeter of a circle | הקף העגלה |
| perimeter of a circle | כמות העגלה |
| noncubic | בלתי מעקב |
| bottom base | תושבת (ה) |
| top base | שטח פיו |
| pyramid | מחודד |
| cube | מעוקב |
| solid, solid body | גשם (ה), מוגשם |
| bodily | גשמי, גשמיות |
| sphere | כדור |
| to encompass | מקיף אותו |
| to draw | נוציא (קו) |
| to pass | יעבור (... על) |
| to halve | נחלק ה... בשני חלקים שוים |
| to divide | חלקנו |
| to be measured | ישוער ב |
| to estimate | תשער |
| א.ה.ב. | |
| friend | אוהבי |
| favorite, preferred | נאהבים |
| א.מ.ר. | |
| to say, to declare, to describe, to note | לומר, לומ' (ש) |
| אומר, אמר, אמרו, אמרנו (ב / ש), נאמ' (ש), נאמר (אותם / ש / ככה / כן ב) | |
| aforementioned | זה שאמרנו, שאמרנו (ש), שאמרנו למעלה, אמרנו למעלה ש |
| aforesaid | האמור, האמורה, האמורה למעלה, האמורות, האמורים, האמורים למעלה, הנאמר |
| as aforesaid | כאמור, כאמור למעלה |
| as aforesaid | כמו שאמרנו (ב), כאשר אמרנו למעלה |
| ולפי מה שאמרנו | |
| כפי שנאמר במקומו | |
| כמו שכבר נאמר ב | |
| ולפי מה שאמרנו למעלה | |
| הדרכים האמורים למעלה | |
| באופן האמור למעלה | |
| בדרך שאמרנו (ב / למעלה) | |
| treatise | מאמרים, מאמר (ה) |
| א.מ.ת. | |
| true meaning | אמתתם |
| correct, true | אמיתי, אמיתית, האמתיים, אמתי, אמת |
| incorrect, erroneous | אינו אמתי, אינו אמת, אינה אמיתית |
| היותר אמתיים | |
| א.פ.ש.ר. | |
| to be possible to | אפשר (ל / ש) |
| possible | אפשרי |
| א.ר.כ. | |
| to elaborate | הארכנו ב |
| lengthiness, extensiveness | אריכות, באריכות |
| ב.א.ר. | |
| to explain | נבאר (איך) |
| to be explained, to be interpreted | מבואר, מבוארים |
| להוסיף ביאור, להוסיף לך ביאור | |
| ב.ד.ל. | |
| distinction | הבדל, הבדליהם |
| difference | הבדל, ההבדל מה... אל ה, ההבדל בין ... ובין, ההבדל שיש בין... ובין |
| ב.ו.א. | |
| to appear, to come out | יבא |
| to result | יבא, יבאו, יבא לנו ה |
| יבא לכל חלק, יבא לכל אחד מהם | |
| ב.ח.נ. | |
| to observe | להבחין, יבחנו כל |
| ב.ח.ר. | |
| preferable | נבחר |
| ב.ט.ל. | |
| to remove | לבטל ה, יבטל |
| ב.י.נ. | |
| to understand | להבין |
| to be understood | יובן, יובן בכל ה, יובנו ב |
| ב.נ.ה. | |
| to generate | יבנו אותו |
| to be generated from | יבנה מ |
| ב.ק.ש. | |
| at the request of | לבקשת |
| to seek, to look for | בקשנו (ה), מבקש, נבקש (ה / ה... כך / ה... ככה ש) |
| to examine, to check | בקשנו |
| sought after, wanted, required | המבוקש , המבוקשים, המספר המבוקש |
| מה שבקשנו, שבקשנו | |
| ג.ד.ר. | |
| to define | גדרנוהו |
| to be defined | יגדר, נגדר |
| definition | גדר, גדרו |
| ג.ז.ר. | |
| to decree | גזר ה... ש |
| ג.מ.ר. | |
| to be complete | יגמר כל ה |
| ד.ב.ר. | |
| saying, words | דברי, דברים |
| to discuss | דברנו (מ / ב), נדבר (ב / מ) |
| to talk about | מדברים מ |
| ד.ר.כ. | |
| method | דרך (ה / ל), דרכים |
| type | דרכים |
| through, by way of | ע"ד, על דרך |
| procedure | הדרך (ה / הזה), בדרך (ה / הזה / זה / זה ש / ש), בזה הדרך (ש), כדרך זה, זה הדרך |
| מדרך ה | |
| ודרך משל | |
| another method | דרך אחר (מ), דרך אחרת מ |
| shortcut | בדרך קצרה, בדרכים הקצרים |
| דרכים מישירים (ב / ל) | |
| דרך כללי שבו | |
| דרך אחד כולל ל | |
| דרכים כוללים | |
| ד.ר.ש. | |
| question, problem | דרושינו, דרושנו |
| required | דרוש |
| ה.ל.כ. | |
| to be shifted | ללכת |
| ה.פ.כ. | |
| to transform | תהפך, תהפכנה |
| vice versa, inversely | בהפך |
| reverse, opposite | הפך |
| ז.כ.ר. | |
| to be remembered, maintained by memorizing | יקויימו בזכירה |
| aforementioned | הנזכר, הנזכרת, הנזכרות, הנזכרים (ב) |
| בדרך המוזכר שלמעלה | |
| בדרך הנזכר | |
| כנזכר | |
| ח.ב.ר. | |
| author | מחבר |
| to compose | חברתי |
| treatise | חבור |
| partnership | חבורה, חבורות, חברה |
| ח.ז.ר. | |
| to turn, to become | יחזור, תחזור, חזרה |
| to repeat the procedure of | נחזור ו, נחזור עוד ו |
| to return again | נחזור שנית ל |
| to fractionalize | החזרנו אותם ל, החזרנום ל, נחזיר ה... ל |
| to convert | נחזירם |
| ח.י.ב. | |
| necessarily | יתחייב ש, מתחייב מ |
| ח.ל.פ. | |
| to convert | נחליפם ל |
| to switch | נחליף ה |
| to exchange | להחליף (ממנו) |
| different | מתחלפים, מתחלפות |
| diversity, variety | חלוף |
| exchange | חלוף |
| change | חלוף |
| חלופים | |
| ח.ל.ק. | |
| aspect | חלקי (ה) |
| portion | חלקים |
| primary element, primary part | חלק ראשון |
| share | חלק ה, בחלקו |
| ח.ש.ב. | |
| to be considered | נחשב |
| ט.ע.ה. | |
| to err | טעינו |
| error | טעות |
| י.ד.ע. | |
| knowledge, knowing | ידיעת (אלה ה / אלו ה), בידיעת (ה) |
| to know (that) | לדעת (אותם / אלו ה / זה / הכל / כל / ש / אם / כמה / מה הם ה), לדעתו (ב) |
| דע (אלו ה / כי / ש), ידענו (ה / ש), ידעת (ש / כל זה), ידעתו, נדע (הכל / ש / מה הוא), נדעהו ב, תדע (ה / כי / ש) | |
| כמו שידעת, כמו שידעתו | |
| לדעתו בדרך הזה ש, דעהו בדרך זה ש, נדעם בדרך זה ש | |
| to be known | ידוע ש, יודע (ב / ש / לנו), יודעו |
| בדרך הזה ידענו | |
| בזה הדרך יודע | |
| ידועים, הידוע, הידועים (לנו) | |
| המספר הידוע | |
| בלתי ידוע, הבלתי ידוע | |
| מספר בלתי ידוע, המספר הבלתי ידוע, המספרים הבלתי ידועים | |
| י.כ.ל. | |
| to be able | יוכל ל, נוכל ל, תוכל ל |
| י.ל.ד. | |
| to produce | יוליד (ה / אותו), יולידו, יולידהו, מוליד (אותו) |
| to be generated | יולד (מ), יולדו (ה / מ) |
| י.פ.ת. | |
| check | מופת (ה / זה ה / ל / לזה) |
| proof | מופת (ש / זה / מה), והמופת על זה (ש) |
| demonstrative, exemplary | מופתיים |
| י.צ.א. | |
| to result | יצא (ה / מ), יצאו |
| יצא לנו (ב / ה) | |
| שיצא ב | |
| שיצא לך | |
| מה שיצא | |
| היוצא, היוצא מהם | |
| to take from, to extract | להוציא ה, נוציא (ב / ה / ממנו / ה... ב / ה... מה / ... ה / ... מה / ... מה ש), הוצאנו |
| נוציא ה... ש, נוציא ה... כך (ש) | |
| י.ר.י. | |
| meaning, signification | הוראתם |
| indication | להוראת |
| to indicate | יורה ש, מורה, תורה |
| שיורה על | |
| indicator | המורות (ה / על) |
| to mean, to signify | תורה |
| י.ת.ר. | |
| remainder, (result of subtraction) | מותר, המותר מ, הנותר (מה / משניהם) |
| כ.ו.ל. | |
| to contain | יכיל |
| כ.ל.ל. | |
| to be included | יוכללו ב |
| comprehensive | כולל, כוללים, כוללות |
| including | כולל, כולל ל |
| inclusive | כולל לכולם |
| consist of | כולל ב |
| כ.נ.ס. | |
| to contribute | הכניס (ה / ל) |
| כ.ר.ח. | |
| necessary | הכרחיים, ההכרחיים |
| necessary | הכרחי (ב / ל) |
| בהכרח | |
| כ.ת.ב. | |
| writing | כתיבתו |
| to write | לכתוב, כתבנו (על / למטה), כתבתי זאת ה, נכתוב (אותו / אותם ב / אותם במקום / אותם על ה / אותה תחת ה / ב / במקום / כנגדו / על ה / עליהם / ה / ה... על ה / ... ב / ה... ב / ... אחר ה / ... אצל ה / ... על / ... על ה / תחת / תחתיה / תחתיו / ... תחת / ... תחתיו) |
| נכתוב כל אחד, נכתוב כל אחד אצל חברו, נכתוב כל אחד בצד חברו | |
| נכתבהו, נכתבם (ב / על ה) | |
| תכתוב... ב | |
| to be written | יכתבו, יכתב (מה ש) |
| written | כתוב ב, הכתובים |
| ל.א.כ. | |
| skill | מלאכה |
| science | מלאכה, מלאכות |
| work | מלאכה |
| ל.מ.ד. | |
| teaching, doctrine | לימוד, למוד (ב / ה / מה), למודים |
| student | לומד |
| teacher | מלמד |
| ל.ק.ח. | |
| to take | לקחת (ב), יקח, לקח (מה), לקחנו (מה), נקח (ב / ה / מ... ה / ... מ / מזה הכל ה), תקח ב |
| to be taken | שילקח, ילקח מ, שלוקחו ממנו |
| לקחנו ל, נקח ל | |
| to consider as | נקח ה... בשם, תקח בשם, תקחהו בשם |
| נקח ה... כמו | |
| to suppose | נקח במחשבתנו |
| מ.ח.ק. | |
| to erase | ימחוק, נמחוק ה |
| מ.נ.ע. | |
| impossible | נמנע ל |
| necessarily, inevitably | לא ימנע מ |
| מ.צ.א. | |
| to find | למצוא (ה / אלה ה), למצא (בהם ה / בו / ה), מצאנו (אותו ה / ה), מצאת, נמצא, נמצאהו כך |
| נמצא ה... כך, ונמצא ה... ככה ש | |
| to find out that, to discover | מצאנו ש, נמצא ש, תמצאנו, תמצא ב... ש |
| to be discovered | ימצא ש |
| to be found | ימצא (ב / ביניהם אותו ה / לו), ימצאו (ה / בו), נמצא, נמצאו אצלנו, נמצאת |
| ימצא ה... כך ש | |
| נמצאת (בש), הנמצאת, הנמצאים, המספרים הנמצאים | |
| finding, discovery | מציאות (ה) |
| existence | מציאות |
| common denominator | שימצאו בו כל אלו השברים, המספר שבו ימצאו כל אלו השברים |
| שימצא בו, שימצאו בו | |
| שנמצא בו אלו ה | |
| נמצאים ב | |
| מ.ש.ל. | |
| to give an example, to illustrate | למשול |
| example | משל (ב / ה / ל), המשל (ב / כי / ל / מ / ש), המשל בזה, המשל לזה |
| המשל לזאת הצורה | |
| משל אחר (ל) | |
| נעשה משל אחר (בש) | |
| נ.ב.ט. | |
| to look | יביט (... מ... ל), מביט ל |
| sight | מבט |
| הבטות | |
| נ.ג.ע. | |
| not exceeding over | שלא הגיע ל |
| to deserve | יגיע לו מ |
| נ.ו.ח. | |
| to leave | בשנניח, הנחנו |
| leaving | בהניחנו |
| let us suppose, for example | נניח, נניח ש, נניח עוד ש |
| הנחנו במחשבה, נניח קודם במחשבה ה | |
| to be supposed | יונחו |
| to place | הנחת, נניח (ה... על / ... על), ננחם ב |
| to be placed | יונח |
| denotation | הנחת |
| to be given | מונחים ה |
| נ.ס.ע. | |
| to shift | לסיע מ, נסייע ה, נסיע ה.... לאחור, נסיעה (ל / לאחור / אות אחת לאחור / אות אחת אצלה) |
| נסיעם כל אחת לאחור אות אחת | |
| נ.צ.ל. | |
| to be saved from | וינצל מ |
| נ.ש.ג. | |
| to get, to obtain, to achieve | להשיג ב, ישיג בו ב, נשיג ב |
| to be achieved, to be obtained | יושג ב |
| נ.ת.נ. | |
| giving | נתינת (דרך / דרכים / משל) |
| to give, to donate | יתן (ל / ... ל), יתנו, נתן (אותו ל / ל), נתנם ל, נתננו ל |
| to yield | נותן |
| ס.ד.ר. | |
| order | סדר, בזה הסדר |
| arrangement, order | סדורם |
| method | סדר, סדרים |
| to order, to arrange | לסדרו, נסדר (אותם), נסדרהו, נסדרם (כך / ככה), סדרנו (ה) |
| נסדר ... כך, נסדר ... ככה | |
| נסדר על שווי, נסדר ה... על שווי ה | |
| arranged, ordered to be ordered, to be arranged | יסודר, יסודרו, מסודרים (ב) |
| and so on | וכסדר הזה |
| and so on successively | וכן כסדר, וכן כסדר הזה, וכן כלם כסדר הזה |
| successively, sequentially | כסדר |
| according to this method | כסדר הזה |
| progression | בסדר המספר |
| ס.כ.ל. | |
| not to know | נסכל ה, סכלנו ה |
| ס.פ.ק. | |
| to be enough, to be sufficient | יספיק, יספיקו ל, מספיק (לכל) |
| וזה יספיק (ב / במה ש), וזה מספיק ב, וזה מספיק בזה (ה) | |
| not enough | זה אינו מספיק |
| יהיה שלא יספיקו ל | |
| ע.ב.ר. | |
| to shift, to move | נעביר, נעבירם ל |
| to proceed to, move forward to | נעבור ל |
| ע.ז.ר. | |
| with, with the help of | בעזר |
| clinging to each other | נעזרות |
| ע.י.נ. | |
| to study, to investigate, to examine, to look carefully | לעיין (ב), נעיין (ב / ה), עיין, תעיין (ב) |
| המעיינים ב | |
| עיון | |
| ע.ל.ה. | |
| to result | יעלו (ל), יעלה (ל), עולה (ל), עלו (כלם), שעלו |
| result | העולה (מ), מה שיעלה (מ), מה שעלה מה, כל מה שיעלה |
| to exceed by | עולה יותר מ |
| not exceeding over | שלא יעלה ל |
| ע.מ.ד. | |
| to stand | יעמוד תחת ה |
| to rest | יעמדו |
| ע.ש.ה. | |
| formation, establishing | העשות, עשיית זה |
| to do, to operate, to make | לעשות (ה / מ), נעשה (ב / בש / כן / כן ה / כן ש / מ / ... ה / ... מה / ... מהם), נעשהו, עושי', עשהו, עשינו (בזה ה), תעשה (ב / ב... ש / כך) |
| to be done | נעשים |
| כמו שעשינו (ב / בזה) | |
| מה שעשינו | |
| שעשינו (מה) | |
| נעשה בדרך זה ש, תעשה בדרך זה ש, נעשה ה... בדרך זה (ש) | |
| בדרך הזה תעשה | |
| נעשה... כך | |
| נעשה ה... כך (ש) | |
| נעשה ה... כן (ש) | |
| נעשה ה... בש, נעשה ה... ככה בש | |
| יעשה ה... כן | |
| to be performed, to be carried out | יעשה (מ), יעשו |
| להעשות (בכל ה) | |
| העשוי מ | |
| to become | יעשה (ה) |
| to convert | נעשה (מ / מה) |
| to yield, to produce | עושה, העושות ה |
| in theory and practice | בעיון ובמעשה |
| פ.ע.ל. | |
| operation | פעלה, פעלת (ה), פעלתו, פעלתנו, פעולתנו |
| תפעול פעולתה | |
| procedure | הפעל |
| deed, action, work | פועלם |
| צ.י.ר. | |
| to be conceived | יצויירו |
| to be formed, to be shaped | יצויירו |
| צ.ר.כ. | |
| should | צריך ש, צריך ל |
| required, needed | צריך, הצריכים (בה / ל), הצריכות ב, צריכות אליה |
| to need | צריכים (מה / ... ל) |
| הוצרכנו ל, נצטרך (ל / ב... ל), מצטרכים ב | |
| כל מה שיצטרך ב | |
| ק.ב.ל. | |
| to be subject to | שיקבל |
| ק.ד.מ. | |
| נקדים | |
| ההקדמה ה, הקדמות | |
| ancient | הקדומים |
| ק.ל.ל. | |
| to make easier, to facilitate | להקל מ |
| easily | בנקלה, יותר בנקל |
| easier | יותר נקל |
| easily | בקלות |
| ק.נ.י. | |
| to acquire | תקנה |
| to bestow, to grant | מקנה |
| ק.צ.ר. | |
| short, brief | קצר |
| brevity, briefness | ובקצור |
| ק.ר.א. | |
| to be named, to be called | יקרא (ה), יקראו, נקרא (ל), נקראת, תקרא (ה) |
| to call, to name, to designate | לקרוא לה, נקראהו |
| ק.ר.י. | |
| to happen, to occur | יקרה (ש / ב), יקרו בהם |
| ר.א.י. | |
| to see | תראה אותם, רואה (ש), ראינו (ש), ראית ש, נראה (ש) |
| יראה ש, יראה מכאן ש, יראה לנו מזה ש | |
| illustration | כמו שיראה בצורה הזאת, כמו שיראה בצורה זו, כמו שנראה זאת הצורה, כמו שנראה ב |
| כנראה בצורה זאת, כנראה בצורה זו | |
| לפי הנראה בצורה זו | |
| seeing, realizing | בראותי |
| visible, can be seen | הנראה |
| as seen, as observed | כמו שיראה (ב) |
| should, it is advisable that | ראוי (ל / ש) |
| הראוי ל, הראויים ל, הראוי לו ב | |
| appropriate | ראויים ל |
| to deserve | יהיה ראוי ל |
| יותר ראויה לזה מה | |
| to deserve | ראוי ה |
| sight | ראות |
| proof | ראיה ש, הראיות |
| ר.ב.י. | |
| רב | |
| to be plenty, to be a lot of | ירבו, ירבו ה... מאד מאד |
| multitude | הרבה |
| multitude | רבוי |
| ר.י.ק. | |
| to be drained | יורק ב, יורקו (ב / ... ב) |
| ר.כ.ב. | |
| to consist of, to be composed of | יורכב מ |
| composed of; consisting on | מורכב מ |
| ר.מ.ז. | |
| to ascribe, to refer to | ירמוז ל, תרמוז אליהם |
| to allude, to refer | רומזים ל, לרמוז על, תרמוז ל |
| alluding, indicating | רומזת, הרומזת ל |
| alluded, indicated | נרמזים ב |
| ר.צ.ה. | |
| to want, to wish | תרצה (ל), רוצה (ל), נרצה (ל / אותה), ירצה (ל), רצינו (ל) |
| כמי שרוצה ל | |
| אי זה שנרצה | |
| אי זה ... שנרצה | |
| אי זה מה... שירצה | |
| מה שרצינו, מה שתרצה | |
| שנרצה, שרצינו, שתרצה | |
| the sought after, wanted, required | וזה מה שרצינו, וזהו מה שרצינו, וזה הוא מה שרצינו |
| כמו שרצינו | |
| whatever you want, and so on as you wish | כל מה שתרצה |
| ר.ש.מ. | |
| רשימת ה | |
| נרשום (אותה / אותה ה / ה) | |
| ש.א.ל. | |
| question, problem | שאלה, שאלות |
| ישאל (על / עליהם), נשאל עליו, נשאל | |
| ישאלו לנו ש | |
| הנשאלים | |
| שואל | |
| ש.א.ר. | |
| remainder | הנשאר, הנשאר מ, הנשארים, שנשאר |
| to remain, to be left | ישאר, ישארו (ה / ... על / ... על ה), נשאר (ל), נשארו |
| ישאר בידינו, ישארו לך, הנשארים לו | |
| מה שישאר, מה שנשאר | |
| to preserve, to leave | נשאיר |
| ישאר אי זה דבר | |
| לא ישאר אלא | |
| the rest | השאר |
| nothing remained, no remainder | לא ישאר דבר, לא נשאר דבר |
| לא ישאר כלום, לא נשאר כלום | |
| לא ישאר מאומה | |
| לא ישאר יותר | |
| לא נשאר שום דבר | |
| no more remains | שלא נשאר יותר |
| ש.ד.ל. | |
| to strive, to make an effort | ישתדל ל |
| ש.ו.ב. | |
| to return | ישובו (ל) |
| to become | ישוב |
| ש.ו.ה. | |
| equal | שוה (ה / ל / כ), שוים (ל), שווים, שוות, שות ל, השוה, ששוה, ששוים (ל), מספר שוה (לכל ה) |
| to be identical to, to be equal to | שוה, שווה ל, ישווה, יהיו שווים, יהיו שוים (ה / ל), יהיו שוות, יהיה שוה (ל), תהיה שוה ל |
| to be worth | שוה (ה / ל), ישוה ה, ישוו, שישוה כל כך ש |
| worth more | שוה יותר מ |
| equal parts | חלקים שוים |
| equally | שוה בשוה |
| value | שווי (ה) |
| highest in value | השוה יותר, ששוה יותר |
| unequal | הבלתי שוה |
| ש.ו.מ. | |
| to place, to mark | נשים (תחת ה / ... ב / ... על), ונשימה אצל ה, נשימם על ה, משים, שמנו (למטה), תשים תחת ה |
| יושם (ב / על / תחת ה) | |
| ש.כ.ל. | |
| learned, intellectual, thinker | משכילי' |
| ש.ל.מ. | |
| completion | תשלום, תשלום הכל, עד תשלום |
| finalization, summing up | תשלום |
| to complete, to finish | נשלים (ה / זה ה) |
| עד שנשלים כלם | |
| to be completed | נשלם (ה) |
| ש.מ.ר. | |
| to keep, to reserve | נשמור (אותה / ה), נשמור אותו, נשמרהו, נשמרם |
| reserved, kept | שמור, השמור אצלנו |
| תשמור כלל זה ש | |
| ש.מ.ש. | |
| to use | תשתמש ב |
| ש.מ.ש. | |
| to weigh | שוקל |
| weight | משקלים |
| ת.ח.ל. | |
| to begin (with), to start | להתחיל (ב / מ), אתחיל, יתחיל ב, נתחיל (ב / ל / מ), תתחיל ב |
| beginning | התחלת |
| at first | תחלה |
| premise, principle | התחלות, התחלות מ, התחלותיה |
| wise, sage, wise man | החכמים |
| with great effort, with great trouble | ובטורח גדול |
| barely, with great difficulty | בקושי גדול |
| to comprehend | יקיף ב |
| useful, beneficial | מועיל (ב), מועילים ב |
| loss of time, waste of time | ומהפסד הזמן |
| to desire, to wish | לבו חפץ |
| arithmetic book | ספר המספר, ספרי המספר |
| book | ספר, ספרי |
| booklet | הספר הקצר |
| section | כלל, כללים, הכלל (ה / ה... מה) |
| chapter | פרק (ה), פרקים, הפרק ה... ב |
| column | טור (ה), טורים |
| row | טור (ה), טורים, שבטור (ה) |
| answer, solution | תשובה, תשובות |
| בקצת שאלות ותשובות מישירות | |
| בקצת שאלות ותשובות | |
| property | סגלה, סגולה, סגלות, סגולותיהם, סגולותיו, סגולתם |
| type | מין, מיני (ה) |
| category, class | מין, מיני (ה), המין (ה / הזה / ש), במין (ה / הזה / זה ש) |
| בזה המין (ש) | |
| מזה המין | |
| באי זה מין הוא | |
| types of operations | מיני (ה) |
| type | סוג (ה), הסוגים ה |
| manner, way | אפני, אופני (ה) |
| באופן ש, באופן זה, באופן אחר | |
| פן (ה), הפן ה, פנים | |
| affair, matter | ענין (ה), ענייני, עניינים |
| element | עניינים |
| property, characteristic | הטבע ש |
| reason | סבה ש, סיבה ש, לסבה ה, לסבות ה |
| principle | שרש |
| on basis of | על שרש |
| form, figure | צורות |
| illustration | צורה, צורות |
| בצורה (זו / הזאת), בזאת הצורה | |
| (זה / זו / זהו) צורתו, זאת היא צורתו, זו היא צורתו, צורתו היא זאת | |
| זו היא הצורה ה, זאת הצורה ה | |
| והנה צורתו, והנה לך צורתו, והנה לך צורה, והנה לך צורתם | |
| שצורתו זאת, שצורתם היא זאת | |
| מהצורה | |
| לצורה זו ש | |
| quantity | הכמה |
| quantity | כמות (ה), כמותו, בכמות ה, בכמות מן ה |
| continuous quantity | כמות המתדבק, כמות מתדבק, הכמה מתדבק, הכמה המתדבק |
| discontinuous quantity | כמות המתחלק, כמות מתחלק, הכמה המתחלק |
| shared by, common to | משותפות ל |
| guiding, leading straight | מישרים, מישירות |
| opinion, assumption | סברת |
| foundation, element | יסוד |
| smallness | למעוטו |
| מעט | |
| מעט יותר | |
| smaller than, less than | פחות (מ / מה / ממנו / מן ה), פחותה מ, פחותים מ |
| smaller number | המספר הפחות |
| no more and no less | לא פחות ולא יותר, לא פחות ולא יתר |
| deficit | הפחות |
| minus | פחות |
| larger, greater than, more than | יותר (ב / מ / מה) |
| more than | יותר... משום |
| excess | היותר |
| plus | ויותר |
| minus | בלתי (ה) |
| plus | עם (ה) |
| plus | בתוספת |
| supplement | התוספת מ |
| excess | התוספת |
| more | עוד |
| further, in addition | עוד |
| another | עוד |
| as a sign that | לאות ש |
| עשרה לאות הסמוכה לה, עשרה עם האות הסמוכה לה | |
| skilled | בקי ב |
| to know by heart | ידע זה הלוח על פה |
| table | לוחות |
| to be identified | יוכרו בטוב |
| remainder | המותר מה, מותר ה |
| empty space | מקום פנוי |
| name, designation | שם (של), שמו, בשם ה, השמות |
| considered as units | בשם |
| decimal position | בשם |
| end, completion | כלות |
| intention | כונתינו (היה ל) |
| meaning | כונת (ה) |
| required | מספר המכוון |
| related | שיוחסו אליו |
| with respect to | מיוחס ל |
| better | יותר טוב |
| into half | באמצע |
| side | צד, צדדים, מהצד ש, בצד |
| to elaborate | הרחבנו בו |
| rule | הכלל ל, זה הכלל |
| rubric | בית (ה) |
| technique | בתחבולה, בזאת התחבולה |
| the same applies | הוא הדין |
| liquid measure | משורות |
| currency | מטבעות |
| geographical location, place | מקום, המקום ה, המקומות |
| flour | קמח |
| bread | לחם |
| לבן, לבנים | |
| king | מלך |
| ליטרין | |
| שקל, שקלים | |
| gold bar | חתיכת זהב |
| profit | ריוח (ה) |
| loss | הפסד |
| amount | לכמות ה |
| amount, total, whole | הכל (ה), כל |
| goods | סחורה |
| man | אדם |
| people | אנשים |
| thing, x | דבר, דברים |
| barrel | חבית, חביות |
| hole | נקב, נקבים |
| day | היום |
| time | זמן |
| as long as | כל זמן ש, בכל זמן ש |
| times | פעם, פעמים (ב / יותר מה / כמו ה) |
| as many times as | שכל כך פעמים... כ |
| essence, element | עצמיות |
| ground | ארץ |
| to look | תטה עיניך ב |
| ray of sight | נצוץ ה |
| eye | עין, עיניך |
| stick | יתד |
| accuracy, exactly | בדקדוק |
| heavenly | השממיות |
| to have | יהיו בידינו, יהיה לו, יהיה לנו, יהיו לה, יהיו לנו, יש ל, יש להם, יש לו, יש לנו, שיש להם, שיש בידינו |
| having | בעל |
| to be, to result | להיות, היותו, היה (ה), היינו, יהיו (ה / ב / מ / מה), יהיה (ה / זה / ב / בו), תהיה, שיהיה, שתהיה ה |
| בהיותך | |
| there is | יש (ב / בו), יש בכאן, שיש (בה / בו) |
| אין, אינו (מ), אינם (מה), שאינו, אין בכאן, אין שם, אין שום, אינו כן ב | |
| אנו, אתה, הנך | |
| הוא (ה / ש / כש / זה), היא (ה / זאת / ש), הם (ה / אלו) | |
| those | ההם, ההיא |
| שהוא (ה), שהיא (ה), שהם (ה) | |
| הזה, זה (ב / ה / ש / הוא / בש), זהו (ה), הזאת, זאת (ה), זו (ה / היא), אלה (ה), אלו (ה / הם / הן), האלו | |
| בזה (ה), באלו ה, מאלה, מאלו (ה) | |
| מזה ה, לזה ה | |
| כזה | |
| any, all, every | כל (ה / אלו ה / זה), כלם, כולם, כולו, הכל, בכל (ה / ... מהם), שבכל, מכל (ה), כל ... ביחד |
| each of | כל אחד (מ / מה / מאלו / מהם), כל אחת (מ / מה), כל א' (מה) |
| מכל אחד מהן, כל א' וא' | |
| for each | לכל, לכל אחד (מ / מה) |
| one of | אחד (מ / מה / מהם / מן ה), אחד מאלו ה, אחת (מ / מאלו ה) |
| what | מה ש, מה שיהיה |
| what is | מהו |
| all that | כל מה ש(יהיה / יהיו) |
| במה (ש / שהם) | |
| whoever | מי ש, למי ש |
| whoever | כל מי ש |
| as someone who | כמי ש |
| whichever, any | שום |
| whichever | כל ... שיהיו, כל ... שיהיה |
| whatever, any of | אי זה (מה / ... ש), אי זה שיהיה, אי זה שיהיו, אי זה שתהיה (מ), אי זה... שיהיה, איזה ... שיהיו, איזה ... שיהיה, אי זה ... שיהיה (מהם) |
| whatever | מאיזה, מאי זה... שיהיה, מאי זו ... שתהיה, מאיזו ... שיהיו |
| באי זה ... ש, באי זה ... שיהיה | |
| whatever | כמו ש |
| anything | מה שהוא |
| itself | עצמו, בעצמה, בעצמו, בפני עצמו |
| same | אותו (ה / ש), אותם (ש / שמ / ה.... ש), באותו (ה), מאותו (ש), מאותם (ש / של), כל אותם שהם |
| whichever | אי זה |
| of | של (ה), שלה, שלהם, שלו |
| of | מן ה |
| of them | שבהם, שבהן, בהם, מהם ש |
| right | ימיני, ימנית |
| left | שמאלי, שמאלית |
| preceding | קודם לה, הקודמת, הקודמת לה, הקודמת להם |
| preceding | שעבר, שעברה, העוברות |
| next, consecutive | הבאה, באות, להבא |
| succeeding, successive, sequential | נמשך אליו, הנמשך לזה, הנמשכת (אליה / אליהן / אחריה / לה) |
| near, closest | הסמוכה, הסמוך (אליה / ל) |
| large, great, large number | גדול, הגדול, המספר הגדול |
| יהיה יותר גדול מ | |
| המספר היותר גדול | |
| היותר גדולה | |
| הגדול מאד | |
| small, small number | קטן, הקטן, הקטון, המספר הקטן, המספר הקטון |
| היותר קטן | |
| הקטן ממנו | |
| mean | אמצעי, מספר אמצעי, המספר האמצעי |
| bottom | תחתון (מה), תחתונה, תחתונות |
| less than, smaller than | תחת |
| upper, top | עליון, עליונה, עליונות |
| other | חברו |
| others | האחרים |
| another, other | אחר, אחרת, אחרים, אחרות |
| the rest | האחרות |
| last | אחרון, אחרונה, אחרונים, אחרונות, המספרים האחרונים |
| corresponding, similar | הדומה (לה), הדומים (ל), הדומות (ל) |
| single | היחידי |
| special | מיוחדות |
| new | חדשה |
| opposite | סותרו |
| separate from | הוא חוץ ל |
| preposition | |
| above, on top | למעלה, כמו למעלה |
| שלמעלה (מהם / ממנו), של מעלה, אותו שלמעלה, אותה שלמעלה הימינה | |
| כמו שלמעלה | |
| מה שלמעלה הימנו, מה שלמעלה מהם | |
| כל מה שלמעלה | |
| upwards | ומעלה |
| beneath, underneath | למטה (מהם) |
| שלמטה (מה), אותו שלמטה, מה שלמטה, מלמטה | |
| by, times, multiplied by | על |
| אל ה, אליה | |
| with | עם, עמה |
| above | על (ה), שעל (ה), שעליה, שעליהם, שעליהן, שעליו, מה שעל ה |
| beneath | תחת (ה), תחתי, שתחת (ה), שתחת תחת ה, מה שתחת ה |
| next to it | שבצד (ה), שבצדה, שבצדו (ה), שבצדם, שמצד (ה) |
| מצד, מהצד ה, מצדה, מצדו | |
| לצד ה | |
| to the right | לצד הימין |
| to the left | מצד שמאל (אליה) |
| in the middle of | באמצע |
| corresponding to | כנגד (ה), שכנגדו, נגדו, הנגדיות |
| ממנו | |
| between | בין ... ו; בין ה... וה, בין... ובין |
| in | בו |
| after | אחר (ה / ש), לאחר (ש), אחריה |
| before | קודם ש, יותר קודם ה, שקודם ה |
| until | עד (ה / ש) |
| מ... עד ה | |
| except for | מלבד |
| as much as | כל מה ש |
| as, as much as | כמו (ש / ה) |
| as well as | כמו |
| such as | כמו |
| as | כפי (ה / ש / מה ש) |
| כמי ש | |
| as, a kind of | מעין ה |
| in order that | כדי (ל / ש) |
| according to | לפי (ה) |
| except | אלא |
| except for | זולת, זולתם, זולת זה מ |
| without | בלתי (ה / ש / שום) |
| אצל ה, שאצלה | |
| adverb | |
| always | לעולם, וכן לעולם |
| always | תמיד |
| every time, whenever | בכל פעם |
| whenever | בכל עת ש |
| then | אז |
| now | עתה |
| still | עדיין |
| infinitely | אל לא תכלית, עד בלתי תכלית |
| then, afterwards | אחר, אחר כך, אח"כ |
| firstly, first of all | קודם כל דבר |
| first, firstly | בראשונה, ראשונה, וראשונה |
| first | קודם |
| here | בכאן |
| together | יחד, ביחד, יחד עם |
| only, alone | לבד, לבדו |
| only | בלבד |
| except that, only | אלא ש |
| a few of | קצת, קצת מ, בקצת (זה) |
| very | מאד |
| therefore | לכן |
| then | אם כן, א"כ |
| also, moreover | וכמו כן |
| also | גם, גם כן, ג"כ, כן ג"כ |
| similarly | וכן |
| similarly | ובדומה לזה |
| et cetera | וכו' |
| similar | בכיוצא לאלו ה |
| so, thus | כן, כך (ה / הוא), ככה, שכך |
| as many as | כל כך, כל כך ... ש, בכל כך |
| how much, how many, by how much | כמה (הוא / הם / היה ה / שהוא / ...יש ב / ...יש לו), בכמה |
| כמה יש עד | |
| כמה יש מ... עד תשלום | |
| thereby | בש |
| how | איך |
| where | ששם |
| there | שם |
| here | הנה (ש / הוא) |
| instead | במקום (ה) |
| anywhere | בכל מקום ש |
| hence | מכאן |
| indeed | האמנם |
| indeed | וכבר |
| already | כבר |
| at the end, finally | באחרונה |
| backward | לאחור |
| forward | לפנים |
| by heart | על פה |
| very well | הרי טוב |
| meaning, i.e. | כלומר, כלומ' |
| i.e., that is to say | ר"ל |
| all the more so | כ"ש |
| conjunction | |
| because, for | למה ש |
| because, for | כי |
| hence | לכן |
| if | אם |
| if not | ואם לאו |
| and so on | וכדומה |
| moreover | וכן |
| yet | אבל |
| but | אבל |
| but | אלא |
| since | היות, להיות ה, להיותו |
| since | אחר ש |
| because, since | בעבור ש |
| provided that | בתנאי זה ש, בתנאי ש |
| whether… or | אם... או, אם ש... או ש |
| אם ... אז | |
| אם... אם לא | |
| בין ... בין | |
| בין ש...בין ש, בין ש... או | |
| even if | ואם |
| when | כש |
| except for | אלא |
| although | ואע"פ ש |
| nothing but, only | אינו אלא, אינם אלא |
| אין ... אלא, אינך ... אלא | |
| אין... שום | |
| לא... אלא (ה / ל) | |
| לא... שום | |
| ואם לא לא | |
| ואכ"כ | |
| first thing | והראשון ש |
| ראשון, ראשונה (מ / מה), ראשונות, ראשונים, מספר ראשון, המספר הראשון | |
| שני, שנית | |
| חצי ה, חציים, חציו ה, החצי מ | |
| שליש, שלשי, שלישי, שלישית, שלשית, שלשיות, שלישיות, שלשיים, שלישי ה | |
| רבעי, רביעי, רביעית, מספר רביעי, רבעיות, רביעיות, רביע, רובע | |
| חמישי, חמשי, חמישית, חמשיות, חמישיות, חומש | |
| ששי, מספר ששי, ששית, ששיות | |
| שביעי, שביעיות | |
| שמני, שמיני | |
| תשיעי, תשיעית, תשיעיות | |
| עשירי, עשירית, עשיריות | |
| decuple, ten‑fold | עשיריתו |
| אליאו גבה בכ"ר אליעזר יצ"ו | |
| son of the honorable Rabbi | בכ"ר |
| God rest his soul | נ"ע |
| with God's help | ובעזר השם, ב"ה , בע"ה, בעה"ו |
| the Spanish | הספרדי |
| city | ממדינת |
| kingdom | ממלכות |
| Alexandria | אלישנדריאה, אלישנדריא', אלכסדריאה |
| Aragon | ארגון |
| Bursa | ברוסה |
| Constantinople | קוסטנטינה, קוסטנדינה, קושטנדינה |
| Oriola | אוריאולה |
| Euclid | אקלידס |
| Archimedes | ארגימידש |
| al-Fārābī | אלפארבי |
| תהלה לאל יתעלה השם | |
| much study is a weariness of the flesh (Ecclesiastes 12, 12) | ולהג הרבה יגיעת בשר |
| the hand of my God which was good upon me (Nehemiah 2, 18) | יד אלהי הטובה עלי |
| shook my lap (Nehemiah 5, 13) | נערתי חצני |
| Be merciful unto me (Psalm 57, 2) | חננני השם |
| as the shining light, that shineth more and more unto the perfect day (Proverbs 4, 18) | כאור נגה הולך ואור עד נכון |
Appendix II: Bibliography
Isaac Ben Moses ‘Eli / ‘Ali
Oriola, Aragon, Spain, 15th century
Meleket ha-Mispar
Manuscripts:
- 1) Leiden, Bibliotheek der Rijksuniversiteit Cod. Or. 1090/3 (IMHM: f 19382), ff. 25v-49r (16th century)
- 2) Oxford, Bodleian Library MS Heb. d. 3 (IMHM: f 22729), ff. 21r-44r (Cat. Neub. 2774, 2); (16th century)
- 3) Oxford, Bodleian Library MS Mich. 141 (IMHM: f 22111), ff. 17r-36r (Cat. Neub. 1297, 2); (15th century)
- 4) Oxford, Bodleian Library MS Poc. 187 (IMHM: f 19350), ff. 9r-46v (Cat. Neub. 2060, 1); (1503)
- Poc. 187
- 5) Paris, Bibliothèque Nationale de France heb. 1029/4 (IMHM: f 15721), ff. 72r-83v (15th-16th century)
- heb. 1029/4
- 6) Paris, Bibliothèque Nationale de France heb. 1095/2 (IMHM: f 15045), ff. 7-49 (15th century)
- heb. 1095/2
- The transcript of the text is based on manuscript Paris 1095.
Bibliography:
- Steinschneider, Moritz. 1893–1901. Mathematik bei den Juden. Berlin-Leipzig-Frankfurt: Kaufmann, p. 208 (h74); repr. Hildesheim: G. Olms, 1964 and 2001.
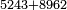
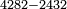
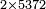
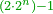
![\scriptstyle{\color{OliveGreen}{2^n\sdot\left[\left(2\sdot2^n\right)-1\right]}}](/mediawiki/images/math/5/3/7/537946adf94cc0f67f53394ebc17be2e.png)
![\scriptstyle{\color{blue}{2\sdot\left[\left(2\sdot2\right)-1\right]=2\sdot3=6}}](/mediawiki/images/math/4/a/d/4ad7cfaee668178995b5434ddc6e77ea.png)
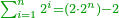
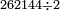
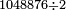
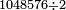
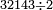
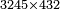
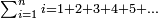
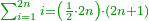
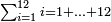
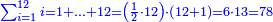
![\scriptstyle{\color{OliveGreen}{\sum_{i=1}^{2n-1} i=\left[\left[\frac{1}{2}\sdot\left(2n-1\right)\right]+\frac{1}{2}\right]\sdot\left(2n-1\right)}}](/mediawiki/images/math/8/a/c/8acf0ea64da5cdcc21c81ce54ae8f855.png)
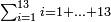
![\scriptstyle{\color{blue}{\sum_{i=1}^{13} i=1+\ldots+13=\left[\left(\frac{1}{2}\sdot13\right)+\frac{1}{2}\right]\sdot13=\left[\left(6+\frac{1}{2}\right)+\frac{1}{2}\right]\sdot13=7\sdot13=91}}](/mediawiki/images/math/9/c/e/9ceefc6ebbbdf0e0aca92452d5ae2149.png)
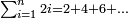
![\scriptstyle{\color{OliveGreen}{\sum_{i=1}^n 2i=2+4+6+\ldots=\left(\frac{1}{2}\sdot2n\right)\sdot\left[\left(\frac{1}{2}\sdot2n\right)+1\right]}}](/mediawiki/images/math/4/6/5/46562373a940e541186c824ae9e20dc4.png)
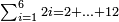
![\scriptstyle{\color{blue}{\sum_{i=1}^6 2i=2+\ldots+12=\left(\frac{1}{2}\sdot12\right)\sdot\left[\left(\frac{1}{2}\sdot12\right)+1\right]=6\sdot\left(6+1\right)=6\sdot7=42}}](/mediawiki/images/math/9/7/8/978a671a457a4cc584dd6a7ba9ad5c41.png)
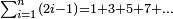
![\scriptstyle{\color{OliveGreen}{\sum_{i=1}^n \left(2i-1\right)=1+3+5+7+\ldots=\left[\left[\frac{1}{2}\sdot\left(2n-1\right)\right]+\frac{1}{2}\right]^2}}](/mediawiki/images/math/b/1/1/b11acf28d1a22904105a43c1759f12be.png)
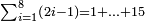
![\scriptstyle{\color{blue}{\sum_{i=1}^8 \left(2i-1\right)=1+\ldots+15=\left[\left(\frac{1}{2}\sdot15\right)+\frac{1}{2}\right]^2=\left[\left(7+\frac{1}{2}\right)+\frac{1}{2}\right]^2=8^2=64}}](/mediawiki/images/math/b/1/4/b14585548b5c68a04f29b88716c0bc65.png)
![\scriptstyle{\color{OliveGreen}{a<b<10\longrightarrow a\times b=\left(10\sdot a\right)-\left[\left(10-b\right)\sdot a\right]}}](/mediawiki/images/math/c/4/e/c4e13c6db94fb5af58a38511245c7d66.png)
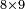
![\scriptstyle{\color{blue}{8<9<10\longrightarrow8\times9=\left(10\sdot8\right)-\left[\left(10-9\right)\sdot8\right]=80-\left(1\sdot8\right)=80-8=72}}](/mediawiki/images/math/a/d/a/ada688c8cf4727a759a5ff8758b8791c.png)
![\scriptstyle{\color{OliveGreen}{a<b<10\longrightarrow a\times b=\left(10\sdot b\right)-\left[\left(10-a\right)\sdot b\right]}}](/mediawiki/images/math/f/d/a/fda2d38c9f0ca67e566915e816849c3b.png)
![\scriptstyle{\color{blue}{8<9<10\longrightarrow8\times9=\left(10\sdot9\right)-\left[\left(10-8\right)\sdot9\right]=90-\left(2\sdot9\right)=72}}](/mediawiki/images/math/1/2/f/12f368ec55a5ad7b76fdc2460670353e.png)
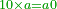
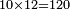
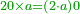
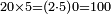
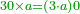
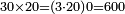
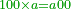
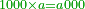
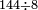
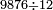








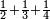
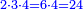
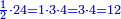
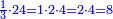
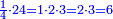
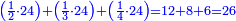
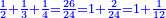
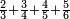

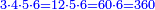
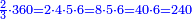
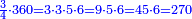
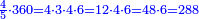
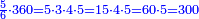
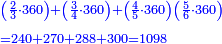
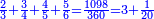
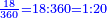

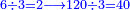
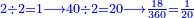
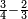



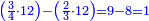
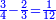
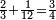
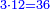
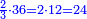
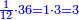
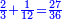
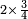
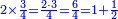
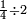
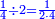
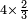

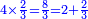
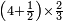

![\scriptstyle{\color{blue}{\left[\left(4\sdot2\right)+1\right]\sdot2=\left(8+1\right)\sdot2=9\sdot2=18}}](/mediawiki/images/math/f/6/7/f6776cd569ed49e4aa40be43566a259b.png)
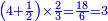
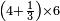
![\scriptstyle{\color{blue}{\left[\left(4\sdot3\right)+1\right]\sdot6=\left(12+1\right)\sdot6=13\sdot6=78}}](/mediawiki/images/math/1/d/9/1d9b723c3e6844776f2e70d9c40e3d4c.png)
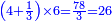
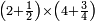
![\scriptstyle{\color{blue}{\left[\left(4\sdot4\right)+3\right]\sdot\left[\left(2\sdot2\right)+1\right]=\left(16+3\right)\sdot\left(4+1\right)=19\sdot5=95}}](/mediawiki/images/math/b/2/f/b2f0b8a3dfc87ea96c0d2ca487f51a03.png)
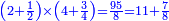
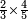
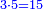
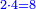
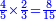
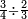

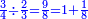
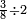
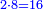
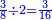
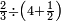
![\scriptstyle{\color{blue}{\left[\left(4\sdot2\right)+1\right]\sdot3=\left(8+1\right)\sdot3=9\sdot3=27}}](/mediawiki/images/math/e/8/e/e8e4a046900922c7247cf2a2064e18a7.png)

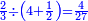
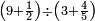
![\scriptstyle{\color{blue}{\left[\left(5\sdot3\right)+4\right]\sdot2=\left(15+4\right)\sdot2=19\sdot2=38}}](/mediawiki/images/math/5/a/2/5a22144368ac484b03473dc5faaf74b3.png)
![\scriptstyle{\color{blue}{\left[\left(9\sdot2\right)+1\right]\sdot5=\left(18+1\right)\sdot5=19\sdot5=95}}](/mediawiki/images/math/8/2/1/82111221272aefe0d07464888b030a03.png)
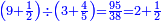
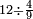
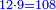
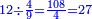
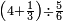

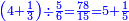
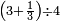
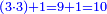
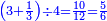
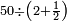
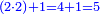

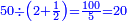
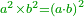
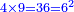
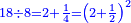
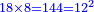
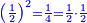
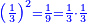
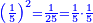
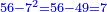
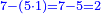
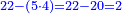
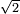

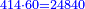
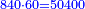
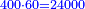

![\scriptstyle{\color{blue}{2^3=2\sdot2^2=2\sdot4=8\longrightarrow\sqrt[3]{8}=2}}](/mediawiki/images/math/a/4/7/a479e56d0ba8e2b21b2a06a055dff0a9.png)
![\scriptstyle{\color{blue}{3^3=3\sdot3^2=3\sdot9=27\longrightarrow\sqrt[3]{27}=3}}](/mediawiki/images/math/c/4/1/c4192879f2aa58718e575cabcfb4515d.png)
![\scriptstyle{\color{blue}{10^3=10\sdot10^2=10\sdot100=1000\longrightarrow\sqrt[3]{1000}=10}}](/mediawiki/images/math/2/5/0/2506e03a640325325cb053de3cb41986.png)
![\scriptstyle\sqrt[3]{12167}](/mediawiki/images/math/a/b/c/abc38f531fb13e4a1ec9492e6194fa3a.png)
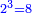


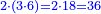

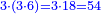

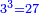
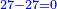
![\scriptstyle\longrightarrow{\color{Violet}{the\ result\ \sqrt[3]{12167}=23}}](/mediawiki/images/math/5/4/5/545f29847e0149872f407d5a9d9b295d.png)
![\scriptstyle\sqrt[3]{571787}](/mediawiki/images/math/3/e/8/3e8cc95dfa131c676806e901de31e5fc.png)
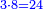

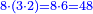

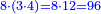
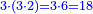
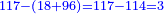
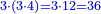

![\scriptstyle\longrightarrow{\color{Violet}{the\ result\ \sqrt[3]{571787}=83}}](/mediawiki/images/math/c/b/4/cb4c1436cb7a06ebcd99307287954f67.png)
![\scriptstyle\sqrt[3]{12812904}](/mediawiki/images/math/0/7/a/07aafd0c5fd061d54bb34d4011050183.png)

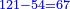
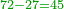
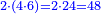

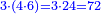
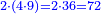
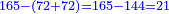
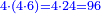
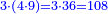
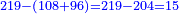
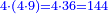
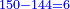
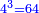

![\scriptstyle\xrightarrow{\begin{align}&\scriptstyle{\color{red}{64-\left(2\times6\times{\color{blue}{4}}\right)=64-\left(2\sdot24\right)=64-48=}}{\color{green}{16}}\\&\scriptstyle{\color{red}{165-\left[\left(3\times6\times{\color{blue}{4}}\right)+\left(2\times9\times{\color{blue}{4}}\right)\right]=}}\\&\scriptstyle{\color{red}{165-\left[\left(3\sdot24\right)+\left(2\sdot36\right)\right]=}}\\&\scriptstyle{\color{red}{165-\left(72+72\right)=165-144=}}{\color{green}{21}}\\&\scriptstyle{\color{red}{219-\left[\left(4\times6\times{\color{blue}{4}}\right)+\left(3\times9\times{\color{blue}{4}}\right)\right]=}}\\&\scriptstyle{\color{red}{219-\left[\left(4\sdot24\right)+\left(3\sdot36\right)\right]=}}\\&\scriptstyle{\color{red}{219-\left(96+108\right)=219-204=}}{\color{green}{15}}\\&\scriptstyle{\color{red}{150-\left(4\times9\times{\color{blue}{4}}\right)=150-\left(4\sdot36\right)=150-144=}}{\color{green}{6}}\\&\scriptstyle{\color{red}{64-{\color{blue}{4}}^3=64-64=}}{\color{green}{0}}\\\end{align}}](/mediawiki/images/math/e/b/e/ebe0f4df388bc732084130a719026f81.png)
![\scriptstyle\longrightarrow{\color{Violet}{the\ result\ \sqrt[3]{12812904}=234}}](/mediawiki/images/math/7/b/1/7b16bd7f1fdac314a617c85aee43a714.png)
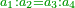
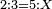
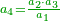
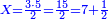
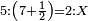
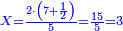
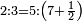
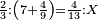
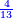

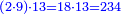
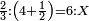
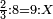
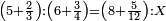
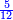
![\scriptstyle{\color{blue}{\left[\left[\left(5\sdot3\right)+2\right]\sdot4\right]\sdot12=\left[\left(15+2\right)\sdot4\right]\sdot12=\left(17\sdot4\right)\sdot12=68\sdot12=816}}](/mediawiki/images/math/b/e/6/be6fd06595fca39aacff31a9abeeba9f.png)
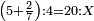


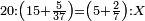
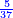
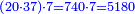
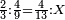
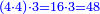
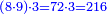
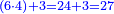
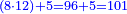
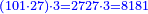
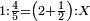
![\scriptstyle{\color{blue}{\left[\left(2\sdot2\right)+1\right]\sdot4=\left(4+1\right)\sdot4=5\sdot4=20}}](/mediawiki/images/math/9/4/3/9438da687c558cf44b88afb73ca06ee9.png)
![\scriptstyle{\color{blue}{\left[\left[\left(4\sdot2\right)+1\right]\sdot6\right]\sdot3=\left[\left(8+1\right)\sdot6\right]\sdot3=\left(9\sdot6\right)\sdot3=54\sdot3=162}}](/mediawiki/images/math/5/8/e/58ef7f28670af1c26a23f2c27ed973e1.png)
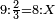

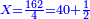

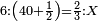
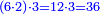
![\scriptstyle{\color{blue}{\left[\left(40\sdot2\right)+1\right]\sdot2=\left(80+1\right)\sdot2=81\sdot2=162}}](/mediawiki/images/math/b/e/b/bebc782632c636f73d7f310f70b46727.png)
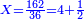
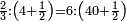
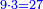
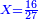
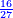
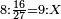
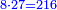
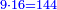
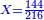
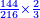
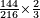
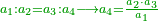
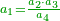
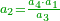
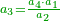
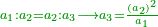
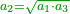
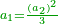
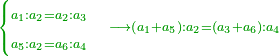
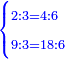
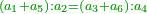

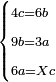
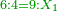
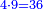
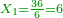
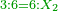
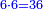
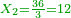
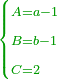
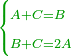
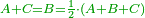
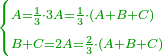
![\scriptstyle{\color{OliveGreen}{C=\left(A+C\right)-A=\left[\frac{1}{2}\sdot\left(A+B+C\right)\right]-\left[\frac{1}{3}\sdot\left(A+B+C\right)\right]=\left(\frac{1}{2}-\frac{1}{3}\right)\sdot\left(A+B+C\right)=\frac{1}{6}\sdot\left(A+B+C\right)}}](/mediawiki/images/math/4/6/3/463f8003a0a182c44dba4a0f25164ab0.png)
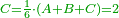
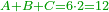
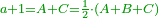
![\scriptstyle{\color{OliveGreen}{a=\left[\frac{1}{2}\sdot\left(A+B+C\right)\right]-1=\left(\frac{1}{2}\sdot12\right)-1=5}}](/mediawiki/images/math/f/3/2/f32487f42bca7d991cbc5e65d30b035c.png)
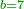
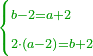
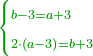
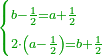
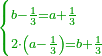
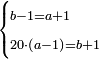
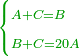
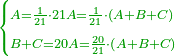
![\scriptstyle{\color{OliveGreen}{C=\left(A+C\right)-A=\left[\frac{1}{2}\sdot\left(A+B+C\right)\right]-\left[\frac{1}{21}\sdot\left(A+B+C\right)\right]=\left(\frac{1}{2}-\frac{1}{21}\right)\sdot\left(A+B+C\right)=\frac{19}{42}\sdot\left(A+B+C\right)}}](/mediawiki/images/math/d/4/0/d4030b405f86d3053694c108ef5e46cc.png)
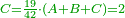
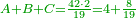
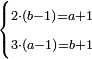
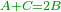
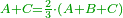
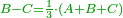
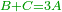
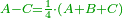
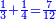
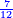
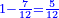
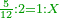
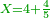

![\scriptstyle{\color{OliveGreen}{B=\left[\frac{1}{3}\sdot\left(4+\frac{4}{5}\right)\right]+1=\left(1+\frac{3}{5}\right)+1=2+\frac{3}{5}}}](/mediawiki/images/math/e/6/b/e6b2ae34ebee80867e7a5bb9cdbbdae0.png)

![\scriptstyle{\color{OliveGreen}{A=\left[\frac{1}{4}\sdot\left(4+\frac{4}{5}\right)\right]+1=\left(1+\frac{1}{5}\right)+1=2+\frac{1}{5}}}](/mediawiki/images/math/a/2/5/a259ab0229cdbeb8e4122bb7f1be987c.png)
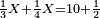
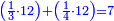
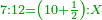
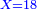
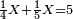
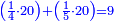
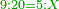

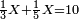
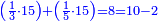
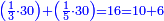
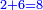
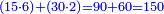
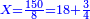
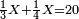
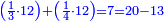
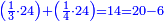
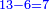
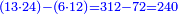
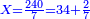
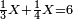
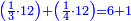
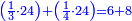
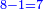
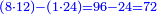
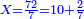

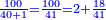
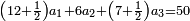
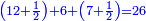
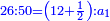
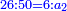
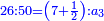
![\scriptstyle2\sdot\left[\left[2\sdot\left(2X-12\right)\right]-12\right]=12](/mediawiki/images/math/2/e/6/2e6830e9068e310a2b310a61c4dc1e73.png)
![\scriptstyle{\color{blue}{X=\frac{1}{2}\sdot\left[12+\frac{1}{2}\sdot\left[12+\left(\frac{1}{2}\sdot12\right)\right]\right]=\frac{1}{2}\sdot\left[12+\left(\frac{1}{2}\sdot18\right)\right]=\frac{1}{2}\sdot\left(12+9\right)=\frac{1}{2}\sdot21=10+\frac{1}{2}}}](/mediawiki/images/math/9/d/8/9d8de09042556dbb485afef4438987c0.png)
![\scriptstyle\left[\left[X-\left(\frac{1}{2}X+1\right)\right]-\left[\left[\frac{1}{2}\sdot\left[X-\left(\frac{1}{2}X+1\right)\right]\right]+1\right]\right]-\left[\left[\frac{1}{2}\sdot\left[\left[X-\left(\frac{1}{2}X+1\right)\right]-\left[\left[\frac{1}{2}\sdot\left[X-\left(\frac{1}{2}X+1\right)\right]\right]+1\right]\right]\right]+1\right]=1](/mediawiki/images/math/b/5/0/b50e38940b92660b687bec29a547c334.png)
![\scriptstyle{\color{blue}{X=2\sdot\left[1+\left[2\sdot\left[1+\left[2\sdot\left(1+1\right)\right]\right]\right]\right]=2\sdot\left[1+\left[2\sdot\left[1+\left(2\sdot2\right)\right]\right]\right]=2\sdot\left[1+\left(2\sdot5\right)\right]=2\sdot\left(1+10\right)=2\sdot11=22}}](/mediawiki/images/math/b/1/f/b1fdc3f3dead1be033d0f81777d572c9.png)