Difference between revisions of "האנציקלופדיה של אבו אלצלת"
From mispar
(→Proportions) |
|||
| Line 5,103: | Line 5,103: | ||
|- | |- | ||
|It is known in this investigation that the geometric relations are added three by three in the gradual progress of the successive "other" with the successive squares. | |It is known in this investigation that the geometric relations are added three by three in the gradual progress of the successive "other" with the successive squares. | ||
| − | |style="text-align:right;"|וידעת כי בזאת החקירה שאלו ההתיחסויות התשברתיות יתחברו שלשה שלשה בהדרגת הזולתיים הנמשכים עם המרבעים הנמשכי' | + | |style="text-align:right;"|וידעת כי בזאת החקירה שאלו {{#annot:term|2097,1770|SC4F}}ההתיחסויות התשברתיות{{#annotend:SC4F}} יתחברו שלשה שלשה בהדרגת הזולתיים הנמשכים עם המרבעים הנמשכי' |
|- | |- | ||
|You know from other places that every two squares may apply these properties. | |You know from other places that every two squares may apply these properties. | ||
| Line 5,720: | Line 5,720: | ||
|- | |- | ||
|Yet, the most beneficial among them in the sciences are mostly only three, which are the arithmetic, the geometric, and the harmonic proportions. | |Yet, the most beneficial among them in the sciences are mostly only three, which are the arithmetic, the geometric, and the harmonic proportions. | ||
| − | |style="text-align:right;"|והמועילים בהם בחכמות על הרוב שלשה לבד והם המתיחסים המספריי' | + | |style="text-align:right;"|והמועילים בהם בחכמות על הרוב שלשה לבד והם המתיחסים המספריי' ו{{#annot:term|2097,1770|ix2l}}התשברתיים{{#annotend:ix2l}} והחבוריים |
|- | |- | ||
|First we will deal with the mentioning of these, then the mentioning of the others among the first ten types will follow. | |First we will deal with the mentioning of these, then the mentioning of the others among the first ten types will follow. | ||
| Line 5,828: | Line 5,828: | ||
| | | | ||
*The geometric proportion: the ratio between the terms is one, but the differences differ as the diversity of the numbers. | *The geometric proportion: the ratio between the terms is one, but the differences differ as the diversity of the numbers. | ||
| − | |style="text-align:right;"|ואולם המתיחסי' התשברתיים הם אשר יהיה היחס אשר בין גבוליהם אחד והמותרות מתחלפות בחלוף המספריים | + | |style="text-align:right;"|ואולם {{#annot:term|2097,1770|Fvij}}המתיחסי' התשברתיים{{#annotend:Fvij}} הם אשר יהיה היחס אשר בין גבוליהם אחד והמותרות מתחלפות בחלוף המספריים |
|- | |- | ||
| | | | ||
Revision as of 06:15, 6 September 2021
Contents
[hide]- 1 Book One
- 2 Book Two
- 3 Music
- 4 Notes
- 5 Appendix: Bibliography
| The Book of Nicomachus on the Numerical Properties | ספר ניקומאכוש בסגלות המספריות |
| Don Benveniste b. Lavi, may his soul rest in heaven, translated it from Arabic to the holy language in the year 195 of creation. | העתיקו בסרגוסא דארגו' השר דון בנבשת בן לביא נ"ע מלשון הגרי ללשון הקדש שנת קצ"ה ליצירה |
| In any place where A"B is written in the work, it means: Benveniste said. | ובכל מקום הכתוב בגיליון א"ב ר"ל אמר בן בנשתי' |
Book One |
|
Introduction - Basic Definitions |
|
|
חכמת המספר חכמה עיונית נושאה המספר המשולח אליו ומיניו והכונה בה העמידה על משיגיו ועל המתחייב אליו וסגלותיו ובכלל מקריו העצמיים |
|
ומהות המספר הנה תאמר המספר קבוץ אחדים וגדרו שהוא כמות מתחלק מתקיים מאחדים |
|
ויש לוקחין האחדותיות תמורת האחדים לפי שהוא יותר מורה על טבע המספר, לפי שקבוץ האחדים אינו המספר עצמו המכוון הנה תאמו וגדרו ובכלל הודעת מהותו אבל הנספרים אשר הם נושאי המספר כקבוץ מהאנשים או מהסוסי' או זולת זה |
|
וקבוץ האחדותיות הוא המספר עצמו המקובץ מהכפלת האחדות אשר בה יאמ' לכל דבר מהנספרים אחד |
|
והמספר המשולח יתחלק ראשנה לשני מינים זוג ונפרד |
|
והזוג הוא כל מספר שיתחלק לשני חלקים שוים כשנים וארבע |
|
והנפרד הוא כל מספר שא"א שיחלק לשני חלקים שוים |
| Our intention is to add the known way of arithmetic to the mathematical science that we have prefaced and what is customary to bring concerning it according to the way that was spread from the Book of Elements that presented many principles in arithmetic, and establishing this way by the realization of this principles. | כונתינו שנחבר אל מה שהקדמנו מהחכמות הלמודיות האופן הידוע בארתימטיקי ומה שפשט המנהג להביאו בו כפי האופן אשר פשט על ספר היסודות כבר נתן שרשים רבים בחכמת המספר והנחת זה האופן אצל ההגעה באותם השרשים |
| Many of the geometric shapes that have relation with the multiplication, division and ratio, may be related to the number and the rules of number of this book may be established upon them. | וכבר אפשר שתתחברנה הרבה מהתמונות התשברתיות אשר להם התלות בהכאה והחלוק ובענייני היחס אל המספר ושתישבו ממנו משפטי המספר זה הספר והנה זה אליך |
| As for the essence of the number - some of it is already known in the Book of Categories and a hint about it was alluded in the Book of Elements, also in metaphysics one reaches to truths about it. | אמנם מהות המספר הנה כבר ידעת בספר קאטיגוריאש ממנו דבר מה ונרמז לך בספר היסודות אליו רמז עוד יבא אליך בחכמה העליונה ממנו אמתות |
| Likewise for its two parts, which are the even number and the odd number. | וכמו כן הענין בשני חלקיו אשר הם הזוג והנפרד |
| You already know the absolute prime, the absolute composite, and the relative composite from the Book of Element. | וכבר ידעת מספר היסודות הראשון והמורכב מוחלטים והמורכב בצרוף |
| You know the even and the odd, the even-times-odd, the even-times-even, and the even-times-even-times-odd, as well as the deficient number, the perfect number and the superabundant number. | וידעת הזוג והנפרד וזוג הנפרד וזוג הזוג וזוג הזוג והנפרד וידעת המספר החסר והשלם והנוסף |
| We are not obligated to simplify [?] the mentioning of these matters for you, but we will endeavor to present the properties to you. | ואיננו מחוייב אלינו הפשת זכרון אלה העניינים לך אבל שנשתדל להביא הסגלות אליך |
Properties of the Absolute Number |
|
| Mentioning the properties of the absolute number: | ונזכור סגלות המספר המשולח |
|
והנה ראשנה שבהם והיותר מפורסמת שכל מספר הנה הוא חצי שתי פאותיו והם שני המספרים הנלוים אליו מצד המעוט והרבוי במרחק שוה |
|
המשל בזה החמשה הנה הוא חצי ששה וארבעה וחצי שבעה ושלשה וחצי שמנה ושנים וחצי תשעה ואחד |
|
והנה יהיה כפלו שוה לשתי פאותיו |
|
וחציו לרביעית שתי פאותיו |
|
וכל מספר יהיה מרובעו שוה להכאת שתי פאותיו הקרובות אחת מהם באחרת עם תוספת אחד |
|
כמו מרובע שנים אשר הוא מהכאת שלשה באחד ותוספת אחד |
|
|
וכמו מרובע שלשה אשר הוא מהכאת ארבעה בשנים ותוספת אחד |
|
|
וכמו מרובע ארבעה אשר הוא מהכאת ג' בחמשה ותוספת אחד |
|
וגם נאמר שכל מספר הנה מרובעו יוסיף על מושטח שתי פאותיו הרחוקות מרחק שוה תהיינה מה שתהיינה אחת מהם באחרת כמרובע מספר המדרגות אשר ביניהם |
| ? | והנה אם תהיינה השתי פאות הקרובות והנה המדרגה היא הראשונה יוסיף כמרובע שלשה |
|
וכל מספר הנה מרחקו במדרגות מכפלו אם כשתקח אותו ראשון למדרגות הנה הוא כמו מספרו ותוספת אחד |
|
ואם כשתקח ראשית המדרגות המספר הנלוה אחריו הנה הוא כמספר מה שבו מן האחדים |
|
המשל בזה שבין ארבעה ושמנה |
|
לפעמים ד' ה' ו' ז' ח' והנה זה חמשה |
|
ולפעמים ה' ו' ז' ח' וזה כמו מספר מה שבו מן האחדים |
|
וכל מספר מרחקו משלשה כפליו הנה הוא בכמו שיעור אחדיו מוכים בשנים |
|
אם בתוספת אחד |
|
אם בזולת תוספת אחד כפי מה שידעת אותו |
|
כמו השנים אשר מרחקם מו' שהוא ג' דמיוניו הוא כמספר הכאתו בשנים בתוספת ובזולת תוספת |
|
וכל מספר מרחקו מד' כפליו הוא כהכאתו בג' מהמספר בתוספת |
|
ובזולת תוספת |
|
|
ובכלל הנה המרחק בכל מקום הוא שנגרע מקריאת הכפלים אחד ונכה המספר במה שנשאר ואח"כ נוסיף או לא נוסיף |
|
|
וכל מספר הנה מרחקו במרובעו בשעור הכאתו במספר אשר לפניו בתוספת אחד או בזולת תוספת |
|
כמו הכאת השנים באחד אשר הוא מרחקו ממרובעו כשלא נוסיף |
|
|
והכאת השלשה בשנים אשר הוא מרחק השלשה ממרובעו בשלא נוסיף |
|
וכמו כן כל מספר הנה מרובעו שוה להכאתו בתוספת אחד במספר אשר לפניו ותוספת אחד |
|
כמו מרובע השנים אשר הוא שוה להכאת השלשה באחד ותוספת אחד |
|
|
ומרובע השלשה אשר הוא שוה להכאת הארבעה בשנים ותוספת אחד |
|
וכל מספר הנה מרחקו מהכאתו במספר אשר לפניו הוא כמו מרבע המספר אשר לפניו כשלא יתוסף |
|
המשל בזה שמרחק השלשה מהכאתו בשלשה הוא כמו מספר מרבע השנים |
|
|
ומרחק הארבעה מהכאתו בשלשה הוא כמו מספר מרבע שלשה רצוני בזה כשלא יתוסף |
|
וכל מספר הנה מרחקו מהכאתו במספר אשר אחריו כמו מספר מרובעו |
|
וכל מספר הנה מרחקו ממעוקבו הוא כמו הנשאר ממעקבו אחר שיהיה בגרע ממנו |
|
כי בין השנים ומעקבו ששה וכמו בין מאלו והלאה עד אין תכלית |
|
וכל מספר הנה בינו ובין מעקבו מהמדרגות כמו הכאתו באשר ימשך אליו אחר כן הכאת זה כלו באשר לפניו |
|
כמו שנים בג' אחר כן באחד |
|
|
ושלשה בארבעה אחר כן בשנים |
|
|
וכל מספר הנה בינו ובין העולה מהכאתו הנקרא בערבי מאל מאלה כמו הכאת מרבעו מחובר אל המספר הנמשך לזה המספר במה שעלה מהכאתו עם המספר אשר לפניו |
|
כמו שבין מאל מאלה של שנים ושנים הוא י"ד ויתחדש מהכאת מרבע שנים מחובר עם שלשה שהוא ז' בהכאת שנים באחד |
| וכמו כן מה שימשך והנה מה שנתקבץ בזה ונשוב אל בחינת סגלות המספרים הנמשכים | |
|
|
וכל מספר מרבעו כאשר נכפל ונוסף עליו שנים הנה הוא שוה למקובץ שני מרובעי פאותיו הקרובות |
|
המשל בזה פי' הכאת עשרה בעצמו בתוספת שנים והוא מאתים ושנים הנה הוא שוה להכאת תשעה בעצמו והוא שמנים ואחד ולהכאת אחד עשר בעצמו והוא מאה ועשרים ואחד |
|
וכל מספר הנה מרובעו כאשר יכפל ויתוסף עליו שמנה הוא שוה למקובץ שני מרובעי שתי פאותיו השניות |
|
המשל בזה עשרה אשר מרובעו כשיעשה בו זה יהיה מאתים ושמנה והוא שוה להכאת שמנה בעצמו |
|
וכל מספר אשר יכפל מרובעו ויתוסף עליו שמנה עשר הנה יהיה שוה לשני מרבעי פאותיו השלישיות |
|
המשל בזה מאתים ושמנה עשר אשר הוא שוה להכאת שבעה בעצמו ושלשה עשר בעצמו |
|
ואמנם בשתי פאות הרביעיות הנה התוספת שנים ושלשי' |
|
ובשתי פאות החמישיות חמשים |
|
והסדר בזה שהתוספת הראשון הוא הכאת הזוג הראשון והוא שנים בנפרד הראשון והוא האחד |
|
והתוספת השני על זה התוספת הוא הכאת הזוג הראשון בנפרד אשר ימשך אל האחד והוא שלשה |
|
והתוספת השלישית על אלו התוספות המקובצות הוא הכאת שנים בנפרד השלישי אחר האחד |
|
|
וכמו כן כל מספר הנה מרובעו כאשר יכפל ויתוסף עליו ד' שוה לשני שטחי פאותיו היורדות ושתי פאותיו העולות כאשר יקובצו |
|
המשל בזה מאתים וארבעה אשר הוא שוה להכאת תשעה בשמנה ואחד עשר בשנים עשר |
|
|
ואמנם המושטחים הנמשכים לשני אלו מהכאת הפאה היורדת השנית ביורדת השלישית והעולה שנית בעולה שלישית הנה יוסיפו על כפל זה בשנים עשר |
|
|
ואשר ימשכו להם בעשרים וארבעה |
|
|
ואשר ימשכו להם בארבעים |
|
והסדר בזה שנכה התוספת הראשון בזוג הראשון ויהיה שמנה ותוסיפם |
|
אח"כ [ת]כה אותו במספר אשר ימשך אליו והוא שלשה ויהיה שנים עשר ותוסיף אותם |
|
אח"כ נכה אותו במספר אשר ימשך אליו והוא ארבעה והנה יהיה ששה עשר ותוסיף אותם |
|
|
וכל מספר הנה כפל מרבעו כאשר יתוסף עליו ששה הוא שוה למושטח פאתו היורדת הקרובה בפאתו היורדת השלישית ולמושטח פאתו העולה הקרובה בפאתו העולה השלישית |
|
המשל בזה מאתים וששה אשר הוא שוה להכאת תשעה בשבעה ואחד עשר בשלשה עשר |
|
|
וכאשר תכה הקרובה אשר בשני צדדיו ברביעית יהיה התוספת שמנה ולא יסורו התוספות להשתנות בשנים שנים |
|
|
[1]כל מספר הנה כפל מרובעו כאשר יתוסף עליו ששה עשר יהיה שוה למשטח הפאה השנית היורדת ברביעית היורדת והשנית העולה ברביעית העולה |
|
המשל בזה מקובץ מושטחי שמנה בששה ושנים עשר בארבעה עשריו הנה זה מאתים וששה עשר |
|
|
וכאשר תכה השניות בחמישיות יהיה התוספת עשרים |
|
|
ואם תכה אותם בששיות יהיה התוספת עשרים וארבעה וכזה ילכו בהדרגה בהעדפת ארבעה ארבעה |
|
|
ואם תהיינה השתי פאות השלישיות הכאה ראשונה בחמישיות יהיה התוספת שלשים שלשים |
|
|
וכאשר תכה אותם בששיות יהיה התוספות שלשים וששה |
|
|
ואם תכה אותם בשביעיות יהיה התוספות שנים וארבעים ולא יסורו התוספות מלכת בהדרגה ששה ששה ועל זה הסדר במה שאחר זה מהפאות |
Arithmetic Progression |
|
| ונתחיל אליך בסגלות המספרים הנמשכים המשכם הטבעי | |
| [The number of] their terms is necessarily either odd or even. | ונאמר שמדרגותיהם הם לא ימלט אם שתהיינה נפרד ואם שתהיינה זוג |
|
ואם תהיינה נפרד ימצא להם אמצעי בלי ספק |
|
וזה האמצעי יהיה תמיד חצי שתי הפיאות מקובצות |
|
ורצוני בשתי פאות שני מספרים או מספר אחד מרחקם בסדר מהאמצעי מרחק שוה אחד מהם מצד החסרון והאחר מצד התוספת |
|
כמו התשעה והאחד אשר הם שתי פאות החמשה וחמשה חצי מקובצם |
|
והוא ג"כ חצי השמנה והשנים אשר הם ג"כ שתי פאותיו |
|
וחצי השבעה והשלשה |
|
והששה והארבעה |
|
והיותר הרחוקות התשעה והאחד |
|
וכל מספר הוא אמצעי הנה הוא חצים |
|
ואם תהיינה המדרגות זוג עד שיהיו תמורת האמצעי האחד שני אמצעיים יחד |
|
הנה יהיו שני האמצעיים מקובצים כמו השתי פאות מקובצות תהיינה מה שתהיינה |
|
המשל בזה הארבעה והחמשה בין האחד והשמנה הנה הם מקובצים שוים לאחד ושמנה ולשנים ושבעה ולשלשה וששה |
It follows necessary from this rule that the [sum of] every two sides of a number is equal to the [sum of] the other corresponding [sides]. 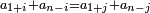
|
ויתחיב מכלל זה שתהיינה כל שתי פאות למספר מה שוות אל האחרות אשר בגילם |
Sums |
|
|
ומהמסגלות הנתלות בקבוץ בעלי המדרגות שאנחנו כאשר נוסיף על הגעת המספר האחרון המתחיל מן האחד אחד ונכה אותו בחצי מספר האחרון המדרגות יהיה העולה שוה לכלל כלם |
|
המשל בזה שיהיה ארבעה הוא האחרונה שבמדרגות |
|
|
והנה אתה כשתוסיף אחד על הארבעה ויהיו חמשה ותכה בחצי מספר המדרגות שהם ארבעה וחציו שנים יהיה העולה עשרה מקובץ מה שבין האחד עד הארבעה |
|
ואם תרצה מן האחד עד החמשה |
|
|
תוסיף על החמשה אחד ויהיו ששה בחצי מספר המדרגו' שהוא שנים וחצי ויהיה העולה חמשה עשר |
|
וגם כן הנה מקובץ כל שתי קצוות מבעלי הדרגה וסדר הן שתהיינה מן האחד או מן זולתו כאשר הוכה בחצי המדרגות או הוכה חציו בכל המדרגות הנה יהיה מה שיתקבץ כמו כלל מקובץ אותם המדרגות |
|
והנה תהיינה הראשונה שבמדרגות שנים והאחרונה ששה |
|
|
ונקבץ אותם ויהיו שמנה ונכה אותם בחצי מספר המדרגו' והוא שנים וחצי והנה הוא עשרים |
|
|
או נכה חצים במספר המדרגות על השלמות ויהיה ארבעה בחמשה וזה עשרים והוא שוה למקובץ שנים ושלשה ארבעה חמשה ששה |
|
ומהסגלות הנתלות בקבוץ שכל מספרים נמשכים ולא ימשך התוספת באחדים אבל על דרך השניות או השלישיות או זולת זה כל עוד שיהיו הולכים על הדרגה ומנהג אחד ותהיה תחילתם איך שתהיה הנה הכאת מספר המדרגות מחוסר ממנו אחד במספר אשר יפול בו ההעדף כמו השניות או השלישיות או זולת זה ממה שיעדיפו בו המדרגות מוסף עליו אשר ממנו ההתחלה הוא שוה למספר האחרון |
|
ואם יתוסף פעם אחרת והוכה במספר המדרגות כמות שהוא הנה יהיה כמו כפל כלל המקובץ |
|
המשל בזה אלו אמר לך אומר חמשה מספרים נמשכים מתחילים מן הארבעה ובין כל שני מספרים שלשה בענין שיהיה ההעדף בארבעה ארבעה מה הוא האחרון שבהם וכמה מקובצם |
|
|
הנה כשתגרע אחד מן החמשה עד שיגיע לך ארבעה ותכה אותו במספר ההעדף והוא ארבעה יהיה ששה עשר וכאשר תוסיף עליו הראשון שבהם יהיה עשרים והנה כבר יצא לך המספר האחרון |
|
לפי שמדרגות המספרי' תהיינה ארבעה אח"כ שמנה אח"כ שנים עשר אח"כ ששה עשר אח"כ עשרים |
|
|
והנה כאשר תוסיף על עשרים ארבעה ג"כ יהיה ארבעה ועשרים ואם תרצה תכה אותו בחמשה ויהיה מאה ועשרים והנה תקח חציו והוא מקובץ המדרגות |
|
ואם תרצה תכה חציו במדרגות או כלו בחצי המדרגות שיעשה הנה הוא תשובת השאלה |
|
ומהסגלות הנתלות בקבוץ שכל מספרים נמשכים מתחילים מן האחד כאשר קובצו מתחילים מן האחד עד האחרון שבהם ואחרי כן דרך חזרה מן האחרון שבהם אל האחד כמו אחד שנים שלשה ארבעה שלשה שנים אחד הנה מקובצם שוה למרובע המספר האחרון |
|
כי מקובץ מה שהמשלנו בו ששה עשר |
|
והנה יגיע זה לפי שמקובץ כפל המספרים אשר תחת הנמשכים האחרונים עם אשר במדרגה האחרונה שוה למרובע המספר האחרון |
|
ומהסגלות הנתלות בקבוץ שאתה כאשר תקבץ מספרים נמשכים מן האחד הנה המקובץ הראשון דמיון וחצי המספר האחרון והמקובץ השני כפל המספר האחרון והמקובץ השלישי כפל וחצי המספר האחרון והמקובץ הרביעי שלשה כפלי המספר האחרון והמקובץ החמישי שלשה כפלים וחצי המספר האחרון וכן לבלתי תכלית |
|
המשל בזה אחד ושנים הנה הוא דמיון וחצי השנים |
|
|
ואחד ושנים ושלשה הנה הוא כפל השלשה |
|
|
ואחד ושנים ושלשה וארבעה הנה הוא כפל וחצי הארבעה |
|
|
ואחד ושנים ושלשה וארבעה וחמשה וששה הנה הוא שלשה כפלים וחצי ששה |
|
וגם כן הנה כל המספרים הנמשכים יקובצו זה הקבוץ הנה המקובץ הראשון יהיה כמו המספר הנמשך אליו והמקובץ השני דמיון וחצי מהמספר הנמשך אליו והמקובץ השלישי כפל המספר הנמשך אליו וכמו כן אל בלתי תכלית |
|
והמשל בזה בהאחד והשנים כמו השלשה |
|
|
והאחד והשנים והשלשה כמו דמיון וחצי מן הארבעה |
|
|
וכאשר תוסיף הארבעה יהיה כפל חמשה |
|
|
וכאשר תוסיף חמשה יהיה כפל וחצי ששה וכן אל בלתי תכלית |
|
ומהסגלות הנתלות בקבוץ שאתה כאשר תקבץ נפרדים נמשכים מתחילים מן האחד ותקבץ אחריהם זוגות נמשכים מן השנים כמספרם הנה המקובץ הראשון מהזוגות יהיה דמיון וחצי המקובץ הראשון מהנפרדים והמקובץ השני דמיון ושלישיתו והמקובץ השלישי דמיון ורביעיתו ויהיה כל מקובץ יוסיף בחלק נקרא על שם מספר מדרגתו ויהיה מספרו מספר מדרגתו |
|
המשל בזה השנים והארבעה הנה יוסיף על האחד והשלשה החצי |
|
|
וכאשר תוסיף בזה ששה ובזה חמשה יהיה זה דמיון ושליש זה |
Types of Numbers |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Returning to the presentation of the properties of the first categorization of the number from the aspect of the quality of its divisibility to equals and unequals, which are the even and the odd. | ונשוב עתה אל הבאת סגלות החלוקה הראשונה מהמספר מצד איכות החלקו אל שוים ובלתי שוים והוא הזוג והנפרד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| What was discussed concerning it in the book of the Elements will also be presented. | ועוד נביא מה שדובר בו בספר היסודות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The natural successive odds and evens are subject to association acquired from their type: | וכבר יפול ביניהם שתוף נקנה מסוגם במה שימשך מהנפרדים והזוגו' המשכות טבעי המשכות מיני המספר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The terms exceed by one excess | וזה כלו שתהיינה המדרגות עודפות בהעדף אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אם העדף ההמשכות הטבעי למיני המספר הנה באחד אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם העדף הנפרדים והזוגות הנמשכים בטבע הנה בשנים שנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
לפי שכל נפרד כאשר יתוסף עליו אחד יהיה זוג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אחר כן כשיתוסף עליו אחד אחד יהיה נפרד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אח"כ כשיתוסף עליו אחד יהיה זוג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויהיה בין הנפרד והנפרד אשר ילוה אליו שנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ובין הזוג והזוג אשר ילוה אליו שנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויחויב שיהיה כל אמצעי במדרגות הנפרדים אשר על ההמשך הטבעי ומדרגות הזוגות אשר על זה ההמשך כמו חצי מקובץ איזה שתי פאות שתהיינה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
לפי שהן פאות זה האמצעי בעצמו בסדור הטבעי למספר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכל שני אמצעיים מקובצים כמו כל שתי פאות מקובצות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
לפי שבאלה השני אמצעיים תהיינה שתי פאות למספר הנופל בסדר המספרים הטבעיים ביניהם והנה יחויב שיהיה שוה מקובצם למקובץ אלה שתי הפאות האחרות כפי מה שקדם באורו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואין זה הענין נוהג בין הנפרדים הנמשכים והזוגות הנמשכי' לבד אבל בין כל המספרים העודפים על השווי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ולזה תמצא זאת הסגלה ג"כ בסדר מדרגות מני הנפרד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Thus, this association should be stated before all the properties. | והנה זה ההשתתפות ראוי שנאמר אותו קודם הסגלות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Now, we will concentrate in mentioning the properties | ונתבודד עתה בזכרון הסגלות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Odd Number |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Starting with the properties of the odd number | ונתחיל בסגלות הנפרד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The known and mentioned properties are that it does not consist of evens at all and not from an even number of odd numbers.
|
ונאמר אמנם הסגלות הידועות והנזכרות מאשר הוא לא יתרכב מזוגות כלל ולא מנפרדים במספר זוג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
There is no number of its type in it, whose remainder is of its type
|
ושלא ימצא בו מסוגו מספר ישאיר מה שאחריו מסוגו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
There is no number of its parallel type in it, whose remainder is of its parallel type
|
ושלא ימצא בו מסוג מקבילו מספר ישאיר מה שאחריו מסוג מקבילו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| What is said about whatever is applied to these properties in the book of the Elements is sufficient. | ומה שירוץ מרוצת אלו הסגלות הנה נסתפק במה שנאמר בספר היסודות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Its properties that will be discussed are the properties related to the sequence, their being successive by the way of succession | ונדבר מסגלותיו סגלות נתלות בסדור היותם נמשכים על דרך ההמשך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומסגלותיו שמקובציו על דרך ההמשך מן האחד יהיה מרובע לעולם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו האחד והשלשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ואח"כ האחד והשלשה והחמשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ואח"כ האחד והשלשה והחמשה והשבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומסגלותיו שכל מרבע מאלו הנה צלעו מספר המדרגות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו הארבעה והוא מקובץ שתי המדרגות והנה גדרו שנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והתשעה והוא מקובץ שלשה מדרגות והנה גדרו שלשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומסגלותיו שאתה כשתרצה לדעת הגעת מספר יפול במדרגה ידועה מן האחד כמו העשירית והאחת עשרה דרך משל וזולת זה הנה תכה מספר המדרגה ותהיה העשירית ומספרה שני עשרה בשנים ויהיו עשרים והנה תגרע מהם אחד ויהיו תשעה עשר והנה הוא מספר המדרגה העשירית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואמנם ענין האמצעי והשני אמצעיים עם השתי פאות הנה הוא ממה שידעת אותו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומסגלותיו שכל אחד מן האחדים ישוב בששי ממנו אליו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
המשל בזה שהאחד ישוב בששי והוא האחד עשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ועוד בששי אחר הששי והוא האחד ועשרים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והשלשה ישוב לששי והוא השלשה עשר וכן על הדרך הזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומסגלותיו שכל נפרד ראשון כאשר תוציא קוו על מספרו יכלה אל מורכב ימשכו אליו ראשונים הם חסרי' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו השלשה כי הנה השלישי ממנו והוא תשעה מורכב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והחמשה כי הנה החמישי ממנו והוא חמשה עשר מורכב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וסגלה אחרת שהראשון שבמספרים הבלתי מורכבים והוא שלשה יביא כשתוציא קוו הראשון אל נגדר אחר כן לא יביא[2] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והשני והוא החמשה יביא בהקוות השני אל נגדר אצל עשרים וחמשה אח"כ לא יבוא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועל הדרך הזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וסגלה אחרת שהרביעי אחר הנגדר הראשון והוא אחד נגדר והוא תשעה והשמיני אחר הנגדר הראשון והשנים עשר אחר הנגדר השני והששה עשר אחר הנגדר השלישי וכן בתוספת ארבעה ארבעה[3] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכל בית ומדרגה שתפול בו נגדר הנה תהיה הכאת זה הנגדר שוה לכפל מספר המדרגה מוסף עליו אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כי המספר המרובע הראשון הוא תשעה והוא במדרגה הרביעי' מן המספרים הנפרדים וכפל הארבעה שמנה והנה תוסיף עליו אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והבית השנים עשר מהשלשה יפול בו חמשה ועשרים והוא שוה לכפל שנים עשר כשתוסיף עליו אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| When the natural successive odds are set in a square table, properties are seen from the aspect of the shape. | וכאשר נניח מהנפרדים הנמשכים בטבע לוח מרובע יראו בו סגלות מצד התמונה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Also, when a triangle table is set. | וכן כאשר נניח לוח משלש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונתחיל במרובע ונשים אותו חמשה על חמשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונאמר שכל שתי וערב ממנו יהיה קטר התמונה או לא יהיה הנה מקובץ שני קטריו הם שוים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אם אשר על הקטר הנה מקובץ כל אחד מהשני קטרים אשר בזאת התמונה קכ"ה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם אשר אינם על הקטר הנה כמו השתי וערב אשר בשתי שורות שאחת מהן ג' ט"ו כ"ז והשנית ז' ט"ו כ"ג כי כל אחד משני אלו הקטרים ארבעים וחמשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונמצא מקובץ שתי קצוות שורה כל שתי וערב שוה למקובץ שתי קצוות השורה האחרת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונמצא מקובץ בתי כל מרובע בנוי מאלה המספרים על המשכם שוה למרבע מרבע מספר בתי הצלע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כי אתה כשתבנה מרבע צלעו שני בתים ויהיו מספריו כזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
יהיה מקובץ זה ששה עשר והוא מרבע מרבע שנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר תהיינה צלעותיו משלשה בתים כזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עד שיהיו מספריו א' ג' ה' ז' ט' י"א י"ג ט"ו י"ז הנה יגיע מקובץ זה לשמנים ואחד והוא מרבע מרבע השלשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונמצא הקטר בכל אלו שוה למעקב זה המספר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
המשל בזה בלוח הגדול אשר בתיו חמשה הנה קטרו קכ"ה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ובשני קטרו שמנה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ובשלישי קטרו כ"ז | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועל הדרך הזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה כאשר תבנה מהם תמונה משלשת על זאת הצורה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תמצא כל המספרים היורדים מן האחד אל נפילת העמוד מרבעים על הסדר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותמצא מקובץ מה שבטור אחד ברחב מעקב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו מקובץ ג' וה' ומקובץ ז' ט' וי"א | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Even Number |
ואמנם מספר הזוג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Whatever is known concerning to it, is known in the book of the Elements. | כבר ידעת בספר היסודות ממנו מה שידעת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Properties that are necessary to its terms will be referred to: | ונרמוז לך אל סגלות יתחיבו למדרגותיו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
מהן שאתה תמצא מקובץ מדרגותיו שוה למרבע מספר המדרגות מצורף אליו צלעו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו שאתה כאשר תתחיל מהשנים ותצרף אליהם הארבעה יהיו ששה והוא כמו מרבע מספר המדרגות שהם שנים וכמו צלעו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכמו שאתה כאשר תתחיל מהשנים ותצרף אליהם הארבעה והששה יהיו שנים עשר והוא כמו מרבע השלשה וכמו צלעו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומסגלותיו שכל זוג יוסיף על הראשון מהנפרדים באחד הנה זה הזוג שוה למקובץ חלקי מרבע זה הראשון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו הארבעה אשר הוא מוסיף על השלשה שהוא ראשון באחד ומרבע השלשה תשעה ולהם מהחלקים שני חלקים תשיעית ושלישית ומקובצם שוה אל הארבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וג"כ הששה יוסיף באחד על החמשה שהוא נפרד ראשון ומרבע זה הראשון עשרים וחמשה ולו מן החלקים חומש וחומש החומש לא זולתם והגעתם ששה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואמנם אם יהיה הזוג באופן שכאשר נגרע ממנו שלשה ישאר נפרד ראשון הנה זה הזוג מורכב מחלקי כפל זה הנפרד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו השמנה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
שהם כאשר נגרע מהם שלשה נשארו חמשה וכפלם עשרה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ולהם חצי וחומש ועשירית ומקובץ זה שמנה רצוני מקובץ החמשה והשנים והאחד |
Types of Even and Odd Numbers |
ונדבר עתה בסגלות מיני הזוג ומיני הנפרד | ||||||||||||
| Starting from the properties of the even number, as their categorization to types is more reasonable than the categorization of the odd numbers. | ונתחיל בסגלות הזוג לפי שחלוקתם אל מינים יותר קרובה מחלוקת הנפרדים | ||||||||||||
Types of Even Numbers |
|||||||||||||
| Starting from the properties of the even-times-even number, since it is simpler. | ונתחיל בסגלות הזוג הזוג לפי שהוא יותר פשוט | ||||||||||||
Even-Times Even |
|||||||||||||
| The quality of its production by way of doubling and other of its properties that are in the book of the Elements, are already known. | וכבר ידעת איכות התילדותו על דרך ההכפלה וסגלות אחרות מהסגלות אשר לו בספר היסודות[4] | ||||||||||||
| Of the properties of the even-times-even number there are parts of properties that were mentioned in the Elements. | [5] מסגלות זוג הזוג מה שהם סעיפים מסגלות נזכרו ביסודות | ||||||||||||
|
שהוא אין חלק לו נקרא בשם מספר נפרד ולא זוג בלתי זוג הזוג[6] | ||||||||||||
|
ואין זוג הזוג שהוא פחות ממנו שלא ימנה אותו | ||||||||||||
|
וכל זוג זוג הנה מרבעו זוג הזוג | ||||||||||||
|
וכאשר חוסר ממנו הזוג הראשון והוא שנים יצא זוג הנפרד[7] | ||||||||||||
|
כמו השמנה שנחסר מהם שנים ויצא זוג הנפרד והוא ששה | ||||||||||||
|
וכל זוג הזוג הנה הוא חסר וחסרונו באחד[8] | ||||||||||||
|
ומסגלות זוג הזוג שמדרגותיו נמשכות על יחס מתדמה תשברתיי[9] | ||||||||||||
|
לפי שהם נמשכות על דרך ההכפל | ||||||||||||
|
והנה לא תהיינה העדפותיהם שוות | ||||||||||||
|
אבל יהיה כל העדף שוה למועדף עליו | ||||||||||||
|
ותהיינה ההעדפות עודפות בזה שביניהם זה ההעדף בעצמו | ||||||||||||
|
ויתחיב מהיות מדרגותיו על היחס האחד שתהיינה מתיחסות כשנחתוך אותם ומתיחסות כשנוסיף עליהם על השווי[10] | ||||||||||||
|
ויתחיב שיהיה הכאת אי זה אמצעי שנקח בעצמו כהכאת אחת מהשתי פאות באחרת | ||||||||||||
|
לפי שיחס הפאה הקטנה אל האמצעי כיחס האמצעי אל הפאה הגדולה | ||||||||||||
|
ויתחיב שתהיה הכאת אחד מהשני אמצעיים באחר כהכאת אחת מהשתי פאות באחרת | ||||||||||||
|
לפי שיחס הפאה הקטנה אל האמצעי הקטן כיחס האמצעי הגדול אל הפאה הגדולה | ||||||||||||
|
והנה תהיינה המדרגות ב' ד' ח' י"ו ל"ב ס"ד | ||||||||||||
|
|
ונמצא ד' בעצמו כמו ב' בח' | ||||||||||||
|
|
וח' בעצמו כמו ב' בל"ב וד' בי"ו | ||||||||||||
|
|
ונמצא ד' בח' כמו ב' בי"ו | ||||||||||||
|
|
וח' בי"ו כמו ד' בל"ב וב' בס"ד | ||||||||||||
|
ולפי שהיו מספרי זוג הזוג מסודרים על יחס מתדבק יחויב שיהיה למרבעים ולמעקבים מהם סדר באשר המרבע יהיה השלישי אליו מרבע והמעקב הרביעי אליו מעקב וילך על הדרך הזה | ||||||||||||
|
ומסגלותיו שהמספרים השלמים יתילדו ממנו[11] | ||||||||||||
|
אמנם המספרים הנאהבים הנה הם המספרים אשר יתרכבו כל אחד מחלקי חברו כמו שיתרכב חברו מחלקיו | ||||||||||||
|
כמו מאתים ועשרים ממאתים ושמנים וארבעה | ||||||||||||
|
|
כי למאתים ושמנים וארבעה חצי והוא קמ"ב | ||||||||||||
|
|
להם רביעית והוא ע"א | ||||||||||||
|
|
ולהם חלק מאחד ושבעים והוא ד' | ||||||||||||
|
|
ולהם חלק ממאה וארבעים ושנים והוא ב' | ||||||||||||
|
|
ולהם חלק ממאתים ושמנים וארבעה והוא א' | ||||||||||||
|
|
ואומר נקבץ אלה החלקים יהיו ר"כ | ||||||||||||
|
| ||||||||||||
|
|
ואמנם חלקי ר"כ הנה להם החצי והוא ק"י | ||||||||||||
|
|
ורביעית והוא נ"ה | ||||||||||||
|
|
וחמישית והוא מ"ד | ||||||||||||
|
|
ועשירית והוא כ"ב | ||||||||||||
|
|
וחלק מאחד עשר והוא עשרים | ||||||||||||
|
|
וחלק מעשרים והוא י"א | ||||||||||||
|
|
וחלק מכ"ב והוא עשרה | ||||||||||||
|
|
וחלק ממ"ד והוא ה' | ||||||||||||
|
|
וחלק מנ"ה והוא ד' | ||||||||||||
|
|
וחלק מק"י והוא ב' | ||||||||||||
|
|
וחלק מר"כ והוא א' | ||||||||||||
|
|
וכאשר תקבץ אלה החלקים יהיו רפ"ד | ||||||||||||
|
ואין לאחד מהם מן החלקים זולת מה שזכרנו | ||||||||||||
|
ואופן התילדותם | ||||||||||||
|
הוא כאשר תקבץ זוג הזוג והאחד עמהם ויקובץ מספר ראשון בתנאי שיהיה כאשר יתוסף עליו האחרון שבהם או יחוסר ממנו אשר לפניו יהיה המגיע אחר התוספת והמגיע אחר החסרון מספר ראשון | ||||||||||||
|
הנה הכאת המגיע הנוסף עליו במגיע המחוסר אחר כן הכאת העולה באחרון שבמקובצים הוא מספר אשר לו אוהב | ||||||||||||
|
ואוהבו הוא המספר אשר יהיה מתוספת הכאת מקובץ הנוסף והמחוסר הנזכרים באחרון שבמקובצים על המספר הנמצא ראשונה אשר הוא אוהב והם נאהבים[12] |
Even-Times Odd |
ואמנם סגלות זוג הנפרד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Whatever is known concerning to it, is known in the book of the Elements. | הנה כבר נודע בספר היסודות ממנו מה שנודע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| It is clear from their rule: | ונתבאר מכללם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
שהוא לא ימנהו זוג אלא במספר נפרד ולא נפרד אלא במספר זוג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וחלקו הזוג נקרא בשם הנפרד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו השנים שהם שלישית הששה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וחלקו הנפרד נקרא בשם הזוג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו השלשה שהוא חצי הששה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ושתוספת הזוג הראשון והוא השנים עליו יוציא זוג הזוג[13] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ודע שהתילדותו מכפל הנפרדים הנמשכים בשנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה תדע מזה שהנופל בין מדרגה ובין המדרגה הנמשכת אליה כפל הנופל אשר היה בנפרדים הטבעיים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויהיה העדף מדרגותיו בארבעה ארבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ושהוא אין נגדר בו ולא מעקב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כי כל נגדר וכל מעקב אם נפרד ימנה בנפרד במספר נפרד ואם זוג ימנה בזוג במספר זוג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכבר ידעת זה לפי שהיה ההעדף בארבעה ארבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וההתחלה אם מהשנים ואם מהששה כפי מה שיתבאר הענין בו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והשנים כאשר נוסיף עליהם ארבעה יהיו ששה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכאשר נוסיף על הששה ארבעה יהיו עשרה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכאשר נוסיף עליהם ארבעה יהיו ארבעה עשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכאשר נוסיף עליהם ארבעה יהיו שמנה עשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכאשר נוסיף עליהם ארבעה יהיו שנים ועשרים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה שבנו אל השנים חוזרים בסבוב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
יחויב שיהיה סבוב אחד האחרים זולת אלו ויחויב שיהיה כל דומה אל הראשון באחדים או גלגל הנקרא ציפרי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר תשים התחלת המדרגות מהששה והששה להם שליש והם הנקראים על שם שלשה הנה כאשר תתחיל אחר הששה תמצא לשלישי אחריו והוא שמנה עשר שליש אמתי ולשלישי כאשר תתחיל אחר השמנה עשר והוא השלשים שליש אמתי ועל הדרך הזה אל בלתי תכלית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר הששה העשרה והחלק שלהם נקרא בשם הנפרד אשר אחר השלשה והוא החמשה כי לעשרה חומש אמתי והנה כאשר תתחיל אחר העשרה תמצא הנגזר לו השם מזה המספר והוא החמישי לו חומש אמתי ועל הדרך הזה עד מה שתרצה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והמספר אשר אחר העשרה הוא הארבעה עשר וחלקו נקרא בשם הנפרד הנמשך אל החמשה כי הנה לו שביעית והנה נמצא השביעי כאשר תתחיל אחריו על הדרך הזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומסגלת אלו המדרגו' שמקובץ השנים והוא הראשון שבזוג הנפרד עם כל מדרגה תהיה נקראת על שם מספר מרובע יוציא מספר מרבע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו קבוצם עם הרביעי מהם והוא ארבעה עשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ועם התשיעי מהם והוא ארבעה ושלשים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנמשך אל שנים והוא הששה והוא זוג הנפרד השני כאשר יקובץ אל מספר כל מדרגה מתחלת מן האחד שתהיה נקראת על שם מספר מרבע הנה יהיה המקובץ מרבע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו הששה עם הרביעי והוא עשרה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ועם התשיעי והוא שלשים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומזה שהכאת הנקרא בשם כל מדרגה בארבעה יהיה כאשר תגרע ממנו המספר הראשון יהיה מספר אותה המדרגה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
המשל בזה שהבית הרביעי נקרא בשם ארבעה וכאשר נכפל בארבעה יהיה ששה עשר תפיל מהם המספר הראשון והוא שנים הנה יהיה ארבעה עשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכבר אפשר לך שתהפך זה ותאמר שכל מספר מהם כאשר תוסיף עליו שנים ותחלק על ארבעה הנה מה שיצא הוא מספר מדרגתו מן הראשון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומזה שכפל הכאת מספר המדרגות בעצמם שוה למקובץ מספרם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה תהיינה המדרגות ארבעה וכפל הכאתם בעצמם שנים ושלשים והנה זה מקובץ שנים ששה עשרה ארבעה עשר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומזה שמקובץ הראשון והשני מעקב ח' ואתה תדענו ותדע מדרגתו ממה שכבר ידעת ועוד מעקב מעקבו ועל הדרך הזה[14] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה נבנה מזוג הנפרד הנמשכים מרבע ששה בששה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומסגלות זה הלוח המרבע שאחדי ראשית התחלת כל שורה ברוחב כמו אחדי הסוף | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם יהיה באחד מהם גלגל הנקרא ספרא הנה באחר גלגל גם כן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומהם שמקובץ שני קצוות הקטר האחר שוה למקובץ שני קצות הקטר האחר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו ב' עם קמ"ב שהם שני קצות הקטר וכ"ב עם קכ"ב והם קצות הקטר האחר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומהם שמקובץ קצות הקטר נגדר לעולם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומהם שכל שני מספרים מרחקם משני קצות הקטר מרחק אחד הנה מקובצם שוה למקובץ שתי קצות הקטר והוא לזה נגדר גם כן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומזה שתוספת כל שורה על התחלת זאת השורה אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כי תוספת כ"ב על מ"ו כתוספת מ"ו על ע' |
Even-Times-Even-Times Odd |
ואמנם עניני זוג הזוג והנפרד הנה נדבר בהם |
|
ונאמר שהוא דומה לזוג הנפרד באשר הוא איננו מקבל ההחצות ההולך בהדרגה בהתמדה עד האחד מזולת שבר |
|
וידמה לזוג הזוג באשר הוא לא יחצה החצותו הראשון אל שני נפרדים ולא יעמד החצותו אצל חלוקה אחרת |
|
ואמנם התילדותו הנה הוא מהכאת זוג הזוג המתחילים מן הארבע בנפרדים הנמשכים |
|
וכל מה שהיה זה הזוג יותר רב יהיה קבלתו להחצות יותר |
|
וכבר יהיו בו הנוסף והחסר והשלם |
|
כי השמנה וששים מספר חסר והוא מכללו |
|
ואמנם השלם הנה כמו השמנה ועשרים |
|
והנוסף בו הרבה כמו השנים עשר |
|
וכבר יפלו בו המרבעים ג"כ |
|
והתילדות אלו המרבעים אשר יפלו במספריהם |
|
הוא שנכה הזוג הראשון בנפרד הראשון עד שיהיה ששה והנה הוא גדר המרבע הראשון |
|
אח"כ נכה אותו בנפרד השני עד שיהיה עשרה והנה הוא גדר המרבע השני |
|
ועל הדרך הזה |
|
וכאשר תגרע הבית מאשר ימשך אליו יצא לך זוג הזוג |
|
כמו השנים עשר מהעשרים |
|
וזה במה שהתילדותו מהכאת הארבעה בנפרדים |
|
וכמו הארבעה ועשרים מן הארבעים |
|
וזה במה שהתילדותו מהכאת השמנה בנפרדים |
| This is what is said on the properties of the types of the even-times-even numbers that are affected by the properties of the odd number. | והנה זה מה שנאמר אותו בסגלות מיני זוג הזוג ונעתק אל מיני סגלות הנפרד |
The Two - is it an even-times-even number or an even-times-odd number? |
|
| The discussion on the first of the numbers, which is two, still remains: is it an even-times-even number, or an even-times-odd number? | וכבר נשאר עלינו הדבור בראשון שבמספרים והוא השנים האם הוא זוג הזוג או זוג הנפרד |
|
וכבר יחשב מצד שהוא לא יכלה בו ההחצות אל זוג שהוא זוג הנפרד |
|
והעבירו קצתם שיהיה זוג הזוג וזוג הנפרד יחד ושיהיה התחלה לשניהם |
[According to the author]:
|
והנראה אלי שזוג באמת הוא המספר המתחלק אל הנפרד אצל ההחצות |
|
וזוג הנפרד באמת הוא המתחלק אל הנפרד אצל ההחצות |
|
והנה הזוג הזוג הוא אשר חציו זוג וכל חצי יחצה אותו זוג זולת האחד |
|
ולא ימלט מהחצות זוג |
|
וזוג הנפרד הוא אשר חציו נפרד ולא יחצה |
|
והנפרד יהיה מספר או יהיה אחד מצד שלא יחלק בשני חלקים |
| ? | והזוג לא יהיה ולא מספר |
| אחר זה הנה ראוי שלא נקפיד בקריאת השמות | |
|
ואם ירצה אחד שנשים השנים ראויים לשני השמות יחד |
|
הנה ראוי שנשים גדר זוג הזוג שהוא אשר לא יחצה אל מספר נפרד |
|
וכן הם השנים אמנם החלוקה לא תהיה על דרך היושר |
|
ואם רצה שנוציא השנים משני השמות יחד |
|
הנה ראוי שנשים גדר זוג הזוג שהוא הנחצה אל מספר זוג |
|
וגדר זוג הנפרד שהוא אשר יחצה אל מספר נפרד |
|
ולא יהיו השנים ראויים אל אחד משני השמות עם יושר החלוקה |
Types of Odd Numbers |
|
| Now the properties of the types of odd numbers will be discussed: | ונדבר עתה בעניני מיני הנפרד |
| Some of the odd numbers are prime and some are composite. | והנפרד ממנו ראשון וממנו מורכב |
| The composite may be relatively prime. | והמורכב כבר יהיה ראשון בהקש אל זולתו |
| All this is already known. | וכבר ידעת כל זה |
Composite Numbers |
|
| When wishing to extract the terms of the composite numbers, one should return to the tables of the successive odd numbers: | וכאשר תרצה שתוציא מדרגות המורכבים בעצמם הנה תשוב אל לוחות המספרים הנפרדים הנמשכים |
|
והנה תמצא כל שלשה אחר השלשה מורכב |
|
וכל חמשה אחר החמשה מורכב |
|
וכן אל בלתי תכלית |
|
דמיון הראשון הט' והט"ו והכ"א |
|
דמיון השני הט"ו והכ"ה והל' |
|
וכמו כן כאשר תתחיל מן השבעה והתשעה על הדרך הזה |
|
ותמצא שם דבר והוא שהשלשה מהם ימנה |
|
המורכב הראשון אשר במדרגותיהם במספר ראשון הנפרדים והוא בעצמו כמו התשעה |
|
והשני בנפרד אשר ימשך אליו כמו החמשה |
|
והשלישי בנפרד השלישי כמו השבעה[15] |
|
והחמשה ג"כ ימנה |
|
אשר ימשך אליו בראשון בנפרדים והוא השלשה כמו החמשה עשר |
|
והשני בעצמו כמו החמשה ועשרים |
|
והשלישי במה שאחריו כמו החמשה ושלשים כי הוא ימנה אותם בשבעה[16] |
Relatively Prime Numbers |
|
|
ואמנם המורכב בעצמו וראשון אצל זולתו |
|
הנה הוא כל מרבע ראשון בהקש אל מרבע ראשון אחר מאלו הנפרדים הנמשכים[17] |
| This is what is said about the properties of the even and the odd numbers. | והנה זה מה שנאמר אותו בעניני הזוג והנפרד |
Superabundant / Deficient / Perfect Numbers |
|
| Another categorization of the number: some number are superabundant, some are deficient, and some are perfect. | והמספר חלוקה אחרת ממנו נוסף וממנו חסר וממנו שלם |
| All this is already known, as well as the quality of the production of the perfect number from the even-times-even numbers. | וכבר ידעת כל זה וידעת איכות התילד המספר השלם מזוגי הזוגות[18] |
| The perfect number is an even number only, because it is produced from the multiplication of an odd number by an even number. | ודע שהמספר השלם לא יהיה אלא זוג לפי שהוא אמנם נתילד מהכאת נפרד בזוג |
|
ונזדמן שהנופל ממנו באחדים אחד והוא ששה |
|
ובעשרות אחד והוא שמנה ועשרים |
|
ובמאות אחד והוא תצ"ו |
|
ובאלפים אחד והוא שמנה אלפים וקכ"ח |
|
וכמו כן בכל מין אחד |
|
לא ימלט מאחדים הם ששה ושמנה ואם לא יתחיב אצל הנסיון בהם שיהיו חוזרים חלילה |
|
ומסגלות המספר השלם שכאשר הוכה בשמנה ונוסף עליו אחד יהיה נגדר |
|
וכאשר יחלק גדרו על ארבעה ויתוסף על מה שיתקבץ רביע יהיה זוג הזוג אשר הוכה בכפלו זולת אחד עד שיצא זה המספר השלם |
|
המשל בזה ששה בשמנה נוסף עליו אחד הוא מ"ט |
|
וגדרו שבעה ורביעיתו אחד ושלשה רביעיו' וכאשר יתוסף עליו רביע יהיה שנים והוא זוג הזוג |
|
|
אשר נפלה ההכאה בכפלו זולת אחד כאשר יצא ששה[19] |
| The superabundant and the deficient numbers are as explained in every chapter [?] | אמנם המספר הנוסף והחסר הנה יהיו כמו שכבר נתבאר בכל שער |
|
והנה בהוצאת השלם והחסר והנוסף בחינה נפלה לקצת האנשים |
|
והיא שכל זוג הזוג כאשר הוכה במספר ראשון איך שיהיה |
|
אחר שיהיה זוג הזוג יותר מחצי זה הראשון בחצי אחד הנה המתקבץ ממנו לעולם מספר שלם |
|
כמו השנים בשלשה |
|
|
והארבעה בשבעה |
|
ואם יהיה יותר מחציו ביותר מחצי אחד הנה המתקבץ ממנו לעולם מספר נוסף |
|
ואם יהיה פחות מחציו איך שיהיה הפחת הנה המספר חסר |
|
משל הראשון הנה ארבעה בחמשה |
|
ומשל השני הארבעה באחד עשר |
|
וכל מספר מהמספרים השלמים הוכה במספר ראשון ולא ימנה זה המספר הראשון זה המספר השלם |
|
כמו הששה כאשר הוכה בשבעה ונתחדש מ"ב |
|
|
ולו מן החלקים החצי והוא כ"א |
|
|
ושליש והוא י"ד |
|
|
והששית והוא ז' |
|
|
והשביעית והוא ו' |
|
|
וחלק מי"ד והוא ג' |
|
|
וחלק מכ"א והוא ב' |
|
|
וחלק ממ"ב והוא א' |
|
וכלל זה נ"ד |
|
הנה מוסיף על מ"ב בי"ב והוא כפל ששה |
|
וכל מספר ימנהו שנים הנה הוא חסר לעולם |
|
וכל המספרים הראשוני' חסרי' בלי ספק |
|
וכל זוגי הזוג חסרים באחד |
|
וכל מספר זולת הששה ימנוהו השנים והשלשה הנה הוא נוסף לעולם |
|
וכל מספר ימנה אותו השנים ושני מספרים יהיה קריאת מקובצם עומדת מקום השליש רצוני שיהיה אחריתם כמו השליש רצוני שיהיה החבור משני יחסי חלקיהם בנכח המוסיף שליש כמו מקובץ שני יחסי המוסיף חומש והמוסיף שביעית אשר הוא לנכח המוסיף שלישית הנה הוא נוסף לעולם |
|
כמו השבעים כי הוא לפי שהוא נמנה עם השנים והחמשה והשבעה יהיה נוסף לעולם |
|
וכל זוג נפרד נמנה עם השנים והחמשה והשבעה יהיה נוסף |
|
וכל זוג נפרד מורכב מנפרד מורכב כמו השמנה עשר והשלשים הנה הוא נוסף תמיד |
|
ואם יהיה מורכב מנפרד ראשון הנה הוא חסר |
|
וכבר ימצאו בזוג הזוג והנפרד חסר ונוסף ושלם |
|
דמיון הנוסף ששה ושלשים |
|
ודמיון החסר ארבעים וארבעה |
|
ודמיון השלם שמנה ועשרים |
|
המספר הנפרד לא יהיה שלם כמו שידעת אבל יהיה חסר |
|
ולא יהיה נוסף אלא שיהיה מורכב מארבעה נפרדים נמשכים על הסדר הטבעי |
|
כמו מה שראשיתו שלשה אח"כ חמשה אח"כ שבעה אח"כ תשעה ומורכבם הוא תשע מאות וארבעים וחמשה והוא המספר הראשון שבנפרדים נוסף בשלישית ואם יניח זה ההמשך לא יתחיב שיהיה נוסף |
| The end of the discussion on this manner of arithmetic - moving on to the manner by which the relation of a number to a number is examined. | ונחתום הנה הדבור בזה האופן מחכמת המספר ונעתק אל האופן אשר יבחן ממנו בצרוף מספר אל מספר |
Book Two |
המאמר הב' |
|---|---|
Ratios |
|
| The number is examined by examination from the aspect of its attention to itself and to the properties that are necessary for it, to what is a number and what is a type of number. | כבר יעויין במספר עיון מצד ההשגחה בעצמו ובעניינים המתחייבים לו במה שהוא מספר ומה שהוא מין מספר |
| It is examined from other aspects, among them from the aspect of being related to another number. | וכבר יעויין בו מצדדים אחרים מהם מצד היותו מצטרף אל מספר אחר |
| This other number is either other from it by number and not by species, or part of the species, so the relation is a relation of changing. | וזה המספר האחר אם יהיה אחר ממנו במספר לא במין או חלק המין יהיה הצרוף צרוף השנוי |
| Every two changing terms - one of them is greater and the other is less | וכל שני משתנים הנה אחד מהם מוסיף והאחר חסר |
| When one knows the properties of the greater to the less, he knows the properties of the less to the greater, according to what the evenness requires in relation. | וכאשר תדע עניני המוסיף אצל החסר תדע עניני החסר אצל המוסיף כפי מה שיחיבהו היושר בהצטרפות |
| The greater is either simple or not simple. | והמוסיף אם פשוט ואם בלתי פשוט |
|
והפשוט אם כפל ואם כפלים ואם מוסיף בחלק או חלקים |
|
והמורכב הוא המוסיף בכפל והחלק או המוסיף בכפל והחלקים או המוסיף בכפלים והחלק או המוסיף בכפלים והחלקים |
|
והחלקים כונתנו בהם מה שהוא יותר מכפל אחד או חלק אחד ואם היה שני כפלים או שני חלקים |
| As for the less, the custom has spread to indicate it by sub-, as saying subsuperparticular | והחסר הנה כבר פשט המנהג שיורו עליו באשר הוא אשר תחת ככה כאמרם אשר תחת המוסיף חלק |
| Sometimes its name is derived from the name of the number of the multiples, such as the third, the quarter, and the twelfth; and sometimes it is called by two ratios, as saying half the sixth, or fifth of a tenth. | ולפעמים יהיה נגזר לו שם משם מספר הכפלים כמו השליש והרביע והחלק משנים עשר ולפעמים יקרא בשני יחסים כאמרם חצי הששית חומש עשירית |
Simple Ratios |
|
Multiple Ratio |
|
|
והנה הנכפל הראשון הוא הנכפל השניי והוא אשר התוספת בו בדמיון האחר |
|
והתחלתו במספרים מן האחד והשנים |
|
ויתוסף החסר על סדר המספרים הנמשכים |
|
והמוסיף והוא הכפל על סדר הזוגות הנמשכים בהעדף שנים שנים |
|
אח"כ הנכפל השלישיי והוא אשר התוספת בו בשני דמיונים |
|
והתחלתו מהשלשה והאחד |
|
ויתוסף החסר על סדר המספרים הנמשכים |
|
והנוסף בשלשה שלשה |
|
כמו שלשה וששה ותשעה ושנים עשר |
| According to this way the less are added one by one in all the multiple ratios and the greater by the number of the multiples. | ועל הדרך הזה יתוסף החסר בכל היחסים בעלי הכפל באחד אחד והנוסף במספר הכפלים |
| The beginning of the less is from 1. | ותהיה התחלת החסר מן האחד |
| The beginning of the greater from the number by which the number of the multiple is denominated [= the multiplier]. | והתחלת הנוסף מהמספר אשר על שמו יקרא מספר הכפלים |
Superparticular Ratio |
|
|
והראשון אשר במוסיף חלק הוא המוסיף על האחר בכמו חציו |
|
והתחלתו מהשלשה והשנים |
|
ויתוסף החסר על סדר הזוגות הנמשכים לפי שיש להם חצי |
|
והמוסיף בשלשה שלשה |
|
כמו השנים עם השלשה אח"כ הארבעה עם הששה אח"כ הששה עם התשעה |
|
ואחר המוסיף חצי הוא המוסיף שליש |
|
והתחלתו מן הארבעה והשלשה |
|
ויתוסף החסר בשלשה שלשה |
|
כמו השלשה והששה והתשעה |
|
והמוסיף בארבעה ארבעה |
| According to this way the matter proceeds always by this order. | ועל הדרך הזה ילך הענין תמיד על זה הסדר |
Table of Multiple and Superparticular Ratios |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Setting a square table with lines, starting from one, the beginnings of its lines are added lengthwise and breadthwise by the sequence of the natural numbers | והנה כאשר נרשום לוח בעל טורים מרובע יתחיל מן האחד ויתוספו ראשי שורותיו בארך וברחב על סדר המספרים הטבעיים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| By this way these ratios are established in it, as well as other propositions that are derived from them. | ועל הדרך הזה תניח בו אלה היחסים ומשפטים אחרים יוצאים מהם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה יהיה זה הלוח הבעל טורים עשרה על עשרה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה נמצא השורה השנית על יחס הכפל לשורה הראשונה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והשלישית על יחס השלשה כפלים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| By this way the excess is found as is said. | ועל הדרך הזה נמצא ההעדף כפי מה שנאמר לך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונמצא השורה השלישית אל השנית על יחס המוסיף חצי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והרביעית אל השלישית על יחס המוסיף שליש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והחמישית אל הרביעית על יחס המוסי' רביע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| According to this way the matter proceeds always. | ועל הדרך הזה הולך הענין תמיד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The excess is found as is said: | ונמצא ההעדף כפי מה שנאמר לך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונמצא תוספת השורה השנית על השורה הראשונה יתחלף במספר ואם לא יתחלף ביחס | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונמצא תוספת הבית הראשון ממנו על הבית הראשון מהשורה הראשונה באחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותוספת הבית השני ממנו על הבית השני מהראשון בשנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| According to this way by the order of the successive numbers. | ועל הדרך הזה על סדר המספרים הנמשכים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועל הדרך הזה ענין כל בית אצל הקודם אליו[20] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונמצא זה כאשר יוקש בין השלישי והראשון בכל סדור על סדר הזוגות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כי הנה נמצא הראשון מכל שלישי יוסיף על ראשון מכל ראשון בשנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והשני בארבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והשלישי בששה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועל הדרך הזה[21] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואמנם תוספת הבית הראשו' מ[הר]ביעי על הבית הראשון מכל ראשון הנה הוא בשלשה שלשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותוספת השני מן הרביעי על השני מן הראשון בששה ששה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועל הדרך הזה תוספת כל בית יוסיף על תוספת הבית בשני צדדין בשלשה שלשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תוספת רביעי על השני וביניהם שורה אחת כתוספת השני על הראשון ביחס | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותוספת הששי על השלישי וביניהם שתי שורות כתוספת השלישי על השני ביחס ועל הדרך הזה[22] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה תמצא כל מספר ממספרי הקטר מרבע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו הד' והט' והי"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונמצא מקבץ כל שני מרבעים נמשכים ומקבץ השני שטחים אשר יפלו ביניהם על האלכסוניות מרבע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו מקבץ הד' והט' עם הו' וו' שעולה כ"ה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונמצא מקבץ כל שני מרבעים נמשכים על מקבץ השני שטחים מוסיף באחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה יחויב שיהיה כפל מקובץ כל שני מרבעים נמשכים מחוסר ממנו אחד מרבע[23][24] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונמצא הכאת כל מספר משורה במספר משורה אחרת שוה להכאת בן גילו בבן גילו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו הב' והוא השני מן הראשונה בכ' והוא האחרון מן השנית אשר הוא כמו הד' אשר הוא השני מן השנית בי' אשר הוא האחרון מן הראשונה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונמצא הכאת כל מספר ממספרי הקטר בבן גילו מהצד האחר מזה הקטר כמו בני גילם אחד מהם באחר רצוני מן הקטר האחר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו הכאת הא' בק' אשר הוא כמו הכאת הי' בי' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וג"כ הכאת ד' בפ"א אשר הוא כמו הכאת י"ח בי"ח | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועל הדרך הזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| As for the other ratios, before examining them in this table, the quality of rule of investigating their first numbers will be referred to. | ואמנם היחסים האחרים הנה אנחנו קודם שנבחין אותם מזה הלוח הבעל טורים נרמוז אל איכות ההנהגה בדרישת מספריהם הראשונים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Their properties will be determined, then their examination in this table will be alluded to. | ונרמוז אל ענינים מסגלים להם אח"כ נרמוז אל בחינתם מזה הלוח |
Superpartient Ratio |
|
| The superbipartient ratio or the superpartient ratio is sometimes absolute and sometimes not absolute. | ונאמר אם יחס המוסיף בשני חלקים או המוסיף בחלקים הנה לפעמים יהיה גמור ולפעמים לא יהיה גמור |
| The absolute, meaning that which is not reduced to the superparticular ratio. | והגמור רצוני מה שאיננו חוזר אל יחס דמיון וחלק |
|
כמו חזרת המוסיף בשני ששיות אל המוסיף שליש |
|
והמוסיף בשני רביעיות אל המוסיף חצי |
|
כל מוסיף בשני חלקים נקראים בשם זוג |
|
וחזרת המוסיף בשלשה ששיות אל החצי אחר כן |
Such as the superbiquintan 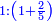 and the supertriquartan and the supertriquartan 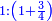 are the [absolute ratios]. are the [absolute ratios].
|
ואבל כמו המוסיף בשני חמישיות והמוסיף בשלש רביעיות הוא הבלתי גמור |
| There is no common order for the absolute ratios, thus any one who measures should examine the sequence. | ולא ימצא לגמור סדור משותף בו אבל יצטרך כל שוער להבחין הסדור |
When it is taken in actu, the order of the realization of its first number is such that the first is that by which the part of the numbers is denominated, so that two is added to it if there are two parts or three if there are three parts.
|
ואמנם כאשר ילקח בשלוח[25] הנה הסדר בהגעת מספרו הראשון הוא שיגיע הראשון אשר בשמו יקרא זה החלק מן המספרי' כדי שנוסיף עליו אם הוא שני חלקים הנה שנים ואם היה שלשה חלקים הנה השלשה |
|
המשל בזה אם היה התוספת בשני שלישיות נניח שלשה ונוסיף עליהם שנים ויהיו חמשה ותהיה התחלתם משלשה וחמשה |
|
ואם יהיה התוספת בשלשה רביעיות נניח ארבעה ונוסיף עליהם שלשה ויהיו ארבעה ושבעה והיא מתחלתם |
|
והנה תמצא המספרים החסרים ביחס הדמיון ושני חלקים |
|
אם ביחס הדמיון ושני שלישיות |
|
הנה החסרים מוסיפים בשלשה |
|
והנוספים בחמשה |
|
|
עד שיהיו שלשה וחמשה אח"כ ששה ועשרה אח"כ תשעה וחמשה עשר |
|
ואמנם ביחס הדמיון ושתי רביעיות והוא בלתי גמור |
|
הנה תמצא החסרים יוסיפו בארבעה ארבעה |
|
והנוספים בששה ששה |
|
|
באלו מספרם על הקש ארבעה וששה ושמנה ושנים עשר |
|
ועל הדרך הזה החסר כמו עצמו והנוסף כמו עצמו |
|
וכפי זה הוא הסדר במוסיף שתי חמישיות |
Comparing [the superbipartient ratios] to each other [![\scriptstyle\left[1:\left(1+\frac{2}{n}\right)\right]:\left[1:\left(1+\frac{2}{n+1}\right)\right]](/mediawiki/images/math/b/1/5/b1597dbddfa7136a5e5ddd7e45afc6c8.png) ]: ]:
|
ואמנם הקש קצתם אל קצת |
|
רצוני הקש המוסיף שתי שלישיות אל המוסיף שתי רביעיות אח"כ המוסיף שתי חמישיות |
|
הנה החסרים יוסיפו באחד אחד |
|
והנוספים ג"כ יוסיפו באחד אחד[26] |
|
וכאשר תבחין הגמורים בזה היחס יהיו על סדר הנפרדים הנמשכים |
|
כמו החמשה אל השלשה והוא המוסיף בשתי שלישיות |
|
והשבעה אל החמשה והוא המוסיף בשתי חמישיות |
|
והתשעה אל השבעה והוא המוסיף בשתי שביעיות |
Comparing between the supermultiplepartient [ ]: ]:
|
ואמנם ההקש בין רבי החלקים |
|
כמו המוסיף בדמיונו ושלשה רביעיות |
|
הנה יוסיפו החסרים מהם והמוסיפים מהם על ההקש הנזכר |
|
|
עד שיהיו ארבעה ושבעה אח"כ שמנה וארבעה עשר |
|
ועל הדרך הזה תוספת שלש חמישיות |
|
|
יהיה חמשה ושמנה ועשרה וששה עשר |
|
ויהיה התיחסות מה שביניהם כפי מה שנאמר בראשונים |
|
כמו ארבעה ושבעה אח"כ חמשה ושמנה אח"כ ששה ותשעה |
| The absolute ratios have unordered properties that should be drawn by examination for each category. | וימצאו לגמורי' סגלות בלתי מסודרות אלא בשער שער יש להוציא אותם עם הבחינה |
Compounded Ratios |
|
Multiple Superparticular Ratio |
|
| When wishing to find the first number in the [multiple] superparticular ratio: | וכאשר נרצה שנמצא ראשון המספרים ליחס הדמיון והחלק[27] |
| Taking that by which the parts are denominated, as two for a half, three for a third, then multiplying this number by two and adding one to it.
|
הנה נקח אשר על שמו יקראו החלקים כמו השנים לחצי והשלשה לשליש ונכפול זה המספר בשנים ונוסיף עליו אחד |
|
כמו הכפל וחצי כי התילדותו מכפל השנים בשנים והתוספת אחד עליו ויהיו שנים וחמשה |
|
והכפל ושליש שהתילדותו מכפילת השלשה בשנים והתוספת אחד עליו ויהיו שלשה ושבעה |
|
והכפל ורביע שיהיו ארבעה ותשעה |
|
ונמצאו המספרים בראשון[28] |
|
יתוסף החסר בשנים שנים על סדר הזוגות הנמשכים |
|
ויתוסף המוסיף בחמשה חמשה |
|
עד שיהיה במוסיף כפל וחצי שנים וחמשה אח"כ ארבעה ועשרה אח"כ ששה וחמשה עשר |
|
ונמצא המספרים בשני והוא יחס הכפל והשליש |
|
יתוספו החסרים בהם בשלשה שלשה |
|
והמוסיפים בשבעה שבעה |
|
כמו שלשה ושבעה אח"כ ששה וארבעה עשר ותשעה ואחד ועשרים |
|
ונמצאו המספרים בשלישי והוא יחס הכפל ורביע |
|
יתוסף החסר בהם בארבעה ארבעה |
|
והמוסיף בתשעה תשעה |
|
עד שיהיו על משך ארבעה ותשעה אח"כ שמנה ושמנה עשר אח"כ שנים עשר ושבעה ועשרים |
| As a rule: the addition of the less and the greater is according to their first number. | ובכלל הנה תוספת החסר והנוסף יהיה על מספרם הראשון |
The relation between their terms, meaning between the double sesquialter ratio and the double sesquitertian ratio [and the double sesquiquartan ratio] [![\scriptstyle\left[1:\left(2+\frac{1}{n}\right)\right]:\left[1:\left(2+\frac{1}{n+1}\right)\right]](/mediawiki/images/math/6/d/7/6d72c1d885f6fce8719102ff81d49e12.png) ] ]
|
ואמנם ההתיחסות במה שבין מדרגותיהם רצוני התיחסות מה שבין הכפל והחצי ובין הכפל והשליש |
|
הנה החסרים יתוספו באחד אחד |
|
והמוסיפים בשנים שנים כפי ההכפלה |
|
עד שיהיו שנים וחמשה שלשה ושבעה ארבעה ותשעה ועל הדרך הזה |
| Thus, the rule of the addition follows the successive odd numbers. | וילך מנהג התוספת על הנפרדים הנמשכים |
Multiple Superpartient Ratio |
|
|
ואמנם יחסי הכפל והשני שלישיות הנה ראוי שנעשה בתולדתם מה שכבר עשינו אותו אלא שאנחנו נוסיף תמורת האחד שנים |
|
ונתחיל אם ביחס הכפל והשתי שלישיות מן השלשה והשמנה |
|
וביחס הכפל והשתי רביעיות והוא בלתי גמור בארבעה והעשרה |
|
וביחס הכפל והשתי חמישיות מן החמשה והשנים עשר |
|
והנה נמצא המוסיפים ג"כ יוסיפו בשנים שנים והחסרים באחד אחד |
|
ונמצא הסדר והמנהג בשער אחד כמו סדר המספרים המונחים לשני דמיונים ושתי שלישיות ונמצא החסרים והמוסיפים יוסיפו על מספרם אלא שאנחנו נמצא מספר החסרים כמו שהיה בדמיון ושליש וכפל ושתי רביעיות וכפל ושתי חמישיות ושאר אלו[29] |
|
וכאשר נרצה הכפל והשלשה חלקים |
|
והראשון שבהם שלשה רביעיות |
|
הנה ההולדה על זה הדרך בעצמו אלא שאנחנו נוסיף למוסיף שלשה חלקים שלשה ולמוסיף ארבעה חלקים ארבעה |
|
והנה הראשון שבכפל ושלשה חלקים הכפל ושלשה רביעיות והתחלתו מן הארבעה והאחד עשר |
|
אח"כ הכפל ושלשה חמישיות והתחלתו מן החמשה ושלשה עשר |
|
ועל הדרך הזה |
|
והנה נמצא תוספת מדרגות המספרים כמו שהיה |
|
וכאשר נתנהג במה שבשער אחד נמצא החסרים והמוסיפים ג"כ יתוספו כמו עצמם |
|
ואמנם מספר החסרים יהיה כמו שהיה ומספר המוסיפים מספר אחד |
|
וכאשר נרצה יחס שלשה כפלים וחלק או שני חלקים אחרים |
|
נעשה בהולדת אלו מה שכבר עשינו אלא שאנחנו לא נכפול פעם אחת לבד אבל במספר אותם הכפלים אח"כ נעשה בחלק והחלקים מה שכבר עשינו |
|
|
|
ונמצא ראשית השלשה כפלים ושליש משלשה ועשרה |
|
וראשית שלשה כפלים ורובע מארבעה ושלשה עשר |
|
ונמצא החסרים יוסיפו באחד אחד והמוסיפים בשלשה שלשה |
|
וכאשר נקח ברחב |
|
נמצא ראשית שלשה כפלים וחצי משנים ושבעה ושנית מארבעה וארבעה עשר |
|
ונמצא ג"כ כלם יתוספו במספרם |
|
והחסר ירוץ על תוספת הזוגות הנמשכים |
|
ונמצא ראשית שלשה כפלים ושליש מהשלשה והעשרה ושנית מהששה ועשרים |
|
ונמצא השרש שמור |
|
וכאשר יבחנו השלשה כפלים והשני חלקים |
|
יהיה ראשיתם שלשה כפלים ושני שלישיות והראשון משלשה ואחד עשר |
|
וראשית שלשה כפלים ושני רביעיות מארבעה וארבעה עשר |
|
וראשית שלשה כפלים ושתי חמישיות מחמשה ושבעה עשר |
|
ונמצא ההעדף בחסרים על משך המספרים הטבעיים והמוסיפים בשלשה שלשה |
|
וכאשר נקח ברוחב |
|
נמצא ראשית שלשה כפלים ושתי שלישיות משלשה ואחד עשר ושנית מששה ושנים ועשרים |
|
והנה שמרו הסדר |
|
וכאשר נבחין השלשה כפלים ושלשה חלקים |
|
היה ראשית זה שלשה כפלים ושלשה רביעיות וראשיתם מארבעה וחמשה עשר |
|
אח"כ שלשה כפלים ושלשה חמישיות וראשיתם מחמשה ושמנה עשר |
|
ונמצא הענין על הדרך הזה |
|
וכאשר נבחין ברוחב |
|
נמצא ראשית שלשה ושלשה רביעיות מארבעה וחמשה עשר ושנית משמנה ושלשים |
|
ונמצא זה הסדור שמור |
Tables of Ratios |
|||||||||||||||||||||||||||||||||||||||||||||||||||
| We should elaborate on this as well as establish the relations of the tens [?] by tens and extract them, but we will be satisfied with this and mention indications from the aspect of the tables with which these are associated. | ולנו שנוסיף בזה ונישב ג"כ התיחסות הכלל בכלל ונוציא אותו אבל אנחנו נסתפק על זה ונזכור רמזים על צד הלוחות ישתתפו בהם אלו | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה מזה שאנחנו כאשר נעשה לוח משתי שורות | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
אחת מהן ימשכו בה הנפרדים הנמשכים מתחילים מן החמשה ויעמדו אצל אחד ועשרים | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
והשנית ימשכו בה מספרים מתחילים משלשה ויעמדו אצל אחד עשר | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויתבאר לנו שבמה שבין אלו יחסים | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר נבחין מה שבכל בית מהלוח הראשון מצורף לבן גילו מהלוח האחר | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה יהיה על יחס הדמיון ושתי שלישיות | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
אח"כ הדמיון ושלשה רביעיות | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
אח"כ הדמיון וארבעה חמישיות | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועל הדרך הזה | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר נבחין סדור מה שבלוח הראשון יהיו על יחס הדמיון ושני חלקים הגמור[30] | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר נבחין סדור מה שבלוח השני יהיו על יחס המוסיף חלק[31] | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר נניח תמורת הבית השני המתחיל מן הג' בית אחר מתחיל מן הב' וילך על משך המספרים אשר בטבע יהיה יחס הבית הראשון מהשורה הראשונה לבן גילו מן השנית על יחס שני דמיונים והחלק | ||||||||||||||||||||||||||||||||||||||||||||||||||
| We should extract from this the tables of the other remaining ratios, since the first column is shared by all the ratios. | ולנו שנוציא מזה הלוחות לשאר היחסים הנשארים עם היות שהלוח הראשון[32] ישתתף לכל היחסי' | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויצא אלינו יחס הדמיון והחלק ממה שכבר ידעת מהטור השלישי והשני | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויחס הדמיון ושני חלקים | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
מהטור החמישי והשלישי והוא הדמיון ושתי שלישיות | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומן הטור הששי והרביעי והוא אל הדמיון ושני רביעיות | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומהטור השביעי והחמישי והוא אל הדמיון ושתי חמישיות | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועל הדרך הזה | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויצא אלינו מן הלוח הטור השביעי והרביעי בהנחת שני טורים יחס הדמיון ושלשה רביעיות | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומן הטור השמיני והחמישי בהנחת שני טורים יחס הדמיון ושלשה חמישיות | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועל הדרך הזה | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויצא אלינו מן הלוח התשיעי והחמישי בהנחת שלשה טורים יחס הדמיון וארבעה חמישיות | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומן הטור העשירי והששי יחס הדמיון וארבעה ששיות | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועל הדרך הזה יצא לנו יחס השני דמיונים וחלק מזה הלוח ג"כ | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
אם הראשון שבהם והנה הוא יחס השני דמיונים והחצי בהנחת שני טורים מהטור החמישי והטור השני | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם השני והוא יחס שני דמיונים ושליש הנה מהטור השביעי והשלישי כאשר תניח שלשה | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם השלישי והוא יחס השני דמיונים ורביע מהטור התשיעי והרביעי כאשר תניח ארבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויצא לנו יחס השני דמיוני' והשני חלקים | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
אם השני שלישיות הנה מהשמיני והשלישי | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
והשני רביעיו' מהעשירי והרביעי | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויצא לנו יחס הדמיון ושלשה חלקים ושאר היחסים כאשר נתנהג בדרך אשר כוננו אליה | ||||||||||||||||||||||||||||||||||||||||||||||||||
Producing the Ratios from Equality |
|||||||||||||||||||||||||||||||||||||||||||||||||||
| The ancients referred to the method of production the ratios from equality and the extraction of the different ratios from the referred ratios. | וכבר רמזו הקדמוני' אל דרך התילד משווי היחסים והביא אל היחסים המתחלפים מהיחסי' הרמוז אליהם | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Which is, that whichever equal numbers, out of which three will be arranged, all ratios can be produced from them by the method employed with them: | והיא כי איזה מספרים שוים יסודרו מהם שלשה אפשר שיתילדו היחסים כלם מהם בדרך נעשה בהם | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה יהיה לוח בו שלשה מספרים אח"כ שלשה מספרים אחרים ויהיו שלשה שלשה | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויתרבו לבחינה וההרחבה בנסיון | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
וימשך אליו ברוחב לוח אחר נחלק בחלקיו | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונאמר שאנחנו כאשר נקח הראשון ונניחהו בבית מכל טור ברחב על שהוא ראשון | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
אח"כ נחבר הראשון והשני ונסדר אותו בבית שני מהלוח השני יהיה מטור האחדים שנים | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
אח"כ נחבר הראשון והשלישי וכפל השני ונסדר אותו בבית השלישי ממנו ויהיה מטור האחדים ארבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
אח"כ נשים הבית השני שרש | ||||||||||||||||||||||||||||||||||||||||||||||||||
| ? | ונחבר ממנו זה החבור ונעתיק אותו אל הבית השלישי זה ההעתק | ||||||||||||||||||||||||||||||||||||||||||||||||||
| The additions of these rubrics proceed continually, so they are four lengthwise. | וילך בהתמדה התוספת הזה באלה הבתים והנה יהיו ארבעה בארך | ||||||||||||||||||||||||||||||||||||||||||||||||||
| If happened first that the ratio of every three numbers on one line is a continuous ratio. | קרה מזה ראשונה שיהיה יחס כל שלשה מספרים בשורה אחת יחס מתדבק | ||||||||||||||||||||||||||||||||||||||||||||||||||
| The required ratios are produced from them. | ויתילדו מהם מהיחסים הדרושים | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ראשונה יחסי הכפולים | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונמצא מה שבבית השני על יחסי השני דמיונים | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומה שבבית השלישי על יחסי השלשה כפלים | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומה שבבית הרביעי על יחסי הארבעה כפלים | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
וילך זה בהתמדה עד אין תכלית | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
וקרה שהיה מספר מה [שבבית השלישי על יחס המוסיף חצי למה] שבבית השני | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומה שבבית הרביעי על יחס המוסיף שליש למה שבבית השלישי | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועל הדרך הזה | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומה שבבית השני מהשורה השנית על יחס ארבעה כפלים למה שבבית הראשון[33] | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומה שבבית השלישי על יחס שני דמיונים ורביע למה שבבית השני | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומה שבבית הרביעי על יחס דמיון ושבעה תשיעיות למה שבבית השלישי | ||||||||||||||||||||||||||||||||||||||||||||||||||
| ? | לא יהיה זה סדור | ||||||||||||||||||||||||||||||||||||||||||||||||||
| When wanting to add to the diagram other ratios instead of the diagram of the multiple ratios: replacing the third column with the first and the first with the third, so the middle remains in its place. | וכאשר נרצה להוסיף לציור היחסים האחרים תמורת ציורנו ליחסי הכפלים נהפוך השורה השנית[34] באורך עד שיפול הראשון השלישי בראשון והראשון בשלישי וישאר האמצעי על ענינו | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר נקח לחבר החבור הנזכר מזה המקום בשנקח הראשון אח"כ נעתיקנו ראשונה בשורה השלישית ויהיה ארבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
אח"כ נחבר הראשון והשני ונעתיק אותו אל השורה השלישית ויהיה ששה | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
אח"כ נחבר הראשון והוא ארבעה והשלישי והוא אחד וכפל השני והוא ארבעה ונעתיק אותו אל הבית השלישי והנה יהיה תשעה | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
וימשכו מספרי השורה על יחס המוסיף חצי וכבר התילדו מיחס הכפל והם הנקראים יחד על שם השנים | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר נעשה זה המעשה בשורה אשר ברחב אשר ליחס השלשה כפלים יצאו לך שלשה מספרים על יחס המוסיף שליש כי שניהם נקראים בשם השלשה | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן הענין בטור הרביעי כי הוא יוציא יחסי המוסיף רביעית | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר תהפך הנחת מספרי המוסיף חצי יולד לך יחס הכפל וחצי | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומהמוסיף שליש יחס הכפל ושליש | ||||||||||||||||||||||||||||||||||||||||||||||||||
| When reversing the numbers of the superparticular ratio and applying the known procedure, the rest of the ratios are produced, and they never cease to be produced from each other endlessly, until the production of all of them from equality is revealed. | וכאשר תהפך מספרי המוסיף חלק ותנהג המנהג הידוע יצאו לך שאר היחסים ולא יסורו מלצאת לך קצתם מקצת אל בלתי תכלית עד שיתגלה התילדות כל אלו מיחס השווי | ||||||||||||||||||||||||||||||||||||||||||||||||||
Reducing the Ratios to Equality |
|||||||||||||||||||||||||||||||||||||||||||||||||||
| One can reverse it and find that all the other ratios are reduced to equality. | ובידך שתהפך ותמצא שאר היחסים כלם ישובו אל יחס השווי | ||||||||||||||||||||||||||||||||||||||||||||||||||
The procedure:
|
המשל בזה שאתה כאשר תניח מספרים ג' על יחס נמשך | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותשמור הקטן בעניינו | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
אח"כ נגרע אותו מן האמצעי ותשים מה שנשאר גבול אמצעי | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
אח"כ תשליך אותו מהגדול כמו הקטן ודמיון כפל השני האמצעי ותשים מה שנשאר גבול שלישי | ||||||||||||||||||||||||||||||||||||||||||||||||||
| One finds a continuous ratio. | תמצא יחס מתדבק | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Apply this procedure on these numbers and terms and another ratio will be produced. | אחר כן תעשה באלה המספרים והגבולים זה הפעל ויצא לך יחס אחר | ||||||||||||||||||||||||||||||||||||||||||||||||||
| According to this way until reaching the equality. | ועל הדרך הזה עד שיביא אותך אל יחס השווי | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון זה שיהיו המספרים ראשונה על יחס שני דמיונים ושתי שלישיות כמו ט' וכ"ד וס"ד | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והנה תשמור ט' | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ותפיל אותם מכ"ד ותשים מה שנשאר והוא ט"ו גבול שני | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והנה תקח כפלו עם ט' ותפיל אותם מס"ד וישארו לך כ"ה והנה תשים אותם שלישי | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
יצאו לך מספרים נמשכים על יחס המוסיף שני שלישים | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
אח"כ תעשה זה המעשה במה שאצלך ויצאו לך ט' וו' וד' והם מספרים נמשכים על יחס המוסיף חצי | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
אח"כ תעשה זה המעשה באלה המספרים ויצאו לד' ב' א' וזה על יחס הכפל | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
אח"כ כשתעשה זה המעשה יצאו לך א' וא' ואחד וחזר אל יחס השווי | ||||||||||||||||||||||||||||||||||||||||||||||||||
| According to this property, when setting the triple ratio, the quadruple ratio and the other ratios that are not mentioned - reducing them to equality by reversing the method by which they were produced. | ובזה הוא הענין כאשר תשים יחס הג' כפלים והד' כפלים ושאר היחסים אשר לא נזכרו התכה בהפך להשיב אותם על יחס השווי מהדרך אשר ממנו הרכבו | ||||||||||||||||||||||||||||||||||||||||||||||||||
Composing a Ratio from Two Ratios |
|||||||||||||||||||||||||||||||||||||||||||||||||||
| Moving on to the composition of a ratio from two ratios. | ונעתק עתה בחבור יחס במספרים משני יחסים | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Prefacing a general introduction enough for examining the property in each ratio, which is that every particular example brought for the composition of a ratio from two ratios, the ratios are already found in this section by a certain description and this rule is possible for all numbers in these ratios. | ונקדים לזה הקדמה כוללת יספיק לנו ממנה בחינת הענין ביחס יחס והיא שכל משל חלקי נביא לחבור יחס במספרים משני יחסים הנה כבר נמצא היחסים בזה החלק על תאר מה והנה זה כלל עובר בכל מספרים יהיו על אלו היחסים | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויהיה א"ב על דרך משל ד' ויהיה א"ג ב' ויהיה א"ד ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויהיה לא"ב אל א"ד יחס והוא יחס המוסיף שליש | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויהיה לא"ד אל א"ג יחס והוא יחס המוסיף חצי | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ולא"ב אל א"ג יחס והוא יחס הכפל והוא מחבר בלי ספק משני אלו היחסים | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה אומר שכל יחס המוסיף חצי יצטרף אליו יחס המוסיף שליש יהיה המקובץ מה שתתקבץ הנה בעינו וכל יחס הכפל הנה יסבול שיחלק לאלו השני יחסים ויפרד אליהם | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
שאם לא | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה יהיה יחס ה"ח לה"ז יחס המוסיף חצי | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויחס ה"ו לה"ח יחס המוסיף שליש | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה אומר שיחס ה"ו לה"ז יחס הכפל | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
כי אתה יודיע שכאשר נחלק הנה ירצה הבדלנו יחס ב"ד ו"ח אל א"ד ה"ח א' | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ובהבדל יחס א"ג ה"ז אל ג"ד ז"ח א' | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה בשווי יחס ב"ד ד"ג כמו יחס ו"ח ח"ז | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויהיה בהרכבה יחס כל ב"ג אל ד"ג וכל ו"ז אל ח"ז א' | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמנם יחס ד"ג ג"א כמו ח"ז ז"ה | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה בדרך השווי יחס ב"ג ג"א כיחס ו"ז ז"ה | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה בדרך ההרחבה יחס א"ב א"ג הוא יחס ה"ו וז"ה | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Also for the supposition of the compound ratio, it is as it is for this part or for whichever ratios. | וגם כן כאשר תהיה ההנחה היחס המורכבת הנה הוא כאשר היה בזה החלק וביחסים כמו שהיה | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
אח"כ נביא איזה שני מספרים שיהיו | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה יהיו ה"ז ה"ו ויהיו על יחס הכפל | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה נאמר שיחס המוסיף חצי יפול בין ז' וח' | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
שאם לא יפול מחוץ כמו ז' ט' | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה כאשר נצרף אליהם היחס האחר כמו ט"ו ישוב היחס המורכב הראשון | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויהיה אז יחס ה"ו ה"ז כמו יחס ה"ו ה"ח כפי מה שבארנו | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
והיה מה שהוא יותר גדול מן ה"ו כמו ה"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה א"כ יפול מבפנים כמו ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||
| ? | ונאמר שיחס ה"ו ה"ח הוא היחס האחר שאם לא הנה יפול ה"ח עם ה"ב או ה"ח או עם ה"ט ויקרה הבטל הנזכר | ||||||||||||||||||||||||||||||||||||||||||||||||||
| We think that we brought a partial proof, as we have mentioned the sesquialter, the sesquitertian and the double ratio, but you should know that this is a general proof. | והלא נחשוב שאנחנו הבאנו מופת חלקי לזכרנו החצי והשליש ויחס הכפל אבל ראוי שתדע שזה המופת כללי | ||||||||||||||||||||||||||||||||||||||||||||||||||
| We brought the example to give the meaning, else you can say that the two numbers AB and AG are two numbers having a certain ratio between them. | ואמנם הבאנו משל לתת המובן שאם לא הנה לך שתאמר ששני מספרי א"ב א"ג שני מספרים חלקים וביניהם יחס מה | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Thus, in this example two ratios AB : AD and AD : AG, were joined into whichever ratio it will be. | וככה חוברנו בזה המשל משני יחסים א"ב א"ד וא"ד א"ג איזה יחס היה | ||||||||||||||||||||||||||||||||||||||||||||||||||
| ? | והנה אם נפל מספר ביניהם קטן מאחד מהם וגדול מאחר אח"כ במופת על הצד הכולל מזולת רמז אל שינוי היחס | ||||||||||||||||||||||||||||||||||||||||||||||||||
| This explanation is enough for endeavoring to confirm the proof of the composition of a ratio from two ratios by numbers as found in the teaching of music after this section. | הנה זה הביאור יספיק ממנו ההשתדלות בקיום המופת על חבור יחס משני יחסים במספרים כאשר נמצא המשלים יוציאו אליו השני יחסים בלמודינו המוסיקי אחר זה האופן | ||||||||||||||||||||||||||||||||||||||||||||||||||
| But, we will endeavor in special explanations [to demonstrate] which ratios are as principals for the other ratios. | ואבל אנחנו נשתדל בבאורים מיוחדים ליחס מה הם כמו ראשים לשאר היחסים | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
מזה שאנחנו נאמר שיחס הכפל ויחס המוסיף חצי יחובר מהם יחס הג' דימיונים א"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
מופת זה | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
שא"ג יכפל א"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה ב"ג כמו א"ב הנה הוא חצי א"ג | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמנם ג"ד חצי א"ג | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה א"ב ב"ג ג"ד שוים קצתם לקצת | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה יהיה כל א"ד ג' דמיוני א"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם יהיה ג"ד שליש א"ג | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה א"ד כפל ושליש א"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה נחלק א"ג אל שלשה חלקים על ה' וז' | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה יהיה א"ה כמו ג"ד והוא שליש א"ג אשר הוא כפל א"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה חצי א"ה שליש א"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה א"ד כמו כפל א"ב רצו' א"ג וכמו שלישית רצו' ג"ד | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם היה יחס א"ג א"ב יחס המוסיף שליש | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה יחס א"ד א"ב יחס הכפל | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה נחלק א"ב בשני חלקים על ה' | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויהיה א"ה כמו ב"ג | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויהיו חלקי א"ה ה"ב ב"ג שוים והם ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
וג"ד כמו א' מג' חלקי א"ג | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה החלקים הד' שוים | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה כלל ב"ד כמו כלל א"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה תוספת א"ד על א"ב בדמיון | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם היה יחס א"ג א"ב יחס המוסיף שליש | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויחס א"ד א"ג יחס המוסיף שמינית | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה יחס א"ד א"ב יחס המוסיף חצי | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה נחלק א"ב לשלישיותיו על ז' וה' | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויהיו חלקי א"ז ז"ה ה"ב ב"ג שוים והם ד' חלקים | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
וחצי כל אחד מהם הוא שמינית א"ג והוא שוה לג"ד | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה יהיה ב"ד שלשה דמיוני ג"ד | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
וא"ב ששה דמיוני ג"ד | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
והוא יחס דמיון וחצי | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויחס ב"ד ד"ג הוא יחס א"ב ב"ג | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ובתמורה יחס ב"ד א"ב יחס ד"ג ב"ג | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
וד"ג חצי ב"ג | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה ב"ד חצי א"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה א"ד א"ב יחס דמיון וחצי | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר היה יחס א"ג א"ב יחס דמיון ורביע | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויחס א"ד א"ג דמיון וחומש | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה יחס א"ד א"ב יחד דמיון וחצי | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
לפי שא"ב כאשר יתחלק ברביעיות היה כל חלק כמו ב"ג והיו החלקים חמשה שוים ויהיה ב"ד כמו חצי א"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר היה יחס א"ג א"ב יחס דמיון וחומש | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויחס א"ד א"ג יחס דמיון וששית | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה יחס א"ד א"ב יחס דמיון ושתי חמשיות | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויתבאר לך זה כשנחלק א"ב לה' חלקים ונעשה מה שעשינו | ||||||||||||||||||||||||||||||||||||||||||||||||||
Therefore, it is clear that:
|
ויתבאר לך מזה שיחס המחובר מדמיון וששית ודמיון ושביעית הוא יחס דמיון ושליש | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
והמחובר מדמיון ושביעית ודמיון והשמינית הוא יחס דמיון ושתי שביעיות | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
והמחובר מדמיון ושמינית ודמיון ותשיעית הוא יחס דמיון ורביעית | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
והמחובר מיחס דמיון ותשיעית ודמיון ועשירית הוא יחס דמיון ושתי תשיעיות | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
והמחובר מדמיון ועשירית ודמיון וחלק מי"א הוא יחס דמיון וחומש | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
והמחובר מדמיון וחלק מי"א ודמיון וחלק מי"ב הוא יחס שני חלקים מי"א | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
והמחובר מדמיון וחלק מי"ב ודמיון וחלק מי"ג הוא יחס הששית | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
והמחובר מדמיון וחלק מי"ג ודמיון וחלק מי"ד הוא יחס משני חלקים מי"ג | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
והמחובר מיחס הדמיון וחלק מי"ד ודמיון וחלק מט"ו הוא יחס דמיון ושביעית | ||||||||||||||||||||||||||||||||||||||||||||||||||
| And so on continually. | ועל הדרך הזה כל ההמשך | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר היו א"ג א"ב על יחס דמיון וחלק מט"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
וא"ד א"ג על יחס המוסיף רביעית | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה יחס א"ד א"ב דמיון ושליש | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה לפי שאתה כאשר תחלק א"ב בט"ו חלקים | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
יהיה כל א"ג י"ו חלקים | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
וג"ד רביעית זה הנה הוא ד' חלקים | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה כל ב"ד ה' חלקים | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
וא"ב [ט]"ו חלקים | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכל א"ד כ' חלקים | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה ב"ד שליש א"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכמו זאת ההנהגה הנה הוא כאשר היה א"ג א"ב על יחס המוסיף חצי | ||||||||||||||||||||||||||||||||||||||||||||||||||
| When following this way it is possible to bring a proof for the rest of the composition in music, as the previous explanation is enough for the endeavoring in all this. | ואפשר לך כאשר תלך בזה הדרך שתביא מופת על שאר מה שבמוסיקי מהחבור לפי שהביאור הקודם יספיק לך השתדלות בזה כלו | ||||||||||||||||||||||||||||||||||||||||||||||||||
| The third section is complete. | נשלם המאמר השלישי' | ||||||||||||||||||||||||||||||||||||||||||||||||||
Numbers as Geometric Shapes |
|
| The properties of the number from the aspect of its quantity by itself were already referred to. | כבר רמזנו לך אל ענייני המספר מצד כמותו בעצמו |
| [Now] the properties of the number from the aspect of its having a quality of combination from units, by which it resembles to the measured shapes, will be referred to. | ורמזנו לך אל עניינים מענייני המספר מצד שיש לו איכות חבור מהאחדיות ידמה בו לתמונות השעוריות |
| The images of the number resemble by combinations to the measures. | כבר ידמו תמונות המספר בחבורים לשעורים |
[They are called]:
|
ויאמר מספרים קוויים |
|
ומספרים שטחיים ומושטחים |
|
ומספרים גשמיים ומוגשמים |
Linear Numbers |
|
| The linear numbers begin from one and follow their natural course. | הנה המספרים הקוויים מתחילים הם מהאחד וילכו כפי מנהגם |
| The first linear number is two, then three and so on. | והמספר הקוי הראשון הוא השנים אח"כ הג' ועל הדרך הזה |
Plane Numbers |
|
| The plane [numbers] are those that can be combined to one another by a combination that resembles to the one that have a geometrical shape. | ואולם המושטחי' הנה הם אשר אפשר שיחובר קצתם אל קצת חבור ידמה קצת השטים הבעל תמונה |
| והמוגשמים | |
Triangular Numbers |
|
| The first plane [numbers] are the triangular numbers. | והמושטחים ראשונים הם המספרים המשלשים |
| They are the numbers that when their units are arranged in a certain arrangement they resemble to a geometrical shape that is encompassed by three sides. | והם המספרים אשר כשיסודרו אחדיהם סדור מה ידמו תמונה יקיפו בה שלש צלעות |
|
והראשון שבהם שלשה וצורתם כזה |
|
אח"כ הששה |
| Their shape is generated from joining a numerical line that exceeds by one over the numerical line [of the preceding triangle] | וצורתם תתחדש מצרוף קו מספריי מוסיף באחד על הקו המספריי אשר הוא כמו שראית |
|
שנים נצטרף אל האחד ונתילד המשלש הראשון והנה יהיה שלשה ותהיה הצורה בזה |
| According to this way, whenever a numerical line is joined, by the sequence of the numbers, a greater triangle will generated. | ועל הדרך הזה כל מה שתצטרף אל זה קו מספריי על סדר המספרים הנמשכים יתחדש משלש יותר גדול |
|
המשל בזה כשתצרף אל זה קו מספריי מארבעה אחדויות יהיה תמונה משלש אחר כזה |
|
והנה הראשון שבמשלשים ג' וצלעו ב' |
|
והמשלש השני ששה וצלעו ג' |
|
והמשלש השלישי י' וצלעו ד' |
|
והמשלש הרביעי ט"ו וצלעו ה' |
|
והנה כל משלש יוסיף על אשר ימשך תחתיו כמו צלע עצמו |
|
ויתחלפו צלעותיהם על סדר המספרים הנמשכים מן האחד עם הא' ואי זה מספר שיתקבץ מזה הנה הוא משלש |
|
וכל משלש הנה צלעו יוסיף על מדרגתו בא' |
|
וכאשר יאמר לך מה הוא צלע המשלש העשירי מראשית המספרים המשלשים |
|
יהיה מספר הצלע ומספר המדרגה אחד |
|
ואם יאמר אליך שתאמר שהוא מרבע או מעקב בכח הנה אינו משלש ולא מחומש ולא דבר מאלו לא בכח ולא בפועל אלא בשתוף השם ולא תשגיח למה שיאמרו |
|
וכל משלש הנה הוא חצי הכאת מדרגתו במוסיף ממנו באחד |
|
עד שאם יאמר לך מהו מספר המשלש החמשי בכח הנה תקח חמשה ותכה אותם במוסיף ממנו באחד ויהיו שלשים ותקח חציים והוא חמשה עשר והוא המשלש החמישי[35] |
|
וכל צלע משלש הנה הוא היותר קטן שבשני מספרים נמשכים יוכה אחד מהם באחר ויהיה ממנו כפל משלשו |
|
עד שאם יאמר לך מה הוא צלע חמשה עשר מהמשלשים |
|
הנה אנחנו נכפול אותו ויהיה שלשים ונבקש שני מספרים נמשכים אשר מושטחם שלשים ונמצא שהם חמשה וששה ונאמר שצלעו חמשה |
Square Numbers |
|
| After the triangular numbers are the square numbers. | ואחר המספרים המשלשים המספרים המרבעים |
| They are as already known. | והם אשר כבר ידעת אותם |
| They are generated from the numerical lines, the value of each of which is equal to the number of units in it. | והנה הם יתחדשו מקוים מספריים שוים מספרם מספר מה שבאחד מהם מן האחדים |
| Their sides are according to the order of the numbers, beginning from one. | וצלעותיהם על סדר המספרים מתחילים מן האחד |
|
כמו האחד שהוא מרבע האחד |
|
|
והארבעה שהוא מרבע השנים |
|
|
והתשעה שהוא מרבע השלשה |
|
|
והששה עשר שהוא מרבע הארבעה |
|
כפי הצורות האלו |
|
והתילדותם מקבוץ הנפרדים הנמשכים עם האחד |
|
כמו השלשה והאחד שהוא ארבעה והוא ראשון המספרים המרבעים[36] |
|
אח"כ האחד והשלשה והחמשה והוא תשעה והוא המספר המרבע השני |
|
אח"כ האחד והשלשה והחמשה והשבעה והוא ששה עשר והוא המספר המרבע השלישי |
|
ומסגלות המרבעים שאתה כאשר תקבץ אותם ממרבע האחד יהיה מקובצם יותר ממרבע האחרון כמו מה שלפניו מן המרבעים |
|
המשל בזה שמקבץ מרבע האחד והשנים יוסיף על מרבע השנים כמו מרבע האחד |
|
ומקובץ מרבעי האחד והשנים והשלשה יוסיף על מרבע השלשה כמו מקבץ שני מרבעי האחד והשנים |
|
וכבר הוציאו להולדת המרבעים דרך יקראוהו רצוא ושוב[37] |
|
והוא שאתה כאשר תתחיל מן האחד ותקבץ מה שתרצה מהמדרגות אח"כ תהיה נוטה יורד ומקבץ הנה מה שיהיה מקובץ זה ההוא מרבע |
|
המשל בזה שיעלה מן האחד אל השנים ויהיו שלשה אח"כ נשוב אל האחד ויהיו ארבעה והוא מרבע ראשון |
|
אחר כן כאשר תקבץ האחד והשנים והשלשה ותצרף אליו השנים והאחד יהיו תשעה והוא מרבע שני |
|
וכאשר תעלה מן האחד והשנים והשלשה והארבעה מקובץ אח"כ תרד ותקבץ השלשה והשנים והאחד יהיה מקובץ זה ששה עשר והוא המרבע השלישי מן המרבעים המספריים |
|
ושלמות זה הדרך שמקובץ כל המספרים הנמשכים עם מקובץ מה שהוא חסר מהם כמו המדרגה האחרונה הנה הוא מרבע |
|
וגם כן כפל מקובץ כל מספרים נמשכים זולת המספר האחרון הנה הוא מרבע |
|
וכל שני משלשים נמשכים יתקבצו מן האחד והשלשה והששה הנה הוא מרבע וזה גם כן התילדות המרבעים |
|
ויהיה כל מרבע ממשלש במדרגתו ומשלש חסר ממדרגתו באחד |
|
וכל שני מרבעים יוכה צלע אחד מהם באחר ויכפל ויקובץ אל השני מרבעים הנה הכל מרבע[38] |
|
כמו הכאת שנים בשלשה כאשר יקובץ כפלו עם ארבעה ותשעה אשר הוא חמשה ועשרים |
|
וכל מרבע יתוסף עליו גדרו פעמים ואחד או יצורף אל דמיונו ודמיון רביעיתו או שלשה דמיוניו או יחוסר ממנו שלשה רביעיותיו הנה מה שיגיע מרבע[39] |
|
ואין מרבע שיהיה חציו או כפלו מרבע |
|
ולא יתקבצו מהמרבעים הנמשכים המתחילים מן האחד מרבע כלל |
| ? | ואין מרבע שיהיה לו שליש מן השלמים |
|
ודע שאחדי המספר הנגדר לא ימלטו אם שיהיו אחד או ארבעה או חמשה או ששה או תשעה |
|
ואם היה אחד הנה אחדי צלעו אם אחד ואם תשעה |
|
ואם היה ארבעה הנה הם שנים או שמנה |
|
ואם היה חמשה הנה הם חמשה |
|
ואם היה ששה הנה הם ארבעה או ששה |
|
ואם היה תשעה הנה הם שלשה או שבעה[40] |
|
ובחינת[41] המרבעים בדרך אנשי הודו הנה לא ימלט אם שיהיה אחד או ארבעה או שבעה או תשעה |
|
והנה לאחד אחד או שמנה |
|
ולארבעה שנים או שבעה |
|
ולשבעה ארבעה או חמשה |
|
ולתשעה שלשה או ששה או תשעה |
Polygonal Numbers |
|
| Following the square numbers are the pentagonal numbers | וימשכו למספרים המרבעים המספרים המחמשים |
|
והראשון שבהם החמשה ויתחברו כזה |
|
והוא המחמש הראשון וצלעו שנים |
|
והמחמש השני הוא אשר צלעו המספר השני והוא שלשה ויהיה המחמש המתקבץ ממנו שנים עשר כזה |
|
והמספר השלישי והוא ארבעה הנה המחומש המתקבץ ממנו הוא שנים ועשרים כזה |
| Likewise the fourth, the fifth, the sixth, and the seventh - the sequence of their sides is as the sequence of the successive numbers. | והרביעי והחמשי והששי והשביעי סדור צלעותיהם על סדור המספרים הנמשכים |
|
והתילדותם מקבוץ המספרים העודפים בשלשה שלשה מתחילים מן האחד |
|
כמו מספרי א' ד' ז' י' י"ג י"ו י"ט כ"ב עם האחד |
|
כי האחד עם הארבעה חמשה והוא המחמש הראשון |
|
והאחד עם הארבעה והשבעה שנים עשר והוא המחמש השני |
|
והאחד עם הארבעה והשבעה והעשרה שנים ועשרים והנה זה המחמש השלישי |
|
וכבר יולדו מקבוץ המרבעים עם המשלשים רצוני קבוץ המרבע אשר במדרגתו עם המשלש אשר הוא למטה ממדרגתו |
|
כמו שתמצא כי מקבוץ המרבע השני שהוא תשעה עם המשלש הראשון שהוא שלשה יולד שנים עשר המחמש השני |
| Indeed, one finds such property in all the measured shapes: | והנה לכל התמונות השעוריות תמצא סגלה כזאת |
|
כי הנה המשושה יתחדש מקבוץ המחמש אשר במדרגתו עם המשלש אשר הוא למטה ממנו במדרגה |
|
כמו המששה השני שהוא חמשה עשר אשר נולד משנים עשר המחמש השני עם שלשה המשלש הראשון |
|
וכן המשבע השני שהוא שמנה עשר יתחדש מהמששה השני שהוא חמשה עשר ומשלשה המשלש הראשון |
|
ועל הדרך הזה |
|
וכבר יולדו המחמשים בלקיחת המרבעים אשר במדרגתם וכפי מספר המדרגות כל כך פעמים נוסיף על המרבע ההוא מספר חצי צלעו |
|
דמיון זה לקחנו ארבעה המרבע הראשון והוספנו עליו חצי צלעו ועלה חמשה המחמש הראשון |
|
ולקחנו תשעה המרבע השני וקבצנו עמו שני פעמים חצי צלעו ועלה שנים עשר המחמש השני |
|
ולקחנו ששה עשר המרבע השלישי והוספנו עליו שלשה פעמים חצי צלעו ועלה שנים ועשרים המחמש השלישי |
| This property is also related to all the measured shapes: | וכן הסגלה הזאת דבקה לכל התמונות השעוריות |
|
אמנם למשושה תמורת חצי צלע נקח צלע |
|
ולמשבע תמורת זה צלע וחצי |
|
ולמשמן שתי צלעות |
| So on, adding half the side by half the side, then multiplying the result by the number of the ranks. | וכן תמיד בתוספת חצי צלע חצי צלע אח"כ בהכפלת המגיע במספר המדרגות |
|
משל זה לקחנו ארבעה המרבע הראשון וקבצנו עמו צלעו פעם ועלה ששה המששה הראשון |
|
לקחנו תשעה המרבע השני וקבצנו עמו צלעו שתי פעמים ועלה חמשה עשר המששה השני |
|
עוד לקחנו ארבע המרבע הראשון וקבצנו עמו צלעו וחצי צלעו פעם ועלה שבעה המשבע הראשון |
|
לקחנו תשעה המרבע השני ועמו קבצנו שני פעמים צלעו וחצי צלעו ועלה שנים עשר המשבע השני ועל הדרך הזה כלם |
| All these are composed from triangles. | וכבר התחברו אלה כלם מהמשלשי' |
|
וכמו שהמרבע יתרכב משני משלשים |
|
כמו כן המחמש יתרכב משלשה |
|
והמששה מארבעה |
|
והמשבע מחמשה |
| In a way that is similar to the composition of the squares. | על דרך דומה לדרך חבור המרבעים |
|
ויהיה דרך משל המחמש השני שהוא י"ב מרכב מהמשלש הראשון שתי פעמים והמשלש השני פעם |
|
והמחמש השלישי מהמשלש השני שתי פעמים והמשלש השלישי פעם |
|
וכן המששה השני שהוא ט"ו מורכב מהמחמש השני המורכב משלשה משלשי' ומהמשלש הראשון אשר למטה ממנו |
|
ואפשר לומר לפי זה שיהיה האחד ג"כ כן במדרגת משלש |
|
וזה כי המחמש הראשון הוא מורכב מארבעה ואחד |
|
וכל מרבע שעוריי יתחלק לשני משלשים ולזה מן הנכון שיהיה האחד כמו כן במקום משלש אחד |
|
וכל מששה משלש ולא יתהפך |
|
כי הנה הששה מששה ראשון הוא המשלש השני |
|
וט"ו המששה השני הוא המשלש הרביעי |
|
וכ"ח המששה השלישי הוא המשלש הששי |
|
ואין כל משלש מששה |
|
כמו ג' י' וכ"א שהם משלשים ואינם מששים |
|
וכל משלש מספרו זוג הנה אין שתוף בינו ובין המששה[42] |
|
וכאשר תרצה שתמצא מדרגת המשלש מהמששה הנה תגרע האחד מכפל מספר מדרגת המששה[43] והפוכו שתוסיף אחד על מספר מדרגת המשלש ותקח חציו |
|
וכל מספר מחמש הנה הוא חצי מה שיתקבץ מהכאת מספר חסר ממדרגתו באחד בתוספת אשר בין המספרים אשר יתילדו מהם[44] והוא שלשה נוסף עליו מה שבין שני מספרים מזה והוא שנים מוכה במספר מדרגתו מהמחמשים המספריים |
|
המשל בזה כאשר תרצה שתדע המחמש הרביעי תכה שלשה בשלשה ויהיו תשעה ותוסיף עליהם שנים ויהיו אחד עשר תכה אותם בארבעה ויהיו ארבעים וארבעה תקח חצים ויהיו שנים ועשרים והוא המחמש הרביעי |
|
וגם כן כי כל מחמש הנה הוא כמו הכאת מספר מדרגתו נמנית מן האחד בעצמו נוסף עליו חצי צלעו בתוספת מדרגתו במחמשים המספריים[45] |
|
המשל בזה בשאלה הנזכרת שנכה ארבעה בארבעה לפי שהוא במדרגה הרביעית מן האחד ויהיו ששה עשר ותוסיף עליו חצי צלעו והוא שנים ושלשה מדרגות ויהיו שנים ועשרים[46] |
| After the pentagons the hexagons | ואחר המחמשים המששים |
|
ויתחברו מקבוץ המספרים העודפים בארבעה ארבעה |
|
כמו א' ה' ט' י"ג י"ז כ"א |
|
על הקש מה שנאמר במחמשים |
| Then the heptagons | אח"כ המשבעים |
|
ויתחברו מקבוץ המספרים העודפים בחמשה חמשה |
| The same is applied to all of them. | וכן תקיש בכלם |
|
ונאמר שכל שטח אחר המשלש כאשר יחובר עם המשלש יתחדש השטח אשר ימשך לזה השטח במספר הצלעות |
|
כמו המשלש הראשון והוא שלשה כשיתחבר עם המרבע השני יהיה מחמש |
|
וכאשר יתחבר עם המחמש השני והוא שנים עשר יהיה מששה והוא החמשה עשר |
|
ועל זה הדרך |
|
ומותר כל שטח על אשר לפניו |
| ? | וכבר נזדמן זה ולא יתהפך |
|
וכל מספר שלם הנה הוא לפניו מששה או משלש |
|
ועוד יהיה מזה דרך נגיע בו אל הוצאת מדרגות המספרים השלמים גם כן |
|
כי כאשר יאמר לך המספר השלם הראשון מאיזה מהמשלשים או מהמששים הוא |
|
הנה תעיין אל הסדור אשר ידעת אותו בזה האחד בפרט |
|
ותמצא הראשון שבזוגי הזוגות יבחן בו הסדור הידוע ארבעה |
|
וכאשר תגרע ממנו אחד ישאר שלשה מספר ראשון ונכון הוא לפעלתך |
|
|
ותקח חציו והוא שנים |
|
ותאמר שהוא המששה השני והמשלש השלישי |
|
וימשך אל הארבעה שמנה |
|
ותמצא השבעה כמו זה מספר ראשון ויתכן למבוקשך |
|
|
ותחלק לחציים השמנה ויהיה ארבעה |
|
ותאמר שהוא המששה הרביעי והמשלש השביעי |
|
וימשך לשמנה ששה עשר |
|
וכאשר תגרע ממנו אחד ישאר מורכב והנה איננו נכון לפעלתך |
|
וימשך אל הששה עשר שנים ושלשים |
|
וכאשר תגרע ממנו אחד ישאר ראשון והוא נכון לפעלתך |
|
|
ותקח חציו והוא ששה עשר |
|
והנה תאמר המששה הששה עשר והמשלש האחד ושלשים |
|
ועל זה ההקש |
| See the wonderful diagram, from which it is clear that all the geometric shapes are produced from the triangle and dissolved to it: | ראה צורה נפלאה יתבאר ממנה שכל התמונות מתילדי' מהמשלש ונתכים אליו |
| מעשרים | מתשעים | משמנים | משבעים | מששים | מחמשים | מרבעים | משלשים |
| י | ט | ח | ז | ו | ה | ד | ג |
| כז | כד | כא | יח | טו | יב | ט | ו |
| נב | מו | מ | לד | כח | כב | יו | י |
| פה | עה | סה | נה | מה | לה | כה | טו |
| קכו | קיא | צו | פא | סו | נא | לו | כא |
| קעה | קנד | קלג | קיב | צא | ע | מט | כח |
| רלב | רד | קעו | קמח | קכ | צב | סד | לו |
| רצז | רסא | רכה | קפט | קנג | קיז | פא | מה |
| שע | שכה | רפ | רלה | קצ | קמה | ק | נה |
| decagon | nonagon | octagon | heptagon | hexagon | pentagon | square | triangle |
| 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 |
| 27 | 24 | 21 | 18 | 15 | 12 | 9 | 6 |
| 52 | 46 | 40 | 34 | 28 | 22 | 16 | 10 |
| 85 | 75 | 65 | 54 | 45 | 35 | 25 | 15 |
| 126 | 111 | 96 | 81 | 66 | 51 | 36 | 21 |
| 175 | 154 | 133 | 112 | 91 | 70 | 49 | 28 |
| 232 | 204 | 176 | 148 | 120 | 92 | 64 | 36 |
| 297 | 261 | 225 | 189 | 153 | 117 | 81 | 45 |
| 370 | 325 | 280 | 235 | 190 | 145 | 100 | 55 |
|
וזה שאתה כשהתחלת מן האחד ראשון המשלשים בכח וצרפת אותו אל השלשה ראשון המשלשים בפעל נתילד מהם ארבעה ראשון המרבעים בפעל |
|
וכאשר צרפת ג' עם ו' הנמשך לו נתילד מהם ט' המרבע השני |
|
וכן תמיד |
|
אח"כ כשתשב אל האחד ראשון המשלשי' בכח וצרפתהו עם ד' ישוב ה' מחמש ראשון בפעל |
|
ובצרוף ג' לט' יתילד י"ב מחמש שני |
|
ומו' וי"ו מחמש שלישי |
|
וכשתשוב לאחד ותצרפהו עם ה' יוליד מששה ראשון בפעל |
|
וג' עם י"ב יוליד מששה שני |
|
וכן תמיד |
Solid Numbers |
|
| Now the solid numbers will be discussed. | ונדבר עתה במספרים המוגשמים |
Pyramids with Sharp Apex |
|
| The first of them are the pyramids. | והראשונים שבהם המחדדים |
| The pyramids are the most famous of the sharp solids, beginning from a broad base, then they do not cease from growing, until reaching the end of the sharp limit, the one. | והמחדדים והם הנודעים במתלהבים הם אשר יתחילו מתושבת מרוחת אח"כ לא יסורו מלצמוח עד שיגיעו אל קצה הגבול מן החדות אל האחד |
|
והראשון שבהם אשר תושבתו משלשת |
|
והראשון מאלו הם הארבעה והנה הם המספר הראשון אשר הוא קויי ושטחיי ומגשם |
Their production:
|
ויתילד מחבור המשלשים על המשכם |
| ?? | הדרכה לחסרים מהם על המוסיף עד שיכלו אל האחד |
|
אח"כ אשר תושבתם ארבעה ויתילדו ומחבור המרבעים על זה התאר |
|
ועל הדרך הזה אשר תושבתם מחמשת ואשר תושבתם משששת |
| ?? | וכל מספר מושטח יתרכבו ממנו יקרא ואשר יחסר מצדו יקרא |
| Their production: | והתילדותם |
|
אם אשר תושבתו משלש |
|
הנה כאשר יצורף אל האחד המשלש הראשון ויהיו ארבעה והנה הוא המחדד הראשון |
|
וכאשר יצורף עם אלו עוד המשלש השני ויהיו עשרה יעלה המחדד השני מזה המין |
|
ואמנם אשר תושבתם מרבע |
|
הנה הראשון שבהם מן האחד והמרבע הראשון |
|
והשני אליו מן האחד והמרבע הראשון והמרבע השני |
|
ואשר תושבתם מחמש ומששה וזולת זה הנה הם על זה ההקש |
| The property of the angles and the sides and their number is according to the rule of the geometric shapes that have magnitude. | ואמנם ענין הזויות והצלעות ומספרם הנה הוא על הקש התמונות בעלות הגודל |
Prisms |
|
| The prism is also among the numerical solid shapes. | והמתגורר גם כן מהתמונות המספריות המוגשמות |
| It is [produced] from multiplying the triangles and their relation to one another. | והוא מהכפלת המשלשים ודבקות קצתם בקצת |
|
והששה המגורר הראשון שיתילד מן המשלש הראשון לו שלשה צלעות כל צלע בעל ארבעה ושתי צלעות כל צלע משלש |
| ? | אמנם הצלעות במספרם |
| The solid shapes encompassed by six surfaces are necessarily: | ואמנם התמונות המגשמות אשר יקיפו בהם ששה שטחים הנה לא ימלטו |
|
אם שיהיו ארכם ורחבם ועמקם שוים ויהיו כמו עשר בעשר אח"כ בעשר ויקרא מעקב |
|
ואם שיהיו שני קטרים מהם שוים וקטר מתחלף |
|
וכאשר יהיה הקטר המתחלף יותר קטן יקרא לבניי |
|
וכאשר יהיה יותר גדול יקרא עמודיי |
|
אם יהיה מושטחו הקטן עגלה יקרא מעגל |
| ?? | כמו חמשה בחמשה אח"כ ביותר מחמשה |
| באשר היה שיהיו השלשה מתחלפים הנה יקרא כפי זאת הצורה | |
|
ודמיון הלבניי ארבעה בארבעה אח"כ בשלשה |
|
ודמיון העמודיי הארבעה בארבעה אח"כ בחמשה |
| ודמיון שלשה בארבעה בחמשה או בשמנה | |
| ומנהגם שיקראו המספר אשר ישוב כשהוכה בעצמו בעצמו אח"כ מה שנתקבץ כעצמו ועל הדרך הזה מספר עגול כמו בס' החמשה והששה | |
|
|
כי החמשה בעצמו חמשה ועשרים |
|
|
אח"כ בחמשה מאה ועשרים וחמשה |
|
|
והששה בעצמו ששה ושלשים |
|
|
אח"כ בששה מאתים וששה עשר |
| יש מן האנשים מי שיקראו משטחו עגלה ומעוגל ומעקבו כדור וכדוריי |
Cube Numbers |
|
| The properties of the cube that should be investigated and what is are already known in the book of The Elements: | ואשר ראוי שנחקור מעניני המעקב וכבר נודע ממנו כלל בספר היסודות |
|
ומסגלות המעקב שעקב כל מספר כאשר הוכה באשר ימשך אליו אח"כ באשר לפניו אח"כ יתוסף אשר לפניו על מה שיתקבץ יהיה שוה לו[47] |
| Their production is when the successive odds are arranged, beginning from the one, then summed according to the rank, thus the cubes are produced successively. | אמנם התילדותם הנה כאשר יסודרו הנפרדים הנמשכים מתחילים מן האחד ואח"כ יקובצו כפי המדרגה הנה יתילדו המעקבים על המשכם |
|
המשל בזה שיסודרו אחד שלשה חמשה שבעה תשעה אחד עשר שלשה עשר |
|
הנה האחד מעקב |
|
ואחריו השלשה והוא במדרגה השנית הנה יחויב שתקבץ שתי מדרגות ותקבץ השלשה והחמשה והנה זה שמנה והוא מעקב |
|
ואחריהם השבעה והוא במדרגה השלישית והנה יחויב שתקבץ שלשה מדרגות והנה יהיו שבעה תשעה אחד עשר וכלל זה שבעה ועשרים והוא המעקב השלישי |
|
ועל זה המנהג |
| When wishing to know the first odd number, from which a known cube is composed, take the number of the rank of the cube from the first number of the cubes, and it is one less than the number of the terms, | וכאשר תרצה לדעת הנפרד הראשון שנתרכב ממנו המעקב הידוע הנה תקח מספר מדרגת המעקב מהמספר הראשון שבמעקבים והנה יהיה זה חסר מן הראשון באחד |
|
ויהיה דמיון שני אלו במעקב השלישי אם הראשון הנה הוא שלשה ואם השני הנה הוא שנים |
| Subtract the second from the square of the first, | ותגרע השני ממרבע הראשון |
|
כמו שתגרע הנה השנים מתשעה והנה הוא הנפרד הראשון אשר ממנו חבור המעקב השלישי וזה הוא שבעה |
|
אח"כ תוסיף אותו עליו והנה יהיה אחד עשר והוא הנפרד האחרון אשר ממנו הרכבתו |
|
ונתרכב מהם וממה שביניהם[48] |
|
והארבעה והחמשה והששה והתשעה חוזרים במעקביהם תמיד אחדים והנה יהיה זה הוראה על אחדי העקב |
|
כמו ארבעה בארבעה אח"כ בארבעה ויהיו ארבעה וששים |
|
|
והתשעה בתשעה אח"כ בתשעה והוא שבע מאות ותשעה ועשרים |
|
אמנם עקב השנים הנה הוא בשמנה תמיד |
|
ועקב השמנה הנה הוא בשנים תמיד |
|
ועקב השבעה בשלשה |
|
ועקב השלשה בשבעה תמיד |
|
והכאת המעקב במעקב וחלוקתו עליו מעקב |
| ?? | והכאת מרבע שני מספרים במרבע מספר אחד יחסים יחס שני מעקבים |
|
החלוק בין שני מעקבים הנמשכים הנה הוא הכאת היותר קטן שבשני המעקבים במספר אשר ימשך אליו ויוסיף עליו באחד כן בשלשה אחר כן תוסיף עליו אחד[49] |
|
וכל מעקב יוסר ממנו עקבו הנה יהיה לנשאר שתות שלם |
|
וכל מעקב זולת אחד הנה ימנה אותו עקבו זולת אחד |
|
וכל מעקב הנה חציו וכפלו בלתי מעקב |
|
וכל מעקב יחובר אליו האחד והכאת המשלש אשר במדרגתו בששה תמיד הנה הוא המעקב אשר ימשך אליו |
|
והנה אפשר שיתילדו מאלו המעקבים |
|
ומסגלות המעקבים שבחינתם אשר כפי מעשה המספר אשר לאנשי הודו יהיה אם אחד ואם שמנה ואם תשעה |
|
ואם היה אחד הנה אחדי הצלעות אחד או ארבעה או שבעה |
|
ואם היה שמנה הנה הוא שמנה או שנים או חמשה |
|
ואם היה תשעה הנה הוא שלשה או ששה או תשעה |
Heteromecic and square numbers |
|
| The numbers that have sides are divided: | וכבר יתחלקו בעלי הצלעות מהמספר |
|
ויאמר שמהם מה שהוא הוא הוא הארך[50] |
|
ומהם מה שהוא זולתיי הארך |
|
ומהם מה שהוא נבדל הארך והנה הוא אשר ההתחלפות בין ארכו ורחבו במה שהוא למעלה מאחד יהיה איך שיהיה |
| The custom of those who discuss arithmetic to bring in this place a discussion that is derived from the people of demonstration, which is very similar to a rhetorical and poetical discussion, but we reject this and we demonstrate it by calling the heteromecic a heteromecic number. | ומנהג המדברים במלאכת המספר שיביאו בזה המקום ובמה שירוץ מרוצתו דבור יוצא ממנהג אנשי המופת ודומה הרבה למאמר ההלציים והשיריים ונברח מזה ונוכיח עליו בקריאתם הזולתיי הארך בזולתיי הארך |
| It seems that the first "otherness" that falls between the numbers is in one, and it is the basis of the heterogeneity and its beginning, as it is the basis of the number itself. | וידמה שיהיה הזולתיות הראשון שיפול בין המספר והמספר הוא באחד ויהיה הוא שרש ההתחלפות והתחלתו כמו שהוא שרש המספר עצמו |
| The heteromecic numbers are those [whose length and breadth] differ by one. | ויהיו המספרי' הזולתיים הארך הם המשתנים באחד |
| The heteromecic surfaces are those that are encompassed by two heteromecic sides. | והשטחים הזולתיים הם אשר יקיפו בהם שתי צלעות זולתיות |
Setting a table:
|
וכאשר נרשום לוח יסודרו בו הנפרדים על המשכם מתחילים מן האחד בשורה אחת |
|
והזוגות על המשכם מתחילים מן השנים בשורה אחרת |
| As is known, by summing the odd numbers, the square numbers are produced. | הנה יולדו מקבוץ הנפרדים כפי מה שידעתו אותו המספרים המרבעים |
| By summing the even numbers, the heteromecic numbers are produced. | ויולדו מקבוץ הזוגות המספרים הזולתיים הארך |
| The "same" squares are produced from the odd numbers and the "others" from the even numbers as a necessary result. | ויתילדו מן הנפרדים המרבעים ההויים ומן הזוגות הזולתיים כפי החיוב |
| The pythagoreans start from this place, in a way that has no perfection. | ויתחילו הפיתגוריים מזה המקום בדרך אין שלמות לו |
| When summing the squares once again in a line, attributes and properties are seen from the position of the two lines: | וכאשר תקבץ המרבעים פעם שנית בשורה יראה משכונת שתי השורות ענינים וסגלות |
|
ומהם שאתה תמצא ראשון הזולתיים על יחס הכפל מראשון המרבעים והוא המוסיף דמיון |
|
והשני אצל השני על יחס המוסיף חצי |
|
והשלישי אצל השלישי על יחס המוסיף שליש |
|
ועל הדרך הזה כלם על דרך המספרים והמדרגות |
|
המשל בזה שהוא לרביעי רובע |
|
ולחמישי חומש |
| One finds the exceedance according to the ratio of the natural numbers: | ותמצא ההעדף על יחס המספרים הטבעיים |
|
כי הנה העדף המדרגה הראשונה אחד |
|
והעדף המדרגה השנית שנים |
|
ועל הדרך הזה |
| When one is omitted and the numbers are set vis-a-vis, the ratio is like this: | וכאשר ישמט האחד ויהיה הנכחיות בין מה שהוא מספר יבא היחס כמו זה |
| The excess is [now] in what was [previously] deficient: | ואמנם התוספת מצד מה שהיה ממנו החסרון |
|
יהיה הארבעה לשנים על יחס הכפל |
|
והתשעה לששה על יחס המוסיף חצי |
|
והששה עשר לשנים עשר על יחס המוסיף שליש |
|
ועל הדרך הזה |
| The difference is according to the ratio of the natural numbers, starting from two. | ויהיה החלוף על יחס המספרים הטבעיים מתחילים מן השנים |
| Arranging the first of the "others" after the first square, starting from one, then their second after the second square. | אח"כ כאשר תסדר ראשון הזולתיים אחר המרבע הראשון מתחיל מן האחד והשני להם אחר המרבע השני |
| The ratio itself is compound: | הנה יבא זה היחס בעצמו מחבר |
|
|
ויהיה יחס השנים אל האחד כיחס הארבעה אל השנים |
|
ויהיה יחס הששה אל הארבעה כיחס התשעה אל הששה והוא יחס המוסיף חצי |
| וכבר יסודרו תמיד ותהיינה השתי קצוות מבלי יחס מספרי כשיקובץ עם כפל האמצעי מרבע | |
| אח"כ כשתקבץ השתי שורות על סדורם | |
| ותתחיל הנפרדים מן האחד יתילדו מהם המספרים המשלשים על סדורם | |
|
ותמצא כל בעל צלע כאשר יחוסר ממנו צלעו יתילד הזולתי אשר הוא בשכונתו מצד החסרון |
|
וכאשר תוסיף עליו צלעו יתילד הזולתיי אשר הוא בשכונתו מצד התוספת |
| וכאשר תגיע[51] צלע המעקב ממנו ישאר צלעותיו ממנו | |
| וכאשר תקח מושטח בין שני מרבעים תמצא המרבע הראשון יקח ממנו יחס והמרבע השני יחס אחר אמנם ישובו אל היחסים הנמשכים מתחילים מן הכפל אח"כ הדמיון והחצי | |
| ועל הדרך הזה אמרו הנה הנפרדים יתנו סבת ההוא הוא ולקח ה[ההויים] | |
| ולכן יתילדו מהם המרבעים והמעקבים וימצאו במדרגות הנפרדי' מרבע ולא ימצאו במדרגות הזוגות כלל | |
| נשלם המאמר השלישי מן אלארתמיטיקי שבח לאל |
Proportions |
|
| It is a common practice to mention at this point the ratios, their types and their properties. | וכבר פשט המנהג לזכור בזה המקום היחסים ומיניהם וסגלותיהם |
| Some people established many types of relations, reaching up to twenty types and some were satisfied with ten, which were translated ancients. | ומן האנשים מי שיחדש להתיחסויות פנים רבים ויגיעו בהם אל עשרים פנים ומהם שנסתפקו על עשרה והוא המועתק מהקדמון |
| The intention is to be satisfied with mentioning these ten and not tending to bring everything they brought and to mention everything they said, because this has no perfection. | ומכונתי שאסתפק בזכר אלו העשרה ועם ההסתפקות בהם לא תטה נפשי אל הבאת כל מה שהביאוהו וזכרון כל מה שאמרו אותו כי זה ממה שאין שלמות לו |
| It should be known that these are the examined relations, and most of their realization is in the diversity between them and the different properties whose diversity is in one order: | ואתה ראוי שתדע שאלו ההתיחסויות הנבחני' ורוב הגעתם במה שיש ביניהם ההתחלפות והענינים המתחלפים אשר ירוץ התחלפותם על סדר אחד |
|
אם מתדבק כמו יחס א' אל ב' כמו ב' אל ג' |
|
או מתחלק כמו יחס א' אל ב' כמו ג' אל ד' |
| Either their similarity and the uniqueness of their arrangement is in the quantity of themselves or in their quantity according to other. | אם שיהיה התדמותם והתיחדות סדורם בכמות נפשם או כמותם אצל זולתם |
| This is the root and the examined. | וזה הוא השרש והנבחן |
|
והתדמות חלוף המספרים בכמות נפשם הוא כמו שיהיה תוספת זה על זה שוה לתוספת השלישי על הרביעי |
|
כמו תוספת הששה על הארבעה והעשרה על השמנה או הארבעה על השנים |
|
ואלו הם ההתיחסויות המספריים |
|
והדמות חלופי המספרים בכמותם אצל זולתם הרי הוא כמו שיהיה כמות תוספת זה על זה כמו כמות זה השלישי על הרביעי או יהיה כמות זה המתחלף אצל המתחלף אליו אחד |
|
כמו ענין הארבעה אצל השנים בהתחלפות הוא כמו ענין העשרה אצל הששה |
|
וזה הוא ההתיחסות התשברתיי |
| These two are in essence two roots | ושני אלו באמתות שני שרשים |
| When someone examines the property of difference of the relative quantity and the difference of the numerical quantity in the arithmetic proportion [and the geometric proportion], they are found different and no harmony is found at all: | אמנם כאשר יבחן אי ענין חלוף הכמות הצרופיי בחלוף הכמות המספריי בהתיחסות המספריי וענין חלוף הכמות הצרופיי נמצאו מתחלפות והנה לא ימצא הנה הסכמה כלל |
|
המשל בזה שנניח יחס תשברתיי כמו ארבעה ששה תשעה |
|
והנה הכמות המצטרף בהם מתדמה והכמות אשר למספר בעצמו בלתי מתדמה כי החלוף באחד מהם שנים ובאחר שלשה |
|
והנה נניח יחס מספריי כמו ארבעה וששה ושמנה |
|
ותמצא חלוף הכמו' בעצמו שוה וחלוף הכמות בהקש בלתי מתדמה |
|
אבל יהיה ששה לארבעה מוסיף חצי |
|
ושמנה לששה אינו מוסיף כי אם בשליש |
|
וימצאו שני היחסים תמיד נמשכים אבל היחס הגדול מהם בין שני המספרים היותר קטנים והקטן מהם בין שני המספרים היותר גדולים |
|
ויחסם מזה הענין אחד והוא שתבקש מספרים חבורם חבור ישים השני יחסים אשר ביניהם נמשכים וישים הגדול בין הגדולים והקטן בין הקטנים |
|
והנה ימצא יחס אחד על זה התאר כמו יחס מה שבין הששה והארבעה והשלשה ויקרא חבוריי לפי שהתועלת בהשגחת אמצעי זה ההתיחסות אמנם יפול במלאכת החבור והוא המוסיקי כפי מה שתדעהו במקומו |
|
וכבר יעבר שיהיה נקרא חבוריי לפי שיחס הקצוות מחובר מיחס המותרות כפי מה שתדע |
|
ויתחיב לו סגלה שיחס מותר הגדול על האמצעי אל מותר האמצעי על הקטן הוא יחס הקצה הגדול אל הקטן |
|
כמו יחס השנים והוא מותר הששה על הארבעה אל אחד אשר הוא מותר השלשה על השנים[52] |
| From this property that is necessary for this ratio, they observed the examination of the excess of the related terms, and gradually moved from them to other relations and proportions that are useful from the aspect of perfection of the division or multiplication of the ratio. | אח"כ הם התבוננו מזאת הסגולה אשר נתחיבה לזה היחס לבחינת התיחסויות מותר הגבולים המתיחסים והלכו בהדרגה מהם אל התיחסויות ואמצעים אחרים אמנם יועילו מצד השלמות חלוקת היחס או רבויו |
| We will begin with each relation and proportion and say a brief statement about them figuratively: | ונתחיל בהתיחסות התיחסות ואמצעי אמצעי ונאמר בהם דבור קצר על דרך העברה |
|
אם האמצעי התשברתיי הנה אמנם יהיה גדר הכאת הקצוות והנה יהיה גדר מה שיתקבץ משתי הקצוות אחד מהם באחר |
|
וכבר ידעת זה ממקום אחר |
|
וידעת כי כשהיה תמורת האמצעי שני אמצעיים הנה הכאת אחד מהם באחר כהכאת אחת משתי הקצוות באחרת |
| This leads you to the investigation of the mean: | וזה יורה אליך אל דרישת האמצעי |
| It is known in this investigation that the geometric relations are added three by three in the gradual progress of the successive "other" with the successive squares. | וידעת כי בזאת החקירה שאלו ההתיחסויות התשברתיות יתחברו שלשה שלשה בהדרגת הזולתיים הנמשכים עם המרבעים הנמשכי' |
| You know from other places that every two squares may apply these properties. | וכבר ידעת גם כן ממקומות אחרים שכל שני מרבעים אפשר שיפלו הודעת אלו הענינים |
|
אמנם ההתיחסות והאמצעי המספרי באחד או בעשרה והנה שם תמצא אותם מתדבקים באמצעי זה ממה שכבר קדם לך |
|
וידעת ענין המשך היחס וכפילת היחס שלהם והוא שילקח חצי מקבץ השתי קצוות כפי מה שידעת ממרבע האמצעי בכמו מרבע המותר |
| כמו שהכאת השנים בששה הוא השנים בעצמו | |
|
אמנם ההתיחסות והאמצעי החבוריי כבר ידעת התנגדותם למספרי במה שימצא ההתנגדות בהם |
|
והוצאת האמצעי בשנכה החלוף אשר בין הגדול והקטן בקטן ונחלק על מקובצם ונוסיף אותו על הקטן ויצא האמצעי |
|
כמו שיהיה תשעה ותחלק על מקובץ השלשה והששה והנה יצא אחד ותוסיף אותו על השלשה ויהיו ארבעה |
| וכאשר יהיה אצלך האמצעי והגדול ותרצה שתמצא הקטן תעיין אל מותר מה שביניהם כמה הוא מן האמצעי כשנחלק עליו האמצעי פעם אחרת והנה מה שיצא נגרע אותו מן האמצעי | |
| וכאשר יהיו הקטן והאמצעי ידועים אצלך ותרצה הגדול תחלק האמצעי על המותר ותגרע ממנו אח"כ תחלק עליו ומה שיצא תוסיף אותו על האמצעי | |
|
ומסגלות זה ההתיחסות שהכאת מקובץ השני קצוות באמצעי כמו כפל אחת הפאות באחרת |
| וג"כ הנה הכאת האמצעי בגדול כמו כפל האמצעי בקטן בשעור הכפלת אחת משתי הקצוות אל האחרת | |
| וכבר חשבו אנשים שזה היחס אמנם נקרא חבוריי לפי שמותרותיו שחלוקותיו אינם בגבולים לבדם ולא במותרות לבדם אבל קצת בזה וקצת בזה וכאלו נפל בזה חבור וזה טורח | |
| וכבר אמרו מה שהוא יותר חזק הטרח מזה | |
| אמנם ההתיחסויות אשר אחר אלו הנה מהם שלשה נודעו ראשונה ומהם ארבעה נודעו שנית ומהם התיחסויות אין מכונתנו שנשגיח אליהם | |
| ואלו הארבעה יודעו בשלישי והרביעי והחמישי והששי | |
| ויקרא הרביעי המתנגד לפי שהוא מנגד לחבוריי באשר הוא הושם בצד | |
| The ratio of the excess of the mean over the smaller to the excess of the greater over the mean is as the ratio of the greater to the smaller
|
והנה יחס מותר האמצעי על הקטן ומותר הגדול על האמצעי כיחס הגדול אל הקטן |
|
כמו חמשה עשר ושמנה וששה |
| והוצאתם בהכאת המותר שבין שתי הקצוות הקטנו' בקטן והחלוקה על מקובצם והכפלת מה שיצא מן הגדול הנה הוא האמצעי סגלותיו שהכאת הגדול באמצעי כפל הכאת באמצעי התיחסות | |
|
והאמצעי החמישי שיהיה האמצעי אצל הקטן כמו מותר השני קטנים אצל מותר השני גדולים |
| ומספרם כאלו נגזר בזה התשברתיי | |
| ודרישת זה האמצעי שתוסיף הקטן על הגדול ותחלק מה שיתקבץ חלוקה תהיה הכאת אחד מהם באחר כהכאת הנשאר מהגדול אחר השלכת הקטן ממנו בקטן וזה נקל למי שידע היחס | |
| ואם אפשר זה זה ואם לא הנה השאלה בטלה | |
| ומה שיצא יחוסר הקטן מהגדול ממנו ומה שנשאר הנה הוא האמצעי | |
| ומסגלותיו שהכאת הגדול באמצעי כפל הכאת הגדול בקטן | |
| ומזה שהאמצעי מהם בהתיחסות הכפליי נגדר לעולם וגדרו הקטן | |
| והקצה הגדול קטן ממקבץ הנשארים באחד | |
|
הששי שיהיה הגדול אצל האמצעי כמו מותר השני קטנים |
| ודמיון זה | |
| והוצאת האמצעי כשנחסר הקטן מן הגדול כמה שיצטרך שיתוסף על הגדול והתוספת עד שיהיה הכאת זה בכל המקובץ מן השרש והשני תוספת כמו המושטח אשר שמר והנה מקובץ השני תוספות הוא האמצעי | |
| ואם נשבר הנה השאלה בטלה | |
| וג"כ הנה אתה כאשר תגרע ותכפול גדרו ותגרע ממנו המוכה ראשונה בעצמו ומה שנשאר תוסיף אותו על הקטן | |
| וכבר יחויב לו מן הסגלות שההתיחסות כשהיה על יחס הדמיון והחלק יהיה האמצעי נגדר | |
| וכאשר יצטרף אליו גדרו יהיה מקבצו הקצה הגדול והקצה הקטן קטן ממנו | |
|
אמנם הארבעה אשר ידעת באחרונה הנה הראשון שבהם הוא השביעית שיהיה יחס המותר בין השתי קצוות אל המותר בין שני הקטנים כיחס הגדול אצל הקטן |
|
המשל בזה הששה והשמנה והתשעה |
|
|
והוצאת האמצעי שלו בהכאת הקטן במותר אשר בינו ובין הגדול וחלוקת המתקבץ על הגדול ותוספת היוצא על הקטן ומה שהגיע הנה הוא האמצעי |
|
והשמיני שיהיה יחס הגדול אל הקטן כיחס מותר שתי הקצוות אל מותר השני גדולים |
|
המשל בזה ששה שבעה תשעה |
| והוא הפך השביעית | |
| והוצאת האמצעי שלו הפך הוצאת זה האמצעי | |
|
|
וזה בהכאת הקטן במותר אשר בין שתי הקצוות וחלוקת היוצא על הגדול ומה שיצא נגרע אותו מהגדול ומה שישאר הנה הוא האמצעי |
|
התשיעי שיהיה יחס מותר הקצוות אל מותר השני קטנים יחס האמצעי אל הקטן |
| כמו הוצאת האמצעי שלו כשנגרע הקטן מהגדול ונחלק השני חלוקה תהיה אחד החלקים אל האחר כיחס האחר אל הקטן אם אפשר ונפיל החלק הראשון מהגדול ומה שישאר הנה הוא האמצעי | |
|
|
ובידך שתקבץ הכאת המותר בקטן אל מרבע חצי הקטן ותקח גדרו ותוסיפהו על חצי הקטן |
| וזה ההתיחסות כאשר יהיה על יחס הדמיון והחלק יהיה הקצה הקטן מרבע תמיד | |
| והתיחסות והאמצעי העשירי שיהיה יחס מותר השתי קצוות אל מותר השני גדולים | |
|
|
כמו יחס האמצעי שלו שתקח מותר מה שבין הקצוות מוכה בקטן מחוסר ממרבע חצי הגדול ותקח גדר זה תוסיפהו על חצי הגדול |
| אלו צריכים בשתי קצוות עם התשברתיי תמיד ולא עם השביעי והשמיני ולא עם החבוריית אל שיהיה הגדול הפך הקטן כמו הרביעי אלא שיהיה הגדול גם כן הפך הקטן והתשבריית לא השמיני ימצאו עם החבוריים ולא עם הרביעי ולא עם השביעי ולא עם השמיני ולא עם התשיעי | |
|
וכאשר הונחו לנו השמנים והעשרים שני גבולים |
|
יהיו החמשים ביניהם אמצעי מספריי |
|
וארבעים אמצעי תשברתיי |
|
ושנים ושלשים אמצעי חבוריי |
|
ושמנה וששים אמצעי רביעי |
|
וחמשה ושלשים אמצעי שביעי |
|
וחמשה וששים אמצעי שמיני |
| The fifth, the sixth, the ninth, and the tenth are extracted: | וכבר הוצאו החמישי והששי והתשיעי והעשירי |
|
והנה נניח ראשון גבולי ההתיחסות החמישי והם |
|
וכאשר חוסר מהקטן אחד ונוסף על הגדול היו והוא ההתיחסות הששי |
|
וכאשר נוסף על כל גבול שנים עד שיהיו יצא ההתיחסות התשיעי |
| וכאשר מן האמצעי אחר זה מה שאמרנוהו בחכמת הארתמיטיקי | |
| וכבר הנחנו ענינים היה המנהג לחברם בזה המקום יוצאים מסדר המלאכה | |
| וכבר אצל המעשה כמו החבור וההקבלה והקבוץ והחלוק ההוריי ומה שירוץ מרוצתם | |
| והראוי בכמו אלו שיזכרו בענפים והנה נסתפק הנה על ההגעה הנזכרת ונקח בחכמת המוסיקי בע"ה | |
| What is done with the number in relation and comparison: | הנעשה במספר על זה ההצטרפות וההקש |
|
כשהוקש אחד משני מספרים אל האחר הנה לא ימלט מאשר יהיו שוים או מתחלפים |
|
ואם היו שוים היה היחס ביניהם יחס השווי והיושר |
|
וידמה שזה היחס הוא התחלה טבעית לשאר היחסים ושהוא אשר אליו יותך כל יחס |
|
ואיך יהיה זה בסדור הניחו בכלם נזכרהו עוד אחר זה |
|
ואם היו מתחלפים לא ימלט אם שיהיה יחס היותר רב שבהם אל היותר מעט יחס הדמיונים כעשרים והשלשים אצל העשרה |
|
או יחס הדמיון המוסיף חלק כעשרה אצל השמנה |
|
או יחס הדמיון המוסיף חלקים כעשרה אצל הששה |
|
או יחס הדמיונים המוסיף חלק כעשרה אצל השלשה |
|
או יחס הדמיוני המוסיף חלקים כחמשה עשר אצל הארבעה |
| These are the categories of the numerical ratios when the greater is related to the smaller. | ואלו הם חלוקות היחסים המספרים כאשר הוקש בהם היותר רב אל היותר מעט |
| When you know this, you know the property of the smaller to the greater. | וכאשר ידעת זה ידעת ענין המעט אצל הרב |
| The less is called the opposite. | ויקרא היותר מעט המקביל |
| The less in the sesquialter ratio, for example, is called the opposite to the sesquialter ratio. | ויקרא היותר מעט ביחס הדמיון המוסיף חצי דרך משל המקביל לדמיון המוסיף חצי |
| In the sesquitertian ratio - the opposite to the sesquitertian ratio. | וביחס הדמיון המוסיף שליש המקביל לדמיון המוסיף שליש |
| And so on for the others. | וכן בשאר |
| It is also [said?] about the less, as beneath so and so, it is said sub-super so and so sub-multiple so and so. | וכבר יולץ ג"כ מן היותר מעט כאשר תחת פלוני ויאמר לו אשר תחת הדמיון המוסיף ככה או הדמיונים המוסיפים ככה |
| The arrangement of the production of all of these ratios is as mentioned. | והסדור בהמצאת אלו היחסים כלם כפי מה שנזכרהו |
|
אם הדמיונים הנה הענין בהם מבואר |
|
והראשון שבהם השניי אחר ימשך אליו השלישיי אחריו הרביעיי אחריו החמישיי וכן תמיד |
|
וזה היחס מתחיל מהשנים והולך על המשך המספר עד אין תכלית |
| The other ratios are found by taking the number by which the additional part or parts are denominated. | אולם היחס אשר זולתו זה הנה אתה תמצאהו בשתקח המספר אשר בשמו יקרא החלק המוסיף או החלקים |
|
ואם תרצה הדמיון המוסיף חלק תוסיף זה החלק על זה המספר אשר יקרא בשמו ויתקבץ לך מה שתרצה |
|
דמיון זה כשתרצה הדמיון ושמינית |
|
הנה תקח המספר אשר בשמו יקרא זה החלק והוא שמנה ותוסיף עליו שמיניתו וזה אחד ויתקבץ מהם תשעה |
|
ויהיה יחס תשעה אל שמנה יחס הדמיון המוסיף שמינית |
|
וכן ג"כ אם תרצה יחס הדמיון המוסיף חלקים |
|
כמו המוסיף שתי חמישיות |
|
הנה תקח חמשה כי בשמו נקראים ותוסיף שני חמישיותיו והוא שנים ויתקבץ שבעה |
|
ויחס שבעה לחמשה יחס הדמיון המוסיף שתי חמישיות |
|
ואולם הדמיונים המוסיפים חלק או חלקים הנה תמצאהו כשתכפול המספר אשר בשמו יקראו החלק או החלקים כמספר הדמיונים המונחים ותוסיף על מה שיתקבץ החלק המבוקש מזה המספר או החלקים ויהיה הכלל כמבוקשך |
|
דמיון זה אם תרצה השלשה דמיונים המוסיף חומש |
|
הנה תקח חמשה ותכפלהו במספר הדמיונים שהם שלשה ויעלה חמשה עשר ותוסיף על זה חומש החמשה שהוא אחד ויעלה ששה עשר והוא היותר רב |
|
ויחסו אל החמשה שהוא היותר מעט יחס השלשה דמיונים המוסיף חומש |
|
וכן תעשה ביחס הדמיונים המוסיף חלקים |
|
|
שתוסיף כאן שנים על החמשה עשר ויהיו שבעה עשר |
|
ויחסם אל חמשה השלשה דמיונים המוסיף שתי חמישיות |
| When the parts are reduced to one part | וכאשר ישובו החלקים אל חלק אחד |
|
כמו שישובו השתי ששיות אל השליש |
|
|
והארבעה שמיניות אל החצי |
|
ומה שדומה לזה |
| Their rule is according to the rule of what they are reduced to. | הנה משפטם בסדור משפט מה שישובו אליו |
| Also, if the superparticular or the superpartient involves fraction of fraction: | וג"כ אם יהיו המוסיף על הדמיון או הדמיונים חלק חלק |
|
כמו שתות השתות |
|
|
וחומש החומש |
|
|
או כשליש העשור |
|
|
וחומש השביע |
|
ומה שהוא יותר דק מזה |
|
|
או אם היה חומש ושתות |
|
|
או שליש ורביע |
|
ומה שדומה לזה |
| All of them are reduced to one part or parts. | הנה אלה כלם ישובו אל החלק האחד או החלקים |
| The fraction of fraction is also a fraction: | וזה כי חלק החלק הוא ג"כ חלק |
|
|
כמו שתות השתות שהוא חלק מששה ושלשים |
|
|
וחומש החומש שהוא חלק מחמשה ועשרים |
|
|
וכן שליש העשור שהוא חלק משלשים |
|
|
וחומש השביע שהוא חלק מחמשה ושלשים |
|
|
וכן השליש והרביע שבעה חלקים משנים עשר |
|
|
והחומש והשתות אחד עשר חלקים משלשים |
| The arrangement discussed concerning the reduction of these ratios to equality: | ואולם הסדור אשר דברנו[53] בהשבת אלו היחסים אל יחס השווי |
|
הוא שנניח זה היחס בשלשה גבולים יהיה יחס הגדול מהם אל האמצעי הוא בעינו יחס האמצעי אל הקטן |
|
ונחסר לעולם מן הגדול כפל האמצעי מחוסר ממנו הקטן |
|
ונחסר מהאמצעי כמו הקטן |
|
ונניח הקטן כמו שהוא |
|
ואם יהיו שוים הגבולים השלשה הנה המבוקש ואם לא תשוב ותעשה כמו מה שעשינו ראשונה עד שיהיו שוים |
|
ודמיון זה ביחס הארבעה דמיוני שיהיה הגדול ס"ד והאמצעי י"ו והקטן ד' |
|
|
הנה כשכפלנו האמצעי ונחסר ממנו הקטן נשארו כ"ח וכאשר נחסר זה מן הגדול נשארו ל"ו |
|
|
וכשנחסר הקטן מן האמצעי נשארו י"ב |
|
|
ונשאיר הקטן בענינו |
|
ויהיו אלו המספרים השלשה אשר הם ל"ו י"ב ד' על יחס השלשה דמיונים |
|
|
וכשנשוב ונחסר ג"כ מן הל"ו כפל הי"ב מחוסר ממנו הד' וזה עשרים נשארו י"ו |
|
|
אחר כן נחסר מן הי"ב הד' נשארו ח' |
|
|
ונשאיר הד' כמו שהם |
|
ויהיו המספרים השלשה אחר זה י"ו ח' ד' על יחס הכפל |
|
|
וכשנשוב שלישית ונחסר כפל הח' מחוסר ממנו הד' וזה י"ב מן הי"ו |
|
|
אח"כ נחסר הד' מן הח' |
|
|
יהיו שוים הגבולים הנשארים ויהיה כל אחד מהם ארבעה |
|
ואתה רואה איך שב המרבע אל המשלש אשר הוא יותר פשוט ממנו |
|
אח"כ המשלש אל השניי אשר הוא יותר פשוט ממנו |
|
ואחר הותך אל יחס השווי |
|
עוד נמשיל ביחס הדמיון וחלק ויהיה החצי |
|
ונשים השלשה מספרים אשר הם על זה היחס י"ח י"ב ח' |
|
|
כפלנו הי"ב וחסרנו ממנו ח' נשארו י"ו וחסרנו זה מי"ח ונשארו ב' |
|
|
וכשנחסר ח' מן י"ב נשארו ד' |
|
|
ונניח ח' כמו שהוא |
|
ויהיה השלשה גבולים ב'ד'ח' על יחס הכפל |
|
|
ונשוב ונחסר מהח' שהוא הגדול כפל האמצעי שהוא ד' מחוסר ממנו הקטן שהוא ב' וזה ו' נשארו מהגדול ב' |
|
|
וכשנחסר מהאמצעי ב' נשאר גם כן ב' |
|
|
ונשאיר הקטן ב' כמו שהוא וזה יחס השווי |
|
ואתה רואה ג"כ איך שב יחס הדמיון והחלק אל יחס השווי |
|
ואיך יותך ראשונה אל יחס הכפל השניי ואחר יותך זה יחס אל יחס השווי |
| The types of proportions: | ומיני המתיחסים |
|
אם שיהיו על צד הדבקות והם אשר יהיה האמצעי משותף בין שתי הקצוות ילקח בהתיחסות פעם נמשך ופעם קודם |
|
וגבוליו תמיד שלשה לא פחות ולא יתר |
|
כאמרנו יחס א' אל ב' כיחס ב' אל ד' |
|
ואם שיהיה על צד ההבדל ולא יהיה בזה אמצעי אחד משותף אבל אמצעיים |
|
כאמרנו יחס א' אל ב' כיחס ד' אל ח' |
|
והגבולים בזה היחס תמיד יותר משלשה |
| The types of proportions are numerous, of them Nicomachus has mentioned only ten types in his book. | ומיני המתיחסים רבים זכר מהם ניקומכוש בספרו עשרה מינים לבד |
| A sect of the ancients endeavored in the investigation of the additional to them and found ten others, so there were twenty types. | ויחתרו כת מן הקדמונים בדרישת מה שנוסף עליהם ומצאו עשרה אחרים והיו בהם מיני היחס עשרים מינים |
| Yet, the most beneficial among them in the sciences are mostly only three, which are the arithmetic, the geometric, and the harmonic proportions. | והמועילים בהם בחכמות על הרוב שלשה לבד והם המתיחסים המספריי' והתשברתיים והחבוריים |
| First we will deal with the mentioning of these, then the mentioning of the others among the first ten types will follow. | ונתעסק בזכרון אלו ראשונה אח"כ ימשך להם זכרון הנשארים מן העשרה מינים הראשונים |
| As for the ten additional, to which the ancients strived, we have no business in mentioning them because they are hardly found. | והעשרה הנוספים אשר טרחו בהם הקדמונים אין לנו עסק בזכרונם הנה למעוט מציאותם |
|
ואולם המתיחסים המספריים הם המתיחסים הנופלים בין גבולים אם שלשה או יותר מזה נמשכים על שווי מה שביניהם מהתוספת והיתרון |
|
כשנים והשלשה והארבעה המוסיפים אחד אחד |
|
וכחמשה והשבעה והתשעה המוסיפים שנים שנים |
|
ואין היחס בין אלו המספרים אחד בכמות רצוני היתרון |
|
כי יחס הארבעה אל השלשה יחס הדמיון המוסיף שליש |
|
ויחס השלשה אל השנים יחס הדמיון המוסיף חצי |
|
ויחס התשעה אל השבעה יחס דמיון המוסיף שתי שביעיות |
|
ויחס השבעה אל החמשה יחס הדמיון המוסיף שתי חמישיות |
|
וכן יהיה ג"כ בנבדלים |
|
כמו השנים והחמשה והארבעה והשבעה והשמנה והאחד עשר |
|
כי היחס אשר בין אלו המספרים הששה יחס מספריי על צד ההבדל והגבולים בו מוסיפים בכמות אחת והוא השלשה |
|
ואולם ההתיחסות אינו אחד |
|
לפי שיחס האחד עשר אל השמנה יחס הדמיון המוסיף רביעית ושמינית |
|
ויחס השבעה אל הארבעה יחס הדמיון המוסיף חצי ורביעית |
|
ויחס החמשה אל השנים יחס הכפל המוסיף חצי |
|
ומסגלות אלו המתיחסים וזה האמצעיות שמקובץ הקצוות במתדבקים מהם כפל האמצעי ובנבדלים שוה למקובץ האמצעיים |
|
ומסגלותם גם כן שהיחס שבין שני הגבולים הקטנים במדובקים מהם והנבדלים יותר גדול תמיד מהיחס אשר בין שני גבולים הגדולים |
|
ומהם שהכאת אחת הקצוות באחרת יותר מעט תמיד ממרובע האמצעי במדובקים כמו מרבע התוספת |
|
ומאלו הסגלות וממה שקדם להם מהידיעה בסגלות המספרים יודע האמצעי באלו המתיחסים מצד שתי הקצוות |
|
וזה במתדבקים כאשר ילקח חצי מקבצם ומה שהיה הוא האמצעי |
|
לפי שכל מספר שוה לחצי מקובץ שתי פאותיו כמו שידעת |
|
ואמנם בנבדלים הנה לו יוגבלו שני האמצעיים מהידיעה בשתי הקצוות לבד אבל כבר אפשר שימצאו ביניהם אמצעיים רבים |
|
ואם יהיו האמצעיי' נעלמים יחד והיה מקובצם ידוע או מותר מה שביניהם ידוע ויחס אחד מהם אל האחר ידוע הנה אפשר מציאות כל אחד מהם על מנינו |
|
ואם לא יהיה דבר מאלו הדברים ידוע יהיה דרך הוצאתם ומציאות כל אחד מהם ממה שאין דרך לזכרו הנה |
|
ואולם המתיחסי' התשברתיים הם אשר יהיה היחס אשר בין גבוליהם אחד והמותרות מתחלפות בחלוף המספריים |
|
כמו האחד והשנים והארבעה במתדבקי' |
|
והאחד והשנים והשלשה והששה בנבדלים |
|
|
וזה שיחס ד' ב' כיחס ב' א' |
|
|
והמותר בין ד' ב' יותר ממותר שבין ב' א' |
|
וכן בו' ג' וב' א' שיחסם אחד ומותרם מתחלפים |
|
ומסגלות אלו המתיחסים וזה האמצעיות שהכאת אחת הקצוות תמיד באחרת שוה למרבע האמצעי במתדבקי' ולהכאת אחד האמצעיים באחר בנבדלים |
|
ולזה היה מציאות האמצעי והוצאתו אם במתדבקים הוא כאשר ילקח שרש הכאת אחת הקצוות באחרת ומה שהיה הוא האמצעי |
|
ואם בנבדלים הנה יצטרך עם הידיעה בכל אחת מהקצוות שיהיה אחד משני האמצעיים ידוע כדי שנדע מזה הצד האמצעי האחר וזה בחלוק הכאת אחת הקצוות באחרת עליו |
|
ואם היו מוסכלים יחד יהיה מקובצם ידוע או מותר מה שביניהם ידוע או יחס אחד מהם אל האחר ידוע הנה אפשר מציאות כל אחד משניהם על מנינו |
|
ואם לא יהיה אחד מאלו הדברים ידוע יהיה דרך הוצאותם ומציאות כל אחד מהם ממה שאין דרכו שיחובר הנה |
|
ואולם ההתיחסות החבוריי הוא אשר יהיה בו יחס גדול שבגבוליו אל הקטן כיחס מותר מה שבין הגדול והאמצעי אל מותר מה שבין האמצעי והקטן |
|
כמו השלשה והארבעה והששה |
|
|
כי יחס הששה אל השלשה כיחס מותר מה שבין הששה והארבעה והוא שנים אל מותר מה שבין הארבעה והשלשה והוא אחד |
|
והצורך אל זה המין ממיני המתיחסים נוגע בחכמת חבור הלחנים הנקרא המוסיקי לפי שיחס המרחקים המסכימים בו אמנם ימצאו בזה המין לבד כפי מה שתאמר עליו אחרי זה ולכן נקרא חבוריי |
|
והוצאת הגבול האמצעי מגבולי ההתיחסות הזה הוא כשנכה לעולם מותר מה שבין הקצוות בקטן שבגבולים ונחלק מה שהתקבץ על מקובץ שתי הקצוות ונוסיף מה שיצא על גבול הקטן ומה שהתקבץ הנה הוא הגבול האמצעי |
|
דמיון זה אם נדע השלשה והששה |
|
|
הנה המותר שלשה נכה שלשה בשלשה יהיה תשעה ומקובץ הקצוות ג"כ תשעה וכשנחלק תשעה על תשעה יעלה אחד לבד נוסיף האחד על השלשה שהוא גבול הקטן ויהיה ארבעה והוא האמצעי |
| These three types of proportions are used in the sciences, and the received is of benefit in them. | הנה אלו השלשה ממיני המתיחסים הם הנעשי' בחכמות והמקובל תועלת בהם |
|
ואולם המין הרביעי הוא אשר יהיה בו יחס הגדול אל הקטן כיחס מותר מה שבין שני הגבולים הקטנים אל מותר מה שבין שני הגבולים הגדולים |
|
כמו השלשה והחמשה והששה |
|
וזה המין מקביל למין החבוריי |
|
ויסגלהו שמוכה הגדול באמצעי כפל מוכה האמצעי בקטן |
|
כמו שיהיה בכאן מוכה ששה בחמשה והוא שלשים כפל מוכה שלשה בחמשה והוא חמשה עשר |
|
ואולם המין החמישי הוא אשר יהיה בו יחס האמצעי אל הקטן כיחס מותר מה שבין שניהם אל מותר מה שבין האמצעי והגדול |
|
כמו השנים והארבעה והחמשה |
|
ויסגלהו שמוכה הגדול באמצעי כפל הכאתו בקטן |
|
כמו שהכאת החמשה בארבעה והוא עשרים כפל הכאת חמשה בשנים אשר הוא עשרה |
|
ואולם המין הששי הנה הוא אשר יהיה בו יחס הגדול אל האמצעי כיחס מותר מה שבין האמצעי והקטן אל מותר מה שבין האמצעי והגדול |
|
כמו האחד והארבעה והששה |
|
ואולם המין השביעי הנה הוא אשר יהיה בו יחס הגדול אל הקטן כיחס מותר מה שבין שניהם אל מותר מה שבין האמצעי והקטן |
|
כמו הששה והשמנה והתשעה |
|
ואולם המין השמיני הנה הוא אשר יהיה יחס הגדול אל הקטן כיחס מותר מה שבין הקצוות אל מותר מה שבין הגדול והאמצעי |
|
כמו הששה והשבעה והתשעה |
|
ואולם המין התשיעי הנה הוא אשר יהיה בו יחס האמצעי אל הקטן כיחס מותר מה שבין הקצוות אל מותר מה שבין האמצעי והקטן |
|
כמו הארבעה והששה והשבעה |
|
ואולם המין העשירי הנה הוא אשר יהיה בו יחס האמצעי אל הקטן כיחס מותר מה שבין שני הקצוות אל מותר מה שבין האמצעי והגדול |
|
כמו השלשה והחמשה והשמנה |
| הנה אלו הם המינים העשרה ממיני המתיחסים שיספיק לנו זכרונם כי אין לאחד מהם מבא בחכמה זולתי מה שזכרנום לפנים ואולם הביאונום על צד שלמות החלוקה והמשכתה וספירת מה שיגיעו אליו צדי ההתיחסות נשלם זה והתהלה לאל ית' שמו |
Music |
|
| האופן הרביעי מן החלק השני בחכמת המוסיקי | |
| אמר אמיה בן עבד היקר אבו אלצלת הנה נסתם מה שקדם מאופני הלמודים באומר בחכמת המוסיקי וזה ספר כבר ספרנוהו לו כמו שעשינו בשאר אופנים וחלקנוהו חלקים שמנוהו הראשון מהם בהתחלות זה האופן ומה שירוץ מרוצת ההתחלות ויכנס בה מן ההכנות וההצעות והמשכנוהו במאמר בספירת הנעימות והמרחקים והסוגים והקבוצים מרובם והמזגתם ואיכות סדר הסוגים בקבוצים עוד בהמצאתם מוחשים בכלים המלאכותיים ובחלקי הכלים ובמיניהם עוד באומר בהעתקות וחלקי הנפילות ומיניהם והלכנו במה שהבאנוהו מזה צד הדרך אשר הלכנו בזה הספר מהבאת מה שאין די זולתו וחסר מה שאין צריך לו ובאל נעזר | |
| המאמר הראשון מזה האופן שני פרקי פרק ראשון בהתחלות זה האופן ומה שירוץ מרוצת ההתחלות ויכנס בה מן ההכנות למלאכת המוסיקא מלאכה נושאה הנעימות וכונתה העיון בם מצד מה שיתקרבו ויתרחקו ובאיכות חבורם כדי שיהיה מהם לחן ותתחלק אל עיונית ומעשית והעיונית היא אשר מדרכה שתחקר מהנעימות ומה המסכים מהם ובלתי מסכים ותעיין בחבור המסכים מהם עד יתכן שיהיה המחובר מהם לחן ותחקר מאי זה מהם יהיה יותר טוב ויותר שלם ומן הדברים אשר יהיו בם יותר טובות ויותר שלמות ותתן עלות זה כלו וסבותיו יתנו סבת ההוא הוא ולכן יתילדו מהם המרבעים והמעקבים וימצאו במדרגות הנפרדים מרבע ולא ימצאו במדרגות הזוגות כלל נשלם המאמר השלישי מן הארתמיטיקי ושבח לאל יתעלה שמו וכבר פשט המנהג לזכור בזה המקום היחסים ומיניהם וסגולותיהם ומן האנשים מי שיחדש להתיחסות פנים רבים ויגיעו בהם אל ב' פנים ומהם שנסתפקו על עשרה והוא המעתק מהקדמון ומכונתי שאסתפק בזכר אלו הי' ועם ההסתפקות בהם ונשלם הספר הזה ספר הארתימיטיקא לאמיה בן עבדו אבו אלצלת היקר תדרוש בסגולות המספרים קצר והוסיף על ספר ניקומאכוש הגרישיני הפיתגוריי לידי הצעיר באלפי הדל אליאו גבה בבר אליעזר יצ"ו בשנת
| |
Notes
- Jump up ↑ MS St. Petersburg beginning
- Jump up ↑ marg. א"ב אם רצה בזה שלא יביא אל נגדר בהקוות השני או שלא יביא אל נגדר באי זה הקוות שיהיה הוא נכון ואולם אם רצה בזה שלא יביא אל נגדר לעולם אין זה צודק כי השלשה אחר י"ג הקוויות יביא אל נגדר אצל פ"א וגם זה יצדק בחמשה ושאר המספרים כאשר תוציא קום
- Jump up ↑ marg.א"ב למעלה קרא נגדר ראשון האחד ובכאן קרא נגדר ראשון התשעה והוא הנכון כי האחד אינו מספר ודבר למעלה דרך העברה והסדר הוא שהראשון שבנגדרים הנפרדים תשעה והשני כ"ה והשלישי מ"ט ועל הדרך הזה
- Jump up ↑ marg. בל"ד מט'
- Jump up ↑ והנה
- Jump up ↑ marg. כי לפי זה יחויב שיהיו השנים נמנים במדרגות זוג הזוג
- Jump up ↑ marg. א"ב לפי זה יהיו השנים זוג הנפרד וזה כי הארבעה זוג הזוג וכאשר נגרע מהם הזוג הראשון שהוא שנים ישארו שנים ואם שנים זוג הנפרד המאמר צודק ולא בזולת זה ובזה תמה כי במקומות מהספר נראה שהוא לוקח השנים במספר זוג הזוג ובמקומות במספר זוג הנפרד
- Jump up ↑ marg. פי' כמו שמנה שהוא זוג הזוג וחלקיו שהם חצי ורביע ושמינית והם ד'ב'א' והגעתם שבעה
- Jump up ↑ marg. ירצה לפי שיש ג' מיני יחסי' יחס מדותיי והוא שהשעורי' מתיחסי' והמותרי' בלתי שוי' ויחס מספרי והוא שהשעורי' בלתי מתיחסי' והמותרי' שוים יחס מוסיף והוא שהשעורי' בלתי מתיחסי' והמותרי' בלתי שוי' אבל יחס השעור הא' אל הג' כיחס מותר מה שבין השעור הא' אל הב' אל מותר מה שבין השעור הב' אל השעו' השלישי כמו מספרי' ג'ד'ו' א"ב ר"ל
- Jump up ↑ marg. ירצה כשנקח מהם חלקי' מתיחסי' על יחס א' הן לתוספת הן למגרעת כמו עד"מ שנקח החצי או הרביע מכל א' מהם או כפל או ג' כפלי כל א' מהם ודומה לזה וישמרו תמיד יחס הכפל עצמו.. א"ב ר"ל
- Jump up ↑ marg. מל"ה מט'
- Jump up ↑ marg. א"ב כדי זה המשפט להביא בו משל והנה נקבץ זוגי הזוג מספרי ב' ד' והאחד עמהם ויהיו ז' והוא מספר ראשון ונוסיף עליו אחרון המקובצי' והוא ד' ויהיו י"א וגם הוא ראשון ונחסר ממנו ר"ל מז' המספר אשר לפני אחרון המקובצים והוא ב' וישאר ה' וגם הוא ראשון ונכה י"א והוא הנוסף בה' שהוא המחוסר ויעלה נ"ה הנה הכאת נ"ה באחרון המקובצים והוא ד' יביא ר"ך והוא המספר אשר לו אוהב והוצאת אוהבו שנוסיף הכאת מקובץ הנוסף והחסר הנזכרי' והוא י"ו בד' שהוא אחרון המקובצים שיעלה ס"ד על ר"ך שהוא האוהב הראשון ויהיה רפ"ד שהוא האוהב השני ושניהם נאהבים ועל הדרך הזה
- Jump up ↑ marg. ר"ל שיחלק יותר מפעם אחת לא זוג הזוג שנאמר ביחוד על המתחלק תמיד עד האחד
- Jump up ↑ marg. לא הבנתי זאת הסגולה ואולי ירצה שקבוץ כל מספרי זוג הנפרד על הסדר שוה לכפלי המרובעי' הטבעיים על הסדר כי קבוץ מספרי ב' ו' שוה לכפל מרובע ב' וקבוץ ב' ו' י' שוה לכפל מרובע ג' וקבוץ ב' ו' י' י"ד שוה לכפל מרובע ד' וכן תמיד על זה הסדר א"ב ד"ל
- Jump up ↑ marg. ר"ל ג' ימנה ט' בג' וימנה ט"ו בה' וימנה כ"א בז'
- Jump up ↑ marg. הה' ימנה ט"ו בג' וכ"ה בה' ול"ה בז'
- Jump up ↑ marg. א"ב ר"ל כל מרבע מספר ראשון בהקש אל מרבע מספר ראשון
- Jump up ↑ marg. מסוף ט' לאקלידס
- Jump up ↑ marg. א"ב ר"ל כי יציאת ששה היתה כאשר לקחנו שנים זוג הזוג והאחד ונתקבץ שלושה מספר ראשון והכינו אותו בשנים ויצא ששה מסוף ט' לאקליד'
- Jump up ↑ marg.א"ב ר"ל שהבית הראשון מהשורה השלישית על הראשון מהשנית יוסיף א' והשני על השני ב' על סדר המספרי' הנמשכים
- Jump up ↑ marg. ר"ל בשורה הראשונה תמצא שכל שלישי לאי זה ראשון שיהיה יוסיף בשנים כמו ג' לא' וד' לב' וה' לג' ובשורה השנית יוסיף בארבעה ובשלישי' בששה
- Jump up ↑ marg. א"ב צ"ע בזה שורה אחת כי יש טעות בלשון ובסברא אפשר לכוין הלשון על צדדים רבים ולכן לא תקננו כי לא יודע אל איזה כיון המחבר
- Jump up ↑ marg.לפי שמקובץ כפל השטחים מרבע בתוספת אחד
- Jump up ↑ marg.כמו כפל ד"ט שהוא כ"ו וכ"ה מרבע
- Jump up ↑ marg.ר"ל מבלי בחינה בין הגמור והבלתי גמור
- Jump up ↑ marg. א"ב לפי שמדרגתם ג"ה ד"ו ה"ז וג"ה יתוסף תמיד בג"ה וד"ו בד"ו וה"ז בה"ז הנה תוספת החסרים והנוספי' אינו רק באחד אחד
- Jump up ↑ marg. א"ב צ"ע כי כפי המשך המשלים נראה שהנכון שיאמר הדמיונים והחלק או הכפל והחלק
- Jump up ↑ marg. ר"ל ביחס הכפל וחצי
- Jump up ↑ marg. א"ב נראה שהרצון הוא כפל מה שהיה בדמיון ושליש כי לא יצדק זה בכפל ושליש במוסיפי' כי אם בחסרים
- Jump up ↑ marg. א"ב ר"ל שיחס כ"א אל י"ט וי"ט לי"ז וי"ז לט"ו הם יחסי הדמיון ושני חלקים והם גמורים וכן השאר
- Jump up ↑ marg.א"ב ר"ל שיחסי י"א אל י' וי' אל ט' וט' אל ח' הם יחסי הדמיון המוסיף חלק וכן השאר
- Jump up ↑ marg. א"ב ר"ל הלוח הגדול הנרשם למעלה בבתי עשר על עשר
- Jump up ↑ marg. ר"ל אם נקח הא' המדרגות החצי
- Jump up ↑ marg. ר"ל האמצעית
- Jump up ↑ marg. א"ב ר"ל בכח כי מספר החמשה עשר שהוא מספר המשלש החמישי אינו משלש בפעל עד שיסודרו סדור ידמה לתמונה המשלשת וישים התושבת ה' ועליהם ד' ועל הד' ג' ועל הג' ב' ועל הב' א'
- Jump up ↑ marg. א"ב ר"ל לפי שהאחד אינו מספר עם היותו מרבע כאשר נזכר למעלה אבל לפי שהאחד הוא הנפרד הראשון יצדק כמו כן אמרנו שמרבע האחד יתילד מדבקותו אל עצמו ואם לא יפול בזה מלת קבוץ
- Jump up ↑ יחזקאל א, יד
- Jump up ↑ marg. א"ב מופת זה המשפט מד' ממאמר שני לאקלידס
- Jump up ↑ marg. א"ב כמו כפל ב' וא' עם ד' ויגיע ט' או כמו י"ו יצורף לדמיונו י"ו ודמיון רביעיתו ד' ויגיע ל"ו או יצורף אל ד' שלשה דמיוניו והוא י"ב ויגיע י"ו או יחוסר מי"ו שלשה רביעיו שההוא י"ב ויגיע ד'
- Jump up ↑ marg. א"ב סבת זה כי לא יצאו אחדים באחרית כי אם מהכאת אחדי' באחדים כי מהכאת עשרות או מאות ושאר המדרגות לא יצאו אחדים וקרה שמהכאת האחדים עד ט' בעצמם היו האחדים הנשארים א' ד' ה' ו' ט' והנה תמצא שמהכאת האמצעי אשר במדרגת האחדי' שהוא ה' בעצמו נשאר ה' אח"כ הנשאר מהפאות הרחוקות מהאמצעי מרחק שוה הנה ישוו אחדי גדריהם כי אחדי פ"א שהוא מרבע ט' ישוה לאחד שהוא אחדי גדר א' וט' וא' רחוקים בשוה מן החמשה וכן אחדי ס"ד וד' למספרי ח' וב' ואחדי מ"ט וט' למספרי ז' וג' ואחדי ל"ו וי"ו למספרי ו' וד'
- Jump up ↑ marg. א"ב צ"ע בבחינה זו פי' במאזניהם
- Jump up ↑ marg. א"ב ר"ל מספר מדרגתו זוג בהתחיל מן האחד כמו ג' וי' שאינם מששים
- Jump up ↑ marg. כמו שתמצא ט"ו שהוא המששה השלישי הנה הוא המשלש החמישי וזה בהתחיל מן האחד
- Jump up ↑ marg.א"ב הם מספרי א'ד'ז'י' הנזכרי' למעלה שהתוספת ג' ג' ומה שבין שני מספרי א' ד' או ד' ז' או ז' י' הוא שנים על משך המספרי' הטבעיי'
- Jump up ↑ marg.א"ב ר"ל נוסף עליו הכאת חצי צלעו במדרגתו מן המחמשים
- Jump up ↑ marg. א"ב נראה שהוא בשלשה מדרגות ור"ל שנכה חצי הצלע והוא שנים בשלשה ויהיה ששה והם עם ששה עשר שנים ועשרים
- Jump up ↑ marg. א"ב המשל בזה שנרצה לדעת מעקב ג' הנה נכה ג' בד' ויהיה י"ב ונכה י"ב בשנים ויהיו כ"ד נוסיף עליו ג' ויהיה כ"ז יהיה שוה למעקבו וירצה באמרו אח"כ יתוסף אשר לפניו אשר לפני אשר ימשך אליו
- Jump up ↑ marg. א"ב משל זה נרצה לדעת המספר הנפרד הראשון שנתרכב ממנו המעקב השלישי שהוא כ"ז הנה תקח מספר מדרגת המעקב הזה מהמספר הראשון שבמעקבים ויהיה ב' וזה חסר ממספר מהמדרגות הראשון שהיה ג' באחד כי כשנתחיל למנות מן האחד יהיו שלשה וכשנתחיל מראשון המספרים המעקבים יהיו שנים וכן תמיד ונגרע ג' שהוא מספר המדרגות השני ממרבע ג' שהוא מספר המדרגות השלישי והוא ט' וישארו ז' והוא הנפרד הראשון אשר ממנו חבור מעקב כ"ז אח"כ נוסיף ב' על המרבע הנזכר ויהיו י"א והוא המספר האחרון משני אלו ממה שביניהם נתרכב כ"ז
- Jump up ↑ marg.א"ב ר"ל המספר אשר ימשך אליו והוא הוא המוסיף עליו באחד
- Jump up ↑ marg.ר"ל הוהיי הארך שמספר הצלעות שוה והם המרבעים
- Jump up ↑ marg. צ"ע כמו שורה אחת
- Jump up ↑ marg. א"ב צ"ע ונראה סיומו כיחס ששה אל שלשה ואפשר שהוא כך אשר הוא מותר הארבעה על השלשה כיחס ששה אל שלשה
- Jump up ↑ זכרנו
Appendix: Bibliography
Abū al-Ṣalt Umayya b. ‘Abd al-‘Azīz al-Andalusī (b. Andalusia ca. 1068 – d. Tunisia ca. 1134)
– Hebrew translation –
Don Benveniste b. Lavi
Sefer Niqomachus ba-Segulot ha-Mispariyot
1395/1435, Saragossa
Manuscripts:
- 1) Oxford, Bodleian Library MS Heb. d. 3/4 (IMHM: f 22729), ff. 47v-59r (cat. Neub. 2774, 4) (16th century)
- 2) St. Petersburg, Inst. of Oriental Studies of the Russian Academy B 103/1 (IMHM: f 44256), ff. 1r-21v (15th century)
- [St.Petersburg103]
Bibliography:
- Langermann, Y. Tzvi. 2001. Studies in Medieval Hebrew Pythagoreanism: Translations and Notes to Nicomachus; Arithmological Texts, Micrologus IX, pp. 219–36.
- Lévy, Tony. 1996. L’histoire des nombres amiables: le témoignage des textes hébreux médiévaux, Arabic Sciences and Philosophy 6, pp. 63–87.
![\scriptstyle n=\frac{1}{2}\sdot\left[\left(n-m\right)+\left(n+m\right)\right]](/mediawiki/images/math/9/c/5/9c5220dd42729dd7ceda90eaea5e82a4.png)
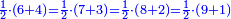
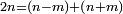
![\scriptstyle\frac{1}{2}\sdot n=\frac{1}{4}\sdot\left[\left(n-m\right)+\left(n+m\right)\right]](/mediawiki/images/math/c/2/3/c2368c2169aef3afd44bbb68b1e44583.png)
![\scriptstyle n^2=\left[\left(n-1\right)\sdot\left(n+1\right)\right]+1](/mediawiki/images/math/b/4/2/b4260f5ae5efcbfb8adcd9588ceef33d.png)
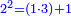
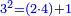
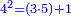
![\scriptstyle n^2-\left[\left(n-m\right)\sdot\left(n+m\right)\right]=m^2](/mediawiki/images/math/c/2/5/c2534a5fa0fa489e9308e83f076f2683.png)
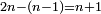
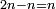
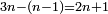
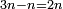
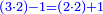
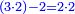
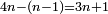
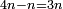
![\scriptstyle\left(m\sdot n\right)-\left(n-1\right)=\left[\left(m-1\right)\sdot n\right]+1](/mediawiki/images/math/8/3/3/833296d312ba1d862ea7a11f65aad7da.png)
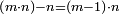
![\scriptstyle n^2-\left(n-1\right)=\left[n\sdot\left(n-1\right)\right]+1](/mediawiki/images/math/2/e/8/2e8f3fd7e6862939836d7c2887fbce6c.png)
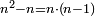
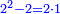
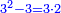
![\scriptstyle n^2=\left[\left(n+1\right)\sdot\left(n-1\right)\right]+1](/mediawiki/images/math/2/2/8/228c62228f173dbb0f8acb2b2842da93.png)
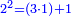
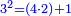
![\scriptstyle\left[n\sdot\left(n-1\right)\right]-\left(n-1\right)=\left(n-1\right)^2](/mediawiki/images/math/f/c/9/fc99bf75bc39bf4caf1eca2000490eb0.png)
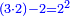
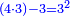
![\scriptstyle\left[n\sdot\left(n+1\right)\right]-n=n^2](/mediawiki/images/math/a/3/e/a3e2be961c71b33740642fb53406703e.png)
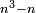 ?
?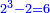
![\scriptstyle n^3-n=\left[n\sdot\left(n+1\right)\right]\sdot\left(n-1\right)](/mediawiki/images/math/a/e/a/aea71daeaade7bda613128faac5a3607.png)
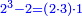
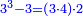
![\scriptstyle n^4-n=\left[n^2+\left(n+1\right)\right]\sdot\left[n\sdot\left(n-1\right)\right]](/mediawiki/images/math/e/f/8/ef8676530f1fd60dcbb1654cced64d45.png)

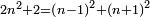
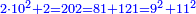
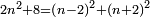

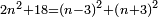
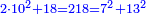
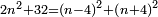
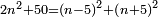
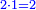
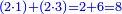
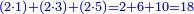
![\scriptstyle2n^2+4=\left[\left(n-2\right)\sdot\left(n-1\right)\right]+\left[\left(n+1\right)\sdot\left(n+2\right)\right]](/mediawiki/images/math/e/d/f/edfd91ae19ebdf94a27e1e45c7240830.png)
![\scriptstyle2n^2+12=\left[\left(n-2\right)\sdot\left(n-3\right)\right]+\left[\left(n+2\right)\sdot\left(n+3\right)\right]](/mediawiki/images/math/4/d/7/4d75349b28ec77646421533f1c00e0bf.png)
![\scriptstyle2n^2+24=\left[\left(n-3\right)\sdot\left(n-4\right)\right]+\left[\left(n+3\right)\sdot\left(n+4\right)\right]](/mediawiki/images/math/1/e/f/1ef27c8af44c80eb913eec6504ba74c5.png)
![\scriptstyle2n^2+40=\left[\left(n-4\right)\sdot\left(n-5\right)\right]+\left[\left(n+4\right)\sdot\left(n+5\right)\right]](/mediawiki/images/math/d/5/1/d514aa0db6374f000dabf24a08200223.png)

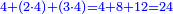
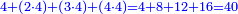
![\scriptstyle2n^2+6=\left[\left(n-1\right)\sdot\left(n-3\right)\right]+\left[\left(n+1\right)\sdot\left(n+3\right)\right]](/mediawiki/images/math/b/6/d/b6d08bfdd80a9ba77cd006f9e9f93d37.png)
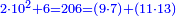
![\scriptstyle2n^2+8=\left[\left(n-1\right)\sdot\left(n-4\right)\right]+\left[\left(n+1\right)\sdot\left(n+4\right)\right]](/mediawiki/images/math/f/d/7/fd72005222fde5847684b4b2d41e0f55.png)
![\scriptstyle2n^2+16=\left[\left(n-2\right)\sdot\left(n-4\right)\right]+\left[\left(n+2\right)\sdot\left(n+4\right)\right]](/mediawiki/images/math/f/f/d/ffd94c709532f4cb997a2fefb55abeab.png)

![\scriptstyle2n^2+20=\left[\left(n-2\right)\sdot\left(n-5\right)\right]+\left[\left(n+2\right)\sdot\left(n+5\right)\right]](/mediawiki/images/math/7/7/e/77e76be56b0d6e6d35b89dfe0d403dbb.png)
![\scriptstyle2n^2+24=\left[\left(n-2\right)\sdot\left(n-6\right)\right]+\left[\left(n+2\right)\sdot\left(n+6\right)\right]](/mediawiki/images/math/6/b/0/6b0255d6e48cb53e70e023418c82b6bf.png)
![\scriptstyle2n^2+30=\left[\left(n-3\right)\sdot\left(n-5\right)\right]+\left[\left(n+3\right)\sdot\left(n+5\right)\right]](/mediawiki/images/math/a/f/6/af6f65bbc997e6a87c8a890a4666eec6.png)
![\scriptstyle2n^2+36=\left[\left(n-3\right)\sdot\left(n-6\right)\right]+\left[\left(n+3\right)\sdot\left(n+6\right)\right]](/mediawiki/images/math/2/b/e/2beba5a6587a3ce96972411b8d33f158.png)
![\scriptstyle2n^2+42=\left[\left(n-3\right)\sdot\left(n-7\right)\right]+\left[\left(n+3\right)\sdot\left(n+7\right)\right]](/mediawiki/images/math/4/b/5/4b5277e92c37684df5b91e14b8a7d025.png)
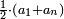
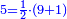
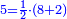
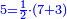
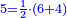
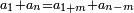

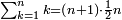
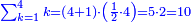
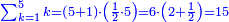
![\scriptstyle\sum_{k=m}^n k=\left(n+m\right)\sdot\left[\frac{1}{2}\sdot\left(n-m+1\right)\right]](/mediawiki/images/math/e/5/a/e5adf0dbee789bd2579afcbe7223033d.png)
![\scriptstyle\sum_{k=m}^n k=\left[\frac{1}{2}\sdot\left(n+m\right)\right]\sdot\left(n-m+1\right)](/mediawiki/images/math/2/0/b/20bebeed8b2d77ce7060b159599d3005.png)
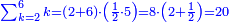
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\sum_{k=2}^6 k=2+3+4+5+6&\scriptstyle=\left[\frac{1}{2}\sdot\left(2+6\right)\right]\sdot5\\&\scriptstyle=\left(\frac{1}{2}\sdot8\right)\sdot5=4\sdot5=20\\\end{align}}}](/mediawiki/images/math/b/5/0/b50b1ddc006e853205d60f33b2e7fb2c.png)
![\scriptstyle a_n=\left[\left(n-1\right)\sdot d\right]+a_1](/mediawiki/images/math/b/c/f/bcf0c1893f245550c7758eb5f74d4294.png)
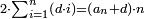
 , starting from 4
, starting from 4  , between every two numbers there are three, so that the excess is four
, between every two numbers there are three, so that the excess is four  , which is the last of them and how much is their sum?
, which is the last of them and how much is their sum?![\scriptstyle{\color{blue}{a_5=\left[\left(5-1\right)\sdot4\right]+4=\left(4\sdot4\right)+4=16+4=20}}](/mediawiki/images/math/d/f/e/dfe4ff338b04a43dffeb392daeb1dbb3.png)
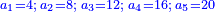
![\scriptstyle{\color{blue}{\sum_{i=1}^5 4i=\frac{1}{2}\sdot\left[\left(20+4\right)\sdot5\right]=\frac{1}{2}\sdot\left(24\sdot5\right)=\frac{1}{2}\sdot120}}](/mediawiki/images/math/b/1/1/b11f9c0c1e45e6acb4bc1ddc924a1cf3.png)
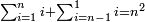
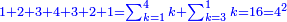
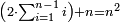
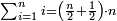
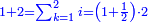
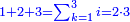
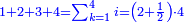

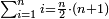
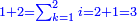
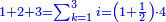

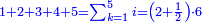
![\scriptstyle\sum_{i=1}^n 2i=\left(1+\frac{1}{n}\right)\sdot\left[\sum_{i=1}^n \left(2i-1\right)\right]](/mediawiki/images/math/c/5/4/c54fadd584df3bbd37e71e4752e5f2bc.png)
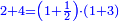
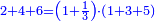
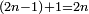 ]
]![\scriptstyle\left[\left(2n-1\right)+1\right]+1=2n+1=\left[2\sdot\left(n+1\right)\right]-1](/mediawiki/images/math/e/a/8/ea8c6a3305842a0ca92cfcea6917294b.png) ]
]![\scriptstyle\left[\left[\left(2n-1\right)+1\right]+1\right]+1=2\sdot\left(n+1\right)](/mediawiki/images/math/3/0/6/306cf0f0b2597dbed70ceb2d26365cf3.png)
![\scriptstyle\left[\left[2\sdot\left(n+1\right)\right]-1\right]-\left(2n-1\right)=2](/mediawiki/images/math/d/c/3/dc3c24da72a3abf4da33ea40880faed4.png)
![\scriptstyle\left[2\sdot\left(n+1\right)\right]-2n=2](/mediawiki/images/math/8/0/b/80b81448159f33d9f7fc0984a9731879.png)
![\scriptstyle n+\left(n+1\right)=\left(n-m\right)+\left[\left(n+1\right)+m\right]](/mediawiki/images/math/1/4/a/14a9c5983a5bc641d63bdb65629ac5c7.png)

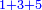

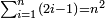
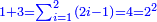
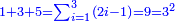
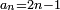
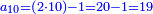
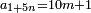


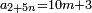
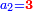

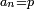 , when extracting from it the interval, whose value is that number, its end
, when extracting from it the interval, whose value is that number, its end 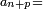 is a composite number that consists of deficient primes.
is a composite number that consists of deficient primes.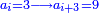 , which is composite.
, which is composite.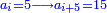 , is composite.
, is composite.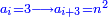 , but afterwards not
, but afterwards not 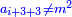
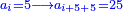 , but afterwards not
, but afterwards not 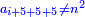
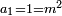 , has a root, which is nine
, has a root, which is nine 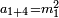 , then the eighth after the first that has a root
, then the eighth after the first that has a root 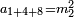 , then the twelfth after the second that has a root
, then the twelfth after the second that has a root 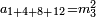 , then the sixteenth after the third that has a root
, then the sixteenth after the third that has a root 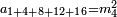 , and so on by adding four
, and so on by adding four 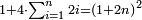
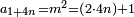
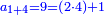

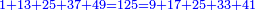 ]
]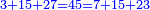
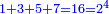 ]
]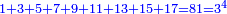 ]
]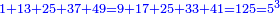 ]
]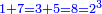 ]
]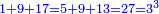 ]
] ; and:
; and: 
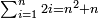
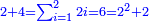
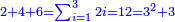
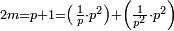
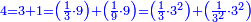
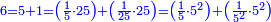
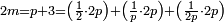
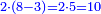
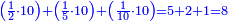
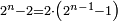 → even-times-odd number
→ even-times-odd number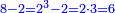
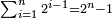 ]
]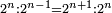
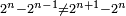
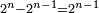
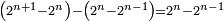
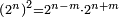
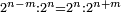
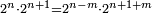
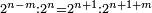
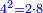

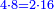

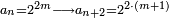
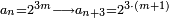
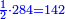
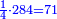
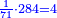
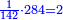
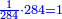
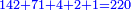



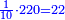
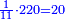
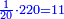
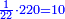


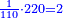

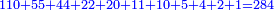
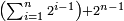 ] and the result of the subtraction [
] and the result of the subtraction [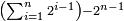 ] are prime numbers.
] are prime numbers.![\scriptstyle a=\left[\left(\sum_{i=1}^n 2^{i-1}\right)+2^{n-1}\right]\sdot\left[\left(\sum_{i=1}^n 2^{i-1}\right)-2^{n-1}\right]\sdot2^{n-1}](/mediawiki/images/math/f/1/a/f1a16a24281539daa583a1502c8fc8f6.png)
![\begin{align}\scriptstyle b&\scriptstyle=\left[\left[\left(\sum_{i=1}^n 2^{i-1}\right)+2^{n-1}\right]\sdot\left[\left(\sum_{i=1}^n 2^{i-1}\right)-2^{n-1}\right]\sdot2^{n-1}\right]\\&\scriptstyle+\left[\left[\left[\left(\sum_{i=1}^n 2^{i-1}\right)+2^{n-1}\right]+\left[\left(\sum_{i=1}^n 2^{i-1}\right)-2^{n-1}\right]\right]\sdot2^{n-1}\right]\\\end{align}](/mediawiki/images/math/c/6/5/c65ed2b72bba8e605ced9a06183a8731.png)
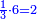
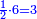
![\scriptstyle\left[2\sdot\left(2n-1\right)\right]+2=2\sdot2n](/mediawiki/images/math/3/2/2/3227327e4c84b9e8b983f435f066a25c.png)
![\scriptstyle\left[2\sdot\left[\left[2\sdot\left(n+1\right)\right]-1\right]\right]-\left[2\sdot\left(2n-1\right)\right]=2\sdot\left[\left[\left[2\sdot\left(n+1\right)\right]-1\right]-\left(2n-1\right)\right]](/mediawiki/images/math/f/f/8/ff8ec7a8ad46e977c80d3201c9f73737.png)
![\scriptstyle\left[2\sdot\left[\left[2\sdot\left(n+1\right)\right]-1\right]\right]-\left[2\sdot\left(2n-1\right)\right]=4](/mediawiki/images/math/7/f/c/7fc2945c117ff0122630cb2b620ad860.png)
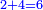
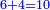
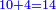
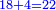
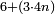 are even-times-odd numbers divisible by 3]
are even-times-odd numbers divisible by 3]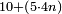 are even-times-odd numbers divisible by 5]
are even-times-odd numbers divisible by 5]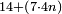 are even-times-odd numbers divisible by 7]
are even-times-odd numbers divisible by 7]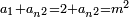
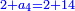
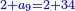
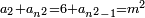
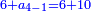
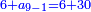
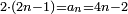
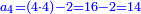
![\scriptstyle n=\frac{\left[2\sdot\left(2n-1\right)\right]+2}{4}=\frac{a_n+2}{4}](/mediawiki/images/math/2/e/a/2ea0a5d7ff15c8af9b5580a5d69e0c0d.png)
![\scriptstyle2n^2=\sum_{i=1}^n \left[2\sdot\left(2i-1\right)\right]](/mediawiki/images/math/3/6/0/3608fbd45e4ae3eb1ccea8b14b38c1a3.png)
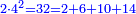
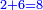 ], and its term is already known, also the cube of the cube and so on [??]
], and its term is already known, also the cube of the cube and so on [??]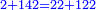

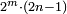
![\scriptstyle\left[2\sdot\left(2n-1\right)\right]^2](/mediawiki/images/math/c/4/a/c4a4088a09b73950cbbc774e7d145e48.png) :
: , which is the root of the first square.
, which is the root of the first square.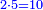 , which is the root of the second square.
, which is the root of the second square.![\scriptstyle\left[2^m\sdot\left[\left[2\sdot\left(n+1\right)\right]-1\right]\right]-\left[2^m\sdot\left(2n-1\right)\right]=2^{m+1}](/mediawiki/images/math/3/0/f/30f8f2ec51a1b51f8404d840fc7f7e5c.png)

![\scriptstyle\left[4\sdot\left[\left[2\sdot\left(n+1\right)\right]-1\right]\right]-\left[4\sdot\left(2n-1\right)\right]](/mediawiki/images/math/2/b/9/2b952ce8d9339a0c1d807877dc17afd5.png)
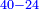
![\scriptstyle\left[8\sdot\left[\left[2\sdot\left(n+1\right)\right]-1\right]\right]-\left[8\sdot\left(2n-1\right)\right]](/mediawiki/images/math/0/f/3/0f3feba94c8998496e3663e08424efe3.png)
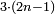
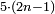



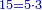
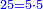
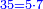
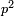 and
and 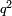 are relatively prime]
are relatively prime]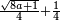 is an even-times-even number; and
is an even-times-even number; and ![\scriptstyle\left(\frac{\sqrt{8a+1}}{4}+\frac{1}{4}\right)\sdot\left[\left[2\sdot\left(\frac{\sqrt{8a+1}}{4}+\frac{1}{4}\right)\right]-1\right]=a](/mediawiki/images/math/2/4/b/24b671f1389b9766f76ad260efe60dd7.png) ]
]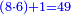
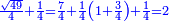 is an even-times-even number
is an even-times-even number![\scriptstyle{\color{blue}{2\sdot\left[\left(2\sdot2\right)-1\right]=6}}](/mediawiki/images/math/7/5/1/7516d3a4e7c3f3303dc7765f59ac0735.png)
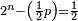 →
→  is a perfect number]
is a perfect number]
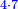
 →
→ 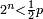 →
→  [
[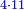 [
[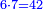
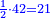

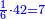
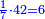
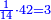
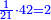
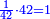
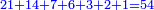
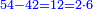
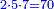
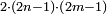 is superabundant
is superabundant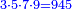

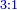
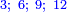

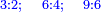

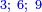
 ]: The second line is in the double ratio to the first line.
]: The second line is in the double ratio to the first line. ]: The third [line] is in the triple ratio.
]: The third [line] is in the triple ratio.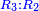 ]: The third line is in the sesquialter ratio to the second line.
]: The third line is in the sesquialter ratio to the second line.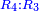 ]: The fourth [line] is in the sesquitertian ratio to the third [line].
]: The fourth [line] is in the sesquitertian ratio to the third [line]. 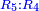 ]: The fifth [line] is in the sesquiquartan ratio to the fourth [line].
]: The fifth [line] is in the sesquiquartan ratio to the fourth [line].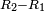 ]: The excesses of the second line over the first line differ by number, but not differ by ratio.
]: The excesses of the second line over the first line differ by number, but not differ by ratio.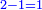

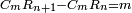 ]
]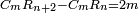 ]: When the third is related to the first in every sequence they are found by the order of the even numbers.
]: When the third is related to the first in every sequence they are found by the order of the even numbers.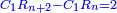
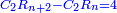
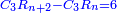
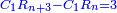
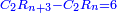
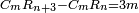 ]
]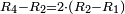 [?]
[?]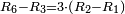 [?]
[?]
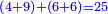
![\scriptstyle\left[2\sdot\left[n^2+\left(n+1\right)^2\right]\right]-1=m^2](/mediawiki/images/math/1/b/5/1b5cf8fdc120fa6c33050cf4008a04b6.png)
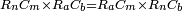
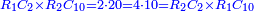
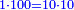
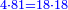
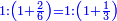
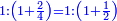
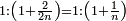 ]
]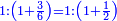
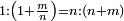 ]
]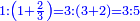 ]
]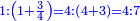 ]
]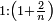 :
: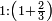
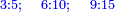
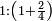 , which is not absolute
, which is not absolute
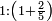
![\scriptstyle\left[1:\left(1+\frac{2}{3}\right)\right];\quad\left[1:\left(1+\frac{2}{4}\right)\right];\quad\left[1:\left(1+\frac{2}{5}\right)\right]](/mediawiki/images/math/8/9/3/8936d012e4df99bde083b4893902cbda.png)
![\scriptstyle\left[1:\left(1+\frac{2}{2n-1}\right)\right]:\left[1:\left(1+\frac{2}{2n+1}\right)\right]](/mediawiki/images/math/8/4/5/8451e01f8feb2bebdca675724dae4f88.png) ]
]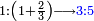
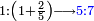
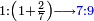
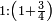

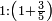
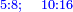
![\scriptstyle\left[1:\left(1+\frac{3}{4}\right)\right];\quad\left[1:\left(1+\frac{3}{5}\right)\right];\quad\left[1:\left(1+\frac{3}{6}\right)\right]](/mediawiki/images/math/7/4/2/7429bd3b015728006a28b251133d1278.png) ]
]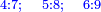
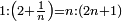
![\scriptstyle{\color{blue}{1:\left(2+\frac{1}{2}\right)=2:\left[\left(2\sdot2\right)+1\right]=2:5}}](/mediawiki/images/math/2/b/1/2b15e422eefe9740ec57253877f5babb.png) ]
]![\scriptstyle{\color{blue}{1:\left(2+\frac{1}{3}\right)=3:\left[\left(2\sdot3\right)+1\right]=3:7}}](/mediawiki/images/math/7/8/b/78b8889b85a9e312e5e794a0afa584f2.png) ]
]![\scriptstyle{\color{blue}{1:\left(2+\frac{1}{4}\right)=4:\left[\left(2\sdot4\right)+1\right]=4:9}}](/mediawiki/images/math/4/8/d/48dc239e9cc60a3aeaeb5d6b389911b7.png) ]
]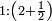 ]:
]: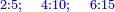
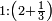 :
: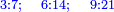
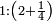 :
: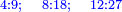
![\scriptstyle\left[1:\left(2+\frac{1}{2}\right)\right];\quad\left[1:\left(2+\frac{1}{3}\right)\right];\quad\left[1:\left(2+\frac{1}{4}\right)\right]](/mediawiki/images/math/0/a/9/0a96ac733bf4e6287b99e10dbe90968b.png) ]
]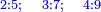 and so on in this way.
and so on in this way.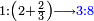
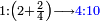
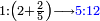
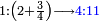
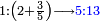
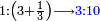
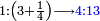


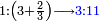
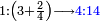
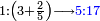

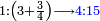
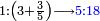

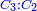 ]:The superparticular ratio is resulted, as already known, from the third and second columns.
]:The superparticular ratio is resulted, as already known, from the third and second columns.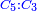 ]: The superbitertian ratio from the fifth and the third columns.
]: The superbitertian ratio from the fifth and the third columns.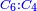 ]: The superbiquartan ratio from the sixth and the fourth columns.
]: The superbiquartan ratio from the sixth and the fourth columns. ]: The superbiquintan ratio from the seventh and the fifth columns.
]: The superbiquintan ratio from the seventh and the fifth columns.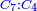 ]: From the seventh and the fourth columns = the supertriquartan ratio.
]: From the seventh and the fourth columns = the supertriquartan ratio.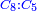 ]: From the eighth and the fifth columns - the supertriquintan ratio.
]: From the eighth and the fifth columns - the supertriquintan ratio.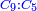 ]: From the ninth and the fifth columns - the superquadriquintan ratio.
]: From the ninth and the fifth columns - the superquadriquintan ratio. ]: From the tenth and the sixth columns - the superquadrisextan ratio.
]: From the tenth and the sixth columns - the superquadrisextan ratio.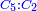 ]: The first of them, the double sesquialter ratio, from the fifth and the second columns.
]: The first of them, the double sesquialter ratio, from the fifth and the second columns.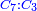 ]: The second, the double sesquitertian ratio, from the seventh and the third columns.
]: The second, the double sesquitertian ratio, from the seventh and the third columns.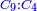 ]: The third, the double sesquiquartan ratio, from the ninth and the fourth columns.
]: The third, the double sesquiquartan ratio, from the ninth and the fourth columns.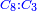 ]: The double superbitertian [ratio], from the eighth and the third [columns].
]: The double superbitertian [ratio], from the eighth and the third [columns].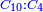 ]: The double superbiquartan [ratio], from the tenth and the fourth [columns].
]: The double superbiquartan [ratio], from the tenth and the fourth [columns]. ]
]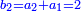 ]
]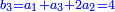 ]
]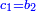 ]
] ]: what is on the second row is in the double ratio.
]: what is on the second row is in the double ratio.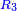 ]: what is on the third row is in the triple ratio.
]: what is on the third row is in the triple ratio.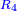 ]: what is on the fourth row is in the quadruple ratio.
]: what is on the fourth row is in the quadruple ratio.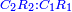 ]: what is in the second rubric of the second row to what is in the first rubric is in the quadruple ratio.
]: what is in the second rubric of the second row to what is in the first rubric is in the quadruple ratio.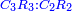 ]: what is in the third rubric to what is in the second rubric is in the double sesquiquartan ratio.
]: what is in the third rubric to what is in the second rubric is in the double sesquiquartan ratio.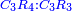 ]: what is in the fourth rubric to what is in the third rubric is in the superseptinona ratio.
]: what is in the fourth rubric to what is in the third rubric is in the superseptinona ratio.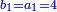 ]
]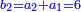 ]
]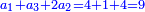 ]
]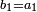 ].
].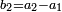 ].
].![\scriptstyle b_3=a_3-\left[2\left(a_2-a_1\right)+a_1\right]=a_3-\left(2b_2+b_1\right)](/mediawiki/images/math/2/8/2/28241de1fdee9a0aaf58885a6fab520b.png) ].
].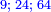
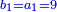
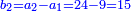
![\scriptstyle{\color{blue}{b_3=a_3-\left[2\left(a_2-a_1\right)+a_1\right]=64-\left[\left(2\sdot15\right)+9\right]=25}}](/mediawiki/images/math/7/1/8/718b329d3f4206cbf8afbf69283299e8.png)
 ] in the superbitertian ratio.
] in the superbitertian ratio. , which are successive numbers in the sesquialter ratio.
, which are successive numbers in the sesquialter ratio. ] by this procedure, and the result are
] by this procedure, and the result are 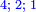 , which are in the double ratio.
, which are in the double ratio. , restored to equality.
, restored to equality.
 ] and the sesquiseptan ratio [
] and the sesquiseptan ratio [ ] is the sesquitertian ratio [
] is the sesquitertian ratio [ ]
] ] is the superbiseptan ratio [
] is the superbiseptan ratio [ ]
] ] is the sesquiquartan ratio [
] is the sesquiquartan ratio [ ]
] ] is the superbinona ratio [
] is the superbinona ratio [ ]
] ] is the sesquiquintan ratio [
] is the sesquiquintan ratio [ ]
] ] is the superbiundecima ratio [
] is the superbiundecima ratio [ ]
] ] is the sesquisextan ratio [
] is the sesquisextan ratio [ ] is the superbitertdecima ratio [
] is the superbitertdecima ratio [ ]
] ] is the sesquiseptian ratio [
] is the sesquiseptian ratio [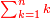 ].
].![\scriptstyle{\color{red}{\sum_{k=1}^n k=\frac{1}{2}\sdot\left[n\sdot\left(n+1\right)\right]}}](/mediawiki/images/math/d/a/3/da36748df8ff59ff88435b913e6c55d2.png) ]
]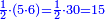 is the fifth triangle [in potential].
is the fifth triangle [in potential].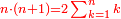 ].
]. → its side is five.
→ its side is five.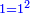
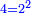
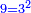
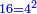
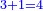 which is the first of the square numbers.
which is the first of the square numbers. which is the second square number.
which is the second square number.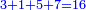 which is the third square number.
which is the third square number.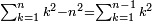 .
.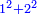 exceeds the square of two
exceeds the square of two 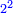 by the square of one
by the square of one 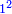 .
.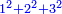 exceeds the square of three
exceeds the square of three 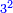 by the sum of the two squares of one and two
by the sum of the two squares of one and two 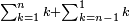 .
.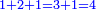 which is the first square number.
which is the first square number. which is the second square number.
which is the second square number.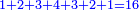 which is the third square of the square numbers.
which is the third square of the square numbers.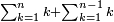 .
.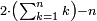 .
.![\scriptstyle n^2+m^2+\left[2\sdot\left(n\sdot m\right)\right]](/mediawiki/images/math/8/2/8/8287d72fc47eefd97b148843d3c9ede1.png) .
.![\scriptstyle{\color{blue}{4+9+\left[2\sdot\left(2\sdot3\right)\right]=25}}](/mediawiki/images/math/0/9/3/0937e73c233767419967902c47ace1a2.png)
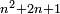 , or when it is added to its same and a quarter of its same
, or when it is added to its same and a quarter of its same 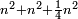 , or thrice its same
, or thrice its same 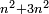 , or when its three quarters are subtracted from it
, or when its three quarters are subtracted from it 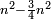 - the results are squares.
- the results are squares.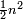 or double
or double 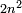 are squares.
are squares. ]: The first of them is the five, which is composed as this:
]: The first of them is the five, which is composed as this: ]: The second pentagonal is that whose side is the second number, which is three, so the pentagonal formed from it is twelve, like this:
]: The second pentagonal is that whose side is the second number, which is three, so the pentagonal formed from it is twelve, like this: ]: The third number, which is four, the pentagonal that is formed from it is twenty two, like this:
]: The third number, which is four, the pentagonal that is formed from it is twenty two, like this: with the one
with the one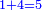 which is the first pentagonal number.
which is the first pentagonal number.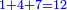 which is the second pentagonal number.
which is the second pentagonal number. which is the third pentagonal number.
which is the third pentagonal number.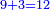 .
.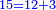 = the second pentagonal number + the first triangular number.
= the second pentagonal number + the first triangular number.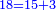 = the second hexagonal number + the first triangular number.
= the second hexagonal number + the first triangular number.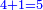 ] = the first pentagonal number.
] = the first pentagonal number.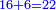 ] = the third pentagonal number.
] = the third pentagonal number. ]
]
 ] = the first hexagonal number.
] = the first hexagonal number.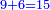 ] = the second hexagonal number.
] = the second hexagonal number.![\scriptstyle{\color{red}{\left(n+1\right)^2+\left[\left(n+1\right)\sdot n\left(1+\frac{1}{2}\right)\right]}}](/mediawiki/images/math/1/2/a/12a39626c58d1b0225254376b46f5fda.png) ]
]
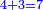 ] = the first heptagonal number.
] = the first heptagonal number. ] = the second heptagonal number.
] = the second heptagonal number. = the first hexagonal number = the second triangular number.
= the first hexagonal number = the second triangular number.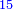 = the second hexagonal number = the fourth triangular number.
= the second hexagonal number = the fourth triangular number. = the third hexagonal number = the sixth triangular number.
= the third hexagonal number = the sixth triangular number. , which are triangles, but not hexagonal numbers.
, which are triangles, but not hexagonal numbers.![\scriptstyle{\color{red}{\frac{1}{2}\sdot\left[\left[\left[3\sdot\left(n-1\right)\right]+2\right]\sdot n\right]}}](/mediawiki/images/math/9/3/e/93e6cc3c933e850b4375b351b8849fde.png) ]
]![\scriptstyle{\color{blue}{\frac{1}{2}\sdot\left[\left[\left(3\sdot3\right)+2\right]\sdot4\right]=\frac{1}{2}\sdot\left[\left(9+2\right)\sdot4\right]=\frac{1}{2}\sdot\left(11\sdot4\right)=\frac{1}{2}\sdot44=22}}](/mediawiki/images/math/a/d/1/ad1bb1cb563e2d2c763ba15700b8a782.png)
![\scriptstyle{\color{red}{n^2+\left[\left(\frac{1}{2}\sdot n\right)\sdot\left(n-1\right)\right]}}](/mediawiki/images/math/1/1/0/1104c405e7db41eab68b7cbee58a5c3a.png) ]
]![\scriptstyle{\color{blue}{\left(4\sdot4\right)+\left[\left(\frac{1}{2}\sdot4\right)\sdot3\right]=16+\left(2\sdot3\right)=22}}](/mediawiki/images/math/1/7/a/17a6757180909a40697a627d465b9a87.png)
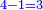 a prime number, appropriate for the procedure.
a prime number, appropriate for the procedure. 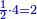
 prime numbe, appropriate for the requested [procedure]
prime numbe, appropriate for the requested [procedure]
 composite number, not appropriate for the procedure
composite number, not appropriate for the procedure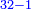 prime number, appropriate for the procedure
prime number, appropriate for the procedure
 .
.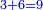 the second square.
the second square.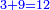 the second pentagon.
the second pentagon.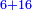 the third pentagon.
the third pentagon. .
.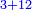 the second hexagon.
the second hexagon. = The first pyramid.
= The first pyramid.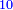 = The second pyramid of this type.
= The second pyramid of this type.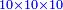 - called cube.
- called cube.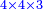
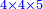
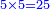


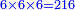
![\scriptstyle\left[n\sdot\left(n+1\right)\sdot\left(n-1\right)\right]+n=n^3](/mediawiki/images/math/a/9/9/a996064cf0852665f551c754512475b1.png)
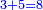 which is a cube.
which is a cube.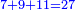 which is the third cube.
which is the third cube.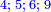 are always recurring in the units of their cubes, this is the instruction of the units of the root of the cube.
are always recurring in the units of their cubes, this is the instruction of the units of the root of the cube.

![\scriptstyle{\color{red}{\left(n+1\right)^3-n^3=\left[n\sdot\left(n+1\right)\sdot3\right]+1}}](/mediawiki/images/math/3/e/6/3e63601006ddff16294ac3b53a745230.png) ]
]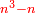 divisible by 6]
divisible by 6] divisible by
divisible by  ]
]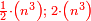 are not cubes]
are not cubes]![\scriptstyle{\color{red}{n^3+1+6\sdot\left[\frac{1}{2}\sdot\left[n\sdot\left(n+1\right)\right]\right]=\left(n+1\right)^3}}](/mediawiki/images/math/7/f/c/7fcce4c6a0816afdc329bdc45d0a7d71.png) ]
]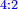 double ratio
double ratio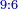 sesquialter ratio
sesquialter ratio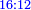 sesquitertian ratio
sesquitertian ratio
 sesquialter ratio
sesquialter ratio



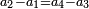
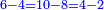
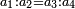
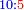
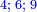
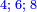
 sesquialter ratio
sesquialter ratio sesquitertian ratio
sesquitertian ratio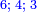 , and it is called harmonic, since the benefit from the observation of this proportion is fulfilled in the art of composition, which is music, as will be known in its place.
, and it is called harmonic, since the benefit from the observation of this proportion is fulfilled in the art of composition, which is music, as will be known in its place.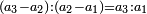
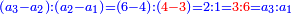
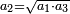
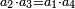
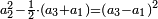
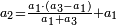
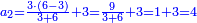
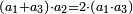
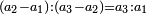
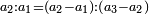
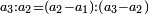
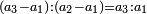
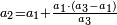
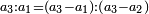
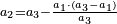
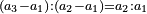
![\scriptstyle\left(\frac{1}{2}\sdot a_1\right)+\sqrt{\left(\frac{1}{2}\sdot a_1\right)^2+\left[\left(a_3-a_1\right)\sdot a_1\right]}](/mediawiki/images/math/e/a/d/eada53cd27cf9472b216bb51d80d9592.png)
![\scriptstyle\left(\frac{1}{2}\sdot a_3\right)+\sqrt{\left(\frac{1}{2}\sdot a_3\right)^2-\left[\left(a_3-a_1\right)\sdot a_1\right]}](/mediawiki/images/math/0/9/f/09fe8930525048d5491e216bfbf3c630.png)
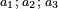 ]
]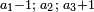 ] and it is the sixth proportion.
] and it is the sixth proportion.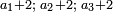 ] the ninth proportion is resulted.
] the ninth proportion is resulted.
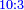
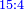
![\scriptstyle\left(1+\frac{1}{n}\right):1=\left[n+\left(\frac{1}{n}\sdot n\right)\right]:n](/mediawiki/images/math/2/9/4/294dfe97e860deae2175a807a062caf2.png)
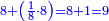
 is the sesquioctavian ratio.
is the sesquioctavian ratio.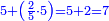
 is the superbiquintan ratio.
is the superbiquintan ratio.![\scriptstyle\left(m+\frac{a}{n}\right):1=\left[\left(m\sdot n\right)+\left(\frac{a}{n}\sdot n\right)\right]:n](/mediawiki/images/math/0/3/c/03cb195620c16cccc85b497ce6b8a366.png)
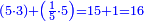 which is the greater.
which is the greater. is the triple sesquiquintan ratio.
is the triple sesquiquintan ratio. 
 is the triple superbiquintan ratio.
is the triple superbiquintan ratio. 

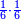
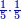
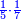
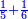
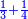
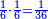
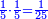
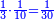
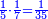
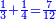
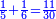
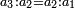 .
.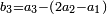 .
.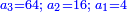
![\scriptstyle{\color{blue}{b_3=a_3-\left(2a_2-a_1\right)=64-\left[\left(2\sdot16\right)-4\right]=64-28=36}}](/mediawiki/images/math/e/d/b/edbc2d3be9a7645d778227d61c7c794f.png)
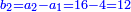
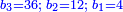 are in the triple ratio.
are in the triple ratio.![\scriptstyle{\color{blue}{c_3=b_3-\left[2b_2-b_1\right]=36-\left[\left(2\sdot12\right)-4\right]=36-20=16}}](/mediawiki/images/math/a/3/8/a381fb3334579961721207bddab4ae86.png)
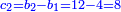
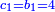
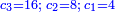 are in the double ratio.
are in the double ratio.![\scriptstyle{\color{blue}{d_3=c_3-\left[2c_2-c_1\right]=16-\left[\left(2\sdot8\right)-4\right]=16-12}}](/mediawiki/images/math/d/1/0/d10ebaae8b410047b51d0823d05b6b68.png)
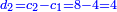
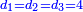
![\scriptstyle{\color{blue}{b_1=a_3-\left[2a_2-a_1\right]=18-\left[\left(2\sdot12\right)-8\right]=18-16=2}}](/mediawiki/images/math/3/f/3/3f342d4f77c4d0edc7a2010a3a55d360.png)
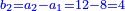
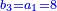
 are in the double ratio.
are in the double ratio.![\scriptstyle{\color{blue}{c_3=b_3-\left[2b_2-b_1\right]=8-\left[\left(2\sdot4\right)-2\right]=8-6=2}}](/mediawiki/images/math/1/a/a/1aacc8a0f3da7e9651e4a4cf6b9858ac.png)
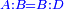

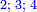 succeeding one by one
succeeding one by one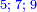 succeeding two by two
succeeding two by two superbiseptian ratio
superbiseptian ratio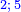 and
and 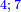 and
and 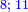
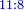 is the same and a quarter and an eighth.
is the same and a quarter and an eighth. is the same and a half and a quarter.
is the same and a half and a quarter. double sesquialter ratio
double sesquialter ratio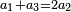 ; and of the discontinuous, it is equal to the sum of the means
; and of the discontinuous, it is equal to the sum of the means 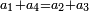 .
. 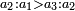 and
and 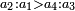
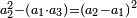 .
. 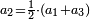 .
.![\scriptstyle n=\frac{1}{2}\sdot\left[\left(n-1\right)+\left(n+1\right)\right]](/mediawiki/images/math/6/6/a/66a4f5c01b212c7e738a63bbb1276d70.png) .
.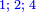 for the continuous.
for the continuous.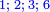 for the discontinuous.
for the discontinuous.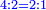

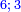 and
and 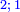 whose ratio is the same, but their differences are different.
whose ratio is the same, but their differences are different.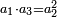 ; and it is equal to the product of one of the means by the other, of the discontinuous
; and it is equal to the product of one of the means by the other, of the discontinuous 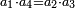 .
. 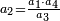 .
.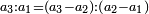
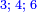 .
.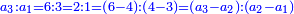
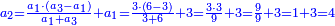
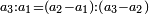
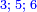 .
.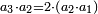 [incorrect for the general case]
[incorrect for the general case]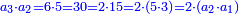
 .
.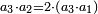 [incorrect for the general case]
[incorrect for the general case]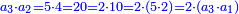
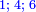 .
.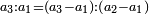
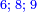 .
.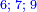 .
.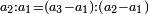
 .
.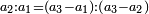
 .
.