Difference between revisions of "ספר היסודות לאקלידס"
(→Proposition 5) |
|||
| Line 695: | Line 695: | ||
|- | |- | ||
|} | |} | ||
| + | {| | ||
| + | |- | ||
| + | | | ||
| + | == Book Fifteen == | ||
| + | |style="text-align:right;"|המאמר החמשה עשר לאספקלאוס | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|אשר יאות לאקלידס החכם | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|א הקדמה לאספקלאוס בהשלמת המאמר על המוגשמים החמשה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כאשר נחלק צלע המשושת על יחס בעל אמצע ושתי קצוות הנה חלק היותר גדול הוא צלע המעושר אשר תקיף בו העגולה אשר תקיף במשושת | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|המשל בזה כי קו א"ב צלע המשושת וכבר נחלק על [יחס] בעל אמצע ושתי קצוות על נקודת ג' וחלקו הגדול ב"ג הנה אומר כי ב"ג צלע המעושר אשר תקיף בו העגולה אשר תקיף במשושת | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|המופת כי כבר התבאר במאמר השלש עשרה [בט' ממנו] כי צלע משושת העגולה ומעושר כאשר נדבקו על יושר אחר כן נחלק הקו על יחס בעל אמצע ושתי קצוות הנה החלק הגדול הוא צלע המשושת והחלק הקטן הוא צלע המעושר ונגיע בקו א"ב צלע המעושר והוא ד"ב הנה קו א"ד כבר נחלק על יחס בעל אמצע ושתי קצוות על נקודת ב' וחלקו הגדול קו א"ב ונרשום קו שוה לקו א"ב והוא קו ה"ו ונחלקהו כיחס בעל אמצע ושתי קצוות על נקודת ז' וחלקו הגדול ו"ז שוה אל קו ב"ג הנה יחס א"ד אל א"ב כיחס ה"ו אל ו"ז וכאשר הבדלנו אחר כן הפכנו הנה [מי"ו מו'] יחס א"ב אל ב"ד כיחס ו"ז אל ז"ה אם כן המרובע אשר יהיה מן א"ב בה"ז כמו המרובע אשר יהיה מן ב"ד בו"ז וא"ב כמו ה"ו ואשר [מי"ו מו'] יהיה מן ה"ו בה"ז שוה לאשר יהיה מן ו"ז בכמוהו אם כן קו ד"ב הוא כמו ו"ז וקו ו"ו כמקומו כמו קו ב"ג וד"ב צלע המעושר אם כן קו ב"ג צלע המעושר וזה מה שרצינו לבאר | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ב נרצה שנרשום בעל ארבעה תושבות משולשות שוות הצלעות במעוקב ידוע ויהיה המעוקב הידוע מעוקב א"ב ג"ד ו"ז ח' ונגיע א"ג ונוציא א"ז וג"ז וא"ה וה"ג וה"ז הנה אומר כי כבר עשינו בעל ארבעה תושבות משולשות שוות הצלעות והוא מוגשם א"ג ז"ה | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|המופת כי א"ג כבר היה מיתר זוית אד"ג הנצבת וא"ז כבר היה מיתר זוית אד"ז הנצבת וג"ז כבר היה מיתר זוית גד"ז הנצבת וא"ה כבר היה מיתר זוית אב"ה הנצבת וג"ה כבר היה מיתר גב"ה הנצבת וה"ז כבר היה מיתר זוית הו"ז הנצבת וקוי א"ד ד"ז ג"ד ג"ב א"ב ב"ה ו"ז שוים אם כן [מד' מא'] צלעות א"ז ז"ג א"ג א"ה ז"ה ג"ה שוות אם כן משולשי אג"ז אה"ג אה"ז הז"ג שוים אם כן מוגשם א"ג ז"ה בעל ארבעה תושבות משולשות שוות הצלעות בתושבת משולש אג"ז וראשו נקודת ה' וזה מה שרצינו לבאר | ||
| + | |} | ||
| + | |||
| + | |||
Notes | Notes | ||
<references group=note/> | <references group=note/> | ||
Revision as of 07:59, 10 July 2020
Contents
Book Two |
המאמר השני[1] מספר אקלידס החכם[2] |
|---|---|
|
[note 1]כל שטח נכחי הצלעות נצב הזויות הנה שני[3] הקוים[4] הישרים המקיפים באחת[5] מזויותיו[6] הנצבות[7] יקרא[8] לשניהם[9] המקיפים[10] בו[11][note 2] |
|
[note 3]וכל[12] שטח[13] נכחי[14] הצלעות הנה[15] יקרא אחד[16] משני[17] השטחים[18] הנכחי[19] הצלעות אשר הם[20] על קוטרו[21] אי זה משניהם היה[22] עם שני השטחים[23] המתמימים[24][note 4] הרושם[25][note 5] |
Proposition 1The distributive law for multiplication over addition:
|
[note 6]א[26] כאשר היו[27] שני קוים ישרים[28] וחולק[29] אחד מהם[30] לחלקים[31] איזה מספר שיהיה[32] הנה[33] השטח הנצב[34] הזויות[35] אשר יקיפו[36] בו[37] השני קוים[38] הישרים[39] שוה[40] לכל השטחים[41] הנצבי[42] הזויות אשר יקיף[43] בכל אחד מהם[44] הקו[45] אשר לא[46] יחלק[47] וכל[48] אחד[49] מן החלקים[50][note 7] |
| גב × א = (דב × א) + (הד × א) + (גה × א) | ויהיו[51] שני[52] קוים ישרים[53] על שניהם[54] א' ב"ג ונחלק ב"ג לחלקים[55] כמה שיהיו[56] על שתי[57] נקודות[58] ד'ה' הנה אומר כי[59] השטח הנצב[60] הזויות[61] אשר יקיפו בו[62] שני[63] קוי[64] א' ב"ג שוה[65] לשטח הנצב[66] הזויות[67] אשר יקיפו בו שני[68] קוי[69] א' ב"ד[70] והשטח הנצב[71] הזויות אשר יקיפו בו שני[72] קוי[73] א' ד"ה[74] והשטח הנצב[75] הזויות[76] גם כן[77] אשר יקיפו בו[78] א' ה"ג[note 8] |
| בז ⊥ בג | ונוציא[79] מנקודת ב' מן קו[80] ב"ג הישר[81] קו ישר[82] על זוית נצבת[83] והוא ב"ז מי”א מא’[84] |
| בז = א | ונשים[85] קו ב"ז[86] הישר שוה[87] לקו א' הישר[88] מג’ מא’[89] |
זח  בג בג
|
ונוציא מנקודת ז' קו ז"ח נכחי[90] לקו ב"ג הישר[91] |
דט, הכ, גח  בז בז
|
ונוציא מן[92] ד'[93] ה' ג'[94] קוים נכחיים לקו ב"ז והם קוי[95] ד"ט ה"כ[96] ג"ח מל”א מא’[97] |
 בט + בט +  דכ + דכ +  הח = הח =  בח בח
|
הנה כל[98] אחד[99] משטחי ב"ט ד"כ[100] ה"ח נכחי הצלעות ושטח[101] ב"ח שוה לשטחי[102] ב"ט[103] ד"כ ה"ח מפתיחת הראשון[104] |
בג × א =  בח → א = בז בח → א = בז
|
ואולם[105] שטח ב"ח הנה הוא[106] שוה לשטח הנצב[107] הזויות[108] אשר יקיפו בו שני[109] קוי א' ב"ג מפני כי קו[110] ב"ז שוה לקו א'[111] |
בד × א =  בט → א = בז בט → א = בז
|
ואולם שטח[112] ב"ט[113] הנה הוא[114] שוה לשטח נצב[115] הזויות[116] אשר[117] יקיפו בו שני[118] קוי[119] א' ב"ד מפני כי קו[120] ב"ז שוה לקו א'[121] |
דה × א =  דכ → א = דט דכ → א = דט
|
ואולם שטח[122] ד"כ[123] הנה הוא[124] שוה[125] לשטח הנצב[126] הזויות[127] אשר יקיפו בו שני קוי[128] א' ד"ה[129] מפני כי קו[130] א' שוה לקו ד"ט |
הג × א =  הח → א = הכ הח → א = הכ
|
ואולם שטח[131] ה"ח הנה הוא[132] שוה[133] לשטח הנצב[134] הזויות[135] אשר יקיפו בו[136] שני קוי[137] א' ה"ג מפני כי קו[138] א' שוה לקו ה"כ[139][note 9] מל”ד מא’[140][note 10] |
| הנה השטח[141] הנצב[142] הזויות[143] אשר יקיפו[144] בו שני[145] קוי[146] א' ב"ג[147] שוה לשטחים נצבי הזויות[148] אשר יקיפו בהם א' ב"ד וא' ד"ה וא' ה"ג[149][note 11] | |
| הנה[150] כאשר[151] היו[152] שני[153] קוים ישרים ונחלק[154] אחד[155] משניהם[156] לחלקים כמה שיהיו[157] הנה השטח[158] הנצב[159] הזויות[160] אשר יקיפו בו[161] שני[162] הקוים[163] הישרים[164] שוה[165] לכל השטחים[166] הנצבים[167] הזויות אשר יקיף[168] בהם[169] הקו אשר לא נחלק[170] וכל[171] אחד[172] מן החלקים[173] | |
| וזה[174] מה שרצינו לבאר[175] | |
Proposition 2in modern notation: |
ב[176] כאשר נחלק[177] קו ישר[178] איך שקרה[179] הנה[180] השטחים[181] נצבי[182] הזויות[183] אשר יקיף[184] בהם הקו כלו וכל אחד מחלקיו[185] שוה למרובע המתהוה[186] מן[187] הקו[188] כלו[189][note 12] |
| ויהיה[190] קו[191] ישר[192] עליו[193] א"ב[194] ויחלק[195] איך שיקרה[196] על נקודת ג'[197] הנה[198] אומר כי[199] השטח[200] הנצב[201] הזויות[202] אשר יקיפו[203] בו שני[204] קוי א"ב[205] ב"ג[206] עם[207] השטח[208] הנצב[209] הזויות[210] אשר יקיפו בו שני[211] קוי[212] א"ב א"ג[213] שוה[214] למרובע המתהוה[215] מן א"ב[216][note 13] | |
| והנה[217] נעשה על קו[218] א"ב[219] מרובע עליו[220] א"דה"ב ממ”ו מא’[221] | |
אד, בה  גז גז
|
ונוציא מנקודת ג' קו ישר נכחי לכל[222] אחד משני[223] קוי [224] א"ד ב"ה והוא ג"ז מל”א מא’[225] |
 אז + אז +  גה = גה =  אה אה
|
הנה כל אחד משני[226] שטחי[227] א"ז ג"ה נכחי הצלעות ושטח א"ה שוה לשני[228] שטחי[229] א"ז ג"ה[230] מא’ מזה[231] |
| אב = אד→
אג × בא = אג × אד = |
ושטח א"ז שוה[232] לשטח נצב[233] הזויות[234] אשר יקיפו[235] בו[236] ב"א [237]א"ג[238] כי הוא[239] יקיפו[240] בו שני[241] קוי א"ד[242] א"ג[243] וקו א"ד[244] שוה לקו א"ב |
אב × בג =  גה → אב = בה גה → אב = בה
|
ושטח ג"ה שוה[245] לשטח הנצב[246] הזויות[247] אשר יקיפו בו[248] שני[249] קוי[250] א"ב ב"ג[251] מפני שא"ב[252] שוה לב"ה[253] |
2אב =  אה אה
|
ושטח א"ה הוא[254] המרובע ההוה[255] מקו א"ב[256] |
| 2אב = (אב × אג)+(אב × בג) | הנה[257] השטח[258] נצב[259] הזויות[260] אשר יקיפו בו[261] שני[262] קוי א"ב[263] א"ג[264] עם השטח הנצב[265] הזויות[266] אשר יקיפו בו[267] שני קוי[268] א"ב ב"ג[269] שוה[270] למרובע[271] המתהוה[272] מן[273] א"ב[274][note 14] |
| הנה[275] כאשר נחלק[276] קו[277] ישר[278] איך שקרה[279] הנה[280] השטחים[281] הנצבי[282] הזויות אשר יקיף בהם[283] הקו כלו וכל אחד[284] מחלקיו[285] שוה למרובע המתהוה[286] מן הקו[287] כלו[288] | |
| וזה מה שרצינו לבאר[289] | |
Proposition 3in modern notation: |
ג[290] כאשר נחלק[291] קו ישר[292] בשני[293] חלקים[294] איך שקרה[295] הנה[296] השטח[297] הנצב[298] הזויות אשר יקיף[299] בו[300] הקו[301] כלו ואחד משני[302] חלקיו[303] שוה לשטח הנצב[304] הזויות[305] אשר יקיפו[306] בו[307]השני[308] חלקים[309] והמרובע[310] המתהוה[311] מן[312] החלק[313] אשר זכרנו[314][note 15] |
| ויהיה[315] קו[316] ישר[317] עליו[318] א"ב[319] ויחלק[320] איך שיקרה[321] על[322] נקודת ג' הנה[323] אומר כי השטח[324] הנצב[325] הזויות אשר יקיפו[326] בו קוי[327] א"ב ב"ג שוה[328] לשטח הנצב[329] הזויות[330] אשר יקיפו בו[331] שני[332] קוי[333] א"ג ג"ב[334] והמרובע המתהוה[335] מן ג"ב[336][note 16] | |
| ונעשה[337] מן קו[338] ג"ב[339] מרובע עליו[340] בגד"ה[341] ממ”ו מא’[342] | |
| ונתמים[343] שטח א"ג ד"ז[344] הנכחי[345] הצלעות[346] מל”א וממ”ב מא’[347] | |
 אד + אד +  גה = גה =  אה אה
|
הנה[348] כל אחד[349] משני[350] שטחי[351] א"ה[352] א"ד[353] נכחי[354] הצלעות[355] ושטח א"ה שוה לשטח א"ד עם ג"ה[356] מא’ מזה[357] |
אב × בג =  אה → בג = בה אה → בג = בה
|
וא"ה שוה לשטח הנצב[358] הזויות[359] אשר יקיפו בו[360] שני[361] קוי א"ב ב"ג[362] מפני כי ב"ג[363] שוה לב"ה |
אג × גב =  אד → בג = גד אד → בג = גד
|
ושטח א"ד שוה לשטח הנצב[364] הזויות אשר יקיפו בו שני[365] קוי[366] א"ג ג"ב[367] מפני כי ב"ג[368] שוה לג"ד[369] |
2גב =  הג הג
|
ושטח ה"ג[370] הוא[371] המרובע[372] המתהוה[373] מן ג"ב[374] |
| 2גב+ (אג × גב) = אב × בג | הנה[375] השטח הנצב[376] הזויות אשר יקיפו בו שני[377] קוי א"ב ב"ג שוה לשטח הנצב[378] הזויות אשר יקיפו בו שני[379] קוי[380] א"ג ג"ב[381] והמרובע[382] המתהוה[383] מן ג"ב[384][note 17] |
| הנה[385] כאשר חולק[386] קו ישר[387] בשני[388] חלקים[389] איך שיקרה[390] הנה[391] השטח הנצב[392] הזויות אשר יקיף[393] בו הקו כלו ואחד משני[394] חלקיו[395] שוה לשטח הנצב[396] הזויות אשר יקיפו בו השני[397] חלקים[398] והמרובע המתהוה[399] מן החלק[400] אשר זכרנו[401] | |
| וזה מה שרצינו לבאר[402] | |
Proposition 4in modern notation: |
ד[403] כאשר חולק[404] קו ישר[405] בשני[406] חלקים[407] איך שיקרה[408] הנה[409] המרובע[410] המתהוה[411] מן[412] הקו[413] כלו שוה לשני[414] המרובעים[415] המתהוים[416] מן השני[417] חלקים[418] וכפל[419] השטח[420] הנצב[421] הזויות אשר יקיפו בו השני[422] חלקים[423][note 18] |
| ויהיה[424] קו ישר[425] עליו[426] א"ב ויחולק[427] איך שיקרה[428] על נקודת ג' הנה[429] אומר כי המרובע[430] המתהוה[431] מן א"ב[432] שוה לשני[433] המרובעים המתהוים[434] מן א"ג[435] ג"ב[436] וכפל[437] השטח[438] הנצב[439] הזויות[440] אשר יקיפו בו שני[441] קוי א"ג ג"ב[442][note 19] | |
| הנה נעשה מן א"ב מרובע א"דה"ב ממ”ו מא’ | |
| ונגיע ד"ב ונוציא מנקודת ג' קו נכחי לשני קוי א"ד ב"ה והוא ג"ז מל”א מא’ | |
| ויחתוך קו ד"ב על נקודת ח' ונוציא מנקודת ח' קו נכחי לשני קוי א"ב ד"ה והוא קו ט"כ הנה מפני כי קו ג"ז נכחי לקו א"ד וכבר נפל על שניהם קו ב"ד הישר תהיה זוית ג'ח'ב' החיצונה שוה לזוית א'ד'ב' הפנימית אשר תקבילה מכ”ט מא’ | |
| אבל זוית א'ד'ב' שוה לזוית ד'ב'א' מפני כי צלע א"ד שוה לצלע א"ב מה’ מא’ | |
| הנה זוית ג'ח'ב' שוה לזוית א'ב'ד' הנה יהיה צלע ג"ח שוה לצלע ג"ב מו’ מא’ | |
| ומפני כי צלע ג"ח שוה לב"כ וג"ב שוה לח"כ יהיו קוי ב"ג ג"ח ח"כ כ"ב הארבעה שוים קצתם אל קצת הנה שטח ג"כ שוה הצלעות מל”ד מא’ | |
| ואומר גם כן כי הוא נצב הזויות הנה מפני כי ג"ח נכחי לב"כ וכבר נפל על שניהם ג"ב יהיו שתי זויות ג'ב'כ' ח'ג'ב' שוות לשתי נצבות מכ”ט מא’ | |
| וזוית כ'ב'ג' נצבת הנה זוית ב'ג'ח' נצבת ויהיו מפני זה שתי זויות ג'ח'כ' ח'כ'ב' המקבילות לשתיהן נצבות מל”ד מא’ | |
| הנה שטח ח"ג כ"ב נצב הזויות וכבר התבאר שהוא שוה הצלעות הנה שטח ג"כ מרובע והוא המתהוה מן ג"ב | |
| וכן התבאר ששטח ט"ז גם כן מרובע והוא המתהוה מן ט”ח אשר הוא שוה לקו א”ג הנה שני שטחי כ"ג ט"ז שני מרובעים והם שוים לשני מרובעים המתהוים מן א"ג ג"ב | |
| אבל ה"ח שוה לא"ח ממ”ג מא’ | |
| וא"ח שוה לשטח הנצב הזויות אשר יקיפו בו א"ג ג"ב מפני שג"ב שוה לג"ח הנה ה"ח שוה לשטח נצב הזויות אשר יקיפו בו א"ג ג"ב הנה שני שטחי א"ח ח"ה שוים לכפל השטח הנצב הזויות אשר יקיפו בו א"ג ג"ב ושני שטחי ט”ז ג”כ שוים לשני המרובעים המתהוים מן קוי א”ג ג”ב הנה כבר התבאר ששטחי ט"ז ג"כ א"ח ח"ה שוים לשני המרובעים המתהוים משני קוי א”ג ג”ב ומכפל השטח הנצב הזויות אשר יקיפו בו א”ג ג”ב אבל שטחי ט”ז ג”כ א”ח ח”ה הם שוים לשטח א"ד ה"ב אשר הוא המרובע המתהוה מן א"ב הנה המרובע המתהוה מן א"ב שוה לשני המרובעים המתהוים מן א"ג ג"ב וכפל השטח הנצב הזויות אשר יקיפו בו א"ג ג"ב[note 20] | |
| הנה כאשר נחלק קו ישר איך שיקרה הנה המרובע המתהוה מן הקו כלו שוה לשני המרובעים המתהוים משני החלקים וכפל השטח הנצב הזויות אשר יקיפו בו השני חלקים | |
| וזה מה שרצינו לבאר | |
| ובכאן התבאר כי כל שטח מרובע הנה שני שטחים הנכחי הצלעות אשר על קוטרו גם כן מרובעים | |
| הנה כבר התבאר מן התמונה הזאת כי השטחים הנכחי הצלעות אשר יהיו על קוטרו שני שטחים מרובעים הם גם כן מרובעים[note 21] | |
| אמר תאבת מצאנו בנסחא אחרת שהוא יתבאר על פנים אחרים כי המרובע המתהוה מן א"ב שוה לשני המרובעים המתהוים מן א"ג ג"ב וכפל השטח הנצב הזויות אשר יקיפו בו שני קוי א"ג ג"ב | |
| הנה מפני שא"ב שוה לא"ד תהיה זוית א'ב'ד' שוה לזוית א'ד'ב' מה’ מא’ | |
| ומפני כי כל משולש הנה זויותיו השלש שוות לשתי נצבות מל”ב מא’ | |
| יהיו זויות א’ד’ב’ א’ב’ד’ ב’א’ד’ השלש ממשולש א'ד'ב' שוות לשתי זויות נצבות וזוית ב'א'ד' נצבת הנה שתי זויות א'ב'ד' א'ד'ב' הנשארות שוות לזוית נצבת ושתיהן שוות מה’ מא’ | |
| הנה כל אחת מהן חצי נצבת וזוית ב'ג'ח' נצבת כי היא שוה לזוית אשר אצל א' אשר תנגדה מכ”ט מא’ | |
| וזוית ג'ב'ח' חצי נצבת הנה זוית ג'ח'ב' הנשארת חצי נצבת הנה זוית ג'ח'ב' אם כן שוה לזוית ג'ב'ח' ויהיה מפני זה צלע ב"ג שוה לצלע ג"ח מו’ מא’ | |
| אבל ג"ב שוה לח"כ מל”ד מא’ | |
| וג"ח שוה לכ"ב הנה שטח ג"כ שוה הצלעות וזוית ב'ג'ח' נצבת הנה ג"כ מרובע והוא המתהוה מן ג"ב ומפני הדברים האלה גם כן התבאר כי ז"ט מרובע והוא שוה למרובע המתהוה מן א"ג הנה ג"כ וט"ז שני מרובעים והם שוים לשני המרובעים המתהוים משני קוי א"ג ג"ב ומפני שא"ח שוה לה"ח ממ”ג מא’ | |
| וא"ח הוא אשר יקיפו בו שני קוי א"ג ג"ב מפני שג"ח שוה לג"ב הנה ה"ח שוה לשטח הנצב הזויות אשר יקיפו בו שני קוי א"ג ג"ב הנה אם כן שני שטחי א"ח ח"ה שוים לכפל השטח הנצב הזויות אשר יקיפו בו א"ג ג"ב ושני שטחי ג"כ ט"ז שוים לשני המרובעים המתהוים משני קוי א"ג ג"ב הנה שטחי ג"כ ט"ז א"ח ח"ה שוים לשני המרובעים המתהוים משני קוי א"ג ג"ב וכפל השטח הנצב הזויות אשר יקיפו בו שני קוי א"ג ג"ב אבל שני שטחי ג"כ ט"ז ושני שטחי א"ח ח"ה הם שטח א"ה הנצב הזויות כלו אשר הוא המרובע המתהוה מן א"ב הנה המרובע המתהוה מן א"ב שוה לשני המרובעים המתהוים מן א"ג ג"ב וכפל השטח הנצב הזויות אשר יקיפו בו שני קוי א"ג ג"ב | |
| וזה מה שרצינו לבאר | |
Proposition 5in modern notation: |
ה[443] כאשר[444] נחלק[445] קו ישר[446] בשני חלקים[447] שוים[448] ושני[449] חלקים[450] בלתי שוים[451] הנה[452] השטח[453] הנצב[454] הזויות אשר יקיפו[455] בו[456] שני חלקי[457] הקו כלו[458] אשר הם בלתי[459] שוים[460] עם המרובע[461] המתהוה מן[462] הקו[463] אשר במה שבין[464] שני[465] מקומות[466] השני חלקים[467] שוה[468] למרובע[469] המתהוה[470] מחצי[471] הקו[note 22] |
| ויהיה[472] קו ישר[473] עליו א"ב ויחלק[474] בשני[475] חלקים שוים[476] על נקודת[477] ג' מי’ מא’[478] | |
| ושני[479] חלקים[480] בלתי שוים[481] על נקודת[482] ד' הנה[483] אומר כי השטח[484] הנצב[485] הזויות אשר יקיפו בו[486] שני[487] קוי א"ד ד"ב עם המרובע המתהוה[488] מן ג"ד[489] שוה[490] למרובע המתהוה[491] מן ג"ב[492][note 23] | |
| ונעשה[493] מקו[494] ג"ב[495] מרובע ג"הז"ב[496] ממ”ו מא’[497] | |
| ונרשום התמונה[498] ונשלים שטח א"גט"ל[499] הנכחי[500] הצלעות מד’ מזה[501] | |
 דז = דז =  גכ → גכ →  חז = חז =  גח גח
|
הנה מפני[502] כי ג"ח[503] שוה לח"ז[504] ונשים ד"כ[505] משותף[506] הנה[507] יהיה ג"כ[508] כלו שוה לד"ז[509] כלו ממ”ג מא’[510] |
 גכ = גכ =  לא → גב = אג לא → גב = אג
|
ומפני שצלע[511] א"ג[512] שוה לצלע ג"ב יהיה שטח ל"א שוה לשטח ג"כ[513] מל”א מא’[514] |
 דז = דז =  לא → לא →  דז = דז =  גכ גכ
|
וכבר היה שטח ג"כ[515] שוה לשטח ד"ז הנה יהיה[516] שטח ל"א[517] שוה לשטח ד"ז[518] מפתיח’ א’[519] |
 מנס = מנס =  אח → אח →
|
ונשים[520] ג"ח[521] משותף[522] הנה[523] א"ח כלו[524] שוה[525] לרושם[526] מנ"ס[527] |
אד × דב =  אח → דח = בד אח → דח = בד
|
אבל א"ח[528] שוה[529] לשטח הנצב[530] הזויות[531] אשר יקיפו בו שני[532] קוי א"ד ד"ב מפני כי ב"ד[533] שוה לד"ח[534] וזה כי ד"כ[535] מרובע[536] משלפניה[537] |
אד × דב =  מנס → מנס →
|
הנה[538] רושם[539] מנ"ס[540] שוה לשטח[541] הנצב[542] הזויות[543] אשר יקיפו בו[544] שני[545] קוי א"ד ד"ב |
→ 2גד =  לע לע
2גד + (אד × דב) = |
ונשים ל"ע אשר הוא שוה[546] למרובע[547] המתהוה[548] מן ג"ד[549] משותף[550] ויהיה[551] רושם מנ"ס[552] ושטח[553] ל"ע כמו השטח הנצב[554] הזויות[555] אשר יקיפו בו[556] שני[557] קוי א"ד ד"ב והמרובע המתהוה[558] מן ג"ד[559] |
 גז = גז =  לע + לע +  מנס מנס
|
אבל[560] רושם[561] מנ"ס ושטח ל"ע[562] הוא[563] שטח ג"ז כלו[564] |
2גב =  גז גז
|
ושטח[565] ג"ז[566] כלו[567] הוא[568] שטח[569] המרובע המתהוה[570] מן ג"ב[571] |
| 2גב = 2גד + (אד × דב) → | הנה[572] השטח[573] הנצב[574] הזויות אשר יקיפו בו[575] א"ד[576] ד"ב עם המרובע המתהוה[577] מן ג"ד[578] שוה למרובע המתהוה[579] מן ג"ב[580][note 24] |
| וכאשר[581] נחלק קו ישר[582] בשני חלקים שוים[583] ושני חלקים בלתי שוים[584] הנה[585] השטח הנצב[586] הזויות אשר יקיפו בו[587] שני[588] חלקי הקו[589] כלו[590] אשר הם בלתי שוים[591] עם המרובע[592] המתהוה[593] מן הקו[594] אשר במה[595] שבין שני מקומות[596] שני[597] החלקים[598] שוה[599] למרובע המתהוה[600] מחצי[601] הקו[602] | |
| וזה מה שרצינו לבאר[603][note 25] | |
Proposition 6in modern notation: |
ו כאשר נחלק קו ישר בחציים ונוסף עליו קו ישר על יושר הנה השטח הנצב הזויות אשר יקיף בו הקו כלו עם התוספת והתוספת עם המרובע המתהוה מחצי הקו שוה למרובע המתהוה מן הקו המורכב מחצי הקו והתוספת[note 26] |
| ויהיה קו ישר עליו א"ב ויחלק בחציים על נקודת ג' מי’ מא’ | |
| ויוסיף עליו קו ישר על יושר והוא ב"ד הנה אומר כי השטח הנצב הזויות אשר יקיפו בו שני קוי א"ד ד"ב עם המרובע המתהוה מן ג"ב שוה למרובע המתהוה מן ג"ד | |
| ונעשה מן ג"ד מרובע ג"ה ז"ד ממ”ו מא’ | |
| ונרשום התמונה ונתמים שטח א"גט"כ הנכחי הצלעות מד’ מזה | |
| הנה מפני כי א"ג שוה לג"ב יהיה שטח א"כ הנכחי הצלעות שוה לשטח ג"ח הנכחי הצלעות אבל ג"ח שוה לח"ז הנה שטח א"כ שוה לשטח ח"ז ממ”ג מא’ | |
| ונשים ג"ל משותף הנה שטח ל"א כלו שוה לרושם מנ"ס כלו אבל השטח הנצב הזויות אשר יקיפו בו שני קוי א"ד ד"ב שוה לשטח ל"א הנצב הזויות מפני שב"ד שוה לד"ל מד’ מזה | |
| הנה רושם מנ"ס שוה לשטח הנצב הזויות אשר יקיפו בו שני קוי א"ד ד"ב ושטח כ"ע שוה למרובע המתהוה מן ג"ב הנה רושם מנ"ס עם שטח כ"ע שוה לשטח אשר יקיפו בו שני קוי א"ד ד"ב והמרובע המתהוה מן ב"ג אבל רושם מנ"ס ומרובע כ"ע הוא ג"ז אשר הוא המרובע המתהוה מן ג"ד | |
| הנה השטח הנצב הזויות אשר יקיפו בו שני קוי א"ד ד"ב עם המרובע המתהוה מן ב"ג שוה למרובע המתהוה מן ג"ד | |
| והנה כאשר נחלק קו ישר בשני חציים והוסף עליו קו ישר על יושר הנה השטח הנצב הזויות אשר יקיף בו הקו כלו עם התוספת והתוספת עם המרובע המתהוה מחצי הקו שוה למרובע המתהוה מן הקו המורכב מחצי הקו והתוספת | |
| וזה מה שרצינו לבאר | |
Proposition 7in modern notation: |
ז כאשר נחלק קו ישר בשני חלקים איך שיקרה הנה המרובע המתהוה מן הקו כלו והמרובע המתהוה מאחד משני חלקים כאשר התקבצו שוים לכפל השטח הנצב הזויות אשר יקיף בו הקו כלו והחלק אשר זכרנו והמרובע המתהוה מן החלק השני[note 27] |
| ויהיה קו ישר עליו א"ב ויתחלק איך שיקרה על נקודת ג' הנה אומר כי שני המרובעים המתהוים משני קוי א"ב ב"ג שוים לכפל השטח הנצב הזויות אשר יקיפו בו שני קוי א"ב ב"ג והמרובע המתהוה מן א"ג | |
| ונרשום מן א"ב מרובע א"דה"ב ממ”ו מא’ | |
| ונבדיל מן ב"ה כמו ב"ג והוא ב"כ מג’ מא’ | |
| ונרשום התמונה הנה שטח א"ז שוה לשטח ז"ה ממ”ג מא’ | |
| ונשים ג"כ משותף הנה יהיה א"כ כלו שוה לג"ה כלו הנה א"כ עם ג"ה כפל א"כ | |
| אבל ג"ה עם א"כ הוא רושם למ"נ ומרובע ג"כ הנה רושם למ"נ ומרובע ג"כ שניהם כפל א"כ וא"כ הוא השטח הנצב הזויות אשר יקיפו בו שני קוי א"ב וב"ג כי הוא יקיפו בו שני קוי א"ב ב"כ וב"כ שוה לב"ג הנה רושם למ"נ ומרובע ג"כ שוים לכפל השטח הנצב הזויות אשר יקיפו בו שני קוי א"ב ב"ג ונשים המרובע המתהוה מן א"ג משותף והוא מרובע ח"ט הנה כפל השטח הנצב הזויות אשר יקיפו בו שני קוי א"ב ב"ג עם המרובע המתהוה מן א"ג שוה לרושם למ"נ ושני שטחי ג"כ ט"ח | |
| אבל רושם למ"נ ושני שטחי ג"כ ט"ח הם א"ה וג"כ וא"ה המרובע המתהוה מן א"ב וג"כ הוא המרובע המתהוה מן ג"ב הנה שני המרובעים המתהוים מן א"ב ב"ג שוים לכפל השטח הנצב הזויות אשר יקיפו בו שני קוי א"ב ב"ג והמרובע המתהוה מן א"ג | |
| הנה כאשר נחלק קו ישר בשני חלקים איך שקרה הנה המרובע המתהוה מהקו כלו והמרובע המתהוה מאחד משני החלקים כאשר התקבצו שוים לכפל השטח הנצב הזויות אשר יקיף בו הקו כלו והחלק אשר זכרנו והמרובע המתהוה מן החלק הנשאר | |
| וזה מה שרצינו לבאר | |
Proposition 8in modern notation: |
ח כאשר נחלק קו ישר בשני חלקים איך שיקרה הנה ארבעה דמיוני[note 28] השטח הנצב הזויות אשר יקיף בו הקו כלו ואחד משני חלקיו עם המרובע המתהוה מן החלק הנשאר שוה למרובע המתהוה מן הקו כלו והחלק אשר קדם זכרו כאשר הושמו שניהם בקו אחד[note 29] |
| ויהיה קו ישר עליו א"ב ויחולק איך שיקרה על נקודת ג' הנה אומר כי ארבעה דמיוני השטח הנצב הזויות אשר יקיפו בו שני קוי א"ב ב"ג עם המרובע המתהוה מן א"ג שוה למרובע המתהוה מן א"ב ב"ג כאשר הושמו בקו אחד | |
| הנה נוציא א"ב אל נקודת ד' מפתי’ א’ | |
| ויהיה ב"ד שוה לב"ג מג’ מא’ | |
| ונעשה מן א"ד מרובע אדה"ז ממ”ו מא’ | |
| ונמשיך ד"ז ונוציא משתי נקודות ג"ב שני קוים נכחיים לשני קוי א"ז ד"ה והם ג"ח ב"ט מל”א מא’ | |
| ויחתוך ב"ט קו ד"ז על נקודת כ' וג"ח על נקודת ק' ונוציא משתי נקודות כ"ק שני קוים נכחיים לשני קוי א"ד ז"ה והם מ"נ ס"ר מל”ד מא’ | |
| הנה מפני כי ג"ב שוה לב"ד וג"ב שוה לכל אחד מפ"כ ק"ע וב"ד שוה לכל אחד מן כ"נ ר"ע יהיה פ"כ שוה אל כ"נ וק"ע לר"ע הנה שטח כ"ג הנכחי הצלעות שוה לשטח ב"נ הנכחי הצלעות מל”ו מא’ | |
| ופ"ע לכ"ר וק"ט גם כן לה"ע ומפני כי ג"כ הנכחי הצלעות שוה לשטח ב"נ הנכחי הצלעות ופ"ע אל כ"ר וג"כ שוה אל כ"ר ממ”ג מא’ | |
| יהיה ב"נ שוה לכל אחד מן פ"ע כ"ר ויהיה פ"ע שוה לכל אחד מן ג"כ ב"נ הנה שטחי ג"כ ב"נ פ"ע כ"ר ארבעה דמיוני ג"כ אבל שטחי ג"כ ב"נ פ"ע כ"ר הם כל שטח ג"ר אשר הוא ארבעה דמיוני שטח ג"כ ומפני כי ג"ב גם כן שוה אל ב"ד וג"ב שוה אל פ"כ אשר יקבילהו והוא גם כן שוה אל פ"ק מפני כי פ"ע מרובע מד’ מזה | |
| וב"ד שוה אל ב"כ ממרובע ב"נ וב"כ הוא גם כן שוה אל ג"פ וג"פ שוה אל פ"ק והנה שטח א"פ שוה לשטח מ"ק מל”ו מא’ | |
| וק"ט שוה אל ר"ט אבל מ"ק שוה אל ק"ט מפני כי שניהם מתמימים ממ”ג מא’ | |
| הנה א"פ שוה אל ר"ט הנה שטחי א"פ מ"ק ק"ט ע"ה הארבעה ארבעה דמיוני שטח א"פ | |
| ושטח ג"ד הנכחי הצלעות ארבעה דמיוני שטח ג"כ הנה כל רושם שת"ת ארבעה דמיוני שטח א"כ וא"כ הוא השטח הנצב הזויות אשר יקיפו בו שני קוי א"ב ב"כ וב"כ שוה אל ב"ג כי הוא שוה אל ב"ד ממרובע ב"ג הנה רושם שת"ת ארבעה דמיוני השטח הנצב הזויות אשר יקיפו בו שני קוי א"ב ב"ג הנה ארבעה דמיוני השטח הנצב הזויות אשר יקיפו בו שני קוי א"ב ב"ג אם כן שוים לרושם שת"ת ונשים המרובע המתהוה מן א"ג משותף והוא ס"ח הנה ארבעה דמיוני השטח הנצב הזויות אשר יקיפו בו שני קוי א"ב ב"ג עם המרובע המתהוה מן א"ג שוה לרושם שת"ת ומרובע ס"ח אבל רושם שת"ת וס"ח שניהם יחד שטח א"ה אשר הוא המרובע המתהוה מן א"ד הנה ארבעה דמיוני השטח הנצב הזויות אשר יקיפו בו שני קוי א"ב ב"ג עם המרובע המתהוה מן א"ג שוה למרובע המתהוה מן א"ד אשר הוא המרובע המתהוה מן א"ב וב"ג כאשר הושמו בקו אחד | |
| הנה כאשר חולק קו ישר בשני חלקים איך שקרה הנה ארבעה דמיוני השטח הנצב הזויות אשר יקיף בו הקו כלו ואחד מחלקיו עם המרובע המתהוה מן החלק הנשאר שוה למרובע המתהוה מן הקו כלו והחלק אשר קדם זכרו כאשר הושמו בקו אחד | |
| וזה מה שרצינו לבאר | |
Proposition 9in modern notation: |
ט כאשר חולק קו ישר לשני חלקים שוים ושני חלקים בלתי שוים הנה שני המרובעים המתהוים משני חלקי הקו כלו אשר הם בלתי שוים שניהם כפל שני המרובעים המתהוים מחצי הקו ומן הקו אשר במה שבין שתי מקומות השני חלקים[note 30] |
| ויהיה קו ישר עליו א"ב ויחלק לשני חלקים שוים על נקודת ג' מי’ מא’ | |
| ושני חלקים בלתי שוים על נקודת ד' הנה אומר כי שני המרובעים המתהוים מן שני קוי א"ד ד"ב כפל שני המרובעים המתהוים מן א"ג ג"ד | |
| ונוציא מנקודת ג' מקו א"ב הישר קו ישר על זוית נצבה והוא ג"ה מי”א מא’ | |
| ונשים ה"ג שוה לכל אחד משני קוי א"ג ג"ב מב’ מא’ ונמשיך קו א"ה ה"ב מפתיח’ א’ | |
| ונוציא מנקודת ד' קו נכחי לקו ג"ה והוא ד"ז מל”א מא’ | |
| ונוציא מנקודת ז' קו נכחי לקו ג"ד והוא ז"ח ונמשיך א"ז | |
| הנה מפני כי ה"ג שוה אל א"ג תהיה זוית גה"א שוה לזוית גא"ה מה’ מא’ | |
| ומפני כי זוית אג"ה נצבת יהיו שתי זויות הא"ג אה"ג הנשארות שוות לזוית נצבת מל”ב מא’ | |
| ושתיהם שוות הנה כל אחת משתי זויות גה"א גא"ה חצי נצבת ומפני כי ה"ג גם כן שוה לג"ב תהיה זוית גה"ב שוה לזוית גב"ה מה’ מא’ | |
| וזוית בג"ה נצבת הנה כל אחת משתי זויות גה"ב גב"ה חצי נצבת אבל כל אחת משתי זויות גה"ב אה"ג חצי נצבת תהיה זוית אה"ז נצבת ומפני כי זוית גב"ה חצי נצבת וזוית זד"ב נצבת תהיה זוית דז"ב חצי נצבת מל”ב מא’ | |
| הנה קו ב"ד שוה לקו ד"ז מו’ מא’ | |
| ולכן גם כן יהיה ז"ח שוה אל ח"ה | |
| ומפני כי ה"ג שוה אל א"ג יהיה המרובע המתהוה מן ה"ג שוה למרובע המתהוה מן א"ג הנה שני המרובעים המתהוים משני קוי ה"ג א"ג כפל המרובע המתהוה מן א"ג הנה המרובע המתהוה מן א"ה שוה לשני המרובעים המתהוים משני קוי ה"ג א"ג ממ”ז מא’ | |
| מפני כי זוית הג"א נצבת הנה המרובע המתהוה מן א"ה כפל המרובע המתהוה מן א"ג ומפני כי ה"ח גם כן שוה אל ז"ח יהיה המרובע ההוה מן ה"ח שוה למרובע ההוה מן ח"ז הנה שני המרובעים ההוים משני קוי ה"ח ח"ז כפל המרובע ההוה מן ח"ז והמרובע ההוה מן ה"ז שוה לשני המרובעים ההוים משני קוי ה"ח ח"ז ממ”ז מא’ | |
| הנה המרובע ההוה מן ה"ז כפל המרובע ההוה מן ח"ז וח"ז שוה אל ג"ד הנה המרובע ההוה מן ה"ז כפל המרובע ההוה מן ג"ד | |
| וכבר התבאר גם כן שהמרובע ההוה מן ה"א כפל המרובע ההוה מן א"ג הנה שני המרובעים ההוים משני קוי א"ה ה"ז כפל שני המרובעים ההוים משני קוי א"ג ג"ד והמרובע ההוה מן א"ז שוה לשני המרובעים ההוים משני קוי א"ה ה"ז ממ”ז מא’ | |
| מפני כי זוית אה"ז נצבת הנה המרובע ההוה מן א"ז כפל שני המרובעים ההוים מן א"ג ג"ד והמרובע ההוה מן א"ז כמו שני המרובעים ההוים מן א"ד ד"ז ממ”ז מא’ | |
| מפני כי זוית אד"ז נצבת הנה שני המרובעים ההוים מן א”ד ד”ז כפל שני המרובעים ההוים משני קוי א”ג ג”ד וז”ד שוה לד”ב הנה שני המרובעים ההוים מן א"ד ד"ב כפל שני המרובעים ההוים משני קוי א"ג ג"ד | |
| הנה כאשר חולק קו ישר לשני חלקים שוים ולשני חלקים בלתי שוים הנה שני המרובעים ההוים משני חלקי הקו כלו אשר הם בלתי שוים שניהם כפל שני המרובעים ההוים מחצי הקו כלו ומן הקו אשר במה שבין שני מקומות השני חלקים | |
| וזה מה שרצינו לבאר | |
Proposition 10in modern notation: |
י כאשר נחלק קו ישר לשני חציים והוסף עליו קו ישר על יושר הנה המרובע ההווה מן הקו כלו עם התוספת והמרובע ההוה מן התוספת כפל שני המרובעים כאשר יחוברו כלומר המרובע ההווה מחצי הקו והמרובע ההווה מן הקו המורכב מחצי הקו והתוספת[note 31] |
| ויהיה הקו הישר א"ב ויחלק לשני חציים על נקודת ג' ויוסיף עליו קו ישר על יושר והוא ב"ד הנה אומר כי שני המרובעים ההוים משני קוי א"ד ד"ב כפל שני המרובעים ההוים משני קוי א"ג וג"ד | |
| ונוציא מנקודת ג' קו ישר על זוית נצבת והוא ג"ה מי”א מא’ | |
| ויושם שוה לכל אחד משני קוי א"ג וג"ב מג’ מא’ | |
| ונגיע קו א"ה ה"ב ונוציא מנקודת ד' קו ישר נכחי לקו ג"ה והוא ד"ז ומנקודת ה' קו ישר נכחי לקו ג"ד והוא ה"ז מל”א מא’ | |
| הנה מפני כי ה"ג נכחי אל ז"ד וכבר נפל על שניהם קו ה"ז הישר יהיו שתי זויות גה"ז הז"ד הפנימיות שוות לשתי זויות נצבות מכ”ט מא’ | |
| הנה שתי זויות בה"ז והז"ד קטנות משתי זויות נצבות והקוים אשר יצאו מפחות משתי זויות נצבות אל לא תכלית יפגשו מפתיחת א’ | |
| הנה קו ה"ב וז"ד כאשר הוצאו אל לא תכלית יפגשו ויפגשו על נקודת ח' ונגיע א"ח הנה מפני כי ה"ג שוה אל א"ג תהיה זוית גה"א שוה לזוית גא"ה מה’ מא’ | |
| וזוית אג"ה נצבת הנה כל אחת משתי זויות גה"א גא"ה חצי נצבת מל”ב מא’ | |
| ומפני כי ה"ג גם כן שוה לג"ב תהיה זוית גה"ב שוה לזוית גב"ה וזוית בג"ה נצבת הנה כל אחת משתי זויות הב"ג וגה"ב חצי נצבת ומפני כי כל אחת משתי זויות אה"ג בה"ג חצי נצבת תהיה זוית אה"ב נצבת ומפני כי זוית הב"ג חצי נצבת תהיה זוית דב"ח חצי נצבת מט”ו מא’ | |
| וזוית בד"ח נצבת כי היא שוה לזוית דג"ה אשר תמירה מכ”ט מא’ | |
| ותשאר זוית דח"ב חצי נצבת | |
| הנה זוית דח"ב אם כן שוה לזוית דב"ח ויהיה מפני זה צלע ב"ד שוה לצלע ח"ד מו’ מא’ | |
| ומפני כי זוית הח"ז גם כן חצי נצבת ואשר אצל ז' נצבת מפני כי היא שוה לאשר תקבילה מל”ד מא’ | |
| והיא אשר אצל ג' תשאר זוית זה"ח חצי נצבת ותהיה זוית הח"ז שוה לזוית זה"ח ולכן יהיה צלע ח"ז שוה לצלע ה"ז | |
| ומפני כי ה"ג שוה אל א"ג יהיה המרובע ההוה מן ה"ג שוה למרובע ההוה מן א"ג ושני המרובעים ההוים משני קוי ה"ג וא"ג כפל המרובע ההוה מן א"ג והמרובע ההוה מן א"ה שוה לשני המרובעים ההוים משני קוי ה"ג א"ג מפני כי זוית הג"א נצבת ממ”ז מא’ | |
| הנה המרובע ההוה מן א"ה כפל המרובע ההוה מן א"ג | |
| ומפני כי ה"ז גם כן שוה אל ז"ח יהיה המרובע ההוה מן ה"ז שוה למרובע ההוה מן ז"ח הנה שני המרובעים ההוים משני קוי ה"ז ז"ח כפל המרובע ההוה מן ה"ז ושני המרובעים ההוים משני קוי ה"ז ז"ח שוים למרובע ההוה מן ה"ח ממ”ז מא’ | |
| הנה המרובע ההוה מן ה"ח כפל המרובע ההוה מן ה"ז | |
| וה"ז שוה אל ג"ד מל”ד מא’ | |
| הנה המרובע ההוה מן ה"ח כפל המרובע ההוה מן ג"ד וכבר התבאר גם כן כי המרובע ההוה מן א"ה כפל המרובע ההוה מן א"ג הנה שני המרובעים ההוים משני קוי א"ה וה"ח כפל שני המרובעים ההוים משני קוי א"ג ג"ד ושני המרובעים ההוים משני קוי א"ה ה"ח שוים למרובע ההוה מן א"ח מפני כי זוית אה"ח נצבת ממ”ז מא’ | |
| הנה המרובע ההוה מן א"ח כפל שני המרובעים ההוים משני קוי א"ג ג"ד והמרובע ההוה מן א"ח שוה לשני המרובעים ההוים משני קוי א"ד ד"ח מפני כי זוית אד"ח נצבת הנה שני המרובעים ההוים משני קוי א"ד וד"ח כפל שני המרובעים ההוים משני קוי א"ג וג"ד | |
| וקו ח"ד שוה לקו ד"ב הנה שני המרובעים ההוים משני קוי א"ד ד"ב כפל שני המרובעים ההוים משני קוי א"ג וג"ד | |
| הנה כאשר חולק קו ישר בשני חציים והוסף עליו קו ישר על יושר הנה המרובע ההווה מן הקו כלו עם התוספת והמרובע ההווה מן התוספת כפל שני המרובעים כאשר יחוברו כלומר המרובע ההווה מחצי הקו והמרובע ההווה מן הקו המורכב מחצי הקו ומן התוספת | |
| וזה מה שרצינו לבאר |
Book Fifteen |
המאמר החמשה עשר לאספקלאוס |
| אשר יאות לאקלידס החכם | |
| א הקדמה לאספקלאוס בהשלמת המאמר על המוגשמים החמשה | |
| כאשר נחלק צלע המשושת על יחס בעל אמצע ושתי קצוות הנה חלק היותר גדול הוא צלע המעושר אשר תקיף בו העגולה אשר תקיף במשושת | |
| המשל בזה כי קו א"ב צלע המשושת וכבר נחלק על [יחס] בעל אמצע ושתי קצוות על נקודת ג' וחלקו הגדול ב"ג הנה אומר כי ב"ג צלע המעושר אשר תקיף בו העגולה אשר תקיף במשושת | |
| המופת כי כבר התבאר במאמר השלש עשרה [בט' ממנו] כי צלע משושת העגולה ומעושר כאשר נדבקו על יושר אחר כן נחלק הקו על יחס בעל אמצע ושתי קצוות הנה החלק הגדול הוא צלע המשושת והחלק הקטן הוא צלע המעושר ונגיע בקו א"ב צלע המעושר והוא ד"ב הנה קו א"ד כבר נחלק על יחס בעל אמצע ושתי קצוות על נקודת ב' וחלקו הגדול קו א"ב ונרשום קו שוה לקו א"ב והוא קו ה"ו ונחלקהו כיחס בעל אמצע ושתי קצוות על נקודת ז' וחלקו הגדול ו"ז שוה אל קו ב"ג הנה יחס א"ד אל א"ב כיחס ה"ו אל ו"ז וכאשר הבדלנו אחר כן הפכנו הנה [מי"ו מו'] יחס א"ב אל ב"ד כיחס ו"ז אל ז"ה אם כן המרובע אשר יהיה מן א"ב בה"ז כמו המרובע אשר יהיה מן ב"ד בו"ז וא"ב כמו ה"ו ואשר [מי"ו מו'] יהיה מן ה"ו בה"ז שוה לאשר יהיה מן ו"ז בכמוהו אם כן קו ד"ב הוא כמו ו"ז וקו ו"ו כמקומו כמו קו ב"ג וד"ב צלע המעושר אם כן קו ב"ג צלע המעושר וזה מה שרצינו לבאר | |
| ב נרצה שנרשום בעל ארבעה תושבות משולשות שוות הצלעות במעוקב ידוע ויהיה המעוקב הידוע מעוקב א"ב ג"ד ו"ז ח' ונגיע א"ג ונוציא א"ז וג"ז וא"ה וה"ג וה"ז הנה אומר כי כבר עשינו בעל ארבעה תושבות משולשות שוות הצלעות והוא מוגשם א"ג ז"ה | |
| המופת כי א"ג כבר היה מיתר זוית אד"ג הנצבת וא"ז כבר היה מיתר זוית אד"ז הנצבת וג"ז כבר היה מיתר זוית גד"ז הנצבת וא"ה כבר היה מיתר זוית אב"ה הנצבת וג"ה כבר היה מיתר גב"ה הנצבת וה"ז כבר היה מיתר זוית הו"ז הנצבת וקוי א"ד ד"ז ג"ד ג"ב א"ב ב"ה ו"ז שוים אם כן [מד' מא'] צלעות א"ז ז"ג א"ג א"ה ז"ה ג"ה שוות אם כן משולשי אג"ז אה"ג אה"ז הז"ג שוים אם כן מוגשם א"ג ז"ה בעל ארבעה תושבות משולשות שוות הצלעות בתושבת משולש אג"ז וראשו נקודת ה' וזה מה שרצינו לבאר |
Notes
- ↑ titled: F137 הקדמות המאמר; Ma1 הקדמות זה המאמר; W66 הקדמה; Lo; Ma1; P1014: marked א
- ↑ E: הקוים המקיפי’ באחת הזוית הנצבות מהשטח נצב הזויות נכחי הצלעות יקראו מקיפים בשטח ההוא [כי] הנה מקביליהם ישוו להם
Mu91 (marg.): פי: ר"ל בשטח ולא יקראו המקיפים בו אם לא שיהיה השטח נצב הזויות בעבור שהשני הקוים לא ישערו השטח אם לא שיהיה השטח נצב הזוית פי' עד כאן
קוים המקיפים בו פי' ר"ל ששני אלו הקוים מודיעים לנו שעור שטח ומגבילים אותו
המשל בזה אם יהיה אחד מן הקוים ארכו ו' אמות ורחב האחר ג' אמות יהיה כל שעור זה השטח י"ח אמות מהכאת האורך ברחב או אם תרצה תכה הרחב באורך ויהיה י"ח גם כן
וכל זה כשיהיה הקו האחד עומד על חבירו על זוית נצבת מה שאין כן בשטח שאינו נצב הזויות
הנה צריך שילקח בזה התנאי שיהיה השטח נצב הזוית שאם לא יהיה כן לא יקראו המקיפים ולא י[...] את השטח השני קוים המקיפים בו
W66: ר"ל ששני אלו הקוים [..] מודיעים לנו שעור השטח ומגבילים אותו
המשל בזה כי אם יהיה אחד מן הקוים ארכו ו' אמות ורחב האחר ג' אמות יהיה כל שעור זה השטח י"ח אמות מהכאת האורך ברחב או הרחב באורך
וכל זה כשיהיה הקו האחד עומד על חברו על זוי' נצבת מה שאין כן בשטח שאינו נצב הזויות
Mu91(marg.), Mu130(marg.), W66: ונקרא השטח בשם שתי אותיות המתנגדות
E: ויקרא השטח בשם שתי אותיות המתנגדות אשר בצד קטרו
P1010 (marg.), PP: ונקרא השטח בשם שתי אותיות הזויות המתנגדות
W194 (marg.): ד"ת ונקרא בשטח בשם שתי אותיות הזויות המתנגדות
Lo (marg.): ונקרא השטח בשם שתי אותיות הזויות המתנגדות בו - ↑ Ma1: marked השנית
- ↑ Lo: והמתמימים באור זה מבואר במ”ג מראשון והרושם הוא שני השטחים המתמימים עם אחד מן השטחים שעל קטרו
- ↑ Mu 246:א כל שטח שוה הצלעות נצב הזויות יסובבנו השני קוים הסובב בזוית הנצבת וכל שטח נגדיי הצלעות נאמ' כי השני שטחים שעל אלכסונו הנגדיי הצלעות והאלכסון יחצבם כשיצטרף אחד מהם לשני השטחים המשלימין שעל שני צדי האלכסון כל זה יקרא עלם
P1011: כל שטח נכחי הצלעות נצב הזויות הנה יקיפו השני קוים המקיפים בזוית הנצבה
וכל שטח נכחי הצלעות הנה השני שטחים אשר יהיו על קטרו [נכח]יי הצלעות והקוטר יחצבם כאשר [...] מהם אל השני שטחים המשלימים אשר [על] צדדי הקוטר יקרא הרושם עד כאן פתי[חה]
E: כל שטח נכחי הצלעות יחתכהו הקוטר והוציאו מנקודו’ ממנו קוים נכחיים לצלעות יחתכם הקוטר ועומדי’ מצדו יקראו השטחי’ אשר יחתכם הקוטר אשר על הקוטר ואשר מצדו המתמימים ומקובץ אחד השטחים שית[ח]כהו הקוטר עם שני המתמימים אשר משני צדיו יקראו הרושם
Ma1: באור להקדמה ב’ הנה נעשה מרובע עליו א’ב’ג’ד’ ובתוכו קוטר אחד והוא קוטר ב”ד ונרשום עליו נקודה איך שתזדמן והיא נקודת ח’ ונגיע מנקודת ח’ קו ט’ח’כ’ על נוכח א”ב וקו ה’ח’ז’ על נוכח ב”ג הנה חלקנו מרובע א’ב’ג’ד’ לארבעה מרובעי’ והם א”ח ה”כ ט”ז ח”ג שנים מהם על קוטר ב”ד ושנים חוצה לו ויאמר שאם נקח אחד משני מרובעי ט”ז ה”כ אשר על הקוטר איזה מהם שנרצה עם שני המרובעי’ אשר חוץ לקוטר הנקראים המשלימים כמבואר בלמוד מ”ג מהמאמר הראשון יקראו אלה השלשה מרובעים רושם ויהיה שעור דבריו כך כל תמונה נכחית הצלעות אחד השטחים וכו’ יקרא הרושם - ↑ F137 titles the propositions’ section: המבוקשים;
- ↑ P1011: כל שני קוים יחלק אחד מהם בחלוקה איך שיהיה הנה אשר יהיה מהכאת אחד משני הקוים באחר כמו אשר יהיה מהכאת הקו אשר לא יחלק בכל חלקי הקו המתחלק חלוקה חלוקה
E: 1 השטח אשר יקיפו בו כל שני קוים שוה למקובץ השטחים יקיפו בם אחד הקוים עם חלקי הקו השני יחד
Mu36 adds a marginal note: כונת זה הדרוש שכשהיו לנו שני קוים מונחי’ כמה שיהיו וחולק האחד מהם לחלקים כמה שהיו שהכאת הקו האחד בכל אחד מהחלקים שחולק הקו השני שוה להכאת הקו ההוא בקו המחולק כלו
The arithmetic version of the proposition is given in marginal notes in a few manuscripts:
Mu91: המשל לתמונת א' משני: כמו עשרה וששה וחולק עשרה לשלשה חלקים כגון חמשה ושלשה ושנים הנה שטח ששה בעשרה שהוא ס' שוה לשטח חמשה בששה שהוא שלשים ולשטח ששה בשלשה שהוא י"ח ולשטח ששה בשנים שהוא י"ב וקבוץ שלשת שטחים אלו הוא ס'
W66: פי’ משל זה במספר כמו עשרה וששה וחולק עשרה לג' חלקים כגון ה' וג' וב' הנה שטח ששה בעשרה שהוא ס' שוה לשטח ששה בחמשה שהוא שלשים ולשטח ששה בשלשה שהוא י"ח ולשטח ששה בשנים שהוא י"ב וקבוץ שלשת שטחים אלו הוא ששים
Numerical example: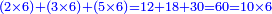
P1010: דמיון במספר כאשר תכה מספר בעצמו יהיה המרובע ההווה ממנו כמרובע ההוה מהכאת המספר ההוא בכל אחד מחלקיו השוים
המשל בזה הכאת י’ בט”ו הוא ק”נ וכשתחלק ט”ו לג’ חלקים שוים שהוא ה’ ותכה עשרה בה’ ה’ יהיה ק”נ
Numerical example: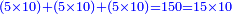
P1014: וכן במספר שה’ עם ד’ הם כ’ וכולו חולק הה’ על ג’ וב’ ותכה הד’ עם השני חלקים יהיו כ’
Numerical example: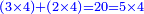
- ↑ C: המשל בזה שקו א' וקו ב"ג נחלק אחד מהם והוא ב"ג על נקודות ד' וה' ואומר שאשר יהיה מהכאת א' בחלק ב"ד ובחלק ד"ה ובחלק ה"ג שוה לאשר יהיה מהכאת א' בב"ג
E: יהיו שני קוי א' ב"ג ונחלק ב"ג על חלקי' איך שנרצה והם ג"ה ה"ד ד"ב ואומ' שהשטח נצב הזויות שיקיפו בו קוי א' ג"ב שוה למקובץ שטחי א'ג"ה וא'ה"ד וא'ד"ב
Mu246: ב שני קוי א'ב"ג חולק ב"ג בחלקי ב"ד ד"ה ה"ג נאמ' כי כפל א' בכל ב"ג ככפל א' בכל אחד מן ב"ד ד"ה ה"ג מקובצי - ↑ AB: פי' זה התבאר מכח מה שאמרנו ששטח ב"ח שוה לשטח ב"ד ד"כ ה"ח
- ↑ C: מופת זה שנוציא מקו ב"ג מנקדת ב' קו על זוית נצבה שוה לקו א' והוא קו ב"ז
ונוציא מנקדת ז' קו נכוחי לקו ב"ג והוא קו ז"ח
ונוציא מנקדת ד' וה' וג' קוים נכוחיים לקו ב"ז והם ד"ט וה"כ וג"ח
וכבר התבאר ששטח ז"ג שוה לשלשת שטחי ז"ד וט"ה וכ"ג וכל השטחים הם נכוחי הצלעות
ושטח ז"ג הוא מהכאת קו א' בקו ב"ג לפי שיקיפו בו קוי ז"ב ב"ג וז"ב שוה לא'
ושטח ז"ד יקיפו בו קוי ז"בוז"ב שוהב"ד וקו ב"ז שוה לקו א'
ושטח ט"ה הוא מהכאת קו א' בקו ד"ה לפי שיקיפו בו קוי ט"ד ד"ה ושקו ט"ד שוה לקו א'
ושטח כ"ג הוא מהכאת א' בה"ג לפי שכ"ה שוה לקו א'
E: מופתו שנוציא מן ג' על קו ג"ב עמוד ג"ח שוה לקו א' ונשלים התמונה
ונוציא מן ה' וד' עמודים על ג"ב והם ה"כ ד"ט
הנה לפי ששטח ב"ח שוה לשלשה שטחי ח"ה ה"ט ט"ב
לפי שמקובץ חלקי השטח שוה לכל השטח ושטח ח"ב שוה לה אשר יקיפו בו א' עם ג"ב
וח"ה שוה לה אשר יקיפו בו א' עם ג"ה
וכן ה"ט לאשר יקיפו בו א' עם ה"ד
וד"ז לאשר יקיפו א' עם ד"ב
Mu246: כיצד נוציא קוי ב"ז כ"ט ה"כ ג"ח על זויות נצבות וכל אחת מהן שוה לקו א'
לפי הדבר נראה כי כל שטח ב"ח הוא כפל א' בב"ג ושטח ב"ט הוא כפל א' בד"ה ושטח ה"ח כפל א' בה"ג - ↑ C: וכבר התבאר שאשר יהיה מהכאת
קקו א' בקו ב"ג שוה לאשר הוא מהכאת קו א' בקו ב"ד ובקו ד"ה ובקו ה"ג וזה מה שרצינו לבאר
E: יהיה השטח שיקיפו בו א' עם ב"ג שהוא כמו ב"ה שוה למקובץ שטחי א' עם ג"ה ה"ד ד"ב שהם כמו שטחי ח"ה ה"ט ט"ב והוא המכוון - ↑ P1011: כל קו יחלק לחלקים הנה אשר יהיה מהכאת הקו בכל חלקיו כמו אשר יהיה מהכאת הקו בעצמו
E: 2 כשנחלק קו ישר לשני חלקי' איך שהזדמן יהיה השטח נצב הזוית שיקיפו בו הקוכלוכלו עם כל אחד מהחלקים שוי' למרובע כל הקו
Mu36: ובנס’ אלחג’אג’ כתו’ כאשר נחלק אי זה מספר שהיה בשני חלקים איך שקרה הנה הכאת המספר כלו בכל אחד מהחלקים להכאת המספר כלו בעצמו
ולפי זאת הנס’ צריך להיות המרובע שוה הצלעו’ כמו זה שלפנינ’
AB: המשל לתמונת ב' כאשר חולק עשרה לשני חלקים כמו ששה וארבעה הנה שטח ששה בעשרה שהוא ס' ושטח ארבעה בעשרה שהוא ארבעים שוה למרובע המתהווה מעשרה אשר הוא מאה
וזה מתבאר מתמונת א' וזה כי בתמונת א' התבאר שהכאת קו ראשון בקו שני כולו כהכאת הקו הראשון בחלקי הקו השני בין שיהיו שני הקוים ר"ל הראשון והשני שוים או בלתי שוים
W66: משל זה במספר כשנחלק עשרה לשני מספרי ו' וד' הנה שטח ו' בי' שהוא ס' ושטח ד' בי' שהוא מ' יחד שוים למרובע המתהוה מי' שהוא מאה
וזהמתפארמתבאר מתמונת א' כי שם התבאר שהכאת קו ראשון בקו שני בקו שני כלו כהכאת הקו הראשון בחלקי הקו השני בין שהיוהשני הקוים ר"ל הראשון והשני שוים או בלתי שוים
Numerical example: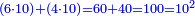
P1014: וכן הח’ אם תחלקהו לו’ וב’ מרובע הכל ס”ד ואם תכה הח’ עם הב’ ועם הב’ יהיו ס”ד וכן בשני המספרים איזה שיהיו
Numerical example: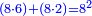
- ↑ C:המשל בזה שקו א"ב נחלק לשני חלקים על נקודת ג' ואומר כי אשר יהיה מהכאת קו א"ב בקו א"ג ובקו ג"ב שוה לאשר יהיה מהכאת א"ב בעצמו
E: יהיה הקו הישר א"ב ויחלק על ג' ואומ' שמרובע א"ב שוה לשטח א"ב בא"ג וא"ב בג"ב - ↑ מופת זה שנצייר על קו א"ב שטח מרובע והוא שטח א"ה ונוציא מנקודת ג' קו עד ז' נכוחי לקוי א"ד וב"ה ויהיו שטחי א"ז וז"ב נכוחי הצלעות והם שוים לשטח א"ה ושטח א"ז הוא
נכוחיאשר היה מהכאת קו ב"א בקו א"ג לפי שיקיפו בו קוי ד"א א"ג וד"א שוה לא"ב ושטח ז"ב הוא אשר היה מהכאת א"ב בג"ב לפי שיקיפו בו ה"ב ב"ג וה"ב שוה לא"ב ושטח א"ה הוא אשר היה מהכאת א"ב בעצמו
וכבר התבאר שאשר היה מהכאת א"ב בא"ג ובג"ב שוה לאשר היה מהכאת א"ב בעצמו
E: מופתו שנעשה על א"ב מרובע א"ה ונוציא ג"ז נכחי לב"ה ולפי ששטח א"ז שוה לשטח שיקיפו בו א"ג בא"ב כי ג"ז כמו א"ב וכן ששטח ג"ה שוה לשטח שיקיף בו א"ב בג"ב ושניהם שוים למרובע א"ה יהיה מרובע א"ה שהוא ההוה מקו א"ב שוה לשני שטחים ההוים מא"ב בא"ג וא"ב בב"ג
וכבר יתבאר זה בצד אחר כשנניח קו ח' שוה לא"ב ותהיה השטח הנצב הזוית שיקיף בו ח' בא"ב שהוא כמו מרובע א"ב משלפניה' שוה לשטח נצב הזוית שיקיף בו ח' בא"ג וח' בג"ב והם כמו שטחי א"ג בא"ב וג"ב בא"ב
Mu246: ג כשיוחלק קו א"ב בחלקי א"ג ג"ב נאמ' כי כפל א"ב בפני עצמו ככפלו בכל אחד מן א"ג ג"ב
והדבר בו ברור כשנעשה על קו א"ב מרובע ואחר כך נוציא בו קו ג"ז עמוד - ↑ E:3 השטח ההוה מקו מה עם אחד מחלקיו שוה לשטח נ"ה שיקיפו בו השני חלקי' ומרובע החלק הנזכר
P1011: כל קו יחלק בשני חלקים הנה אשר יהיה מהכאת כל הקו באחד החלקים כמו אשר יהיה מאחד מהחלקים בשני והכאת החלק אשר בו הוכה הקו בעצמו
Mu36: נס’ אלחג’אג’ כאשר נחלק מספר בשני חלקים איך שקרה הנה הכאת המספר כלו באחד מחלקיו שוה להכאת שני החלקים הא[חד] בחבירו עם הכאת החלק ההוא בעצמו
W66: משל זה במספר כשחולק קו עשרה לשני חלקים כמו ששה וארבעה הנה שטח ד' בי’ שהוא מ’ שוה לשטח ו' בד’ שהוא כ”ד עם מרובע ד’ שהוא י”ו
Mu91: המשל לתמונת ג' כאשר חולק קו עשרה לשני חלקים כמו ששה וארבעה הנה שטח ארבעה בעשרה שהוא מ’ שוה לשטח ששה בארבעה שהוא כ”ד עם מרובע ד’ שהוא י”ו
וזה מתבאר מתמונת א’ וזה כי בתמונת א’ התבאר שהכאת קו ראשון בקו שני כמו הכאת קו ראשון עם חלקי הקו השני
וכן בתמונה הזאת כי הכאת קו ארבע שהוא הראשון עם עשרה השני כהכאת הקו ד’ הראשון עם ששה וארבעה שהם חלק הקו השני
Numerical example: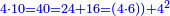
Mu130: יהיה הקו כלו עשרה ונחלק לשבעה וג’ הנה הכאת עשרה בג’ שהם ל’ כמו הכאת ז’ בג’ שהם כ”א עם הכאת ג’ בעצמו שהם ט’ שהמקובץ מכ”א וט’ יעלו ל’
Another example: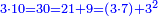
P1010: דמיון במספר המרובע המתהוה מהכאת עשרה בששה כמרובע ההווה מהכאת ששה בארבעה שהוא כ”ד וכמרובע ההווה מששה בעצמו שהוא החלק אשר זכרנו והיה ל”ו והכל ששים וכך מרובע עשרה בששה
Example: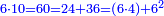
P1014: וכן הח’ על ו’ וב’ הח’ עם הב’ יעלו י”ו וכן הו’ בב’ ומרובע הב’ יעלו י”ו וכן בכל מן מספר
Example: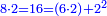
- ↑ C: המשל בזה שקו א"ב נחלק לשני חלקים על נקודת ג' ואומר שאשר יהיה מהכאת קו א"ב בא"ג שוה לאשר יהיה מהכאת א"ג בג"ב ומהכאת א"ג בעצמו
E: יהיה הקו א"ב ונחלק על נקודת ג' ואומ' ששטח א"ב באחד מחלקיו ויהיה ב"ג שוה למרובע ב"ג עם שטח א"ב בב"ג - ↑ C: מופת זה שנצייר על קו א"ג שטח מרובע עליו א"ז ונוציא קו ז"ד אל ה' ונוציא מב'
מביתקו נכוחי לקוי א"ד וג"ד והוא קו ב"ה ושטחי ז"ב וז"א נכוחי הצלעות ושטח ב"ד גם כן נכוחי הצלעות והוא שטח ז"ב ושטח ז"א יחד וז"ב הוא שהיה מהכאת א"ג בג"ב לפי שיקיפו בו ב"ג ג"ז וז"ג שוה לג"א וב"ד הוא שהיה מהכאתא"ג בג"בא"ב בא"ג לפי שיקיפו בו ב"א א"ד וג"א שוה לא"ד וא"ד הוא שהיה מהכאת א"ג בעצמו
והתבאר כבר שאשר היה מהכאת ב"א בא"ג שוה לאשר היה מהכאת א"ג בג"ב ומהכאת א"ג בעצמו
E: מופתו שנעשה על ב"ג מרובע והוא ב"ד ונוציא קו ד"ה על יושר ונשלים שטח א"ה ויהיה שטח א"ה שוה לשני שטחי א"ד ד"ב ושטח א"ה שוה לשטח שיקיפו בו א"ב ב"ג כי ב"ג שוה לב"ה ושטח א"ד שוה לשטח שיקיפו בו א"ג ג"ב כי ג"ד שוה לג"ב ושטח ג"ה שוה למרובע ג"ב הנה שטח א"ב ב"ג שוה לשני שטחי א"ג בג"ב ומרובע ג"ב
וכבר יתבאר זה בהניחנו קו ח' שוה לקו ג"ב ויהיה שטח ח' בא"ב שוה לשני שטחי ח' בא"ג וח' בג"ב וח' בג"ב הוא כמו מרובע ג"ב כי ח' שוה לג"ב וא"ג בח' כמו שטח א"ג בג"ב הנה שטח א"ב בב"ג שוה לשטחי א"ג בג"ב ומרובע ג"ב
Mu246: ד [כמו של מעלה] קו א"ב חולק בשני חלקי' על ג' נאמ' כי כפל א"ב בא"ג ככפל א"ג בג"ב וכפל א"ג [בפני] עצמו מקובצי' נוציא עמוד א"ד שוה לא"ג וכמו כן כיוצא ב"ה ג"ז והוא כפל א"ג בפני עצמו ושטח ג"ה הוא א"ג בג"ב וכל שטח א"ה הוא כפל א"ב בא"ג - ↑ P1011: כל קו יחלק בחלקים הנה אשר יהיה מהכאת הקו בעצמו כמו אשר יהיה מהכאת כל חלק בעצמו ומהכאת אחד החלקים באחר שני פעמים
E: 4 מרובע כל קו נחלק לשני חלקים שוה למרובעי שני חלקיו וכפל שטח אחד מהם באחר Mu36: נס’ אלחג’אג’ כאשר חולק איזה מספר שיהיה בשני חלקים איך מה שקרה הנה הכאת המספר ההוא בעצמו שוה להכאת כל אחד מהחלקים בעצמו ולהכאת כל אחד משני החלקים בחבירו
Mu130: יהיה הקו עשרה נחלק על שלשה וז’ נכה שלשה בשבעה עלו כ”א והכפל מ”ב ומרובע שבעה מ”ט נוסיפם עלו צ”א נוסיף מרובעכל הקוג’ שהוא ט’ עלו מאה וכן מרובע כל הקו מאה
Numerical example:![\scriptstyle{\color{blue}{\left[2\sdot\left(3\sdot7\right)\right]+72+32=\left(2\sdot21\right)+49+9=42+49+9=91+9=100=102}}](/mediawiki/images/math/1/1/3/113ef37869cb07a63959a68cc09af144.png)
P1010: דמיון במספר כאשר תכה עשרה על דרך משל בעצמו יהיה מאה אחר כן תחלק עשרה לשני חלקים על דרך משל לז’ וג’ ותרבע ז’ בעצמו יהיה מ”ט עוד ג’ בעצמו יהיה ט’ והכל נ”ח עוד תכה ג’ בז’ ב’ פעמים יהיה מ”ב הכל מאה
Numerical example:![\scriptstyle{\color{blue}{\left[2\sdot\left(3\sdot7\right)\right]+72+32=\left(2\sdot21\right)+49+9=42+58=100=102}}](/mediawiki/images/math/4/1/c/41c82e0003478bf24398273435235086.png)
P1014: העשרה כלו חולק על ו’ וד’ מרובע הכל ק’ שוה למרובע הו’ והד’ וכפל שטח ו' בד’ וכן בשיעורים
Numerical example:![\scriptstyle{\color{blue}{102=100=\left[2\sdot\left(6\sdot4\right)\right]+62+42}}](/mediawiki/images/math/2/e/6/2e682b264718f78a3fc3fde0b8b0dbbd.png)
- ↑ C: המשל בזה שקו א"ב נחלק לשני חלקים על נקודת ג' ואומר שאשר יהיה מהכאת א"ב בעצמו שוה לאשר יהיה מהכאת א"ג בעצמו וג"ב בעצמו וא"ג בג"ב פעמים
E: יהיה הקו הנחלק א"ג וחלקיו א"ב א"ג אומ' שמרובע א"ג כמו שני מרובעי א"ב ב"ג וכפל שטח א"ב [ב]ב"ג - ↑ E: מופתו שנעמיד על קו א"ג מרובע א"ה ונוציא בו קוטר א"ה ומן ב' עמוד ב"ד נכחי לג"ה יחתוך קוטר א"ה על ז' ונוציא מז' קו נכחי לקו א"ג והוא ח'ז'ט' ויתבאר ששטחי א"ז ז"ה שעל הקוטר מרובעים לפי שזוית ג' נצבת וזויות ג'א'ה' ג'ה'א' שוות כי קוי ג"א ג"ה שוות הנה כל אחת מהן חצי נצבת הנה קוי א"ב ב"ז שוים ולכן א"ז מרובע וכן קוי ז"ט ט"ה שוים ולכן ז"ה מרובע וקו ז"ט שוה לקו ב"ג הנה שטח ז"ה כמו מרובע ב"ג ולפי שמרובע א"ה ההוה מן א"ג שוה לשני מרובעי א"ז ז"ה ושני מתמימים כ"ט ח"ד ושני אלה המרובעים הם כמו מרובעי א"ב ב"ג ומתמים כ"ט כמו השטח שיקיף בו ב"ג בב"ז השוה לא"ב והוא שוה למתמים ח"ז יהיה מרובע א"ג שוה לשני המרובעים ההווים מן א"ב ב"ג וכפל שטח א"ב בב"ג
ולו מופת קרוב והוא שנניח קו דה"ז שוה לא'ב'ג' ד"ה שוה לא'ב'ג' וה"ז לב"ג והנה יהיה שטח א"ב בכל ד"ז שוה לשטח א"ג בד"ה וא"ג בה"ז ואבל שטח א"ג בד"ה כמו שטח א"ב בד"ה שהוא כמו מרובע א"ב וב"ג בד"ה וכן שטח א"ג בה"ז שוה לשטח ב"ג בה"ז שהוא כמו מרובע ב"ג ושטח א"ב בה"ג הנה שטח א"ג בד"ז השוה לא"ג כמו מרובע א"ב ומרובע ב"ג וכפל שטח א"ב בב"ג ומשל - ↑ E: והתבאר בזה שהשטחים שעל קוטר המרובע הם מרובעים ואם הם מרובעי' הקוטר קוטר למרובעי' ושמרובע כל קו ד' דמיוני מרובע חציו וט' דמיוני מרובע שלישיתו
- ↑ P1011: כל קו יחלק בחציים ואחר יחלק בחלקים מתחלפים הנה אשר יהיה מהכאת החלק היותר ארוך בחלק היותר קטן ומהכאת יתרון חצי הקו על החלק היותר קצר בעצמו הוא כמו אשר יהיה מהכאת חצי הקו בעצמו
For any line divided in half and then divided into two unequal parts, the [sum] of the product of the larger part by the smaller part and the product of the excess of half the line over the smaller part by itself is equal to the product of half the line by itself
E:
5 הקו הנחלק לחצאיים ולחלקי' בלתי שוים בשטח שיקיפו בו החלקים הבלתי שוים עם מרובע הקו שבן שני המקומות שוים למרובע חצי הקו
Mu36:ובנס’ אלחג’אג’ כאשר חולק אי זה מספר שיהיה בשני חלקים שוים ובשני חלקים בלתי שוים הנה הכאת החלקים הבלתי שוים כל אחד בחבירו עם הכאת המספר אשר מה שבין בעצמו שוים להכאת חצי המספר בעצמו
In the version of al-Ḥajjāj: when a number is divided into two equal parts and into two unequal parts, [the sum of] the product of the unequal parts one by the other together with the product of the number that is the difference by itself [is] equal to the product of half the number by itself
Mu130:
יהיה הקו עשרה ונחלק בשווי על חמשה ובבלתי שיווי על שלש נכה שלשה בשבעה עלה כ”א נוסיף מרובע שבין שלשה וחמשה והוא ארבע כי המרחק שנים עלו כ”ה וכן מרובע חצי הקו שהוא חמשה עולה כ”ה
P1010:דמיון במספר כשנחלק עשרה על ה’ ה’ חלקים שוים עוד נחלק עשרה לג’ וז’ על [דרך] משל הנה המרובע המתהוה מחלק השוה באחר שהוא [...] כ”ה [...] המרובע המתהוה מג’ על ז’ שהוא כ”א עם המרובע המתהוה מתוספת ז’ על ה’ שהוא ב’ ומרובעו ד’ והכל כ”ה
Numerical example:
P1014:![\scriptstyle{\color{blue}{\left(3\sdot7\right)+\left[\left(\frac{1}{2}\sdot10\right)-3\right]^2=21+\left(5-3\right)^2=21+2^2=21+4=25=5^2=\left(\frac{1}{2}\sdot10\right)^2}}](/mediawiki/images/math/1/5/3/153fd747e25cb09c6de8b6414c49e8d6.png) העשרה אם תחלקהו על ה’ ועל ו’ וד’ הנה שטח ו’ בד’ עם מרובע אחד שבין ה' לו’ שוה למרובע ה’ה’ שהם כ”ה וכן בשיעורים
העשרה אם תחלקהו על ה’ ועל ו’ וד’ הנה שטח ו’ בד’ עם מרובע אחד שבין ה' לו’ שוה למרובע ה’ה’ שהם כ”ה וכן בשיעורים
Numerical example:
![\scriptstyle{\color{blue}{\left(6\sdot4\right)+\left[6-\left(\frac{1}{2}\sdot10\right)\right]^2=24+\left(6-5\right)^2=24+1^2=24+1=25=5^2=\left(\frac{1}{2}\sdot10\right)^2}}](/mediawiki/images/math/1/5/3/153a80898ac8207e134965131113b24f.png)
- ↑ C: המשל בזה שקו א"ב נחלק לחלקים שוים על נקדת ג' ולחלקים מתחלפים על נקודת ד' ואומר שאשר היה מהכאת א"ד בד"ב ומהכאת ג"ד בעצמו יחד שוה לאשר יהיה מהכאת ג"ב בעצמו
E: ויהיה קו ישר א"ב ויחלק לחלקי' שוים על ג' ולבלתי שוים על ד' הנה אומר ששטח א"ד בד"ב עם מרובע ג"ד שוה למרובע ג"ב - ↑ C: מופת זה שנצייר על קו ג"ב שטח מרובע עליו ג"ה[ז"ב] ונדביק ב' בה' ונוציא מד' קו אל ט' נכוחי לקוי ג"ה וב"ז עליו ד'ח'ט' ונוציא מח' קו נכוחי לקוי א"ב וה"ז עליו לח"ב ונוציא מא' קו נכוחי לקוי ג"ל וד"ח וב"כ והוא א"מ ונמשוך קו כ"ל אל מ' ושטח ג"ח המשלים שוה לשטח ח"ז המשלים ויהיה שטח ד"כ משותף ויהיה יחד שטח ג"כ שוה לשטח ד"ז יחד ואמנם ג"כ שוה לג"מ לפי שהם על שתי תושבות שוות ב"ג וג"א ובין שני קוים נכוחים ב"א וכ"מ
ואם כן שטח ג"מ שוה לשטח ד"ז ויהיה ד"ל משותף ויהיה יחד מ"ד שוה לנס"ע המסומן ומ"ד הוא שהיה מהכאת א"ד בד"ב לפי שיקיפו בו א"ד ד"ח וח"ד שוה לב"ד ויהיה נ'ס'ע' המסומן שוה לאשר יהיה מהכאת א"ד בד"ב ונשים אשר יהיה מהכאת ג"ד בעצמו משותף והוא שטח ל"ט המרובע
ויתבאר שאשר היה מהכאת א"ד בד"ב ומהכאת ג"ד בעצמו יחד שוה לשטח ג"ז שהיה מהכאת ג"ב בעצמו שהוא חצי הקו [ר”ל מהתבארות צורת ד’ מזה השער]
E: מופתו שנעשה על ג"ב מרובע ג"ז ונוציא ד"ע עמוד על א"ב וקוטר ה"ב ויתחתכו על ח' ונוציא קו ט'ח'ב' נכחי לא"ב ונשלים התמונה הנה מרובע ג"ז ההוה מקו ג"ב שוה לשני מתמימי ג"ח ח"ז עם מרובעי ב"ח ח"ד ולפי שמתמים ג"ח עם [מרובע] ד"כ העושה שטח ג"כ ישוה לשטח ג"ט יהיה שטח ג"ט עם מתמימי ח"ז שהוא כמו שטח א"ח עם מרובע ח"ה [שוה לשטח ג"כ [עם] מרובע ח"ה ומת[מים] ח"ז אבל שטח ג[כ] עם מרובע ח"ה] ומתמים ח"ז כמו המרובע ההווה מן ג"ב ושטח א"ח הוא ההווה מהכאת א"ד בד"ב [כי] ד"ח ד"ב שוים ומרובע ח"ה הוא כמו המרובע ההווה מן ג"ד הנה שטח [א"ד] בד"ב עם מרובע ג"ד כמו המרובע ההווה מן ג"ב
ויתבאר גם כן שלפי שג"ב נחלק בנקודת ד' איך שיזדמן היה מרובע ג"ב כמו המרובע ההווה מן ג"ד עם [כפל] שטח ג"ד בד"ב ומרובע ד"ב [כפל] ושטח ג"ד בד"ב עם מרובע ד"ב כמו שטח ג"ד בב"ד והוא כמו שטח א"ג בד"ב [הנה] שטח א"ג בד"ב עם שטח ג"ד בד"ב שזה כמו א"ד בד"ב כשקובץ עם מרובע ג"ד היה כמו מרובע ג"ב
Mu246: ו קו א”ב חולק בחציו על ג’ ובשני חלקים שאינם שוים על ד’ נאמ’ כי כפל א”ד בד”ב וכפל ג”ד בפני עצמו מקובצים ישוו לג”ב בפני עצמו
נעשה על ג”ב מרובע ג”ז ונחוק בו מרובע ב”ח ושני שטחי ג”ח ח”ז וגם נעשה שטח א”ל על יושר קו מל”כ וקו א”מ כמו ד”ב ומפני שא”ג שוה לב”ז הילכך שטח א”ל כמו ד”ז וכפל א”ד בד”ב הוא שטח א”ח ונשים שטח ג”ח שותף ויהא נס”ע שוה לשטח א”ח שהוא כפל א”ד בד”ב ומרובע ה”ח הוא כפל ג”ד בעצמו - ↑ C adds: והתבאר לך הנה ששני מרובעי החלקים המתחלפים יעדפו על כפל שטח נצב הזויות שיקיפו בו החלקים ארבעה דמיוני מרובע הקו שבין מקומות החלקים
תקון המעתיק ועוד יתבאר לך הנה כי כשיחלק קו בשני מקומות לחלקים שאינם שוים שהשטח שיקיפו בו שני קוי החלוקה האחד בלתי שוה לשטח שיקיפו בו שני קוי החלוק האחר
כי כל אשר ירחק מקום החלוק מחצי הקו יחסר השטח שיקיפו בו שני קוי החלוק
ומתוך הצורה אשר לפני זו התבאר כי כשיעור אשר יחסר כפל שטח שיקיפו בו קוי החלוק האחד מן האחר יוסיפו שני מרובעי הקוים ההם על שני מרובעי הקוים האחרים ולפי ביאור זה נעשו מופתים רבים בשער העשירי - ↑ P1011: כל קו יחלק בחציים עוד נוסף עליו קו אחר בארכו הנה אשר יהיה מהכאת כל זה בקו הנוסף ומהכאת חצי הקו הראשון בעצמו הוא כמו אשר יהיה מחצי הקו הראשון כאשר יחובר הקו הנוסף ואחר הוכה כלו בעצמו יחד
Mu36: נ’ אלחג’אג’ כאשר נחלק אי זה מספר שהונח בחציים והוספנו עליו מספר מו[נח] הנה הכאת המספר המקובץ במספר הנוסף עם מרובע חצי המ[ספר] שוים למרו[בע] חצי המספ[ר] והתוספת כשחוברו והושמו מ[ספר] אחד
Mu130: [...] יהיה הקו עשרה ונוסיף עליו ארבע נכה ארבע
P1010: דמיון במספר כשנחלק עשרה לחציין והוא ה’ ותוסיף על עשרה שנים על דרך משל הנה מרובע המתהוה מהמספר כולו שהוא י”ב כאשר תכה אותו בשנים שהוא התוספת ויהיו עשרים וארבע [..] המרובע המתהוה מ[חצי] [מספר] הראשון שהוא ה’ ומרובעו כ”ה והכל מ”ט כמרובע המתהוה מחצי המספר עם התוספת שהוא ז’ ומרובעו מ”ט
Numerical example:![\scriptstyle{\color{blue}{\left[\left(10+2\right)\sdot2\right]+\left(\frac{1}{2}\sdot10\right)^2=\left(12\sdot2\right)+5^2=24+25=49=7^2=\left(5+2\right)^2=\left[\left(\frac{1}{2}\sdot10\right)+2\right]^2}}](/mediawiki/images/math/d/3/1/d31d0d74b15499bed8abd54a866f974f.png)
P1014: וכן במספר אם תחלק הי”ב ות[ו]סיף עליו ב’ הנה השטח י”ד עם ב’ ומרובע ו' שהו’ חצי י”ב והכל ס”ד שוה למרובע הח’ שהו’ תוספת הקו עם חציו כמש[.] התמונה וכן בשיעורים
Numerical example:![\scriptstyle{\color{blue}{\left[\left(12+2\right)\sdot2\right]+\left(\frac{1}{2}\sdot12\right)^2=\left(14\sdot2\right)+6^2=64=8^2=\left(6+2\right)^2=\left[\left(\frac{1}{2}\sdot12\right)+2\right]^2}}](/mediawiki/images/math/d/b/f/dbff83c5299277fd73a904ad1f1f3a68.png)
- ↑ P1011: כל קו יחלק בחלקים הנה אשר יהיה מהכאת הקו בעצמו והכאת אחד משני החלקים בעצמם יחד הוא כמו אשר יהיה מהכאת הקו כלו בחלק אשר תכה בעצמו שני פעמים ומהכאת החלק האחד בעצמו
Mu36: נס’ אל חג’אג’ כאשר נחלק אי זה מספר שיהיה בשני חלקים איך מה שקרה ה[נה] המרובעי’ ההווים מהמספר כלו ומאחד מהחלקים כאש[ר] קובצו שוים לכפל הכאת המספר כלו בחלק אשר זכרנו [עם] הכאת החלק הנשאר בעצמו
Mu130: ויהיה הקו עשרה ויחלק על ששה נכה ששה בעשרה עלה ס’ וכפלו ק”כ ועם מרובע ארבע שהוא י”ו עלה [...] קל”ו וכן מרובע כל הקו שהוא עשרה עם מרובע החלק הנזכר שהוא ששה עלו [...]
P1010: דמיון במספר כשנחלק מספר עשרה לד’ ו’ יהיה המרובע המתהוה מכל המספר מאה והמרובע המתהוה מו’ על דרך משל ל”ו והכל קל”ו ויהיה שוה למרובע המתהוה מהכאת עשרה בששה שני פעמים שהם ק”כ והמרובע המתהוה מן החלק הנשאר שהוא ד’ ומרובעו י”ו ועם ק”כ יהיו קל”ו
Numerical example:![\scriptstyle{\color{blue}{10^2+6^2=100+36=136=120+16=\left(2\sdot60\right)+16=
\left[2\sdot\left(10\sdot6\right)\right]+4^2}}](/mediawiki/images/math/3/a/b/3ab19fd72438ca4bb72c921369fc9aaa.png)
P1014: וכן עשרה אם חולק על ח’ וב’ מרובע הי’ שהו’ ק’ ומרובע הב’ שהו’ ד’ והכל ק”ד שוה לכפל י’ עם ב’ שהו’ מ’ ומרובע ח’ בין הכל ג”כ ק”ד וכן בשיעורים
Numerical example:![\scriptstyle{\color{blue}{10^2+2^2=100+4=104=40+64=
\left[2\sdot\left(10\sdot2\right)\right]+8^2}}](/mediawiki/images/math/5/0/c/50ca39d8b1c1632a6ce0b882cb22620d.png)
- ↑ דמיוני: AB פי’ כפולי
- ↑ P1011: כל קו יחלק בחלקים עוד נוסף באורך הקו כמו אחד מהחלקים הנה אשר יהיה מהכאת כל זה בעצמו כמו אשר יהיה מהכאת הקו הראשון בחלק הנוסף ארבע פעמים והכאת החלק האחד בעצמו
Mu36: נס’ אל חג’אג’ כאשר חולק אי זה מספר שיהיה בשני חלקים איך שקרה הנה ארבעה דמיוני כפל המספר כלו באחד משני חלקיו עם הכאת החלק הנשאר בעצמו שוי[ם] למרובע המספר הנקבץ מהמספר המונח והחלק אשר זכרנו
Mu130: [יהיה הקו עשרה ונחלקהו על ג’ ונכה ד’] פעמים ג’ בעשרה עלה ק”ך [נרבע] שבעה ויעלה מ”ט נוסיפהו על ק”ך עלה קס”ט וכן [מרובע] כל הקו המונח שהוא עשרה א”כ נוסיף עליו שלושה שחולק עליו יהיה כל הקו י”ג ומרובעו קס”ט
Numerical example:![\scriptstyle{\color{blue}{\left[4\sdot\left(10\sdot3\right)\right]+7^2=120+49= 169=13^2=\left(10+3\right)^2}}](/mediawiki/images/math/1/1/9/119c63c57a6f45b75bf018ff924f1131.png)
P1010: דמיון במספר כש[נחלק] עשרה על דרך משל לב’ וח’ ונוסיף [על] עשרה שנים שה[ם] כמו החלק ה[...] ויהיה הכל י”ב ומרובעו קמ”[ד] ויהיה שוה להכאת המספר הראש[ון] שהוא עשרה ב[שנים] שהוא החלק הנ[שאר] ד’ פעמים שה[ם] שמנים ומרוב[ע] החלק עשרה הנשאר שמנה ומרובעו ס”ד והכל קמ”ד
Numerical example:![\scriptstyle{\color{blue}{\left[4\sdot\left(10\sdot2\right)\right]+8^2=80+64=144 =12^2=\left(10+2\right)^2}}](/mediawiki/images/math/3/5/7/3572c6c2fff1368f77750977b208cbff.png)
P1014: אם הי’ יחולק לו’ וד’ הנה ד’ פעמי’ הי’ עם הד’ שהם ק”ס עם מרובע הו’ ס”ד ובין הכל קצ”ו שוה למרובע י”ד שהו’ ג”כ קצ”ו וכן בשיעורים
Numerical example:![\scriptstyle{\color{blue}{\left[4\sdot\left(10\sdot4\right)\right]+6^2=160+36=196 =14^2=\left(10+4\right)^2}}](/mediawiki/images/math/b/c/6/bc69367f2c839dd02ac2d7e8e1216d85.png)
- ↑ P1011: כל קו יחלק בחציים עוד יתחלק גם כן לחלקים מתחלפים הנה אשר יהיה מהכאת שני החלקים המתחלפים כל אחד מהם בעצמו הוא כפל מה שיהיה מהכאת חצי הקו בעצמו וכפל מה שיהיה מהכאת חצי הקו על החלק היותר קצר בעצמו יחד
Mu36: נס’ אל חג’אג’ כאשר חולק אי זה מספר שיהיה בשני חלקים שוים ושני חלקים בלתי שוים הנה הכאת כל אחד מהשני חלקים הבלתי שוים בעצמו מקובצים הנה הם שוים להכאת חצי המספר בעצמו עם הכאת המספר אשר מה שבין בעצמו
Mu130: [...]
P1010: דמיון במספר כשנחלק עשרה לה’ ה’ שהם שנים ונחלקהו לז’ וג’ שהם חלקים בלתי שוים הנה המרובע המתהוה מהכאת ז’ בעצמו שהוא מ”ט ומהכאת ג’ בעצמו שהוא ט’ והכל נ”ח כמרובע המתהוה מחצי הקו שהוא ה’ ורבועו כ”ה וכפלו נ’ ועוד כפל מרובע מותר החלק הגדול הבלתי שוה על החלק השוה שהיה המותר ב’ ורבועו ד’ וכפלו ח’ והכל נ”ח
Numerical example: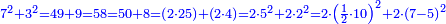
P1014: וכן הי”ד אם חולק לז’ ז’ וחולק לח’ וו’ מרובעי ח’ ס”ד ומרובע ו’ ל”ו בין הכל הו’ ק’ שוה לכפל מרובע ז’ שהם צ”ח וכפל מרובע א’ ובין הכל ק’ וכן בשיעורים
Numerical example: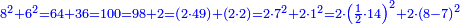
- ↑ P1011: כל קו יחלק בחציים עוד נוסף באורך הקו קו אחר הנה אשר יהיה מהכאת זה כלו בעצמו והקו הנוסף בעצמו מקבצים הוא כפל מה שיהיה מחצי הקו הראשון כאשר תחבר אליו הקו הנוסף ותכה בעצמו והכאת חצי הקו הראשון בעצמו
Mu36: נ’ אל חג’אג’ כאשר נחלק אי זה מספר מונח שיהיה בשני חלקים שוים והוספנו עליו אי זה מספר מונח שהיה הנה המרובע ההווה מהמספרהמונחהמקובץ מהמספר המונח והמספר המוסף עם הכאת המספר המוסף בעצמו הנה הם כפל המרובע ההווה מחצי המספר המונח עם הכאת המספר המקובץ מחצי המספר המונח והתוספת בעצמו
Mu130: [...]
P1010: דמיון במספר כשנחלק מספר עשרה על דרך משל לה’ ה’ והוסף עליו מספר [ב'] והוא י”ב יהיה הכאת י”[ב] שה[וא] המספר עם התוספת בעצמו והוא קמ”ד ורבוע התוספת שהוא ב’ ורבועו ד’ והכל קמ”ח שוה לכפל מרובע ההוה מחצי המספר הבלתי נוסף שהיה חציו ה’ ורבועו כ”ה וכפלו נ’ עם כפל מרובע ה’ מורכב עם ב’ שהוא הנוסף והכל ז’ ורובעו מ”ט וכפלו צ”ח והכל קמ”ח
Numerical example:![\scriptstyle{\color{blue}{\left(10+2\right)^2+2^2=12^2+2^2=144+4=148=50+98=
\left(2\sdot25\right)+\left(2\sdot49\right)=\left(2\sdot5^2\right)+\left(2\sdot7^2\right)=\left(2\sdot5^2\right)+\left[2\sdot\left(5+2\right)^2\right]=\left[2\sdot\left(\frac{1}{2}\sdot10\right)^2\right]+\left[2\sdot\left[\left(\frac{1}{2}\sdot10\right)+2\right]^2\right]}}](/mediawiki/images/math/b/a/9/ba91ead41879ce09af12af17781c287b.png)
P1014: הי’ אילו חולק לה’ ה’ והוסף עליו ד’ שהו’ י”ד הנה מרובע הכל שהו’ קצ”ו עם י”ו שהו’ מרובע ד’ בין הכל רי”ב שוה לכפל מרובע הה’ שהו’ נ’ ולכפל מורכב מה’ וד’ שהו’ ט’ וכפל מרו’ ט’ יהיה קס”ב ובין הכל רי”ב וכן בשיעורים
Numerical example:![\scriptstyle{\color{blue}{\left(10+4\right)^2+4^2=14^2+4^2=196+16=212=50+162=
\left(2\sdot25\right)+\left(2\sdot81\right)=\left(2\sdot5^2\right)+\left(2\sdot9^2\right)=\left(2\sdot5^2\right)+\left[2\sdot\left(5+4\right)^2\right]=\left[2\sdot\left(\frac{1}{2}\sdot10\right)^2\right]+\left[2\sdot\left[\left(\frac{1}{2}\sdot10\right)+4\right]^2\right]}}](/mediawiki/images/math/f/8/9/f891e0ea124a956a8e6d7ca572734a4f.png)
Apparatus
- ↑ E: ’מאמר ב; Mu246: מאמר שני
- ↑ מספר אקלידס החכם| Mu246; P1011; P1013; P1014: om.; Mu130: מספר היסודות; Ma1: מספר היסודות לאקלידס; C, AB; P1012: מספר אקלידס; O16: מספר אוקלידיס; W66: מספר אלקידוס; F137: מספר אוקלידס בשרשים
- ↑ הנה שני: C, Ma1 om.; F137(marg.), P1012, P1014 הנה כל שני; P1007 הנה ב'
- ↑ הקוים: A1, AB, P1010, P1012, P1014 קוים
- ↑ באחת: A2 באחד; Ma1 אחת
- ↑ מזויותיו: B(except for W66) מזויות; W66 מזויותיה; P1012, P1014 מהזויות
- ↑ הנצבות: O16 נצבות; W66 om.
- ↑ יקרא: C, F יאמר
- ↑ לשניהם: B, C, F להם; P1007 לשניהן
- ↑ המקיפים: P1012 לשון המקיפים
- ↑ בו: O16 om.
- ↑ וכל: F כל; O16 ובכל
- ↑ שטח: F תמונה
- ↑ נכחי: F נכחית
- ↑ הנה: C, F, O16 om.
- ↑ אחד: Ma1 אחד [נ"ל כשאחד]
- ↑ משני: C, F om.; P1007 מב'
- ↑ משני השטחים: B(except for Mu130) מהשני שטחים; F137
הצלעותמהשטחים - ↑ הנכחי: B(except for Mu130), F נכחיי; C נכוחי
- ↑ הם: C, F om.
- ↑ קוטרו: C אלכסונו
- ↑ משניהם היה: B שיהיה משניהם; C, F מהם שיהיה; P1007 משניהן היה
- ↑ שני השטחים: A2 השני שטחים; W66 השטחים; P1007 ב' השטחי'
- ↑ המתמימים: B, C, F המשלימים
- ↑ הרושם: C המסומן
- ↑ א: F137, Lo, O16, P1012 mark is missing; Mu130 למוד א'
- ↑ כאשר היו: C כשיהיו; F כאשר יהיו
- ↑ קוים ישרים: F137 הקוין הישרים; P1013 הקוים הישרים; B(except for W66), C קוים ישרים מונחים
- ↑ וחולק: B, C ונחלק
- ↑ מהם: Lo, PP משניהם; P1013 מהן
- ↑ אחד מהם לחלקים: O16
אותםלחלקים אחד מהם; C אחד מהם חלקים - ↑ איזה מספר שיהיה: B, F כמה שיהיו/שהיו; C כמות שהן
- ↑ הנה: C יהיה
- ↑ הנצב: B, C, F, P1014 נצב
- ↑ הזויות: P1010 הזוית
- ↑ אשר יקיפו: C שיקיפו
- ↑ בו: A1 בה; O16, P1012 om.
- ↑ השני קוים: B, C, F שני הקוים; P1007 ב' הקוים
- ↑ הישרים: C; O16 הישרים המונחים
- ↑ שוה: F יהיה שוה
- ↑ לכל השטחים: F לשטחים; W66 לכלל השטחים; O16 כלו לשטחים
- ↑ הנצבי: B, C, F נצבי; P1012 הנצבים
- ↑ אשר יקיף: C שיקיפו; O16 אשר יקיפו
- ↑ בכל אחד מהם: F בהם
- ↑ הקו: A2 הקו הישר
- ↑ אשר לא: C שלא
- ↑ יחלק: F יתחלק; C, AB, P1012, P1014 נחלק
- ↑ וכל: A2, P1012, P1014 עם כל; P1013 לכל
- ↑ וכל אחד: C ואחד
- ↑ מן החלקים: B, P1007 מהחלקים
- ↑ ויהיו: F המשל יהיו; B הנה יהיה/יהיו
- ↑ שני: P1007 ב'
- ↑ קוים ישרים: A2, F הקוים הישרים; B(except for W66) קוים ישרים מונחים
- ↑ על שניהם: B, F עליהם
- ↑ לחלקים: F137 חלקים
- ↑ כמה שיהיו: B(except for W66) om.; A2 כמה שהוא
- ↑ שתי: F om.; P1012, P1014 שני; P1007, P1013 ב'
- ↑ נקודות: Ma1 נקודת
- ↑ הנה אומר כי השטח: B הנה נאמר שהשטח; F אומר כי השטח; P1007 הנה אומר כי שטח
- ↑ הנצב: B, F, P1007 נצב
- ↑ הזויות: A2, B(except for W66), P1012 הזוית
- ↑ בו: A1 בה
- ↑ שני: F om.; P1007 ב'
- ↑ קוי: P1013 קוים
- ↑ שוה: Mu130 שוים
- ↑ הנצב: B, F נצב
- ↑ הזויות: Mu130 הזוית
- ↑ שני: P1007 ב'
- ↑ שני קוי: F om.| א' ב"ג ... שני קוי: P1012 om.
- ↑ א' ב"ד: P1013 אב"ג אב"ד
- ↑ והשטח הנצב: B, F ולשטח נצב
- ↑ בו שני: F om.; P1007 בו ב'
- ↑ שני קוי: Mu130, P1014 om.
- ↑ ד"ה: Lo, PP ה"ד
- ↑ והשטח הנצב: B, F ולשטח נצב
- ↑ הזויות: B(except for O16) הזוית
- ↑ גם כן: B, F om.
- ↑ בו: A2, P1010, P1013, PP om.; B בו שני קוי; F בו קוי
- ↑ ונוציא: A2, B הנה נוציא; F המופת נוציא
- ↑ מן קו: A1, B, F, P1007 מקו
- ↑ הישר: A1, F om.
- ↑ ישר: P1014 om.
- ↑ זוית נצבת: B זוית נצבה; A1, F, Lo, P1010, PP זויות נצבות; P1012 זוית קו נצבת
- ↑ מי"א מא': Ma1, E, O16, P1007, P1012 om.; AB מי' מא'; F137, Lo, P1010, P1013, PP, W194 מי"א מראשון
- ↑ ונשים: B(except for Mu130) ויהיה
- ↑ ונשים קו ב"ז: A1, Ma1 om.
- ↑ שוה: P1010 om.
- ↑ הישר: A1, W66 om.
- ↑ מג' מא': C, Ma1, E, Mu36, O16, P1007, P1012 om.; F137, P1010, P1013, PP, W194 מב' מראשון; Mu130, P1014 מב' מא'
- ↑ נכחי: P1013 נכוחי ה[צלע]?
- ↑ קו ז"ח ... הישר: B קו נכחי לקו ב"ג הישר והוא קו ז"ח; AB קו ז”ח נכחי לקו ב”ג הישר והוא קו ז”ח| הישר: Lo om.
- ↑ מן: B, F מנקודות
- ↑ מן ד': P1007 מד'
- ↑ ד' ה' ג': A1 ד'ה'ג' הישר; F137 ד' ה' וג'
- ↑ קוי: O16 om.
- ↑ ה"כ: AB, P1012, P1014 כ"ה
- ↑ מל"א מא': Ma1, E, P1007, P1012 om.; F137, Lo, P1010, P1013, PP, W194 מל"א מראשון
- ↑ הנה כל: B(except for W66) וכל
- ↑ אחד: P1013 אחת
- ↑ ד"כ: AB
דהד"כ - ↑ ושטח: P1013 om.
- ↑ לשטחי: O16 לשטח
- ↑ שוה לשטחי ב"ט: W194 twice
- ↑ מפתיחת הראשון: according to F137, W194| AB, מפתיחת א'; O561 מהפתיחה מא'; P1010 מפ' מרא'; P1014 מפת' מא'; PP מפתיחת ראשון; W66 מפתיח' א'
- ↑ ואולם: F אבל
- ↑ הנה הוא: F om.
- ↑ הנצב: A1, B, F נצב
- ↑ הזויות: Mu130, P1007 הזוית
- ↑ שני: F om.; P1007 ב'
- ↑ מפני כי קו: B מפני שקו; F לפי שקו; AB מפני כי קו
י; P1012, P1014 מפני כי קוי; PP מפני כי - ↑ ואולם ... לקו א': P1007 twice, the second recurrence is erased| א': O16
ג'א' - ↑ ואולם שטח: F ושטח
- ↑ ב"ט: PP marg.
- ↑ הנה הוא: F om.; A2, P1007, P1010 הנה
- ↑ נצב: F137 הזויות נצב; P1014 הנצב
- ↑ הזויות: Mu130 הזוית
- ↑ אשר: F om.
- ↑ שני: F om.; P1007 ב'
- ↑ שני קוי: A2, Lo, P1010, P1012, PP om.; AB שני קוי
- ↑ מפני כי קו: B מפני שקו
- ↑ מפני כי קו ב"ז ... א': F om.
- ↑ ואולם שטח: F ושטח
- ↑ ד"כ: P1014 marg.
- ↑ הנה הוא: F om.
- ↑ שוה: P1010 שוה
- ↑ הנצב: B, A1, F, P1014 נצב
- ↑ הזויות: Mu130 הזוית
- ↑ שני קוי: A2, F, Lo, P1007, P1010, P1014, PP om.; AB שני קוי
- ↑ א' ד"ה: P1014 marg.
- ↑ מפני כי קו: B מפני שקו; F לפי שקו
- ↑ ואולם שטח: F ושטח
- ↑ הנה הוא: F, P1014 om.
- ↑ שוה: P1010 שוה
- ↑ הנצב: B, A1, F נצב
- ↑ הזויות: Mu130 הזוית
- ↑ בו: P1013 בהם
- ↑ א' ד"ה ... שני קוי: P1012 om.| שני קוי: Ma1, O16, P1014 om.; F137 קוי; P1007 ב' קוי
- ↑ מפני כי קו: B מפני שקו; F לפי שקו
- ↑ לקו ה"כ: A1 לה"כ; Mu130 לקו ה"ד; O16 לקו ה"ג
- ↑ מל"ד מא': A1, Ma1, E, O16, P1007, P1012, P1014 om.; F137, Lo, P1010, P1013, PP, W194 מל"ד מראשון
- ↑ הנה השטח: F והשטח
- ↑ הנצב: B, F, P1007 נצב
- ↑ הזויות: O16 הזוית
- ↑ יקיפו: P1012 om.; P1014 marg.
- ↑ שני: F137 om.; AB שני; P1007 ב'
- ↑ שני קוי: Ma1 om.
- ↑ א' ב"ג: O16 ב"ג א'
- ↑ הזויות: P1007 הזויות
- ↑ ה"ג: P1012 ג"ה|
לשטחים ... וא' ה"ג: F לשטח נצב הזויות אשר יקיפו בו קוי א' ב"ד והשטח נצב הזויות אשר יקיפו בו קוי א' ד"ה והשטח נצב הזויות אשר יקיפו בו קוי א' ה"ג
B לשטח נצב הזויות אשר יקיפו בו שני קוי א' ב"ד ולשטח נצב הזויות אשר יקיפו בו שני קוי א' ד"ה ולשטח נצב הזויות אשר יקיפו בו שני קוי א' ה"ג [הזויות: Mu130 הזוית]
AB לשטחים נצבי הזויות אשר יקיפו בהם שני קוי א' ב"דוא' ד"ה וא' ה"גולשטח נצב הזויות אשר יקיפו בו שני קוי א' ד"ה ולשטח נצב הזויות אשר יקיפו בו שני קוי א' ה"ג - ↑ הנה: F137 וא"כ
- ↑ הנה כאשר: AB הנה התבאר כי כאשר
- ↑ היו: F137 יהיו
- ↑ שני: P1007 ב'
- ↑ ונחלק: F137 וחולק
- ↑ Mu130: F137 א'
- ↑ משניהם: F137, B(except for W66), P1010 מהם
- ↑ לחלקים כמה שיהיו: A2 בחלקים כמה שהיו; Mu130 לאי זה חלק שיהיה; O16 לאי זה חלקים שיהיו; P1007 לחלקים כמה שיהי
הו - ↑ השטח: P1007 om.
- ↑ הנצב: F137, B(except for W66) נצב
- ↑ הזויות: Mu130 הזוית, P1007 הזויות
- ↑ בו: P1007 בהם, P1010 בו
- ↑ שני: P1007 ב'
- ↑ הקוים: F137 הקוין; P1007 קוים
- ↑ הישרים: B(except for W66) הישרים המונחים; AB הישרים המונחים, A1 om.
- ↑ שוה: F137 יהיה שוה; O16 שוים
- ↑ לכל השטחים: F137, B(except for W66) לשטחים
- ↑ הנצבים: F137, B(except for W66) נצבי; A1, A2 הנצבי
- ↑ יקיף: B(except for W66), A2, P1007, P1012 יקיפו
- ↑ בהם: B(except for W66) בהן
- ↑ נחלק: F137 יתחלק; Mu130 תחלק; O16 יחלק
- ↑ וכל: P1014 לכל
- ↑ וכל אחד: P1012 לאחד
- ↑ מן החלקים: B(except for W66), P1007 מהחלקים|
הנה כאשר ... מן החלקים: C, Ma1, E, W66 om. - ↑ וזה: F137 וזהו
- ↑ וזה מה שרצינו לבאר: E והוא המכוון; Mu130 ומש"ל; P1007 וזמש"ל; Ma1, P1014 וזה מש"ל; P1010 וזה מה שרצינו לבארו; O16 om.
- ↑ ב: O16, P1007, P1012 mark is missing; Mu130 למוד ב'
- ↑ כאשר נחלק: C כשיחלק; F כאשר יתחלק
- ↑ ישר: C, B ישר מונח; AB ישר מונח
- ↑ איך שקרה: C בחלקים כפי אשר קרה; B איך שהזדמן; F איך שיזדמן
- ↑ הנה: C, F יהיו; AB הנה
- ↑ השטחים: Mu130 שני השטחים; O16 השני שטחים
- ↑ נצבי: A1 הנצבי
- ↑ הזויות: C הזוייות
- ↑ אשר יקיף: C שיקיפו; P1007 אשר יקיפו
- ↑ מחלקיו: Mu130, O16 מהחלקים; W66 מן חלקיו
- ↑ המתהוה: A2, B, F ההוה
- ↑ המתהוה מן: C om.
- ↑ מן הקו: P1007, W66 מהקו; O561 מן
כלוהקו - ↑ כלו: Mu130 om.
- ↑ ויהיה: F137 יהיה; Ma1 המשל יהיה; B הנה יהיה
- ↑ קו: F, O16, P1014 הקו
- ↑ ישר: F, P1014 הישר; O16 הישר המונח; Mu130, W66 ישר מונח; AB ישר מונח
- ↑ עליו: A1, A2, P1012, P1014 om.; AB, P1010 עליו
- ↑ א"ב: Mu130, P1014 קו א"ב
- ↑ ויחלק: F ויתחלק; O16 נחלק; Mu130 ונחלק; W66 שנחלק
- ↑ איך שיקרה: B איך שהזדמן; F איך שיזדמן; P1013 איך שקרה; O561 איך שיקרה
- ↑ ג': W66 א'
- ↑ הנה: F om.
- ↑ אומר כי: B אומר ש
- ↑ השטח: P1007, P1014 שטח
- ↑ הנצב: B, F, P1013 נצב
- ↑ הזויות: Mu130 הזוית
- ↑ יקיפו: O16 יקיף
- ↑ שני: F, O16 om.; P1007 ב'
- ↑ א"ב: F, B(except for W66) ב"א
- ↑ ב"ג: F, B(except for W66), P1007 א"ג; Lo
ג"דב"ג - ↑ עם: P1007
שוה למרובע המתהווהעם; P1012 וגם - ↑ השטח: A2 שטח
- ↑ הנצב: B, F, A2 נצב
- ↑ הזויות: Ma1, B(except for W66) הזוית
- ↑ שני: P1007 ב'; P1012 שתי
- ↑ שני קוי: F om.; Mu130 שני קו; P1013 שני קוים
- ↑ א"ג: B(except for W66), F ב"ג; P1010 א"ג
- ↑ שוה: B(except for W66) שוים; W66 שוהים
- ↑ המתהוה: B, F ההוה; O561 המתהווה
- ↑ מן א"ב: B(except for W66), F, P1007 מא"ב; W66
מהקו כלומא"ב - ↑ והנה: Ma1 המופת; B הנה; F137 om.
- ↑ על קו: B מקו; AB
עלמקו - ↑ על קו א"ב: F מא"ב
- ↑ עליו: O561 marg.
- ↑ ממ"ו מא': C בצורת מ"ו; A1, F137, Lo, P1010, PP ממ"ו מראשון; AB מ"ו מראשון; Ma1, E, P1007, P1012, W66 om.
- ↑ לכל: Mu36, Mu130 לכל; Mu91
לקולכל; O561 כל - ↑ משני: P1007 מב'
- ↑ משני קוי: F, B(except for Mu130) מקוי
- ↑ מל"א מא': A1, F137, Lo, P1010, PP מל"א מראשון; Mu130 מל"א; AB, C, Ma1, E, P1007, P1012, W66 om.
- ↑ הנה כל אחד משני: P1014
הנה כל אחד משני קוי א"ד ב"ה והוא ג"זהנה כל אחד משני; P1007 הנה כל אחד מב' - ↑ משני שטחי: F, B משטחי
- ↑ לשני: A2 לשתי; P1007 לב'
- ↑ לשני שטחי: F137 לשטחי; Ma1 לשטח; W66 לשתי שטחים
- ↑ א"ז ג"ה: AB, P1010 א"ז ג"ה נכחיי הצלעות; PP, W66 א"ז ג"ה נכחיי הצלעות
- ↑ מא' מזה: A2 מהקודמת; AB מפתיחת א'; P1010 מא'; B, C, Ma1, E, P1007, P1012, P1014 om.
- ↑ שוה: O16 om.
- ↑ נצב: O16 הנצב
- ↑ הזויות: Mu130, P1010 הזוית
- ↑ יקיפו: B(except for Mu130) יקיף
- ↑ בו: O561 בו
- ↑ ב"א: A2, P1007 א"ב
- ↑ ב"א א"ג: F137
א"ב ג"בmarg. ב"א א"ג; E א"ג בא"ב; A1 ב"א וא"ג - ↑ כי הוא: F, B מפני ש
- ↑ יקיפו: F, B(except for Mu130) מקיף; Mu130 מקיפים
- ↑ שני: Ma1 om.; P1007 ב'
- ↑ א"ד: F, B ד"א
- ↑ כי הוא ... א"ד א"ג: Mu36 om.; O561 marg. בו א"ד א"ג וקו א"ד שוה לקו א"ב ושטח ג"ה שוה לשטח
א"ג: P1007 ב"ג; A1 וא"ג - ↑ א"ד: F, B ד"א
- ↑ שוה: P1012 om.
- ↑ הנצב: AB, B, P1013 נצב
- ↑ הנצב הזויות: F om.
- ↑ ב"א א"ג ... יקיפו בו: P1014 om.
בו: P1010 om. - ↑ שני: P1007 ב'
- ↑ שני קוי: Ma1, A1 om.
- ↑ ב"א א"ג ... א"ב ב"ג: F137 marg.
ב"ג: Ma1 ג"ב; ABב"גב"ג; P1007, P1014 א"ג; P1013 ה"ג - ↑ מפני שא"ב: A2 מפני כי א"ב; P1014 מפני שא"ד; O16 הנה מפני שא"ב
- ↑ לב"ה: P1014 לב"א
מפני ש... לב"ה: F137 added on top of the line - ↑ הוא: O16 om.
- ↑ ההוה: P1010, P1012, PP הווה
- ↑ מקו א"ב: F137 מא"ב
- ↑ הנה: F ואם כן
- ↑ השטח: F השטחים
- ↑ נצב: F נצבי; B(except for Mu130), AB, Lo הנצב
- ↑ הזויות: O561 הזויות
- ↑ בו: F בהם; P1007, P1010, W194 om.; O561 בו
- ↑ שני: F om.; P1007 ב'
- ↑ א"ב: B(except for Mu130) ב"א
- ↑ א"ג: A1 ב"ג
- ↑ הנצב: B, F, P1013 נצב
- ↑ הזויות: Ma1 הזויות; O561 הזוית
- ↑ בו: A2, P1007, P1010, PP om.
- ↑ שני קוי: F om.
- ↑ ב"ג: A1 א"ג
- ↑ שוה: F שניהם שוים
- ↑ למרובע: Lo עם המרבע
- ↑ המתהוה: B, Lo, P1007 ההוה
- ↑ המתהוה מן: F om.
- ↑ מן א"ב: B(except for Mu130), P1007 מא"ב; F אדה"ב; Mu130 מן הקו כלו
- ↑ הנה: F137 ואם כן
- ↑ נחלק: F137 יתחלק
- ↑ קו: O16 om.
- ↑ ישר: AB ישר מונח; O16 ישר מונח
- ↑ איך שקרה: F137 איך שיזדמן; O16 איך שהזדמן
- ↑ הנה: F137 יהיו
- ↑ השטחים: O16 שני השטחים
- ↑ הנצבי: F137, O16, P1012, P1014 נצבי
- ↑ בהם: P1007 בו
- ↑ אחד: P1007 א'
- ↑ מחלקיו: O16 מהחלקים
- ↑ המתהוה: F137, O16 ההוה; PP המהווה
- ↑ מן הקו: P1007 מהקו; P1013 מן קו
- ↑ הנה ... כלו: C, Ma1, E, B(except for O16) om.
- ↑ וזה מה שרצינו לבאר: E, Mu130 ומש"ל; P1007 וזמש"ל; F, P1012 וזהו מה שרצינו לבאר; Mu36, P1014 וזה מש"ל; P1010 וזה מה שרצינו בארו
- ↑ ג: P1007, P1012 mark is missing; Ma1 ד'; Mu130 למוד ג'; O561 marg. at the end of proposition 2 חסר מכאן תמונת ג’ והיא [...]
- ↑ כאשר נחלק: C כשיחלק; F כאשר יתחלק
- ↑ ישר: C, B ישר מונח; AB ישר מונח
- ↑ בשני: P1007 לב'
- ↑ בשני חלקים: F137 marg.; Ma1 om.
- ↑ איך שקרה: C כמו שקרה; F137 איך מה שיזדמן; Ma1 איך שהזדמן; B איך שיזדמן
- ↑ הנה: C, F יהיה
- ↑ השטח: C שטח
- ↑ הנצב: B, C, F נצב
- ↑ אשר יקיף: C שיקיפו; B אשר יקיפו
- ↑ בו: Mu130 om.
- ↑ הקו: PP קו
- ↑ משני: F137 marg.; P1007 מב'
- ↑ משני חלקיו: C, Ma1 מחלקיו; B(except for Mu130) מן החלקים
- ↑ הנצב: B, C, Ma1, W194 נצב; F137
נצב לשטחנצב - ↑ אשר יקיף ... הזויות: P1013 om.
- ↑ אשר יקיפו: C שיקיפו
- ↑ בו: C, P1010 בו
- ↑ השני: B(except for W66), C, F, Lo שני; W66 שתי; P1007, P1013 הב'
- ↑ חלקים: B, C, F, Lo החלקים
- ↑ והמרובע: C ומרובע
- ↑ המתהוה: B, F, Lo ההוה
- ↑ המתהוה מן: C om.
- ↑ מן החלק: B(except for Mu130), P1007 מהחלק
- ↑ אשר זכרנו: C שהזכרנו
- ↑ ויהיה: B הנה יהיה; F המשל יהיה
- ↑ קו: Ma1 הקו
- ↑ ישר: B ישר מונח; AB ישר מונח; Ma1 הישר
- ↑ עליו: A1 om.
- ↑ א"ב: A1 om.
- ↑ ויחלק: AB, B(except for W66) ונחלק; W66 ונחלק אותו; F ויתחלק
- ↑ איך שיקרה: F איך שיזדמן; B איך שהזדמן; P1007 איך שקרה
- ↑ על: P1010
עליועל - ↑ הנה: F om.
- ↑ כי השטח: B שהשטח; Ma1 ששטח; F137 כי שטח
- ↑ הנצב: B, F נצב
- ↑ יקיפו: Mu130 יקיף
- ↑ קוי: A2, B, P1014 שני קוי; AB שני קוי; A1, P1007 קו
- ↑ שוה: Ma1 שוים
- ↑ הנצב: B, F נצב
- ↑ הזויות: P1014 הזוית
- ↑ בו: Mu130, W194 om.
- ↑ שני: F om.; P1007 ב'
- ↑ א"ב ב"ג ... שני קוי: W66 marg.
- ↑ ג"ב: Mu36, P1007, P1014 ב"ג
- ↑ המתהוה: B, F ההוה
- ↑ מן ג"ב: F מב"ג; P1007 מג"ב; Mu36 מן
ג"בג"ב - ↑ ונעשה: F137 נעשה; Ma1 מופת זה נעשה; B(except for W66) הנה נעשה
- ↑ מן קו: F על; A1, B, Lo, P1010, PP מקו; P1007 הקו; Mu36 מן קו
- ↑ ג"ב: F ב"ג
- ↑ עליו: F om.
- ↑ בגד"ה: W66 ה"ג
- ↑ ממ"ו מא': AB מ"ו מראשון; A1, F137, Lo, P1010, PP ממ"ו מראשון; Mu130 ממ"ו; C, Ma1, E, Mu36, P1007, P1012 om.
- ↑ ונתמים: B(except for W66), F ונשלים; Lo, AB, P1010, PP ונתמם
- ↑ א"ג ד"ז: F אזד"ג; B(except for W66) ג"א ז"ד
- ↑ הנכחי: F נכחי
- ↑ הנכחי הצלעות: B(except for W66) הנכחי הצלעות נצב הזויות
- ↑ מל"א וממ"ב מא': F137, Lo, P1013, PP מל"א ומ"ב מראשון; P1010 מל"א מרא'; W66 מב"א ומ"ב מא'; W194 מל"א ומ"ה מראשון; AB, B(except for W66), C, Ma1, E, Mu36, P1007, P1012 om.
- ↑ הנה: O16 marg.
- ↑ אחד: AB
שטחאחד - ↑ משני: P1007 מב'; P1010
משטימשני - ↑ משני שטחי: F משטחי
- ↑ א"ה: A1, Mu130 ג"ה
- ↑ א"ה א"ד: Mu36, P1014 א"ד ג"ה
- ↑ נכחי: F נכחיי
- ↑ נכחי הצלעות: B(except for W66) נכחי הצלעות נצב הזויות
- ↑ ג"ה: F שטח ה"ג; B(except for W66), Mu36 שטח ג"ה
- ↑ מא' מזה: P1010 מא'; AB, B, C, Ma1, E, P1007, P1012, P1013 om.
- ↑ הנצב: AB, B נצב
- ↑ הנצב הזויות: F om.
- ↑ בו: P1013
שבו - ↑ שני: F om.; P1007 ב'
- ↑ ב"ג: Mu130 ג"ב
- ↑ מפני כי ב"ג: F לפי שב"ג; Mu130 מפני שב"ג
- ↑ הנצב: A1, B, F נצב
- ↑ שני: F om.
- ↑ א"ב ב"ג ... שני קוי: O16 marg.; P1007 om.
- ↑ ג"ב: F, Mu36 ב"ג
- ↑ מפני כי ב"ג: F לפי שב"ג; B(except for W66) מפני שג"ב; P1013 מפני ב"ג
- ↑ ושטח א"ד ... לג"ד: Mu130 moved below; P1014 marg.
- ↑ ה"ג: F ג"ה
- ↑ הוא: Mu36 om.
- ↑ המרובע: Mu36 מרובע; AB המרובע
- ↑ המתהוה: B(except for W66), Ma1 ההוה; F137
המההווה; Mu36 מתהוה - ↑ מן ג"ב: F, Mu36, P1007 מג"ב
ושטח ה"ג ... מן ג"ב: P1014 ושטח מרובע מתהוה מן ב"ג; marg. ושטח ה"ג הוא המרובע המתהוה מן ג"ב - ↑ הנה: F אם כן; Mu130 ושטח א"ד [...] לג"ד הנה
- ↑ הנצב: B(except for W66), F, Mu36 נצב
- ↑ שני: F om.
- ↑ הנצב: B(except for W66), F, P1013 נצב
- ↑ שני: P1007 ב'
- ↑ שני קוי: A1, F om.
- ↑ א"ג ג"ב: P1012 א"ב ב"ג; F א"ג ב"ג
- ↑ והמרובע: Ma1 ומרובע
- ↑ המתהוה: B(except for W66), A1, AB, F ההוה
- ↑ מן ג"ב: F מב"ג; P1007 מג"ב
- ↑ הנה: F137 א"כ
- ↑ חולק: F137 יתחלק; O16 נחלק
- ↑ ישר: Mu36, O16 ישר מונח; AB ישר מונח; Mu130 ישר
עלמונח - ↑ בשני: P1007 בב'
- ↑ בשני חלקים: F137 om.
- ↑ איך שיקרה: F137 איך מה שיזדמן; B(except for W66) איך שהזדמן; P1013 איך שקרה
- ↑ הנה: F137 יהיה
- ↑ הנצב: F137, B(except for W66) נצב
- ↑ יקיף: Mu36, O16 יקיפו
- ↑ משני: P1007 מב'
- ↑ משני חלקיו: F137 מחלקיו; O16 מחלקיו
- ↑ הנצב: F137, B(except for W66) נצב
- ↑ השני: F137, O16 שני; P1007 הב'
- ↑ חלקים: F137, O16 החלקים
- ↑ המתהוה: F137, O16 ההוה
- ↑ מן החלק: O16, P1007, P1012 מהחלק
- ↑ אשר זכרנו: F137 שזכרנו
הנה כאשר ... זכרנו: C, Ma1, E, W66 om. - ↑ וזה מה שרצינו לבאר: F137, E, Mu130 ומש"ל; Ma1, P1007 וזה מש"ל; Lo, P1010, PP, W194 וזה מה שרצינו באורו; C וזה מה שרצינו
- ↑ ד: P1007, P1012 mark is missing; Ma1 ג'; Mu130 למוד ד'
- ↑ כאשר חולק: B כאשר נחלק; C כשיחלק; F כאשר יתחלק
- ↑ ישר: B(except for Mu130), C, P1012; P1014 ישר מונח
- ↑ בשני: C לשני; P1007 בב'
- ↑ חלקים: Ma1 חצאים
- ↑ איך שיקרה: B איך שהזדמן; C כמו שקרה; F איך שיזדמן; O561 איך שיקרה; P1007 איך שקרה; PP איך מה שיקרה
- ↑ הנה: C, F יהיה
- ↑ המרובע: C מרובע
- ↑ המתהוה: B(except for Mu130), C ההוה
- ↑ המתהוה מן: C om.
- ↑ מן הקו: B(except for Mu130), P1007 מהקו; PP מן קו
- ↑ לשני: P1007 לב'
- ↑ המרובעים: C מרובעי
- ↑ המתהוים: B(except for Mu130), F ההוים; C om.
מן ... המתהוים: O561 marg. - ↑ מן השני: B(except for Mu130), F, Lo, P1012, P1013, P1014 משני; C שני; P1007 מהב'; W194 מן שני
- ↑ חלקים: C, F, Lo, O16, P1012, P1014 החלקים; W66 החלקים
- ↑ וכפל: C ולכפל; Mu36, O16, P1012, P1014 ומכפל; O561 ומכפל
- ↑ השטח: C שטח
- ↑ הנצב: B(except for Mu130), C, F נצב; P1014 om.
- ↑ השני: B(except for Mu130), C, F, PP שני; O561 השני; P1007 ב'
- ↑ חלקים: B(except for Mu130), C, F החלקים
- ↑ ויהיה: B(except for Mu130) הנה יהיה; F137 יהיה; Ma1 המשל יהיה
- ↑ קו ישר: F, Lo הקו הישר; O16 קו
- ↑ עליו: B(except for Mu130) מונח עליו
- ↑ ויחולק: F ויתחלק; O16 נחלק; W66 ונחלק
- ↑ איך שיקרה: B(except for Mu130) איך שהזדמן; F איך שיזדמן; P1007 איך שקרה
- ↑ הנה: F om.
- ↑ המרובע: Mu36 המרובע
- ↑ המתהוה: B(except for Mu130), F ההוה
- ↑ מן א"ב: B(except for Mu130), F, P1007 מא"ב
- ↑ לשני: P1007 לב'
- ↑ המתהוים: A1, B(except for Mu130), F ההוים
- ↑ מן א"ג: B(except for Mu130), F, P1007 מא"ג
- ↑ ג"ב: F ב"ג
- ↑ וכפל: P1014 ומכפל
- ↑ השטח: W66 שטח
- ↑ הנצב: B(except for Mu130), F נצב
- ↑ הזויות: Ma1 הזוית
- ↑ שני: F om.; P1007 ב'
- ↑ ג"ב: F ב"ג
- ↑ ה: P1007, P1012 mark is missing; Mu130 למוד ה'
- ↑ כאשר: F om.
- ↑ כאשר נחלק: C כשיחלק
- ↑ נחלק ... ישר: F כל קו ישר יתחלק
- ↑ בשני חלקים: C לשני חלקים; O16 בחלקים; F לשני חצאים
- ↑ שוים: F137 שוים; Ma1 om.
- ↑ ושני: C ולשני; F ובשני; P1007 ולב'
- ↑ ושני חלקים: O16 וחלקים
- ↑ בלתי שוים: C שאינם שוים; F מתחלפים
- ↑ הנה: C; F יהיה
- ↑ השטח: C שטח
- ↑ הנצב: B(except for Mu130), C, F137 נצב
- ↑ אשר יקיפו: C שיקיפו; P1007 אשר יקיף
- ↑ בו: P1012 om.
- ↑ שני חלקי: C החלקים; F חלקי; P1007 ב' חלקי; AB שני
קויחלקי - ↑ הקו כלו: C om.
- ↑ אשר הם בלתי: C שאינם; O16 הבלתי
- ↑ אשר הם בלתי שוים: F המתחלפים
- ↑ עם המרובע: C עם מרובע; F ומרובע; P1013 מן המרובע; W194
מןנ' עם המרובע - ↑ המתהוה מן: C om.; B(except for Mu130) ההוה מן
- ↑ מן הקו: O16, P1007 מהקו; W66
מן הקומהקו - ↑ אשר במה שבין: C כלו שהוא בין; Mu130 אשר במה
שנישבין - ↑ שני: B (except for O16), C om.; P1007 ב'; P1013 שכל; P1014 שתי
- ↑ מקומות: P1007 המקומות
- ↑ השני חלקים: C
שוההחלקים; B(except for Mu130) החלקים
המתהוה מן ... השני חלקים: F יתרון חצי הקו על החלק היותר קצר - ↑ שוה: B(except for Mu 130), F, P1012 שוים
- ↑ למרובע: W66 מרובע
- ↑ המתהוה: C, F om.; A1, B(except for Mu130), P1014 ההוה
- ↑ מחצי: C, F חצי; Mu130 מן חצי
- ↑ ויהיה: B (except for Mu130) הנה יהיה; F137 יהיה; Ma1 המשל יהיה
- ↑ קו ישר: F הקו הישר
- ↑ ויחלק: F ויתחלק; B(except for Mu130) ונחלק
- ↑ בשני: A2, P1014 לשני; P1007 בב'
- ↑ בשני חלקים שוים: F לחצאים; O16 בחלקים שוים
- ↑ נקודת: F om.; P1013 מקומות נקודת
- ↑ מי' מא': according to AB, W66
- ↑ ושני: Mu130, P1007 וב'; W66 ולשני
- ↑ ושני חלקים: F, O16 ובחלקים
- ↑ בלתי שוים: F מתחלפים
על נקודת ג' ... בלתי שוים: Mu130 marg. - ↑ נקודת: F om.
- ↑ הנה: F om.
- ↑ כי השטח: B(except for Mu130), Ma1 שהשטח
- ↑ הנצב: B, F נצב
- ↑ בו: P1012 om.
- ↑ שני: F om.
- ↑ המתהוה: B(except for Mu130), F ההוה
- ↑ מן ג"ד: B(except for Mu130), P1007 מג"ד; F מד"ג; Mu130 ג"ד illegible
- ↑ שוה: F שוים
- ↑ המתהוה: B(except for Mu130), F, P1014 ההוה
- ↑ מן ג"ב: B(except for Mu130), P1007, P1013 מג"ב; F מב"ג; AB מן
ג"א או מןג"ב; Mu130 מן ג"א או ג"ב; P1012 מן ג"א או מן ג"ב - ↑ ונעשה: F137 נעשה; Ma1 המופת נעשה; B(except for Mu130) הנה נעשה
- ↑ מקו: AB, Mu130, P1012, P1014 מן קו
- ↑ ג"ב: F ב"ג
- ↑ ג"הז"ב: F ב'ג'ה'ז' ונעשה מב"ד מרובע ד'ב'כ'ח'; P1010
ד"הג"ה ז"ב - ↑ ממ"ו מא': A2, C, E, Ma1, Mu130, P1007, P1012 om.; A1, AB, F137, Lo, P1010, PP ממ"ו מראשון; O16 ממ"ו
- ↑ התמונה: F התבנית
- ↑ א"גט"ל: F א'ט'ל'ג'
- ↑ הנכחי: F נכחי; P1013 [..] נכוחי
- ↑ מד' מזה: A2, B(except for W66), C, E, Ma1, P1007, P1014 om.; Lo, P1010, P1012 מד'
- ↑ הנה מפני: P1012 twice
- ↑ מפני כי ג"ח: F לפי שג"ח; B(except for Mu130) מפני שג"ח
ג"ח: P1012 ג"ה - ↑ לח"ז: P1012 לה"ז
- ↑ ד"כ: Mu130 ח"ב
- ↑ משותף: O16 משותפת
- ↑ הנה: F om.; W66
ההנה - ↑ ג"כ: Mu130 ל"ב
- ↑ לד"ז: Ma1 לשטח ד"ז
- ↑ ממ"ג מא': A1, E, F137, P1007, P1010, P1012, PP om.; C מצורת מ"ג מן הראשון; Ma1 מג' מזה המאמר; Lo ממ"ג מראשון; O16 ממ"ג
- ↑ ומפני שצלע: AB, P1007, P1012, PP ומפני כי צלע
- ↑ א"ג: O561
ג"הא"ג - ↑ ג"כ: Mu130 ל"ב; PP marg. כ"ג
- ↑ מל"א מא': according to W66; AB מל"ו מראשון
- ↑ ג"כ: Mu130 ל"ב; PP ל"ג
- ↑ הנה יהיה: B(except for Mu130), AB, F אם כן
- ↑ ל"א: B(except for Mu130), AB, F א"ל
- ↑ ומפני שצלע א"ג ... לשטח ד"ז: F137 marg. with the note ונשמט
וכבר היה ... ל"א שוה לשטח ד"ז: AB, PP marg.
הנה יהיה ... לשטח ד"ז: P1012 om. - ↑ מפתיח' א': according to W66; AB מפתיחת א'
- ↑ ונשים: Mu31 starts here (247v; line 2 from the bottom) ונשום
- ↑ ג"ח: Lo ד"ח ג"ח
- ↑ משותף: B(except for Mu130) משותפת
- ↑ הנה: F יהיה
- ↑ כלו: Mu31 ג כלנו
- ↑ שוה: Mu31 שוים; P1012 om.
- ↑ לרושם: Mu31 om.; Mu130
לשטחלרושם - ↑ מנ"ס: P1012 מנ"ח
- ↑ א"ח: Mu31; Mu130 שטח א"ח
- ↑ שוה: P1012 שוה לשטח ג”כ וכבר היה שטח ג”כ שוה לשטח ד”ז ונשים ג”ח משותף הנה א”ח כלו לרושם מנ”ח אבל א”ח שוה
- ↑ הנצב: B, F נצב; P1007 ה[.] הנצב
- ↑ הזויות: P1007 הזוית
- ↑ שני: B(except for Mu130), F om. P1007 ב'
- ↑ מפני כי ב"ד: B(except for Mu130) מפני שב"ד; F לפי שד"ב; O561 marg.; P1007 הנה מפני כי ב"ד; P1012 ומפני כי ב"ד
- ↑ לד"ח: O16
לשטחלד"ח - ↑ וזה כי ד"כ: B(except for Mu130) וזה שד"כ
- ↑ וזה כי ד"כ מרובע: Ma1 om.
- ↑ משלפניה: according to B(except for Mu130); C מלפניה; Ma1 מג' מזה; AB מאשר לפניה; O561 מהקודמת; P1014 מסוף תמונה אשר לפניה
- ↑ הנה: F אם כן
- ↑ רושם: AB
כירושם - ↑ מנ"ס: P1012 מנ"ד
- ↑ שוה לשטח: O561 twice
- ↑ הנצב: B, F נצב
- ↑ הזויות: W66 הזויות
- ↑ בו: Mu31, P1007, P1010, PP om.
- ↑ שני: B(except for Mu130), F om.; P1007 ב'
- ↑ אשר הוא שוה: Mu31 אשר ראשונה; O16 שהוא כמו
- ↑ למרובע: O16 השטח המרובע
- ↑ המתהוה: B(except for Mu130), F ההוה
- ↑ מן ג"ד: B(except for Mu130), F, P1007 מג"ד
- ↑ משותף: O16 משותפת
- ↑ ויהיה: B(except for Mu130) הנה יהיה; F יהיה
- ↑ מנ"ס: P1012 מנ"ד
- ↑ ושטח: F עם
- ↑ הנצב: F, W66 נצב
- ↑ הזויות: O16 הזוית
- ↑ יקיפו בו: Lo יקיפוהו; A2, F, P1007, P1010, PP, W194 יקיפו
- ↑ שני: B(except for Mu130), F om.; P1007 ב'
- ↑ המתהוה: A1, B(except for Mu130), F ההוה
- ↑ מן ג"ד: B(except for Mu130), F, P1007 מג"ד
- ↑ אבל: A2, AB, Lo, Mu31, Mu130, P1010, P1012, PP, W194 ויהיה
- ↑ רושם: PP marg.
- ↑ כמו השטח הנצב ... ושטח ל"ע: P1012, P1014 om.
- ↑ הוא: F הם
- ↑ כלו: AB om.
- ↑ ושטח: O561 ג ושטח
- ↑ ג"ז: Mu31 כ"ז
- ↑ ושטח ג"ז כלו: P1012 om.
- ↑ ושטח ג"ז כלו הוא: F והוא
- ↑ שטח: B(except for Mu130), F, Mu31 om.; P1007 השטח
- ↑ המתהוה: B(except for Mu130), F ההוה
- ↑ מן ג"ב: AB, B(except for Mu130), P1007, P1012 מג"ב; F מב"ג
- ↑ הנה: F אם כן
- ↑ השטח: Mu31 השוה; Mu130 שטח
- ↑ הנצב: B(except for Mu130), F נצב
- ↑ בו: A1 om.
- ↑ א"ד: F קוי א"ד; P1007 ב' קוי א"ד
- ↑ המתהוה: B(except for Mu130), F, P1007 ההוה
- ↑ מן ג"ד: O16, P1007, P1012, P1014 מג"ד; F מד"ג
- ↑ המתהוה: B(except for Mu130), F, P1007 ההוה
- ↑ מן ג"ב: O16, P1007 מג"ב; F מב"ג, AB
מג"א אומן ג"ב; Mu130 מן ג"א או ג"ב; P1010 מןג"חג"ב; P1012, P1013 מן ג"א ג"ב; W194 מן ג"א ג"ב [נ' שהוא אחד] - ↑ וכאשר: F137 ואם כן; B(except for W66) הנה כאשר; O561 וכאשר
- ↑ נחלק קו ישר: F137 כל קו ישר יתחלק
- ↑ בשני חלקים שוים: F137 לשני חצאים; O16 בחלקים שוים; P1007 בב' חלקים שוים
- ↑ ושני חלקים בלתי שוים: A2 ובלתי שוים; F137 ובשני חלקים מתחלפים; O16 וחלקים בלתי שוים; P1007 om.
- ↑ הנה: F137 יהיה
- ↑ הנצב: F137, O16, P1013 נצב
- ↑ בו: P1010 om.
- ↑ שני: F137 om.; P1007 ב'
- ↑ חלקי הקו: Mu31 חלקו ההן; AB חלק קו
- ↑ כלו: O16 om.
- ↑ אשר הם בלתי שוים: F137 המתחלפים; O16 אשר אינם שוים
- ↑ עם המרובע: F137 ומרובע
- ↑ המתהוה: O16 ההוה
- ↑ מן הקו: O16, P1007 מהקו
- ↑ אשר במה: Mu31 twice
- ↑ מקומות: P1013 המקומות
- ↑ שני: O16 om.; PP marg.
- ↑ שני מקומות שני החלקים: A2 שני המקומות שני חלקים; P1007 ב' מקומות ב' החלקים; P1014 שתי מקומות השני חלקים
המתהוה מן הקו אשר במה שבין שני מקומות שני החלקים: F137 יתרון חצי הקו על החלק היותר קצר - ↑ שוה: F137 שוים
- ↑ המתהוה: F137 om.; O16 ההוה
- ↑ מחצי: F137 חצי; P1012 מהם
- ↑ וכאשר ... מחצי הקו: C, E, Ma1, W66 om.
- ↑ וזה מה שרצינו לבאר: E om.; Mu130 ומש"ל; P1007 וזמש"ל; W66 וזה מה שרצינו לבאר ונשלם באורו; Ma1, P1014 וזה מש"ל; F137 וזהו מה שרצי' לבאר
Appendix: Bibliography
Manuscripts:
A) Moses ibn Tibbon - the main translation
- 1) London, British Library Add. 20746 (IMHM: f 5053), (cat. Margo. 1001) (15th century)
- translation: 6 September 1270; Book X – 2 August 1270
- Lo
- translation: 6 September 1270; Book X – 2 August 1270
- 2) Paris, Bibliothèque Nationale de France heb. 1007/3 (IMHM: f 15710), ff. 37r-65v (16th century)
- 3) Paris, Bibliothèque Nationale de France heb. 1010 (IMHM: f 15712), (15th-16th century)
- translation: 6 September 1270; Book X – 2 August 1270
- P1010
- translation: 6 September 1270; Book X – 2 August 1270
- 4) Paris, Bibliothèque Nationale de France heb. 1012/1 (IMHM: f 15713), ff. 1-254 (15th century)
- translation: 16 September 1270
- P1012
- translation: 16 September 1270
- 5) Paris, Bibliothèque Nationale de France heb. 1014/1 (IMHM: f 15714), ff. 1r-157r (16th century)
- 6) Paris, Private collection (IMHM: f 39116) (1470-1475)
- A1)
- 1) Paris, Bibliothèque Nationale de France heb. 1013 (IMHM: f 15018), (15th century)
- 2) Wien, Öesterreichische Nationalbibliothek Cod hebr. 194/1 (IMHM: f 1456), ff. 1-82 (16th century)
- A2)
- 1)München, Bayerische Staatsbibliothek, Cod. hebr. 36/3 (IMHM: f 1166), ff. 8r-17r, 22r-85r, 87r-100r (Istanbul, 1485)
- translation: 16 September 1270
- Mu36
- translation: 16 September 1270
- 2) Oxford, Bodleian Library MS Hunt. 561 (IMHM: f 19288) (cat. Neub. 2003) (Candia, 1375)
Unchecked
- Jerusalem, Jewish National and University Library Ms. Heb. 8°2339 (IMHM: B 449 (8°2339)), (19th century)
- Leiden, Bibliotheek der Rijksuniversiteit Cod. Or. 4785 (IMHM: f 27910) (14th-15th century) (similar to MS Oxford 405?)
- Madrid, Biblioteca Nacional 5474/1 (IMHM: f 7233), 1-190 (14th-15th century)
- translation: 16 September 1270
- Montecassino, Archivio di Stato 510/1 (IMHM: f 34894), ff. 1v-132v (15th century)
- translation: 2 August 1270
- translation: 2 August 1270
- New York, Jewish Theological Seminary Ms. 2613 (IMHM: f 28866), ff. 1r-30r (list of propositions of Books I-XV); 31r-38r (Book I until proposition 19) (18th century)
- New York, Jewish Theological Seminary Ms. 9545/2 (IMHM: f 49965), ff. 16r, 18v-21v (15th century)
- Oxford, Bodleian Library MS Mich. 358/1 (IMHM: f 19289) (cat. Neub. 2004, 1), ff. 1r-72v, (13th-14th century)
- Oxford, Bodleian Library MS Mich. 400/1 (IMHM: f 19291) (cat. Neub. 2006, 1), 1r-10v, (15th century) (list of definitions and propositions)
- Oxford, Bodleian Library MS Mich. 405 (IMHM: f 19287) (cat. Neub. 2002) (1573) (similar to MS Leiden?)
- Philadelphia, University of Pennsylvania Ms. Codex 1787
- Roma, Accademia Nazionale dei Lincei, Biblioteca Corsiniana, Or. 259/1 (IMHM: f 73284), ff. 1r-68v, (Mantova, 1441)
- Roma, Biblioteca Nazionale Centrale Vittorio Emanuele II Or. 78 (IMHM: f 415) (15th century) (with comments by Gersonides)
- St. Petersburg, Inst. of Oriental Studies of the Russian Academy B 16 (IMHM: f 52919), (15th century)
- St. Petersburg, Inst. of Oriental Studies of the Russian Academy B 191/2 (IMHM: f 53338), ff. 167v-178v (Volga, 1392)
- St. Petersburg, Inst. of Oriental Studies of the Russian Academy C 127 (IMHM: f 69382), (Istanbul, 17th century)
B) Jacob ben Makir - revision of ibn Tibbon's translation
- 1) München, Bayerische Staatsbibliothek, Cod. hebr. 130 (IMHM: f 1195), (15th century)
- 2) Oxford, Bodleian Library MS Hunt. 16/1 (IMHM: f 19290) (cat. Neub. 2005, 1), 1r-89v, (15th century)
- 3) Wien, Öesterreichische Nationalbibliothek Cod hebr. 66/3 (IMHM: f 1343), ff. 157-233 (16th century)
AB)
- München, Bayerische Staatsbibliothek, Cod. hebr. 91/1 (IMHM: f 1157), ff. 1r-141v (14th century)
C)
- Cambridge, Trinity College R 14 61 (IMHM: f 12598), (14th century)
F)
- 1) Firenze, Biblioteca Nazionale Centrale Magl. III. 137/1 (IMHM: f 11976), ff. 4v-199r (15th century)
- translation: 6 September 1270
- F137
- translation: 6 September 1270
- 2) Mantova, Comunita Israelitica MS ebr. 1 (IMHM: f 782) (15th century)
- translation: 6 September 1270
- Ma1
- translation: 6 September 1270
E)
- Mantova, Comunita Israelitica MS ebr. 2 (IMHM: f 783) (14th-15th century)
lists
- München, Bayerische Staatsbibliothek, Cod. hebr. 246/6 (IMHM: f 1102), ff. 56r-64r (1429-1431)
- Paris, Bibliothèque Nationale de France heb. 1011/1 (IMHM: f 15017), ff. 1r-64r (13th-14th century)
Campanus de Novare?
- Moscow, Russian State Library, Ms. Guenzburg 539/2 (IMHM: f 47860), ff. 67r-91r (16th century) (Moses Provenṣali ?)
- München, Bayerische Staatsbibliothek, Cod. hebr. 31/3; 31/5 (IMHM: f 1165), ff. 113r-122v; 242v-254r (16th century)
- Paris, Bibliothèque Nationale de France heb. 1015/1 (IMHM: f 15019), ff. 1-29 (16th century)
Bibliography:
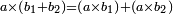
![\scriptstyle\left[\left(a+b\right)\sdot a\right]+\left[\left(a+b\right)\sdot b\right]=\left(a+b\right)^2](/mediawiki/images/math/9/c/9/9c9305cbc3ba9b0e4edc1ee228e83fa9.png)
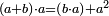
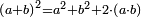
![\scriptstyle\left(a\sdot b\right)+\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]^2=\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2](/mediawiki/images/math/6/2/4/6240a40a1b55eec2eca043f4e2218ca7.png)
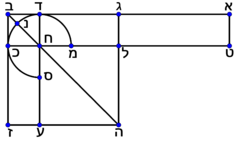
![\scriptstyle\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2](/mediawiki/images/math/a/0/b/a0b403dd8b7c15a5cb1dc47a5f8ca5bb.png)
![\scriptstyle\left(a+b\right)^2+a^2=2\sdot\left[\left(a+b\right)\sdot a\right]+b^2](/mediawiki/images/math/5/e/f/5ef738b800e1b84fc257df70a83fb86b.png)
![\scriptstyle4\sdot\left[\left(a+b\right)\sdot a\right]+b^2=\left[\left(a+b\right)+a\right]^2](/mediawiki/images/math/f/6/2/f62f5f20431f619df80a01a1d97e57cf.png)
![\scriptstyle a^2+b^2=2\sdot\left[\left[\frac{1}{2}\sdot\left(a+b\right) \right]^2+\left[b-\left[\frac{1}{2}\sdot\left(a+b\right)\right]\right]^2\right]](/mediawiki/images/math/d/a/a/daab00123b1a8516078d128698e4b24d.png)
![\scriptstyle\left(a+b\right)^2+b^2=2\sdot\left[\left(\frac{1}{2}\sdot a\right)^2+\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2\right]](/mediawiki/images/math/b/7/d/b7dd112f5309b8cd4f778bd6269c21f3.png)