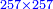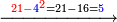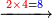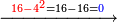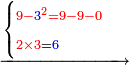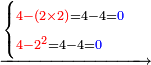|
|
| Line 1,367: |
Line 1,367: |
| | |- | | |- |
| | | | | | |
| − | *<math>\scriptstyle{\color{red}{x+y<10\quad x\sdot y=\left[\left(10-y\right)\sdot\left(10-x\right)\right]+\left[10\sdot\left(x+y\right)\right]-\left(10\sdot10\right)}}</math> | + | *If the numbers that you want to multiply one by the other are less than 10, when you sum them together: |
| | + | :<math>\scriptstyle{\color{red}{x+y<10\quad x\sdot y=\left[\left(10-y\right)\sdot\left(10-x\right)\right]+\left[10\sdot\left(x+y\right)\right]-\left(10\sdot10\right)}}</math> |
| | :[MS Oxford 60, 151v, 161r] | | :[MS Oxford 60, 151v, 161r] |
| − | |style="text-align:right;"|ואם יהיה המספר אשר תרצה {{#annot:|185|mkj8}}לכפול{{#annotend:mkj8}} זע"ז פחות מי' כשתצרף שני המספרים יחד | + | |style="text-align:right;"|ואם יהיה המספר אשר תרצה {{#annot:term|185|mkj8}}לכפול זע"ז{{#annotend:mkj8}} פחות מי' כשתצרף שני המספרים יחד |
| | |- | | |- |
| | | | | | |
| Line 1,381: |
Line 1,382: |
| | |<math>\scriptstyle\xrightarrow{{\color{red}{\left(10-4\right)\sdot\left(10-3\right)=6\sdot7}}={\color{blue}{42}}}</math>||<span style="color:#0000FF>42</span>||<math>\scriptstyle\xrightarrow{{\color{red}{4+3}}={\color{blue}{7}}}</math>||<span style="color:#0000FF>7</span>42||<math>\scriptstyle\xrightarrow{{\color{red}{\left(7+4\right)-10}}={\color{blue}{1}}}</math>||<span style="color:#0000FF>1</span>2 | | |<math>\scriptstyle\xrightarrow{{\color{red}{\left(10-4\right)\sdot\left(10-3\right)=6\sdot7}}={\color{blue}{42}}}</math>||<span style="color:#0000FF>42</span>||<math>\scriptstyle\xrightarrow{{\color{red}{4+3}}={\color{blue}{7}}}</math>||<span style="color:#0000FF>7</span>42||<math>\scriptstyle\xrightarrow{{\color{red}{\left(7+4\right)-10}}={\color{blue}{1}}}</math>||<span style="color:#0000FF>1</span>2 |
| | |} | | |} |
| − | | + | | |
| − | |style="text-align:right;"|אז תקח המרחק מן י' מכל אחד דהיינו מד' עד י' ו' ומג' עד י' ז זפ"ז ב"ד אותו ב"ד כתו' לזכרון<br> | + | |- |
| − | [בד]<br> | + | | |
| − | ואח"כ צרוף ד' ג' יחד ויהיה ז' אות ז' כתוב לצד שמאל אצל ב"ד כזה<br> | + | ::*Take the difference of each from 10, i.e. from 4 to 10, it is 6 and from 3 to 10, it is 7 |
| − | [בדז]<br> | + | :::6 times 7 is 42. <math>\scriptstyle{\color{blue}{\left(10-4\right)\times\left(10-3\right)=6\times7=42}}</math> |
| − | ואח"כ השלך י' מצד אותיות של שמאל וישאר ב'א' היינו החשבון אשר בקשת לידע וכפי זה תקיש והנה כתבתי זה אף כי הוא מושכל ראשון החשבון אשר בקשת להודיעך שאין בדרך הזה [...] | + | |style="text-align:right;"|אז תקח המרחק מן י' מכל אחד דהיינו מד' עד י' ו' ומג' עד י' ז‫'<br> |
| | + | ופ"ז ב"ד |
| | + | |- |
| | + | | |
| | + | :::Write this 42 for remembrance. |
| | + | |style="text-align:right;"|אותו ב"ד כתו' לזכרון<br> |
| | + | [בד] |
| | + | |- |
| | + | | |
| | + | |style="text-align:right;"|ואח"כ צרוף ד' ג' יחד ויהיה ז' אות ז' כתוב לצד שמאל אצל ב"ד כזה<br> |
| | + | [בדז] |
| | + | |- |
| | + | | |
| | + | |style="text-align:right;"|ואח"כ השלך י' מצד אותיות של שמאל וישאר ב'א' היינו החשבון אשר בקשת לידע וכפי זה תקיש והנה כתבתי זה אף כי הוא מושכל ראשון החשבון אשר בקשת להודיעך שאין בדרך הזה [...] |
| | |- | | |- |
| | | | | | |
| Line 9,202: |
Line 9,216: |
| | |- | | |- |
| | |to multiply | | |to multiply |
| − | |style="text-align:right;"|לחשוב | + | |style="text-align:right;"|לחשוב, לכפול זע"ז |
| | |- | | |- |
| | | | | | |
| Line 9,272: |
Line 9,286: |
| | | | | | |
| | |style="text-align:right;"|צירופו | | |style="text-align:right;"|צירופו |
| | + | |- |
| | + | | |
| | + | |style="text-align:right;"|תצרף |
| | |- | | |- |
| | | | | | |
| Line 9,287: |
Line 9,304: |
| | | | | | |
| | |style="text-align:right;"|מה שבא מן הכפל | | |style="text-align:right;"|מה שבא מן הכפל |
| | + | |- |
| | + | | |
| | + | |style="text-align:right;"|תקח ה |
| | + | |- |
| | + | | |
| | + | |style="text-align:right;"|מרחק מן |
| | + | |- |
| | + | | |
| | + | |style="text-align:right;"|מכל אחד |
| | + | |- |
| | + | | |
| | + | |style="text-align:right;"|דהיינו |
| | |- | | |- |
| | | | | | |
| Line 9,353: |
Line 9,382: |
| | | | | | |
| | |style="text-align:right;"|תמצא, נמצא | | |style="text-align:right;"|תמצא, נמצא |
| | + | |- |
| | + | | |
| | + | |style="text-align:right;"|לזכרון |
| | |- | | |- |
| | | | | | |
| Line 9,359: |
Line 9,391: |
| | | | | | |
| | |style="text-align:right;"|הוי אומר | | |style="text-align:right;"|הוי אומר |
| | + | |- |
| | + | | |
| | + | |style="text-align:right;"|ודוק |
| | |- | | |- |
| | | | | | |
Prologue
|
|
| [MS Paris, Séminaire Israélite de France (École Rabbinique) 158/1 (IMHM 4102) f. 197r, lines 1-16]
|
|
|
|
זה ספר חכמת התשבורת [הנקרא] טשיפרא
|
|
|
סיבתו אני את לבי גם מנעורי גרסה נפשי לדעת חכמה ובקש חשבון ומי יתן ואמצאם בספר ויחקו בעט סופר מהיר [1]. ולסבה שזאת היא חכמת החיצוניות לא נמצאת לפנינו בישראל, והמיעוט שבמיעוט הנמצא נאסף אל תוך הבית בחדרי חדרים, לכן העירוני רעיוני ללקט האמרים מיד כל אשר ימצא אתו ולכל[...] לזכרון
|
|
|
וקודם שאתחיל אבקש מיד כל רואיו לבל יכרעני לכף חובה ולומר מה לך פה כלך בהוייות דאביי ורבא חלילה וחס [לי'] לזרעא דאבא, כי לא לקחתי זאת לשום עיקר ותכלית, רק לחדד השכל ולבא בחשבון במקרה ושנייה ובחידוד דאביי ורבא בעצם וראשונה ועל זאת אמרו המושלים באו חשבון [2] כמו שכתוב הרמבם ז"ל פרק חמישי מה[קדמת] ה פרקי אבות [3] וז"ל
|
|
|
ומה שאין בו תועלת לו בתכלית ההוא כשאלות החשבון וספר החר[וט]ים והתחבולות הרבות משאלות אל ההנד[ס]ה ומשיכת המשקלים והרבה כיוצא בא[ילו] יהיה הכוונה בהם לחדד השכל ולהרגיל כח השכלי בדרכי המופת עד שיגיע לו לאדם קניין ידיעת ההיקש המופתי מזולתו ויהיה לו זה הדרך שיגיע בה לידעת אמיתות מציאתו ית' עכל'
|
Introduction
|
|
| With good luck
|
בטוב גדא
|
| I shall start this
|
אתחיל דא
|
| Sefer Ṣifra
|
ספר ציפרא
|
| To know and explain the book of number that has 9 chapters.
|
לידע ולפרש ספר המספר שיש בו ט' שערים
|
| First I shall explain the teachings that the one who calculates should know, so that he can know all the calculations [practice].
|
ואפרש תחילה הקבלות אשר צריך לידע המחשב הוא המפתח ויכול אחר כך לידע כל החשבונות
|
The Positional Decimal System
|
|
| The numerals
|
|
| Know that you do not have any number [= numeral] smaller than one and you do not have any number [= numeral] greater than nine.
|
דע כי אין לך חשבון קטן מן א' שהוא אחד
ואין לך חשבון גדול מן ט'
|
| By these nine numerals from א to ט [the nine first Hebrew letters] all numbers in the world [are formed] infinitely. How?:
|
ובאלו ט' אותיות מן א' ועד ט' יש בו כל החשבונות שבעולם עד אין מספר כיצד
|
| The written ranks [= decimal places]
|
|
- Units: the first rank is called the rank of units, for as the digit is named so is its numerical value, meaning: 1 is one; 2 is two; 3 is three; and so on until 9, which is nine.
|
מעלה הראשונה היא נקראת מעלת היחידים כי כאשר יקראו האות כך מניינם פי' א' אחד ב' שנים ג’ שלש וכן עד ט' שהיא תשע
|
|
|
|
- Zero – placeholder digit: when you calculate ten you should write two ranks - 1 in the second rank
|
וכשתחשוב עשרה אז צריך אתה לכתוב ב' מעלות א' במעלה שנייה
|
- and before it a numeral, which is a zero [lit. wheel], like this 0, that has no substance but is a place holder and a remnant of a thing like a wheel, [like stubble] before the wind [Psalms 83, 14].
|
ולפניו ציפרא שהוא גלגל כזה 0 שאין בו ממש אלא שומר המעלות וזכר לדבר כגלגל לפני רוח [4]
|
|
|
|
|
- For the first א of the units is in the first rank and the second א is of the tens, hence 11.
|
כי הא' הראשונה מן היחידים שהיא במעלה ראשונה וא' שנייה היא מן העשיריות הרי י"א
|
|
|
|
|
- and so on until טא which is 19.
|
|
|
|
|
|
|
|
- and so on until twenty-nine, which is טב.
|
|
- Hundreds: the third rank is the rank of the hundreds, like this:
|
ומעלה השלישית היא מעלת המאות כזה
|
|
|
|
|
|
|
- and so on until 9 hundred, which is ט00.
|
|
|
|
|
|
- Thousands: the fourth rank is the rank of thousands.
|
ומעלה הרביעית היא מעלת האלפים
|
|
|
|
|
|
|
- and so on until 9 thousand, which is ט000.
|
וככה עד ט' אלפים שהוא 000"ט
|
- Tens of thousands: the fifth rank is the rank of tens of thousands.
|
ומעלה החמישית היא מעלת הרבבות שהוא י' אלפים
|
- Hundreds of thousands: the sixth rank is the rank of hundreds of thousands.
|
ומעלה ששית היא מעלת מאה אלפים
|
- Thousands of thousands: the seventh rank is the rank of thousands of thousands [= millions].
|
ומעלה שביעית היא מעלת אלף אלפים
|
| And so you can write endlessly.
|
וככה עד אין מספר תוכל לכתוב
|
| Every rank is ten times the preceding rank.
|
וכל מעלה היא עשרה פעמים יותר מן המעלה שלפניה
|
- Example: if one asks you: how much is 3020?
|
|
- Note that the zero has no numerical value but is a place holder, so the number is three thousand and twenty.
|
תשיב אל לבך כי הגלגל אין לו מניין רק שומר המעלות והנה החשבון עשרים וג' אלפים
|
| Thus, I have explained to you the number and the meaning of the writing.
|
והנה ביארתי לך מניין ועניין הכתיבה
|
| 1 2 3 4 5 6 7 8 9 0 10 20 30
|
| 0ג |
0ב |
0א |
0 |
ט |
ח |
ז |
ו |
ה |
ד |
ג |
ב |
א
|
|
|
Chapter One: Multiplication of Units - Shortcuts
|
שער הכפל הקטן
|
| If you wish to know how much is the result of 9 times 9, or 9 times 8, or 5 times 9, or 6 times 9 and so on for all that is less than ten, I will teach you:
|
אם תרצה לידע כמה עולה ט' פעמים ט' או ט' פעמים ח' או ה' פעמים ט' או ו' פעמים ט' וכן כל כיוצא בזה שכל אחד פחות מעשרה אשכילך
|
- If you wish to know how much is 9 times 9
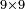
|
אם תחפוץ לידע כמה ט’ פעמים ט’
|
- Write like this:
|
אז כתוב כזה
|
-
|
|
|
|
- Think by how much it exceeds over ten, it is 8.
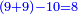
|
ואחר כך חשוב כמה יותר על עשרה ויהיה ח' ואותה ח'
|
- Write [it] next to the upper 9 to the left, like this:
|
כתוב אצל הט' העליונה בצד שמאל כזה
|
-
|
|
- Then, think by how much the upper 9 exceeds over the 8, you will find only 1.

|
ואחר כך חשוב כמה ט' העליונה יותר על ח' ותמצא רק אחד
|
- Write this 1 next to the bottom 9:
|
אותו א’ כתוב בצד ט’ התחתונה
|
-
|
|
- Then, think by how much the bottom 9 exceeds over the 8, it is 1.

|
ואחר כך חשוב כמה ט’ התחתונה יותר על הח’ ויהיה א’
|
- Write this 1 also next to the bottom 9, like this:
|
כתוב אותה א’ ג”כ בצד ט’ תחתונה כזה
|
-
|
|
- Think how much is 1 times 1, it is 1.
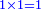
|
ותחשוב א' פעמים א' היינו אחד
|
- Write 1 before the 8, like this:
|
כתוב א' לפני הח' כזה
|
-
|
|
- Erase the bottom and the upper 9, so they are eighty-one.
|
ומחוק הט' למטה ולמעלה ויהיו אחד ושמונים
|
- Also if you want to know how much is 9 times 8
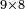
|
וכן אם תרצה לידע כמה ט' פעמים ח'
|
- Write like this:
|
כתוב כזה
|
-
|
|
|
|
- Think by how much 9+8 exceeds over ten, it is 7.
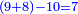
|
וחשוב כמה ח'ט' יותר על עשרה דהיינו ז'
|
- Write the 7 next to the 9, like this:
|
כתוב הז' אצל הט' כזה
|
-
|
|
- Think by how much the 9 exceeds over the 7, it is 2.

|
וחשוב כמה הט' עודף על הז' דהיינו ב'
|
- By how much the 8 exceeds over the 7, [it is] 1.

|
וכמה הח' עודף על ז' א'
|
- Write like this:
|
וכתוב כזה
|
-
|
|
- Multiply 1 by 2, it is 2.
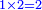
|
תכפול א' על ב' היינו ב'
|
- Write this 2 before the 7, like this:
|
אותה ב' כתוב קודם הז’ כזה
|
-
|
|
- We find that 9 times 8 is 72.
|
נמצא ט' פעמים ח' יהיה ע"ב
|
- Example: if you wish to know how much is 6 times 6 [MS Paris 1088, 4v]
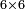
|
דומיון אם תחפוץ לידע כמה ו' פעם ו'
|
- Write the 6 beneath the 6, like this:
|
אז כתו' הו' תחת הו' כזה
|
-
|
|
| 6 |
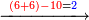 |
26 |
 |
[26] |
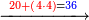 |
36
|
| 6 |
6 |
[6] |
6
|
| |
|
[44] |
|
|
|
- Say: by how much the two 6 exceed over 10, it is 2.
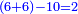
|
ואז תאמר כמה השני ו' למעלה מי' זהו ב'
|
- Write this 2 after the 6, like this:
|
ואותו ב' תכתו' לאחר הו' כזה
|
-
|
|
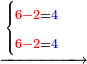
- Then, say: by how much the 6 exceeds over 2, it is 4.

|
ואז תאמ' כמה הו' יתיר על הב' זהו ד'
|
- The second 6 also exceeds over 2 by 4.

|
והו' השנייה נמי למעל' מב' זהו ד'
|
- Multiply 4 times 4, it is 16, meaning sixteen.
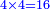
|
ואז תכפול ד' פעמי' ד' זהו ו"א פי' י"ו
|
- Add the 1 to the 2, because the 2 is in the second rank, it is 3.
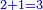
|
ואז תכתוב שים הא' על הב' כי הב' מעלה שניי' ויהיה ג'
|
- There is also 6, write the 6 before the 3, like this:
|
ועוד הוה ו' ואות' ו' תכתו' לפני הג' כזה
|
-
|
|
- We find that 6 times 6 is 36.
|
נמצא שו' פעמ' ו' עולה ו"ג פי' ל"ו
|
| Always do as this.
|
וכן עשה לעולם
|
| Multiply always the excess of this by the excess of this and write the result before the excess [of the sum of the multipliers over ten], then you will become wise in all that you do.
|
וכן לעולם תכפול המותר מזה ומזה והעולה כתוב קודם העודף עליו ואז תשכיל בכל אשר תעשה
|
- Another example that I translated from a Latin book [MS Paris 158, 198r]:
|
דמיון אחר שהעתקתי מספר גלחות
|
- Sum together the two numerals, subtract a ten, then write the small number.
- Multiply together the differences of each from ten and write [the product] before the small number that you have.
- If this product is of two ranks, add the second rank to the number that you have.
![\scriptstyle{\color{red}{x,y<10\quad x\sdot y=\left[10\sdot\left[\left(x+y\right)-10\right]\right]+\left[\left(10-y\right)\sdot\left(10-x\right)\right]}}](/mediawiki/images/math/b/a/4/ba47b3ce6e602ae8b4e44a762172704c.png)
|
חברם יחד הב' אותיות והשליך עשרה והמניין הקטון כתוב
ואח"כ תכפול יחד החשבון שיש מכל אחד עד עשרה וכתוב זה לפני המנין הקטן שבידך
ואם בא לידך מהכפל הזה ב' מעלות אז תחבר המעלה שנייה אל המניין שבידך
|
- As these calculations that are written in front of you, from which you will become wiser:
|
כגון אילו החשבונות החרו[ת]ים לפניך ממנו תשכיל ותחכם עוד
|
 |
 |

|
| 8 |
2 |
7 |
3 |
6 |
4
|
| 9 |
1 |
8 |
2 |
7 |
3
|
| 72 |
56 |
42
|
|
| 8 |
2 |
7 |
3 |
6 |
4
|
| 9 |
1 |
8 |
2 |
7 |
3
|
| 72 |
56 |
42
|
|
- Or in this way: write zero 0 before the smaller of the two numerals [MS Paris 158, 198r]:
![\scriptstyle{\color{red}{x<y<10\quad x\sdot y=\left(x\sdot10\right)-\left[x\sdot\left(10-y\right)\right]}}](/mediawiki/images/math/3/7/9/379821fa6258d1d24574dbe3c30f6dca.png)
|
או כלך לדרך זו כתוב לפני המניין קטון שבשני אותיות גלגל כזה 0
|
- Example: if you wish to know [how much is] 7 times 8.
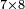
|
כגון את"ל ז'פ'ח'
|
|
כתוב כזה 0ז
|
- Subtract from it the product of the difference of the greater numeral from ten by the smaller numeral.
|
וקח ממנו מה שבא מן הכפל שתכפול המניין מאות הגדול עד עשרה עם האות הקטן
|
- As what is infront of you: say 7 times 2 are 14.
- Subtract 14 from 70, the remainder is 56.
![\scriptstyle{\color{blue}{7\times8=\left(7\sdot10\right)-\left[7\sdot\left(10-8\right)\right]=70-\left(7\sdot2\right)=70-14=56}}](/mediawiki/images/math/c/f/8/cf82d668175564f785f54108257ef5e3.png)
|
כגון מה שלפניך אמור ז'פ'ב' הם ד"א
ותקח ד"א מן 0"ז ונשאר ו"ה
|
|
וכגון אילו
|
 |
 |
 |

|
| 8 |
0 |
6 |
0 |
4 |
0 |
5 |
0
|
| 8 |
2 |
7 |
3 |
9 |
1 |
8 |
2
|
| 64 |
42 |
36 |
40
|
|
| ח |
0 |
ו |
0 |
ד |
0 |
ה |
0
|
| ח |
ב |
ז |
ג |
ט |
א |
ח |
ב
|
| דו |
בד |
וג |
0ד
|
|
- If you want to know and calculate how much is 3 times 3, or 4 times 4, et cetera, which even their sum does not reach ten, I will teach you how to do so:
![\scriptstyle{\color{red}{x+y<10\quad x\sdot y=10+\left[\left(x-1\right)\sdot\left(y-1\right)\right]-\left[11\left(x+y\right)\right]}}](/mediawiki/images/math/d/e/b/deb3a15bab1027d790aee3e499ce8951.png)
|
ואם תרצה לידע ולחשוב כמה ג' פעמים ג' או ד' פעמים ד' וכן כל כיוצא בזה שאפילו צירופו אינו מגיע לעשרה אשכילך לעשות
|
- Lend to it as much as needed so that it will be one more than ten.
|
שתלוה לו כמה שצריך שיהיה בכל פעם אחד יותר מעשרה
|
- When your calculation is complete, subtract what you have lent to it and the required remains.
|
וככלות חשבונך קח מה שהלוית לו וישאר מתכונך
|
- Example: we want 4 times 4.
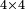
|
דמיון בקשנו ד' פעמים ד'
|
- Like this:
|
כזה
|
-
|
|
- Lend to it 3, so that it becomes 11.
![\scriptstyle{\color{blue}{4+4+\left[11-\left(4+4\right)\right]=4+4+3=11}}](/mediawiki/images/math/b/4/2/b42c664ab942373f7f7104da31b46a3d.png)
|
והנה תלוה לו ג' שיעלה י"א
|
- Subtract ten, 1 remains in your hand.
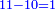
|
והשלך עשרה וישאר בידך א'
|
- Write it like this:
|
ורשום כזה
|
-
|
|
- Think by how much the first 4 exceeds over the 1, that is to say 3.
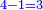
|
ואחר כך חשוב כמה ד' הראשונה יותר על הא' הוי אומר ג'
|
- So, the second 4 also exceeds by 3.
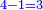
|
וכן ד' השנייה גם כן יותר ג'
|
-
|
|
- Multiply 3 by 3, it is 9.

|
כפול ג' על ג' הרי ט'
|
- Write the 9 before the 1, like this:
|
כתוב הט' לפני הא’ כזה
|
-
|
|
- Subtract 3 that you have lent to it and 16 remain, which are sixteen.

|
והנה קח ג' שהלוית לו וישאר ו"א והם י"ו
|
- You will find that your calculation is correct.
|
ותמצא חשבונך מכוון
|
-
|
|
- Another property: if you want to know how much is 3 times 3, or 4 times 4, et cetera, which even their sum does not reach ten, I will teach:
![\scriptstyle{\color{red}{x+y<10\quad x\sdot y=\left[\left(10-y\right)\sdot\left(10-x\right)\right]-\left[10\sdot\left[10-\left(x+y\right)\right]\right]}}](/mediawiki/images/math/f/a/5/fa50d116d61f078f4565958da778fb21.png)
|
עניין אחר אם תרצה לידע כמה ג’ פעמים ג’ או ד’ פעמים ד’ וכן כל כיוצא בזה שאפילו צירופו אינו מגיע לעשרה אשכילך
|
- I will teach you an example: if you want to multiply 4 times 4.
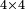
|
דמיון אם תרצה לחשוב ד’ פעמים ד’
|
- Write it like this:
|
אז תכתוב אותו כזה
|
-
|
|
| 4 |
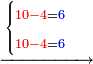 |
[4] |
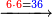 |
[36] |
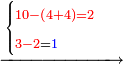 |
16
|
| 4 |
[4] |
[4] |
|
| |
[66] |
[66] |
|
|
|
- Think by how much the first 4 is less than 10, it is 6.
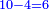
|
וחשוב כמה ד’ ראשונה פחות מי’ ויהיה ו’
|
- Think also by how much the second [4] is less than 10, you find it is also 6.
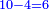
|
וחשוב גם השנייה כמה השנייה פחות מי’ ותמצא ג”כ ו’
|
- Multiply 6 by 6, the result is 36.

|
ואז תכפול ו’ על ו’ ויעלה בידך ו”ג
|
- Think by how much the two 4 are less than ten, it is 2.
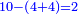
|
אז חשוב כמה השני ד’ פחותים מעשרה ויהיה ב’
|
- Subtract 2 in the second rank from 3, you are left with 16
|
השלך ב’ ממעלה שנייה מהג’ וישאר לך ו”א
|
- We find that 4 times 4 is 16.
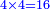
|
נמצא ד’ פעמים ד’ הוא ו”א
|
- The same for all.
|
וכן כולם ודוק
|
- If the numbers that you want to multiply one by the other are less than 10, when you sum them together:
![\scriptstyle{\color{red}{x+y<10\quad x\sdot y=\left[\left(10-y\right)\sdot\left(10-x\right)\right]+\left[10\sdot\left(x+y\right)\right]-\left(10\sdot10\right)}}](/mediawiki/images/math/0/0/9/009964355db1dd5f0f49cfb6586fc299.png) - [MS Oxford 60, 151v, 161r]
|
ואם יהיה המספר אשר תרצה לכפול זע"ז פחות מי' כשתצרף שני המספרים יחד
|
- Example: if you want to multiply 4 by 3.
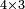
|
דימיון אם בקשת לכפול ד' על ג'
|
|
|
- Take the difference of each from 10, i.e. from 4 to 10, it is 6 and from 3 to 10, it is 7
- 6 times 7 is 42.
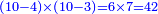
|
אז תקח המרחק מן י' מכל אחד דהיינו מד' עד י' ו' ומג' עד י' ז'
ופ"ז ב"ד
|
- Write this 42 for remembrance.
|
אותו ב"ד כתו' לזכרון
[בד]
|
|
|
ואח"כ צרוף ד' ג' יחד ויהיה ז' אות ז' כתוב לצד שמאל אצל ב"ד כזה
[בדז]
|
|
|
ואח"כ השלך י' מצד אותיות של שמאל וישאר ב'א' היינו החשבון אשר בקשת לידע וכפי זה תקיש והנה כתבתי זה אף כי הוא מושכל ראשון החשבון אשר בקשת להודיעך שאין בדרך הזה [...]
|
- [MS New York, 94r-v; MS Oxford 60, 161r; MS Oxford 440, 115r, 124r]
- taken from another book
|
דרך אחרת לכפל קטן בספר אחר מצאתי או כלך בדרך זו קח המרחק עד י’ מן כל אחד ואחד שתרצה לכפול יחד וחשוב אותו ב’ מרחקים זה על זה ומה שיעלה בידך כתוב לזכרון
אחר כך צורפם יחד בשער החיבור והעולה בידך קח מה שלמטה מן י’ וי’ השלך מידך וכתוב אותו למטה בצד שמאל למה שכתבת כבר ויהיה חשבונך מכוון
|
- Example: you wish to multiply 7 times 9.
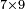
|
דמיון הנה רצונך לכפול ז’ פעמים ט’
|
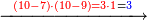 |
3 |
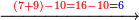 |
63
|
|
קח המרחק מן הז' עד י' דהיינו ג' והמרחק מן ט’ עד י’ דהיינו א’ ואמור ג’ פעמים א’ היינו ג’ אותו ג’ כתוב לזכרון כזה
ג
אחר כך חבור ז' על ט' ויעלה ו"א פי' י"ו השלך הי’ והו’ קח בידך וכתוב אותה בצד שמאל אצל הג’ הנשארת ויהיה כזה
גו
ששי' ושלש ועיין
|
- Another example: you wish to multiply 6 times 8.
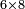
|
דמיון אחר הנה רצונך לכפול ו’ פעמים ח’
|
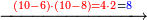 |
[8] |
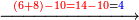 |
[48]
|
|
קח המרחק מן ו’ עד י’ דהיינו ד’ והמרחק מן ח’ היינו ב’ ואמור ב’ פעמים ד’ היינו ח’ אותו ח’ כתוב לזכרון
[ח]
אחר כך חבור ו’ על ח’ ויעלה י”ד השלך י’ וקח ד’ בידך וכתוב ד’ בצד שמאל אל ח’ אשר כתבת כבר ויעלה מ”ח היינו חשבון ח’פ’ו’ עיין ודוק
[חד]
|
- Another example: if you want to know 5 times 6 [MS Oxford 440, 115r].
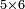
|
דמיון אחר אם תרצה לידע הפ"ו
|
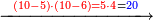 |
[20] |
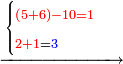 |
[30]
|
|
קח המרחק מן ה' עד י' ויהיה ה' צרפם יחד הה’ והו’ ויהיה א' השלך עשרה ונשאר לך א' צרפם 0"ב ויהיה ג' נמצא ל' ודוק
|
| Multiplication Table
|
|
- multiplication table of 1 to 9
|
והנה ארשום לך לוח מתוקנת על שער הכפל קטן כדי שתוכל לראות בקלות כל מה שתרצה בלא שום חשבון מן א' פעמים א' עד ט' פעמים ט' ודוק
|
- half multiplication table
- [MS Oxford 440, 115r; Oxford 60, 175r]
|
והחצי לוח עשיתי למצוא כל חשבון ואינך צריך הרבה כל כך
|
|
|
סליק שער כפל קטן ואז תשכיל כל אשר תעשה
|
Chapter Six: Division
|
שער החילוק
|
| Dividing a large number into a few smaller numbers
|
והוא טוב לחלק חשבון גדול לכמה חשבונות קטנים
|
|
|
ועתה ידוע תדע שאין כותבין בשער זה כמו בשער הכפל אות ראשונה משורה תחתונה נגד אות אחרונה משורה עליונה אלא כותבין שורה עליונה כפי מעלותיה ושורה תחתונה כמו כן כפי מעלותיה ויכוון אות אחרונה שבשורה תחתונה נגד אות אחרונה שבשורה עליונה
|
- The digit in the highest rank of the dividend is smaller than the digit of the highest rank of the divisor - shifting the divisor to the lower rank to the right
|
ואם אות אחרונה שבשורה תחתונה יותר מאות אחרונה שבשורה עליונה אז יסיג שורה תחתונה מעלה אחת לאחוריה אלא א"כ דאותו שורה תחתונה יש בה יותר מאות אחת
|
- The digit in the highest rank of the dividend is the same as the digit of the highest rank of the divisor and the divisor consists of one digit only - no need to shift the divisor to the lower rank to the right
|
אבל אם עלו שוות לא יסוג לאחריה אלא אם כן דאותו שורה יש בה יותר מאות אחת
|
- Shifting the divisor to the lower rank to the right and dividing the dividend by it
|
וכשיש בה יותר מאות אחת יסיג כל השורה מעלה אחת לאחוריה ואז יכול לחלק אותיות עליונה על אותיות תחתונות
|
- The place of the result of division
|
והחילוק שחילקו יכתוב נגד מעלה ראשונה שבשורה תחתונה הן אם אותו מעלה אות או גלגל
|
| All the digits of the divisor should be subtracted from the dividend the same number of times as the digit in the highest rank is subtracted
|
וכשתחלוק ב' אותיו' פי' שהיו בשורה תחתונה ב' אותיות אז אין חילוק של שתיהם רק מנין אחד יהיה ג' אותיות או ד' וכן עד סוף כל הדורות וכל כך כמה פעמים שחלקת האות האחרונה מן החשבון כן תקח כל שאר אותיות ול"ד
|
| Examples
|
ועתה אכתוב דמיונים למען יבין המבין ותן לחכם ויחכם עוד ויוסיף לקח
|
|
|
ועתה אתחיל בחילוק קטן אם ישאל השואל כמה פעמים ז' יש במאתים וי"ח
|
- [Illustration of the procedure:]
| |
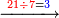 |
3 |
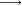 |
3 |
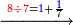 |
31
|
| 218 |
218 |
8 |
1
|
| 7 |
7 |
7 |
7
|
|
הילך היאך תעשה כתוב המאתים וי"ח כזה
|
-
|
|
|
|
והז' היה מן הדין לכתוב תחת הב' כדי לחלק הב' לז' ז' פי' למנה כמה פעמים ז' יש בב' אלא שאין הב' מגיע לחילוק של ז' לכן נסוג הז' לאחור כדי שתהא הב' במעלה שנייה לה ותעלה לנגדה עשרים ואחת כזה
|
-
|
|
|
|
ואותו עשרים ואחת תחלוק לז'ז' פי' מנה כמה פעמים ז' יש באחת ועשרים ונמצא שיש בהם ג' פעמים ז' אותו ג' כתוב למעלה על הא' שבשורה עליונה נגד ז' שבשורה התחתונה כזה
|
-
|
|
|
|
ואחר כך מחוק הא"ב שמצאת בהם ג' פעמי' ז' ואחר כך סוג הז' מעלה אחת לאחוריה ויהיה תחת הח' כזה
|
-
|
|
|
|
ומנה כמה פעמי' ז' יש בח' ולא מצאת בה רק פעם אחת ז' ועוד יש א' יותר אז כתוב א' נגד הז' על הח' כזה והאחד העודפת כתוב במקום הח' כזה
|
-
|
|
|
|
נמצא ברי"ח יש ל"א פעמים ז' וישאר אחת וכן לעולם ועיין
|
- Word problem: I have 10127 pazan(?) and I want to know how many zehuvim are they, if each [zahuv] is 15 pazan
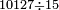
|
דמיון אחר הנה יש לי עשרת אלפים פצין ומאה ועשרים ושבע פצין ואבקש לידע כמה זהובי' יש בתוכם שכל אחד יש ט"ו פצין
|
|
|
והנה רשומיהו כזה
|
-
|
|
- [Illustration of the procedure:]
| |
 |
6 |
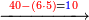 |
6
|
| 10127 |
4127 |
1127
|
| 15 |
5
|
|
והנה רשום תחת זה הז'ב'א'0'א' החשבון ה'א' ואם תכתבהו תחת הסופיים כמחוייב נמצא א' תחת א' ולא ישאר לך דבר וא"כ מאין תקח ה'פעמים א' כי כמה פעמים שתקח אות אחת כמו כן תקח חבירתה כמו שכתבתי לעיל וא"כ סוג ה'א' אחור וכתו' א' תחת גלגל וכתו' ה' תחת א' שלפני גלגל ויהיה כזה
|
-
|
|
|
|
והנה צריכין אנו לשער באם נקח הא' מהאותיות שעליו שגם יעדיף למצא הה' בעודף בחשבון הזה ואם תרצה לומר ליקח ט' פעמים מן י' א"כ לא ישאר רק אחד ותבא א' במקום גלגל ויהיה א"א ומעתה לא תוכל ליקח ט' פעמים ה' מן א"א וכן אם תקח ח' פעמים א' לא ישאר רק ב' ולא תוכל ליקח ח' פעמים ה' מן ב"א וכן אם תיקח ז' לא ישאר רק ג' ולא תוכל ליקח ז' פעמים ה' מן ג"א אלא קח ו' וישאר ד' כתוב ו' על הא' ויהיה כזה
|
-
|
|
|
|
ואז תוכל ליקח ו' פעמים ה' מן א"ד וישאר לך מן הד' שהיא א' עשרה ואם כן כתוב א' במקום הד' ומחק ה' ויהיה כזה
|
-
|
|
- [Illustration of the procedure:]
| 6 |
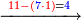 |
67 |
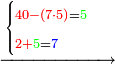 |
67
|
| 1127 |
427 |
77
|
| 15 |
5 |
|
|
ואחר כך בקשנו ליקח הא' מן החשבון הזה י' פעמים לא תוכל ליקח כמו שפירשתי וגם זה הכלל נקוט בידך לעולם לא תוכל ליקח י' רק ט' או ח' או ז' ולמטה לכן עשה כך: כתוב ה'א' תחת ב'א' כזה
|
-
|
|
|
|
וקח ז' פעמים וישאר ד' שעודף י"א על ז' ד' וכתוב ז' למעלה נגד הה' תחתונה ומחק הא' תחתונה ומחק ג"כ הא'א' עליונה וכתב תחתיהן ד' כזה
|
-
|
|
- [Illustration of the procedure:]
| 67 |
 |
675 |
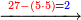 |
675
|
| 77 |
27 |
2
|
| 15 |
5 |
15
|
|
והנה קח ז' פעמים ה' מן ד' שבצידה דהיינו ל"ה וישאר ה' כי הד' היא במעלה שנייה מן הה' עולה ארבעים ועתה קח ממנה ל"ה וישאר ה' צרוף הה' אל הב' שלפניה ויהיה ז' כזה
|
-
|
|
|
|
וקח ה' פעמים א' מן ז' כי ז' פעמים לא נוכל ליקח כמו שפי' לעיל שאז לא נוכל ליקח ז' פעמים או ו' פעמים ה' ודו"ק לכן קח ה' פעמי' וכתוב למעלה ה' בצד הז' נגד ה' תחתונה ויעדיף ב' אותו ב' כתוב במקום ז' כזה
|
-
|
|
|
|
והנה קח ה' פעמי' ה' מן ז"ב וישאר ב' שאינו מגיע לחשבון הא' וצורתו כזה
|
-
|
|
|
|
נמצא מכוון שעשרת אלפים ומאה וכ"ז פצין עולה ה' זהו' וגם ת"ר זהו' ושני פצין
|
Checking Methods
|
ואם לבך מגמגם כפול העודף האחרון על ה'א' ויצא לך חשבון הראשון ששאלת
|
| The checking method of division is multiplication and the checking method of multiplication is division
|
וזהו מאזני צדק על שער החילוק נמצא כפל מברר החילוק והחילוק מברר הכפל
|
Chapter Seven: Proportions
|
שער הערכין
|
| The purpose of this chapter - deducing and estimating a thing from another thing
|
הילך שער נכבד הנקרא שער הערך אשר לכולא עלמא צריך למנות ולחשוב ולהחכים ולהשכיל ולדעת ולהבין דבר מתוך דבר ולהעריך דבר אחר דבר ולעמוד על יסודו ועל בוריו
|
- Estimating the price of a small amount of goods based on the given price of a larger amount of the same goods
|
כיצד אם לקחת מקח גדול בדמים מרובים ואתה רוצה להעריך מקח קטון לפי אותן דמים פי’ כמה מגיע מן הדמים למקח הקטון שקנית
|
- Estimating the price of a large amount of goods based on the given price of a smaller amount of the same goods
|
או להפך שקנית מקח קטון בדמים מועטים ואתה תרצה להעריך מקח גדול אחריו
|
| The procedure:
|
הילך היאך תעשה ותמנה ותעריך
|
- Calculating the price of a small amount of goods based on a given price of a larger amount of the goods:
|
תכתוב המקח הגדול וסכום הדמים מן הגדול תכתוב תחת המקח הגדול ואחר כך כתוב המקח קטון תחת הסכום
|
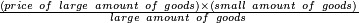
|
וכפול דמי המקח הגדול אשר כתבת למעלה אחר המקח הגדול על מניין המקח הקטון והעולה קח בידך ותחלוק אותו בשער החילוק על המקח הגדול ומה שיעלה בידך כך ערך המקח הקטן
|
- If there is a remainder - the price is represented by [an integer and] fractions
|
ואם יותר לך חלקים שלא יעלה לחלק המבוקש אז תאמר עוד נשאר לי חלקים כך וכך שסכום כך וכך עולה לחלק א' המבוקש
|
- Calculating the price of a large amount of goods based on a given price of a smaller amount of the goods:
|
ואם להיפך שאתה רוצה להעריך חשבון מקח גדול אחר חשבון מקח קטן אז כתוב חשבון הקטן למעלה ואחריו כתוב דמים הידועים לאותו מקח לחשבון הגדול כתו' למטה תחת דמיו של חשבון הקטון
|
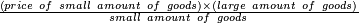
|
וכפול חשבון הגדול על דמים הידועים של מקח הקטון והעולה תחלק בשער החילוק על המקח הקטון כדלעיל
|
The writing rule of the calculation procedure:
- the given amount of goods
- its price
- the amount of goods of which the price is unknown
|
זה הכלל:
המקח אשר ידעת כתוב תחילה
ואחר כך כתוב דמיו
ואחר כך המקח אשר בקשת לידע ולהעריך ותכפול ואחר כך תעריך כמו שצויתיך
|
Word Problems
|
|
| Now I will write two or three examples so you may understand and become wise.
|
ועתה אכתוב לך ב' או ג' דמיונות כדי שתוכל להבין ולהשכיל
|
Pricing Problems - Find the Price
|
|
- A man who asks you: I bought 70 cubits of cloth for 40 dinar, how much will 55 cubits cost?
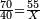
|
איש אשר ישאלך הנה קניתי ע' אמות בגד בעד מ' דינרין כמה מגיע לנ"ה אמות
|
- First write 70 cubits, then the price of the bargain, and then the 55 cubits, whose price you wish to know, as this:
|
אז תכתוב תחילה ע' אמות ואחר כך דמי המקח ואחר נ"ה אמות אשר בקשת לידע עירוכיהן כזה
|
-
|
|
- Rule of Four
- Multiply 55 by 40 and the result is 2200, as this:
|
וכפול נ"ה על מ' ועולה הוא ב' אלפים וב' מאות כזה
|
-
|
|
- Then, divide 2200 by 70, meaning, divide according to the chapter of division: how many times 70 is in it? The division is 31 times 70 and 30 smaller parts of which 70 are a whole unit, i.e. a dinar.
|
ואחר כך תחלק ב' אלפים וב' מאות לע'ע' פי' חלוק בשער החילוק כמה פעמים ע' יש בהן והחילוק הוא ל"א פעמים ע' ועוד ל' חלקים קטנים שע' מהם הם חלוק שלם דהיינו דינר
|
- We find the question that you were asked: when 70 cubits were bought for 40 dinar, how much will 55 cubits cost? [is solved by:] 31 dinar and 30 parts of which 70 are one dinar.
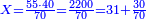 dinar dinar
|
נמצא השאלה ששואל לך כשקנה ע' אמות עבור מ' דינרין כמה מגיע לנ"ה אמות ל"א דינרין ועוד ל' חלקים שע' עושין חלק שלם שהוא דינר
|
- Check:
- If you think: where it is proven and where we are told it is so? Lest the ratio is not as you had calculated.
|
ואם תעלה על דעתך מאן מוכח ומאן לימא לן שכך הוא שמא הערך אינו כמו שחשבת
|
- Think about the 15 cubits that exceed the 55, for from 55 to 70 there are 15.

|
אז צא וחשוב ט"ו אמות העודפים על נ"ה כי מן נ"ה עד ע' יש ט"ו
|
- Evaluate: how much will 15 cubits cost, when 70 cubits are bought for 40 dinar?
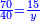
|
ותעריך כמה מגיע לט"ו אמות כשע' אמות באו עבור מ' דינרין
|
- Here is how you do it:
|
והילך היאך תעשה
|
- Write 70 cubits, then 15 cubits, as this:
|
כתוב ע' אמות ואחר כך ט"ו אמות כזה
|
-
|
|
- Rule of Four
- Multiply 15 by 40, meaning: think how much is 15 times 40? The result is 600
|
וכפול ט"ו על מ' פי' חשוב כמה ט"ו פעמים מ' ועולה ו' מאות
|
- Divide 600 to 70, meaning: count how many times 70 is in 600? The result is eight times 70 and 40 parts remain, of which 70 are a whole unit, meaning one dinar.
|
ואחר חלוק ו' מאות לע"ע פי' מנה כמה פעמים ע' יש בו' מאות ויעלה שמונה פעמים ע' ועוד ישארו מ' חלקים שע' מהם עושין חלק שלם פי' דינר אחד
|
- We find that when you buy 70 cubits for 40 dinar, 15 cubits are cost 8 dinar and 40 parts of which 70 are one dinar.
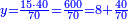 dinar dinar
|
נמצא כשקנית ע' אמות בעד מ' דינרין מגיע לט"ו אמות ח' דינרין ומ' חלקים שע' מהם עושין דינר שלם
|
- Above we calculated that 55 cost 31 dinar and 30 parts of which 70 are one dinar. Now sum the prices together: 31 dinar and 8 dinar are 39 dinar; sum the 40 parts that remain for the 15 cubits with the 30 parts that remain for the 55, they are 70, i.e. a whole dinar. Add this dinar to the 39 and they are 40. We find that 55 cubits and 15 cubits cost 40 dinar.
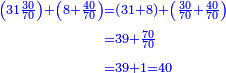
|
ולמעלה חשבנו שמגיע לנ"ה אמות ל"א דינרין ול' חלקים שע' מהם עושין דינר שלם
עתה חבור הערך יחד ל"א דינרין וח' דינרין הרי ל"ט דינרין
ומ' חלקים הנותרים בט"ו אמות ול' חלקים הנותרים בנ"ה
צרפם יחד ויהיה ע' דהיינו דינר שלם
תן אותו דינר עם הל"ט ויהיה מ'
נמצא שנ"ה אמות וט"ו אמות באו בעד מ' דינרין
|
- Sum 55 and 15, it is 70.
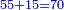
|
צרוף נ"ה וט"ו ויהיה ע'
|
- We find that now you know and understand that you calculated rightly and correctly.
|
נמצא שעכשיו אתה יודע ומבין שחשבת כדין וביושר ול"ד ע"א
|
- Another example: If a person asks you: I bought 100 barrels for 90 liṭra, how much will one barrel cost?
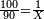
|
דמיון אחר אם ישאלך אדם הנה קניתי ק' חבית בעד צ' ליטרות כמה מגיע לחבית אחת
|
- First write 100 barrels, then their price, i.e. 90 liṭra and beneath the 90 liṭra write one barrel, like this:
|
אז כתוב תחילה ק' חבית ואחר כך דמיהם דהיינו צ' ליטרות ותחת צ' ליטרו' כתוב החבית האחד כזה
|
-
|
|
- Rule of Four
- Multiply the bottom 1 by 90 that is above it, 1 times 90, the result is 90.
|
וכפול א' התחתונה על צ' שלמעלה הימנה א' פעמים צ' יעלה צ'
|
- Then divide the 90 by 100, meaning: how many times 100 is in 90? You will not get even one time 100. On the contrary, you are missing ten and this is the price of one barrel: 90 parts of which 100 are one liṭra.
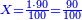
|
ואחר כך תחלק אותו צדיק לק"ק פי' כמה פעמים ק' יש בצ' ולא תשיג ידך אפי' פעם אחת ק' אדרבה חסר לך עשרה וזה הערך המגיע לחבית אחד צדיק חלקי' שק' מהן עולין ליטרו'
|
- This our teacher R. Wiesel found in another book, in these words.
|
זה מוצא מהר"ר וייזל בספר אחר וזה לשונו
|
- In my opinion there is no need for this premise, as a person does not think of dividing 90 parts of which 100 are a whole unit.
|
ולפי דעתי שאין צריך לטעם זה כי אין מחשבתו של אדם לחלק צ' חלקים שק' מהן חלק א'
|
- The premise that is more appropriate, in my opinion, in the Gentile calculations also, is as I will write below concerning the question "100 barrels for 90 liṭra, how much will one [barrel] cost?"
|
וזה הטעם ראוי יותר בעיני גם חשבונות של גוים נמי כזה שאכתוב הנה שאלת ק' חבית בעד צ' ליטרו' כמה מגיע לאחד
|
|
כתוב כזה
|
-
|
|
- Think in your mind: how many pešuṭim there are in 90 liṭra, if in one liṭra there are 20 pešuṭim?
|
חשוב בדעתך כמה פשוטים יש בצ' ליטרו' אם היה בליטר' כ' פשוטים
|
- Rule of Four
- Multiply 20 times 90, the result is 1800, as this:
|
חשוב כ' פעמים צ' ויעלה ח' מאות ואלף כזה
|
-
|
|
- Think according to the chapter of division: how many times 100 is in 1800? You will find 18 times exactly and so is the price: 18 pešuṭim for one barrel.
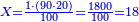
|
חשוב בשער החילוק כמה פעמים מאה יש באלף וח' מאות ותמצא י"ח פעמים מכוון כך היא החשבון י"ח פשיטי' לחבית אחד
|
- And if you have small parts remaining, say: such and such parts, of which so and so are a whole unit, meaning one pašuṭ.
|
ואם ישארו לך חלקי' קטנים אמור כך וכך חלקים שכך וכך עולה לחלק שלם פי' פשי' ודוק ע"א
|
| We wish to evaluate:
|
הנה בקשנו להעריך
|
- If a person asks: I bought 19 cubits of cloth for 13 dinar, how much will 13 cubits cost?
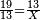
|
אם ישאל אדם קניתי י"ט אמות בגד עבור י"ג דינרין כמה מגיע לי"ג אמות
|
- Evaluate as follows:
|
אז תערוך כך
|
- First write 19 cubits, then their price, i.e. 13 dinar, then 13 cubits, like this:
|
וכתוב תחילה י"ט אמות אחר כך דמיו דהיינו י"ג דינרין ואחר כך י"ג אמות כזה
|
-
|
|
- Rule of Four
- Multiply 13 above by 13 below, meaning: calculate how much is 13 times 13, you will find that the result is 169, as this:
|
וכפול י"ג שלמעלה על י"ג שלמטה פי' מנה כמה עולה י"ג פעמים י"ג ותמצא שיעלה קס"ט כזה
|
-
|
|
- Then, divide 169 by 19, meaning: how many times 100 is in 1800? You will find that there are 8 times 19 in it and 17 parts remain, of which 19 are a whole unit.
|
ואז תחלק קס"ט לי"ט י"ט פי' כמה פעמים י"ט יש בקס"ט ותמצא שיש בו ח' פעמים י"ט ונשארו י"ז חלקים שי"ט מהן עולה חלק אחד
|
- This is the price of 13 cubits: when 19 cubits are bought for 13 dinar, 13 cubits cost 8 dinar and 17 parts, of which 19 are a whole unit, i.e. one dinar.
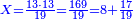 dinar dinar
|
וזה הערך המגיע לי"ג אמות כשקונין י"ט אמות בעד י"ג דינרין אז מגיע לי"ג אמו' ח' דינרין וי"ז חלקים שי"ט מהן עושין חלק שלם דהיינו דינר אחד ול"ד
|
| Likewise, if you wish to evaluate a large amount of merchandise through a small amount of merchandise, I will teach how:
|
וכן אם תרצה להעריך מקח גדול אחר מקח קטן אשכילך היאך
|
- I bought 21 cubits of cloth for 43 dinar, how much will 65 cubits cost?
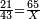
|
הנה קנית כ"א אמות מ"ג דינרין כמה מגיע לס"ה אמות
|
- First write 21 cubits, then 43 dinar, then 65 cubits that you wish to evaluate, like this:
|
כתוב בתחילה כ"א אמות ואח"כ מ"ג דינרין ואחר כך ס"ה אמות אשר בקשת לערוך כזה
|
| small amount of merchandise |
21
|
| price |
43
|
| large amount of merchandise |
65
|
|
|
| מקח קטן |
אב
|
| מעות |
גד
|
| מקח גדול |
הו
|
|
|
- Rule of Four
- Multiply 65 by 43, meaning how much is 43 times 65, the result is 2795.
|
וכפול ה"ו על ג"ד פי' כמה עולה ג"ד פעמים ה"ו ויעלה ה'ט'ז'ב'
|
- Then, divide 2795 according to the chapter of division: how many times 21 is [in it]? You find that there are 133 times 21 in it and 2 parts remain, of which 21 are a whole unit, i.e. one dinar.
|
ואחר כך חלוק ה'ט'ז'ב' בשער החילוק כמה פעמים א"ב יש ותמצא גג"א פעמים א"ב שיש בהן ועוד נשארו ב' חלקים שא"ב מהן עושין חלק שלם דהיינו דינר
|
- We find that if you bought 21 cubits for 43 dinar, 65 cubits cost 133 dinar and 2 parts, of which 21 are one dinar.
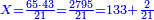
|
נמצא אם קנית א"ב אמות בעד ג"ד דינרין מגיע לה"ו אמות ג'ג'א' דינרין וב' חלקים שא"ב מהן דינר שלם
|
- Check:
- If you wish to know if you calculated correctly or not.
|
ואם תרצה לידע אם אמת חשבת אם לאו
|
- See by how much 65 exceeds 21, i.e. by 44.
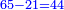
|
ראה כמה ה'ו' עולה יותר מן א'ב' היינו ד'ד'
|
- Rule of Four
- [Multiply] 44 by 43, according to the chapter of division, meaning: 43 times 44, i.e. 1892.
|
השלך ד"ד בשער הכפל על ג"ד פי' ג"ד פעמים ד"ד דהיינו ב'ט'ח'א'
|
- Then, divide it, according to the chapter of division: how many times 21 is in it? We find 90 times and 2 small parts remain, of which 21 is a whole unit.
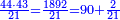
|
ואחר כך חלקהו בשער החילוק כמה פעמים שיש בהם א"ב נמצא 0"ט פעמים ועוד נשאר ב' חלקים קטנים שא"ב מהן חלק אחד
|
- Add 90 and 2 small parts to 43, i.e. the dinar for the 21 cubits, and it is 133 and 2 small parts, like this:
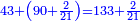
|
חבור 0"ט וב' חלקים קטנים על ג"ד דהיינו דינרין השייכי' לא"ב אמות ויהיה גג"א וב' חלקים קטנים כזה
|
-
|
|
- So, the calculation is correct.
|
והיינו כוונת החשבון ול"ד ודוק
|
Boiling Problem
|
|
- A question that is derived from this chapter on proportion:
|
שאלה היוצא משער הערך הזה
|
- You have 50 se'ah [1 se'ah = ca. 22 liter], and you say: when I boil them on fire, while boiling 7 se'ah evaporate each day, if 5 se'ah overflowed, and we reduce the heat accordingly, how much will be evaporated from the remaining 45 se'ah each day?
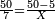 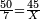
|
הנה לפניך נ' סאין ועתה שואלין אם נשפכו ה' סאין ואינו ממעטי' האור לפי זה כמה יחסרו מה' סאין הנותרות ביום אחד
|
- Here is how you do it:
|
הילך היאך תעשה
|
- First write 50 se'ah, then write 7 se'ah that evaporate each day and beneath the 7 se'ah write the remaining 45 se'ah, like this:
|
כתוב תחילה נ' סאין ואחר כך כתוב ז' סאין הנחסרים ביום אחד ותחת ז' סאין כתוב מ"ה סאין הנותרות כזה
|
-
|
|
- Rule of Four
- Multiply what is beneath by 7 that is above it, meaning, calculate: how much is 45 times 7? The result is 315.
|
וכפול מה שלמטה על ז' שלמעלה הימנה פירו' חשוב כמה עולה מ"ה פעמים ז' ויעלה שט"ו
|
- Divide it by 50, meaning, calculate: how many times 50 there are in 315? You find in it 6 times 50 and 15 parts remain, of which 50 is a whole unit.
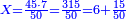
|
חלק אותו לנ'נ' פי' חשוב כמה פעמים נ' יש בשט"ו ותמצא בו ו' פעמים נ' ועוד נשארו ט"ו חלקים שנ' מהן עושה חלק שלם
|
- We find that when 50 se'ah are reduced by 7 se'ah each day, 45 se'ah are reduced by 6 se'ah and 15 parts, of which 50 are a whole unit.
|
נמצא כשנ' סאין יחסרו ז' סאין ביום אחד מ"ה סאין יחסרו ו' סאין וט"ו חלקים שנ' מהן עושה חלק שלם
|
- Another question:
|
עוד שאלה
|
- If one asks: there are 91 se'ah of water, when boiling on fire 9 se'ah evaporate each day, if we add to them 11 se'ah more, so there are now 102 se'ah and we increase the heat accordingly - since, if we would not increase the heat, the water would not evaporate according to this calculation, as the heat is not dominant much when the water is plentiful as when the water is low, hence when adding water, one should increase the heat, and if the water is reduced, one should reduce the heat - back to the question asked: how much will be evaporated from the 102 se'ah each day?
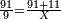 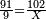
|
אם ישאל השואל הנה יש צ"א סאין מים ואם יתבשלו על האור יחסרו ביום א' ט' סאין ואם נוסיף עליהן עוד י"א סאין שיהיה הכל ק"ב סאין ואנו מרבים את האש לפי זה שאם לא היינו מרבים את האש אז לא היו המים מתמעטים וחסרים לפי חשבון זה כי האור אינו שולט כל כך כשהמים הרבה כמו שאם היו המים מעט לפיכך כשמרבים מים אז צריכי' להרבות אש או אם מתמעטים המים צריכין למעט האש נחזור לשאלה ששאלנו כמה יחסרו ק"ב סאין ביום אחד כשצ"א סאין חסירין סאין
|
- Here is how you do it:
|
הילך היאך תעשה
|
- First write 91 se'ah, then write 9 se'ah, then 102 beneath, like this:
|
כתוב תחילה צ"א סאין ואחר כך ט' סאין ולאחר כך ק"ב למטה כזה
|
-
|
|
- Rule of Four
- Multiply 102 beneath by 9 above, meaning: how much is 9 times 102? The result is 918.
|
וכפול ק"ב שלמטה על ט' שלמעלה פי' כמה ט' פעמים ק"ב ויעלה תתקי"ח
|
- Divide 918 by 91, meaning: how many times 91 there are in 918? There are 10 times 91 and 8 small parts, of which 91 is a whole unit.
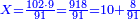
|
תחלק תתקי"ח לצ"א פי' כמה פעמים צ"א יש בתתקי"ח והיינו י' פעמים צ"א וח' חלקים קטני' שצ"א מהן עושה חלק שלם
|
- We find that when 91 [se'ah] are reduced by 9 se'ah each day, 102 [se'ah] are reduced by 10 se'ah and [8] parts, of which 91 are a whole unit.
|
נמצא כשצ"א חסרין ביום אחד ט' סאין יחסרו ק"ב י' סאין וחלקים שצ"א מהן עושה חלק שלם
|
| The checking procedure is as written above regarding the cloth.
|
והמאזנים על זה כמו שכתבתי לעיל עם הבגדים
|
| This is the rule: the [boiling] water problems are similar to the cloth [pricing] problems, therefore their checking procedure and solving method are similar.
|
זה הכלל זה השאלות עם המים כמו השאלות עם הבגד לכן יש להם מאזני צדק אחד וחשבון אחד ול"ד
|
Find a Quantity Problems - Whole from Parts
|
|
| Many sciences and problems are derived from this chapter that cannot be counted.
|
והרבה חכמות ושאלות יוצאין משער זה אשר לא יוכל הסופר לספר
|
| Now, a few of them will be explained
|
ועתה אפרש קצת מהם
|
| I start by saying:
|
ובזה אתחיל ואומר
|
- A tree - a half of it is [ingrained] in the soil, a third of it is in the water, and 5 cubits of it are up above the water, how much is the length of the whole tree?
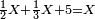
|
הנה לך אילן שחציו בארץ ושלישיו במים ומעל המים הוא גבוה ה' אמות כמה אורכה של כל האילן
|
- Here is how you do and understand the matter:
|
הילך היאך תעשה ותבין העניין
|
- Common denominator: think, which is the smallest number that is divisible into 2 parts and 3 parts? It is 6.
|
חשוב כל כך איזה חשבון הקרוב שיכולין לחלק לב' חלקים ולג' חלקים זהו ו'
|
- Subtract a half from 6, the remainder is 3. Subtract also a third, the remainder is 1.
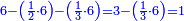
|
חסר מן ו' החצי' וישאר ג' חסר ג"כ השליש וישאר א' אותו א'
|
- Write 1 to the left of 6, and write 5 cubits beneath 1, like this:
|
כתוב בצד שמאל אצל א' כתוב ו' ותחת א' כתוב ה' אמות כזה
|
-
|
|
- Rule of Four
- Multiply 5 that is beneath 1 by 6 that is next to 1 on the top row, meaning: count how much is 5 times 6. The result is 30.
|
וכפול ה' שתחת א' על ו' אצל א' בשיטה עליונה פי' מנה כמה עולה ה' פעמים ו' והעולה הוא ל'
|
- Divide the 30 by 1, meaning: count how many times 1 there are in 30. It is a thing that is known to all that there are 30 times 1 in 30. Thus, this is the length of the tree, about which you asked: if its half is [ingrained] in the soil, a third [of it] is in the water, and 5 cubits [of it] are up above the water, how much is its length? Its length is 30 cubits, as this:
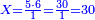
|
אותו ל' תחלק לא'א' פי' מנה כמה פעמים א' יש בל' ודבר ידוע לכל שיש בל' ל' פעמים א' וזהו אורך האילן אשר שאלת אם חציו בארץ ושליש עומד במים ומעל לארץ הוא ה' אמות ושאלת כמה ארכו הנה ארכו ל' אמות ודמיון כזה
|
-
|
|
- Check:
- If you fear that is not so, take a lance, whose length is 30 cubits.
|
ואם אתה ירא שמא אינו כך אז קח רומח שארכו ל' אמות
|
- Subtract 15 from it, which is its half, then subtract a third from it, which is ten.
- Ten and 15 are 25.
- We find that the remainder is but 5 cubits.
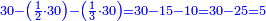
|
חסר ממנו ט"ו זהו חציו אחר כך חסר ממנו שליש זהו עשרה
עשרה וט"ו הרי כ"ה
נמצא שאין נשאר כי אם ה' אמות
|
| Another example, in order that the reader will be well taught in it and understand its virtues and profit, and it is the question asked:
|
דמיון אחר למען ירוץ הקורא בו ויבן מעלותיו וטובו והוא שאלה ששואלין
|
- A lance is embedded one third, a quarter, and one fifth in the earth, and it is 7 cubits above the earth, how much is the length of the whole lance?
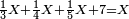
|
והנה לך רומח שעמד השליש והרביעי והחומש בארץ ולמעלה מן הארץ ארכו ז' אמות כמה ארכו של כל הרומח
|
- Common denominator: think of a number that has a third, a quarter and a fifth, that is divisible by 3, 4 and 5.
|
אז חשוב שיש בו שליש ורביעי וחומש וזהו שיכולי' לחלק לג' לד' לה'
|
- Subtract from 60 a third, which is 20.

|
חסר מן ס' שליש זהו כ'
|
- Subtract also a quarter, which is 15.

|
חסר כמו ג"כ רביעי זהו ט"ו
|
- Subtract also a fifth, which is 12.

|
חסר ג"כ החמישי והוא י"ב
|
- The total is 47.

|
סך הכל מ"ז
|
- 13 remains from the 60.
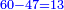
|
עוד נשאר לך מן ס' י"ג
|
- First write the remaining 13, write it next to 60 slightly far from it and beneath the 13 write 7 cubits, like this:
|
אז כתוב תחילה י"ג שנשאר לך ואת י"ג כתו' בצדו רחוק מעט ס' ותחת י"ג כתוב ז' אמות ויהיה כזה
|
-
|
|
- Rule of Four
- Multiply 7 that is beneath by 60 on the top row, meaning: count how much is 7 times 60. The result is 420.
|
כפול ז' שלמטה על ס' שבשיטה עליונה פי' חשוב ומנה כמה פעמים עולה ז' פעמים ס' ויעלה ת"ך
|
- Divide the 420 by 13, meaning: count how many 13 there are in 420. You find that there are 32 times 13 in it and 4 remain that cannot become 13, which are 4 parts, of which 13 are a whole unit.
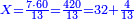
|
תחלק ת"ך לי"ג פי' חשוב כמה י"ג יש בת"ך ותמצא שיש בו ל"ב פעמים י"ג ועוד נשארו ד' שלא יכולנו לעשו' מהם י"ג והם ד' חלקים שי"ג מהן עושין חלק שלם
|
- We find that the lance that is [embedded] one third, a quarter, and one fifth in the earth, and it is 7 cubits above the earth, about which you were asked how much is the length of the whole lance? - is 32 cubits [long] and 4 parts, of which 13 is a whole unit.
|
נמצא שהרומח ששאלת בשליש וברביעי ובחומש בארץ ולמעלה מן הארץ ז' אמות ארכו וששאלת כמה אורך של כל הרומח ל"ב אמות וד' חלקים שי"ג מהן חלק שלם ודוק
|
- Another question: a wall whose base is buried 5 cubits in the ground, and it is a half, one third, and a seventh up above the ground, how much is the height of the whole wall?
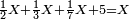
|
שאלה אחרת הנה חומה שיסודה שקוע בארץ ה' אמות ולמעלה מן הארץ היא גבוה החצי' והשליש והשביעי כמה גבהו של כל החומה
|
- Common denominator: think, which is the number that can be easily divided by 2, 3 and 7.
- Here is a way to calculate this number that is divisible by 2, 3 and7: count 7 times 3, the result is 21. 21 times two are 42. Thus, 42 is divisible by two, three and seven.
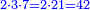
|
אז חשוב איזה חשבון שיכול לחלק לב' לג' לז' בקל לפי רגע והנה לך דרך היאך תעשה אותו חשבון המתחלק לב' לג' לז' מנה ז"פ ג' באה כ"א כ"א פעמים שנים הרי הן מ"ב הרי מ"ב מתחלק לשנים לשליש ולשביעי
|
- Or by this way and all is the same: 2 times 3 are 6; 6 times 6 are 36; and you already have a 6, so sum 6 with 36, it is 42.
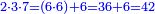
|
או כלך לדרך זו והכל אחד ב' פעמים ג' הרי ו' ו' פעמים ו' הרי ל"ו וכבר היו לך ו' צרוף ו' עם ל"ו הרי מ"ב הוא
|
- Or by this way and all is the same: calculate 2 times 3 are 6; 6 times 7 are 42.
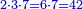
|
או נלך לדרך זו והכל אחד חשוב בפ"ג הרי ו' ו'פ"ז הרי מ"ב
|
- We find that it is 42.
|
נמצא שמ"ב הוא
|
- Finding the least common multiple: likewise, when you are asked for a thing that is divisible by seven, nine, ten, or any thing else that is divisible, always multiply this divisor by the other.
|
וכן לעולם כשישאלך דבר המתחלק לשביעי ולתשיעי ולעשירי או לכל דבר המתחלק אז כפול אותו חילוק על האחר
|
- For instance, if one asks for a thing that is divisible by ten and nine: multiply 10 by 9, meaning: count how much is 10 times 9.
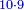
|
כגון אם שאל דבר המתחלק לעשרה ולתשעה אז כפול י' על ט' פי' מנה כמה עולה י' פעמים ט'
|
- If you are asked for a thing that is divisible by five and four, or hundreds, or thousands; or any thing that is divisible by 3, 4 and 5: first multiply 3 by 4, then multiply the result by 5; or vice versa, multiply 5 by 4, then multiply the result by 3.
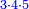
|
ואם ישאלך דבר המתחלק לחמישי ולרביעי או למאות או לאלפים או לכל דבר המתחלק לג' לד' לה' אז כפול תחילה ג' על ד' והעולה כפול על ה' או איפכה כפול ה' על ד' והעולה בידך כפול על ג'
|
- Returning to our question above: the wall that is a half, one third, and a seventh up above the ground and its base is buried 5 cubits in the ground, how much is the height of the whole wall?
|
ועתה נחזו' לשאילתינו דלעיל החומה אשר היא חצי' ושלישית ושביעית גבוה מן הקרקע ויסודה שקועה בקרקע ה' אמות כמה גובה של כל החומה
|
- We find that the thing we have asked for, which is divisible by 2, 3 and 7, is 42.
|
נמצא ששאלנו על דבר המתחלק לב' לג' לז' זהו מ"ב
|
- Now, subtract from 42 a half, which is 21.
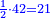
|
ועתה סור מן מ"ב החצי' זהו כ"א
|
- We subtract also a third, which is 14.

|
נסיר כמו כן השליש זהו י"ד
|
- We subtract also a seventh, which is 6.
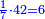
|
נסיר כמו כן השביעי' ויהיה ו'
|
- The total is 41.
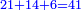
|
סך הכל מ"א
|
- 1 remains from the 42.
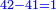
|
עוד נשאר מן מ"ב א'
|
- We find that if we would have asked for the height of a wall whose base is on the ground, the height of the whole wall would have been 42 cubits.
|
נמצא אם היינו שואלין גבוה החומה שיסודה בקרקע אז יהיה גבוה של כל החומה מ"ב אמות
|
- Now, we need to learn and evaluate how much it is for 5 cubits, meaning when it is buried 5 cubits in the ground.
|
עכשיו צריכין אנו ללמוד ולהעריך כמה מגיע לה' אמות פי' שהוא שקוע בקרקע ה' אמות
|
- Do the ratio as follows:
|
וכן עשה הערך
|
- First write one cubit, then, slightly far from it, write 42 cubits, and beneath the one cubit write the 5 cubits we have asked for, like this:
|
כתוב תחילה אמה אחת ואחר רחוק ממנו מעט כתוב מ"ב אמות תחת האמה אחת כתוב ה' אמות ששאלנו ויהיה כזה
|
-
|
|
- Rule of Four
- Multiply 5 by 42, meaning: how much is 5 times 42. The result is 210.
|
כפול ה' על מ"ב פי' כמה עולה ה' פעמים מ"ב והעולה הוא ר"י
|
- Divide 210 by 1, meaning: count how many 1 there are in 210. We find that there are 210 times 1 in it and this is the height we asked for. The image is like this:
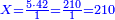
|
חלוק ר"י לא'א' פי' מנה כמה פעמים א' יש בר"י ונמצא ר"י פעמי' א' יש בתוכה לזה גבוה ששאלנו והדמיון כזה
|
-
|
|
- Another short way how you can know the height of the whole wall, when is buried 5 cubits in the ground, and it is a half, one third, and a seventh up above the ground:
|
וזה לך דרך אחר בקיצר היאך תוכל לידע גבוה של כל החומה כשהיא משוקעת בארץ ה' אמות ולמעלה מן הארץ היא גבוה החצי' והשליש והשביעי
|
- Take 2 times 5, it is 10; 10 times 3, it is 30; 30 times 7, it is 210.
|
קח ב' פעמים ה' הרי י' י' פעמים ג' הרי ל' ל' פעמים ז' הרי ר"י
|
- Or, 2 times 5, it is 10; 10 times 3, it is 30; 30 times 7, it is 210.
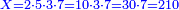
|
או כלך לדרך זה ב' פעמים ה' הרי י' י' פעמים ג' הרי ל' ל' פעמים ז' הרי ר"י ול"ד ודוק
|
Joint Purchase Problems - If You Give Me
|
|
- Another question: there is a fish to sell, and 3 people want to buy it.
- One of them said to his friends: I will give all that I have and each of you will give a half of his and the fish is paid.
- The second said: I will give all that I have and each of you will give one third.
- The third said: I will give all that I have and each of you [will give] a quarter.
- Now it is asked: for how much is the fish being sold and how much does each of them have?
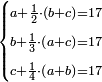
|
שאלה אחרת אם אדם אחד אמר לך הנה יש כאן דג אחד למכור והנה ג' בני אדם רוצים לקנות הדג
ואחד מהם אומר לחבירו אתן כל אשר לי וכל אחד מכם יתן החצי' ממה שלו ואז פרוע
והשני אמר אתן כל אשר לי ואתם יתנו שליש ואז יהיה פרוע
והשלישי אמר אתן כל אשר לי ואתם תנו כל אחד רביעי'
ועתה שואלין בכמה רוצין ליתן הדג או כמה מעות יש לכל אחד
|
- Answer:
- The fish is given for 17 pešuṭim
|
תשובה הדג רוצה ליתן בעד י"ז פשוטי'
|
- The first has 5 pešuṭim

|
הראשון יש לו ה' פשוטי'
|
- The second has 11 pešuṭim
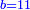
|
והשני יש לו י"א פשוטי'
|
- The third has 13 pešuṭim
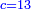
|
והשלישי יש לו י"ג פשוטי'
|
- This is for integers.
|
זהו בשלימים
|
- But, for fractions: such as if one asks when the fish is bought for 8 pešuṭim, or for 9 pešuṭim , or for 30 pešuṭim , or for 1 pašuṭ, or for whichever amount of money he wish to ask, and for that amount asked:
- One said: I will give all that I have and you will give a half of yours.
- The second said: I will give all that I have and you will give one third of yours.
- The third said: I will give all that I have and you will give a quarter of yours.
- How much does each of them have, given that this is the amount?
|
אבל בשבורי' כגון אם ישאל השואל כשהדג נקנה בעד ח' פשוטי' או בעד ט' פשוטים או ל' פשוטי' או א' פשוטי' או איזה סכום שירצה לשאול ולאותו סכום ששאל
אמר אחד אתן כל אשר לי ואתם תנו החצי' שלכם
והשני אמר אתן כל אשר לי ואתם תנו השליש שלכם
והשלישי אמר אתן כל אשר לי ואתם תנו רביעית שלכם
כמה יהיה לכל אחד ואחד שיהיה הסכום שזה
|
- Here I will write you two or three examples so you can understand everything such as that:
|
והנה אכתוב לך שנים או שלשה דמיונים כדי שתוכל להבין כל כיוצא בזה
|
- When the fish is bought for 8 pešuṭim and the first says as above and so does the second and the third
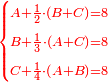
|
כשנקנה הדג בעד ח' פשוטי' ואמר הראשון כדלעיל וכן השיני וכן השלישי
|
- The first should have 2 pešuṭim and six parts, of which 17 are a whole unit.
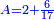
|
צריך שיהא לראשון ב' פשוטים וששה חלקים שי"ז עושין חלק שלם
|
- The second should have 5 pešuṭim and 3 parts, of which 17 are a whole unit.

|
ולשני ה' פשיטי' וג' חלק שי"ז עושין חלק שלם
|
- The third should have 6 pešuṭim and 2 parts, of which 17 are a whole unit.
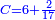
|
ולשלישי ו' פשיטי' וב' חלקים שי"ז עושין חלק שלם
|
- Now, I will show you the way, by which you will see that it is so:
|
ועתה אראה לך הדרך שתראה שכן הוא
|
- Rule of Four
- If it were in integers, the first would have had 5 pešuṭim, as explained above. Now that it is in fractions and it is asked when the fish is bought for 8 pešuṭim:
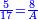
|
הנה אם היה בשלימות אז היה לראשון ה' פשוטים כמו שפרשתי לעיל
עתה שהוא בשבורים ואתה שואל כשהדג נקנה בעד ח' פשוטים
|
- You should multiply, according to the chapter of multiplication, 8 times 5, it is 40.
|
אז צריך אתה לכפול בשער הכפל ח' פעמי' ה' הרי זו מ'
|
- Then, you should divide it, according to the chapter of division: how many times 17 there are in 40? There are 2 times and six remain, which are less than 17 that are a whole unit.
|
ואחר כך צריך אתה להטותו בשער החילוק כמה פעמים י"ז יש במ' והנה יש ב' פעמים וששה עודפת שלא הגיע לי"ז שהן חלק שלם
|
- We find that the first has 2 pešuṭim and six parts, of which 17 are a whole unit.
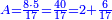
|
נמצא שיש לראשון ב' פשיטים וששה חלקים שי"ז מהן חלק שלם
|
- Now, I will show you the way [to find out] how much does the second have.
|
ועתה אראה לך הדרך כמה יש לשני
|
- Rule of Four
- If it were in integers, he would have had 11 pešuṭim. Now that it is in fractions, say as you have said for the first:
|
הנה אם היה בשלימות אז היה לו י"א פשוטי'
ועתה שהוא בשברים אז תאמר כמו שאמרת לראשון
|
- For the first you have said: "8 times 5". So, for this one say: 8 times 11, the result is 88.
|
לראשון אמרת ח' פעמים ה' כן תאמר לזה ח' פעמים י"א ויעלה פ"ח
|
- Then, divide by 17, meaning: how many times 17 there are in 88? There are 5 times 17 in it and 3 remain.
|
ואחר כך תחלק לי"ז פי' כמה פעמים י"ז יש בפ"ח והנה יש בו ה' פעמים י"ז וג' עודפת
|
- We find that the second has 2 pešuṭim and 3 parts, of which 17 are a whole unit.
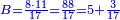
|
נמצא שיש לשני ה' פשוטי' וג' חלקים שי"ז מהן עושין חלק שלם
|
- Do the same for the third.
|
וכן תעשו לשלישי
|
- Rule of Four
- Say: if it were in integers, he would have had 13 pešuṭim. Now that it is in fractions:
|
ותאמר אם היה בשלימו' היה לו י"ג פשוטי' עכשיו שהוא בשברים
|
- Say: 8 times 13, it is 104.
|
אז תאמר לו ח' פעמי' י"ג הרי ק"ד
|
- Then, divide by 17, meaning: how many times 17 there are in 104? You find that there are 6 times 17 in it and 2 remain.
|
ואחר כך תחלק לי"ז פי' כמה פעמים י"ז יש בק"ד ותמצא בו ו' פעמים י"ז וב' עודפות
|
- We find that the third has 6 pešuṭim and 2 remain, of which 17 are a whole unit.
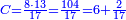
|
נמצא שיש לשלישי ו' פשיטי' וב' עודפות שי"ז מהן עושין חלק שלם
|
- If the question concerns a fish that is bought for 30 pešuṭim.
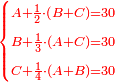
|
ואם בשאלה מדג שנקנה בעד ל' פשוטי'
|
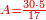
|
אז אמור ל' פעמים ה' לראשון והעולה כתיב ואחר כך תסלקהו לי"ז כמו שצויתיך
|
|
|
וכן לשני וכן לשלישי כדלעיל
|
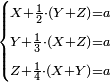

|
ועתה כתבתי לעיל שיש לראשון ה' פשיטים ולשני י"א ולשלישי י"ג בשלמים הנה אראך הדרך שתמצא שהכלל כן הוא שלכולם יש כ"ט
|
|
|
קח ג' חשבונות כשתסיר מהם החצי' והשליש והרביעית וישאר בידך ג' ואלו הן ד' ד' וחצי ו'
|
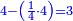
|
תסיר הרביעי מן ד' וישאר ג'
|
![\scriptstyle{\color{blue}{\left(4+\frac{1}{2}\right)-\left[\frac{1}{3}\sdot\left(4+\frac{1}{2}\right)\right]=3}}](/mediawiki/images/math/b/2/c/b2c7654e9e36456843cf38a9cefba0f9.png)
|
השליש מן ד' וחצי וישאר ג'
|
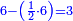
|
חצי מן ו' וישאר ג' מכל אחד ואחד וזה המורה תועי רוח בינה [5]
|
|
|
ועתה יען כי אין במורה שלימי' כי אין ד' וחצי שלם
|
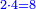
|
כפול ד' ויהיה ח'
|
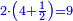
|
כפול ד' וחצי ויהיה ט'
|
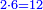
|
כפול ו' ויהיה י"ב
|
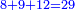
|
סך הכל כ"ט
|
|
|
ועדיין אין אנו יודעין כמה יש לכל אחד לחלקו ועתה אשכילך
|
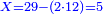
|
הסר ב' פעמים י"ב מן כ"ט וישאר ה' והוא חלקו של ראשון
|
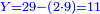
|
וכן הסר ב' פעמים ט' וישאר י"א והוא חלקו של שני
|
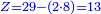
|
וכן הסר ב' פעמים ה' וישאר י"ג והוא חלוק של שלישי
|
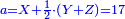
|
נמצא כשראשון יתן כל אשר לו וכל אחד מהם יתן החצי' ויהיה ס"ה י"ז נמצא שהדג נקנה בעד י"ז פשוטי' וכן כולם ודו"ק
|
|
|
וכן אם הקונים ד' או ה' עד אין קץ הרוצים לקנות הדג קח מנין השוה לכולם פי' אם קונין ג' או קח מנין כשתסיר השליש לרביעי וחצי וישאר ג' אם הקונים ד' קח מנין כשתסיר חצי' ושליש ורביעי וחומש וישאר ד' וכן לכולם כשאין המנין בשלימות כפול אותו שיהיו חשבון שלם ואחר כך כטעית החשבון שלם אם הקונין ג' תסיר ב' פעמים ואם הן ד' תסיר ג' פעמים הכפל וכן לכולם
|
|
[MS P1088: margin]
- If the buyers are four and the fourth says: I will give all that I have and you will give only a fifth
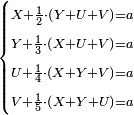
|
ואם הקוני' ד' והרביעי אומ' אתן כא"ל וכל אחד יתן רק החומש
|
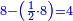
|
אז קח ד' מנינים אחר תסיר ממנו חצי וישאר ד' וזהו ח'
|
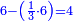
|
ואחר תסיר ממנו שליש וישאר ד' זהו ו'
|
![\scriptstyle{\color{blue}{\left(5+\frac{1}{3}\right)-\left[\frac{1}{4}\sdot\left(5+\frac{1}{3}\right)\right]=4}}](/mediawiki/images/math/2/f/8/2f8b0ce274ed2357653f5bbb5b2e2059.png)
|
ואחר תסיר ממנו רביעי וישאר ד' זהו ה' ושלישי
|
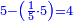
|
ואחר תסיר ממנו החומש וישאר ד' זהו ה'
|
|
|
וצריך לקח' זה החשבונות ג' פעמים ואז יהא השליש שלם
|
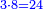
|
ועתה קח ח' ג' פעמי' זהו ד"ב
|
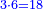
|
קח ו' ג"פ זהו ח"א
|
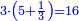
|
קח ה' ושלי' ג"פ זהו ו"א
|
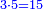
|
קח ה' ג"פ זהו ה"א
|
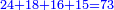
|
סך הכל ג"ז
|

|
ועתה הסר ג"פ ד"ב מג"ז וישאר א' נמצא ש[......] ראובן א'
|
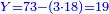
|
והסר ג"פ ח"א מג"ז וישאר ט"א זה סך שמעון
|
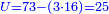
|
והסר ו"א ג"פ מג"ז וישאר ה"ב זהו סך לוי
|
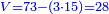
|
והסר ה"א ג"פ מג"ז וישאר ח"ב זהו סך יודא
|
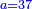
|
הכל ג"ז והדג נקנה בעד ז"ג ודוק ותמצא
|
- Question: three people - Reuven, Shimon, and Levi – are going to the market to buy something.
- Reuven said: I will give all that I have and each of you will give one third of what is in his pocket.
- Shimon said: I will give all that I have and each of you will give a sixth of what is in his pocket.
- Levi said: I will give all that I have and each of you will give a ninth of what is in his pocket
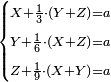
|
שאלה הנה ג' אנשים הולכים על השוק ראובן שמעון לוי ורוצים לקנות דבר
והנה ראובן אומר אתן כל אשר לי ואתם יתן כל אחד מכם שליש שבכיסו
שמעון אומר אתן כל אשר לי וכל אחד מכם יתן שישית שבכיסו
ולוי אומר אתן כל אשר לי ואתם יתן כל אחד התשיעי' שבכיסו
|
|
|
ועתה אשכילך הדרך הנה יש לך ג' אנשים ראובן שמעון לוי ראובן שאל שליש שמעון שישית לוי תשיעית נגדו כתוב ג' אותיות כנגד שאלת כזה
|
-
|
|
![\scriptstyle{\color{blue}{\left(4+\frac{1}{2}\right)-\left[\frac{1}{3}\sdot\left(4+\frac{1}{2}\right)\right]=3}}](/mediawiki/images/math/b/2/c/b2c7654e9e36456843cf38a9cefba0f9.png)
|
וקח חשבון המיעוט שתקח ממנו שליש וישאר ג' נגד בני החידה וזהו ד' וחצי וכתבו תחת ג' כזה
|
-
|
|
![\scriptstyle{\color{blue}{\left(3+\frac{3}{5}\right)-\left[\frac{1}{6}\sdot\left(3+\frac{3}{5}\right)\right]=3}}](/mediawiki/images/math/d/b/8/db875db8eb50eca9108eb5f305313319.png)
|
וקח חשבון המיעוט שתקח ממנו שישית וישאר ג' נגד בני החידה וזהו ג' וג' חומשין וכתבהו תחת ו' כזה
|
-
|
|
![\scriptstyle{\color{blue}{\left(3+\frac{3}{8}\right)-\left[\frac{1}{9}\sdot\left(3+\frac{3}{8}\right)\right]=3}}](/mediawiki/images/math/7/f/1/7f1cf2e5edc0dd92725597fe77ab6fbe.png)
|
וקח חשבון המיעוט שתקח ממנו תשיעית וישאר ג' נגד בני החידה זה ג' וג' שמינית וכתבו תחת ט' כזה
|
-
|
|
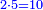
|
ועתה קח חשבון המיעוט שתמצא בו חשבון שלם נגד אותן חלקים שברים כגון חצי' עתה קח חשבון שתמצא בו חצי' שלם זהו ב' קח חשבון המעוט שתמצא חמשית שלם זהו ה' וגם קח חשבון המיעוט שתמצא בו שמינית שלם זהו ח' כפול ב' על ה' ויהיה עשרה כזה
|
-
|
|
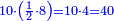
|
בזה תמצא שניהם שלם חצי שלם וחמישית שלם עתה כפול ותאמר י' פעמים ד' דהיינו חצי ח' זהו מ' כזה
|
-
|
|

|
בזה תמצא חצי שלם וחמישית שלם ושמינית שלם ובדין היה לכפול ח' עם עשרה נגד חלקים שערים דהן ג' שמינית ואז היה עולה כזה
|
-
|
|
- Least common multiple: LCM(2,5,8) = 40
|
אך היתה מוצא יותר מצרכיך כי בא תמצא החשבון כמו ב"פ ולעולם קח חשבון המועט תפשת מרובה לא תפשת תפשת מועט תפשת[6]
|
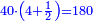
|
ועתה כפול על מ' מה שכתוב תחת כל אחד הנה מצאת תחת ראובן ד' וחצי כפול 0'ד' על ד' וחצי ויעלה כזה
|
-
|
|
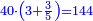
|
וכפול 0"ד על שכתוב תחת לוי דהיינו ג' וג' חומשין ויעלה כזה
|
-
|
|
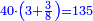
|
וכפול 0'ד' על מה שכתוב תחת שמעון דהיינו ג' וג' שמינית ויהיה כזה
|
-
|
|

|
עתה חיבור אלו ג' חשבונות יחד ויעלה כזה
|
-
|
|
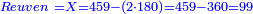
|
והוא זה המורה את החידה כפול 0'ח'א' ב' פעמים ויעלה 0'ו'ג' ונכהו מן המורה את החידה שהוא ט'ה'ד' ויותר לך ט'ט' כך מעות יש לראובן
|
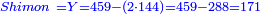
|
ואחר כך כפול ב' פעמים ד'ד'א' והוא היה כפול של שמעון ועולה ח'ח'ב' תנכהו מן המורה ויותר לך א'ז'א' כך מעות יש לשמעון
|
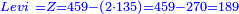
|
ואחר כך כפול ב' פעמים ה'ג'א' שהוא כפול של לוי ויעלה 0'ז'ב' תנכהו מן המורה ויותר לך ט'ח'א' כך מעות יש ללוי
|
|
|
עתה מצאת הכל לראובן ט'ט' לשמעון א'ז'א' ללוי ט'ח'א' והמבין יבין וק"ל ודוק ול"ד
|
Find a Quantity Problems - Whole from Parts
|
|
- Question: a tree - its third, its fifth, and its ninth are planted in the soil and 10 cubits remain up above the ground, how long is it?
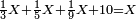
|
שאלה אילן התקוע בארץ שלישיתו וחמישיתו ותשיעתו ונותר למעלה מן הארץ עשרה אמות כמה היה תחילתו
|
|
|
והא לך דמות אשר תערוך כתוב כזה דהיינו נגד החלקים ששאלת
|
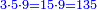
- Least common multiple: LCM(3,5,9) = 45
|
עתה שים דעתך למצא חשבון המועט שנמצא בו החלקים ששאלת שליש שלם חמישית שלם תשיעית שלם וכה תאמר ג' פעמים ה' היינו ה"א ט' פעמי' ה"א יעלה הג"א ואינך צריך כ"כ כי תמצאנה בה"ד שהוא שליש מן הג"א קח המועט ולא המרובה
|
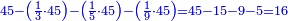
|
חסור מן ה"ד כל החלקים ששאלת דהיינו שלישית חמישית תשיעית שליש מן ה"ד זהו ה"א חמישית ט' תשיעית ה' חסור כולם מן המורה שהוא ה"ד וישאר ו'א'
|
- Rule of Four
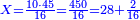
|
עתה כפול האמות הנותרים למעלה מן הארץ והם 0"א על המורה שהוא ה"ד ויעלה 0'ה'ד'
|
|
|
style="text-align:right;"עתה חלוק ממנו ו"א הנותרים בשער החילוק פי' כמה פעמים יש ו"א ב0'ה'ד' ויעלה החילוק ח'ב' וב' חלקים שו'א' עושין חלק שלם
|
|
|
style="text-align:right;"וכן כל האילן ח"ב אמות וב' חלקים שו'א' מהן עושין חלק שלם
|
- Question: a lance - one sticks a half of the whole lance in the ground, then another comes and raises a third of the whole lance, another one comes and sticks a quarter of the whole lance, and one more comes and raises a sixth of the whole lance. After lowering the high and raising the low, 11 cubits remain above the ground. How many cubits are the length of the whole lance?
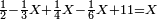
|
שאלה הנה רומח לפניך ובא אחד ותוקעו בארץ חציו של כל הרומח ובא אחד והגביה שלישיתו של כל הרומח ובא אחד ותוקעו רביעיתו של כל הרומח ובא אחד והגביה שישיתו של כל הרומח ולאחר מן הארץ הגבהה וזה הגביה הנמוך נותר למעלה מן הארץ א'א' אמות כמה אמות ארכו של כל הרומח
|
|
|
וזה לך הדרך כתוב נגד החלקים ששאלת נגד החצי' ב' נגד שליש ג' נגד רביעי' ד' נגד שישית ו' כתוב עליו א'א' אמות הנותרים כזה
|
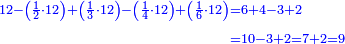
|
וקח חשבון המעט שתמצא בו אלו דהיינו ב"א וזה המורה חסר מן ב'א' חצי' וישאר ו' הוסיף שליש מן ב"א על ו' דהיינו ד' ויהיה 0"א חסר הרביעי' מן ב"א דהיינו ג' וקח אותם מן 0"א וישאר ז' הוסיף השישית של ב"א דהיינו ב' על ז' ויהיה ט' אותו ט' כתוב בצד אחר ויהיו עיניך רואות את פני מוריך [7] שהוא ב"א
|
- Rule of Four
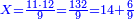
|
וכפול עליו א'א' הנותרים למעלה מן הארץ ויעלה כזה
חלוק ממנו בשער החילוק מה שנותר לך מן המורה לאחר שחסרת והוספת כל החלקים זהו ט' כמה פעמים ט' יש בה'ג'א' זהו ד"א פעמים ונותרים ו' שאינו מגיע לכלל ט' וכן אורך הרומח ד"א אמות ו' חלקים שט' מהן עושין חלק שלם דהיינו אמה
|
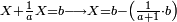
|
זה כלל כשתאמר שים שליש עליו או חמישית או רביעית או כל כמה שתרצה ויהיה כך וכך כמה היה בתחילה אראה לך הדרך אשר תלך בה לעולם חסר מן החשבון המפורש חלק אחד יותר מחשבון הנעלם שדעתך לצרף עליו
|
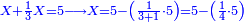
|
כגון אם תאמר עשה שליש עליו ויהיה ה' זה המפורש כמה היה בתחילה אז חסר מן הה' המפורש רביעי' זהו חלק אחד יותר ממה שבדעתך לצרף עליו כי היה בדעתך לצרף שליש וזהו רביעי' תסיר מן ה' רביעי' אז הנשא הוא המבוקש וכשתעשה עליו שליש יהיה ה'
|
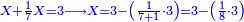
|
או אם תאמר עשה שביעית עליו ויהיה ג' זה המפורש אז הסר מן ג' המפורש שמינית ומה שנשאר הוא הסכום מה שיהיה בתחילה
|
|
|
ואם תרצה לידע אם אמת חשבת צרוף השביעית על הנשאר ויהיה ג' וכן לעולם עשה כאשר הראיתיך
|
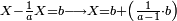
|
אבל אם ת"ל כשתקח שליש וישאר כך וכך או תקח ממנו כל מה שתרצה וישאר כך וכך כמה היה בתחילה אז תחלוק חשבון הנשאר לחלק אחת פחות ממה שחסרת ממנה וחלק אחד מן החלקים צרוף עם זה הנשאר ותמצא כמה שהיה בתחילה
|
Multiple Quantities Problems
|
|
| Multiple Quantities - Women Selling Eggs
|
|
- Pose a riddle: three women are selling eggs. One has 10 eggs, the second has 30, and the third has 50. Each of them gives a certain amount of eggs for one ḥalish and they earns the same amount of money
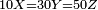
|
חוד חידה ג' נשים מוכרות ביצות לאחת יש עשרה ביצת לשנייה יש ל' בצים ולשלישי יש וכל אחת תתן סך בצים בחליש אחד כמו חברתה ויפדו מעות שוות
|
- each one will give 7 eggs for one ḥalish and what remained - one egg for 3 ḥalish
![\scriptstyle{\color{red}{\begin{cases}\scriptstyle1+\left[3\sdot\left[10-\left(1\sdot7\right)\right]\right]=1+\left[3\sdot\left(10-7\right)\right]=1+\left(3\sdot3\right)\\\scriptstyle4+\left[3\sdot\left[30-\left(4\sdot7\right)\right]\right]=4+\left[3\sdot\left(30-28\right)\right]=4+\left(3\sdot2\right)\\\scriptstyle7+\left[3\sdot\left[50-\left(7\sdot7\right)\right]\right]=7+\left[3\sdot\left(50-49\right)\right]=7+\left(3\sdot1\right)\end{cases}}}](/mediawiki/images/math/e/5/6/e56f405103a32d25d75437a6af1375fc.png)
|
תשובה כל אחת תתן ז' בחליש כל מה שנותר על השביעית תתן ביצה אחת בחליש
|
- If they are four [women]. The fourth has 70.
- the calculation is the same
|
ואם היתה ארבע לרביעי' יש לה ע' וחשבון כמו כן
|
| Multiple Quantities - Brothers Sharing an Inheritance
|
|
- Question: an inheritance was given to three brothers.
- The first took as much as he wanted, and so did the second and the third.
- Then the second and the third returned to first and complained against him: you took more than you deserved, therefore you should share with us equally.
- He answered: do not judge me, I will give each of you the same amount as he has, be it is much or less; and so he did.
- Later the first and the third returned to the second and he answered them the same as the first.
- Afterwards the first and the second returned to the third and he too said the same as the previous.
- Now the division between them became equal.
- How much did each of them took at the beginning and how much is the whole amount of the money?
|
שאלה אם נפלה ירושה לפני ג' אנשים אחים
ראשון לוקח כל מה שרוצה וכן השני וכן השלישי
ואחר כך חזרו השני והשלישי על ראשון וטוענין אותו לא נטלת מן הראוי לך לכן חלוק עמנו שוה בשוה
והוא אומר אל תדונו עמי אתן לכל אחד מכם כמה שיש לכם כבר הן רב והן מעט וכן עשה
ואחר כך חזרו הראשון והשלישי על השני והוא משיב להם ג"כ כמו הראשון
ואחר כך חזרו הראשון והשני על השלישי והוא אומר ג"כ כמו הראשונים
ואז יהיה החלוקה שוה ביניהם
חוד כמה לקח כל אחד בתחילה או כמה סך מעות ביחד
|
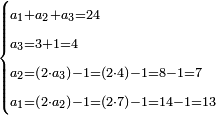
|
תשובה הכל יהיה כ"ד הראשון לקח י"ג והשני ז' והשלישי ד' והילך המורה את החידה
אם הם רק ג' אז קח לאחרון ג' ואחד יותר זהו ד'
ולאמצע קח כפלים כמו לאחרון זהו ח' רק אחת תסיר ויהיה ז'
ולראשון קח כפלים כמו לאמצע דהיינו י"ד תסיר אחד ויהיה י"ג
|
|
|
וכן לעולם כמה הן אז קח לאחרון כמניין כולם ואחד יותר ואחר כך כפול המבוקש ותסיר א'
|
- If they were four brothers
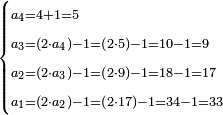
|
וכן אם הם ד' קח לאחרון ד' ואחד יותר וזה ה'
ולשלישי עשרה ואחד תסיר וזהו ט'
ולשני י"ח ואחד תסיר זהו י"ז
לראשון ל"ד ואחד תסיר זהו ל"ג בין תבין את אשר לפניך[8]
|
- Payment Problem - Digging a Hole - a worker was hired to dig a hole with a length of 17 cubits and a width of 7 cubits for 33 zehuvim (golden coins), but the worker dug [a hole with a width of] 3 cubits and a length of 17 cubits. How much should be his payment?
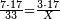
|
השוכר את הפועל לחפור בור ארוכה י"ז אמות ברוחב ז' אמות בעד ל"ג זהו' והפועל חופר ג' אמות במשוך יז' כמה שכרו של פועל זה
|
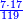
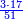
|
תשובה כפול בתחלה בשער הכפל ז' פעמים י"ז ויעלה ט'א'א' נמצא שהשוכר את הפועל לחפור קי"ט אמות ברוחב אמה בעד ל"ג זהו'
והפועל חופר ג' אמות במשוך י"ז כפול ג' על י"ז ויעלה א"ה נמצא שלא חפר רק נ"א אמות והיה לחפור קי"ט אמות
|
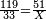
|
אחר כך כתוב קי"ט אמות למטה ממנו כתוב נ"א כזה
|
-
|
|
- Rule of Four
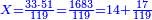
|
וכפול בשער הכפל א"ה על ג'ג' ויעלה ג"חו"א חלוק ג"חו"א לקי"ט פי' כמה פעמים קי"ט יש בגחו"א ותמצא י"ד פעמים קי"ט וי"ז חלקים שקי"ט מהן עושין חלק שלם נמצא שכר הפועל י"ד זהו' וי"ז חלקים שקי"ט מהן חלק שלם דהיינו זהוב
|
- Find a Quantity Problem - Stolen Amount of Money - a man gave his purse with some money to his friend for safekeeping and it was stolen. Both the depositor and the keeper do not know how much money was in the purse. The depositor remembers that when he counted the money by two 1 remained, by three 1 remained, by four 1 remained, by five 1 remained, by six 1 remained, and by seven nothing remained.
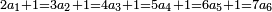
|
אדם הפקיד לחבירו כיסו מלא מעות וגנבו בפשיעה והמפקיד והנפקד אינם יודעי' סכום המעות שהיה בו אלא המפקיד זכר המעות ב'ב'ב' נשאר א' ג'ג' נשאר א' ד'ד' נשאר א' ה'ה' נשאר א' ו'ו' נשאר א' ז'ז' יצא מכוון והנה חוד כמה היו המעות הללו
|
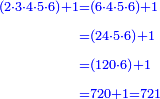
|
תשובה המעות היו אחת וג' מאות או ת'ש'כ'א' היו המעות והנה אשכילך הדרך היאך תעשה כתוב כנגד כל מניין השאלה מספר המועט שתמצא בו השאלה פי' שאילתך מניין הנמנה ב'ב' וישאר א' נגד זה כתו' ב' ושאלת מניין הנמנה ג'ג' נגדו כתו' ג' ושאלת מניין הנמנה ד'ד' נגדו כתוב ד' ושאלת מניין הנמנה ה'ה' כתוב ה' ושאלת מניין הנמנה ו'ו' כתוב ו'
אחר כך כפול ב' על ג' ויעלה ו'
כפול ו' על ד' ויעלה ד'ב'
כפול ד'ב' על ה' ויעלה 0'ב'א'
כפול 0'ב'א' על ו' ויעלה 0'ב'ז' פי' עשרים וז' מאות זהו מספר המחלק לב' לג' לד' לה' לו'
ובהוסיפך עוד אחד שיהיה אב"ז אז כשתחלקהו לב'ג'ד' ה"ו ישאר בכל מנין א' חלקהו לז'ז' יוצא מכוון
|
- If the number is divided by 2-8 with a remainder of 1 and by 9 with no remainder
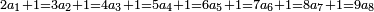
|
וכן אם ישאלך השואל מספר המחלק לב'ג"ד ה"ו ז"ח וישאר א' ובט' יוצא מכוון
|
![\scriptstyle{\color{blue}{\left[720\sdot\left(7\sdot8\right)\right]+1=\left(720\sdot56\right)+1}}](/mediawiki/images/math/4/7/7/4771f98330aab4d54b098ef66e8365c0.png)
|
אזי כפול ז' על ח' ויעלה ו"ה כפול זה על 0'ב"ז והעולה הוא מתחלק לב"ג"ד ה"ו ז"ח ובהוסיפך אחת ישאר א' בכל מניין ובט' יוצא מכוון
|
- If the remainder from division by all the numbers 2-6 is 3
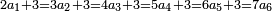
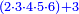
|
ואם ישאל השואל מניין הנותר ג' בכל מניינם אזי תוסיף ג' על העולה אחר כפלך מספרם המועטים
|
- If the remainder from division by all the numbers 2-6 is 4
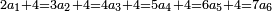
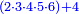
|
וכן אם ישאלך מניין הנותר ד' אזי תוסיף ד' וכן לעולם בדרך זו ודוק
|
- Find a Quantity Problem - How Much Problem - Amount of Money - we add to it its half, its third, its quarter, its fifth, and its sixth, and the total is 40. How much was the original amount of money?
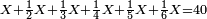
|
שאלה ממון הוספנו עליו מחציתו שלישיתו רביעיתו וחמישיתו שישיתו והכל הוא ארבעים כמה היה הממון
|
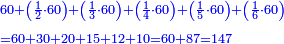
|
בתחילה אשכילך קח מספר המועט המתחלק לחצאין לשליש לרביעי לחומש לשישית וזהו 0"ו ששים ותוסיף על ששים כל החלקים ששאלת החצי' הוא ל' והשליש כ' הרביעי ט"ו והחמישית י"ב והשישית י' וצרפם הכל יחד ויהיה פ"ז חבור פ"ז עם ששים ויעלה קמ"ז נמצא אם היו שואלין אותך ממון שהוספנו עליו מחציתו שלישיתו רביעיתו חמישיתו ששיתו ובין הכל קמ"ז כמה תחילת הממון היינו משיבין תחילתו ששים
|
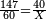
|
ועתה שהוא סך הכל רק א' כמה תחילתו אז כתוב אותו קמ"ז בטור העליון ורחוק ממנו קצת כתוב הששים ותחת ס' כתוב מ' שאנו שואלין ויהיה כזה
|
-
|
|
- Rule of Four
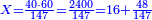
|
כפול 0"ד על 0"ו שעליה ויעלה 0'0'ד'ב' פי' כ"ד מאות חלוק בשער החילוק כמה פעמים זד"א יש בכ"ד מאות ותמצא שיש בו י"ו פעמים זד"א ונותר מ"ח חלקים קטנים שאינן עולין לזד"א נמצא שתחילת הממון היו י"ו שלמים ומ"ח חלקים קטנים שזד"א מהן חלק שלם
|
- Check:
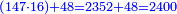
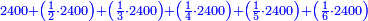
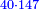
|
ואם תחפוץ לשקול חשבונך אם הוא מכוון אז כפול זד"א על י"ו פי' ב' אלפים ג' מאות נ"ב חבור עמהם מ"ח חלקים הנותרים למעלה שלא עולה לזד"א ויהיה 0'0'ד'ב' פי' כ"ד מאות
תוסיף עליהם החצי' השליש הרביעי החומש השישית וחיבור הכל עם כ"ד מאות
ואחר כך כפול 0ד פי' מ' עם זד"א
ואם תמצא מכוון מה שיעלה לך אחר שתכפול מ' על קמ"ז כמו חשבון שמצאת בהוסיפך בג"דה"ו על כ"ד מאות אז חשבונך מכוון ואם לאו ודאי טעית ודוק
|
- Divide a Quantity - Loans Repayment - Reuven and Shimon lent two loans: Reuven lent 37 zehuvim with an interest of one pašuṭ for each zahuv every week for 55 weeks. Shimon lent to the same borrower 23 zehuvim for 33 weeks. Then came the borrower and said to them: I will give both of you 13 zehuvim together and you will compromise. How much should Reuven receive and how much should Shimon receive from the 13 zehuvim?
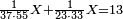
|
שאלה אם ישאל השואל הנה ראובן ושמעון הלא שני חובות ראובן הלווה ל"ז זהו' ועולה על כל זהו' פשוט לשבועה ועומד נ"ה שבועות ושמעון הלווה לאותן חוב כ"ג זהו' ועומד ל"ג שבועות ואחר כך בא הבעל חוב ואמר להם אתן לכם י"ג זהו' רבית מן הכל ואתם התפשרו התפשרו יחד
|
|
|
ואשכילך הדרך אשר תמצא בו כמה מגיע לראובן וכמה מגיע לשמעון מן הי"ג זהו' כאשר קבלתי מרבי'
|
- Reuven's interest:
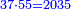
|
חשוב כמה רבית של ראובן שהוא ל"ז על נ"ה ויעלה ה"ג0"ב פשי' פירו' ב' אלפים ועוד ל"ה זה היה ריבית שהיה שייך מן הדין לראובן
|
- Shimon's interest:

|
ואחר כך כפול כ"ג זהו' של שמעון על ל"ג שבועות ויעלה ט'ה'ז' שהוא ריבית שהיה שייך מן הדין לשמעון
|
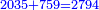
|
ואחר כך חבור ט'ה'ז' עם ה'ג'0'ב' ויעלה ד'ט'ז'ב' וזה המורה את החידה
|
- Reuven:

|
אחר כך כפול י"ג זהו' על ה"ג0"ב שהוא ריבית שהיה שייך לראובן ויעלה ה'ה'ד'ו'ב' אחר כך נכהו שהוא ד'ט'ז'ב' פי' כמה פעמים ד'ט'ז'ב' יש בה'ה'ט'ו'ב' ותמצא שיש בו ט' פעמים ונותרים עדיין ט'0'ג'א' שלא יעלה למניין ד'ט'ז'ב' נמצא שלראובן שייך מן י"ג זהו' ט' זהו' ואלף ועוד ש"ט חלקים שלא הגיע הכלל ד'ט'ז'ב'
|
- Shimon:
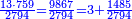
|
ואת"ל כמה מגיע לשמעון על דרך שאמרנו לראובן אז כפול י"ג על ט'ה'ז' ויעלה ז'ו'ח'ט' נכהו מן המורה שהוא ד'ט'ז'ב' פי' כמה פעמים ד'ט'ז'ב' יש בז'ו'ח'ט' נמצא שיש בו ג' פעמים ונותרים ה'ח'ד'א' חלקים שד'ט'ז'ב' מהן עושין חלק שלם דהיינו זהו' נמצא ששייך לשמעון ג' זהו' ועוד ה'ח'ד"א חלקים שד"טז"ב מהן עושין חלק שלם
|
- Check:
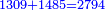
|
חיבור ה'ח'ד'א' עם ט'0'ג'א' שנותרים לראובן ויעלה ד'ט'ז'ב'
|
|
|
ואם תחפוץ לידע חשבון בצמצום אז חלק הי"ג זהו' לפשוטים ואחר כך כפול בהם ה'ה'ד'ו'ב' ריביתו של ראובן או ד"טז"ב ריביתו של שמעון ואז חלוק ד'ט'ז'ב' לחלקי פשוטים ודו"ק
|
- Multiple Quantities - Dividing a Total Weight to Several Weights - finding four weights weighing together 40, or 5 weights weighing together 121, so that you can weigh with them the heavy as well as the light up to 40. How much will each of them weigh by itself?
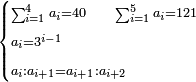
|
שאלה אם ישאלך השואל איך תמצא ארבע משקלות שמשקל כולם רק ארבעים ליטרות ואתה תוכל לשקול בו הן רב הן מעט עד ארבעים כמה משקל כל אחד בפני עצמו או אם ה' משקלות שמשקלותם קכ"א ואתה תוכל לשקול בו הן רב הן מעט כמה משקל כל אחד בפני עצמו
|
|
|
כה תעשה אם תחפוץ להוסיף משקלות: הראשון משקלו ליטרא, השני משקלו ג' ליטרות, השלישי משקלו ט' לטרי', הרביעי משקלו כ"ז לטרין, חמישי משקלו פ"א
|
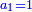
|
וככה עשה כתוב בתחילה א' משקלו של הראשון ואחר כך כתוב עוד אחת תחתיו כזה
|
-
|
|

|
חברם יחד ויהיה ב' תוסיף עוד אחת עליהן ויהיה ג' ליטרי' זהו משקל השני אחר כך כתוב ג' ועוד ג תחתיו כזה
|
-
|
|

|
חברם יחד ויהיה ח' תוסיף עוד אחת ויהיה ט' ליטרו' זהו משקל השלישי אחר כך כתוב ט' ועוד ט' אחד תחתיה כזה
|
-
|
|
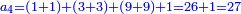
|
חברם יחד ויהיה כ"ו תוסיף עוד אחת ויהיה כ"ז זהו משקל הרביעי ואם תרצה לידע משקל החמישי כתוב זב תחת זב כדלעיל כזה
|
-
|
|
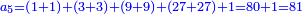
|
חברם יחד ויהיה פ' תוסיף עוד ויהיה פ"א זהו משקל חמשי
|
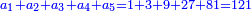
|
סך הכל קכ"א ועל דרך זה תוכל להוסיף
|
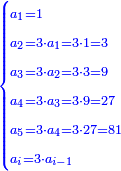
|
או כלך אצל דרך זה למשקל הראשון קח א' לשני ג' פעמי' א' לשלישי ג"פ ג' לרביעי ג' פעמים ט' לחמישי ג"פ כ"ז וכן לעולם וסימניך ושלישים על כולו פי' ג"פ וק"ל ודוק
|
- Divide a Quantity - Money - if you want to divide 5 pešiṭim to one third and one quarter so that nothing remains
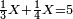
|
שאלה אם תרצה לחלוק ה' פשוטים לשליש ולרביעי ולא ישאר מהם כלום
|
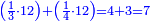
|
אמור תחילה שליש ורביעי בכמה ימצאון בי"ב השליש הוא ד' הרביעי הוא ג' חברם יחד הרי ז' וזהו המורה
|
- Rule of Four
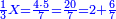
|
אם ת"ל כמה מגיע לזה שיש לו שליש שהוא ד' כפול ד' על ה' הרי 0"ב חלוק אותו ז' ותמצא בו ב' פעמים ז' ועוד ששה חלקים שז' מהם עושין חלק שלם הרי שיש לזה ב' פשוטים שלימי' ו' חלקי' שבורים שז' מהן עושין חלק שלם
|
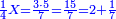
|
ומי שיש לו רביעי כפול ג' על ה' ויעלה ט"ו תחלק ממנו ז' ויעלה ב' פשוטים וחלק א' שז' מהן חלק שלם דהיינו פשוט
|
|
|
הרי שנחלקו ה' פשוטים לג' ולד' ולא נשאר מהם כלום
|
- Divide a Quantity - Money - if you have 12 and you wish to divide them to a third, a half, and a quarter, so that nothing remains
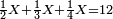
|
וכן אם בידך י"ב פשוטים ותרצה לחלקם לחצאין לשליש לרביעי ולא ישאר כלום
|
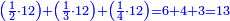
|
אמור חצי שליש ורביע אנא ימצאון בי"ב החצי ו' השליש ד' הרביע ג' צורפם יחד הרי י"ג וזהו המורה
|
- Rule of Four
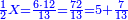
|
אחר כך כפול ו' שהיא החציה על י"ב ותמצא ב"ז חלוק כמה פעמים י"ג יש בו ותמצא ה' פעמים וז' שבורים שי"ג מהן פשוט שלם
|
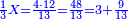
|
אחר כך כפול השליש שהוא ד' על י"ב ויעלה ח"ד חלוק ממנו י"ג ותמצא ג' ועוד ט' שבורים שי"ג מהן פשוט שלם
|
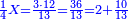
|
וכן כפול ג' על י"ב ויעלה ו"ג חלוק מהן י"ג ותמצא ב' פעמים וי' שבורים שי"ג מהן חלק שלם וכן לעולם ול"ד
|
- Find a Quantity Problem - Whole from Parts - Fish - its body weighs 10 liṭra and its tail and head weigh a third, a quarter, a fifth, and a sixth of its whole. How much is the weight of the whole [fish]?
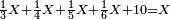
|
שאלה הרי יש לפניך דג שמשקל גופו עשרה לטרות ומשקל זנבו וראשו שלישיתו רביעיתו חמישתו שישיתו כמה כל משקלו
|
![\scriptstyle{\color{blue}{60-\left[\left(\frac{1}{3}\sdot60\right)+\left(\frac{1}{4}\sdot60\right)+\left(\frac{1}{5}\sdot60\right)+\left(\frac{1}{6}\sdot60\right)\right]=60-57=3}}](/mediawiki/images/math/a/f/0/af01839e49ad14fc9850f6d812f5b8cb.png)
|
תשובה מנה מספר המתחלק לג"ד ה"ו וזה 0'ו' כשתסיר מן 0"ו ג"דה"ו פי' שליש רביעי' חמישית שישית וצרפם יחד ויעלה ז"ה ועודף ג' וזהו המורה
|
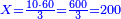
|
כפול 0"א על 0"ו ויעלה 00"ו חלוק ממנו ג' ותמצא בו מאתים פעמים ג' וכן כל משקל של דג ששאלת מאתים ליטרות
|
- Multiple Quantities - Boys Selling Cubits of a Cloth - a man gave his three sons 30 cubits of cloth to sell. One sold one cubit for 4 zehuvim, the second for 5 zehuvim, and the third for 6 zehuvim. All of them earned the same amount of money. How much money did each of them get from the sale and how many cubits did each of them sell?
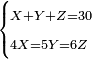
|
שאלה אדם נותן לג' בניו בגד למכור ל' אמות והאחד מכר אמה בעד ד' זהו' השני בעד ו' זהו' והג' עבור ו' זהו' וכולם מביאין מעות שוות זה כזה. חוד כמה מעות גובה מן המקח וכמה אמות מכר כל אחד
|
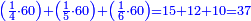
|
תשובה בתחילה אראך כמה שהיה לזה שנותן אמה בעד ד' זהו' אמור תחילה רביעית חמישית ששית בכמה ימצאון בס' רביעי' ט"ו חומש י"ב שתות י' חברם יחד ויהיה ל"ז זה המורה
|
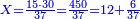
|
אחר כך כפול ט"ו שהוא רביעי' על ל' כמידת הבגד ותמצא 0'ה'ד' חלוק אותם על ל"ז ותמצא בו ב"א פעמים ל"ז וששה חלקים של"ז חלק שלם
|
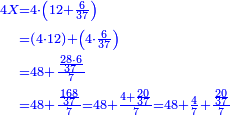
|
ואת"ל כמה מעות יש לזה שנותן אמה בעד ד' זהו' י"ב אמות היה לו וששה חלקים של"ז מהן אמה שלימה הרי י"ב פעמים ד' עולה מ"ח ומן ו' חלקים הנותרים עשה כך חלוק כל זהו' על ז' תפוחים ותאמר כך אילו היו אלו ו' חלקי ל"ז דהיינו דמיהם של בגד אמה אז היה דמיהם כ"ח תפוחים עתה שהם רק ו' כמה אז כפול ו' על כ"ח ויעלה ח'ו'א' חלוק אותם לל"ז ותמצא בו ד' פעמים ל"ז ועשרים חלקים של"ז מהן תפוח שלם נמצא שזה גובה מ"ח זהו' וד' תפוחים ועשרים חלקים של"ז מהן תפוח שלם
|
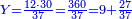
|
לדעת כמה אמות מכר זה שנתן אמה בעד ה' זהו' עשה כך כפול החומש מששים דהיינו י"ב על מנין אמות הבגד שהוא ל' ויעלה 0'ו'ג' וחלוק אותם ל"ז שהוא המורה ותמצא בו ט' פעמים דהיינו ט' אמות וכ"ז חלקים של"ז עושין אמה שלימה
|
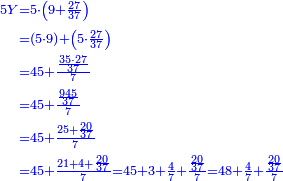
|
ואת"ל כמה מעות גבה ט' אמות היינו מ"ה זהו' וכ"ז חלקים אלו היה ל"ז היו נמכרים בעד ל"ה תפוחים כשתעריך כל זהו' בעד ז' תפוחים כדלעיל עתה שהוא רק כ"ז כמה כפול כ"ז על ל"ה ויעלה הד"ט חלוק אותם ל"ז ותמצא בו כ"ה תפוחים ועשרים חלקים של"ז עושה תפוחים שלם עשה מן כ"א תפוחים ג' זהו' וחברם יחד עם מ"ה ויהיה מ"ח ויותרו לך ד' תפוחים ועשרים חלקים של"ז תפוח שלם נמצא מעות השני כראשון
|
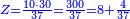
|
לדעת מעות ואמות המוכר אמה בעד ו' זהו' כפול חלק שישית מן ס' על מנין האמות דהיינו ל' ויעלה 0'0'ג' חלוק אותם ל"ז ותמצא בו ח' אמות וגם ד' חלקים של"ז מהן עושין חלק שלם
|
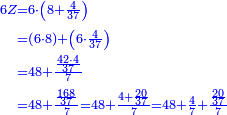
|
לדעת כמה מעותיו ח' פעמים ו' דהיינו מ"ח זהו' ד' חלקים הנותרים אילו היה ל"ז היו נמכרים בעד מ"ב תפוחים עתה שהם רק ד' בכמה כפול ד' על מ"ב ויעלה חו"א חלוק אותם ל"ז ותמצא בו ד' תפוחים ועשרים חלקים של"ז מהן תפוח שלם
|
|
|
נמצא שאין בין זה לזה במנין המעות והראשון מכר י"ב אמו' יותר ו' חלקים ושני מכר ט' אמות וכ"ז חלקים ושלישי מכר ח' אמות וד' חלקים וזהו סימנם
|
- Divide a Quantity - Amount Given by a Group of People - three friends want to donate together as a group 40 liṭra zehuvim. The first has gold that worth 3 zehuvim per liṭra, the second [has gold that] worth 5 zehuvim [per liṭra], and the third has gold that worth 8 zehuvim per liṭra. How many liter does each of them has equally?
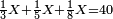
|
שאלה שלשה חברים רוצים לתת בחבורה מ' ליטרי' זהו' לראשון יש לו זהב ששוה הליטרא ג' זהו' והשני יש לו זהב ששוה הליטרא ה' זהו' ולשלישי יש לו זהב ששוה הליטרא ח' זהו' כמה יש לכל אחד ליטרין שוה בשוה
|
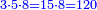
|
תשובה עשה מספר המתחלק לג'ה'ח' כפול ג' על ה' ויעלה ט"ו כפול ח' על ט"ו ויעלה ק"כ
|
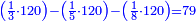
|
חסר מק"כ שליש חומש שמינית וחברם יחד ויהיה ע"ט וזה המורה
|
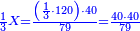
|
לדעת כמה ליטרן יש לשום זה שזה שוות ג' זהו' קח השליש מן ק"כ וזהו מ' כפול מ' על מ' מנין הליטרין ומן העולה חלוק ע"ט וכן לכולם
|
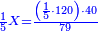
|
לשני כפול החומש מן ק"כ על מ' כבר הארכתי בעניין זה ודוק
|
- Multiple Quantities - Coins that Worth an Amount of Money - four coins are worth 40 pešuṭim: the first is equal to a half and a sixth of the second. What is left from the second equals two thirds of the third. The third is equal to a third, a quarter, and a sixth of the first. The fourth is equal to four fifths of the third. How much does each [of the coins] worth?
![\scriptstyle\begin{cases}\scriptstyle\sum_{i=1}^4 a_i =40\\\scriptstyle a_1=\left(\frac{1}{2}+\frac{1}{6}\right)\sdot a_2\\\scriptstyle a_2-\left[\left(\frac{1}{2}+\frac{1}{6}\right)\sdot a_2\right]=a_2-a_1=\frac{2}{3}a_3\\\scriptstyle a_3=\left(\frac{1}{3}+\frac{1}{4}+\frac{1}{6}\right)\sdot a_1\\\scriptstyle a_4=\frac{4}{5}\sdot{\color{red}{a_3}}\end{cases}](/mediawiki/images/math/c/1/e/c1e254f07692c6845aa08397f170e7e7.png)
|
שאלה הרי שיש לפניך ד' מטבעות ששוים מ' פשוטים
הראשונה שוה החצי והשתות מן השנייה
והנשאר מן השני הוא ב' שלישים מן השלישית
והשלישי שוה שליש ורביעית ושתות מן הראשונ'
והרביעי' שוה ד' חומשין מן השניה
לדעת כמה שוה אחד מחבירו בקיצור
|
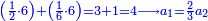
|
עשה כך הראשונה ששוה חצי' ושתות מן השניי' באיזה מספר תמצא חצי ושתות שלמים בששה החציה ג' והשתות א' הרי ד' מו' הרי כאלו אמר הראשונה ב' שלישים מן השני
|
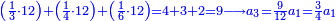
|
ושלישית ששוה שליש ורביעי ושתות מן הראשון אלו החלקים בכמה נמצאין בי"ב שליש ד' רביעית ג' שתות ב' הרי ט' מן י"ב הוי כאלו אמר השליש ג' רביעי' מן הראשון
|
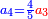
|
והד' שוה ד' חומשין מן השני אין צריך ביאור דהא מבואר היטב
|
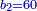
|
לדעת איך תמצא החלקים בפירוש הבן איזה חלקי' הזכרנו בשאל' חצי ושתות ובכל מקום שתמצא שתות תמצא גם שליש גם הוזכרנו רביעי' וחומש וכל אלו החלקים נמצאים בששי' נמצא מטבע שנייה ס'
|
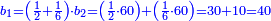
|
החצי ל' והשתות י' כללם יחד ויהיה מ' זהו' מטבע ראשונה
|
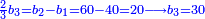
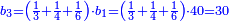
|
כמה עודף ס' על מ' כ' זהו' שאמרנו בשאלה והנשאר מן השני עודף על הראשון הוא שני שליש מן השלישי כי מטבע שלישי ל' כשתסיר גד"ו פי' שליש רביעי שתות מן מ' תמצא שלישי
|
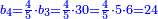
|
לדעת מטבע רביעית תחלוק לה' חלקים נמצא ל' ה' פעמי' ו' ד' חומשין מל' הרי כ"ד
|
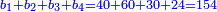
|
וזהו סידורן מ' ס' ל' כ"ד חבור אותם יחד קנ"ד וזה המורה את החידה
|
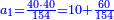
|
לדעת כמה מטבע ראשונה למלאות מנין ארבעים כפול מ' על מ' שהוא מנין המעות ומן העולה תחלוק קנ"ד ותמצא צורתו כזה פי' י' פשוטים וששים חלקים שקנ"ד מן פשוטים שלם זהו סך מטבע ראשונה
|
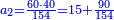
|
אחר כך כפול ס' על מ' ומן העולה חלוק קנ"ד ויהיה צורתו כזה פי' ט"ו פשוטי' וצ' חלקים שקנ"ד מן פשוט שלם זה סך מטבע שני'
|
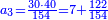
|
אחר כך כפול ל' על מ' וחלוק לקנ"ד וצורתו כזה פי' ז' פשוטי' קכ"ב חלקים שקנ"ד מהן חלק שלם זהו מטבע שלישית
|
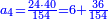
|
אחר כך כפול כ"ד על מ' ומן העולה תחלק קנ"ד וצורתו כזה פי' ו' פשוטי' ל"ו חלקים שקנ"ד מהן פשוט שלם
|
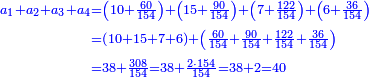
|
צרוף יחד י' וט"ו וז' ועוד ו' הרי ל"ח וצרוף יחד החלקים שתחתיהן ויעלה ח' וג' מאות היינו ב' פעמים קנ"ד וזהו ב' פשוטי' ול"ד
|
- Divide a Quantity - Boys Sharing Property of Their Father - a rich man talking to his sons, divided his assets and said to one of his sons: take from my purse one zahuv first, and then take a tithe of the remaining. To the second he said: take two zehuvim and a tithe of the remaining. To the third he said: take three zehuvim and a tithe of the remaining. And so on to all, first one zahuv more than the preceding should be taken, and then a tithe. How much is the money and how many are the sons, so that when they took according to their father's instruction each received as the other?
![\scriptstyle1+\left[\frac{1}{10}\sdot\left(X-1\right)\right]=2+\frac{1}{10}\sdot\left[X-\left[\left[1+\left[\frac{1}{10}\sdot\left(X-1\right)\right]\right]+2\right]\right]](/mediawiki/images/math/0/4/e/04ec9fa2f7109a05d7c4e8fa7ce5d879.png)
|
חידה אדם עשיר המחלק נכסיו על פיו ואמר לאחד מבניו טול מנכסי זהו' בראש ואחר כך טול המעשר מן הנותר ולשני אמר טול אתה ב' זהו' ועישור נכסי מן הנותרים ולשליש אמר טול אתה ג' ועישור נכסי' מן הנותרים וכן לכולם הוסיף ליקח זהו' יותר בראש מן הקדמון ואחר כך עישור חוד כמה המעות כמה הבני' וכשנטלו כאשר ציום אביהם הגיע לזה כזה
|
- number of sons:
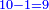
|
תשובה אמור לפי החשבון השבור שבזה הוא עשרה תפחות א' מעשרה ויהיה ט' הרי ט' היו הבנים
|
- number of zehuvim:
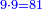
|
אמור אחר זה ט' פעמים ט' ויעלה פ"א הרי פ"א היו הזהובים
|
- number of zehuvim each one received:

|
ולכל אחד הגיע ט' זהו'
|
|
|
וכן לעולם היאך שהיה השבור שאמר לבניו ליקח אחד קח אחת פחות ועשה כמו שצויתיך ודוק
|
| Motion Problem - Pursuit
|
|
- Question: a man is walking ten miles a day. His friend is walking one mile on the first day, two miles on the second day, and so on in each day he goes on walking one mile more. In how many days will he reach the one who walks 10 miles?
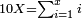
|
שאלה אדם שמהלך בכל יום י' מילין וחבירו הולך ביום ראשון מיל יום שני ב' מילין וכן בכל יום מוסיף והולך מיל בכמה ימים מגיע למהלך י' מיל
|
- Answer: sum 10 with 10, the result is 20. Subtract one and 19 remain, so he will reach his friend in 19 days.
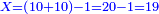
|
תשובה חבר י' עם י' ויעלה כ' חסר אחד וישאר י"ט הרי בי"ט ימים מגיע לחבירו
|
- Thus, always double the walk of the one who walks in a constant [velocity], then subtract 1 and this is [the number of] days within which he will reach him.
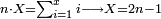
|
וכן לעולם כפול מהלכו של המהלך קביעתו והסר א' ובאלו הימים הגיעו
|
- If the second is walking 1; 3; 5; 7.
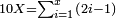
|
ואם השני מהלך א'ג'ה'ז'
|
- Subtract 10 from the walk and he will reach him in
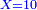 days. days.
|
תחוסר מן המהלך י' וישיגו בי' ימים
|
- If he [= the second] is walking 2; 4; 6; 8.
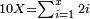
|
ואם הוא מהלך ב'ד'ו'ח'
|
- He will reach him in
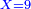 days. days.
|
ישיגו בט' ימים
|
|
|
וזה לך סימן לעולם על המהלך א'ב'ג' שתדע בקיצור כמה מילין הלך
|
- Sums - Stock of Coins - arranged in sequence: 1, 2, 3, 4, 5, 6,... → finding their sum
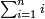
|
שאלה אם ישאלך השואל הנה צבור מעות מונחים כאן וכולן מונחים על דרך א'ב'ג'ד'ה'ו'
|
|
תבין בסוף השיטה אם סוף השיטה ט'
|
![\scriptstyle{\color{blue}{\sum_{i=1}^9 i={\color{red}{\left[\frac{1}{2}\sdot\left(9+1\right)\right]\sdot9}}=5\sdot9=45}}](/mediawiki/images/math/1/7/c/17c86b679997e03988c770bad30550d2.png)
|
אז קח אמצעית אותו שיטה שהוא חמשה ואמור ה' פעמים ט' הרי מ"ה וכך המעות מ"ה
|
|
ואם סוף השיטה י'
|
![\scriptstyle{\color{blue}{\sum_{i=1}^{10} i=\left[\left(\frac{1}{2}\sdot10\right)\sdot10\right]+\left(\frac{1}{2}\sdot10\right)=\left(5\sdot10\right)+5=50+5=55}}](/mediawiki/images/math/8/0/b/80b5dca53c99289503b8c13b342ab214.png)
|
אז קח אחת מאמצעי' השיטה ואמור ה' פעמים י' הרי זה נ' ותוסיף עוד חצי שיטה היינו ה' והיינו הכל נ"ה
|
| The rule:
|
נקט האי כללא בידך
|
![\scriptstyle n=2m\longrightarrow\sum_{k=1}^n k=\left[\left(\frac{1}{2}\sdot n\right)\sdot n\right]+\frac{1}{2}n](/mediawiki/images/math/a/8/a/a8a5babcd3a6eea49bd9b762c7395e9b.png)
|
כשסוף השיטה בזוגות אז כפול אמצעית השיטה על השיטה השלימה ותוסיף חצי השיטה
|
![\scriptstyle n=2m+1\longrightarrow\sum_{k=1}^n k=\left[\frac{1}{2}\sdot\left(n+1\right)\right]\sdot n](/mediawiki/images/math/1/e/4/1e4ea38423bb671340fbd2275e275e63.png)
|
ואם סוף השיטה בפרודות כגון ז' ט' י"א י"ג ט"ו אז כפול אמצעי השיטה על כל השיטה ואינך צריך להוסיף דבר ודוק
|
- Divide a Quantity - Sharing Food - two sat down to eat some bread. One had three loafs of bread and the second had two loafs of bread. A third came and ate with them. At the end of the meal, he went leaving five pešiṭim for the two. How should these two share the five pešiṭim?
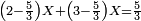
|
חידה שנים הסיבו לאכול לחם ואחד יש לו ג' ככרות והשני יש לו ב' ככרות ובא עוד שלישי ואכל עמהם ובגמר הסעודה הלך לו והניח לפני השנים ה' פשוטים חוד איך יחלקו אלו השנים הה' פשוטים
|
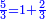
|
ודע והבין כמה מגיע לכל אחד מן הלחם צריך לומר כיכר שלם ושני שלישית
|
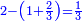
|
כמה הפסיד בעל ב' ככרות רק שליש
|
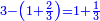
|
וכמה הפסיד בעל ג' ככרות ככר ושליש
|
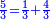
|
נמצא שנתן בעד ה' שלישיות ה' פשוטים זה נוטל ארבע פשי' וזה נוטל פשוט
|
- Multiple Quantities - Men, Women, and Children as Guests - people came to eat. Among them, there were men, women, and children. All in all 20 [people]. The host came and said to them: every man should give me three pešiṭim, every woman – two pešiṭim, and every child – a half pašuṭ, and so they did. The total amount of money [paid by] all of them together was 20. How many men, women, and children were there?
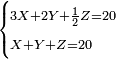
|
חוד חידה הנה באו הנה נפשות לאכול ויש ביניהם אנשים ונשים וטף וסך כולם עשרים ובא להן בעל הבית ואמר להן תנו לי איש אחד מכם ג' פשוטים ואשה ב' פשוטים ותינוק חצי פשוט וכן עשו ועלה הסך של מעות כולם עשרים פשוטים חוד כמה היו האנשים וכמה הנשים וכמה הטף
|
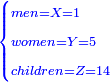
|
תשובה איש אחד חמשה נשים י"ד תינוקות ודוק
|
- Multiple Quantities - Men, Women, and Children as Guests - a hundred people came to a guesthouse and sat to eat together. Among them, there were men, women, and children. The host came and said to them: every man should give me ten pešiṭim, every woman – five pešiṭim, and every child – a half pašuṭ, and so they did. The total amount of money [paid by] all of them together was 100 pešiṭim. How many men, women, and children were there?
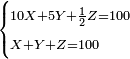
|
דרך אחר הנה באו מאה נפשות למלון אחד וישבו יחד לאכול והיה ג"כ ביניהם אנשים ונשים וטף ובא ג"כ להם בעל אושפיזין ואמר להם תנו לי כל איש עשרה פשוטי' ואשה ה' פשוט ותינוק חצי פשי' וכן עשו והיה הסך של מעות מאה פשוטי' חוד כמה היו אנשים וכמה הנשים וכמה טף
|
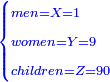
|
תשובה איש אחד ט' נשים צ' תינוקות
|
Moscow, Russian State Library, Ms. Guenzburg 714/4
|
|
|
|
שאלה הנה שוורים הרבה בזה אחר זה וב[...] זה . בכל פעם כשקניתי הראשון [.....] א' אז קניתי אותו שור של [...] בעד [...] וכן [...] אותו [...]
|
|
|
כגון הא' קניתי השור א' זהוב הב' בב' זהובי' הג' בד' וכן כולם והנה השאלה כמה כל המעות הללו בסך אחת
|
|
|
תשובה זאת ועוד אחרת דוגמא זה למצוא ולחשוב ולעמוד על בוריו תעשה בענין זה ואופן זה בתחלה תראה ותבין כמה הוא סך הראשון שקנית בו השור הראשון ואח"כ תראה ג"כ כמה הוא הסך האחרון ב' פעמים בשער הכפל גדול ותחסר ממנו בשער החיסור הסך הראשון שקנית בו השור הראשון ומה שישאר בידך כשחסרת ממנו הסך הא' הוא סכום כל המעות שקנית בהם [אלה] השוורים
|
|
|
והנה לך הדמיון כגון הראשון קנית בעד א' זהוב והשני בעד ב' והשלישי בעד ד' והרביעי בעד ח' והה' בעד י"ו והו' בעד ל"ב והז' בעד ס"ד . והנה תראה אתה שהסך האחרון שקנית בו השור הז' היינו השור האחרון הוא ס"ד זהובים א"כ תחשוב הכפול הגדול ב' פעמים ס"ד ויהיה ס"ד ויהיה קכ"ח אז החסר מן קכ"ח הסך הראשון שקנית בו השור הא' שהוא א' זהוב וישאר בידך קכ"ז זה כל כך מעות קנית [האלה] השוורים [...] מן הסך [...] הראשון [...]קא אם הסך הראשון א' שהוא [...] אם הסך הא' ב' או ג' או ד' או כמה שהוא בתחלה ת[חסר] מן הסך האחרון כשכפלת אותו ב"פ ואל תש[.]ה מעניין זה כי חשבון א' הוא ואמת
|
|
|
שאלה אם תרצה לידע ולחשוב חשבון מה שתרצה בעניין זה בכל פעם אותו חשבון שלאחריו הוא ד' פעמים כמו אותו חשבון שלפניו כגון א' ד' י"ו . ס"ד . ס"ד . רנ"ו . ותרצה לידע ולחשוב כמה הוא סך אחד . אשכילך בדרך זו הילך למען תצליח שתשכיל . והנה אראך הדרך אשר תלך בה בתחלה תראה ותבין ג"כ על הסך הראשון ועל הסך האחרון כמה הם אמנם אינו צריך לכפול סך האחרון כמו שהראיתיך לעיל . רק קח בידך כמו שתמצא אותו עתה ותחסר ממנו סך הראשון מן סך האחרון אז תוכל לחלק הנשאר בידך לג' חלקים שוים וזה קל להבין לכל בר משכיל אשר הערה את נפשו למלאכה היקרה הזאת . כי אמשול לך משל בדמיון קטן ואשכילך בו למען הבין ממנו ותראה בעיניך שתוכל לחלק הנשאר אז בידך לג' חלקים אחרי שחסרת ממנו הסך הראשון [..]
|
|
|
והנה לך הדמיון [...] [...] תראה [...] האחרון הוא רנ"ו והסך הא' הוא א' ותרצה לחשוב כל הסכומין בסך אחד אז קח הסך האחרון היינו רנ"ו ותחסר ממנו הסך הראשון היינו א' וישאר לך רנ"ה ואח"כ תחלק בשער החלוק כמה יש ברנ"ה הג' כ[.] תמצא שיצא החשבון לג' חלקים שוים ולא ישאר לך מהם כלום . אחר אשר חסרת ממנו הסך הראשון היינו א' . ואם אתה עושה כן תמצא שיש בו פ"ה פעמים ג' ברנ"ה והיינו השליש מן הרנ"ה כי פ"ה פעמים ג' היינו רנ"ה . אם כן תראה עתה שיצא החשבון בג' חלקים שוים אחרי שחסרת ממנו הסך הראשון אח"כ קח אותו השליש מן רנ"ה דהיינו פ"ה וחבר אותו אל רנ"ו כי כן היה הסך האחרון מתחלה קודם שחסרת ממנו הסך הראשון ותמצא אחר החיבור שיצא לך תר"ל (?) והיינו כל החשבון אשר חפצת לידע כי כשתחבר ביחד א' ד' י"ו ס"ד ס"ד רנ"ו יעלה לך תר"ל (?) . ותן לבך להבין ולא לשכוח בכל פעם לחסר החשבון הראשון מן סך האחרון ויצא אחר החיסור לג' חלקים שוים אח"כ תוכל ליקח [החלק] הג' היינו השליש ולחברו אל הסך [...] בתחלה [...] [...] אם הסך הראשון ב' או ג' או [...] או כמה שתרצה . תוכל בכל פעם לחסר אותו מן הסך האחרון ויצא לך הסך בכל פעם אחר החיסור לג' חלקים שוים וחבור אותו השליש לסך האחרון כמו שהיה בתחלה וזהו חשבון ודוק תם
|
|
|
אדם הלך לשוק [...] והוציא [...] פשוטים [...] [...] [...] [....] כמה היה הקרן שהוליך כמו בשוק הראשון עשה כך בעבור הראשון נצטרך להוציא החצי מן הי"ב שהוציא ובעבור השני נקח הרביעי ובעבור השלישי נקח השמינית מי"ב שהוא פשוט וחצי הסר א' פשוט וחצי מי"ב ישארו י' וחצי וכן היה הקרן שהוליך לשוק הראשון ועל זה הדרך תוכל לעשות ואם ילך לכמה שווקים כי בעבור השוק הרביעי נסיר מן הי"ב פ' שהיה מוציא בכל פעם חלק א' מי"ו ובעבור החמישי נסיר חלק א' מל"ב ובעבור השישי נסיר חלק א' מס"ד וכאשר תרבה השווקים כן תכפול מה שיש בידך ועל הכפול חלק מה שהוציא ומה שיעלה בחילוק הסר ממה שהוציא והוא המבוקש
|
|
|
אדם א' הלך לפרדס א' ללקוט תפוחים ויש לו ללקוט מהם כל כך שיתן לשוער הפנימי של הפרדס חצי התפוחים שלקט וא' יותר ולשוער השני מן השער הב' יש לו ליתן החצי מן [התפוחים הנותרים] וא' יותר וכן יש לו [...] לכל שוער החצי וא' [יותר] [...] תפוחים לא פחות ולא יותר עשה כך תפוש מספר הה' שהוא חייב להביא ותוסיף עליו א' הרי ו' כפול ו' ויהא י"ב הרי שער א' הוסיף עליו א' הרי י"ג כפול אותם ויהיו כ"ו הרי ב' שערים תוסיף עליו א' ויהיו כ"ז כפול אותם ויהיו נ"ד הרי ג' שערים תוסיף עליהם א' ויהיו נ"ה כפול אותם ויהיו ק"י הרי ד' שערים תוסיף עליהם א' ויהיו קי"א כפול אותם ויהיו רכ"ב הרי ה' שערים תוסיף עליהם א' ויהיו רכ"ג כפול אותם ויהיו תמ"ו הרי ו' שערים הרי שיש לו ללקט תמ"ו תפוחים בין הכל וישארו בידו ה' תפוחים להביא לא פיחות ולא יותר ואם יש לו ללקט מהם כל כך שיתן לשוער הפנימי החצי ממה שלקט וא' יותר ולשוער הב' חצי הנשאר וב' יותר ולשוער הג' חצי הנשאר וג' יותר ולשוער הד' חצי הנשאר וד' יותר וד' תפוחים יש לו להביא לא פחות ולא יותר ע[...] משער הד' [...] לש[...הרי שער] א' [הוסף] [עליהם א' ויהיו] י"ט כפלם ויהיו ל"ח . הרי ב' שערים הוסף עליהם ב' ויהיו מ' כפלם ויהיו פ' הרי ג' שערים הוסף עליהם א' יהיו פ"א כפלם ויהיו קס"ב הרי ד' שערים והתפוחים שלקט היו קס"ב והנשארים בידו ד' תפוחים
|
|
|
חנית מעוכה בארץ שלישיתה ורביעיתה ולמעלה מן הארץ היא פ' אמה כמה אמות היא בין כולה עשה כך תמצא מספר שיש לו שליש ורביע והוא י"ב ושליש ורביע מי"ב הוא ז' והוא התחוב בארץ ולמעלה מן הארץ נשאר ה' אם כך אמור כך אם ה' שווה י"ב כמה ישוה כ' כפול אותם כ"פ י"ב יעלו ר"מ חלקם על ה' יעלו מ"ח בחלוק א"כ אורך החנית מ"ח אמות
|
Reuven hired Shimon to build him a house in 30 days - for a day working in construction he will earn 9 liṭra, and for an unemployment day he will lose 4 liṭra. At the end of 30 days he did not earn or lose. How many days did he work and how many days he did not work?
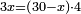
|
ראובן שכר שמעון שיבנה לו בית א' בל' יום והיום שיעבוד בבנין ירויח ג' ליט' והיום שלא יעבוד יפסיד ד' ליט' ובסוף ל' יום לא הרויח ולא הפסיד כלום כמה ימים עבד וכמה ימים לא עבד
|
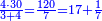
|
[י"ב ימים חלקים של ז' והם הימים שלא עבד בה ואחר הכפיל ד"פ ל' ויעלו ק"כ חלקם עם ז' ויעלו י"ז יום וחלק א' מז' ביום]
|
|
|
עשה כך אין ספק כי מה שירויח בד' ימים לחשבון ג' ליט' [ליום] יפסיד בג' ימים לחשבון ד' ליט' ל[...] [...] וכן ימים עבד [...]
|
If for a day working in building the house he will earn 36 pešuṭim, for an unemployment day he will lose 41 pešuṭim and at the end of 30 days he did not earn or lose
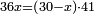
|
ואם יאמר כי היום שיעבוד בבית ירויח ל"ו פשוט והיום שלא יעבוד יפסיד מ"א פשוטים ובסוף ל' יום לא הרויח ולא הפסיד כלום
|
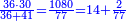
|
עשה כך אין ספק כי מה שירויח במ"א יום לחשבון ל"ו פשוטים ליום יפסיד בל"ו יום לחשבון מ"א פשוטים ליום תחבר ל"ו עם מ"א יעלו ע"ז כפול ל"ו פעמים ל' יהיו לך י"ד יום שלמים יעלה לך אלף ופ' חלקם על ע"ז ויעלו בחלוק י"ד יום שלם וב' חלקים מע"ז ביום וכך ימים לא עבד בבית
|
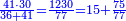
|
ועוד כפול מ"א פעמים ל' ויעלה אלף ור"ל חלקם על ע"ז ויעלו בחלוק ט"ו ימים שלמים וע"ה חלקים מע"ז ביום
|
- Divide a Quantity - Sharing Food
Two men sat down to eat. One had two loafs of bread and the second had three loafs of bread. A third came and ate with them. [The three ate the five loafs of bread and after they ate and drank, the third who came to eat with them gave five pešiṭim for the two. How should they share the five pešiṭim]?
![\scriptstyle\left[\left(2-\frac{5}{3}\right)\sdot X\right]+\left[\left(3-\frac{5}{3}\right)\sdot X\right]=5](/mediawiki/images/math/b/3/9/b39a89f5f9f01ae578ff87165913ffb8.png)
|
ב' אנשים היו יושבין לאכול לאחד היו ב' לחמים ולשני ג' לחמים בא אדם שלישי ואכל עמהם וא[.] ליתן של[...] אלו [...] לפשוט לאמרו שאכלו [...] [...]ם [...] חלק מכל לחם אכל כל א' מהם א' לחם וב' שלישיות מלחם א"כ אותו שהיו לו ב' לחמים ואכל א' לחם וב' שלישיות לא הפסיד כי אם שליש לחם ואותו שהיו לו ג' לחמים ואכל א' לחם וב' שלישיות הפסיד א' לחם ושליש שהם ד' שלישיות לחם א"כ אותו שהיו לו ב' לחמים יקח א' פשוט כי הפסיד שליש לחם ואותו שהיו לו ג' לחמים יקח ד' פשוטים כי הפסיד לחם א' ושליש שהם ד' שלישי לחם
|
- Motion Problem - To and From - an Ant Climbing a Tower
A tower is 20 cubits tall. An ant wants to climb up. Every day it climbs up one third of a cubit and every night it goes down a quarter of a cubit. How much further up it moves each day and in how many days it will reach to the top?
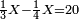
|
מגדל שהוא גבוה כ' אמה ונמלה א' רוצה לעלות למעלה ובכל יום עולה שליש אמה ובכל לילה יורדה רביע אמה כמה יתרון יש לה בכל יום ובכמה ימים תעלה למעלה
|
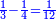
|
אמור תחלה כמה הוא יותר השליש מן הרביע א' חלק מי"ב
|
|
|
הרי שבי"ב ימים היא עולה א' אמה
|
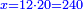
|
ובעבור שהמגדל היא גבוה כ' אמות אמור י"ב פעמים כ' הרי ר"מ הרי שבר"מ ימים היא עולה לראש המגדל
|
|
You have some money. You take a third, a quarter, and a fifth of it and their sum is nine. How much remains?
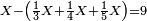
|
הרי שיש לך מעות והוצאת מהם השליש והרביע והחומש והחומש והם ט' פשוטים כמה יהיו הנשארים
|
|
|
אמור [מ]כלם שליש ורביע וחומש ימצאו בס' השליש הוא כ' ה[רביע] הוא [ט"ו] החומש הוא י"ב וכללם יהיו מ"ז הרי שה[...] חלקים מס' נמצא שהנשאר [...] ולכן אמור אם מ"ז חלקים מס' שוים ט' פשוטים י"ג חלקים מס' כמה שוים אמור י"ג פעמים ט' הם קי"ז חלקם במ"ז יבואו (ב' ו)כ"ג חלקים ממ"ז נמצא שהיו בכיס י"א פשוטים וכ"ג חלקים ממ"ז ומה שהוציא הוא ט' ומה שנשאר היו ב' וכ"ג חלקים ממ"ז וכן לכל חשבון שתרצה
|
| A man has a jug with maximum capacity of 8 cups of wine and he wants to divide its content between two people, giving each 4 cups, but he has only two jars – one with a maximum capacity of 3 cups and the other [with a maximum capacity of] 5 [cups]. How will he divide it, giving each 4 [cups]?
|
אדם א' יש לו קנקן שמחזיק ח' כוסות של יין ורוצה לחלקו לשני אנשים וליתן לכל א' ד' כוסות ואין לו רק שני כלים שהא' מחזיק ג' כוסות וא' ה' היאך יעשה לחלק אותם וליתן ד' לכל א'
|
- Filling the small jar [3 cups] and pouring its content to the medium jar [5 cups]
- 3 cups - medium jar
5 cups - large jug
|
תחלה ימלא הכלי שמחזיק ג' כוסות וישים אותם בתוך הכלי המחזיק ה'
|
- Filling the small jar once more, pouring its content to the medium jar until it is full
- 1 cup - small jar
5 cups - medium jar
[2 cups - large jug]
|
ואח"כ ימלא פעם אחר הכלי המחזיק ג' ויריק כמו כן באותו הכלי המחזיק ה' הרי שהכלי המחזיק ה' מלא ונשאר בכלי המחזיק ג' כוס א'
|
- Pouring the content of the medium jar to the large jug [8 cups]
- 1 cup - small jar
[7] cups - large jug
|
אח"כ יריק הכלי מלא של ה' כוסות בתוך הקנקן המחזיק ח' ונמצא שבתוך הקנקן גדול יש בו ה' כוסות ובכלי המחזיק ג' יש בו כוס א'
|
- Pouring the content of the small jar [1 cup] to the medium jar, then filling the small jar once again from the large jug and pouring the content of the small jar [3 cup] to the medium jar
- 4 cups - medium jar
4 cups - large jug
|
אח"כ יריק הכלי של ג' כוסות שיש בו מהם א' בתוך הכלי המחזיק [ה'] [...] וימלא הכלי המחזיק ג' מתוך הכלי המחזיק ח' ויריק בתוך הכלי המחזיק ה' ונמצא עכשיו ד' כוסות בתוך הכלי המחזיק ח' וד' כוסות בתוך הכלי המחזיק ה' ועם זה היין חלוק בשוה
|
- Joint Purchase Problem - If You Give Me - Amounts of Money
- Three friend, one said to his two friends: know that all I have in my purse with a half of what the both of you have is 60. The second answers and says: all I have in my purse and a quarter of what the both of you have is 60. The third answers: all I have in my purse and a third of what the both of you have is 60.
![\scriptstyle\begin{cases}\scriptstyle X+\left[\frac{1}{2}\sdot\left(Y+Z\right)\right]=60\\\scriptstyle Y+\left[\frac{1}{4}\sdot\left(X+Z\right)\right]=60\\\scriptstyle Z+\left[\frac{1}{3}\sdot\left(X+Y\right)\right]=60\end{cases}](/mediawiki/images/math/f/7/e/f7ed4efec08d6ecaa27c9fc465bdae6d.png)
|
שלשה חברים היו ואמר הא' לשני חבריו דעו כי כל מה שבכיסי והחצי משניכם עולה ס' ויען השני ויאמר כל מה שבכיסי ורביע משניכם עולה ס' ויען השלישי כל מה שבכיסי ושליש משניכם עולה ס'
|
- False Position: we found 3 numbers - 5, 11 and 13, which are a sort of [an answer to] this question.
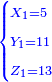
|
מצאנו ג' מספרים והם ה' י"א וי"ג שהם כעין השאלה הזאת
|
- For, 5 says to 11 and 13: me and a half of both of you is 17.
- 11 says to 5 and 13: me and a third of both of you is 17.
- 13 says to 5 and 11: me and a quarter of you is 17.
![\scriptstyle{\color{blue}{\begin{cases}\scriptstyle X_1+\left[\frac{1}{2}\sdot\left(Y_1+Z_1\right)\right]=17\\\scriptstyle Y_1+\left[\frac{1}{4}\sdot\left(X_1+Z_1\right)\right]=17\\\scriptstyle Z_1+\left[\frac{1}{3}\sdot\left(X_1+Y_1\right)\right]=17\end{cases}}}](/mediawiki/images/math/9/7/d/97d57b8ac4e8a9dbe8f698d6b961bdee.png)
|
כי ה' אומר לי"א ולי"ג אני וחצי שניכם י"ז
וי"א אומר לה' ולי"ג אני ושליש שניכם י"ז
וי"ג אומר לה' ולי"א אני ורביע שניכם י"ז
|
- Rule of Four: you see that if they would have said: "the sum of all three of us is 17", the first would have 5, the second 11 and the third 13.
|
והנך רואה שאלו אמרו מחובר שלשתנו י"ז יהיה לא' ה' ולשני י"א ולשלישי י"ג
|
- Now, that they say: "the sum of all three of us together is 60", we turn to the ratios and say:
|
ועכשיו שאמרו מחובר שלשתנו יחד ס' נשוב לערכים ונאמר
|
- As the ratio of 5 to 17 so is the ratio of the smaller to 60, i.e. the one who asked a half of his friends.
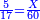
|
כערך ה' לי"ז כן ערך הקטן אל ס' הוא ששאל לחבריו החצי
|
- As the ratio of 11 to 17 so is the ratio of the second to 60, i.e. the one who asked a third of his friends.
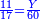
|
וכערך י"א לי"ז כן ערך השני לס' והוא ששאל לחבריו השליש
|
- As the ratio of 13 to 17 so is the ratio of the greater to 60, i.e. the one who asked a quarter of his friends.
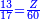
|
וכערך י"ג לי"ז כן ערך הגדול אל ס' [והוא] ששאל לחביריו הרביע
|
|
|
וכן תערוך לכל הס' [...]הם תשים המורה [...] וי"ג ודרך הערכים הוא [...]
|
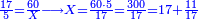
|
אמור אם בעת שהמחובר הוא י"ז יהיה חלק הקטן ה' בהיות המחובר ס' כמה הם חלקיו אמור ספ"ה הוא ש' וחלקם בי"ז יהיו י"ז וי"א חלקים מי"ז
|
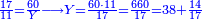
|
ולדעת החלק האמצעי אמור אם בעת שהמחובר הוא י"ז שוה חלק האמצעי י"א בהיות המחובר ס' כמה הם חלקו אמור ס"פ י"א הם תר"ס חלקם בי"ז יהיו ל"ח וי"ד חלקים מי"ז
|
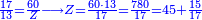
|
ולדעת חלקי הגדול אמור אם בעת שהמחובר הוא י"ז יהיה החלק הגדול י"ג בהיות המחובר ס' כמה יהיה חלקו אמור ס"פ י"ג תש"פ חלקם בי"ז יהיו מ"ה וט"ו חלקים מי"ז
|
- Check:
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle X+\left[\frac{1}{2}\sdot\left(Y+Z\right)\right]&\scriptstyle=\left(17+\frac{11}{17}\right)+\left[\frac{1}{2}\sdot\left[\left(38+\frac{14}{17}\right)+\left(45+\frac{15}{17}\right)\right]\right]\\&\scriptstyle=\left(17+\frac{11}{17}\right)+\left(19+\frac{7}{17}\right)+\left(22+\frac{16}{17}\right)=60\\\end{align}}}](/mediawiki/images/math/1/1/5/1151c1953e5eeefb1128f4a9ae687afb.png)
|
ויהיה סדר הענין כך אומר הקטן אני שאני י"ז וי"א חלקים וחצי האמצעי שהם י"ט וז' חלקים מי"ז וחצי הגדול שהם כ"ב וי"ו חלקים מי"ז מחובר שלשתם ס'
|
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle Y+\left[\frac{1}{3}\sdot\left(X+Z\right)\right]&\scriptstyle=\left(38+\frac{14}{17}\right)+\left[\frac{1}{3}\sdot\left[\left(17+\frac{11}{17}\right)+\left(45+\frac{15}{17}\right)\right]\right]\\&\scriptstyle=\left(38+\frac{14}{17}\right)+\left(5+\frac{15}{17}\right)+\left(15+\frac{5}{17}\right)=60\\\end{align}}}](/mediawiki/images/math/8/c/5/8c51fcde67c49f9f297096f4fcd9e029.png)
|
ואומר האמצעי אני שאני ל"ח וי"ד חלקים מי"ז ושליש הקטן שהם ה' וט"ו חלקים מי"ז ושליש הגדול שהם ט"ו וה' חלקים מי"ז מחובר שלשתנו ס'
|
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle Z+\left[\frac{1}{4}\sdot\left(X+Y\right)\right]&\scriptstyle=\left(45+\frac{15}{17}\right)+\left[\frac{1}{4}\sdot\left[\left(17+\frac{11}{17}\right)+\left(38+\frac{14}{17}\right)\right]\right]\\&\scriptstyle=\left(45+\frac{15}{17}\right)+\left(4+\frac{7}{17}\right)+\left(9+\frac{12}{17}\right)=60\\\end{align}}}](/mediawiki/images/math/5/a/2/5a2cd999d16458b3c413355c1586917a.png)
|
ואומר הגדול אני שאני מ"ה וט"ו חלקים מי"ז ורביע הקטן שהוא ד' וז' חלקים מי"ז ורביע האמצעי שהוא ט' וי"ב חלקים מי"ז מחובר שלושתנו עולה ס'
|
| Jacob divided [a certain amount] between his three sons. The share of Reuven was greater than the share of Shimon and the share of Shimon was greater than the share of Levi. Reuven gave his two brothers from his shares as much as their shares, Shimon gave his brothers also as much as their shares and Levi gave his brothers also as much as their shares, then the shares of the three were equal. How much was the [original] share of each?
|
שאלה יעקב חלק לבניו [ג'] והיה חלק ראובן גדול [משל שמעון וחלק] שמעון גדול משל לוי נתן ראובן לשני אחיו מחלקו כפי מה שהיה חלקם ושמעון גם הוא נתן לאחיו כפי חלקם ולוי גם כן נתן לאחיו כפי חלקם ואז נמצא חלק שלשתם שוה כמה היה חלק כל א' מהם
|
|
|
אמור כי חלק הראשון היה ד' וחלק השני ז' וחלק השלישי י"ג ונמצא בסוף חלקם שוה והיה ח' פשוטים לכל א' כיצד דרך משל חלק ראובן היה י"ג וחלק שמעון ז' וחלק לוי ד' והנה התחיל ראובן ונתן מחלקו לשמעון ז' כפי שהיה לו וללוי ד' ושנים נשאר בידו ואח"כ שמעון שעכשיו היה לו י"ד נתן ללוי ח' כפי מה שהיה בידו ולראובן ב' כפי מה שהיה עכשיו בידו ואח"כ לוי שעכשיו היה לו י"ו נתן מאלו לראובן ד' ונמצא שיש לו ח' וד' לשמעון ועם זה נמצא שביד כולם יש ח' פשוט' וחלקם שוה
|
| A man said: here are two baskets of figs in each there are 100 figs, the fine are [sold at a rate of] 20 for one pašuṭ, the defective are [sold at a rate of] 30 for one pašuṭ. Their total price is 8 pešuṭim and one third.
|
אדם א' אמר הנה שני כלכלות של תאנים ובכל א' יש ק תאנים משל היפות כ' לפשוט והרעות ל' לפשוט עולה חשבונם ח' פשוטים ושליש בא א' [לקצוב] ואמר היאך אתה מוכר אמר מאלו אתן לך ל' ומאלו כ' השיב הקונה אם כן תן לי מאלו ומאלו ב' בב' פשוטים ונתן הכל בח' פשוטים [...]
|
|
|
אדם שכר שכיר לל' יום בשכר [...] פשוט לכל יום והיה צריך לפרוע מידי יום ביום ולא היה לו כי אם ששה מטבעות ששוויים בין הכל ל' פשוטים ועכשיו שואלים מה יהיה שווי המטבעות כדי שיוכל לפרוע מידי יום ביומו
|
|
|
תשובה שיווי המטבעות צריך להיות כזה א' ב' ג' ד' ח' י"ב
|
- A man had a wolf, a goat, and a cabbage, and he had to move them across the water. He had nothing but a small boat that could contain only the person and one more thing. If he will leave the goat and the cabbage and move the wolf the goat will eat the cabbage, if he will move the cabbage and leave the wolf with the goat the wolf will eat the goat
|
אדם היה לו זאב ועז וכרוב והיה לו לעבור מעבר מים ולא היה כי אם ספינה קטנה מאד שאינה מחזיק כי אם האדם ודבר אחד ולא יותר
ואם תניח העז והכרוב ויעביר הזאב העז אכל הכרוב
ואם הכרוב יעביר הכרוב ויניח הזאב אצל העז הזאב יאכל העז
וכמו כן אם יעביר הא' ויחזור ליקח השני להעביר בעוד שיבא ליקח א' יאכל א' חבירו ואם כן כיצד יעשה
|
- He should move first the goat, leaving the wolf and the cabbage, then move the cabbage and bring the goat back with him, then he should move the wolf to the other side and go back to move the goat with him to the other side
|
תחלה יעביר העז ויניח הזאב והכרוב
ואחר יעביר הכרוב ויחזור להעביר העז עמו למקום הראשון
ויעביר הזאב לעבר האחר ויחזור להעביר העז עמו לעבר הא' ויעביר הכרוב ויניח העז ואחר יחזור ליקח העז
|
- Joint Purchase Problem - "If You Give Me"
- Reuven told Shimon: if you will give me one thousand zehuvim my amount will be equal to your amount of money.
Shimon answered Reuven: if you will give me one thousand zehuvim my money will be double your amount of money.
How much money did each of them have?
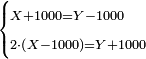
|
ראובן אמר לשמעון אם אתה נותן לי אלף זהובים יעלה הקרן שלי כסכום מעותיך
ושמעון משיב לראובן ואם אתה נותן לי אלף זהובים אני אכפול מעותי לסכום מעותיך
כמה מעות יש לכל אחד
|
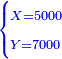
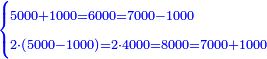
|
תשובה ראובן יש לו ה' אלפים זהובים ושמעון יש לו ז' אלפים
וזה פי' ראובן שואל לשמעון אלף זהובים ואם שמעון יתן לו נשאר ביד שמעון ו' אלפים וראובן שהיה לו ה' אלפים תחלה עכשיו עם האלף שנותן לו שמעון יש לו ו' אלפים נמצא שלכל א' יש להם ו' אלפים
ושמעון אומר לראובן אם אתה תתן לי אלף זהובים נמצא שישאר ביד ראובן ד' אלפים והקרן של שמעון שהיה ז' אלפים נמצא עכשיו עולה לסכום ח' אלפים והיינו הכפל ממה שנשאר ביד ראובן
|
![\scriptstyle\xrightarrow{{\color{red}{\left[4+4+\left[11-\left(4+4\right)\right]\right]-10}}={\color{blue}{1}}}](/mediawiki/images/math/3/f/a/3faacadf1089c902d319654aa049b711.png)
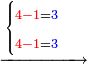
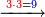
![\scriptstyle\xrightarrow{{\color{red}{9-\left[11-\left(4+4\right)\right]}}={\color{blue}{6}}}](/mediawiki/images/math/2/1/1/211ec1ed49b06c80e5f87cd6b93c9500.png)
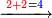
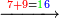

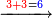
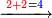
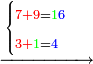
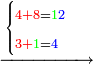
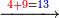
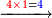
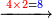
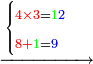
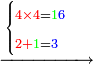
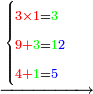
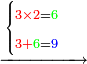
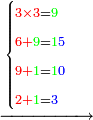
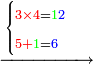
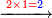
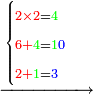
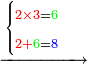
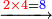
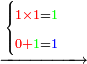
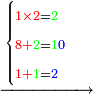
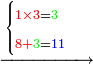
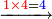
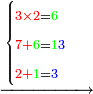
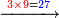
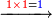
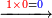
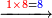
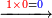
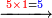
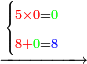
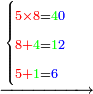
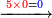
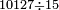 → Check:
→ Check: 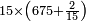
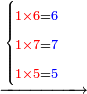
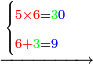

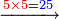

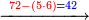
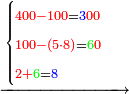

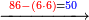


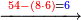
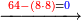
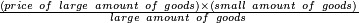
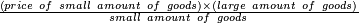
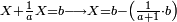
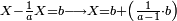
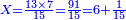
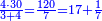
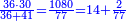
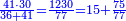
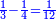
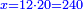
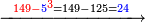
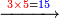
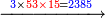
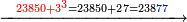

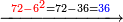
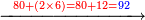
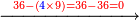
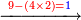
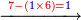
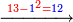
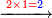
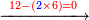
![\scriptstyle{\color{red}{x,y<10\quad x\sdot y=\left[10\sdot\left[\left(x+y\right)-10\right]\right]+\left[\left[x-\left[\left(x+y\right)-10\right]\right]\sdot\left[y-\left[\left(x+y\right)-10\right]\right]\right]}}](/mediawiki/images/math/9/4/f/94f68b3edd7a5de8373da91368968ab4.png)
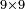
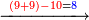
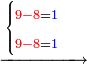

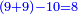

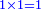
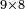
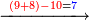
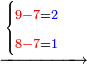
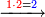
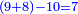


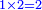
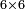
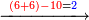

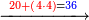
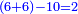

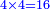
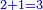
![\scriptstyle{\color{red}{x,y<10\quad x\sdot y=\left[10\sdot\left[\left(x+y\right)-10\right]\right]+\left[\left(10-y\right)\sdot\left(10-x\right)\right]}}](/mediawiki/images/math/b/a/4/ba47b3ce6e602ae8b4e44a762172704c.png)



![\scriptstyle{\color{red}{x<y<10\quad x\sdot y=\left(x\sdot10\right)-\left[x\sdot\left(10-y\right)\right]}}](/mediawiki/images/math/3/7/9/379821fa6258d1d24574dbe3c30f6dca.png)
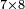
![\scriptstyle{\color{blue}{7\times8=\left(7\sdot10\right)-\left[7\sdot\left(10-8\right)\right]=70-\left(7\sdot2\right)=70-14=56}}](/mediawiki/images/math/c/f/8/cf82d668175564f785f54108257ef5e3.png)



![\scriptstyle{\color{red}{x+y<10\quad x\sdot y=10+\left[\left(x-1\right)\sdot\left(y-1\right)\right]-\left[11\left(x+y\right)\right]}}](/mediawiki/images/math/d/e/b/deb3a15bab1027d790aee3e499ce8951.png)
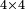
![\scriptstyle{\color{blue}{4+4+\left[11-\left(4+4\right)\right]=4+4+3=11}}](/mediawiki/images/math/b/4/2/b42c664ab942373f7f7104da31b46a3d.png)
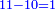
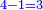


![\scriptstyle{\color{red}{x+y<10\quad x\sdot y=\left[\left(10-y\right)\sdot\left(10-x\right)\right]-\left[10\sdot\left[10-\left(x+y\right)\right]\right]}}](/mediawiki/images/math/f/a/5/fa50d116d61f078f4565958da778fb21.png)
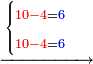
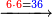
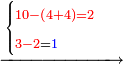
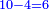

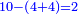
![\scriptstyle{\color{red}{x+y<10\quad x\sdot y=\left[\left(10-y\right)\sdot\left(10-x\right)\right]+\left[10\sdot\left(x+y\right)\right]-\left(10\sdot10\right)}}](/mediawiki/images/math/0/0/9/009964355db1dd5f0f49cfb6586fc299.png)
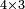
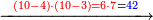
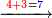
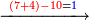
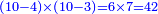
![\scriptstyle{\color{red}{x,y<10\quad x\sdot y=\left[\left(10-y\right)\sdot\left(10-x\right)\right]+\left[10\sdot\left[\left(x+y\right)-10\right]\right]}}](/mediawiki/images/math/0/a/6/0a68457b8baa2872f5fd92e1bf4d30a1.png)
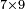
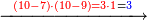
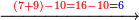
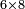
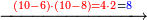
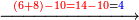
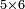
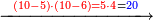

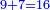
 :
: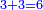
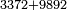



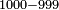
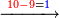
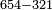
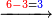
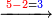
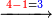
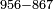
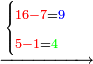
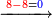
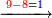
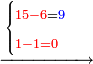
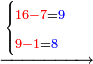
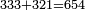
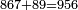
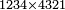
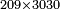
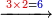
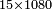
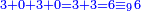
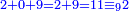
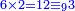

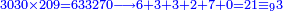
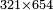
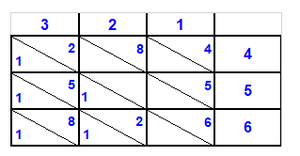
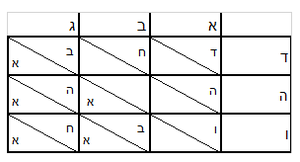
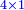


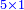


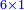


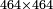
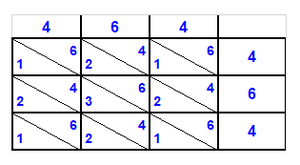
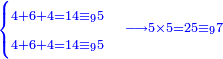
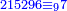
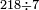
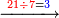
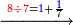

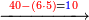
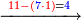
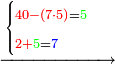

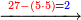
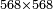 → Check:
→ Check: 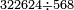
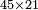 → Check:
→ Check: 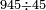

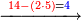

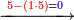
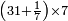
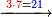
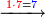
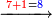
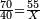
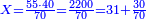 dinar
dinar
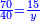
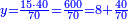 dinar
dinar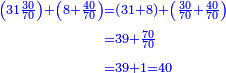
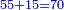
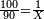
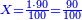
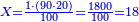
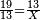
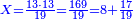 dinar
dinar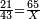
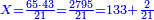
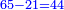
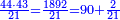
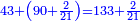
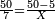
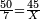
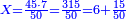
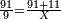
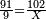
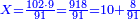
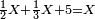
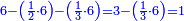
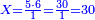
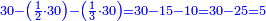
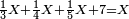




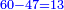
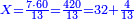
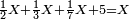
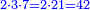
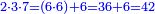
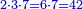
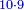
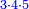
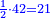

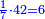
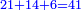
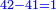
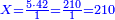
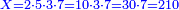
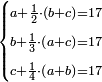

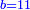
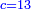
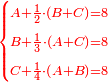
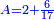

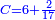
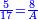
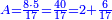
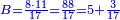
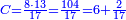
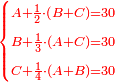
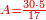
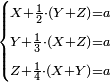

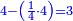
![\scriptstyle{\color{blue}{\left(4+\frac{1}{2}\right)-\left[\frac{1}{3}\sdot\left(4+\frac{1}{2}\right)\right]=3}}](/mediawiki/images/math/b/2/c/b2c7654e9e36456843cf38a9cefba0f9.png)
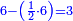
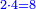
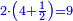
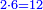
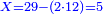
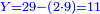
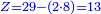
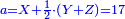
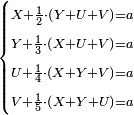
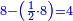
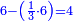
![\scriptstyle{\color{blue}{\left(5+\frac{1}{3}\right)-\left[\frac{1}{4}\sdot\left(5+\frac{1}{3}\right)\right]=4}}](/mediawiki/images/math/2/f/8/2f8b0ce274ed2357653f5bbb5b2e2059.png)
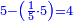
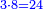
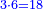
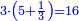
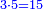
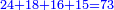

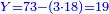
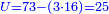
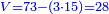
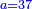
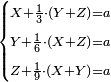
![\scriptstyle{\color{blue}{\left(3+\frac{3}{5}\right)-\left[\frac{1}{6}\sdot\left(3+\frac{3}{5}\right)\right]=3}}](/mediawiki/images/math/d/b/8/db875db8eb50eca9108eb5f305313319.png)
![\scriptstyle{\color{blue}{\left(3+\frac{3}{8}\right)-\left[\frac{1}{9}\sdot\left(3+\frac{3}{8}\right)\right]=3}}](/mediawiki/images/math/7/f/1/7f1cf2e5edc0dd92725597fe77ab6fbe.png)
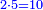
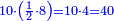

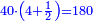
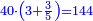
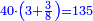

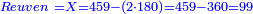
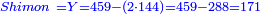
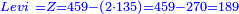
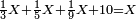
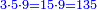
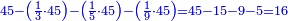
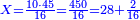
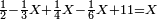
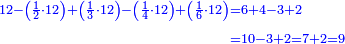
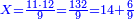
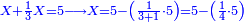
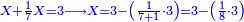
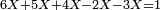

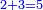
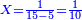
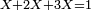

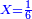
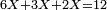
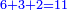
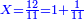
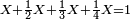
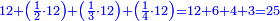
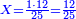
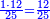
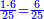
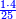
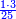
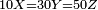
![\scriptstyle{\color{red}{\begin{cases}\scriptstyle1+\left[3\sdot\left[10-\left(1\sdot7\right)\right]\right]=1+\left[3\sdot\left(10-7\right)\right]=1+\left(3\sdot3\right)\\\scriptstyle4+\left[3\sdot\left[30-\left(4\sdot7\right)\right]\right]=4+\left[3\sdot\left(30-28\right)\right]=4+\left(3\sdot2\right)\\\scriptstyle7+\left[3\sdot\left[50-\left(7\sdot7\right)\right]\right]=7+\left[3\sdot\left(50-49\right)\right]=7+\left(3\sdot1\right)\end{cases}}}](/mediawiki/images/math/e/5/6/e56f405103a32d25d75437a6af1375fc.png)
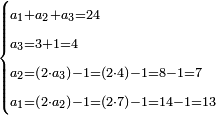
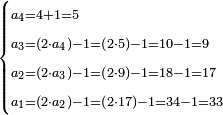
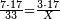
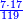
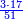
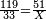
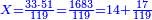
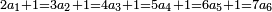
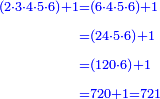
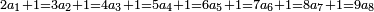
![\scriptstyle{\color{blue}{\left[720\sdot\left(7\sdot8\right)\right]+1=\left(720\sdot56\right)+1}}](/mediawiki/images/math/4/7/7/4771f98330aab4d54b098ef66e8365c0.png)
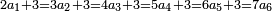
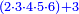
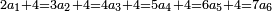
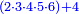
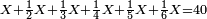
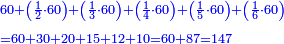
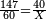
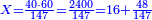
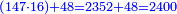
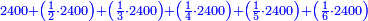
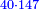
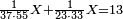
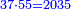

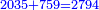

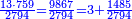
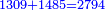
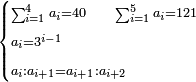
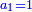


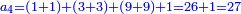
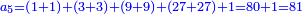
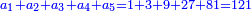
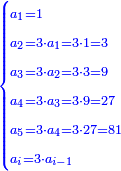
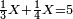
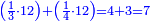
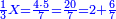
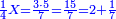
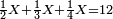
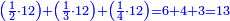
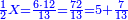
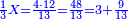
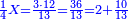
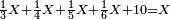
![\scriptstyle{\color{blue}{60-\left[\left(\frac{1}{3}\sdot60\right)+\left(\frac{1}{4}\sdot60\right)+\left(\frac{1}{5}\sdot60\right)+\left(\frac{1}{6}\sdot60\right)\right]=60-57=3}}](/mediawiki/images/math/a/f/0/af01839e49ad14fc9850f6d812f5b8cb.png)
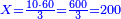
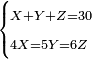
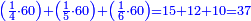
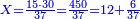
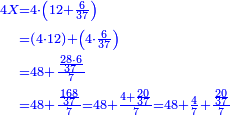
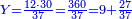
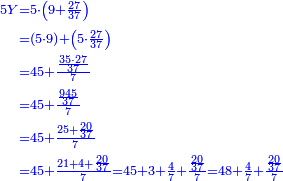
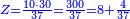
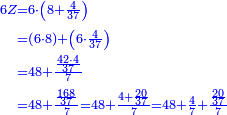
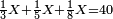
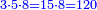
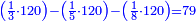
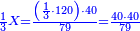
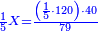
![\scriptstyle\begin{cases}\scriptstyle\sum_{i=1}^4 a_i =40\\\scriptstyle a_1=\left(\frac{1}{2}+\frac{1}{6}\right)\sdot a_2\\\scriptstyle a_2-\left[\left(\frac{1}{2}+\frac{1}{6}\right)\sdot a_2\right]=a_2-a_1=\frac{2}{3}a_3\\\scriptstyle a_3=\left(\frac{1}{3}+\frac{1}{4}+\frac{1}{6}\right)\sdot a_1\\\scriptstyle a_4=\frac{4}{5}\sdot{\color{red}{a_3}}\end{cases}](/mediawiki/images/math/c/1/e/c1e254f07692c6845aa08397f170e7e7.png)
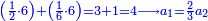
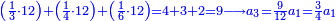
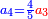
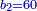
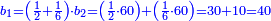
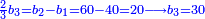
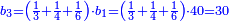
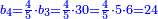
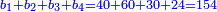
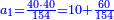
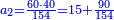
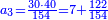
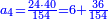
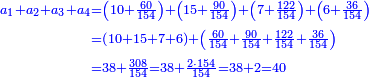
![\scriptstyle1+\left[\frac{1}{10}\sdot\left(X-1\right)\right]=2+\frac{1}{10}\sdot\left[X-\left[\left[1+\left[\frac{1}{10}\sdot\left(X-1\right)\right]\right]+2\right]\right]](/mediawiki/images/math/0/4/e/04ec9fa2f7109a05d7c4e8fa7ce5d879.png)
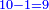
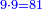

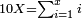
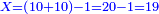
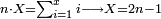
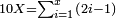
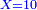 days.
days.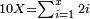
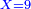 days.
days.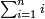
![\scriptstyle{\color{blue}{\sum_{i=1}^9 i={\color{red}{\left[\frac{1}{2}\sdot\left(9+1\right)\right]\sdot9}}=5\sdot9=45}}](/mediawiki/images/math/1/7/c/17c86b679997e03988c770bad30550d2.png)
![\scriptstyle{\color{blue}{\sum_{i=1}^{10} i=\left[\left(\frac{1}{2}\sdot10\right)\sdot10\right]+\left(\frac{1}{2}\sdot10\right)=\left(5\sdot10\right)+5=50+5=55}}](/mediawiki/images/math/8/0/b/80b5dca53c99289503b8c13b342ab214.png)
![\scriptstyle n=2m\longrightarrow\sum_{k=1}^n k=\left[\left(\frac{1}{2}\sdot n\right)\sdot n\right]+\frac{1}{2}n](/mediawiki/images/math/a/8/a/a8a5babcd3a6eea49bd9b762c7395e9b.png)
![\scriptstyle n=2m+1\longrightarrow\sum_{k=1}^n k=\left[\frac{1}{2}\sdot\left(n+1\right)\right]\sdot n](/mediawiki/images/math/1/e/4/1e4ea38423bb671340fbd2275e275e63.png)
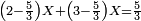
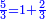
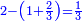
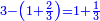
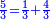
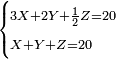
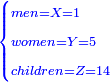
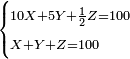
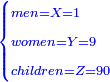
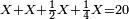
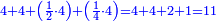
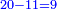
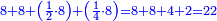

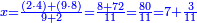
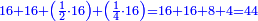

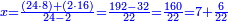
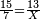
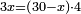
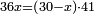
![\scriptstyle\left[\left(2-\frac{5}{3}\right)\sdot X\right]+\left[\left(3-\frac{5}{3}\right)\sdot X\right]=5](/mediawiki/images/math/b/3/9/b39a89f5f9f01ae578ff87165913ffb8.png)
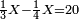
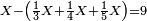
![\scriptstyle\begin{cases}\scriptstyle X+\left[\frac{1}{2}\sdot\left(Y+Z\right)\right]=60\\\scriptstyle Y+\left[\frac{1}{4}\sdot\left(X+Z\right)\right]=60\\\scriptstyle Z+\left[\frac{1}{3}\sdot\left(X+Y\right)\right]=60\end{cases}](/mediawiki/images/math/f/7/e/f7ed4efec08d6ecaa27c9fc465bdae6d.png)
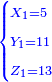
![\scriptstyle{\color{blue}{\begin{cases}\scriptstyle X_1+\left[\frac{1}{2}\sdot\left(Y_1+Z_1\right)\right]=17\\\scriptstyle Y_1+\left[\frac{1}{4}\sdot\left(X_1+Z_1\right)\right]=17\\\scriptstyle Z_1+\left[\frac{1}{3}\sdot\left(X_1+Y_1\right)\right]=17\end{cases}}}](/mediawiki/images/math/9/7/d/97d57b8ac4e8a9dbe8f698d6b961bdee.png)
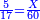
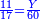
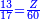
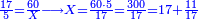
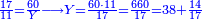
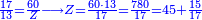
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle X+\left[\frac{1}{2}\sdot\left(Y+Z\right)\right]&\scriptstyle=\left(17+\frac{11}{17}\right)+\left[\frac{1}{2}\sdot\left[\left(38+\frac{14}{17}\right)+\left(45+\frac{15}{17}\right)\right]\right]\\&\scriptstyle=\left(17+\frac{11}{17}\right)+\left(19+\frac{7}{17}\right)+\left(22+\frac{16}{17}\right)=60\\\end{align}}}](/mediawiki/images/math/1/1/5/1151c1953e5eeefb1128f4a9ae687afb.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle Y+\left[\frac{1}{3}\sdot\left(X+Z\right)\right]&\scriptstyle=\left(38+\frac{14}{17}\right)+\left[\frac{1}{3}\sdot\left[\left(17+\frac{11}{17}\right)+\left(45+\frac{15}{17}\right)\right]\right]\\&\scriptstyle=\left(38+\frac{14}{17}\right)+\left(5+\frac{15}{17}\right)+\left(15+\frac{5}{17}\right)=60\\\end{align}}}](/mediawiki/images/math/8/c/5/8c51fcde67c49f9f297096f4fcd9e029.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle Z+\left[\frac{1}{4}\sdot\left(X+Y\right)\right]&\scriptstyle=\left(45+\frac{15}{17}\right)+\left[\frac{1}{4}\sdot\left[\left(17+\frac{11}{17}\right)+\left(38+\frac{14}{17}\right)\right]\right]\\&\scriptstyle=\left(45+\frac{15}{17}\right)+\left(4+\frac{7}{17}\right)+\left(9+\frac{12}{17}\right)=60\\\end{align}}}](/mediawiki/images/math/5/a/2/5a2cd999d16458b3c413355c1586917a.png)
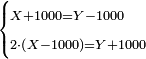
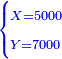
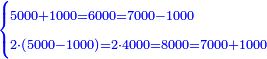
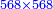

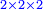
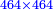

![\scriptstyle{\color{blue}{\sqrt[3]{149721291}}}](/mediawiki/images/math/2/8/8/28889c07ec72df83ee96c8d036f89e7d.png)

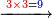


![\scriptstyle{\color{blue}{\sqrt[3]{99897344}}}](/mediawiki/images/math/7/3/e/73e3d56a32f3f45e418253824810fdba.png)
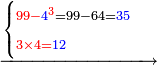
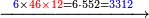
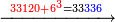

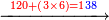
![\scriptstyle\xrightarrow{{\color{red}{\left[\left[4\times\left(464\times138\right)\right]\sdot10\right]+4^3}}={\color{blue}{2561344}}}](/mediawiki/images/math/9/8/5/98577a9d90a199749f7fe8e04eebab1f.png)