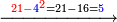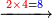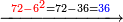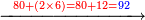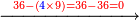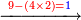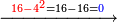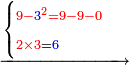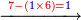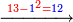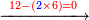Difference between revisions of "ספר ציפרא"
(→Chapter Six: Division) |
(→Chapter Six: Division) |
||
| Line 3,068: | Line 3,068: | ||
|- | |- | ||
| | | | ||
| − | :{| | + | ::<span style=color:red>[Illustration of the procedure:]</span> |
| + | ::{| | ||
|- | |- | ||
| ||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{10-\left({\color{blue}{6}}\sdot1\right)}}={\color{blue}{4}}}</math>|| <span style="color:#0000FF>6</span>  ||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{40-\left(6\sdot5\right)}}={\color{blue}{1}}{\color{red}{0}}}</math>|| 6   | | ||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{10-\left({\color{blue}{6}}\sdot1\right)}}={\color{blue}{4}}}</math>|| <span style="color:#0000FF>6</span>  ||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{40-\left(6\sdot5\right)}}={\color{blue}{1}}{\color{red}{0}}}</math>|| 6   | ||
| Line 3,164: | Line 3,165: | ||
|- | |- | ||
| | | | ||
| − | :{| | + | ::<span style=color:red>[Illustration of the procedure:]</span> |
| + | ::{| | ||
|- | |- | ||
| 6  ||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{11-\left({\color{blue}{7}}\sdot1\right)}}={\color{blue}{4}}}</math>||6<span style="color:#0000FF>7</span> ||rowspan="3"|<math>\scriptstyle\xrightarrow{\begin{cases}\scriptstyle{\color{red}{40-\left(7\sdot5\right)}}={\color{green}{5}}\\\scriptstyle{\color{red}{2+}}{\color{green}{5}}={\color{blue}{7}}\end{cases}}</math>||67  | | 6  ||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{11-\left({\color{blue}{7}}\sdot1\right)}}={\color{blue}{4}}}</math>||6<span style="color:#0000FF>7</span> ||rowspan="3"|<math>\scriptstyle\xrightarrow{\begin{cases}\scriptstyle{\color{red}{40-\left(7\sdot5\right)}}={\color{green}{5}}\\\scriptstyle{\color{red}{2+}}{\color{green}{5}}={\color{blue}{7}}\end{cases}}</math>||67  | ||
| Line 3,236: | Line 3,238: | ||
|- | |- | ||
| | | | ||
| − | :{| | + | ::<span style=color:red>[Illustration of the procedure:]</span> |
| + | ::{| | ||
|- | |- | ||
|67 ||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{7-\left({\color{blue}{5}}\sdot1\right)}}={\color{blue}{2}}}</math>||67<span style="color:#0000FF>5</span>||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{27-\left(5\sdot5\right)}}={\color{blue}{2}}}</math>||675 | |67 ||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{7-\left({\color{blue}{5}}\sdot1\right)}}={\color{blue}{2}}}</math>||67<span style="color:#0000FF>5</span>||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{27-\left(5\sdot5\right)}}={\color{blue}{2}}}</math>||675 | ||
| Line 3,348: | Line 3,351: | ||
|} | |} | ||
*<math>\scriptstyle10127\div15</math>→ Check: <math>\scriptstyle15\times\left(675+\frac{2}{15}\right)</math><br> | *<math>\scriptstyle10127\div15</math>→ Check: <math>\scriptstyle15\times\left(675+\frac{2}{15}\right)</math><br> | ||
| − | :{| | + | ::<span style=color:red>[Illustration of the procedure:]</span> |
| + | ::{| | ||
|- | |- | ||
|  <span style="color:red>1</span>5||rowspan="2"|<math>\scriptstyle\xrightarrow{\begin{cases}\scriptstyle{\color{red}{1\times6}}={\color{blue}{6}}\\\scriptstyle{\color{red}{1\times7}}={\color{blue}{7}}\\\scriptstyle{\color{red}{1\times5}}={\color{blue}{5}}\end{cases}}</math>||<span style="color:#0000FF>675</span><span style="color:red>5</span>||rowspan="2"|<math>\scriptstyle\xrightarrow{\begin{cases}\scriptstyle{\color{red}{5\times6}}={\color{green}{3}}{\color{blue}{0}}\\\scriptstyle{\color{red}{6+}}{\color{green}{3}}={\color{blue}{9}}\end{cases}}</math>||<span style="color:#0000FF>9</span>75<span style="color:red>5</span>||rowspan="2"|<math>\scriptstyle\xrightarrow{\begin{cases}\scriptstyle{\color{red}{5\times7}}={\color{green}{35}}\\\scriptstyle{\color{red}{5+}}{\color{green}{35}}={\color{green}{4}}{\color{blue}{0}}\\\scriptstyle{\color{red}{7+}}{\color{green}{4}}={\color{green}{1}}{\color{blue}{1}}\\\scriptstyle{\color{red}{9+}}{\color{green}{1}}={\color{blue}{10}}\end{cases}}</math>||<span style="color:#0000FF>1010</span><span style="color:red>5</span>||rowspan="2"|<math>\scriptstyle\xrightarrow{\scriptstyle{\color{red}{5\times5}}={\color{blue}{25}}}</math>||101<span style="color:#0000FF>25</span>||rowspan="2"|<math>\scriptstyle\xrightarrow{\scriptstyle{\color{red}{5+2}}={\color{blue}{7}}}</math>||1012<span style="color:#0000FF>7</span> | |  <span style="color:red>1</span>5||rowspan="2"|<math>\scriptstyle\xrightarrow{\begin{cases}\scriptstyle{\color{red}{1\times6}}={\color{blue}{6}}\\\scriptstyle{\color{red}{1\times7}}={\color{blue}{7}}\\\scriptstyle{\color{red}{1\times5}}={\color{blue}{5}}\end{cases}}</math>||<span style="color:#0000FF>675</span><span style="color:red>5</span>||rowspan="2"|<math>\scriptstyle\xrightarrow{\begin{cases}\scriptstyle{\color{red}{5\times6}}={\color{green}{3}}{\color{blue}{0}}\\\scriptstyle{\color{red}{6+}}{\color{green}{3}}={\color{blue}{9}}\end{cases}}</math>||<span style="color:#0000FF>9</span>75<span style="color:red>5</span>||rowspan="2"|<math>\scriptstyle\xrightarrow{\begin{cases}\scriptstyle{\color{red}{5\times7}}={\color{green}{35}}\\\scriptstyle{\color{red}{5+}}{\color{green}{35}}={\color{green}{4}}{\color{blue}{0}}\\\scriptstyle{\color{red}{7+}}{\color{green}{4}}={\color{green}{1}}{\color{blue}{1}}\\\scriptstyle{\color{red}{9+}}{\color{green}{1}}={\color{blue}{10}}\end{cases}}</math>||<span style="color:#0000FF>1010</span><span style="color:red>5</span>||rowspan="2"|<math>\scriptstyle\xrightarrow{\scriptstyle{\color{red}{5\times5}}={\color{blue}{25}}}</math>||101<span style="color:#0000FF>25</span>||rowspan="2"|<math>\scriptstyle\xrightarrow{\scriptstyle{\color{red}{5+2}}={\color{blue}{7}}}</math>||1012<span style="color:#0000FF>7</span> | ||
| Line 3,357: | Line 3,361: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|דמיון למאזנים כתוב ה'א' וכתוב תחתיו ה'ז'ו' הנשאר באחרונה חוץ מן הב' שלא הגיע לחשבון ט"ו אל תצטרף עמהן עד סופו חיבורו לאות ראשונה כזה | + | |style="text-align:right;"|דמיון למאזנים כתוב ה'א' וכתוב תחתיו ה'ז'ו' הנשאר באחרונה חוץ מן הב' שלא הגיע לחשבון ט"ו אל תצטרף עמהן עד סופו חיבורו לאות ראשונה כזה |
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px;" | ||
| + | |- | ||
| + | | || ||1||5 | ||
| + | |- | ||
| + | |6||7||5|| | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px;" | ||
| + | |- | ||
| + | | || ||א||ה | ||
| + | |- | ||
| + | |ו||ז||ה|| | ||
| + | |} | ||
| + | |- | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|כפול ו' על א' יעלה ו' כפול ז' על א' יעלה ז' כפול ה' על א' ויעלה ה' כזה | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
{|style="margin-left: auto; margin-right: 0px;" | {|style="margin-left: auto; margin-right: 0px;" | ||
|- | |- | ||
| − | | | + | |6||7||5||5 |
| + | |} | ||
|- | |- | ||
| − | |||
|} | |} | ||
| − | + | | | |
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
{|style="margin-left: auto; margin-right: 0px;" | {|style="margin-left: auto; margin-right: 0px;" | ||
|- | |- | ||
| − | + | |ו||ז||ה||ה | |
| + | |} | ||
| + | |- | ||
|} | |} | ||
| − | והנה כתוב ה'ז'ו' תחת ה' של ה'א' כזה | + | |- |
| + | | | ||
| + | |style="text-align:right;"|והנה כתוב ה'ז'ו' תחת ה' של ה'א' כזה | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
{|style="margin-left: auto; margin-right: 0px;" | {|style="margin-left: auto; margin-right: 0px;" | ||
|- | |- | ||
| − | | | + | |6||7||5||5 |
|- | |- | ||
| − | + | | ||6||7||5 | |
|} | |} | ||
| − | + | |- | |
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
{|style="margin-left: auto; margin-right: 0px;" | {|style="margin-left: auto; margin-right: 0px;" | ||
|- | |- | ||
| − | | | + | |ו||ז||ה||ה |
| + | |- | ||
| + | | ||ו||ז||ה | ||
| + | |} | ||
|- | |- | ||
| − | |||
|} | |} | ||
| − | + | |- | |
| + | | | ||
| + | |style="text-align:right;"|כפול ו' על ה' ויעלה ל' חבור על ז' שעליו כמו שצויתיך בשער הכפול אם כן צריך אתה ליתן הג' אל הו' ויהיה ט' כזה | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
{|style="margin-left: auto; margin-right: 0px;" | {|style="margin-left: auto; margin-right: 0px;" | ||
|- | |- | ||
| − | | | + | |9||7||5||5 |
| + | |- | ||
| + | | || ||7||5 | ||
| + | |} | ||
|- | |- | ||
| − | |||
|} | |} | ||
| − | ואחר כך כפול ה' על ה' ויעלה ה"ב כתוב ה' במקום ה' העליונה ואל תצטרף ה' ראשונה עליה כמו שצויתיך בשער הכפל ואחר כך כתוב ב' במקום גלגל כזה | + | | |
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px;" | ||
| + | |- | ||
| + | |ט||ז||ה||ה | ||
| + | |- | ||
| + | | || ||ז||ה | ||
| + | |} | ||
| + | |- | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואחר כך כפול ז' על ה' ויעלה ה"ג ועליו ה' דהיינו 0"ד עשה גלגל במקום ה' ותן ד' לז' ויהיה א"א כתוב במקום ז"א ותן א' על הט' ויהיה י' אז צריך אתה לעשות גלגל במקום הט' ואחריו א' כזה | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px;" | ||
| + | |- | ||
| + | |1||0||1||0||5 | ||
| + | |- | ||
| + | | || || || ||5 | ||
| + | |} | ||
| + | |- | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px;" | ||
| + | |- | ||
| + | |א||0||א||0||ה | ||
| + | |- | ||
| + | | || || || ||ה | ||
| + | |} | ||
| + | |- | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואחר כך כפול ה' על ה' ויעלה ה"ב כתוב ה' במקום ה' העליונה ואל תצטרף ה' ראשונה עליה כמו שצויתיך בשער הכפל ואחר כך כתוב ב' במקום גלגל כזה | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px;" | ||
| + | |- | ||
| + | |style="text-align:right;"|1||0||1||2||5 | ||
| + | |} | ||
| + | |- | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
{|style="margin-left: auto; margin-right: 0px;" | {|style="margin-left: auto; margin-right: 0px;" | ||
|- | |- | ||
|style="text-align:right;"|א||0||א||ב||ה | |style="text-align:right;"|א||0||א||ב||ה | ||
|} | |} | ||
| − | והנה חבר ב' שלא הגיע לכלל ט"ו אל הה' הראשונה ויהיה ז' ואז יהיה החשבון כזה | + | |- |
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|והנה חבר ב' שלא הגיע לכלל ט"ו אל הה' הראשונה ויהיה ז' ואז יהיה החשבון כזה | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="color:blue; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px;" | ||
| + | |- | ||
| + | |style="text-align:right;"|1||0||1||2||7 | ||
| + | |} | ||
| + | |- | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
{|style="margin-left: auto; margin-right: 0px;" | {|style="margin-left: auto; margin-right: 0px;" | ||
|- | |- | ||
|style="text-align:right;"|א||0||א||ב||ז | |style="text-align:right;"|א||0||א||ב||ז | ||
|} | |} | ||
| − | והיינו כיון השאלה | + | |- |
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|והיינו כיון השאלה | ||
|- | |- | ||
| | | | ||
| Line 3,416: | Line 3,558: | ||
|} | |} | ||
| + | ::<span style=color:red>[Illustration of the procedure:]</span> | ||
::{| | ::{| | ||
|- | |- | ||
| Line 3,463: | Line 3,606: | ||
|} | |} | ||
| + | ::<span style=color:red>[Illustration of the procedure:]</span> | ||
::{| | ::{| | ||
|- | |- | ||
| Line 3,511: | Line 3,655: | ||
|- | |- | ||
| | | | ||
| − | :{| | + | ::<span style=color:red>[Illustration of the procedure:]</span> |
| + | ::{| | ||
|- | |- | ||
| 56 ||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{45-\left({\color{blue}{8}}\sdot5\right)}}={\color{blue}{5}}}</math>||56<span style="color:#0000FF>8</span>||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{54-\left(8\sdot6\right)}}={\color{blue}{6}}}</math>||568||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{64-\left(8\sdot8\right)}}={\color{blue}{0}}}</math>||568 | | 56 ||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{45-\left({\color{blue}{8}}\sdot5\right)}}={\color{blue}{5}}}</math>||56<span style="color:#0000FF>8</span>||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{54-\left(8\sdot6\right)}}={\color{blue}{6}}}</math>||568||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{64-\left(8\sdot8\right)}}={\color{blue}{0}}}</math>||568 | ||
| Line 3,575: | Line 3,720: | ||
|- | |- | ||
| | | | ||
| − | :{| | + | ::<span style=color:red>[Illustration of the procedure:]</span> |
| + | ::{| | ||
|- | |- | ||
| ||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{9-\left({\color{blue}{2}}\sdot4\right)}}={\color{blue}{1}}}</math>|| <span style="color:#0000FF>2</span> ||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{14-\left(2\sdot5\right)}}={\color{blue}{4}}}</math>||2  | | ||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{9-\left({\color{blue}{2}}\sdot4\right)}}={\color{blue}{1}}}</math>|| <span style="color:#0000FF>2</span> ||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{14-\left(2\sdot5\right)}}={\color{blue}{4}}}</math>||2  | ||
| Line 3,608: | Line 3,754: | ||
|- | |- | ||
| | | | ||
| − | :{| | + | ::<span style=color:red>[Illustration of the procedure:]</span> |
| + | ::{| | ||
|- | |- | ||
|2 ||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{4-\left({\color{blue}{1}}\sdot4\right)}}={\color{blue}{0}}}</math>||2<span style="color:#0000FF>1</span>||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{5-\left(1\sdot5\right)}}={\color{blue}{0}}}</math>||21 | |2 ||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{4-\left({\color{blue}{1}}\sdot4\right)}}={\color{blue}{0}}}</math>||2<span style="color:#0000FF>1</span>||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{5-\left(1\sdot5\right)}}={\color{blue}{0}}}</math>||21 | ||
| Line 3,642: | Line 3,789: | ||
|- | |- | ||
| | | | ||
| − | :{| | + | ::<span style=color:red>[Illustration of the procedure:]</span> |
| + | ::{| | ||
|- | |- | ||
|<span style="color:red>3</span>1||rowspan="2"|<math>\scriptstyle\xrightarrow{{\color{red}{3\sdot7}}={\color{blue}{21}}}</math>||<span style="color:#0000FF>21</span><span style="color:red>1</span>||rowspan="2"|<math>\scriptstyle\xrightarrow{{\color{red}{1\sdot7}}={\color{blue}{7}}}</math>||21<span style="color:#0000FF>7</span>||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{7+1}}={\color{blue}{8}}}</math>||21<span style="color:#0000FF>8</span> | |<span style="color:red>3</span>1||rowspan="2"|<math>\scriptstyle\xrightarrow{{\color{red}{3\sdot7}}={\color{blue}{21}}}</math>||<span style="color:#0000FF>21</span><span style="color:red>1</span>||rowspan="2"|<math>\scriptstyle\xrightarrow{{\color{red}{1\sdot7}}={\color{blue}{7}}}</math>||21<span style="color:#0000FF>7</span>||rowspan="3"|<math>\scriptstyle\xrightarrow{{\color{red}{7+1}}={\color{blue}{8}}}</math>||21<span style="color:#0000FF>8</span> | ||
Revision as of 12:32, 27 January 2020
Contents
- 1 Prologue
- 2 Introduction
- 3 Chapter One: Multiplication of Units - Shortcuts
- 4 Chapter Two: Addition
- 5 Chapter Three: Subtraction
- 6 Chapter Four: Multiplication
- 7 Chapter Five: Gelosia
- 8 Chapter Six: Division
- 9 Chapter Seven: Proportions
- 10 Chapter On Cubic Roots [P1088 2r-v]
- 11 Chapter on Square Roots [P1088 6v-7v]
- 12 Notes
- 13 Appendix: Bibliography
Prologue |
|||||||||||||||
| [MS Paris, Séminaire Israélite de France (École Rabbinique) 158/1 (IMHM 4102) f. 197r, lines 1-16] | |||||||||||||||
| זה ספר חכמת התשבורת [הנקרא] טשיפרא סיבתו: אני את לבי גם מנעורי גרסה נפשי לדעת חכמה ובקש חשבון ומי יתן ואמצאם בספר ויחקו בעט סופר מהיר [1]. ולסבה שזאת היא חכמת החיצוניות לא נמצאת לפנינו בישראל, והמיעוט שבמיעוט הנמצא נאסף אל תוך הבית בחדרי חדרים, לכן העירוני רעיוני ללקט האמרים מיד כל אשר ימצא אתו ולכל[...] לזכרון. | |||||||||||||||
| וקודם שאתחיל אבקש מיד כל רואיו לבל יכרעני לכף חובה ולומר מה לך פה כלך בהוייות דאביי ורבא חלילה וחס [לי'] לזרעא דאבא, כי לא לקחתי זאת לשום עיקר ותכלית, רק לחדד השכל ולבא בחשבון במקרה ושנייה ובחידוד דאביי ורבא בעצם וראשונה ועל זאת אמרו המושלים באו חשבון [2] כמו שכתוב הרמבם ז"ל פרק חמישי מה[קדמת] ה פרקי אבות [3] וז"ל: | |||||||||||||||
| ומה שאין בו תועלת לו בתכלית ההוא כשאלות החשבון וספר החר[וט]ים והתחבולות הרבות משאלות אל ההנד[ס]ה ומשיכת המשקלים והרבה כיוצא בא[ילו] יהיה הכוונה בהם לחדד השכל ולהרגיל כח השכלי בדרכי המופת עד שיגיע לו לאדם קניין ידיעת ההיקש המופתי מזולתו ויהיה לו זה הדרך שיגיע בה לידעת אמיתות מציאתו ית' עכל' | |||||||||||||||
Introduction |
|||||||||||||||
| בטוב גדא | |||||||||||||||
| אתחיל דא | |||||||||||||||
| ספר ציפרא | |||||||||||||||
| The book contains nine chapters | לידע ולפרש ספר המספר שיש בו ט' שערים | ||||||||||||||
| The basic conventions needed for the calculation practice | ואפרש תחילה הקבלות אשר צריך לידע המחשב הוא המפתח ויכול אחר כך לידע כל החשבונות | ||||||||||||||
The Positional Decimal System |
|||||||||||||||
| The numerals | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
דע כי אין לך חשבון קטן מן א' שהוא אחד | ||||||||||||||
|
ואין לך חשבון גדול מן ט' | ||||||||||||||
| The nine numerals from which all numbers are formed - the nine first Hebrew letters | ובאלו ט' אותיות מן א' ועד ט' יש בו כל החשבונות שבעולם עד אין מספר | ||||||||||||||
| The written ranks [= decimal places] | |||||||||||||||
| Units | כיצד מעלה הראשונה היא נקראת מעלת היחידים כי כאשר יקראו האות כך מניינם פי' א' אחד ב' שנים ג’ שלש וכן עד ט' שהיא תשע | ||||||||||||||
| Tens | וכשתחשוב עשרה אז צריך אתה לכתוב ב' מעלות א' במעלה שנייה ולפניו ציפרא | ||||||||||||||
| Zero – placeholder digit | שהוא גלגל כזה 0 שאין בו ממש אלא שומר המעלות וזכר לדבר כגלגל לפני רוח [4] | ||||||||||||||
|
| ||||||||||||||
|
| ||||||||||||||
| כי הא' הראשונה מן היחידים שהיא במעלה ראשונה וא' שנייה היא מן העשיריות הרי י"א | |||||||||||||||
|
| ||||||||||||||
|
| ||||||||||||||
|
| ||||||||||||||
|
| ||||||||||||||
|
| ||||||||||||||
|
| ||||||||||||||
|
| ||||||||||||||
| Hundreds | ומעלה השלישית היא מעלת המאות כזה | ||||||||||||||
|
| ||||||||||||||
|
| ||||||||||||||
|
| ||||||||||||||
|
| ||||||||||||||
|
| ||||||||||||||
|
| ||||||||||||||
| Thousands | ומעלה הרביעית היא מעלת האלפים | ||||||||||||||
|
| ||||||||||||||
|
| ||||||||||||||
|
| ||||||||||||||
| וככה עד ט' אלפים שהוא 000"ט | |||||||||||||||
| Tens of thousands | ומעלה החמישית היא מעלת הרבבות שהוא י' אלפים | ||||||||||||||
| Hundreds of thousands | ומעלה ששית היא מעלת מאה אלפים | ||||||||||||||
| Thousands of thousands | ומעלה שביעית היא מעלת אלף אלפים | ||||||||||||||
| and so on endlessly | וככה עד אין מספר תוכל לכתוב | ||||||||||||||
| Every rank is ten times the preceding rank | וכל מעלה היא עשרה פעמים יותר מן המעלה שלפניה | ||||||||||||||
|
| ||||||||||||||
| תשיב אל לבך כי הגלגל אין לו מניין רק שומר המעלות והנה החשבון עשרים וג' אלפים | |||||||||||||||
| This is the meaning of the written numerals and their numerical value | והנה ביארתי לך מניין ועניין הכתיבה | ||||||||||||||
| 1 2 3 4 5 6 7 8 9 0 10 20 30 |
|
Chapter One: Multiplication of Units - Shortcuts |
שער הכפל הקטן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
אם תרצה לידע כמה עולה ט' פעמים ט' או ט' פעמים ח' או ה' פעמים ט' או ו' פעמים ט' וכן כל כיוצא בזה שכל אחד פחות מעשרה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
אשכילך אם תחפוץ לידע כמה ט’ פעמים ט’ אז כתוב כזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר כך חשוב כמה יותר על עשרה ויהיה ח' ואותה ח' כתוב אצל הט' העליונה בצד שמאל כזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואחר כך חשוב כמה ט' העליונה יותר על ח' ותמצא רק אחד אותו א’ כתוב בצד ט’ התחתונה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואחר כך חשוב כמה ט’ התחתונה יותר על הח’ ויהיה א’ כתוב אותה א’ ג”כ בצד ט’ תחתונה כזה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ותחשוב א' פעמים א' היינו אחד כתוב א' לפני הח' כזה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ומחוק הט' למטה ולמעלה ויהיו אחד ושמונים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכן אם תרצה לידע כמה ט' פעמים ח' כתוב כזה
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וחשוב כמה ח'ט' יותר על עשרה דהיינו ז' כתוב הז' אצל הט' כזה
וחשוב כמה הט' עודף על הז' דהיינו ב' וכמה הח' עודף על ז' א' וכתוב כזה
תכפול א' על ב' היינו ב' אותה ב' כתוב קודם הז’ כזה
נמצא ט' פעמים ח' יהיה ע"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דומיון אם תחפוץ לידע כמה ו' פעם ו' אז כתו' הו' תחת הו' כזה
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואז תאמר כמה השני ו' למעלה מי' זהו ב' ואותו ב' תכתו' לאחר הו' כזה
ואז תאמ' כמה הו' יתיר על הב' זהו ד' והו' השנייה נמי למעל' מב' זהו ד' ואז תכפול ט ד' פעמי' ד' זהו ו"א פי' י"ו ואז תכתוב שים הא' על הב' כי הב' מעלה שניי' ויהיה ג' ועוד הוה ו' ואות' ו' תכתו' לפני הג' כזה
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נמצא שו' פעמ' ו' עולה ו"ג פי' ל"ו וכן עשה לעולם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן לעולם תכפול המותר מזה ומזה והעולה כתוב קודם העודף עליו ואז תשכיל בכל אשר תעשה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון אחר שהעתקתי מספר גלחות: חברם יחד הב' אותיות והשליך עשרה והמניין הקטון כתוב ואח"כ תכפול יחד החשבון שיש מכל אחד עד עשרה וכתוב זה לפני המנין הקטן שבידך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
או כלך לדרך זו כתוב לפני המניין קטון שבשני אותיות גלגל כזה 0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
כגון את"ל ז'פ'ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
כתוב כזה 0ז' וקח ממנו מה שבא מן הכפל שתכפול המניין מאות הגדול עד עשרה עם האות הקטן כגון מה שלפניך אמור ז'פ'ב' הם ד"א | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ואם תרצה לידע ולחשוב כמה ג' פעמים ג' או ד' פעמים ד' וכן כל כיוצא בזה שאפילו צירופו אינו מגיע לעשרה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אשכילך לעשות שתלוה לו כמה שצריך שיהיה בכל פעם אחד יותר מעשרה וככלות חשבונך קח מה שהלוית לו וישאר מתכונך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
דמיון בקשנו ד' פעמים ד' כזה
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4 ![\scriptstyle\xrightarrow{{\color{red}{\left[4+4+\left[11-\left(4+4\right)\right]\right]-10}}={\color{blue}{1}}}](/mediawiki/images/math/3/f/a/3faacadf1089c902d319654aa049b711.png)
14 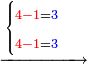
14 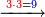
19 ![\scriptstyle\xrightarrow{{\color{red}{9-\left[11-\left(4+4\right)\right]}}={\color{blue}{6}}}](/mediawiki/images/math/2/1/1/211ec1ed49b06c80e5f87cd6b93c9500.png)
16 4 4 4 4 4 33
והנה תלוה לו ג' שיעלה י"א והשלך עשרה וישאר בידך א' ורשום כזה
ואחר כך חשוב כמה ד' הראשונה יותר על הא' הוי אומר ג' וכן ד' השנייה גם כן יותר ג'
כפול ג' על ג' הרי ט' כתוב הט' לפני הא’ כזה
והנה קח ג' שהלוית לו וישאר ו"א והם י"ו ותמצא חשבונך מכוון
| ||||||||||||||||
|
|
עניין אחר אם תרצה לידע כמה ג’ פעמים ג’ או ד’ פעמים ד’ וכן כל כיוצא בזה שאפילו צירופו אינו מגיע לעשרה | |||||||||||||||
|
|
אשכילך דמיון אם תרצה לחשוב ד’ פעמים ד’ אז תכתוב אותו כזה
| |||||||||||||||
|
וחשוב כמה ד’ ראשונה פחות מי’ ויהיה ו’ וחשוב גם השנייה כמה השנייה פחות מי’ ותמצא ג”כ ו’ ואז תכפול ו’ על ו’ ויעלה בידך ו”ג | |||||||||||||||
|
ואם יהיה המספר אשר תרצה לכפול זע"ז פחות מי' כשתצרף שני המספרים יחד | |||||||||||||||
|
|
דימיון אם בקשת לכפול ד' על ג' | |||||||||||||||
|
אז תקח המרחק מן י' מכל אחד דהיינו מד' עד י' ו' ומג' עד י' ז זפ"ז ב"ד אותו ב"ד כתו' לזכרון [בד] | |||||||||||||||
|
דרך אחרת לכפל קטן בספר אחר מצאתי או כלך בדרך זו קח המרחק עד י’ מן כל אחד ואחד שתרצה לכפול יחד וחשוב אותו ב’ מרחקים זה על זה ומה שיעלה בידך כתוב לזכרון אחר כך צורפם יחד בשער החיבור והעולה בידך קח מה שלמטה מן י’ וי’ השלך מידך וכתוב אותו למטה בצד שמאל למה שכתבת כבר ויהיה חשבונך מכוון | |||||||||||||||
|
|
דמיון הנה רצונך לכפול ז’ פעמים ט’ | |||||||||||||||
|
קח המרחק מן הז' עד י' דהיינו ג' והמרחק מן ט’ עד י’ דהיינו א’ ואמור ג’ פעמים א’ היינו ג’ אותו ג’ כתוב לזכרון כזה ג | |||||||||||||||
|
|
דמיון אחר הנה רצונך לכפול ו’ פעמים ח’ | |||||||||||||||
|
קח המרחק מן ו’ עד י’ דהיינו ד’ והמרחק מן ח’ היינו ב’ ואמור ב’ פעמים ד’ היינו ח’ אותו ח’ כתוב לזכרון [ח] | |||||||||||||||
|
דמיון אחר אם תרצה לידע הפ"ו | |||||||||||||||
|
קח המרחק מן ה' עד י' ויהיה ה' צרפם יחד הה’ והו’ ויהיה א' השלך עשרה ונשאר לך א' צרפם 0"ב ויהיה ג' נמצא ל' ודוק | |||||||||||||||
| Multiplication Table | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
והנה ארשום לך לוח מתוקנת על שער הכפל קטן כדי שתוכל לראות בקלות כל מה שתרצה בלא שום חשבון מן א' פעמים א' עד ט' פעמים ט' ודוק | |||||||||||||||
|
והחצי לוח עשיתי למצוא כל חשבון ואינך צריך הרבה כל כך | |||||||||||||||
| סליק שער כפל קטן ואז תשכיל כל אשר תעשה |
Chapter Two: Addition |
שער החיבור | ||||||||||||||||||
|
אם תרצה לחבר שנים ושבעים וג' מאות וג' אלפים עם שנים ותשעים וג' מאות וג' אלפים | ||||||||||||||||||
|
תכתוב כזה | ||||||||||||||||||
|
|
- [Illustration of the procedure:]
3372 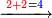
[3372] 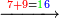
[3372] 
[3372] 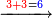
[3372] 3392 [3392] [3392] [3392] [3392] 4 64 764 6764
|
תחבר ב' תחתונה על ב' עליונה ויהי ד' | ||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
|
תחבר ט' תחתונה על ז' עליונה ויהיה ו"א הו' כתוב במעלה שניה אחר ד' שכתבת כזה | ||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
|
והא' הנשארת חבור אל הג'ג' שלאחריו שהם למעלה מזו כזה במעלה השלישי | ||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
|
ויהיה הכל ז' כזה | ||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
|
ואחר כך תחבר שני הג'ג' האחרונים במעלה הרביעי' ויהיה חבורם ו' אות' ו' כתוב במעלה הרביעי' אחר דוז שכתבת כזה | ||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
|
ותשלם המלאכה ויהיה חבורו ארבע וששי' ז' מאות ו' אלפי' דהיינו כזה | ||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| The highest rank of the sum exceeds the addend by one rank to the left at most, sometimes it does not exceed [its ranks] at all. | לעולם לא תמצא הטור מן החיבור אשר בעליונה שעברת על המחובר רק מעלה לשמאל לכל היותר ולפעמים לא תעבור כלל | ||||||||||||||||||||||||||
| [MS Paris 1088, 7v:] Here follows a chapter on addition, to add every thing and to establish its methods | הילך שער חיבור לחבר כל דבר [..] ולישב על אופניו | ||||||||||||||||||||||||||
| Such as, if you wish to sum some numbers together. | כגון אם תרצה לחבר כמה חשבונות יחד | ||||||||||||||||||||||||||
| Now, I sum one number and according to this you shall apply for others: | ועתה אחבר חשבון אחד ומהם תבין אחר | ||||||||||||||||||||||||||
|
ותכתו' אות תחת אות ולא תכתו' כאשר כותבין בשער כפל אלא תכתו' כזה שאראך בע"ה | ||||||||||||||||||||||||||
|
דומיון בקשנו לחבר ע"ב וג' מאות וג' אלפי' עם צ"ב וח' מאות וט' אלפים | ||||||||||||||||||||||||||
|
הילך היאך תכתוב אותו וצורתו כזה | ||||||||||||||||||||||||||
|
|
- [Illustration of the procedure:]
3372 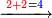
3372 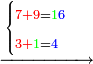
3472 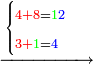
4472 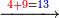
3372 9892 9892 9892 9892 9892 4 64 264 13264
| נחבר ב' תחתונ' עם ב' עליונ' הרי ד' אות' ד' נכתוב נגד ב' תחתונ' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נחבר כמו כן ט' תחתונ' עם ז' עליונ' ויעלה ו"א נכתוב ו' תחת הט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונוסיף א' על אות שבשיט' עליונ' הסמוכ' לה ושם יש ג' ונוסיף א' עליה ויהיה כאילו נכתו' ד' במקום ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונחבר ד' עליונ' עם ח' תחתונ' ויעלה ב"א נכתו' ב' למטה תחת הח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונוסיף א' על אות הסמוך לד' עליונ' ושם יש ג' ונוסיף א' עליה ויהא ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נחבר ד' עליונ' על ט' שלמטה ויעלה ג"א נכתוב ג' למט' תחת הט' וא' נכתוב לאחריה ויהיה כזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| זה הכלל לא ימוש מפיך כשמותר הא' משיט' ראשונ' אני מוסיף אות' על שיט' שלאחריה כי הא' הנותרת לי היא כמו כן מן העשיריות נגד שיט' ראשונ' לכך אני מוסיף אות' תדיר עליה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [MS Paris158, 198v] | ציור זה בגלחת ונקרא אדירין | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Checking Methods |
ועתה תדע שאכתוב לך שני משקלים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [MS Paris158, 198v] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הא' השלך ט"ט כל כמה שתוכל מב' שיטות עליונות ומה שנשמר לך למטה מט' קח בידך לאבני המשקל ואח"כ השלך ג"כ השיטה התחתונה בט"ט ומה שנשאר לך אם משקלו כאבן הראשון דע שכוינת חשבונך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
משקל השני יקח השני שיטות העליונות מהשיטה התחתונה אם יצא במבוקש בלי חסרון ויתרון אז חשבונך מכוון ודוק ותמצא |
Chapter Three: Subtraction |
שער החיסור | ||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| אם תרצה לחסור ולנכות חשבון מן חשבון הילך איך תעשה: תכתוב החשבון שאתה רוצה לנכות ולחסר ממנו אותו חשבון כתוב למעלה כפי מעלותיו והחשבון שאתה מנכה הימנו כתוב למטה כפי מעלותיו ואחר כך תנכה מן החשבון שלמעלה | |||||||||||||||||||||||||||
|
|
ועתה אכתוב לך הדמיון להשכילך: הנה בקשנו לחסור ט' מאות ותשעים ותשע מאלף הילך היאך תכתוב אותו כזה
| ||||||||||||||||||||||||||
|
נמצא הא' שבשיטה העליונה במעלה רביעי' עולה עשרה לגבי ט' שלישית שבתחתונה עתה נחסר מאותו עשרה ט' וישאר לך א' אותו א' כתוב במקום גלגל השלישי נגד הט' שחסרת ואותו ט' מחוק כזה
ועכשיו כמו כן הא' שבמעלה שלישית שבשיטה העליונה עולה עשרה לגבי ט' שבשיטה תחתונה נחסר ט' שנייה ונשאר א' ואותו א' כתוב במקום הגלגל השני ותמחוק ט' שנייה שחסרנו וגם תמחוק הא' העליונה שבמעלה שלישית שחסרנו ממנו ויהיה כזה
שוב נחסר ט' תחת הגלגל מן א' שלמעלה במעלה השנייה כי גם היא עולה עשרה לגבי ט' כדלעיל והנה כשנחסר ט' מן י' וישאר א' אותו א' כתוב במקום הגלגל ומחק הא' העליונה אשר במעלה שנייה וגם הט' מחק ואז נשאר רק א' | ||||||||||||||||||||||||||
|
|
דמיון אחר אם בקשנו לחסור אב"ג מן דה"ו כתוב כזה:
| ||||||||||||||||||||||||||
|
נחסר ג' התחתונה מן ו' העליונה שכנגדה וישאר ג' מחק הו' וכתוב במקומה הג' שנשאר ומחק גם כן הג' שנשאר שלמטה ויהיה כזה
שוב נחסר ב' התחתונה מן ה' עליונה שכנגדה וישאר ג' אותו ג' כתוב במקום הה' ומחק הב' שלמטה וגם ה' שלמעלה ויהיה כזה
שוב נחסר א' התחתונה מן ד' עליונה שכנגדה וישאר ג' ומחוק ד' שלמעלה וגם א' שלמטה וכתוב ג' במקום ד' שלמעלה ויהיה כזה
נמצא כשחסרנו אב"ג מן דה"ו לא נשאר כי אם ג'ג'ג' | ||||||||||||||||||||||||||
|
וכאשר תמצא שהאות העליון אשר בקשנו לחסר ממנו פחות מן האות התחתון שתרצ' לחסר | ||||||||||||||||||||||||||
|
|
כגון אם תרצ' לחסר ז ו ח מן ו ה ט כזה:
| ||||||||||||||||||||||||||
|
היאך תחסור מרובה ממועט כזה ז' מן ו' לא תוכל וכן ו' מן ה' בדרך זה תעשה: טול א' מן ה' אשר אצל ו' ומחוק הה' וכתוב ד' אותו א' כמה עולה לחבירו עם הו' י"ו כי היא במעלה שנייה מן הו' הרי י"ו חסר ז' אשר בטור השפל מן י"ו וישאר ט' אחר כך צריך לחסר ו' מן ד' עשר ג"כ כמו שצויתיך מחוק א' מן ט' ויהיה במעלה שלפניו י"ד וחסר ממנו ו' וישאר ח' ול"ד זה שייך לשער הכפל קטון | ||||||||||||||||||||||||||
| [MS Oxford 60, 153r-v] | |||||||||||||||||||||||||||
|
אשכילך היאך תעשה כי לא תוכל לחסר ז' מן ו' וכן ו' מה' בדרך זה תעשה: בתחילה חסר ח' תחתונה מט' עליונ' וישאר א' מחוק הט' וכתוב א' במקומ' גם ח' תחתונ' מחוק ויהיה כזה
עתה צריכין אנו לחסר ו' תחתונ' מה' עליונ' ולא יכולנ' לכן לך לך אל הא' אשר לשמאל ה' עליונ' וצרפ' יחד א' וה' ויהיה ט"ו ונחסור הו' ממנו וישאר ט' מחוק הא' העליונ' גם ה' העליונ' וכתוב במקומם ט' גם ו' תחתונ' תמחוק וישאר כזה
שוב צריכין אנו לחסר ז' תחתונ' מו' ולא יכולנ' עתה לך לך וקח אחד מן הט' שבצד הו' בשיט' עליונ' וצרפ' יחד הו' גם הא' והיא עשרה אצל הו' ויהיה י"ו ועתה חסר ז' מן י"ו וישאר ט' מחק ו' ט' עליונ' וכתוב ט' ח' במקומם כאשר ציויתיך ומחוק ג"כ הז' התחתונ' ויהיה כזה
ותשלם המלאכה עיין היטב | ||||||||||||||||||||||||||
Checking Methods |
|||||||||||||||||||||||||||
|
ואם תרצה לידע אם אמת חשבת אז תחבר בשער החיבור אב"ג עם גג"ג אז תמצא דה"ו אז החיסור מכוון | ||||||||||||||||||||||||||
|
ואם תרצ' לידע אם אמת חשבת אז חבר בשער החיבור ז ו ח עם ט ח הנשארי' ואם תמצא ו ה ט אז כיוונת | ||||||||||||||||||||||||||
| The checking method of addition is subtraction and the checking method of subtraction is addition | זה הכלל שער החיסור מאזני צדק לשער החיבור ושער החיבור מאזני צדק לשער החיסור | ||||||||||||||||||||||||||
Chapter Four: Multiplication |
שער הכפל | ||||||||||||||||||||||||||
|
אם תרצה לכפול רל"ד ואלף על ד' אלפים ושכ"א |
- [Illustration of the procedure:]
4321 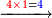
4 4321 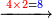
48 4321 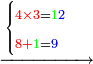
4924321 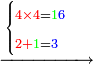
4936321 1234 234 34 4
| הילך צורתו כאשר תכתבנו חשבון האחד בצד השני ומכוון אות ראשון בחשבון התחתון תחת אות האחרון שבחשבון העליון כזה | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| וכפול א' תחתונה על ד' עליונה פי' חשוב א' פעמים ד' זה ד' אות ד' כתוב נגד א' התחתונה ומחוק א' תחתונה כזה | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| עוד כפול ב' תחתונה על ד' עליונה ויעלה ח' אותו ח' כתוב נגד ב' התחתונה ומחק ב' התחתונה כזה | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| עוד נכפל ג' תחתונה על ד' עליונה ויעלה ב"א פי' י"ב עתה כתוב ב' נגד ג' תחתונה וא' על ח' אחריה ויעלה ט' כי הוא מעלה אחת שהיא עשרה אחר ב' שלפניה ומחוק ג' תחתונה כזה | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| עוד נכפל ד' תחתונה על ד' עליונה ויעלה ו"א פי' י"ו עתה נכתב ו' נגד ד' תחתונה במקום ד' עליונה כי עתה חשבנו ד' עליונה בכל חלקים וכתוב א' על ב' שלאחריה ויהיה ג' כזה | |||||||||||||||||||||||||||||||
|
|
- [Illustration of the procedure:]
4936321 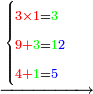
5236321 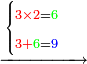
5296321 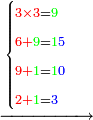
5305321 1234 234 34 4
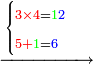
5306221
| ועתה נמשך ד"ג ב"א מעלה לאחורית תחת ג' עליונה כדי לחשוב ג' עליונה כדי לחשוב ג' גם בכל תוצאותיה ד"גב"א כזה | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| כפול א' תחתונה על ג' עליונה פי' ג' פעמים א' זהו ג' ושים אותו ג' על ט' שעל א' התחתונה ויעל ב"א פי' י"ב עתה כתוב ב' במקום ט' א' שהיא עשרה שים אותו במעלה שנייה דהיינו ד' ועשה ד' אחרונה ה' ומחוק א' תחתונה כזה | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| עוד כפול ב' תחתונה על ג' עליונה ויעלה ב' פעמים ג' דהיינו ו' ושים אותו ו' על ג' שעליה ויהיה ט' ומחוק ב' תחתונה כזה | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| עוד כפול ג' תחתונה על ג' עליונה ג' פעמים יעלה ט' ושים אותו ט' על ו' שעליה ויעלה ה"א ה' כתוב במקום ו' א' כתוב במעלה שנייה דהיינו אל ט' שלאחריה ויהיה עשרה אך אין ראוי לכתוב עשרה כי אין כותבין בחשבונות הציפרא עשרה רק ט' לכן כתוב גלגל כזה במקום ט' וכת' א' במעלה שלאחריה דהיינו אל ב' | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| ועתה יהיה ג' מחוק ג' תחתונה כזה עוד כפול ד' תחתונה על ג' עליונה ויעלה ב"א עתה כתב ב' במקום ג' עליונה כי חשבונו גם כן ג' בכל חילוקה א' כתוב במעלה שנייה אל ה' ויהיה ו' ומחוק ד' תחתונה כזה | |||||||||||||||||||||||||||||||
|
|
- [Illustration of the procedure:]
5306221 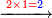
5326221 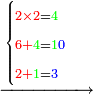
5330221 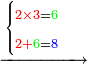
5330821 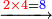
5330881 1234 234 34 4
| ועתה נמשך ד"ג ב"א מעלה אחת לאחורית תחת ב' עליונה כזה | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| עוד כפול א' תחתונה על ב' עליונ' א' פעמים ב' דהיינו ב' כתוב אותו ב' נגד א' תחתונה במקום גלגל ומחוק א' תחתונה כזה | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| שוב כפול תחתונה על ב' עליונה ב' פעמים ב' היינו ד' אותו ד' כתוב למעלה נגד ב' תחתונה דהיינו אל ו' הרי י' כתוב במקום ו' גלגל ואחר הגלגל תוסיף א' היינו אל ב' ויהיה כזה | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| שוב כפול ג' תחתונה על ב' עליונה ג' פעמים ב' היינו ו' אותה ו' כתו' נגד ג' תחתונה דהיינו אל ב' עליונה ויהיה ח' ומחוק ג' תחתונה כזה | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| שוב כפול ד' תחתונה על ב' עליונה ד' פעמים ב' ויעלה ח' כתוב ח' במקום ב' עליונה כי חשבנו ב' בכל חילוקיה ומחוק ד' תחתונה כזה | |||||||||||||||||||||||||||||||
|
|
- [Illustration of the procedure:]
5330881 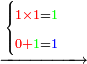
5331881 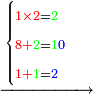
5332081 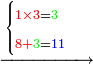
5332111 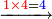
5332114 1234 234 34 4
| ועתה נמשך דגב"א מעלה לאחורית כדי לכפול אותו על א' ראשונה ויהיה כזה | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| כפול א' תחתונה על א' עליונה א' פעמים א' זה א' אותו א' כתוב נגד א' תחתונה במקום גלגל ומחק א' תחתונה כזה | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| שוב כפול ב' תחתונה על א' עליונה ב' פעמים א' היינו ב' אותו ב' כתוב על התחתונה דהיינו אל ח' ויהיה עשרה כתוב במקום ח' גלגל אחר גלגל תוסיף א' על א' ויהיה ב' ומחוק ב' תחתונה כזה | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| שוב כפול ג' תחתונה על א' עליונה ג' פעמים א' זה ג' אותו ג' כתוב נגד ג' תחתונה דהיינו אל ח' הרי י"א מחוק ח' וכתוב במקומה א' ואחריה במקום גלגל א' ומחוק ג' תחתונה כזה | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| שוב כפול ד' תחתונה אל א' עליונה ד' פעמים א' היינו ד' אותו ד' כתוב במקום א' שכנגדה אבל לא תצרף אותו א' עם ד' כמו שצויתיך כבר כי על אותו א' כפלנו עכשיו דגב"א ולא היתה א' רק לסימן לכן לא חיידיא לצירוף ומחוק ד' תחתונה כזה | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| נמצא כי א"בג"ד פעמים דגב"א עולה בחשבון דא"אב"ג ג"ה היינו י"ד ומאה וגם ב' אלפים גם ל' אלפים וגם מאה אלפים וגם ה' מאות רבבות וד"ל |
|
דמיון אחר הנה בקשנו לכפול ט' ומאתים על ג' אלפים ושלשים | ||||||||||||||||||||||||||
|
הילך היאך תכתוב צורתו כזה | ||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| כפול ב' תחתונה על ג' עליונה ב' פעמים ג' היינו ו' אותו ו' כתוב נגד ב' תחתונה ומחוק ב' תחתונה וגם הגלגל שלפני ב' מחוק וכתוב גלגל לפניו כזה כי נכפול גלגל ג' פעמים ויהיה גלגל | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| שוב כפול ט' על ג' שעליה ט' פעמים ג' היינו ז"ב אותו ז' כתוב למעלה במקום ג' אחרונה ויהיה ז' במקום וגם ב' כתוב במקום גלגל ומחק ט' תחתונה כזה | |||||||||||||||||||||||||||
|
|
- [Illustration of the procedure:]
627030 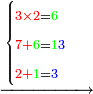
633030 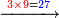
633270 209 9
| ועתה משוך 0ט"ב לאחוריו ב' מעלות כדי שתהא ט' תחתונה שהיא אות ראשונה שבשיטה תחתונה נגד ג' עליונה כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| ואת"ל למה לא כתבנו ט0"ב תחת גלגל עליון ודאי עשינו כך אבל מ"מ לא עלה יותר מגלגל כי כאשר תמצא אותיות כתובים ואת' צריך לצרף עמהם גלגל אין צירופין עמהם ול"ד כמו שפי' לקמן | |||||||||||||||||||||||||||
| כפול ב' תחתונה על ג' עליונה ב' פעמים ג' היינו ו' אותו ו' כתוב נגד ב' תחתונה דהיינו אל ז' ויהיה י"ג מחוק ז' וכתוב במקומה ג' ואחריה תוסיף א' על ב' כי הוא עשרה כמו שכתבתי לעיל ויהיה ג"כ ג' ומחוק ב' תחתונה וגם גלגל שלפניה | |||||||||||||||||||||||||||
| Zero cannot replace a non-zero digit in the upper line (the result line) in this erasing and shifting procedure -as this will decrease the numerical value of the rank, and there is no need for the zero as a place holder, since the current non-zero digit is already holding the place | ואין אתה צריך לצייר אותו הגלגל למעלה כמו שעשית כבר כי בלאו הכי יש גלגל כנגדו וכ"ש אם היה אות נגד הגלגל שלא היינו מוחקים האות לצייר שם גלגל שאם היינו מוחק' האות כדי לצייר שם גלגל אז היינו ממעטים החשבון ואם לעשות כדי להרחיק המעלה זה אינו כי בלאו הכי האות מרחיק המעלה כללא דמילתא לעולם אין אנו מציירין גלגל התחתון למעלה אלא אם אין כנגדו שום דבר | ||||||||||||||||||||||||||
| Zero does not need to replace a zero in the upper line as it is only a place holder, and the rank is already held by the current zero | אבל אם יש שום גלגל או אות נגד אותו גלגל התחתון אז אין אנו צריכין לצייר שום גלגל כי ציורו אינו אלא שומר המעלה כמו שכתבתי לעיל כי הגלגל מודיע שאות אחריו עולה מעלה אחת יותר ממה שהיית עושה אם לא היית שם שום ציור גלגל | ||||||||||||||||||||||||||
| ועתה נחזור לחשבון דלעיל כמו שפרטתי אז יהיה כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| שוב כפול ט' תחתונה על ג' עליונה ט' פעמים ג' היינו ז"ב כתוב במקום ג' עליונה ז' ואחריה במקום גלגל כתוב ב' ומחק ט' תחתונה כזה וגם ג' עליונה מחק | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| תמצא שמאתים וט' פעמים ג' אלפים ול' יש ס"ג רבבות וג' אלפים ומאתים ושבעים | |||||||||||||||||||||||||||
| הנה אראך בדרך אחר לכפול | |||||||||||||||||||||||||||
|
אם תרצה לידע כמה ט"ו פעמים תתר"ף |
- [Illustration of the procedure:]
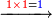
1 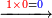
10 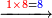
108 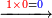
1080 1080 1080 1080 1080 1080 15 15 15 15 15
| עשה טור ראשון מתתר"ף ושים תחתיו ט"ו ה' תחת הא' וא' לשמאלו כזה | |||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
| אז תכפול הא' על כל הטור העליון ואחר כך ה' על כל הטור העליון וכה תאמר א' פעם א' הרי א' שים א' כנגד א' השפל מן הכפלות כל כך גבוה שיהא הוא למעלה מן התתר"ף מכוון כנגד הא' התחתונ' ויהיה צורת' כזה | |||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
| ואחר כך כפול א' פעמי' גלגל הרי גלגל שים אותו גלגל לפני הא' אשר כתבתי למעלה מן התתר"ף מכוונ' נגד הא' בשיט' ראשונ' ויהיה כזה | |||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
| ואחר כך כפול א' פעמי' ח' יעלה ח' כתוב ח' לפני ה0' שכתבת בשיט' עליונ' מכוונת נגד הציפר' שבשיט' אמצעי' ויהיה כזה | |||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
| ואחר כך כפול א' פעם 0' ויעלה 0' שימהו לפני הח' אשר כתבת בשיט' עליונ' מכוון נגד 0' שבשיט' אמצעי' גם תמחוק הא' כי נכפל על כל התתר"ף ויהיה כזה דמיונו | |||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
| והנה כפלת הא' על כל התתר"ף |
- [Illustration of the procedure:]
1080 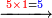
1580 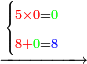
1580 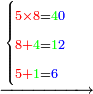
1620 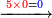
16200 1080 1080 1080 1080 15 15 15 15
| ואחר כך כפול הה' על כל התתרף ותתחיל לכופלו כנגדו ממש למעלה כאשר התחלת לכפול הא' כנגד א' כן תכפול הה' ועלה כך ה' פעמים א' היינו ה' שים אות ה' נגד הא' למעלה הימנו דהיינו במקום גלגל כזה | |||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
| ואחר כך אמור ה' פעמים 0' אם לא היה נכתב מאומה על הגלגל היית נותן שם גלגל עכשיו שרשום עליו ח' לא תעשה מהגלגל כלום כי אוחז מקומו ואחר כך אמור ה' פעמים ח' יעלה ארבעים ולא תשימהו במקום הגלגל כי תצטרך לגלגל אלא כתוב ד' על הח' לשמאל אז תמצא ד"ח זה על זה תמחוק שניהם ותכתוב במקומו ב' ועל הה' אשר כתבת לשמאל כתוב א' הרי ו' כזה | |||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
| ואחר כך אמור ה' פעמים גלגל היינו גלגל שים גלגל על גלגל ויהא דמיונו כזה | |||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
| תבין שלא נשלם הטור העליון נגד הטור השפל עד אשר תכפול כל האותיות מן הכפולות על כל החשבון ולמבין די ודו"ק |
Checking Methods |
ואם לבך מפקפק לומר מאן יאמר שכך הוא הילך מאזני צדק היאך תשקול ותבחין אם טעות אם לאו |
|
בראשונה קח חשבון שבשיטה העליונה אשר בקשת לכפול והשלך אותו ט"ט והמותר קח בידך |
| ואם לא תמצא אפילו פעם אחת ט' אז תקח הכל | |
| ואחר כך קח החשבון התחתון והשלך גם כן בט"ט | |
| ומה שנשאר בידך קח נא והשלך אותו בשער הכפל על מה שנשאר לך בשיטה עליונה אחר שהשלכת ממנו ט"ט ומה שיעלה בידך השלך אותו ג"כ בט"ט ומה שנשאר שלא הגיע לכלל ט' קח נא בידך | |
| ואחר כך קח החשבון היוצא לך כבר כשכפלת הב' חשבונות יחד והשלך ג"כ אותו בט"ט | |
| ומה שנשאר בידך אם הוא מכוון כנגד מה שנשאר לך כבר ידוע תדע שאמת חשבת ואם לאו בודאי טעית | |
|
|
ועתה שקול חשבון דלעיל למען יבין המבין ויוסיף לקח הדמיון היה 0"ג0"ג פעמים ט0"ב |
|
|
בתחילה נחבר ב' פעמים ג' היינו ו' ואין כאן אפילו פעם אחת ט' |
|
|
ואחר כך חבר חשבון התחתון דהיינו ט0"ב חיבור ט"ב היינו י"א השלך ט' וישאר ב' |
|
|
כפול ב' על ו' ב' פעמים ו' היינו י"ב השלך ט' וישאר ג' וזה יהיה לך לזכרון |
|
|
זה הכלל ראה בכפל מה שנשאר לך כגון עתה הוצרכת לכפול ב' פעמים ו' ויהיה י"ב כתוב י"ב בציפור ויהיה ב"א היינו יתיר על ט' ג' וכן לעולם |
|
|
ואחר כך ראה מה שיעלה בידך כשכפלתה 0"ג0"ג על ט0"ב דהיינו 0'ז'ב'ג'ג'ו' חבור אותו יחד ויהיה כ"א השלך אותו ט"ט וישאר ג' כמו שנשאר לך כבר ואם כן החשבון מכוון |
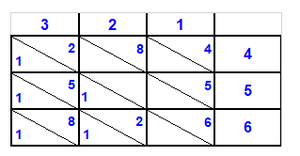
Chapter Five: Gelosia |
שער הכפל בסולם |
|---|---|
| ציור נקרא סולם ויפה לשער הכפל גדול | |
| The number of cells corresponds to the number of ranks of the multiplicands | וכמה שתרצה לכפול חשבון על חשבון כן עשה מניין הבתים |
|
אם תכפול חשבון בן ג' מעלות על ג' מעלות כמו כן תצייר שליבות הסולם ג' בתים לארכה ולרחבה |
|
ואם תכפל סך בן ג' אותיות על ב' אותיות עשה ג' בתים לרחבה וב' בתים לארכה |
| וכן להיפך מלמעלה למטה אחד המרבה ואחד הממעיט ובלבד שיכווין לבו כל אות במקומו לפי הציור | |
|
|
דמיון אם תרצה לידע כמה כ"א וג' מאות פעמים נ"ד וגם ת"ר שרשימתו א'ב'ג' ד'ה'ו' |
| The multiplier is written in the top line and the multiplicand in the rightmost column | רשום למעלה על הבתים כאשר תראה בסולם שרשמתי והנכפול כתוב בצדו זה תחת זה כמצוייר |
|
ובראשונה חשוב כמה ד' פעמים א' ויעלה ד' וכתוב אות בחצי הבית ראשון שמכוון תחת הא' וגם נגד הד' |
| Every cell is divided to two: the upper part is for the units of the interim product and the bottom part is for the tens | כי כל בית נחלק מחציתו העליון אחדים והתחתוני' עשיריים |
|
|
ואחר כך חשוב כמה ד' פעמים ב' ויעלה ח' רשומיהו בחצי בית העליון שתחת ב' |
|
|
ואחר כך חשוב כמה ד' פעמים ג' ויעלה ב"א רשומיהו באותו בית שתחת הג' וכתוב ב' בחצי' בית העליון וא' בחצי השניי' |
| ומעתה מחוק הד' כי היא נחשבת בכל חילוקים | |
|
מעתה תצטרך לחשוב ה' פעמים א' ויעלה ה' רשומיהו בבית שבצד הה' מכוון תחת הא' |
|
|
ואחר כך חשוב ה' פעמים ב' ויעלה 0"א רשומיהו בחצי בית התחתון בבית חמישי |
|
|
ואחר כך חשוב ה' פעמים ג' ויעלה ה"א רשומיהו בבית ששי ה' בחצי העליון א' בחצי תחתון |
| ומעתה מחוק ה' | |
|
והנה חשוב ו' פעמים א' ויעלה ו' רשומיהו בצדו מכוון בטור שתחת הא' |
|
|
ו' פעמים ב' כ"א רשומיהו בבית השמיני |
|
|
ו' פעמים ג' היינו ח"א רשומיהו בבית האחרון |
| והנה כפלנו כולה | |
| ואשכילך כמה יעלה סכום שלה קח אות ראשון שבבית ראשון שהיא ד' וכתביהו במקום מיוחד | |
| ואחר כך חשוב בשליבה שנייה בכל השיפוע מאות ח' עד אות ה' וצירוף אות הה' עם הח' ויעלה ג'א' הג' כתוב בצד הד' הנרשמת כבר כזה ד ג | |
| וגם הא' שהיא עשרה צרוף לשליבה שתחתיו וחבריהו אל הב' בתחילת שליבה שלישית ויעלה ג' וחבור אחר כך גם הו' שבסוף השיפוע ויהיה ט' רשומיהו אצל ד"ג כזה ד ג ט | |
| ואחר כך חשוב וצרוף אותיות שבשליבה רביעי' מראש ועד סוף ויעלה ט' כתוב ט' אצל דג"ט כזה ד ג ט ט | |
| והנה חשוב אותיות שבשליבה חמישית בשיפוע ויעלה צירופו עשרה | |
| The tens in the sum of the interim products are added to the subsequent sum of interim products | וכבר אמרתי שלעולם העשירי מצטרף לשליבה שתחתיו ואין רושמין אותה בצד המיוחדין |
| If there are no units left in the sum - zero should be written in order to hold the rank | אבל תצטרך להשיב גלגל במקום העשרה לשמור המעלה הואיל ולא נשאר אפילו אחד לשמור המורה המעלה |
| והנה כשתצטרף העשרה לא' שבשליבה אחרונה יעלה ב' וכתביהו בצד ד'ג'ט'ט' המיוחדים ויהיה כזה ד ג ט ט 0 ב | |
| זה מכוון חשבון של כפולת אב"ג על דה"ו | |
| The checking method of the result is the same method as in the previous chapter on multiplication | ומאזנים שלו כמו שכתבתי לעיל בשער הכפל הגדול |
|
|
ד'ו'ד' פעמים ד'ו'ד' עולה חשבונו ו'ט'ב'ה'א'ב' ודוק |
| סליק שער הכפל |
Multiplication - CheckMS Mantova f. 69r |
כשתרצה לידע משקל אם אתא שפיר כשיש לפניך הכפל |
|---|---|
|
|
כגו' א דוד פעם דוד כגו' ו'ט'ב'ה'א'ב' או כל כפלים אם הן שפיר או לאו |
|
|
אז קח לפניך דוד במניין נמצא י"ד ואמ' כמה הוא יותר מט' נמצא ה' ותשליך הט' ממך ואמ' כמה ה' פעמי' ה' נמצא כ"ה ותשליך ממך כל הט' שבתוך כ"ה ויתר לך ז' |
|
|
אז תשליך נמי ו'ט'ב'ה'א'ב' בט' אז ישאר לך ז' וכן תעשה לכל הכפולים שבעולם ודו"ק |
Chapter Six: Division |
שער החילוק | ||||||||||||||||||||||||||
| Dividing a large number into a few smaller numbers | והוא טוב לחלק חשבון גדול לכמה חשבונות קטנים | ||||||||||||||||||||||||||
| ועתה ידוע תדע שאין כותבין בשער זה כמו בשער הכפל אות ראשונה משורה תחתונה נגד אות אחרונה משורה עליונה אלא כותבין שורה עליונה כפי מעלותיה ושורה תחתונה כמו כן כפי מעלותיה ויכוון אות אחרונה שבשורה תחתונה נגד אות אחרונה שבשורה עליונה | |||||||||||||||||||||||||||
|
ואם אות אחרונה שבשורה תחתונה יותר מאות אחרונה שבשורה עליונה אז יסיג שורה תחתונה מעלה אחת לאחוריה אלא א"כ דאותו שורה תחתונה יש בה יותר מאות אחת | ||||||||||||||||||||||||||
|
אבל אם עלו שוות לא יסוג לאחריה אלא אם כן דאותו שורה יש בה יותר מאות אחת | ||||||||||||||||||||||||||
|
וכשיש בה יותר מאות אחת יסיג כל השורה מעלה אחת לאחוריה ואז יכול לחלק אותיות עליונה על אותיות תחתונות | ||||||||||||||||||||||||||
|
והחילוק שחילקו יכתוב נגד מעלה ראשונה שבשורה תחתונה הן אם אותו מעלה אות או גלגל | ||||||||||||||||||||||||||
| All the digits of the divisor should be subtracted from the dividend the same number of times as the digit in the highest rank is subtracted | וכשתחלוק ב' אותיו' פי' שהיו בשורה תחתונה ב' אותיות אז אין חילוק של שתיהם רק מנין אחד יהיה ג' אותיות או ד' וכן עד סוף כל הדורות וכל כך כמה פעמים שחלקת האות האחרונה מן החשבון כן תקח כל שאר אותיות ול"ד | ||||||||||||||||||||||||||
| Examples | ועתה אכתוב דמיונים למען יבין המבין ותן לחכם ויחכם עוד ויוסיף לקח | ||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
ועתה אתחיל בחילוק קטן אם ישאל השואל כמה פעמים ז' יש במאתים וי"ח | ||||||||||||||||||||||||||
|
הילך היאך תעשה כתוב המאתים וי"ח כזה | ||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| והז' היה מן הדין לכתוב תחת הב' כדי לחלק הב' לז' ז' פי' למנה כמה פעמים ז' יש בב' אלא שאין הב' מגיע לחילוק של ז' לכן נסוג הז' לאחור כדי שתהא הב' במעלה שנייה לה ותעלה לנגדה עשרים ואחת כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| ואותו עשרים ואחת תחלוק לז'ז' פי' מנה כמה פעמים ז' יש באחת ועשרים ונמצא שיש בהם ג' פעמים ז' אותו ג' כתוב למעלה על הא' שבשורה עליונה נגד ז' שבשורה התחתונה כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| ואחר כך מחוק הא"ב שמצאת בהם ג' פעמי' ז' ואחר כך סוג הז' מעלה אחת לאחוריה ויהיה תחת הח' כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| ומנה כמה פעמי' ז' יש בח' ולא מצאת בה רק פעם אחת ז' ועוד יש א' יותר אז כתוב א' נגד הז' על הח' כזה והאחד העודפת כתוב במקום הח' כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| נמצא ברי"ח יש ל"א פעמים ז' וישאר אחת וכן לעולם ועיין | |||||||||||||||||||||||||||
|
דמיון אחר הנה יש לי עשרת אלפים פצין ומאה ועשרים ושבע פצין ואבקש לידע כמה זהובי' יש בתוכם שכל אחד יש ט"ו פצין | ||||||||||||||||||||||||||
| והנה רשומיהו כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
|
והנה רשום תחת זה הז'ב'א'0'א' החשבון ה'א' ואם תכתבהו תחת הסופיים כמחוייב נמצא א' תחת א' ולא ישאר לך דבר וא"כ מאין תקח ה'פעמים א' כי כמה פעמים שתקח אות אחת כמו כן תקח חבירתה כמו שכתבתי לעיל וא"כ סוג ה'א' אחור וכתו' א' תחת גלגל וכתו' ה' תחת א' שלפני גלגל ויהיה כזה | ||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| והנה צריכין אנו לשער באם נקח הא' מהאותיות שעליו שגם יעדיף למצא הה' בעודף בחשבון הזה ואם תרצה לומר ליקח ט' פעמים מן י' א"כ לא ישאר רק אחד ותבא א' במקום גלגל ויהיה א"א ומעתה לא תוכל ליקח ט' פעמים ה' מן א"א וכן אם תקח ח' פעמים א' לא ישאר רק ב' ולא תוכל ליקח ח' פעמים ה' מן ב"א וכן אם תיקח ז' לא ישאר רק ג' ולא תוכל ליקח ז' פעמים ה' מן ג"א אלא קח ו' וישאר ד' כתוב ו' על הא' ויהיה כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| ואז תוכל ליקח ו' פעמים ה' מן א"ד וישאר לך מן הד' שהיא א' עשרה ואם כן כתוב א' במקום הד' ומחק ה' ויהיה כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
|
ואחר כך בקשנו ליקח הא' מן החשבון הזה י' פעמים לא תוכל ליקח כמו שפירשתי וגם זה הכלל נקוט בידך לעולם לא תוכל ליקח י' רק ט' או ח' או ז' ולמטה לכן עשה כך: כתוב ה'א' תחת ב'א' כזה | ||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| וקח ז' פעמים וישאר ד' שעודף י"א על ז' ד' וכתוב ז' למעלה נגד הה' תחתונה ומחק הא' תחתונה ומחק ג"כ הא'א' עליונה וכתב תחתיהן ד' כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
|
והנה קח ז' פעמים ה' מן ד' שבצידה דהיינו ל"ה וישאר ה' כי הד' היא במעלה שנייה מן הה' עולה ארבעים ועתה קח ממנה ל"ה וישאר ה' צרוף הה' אל הב' שלפניה ויהיה ז' כזה | ||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| וקח ה' פעמים א' מן ז' כי ז' פעמים לא נוכל ליקח כמו שפי' לעיל שאז לא נוכל ליקח ז' פעמים או ו' פעמים ה' ודו"ק לכן קח ה' פעמי' וכתוב למעלה ה' בצד הז' נגד ה' תחתונה ויעדיף ב' אותו ב' כתוב במקום ז' כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| והנה קח ה' פעמי' ה' מן ז"ב וישאר ב' שאינו מגיע לחשבון הא' וצורתו כזה | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| נמצא מכוון שעשרת אלפים ומאה וכ"ז פצין עולה ה' זהו' וגם ת"ר זהו' ושני פצין | |||||||||||||||||||||||||||
Checking Methods |
ואם לבך מגמגם כפול העודף האחרון על ה'א' ויצא לך חשבון הראשון ששאלת | ||||||||||||||||||||||||||
| The checking method of division is multiplication and the checking method of multiplication is division | וזהו מאזני צדק על שער החילוק נמצא כפל מברר החילוק והחילוק מברר הכפל |
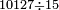 → Check:
→ Check: 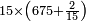
- [Illustration of the procedure:]
15 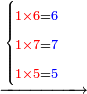
6755 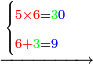
9755 
10105 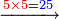
10125 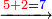
10127 675 675 75 5
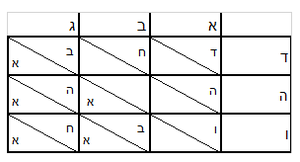
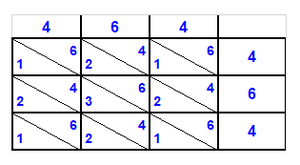
| דמיון למאזנים כתוב ה'א' וכתוב תחתיו ה'ז'ו' הנשאר באחרונה חוץ מן הב' שלא הגיע לחשבון ט"ו אל תצטרף עמהן עד סופו חיבורו לאות ראשונה כזה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![\scriptstyle x,y<10\quad x\sdot y=\left[10\sdot\left[\left(x+y\right)-10\right]\right]+\left[\left[x-\left[\left(x+y\right)-10\right]\right]\sdot\left[y-\left[\left(x+y\right)-10\right]\right]\right]](/mediawiki/images/math/c/5/3/c53bdf7d0d05eee10ddfd41a4484bd4b.png)
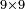
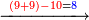

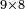
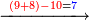
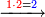
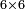
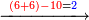
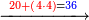
![\scriptstyle x,y<10\quad x\sdot y=\left[10\sdot\left[\left(x+y\right)-10\right]\right]+\left[\left(10-y\right)\sdot\left(10-x\right)\right]](/mediawiki/images/math/a/f/e/afe955d77e980c543eb318dccb42a0f3.png)



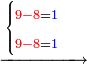
![\scriptstyle x<y<10\quad x\sdot y=\left(x\sdot10\right)-\left[x\sdot\left(10-y\right)\right]](/mediawiki/images/math/5/9/b/59bef0eba0fe04dc9bf9ce5cf50e92cd.png)
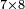
![\scriptstyle{\color{blue}{7<8<10\quad 7\times8=\left(7\sdot10\right)-\left[7\sdot\left(10-8\right)\right]=70-\left(7\sdot2\right)=70-14=56}}](/mediawiki/images/math/0/f/0/0f0b2311629a5458a2e7bbbe2497fcba.png)



![\scriptstyle x+y<10\quad x\sdot y=10+\left[\left(x-1\right)\sdot\left(y-1\right)\right]-\left[11\left(x+y\right)\right]](/mediawiki/images/math/4/8/a/48af587987c57b4bd9afe276050f32df.png)
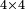
![\scriptstyle x+y<10\quad x\sdot y=\left[\left(10-y\right)\sdot\left(10-x\right)\right]-\left[10\sdot\left[10-\left(x+y\right)\right]\right]](/mediawiki/images/math/1/c/f/1cfea8153eb9c60eca5149ee3b1fa038.png)
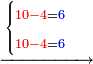
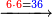
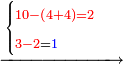
![\scriptstyle x+y<10\quad x\sdot y=\left[\left(10-y\right)\sdot\left(10-x\right)\right]+\left[10\sdot\left(x+y\right)\right]-\left(10\sdot10\right)](/mediawiki/images/math/9/b/7/9b71666c0f526fd5ea112fcf1db9a61d.png)
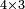
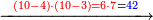
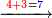
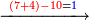
![\scriptstyle x,y<10\quad x\sdot y=\left[\left(10-y\right)\sdot\left(10-x\right)\right]+\left[10\sdot\left[\left(x+y\right)-10\right]\right]](/mediawiki/images/math/9/f/d/9fd75869b4462d349309f85b6504290b.png)
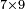
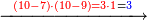
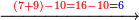
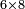
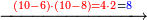
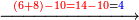
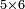
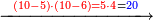
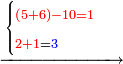
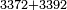

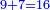
 :
: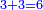
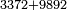



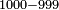
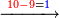
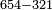
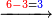
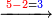
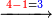
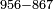
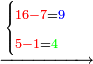
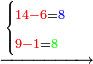
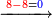
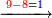
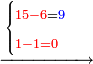
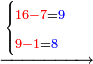
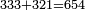
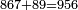
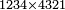
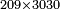
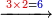
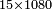
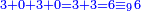
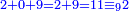
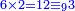

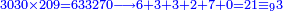
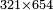
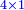


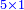


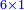


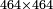
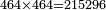
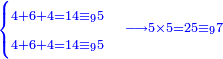
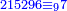
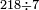
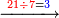
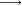
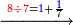

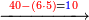
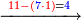
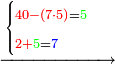

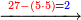
 → Check:
→ Check: 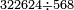

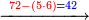



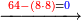
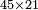 → Check:
→ Check: 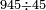

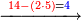

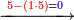
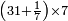
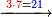
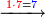
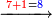
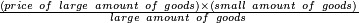
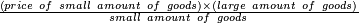
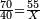
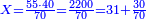

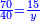
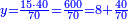
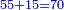
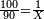
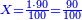
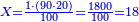
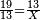
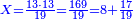
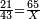
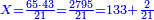
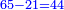
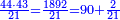
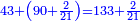
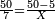
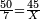
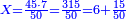
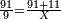
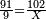
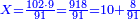
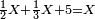
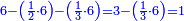
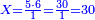
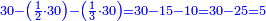
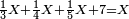
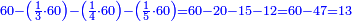
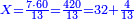
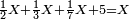
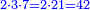
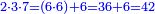
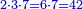
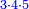
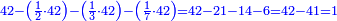
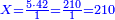
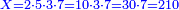
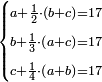
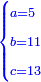
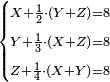
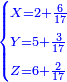
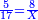
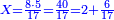
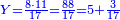
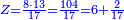
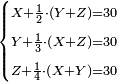
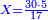
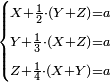

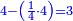
![\scriptstyle{\color{blue}{\left(4+\frac{1}{2}\right)-\left[\frac{1}{3}\sdot\left(4+\frac{1}{2}\right)\right]=3}}](/mediawiki/images/math/b/2/c/b2c7654e9e36456843cf38a9cefba0f9.png)
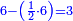
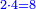
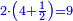
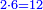
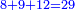
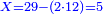
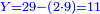
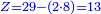
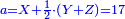
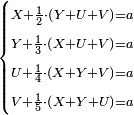
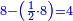
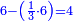
![\scriptstyle{\color{blue}{\left(5+\frac{1}{3}\right)-\left[\frac{1}{4}\sdot\left(5+\frac{1}{3}\right)\right]=4}}](/mediawiki/images/math/2/f/8/2f8b0ce274ed2357653f5bbb5b2e2059.png)
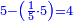
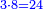
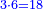
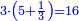
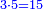
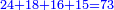

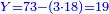
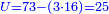
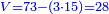
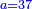
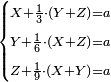
![\scriptstyle{\color{blue}{\left(3+\frac{3}{5}\right)-\left[\frac{1}{6}\sdot\left(3+\frac{3}{5}\right)\right]=3}}](/mediawiki/images/math/d/b/8/db875db8eb50eca9108eb5f305313319.png)
![\scriptstyle{\color{blue}{\left(3+\frac{3}{8}\right)-\left[\frac{1}{9}\sdot\left(3+\frac{3}{8}\right)\right]=3}}](/mediawiki/images/math/7/f/1/7f1cf2e5edc0dd92725597fe77ab6fbe.png)
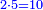
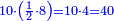

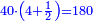
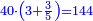
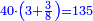

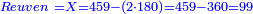
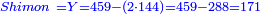
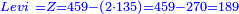
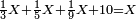
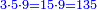
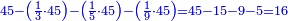
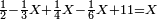
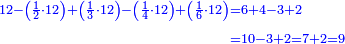
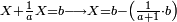
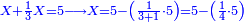
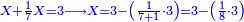
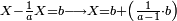

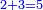
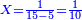
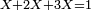

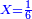
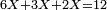
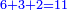
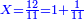
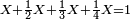
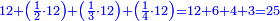
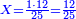
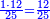
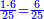
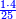
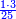
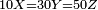
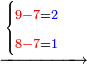
![\scriptstyle{\color{red}{\begin{cases}\scriptstyle1+\left[3\sdot\left[10-\left(1\sdot7\right)\right]\right]=1+\left[3\sdot\left(10-7\right)\right]=1+\left(3\sdot3\right)\\\scriptstyle4+\left[3\sdot\left[30-\left(4\sdot7\right)\right]\right]=4+\left[3\sdot\left(30-28\right)\right]=4+\left(3\sdot2\right)\\\scriptstyle7+\left[3\sdot\left[50-\left(7\sdot7\right)\right]\right]=7+\left[3\sdot\left(50-49\right)\right]=7+\left(3\sdot1\right)\end{cases}}}](/mediawiki/images/math/e/5/6/e56f405103a32d25d75437a6af1375fc.png)
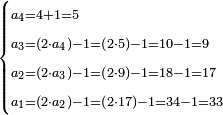
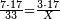
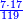
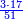
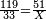
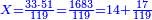
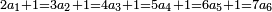
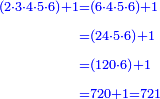
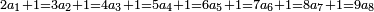
![\scriptstyle{\color{blue}{\left[720\sdot\left(7\sdot8\right)\right]+1=\left(720\sdot56\right)+1}}](/mediawiki/images/math/4/7/7/4771f98330aab4d54b098ef66e8365c0.png)
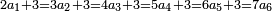
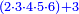
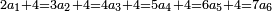
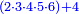
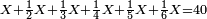
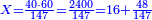
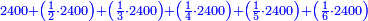
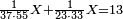
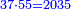

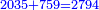

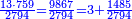
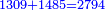
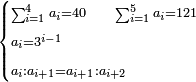
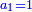


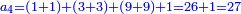
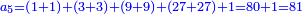
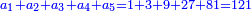
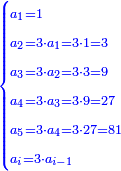
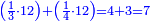
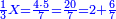
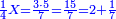
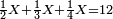
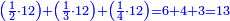
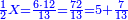
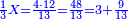
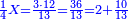
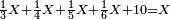
![\scriptstyle{\color{blue}{60-\left[\left(\frac{1}{3}\sdot60\right)+\left(\frac{1}{4}\sdot60\right)+\left(\frac{1}{5}\sdot60\right)+\left(\frac{1}{6}\sdot60\right)\right]=60-57=3}}](/mediawiki/images/math/a/f/0/af01839e49ad14fc9850f6d812f5b8cb.png)
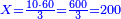
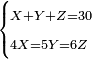
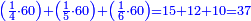
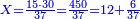
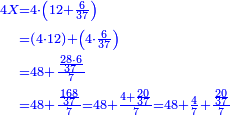
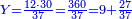
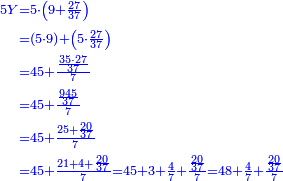
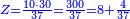
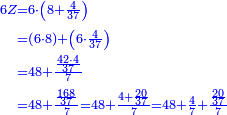
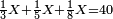
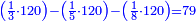
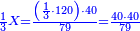
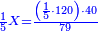
![\scriptstyle\begin{cases}\scriptstyle\sum_{i=1}^4 a_i =40\\\scriptstyle a_1=\left(\frac{1}{2}+\frac{1}{6}\right)\sdot a_2\\\scriptstyle a_2-\left[\left(\frac{1}{2}+\frac{1}{6}\right)\sdot a_2\right]=a_2-a_1=\frac{2}{3}a_3\\\scriptstyle a_3=\left(\frac{1}{3}+\frac{1}{4}+\frac{1}{6}\right)\sdot a_1\\\scriptstyle a_4=\frac{4}{5}\sdot{\color{red}{a_3}}\end{cases}](/mediawiki/images/math/c/1/e/c1e254f07692c6845aa08397f170e7e7.png)
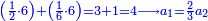
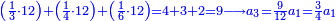
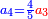
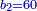
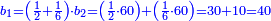
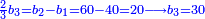
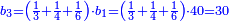
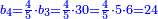
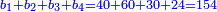
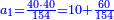
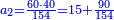
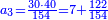
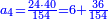
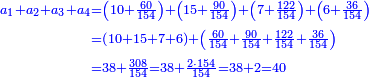
![\scriptstyle1+\left[\frac{1}{10}\sdot\left(X-1\right)\right]=2+\frac{1}{10}\sdot\left[X-\left[\left[1+\left[\frac{1}{10}\sdot\left(X-1\right)\right]\right]+2\right]\right]](/mediawiki/images/math/0/4/e/04ec9fa2f7109a05d7c4e8fa7ce5d879.png)
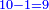

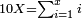
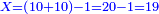
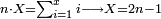
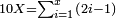
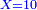
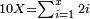
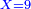
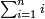
![\scriptstyle{\color{blue}{\sum_{i=1}^9 i={\color{red}{\left[\frac{1}{2}\sdot\left(9+1\right)\right]\sdot9}}=5\sdot9=45}}](/mediawiki/images/math/1/7/c/17c86b679997e03988c770bad30550d2.png)
![\scriptstyle{\color{blue}{\sum_{i=1}^{10} i=\left[\left(\frac{1}{2}\sdot10\right)\sdot10\right]+\left(\frac{1}{2}\sdot10\right)=\left(5\sdot10\right)+5=50+5=55}}](/mediawiki/images/math/8/0/b/80b5dca53c99289503b8c13b342ab214.png)
![\scriptstyle n=2m\longrightarrow\sum_{k=1}^n k=\left[\left(\frac{1}{2}\sdot n\right)\sdot n\right]+\frac{1}{2}n](/mediawiki/images/math/a/8/a/a8a5babcd3a6eea49bd9b762c7395e9b.png)
![\scriptstyle n=2m+1\longrightarrow\sum_{k=1}^n k=\left[\frac{1}{2}\sdot\left(n+1\right)\right]\sdot n](/mediawiki/images/math/1/e/4/1e4ea38423bb671340fbd2275e275e63.png)
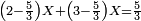
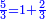
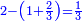
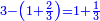
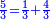
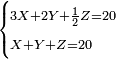
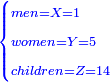
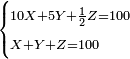
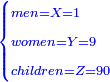
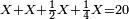
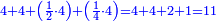
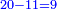
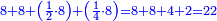

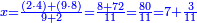
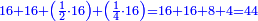

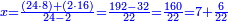
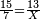
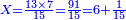
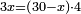
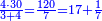
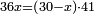
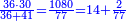
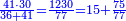
![\scriptstyle\left[\left(2-\frac{5}{3}\right)\sdot X\right]+\left[\left(3-\frac{5}{3}\right)\sdot X\right]=5](/mediawiki/images/math/b/3/9/b39a89f5f9f01ae578ff87165913ffb8.png)
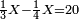
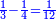
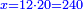
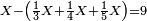
![\scriptstyle\begin{cases}\scriptstyle X+\left[\frac{1}{2}\sdot\left(Y+Z\right)\right]=60\\\scriptstyle Y+\left[\frac{1}{4}\sdot\left(X+Z\right)\right]=60\\\scriptstyle Z+\left[\frac{1}{3}\sdot\left(X+Y\right)\right]=60\end{cases}](/mediawiki/images/math/f/7/e/f7ed4efec08d6ecaa27c9fc465bdae6d.png)
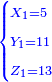
![\scriptstyle{\color{blue}{\begin{cases}\scriptstyle X_1+\left[\frac{1}{2}\sdot\left(Y_1+Z_1\right)\right]=17\\\scriptstyle Y_1+\left[\frac{1}{4}\sdot\left(X_1+Z_1\right)\right]=17\\\scriptstyle Z_1+\left[\frac{1}{3}\sdot\left(X_1+Y_1\right)\right]=17\end{cases}}}](/mediawiki/images/math/9/7/d/97d57b8ac4e8a9dbe8f698d6b961bdee.png)
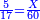
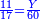
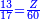
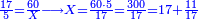
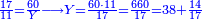
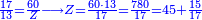
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle X+\left[\frac{1}{2}\sdot\left(Y+Z\right)\right]&\scriptstyle=\left(17+\frac{11}{17}\right)+\left[\frac{1}{2}\sdot\left[\left(38+\frac{14}{17}\right)+\left(45+\frac{15}{17}\right)\right]\right]\\&\scriptstyle=\left(17+\frac{11}{17}\right)+\left(19+\frac{7}{17}\right)+\left(22+\frac{16}{17}\right)=60\\\end{align}}}](/mediawiki/images/math/1/1/5/1151c1953e5eeefb1128f4a9ae687afb.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle Y+\left[\frac{1}{3}\sdot\left(X+Z\right)\right]&\scriptstyle=\left(38+\frac{14}{17}\right)+\left[\frac{1}{3}\sdot\left[\left(17+\frac{11}{17}\right)+\left(45+\frac{15}{17}\right)\right]\right]\\&\scriptstyle=\left(38+\frac{14}{17}\right)+\left(5+\frac{15}{17}\right)+\left(15+\frac{5}{17}\right)=60\\\end{align}}}](/mediawiki/images/math/8/c/5/8c51fcde67c49f9f297096f4fcd9e029.png)
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle Z+\left[\frac{1}{4}\sdot\left(X+Y\right)\right]&\scriptstyle=\left(45+\frac{15}{17}\right)+\left[\frac{1}{4}\sdot\left[\left(17+\frac{11}{17}\right)+\left(38+\frac{14}{17}\right)\right]\right]\\&\scriptstyle=\left(45+\frac{15}{17}\right)+\left(4+\frac{7}{17}\right)+\left(9+\frac{12}{17}\right)=60\\\end{align}}}](/mediawiki/images/math/5/a/2/5a2cd999d16458b3c413355c1586917a.png)
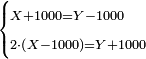
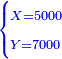
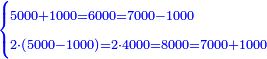
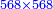


![\scriptstyle{\color{blue}{\sqrt[3]{149721291}}}](/mediawiki/images/math/2/8/8/28889c07ec72df83ee96c8d036f89e7d.png)
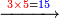
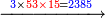

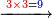


![\scriptstyle{\color{blue}{\sqrt[3]{99897344}}}](/mediawiki/images/math/7/3/e/73e3d56a32f3f45e418253824810fdba.png)
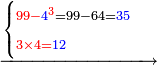
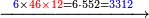

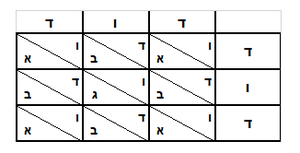
![\scriptstyle\xrightarrow{{\color{red}{\left[\left[4\times\left(464\times138\right)\right]\sdot10\right]+4^3}}={\color{blue}{2561344}}}](/mediawiki/images/math/9/8/5/98577a9d90a199749f7fe8e04eebab1f.png)