|
|
| זוג הזוג
|
זוג הזוג הוא המתחלק בשני חצאים וכל חצי לחצאים עד האחד ודימיונו
|
ס"ד
|
| הזוג הנפרד
|
הזוג הנפרד הוא הנחלק פעם אחת לשני חצאים ויעמד בנפרד ודמיונו
|
י"ד
|
|
|
זוג הזוג והנפרד הוא החלק יותר מפעם אחת ולא יכלה לאחד הנפרד הזוג ודמיונם כ"ד
|
|
|
הנפרד הראשון הבלתי מורכב הוא אשר לא ימנהו מספר כלל אין ראשון ראשון חלק לו אלא האחת י"א
|
|
|
הנפרד השני המורכב הוא אשר לו מספר ימנהו ולא יהיה המספר לו שני אלא נפרד ודמיונו ט"ו
|
|
|
מורכב המין המניין המקרי הוא מהקשת שני נפרדים מורכבים אין להם מספר ט' הג' להם בהצטרף משותף כלל כ"ה
|
|
Second Categorization of Even Numbers
|
חלוקה שנית למספר הזוג
|
| three types of even numbers
|
המספר והזוג יחלק לשלשה חלקים
|
- Superabundant number = the sum of its parts exceeds the whole number
|
אם נוסף ר"ל שהגעת כלל חלקיו מוסיף על כלו
|
- Deficient number = the sum of its parts is less than the whole number
|
ואם חסר ר"ל שהגעת כלל חלקיו יחסרו מכלו
|
- Perfect number = the sum of its parts is equal to the whole number
|
ואם שוה ר"ל שהגעת כלל חלקיו שוה לכלו
|
|
|
וזה המין השלישי כאמצעי בין שני המינים הראשונים אשר הם בדמות קצוות נבדלים אחר שהם בתכלית ההבדל לעברם השווי בתוספת ובחסרון
|
|
|
ונאמ' במספר הנוסף שהוא כמו הבעל חיים שאיבריו הם נוספים במקרה על האיברים הטבעיים לו ולכל אישי צורתו
|
|
|
וזה כמו י"ב וכ"ד והדומה להם
|
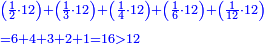
|
כי לי"ב חצי ושליש ורובע ושתות וחלק מי"ב ואלו החלקים מי"ב הם ששה וארבעה וג' ושנים ואחד וכלל זה י"ו והנה י"ו יותר מי"ב והם חלקיו
|
|
|
אמנם המספר החסר הנה הוא המתחלף בתאר למספר הנוסף והוא אשר הגעת חלקיו פחות מכלו
|
|
|
וידמה לזה המספר הבעל חיים שאיבריו הטבעיים חסרים משוויים הנמצא בכל אחדי צורתו בטבע
|
|
|
וזה כמו מספר ח' וי"ד והדומה להם
|
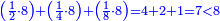
|
כי לשמנה מן החלקים חצי ורביעית ושמינית והם ד' ב' א' וכלם ז' וז' פחות מח' אשר ז' כלל חלקיו
|
|
|
וכמו שהיציאה מהשווי בתוספת אי אפשר לעמד על תכליתו בטבע כמו שנאמ' בפתיחת הספר כן החסרון בכמות בעל הגודל בלתי מוגבל התכלית אחר שהוא בהצטרף אלא במאמר כולל והשווי אחד אמצעי בין שני דברים אי אפשר לעמד על תכליתם כן רבוי שני המינים אשר זכרנום מהנוסף והחסר בטבע המספר הזוג ואמנ' השוה אמנם ימצא מעט לא הרבה כמו שיתרבו שני המינים הראשונים וזה שאנו אמנם נמצא מהמספר הזוג השוה מה שנגיע אליו לבד בתחבולה אשר נזכרה עתה בג"ה
|
The Discussion on the Quality of the Perfect Number
|
הדבור בתאר המספר השוה
|
|
|
והוציאו כבר אמרנו שהמספר השוה הוא אשר הגעת כלל חלקיו שוה לכלו וזה המספר ידמה בעל חיים שוה האיברים ממוצע הצורה
|
|
|
וזה כמו מספר ו' ומספר כ"ח
|
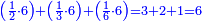
|
כי ששה יש לו חצי ושליש ושתות והם ג' ב' א' וכלם ששה הנה אלו הששה שוים לששה אשר הם חלקיו לא יוסיפו ולא יחסרו
|
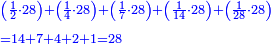
|
וכמו כן גם כן כ"ח יש לו מהחלקים חצי ורביעית ושביעית וחלק מי"ד וחלק מכ"ח והם י"ד ז' ד' ב' א' ואלו כלם שוים למספר כ"ח אשר הם כלל חלקיו לא יוסיפו ולא יחסרו מהם
|
|
|
ואמנם איך יתילדו אל המספרים השווים ואיך נעמוד על המספר הנמצא מהם וכמה מספרים ימצאו מהם בכל מספר מונח הנה הוא במה שאתאר וזה שנניח מדרגות מספרי זוג הזוג אשר התחלתם מהאחד בטור ותהיה המדרגה הראשונה א' והשנית ב' ונעזוב המדרגה הראשונה עוד נתחיל מב' ונניח תחתיה כלל מה שיתקבץ ממנה וממה שלפניה וזה ג' וכן תעשה במה שילוה לה מן המדרגות זוג הזוג תניח תחת כל מדרגה כלל מה שיתקבץ ממנה וממה שלפניה הנה בהכרח שיהיו המספרים המונחים תחת מדרגות זוג הזוג נפרדים לפי שהמדרגה הראשונה האחד והמדרגות אשר אחריה זוגות והזוג כאשר יוסף עליו האחד ישוב נפרד הנה יוכרו מאלו המספרים הנפרדים כל מספר ראשון בלתי מורכב ונרשום עליו רושם ונעזוב מה שזולתו עוד נכה כל מספר שרשמנו עליו במה שלמעלה ממנו עליו ר"ל במספר הזוג אשר תחתיו אותו הנפרד הראשון הבלתי מורכב ונעמיד מה שיצא מן ההכאה תחת אותו הנפרד הראשון הבלתי מורכב כדי שיסודרו גם כן הגעות המוכים כפי מדרגותיהם בטור שלישי וכאשר תחפש בזאת התחבולה כל מה שהנחת ממדרגות מספרי זוג הזוג הנה כבר הוצאת כל המספרים השלמים אשר הם נכללים תוך מספר המדרגה האחרונה ממה שהוצאת מהם ואותם המספרים הם אשר העמדתם בטור השלישי תחת הנפרדים הראשונים הבלתי מורכבים והם נלוים על משך סדרם בטבע לא ידולג ביניהם מספר שלם כלל וכבר יתחייב לאלו המספרים השלמים שיהיה הפרט העודף הם על עשרה פעם ו' פעם ח' וכן תמיד ימצאו אלו המספרים בזה התאר ובחן כל מה שזכרתי לך מתארם ודרך הוצאתם בזאת הצורה בג"ה
|
The Discussion on the Quality of the Relative Quantity and its Division into the Equal and the Unequal
|
הדבור בתאר הכמה הצירופיי והחלקו אל השוה ובלתי שוה
|
| After elaborating the discussion on the absolute quantity, completing its discription and the explanation of its interprations, now the relative quantity will be discussed, and described by a proper description in accordance with what was described beforehand
|
ואחר אשר הרחבנו המאמר על הכמה הנפרד והשלמנו תאריו ובאור פירושיו אנו נקח עתה לדבר בכמה המצטרף ונתארהו תאר נאות ומסכים למה שתארנו בו מה שקדם לפניו
|
| The relative quantity is divided in the first division into two parts: one is the equality, and the other is inequality.
|
והכמה המצטרף יחלק חלוקה ראשונה לשני חלקים אחד מהם השווי והאחר לא שווי
|
| For, every number is related to a number that is either equal to it, or unequal, with no third species in this division at all.
|
כי כל מספר יחובר אל מספר אם שיהיה שוה לו ואם שיהיה מבלתי שוה מבלתי שיהיה בזאת החלוקה מין שלישי כלל
|
| There is no supplement nor deficiency in equality, but one of the two relatives is equal to the other.
|
הנה השווי אין תוספת בו ולא חסרון אבל יהיה בו אחד מן ב' המצטרפים שוה לאחר
|
- As the hundred, when compared with the hundred, the ten with the ten,
|
כמו המאה כאשר הוקשו אל המאה והעשרה אל העשרה
|
- And the similar of the equal to what is related to it among those that are related to it by matter of quantity, whose property is "equal" and "unequal".
|
והדומה לזה ממה שהוא שוה למה שהוקש אליו ממה שהוקשו אליו בענין הכמה אשר סגולתו שוה ולא שוה
|
| The evenness is not to be divided into species at all, since the matter of evenness is the equal, the equal is equal to the equal, and the even is even to its even.
|
והישר לא יחלק למינים כלל לפי שאמנם ענין הישר השוה והשוה שוה לשוה והישר ישר למיושר לו
|
| The species of the given numbers that differ in comparison with one another, in inequality, is divided in a second division, into two parts - one of them is greater, and the other is smaller, and they are different by name and antithetical by matter.
|
ואמנם המספרים המונחים המתחלפים עם הצטרף קצתם אל קצת ביציאה מהשווי הנה מינם יחלק בחלוקה השנית לשני חלקים אחד מהם גדול והאחר קטן והם מתחלפים בשם ונבדלים בענין
|
| The greater relation is divided in a third division into five parts: the multiple to the related to it, the superpaticular to the related to it, the superpartient to the related to it, the multiple superparticular to the related to it, and the multiple superpartient to the related to it.
|
וההצטרפות הגדול יחלק בחלוקה השלישית לחמשה חלקים מהם בעל הכפלים למה שהוקש אליו ומהם המוסיף חלק למה שהוקש אליו ומהם המוסיף חלקים למה שהוקש אליו ומהם בעל הכפלים המוסיף חלק למה שהוקש אליו ומהם בעל הכפלים המוסיף חלקים למה שהוקש אליו
|
| The smaller is divided, like the greater related to it, into five species, each species is parallel to a species of the greater, ascribed and named according to its corresponding, i.e. the species of the smaller are called: the submultiple, the subsuperpaticular, the subsuperpartient, the submultiple-superparticular, and the submultiple-superpartient.
|
ואמנם הקטן יחלק כמו הגדול ההקש בו לחמשה מינים יקביל כל מין מהם מין מהגדול ייוחס ויקרא בהקבלתו ר"ל שיקראו מיני הקטן כשיאמר מין תחת בעל הכפלים ומין תחת המוסיף חלק ומין תחת המוסיף חלקים ומין תחת בעל הכפלים המוסיף חלק ומין תחת בעל הכפלים המוסיף חלקים
|
[Simple Ratios]
|
|
| Said Abū Yusūf: two of these five ratios are simple: the multiple ratio and the superparticular ratio
|
אמר אבו יוסף ומאלו היחסים החמש שנים מהם פשוטים והם בעל הכפלים והמוסיף חלק
|
- He did not mean by superparticular ratio to the multiple superparticular ratio, but he meant the ratio between the two numbers, of which the greater is as the smaller once and as a part of the smaller.
|
ולא ירצה במוסיף חלק בעל הכפלים המוסיף חלק אמנם רצה היחס אשר בין שני המספרים אשר הגדול מהם כמו הקטן פעם אחת וכמו חלק מהקטן
|
| This is clear in what was clarified for you by Plato, in the book that is attributed to the causes of the capacities that are ascribed to the supreme individuals.
|
וזה מבואר במה שביארו אליך אפלטון בספר המיוחס אל עלות הכחות המיוחסות אל האישים העליונים
|
- This is because he mentioned the numbers that are ascribed to the nine spheres, and related between them, relating to each supreme sphere, conceived by the intellect, their natures, of which the numbers ascribed, are of the numbers that are given to the spheres of the four elements.
|
וזה שלמה שזכר המספרים המיוחסים אל הכדורים התשעה וייחס ביניהם לחבר אל כל כדור עליון הדמוי בשכל מטבעיהם מה שיוחסו מספריהם מהמספרים המונחים לכדורי היסודות הארבעה
|
- to the sphere of the earth and the water - 24
|
וייחס אל כדור הארץ והמים כ"ד
|
- to the sphere of the fire and the air - 27
|
וייחס אל כדור האש והאויר כ"ז
|
- the sphere of the moon - 36
|
וייחס אל כדור הירח ל"ו
|
- the sphere of Mercury and Venus - 48
|
וייחס אל כדור כוכב ונוגה מ"ח
|
- Since he explained why the sphere of these two stars is one and the number ascribed to them is one, by saying that these two stars are included in one matter, which is that their distance from the sun is only in the circles of their encirclements, and the sum of the movments of their centers and the sun is one, therefore one number is ascribed to them.
|
אחר שבאר למה היו שני אלו הכוכבים כדורם אחד והמספר המיוחס אליהם אחד בשאמר ששני אלו הכוכבים יכללם ענין אחד והוא שמרחקיהם מן השמש אמנם הוא בגלגלי הקפותיהם לבד ואמנם מרכזיהם הנה סך תנועותיהם והשמש אחד ולזה נתייחס אליהם מספר אחד
|
- the sphere of the sun - 54
|
ונתייחס אל כדור השמש נ"ד
|
- the sphere of the Mars - 64
|
ולכדור מאדים ס"ד
|
- the sphere of the Jupiter - 72
|
ולכדור צדק ע"ב
|
- the sphere of the Saturn - 72
|
ולכדור שבתאי צ"ו
|
- the sphere of the fixed stars - 108
|
ולכדור הכוכבים הקיימים ק"ח
|
- His theory about the attributions to these spheres, that ascribed these numbers, was not by accident, without a nesessary reason, but it was resulted from a necessary discussion that approves that this is the greater first relation described of these numbers to these spheres in this ratio.
|
ולא היתה הנחתו לאלו היחסים אל אלו הכדורים אשר חייבו זה המספר בהזדמן מבלתי טעם ראוי אבל אמנם נתחייב זה במאמר הכרחי המאמת שזה הוא היותר ראשון במה שיתואר מהצטרפות אלו המספרים אל אלו הכדורים בזה היחס
|
- When he related between these numbers, he mentioned that
 is not a simple ratio. is not a simple ratio.
|
וכאשר ייחס בין אלו המספרים זכר שק"ח מכ"ד אינו ביחס פשוט
|
- He [= Nicomachus] said: because of this we say that the fixed stars are far from the corporeal activities, that have essence.
|
אמר ולזה נאמר שהכוכבים הקיימים רחוקים מהפעולות הגשמיות בעלות ההויה
|
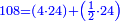 → this is the double sesquialter ratio, which is not a simple ratio. → this is the double sesquialter ratio, which is not a simple ratio.
|
וק"ח כמו ארבעה דמיוני כ"ד וכמו חציים וזהו הכפל המוסיף חלק הנה לא יהיה זה היחס פשוט
|
| This is the explanation of that he did not mean by superparticular ratio to the multiple superparticular ratio.
|
זהו ביאור שלא רצה במוסיף חלק בעל הכפלים המוסיף חלק
|
| I did not elaborate this discussion, thinking that the similar of the author's discussions were [not] unknown to you, in your casuistry and diligence when studying his talk, and your love to this craft, all the more so that you are of those who have his books
|
ולא הארכתי בזה המאמר הנה לחשבי שכמו זה ממאמרי המחבר נעלם ממך עם פילפולך ושקידתך בעיון דבריו ואהבתך לזאת המלאכה וכל שכן שאתה ממי שספריו אצלו
|
| But, I wanted to remind you of it.
|
אבל ראיתי להזכירך זה
|
| I have no doubt that our book will fall into the hand of the one who is ignorant concerning the teacher's opinion, of which you yourself know.
|
ולא אספק שספרנו זה יפול אצל מי שסכל מסברת המלמד מה שתדעהו אתה
|
| And when the discussion has no capacity of bringing to the essence of the thesis, the thoughts become confused, the conception falls, the truths disappear, and the axioms are non-existent.
|
וכאשר לא היה בכח המאמר שיביא אל האמתת הדרוש יתבלבלו המחשבות ויפול הדמוי ויעלמו האמתיות ויעדרו הידיעות
|
| May God lead you straight in the light of his explanation, to reach the brightness of his high rank.
|
יישירך האל לאור באורו ולהשיג זיו יקרו
|
The Discussion on the Multiple Ratio - its Nature and it Production
|
הדבור ביחס בעל הכפלים וטבעו והתילדו
|
| Now, we shall preface the discussion on the multiple ratio, since it is anterior by nature to the other four remaining ratios.
|
ואמנם עתה נקדים המאמר על יחס בעל הכפלים אחר שהוא היותר קודם בטבע משאר היחסים הארבעה הנשארים
|
- When relating the beginning of the numbers, which is 2, to 1, which is the cause of the number, its double is found, and this is called the double ratio.

|
וזה שאנו כאשר הקשנו תחלת המספרים אשר הוא ב' אל האחד אשר הוא עלת המספר מצאנוה כפל לו וזה הוא הנקרא הכפל השניי
|
- If relating 1 also to the second number, which is 3, the triple ratio is created.
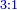
|
ואם הקשנו האחד גם כן אל המספר השני אשר הוא ג' יתחדש הכפל השלישי
|
- If it is related to the third number, which is 4, the quadruple ratio is created.
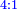
|
ואם הקשנוהו אל המספר השלישי והוא ד' יתחדש הכפל הרביעי
|
- Likewise when it is related to the terms of the natural numbers, the multiple ratios are created, named by the number to which the one is related.
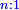
|
עוד כן כאשר יוקש אל מדרגות המספרים הטבעיים יתחדשו כפליים יקרא בשם המספר אשר אליו יוקש האחד
|
| It is clarified that the first ratio that subsists in number is the double ratio, when the beginning of the numbers, which is 2, is in comparison with the one, whose duplication generates the number.
|
הנה התבאר שהיחס הראשון שיפל במספר הוא יחס הכפלים בהצטרף תחלת המספרים אשר הוא ב' אל האחד אשר מהכפלו יהיה המספר
|
| It is clarified also that the double ratio is the first of the multiple ratios by nature, as it is by relating the one to the beginning of the numbers.
|
והתבאר שהכפל השניי ראשון למיני הרב הכפליים בטבע לפי שהוא מהקשת האחד אל תחלת המספרים
|
| The species of the multiple ratios are endless in potentia, as they are growing with the growth of the natural numbers.
|
ואין למיני הכפלים תכלית בכח להתרבותם עם התרבות המספרים הטבעיים
|
| We will start first with the description of the production the multiples, without the rest of the ratios
|
ונתחיל ראשונה בספור התילד בעל הכפלים בלתי שאר היחסים
|
- The first of them by nature will prefaced:
|
ונקדים ממנו הראשון מהם בטבע
|
- The double ratio is that which is generated by relating the double of any number to that number:
|
ונאמר שהכפל השניי הוא אשר יתחדש מיחס כפל כל מספר אליו
|
- Such as:
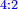 and and 
|
כמו ד' אצל ב' וכמו ח' אצל ד'
|
- Hence, it is already clarified how the double ratio grows:
|
הנה אם כן כבר התבאר איך יצמח הכפל השניי
|
- The natural numbers are lined up by the succession of the natural order.
|
וזה כשיסודרו המספרים על משך סדר הטבע
|
- Such as: 1; 2; 3; 4; 5; 6; 7; as much as one wishes to set.
|
כמו א' ב' ג' ד' ה' ו' ז' עד מה שנרצה להניח
|
- The natural even numbers are lined up by the succession of the natural order in a line parallel to the first line.
|
עוד נסדר הזוגות הטבעיים על משך סדר הטבע בטור נכחיי לטור הראשון
|
- Such as: 2; 4; 6; 8; 10; 12; 14
|
כמו ב' ד' ו' ח' י' י"ב י"ד
|
- Its terms are as the number of the terms that were set in the line of the sequence of the natural numbers.
|
ויהיו מדרגותיו כמספר המדרגות אשר סדרת אותם בטור סדר המספרים הטבעיים
|
- Then, the first of the terms of the natural evens is related to the first of the terms of the natural numbers; the second to the second; the third to the third; and so on in what follows - we find all of them together in the double ratio.
|
עוד תקיש הראשון ממדרגות הזוג הטבעי בראשון ממדרגות המספר הטבעי והשני בשני והשלישי בשלישי וכן במה שאחר זה שאנו נמצאם יחד ביחס הכפל השני
|
- Such as:
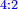 ; ;  ; ;  ; and so on. ; and so on.
|
כמו ד' אצל ב' וו' אצל ג' וח' אצל ד' וכן כלם
|
- The triple ratio is that in which the greater among the two given numbers is thrice the smaller number.
|
אמנם הכפל השלישי הוא שיהיה בגדול משני המספרים המונחים שלשה דמיוני המספר הקטן
|
- Hence, it is clarified how the triple ratio is produced:
|
אם כן הוא מבואר לך איך יתילד הכפל השלישי
|
- The natural numbers are lined up by the succession of the natural order.
|
וזה כשתסדר המספרים כטבעיים על משך סדר הטבע בטור
|
- Such as: 1; 2; 3; 4; 5; 6; 7; 8; 9
|
כמו א' ב' ג' ד' ה' ו' ז' ח' ט'
|
- Then, two terms are skipped and the third is taken and placed at the beginning of another line.
|
עוד נתחיל ונעבור שני מדרגות ונקח השלישית ונשימה ראש מדרגות טור אחד
|
- The two terms that follow this term are skipped and the third is taken and placed second in the other line.
|
עוד נעבור גם כן שתי מדרגות אחר אותה המדרגה תקח המדרגה השלישית ונשימה ראש מדרגות השנית מהטור האחר
|
- Likewise, the two terms that follow each taken term are skipped and the third is taken and arranged in the terms of the other line.
|
עוד כן נדלג שתי מדרגות אחר כל מדרגה שנקח ונחזיק בשלישית ממנה ונסדרם במדרגות אשר בטור האחר
|
- Thereafter, the [first] term of the resulted line is related to the first term of the natural numbers; the second to the second; the third to the third - we find them in the triple ratio.
|
ואחר נקיש בין המדרגות מהטור המוצא ובין המדרגה הראשונה מטור המספר הטבעיי עוד השנית בשנית והשלישית בשלישית הנה אנו נמצאם ביחס הכפל השלישי
|
- Such as:
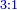 ; ;  ; ;  ; and so on until the end of the numbers that were set. ; and so on until the end of the numbers that were set.
|
כמו ג' אצל א' ו' אצל ב' וט' אצל ג' וכן תמיד עד סוף שהנחת מן המספרים
|
- Thus it is clear that the triple ratio is generated by multiplying each of the terms of the natural numbers by three and placing these products in the terms of another line.
|
הנה אם כן כבר התבאר שאמנם יתחדש יחס הכפל השלישיי מהכאת כל מדרגה ממדרגות המספרים הטבעיים בשלשה והעמדת אלו ההגעות במדרגות טור אחר
|
- It is necessary for the line of the greater numbers in this ratio, and any ratio that is derived from the duplication of an odd number to a number, that it will be an odd number, then an even number, then another odd number, as the observation shows.
|
וכבר יתחייב לטור אשר בו מדרגות המספרים הגדולים מזה היחס ובכל יחס נגזר ההכפלה ממספר נפרד אל מספר שיהיה נפרד ואחר כן זוג עוד נפרד כפי מה שתראה אותך הבחינה
|
- It is also necessary, in this ratio alone, that between each two odd numbers there will be two means of the natural odd numbers that were skipped.
|
וכבר יתחייב גם כן בזה היחס לבד שיהיה בין כל נפרד ונפרד שני אמצעיים מן הנפרד הטבעי כבר עברו
|
- Such as 5 and 7 of the natural odd numbers, which were skipped, between 3 and 9.
|
כמו ה' וז' אשר כבר עברו מהנפרד הטבעי בין ג' וט'
|
- Likewise it is necessary that between each two even numbers there will be two means of the natural even numbers that were skipped.
|
וכן יחוייב גם כן שיהיה בין הזוג שני אמצעיים כבר עברו מהזוג הטבעי
|
- Such as 8 and 10, which were skipped, between 6 and 12; as well as 14 and 16, which are between 12 and 18.
|
והזוג כמו ח' וי' אשר כבר עברו בין ו' וי"ב וכמו י"ד וי"ו בין י"ב וי"ח
|
- The quadruple ratio is generated by multiplying each of the terms of the natural numbers by 4 and relating the product to the same term.
|
אמנם הכפל הרביעיי אמנם יתחדש מהכאת כל מדרגה ממדרגות המספר הטבעי בד' עוד יוקיש מה שיצא מן ההכאה אל אותה המדרגה
|
- The same for the quintuple ratio and any of the species of the following multiple ratios that one wishes.
|
וכן החמשיי ומה שאחריו ממה שתרצה ממיני הכפלים
|
| Yet, if the multiple is named by an even number, all of its terms are even numbers.
|
אלא שכאשר היה הכפל נקרא למספר הזוג היו כל מדרגותיו זוגות
|
- Such as the quadruple ratio, of which the beginning of the terms is 4; 8; 12; 16.
|
כמו הכפל הרבעיי אשר תחלת מדרגותיו ארבעה עוד ח' י"ב י"ו
|
| If the multiple is named by an odd number, its terms are an even number then an odd number.
|
ואם היה הכפל נקרא למספר נפרד היו מדרגותיו אחת זוג ואחרת נפרד
|
- Such as the quintuple ratio, of which the beginning of the terms is 5; 10; 15; 20.
|
כמו הכפל החמשיי אשר תחלת מדרגותיו ה' עוד י' עוד ט"ו עוד כ'
|
| This species is named by the greater a multiple ratio and by the smaller a submultiple ratio.
|
וראוי שיקרא זה המין מן הגדול בעל הכפלים ומהקטן תחת בעל הכפלים
|
The Discussion on the Second Simple Ration which is the Superparticular Ratio
|
הדבור ביחס השני הפשוט והוא יחס המוסיף חלק
|
| Since the discussion on the multiple ratio has already been brought, because it is simplier, and anterior by nature, as been explained, its successive by natural succession, which is the superparticular ratio is discussed:
|
ואחר שכבר הבאנו הדבור על יחס הכפלים אחר שהוא יותר פשוט ויותר קודם בטבע כמו שבארנו נאמ' על אשר ימשך לו המשכות טבעי והוא המוסיף חלק
|
When comparing the beginning of the numbers, which is 2, with its successive, which is 3, the three is to two as its similar and its half.[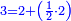 ] ]
|
וזה שאנו כאשר הקשנו בין תחלת המספרים אשר הוא ב' ובין המספר אשר ימשך לו והוא ג' היה ג' אצל ב' כמהו וכמו חציו
|
| Hence, the superparticular ratio is formed by comparing the beginning of the numbers with its successive.
|
הנה יתחדש המוסיף חלק מההקשה בין תחלת המספרים ואשר ימשך לו
|
- the first superparticular ratio by nature: sesquialter ratio
|
והתבאר שהחלק הראשון בטבע הוא המוסיף חצי
|
- sesquitertian ratio: the ratio of the third number, which is 4, to the second number, which is 3
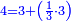
|
עוד המוסיף שליש בהקשת המספר השלישי אשר הוא ד' אל המספר השני אשר הוא ג' כי ד' כמו ג' וכמו שלישיתו
|
|
|
עוד המוסיף רביע
|
|
|
עוד המוסיף חומש
|
| the ratio of each number to its preceding of the natural numbers
|
בהקשת כל מספר אל אשר לפניו מהמספרים הטבעיים
|
- Hence, it is necessary to mention the sesquialter ratio:
|
הנה אם כן יחוייב שנזכיר המוסיף חלק חצי
|
- This ratio is produced by setting the natural even numbers beginning from 2 in a line successively, which is the line that is produced by the double ratio.
|
ונאמר שזה היחס יתילד בשנסדר הזוג הטבעי אשר התחלתו ב' והוא הטור אשר נעשה בכפל השניי בטור ימשך קצתו לקצת
|
- Setting the numbers that result from the multiplication of each of the terms of the natural numbers by three in a line successively, which is the visible from the triple ratio.
|
עוד נסדר המספרים אשר מהכאת מדרגות המספרים הטבעיי' כל א' בג' והוא אשר נראה בכפל השלישיי בטור ימשכו קצתם לקצת
|
- Then each term of this line is related to its corresponding in the other line, so the terms illustrate the sesquialter ratio, as seen in the following diagram:
|
עוד יוקש בין כל מדרגה מזה הטור ובין דומה לה מהטור האחר במספר המדרגות כי יראו המדרגות יחס המוסיף חלק החציי כמו שתראה בזאת הצורה
|
| לב |
ל |
כח |
כו |
כד |
כב |
כ |
יח |
יו |
יד |
יב |
י |
ח |
ו
|
| מח |
מה |
מב |
לט |
לו |
לג |
ל |
כז |
כד |
כא |
יח |
טו |
יב |
ט
|
- The sesquitertian ratio is generated by setting this line of the multiplication of each of the terms of the natural numbers by three parallel to the line that is generated from the multiplication of the natural numbers by four, which is the line that is produced by the quadruple ratio.
|
ואמנם המוסיף שליש הוא אמנם יתחדש בסדור זה הטור אשר מהכאת מדרגות המספרים הטבעיים בג' נכחיי לסדר הטור אשר יתחדש מהכאת המספרים הטבעיים בד' והוא הטור אשר חודש בכפל הרבעיי
|
- Likewise the sesquiquintan ratio, for one of its lines is the line of the quadruple ratio and the other is the line of the quintuple ratio.
|
וכמו כן המוסיף רביע כי אחד מטוריו טור הכפל הרבעיי והאחר טור החמשיי
|
| The same for any superparticular ratio wished, according to the example described.
|
וכמו כן כל מה שתרצה מהמוסיף חלק הוא כמו זה המשל אשר תארתי לך
|
| The greater compared in this species is called superparticular and the smaller subsuperparticular.
|
וכבר יתכן שיקרא המוקש בזה המין אם הגדול המוסיף חלק ואם הקטן תחת המוסיף חלק
|
| So, for any species the smaller compared is called sub of the greater compared, which is called by a special name.
|
וכמו כן יקרא המוקש הקטן מכל מין כאשר הוא תחת מה שלמעלה ממנו מההצטרפות הגדול הנקרא בשם מיוחד
|
| The multiple and superparticular ratios mentioned and what is properly to say are written also in this diagram:
|
וכבר רשמתי מה שזכרתי לך מהכפלים והמוסיף חלק ומה שיאות לומר גם בזאת הצורה
|
|
|
| י |
ט |
ח |
ז |
ו |
ה |
ד |
ג |
ב |
א
|
| כ |
יח |
יו |
יד |
יב |
י |
ח |
ו |
ד |
ב
|
| ל |
כז |
כד |
כא |
יח |
טו |
יב |
ט |
ו |
ג
|
| מ |
לו |
לב |
כח |
כד |
כ |
יו |
יב |
ח |
ד
|
| נ |
מה |
מ |
לה |
ל |
כה |
כ |
טו |
י |
ה
|
| ס |
נד |
מח |
מב |
לו |
ל |
כד |
יח |
יב |
ו
|
| ע |
סג |
נו |
מז |
מב |
לה |
כח |
כא |
יד |
ז
|
| פ |
עב |
סד |
נו |
מח |
מ |
לב |
כד |
יו |
ח
|
| צ |
פא |
עב |
סג |
נד |
מה |
לו |
כז |
יח |
ט
|
| ק |
צ |
פ |
ע |
ס |
נ |
מ |
ל |
כ |
י
|
|
- [
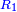 ]: Starting by arranging the numbers by natural order, from one to ten, in the first line widthwise. ]: Starting by arranging the numbers by natural order, from one to ten, in the first line widthwise.
|
וזה שאנו נתחיל ונסדר בטור הראשון הלוקח ברחב המספרים על סדר הטבע מא' עד עשרה
|
- [
 ]: The double ratio in the second line, following the first line. ]: The double ratio in the second line, following the first line.
|
ובטור השני הכפל השני נלוה לטור הראשון
|
- [
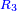 ]: The triple ratio in the third line. ]: The triple ratio in the third line.
|
ובטור השלישי הכפל השלישי
|
- [
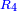 ]: The quadruple ratio in the fourth line. ]: The quadruple ratio in the fourth line.
|
ובטור הרביעי הכפל הרביעי
|
- So on, in ten lines, and the decuple ratio. [
 ] ]
|
וכן עשרה טורים ויהיה הכפל העשריי סופם
|
It is clear in this figure that:
- the two lines [
 ] that meet on the square 1 and extend to the surface 1-100 ] that meet on the square 1 and extend to the surface 1-100
|
וגלוי בזאת הצורה ששני הטורים אשר יפגשו על מרובע א' ויתרחבו עד שטח א'ק'
|
- the two lines [
 ] that meet on the square 4 and extend to the surface 1-100 ] that meet on the square 4 and extend to the surface 1-100
|
ושני הטורים אשר יפגשו על מרובע ד' ויתרחבו עד שטח א'ק'
|
- the two lines [
 ] that meet on the square 9 and extend to the surface 1-100 ] that meet on the square 9 and extend to the surface 1-100
|
ושני הטורים אשר יפגשו על מרובע ט' ויתרחבו עד שטח א'ק'
|
| Their ratio is one, i.e. the ratio of each term to its preceding in each two lines that meet on one of the squares that are on the diagonal, i.e. the main diagonal of the whole figure, is as the ratio of its corresponding term on the other line to its preceding as well.
|
יחסם אחד ר"ל ששעור כל מדרגה מאשר לפניה מאחד מכל שני טורים מהם יפגשו על מרובע מן המרובעים אשר על הקוטר ר"ל קוטר הצורה הגדולה כשעור המדרגה אשר היא דומה לה מהטור האחר מאשר היא גם כן לפניה
|
Except that:
- Each term of the two first lines [
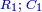 ] adds one to its consecutive. ] adds one to its consecutive.
|
אלא ששני הטורים הראשונים תוסיף כל מדרגה מהם על אשר ילוה לה מכל אחד משני הטורים אחד
|
- Each term of the two second lines [
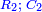 ] adds two to its consecutive. ] adds two to its consecutive.
|
ושני הטורים השניים תוסיף כל אחת ממדרגותיהם על אשר תלוה לה שנים שנים
|
- Each term of the two third lines [
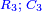 ] adds three to its consecutive. ] adds three to its consecutive.
|
ושני הטורים השלישיים תוסיף כל אחת ממדרגותיהם על אשר תלוה שלשה שלשה
|
- The fourth [
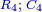 ] by four. ] by four.
|
והרביעיים ארבעה ארבעה
|
| The ratios of the terms of these lines, the ratio of any term wished to its preceding is one and the same, as they are similar.
|
ויחסי המדרגות מאלו הטורים יחס כל מדרגה אל אשר לפניה שתרצה אחד אחר שיהיו דומים
|
For example:
- the ratio of 42 on the seventh line breadthwise [
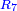 ] to its preceding 36 on this line is as the ratio of 7 on the first line breadthwise [ ] to its preceding 36 on this line is as the ratio of 7 on the first line breadthwise [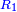 ] to its preceding 6 [ ] to its preceding 6 [ ] ]
|
משל זה שיחס מ"ב מהטור השביעי הלוקח ברחב אל ל"ו אשר לפניה מזה הטור כיחס ז' מהטור הראשון הלוקח ברחב אל ו' אשר לפניו
|
- the ratio of 7 on the first line lengthwise [
 ] to its preceding 6 on this line is as the ratio of 42 on the seventh line lengthwise [ ] to its preceding 6 on this line is as the ratio of 42 on the seventh line lengthwise [ ] to its preceding 36 of the same line [ ] to its preceding 36 of the same line [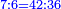 ] ]
|
ועוד יחס ז' מהטור הראשון הלוקח באורך אל ו' אשר לפניו בזה הטור כיחס מ"ב מהטור הז' הלוקח באורך אל ל"ו אשר לפניו מאותו הטור
|
- Since the column that goes lengthwise from 6 on the first row breadthwise [
 ] and the row that goes breadthwise from 6 on the first column lengthwise [ ] and the row that goes breadthwise from 6 on the first column lengthwise [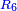 ] meet on the square 36, and 36 is one term first to each of the terms of 42 on both cross-lines, as both lines intersect on the square 36. ] meet on the square 36, and 36 is one term first to each of the terms of 42 on both cross-lines, as both lines intersect on the square 36.
|
לפי שהטור אשר יצא מו' מהטור הראשון ההולך ברחב הולך באורך והטור אשר יצא מו' מהטור הראשון ההולך באורך הולך ברחב יפגשו על מרובע ל"ו והיה ל"ו לכל אחת משתי המדרגות אשר בכל אחת מהן מ"ב משני הטורים המתחלפים מדרגה ראשונה לפי ששני הטורים יתחתכו על מרובע ל"ו
|
- Likewise, each cross-lines lengthwise and breadthwise [
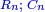 ] meet on a square of the squares on the main diagonal of the great square, and the square on which they meet is common to both. ] meet on a square of the squares on the main diagonal of the great square, and the square on which they meet is common to both.
|
וכן כל שני טורים מתחלפים באורך וברחב יפגשו על מרובע מן המרובעים אשר על קוטר המרובע הגדול הנה המרובע אשר יפגשו עליו משותף להם
|
| Hence, it is already clarified how the multiple ratio is produced from what is compared to it:
|
הנה אם כן כבר התבאר איך יתילד בעל הכפלים למה שיוקש אליו
|
- Since the second line of whichever side wished, the length or breadth, to the first line in the same side is a double ratio. [
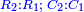 ] ]
|
לפי שהטור השני מטורי אי זה משני צדי האורך והרחב שתרצה אל הטור הראשון מאותו הצד כפל שניי
|
- The third to it is triple ratio. [
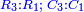 ] ]
|
והשלישי אליו שלשיי
|
- The fourth to it is quadruple ratio [
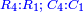 ] ]
|
והרביעי אליו רבעיי
|
| So on always orderly by the natural succession.
|
וכן תמיד כפי סדר על משך הטבע
|
| This is the explanation of the multiple ratios in this diagram.
|
וזה הוא המאמר על הכפלים בזאת הצורה
|
| As for the superparticular ratio:
|
אמנם המוסיף חלק
|
- The two lines, one of which lengthwise and the other breadthwise, that go out from the two squares of 30 and meet on the square of 9, when their terms are related to the terms of both lines lengthwise and breadthwise that go out from the two squares of 20 and meet on the square of 4, each term to its consecutive. [
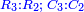 ] ]
|
הנה שני הטורים שלוקח אחד מהם באורך והאחר ברחב וכבר יצאו משני מרובעי ל' ל' ויפגשו על מרובע ט' כאשר יוחסו מדרגותיהם אל מדרגות שני הטורים הלוקחים באורך והרחב וכבר יצאו משני מרובעי כ' כ' ויפגשו על מרובע ד' כל מדרגה אל אשר ילוה לה
|
- This is found in sesquialter ratio.
|
תמצא זה ביחס המוסיף חלק החציי
|
- So the ratio of the rest of the terms of these four lines to their precedings, i.e. the second and the third columns lengthwise; and the second and the third rows breadthwise.
|
וכן יחס שאר מדרגות אלו הטורים הארבעה אל התחלותיהם ר"ל אל שני בתי ב' וג' משני הטורים הלוקחים באורך ואל שני בתי ב' וג' משני הטורים הלוקחים ברחב
|
|
|
ואמנם יחס המוסיף חלק השלישי
|
- The two lines, one of which lengthwise and the other breadthwise, that go out from the two squares of 40 and meet on the square of 16, when their terms are related to the terms of both lines lengthwise and breadthwise that go out from the two squares of 30 and meet on the square of 9, each term to its preceding in the other line. [
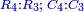 ] ]
|
הנה שני הטורים שלוקח אחד מהם באורך והאחר ברחב וכבר יצאו משני מרובעי מ' מ' ויפגשו על מרובע י"ו כאשר יוחסו מדרגותיהם אל מדרגות שני הטורים הלוקחים באורך והרחב היוצאים משני מרובעי ל' ל' ויפגשו על מרובע ט' כל מדרגה אשר לפניה מהטור האחר
|
- This is found in sesquitertian ratio, as in the same explanation mentioned for the sesquialter ratio.
|
תמצא זה ביחס המוסיף חלק השלישי בכמו אותו הביאור אשר זכרנו כמוסיף חלק החציי
|
- Likewise for the sesquiquartan ratio.
|
וכן המוסיף חלק הרביעי
|
- Likewise for sesquiquintan ratio.
|
וכן המוסיף חלק החמשיי
|
| The species of the superparticular ratio that follow are found in this technique following the derivation of its name from the sequence of the natural numbers that are produced by the addition of the units.
|
ומה שאחר זה ממיני המוסיף חלק תמצאהו בזאת המלאכה נמשך בגזרת שמו ממשך המספרים הטבעיים המתילדים מהוספת האחדים
|
| Hence it is already clarified to the sense that the most anterior of these ratios by nature and not by will and assumption is the multiple ratio, due to what was ascribed to it.
|
הנה אם כן כבר התבאר לחוש מהיותר קודם באלו היחסים בטבע לא ברצון והנחה בעל הכפלים למה שיוחס אליו
|
| And the most anterior of [the multiple ratios] is the double ratio, then the triple ratio, and so on always according to the description of the derivation of the numbers as they are in the natural order.
|
ושהקודם יותר בזה השניי עוד השלישי וכן תמיד כפי תואר הגזר המספרים כמו שהם בסדר הטבע
|
| The superparticular ratio is what follows the multiple ratio
|
ושאשר ימשך לבעל הכפלים הוא המוסיף חלק
|
| And the beginning of the [superparticular ratios] is the sesquialter ratio, then the sesquitertian ratio, then the sesquiquartan ratio and so on always according to the derivation of the numbers as they are in the natural order.
|
ושתחלת זה הוא החציי עוד השלישי ועוד הרביעי עוד כן תמיד כפי הגזרה מהמספרים כמו שהם בסדר הטבע
|
What can be apprehended from this diagram is that the terms of the numbers on the main diagonal that goes out from 1 to 100, written oppositely, each one is rooted, i.e. has an expressible root, which when multipled by itself, i.e. by the measure of its units, it is equal to the total. [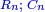 ] ]
|
וממה שישיג סדר זאת הצורה שמדרגות המספרים אשר על קוטר היוצא מא' אל ק' הכתוב נגדו כל אחת נגזרת ר"ל שיש לו שורש וידובר בו בשיכפל בעצמו ר"ל בשעור אחדיו היה שוה לכלם
|
- Such as: 1; 4; 9; 16; 25; 36; 49; 64; 81; 100
|
כמו א' ד' ט' י"ו כ"ה ל"ו מ"ט ס"ד פ"א ק'
|
- For each of these is a rooted number in actu.
|
כי כל אחד מאלו מספר נגזר בפעל
|
- Except for the one, which is rooted in potentia and its root is one, as it is one itself.
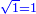
|
מלבד האחד שהוא נגזר בכח וגדרו אחד לפי שהוא אחד בעצמו
|
|
וגדר ד' ב'
|
|
וגדר ט' ג'
|
| If the roots of these terms are taken and arranged in a line, they are found in the order of their terms, by the order of the sequence of the natural numbers, such as 1, 2, 3, 4, 5, 6, until the end of the rooted numbers that were set on the main diagonal of the square.
|
ואם לקחת גדרי אלו המדרגות ותסדרם בטור תמצאם בסדר מדרגותיהם על סדר משך המספרים הטבעיים כמו א' ב' ג' ד' ה' ו' עד תכלית מה שהנחת מן המספרים הנגדרים באלכסון המרובע
|
| Abū Yusūf said: we have found these rooted numbers produced and grow from the sum of the natural odd numbers to each other by their successive order, beginning from the one, which is an odd number in potantia.
|
אמר אבו יוסף מצאנו אלו המספרים הנגדרים אמנם יתחדשו ויצמחו מתוספת הנפרדים הטבעיים על משך סדרם אשר התחלתם מהאחד אשר הוא נפרד בכח על קצתם על קצת
|
|
ג' כאשר נוסף על האחד יתקבץ מספר נגדר והוא ד' וגדרו ב'
|
|
וכאשר נוסף על ד' הנפרד אשר ימשך לג' והוא ה' יתקבץ מספר נגדר והוא ט' וגדרו ג'
|
|
וכאשר נוסף הנפרד אשר ימשך לה' והוא ז' על ט' יתקבץ מספר נגדר והוא י"ו ושרשו ד'
|
|
וכן תמיד הנה
|
| Thus, it is already clarified that when the natural odd numbers, beginning from the one, which is odd in potentia, are added to each other by their successive order, the natural rooted numbers are produced by their successive order.
|
אם כן כבר התבאר שכאשר נוספו הנפרדים הטבעיים אשר התחלתם האחד אשר הוא נפרד בכח קצתם על קצת על משך סדרם יתילדו המספרים הנגדרים הטבעיים על משך סדרם
|
| Their roots that are extracted from them are by their successive order of the natural numbers
|
והיו שרשיהם לקוחים מהם על משך סדרם על המספר הטבעי
|
| The terms of the two secondary diagonals that follow the main diagonal are heteromecic, i.e. the two numbers that the term is a product of their multiplication one by the other - one of them exceeds the other by one, as they are conceived as close to the root of the term that has a root, which is an expressible number.
|
ואמנם שני הטורים אשר ימשכו וילוו לקוטר הנה מדרגותיהם זולתיות האורך ר"ל ששני המספרים אשר התקבצה המדרגה מהכאת אחד מהם באחר יוסיף אחד מהם על האחר באחד בשיודמו שכבר קרבו מגדר המדרגה אשר היה להם גדר מספר ידובר בו
|
|
והמספרים הזולתיים כמו ו' כי הוא מהכאת ב' בג'
|
|
וכמו י"ב שהוא מהכאת ג' בד'
|
| So they are always found in the two secondary diagonals that are on both sides of the main diagonal.
|
עוד כן נמצאם תמיד בשני הטורים אשר משני צדי הקוטר כלם
|
What can be apprehended from this diagram is that the two lines that go out from the square of 1, lengthwise and breadthwise - their terms are added one by one until each of them reaches to ten that is the end of all their terms. [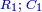 ] ]
|
וממה שישיג זאת הצורה ששני הטורים היוצאים ממרובע א' באורך והרחב יתוספו מדרגותיהם אחד אחד עד שיגיע כל אחד מהם אל העשרה אשר הם סוף כל המדרגות בם
|
And that the two lines that go out from the squares of 10 and meet on the square of 100 - their terms are added ten by ten. [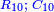 ] ]
|
וששני הטורים היוצאים משני מרובעי י"י ויפגשו על מרובע ק' יתוספו מדרגותיהם י' י'
|
| Furthermore, if what is on the four angles of this diagram is summed, one finds this sum a rooted number.
|
ואם קובץ מה שבזויות זאת הצורה הארבעה תמצא כלל זה המספר נגדר
|
| What can be apprehended from this diagram is that the sum of each square whose main diagonal differs from the opposite main diagonal, is rooted.
|
וממה שישיג זאת הצורה שכלל מדרגות כל מרובע יהיה קטרו נבדל מקוטר הצורה הוא נגדר
|
| Abū Yusūf said: what is apprehended concerning the other main diagonal, whose ends are ten, and the number of its terms is even, is that it has two means, which are 30.
|
אמר אבו יוסף וממה שישיג הקוטר האחר אשר תכליותיו עשרה עשרה ומספר מדרגותיו זוג שיש לו שני אמצעיים והם ל' ל'
|
| The terms that are between one of the two ends and one of the two means, the ratio between them, and the values of their numbers are in the same ratio of what is between the other end and the other mean.
|
והמדרגות אשר בין אחד משני התכליות עד אחד משני האמצעיים ביחס קצתם אל קצת והגעות מספריהם כיחס מה שבין התכלית האחר והאמצעי האחר
|
| The philosopher, the author of this book [= Nicomachus] said: The executed in this diagram is found when its investigation is precise, for it has more beneficial and purity things than what was described, but they will not be investigated in this introduction, as there was no intention to investigate them here.
|
אמר הפילוסוף מניח הספר כבר נמצא המקויים בזאת הצורה כאשר ידוקדק העיון בה כי בה דברים מהתועלות והזכיות יותר מאשר תארנו אלא שאנו לא נחקרם בזה המבוא לפי שאין כונתנו בו לחקרם
|
| It is necessary to move forward to the explanation of what is firmly agreed upon, concerning the account on the five ratios that we started discuss on
|
וראוי שנעתק אל המאמר על מה שהוא חזק ההאותות למה שהחלונו לדבר בו מזכר היחסים החמש
|
| Now, it should be said that the discussion on the superpartient to what is related to it should be preceded, as it is simpler than the two remaining ratios:
|
ונאמר עתה שהמוסיף חלקים למה שהוקש אליו יותר ראשון להקדים המאמר עליו לפי שהוא יותר פשוט משני היחסים הנשארים
|
- The multiple superparticular ratio consists of two ratios.
|
וזה שבעל הכפלים המוסיף חלק הוא מורכב משני יחסים
|
- The multiple superpartient ratio consists of two ratios as well.
|
ובעל הכפלים המוסיף חלקים מורכב גם כן משני יחסים
|
| Furthermore, when the beginning of the odds, which is 3, is added to the secont odd number, which is 5, the superbipartient is generated, which is the beginning of the species of the superpartient ratios.
|
ועוד שאנו כאשר חברנו ראש הנפרדים אשר הוא ג' אל הנפרד השני אשר הוא ה' יתחדש המוסיף שני חלקים והוא תחלת מיני המוסיף חלקים
|
| Therefore, it is necessary to put the discussion on this ratio following to what was said about the two first simple ratios.
|
ולזה יחוייב שנשים המאמר על זה היחס נמשך למה שאמרנו משני היחסים הראשונים הפשוטים
|
| In relation, by the natural order, the multiple superparticular ratio is seen prior to the superpartient ratio.
|
ואמנם בהצטרף על סדר הטבע הנה הכפל המוסיף חלק יראה קודם מהמוסיף חלקים
|
- This is when relating first two numbers of the terms of the natural numbers, which by their relation a third ratio is generated.
|
וזה כשנקיש תחלה שני מספרים ממדרגות המספרים הטבעיים יתחדש בהקשתם יחס שלישי
|
- Such as, relating 5 to 2, for 5 is the same as double 2 plus its half, and its half is a part of it.
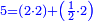
|
והוא כמו צרוף ה' אל ב' כי ה' כמו כפל ב' וכמו חציו וחציו חלק ממנו
|
- and 5:2 are the first two numbers of the terms of the natural numbers, which by the relation of one of them to the other a third ratio is generated.
|
וה' ב' ראשוני שני מספרים ממדרגות המספרים הטבעיים יתחדש בהצטרף אחד מהם אל האחר יחס שלישי
|
| Yet, it is clear and obvious that the superpartient ratio is simpler than the multiple superparticular ratio.
|
אבל הוא מבואר נגלה שיחס המוסיף חלקים יותר פשוט מיחס הכפל המוסיף חלק
|
| The simple is anterior to the compound by natural precedence.
|
והפשוט יותר קודם מהמורכב קדימה טבעית
|
| Hence, it is necessary to preface the discussion on the superpartient to what is related to it.
|
הנה אם כן יחוייב שנקדים המאמר על המוסיף חלקים אל מה שיוקש אליו
|
| And among its species, the superbipartient will be preceded, since it is the first of its species.
|
ונקדים ממיניו המוסיף שני חלקים אחר שהוא ראש מיניו
|
The Discussion on the Third Ratio which is the Superpartient Ratio
|
הדבור ביחס השלישי והוא היחס המוסיף חלקים
|
| Nicomachus said: there is no superpartient ratio less than the superbipartient ratio
|
אמר ניקומאכוש לא יהיה היחס המוסיף חלקים בפחות מהמוסיף שני חלקים
|
| Hence, this ratio is formed from the sequence of the natural numbers beginning with three in a line.
|
ולזה אמנם יתילד זה היחס מסדר המספרים הטבעיים אשר התחלתם השלשה בטור
|
| Because, the number prior to three has no two parts that are smaller than it, since its parts are equal to it.[?]
|
לפי שהמספר אשר קודם השלשה אין לו שני חלקים יהיו פחות ממנו אחר שחלקיו שוים לו
|
| He said: the terms of the natural odd numbers are arranged beneath the terms of the mentioned line, beginning with the consecutive of 3, which is 5.
|
אמר ויסודר תחת מדרגות הטור הנזכר מדרגות הנפרדים הטבעיים אשר הראשון מהם ימשך לג' והוא ה'
|
| Then, each term is compared with the one that above it.
|
עוד נקיש בין כל מדרגה ואשר למעלה ממנו
|
| Thus, all successive species of the superpartient ratio are revealed, according to the rule of their succession in nature.
|
ויראו לנו כל מיני המוסיף חלקים נמשכים כפי משפט המשכם בטבע
|
| If one wishes to see the production of each species of this ratio:
|
ואמנם כאשר תרצה שתראה איך צמיחת כל מין ממיני זה היחס
|
- Placing the two first productive numbers of that species in one term, the smaller above the greater.
|
הנה עתה תעמיד שני המספרים הראשונים הפועלים למין ההוא במדרגה אחת ותניח הקטן למעלה מהגדול
|
- Multiplying each by 2, then placing the two products in the successive term after the two first numbers, each follows its corresponding, the greater follows the greater and the smaller follows the smaller.
|
עוד תכה כל אחד מהם בב' ותעמיד שני המספרים המגיעים אחר ההכאה במדרגה תמשך לשני המספרים הראשונים כל אחת מהן תמשך לדומה לה הגדול ימשך לגדול והקטן ימשך לקטן
|
- Multiplying again each of the first two numbers by 3, then placing the [products] in the third successive term, as the two numbers were placed in the second term.
|
עוד תשוב אל שני המספרים הראשונים ותכה אותה גם כן בג' ותעמידם במדרגה שלישית על הצד אשר העמדת בו שני המספרים במדרגה השנית
|
- Multiplying each of the first two numbers also by 4, then placing the [products] according the above concept, in the successive term, denominated by the number by which the two first numbers were multiplied.
|
וכן גם כן תכה שני המספרים הראשונים בד' ותעמידם כפי הגדר הנזכר במדרגה הנגזרת השם מהמספר אשר הכית שני המספרים הראשונים בו
|
| The same is done always when wishing to produce any species of the superpartient ratio.
|
וכן תעשה תמיד כאשר תרצה להצמיח מין ממיני המוסיף חלקים
|
| Setting up the first active numbers of the species of the superpartient ratio by the order of these natural species, so that no species of them would fall in the vacum of the given numbers - it is as mentioned in the introduction of this chapter, and as the first active numbers of the species of the superpartient ratio that are already illustrated below.
|
ואמנם איך תניח המספרים הראשונים הפועלים למיני המוסיף חלקים על סדר אותם המינים הטבעיים עד שלא יפול מהם מין בפנוי מה שיונח מהמספרים הנה הוא כמו שנזכר בפתיחת זה הפרק וכמו שכבר המשלנו תחת זה המספרים הראשונים הפועלים למיני יחס המוסיף חלקים
|
| This is the diagram:
|
וזאת הצורה ועד כאן דברי מחבר הספר
|
| יט |
יח |
יז |
יו |
טו |
יד |
יג |
יב |
יא |
י |
ט |
ח |
ז |
ו |
ה |
ד |
ג
|
| לז |
לה |
לג |
לא |
כט |
כז |
כה |
כג |
כא |
יט |
יז |
טו |
יג |
יא |
ט |
ז |
ה
|
| Until here the author's words.
|
ועד כאן דברי מחבר הספר
|
| How the other similar species are extracted from whichever of these first species that one wishes:
|
אמנם איך יוצאו שאר המינים הדומים באי זה מין שנרצה מאלו המינים הראשונים
|
- Such as, for example, the superbitertian ratio, under the superbiquintan ratio, the superbiseptian ratio, and the rest of what falls under the superbipartient ratios.
|
כמו הדומה דרך משל במוסיף שני שלישים תחת המוסיף שני חומשים ושני שביעים ושאר מה שיפל תחת המוסיף שני חלקים
|
- Or those that are similar by falling under the supertripartient ratios.
|
או במתדמים לנפלם תחת המוסיפים שלשה חלקים
|
- Or whichever of the species of the superpartient ratios other than these two.
|
או בלתי שני אלו מאי זה ממיני המוסיף חלקים
|
| The obvious way for finding this is by arranging the natural numbers in a line, such that the first of its term is the number that is the number of the additional parts of the species intended to be added to its similar extracted.
|
הנה הדרך הגלוי אל מציאות זה הוא בסדור המספרים הטבעיים בטור יהיה ראש מדרגותיו המספר אשר הוא מספר החלקים הנוספים במין המכוון להוסיף להוצאת הדומים לו
|
- The first term is added to the second, and the sum is placed under the second.
|
ותנשא המדרגה הראשונה על השנית ויונח מה שיתקבץ תחת השנית
|
- The first term is [summed] also with the third, [and the sum is placed] under the third
|
עוד נניח המדרגה הראשונה גם כן עם השלישית תחת השלישית
|
- Also the first with the fourth placed under the fourth.
|
וכן תונח הראשונה עם הרביעית תחת הרביעית
|
- Proceeding likewise until the given end of the natural numbers.
|
ונעשה זה תמיד עד תכלית המונח מן המספרים הטבעיים
|
- Then each of the terms is related to its corresponding.
|
עוד תקיש בין כל מדרגה ממנה והדומה לה
|
| An example was given of the superquadripartient ratio, in order that the mathematician will examine it and will be led straight by it in other [cases].
|
וכבר הנחתי לזה משל מהמוסיף ארבעה כדי שיבחנהו החושב ויתישר בו בזולתו
|
| There are species of superpartient ratio that are included in other species of superpartient ratio:
|
ודע שמהמוסיף חלקים מה שיכנס במין אחר מהמוסיף חלקים
|
- 6 and 10 are in the superquadrisextan ratio [
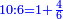 ] ]
|
כמו ו' וי' כי הם בהצטרף המוסיף הארבעה שתויות
|
- they are also in superbitertian ratio [
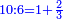 ] ]
|
והם גם כן בהצטרף המוסיף שני שלישים
|
| There are species that are included in a ratio of another type i.e. the superparticular ratio:
|
וממנו גם כן מה שיכנס בזולת סוגו ר"ל במוסיף חלק
|
- 8 and 12 are in the superquadrioctan ratio [
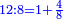 ] ]
|
כמו ח' וי"ב שהם בהצטרף המוסיף הארבעה שמיניות
|
- they are also in a superparticular ratio, i.e. sesquialter ratio [
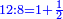 ] ]
|
והם גם כן בצרוף המוסיף חלק ר"ל חצי
|
| If one wishes to recognize the absolute ratios in a certain species that are not included in other than their species, al-Kindī's bother to set a special technique for each species is not enough, since he strived in what is impossible to arrive to its end.
|
ואם תרצה במין מה להכיר הצרופים הגמורים אשר לא יכנסו בזולת מינם לא יספיק בזה מה שטרח בו אלכנדי מהניח מלאכה מיוחדת לכל מין לפי שהוא השתדל במה שלא נוכל לבא עד תכליתו
|
| However, the general technique for all that was brought of this is to skip each term of the terms of the natural numbers, whose number is commensurable with the number of the additional parts.
|
אבל המלאכה הכוללת לכל מה שהובא מזה היא שנדלג ממדרגות המספרים הטבעיים כל מדרגה שיהיה מספרה משותף למנין החלקים הנוספים
|
| The meaning of commensurability is that one of the two numbers is part of the other, and this is only if they have a common divisor, other than one, that counts both of them.
|
ור"ל בהשתתפות שיהיה אחד משני המספרים חלק לאחר ולא יהיה זה אלא אם להם חלק משותף בלתי האחד ימנם יחד
|
| Its explanation was already introduced in the account on the even number and the account on the composite odd number.
|
וזה כבר עבר ביאורו בזכירת המספר הזוג וזכירת המספר הנפרד המורכב
|
| Here, a technique is required for recognizing the terms that should be skipped.
|
ומכאן תבוקש התחבולה בהכרת המדרגות אשר נצטרך הנה לדלגם
|
| It is as said - the terms - either the number of the additional parts are of each of their numbers, since their ratios are icluded in the superparticular ratio, or the number of the additional parts is not a part of each of their numbers, since their numbers and the number of the additional parts have a common part, other than one, that counts them together.
|
והיה כמו שאמרנו המדרגות אשר אם שיהיה מנין החלקים המוסיפים מכל אחד ממספריהם כי צירופי אלו יכנסו במוסיף חלק ואם שלא יהיה מנין החלקים המוסיפים חלק מכל אחד ממספריהם אלו שמספריהם ולמנין החלקים הנוספים חלק משותף להם בלתי האחד ימנה אותם יחד
|
| For, these ratios, even if the are not included in other than their species, i.e. the superparticular ratio, they are included in a species other than their species of the superpartient ratio.
|
כי צירופי אלו ואם לא יכנסו בבלתי סוגם ר"ל במוסיף חלק הנה יכנסו במין בלתי מינם מהמוסיף חלקים
|
| Hence, when the terms that are common by the number of the parts are skipped, the terms, whose ratios are not included in other than their species, remain, and they are the absolute of the terms of the superpartient ratio.
|
הנה כאשר תדלג אלו המדרגות המשותפות למנין החלקים הנה כבר השארת המדרגות אשר לא יכנסו צרופיהם בבלתי מינם והם הגמורים ממדרגות המוסיף חלקים
|
|
|
וכבר תארנו משל זה שאמרנו בזאת הצורה עם רושם השותפים הנזכרים בה
|
| שתוף |
|
שתוף |
|
שתוף |
|
שתוף |
|
שתוף |
|
שתוף |
|
שתוף |
|
שתוף |
|
שתוף |
|
שתוף |
|
שתוף |
|
שתוף |
|
|
| כח |
כז |
כו |
כה |
כד |
כג |
כב |
כא |
כ |
יט |
יח |
יז |
יו |
טו |
יד |
יג |
יב |
יא |
י |
ט |
ח |
ז |
ו |
ה |
ד
|
| לב |
לא |
ל |
כט |
כח |
כז |
כו |
כה |
כד |
כג |
כב |
כא |
כ |
יט |
יח |
יז |
יו |
טו |
יד |
יג |
יב |
יא |
י |
ט |
|
[Compound Ratios]
|
|
The Discussion on the Fourth Ratio which is the Multiple Superparticular Ratio
|
הדבור ביחס הרביעי והוא יחס הכפל המוסיף חלק
|
| The author of this book [= Nicomachus] said: The simple species among the species of the relative quantity are the species of the three ratios of the preceding discussion.
|
אמר מניח הספר אמנם המינים הפשוטים ממיני הכמה המצטרף הנה הם מיני שלשת היחסים אשר קדם המאמר עליהם
|
| For, they are as causes and principles for the two remaining species, i.e. the multiple superparticular ratio, and the multiple superpartient ratio.
|
כי הם כהתחלות וכפנות לשני המינים הנשארים ר"ל מין הכפל המוסיף חלק מן הכפלים המוסיף חלקים
|
| Since these two species are produced from the first species and dissolved to them.
|
אחר ששני אלו המינים כבר יתילדו מהמינים הראשונים ויותכו אליהם
|
| The simple has also another aspect, by which the species of the multiple ratio and the superparticular ratio are set aside from the superpartient ratio, in that the first is said to resemble to the second.
|
ולפשוט גם כן צד אחר ייוחד בו מין הכפל ומין המוסיף חלק בלתי מין המוסיף חלקים והוא בשיאמר שהוא יתדמה הראשון ממנו לשני
|
| It is said to be simple, since its meaning is of the two numbers that relate in each of these two species by assimilation of themselves:
|
ויאמר לו פשוט לפי שעניינו אמנם הוא של שני המספרים המצטרפים בכל אחד מאותם שני המינים התדמות בעצמם
|
- Either the assimilation of two numbers in the multiple ratio is such that the greater is composed from the smaller;
|
אם התדמות שני המספרים במין הכפל באשר הגדול מחובר מהקטן
|
- Or the assimilation of two numbers in the superparticular ratio is such that they are composed together from a principle, which is the difference between them.
|
ואם התדמות שני המספרים במין המוסיף חלק באשר הם יחד מחוברים מפנה אחת והוא המותר אשר ביניהם
|
| Therefore, the ancients related the natural things by relation of these two species alone, and did not relate them by the third species that is said to be simple as well, i.e. the superpartient ratio.
|
ולזה הקישו הראשונים הדברים הטבעיים החבור בשני אלו המינים לבד ולא יקישו אותם במין השלישי אשר יאמר לו שהוא פשוט גם כן ר"ל במין המוסיף חלקים
|
| The two compound species:
|
ואמנם שני המינים המורכבים
|
- One of them consists of the multiple ratio and the superparticular ratio.
|
הנה אחד מהם מורכב מבעל הכפלים ומהמוסיף חלק
|
- The other consist of the multiple ratio and the superpartient ratio.
|
ואמנם האחר מורכב מבעל הכפלים ומהמוסיף חלקים
|
| Since the part is anterior by nature to the parts, the multiple superparticular ratio is anterior to the multiple superpartient ratio.
|
ולפי שהחלק קודם בטבע על החלקים היה הכפל המוסיף חלק קודם על הכפל המוסיף חלקים
|
| Therefore, it is necessary the preface the discussion on the multiple superparticular ratio.
|
ולזה יחוייב להקדים המאמר על הכפל המוסיף חלק
|
| It is said that this ratio is conceived of two numbers, one of them is greater by once or many times the other and as a part of its.
|
ונאמר שזה היחס יראה משני מספרים אחד מהם יותר לאחר מדמיון אחד או דמיונים הרבה וכמו חלק ממנו
|
- Such as: the five when they are related to the two, for the five are twice the two plus their half.
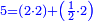
|
כמו החמשה כאשר יוקשו אל שנים כי החמשה שני דמיוני שנים וכמו חציים
|
| This species assumes the similarity from the two species of which it consists:
|
וכבר יקח זה המין הדמוי משני המינים אשר הוא מורכב מהם
|
- What it assumes from the multiple ratio: the multiplicity of its multiple and the unconverted one part.
|
אמנם מה שיקח מיחס הכפל הנה ברבות כפלו והחלק אחד בלתי מומר
|
- Such as: the double sesquialter ratio, the triple sesquialter ratio, the quadruple sesquialter ratio
|
כמו הכפל השניי המוסיף חצי והכפל השלישיי המוסיף חצי והכפל הרביעיי המוסיף חצי
|
- and so on always, the multiples are multiplied and the one part is not converted.
|
וכן תמיד ברבות הכפלים והחלק אחד לא יומר
|
- What it assumes from the superparticular ratio: its parts are converted, but its multiples are not multiplied.
|
ואמנם מה שיקחהו מדמיון המוסיף חלק יומרו חלקיו ולא יתרבו כפליו
|
- Such as: the double sesquialter ratio, the double sesquitertian ratio, the double sesquiquartan ratio, the double sesquiquintan ratio
|
כמו הכפל השניי המוסיף חצי והכפל השניי המוסיף שליש והכפל השניי המוסיף רביע והכפל השניי המוסיף חומש
|
- and so on, its parts are converted and its multiples are not multiplied.
|
עוד כן יומרו חלקיו ולא יתרבו כפליו
|
- It is composed from the sum of their two properties: when its multiples are multiplied and its parts are converted.
|
וכבר יתחדש לו והתרכבו מהם קבוץ שני סגולותיהם כאשר יתרבו כפליו ויומרו חלקיו
|
- Such as: the double sesquialter ratio, the triple sesquitertian ratio, the quadruple sesquiquartan ratio
|
כמו הכפל השניי המוסיף חצי והכפל השלישי המוסיף שליש והכפל הרביעיי המוסיף רביע
|
- and so on, its multiples are multiplied and its parts are converted.
|
וכן תמיד יתרבו כפליו ויומרו חלקיו
|
| Forming the species by the similarity to the superparticular ratio:
|
ואמנם יתחדש המין האחד לדמוי מהמוסיף חלק לבד
|
- Arranging the natural numbers, beginning from 2, in a line.
|
באשר תסדר המספרים הטבעיים אשר התחלתם ב' בטור
|
- Arranging the natural odd numbers, beginning from 5, in a line.
|
עוד תסדר הנפרדים הטבעיים אשר התחלתם ה' בטור
|
- Then, each term is related to its corresponding, as seen in the example of the following diagram:
|
ונקיש כל מדרגה אל הדומה לה כמו שתראה בזה הדמיון בזאת הצורה צורת הדמיון שנזכרנו
|
| כז |
כו |
כה |
כד |
כג |
כב |
כא |
כ |
יט |
יח |
יז |
יו |
טו |
יד |
יג |
יב |
יא |
י |
ט |
ח |
ז |
ו |
ה |
ד |
ג |
ב
|
| נה |
נג |
נא |
מט |
מז |
מה |
מג |
מא |
לט |
לז |
לה |
לג |
לא |
כט |
כז |
כה |
כג |
כא |
יט |
יז |
טו |
יג |
יא |
ט |
ז |
ה
|
| Finding the species by the similarity to the multiple ratio:
|
ותמצא המין האחד לדמוי מהכפל לבד
|
- Arranging a line lengthwise, its beginning are the two active numbers of the multiple superparticular ratio, which are 2 and 5 beneath it.
|
כשתסדר טור באורך יהיה ראשיתו שני המספרים הפועלים ביחס הכפל המוסיף חלק והם ב' ותחתיו ה'
|
- Arranging beneath the 5 the subsequent terms of the natural odds successively downwards, so that these terms begin the lines breadthwise.
|
עוד תסדר תחת הה' מה שימשך לו ממדרגות הנפרד הטבעי ימשכו קצתם לקצת יורדים ותשים אלו המדרגות יתחילו בטורים לוקחים ברחב
|
- The terms of each line are added by the number of its first term.
|
יתוספו מדרגות כל טור מהם כמנין המדרגה הראשונה ממנו
|
- Then, each of the terms of this table is related to its corresponding, which is its parallel in the first line.
|
עוד תקיש כל אחת ממדרגות זה המרובע באשר נכח לו והוא מקבילו מהטור הראשון
|
- One finds that the multiple ratio is set in it, without the growth of the part, as seen here:
|
שאתה תמצא בזה כבר העמדת בו יחס הכפל מבלתי שיצמח החלק וזה כמו שתראה בכאן
|
|
|
| כ |
יח |
יו |
יד |
יב |
י |
ח |
ו |
ד |
ב
|
| נ |
מה |
מ |
לה |
ל |
כה |
כ |
טו |
י |
ה
|
| ע |
סג |
נו |
מט |
מב |
לה |
כח |
כא |
יד |
ז
|
| צ |
פא |
עב |
סג |
נד |
מה |
לו |
כז |
יח |
ט
|
| קי |
צט |
פח |
עז |
סו |
נה |
מד |
לג |
כב |
יא
|
| קל |
קיז |
קד |
צא |
עח |
סה |
נב |
לט |
כו |
יג
|
| קנ |
קלה |
קכ |
קה |
צ |
עה |
ס |
מה |
ל |
טו
|
| קע |
קנג |
קלו |
קיט |
קב |
פה |
סח |
נא |
לד |
יז
|
| קצ |
קעא |
קנב |
קלג |
קיד |
צה |
עו |
נז |
לח |
יט
|
| רי |
קפט |
קסח |
קמז |
קכו |
קה |
פד |
סג |
מב |
כא
|
|
| Forming the species to a ratio by its two principles, of which it consists
|
ויתחדש זה המין האחד ליחס משני פנותיו אשר הוא מורכב מהם
|
| It is that whose multiples are multiplied and whose parts are converted.
|
והוא אשר יתרבו כפליו ויומרו חלקיו
|
- Arranging the natural odd numbers, beginning from 5, in a line written in red.
|
באשר תסדר הנפרדים הטבעיים אשר התחלתם מה' בטור הנרשם באודם
|
- It is not related, but it is set as a description from which an example is taken.
|
ולא נרצה להקיש בו אבל לשומו רושם לקחת דמיון ממנו
|
|
וזה שאנו נסדר טור אחד
|
- The beginning of its terms is also 5.
|
יהיה ראש מדרגותיו גם כן ה'
|
- The second term as its preceding, i.e. as 5, to which what is above it is added, i.e. from the first preceding red line.
|
והמדרגה השנית כמו אשר לפניה ר"ל כמו ה' מוסף עליו מה שלמעלה ממנו ר"ל מהטור הראשון האדום אשר לפניה
|
- The third term as its preceding, i.e. as 10, to which what is above it is added, i.e. the second term of the red line.
|
והמדרגה השלישית כמו אשר לפניה ר"ל כמו י' מוסף עליו מה שהוא למעלה ממנו ר"ל המדרגה השנית מהטור האדום
|
- Proceeding likewise, until the end of the numbers that were set in the red line.
|
וכן תעשה עד שיכלה אל סוף מה שהנחת מהמספרים בטור האדום
|
- As this second line is produced, so a line of the natural numbers beginning from 2 is set parallel to it.
|
וכאשר הולדנו זה הטור השני כן סדרנו נכחו טור המספרים הטבעיים והתחלתו מב'
|
- Then, its terms are related to the terms of the line that was produced, leaving aside the red line.
|
עוד נקיש בין מדרגותיו ובין מדרגות הטור אשר הולדנו ונעזוב הטור האדום
|
|
|
ויראה בהקשתם איך יתילד המין הלוקח הדמוי משני פאותיו וזה המין השלישי ממיני הכפל המוסיף חלק ותבחנהו בצורה שעשינו והתישר בו
|
| נט |
נז |
נה |
נג |
נא |
מט |
מז |
מה |
מג |
מא |
לט |
לז |
לה |
לג |
לא |
כט |
כז |
כה |
כג |
כא |
יט |
יז |
טו |
יג |
יא |
ט |
ז |
ה |
|
| תתקא |
תתמב |
תשפה |
תשל |
תרעז |
תרכו |
תקעז |
תקל |
תפה |
תמב |
תא |
שסב |
שכה |
רצ |
רנז |
רכו |
קצז |
קע |
קמה |
קכב |
קא |
פב |
סה |
נ |
לז |
כו |
יז |
י |
ה
|
| ל |
כט |
כח |
כז |
כו |
כה |
כד |
כג |
כב |
כא |
כ |
יט |
יח |
יז |
יו |
טו |
יד |
יג |
יב |
יא |
י |
ט |
ח |
ז |
ו |
ה |
ד |
ג |
|
The Discussion on the Fifth Ratio which is the Multiple Superpartient Ratio
|
הדבור ביחס החמישי והוא יחס הכפלים המוסיף חלקים
|
| As been said, it is composed from the multiple ratio and the superpartient ratio.
|
הוא כמו שאמרנו מורכב מיחס הכפל ומיחס המוסיף חלקים
|
| Therefore, the technique of the production of this ratio is divided into three parts:
|
ולזה גם כן כבר תחלק המלאכה בהולדת זה היחס לשלשה חלקים
|
- Striving to reveal the quality of the multiple ratio by augmenting its multiples, without changing the added parts.
|
אם שתשתדל בם להראות סגולת הכפל ברבות כפליו מבלתי השתנות החלקים הנוספים או תמורתם
|
- Teaching to reveal the quality of the superpartient ratio by converting the parts, without augmenting the multiples.
|
ואם שתתחכם בם להראות סגולת המוסיף חלקים בהמרת החלקים בלתי רבות הכפלים
|
- Revealing both qualities in a continuous evident ratio as it is by nature.
|
ואם שיראו בם שתי הסגולות יחס הראות נמשך כמו שהוא בטבע
|
| The species whose multiples are augmented, while its parts do not change, is created when placing the two first productive numbers of whichever multiple superpartient ratio one wishes:
|
הנה המין אשר יצמחו כפליו ולא ישתנו חלקיו יתחדש כשנניח שני המספרים הראשונים הפועלים ליחס אי זה הכפל המוסיף חלקים שנרצה
|
| לז |
לה |
לג |
לא |
כט |
כז |
כה |
כג |
כא |
יט |
יז |
טו |
יג |
יא |
ט |
ז |
ה |
|
| שסב |
שכה |
רצ |
רנז |
רכו |
קצז |
קע |
קמה |
קכב |
קא |
פב |
סה |
נ |
לז |
כו |
יז |
י |
ה
|
| יט |
יח |
יז |
יו |
טו |
יד |
יג |
יב |
יא |
י |
ט |
ח |
ז |
ו |
ה |
ד |
ג |
ב
|
| For example: the multiple superbitertian ratio
|
וכאלו נרצה יחס הכפל המוסיף שני שלישים
|
- Placing their two first productive numbers, which are 3 and 8.
|
הנה נניח שני המספרים הראשונים הפועלים להם והם ג' וח'
|
- For the rest of the multiple superbitertian ratios: leaving the smaller, and arranging a line beneath the 8 lengthwise, whose terms begin from 8 and are added by the smaller number, i.e. added by threes.
|
וכאשר נרצה שאר הכפלים המוסיפים שני שלישים נעזוב הקטן על ענינו ונסדר תחתיו טור באורך לוקח תחת ח' יתחילו מדרגותיו מח' יתוספו במניין אחרי המספר הקטן ר"ל שיתוספו ג' ג'
|
- Relating each of them to the first term, i.e. to the first number, which is 3, because they are related to it by the multiple superbitertian ratio.
|
עוד נקיש כלם במדרגה הראשונה ר"ל במספר הקטן אשר הוא ג' כי הם יהיו אליו ביחס הכפל המוסיף אותם החלקים הראשונים
|
- Thus the multiples are produced according to their natural succession, without the parts being added or converted.
|
וכבר התילדו הכפלים כפי המשכם בטבע מבלתי שיתוספו החלקים או יומרו
|
| By this technique whichever multiple superpartient ratio one wishes is produced.
|
ובזאת המלאכה יתילדו איזה מן הכפלים המוסיף חלקים שתרצה
|
| Such as: the multiple supertriquartan ratio, or the multiple supertriquintan ratio, or whichever one wishes of this.
|
כמו הכפל המוסיף שלשה רביעיות או שלשה חמשיות או מה שתרצה מזה
|
| You will be well guided in it in the example given here.
|
ותתישר בו במשל אשר המשלתיו לך הנה
|
| The production of the species whose parts are converted and reproduced by a natural successive reproduction, as the number, from which their names are derived [= the denominator], is augmented, while the number of its multiples does not change:
|
ואמנם איך יתילד המין אשר יומרו חלקיו ויעתקו ברבות המספר אשר ממנו יגזרו שמותיהם העתק נמשך בטבע מבלתי שיומר מנין כפליו
|
| Its technique is divided also into two parts
|
זה גם כן תחלק מלאכתו לשני חלקים
|
- Following the production of the first species of the superpartient ratio, as their natural succession.
|
לפי שאנו אם שנלך בזה אל תולדת המינים הראשונים מהמוסיף חלקים כפי המשכם בטבע
|
- Such as: the superbipartient ratio, the supertripartient ratio, the superquadripartient ratio, and what follows.
|
כמו המוסיף שני חלקים עוד המוסיף שלשה חלקים עוד המוסיף ארבעה חלקים עוד מה שילווה לזה
|
- Following the production of one species of them, by extracting each ratio that is denoted by the name of that same ratio.
|
ואם שנלך אל הולדת מין אחת מהם בהוצאת כל יחס יפל תחת שם אותו המין
|
- Such as: the superbipartient ratio alone, or the supertripartient ratio alone.
|
כמו המוסיף שני חלקים לבד והמוסיף שלשה חלקים לבד
|
| The technique that leads to the first species of the superpartient ratio, as their natural succession, without augmenting the multiples:
|
אבל המלאכה אשר תביא אל המינים הראשונים מהמוסיף חלקים כפי המשכם בטבע מבלתי שירבו הכפלים
|
- Arranging the natural numbers in a line, beginning from 3.
|
אמנם היא כשנסדר המספרים הטבעיים שהתחלתם ג' בטור
|
- Placing beneath 3 the number that produces with it the beginning of the superpartient ratio.
|
ותניח תחת ג' המספר אשר יפעל עמם תחלת יחס המוסיף חלקים
|
- Completing the greater line with terms added by threes.
|
עוד נשלים הטור הגדול במדרגות יתוספו ג' ג'
|
- Once - if wishing for the double ratio.
|
פעם א' אם רצינו שיהיה הכפל שניי
|
- twice - if wishing for the triple ratio.
|
ואם רצינו אותו שלישיי כזה שני פעמים
|
- thrice - if wishing for the quadruple ratio
|
ואם רצינו אותו רביעיי שלשה פעמים
|
|
וכן מה שאחר זה
|
- Relating each term to what is above it, i.e. its corresponding in the first line
|
עוד נקיש כל מדרגה באשר למעלה ממנה ר"ל הדומה לה מהטור הראשון
|
| Thus, the multiple superpartient ratio is revealed according to the natural production of the first species of the superpartient ratio, without augmenting the multiples.
|
הנה יראה לנו יחס הכפל המוסיף חלקים כפי התילד המינים הראשונים מהמוסיף חלק בטבע בלתי שיתרבו הכפלים
|
| As seen in this example - examine it and you will find it with God's help.
|
וזה כפי מה שתראה בזה המשל ותבחנהו ותמצאהו בע"ה
|
| |
יח |
יז |
יו |
טו |
יד |
יג |
יב |
יא |
י |
ט |
ח |
ז |
ו |
ה |
ד |
|
| נג |
נ |
מז |
מד |
מא |
לח |
לה |
לב |
כט |
כו |
כג |
כ |
יז |
יד |
יא |
ח |
ג
|
| The production of the species of the multiple superbipartient for example, or the species of the multiple supertripartient, or the species of the multiple superquadripartient, or others, without augmenting the multiples and without changing the number of the parts, yet the number, from which they are derived, is changing by a natural production:
|
ואמנם איך יתילדו מיני הכפלים המוסיפים שני חלקים דרך משל או מיני הכפל המוסיף שלשה חלקים או מיני המוסיף ארבעת חלקים או זולת אלו מבלתי שיתרבו הכפלים ולא ישתנה מנין החלקים אבל ישתנה בצמיחה הטבעית המנין אשר הם נגזרים ממנו
|
- Extracting the similar by their multiples beneath the superpartient ratio of these parts, as discovered in the chapter of the superpartient ratio.
|
וזה כשנוציא המתדמים בכפלם תחת המוסיף אותם החלקים כמו שכבר גלינו בשער המוסיף חלקים
|
- the smaller number in each term is raised above the greater corresponding to it - if wishing for the double ratio.
|
עוד ינשא המספר הקטן מכל מדרגה על הגדול אשר נכחו אם תרצה שיהיה הכפל השניי
|
- double the smaller - if wishing for the triple ratio.
|
ואם תרצה שיהיה שלישיי תשא כפל הקטן
|
- thrice the smaller number is raised above - if wishing for the quadruple ratio.
|
ואם תרצה אותו רבעיי תשא שלשה כפלי הקטן
|
- And so for all that follows. in all the terms of the greater line.
|
וכן מה שאחר זה בכל מדרגות הטור הגדול
|
- Relating each term to its corresponding.
|
עוד נקיש כל מדרגה בנכחית לה
|
| The superpartient ratio of these parts is found without augmenting the multiples or reproducing the number that one wishes.
|
שאתה תמצא המוסיף אותם החלקים בלתי שיוסיפו הכפלים או יעתקו מהמנין אשר תרצה
|
| Examine what was mentioned in both descriptions in the chaper of the superpartient ratio, which are the species of the superpartient ratio, whose number does not change, and you will be well guided in them for the production of this species of the multiple superpartient ratio, by observing carefully what was noted.
|
ובחן מה שזכרתיו לך בשני הרשמים לפניך בשער המוסיף חלקים והם טור מיני המוסיף חלקים לא יומר מנינם ותתישר מהם להולדת זה המין מהכפל המוסיף חלקים כאשר תטיב להתבונן במה שזכרנוהו
|
| The third type of the first division mentioned in the beginning of this chapter - the production of the species whose multiples are augmented and whose parts are changed:
|
ואמנם המין השלישי מהחלוקה הראשונה הנזכרת בפתיחת זה הספר והוא איך יתילדו המינים אשר יצמחו כפליהם וישתנו חלקיהם
|
| Since the change of the parts is either by the constancy of their number and the increasing of their values in a natural growth, or by the increasing of their number as well as the increasing of their values together, the technique of extracting them is necessary divided into two parts:
|
הנה לפי שהשתנות החלקים אם שיהיה בקיום מנינם והתרבות הגעותיהם התרבות טבעי ואם שיהיה בהתרבות מנינם והתרבות הגעותיהם יחד יחוייב שתחלק המלאכה בהוצאת זה לשני חלקים
|
- The production of the type in which the number of the parts is constant while their values change in the natural growth:
|
אבל יתילד המין אשר יתקיים בו מניין החלקים וישתנו הגעותיהם בהתרבות הטבעיי
|
- Its technique is by extracting two lines of the superpartient ratio whose number, i.e. the number of the added parts, is as the number you wish to ascribe.
|
תהיה מלאכתו כאשר נוציא שני טורים מיחס המוסיף חלקים מנינם ר"ל מנין החלקים הנוספים כמניין אשר תרצה לחייבו
|
- You will be well guided by it in the two written lines, similarly in the chapter of the superpartient ratio, which are the two lines in which the commensurability and incommensurability are recognized.
|
ותתישר בזה בשני הטורים הנרשמים בדומה זה בשער המוסיף חלקים והם שני הטורים אשר הוכר בם השתוף מהבלתי שתוף
|
- Then, above each of the terms of the greater numbers, raised the product of its corresponding in the terms of the smaller numbers by the number of the values of the parts minus one.
|
עוד ינשא על כל מדרגה מן המספרים הגדולים מה שבדומה לה מן המדרגות המספרים הקטנים מוכה במנין הגעות החלקים אלא אחד
|
- When this is done for all the terms of the greater line - each term of which is related to its corresponding in the terms of the smaller line, i.e. whose numbers are the smaller - one finds all this in the multiple superpartient ratio, while the values of their parts are the numbers of the multiples, i.e. the number of the parts does not change.
|
וכאשר עשית זה בכל מדרגות הטור הגדול הקשת בין כל מדרגה ממנו ודומה לה ממדרגות הטור הקטן ר"ל בעל המספרים הקטנים שאתה תמצא כל זה ביחס הכפל המוסיף חלקים הגעתם הוא מנין הכפלים ר"ל שמנין החלקים לא יומרו
|
- The second part of this type - in which the multiples, the number of the parts and their values increase together.
|
ואמנם החלק השני מזה המין והוא אשר יתרבו בו הכפלים ומנין החלקים והגעתם יחד
|
- Their production technique:
- Placing the natural numbers, beginning from three, in a line.
|
הנה מלאכת הולדתם בהנחת המספרים הטבעיים אשר התחלתם ג' בטור
|
- Placing 8 beneath the 3 and completing the second line, whose beginning is 8, by adding the natural odd numbers, beginning from 7:
|
עוד תניח תחת ג' ח' ותשלים הטור השני אשר התחלתו ח' בתוספת הנפרדים הטבעיים אשר התחלתם ז'
|
- secone term:

|
ותוסיף ז' על ח' ותעמיד מה שהתקבץ במדרגה השנית וזה ט"ו
|
- [third] term:

|
עוד תוסיף על ט"ו ט' ותעמיד מה שהתקבץ במדרגה
|
- fourth term: third term + 11
|
וכן תוסיף על השלישית י"א ותעמיד מה שהתקבץ ברביעית
|
- Proceeding like this in the rest of the terms of the second line, until reaching the corresponding to the end of the natural numbers placed in the first line.
|
ותעשה כמו זה בשאר מדרגות הטור השני עד שתגיע לנכח סוף מה שהנחת מן המספרים הטבעיים בטור הראשון
|
- Relating each term to its similar, as seen in these two lines:
|
עוד נקיש כל מדרגה בדומה לה כמו שתראה בשני אלו הטורים
|
| טו |
יד |
יג |
יב |
יא |
י |
ט |
ח |
ז |
ו |
ה |
ד |
ג
|
| רכד |
קצה |
קסח |
קמג |
קכ |
צט |
פ |
סג |
מח |
לה |
כד |
טו |
ח
|
| The species of the multiple superpartient ratio, of which the multiples, the number of the parts and their values as well, increase by a natural successive growth, are revealed with God's help.
|
ויראו לך בע"ה מיני הכפל המוסיף חלקים אשר התרבו כפליהם ומנין חלקיהם והגעות חלקיהם כמו כן התרבות טבעי נמשך
|
| Thus, the five ratios and the ten numeral relations were already discussed and stated in a remarkable discussion, as needed, without multiplicity and lengthiness.
|
הנה כבר דברנו על היחסים החמש וההקשות המספריות העשרה ואמרנו בם מאמר מופלג כפי הצורך מבלתי רבוי ואריכות
|
The Discussion on the Technique of Producing the Ratios from Equality
|
המאמר על התחבולה בהולדת היחסים מן השווי
|
| What follows from the aforesaid is that the way to produce these five ratios from equality will be brought with a basic valid coherent technique that imagines the natural matters in its wider sense and the true meaning of its interpretation.
|
וכבר ימשך למה שקדם מדברינו שנביא הצד בהולדת אלו היחסים החמש מן השווי בתחבולה שרשית קיימת בלתי מבולבלת תדמה הענינים הטבעיים בכללותה ואמתת פירושה
|
| The fruit of what will be noted of this is very precious and honorable.
|
והפרי במה שנזכור מזה יקר ונכבד מאד
|
| All the more so by the one who examines the metaphor of the knowledge of good, which is investigated.
|
וכל שכן אצל מי שבחן מה שאעיין בו מדמיון הידיעה לטוב
|
| For the good is defined by the soul, its allegory and relation are known, and the souls are drawn to it.
|
כי הטוב אצל הנפש מוגבל וידוע המשלו וחברו ונמשכו לו הנפשות
|
| Know, that it is first for all that is uncompounded by itself, preserving the perception, among all that is generated by its nature, and that the evil, in its disgrace, is infinite, does not reach a limit, does not branch out from a root, and is not subsequent of interpretation, indeed it is a change of the nature that is good.
|
ותדע שהוא ראשון לכל מה שיתפרד מעצמו מתמיד ההרגש בכל מה שיתילד מטבעו ושהרע בגנותו בלתי בעל תכלית ולא מגיע אל גבול ולא יסתעף משרש ולא נמשך על פירוש אמנם הוא שנוי הטבע אשר הוא טוב
|
| Their deviation from their primary nature is a different deviation, not included in a limit, and not existing in order.
|
הנה היציאה מטבעם הראשון להם יציאה מתחלפת לא תכלל בגבול ולא תתקיים בסדר
|
| Therefore, a rational capacity does not hold them by a rational hold, but recognizes them when they deviate from their nature.
|
ולזה לא יאחזהו כח מדבר אחיזה מושכלת אבל יכירהו בהתחלפו לטבע
|
| For example: the rust in the transparent mirror and the injustice of the straight soul that are incomprehensible by way of definition and limitation, since they have no essence, but they are known by the change of the substance in which they were set and embedded.
|
דרך משל אומר כחלודה במראה הספירית והעול בנפש הישרה שהם בלתי מושגים בדרך הגדר וההגבלה אחר שאין עצמיות להם ואמנם יודעו בהשתנות העצם אשר נקבעו ונטבעו בו
|
| Yet, if limited ways were found for these five ratios, by which they are produced from equality and reduced to equality by their reverse, and equality is undoubtedly good and virtue, the ratios also share the same virtue and joined together by the same good.
|
אבל אם אנחנו מצאנו לאלו היחסים החמש דרכים מוגבלים בהם יתילדו מהשווי ויותכו בהפוכם אל השווי והיה השווי בלי ספק טוב וחשיבות היו היחסים גם כן משותפים לאותו החשיבות ונקשרים באותו הטוב
|
| Since their production from it is arranged, subsequent of a limit, preserving the capacity of their root, from which they are produced, as the seed preserves the capacity of the tree, since the seed becomes a tree also.
|
אחר שהיה התילדם ממנו מסודר נמשך על גבול שומר לכח שרשם אשר ממנו יתילדו כמו שישמור הגרגיר כח האילן אחר שכבר ישוב גם כן הגרגיר אילן
|
| So these ratios are produced from equality and return to equality, however this is not by accident, but a technique and a correlation are needed, as the cultivation of land is needed in the matter of the seed and the tree before it sprouts.
|
וכן אלו היחסים יתילדו מן השווי וישובו כמו כן אל השווי אבל לא יהיה זה בהזדמן אבל כבר נצטרך בו אל מלאכה וחבור כמו שנצטרך בענין הזרע והאילן על עבודת הקרקע קודם שיצא
|
| For it is impossible to reach the end of an assumption, be it a theoretical assumption or a practical assumption, unless using the assistance of things from the outside, which have some similarity to that assumption, that are related in some limited order, through which by guidance the assumption is reached.
|
כי אי אפשר להגיע אל תכלית דרוש מן הדרושים דרוש מדעי היה או דרוש מעשי אם לא בהעזר מדברים מחוץ יהיה להם קצת התדמות לאותו הדרוש ויחוברו על סדר מה מוגבל נגיע עם ההדרכה עליהם אל הדרוש
|
| Because of this, Euclid stated the relation as one of the things from which knowledge exists and by which the practice is reached.
|
ולזה שם אקלידס החבור אחד מהדברים אשר מהם תהיה הידיעה ובהם נגיע אל המעשה
|
| Therefore, in the production of each of these ratios also, three numbers are placed in three terms, in order to reach the relation through them.
|
ולזה גם כן נניח אנחנו בהולדת כל אחד מאלו היחסים שלשה מספרים בשלשה מדרגות להגיע בם אל ההתיחסות
|
| For the least relation possible is in three limits.
|
כי ההתיחס בפחות מה שיהיה הוא בשלשה גבולים
|
| In relation, one is assisted by things that are apart from that by which the similarity of the ratio is.
|
ואמנם יעזרו בהתיחסות מהדברים אשר מחוץ למה שבו מהתדמות היחס
|
| Since it was already said that the things, by which one is assisted, are apart from the investigation of the assumption, they should be homogeneous with the assumption.
|
ולפי שאנו כבר אמרנו שהדברים אשר נעזר בם מחוץ אל החקירה מהדרוש ראוי שיהיו מתדמים לדרוש
|
| These three terms are called first, second and third.
|
ויקראו אלו שלשת המדרגות ראשונה ושניה ושלישית
|
| Each term of them is based on a limit, beyond which it does not pass:
|
ותדבק כל מדרגה מהן בגבול לא תעברהו
|
- The limit of the first term is that one should always place beneath it the same as the number in it. [
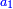 ] ]
|
אם הגבול במדרגה הראשונה הוא שנניח תחתיה לעולם כמו המספר אשר בה
|
- The limit of the second term is that one should always place beneath it the same as the number in it plus the same as the number in the first term. [
 ] ]
|
ואמנם הגבול במדרגה השנית הוא שנניח תחתיה לעולם כמו המספר אשר בה וכמו המספר אשר במדרגה הראשונה
|
- The limit of the third term is that one should always place beneath it the same as the number in it plus the same as the number in the first term and double of what in the second term. [
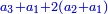 ] ]
|
ואמנם הגבול אשר במדרגה השלישית הוא שנניח תחתיה כמו המספר אשר בה וכמו המספר אשר במדרגה הראשונה וכפל אשר במדרגה השנית
|
| This is the general in the technique by which each of these ratios is produced.
|
זה הוא מה שהוא כולל במלאכה אשר בה יתילד כל אחד מאלו היחסים
|
| Yet, what is particular in it for each of these ratios is:
|
ואמנם מה שהוא מיוחד בה לכל אחד מאלו היחסים
|
- The particular in this technique for the production of the multiple ratio is that the first given numbers in the three terms, from which this ratio is produced, are equal numbers, preserving equality in their relation.
|
כי אשר תיחד המלאכה בהולדת יחס הכפל השווי שיהיו המספרים הראשונים המונחים במדרגות הג' אשר מהם יתילד זה היחס מספרים שוים שומרים השווי בהצטרפם
|
- When the aforementioned general condition is kept, the numbers in the double ratio are revealed, and this is the first of the species of this ratio.
|
וכשנשמור בם התנאי הכולל הנזכר יראו אלינו מספרים ביחס הכפל השניי והיה המין הראשון ממיני זה זה היחס
|
- If the visible species is stated as given, and the aforementioned general condition is added, i.e. the formation of the three limits in the three terms, the second species of the multiple species, which is the triple ratio, is revealed.
|
ואם שמנו זה המין הנראה מונח והוספנו בו התנאי הכולל הנזכר ר"ל העשות הגבולים השלשה במדרגות השלשה יראה לנו המין השני ממיני הכפל והוא הכפל השלישיי
|
- If it was stated as given, and the first procedure was repeated on it, the third species, which is the quadruple ratio, is revealed.
|
ואם שמנוהו גם כן מונח והשבנו בו במעשה הראשון יראה לנו המין השלישי והוא הכפל הרביעיי
|
- According to this way, the procedure does not cease, so the species of the multiple ratio are revealed in their natural succession.
|
וכפי זה הדרך לא נסור מזה המעשה יראו לנו מיני הכפל ראשון ראשון כפי המשכם בטבע
|
- Examine this in these two lines:
|
ובחן זה בשני טורים אלו
|
|
|
| א |
א |
א |
|
| ד |
ב |
א |
ראשון
|
| ט |
ג |
א |
שני
|
| יו |
ד |
א |
ג
|
|
- Take them as a basis for what follows them.
|
וקחם לשרש למה שימשך להם
|
- The particular in this technique for the production of the superparticular ratio is that the given numbers, from which one wishes to produce the superparticular ratio, are related in the multiple ratio, the greater is in the first place, and the smaller is in the third place, then one employs the aforementioned general repetition.
|
ואמנם אשר הוא מיוחד בזאת המלאכה להוליד יחס המוסיף חלק הנה הוא שיהיו המספרים המונחים אשר מהם תרצה להוליד המוסיף חלק מתיחסים ביחס הכפל ויהיה הגדול מהם במקום הראשון והקטן מהם במקום השלישי עוד תעשה בם הסבוב הכולל אשר זכרנו
|
- For, what follows from this is that the species of the superparticular ratio are seen according to their natural succession.
|
כי ימשך לזה שיראו אלינו מיני המוסיף חלק כפי המשכם בטבע
|
- If the given numbers were of the first species of the multiple ratio, i.e. the double ratio, the [first] species of the superparticular ratio will be seen from them, i.e., the sesquialter ratio.
|
ר"ל שהמספרים המונחים אם היו עליהם תחלת מיני הכפל ר"ל השניי יראו מהם מיני המוסיף חלק ר"ל המוסיף חצי
|
- If they were of the second species of the multiple ratio, i.e. the triple ratio, the second species of the superparticular ratio will be seen from them, i.e., the sesquitertian ratio.
|
ואם היו על היחס השני ממיני הכפל ר"ל השלישיי יראה לנו גם כן השני מהמוסיפי חלק ר"ל המוסיף שליש
|
- The same for what follows.
|
וכמו כן מה שאחר זה
|
| Examine it from this diagram:
|
ותבחנהו מזאת הצורה
|
- The particular for the production of the superpartient ratio is that the given numbers are related in the superparticular ratio, the greater is in the first place, and the smaller is in the third place, then one employs the aforementioned general repetition.
|
ואשר ייחד תולדת המוסיף חלקים הוא שיהיו המספרים המונחים מתיחסי' ביחס המוסיף חלק ויהיה הגדול מהם במקום הראשון והקטן מהם במקום השלישי עוד נעשה בם הסבוב הכולל הנזכר
|
- For, it reveals the numbers in a species of the superpartient ratio, arranged naturally approximated according to the arrangement of the given superparticular ratio, as this:
|
כי הוא יראה לנו המספרים על יחס מין מהמוסיף חלקים מסודרים בקירוב מהטבע בסדור המוסיף חלק המונח וזה יהיה כן
|
- The particular for the production of the multiple superparticular ratio is that the given numbers are related also in the superparticular ratio, only the greater is in the third place, and the smaller is in the first place, then one employs the aforementioned general repetition.
|
ואשר ייחד הולדת יחס הכפל המוסיף חלק הוא שיהיו המספרים המונחים מתיחסים ביחס המוסיף חלק גם כן אלא שהגדול מהם יהיה במקום השלישי והקטן מהם במקום הראשון
|
- The general conditional repetition reveals a species of the multiple superparticular ratio naturally approximated, i.e. from the beginning of the species of the multiple superparticular ratio, according to the terms of the given species of the superparticular ratio, and so it is:
|
ויראה לנו הסבוב הכולל המותנה מין מהכפל המוסיף חלק הוא בקרוב מהטבע ר"ל מהתחלת מיני הכפל המוסיף חלק בכמו מדרגת המין המוסיף חלק המונח ויהי כן
|
- The particular for the production of the multiple superpartient ratio is that the given numbers are related in the superpartient ratio, the smaller is in the first place, and the greater is in the third place.
|
ואשר ייחד הולדת יחס הכפל המוסיף חלקים הוא שיהיו המספרים המונחים מתיחסים יחס המוסיף חלקים ויהיה הקטן מהם במקום הראשון והגדול מהם במקום השלישי
|
- When the procedure that is general for all ratios is repeated on them, a species of the multiple superpartient ratio is revealed, arranged in its type, according to the arrangement of the given superpartient ratio in its type, as can be seen here:
|
וכאשר נסובב בהם המעשה אשר הוא כולל לכל היחסים יראה לנו מין מהכפלים המוסיף חלקים מסודרים בסוגו כסדר המוסיף חלקים המונח כסוגו וזה כמו שתראה הנה
|
| It has already become clear that all these ratios that were brought here as an example, were produced from the line of the three equal terms, which is the line of the units written in red.
|
הנה כבר התבאר שכל אלו היחסים שהמשלנו אותם בכאן אמנם יתילדו מהטור השוה המדרגות השלשה והוא טור האחדים הנכתבים באודם
|
| If others than the units were placed in this line, provided that they were equal numbers, and they were employed in the described ways, all the matters necessitated in the production of these ratios that were seen, will necessary follow, except that what will be seen from this is not its cause, but its cause is the equality of the units.
|
ואלו הנחנו כמו כן באותו הטור בלתי האחדים רק שיהיו מספרים שוים ועשינו בם מה שעשינו אותו בדרכים אשר תארנו יחוייב שימשך לזה כל מה שנראה לנו מהענינים המתחייבים בהולדת אלו היחסים אלא שאשר נראה מזה אינו עלתו אבל עלתו שווי האחדים
|
| It can be known that the species of the superpartient ratio produced by this technique are indeed the first of these ratios.
|
וכבר יתכן לנו שנדע כי מיני המוסיף חלקים אשר יתילדו בזאת המלאכה אמנם הם המינים הראשונים מאלו היחסים
|
| The intention in the first species is to those whose values of their parts exceed their denominator by one, as the superbitertian ratio, the supertriquartan ratio, the superquadriquintan ratio, the superquintisextan ratio, and the similar that is possible.
|
ורצוני במינים הראשונים מאלו מהם אשר יהיו הגעות חלקיהם יותר מוסיפים ממנין חלקיהם באחד כמו המוסיף שני שלישים והמוסיף שלשה רביעיות והמוסיף ארבעה חומשים והמוסיף חמשה שתויות ומה שיעבור זה ממה שידמהו
|
| The rest of the species of the superpartient ratio, such as the superbiquintan ratio, the supertriquintan ratio, or the supertriseptan ratio, or what is similar - the technique for their production is as is stated about it for the measure of the superpartient ratio.
|
ואמנם שאר מיני המוסיף חלקים כמו המוסיף שני חומשים והמוסיף שלשה חומשים או המוסיף שלשה שבעיות או מה שהוא דומה זה הנה המלאכה בהולדתם אמנם היא כמו מה שהגדנו עליה בשעור המוסיף חלקים
|
| When the species of the multiple superpartient ratio are wished in this technique, it is necessary that the given species of the superpartient ratio to produce it will be the first species mentioned, whose value of their parts exceeds the number of their parts by one.
|
וכן גם כן ראוי לנו כשנרצה מיני הכפל המוסיף חלקים בזאת המלאכה שיהיו המינים המונחים מהמוסיף חלקים להוליד זה הם המינים הראשונים אשר זכרנו שהגעת חלקיהם תוסיף על מנין חלקיהם אחד
|
| This alone is a sufficient discussion on the instruction of whichever species of the multiple superparticular ratio and whichever species of the multiple superpartient ratio are produced in the mentioned explanation, and which the rest of the types of these ratios are far from the way of their types, and because of this may be they are not visible except by a technique of much more complexity than the one whose mention is completed now.
|
וזה בלבד מאמר מספיק בהוראה על אי זה מיני הכפל המוסיף חלק ואי זה מיני הכפל המוסיף חלקים יתילדו בבאור הנזכר וששאר סוגי אלו היחסים יתרחקו מדרך סוגיהם ולזה אולי לא יראו אלא במלאכה היא יותר רבת ההרכבה מזאת אשר השלמנו לזכרה עתה
|
| God is the Knower.
|
והאל היודע
|
| This is for you the conception of the categorization of the relative quantity
|
וזה לך ציור חלוקת הכמה המצטרף
|
|
|
הנה זה יישירך השם מספיק בסוף המאמר הראשון מספר הארתמאיטיקא כפי מה שתיארו ניקמאכוש אלגהר שיני הפתאגורי
|
| Revised in al-Andalus by Abū Sulaymān Rabīʽ ben Yaḥyā usquf Elvira.
|
ותקנו באנדלס אבו סלימאן רביע בן יחיי אסקף אלבירה
|
|
|
והעזר בעיון וההגיה בו והאל ברחמיו יישירך להבין ולמצוא חפציך בו המועילים לאחריתך אמן
|
|
|
נשלם המאמר הראשון מספר הארתמאטיקא והתהלה לאל יבא אחריו המאמר השני בג"ה
|
Book Two
|
המאמר השני מספר הארתמאטיקא
|
The First Section: Reducing the Ratios to Equality
|
המאמר הראשון ממנו בהתכת היחסים אל השווי
|
| He [= Nicomachus] said: the principle and the foundation is the thing from which another thing is composed and into which another thing is decomposed.
|
אמר שהפנה והיסוד הוא הדבר אשר הורכב ממנו דבר אחר ויותך אליו דבר אחר
|
For example:
- The Alpha Beta letters, as it is said about them that they are elements of the given writings that are composed from them and decomposed into them.
|
כמו אותיות האלפא ביתא כי יאמר בם שהן פנות לכתבים המונחים המחוברים מהם הנתכים אליהם
|
- The sounds are elements of the melodies, for the melodies are composed from them and decomposed into them.
|
וכן הנעימות הן פנות לכל הלחנים אחר שהיו הלחנים מחוברים מהם נתכים אליהם
|
- The four elements, i.e. the fire, air, water, and earth, are said to be principles and simple elements of for all that is subject to the generation and corruption, for they are composed from them and decomposed into them.
|
וכן גם כן אלו היסודות הארבעה ר"ל האש והאויר והמים והארץ יאמר שהם פנות ופשוטים לכל הנופלים תחת ההויה וההפסד אחר שחבורם מהם והתכתם אליהם
|
| These propositions were brought forward to demonstrate that equality is a principle of the relative quantity, from which it increased and to which it is reduced.
|
ואמנם הקדמנו אלו ההקדמות להראות שהשווי פנה לכמות המצטרף ושהוא ממנו צמח ואליו יותך
|
| As for the absolute quantity, its first principle, from which it is produced, and which can be added infinitely, is the one.
|
ואמנם הכמה הנפרד הנה פנתו הראשונה ובו התילד ואיפשר להוסיף בו אל מה שאין תכלית לו הוא אחד
|
| What is produced from equality, and reduced to it, is common to all the relations.
|
ואמנם מה שיתילד מן השווי ויותך אליו הנה הוא כולל לכל הצרופים
|
| A proof will be brought, by demonstration and true meaning, that equality is a cause of the relative quantity, from which its production is, by which it increases when added, and into which it is consumed and dissolved when subtracted.
|
ונביא ראיה במופת ואמתות שהשווי סבה לכמות המצטרף אשר ממנו היה הולדתו ובו צמח בהתוספו ואליו יכלה כאשר חוסר ונתך
|
From the general technique one knows that when setting three numbers, such that the ratio of the first of them to the second is as the ratio of the second to the third [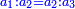 ], in any species of the five ratios mentioned in the first section, these three given numbers, the ratio of the third to the second is also as the ratio of the second to the first [ ], in any species of the five ratios mentioned in the first section, these three given numbers, the ratio of the third to the second is also as the ratio of the second to the first [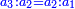 ], when the first is the smaller, the second is the mean, and the third is the greater. ], when the first is the smaller, the second is the mean, and the third is the greater.
|
ומהתחבולה הכוללת לזה הוא שתדע שכאשר תניח שלשה מספרים יחס הראשון מהם אל השני כיחס השני אל השלישי באי זה מהמינים היה מהיחסים החמש אשר זכרנום במאמר הראשון הנה אלו מספרים שלשה אם הונחו כן היה יחס גם כן השלישי אל השני כיחס השני אל הראשון והראשון הוא הקטן והשני הוא האמצעי והשלישי הוא הגדול
|
- If one wishes to restore them to equality: subtract the smaller from the mean, then subtract from the greater the mean and what remained from the mean. [
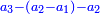 ] ]
- [
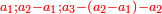 ] ]
|
ואם רצה רוצה להשיבם אל השווי הנה ישליך מהאמצעי כמו הקטן עוד ישליך מהגדול כמו מה שישאר מהאמצעי וכמו מהאמצעי
|
- If the three numbers are equalized, it is the required.
|
ואם השתוו המספרים השלשה הנה כבר היה מה שרצינו
|
- If not, they departed from the species of their ratio, and restored to another species anterior by nature to the ratio in which they were first.
|
ואם לא הנה כבר יצאו ממין צרופם ושבו אל מין אחר הוא יותר קודם בטבע ממין היחס אשר היו ממנו ראשונה
|
- Proceed as the first procedure.
|
עוד תעשה בו כמו המעשה הראשון
|
- If they are equalized, the required is found.
|
ואם השתוו הנה מצאנו מבוקשנו
|
- If not, they departed from that species also and restored to a species even prior by nature to the first.
|
ואם לא הנה כבר יצאו מאותו המין גם כן אל מין יותר רחוק מן הראשון בטבע
|
- One does not cease to do so, until they are equalized.
|
ולא תסור מעשות כן תמיד עד שישתוו
|
| Example:
|
ומשל זה
|
- Placing the equality in a line of three ranks.
|
נניח השווי בטור בעל שלשה מדרגות
|
- Arranging a second line of multiple ratio
|
ונסדר אליו טור שני מתיחס ביחס הכפל
|
- Arranging a third line of superparticular ratio
|
עוד נסדר בם טור שלישי על יחס המוסיף חלק
|
- Continuing with a fourth line of superpartient ratio
|
ונמשיך בזה טור רביעי על יחס המוסיף חלקים
|
- Placing in a fifth line numbers that relate in a multiple superparticular ratio
|
עוד נניח בטור החמשי מספרים מתיחסים ביחס הכפל המוסיף חלק
|
- Completing the diagram with a sixth line relating the ranks in a multiple superpartient ratio.
|
ונחתום הצורה בטור ששי מתיחס המדרגות ביחס הכפל המוסיף חלקים
|
| As in this diagram:
|
כפי מה שבצורה
|
- This line, with which these lines are confronted, and on which the mentioned reduction operation is done, is restored to the ratio of a line that is closer than it to equality, i.e. closer to the line of the equal terms.
|
הנה זה הטור שנכוין אליו מאלו הטורים ועשינו בו מלאכת ההתכה אשר זכרנוה נשיבהו בזה אל יחס טור הוא יותר קרוב ממנו אל השווי ר"ל שהוא יותר קרוב אל טור הגבולים השוים
|
- One does not cease to operate so, until its ranks are restored to the ratio of the line of equality itself.
|
עוד לא נסור מעשות זה בו עד שישובו מדרגותיו אל יחס טור השווי עצמו
|
| What was said is more sufficient than the extending of the examples and the long repetition that are not adequate for the one who knows that the completion of the operations is not by multitude of examples, but by restoration of the terms.
|
ויספיק לך מה שאמרנו מלהרבות ההמשלים וההכפלה הארוכה אשר לא יאותו למי שידע שהשלמת המלאכות לא תהיה ברבוי ההמשלים אבל בתקון הגבולים
|
| It is already clear that the procedure that was brought forward in the first section, for the production of the ratios, is reversed by itself, when trying to reduce the ratios to equality.
|
וכבר התבאר כי המעשה אשר הקדמנוהו להולדת היחסים במאמר הראשון הוא בעצמו יתהפך הנה כאשר נשתדל להתיך אותם היחסים אל השווי
|
The Discussion on the Arrangement of the Terms of each Ratio of two Given Numbers the of Superparticulars
|
הדבור בסדור גבולי כל יחס מונח שני המספרים מיחסי המוסיף חלק
|
| Since we very much need to set successive proportional numbers of the sesquialter ratio, the sesquitertian ratio, the sesquiquartan ratio, or other ratio of the superparticular ratios, we should bring an artificial extraction procedure for it and a technique that will verify the assumption of it, in order that the investigation of what we investigate will be without confusion.
|
וראוי אחר שכבר נצטרך הרבה אל שנניח מספרים נמשכים מתיחסים מהמוסיף חצי או המוסיף שליש או המוסיף רביע או זולת מה מהמוסיף חלק אחר שנביא הוצאה מלאכותית לזה ותחבולה תאמת לנו הסברא בה כדי שתהיה דרישתנו למה שנדרשנו מזה מבלתי בלבול
|
- It is said that the sesquialter ratio is the first of the superparticular ratios, as is visible in the above.
|
ונאמר שיחס המוסיף חצי הוא ראש יחסי המוסיף חלק כמו שנגלה במה שקדם
|
- The first two productive numbers of the sesquialter ratio are two and three.
|
ושתחלת שני מספרים פועלים יחס המוסיף חצי הם שנים ושלשה
|
- When wishing to explain how the succeeding terms of this ratio are extracted:
|
וכאשר נרצה לבאר איך נוציא הגבולים הנלוים בזה היחס
|
- Arranging the ranks of the double ratio, which are the ranks of the even-times-even numbers, in a line
|
נסדר מדרגות הכפל השניי בטור והם מדרגות זוג הזוג
|
- Leaving out the first rank, since it is one, which has no half.
|
ונשליך המדרגה הראשונה לפי שהיא האחד ואין חצי לו
|
- Placing beneath each rank the number that produces with it the sesquialter ratio, so a second line is generated that is one rank shorter than the first line, as one was subtracted from the corresponding.
|
עוד נניח תחת כל מדרגה המספר הפועל עמה יחס הדמיון וחצי ר"ל יחס המוסיף חצי ויתחדש טור שני חסר מהטור הראשון מדרגה והיא אשר השלכנו בנוכח האחד
|
- Leaving out again the first rank of this second line, since it is three, which has no half.
|
עוד נשוב ונשליך כמו כן המדרגה הראשונה מזה הטור השני לפי שהוא שלשה ואין חצי לו
|
- Placing beneath each of its remaining ranks the number that produces with it the sesquialter ratio, so a third line is generated that is one rank shorter than the second line, which is the subtracted corresponding the three.
|
ונניח תחת כל אחת ממדרגותיו הנשארות המספר הפועל עמו יחס המוסיף חצי ויתחדש טור שלישי חוסר מהטור השני מדרגה והיא המושלכת נגד השלשה
|
- Leaving out again the first rank of this third line, since it is nine, which has no half.
|
עוד נשוב גם כן ונשליך המדרגה הראשונה מזה הטור השלישי לפי שהוא תשעה ואין לו חצי
|
- Placing beneath each of its ranks the number that produces with it the sesquialter ratio, so a fourth line is generated that is one rank shorter than the third line, which is the subtracted corresponding the nine.
|
ונניח תחת כל אחת ממדרגותיו המספר הפועל עמו יחס המוסיף חצי הנה יתחדש טור רביעי חוסר מהטור השלישי מדרגה והיא אשר השלכנו כנגד התשעה
|
- Creating also the fifth and the sixth lines and upwards as is seen in this diagram:
|
וכמו כן נחדש טור חמישי וששי ולמעלה מזה כמו שתראה בזאת הצורה
|
|
|
| לב |
יו |
ח |
ד |
ב |
א
|
| מח |
כד |
יב |
ו |
ג
|
| עב |
לו |
יח |
ט
|
| קח |
נד |
כז
|
| קסב |
פא
|
| רמג
|
|
- It is clear that the beginning of the sesquialter ratio is in two terms.
|
וכבר התבאר שתחלת מה שימצא יחס המוסיף חצי בשני גבולים
|
- It is also clear from this diagram how it is found in three, four, five, or six terms.
|
עוד התבאר בזאת הצורה איך נמצאהו בשלשה גבולים עוד בארבעה עוד בחמשה עוד בששה
|
| Through the technique, by which this diagram is done, terms are added in this ratio endlessly, and no term is missing in any empty space in which this technique is not evident.
|
והמלאכה שנעשית בה זאת הצורה כבר יתוספו בה הגבולים בזה היחס אל מה שאין תכלית לו ולא יבצר מהם גבול בשום פנוי שלא תראה בו התחבולה
|
- If wishing to produce numbers according to this example in the sesquitertian ratio:
|
ואם רצינו להוליד מספרים כפי זה המשל ביחס המוסיף חלק השלישי
|
- Arranging what is in the line of the successive triple ratio: 1; 3; 9; 27; 81; 243.
|
נסדר מה שבטור הכפל השלישי הנמשך על יחס דמיון א' ג' ט' כ"ז פ"א רמ"ג
|
- Arranging lines beneath this line, placing under each number a similar to it plus its one third.
|
ונסדר טורים תחת זה הטור נעמיד תחת כל מספר כמהו וכמו שלישיתו מה שאפשר בו זה
|
- Drawing a diagram, as was illustrated previously at first, in which the terms of the sesquitertian ratio are seen, without missing out any of the terms, as one sees in the following diagram:
|
ונצייר צורתו כמו מה שציירנו הראשונה אשר לפניה ויראו בה מדרגות הגבולים ביחס המוסיף שליש מבלתי שיחטא בגבול מהם כמו שתראה בזאת הצורה אשר לפניך
|
|
|
| רמג |
פא |
כז |
ט |
ג |
א
|
| שכד |
קח |
לו |
יב |
ד
|
| תלב |
קמד |
מח |
יו
|
| תקעו |
קצב |
סד
|
| תשסח |
רנו
|
| אלף כד
|
|
- Likewise when we wish the sesquiquartan ratio: 1; 4; 16; 64
|
וכמו כן כאשר נרצה ביחס המוסיף חלק הרביעיי הנמשך על יחס דמיון א' ד' י"ו ס"ד
|
- Also for any type of the types of the superparticular ratios that follow.
|
וכמו כן מה שילוה לזה מין ממיני המוסיף חלק
|
| The basis of the technique of this diagram is to place the successive terms of the first line in the multiple ratio, by which the superparticular ratio of the required terms is called, i.e. the multiple by which the denominator of the part is denominated.
|
ואמנם היסוד במלאכת זאת הצורה שנשים מדרגות הטור הראשון נמשכים על יחס הכפל אשר הוא נקרא ליחס הדרוש הגבולים מיחסי המוסיף חלק ר"ל הכפל אשר ממנו מעמד אותו החלק
|
| When it is produced in this diagram by the mentioned technique, it is evident and clear that the numbers that are placed in the angles [the main diagonal] of each diagram are the numbers that are in the first given line of the following diagram.
|
וכאשר עשית אותו מזאת הצורה במלאכת הנזכרת הוא גלוי מבואר שהמספרים אשר יפלו בזויות מכל צורה הם המספרים אשר בטור הראשון המונח בצורה אשר תמשך לה
|
| Here are other notable and wonderful properties that you will understand through your good examination by the will of God.
|
ובכאן עניינים אחרים נכבדים ונפלאים תעמוד עליהם עם טוב בחינתך בהם ברצון השם
|
| Revealing which ratio of the superparticular ratios is found in a composition, i.e. from the composition of which of the ratios follows whichever multiple ratio required.
|
על גלוי אי זה יחס מיחסי המוסיף חלק הנמצא בחבור ר"ל נמצא בחבוריהם יחס מונח ופי' איזה יחסים הם אשר יתחייב מחבורם יחס איזה כפל שתדרוש בחבור יחס מונח מיחסי בעל הכפלים
|
- The first type of the multiple ratios, which is the double ratio, is composed and produced through the first two types of the superparticular ratios, which are the sesquialter ratio and the sesquitertian ratio.
|
אמנם המין הראשון מבעל הכפלים והוא השניי הנה הוא יתחבר ויתילד באמצעות שני המינים הראשונים ממיני המוסיף חלק והם המוסיף חצי והמוסיף שליש
|
- For example:
|
משל זה שהארבעה כמו השלשה וכמו שלישיתם
|
|
והשלשה כמו השנים וכמו חציו
|
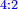 in the double ratio, as one sees in this diagram. in the double ratio, as one sees in this diagram.
|
והנה הארבעה אצל השנים ביחס הכפל השניי כמו שתראה בזאת הצורה
|
- By the reverse explanation it is clear that the double ratio is dissolved to the sesquialter ratio and the sesquitertian ratio.
|
ובהפך זה המאמר יתבאר שהכפל השניי יותך אל המוסיף חצי והמוסיף שליש
|
- For example: if we take two numbers in the double ratio, such as 6 and 3, we will find a mean number between them, by which the double ratio of the two given extremes is dissolved to the two mentioned ratios of the superparticular ratios.
|
משל זה שאם לקחנו שני מספרים ביחס הכפל השניי כמו הששה והשלשה שאנו נמצא ביניהם אמצעי מן המספר יותך אצלו יחס שני הקצוות המונחים מהכפל השניי על שני היחסים הנזכרים מיחסי המוסיף ואם כן יותך אליהם חלק
|
- The mean between 6 and 3 is 4:
|
והאמצעי בין הששה והשלשה הם ארבעה
|
 sesquialter ratio sesquialter ratio
|
הנה הששה כאשר הוקשו אל הארבעה היה המוסיף חצי
|
 sesquitertian ratio sesquitertian ratio
|
והארבעה אצל השלשה תוסיף שליש
|
- And when it is dissolved, it is dissolved to them.
|
וכאשר יותך אמנם יותך אליהם
|
- The second type of the multiple ratios, i.e. the triple ratio, is produced from the first type of the superparticular ratios, i.e. the sesquialter ratio, and the first type of the multiple ratios, i.e. the double ratio.
|
ואמנם המין השני מבעל הכפלים ר"ל הכפל השלישיי אמנם יולד מהמין הראשון המוסיף חלק ר"ל החצי והמין הראשון מבעל הכפלים ר"ל השניי
|
- For example:
|
משל זה שי"ח כמו י"ב וכמו חציו
|
|
וי"ב כפל ו'
|
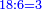 triple ratio triple ratio
|
אבל י"ח אצל ו' כיחס הכפל השלישיי
|
- You will find it the same, however, it is not necessary to define 12, which is double 6, as the mean, but 9, which is the same as 6 plus its half, can be set instead.
|
וכמו כן גם כן תמצאהו אלא שלא יחוייב שנשים האמצעי י"ב אשר הוא כפל ו' אבל נשים במקומו ט' אשר הוא כמו ו' וכמו חציו
|
- Both forms are already demonstrated.
|
וכבר המשלתי לך שתי הצורות
|
- By the reverse explanation it is clear that the triple ratio, when it is dissolved, it is dissolved to the double ratio and the sesquialter ratio.
|
ובהפך זה המאמר יתבאר שהכפל השלישי כאשר יותך אמנם יותך אל הכפל השניי והמוסיף חצי
|
- Examine it with whichever of the two numbers you wish by setting them in the triple ratio, and you will find it so.
|
ובחן זה באי זה משני מספרים תרצה אם תניחם ביחס הכפל השלישיי ותמצאהו כן
|
- If the triple ratio and the second type of the superparticular ratio are composed, the quadruple ratio is produced.
|
ואמנם אם יחובר הכפל השלישיי והמין השני מהמוסיף חלק יתילד מזה הכפל הרביעיי
|
- And if the quadruple ratio is dissolved, it is dissolved to the triple ratio and to the second type of the superparticular ratio.
|
וכאשר יותך הכפל הרביעיי הנה הוא יותך אל הכפל השלישיי ואל המוסיף חלק השניי
|
| The rule of the discussion is that every type of the multiple ratios, when it is composed with its corresponding type of the superparticular ratios, the closest type that follows it of the multiple ratios is composed from them.
|
וכלל המאמר שכל מין ממיני הכפל כאשר הורכב עם דומה לו במדרגה ממיני המוסיף חלק הנה יתחבר מהם המין אשר ילוה אליו בקרוב שבמדרגות אליהם ממיני הכפל
|
| This is the rule of the discussion on the relative quantity with all the aspects of its relations, while keeping as much as possible the completion of the properties by a brief discussion about what the scholars cannot do without it.
|
זהו כלל המאמר בכמה המצטרף על כל צדי צירופיו עם תכלית מה שאיפשר מהשמירה בהשלמת הענינים עם קצור המאמר במה שאי אפשר למתלמדים בלעדיו
|
[Absolute Quantity]
|
|
The Discussion on the Quality of the Absolute Numbers that are Potentially Commensurable with the Geometric Shapes
|
הדבור בתואר המספרים הנפרדים המשותפים בכחם לתמונות המידותיות
|
| The beginning of this discussion on the geometrical shapes:
|
ותחלת זה הדבור בתמוניות
|
| Now what remains of the things that belong to the absolute quantity is noted, which require a more intensive investigation than all the discussed in the first section.
|
אמנם עתה הנה אנחנו זוכרים מה שנשאר מהדברים המתחייבים לכמה הנפרד ממה שיצטרך לחקירה יותר חזקה מכל מה שדברנו עליו במאמר הראשון
|
| For when one wishes to mention it, it is a thing that is necessary in order to assume from it an evidence for another.
|
כי כאשר אנחנו רוצים לזכרו הנה הוא דבר נצטרך אליו לקחת ממנו ראיה על זולתו
|
| The wise men used to praise the explanation of some sciences through others.
|
והחכמים היו משבחים מאד לפרש קצת החכמות בקצת
|
| Of the things whose explanation should be prefaced, it should be said that:
|
ומהדברים אשר ראוי להקדים בבאורם שנאמר כי
|
- Some of the numbers are similar to lines in their arrangement.
|
מהמספרים מה שהוא דומה לקוים בסדרם
|
- Some of them are similar to a surface.
|
ומהם מה שהוא דומה לשטח
|
- Some of them are similar to a cube.
|
ומהם מה שהוא דומה למעוקב
|
- Some of them are similar to a sphere.
|
ומהם מה שהוא דומה לכדור
|
- Some of them are similar to a brick, in the deficiency of the height compared with the length and width.
|
ומהם מה שהוא דומה ללבנה בחסרון הגובה מהאורך והרחב
|
- Some of them are similar to a pillar, in the deficiency of the length and width compared with the height.
|
ומהם מה שהוא דומה לעמוד בחסרון האורך והרחב מהגובה
|
- Some of them are similar to an arc.
|
ומהם מה שהוא דומה לקשת
|
| Likewise for each of the things of geometry, i.e. the measures - these shapes have similarity in numbers.
|
וכמו כן לכל אחד מהדברים אשר להנדסה ר"ל המדות יש דמיון לאותם התמונות במספרים
|
| For geometry is based on quality more than on quantity.
|
כי ההנדסה לאיכות יותר דבקה מאשר לכמות
|
| Look carefully on what was mentioned about the precedence of the number over the measures in the introduction to the number, because it was noticed and discussed there.
|
ותעיין מה שזכרנו מקדימת המספר למדות בפתיחת המספר כי שם שמנו אליו לב ודברנו בו
|
| Before discussing the similarity of these mentioned boundaries to the numbers, it is said that the meaning of the alpha beta letters as designating the numbers that are marked by them, which are the shapes that are seen, that the people call decimal calculation, is not by their nature, nor by their law, but they designate them only by convention and positioning.
|
וקודם שנדבר על דמיון אלו הגבולים אשר זכרנום מהמספרים נאמר שהוראת אותיות האלפא ביתא על מה שיורו עליו מן המספרים הנרשמים בם והם הרשמים אשר אנו רואים שיקראום האנשים חשבון הכללים אינו בטבע להם ולא בדין להם כך אבל הם מורים בהסכמה ובהנחה ממנו לא זולתו
|
| Those that are indicators by nature are as the seen by the sense.
|
ואמנם המורים בטבעם הנה הם כמו הנראים לחוש
|
- If one wishes to write one - setting one sign.
|
והוא שאנו כאשר נרצה לרשום אחד נניח סימן אחד
|
- If one wishes to write two - setting two signs.
|
וכשנרצה לרשום שנים נניח שני סמנים
|
- If one wishes [to write] three - setting three signs.
|
וכן אם נרצה שלשה נניח שלשה סמנים
|
| These will be the form of the one, the form of the two, the form of the three, and so on for what follows.
|
ותהיה צורת האחד וצורת השנים וצורת השלשה וכן מה שאחר זה
|
| When this condition is brought, it is said that the one is assumed in this craft as the beginnig of the number, as the rank of the point in the science of geometry, which is the beginning of the line, but not that the point or the one being a line or a number.
|
וכאשר הבאנו זה התנאי נאמר שאנו נניח האחד בזאת המלאכה התחלה למספר כמדרגת הנקודה במלאכת המדות אשר היא התחלת הקו מבלתי שתהיה הנקודה או האחד קו או מספר
|
| As when the point is multiplied by itself, no other quantity is generated.
|
הנה כמו שהנקדה כאשר נכפלה בעצמה לא יתחדש גודל אחר
|
| Because, when what has no quantity is multiplied by what has no quantity, no quantity is generated
|
שמה שאין גודל לו כאשר נכפל במה שאין גודל לו לא יתחדש גודל
|
| Since no being existes from non-being.
|
לפי שלא יהיה יש מלא יש
|
| Likewise the one, which is not a number, when it is multiplied by itself, no number is generated, as no being is generated from the multiplication of nothing.
|
כמו כן האחד אשר אינו מספר כאשר נכפל בעצמו לא יתחדש מספר לפי שלא יתחדש יש מכפל אין
|
| Hence, the essence of the one, as it is said, is that it is the beginning of the number, but it is not a number.
|
הנה אם כן אמתת האחד כמו שאמרנו שהוא תחלת המספר ואינו מספר
|
Plane Numbers
|
|
The Discussion on the Similarity Aspect of the Number to the Line
|
הדבור בצד התדמות המספר לקו
|
| The beginning of its continuity is found in the duality.
|
ואמנם תחלת המשכותו אמנם ימצא בשניות
|
| Furthermore, it increases continually according to the measure of the addition of the natural numbers and their production.
|
עוד יתרבה בהמשכות כפי שעור הוספת המספרים הטבעיים וצמיחתם
|
| As the number is generated by assuming two different units such that the number is from their difference, so the line is generated by assuming two different point, such that the line is from their difference.
|
הנה כמו שהמספר יתחדש בהנחת שני אחדים נבדלים ויהיה מהבדלם המספר כן הקו אמנם יתחדש בהנחת שתי נקודות נבדלות הנה יהיה מהבדלם הקו
|
- The line has one dimension.
|
והקו בעל משך אחד
|
- The two-dimensional is the surface.
|
ומה שהיה בעל שני המשכים הוא שטח
|
- The three-dimensional is the body.
|
ומה שהיה בעל שלשה המשכים הוא גשם
|
| The three-dimensional has six directions, which are said to be necessarily in every body, i.e. up, down, right, left, forward, backward.
|
ולבעל השלשה המשכים מה שיתחדש השש פאות אשר יאמר שהן מתחייבות לכל גשם ר"ל מעלה ומטה וימין ושמאל ופנים ואחור
|
| By these six directions the motion divides the places.
|
ובאלו השש פאות תחלק התנועה המקומות
|
| For it is necessarily follows that each dimension has two opposite directions, whether one has the two directions up and down, or another forward and backward, or another right and left.
|
כי בהכרח שיתחייב לכל משך שתי תכליות מקבילים אם לאחד משתי התכליות מעלה ומטה ואם לאחר פנים ואחור ואם לאחר ימין ושמאל
|
- One may argue by saying in a general statement that any thing that has length, breadth, and depth is a body, and every body has length, breadth, and depth.
|
ואולי יהיה לטוען שיאמר הנה במאמר כולל שכל בעל אורך ורוחב ועומק הוא גשם וכל גשם בעל אורך ורחב ועומק
|
- Likewise, one may say that what has only length and breadth is a surface, and the surface is that which has only length and breadth.
|
וכמו כן יאמר מה שהיה לו אורך ורחב לבד הוא שטח והשטח הוא מה שהיה לו אורך ורחב לבד
|
- The line is that which has only length, and that which has only length is a line.
|
והקו מה שהיה לו אורך לבד ומה שהיה לו אורך לבד הוא קו
|
Hence:
- The surface is one dimension less than the body.
|
הנה השטח חסר מהגשם במשך אחד
|
- The line is one dimension less than the surface.
|
והקו מהשטח במשך אחד
|
- The point is one dimension less than the line.
|
והנקודה חסרה מהקו במשך אחד
|
| Hence, the point has no dimension at all.
|
הנה אם כן הנקודה אין מרחק לה כלל
|
- It is the beginning of the line, but it is not a line.
|
ואמנם היא התחלת הקו ואיננה קו
|
- The line is the beginning of the surface, but it is not a surface.
|
וכמו כן הקו התחלת השטח ואיננו שטח
|
- It is the beginning of the two dimensions, but it is not two-dimensional.
|
והתחלת שני המשכים ואיננו שני המשכים
|
- The surface is the beginning of the body, but it is not a body.
|
וכמו כן השטח התחלת הגשם ואיננו גשם
|
- It is the beginning of the three dimensions.
|
והתחלת שלשה המשכים
|
| Thus, the numbers are also similar to these boundaries, as will be described.
|
הנה אכן גם כן המספרים הם דומים לאלו הגבולים כפי מה שאתאר
|
| This is because the linear numbers are all those that are set to begin with two and increase by one by the order of the natural succession.
|
וזה שהמספרים הקויים הם כל מה שתניח התחלתו מהשנים עוד יתרבו באחד על סדר משך הטבע
|
The Discussion about the Triangle as the Foundation of All Rectilinear Surfaces
|
הדבור באשר המשולש יסוד לכל השטחים ישרי הקוים
|
| The first of the rectilinear surfaces is the triangle.
|
ואמנם השטחים ישרי הקוים הראשון מהם המשולש
|
| It is the one that has three angles.
|
והוא בעל השלש זויות
|
| It is as a root and a beginning of all regular surfaces, such as the square, the pentagon, the hexagon, and their similar.
|
והוא כשרש וכהתחלה לכל השטחים הישרים כמו המרובע והמחומש והמשושה והדומה להם
|
| For all of them are dissolved into a triangle.
|
כי כלם יותכו אל המשולש
|
| The triangle does not dissolved except into its shape.
|
וזה המשולש לא יותך אל בלתי תמונתו
|
| This is clear from that when drawing lines from the angles of whichever regular shapes one wishes to their center, the shape, whichever it may be, will be divided into triangles.
|
וזה מבואר מאשר כשתוציא מאיזה מהתמונות הישרות הקוים שתרצה קוים ישרים מזויותיהם אל מרכזה תחלק איזו תמונה שתהיה אל המשולשים
|
| One finds that the triangle is also divided into its own [type], not different by its nature, and not deviates from its type.
|
ותמצא המשולש יחלק גם כן עצמו אל עצמו בלתי נבדל מטבעו ולא יצא מסוגו
|
| It is already seen in this figure, to sense that the triangle, the square, the pentagon, and the rectilinear shapes that follow them, when drawing in them the described lines from their centers to their angles, all of them are dissolved into triangles.
|
וכבר תראה זה בזאת הצורה לחוש שהמשולש והמרובע והמחומש ומה שאחריהם מהתמונות הישרות הקוים כאשר הוצאנו בם ממרכזיהם אל זויותיהם הקוים אשר תארנו יותכו כלם אל משולשים
|
| It has already been clarified that the triangle is a root and a beginning of all the shapes.
|
הנה כבר התבאר שהמשולש שרש והתחלה לכל התמונות כלן
|
The Discussion on the Triangular Numbers, their Production and their Sides
|
הדבור במשולשים המספריים וצמיחתם וצלעותיהם
|
| The triangular numbers are sums of the natural numbers beginning from the one.
|
ואמנם המשולשים הם הוספות המספרים הטבעיים אשר התחלתם האחד קצתם על קצת
|
- The one, when it is written, is a triangle in potentia.
|
הנה האחד כאשר נרשם הנה הוא משולש בכח
|
- When two is added to the one, the three are the beginning of the triangles in actu.

|
וכאשר נוסיף על האחד השנים היו השלשה ראשית המשולשים בפעל
|
- When adding three, the consecutive of two, to the first actual triangle the result is the second actual triangle, which is 6.
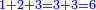
|
עוד תוסיף שלשה אשר ימשכו לשנים על המשולש הראשון בפעל ויהיה המשולש השני בפעל והוא ששה
|
- When adding four the result is the third actual triangle, which is 10.
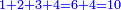
|
עוד תוסיף ארבעה ויהיה המשולש השלישי בפעל והוא עשרה
|
| So on, the production of the triangles is generated from the addition of the natural numbers to each other.
|
עוד כן תתחדש תולדת המשלשים בתוספת המספרים הטבעיים קצתם אל קצתם
|
| From what is examined in this diagram, the triangular numbers are produced from the addition of the natural numbers to each other.
|
וממה שתבחנהו בזאת הצורה שהמספרים המשולשים יתילדו מחבור המספרים הטבעיים קצתם על קצת
|
|
|
כמו ג' שתשא חבור ב' וא'
|
|
|
א' ג' ו' י' ט"ו כ"א וכו'
|
| The production of the sides of these triangles is as the production of the natural numbers according to their succession:
|
ואמנם התילד צלעות אלו המשולשים הוא כפי התילד המספרים הטבעיים על המשכם
|
- The side of the first in potentia is 1.
|
הנה יהיה צלע הראשון בכח האחד
|
- The side of the first in actu is 2.
|
וצלע הראשון בפעל ב'
|
- The side of the second in actu is 3.
|
וצלע השני בפעל ג'
|
- The side of the third in actu is 4.
|
וצלע השלישי בפעל ד'
|
| In this way, each side of the triangles is produced from the production of the natural numbers.
|
ובזה הצד מהתילד המספרים הטבעיים יתילד כל צלע מצלעות המשולשים
|
- Beginning from placing the one first.
|
וזה כאשר נתחיל להניח האחד תחלה
|
- Then, each number of the natural numbers is produced by itself in the successive lines beneath the one, as seen illustrated in this diagram:
|
עוד יתילד כל מספר מהמספרים הטבעיים בפני עצמו בטורים ימשכו קצתם לקצת תחת האחד כפי מה שתראה מצוייר בזאת הצורה
|
|
|
|
- The first potential triangle is 1, and its side is 1.
|
המשולש הראשון בכח אחד וצלעו אחד
|
- The first actual triangle is 3, and its side is 2.
|
והמשולש הראשון בפעל שלשה וצלעו השני'
|
- The second actual triangle is 6, and its side is 3.
|
והמשלש השני בפועל ששה וצלעו שלשה
|
- The third actual triangle is 10, and its side is 4.
|
והמשלש השלישי בפעל עשרה וצלעו ארבעה
|
- The fourth actual triangle is 15, and its side is 5.
|
והמשלש הרביעי בפעל ט"ו וצלעו חמשה
|
| What should be examined concerning these triangular numbers is that each triangular of them encompasses the geometrical triangles by a number that is equal to the number of the preceding square, i.e. preceding by one rank, and so on infinitely.
|
ומה שראוי שתבחנהו באלו המספרים המשולשים שכל משולש מהם יקיף מהמשלשים המדותיים במניין שוה למספר המרובע הקודם ר"ל במדרגה אחת וכן תמיד
|
The Discussion on the Square Numbers, their Sides and their Production
|
הדבור במרובעים המספריים וצלעותיהם והתילדם
|
| The regular square shapes are not produced as the triangles are produced from the three.
|
ואמנם התמונות המרובעות הישרות לא יתילדו כמו שיתילדו המשולשות מן השלשה
|
| This is because they have four sides and four angles.
|
וזה שהן בעלות ארבע צלעות וארבע זויות
|
| Such as: 4; 9; 16; 25; 36
|
כמו ד' ט' י"ו כ"ה ל"ו
|
| The shapes of these numbers are the square and the equilateral, according to this example, i.e. the illustrated at the end of the chapter, which is a diagram in which there are always regular squares.
|
ורשמי אלו המספרים על הרבוע והשווי יהיה כפי זה המשל ר"ל המצוייר בסוף זה השער והיא התמונה אשר עליה יהיו המרובעים השוים תמיד
|
| It is clarified from the illustrated example below that the sides of the square numbers according to their succession are added according to the root of the production of the natural numbers:
|
ומבואר נגלה מהדמיון המצוייר למטה שצלעות המרובעים המספריים כפי המשכם יתוספו כפי שרש צמיחת המספרים הטבעיים
|
- The side of the first in potenti, which is 1, is 1.
|
כי צלע הראשון בכח אשר הוא האחד אחד
|
- The side of the first in actu is 2.
|
וצלע הראשון בפעל ב'
|
- The side of the second in actu is 3.
|
וצלע השני בפעל ג'
|
- The side of the third in actu is 4.
|
וצלע השלישי בפעל ד'
|
| And so is their production always.
|
וכן צמיחתם תמיד
|
| It is already said in the first chapter how the equilateral numbers are produced, as it was mentioned there.
|
וכבר אמרנו במאמר הראשון איך יתילדו המספרים השוי הצלעות למה שקרה שם זכרו
|
| Yet, it is necessary to return the discussion to it, since this is the place in which it is especially mentioned.
|
ואמנם מחוייב להשיב המאמר עליו הנה אחר שהוא מקום זכרו המיוחד בו
|
| It is said that the production of the square numbers is from the successive addition of the natural odd numbers.
|
ונאמר שצמיחת אלו המרובעים מהוספת הנפרדים הטבעיים קצתם על קצת
|
- Their beginning is the one, which is an odd in potentia and a square in potentia.
|
אחר שהתחלתם האחד אשר הוא נפרד בכח ומרובע בכח
|
- The three, which are the first odd, when added to the one, the result is four, which is the first actual square.

|
כי השלשה אשר הם נפרד ראשון כאשר נוספו על האחד היה הגעת זה ארבעה והוא המרובע הראשון בפעל
|
- When the second odd number, which is five, is added to the first actual square, the result is nine, which is the second actual square.
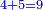
|
וכאשר נוסף על המרובע הראשון בפעל הנפרד השני אשר הוא חמשה היה הגעת זה תשעה והוא המרובע השני בפעל
|
| Since it was already mentioned once, there is no need to elaborate about it more than saying that the production of the equilateral squares is by adding the natural odd numbers to each other.
|
ולפי שאנו כבר זכרנו זה פעם אחת אין צורך לנו להאריך ביותר מאשר נאמר שהולדת המרובעים השוי הצלעות אמנם תהיה בתוספת הנפרדים הטבעיים קצתם על קצת
|
| Each side of any square of them is a root of that square, i.e. when it is counted by the measure of the units that are in it, the result is that square.
|
וכל צלע מצלעות כל מרובע מהם הוא שרש אותו המרובע ר"ל כאשר ימנה בשעורי מה שבו מהאחדים היה כללו הגעת אותו המרובע
|
| When the roots of these squares are set successively, they are according to the order of the succession of the natural numbers.
|
וכאשר הונחו שרשי אלו המרובעים ילוו קצתם לקצת היו על סדר המספרים הטבעיים ימשכו קצתם לקצת
|
| The rule of this discussion is in accordance with this.
|
וכלל זה המאמר על זה
|
| This is the diagram of the squares, which was intended to be brought at the end of the discussion:
|
וזה צורת המרובעים אשר יעדנו להביאה בסוף הדברים
|
|
|
|
- The first potential square is one, which is written in black, on the right upper angle, upon which א is written.
|
המרובע הראשון בכח הוא האחד הנרשם בשחרות בזוית העליונה מצד הימין והוא הנרשם עליו א'
|
- The first actual square is the summed from this one and from the three red units that follow, by the property of the geometrical shape.
|
והמרובע הראשון בפעל הוא המתקבץ מזה האחד ומשלשת האחדים האדומים אשר ילוו עליהם על תכונת תמונת הרושם
|
- The second square is the summed from this first actual square and from five units.
|
והמרובע השני הוא המתקבץ מזה המרובע הראשון בפועל ומחמשת אחדים
|
- The third actual square is the summed from this second actual square and from the seven red units that follow, by the property of the geometrical shape.
|
והמרובע השלישי בפעל הוא המתקבץ מזה המרובע השני בפעל ומשבעה האחדים האדומים הנלוים עליהם על תכונת תבנית הרושם
|
- The four actual square is the summed from this third actual square and from the nine black units that follow, by the property of the geometrical shape.
|
והמרובע הרביעי בפעל הוא המתקבץ מזה המרובע השלישי בפעל ומתשעת האחדים השחורים הנלוים עליהם על תכונת תבנית הרושם
|
| It should be examined that the geometrical shapes in this diagram are the natural odd numbers, according to their succession in the natural order.
|
וממה שראוי לך שתבחנהו שתמונות הרושם בזאת הצורה הם הנפרדים הטבעיים כפי המשכם בסדר הטבע
|
The Discussion on the Pentagonal Numbers, their Production and their Sides
|
הדבור במחומשים המספרים והתילדם וצלעותיהם
|
| The pentagonal number, i.e. all pentagonal numbers, their production is not through the production of the triangle and the square, since the pentagon has five sides and five angles, such as: 1, 5, 12, 22, 35, 51, and the descriptions of these numbers by the quintuple and equality are as drawn at the end of this chapter.
|
ואמנם המספר המחומש ר"ל כלל המחומשים המספרים אין צמיחתם בצמיחת המשלש והמרובע כי המחומש לו חמשה צלעות וחמשה זויות כמו א' ה' י"ב כ"ב ל"ה נ"א ורשמי אלו המספרים על החמוש והשווי הם כפי מה שציירתי לך בסוף זה השער
|
- The side of the first actual pentagonal, which is 5, is 2.
|
הנה צלע המחומש הראשון בפעל והוא ה' שנים
|
- The side of the second actual pentagonal, which is 12, is 3.
|
וצלע המחומש השני בפעל והוא י"ב שלשה
|
- The side of the third actual pentagonal, which is 22, is 4.
|
וצלע המחומש השלישי בפעל והוא כ"ב ארבעה
|
| It necessary follows that the sides of these pentagonals follow each other by the sequence of the natural numbers, as clarified concerning the triangular and the square numbers.
|
וכן יחוייב שיהיו צלעות אלו המחומשים נמשכים יחד על סדר המספרים הטבעיים כפי מה שהתבאר במשולש והמרובע
|
| The production of the pentagonal numbers:
|
ואמנם התילד המחומש
|
- It is already clarified that, since the first actual pentagonal is 5, the second is 12, and the third is 22, what is added to the first potential pentagonal, which is 1, until it becomes the first actual pentagonal, is 4.
|
הנה כבר התבאר כי אחר שהיה המחומש הראשון בפעל ה' והשני י"ב והשלישי כ"ב שאשר הוספנו אותו על המחומש הראשון אשר הוא א' בכח ארבעה עד שהיה המחומש הראשון בפעל
|
- When 7 is added to the first actual, which is 5, until it becomes 12, which is the second actual, the excess of the 7, which was added at the end, over the 4, which was added first, is 3.
|
וכאשר הוספנוהו על הראשון בפעל והוא ה' ז' עד שהיה י"ב והוא השני בפעל הנה מותר השבעה אשר הוספנום לסוף על הארבעה אשר הוספנום ראשונה שלשה
|
- The second actual pentagonal number is 12, and the third actual is 22.
|
והמחומש השני בפעל י"ב והשלישי בפועל כ"ב
|
- What is added to the second actual, until it becomes the third actual, is 10, and 10 exceeds 7 by 3.
|
ואשר הוספנוהו על השני בפועל עד שיהיה השלישי בפעל עשרה ועשרה יותר משבעה שלשה
|
| Hence, it is already clarified that the production of the pentagonal numbers is always by adding three to what was added to the preceding pentagonal number and so it will be found always.
|
הנה אם כן כבר התבאר שתולדת המחומשים בתוספת שלשה לעולם על מה שהוספנוהו במחומש אשר לפניו וכן ימצא תמיד
|
- The fourth pentagonal number is 35, and 35 exceeds 22 by the addition of 13, and 13 exceeds 10 by 3.
|
כי הנה המחומש הרביעי ל"ה ול"ה יותר מכ"ב בתוספת י"ג וי"ג יותר מי' שלשה
|
| Thus, it has already been clarified how the pentagonal numbers are produced.
|
הנה אם כן כבר התבאר איך יתילדו המחומשים
|
| Furthermore, it is already clear from all that is said, how the hexagonal and the heptagonal numbers and the others are composed:
|
וגם כן כבר יתבאר מכל מה שאמרנו איך יתרכבו כמו כן המשושים והמשובעים וזולתם
|
- It was already explained that the triangular numbers are generated from the successive addition of the natural numbers, and the natural numbers are added one by one.
|
וזה שאנו כבר בארנו שהמשלשים יתחדשו בתוספת המספרים הטבעיים קצתם על קצת והמספרים הטבעיים יתוספו באחד אחד
|
- It was also explained that the square numbers are generated from the successive addition of the odd numbers, and the odd numbers are added two by two.
|
ובארנו גם כן כי המרובעים יתחדשו בתוספת המספרים הנפרדים קצתם על קצת והנפרדים יתוספו שנים שנים
|
- It was explained that the pentagonal numbers are generated from the addition of the numbers that are added successively three by three.
|
ובארנו שהמחומשים יתחדשו בתוספת המספרים אשר יתוספו קצתם על קצת שלשה שלשה
|
- It is said that the hexagonal numbers are generated from the addition of the numbers that are added successively four by four.
|
ונאמר שהמשושים יתחדשו בתוספת המספרים אשר יתוספו קצתם על קצת ארבעה ארבעה
|
- The heptagonal numbers are generated from the addition of the numbers that are added successively five by five.
|
והמשובעים יתחדשו בהוספת המספרים אשר יתוספו קצתם על קצת חמשה חמשה
|
| So also for the octagonal and the nonagonal numbers, or whatever one wishes of these, they are generated as this drawn description.
|
וכן המשומין והמתושע או מה שתרצה מזה אמנם יתחדש בזה התאר המצוייר
|
| Examples were already given for the pentagonal, hexagonal, heptagonal, and octagonal numbers.
|
הנה כבר המשלנו דמיונים למחומשים ולמשושים ולמשובעים ולמשומנים
|
- The numbers by which each plane number of them exceeds its preceding are distinguished by two colors.
|
והבדלנו בחלוק שני גוונים המספרים אשר בם יוסיף כל מספר משוטח מהם על אשר לפניו
|
| These numbers were assumed as an image of geometrical shapes, in order that what was mentioned will be clarified about them, that the shapes of each species of the plane right angled numbers are produced from the addition of numbers that exceed by one number that never changes forever.
|
והנחנו אותם המספרים כדמות תבניות הרושם כדי שיתבאר בם מה שזכרנו מאשר כל מין ממיני המספרים המשוטחים בעלי הזויות השוות אמנם יתילדו תמונותיו בתוספת מספרים יעדיפו במספר אחד לא ישתנה לעולם אל בלתי תכלית
|
- The squares - the numbers that are added in them, i.e. the excess of numbers of the shapes that complete them at the ends of the geometrical shapes is two by two.
|
אמנם המרובעים המספרים אשר יתוספו בם ר"ל מספרי התמונות אשר ישלימו אותם על גבולי תמונות הרושם תהיה העדפתם שנים שנים
|
- The pentagonals - the excess mentioned with regard to them is three by three.
|
ואמנם המחומשים הנה העודף הנזכר בם יהיה שלשה שלשה
|
| Likewise, for any rank shifted forwards in the ranks of the species of the plane numbers, the excess mentioned exceeds by one.
|
וכמו כן כל מה שתעתיק מדרגה אחת במדרגות מיני המספרים המשוטחים יוסיף היתרון הנזכר באחד
|
| משולש ח |
משולש ז |
משולש ו |
משולש ה |
משולש ד |
משולש ג |
משולש ב |
משולש א
|
|
|
|
|
|
|
|
|
א
|
| מרובע ח |
מרובע ז |
מרובע ו |
מרובע ה |
מרובע ד |
מרובע ג |
מרובע ב |
מרובע א
|
|
|
|
|
|
|
|
|
א
|
| מחומש ח |
מחומש ז |
מחומש ו |
מחומש ה |
מחומש ד |
מחומש ג |
מחומש ב |
מחומש א
|
|
|
|
|
|
|
|
|
א
|
| משושה ח |
משושה ז |
משושה ו |
משושה ה |
משושה ד |
משושה ג |
משושה ב |
משושה א
|
|
|
|
|
|
|
|
|
א
|
All Plane Polygonals Consist of and Resolved into Triangles
|
הדבור באשר כל המשוטחים בעלי הזויות השוות מהמשולשים יתרכבו ואליהם יותכו
|
|
|
וכבר קרה מזה ביאור מה שאמרנו לפנים שבעלי המספרים הישרי הקוים השוי הזויות הם מורכבים מהמשולשים ונתכים אליהם וזה שכבר נראה לנו שהמרובעים אמנם חודשו מהרכבת המשולשים כאשר הנחנו המשולשים על סדר כמו א'ג'ו'י' ט"ו
|
- When the first potential triangle is added to the first actual triangle, which is 3, the first actual square is created, which is 4.

|
עוד חברנו המשלש הראשון בכח אל המשלש הראשון בפעל והוא ג' יחודש המרובע הראשון בפעל והוא ד'
|
- When the first actual triangle, which is 3, is added to the second actual triangle, which is 6, the second actual square is created, which is 9.
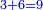
|
וכאשר חברנו המשולש הראשון בפעל אשר הוא ג' אל השני בפעל אשר הוא ו' יתחדש המרובע השני בפעל אשר הוא ט'
|
- When the second actual triangle, which is 6, is added to the third actual triangle, which is 10, the third actual square is created, which is 16.
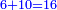
|
וכן כאשר חברנו המשולש השני בפעל והוא ו' אל המשולש השלישי בפועל והוא י' יחודש המרובע השלישי והוא י"ו
|
|
|
וכן תמצא זה תמיד מתרכב מכל שני משולשים מהם מרובע כפי זה הסדר אשר המשלנו ובהפך זה המאמר יותך כל מרובע מהמרובעים אל המשולשים אשר מהם הורכב כי הארבעה אשר הוא מרובע יותך אל אחד ושלשה והם שני משולשים והתשעה אל שלשה וששה הם שני משולשים הנה כבר התבאר איך יתרכבו המרובעים מן המשולשים ויתכו אליהם
|
|
|
ואמנם המחומשים כפי מה שאתאר וזה שהם יתרכבו מהמשולשים והמרובעים כאשר סדרנו המשולשים בטור כמו א'ג'י'ו' ט"ו
|
|
|
עוד נסדר המרובעים בטור כמו ד' ט' י"ו כ"ה ל"ו
|
|
|
עוד נחבר כל מדרגה עם נכחה
|
- The result of the sum of the first potential triangle, which is 1, with the first actual square, which is 4, is the first actual pentagonal, which is 5.
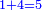
|
הנה יתקבץ מחבור המשלש הראשון בכח אשר הוא א' עם המרובע הראשון בפעל אשר הוא ד' המחומש הראשון בפעל אשר הוא ה'
|
|
|
וכן תמצאהו תמיד כאשר תרכיבהו כפי זה הסדר ובהפך זה המאמר יתבאר שהמחומשים יותכו אל המשולשים ואל מה שיורכב מהמשולשים ר"ל המרובעים כי החמשה יותך אל אחד וארבעה והי"ב אל שלשה ותשעה וכן מה שאחר זה הנה כבר התבאר איך יתרכבו המחומשים מהמשולשים ויותכו אליהם
|
|
|
וכן תמצא גם כן שיתילדו המשושים מהרכבת המשולשים עם מה שיהיה נכחם בטור המחומשים כאשר הורכבו על דמיון מה שבארנו אלא שיהיה לעולם ראש הנחת המשולשים המשולש הראשון בכח אשר הוא אחד וראש מדרגות מספרי השטחים האחרים הראשון מהם בפעל
|
- The first actual hexagonal is created from the combination of the first potential triangle, which is 1, with the first actual pentagonal, which is 5.
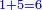
|
והמשושה הראשון בפעל אמנם יחודש מהרכבת המשלש הראשון בכח אשר הוא האחד עם המחומש הראשון בפעל אשר הוא חמשה
|
- The second hexagonal [is created] from the combination of the first actual triangle, which is 3, with the second actual pentagonal, which is 12.
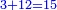
|
והמשושה השני מהרכבת המשלש הראשון בפעל אשר הוא ג' עם המחומש השני בפעל אשר הוא י"ב
|
- The first actual heptagonal is created from the combination of the first potential triangle, which is 1, with the first actual hexagonal.
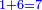
|
וכן המשובע גם כן יתחדש הראשון ממנו בפעל מהרכבת המשלש הראשון בכח אשר הוא א' עם המשושה הראשון בפעל
|
- The second heptagonal [is created] from the combination of the first actual triangle, with the second actual hexagonal.
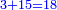
|
והמשובע השני בפעל מהרכבת המשולש הראשון בפעל עם המשושה השני בפעל
|
|
|
וכן ימצאו כלם תמיד המשומנים והמתושעים וזולתם מבעלי הזויות ותולדותם מן המשולשים והתכתם אל המשולש
|
|
|
ולבאר זה לחוש נניח לו צורה מטורים נכחים הטור הראשון למשולשים והשני למרובעים והשלישי למחומשים והרביעי למשושים והטור החמישי למשובעים והטור השני למשומנים ומי שירצה להוסיף בזאת הצורה מספרים מבעלי השטחים ידבק בסדור אשר נשעננו וכוננו אליו
|
|
|
וממה שיתבאר בזאת הצורה שהמינים הראשונים בפעל ר"ל המשוטחים המספריים יעדיפו על המשכם ברחב הצורה במשלש הראשון בכח והוא האחד
|
|
|
והמינים השניים בפעל יעדיפו על המשכם ברחב הצורה במשולש הראשון בפעל ר"ל בשלשה
|
|
|
והמינים השלישים בפעל יעדיפו על המשכם ברחב הצורה במשולש השני בפעל
|
|
|
וכן המינים הרביעים בפעל יעדיפו על המשכם במשלש השלישי בפעל וכן מה שאחר זה
|
|
|
וכבר נשלם המאמר במספרים המשוטחים בעלי הזויות
|
The Discussion on the Solid Numbers
|
הדבור במספרים הגרמיים
|
| The distinction between the solid and the surface has already been explained in the previous discussion
|
כבר בארנו במה שקדם מן המאמר מה ההפרש בין הגרם והשטח
|
| It was said that the solid adds a dimension of depth to the surface, since the surface has only length and breadth
|
ואמרנו שהגרם הוא אשר יוסיף משך בעומק על השטח אחר שהשטח אורך ורחב לבד
|
- Saying depth or height is the same.
|
ואמרנו עומק או גובה הכל שוה
|
| People have said it all before.
|
וכבר אמרו כל זה אנשים
|
| Since the discussion on triangles in the section on surface previously was more worthy of precedence, because of the described reason, as they are a principle and a root for all the surfaces, the pyramids are prefaced in the discussion on solid numbers.
|
ואחר שהיה קודם במאמרנו על השטח הדבור על משולשים לעלה אשר תארנו מהיותר ראוי לקדימה אחר שהם פנה לכל השטחים ושרש יהיה הקדימנו המאמר הזה בגרמים על המזונבים
|
| The meaning of the pyramids is those that begin in an equilateral plane base, rising in height, until ending in one.
|
ורצוני במזונבים אשר יתחילו מתושבת משוטח ישר הקוים ר"ל הצלעות עוד יעלו בגובה עד שיכלו אל האחד
|
| All the surfaces of this shape are triangles except its base, since the bases of the pyramid species are either triangles, or squares, or pentagons, or hexagons, or others of the mentioned surfaces, but its [other] surfaces are triangles only.
|
כי זאת התמונה אם שיהיו שטחיה כלם משלשים מלבד תושבתה כי התושבות לזה המין המזונב כבר יהיו משולשים או מרובעים או מחומשים או משושים או זולת זה מהשטחים אשר זכרנו ואמנם בשטחיו כאשר היה מזונב הם משולשים לבד
|
| Since the pyramid whose bases are all triangles, i.e. the triangular pyramid is a principle and a root for all the pyramids, as they are composed from it and dissolved to it, it is necesary to begin with its description.
|
ומפני שהמזונב אשר תושבותיו יחד משולשים ר"ל הגרם המשולש פנה ושרש לכל הגרמים בעלי הזויות אחר שהרכבתם ממנו והתכתם אליו יחוייב שנתחיל בו לתארו
|
| This solid is encompassed by four triangles.
|
ונאמר שזה הגרם יקיפו בו ארבעה משולשים
|
- If one imagines solid shapes from the two-dimensional shapes: an equilateral triangle of three dimensions that are lengthwise equal to its sides, going from the angles of its base, converging to one point, parallel to the center, in the falling of the height, a pyramid is conceived, having four equal surfaces, one of them is the base, and the remaining three are encompassing it.
|
כי אלו ידמה מדמה מהתמונות הגרמיות מהמדתיות משולש שוה הצלעות בעל שלשה המשכים שוים באורך לצלעותיו יצאו מזויות תושבתו עוד יפגשו על נקדה נכחית למרכז בנפילת עמוד יהיה כבר ידומה גרם מזדנב לו ארבעה שטחים שוים אחד מהם התושבת והשלשה הנשארים המקיפים בו
|
- If one imagines a square, four sides are going from its angles, one from each side of its base, and all converging to one point, parallel to the center, in the falling of the height of the square, a pyramid is conceived, i.e. a pyramid that has five surfaces, as this figure, one of them is a square surface, which is its base, and the remaining four are triangles that encompassing it.
|
וכמו כן גם כן אלו ידמה מדמה מרובע שוה יצאו מזויותיו ארבע צלעות כל אחד מהם לצלע מצלעות תושבתו ויפגשו כלם על נקדה נכחית למרכז בנפילת עמוד המרובע ידומה גרם המזדנב ר"ל מחודד לו חמשה שטחים כמו זאת הצורה אחד מהם שטח מרובע והוא תושבתו והארבעה הנשארים משולשים והם המקיפים בו
|
- Likewise if one imagines the same for a pentagon, or a hexagon, or a heptagon, or other than this, such that lines are going from their angles, converging to one point, parallel to their center, triangles will be generated from the lines that are going from the angles and the ends of their base, and it will be a pyramid.
|
וגם כן אלו ידמה מדמה כמו זה במחומש והמשושה והמשובע וזולתם ימצא בכל אחד מהם המשכים יצאו מזויותיהם ויפגשו על נקדה לנגד מרכזיהם יחדשו באותם הקוים היוצאים מהזויות ותכליות תושבתם משולשים ויהיה הגרם מזדנב ר"ל מחודד
|
| If wishing to examine it, one can look at the examples drawn previously in the chapter of the discussion about the triangle as a principle for all the two-dimensional regular surfaces.
|
וכאשר תרצה לבחון זה עיין בדמיונים המצויירים קודם זה בשער הדבור על שהמשולש פנה לכל בעלי הזויות והקוים הישרים מהשטחים המדותיים
|
| Again, it is said that the production and increasing of every absolute number, as the line, is from the one, such as 1, 2, 3, 4, 5, 6, to what is added infinitely.
|
ונשוב עתה ונאמר שכל מספר מוגבל כמו הקו הנה תולדתו וצמיחתו מהאחד וזה כמו א' ב' ג' ד' ה' ו' אל מה שיתוסף מזה תמיד
|
| From the linear numbers the angled surfaces and solids are composed, except that they are not produced and composed accidentally from the imaginary construction, but according to a definition and order, as revealed previously when defining the production of the surfaces.
|
ומאלו המספרים הקויים מה שיתרכבו בעלי הזויות מהשטחים והגרמים אלא שלא יתילד ויתרכב איך שיזדמן מההרכבה במחשבה אבל על גבול וסדר כמו שכבר גלינו במה שקדם בהגבילנו צמיחת השטחים
|
| The production of the solid numbers and their growth
|
ואמנם התילד המוגשמים וצמיחתם
|
- The triangular pyramid, i.e. the trianlular solid, is produced by placing one on top, then placing beneath it the triangular numbers that were already mentioned, each beneath its preceeding in rank by order successively. This is done always when wishing to form the triangular pyramid.
|
הנה המשלש המזדנב ר"ל הגרם המשלש התילדו בהנחת האחד בגובה עוד תניח תחתיו המשולשים המספריים אשר כבר זכרנום כל אחד תחת אשר לפניו במדרגה וסדר כפי המשכם ונפעל זה תמיד מה שנרצה להוליד המזדנבים כי יתחדש גוף מחודד משולש
|
- The square pyramids are generated by arranging the aforementioned numerical square surfaces, placing one as their first, then placing beneath it the squares by order successively, and from this a square pyramid is generated.
|
ואמנם המרובעים המזדנבים ר"ל המחודדים הנה הם יתחדשו כאשר תסדר אותם השטחים המרובעים המספריים אשר זכרנום לפנים והנחת האחד ראשון להם עוד תשים המרובעים תחתיו ימשכו קצתם לקצת יתחדש מזה מרובע מזדנב
|
| Likewise for the pentagonal pyramid, the hexagonal pyramid, the heptagonal pyramid, and what is similar to this.
|
וכן המחומש והמשושה והמשובע ומה שידמה זה
|
- The triangular pyramids - the ranks of their formation are as the sequence of these numbers: 1, 4, 10, 20, 35, 56.
|
הנה הגרמיים המזדנבי' המשולשים ר"ל המחודדים יהיו מדרגות חדושם כפי משך אלו המספרים א' ד' י' כ ל"ה נ"ו
|
- Each of these numbers is produced from the arrangement of the numbers one beneath the other.
|
הנה כל אחד מאלו המספרי' אמנם יתילד מסדר המספרים קצתם תחת קצת מאחד האחד עוד האחד עד אשר תרצה
|
- One is the potential triangular pyramid
|
ואמנם האחד הנה הוא גרם המחודד המשולש בכח
|
- Four is the second, which is a construction of two triangles - one and three
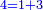
|
ואמנם הארבעה הנה הוא השיני והוא הרכבת שני משולשים האחד והשלשה
|
- ten is a construction of three triangles - one, three and six
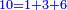
|
ואמנם העשרה הוא מהרכבת שלשה משולשים אחד ושלשה וששה
|
- And so the rest in this order are found by this description.
|
וכן הנשארים כפי זה הסדר נמצא בזה התאר
|
- The ranks of the formation of the square pyramids in their succession are as the sequence of these numbers: 1, 5, 14, 30, 55.
|
ואמנם מדרגות התחדש הגרמים המרובעים המחודדים כפי המשכם הנה על משך אלו המספרים א' ה' י"ד ל' נ"ה
|
- Each of these numbers is produced from the construction of the simple squares introduced above, one upon the other, as said about the the triangular pyramid.
|
כי כל אחד מאלו המספרים אמנם התילד מהרכבת המרובעים הפשוטים אשר אמרנו עליהם לפנים קצתם על קצת כמו שאמרנו במשולש המחודד
|
| As this described instance, so are the pentagonal pyramid, the hexagonal pyramid and others.
|
וכפי זה המשל אשר תארנו יהיה המחומש המחודד והמשושה וזולתם
|
| It is clarified from all that was noted, that the units that are in each of the sides of the pyramids are equal to the number of the surfaces arranged in them, whatever they may be, from the one to the surface of the base.
|
ומבואר מכל מה שזכרנו שכל צלע מצלעות מנין המחודדים יחד שוה מה שבם מהאחדים למנין השטחים המסודרים בם היו מה שהיו מהאחד עד שיגיע אל שטח התושבת
|
| It is not invisible from all that was mentioned, that the simple triangle is the principle and the root of all the surfaces.
|
ולא יעלם ממה שזכרנו שהמשולש הפשוט הוא הפנה והשרש לכל השטחים
|
| The triangular pyramid is the principle of all pyramids.
|
והמשולש המוגשם המחודד הוא הפנה לכל המחודדים
|
| After mentioning the pyramids among the solids, now the one that is called truncated is discussed, which is every angled solid, whose arrangement and construction are according to the arrangement of the construction of the pyramids, except that its height does not end in one, which is the apex of the pyramid, and the angles of its top base are equal in number to the angles of its bottom base, this species is called the truncated.
|
ואחר שכבר הבאנו בזכירת המזונב מהמוגשמים נדבר על אשר נקראהו מחוסר והוא כל גשם בעל זויות היה בסדורו והרכבתו על סדר הרכבת המחודדים אלא שלא יכלה בגבהו אל האחד אשר הוא עליון שבמחודד והיו זויות שטח עליונו שוות במספר לזויות שטח תושבתו הנה זה המין יקרא המחוסר
|
- If the pyramid is deficient by one alone, which is apex of the pyramid, it is called truncated.
|
וזה אם היה חסר מהמחודד באחד לבד אשר הוא עליון המחודד יקרא מחוסר אחד
|
- If it is deficient by one surface [= one + the first actual polygon], it is called bi-truncated.
|
ואם היה חסר מהאחד שטח אחד יקרא מחוסר שנים
|
- If it is deficient by a third surface [= one + the first actual polygon + the second actual polygon], it is called tri-truncated.
|
ואם היה חסר שטח שלישי יקרא מחוסר שלשה
|
- If it is deficient by four surfaces [= one + the first actual polygon + the second actual polygon + the third actual polygon], it is called quadri-truncated.
|
וכן המחוסר ארבעה אם היה חסר ארבעה שטחים
|
| So it is always found.
|
וכן תמצאהו תמיד
|
| Since the production of this truncated solid is already clarified,as there is no difference between it and what was already explained before about the construction of the pyramid, except that a surface or surfaces are subtracted from the apex of the pyramid, which is the one, this is rule of the discussion.
|
ואחר שכבר התבאר איך צמיחת זה הגשם המחוסר אחר שאין הפרש בינו ובין מה שבארנו לפנים מהרכבת המוגשם המחודד אלא שאנו נחסרהו מעליון המחודד אשר הוא האחד שטח או שטחים הנה זה כלל המאמר על זה
|
| This is the time to begin the discussion on the rest of the aforementioned solids, which are the cubes, the bricks, the wedges, the circulars, the sphericals, the scalene, and the heteromecic, while endeavoring to explain it, with the help of God.
|
ואמנם המאמר על שאר הגרמים אשר זכרנום לפנים והם המעוקבים והלבנים והאריחיים והקשתיים והכדוריים והמתחלפי הצלעות והזולתיים באורך הנה זה עת להתחיל בו ונשתדל לפרשו בג"ה
|
The Discussion on the Cube Number
|
הדבור במספר המעוקב
|
| The square equilateral plane numbers discussed above, such as 1, 4, 9, 16, 25, 36, when each one of these surfaces is composed with a surface similar to it in quantity, so that the number of the surfaces composed with each other is as the units of the length and the breadth of the base surface, it is called a cube number.
|
ונאמר עתה שהמספרים המרובעים השוים המשוטחים אשר דברנו עליהם לפנים והם כמו א' ד' ט' י"ו כ"ה ל"ו כאשר הורכב כל אחד מאלו השטחים לדומה לו מהשטחים בכמות עד שיהיה מספר השטחים המורכב קצתם על קצת כמו אחדי אורך ורחב שטח התושבת יקרא מעוקב
|
| The rule of the discussion: the cube is that whose length, breadth and depth are equal to each other.
|
וכלל המאמר כי המעוקב הוא אשר ארכו ורחבו ועמקו שוה קצתו לקצתו
|
- The four, which is an equilateral number, each side of it is two
 , when four units are composed with them , when four units are composed with them 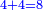 , the sum is eight, eight is two by two by two , the sum is eight, eight is two by two by two  , and this is equal in the three dimension, i.e. the length, breadth and depth. , and this is equal in the three dimension, i.e. the length, breadth and depth.
|
כי הארבעה אשר הם מספר שוה כל צלע ממנו שנים כאשר הורכב עליהם ארבעה אחדים היה כלל שמנה ושמנה שנים בשנים עוד בשנים וזה שוה המרחקים בשלשה ר"ל האורך והרחב והעמק
|
- The nine, each side of which is three
 , when two surfaces equal to them are composed with them, the sum is 27 , when two surfaces equal to them are composed with them, the sum is 27 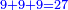 , which is the product of three by three by three , which is the product of three by three by three 
|
וכן גם כן התשעה אשר כל צלע מצלעיותיו שלשה כאשר הרכבו עליהם שני שטחים אחרים שוים להם היה הכלל כ"ז הוא הגעת מוכה ג' בג' עוד בג'
|
| So for the rest of the cube numbers according to this description.
|
וכן שאר המספרים המעוקבים כפי זה התאר
|
| Their general rule: each number is multiplied by the measure of its units, then the product is multiplies again by the measure of the units of the first number, so the total sum is a cube number.
|
והכלל הכולל בהם שכל מספר נכפל בשעור אחדיו עוד נכפל הכל בשעור אחדי המספר הראשון שנית הנה הכלל יהיה מספר מעוקב
|
| From these it is known that any plane square is a surface that has four angles and four sides.
|
הנה כבר קרה מזה שנדע שכל מרובע פשוט הוא שטח ולו ארבע זויות וארבע צלעות
|
| Any cube has six equal surfaces, eight equal angles, and twelve equal sides.
|
וכל מעוקב לו ששה שטחים שוים ושמנה זויות שוות ושתים עשרה צלעות שוות
|
| It is said that the sides, the angles, the surfaces, and the lines of the cube are in a harmonic proportion.
|
ואמנם מה שנאמר בו כי צלעות המעוקב וזויותיו ושטחיו וצלעותיו ר"ל קוויו ביחס חבוריי
|
- The ratio of the surfaces, which are 6, to the angles, which are 8, is a sesquitertian ratio
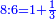
|
וזה שיחס השטחים והם ששה אל הזויות והם שמנה ביחס המוסיף שליש
|
- The ratio of the angles, which are 8, to the sides, which are 12, is a sesquialter ratio
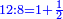
|
ויחס הזויות והם שמנה אל הצלעות והם י"ב ביחס המוסיף חצי
|
- The ratio of the surfaces, which are 6, to the sides, which are 12, is a double ratio
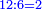
|
הנה יחס השטחים והם ששה אל הצלעות והם שתים עשרה ביחס הכפל השניי
|
| These two ratios, i.e. the superparticular ratio and the multiple ratio, are the species of the simple ratios, as already clarified above.
|
ושני אלו היחסים ר"ל המוסיף חלק והכפל הם מיני היחסים הפשוטים החבורים כמו שכבר התבאר זה לפנים
|
| Hence, the solid number whose dimensions are equal, i.e. the length, breadth and depth, is necessarily the cube number.
|
הנה אם כן המספר הגרמי השוה המרחקים ר"ל האורך והרחב והעומק הוא המעוקב בהכרח
|
The Discussion on the Scalene Numbers
|
הדבור במספרים הגרמיים המתחלפי המרחקים השלשה
|
| Now we should discusses the body that is opposed to the cube, that is, the unequal in all dimensions, i.e. whose length differs from its breadth, and both together differ from its height.
|
וממה שראוי שנדבר עתה הוא בגרם אשר יקביל המעוקב והוא המתחלף המרחקים יחד ר"ל אשר ארכו מתחלף לרחבו והם יחד מתחלפים לגבהו
|
| For example: breadth = 2, length = 2, height = 4; or length = 3, breadth = 4, depth = 5.
|
משל זה שיהיה הרחב ב' והאורך ג' והגובה ד' או יהיה האורך ג' והרחב ד' והעומק ה'
|
| Or other modes of diversity of the excess of some sides over others.
|
או זולת זה מאופני החלוף בתוספת קצת הצלעות על קצת
|
| The rule of this discussion is that none of its dimensions is equal to its other dimension.
|
וכלל המאמר שלא יהיה דבר ממרחקיו שוה למרחק אחר ממנו
|
| This number is called by many names:
|
וזה המספר יקרא בשמות רבים
|
- Some people call it scale, as it extended from its breadth to its length and from its length to its height.
|
מהם שאנשים יקראוהו הסולמיי מפני שיעלה בהוספה מרחבו לארכו ומארכו לגבהו
|
- Other call it wedge, because of the similarity to the wedge that is a body of different surfaces in its three dimensions.
|
ויקראהו אחרים הארחיי להתדמות לאריח שהוא גוף מתחלף השטחים בשלשת מרחקיו
|
| This is an example of their shape and their order according to their natural succession:
|
וזה לך דמיון תמונתם וסדורם כפי המשכם בסדר הטבע
|
- Set a table breadthwise, i.e. the ranks of the breadth of the table are divided into the ranks of the numbers according to their natural succession.
|
תניח לוח הולך ברחב ר"ל רחב הלוח נרשם מחולק במדרגותיו מדרגות המספרים כפי סדרם בטבע
|
- Set beneath it a second table that is one less rank on the side of the beginning of the ranks, placing in each of its ranks the product of the multiplication of what is above it in the first table by the preceding.
|
ונניח תחתיו לוח שני יותר חסר ממנו במדרגה מצד התחלת המדרגות עוד נעמיד בכל מדרגה ממנו מה שיתקבץ מהכאת אשר למעלה ממנו מהלוח הראשון עם אשר לפניו
|
- Set beneath them a third table, same as the second table and as its ranks, placing beneath each rank of the table the product of the multiplication of the rank that above it by the third rank of the first table above it, until the third line is completed by this and all of its ranks are scalene numbers, according to their natural succession, without missing any of them by emptying two of their ranks [?].
|
ותניח גם כן תחתיהם לוח שלישי כמו הלוח השני וכפי מנין מדרגותיו ונעמיד בו תחת כל מדרגה מהלוח מה שיתקבץ ממדרגה אשר עליה ומהכאתה במדרגה השלישית אשר עליה מהלוח הראשון עד שישלם בזה הטור השלישי ויהיו מדרגותיו כלם הם מספרי הגרמים הסולמיים כפי המשכם בטבע מבלתי שיחטא בם באחד מהם בפנוי ב' ממדרגותיהם
|
| Examine it in this diagram written here:
|
ותבחן זה בזאת הצורה אשר רשמנו בכאן
|
The Discussion on the Parallelepipedon Numbers
|
הדבור במספרים הגרמים הזולתיים
|
| Since these two species, i.e. the cube and the scalene numbers correspond to the parallelism of the two extremes, as the cube is equal on its three sides, and the other is unequal on its three sides, the mean between these two are the solid numbers that are called parallelepipedons, i.e. their surfaces are heteromecic.
|
ואחר שהיו שני אלו המינים ר"ל המעוקב והמתחלף הצלעות יוקבלו בהקבלת שני הקצוות אחר שהמעוקב שוה הצלעות השלשה והאחר מתחלף הצלעות השלשה הנה האמצעי בין שני אלו הם המספרים הגרמיים אשר יקראו הזולתיים האורך ר"ל אשר פשוטיהם זולתיי האורך
|
| As will soon be stated, the heteromecic number is the number whose measure is defined in a plane as a quadrangular right-angled shape, whose breadth is shorter than its length by one, such as: 2, 6, 12, 20, 30, 42 and their similar.
|
הנה המספר הזולתי האורך כבר יאמר שהוא המספר אשר ירשם שעורו בפשוט רושם מרובע נצב הזויות ורחבו פחות מארכו אחד כמו ב' ו' י"ב כ' ל' מ"ב והדומה להם
|
| When each of these heteromecic surfaces is given a height that is same as one of its sides - the parallelepipedon numbers are produced.
|
הנה כאשר שמנו לכל אחד מאלו הפשוטים הזולתיי האורך גובה באחד מצלעותיו יתילדו מזה המספרים הגרמיים הזולתיים
|
| This is an example of their positioning:
|
וזה לך דמיון הנחתם
|
- Two lines of them - the first and the second - are of the three previous line in the chapter on the extraction of the scalene numbers.
|
שני טורים מהם הראשון והשני הם משלשת הטורים הקודמים בשער הוצאת המספרים הגרמיים הסולמיים
|
- Multiplying each of the ranks of the second line of them by each of those that are above it in the first line, i.e. the one that results from the multiplication of one by the other.
|
ונכה כל מדרגה ממדרגות הטור השני מהם בכל אחת מאשר עליה בטור הראשון ר"ל אשר עמדה מהכאת אחת מהן באחרת
|
- Placing each of the two products in two different ranks, the smaller of them precedes the greater, and both are beneath the multiplicand rank of the second line.
|
ונעמיד שני הכללים בשתי מדרגות נבדלות הקטנה מהן קודמת לגדולה ושתיהן תחת המדרגה הנעשית בהכאה מהטור השני
|
- When this table is completed in this technique, the ranks set at the third line are twice the ranks of the second line.
|
וכאשר תשלים הלוח בזאת המלאכה הנה כבר שמת מדרגות הטור השלישי כפל מדרגות הטור השני
|
| Thus, all parallelepipedon numbers are reproduced according to their natural succession, none of them is missing.
|
וכבר העמדנו בו כל המספרים הגרמים הזולתיים כפי המשכם בסדר הטבע לא יבצר מהם אחד
|
If some of the sides exceed some of them by more than one, i.e. by two, or three, or four, such as  , ,  , or , or  , or more than that, it is not called heteromecic number but an oblong number. , or more than that, it is not called heteromecic number but an oblong number.
|
ואמנם אם יוסיפו קצת הצלעות על קצת ביותר מאחד ר"ל שנים או שלשה או ארבעה כמו שנים בארבעה וארבעה בששה או חמשה בשבעה או מה שלמעלה מזה לא יקרא מה שהוא כן זולתיי האורך אבל יקרא המוסיף האורך
|
| Know that two of the quadrangular surfaces of the parallelepipedon numbers are parallel and the rest of their surfaces, i.e. the four remaining surfaces of any of the solid numbers among them, each of them is a heteromecic number, its four sides are equal, of one measure, and its eight sides are equal, of one measure differs from the measure of the four by one, additional or deficient.
|
ודע שהמספרים הגרמיים הזולתיים יהיו לעולם שני שטחים משטחיהם מרובעים מקבילים ושאר שטחיהם ר"ל הארבעה שטחים הנשארים בכל מספר גרמיי מהם הנה כל אחד מהם יהיה זולתיי האורך ויהיו ארבעת צלעותיו שוים על שעור אחד ושמנה מצלעותיו שוים על שעור אחד מתחלף לשעור הארבעה באחד אם מוסיף ואם חסר
|
The Discussion on the Natural Root of the Numerical “Sameness” and Numerical “Otherness”
|
הדבור בשורש הטבעיי להוא הוא והזולתיות המספריים
|
| The "same" is the number, whose breadth is in the value of its length
|
אמנם ההוא הוא הנה הוא המספר אשר רחבו הוא ארכו בהגעה
|
| The root of the "sameness", according to the ancients of the pythagoreans, is 1, since when it is multiplied by 1, the length is the breadth, and the product is each of them not extrinsic at all.
|
ואמנם היה שרש ההוא הוא אצל הקדמונים מכת פתאגורוש האחד לפי שהוא כאשר יוכה באחד היה האורך הוא הרחב והמתקבץ הוא כל אחד מהם לא יצא מעצמו כלל
|
| The square numbers are called "same", as they partake this conception, since their length is their breadth.
|
עוד נקראו המספרים המרובעים הוא הויים ללקחם הדמוי מזה לפי שארכם הוא רחבם
|
| The more appropriate among the numbers to be the root of the otherness, is the one which does not differ from the above mentioned true fundamental "same", except by one.
|
והיה היותר ראוי מהמספרים להיות שרש לזולתיי הוא אשר לא ישתנה מההוא הוא האמתי השרשיי הנזכר לפנים אלא באחד
|
| Therefore, the root of the "other" numbers is necessary the second number
|
הנה בראוי אם כן יהיה שרש המספרים הזולתיים הוא המספר השניי
|
| י |
ט |
ח |
ז |
ו |
ה |
ד |
ג |
ב |
א
|
| צ |
עב |
נו |
מב |
ל |
כ |
יב |
ו |
ב |
|
| תתק |
תתי |
תרנב |
תקעו |
תמח |
שצב |
רצד |
רנב |
קף |
קנ |
ק |
פ |
מח |
לו |
יח |
יב |
ד |
ב |
|
| According to this the "same" and the "other" are drawn.
|
הנה כפי זה היו מקישים ההוא הוא והזולת
|
It is already clear from what was precede and explained:
- that the one is particular for the odd numbers, since one is always mean between its two parts.
|
וכבר היה שתבאר ממה שהקדמנו ובארנו שכל נפרד הנה האחד מיוחד לו אחר שבין שני חלקיו האחד לעולם
|
- One of its two parts necessarily exceeds by one.
|
בהכרח הם יעדיף אחד משני חלקיו לאחד
|
- And that the duality is particular for every even numbers, since it is divided into two similar parts.
|
ושכל זוג הנה השניות מיוחד לו אחר שיחלק בשני חלקים דומים נמשלים
|
| It is necessary to say that the odd number, as it is the root of the "same", is particular for the nature of the "same".
|
ובראוי נאמר כי הנפרד מיוחד אחר שזאת שהוא שורש ההוא הוא מיוחד לו לטבע ההוא הוא
|
| And the even number is particular for the "other".
|
והזוג מיוחד לטבע הזולת
|
| Since, from the successive addition of the odd numbers, beginning with the one, the "same" numbers are generated, i.e. the squares, that are equal by the measure of the length and the breadth, as explained a few times.
|
כי בתוספת הנפרדים קצתם על קצת ובהקדים האחד בהנחה ראשונה להם יצמחו מספרי ההוא הוא ר"ל המרובעים השוים במרחק האורך והרחב כמו שבארנו זה פעמים
|
| And from the successive addition of the natural even numbers, beginning with the two, the "other" numbers are produced.
|
ובתוספת הזוגות הטבעיים קצתם על קצת ובהקדים השנים ראשונה להם בהנחה יתילדו הזולתיים
|
- The numbers that are equal by length and breadth are called "the same" numbers, as they partake the conception of the "sameness" of the one.
|
ואמנם קראנו אלו המספרים השוים באורך וברחב מספרי הוא הוא ללקחם דמוי הוא הוא האחד
|
- The numbers that differ in length and breadth by one are called heteromecic, as they partake the conception of the "duality" that is actualized by the nature of the true "sameness" in the one.
|
וקראנו המתחלפים באורך וברחב באחד זולתיים ללקחם דמוי השניות היוצא מטבע ההוא הוא האמיתי באחד
|
| When comparing the terms of the "same" numbers and the terms of the "other" numbers in two lines, each term compared to its corresponding, one finds that the excess of the "other" term over the corresponding "same" rank is the number, from which the name the term is derived.
|
וכאשר תקביל בשני טורים בין מדרגות המספרים ההוא הויים ומדרגות המספרים הזולתיים כל מדרגה במקביליה תמצא מותר המדרגה הזולתיית על הנכחיית לה ההוא הויית הוא המניין אשר ממנו נגזר שם המדרגה
|
|
|
|
The Discussion on the Brick Numbers
|
הדבור על המספרים הלבניים והמגודרים
|
| The numbers that are similar to bricks are of a species of the parallelepipedon numbers, which the measure of their four equal sides is one less than the measure of their eight equal sides.
|
ואמנם המספרים הדומים ללבנים הוא המין מהמספרים הגרמיים הזולתיים אשר יהיה שעור צלעותיו הארבעה השוים פחות אחד משעור צלעותיו השמנה השוים
|
| Those are the terms whose explanation is written in the column of the parallelepipedon numbers.
|
והם המדרגות הנרשם עליהם באורם בטור המספרים הגרמיים והזולתיים
|
| These are those whose length and breadth are equal and the height is one less than each of them.
|
והם אשר ארכם ורחבם שוה ויחסר הגובה מכל אחד מהם אחד
|
| If its height exceeds the length and breadth that are equal by the excess of the "other", i.e. by one, or by the excess of the oblong number, i.e. by more than one, such numbers, whose one of the three dimensions exceeds the others, are called beam solids.
|
ואמנם אם יוסיף בגובה על האורך והרחב השוים תוספת הזולתיי ר"ל אחד או תוספת המוסיף באורך ר"ל יותר מאחד היו מה שהיה המספר הנוסף באחד מהמרחקים השלשה הנה כל אלו יקראו מוגשמים אריחיים
|
Such as:
|
כמו ג' בג' בד'
|
|
או ה' בה' בו'
|
| Or as much as one wishes, as long as the height is longer than both the length and the breadth.
|
או כמה שתרצה אחר שיהיה הגובה יותר ארוך מכל אחד מהאורך והרחב
|
The Discussion on the Circular and Spherical Numbers
|
הדבור במספרים הסבוביים והכדוריים
|
| After describing the quality of the solids whose surfaces are of straight lines:
|
ואחר שכבר הבאנו תאר הגרמים בעלי השטחים הישרי הקוים
|
| We say, as we said that the cube number is of equal dimensions, i.e. the length, the breadth, and the depth, it is divided into two parts:
|
הנה נאמר כמו שאמרנו שהמספר המעוקב הוא השוה המרחקים ר"ל האורך והרחב והעומק וזה יחלק לשני חלקים
|
- The number that is the root of each of its surfaces, mentioned in the total surface, then mentioned in the total body recurrently, then mentioned also in the total body when multiplied by it once, or twice, or more.
|
אם שיהיה המספר אשר הוא שרש כל אחד משטחיו נזכר בכלל השטח עוד נזכר בכלל הגרם חוזר על עצמו עוד נזכר גם כן בכלל הגרם כאשר הוכה בו פעם או שני פעמים או יותר מזה
|
|
|
ואם שלא יהיה כן
|
| Those, whose roots are mentioned in their total in the pronunciation, their realization in these cube numbers, that are called spherical numbers.
|
הנה אשר שרשיהם נזכרים בכללם במבטא הגעתם מאלו המספרים המעוקבים הם אשר יקראו המספרים הכדוריים
|
| Since they revolve, reversible as a sphere, to the number from which their beginning is.
|
אחר שיסבבו מתהפכים כמו הכדור אל המספר אשר ממנו התחלתם
|
| Such as the cube number, whose side is 5 or 6, for as much as one multiplies one of them by the same, and the product by its root, it will be found as described.
|
כמו המספר המעוקב אשר הצלע מצלעותיו חמשה או ששה כי כל מה שתכה אחד משני אלו בכמהו עוד מה שיתקבץ בשרשו יהיה נמצא כמו שתארנו
|
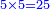 the five returns, expressed in the total. the five returns, expressed in the total.
|
וזה שאנו אם נכה חמשה בחמשה היה המתקבץ כ"ה וישוב החמשה מבוטא בו בכלל וישוב אליו
|
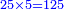 the five is again expressed in the total. the five is again expressed in the total.
|
עוד נכה החמשה גם כן בכ"ה ותמצא החמשה גם כן מבוטא בו בכללם והוא קכ"ה
|
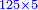
|
וכן אם תכה הקכ"ה בחמשה
|
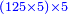
|
ומה שהתקבץ גם כן בחמשה
|
- It will be found always with this quality.
|
תמצאהו בזה התאר לעולם
|
- So also the six in this matter, its rule is the rule of the five.
|
וכן גם כן הששה בזה הענין משפטם משפט החמשה
|
- It is also found in the one, since one by the same is the same
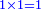
|
וכן תמצא זה באחד כי האחד בכמהו
|
- then by the same, and again by the same, always not extrinsic, but cyclic.
|
עוד בכמוהו עוד בכמהו עוד כן תמיד בלתי יוצא מעצמו אבל סובב על עצמו
|
| Since what was described is already clear, it is said that the circular number is by multiplying the number once by itself:
|
ואחר שכבר התבאר מה שתארנו נאמר שהמספר הסבוביי מזה שתכה המספר פעם אחת בעצמו
|
|
כמו א' בא'
|
|
וה' בה'
|
|
וו' בו'
|
| If it is multiplied more than once, it is a spherical number.
|
ואם הוכה יותר מפעם הנה הוא מספר כדורי
|
| Since the circles are surfaces, and the spheres are bodies.
|
אחר שהעגולים פשוטים והכדורים גרמיים
|
| This is the end of the discussion concerning the solid numbers.
|
וזה סוף המאמר על המספרים הגרמיים
|
The Discussion on the Indications of the Ancients that the Beginning of Numbers is similar to the Beginning of the Universe
|
הדבור ברמזי הראשונים על ההתחלות המספריות הדומות להתחלות העולם
|
|
|
וכבר ימשך למה שאמרנו לפנים על המספרים הזולתיים ההפרש בם מהמספרים המוסיפים באורך שאנו כבר בארנו כי הזולתיים הוא אשר אחד ממרחקיו השנים יותר מהאחד באחד
|
|
|
ואמנם המוסיף הוא מה שהיתה צמיחתו כפי זה הצד אלא שתוספת אחד ממרחקיו על האחר יותר מאחד
|
|
|
כמו ח' המתקבץ מהכאת ב' בד'
|
|
|
וכמו י"ח אשר יתקבץ מהכאת ג' בו'
|
|
|
והדומה לזה ממה שהחלוף בו בין שני המספרים אשר יוכה אחד מהם באחר ביותר מאחד
|
| He [= Nicomachus] said:
|
אמר ולחלוף אלו המספרים ר"ל ההוא הויים ר"ל השרשיים והזולתיים ר"ל אשר יוסיף ארכם על רחבם יותר מאחד חודשה ההפרדה וההחלק והסתעפות מה שבמספר מהמינים
|
| He [= Nicomachus] said: it is appropriate that the ancients began the principles of number by starting the discussion about the nature of the world.
|
אמר ובראוי מה שהתחילו הקדמונים הראשיות במספר בהתחילם המאמר על טבע העולם
|
| Plato mentioned that the nature of the world is of three ends:
|
אם אפלאטון הנה זכר שטבע העולם משלשה גבולים
|
- 1) the same
|
אחד מהם ההוא הוא
|
- 2) the other
|
והשני הזולת
|
- 3) the substance that is indivisible
|
והשלישי מהעצם אשר אינו מתחלק
|
|
|
וזה המאמר יישירך השם רחוק העול מאד דק הענין
|
|
|
ואפלאטון ירמז בו אל ראשיות העולם
|
|
|
וזה דבר חוץ ממלאכת המספר
|
|
|
ולולא שאני הסכמתי שלא אערב דבר בחכמת זה הספר עבדתי זה השער
|
|
|
ולולא שאני בטוח שלא ידומה עלי לאדיבות לבלתי תועלת וגם בטחוני במדרגתך היום מהעיון לא זכרתי לך שתחת זה המאמר רמז ולא שהוא רחוק העול ודק הענין
|
| The author of this book [= Nicomachus] said: Philolaus says that all the things that exist are necessarily either limited, or limitless, or limited and limitless together.
|
אמר מניח הספר אמנם פילולאוש יאמר שכל הדברים אשר הם נמצאים הנה הם בהכרח אם מוגבלים נכללים ואם בלתי מוגבלים ואם מוגבלים ובלתי מוגבלים יחד
|
| It is said: and this third saying is about the manner of the number and its image.
|
אמר וזה המאמר השלישי אמנם הוא מאופן המספר ודמיונו
|
| For the number is composed of the units, and its species are even and odd, which indicate the equality and inequality, the "sameness" and "otherness", the bound and boundless, the defined and undefined
|
כי המספר מורכב מהאחדים ומיניו זוג נפרד והם מורים על השווי והחלוף וההוא הויים והזולתיים וההקפה ובלתי הקפה וההגדרה ובלתי הגדרה
|
|
|
ויהיה מה שנאמר מבואר יאמר שהדברים אשר הם נמצאים התילדו ועמדו מהמתנגדים המתחלפים הדומים ובראוי מה שהראו החבור וההסכמה כי החבור אמנם יהיה בלי ספק כמו שבארנו בפתיחת המאמ' הראשון מזה הספר מהדברים המתחלפים הדומים הנמצאים כי החבור אמנם הוא ערוב דברים מתחלפי הגדרים דומי הסוגים
|
| Abū Yusūf said:
|
אמר אבו יוסף אמנם אמר זה המאמר והוא ימשיל המוגבל מהדברים במספרים הנגדרים שהם מוגבלים אחר שידובר בגדרם ר"ל שרשם שאחד שימנה בעצמו יחודש ויראו
|
|
|
וימשיל הבלתי מוגבלים מהדברים הזולתיים שהם אלמים לא ידובר בשרש דבר מהם
|
|
|
ורצה במוגבל ובלתי מוגבל יחד המוסיף האורך כי ממנו שרשי וממנו בלתי שרשיי הנה השרשיי מוגבל ובלתי שרשיי בלתי מוגבל
|
Properties of the Types of Numbers and their Mutual Harmony
|
הדבור בקצת סגולות מיני המספרים ומה שיראה בהתילדם והקבלת קצתם לקצת
|
| We have already brought in the propositions what we wanted to preface.
|
כבר הבאנו בהקדמות מה שרצינו להקדימו
|
| Now, it will be shown how many of those described in the description of the "same" and "other" numbers are produced:
|
ונראה איך יתילדו הרבה ממה שתארנו מתואר המספרים ההוא הויים והזולתיים
|
- Arranging the square numbers that were produced by summing the natural odd numbers successively, i.e. the rootable in a line.
|
וזה בשנסדר המספרים המרובעים אשר נולדו בהוספת הנפרדים הטבעיים קצתם על קצת ר"ל הנגדרים בטור
|
- Arranging the heteromecic numbers, i.e. those that were produced by summing the even numbers, successively in a second line.
|
עוד נסדר הזולתיי האורך ר"ל אשר התילדו מתוספת הזוגות המתילדים קצתם על קצת בטור שני
|
| For this way of action is truly seen visible in the nature of all.
|
כי זה האופן מן הפועל באמת כבר נראהו גלוי בטבע הכל
|
| The line according to this example is:
|
ויהיה הטור כפי זה המשל
|
| קמד |
קכה |
ק |
פא |
סד |
מט |
לו |
כה |
יו |
ט |
ד |
א
|
| קנו |
קלב |
קי |
צ |
עב |
נו |
מב |
ל |
כ |
יב |
ו |
ב
|
| It is clear from the wonders of the nature's action that the first of the "others" is in the double ratio to the first of the "same"; the second to the second are in the sesquialter ratio; the third to the third are in the sesquitertian ratio; the fourth to the fourth are in the sesquiquartian ratio; and so on, one finds them together according to this description.
|
והוא מבואר מפליאות פועל הטבע שהראשון מהזולתיים ביחס הכפל השניי אצל הראשון מן ההוא הויים וכשני אל השני ביחס המוסיף חצי והשלישי אל השלישי ביחס המוסיף שלישי וכן הרביעי אל הרביעי ביחס המוסיף רביע וכן תמצאם תמיד יחד בכמו זה התאר
|
| What was said afore is also clarified in these two lines, that if the excess of each term of the "others" over its corresponding term of the "same" is taken and set in a third line successively, the terms are found to be the numbers by the natural succession.
|
והתבאר גם כן בשני אלו הטורים מה שכבר אמרנו במה שקדם שאנו אם לקחנו תוספת כל מדרגה מהזולתיים על נכחה מהמדרגות ההוא הויים והנחנוהו בטור שלישי כפי המשכיה מצאנו מדרגות זה הם המספרים על סדר הטבע
|
This is found also by:
- Taking the terms of the "same", beginning with four.
|
וכן תמצאהו כאשר תתחיל במדרגות ההוא הויים ותשים ראש מדרגותיהם ארבעה
|
- Adding the excess of each term of them over its corresponding among the terms of the "others".
|
עוד תוסיף תוספת כל מדרגה מהם על נכחה ממדרגות הזולתיי
|
- Arranging them in a third line successively - they are found in the succession of the natural numbers.
|
עוד תסדרם בטור שלישי כפי המשכיהם תמצא זה בסדר המספרים הטבעיים
|
- The excess of 4 over 2 is 2.

|
כי תוספת ד' על ב' ב'
|
- The excess of 9 over 6 is 3.

|
ותוספת ט' על ו' ג'
|
- And so on, one finds it always according to this description.
|
וכן תמצאהו תמיד בזה התאר
|
| If one relates between them, when they are according to this position - when wishing to relate them, they are found in the same ratios, by which they are seen at first:
|
ואמנם אם תקיש ביניהם והם כפי זאת ההנחה ותרצה ליחסם תמצאם באותם היחסים אשר נראו בראשונה בעצמם
|
- 4 to 2 is in double ratio.

|
וזה שד' אצל ב' בייחסם הכפל השניי
|
- 9 to 6 is in sesquialter ratio.
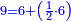
|
וט' אצל ו' ביחס המוסיף חצי
|
- 16 to 12 is in sesquitertian ratio.
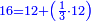
|
וי"ו אצל י"ב ביחס המוסיף שליש
|
- Likewise it is found always according to the first property.
|
וכמו זה תמצאהו תמיד על צד הענין הראשון
|
| It is clear that the additions of the "same" to each other are the natural odds
|
ואמנם תוספת מדרגות ההוא הויים קצתם על קצת הוא מבואר שהם הנפרדים הטבעים
|
| ?
|
והנפרדים הטבעיים והזוגות הטבעיים ויחס הכפל ויחס המוסיף חלק
|
- Setting the first of the "others" as mean between the first two of the squares, i.e. two between one and four.
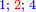
|
ואמנם אם תניח הראשון מהזולתיים אמצעי בין שני הראשונים מן המרובעים ר"ל שנים בין אחד וארבעה
|
- Setting the second of the "others" as mean between the consecutive of the squares, i.e. six between four and nine.
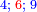
|
ותניח השני מן הזולתיים אמצעי בין אשר אחריהם מן המרובעים ר"ל ו' בין ד' וט'
|
- [Setting] the third "other" between two others of the squares, following those that were set.
|
וכן השלישי הזולתיי בין שני המרובעים אחרים אחר אשר הנחת
|
- Proceeding likewise for each term of the "others" successively.
|
וכן תעשה כל מדרגה ממדרגות הזולתיי כפי המשכם
|
- One finds that it is in the ratio of the terms of the even-times-even numbers
|
תמצא זה ביחס מדרגות זוג הזוג
|
- The measure of the first to the second is as the measure of the second to the third
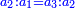
|
שעור הראשון אצל השני כשעור השני אצל השלישי
|
- Every three numbers of them, i.e. of those whose mean between every two terms of the "same" among them is a term of the "others", according to the explained order, are found in this ratio, i.e. the measure of the first to the second is as the measure of the second to the third
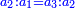 ; and vice versa, the third to the second is as the second to the first ; and vice versa, the third to the second is as the second to the first 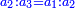 . .
|
וכן תמצא כל שלשה מספרים מהם ר"ל מאלו אשר הממצע בין כל שתי מדרגות מההוא הויים מהם מדרגה מהזולתיים כפי סדרם אשר בארנו בזה היחס ר"ל ששעור הראשון מן השני כשעור השני מן השלישי ובהפך גם כן השלישי אצל השני כשני אצל הראשון
|
- It is clear that when these terms are in this order, the excesses of their terms one over the other are unequal.
|
ומבואר שאלו המדרגות כאשר היו כפי זה הסדר לא יהיה תוספת ממדרגותיהם קצתם על קצת שוים
|
- This is their diagram:
|
וזה צורתו
|
| פא |
עב |
סד |
נו |
מט |
מב |
לו |
ל |
כה |
כ |
יו |
יב |
ט |
ו |
ד |
ב |
א
|
| The property of terms of the even-times-odd numbers, is that when they are arranged successively in a special line, they are in the succession of the natural numbers.
|
ואמנם זוג הנפרד הנה סגולת מדרגותיו בסדורם כפי המשכם בטור מיוחד סדור המספרים הטבעיים
|
| That is, the excesses of the terms of the even-times-odd numbers one over the other are equal:
|
וזה שזוג הנפרד הגעות תוספת מדרגותיו קצתם על קצת שוים
|
- The excess of 10 over 6 is as the excess of 14 over 10.
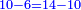
|
כי תוספת י' על ו' כמו תוספת י"ד על י'
|
- The excess of 2 over 1 is as the excess of 3 over 2.

|
וכן תוספת ב' על א' כמו תוספת ג' על ב'
|
- From these two is is understood that double the mean is as the sum of the two extremes
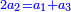 , and this and its similar were already explained in the first section. , and this and its similar were already explained in the first section.
|
וישיג שני אלו יחד שיהיה האמצעי נכפל כמו שני הקצוות מקובצים וכבר בארנו זה ודומה לו במאמר הראשון
|
| The triangular numbers are generated from the combination of the "same" and the "others", each term with its corresponding, successively.
|
ונאמר שהמספרים המשולשים אמנם יתחדשו מהרכבת ההוא הויים והזולתיים כל מדרגה עם נכחה על משך מדרגותיהם
|
- The first term of the "same", which is one, when it is set up with the first term of the "others", which is two, the first actual triangle is generated, which is three.

|
כי המדרגה הראשונה מההוא הויים והוא האחד כאשר הורכבה עם המדרגה הראשונה מהזולתיים והוא ב' יחודש המשולש הראשון בפעל והוא ג'
|
- When the first term of the "others", which is two, is set up with the second term of the "same", which is four, the second actual triangle is generated, which is six.
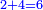
|
וכאשר תרכיב המדרגה הראשונה מהזולתיים והיא ב' עם המדרגה השנית מהוא הויים והוא ד' יחודש המשולש השני בפעל והוא ו'
|
- So the combination of these terms is found always according to this description.
|
וכן תמצא הרכבת אלו המדרגות בזה התאר תמיד
|
| It is visible from what was described and explained before, that when one of the dimensions of the square becomes different from the other by one, whether by addition to it or by subtraction from it, it becomes an "other".
|
ויראה ממה שתארנו ובארנו קודם שהמרובע כאשר יתחלף באחד משני מרחקיו לאחד באחד אם בתוספת עליו ואם בחסרון ממנו יצא אל הזולתיי
|
|
|
הנה אם כן מדרגת המרובע השוה לזולתיי כמדרגת השוה להקשות החמש אשר הקדמנו זכרם אחר שאחד משני המספרים נוסף על האחר והאחד חוסר ממנו והשווי פינה להם
|
| It was also said that the true "same" is the one, and the true "other" is the duality.
|
וכבר אמרנו גם כן שההוא הוא האמתי הוא האחד והזולתיי האמתי הוא השניות
|
| In addition, the odd is similar to the "same" and the even to the "other", therefore, the regular square is similar to the "same", since it consists of the odds, and the [heteromecic number], whose two dimensions differ by one, is similar to the "other", since it consists of the evens.
|
עוד אחר זה כבר ידמה הנפרד להוא הוא והזוג לזולת ולזה בעצמו כבר ידמה המרובע השוה ההוא הוא אחר שהוא מורכב מהנפרדים וידמה המתחלף שני המרחקים באחד הזולתיי אחר שהוא מורכב מהזוגות
|
| Returning to what was mentioned about the evident from these two species, i.e. the "same" and the "other", when they are arranged successively as aforementioned, which is the succession of the two species together in one line, so that their terms are such that each term of one of the two species is between two terms of the other species successively.
|
אמנם עתה נשוב אל מה שזכרנוהו ממה שיראה משני אלו המינים ר"ל ההוא והזולתיי כאשר יסודר כפי הסדר אשר זכרנוהו לפנים והוא סדר שני המינים יחד בטור אחד בסדר שיהיו מדרגותיהם כן כל מדרגה מאחד משני המינים בין שתי מדרגות מהמין האחד על המשך
|
- Such as: 1; 2; 4; 6; 9; and so on.
|
כמו א' ב' ד' ו' ט' וכן תמיד
|
| One finds that every three terms of this line, when it is arranged by this order, when they are equal in ratio, they differ in their additions to each other; and when they are equal in their additions to each other, they differ in their ratio.
|
הנה זה הטור כאשר יסודר זה הסדר תמצא כל שלשה מדרגות מהם כאשר השתוו ביחס יתחלפו בהגעות תוספותיהם קצתם על קצת וכאשר ישתוו בהגעות תוספות קצתם על קצת יתחלפו ביחס
|
- 1; 2; 4 - are in the double ratio [
 ], but the excess of 4 over 2 is two [ ], but the excess of 4 over 2 is two [ ], and the excess of 2 over 1 is 1 [ ], and the excess of 2 over 1 is 1 [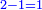 ] - the ratio is one and the same, while the additions are different. ] - the ratio is one and the same, while the additions are different.
|
כי א' ב' ד' ביחס הכפל השניי אבל תוספת ד' על ב' ב' ותוספת ב' על א' א' הנה היחס אחד והתוספות מתחלפות
|
- 2; 4; 6 - the excess of 6 over 4 is the same as the excess of 4 over 2 [
 ], but the ratio differs, as the ratio of 6 to 4 is not the ratio of 4 to 2 [ ], but the ratio differs, as the ratio of 6 to 4 is not the ratio of 4 to 2 [ ]. ].
|
אמנם שלשה המדרגות אשר הן ב' ד' ו' תוספת ו' על ד' כמו תוספת ד' על ב' אלא שהיחס יתחלף לפי שיחס ו' אל ד' בלתי יחס ד' אל ב'
|
- 4; 6; 9 - are in one ratio, but their additions are unequal.
|
וכן גם כן שלשת המדרגות אשר הן ד' ו' ט' שהן ביחס אחד ואין התוספות שוות
|
- 6; 9; 12 - their additions [are equal], but they differ in their ratio.
|
וכן גם כן שלשת מדרגות ו' ט' י"ב בהגעות התוספות מתחלפות ביחס
|
- Likewise, every three terms of this line which is compounded from the "same" and the "others", are found according to the combination described in this description above.
|
וכן תמצא כל שלשה מדרגות מזה הטור המורכב מן ההוא הויים והזולתיים כפי ההרכבה אשר תארנו לפנים בזה התאר
|
| It is clarified from what was mentioned, that when the "other" and the "same" are such that the two dimensions of the "other" differ by that the length exceeds the breadth by one, for every three terms of this line that are matching in ratio, but differ in the excesses, the difference of the excesses is also one.
|
ויתבאר ממה שזכרנו שכאשר היה הזולתיי וההוא הוא אלו ששני מרחקי הזולתיי יתחלפו בתוספת אחד באורך על הרחב שיהיו כל שלשה מדרגות מזה הטור שיסכימו ביחס ויתחלפו בהגעת התוספת שיהיה חלוף התוספות גם כן באחד
|
- For, 2, which is the difference between 4 and 2 exceeds the one, which is the difference between 1 and 2, by one [
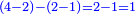 ], and so on. ], and so on.
|
כי ב' אשר הוא המותר בין ד' וב' יוסיף על האחד אשר הוא המותר אשר הוא בין א' וב' אחד וכן תמיד
|
|
|
ונאמר עוד שממה שיחזק עם מה שזכרנוהו קודם כי הנפרדים יותר חזקי ההאמתה בטבע ההוא ר"ל הנגדרים מה שאנחנו זוכרים אותו
|
- Arranging the numbers that begin with the one, and proceeding by the double ratio, such as: 1; 2; 4; 8; 16; 32; 64.
|
וזה שאנו נסדר המספרים אשר התחלתם מהאחד והמשכם ביחס הכפל השניי בטור כמו א' ב' ד' ח' י"ו ל"ב ס"ד
|
- Arranging also the numbers that begin with the one, and proceeding by the triple ratio, such as: 1; 3; 9; 27; 81; 243.
|
ונסדר גם כן המספרים אשר התחלתם מהאחד והמשכם על יחס הכפל השלישיי כמו א' ג' ט' כ"ז פ"א רמ"ג
|
| One finds that the odd terms in each of the two lines are of the "same", i.e. necessarily rooted, i.e. the terms that are in places of an odd number of terms, their values are rooted; those that are in places of an even number of terms, their values are not rooted.
|
ונמצא מדרגות הנפרדים מכל אחד משני הטורים מספרים הוא הויים ר"ל שרשיים בהכרח ר"ל שהמדרגות אשר תהיינה במקום נפרד ממנין המדרגות הגעותיהם נגדרות ואשר הם במקום זוג ממנין המדרגות הגעותיהם בלתי נגדרות
|
| It is further said that the solid cube numbers, since they are also similar to the "same", as their dimensions are equal, they are also produced from the odd numbers.
|
ונאמר עוד שהמספרים הגרמיים המעוקבים אחר שהם גם כן דומים להוא הויים לפי שמרחקיהם שוים הנה הם יתילדו מהנפרדים גם כן
|
| This is found by the natural wonderful technique that is easy to execute:
|
וימצא זה בזאת התחבולה הנפלאה בטבע הנקלה במעשה
|
- Arranging the natural odds in a line.
|
וזה שאנו נסדר הנפרדים הטבעיים בטור
|
- The first potential cube, which is one, is the first potential odd
|
וימצא המעוקב הראשון בכח אשר הוא האחד הוא הנפרד הראשון בכח אשר הוא א'
|
- The second potential cube, which is eight, is from the combination of the two terms of the odds following the one, which are 3 and 5
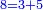 . .
|
והמעוקב השני בכח הוא ח' מהרכבת שתי מדרגות ימשכו לאחד מהנפרדים והם ג' וה'
|
- The third cube, which is 27, is from the combination of the three terms of the odds following the the two terms, from which the second cube is compounded, and they are 7, 9, 11, for their sum is 27.
 . .
|
והמעוקב השלישי אשר הוא כ"ז מהרכבת שלשה מדרגות ממדרגות הנפרדים ילוו לשתי המדרגות אשר הורכב מהם המעוקב השני והם ז' ט' י"א כי כל זה כ"ז
|
| So, one always finds, whenever skipping to a cube, that its combination is from odd terms, whose number are the same as the number of its place among the terms of the cubes, i.e. that the second cube consists of two odds, the third consists of three odds, and so on for what follows.
|
וכן תמצא זה תמיד כל מה שתדלג אל מעוקב תמצא כי הרכבתו ממדרגות נפרדים מנינם כמו מקומו ממנין מדרגות המעוקבים ר"ל כי המעוקב השני מהרכבת שני נפרדים והשלישי מהרכבת שלשה נפרדים וכן מה שאחר זה
|
| Yet, for every cube, the first of the odds, from which it is compounded, is following the end of the terms, from which its preceding cube is compounded, and the terms are taken successively by the order of the natural odd numbers.
|
אלא שכל מעוקב הנה ראש הנפרדים אשר מהם יורכב אחר סוף מדרגה מהמדרגות אשר הורכב מהם המעוקב אשר לפניו עוד המדרגות לקוחות על משך סדר הנפרדים הטבעיים
|
| This is the rule of the discussion about it, and its diagram is as it is seen:
|
הנה זה כלל המאמר על זה וצורתו כמו שתראה
|
| מא |
לט |
לז |
לה |
לג |
לא |
כט |
כז |
כה |
כג |
כא |
יט |
יז |
טו |
יג |
יא |
ט |
ז |
ה |
ג |
א
|
| המעוקב הששי |
המעוקב החמישי |
המעוקב הרביעי |
המעוקב השלישי |
המעוקב השני |
המעוקב הראשון
|
| ריו |
קכה |
סד |
כז |
ח |
א
|
[Relative Quantity]
|
|
The Discussion on The Ten Proportions
|
הדבור על האמצעיים העשרה
|
| It is what the author of this book in Arabic calls al-ʽIyād.
|
וזה אשר יקרא אותו בעל זה הספר בערבי אלעיאד
|
| Its meaning: a limitation of two ratios or more between two given terms,
|
ומשמעותו הגבלת שני יחסים או יותר מזה בין גבולים מונחים
|
- either by themselves, i.e. that the limitation is actualized from the terms themselves to each other.
|
אם מעצמם ר"ל שתהיה ההגבלה מוצאת מעצמי הגבולים עצמם קצת אל קצת
|
- or by the excess of one over the other
|
ואם מיתרון קצתם על קצת
|
- or by both properties together.
|
ואם משני העניינים יחד
|
| The ratio is an existence of two given defined terms one to the other.
|
והיחס הוא ישות שני גבולים מוגבלים מונחים אחד מהם אצל האחר
|
| The least proportion is in three terms.
|
ובפחות מה שיהיה ההתיחסות בשלשה גבולים
|
- Such as: 4; 2; 1
|
כמו ד' וב' וא'
|
- For, the measure of 4 to 2 is as the measure of 2 to 1

|
כי שעור ד' אצל ב' כשעור ב' אצל א'
|
- Also vice versa, the limitation that is called al-ʽIyād, which is between 1 and 2 to 4, their ratio is one [
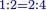 ] ]
|
וכמו כן בהפך הנה ההגבלה הנקראת אלאיעד אשר בין א' וב' אצל ד' הוא יחסם אחד
|
| This al-ʽIyād is essentially the given number itself.?
|
וזה אלאיעד הוא בעצם המספר המונח עצמו
|
| The numbers in this ratio can always be added by units, as explained before, more than once, in this book, so that the numbers will be four, or five, or six, or more, as one wishes.
|
וזה היחס כבר אפשר שיתוספו מספריו תמיד באחדות כאשר קדם פירושינו לו יותר מפעם בספרנו זה כמו שיהיו המספרים כאשר היו ארבעה או חמשה או ששה או יותר מזה כפי מה שתרצה
|
- Such as setting 1; 2; 4; 8; 16; 32; 64 - since all of them are in the ratio mentioned at first between the three terms.
|
כמו שתניח א' ב' ד' ח' י"ו ל"ב ס"ד כי אלו כלם ביחס הנזכר בין שלשת הגבולים תחלה
|
| The proportion that is subject to addition:
|
ואמנם ההתיחס אשר יפול ביתרון
|
- Such as: 1; 2; 3
|
כמו א' ב' ג'
|
- For the measure of 1 to 2 is not as the measure of 2 to 3 [
 ]. ].
|
כי אין שעור האחד מב' כשעור ב' מג'
|
- Yet, the measure of the excess of 3 over 2 is the measure of the excess of 2 over 1 [
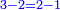 ]; and vice versa. ]; and vice versa.
|
אבל שעור תוספת ג' על ב' הוא השעור אשר בו יוסיף ב' על האחד וכן הוא גם כן בהפך
|
| It is al-ʽIyād even if the given numbers are numerous:
|
וזה אלאיעד גם כן אם ירבו המספרים המונחים
|
- The measures of the excesses are found in diversity also according to this example: 2; 3; 4; 5 [
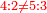 ]. ].
|
הנה כפי זה המשל ימצאו שעורי התוספות בחלוף כפי זה המשל גם כן כמו ב' וג' וד' וה'
|
- Yet, the excess of 5 over 3 is as the excess of 4 over 2 [
 ]; and vice versa. ]; and vice versa.
|
כי תוספת ה' על ג' כמו תוספת ד' על ב' וכן ימצא גם כן בהפך
|
| It is said that the proportions that are acknowledged by all the ancients - Pythagoras, Plato and others - are three:
|
ונאמר שהאמצעיים אשר יודו בם כל הקדמונים ר"ל פיתאגורש ואפלאטון וזולתם הם שלשה
|
- 1) for arithmetic
|
האחד מהם לחשבון
|
- 2) for geometry
|
והשני למדות
|
- 3) for music
|
והשלישי לחבור הנגונים
|
- The geometric and the harmonic proportions have three subcontrary proportions:
|
ולאמצעי המדות והחבור מקבילים אחרים שלשה
|
- The harmonic proportion has one contrary
|
לחבור הקבלה אחת
|
- The geometric proportion has two contraries
|
ולמדות שתי הקבלות
|
- These do not have names, they are called by their numbers: fourth, fifth, sixth.
|
אלא שהם אינם בעלות שמות כמו אלו ונקראו מהמספר ונקראו רביעית וחמישית וששית
|
| four other proportions were added to these six proportions constituting the ten proportions, as the perfect ten of Pytagoras
|
וכבר אמרו אחר זה המאמר הקדום שהאמצעיים עשרה והוסיפו על אלו הששה ארבעה אחרים להשלים האמצעיים העשרה להיות לעשרה שלמות אצל פיתאגורש
|
|
|
ונדבר בתאר אלו האמצעיים
|
The Arithmetic Proportion
|
וניחד המאמר תחלה במצוע המספריי
|
| The discussion about the priority of the number in the four sciences is already completed.
|
ונאמר הנה כבר נשלם מאמרנו בהיות המספר ראוי בקדימה באומניות הארבעה
|
| The numbers given in the arithmetic proportion are according to the natural succession, or similarly to the natural succession.
|
ועם זה הנה המספרים המונחים לאמצעי החשבון הם כפי סדר הטבע או מה שהיה דומה לסדר הטבע
|
| Hence, it is necessary to precede this proportion to the other proportions, since it is antecedent to the other antecedent proportions, all the more to their opposites.
|
הנה אם כן יחוייב בהכרח שנקדים זה האמצעי על שאר האמצעיים שאחר שהיה קודם על שאר האמצעיים הקודמים הנה יותר ראוי מזה שיקדם על המקבילים להם
|
- The arithmetic proportion is when three numbers or more are given, set according to the natural addition successively.
|
הנה האמצעי המספריי יהיה כאשר תניח שלשה מספרים או יותר מזה והונחו כפי חבור הטבע ימשכו קצתם לקצת
|
- Such as: 1; 2; 3; 4; 5
|
כמו א' ב' ג' ד' ה'
|
- For, excess of each of these numbers over its preceding number is one.
|
כי אלו המספרים בהכרח תוספת כל אחד מהם על מה שלפניו אחד
|
| If one wishes to arrange them according to this ratio, which is equality of the difference:
|
ואם תרצה לסדרם בזה היחס אשר הוא שווי היתרון
|
- Setting the natural numbers in a line.
|
אתה תסדר המספרים הטבעיים בטור
|
- Starting with the number that is wished to be set as the first term, then examining how much there are between it and the number that is wished to be set as the mean term according to the natural succession, so that the terms between the mean and the third term will succeed by the same number, and also between the third and the fourth, or whichever terms that are set in this ratio.
|
עוד תתחיל במספר אשר תרצה לשומו בגבול הראשון ותעיין כמה בינו ובין המספר אשר תרצה לשומו אמצעי מהמדרגות אשר על סדר הטבע וימשכו כמו אותו המנין מהמדרגות בין האמצעי והגבול השלישי וכן בין השלישי והרביעי או במה שתניח מהמדרגות בזה היחס
|
- Such as: setting the first term as 2 and the second term as 4.
|
כמו שתניח הגבול הראשון ב' והגבול השני ד'
|
- No doubt that the third term will be set as similar to the interval from 4 to 2, which is the interval from 6 to 4, i.e. the two terms interval.
|
ואין ספק שתניח הגבול השלישי על דמיון מרחק ד' מב' והוא מרחק ו' מד' ר"ל על מרחק שתי מדרגות
|
- Also, when setting a fourth term, it is the one that is far from 6 by two terms, which is 8.
|
וכן אם תניח גבול רביעי היה הוא אשר ירחק מו' בשתי מדרגות והוא ח'
|
| According to this way the terms are set, when wishing to increase them, their addition is always by adding one.
|
וכפי זה הדרך תניח הגבולים כאשר תרצה להרבותם הנה תהיה הוספתם לעולם בתוספת אחד
|
- The property of this proportion, i.e. the arithmetic proportion, that is necessary for it and not the other: its mean term, when it is doubled, if the given terms have one mean, it equals the sum of the two extremes,
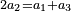
|
ובפרט זה האמצעי ר"ל אמצעי החשבון המתחייב לאלו בלתי זולתם שהגבול האמצעי מהם כשיכפל על ב' אם היו המדרגות המונחות להם אמצעי אחד ישוה שני הקצוות כאשר יקובצו
|
- and if the terms have two mean terms, the sum of the two means equals the sum of the two extremes:
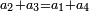
|
אם היו המדרגות בעלות שני אמצעיים הנה קבוץ שני האמצעים כמו קבוץ שני הקצוות
|
- This proportion has a second property: the ratio of each term to itself is equal to the ratio of the differences of the terms to each other.
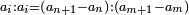
|
ולהם סגולה שנית גם כן והיא שיחס כל אחד אל עצמו כמו יחס מותרי הגבולים אלו על אלו קצתם על קצת
|
- Also a third property, which is more difficult and hidden from the understanding of many: the product of the two extremes one by the other compared to the product of the mean [by itself] is smaller by the product of the differences of the terms by each other, whether the terms are odd in number, or whichever number they are, so that when they are summed they are more than the two extremes together.
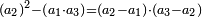
|
עוד סגולה שלישית והיא היותר קשה ונעלמת מדעת רבים והיא כי כפילת שתי הקצוות האחד על האחר כאשר נערכהו אל כפילת האמצעי הוא יותר פחות בערך כפילת מותרי הגבולים אלו על אלו בין שיהיו הגבולים נפרדים במספרם ובין שיהיו איזה מספר שיהיה כאשר יקובצו היו יותר משני הקצוות יחד
|
- This proportion has a fourth property, mentioned by the ancients: the ratio between the smaller terms is larger than the ratio between the greater terms
|
ולהם סגולה רביעית והיא ממה שזכרנוהו הראשונים מתאריהם והיא שיחס אשר בין הגבולים הקטנים מהם יותר גדול מיחס אשר בין הגבולים הגדולים
|
- Such as: 2; 3; 4 - which are in this proportion.
|
כי שנים ושלשה וארבעה אשר הם בסדר זה האמצעי
|
- The measure of 4, which is the greater term, to 3 is as the sesquitertian ratio
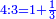
|
שעור ארבעה מהם והוא הגבול הגדול אצל השלשה כיחס המוסיף חלק השלישי
|
- The measure of 3 to 2, which is the smaller term, is as the sesquialter ratio
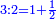
|
ושעור שלשה אצל השנים והוא הגבול הקטן כיחס המוסיף חלק החציי
|
- This ratio [= the sesquialter] is greater than the first [= the sesquitertian] as the measure of the excess of the half over the third.
|
וזה היחס גדול מהראשון כשעור תוספת החצי על השליש
|
- The opposite is seen in the harmonic proportion, in which the ratio between the greater terms is larger than the ratio between the smaller [terms].
|
וזה יראה ביחס הניגוניי בהפך כי היחס אשר בין הגבולים הגדולים יותר גדול מהיחס אשר הקטנים
|
- Because of this, the arithmetic proportion is subcontrary to the harmonic proportion,
|
מפני זה אמצעי המספר הם הפכים לאמצעי הנגון
|
- and the geometric proportion is mean between these opposites, for [in this proportion] the ratio between the greater terms is equal to the ratio between the smaller [terms]
|
ואמצעי המדות הם אמצעיי בין אלו ההפכים כי יחס אשר בין הגבולים הגדולים הוא שוה ליחס אשר בין הקטנים
|
| This is the end of the discussion on the arithmetic proportion.
|
זה הוא סוף המאמר על האמצעי המספרי
|
The Geometic Proportion
|
ואמנם האמצעי המדותיי
|
- It is when there are three numbers or more, such that the measure of the first of them to the second is as the measure of the second to the third and vice versa.

|
הוא כאשר יהיו שלשה מספרים או יותר מזה והיה שעור הראשון מהם אצל השני כשעור השני אצל השלישי וכן בהפך
|
- Such as: 4; 8; 16 - which are by this description in the geometic proportion.
|
כמו ד' ח' י"ו שהם בזה התאר בהתיחסות המדותיי
|
| These given numbers in the geometric proportion differ from the given numbers in the arithmetic proportion, since these terms themselves are proportional and their differences between each other are unequal, while the differences of those are equal and their terms are disproportional.
|
וכבר יתחלפו אלו המספריים המונחים לאמצעי ההנדסה למספרים המונחים באמצעי המספר לפי שאלו המדרגות עצמן מתיחסות ומותרי קצתם על קצת בלתי שוה ואותן היו מותריהם שוים ומדרגותיהם בלתי מתיחסות
|
- The property of the geometric proportion is that the ratio of the excesses of the terms one over the other is the same as the ratio of the terms themselves.
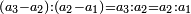
|
וסגלת זה האמצעי ההנדסיי כי למותרי הגבולים קצתם על קצת מהיחס כמו מה של גבולים עצמם מהיחס
|
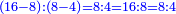
|
כי יחס מותרי י"ו על ח' והוא ח' אל מותרי ח' על ד' והוא ד' כמו יחס י"ו אל ח' וח' אל ד'
|
- Also if the terms are in triple ratio, such as: 3; 9; 27
|
וכן אם היו גם כן הגבולים ביחס הכפל השלישיי כמו ג' ט' כ"ז
|
- Likewise alway, for any given terms in whichever of the five ratios that one wishes, since the terms are following by the ratio, understand this.
|
וכן הוא תמיד כל מה שתניח מן המדרגות באי זה מן היחסים החמש שתרצה אחר שיהיו הגבולים נמשכים ביחס והבן זה
|
- This proportion has a second property: the product of the mean term by itself is as the two extremes multiplied one of them by the other.
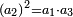
|
ולזה האמצעי סגולה שנית והוא שמוכה הגבול האמצעי בעצמו כמו שני הקצוות מוכה אחד מהם באחר
|
| It should be noticed to what was said before, concerning the "same" and "other" numbers, that between each term of one of them there is a mean term of the other successively in the natural order.
|
וראוי שנשים לב למה שאמרנו לפנים שמספרי ההוא הוא והזולת בין כל מדרגה מאחד מהם ומדרגה מן האחר אמצעי על המשכם בסדר הטבע
|
- Such as: 4; 6; 9; 12; 16
|
כמו ד' ו' ט' י"ב י"ו
|
| Since every three terms that are taken of them, are proportional.
|
כי כל שלשה מספרים יוקחו מהם מתיחסים
|
| If the first term of them is "other" the differences are equal.
|
ואם יהיה הגבול הראשון מהם זולתיי יהיה שווי היתרון
|
| The rule of this statement: between every two sequential "same" numbers there is one "other" number that follows the same ratio with them, which is less than for the cube "same" numbers.
|
וכלל זה המאמר שיפל בין כל שני מספרים הוא הויים נלוים מספר אחד זולתיי ימשך עמם על יחס בפחות מההוא הויים המעוקבים
|
| Since, between every two sequential cubes of them there are two numbers that follow the same ratio.
|
כי בין כל שני מעוקבים נלוים מהם שני מספרים ימשכו עמם על יחס
|
- Because the first actual cube is 8, the second cube is 27, and between these two cube numbers there are two numbers, which are 18 and 12, and these four are in the same ratio.
|
כי המעוקב הראשון בפעל ח' והמעוקב השני כ"ז ובין שני אלו המספרים המעוקבים שני מספרים והם י"ח וי"ב וכבר יתיחסו אלו הארבעה ביחס אחד
|
| This is what was necessary to be said here.
|
וזה ממה שיחוייב שנאמר אותו הנה
|
|
|
דע שכל מספר מרובע הוכה במספר מרובע הנה המקובץ מרובע
|
|
|
וכל מספר מרובע יוכה במספר בלתי מרובע יהיה המתקבץ מספר מעוקב
|
- Such as:
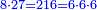
|
כמו ח' בכ"ז שהוא רי"ו כי זה מהכאות בו' עוד בו'
|
|
|
ואם תכה מעוקב בזולתיי לא יתקבץ מעוקב
|
- Such as:
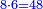 , 48 is not a cube and not a rooted surface. , 48 is not a cube and not a rooted surface.
|
כמו ח' בו' שהוא מ"ח ומ"ח אינו מעוקב ולא שטח נגדר
|
- "other" × "other" = not necessarily a square or a cube
|
ואם תכה מספר זולתיי במספר אחר זולתיי לא יחוייב שיתקבץ מרובע פשוט ולא גם כן מעוקב
|
|
|
ואם תכה זוג בזוג יהיה המתקבץ זוג
|
|
|
ואם תכה נפרד בנפרד יהיה מה שיתקבץ נפרד
|
| The author of this book [= Nicomachus] said: Plato has already explained it in his book that is called in Greek language politeia.
|
אמר מניח הספר וכבר באר זה אפלאטון בספרו אשר יכונה בלשון יוני בולוטיא
|
The Harmonic Proportion
|
ואמנם האמצעי החבוריי
|
When there are three given numbers, which are not in one ratio to each other, as the terms in the geometric proportion, and the excesses of each over the other are not equal, as [those of] the terms in the arithmetic proportion, but the measure of the greater term to the measure of the smaller term is as the measure of the excess of the greater term over the mean term to the excess of the mean over the smaller.
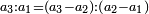
|
הנה הוא כאשר היו שלשה מספרים מונחים ולא יהיה לקצתם אל קצת יחס אחד כמו הגבולים המדותיים לא יתרוני קצתם על קצת שוים כמו הגבולים המספרים אבל יהיה השעור הגבול הגדול אצל שעור הגבול הקטן כשעור מותר הגבול הגדול על הגבול האמצעי אל מותר האמצעי על הקטן
|
- Such as: 3; 4; 6
|
כמו ג' ד' ו'
|
| Also, the measure of the greater term to the greater excess is as the measure of the smaller term to the smaller excess.
|
וכן גם כן שעור הגבול הגדול אצל גדול שני המותרים כשעור הגבול הקטן אצל קטן שני המותרים
|
- The property of these terms is opposite to the terms of the arithmetic and the geometric proportion together.
|
וסגולת אלו הגבולים הפכית לגבולי אמצעי החשבון והמדות יחד
|
- Since the ratio of the smaller of these terms to the mean is greater than the ratio of the mean to the greater.
- [
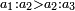 ] ]
|
לפי שאלו הגבולים יחס הגבול הקטן מהם אל האמצעי גדול מיחס האמצעי אל הגדול
|
- While in the terms of the arithmetic proportion, the ratio of the smaller to the mean is less than the ratio of the mean to the greater.
- [
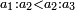 ] ]
|
וגבולי האמצעי החשבון יחס הקטן אל האמצעי פחות מיחס האמצעי אל הגדול
|
- And in the terms of the geometric proportion, if three terms of them are given according to their condition, all of them are in one ratio.
- [
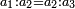 ] ]
|
ואמנם גבולי אמצעי המדות אם היו שלשה גבולים מהם מונחים כפי תנאם יהיו כלם ביחס אחד
|
- The harmonic proportion has another property, which is that the sum of the products of each of the two extreme terms by the mean is as double the product of the two extremes multiplied by each other.
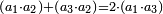
|
ולאמצעי חבוריי סגלה אחרת והיא שהכאת כל אחד משני הקצוות מגבוליו באמצעי מקובצים כמו כפל מה שיהיה משני הקצוות מוכה אחד מהם באחר
|
[Extracting a Third Term in the Arithmetic, Geometric, and Harmonic Proportions]
|
|
| Now it will be explained how the third term is extracted for each of these three proportions, when two of the terms are given:
|
ונבאר עתה איך יוצא הגבול השלישי לכל אחד מאלו השלשה אמצעיים כאשר היו שני חלקים מהם מונחים
|
- If two successive terms of the arithmetic proportion are given and the third term is required:
|
וזה שאם היו שני חלקים מאמצעי החשבון נלוים מונחים ונבקש הגבול השלישי
|
- If the required is the greater term
- It is defined as a number such that the measure of its excess over the mean is as the measure of the excess of the mean over the smaller.
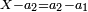
|
הנה אנו נשימהו אם היה הדרוש הגבול הגדול מספר ששעור תוספתו על האמצעי כשעור תוספת האמצעי על הקטן
|
- The third term is found also, when it is the greater, by multiplying the mean, then subtracting from it the smaller term, and the remainder is the greater term.
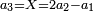
|
ונמצא גם כן הגבול השלישי כאשר היה הגדול כאשר נכפול האמצעי עוד נשליך ממנו הגבול הקטן ומה שישאר הוא הגבול הגדול
|
- It was already said that the arithmetic proportion is that, whose terms exceed one over the other equally, but the terms are not proportional.
|
הנה כבר נאמר שאמצעי החשבון הוא אשר יוסיפו גבוליו קצתם על קצת בשוה ואינם מתיחסים הגבולים
|
- Furthermore, it was said that double the mean is as the two extremes together.
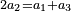
|
ואמרנו שכפל האמצעי מגבוליו כמו שני קצוותיו יחד
|
- If the required is the smaller term
- It is defined similarly as a number such that its subtraction from the mean is as the subtraction of the mean from the greater.
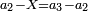
|
וכדמיון זה נוציא הגבול הקטן אם היה הדרוש וזה שאנו נשים הגבול הקטן מספר יהיה חסרונו מהאמצעי כשעור חסרון האמצעי מהגדול
|
- Or, subtracting the greater term from double the mean and the remainder is the smaller term.
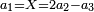
|
או כפל האמצעי הנה נשליך ממנו הגבול הגדול ומה שישאר הוא הגבול הקטן
|
- If the required is the mean
|
אמנם אם היה הדרוש באמצעי
|
- Taking half the sum of the two extremes and it is the mean.
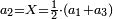
|
אנו נקח חצי שני הקצוות מקובצים והוא האמצעי
|
- Extracting the third term in the geometric proportion:
|
ואמנם איך יוצא הגבול השלישי אל אמצעי המדות
|
- If the required is the greater term
|
הנה אם היה דרושנו הגבול הגדול
|
- It is defined as a number such that the ratio of the mean to it is as the ratio of the smaller to the mean.
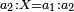
|
אנו נשימהו מספר יחס האמצעי אליו כיחס הקטן אל האמצעי
|
- Or, multiplying the mean by itself, then dividing the product by the smaller term, and the result of division is the greater term.
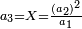
|
או נכה האמצעי בעצמו ומה שיצא נחלקהו על הגבול הקטן ומה שיצא בחלוק הוא הגבול הגדול
|
- It was already explained before that the geometric proportion is that, whose terms are proportional, but their excesses are unequal.
|
וכבר בארנו לפנים שאמצעי המדות הוא אשר גבוליו מתיחסים ואין תוספתם שוה
|
- It was further explained that the product of the mean by itself is as the product of the two extremes multiplied one by the other.
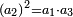
|
ובארנו הכאת שהאמצעי בעצמו כמו שני הקצוות מוכה אחד מהם באחר
|
- For the number that is the quotient resulted from the division of that number by one of the two numbers that are multiplied one by the other, is equal to the one of them, by which it is not divided.
- [
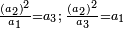 ] ]
|
כי המספר אשר יצא מחלוקת אותו המספר על אחד משני המספרים המוכה אחד מהם באחר שוה לאשר לא יחלק עליו מהם
|
- If the required is the mean term
|
ואם היה הדרוש הגבול האמצעי
|
- Extracting the root of the product of one of the numbers by the other is defined as the mean.
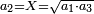
|
הנה אנו נקח שורש המתקבץ מהכאת אחד משני המספרים באחר ונשימהו האמצעי
|
- Extracting the third term in the harmonic proportion
|
ואמנם איך נוציא הגבול השלישי מאמצעי החבור
|
- It is impossible to extract one of the two extreme terms.
|
הנה אין אחד משני גבולי הקצוות אפשרי להוציאו
|
- This is because the extraction of each of them requires knowing two unknowns of the four proportional dividends in the ratio:
|
וזה שיצטרך בהוצאת כל אחד מהם אל שתי ידיעות מוסכלות מארבעה מתיחסים חלוקים ביחס
|
- One of them is the unknown term itself.
|
אחד מהם בגבול המוסכל עצמו
|
- The other is the excess of the unknown term over the mean term, if the unknown term is the greater term.
|
והשני מותר הגבול המוסכל על הגבול האמצעי אם היה הגבול המוסכל הוא הגבול הגדול
|
- Or the excess of the mean over the smaller, if the unknown is the smaller.
|
או מותר האמצעי על הקטן אם היה המוסכל הוא הקטן
|
|
ואמנם הוצאת האמצעי
|
- It is already known that this is when the excess of the greater over the smaller is taken and divided into two parts, such that the ratio of one of them to the other is as the ratio of the greater to the smaller.
|
הנה כבר נודע שהוא כאשר לוקח מותר הגדול על הקטן וחולק בשני חלקים יחס א' מהם אל האחר יחס הגדול אל הקטון
|
- For, the smaller of the two parts of the excess, when it is added to the smaller of the two extremes, the result is the mean, and when the greater part of the two parts of the excess is subtracted from the greater term, it is also the mean.
|
כי הקטון משני חלקי המותר כאשר נוסף על הקטן משני הקצוות היה המתקבץ הוא האמצעי וכאשר חוסר החלק הגדול משני חלקי המותר מהגבול הגדול היה גם כן הוא האמצעי
|
- Another way is by multiplication: multiplying one of the two extremes by the other, doubling the product, then dividing the result by the sum of the two extremes, and the quotient is the mean.
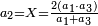
|
ואמנם אופן אחר ההכאה בם אנו נכה אחד משני הקצוות באחר ועוד נכפל מה שיתקבץ ונחלק מה שיתקבץ על שני הקצוות מקובצים ומה שיצא מהחלוקה הוא האמצעי
|
| This is enough for the description of the three proportions that are recognized by the ancients.
|
וזה מספיק בתאר האמצעים השלשה המפורסמים אצל הקדמונים
|
| The discussion on the remaining will be brief, as the ancients rarely used them.
|
ואמנם הנשארים נקצר המאמר עליהם למעוט השתמש הקדמונים מהם
|
The Fourth Proportion
|
האמצעי הרביעי
|
- It is the first of the seven remaining proportions.
|
הוא הראשון מהשבעה האמצעים הנשארים
|
- It is the one that is said to be opposite to the harmonic proportion.
|
והוא אשר יאמר לו מקביל האמצעי החבוריי
|
When there are three terms, the ratio of the excess of the mean over the smaller to the excess of the greater over the mean is as the ratio of the greater to the smaller.
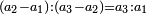
|
והוא שיהיו שלשה גבולים יחס מותר האמצעי על הקטן אל מותר הגדול על האמצעי כיחס הגדול אל הקטן
|
- Such as: 3; 5; 6
|
כמו ג' ה' ו'
|
- Its property: the product of the greater by the mean is double the smaller by the mean.
- [the general property
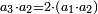 is incorrect] is incorrect]
|
וסגולת זה האמצעי הוא שהכאת הגדול באמצעי כפל הקטן באמצעי
|
The Fifth Proportion
|
והאמצעי החמשי
|
- One of the two proportions that are opposite to the geometrical proportion.
|
והוא אחד משני המקבילים לאמצעי המדותיי
|
When there are three terms, the ratio of the excess of the greater over the mean to the excess of the mean over the smaller is as the ratio of the smaller to the mean.
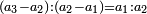
|
הוא כאשר יהיו שלשה גבולים יחס מותר הגדול על האמצעי אל מותר האמצעי על הקטן כיחס הקטן אל האמצעי
|
- Such as: 2; 4; 5
|
כמו ב' ד' ה'
|
- Its property: the product of the greater by the mean is double the product of the greater by the smaller.
- [the general property
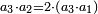 is incorrect] is incorrect]
|
וסגלת זה שמה שיתקבץ מהכאת הגדול באמצעי כפל המתקבץ מהכאת הגדול בקטן
|
- It follows necessary that the ratio of the mean to the smaller is the double ratio.
- [
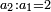 is also incorrect] is also incorrect]
|
ויתחייב מזה שיהיה לעולם יחס האמצעי אל הקטן הוא יחס הכפל
|
The Sixth Proportion
|
ואמנם האמצעי הששי
|
- The second of the two proportions that are opposite to the geometrical proportion.
|
והוא השני לשני המקבילים לאמצעי המדותי
|
When there are three terms, the ratio of the excess of the mean over the smaller to the excess of the greater over the mean is as the ratio of the greater to the mean.
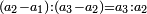
|
הנה הוא כאשר היו שלשה גבולים יחס מותר האמצעי על הקטן אל מותר הגדול אל האמצעי כיחס הגדול אל האמצעי
|
- Such as: 1; 4; 6
|
כמו א' ד' ו'
|
- Its property: the product of the greater excess by the mean term is equal to the product of the smaller excess by the greater term.
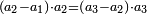
|
וסגלת זה שמה שיתקבץ מהכאת המותר הגדול בגבול האמצעי שוה למה שיתקבץ מהכאת המותר הקטן בגבול הגדול
|
| The proportions that were used from after Pythagoras until Plato's time are the three first proportions.
|
הנה האמצעים הנעשים מאחר פיתאגוריש עד זמן אפלאטון הם השלשה הראשונים
|
| The other three are their opposites.
|
ואלו השלשה האחרים הם מקבילים
|
| The four remaining were mentioned by the contemporaries and found to a small extent in the writings of the ancients.
|
ואמנם הארבעה הנשארים אשר זכרום החדשים ומעט מה שימצאו בספרי הקדמונים
|
| Since they were mentioned literally, it is necessary to mention them - lest the author will be considered ignorant concerning them.
|
וכאשר נזכרו זכר פשוט כבר יחוייב שנזכירם כדי שלא יחשוב חושב שאנו עזבנום להכלותנו בם והם אלו
|
The Seventh Proportion
|
האמצעי השביעי
|
When there are three terms, the ratio of the excess of the greater over the smaller to the excess of the mean over the smaller is as the ratio of the greater to the smaller.
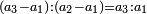
|
הוא כאשר היו שלשה גבולים יחס מותר הגדול על הקטן אל מותר האמצעי על הקטן כיחס הגדול אל הקטן
|
- Such as : 6; 8; 9
|
כמו ו' ח' ט'
|
The Eighth Proportion
|
והאמצעי השמיני
|
When the setting of the terms is such that the ratio of the greater to the smaller is as the ratio of the excess of the greater over the smaller to the excess of the greater over the mean.
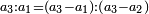
|
הנה הוא כאשר היתה הנחת הגבולים כן יחס הגדול אל הקטן כיחס מותר הגדול על הקטן אל מותר הגדול על האמצעי
|
- Such as: 6; 7; 9
|
כמו ו' ז' ט'
|
The Ninth Proportion
|
והאמצעי התשיעי
|
When there are three terms, the ratio of the excess of the greater over the smaller to the excess of the mean over the smaller is as the ratio of the mean to the smaller.
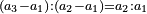
|
הוא כאשר היו שלשה גבולים יחס מותר הגדול על הקטן אל מותר האמצעי על הקטן כיחס האמצעי אל הקטן
|
- Such as: 4; 6; 7
|
כמו ד' ו' ז'
|
The Tenth Proportion
|
אמנם האמצעי הי
|
When there are three terms, the ratio of the excess of the greater over the smaller to the excess of the greater over the mean is as the ratio of the mean to the smaller.
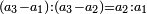
|
כאשר היו ג' גבולים יחס מותר הגדול על הקטן אצל מותר הגדול על האמצעי כיחס האמצעי אל הקטן
|
- Such as: 3; 5; 8
|
כמו ג' ה' ח'
|
|
|
והנה השלמנו כלם בזאת הצורה
|
The Perfect Proportion that encompasses the body
|
הדבור באמצעי השלם המקיף במוגשם
|
| The proportion that has three terms, as the boundary of its ends is composed of two intervals, which are:
|
האמצעי בעל הג' גבולים מפני שהקפת תכליותיו מורכבת מב' המרחקים והם
|
- the interval of what is between the greater and the mean.
|
מרחק מה שבין הגדול והאמצעי
|
- the interval of what is between the mean and the smaller
|
ומרחק מה שבין אמצעי והקטן
|
| As these in the surface that is composed of length and breadth.
|
כמו אותם אל הפשוט אשר הוא מורכב מהארך והרחב
|
| The proportions that are imagined in the body are more perfect proportions, and it is impossible that there would be a proportion that deserves to be named perfect more than them, as the perfection of the body ends, since it is impossible by nature that it will receive addition to the three dimentions, which are the length, the breadth, and the depth.
|
ואמנם האמצעים המדומים בגשם הנה הם יותר שלמים האמצעיים וא"א להיות אמצעי יותר ראוי בשם השלימות מהם כמו שהמוגשם כבר יכלה שלמותו אחר שאי אפשר בטבע שיקבל תוספת על המרחקים הג' אשר הם הארך והרחב והעומק
|
| Therefore, the proportion that has four terms, as the boundary of its ends is composed of three intervals, which are:
|
הנה אם כן האמצעי בעל הד' גבולים מפני שההקפה אשר לתכליותיו היא מורכבת מג' מרחקים והם
|
- the interval of what is between the first and the second.
|
מרחק מה שבין הראשון והב'
|
- the interval of what is between the second and the third.
|
ומרחק מה שבין הב' לשלישי
|
- the interval of what is between the third and the fourth.
|
ומרחק מה שבין הג' לד'
|
| It is by reason and necessary the perfect proportion imagined in the body.
|
היה בדין ובראוי הוא האמצעי השלם הדומה במוגשם
|
| It has this analogy by reason, since the three dimensions of the body are in four limits, which are the unit, the side, the surface, and the body.
|
ובדין לו זה הדמיון כי היו מרחקי הגשם הג' אמנם עמדו מד' גבולים והם האחדות והצלע והפשוט והגשם
|
| For, the space between the unit and the body is the body itself and it consists of the three spaces, which are: the space between the unit and the side, the space between the side and the surface, and the space between the surface and the body.
|
כי מרחק מה שבין האחדות והגשם הוא המוגשם עצמו והוא מורכב מהג' רחקים אשר הם מרחק מה שבין האחדות והצלע ומרחק מה שבין הצלע והפשוט ומרחק מה שבין הפשוט והגשם
|
| Also the perfect proportion that has four limits is the boundary of its ends, and one finds that this boundary consists of the three intervals, which are: the interval from the first term to the second, the interval from the second to the third, and the interval from the third to the fourth.
|
וכן האמצעי השלם בעל הד' גבולים הוא הקפת תכליותיו ותמצא אותה ההקפה מורכבת מג' המרחקים אשר הם מרחק הגבול הראשון מהב' ומרחק הב' מהג' והמרחק הג' מהד'
|
|
|
וכבר הניח ניקומכוש לזה האמצעי השלם המוגשם המקיף דמיון משל א' הראנו כי ההקפה בסגולות האמצעיי' הג' ר"ל אמצע החשבון ואמצע המדות אמצע החבור וזה צורתו המשל שהביא ניקומאכוש ו ח ט יב
|
- The property of the arithmetic proportion that exists in this perfect proportion that encompasses the body, is seen in three of the terms, which are the first, the third, and the fourth [= 6; 9; 12], since the excess of the fourth over the third is the excess of the third over the first; also the sum of the first and the fourth is as double the mean, and this is the mentioned property. Since this is so, all the properties mentioned above for the arithmetic proportion are undertaken by it.
- [
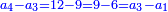 ] ]
- [
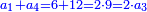 ] ]
|
ואמנם סגולת האמצעי החשבון הנמצאת בזה האמצעי השלם המוגשם המקיף הנה יראה בג' גבולי' מהם והם הראשון והג' והד' וזה לפי שמותר הרביעי על הג' הוא מותר הג' על הראשון ושהראשון והד' מקובצים כמוכפל האמצעי והיא הסגולה שזכרנו וכאשר היה זה כן הנה כבר יתחייבו לו כל הסגולות אשר קדם זכרם לאמצע החשבון
|
- The property of the geometric proportion that exists in this perfect proportion that encompasses the body, is seen in the four terms together [= 6; 8; 9; 12], when the first is related to the third, and the second to the fourth. This is because the ratio will then be one, and the product of the two extremes one by the other is as the product of the two means one by the other. Since this is so, the rest of the properties that exist in the geometric proportion are undertaken by it.
- [
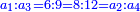 ] ]
- [
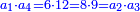 ] ]
|
ואמנם סגולת אמצע המדות הנמצאת בזה האמצעי השלם המוגשם המקיף תראה בגבולי' הד' יחד כאשר יוחס הראשון אל הג' והב' אל הד' וזה לפי שהיחס יהיה אז אחד ויהיה מוכה ב' הקצוות א' מהם באחר כמוכה ב' האמצעיי' א' מהם באחר וכאשר היה זה כן יתחייבו לו שאר הסגולות הנמצאות לאמצעי המדות
|
- The property of the harmonic proportion that is found in this perfect proportion that encompasses the body, is seen in three of these terms, as seen in the arithmetic proportion, and the evidence of this is when the fourth is related to the second, and the second to the first [= 6; 8; 12], for then the ratio of the excess of the fourth over the second to the fourth is as the ratio of the excess of the second over the first [to the first]. Since this is so, the rest of the properties that exist in the harmonic proportion are also undertaken by it.
- [
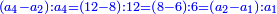 ] ]
|
ואמנם סגולת האמצעי החבור אשר תמצא בזה האמצעי השלם המוגשם המקיף תראה בג' מגבוליו כמו שנראה באמצעי החשבון והראות זה יהיה כאשר ייוחס הד' אל הב' והב' אל הראשון כי יהיה אז יחס מותר הד' על הב' אל הד' כיחס מותר הב' על הראשון וכאשר היה זה כן הנה יתחייבו לו ג"כ שאר הסגולות הנמצאו' אל אמצעי החבור
|
|
|
ואמנם נראו סגולות אמצעי החשבון בג' גבולים וסגולות אמצעי החבור בג' גבולים וחלוף זה הראות סגולות אמצעי המדות כאשר השתמש בהראותם ד' גבולי' יחד לפי שהמדה באלו היא אמצעית בין ב' המלאכות האחרות ותקח הראוי מהן יחד והנה יתקבץ בם מה שתפריש בם
|
|
|
וזולת זה אנו נאמר כי כבר יראה בזה האמצעי השלם המוגשם המקיף כל ההסכמות הנמצאות במלאכת החבור
|
- The diatessaron, which is in the sesquitertian ratio, is seen in the ratio of the first to the second, as well as the ratio of the third to the fourth.
- [
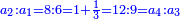 ] ]
|
אם ההסכמה בד' והיא על יחס דמיון ושליש תראה מהקשת הראשון אל הב' ותרא' ג"כ מהקשת הג' אל הד'
|
- The diapente, which is in the sesquialter ratio, is seen in the ratio of the first to the third, as well as the ratio of the second to the fourth..
- [
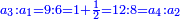 ] ]
|
ואמנם ההסכמה בחומש והוא על יחס דמיון וחצי תרא' מהקשת הראשון אל הג' ותראה גם כן מהקשת השני אל הרביעי
|
- The diapason, which is in the double ratio, is seen in the ratio of the first to the fourth.
- [
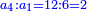 ] ]
|
ואמנם ההסכמה בכל והוא על יחס הכפל השניי תראה מהקשת הראשון אל הד'
|
- The interval of a tone, which is in the sesquioctavian ratio, is seen in the ratio of the second and the third.
- [
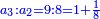 ] ]
|
ואמנם הזמן והוא על יחס דמיון ושמינית תראה מהקשת מה שבין הב' והג'
|
- This interval of a tone is a measure common to all melodies, and it is the smallest interval in the melodies.
|
וזה הזמן הוא שעור משותף לכל הליחנים והוא הפחות שבמרחקים המקבילים בליחנים להחלק
|
- It is the difference between the diapente and the diatessaron, as the superoctave is the difference between the sesquialter and the sesquitertian
- [
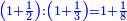 ] ]
|
והוא היתרון אשר בין ההסכמה בחומש וההסכמה בד' כמו שהשמינית הוא המותר בין המוסיף חצי ובין המוסיף שליש
|
|
|
וכבר השלמתי לך איך יראו אלו ההסכמות מזה האמצעי השלם המקיף המוגשם בצורה זו
|
|
|
תם ונשלם שבח לכל בורא עולם]
|
|
|
Appendix: Bibliography
Nicomachus of Gerasa
2nd century C. E
’Αριθμητικής είσαγωγής βιβλία β – Introduction to Arithmetic
Critical Edition:
- Nicomachus of Gerasa. Introduction to Arithmetic. trans. Martin L. D'Ooge. Chicago IL: Encyclopaedia Britannica, 1955.[Great Books of the Western World, vol.11], pp. 811 – 848.
– Hebrew translation –
Qalonymos ben Qalonymos (known as Maestro Calo or Callus)
South of France, 1286/7-after 1329
Sefer ha-Aritmitiqa / Aritmaiti
1317
Manuscripts:
- 1) Halle, Universitätsbibliothek Yb Qu. 5/1 (IMHM: f 71790), ff. 1r-54r (15th century)
- 2) München, Bayerische Staatsbibliothek, Cod. hebr. 36/14 (IMHM: f 1166), ff. 144r-164r (Istanbul, 1485)
- 3) New York, Jewish Theological Seminary Ms. 2449/2 (IMHM: f 28702), ff. 107r-153r (15th century)
- 4) Paris, Bibliothèque Mazarine 4478/1 (IMHM: f 4414), ff. 194-296 (15th century)
- 5) Paris, Bibliothèque Nationale de France heb. 1028/1 (IMHM: f 15720), ff. 1r-54r (1342)
- 6) Paris, Bibliothèque Nationale de France heb. 1029/1 (IMHM: f 15721), ff. 1r-30v (15th – 16th century)
- 7) Paris, Bibliothèque Nationale de France heb. 1093/2 (IMHM: f 15043), ff. 127r-155v (15th century)
- 8) Paris, Bibliothèque Nationale de France heb. 1095/8 (IMHM: f 15045), ff. 177-226 (15th century)
Bibliography:
- Freudenthal, Gad et Lévy Tony. 2004. De Gérase à Bagdad: Ibn Bahriz, al-Kindi, et leur recension arabe de l’Introduction arithmétique de Nicomaque, d’après la version hébraïque de Qalonymos ben Qalonymos d’Arles, In R. Morelon et A. Hasnawi eds. De Zénon d’Elée à Poincaré. Recueil d’études en hommage à Roshdi Rashed. Louvain-Paris. pp. 479-544.
- Freudenthal, Gad and Mauro Zonta. 2007. Remnants of Habīb ibn Bahrīz’s Arabic translation of Nicomachus of Gerasa’s Introdaction to Arithmetic, in Y. Tzvi Langermann and Josef Stern eds. Adaptations and Innovations: Studies on the interaction between Jewish and Islamic thought and literature from the early Middle Ages to the late twentieth century, dedicated to Professor Joel L. Kraemer. Paris, Louvain and Dudley: Peeters, 2007. pp.67-82.
- ———. 2009. Nicomachus of Gerasa in Spain, Circa 1100: Abraham bar Ḥiyya’s Testimony, Aleph 9.2 (2009), pp. 189-224.
- Langermann, Y. Tzvi. 2001. Studies in Medieval Hebrew Pythagoreanism: Translations and Notes to Nicomachus; Arithmological Texts, Micrologus IX, pp. 219–36.
- Sarfatti, Gad ben ‛Ami. 1968. Mathematical Terminology in Hebrew Scientific Literature of the Middle Ages. Jerusalem: Magnes Press, pp. 200-214.
- Steinschneider, Moritz. 1894. Miscellen 26. Nikomachus, Arithmetik, Monatsschrift für die Geschichte und Wissenschaft des Judenthums 38, pp. 68–77.
– Summary –
Manuscript:
- Oxford, Bodleian Library MS Mich. 29/3 (IMHM: f 20994), ff. 131v-158r (cat. Neub. 2302, 3; 18th century)
– Commentaries on the Introduction to Arithmetic by Nicomachus –
Caleb Afendopolo
Constantinople, 1499
Manuscript:
- Berlin, Staatsbibliothek (Preußischer Kulturbesitz) Or. Qu. 760 (IMHM: f 1742) (1499)
Bibliography:
- Steinschneider, Moritz. 1896. Miscellen 36. Kaleb Afednopolo's encyklopädische Einteilung der Wissenschaften, Monatsschrift für die Geschichte und Wissenschaft des Judenthums 40, pp. 90–94.
A certain Yosef
Manuscript:
- Moscow, Russian State Library, Ms. Guenzburg 340/1 (IMHM: f 47750), ff. 2r-18v (16th century)
Abraham Yerushalmi
Manuscripts:
- Moscow, Russian State Library, Ms. Guenzburg 340/2 (IMHM: f 47750), ff. 19r-23r (16th century)
|
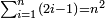 .
.
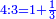 ]
]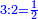 ]
]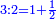 ]
] ]
]![\scriptstyle n=\frac{1}{2}\sdot\left[\left(n+1\right)+\left(n-1\right)\right]](/mediawiki/images/math/0/8/a/08a331a4b14c89dd6b9cea191a31ef06.png)
![\scriptstyle n=\frac{1}{2}\sdot\left[\left(n+2\right)+\left(n-2\right)\right]](/mediawiki/images/math/3/8/0/380f7d2cc486e55ce5fc116c2f382b67.png)
![\scriptstyle n=\frac{1}{2}\sdot\left[\left(n+m\right)+\left(n-m\right)\right]](/mediawiki/images/math/d/1/f/d1f23c2ce19c992ceead63ae37670955.png)
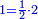

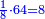 → 8 is even-times-even
→ 8 is even-times-even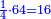 → 4 and 16 are even-times-even
→ 4 and 16 are even-times-even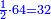 → 2 and 32 are even-times-even
→ 2 and 32 are even-times-even which is derived from 9
which is derived from 9 which is derived from 3
which is derived from 3

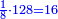
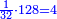
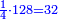
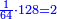
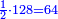

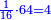
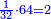
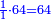
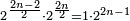
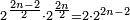
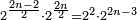
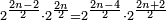
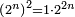
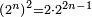
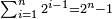
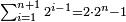
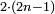

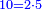
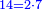
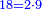
 ], as illustrated in their terms.
], as illustrated in their terms.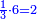
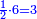
 , and whose half is 4:
, and whose half is 4: 
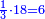
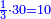
![\scriptstyle\left[2\sdot\left(2n+1\right)\right]+\left[2\sdot\left[\left[2\sdot\left(n+1\right)\right]+1\right]\right]=\left[2\sdot\left(2+1\right)\right]+\left[2\sdot\left[\left(2\sdot2n\right)+1\right]\right]](/mediawiki/images/math/0/3/b/03b1aebe88db1e369e31ef8013f61229.png)
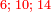 ] When setting 6 as the smaller extreme of the even-times-odd numbers and 14 as the greater extreme, their sum is 20, and the mean, which is 10, when it is doubled is the same.
] When setting 6 as the smaller extreme of the even-times-odd numbers and 14 as the greater extreme, their sum is 20, and the mean, which is 10, when it is doubled is the same.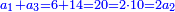
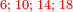 ] When setting 18 as the greater extreme, the sum of the two extremes is 24, and the two means, which are 10 and 14, are also 24.
] When setting 18 as the greater extreme, the sum of the two extremes is 24, and the two means, which are 10 and 14, are also 24.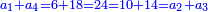
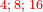 ] When setting 4 as the smaller extreme of [the even-times-even numbers] and 16 as the greater extreme, the product of 4 by 16 is equal to the product of the mean, which is 8, by itself, which is 64.
] When setting 4 as the smaller extreme of [the even-times-even numbers] and 16 as the greater extreme, the product of 4 by 16 is equal to the product of the mean, which is 8, by itself, which is 64.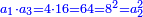
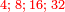 ] When setting 32 as the greater extreme, the product of 4 by 32 is 128 and it is equal to the product of the two means one by the other, which are 8 and 16.
] When setting 32 as the greater extreme, the product of 4 by 32 is 128 and it is equal to the product of the two means one by the other, which are 8 and 16.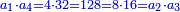
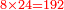 ] is far from 24 by two intermediary terms [breadthwise], yet it is not far by two intermediary terms from the product [of the first term of the even-times-even numbers by the first term in the second column of the even-times-even-times-odd numbers], but from the multiplied [i.e. by the first term in the second column of the even-times-even-times-odd numbers] itself.
] is far from 24 by two intermediary terms [breadthwise], yet it is not far by two intermediary terms from the product [of the first term of the even-times-even numbers by the first term in the second column of the even-times-even-times-odd numbers], but from the multiplied [i.e. by the first term in the second column of the even-times-even-times-odd numbers] itself. → from 7
→ from 7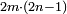 .
.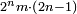 .
.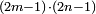 , so that the multiplied odd number divides it by the number of times by which it is multiplied, and the number of times, by which the prime incomposite odd number divides the multiplied odd number, divides also the product.
, so that the multiplied odd number divides it by the number of times by which it is multiplied, and the number of times, by which the prime incomposite odd number divides the multiplied odd number, divides also the product. .
.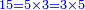 .
.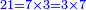 .
.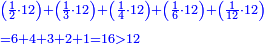
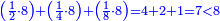
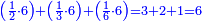
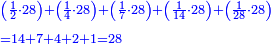
 is not a simple ratio.
is not a simple ratio.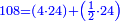 → this is the double sesquialter ratio, which is not a simple ratio.
→ this is the double sesquialter ratio, which is not a simple ratio.
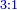
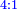
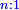
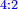 and
and 
 ;
;  ;
;  ; and so on until the end of the numbers that were set.
; and so on until the end of the numbers that were set.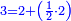 ]
]
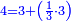
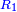 ]: Starting by arranging the numbers by natural order, from one to ten, in the first line widthwise.
]: Starting by arranging the numbers by natural order, from one to ten, in the first line widthwise. ]: The double ratio in the second line, following the first line.
]: The double ratio in the second line, following the first line.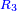 ]: The triple ratio in the third line.
]: The triple ratio in the third line.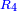 ]: The quadruple ratio in the fourth line.
]: The quadruple ratio in the fourth line.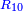 ]
] ] that meet on the square 1 and extend to the surface 1-100
] that meet on the square 1 and extend to the surface 1-100 ] that meet on the square 4 and extend to the surface 1-100
] that meet on the square 4 and extend to the surface 1-100 ] that meet on the square 9 and extend to the surface 1-100
] that meet on the square 9 and extend to the surface 1-100  ] by four.
] by four.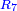 ] to its preceding 36 on this line is as the ratio of 7 on the first line breadthwise [
] to its preceding 36 on this line is as the ratio of 7 on the first line breadthwise [ ]
] ] to its preceding 6 on this line is as the ratio of 42 on the seventh line lengthwise [
] to its preceding 6 on this line is as the ratio of 42 on the seventh line lengthwise [ ] to its preceding 36 of the same line [
] to its preceding 36 of the same line [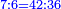 ]
] ] and the row that goes breadthwise from 6 on the first column lengthwise [
] and the row that goes breadthwise from 6 on the first column lengthwise [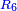 ] meet on the square 36, and 36 is one term first to each of the terms of 42 on both cross-lines, as both lines intersect on the square 36.
] meet on the square 36, and 36 is one term first to each of the terms of 42 on both cross-lines, as both lines intersect on the square 36.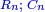 ] meet on a square of the squares on the main diagonal of the great square, and the square on which they meet is common to both.
] meet on a square of the squares on the main diagonal of the great square, and the square on which they meet is common to both.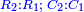 ]
]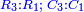 ]
]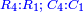 ]
]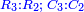 ]
]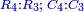 ]
]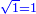
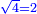
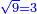
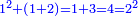
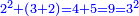
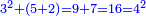


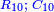 ]
]
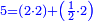
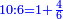 ]
]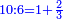 ]
]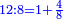 ]
]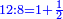 ]
]
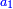 ]
] ]
]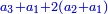 ]
]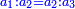 ], in any species of the five ratios mentioned in the first section, these three given numbers, the ratio of the third to the second is also as the ratio of the second to the first [
], in any species of the five ratios mentioned in the first section, these three given numbers, the ratio of the third to the second is also as the ratio of the second to the first [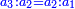 ], when the first is the smaller, the second is the mean, and the third is the greater.
], when the first is the smaller, the second is the mean, and the third is the greater.
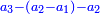 ]
]
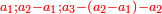 ]
] sesquialter ratio
sesquialter ratio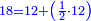
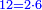
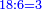 triple ratio
triple ratio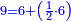

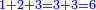
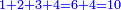
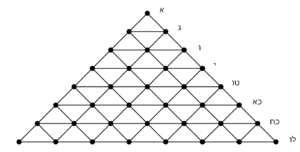

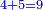
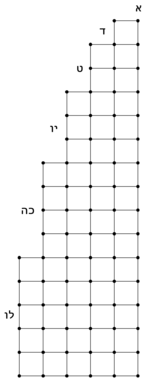
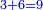
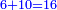
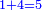
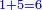
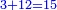
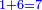
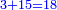
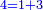
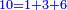
 , when four units are composed with them
, when four units are composed with them 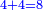 , the sum is eight, eight is two by two by two
, the sum is eight, eight is two by two by two  , and this is equal in the three dimension, i.e. the length, breadth and depth.
, and this is equal in the three dimension, i.e. the length, breadth and depth.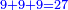 , which is the product of three by three by three
, which is the product of three by three by three 
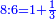
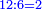
 ,
,  , or
, or  , or more than that, it is not called heteromecic number but an oblong number.
, or more than that, it is not called heteromecic number but an oblong number.

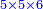
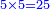 the five returns, expressed in the total.
the five returns, expressed in the total. the five is again expressed in the total.
the five is again expressed in the total.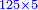
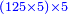
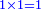
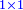







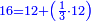
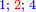
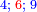
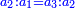
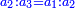 .
.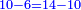

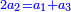 , and this and its similar were already explained in the first section.
, and this and its similar were already explained in the first section.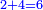
 ], but the excess of 4 over 2 is two [
], but the excess of 4 over 2 is two [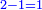 ] - the ratio is one and the same, while the additions are different.
] - the ratio is one and the same, while the additions are different.  ], but the ratio differs, as the ratio of 6 to 4 is not the ratio of 4 to 2 [
], but the ratio differs, as the ratio of 6 to 4 is not the ratio of 4 to 2 [ ].
].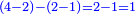 ], and so on.
], and so on.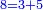 .
. .
.
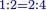 ]
] ].
].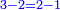 ]; and vice versa.
]; and vice versa.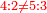 ].
]. ]; and vice versa.
]; and vice versa.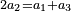
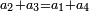
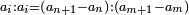
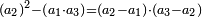

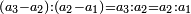
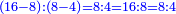
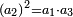
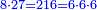
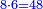 , 48 is not a cube and not a rooted surface.
, 48 is not a cube and not a rooted surface.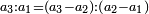
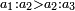 ]
]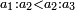 ]
]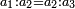 ]
]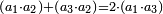
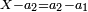
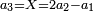
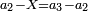
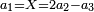
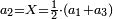
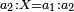
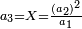
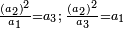 ]
]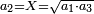
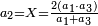
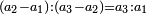
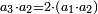 is incorrect]
is incorrect]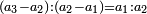
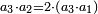 is incorrect]
is incorrect]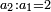 is also incorrect]
is also incorrect]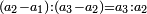
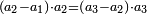
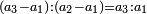
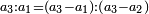
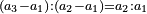
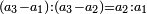
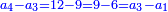 ]
]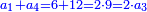 ]
]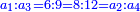 ]
]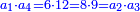 ]
]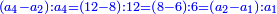 ]
]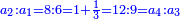 ]
]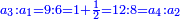 ]
]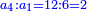 ]
]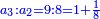 ]
]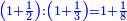 ]
]