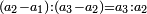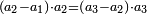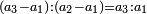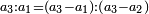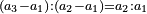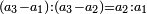Difference between revisions of "האריתמטיקה של ניקומכוס"
(→Simple Ratios) |
(→Simple Ratios) |
||
| Line 1,717: | Line 1,717: | ||
|- | |- | ||
| | | | ||
| − | ::<math>\scriptstyle{\color{blue}{108=\left(4\sdot24\right)+\left(\frac{1}{2}\sdot24\right)}}</math> | + | ::<math>\scriptstyle{\color{blue}{108=\left(4\sdot24\right)+\left(\frac{1}{2}\sdot24\right)}}</math> this is the double sesquialter ratio, which is not a simple ratio. |
|style="text-align:right;"|וק"ח כמו ארבעה דמיוני כ"ד וכמו חציים וזהו הכפל המוסיף חלק הנה לא יהיה זה היחס פשוט | |style="text-align:right;"|וק"ח כמו ארבעה דמיוני כ"ד וכמו חציים וזהו הכפל המוסיף חלק הנה לא יהיה זה היחס פשוט | ||
|- | |- | ||
Revision as of 09:40, 5 October 2019
Contents
- 1 Book One
- 2 Book Two
- 2.1 Reducing the Ratios to Equality
- 2.2 Setting Up Series of Superparticulars
- 2.3 Absolute Quantity
- 2.4 Relative Quantity
- 3 Appendix: Bibliography
Book One |
המאמר הראשון מספר הארתמאיטי |
|---|---|
Prologue by al-Kindī's Student |
|
| ימלא הבורא משאלותיך ויפיק זממיך ויוסיף חסדו ונעמו אצלך | |
| The history of the successive translations of the text: | הבינותי יתמיד האל כבודך מה שזכרת עיינת בספר הארתמאיטיקא הידוע אשר בינינו |
|
אשר הניחו וחברו ניקומאכוש אלגהר שיני הפיתאגורי |
|
בנסחא אשר תקננו זה הספר ממנה על דעת מלמדנו המעולה יעקב בן אסחק אלצבאה אלכנדי |
|
משבש מחשבות חביב בן בהריז אלנסטורי אשר תרגמו מהסריאני אל הערבי לבעל שני הימינים טאהר בן אלחסין |
| A reader received al-Kindī's recension of the text without the opening chapters and asked al-Kindī's student to send him the missing part | ואתה ראית לתקנו במאמר הראשון ממקום המספרים והלאה לפי שהוא אמנם תקון מזה המקום נשען למי שכבר קדם לו בחכמת ההגיון מה שיעזרהו להבין פתיחתו הקודמת לפני זכירת המספר ושזאת הפתיחה לא נפלה אליך ולא ידעת כוונתה ולא מה זכר בה מניחה |
| The student explains that he did not need to interpret Nicomachus' words at length since he had heard al-Kindī's short commentaries | ואשר שאלת מזה הנו מפורש לך כמו שפירשתי בשאר פירושינו הנשארים בספר |
| וקצרינו לעניניו במאמר קצר מבלתי אריכות והכפלה | |
| ואתה חושב שבזה תועלת יקרה והערה נפלאה ואני מודיעך יכבדך האל אולי ארצה הרבה פעמים לתאר דבר בהפלגה ואריכות כדי להגיע בו אל כוונת מניח הספר | |
| ויזדמן לי מאמר קצר שמעתיו ממלמדנו אבו יוסף לבאר מה ששאלת לבארו ולפרש מה שכוונת לפרשו כבר הגיע ממנו עם קצורו באשר לא יגיעהו מאמר מאריך ולא יעברהו תאר מפליג ואעזוב מה שראיתי לגלותו בדברים מרובים בעבור מאמרו הקצר ובעבור זה אמנע אני מליפות הספר ולקשטו ביותר | |
| Al-Kindī's opinion that the introduction to Ptolemy's Almagest and the introduction to arithmetic by Nicomachus are of great philosophical importance | וממה ששמעתיו ממלמדנו יותר מפעם אחת כשיאמר שהיותר ראוי ממה שתתבאר בו פילוסופית שני אלו האנשים ר"ל בטלמיוס וניקומאכוש הוא בפתיחת נושאיהם אם בטלמיוס בפתיחתו לספר המגסטי ואם ניקומאכוש בפתיחת ספר הארתמאיטיקא כי פתיחות שני אלו הספרים מעוררות על מקומות עליונים בפילוסופייא ומדרגתם יקרה בידיעה |
| Al-Kindī's student supports the reader's thought concerning the importance of the introduction of the book | ולא כזבה מחשבתך בזה ואמנם אחשוב אותה חי השם שהיא אמתית למה שהתאמת אצלך גודל מעלת פתיחת זה הספר ומעלת שעור תועלתו וטובו |
| At the reader's request, al-Kindī's student prepared a prologue of his own to the book and completed the missing part of the book with the commentary, remaining faithful to the wording of the Arabic translator, the order of writing by Nicomachus, and the opinions of his master Abū Yusūf al-Kindī | ואני השיבותיך יפארך השם למה ששאלת נמשך להפיס דעתך בכל מה שאוכל להועילך |
| ובכאן עת להתחיל במה ששאלת והיה בו מצליח יישירך השם יתע' למה שתושע בו נפשך | |
Introduction |
|
| According to the ancients, philosophy is the love of wisdom, derived from the linguistic meaning of the word (philo-sophia) | אמר ניקומאכוש שהקדמונים הראשונים אשר דקדקו בחכמה והעמיקו בה והיה הראשון להם פיתאגורש גדרו הפילוסופייא כשאמרו שהפילוסופיאה אהבת החכמה כמו ששמה מורה על זה ממנה כי העתקתו אהבת החכמה |
| ירצה באומרו שמה מורה על זה ממנה לפי ששם הפילוסופיאה מורכב משתי מלות פילו וסופיה ופילו אוהב וסופיה חכמה הנה שמה מורכב מאוהב החכמה | |
| Before Pythagoras, anyone who was versed in any craft or medicine was called 'wise' | אמר וכבר היה אשר היו קודם פיתאגוריש וקראו כל מי שהיה פקח בדבר מהמלאכות או הרפואה חכם בשם משולח מבלתי שיחקרו על השורש אשר בו ראוי להקרא בשם החכמה |
| Pythagoras restricted the definition of wisdom to the true knowledge of permanent things | אמנם פיתאגוריש למה שייחד זה השני לעיניינו והשרש אשר ממנו נגזר קרא אמתת הידיעה בדברים המתמידים ר"ל המינים והסוגים החכמה בפרט מבלתי מה שיצא מזה מן החכמות |
| אמר והראוי מי שקרא החכמה סופיה והאהבה לה הפילו סופיה ר"ל אהבת החכמה | |
| The definition that is based on the linguistic derivation of the term is the more accurate definition | אמר הנה יותר ראשון שיצדק המאמר בגדרה ויותר ראוי בשנקבל ממנו בלתי מי שגדרה נגזר משמה |
| Al-Kindī presents a list of definitions of philosophy given by the ancients: | אמר אבו יוסף כי הקדמונים גדרו הפילוסופיה במספר גדרים |
|
אם מגזרת שמה כמו אוהב החכמה לפי שפילוסוף הוא מורכב מפילו והוא אוהב וסופיה והוא החכמה |
|
ואם שגדרוה מפעולתה ואמרו שהפילוסופיאה ההתדמות בבורא ית' כפי יכולת האדם ירצה בזה שיהיה האדם שלם בחשיבות |
|
וגדרוה עוד מצד פעולתה ואמרו שהיא ההשגחה במות והמות אצלם שתי מיתות: |
|
וגדרו גם כן הפילוסופיאה היא מלאכת המלאכות וחכמת החכמות |
|
וגדרו גם כן הפילוסופיה כשאמרו כי היא ידיעת האדם עצמו |
| וזה מאמ' נכבד ורחוק מהעול מאד | |
| ודרך משל אומ' שבדברים אחר שהיו גשמים ולא גשמים והיו הגשמים עצמים והיו לא גשמים אם עצמים ואם מקרים והיה האדם הוא בעל הנפש והגשם והמקרה והיתה הנפש עצם לא גשם הנה כשידע האדם עצמו ידע הגשם במקריו והמקרה בראשון והעצם אשר הוא לא גשם וכאשר ידע זה יחד הנה כבר ידע הכל ולזאת העלה קראו החכמים האדם עולם קטן | |
| Al-Kindī's definition of philosophy: knowledge of the eternal universal things, their existences, essences, causes, and perfections, according to the human perception capacity | ואמנם מה שנגדור בו אנחנו הפילוסופיה הוא שהפילוסופיה היא ידיעת הדברי' הנצחיים הכוללים ישתויותיהם ומהיותיהם ועלותיהם ולמויותיהם כפי יכולת האדם להשיגו |
| שלמו דברי אבו יוסף | |
| The definition of wisdom as the true knowledge of permanent things, means the apprehension of the purpose of the permanent things, that never depart from their existence, unchangeable in their essence, and are never released from their quality. These naturally primary species and types when associating with the existing things and describing them are said to be existing. | אמר מניח הספר ועוד שהוא גדר החכמה בשאמר שהחכמה אמיתת הידיעה בדברים התמידים |
| עוד גדר הידיעה כשאמר שהידיעה היא השגת תכלית הדברים המיוחסים לידיעה ר"ל אותם התמידיים אשר לא יעתקו מעניין מציאותם ולא ישיגם שינוי בישותם ולא יותרו מתכונתם והם המינים והסוגים הראשונים בטבע אשר בהשתתפות האישים להם וכשהם מתוארים בם היו ראויים לשם הנמצא אחר שיתנו מיניהם שמותיהם וגדריהם | |
| The bodily perceptible existing things are in a continuous decomposition and change assimilating the nature and the primary quality – the element, the changeable wheel – of the primeval matter from which they were created | ואמנם האישים המוחשים הגשמיי' הנה הם בהתוך מתמיד ובשנוי מדובק והנה עם זה מתדמי הטבע והסגולה אל הסגולה הראשונה מן ההיולי אשר בו התוו ורצוני בסגלה היסוד כי היסוד כלו היה גלגל אחד השתנה והותר |
| Al-Kindī:
God founded some of the qualities as causes for some of the things |
אמר אבו יוסף ירצה בזה שהבורא ית' שם קצת תכונה לקצת עלות |
| ודרך משל אומ' כראות אשר שמו עלה לנראים מהגוונים והשמע אשר שמו עלה למציאות הנשמעים | |
| He founded nature as the cause for the motions of the bodies. Since they are moving and resting by nature, they are always subject to motion and change | וכן שם הכח אשר יקרא הטבע עלה לתנועות המתנועעים הנחים אחר התנועה |
| והמתנועעים הם הגשמים ולזה יקראו הגשמים טבע לפי שאשר יקבלו מהתנועה והמנוחה אמנם יקבלוהו מן הטבע הנה הם בזה בחסרון לעולם ובתמורה | |
| וכן הגשמים המוחשים ר"ל האישים יקרה להם ההעתק והתמורה תמיד | |
| Those that exist they change in their essence according to their nature | ואמנם אשר תחת ההויה מהם הנה התמורה תקרה להם בעצם ובטבע ואמנם הגלגל ומה שבו הנה תקרה להם ההעתקה במקום ואמנם האש והאויר והמים והארץ יקרה להם ההעתק והתמורה בקצת בלתי הכל |
| Those that are subject to change are so as long as they exist | וכל אחד מאלו אשר תארנום במה שיקרה להם מהתמורה הנה הם בו כל ימי היותם |
| According to Al-Kindī, the primary quality of the primeval matter is the possibility of the existence of the non-existing | ואמרו הסגלה הראשונה מן ההיולי ירצה בו אויש המתייאשים שהם יומרו מה שהיו מלא אל יש והיסוד הוא האפשרות |
| The accidents of the nine categories by their own are unchangeable and do not cease from their qualities | אמר מניח הספר ואמנ' אשר אינם גשמים והם מה שימצא ר"ל מאמרות התשעה המקרים הנה הם בגדר הפרדתם בלתי סרים מתכונתם ולא משתנים מענינם ירצה המקרים השיניים כי הם מושכלים יחד |
| When they exist and are associated with the body that carry them, these accidents are subject to change through the changes of the body, and their knowledge then is not considered wisdom | אבל מה שישיג אישי אלו המקרים המוחשים כמו לובן פלני ותנועת פלני מהשנוי והתמורה הנה הם להשתתפם לעצם הנושא אותם ר"ל כשהם עומדים ישיגם השינוי והתמורה בתוסדתו ושינויו ולזה ידיעתם לא תקרא חכמה |
| The knowledge of the accidents and the spiritual being is the wisdom | אבל העצמים השניים והמקרים השניים הנה הם אשר ידיעתם בפרט היא החכמה |
| The knowledge of the existing things is called wisdom metaphorically, since it is the way for the knowledge of those permanent eternal primary things, which are unchangeable and do not cease from their nature, which are said to be truly and clearly existing | ואמנ' על ההעברה הנה תקרא ידיעת האישים חכמה אחר שהיא הדרך אל ידיעת אותם הדברים המתמדיים הנצחיים הראשונים אשר לא ישיגם שנוי ולא הסרה מטבעם אשר יאמ' שהם נימצאים באמת ובברור |
| The existing things that are subject to the six motions – birth and destruction, growth and diminution, change and movement – are said to be existing because of the existence of their species that define them and give them their names. Yet they are not existing by their own nature, since they are always in motion and change and do not stay even for a moment in one condition. | אבל האישים הנופלים תחת התנועות השש אשר הן ההויה וההפסד והגדול והחסרון וההשתנות וההעתק הנה אמנם יאמרו שהם נימצאים מפני מציאות מיניהם אחר שמיניהם כמו שבארנו יתנו להם שמותיהם וגדריהם ואמנם כאשר נכוון אל אחד מאישיהם לא ימצא בטבעו נמצא לפי שלא יתקיים כהרף עין אל עניין אחד אחר שהאישים בכל עת להם תנועה ותמורה |
| The everlastingly homogeneous types and species, which are not subject to existence, and are apprehended by reason through guidance of the senses – things that exist forever but have no becoming. The existing things that are thought to exist at one time but are not so, since they come to be and change, so that they are not found in one condition at two occasions – things that are always coming to be but have no existence. |
ולזה אמ' אפלטון בספר טימאוש מה הדבר אשר הוא נמצא לעולם ואין לו התהוות כלל ומה הדבר אשר יתהווה לעולם ואין לו מציאות כלל ירצה בראשון הסוגים והמינים המתדמים לנצח אשר לא תשיגם הויה אמנם יושגו בשכל ר"ל בהדרכה מהמוחשות |
|
Human perfection and immortality is achieved by philosophy alone, i.e. by the love of wisdom, which is the the true knowledge of the existing things |
אמר הנה כבר ראוי לנו ויחוייב עלינו אם היינו נכספים לשלמות האדם אשר כפי יכלתו וההשארות המתמיד והיה זה אמנם יהיה בפילוסופיה לבדה לא בדבר זולתה והפילוסופיה כמו שזכרנו אהבת החכמה |
The existing things:
|
והדברים הנימצאים מהם מה שיאמ' לא נמצא באמת ומהם מה שיאמ' זה בשתוף השם נוכל שנחקור מהדברים הנמצאים ונבארם באמתות |
The perceptible existences:
|
ונאמ' שהנמצאות המוחשות מה שהם מתאחדי החלקים מחוברי האיברים במדרגת החי אשר חלקיו מתאחדים בו וכמו כן האילן והדומה להם ואילו יאמ' להם גדלים באמתות ומהם מה שהם מפורדים והם בהתקרב מקומותיהם ובהתקבצם יקראו כללים ורבויים ואם לא יהיו מתאחדי החלקים כמו עדרי הצאן ושורות האנשים הנה כבר התבאר שמהמוחשים מהם מה שהוא נופל תחת הרבוי אלא ששני הגודל ומהם מה שהוא נופל תחת הרבוי |
Both kinds are infinite by nature:
|
אלא ששני אלו המינים אין תכלית להם בטבע כאשר יאמרו מאמ' משולח כי הרבוי כאשר יתחיל משרש מוגבל ויכפיל לא יהיה לו תכלית בטבע יעמד אצלו ולא יהיה לו כפל אחר אבל יוסיף ויצמח תמיד |
| Therefore, the knowledge of these two kinds of existences cannot be truly achieved – the knowing the infinite is impossible | הנה אין ידיעת שני אלו נמצאות על האמת אחר שידיעת מה שאין תכלית לו בלתי נמצאת |
| The true meaning of knowledge is the knowledge of inclusive limited things | ואמנ' הידיעה על אמיתתו ידיעת הדברים הניכללים המוגבלים |
| Since the absolute multitude is infinite, it is limitless, and thus cannot be grasp by knowledge | הנה כבר התבאר שהידיעה לא תעמד אצל הרבוי המשולח לפי שהוא בלתי ב"ת ומה שהוא בב"ת הוא בלתי מוגבל אין דרך אל הידיעה בו כלל |
| The multitude is knowable in comparison with the less: The multiple is great in comparison with what is less and less in comparison with what is greater |
ואמנם אם נאמ' הרבוי בהצטרף אל המיעוט ונקרא שני המצטרפים בשמותם המיוחדים היו אז ידועים לפי שהרב אמנם יהיה רב אצל מה שהוא פחות ממנו וכמו כן המעט אמנם הוא מעט אצל מה שהוא יותר ממנו (והמעט אצל מה שהוא יותר ממנו) והמעט אצל מה שהוא יותר ממנו ממעט אצל מה שהוא יתר ממנו הוא הרב אצל מה שהוא פחות ממנו כמו העשרה שהוא הרבה אצל מה שהוקש אל מה שתחתיו ומעט כשהוקש אל מה שעליו |
| Although multitude and magnitude are infinite, they are finite by comparison | הנה כבר התבאר משני אלו הצדדים שאפלו היו בלתי מוגבלים בעצמם הנה הם עם ההצטרף אליהם מוגבלים |
The numerical quantity is divided into two kinds:
|
ונאמ' עתה שהכמה המספרי יחלק לשני חלקים אחד מהם הוא אחד מה שחוייב לו יחוייב לו לבדו ובטבעו והאחד הוא שמה שיחוייב לו יחוייב לו לבד בהצטרף אמנ' המחוייב לו בטבע כמו הזוג והנפרד וזוג הזוג וזוג הנפרד והנפרד הראשון בלתי המורכב והשני המורכב כי אלו אמנם יחוייבו לכמה המספרי בטבעו לא מפני הצטרפו אל זולתו כי אין הזוג מתחלק לשני חלקים מתמשלי האחדים מפני הצטרפו אל דבר אחר |
The wisdom of quantity is investigated by two arts:
|
הנה אם כן התבאר שהכמה חכמה יחקרוה שתי מלאכות הם: הארתמאיתיקא והיא תחקור מהכמה הניפרד |
The natural quality is divided to two kinds:
|
ואמנם איכות הדברים הטבעיים יחלק לשני חלקים אם איכות מתנועע ואם איכות נח |
[The wisdom of quality is investigated by two arts]:
|
והמתנועע הוא מה שיחקור במלאכת האסטרונומייא ר"ל התכונה והנח הוא מה שיחקר במלאכת הגאומטר' ר"ל ההנדסה |
| The knowledge of the kinds that truly exist is achieved only through these four arts: arithmetic, geometry, astronomy, and music | אמר הנה אין דרך אל ידיעת מיני מה שנאמר שהם נימצאים באמת רק באלו האומניות הד' אשר הם הארתמאיטיקא וההנדסה והתכונה וחבור הנגונים |
| Philosophy is achieved only through mastery of these four arts | ולא ימצא דרך אל הפילוסופיה אלא בם |
| וכמו שכל מלאכה מן המלאכות יצטרך עושה אל בקיאות במלאכתו ודמיון יתישר ממנו בהוצאת דרושו כן אלו החכמות במלאכת הפילוסופיה אשר היא מלאכת המלאכות | |
| וכבר יאמ' זה המאמ' אנדרוקודיס הפיתאגוריי וכן יאמר גם כן ארגוטאלס אל אטראנטיני כאשר התחיל במלאכת חבור הליחנים שהוא אמ' הביטו הראשונים במה שראו מענין אלו החכמות כי אינו בלתי אפשר כלל שיהיה להם דבר סברה אחת אמיתית | |
| הנה כמו שהם כבר הביטו במה שראו מענין טבע הכל כן היו מוכל מוכנים לסבור בכל א' מן החלקים סברא אמיתית כי הם הקנו לה בשערי המדות והתכונה חכמה גלויה ומבוארת ולא קצרו גם כן מזה במה שהועילונו מעלות מלאכת הליחני | |
| וכבר ידומה שאלו החכמות הארבעה אחים | |
| ואם היו כבר ישובו אל שני המינים הראשונים אשר הם הכמות והאיכות כמו שביארנו לפנים | |
| עם שאפלטון בסוף האופן השלשה עשר מהספר אשר הניח בנימוסים והוא הספר אשר יקראוהו האנשים הפילוסופיא בחקרו וגדרו איך ראוי שיהיה אשר הוא פילוסוף באמת כן בידיעת אלו הארבעה אחר כן שב ואמ' בקצרה אחר שהפליג בזה והקדים שכל תמונה וקיבוץ מספר והסכמת חבור ומה שיורו בו ממרוצות הכוכבים אמנם ראוי שיורגל ידיעתו כפי שעור חבורם אחד אחד | |
| וכבר יתבאר עלה מה שזכרנוהו כי כאשר היה האדם אמנם יתלמד הרבה להשיג בם ידוע אחד הוא כונתו מהם הנה אמנם הם דבר אחד ואם רבו | |
| ואמנ' אם יחליף האדם זה הדרך בחכמת הפילוסופיא אין דרך לו אליה לפי שזה האופן אשר ממנו יבא הדרך אשר ממנו המציאות אין דרך לו זולת כלל ר"ל החכמות הארבעה אשר זכרנו קשות היו או קלות רבות היו או מועטות אין ראוי להתרשל בקניניהם כי מי שקיבץ אלו החכמות על צד שתארתי הוא אשר אקראהו אני חכם אמתי ואתארהו שש בחכמתו | |
| Through these wisdoms, the thoughts are carried from the perceptible apprehended material things to the rational theological subtle things | כי לא יעלם שאלו החכמות הם כמו גשרים בם יעברו מחשבותינו מאלו הדברים המוחשים המחושבים אל הדברים הנימצאים המושכלים ויעבירו דעותנו מאלו הדברים הגשמיים אשר גדלנו בם והרגלנום אל הדברים תורים אצלנו אשר לא הרגילום ראשנו ואשר הם בדקותם דומים לנפשותינו |
| These wisdoms are useful for the improvement of human life: | והיותר ראוי ממה שבחרנוהו בהקדמת העיון בחכמות וקנינם מה שזכרו אפלאטון בספר הנימוסים שסקראט אמ' לו והוא יתחכם כשיביא עלות אמיתיות מועילות בענין אלו החכמות מתחייבות מצד החוכמות מועילות בתיקון חיי בני אדם אמ' שיאמ' |
|
אמנם מלאכת החשבון אמנם נצטרך אליה בחשבונות או בחלוקות ובתבואות ובהוצאות ופרעון החובות והשותפיות |
|
אמנם המדות בהשואת המחנות ובניין המדינות וההיכלות ומדידת השדות |
|
אמנ' חכמת הכוכבים בידיעת עיתות עבודת הקרקעות ורכיבת הים וזולת זה מבחירות עיתות התחלות המלאכות ופרק הזמנים |
|
אמנם חכמת הניגונים להודות בם הבורא ית' או לשמוח במקהלות או בצניעה |
| Only through these wisdoms the eye of the soul, which is blinded and hidden by the bodily acts, is open and awaken to see the truths of the things | ולזה יאמ' אפלאטון משיב לו והוא יוכיחהו כתחשבני כי תראה שאחמול עליך שלא תחלק עמך הנני אומ' שאלו החכמות אין לדקדק בם שזה אחלוק יקשה מאד מכל צד אבל אוסיפך חזוק שאין דרך לאחד לומ' זה כי עין הנפש ר"ל כאשר יעצומוהו ויסתמוהו שאר הפעולות הגופיות וישימו עליך מסך הנה הוא יפקח ויעור באלו החכמות ואמתת עין הנפש יותר משובח מאמתת עשרת אלפים עינים מהעינים הגופים כי בו לבדו יראו אמתויות הדברים |
The learning order of the natural sciences:
|
אמר והיותר ראשונה מאלו סדר המדעים המתמטיים החכמות הארבעה והיותר קודמת על הנשארות בטבע והיותר חזקת האמונה והיא להם כמדרגת המולידה אשר ממנה התחלה היותן ושרש צמיחתן הוא מלאכת החשבון |
|
אין זה לפי שהיא היא אשר התקיים בהצעת הבורא אבל לפי שהיא במדרגת ההמשל היתה ראשונה במחשבת האל והדמיון אשר ממנו יקחו תכונת הדברים אשר הצמיחם ית' מהיסוד והשלימם על הענינים המיוחדים אשר עליהם כל אחד מהם |
|
אמר מניח הספר ויורה על מלאכת החשבון ג"כ יותר קודמת בטבע מזולתה שהיא תשים זולתה מאלו החכמות אובד באבדה מבלתי שתאבד היא באבדן דבר מהן כי אם יסתלק המספר קודמת מבחינה טבעית יעדרו הספורים ולא אם יעדרו הספורים יאבד המספר |
| כאמרנו בחי שהוא יותר קודם מן האדם קדימה טבעית שכאשר יעלה החי יעלה האדם בהעלותו ולא כשיעלה האדם יעלה החי וכן כל דבר יותר קודם מדבר אחר קדימה טבעית כשיעלה הקודם יעלה בהעלותו זולתו ולא יעלה הוא בהעלות דבר ממה שהוא יותר קודם ממנו | |
| וכן כאשר תהפך המאמ' תמצא הענין כפי זה כשיחויב דבר יחויב בחיובו מה שהוא יותר קודם ממנו קדימה טבעית ולא כשיחויב הקודם יהיה הכרח שיחויב בחיובו מה שהוא תחתיו בקדימה כמו האדם והמשורר כי האדם יותר קודם מהמשורר וכשיחויב משורר יחויב שיהיה אדם ואין הכרח כשיחויב אדם שיהיה בלי ספק משורר | |
|
הנה כפי זה הסדר אלו החכמות הארבעה אשר זכרנו כאשר תהיה המדידה אין ספק שיהיה החשבון עמה כי כשיחויב במדות משולש ומרובע ובעל שמנה תושבות או חמש עשרה תושבות |
| ואמנם אם תהפך המאמ' תמצא השלשה והארבעה וזולתה מהמספרים כבר נתקיימו בטבע והמחשבה ואם לא היו הגדולים הניגודי השמות מהם ידועים או נמצאים הנה כבר התבאר אם כן שהמספר יותר קודם מן המדות קדימה טבעית,br> אחר שבסור החשבון תסור המדידה ולא יסור החשבון בסורה | |
|
וכן גם כן בכמו זה הבאור יתבאר שמלאכת החשבון יותר קודמת ממלאכת הלחנים לפי שהעצם יותר קודם מההצטרפות |
|
וכמו כן גם כן מלאכת החשבון בזה הבאור יתבאר שהיא קודמת ממלאכת התכונה וזה גלוי אחר שבחשבון והמדות יושגו כל דרושיה |
|
וכבר יתבאר גם כן שהמדה יותר קודמת מהתכונה מצד שהתנועה אמנם תהיה אחר המנוחה |
|
ועוד שכבר יאמ' שתנועות הכוכבים הם נגונים נערכים ר"ל הן בייחס דבוריי פשוט ר"ל בפשיטות יחס בעל הכפלים ויחס המוסיף חלק וכאשר היה זה כן הנה החבור הנגוני יותר הקודם מהתכונה |
|
ואמנ' זריחות הכוכבים ועריבותיהם וקדריותיהם והסתרתם והראותם לא יעלם שכבר יושב במדה |
| Since arithmetic is prior to all other [sciences], it should be treated firstly in this treatise | וכאשר היתה מלאכת החשבון יותר קודמת מזולתה בראוי אם כן ממנה מה שהקדמנו לפנים שהמאמ' עליה ומשפטי הדבור בה יותר ראשונים בקדימה ואנחנו בזה מכאן |
| הנה לך אחי שלמות פתיחת זה הספר כאשר שאלת עד מקום המספר ממנו | |
| והיה בו ובכל מה שהשיב הבורא עליך מצליח והוא בחסדו יישירך לרצונו אמן | |
Absolute Quantity - Arithmetic |
|
The Nature of Number |
הדבור בטבע המספר |
|---|---|
| all things that are summed by nature are subject to a numerical order | כל הדברים שתיקן הטבע חבורם ימצאו נופלים תחת סדר המספר |
| כמו היסודות והזמנים ותנועות השמים ושאר התקונים הטבעיים | |
| הנה בזה ראוי שיהיה המספר במדרגת ההמשל והדמיון אשר ממנו יוקח הדבר | |
| וחדשו הבורא ית' ראשון בטבע | |
| ואמנם חבור המספר עצמו אין סדר לו זולתו לפי שהוא בתכונתו נצחי בעצמו לא עומד בזולתו | |
| אבל לפי שכל מחובר אמנם הוא מחובר מדברים מתחלפים בלי ספק ומדברים הם גם כן נמצאים אחר שאשר אינם נמצאים אין לשער חבורם ולא אשר הם ואפי' היו נמצאים אלא לפי שהם בלתי דומים אי אפשר חבורם | |
| הנה נמשך לזה שהדברים המחוברים אמנם יחוברו מדברים נמצאים מתחלפים נאותים | |
| לפי שאם לא יהיו מתחלפים הנה הם אחד לא יצטרכו אל חבור | |
| ואם לא יהיו נאותים לא יהיו מתדמים | |
| ואם לא יהיו מתדמים אלא שהם הפכיים לא יפול בם החבור | |
| הנה המספר יהיה גם כן מתחלף ונאות כך אחר שהוא מחובר וזה אמת אחר שבו שתי מינים ראשונים מתחלפים נאותים דומים ר"ל הזוג והנפרד כי הבורא ית' חברם עם חלופם חבור מסתבך אין הפרדה בו כמו שיתבאר זה במה שיבא אחר זה | |
The Definition of Number and its Types |
הדבור בגדר המספר וחלוקתו |
| number - a sum of units or a total quantity that consists of units | המספר בהעברה מן המאמ' הוא קבוץ האחדים או כלל הכמות המורכב מהאחדים |
| the first division of number: even and odd | והמספר יחלק חלוקה ראשונה אל שני חלקים אחד מהם הזוג והאחר הנפרד |
|
והזוג יחלק לשני חלקים שוים אין ביניהם אחדות אמצעי יעדיף בו אחד מהם על האחר |
|
והנפרד הוא אשר אין דרך אל שיחלק בשני חלקים שוים אבל בהכרח כשיחלק בשני חלקים בתכלית הקירוב מן השווי היה בין חלקיו אחדות יעדיף בו אחד משני חלקיו על האחר |
|
וזה הוא הגדר כפי מה שיראו ההמון |
| according to Pythagoras | ואמנם כפי מאמ' פיתאגוריש |
|
הנה המספר הזוג הוא אשר יחלק חלוקה יראה בה היחס המקיף בתחלת המיעוט ותחלת הרבוי |
|
ירצה ביחס המקיף בתחלת המיעוט ותחלת הרבוי יחס הכפל והחצי אחר שלא יראה אלא בחלוקת המספר הזוג ר"ל המתחלק בשני חלקים שוים |
|
אמר ואמנם הנפרד הנה הוא אשר לא יקבל זה אבל הוא יחלק בשני חלקים בלתי שוים לעולם |
| according to ancients | וכפי צד מאמר הראשונים גם כן |
| הנה המספר הזוג הוא אשר יחלק בשני חלקים שוים ויחלק גם כן בשני חלקים בלתי שוים בתוספת והחסרון | |
| מלבד השנים מהמספר הזוג שהם כאשר נחלקו יותכו אל האחדים ולא יסבלו חלקיהם התוספת והחסרון | |
| ולא יעבור הזוג בהחלקו בשני חלקים שוים מן אחד מן המספר ר"ל אם היה אחד משני חלקיו זוג היה האחר זוג ואם היה אחד מהם נפרד היה האחר נפרד | |
| והמספר הנפרד הוא אשר איך שתחלקהו לא ישתוו חלקיו ולא ימנעו מחלקיו הזוג והנפרד יחד ר"ל שאם היה אחד מחלקיו נפרד היה האחר זוג | |
| אם כן הוא מבואר שהיותר קרוב מה שיהיו חלקי הנפרד מן השווי כאשר היה בין שני חלקיו אחדות יעדיף בו אחד מהם לאחד | |
| ואמנם בגדר אשר יקרא דיאלילש וענינו ידיעת אחד משני המוסכלים באחד כי המספר הנפרד הוא המתחלף משני צדדיו לזוג באחדות אם בתוספת עליו ואם בחסרון ממנו הנה אם כן בזה הגדר לא יודע הנפרד אשר הוא מוסכל עד שיודע הזוג אשר הוא מוסכל ולא יודע הזוג אשר הוא מוסכל עד שיודע הנפרד אשר הוא מוסכל | |
The Units |
הדבור באחדים ושררת האחדות |
| every number is half the sum of its two sides | כל מספר הוא חצי שתי פאותיו כאשר יקובצו |
|
|
ר"ל מה שהוא מוסיף מאותו המספר באחד ופוחת ממנו באחד כאשר יקובצו |
| and half the sum of the two sides of its sides |
וכמו כן הוא חצי שתי פאות פאותיו |
|
|
וחצי גם כן מה שאחר זה כאשר היה מה שיחסר מאחת משתי הפיאות כשעור מה שיוסיף באחרת |
| וכן יהיה תמיד עד שיגיע החסרון מהפאה הקטנה אל האחדות אשר לא יוכל לעברו | |
| unit is preceded by the smallest number which is two | ואמנם האחדות הנה לא ילוה לו רק הפחות במספרים אשר הוא שנים |
| unit is not a number that has two sides, therefore it is half of its one side |
ולפי שאינו מספר שיהיו לו שתי פיאות היה חצי פאתו האחת ר"ל חצי השנים |
|
אחר שתולדת השנים מכפלו |
| unit is the cause of number | הנה כבר התבאר מה שהאחדות עלת המספר בצמיחתו |
Even Number |
הדבור בחלקי הזוג וסגולתו זוג הזוג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| the even numbers are divided into three types: 1) even-times-even |
המספר הזוג יחלק לשלשה חלקים: אחד מהם זוג הזוג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה אם כן שני החלקים הראשונים אשר הם זוג הזוג וזוג הנפרד נבדלים להבדל הזוג והנפרד בגדר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והחלק השלישי אשר הוא זוג הזוג והנפרד כאמצעי משני הקצוות ללקחו השם מורכב משמות שני החלקים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Even-Times-Even |
הנה זוג הזוג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הוא מורכב מהכפלת האחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אם כן הוא אשר איפשר שיחלק בשני חלקים שוים הם חצאיו וכל חצי מהם לשני חצאים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה אם כן כבר התבאר שכל אחד מחצי זוג הזוג זוג הזוג
וכן חצי חצייו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועוד כי חלקי זוג הזוג נמצאים לעולם נגזרי השם מזוג הוא זוג הזוג והגעתם ג"כ זוג הזוג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו שמינית ס"ד אשר הוא נגזר משמנה אשר הוא זוג הזוג והגעתו שמנה והוא זוג הזוג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
גם כן כמו רביעיתם הנגזר בארבעה והוא זוג הזוג והגעתו י"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן חצים והוא נגזר משנים והוא זוג הזוג והגעתו ל"ב והוא זוג הזוג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ולא ימצא לזוג הזוג חלק נגזר השם ממספר נפרד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו התשיעית הנגזר מתשעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והשלישית הנגזר מג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכבר יחשב שזה המספר אמנם נקרא זוג הזוג לפי שחלקיו נגזרי השמות ממספרים זוגות והגעתם זוגות גם כן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונמצא מסגולת זוג הזוג שחלקיו אחר שהם נגזרי השמות ממספרי זוג הזוגות שאותם הזוגות גם כן הם הגעות חלקי זוגות זוגות מן המספר אשר הם לו חלקי' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
כמו החצי הנגזר מב' והגעתו ל"ב מס"ד אשר החלק מל"ב מהם ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר הנחנו מדרגות מספרי זוג הזוג בהכפלה מהאחד כפי זה הסדר א' ב' ד' ח' י"ו ל"ב ס"ד קכ"ח | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
היו שמנה מדרגות הראשונה א' והשמינית קכ"ח | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והיו להם שני אמצעיים והם ח' וי"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והיה החלק מי"ו מקכ"ח ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ושמינית קכ"ח י"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכמו כן החלק מל"ב מהם ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ורביע קכ"ח ל"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכמו החלק מס"ד מהם ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וחציים ס"ד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכמו כן הם באחדות פעם אחת קכ"ח כמו שהאחד בם קכ"ח פעם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה כבר התבאר במספרי זוג הזוג חלקיהם נגזרי השמות ממה שבתוכם מהגעתם כפי ההכפלה אשר תארנוה לפנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכמו כן גם כן אם יושלך ממדרגותיהם מדרגה עד שיהיה מספר מדרגותיהם נפרד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויהיה הקצה הגדול מהם ס"ד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תמצא שלא יבצר דבר ממה שתארנו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויהיה שמיניתו ח' אשר הוא האמצעי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וחלק מי"ו מהם ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ורביעיתם י"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והחלק מל"ב מהם ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וחציים ל"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וס"ד באחד ס"ד פעם כמו שהאחד בו ס"ד פעם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועוד יתחייב למדרגות זוג הזוג כאשר יונחו על הסדר אשר המשלנו והיו המדרגות זוג ויחויב שיהיו להם שני אמצעיים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
יהיה מה שיתקבץ מהכאת אחד משני האמצעיים באחר שוה למה שיתקבץ מהכאת שני הקצוות אחד מהם באחר וכן מה שילווה לשני הקצוות אחד מהם באחר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ותבחן הקש בזה במדרגות אשר ספרנום שיהיה מספרם זוג והם אשר תחלתם אחד וסופם קכ"ח ותמצא כמו שאמרנו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר היה מספר המדרגות נפרד היה להם אמצעי אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויהיה כח מוכה האמצעי בעצמו כהכאת שני הקצוות אחד מהם באחר וכן מה שימשך להם כמו שבארנו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכבר יתחייב למדרגת זוג הזוג שיהיו כאשר נכללו מן האחד היה הגעת כלם פחות מהקצה הגדול באחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ואם לוקח עמם הקצה הגדול היה כל זה פחות מכפל הקצה הגדול באחד וזה יתחייב למדרגות ימעטו או ירבו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומבואר מזה שמדרגות זוג הזוג כשנכללו מן האחד היה הגעתם נפרד לפי שהם פחות מהקצה הגדול אשר הוא לעולם זוג באחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והחסר מהזוג אחד הוא הנפרד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Even-Times-Odd |
הדבור בזוג הנפרד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| an even-times-odd number is divided once into two equal parts by the nature of its being an even number, but its halves cannot be divided once more into halves | המספר אשר הוא זוג הנפרד יחלק לשני חלקים דומי האחדים למה שהקנהו מטבע סוגו אחר שהוא זוג ושם יעמוד ולא יתחלק פעם שנית אחד מחלקיו בשני חצאים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה אם כן זוג הנפרד הוא הכפלת הנפרד פעם אחת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו ששה ועשרה וארבעה עשר וי"ח וכ"ב וכ"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
כי ששה מכפל ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ועשרה מכפל ה' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וי"ד מכפל ז' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וי"ח מכפל ט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The production of the even-times-odd numbers: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה אם כן כשיסודרו הנפרדים הטבעיים ר"ל על משך סדר הטבע ויתחילו מתחלת הנפרדים אשר הוא ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו ג' ה' ז' ט' י"א י"ג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והיה תוספת הנפרד על הנפרד אשר לפניו מהם שנים שנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עוד תכפול אלו הנפרדים על המשכם ותסדרם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו ו' י' י"ד י"ח | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תוסיף כל פעם על אשר לפניו ד"ד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
לפי שהנפרדים הטבעיים אשר חדשו אלו הזוגות מכפלם היו נוספים שנים שנים וכאשר נכפלו יכפלו התוספת והיו ד"ד כמו שהמשלנוהו ממדרגותיהם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומבואר שהם אמנם יתחדשו על משך טבעם מהכפלת הנפרדים הטבעיים פעם אחת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכבר יתחייב לזוג הנפרד שיהיה כל אחד מחלקיו מתחלף ההגעת לשמות גזרתו בסוג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ר"ל שאם היה החלק נגזר השם ממספר נפרד היה הגעתו זוג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם היה החלק נגזר השם ממספר זוג היה הגעתו נפרד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו ששה מזוג הנפרד כי שלישיתו הנגזר מג' והוא נפרד ב' וחציו הנגזר מב' והוא זוג ג' והוא נפרד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אם כן כבר התבאר שזוג הזוג מתחלף לזוג הנפרד לפי שזוג הזוג חלקיו נגזרי השמות מסוג הגעתם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
כמו ח' אשר רביעיתם ב' וחציים ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכבר יחשב שלזה נקרא זה המין זוג הנפרד אחר שהיו חלקיו מתחלפים בשם ובהגעה בסוג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| the even-times-odd numbers that have a third [= that are divisible by 3]: | וכבר יתחייב לזוג הנפרד שלא יהיה לדבר ממנו שליש אלא למה שאתאר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה שתניח מדרגות זוג הנפרד אשר התחלתם ו' על הדמיון המתואר קודם זה והם ו' י' י"ח כ"ב כ"ו ל' ל"ד ל"ח מ"ב מ"ו נ' נ"ד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עוד נעבור שלשה מדרגות מתחלת המדרגות הנה הרביעית יש לה שליש והיא י"ח ושלישיתה ו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עוד תתרחק מי"ח שלשה מדרגות והרביעית יש שליש והיא ל' ושלישיתה י' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תמיד ולא ימלטו ממך מזוג הנפרד מה שיש לו שליש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The production of the even-times-odd numbers from the sequence of even numbers that are divisible by 3: | אמר אבו יוסף ואתה כאשר תקח הזוגות אשר להם שליש מתחלתם ותסדרם ימשכו קצתם לקצת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו י"ח ל' ומ"ב ונ"ד וס"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותקח שליש כל אחד מהם על המשך ותסדרם ימשכו קצתם לקצת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו ו' י' י"ד י"ח כ"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תמצא שלשיותיהם על משך סדרם הם מדרגות זוג הנפרד מתחלתם על סדרם לא יבצר מהם דבר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The sequence of the even-times-odd numbers | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכבר ישיג לזוג הנפרד שמדרגותיו כאשר היה מספרם זוג והיו להם שני אמצעיים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו שני הקצוות מקובצים וכמו אשר ילוה לשני הקצוות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו שבארנו לפנים במדרגות זוג הזוג אלו שהענין יהיה שם בהכאה ובכאן יהיה בחבור | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם היו מספר המדרגות נפרד היה להם אמצעי אחד לבד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותהיה הכפלת האמצעי האחד ממדרגות זוג הנפרד כמו מקובץ שני הקצוות וכן מה שימשך לשני הקצוות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| the even-times-even numbers and the even-times-odd numbers differ from each other with regard to the sum/product of the two extremes, the single mean, or the two means | הנה כבר התבאר הנה חלוף זוג הזוג וזוג הנפרד בהתחלף ענין ההכאה וענין החבור בשני הקצוות והאמצעי ושני האמצעיים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| the even-times-even number and the even-times-odd number differ from each other also in that the even-times-odd number alone is divisible [= its other divisors are indivisible], while the only indivisible part of the even-times-even number is the smallest part, i.e. 1 [= its other divisors are divisible] | וכבר יתחלף זוג הזוג לזוג הנפרד גם כן כאשר המתחלק מזוג הנפרד קצהו הגדול לבד ושהבלתי מתחלק מזוג הזוג קצהו הקטן לבד אשר הוא האחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Even-Times-Even-Times-Odd |
הדבור בתאר זוג הזוג והנפרד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| the third type of even numbers | אמנם המספר אשר הוא זוג הזוג והנפרד והוא המין השלישי ממיני הזוג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| as a mean between the other types of even numbers and consists of them, since it adopts from each of them its property | כאמצעי להם ומורכב מהם ללוקחו מכל אחד כמו סגלתו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמנם מה שלקח מדמיון זוג הזוג שהוא יחלק לשני חלקים מתמשלי האחדים בטבע אשר הקנהו סוגו עוד יחלק כל אחד משני חלקיו שנית בשני חלקים מתמשלי האחדים בטבע אשר הקנהו בהכרח | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה במה שיחלק לשני חלקים מתמשלי האחדים יותר מפעם אחת ידמה לזוג הזוג ויתחלף לזוג הנפרד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ובאשר לא יכלה בחצוי אל האחד ידמה לזוג הנפרד ויתחלף לזוג הזוג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| by every property which it is similar to one of the two types it differs from the other type | הנה כל מה שידמה בו אחד משני המינים יתחלף באותו הענין למין האחר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותבחן זה במספרי זוג הזוג והנפרד כמו י"ב וכ' וכ"ד ותמצאהו כן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| the even-times-even-times-odd number has properties that the even-times-even and the even-times-odd numbers do not have; and it has properties that are shared by them as well |
וכבר ישיג מספר זוג הזוג והנפרד שימצאו לו הסגלות אשר נאמרו שלא ימצאו לזוג הזוג ולא לזוג הנפרד ושימצאו לו ג"כ אותם הסגלות אשר ימצאו אליהם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמנם אשר ישיגהו ממה שלא ישיגם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
מזה שהמתחלק מזוג הנפרד קצהו הגדול לבד והבלתי מתחלק מזוג הזוג קצהו הקטן לבד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואמנם מה שישיגהו ממה שישיגם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הוא שבו חלקים נגזרי השמות ממספר מין הגעתם דומה בזה לזוג הזוג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ובו חלקים מתחלפים הגזרה במין להגעתם ידמה בזה לזוג הנפרד ותבחן זה ותמצאהו כן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The production of the even-times-even-times-odd numbers | ואמנם איך יתילד זה המין ואיך יצמח | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| since it shares similarities with the even-times-even number and the even-times-odd number, it consists of what they both consist of | הנה למה שהיה לוקח הדמוי לזוג הזוג ולזוג הנפרד יודע שהוא יורכב ממה שהורכבו ממנו יחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה המספר אשר הוא זוג הנפרד אמנם יתילד מהכפלת הנפרדים הטבעיים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והמספר אשר הוא זוג הזוג אמנם יתילד מהכפלת האחדים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| generating the third type - the even-times-even-times-odd numbers: | הנה כאשר תרצה להוליד זה המין השלישי אשר הוא זוג הזוג והנפרד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תסדר הנפרדים הטבעיים אשר התחלתם שלשה ימשכו קצתם לקצת בטור הארוך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עוד תסדר מדרגות זוג הזוג אשר הכפלתם מד' ר"ל בזה הצד לפי שאחר הנפרד הראשון מהנפרדים הטבעיים התחלת זוג הזוג ימשכו קצתם לקצת בטור הרחב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עוד תתחיל ותכה המדרגה הראשונה מאי זה משני הטורים שתרצה בכל מדרגות הטור האחר אחד אחד עוד תעמיד כל מה שיצא לך על מדרגותיו בטור שלישי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עוד אחר זה תשוב אל המדרגה הנמשכת למדרגה אשר הכית בכל מדרגות הטור האחד ותעשה בם גם כן כמו שעשית באשר לפניה ותכה אותה בכל מדרגות הטור האחד ותעמיד מה שיצא לך גם כן ג"כ מסודר בטור רביעי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן תעשה במדרגה השלישית והרביעית או מה שהנחת מהמדרגות ותסדר זה כלו כמו שאתה מראה בזאת הצורה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכבר הוספנו ברחב לוח הולך באורך ילוה ללוח אשר בו הנפרד הטבעי העמדנו בו זוג הנפרד על סדר מדרגותיו אשר התחלתם ששה כדי להראות בזה כל מה שזכרנו מהסגולות למיני הזוג השלשה אחר שזאת הצורה תקיף עליהם יחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| even-times-odd numbers: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כי אתה כאשר תשים הקצה הקטן מזוג הנפרד ששה והקצה הגדול ממנו י"ד תמצאם מקובצים כ' ותמצא האמצעי אשר הוא י' כאשר תכפלהו כמו זה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן אם שמת הקצה הגדול י"ח תמצא שני הקצוות מקובצים כ"ד וכן שני האמצעיים והם י' וי"ד כ"ד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| even-times-even numbers | ואמנם זוג הזוג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה אתה אם שמת הקצה הקטן ממנו ד' והגדול י"ו תמצא מה שיתקבץ מהכאת ד' בי"ו שוה למה שיתקבץ ממוכה האמצעי והוא בעצמו והוא ס"ד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם שמת הקצה הגדול ל"ב תמצא כלל הכאת ד' בל"ב קכ"ח והוא שוה למה שיהיה מהכאת שני האמצעיים אחד מהם באחד והם ח' וי"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| even-times-even-times-odd numbers | הנה כבר התבאר ממה שבארנו לפנים מסגולות זוג הזוג וזוג הנפרד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וממה שנמצאהו משיג לזאת הצורה אחרי השלמה שאתה כשתכה תחלת מדרגה ממדרגות הנפרד הטבעי במדרגה הראשונה ממדרגות זוג הזוג והנפרד מאי זה מן הטורים ההולכים באורך המתחילים מן הרחב שתרצה תמצא ההגעה כבר תתרחק מאותה המדרגה שני אמצעיים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תכה המדרגה השנית ממדרגות הנפרד באותה המדרגה הראשונה ממדרגות זוג הזוג והנפרד תמצא ההגעה מתרחקת מאותה המדרגה הראשונה ממדרגת זוג הזוג והנפרד חמש אמצעיים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכמו כן ישיג כל מדרגות הנפרד שכל מה שתרד בם מדרגה תעבור הגעת אשר לפניה בשני אמצעיים באורך כאשר היתה המדרגה המוכה בה מדרגות הנפרד ממדרגות זוג הזוג והנפרד לבדו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואמנם אם תכה המדרגה הראשונה מזוג הזוג במדרגה הראשונה מזוג הזוג והנפרד מאי זה מהטורים ההולכים ברחב שתרצה תעבור אמצעי מהמדרגה המוכה בה מזוגות הזוגות והנפרד והיית בעברך האמצעי לוקח ברחב מכוין למה שהיית עושה בהכאת מדרגות הנפרד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תכה המדרגה השנית ממדרגות זוג הזוג במה שהכית בו ממדרגות זוג הזוג והנפרד ר"ל המדרגה הראשונה מזוג הזוג והנפרד תמצא ההגעה כבר נתרחקה מן המדרגה המוכה בה מזוג הזוג והנפרד שני אמצעיים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וגם כן אם תכה המדרגה השנית מזוג הזוג והיא ח' במדרגה השנית ברחב מזוג הזוג והנפרד והיא כ"ד תמצא ההגעה מתרחקת מכ"ד שני אמצעיים גם כן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה אם כן כבר התבאר שמוכה המדרגה הראשונה ממדרגות זוג הזוג כשהוכה במדרגות טור מטורי זוג הזוג והנפרד ההולכים ברחב כל מה שירד מדרגה ירד אחרת מההגעה הראשונה לוקח ברחב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ושהמדרגה הראשונה ממדרגות טורי זוג הזוג והנפרד כאשר תוכה בכל מדרגות זוג הזוג ויצאו ההגעות ימשכו קצתם לקצת בלא אמצעי בטור אשר התחלתו היא המדרגה מזוג הזוג והנפרד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה זה סוף המאמר בחלקי הזוג השלשה הנראים בחלוקה אשר זכרנו לפנים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אמנם זכירת הזוג השוה והנוסף והחסר הוא בזולת זה המקום יותר ראוי באשר זכרו מניח הספר ושם נדבר עליו ברצון השם יתע' |
Odd Number |
בזכירת המספר הנפרד ובאור חלוקותיו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| odd number = is divided by any division into two unequal parts greater and less, and as its division is closer as possible to equality, one of them exceeds the other by one | המספר הנפרד כמו שאמרנו לפנים הוא אשר איך שחולק חלק בשני חלקים מתחלקים בתוספת וחסרון וכשיקרבו חלוקותיו מהשווי תכלית מה שאיפשר היה ביניהם אחד יעדיף אחד מהם על האחר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| odd numbers are divided naturally into two types and a third type occasionally occurs | והוא יחלק בטבע לשני חלקים ויקרה לו שיהיה לו חלק שלישי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואמנם האחד מהשנים אשר בטבע יאמר לו ראשון בלתי מורכב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואמנם האחר יאמר לו שני מורכב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואמנם השלישי הנה יקרה משני אלו החלקים בהצטרף והוא שיהיה נפרד שני מורכב יצורף אל נפרד שני מורכב ויהיה כל אחד מהם אצל חבירו ראשון בלתי מורכב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
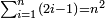
|
וכבר ישיג הנפרד הטבעי שכל מספר מדרגותיו כמו הכאת מספרי המדרגות בעצמם ותבחן זה בצורה הזאת א' ג' ה' ז' ט' י"א י"ג ט"ו י"ז י"ט כ"א כ"ג כ"ה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Prime Incomposite Number |
בזכירת הנפרד הראשון הבלתי מורכב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| the first type of odd numbers is incomposite, that has no divisor but the one | המספר הנפרד הראשון שהוא בלתי מורכב אשר אין לו חלק ימנהו בלתי האחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| such as: 3; 5; 7; 11; 13; 17 | כמו ג' ה' ז' י"א י"ג י"ז | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| these numbers and others like them has no divisor and no fractional part but that of which the numerator is one and the denominator is derived from the whole number itself | אלו המספרים ומה שימצא כמותם לא ימצא להם מספר ימנם ואין להם חלק כלל ימנם בלתי האחדים שנגזר להם חלק מכלל המספר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו השלישי מג' והשביעית מז' אשר הוא האחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| it is prime because it is measured only by the unit | הנה בראוי אם כן נאמר שהוא ראשון אחר שלא ימנהו בלתי האחדות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| it is incomposite because it cannot be divided into equal parts since it is produced from the sequence of units | ושהוא בלתי מורכב אחר שאי אפשר שיחלק בחלקי מספרים שוים לפי שהוא אמנם התילד מסדר האחדים והמשכם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| an odd number has a divisor if it is a product of this type of odd number, i.e. a prime incomposite odd number | ואמנם יהיה למספר הנפרד חלק ימנהו כאשר היה נכפל מזה המין מהנפרד ר"ל הנפרד הראשון הבלתי מורכב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כי אם נכפל פעמים מספרם זוג יתילד מהם מספר הזוג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והמספר הזוג לו מספר ימנהו בהכרח לפי שאפילו ימעטו חלקיו המונים אותו מאד הנה השנים ימנהו וימנהו גם כן כלל אחדי הפעמים אשר בם ימנוהו השנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם היו הפעמים הזוג אשר נכפל בם הנפרד שנים לבד יתחדש מכל נפרד מהם זוג הנפרד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם נכפל הנפרד מספר פעמים והיה מספר הפעמים זוג והיה הזוג יותר משנים הנה המתחדש מהם זוג הזוג והנפרד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם נכפל פעמים מספרם נפרד יחודש ממנו נפרד ימנהו אותו המספר הנפרד הנכפל בשעור אחדי הפעמים אשר נכפל בם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Composite Odd Number |
בזכר המספר הנפרד השני המורכב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| composite odd number = has a divisor beside one, and that number is a fractional part of it | המספר הנפרד המורכב הוא אשר לו עם האחד מספר ימנהו וזה המספר הוא חלק לו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכבר אמרנו שהמספר הנפרד הראשון אמנם התילד מהמשך האחדים לבד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואמנם אם יהיה המספר נפרד נכפל הנה לא יהיה ואמנם זה הנה אמנם יצמח ויתילד מהכפלת הנפרדים הראשונים כשנכפלו פעמים מספרם נפרד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| this type of odd number consists of the prime odd number | הנה זה הנפרד אם כן מורכב מהנפרד הראשון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה הוא אם כן שני לפי שהוא אמנם חודש מהראשון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והוא מורכב לפי שהנפרד הראשון חלק לו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| such as: 9; 15; 25; 27 | וזה כמו ט' וט"ו וכ"ה וכ"ז | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
כי ט' מורכב מהכפלת ג' שלשה פעמים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וט"ו מורכב מהכפלת ה' שלשה פעמים או מהכפלת ג' חמשה פעמים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכמו כן כ"א מהכפלת ז' שלשה פעמים או מכפל ג' שבעה פעמים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה אם כן כבר יכלול זה המין מהנפרד והמין הראשון שיש לו חלק נגזר השם משמו אינו מספר והוא האחדות כי זה סגולת סוג הסוגים אשר הוא המספר ר"ל שהוא מורכב מהאחדים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם מה שנתיחד בו השני המורכב הנה הוא שיש לו חלק אינו נגזר משמו ימנהו כמו ט' כי הוא ואם היה לו חלק נגזר משמו הוא האחד אשר הוא תשיעית התשעה יש לו שליש גם כן הוא השלשה וכמו כן ט"ו יש לו חומש והוא ג' ושליש ה' עם החלק מט"ו אשר הוא האחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Relatively Prime |
תאר המין השלישי מהמספר הנפרד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שזה המין יתחדש לנפרד במקרה לפי שהוא אמנם יהיה עם ההקשה בין שני המספרים המורכבים אין להם מספר משותף ימנה אותם ולכל אחד מהם כאשר הושב אל טבעו מספר ימנהו הוא חלק לו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה כמו ט' אשר הם מורכבים כמו שאמרנו מהכפלת ג' שלשה פעמים הנה כאשר הוקשו אל כ"ה אשר הם מורכבים מה' חמשה פעמים הנה כל אחד משני אלו המספרים אצל חבירו ראשון בלתי מורכב לפי שאין להם מספר משותף ימנם ואמנם היה שיהיה להם מספר משותף אלו היה החלק לאחד מהם חלק לאחד אחר שהחלק הוא המונה לכל ואין השלשה אשר הם חלק לתשעה חלק לחמשה ועשרים שימנום ולא החמשה אשר הם חלק לחמשה ועשרים חלק לתשעה שימנום ואמנם ישתתפו באחד אשר אינו מספר ואמנם הוא עלה למספר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אמנם איך יוכרו אלו המינים אשר הם מיני הנפרד ואיך יוברר מין מין מהם מהנפרד הטבעי עד שיודע הראשון הבלתי מורכב מהשני המורכב הנה זה בתחבולה יקראה ארסטשאש המכבר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והיא שתקח הנפרדים הטבעיים אשר התחלתם ג' על סדרם הטבעי ימשכו קצתם לקצת כפי מה שבלוח אשר למעלה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכשתרצה השני המורכב מאלו הנפרדים תתחיל ותעזוב שני אמצעיים אחר המדרגה הראשונה והמדרגה הרביעית מספר שיני מורכב והמדרגה הראשונה ג' והרביעית ט' והיא שני מורכב לפי שהיא מורכבת מג' שלשה פעמים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד עזוב ממנו שני אמצעיים והמדרגה הרביעית גם כן ממנה נפרד מורכב והיא ט"ו מורכב מה' שלשה פעמים או מג' חמשה פעמים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תעשה תמיד ותעזוב שני אמצעיים והרביעי מספר נפרד שני מורכב עד שתגיע אל סוף מה שהנחת מהנפרדים הטבעיים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אחר תשוב תתחיל מחמשה והיא המדרגה השנית מהנפרדים הטבעיים ותעזוב אחריה ארבע אמצעיים והמדרגה הששית ממנה נפרד שני מורכב והיא ט"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד המדרגה השנית מט"ו והיא כ"ה וכ"ה מורכב מהכפלת ה' חמשה פעמים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד תעזוב ארבע אמצעיים גם כן אחר כ"ה והמדרגה הששית ממנה היא מספר נפרד שני מורכב עד שיכלה לאשר הנחת מהמספרים הנפרדים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תעשה כל מה שתרד מן ההתחלה מדרגה תוסיף בה שיותירו שני האמצעיים שנים לכל מדרגה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי כשתעשה זה ורשמת על מדרגת הנפרד השני המורכב אשר תעמד עליהם בזאת התחבולה לא יבצר ממך דבר והיה מה שישאר אחר כלותך מזה ולקיחתו כפי זה הרושם אשר תארתי לך מאשר לא יפל בם סימן הם נפרדים ראשונים בלתי מורכבים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ודע שכאשר החלות במדרגה הראשונה ותעזוב שני אמצעים בין כל שני מורכב ושני מורכב תהיה המדרגה המורכבת הראשונה תצא מורכבת מן המדרגה אשר ממנה התחילה נכפלת בעצמה ר"ל בשיעור אחדיה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והמדרגה השנית המורכבת מורכבת מהמדרגה הראשונה נכפלת במדרגה השנית | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והמדרגה השלישית המורכבת היא מורכבת מהמדרגה הראשונה נכפלת במדרגה השלישית | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תתחיל מן המדרגה השנית ותדלג ארבע אמצעיים בין כל מורכב ומורכב יהיו המורכבים היוצאים מורכבים מהמדרגה השנית אשר החלות ממנה נכפלת בכל אחד מהאחדים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכל מדרגה ראשונה מורכבת שתצא היא מן המדרגה אשר ממנה הוחל נכפלת במדרגה הראשונה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והמורכב השני מורכב מהמדרגה השנית נכפלת בעצמה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והמורכב השלישי מורכב מהמדרגה השנית אשר ממנה הוחל נכפלת במדרגה השלישית מראש המדרגות והיא המדרגה השלישית מאשר ממנה הוחל וכבר ציירתי לך המכבר לבחון בו כל אלו הענינים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואחר שכבר התבאר לך איך תברור בזה המכבר המספרים השניים המורכבים מהנפרדים הראשונים הבלתי מורכבים עד שיוכרו שני המינים הטבעיים ממיני הנפרד כל אחד מהם לבדו נמשיך לזה הכרת המין השלישי המקרי ונגלה איך יודע כשנקיש בין שני מספרים כל אחד מהם בעצמו שני מורכב אם הם עם ההקשה כל אחד מהם אצל חברו ראשון ר"ל שאין להם מספר משותף ימנם ואם היה להם מספר משותף ימנם איך נמצאהו כי אנו כשנרצה לידע זה בשני מספרים הנה אנו נשליך מגדול המספרים המונחים מה שבו מדמיוני הקטן | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכאשר ישאר מהגדול פחות מן הקטן נשליך מן הקטן מה שהוא מדמיוני הנשאר מהגדול | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד נשליך מהנשאר מן הגדול מה שבו מדמיוני הנשאר מהקטן עוד כן לא נסור מחסר מה שביתר מדמיוני הפחות עד שנגיע אם אל האחדות או אל שני מספרים הקטן מהם ימנה הגדול | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם יגיעו אל האחדות הנה כל אחד מהם אצל האחר ראשון בלתי מורכב ואם הגענו אל שני מספרים הקטן מהם ימנה הרב הנה הקטן הוא המספר המשותף אשר ימנה שני המספרים אשר הוקש אחד מהם אל האחר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| משל זה במספרים אשר כל אחד מהם בעצמו שני מורכב ובהקש אל האחר ראשון בלתי מורכב מספר ט' וכ"ה שאנו נשליך בכ"ה מדמיוני ט' וישאר ז' נשליך מה שבט' מדמיוני ז' ישאר ב' נשליך מה שבז' מדמיוני ב' ישאר אחד והאחד ימנה השנים ואין האחד מספר הנה ט' וכ"ה כל אחד מהם אצל חברו ראשון בלתי מורכב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם דמיון המספרים אשר כל אחד מהם שני מורכב ובהקשה ביניהם להם מספר משותף ימנם והם בו שניים מורכבים הם כמו מספר כ"א ול"ה כי אנו נשליך מה שבל"ה מדמיוני כ"א וישאר י"ד עוד נשליך מה שבכ"א מדמיוני י"ד וישאר ז' וז' ימנה י"ד הנה כ"א ול"ה להם מספר משותף ימנה אותם והוא ז' והם בו עם ההקשה שניים מורכבים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אם כן כבר התבאר איך יוצא המין השלישי המקרי מחלקי הנפרד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנה נשלם המאמר על מיני המספר יחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה צורת חלוקת מה שדברנו עליו מתחלת ספרנו עד זה המקום | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| זוג הזוג הוא המתחלק בשני חצאים וכל חצי לחצאים עד האחד ודימיונו ס"ד הזוג זוג הזוג הנפרד הוא הנחלק פעם אחת לשני חצאים ויעמד בנפרד י"ד הנפרד זוג זוג הזוג והנפרד הוא החלק יותר מפעם אחת ולא יכלה לאחד הנפרד הזוג ודמיונם כ"ד והנפרד נפרד הנפרד הראשון הבלתי מורכב הוא אשר לא ימנהו מספר כלל אין ראשון ראשון חלק לו אלא האחת י"א נפרד הנפרד השני המורכב הוא אשר לו מספר ימנהו ולא יהיה המספר לו שני אלא נפרד ודמיונו ט"ו מורכב המין המניין המקרי הוא מהקשת שני נפרדים מורכבים אין להם מספר ט' הג' להם בהצטרף משותף כלל כ"ה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Second Categorization of Even Numbers |
חלוקה שנית למספר הזוג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| three types of even numbers | המספר והזוג יחלק לשלשה חלקים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אם נוסף ר"ל שהגעת כלל חלקיו מוסיף על כלו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם חסר ר"ל שהגעת כלל חלקיו יחסרו מכלו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם שוה ר"ל שהגעת כלל חלקיו שוה לכלו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה המין השלישי כאמצעי בין שני המינים הראשונים אשר הם בדמות קצוות נבדלים אחר שהם בתכלית ההבדל לעברם השווי בתוספת ובחסרון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונאמ' במספר הנוסף שהוא כמו הבעל חיים שאיבריו הם נוספים במקרה על האיברים הטבעיים לו ולכל אישי צורתו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה כמו י"ב וכ"ד והדומה להם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
כי לי"ב חצי ושליש ורובע ושתות וחלק מי"ב ואלו החלקים מי"ב הם ששה וארבעה וג' ושנים ואחד וכלל זה י"ו והנה י"ו יותר מי"ב והם חלקיו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אמנם המספר החסר הנה הוא המתחלף בתאר למספר הנוסף והוא אשר הגעת חלקיו פחות מכלו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וידמה לזה המספר הבעל חיים שאיבריו הטבעיים חסרים משוויים הנמצא בכל אחדי צורתו בטבע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה כמו מספר ח' וי"ד והדומה להם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
כי לשמנה מן החלקים חצי ורביעית ושמינית והם ד' ב' א' וכלם ז' וז' פחות מח' אשר ז' כלל חלקיו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכמו שהיציאה מהשווי בתוספת אי אפשר לעמד על תכליתו בטבע כמו שנאמ' בפתיחת הספר כן החסרון בכמות בעל הגודל בלתי מוגבל התכלית אחר שהוא בהצטרף אלא במאמר כולל והשווי אחד אמצעי בין שני דברים אי אפשר לעמד על תכליתם כן רבוי שני המינים אשר זכרנום מהנוסף והחסר בטבע המספר הזוג ואמנ' השוה אמנם ימצא מעט לא הרבה כמו שיתרבו שני המינים הראשונים וזה שאנו אמנם נמצא מהמספר הזוג השוה מה שנגיע אליו לבד בתחבולה אשר נזכרה עתה בג"ה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Perfect Number |
הדבור בתאר המספר השוה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והוציאו כבר אמרנו שהמספר השוה הוא אשר הגעת כלל חלקיו שוה לכלו וזה המספר ידמה בעל חיים שוה האיברים ממוצע הצורה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה כמו מספר ו' ומספר כ"ח | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
כי ששה יש לו חצי ושליש ושתות והם ג' ב' א' וכלם ששה הנה אלו הששה שוים לששה אשר הם חלקיו לא יוסיפו ולא יחסרו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכמו כן גם כן כ"ח יש לו מהחלקים חצי ורביעית ושביעית וחלק מי"ד וחלק מכ"ח והם י"ד ז' ד' ב' א' ואלו כלם שוים למספר כ"ח אשר הם כלל חלקיו לא יוסיפו ולא יחסרו מהם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם איך יתילדו אל המספרים השווים ואיך נעמוד על המספר הנמצא מהם וכמה מספרים ימצאו מהם בכל מספר מונח הנה הוא במה שאתאר וזה שנניח מדרגות מספרי זוג הזוג אשר התחלתם מהאחד בטור ותהיה המדרגה הראשונה א' והשנית ב' ונעזוב המדרגה הראשונה עוד נתחיל מב' ונניח תחתיה כלל מה שיתקבץ ממנה וממה שלפניה וזה ג' וכן תעשה במה שילוה לה מן המדרגות זוג הזוג תניח תחת כל מדרגה כלל מה שיתקבץ ממנה וממה שלפניה הנה בהכרח שיהיו המספרים המונחים תחת מדרגות זוג הזוג נפרדים לפי שהמדרגה הראשונה האחד והמדרגות אשר אחריה זוגות והזוג כאשר יוסף עליו האחד ישוב נפרד הנה יוכרו מאלו המספרים הנפרדים כל מספר ראשון בלתי מורכב ונרשום עליו רושם ונעזוב מה שזולתו עוד נכה כל מספר שרשמנו עליו במה שלמעלה ממנו עליו ר"ל במספר הזוג אשר תחתיו אותו הנפרד הראשון הבלתי מורכב ונעמיד מה שיצא מן ההכאה תחת אותו הנפרד הראשון הבלתי מורכב כדי שיסודרו גם כן הגעות המוכים כפי מדרגותיהם בטור שלישי וכאשר תחפש בזאת התחבולה כל מה שהנחת ממדרגות מספרי זוג הזוג הנה כבר הוצאת כל המספרים השלמים אשר הם נכללים תוך מספר המדרגה האחרונה ממה שהוצאת מהם ואותם המספרים הם אשר העמדתם בטור השלישי תחת הנפרדים הראשונים הבלתי מורכבים והם נלוים על משך סדרם בטבע לא ידולג ביניהם מספר שלם כלל וכבר יתחייב לאלו המספרים השלמים שיהיה הפרט העודף הם על עשרה פעם ו' פעם ח' וכן תמיד ימצאו אלו המספרים בזה התאר ובחן כל מה שזכרתי לך מתארם ודרך הוצאתם בזאת הצורה בג"ה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Relative Quantity |
הדבור בתאר הכמה הצירופיי והחלקו אל השוה ובלתי שוה |
|---|---|
| After elaborating the discussion on the absolute quantity, completing its discription and the explanation of its interprations, now the relative quantity will be discussed, and described by a proper description in accordance with what was described beforehand | ואחר אשר הרחבנו המאמר על הכמה הנפרד והשלמנו תאריו ובאור פירושיו אנו נקח עתה לדבר בכמה המצטרף ונתארהו תאר נאות ומסכים למה שתארנו בו מה שקדם לפניו |
| The relative quantity is divided in the first division into two parts: one is the equality, and the other is inequality. | והכמה המצטרף יחלק חלוקה ראשונה לשני חלקים אחד מהם השווי והאחר לא שווי |
| For, every number is related to a number that is either equal to it, or unequal, with no third species in this division at all. | כי כל מספר יחובר אל מספר אם שיהיה שוה לו ואם שיהיה מבלתי שוה מבלתי שיהיה בזאת החלוקה מין שלישי כלל |
| There is no supplement nor deficiency in equality, but one of the two relatives is equal to the other. | הנה השווי אין תוספת בו ולא חסרון אבל יהיה בו אחד מן ב' המצטרפים שוה לאחר |
|
כמו המאה כאשר הוקשו אל המאה והעשרה אל העשרה |
|
והדומה לזה ממה שהוא שוה למה שהוקש אליו ממה שהוקשו אליו בענין הכמה אשר סגולתו שוה ולא שוה |
| The evenness is not to be divided into species at all, since the matter of evenness is the equal, the equal is equal to the equal, and the even is even to its even. | והישר לא יחלק למינים כלל לפי שאמנם ענין הישר השוה והשוה שוה לשוה והישר ישר למיושר לו |
| The species of the given numbers that differ in comparison with one another, in inequality, is divided in a second division, into two parts - one of them is greater, and the other is smaller, and they are different by name and antithetical by matter. | ואמנם המספרים המונחים המתחלפים עם הצטרף קצתם אל קצת ביציאה מהשווי הנה מינם יחלק בחלוקה השנית לשני חלקים אחד מהם גדול והאחר קטן והם מתחלפים בשם ונבדלים בענין |
| The greater relation is divided in a third division into five parts: the multiple to the related to it, the superpaticular to the related to it, the superpartient to the related to it, the multiple superparticular to the related to it, and the multiple superpartient to the related to it. | וההצטרפות הגדול יחלק בחלוקה השלישית לחמשה חלקים מהם בעל הכפלים למה שהוקש אליו ומהם המוסיף חלק למה שהוקש אליו ומהם המוסיף חלקים למה שהוקש אליו ומהם בעל הכפלים המוסיף חלק למה שהוקש אליו ומהם בעל הכפלים המוסיף חלקים למה שהוקש אליו |
| The smaller is divided, like the greater related to it, into five species, each species is parallel to a species of the greater, ascribed and named according to its corresponding, i.e. the species of the smaller are called: the submultiple, the subsuperpaticular, the subsuperpartient, the submultiple-superparticular, and the submultiple-superpartient. | ואמנם הקטן יחלק כמו הגדול ההקש בו לחמשה מינים יקביל כל מין מהם מין מהגדול ייוחס ויקרא בהקבלתו ר"ל שיקראו מיני הקטן כשיאמר מין תחת בעל הכפלים ומין תחת המוסיף חלק ומין תחת המוסיף חלקים ומין תחת בעל הכפלים המוסיף חלק ומין תחת בעל הכפלים המוסיף חלקים |
Simple Ratios |
|
| Said Abū Yusūf: two of these five ratios are simple: the multiple ratio and the superparticular ratio | אמר אבו יוסף ומאלו היחסים החמש שנים מהם פשוטים והם בעל הכפלים והמוסיף חלק |
|
ולא ירצה במוסיף חלק בעל הכפלים המוסיף חלק אמנם רצה היחס אשר בין שני המספרים אשר הגדול מהם כמו הקטן פעם אחת וכמו חלק מהקטן |
| This is clear in what was clarified for you by Plato, in the book that is attributed to the causes of the capacities that are ascribed to the supreme individuals. | וזה מבואר במה שביארו אליך אפלטון בספר המיוחס אל עלות הכחות המיוחסות אל האישים העליונים |
|
וזה שלמה שזכר המספרים המיוחסים אל הכדורים התשעה וייחס ביניהם לחבר אל כל כדור עליון הדמוי בשכל מטבעיהם מה שיוחסו מספריהם מהמספרים המונחים לכדורי היסודות הארבעה |
|
וייחס אל כדור הארץ והמים כ"ד |
|
וייחס אל כדור האש והאויר כ"ז |
|
וייחס אל כדור הירח ל"ו |
|
וייחס אל כדור כוכב ונוגה מ"ח |
|
אחר שבאר למה היו שני אלו הכוכבים כדורם אחד והמספר המיוחס אליהם אחד בשאמר ששני אלו הכוכבים יכללם ענין אחד והוא שמרחקיהם מן השמש אמנם הוא בגלגלי הקפותיהם לבד ואמנם מרכזיהם הנה סך תנועותיהם והשמש אחד ולזה נתייחס אליהם מספר אחד |
|
ונתייחס אל כדור השמש נ"ד |
|
ולכדור מאדים ס"ד |
|
ולכדור צדק ע"ב |
|
ולכדור שבתאי צ"ו |
|
ולכדור הכוכבים הקיימים ק"ח |
|
ולא היתה הנחתו לאלו היחסים אל אלו הכדורים אשר חייבו זה המספר בהזדמן מבלתי טעם ראוי אבל אמנם נתחייב זה במאמר הכרחי המאמת שזה הוא היותר ראשון במה שיתואר מהצטרפות אלו המספרים אל אלו הכדורים בזה היחס |
|
וכאשר ייחס בין אלו המספרים זכר שק"ח מכ"ד אינו ביחס פשוט |
|
אמר ולזה נאמר שהכוכבים הקיימים רחוקים מהפעולות הגשמיות בעלות ההויה |
|
וק"ח כמו ארבעה דמיוני כ"ד וכמו חציים וזהו הכפל המוסיף חלק הנה לא יהיה זה היחס פשוט |
| This is the explanation of that he did not mean by superparticular ratio to the multiple superparticular ratio. | זהו ביאור שלא רצה במוסיף חלק בעל הכפלים המוסיף חלק |
| ולא הארכתי בזה המאמר הנה לחשבי שכמו זה ממאמרי המחבר נעלם ממך עם פילפולך ושקידתך בעיון דבריו ואהבתך לזאת המלאכה וכל שכן שאתה ממי שספריו אצלו אבל ראיתי להזכירך זה ולא אספק שספרנו זה יפול אצל מי שסכל מסברת המלמד מה שתדעהו אתה וכאשר לא היה בכח המאמר שיביא אל האמתת הדרוש יתבלבלו המחשבות ויפול הדמוי ויעלמו האמתיות ויעדרו הידיעות יישירך האל לאור באורו ולהשיג זיו יקרו |
Multiple Ratio |
הדבור ביחס בעל הכפלים וטבעו והתילדו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| prior to the other ratios | ואמנם עתה נקדים המאמר על יחס בעל הכפלים אחר שהוא היותר קודם בטבע משאר היחסים הארבעה הנשארים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה שאנו כאשר הקשנו תחלת המספרים אשר הוא ב' אל האחד אשר הוא עלת המספר מצאנוה כפל לו וזה הוא הנקרא הכפל השניי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם הקשנו באחד גם כן אל המספר השני אשר הוא ג' יתחדש הכפל השלישי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם הקשנוהו אל המספר השלישי והוא ד' יתחדש הכפל הרביעי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עוד כן כאשר יוקש אל מדרגות המספרים הטבעיים יתחדשו כפליים יקרא בשם המספר אשר אליו יוקש האחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה התבאר שהיחס הראשון שיפל במספר הוא יחס הכפלים בהצטרף תחלת המספרים אשר הוא ב' אל האחד אשר מהכפלו יהיה מספר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והתבאר שהכפל השניי ראשון למיני הרב הכפליים בטבע לפי שהוא מהקשת האחד אל תחלת המספרים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואין למיני הכפלים תכלית בכח להתרבותם עם התרבות המספרים הטבעיים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| generating the multiples | ונתחיל ראשונה בספור התילד בעל הכפלים בלתי שאר היחסים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונקדים ממנו הראשון מהם בטבע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונאמר שהכפל השניי הוא אשר יתחדש מיחס כפל כל מספר אליו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו ד' אצל ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכמו ח' אצל ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה אם כן כבר התבאר איך יצמח הכפל השניי וזה כשיסודרו המספרים על משך סדר הטבע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו א' ב' ג' ד' ה' ו' ז' עד מה שנרצה להניח | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עוד נסדר הזוגות הטבעיים על משך סדר הטבע בטור נכחיי לטור הראשון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו ב' ד' ו' ח' י' י"ב י"ד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ויהיו מדרגותיו כמספר המדרגות אשר סדרת אותם בטור סדר המספרים הטבעיים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד תקיש הראשון ממדרגות הזוג הטבעי בראשון ממדרגות המספר הטבעי והשני בשני והשלישי בשלישי וכן במה שאחר זה שאנו נמצאם יחד ביחס הכפל השני | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו ד' אצל ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וו' אצל ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וח' אצל ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן כלם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אמנם הכפל השלישי הוא שיהיה בגדול משני המספרים המונחים שלשה דמיוני המספר הקטן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אם כן הוא מבואר לך איך יתילד הכפל השלישי וזה כשתסדר המספרים כטבעיים על משך סדר הטבע בטור | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו א' ב' ג' ד' ה' ו' ז' ח' ט' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד נתחיל ונעבור שני מדרגות ונקח השלישית ונשימה ראש מדרגות טור אחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד נעבור גם כן שתי מדרגות אחר אותה המדרגה תקח המדרגה השלישית ונשימה ראש מדרגות השנית מהטור האחר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד כן נדלג שתי מדרגות אחר כל מדרגה שנקח ונחשק בשלישית ממנה ונסדרם במדרגות אשר כטור האחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואחר נקיש בין המדרגות מהטור המוצא ובין המדרגה הראשונה מטור המספר הטבעיי עוד השנית בשנית והשלישית בשלישית | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה אנו נמצאם ביחס הכפל השלישי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו ג' אצל א' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ו' אצל ב' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וט' אצל ג' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תמיד עד סוף שהנחת מן המספרי' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה אם כן כבר התבאר שאמנם יתחדש יחס הכפל השלישיי מהכאת כל מדרגה ממדרגות המספרים הטבעיים בשלשה והעמדת אלו ההגעות במדרגות טור אחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכבר יתחייב לטור אשר בו מדרגות המספרים הגדולים מזה היחס ובכל יחס נגזר ההכפלה ממספר נפרד אל מספר שיהיה נפרד ואחר כן זוג עוד נפרד כפי מה שתראה אותך הבחינה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכבר יתחייב גם כן בזה היחס לבד שיהיה בין כל נפרד ונפרד שני אמצעיים מן הנפרד הטבעי כבר עברו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו ה' וז' אשר כבר עברו מהנפרד הטבעי בין ג' וט' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן יחוייב גם כן שיהיה בין הזוג שני אמצעיים כבר עברו מהזוג השביעי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והזוג כמו ח' וי' אשר כבר עברו בין ו' וי"ב כמו י"ד וי"ו בין י"ב וי"ח | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אמנם הכפל הרביעיי אמנם יתחדש מהכאת כל מדרגה ממדרגות המספר הטבעי בד' עוד יוקיש מה שיצא מן ההכאה אל אותה המדרגה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן החמשיי ומה שאחריו ממה שתרצה ממיני הכפלים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אלא שכאשר היה הכפל נקרא למספר הזוג היו כל מדרגותיו זוגות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו הכפל הרבעיי אשר תחלת מדרגותיו ארבעה עוד ח' י"ב י"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם היה הכפל נקרא למספר נפרד היו מדרגותיו אחת זוג ואחרת נפרד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו הכפל החמשיי אשר תחלת מדרגותיו ה' עוד י' עוד ט"ו עוד כ' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וראוי שיקרא זה המין מן הגדול בעל הכפלים ומהקטן תחת בעל הכפלים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Superparticular Ratio |
הדבור ביחס השני הפשוט והוא יחס המוסיף חלק | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואחר שכבר הבאנו הדבור על יחס הכפלים אחר שהוא יותר פשוט ויותר קודם בטבע כמו שבארנו נאמ' על אשר ימשך לו המשכות טבעי והוא המוסיף חלק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
the ratio between the beginning of the numbers, which is 2, and its successive, which is 3 
|
וזה שאנו כאשר הקשנו בין תחלת המספרים אשר הוא ב' ובין המספר אשר ימשך לו והוא ג' היה ג' אצל ב' כמהו וכמו חציו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה יתחדש המוסיף חלק מההקשה בין תחלת המספרים ואשר ימשך לו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והתבאר שהחלק הראשון בטבע הוא המוסיף חצי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עוד המוסיף שליש בבקשת המספר השלישי אשר הוא ד' אל המספר השני אשר הוא ג' כי ד' כמו ג' וכמו שלישיתו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עוד המוסיף רביע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עוד המוסיף חומש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| the ratio of each number to its preceding of the natural numbers | בהקשת כל מספר אל אשר לפניו מהמספרים הטבעיים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה אם כן יחוייב שנזכיר המוסיף חלק חצי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונאמ' שזה היחס יתילד בשנסדר הזוג הטבעי אשר התחלתו ב' והוא הטור אשר נעשה בכפל השניי בטור ימשך קצתו לקצת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד נסדר המספרים אשר מהכאת מדרגות המספרים הטבעיי' כל א' בג' והוא אשר נראה בכפל השלישיי בטור ימשכו קצתם לקצת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד יוקש בין כל מדרגה מזה הטור ובין דומה לה מהטור האחר במספר המדרגות כי יראו המדרגות יחס המוסיף חלק החציי כמו שתראה בזאת הצורה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם המוסיף שליש הוא אמנם יתחדש בסדור זה הטור אשר מהכאת מדרגות המספרים הטבעיים בג' נכחיי לסדר הטור אשר יתחדש מהכאת המספרים הטבעיים בד' והוא הטור אשר חודש בכפל הרבעיי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכמו כן המוסיף רביע כי אחד מטוריו טור הכפל הרבעיי והאחר טור החמשיי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכמו כן כל מה שתרצה מהמוסיף חלק הוא כמו זה המשל אשר תארתי לך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכבר יתכן שיקרא המוקש בזה המין אם הגדול המוסיף חלק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם הקטן תחת המוסיף חלק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכמו כן יקרא המוקש הקטן מכל מין כאשר הוא תחת מה שלמעלה ממנו מההצטרפות הגדול הנקרא בשם מיוחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכבר רשמתי מה שזכרתי לך מהכפלים והמוסיף חלק ומה שיאות לומר גם בזאת הצורה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה שאנו נתחיל ונסדר בטור הראשון הלוקח ברחב המספרים על סדר הטבע מא' עד עשרה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובטור השני הכפל השני נלוה לטור הראשון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובטור השלישי הכפל השלישי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובטור הרביעי הכפל הרביעי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן עשרה טורים ויהיה הכפל העשריי סופם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וגלוי בזאת הצורה ששני הטורים אשר יפגשו על מרובע א' ויתרחבו עד שטח א'ק' ושני הטורים אשר יפגשו על מרובע ד' ויתרחבו עד שטח א'ק' ושני הטורים אשר יפגשו על מרובע ט' ויתרחבו עד שטח א'ק' יחסם אחד ר"ל ששעור כל מדרגה מאשר לפניה מאחד מכל שני טורים מהם יפגשו על מרובע מן המרובעים אשר על הקוטר ר"ל קוטר הצורה הגדולה כשעור המדרגה אשר היא דומה לה מהטור האחר מאשר היא גם כן לפניה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אלא ששני הטורים הראשונים תוסיף כל מדרגה מהם על אשר ילוה לה מכל אחד משני הטורים אחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ושני הטורים השניים תוסיף כל אחת ממדרגותיהם על אשר תלוה לה שנים שנים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ושני הטורים השלישיים תוסיף כל אחת ממדרגותיהם על אשר תלוה שלשה שלשה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והרביעיים ארבעה ארבעה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ויחסי המדרגות מאלו הטורים יחס כל מדרגה אל אשר לפניה אל היחס שתרצה אחד אחר שיהיו דומים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| משל זה שיחס מ"ב מהטור השביעי הלוקח ברחב אל ל"ו אשר לפניה מזה הטור כיחס ז' מהטור הראשון הלוקח ברחב אל ו' אשר לפניו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ועוד יחס ז' מהטור הראשון הלוקח באורך אל ו' אשר לפניו בזה הטור כיחס מ"ב מהטור הז' הלוקח באורך אל ל"ו אשר לפניו מאותו הטור | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| לפי שהטור אשר יצא מו' מהטור הראשון ההולך ברחב הולך באורך והטור אשר יצא מו' מהטור הראשון ההולך באורך הולך ברחב יפגשו על מרובע ל"ו והיה ל"ו לכל אחת משתי המדרגות אשר בכל אחת מהן מ"ב משני הטורים המתחלפים מדרגה ראשונה לפי ששני הטורים יתחתכו על מרובע ל"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן כל שני טורים מתחלפים באורך וברחב יפגשו על מרובע מן המרובעים אשר על קוטר המרובע הגדול הנה ממרובע אשר יפגשו עליו משותף להם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה אם כן כבר התבאר איך יתילד בעל הכפלים למה שיוקש אליו לפי שהטור השני מטורי אי זה משני צדי האורך והרחב שתרצה אל הטור הראשון מאותו הצד כפל שניי והשלישי אליו שלשיי והרביעי אליו רבעיי וכן תמיד כפי סדר ועל הטבע וזה הוא המאמ' על הכפלים בזאת הצורה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אמנם המוסיף חלק הנה שני הטורים שלוקח אחד מהם באורך והאחר ברחב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכבר יצאו משני מרובעי ל' ל' ויפגשו על מרובע ט' כאשר יוחסו מדרגותיהם אל מדרגות שני הטורים הלוקחים באורך והרחב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכבר יצאו משני מרובעי כ' כ' ויפגשו על מרובע ד' כל מדרגה אל אשר ילוה לה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תמצא זה ביחס המוסיף חלק החציי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן יחס שאר מדרגות אלו הטורים הארבעה אל התחלותיהם ר"ל אל שני בתי ב' וג' משני הטורי' הלוקחים באורך ואל שני בתי ב' וג' משני הטורים הלוקחים ברחב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם יחס המוסיף חלק השלישי הנה שני הטורים שלוקח אחד מהם באורך והאחר ברחב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכבר יצאו משני מרובעי מ' מ' ויפגשו על מרובע י"ו כאשר יוחסו מדרגותיהם אל מדרגות שני הטורים הלוקחים באורך והרחב היוצאים משני מרובעי ל' ל' ויפגשו על מרובע ט' כל מדרגה אשר לפניה מהטור האחר תמצא זה ביחס המוסיף חלק השלישי בכמו אותו הביאור אשר זכרנו כמוסיף חלק החציי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן המוסיף חלק הרביעי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן המוסיף חלק החמשיי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ומה שאחר זה ממיני המוסיף חלק תמצאהו בזאת המלאכה נמשך בגזרת שמו ממשך המספרים הטבעיים המתילדים מהוספת האחדים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה אם כן כבר התבאר לחוש מהיותר קודם באלו היחסים בטבע לא ברצון והנחה בעל הכפלים למה שיוחס אליו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ושהקודם יותר בזה השניי עוד השלישי וכן תמיד כפי הגזר המספרים כמו שהם בסדר הטבע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ושאשר ימשך לבעל הכפלים הוא המוסיף חלק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ושתחלת זה הוא החציי עוד השלישי ועוד הרביעי עוד כן תמיד כפי הגזרה מהמספרים כמו שהם בסדר הטבע ממה שישיג סדר זאת הצורה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שמדרגות המספרים אשר על קוטר הוצא מא' אל ק' הכתוב נגדו כל אחת נגזרת ר"ל שיש לו שורש וידובר בו כשיכפל בעצמו ר"ל בשעור אחדיו היה שוה לכלם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו א' ד' ט' י"ו כ"ה ל"ו מ"ט ק"ד פ"א ק' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי כל אחד מאלו מספר נגזר בפעל | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| מלבד האחד שהוא נגזר בכח וגדרו אחד לפי שהוא אחד בעצמו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וגדר ד' ב' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וגדר ט' ג' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם לקחת גדרי אלו המדרגות ותסדרם בטור תמצאם כסדר מדרגותיהם על סדר משך המספרים הטבעיים כמו א"ב ג"ד ה"ו עד תכלית מה שהנחת מן המספרים הנגדרים באלכסון המרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אמר אבו יוסף מצאנו אלו המספרים הנגדרים אמנם יתחדשו ויצמחו מתוספת הנפרדים הטבעיים על משך סדרם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אשר התחלתם מהאחד אשר הוא נפרד בכח על קצתם על קצת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ג' כאשר נוסף על האחד יתקבץ מספר נגדר והוא ד' וגדרו ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכאשר נוסף על ד' הנפרד אשר ימשך לג' והוא ה' יתקבץ מספר נגדר והוא ט' וגדרו ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכאשר נוסף הנפרד אשר ימשך לה' והוא ז' על ט' יתקבץ מספר נגדר והוא י"ו ושרשו ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תמיד הנה אם כן כבר התבאר שכאשר נוספו הנפרדים הטבעיים אשר התחלתם האחד אשר הוא נפרד בכח קצתם על קצת על משך סדרם יתילדו המספרים הנגדרים הטבעיים על משך סדרם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והיו שרשיהם לקוחים מהם על משך סדרם על סדר מספר הטבעי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם שני הטורים אשר ימשכו וילוו לקוטר הנה מדרגותיהם זולתיות האורך ר"ל ששני המספרים אשר התקבצה מהכאת אחד מהם באחר יוסיף אחד מהם על האחר באחד ברישומו שכבר קרבו מגדר המדרגה אשר היה להם גדר מספרי ידובר בו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והמספרים הזולתיים כמו ו' כי הוא מהכאת ב' בג' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכמו י"ב שהוא מהכאת ג' בד' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד כן נמצאם תמיד בשני הטורים אשר משני צדי הקוטר כלם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וממה שישיג זאת הצורה ששני הטורים היוצאים ממרובע א' באורך והרחב יתוספו מדרגותיהם אחד אחד עד שיגיע כל אחד מהם אל העשרה אשר הם סוף כל המדרגות בם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וששני הטורים היוצאים משני מרובעי י"י ויפגשו על מרובע ק' יתוספו מדרגותיהם י' י' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם קובץ מה שבזויות זאת הצורה הארבעה תמצא כלל זה המספר נגדר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וממה שישיג זאת הצורה שכלל מדרגות כל מרובע יהיה קטרו נבדל מקוטר הצורה הוא נגדר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אמר אבו יוסף וממה שישיג הקוטר האחד אשר תכליותיו עשרה עשרה ומספר מדרגותיו זוג שיש לו שני אמצעיים והם ל' ל' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והמדרגות אשר בין אחד משני התכליות עד אחד משני האמצעיים ביחס קצתם אל קצת והגעות מספריהם כיחס מה שבין התכלית האחר והאמצעי האחר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אמר הפילוסוף מניח הספר כבר נמצא המקויים בזאת הצורה כאשר ידוקדק העיון בה כי בה דברים מהתועלות והזכיות יותר מאשר תארנו אלא שאנו לא נחקרם בזה המבוא לפי שאין כונתנו בו לחקרם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וראוי שנעתק אל המאמר על מה שהוא חזק ההאותות למה שהחלונו לדבר בו מזכר היחסים החמש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונאמ' עתה שהמוסיף חלקים למה שהוקש אליו יותר ראשון להקדים המאמר עליו לפי שהוא יותר פשוט משני היחסים הנשארים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה שבעל הכפלים המוסיף חלק הוא מורכב משני יחסים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובעל הכפלים המוסיף חלקים מורכב גם כן משני יחסים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ועוד שאנו כאשר חברנו ראש הנפרדים אשר הוא ג' אל הנפרד השני אשר הוא ה' יתחדש המוסיף שני חלקים והוא תחלת מיני המוסיף חלקים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולזה יחוייב שנשים המאמר על זה היחס נמשך למה שאמרנו משני היחסים הראשונים הפשוטים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם בהצטרף על סדר הטבע הנה הכפל המוסיף חלק יראה קודם מהמוסיף חלקים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה כשנקיש תחלת שני מספרים ממדרגות המספרים יתחדש בהקשתם יחס שלישי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והוא כמו צרוף ה' אל ב' כי ה' כמו כפל ב' וכמו חציו וחציו חלק ממנו וה' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וב' ראשוני שני מספרים ממדרגות המספרים הטבעיים יתחדש בהצטרף אחד מהם אל האחר יחס שלישי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אבל הוא מבואר נגלה שיחס המוסיף חלקים יותר פשוט מיחס הכפל המוסיף חלק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והפשוט יותר קודם מהמורכב קדימה טבעית | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה אם כן יחוייב שנקדים המאמר על המוסיף חלקים אל מה שיוקש אליו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונקדים ממיניו המוסיף שני חלקים אחר שהוא ראש מיניו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Superpartient Ratio |
הדבור ביחס השלישי והוא היחס המוסיף חלקים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אמר ניקומאכוש לא יהיה היחס המוסיף חלקים בפחות מהמוסיף שני חלקים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולזה אמנם יתילד זה היחס מסדר המספרים הטבעיים אשר התחלתם השלשה בטור | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| לפי שהמספר אשר קודם השלשה אין לו שני חלקים יהיו פחות ממנו אחר שחלקיו שוים לו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אמר ויסודר תחת מדרגות הטור הנזכר מדרגות הנפרדים הטבעיים אשר הראשון מהם ימשך לג' והוא ה' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד נקיש בין כל מדרגה ואשר למעלה ממנו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ויראו לנו כל מיני המוסיף חלקים נמשכים כפי משפט המשכם בטבע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם כאשר תרצה שתראה איך צמיחת כל מין ממיני זה היחס | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה עתה תעמיד שני המספרים הראשונים הפועלים למין ההוא במדרגה אחת ותניח הקטן למעלה מהגודל | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד תכה כל אחד מהם בב' ותעמיד שני המספרים המגיעים אחר ההכאה במדרגה תמשך לשני המספרים הראשונים כל אחת מהן תמשך לדומה לה הגדול ימשך לגדול והקטן ימשך לקטן | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד תשוב אל שני המספרים הראשונים ותכה אותה גם כן בג' ותעמידם במדרגה שלישית על הצד אשר העמדת בו שני המספרים במדרגה השנית | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן גם כן תכה שני המספרים הראשונים בד' ותעמידם כפי הגדר הנזכר במדרגה הנגזרת השם מהמספר אשר הכית שני המספרים הראשונים בו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תעשה תמיד כאשר תרצה להצמיח מין ממיני המוסיף חלקי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם איך תניח המספרים הראשונים הפועלים למיני המוסיף חלקים על סדר אותם המינים הטבעיים עד שלא יפול מהם מין בפנוי מה שיונח מהמספרים הנה הוא כמו שנזכר בפתיחת זה הפרק וכמו שכבר המשלנו תחת זה המספרים הראשונים הפועלים למיני יחס המוסיף חלקים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזאת הצורה וע"כ דברי מחבר הספר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אמנם איך יוצאו שאר המינים הדומים באי זה מין שנרצה מאלו המינים הראשונים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו הדומה דרך משל במוסיף שני שלישים תחת המוסיף שני חלקים שני חומשים ושני שביעים ושאר מה שיפל תחת המוסיף שני חלקים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| או במתדמים לנפלם תחת המוסיפים שלשה חלקים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| או בלתי שני אלו מאי זה ממיני המוסיף חלקים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה הדרך הגלוי אל מציאות זה הוא בסדור המספרים הטבעיים בטור יהיה ראש מדרגותיו המספר אשר הוא מספר החלקים הנוספים במין המכוון להוצאת הדומים לו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ותנשא המדרגה הראשונה על השנית ויונח מה שיתקבץ תחת השנית | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד נניח המדרגה הראשונה גם כן עם השלישית תחת השלישית | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תונח הראשונה עם הרביעית תחת הרביעית | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונעשה זה תמיד עד תכלית המונח מן המספרים הטבעיים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד תקיש בין כל מדרגה ממנה והדומה לה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכבר הנחתי לזה משל מהמוסיף ארבעה כדי שיבחנהו החושב ויתישר בו בזולתו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ודע שמהמוסיף חלקים מה שיכנס במין אחד מהמוסיף חלקים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו ו' וי' כי הם בהצטרף המוסיף הארבעה שתויות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והם גם כן בהצטרף המוסיף שני שלישים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וממנו גם כן מה שיכנס בזולת סוגו ר"ל במוסיף חלק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו ח' וי"ב שהם בהצטרף המוסיף הארבעה שמיניות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והם גם כן בצרוף המוסיף חלק ר"ל חצי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תרצה במין מה להכיר הצרופים הגמורים אשר לא יכנסו בזולת מינם לא יספיק בזה מה שטרח בו אלכנדי מהניח מלאכה מיוחדת לכל מין לפי שהוא השתדל במה שלא נוכל עד תכליתו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אבל המלאכה הכוללת לכל מה שהובא מזה היא שנדלג ממדרגות המספרים הטבעיים כל מדרגה שיהיה מספרה משותף למנין החלקים הנוספים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ור"ל בהשתתפות שיהיה אחד משני המספרים חלק לאחר ולא יהיה זה אלא אם להם חלק משותף בלתי האחד ימנם יחד וזה כבר עבר ביאורו בזכירת המספר הזוג וזכירת המספר הנפרד המורכב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ומכאן תבוקש התחבולה בהכרת המדרגות אשר נצטרך הנה לדלגם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והיה כמו שאמרנו המדרגות אשר הם שיהיה מנין החלקים המוסיפים מכל אחד ממספריהם ולמנין החלקים חלק משותף להם בלתי האחד ימנה אותם יחד כי צירופי אלו ואם לא יכנסו בבלתי סוגם ר"ל במוסיף חלק הנה יכנסו במין בלתי מינם מהמוסיף חלקים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה כאשר תדלג אלו המדרגות המשותפות למנין החלקים הנה כבר השארת המדרגות אשר לא יכנסו צרופיהם בבלתי מינם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והם הגמורים ממדרגות המוסיף חלקים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכבר תארנו משל זה שאמרנו בזאת הצורה עם רושם השותפים הנזכרים בה |
| שתוף | שתוף | שתוף | שתוף | שתוף | שתוף | שתוף | שתוף | שתוף | שתוף | שתוף | שתוף | |||||||||||||
| כח | כז | כו | כה | כד | כג | כב | כא | כ | יט | יח | יז | יו | טו | יד | יג | יב | יא | י | ט | ח | ז | ו | ה | ד |
| לב | לא | ל | כט | כח | כז | כו | כה | כד | כג | כב | כא | כ | יט | יח | יז | יו | טו | יד | יג | יב | יא | י | ט |
Compounded Ratios |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Multiple Superparticular Ratio |
הדבור ביחס הרביעי והוא יחס הכפל המוסיף חלק | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| אמר מניח הספר אמנם המינים הפשוטים ממיני הכמה המצטרף הנה הם מיני שלשת היחסים אשר קדם המאמר עליהם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי הם כהתחלות וכפנות לשני המינים הראשונים ר"ל מין הכפל המוסיף חלק מן הכפלים המוסיף חלקים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אחר ששני אלו המינים כבר יתילדו מהמינים הראשונים ויותכו אליהם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולפשוט גם כן צד אחר ייוחד בו מין הכפל ומין המוסיף חלק בלתי מין המוסיף חלקים והוא בשיאמר שהוא יתדמה הראשון ממנו לשני | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ויאמר לו פשוט לפי שעניינו אמנם הוא של שני המספרים המצטרפים בכל אחד מאותם שני המינים התדמות בעצמם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אם התדמות שני המספרים במין הכפל באשר הגדול מחובר מהקטן | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם התדמות שני המספרים במין המוסיף חלק כאשר הם יחד מחוברים מפנה אחת והוא המותר אשר ביניהם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולזה הקישו הראשונים הדברים הטבעיי החבור בשני אלו המינים לבד ולא יקישו אותם במין השלישי אשר יאמר לו שהוא פשוט גם כן ר"ל במין המוסיף חלקים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם שני המינים המורכבים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה אחד מהם מורכב מבעל הכפלים ומהמוסיף חלק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם האחר מורכב מבעל הכפלים ומהמוסיף חלקים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולפי שהחלק קודם בטבע על החלקים היה הכפל המוסיף חלק קודם על הכפל המוסיף חלקים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולזה יחוייב להקדים המאמר על הכפל המוסיף חלק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונאמ' שזה היחס יראה משני מספרים אחד מהם יותר לאחד מדמיון אחד או דמיונים הרבה וכמו חלק ממנו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו החמשה כאשר יוקשו אל שנים כי החמשה שני דמיוני שנים וכמו חציים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכבר יקח זה המין הדמוי משני המינים אשר הוא מורכב מהם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אמנם מה שיקח מיחס הכפל הנה ברבות כפלו והחלק אחד בלתי מומר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו הכפל השניי המוסיף חצי והכפל השלישיי המוסיף חצי והכפל הרביעיי המוסיף חצי וכן תמיד ברבות הכפלים והחלק אחד לא יומר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם מה שנקחהו מדמיון המוסיף חלק יומרו חלקיו ולא יתרבו כפליו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו הכפל השניי המוסיף חצי והכפל השניי המוסיף שליש והכפל השניי המוסיף רביע והכפל השניי המוסיף חומש עוד כן יומרו חלקיו ולא יתרבו כפליו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכבר יתחדש לו והתרכבו מהם קבוץ שני סגולותיו כאשר יתרבו כפליו ויומרו חלקיו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו הכפל השניי המוסיף חצי והכפל השלישי המוסיף שליש והכפל הרביעיי המוסיף רביע וכן תמיד יתרבו כפליו ויומרו חלקיו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם יתחדש המין האחד לדמוי מהמוסיף חלק לבד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| באשר תסדר המספרים הטבעיים אשר התחלתם ב' בטור | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד תסדר הנפרדים הטבעיים אשר התחלתם ה' בטור | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונקיש כל מדרגה אל הדומה לה כמו שתראה בזה הדמיון בזאת הצורה צורת הדמיון שנזכרנו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ותמצא המין האחר לדמוי מהכפל לבד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כשתסדר טור באורך יהיה ראשיתו שני המספרים הפועלים ביחס הכפל המוסיף חלק והם ב' ותחתיו ה' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד תסדר תחת הה' מה שימשך לו ממדרגות הנפרד הטבעי ימשכו קצתם לקצת יורדים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ותשים אלו המדרגות יתחילו בטורים לוקחים ברחב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| יתוספו מדרגות כל טור מהם כמנין המדרגה הראשונה ממנו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד תקיש כל אחת ממדרגות זה המרובע באשר נכח לו והוא מקבילו מהטור הראשון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שאתה תמצא בזה כבר העמדת בו יחס הכפל מבלתי שיצמח החלק וזה כמו שתראה בכאן | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ויתחדש זה המין האחד ליחס משני פנותיו אשר הוא מורכב מהם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והוא אשר יתרבו כפליו ויומרו חלקיו באשר תסדר הנפרדים הטבעיים אשר התחלתם מה' בטור הנרשם באודם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולא נרצה להקיש בו אבל לשומו רושם לקחת דמיון ממנו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה שאנו נסדר טור אחד יהיה ראש מדרגותיו גם כן ה' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והמדרגה השנית כמו אשר לפניה ר"ל כמו ה' מוסף עליו מה שלמעלה ממנו ר"ל מהטור הראשון האדום אשר לפניה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והמדרגה השלישית כמו אשר לפניה ר"ל כמו י' מוסף עליו מה שהוא למעלה ממנו ר"ל המדרגה השנית מהטור האדום | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תעשה עד שיכלה אל סוף מה שהנחת מהמספרים בטור האדום |
| נט | נז | נה | נג | נא | מט | מז | מה | מג | מא | לט | לז | לה | לג | לא | כט | כז | כה | כג | כא | יט | יז | טו | יג | יא | ט | ז | ה | |
| תתקא | תתמב | תשפה | תשל | תרעז | תרכו | תקעז | תקל | תפה | תמב | תא | שסב | שכה | רצ | רנז | רכו | קצז | קע | קמה | קכב | קא | פב | סה | נ | לז | כו | יז | י | ה |
| ל | כט | כח | כז | כו | כה | כד | כג | כב | כא | כ | יט | יח | יז | יו | טו | יד | יג | יב | יא | י | ט | ח | ז | ו | ה | ד | ג |
| וכאשר הולדנו זה הטור השני כן סדרנו נכחו טור המספרים הטבעיים והתחלתו מב' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד נקיש בין מדרגותיו ובין מדרגות הטור אשר הולדנו ונעזוב הטור האדום | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ויראה בהקשתם איך יתילד המין הלוקח הדמוי משני פאותיו וזה המין השלישי ממיני הכפל המוסיף חלק ותבחנהו בצורה שעשינו והתישר בו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
Multiple Superpartient Ratio |
הדבור ביחס החמישי והוא יחס הכפלים המוסיף חלקים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| הוא כמו שאמרנו מורכב מיחס הכפל ומיחס המוסיף חלקים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולזה גם כן כבר תחלק המלאכה בהולדת זה היחס לשלשה חלקים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אם שתשתדל בם להראות סגולת המוסיף חלקים בהמרת החלקים הכפל ברבות כפליו מבלתי השתנות החלקים הנוספים או תמורתם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם שתתחכם בם להראות סגולת המוסיף חלקים בהמרת החלקים בלתי רבות הכפלים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם שיראו בם שתי הסגולות יחד הראות נמשך כמו שהוא בטבע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה המין אשר יצמחו כפליו ולא ישתנו חלקיו יתחדש כשנניח שני המספרים הראשונים הפועלים ליחס אי זה הכפל המוסיף חלקים שנרצה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכאלו נרצה יחס הכפל המוסיף שני שלישים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה נניח שני המספרים הראשונים הפועלים להם והם ג' וח' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכאשר נרצה שאר הכפלים המוסיפים שני שלישים נעזוב הקטן על ענינו ונסדר תחתיו טור באורך לוקח תחת ח' יתחילו מדרגותיו מח' יתוספו במניין אחרי המספר הקטן ר"ל שיתוספו ג' ג' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד נקיש כלם במדרגה הראשונה ר"ל במספר הקטן אשר הוא ג' כי הם יהיו אליו ביחס הכפל המוסיף אותם החלקים הראשונים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכבר התילדו הכפלים כפי המשכם בטבע מבלתי שיתוספו החלקים או יומרו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובזאת המלאכה יתילדו איזה מן הכפלים המוסיף חלקים שתרצה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו הכפל המוסיף שלשה רביעיות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| או שלשה חמשיות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| או מה שתרצה מזה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והתישר בו במשל אשר המשלתיו לך הנה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם איך יתילד המין אשר יומרו חלקיו ויעתקו ברבות המספר אשר ממנו יגזרו שמותיהם העתק נמשך בטבע מבלתי שיומר מנין כפליו זה גם כן תחלק מלאכתו לשני חלקים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| לפי שאנו אם שנלך בזה אל תולדת המינים הראשונים מהמוסיף חלקים כפי המשכם בטבע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו המוסיף שלשה חלקים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד המוסיף ארבעה חלקים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד מה שילווה לזה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם שנלך אל הולדת מין אחת מהם בהוצאת כל יחס יפל תחת שם אותו המין | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו המוסיף שני חלקים לבד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והמוסיף שלשה חלקים לבד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אבל המלאכה אשר תביא אל המינים הראשונים מהמוסיף חלקים כפי המשכם בטבע מבלתי שירבו הכפלים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אמנם היא כשנסדר המספרים הטבעיים שהתחלתם ג' בטור | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ותניח תחת ג' המספר אשר יפעל עמם תחלת יחס המוסיף חלקים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד נשלים הטור הגדול במדרגות יתוספו ג' ג' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| פעם א' אם רצינו שיהיה הכפל שניי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם רצינו אותו שלישיי כזה שני פעמים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם רצינו אותו רביעיי שלשה פעמים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן מה שאחר זה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד נקיש כל מדרגה באשר למעלה ממנה ר"ל הדומה לה מהטור הראשון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה יראה לנו יחס הכפל המוסיף חלקים כפי התילד המינים הראשונים מהמוסיף חלק בטבע בלתי שיתרבו הכפלים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה כפי מה שתראה בזה המשל ותבחנהו ותמצאהו בע"ה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם איך יתילדו מיני הכפלים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המוסיפים שני חלקים דרך משל | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| או מיני הכפל המוסיף שלשה חלקים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| או זולת אלו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| מבלתי שיתרבו הכפלים ולא ישתנה מנין החלקים אבל ישתנה בצמיחת הטבעית המנין אשר הם נגזרים ממנו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה כשנוציא המתדמים בכפלם תחת המוסיף אותם החלקים כמו שכבר גלינו בשער המוסיף חלקים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד ינשא המספר הקטן מכל מדרגה על הגדול אשר נכחו אם תרצה שיהיה הכפל השניי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תרצה שיהיה שלישיי תשא כפל הקטן | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תרצה אותו רבעיו תשא שלשה כפלי הקטן | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן מה שאחר זה ככל מדרגות הטור הגדול | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד נקיש כל מדרגה בנכחית לה שאתה תמצא המוסיף אותם החלקים בלתי שיוסיפו הכפלים או יעתקו מהמנין אשר תרצה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובחן מה שזכרתיו לך בשני הרשמים לפניך בשער המוסיף חלקים והם טור מיני המוסיף חלקים לא יומר מנינם ותתישר מהם להולדת זה המין מהכפל המוסיף חלקים כאשר תטיב להתבונן במה שזכרנוהו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם המין השלישי מהחלוקה הראשונה הנזכרת בפתיחת זה הספר והוא איך יתילדו המינים אשר יצמחו כפליהם וישתנו חלקיהם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה לפי שהשתנות החלקים אם שיהיה בקיום מנינם והתרבות הגעותיהם התרבות טבעי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם שיהיה בהתרבות מנינם והתרבות הגעותיהם יחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| יחוייב שתחלק המלאכה בהוצאת זה לשני חלקים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אבל יתילד המין אשר יתקיים בו מניין החלקים וישתנו הגעותיהם בהתרבות הטבעיי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תהיה מלאכתו כאשר נוציא שני טורים מיחס המוסיף חלקים מנינם ר"ל מנין החלקים הנוספים אשר תרצה לחייבו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ותתישר בזה בשני הטורים הנרשמים בדומה זה בשאר המוסיף חלקיים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והם שני הטורים אשר הוכר בם השתוף מהבלתי שתוף | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד ינשא על כל מדרגה מן המספרים הגדולים מה שבדומה לה מן המדרגות המספרים הקטנים מוכה במנין הגעות החלקים אל האחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכאשר עשית זה בכל מדרגות הטור הגדול הקשת בין כל מדרגה ממנו ודומה לה ממדרגות הטור הקטן ר"ל בעל המספרים הקטנים שאתה תמצא כל זה ביחס הכפל המוסיף חלקים הגעתם הוא מנין הכפלים ר"ל שמנין החלקים לא יומרו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם החלק השני מזה המין והוא אשר יתרבו בו הכפלים ומנין החלקים והגעתם יחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה מלאכת הולדתם בהנחת המספרים הטבעיים אשר התחלתם ג' בטור | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד תניח תחת ג' ח' ותשלים הטור השני אשר התחלתו ח' בתוספת הנפרדים הטבעיים אשר התחלתם ז' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ותוסיף ז' על ח' ותעמיד מה שהתקבץ במדרגה השנית וזה ט"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד תוסיף על ט"ו ט' ותעמיד מה שהתקבץ ברביעית | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ותעשה כמו זה בשאר מדרגות הטור השני עד שתגיע לנכח סוף מה שהנחת מן המספרים הטבעיים בטור הראשון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד נקיש כל מדרגה בדומה לה כמו שתראה בשני אלו הטורים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ויראו לך בע"ה מיני הכפל המוסיף חלקים אשר התרבו כפליהם ומנין חלקיהם והגעות חלקיהם כמו כן התרבות טבעי נמשך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה כבר דברנו על היחסים החמש וההקשות המספריות העשרה ואמרנו בם מאמר מופלג כפי הצורך מבלתי רבוי ואריכות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
Producing the Ratios from Equality |
המאמר על התחבולה בהולדת היחסים מן השווי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכבר ימשך למה שקדם מדברינו שנביא הצד בהולדת אלו היחסים החמש מן השווי בתחבולה שרשית קיימת בלתי מבולבלת תדמה הענינים הטבעיים בכללותה ואמתת פירושה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והפרי במה שנזכור מזה יקר ונכבד מאד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכל שכן אצל מי שבחן מה שאעיין בו מדמיון הידיעה לטוב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי הטוב אצל הנפש מוגבל וידוע המשלו וחברו ונמשכו לו הנפשות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ותדע שהוא ראשון לכל מה שיתפרד מעצמו מתמיד ההרגש בכל מה שיתילד מטבעו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ושהרע בגנותו בלתי בעל תכלית ולא מגיע אל גבול ולא יסתעף משרש ולא נמשך על פירוש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אמנם הוא שנוי הטבע אשר הוא טוב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה היציאה מטבעם הראשון להם יציאה מתחלפת לא תכלל בגבול ולא תתקיים בסדר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולזה לא יאחזהו כח מדבר אחיזה מושכלת אבל יכירהו בהתחלפו לטבע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דרך משל אומר כחלודה במראה הספירית | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והעול בנפש הישרה שהם בלתי מושגים בדרך הגדר וההגבלה אחר שאין עצמיות להם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם יודעו בהשתנות העצם אשר נקבעו ונטבעו בו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אבל אם אנחנו מצאנו לאלו היחסים החמש דרכים מוגבלים בהם יתילדו מהשווי ויותכו בהפוכם אל השווי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והיה השווי בלי ספק טוב וחשיבות היו היחסים גם כן משותפים לאותו החשיבות ונקשרים באותו הטוב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אחר שהיה התילדם ממנו מסודר נמשך על גבול שומר לכח שרשם אשר ממנו יתילדו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו שישמור הגרגיר כח האילן אחר שכבר ישוב גם כן הגרגיר אילן | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן אלו היחסים יתילדו מן השווי וישובו כמו כן אל השווי אבל לא יהיה זה בהזדמן אבל כבר נצטרך בו אל מלאכה וחבור כמו שנצטרך בענין הזרע והאילן על עבודת הקרקע קודם שיצא כי אי אפשר להגיע אל תכלית דרוש מן הדרושים דרוש מדעי היה או דרוש מעשי אם לא בהעזר מדברים מחוץ יהיה להם קצת התדמות לאותו הדרוש ויחוברו על סדר מה מוגבל נגיע עם ההדרכה עליהם אל הדרוש ולזה שם אקלידס החבור אחד מהדברים אשר מהם תהיה הידיעה ובהם נגיע אל המעשה ולזה גם כן נניח אנחנו בהולדת כל אחד מאלו היחסים שלשה מספרים בשלשה מדרגות להגיע בם אל ההתיחסות כי ההתיחס בפחות מה שיהיה הוא בשלשה גבולים ואמנם נעזרנו בהתיחסות מהדברים אשר מחוץ למה שבו מהתדמות היחס ולפי שאנו כבר אמרנו שהדברים אשר נעזר בם מחוץ עם החקירה מהדרוש ראוי שיהיו מתדמים לדרוש ויקראו אלו שלשת המדרגות ראשונה ושניה ושלישית ותדבק כל מדרגה מהן בגבול לא תעברהו אם הגבול במדרגה הראשונה הוא שנניח תחתיה לעולם כמו המספר אשר בה ואמנם הגבול במדרגה השנית הוא שנניח תחתיה לעולם כמו המספר אשר בה וכמו המספר אשר במדרגה הראשונה ואמנם המדרגה השלישית הוא שנניח תחתיה כמו המספר אשר בה וכמו המספר אשר במדרגה הראשונה וכפל אשר במדרגה השנית זה הוא מה שהוא כולל במלאכה אשר בה יתילד כל אחד מאלו היחסים ואמנם מה שהוא מיוחד בם לכל אחד מאלו היחסים כי אשר תיחד המלאכה בהולדת יחס הכפל השניי שיהיו המספרים הראשוני' המונחים במדרגות הג' אשר מהם יתילד זה היחס מספרים שוים שומרים השווי בהצטרפם וכשנשמור בם התנאי הכולל הנזכר יראו אלינו מספרים ביחס הכפל השניי והיה המין הראשון ממיני זה זה היחס ואם שמנו זה המין הנראה מונח והוספנו בו התנאי הכולל אל הנזכר ר"ל העשות הגבולים השלשה במדרגות השלשה יראה לנו המין השני ממיני הכפל והוא הכפל השלישיי ואם שמנוהו גם כן מונח והשבט בו במעשה הראשון יראה לנו המין השלישי והוא הכפל הרביעיי וכפי זה הדרך לא נסור מזה המעשה יראו לנו מיני הכפל ראשון ראשון כפי המשכם בטבע ובחן זה בשני טורים אלו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וקחם לשרש למה שימשך להם ואמנם אשר הוא מיוחד בזאת המלאכה להוליד יחס המוסיף חלק הנה הוא שיהיו המספרים המונחים אשר מהם תרצה להוליד המוסיף חלק מתיחס ביחס הכפל ויהיה הגדול מהם במקום הראשון והקטן מהם במקום השלישי עוד תעשה בם הסבוב הכולל אשר זכרנו כי ימשך לזה שיראו אלינו מיני המוסיף חלק כפי המשכם בטבע ר"ל שהמספרים המונחים אם היו עליהם תחלת מיני הכפל ר"ל השניי יראו מהם מיני המוסיף חלק ר"ל המוסיף חצי ואם היו על היחס השני ממיני הכפל ר"ל השלישיי יראה לנו גם כן השני מהמוסיפי חלק ר"ל המוסיף שליש וכמו כן מה שאחר זה ותבחנהו מזאת הצורה ואשר ייחד תולדת המוסיף חלקים ט טו כה הוא שיהיו המספרים המונחים ט כד סד מתיחסי' ביחס המוסיף חלק ויהיה הגדול מהם במקום הראשון והקטן מהם במקום השלישי עוד נעשה מוסיף חלק מוסיף חלקים בם הסבוב הכולל הנזכר כי הוא יראה לנו המספרים על יחס מין מהמוסיף חלקים מסודרים הקרוב מהטבע בסדור המוסיף חלק המונח וזה יהיה כן : ואשר ייחד הולדת יחס הכפל מוסיף חלק כפל מוסיף חלק המוסיף חלק הוא שיהיו המספרים המונחים מתיחסים ביחס המוסיף חלק גם כן אלא שהגדול מהם יהיה במקום השלישי והקטן מהם במקום הראשון ויראה לנו הסבוב הכולל המותנה מין מהכפל המוסיף חלק הוא בקרוב מהטבע ר"ל מהתחלת מיני הכפל המוסיף חלק בכמו מדרגת המין המוסיף חלק המונח ויהי כן ואשר ייוחס הולדת יחס הכפל המוסיף חלקים ד ו ט הוא שיהיו המספרים המונחים ; ד י כה מתיחסים יחס המוסיף חלקים ויהיה הקטן מהם במקום הראשון והגדול מהם מוסיף חלקים כפל מוסיף חלקים במקום השלישי וכאשר נסובב בהם המעשה אשר הוא כולל לכל היחסים יראה לנו מן הכפלים המוסיף חלקי' מסודרי' בסוגו כסדר המוסיף חלקים המונח כסוגו וזה כמו שתראה הנה ט טו כה הנה כבר התבאר שכל אלו היחסים ט כד סד שהמשלנו אותם יתילדו מהטור השוה המדרגות השלשה והוא טור האחדים הנכתבים באודם ואלו הנחנו כמו כן באותו הטור בלתי האחדים רק שיהיו מספרים שוים ועשינו בם מה שעשינו אותו בדרכים אשר תארנו יחוייב שימשך לזה כל מה שנראה לנו מהענינים המתחייבים בהולדת אלו היחסים אלא שאשר נראה מזה אינו עלתו אבל עלתו שווי האחדים וכבר יתכן לנו שנדע כי מיני המוסיף חלקים אשר יתילדו בזאת המלאכה אמנם הם המינים הראשונים מאלו היחסים ורצוני במיני הראשונים מאלו מהם אשר יהיו הגעות חלקיהם יותר מוסיפים ממנין חלקיהם באחד כמו המוסיף שני שלישיים והמוסיף שלשה רבעיות והמוסיף ארבעה חומשים והמוסיף חמשה שתויות ומה שיעבור זה ממה שידמהו ואמנם שאר מיני המוסיף חלקים כמו המוסיף שני חומשים והמוסיף שלשה חומשים או שלשה שבעיות או מה שהוא דומה זה הנה המלאכה בהולדתם אמנם היא כמו שהגדנו עליה בשאר המוסיף חלקים וכן גם כן ראוי לנו כשנרצה מיני הכפל המוסיף חלקים בזאת המלאכה שיהיו המינים המונחים מהמוסיף חלקים להוליד זה הם המינים הראשונים אשר זכרנו שהגעת חלקיהם תוסיף על מנין חלקיהם אחד וזה בלבד מאמר מספיק בהוראה על אי זה מיני הכפל המוסיף חלק ואי זה מיני הכפל המוסיף חלקים יתילדו בבאור הנזכר וששאר מיני סוגי אלו היחסים יתרחקו מדרך סוגיהם ולזה אולי לא יראו אלא במלאכה היא יותר רבת ההרכבה מזאת אשר השלמנו לזכרה עתה והאל היודע וזה לך ציור חלוקת הכמה המצטרף והיתרון והוא נחלק לשני חלקים השווי באחד אל אחד ומאה אל מאה הכמה המצט[רף] יחלק הקטן והוא ה' חלקי' הגדול והוא ה' חלקים א א ק ק לשני חלקים הנה זה יישירך תחת בעל הכפלים המוסיף חלקים תחת בעל הכפלים המוסיף חלק תחת המוסיף חלקים תחת המוסיף חלק תחת בעל הכפלים בעל הכפלים המוסיף חלקים בעל הכפלים המוסיף חלק המוסיף חלקים המוסיף חלק בעל הכפלים כד ח ט ד א סד פה טו ו ב השם מספיק בסוף המאמר הראשון מספר הארתמאיטיקא כפי מה שתיארו ניקמאכוש אל גהר שיני הפתאגורי ותקנו באנדלס אבו סלימאן רביע בן יחיי אסקף אלכידה והעזר בעיון וההגיה בו והאל ברחמיו יישירך להבין ולמצוא חפציך בו המועילים לאחריתך אמן נשלם המאמר הראשון מספר הארתמאטיקא והתהלה לאל יבא אחריו המאמר השני בג"ה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
Book Two |
המאמר השני מספר הארתמאטיקא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Reducing the Ratios to Equality |
המאמר הראשון ממנו בהתכת היחסים אל השווי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| יאמ' שהפנה והיסוד הוא הדבר אשר הורכב ממנו דבר אחד ויתך אליו דבר אחר כמו אותיות האלפא ביתא כי יאמר בם שהן פנות לכתבים המונחים המחוברים מהם הנתכים אליהם וכן הנעמות הן פנות לכל הלחנים אחר שהיו הלחנים מחוברים מהם נתכים אליהם וכן גם כן אלו היסודות הארבעה ר"ל האש והאויר והמים והארץ יאמר שהם פנות ופשוטים לכל הנופלים תחת ההויה וההפסד אחר שחבורם מהם והתכתם אליהם ואמנם הקדמנו אלו ההקדמות להראות שהשווי פנה לכמות המצטרף ושהוא ממנו צמח ואליו יותך ואמנם הכמה הנפרד הנה פנתו הראשונה וכן התילד ואיפשר להוסיף בו אל מה שאין תכלית לו הוא האחד ואמנם מה שיתילד מהשווי ויותך אליו הנה הוא כולל לכל הצרופים ונביא ראיה במופת ואמתות שהשווי יפנה לכמות המצטרף אשר ממנו היה התחלת מולדתו ובו צמח בהתוספו ואליו יכלה כאשר חוסר ונתך ומהתחבולה הכוללת לזה הוא שתדע שכאשר תניח שלשה מספרים יחס הראשון מהם אל השני כיחס השני אל השלישי באי זה מהמינים היה מהיחסים החמש אשר זכרנום במאמר הראשון הנה אלו מספרים שלשה אם הונחו כן היה יחס גם כן השלישי אל השני כיחס השני אל הראשון והראשון הוא הקטן והשני הוא האמצעי והשלישי הוא הגדול ואם רצה רוצה להשיבם אל השווי הנה ישליך מהאמצעי כמו הקטן עוד ישליך מהגדול כמו מה שישאר מהאמצעי וכמו מהאמצעי ואם השתוו המספרים השלשה הנה כבר היה מה שרצינו ואם לא הנה כבר יצאו ממין צרופם ושבו אל מין אחר הוא יותר קודם בטבע ממין היחס אשר היו ממנו ראשונה עוד תעשה בו כמו המעשה הראשון ואם השתוו הנה מצאנו מבוקשנו ואם לא הנה כבר יצאו מאותו המין גם כן אל מין יותר רחוק מן הראשון בטבע ולא תסור מעשות כן תמיד עד שישתוו ומשל זה נניח השווי בטור בעל שלשה מדרגות ונסדר אליו טור שני מתיחס ביחס הכפל עוד נסדר בם טור שלישי על יחס המוסיף חלק ונמשיך בזה טור רביעי על יחס המוסיף חלקים עוד נניח בטור החמשי מספרים א א א מתיחסים ביחס הכפל המוסיף א ב ד חלק ונחתום הצורה בטור ד ו ט ששי מתיחס המדרגות ט טו כה ביחס הכפל המוסיף חלקים ד [י] כה ט כד סד כפי מה שבצורה הנה זה הטור שנכוין אליו מאלו הטורים ועשינו בו מלאכת ההתכה אשר זכרנוה נשיבהו בזה אל יחס טור הוא יותר קרוב ממנו אל השווי ר"ל שהוא יותר קרוב אל טור הגבולים השוים עוד לא נסור מעשות זה בו כמו עד שישובו מדרגותיו אל יחס טור השווי עצמו ויספיק לך מה שאמרנו מלהרבות ההמשלים וההכפלה הארוכה אשר לא יאותו למי שידע שהשלמת המלאכות לא תהיה ברבוי ההמשלים אבל בתקון הגבולים וכבר התבאר כי המעשה אשר הקדמנוהו להולדת היחסים במאמר הראשון הוא בעצמו יתהפך הנה כאשר נשתדל להתיך אותם היחסים אל השווי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Setting Up Series of Superparticulars |
הדבור בסדור גבולי כל יחס מונח שני המספרים מיחסי המוסיף חלק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וראוי אחר שכבר נצטרך הרבה אל שנניח מספרים נמשכים מתיחסים מהמוסיף חצי או המוסיף שליש או המוסיף רביע או זולת מה מהמוסיף חלק אחר שנביא הוצאה מלאכותית לזה ותחבולה תאמת לנו הסברא בה כדי שתהיה דרישתנו למה שנדרשנו מזה מבלתי בלבול | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונאמר שיחס המוסיף חצי הוא ראש יחסי המוסיף חלק כמו שנגלה במה שקדם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ושתחלת שני מספרים פועלים יחס המוסיף חצי הם שנים ושלשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכאשר נרצה לבאר איך נוציא הגבולים הנלוים בזה היחס נסדר מדרגות הכפל השניי בטור והם מדרגות זוג הזוג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונשליך המדרגה הראשונה לפי שהיא האחד ואין חצי לו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד נניח תחת כל מדרגה המספר הנכפל הפועל עמה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי בהניחנו תחת כל מדרגה אותה המדרגה ושלפניה אשר היא חציה הנה שמנו יחס הדמיון וחצי ר"ל יחס המוסיף חצי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ויתחדש טור שני חסר מהטור הראשון מדרגה והיא אשר השלכנו בנוכח האחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד נשוב ונשליך כמו כן המדרגה הראשונה מזה הטור השני לפי שהוא שלשה ואין חצי לו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונניח תחת כל אחת ממדרגותיו הנשארות המספר הפועל עמו יחס המוסיף חצי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ויתחדש טור שלישי חוסר מהטור השני מדרגה והיא נגד השלשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד נשוב גם כן ונשליך המדרגה הראשונה מזה הטור השלישי לפי שהוא תשעה ואין לו חצי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונניח תחת כל אחת ממדרגותיו המספר הפועל עמו יחס המוסיף חצי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה יתחדש טור רביעי חוסר מהטור השלישי מדרגה והיא אשר השלכנו כנגד התשעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכמו כן נחדש טור חמישי וששי ולמעלה מזה כמו שתראה בזאת הצורה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכבר התבאר שתחלת מה שימצא יחס המוסיף חצי בשני גבולים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד התבאר בזאת הצורה איך נמצאהו בשלשה גבולים עוד בארבעה עוד בחמשה עוד בששה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והמלאכה שנעשית בה זאת הצורה כבר יתוספו בה הגבולים בזה היחס אל מה שאין תכלית לו ולא יבצר מהם גבול בשום כנוי שלא תראה בו התחבולה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם רצינו להוליד מספרים כפי זה המשל ביחס המוסיף חלק השלישי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נסדר מה שבטור הכפל השלישי הנמשך על יחס דמיון א'ג'ט' כז פא רמג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונסדר טורים תחת זה הטור נעמיד תחת כל מספר כמהו וכמו שלישיתו מה שאפשר בו זה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונצייר צורתו כמו מה שציירנו הראשונה אשר לפניה ויראו בה מדרגות הגבולים ביחס המוסיף שליש מבלתי שיחטא בגבול מהם כמו שתראה בזאת הצורה אשר לפניך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכמו כן כאשר נרצה ביחס המוסיף חלק הרביעיי הנמשך על יחס דמיון א'ד' י"ו ס"ו וכמו כן מה שילוה לזה מין ממיני המוסיף חלק | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם היסוד במלאכת זאת הצורה שנשים מדרגות הטור הראשון נמשכים על יחס הכפל אשר הוא נקרא ליחס הדרוש הגבולים מיחסי המוסיף חלק ר"ל הכפל אשר ממנו מעמד אותו החלק | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכאשר עשית אותו מזאת הצורה במלאכת הנזכרת הוא גלוי מבואר שהמספרים אשר יפלו בזויות מכל צורה הם המספרים אשר בטור הראשון המונח בצורה אשר תמשך לה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובכאן עניינים אחרים נכבדים ונפלאים תעמוד עליהם עם טוב בחינתך בהם ברצון השם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| על גלוי אי זה יחס מיחסי המוסיף חלק הנמצא בחבור ר"ל נמצא בחבוריהם יחס מונח | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ופי' איזה יחסים הם אשר יתחייב מחבורם יחס איזה כפל שתדרוש בחבור יחס מונח מיחסי בעל הכפלים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אמנם המין הראשון מבעל הכפלים והוא השניי הנה הוא יתחבר ויתילד באמצעות שני המינים הראשונים ממיני המוסיף חלק והם המוסיף חצי והמוסיף שליש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| משל זה שהארבעה כמו השלשה וכמו שלישיתם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והשלשה כמו השנים וכמו חציו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנה הארבעה אצל השנים ביחס הכפל השניי כמו שתראה בזאת הצורה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובהפך זה המאמר יתבאר שהכפל השניי יותך אל המוסיף חצי והמוסיף שליש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| משל זה שאם לקחנו שני מספרים ביחס הכפל השניי כמו הששה והשלשה שאנו נמצא ביניהם אמצעי מן המספר יותך אצלו יחס שני הקצוות המונחים מהכפל השניי על שני היחסים הנזכרים מיחסי המוסיף ואם כן יותך אליהם חלק | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והאמצעי בין הששה והשלשה הם ארבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה הששה כאשר הוקשו אל הארבעה היה המוסיף חצי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והארבעה אצל השלשה תוסיף שליש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכאשר יותך אמנם יותך אליהם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם המין השני מבעל הכפלים ר"ל הכפל השלישיי אמנם יולד מהמין הראשון המוסיף חלק ר"ל החצי והמין הראשון מבעל הכפלים ר"ל השניי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| משל זה שי"ח כמו י"ב וכמו חציו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וי"ב כפל ו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אבל י"ח אצל ו' כיחס הכפל השלישיי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכמו כן גם כן תמצאהו אלא שלא יחוייב שנשים האמצעי י"ב אשר הוא כפל ו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אבל נשים במקומו ט' אשר הוא כמו ו' וכמו חציו וכבר המשלתי לך שתי הצורות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובהפך זה המאמר יתבאר שהכפל השלישי כאשר יותך אמנם יותך אל הכפל השניי והמוסיף חצי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובחן זה באי זה משני מספרים תרצה אם תניחם ביחס הכפל השלישיי ותמצאהו כן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם אם יחובר הכפל השלישיי והוא והמין השני מהמוסיף חלק יתילד מזה הכפל הרביעיי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכאשר יותך הכפל הרביעיי הנה הוא יותך אל הכפל השלישיי ואל המוסיף חלק השניי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכלל המאמר שכל מין ממיני הכפל כאשר הורכב עם דומה לו במדרגה ממיני המוסיף חלק הנה יתחבר מהם המין אשר ילוה אליו בקרוב שבמדרגות אל יחס ממיני הכפל וממיני המוסיף חלק | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| זהו כלל המאמר בכמה המצטרף על כל צדי צירופיו עם תכלית מה שאיפשר מהשמירה בהשלמת הענינים עם קצור המאמר במה שאי אפשר למתלמדים בלעדיו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Absolute Quantity |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Numbers as Geometric Shapes |
הדבור בתואר המספרים הנפרדים המשותפים בכחם לתמונות המידותיות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ותחלת זה הדבור בתמוניות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אמנם עתה הנה אנחנו זוכרים מה שנשאר מהדברים המתחייבים לכמה הנפרד ממה שיצטרך לחקירה יותר חזקה מכל מה שדברנו עליו במאמר הראשון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי כאשר אנחנו רוצים לזכרו הנה הוא דבר נצטרך אליו לקחת ממנו ראיה על זולתו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והחכמים היו משבחים מאד לפרש קצת החכמות בקצת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ומהדברים אשר ראוי להקדים בבאורם שנאמר כי מהמספרים מה שהוא דומה לקוים בסדרם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ומהם מה שהוא דומה לשטח | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ומהם מה שהוא דומה למעוקב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ומהם מה שהוא דומה לכדור | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ומהם מה שהוא דומה ללבנה בחסרון הגובה מהאורך והרחב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ומהם מה שהוא דומה לעמוד בחסרון האורך והרחב מהגובה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ומהם מה שהוא דומה לקשת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכמו כן לכל אחד מהדברים אשר להנדסה ר"ל המדות יש דמיון לאותם התמונות במספרים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי ההנדסה לאיכות יותר דבקה מאשר לכמות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ותעיין מה שזכרנו מקדימת המספר למדות בפתיחת המספר כי שם שמנו אליו לב ודברנו בו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וקודם שנדבר על דמיון אלו הגדולים אשר זכרנום מהמספרים נאמר שהוראת אותיות האלפא ביתא על מה שיורו עליו מן המספרים הנרשמים בם והם הרשמים אשר אנו רואים שיקראום האנשים חשבון הכללים אינו בטבע להם ולא בדין להם כך אבל הם מורים בהסכמה ובהנחה ממנו לא זולתו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם המורים בטבעם הנה הם כמו הנראים לחוש והוא שאנו כאשר נרצה לרשום אחד נניח סימן אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכשנרצה לרשום שנים נניח שני סמנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן אם נרצה שלשה סמנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ותהיה צורת האחד וצורת השני וצורת השלשה וכן מה שאחר זה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכאשר הבאנו זה התנאי נאמ' שאנו נניח האחד בזאת המלאכה התחלה למספר כמדרגת הנקודה במלאכת המדות אשר היא התחלת הקו מבלתי שתהיה הנקודה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| או האחד קו או מספר הנה כמו שהנקדה כאשר נכפלה בעצמה לא יתחדש גודל אחר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שמה שאין גודל לו כאשר נכפל במה שאין גודל לו לא יתחדש גודל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| לפי שלא יהיה יש מלא יש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו כן האחד אשר אינו מספר כאשר נכפל בעצמו לא יתחדש מספר לפי שלא יתחדש יש מכפל אין | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה אם כן אמתת האחד כמו שאמרנו שהוא תחלת המספר ואינו מספר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Plane Numbers |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Number as a Line |
הדבור בצד התדמות המספר לקו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם תחלת המשכותו אמנם ימצא בשניות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד יתרבה ההמשכות כפי שעור הוספת המספרים הטבעיים וצמיחתם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה כמו שהמספר יתחדש בהנחת שני אחדים נבדלים ויהיה מהבדלם המספר כן הקו אמנם יתחדש בהנחת שתי נקודות נבדלות הנה יהיה מהבדלם הקו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והקו בעל משך אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ומה שהיה בעל שני המשכים הוא שטח | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ומה שהיה בעל שלשה המשכים הוא גשם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולבעל השלשה המשכים מה שיחדש השש פאות אשר יאמר שהן מתחייבות לכל גשם ר"ל מעלה ומטה וימין ושמאל ופנים ואחור | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובאלו השש פאות תחלק התנועה המקומית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי בהכרח שיתחייב לכל משך שתי תכליות מקבילים אם לאחד משתי התכליות מעלה ומטה ואם לאחר פנים ואחור ואם לאחר ימין ושמאל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואולי יהיה לטוען שיאמר הנה במאמר כולל שכל בעל אורך ורוחב ועומק הוא גשם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכל גשם בעל אורך ורחב ועומק | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכמו כן יאמר מה שהיה לו אורך ורחב לבד הוא שטח | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והשטח הוא מה שהיה לו אורך ורחב לבד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והקו מה שהיה לו אורך לבד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ומה שהיה לו אורך לבד הוא קו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה השטח חסר מהגשם במשך אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והקו מהשטח במשך אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנקודה חסרה מהקו במשך אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה אם כן הנקודה אין מרחק לה כלל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם היא התחלת הקו ואיננה קו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכמו כן הקו התחלת השטח ואיננו שטח | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והתחלת שני המשכים ואיננו שני המשכים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכמו כן השטח התחלת הגשם ואיננו גשם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והתחלת שלשה המשכים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה אכן גם כן המספרים הם דומים לאלו הגבולים כפי מה שאתאר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה שהמספרים הקויים הם כל מה שתניח התחלתו מהשנים עוד יתרבו באחד על סדר משך הטבע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Triangle as the Foundation of All Rectilinear Shapes |
הדבור באשר המשולש יסוד לכל השטחים ישרי הקוים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם השטחי' ישרי הקוים הראשון מהם המשולש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והוא בעל השלש זויות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והוא כשרש וכהתחלה לכל השטחים הישרים כמו המרובע והמחומש והמשושה והדומה להם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי כלם יותכו אל המשולש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה המשולש לא יותך אל בלתי תמונתו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה מבואר מאשר כשתוציא מאיזה מהתמונות הישרות הקוים שתרצה קוים ישרים מזויותיהם אל מרכזה תחלק איזו תמונה שתהיה אל המשולשים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ותמצא המשולש יחלק גם כן עצמו אל עצמו בלתי נבדל מטבעו ולא יצא מסוגו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכבר תראה זה בזאת הצורה לחוש שהמשולש המרובע והמחומש ומה שאחריהם מהתמונות הישרות הקוים כאשר הוצאנו בם ממרכזיהם אל זויותיהם הקוים אשר תארנו יותכו כלם אל משולשים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה כבר התבאר שהמשולש שרש והתחלה לכל התמונות כלן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Triangular Numbers |
הדבור במשולשים המספריים וצמיחת' וצלעותיהם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם המשולשים הנה הוספות המספרים הטבעיים אשר התחלתם האחד קצתם על קצת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה האחד באשר נרשם הנה הוא משולש בכח | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר נוסיף על האחד השנים היו השלשה ראשית המשולשים בפעל | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עוד תוסיף שלשה אשר ימשכו לשנים על המשולש הראשון בפעל ויהיה המשולש השני בפעל והוא ששה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עוד תוסיף ארבעה ויהיה המשולש השלישי בפעל והוא עשרה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד כן תתחדש תולדת המשלשים בתוספת המספרים הטבעיים קצתם אל קצתם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וממה שתבחנהו בזאת הצורה שהמספרים המשולשים יתילדו מחבור המספרים הטבעיים קצתם על קצת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו ג' שתשא חבור ב' וא' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| א' ג' ו' י' ט"ו כ"א וכו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם התילד צלעות אלו המשולשים הוא כפי התילד המספרים הטבעיים על המשכם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה יהיה צלע הראשון כמו האחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וצלע האחרון בפעל ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וצלע השני בפעל ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וצלע השלישי בפעל ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובזה הצד מהתילד המספרים הטבעיים יתילד כל צלע מצלעות המשולשים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה כאשר נתחיל להניח האחד תחלה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד יתילד כל מספר מהמספרים הטבעיים בפני עצמו בטורים ימשכו קצתם לקצת תחת האחד כפי מה שתראה מצוייר בזאת הצורה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשולש הראשון בכח אחד וצלעו אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והמשולש הראשון בפעל שלשה וצלעו השני' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והמשלש השני בפועל ששה וצלעו שלשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והמשלש השלישי בפעל עשרה וצלעו ארבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והמשלש הרביעי בפעל ט"ו וצלעו חמשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וממה שראוי שתבחנהו באלו המספרים המשולשים שכל משולש מהם יקיף מהמשלשים המדותיים במניין שוה למספר המרובע הקודם ר"ל במדרגה אחת וכן תמיד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Square Numbers |
הדבור במרובעים המספריים וצלעותיהם והתילדם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם התמונות המרובעות הישרות לא יתילדו כמו שיתילדו המשולשות מן השלשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה שהן בעלות ארבע צלעות וארבע זויות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו ד' ט' י"ו כ"ה ל"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ורשמי אלו המספרים על הרבוע והשווי יהיה כפי זה המשל ר"ל המצוייר בסוף זה השער והיא התמונה אשר עליה יהיה המרובעים השוים תמיד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ומבואר נגלה מהדמיון המצוייר למטה שצלעות המרובעים המספריים כפי המשכם יתוספו כפי שרש צמיחת המספרים הטבעיים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי צלע הראשון בכח אשר הוא האחד אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וצלע הראשון בפעל ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וצלע השני בפעל ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וצלע השלישי בפעל ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן צמיחתם תמיד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכבר אמרנו במאמר הראשון איך יתילדו המספרים השוי הצלעות למה שקרה שם זכרו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם מחוייב להשיב המאמר עליו הנה אחר שהוא מקום זכרו המיוחד בו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונאמר שצמיחת אלו המרובעים מהוספת הנפרדים הטבעיים קצתם על קצת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אחר שהתחלתם האחד אשר הוא נפרד בכח ומרובע בכח | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי השלשה אשר הם נפרד ראשון כאשר נוספו על האחד היה הגעת זה ארבעה והוא המרובע הראשון בפעל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכאשר נוסף על המרובע הראשון בפעל הנפרד השני אשר הוא חמשה היה הגעת זה תשעה והוא המרובע השני בפעל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולפי שאנו כבר זכרנו זה פעם אחת אין צורך לנו להאריך ביותר מאשר נאמר שהולדת המרובעים השוי הצלעות אמנם תהיה בתוספת הנפרדים הטבעיים קצתם על קצת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכל צלע מצלעות כל מרובע מהם הוא שרש אותו המרובע ר"ל כאשר ימנה בשעורי מה שבו מהאחדים היה כללו הגעת אותו המרובע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכאשר הונחו שרשי אלו המרובעים ילוו קצתם לקצת היו על סדר המספרים הטבעיים ימשכו קצתם לקצת וכלל זה המאמר על זה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה צורת המרובעים אשר יעדנו להביאה בסוף הדברים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המרובע הראשון בכח הוא האחד הנרשם בשחרות בזויות העליונה מצד הימין והוא הנרשם עליו א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והמרובע הראשון בפעל הוא המתקבץ מזה האחד ומשלשת האחדים האדומים אשר ילוו עליהם על תכונת תמונת הרושם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והמרובע השני הוא המתקבץ מזה המרובע הראשון בפועל ומחמשת אחדים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והמרובע השלישי בפעל הוא המתקבץ מזה המרובע השני בפעל ומשבעה האחדים האדומים הנלוים עליהם על תכונת תבנית הרושם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והמרובע הרביעי בפעל הוא המתקבץ מזה המרובע השלישי בפעל ומתשעת האחדים השחורים הנלוים עליהם על תכונת תבנית הרושם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וממה שראוי לך שתבחנהו שתמונות הרושם בזאת הצורה הם הנפרדים הטבעיים כפי המשכם בסדר הטבע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Pentagonal Numbers |
הדבור במחומשים המספרים והתילדם וצלעותיהם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם המספר המחומש ר"ל כלל המחומשים המספרים אין צמיחתם בצמיחת המשלש והמרובע כי המחומש לו חמשה צלעות וחמשה זויות כמו א' ה' י"ב כ"ב ל"ה נ"א ורשמי אלו המספרים על החמוש והשווי הם כפי מה שציירתי לך בסוף זה השער | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה צלע המחומש הראשון בפעל והוא ה' שנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וצלע המחומש השני בפעל והוא י"ב שלשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וצלע המחומש השלישי בפעל והוא כ"ב ארבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן יחוייב שיהיו צלעות אלו המחומשים נמשכים יחד על סדר המספרים הטבעיים כפי מה שהתבאר במשולש והמרובע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם התילד ממחומש הנה כבר התבאר כי אחר שהיה המחומש הראשון בפעל ה' והשני י"ב והשלישי כ"ב שאשר הוספנו אותו על המחומש הראשון אשר הוא א' בכח ארבעה עד שהיה המחומש הראשון בפעל אשר הוספנוהו על הראשון בפעל והוא ה' ז' עד שהיה י"ב וקרא השני בפעל הנה מותר השבעה אשר הוספנום לסוף על הארבעה אשר הוספנום ראשונה שלשה והמחומש השני בפעל י"ב והשלישי בפועל כ"ב ואשר הוספנו על השני בפועל עד שהיה השלישי בפעל עשרה ועשרה יותר משבעה שלשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה אם כן כבר התבאר שתולדת המחומשי' בתוספת שלשה לעולם על מה שהוספנוהו במחומש אשר לפניו וכן ימצא תמיד כי הנה כמחומש הרביעי ל"ה ול"ה יותר מכ"ב בתוספת י"ג וי"ג יותר מי' שלשה הנה אם כן כבר התבאר איך יתילדו המחומשים וגם כן כבר יתבאר מכל מה שאמרנו איך יתרכבו כמו כן המשושים והמשובעים וזולתם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה שאנו כבר בארנו שהמשלשים יתחדשו בהוספת המספרים הטבעיים קצתם על קצת והמספרים הטבעיים יתוספו באחד אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובארנו גם כן כי המרובעים יתחדשו בהוספת המספרים אשר יתוספו קצתם על קצת שלשה שלשה (?) ונאמר שהמשושים הנפרדים קצתם על קצת והנפרדים יתוספו שנים שנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובארנו שהמחומשים יתחדשו בהוספת המספרים אשר יתוספו קצתם על קצת שלשה שלשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונאמר שהמ[שו]שים יתחדשו בהוספת המספרים אשר יתוספו קצתם על קצת ארבעה ארבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והמשובעים יתחדשו בהוספת המספרים אשר יתוספו קצתם על קצת חמשה חמשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן המשומין והמתושע או מה שתרצה מזה אמנם יתחדש בזה התאר המצוייר הנה כבר המשלנו דמיונים למחומשים ולמשושים ולמשובעים ולמשומנים והבדלנו בחלוק שני גוונים המספרים אשר בם יוסיף כל מספר משוטח מהם על אשר לפניו והנחנו אותם המספרים כדמות תבניות הרושם כדי שיתבאר בם מה שזכרנו מאשר כל מין ממיני המספרי' המשוטחים בעלי הזויות השוות אמנם יתילדו תמונותיו בתוספת מספרים יעדיפו במספר אחד לא ישתנה לעולם אל בלתי תכלית אמנם המרובעים המספרים אשר יתוספו בם ר"ל מספרי התמונו' אשר ישלימו אותם על גבולי תמונות הרושם תהיה העדפתם שנים שנים ואמנם המחומשים הנה העודף הנזכר בם יהיה שלשה שלשה וכמו כן כל מה שתעתק מדרגה אחת במדרגות מיני המספרים המשוטחים יוסיף היתרון הנזכר באחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
All Plane Polygonals Consist of and Resolved into Triangles |
הדבור באשר כל המשוטחים בעלי הזויות השוות מהמשולשים יתרכבו ואליהם יותכו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכבר קרה מזה ביאור מה שאמרנו לפנים שבעלי המספרים הישרי הקוים השוי הזויות הם מורכבים משלש א משולש ב משולש ג משולש ד משולש ה משולש ו משולש ז משולש ח מרובע א מרובע ב מרובע ג מרובע ד מרובע ה מרובע ו מרובע ז מרובע ח מחומש א מחומש ב מחומש ג מחומש ד מחומש ה מחומש ו מחומש ז מחומש ח משושה א משושה ב משושה ג משושה ד משושה ה משושה ו משושה ז משושה ח מהמשולשים ונתכים אליהם וזה שכבר נראה לנו שהמרובעים אמנם חודשו מהרכבת המשולשים כאשר הנחנו המשולשים על סדר כמו א'ג'ו'י' ט"ו עוד חברנו המשלש הראשון בכח אל המשלש הראשון בפעל והוא ג' יחודש המרובע הראשון בפעל והוא ד' וכאשר חברנו המשולש הראשון בפעל אשר הוא ג' אל השני בפעל אשר הוא ו' יתחדש המרובע השני בפעל אשר הוא ט' וכן כאשר חברנו המשולש השני בפעל והוא י' יחודש המרובע השלישי והוא י"ו וכן תמצא זה תמיד מתרכב מכל שני משולשים מהם מרובע כפי זה הסדר אשר המשלנו ובהפך זה המאמר יותך כל מרובע מהמרובעים אל המשולשים אשר מהם הורכב כי הארבעה אשר הוא מרובע יותך אל אחד ושלשה והם שני משולשים והתשעה אל שלשה וששה הם שני משולשים הנה כבר התבאר איך יתרכבו המרובעים מן המשולשים ויתכו אליהם ואמנם המחומשים כפי מה שאתאר וזה שהם יתרכבו מהמשולשים והמרובעים כאשר סדרנו המשולשים בטור כמו א'ג'י'ו' ט"ו עוד נסדר המרובעים בטור כמו ד' ט' י"ו כ"ה ל"ו עוד נחבר כל מדרגה עם נכחה הנה יתקבץ מחבור המשלש הראשון בכח אשר הוא א' עם המרובע הראשון בפעל אשר הוא ד' המחומש הראשון בפעל אשר הוא [ ] ב' וכן תמצאהו תמיד כאשר תרכיבהו כפי זה הסדר ובהפך זה המאמר יתבאר שהמחומשים יותכו אל המשולשים ואל מה שיורכב מהמשולשים ר"ל המרובעים כי החמשה יותך אל אחד וארבעה והי"ב אל שלשה ותשעה וכן מה שאחר זה הנה כבר התבאר איך יתרכבו המחומשים מהמשולשים ויותכו אליהם וכן תמצא גם כן שיתילדו המשושים מהרכבת המשולשים עם מה שיהיה נכחם בטור המחומשים כאשר הורכבו על דמיון מה שבארנו אלא שיהיה לעולם ראש הנחת המשולשים המשולש הראשון בכח אשר הוא אחד וראש מדרגות מספרי השטחים האחרים הראשון מהם בפעל והמשושה הראשון בפעל אמנם יחודש מהרכבת המשלש הראשון בכח אשר הוא האחד עם המחומש הראשון בפעל אשר הוא חמשה והמשושה השני מהרכבת המשלש הראשון בפעל אשר הוא ג' עם המחומש השני בפעל אשר הוא י"ב וכן המשובע גם כן יתחדש הראשון ממנו בפעל מהרכבת המשלש הראשון בכח אשר הוא א' עם המשושה הראשון בפעל והמשובע השני בפעל מהרכבת המשולש הראשון בפעל עם המשושה השני בפעל וכן ימצאו כלם תמיד המשומנים והמתושעים וזולתם מבעלי הזויות ותולדותם מן המשולשים והתכתם אל המשולש ולבאר זה לחוש נניח לו צורה מטורים נכחים הטור הראשון למשולשים והשני למרובעים והשלישי למחומשים והרביעי למשושים והטור החמישי למשובעים והטור השני למשומנים ומי שירצה להוסיף בזאת הצורה מספרים מבעלי השטחים ידבק בסדור אשר נשעננו וכוננו אליו / מספר מספר הצלעות השטחים ב ג ד ה ו ז ח ט י יא א המשולשים א ג א ו ג י ו טו י כא טו כח כא לו כח מה ל[ו] נה מא סו נה ב המרובעים א ד ט יו כה לו מט סד פא ק קכא ג המחומשים א ה יב כב לה נא ע צב קיז קמה קע ד המשושים א ו טו כח נה סו צא קכ קנג קץ רלה ה המשובעים א ז יח לד מה פא קיב קמח קפט רלט רפ ו המשומנים א ח כא מ סה צו קלג קעו רכה רפ ש וממה שיתבאר בזאת הצורה שהמינים הראשונים בפעל ר"ל המשוטחים המספריים יעדיפו על המשכם ברחב הצורה במשלש הראשון בכח והוא האחד והמינים השניים בפעל יעדיפו על המשכם ברחב הצורה במשולש הראשון בפעל ר"ל בשלשה והמינים השלישים בפעל יעדיפו על המשכם ברחב הצורה במשולש השני בפעל וכן המינים הרביעים בפעל יעדיפו על המשכם במשלש השלישי בפעל וכן מה שאחר זה וכבר נשלם המאמר במספרים המשוטחים בעלי הזויות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Solid Numbers |
הדבור במספרים הגרמיים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כבר בארנו במה שקדם מן המאמר מה ההפרש בין הגרם והשטח ואמרנו שהגרם הוא אשר יוסיף משך בעומק על השטח אחר שהשטח אורך ורחב לבד ואמרנו עומק או גובה הכל שוה וכבר אמרו כל זה אנשים ואחר שהיה קודם במאמרנו על השטח הדבור על משולשים לעלה אשר תארנו מהיותר ראוי לקדימה אחר שהם פנה לכל השטחים ושרש יהיה הקדימנו המאמר הזה בגרמים על המזונבים ורצוני במזונבים אשר יתחילו מתושבת משוטח ישר הקוים ר"ל הצלעות עוד יעלו בגובה עד שיכלו אל האחד כי זאת התמונה אם שיהיו שטחיה כלם משלשים והיא אשר תושבתו כי התשבות לזה המין המזונב כבר יהיו משולשים או מרובעים או משוששים או זולת זה מהשטחים אשר זכרנו ואמנם בשטחיו כאשר היה מזונב הם משולשים לבד ומפני שהמזונב אשר תושבותיו יחד משולשים ר"ל פרמידה עם בסיס משולש הגרם המשולש פנה ושרש לכל הגרמים בעלי הזויות אחר שהרכבתם ממנו והתכתם אליו יחוייב שנתחיל בו לתארו ונאמ' שזה הגרם יקיפו בו ארבעה משולשים כי אלו ידמה מדמה מהתמונות הגרמיות מהמדתיות משולש שוה הצלעות בעל שלשה המשכים שוים באורך לצלעותיו יצאו מזויות תושבתו עוד יפגשו על נקדה נכחית למרכז בנפילת עמוד יהיה כבר ידומה גרם מזדנב לו ארבעה שטחים שוים אחד מהם התושבת והשלשה הנשארים המקיפים בו וכמו כן גם כן אלו ידמה מדמה מרובע שוה יצא מזויותיו ארבע צלעות כל אחד מהם לצלע מצלעות תושבתו ויפגשו כלם על נקדה נכחית בנפילת עמוד למרכז המרובע ידומה גרם המזדנב ר"ל מחודד לו חמשה שטחים פרמידה עם בסיס מרובע כמו זאת הצורה אחד מהם שטח מרובע והוא תושבתו והארבעה הנשארים משולשים והם המקיפים וגם כן אלו ידמה מדמה כמו זה במחומש והמשושה והמשובע וזולתם ימצא בכל אחד מהם המשכים יצאו מזויותיהם ויפגשו על נקדה לנגד מרכזיהם יחדשו באותם הקוים היוצאים מהזויות ותכליות תושבתם משולשים ויהיה הגרם מזדנב ר"ל מחודד וכאשר תרצה לבחון זה ע[] עיין בדמיונים המצויירים קודם זה בשער הדבור על שהמשולש פנה לכל בעלי הזויות והקוים הישרים מהשטחים המדותיים ונשוב עתה ונאמ' שכל מספר מוגבל כמו הקו הנה תולדתו וצמיחתו מהאחד וזה כמו א"ב ג"ד ה"ו אל מה שיתוסף מזה תמיד ומאלו המספרים הקויים מה שיתרכבו בעלי הזויות מהשטחים והגרמים אלא שלא יתילד ויתרכב איך שיזדמן מההרכבה במחשבה אבל על גבול וסדר כמו שכבר גלינו במה שקדם בהגבילנו צמיחת השטחים ואמנם התילד המוגשים וצמיחתם הנה המשלש המזדנב ר"ל הגרם יצירת הפירמידה המשולשת המשלש התילדו בהנחת האחד בגובה עוד תניח תחתיו המשולשים המספריים אשר כבר זכרנום כל אחד תחת אשר לפניו במדרגה וסדר כפי המשכם ונפעל זה תמיד מה שנרצה להוליד המזדנבים כי יתחדש גוף מחודד משולש ואמנם המרובעים המזדנבים ר"ל המחודדים הנה הם יתחדשו כאשר יצירת הפירמידה המרובעת תסדר אותם השטחים המרובעים המספריים אשר זכרנום לפנים והנחת האחד ראשון להם עוד תשים המרובעים תחתיו ימשכו קצתם לקצת יתחדש מזה מרובע מזדנב וכן המחומש והמשושה והמשובע ומה שידמה זה הנה הגרמיים המזדנבי' המשולשים ר"ל המחודדים יהיו מדרגות חדושם כפי משך אלו המספרים א"ד י"כ ל"[ה] נ"ו הנח כל אחד מאלו המספרי' אמנם יתילד מסדר המספרים קצתם תחת קצת מאחד האחד עוד האחד עד אשר תרצה ואמנם האחד הנה הוא גרם המחודד המשולש בכח ואמנם הארבעה הנה הוא השיני והוא הרכבת שני משולשים האחד והשלשה ואמנם העשרה הוא מהרכבת שלשה משולשים אחד וששה ושלשה וכן הנשארים כפי זה הסדר נמצא בזה התאר ואמנם מדרגות התחדש הגרמים המרובעים המחודדים כפי המשכם הנה על משך אלו המספרים א"ה י"ד ל' נ"ה כי כל אחד מאלו המספרים אמנם התילד מהרכבת המרובעים הפשוטים אשר אמרנו עליהם לפנים קצתם על קצת כמו שאמרנו במשולש המחודד וכפי זה המשל אשר תארנו יהיה המחומש המחודד והמשושה וזולתם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ומבואר מכל מה שזכרנו שכל צלע מצלעות מנין המחוברים יחד שוה מה שבם מהאחדים למנין השטחים המחודדים בם היו מה שהיו מהאחד עד שיגיע אל שטח התושבת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולא יעלם ממה שזכרנו שהמשולש הפשוט הוא הפנה והשרש לכל השטחים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והמשולש המוגשם המחודד הוא הפנה לכל המחודדים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואחר שזכרנו שכבר הבאנו בזכירת המזונב מהמוגשמים נדבר על אשר נקראהו מחוסר פרמידה קטומה והוא כל גשם בעל זויות היה בסדורו והרכבתו על סדר הרכבת המחודדים אלא שלא יכלה בגבהו אל האחד אשר הוא עליון שבמחודד והיו זויות שטח עליונו שוות במספר לזויות שטח תושבתו הנה זה המין יקרא המחוסר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה אם היה חסר מהמחודד באחד לבד אשר הוא עליון המחודד יקרא מחוסר אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם היה חסר מהאחד שטח אחד יקרא מחוסר שנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם היה חסר שטח שלישי יקרא מחוסר שלשה וכן המחוסר ארבעה אם היה חסר ארבעה שטחים [וכן] וכן תמצאהו תמיד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואחר שכבר התבאר איך צמיחת זה הגשם המחוסר אחר שאין הפרש בינו ובין מה שבארנו לפנים מהרכבת המוגשם המחודד אלא שאנו נחסרהו מעליון המחודד אשר הוא האחד שטח או שטחים הנה זה כלל המאמר על זה ואמנ' המאמ' על שאר הגרמים אשר זכרנום לפנים והם המעוקבים והלבנים והאריחיים והקשתיים והכדוריים והמתחלפי הצלעות והזולתיים באורך הנה זה עת להתחיל בו ונשתדל לפרשו בג"ה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Cube Numbers |
הדבור במספר המעוקב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונאמ' עתה שהמספרים המרובעים השוים המשוטחים אשר דברנו עליהם לפנים והם כמו א"ד ט' י"ו כ"ה ל"ו כאשר הרכב כל אחד מאלו השטחי' לדומה לו מהשטחים בכמות עד שיהיה מספר השטחים המורכב קצתם על קצת כמו אחדי אורך ורחב שטח התושבת יקרא מעוקב וכלל המאמר כי המעוקב הוא אשר ארכו ורחבו ועמקו שוה קצתו לקצתו כי הארבעה אשר הם מספר שוה כל צלע ממנו שנים כאשר הורכב עליהם ארבעה אחדים היה כלל שמנה ושמנה שנים בשנים עוד בשנים וזה שוה המרחקים בשלשה ר"ל האורך והרחב והעמק וכן גם כן התשעה אשר כל צלע מצלעיותיו שלשה כאשר הרכבו עליהם שני שטחים אחרים שוים להם היה הכלל כ"ז הוא הגעת מוכה ג' בג' עוד בג' וכן שאר המספרים המעוקבים כפי זה התאר והכלל הכולל בהם שכל מספר נכלל נכפל בשעור אחדיו עוד נכפל הכל בשעור אחדי המספר הראשון שנית הנה הכלל יהיה מספר מעוקב הנה כבר קרה מזה שנדע שכל מרובע פשוט הוא שטח ולו ארבע זויות וארבע צלעות וכל מעוקב לו ששה שטחים שוים ושמנה זויות שוות ושתים עשרה צלעות שוות ואמת מה שנאמר בו כי צלעות המעוקב וזויותיו ושטחיו וצלעותיו ר"ל קוויו ביחס חבוריי וזה שיחס השטחים והם ששה אל הזויות והם שמנה ביחס המוסיף שלש ויחס הזויות והם שמנה אל הצלעות והם י"ב ביחס המוסיף חצי הנה יחס השטחים והם ששה אל הצלעות והם שתים עשרה ביחס הכפל השניי ושני אלו היחסים ר"ל המוסיף חלק והכפל הם מיני היחסים הפשוטים החבורים כמו שכבר התבאר זה לפנים הנה אם כן המספר הגרמי השוה המרחקים ר"ל האורך והרחב והעומק הו המעוקב בהכרח | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Scalene Numbers |
הדבור במספרים הגרמיים המתחלפי המרחקים השלשה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Now we should discusses the body that is opposed to the cube, that is, the unequal in all dimensions, i.e. whose length differs from its width, and both together differ from its height. | וממה שראוי שנדבר עתה הוא בגרם אשר יקביל המעוקב והוא המתחלף המרחקים יחד ר"ל אשר ארכו מתחלף לרחבו והם יחד מתחלפים לגבהו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| משל זה שיהיה הרחב ב' והאורך ג' והגובה ד' או יהיה האורך ג' והרחב ד' והעומק ה' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| או זולת זה מאופני החלוף בתוספת קצת הצלעות על קצת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכלל המאמר שלא יהיה דבר ממרחקיו שוה למרחק אחר ממנו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה המספר יקרא בשמות רבים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| מהם שאנשים יקראוהו הסולמיי מפני שיעלה בהוספה מרחבו לארכו ומארכו לגבהו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ויקראהו אחרים הארחיי להתדמות לאריח שהוא גוף מתחלף השטחי' בשלשת מרחקיו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה לך דמיון תמונתם וסדורם כפי המשכם בסדר הטבע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תניח לוח הולך ברחב ר"ל רחב הלוח נרשם מחולק במדרגותיו מדרגות המספרים כפי סדרם בטבע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונניח תחתיו לוח שני יותר חסר ממנו במדרגה מצד התחלת המדרגות עוד נעמיד בכל מדרגה ממנו מה שיתקבץ מהכאת אשר למעלה ממנו מהלוח הראשון עם אשר לפניו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ותניח גם כן תחתיהם לוח שלישי כמו הלוח השני וכפי מנין מדרגותיו ונעמיד בה תחת כל מדרגה מהלוח מה שיתקבץ ממדרגה אשר עליה ומהכאתה במדרגה השלישית אשר עליה מהלוח הראשון עד שישלם בזה הטור השלישי ויהיו מדרגותיו כלם הם מספרי הגרמים הסולמיים כפי המשכם בטבע מבלתי שיחטא בם באחד מהם בפנוי ממדרגותיהם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ותבחן זה בזאת הצורה אשר רשמנו בכאן א ב ג ד ה ו ז ח ט י | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Parallelepipedon Numbers |
הדבור במספרים הגרמים הזולתיים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואחר שהיו שני אלו המינים ר"ל המעוקב והמתחלף הצלעות יוקבלו בהקבלת שני הקצוות אחר שהמעוקב שוה הצלעות השלשה והאחר מתחלף הצלעות השלשה הנה האמצעי בין שני אלו הם המספרים הגרמיים אשר יקראו הזולתיים האורך ר"ל אשר פשוטיהם זולתיי האורך הנה המספר הזולתי האורך כבר יאמר שהוא המספר אשר ירשם שעורו בפשוט רושם מרובע נצב הזויות ורחבו פחות מארכו אחד כמו ב' וי"ב כ' ל' מ"ב והדומה להם הנה כאשר שמנו לכל אחד מאלו הפשוטים הזולתיי האורך גובה באחד מצלעותיו יתילדו מזה במספרים הגרמיים הזולתיים וזה לך דמיון הנחתם שני טורים מהם הראשון והשני הם משלשת הטורים הקודמים בשער הוצאת המספרים הגרמיים הסולמיים א ב ג ד ה ו ז ח ט ב ו יב כ ל מב נו עב ב ד יב יח לו מח פ ק קנ קפ רנב רצד שצב תמח תקעו תרמח ונכה כל מדרגה ממדרגות הטור השני מהם בכל אחת מאשר עליה בטור הראשון ר"ל אשר עמדה מהכאת אחת מהן באחרת ונעמיד שני הכללים בשתי מדרגות נבדלות הקטנה מהן קודמת לגדולה ושתיהן תחת המדרגה הנעשית בהכאה מהטור השני וכאשר תשלים הלוח בזאת המלאכה הנה כבר שמת מדרגות הטור השלישי כפל מדרגות הטור השני וכבר העמדנו בו כל המספרים הגרמים הזולתיים כפי המשכם בסדר הטבע לא יבצר מהם אחד ואמנם אם יוסיפו קצת הצלעות על קצת ביותר מאחד ר"ל שנים או שלשה או ארבעה כמו שנים בארבעה וארבעה בששה או חמשה בשבעה או מה שלמעלה מזה לא יקרא מה שהוא כן זולתיי האורך אבל יקרא המוסיף האורך ודע שהמספרים הגרמיים הזולתיים יהיו לעולם שני שטחים משטחיהם מרובעים מקבילים ושאר שטחיהם ר"ל הארבעה שטחים הנשארי' בכל מספר גרמיי מהם הנה כל אחד מהם יהיה זולתיי האורך ויהיו ארבעת צלעותיו א ב ג ד ה ו ז ח ט י שוים על שעור ב ו יב כ ל מב נו עב צ אחד ושמנה מצלעותיו שוים על שעור אחד מתחלף לשעור הארבעה באחד אם מוסיף ואם חסר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Numerical “Sameness” and Numerical “Otherness” |
הדבור בשורש הטבעיי להוא הוא והזולתיות המספריים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אמנם ההוא הוא הנה הוא המספר אשר רחבו הוא ארכו בהגעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם היה שרש ההוא הוא אצל הקדמונים מכת פתאגורוש האחד לפי שהוא כאשר יוכה באחד היה האורך הוא הרחב והמתקבץ הוא כל אחד מהם לא יצא מעצמו כלל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד נקראו המספרים המרובעים הוהויים ללקחם הדמיו מזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| לפי שארכם הוא רחבם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והיה היותר ראוי מהמספרים להיות שרש לזולתיי הוא אשר לא ישתנה מה הוא הוא האמתי השרשיי הנזכר לפנים אלא באחד הנה בראוי אם יהיה שרש המספרים הזולתיים הוא המספר השניי הנה כפי זה היו מקישים ההוא הוא והזולת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכבר היה שתבאר ממה שהקדמנו ובארנו שכל נפרד הנה האחד מיוחד לו אחר שבין שני חלקיו האחד לעולם בהכרח הם יעדיף אחד משני חלקיו לאחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ושכל זוג הנה השניות מיוחד לו אחר שיחלק בשני חלקים דומים נמשלים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובראוי נאמר כי הנפרד מיוחד אחר שזאת שהוא שורש ההוא הוא מיוחד לו לטבע ההוא הוא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והזוג מיוחד לטבע הזולת כי בתוספת הנפרדים קצתם על קצת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובהקדים האחד בהנחה ראשונה להם יצמחו מספרי ההוא הוא ר"ל המרובעים השוים במרחק האורך והרחב כמו שבארנו זה פעמים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ומסגולת המספרים הזולתיים אשר הם חבורי הטבעיים אשר הם יולידו המספרים ההוהויים וצלעותיהם ובתוספת הזוגות הטבעיים קצתם על קצת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובהקדים השנים ראשונה להם בהנחה יתילדו הזולתיים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם קראנו אלו המספרי' השוים באורך וברחב מספרי הוא הוא ללקחם דמוי הוא הוא האחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וקראנו המתחלפים באורך וברחב באחד זולתיים ללקחם דמוי השניות היוצא מטבע ההוא הוא האמיתי באחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכאשר תקביל בשני טורים בין מדרגות המספרים ההוא הויים ומדרגות המספרים הזולתיים כל מדרגה במקביליה תמצא מותר המדרגה הזולתיית על הנכחיית לה ההוא הויית הוא המניין אשר ממנו נגזר שם המדרגה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Brick Numbers |
הדבור על המספרים הלבניים והמגודרים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם המספרי' הדומים ללבנים הוא המין מהמספרים הגרמיים הזולתיים אשר יהיה שעור צלעותיו הארבעה השוים פחות אחד משעור צלעותיו השמנה השוים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והם המדרגות הנרשם עליהם באורם בטור המספרים הגרמיים והזולתיים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והם אשר ארכם ורחבם שוה ויחסר הגובה מכל אחד מהם אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם אם יוסיף בגובה על האורך והרחב השוים תוספת הזולתיי ר"ל אחד או תוספת המוסיף באורך ר"ל יותר מאחד היו מה שהיה המספר הנוסף באחד מהמרחקים השלשה הנה כל אלו יקראו מוגשמים אריחיים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו ג' בג' בד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| או ה' בה' בו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| או במה שתרצה אחר שיהיה הגובה יותר ארוך מכל אחד מהאורך והרחב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Circular and Spherical Numbers |
הדבור במספרים הסבוביים והכדוריים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואחר שכבר הבאנו תאר הגרמים בעלי השטחים הישרי הקוים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה נאמר כמו שאמרנו שהמספר המעוקב הוא השוה המרחקים ר"ל האורך והרחב והעומק | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה יחלק לשני חלקים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אם שיהיה המספר אשר הוא שרש כל אחד משטחיו נזכר בכלל השטח עוד נזכר בכלל הגרם חוזר על עצמו עוד נזכר גם כן בכלל הגרם כאשר הוכה בו פעם או שני פעמים או יותר מזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם שלא יהיה כן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה אשר שרשיהם נזכרים בכללם כמבטא הגעתם מאלו המספרים המעוקבים הם אשר יקראו המספרים הכדוריים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אחר שיסבבו מתהפכים כמו הכדור אל המספר אשר ממנו התחלתם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו המספר המעוקב אשר הצלע מצלעותיו חמשה או ששה כי כל מה שתכה אחד משני אלו בכמהו עוד מה שיתקבץ בשרשו יהיה נמצא כמו שתארנו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה שאנו אם נכה חמשה בחמשה היה המתקבץ כ"ה וישוב החמשה מבוטא בו בכלל וישוב אליו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד נכה החמשה גם כן בכ"ה ותמצא החמשה גם כן מבוטא בו בכללם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן אם תכה הקכ"ה בחמשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ומה שהתקבץ גם כן בחמשה תמצאהו בזה התאר לעולם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן גם כן הששה בזה הענין משפטם משפט החמשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תמצא זה באחד כי האחד בכמהו עוד בכמוהו עוד בכמהו עוד כן תמיד בלתי יוצא מעצמו אבל סובב על עצמו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואחר שכבר התבאר מה שתארנו נאמר שהמספר הסבוביי מזה שתכה המספר פעם אחת בעצמו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו א' בא' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וה' בה' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וו' בו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם הוכה יותר מפעם הנה הוא מספר כדורי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אחר שהעגולים פשוטים והכדורים גרמיים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה סוף המאמר על המספרים הגרמיים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Indications of the Ancients that the Beginning of Numbers is similar to the Beginning of the Universe |
הדבור ברמזי הראשונים על ההתחלות המספריות הדומות להתחלות העולם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכבר ימשך למה שאמרנו לפנים על המספרים הזולתיים ההפרש בם מהמספרים המוסיפים באורך שאנו כבר בארנו כי הזולתיים הוא אשר אחד ממרחקיו השנים יותר מהאחד באחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם המוסיף הוא מה שהיתה צמיחתו כפי זה הצד אלא שתוספת אחד ממרחקיו על האחר יותר מאחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו ח' המתקבץ מהכאת ב' בד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכמו י"ח אשר יתקבץ מהכאת ג' בו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והדומה לזה ממה שהחלוף בו בין שני המספרים אשר יוכה אחד מהם באחר ביותר מאחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אמר ולחלוף אלו המספרים ר"ל ההוא הויים ר"ל השרשיים והזולתיים ר"ל אשר יוסיף ארכם על רחבם יותר מאחד חודשה ההפרדה וההחלק והסתעפות מה שבמספר מהמינים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אמר ובראוי מה שהתחילו הקדמונים הראשיות במספר בהתחילם המאמר על טבע העולם אם אפלאטון הנה זכר שטבע העולם משלשה גבולים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אחד מהם ההוא הוא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והשני הזולת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והשלישי מהעצם אשר אינו מתחלק | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה המאמר יישירך השם רחוק העול מאד דק הענין | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואפלאטון ירמז בו אל ראשיות העולם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה דבר חוץ ממלאכת המספר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולולא שאני הסכמתי שלא אערב דבר בחכמת זה הספר עבדתי זה השער | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולולא שאני בטוח שלא ידומה עלי לאדיבות לבלתי תועלת וגם בטחוני במדרגתך היום מהעיון לא זכרתי לך שתחת זה המאמר רמז ולא שהוא רחוק העול ודק הענין | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אמר מניח הספר אמנם פילולאוש יאמר שכל הדברים אשר הם נמצאים הנה הם בהכרח אם מוגבלים נכללים ואם בלתי מוגבלים ואם מוגבלים ובלתי מוגבלים יחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אמר וזה המאמר השלישי אמנם הוא מאופן המספר ודמיונו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי המספר מורכב מהאחדים ומיניו זוג נפרד והם מורים על השווי והחלוף וההוא הויים והזולתיים וההקפה ובלתי הקפה וההגדרה ובלתי הגדרה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ויהיה מה שנאמר מבואר יאמר שהדברים אשר הם נמצאים התילדו ועמדו מהמתנגדים המתחלפים הדומים ובראוי מה שהראו החבור וההסכמה כי החבור אמנם יהיה בלי ספק כמו שבארנו בפתיחת המאמ' הראשון מזה הספר מהדברים המתחלפים הדומים הנמצאים כי החבור אמנם הוא ערוב דברים מתחלפי הגדרים דומי הסוגים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אמר אבו יוסף אמנם אמר זה המאמר והוא ימשיל המוגבל מהדברים במספרים הנגדרים שהם מוגבלים אחר שידובר בגדרם ר"ל שרשם שאחד שימנה בעצמו יחודש ויראו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וימשיל הבלתי מוגבלים מהדברים הזולתיים שהם אלמים לא ידובר בשרש דבר מהם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ורצה במוגבל ובלתי מוגבל יחד המוסיף האורך כי ממנו שרשי וממנו בלתי שרשיי הנה השרשיי מוגבל ובלתי שרשיי בלתי מוגבל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Properties of the Types of Numbers and their Mutual Harmony |
הדבור בקצת סגולות מיני המספרים ומה שיראה בהתילדם והקבלת קצתם לקצת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכבר הבאנו בהקדמת מה שרצינו להקדימו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונראה איך יתילדו הרבה ממה שתארנו מתאר המספרים ההוא הויים והזולתיים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה בשנסדר המספרים המרובעים אשר נולדו בהוספת הנפרדים הטבעיים קצתם על קצת ר"ל הנגדרים בטור | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד נסדר הזולתיי האורך ר"ל אשר התילדו מתוספת הזוגות המתילדים קצתם על קצת בטור שני | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי זה האופן מן הפועל באמת כבר נראהו גלוי בטבע הכל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ויהיה הטור כפי זה המשל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והוא מבואר מפליאת בעל הטבע שהראשון מהזולתיים ביחס הכפל השניי אצל הראשון מן ההוא הויים וכשני אל השני ביחס המוסיף חצי והשלישי אל השלישי ביחס המוסיף שלישי וכן הרביעי אל הרביעי ביחס המוסיף רביע וכן תמצאם תמיד יחד בכמו זה התאר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והתבאר גם כן בשני אלו הטורים מה שכבר אמרנו במה שקדם שאנו אם לקחנו תוספת כל מדרגה מהזולתיים על נכחה מהמדרגות ההוא הויים והנחנוהו בטור שלישי כפי המשכיה מצאנו מדרגות זה הם המספרים על סדר הטבע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תמצאהו כאשר תתחיל במדרגות ההוא הויים ותשים ראש מדרגותיהם ארבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד תוסיף תוספת כל מדרגה מהם על נכחה ממדרגות הזולתיי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד תסדרם בטור שלישי כפי המשכיהם תמצא זה בסדר המספרים הטבעיים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי תוספת ד' על ב' ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ותוספת ט' על ו' ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תמצאהו תמיד בזה התאר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם אם תקיש ביניהם והם כפי זאת ההנחה ותרצה ליחסם תמצאם באותם היחסים אשר נראו בראשונה בעצמם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה שד' אצל ב' בייחסם הכפל השניי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וט' אצל ו' ביחס המוסיף חצי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וי"ו אצל י"ב ביחס המוסיף שליש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכמו זה תמצאהו תמיד על צד הענין הראשון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם תוספת מדרגות ההוא הויים קצתם על קצת הוא מבואר שהם הנפרדים הטבעים והנפרדים הטבעיים והזוגות הטבעיים ויחס הכפל ויחס המוסיף חלק | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם אם תניח הראשון מהזולתיים אמצעי בין שני הראשונים מן המרובעים ר"ל שנים בין אחד וארבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ותניח השני מן הזולתיים אמצעי בין אשר אחריהם מן המרובעים ר"ל ו' בין ד' וט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן השלישי הזולתיי בין שני המרובעים אחדים אחר אשר הנחת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תעשה כל מדרגה ממדרגות הזולתיי כפי המשכם תמצא זה ביחס מדרגות זוג הזוג שעור הראשון אצל השני כשעור השני אצל השלישי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תמצא כל שלשה מספרים מהם ר"ל מאלו אשר הממצע בין כל שתי מדרגות מההוא הויים מהם מדרגה מהזולתיים כפי סדרם אשר בארנו בזה היחס | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל ששעור הראשון מן השני כשעור השני מן השלישי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובהפך גם כן השלישי אצל השני כשני אצל הראשון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ומבואר שאלו המדרגות כאשר היו כפי זה הסדר לא יהיה תוספת ממדרגותיהם קצתם על קצת שוים וזה צורתו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמנם זוג הנפרד הנה סגולת מדרגותיו בסדורם כפי המשכם בטור מיוחד סדור המספרים הטבעיים וזה שזוג הנפרד הגעות תוספת מדרגותיו קצתם על קצת שוים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי תוספת י' על ו' כמו תוספת י"ד על י' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תוספת ב' על א' כמו תוספת ג' על ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וישיג שני אלו יחד שיהיה האמצעי נכפל כמו שני הקצוות מקובצים וכבר בארנו זה ודומה לו במאמר הראשון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונאמר שהמספרים המשולשים אמנם יתחדשו מהרכבת ההוא הויים והזולתיים כל מדרגה עם נכחה על משך מדרגותיהם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי המדרגה הראשונה מההוא הויים והוא האחד כאשר הורכבה עם המדרגה הראשונה מהזולתיים והוא ב' יחודש המשולש הראשון בפעל והוא ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכאשר תרכיב המדרגה הראשונה מהזולתיים והיא ב' עם המדרגה השנית מהוא הויים והוא ד' יחודש המשולש השני בפעל והוא ו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תמצא הרכבת אלו המדרגות בזה התאר תמיד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ויראה ממה שתארנו ובארנו קודם שהמרובע כאשר יתחלף באחד משני מרחקיו לאחד באחד אם בתוספת עליו ואם בחסרון ממנו יצא אל הזולתיי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה אם כן מדרגת המרובע השוה לזולתיי כמדרגת השוה להקשות החמש אשר הקדמנו זכרם אחר שאחד משני המספרים נוסף על האחר והאחד חוסר ממנו והשווי פינה להם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכבר אמרנו גם כן שההוא הוא האמתי הוא האחד והזולתיי האמתי הוא השניות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד אחר זה כבר ידמה הנפרד להוא הוא והזוג לזולת ולזה בעצמו כבר ידמה המרובע השוה ההוא הוא אחר שהוא מורכב מהנפרדים וידמה המתחלף שני המרחקים באחד הזולתיי אחר שהוא מורכב מהזוגות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אמנם עתה נשוב אל מה שזכרנוהו ממה שיראה משני אלו המינים ר"ל ההוא והזולת כאשר יסודר כפי הסדר אשר זכרנוהו לפנים והוא סדר שני המינים יחד בטור אחד בסדר שיהיו מדרגותיהם כן כל מדרגה מאחד משני המינים בין שתי מדרגות מהמין האחד על המשך כמו א'ב'ד' ו'ט' וכן תמיד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה זה הטור כאשר יסודר זה הסדר תמצא כל שלשה מדרגות מהם כאשר השתוו ביחס יתחלפו בהגעות תוספותיהם קצתם על קצת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכאשר ישתוו בהגעות תוספות קצתם על קצת יתחלפו ביחס | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי א'ב'ד' ביחס הכפל השניי אבל תוספת ד' על ב' ב' ותוספת ב' על א' א' הנה היחס אחד והתוספות מתחלפות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אמנם שלשה המדרגות אשר הן ב'ד'ו' תוספת ו' על ד' כמו תוספת ד' על ב' אלא שהיחס יתחלף לפי שיחס ו' אל ד' בלתי יחס ד' אל ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן גם כן שלשת המדרגות אשר הן ד'ו'ט' שהן ביחס אחד ואין התוספות שוות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן גם כן שלשת מדרגות וט' י"ב בהגעות התוספות מתחלפות ביחס | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תמצא כל שלשה מדרגות מזה הטור המורכב מן ההוא הויים והזולתיים כפי ההרכבה אשר תארנו לפנים בזה התאר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ויתבאר ממה שזכרנו שכאשר היה הזולתיי וההוא הוא אלו ששני מרחקי הזולתיי יתחלפו בתוספת אחד באורך על הרחב שיהיו כל שלשה מדרגות מזה הטור שיסכימו ביחס ויתחלפו בהגעת התוספת שיהיה חלוף התוספת גם כן באחד כי ב' אשר הוא המותר בין ד' וב' יוסיף על האחד אשר הוא המותר אשר הוא בין א' וב' אחד וכן תמיד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונאמ' עוד שממה שיחזק עם מה שזכרנוהו קודם כי הנפרדים יותר חזקי ההאמתה בטבע ההוא ר"ל הנגדרים מה שאנחנו זוכרים אותו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה שאנו נסדר המספרים אשר התחלתם מהאחד והמשכם ביחס הכפל השניי בטור כמו א"ב ד"ח י"ו ל"ב ס"ד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונסדר גם כן המספרים אשר התחלתם מהאחד והמשכם על יחס הכפל השלישיי כמו א'ג'ט' כ"ח פ"א רמ"ג ונמצא מדרגות הנפרדים מכל אחד משני הטורים מספרים הוא הויים ר"ל שרשיים בהכרח ר"ל שהמדרגות אשר תהיינה במקום נפרד ממנין המדרגות הגעותיהם נגדרות ואשר הם במקום זוג ממנין המדרגות הגעותיהם בלתי נגדרות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונאמר עוד שהמספרים הגרמיים המעוקבים אחר שהם גם כן דומים להוא הויים לפי שמרחקיהם שוים הנה הם יתילדו מהנפרדים גם כן וימצא זה בזאת התחבולה הנפלאה בטבע הנקלה במעשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה שאנו נסדר הנפרדים הטבעיים בטור | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וימצא המעוקב הראשון בכח אשר הוא האחד הוא הנפרד הראשון בכח אשר הוא א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והמעוקב השני בכח הוא ח' מהרכבת שתי מדרגות ימשכו לאחד מהנפרדים והם ג' וה' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והמעוקב השלישי אשר הוא כ"ז מהרכבת שלשה מדרגות ממדרגות הנפרדים ילוו לשתי המדרגות אשר הורכב מהם המעוקב השני והם ז'ט' י"א כי כל זה כ"ז | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תמצא זה תמיד כל מה שתדלג אל מעוקב תמצא כי הרכבתו ממדרגות נפרדים מנינם כמו מקומו ממנין מדרגות המעוקבים ר"ל כי המעוקב השני מהרכבת שני נפרדי' והשלישי מהרכבת שלשה נפרדים וכן מה שאחר זה אלא שכל מעוקב הנה ראש הנפרדים אשר מהם יורכב אחר סוף מדרגה מהמדרגות אשר הרכב מהם המעוקב אשר לפניו עו' המדרגות לקוחות על משך סדר הנפרדים הטבעיים הנה זה כולל המאמר על זה וצורתו כמו שתראה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Relative Quantity |
|
The Ten Proportions |
הדבור על האמצעיים העשרה |
|---|---|
| וזה אשר יקרא אותו בעל זה הספר בערבי אלעיאד | |
| Its meaning: a limitation of two ratios or more between two given terms. | ומשמעותו הגבלת שני יחסים או יותר מזה בין גבולים מונחים |
| אם מעצמם ר"ל שתהיה ההגבלה מוצאת מעצמי הגבולים עצמם והוא יחס הבעל | |
| ויקרא הנדסייא להדבקותו הנדסייא קצתם אצל קצת | |
| ואם מיתרון והוא יחס המוסיף חלק קצתם חשבון על קצת | |
| ואם משני העניינים חבור יחד | |
| והיחס הוא ישות שעור שני גבולים מהגבולי' מונחים אחד מהם אצל האחר ובפחות מה שיהיה ההתיחסות אבל היחס ב'ב' כי היחס בלתי ההתיחסות בשלשה גבולים כמו ד' וב' וא' כי שעור ד' אצל ב' כשעור ב' אצל א' וכמו כן בהפך הנה ההגבלה הנקראת אלאיעד אשר בין א' וב' וד' הוא יחסם אחד וזה אלאיעד הוא בעצם המספר המונח עצמו וזה היחס כבר אפשר שיתוספו מספריו תמיד באחדות באשר קדם פירושינו לו יותר מפעם בספרנו זה כמו שיהיו המספרים כאשר היו ארבעה או חמשה או ששה או יותר מזה כפי מה שתרצה כמו שתניח א'ב'ד' ח' י"ו ל"ב ס"ד כי אלו כלם ביחס הנזכר בין שלשת הגבולים תחלה | |
| ואמנם ההתיחס אשר יפול ביתרון כמו א'ב'ג' כי אין שעור האחד מב' כשעור ב' מג' אבל שעור תוספת ג' על ב' הוא השעור אשר בו יוסיף ב' על האחד וכן הוא גם כן בהפך וזה אלאיעד גם כן אם ירבו המספרים המונחים הנה כפי זה המשל ימצאו שעורי התוספת בחלוף כפי זה המשל גם כן כמו ב' וג' וד' וה' כי תוספת ה' על ג' כמו תוספת ד' על ב' וכן ימצא גם כן בהפך | |
| all the ancients - Pythagoras, Plato and others - acknowledged three proportions: | ונאמ' שהאמצעיים אשר יודו בם כל הקדמונים ר"ל פיתאגורש ואפלאטון וזולתם הם שלשה |
|
האחד מהם לחשבון |
|
והשני למדות |
|
והשלישי לחבור הנגונים |
| the geometric and the harmonic proportions have three subcontrary proportions | ולאמצעי המדות והחבור מקבילים אחרים שלשה |
|
לחבור הקבלה אחת |
|
ולמדות שתי הקבלות |
| these [three contrary proportions] do not have names, they are called by their numbers: fourth, fifth, sixth | אלא שהם אינם בעלות שמות כמו אלו ונקראו מהמספר ונקראו רביעי' וחמישית וששית |
| four other proportions were added to these six proportions constituting the ten proportions, as the perfect ten of Pytagoras | וכבר אמרו אחר זה המאמר הקדום שהאמצעיים עשרה והוסיפו על אלו הששה ארבעה אחרים להשלים האמצעיים העשרה להיות לעשרה שלמות אצל פיתאגורש |
| ונדבר בתאר אלו האמצעיים | |
|
וניחד המאמר תחלה במצוע המספריי |
| ונאמ' הנה כבר נשלם מאמרנו בהיות המספר ראוי בקדימה באומניות הארבעה | |
| ועם זה הנה המספרים המונחים לאמצעי החשבון הם כפי סדר הטבע או מה שהיה דומה לסדר הטבע | |
| הנה אם כן יחוייב בהכרח שנקדים זה האמצעי על שאר האמצעיים שאחר שהיה קודם על שאר האמצעיים הקודמים הנה יותר ראוי מזה שיקדם על המקבילים להם | |
| הנה האמצעי המספריי יהיה כאשר תניח שלשה מספרים או יותר מזה והונחו כפי חבור הטבע ימשכו קצתם לקצת | |
|
כמו א"ב ג'ד'ה' |
|
כי אלו המספרים בהכרח תוספת כל אחד מהם על מה שלפניו אחד |
| equality of the difference | ואם תרצה לסדרם בזה היחס אשר הוא שווי היתרון |
|
אתה תסדר המספרים הטבעיים בטור עוד תתחיל במספר אשר תרצה לשומו בגבול הראשון ותעיין כמה בינו ובין המספר אשר תרצה לשומו אמצעי מהמדרגות אשר על סדר הטבע וימשכו כמו אותו המנין מהמדרגות בין האמצעי והגבול השלישי וכן בין השלישי והרביעי או במה שתניח מהמדרגות בזה היחס |
|
כמו שתניח הגבול הראשון ב' והגבול השני ד' |
|
|
ואין ספק שתניח הגבול השלישי על דמיון מרחק ד' מב' והוא מרחק ו' מד' ר"ל על מרחק שתי מדרגות |
|
|
וכן אם תניח גבול רביעי היה הוא אשר ירחק מו' בשתי מדרגות והוא ח' |
|
וכפי זה הדרך תניח הגבולי' כאשר תרצה להרבותם הנה תהיה הוספתם לעולם בתוספת אחד |
|
ובפרט זה האמצעי ר"ל אמצעי החשבון המתחייב לאלו בלתי זולתם שהגבול האמצעי מהם כשיכפל על ב' אם היו המדרגות המונחות להם אמצעי אחד ישוה שני הקצוות כאשר יקובצו |
|
אם היו המדרגות בעלות שני אמצעיים הנה קבוץ שני האמצעים כמו קבוץ שני הקצוות |
|
ולהם סגולה שנית גם כן והיא שיחס כל אחד אל עצמו כמו יחס מותרי הגבולים אלו על אלו קצתם על קצת |
|
עוד סגולה שלישית והיא היותר קשה ונעלמת מדעת רבים |
|
והיא כי כפילת שתי הקצוות האחד על האחר כאשר נערכהו אל כפילת האמצעי הוא יותר פחות בערך כפילת מותרי הגבולים אלו על אלו בין שיהיו הגבולים נפרדים במספרם ובין שיהיו אי זה מספר שיהיה כאשר יקובצו היו יותר משני הקצוות יחד |
|
ולהם סגולה רביעית והיא ממה שזכרנוהו הראשונים מתאריהם |
|
והיא שיחס אשר בין הגבולים הקטנים מהם יותר גדול מיחס אשר בין הגבולים הגדולים |
|
כי שנים ושלשה וארבעה אשר הם בסדר זה האמצעי |
|
|
שעור ארבעה מהם והוא הגבול הגדול אצל השלשה כיחס המוסיף חלק השלישי ושעור שלשה אצל השנים והוא הגבול הקטן כיחס המוסיף חלק החציי |
|
וזה יראה ביחס הניגוניי בהפך כי היחס אשר בין הגבולים הגדולים יותר גדול מהיחס אשר הקטנים |
|
מפני זה אמצעי המספר הם הפכים לאמצעי הנגון |
|
ואמצעי המדות הם אמצעיי בין אלו ההפכים כי יחס אשר בין הגבולים הגדולים הוא שוה ליחס אשר בין הקטנים |
| זה הוא סוף המאמר על האמצעי המספרי | |
|
ואמנם האמצעי המדותיי |
|
הוא כאשר יהיו שלשה מספרים או יותר מזה והיה שעור הראשון מהם אצל השני כשעור השני אצל השלישי וכן בהפך |
|
כמו ד' ח' י"ו שהם בזה התאר בהתיחסות המדותיי |
| וכבר יתחלפו אלו המספריים המונחים לאמצעי ההנדסה למספרים המונחים באמצעי המספר לפי שאלו המדרגות עצמן מתיחסות ומותרי קצתם על קצת בלתי שוה ואותן היו מותרי הם שוים ומדרגותיהם בלתי מתיחסות | |
| וסגלת זה האמצעי ההנדסיי כי למותרי הגבולים קצתם על קצת מהיחס כמו מה של גדולים עצמם מהיחס | |
|
|
כי יחס מותרי י"ו על ח' והוא ח' אל מותרי ח' על ד' והוא ד' כמו יחס י"ו אל ח' וח' אל ד' |
|
וכן אם היו גם כן הגדולים ביחס הכפל השלישיי כמו ג' ט' כ"ז |
| וכן הוא תמיד כל מה שתניח מן המדרגות באי זה מן היחסים החמש שתרצה אחר שיהיו הגבולים נמשכים ביחס והבן זה | |
| ולזה האמצעי סגולה שנית והוא שמונה הגבול האמצעי בעצמו וכמו שני הקצוות מוכה אחד מהם באחר | |
| וראוי שנשים לב למה שאמרנו לפנים שמספרי ההוא הוא והזולת בין כל מדרגה מאחד מהם ומדרגה מן האחר אמצעי על המשכם בסדר הטבע | |
| כמו ד'ו'ט'י"ב י"ו | |
| כי כל שלשה מספרים יוקחו מהם מתיחסים | |
| ואם יהיה הגבול הראשון מהם זולתיי יהיה שווי היתרון | |
| וכלל המאמ' שיפל בין כל שני מספרים הוא הויים נלוים מספר אחד זולתיי ימשך עמם על יחס בפחות מההוא הויים המעוקבים | |
| כי בין כל שני מעוקבים נלוים מהם שני מספרים ימשכו עמם על יחס | |
| כי המעוקב הראשון בפעל ח' והמעוקב השני כ"ז ובין שני אלו המספרים המעוקבים שני מספרים והם י"ח וי"ב וכבר יתיחסו אלו הארבעה ביחס אחד | |
| וזה ממה שיחוייב שיאמ' אותו הנה דע שכל מספר מרובע הוכה במספר מרובע הנה המקובץ מרובע | |
| וכל מספר מרובע יוכה במספר בלתי מרובע יהיה המתקבץ מספר מעוקב | |
| כמו ח' בכ"ז שהוא רי"ו כי זה מהכאות בו' עו' בו' | |
| ואם תכה מעוקב בזולתיי לא יתקבץ מעוקב | |
| כמו ח' בו' שהוא מ"ח ומ"ח אינו מעוקב ולא שטח נגדר | |
| ואם תכה מספר זולתיי במספר אחר זולתיי לא יחוייב שיתקבץ מרובע פשוט ולא גם כן מעוקב | |
| ואם תכה זוג בזוג יהיה המתקבץ זוג | |
| ואם תכה נפרד בנפרד יהיה מה שיתקבץ נפרד | |
| אמר מניח הספר וכבר באר זה אפלאטון בספרו אשר יכונה בלשון יוני כולוטיא | |
|
ואמנם האמצעי החבוריי |
| הנה הוא כאשר היו שלשה מספרים מונחים ולא יהיה לקצתם אל קצת יחס אחד כמו הגבולים המדותיים לא יתרוני קצתם על קצת שוים כמו הגבולים המספרים אבל יהיה השעור הגבול הגדול אצל שעור הגבול הקטן כשעור מותר הגבול הגדול על הגבול האמצעי אל מותר האמצעי על הקטן | |
|
כמו ג'ד'ו' |
| וכן גם כן שעור הגדול אצל גדול שני המותרים כשעור הגבול הקטן אצל קטן שני המותרים | |
| וסגולת אלו הגבולים הפכים לגבולי אמצעי החשבון והמדות יחד לפי שאלו הגבולים הפכית לגבולי אמצעי החשבון והמדות יחד לפי שאלו הגבולים יחס הגבול הקטן מהם אל האמצעי גדול מיחס האמצעי אל הגדול וגבולי האמצעי החשבון יחס הקטן אל האמצעי פחות מיחס האמצעי אל הגדול | |
| ואמנם גבולי אמצעי המדות אם היו שלשה גבולים מהם מונחים כפי תנאם יהיו כלם ביחס אחד | |
| ולאמצעי חבוריי סגלה אחרת והיא שהכאת כל אחד משני הקצוות מגבוליו באמצעי מקובצים כמו כפל מה שיהיה משני הקצוות מוכה אחד מהם באחר | |
| ונבאר עתה איך יוצא הגבול השלישי לכל אחד מאלו השלשה אמצעיים כאשר היו שני חלקים מהם מונחים | |
| וזה שאם היו שני חלקים מאמצעי החשבון נלוים מונחים ונבקש הגבול השלישי | |
| הנה אנו נשימהו אם היה הדרוש הגבול הגדול מספר ששעור תוספתו על האמצעי כשעור תוספת האמצעי על הקטן | |
| ונמצא גם דרך אחרת הגבול השלישי כאשר היה הגדול כאשר נכפול האמצעי עוד נשליך ממנו הגבול הקטן ומה שישאר הוא הגבול הגדול | |
| הנה כבר נאמ' שאמצעי החשבון היא אשר יוסיפו גבוליו קצתם על קצת בשוה ואינם מתיחסים הגבולים | |
| ואמרנו שכפל האמצעי מגבוליו כמו שני קצוותיו יחד | |
| וכדמיון זה נוציא הגבול הקטן אם היה הדרוש וזה שאנו נשים הגבול הקטן מספר יהיה חסרונו מהאמצעי כשעור חסרון האמצעי מהגדול או בכפל האמצעי הנה נשליך ממנו הגבול הגדול ומה שישאר הוא הגבול הקטן | |
| אמנם אם היה הדרוש באמצעי אנו נקח חצי שני הקצוות מקובצים והוא האמצעי | |
| ואמנם איך יוצא הגבול השלישי אל אמצעי המדות | |
| הנה אם היה דרושנו הגבול הגדול אנו נשימהו מספר יחס האמצעי אליו כיחס הקטן אל האמצעי | |
| או נכה האמצעי בעצמו ומה שיצא נחלקהו על הגבול הקטן ומה שיצא בחלוק הוא הגבול הגדול | |
| וכבר בארנו לפנים שאמצעי המדות הוא אשר גבוליו מתיחסים ואין תוספתם שוה | |
| ובארנו הכאת שהאמצעי בעצמו כמו שני הקצוות מוכה אחד מהם באחר כי המספר אשר יצא מחלוקת אותו המספר על אחד משני המספרים המוכה אחד מהם באחר שוה לאשר לא יחלק עליו מהם | |
| ואם היה הדרוש הגבול האמצעי הנה אנו נקח שורש המתקבץ מהכאת אחד משני המספרים באחר ונשימהו האמצעי | |
| ואמנם איך נוציא הגבול השלישי מאמצעי החבור | |
| הנה אין אחד משני גבולי הקצוות אפשרי להוציאו וזה שיצטרך בהוצאת כל אחד מהם אל שתי ידיעות מוסכלות מארבעה מתיחסים חלוקים ביחס אחד מהם בגבול המוסכל עצמו והשני מותר הגבול המוסכל על הגבול האמצעי אם היה הגבול המוסכל הוא הגבול הגדול | |
| או מותר האמצעי על הקטן אם היה המוסכל הוא הקטן | |
| ואמנם הוצאת האמצעי הנה כבר נודע שהוא כאשר לוקח מותר הגדול על הקטן וחולק בשני חלקים יחס א' מהם אל האחר יחס הגדול אל הקטון כי הקטון משני חלקי המותר כאשר נוסף על הקטן משני הקצוות היה המתקבץ הוא האמצעי וכאשר חוסר החלק הגדול משני חלקי המותר מהגבול הגדול היה גם כן הוא האמצעי | |
| ואמנם אופן אחר ההכאה בם אנו נכה אחד משני הקצוות באחר ועוד נכפל מה שיתקבץ ונחלק מה שיתקבץ על שני הקצוות מקובצים ומה שיצא מהחלוקה הוא האמצעי וזה מספיק בתאר האמצעים השלשה המפורסמים אצל הקדמונים | |
| ואמנם הנשארים נקצר המאמר עליהם למעוט השתמש הקדמונים מהם | |
|
האמצעי הרביעי הוא הראשון מהשבעה האמצעים הנשארים |
|
והוא אשר יאמר לו מקביל האמצעי החבוריי |
|
|
והוא שיהיו שלשה גבולים יחס מותר האמצעי על הקטן אל מותר הגדול על האמצעי כיחס הגדול אל הקטן |
|
כמו ג'ה'ו' |
|
וסגולת זה האמצעי הוא שהכאת הגדול באמצעי כפל הקטן באמצעי |
|
והאמצעי החמשי |
|
והוא אחד משני המקבילים לאמצעי המדותיי |
|
|
הוא כאשר יהיו שלשה גבולים יחס מותר הגדול על האמצעי אל מותר האמצעי על הקטן כיחס הקטן אל האמצעי |
|
כמו ב'ד'ה' |
|
וסגלת זה שמה שיתקבץ מהכאת הגדול באמצעי כפל המתקבץ מהכאת הגדול בקטן |
|
ויתחייב מזה שיהיה לעולם יחס האמצעי אל הקטן הוא יחס הכפל |
|
ואמנם האמצעי הששי |
|
והוא השני לשני המקבילים לאמצעי המדותי |
|
|
הנה הוא כאשר היו שלשה גבולים יחס מותר האמצעי על הקטן אל מותר הגדול אל האמצעי כיחס הגדול אל האמצעי |
|
כמו א'ד'ו' |
|
וסגלת זה שמה שיתקבץ מהכאת המותר הגדול בגבול האמצעי שוה למה שיתקבץ מהכאת המותר הקטן בגבול הגדול |
| the first three proportions were used from Pythagoras until Plato | הנה האמצעים הנעשים מאחר פיתאגוריש עד זמן אפלאטון הם השלשה הראשונים |
| the other three are their opposites | ואלו השלשה האחרים הם מקבילים |
| the four remaining were mentioned by the contemporaries and found to a small extent in the writing of the ancients | ואמנם הארבעה הנשארים אשר זכרום החדשים ומעט מה שימצאו בספרי הקדמונים |
| since they were mentioned they must be mentioned here - lest the author will be considered ignorant concerning them | וכאשר נזכרו זכר פשוט כבר יחוייב שנזכירם כדי שלא יחשוב חושב שאנו עזבנום להכלותנו בם והם אלו |
|
האמצעי השביעי |
|
|
הוא כאשר היו שלשה גבולים יחס מותר הגדול על הקטן אל מותר האמצעי על הקטן כיחס הגדול אל הקטן |
|
כמו ו'ח'ט' |
|
והאמצעי השמיני |
|
|
הנה הוא כאשר היתה הנחת הגבולים כן יחס הגדול אל הקטן כיחס מותר הגדול על הקטן אל מותר הגדול על האמצעי |
|
כמו ו'ז'ט' |
|
והאמצעי התשיעי |
|
|
הוא כאשר היו שלשה גבולים יחס מותר הגדול על הקטן אל מותר האמצעי על הקטן כיחס האמצעי אל הקטן |
|
כמו ד'ו'ז' |
|
אמנם האמצעי הי' |
|
|
כאשר היו ג' גבולי' יחס מותר הגדול על הקטן אצל מותר הגדול על האמצעי כיחס האמצעי אל הקטן |
|
כמו ג'ה'ח' |
| והנה השלמנו כלם בזאת הצורה |
The Perfect Proportion that encompassing the body |
הדבור באמצעי השלם המקיף במוגשם |
|---|---|
| the proportion that has three dimensions - | האמצעי בעל הג' גבולי' מפני שהקפת תכליותיו מורכבת מב' המרחקי' והם |
| מרחק מה שבין הגדול והאמצעי | |
| ומרחק מה שבין אמצעי והקטן כמו אותו אל הפשוט אשר הוא מורכב מהארך והרחב | |
| ואמנם האמצעי' המדומים בגשם הנה הם יותר שלימי' האמצעיים וא"א להיות אמצעי יותר ראוי בשם השלימות מהם כמו שהמוגשם כבר יכלה שלמותו אחר שאי אפשר בטבע שיקבל תוספת על המרחקי' הג' שאר הם הארך והרחב והעומק | |
| הנה א"כ האמצעי בעל הד' גבולים מפני שההקפה אשר לתכליותיו היא מורכבת מג' מרחקים והם מרחק מה שבין הראשון והב' ומרחק מה שבין הב' לשלישי | |
| ומרחק מה שבין הג' לד' היה בדין ובראוי הוא האמצעי השלם הדומה במוגשם ובדין לו זה הדמיון כי היו מרחקי הגשם הג' אמנם עמדו מד' גבולי' והם האחדות והצלע והפשוט והגשם | |
| כי מרחק מה שבין האחדות והגשם הוא המוגשם עצמו והוא מורכב מהג' רחקי' אשר הם מרחק מה שבין האחדות והצלע ומרחק מה שבין הצלע והפשוט ומרחק מה שבין הפשוט והגשם | |
| וכן האמצעי השלם בעל הד' גבולי' הוא הקפת תכליותיו ותמצא אותה ההקפה מורכבת מג' המרחקים אשר הם מרחק הגבול הראשון מהב' ומרחק הב' מהג' והמרחק הג' מהד' | |
| וכבר הניח ניקומכוש לזה האמצעי השלם המוגשם המקיף דמיון משל א' הראנו כי ההקפה בסגולות האמצעיי' הג' ר"ל אמצע החשבון ואמצע המדות אמצע החבור וזה צורתו המשל שהביא ניקומאכושו ח ט יב | |
| ואמנם סגולת האמצעי החשבון הנמצאת בזה האמצעי השלם המוגשם המקיף הנה יראה בג' גבולי' מהם | |
| והם הראשון והג' והד' וזה לפי שמותר הרביעי על הג' הוא מותר הג' על הראשון ושהראשון והד' מקובצים כמוכפל האמצעי והיא הסגולה שזכרנו | |
| וכאשר היה זה כן הנה כבר יתחייבו לו כל הסגולות אשר קדם זכרם לאמצע החשבון | |
| ואמנם סגולת אמצע המדות הנמצאות בזה האמצעי השלם המוגשם המקיף תראה בגבולי' הד' יחד | |
| כאשר יוחס הראשון אל הג' והב' אל הד' וזה לפי שהיחס יהיה אז אחד ויהיה מוכה ב' הקצוות א' מהם באחר כמוכה ב' האמצעיי' א' מהם באחר וכאשר היה זה כן יתחייבו לו שאר הסגולות הנמצאות לאמצעי המדות | |
| ואמנם סגולת האמצעי החבור אשר תמצא בזה האמצעי השלם המוגשם המקיף תראה בג' מגבוליו | |
| כמו שנראה באמצעי החשבון והראות זה יהיה כאשר ייוחס הד' אל הב' והב' אל הראשון כי יהיה אז יחס מותר הד' על הב' ועל הד' כיחס מותר הב' על הראשון | |
| וכאשר היה זה כן הנה יתחייבו לו ג"כ שאר הסגולות הנמצאו' אל אמצעי החבור | |
| ואמנם נראו סגולות אמצעי החשבון בג' גבולים וסגולות אמצעי החבור בג' גבולים וחלוף זה הראות סגולות אמצעי המדות כאשר השתמש בהראותם ד' גבולי' יחד לפי שהמדה באלו היא אמצעית בין ב' המלאכות האחרות ותקח הראוי מהן יחד והנה יתקבץ בם מה שתפריש בם | |
| וזולת זה אנו נאמר כי כבר יראה בזה האמצעי השלם המוגשם המקיף כל ההסכמות הנמצאות במלאכת החבור | |
| אם ההסכמה בד' והיא על יחס דמיון ושליש תראה מהקשת הראשון אל הב' ותרא' ג"כ מהקשת הג' אל הד' | |
| ואמנם ההסכמה בחומש והוא על יחס דמיון וחצי תרא' מהקשת הראשון אל הג' | |
| ואמנם ההסכמה בכל והוא על יחס הכפל השניי תראה מהקשת הראשון אל הד' | |
| ואמנם הזמן והוא על יחס דמיון ושמינית תראה מהקשת מה שבין הב' והג' | |
| וזה הזמן הוא שעור משותף לכל הליחנים והוא הפחות שבמרחקים המקבילים בליחנים להחלק | |
| והוא היתרון אשר בין ההסכמה בחומש וההסכמה בד' כמו שהשמינית הוא המותר בין המוסיף חצי ובין המוסיף שליש | |
| וכבר השלמתי לך איך יראו אלו ההסכמות מזה האמצעי השלם המקיף המוגשם בצורה זו | |
| תם ונשלם שבח לכל בורא עולם] | |
Appendix: Bibliography
Nicomachus of Gerasa
2nd century C. E
’Αριθμητικής είσαγωγής βιβλία β – Introduction to Arithmetic
Critical Edition:
- Nicomachus of Gerasa. Introduction to Arithmetic. trans. Martin L. D'Ooge. Chicago IL: Encyclopaedia Britannica, 1955.[Great Books of the Western World, vol.11], pp. 811 – 848.
– Hebrew translation –
Qalonymos ben Qalonymos (known as Maestro Calo or Callus)
South of France, 1286/7-after 1329
Sefer ha-Aritmitiqa / Aritmaiti
1317
Manuscripts:
- 1) Halle, Universitätsbibliothek Yb Qu. 5/1 (IMHM: f 71790), ff. 1r-54r (15th century)
- 2) München, Bayerische Staatsbibliothek, Cod. hebr. 36/14 (IMHM: f 1166), ff. 144r-164r (Istanbul, 1485)
- 3) New York, Jewish Theological Seminary Ms. 2449/2 (IMHM: f 28702), ff. 107r-153r (15th century)
- 4) Paris, Bibliothèque Mazarine 4478/1 (IMHM: f 4414), ff. 194-296 (15th century)
- 5) Paris, Bibliothèque Nationale de France heb. 1028/1 (IMHM: f 15720), ff. 1r-54r (1342)
- 6) Paris, Bibliothèque Nationale de France heb. 1029/1 (IMHM: f 15721), ff. 1r-30v (15th – 16th century)
- 7) Paris, Bibliothèque Nationale de France heb. 1093/2 (IMHM: f 15043), ff. 127r-155v (15th century)
- 8) Paris, Bibliothèque Nationale de France heb. 1095/8 (IMHM: f 15045), ff. 177-226 (15th century)
Bibliography:
- Freudenthal, Gad et Lévy Tony. 2004. De Gérase à Bagdad: Ibn Bahriz, al-Kindi, et leur recension arabe de l’Introduction arithmétique de Nicomaque, d’après la version hébraïque de Qalonymos ben Qalonymos d’Arles, In R. Morelon et A. Hasnawi eds. De Zénon d’Elée à Poincaré. Recueil d’études en hommage à Roshdi Rashed. Louvain-Paris. pp. 479-544.
- Freudenthal, Gad and Mauro Zonta. 2007. Remnants of Habīb ibn Bahrīz’s Arabic translation of Nicomachus of Gerasa’s Introdaction to Arithmetic, in Y. Tzvi Langermann and Josef Stern eds. Adaptations and Innovations: Studies on the interaction between Jewish and Islamic thought and literature from the early Middle Ages to the late twentieth century, dedicated to Professor Joel L. Kraemer. Paris, Louvain and Dudley: Peeters, 2007. pp.67-82.
- ———. 2009. Nicomachus of Gerasa in Spain, Circa 1100: Abraham bar Ḥiyya’s Testimony, Aleph 9.2 (2009), pp. 189-224.
- Langermann, Y. Tzvi. 2001. Studies in Medieval Hebrew Pythagoreanism: Translations and Notes to Nicomachus; Arithmological Texts, Micrologus IX, pp. 219–36.
- Sarfatti, Gad ben ‛Ami. 1968. Mathematical Terminology in Hebrew Scientific Literature of the Middle Ages. Jerusalem: Magnes Press, pp. 200-214.
- Steinschneider, Moritz. 1894. Miscellen 26. Nikomachus, Arithmetik, Monatsschrift für die Geschichte und Wissenschaft des Judenthums 38, pp. 68–77.
– Summary –
Manuscript:
- Oxford, Bodleian Library MS Mich. 29/3 (IMHM: f 20994), ff. 131v-158r (cat. Neub. 2302, 3; 18th century)
– Commentaries on the Introduction to Arithmetic by Nicomachus –
Caleb Afendopolo
Constantinople, 1499
Manuscript:
- Berlin, Staatsbibliothek (Preußischer Kulturbesitz) Or. Qu. 760 (IMHM: f 1742) (1499)
Bibliography:
- Steinschneider, Moritz. 1896. Miscellen 36. Kaleb Afednopolo's encyklopädische Einteilung der Wissenschaften, Monatsschrift für die Geschichte und Wissenschaft des Judenthums 40, pp. 90–94.
A certain Yosef
Manuscript:
- Moscow, Russian State Library, Ms. Guenzburg 340/1 (IMHM: f 47750), ff. 2r-18v (16th century)
Abraham Yerushalmi
Manuscripts:
- Moscow, Russian State Library, Ms. Guenzburg 340/2 (IMHM: f 47750), ff. 19r-23r (16th century)
![\scriptstyle n=\frac{1}{2}\sdot\left[\left(n+1\right)+\left(n-1\right)\right]](/mediawiki/images/math/0/8/a/08a331a4b14c89dd6b9cea191a31ef06.png)
![\scriptstyle n=\frac{1}{2}\sdot\left[\left(n+2\right)+\left(n-2\right)\right]](/mediawiki/images/math/3/8/0/380f7d2cc486e55ce5fc116c2f382b67.png)
![\scriptstyle n=\frac{1}{2}\sdot\left[\left(n+m\right)+\left(n-m\right)\right]](/mediawiki/images/math/d/1/f/d1f23c2ce19c992ceead63ae37670955.png)
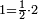
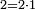
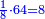 → 8 is even-times-even
→ 8 is even-times-even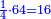 → 4 and 16 are even-times-even
→ 4 and 16 are even-times-even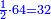 → 2 and 32 are even-times-even
→ 2 and 32 are even-times-even which is derived from 9
which is derived from 9 which is derived from 3
which is derived from 3

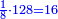
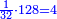
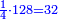
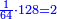
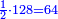

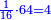
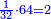
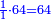
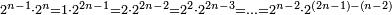
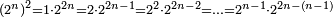
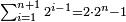
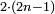

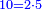
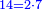
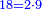


![\scriptstyle\left[2\sdot\left(2n+1\right)\right]+\left[2\sdot\left[\left[2\sdot\left(n+1\right)\right]+1\right]\right]=\left[2\sdot\left(2+1\right)\right]+\left[2\sdot\left[\left(2\sdot2n\right)+1\right]\right]](/mediawiki/images/math/0/3/b/03b1aebe88db1e369e31ef8013f61229.png)

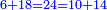
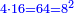

 → from 7
→ from 7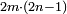
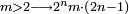
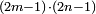

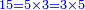
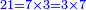
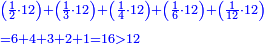
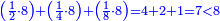
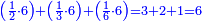
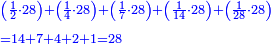
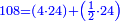 this is the double sesquialter ratio, which is not a simple ratio.
this is the double sesquialter ratio, which is not a simple ratio.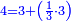
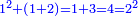
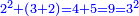
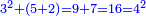

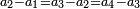

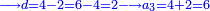
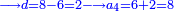
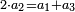
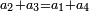
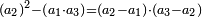
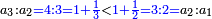

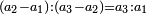
 is incorrect]
is incorrect]
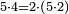
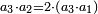 is incorrect]
is incorrect] is also incorrect]
is also incorrect]