Difference between revisions of "ספר החשבון לאל חצאר"
(→written extraction of roots) |
(→written extraction of roots) |
||
| Line 287: | Line 287: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|{{#annot:|147| | + | |style="text-align:right;"|{{#annot:|147|c05l}}הנה כבר הושם המספר על<ref>על: MS V om.</ref> שתים עשרה שמות והם התשעה שמות אשר לאחדים והעשירי לעשרות<ref>לעשרות: MS V השמו'</ref> והאחד עשר המאות והשתים עשרה<ref>עשרה: MS V עשרי</ref> האלפים {{#annotend:c05l}} |
|- | |- | ||
| | | | ||
| Line 940: | Line 940: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|{{#annot:|172| | + | |style="text-align:right;"|{{#annot:|172|676N}}דע כי קבוץ מספר<ref>מספר: MS V המספר</ref> אל המספר<ref>המספר: MS V מספר</ref> אמנם הוא שתקובץ כל מדרגה אל סוגה כלומר האחדים אל האחדים והעשרות אל העשרות והמאות אל המאות והאלפים אל האלפים{{#annotend:676N}} |
|- | |- | ||
|The procedure starts from the rank of units | |The procedure starts from the rank of units | ||
| − | |style="text-align:right;"|תתחיל תמיד {{#annot:|178| | + | |style="text-align:right;"|תתחיל תמיד {{#annot:|178|kYNn}}לקבץ{{#annotend:kYNn}} מן<ref>מן: MS V om.</ref> המדרגה הראשונה |
|- | |- | ||
| | | | ||
*The sum of the digits in the first rank is equal to ten | *The sum of the digits in the first rank is equal to ten | ||
| − | |style="text-align:right;"|אם<ref>אם: MS V ואם</ref> {{#annot:|180| | + | |style="text-align:right;"|אם<ref>אם: MS V ואם</ref> {{#annot:|180|BnYv}}יעלה{{#annotend:BnYv}} ממנו עשרה הגביהנו<ref>הגביהנו: MS V הגביהו</ref> אל העשרות |
|- | |- | ||
| | | | ||
| Line 977: | Line 977: | ||
| | | | ||
|style="text-align:right;"|הניח<ref>הניח: MS V תניח</ref> החמשה ושבעים ושמנה מאות בשטה<br> | |style="text-align:right;"|הניח<ref>הניח: MS V תניח</ref> החמשה ושבעים ושמנה מאות בשטה<br> | ||
| − | אחר כן תניח השמנה ותשעים ושבע מאות תחת {{#annot:|179| | + | אחר כן תניח השמנה ותשעים ושבע מאות תחת {{#annot:|179|PT9E}}המספר המקובץ אליו{{#annotend:PT9E}} בשטה אחרת<br> |
ויהיו האחדים תחת האחדים והעשרות תחת העשרות והמאות תחת המאות על זאת הצורה | ויהיו האחדים תחת האחדים והעשרות תחת העשרות והמאות תחת המאות על זאת הצורה | ||
|- | |- | ||
| Line 1,011: | Line 1,011: | ||
|style="text-align:right;"|ואחר<ref>ואחר: MS V אחר</ref> כן תמשוך על המספר קו ותחת המספר<ref>המספר: MS V om.</ref> קו אחר<br> | |style="text-align:right;"|ואחר<ref>ואחר: MS V אחר</ref> כן תמשוך על המספר קו ותחת המספר<ref>המספר: MS V om.</ref> קו אחר<br> | ||
ואחר<ref>ואחר: MS V אחר</ref> כן קבץ החמשה אל השמנה יהיו שלשה עשר והעמיד השלשה על האחדים על הקו העליון והגביה העשרה אל מדרגת העשרות והעמידהו תחת הקו התחתון<br> | ואחר<ref>ואחר: MS V אחר</ref> כן קבץ החמשה אל השמנה יהיו שלשה עשר והעמיד השלשה על האחדים על הקו העליון והגביה העשרה אל מדרגת העשרות והעמידהו תחת הקו התחתון<br> | ||
| − | אחר כן קבץ העשרות וזה שבעה ותשעה ואחד<ref>ואחד: MS O om.</ref> ויהיה {{#annot:|180| | + | אחר כן קבץ העשרות וזה שבעה ותשעה ואחד<ref>ואחד: MS O om.</ref> ויהיה {{#annot:|180|NS56}}המקובץ{{#annotend:NS56}} שבעה עשר עם האחד שהיה לנו מן האחדים<ref>עם ... האחדים: MS V om.</ref> והעמיד השבעה על מדרגת העשרות על הקו העליון והעתיק<ref>והעתיק: MS V ותעתיק</ref> אותם העשרה המורמת מהם אל מדרגת המאות והעמידם תחת הקו התחתון<br> |
אחר כן קבץ המאות וזה שמנה ושבעה ואחד<ref>ואחד: MS O באחד</ref> יהיה זה ששה עשר והעמיד הששה על המאות על הקו העליון והרם<ref>והרם: MS V ותרים</ref> העשרה באחד אל מדרגת האלפים לבדו<br> | אחר כן קבץ המאות וזה שמנה ושבעה ואחד<ref>ואחד: MS O באחד</ref> יהיה זה ששה עשר והעמיד הששה על המאות על הקו העליון והרם<ref>והרם: MS V ותרים</ref> העשרה באחד אל מדרגת האלפים לבדו<br> | ||
| − | ויהיה {{#annot:|180| | + | ויהיה {{#annot:|180|49EH}}היוצא{{#annotend:49EH}} שלשה ושבעים ושש מאות ואלף |
{|style="margin-left: auto; margin-right: 0px;" | {|style="margin-left: auto; margin-right: 0px;" | ||
|- | |- | ||
| Line 1,091: | Line 1,091: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|תשים<ref>תשים: MS O השיב</ref> אלו השלשה מספרים בשלש שטות ושים כל {{#annot:|188| | + | |style="text-align:right;"|תשים<ref>תשים: MS O השיב</ref> אלו השלשה מספרים בשלש שטות ושים כל {{#annot:|188|OsBR}}סוג{{#annotend:OsBR}}<ref>סוג: MS O מין סוג</ref> תחת סוגו על הצורה הזאת |
|- | |- | ||
| | | | ||
| Line 1,244: | Line 1,244: | ||
אחר כן קבץ העשרות והם תשעה וחמשה וששה ושנים יהיה שנים ועשרים ושים השנים על העשרות על הקו ושים השתי עשרות תחת המאות<br> | אחר כן קבץ העשרות והם תשעה וחמשה וששה ושנים יהיה שנים ועשרים ושים השנים על העשרות על הקו ושים השתי עשרות תחת המאות<br> | ||
אחר כן קבץ המאות והם ששה ואחד ושמנה ושנים יהיו<ref>יהיו: MS V יהיה</ref> שבעה עשר והעמד השבעה על המאות על הקו והעמיד העשרה תחת האלפים<br> | אחר כן קבץ המאות והם ששה ואחד ושמנה ושנים יהיו<ref>יהיו: MS V יהיה</ref> שבעה עשר והעמד השבעה על המאות על הקו והעמיד העשרה תחת האלפים<br> | ||
| − | אחר כן קבץ האלפים והם שבעה ואחד ושים אותם על הקו יהיה שמנה ב{{#annot:|188| | + | אחר כן קבץ האלפים והם שבעה ואחד ושים אותם על הקו יהיה שמנה ב{{#annot:|188|IiQ2}}בית{{#annotend:IiQ2}} האלפים<br> |
יהיה היוצא שנים ועשרים ושבע מאות ושמנת אלפים | יהיה היוצא שנים ועשרים ושבע מאות ושמנת אלפים | ||
{|style="margin-left: auto; margin-right: 0px;" | {|style="margin-left: auto; margin-right: 0px;" | ||
| Line 1,328: | Line 1,328: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|{{#annot:|173| | + | |style="text-align:right;"|{{#annot:|173|X86n}}דע כי הוצאת המספרים קצתם מקצת אמנם הוא שיוצא<ref>שיוצא: MS O om.</ref> כל סוג מסוגו{{#annotend:X86n}} |
|- | |- | ||
|Example: <math>\scriptstyle6475-2343</math> | |Example: <math>\scriptstyle6475-2343</math> | ||
| − | |style="text-align:right;"|דמיון זה {{#annot:|181| | + | |style="text-align:right;"|דמיון זה {{#annot:|181|yl1d}}הוצא{{#annotend:yl1d}} שלשה וארבעים ושלש מאות ואלפים מחמשה ושבעים וארבע מאות וששת אלפים |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|שים {{#annot:|183| | + | |style="text-align:right;"|שים {{#annot:|183|jzGO}}המספר המוצא{{#annotend:jzGO}} בשטה ו{{#annot:|182|3GBe}}המוצא ממנו{{#annotend:3GBe}} בשטה גם כן<ref>גם כן: MS O ג"כ</ref> כל סוג נכחי אל סוגו על<ref>על: MS O אל</ref> הצורה הזאת |
|- | |- | ||
| | | | ||
| Line 1,366: | Line 1,366: | ||
אחר כן הוצא<ref>הוצא: MS V תוציא</ref> העשרות מן העשרות וזה ארבעים משבעים הנשאר שלשים ושים אותם על ראשם שלשה<br> | אחר כן הוצא<ref>הוצא: MS V תוציא</ref> העשרות מן העשרות וזה ארבעים משבעים הנשאר שלשים ושים אותם על ראשם שלשה<br> | ||
אחר כן הוצא<ref>הוצא: MS V תוציא</ref> האחדים מן האחדים וזה שלשה מחמשה הנשאר שנים ושים אותם על ראשם שנים‫<ref>שנים: MS V om.</ref><br> | אחר כן הוצא<ref>הוצא: MS V תוציא</ref> האחדים מן האחדים וזה שלשה מחמשה הנשאר שנים ושים אותם על ראשם שנים‫<ref>שנים: MS V om.</ref><br> | ||
| − | ויהיה {{#annot:|184| | + | ויהיה {{#annot:|184|i0nS}}הנשאר{{#annotend:i0nS}} אחר ההוצאה שנים ושלשה ואחד וארבעה |
{|style="margin-left: auto; margin-right: 0px;" | {|style="margin-left: auto; margin-right: 0px;" | ||
|- | |- | ||
| Line 1,384: | Line 1,384: | ||
|- | |- | ||
|Example: <math>\scriptstyle9385-5496</math> | |Example: <math>\scriptstyle9385-5496</math> | ||
| − | |style="text-align:right;"|ואם יאמר {{#annot:|181| | + | |style="text-align:right;"|ואם יאמר {{#annot:|181|rC7m}}השלך{{#annotend:rC7m}} ששה ותשעים וארבע מאות וחמשת אלפים מחמשה ושמנים ושלש מאות ותשעה אלפים |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|הניח<ref>הניח: MS V תניח</ref> שני המספרים בשתי שטות כמו שקדם ויהיה {{#annot:|183| | + | |style="text-align:right;"|הניח<ref>הניח: MS V תניח</ref> שני המספרים בשתי שטות כמו שקדם ויהיה {{#annot:|183|vJsA}}המספר המושלך{{#annotend:vJsA}} תחת {{#annot:|182|4BYH}}המושלך ממנו{{#annotend:4BYH}} על זאת הצורה‫<ref>זאת הצורה: MS V הצורה הזאת</ref> |
|- | |- | ||
| | | | ||
| Line 1,416: | Line 1,416: | ||
אחר כן השלך<ref>השלך: MS V תשליך</ref> המאות השליך ארבעה משלשה<ref>משלשה: MS V מה שלשה</ref> לא יושלך וקח מן האלפים אלף ויהיה<ref>ויהיה: MS V om.</ref> הנשאר שלשת אלפים ושים אותם על ראש האלפים<br> | אחר כן השלך<ref>השלך: MS V תשליך</ref> המאות השליך ארבעה משלשה<ref>משלשה: MS V מה שלשה</ref> לא יושלך וקח מן האלפים אלף ויהיה<ref>ויהיה: MS V om.</ref> הנשאר שלשת אלפים ושים אותם על ראש האלפים<br> | ||
אחר כן חבר<ref>חבר: MS V צרף נ' חבר</ref> האלף בעשרה אל מדרגת המאות וחברם אל השלשה<ref>אל השלשה: MS O בשלשה</ref> אשר מצאת בהם יהיו שלשה עשר והשליך מהם ארבעה והנשאר<ref>והנשאר: MS V הנשאר</ref> תשעה והעמידם על המאות<br> | אחר כן חבר<ref>חבר: MS V צרף נ' חבר</ref> האלף בעשרה אל מדרגת המאות וחברם אל השלשה<ref>אל השלשה: MS O בשלשה</ref> אשר מצאת בהם יהיו שלשה עשר והשליך מהם ארבעה והנשאר<ref>והנשאר: MS V הנשאר</ref> תשעה והעמידם על המאות<br> | ||
| − | אחר כן השלך<ref>השלך: MS V תשליך</ref> העשרות השליך<ref>השליך: MS V תשליך</ref> תשעה משמנה לא יושלך ו{{#annot:|190| | + | אחר כן השלך<ref>השלך: MS V תשליך</ref> העשרות השליך<ref>השליך: MS V תשליך</ref> תשעה משמנה לא יושלך ו{{#annot:|190|9cyd}}התיר{{#annotend:9cyd}} מן המאות מאה נשארו<ref>נשארו: MS V ישארו</ref> שמנה<ref>שמנה: MS V שמנה מאות</ref> ושים אותם על המאות‫<ref>המאות: MS V מאות</ref><br> |
אחר כן חבר<ref>חבר: MS V חבר נ' צרף</ref> המאה ההוא בעשרה אל העשרות ובהם שמנה ויהיה זה שמנה עשר והשליך מהם תשעה והנשאר<ref>והנשאר: MS V הנשאר</ref> תשעה ושים אותם על ראש העשרות<br> | אחר כן חבר<ref>חבר: MS V חבר נ' צרף</ref> המאה ההוא בעשרה אל העשרות ובהם שמנה ויהיה זה שמנה עשר והשליך מהם תשעה והנשאר<ref>והנשאר: MS V הנשאר</ref> תשעה ושים אותם על ראש העשרות<br> | ||
ואחר<ref>ואחר: MS V אחר</ref> כן השליך<ref>השליך: MS V תשליך</ref> האחדים מן<ref>מן: MS O על</ref> האחדים והשליך ששה מחמשה לא יושלך והתיר מן העשרות עשרה ישארו שמנה והעמידם בעשרות<br> | ואחר<ref>ואחר: MS V אחר</ref> כן השליך<ref>השליך: MS V תשליך</ref> האחדים מן<ref>מן: MS O על</ref> האחדים והשליך ששה מחמשה לא יושלך והתיר מן העשרות עשרה ישארו שמנה והעמידם בעשרות<br> | ||
| − | אחר כן {{#annot:|178| | + | אחר כן {{#annot:|178|gktc}}חבר{{#annotend:gktc}} העשרה ההוא אל החמשה ויהיו<ref>ויהיו: MS V יהיו</ref> חמשה עשר ו{{#annot:|181|ulhP}}הפיל{{#annotend:ulhP}} מהם ששה נשאר<ref>נשאר: MS V הנשאר</ref> תשעה והעמידם על האחדים<br> |
ויהיה הנשאר מן ההשלכה תשעה ושמנה ושלשה | ויהיה הנשאר מן ההשלכה תשעה ושמנה ושלשה | ||
{|style="margin-left: auto; margin-right: 0px;" | {|style="margin-left: auto; margin-right: 0px;" | ||
| Line 1,491: | Line 1,491: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|{{#annot:|174| | + | |style="text-align:right;"|{{#annot:|174|4gjS}}דע כי ענין ההכאה הוא שתכפול אחד משני המספרים כשעור מה שבמספר<ref>שבמספר: MS O ממספר</ref> האחד המוכה בו מן האחדים{{#annotend:4gjS}} |
|- | |- | ||
|Example: <math>\scriptstyle3\times4</math> | |Example: <math>\scriptstyle3\times4</math> | ||
| − | |style="text-align:right;"|ודמיון זה כאשר תרצה {{#annot:|185| | + | |style="text-align:right;"|ודמיון זה כאשר תרצה {{#annot:|185|MqIe}}להכות{{#annotend:MqIe}} שלשה בארבעה הנה ענינו<ref>ענינו: MS V ענין כן</ref> ש{{#annot:|191|1gok}}תכפול{{#annotend:1gok}} הארבעה שלשה פעמים והשלשה ארבעה פעמים |
|- | |- | ||
| | | | ||
| Line 1,500: | Line 1,500: | ||
|- | |- | ||
|Multiplication by 1 | |Multiplication by 1 | ||
| − | |style="text-align:right;"|ודע כי כל מספר תכהו באחד או תכה האחד<ref>האחד: MS V אחד</ref> בו הנה המספר ההוא לא יכפל ולא {{#annot:|191| | + | |style="text-align:right;"|ודע כי כל מספר תכהו באחד או תכה האחד<ref>האחד: MS V אחד</ref> בו הנה המספר ההוא לא יכפל ולא {{#annot:|191|gjSo}}יעתק{{#annotend:gjSo}} מגדרו וכן גם כן<ref>גם כן: MS O ג"כ</ref> הכאת האחד בנפשו לא יכפל אמנם הוא אחד |
|- | |- | ||
| | | | ||
| Line 2,955: | Line 2,955: | ||
| | | | ||
*if there are zeros in the number - its root has half the number of the zeros | *if there are zeros in the number - its root has half the number of the zeros | ||
| − | |style="text-align:right;"|ואם תרצה לקחת גדר מספר יהיה | + | |style="text-align:right;"|ואם תרצה לקחת גדר מספר יהיה צפרים עשה בצפר כמו שקדם בלקיחת הגדרים וקיים הצפרים וקח חצי מספרם וחצי מה שכפלת וחברהו אל הצפרים יהיה הגדר |
|- | |- | ||
| | | | ||
:Example: <math>\scriptstyle\sqrt{10000}</math> | :Example: <math>\scriptstyle\sqrt{10000}</math> | ||
| − | |style="text-align:right;"|המשל בזה | + | |style="text-align:right;"|המשל בזה כאשר תרצה לקחת גדר עשרת אלפים |
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"|הוריד העשרת אלפים ארבעה | + | |style="text-align:right;"|הוריד העשרת<ref>העשרת: MS O עשרת</ref> אלפים ארבעה צפרים ואחד כמו שקדם באותיות האבק על הצורה הזאת |
|- | |- | ||
| | | | ||
| Line 2,978: | Line 2,978: | ||
|- | |- | ||
| | | | ||
| − | |style="text-align:right;"| | + | |style="text-align:right;"|ואחר כן מנה המדרגות תמצאם נפרד והתחיל במדרגה האחרונה<br> |
| + | אחר כן תאמר איזה מספר אכהו בדומה לו ונפיל המקובץ מן האחד ויכלה תמצא אחד ועמך מן הצפרים ארבעה קח חציים וזה שנים ויהיה הגדר שני צפרים ואחד על זאת הצורה | ||
| + | |- | ||
| + | | | ||
| + | :<span style="color:#0000FF>1 0 0</span> | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | | | ||
| + | {|style="margin-left: auto; margin-right: 0px;" | ||
| + | |- | ||
| + | |א||‫0||‫0 | ||
| + | |} | ||
| + | |- | ||
| + | |} | ||
|- | |- | ||
| | | | ||
Revision as of 16:23, 19 April 2018
Contents
- 1 Prologue
- 2 Table of Contents
- 3 Section One – Integers
- 3.1 Chapter One – Numeration
- 3.2 Chapter Two – Positional Decimal System
- 3.3 Chapter Three – Addition
- 3.4 Chapter Four – Subtraction
- 3.5 Chapter Five – Multiplication
- 3.6 Chapter Six – Dividing a Small Number by a Larger Number
- 3.7 Chapter Seven – Division
- 3.8 Chapter Eight – Halving
- 3.9 Chapter Nine – Doubling
- 3.10 Chapter Ten – Extracting Roots
- 4 Section Two – Fractions
- 4.1 Multiplication of Fractions
- 4.1.1 Chapter One – Forms of Fractions
- 4.1.2 Chapter Two – Multiplication of Fraction by Integer
- 4.1.3 Chapter Three – Multiplication of Fraction and Fraction of Fraction by Integer
- 4.1.4 Chapter Four – Multiplication of Fraction of Fraction by Integer
- 4.1.5 Chapter Five – Multiplication of Two Different Fractions by Integer
- 4.1.6 Chapter Six – Multiplication of Fraction by Integer and Fraction
- 4.1.7 Chapter Seven – Multiplication of Fraction and Fraction of Fraction by Integer and Fraction
- 4.1.8 Chapter Eight – Multiplication of Fraction of Fraction by Integer and Fraction
- 4.1.9 Chapter Nine – Multiplication of Two Different Fractions by Integer and Fraction
- 4.1.10 Chapter Ten – Multiplication of Fraction by Integer and Fraction and Fraction of Fraction
- 4.1.11 Chapter Eleven – Multiplication of Fraction by Integer and Fraction of Fraction
- 4.1.12 Chapter Twelve – Multiplication of Fraction by Integer and Two Different Fractions
- 4.1.13 Chapter Thirteen – Multiplication of Fraction and Fraction of Fraction by Integer and Fraction and Fraction of Fraction
- 4.1.14 Chapter Fourteen – Multiplication of Fraction and Fraction of Fraction by Integer and Fraction of Fraction
- 4.1.15 Chapter Fifteen – Multiplication of Fraction and Fraction of Fraction by Integer and Two Different Fractions
- 4.1.16 Chapter Sixteen – Multiplication of Fraction of Fraction by Integer and Fraction and Fraction of Fraction
- 4.1.17 Chapter Seventeen – Multiplication of Fraction of Fraction by Integer and Fraction of Fraction
- 4.1.18 Chapter Eighteen – Multiplication of Fraction of Fraction by Integer and Two Different Fractions
- 4.1.19 Chapter Nineteen – Multiplication of Two Different Fractions by Integer and Fraction and Fraction of Fraction
- 4.1.20 Chapter Twenty – Multiplication of Two Different Fractions by Integer and Fraction of Fraction
- 4.1.21 Chapter Twenty One – Multiplication of Two Different Fractions by Integer and Two Different Fractions
- 4.1.22 Chapter Twenty Two – Multiplication of Integer and Fraction by Integer and Fraction
- 4.1.23 Chapter Twenty Three– Multiplication of Integer and Fraction and Fraction of Fraction by Integer and Fraction and Fraction of Fraction
- 4.1.24 Chapter Twenty Four – Multiplication of Integer and Two Different Fractions by Integer and Two Different Fractions
- 4.1.25 Chapter Twenty Five – Multiplication of Integer and Two Different Fractions and Fraction of Fraction by Integer and Two Different Fractions and Fraction of Fraction
- 4.1.26 Chapter Twenty Six – Multiplication of Integer and Three Different Fractions by Integer and Three Different Fractions
- 4.1.27 Chapter Twenty Seven – Multiplication of Integer and Three Different Fractions and Fraction of Fraction
- 4.1.28 Chapter Twenty Eight – Multiplication of Fraction by Fraction
- 4.1.29 Chapter Twenty Nine – Multiplication of Fraction and Fraction of Fraction by Fraction
- 4.1.30 Chapter Thirty – Multiplication of Two Different Fractions by Fraction
- 4.1.31 Chapter Thirty One – Multiplication of Fraction and Fraction of Fraction by Fraction and Fraction of Fraction
- 4.1.32 Chapter Thirty Two – Multiplication of Two Different Fractions by Fraction and Fraction of Fraction
- 4.1.33 Chapter Thirty Three – Multiplication of Two Different Fractions by Two Different Fractions
- 4.1.34 Chapter Thirty Four – Multiplication of Fraction by Fraction of Fraction
- 4.1.35 Chapter Thirty Five – Multiplication of Two Different Fractions and Fraction of Fraction by the Same
- 4.1.36 Chapter Thirty Six – Multiplication of Three Different Fractions by Three Different Fractions
- 4.1.37 Chapter Thirty Seven – Multiplication of Three Different Fractions and Fraction of Fraction by the Same
- 4.1.38 Chapter Thirty Eight – Multiplication of Fraction of Integer by Fraction of Integer
- 4.1.39 Chapter Thirty Nine – Multiplication of Fraction and Fraction of Fraction of Integer by Fraction and Fraction of Fraction of Integer
- 4.1.40 Chapter Forty – Multiplication of Different Fractions of Integer by Different Fractions of Integer
- 4.1.41 Chapter Forty One – Multiplication of Fraction of Fraction of Integer by Fraction of Fraction of Integer
- 4.1.42 Chapter Forty Two – Multiplication of Fraction of Integer and Fraction by Fraction of Integer and Fraction
- 4.1.43 Chapter Forty Three – Multiplication of Fraction of Integer and Fraction and Fraction of Fraction by the Same
- 4.1.44 Chapter Forty Four – Multiplication of Fraction of Integer and Two Different Fractions by the Same
- 4.1.45 Chapter Forty Five – Multiplication of Fraction of Integer and Fraction of Fraction by Fraction of Integer and Fraction of Fraction
- 4.1.46 Chapter Forty Six – Multiplication of Fraction of Fraction of Integer and Fraction by Fraction of Fraction of Integer and Fraction
- 4.1.47 Chapter Forty Seven– Multiplication of Fraction of Fraction of Integer and Fraction and Fraction of Fraction by the Same
- 4.1.48 Chapter Forty Eight – Multiplication of Fraction of Fraction of Integer and Two Different Fractions by Fraction of Fraction of Integer and Two Different Fractions
- 4.1.49 Chapter Forty Nine – Multiplication of Two Different Fractions of Integer and Fraction by Two Different Fractions of Integer and Fraction
- 4.1.50 Chapter Fifty – Multiplication of Two Different Fractions of Integer and Two Different Fractions by the Same
- 4.1.51 Chapter Fifty One – Multiplication of Fraction and Fraction of Fraction of Integer and Fraction and Fraction of Fraction by the Same
- 4.1.52 Chapter Fifty Two – Multiplication of Fraction of Fraction of Integer and Fraction of Fraction by the Same
- 4.1.53 Chapter Fifty Three – Multiplication of Fraction of Integer and Fraction of Integer by the Same
- 4.1.54 Chapter Fifty Four – Multiplication of Fraction of Integer and Fraction of Integer and Fraction by the Same
- 4.1.55 Chapter Fifty Five – Multiplication of Integer and Fraction and Integer and Fraction by the Same
- 4.1.56 Chapter Fifty Six – Multiplication of Integer and Two Different Fractions and Integer and Two Different Fractions and Integer by the Same
- 4.1.57 Chapter Fifty Seven – Multiplication of Integer and Fraction of Fraction and Integer and Fraction of Fraction and Integer by the Same
- 4.1.58 Chapter Fifty Eight – Multiplication of Fraction and Integer and Two Different Fractions and Integer and Fraction by the Same
- 4.1.59 Chapter Fifty Nine – Multiplication of Fraction and Fraction of fraction and Integer and Two Different Fractions and Integer and Fraction and Integer and Fraction and Fraction of Fraction by the Same
- 4.1.60 Chapter Sixty – Multiplication of Fractions
- 4.1.61 Chapter Sixty One – Multiplication of Fractions
- 4.1.62 Chapter Sixty Two – Multiplication of Fraction of fraction of Integer by the Same
- 4.1.63 Chapter Sixty Three – Multiplication of Fraction of Fraction and Fraction of Integer by the Same
- 4.1.64 Chapter Sixty Four – Multiplication of Fraction of Fraction of Integer and Fraction by the Same
- 4.1.65 Chapter Sixty Five – Multiplication of Fraction of Fraction of Integer and Fraction and Fraction of Fraction by the Same
- 4.1.66 Chapter Sixty Six – Multiplication of Integer and Fraction of Fraction by the Same
- 4.1.67 Chapter Sixty Seven – Multiplication of Integer and Fraction of Fraction and Fraction by the Same
- 4.1.68 Chapter Sixty Eight – Multiplication of Fraction of Fraction and Integer and Fraction of Fraction by the Same
- 4.1.69 Chapter Sixty Nine – Multiplication of Two Different Fractions and Integer and Fraction of Fraction and Integer and Fraction and Fraction of Fraction and Integer and Fraction of Fraction and Integer and Fraction
- 4.1.70 Chapter Seventy – Multiplication of Integer and Fraction by Integer and Fraction by Integer and Fraction and so on
- 4.1.71 Chapter Seventy One– Multiplication of Reduced Fractions
- 4.1.72 Chapter Seventy Two – Multiplication of Reduced Fractions of Integers
- 4.2 Converting Fractions to Lower Fractions
- 4.3 Addition of Fractions
- 4.3.1 Chapter One – Adding One Fraction to Another
- 4.3.2 Chapter Two – Adding Two Fractions to Two Fractions
- 4.3.3 Chapter Three – Adding Fraction and Fraction of Fraction to Two Different Fractions
- 4.3.4 Chapter Four – Adding Fraction and Fraction of Fraction to Fraction and Fraction of Fraction
- 4.3.5 Chapter Five – Adding Integer and Fraction to Integer and Fraction
- 4.3.6 Chapter Six – Adding Integer and Fraction and Fraction of Fraction to Integer and Two Different Fractions
- 4.3.7 Chapter Seven – Adding Fraction of Integer to Integer
- 4.3.8 Chapter Eight – Adding Fraction of Integer to Fraction of Integer
- 4.3.9 Chapter Nine – Adding Fraction of Integer and Fraction to Fraction of Integer and Fraction
- 4.3.10 Addition of Unknown Amounts
- 4.3.11 Sums
- 4.3.12 Geometrical Progression of Doubles – Squares of Chessboard
- 4.4 Subtraction of Fractions
- 4.4.1 Subtraction of Integer and Fraction from Integer and Fraction/s
- 4.4.2 Subtraction of Three Different Fractions from Integer and Fraction
- 4.4.3 Subtraction of Fraction of Integer from Fraction of Integer
- 4.4.4 Subtraction of Fraction of Integer and Fraction from Fraction of Integer and Fraction
- 4.4.5 Subtraction of Unknown Amounts
- 4.5 Division of Fractions
- 4.5.1 Division of the smaller by the larger
- 4.5.1.1 Division of Fraction and Fraction of fraction by Integer
- 4.5.1.2 Division of Two Different Fractions by Integer
- 4.5.1.3 Division of Fraction by Integer and Fraction
- 4.5.1.4 Division of Fraction by Integer and Fraction and Fraction of Fraction
- 4.5.1.5 Division of Fraction by Integer and Two Different Fractions
- 4.5.1.6 Division of Fraction and Fraction of Fraction by Integer and Fraction
- 4.5.1.7 Division of Integer by Integer and Fraction
- 4.5.1.8 Division of Integer and Fraction by Integer and Fraction
- 4.5.1.9 Division of Fraction by Fraction
- 4.5.1.10 Division of Fraction and Fraction of Fraction by Fraction
- 4.5.1.11 Division of Two Different Fractions by Fraction
- 4.5.1.12 Division of Fraction by Fraction and Fraction of Fraction
- 4.5.1.13 Division of Fraction by Two Different Fractions
- 4.5.1.14 Division of Fraction and Fraction of Fraction by Fraction and Fraction of Fraction
- 4.5.1.15 Division of Two Different Fractions by Two Different Fractions
- 4.5.1.16 Division of Fraction of Fraction by Integer
- 4.5.1.17 Division of Fraction of Fraction by Integer and Fraction
- 4.5.1.18 Division of Fraction of Fraction by Integer and Fraction and Fraction of Fraction
- 4.5.1.19 Division of Fraction of Fraction by Integer and Two Different Fractions
- 4.5.1.20 Division of Fraction of Fraction by Fraction
- 4.5.1.21 Division of Fraction of Fraction by Fraction and Fraction of Fraction
- 4.5.1.22 Division of Fraction of Fraction by Two Different Fractions
- 4.5.2 Division of the larger by the smaller
- 4.5.2.1 Division of Integer by Fraction
- 4.5.2.2 Division of Integer by Fraction of Fraction
- 4.5.2.3 Division of Integer by Fraction and Fraction of Fraction
- 4.5.2.4 Division of Integer by Two Different Fractions
- 4.5.2.5 Division of Integer and Fraction by Fraction
- 4.5.2.6 Division of Integer and Fraction by Fraction of Fraction
- 4.5.2.7 Division of Integer and Fraction by Fraction and Fraction of Fraction
- 4.5.2.8 Division of Integer and Fraction by Two Different Fractions
- 4.5.2.9 Division of Integer and Fraction and Fraction of Fraction by Fraction
- 4.5.2.10 Division of Integer and Fraction and Fraction of Fraction by Fraction of Fraction
- 4.5.2.11 Division of Integer and Fraction and Fraction of Fraction by Fraction and Fraction of Fraction
- 4.5.2.12 Division of Integer and Fraction and Fraction of Fraction by Two Different Fractions
- 4.5.2.13 Division of Integer and Two Different Fractions by Fraction
- 4.5.2.14 Division of Integer and Two Different Fractions by Fraction of Fraction
- 4.5.2.15 Division of Integer and Two Different Fractions by Fraction and Fraction of Fraction
- 4.5.2.16 Division of Integer and Two Different Fractions by Two Different Fractions
- 4.5.2.17 Division of Integer and Two Different Fractions by Integer and Two Different Fractions
- 4.5.2.18 Division of Fraction by Fraction
- 4.5.2.19 Division of Fraction by Fraction of Fraction
- 4.5.2.20 Division of Fraction by Fraction and Fraction of Fraction
- 4.5.2.21 Division of Fraction by Two Different Fractions
- 4.5.2.22 Division of Fraction and Fraction of Fraction by Fraction and Fraction of Fraction
- 4.5.2.23 Division of Two Different Fractions by Two Different Fractions
- 4.5.2.24 Division of Integer and Fraction by Integer and Fraction
- 4.5.2.25 Division of Integer and Fraction and Fraction of Fraction by Integer and Fraction and Fraction of Fraction
- 4.5.2.26 Division of Integer and Two Different Fractions by Integer and Two Different Fractions
- 4.5.1 Division of the smaller by the larger
- 4.6 Completion of Fractions
- 4.7 Degrading
- 4.8 Extracting Roots of Integer and Fraction
- 4.9 Additional Chapters
- 4.9.1 Multiplication of Fraction by Integer
- 4.9.2 Multiplication of Fraction and Fraction of Fraction by Fraction and Fraction of Fraction
- 4.9.3 Multiplication of Integer and Two Fractions by Integer and Fraction
- 4.9.4 Multiplication of Fraction of Integer and Fraction by Fraction of Integer and Fraction
- 4.9.5 Multiplication of Integers
- 4.9.6 Gelosia (MS Oxford)
- 4.9.7 Degrading the Ranks of Sexagesimal Fractions (MS Guenzburg)
- 4.9.8 MS Vatican - Additional Excerpt
- 4.9.9 Extracting Cubic Roots of Integer (MS Vatican)
- 4.1 Multiplication of Fractions
- 5 Notes
- 6 Appendix: Bibliography
Prologue |
|
| אמר[1] המלמד אבו בכר מחמד בן עבד אללה בן עבאס בן חצאר[2] | |
| תהלה לאל אשר אין אלוה בלעדיו בורא כל ויודע כל ומקיף על כל דבר ידיעה ומונה הכל במספר | |
| ואחר[3] ההודאה לשם ית'[4] המדריך אל היושר ואל הסדר | |
| הנה אני מפני שראיתי החוכמו' והמוסרים | |
| וראיתי כי היותר נכבדת[5] מהם חכמת המספר והחשבון[6] אחר ידיעת הדת והתורה | |
| והנה האל שם במספר רמז להגיע[7] בו אל ידיעת אחדותו וסדר בריאותיו | |
| ולדעת בו כל דבר סתום ונסתר | |
| להיות הישרה למתחילים וזכרון לשלמים | |
| חברתי הספר הזה | |
| וכל מה שסברתי[8] בו וספרתיו | |
| ובארתיו ופרשתיו | |
| והנה[9] ממאמרי החכמים לקחתיו | |
| וספרי הקודמים קבצתיו ואספתיו[10] | |
| ובהקשים אמתיים[11] הוצאתיו והולדתיו | |
| ומאלהים[12] אשאל לשמור אותי מן הטעות והשגיאה | |
| ולהדריכני אל היושר והצדק במאמר ובמעשה | |
| כי אין אלוה זולתו | |
| ואין נעבד בלתו | |
Table of Contents |
וסדרתי החבור הזה לשערים |
| השער הראשון מהם אזכור[13] בו כל מעשה המספר השלם | |
| השער[14] השני אזכור[15] בו כל מעשה השברים | |
| ואולם השער הראשון והוא אשר אזכור בו כל מעשה[16] המספר השלם הנה הוא יחלק אל עשרה שערים | |
| השער[17] הראשון מהם במדרגות[18] המספר ושמותיהם | |
| השער השני בצורות האבק ושמושו על מדרגות[19] המספר | |
| השער השלישי בקבוץ המספרים קצתם עם קצת | |
| השער הרביעי בהשליך המספרים קצתם מקצת | |
| השער החמשי בהכאה | |
| השער השישי ביחס בלקיחת השם[20] והוא אלתסמיה בער'[21] | |
| השער[22] השביעי בחלוק | |
| השער השמיני באלפלג[23] | |
| השער התשיעי בכפילה | |
| השער העשירי בהגדרה[24] | |
Section One – Integers |
|
Chapter One – Numeration |
השער הראשון במדרגות המספר ושמותיו |
|---|---|
| The twelve names of numbers | דע כי שמות המספר הם[25] שתים עשרה[26] שמות |
| Units | |
|
הראשון האחד אשר הוא שורש המספר ותכליתו וצמיחתו |
|
אחר כן תוסיף על האחד אחד אחר[27] והיה זה שנים והוא ראשית המספר כי האחד איננו[28] מספר |
|
ואחר[31] כן הוסף[32] על השנים[33] אחד ונקרא זה שלשה |
|
ואחר[34] כן הוסף[35] על השלשה אחד ונקרא זה ארבעה |
|
אחר כן הוסף[36] על הארבעה אחד ונקרא זה חמשה |
|
אחר כן הוסף[37] על החמשה אחד ונקרא זה ששה |
|
אחר כן הוסף[38] על הששה אחד ונקרא זה שבעה |
|
אחר כן הוסף[39] על שבעה[40] אחד ונקרא זה שמנה |
|
אחר כן הוסף[41] על שמנה[42] אחד ונקרא זה תשעה |
| these nine numbers are the units which are the first rank | ואלו[43] המספרים התשעה הם האחדים והם המדרגה הראשונה |
| Tens | |
|
אחר כן הוסף[44] אחד על התשעה[45] ונקרא זה עשרה ואלו[46] העשרה הוא ראשית העשרות והם במדרגת העשרות כמדרגת האחד באחדים |
|
אחר כן הוסף[47] על העשרה עשרה שנית ונקרא זה עשרים |
|
אחר כן הוסף[48] על העשרים[49] עשרה ונקרא זה שלשים |
|
אחר כן הוסף[50] על השלשים[51] עשרה ונקרא זה ארבעים |
|
אחר כן תוסף[52] על הארבעים עשרה ונקרא זה חמשים |
|
אחר כן הוסף[53] על החמשים עשרה ונקרא זה ששים |
|
אחר[54] כן הוסף[55] על הששים עשרה ונקרא זה שבעים |
|
אחר כן הוסף[56] על השבעים עשרה ונקרא זה שמונים |
|
אחר כן הוסף[57] על השמונים עשרה ונקרא זה תשעים |
| the names of the nine tens are derived from their similar in the rank of the units | ואלו התשע עשרות הם שמות לקוחים מן הדומים[58] להם מן האחדים |
|
כי[59] העשרה הוא כמו[60] האחד באחדים |
|
והעשרים כמו השנים באחדים |
|
והשלשים כמו השלשה באחדים |
|
והארבעים כמו הארבעה[61] באחדים |
|
והחמשים כמו החמשה[62] באחדים |
|
והששים כמו הששה באחדים |
|
והשבעים כמו השבעה באחדים |
|
והשמנים כמו השמונה באחדים |
|
והתשעים כמו התשעה באחדים |
| these ranks are the rank of tens which is the second rank | ואלו המדרגות עד תשעה הם מדרגת[63] העשרות והוא המדרגה השנית |
| Hundreds | |
|
אחר כן הוסף[64] על תשעים עשרה ונקרא זה מאה והוא ראשון למדרגת[65] המאות כמו האחד[66] באחדים וכמו העשרה[67] בעשרות |
|
אחר כן הוסף[68] על המאה מאה שני ונקרא זה מאתים ואלו המאתים[69] כמו שנים באחדים וכמו עשרים בעשרות |
|
וכן ההרכבה הזאת יהיו השלש מאות והארבע מאות והחמש מאות והשש מאות והשבע מאות והשמנה מאות והתשע מאות |
| ואלו השמות כלם אמנם הם[70] לקוחים מדומיהם באחדים כלומ' המאה כמו האחד[71] באחדים והמאתים כמו שנים באחדים[72] וכן עד תשע מאות כמו תשעה | |
| ואלו[73] המדרגות התשע הן[74] גם כן[75] מדרגות המאות והיא[76] המדרגה השלישית | |
| Thousands | |
|
אחר כן הוסף[77] על התשע מאות מאה אחת והיה זה אלף והאלף הזה[78] כמו[79] אחד באחדים וכמו העשרה[80] בעשרות וכמו המאה[81] במאות |
|
אחר כן[82] הוסף[83] על האלף אלף אחד[84] ונקרא זה אלפים ואלו[85] האלפים כמו שנים באחדים וכמו עשרים בעשרות וכמו מאתים במאות |
|
וכן שלשת[86] אלפים וארבעת אלפים וחמשת אלפים וששת אלפים ושבעת אלפים ושמנת אלפים ותשעת אלפים כמו תשעה |
| ואלו התשעה הם מדרגת[87] האלפים והיא המדרגה הרביעית | |
| הנה כבר הושם המספר על[88] שתים עשרה שמות והם התשעה שמות אשר לאחדים והעשירי לעשרות[89] והאחד עשר המאות והשתים עשרה[90] האלפים | |
| ומה שלמעלה מזה אמנם הוא מורכב מאלה[91] השמות | |
| וזה כי האלפים הושמו כי האחדים[92] | |
| ועשרות[93] האלפים הושמו כמו העשרות | |
| ומאות האלפים הושמו כמו המאות | |
| עוד אחר זה נאמר בו אלף אלפים כפולים | |
| עוד אחר זה ישוב אל העשרות מהם ויאמר בזה עשרות אלף אלפים | |
| עוד אחר זה ישוב אל המאות ויאמר בזה מאות אלף אלפים[94] | |
| עוד יכפל כפל אחר ויאמר בו[95] אלף אלפי אלפים כפולים אלף פעם ומה שהתקבץ אלף[96] פעם והתקצר[97] זה להראות הענין[98] ונאמר בו אלף אלפי אלפים | |
| וכן אל מה שאין תכלית לו מן המספר | |
| הנה כבר התבאר מזכרנו[99] אלו המדרגות כי אחר שלש מדרגות יפלו האלפים ואחר שלש המדרגות[100] יגיע אל אלף אלפים[101] ואחר שלש מדרגות יגיע אל אלף אלפי אלפים | |
| וכן יכפל אל מה שאין לו תכלית[102] מאחר שלש מדרגות | |
| First Rank: Units | ומפני שיהיו[103] האחדים במדרגה[104] הראשונה נאמר בה אחדים כלומ' היא המדרגה הראשונה שמה אחד |
| Second Rank: Tens | והעשרות שמם[105] שנים כלומר היא המדרגה השנית |
| Third Rank: Hundreds | והמאות שמם שלשה כלומ' הם[106] במדרגה השלישית |
| Fourth Rank: Thousands | וכן האלפים שמם ארבעה[107] כלומר הם[108] במדרגה הרביעית[109] |
| Fifth Rank: Tens of Thousands | וכן עשרות האלפים הם חמשה כלו' שהם[110] במדרגה החמשית |
| Sixth Rank: Hundreds of Thousands | וכן מאות האלפים שמם ששה כלומ' הם במדרגה הששית |
| Seventh Rank: Thousands of Thousands | וכן[111] אלפי[112] האלפים[113] שמם שבעה כלומ' הם במדרגה השביעית |
| Eighth Rank: Tens Thousands of Thousands | ועשרות[114] האלף האלפים[115] שמם שמנה כלומ' הם במדרגה השמינית |
| Ninth Rank: Hundreds Thousands of Thousands | ומאות האלף אלפים[116] שמם תשעה כלומ' הם במדרגה התשיעית |
| Tenth Rank: Thousands Thousands of Thousands | ואלף אלפי אלפים שמם[117] עשרה כלומ' הם במדרגה העשירית |
| וכן אל[118] מה שאין תכלית לו | |
| ובעלי החשבון יקראו השער הזה שער היסוד והוא[119] שער המדרגות ג"כ[120] והבין זה[121] | |
Chapter Two – Positional Decimal System |
השער השני בצורות[122] האבק ושמושו על דמיון המספר[123] | |||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Units | דע כי אותיות האבק[124] אשר[125] ישתמשו אצלנו בחשבון הם תשע אותיות ולהם צורות מתחלפות על הצורה הזאת[126] | |||||||||||||||||||||||
| 1 2 3 4 5 6 7 8 9 |
| |||||||||||||||||||||||
| הנה[127] הם[128] תשע צורות ולהם תשע מדרגות כמו האחדים[129] אשר הם מאחד ועד[130] תשעה וכמו העשרות אשר הם[131] מעשרה ועד[132] תשעים | ||||||||||||||||||||||||
| Tens | וכאשר תרצה לצייר העשרה הנה כבר ידענו כי העשרה הם במדרגה השנית מן המספר ויצטרך שיקדם[133] במדרגת האחדים דבר[134] יחזיק[135] המדרגה כדי שיודע בו כי מדרגת האחדים אין בה דבר | |||||||||||||||||||||||
|
והסכימו בעלי החשבון שישימו בה צפר והיא[136] תמונת עגולה קטנה אשר[137] כן ישימו אל מה שילוה לצפר מצד[138] השמאל ויהיה זה צפר[139] | |||||||||||||||||||||||
| 10 |
| |||||||||||||||||||||||
| 20 | ואם הושם במקום האחד שנים נאמר בו[141] עשרים מפני שהם שנים במדרגה השנית ושנים במדרגה[142] השנית הם עשרים לפי מה שקדם
| |||||||||||||||||||||||
| 30 | ואם הושם במקום השנים שלשה נאמר בו[143] שלשים מפני שהוא שלשה במדרגה השנית[144] ושלשה במדרגה[145] השנית הם שלשים
| |||||||||||||||||||||||
| 40 | וכן[146] ארבעים[147] הם צפר וארבעה | |||||||||||||||||||||||
| 50 | וחמשים[148] הם[149] צפר וחמשה | |||||||||||||||||||||||
| 60 | וששים[150] הם[151] צפר וששה | |||||||||||||||||||||||
| 70 | ושבעים[152] הם[153] צפר ושבעה | |||||||||||||||||||||||
| ושמונים[154] הם[155] צפר ושמנה | ||||||||||||||||||||||||
| 90 | ותשעים[156] צפר ותשעה | |||||||||||||||||||||||
| ודע כי אתה[157] אמנם תקרא המספר בשם המדרגה אשר תמצאהו בה אם היה באחדים תקראהו בשמו | ||||||||||||||||||||||||
| ואם היה במדרגת העשרות תקראהו בשמם וצורתו | ||||||||||||||||||||||||
| Units and Tens | ואם היו עמך אחדים ועשרות תפיל הצפר אשר היית מניחו במדרגת האחדים ושמת במקומו מספר האחדים אשר לך אחר כן תשים העשרות גם כן[158] במדרגותם | |||||||||||||||||||||||
| 12 | דמיון זה אם תרצה שתניח שתים עשרה הניח[159] תחלה השנים במדרגת האחדים ותניח האחד במדרגה השנית
| |||||||||||||||||||||||
| 25 | וכן אם היו חמשה ועשרים
וזה כי[161] חמשה במדרגת האחדים ושנים במדרגת העשרות | |||||||||||||||||||||||
| 76 | וכן ששה ושבעים אמנם הם ששה במדרגת הראשונה ושבעה במדרגה[162] השנית
| |||||||||||||||||||||||
| 99 | וכן גם כן[164] תשעה ותשעים[165] אמנם הם תשעה במדרגת האחדים ותשעה במדרגת העשרות
| |||||||||||||||||||||||
| Hundreds | ואולם המאות הנה כבר קדם בשער המדרגות שאמנם הם במדרגה השלישית ותניח במדרגה הראשונה צפר ובמדרגה השנית[167] צפר גם כן[168] אחר כן תניח במדרגה השלישית מספר מה שעמך מן המאות | |||||||||||||||||||||||
| 100 | רצוני לו'[169] אם היו[170] מאה תניח אחד ויהיה תמונת[171] המאה שני צפרי ואחד
| |||||||||||||||||||||||
| 200 | ואם היו עמך מאתים תניח במקום האחד שנים
| |||||||||||||||||||||||
| 300 | וכן השלוש[174] מאות שני צפרי ושלשה | |||||||||||||||||||||||
| 900 |
| |||||||||||||||||||||||
| Units and Hundreds | ואם היו עמך אחדים ומאות תניח האחדים במקום הצפר הראשון אשר הוא במדרגת האחדים ותניח אחר זה צפר יהיה במדרגת העשרות ותניח אחר זה המאות אשר עמך | |||||||||||||||||||||||
| 205 | דמיון זה אילו[176] היה עמך חמשה ומאתים
| |||||||||||||||||||||||
| Tens and Hundreds | ואם היו עמך עשרות ומאות הנה תניח במקום[177] האחדים צפר ואחר כן תניח מה שעמך מן העשרות במדרגה השנית ואחר זה מספר מה שעמך מן המאות | |||||||||||||||||||||||
| 620 | דמיון זה אלו היו[178] עמך עשרים ושש מאות
| |||||||||||||||||||||||
| Units, Tens and Hundreds | ואם היו[179] עמך אחדים ועשרות ומאות הנה תניח האחדים תחלה במדרגת הראשונה ותניח העשרות במדרגה[180] השנית ותניח המאות במדרגה השלישית | |||||||||||||||||||||||
| 864 | דמיון זה[181] אילו[182] רצית ארבעה וששים ושמנה[183] מאות תניח ראשונה הארבעה ותניח אחריהם ששה ותניח אחריהם שמנה
| |||||||||||||||||||||||
| Thousands | ואולם האלפים הנה כבר ידעת שהם במדרגה הרביעית | |||||||||||||||||||||||
| 1000 | דמיון זה אלו היה עמך אלף תניח במדרגה הראשונה צפר וכן בשנית וכן בשלישית ואחד ברביעית[184]
| |||||||||||||||||||||||
| 2000 |
| |||||||||||||||||||||||
| 9000 |
| |||||||||||||||||||||||
| Units and Thousands | ואם היו[186] עמך אחדים ואלפים | |||||||||||||||||||||||
| 5006 | כמו ששה וחמשת אלפים תניח תחלה ששה ותניח אחריה שני צפרי וחמשה[187]
| |||||||||||||||||||||||
| Tens and Thousands | ||||||||||||||||||||||||
| 4020 | וכן אלו היה עמך עשרים וארבעת אלפים תניח צפרי ואחריו שנים ואחרי השנים[188]צפר ואחריו ארבעה
| |||||||||||||||||||||||
| Hundreds and Thousands | ||||||||||||||||||||||||
| 8300 | וכן אלו היו[190] עמך שלש מאות ושמונת אלפים תניח תחלה שני צפרי ואחריהם שלשה ואחריהם[191] שמנה
| |||||||||||||||||||||||
| Units, Tens and Thousands | וכן אלו היו עמך אחדים ועשרות ואלפים | |||||||||||||||||||||||
| 9075 | כמו חמשה ושבעים ותשעה[192] אלפים תניח חמשה ושבעה ואחריהם צפר ואחריו תשעה
| |||||||||||||||||||||||
| Units, Hundreds and Thousands | וכן אלו היו[193] עמך אחדים ומאות ואלפים | |||||||||||||||||||||||
| 5701 | כמו אחד ושבע מאות וחמשת אלפים תניח אחד ואחריו צפר ואחריו שבעה[194] ואחריו חמשה
| |||||||||||||||||||||||
| Tens, Hundreds and Thousands | וכן אלו היו עמך עשרות ומאות ואלפים | |||||||||||||||||||||||
| 1960 | כמו ששים ותשע מאות ואלף[195] תניח תחלה צפר[196] וששה ותשעה ואחד
| |||||||||||||||||||||||
| Units, Tens, Hundreds and Thousands | ||||||||||||||||||||||||
| 6372 | וכן אילו[197] היו[198] שנים ושבעים ושלש מאות וששת אלפים
| |||||||||||||||||||||||
| ודע כי אתה כאשר תניח[199] המספר במדרגה אחר מדרגה תניח מספר האחדים במדרגה הראשונה ואחריו העשרות והמאות והאלפים | ||||||||||||||||||||||||
| ודע כי המספר יתרבה ויתוסף אל מה שאין תכלית לו כמו מדרגות המספר אשר[200] יתרבה[201] ויתוסף אל מה שאין תכלית לו | ||||||||||||||||||||||||
| ואם היה עמך מספר גדול ומדרגות רבות[202] ותרצה למנותם | ||||||||||||||||||||||||
| דמיון זה אלו היה עמך עשרים מדרגות מן המספר[203] ורצית לדעת אותם בכפל התחיל[204] במדרגה הראשונה ומנה ממנה שלשה והניח[205] על המדרגה הרביעית אחד יהיה אות ראשית הכפל | ||||||||||||||||||||||||
| עוד מנה ממקום האות שלש מדרגות והנח[206] על המדרגה[207] הרביעית אות ויהיה ראיה על אלף אלפים כפולים שני פעמים | ||||||||||||||||||||||||
| עוד מנה ממקום האות שלש מדרגות[208] ותניח על המדרגה הרביעית אות שלישית ויהיה ראיה על האלפים כפולים שלש[209] פעמים | ||||||||||||||||||||||||
| וכן תמנה תמיד ממקום האות האחרון ותניח על המדרגה הרביעית ותוסיף אותות[210] באחד אחד מה שאין תכלית לו כמו שהמספר יוסיף[211] באחד תמיד כמו שקדם והמדרגות באחד אחד וכן אותות הכפל יוסיפו[212] אחד אחד | ||||||||||||||||||||||||
| ואם ישאר אחרי[213] האותיות[214] אחד הנה הם עשרת אלפים כפולים במספר האותות אשר לפניהם | ||||||||||||||||||||||||
| ואם ישארו שנים הנה הם מאות אלפים כפולים במספר האותיות אשר לפניהם[215] | ||||||||||||||||||||||||
| ואם לא ישאר כלום הנה הם אלף כפולים במספר האותות אשר לפניהם[216] | ||||||||||||||||||||||||
| ||||||||||||||||||||||||
Chapter Three – Addition |
השער השלישי בקבוץ המספרים קצתם אל קצת | ||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| דע כי קבוץ מספר[217] אל המספר[218] אמנם הוא שתקובץ כל מדרגה אל סוגה כלומר האחדים אל האחדים והעשרות אל העשרות והמאות אל המאות והאלפים אל האלפים | |||||||||||||||||||||||||||||||||||||
| The procedure starts from the rank of units | תתחיל תמיד לקבץ מן[219] המדרגה הראשונה | ||||||||||||||||||||||||||||||||||||
|
אם[220] יעלה ממנו עשרה הגביהנו[221] אל העשרות | ||||||||||||||||||||||||||||||||||||
|
והעמיד אחדים[222] במקומם אם יהיו עמך אחדים | ||||||||||||||||||||||||||||||||||||
|
ואם לא שים במקום האחדים צפר אחד[223] | ||||||||||||||||||||||||||||||||||||
| אחר כן קבץ העשרות עם העשרות אשר עלו מן האחדים | |||||||||||||||||||||||||||||||||||||
| ואם התקבץ[224] מהם מאה הגביהם אל מדרגת המאות וקיים מה שעמך מן העשרות במדרגתם | |||||||||||||||||||||||||||||||||||||
| ואם לא יהיה בהם עשרות נניח ג"כ במדרגת העשרות צפר | |||||||||||||||||||||||||||||||||||||
| אחר כן קבץ המאות והמאות אשר עלו מן העשרות | |||||||||||||||||||||||||||||||||||||
| ואם התקבץ מהם אלף הגביהם על מדרגת האלפים לפי מה שקדם מן המאמר | |||||||||||||||||||||||||||||||||||||
Example: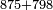
|
והדמיון קבוץ[225] חמשה ושבעים ושמונה מאות אל שמנה ותשעים ושבע מאות | ||||||||||||||||||||||||||||||||||||
| הניח[226] החמשה ושבעים ושמנה מאות בשטה אחר כן תניח השמנה ותשעים ושבע מאות תחת המספר המקובץ אליו בשטה אחרת | |||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||
|
ואחר[227] כן תמשוך על המספר קו ותחת המספר[228] קו אחר ואחר[229] כן קבץ החמשה אל השמנה יהיו שלשה עשר והעמיד השלשה על האחדים על הקו העליון והגביה העשרה אל מדרגת העשרות והעמידהו תחת הקו התחתון
| ||||||||||||||||||||||||||||||||||||
| ואם היו[235] כאשר התקבצו האחדים אל האחדים[236] שיתקבץ[237] מזה פחות מעשרה העמידם במקומם ולא תרים אל העשרות דבר וכן תעשה אל[238] העשרות כאשר התקבץ מן העשרות פחות ממאה העמידם במקומם | |||||||||||||||||||||||||||||||||||||
Example: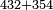
|
דמיון זה קבץ שנים ושלשים וארבעה[239] מאות אל ארבעה וחמשים ושלש מאות | ||||||||||||||||||||||||||||||||||||
| שים השנים ושלשים וארבע מאות בשטה אחת[240] והארבעה וחמשים ושלש מאות בשטה אחרת כמו שקדם ויהיו האחדים תחת האחדים והעשרות תחת העשרות והמאות תחת המאות ומשוך עליהם קו ותחתיהם[241] קו אחר על זאת הצורה[242] | |||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||
|
ואחר[243] כן תקבץ[244] האחדים וזה ארבעה אל[245] שנים יהיו[246] ששה והעמידם על הקו על האחדים אחר כן קבץ העשרות וזה חמשה ושלשה יהיו שמנה והעמידם על העשרות על הקו[247]
| ||||||||||||||||||||||||||||||||||||
| A sum of three numbers | ואם תרצה לקבץ שלש שטות מן המספרים | ||||||||||||||||||||||||||||||||||||
Example: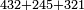
|
דמיון זה קבץ שנים ושלשים וארבע מאות אל חמשה וארבעים ומאתים אל אחד ועשרים ושלש מאות | ||||||||||||||||||||||||||||||||||||
| תשים[250] אלו השלשה מספרים בשלש שטות ושים כל סוג[251] תחת סוגו על הצורה הזאת | |||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||
|
אחר כן התחיל[252] לקבצם מן האחדים כמו שקדם וקבץ תחלה אחד וחמשה ושנים יהיה המקובץ שמנה והעמידם על הקו על[253] ראש האחדים אחר כן[254] קבץ העשרות וקבץ שנים וארבעה ושלשה יהיה זה תשעה והעמידם על ראש העשרות על הקו
| ||||||||||||||||||||||||||||||||||||
| ואם קבצת מספר יהיה[255] בו צפר אל המספר האחר[256] עם צפר ג"כ | |||||||||||||||||||||||||||||||||||||
Example: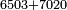
|
כמו שתקבץ שלשה וחמש מאות וששת אלפים | ||||||||||||||||||||||||||||||||||||
| שים[257] שלשה במקום האחדים[258] וצפר במקום העשרות אחר כן חמשה אחר כן ששה אחר כן שים תחתיו המספר המקובץ אליו והוא עשרים[259] ושבעת אלפים שים צפר תחת מדרגת האחדים ושנים וצפר ושבעה ותהיה עמידתם[260] על זאת הצורה | |||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||
|
אחר כן שים השלשה אשר הם האחדים על הקו העליון[261] במדרגתם אחר כן שים השנים אשר הם שתי עשרות על[262] העשרות על הקו
וזה שלשה ועשרים וחמש מאות ושלשה עשר אלפים | ||||||||||||||||||||||||||||||||||||
Example: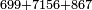
|
ואם יאמר לך קבץ תשעה ותשעים ושש מאות אל ששה וחמשים ומאה ושבעת אלפים אל שבעה וששים ושמנה מאות | ||||||||||||||||||||||||||||||||||||
| שים[267] אותם שטות כמו שקדם על הצורה הזאת | |||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||
|
אחר כן קבץ האחדים והם תשעה וששה ושבעה יהיו שנים ועשרים[268] ושים השנים על האחדים על הקו ושים השתי עשרות[269] תחת העשרות אחר כן קבץ העשרות והם תשעה וחמשה וששה ושנים יהיה שנים ועשרים ושים השנים על העשרות על הקו ושים השתי עשרות תחת המאות
| ||||||||||||||||||||||||||||||||||||
Example: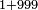
|
ואם יאמר[271] לך[272] קבץ אחד אל תשעה ותשעים ותשע מאות | ||||||||||||||||||||||||||||||||||||
| הניחם בשתי שטות כמו שקדם על הצורה הזאת | |||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||
|
אחר כן קבץ האחדים וזה תשעה ואחד יהיו עשרה ולא תשים על האחדים דבר כי אם הצפר[273] מפני כי לא נפלו לך אחדים ושים העשרה תחת העשרות וקבץ העשרות וזה אחד ותשעה יהיו עשרה ושים אותם תחת המאות ושים על העשרות צפר
| ||||||||||||||||||||||||||||||||||||
Chapter Four – Subtraction |
השער הרביעי בהוציא[279] המספרים קצתם מקצת | |||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| דע כי הוצאת המספרים קצתם מקצת אמנם הוא שיוצא[280] כל סוג מסוגו | ||||||||||||||||||||||||||||||||
Example: 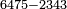
|
דמיון זה הוצא שלשה וארבעים ושלש מאות ואלפים מחמשה ושבעים וארבע מאות וששת אלפים | |||||||||||||||||||||||||||||||
| שים המספר המוצא בשטה והמוצא ממנו בשטה גם כן[281] כל סוג נכחי אל סוגו על[282] הצורה הזאת | ||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
|
אחר כן תתחיל המוצא מאחת[283] המדרגות כלומר האלפים[284] והוצא[285] האלפים[286] מששת אלפים והנשאר[287] ארבעת אלפים ושים אותם על מדרגת האלפים אחר כן הוצא[288] המאות מן המאות וזה שלש מאות מארבע מאות והנשאר[289] מאה ושים אותם על קו אחד
| |||||||||||||||||||||||||||||||
Example: 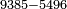
|
ואם יאמר השלך ששה ותשעים וארבע מאות וחמשת אלפים מחמשה ושמנים ושלש מאות ותשעה אלפים | |||||||||||||||||||||||||||||||
| הניח[293] שני המספרים בשתי שטות כמו שקדם ויהיה המספר המושלך תחת המושלך ממנו על זאת הצורה[294] | ||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
|
אחר כן תתחיל מן האלפים בהשלכה והשליך[295] חמשה מתשעה ויהיה[296] הנשאר ארבעה ושימם על מדרגת האלפים אחר כן השלך[297] המאות השליך ארבעה משלשה[298] לא יושלך וקח מן האלפים אלף ויהיה[299] הנשאר שלשת אלפים ושים אותם על ראש האלפים
| |||||||||||||||||||||||||||||||
Example: 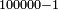
|
ואם יאמר לך השלך אחד ממאה אלף | |||||||||||||||||||||||||||||||
|
שים המאה אלף חמשה צפר ואחד[315] אחר[316] כן התיר מן המאה אלף עשרת אלפים הנשאר תשעים אלף שימם על מדרגת עשרות[317] האלפים בתשעה
| |||||||||||||||||||||||||||||||
Chapter Five – Multiplication |
השער החמשי בהכאת המספרים קצתם בקצתם[328] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| דע כי ענין ההכאה הוא שתכפול אחד משני המספרים כשעור מה שבמספר[329] האחד המוכה בו מן האחדים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Example: 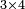
|
ודמיון זה כאשר תרצה להכות שלשה בארבעה הנה ענינו[330] שתכפול הארבעה שלשה פעמים והשלשה ארבעה פעמים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן הוא כל הכאת המספרים על הדמיון הזה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Multiplication by 1 | ודע כי כל מספר תכהו באחד או תכה האחד[331] בו הנה המספר ההוא לא יכפל ולא יעתק מגדרו וכן גם כן[332] הכאת האחד בנפשו לא יכפל אמנם הוא אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכאשר תרצה להכות המספר במספר באותיות האבק הוא צריך על כל פנים[333] לדעת הכאת האחדים קצתם בקצתם[334] והעמידה עליו ואחר ישתמש בהם בתמונות האבק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Multiplication of Units | שער בהכאת האחדים קצתם בקצתם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Units by 1 | כבר קדם לנו כי כל מספר תכהו באחד או תכה האחד[335] בו הנה המספר ההוא לא יכפל ולא יעתק מענינו[336] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון זה אחד באחד אחד אחד בשנים שנים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Units by 2 | שער השנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שנים בשנים ארבעה שנים בשלשה ששה[337] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Units by 3 | שער השלשה[338] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שלשה בשלשה תשעה שלשה בארבעה שנים[339] עשר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Units by 4 | שער הארבעה[341] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ארבעה בארבעה ששה עשר ארבעה בחמשה עשרים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Units by 5 | שער החמשה[345] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חמשה בחמשה חמשה ועשרים חמשה בששה שלשים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Units by 6 | שער הששה[346] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ששה בששה ששה ושלשים ששה בשבעה שנים וארבעים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Units by 7 | שער השבעה[348] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שבעה בשבעה תשעה וארבעים שבעה בשמנה ששה וחמשים[349] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Units by 8 | שער שמנה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שמנה בשמנה ארבעה וששים שמנה בתשעה שבעים ושנים[351] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Units by 9 | שער התשעה[352] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תשעה בתשעה אחד ושמנים[353] תשעה בעשרה תשעים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Units by 10 | שער העשרה[354] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עשרה בעשרה מאה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכאשר ידע התלמיד השער הזה ועמד עליו אז ישמשהו[355] בכל מה שיצטרך אליו ממה שיבא מן המעשה[356] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Example: 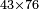
|
וכאשר[357] יאמר לך הכה שלשה וארבעים בששה ושבעים[358] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הניח השלשה וארבעים בשטה כמו שקדם אחר כן תשים[359] תחתיו ששה ושבעים בשטה אחרת ותהיה המדרגה הראשנה מן השטה התחתונה תחת המדרגה האחרונה מן השטה[360] העליונה והמדרגה הנשארת מן השטה התחתונה קודמת אל מה שילוה לשמאל על הצורה הזאת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אחר כן תכה[361] המדרגה האחרונה מן השטה העליונה במדרגה האחרונה[362] מן השטה התחתונה והוא ארבעה בשבעה והוא שמנה ועשרים ושים השמנה על ראש השבעה ויהיה השמנה[363] בשטה עם השטה העליונה והקדים העשרים בשנים אל מה שילוה אל[364] השמאל אחר כן הכה הארבעה בעצמם בששה אשר תחתיו יהיו ארבעה ועשרים והנה לך ארבעה במקומם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אחר כן תקח השלשה[374] אשר הם מדרגה[375] ראשנה מן השטה העליונה והכה אותם בשבעה אשר הם המדרגה האחרונה מן השטה התחתונה יהיה זה אחד ועשרים וקבץ אליהם[376] הארבעה אשר על ראש השבעה יהיה כל זה חמשה[377] ועשרים ומחה הארבעה ושים במקומם חמשה[378] ואחר[379] כן הקדים[380] העשרים בשנים אל מקום הצפר ותמחה הצפר ושים במקומו השנים
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה שמנה וששים ומאתים ושלשת אלפים והוא היוצא מהכאת[386] שלשה וארבעים בששה ושבעים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ודע כי אתה אמנם תקח המדרגה האחרונה[387] מן הקו העליון ותכהו בכל אחת[388] ממדרגות הקו התחתון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תתחיל ראשונה באחרון ממה שילוה השמאל ותשים מה שיצא מן ההכאה על ראשו[389] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אחר כן תכה אותה גם כן במספר אשר ילוה המדרגה ההיא אל הימין ותשים מה שיצא מן ההכאה על ראשו[390] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כן תכה בכל מדרגה ממדרגות השטה התחתונה עד שתגיע אל המדרגה הראשונה אשר תחת המדרגה אשר הוכתה במספר התחתון ותכה בה גם כן[391] ותשים מה שיצא במקום אותה המדרגה בעינה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אחר כן תעתיק השטה[392] התחתונה בכללה מדרגה אחת ממדרגות השטה העליונה אל מה שילוה אל[393] הימין | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אחר כן תכה המדרגה ההיא אשר נעתק המספר ממנה בכל מדרגות השטה התחתונה ותתחיל באחרונה כמו שקדם ומה שהתקבץ לך מן ההכאה תחברהו[394] על מה שעל המדרגה ההיא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תעשה בשנית והשלישית עד שתשלם ההכאה בכל מדרגות השטה התחתונה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אחר כן תעתיק השטה התחתונה על דמיונו אל המדרגה האחרונ'[395] ממה[396] שילוה[397] הימין ממדרגות השטה העליונה ותעשה[398] כמו מה שעשית במה שקדם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן לא תסור[399] להעתיק המספר התחתון תחת כל מדרגה ממדרגות השטה העליונה ותעשה בו מה[400] שזכרנו עד שתכלינה[401] מדרגות המספר העליון וכאשר עשית זה הנה כבר השלמת להכות השאלה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונמשיל מזה משל בהכאת שלשה מדרגות כדי שתלקח ראיה בזה[402] על מה שאמרנו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Example: 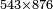
|
הכה שלשה וארבעים וחמש מאות בששה ושבעים ושמנה מאות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכאשר רצית זה שים אותם בשתי שטות[403] תהיה אחת[404] מהן נגד השנית ותהיה המדרגה הראשונה מן המספר התחתון תחת המדרגה האחרונה מן המספר העליון על הצורה הזאת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואחר[405] כן הכה החמשה אשר[406] הם המדרגה האחרונה מן המספר העליון בשמנה אשר הוא המדרגה האחרונה מן[407] המספר התחתון[408] יהיה זה ארבעים ושים צפר על השמנה וקדם ארבעה אל מה שילוה השמאל אחר כן הכה החמשה פעם שנית בשבעה אשר ילוה השמנה ממה שילוה אל[409] הימין יהיה זה חמשה ושלשים ושים החמשה על ראש השבעה והקדים השלשים אל מקום הצפר ותמחה[410] הצפר והעמיד שלשה[411] במקומו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אחר כן תעתיק המספר התחתון בכללו תחת מדרגה אחרת ממה שילוה הימין ממדרגות המספר העליון וזה שתעתיק הששה תחת הארבעה והשבעה תחת הצפר והשמנה תחת השמנה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אחר כן תעתיק המספר התחתון בכללו תחת השלשה אשר הם המדרגה הראשונה ממדרגות המספר העליון ותעתיק[423] הששה תחת השלשה והשבעה תחת הארבעה והשמנה תחת הצפר אחר כן תכה[424] השלשה בשמנה יהיו ארבעה ועשרים ועל ראש השמנה צפר מחה[425] אותו ושים במקומו ארבעה וקדם העשרים בשנים אל השלשה אשר ילוה[426] השמאל יהיו חמשה ושים אותם במקום השלשה
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והם שמנה וששים ושש מאות וחמשת אלפים ושבעים אלף וארבע מאות אלפים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ועל הדמיון הזה תהיה הכאת[435] המדרגות באבק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Chapter Six – Dividing a Small Number by a Larger Number |
השער הששי בשומא[436] וידיעת[437] השם והוא חלוקת המספר הקטן על הגדול |
|---|---|
| ודע כי לשער הזה הקדמה ראוי למבקש לדעת אותה והאימות בה והוא שער גדול התועלת בכל מעשה החשבון[438] ובו יוצא מאיזו[439] הכאה יעמדו המספרים | |
| ובו[440] יודע[441] אם המספר ההוא[442] מורכב או בלתי מורכב | |
| והמספר המורכב הוא המקובץ מהכאת המספר[443] במספר | |
| והבלתי מורכב הוא אשר לא ימנהו[444] מספר כי אם האחד | |
Casting Out |
הקדמה בהשלכה |
| דע כי כל מספר אין בתחלתו אחדים הנה יש[445] לו עשור | |
| ודע כי המספר כלו יחלק לשני[446] חלקים אם זוג ואם נפרד | |
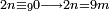
|
והמספר הזוג השליכהו תשעה תשעה ואם יושלך הנה התשיעית לו |
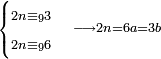
|
ואם לא יושלך ונשאר ממנו שלשה או ששה הנה השלישית[447] לו |
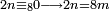
|
ואם נשאר זולת זה השליכהו שמנה שמנה ואם יושלך הנה השמינית לו |
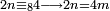
|
ואם לא יושלך ונשאר ממנו ארבעה הנה הרביעית לו[448] |
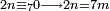
|
ואם נשאר זולת זה השליכהו שבעה שבעה ואם הושלך הנה השביעית לו |
| ואם לא יושלך הנה אין לו שם כי אם החצי | |
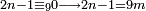
|
והמספר הנפרד השליכהו תשעה תשעה ואם הושלך הנה התשיעית לו |
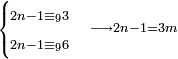
|
ואם לא הושלך ונשאר ממנו שלשה או ששה הנה השלישית לו |
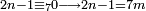
|
ואם נשאר זולת זה השליכהו[449] שבעה שבעה ואם הושלך הנה השביעית לו |
| ואם לא הושלך[450] אין לו שם ובקשהו בחלקים | |
| ודע כי כל מספר בתחלתו חמשה[451] הנה החומש[452] לו | |
Casting Out by 9 |
שער השלכת תשעה |

|
דע[453] כי השלכת תשעה ישאר מכל עשרה אחד |
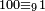
|
ומכל מאה אחד |
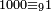
|
ומכל אלף אחד |
| וכן תקח כל מספר[454] בשמו כמו שתעשה בו עם ההכאה | |
Casting Out by 8 |
שער השלכת שמנה |
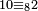
|
דע כי השלכת שמנה ישאר מכל עשרה שנים |
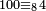
|
ומכל מאה ארבעה |
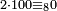
|
וזוגות[455] המאות נשלכים |
| וכן האלפים ומה שיכלה המספר | |
Casting Out by 7 |
שער השלכת שבעה |
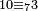
|
דע כי השלכת שבעה ישאר מכל עשרה שלשה |
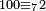
|
ומכל מאה שנים |
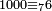
|
ומכל אלף ששה |
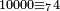
|
ומכל עשרת אלפים ארבעה |
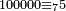
|
ומכל מאה[456] אלף חמשה |
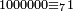
|
ומכל אלף אלפים אחד |
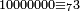
|
ומכל עשרת אלפי אלפים שלשה |
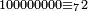
|
ומכל מאת[457] אלפי אלפים שנים |
| וכן יכפל השלכת שבעה[458] אצל כל שני כפלים וישוב כמו אחדים ועשרות ומאות | |
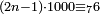
|
ודע כי כל אלף[459] יהיה כפלם נפרד הנה הנשאר מהם ששה |
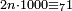
|
ואם כפלם[460] זוג הנה הנשאר מהם אחד |
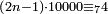
|
וכל עשרת[461] אלפים יהיה כפלם נפרד יהיה[462] הנשאר מהם ארבעה |
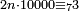
|
ואם היה כפלם זוג הנה הנשאר מהם שלשה |
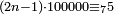
|
וכל מאה אלף יהיה כפלם נפרד הנה הנשאר מהם חמשה |
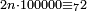
|
ואם היה כפלם זוג הנה הנשאר מהם שנים |
| והמספר הזוג הוא אשר תחלתו[463] שנים או ארבעה או ששה או שמנה | |
| והמספר הנפרד הוא אשר בתחלתו אחד או שלשה או חמשה או שבעה או תשעה | |
Divisors |
ודע כי כל מספר אין חצי לו אין רביעית לו ואין[464] שמינית לו[465] ואין[466] שתות לו |
| וכל מספר אין שליש לו אין שתות לו ולא תשיעית לו | |
| כ"א וכל מספר אין שתות לו אין שלישית לו ולא חצי לו[467] | |
| וכל מספר אין חומש לו אין עשירית לו | |
Dividing a Small Number by a Larger Number |
ואחר אשר כבר[468] הגענו על ההקדמה הנה נשוב אל שער ידיעת השם ונאמר כי[469] יחס המספר הקטן מן המספר הגדול הוא ממנו חלק[470] אחד[471] או חלקים[472] | ||||||||
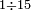
|
דמיון זה כאשר נאמר לך שם אחד מחמשה עשר | ||||||||
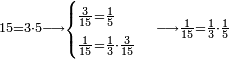
|
הנה כבר ידעת כי החמשה עשר מספר מורכב מהכאת השלשה[473] בחמשה אם כן[474] השלשה מהם חומש ואחד[475] מן השלשה[476] שלישיתו אם כן[477] האחד מן החמשה עשר שליש החומש[478] | ||||||||
| ויצטרך גם כן[479] אל שנקדים בזה הקדמה | |||||||||
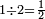
|
ואומר כי יחס האחד מן השנים חצי | ||||||||
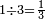
|
ומן השלשה[480] שליש | ||||||||
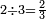
|
ושנים מהם שני שלישים | ||||||||
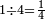
|
ואחד מן ארבעה רביע[481] | ||||||||
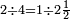
|
ושנים חצי רביע[482] כי יחס שנים מן הארבעה[483] כיחס אחד מן השנים[484] | ||||||||
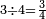
|
והשלשה מהם שלשה רביעים | ||||||||
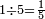
|
ואחד מחמשה חומש | ||||||||
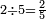
|
ושנים שני חומשים | ||||||||
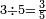
|
ושלשה שלשה חומשים | ||||||||
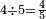
|
וארבעה ארבעה חומשים | ||||||||
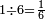
|
ואחד מששה שתות | ||||||||
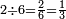
|
ושנים שני שתותים ואם תרצה תאמר שליש | ||||||||
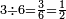
|
ושלשה שלשה[485] שתותים ואם תרצה תאמר חצי | ||||||||
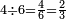
|
וארבעה ארבעה שתותים ואם תרצה תאמר שני שלישים | ||||||||
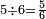
|
וחמשה מהם חמשה שתותים[486] | ||||||||
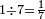
|
ואחד משבעה שביעית | ||||||||
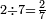
|
ושנים שתי[487] שביעיות | ||||||||
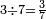
|
ושלשה שלשה שביעיות | ||||||||
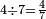
|
וארבעה ארבע[488] שביעיות | ||||||||
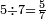
|
וחמשה חמש[489] שביעיות | ||||||||
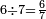
|
וששה שש[490] שביעיות | ||||||||
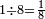
|
ואחד משמנה שמינית | ||||||||
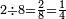
|
ושנים שתי שמיניות ואם תרצה תאמר רביע | ||||||||
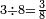
|
ושלשה שלש[491] שמיניות | ||||||||
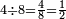
|
וארבעה ארבע[492] שמיניות ואם תרצה תאמר[493] חצי | ||||||||
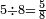
|
וחמשה חמש[494] שמיניות | ||||||||
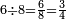
|
וששה שש[495] שמיניות ואם תרצה תאמר[496] שלש[497] רביעיות | ||||||||
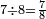
|
ושבעה מהם שבע[498] שמיניות[499] | ||||||||
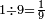
|
ואחד מתשעה תשיעית | ||||||||
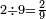
|
ושנים שתי תשיעיות | ||||||||
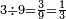
|
ושלשה שלש[500] תשיעיות ואם תרצה תאמר[501] שליש[502] | ||||||||
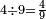
|
וארבעה[503] ארבע תשיעיות | ||||||||
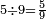
|
וחמשה חמש תשיעיות | ||||||||
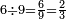
|
וששה שש תשיעיות ואם תרצה תאמר[504] שני שלישים | ||||||||
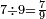
|
ושבעה שבע[505] תשיעיות | ||||||||
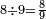
|
ושמנה שמנה[506] תשיעיות | ||||||||
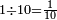
|
ואחד מעשרה עשירית | ||||||||
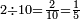
|
ושנים שתי עשיריות ואם תרצה תאמר[507] חמשית[508] | ||||||||
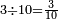
|
ושלשה שלש עשיריות | ||||||||
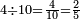
|
וארבעה ארבע[509] עשיריות ואם תרצה תאמר[510] שני חומשים | ||||||||
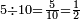
|
וחמשה חמש עשיריות ואם תרצה תאמר[511] חצי | ||||||||
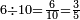
|
וששה שש[512] עשיריות ואם תרצה תאמר[513] שלשה חומשים | ||||||||
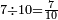
|
ושבעה שבע[514] עשיריות | ||||||||
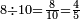
|
ושמנה מהם שמנה עשיריות ואם תרצה ארבעה חומשים | ||||||||
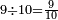
|
ותשעה תשע[515] עשיריות | ||||||||
| Written division of a small number by a larger number - Written fractions | |||||||||
|---|---|---|---|---|---|---|---|---|---|
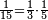
|
ואחר שהקדמנו[516] מה שראוי[517] להקדימו הנה[518] נשוב אל מה שהיינו בו כי אחד מחמשה עשר שליש חומש [519]וכאשר תרצה שתקראהו[520] באבק הנה כבר[521] ידעת כי החמשה[522] עשר מורכב מחמשה ושלשה ושים בקצה[523] הלוח החמשה והשלשה ויהיו השלשה על החמשה ואשר[524] תרצה שנקראהו מחמשה[525] עשר שים אותו על השלשה | ||||||||
| |||||||||
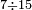
|
דמיון זה אלו רצית שתקרא[530] מהם השבעה[531] | ||||||||
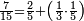
|
שים אלו השבעה על השלשה אחר כן בקש מספר תשימהו על החמשה ואחר[532] תכהו בשלשה ותפיל המקובץ[533] מן השבעה ויכלה או ישאר[534] מה שהוא פחות מן השלשה[535] נמצא שנים[536] ושים אלו השנים על החמשה[537] | ||||||||
| תיחס תמיד מה שעל רוב[549] הסכום[550] אל מה שתחתיו אחר כן תיחס מה[551] שעל השני אל מה שתחתיו ואל מה שילוה אליו מן הסכום[552] | |||||||||
| ויהיה היוצא[553] מן השאלה הזאת על זאת הצורה | |||||||||
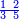
|
| ||||||||
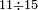
|
ואם תרצה שתקרא מן החמשה עשר אחד[554] עשר | ||||||||
|
שים אלו האחד עשר על השלשה אשר הם בקצה הלוח אחר כן בקש מספר תשימהו על החמשה ותכהו בשלשה ותפיל המקובץ מן האחד עשר ויכלה או ישאר מה שהוא פחות מן השלשה תמצא שלשה שים אותם על החמשה[555] | ||||||||
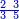
|
| ||||||||
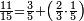
|
והם שלשה חומשים ושני שלישי חומש | ||||||||
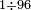
|
ואם יאמר לך קרא אחד[565] מששה ותשעים | ||||||||
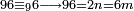
|
הוצא ששה ותשעים תשעה תשעה[566] הנשאר מהם ששה הנה להם[567] שתות לפי מה שקדם בשער ההשלכה מפני שהוא מספר זוג | ||||||||
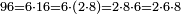
|
ובקש מספר תכהו בששה ויהיה ששה ותשעים תמצא זה ששה עשר והששה[568] עשר מורכב משנים ושמנה[569] הנה כל הששה ותשעים מורכב מהכאת שנים בשמנה ומה שהתקבץ בששה[570]
ואם תרצה תכה שנים בששה ומה שהתקבץ בשמנה ושים בקצה הלוח השנים ותחתיהם[571] הששה ותחת הששה השמנה | ||||||||
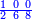
|
| ||||||||
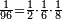
|
אחר כן תיחס האחד אל השנים אחר כן תסמכהו אל הששה ותסמוך הכל אל השמנה יהיה זה חצי שתות השמינית והוא יחס האחד אל הששה ותשעים | ||||||||
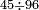
|
ואם תרצה שתקרא מהם חמשה וארבעים | ||||||||
|
שים החמשה וארבעים בקצה הלוח על השנים המקוימים[576] בו[577] אחר כן בקש מספר תכהו בשנים ותפילהו מן החמשה וארבעים ויכלה או ישאר מה שהוא פחות מן השנים תמצאהו שנים ועשרים וישאר מן החמשה וארבעים אחד ותוריד אלו השנים ועשרים על[578] הששה אחר כן תקים האחד הנשאר על השנים עוד שוב ובקש מספר תכהו[579] בששה ותפיל המקובץ מן השנים ועשרים ויכלה או ישאר פחות מששה תמצא שלשה הורידם על השמנה והכה[580] שלשה בששה יהיו[581] שמנה עשר והפילם[582] משנים ועשרים יהיה[583] הנשאר ארבעה וקיים[584] אותם על[585] הששה[586] הנה כבר יצא על השמנה שלשה[587] ועל הששה ארבעה ועל השנים אחד אחר כן[588] תמשוך[589] קו וכתוב[590] תחתיו זה הסכום לפי מה שקדם מן הסדר[591] וקיים על כל סכום[592] מה שיצא וזה על השמנה שלשה ועל הששה ארבעה ועל השנים אחד וזה שלש[593] שמיניות וארבעה שתותים משמינית וחצי שתות שמינית וזו[594] צורתם | ||||||||
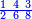
|
| ||||||||
Check: 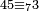
|
ובחינת השאלה הזאת הוא שתשליך המספר הנקרא שבעה שבעה והוא חמשה וארבעים הנשאר שלשה ושמרם[595] בידך | ||||||||
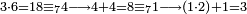
|
אחר כן הכה[596] השלשה[597] אשר על השמנה בששה אשר הוא הסכום וזה שמנה עשר הנשאר מהם ארבעה והשיא[598] עליהם הארבעה אשר על הששה יהיה זה שמנה הפיל[599] מהם שבעה הנשאר אחד אחר כן[600] הכהו[601] בשנים והשיא[602] מה שעליהם יהיה[603] זה שלשה והוא שוה לשלשה אשר שמרת בידך והוא הנשאר מן המספר הנקרא וכבר[604] נתאמתה השאלה | ||||||||
Chapter Seven – Division |
השער השביעי בחלוקת המספרים קצתם על קצת | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Two kinds of division | דע כי השער הזה יחלק לשני חלקים | |||||||||||||||
|
אחד מהם חלוקת הדבר על סוגו | |||||||||||||||
|
והשני חלוקת[605] הדבר על זולת סוגו[606] | |||||||||||||||
|
ואולם חלוק הדבר על סוגו הנה הוא חלוקת מספר[607] שלם על מספר שלם כמוהו | |||||||||||||||
|
והחלוק השני הוא[608] חלוק הדבר על זולת סוגו[609] הנה הוא חלוק השלם על השבר | |||||||||||||||
| והמבוקש[610] בשני הפנים[611] אמנם הוא מה שראוי לאחד תמיד | ||||||||||||||||
| ודע כי אתה[612] כאשר תרצה שתחלק מספר על מספר הנה השער הזה יסבול כמעשה במאמר[613] | ||||||||||||||||
|
|
פעם אחד[614] מהם שתקרא[615] אחד[616] מן הנחלק עליו ותקח[617] היחס ההוא מן הנחלק ומה שיהיה הנה[618] הוא מה שראוי לאחד | |||||||||||||||
|
דמיון זה כשיאמר לך אדם[619] חלק עשרים על ארבעה | |||||||||||||||
|
|
קרא אחד מן הארבעה[620] תמצא זה רביע וקח רביע העשרים וזה חמשה והוא מה שיצא והוא הראוי לכל אחד מן הארבעה | |||||||||||||||
|
|
והענין השני שתשיב הנחלק והנחלק עליו אל חלק שישתוו בו | |||||||||||||||
|
|
כלומ' אם היה לכל אחד משניהם[621] רביע השב[622] אותם אל רביעית שניהם אחר כן חלק רביע הנחלק על רביע הנחלק עליו ומה שיצא הנה[623] הוא המבוקש | |||||||||||||||
|
דמיון זה חלק חמשה ושלשים על חמשה עשר | |||||||||||||||
|
|
הנה לכל אחד מהם חלק ישתתפו[624] בו והוא החומש וקח חומש החמשה[625] עשר וזה שלשה וקח חומש החמשה ושלשים והוא שבעה וחלקם על השלשה יצא זה שנים ושליש והוא מה שיצא מחלוקת החמשה[626] ושלשים על החמשה[627] עשר | |||||||||||||||
| והמין[628] השלישי מן החלוק יחלק לשני חלקים והוא אם[629] שיהיה המספר הנחלק עליו ראשון או מורכב | ||||||||||||||||
|
|
ואם היה ראשון תבקש מספר תכהו בנחלק עליו ויסבלהו[630] ותפילהו מן הנחלק ויכלה או ישאר מה שהוא פחות מן הנחלק עליו ומה שהתקבץ הנה הוא היוצא מן החלוקה | |||||||||||||||
|
דמיון[631] זה חלק חמשים[632] על אחד עשר | |||||||||||||||
|
|
הנה כבר ידעת כי האחד עשר מספר בלתי מורכב לא ימנהו[633] כי אם האחד ובקש מספר תכהו באחד עשר ותפיל העולה ממנו מן החמשים[634] ויכלו בהם כל החמשים או ישאר מהם מה שהוא פחות מן האחד עשר תמצא ארבעה והכם[635] באחד עשר יהיו ארבעה וארבעים והפילם[636] מן החמשים הנשאר ששה | |||||||||||||||
|
|
וקרא אותם מן האחד עשר וזה ששה חלקים מאחד עשר הנה אם כן היוצא[637] ארבעה וששה חלקים מאחד עשר וזה צורתם | |||||||||||||||
|
|
| |||||||||||||||
|
|
ואם יהיה המספר הנחלק[638] עליו מורכב התירהו אל מספריו אשר הורכב מהם אחר כן חלק המספר הנחלק על[639] כל אחד מאלו המספרים הנזכרים יחלק[640] ראשונה על הקטן מהם ומה שיצא בחלוקה תחלקהו על היותר גדול עד שישלמו אלה[641] המספרים הנזכרים[642] ומה שיצא על האחרון מהם הנה הוא[643] המבוקש | |||||||||||||||
|
ודמיון זה חלק ששים על שמנה עשר | |||||||||||||||
|
|
הנה כבר ידעת כי השמנה עשר מספר מורכב מן השנים בתשעה וחלק הששים על השנים יצא[644] שלשים וחלק אלו השלשים על התשעה יצא לך שלשה וישאר על התשעה שלשה והם שלש[645] תשיעיות הנה יהיה היוצא מן החלוקה שלשה ושלש תשיעיות[646] | |||||||||||||||
written division |
ואם ירבה[647] המספר הנחלק וירבו מדרגותיו חלקם באותיות האבק | |||||||||||||||
|
|
דמיון זה חלק ארבעה וחמשים ושמנה מאות על שלשה[648] | |||||||||||||||
| הוריד הארבעה והחמישים[649] ושמנה מאות בשטה על זאת[650] הצורה | ||||||||||||||||
|
| |||||||||||||||
|
אחר כן הוריד המספר הנחלק עליו תחת השמנה[651] אשר הם אחרית[652] המספר[653] מן הנחלק והוריד השלשה תחתיהם אחר כן בקש מספר הורידהו[654] תחת השמנה[655] ותכהו בשלשה[656] ותפילהו מן השמנה תמצא שנים הכם[657] בשלשה יהיו ששה והפילם[658] מן השמנה נשאר[659] שנים והורידם במקום[660] השמנה אחר שתסיר השמנה מהם | |||||||||||||||
|
|
| |||||||||||||||
|
ואם תרצה בחינת השאלה הזאת השלך המספר הנחלק שבעה שבעה תמצאהו מושלך | |||||||||||||||
|
|
אחר כן שוב אל המספר היוצא מן החלוקה והשליכהו שבעה שבעה הנשאר ממנו ארבעה הכהו[677] בשלשה אשר נחלק עליו יהיו[678] שנים עשר השלך מהם שבעה הנשאר חמשה והשיא[679] עליהם השנים אשר על השלשה יהיו שבעה מושלכים גם כן[680] | |||||||||||||||
|
|
ואם יאמר חלק ששה וארבעים ושבע מאות ושמנת אלפים ותשעים אלף על ששה ושלשים | |||||||||||||||
| הוריד המספר הנחלק בשטה על זאת הצורה | ||||||||||||||||
|
| |||||||||||||||
|
|
ודע כי הששה ושלשים מספר מורכב מן ארבעה[681] ותשעה[682] וחלק המספר[683] הנזכ' על ארבעה אשר הם פחות תחלה לפי מה שקדם[684] בשאלה[685] קודם זה יצא לך בחלוק ששה ושמנים ושש מאות וארבע ועשרים אלף וישאר על הארבעה שנים אחר כן חלק הששה ושמנים ושש מאות וארבעה ועשרים על תשעה גם כן[686] לפי מה שקדם יצא לך בחלוק שנים וארבעים[687] ושבע מאות ושני אלפים וישאר על הארבעה שנים ועל[688] התשעה[689] שמנה | |||||||||||||||
|
|
| |||||||||||||||
| ויהיה היוצא מן החלוקה שנים וארבעים ושבע מאות ואלפים ושמנה תשיעיות ושני[694] רביעי תשיעיות[695] והוא חצי תשיעית | ||||||||||||||||
| ואמנם אמרנו שתי רביעיות[696] להקל עלינו בבחינה | ||||||||||||||||
|
ובחינת זאת השאלה הוא שתשליך המספר הנחלק שבעה שבעה ישאר ממנו ארבעה ושמרם | |||||||||||||||
|
|
אחר כן שוב[697] אל המספר היוצא והשליך השלם ממנו ישאר מזה חמשה והכם[698] בנשאר מן התשעה וזה שנים יהיו עשרה ישאר מהם שלשה והשיא[699] עליהם הנשאר מן השמנה אשר על התשעה וזה אחד יהיה זה ארבעה והכם[700] בארבעה אשר[701] הם הסכום והיו[702] ששה עשר הנשאר מהם[703] שנים ועל הארבעה שנים יהיו ארבעה והוא שוה לארבעה אשר נשארו מן המספר הנחלק וכבר התאמתה השאלה | |||||||||||||||
| ואולם החילוק על החלקים כמו אחד עשר ושלשה עשר ושבעה עשר הנה המעשה בהם לפי מה שזכרנו[704] | ||||||||||||||||
|
|
ודמיון זה חלק ששה ושבעים ומאתים על אחד עשר | |||||||||||||||
| הוריד זה המספר הנזכר בשטה כמו שקדם אחר כן הוריד האחד עשר תחת שבעה ועשרים וזה צורתם | ||||||||||||||||
| ||||||||||||||||
|
אחר כן בקש מספר תורידהו[705] תחת האחד[706] אשר הוא[707] אחד והוא גם כן[708] תחת השבעה ותכהו באחד אשר הוא עשרה עוד באחד אשר הוא אחד ויכלה בזה כל מה אשר על ראשו תמצא שנים הפילם[709] מן השנים אשר על ראשם יכלה אחר כן הכה[710] אלו השנים באחד אשר הוא תחתיו יהיו שנים הפילם[711] מן השבעה אשר על ראשם ישארו חמשה וקיים אותם במקום השבעה | |||||||||||||||
|
|
| |||||||||||||||
|
ובחינת זאת השאלה שתשליך הששה ושבעים ומאתים הנחלקים שבעה שבעה וישאר מהם שלשה ושמרם[720] | |||||||||||||||
|
|
אחר כן השליך[721] החמשה[722] ועשרים אשר יצאו מן החלוקה שבעה שבעה ישאר מהם ארבעה והכם[723] בנשאר מן האחד עשר והוא ארבעה ויהיו[724] ששה עשר ישאר מהם שנים והשיא עליהם החלק אשר על האחד עשר שהוא אחד יהיו שלשה והוא שוה לשלשה אשר נשאר מן הנחלק | |||||||||||||||
| ועל הדמיון הזה הוא החלוק על שלשה[725] עשר ועל שבעה עשר והבין[726] ותמצא בעז' האל יתעלה[727] | ||||||||||||||||
Chapter Eight – Halving |
השער השמיני בחצית[728] איזה מספר שתרצה[729] | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
דע כי השער הזה מין ממיני החלוק וכאשר תרצה לקחת חצי מספר חלקהו על השנים[730] ומה שיצא מן החלוק הוא חצי המספר הנחלק | |||||||||||||||||||
|
ודמיון זה כאשר תרצה לקחת חצי ארבעה וששים ושבע מאות ושמנת אלפים | |||||||||||||||||||
| הוריד[731] המספר הזה בשטה כמו שקדם והוריד תחלה הארבעה אחר כן הששה אחר כן השבעה אחר כן השמנה וזה צורתם | ||||||||||||||||||||
|
| |||||||||||||||||||
|
אחר כן הוריד השנים תחת השמנה אשר הם המדרגה האחרונה אחר כן בקש מספר[732] תורידהו[733] תחת השנים ותכהו בשנים ויכלו בו השמונה תמצא ארבעה והורידהו תחת השנים[734] | |||||||||||||||||||
|
| |||||||||||||||||||
|
ודע כי כל מספר שיהיה[743] תחלתו נפרד הנה הוא אין לו חצי שלם כי אם בשבר | |||||||||||||||||||
|
ודע כי אתה כאשר תרצה שתקח שליש מספר הנה תחלקהו[744] על שלשה | |||||||||||||||||||
|
או ארבעה[745] ותחלקהו על ארבעה | |||||||||||||||||||
| ועל הדמיון הזה עד[746] עשרה | ||||||||||||||||||||
Chapter Nine – Doubling |
השער התשיעי בהכפיל[747] איזה מספר שתרצה | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
דע כי השער[748] הזה מין ממיני הקבוץ והוא קבץ מספר אחד[749] אל מספר[750] אחר כמוהו[751] | |||||||||||||||
|
דמיון זה כפול אחד ועשרים וארבע מאות | |||||||||||||||
| וקיים אותם בשטה על זאת הצורה[752] | ||||||||||||||||
|
| |||||||||||||||
| אחר כן קיים תחת השטה שטה אחרת כמוה תוריד כל סוג תחת סוגו תוריד[753] האחד[754] תחת האחד[755] והעשרים[756] תחת העשרים והארבע מאות תחת הארבע מאות על זאת הצורה[757] | ||||||||||||||||
| ||||||||||||||||
|
ואחר[758] כן תתחיל לקבץ מן האחדים וקבץ האחד עם האחד יהיו שנים וקיים אותם על הקו כמספר האחדים[759] אחר כן קבץ הארבעה אל הארבעה יהיו שמנה וקיים אותם גם כן[760] על הקו על המאות ויתקבץ לך על הקו שנים וארבעים ושמנה מאות והוא כפל האחד ועשרים וארבע מאות | |||||||||||||||
Chapter Ten – Extracting Roots |
השער העשירי בלקיחת גדר המספרים | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Square number - number that has a root | דע כי המספרים הנגדרים הם המספרים המרובעים ושרשיהם הם הגדרים | |||||||||||||||||
| ודע כי מדרגות המספר מדרגה מהן[761] נגדרת[762] ושנית לה בלתי נגדרת | ||||||||||||||||||
|
וזה כי מדרגת האחדים היא תחלת המדרגה הראשונה ממדרגות המספרים ותחלתה האחד ולו גדר והוא אחד | |||||||||||||||||
|
והמדרגה השנית העשרות ותחלתה העשרה ואין לו[763] גדר | |||||||||||||||||
|
והמדרגה השלישית המאות ותחלתה המאה[764] ולו גדר והוא העשרה[765] | |||||||||||||||||
|
והמדרגה הרביעית האלפים ותחלתה האלף[766] ואין לו[767] גדר | |||||||||||||||||
|
והמדרגה החמשית עשרת[768] אלפים ולו גדר וגדרו[769] מאה | |||||||||||||||||
|
ועל הסדר הזה מדרגה[770] תמיד נגדרת ושנית לה[771] בלתי נגדרת | |||||||||||||||||
written extraction of roots |
||||||||||||||||||
| description of the procedure | וכאשר תרצה לדעת איך תקח גדר[772] מספר נגדר הוריד המספר ההוא[773] על מדרגותיו כמו שקדם אחר כן תתחיל מן המדרגה הראשונה הנה לה גדר והשנית אין לה גדר | |||||||||||||||||
|
ודמיון זה כאשר תרצה לקחת גדר חמשה ועשרים ושש מאות | |||||||||||||||||
| הורידם על הצורה הזאת | ||||||||||||||||||
|
| |||||||||||||||||
|
אחר כן[786] התחיל בתחלת מדרגה שיש לה[787] גדר והשנית אין לה גדר[788] והשלישית יש לה גדר ובקש מספר תורידהו[789] תחת הששה ותכהו בנפשו יכלו בו[790] הששה[791] תמצא שנים והכם[792] בדומה להם יהיו ארבעה והפילם מן הששה[793] אשר על ראשם הנשאר שנים וקיים אותם במקום הששה | |||||||||||||||||
|
ואם רצית לקחת גדר ששה[802] ותשעים[803] ושש מאות ושלשת אלפים ושמנים אלף וחמש מאות אלפים | |||||||||||||||||
| הורידם בשטה על זאת הצורה[804] | ||||||||||||||||||
|
| |||||||||||||||||
| אחר כן מנה המדרגות תמצאם זוג[805] והניח המדרגה האחרונה מפני שהיא בלתי נגדרת וחזור אל אשר תלוה אליה אל הימין | ||||||||||||||||||
| ואם[806] יהיו[807] מספר המדרגות נפרד הנה המדרגה האחרונה נגדרת | ||||||||||||||||||
|
הנה כבר מצאת מספר אלו זוג ועזוב המדרגה האחרונה מהם ובקש מספר תורידהו[808] תחת השמנה[809] וחמשים תמצא שבעה והכם[810] בדומה להם יהיו תשעה וארבעים הפילם[811] מן השמנה וחמשים הנשאר תשעה אחר כן מחה השמנה וחמשים וקיים התשעה מקום השמנה[812] | |||||||||||||||||
|
אחר כן בקש מספר תורידהו תחת הששה ותכהו באחד האחרון ובארבעה ובנפשו ותפיל כל זה ממה שעל ראשו תמצא ששה[816] ותכם[817] באחד[818] יהיו ששה[819] ותפילם מן התשעה הנשאר שלשה וקיים אותם במקום התשעה אחר כן הכה[820] הששה בארבעה יהיו ארבעה ועשרים והפילם[821] מן השלשה[822] ושלשים הנשאר תשעה על ראש הארבעה | |||||||||||||||||
|
ואחר[829] כן בקש מספר תורידהו[830] תחת הששה אשר הם מדרגה ראשונה מן המספר הנגדר ותכהו באחד האחרון ובחמשה ובשנים ובנפשו ויכלה[831] בו כל מה שנשאר מן המספר תמצא[832] ארבעה ותכה אותם באחד יהיו ארבעה תפילם מן הששה אשר על ראשם ישארו שנים אחר כן תכה הארבעה בשנים יהיו שמנה ותפילם מן התשעה אשר על ראשם ישאר אחד והעתיקהו במקום הששה | |||||||||||||||||
|
ואם תרצה לקחת גדר מספר יהיה צפרים עשה בצפר כמו שקדם בלקיחת הגדרים וקיים הצפרים וקח חצי מספרם וחצי מה שכפלת וחברהו אל הצפרים יהיה הגדר | |||||||||||||||||
|
המשל בזה כאשר תרצה לקחת גדר עשרת אלפים | |||||||||||||||||
| הוריד העשרת[838] אלפים ארבעה צפרים ואחד כמו שקדם באותיות האבק על הצורה הזאת | ||||||||||||||||||
|
| |||||||||||||||||
| ואחר כן מנה המדרגות תמצאם נפרד והתחיל במדרגה האחרונה אחר כן תאמר איזה מספר אכהו בדומה לו ונפיל המקובץ מן האחד ויכלה תמצא אחד ועמך מן הצפרים ארבעה קח חציים וזה שנים ויהיה הגדר שני צפרים ואחד על זאת הצורה | ||||||||||||||||||
|
| |||||||||||||||||
| והם מאה וקבץ תמצא | ||||||||||||||||||
Section Two – Fractions |
||||||||||
Multiplication of Fractions |
ואחר שכבר הגענו אל מה שאמרנו מאלו העשרה שערים הנה נתחיל עתה בהכאת השברים באבק | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| והנה עשינו שערים גם כן בהכאת השברים באבק שנים ושבעים שערים | ||||||||||
Chapter One – Forms of Fractions |
השער הראשון בצורת השברים באבק | |||||||||
| simple fractions | דע כי ראשון השברים החצי ואחריו השליש והרביע והחומש והשתות והשביעית והשמינית והתשיעית והעשור הנה אלו פשוטים | |||||||||
| וכאשר תרצה לצייר החצי תצייר שנים ועליהם קו ועל הקו אחד על הצורה הזאת: | ||||||||||

|
| |||||||||
| והשליש שלשה עליהם אחד על זאת הצורה: | ||||||||||

|
| |||||||||
| וכאשר תרצה שני שלישים תשים במקום האחד שנים ויהיו שני שלישים כזה: | ||||||||||

|
| |||||||||
| והרביע אחד על ארבעה על זאת הצורה: | ||||||||||

|
| |||||||||
| וכן העשירית אחד על העשרה על זאת הצורה: | ||||||||||
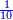
|
| |||||||||
| ויהיה ביניהם קו תמיד | ||||||||||
| וכן תשע עשיריות יהיו תשעה על עשרה וביניהם קו | ||||||||||
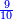
|
| |||||||||
| ומאלו הפשוטים גם כן החלקים ומהם חלק מאחד עשר תוריד אחד עשר ועליהם קו ועל הקו אחד על זאת הצורה: | ||||||||||
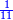
|
| |||||||||
| ואם יהיו שני חלקים תשים במקום האחד שנים | ||||||||||
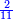
|
| |||||||||
| ותשעה חלקים תשים במקום אחד תשעה | ||||||||||
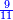
|
| |||||||||
| או עשרה חלקים תשים במקום האחד עשרה ויהיו עשרה חלקים מאחד עשר | ||||||||||
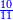
|
| |||||||||
| וכן תעשה החלקים כולם כמו שלשה עשר ותשעה עשר תוריד מקום החלק אחר כן תמשוך קו ועל הקו מספר מה שעמך מן החלקים עוד תשנה ג"כ אלו החלקים | ||||||||||
| fractions of fractions | ויהיה מהם שם מחובר משנים | |||||||||
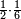
|
כמו חצי שתות הנה השם הזה מחובר מן החצי והשתות ורשום מקום השתות ומקום החצי תחת קו ויהיו ששה ראשונה והשנים אחרונים ותוריד על השנים אחד על זאת הצורה: | |||||||||
|
| |||||||||
| הנה זאת צורת חצי שתות | ||||||||||
|
וכן רביע שביעית תשים ארבעה ושבעה תחת קו ועל הארבעה אחד על זאת הצורה: | |||||||||
|
| |||||||||
| ואלו הצורות הם שברי השברים | ||||||||||
| ואם יהיה שבר נשבר רשום שני המקומות תחת קו ורשום על כל אחד מהם גדרו הנזכר | ||||||||||
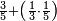
|
דמיון זה אלו יאמר לך שלשה חומשים ושליש החומש | |||||||||
| הוריד החמשה והשלשה תחת קו אחד כמו שסדרנו ורשום על החמשה שלשה ועל השלשה אחד על זאת הצורה: | ||||||||||
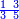
|
| |||||||||
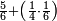
|
וכן חמשה שתותים ורביע שתות | |||||||||
| הוריד הארבעה והששה תחת קו ועל הששה חמשה ועל הארבעה אחד על זאת הצורה: | ||||||||||
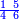
|
| |||||||||
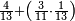
|
וכן שתוף החלקים כמו ארבעה חלקים משלשה עשר ושלשה חלקים מאחד עשר בחלק משלשה עשר | |||||||||
| הוריד השלשה עשר והאחד עשר תחת קו ועל השלשה עשר ארבעה ועל האחד עשר שלשה ויהיו ארבעה חלקים משלשה עשר ושלשה חלקים מאחד עשר בחלק משלשה עשר וזה צורתם: | ||||||||||
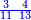
|
| |||||||||
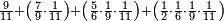
|
וכן ישתתף בשלשה שמות וארבעה שמות כמו תשעה חלקים מאחד עשר ושבע תשיעיות החלק מאחד עשר וחמשה שתותים תשיעית החלק מאחד עשר וחצי שתות תשיעית החלק מאחד עשר משוך קו וכתוב תחלה מקום החלק ואחריו מקום התשיעית אל מה שילוה אל השמאל ואחריו מקום השתות ואחריו מקום החצי אחר כן תכתוב על כל אחד מהם מספר חלקיו וזה על האחד עשר תשעה ועל התשעה שבעה ועל הששה חמשה ועל השנים אחד וזה צורתם: | |||||||||
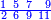
|
| |||||||||
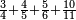
|
ומאלו השברים מה שהוא מתחלף לא ייוחס אחד מהם אל השני כמו שלשה רביעים וארבעה חמישיים וחמשה שתותים ועשרה חלקים מאחד עשר כל אחד מיוחס אל האחד הנה אתה תפריד הקו ביניהם ולא יהיה דבק על הצורה הזאת: | |||||||||
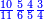
|
| |||||||||
| ומאלו השברים מה שהוא מיוחס במלה בחסרון הוו' והוא לקיחת השבר מן השבר | ||||||||||
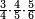
|
דמיון זה שלשה רביעים ארבעה חומשים חמשה שתותים הנה צורת אלו כמו צורת המתיחסי' באחד ומשוך קו ורשום תחתיו תחלה הארבעה אחר כן החמשה אחר כן הששה ורשום על כל אחד מהם מספר החלקים הנזכ' וזה על הארבעה שלשה ועל החמשה ארבעה ועל הששה חמשה על זאת הצורה: | |||||||||
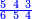
|
| |||||||||
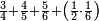
|
ופעמים יבואו מאלו השברים מה שהוא מתחלף ומתייחס כמו שלשה רביעים וארבעה חומשים וחמשה שתותים וחצי שתות תחת קו אחד כמו שקדם וזה צורתם: | |||||||||

|
| |||||||||
| ומהם מה שהוא שבר מיוחס אל זולת אחד מן השברים המתחלפים | ||||||||||
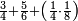
|
דמיון זה שלשה רביעים וחמשה שתותים ורביע שמינית | |||||||||
| הוריד השלשה רביעים והחמשה שתותים תחת שני קוים ורביע השמינית תחת קו בעצמו וזה צורתם: | ||||||||||
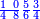
|
| |||||||||
| וכמו המעשה הזה תקיש כל מה שיבא עליך בע"ה | ||||||||||
|
Chapter Two – Multiplication of Fraction by Integer |
השער השני בהכאת השבר במספר השלם | |||||
|---|---|---|---|---|---|---|
|
|
כאשר יאמר לך הכה חמשה שתותים בעשרה | |||||
| הוריד החמשה שתותים בשטה והוריד תחתיו בשטה אחרת העשרה על זאת הצורה: | ||||||
|
|
| |||||
|
|
אחר כן תתחיל בשטה העליונה וקח החמשה אשר על הששה והכה אותם בעשרה יהיו חמישים וחלקם על הששה אשר הם במעמד והם גם כן תחת הקו יצא לך שמונה ושני שתותים וזה צורתם: | |||||
|
|
| |||||
|
ואם תרצה לבחון אותו השלך העשרה בהשלכת שבעה ישארו מהם שלשה והכם בחמשה אשר הכית בהם העשרה יהיו חמשה עשר והשליכם שבעה הנשאר אחד והוא התשובה ושמרהו | |||||
|
|
אחר כן חזור אל היוצא והוא שמונה והשליך מהם שבעה הנשאר אחד והכהו בששה אשר הם המורה והשיא מה שעל ראשם וזה שנים יהיו שמונה והשליך מהם שבעה הנשאר אחד והוא שוה אל האחד השמור | |||||
Chapter Three – Multiplication of Fraction and Fraction of Fraction by Integer |
השער השלישי בהכאת השבר ושבר השבר במספר השלם | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
|
כאשר יאמר לך הכה חומש וחצי חומש בשנים עשר | |||||||||
| הוריד החומש וחצי חומש בשטה והשנים עשר בשטה אחרת תחתיו על זאת הצורה: | ||||||||||
|
|
| |||||||||
|
|
אחר כן תתחיל בשטה העליונה והכה האחד אשר על החמשה בשנים והשיא על המקובץ האחד אשר על השנים יהיו שלשה והכם בשנים עשר יהיו ששה ושלשים וחלקם על המורה אשר הם שנים וחמשה יצא לך המבוקש שלשה ושלשה חומשים וזאת צורתם: | |||||||||
|
|
| |||||||||
|
ובחינת זאת השאלה כמו שקדם במעשה וזה שתכה האחד בשנים ותשיא מה שעל ראשם כמו שקדם במעשה יהיה זה שלשה אחר כן תשליך מן השנים עשר שבעה הנשאר חמשה והכם בשלשה אשר על הקו העליון יהיו חמשה עשר השליכם שבעה שבעה הנשאר מהם אחד | |||||||||
|
|
אחר כן חזור אל היוצא בתשובה והוא שלשה והכם בחמשה אשר הם המורה יהיו חמשה עשר וישאר מהם אחר ההשלכה אחד וקבצהו עם השלשה אשר על החמשה יהיו ארבעה הכם בשנים אשר הם הסכום השני יהיו שמונה ישאר מהם אחד והוא נאות לתשובה | |||||||||
Chapter Four – Multiplication of Fraction of Fraction by Integer |
השער הרביעי בהכאת שבר השבר במספר השלם | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
|
כאשר יאמר לך הכה שליש השביעית בחמשה ועשרים | |||||||||
|
|
| |||||||||
| הוריד שליש השביעית בשטה וחמשה ועשרים בשטה אחרת תחתיו על זאת הצורה: | ||||||||||
|
|
אחר כן הכה האחד אשר על הקו העליון בחמשה ועשרים יהיו חמשה ועשרים וחלקם על הסכום יצא לך המבוקש וזה אחד ושביעית ושליש ושביע וזה צורתו: | |||||||||
|
|
| |||||||||
|
ובחינת זאת השאלה כמו שקדם במעשה והוא שתשליך החמשה ועשרים שבעה שבעה הנשאר מהם ארבעה והכם באחד אשר על הסכום יהיו ארבעה והוא התשובה ושמרהו | |||||||||
|
|
אחר כן חזור אל היוצא והוא אחד והכהו בשבעה יהיה ההשלכה ועל ראשו אחד והכהו בשלשה והשיא מה שעל ראשם יהיו ארבעה וזה נאות לתשובה | |||||||||
Chapter Five – Multiplication of Two Different Fractions by Integer |
השער החמישי בהכאת שני השברים המתחלפים במספר השלם | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך הכה שלשה רביעים וארבעה חומשים בחמשה עשר | |||||||||
|
|
| |||||||||
| הוריד השלשה רביעים והארבעה חומשים בשטה והוריד תחתיו החמשה עשר על זאת הצורה: | ||||||||||
|
|
אחר כן התחיל בשטה העליונה והכה מה שעל החמשה בסכום אשר תחת השלשה והוא ארבעה עוד הכה מה שעל הארבעה בחמשה וקבץ שתי ההכאות יהיה זה אחד ושלשים והכם בחמשה עשר יהיה זה חמשה ושישים וארבע מאות וחלקם על הארבעה יצא לך בחלוקה ששה עשר ומאה וישאר על הארבעה אחד אחר כן חלק הששה עשר ומאה על החמשה אשר הם הסכום השני יצא לך בחלוקה שלשה ועשרים וחומש אחד ורביע חומש על זאת הצורה: | |||||||||
|
|
| |||||||||
|
ובחינת השאלה הזאת כמו שקדם בהכאתה וזה שתכה השלשה אשר על הארבעה בחמשה אשר תחת הקו יהיו חמשה עשר ישאר מהם אחד אחר כן הכה הארבעה אשר על החמשה בארבעה אשר הם הסכום יהיו ששה עשר ישאר מהם שנים וקבצם אל האחד השמור יהיה זה שלשה והכם בנשאר מן החמשה עשר והוא אחד יהיה זה שלשה ושמרהו והוא התשובה | |||||||||
|
|
אחר כן חזור אל היוצא והוא שלשה ועשרים ישאר מהם שנים והכם בחמשה אשר הם הסכום יהיו עשרה ישאר מהם שלשה השיא עליהם האחד אשר על החמשה יהיו ארבעה והכם בארבעה אשר הם הסכום השני יהיו ששה עשר הנשאר מהם שנים ועל ראשם אחד יהיו שלשה והוא שוה לתשובה השמורה | |||||||||
Chapter Six – Multiplication of Fraction by Integer and Fraction |
השער השישי בהכאת השבר בשלם והשבר | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כאשר יאמר לך הכה שלשה חומשים בתשעה ושליש | ||||||||||
| הוריד השלשה חומשים בשטה אחת והתשעה ושליש בשטה אחרת תחתיו על זאת הצורה: | |||||||||||
|
|
| ||||||||||
|
|
אחר כן [הכה] [התשעה] בג' אשר תחת הקו מן השטה התחתונה והשיא מה שעל ראשם יהיו שמונה ועשרים והכם בשלשה אשר על החמשה יהיו ארבעה ושמונים וחלקם על הסכום אשר תחת הקוים יצא לך המבוקש וזה חמשה ושלשה חומשים על זאת הצורה: | ||||||||||
|
|
| ||||||||||
|
ואם תרצה הבחינה השלך התשעה ישאר מהם שנים והכם בשלשה אשר הם הסכום והשיא מה שעל ראשם יהיו שבעה והכם בשלשה אשר על החמשה יהיו גם כן שלשה ותשובתם השלכה | ||||||||||
|
|
אחר כן חזור אל היוצא מן ההכאה והוא חמשה והכם בחמשה אשר הם הסכום יהיו חמשה ועשרים הנשאר ארבעה ועל ראשם שלשה יהיו שבע' והם נשלכים והכם במקום השליש יהיה גם כן השלכה ותשובת זאת השאלה השלכה הנה כבר נתאמתה השאלה | ||||||||||
| ודע כי המלאכה המעשה הראשון בכל שאלה כמו מלאכת ההכאה | |||||||||||
Chapter Seven – Multiplication of Fraction and Fraction of Fraction by Integer and Fraction |
השער השביעי בהכאת השבר ושבר השבר בשלם והשבר | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך: הכה חמשה שתותים וחצי שתות בששה ושלשה חומשים | ||||||||||
| הוריד החמשה שתותים וחצי שתות בשטה והששה ושלשה חומשים בשטה אחרת תחתיו על זאת הצורה: | |||||||||||
|
|
| ||||||||||
|
|
אחר כן תתחיל בקו העליון והכה החמשה בשנים והשיא מה שעל ראשם יהיו אחד עשר ושמרם אחר כן תכה הששה אשר בקו התחתון בחמשה אשר תחת הג' והשיא מה שראשם ויעלה שלשה ושלשים והכם באחד עשר השמורים יהיו שלשה ושישים ושלש מאות וחלקם על הסכום יצא לך המבוקש וזה ששה וחומש שתות וחצי חומש שתות על זאת הצורה: | ||||||||||
|
|
| ||||||||||
|
והבחינה בשאלה הזאת כמו שקדם בהכאתה ישאר מן הקו העליון ארבעה ומן הקו התחתון חמשה אחר כן הכה הארבעה אשר נשארו מן השטה העליונה בחמשה אשר נשארו מן השטה התחתונה יהיו עשרים הנשאר מהם ששה והוא התשובה | ||||||||||
|
|
אחר כן חזור אל היוצא והוא ששה והכהו במקום השתות יהיו ששה ושלשים הנשאר מהם אחד והכהו בחמשה מקום החומש והשיא מה שעל ראשם יהיו ששה והכם בשנים ותשיא מה שעל ראשם יהיו שלשה עשר הנשאר מהם ששה כמו התשובה | ||||||||||
Chapter Eight – Multiplication of Fraction of Fraction by Integer and Fraction |
השער השמיני בהכאת שבר השבר בשלם והשבר | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כאשר יאמר לך: הכה חצי שביעית בעשרה ושלשה חומשים | ||||||||||
| הוריד חצי השביעית בשטה והעשרה ושלשה חומשים בשטה תחתיה בצורה הזאת: | |||||||||||
|
|
| ||||||||||
|
|
אחר כן הכה העשרה אשר בקו התחתון בחמשה והשיא מה שעל ראשם יהיו שלשה וחמישים והכם באחד אשר על הקו העליון יהיו שלשה וחמשים בעצמם וחלקם על הסכום יצא לך המבוקש חמשה שביעיות וחומש שביע וחצי חומש שביע על זאת הצורה: | ||||||||||
|
|
| ||||||||||
| ובחינתה כמו שקדם והתשובה בה היא ארבע בהשלכת שבעה | |||||||||||
Chapter Nine – Multiplication of Two Different Fractions by Integer and Fraction |
השער התשיעי בהכאת שני השברים המתחלפים בשלם והשבר | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך: הכה שלשה רביעים וארבעה חומשים בחמשה וחמשה שתותים | ||||||||||
| הוריד השלשה רביעים והארבעה חומשים בשטה כמו שקדם בשער הראשון בצורות השברים המתחלפים אחר כן הוריד בשטה תחתיו החמשה והחמשה שתותים על זאת הצורה: | |||||||||||
|
|
| ||||||||||
|
|
אחר כן תתחיל בשטה העליונה והכה מה שעל הארבעה בחמשה ומה שעל החמשה בארבעה וקבץ שתי ההכאות יהיה זה אחד ושלשים ושמרם אחר כן חזור אל הקו התחתון והכה החמשה בששה והשיא מה שעל ראשם יהיו חמשה ושלשים והכם באחד ושלשים יהיו חמשה ושמונים ואלף וחלקם במאה ועשרים יצא לך המבוקש וזה תשעה וחומש שתות ורביע חומש שתות וזה צורתו: | ||||||||||
|
|
| ||||||||||
| ובחינתה על תואר הכאתה והתשובה בזה השלכה | |||||||||||
| וכל בחינה אמנם יצטרך בה אל השלכת שבעה | |||||||||||
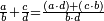
|
ודע כי שני השברים המתחלפים כאשר תכה אמנם תקח מה שעל הקו הראשון והכה מה שבקו השני וקבץ שתי ההכאות והשברים המתיחסים תקח מה שעל גבול הסכום ותכהו בסכום אשר ייוחס אליו ותשיא מה שעל ראשם והבן תמצא בע"ה | ||||||||||
Chapter Ten – Multiplication of Fraction by Integer and Fraction and Fraction of Fraction |
השער העשירי בהכאת השבר בשלם והשבר ושבר השבר | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כאשר יאמר לך: הכה שלשה רביעיות בחמשה ושבעה שמיניות ושתות שמינית | ||||||||||||||
| הוריד השלשה רביעיות בשטה והחמשה ושבעה שמניות ושתות שמין בשטה תחתיה על הצורה הזאת: | |||||||||||||||
|
|
| ||||||||||||||
|
|
אחר כן התחיל בשטה התחתונה והכה החמשה בשמונה והשיא מה שעל ראשם ומה שהתקבץ [פי' שהוא מ"ז] תכהו בששה ותשיא מה שעל ראשם יהיו ג' ושמונים ומאתים ותכם בשלשה אשר על הארבעה יהיה זה תשעה וארבעים ושמונה מאות וחלקם על הסכום יצא לך המבוקש וזה ארבעה ושלש שמיניות ושתות שמינית על זאת הצורה: | ||||||||||||||
|
|
| ||||||||||||||
| ואולם הבחינה הנה היא על צורת המעשה והתשובה בה שנים | |||||||||||||||
![\scriptstyle n+\frac{a_1}{b_1}+\left(\frac{a_2}{b_2}\sdot\frac{1}{b_1}\right)=\frac{\left[\left[\left(n\sdot b_1\right)+a_1\right]\sdot b_2\right]+a_2}{b_1\sdot b_2}](/mediawiki/images/math/c/9/d/c9db4fa0c85cc5f4c8ed8387974743ac.png)
|
והבין ודע כי כאשר יביאך השלם והשבר ושבר השבר הנה אמנם המעשה בו שתכה השלם בשבר ותשיא מה שעל ראשו ומה שהתקבץ הכהו במקום השבר השני והשיא מה שעל ראשו והבין תמצא זה בע"ה | ||||||||||||||
Chapter Eleven – Multiplication of Fraction by Integer and Fraction of Fraction |
השער האחד עשר בהכאת השבר בשלם ושבר השבר | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך: הכה חמשה שתותים בשמונה וחמש שביעיות התשיעית | ||||||||||||||
| הוריד החמשה שתותים בשטה והשמונה וחמש שביעיות התשיעית בשטה תחתיו על הצורה הזאת: | |||||||||||||||
|
|
| ||||||||||||||
|
|
אח"כ תתחיל מן הקו התחתון והכה השמונה בתשעה ומה שהתקבץ בשבעה והשיא מה שעל ראשם יהיה זה תשעה וחמש מאות והכם בחמשה אשר על הששה יעלה חמשה וארבעים וחמש מאות ושני אלפים וחלקם על הסכום יצא לך המבוקש והוא ששה ושש תשיעיות וארבעה שביעי התשיעית ושתות שביע התשיעית על זאת הצורה: | ||||||||||||||
|
|
| ||||||||||||||
| והבחינה בה על תואר המעשה והתשובה בה ארבעה | |||||||||||||||
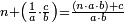
|
ודע כי כאשר יביאך שלם ושבר שבר תכה השלם תחלה בשבר הראשון ומה שהתקבץ בשבר השני ותשיא מה שעל ראשו | ||||||||||||||
Chapter Twelve – Multiplication of Fraction by Integer and Two Different Fractions |
השער השנים עשר בהכאת השבר בשלם והשברים המתחלפים | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כאשר יאמר לך: הכה שני שלישים בתשעה ושלשה שביעיות וארבעה חומשים | ||||||||||||||
| הוריד השאלה על זאת הצורה: | |||||||||||||||
|
|
| ||||||||||||||
|
|
אחר כן תתחיל בשטה התחתונה והכה התשעה בשבעה ומה שהתקבץ בחמשה יהיה זה חמשה עשר ושלש מאות אחר כן הכה מה שעל השבעה בחמשה ומה שעל החמשה בשבעה ויקבץ שתי ההכאות יהיה זה שלשה וארבעים וקבצם אל החמשה עשר ושלש מאות יהיה זה שמונה וחמישים ושלש מאות והכם בשנים אשר על השלשה יהיה המקובץ ששה עשר ושבע מאות וחלקם על הסכום יצא לך המבוקש והוא ששה וחמש שביעיות ושלשה חומשי השביעית ושני שלישי חומש השביעית על זאת הצורה: | ||||||||||||||
|
|
| ||||||||||||||
| והתשובה בה בהשלכה שנים | |||||||||||||||
|
ודע כי כאשר יביאך שלם ושברים מתחלפים הכה השלם במקום האחד ומה שהתקבץ הכהו בשני מן המקומות ותשמור המקובץ אחר כן שוב אל השברים המתחלפים ותעשה בהם כמו שקדם בשני השברים המתחלפים ומה שהתקבץ קבצהו אל המספר השמור | ||||||||||||||
Chapter Thirteen – Multiplication of Fraction and Fraction of Fraction by Integer and Fraction and Fraction of Fraction |
השער השלשה עשר בהכאת השבר ושבר השבר בשלם והשבר ושבר השבר | ||||||||||||
|
|
דמיון זה כאשר יאמר לך: הכה חמשה שתותים וחצי שתות בשמונה וחמש שביעיות וחומש שביעית | ||||||||||||
| הוריד החמשה שתותים וחצי שתות בשטה אחר כן הוריד תחתיו השמונה וחמש שביעיות וחומש שביע בשטה על זאת הצורה: | |||||||||||||
|
|
| ||||||||||||
|
|
אחר כן התחיל בשטה העליונה והכה החמשה בשנים והשיא מה שעל ראשם יהיה זה אחד עשר ושמרם אחר כן חזור אל הקו התחתון והכה השמונה בשבעה והשיא מה שעל ראשם ומה שהתקבץ הכם עם החמשה שתחת האחד והשיא מה שעל ראשם יהיה זה ששה ושלש מאות והכם באחד עשר הנזכרים אשר שמרת יהיה המקובץ ששה ושישים ושלש מאות ושלשת אלפים וחלקם על הסכום ויצא לך המבוקש וזה שמונה ושלשה חומשי שתות שביעית והשנים אין על ראשם כלום על זאת הצורה: | ||||||||||||
|
|
| ||||||||||||
| ותשובת השאלה הזאת בבחינת הששה | |||||||||||||
| ודע כי אתה כאשר הגעת בבחינה כיוצא מן השאלה שתכה בחמשה ותשיא מה שעל ראשם והמקובץ הכהו בשנים אשר אין על ראשם דבר והושלך כל מה שעמך הנה אם השתוו הנה כבר מצאת ואם התחלפו הנה טעית ודעהו | |||||||||||||
Chapter Fourteen – Multiplication of Fraction and Fraction of Fraction by Integer and Fraction of Fraction |
השער הארבעה עשר בהכאת השבר ושבר השבר בשלם ושבר השבר | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
דמיון זה הכה חמשה שתותים וחצי שתות בתשעה ושתות שביעית | ||||||||||||
| הוריד החמשה שתותים וחצי שתות בשטה והתשעה ושתות שביעית בשטה תחתיו על זאת הצורה: | |||||||||||||
|
|
| ||||||||||||
|
|
אחר כן עשה בחמשה שתותים וחצי שתות כמו שקדם יהיה המקובץ אחד עשר ושמרם ועשה בתשעה ושתות שביעית כמו שקדם גם כן ויהיה המקובץ תשעה ושבעים ושלש מאות והכם באחד עשר ויתקבץ לך מזה תשעה ושישים ומאה וארבעת אלפים וחלקם על הסכום ויצא לך המבוקש והוא שמונה ושביעית ושני חומשי שתות השביעית ושני שתות השביע וחצי שתות השביע על זאת הצורה: | ||||||||||||
|
|
| ||||||||||||
| והתשובה בה בבחינה ארבעה והקש תמצא בע"ה | |||||||||||||
Chapter Fifteen – Multiplication of Fraction and Fraction of Fraction by Integer and Two Different Fractions |
השער החמשה עשר בהכאת השבר ושבר השבר בשלם ושני השברים המתחלפים | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
דמיון זה כשיאמר לך: הכה חמשה שתותים וחצי שתות בשמונה ותשע עשיריות ועשרה חלקים מאחד עשר | ||||||||||||
| הוריד החמשה שתותים וחצי שתות בשטה והשמונה ותשע עשיריות ועשרה חלקים מאחד עשר בשטה אחרת תחתיו על זאת הצורה: | |||||||||||||
|
|
| ||||||||||||
|
|
אחר כן התחיל בשטה העליונה כמו שקדם יצא לך אחד עשר אחר כן שוב אל השטה התחתונה והכה השמונה בעשרה ומה שהתקבץ באחד עשר יתקבץ לך מזה שמונים ושמונה מאות ושמרם אחר כן הכה התשעה באחד עשר ועשרה בעשרה יהיה כל זה תשעה ותשעים ומאה וקבצם אל השמונים ושמונה מאות יהיה כל זה תשעה ושבעים ואלף והכם באחד עשר אשר יצאו מן השטה העליונה יהיה כל זה תשעה ושישים ושמונה מאות ואחד עשר אלפים וחלקם על הסכום יצא לך המבוקש וזה שמונה ועשרה חלקים מאחד עשר ותשעה עשיריות החלק מאחד עשר וחצי שתות עשירית החלק מאחד עשר וזה צורתו: | ||||||||||||
|
|
| ||||||||||||
| והתשובה בזה ארבעה | |||||||||||||
Chapter Sixteen – Multiplication of Fraction of Fraction by Integer and Fraction and Fraction of Fraction |
השער הששה עשר בהכאת שבר השבר בשלם והשבר ושבר השבר | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
דמיון זה: הכה שני שלישי שביעית בששה ותשעה עשיריות וארבעה חומשי העשור | ||||||||||||
| הוריד שני שלישי השביעית בשטה והוריד תחתיו בשטה אחרת הששה ותשע עשיריות וארבעה חומשי העשור על זאת הצורה: | |||||||||||||
|
|
| ||||||||||||
|
|
אחר כן התחיל בקו התחתון והכה התשעה בעשרה והשיא מה שעל ראשם יהיה זה תשעה ושישים והכם בחמשה והשיא מה שעל ראשו יהיה זה תשעה וארבעים ושלש מאות והכם בשנים אשר על הקו העליון יהיה זה שמונה ותשעים ושש מאות וחלקם על הסכום יצא לך המבוקש וזה שש עשיריות וארבע שביעיות העשירית ושני חומשי שביעית העשירית ושני שלישי חמישית שביעית העשור וזה צורתו: | ||||||||||||
|
|
| ||||||||||||
| והבחינה כמו שקדם והתשובה חמשה | |||||||||||||
Chapter Seventeen – Multiplication of Fraction of Fraction by Integer and Fraction of Fraction |
[ה]שער השבעה עשר בהכאת שבר השבר בשלם ושבר השבר | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
דמיון זה כשיאמר לך הכה שלשה רביעי התשיעית בשמונה וחמשה שתותי השביעית | ||||||||||||
| הוריד השלשה רביעי התשיעית בשטה והוריד תחתיו השמונה וחמשה שתותי השביעית בשטה גם כן על זאת הצורה: | |||||||||||||
|
|
| ||||||||||||
|
|
אחר כן התחיל בשטה התחתונה והכה השמונה בשבעה ומה שהתקבץ בששה והשיא מה שעל ראשו יהיה זה אחד וארבעים ושלש מאות והכם בשלשה אשר על הקו העליון יהיה זה שלשה ועשרים ואלף וחלקם על הסכום ויצא לך המבוקש והוא ששה תשיעיות שתותי שביע התשיעית ושלשה רביעי שתות שביע התשיעית וזה צורתו: | ||||||||||||
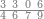
|
| ||||||||||||
| ותשובת השאלה הזאת אחת | |||||||||||||
Chapter Eighteen – Multiplication of Fraction of Fraction by Integer and Two Different Fractions |
השער השמונה עשר בהכאת שבר השבר בשלם ושני השברים המתחלפים | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך הכה חמשה שתותי השמינית בששה ושלשה רביעים וארבעה חומשים | ||||||||||||
| הוריד החמשה שתותי השמינית בשטה והוריד המספר השני תחתיו בשטה אחרת על זאת הצורה: | |||||||||||||
|
|
| ||||||||||||
|
|
אחר כן התחיל בקו התחתון והכה הששה בארבעה ומה שהתקבץ בחמשה יהיה זה מאה ועשרים ושמרם אחר כן הכה מה שעל הארבעה בחמשה ומה שעל החמשה בארבעה וקבץ שתי ההכאות יהיה זה אחד ושלשים וקבצם אל המאה ועשרים יהיה זה אחד וחמישים ומאה והכם בחמשה אשר על הקו העליון יהיה זה חמשה וחמישים ושבע מאות וחלקם על הסכום יצא לך המבוקש וזה ששה שמיניות ושתות שמין ושלשה חומשי שתות השמינית ושלשה רביעי חמשית שתות השמינית וזה צורתו: | ||||||||||||
|
|
| ||||||||||||
Chapter Nineteen – Multiplication of Two Different Fractions by Integer and Fraction and Fraction of Fraction |
השער התשעה עשר בהכאת שני שברים מתחלפים בשלם והשבר ושבר השבר | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כאשר יאמר לך הכה שלשה רביעים וארבעה חומשים בששה ושבע שמיניות ושתות השמינית | ||||||||||||
| הוריד השלשה רביעים והארבעה חומשים בשטה והששה ושבע שמיניות ושתות השמינית בשטה אחרת תחתיה על זאת הצורה: | |||||||||||||
|
|
| ||||||||||||
|
|
אחר כן התחיל בשטה העליונה והכה אותה כמו שקדם בשני השברים המתחלפים ויתקבץ לך ממנו אחד ושלשים ושמרם אחר כן חזור אל השטה התחתונה ועשה בה כמו שקדם בשלם והשברים המתיחסים ויתקבץ לך מזה אחד ושלשים ושלש מאות והכם באחד ושלשים השמורים בקו העליון יתקבץ לך מזה אחד ושישים ומאתים ועשרת אלפים וחלקם על הסכום יצא לך המבוקש וזה עשרה וחמשה שמיניות ושלשה שתותי השמינית ורביע חומש שתות השמינית וזה צורתו: | ||||||||||||
|
|
| ||||||||||||
| והתשובה שניה | |||||||||||||
Chapter Twenty – Multiplication of Two Different Fractions by Integer and Fraction of Fraction |
השער העשרים בהכאת שני השברים המתחלפים בשלם ושבר השבר | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כאשר יאמר לך הכה שלשה רביעים וארבעה חומשים בששה ושביעית השמינית | ||||||||||||
| הוריד השלשה רביעים וארבעה חומשים בשטה והוריד תחתיה הששה ושביעית שמינית בשטה אחרת על זאת הצורה: | |||||||||||||
|
|
| ||||||||||||
|
|
אחר כן התחיל בשטה העליונה ועשה בו כמו שעשית בשני השברים המתחלפים ויתקבץ לך אחד ושלשים ושמרם אחר כן חזור אל השטה התחתונה ועשה בו מה שעשית בשלם ושבר השבר יתקבץ לך ממנו שבעה ושלשים ושלש מאות והכם באחד ושלשים השמורים יתקבץ לך שבעה וארבעים וארבע מאות ועשרת אלפים וחלקם על הסכום יצא לך המבוקש והוא תשעה ושתי שמיניות וארבע שביעיות השמינית וחומש שביעית השמינית ושלשה רביעי חומש שביע השמינית וזה צורתו: | ||||||||||||
|
|
| ||||||||||||
| והתשובה בשאלה הזאת שלשה | |||||||||||||
Chapter Twenty One – Multiplication of Two Different Fractions by Integer and Two Different Fractions |
שער אחד ועשרים בהכאת שני השברים המתחלפים בשלם ושני השברים המתחלפים | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
המשל בו: הכה חצי ושני שלישים בחמשה ושש שביעיות ושמונה תשיעיות | ||||||||||||
| הוריד החצי והשני שלישים בשטה והוריד החמשה והשש שביעיות והשמנה תשיעיות בשטה אחרת תחתיו על זאת הצורה: | |||||||||||||
|
|
| ||||||||||||
|
|
אחר כן תתחיל בשטה העליונה ועשה בו מה שעשית בב' השברים המתחלפים יתקבץ לך בו שבעה ושמרם אחר כן חזור אל השטה התחתונה ועשה בו מה שעשית בשלם ושני השברים המתחלפים ויתקבץ לך מזה חמשה ועשרים וארבע מאות והכם בשבעה השמורים ויתקבץ לך מזה חמשה ושבעים ותשע מאות ושני אלפים וחלקם על הסכום יצא לך המבוקש וזה שתכה מקום החצי במקום השליש יהיה ששה ויהיה הסכום ששה ושבעה ותשעה וחלק עליהם המספר הנזכר ויצא לך המבוקש וזה שבעה ושבע תשיעיות וחמש שביעיות התשיעית וחמשה שתותי שביעית התשיעית על הצורה הזאת: | ||||||||||||
|
|
| ||||||||||||
| וזאת השאלה נשלכת אצל הבחינה | |||||||||||||
Chapter Twenty Two – Multiplication of Integer and Fraction by Integer and Fraction |
שער שנים ועשרים בהכאת השלם והשבר בשלם והשבר | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
|
כאשר יאמר לך הכה שלשה וחומש בשבעה ושלש שמיניות | |||||||||
| הוריד השלשה וחומש בשטה והשבעה ושלש שמיניות בשטה תחתיו על הצורה הזאת: | ||||||||||
|
|
| |||||||||
|
|
אחר כן התחיל בשטה העליונה והכה השלשה בחמשה והשיא מה שעל ראשם יהיה המקובץ ששה עשר ושמרם אחר כן שוב אל השטה התחתונה והכה השבעה בשמונה והשיא מה שעל ראשם יהיה תשעה וחמישים והכם בששה עשר השמורים יתקבץ לך מזה ארבעה וארבעים ותשע מאות וחלקם על הסכום יצא לך המבוקש וזה שלשה ועשרים וארבע שמיניות וארבעה חומשי השמינית וזה צורתו: | |||||||||
|
|
| |||||||||
| ותשובת הבחינה בה ששה ומלאכתו כמלאכת המעשה | ||||||||||
Chapter Twenty Three– Multiplication of Integer and Fraction and Fraction of Fraction by Integer and Fraction and Fraction of Fraction |
שער שלשה ועשרים בהכאת השלם והשבר ושבר השבר בשלם והשבר ושבר השבר | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
המשל כשיאמר לך: הכה שנים ושלשה חומשים וחצי חומש בארבעה ושבעה תשיעיות ושש שמיניות התשיעית | |||||||||||||
| הוריד השנים ושלשה חומשים וחצי חומש בשטה והארבעה ושבע תשיעיות ושש שמניות התשיעית בשטה תחתיו על זאת הצורה: | ||||||||||||||
|
|
| |||||||||||||
|
|
אחר כן התחיל בשטה העליונה והכה השנים בחמשה והשיא מה שעל ראש החמשה ומה שהתקבץ הכהו בשנים אשר תחת הקו והשיא מה שעל ראשם ויתקבץ לך מזה שבעה ועשרים ושמרם אחר כן חזור אל השטה התחתונה והכה הארבעה בתשעה והשיא מה שעל ראשם והכה מה שהתקבץ בשמנה והשיא מה שעל ראשם יתקבץ לך חמישים ושלש מאות והכם בתשעה ועשרים השמורים יתקבץ מזה חמישים וארבע מאות ותשעה אלפים וחלקם על הסכום יצא לך המבוקש והוא שלשה עשר ותשיעית ושמינית התשיעית ושאר הסכום פנוי וזה צורתו: | |||||||||||||
|
|
| |||||||||||||
| וזאת השאלה אצל הבחינה נשלכת | ||||||||||||||
Chapter Twenty Four – Multiplication of Integer and Two Different Fractions by Integer and Two Different Fractions |
שער ארבעה ועשרים בהכאת השלם ושני השברים המתחלפים בשלם ושני השברים המתחלפים | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כאשר יאמר לך: הכה ששה ושתי שלישיות ושלשה חומשים בתשעה וחמשה שתותים ושבע שמיניות | |||||||||||||
| הוריד המספר הראשון בשטה והוריד השני בשטה אחרת תחתיו על זאת הצורה: | ||||||||||||||
|
|
| |||||||||||||
|
|
אחר כן התחיל בשטה העליונה והכה הששה בשלשה ומה שהתקבץ בחמשה יהיה זה תשעים אחר כן הכה מה שעל השלשה בחמשה ומה שעל החמשה בשלשה ותקבץ שתי ההכאות ותחבר עמהן התשעים יהיה זה תשעה ומאה ושמרם אחר כן שוב אל השטה התחתונה והכה התשעה בששה ומה שהתקבץ בשמונה והכה גם כן מה שעל הששה בשמונה ומה שעל השמונה בששה וקבץ ההכאות השלש יהיה זה ארבעה עשר וחמש מאות והכם בתשעה ומאה השמורים יתקבץ לך מזה ששה ועשרים וששה ועשרים אלף וחלקם על הסכום יצא לך המבוקש וזה שבעה ושבעים ושש שמיניות ושלשה שתותי השמינית ושליש חומש שתות השמינית על זאת הצורה: | |||||||||||||
|
|
| |||||||||||||
| והתשובה בה חמשה | ||||||||||||||
Chapter Twenty Five – Multiplication of Integer and Two Different Fractions and Fraction of Fraction by Integer and Two Different Fractions and Fraction of Fraction |
שער חמשה ועשרים בהכאת השלם ושני השברים המתחלפים ושבר השבר בשלם ושני השברים המתחלפים ושבר השבר | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| דע כי השער הזה יחלק לשני חלקים: | ||||||||||||||||||||||
| אם שיהיה שבר השבר מיוחס אל אחד משני השברים אשר הונחו בשאלה | ||||||||||||||||||||||
| ואם שיהיה מיוחס אל שבר אחד | ||||||||||||||||||||||
| ואולם אם היה מיוחס אל אחד משברי השאלה | ||||||||||||||||||||||
|
|
הנה דמיון זה שתכה שנים ושלשה רביעים וארבעה חומשים וחצי חומש בששה ושש שביעיות ותשע עשריות ושלש שמיניות העשור | |||||||||||||||||||||
| המעשה בזה שתוריד השנים והשלשה רביעים וארבעה חומשים וחצי חומש בשטה אחר כן הורד הששה ושש שביעיות ותשע עשיריות ושלש שמיניות העשירית בשטה אחרת תחתיה על זו הצורה: | ||||||||||||||||||||||
|
|
| |||||||||||||||||||||
|
|
אחר כן התחיל מן השטה העליונה והכה השנים בארבעה אשר הם הסכום ומה שהתקבץ בה' ומה שהתקבץ בשני אשר עם החמשה אשר תחת הקו יתקבץ לך מזה שמונים ושמרם אחר כן הכה מה שעל הארבעה בחמשה ומה שיתקבץ בשנים אשר עם החמשה תחת הקו ויהיה זה שלשים אחר כן תכה הארבעה אשר על החמשה בשנים אשר תחת הקו והשיא מה שעל ראשו והכה המקובץ בארבעה אשר תחת הקו הראשון יתקבץ מזה ששה ושלשים וחברם אל השלשים והשמונים השמורים יהיה זה ששה וארבעים ומאה ושמרם אחר כן חזור אל הקו התחתון והכה הששה אשר הם השלמים בכל הסכום אשר תחת הקוים בשיטתם לפי מה שקדם בשטה העליונה יתקבץ מזה שישים ושלש מאות ושלשת אלפים אחר כן הכה מה שעל השבעה בעשרה ובשמונה יהיה זה שמונים וארבע מאות אחר כן הכה מה שעל העשרה בשמונה והשיא מה שעל ראשם והכהו בשבעה יתקבץ מזה חמשה ועשרים וחמש מאות וקבצם אל השמונים וארבע מאות והשישים ושלש מאות ושלשת אלפים יהיה זה המקובץ חמשה ושישים ושלש מאות וארבעת אלפים והכם באשר יצא בשטה העליונה יתקבץ לך תשעים ומאתים ושבע' ושלשים אלפים ושש מאות אלפים וחלקם על הסכום יצא לך המבוקש וזה שמונה ועשרים וארבע עשיריות וארבע שמיניות העשירית וחומש שביעית שמינית העשור ורביע חומש שביעית השמינית העשור וזה צורתה: | |||||||||||||||||||||
|
|
| |||||||||||||||||||||
| והתשובה בה שלשה | ||||||||||||||||||||||
| ואם תרצה בזאת השאלה כאשר הכית השלם במקומות השברים אחר כן הכה מה שעל ראשון הסכום במה שתחת זולתו מן הקוים ותקח ג"כ מה שעל הסכום השני ותכהו בסכום הראשון ומה שהתקבץ תכהו במקום השבר אחר כן תקח מה שעל מקום שבר השבר ותניח המקום המיוחס הוא אליו ותכהו בזולתו ירבו המקומו' או ימעטו | ||||||||||||||||||||||
| ודע כי השברים המתחלפים אמנם הורידם תחת קוים נפרדים בשטה אחת אחר כן תקח מה שעל הקו הראשון ותעזוב המקום אשר תחתיו ותכהו בשאר המקומות הקודמים ממנו אחר כן תקח מה שעל הקו השני ועזוב המקום אשר תחתיו ותכהו במקום הראשון ובשאר המקומות הקודמים לו כלומ' בהכאה אלא המקום אשר תחת הקו שלו | ||||||||||||||||||||||
| ואם היה עמך שבר השבר תקח מה שעל מקום שבר השבר ועזיבת מה שתחת הקו אשר הוא עליו ותכה אותו בשאר הסכום | ||||||||||||||||||||||
| והפנים השניים מן השאלה הקודמת והוא שיהיה שבר השבר בלתי מיוחס אל אחד מן השברים המתחלפים | ||||||||||||||||||||||
|
|
דמיון זה הכה שנים ושליש וחומש ושביעית שמינית בשלשה ותשיעית ועשירית ושתות חלק מאחד עשר | |||||||||||||||||||||
| הוריד השנים והשליש והחומש ושביעית השמינית בשטה אחר כן הוריד תחתיה בשטה אחרת השלשה והתשיעית והעשירית ושתות חלק מאחד עשר על הצורה הזאת: | ||||||||||||||||||||||
|
|
| |||||||||||||||||||||
|
|
אחר כן התחיל בשטה העליונה והכה השנים אשר הם השלמים בכל מקומות השברים אשר בשטה ושמרם אחר כן תקח מה שעל השלשה ותעזוב ההכאה בשלשה ותכה מה שעליהם ובשאר המקומות ותשמרהו אחר כן תקח מה שעל החמשה ותעזוב החמשה ותכה מה שעליהם בשאר המקומות אשר תחת זולתו מן הקוים אחר כן תקח מה שעל השבעה ותעזוב מה שתחת הקו אשר הוא עליו ואילו היו שלשה הסכומים או יותר מזה לא תכהו באחד מהם אחר כן תכהו בשאר המקומות אשר תחת קו זולתו וקבץ זה כלו יתקבץ לך מזה שלשה וארבעים ומאה ושני אלפים ושמור זה הנה הוא אשר יצא מן השטה העליונה אחר כן חזור אל השטה התחתונה ותכה השלשה השלמים בכל מקומות השברים אחד אחד ושמרהו אחר כן הכה מה שעל התשעה במה שתחת הקוים זולת הקו אשר הוא עליו וכן תעשה בעשרה ותקח האחד אשר עליהם ותעזוב העשרה ותכהו בזולת זה מן המקומות וכן תעשה באחד אשר על הששה תעזוב כל מה שהוא תחת הקו אשר הוא עליו ותכה במה שתחת הקוים הנשארים מן הסכום ותקבץ זה כלו יהיה ארבעה ושישים ומאה ותשעה עשר אלפים ותכהו באשר יצא מן השטה העליונה יתקבץ מזה שנים וחמישים וארבע מאות ושמונה ושישים אלף וציפרא ואחד וארבעים אלף וחלקהו על הסכום יצא לך שמונה ושני חלקים מאחד עשר וחמש עשיריות החלק מאחד עשר וארבע שמיניות תשיעית עשירית החלק וארבעה חומשי שתות שביעית שמינית תשיעית עשירית חלק מאחד עשר וזה צורתו: | |||||||||||||||||||||
|
|
| |||||||||||||||||||||
| ותשובתו חמשה | ||||||||||||||||||||||
| ומעשה הבחינה בה כמו מה שעשית בהכאתה | ||||||||||||||||||||||
Chapter Twenty Six – Multiplication of Integer and Three Different Fractions by Integer and Three Different Fractions |
שער ששה ועשרים בהכאת שלם ושלשה שברים מתחלפים בשלם ושלשה שברים מתחלפים | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
דמיון זה: הכה שנים ושליש וחומש ושתות בארבעה ושביעית ושמינית ותשיעית | |||||||||||||||||
| הוריד שני אלו המספרים בשתי שטות אחת תחת אחרת על זאת הצורה: | ||||||||||||||||||
|
|
| |||||||||||||||||
|
|
אחר כן התחיל בשטה העליונה והכה השנים בכל מקומות השברים אשר תחת הקוים בשלשה ומה שיתקבץ בחמשה ומה שיתקבץ בששה ושמרהו אחר כן קח מה שעל השלשה והכהו בחמשה ובששה ותשמרהו אחר כן תקח מה שעל החמשה ותכהו בששה והשלשה אחר כן תקח מה שעל הששה ותכהו בחמשה והשלשה אחר כן תקבץ אלו ההכאות הארבע יתקבץ מזה שלשה וארבעים ומאתים והוא היוצא מן השטה העליונה ושימהו אל צד אחר כן חזור אל השטה התחתונה ותעשה בו כמו שעשית בשטה העליונה ותקבץ ההכאות כלם יהיו שבעה ומאתים ושני אלפים ותכהו באשר יצא מן השטה העליונה מהקוים אל צד יתקבץ לך מזה אחד ושלש מאות וששה ושלשים אלפים וחמש מאות אלפים וחלקהו על הסכום יצא לך המבוקש וזה אחד עשר ושבע תשיעיות ושלש שמיניות התשיעית ושבעה שמיניות התשיעית וחמשה שתותי שביעית שמינית התשיעית ושני חומשי שתות שביעית שמינית התשיעית על הצורה הזאת: | |||||||||||||||||
|
|
| |||||||||||||||||
| ותשובת השאלה והמלאכה כבחינה והמעשה אחד | ||||||||||||||||||
Chapter Twenty Seven – Multiplication of Integer and Three Different Fractions and Fraction of Fraction |
שער שבעה ועשרים בהכאת השלם ושלשה שברים מתחלפים ושבר השבר בכמוהו |
|---|---|
| דע כי הקש השער הזה כמו הקש הכאת השלם ושני השברים ושבר השבר | |
| ומעשהו כמו שקדם בשער חמשה ועשרים ומי שהבין אותו והנהיגו לא יעלם ממנו מה שיבוא אחריו מן השברים המתחלפים והבן תמצא בע"ה | |
Chapter Twenty Eight – Multiplication of Fraction by Fraction |
שער שמונה ועשרים בהכאת השבר בשבר | |||||||
|---|---|---|---|---|---|---|---|---|
|
|
כאשר יאמר לך הכה שבעה שמיניות בתשעה עשיריות | |||||||
| הוריד השבעה שמיניות בשטה והתשעה עשיריות בשטה אחרת תחתיה על זאת הצורה: | ||||||||
|
|
| |||||||
|
|
אחר כן הכה השבעה אשר על השמונה בתשעה אשר על העשרה יהיו שלשה ושישים וחלקם על הסכום יצא לך המבוקש וזה שבע עשיריות ושבע שמיניות העשירית וזאת הצורה: | |||||||
|
|
| |||||||
|
ובחינתו כמעשהו וזה שתקח מה שעל השמונה והוא שבעה והשלך וכאשר תכהו בתשעה יהיה כל זה נשלך הנה תשובת השאלה נשלך | |||||||
|
|
אחר כן חזור אל היוצא מן ההכאה והוא שבעה עשיריות הנה השבעה השלכה מוכים בשמונה יושלך ועל ראשו שבעה והוא השלכה הנה כל היוצא השלכה והוא נאות לתשובה | |||||||
|
|
ואם יאמר הכה עשרה חלקים מאחד עשר בשנים עשר חלקים משלשה עשר | |||||||
| הורידם בשתי שטות על זאת הצורה: | ||||||||
|
|
| |||||||
|
|
אחר כן הכה העשר' אשר על האחד עשר בשנים עשר אשר על השלשה עשר יהיו עשרים ומאה וחלקם על הסכום יצא לך המבוקש וזה עשרה חלקים משלשה עשר ועשרה חלקים מאחד עשר בחלק משלשה עשר וזה צורתו: | |||||||
|
|
| |||||||
| ותשובתו אחד והבן תמצא | ||||||||
Chapter Twenty Nine – Multiplication of Fraction and Fraction of Fraction by Fraction |
שער תשעה ועשרים בהכאת השבר ושבר השבר בשבר | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך הכה שש שביעיות ושליש שביעית בשמונה תשיעיות | |||||||||||
| הוריד השש שביעיות ושליש שביעית בשטה והשמונה תשיעיות בשטה תחתיה על זאת הצורה: | ||||||||||||
|
|
| |||||||||||
|
|
אחר כן תתחיל בשטה העליונה והכה הששה אשר על השבעה בשלשה אשר תחת הקו ותשיא מה שעל ראשם יהיה זה תשעה עשר והכם בשמונה אשר על התשעה בשטה התחתונה יתקבץ לך מזה שנים וחמישים ומאה וחלקם על הסך יצא לך המבוקש וזה שבע תשיעיות ושביעית התשיעית ושני שלישי שביעיות התשיעית וזה צורתו: | |||||||||||
|
|
| |||||||||||
|
|
ואם יאמר לך: הכה חלק מאחד עשר וחצי חלק מאחד עשר בשנים עשר חלק משלשה עשר | |||||||||||
| הוריד החלק וחצי חלק בשטה והשנים עשר חלק משלשה עשר תחתיו על הצורה הזאת: | ||||||||||||
|
|
| |||||||||||
|
|
אחר כן התחיל בשטה העליונה כמו שקדם והכה האחד אשר על האחד עשר בשנים והשיא מה שעל ראשם יהיו שלשה והכם בשנים עשר יהיו ששה ושלשים וחלקם על הסכום יצא לך המבוקש והוא חלק משלשה עשר ושבעה חלקים מאחד עשר בחלק משלשה עשר וזה צורתו: | |||||||||||
|
|
| |||||||||||
| ותשובתו אחד והבין תמצא | ||||||||||||
Chapter Thirty – Multiplication of Two Different Fractions by Fraction |
שער שלשים בהכאת שני שברים המתחלפי' בשבר | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך הכה שני שלישים וארבע שביעיות בעשרה חלקים מאחד עשר | |||||||||||
| הורידם על זאת הצורה: | ||||||||||||
|
|
| |||||||||||
|
|
אחר כן עשה בשטה העליונה כמו שקדם בשני השברים המתחלפים וזה שתכה מה שעל השלשה בשבעה ומה שעל השבעה בשלשה ותקבץ שתי ההכאות יהיה זה ששה ועשרים והכם בעשרה אשר על האחד עשר יהיה שישים ומאתים וחלקם על הסכום יצא לך המבוקש וזה אחד וחלק מאחד עשר ושתי שביעיות חלק מאחד עשר ושתי שלישיות שביעית החלק מאחד עשר וזה צורתו: | |||||||||||
|
|
| |||||||||||
| והתשוב' בה אחד | ||||||||||||
Chapter Thirty One – Multiplication of Fraction and Fraction of Fraction by Fraction and Fraction of Fraction |
שער אחד ושלשים בהכאת השבר ושבר השבר בשבר ושבר השבר | ||||||
|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך הכה חמשה שתותים וחצי שתות בתשע עשיריות ושבע שמיניות העשירית | ||||||
| הוריד החמשה שתותים וחצי שתות בשטה והוריד בשטה אחרת תחתיה התשעה עשיריות ושבע שמיניות העשירית על זאת הצורה: | |||||||
|
|
| ||||||
|
|
אחר כן התחיל בשטה העליונה והכה החמשה בשנים והשיא מה שעל ראשם יהיה אחד עשר ושמרם אחר כן חזור אל השטה התחתונה והכה התשעה בשמונה והשיא מה שעל ראשם יהיה תשעה ושבעים והכם באחד עשר יהיה זה תשע ושישים ושמונה מאות וחלקם על הסכום יצא לך תשע עשיריות ושני שתותי שמינית העשירית וחצי שתות שמינית העשירית וזה צורתו: | ||||||
|
|
| ||||||
| והתשובה בה אחד | |||||||
Chapter Thirty Two – Multiplication of Two Different Fractions by Fraction and Fraction of Fraction |
שער שנים ושלשים בהכאת שני השברים המתחלפים בשבר ושבר השבר | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך הכה שלש רביעיות וארבעה חומשים בעשרה חלקים מאחד עשר ושמונה תשיעיות החלק מאחד עשר | ||||||||||
| הורידם על זאת הצורה: | |||||||||||
|
|
| ||||||||||
|
|
אחר כן עשה בשטה העליונה כמו שקדם בשני השברים המתחלפים יתקבץ לך מזה אחד ושלשים ועשה בשטה התחתונה כמו שקדם בשבר ושבר השבר יתקבץ לך שמונה ותשעים והכם באחד ושלשים השמורים וחלק המקובץ על הסכום יצא לך המבוקש וזה אחד וחמשה חלקים מאחד עשר ושבע תשיעיות החלק וארבעה חומשי תשיעית החלק ושני רביעי חומשי תשיעית החלק מאחד עשר והוא חצי וזה צורתו: | ||||||||||
|
|
| ||||||||||
| והם נשלכים | |||||||||||
Chapter Thirty Three – Multiplication of Two Different Fractions by Two Different Fractions |
שער שלשה ושלשים בהכאת שני השברים המתחלפים בשני השברים המתחלפים | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך הכה שני שלישי' ושלשה חומשים בשביעית ושתי תשיעיות | ||||||||||
| הוריד השאלה בשתי שטות כמו שקדם על זאת הצורה: | |||||||||||
|
|
| ||||||||||
|
|
אחר כן עשה בשטה העליונה כמו שקדם בשני השברים המתחלפים יתקבץ בו ארבעה עשר וכן תעשה בשטה השנית יתקבץ בו שלשה ועשרים והכם בארבעה עשר וחלק המקובץ על הסכום ומה שיצא הנה הוא המבוקש וזה שלשה תשיעיות ושני חומשי שביעית התשיעית ושליש חומש שביעית התשיעית וזאת צורתו: | ||||||||||
|
|
| ||||||||||
| ותשובתו נשלכת והבן | |||||||||||
Chapter Thirty Four – Multiplication of Fraction by Fraction of Fraction |
שער ארבעה ושלשים בהכאת השבר בשבר השבר | ||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
כאשר יאמר לך: הכה שני שלישים בארבעה חומשי התשיעית | ||||||||
| הורידם על זאת הצורה: | |||||||||
|
|
| ||||||||
|
|
אחר כן הכה השנים אשר על השלשה מן השטה העליונה בארבעה אשר על החמשה בשטה התחתונה יהיה זה שמונה וחלקם על הסכום יצא לך המבוקש וזה שני חומשי תשיעית ושני שלישי חמישית התשיעית וזה צורתו: | ||||||||
|
|
| ||||||||
| והנה תשובתו אחד | |||||||||
Chapter Thirty Five – Multiplication of Two Different Fractions and Fraction of Fraction by the Same |
שער חמשה ושלשים בהכאת שני השברים המתחלפים ושבר השבר בכמוהו | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| זאת השאלה אם שיהיה שבר השבר מיוחס אל אחד השברים המתחלפים או יחסו אל זולתם | |||||||||||||||
| ואולם אם היה מיוחס אל אחד מהם | |||||||||||||||
|
|
הנה דמיון זה: הכה שני שלישים וחמש שביעיות ושתות שביעית בארבעה חומשים ותשע עש[י]ר[י]ות ושמינית תשיעית העשירי' | ||||||||||||||
| והוריד שני השלישים וחמש שביעיות ושתות שביעית בשטה והוריד השני בשטה תחתיה על זאת הצורה: | |||||||||||||||
|
|
| ||||||||||||||
|
|
אחר כן התחיל בשיטה העליונה והכה השנים בשבעה ומה שהתקבץ בששה יהיה זה ארבע' ושמונים אחר כן הכה החמשה אשר על ראש השבעה בששה והשיא מה שעל ראשם והכהו בשלשה יהיה זה שלשה ותשעים וקבצם עם הארבעה ושמנים יהיה זה שבעה ושבעים ומאה ושמרם אחר כן חזור אל הקו התחתון והכה הארבעה אשר על החמשה בעשרה ומה שיתקבץ בתשעה יהיה זה ששים ושלוש מאות אחר כן הכה התשעה אשר על העשרה בתשעה אשר תחת הקו והשיא מה שעל ראשם ומה שיתקבץ הכהו בחמשה יהיה זה חמשה וארבעים וארבע מאות וקבצם אל השישים ושלש מאות יהיה זה חמשה ושמונה מאות והכם באשר יצא מן הקו העליון ותחלק המקובץ על הסכום יצא לך המבוקש והוא שנים וחמש עשיריות ותשיעית עשירית ושביעית תשיעית העשירית ושתות שביעית תשיעית העשירית וזה צורתו: | ||||||||||||||
|
|
| ||||||||||||||
| והיא נשלכת בבחינה | |||||||||||||||
| ואולם המין השני הנה הוא אשר יהיה שבר השבר בלתי מיוחס אל אחד מן השברים המתחלפים אשר בשאלה | |||||||||||||||
|
|
דמיון זה: כשיאמר לך הכה שלשה רביעים וארבעה חומשים וחצי שביעית בשבע שמיניות ושמונה תשיעיות ושלש עשיריות | ||||||||||||||
| הוריד השאלה על זאת הצורה: | |||||||||||||||
|
|
| ||||||||||||||
|
|
הנה זאת השאלה תקח מה שעל הקו הראשון מן השטה העליונ' וזה שלשה ותכם בחמשה ומה שהתקבץ בשבעה ומה שהתקבץ בשנים יהיה זה עשרה ומאתים ושמרם אחר כן הכה מה שעל החמשה והוא ארבעה בארבעה אשר הם המעמד ומה שהתקבץ בשבעה והשנים יהיה זה ארבעה ועשרי' ומאתים ושמרם גם כן אחר כן הכה האחד אשר על השנים בחמשה והארבעה יהיה זה עשרים וקבץ שלש הכאות אלה יהיה זה ארבעה וחמישים וארבע מאות ושמרם והוא היוצא מן השטה העליונה אחר כן חזור אל הקו התחתון ועשה בו כמו שעשית בשני יתקבץ לך בו שנים ושמונים ושמונה מאות ושלשת אלפים והכם באשר יצא מן הקו העליון ומה שהיה הנה הוא המקובץ חלקהו על הסכום יצא לך בחלוקה שנים ותשע עשיריות ותשיעית העשירית ושתי שמיניות תשיעית העשירי' ושביעית שמינית תשיעית העשירית וחמישית שביעית שמינית תשיעית העשירית וזה צורתם: | ||||||||||||||
|
|
| ||||||||||||||
| והתשובה בה שלשה ובחינתה כמו המעשה בה אין הפרש בין שניהם | |||||||||||||||
Chapter Thirty Six – Multiplication of Three Different Fractions by Three Different Fractions |
שער ששה ושלשים בהכאת שלשה שברים מתחלפים בשלשה שברים מתחלפים | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך: הכה שני שלישים ושלשה חומשים וארבעה שתותים בחמש שביעיות ושבע שמיניות ותשעה חלקים מאחד עשר | ||||||||||||||
| הוריד שני מספרים אלו בשתי שטות על זאת הצורה: | |||||||||||||||
|
|
| ||||||||||||||
|
|
אחר כן התחיל בשטה העליונה ותקח מה שעל הראשון ממנו ותעזוב המעמד אשר תחתיו ותכהו במעמד השני ומה שהתקבץ בשלישי אחר כן תקח מה שעל הקו השני ותעזוב גם כן מה שתחתיו ותכהו בשאר המעמדים הקודמים והמתאחרים אחר כן תקח מה שעל הקו השלישי ותעזוב מה שתחתיו ותכהו במה שתחת זולתו מן הקוים ותקבץ אלו ההכאות השלש יהיה זה ארבעה ועשרים ומאה ושמרם אחר כן עשה בשטה התחתונה כמו מה שעשית בה הנה מה שהתקבץ לך בו שלשה ושמונים וארבע מאות ואלף והכהו באשר יצא מן הקו העליון ומה שהתקבץ חלקהו על הסכום יצא לך המבוקש והוא ארבעה ושבעה מאחד עשר ושמינית החלק וארבע שביעיות שמינית החלק וארבעה חומשים משתות שביעית שמינית החלק מאחד עשר וזו היא צורתם: | ||||||||||||||
|
|
| ||||||||||||||
| והתשובה בה שלשה | |||||||||||||||
Chapter Thirty Seven – Multiplication of Three Different Fractions and Fraction of Fraction by the Same |
שער שבעה ושלשים בהכאת שלשה שברים מתחלפים ושבר שבר בכמוהו |
|---|---|
| הנה הענין והמעשה בשער הזה כמו שקדם בהכאת שני השברים ושבר השבר | |
Chapter Thirty Eight – Multiplication of Fraction of Integer by Fraction of Integer |
שער שמונה ושלשים בהכאת שבר המספר השלם בשבר המספר | ||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
כאשר יאמר לך: הכה שלשה רביעי חמשה בחמשה שתותי שבעה | ||||||||
| הוריד השלשה רביעים תחלה והחמשה אחריהם בשטה אחר כן הוריד החמשה שתותים והשבעה אחריהם על זאת הצורה: | |||||||||
|
|
| ||||||||
|
|
אחר כן התחיל בשטה העליונה הכה השלשה אשר על הארבעה בחמשה אשר הם השלמים ושמור זה אחר כן חזור אל השטה התחתונה והכה החמשה אשר על הששה בשבעה והכה המקובץ במקובץ וחלקם על הסכום יצא לך המבוקש וזה אחד ועשרים וחמשה שתותים ורביע שתות וזה צורתו: | ||||||||
|
|
| ||||||||
|
ובחינת השאלה הזאת כמו המעשה אין הפרש בין שניהם וזה שתתחיל בשאלה מן הקו העליון והכה השלשה אשר על ראש הארבעה בחמשה אשר הם השלם יהיו חמשה עשר ישאר מהם אחד אחר כן חזור אל הקו השני והכה החמשה אשר על הששה בשבעה יהיו חמשה ושלשים והם נשלכים והכם באחד אשר נשאר מן הקו העליון יהיה כל זה השלכה הנה השאלה אם כן בכללה נשלכת | ||||||||
|
|
אחר כן חזור אל היוצא מן השאלה והוא אחד ועשרים והוא השלכה אחר כן הכהו בששה יהיה כל זה השלכה אחר כן קח החמשה אשר על הששה והכם בארבעה אשר הם הסכום המעמד יהיה זה עשרים ועל הארבעה אחד והשיא מה שעל ראשם יהיה אחד ועשרים והם נשלכים והם נאותים לראשון בהשלכה | ||||||||
Chapter Thirty Nine – Multiplication of Fraction and Fraction of Fraction of Integer by Fraction and Fraction of Fraction of Integer |
שער תשעה ושלשים בהכאת שבר ושבר השבר מן המספר השלם בשבר ושבר שבר המספר השלם | ||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
כאשר יאמר לך: הכה חמשה שתותים וחצי שתות שמונה בשמונה תשיעיות וחומש תשיעית שנים עשר | ||||||||
| הוריד החמשה שתותים וחצי שתות והשמונה בשטה והשמונה תשיעיות וחומש תשיעית שנים עשר בשטה תחתיה על זאת הצורה: | |||||||||
|
|
| ||||||||
|
|
אחר כן התחיל בשטה העליונה והכה החמשה אשר על הששה בשנים מעמד החצי והשיא עליהם האחד יהיה זה אחד עשר והכם בשמונה השלמים יהיה זה שמונה ושמונים ושמרם אחר כן חזור אל השטה התחתונה והכה השמונה בחמשה והשיא עליהם האחד יהיה זה אחד וארבעים והכם בשנים עשר יתקבץ לך מזה שנים ותשעים וארבע מאות והכם בשמונה ושמונים יתקבץ לך מזה ששה ותשעים ומאתים ושלשה וארבעים וחלקם על הסכום יצא לך בחלוקה שמונה ותשיעית ושלשה שתותי התשיעית ושלשה חומשי שתות התשיעית וזה צורתו: | ||||||||
|
|
| ||||||||
| ותשובתה בהשלכה אחד ומלאכת הבחינה כמעשה אין הפרש בין שניהם | |||||||||
Chapter Forty – Multiplication of Different Fractions of Integer by Different Fractions of Integer |
שער הארבעים בהכאת שברי המספר בשברי המספר | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כאשר יאמר לך הכה שני שלישים ושלשה חומשי שמונה בששה שביעיות וחמש תשיעיות ארבעה | ||||||||||||
| הוריד השני שלישים והשלשה חומשים והשמנה בשטה והוריד תחתיו הששה שביעיות והחמש תשיעיות והארבעה בשטה אחרת על זאת הצורה: | |||||||||||||
|
|
| ||||||||||||
|
|
אחר כן התחיל בשטה העליונה ועשה בשני השברים כמו שקדם בהכאת שני השברים המתחלפים ומה שהתקבץ הכהו בשמנה ושמרהו אחר כן עשה כן בשטה התחתונה ומה שהתקבץ חלקהו על הסכום יצא לך המבוקש והוא שבעה וחמישים ושתי תשיעיות ושתי שביעיות התשיעית ושני חומשי שביעית התשיעית וזה צורתו: | ||||||||||||
|
|
| ||||||||||||
| והבחינה בה כמו שעשית והתשובה בשנים | |||||||||||||
Chapter Forty One – Multiplication of Fraction of Fraction of Integer by Fraction of Fraction of Integer |
שער אחד וארבעים בהכאת שבר שבר המספר בשבר שבר המספר | ||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
כאשר יאמר לך הכה שלשה רביעי חמישית השמונה בחמשה שתותי שביעית חמשה עשר | ||||||||
| הוריד השלשה רביעי חמישית והשמונה בשטה והוריד החמשה שתותי שביעית והחמשה עשר בשטה תחת הראשונה על זאת הצורה: | |||||||||
|
|
| ||||||||
|
|
אחר כן התחיל בשטה העליונה והכה השלשה בשמונה ושמרהו אחר כן חזור אל השט' התחתונה והכה החמשים בחמשה עשר מה שהתקבץ הכהו בשמור ומה שהתקבץ חלקהו על הסכום יצא לך המבוקש וזה שנים ושביעית ושאר הסכום פנוי וזה צורתו: | ||||||||
|
|
| ||||||||
| והתשובה אחד | |||||||||
| וענין אלו השאלות שתקח שם השבר מכל מספר ומה שהיה הכה אחד משניהם בשני כמו שקדם כל אחד משניהם בשערו | |||||||||
Chapter Forty Two – Multiplication of Fraction of Integer and Fraction by Fraction of Integer and Fraction |
שער שנים וארבעים בהכאת שבר המספר השלם והשבר בכמוהו | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כאשר יאמר לך הכה שני שלישי חמשה וחמשה שתותים בחמש שביעיות שמונה וארבע תשיעיות | ||||||||||||
| הוריד השני שלישים והחמשה שתותים בשטה והוריד תחתיו השש שביעיות והשמונה והארבע תשיעיות בשטה תחת הראשון על זאת הצורה: | |||||||||||||
|
|
| ||||||||||||
|
|
אחר כן התחיל בשטה העליונה והכה החמשה אשר הם השלמים בששה והשיא מה שעל ראשם יתקבץ לך מזה חמשה ושלשים והכם בשנים אשר על ראש השלשה אשר הם ראשית השטה יהיה זה שבעים ושמרם אחר כן חזור אל השטה התחתונה והכה השמונה בתשעה והשיא מה שעל ראשם יהיה זה ששה ושבעים והכם בששה אשר על ראש השבעה יהיה זה ששה וחמישים וארבע מאות והכם בשבעים השמורים ומה שהתקבץ חלקהו על הסכום אשר תחת הקוים יצא לך המבוקש וזה שמונה ועשרים ותשיעית ושתי שביעיות התשיעית ושני שתותי שביעית התשיעית וזה צורתו: | ||||||||||||
|
|
| ||||||||||||
| והתשובה בה בהשלכה והמלאכה בבחינה אחד כמעשה | |||||||||||||
| וענין השאלה הזאת שהוא רוצה שיקח מן החמשה וחמשה שתותים שני שלישיהם ומן השמונה וארבעה תשיעיות שש שביעיותיו והכה המקובץ במקובץ כמו שקדם והבן | |||||||||||||
Chapter Forty Three – Multiplication of Fraction of Integer and Fraction and Fraction of Fraction by the Same |
שער שלשה וארבעים בהכאת שבר המספר השלם והשבר ושבר השבר בדומה לו | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
דמיון זה הכה שלשה רביעי חמשה וששה שביעיות ושתות שביעית בשבע שמיניות שלשה ושלש עשיריות ותשיעית העשירית | ||||||||||||
| תוריד השלשה רביעיות והחמשה והשש שביעיות ושתות השביעית בשטה אחר כן הוריד בשטה אחרת תחתיה השבע שמיניות והשלשה ושלשה עשיריות ותשיעית העשירית על זאת הצורה: | |||||||||||||
|
|
| ||||||||||||
|
|
אחר כן התחיל בשטה העליונה והכה החמשה אשר הם השלמים בשבעה אשר הם תחת הקו והשיאן על מה שהתקבץ הששה אשר על השבעה ומה שהתקבץ הכהו בששה והשיא מה שעל ראשם ומה שהתקבץ הכהו בשלשה אשר על הארבעה בתחלת השטה ושמור מה שהתקבץ וזה אחד וארבעים ושבע מאות והוא היוצא מן השטה העליונה אחר כן חזור אל השטה התחתונה והכה השלשה השלמים אשר בין שני הקוים בעשרה והשיא מה שעל ראשם והכה מה שהתקבץ בשבעה אשר על ראש השמונה ויתקבץ לך מזה ששה ושמונים ושני אלפים והכהו באשר יצא מן השטה העליונה ומה שיצא חלקהו על הסכום יצא לך המבוקש וזה שנים עשר ושבע עשיריות ושבע' שמיניות העשירית וחמש שביעיות שמינית תשיעית העשירית ושתות שביעית שמינית תשיעית העשירית ושני רביעי שתות שביעית שמינית תשיעית העשירית וזה צורתו: | ||||||||||||
|
|
| ||||||||||||
| והתשובה בה בהשלכה והמלאכה אחת | |||||||||||||
| וענין זאת השאלה שהוא רוצה שיקח מן חמשה ושש שביעיות ושתות שביעית שלשה רביעיהם ויקח ג"כ משלשה ושלש עשיריות ותשיעית עשירית שבע שמיניותיו והכה היוצא ביוצא | |||||||||||||
Chapter Forty Four – Multiplication of Fraction of Integer and Two Different Fractions by the Same |
שער ארבעה וארבעים בהכאת שבר המספר והשבר המתחלף בדומה לו | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך: הכה חצי שנים וחומש ושתות בשביעית שלשה ושמינית ותשיעית | ||||||||||||||||
| הוריד החצי והשנים והחומש והשתות בשטה אחת ואחר כן הוריד השביעי' והשלשה והשמינית והתשיעית בשטה אחרת תחתיה על זאת הצורה: | |||||||||||||||||
|
|
| ||||||||||||||||
|
|
אחר כן התחיל בשטה העליונה ותקח השנים והחומש והשתות ותעשה בו כמו שעשית בהכאת השלם ושני השברים המתחלפים ומה שהתקבץ הכהו באחד אשר על השנים בתחלת הקו ויתקבץ לך מזה אחד ושמרם אחר כן עשה בשטה השנית כן יתקבץ לך שלשה ושלשים ומאתים והכם בשמור וחלק מה שיצא על הסכום יצא לך המבוקש וזה ארבע תשיעיות ושבע שמיניות תשיעית ושתי שביעיות שמינית תשיעית וארבעה שתותי שביעית שמינית התשיעית וזה צורתו: | ||||||||||||||||
|
|
| ||||||||||||||||
| והתשובה בה שנים | |||||||||||||||||
| והענין עצמו בו כמו שיקדם מן השברים כי הכונה אחת | |||||||||||||||||
Chapter Forty Five – Multiplication of Fraction of Integer and Fraction of Fraction by Fraction of Integer and Fraction of Fraction |
שער חמשה וארבעים בהכאת שבר המספר ושבר השבר בשבר המספר ושבר השבר | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך הכה שש שביעיות חמשה וחצי שתות בשבעה שמיניות ושלשה חומשי התשיעית | ||||||||||||
| הורד השש שביעיות והחמשה וחצי שתות בשטה והוריד תחתיו בשטה אחרת השבע שמיניות והשלשה ושלשה חומשי התשיעית בשטה על זאת הצורה: | |||||||||||||
|
|
| ||||||||||||
|
|
אחר כן התחיל בשטה העליונה והכה החמשה בששה ומה שהתקבץ בשנים והשיא מה שעל ראשם ומה שהתקבץ הכהו בששה אשר על השבעה יהיה כל זה ששה ושישים ושלש מאות ושמרם אחר כן עשה בשטה התחתונה כמו מה שעשית בשטה העליונה יתקבץ לך ששה ושישים ותשע מאות והכהו בשמור הראשון ומה שהתקבץ חלקהו על הסכום יצא לך המבוקש והוא אחד עשר ושש תשיעיות ושמינית תשיעית וחמש שביעיות שמינית התשיעית ושלשה שתותים ושלשה חומשי שתות שביעית שמינית התשיעית וזו צורתו: | ||||||||||||
|
|
| ||||||||||||
| והתשובה בהשלכה | |||||||||||||
| והוא העניין בשאלה הזאת שהוא רוצה שתקח מן החמשה וחצי שתות שש שביעיות ותקח גם כן מהשלשה ושלשה חומשי התשיעית שבע שמיניותיו והכה המקובץ במקובץ כמו שקדם | |||||||||||||
Chapter Forty Six – Multiplication of Fraction of Fraction of Integer and Fraction by Fraction of Fraction of Integer and Fraction |
שער ששה וארבעים בהכאת שבר שבר המספר והשבר בשבר שבר המספר והשבר | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך הכה שני שלישי חומש שמונה ושתות בחמש שביעיות שמינית ששה ותשיעית | ||||||||||||
| הוריד שני שלישי ושמונה ושתות בשטה והוריד תחתיו בשטה חמש שביעיות שמינית וששה ותשיעית על זאת הצורה: | |||||||||||||
|
|
| ||||||||||||
|
|
אחר כן התחיל בשטה העליונה והכה השמונה בששה והשיא מה שעל ראשם ומה שהתקבץ הכהו בשנים אשר על השלשה בתחלת הקו יתקבץ לך מזה שמונה ותשעים ושמרהו אחר כן עשה בשטה התחתונה כמו זה יתקבץ לך בו חמשה ושבעים ומאתים והכהו בשמונה ותשעים וחלק מה שיתקבץ לך על הסכום יצא לך מזה חמש תשיעיות ושני שמיני תשיעית וחמש שביעיות שמינית תשיעית ושתות שביעית שמינית התשיעית ושלשה חומשים ושליש חומש שתות שביעית שמינית התשיעית וזה צורתו: | ||||||||||||
|
|
| ||||||||||||
| והתשובה בה בהשלכה | |||||||||||||
Chapter Forty Seven– Multiplication of Fraction of Fraction of Integer and Fraction and Fraction of Fraction by the Same |
שער שבעה וארבעים בהכאת שבר שבר המספר והשבר ושבר השבר בכמוהו | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך: הכה שלשה רביעי חומש בששה ושלשה חלקים מאחד עשר וחמש שתותי החלק מאחד עשר בחמש שביעיות תשיעית שנים עשר וששה חלקים משלשה עשר ושלש שמיניות החלק משלשה עשר | ||||||||||||
| הוריד השאלה הזאת על זאת הצורה: | |||||||||||||
|
|
| ||||||||||||
|
|
אחר כן תקח הששה אשר בין שני הקוים והכם באחד עשר והשיא מה שעל ראשם והכה מה שהתקבץ בששה אשר תחת הקו והשיא מה שעל ראשם ומה שהתקבץ הכהו בשלשה אשר על הקו הראשון והם על הארבעה יתקבץ לך מזה שבעה וחמישים ומאתים ואלף ועשה המלאכה הזאת בשטה התחתונה יתקבץ לך בו חמשה ותשעים וארבע מאות וששת אלפים והכם בשמור הראשון ומה שהתקבץ חלקהו על הסכום יצא לך המבוקש בחלוקה שנים עשר חלקים משלשה עשר ושני חלקים מאחד עשר בחלק משלשה עשר ושמונה תשיעיות החלק מאחד עשר בחלק משלשה עשר ושבע שמיניות ושני שביעי שמיניות תשיעית החלק מאחד עשר בחלק משלשה עשר ושלשה חומשי ושלשה רביעי חמישית שתותי שביעית שמינית תשעית החלק מאחד עשר בחלק משלשה עשר וזה צורתו: | ||||||||||||
|
|
| ||||||||||||
| והתשובה בה שלשה | |||||||||||||
Chapter Forty Eight – Multiplication of Fraction of Fraction of Integer and Two Different Fractions by Fraction of Fraction of Integer and Two Different Fractions |
שער שמונה וארבעים בהכאת שבר שבר המספר ושני השברים המתחלפים בשבר שבר המספר ושני השברים המתחלפים | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך הכה שני שלישי חומש שמונה ושלשה שתותים וארבעה שביעיות בארבע תשיעיות עשירית שמונה עשר וששה חלקים מאחד עשר וחמש שמיניות | ||||||||||||||||
| הוריד זאת השאלה על זאת הצורה: | |||||||||||||||||
|
|
| ||||||||||||||||
|
|
אחר כן בא אל השמונה והשלשה שתותים והארבע שביעיות ותעשה בהם כמו שעשית בשלם ושני השברים המתחלפים ומה שהתקבץ מזה הכהו בשנים אשר על השלשה יתקבץ לך מזה שנים וששים ושבע מאות וכן תעשה בשתה השנית יתקבץ בו שמונה וארבעים ושבע מאות וששת אלפים והכם במספר הראשון וחלק מה שיתקבץ על הסכום יצא לך המבוקש וזה אחד ושלש עשיריות החלק מאחד עשר ושלש תשיעיות עשירית החלק מאחד עשר ושמינית תשיעית עשירית החלק מאחד עשר ושלש שביעיות שמינית תשיעית עשירית החלק מאחד עשר ושני חומשי שתות שביעית שמינית תשיעית עשירית החלק מאחד עשר וזה צורתו: | ||||||||||||||||
|
|
| ||||||||||||||||
| ותפיל הששה בתחילת החלוקה והתשובה בה בהשלכה | |||||||||||||||||
Chapter Forty Nine – Multiplication of Two Different Fractions of Integer and Fraction by Two Different Fractions of Integer and Fraction |
שער תשעה וארבעים בהכאת שני שברי המספר והשבר בדומה לו | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך הכה שני שלישים ושלשה חומשי תשעה וחמשה שתותים בשלשה שביעיות ושבע שמיניות שנים עשר ושבע תשיעיות | ||||||||||||||||
| הורידם בשטה על זאת הצורה: | |||||||||||||||||
|
|
| ||||||||||||||||
|
|
כאשר תשלים בשטה העליונה שני שברים מתחלפים ושלם כמו שקדם יתקבץ בו תשעה עשר ועמך שלם ושבר ועשה בו כמו שקדם בשלם והשבר יתקבץ ממנו תשעה וחמישים והכם בתשעה עשר יתקבץ מזה אחד ועשרים ומאה ואלף וזה הוא היוצא מן השטה העליונה ושמרהו אחר כן עשה בשטה השנית כן יתקבץ בה חמשה ותשעים ושלש מאות ושמונה אלפים והכם בשמור הראשון וחלק מה שהתקבץ בסכום יצא לך המבוקש וזה שבעה ומאתים וארבע תשיעיות ושמינית תשיעי' וחמש שביעיות שמינית מתשיעית ושני שתותים ושליש שתות שביעית שמינית תשיעית ותפיל החמשה בתחילת החלוקה וזה צורתו: | ||||||||||||||||
|
|
| ||||||||||||||||
| והתשובה בה שנים והבחינה בה כמו המעשה | |||||||||||||||||
Chapter Fifty – Multiplication of Two Different Fractions of Integer and Two Different Fractions by the Same |
שער חמישים בהכאת שני שברי המספר ושני שברים בדומה לו | ||||||||||||||||||||
|
|
כשיאמר לך: הכה שני שלישים ושלשה חומשי שבעה ושלשה רביעים ושלשה חומשים בחמשה שתותים וחמש שמיניות ארבעה וחמש שתותים ותשע עשיריות | ||||||||||||||||||||
| הורידם על זאת הצורה: | |||||||||||||||||||||
|
|
| ||||||||||||||||||||
|
|
אחר כן התחיל בשטה העליונה תמצא בה שני שברים מתחלפי' ושלם ושני שברים מתחלפים ותחלק השטה בשני חלקים ותעשה החלק האחד שני השברים המתחלפים הראשונים והחלק השני השלם ושני השברים המתחלפים אחר כן עשה בחלק הראשון כמו שתעשה בשני השברים המתחלפים בשער החמישי מן השברי' יתקבץ בו תשעה עשר ושמרם והגביהם על ראשם אחר כן עשה בחלק השני כמו שעשית בשלם ושני השברים המתחלפים בשער הארבעה ועשרים יתקבץ ממנו שבעה ושישים ומאה והכם בתשעה עשר יהיה המקובץ שלשה ושבעים ומאה ושלשת אלפים והוא היוצא מן השטה העליונה כלה אחר כן תעשה בשטה התחתונה כמו מה שעשית בשטה העליונה יתקבץ לך בה שמונים וארבע מאות ועשרים אלף והכהו בשמור הראשון וחלק מה שיצא על הסכום אחר שתשימם על זולתם תשוב אחר השמוש עשרה שלוש פעמים ותשעה ושמונה וששה ושנים והמספר הנחלק לו שמינית ועשירית וחלק תחילה על עשרה ושמונה ולא יצא לך על הסכום הזה שארית אחר כן חלק שארית המספר על שארית הסכום יצא לך היוצא שמונה ושמונים וארבע עשיריות ושלוש עשיריות העשירית ושתי תשיעיות עשירית העשירית ושני שתותים וחצי שתות תשיעית עשירית העשירית וזה צורתו: | ||||||||||||||||||||
|
|
| ||||||||||||||||||||
| והתשובה בה השלכה | |||||||||||||||||||||
Chapter Fifty One – Multiplication of Fraction and Fraction of Fraction of Integer and Fraction and Fraction of Fraction by the Same |
שער אחד וחמישים בהכאת שבר ושבר שבר מספר ושבר שבר בדומה לו | ||||||||||||
|
|
כאשר יאמר לך: הכה שלשה חומשים וחצי חומש ארבעה ושתות וחצי שתות בששה שביעיות ושני חומשי שביעית שלשה וחמשה חלקים מאחד עשר וחמש שמיניות החלק מאחד עשר | ||||||||||||
| הנה כאשר תרצה זה הורידם על זאת הצורה: | |||||||||||||
|
|
| ||||||||||||
|
|
אחר כן התחיל בשטה העליונה תמצא בה שבר ושבר בקו אחד ותמצא ארבעה משלם ושבר ושבר שבר אחר זה ותחלק השטה בשני חלקים תשים החלק האחד השלשה חומשים וחצי חומש ועשה בו כמו שעשית בשער השלישי יתקבץ בה שבעה ושמרם אחר כן חזור אל החלק השני מן השטה העליונה והוא ארבעה שתותים וחצי שתות ועשה בו כמו שעשית בשער שלשה ועשרים יהיה מה שיתקבץ אחד וחמישים הכם בשבעה השמור יהיה המתקבץ שבעה וחמישים ושלש מאות והוא היוצא מן השטה העליונה אחר כן עשה בשטה התחתונה כמו זה יתקבץ בה שמונה ושמונים ושמונה מאות ותשעת אלפים והכם בשמור הראשון וחלק מה שהתקבץ על הסכום אחר שתצרפם יהיה היוצא תשעה וששה חלקים מאחד עשר ושש עשיריות עשירית החלק מאחד עשר וזה צורתו: | ||||||||||||
|
|
| ||||||||||||
| והתשובה בה בהשלכה | |||||||||||||
Chapter Fifty Two – Multiplication of Fraction of Fraction of Integer and Fraction of Fraction by the Same |
שער שנים וחמישים בהכאת שבר שבר מספר ושבר שבר בדומה לו | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך הכה שני שלישי חמישית שמנה הרביע שתות בשלש שביעיות שמינית שנים עשר וחצי חלק משלשה עשר | ||||||||||||
| הנה כאשר תרצה זה הוריד השאלה על זאת הצורה: | |||||||||||||
|
|
| ||||||||||||
|
|
אחר כן תתחיל בשטה העליונה תמצא בה שבר שבר ראשונים ושלם ושבר שבר אחר זה ועשה בשלם ושבר השבר כמו שקדם והכם בשנים אשר על הקו הראשון יהיה זה ששה ושמוני' ושלש מאות והוא היוצא מן השטה העליונה ותעשה בשטה השנית כן יתקבץ בו תשעה ושלשים ותשע מאות והכם בראשון וחלק על הסכום אחר שמושם יצא לך המבוקש והוא שמונה חלקים משלשה עשר ותשע עשיריות החלק משלשה עשר ושמונה תשיעיות עשירית החלק משלשה עשר ושלשה שמיניות שמינית תשיעית עשירית חלק משלשה עשר ושביעית שמינית שמינית תשיעית עשירית חלק משלשה עשר וזה צורתו: | ||||||||||||
|
|
| ||||||||||||
| והתשובה בה אחד | |||||||||||||
Chapter Fifty Three – Multiplication of Fraction of Integer and Fraction of Integer by the Same |
שער שלשה וחמישים בהכאת שבר המספר ושבר השבר בדומה לו | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך הכה שלשה חומשי חמשה וחמשה שתותי שבעה בשני שלישי ארבעה וחצי חמשה | ||||||||||||||
| הורידם על זאת הצורה: | |||||||||||||||
|
|
| ||||||||||||||
|
|
הנה זאת השאלה כל קו ממנה מורכב משתי שאלות משאלות השער השמונה ושלשים וכאשר חלקת אותו תעשה השבר הראשון עם השלם כחלק ותשים גם כן השבר השני עם השלם בחלק ותעשה בחלק הראשון כמו שעשית בשער שמונה ושלשים ומה שהתקבץ הכהו בסכום אשר תחת הקו הקודם מן השטה העליונה יתקבץ ממנו תשעים אחר כן תעשה בחלק השני כמו שעשית בחלק הראשון ומה שהתקבץ הכהו בסכום אשר תחת הקו הראשון מן השטה העליונה יתקבץ לך מזה חמשה ושבעים ומאה וקבצם אל התשעים יתקבץ מזה חמשה ושישים ומאתים והוא היוצא מן השטה העליונה ותעשה כן בשטה התחתונה יתקבץ לך בו אחד ושלשים ותכהו במספר הראשון וחלק אותו על כל הסכום יהיה היוצא חמשה ושש עשיריות ושני שתותי העשירית ושליש שתות העשירית וזו צורתו: | ||||||||||||||
|
|
| ||||||||||||||
| והתשובה בה ארבעה | |||||||||||||||
|
|
ואם תרצה בזאת השאלה פנים אחרים מן המעשה יותר נראה מזה והוא שתבוא אל השטה העליונה ותקח מן השבעה חמשת שתותים ותקח מן החמשה שלושת חומשיהם והוא שלשה ושמרם אחר כן חזור אל השטה התחתונה ותקח מן החמשה חציים והוא שנים וחצי ותקח מן הארבעה שני שלישיהם והוא שנים ושני שלישים ותקבצם אל השנים וחצי כמו שנתבאר בשער הקבוץ יהיה זה חמשה ושתות והכם בשמונה וחמשה שתותים כמו שקדם בשער שנים ועשרים יצא לך המבוקש | ||||||||||||||
Chapter Fifty Four – Multiplication of Fraction of Integer and Fraction of Integer and Fraction by the Same |
שער ארבעה וחמישים בהכאת שבר השלם ושבר השלם והשבר בדומה לו | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך הכה שלשה חומשי שלשה ושלשה רביעי שנים ושני שלישים בארבעה חומשי שנים וחמשת שביעיות שלשה וחצי האחד | ||||||||||||||||||
| והורד השאלה בדמותה על זאת הצורה: | |||||||||||||||||||
|
|
| ||||||||||||||||||
|
|
הנה בזאת השאלה כל קו ממנה יחלק לשני חלקים הראשון ממנו השלשה חומשים והשלשה והוא שבר שלם והחלק השני השלוש רביעים והשנים והוא שבר שלם ותעשה בחלק הראשון כמו שקדם ומה שהתקבץ לך הכהו בסכום החלק השני והוא ארבעה ושלשה יהיה המקובץ ממנו שמונה ומאה ושמרם אחר כן עשה בחלק השני כמו שקדם בהכאת שבר השלם והשבר בשער שנים וארבעים ומה שהתקבץ תכהו בסכום החלק הראשון והוא חמשה יתקבץ מזה עשרים ומאה וקבצם אל השמונה ומאה יהיה המקובץ שמונה ועשרים ומאתים והוא היוצא מן השטה העליונה והמשיך המלאכה הזאת בשטה התחתונה יתקבץ בה שנים וחמישים ומאתים והכהו בראשון וחלק על הסכום יצא לך המבוקש והוא שלשה עשר ושש עשיריות ושמונה עשיריות העשירית וזו צורתם: | ||||||||||||||||||
|
|
| ||||||||||||||||||
| והתשובה בה בהשלכה | |||||||||||||||||||
| ואם תרצה תמשיך המעשה הראשון בשאלה והבן | |||||||||||||||||||
Chapter Fifty Five – Multiplication of Integer and Fraction and Integer and Fraction by the Same |
שער חמשה וחמישים בהכאת שלם ושבר ושלם ושבר בכמוהו | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כאשר יאמר לך: שלשה וחצי וחמשה ושני שלישים בארבעה ושלשה רביעים וששה וארבעה חומשים | ||||||||||||||
| הנה כאשר תרצה זה הורידם על זאת הצורה: | |||||||||||||||
|
|
| ||||||||||||||
|
|
אחר כן הביט אל השטה העליונה תמצא בה שלם ושבר ושלם ושבר וחלק השטה בשני חלקים ויהיה החלק הראשון שלשה וחצי והחלק השני חמשה ושליש ועשה בחלק הראשון כמו שקדם מהכאת השלם והשבר ומה שהתקבץ הכהו בסכום החלק השני יהיה זה אחד ועשרי' אחר עשה בחלק השני כמו שקדם בשערו ומה שהתקבץ הכהו בסכום החלק הראשון יתקבץ שנים ושלשים וקבצם אל האחד ועשרים יהיה זה שלשה וחמישים והוא היוצא מן השטה הראשונה ותעשה בשטה השנית כמו מה שעשית בראשונה יתקבץ בה אחד ושלשים ומאתים והכהו במספר הראשון וחלק מה שיתקבץ על הסכום יהיה היוצא שנים ומאה ושלשה רביעיות חמישית שתות וזה צורתו: | ||||||||||||||
|
|
| ||||||||||||||
|
|
ואם תרצה קבץ השלשה וחצי והחמשה ושליש כמו שהתבאר בשער קבוץ השברים יתקבץ בו שמונה וחמשה שתותים ושמרם אחר כן קבץ הארבעה ושלשה רביעי חמישית והכם בשמונה וחמשה שתותים כמו שקדם | ||||||||||||||
| ועניין זאת השאלה כי כשירצה שיקבץ שני השלמים ושני השברים משני הקוים ותכה המקובץ במקובץ | |||||||||||||||
|
|
ולה עניין שני והוא כי כאשר ירצה שיקח מן השטה העליונה מן החמשה ושליש חציה ונחברהו אל השלשה ומן השטה התחתונה תקח מן הששה וארבעה חומשי שלשה רביעיתם ותחברם אל הארבעה ותכהו בראשון | ||||||||||||||
|
|
והמעשה בזאת השאלה שתתחיל בשטה העליונה ותכה השלשה הראשונים בסכום הראשון ומה שהתקבץ בשני יהיה זה שמונה עשר אחר כן הכה החמשה בשלשה אשר ילוו אליהם ותשיא עליהם מה שעל השלשה ומה שהתקבץ הכהו באחד אשר על השנים יהיה זה ששה עשר נקבצם אל השמונה עשר יהיה זה ארבעה ושלושים והוא היוצא מן הקו העליון ושמרהו אחר כן עשה בשטה הב' כמו זה יתקבץ בו שנים ושמונים ומאה והכם במספר השמור וחלקהו על הסכום יצא לך המבוקש והוא אחד וחמישים ושלשה שתותים ושני חומשי שתות | ||||||||||||||
Chapter Fifty Six – Multiplication of Integer and Two Different Fractions and Integer and Two Different Fractions and Integer by the Same |
שער ששה וחמישים בהכאת השלם ושני השברים המתחלפים והשלם ושני השברים המתחלפים בדומה לו | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך הכה שנים ושני שלישים ושלשה רביעי שלשה וארבעה חומשים וחמשה שתותי ארבעה באחד ושלשה חלקים מאחד עשר ושבע עשיריות שלשה | ||||||||||||||||||||||||
| הורידם על זאת הצורה: | |||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||
|
|
אחר כן הבט אל השטה העליונה תמצא בה מספר שלם בשלשה מקומות בתחלת השאלה ואמצעה וסופה וחלק השטה העליונה על שלשה חלקים יהיו השנים תחלה חלק ושני השברים עם השלשה חלק אחר ושני השברים השניים עם הארבעה חלק שלישי הנה כל אחד מן החלק השני והשלישי אמנם המבוקש הוא שתקח אותם השני שברים מן השלם אשר ילוה אליהם ותקבץ אותם המספרים אל השנים אשר בתחלת השאלה והמעשה לפי מה שזכרנו שתעשה בחלק האמצעי כמו שזכרנו במה שקדם בשער הארבעים ומה שהתקבץ הכהו בסכום החלק השלישי יתקבץ מזה שלשים וחמש מאות ואלף אחר כן תעשה בחלק השלישי כמו שקדם בשער הנזכר ומה שהתקבץ הכהו בסכום החלק השני יתקבץ מזה שנים וחמישים ושלש מאות ואלפים אחר כן תקח השנים אשר בתחלת השאלה והכם בכל סכום השטה כלה יתקבץ מזה עשרים ושבע מאות וקבץ אלו ההכאות השלש יהיה זה שנים ושבע מאות וארבעת אלפים והוא היוצא מן השטה העליונה אחר כן תעשה כן בשטה התחתונה יתקבץ בה תשעים ושלש מאות ושבעת אלפים והכם במספר הראשון וחלק מה שהתקבץ על הסכום יצא לך המבוקש והוא חמשה ושמונים ותשעה חלקים מאחד עשר ושש עשיריות החלק מאחד עשר ושמונה עשיריות עשירית החלק וחמשה שתותי עשירית עשירית החלק וזה צורתו: | ||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||
|
|
ולזאת השאלה פנים אחרים והוא שתבקש בשאלה שתחבר השנים הראשונים מן השטה העליונה אל שני השברים אשר ילוו אליהם ותחבר ג"כ השלשה אל שני השברים אשר ילוו אליהם ויהיו הארבעה נוספים אל הכל הנה כבר נחלקה השטה ג"כ בשלשה חלקים החלק הראשון שלם ושני שברים וכן השני והשלישי שלם נפרד | ||||||||||||||||||||||||
|
|
ותעשה בחלק הראשון כמו שקדם בשער הארבעה ועשרים ומה שהתקבץ הכהו בסכום החלק השני וכן תעשה בחלק השני כמו שקדם בשער ארבעה ועשרים ומה שהתקבץ הכהו בסכום החלק הראשון אחר כן תקח הארבעה אשר באחרית השטה והכם בכל סכום השטה כלה ותקבץ כל אלו ההכאות השלש יהיה זה שמונה ושלשים ושלש מאות וארבעת אלפים אחר כן עשה כן בשטה השנית יתקבץ בה מאה ותשעת אלפים והכם במספר הראשון וחלק מה שיתקבץ על הסכום יצא לך המבוקש והוא תשעה ותשעים ושבעה חלקים מאחד עשר וחמש עשיריות החלק מאחד עשר וחצי עשירית החלק מאחד עשר וזה צורתם: | ||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||
| והנה התשובה בה בהשלכה והפנים הראשונים באחד והנה תחלק זאת השאלה בחלקים אחרים ומי שהבין שני חלקים אלו יבין הצורה בכל מה שיקרה מזה וכזה ואלהים העוזר | |||||||||||||||||||||||||
Chapter Fifty Seven – Multiplication of Integer and Fraction of Fraction and Integer and Fraction of Fraction and Integer by the Same |
שער שבעה וחמישים בהכאת השלם ושבר השבר והשלם ושבר השבר והשלם בדומה לו | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך הכה שנים וחצי חמישית שלשה ושני שלישי שתות חמשה בשלשה רביעי שביעית ארבעה וחמשה שתותים משמינית שנים | ||||||||||||||||
| הוריד השאלה על זאת הצורה: | |||||||||||||||||
|
|
| ||||||||||||||||
|
|
אחר כן חלק השטה העליונה בשלשה חלקים ויהיו שנים תחלה חלק וחצי חמישית השלשה חלק אחר ושני שלישי שתות חמשה חלק שלישי ותעשה בכל אחד מן החלק השני והשלישי כמו שקדם בשער אחד וארבעים ומה שהתקבץ מן השני הכהו בסכום החלק השלישי ומה שהתקבץ ג"כ מהשלישי הכהו בסכום החלק השני ושמור זה אחר כן תקח השנים אשר בתחלת השאלה והכה אותם בסכום על הששה ותקבץ אלו ההכאות השלש יהיה זה ארבעה עשר וחמש מאות ויצא לך מן השטה השנית כמו שספרנו בתחלה ארבעה וחמש מאות וארבעת אלפים ותכה אחד משני המספרים בשני ותחלק על הסכום יצא לך המבוקש והוא תשעה וחמש עשיריות ושש תשיעיות העשירית ושתי שמיניות תשיעית העשירית ושתי שביעיות שמינית שמינית תשיעית העשירית וארבעה שתותי שביעית שמינית תשיעית העשירית וזה צורתו: | ||||||||||||||||
|
|
| ||||||||||||||||
| והתשובה שנים | |||||||||||||||||
|
|
ולה עניין אחר והוא שתחלק השטה העליונה בשלשה חלקים על זולת מה שחלקתי תשים החלק הראשון שנים וחצי חומש והשני שלשה ושני שלישי שתות והחלק השלישי החמשה ותחלק השטה התחתונה כמו שחלקתי בו השני | ||||||||||||||||
|
|
ויהיה בשטה העליונה על החלק הראשון שלם ושבר השבר וכן השני תעשה כל אחד מהם כמו שקדם בהכאת השלם ושבר השבר ומה שהתקבץ מן החלק הראשון הכהו בסכום החלק השני וכן מה שהתקבץ מן החלק השני תכהו בסכום החלק הראשון אחר כן תקח השלם אשר בסוף השאלה ותכהו בכל סכום השטה ותקבץ זה כלו יהיה זה שמונה ושלשים ושמונה מאות ואלף ומן השטה השנית ארבעה ושמונים ומאתים ושנים עשר אלף והכה אחד משני המספרים בשני וחלק על הסכום יצא לך המבוקש והוא שלשה ותשעים ושלש עשיריות ושתי תשיעיות שמינית תשיעית העשירית ושתי שביעיות שמינית תשיעית העשירית וחמשה שתותי שביעית שמינית תשיעית העשירית וזה צורתו: | ||||||||||||||||
|
|
| ||||||||||||||||
| והתשובה בשלש' | |||||||||||||||||
Chapter Fifty Eight – Multiplication of Fraction and Integer and Two Different Fractions and Integer and Fraction by the Same |
שער שמנה וחמישים בהכאת השבר והשלם ושני השברים המתחלפים והשלם והשבר בדומה לו | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כאשר יאמר לך: הכה שלשה רביעי חמשה וחצי וחמשה שתותי שלשה ושני חומשים בשני שלישי ארבעה ושביעית ושלש שמיניות שנים ושלשה חלקים מאחד עשר | ||||||||||||||||||||||
| הוריד השאלה על זאת הצורה: | |||||||||||||||||||||||
|
|
| ||||||||||||||||||||||
|
|
אחר כן חלק השטה העליונה בשני חלקים יהיה בחלק האחד שלש רביעיות חמשה וחצי ובחלק השני חמשה שתותי שלשה ושני חומשים וכל אחד משני חלקים אלו הוא משער שנים וארבעים ותעשה בכל חלק מהם כמו שקדם בשערו ותכה מה שיצא בחלק הראשון בסכום החלק השני ומה שיצא מן החלק השני בסכום החלק הראשון ותקבץ שתי הכאות אלו יהיה זה שבעים ושש מאות ואלף ומן השטה התחתונה תשעה ושבעים ושש מאות וששת אלפים והכה אחד משני המספרים בשני ותחלק מה שהתקבץ על הסכום יצא חמשה ועשרים וחלק מאחד עשר וחמש תשיעיות החלק מאחד עשר וחמש שמיניות שמינית תשיעית החלק מאחד עשר וחמש שמיניות שמינית תשיעית החלק מאחד עשר ושש שביעיות שמינית שמינית תשיעית החלק מאחד עשר וזה צורתו: | ||||||||||||||||||||||
|
|
| ||||||||||||||||||||||
| והתשובה בארבעה | |||||||||||||||||||||||
|
|
ולזאת השאלה פנים אחרים והוא שתקח החמשה שתותים מן החלק השני ותחברם אל החלק הראשון ויהיה בחלק הראשון שבר מספר ושני שברים מתחלפים והוא משער ארבעה וארבעים | ||||||||||||||||||||||
| ותעשה בכל חלק כמו שקדם בשערו והיוצא מן החלק הראשון הכהו בסכום החלק השני וכן היוצא מן החלק השני הכהו בסכום החלק הראשון ותקבץ שתי ההכאות ותעשה כן בשטה התחתונה ותכה המקובץ במקובץ ותחלק מה שיצא לך על הסכום יצא לך המבוקש | |||||||||||||||||||||||
| ודע כי העקר באלו השאלות כאשר חלקת אותם בשני חלקים או שלשה או בארבעה או בחמשה או מה שיסבול מן הענינים | |||||||||||||||||||||||
| אחר כן תעשה בכל חלק כמו שקדם בשערו וזה שתקח המקובץ מן החלק הראשון ותכה בשארית סכום השטה הקודמת כלה ותקח המקובץ מן החלק השני ותכהו בסכום החלק הנשאר הקודם והמתאחר וכן תעשה בשלישי והרביעי | |||||||||||||||||||||||
| ואם היה אחד מן החלקים שלם הנה כבר הכית אותו בסכום השטה כולה ולא תקפיד זה החלק באיזה מקום יהיה אם בתחלת השאלה או באמצעה או בסופה ועל זה העקר תבנה כל מה שקדם מן השברים ומה שנשאר מהם עד סופם בע"ה | |||||||||||||||||||||||
| פרק | |||||||||||||||||||||||
|
|
והנה תחלק זאת השאלה בשני חלקים אחרים כלומ' שאלת שמנה וחמישים והוא כי אתה כבר חלקת השאלה תחלה בשני חלקים והיה בחלק הראשון שלשה רביעי חמשה וחצי והחלק השני חמשה שתותי שלשה ושני חומשים | ||||||||||||||||||||||
| וקח החצי כלומ' השבר מן החלק הראשון ותחברהו אל החלק השני | |||||||||||||||||||||||
|
|
והנה כבר נחלקה השטה בשני חלקים אחרים ובחלק הראשון שלשה רביעי חמשה והיא שאלה משער שבעה ושלשים ובחלק השני חצי וחמשה שתותי שלשה ושני חומשים והיא שאלה משער תשעה וארבעים | ||||||||||||||||||||||
| ותעשה בכל חלק כמו שקדם בשערו ולפי מה שהתנינו בשער הזה מן השרשים ובשטה השנית כמו מה שעשית בראשנה והכה המקובץ במקובץ ותחלק על הסכום | |||||||||||||||||||||||
|
|
ואם חלקת זאת השאלה בשלשה חלקים תשים בחלק הראשון שלשה רביעים לבד ובחלק השני חמשה וחצי וחמשה שתותים ובחלק השני שלשה ושני חומשים והם משער ארבעה ועשרים | ||||||||||||||||||||||
| ותעשה בכל חלק כמו שקדם בשערו ועל התנאים אשר התנינו בשער הזה אבל כי החלק הראשון לא יתבאר בו והוא שבר לבד ותקח מה שעל ראשו ותכהו בשארית הסכום | |||||||||||||||||||||||
| וכן כאשר יבוא לך באחד מן החלקים שבר לבד היה בתחלת השאלה או אמצעה או אחריתה אמנם תקח מה שעל הקו ותכהו בשארית סכום השטה כלה הקודם ממנה והמתאחר ותבנה כמו שקדם | |||||||||||||||||||||||
|
|
והנה יחלק גם כן השער הזה בשלשה חלקים תשים בחלק הראשון שלשה רביעים והוא משער שבעה ושלשים ובחלק השני חצי וחמשה שתותי שלשה והוא משער ארבעה ושלשים ובחלק השלישי שלשה חומשים | ||||||||||||||||||||||
| ותעשה בכל חלק כמו שקדם בשערו בשבר הנפרד כמו שזכרנו ותשלים השאלה על התנאים אשר הקדמנו בשער הזה | |||||||||||||||||||||||
|
|
והנה תחלק זאת השאלה בשלשה חלקים אחרים והוא שתשים החלק הראשון שלשה רביעי חמשה וכבר זכרנו שערו ובחלק השני חצי וחמשה שתותים והוא משער שלשה ושלשים ובחלק השלישי שלשה ושני חומשים | ||||||||||||||||||||||
| ותעשה בכל חלק כמו שקדם בשערו וכפי מה שהתנינו בשער הזה מן השרשים | |||||||||||||||||||||||
Chapter Fifty Nine – Multiplication of Fraction and Fraction of fraction and Integer and Two Different Fractions and Integer and Fraction and Integer and Fraction and Fraction of Fraction by the Same |
שער תשעה וחמישים בהכאת השבר ושבר השבר והשלם ושני השברים המתחלפים והשלם והשבר והשלם והשבר ושבר השבר בדומה לו | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כאשר יאמר לך: הכה חמשה שתותים וחצי שתות שלשה ושלשה רביעים וארבעה חומשי שנים ושלש שמיניות ארבעה ושלש תשיעיות ושני שלישי תשיעית | |||||||||||||
| הוריד השאלה על זאת הצורה: | ||||||||||||||
|
|
| |||||||||||||
|
|
אחר כן חלק זאת השטה תחלה בשני חלקים יהיו השנים ממנו בחלק הראשון ושאר השאלה בחלק השני ונקיש על החלק משער ששה וחמישים ועל החלק השני משער שלשה וארבעים ותשלים השאלה על התנאים הקודמים | |||||||||||||
| ואם תרצה תשיב השנים מן החלק השני ותקיש על החלק הראשון משער חמישים ועל החלק השני משער חמשה וחמישים ותשלים השאלה על הקש שלהם | ||||||||||||||
| ואם תרצה חלק השאלה על שני זולת אלו השני חלקים והוא שתשים הארבעה חומשים מן החלק השני ותקיש על השאלה בחלק הראשון משער שבעה וארבעים ובחלק השני משער ארבעה וחמישים ותעשה כמו שקדם | ||||||||||||||
| פרק | ||||||||||||||
| והנה תחלק השאלה הזאת בשלשה חלקים וחלוקתה בשלשה חלקים עניין קטן והנה תחלק זאת השאלה על זולת זה והבין תמצא בע"ה | ||||||||||||||
Chapter Sixty – Multiplication of Fractions |
שער שישים בהכאת השבר בחסרון הוו' והוא שבר לקוח משבר | ||||||
|---|---|---|---|---|---|---|---|
| והנה יחלק השער הזה לשני חלקים נדבק ונבדל | |||||||
| והנבדל ממנו הוא שיהיו מעמדות השברים בו ההוספה באחד וכן מה שעל כל מעמד יתוסף באחד ויהיה אשר על כל מעמד פחות ממנו באחד ויהיה אשר על כל מעמד הוא הנבדל | |||||||
|
|
והמשל בו כשיאמר לך הכה שני שלישי שלשה רביעי ארבעה חומשי חמשה שתותי שש שביעיות שבעה שמיניות שמונה תשיעיות תשע עשיריות עשרה חלקים מאחד עשר בדומה לו | ||||||
| הנה משפט זאת השאלה שיהיו המעמדות כולם תחת קו אחד בשטה העליונה והתחתונה על זאת הצורה: | |||||||
|
|
| ||||||
| הנה לזאת השאלה מן המעשה שני פנים יביאך אל דבר אחד מן היוצא | |||||||
|
|
והמעשה האחד מהם שתקח מה שעל הסכום הראשון והוא שנים ותכהו במה שעל הסכום השני והוא שלשה ומה שהתקבץ הכהו במה שעל הסכום השלישי ומה שהתקבץ הכהו במה שעל הסכום הרביעי וכן במה שעל החמישי והשישי עד אחריתם יתקבץ לך בו שמונה מאות ושמונה ועשרים אלף ושש מאות אלפים ושלשת אלפי אלפים וכן יצא מן השטה השנית ותכה המקובץ במקובץ וחלק על הסכום ויצא לך המבוקש וזה ארבעה חלקים מאחד עשר בחלק מאחד עשר והמעשה הזה יתחבר עמך בכל זה המין מדובק או נבדל | ||||||
| והמעשה השני הוא שתקח מה שעל הראשון הסכום מן השטה העליונ' והוא שנים ותקח גם כן מה שעל ראשון הסכום מן השטה התחתונה והוא ג"כ שנים ותכם בשנים הראשונים יהיו ארבעה ותחלקם על האחרון הסכום מן השטה העליונה ועל אחרון הסכום מן השטה התחתונה יהיה היוצא מה שזכרנו | |||||||
|
|
ועניין זאת השאלה שתקח אחד ותחלקהו באחד עשר חלקים אשר הוא אחרית הסכום ותקח מהם עשרת חלקיהם בעשרה חלקים ותקח מהם תשע עשיריותיהם בתשעה חלקים ותקח מהם שמונה תשיעיותיהם בשמונה חלקים ותקח מהם שבעה חלקיהם בשבעה חלקים ותקח מהם שש שביעיותיהם בששה חלקים ותקח מהם חמשת שתותיהם בחמשה חלקים ותקח מהם ארבעת חומשיהם בארבעה חלקים ותקח מהם שלשת רביעיותיהם בשלשה חלקים ותקח מהם שני שלישיהם שני חלקים והוא המבוקש שמן השטה העליונה שני חלקים מאחד עשר וכן מן השני מפני שהוא כמוהו ותכה שני חלקים מאחד עשר כמו שקדם מהכאת השבר בשבר בשער שמונה ועשרים | ||||||
| פרק | |||||||
| ואולם החלק השני מן השער הזה והוא הנבדל והוא שיהיו המעמדים לא יתוספו בשעור אחד ולא מה שעל ראשיהם יתוספו ג"כ בשעור אחד הנה אמנם יתחבר עמך בו המעשה הראשון מזאת השאלה והוא שתקח מה שעל הסכום הראשון ותכהו במה שעל השני ומה שהתקבץ במה שעל השלישי ומה שהתקבץ במה שעל הרביעי עד אחריתם וכן בשטה השנית ותכה המקובץ במקובץ ותחלק על כל סכום השאלה | |||||||
|
|
ודמיון זה כשיאמר לך: הכה שלשה חומשי שלש שביעיות שתי תשיעיות עשרה בשני שלישי שש שביעיות ארבעה חומשי שבע תשיעיות | ||||||
| הוריד השאלה על זאת הצורה: | |||||||
|
|
| ||||||
|
|
אחר כן התחיל בשטה העליונה והכה מה שעל הקו קצתו בקצת יתקבץ בו שמונה עשר ותכה גם כן מה שעל השטה התחתונה קצתו בקצת יתקבץ בו ששה ושלשים ושלש מאות ותכם בשמונה עשר וחלק על הסכום יצא לך שביעית תשיעית עשירית וחומש שביעית תשיעית עשירית ושני חומשי חמישית שביעית תשיעית העשירית וזו צורתו: | ||||||
|
|
| ||||||
| והתשוב' בהשלכה | |||||||
Chapter Sixty One – Multiplication of Fractions |
שער אחד ושישים בהכאת השברים המתחלפים בחסרון הוו' | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך הכה שלשה רביעי ארבעה חומשים וחמשה שתותי שש שביעיות ושבע שמיניות שמונה תשיעיות בשני שלישי שלשה רביעי ארבעה חומשי חמשה שתותים ושש שביעיות שבע שמיניות | ||||||||||||||
| הוריד השאלה על זאת הצורה: | |||||||||||||||
|
|
| ||||||||||||||
|
|
אחר כן התחיל בשטה העליונה ותמצא בה שלשה קוים תחת כל קו שני סכומים אחר כן תקח מה שעל הקו הראשון ותכה המספרים אשר עליו קצתם בקצת ומה שהתקבץ תכהו בשאר סכום השטה וכן תעשה בקו השני והשלישי ותקבץ ההכאות השלש יהיה זה שמונה ועשרים וחמש מאות ושש ועשרים אלף ומאה אלף ויצא מן הקו התחתון ארבעים ושש מאות ושמונה ושלשים אלפים ותכם במספר הראשון ותחלק על הסכום יצא ארבעה ושש שביעיות תשיעית העשירית ושתות שביעית תשיעית העשירית | ||||||||||||||
|
|
| ||||||||||||||
| והתשובה בה בהשלכה | |||||||||||||||
|
|
ואם תרצה בזאת השאלה שתעשה ביותר קרוב מזה והוא שתקח מן הארבעה חומשים אשר בתחלת הקו מן השטה הראשנה תקח מהם שלשה רביעיהם וזה שלשה חומשים ותקח מן הששה שביעיות חמשה שתותים וזה חמש שביעיות ותקח מן השמונה תשיעיות שבע שמיניות והוא שבע תשיעיות והם שלשה שברים מתחלפים אחר כן תחזור אל השטה התחתונה ותקח מן השלשה רביעים שני שלישי' וזה חצי ותקח מן החמשה שתותים ארבע חומשיהם והוא שני שלישים ותקח מן השבעה שמיניות שש שביעיותיהם והוא שלשה רביעים ויהיה בשטה השנית שלשה שברים מתחלפים והם חצי ושני שלישים ושלשה רביעים ותעשה בשאלה הזאת כמו שקדם בשער ששה ושלשים והיוצא מהם כמו מה שיצא במעשה הראשון | ||||||||||||||
Chapter Sixty Two – Multiplication of Fraction of fraction of Integer by the Same |
שער שנים ושישים בהכאת השבר בחסרון הוו' והשלם בכמוהו | ||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך: הכה שני שלישים שלשה רביעי ששה בשלשה רביעי ארבעה שביעיות שמונה | ||||||||
| הוריד השאלה על הצורה הזאת: | |||||||||
|
|
| ||||||||
|
|
אחר כן התחיל בשטה הראשונה ותבנה בשבר הזה אשר בו כמו שקדם בשער השישים והוא שתכה השנים אשר על השלשה בשלשה אשר על הארבעה ומה שהתקבץ תכהו בששה אשר הם השלם מפני כי זאת השאלה דומה בשאלה אשר בשער שבעה ושלשים מפני כי זאת השאלה אמנם היא שבר מספר בשבר מספר אחר כן תקבץ ההכאה יתקבץ בה ששה ושלשים ובשטה השנית ששה ותשעים ותכה האחד בשני ותחלק על הסכום יצא לך עשרה ושתי שביעיות | ||||||||
|
|
| ||||||||
| והתשובה בחמשה והבן תמצא זה בע"ה | |||||||||
Chapter Sixty Three – Multiplication of Fraction of Fraction and Fraction of Integer by the Same |
שער שלשה ושישים בהכאת השבר בחסרון הוו' והשבר הנפרד והשלם | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך: הכה שני חומשי חמשה שתותים וחצי שלשה בשני שלישי שש שביעיות ושלשה חומשי עשרה | ||||||||||||
| הוריד השאלה על זאת הצורה: | |||||||||||||
|
|
| ||||||||||||
|
|
אחר כן התחיל בשטה העליונה ותקח מה שעל הקו הראשון והוא שנים וחמשה ותכה השנים בחמש' מפני שהם בחסרון הוו' ומה שהתקבץ הכהו במה שתחת הקו השני והוא שנים ותשמרהו ותקח מה שעל הקו השני ותכהו בסכום הקו הראשון ותקבץ שתי ההכאות ותכה המקובץ בשלשה אשר הם השלם יהיה כל זה חמישים ומאה ויצא מן השטה השנית שלשים ומאתים ואלף ותכם בחמישים ומאה ותחלק על הסכום יצא לך המבוקש והוא תשעה ועשרים ושתי שביעיות וזה צורתו: | ||||||||||||
|
|
| ||||||||||||
| והתשובה באחד | |||||||||||||
Chapter Sixty Four – Multiplication of Fraction of Fraction of Integer and Fraction by the Same |
שער ארבעה ושישים בהכאת השבר בחסרון הוו' והשלם והשבר | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך: הכה שני שלישי ששה תשיעיות של ששה ושלשה רביעים בשלשה רביעי שמונה תשיעיות שנים ושני חומשים | ||||||||||||
| הוריד השאלה על זאת הצורה: | |||||||||||||
|
|
| ||||||||||||
|
|
אחר כן התחיל בשטה הראשונה והכה השנים אשר על הקו הראשון בששה אשר עמהם על קו אחד יהיו שנים עשר ושמרם אחר כן הכה הששה אשר הם השלם בארבעה והשיא מה שעל ראשם יהיו שבעה ועשרים והכם בשנים עשר יהיו ארבעה ועשרים ושלש מאות והוא היוצא מן השטה העליונה ותמשיך זאת המלאכה בשטה השנית יתקבץ בה שמונה ושמונים ומאתים ותכם במספר הראשון וחלק על הסכום יצא לך המבוקש והוא ארבעה וארבעה חומשים והתשובה בה שנים וזאת צורתם: | ||||||||||||
|
|
| ||||||||||||
| ודע כי זאת השאלה דומה בשאלה אשר בשער שנים וארבעים | |||||||||||||
Chapter Sixty Five – Multiplication of Fraction of Fraction of Integer and Fraction and Fraction of Fraction by the Same |
שער חמשה ושישים בהכאת השבר בחסרון הוו' והשלם והשבר ושבר השבר | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך הכה שלשה חומשי ארבעה שביעי שלשה וחמשה שתותי וחצי שתות בשני שלישי חמשה שתותי ששה ושבע שמיניות ושני שלישי שמינית | ||||||||||||
| הוריד השאלה על זאת הצורה: | |||||||||||||
|
|
| ||||||||||||
|
|
אחר כן חלק השטה העליונה בשני חלקים יהיה בחלק האחד השבר בחסרון הוו' אשר בתחלת השאלה ותעשה בו כמו שקדם בשער שישים יתקבץ בו שנים עשר והחלק השני שלשה וחמשה שתותים וחצי שתות ותעשה בו כמו שקדם בשער שלשה ועשרים יתקבץ בו שבעה וארבעים ותכם בשנים עשר השמורים יהיה כל זה ארבעה ושישים וחמש מאות והוא היוצא מן השטה העליונה אחר כן תמשיך זה המעשה בשטה השנית יתקבץ לך בה שבעים ושש מאות ואלף והכם במספר הראשון וחלק על הסכום יצא לך חמשה ותשיעית וחמשה שמיניות תשיעית וחמש שביעיות שמינית תשיעית ושליש שביעית שמינית תשיעית וזה צורתו: | ||||||||||||
|
|
| ||||||||||||
| והתשובה בה בשנים | |||||||||||||
| פרק | |||||||||||||
| ואם היה עמך במקום שבר השבר שני שברים מתחלפים | |||||||||||||
| הנה תעשה בשבר הראשון אשר הוא בחסרון הוו' כמו שקדם ותעשה בשלם ושני השברים כמו שקדם בשער ארבעה ועשרים והכה המקובץ במקובץ ומה שהתקבץ הנה הוא היוצא מן השטה העליונה וכן תעש' בשנית והשלים השאלה בע"ה | |||||||||||||
Chapter Sixty Six – Multiplication of Integer and Fraction of Fraction by the Same |
שער ששה וששים בהכאת השלם והשברים בחסרון הוו' | ||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך הכה שלשה ושלשה חומשי חמשה שתותים בארבעה ושתי שביעיות שלש שמיניות | ||||||||
| תוריד השאלה על זאת הצורה: | |||||||||
|
|
| ||||||||
|
|
אחר כן תקח השלשה השלמים אשר בתחלת השאלה ותכם בכל השטה בחמשה תחלה ומה שהתקבץ בששה ותניחהו לצד אחר כן הכה מה שעל הקו קצתן בקצת ותחברהו אל אותו המספר המוצנע יתקבץ בו חמשה ומאה ויתקבץ מן השטה השנית על זה המעשה שלישים ושתי שלישיות והכה אחד משניהם בשני וחלק על הסכום יצא ארבעה עשר ושלש' שמניות וזה צורתם: | ||||||||
|
|
| ||||||||
| והתשובה בהשלכה והבין | |||||||||
Chapter Sixty Seven – Multiplication of Integer and Fraction of Fraction and Fraction by the Same |
שער שבעה ושישים בהכאת השלם ושני השברים בחסרון הוו' והשבר הנפרד | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך הכה שנים ושלש שביעיות שלשה חומשים ושני שלישים בשלשה ושלש רביעיות חמשה שתותים וחצי | ||||||||||||
| הוריד השאלה על זאת הצורה: | |||||||||||||
|
|
| ||||||||||||
|
|
אחר כן התחיל בשטה העליונה והכה השנים אשר בתחלת השאלה בכל השטה אחר כן הכה מה שעל הקו קצתו בקצת ומה שהתקבץ בסכום אשר תחת הקו השני אחר כן תקח מה שעל השבר הנפרד ותכהו בסכום אשר תחת הקו הראשון ותקבץ אחר זה אלו ההכאות השלש יהיה שבעה ושלש מאות ומן הקו השני שמונה ותשעים ומאה והכה אחד משניהם בשני יצא לך ששה ושמנים ושבע מאות ושישים אלף וחלק על הסכום יצא לך שנים עשר ושלש שביעיות השמינית ושני חומשי שביעית השמינית וזה צורתם: | ||||||||||||
|
|
| ||||||||||||
| והתשובה בחמשה | |||||||||||||
Chapter Sixty Eight – Multiplication of Fraction of Fraction and Integer and Fraction of Fraction by the Same |
שער שמנה ושישים בהכאת השבר בחסרון הוו' והשלם והשבר בחסרון הוו' | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך הכה שלשה רביעי שלשה חומשי שנים ושלש תשיעיות חמשה שתותים בחצי שלשה רביעי שלשה ושני חומשי ארבע תשיעיות | ||||||||||||
| הוריד השאלה על זאת הצורה: | |||||||||||||
|
|
| ||||||||||||
| וחלק זאת השאלה בשני חלקים כלומ' הקו הראשון והוא שתים והשנים אשר הוא השלם והוא באמצע השאלה אם שתשימם בחלק הראשון או מן החלק השני | |||||||||||||
|
|
ואם תשימהו מן החלק השני יהיה החלק השני משער ששה וששים והראשון משער שישים ותשים בכל אחד משני אלו החלקים כמו שקדם בשערו ומה שהתקבץ מן החלק הראשון תכהו בסכום החלק השני ומה שהתקבץ מן החלק השני תכהו בסכום החלק הראשון וקבצת שתי ההכאות ועשה כן בשטה השנית והכה המקובץ במקובץ וחלקהו על הסכום יצא לך המבוקש | ||||||||||||
|
|
ואם תשיב השנים אל החלק הראשון הנה יהיה החלק הראשון משער שנים וששים ותעשה כמו שקדם | ||||||||||||
| ואם לא תחלק השאלה ונשארה על ענינה ורצית שתקח מן השנים ושלש שביעיות חמשה שתותים שלשה רביעי שלשת חומשיהם | |||||||||||||
|
|
הנה תוריד השאלה על דמותה אחר כן תכה מה שעל הקו הראשון קצתו בקצת ותשמרהו אחר הכה השנים בשבעה ומה שהתקבץ בששה ותכה מה שעל הקו האחר קצתו בקצתו ותחברהו אל הכאת השנים בסכום ומה שהתקבץ תכהו במספר השמור ויתקבץ מזה כלו אחד ותשעים ושמנה מאות ומן השטה השנית תשעה ועשרים וארבע מאות ותכה אחד משניהם בשני ותחלק על הסכום יצא לך המבוקש והוא אחד ועשרים ושש עשיריות העשירית ושלש שמיניות עשירית העשירית ושביעית וחצי שביעית שמינית עשירית העשירית | ||||||||||||
| והתשובה בארבעה | |||||||||||||
Chapter Sixty Nine – Multiplication of Two Different Fractions and Integer and Fraction of Fraction and Integer and Fraction and Fraction of Fraction and Integer and Fraction of Fraction and Integer and Fraction |
שער תשעה ושישים בהכאת שני השברים המתחלפים והשלם והשבר בחסרון הוו' והשלם והשבר ושבר השבר והשלם והשבר בחסרון הוו' והשלם והשבר | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך הכה שלשה רביעי וחמשה שתותי ארבעה ושלש' חומשי שלשה וחמשה שתותים וחצי שתות ארבעה ושבע שמיניות שמנת תשיעיות שלשה וחצי במספר אחד ושבר כמו זה או פחות ממנו | ||||||||||||||||||||
| הוריד השאלה על זאת הצורה: | |||||||||||||||||||||
|
|
| ||||||||||||||||||||
| דע כי זאת השאלה לא תעשה על עניינה אלא שתשוב אל עניין ותקצר כל מה שזכרנו מן השברים ולזאת השאלה עניינים רבים | |||||||||||||||||||||
| אחד מענייניהם: שהוא רצה מן השלשה וחצי אשר בסוף השאלה שבע שמיניות שמינית תשיעיותיהם | |||||||||||||||||||||
|
|
וזאת השאלה משער ארבעה ושישים ויבקש ג"כ מן הארבעה אשר ילוו לאלה הנזכרים חמשת שתותיהם וחצי שתותיהם וזאת השאלה משער תשעה ושלשים ותבקש ג"כ מן השלשה אשר ילוו אלו השברים שלשת חמשיות ששת שביעיותיהם וזאת השאל' משער שנים ושישים ויבקש ג"כ מן הארבעה אשר ילוו אלו השברים חמשת שתותיהם ושלשת רביעיותיהם וזאת השאלה משער ארבעים וירצה שיקבץ זה כלו ויכהו בכמוהו אם ירצה או בזולת כמוהו | ||||||||||||||||||||
| והמעשה בזאת השאלה שתעשה בכל חלק חלוקה בה השאלה וזכרנו שערה כמו שזכרנוהו בשערו ומה שהתקבץ תכהו בסכום החלקים הנשארים בו ותקבץ אחר כן ההכאות השלש ותעשה כמו שקדם | |||||||||||||||||||||
| וכן אם תרצה שתחלק זאת השאלה בזולת אלו החלקים הנה תעשה בכל חלק כמו שקדם בשערו | |||||||||||||||||||||
| ודע כי זאת השאלה לה יותר מעשרים פנים מן המעשה ולכל פנים ענין ישוב אליו ומי שהבין מה שזכרנו באלו הפנים ינהיגם כולם והבין תמצא בע"ה | |||||||||||||||||||||
Chapter Seventy – Multiplication of Integer and Fraction by Integer and Fraction by Integer and Fraction and so on |
השער השבעים בהכאת המספר והשבר במספר והשב' ומה שהתקבץ במספר ושבר ומה שהתקבץ במספ' ושבר אל מה שאין תכלית לו | |||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
המשל בו: הכה אחד וחצי באחד ושליש באחד ורביע באחד וחומש באחד ושתות באחד ושביעית באחד ושמינית באחד ותשיעית באחד ועשירית | |||||||||||||||||||||||||||
| הנה אלו תשע שאלות משלם ושבר והורידם כולם בשטה אחת על הצורה הזאת: | ||||||||||||||||||||||||||||
|
|
| |||||||||||||||||||||||||||
|
|
אחר כן תקח האחד אשר בתחלת השאלה ותכהו בשנים אשר הם מעמד השבר ותשיא מה שעליהם כמו שקדם בשער הכאת המספר והשבר במספר והשבר יהיה זה שלשה וקיימם תחתיהם ותעשה בשאלה השנית כן יתקבץ בה ארבעה וקיימם ג"כ תחתיהם ויתקבץ לך בשאלה השלישית חמשה וברביעית ששה ובחמישית שבעה ובשישית שמונה ובשביעית תשעה ובשמינית עשרה ובתשיעית אחד עשר והכה אלו המספרים קצתם בקצת ומה שהתקבץ חלקהו על הסכום יצא לך המבוקש והוא חמשה וחצי | |||||||||||||||||||||||||||
|
|
ואם תרצה תקח ראשית השאלה והוא אחד וחצי ותשימם כולם חציים יהיו שלשה חציים ותכם באחד ושליש יהיו ארבעה חציים ותכם באחד ורביע יהיו חמשה חציים ותכם באחד וחומש יהיו ששה חציים ותכם באחד ושתות יהיו שבעה חציים ותכם באחד ושביעית יהיו שמונה חציים והכם באחד ושמינית יהיו תשעה חציים והכם באחד ותשיעית יהיו עשרה חציים והכם באחד ועשירית יהיו אחד עשר חציים והשיבם אחדים יהיו חמשה וחצי | |||||||||||||||||||||||||||
Chapter Seventy One– Multiplication of Reduced Fractions |
שער אחד ושבעים בהכאת השבר בתנאי | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| כשיאמר לך: הכה שלשה רביעים חסר שתות בארבעה חומשים אלא שליש | |||||||||||||
| הוריד השאלה על זאת הצורה: | |||||||||||||
|
| ||||||||||||
| הנה זאת השאלה תסבול שני עניינים: | |||||||||||||
|
|
אחד משניהם שהוא רצה שיקח שלשה רביעי אחד אלא שתות אחד וישמור הנשאר אחר כן יקח ג"כ ארבעה חומשי אחד ויפיל מהם שליש אחד ותכה הנשאר בנשאר | ||||||||||||
|
|
הנה אופן המעשה בפנים האלו שתכה מה שעל ראש הארבעה בששה יהיו שמונה עשר אחר כן תקח מה שעל ראש הששה ותכהו בארבעה יהיו ארבעה תפילם מן השמונה עשר הנשאר ארבעה עשר והוא המבוקש מן השטה העליונה אחר כן תכה ג"כ בשטה התחתונה מה שעל החמשה בשלשה יהיו שנים עשר ותכה מה שעל השלשה בחמשה ותפיל מן השנים עשר הנשאר שבעה והכם בארבעה עשר השמורים וחלק על הסכום יצא לך שתי תשיעיות ושלשה שמיניות התשיעית ושלשה חומשי שמינית התשיעית | ||||||||||||
|
|
ואולם הפנים השניים הוא שתקח שלשה רביעי אחד ותפיל מהם שתותיהם וכן בשט' השנית תקח ארבעה חומשי אחד ותפיל מהם שלישיהם ותכה הנשאר בנשאר | ||||||||||||
|
|
והנה אופן המעשה בשער הזה שתכה השלשה בששה יהיו שמנה עשר ותקח מה שעל הששה ותכם בארבעה והם שלש' ותפילם מן השמנה עשר הנשאר חמשה עשר והנשאר על זה המעשה מן השטה השנית שמנה והכם בחמשה עשר וחלקם על הסכום יצא לך המבוקש | ||||||||||||
Chapter Seventy Two – Multiplication of Reduced Fractions of Integers |
שער שנים ושבעים בהכאת שבר המספר בתנאי | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| כשיאמ' לך הכה שלשה רביעי חמשה אלא שתות בארבעה חומש שלשה אלא רביעית | |||||||||||||||
| הוריד על זאת הצורה: | |||||||||||||||
|
| ||||||||||||||
| השאלה הנה זאת השאלה סובלת שלשה עניינים: | |||||||||||||||
|
|
אחד מהם שהוא רוצה שתקח מן החמשה שלשה רביעי' ותפיל מן המקובץ שתות החמשה ורצה מן השטה השנית כמו זה שתקח ארבעה חומשי השלשה ותפיל מהם רביע השלשה ותכה הנשאר בנשאר | ||||||||||||||
|
|
הנה המעשה בפנים האלה שתכה השלשה אשר על הארבעה בחמשה ומה שהתקבץ בששה אשר הוא הסכום השני יהיה זה תשעים אחר כן תקח האחד אשר על הששה ותכהו בחמשה ומה שהתקבץ בארבעה אשר הם הסכום הראשון יהיה זה עשרים ותפילם מן התשעים הנשאר שבעים והנשאר מן השטה השנית במעשה הזה שלשה ושלשים והכם בשבעים וחלק מה שהתקבץ על הסכום יצא לך המבוקש והוא: | ||||||||||||||
| |||||||||||||||
| והבין | |||||||||||||||
|
|
השני שהוא רצה שיקח שלשה רביעי החמש ויפיל מהם שתותם ויקח ג"כ ארבעה חומש השלשה ויפיל מהם רביעם ויכה הנשאר בנשאר | ||||||||||||||
|
|
ואופן המעשה שתכה השלשה בחמשה ומה שהתקבץ בששה יהיו תשעים כמו שקדם אחר כן תקח האחד אשר על הששה ותכהו בחמשה ומה שהתקבץ בששה יהיו תשעים כמו שקדם אחר כן בשלשה אשר על הארבעה יהיה חמשה עשר ותפילם מן התשעי' הנשאר חמשה ושבעים והנשאר מן השטה השנית במעש' הזה ששה ושלשים והכה אחד משני המספרים בשני ותחלק מה שהתקבץ על הסכום | ||||||||||||||
|
|
ואולם האופן השלישי הנה הוא שתקח שלשה רביעי החמשה ותפיל שתות אחד ותקח ג"כ ארבעה חומשי השלשה ותפיל מהם רביע אחד והכה הנשאר בנשאר | ||||||||||||||
|
|
ואופן המעשה שתכה השלשה בחמשה ומה שהתקבץ בששה כמו שקדם באופן הראשון יהיו תשעים אחר כן הכה האחד אשר על הששה בארבעה אשר הם הסכום הראשון ותפיל מן התשעים הנשאר ששה ושמונים והנשאר מן השטה השנית בזה המעשה שלשה וארבעים והכה המספר האחד בשני וחלק מה שהתקבץ על הסכום יצא לך המבוקש | ||||||||||||||
| וכבר הבנו מהכאת השברים מה שבו די למי שיתנהג בהם וידע הנרצה מהם וקצרנו מהם מה שלא יוכל אחד לסובלו ועזבנו האריכות ומה שזכרנו מהם יוקש עליו כל מה שיבוא אחריו למי שהבין השורש וחקר עליו וידע שעור מה שבהם מן התועלת בכל ידיעת החשבון והאל המדריך אל היושר | |||||||||||||||
Converting Fractions to Lower Fractions |
שער פריטת השברים קצתם אל קצת |
|---|---|
| דע כי השער הזה אמנם עניינו שתשיב השבר משם אל שם אחר אם יותר דק ממנו בחלק ואם יותר גדול | |
| והטוב מהם שתפרוט השברים כולם תמיד אל חלק יותר דק והוא שתשיב השלישים אל רביעים או חומשים או עשריים ושתשיב השתותים אל שביעיים הנה הוא יותר טוב אם לא שיבוא אליו ההכרח אצל קבוץ השברים או השלכתם והנה נבארהו במקומו | |
Simple fraction to simple fraction |
השער הראשון מן הפריטה והוא פריטת השבר אל השבר | |||
|---|---|---|---|---|
|
|
כשיאמר לך חמשה שתותים כמה שביעיים יהיו בהם | |||
| הוריד החמשה שתותים בשטה והוריד מעמד השביעית והוא שבעה בשטה תחתיה ומשוך עליו קו על זאת הצורה: | ||||
|
|
| |||
|
|
אחר כן תכה החמשה אשר על הששה בשבעה אשר תחת הקו התחתון יהיה זה חמשה ושלשים וחלקם על הששה אשר הם מעמד הסכום בקו העליון ומה שיצא תחלקהו על השבעה אשר הם מעמד השביעית יצא לך בחלוקה חמש שביעיות וחמשה שתותי השביעית על זאת הצורה: | |||
|
|
| |||
|
|
ואם אמר: שלשה שמיניות כמה תשיעיות יהיו בהם | |||
|
|
הכה מספר השמניות בתשעה אשר נרצה שנפרוט אליהם השמיניות יהיו שבעה ועשרים חלקם על השמונה אשר הם מעמד השמינית הנה הם שלשה וישארו שלשה הנה השלשה היוצאים הם תשיעיות והשלשה הנשארים הם שמיניות תשיעיות הנה הם אם כן שלש תשיעיות ושלש שמיני התשיעית | |||
|
|
| |||
| ודע כי כל מעשה השער הזה אמנם הם שתקח מספר השבר המפורט ותכהו תמיד במעמד המפורט אליו וזה המעשה כולל בכל שער הפריטה | ||||
|
|
ואם אמר תשע עשיריות כמה חלקים יהיו בהם מאחד עשר | |||
| הורידם על זאת הצורה: | ||||
|
|
| |||
|
|
אחר כן הכה התשעה באחד עשר וחלק מה שיצא על העשרה תחלה ומה שיצא על האחד עשר ג"כ יצא לך תשעה חלקים מאחד עשר ותשע עשיריות החלק מאחד עשר | |||
|
|
| |||
Fraction and fraction of fraction to fraction |
שער אחר ממנו | |||
|---|---|---|---|---|
|
|
כשיאמר לך חמשה שתותים וחצי כמה עשיריות יהיו בהם | |||
| הוריד החמשה שתותים וחצי שתות בשטה והעשירית בשטה תחתיה על זאת הצורה: | ||||
|
|
| |||
|
|
אחר כן עשה בחמשה שתותים וחצי שתות כמו שקדם בשער השברים יתקבץ בו אחד עשר והכם בעשרה יחלק מה שהתקבץ על הסכום השטה העליונה תחלה אחר כן מה שיצא על העשרה יצא לך המבוקש והוא תשע עשרות ושתות העשירית | |||
|
|
| |||
|
|
ואם יאמ' חמש שמיניות ושליש שמינית כמה חלקים יהיו משלשה עשר | |||
| הוריד החמש שמיניות ושליש שמינית בשטה והוריד תחתיה בשטה אחרת מעמד החלק משלשה עשר תחת קו על זאת הצור': | ||||
|
|
| |||
|
|
אחר כן עשה בחמש שמניות ושליש שמינית כמו שקדם ומה שהתקבץ הכהו בשלשה עשר יתקבץ לך מזה שמנה ומאתים וחלקם על הסכום הקו העליון ומה שיצא על השלשה עשר יצא לך בחלוקה שמנה חלקי' משלשה עשר וחמש שמינייות החלק משלשה עשר ושליש שמינית החלק משלשה עשר | |||
Fraction and fraction to fraction |
שער אחר ממנו | |||
|---|---|---|---|---|
|
|
שני שלישים וחמשה שתותים כמה עשיריות יהיו בהם | |||
|
|
הנה זאת השאלה יתקבצו בה מן העשירות יותר מעשר מפני כי השני שלישים כאשר תפרטם לשתותים יהיו ארבעה שתותים ופה [ועמך] בשבר השני חמשה שתותים הנה כולם תשעה שתותים | |||
| וכאשר תרצה שתפרוט זאת השאלה עשיריים הוריד השני שלישים והחמשה שתותים בשטה והוריד תחת מעמד העשירית בשטה אחרת תחת קו על זאת הצור': | ||||
|
|
| |||
|
|
אחר כן עשה בשני שלישים וחמשה שתותים כמו שקדם מהכאת שני השברי' המתחלפים ומה שהתקבץ תכהו בעשר' ותחלק מה שהתקבץ על סכום השטה העליונה ומה שיצא על העשר יצא לך חמשה עשר עשירייות והוא אחד וחצי | |||
Fraction of fraction to fraction of fraction |
שער אחר ממנו | |||
|---|---|---|---|---|
|
|
כשיאמר לך שליש חומש כמה רביעי חומש יהיה בהם | |||
| תפילם על זאת הצורה: | ||||
|
|
| |||
|
|
הנה זאת השאלה ישתתף החומש בשני הפנים במפורט ובמפורש אליו ותפיל חלק החומש משני הפנים כאשר יקרו תמיד אחר כן תאמר שליש כמה רביע | |||
|
|
ויחס אותו יהיה בהם ותעש' כמו שקדם בשער הראשון מן הפריטת יצא לך רביע ושליש רביע | |||
|
|
ויחס אותו לאל חמישית אחד מאותם החומשים אשר הפלנו זכרם ויהיה רביע חומש ושליש רביע חומש וזה צורתו: | |||
|
|
| |||
|
|
וכן אם יאמר רביע שביעית כמה חמישית שביעית יהיה בהם | |||
|
|
הנה תפיל השביעית בשביעית ותאמ' רביע כמה חומש יהיה בהם | |||
|
|
ותפיל השביעית האחד ותעשה כמו שקדם יצא לך חומש ורביע חומש | |||
|
|
והוא חומש שביעית ורביע חומש שביעית | |||
|
|
| |||
|
|
ואם אמר חמישית שמינית כמה שביעית תשיעית יהיו | |||
| הוריד החמשית שמינית בשטה והוריד תחתיו השביעית תשיעית על זאת הצורה: | ||||
|
|
| |||
|
|
אחר כן תקח האחד אשר הוא החמשית מן הקו העליון ותכהו בסכום הקו התחתון ומה שהתקבץ תחלקהו על הסכום הקו העליון ומה שיצא על הסכום הקו התחתון יצא לך שביעית התשיעית וארבע שמנייות שביעית התשיעית ושלשה חומשי שמינית שביעית התשיעית | |||
|
|
| |||
Fractions of fractions to fraction |
שער אחר ממנו | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך שלשה רביעיות חמשית וחמשה שתותי שביעית ושבע שמניות תשיעית | |||||||||
| בשטה אחת אחר כן הוריד מעמד העשירית בשטה אחרת תחתיו ותמשוך עליו קו על זאת הצורה: | ||||||||||
|
|
| |||||||||
|
|
ותעשה בזאת השאלה כלומר בשטה העליונה מה שקדם בהכאת השברים השלשה בשלשה השברים המתחלפים בכמותם והוא שתקח השלשה אשר על הקו הראשון מן השטה העליונה ותכם בסכום אשר תחת הקו השני ומה שהתקבץ בסכום הקו השלישי, אחר כן תקח מה שעל הקו השלישי ותכהו בסכום השני ומה שהתקבץ בסכום הקו הראשון ותקבץ כל ההכאות השלשה ותכם בעשר' אחר כן תחלק על סכום השטה העליונה תחלה ומה שיצא ה' על העשרה | |||||||||
Addition of Fractions | |
| ואחר שכבר הכאת ממיני השברים מה שבו ספוק למי שירגילם הנה תתחיל עתה בקבוץ השברים ואחר זה בהשלכתם ונמשיך בו רק הקצור ועזיבת האריכות עם מה שיחובר אליהם מדמיונם במה שיצטרך אליו בקבוץ בעזרת האל | |
Chapter One – Adding One Fraction to Another |
השער הראשון מקבוץ השברים קצתם אל קצת | ||||||
|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך קבץ שלשה רביעים אל ארבעה חומשים | ||||||
| הוריד השלשה רביעים בשטה והארבע' חומשים בשטה אחרת על זאת הצורה: | |||||||
|
|
| ||||||
|
|
אחר כן הכהו מה שעל הקו העליון נ' הראשון במה שתחת הקו התחתון נ' השני ומה שעל התחתון במה שתחת הקו העליון כמו שקדם מהכאת שני השברי' המתחלפים ותקבץ שתי ההכאות יהיה זה כלו אחד ושלשים וחלקם על הסכום על הארבעה ומה שיצא על החמשה יצא לך המבוקש והוא אחד ושני חומשים ושלשה רביעי החומש | ||||||
|
|
| ||||||
| ובחינתו כמו שקדם בהכאת השברים בשוה והמעשה בהם אחד | |||||||
|
|
ולהם פנים אחרים והוא שתפרוט השלשה רביעי חומשים יהיו שלשה חומשים ושלשה רביעי החומש ותקבצם אל הארבעה חומשים יהיו שבעה חומשים תפיל מהם חמשה באחד ישארו שני חומשים ושלשה רביעי החומש הנה המקובץ אם כן מהם אחד ושני חומשים ושלשה רביעי החומש | ||||||
Chapter Two – Adding Two Fractions to Two Fractions |
שער קבוץ שני השברים אל שני השברים | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמ' לך קבץ שלשה רביעים וארבעה חומשים אל חמשה שתותים והשש שביעיות | ||||||||||
| על זאת הצורה: | |||||||||||
|
|
| ||||||||||
|
|
אחר כן תעשה בשטה העליונה כמו שקדם בהכאת שני השברים המתחלפים בשערם יתקבץ מזה אחד ושלשים ושלש מאות ואלף ושמרם אחר כן חזור אל השטה העליונה התחתונה ועשה כמו שקדם בשטה העליונה ומה שהתקבץ הכהו בסכום השטה העליונה יתקבץ מזה עשרים וארבע מאות ואלף וקבצם אל המספר השמור הראשון יהיה זה שנים ועשרים ושבע מאות ושני אלפים וחלקם על הסכום יצא לך בחלוקה שלשה ושביעית וארבע שתותי השביעית וחצי חומש שתות השביעית | ||||||||||
| פרק | |||||||||||
| דע כי כל המעשה בכל השברים או השלמים והשברים קצתם אל קצת אמנם השורש בהם שתעשה בכל מספר כמו שעשית בו בשערו בהכאה ומה שהתקבץ לך תכהו בסכום השטה התחתונה ומה שהתקבץ מן השטה התחתונה תכהו בסכום השטה העליונה ואחר כן תקבץ שני מספרים אלו ותחלקם על הסכום | |||||||||||
| ואם תהיה בהשלכה תשליך אחד משני המספרים אלו מן האחר ותחלק הנשאר על הסכום | |||||||||||
| ואם היתה בחלוקה חלקת אחד משני אלו המספרים על השני יצא לך המבוקש והנה נבאר מן הנחלק מהם על חבירו בשער החלוקה | |||||||||||
| ודע כי המעשה הזה יתחבר עמך בקבוץ וההשלכה והעליה [אל גבר] בקצת השאלות וכן הירידה [אלחט] והחלוק | |||||||||||
Chapter Three – Adding Fraction and Fraction of Fraction to Two Different Fractions |
שער קבוץ השבר ושבר השבר אל שני השברים המתחלפים | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך קבץ חמש' שתותים וחצי שתות אל שבע שמיניות שמנה תשיעיות | ||||||||||
| הוריד השאלה על זאת הצורה: | |||||||||||
|
|
| ||||||||||
|
|
אחר כן עשה החמשה שתותי' וחצי שתות כמו שקדם בהכאת השבר ושבר השבר ומה שהתקבץ תכהו בסכום השטה התחתונה יתקבץ מזה שנים ותשעים ושבע מאות ושמרם אחר כן עשה בשני השברים כמו שקדם בשערם ומה שהתקבץ הכהו בסכום הקו העליון יתקבץ מזה ארבעה ועשרים וחמש מאות ואלף וקבצהו אל השמור הראשון יתקבץ מזה ששה עשר ושלש מאות ושני אלפים וחלקם על הסכום כלו העליונה ותחתונה כלומר מה שתחת שני קויהם כמו שביארנו בשער ההכאה יצא לך המבוקש והוא שנים ושש תשיעיות ושמינית תשיעית על זאת הצורה: | ||||||||||
|
|
| ||||||||||
Chapter Four – Adding Fraction and Fraction of Fraction to Fraction and Fraction of Fraction |
שער קבוץ השבר ושבר השבר אל השבר ושבר השבר | ||||||
|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך קבץ חמשה חלקים מאחד עשר ושלשה רביעי החלק מאחד עשר על עשרה חלקים משלשה עשר ושמונה תשיעיות החלק משלשה עשר | ||||||
| והורידם על זאת הצורה: | |||||||
|
|
| ||||||
|
|
אחר כן עשה כל שטה מהם כמו שקדם בשערו ומה שהתקבץ מן השטה העליונה הכהו בסכום השטה התחתונה ותקבץ שתי ההכאות ותחלקם על הסכום יצא לך אחד וארבעה חלקים משלשה עשר ושבעה חלקים מאחד עשר וארבע תשיעיות החלק ושלשה רביעי תשיעית החלק מאחד עשר בחלק משלשה עשר וזה צורתו: | ||||||
|
|
| ||||||
Chapter Five – Adding Integer and Fraction to Integer and Fraction |
שער קבוץ השלם והשבר אל השלם והשבר | ||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמ' לך: קבץ שנים וחצי אל שלשה ושני חומשים | ||||||||
| הוריד השאלה על זאת הצורה: | |||||||||
|
|
| ||||||||
|
|
אחר כן עשה בכל שטה מהם כמו שקדם בשער שנים ועשרים מהכאת השלם והשבר בשלם והשבר ומה שהתקבץ לך מן הקו העליון תכהו בחמשה אשר הם סכום הקו התחתון ומה שהתקבץ גם כן מן הקו התחתון תכהו בשנים אשר הם סכום הקו העליון וקבץ שתי ההכאות יהיו תשעה וחמישים וחלקם על הסכום יצאו חמשה וארבעה חומשים וחצי חומש וזה צורתו: | ||||||||
|
|
| ||||||||
|
|
ואם תרצה קבץ השנים אל השלשה יהיו חמשה אחר כן קבץ חצי אל שני חומשים כמו שקדם יהיו ארבעה חומשים וחצי חומש וחברם אל החמשה יהיו חמשה וארבעה חומשים וחצי חומש | ||||||||
Chapter Six – Adding Integer and Fraction and Fraction of Fraction to Integer and Two Different Fractions |
שער קבוץ השלם והשבר ושבר השבר אל השלם ושני השברים המתחלפים | ||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך קבץ שמונה וחמשה שתותים וחצי שתות אל ששה וחמשה שביעיות ועשרה חלקים מאחד עשר | ||||||||
| הורידם על זאת הצורה: | |||||||||
|
|
| ||||||||
|
|
אחר כן התחיל בשטה העליונה והכה השמונה בחמשה והשיא מה שעל ראשם ומה שהתקבץ הכהו בסכום השטה התחתונה ותשמרהו אחר כן חזור אל השטה התחתונה והכה הששה בשבעה ומה שהתקבץ באחד עשר אחר כן הכה החמשה באחד עשר והעשרה בשבעה ותקבץ אלו ההכאות השלש והכה זה בסכום השטה העליונה ומה שהתקבץ מהם תקבצהו עם השמור הראשון ותחלק הכל על הסכום יצא לך ששה עשר וחמשה חלקים מאחד עשר וששה שביעיות החלק מאחד עשר ושלשה שתותי שביעית החלק מאחד עשר וחצי שתות שביעית החלק מאחד עשר וזו צורתו: | ||||||||
|
|
| ||||||||
Chapter Seven – Adding Fraction of Integer to Integer |
שער אחר ממנו | ||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך קבץ שלשה רביעי חמשה אל דומה לו | ||||||||
| הוריד השאלה על זאת הצורה: | |||||||||
|
|
| ||||||||
|
|
אחר כן הכה השלשה אשר על הקו בחמשה והכה השלש' בארבעה וקבץ שתי ההכאות וחלק על ארבעה יצא לך תשעה ושלשה רביעים | ||||||||
|
|
ואם תרצה קח שלשה רביעי החמשה והוא שלשה ושלשה רביעים וקבצם אל הששה | ||||||||
Chapter Eight – Adding Fraction of Integer to Fraction of Integer |
שער אחר ממנו | ||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך קבץ שני שלישי שבעה אל שבע שמיניות תשעה | ||||||||
| הוריד השאלה על זאת הצורה: | |||||||||
|
|
| ||||||||
|
|
אחר כן עשה בזאת השאלה כמו שקדם בשער הכאת שבר המספר והוא שתכה השנים בשבעה ומה שהתקבץ הכהו בסכום הקו התחתון והוא שמונה לפי מה שהתניתו בראשית המין הזה אחר כן הכה גם כן השבעה אשר על השמונה בתשעה ומה שהתקבץ בשלשה והוא סכום הקו העליון ותקבץ שתי ההכאות וחלק על הסכום יצא לך המבוקש והוא שנים עשר וארבע שמיניות ושליש שמיניות | ||||||||
|
|
ואם תרצה הכה שני שליש בשבעה יצא לך ארבעה ושני שלישים אחר כן הכה שבע שמיניות בתשעה יצא שבעה ושבע שמיניות וקבצם אל הארבעה ושני שלישים כמו שקדם | ||||||||
Chapter Nine – Adding Fraction of Integer and Fraction to Fraction of Integer and Fraction |
שער אחר ממנו | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך קבץ שלשה רביעי חמשה וחצי אל חמשה שתותי ששה ושליש | ||||||||||||
| הורידם על זאת הצורה: | |||||||||||||
|
|
| ||||||||||||
|
|
אחר כן עשה בכל שטה מזאת השאלה כמו שקדם בשער שנים וארבעים מהכאת השברים ומה שהתקבץ מכל שטה מהם הכה היוצא מן השטה העליונה בסכום השט' התחתונה והיוצא מן השטה התחתונה הכהו בסכום השטה העליונה וקבץ שתי ההכאות וחלקהו על הסכום יצא לך המבוקש והוא תשעה ושלשה שמיניות ושתות שמינית ושליש שתות שמינית על הצורה הזאת: | ||||||||||||
|
|
| ||||||||||||
| והבן | |||||||||||||
Addition of Unknown Amounts |
שער קבוץ הממונות |
|---|---|
|
|
כשיאמר לך: קבץ מהממון שלישיתו ורביעיתו ודע כמה הנשאר |
|
|
הנה זאת השאלה כאלו אמר: קבץ שליש אל רביע |
|
|
ועשה כמו שקדם יצא לך שלשה שתותים וחצי שתות |
|
|
ואם אמר לך: קבץ מעשרה דרהם שלישיתם ורביעיתם ודע כמה המקובץ |
|
|
כאלו אמר: הכה שליש ורביע בעשרה |
|
|
ותעשה כמו שקדם יצא חמשה וחמש שתותים |
|
|
ואם תרצה קבץ שליש אל רביע והכה מה שיצא בעשרה |
|
|
ואם אמר קבץ מעשרה דרהם שלישיתם ורביעיתם וחומש מה שנשאר |
|
|
הנה המעשה בזאת השאלה שתעמיד השליש משלשה והרביע מארבעה אחר כן הכה השלשה בארבעה יהיו שנים עשר וקחם סכום אחר כן תקח מן השנים עשר שלישיתם ורביעיתם והם שבעה הנשאר חמשה ותקח מהם חמישיתם לאומרו חומש הנשאר והוא אחד ותחברהו אל השבעה יהיו שמונה והכם בעשרה דרהם וחלק מה שהתקבץ על השנים עשר אשר הם הסכום יצא לך ששה ושני שלישים |
| ואם תרצה קרא שם העשרה מן השנים עשר ותקח היחס ההוא מן השמנה | |
|
|
ואם תרצה תקרא השמנה מן השנים עשר ותקח היחס ההוא מן העשרה |
|
|
ואם אמר קבץ מעשרה דרהם שלישיתם ורביעיתם ודרהם |
| הכה שלישית ורביע בעשרה ומה שיצא תוסיף עליו דרהם | |
|
|
ואם תרצה העמד השליש והרביע משנים עשר ותקח שלישיתם ורביעיתם והוא שבעה ותכם בעשרה יהיו שבעים אחר כן הכה הדרהם בשנים עשר והשיאהו על השבעים יהיה זה שנים ושמונים וחלקם על השנים עשר אשר הם הסכום יצא לך ששה וחמשה שתותי' |
|
|
ואלו אמר שלישיתם ורביעתם אלא דרהם |
|
|
תהיה מפיל השנים עשר מן השבעים ומה שנשאר תחלקהו על הסכום יצא לך ארבעה וחמשה שתותים |
Word Problems: How Much or How Many |
שער אחר מקבוץ הממונות |
|---|---|
|
אם יאמר לך אדם: ממון קבצת שלישיתו ורביעיתו והיה אחד ועשרים דרהם |
|
|
הנה המעשה בזאת השאלה שתעמיד השליש והרביע משנים עשר אחר כן תקח מן השנים עשר שלישיתם ורביעיתם והוא שבעה הנה יחס אלו השבעה מן השנים עשר אשר הם הסכום כיחס האחד ועשרים מן הממון המבוקש |
|
|
והכה השנים עשר באחד ועשרים ותחלק מה שיצא על השבעה יצא לך ששה ושלשים והוא הממון |
|
ואם תרצה עשה אותו בעליה [באלגבר] |
|
|
והוא שתשים הממון דבר ותקח ממנו שלישיתו ורביעיתו והוא שלשה שתותי דבר וחצי שתות דבר הנה הוא שוה האחד ועשרים |
|
|
ותאמר בכמה תעלה השלשה שתותים וחצי שתות עד שיהיה דבר שלם תמצא זה בהכותו באחד וחמש שביעיות |
|
|
והנה ביארנוהו בשער עליית [חיתום] השברים ותכה אחד וחמשה שביעיות באחד ועשרים יצא לך ששה ושלשים והוא הממון |
|
ואם תרצה תעשהו בחפנים |
|
והוא שתקח איזה מספר שתרצה לסכום כי הנה אפשר זה ותשים הסכום החופן האחד שלשה ותקח שלישיתם ורביעיתם והוא אחד ושלש רביעיות ותקבל בהם האחד ועשרים תמצא אותם פחות מהם הנה טעית בחופן שלש תשעה עשר ורביע חסר ושמור זה הטעות |
|
אחר כן תקח חופן שני והוא ארבעה ותקח שלישיתם ורביעיתם והוא שנים ושליש ותקביל בהם האחד ועשרים הנה טעית בחופן ארבעה בשמונה עשר ושני שלישים |
|
|
וחסר ותכה טעות חופן הראשון אשר הוא תשעה עשר ורביע בחופן השני אשר הוא ארבעה יהיה זה שבעה ושבעים ושמרם אחר כן הכה טעות החופן השני אשר הוא שמונה עשר ושני שלישים בחופן הראשון אשר הוא שלשה יתקבץ מזה ששה וחמישים והשליכם מן השבעה ושבעים הנשאר אחד ועשרים אחר כן השליך הפחות משתי הטעיות מן היותר גדול מהם הנשאר שלשה שתותים וחצי שתות וחלק עליהם האחד ועשרים יצא לך ששה ושלושים והוא הממון והנה נבאר היחס הזה בשערו |
| שער אחר ממנו | |
|
ממון קבצת שלישיתו ורביעיתו וחצי מה שנשאר והיו עשרה דרהם כמה הממון |
|
|
הנה המעשה בזה שתעמיד השליש והרביע והחצי מארבעה ועשרים ותקח שלישיתם ורביעיתם והוא ארבעה עשר ותפילם מן הארבעה ועשרים ישארו עשרה ותקח חציים וחצי מה שנשאר ישאר חמשה אחר כן חברם אל הארבעה עשר יהיו תשעה עשר וקחם סכום האחד אחר כן הכה העשרה בארבעה ועשרים ותחלק מה שהתקבץ על הסכום יצא לך שנים עשר ושנים עשר חלקים מתשעה עשר חלק והוא הממון |
|
ובחינת זאת השאלה שתקבץ משנים עשר ושנים עשר חלק מתשעה עשר שלישיתם ורביעיתם וחצי מה שנשאר ותעשה כמו שקדם |
| ואם יהיה היוצא עשרה הנה כבר התאמת המעשה הראשון | |
|
ואם תרצה תעשה אותו בחתום |
|
|
והוא שתשים הממון דבר ותקח שלישיתו ורביעיתו וחצי מה שנשאר והיו ארבעה שתותי דבר וחצי שתות הנה הוא ישוה עשרה |
|
|
ותאמר בכמה תחתים ארבעה שתותים ושלשה רביעי שתות עד שיהיה אחד תמצא זה בהכותם באחד וחמשה חלקים מתשעה עשר |
|
|
ותכה אחד וחמשה חלקים מ[תשעה] עשר בעשרה ומה שהתקבץ הנה הוא הממון |
|
ואם תרצה תעשה אותו בחופנים |
|
והוא שתקח חופן מששה ותקח מהם שלישיתם ורביעיתם וחצי מה שנשאר יהיה זה ארבעה ושלשה רביעים ותקביל העשרה הנה כבר טעית בחופן ששה בחמשה ורביע חסר ושמרם |
|
אחר כן תקח חופן אחד משמונה וקח שלישיתם ורביעיתם וחצי מה שנשאר יהיה זה ששה ושני שלישים ותקביל בהם העשרה הנה כבר טעית בחופן שמנה בשלשה ושני שלישים חסרים |
|
|
והכה טעות החופן הראשון אשר הוא חמשה ורביע בחופן השני אשר הוא שמונה יהיו שנים וארבעים אחר כן תכה טעות החופן השני אשר הם שלשה ושני שלישים בחופן הראשון אשר הוא ששה יהיו עשרים ותפילם מן השנים וארבעים הנשאר עשרים הפיל הפחות מן הטעיות מן היותר גדול והנה נבארהו בשער ההשלכה ישאר אחד ושלשה שתותים וחצי שתות וחלק עליהם העשרים יצא שנים עשר ושנים עשר חלק מתשעה עשר והוא הממון |
|
ואם תרצה תקח מאחד שלישיתו ורביעיתו וחצי מה שנשאר יהיה זה ארבעה שתותים ושלשה רביעי שתות הנה יחס אלו הארבעה שתותים ושלשה רביעיות שתות אל אחד כיחס עשרה מן המבוקש הנה אלו הארבעה מספרים מתיחסים הראשון מהם ארבעה שתותים ושלשה רביעי שתות והשני אחד והשלישי עשרה והרביעי הנעלם |
|
|
ותכה השני והוא אחד בשלישי והוא עשרה ותחלק המקובץ על הראשון והוא ארבעה שתותים ושלשה רביעי שתות והנה נבאר היחס הזה בשער חלוקת השברים |
| שער אחר ממנו | |
|---|---|
|
כשיאמר לך ממון קבצת שלישיתו ורביעיתו ודרהם והיו חמשה עשר דרהם כמה הממון |
|
|
הפיל הדרהם מן החמשה עשר הנשאר ארבעה עשר |
|
והוא כאלו אמר ממון קבצת שלישיתו ורביעיתו והיו ארבעה עשר דרהם |
|
|
הנה תעשה כמו שקדם יצא הממון ארבעה ועשרים |
|
ואם אמר ממון קבצת שלישיתו ורביעיתו אלא שני דרהם והיו שנים עשר דרהם |
|
|
הנה תוסיף השני דרהם על השנים עשר יהיו ארבעה עשר |
|
והוא כאלו אמר ממון קבצת שלישיתו ורביעיתו והיו ארבעה עשר דרהם |
| ותעשה כמו שקדם | |
|
ואם אמר: ממון קבצת שלישיתו וארבעה דרהם וחמישיתו אלא שני דרהם והיה עשרה דרהם |
|
|
הנה עמך ארבעה דרהם נוספים ושני דרהם חסרים והפיל השני דרהם החסרים מהד' נוספים והנשאר שני דרהם נוספים והפילם מן העשר' הנשאר שמונה |
|
והוא כאלו אמר: ממון קבצת שלישיתו וחמשיתו והיו שמנה |
|
|
ותעשה כמו שקדם יצא הממון חמשה עשר |
|
ואם אמר ממון קבצת חמישיתו וששה דרהם ושתותו אלא שמונה דרהם והיה שמונה דרהם |
|
|
הנה תפיל מן השמונה דרהם הששה דרהם הנשאר שני דרהם והם חסרים |
|
והוא כאלו אמר: ממון קבצת חמישיתו ושתותו והיו עשרה דרהם |
| ותעשה כמו שקדם | |
| ודע כי כאשר היו הדראהם המונחים עם השליש והשתות והחלק המונח נוסף ותפילם מן המספר אשר זכר שהוא התקבץ לו מן החלקים ואם היו חסרים הוסיפם אחר כן עשה כזה כמו שקדם | |
| שער אחר ממנו | |
|
ממון קבצת שלישיתו ורביעיתו והכיתו בדומה ושב הממון |
|
|
העמיד השליש והרביע משנים עשר אחר כן תקח שלישיתם ורביעיתם והוא שבעה והכם בדומה להם יהיו תשעה וארבעים והוא הסכום אחר כן תכה השנים עשר בדומה להם וחלקם על הסכום יצא לך בחלוק שנים ושש שביעיות וארבעה שביעיות השביעית |
|
ואם תרצה עשה אותו בחתום |
|
|
והוא שתשים הממון דבר ותקח שלישיתו ורביעיתו והוא שלשה שתותי דבר וחצי שתות דבר והכם בדומה להם יהיו שלשה תשיעי ממון וחצי שמינית תשיעית ממון הנה זה ישוה דבר |
| ותחתים דבר ותקביל יצא לך הממון אשר זכרנו | |
|
ואלו אמר ממון קבצת שלישיתו ורביעיתו ותכהו בדומה לו וחזר הממון וכמו שלישיתו |
|
|
העמיד השליש והרביע משנים עשר אחר כן תקח שלישיתו ורביעיתו בשבעה והכם בדומה להם יהיו תשעה וארבעים הנה הוא הסכום אחר כן הכה השנים עשר בדומה להם והשיא על מה שהתקבץ שלישיתו יהיה זה ארבעים ומאתים וחלקהו על הסכום יצא לך הממון ארבעה ושש שביעיות ושני שביעי השביעית |
|
ואם אמר ממון קבצת שלישיתו וחמישיתו ולקחת רביע מה שקבצת וחצי מה שנשאר והיה אחד עשר |
|
|
העמיד השליש והרביע והחומש משישים ולא נהיה צריכים להעמיד החצי כי הוא ימצא ברביע וקח מן השישים שלישיתם וחמישיתם והוא שנים ושלשים הנשאר מן השישים שמונה ועשרים ותקח חציים והוא ארבעה עשר ותקח רביע השנים ושלשים אשר נקבצו תחלה והם שמנה ותחברם אל הארבעה עשר יהיו שנים ועשרים והוא הסכום אחר כן הכה האחד עשר בששים וחלקם על הסכום יצא שלשים והוא הממון |
|
|
ואם תרצה תחלק תחלה האחד עשר על השנים ועשרים יצא חצי ותכהו בששים |
|
|
תרצה תחלקהו בששים על השנים ועשרים ומה שיצא תכהו באחד עשר |
|
ואם אמר ממון קבצת חציו ושלישית מה שנשאר ורביע מה שנשאר וחומש מה שנשאר והיו עשרים דרהם כמו הממון |
|
|
העמיד השליש והרביע והחומש מששים ותקח חציים שהוא שלשי' ותקח שליש מה שנשאר שהוא עשרה הנשאר עשרים ותקח רביע מה שנשאר שהוא חמשה הנשאר חמשה עשר ותקח חמשיתם והוא שלשה אחר כן קבץ השלשים עם העשרה והחמשה והשלשה ותקבץ זה כלו יהיו שמנה וארבעים הנה הוא הסכום אחר כן הכה העשרי' בששים ותחלק מה שהתקבץ על הסכום יצא לך המבוקש חמשה ועשרים |
|
|
ואם תרצה תחלק הששים על השמנה וארבעי' ומה שיצא תכהו בשישי' |
|
|
ואם תרצה תחלק השמנה וארבעים על העשרים יצא שנים ושני חומשים ותחלק הששים עליהם יצא לך הממון |
Two Unknowns |
שער אחר ממנו |
|---|---|
|
|
שני מספרים מתחלפים קבצת שליש אחד משניהם אל רביע השני והיה ששה |
| זאת השאלה יש לה הישרות רבות | |
|
|
ואחת מההיישרות שתקח מן הששה כמה שתרצה ותשימהו שליש אחד משני המספרים יהיה הנשאר מן הששה רביע המספר השני |
|
|
ואם תשים הלקוח מן הששה הראשון רביע אחד משני המספרים יהיה הנשאר שליש השני |
|
|
כאלו אתה תקח מן הששה שנים ותשימם שליש אחד משני המספרים ויהיה המספר אשר יהיו השנים שלישיתו ששה אחר כן תפיל השנים מן הששה הנשאר ארבעה והם רביע המספר השני הנה המספר השני אם כן ששה עשר אם כן אחד משני המספרים ששה והשני ששה עשר |
|
|
ואם תרצה שיהיה אחד משני המספרים שמנה והשני שנים עשר |
|
|
או יהיה אחד מהמספרים ארבעה והשני חמשה עשר |
|
|
או יהיה אחד משני המספרים תשעה והשני שנים עשר |
Sums |
שער מן הקבוץ ג"כ והוא קבוץ המספרים |
|---|---|
|
|
כשיאמר לך קבץ מאחד עד עשרה על המשך המספר |
|
|
השיא אחד על עשרה יהיו אחד עשר והכם בחצי העשרה והוא חמשה יהיו חמשה וחמישים והוא המבוקש |
| שער | |
|
ודע כי כאשר נאמר לך קבץ מאחד עד מספר על המשך המספר השיא תמיד חצי אחד על המספר ותכה המקובץ בחצי המספר הראשון ומה שהתקבץ הוא המבוקש |
| שער | |
|
|
ואם אמר לך: קבץ מחמשה עד עשרה |
|
|
קבץ תחלה מאחד עד עשרה כמו שקדם יהיו חמשה וחמשים אחר כן תפיל אחד תמיד מן זה הששה הנשאר ארבעה וקבץ מאחד עד ארבעה יהיו עשרה ותפילם מן החמשה וחמשים הנשאר חמשה וארבעי' והוא אשר יתקבץ מחמשה עד עשרה |
| שער אחר ממנו | |
|
|
קבץ מאחד עד מספר בלתי ידוע על המשך המספר והגיע חמשה וחמישים כמה המספר הבלתי ידוע |
|
|
הנה הקשו שתכה החמשה וחמשים בשנים תמיד יהיו עשרה ומאה ושמרם אחר כן קח חצי האחד אשר התחלת הקבוץ ממנו הוא חצי והכהו בדומה לו יהיה רביע והשיאהו על העשרה ומאה ורביע ותקח גדרו והנה נבאר זה בשער הגדר יהיה עשרה וחצי ותפיל מהם החצי אשר הכית בדומ' הנשאר עשרה והוא המספר הבלתי ידוע |
|
ואם תרצה בחיתום |
|
|
שים המספר דבר והשיא עליו אחד יהיה אחד ודבר והכהו בחצי הדבר אשר הוא המספר הראשון יהיה חצי ממון וחצי דבר ישוה חמשה וחמשים |
|
|
ותחתים הממון ותכהו בשנים ותכה כל המשוה בשנים יהיה עמך ממון ודבר ישוה מאה ועשרה הנה כבר יצאת אל האופן הראשון מאופני החיתום ותעשה כמו שנזכ' במקומו בע"ה |
Odds |
שער אחר ממנו |
|---|---|
|
|
קבץ מאחד עד תשעה עשר על המשך הנפרדים |
|
|
הקשו שתשיא אחד ממנו תמיד על התשעה עשר יהיו עשרים ותקח חציים והוא עשרה ותכם על עצמם יהיו מאה והוא המספר אשר יתקבץ מאחד עד תשעה עשר על המשך הנפרדים |
| פרק | |
| ואלו אמר בזאת השאלה קבץ מאחד עד עשר' או עד שנים עשר על המשך הנפרדים לא יחתום מפני כי העשרה מן המספר הזוג ואינו מן המספר הנפרד | |
|
|
ואם אמר קבץ משבעה עד שלשה עשר על המשך הנפרדים |
|
|
קבץ מאחד עד שלשה עשר יתקבץ בו תשעה וארבעים אחר כן תפיל מהשבעה שנים הנשאר חמשה וקבץ מאחד עד חמשה על המשך הנפרדים יהיו תשעה ותפילם מן התשעה וארבעים הנשאר ארבעים |
|
|
ואם אמר קבץ מאחד עד מספר בלתי ידוע על המשך והתקבץ ששה ושלשים כמה המספר הנפרד |
|
|
הקישו שיקח גדר שש' ושלשים והוא ששה וכפלם יהיו שנים עשר ותפיל מהם אחד הנשאר אחד עשר והוא המספר הנפרד אשר התקבץ אליו |
|
ואם תרצה שים המספר דבר והשיא עליו אחד יהיה אחד ודבר ותקח חציו והוא חצי אחד וחצי דבר והכהו בכמוהו רביע ממון וחצי דבר ורביע אחד הנה זה ישוה ששה ושלשי' |
|
|
ותפיל הרביע אחד הנשאר חמשה ושלשים ושלשה רביעים הנה עמך רביע ממון וחצי דבר ישוה חמשה ושלשים ושלש' רביעים |
|
|
ותחתים רביע הממון והוא שתכהו בארבעה ותכה כל ההשואת בארבעה יהיו ממון וששים ישוה מאה ושלש וארבעים הנה כבר יצא אל המין הרביעי מן החיתום ותעשה כמו שקדם יצא הדבר אחד עשר והוא המספר הבלתי ידוע |
|
|
ואם תרצה תכה הששה ושלשים בארבעה תמיד ותקח גדר מה שיצא ותפיל ממנו אחד |
| ודע כי אתה אם תעשה זאת השאלה באופן החיתום ויצא השאלה בלתי מדברת הנה המעשה טעות | |
Evens |
שער אחר ממנו |
|---|---|
|
|
כשיאמר לך קבץ משנים עד עשרה על המשך הזוגות |
|
|
השיא השנים על העשרה תמיד יהיו שנים עשר ותקח חציים ותכהו בחצי העשרה יהיה זה שלשים והוא המספר אשר תרצה |
|
|
ואם תרצה קח רביע השנים עשר ותכהו בעשרה או תקח רביע העשרה ותכהו בשנים עשר |
|
|
ואם אמר קבץ מששה עד שנים עשר על המשך הזוגות |
|
|
הקשו שתקבץ משנים עד שנים עשר יהיו שנים וארבעים אחר כן תפיל מן השש שנים הנשאר ארבעה וקבץ מן השנים עד ארבעה יהיו ששה ותפילם מן השנים וארבעים הנשאר ששה ושלשים והוא המספר המבוקש |
|
|
ואם אמר קבץ משנים אל מספר זוג על המשך הזוגות והתקבץ שלשים כמה המספר הבלתי ידוע אשר התקבץ אליו |
|
|
הקשו שתכה השלשים בארבעה תמיד יהיו מאה ועשרים אחר כן תקח חצי השנים תמיד ותכהו בדומה לו יהיה אחד והשיאהו על המאה ועשרים יהיה אחד ועשרים ומאה וקח גדרו והוא אחד עשר ותפיל מהם האחד אשר הכית אותו בדומה לו ישארו עשרה והוא המספר המושכל |
|
ואם תרצה שים המספר דבר והשיא עליו שנים יהיו שנים ודבר ותקח מהם חציים והוא חצי דבר ואחד ותכהו בחצי הדבר יהיה רביע הממון ישוה שלשים |
|
|
ותחתים ותקביל יצא הדבר עשרה והוא מה שרצית |
Squares |
שער אחר ממנו |
|---|---|
|
|
קבץ ממרובע אחד עד מרובע עשרה על המשך המספר |
|
|
הקשו שתקבץ מאחד עד עשרה כמו שקדם יהיו חמשה וחמישים אחר כן תקח שני שלישי העשרה בתוספת שליש אחד תמיד יהיו שבעה והכם בחמשה וחמישים יהיו חמשה ושמונים ושלש מאות והוא מה שרצית |
|
|
ואם אמר קבץ ממרובע חמשה עד מרובע שנים עשר |
|
|
קבץ תחלה ממרובע אחד עד מרובע שנים עשר ומה שהתקבץ שמרהו אחר כן תפיל אחד תמיד מן החמשה הנשאר ארבעה ותקבץ ממרובע אחד עד מרובע ארבעה ומה שהתקבץ הפילהו מן השמור הראשון ומה שנשאר הנה הוא המבוקש |
Squares of Evens |
שער אחר ממנו |
|---|---|
|
|
קבץ ממרובע שנים עד מרובע עשרה על המשך הזוגות |
|
|
הקשו שתקבץ משנים עד עשרה יהיו שלשים אחר כן תקח שני שלישי העשרה בתוספת שני שלישי אחד והוא שבעה ושליש ותכהו בשלשים יהיו עשרים ומאתים והוא מה שרצית |
|
|
ואם תרצה הנה תקח מן השלשים שני שלישיתם יהיו עשרים אחר כן תקח העשרה ותשיא אחד יהיו אחד עשר והכם בעשרים |
|
|
ואם אמר קבץ ממרובע ששה עד מרובע ששה עשר |
|
|
קבץ ממרובע שנים עד מרובע ששה עשר ומה שהתקבץ שמרהו אחר כן הפיל מן הששה השנים הנשאר ארבעה וקבץ ממרובע שנים עד מרובע ארבעה ותפיל מן השמור ומה שנשאר הנה הוא המבוקש |
| ואם אמר קבץ ממרובע אחד עד מרובע ארבעה | |
| והפיל מן השמור ומה שנשאר הוא המבוקש | |
Squares of Odds |
|
|
|
ואם אמר קבץ ממרובע אחד עד מרובע תשעה על המשך הנפרד |
|
|
הקשו שתשיא על התשעה שנים יהיו אחד עשר אחר כן השיא על התשעה אחד יהיו עשרה וקח חציים ותכהו בחצי האחד עשר ומה שהתקבץ הכהו בשני שלישי התשעה יהיה זה חמשה ושישים ומאה והוא מה שרצית |
|
|
ואם תרצה קבץ מאחד עד תשעה יהיו חמשה ועשרים ותפיל מהם שלישיתם בתוספת שתות אחד הנשאר ששה עשר וחצי אחר כן השיא אחד על התשעה יהיו עשרה והכם בששה עשר וחצי |
|
|
ואם תרצה השיא על התשעה אחד והכה מה שהתקבץ בחצי התשעה ומה שהתקבץ הכהו בשליש התשעה בתוספת שני שלישי אחד ומה שהתקבץ הנה הוא מה שרצית |
|
|
ואם תרצה הנה תקח חצי התשעה ותשמרהו ותקח שליש התשעה בתוספת שני שלישי אחד ותשמרהו ג"כ אחר כן תשיא על התשע' אחד יהיו עשרה אחר כן תכה הארבעה וחצי בשלשה ושני שלישים ומה שהתקבץ בעשרה |
Cubics |
שער אחר ממנו |
|---|---|
|
|
קבץ מן מעוקב אחד עד מעוקב עשרה על המשך המספר |
|
|
המעשה בזה שתקבץ מאחד עד עשרה על המשך המספר יהיו חמשה וחמישים והכם בכמוהם והוא מה שרצית |
|
|
ואם אמר קבץ ממעוקב ארבעה עד מעוקב עשרה |
|
|
תפיל מן הארבעה אחד הנשאר שלשה אחר כן קבץ מן מעוקב אחד עד מעוקב עשרה וקבץ ג"כ ממעוקב אחד עד מעוקב שלשה והפיל הפחות מן היותר ומה שנשאר הנה הוא המבוקש |
|
|
ואם אמר קבץ ממעוקב אחד עד מעוקב מספר מושכל והגיע חמשה ועשרים ושלשת אלפים כמה המספר המוסכל |
|
|
הקשו שתקח גדר החמשה ועשרים ושלשת אלפים יהיו חמשה וחמשי' |
| וכאלו אמר לך קבץ מאחד עד מספר מושכל והגיע חמשה וחמשי' כמה המספר המושכל | |
|
|
ותעשה כמו שקדם יצא המספר עשרה |
| פרק | |
| ודע כי כאשר היה בשער הזה המספר המונח אין לו גדר הנה השאלה טעות | |
| ואם תרצה תעשה אותה בחיתום כמו שקדם בשורש המעשה תחלה | |
Cubics of Odds |
שער אחר ממנו |
|---|---|
|
|
קבץ ממעוקב אחד עד מעוקב תשעה על המשך הנפרד |
|
|
הקשו שתקבץ מאחד עד תשעה יהיו חמשה ועשרים והכם בכפלם אלא אחד ומה שהתקבץ הנה הוא מה שרצית והוא חמשה ועשרים ומאתים ואלף |
|
|
ואם אמר קבץ ממעוקב שבעה עד מעוקב אחד עשר |
|
|
הפיל מן השבעה שנים הנשאר חמשה וקבץ ממעוקב אחד עד מעוקב אחד עשר וקבץ ג"כ מן מעוקב אחד עד מעוקב חמשה והפילהו מן הראשון ותפיל הפחות מן היותר ומה שנשאר הוא המבוקש והוא שני אלפים וארבע מאות ושלשה |
| שער אחר ממנו | |
|
|
קבץ ממעוקב אחד עד מעוקב מושכל על המשך הנפרדים והתקבץ חמשה ועשרים ומאתים ואלף כמה המספר המושכל |
|
|
הקשו שתקח חצי המספר תמיד יהיו שנים עשר ושש מאות וחצי אחר כן תקח מן האחד רביעיתו ותכהו בכמוהו יהיה חצי שמינית והשיאהו על השנים עשר ושש מאות וחצי וקח גדר מה שיצא יהיו ארבעה ועשרים ושלש רביעיות והשיא עליו הרביע אשר לקחת מן האחד יהיו חמשה ועשרים והכם בארבעה ותקח גדר מה שיצא ותפיל ממנו אחד הנשאר תשעה והוא המספר |
|
ואם תרצה בחיתום |
|
|
וזה שתשים המספר דבר ותשיא עליו אחד ותקח חצי המקובץ ותכהו בעצמו ומה שהתקבץ בכפלו אלא אחד ותקביל במקובץ המספר |
|
|
יצא הדבר תשעה והוא המספר |
|
|
ואם תרצה תשים המספר המוכה בכפלו אלא אחד והוא שני דברים אלא אחד ותקביל במקובץ המספר הנזכר |
|
|
יצא הדבר חמשה ועשרי' אחר כן תאמר קבץ מאחד עד מספר נפרד על המשך הנפרד והגיע חמשה ועשרים כמה המספר הנפרד |
|
|
הנה תעשה כמו שקדם יצא תשעה והוא המספר |
Cubics of Evens |
שער אחר ממנו |
|---|---|
|
|
קבץ ממעוקב שנים עד מעוקב עשר' על המשך הזוגות |
|
|
קבץ תחלה משנים עד עשרה כמו שקדם יצאו שלשים והכם בכפלם יהיו אלף ושמנה מאות והוא מה שרצית |
|
|
ואם אמר קבץ ממעוקב שמנה עד מעוקב ששה עשר |
|
|
הפיל מן השמנה שנים תמיד אחר כן קבץ ממעוקב שנים עד מעוקב ששה עשר אחר כן קבץ ממעוקב שנים עד מעוקב ששה והפילהו מן הראשון הנה מה שנשאר הוא המבוקש |
|
|
ואם אמר קבץ ממעוקב שנים עד מעוקב מספר מוסכל על המשך הזוגות והגיע שני אלפים ושמנה מאות כמה המספר המוסכל |
|
|
המעשה בזה שתקח חצי המספר המונח ותקח גדרו יהיו שלשים |
| והוא כאלו יאמר לך קבץ משנים עד מספר זוג על המשך הזוגות והגיע שלשים כמה המספר הזוג | |
|
|
הנה תעשה כמו שקדם ויצא המספר עשרה |
Geometrical Progression of Doubles – Squares of Chessboard |
המאמר בכפול בתי הנרדשיר הוא האשקקור |
|---|---|
| וקבץ מה שבהם עד שיהיה בבית הראשון אחד ובשני שנים ובשלשי ארבעה וברביעי שמנה ובחמשי ששה עשר | |
| וכן תכפול המספר לכל בית עד שישתוו בכל הארבעה וששים בית | |
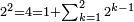
|
וכאשר תרצה זה תשים מה שבבית הראשון שנים והכם בכמותם יהיו ארבעה והוא מה שבבית הראשון והשני בתוספת אחד |
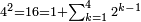
|
אחר כן הכה הארבעה בכמותם יהיו ששה עשר והוא מה שבבית הרביעי וכן כל מה שלפניו בתוספת אחד |
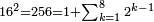
|
אחר כן הכה הששה עשר בכמותם יהיו ששה וחמישים ומאתים והוא מה שבבית השמיני וכל מה שלפניו בתוספת אחד |
| 2 5 6 | ו ה ב |
| והכה הששה וחמישים ומאתים בכמותם יהיו ששה ושלשים וחמש מאות וחמשה וששים אלף וזה צורתם: | |
| 6 5 5 3 6 | ו ג ה ה ו |
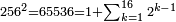
|
והוא מה שבבית השש עשרה וכל מה שלפניו בתוספת אחד |
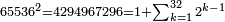
|
אחר כן הכה השש עשרה בכמותו יהיה היוצא ששה ותשעים ומאתים ושבעה ושישים אלף ותשע מאות אלפים וארבעה ותשעים אלף אלפים ומאתים אלף אלפים וארבעת אלפי אלף אלפים והוא מה שבבית השנים ושלשים וכל מה שלפניו וזה צורתם: |
| 4 2 9 4 9 6 7 2 9 6 | ו ט ב ז ו ט ד ט ב ד |
| אחר כן הכה הבית השנים ושלשים בכמוהו יהיה היוצא ששה עשר ושש מאות ואחד וחמישים אלף וחמש מאות אלפים ותשעת אלפי אלפים ושבע מאות אלפי אלפים ושלשה ושבעים אלף כפולים שלשה וארבעה וארבעים אלף כפולים ארבעה ושבע מאות אלף כפולים ארבעה וששה וארבעים אלף כפולים חמשה וארבע מאות אלף כפולים חמשה ושמונה עשר אלף כפולים ששה וזה צורתם: | |
| 1 °8 4 4 °6 7 4 °4 0 7 °3 7 0 °9 5 5 °1 6 1 6 | ו א ו א° ה ה ט° 0 ז ג° ז 0 ד° ד ז ו° ד ד ח° א |
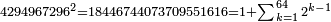
|
והוא כל מה שבבתי הנדרשיר הארבעה וששים ונוסף עליהם אחד |
| הפיל מהם האחד יהיה ראשון השאלה חמשה עשר | |
Subtraction of Fractions |
שער ההשלכה | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| דע כי כל מה ששמשת מן המעשים בשער הקבוץ תשתמש בשער ההשלכה | |||||||||||
| דמיון זה כי כאשר תרצה שתשליך מספר ושבר | |||||||||||
| הנה אתה תעשה במספר והשבר כמו שקדם בשער ההכאה ומה שהתקבץ הכהו בסכום הקו התחתון אחר כן תשמרהו אל צד אחד כן תעשה ג"כ בשטה התחתונה כמו שקדם בשער ההכאה ומה שהתקבץ הכהו בסכום השטה העליונה ומה שהתקבץ תשליך ממנו המספר הראשון השמור ומה שישאר תחלקהו על הסכום ומה שיצא הנה הוא המבוקש | |||||||||||
|
|
כשיאמר לך השלך רביע חמשה שתותים | ||||||||||
| הוריד הרביע בשטה והוריד החמשה שתותים בשטה אחרת תחתיה על זאת הצורה: | |||||||||||
|
|
| ||||||||||
|
|
אחר כן הכה האחד אשר על הקו העליון בששה אשר הם סכום הקו התחתון יהיו ששה ושמרם אחר כן הכה החמשה אשר על הקו התחתון בארבעה אשר הם סכום הקו העליון יהיו עשרים והפיל מהם הששה הנשאר ארבעה עשר וחלקם על הסכום יצא לך המבוקש והוא שלשה שתותים וחצי שתות | ||||||||||
|
|
| ||||||||||
|
|
ואם אמר: השלך ארבעה חומשים וחצי חומש מעשרה חלקים מאחד עשר | ||||||||||
| הוריד השאלה על זאת הצורה: | |||||||||||
|
|
| ||||||||||
|
|
אחר כן עשה בשטה העליונה כמו שקדם בהכאת השבר ושבר השבר ומה שהתקבץ הכהו בסכום הקו התחתון יהיו תשעה ותשעים ושמרם אחר כן הכה העשרה אשר על הקו התחתון בסכום הקו העליון יהיו מאה והשליך מהם התשעה ותשעים הנשאר אחד וחלקהו על הסכום יצא לך חצי חומש חלק מאחד עשר | ||||||||||
|
|
| ||||||||||
|
|
ואם יאמר לך: השלך שבעה שמיניות ושליש שמינית מתשע עשיריות ושלוש רביעיות העשירית | ||||||||||
| הוריד השאלה על זאת הצורה: | |||||||||||
|
|
| ||||||||||
|
|
אחר כן עשה בשטה העליונה והשטה התחתונה כמו שקדם בהכאת השבר ושבר השבר ומה שהתקבץ מן הקו העליון הכהו בסכום הקו התחתון ומה שהתקב' מן הקו התחתון הכהו בסכום הקו העליון ותפיל הפחות מן היותר ומה שנשאר תחלקהו על הסכום יצא לך המבוקש הנשאר ארבע שמיניות העשירית וארבעה שתותי שמינית העשירית | ||||||||||
|
|
| ||||||||||
|
|
ואם אמר לך אדם: השלך שני שלישיות ושתי רביעיו' מתשע עשיריות | ||||||||||
| הנה הוריד השאלה על זאת הצורה: | |||||||||||
|
|
| ||||||||||
|
|
אחר כן עשה בשטה העליונה כמו שקדם מהכאת שני השברים המתחלפים ומה שהתקבץ מן הקו העליון הכהו בסכום הקו התחתון יהיה זה שבעים ושמרם אחר כן הכה התשעה אשר על העשרה בסכום הקו העליון יהיה זה שמונה ומאה השלך מהם השבעים הנשאר שמונה ושלשים וחלקם על הסכום יצא לך המבוקש והוא שלשה עשיריות ושתות העשירית והוא הנשאר המבוקש | ||||||||||
|
|
ואם אמר השלך שלשה חומשים ושליש משש שביעיות ושמינית | ||||||||||
| הוריד השאלה על זאת הצורה: | |||||||||||
|
|
| ||||||||||
|
|
אחר כן עשה בשטה העליונה והתחתונה כמו שקדם מהכאת שני השברים המתחלפים ומה שהתקבץ מן הקו העליון הכהו בסכום הקו התחתון ומה שהתקבץ מן הקו התחתון הכהו בסכום הקו העליון אחר כן השליך היוצא מן הקו העליון מן היוצא מן השטה התחתונה ומה שנשאר תחלקהו על הסכום יצא לך המבוקש | ||||||||||
Subtraction of Integer and Fraction from Integer and Fraction/s |
שער אחר ממנו | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך: השליך חמשה ושליש משבעה ושלשה רביעיות | ||||||||||||
| הוריד השאלה על זאת הצורה: | |||||||||||||
|
|
| ||||||||||||
|
|
אחר כן עשה בכל אחד מן הקו העליון והתחתון כמו שעשית בהכאת השלם והשבר והכה היוצא מן הקו העליון בסכום הקו התחתון וכן מה שיצא מן הקו התחתון הכהו בסכום הקו העליון אחר כן הפיל הפחות מן היותר הנשאר תשעה ועשרים וחלקם על הסכום יצא שנים ושני שתותים וחצי שתות והוא הנשאר | ||||||||||||
|
|
| ||||||||||||
|
|
ואם אמר: השלך חמשה ושבע שמיניות משמונה ותשעה חלקים מאחד עשר ושלשה רביעיות | ||||||||||||
| הוריד השאלה על זאת הצורה: | |||||||||||||
|
|
| ||||||||||||
|
|
אחר כן עשה בשטה העליונה כמו שקדם מהכאת השלם והשבר ומה שהתקבץ הכהו בסכום הקו התחתון ושמרהו אחר כן עשה בשטה התחתונה כמו שקדם מהכאת השלם ושני השברים המתחלפים ומה שהתקבץ הכהו בסכום הקו העליון ומה שהתקבץ השליך ממנו המספר הראשון ומה שנשאר תחלקהו על הסכום ומה שיצא הנה הוא המבוקש הנשאר | ||||||||||||
Subtraction of Three Different Fractions from Integer and Fraction |
שער אחר ממנו | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
השליך חצי ושני חלקים מאחד עשר וחמשה שתותים משמנה ותשע עשיריות | |||||||||||
| הוריד השאלה על זאת הצורה: | ||||||||||||
|
|
| |||||||||||
|
|
אחר כן בשטה העליונה כמו שקדם בשברי' השלשה המתחלפים ומה שהתקבץ הכהו בסכום הקו התחתון אחר כן עשה בשטה התחתונה כמו שקדם בשלם והשבר ומה שהתקבץ הכהו בסכום הקו העליון ומה שהתקבץ תשליך ממנו הראשון ומה שנשאר חלקהו על הסכום יצא לך המבוקש | |||||||||||
Subtraction of Fraction of Integer from Fraction of Integer |
שער אחר ממנו | ||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך: השלך שלשה רביעי חמשה משבע שמיניות תשעה | ||||||||
| הוריד השאלה על זאת הצור': | |||||||||
|
|
| ||||||||
|
|
אחר כן הכה השלשה אשר על הארבעה בחמשה ומה שהתקבץ הכהו בשמונה אשר הם סכום הקו התחתון ושמרהו אחר כן הכה השבעה בתשעה ומה שהתקבץ בארבעה אשר הם סכום הקו העליון ומה שהתקבץ תשליך ממנו הראשון השמור ומה שנשאר תחלקהו על הסכום יצא לך המבוקש | ||||||||
Subtraction of Fraction of Integer and Fraction from Fraction of Integer and Fraction |
שער אחר ממנו | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
השלך שלשה רביעי חמשה וחצי מחמשה שתותי שבעה ושמינית | ||||||||||||
| הורידם על זאת הצורה: | |||||||||||||
|
|
| ||||||||||||
|
|
אחר כן עשה בשטה העליונה כמו שקדם בהכאת השבר בשער אחד וארבעים ומה שהתקבץ מן השטה העליונה הכהו בסכום השטה התחתונה ושמרהו והיוצא ג"כ מן השטה התחתונה הכהו בסכום השטה העליונה ומה שהתקבץ תשליך ממנו המספר הראשון ומה שנשאר תחלקהו על הסכום יצא לך המבוקש | ||||||||||||
Subtraction of Unknown Amounts |
שער אחר ממנו מן ההשלכה ג"כ |
|---|---|
|
|
השלך מעשרה דרהם שלישיתם ורביעיתם ודע כמה הנשאר |
|
|
הנה המעשה בזה שתעמיד השליש והרביע משנים עשר והשלך מהם שלישיתם ורביעיתם והם ז' הנשאר חמשה הנה יחס אלו החמשה מן השנים עשר אשר הם המעמד כיחס המבוקש מן העשרה ותאמר אם ה' שוים ז' עשרה כמה ישוו והכה החמשה בעשרה וחלק המקובץ על השנים עשר יצא לך ארבע' ושתות והוא הנשאר מן העשרה |
| ואם תרצא תכה שליש ורביע בעשרה ומה שיצא תשליך ממנו העשרה ומה שנשאר הנה הוא המבוקש | |
|
|
ואם תרצה קבץ שליש אל רביע יהיה זה שלשה שתותים וחצי שתות ותפילם מאחד יצא שני שתותים וחצי שתות והכם בעשרה וחלק המקובץ על אחד יצא המבוקש |
|
|
ואם תרצה במעשה הראשון תחלק החמשה על השנים עשר ותכה מה שיצא בעשרה ויצא לך המבוקש |
|
|
ואם אמר השלך מעשרה דרהם שלישי' ורביעיתם ושלשה דרהם ודע כמה הנשאר |
|
|
תעמיד השליש והרביע משנים עשר והוא הסכום אחר כן תקח שלישיתם ורביעיתם ותפיל מן השנים עשר השבעה הנשאר חמשה והכם בעשרה יהיו חמשים ושמרם אחר כן תקח השלשה דרהם הנזכרים והכם בשנים עשר והשליך מה שהתקבץ מן החמשים הנשאר ארבעה עשר וחלקם על השנים עשר יצא אחד ושתות והוא הנשאר ואם תחלק החמשים על הסכום |
Chapter |
שער אחר ממנו |
|---|---|
|
|
ואם אמר השליך מעשרה דרהם שלישית' ורביעיתם אלא שני דרהם |
|
|
העמיד השליש והרביע משנים עשר אחר כן השליך שלישיתם ורביעיתם הנשאר חמשה והכם בעשרה יהיו חמשים ושמרם אחר כן הכה שני דרהם בשנים עשר והשיאם על החמשים יהיו ארבעה ושבעים וחלקם על הסכום אשר הוא שנים עשר יצא ששה ושתות והוא הנשאר |
| ואם תרצה הכה שליש ורביע בעשרה ומה שיצא תשליך ממנו השני דרהם ומה שנשאר תפילהו מן העשרה והנשאר הוא המבוקש | |
Chapter |
שער אחר ממנו |
|---|---|
|
|
השליך מממון שלישיתו ורביעיתו ודע כמה הנשאר |
|
|
קבץ שליש אל רביע יהיו שלשה שתותים וחצי שתות ותפילם מאחד תמיד ומה שנשאר הנה הוא המבוקש והוא שני שתותים וחצי שתות |
|
|
ואם אמר השלך מממון שלישיתו ורביעיתו והשיא על מה שנשאר חמשה ודע כמה הוא |
|
|
העמיד השליש והרביע והחומש מששים ותפיל מהם שלישיתם ורביעיתם הנשאר חמשה ועשרים והשיא עליהם חמשה יהיו שלשים וחלקם על הסכום יצא חצי והוא הנשאר |
Word Problems: First from Last |
שער אחר ממנו והוא השלכת הממונות |
|---|---|
|
ממון השלכת שלישיתו ורביעיתו ונשאר עשר כמה הממון |
|
|
העמיד השליש והרביע משנים עשר אחר כן תפיל מהם שלישיתם ורביעיתם הנשאר חמשה והוא הסכום אחר כן הכה העשרה דרהם בשנים עשר וחלק מה שהתקבץ על הסכום יצא ארבעה ועשרים והוא הממון |
|
ואם תרצה בחיתום |
|
|
שים הממון דבר והשליך שלישיתו ורביעיתו הנשאר שני שתותי דבר וחצי שתות דבר הנה זה ישוה העשרה |
|
|
ותאמר בכמה אחתים שני שתות דבר וחצי שתותי דבר עד שיהיה אחד תמצא זה כשתכהו בשנים ושני חומשים |
|
|
ותכה העשרה בשנים ושני חומשים יהיו ארבעה ועשרים והוא הממון |
|
ואם תרצה בחפנים |
|
והוא שתקח אי זה מספר שתרצה סכום כאלו אתה תקח שנים עשר ותפיל שלישיתם ורביעיתם הנשאר חמשה ותקביל בהם העשרה הנה כבר טעית בחופן נ' כאומר שנים עשר בחמש' חסרים |
|
אחר כן תקח חופן אחר משמנה עשר ותפיל שלישיתם ורביעיתם הנשאר מהם שבעה וחצי ותקביל בהם העשר' הנה כבר טעית בחופן שמנה עשר בשנים וחצי |
|
|
הסרם והנה טעות החופן הראשון אשר הוא חמשה בחופן השני אשר הוא שמנה עשר יהיה זה תשעים אחר כן הכה טעות החופן השני אשר הוא שנים וחצי בחופן הראשון אשר הוא שנים עשר יהיו שלשים הפילם מן התשעים הנשאר ששים והפיל הפחות משני הטעייות מן היותר גדול הנשאר שנים וחצי וחלק עליהם הששים ויצא ארבעה ועשרים והוא הממון |
| פרק | |
|
ודע כי כאשר היו שני הטעיות חסרים תפיל הפחות משתי הרבאות מן היותר גדולה מהם ותפיל גם כן הפחות משתי הטעיות מן היותר גדול מהם ומה שנשאר חלק עליו הנשאר משתי ההכאות |
|
וכן תעשה כאשר יהיו שתי הטעוייות נוספים |
|
ואם היה אחד משתי הטעויות נוסף והאחר חסר קבץ שתי ההכאות וקבץ ג"כ שתי הטעיות וחלק על השתי ההכאות על כל שתי הטעויות ומה שיצא הנה הוא המבוקש |
| פרק | |
|
דע כי כאשר היו שתי הטעיות חסר והנה הממון יותר משני החופנים |
|
ואם היה אחד משתי הטעיות נוסף והאחר חסר הנה הממון במה שבין שני החופנים |
| שער אחר ממנו | |
|
השלכת שלישיתו ורביעיתו ושלשה דרהם וחמשיתו ושלשה דרהם ונשאר עשרה דרהם כמה הממון |
|
|
העמיד השליש והרביע והחומש מששים והוא המעמד אחר כן השליך שלישיתם ורביעיתם וחמישיתם הנשאר שמנה עשר והוא הסכום אחר כן קבץ הדרהם והם ששה והשיאם על העשר יהיו ששה עשר והכם בששים וחלק המקובץ על הסכום יצא המבוקש שלשה ושבעים ואחד עשר חלק משלשה עשר |
| פרק | |
|
ודע כי הדרהם כאשר היו נוספים הוסיפם על הדרהם הנשארים |
|
ואם היו חסרים חסרם מן המספר הנשארי' |
| אחר כן תעשה כמו שקדם בשער הזה | |
|
ואולם שער הקבוץ הנ[.] כאשר היו הדראהם המונחים עם השליש והרביע והחלק הנזכר נוספים חסרם מן המספר ואם היו הדראהם חסירים הוסיפם ועשה כמו שקדם |
| שער אחר ממנו | |
|
כשיאמר לך: מממון השלכת שלישיתו אלא דרהם ורביעיתו אלא שני דרהם ונשארו עשרה |
|
|
הדרך שתקבץ אלו הדראהם והם שלשה חסרים ותפילם מן העשרה דרהם הנשאר שבעה |
|
|
ותעשה כמו שקדם בשאלה הראשונה מהשלכת הממונות יצא הממון ששה עשר וארבעה חומשים |
| שער אחר ממנו | |
|
ממון חוסר שלישיתו והכית מה שנשאר בכמוהו ושב הממון כמו שהיה |
|
|
הנה המעשה בזה שתעמיד השליש משלשה ותסיר שלישיתו הנשאר שנים והכם בכמותם יהיו ארבעה והוא הסכום אחר כן הכה השלשה בכמותם יהיו תשעה וחלקם על הסכום יצא שנים ורביע והוא הממון |
|
ואם אמר: ממון חוסר שלישיתו וחצי מה שנשאר והכית מה שנשאר במה שהלך וחזר הממון |
|
|
העמד השליש משלשה אחר כן הפיל שלישיתם הנשאר שנים וחצי מה שנשאר אחד וכבר הוסרו שנים והכה האחד הנשאר בשנים המוסרים יהיו שנים והוא הסכום אחר כן הכה השלשה בכמותם וחלקם על הסכום יצאו ארבעה וחצי והוא הממון |
|
ואם אמר: ממון הלך שלישיתו והוכה מה שנשאר בכמוהו וחזר ששה דמיוני הממון ושני שלישי כמותו |
|
|
העמד השליש משלשה וחסר שלישיתו הנשאר שנים והכם בכמותם יהיו ארבעה והוא הסכום אחר כן הכה השלשה בכמותם ומה שהתקבץ בששה ושני שלישים יהיו שישים חלקם על הסכום יצא חמשה עשר והוא הממון |
Word Problems: Whole from Parts |
שער מן הקנה |
|---|---|
|
קנה בטיט שלישיתו ובמים רביעיתו ועל המים עשרה זרתות כמה מדת הקנה |
|
הנה זאת השאלה כאומרך ממון הלך שלישיתו ורביעיתו ונשאר עשרה |
|
|
הנה תעשה כמו שקדם יצא ארבעה ועשרים והוא אורך הקנה |
|
ואם אמר: קנה כיון שלישיתו ושתי אמות ובמים רביעיתו ושלש אמות ועל המים עשר אמות |
|
הנה זאת השאלה כאמרך ממון הלך שלישיתו ושני דרהם ורביעיתו ושלשה דרהם ונשאר עשרה כמה הממון |
|
|
ותעשה כמו שקדם יצא אורך הקנה ששה ושלשים |
|
ואם דג בראשו שלישיתו בזנבו רביעיתו ובאמצעו עשרה ליטרי' כמה משקל הדג |
|
הנה זה כאלו אמר ממון השלכת שלישיתו ורביעיתו ונשאר עשרה |
|
|
ותעשה כמו שקדם יצא ארבעה ועשרים והוא משקל הדג |
|
וכן אלו אמרת שלישיתו וליטרי' ורביעיתו ולטרין |
| הנה אלו השאלות כולם אמנם יצא מן השער הזה | |
Division of Fractions |
שער החלוקה |
|---|---|
| דע כי השער הזה ילך על דרך הקבוץ וההשלכה וענינו שתשוב הנחלק והנחלק עליו מסוג אחד והוא שתשיבם יחד אל היותר דק שבשיבר השאלה עוד תחלק אחר זה אחד משניהם על השני ומה שהתקבץ הוא מה שיגיע לאחד | |
| וזאת החלוקה תחלק לשני חלקים: | |
| חלק מעט על רב ויקרא השומא נ' קריאת השם | |
| והחלק השני חלוק הרב על המעט | |
Division of the smaller by the larger |
ויתחיל בה בחלוקת המעט על הרב תחלה כמו שסדרנו במספר השלם | |||||
|
|
המשל בו חלק שליש דרהם על ארבעה אנשים | |||||
| והוריד השאלה על זאת הצורה: | ||||||
|
|
| |||||
|
|
אחר כן קח הארבעה אשר הם השלם והכם במעמד השליש מן השטה העליונה יהיו שנים עשר והוא הסכום אחר כן קרא שם ממנין האחד אשר על השלשה יהיה חצי שתות הדרהם | |||||
| פרק | ||||||
|---|---|---|---|---|---|---|
|
|
ודע כי הכאת כל מה שבשטה התחתונה מן המספר כאשר הוכה במקומות השברים מן השטה העליונה מן המקובץ מזה הוא הסכום אשר יחלק עליו אחר כן אם היית מחלק רב על מספר תקח מה שעל השברים ותחלקהו על הסכום כמו שעשינו בזאת השאלה ומה שיבוא אחריה כשיאמר לך חלק חמשה שתותים על שמנה הורידם על זאת הצורה: | |||||
|
|
| |||||
|
|
אחר כן הכה השמנה בששה יהיו שמנה וארבעים וקרא שם מהם החמשה יהיו חמשה שתותים שמינית והוא היוצא מן החלוקה | |||||
|
|
ואם יאמר לך חלק חמשה חלקים מאחד עשר על שבעה | |||||
| הוריד השאלה על זאת הצורה: | ||||||
|
|
| |||||
|
|
אחר כן הכה השבעה באחד עשר יהיו שבעה ושבעי' והוא הסכום אחר כן קרא שם מהם החמשה יהיו חמשה שביעייות החלק מאחד עשר ואם תרצה חמשה חלקים מאחד עשר בשביעית | |||||
| פרק | ||||||
| היותר קרוב ממה שיעשה בשער הזה שתחזיר השלם תמיד מקום שבר תחת הקו ותיחס אליהם כל השברים הנחלקים | ||||||
|
|
המשל בו חלק שבע תשיעייות על שבעה עשר: | |||||
| הוריד השאלה על זאת הצורה: | ||||||
|
|
| |||||
|
|
אחר כן תקח השבעה עשר ותשיבם מקום שבר תחת הקו העליון אל מה שילוה הימין ויבוא צורך כל זה שבע תשיעיות החלק משבעה עשר על זאת הצורה: | |||||
|
|
| |||||
| וזהו היוצא מן החלוקה | ||||||
Division of Fraction and Fraction of fraction by Integer |
שער חלוקת השבר ושבר השבר על השלם והוא קריאת שם | |||||
|---|---|---|---|---|---|---|
|
|
המשל בו חלק חמשה שתותים וחצי שתות על חמשה | |||||
| הוריד החמשה שתותים וחצי שתות בשטה והוריד תחתיה בשטה אחרת החמשה על זאת הצורה: | ||||||
|
|
| |||||
|
|
אחר כן התחיל בשטה התחתונה והכה החמשה אשר בה בראשית השטה העליונה בששה ומה שהתקבץ בשנים יהיו ששים והוא הסכום, אחר כן תחזור אל השטה העליונה ותכה החמשה אשר על הששה בשנים ותשיא מה שעל ראשם יהיו אחד עשר וקרא שמם מן הסכום אשר הוא ששים יצא עשרה וחמשה שתותי העשור וזהו היוצא מן החלוקה | |||||
|
|
ואם אמר חלק עשרה חלקים מאחד עשר ושלש' חומשי החלק מאחד עשר על שלשה ושישים | |||||
| הוריד השאלה על זאת הצורה: | ||||||
|
|
| |||||
|
|
אחר כן הכה השלשה וששים באחד עשר ומה שהתקבץ בחמשה אחר כן שוב והכה יהיה כל זה חמשה וששים וארבע מאות ושלשת אלפים והוא הסכום אחר כן שוב והכה העשרה אשר על האחד עשר בחמשה ותשיא מה שעל ראשם יהיו שלשה וחמשים וקרא אותם מן הסכום יצא תשיעית החלק מאחד עשר ושלשה שביעייות תשיעית החלק מאחד עשר ושלשה חומשי שביעית תשיעית החלק מאחד עשר | |||||
|
|
| |||||
Division of Two Different Fractions by Integer |
שער חלוקת שני השברים המתחלפים על השלם | ||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך חלק שלשה חומשים ושבע שמינייות על ששה | ||||||||
| הוריד השלשה חומשים והשבע שמינייות בשטה והוריד הששה בשטה אחרת על זאת הצורה: | |||||||||
|
|
| ||||||||
|
|
אחר כן התחיל בשטה התחתונה והכה הששה אשר בשטה התחתונה בסכום השטה העליונה הכה תחלה בחמשה ומה שהתקבץ בשמנה יהיה זה ארבעים ומאתים והוא הסכום אחר כן עשה בשטה העליונה כמו שתעשה בשני השברים המתחלפים והוא שתכה מה שעל החמשה והוא שלשה בשמנה יהיו ארבעה ועשרים ותכה ג"כ מה שעל השמנה בחמשה והוא שבעה בחמשה יהיו חמשה ושלשים וקבצם אל הארבעה ועשרים יהיו תשעה וחמשים וחלקם על הסכום יצא לך בחלוקה שתי עשירייות ושלש שמינייות העשירית ושתי שלישייות שמינית העשירית וזאת החלוקה אמנם היא קריאת שם | ||||||||
|
|
ואם תרצה קבץ השלשה חומשים אל השבע שמנייות יהיה כל זה אחד ושלש שמניות וארבעה חמשי השמינית אחר כן קרא שם אחד מן הששה הנחלק עליהם תמצאהו שתות והכה שתות באחד ושלשת שמינייות וארבעה חומשי השמינית ומה שיצא הנה הוא המבוקש | ||||||||
|
|
ואם תרצה הכה שתות בשלשה חומשים ושבע שמנייות ומה שיצא הנה הוא המבוקש וזה נכלל בכל החלוקה מה שקדם ממנה ומה שהתאחר | ||||||||
Division of Fraction by Integer and Fraction |
שער חלוקת השבר על השלם והשבר | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
|
חלק ששה שביעייות על חמשה וחצי | |||||||||
| הוריד השאלה על זאת הצורה: | ||||||||||
|
|
| |||||||||
|
|
אחר כן התחיל בשטה התחתונה והכה החמשה בשנים והשיא מה שעל ראשם יהיה אחד עשר והכם בשבעה אשר הם מעמד השבר בשטה העליונה יהיו שבעה ושבעים והוא הסכום אחר כן הכה הששה אשר על השבעה בשטה העליונה בשנים מעמד השבר בשטה התחתונה יהיו שנים עשר וחלקם על הסכום ומה שיצא הנה הוא המבוקש והוא חלק מאחד עשר וחמשה שביעייות החלק מאחד עשר והוא המבוקש | |||||||||
|
|
ואם תרצה [..] חלק אחד מחמשה וחצי תמצאהו שני חלקים מאחד עשר והכה שני חלקים מאחד עשר בששה שביעייות ומה שיצא הנה הוא מה שרצית | |||||||||
| פרק | ||||||||||
| ודע כי אתה כשתרצה שתחלק אחד על מספר קרא שם האחד מן המספר ומה שתהיה קריאת השם כזה הוא היוצא מן החלוקה | ||||||||||
|
|
דמיון זה חלק אחד על שלשה | |||||||||
| קרא שם אחד משלשה תמצאהו שני שלישים ואם כן שליש הוא היוצא מן החלוקה | ||||||||||
| ואם חלקתה אחד על מספר ושבר | ||||||||||
| הכה האחד במעמד השבר ושמרהו הנה הוא הנקרא אחר כן הכה המספר במעמד שברו והשיא השבר הנזכר ומה שהתקבץ תקראהו ממנו המספר השמור ומה שיצא הנה הוא היוצא מן החלוקה | ||||||||||
|
|
דמיון זה חלק אחד על שלשה ושליש | |||||||||
|
|
הכה האחד במעמד השליש יהיה תשעה והשיא עליהם השליש הנזכר יהיו עשרה וקרא מהם שם השלשה יצא שלש עשיריות והוא מה שיצא מחלוקת אחד על שלשה ושליש | |||||||||
| וענינן שתשיב הנחלק והנחלק עליו אל סוג אחד מן השבר היותר דק שבשאלה אחר כן חלק האחד על השני | ||||||||||
|
|
ודמיון זה חלק אחד על ששה ורביע | |||||||||
|
|
השיב האחד רביעיים יהיו ארבעה אחר כן השיב הששה ורביע רביעיים יהיו חמשה ועשרים וקרא מהם שם הארבעה יהיו ארבעה חומשי החומש והוא מה שיצא מחלוקת אחת על ששה ורביע | |||||||||
|
|
אחר כן חזור אל השאלה ותאמר חלק אחד על חמשה וחצי השיב האחד חציים יהיו שנים אחר כן השיב החמשה וחצי חציים יהיו אחד עשר חציים וקרא שם שנים מאחד עשר והוא שני חלקים מאחד עשר ותכם בשש שביעיות ומה שיצא הנה הוא היוצא מחלוקת ששה שביעיות על חמשה וחצי | |||||||||
| שער אחר ממנו | ||||||||||
|
|
חלק עשרה חלקים מאחד עשר על ששה ושני שלישים | |||||||||
| הוריד השאלה על זאת הצורה: | ||||||||||
|
|
| |||||||||
|
|
אחר כן התחיל בשטה התחתונה והכה הששה בשלשה והשיא מה שעל ראשם יהיו עשרים והכם באחד עשר אשר הם הסכום בשטה העליונה יהיו עשרים ומאתים והוא הסכום אחר כן הכה העשרה אשר על האחד עשר בשלשה אשר הם הסכום בקו התחתון יהיו שלשים וחלקם על הסכום יצא חלק מאחד עשר וחמשה עשיריות החלק מאחד עשר והוא קריאת שם | |||||||||
|
|
ואם תרצה קרא שם אחד מששה ושלשים תמצא עשירית וחצי עשירית והכה עשירית וחצי עשירית בעשרה חלקים מאחד עשר ומה שיצא הנה הוא המבוקש | |||||||||
Division of Fraction by Integer and Fraction and Fraction of Fraction |
שער חלוקת השבר על השלם והשבר ושבר השבר | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך חלק ארבעה חומשים על שלשה ושש שביעיות וחצי שביעית | |||||||||||
| הורידם על זאת הצורה: | ||||||||||||
|
|
| |||||||||||
|
|
אחר כן התחיל בשטה התחתונה והכה השלשה בשבעה והשיא מה שעל ראשם ומה שהתקבץ הכהו בשנים והשיא מה שעל ראשם יתקבץ לך מזה חמישה וחמישים והכם בחמשה אשר הם הסכום בשטה העליונה יהיו חמשה ושבעים ומאתים והוא הסכום אחר כן הכה הארבעה אשר על החמשה בשטה העליונה יהיו במעמדות השברים בשטה התחתונה הכם תחלה בשנים ומה שהתקבץ הכהו בשבעה יהיו ששה וחמישים וקרא להם שם מן הסכום ומה שיצא הנה הוא המבוקש והוא שני חלקים מאחד עשר וחומש החלק מאחד עשר וחמישית חמישית החלק מאחד עשר | |||||||||||
|
|
| |||||||||||
Division of Fraction by Integer and Two Different Fractions |
שער חלוקת השבר על השלם ושני השברים המתחלפים | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך חלק ששה חלקים משלשה עשר על ארבעה ושליש וששה חלקים מאחד עשר | |||||||||||||
| הוריד השאלה על זאת הצורה: | ||||||||||||||
|
|
| |||||||||||||
|
|
אחר כן התחיל בשטה התחתונה ועשה בה כמו שעשית בהכאת השלם ושני השברים המתחלפים והוא שתכה הארבעה בשלשה ומה שהתקבץ באחד עשר אחר כן הכה מה שעל השלשה באחד עשר ומה שעל האחד עשר בשלשה וקבץ ההכאות השלשה יהיו אחד ושישים ומאה והכם בשלשה עשר אשר הם מעמד השבר בשטה העליונה יהיה זה שלשה ותשעים ושני אלפים והוא הסכום אחר כן תקח הששה אשר על השלשה עשר בשטה העליונה ותכם במעמד השבר בשטה התחתונה כלה יתקבץ לך מזה שמונה ותשעים ומאה וקרא להם שם מן הסכום והוא שני חלקים מאחד עשר ושתי עשיריות ושני חלקים משלשה עשר בחלק משלשה ועשרים ושתי שביעיות החלק משלשה עשר בחלק משלשה ועשרי' ושתי שביעיות החלק משלשה עשר בחלק משלשה ועשרים והוא היוצא מן החלוקה | |||||||||||||
Division of Fraction and Fraction of Fraction by Integer and Fraction |
שער חלוקת השבר ושבר השבר על השלם והשבר | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך חלק שבע שמיניות ושליש שמינית על שלשה וחצי | |||||||||
| הוריד השאלה על זאת הצורה: | ||||||||||
|
|
| |||||||||
|
|
אחר כן התחיל בשטה התחתונה והכה השלשה אשר הם השלם בשנים והשיא מה שעל ראשם יהיו שבעה הכם בסכום הקו העליון יהיה זה שמונה ושישים ומאה והוא הסכום אחר כן חזור אל השטה העליונה והכה השבעה בשלשה והשיא מה שעל ראשם יהיו שנים ועשרים והכם בסכום הקו התחתון אשר הוא שנים יהיו ארבעה וארבעים וקרא להם שם מן הסכום יצא בחלוקה שתי שמניות ושני שלישי שביעית השמינית והוא היוצא מן החלוקה | |||||||||
|
|
ואם תרצה קרא שם אחר משלשה וחצי תמצא שבעים והכה שבעים בשבע שמיניות ושליש יצא לך שתי שמיניות ושני שלישי שביעית השמינית | |||||||||
Division of Integer by Integer and Fraction |
שער חלוקת השלם על השלם והשבר והוא משער קריאת השם | |||||||
|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך חלק שנים על חמשה וחצי | |||||||
| הוריד השנים בשטה והוריד החמשה וחצי בשטה אחרת תחתיה על זאת הצורה: | ||||||||
|
|
| |||||||
|
|
אחר כן התחיל בשטה התחתונה והכה החמשה בשנים והשיא מה שעל ראשם יהיו אחד עשר והוא הסכום אחר כן הכה השנים אשר בשטה העליונה בשנים אשר הם מעמד השבר בשטה התחתונה ומה שהתקבץ תקרא לו שם מן הסכום יצא ארבעה חלקים מאחד עשר והוא היוצא מן החלוקה | |||||||
|
|
ואם תרצה תקרא שם אחר מחמשה וחצי תמצאהו שני חלקים מאחד עשר והכה חלק מאחד עשר בשנים ומה שיצא הנה הוא המבוקש | |||||||
Division of Integer and Fraction by Integer and Fraction |
שער בחלוקת השלם והשבר על השלם והשבר והוא משער קריאת השם | ||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך חלק ששה ורביעית על שמונה ושליש | ||||||||
| הוריד השאלה על זאת הצורה: | |||||||||
|
|
| ||||||||
|
|
אחר כן התחיל בשטה התחתונה והכה השמונה בשלשה והשיא מה שעל ראשם יהיו חמשה ועשרים והכם בסכום השטה העליונה והוא ארבעה יהיו מאה והוא הסכום אחר כן חזור אל השטה העליונה והכה הששה בארבעה והשיא מה שעל ראשם יהיו חמשה ועשרים והכם בסכום הקו התחתון אשר הוא שלשה יהיו חמשה ושבעים וקרא להם שם מן הסכום אשר הוא מאה יצא שלשה רביעיות | ||||||||
| ואלו השעורים הקודמים מן החלוקה אמנם הם כלם קריאת שם וישוה עליו כשיאמר חלק או קרא שם מכך ומכך כשיהיה הנחלק פחות מן הנחלק עליו | |||||||||
Division of Fraction by Fraction |
שער חלוקת השבר על שבר משער קריאת השם | ||||||
|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך: חלק שליש על שלשה רביעים | ||||||
| הוריד שליש בשטה והוריד השלשה רביעים בשטה אחרת תחתיה על זאת הצורה: | |||||||
|
|
| ||||||
|
|
אחר כן התחיל בשטה התחתונה והכה השלשה אשר על הארבע' בסכום הקו העליון והוא שלשה יהיו תשעה ושמרם והוא הסכום אחר כן תקח האחד אשר הוא מעמד השבר בשטה העליונה והכהו בארבעה אשר הם מעמד השבר בשטה התחתונה יהיה זה ארבעה וקרא להם שם מן הסכום יצא ארבע תשיעיות והוא היוצא מן החלוקה | ||||||
|
|
וכן אילו אמר: שני שליש משלשה רביעים | ||||||
|
|
הנה יהיה המעשה כמו שספרנו ויהיה היוצא מקריאת השם ארבעה תשיעיות | ||||||
|
|
ואם אמר חלק שלשה חומשים על שבע תשיעיות | ||||||
| הוריד השאלה על זאת הצורה: | |||||||
|
|
| ||||||
|
|
אחר כן התחיל בשטה התחתונה והכה השבעה בחמשה אשר הם סכום הקו העליון יהיו חמשה ושלשים והוא הסכום אחר כן הכה השלשה אשר על החמשה בקריאת השם אשר הם סכום השטה התחתונה יהיו שבעה ועשרים וקרא להם שם מן הסכום יצא חמש שביעיות ושתי חמישיות שביעית | ||||||
|
|
ואלו אמר לך: חלק שני חלקים משלשה עשר על תשע עשיריות | ||||||
| הורידם על הצורה הזאת: | |||||||
|
|
| ||||||
|
|
אחר כן הכה התשעה בשלשה עשר יהיה הסכום אחר כן הכה השנים בעשרה וחלקהו על הסכום יצא לך שני חלקים משלשה עשר ושתי תשיעיות חלק משלשה עשר | ||||||
|
|
ואם אמר חלק חמשה חלקים מאחד עשר על תשעה חלקים משבעה עשר | ||||||
| הוריד השאלה על זאת הצורה: | |||||||
|
|
| ||||||
|
|
אחר כן התחיל בשטה התחתונה והכה התשעה באחד עשר יהיה זה הסכום אחר כן הכה החמשה בשבעה עשר חלק על הסכום ומה שיצא הנה הוא מה שרצית והוא תשעה חלקים מאחד עשר וארבעה תשיעיות החלק מאחד עשר | ||||||
Division of Fraction and Fraction of Fraction by Fraction |
שער חלוקת השבר ושבר השבר על השבר משער קריאת השם | ||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך חלק שתי שמיניות וחצי שמינית על תשע עשרות | ||||||||
| הוריד השאלה על זאת הצורה: | |||||||||
|
|
| ||||||||
|
|
אחר כן התחיל בשטה התחתונה והכה התשעה אשר על העשרה בסכום השטה העליונה יתקבץ מזה ארבעה וארבעים ומאה והוא הסכום אחר כן חזור אל השטה העליונה והכה השנים אשר על השמונה בשנים אשר הם המעמד והשיא מה שעל ראשם יהיו חמשה והכם בעשרה אשר הם סכום השטה התחתונה יהיו חמישים וקרא להם שם מן הסכום יצא שלשה שביעיות ושמינית תשיעית | ||||||||
Division of Two Different Fractions by Fraction |
שער חלוקת שני השברים על שני השברים משער קריאת השם | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
חלק שליש ושביעית על עשרה חלקים מאחד עשר | ||||||||||
| הוריד השאלה על זאת הצורה: | |||||||||||
|
|
| ||||||||||
|
|
אחר כן התחיל בשטה התחתונה והכה העשרה בסכום השטה העליונה יהיו עשרה ומאתים והוא הסכום אחר כן עשה בשטה העליונה כמו שתעשה בהכאת שני השברים יתקבץ לך עשרה והכם באחד עשר וקרא שם למה שיצא מן הסכום יצא חמש עשיריות ושביעית עשירית ושני שלישי שביעית עשירית | ||||||||||
| ואם תרצה שלשה שביעיות ושליש שביעית | |||||||||||
Division of Fraction by Fraction and Fraction of Fraction |
שער חלוקת השבר על השבר ושבר השבר משער קריאת השם | ||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
חלק שני שלישים על תשע עשרות וחמש שמיניות העשירית | ||||||||
| הורידם על הצורה הזאת: | |||||||||
|
|
| ||||||||
|
|
אחר כן התחיל בשטה התחתונה ותעשה בה כמו שקדם בשבר ושבר השבר יתקבץ בה שבעה ושבעים והכם בשלשה אשר הם הסכום בשטה העליונה יהיו אחד ושלשים ומאתים והוא הסכום אחר כן הכה השנים אשר בשטה העליונה על השלשה בסכום השטה התחתונה יהיו שישים ומאה וקרא להם שם מן הסכום יצא שבעה חלקים מאחד עשר וארבע שביעיות החלק מאחד עשר ושליש שביעית החלק מאחד עשר | ||||||||
Division of Fraction by Two Different Fractions |
שער חלוקת השבר על שני השברים משער קריאת השם | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
חלק שבע תשיעיות על שלשה רביעיות ושבע שמיניות | ||||||||||
| הורידם על זאת הצורה: | |||||||||||
|
|
| ||||||||||
|
|
אחר כן התחיל בשטה התחתונה ועשה בו כמו שעשית בשני השברים המתחלפים יתקבץ לך שנים וחמישים והכם בסכום השטה העליונה והוא תשעה יהיה זה שמונה ושישים וארבע מאות והוא הסכום אחר כן הכה השבעה אשר על התשעה בשטה העליונה בסכו' השטה התחתונה והם שמונה יהיו ארבעה ועשרים ומאתים וקרא להם שם מן הסכום יצא ששה חלקים מאחד עשר ושתי תשיעיות חלק משלשה עשר | ||||||||||
Division of Fraction and Fraction of Fraction by Fraction and Fraction of Fraction |
שער חלוקת השבר ושבר השבר על השבר ושבר השבר משער קריאת השם | ||||||
|---|---|---|---|---|---|---|---|
|
|
חלק ארבע תשיעיות וחצי תשיעית על שבע שמיניות ושליש שמינית | ||||||
| הוריד השאלה על זאת הצורה: | |||||||
|
|
| ||||||
|
|
אחר כן התחיל בשטה התחתונה ועשה בה כמו שתעשה בשבר ושבר השבר ומה שהתקבץ הכהו בסכום השטה העליונה יהיה זה ששה ותשעי' ושלש מאות והוא הסכום אחר כן עשה בשטה העליונה כמו שקדם בהכאת השבר ושבר השבר ומה שהתקבץ הכהו בסכום השטה התחתונה יהיה זה ששה עשר ומאתים וקרא להם שם מן הסכום יהיה ששה חלקים מאחד עשר | ||||||
Division of Two Different Fractions by Two Different Fractions |
שער חלוקת שני השברים המתחלפים על שני השברים המתחלפים משער קריאת השם | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
חלק שני שלישים ושלשה חומשים על תשע עשיריות ועשרה חלקים מאחד עשר | ||||||||||
| הורידם על זאת הצורה: | |||||||||||
|
|
| ||||||||||
|
|
אחר כן התחיל בשטה התחתונה ועשה בה כמו שתעשה בשני השברים המתחלפים בשער ההכאה יהיה זה תשעה ותשעים ומאה והכם בסכום השטה העליונה יהיה זה חמשה ושמונים ותשע מאות ושני אלפים והוא הסכום אחר כן חזור אל השטה העליונה ותמשיך בה מעשה שני השברים המתחלפים ומה שהתקבץ הכהו בסכום השטה התחתונה יהיה זה תשעים ושני אלפים וקרא להם שם מן הסכום יהיה זה תשעה ושלשים ומאה חלק מתשעה ותשעים ומאה וחומש ושני שלישי חומש וזה צורתו: | ||||||||||
|
|
| ||||||||||
Division of Fraction of Fraction by Integer |
שער חלוקת שבר השבר על השלם משער קריאת השם | |||||
|---|---|---|---|---|---|---|
|
|
חלק שני שלישי חומש על שבעה | |||||
| הוריד השאלה על זאת הצורה: | ||||||
|
|
| |||||
|
|
אחר כן הכה השבעה בסכום הקו העליון ומה שהתקבץ הנה הוא הסכום והוא חמשה ומאה אחר כן קרא שם השנים אשר על קו השטה העליונה תמצא זה שני שלישי חומש שביעית | |||||
Division of Fraction of Fraction by Integer and Fraction |
שער חלוקת שבר השבר על השלם והשבר משער קריאת השם | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך: חלק שבעה שמיניות תשיעית על שלשה וחצי | |||||||||
| הוריד השאלה על זאת הצורה: | ||||||||||
|
|
| |||||||||
|
|
אחר כן התחיל בשטה התחתונה והכה השלשה בשנים והשיא מה שעל ראשם יהיו שבעה והכם בסכום הקו העליון יהיה זה ארבעה וחמש מאות והוא הסכום אחר כן הכה השבעה אשר על הקו העליון בשנים מעמד השבר בקו התחתון יהיה זה ארבעה עשר וקרא להם שם מן הסכום יצא שני שמיניות תשיעית | |||||||||
Division of Fraction of Fraction by Integer and Fraction and Fraction of Fraction |
שער חלוקת שבר השבר על השלם והשבר ושבר השבר | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך חלק תשע עשיריות חלק משלשה עשר על ששה ושלש שמיניות ושליש שמינית | |||||||||
| הוריד השאלה על זאת הצורה: | ||||||||||
|
|
| |||||||||
|
|
אחר כן התחיל בשטה התחתונה ותמשיך בה מעשה הכאת השלם והשבר ושבר השבר יתקבץ בו ארבעה וחמשים ומאה והכם בסכום הקו העליון יהיה זה עשרים ועשרים אלף והוא הסכום אחר כן הכה התשעה אשר על הקו העליון בסכום הקו התחתון יהיו ששה עשר ומאתים וקרא שמם מן הסכום יצא חלק מאחד עשר בחלק משלשה עשר וחמש עשיריות ושלש שביעיות עשירית חלק מאחד עשר בחלק משלשה עשר | |||||||||
Division of Fraction of Fraction by Integer and Two Different Fractions |
שער חלוקת שבר השבר על השלם ושני השברים המתחלפים | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך חלק שלשה חומשי השביעית על אחד וחמשה שתותים ושני שלישים | |||||||||||||
| הוריד השאלה על זאת הצורה: | ||||||||||||||
|
|
| |||||||||||||
|
|
אחר כן עשה בשטה התחתונה כמו שתעשה בשלם ושני השברים המתחלפים ומה שהתקבץ הכהו בסכום השטה העליונה יהיה הכל חמשה ושבעים וחמש מאות ואלף והוא הסכום אחר כן הכה השלשה אשר על הקו העליון בסכום השטה התחתונה יהיו ארבעה וחמישים וקרא שמם מן הסכום יצא שתי שביעיות תשיעית וארבעה חומשי חמישית שביעית תשיעית | |||||||||||||
Division of Fraction of Fraction by Fraction |
שער חלוקת שבר השבר על השבר | ||||||
|---|---|---|---|---|---|---|---|
|
|
חלק חמש תשיעיות העשירית על שלשה חומשים | ||||||
| הורידם על זאת הצורה: | |||||||
|
|
| ||||||
|
|
אחר כן הכה השלשה אשר על הקו התחתון בסכום השטה העליונה יהיה זה שבעים ומאתים והוא הסכום אחר כן הכה החמשה אשר על הקו העליון בסכום הקו התחתון והוא חמשה יהיו חמשה ועשרים וקרא שמם מן הסכום יהיו שמונה תשיעיות העשירית ושליש תשיעית העשירית | ||||||
Division of Fraction of Fraction by Fraction and Fraction of Fraction |
שער חלוקת שבר השבר על השבר ושבר השבר | ||||||
|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך: חלק שלש רביעיות חמישית על שלשה שתותים וחצי שתות | ||||||
| הורידם על זאת הצורה: | |||||||
|
|
| ||||||
|
|
אחר כן עשה בשטה התחתונה כמו שקדם בשבר ושבר השבר ומה שהתקבץ הכהו בסכום השטה העליונה יהיה זה מאה וארבעים והוא הסכום אחר כן הכה השלשה אשר על הקו העליון במעמדי השטה התחתונה והם שנים וששה יהיו ששה ושלשים וקרא שמם מן הסכום יצא שתי עשיריות וארבעה שביעיות העשירית | ||||||
Division of Fraction of Fraction by Two Different Fractions |
שער חלוקת שבר השבר על שני השברים המתחלפים | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
חלק חצי שביעית על שלש רביעיות ושלשה חומשים | ||||||||||
| הורידם בשתי שטות על זאת הצורה: | |||||||||||
|
|
| ||||||||||
|
|
אחר כן עשה בשטה התחתונה כמו שתעשה בשני השברים המתחלפים בשער ההכאה יהיו שבעה ועשרים והכם בסכום השטה העליונה יהיה זה שמונה ושבעים ושלש מאות והוא הסכום אחר כן הכה האחד אשר על הקו העליון בסכום השטה התחתונה ותקרא שם מה שהתקבץ מן הסכום יצא שלשה שביעיות התשיעית ושתות שביעית התשיעית | ||||||||||
Division of the larger by the smaller |
|
| ובמה שהקדמנו מחלוקת המעט על הרב אשר הוא קריאת השם מהשבור יקח ראיה בו על כל מה שיבוא מן הדומה לו ושוה ומזה שיאמר באלו השאלות הקודמות חלק או קרא שם כל זה שבר בהם והשער הזה יקראוהו בעלי החשבון שער קריאת שם השברים | |
| וימשך אחר השער הזה חלוקת הרב על המעט והוא שער חלוקת השברים ג"כ אצל בעלי החשבון ונביא בו השאלות לפי מה שהבאנו בשער הקודם | |
|
א' חלוקת השבר על השלם |
|
ב' חלוקת השבר ושבר השבר על השלם |
|
ג' חלוקת שני השברים המתחלפים על השלם |
|
ד' חלוקת השבר על השלם והשבר |
|
ה' חלוקת השבר על השלם ושני השברים המתחלפים |
|
ו' חלוקת השבר ושבר השבר על השלם והשבר |
|
ז' בחלוקת השלם על השלם והשבר |
|
ח' בחלוקת השלם והשבר על השלם והשבר |
|
ט' בחלוקת השבר על שני השברים מתחלפים |
|
י' בחלוקת השבר ושבר השבר על השבר |
|
י"א בחלוקת שני השברים על שני השברים |
|
י"ב בחלוקת השבר על השבר ושבר השבר |
|
י"ג בחלוקת השבר על שני השברים |
|
י"ד בחלוקת השבר ושבר השבר על השבר ושבר השבר |
|
ט"ו בחלוקת שני השברים המתחלפים על שני השברים המתחלפים |
|
י"ו בחלוקת שבר השבר על השלם |
|
י"ז בחלוקת שבר השבר על השלם והשבר |
|
י"ח בחלוקת שבר השבר על השלם והשבר ושבר השבר |
|
י"ט בחלוקת שבר השבר על השלם ושני השברים המתחלפים |
|
כ' בחלוקת שבר השבר על השבר |
|
כ"א בחלוקת שבר השבר על השבר ושבר השבר |
|
כ"ב בחלוקת שבר השבר על שני השברים המתחלפים |
| שער חלוקת הרב על המעט | |
|---|---|
| דע כי השער הזה כל מעשיו שוים לכל מעשי הקודם והוא שתתחיל ראשונה בשטה התחתונה ותמשיך בה המעשה כמו שקדם בשער הקודם ומה שהתקבץ הכהו בסכום השטה העליונה יהיה זה המקובץ הסכום אשר עליו החלוקה עוד תעשה ג"כ בשטה העליונה כמו שקדם בשערו ובשער ההכאה ומה שהתקבץ תכהו בסכום השטה התחתונה ומה שהתקבץ תחלקהו על הסכום ומה שיצא הוא המבוקש וזה המעשה כולל במה שיבוא אחר זה בע"ה | |
Division of Integer by Fraction |
שער חלוקת השלם על השבר | |||||
|---|---|---|---|---|---|---|
|
|
כשיאמר לך חלק עשרה על חומש | |||||
| הוריד השאלה על זאת הצורה: | ||||||
|
|
| |||||
|
|
אחר כן הכה העשרה בחמשה וחלקהו על האחד יצא חמשים והוא היוצא מן החלוקה | |||||
| ועניין זאת השאלה כי כאשר התחייב לחומש אחד עשרה יתחייב לאחד השלם אם כן חמשים והמבוקש בחלוקה תמיד אמנם הוא מה שראוי לאחד | ||||||
| וזה השער ג"כ יחלק לשני חלקים: אם שיהיה חלוקת השלם על חלק וחלקים רבים | ||||||
| ואם היתה חלוקתו על חלק אחד הכה השלם במעמד אותו החלק ומה שיצא הנה הוא היוצא מן החלוקה והוא הראוי לאחד | ||||||
| ואם היתה החלוקה על חלקים הכה השלם במעמדות החלק ההוא וחלק מה שהתקבץ על מספר החלקים ומה שיצא הנה הוא הראוי לאחד | ||||||
| ואם אמר חלק ששה על תשעה הכה ששה בתשעה יהיו ארבעה וחמשים והוא היוצא מן החלוקה | ||||||
| וכן אלו אמר חלק עשרים על עשרה הכה העשרי' בעשרה יהיו מאתים והוא היוצא מן החלוקה | ||||||
| ואולם חלוקת השלם על החלקים | ||||||
|
|
הנה דמיונו חלק ששה על שני שלישים | |||||
| הוריד השאלה על זאת הצורה: | ||||||
|
|
| |||||
|
|
אחר כן הכה הששה בשלשה וחלקהו על השנים יצא תשעה | |||||
|
|
ואלו אמר חלק תשעה על שלש שמיניות | |||||
| הוריד השאלה על זאת הצורה: | ||||||
|
|
| |||||
|
|
אחר כן הכה התשעה בשמנה וחלקם על השלשה יצא ארבעה ועשרים | |||||
|
|
ואלו אמר חלק חמשה עשר על עשרה חלקים מאחד עשר | |||||
| הורידם על זאת הצורה: | ||||||
|
|
| |||||
|
|
אחר כן הכה החמשה עשר באחד עשר וחלק מה שיצא על העשרה יהיה זה ששה עשר וחצי | |||||
| הנה הוצאת הסכום אשר יחלק עליו בכל זה המין אמנם הוא שתקח החלקים אשר על הקו התחתון ותקחם סכום ותעשה כמו שקדם והבין ותמצא בע"ה | ||||||
Division of Integer by Fraction of Fraction |
שער חלוקת השלם על שבר השבר | |||||
|---|---|---|---|---|---|---|
| דע כי כל המעשה בזה השער והשער אשר קדם מעשה אחד והוא יחלק לשני חלקים: | ||||||
| אם שיהיה השבר הנחלק עליו חלק אחד | ||||||
| ואם היה חלק אחד הכה המספר הנחלק במעמד השבר והוא היוצא מן החלוקה | ||||||
| ואם היה השבר הנחלק עליו חלקים הנה אתה תכה המספר הנחלק במעמדי השבר ההוא ותחלק מה שהתקבץ על מספר החלקים ומה שיצא הנה הוא המבוקש | ||||||
|
|
ודמיון זה בחלוקה על חלק אחד: חלק עשרה על שליש חומש | |||||
| הוריד השאלה על זאת הצורה: | ||||||
|
|
| |||||
|
|
אחר כן הכה העשרה בסכום השטה התחתונה ומה שיצא הנה הוא היוצא מן החלוקה והבין זה והוא חמשים ומאה ויהיה עקר המעשה שתחלק המאה וחמשים על האחד אשר על השלשה אבל החלוקה על אחד לא יכפול כמו שההכאה באחד לא יכפול הפלנו אנחנו מלת החלוקה על אחד וגם כן הנה המבוקש בחלוקה אמנם הוא מה שראוי לאחד ולרבים ונחלק עליהם המספר וכאשר נחלק מספר על אחד ינתן אותו המספר כלו לאחד ולא נצטרך לחלק ההכאה וההכאה בו | |||||
| ואולם החלוקה על החלקים מזה השער | ||||||
|
|
הנה דמיונו: חלק תשעה על שני שלישי שמינית | |||||
| הורידם על זאת הצורה: | ||||||
|
|
| |||||
|
|
אחר כן הכה התשעה בסכום השטה התחתונה ומה שהתקבץ חלקהו על הסכום והוא השנים אשר הם שני השלישים יצא שמנה ומאה | |||||
|
|
ואלו אמר חלק תשעה עשר על שלשה רביעי חומש | |||||
| הורידם על זאת הצורה: | ||||||
|
|
| |||||
|
|
אחר כן הכה התשעה עשר בסכום השטה התחתונה וחלק מה שהתקבץ על השלשה אשר הם הרביעיות יצא מאה וששה ועשרים ושני שלישים והבין | |||||
Division of Integer by Fraction and Fraction of Fraction |
שער חלוקת השלם על השבר ושבר השבר | |||||
|---|---|---|---|---|---|---|
|
|
חלק ארבעה על שלשה חומשים ושליש חומש | |||||
| הוריד השאלה על זאת הצורה: | ||||||
|
|
| |||||
|
|
אחר כן התחיל בשטה התחתונה ועשה בה כמו שתעשה בשער הכאת השבר ושבר השבר והוא שתכה השלשה אשר על החמשה בשלשה אשר הם מעמד השליש והשיא מה שעל ראשם והוא אחד יהיה כל זה עשרה והוא הסכום אחר כן הכה הארבעה הנחלקים במעמדי השברים יהיו ששים וחלקם על הסכום יצא ששה והוא היוצא מן החלוקה | |||||
|
|
ואם תחלק חמשה על עשרה חלקים מאחד עשר וחצי חלק מאחד עשר | |||||
| הורידם על זאת הצורה: | ||||||
|
|
| |||||
|
|
אחר כן התחיל בשטה התחתונה והכה העשרה בשנים והשיא מה שעל ראשם יהיו אחד ועשרים והוא הסכום אחר כן הכה החמשה באחד עשר ובשנים ותחלק מה שהתקבץ על הסכום יצא חמשה ושביעית ושני שלישי שביעית | |||||
Division of Integer by Two Different Fractions |
שער חלוקת השלם על שני השברים המתחלפים | ||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
חלק שמנה על שליש ושלשה רביעים | ||||||||
| הורידם על זאת הצורה: | |||||||||
|
|
| ||||||||
|
|
אחר כן עשה בשטה התחתונה כמו שתעשה בשני השברים המתחלפים יתקבץ בו שלשה עשר והוא הסכום אחר כן הכה השמנה בסכום השטה התחתונה ותחלקהו על הסכום יצא שבעה וחמשה חלקים משלשה עשר | ||||||||
|
|
ואם אמר חלק עשרה על שלשה חומשים ושלש שמניות | ||||||||
| הוריד השאלה על זאת הצורה: | |||||||||
|
|
| ||||||||
|
|
אחר כן התחיל בשטה התחתונה ועשה בו כמו שקדם בשני השברים המתחלפים יהיו תשעה ושלשים והוא הסכום אחר כן הכה העשרה במעמדי שבר הקו התחתון והכהו בחמשה תחלה ומה שהתקבץ הכהו בשמונה יהיה זה ארבע מאות וחלקם על הסכום יצא עשרה ושלשה חלקים משלשה עשר ושליש חלק משלשה עשר | ||||||||
Division of Integer and Fraction by Fraction |
שער חלוקת השלם והשבר על השבר | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| כשתרצה לחלק שלם ושבר על שבר הוריד השאלה בשתי שטות הנחלק בשטה העליונה והנחלק עליו בשטה התחתונה אחר כן עשה בשטה התחתונה כמו שקדם בשערו בהכאת השלם והשבר ומה שהתקבץ לך בה הכהו בסכום הקו התחתון ואמרנו סכום הקו התחתון אמנם המבוקש בו מעמד השבר אשר בשטה ההיא וכן כל מה שיבוא אחריו וכל מה שקדם לנו מן המעשה אחר כן הכה המספר אשר על מעמד השבר מן הקו התחתון והוא מספר החלקים בסכום השטה העליונה ומה שהתקבץ הנה הוא הסכום וחלק עליו המספר הראשון | ||||||||||||
|
|
והמשל בו אלו נאמר לך: חלק עשרה וחצי על חמשה שתותים | |||||||||||
| הורידם על זאת הצורה: | ||||||||||||
|
|
| |||||||||||
|
|
אחר כן הכה החמשה אשר על הקו התחתון בסכום הקו העליון ותעשה בו כמו שקדם בהכאת השלם והשבר והוא שתכה העשרה בשנים ותשיא מה שעל ראשם יהיו אחד ועשרים והכם בסכום הקו התחתון יהיו ששה ועשרים ומאה וחלקם על הסכום אשר הוא עשרה יצא שנים עשר ושש עשיריות | |||||||||||
|
|
ואם אמר: חלק עשרים ורביע על שלשה חומשים | |||||||||||
| הורידם על זאת הצורה: | ||||||||||||
|
|
| |||||||||||
|
|
והכה השלשה אשר על הקו התחתון בסכום הקו העליון יהיו שנים עשר והוא הסכום אשר יחלק עליו אחר כן חזור אל הקו העליון והכה העשרים בארבעה והשיא מה שעל ראשם והכהו על סכום הקו התחתון יהיה זה חמשה וארבע מאות וחלקם על הסכום יצא שלשה ושלשים וארבעה שתותים וחצי שתות | |||||||||||
Division of Integer and Fraction by Fraction of Fraction |
שער חלוקת השלם והשבר על שבר השבר | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
|
חלק חמשה ושליש על שלשה רביעי חמישית | |||||||||
| הורידם על זאת הצורה: | ||||||||||
|
|
| |||||||||
|
|
אחר כן הכה השלשה אשר על הקו התחתון בשלשה אשר הם סכום הקו העליון יהיו תשעה והוא הסכום אחר כן חזור אל השטה העליונה והכה החמשה בשלשה והשיא מה שעל ראשם יהיו ששה עשר והכם בסכום הקו התחתון יהיה כל זה עשרים ושלש מאות וחלקם על הסכום יצא חמשה ושלשים וחמש תשיעיות | |||||||||
|
|
ואם אמר: חלק שמונה ושלשה חלקים משלשה עשר על שלשה חומשי שביעית | |||||||||
| הוריד השאלה על זאת הצורה: | ||||||||||
|
|
| |||||||||
|
|
אחר כן הכה השלשה אשר על הקו התחתון בשלשה עשר יהיה זה תשעה ושלשים והוא הסכום אחר כן הכה השמונה בשלשה עשר והשיא מה שעל ראשם ומה שהתקבץ הכהו בסכום הקו התחתון יהיה זה חמשה וארבעים ושבע מאות ושלשת אלפים וחלקם על הסכום יצא ששה ושתי תשיעיות וחלק מתשע ושלשים | |||||||||
Division of Integer and Fraction by Fraction and Fraction of Fraction |
שער חלוקת השלם והשבר על השבר ושבר השבר | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
|
חלק ששה וחצי על ארבעה חומשים וחצי חומש | |||||||||
| הורידם על זאת הצורה: | ||||||||||
|
|
| |||||||||
|
|
אחר כן התחיל בשטה התחתונה ותעשה בה כמו שקדם בהכאת השבר ושבר השבר יהיו תשעה והכם במעמד השבר מן השטה העליונה יהיה זה שמנה עשר והוא הסכום אחר כן חזור אל השטה העליונה ותעשה בו כמו שקדם בהכאת השלם והשבר ומה שהתקבץ הכהו בסכום השטה התחתונה יהיו שלשים ומאה וחלקם על הסכום יצא שבעה ושתי תשיעיות | |||||||||
Division of Integer and Fraction by Two Different Fractions |
שער חלוקת השלם והשבר על שני השברים המתחלפים | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
חלק עשרה ושליש על שני חומשים ושתות | |||||||||||
| הורידם על זאת הצורה: | ||||||||||||
|
|
| |||||||||||
|
|
אחר כן עשה בשטה התחתונה כמו שקדם בשני השברי' המתחלפים יהיה המקובץ בו שבעה עשר והכם במעמד השליש מן הקו העליון יהיה אחד וחמשים והוא הסכום אחר כן הכה העשרה בשלשה והשיא מה שעל ראשם יהיה זה שלשי' ותשע מאות וחלקם על הסכום יצא שמנה עשר וארבעה חלקי' משבעה עשר | |||||||||||
Division of Integer and Fraction and Fraction of Fraction by Fraction |
שער חלוקת השלם והשבר ושבר השבר על השבר | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
|
חלק ארבעה ושלש שמיניות וחצי שמינית על שלשה חומשים | |||||||||
| הורידם על זאת הצורה: | ||||||||||
|
|
| |||||||||
|
|
אחר כן התחיל בשטה התחתונה והכה השלשה אשר על החמש' בסכום השטה העליונה יהיו שמונה וארבעים והוא הסכום אחר כן חזור אל השטה העליונה ועשה בה כמו שתעשה בהכאת השלם והשבר ושבר השבר והוא שתכה הארבעה בשמונה והשיא מה שעל ראשם והכה המקובץ בשנים והשיא מה שעל ראשם יהיה זה אחד ושבעים והכם בחמשה אשר הם מעמד השבר בשטה התחתונה יהיה זה חמשה וחמישים ושלש מאות וחלקם על הסכום יצא לך בחלוקה שבעה ושלש שמיניות ושתות שמינית | |||||||||
Division of Integer and Fraction and Fraction of Fraction by Fraction of Fraction |
שער חלוקת השלם והשבר ושבר השבר על שבר השבר | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
|
חלק שנים ושש שביעיות ושני שלישי שביעית על ארבעה חומשי השתות | |||||||||
| הורידם על זאת הצורה: | ||||||||||
|
|
| |||||||||
|
|
אחר כן קח הארבעה אשר על הקו התחתון והכם בסכום הקו העליון יהיה זה ארבעה ושמנים והוא הסכום אחר כן עשה בשטה העליונה כמו שקדם בהכאת השלם והשבר ושבר השבר ומה שהתקבץ הכהו בסכום הקו התחתון יהיה זה ששים ושמונה מאות ואלף וחלקם על הסכום יצא לך שנים ועשרים ושביעית | |||||||||
Division of Integer and Fraction and Fraction of Fraction by Fraction and Fraction of Fraction |
שער חלוקת השלם ושבר ושבר השבר על השבר ושבר השבר | |||||||
|---|---|---|---|---|---|---|---|---|
|
|
כשיאמ' לך חלק תשעה וחמשה שתותים ורביעית שתות על שביעית וחצי שביעית | |||||||
| הורידם על זאת הצורה: | ||||||||
|
|
| |||||||
|
|
אחר כן התחיל בשטה התחתונה והכה באחד אשר על השבעה בשנים והשיא מה שעל ראשם ומה שהתקבץ הכהו בסכום הקו העליון יהיה זה שנים ושבעים והוא הסכום אחר כן עשה בשטה העליונה כמו שקדם בשערו ומה שהתקבץ הכהו בסכום השטה התחתונה יהיה זה שמנה עשר ושלש מאות ושלשת אלפים וחלקם על הסכום יצא ששה וארבעי' ושש שמיניות התשיעית | |||||||
Division of Integer and Fraction and Fraction of Fraction by Two Different Fractions |
שער חלוקת השלם והשבר ושבר השבר על שני השברים המתחלפים | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
|
חלק שלשה ושלש עשיריות וחצי עשירית על שלש רביעיות ושלשה חלקים מאחד עשר | |||||||||
| הורידם על זאת הצורה: | ||||||||||
|
|
| |||||||||
|
|
אחר כן עשה בשטה התחתונה כמו שקדם בהכאת שני השברים המתחלפים ויתקבץ בה חמשה וארבעים והכם בסכום הקו העליון יהיו תשע מאות והוא הסכום אחר כן חזור אל הקו העליון והכה השלשה אשר הם השלמים בעשרה והשיא מה שעל ראשם ומה שהתקבץ הכהו בשנים והשיא מה שעל ראשם ומה שהתקבץ הכהו בסכום השטה התחתונה יצא זה שמנה וארבעים ותשע מאות ושני אלפים וחלקם על הסכום יצא שלשה ועשרים ושבע עשיריות העשירית וחמש תשיעיות עשירית העשירית | |||||||||
Division of Integer and Two Different Fractions by Fraction |
שער חלוקת השלם ושני השברים המתחלפים על השבר | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
חלק חמשה ושלישית ורביעית על שני חומשים | |||||||||||
| הורידם על זאת הצורה: | ||||||||||||
|
|
| |||||||||||
|
|
אחר כן הכה השנים אשר על החמשה בשטה התחתונה בסכום השטה העליונה יהיה זה ארבעה ועשרים והוא הסכום אחר כן עשה בשטה העליונה כמו שקדם מהכאת השלם ושני השברים המתחלפים יהיה זה שבעה ושישים והכם בחמשה אשר הם מעמד החומש בשטה התחתונה יהיה זה חמשה ושלשים ושלש מאות וחלקם על הסכום יצא שלשה עשר ושבע שמיניות ושני שלישי השמינית | |||||||||||
Division of Integer and Two Different Fractions by Fraction of Fraction |
שער חלוקת השלם ושני השברים על שבר השבר | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
חלק שנים ושלשה חומשים וארבע תשיעיות על שלשה רביעי השמינית | |||||||||||||
| הורידם על זאת הצורה: | ||||||||||||||
|
|
| |||||||||||||
|
|
אחר כן הכה השלשה אשר על השטה התחתונה בסכום השטה העליונה יהיה זה חמשה ושלשים ומאה והוא הסכום אחר כן עשה בשטה העליונה כמו שקדם בשערו כלומר הכאת השלם ושני השברים ומה שהתקבץ הכהו בסכום השטה התחתונה יהיה זה ארבעה ושמנים ושלש מאות וארבעת אלפים וחלקם על הסכום יצא שנים ושלשים וארבעה תשיעיות וחמישית תשיעית ושליש חמישית תשיעית | |||||||||||||
Division of Integer and Two Different Fractions by Fraction and Fraction of Fraction |
שער חלוקת השלם ושני השברים על השבר ושבר השבר | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
חלק שמונה משלשה חלקים מאחד עשר וחמשה שביעיות על חמש שמיניות ושליש שמינית | |||||||||||||
| הורידם על זאת הצורה: | ||||||||||||||
|
|
| |||||||||||||
|
|
אחר כן התחיל בשטה התחתונה והכה החמשה אשר על ראש השמונה בשלשה והשיא מה שעל ראשם יהיה ששה עשר והכם בסכום השטה העליונה יהיה זה שנים ושלשים ומאתים ואלף והוא הסכום אחר כן חזור אל השטה העליונה והכהו כמו שקדם בהכאת השלם ושני השברים המתחלפים ומה שהתקבץ הכהו בסכום השטה התחתונה יהיה זה שמונה ושש מאות וששה עשר אלף וחלקם על הסכום יצא שלשה עשר וחמשה חלקים מאחד עשר ושתי שמיניות חלק מאחד עשר ושתי שביעיות שמינית חלק מאחד עשר | |||||||||||||
Division of Integer and Two Different Fractions by Two Different Fractions |
שער חלוקת השלם ושני השברים המתחלפים על שני השברי' המתחלפים | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
חלק עשרה וששה חלקי' משלשה עשר ושבע שמנייות על תשע עשרייות ושבעה חלקי' מאחד עשר | |||||||||||
| והורידם על זאת הצורה: | ||||||||||||
|
|
| |||||||||||
|
|
אחר כן התחיל בשטה התחתונה ועשה בו כמו שתעשה בהכאת שני השברים המתחלפי' ומה שהתקבץ הכהו בסכום השטה העליונה יהיה זה ששה ושבעי' וחמש מאות ושבעה עשר אלף והוא הסכום אחר כן עשה בשטה העליונה כמו שקדם בהכאת השלם ושני השברים ומה שהתקבץ הכהו בסכום השטה התחתונה יהיה זה תשעים ושש מאות ותשעה ועשרים אלף ומאה אלף וחלקם על הסכום יצא שבעה וארבעה חלקי' משלשה עשר ושנים עשר חלקי' משלשה עשר ושנים עשר חלקים משלשה עשר בחלק משלשה עשר | |||||||||||
Division of Integer and Two Different Fractions by Integer and Two Different Fractions |
שער חלוקת השלם ושני השברים המתחלפים על השלם ושני השברים המתחלפים | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמ' לך חלק עשרה וששה חלקי' משלשה עשר ושבע שמנייות על תשע' ותשע עשרייות ותשעה חלקי' מאחד עשר | ||||||||||||
| והורידם על זאת הצורה: | |||||||||||||
|
|
| ||||||||||||
|
|
אחר כן התחיל בשטה התחתונה ותעשה בו כמו שקדם בהכאת השלם ושני השברים המתחלפים ומה שהתקבץ הכהו בסכום השטה העליונה יהיה זה ששה ושלשים וחמש מאות ועשרים אלף ומאה אלף והוא הסכום אחר כן עשה בשטה העליונה כמו שקדם בהכאת השלם ושני השברים המתחלפים ומה שהתקבץ הכהו בסכום השטה התחתונה יהיה זה תשעים ושש מאות ותשעה ועשרים אלף ומאה אלף וחלקם על הסכום יצא שבעה וארבעה חלקי' משלשה עשר ושנים עשר חלק משלשה עשר בחלק משלשה עשר ושתי שמניות חלק משלשה עשר בחלק משלשה עשר | ||||||||||||
Division of Fraction by Fraction |
שער חלוקת השבר על השבר | ||||||
|---|---|---|---|---|---|---|---|
|
|
חלק שש שביעיות על שלש שמיניות | ||||||
| הוריד השאלה על זאת הצורה: | |||||||
|
|
| ||||||
|
|
אחר כן התחיל בשטה התחתונה והכה השלשה אשר על השמנה בשבעה אשר הם סכום השטה העליונה יהיה אחד ועשרים והוא הסכום אחר כן הכה הששה אשר על הקו העליון בשמונה אשר הם סכום הקו התחתון יהיה זה שמונה וארבעים וחלקם על הסכום יצא שנים ושתי שבעיות | ||||||
Division of Fraction by Fraction of Fraction |
שער חלוקת השבר על שבר השבר | ||||||
|---|---|---|---|---|---|---|---|
|
|
חלק תשע עשרות על שני שלישי שביעית | ||||||
| הורידם על זאת הצורה: | |||||||
|
|
| ||||||
|
|
אחר כן התחיל בשטה התחתונה והכה השנים אשר על הקו התחתון בעשרה אשר הם סכום הקו העליון יהיו עשרים והוא הסכום אחר כן הכה התשעה אשר על הקו העליון בסכום הקו התחתון יהיו תשעה ושמונים ומאה וחלקם על הסכום יצא תשעה וארבע עשיריות וחצי עשירית | ||||||
Division of Fraction by Fraction and Fraction of Fraction |
שער חלוקת השבר על השבר ושבר השבר | ||||||
|---|---|---|---|---|---|---|---|
|
|
חלק שנים עשר חלקים משלש' עשר על שמינית ושליש שמינית | ||||||
| הורידם על זאת הצורה: | |||||||
|
|
| ||||||
|
|
אחר כן עשה בשטה התחתונה כמו שקדם בשבר ושבר השבר ומה שהתקבץ הכהו בסכום הקו העליון יהיו שנים וחמישים והוא הסכום אחר כן תקח השנים עשר אשר על הקו העליון יהיה שנים וחמשים והוא הסכום והכם בסכום הקו התחתון יהיו שמונה ושמונים ומאתים וחלקם על הסכום יצא לך חמשה ושבעה חלקים משלשה עשר | ||||||
Division of Fraction by Two Different Fractions |
שער חלוקת השבר על שני השברים המתחלפים | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
חלק שבע שמיניות על שתי תשיעיות ושלש שמיניות | ||||||||||
| הורידם על זאת הצורה: | |||||||||||
|
|
| ||||||||||
|
|
אחר כן התחיל בשטה התחתונה ותעשה בה כמו שתעשה בשני השברים המתחלפים ומה שהתקבץ הכהו בסכום הקו העליון יהיה זה ארבעה וארבעים ושלש מאות והוא הסכום אחר כן הכה השבעה אשר על הקו העליון בסכום השטה התחתונה יהיה זה ארבעה וחמש מאות וחלקם על הסכום יצא אחד שלם ועשרה חלקים משלשה וארבעים | ||||||||||
Division of Fraction and Fraction of Fraction by Fraction and Fraction of Fraction |
שער חלוקת השבר ושבר השבר על השבר ושבר השבר | ||||||
|---|---|---|---|---|---|---|---|
|
|
חלק תשעה חלקי' מאחד עשר וחצי חלק מאחד עשר על חומש וחצי חומש | ||||||
| הורידם על זאת הצורה: | |||||||
|
|
| ||||||
|
|
אחר כן עשה בכל אחד משתי השטות כמו שקדם בשער הכאת השבר ושבר השבר ומה שהתקבץ מן השטה התחתונה הכהו בסכום השט' העליונה יהיה זה הסכום ומה שהתקבץ מן השט' העליונה תכהו בסכום השטה התחתונה וחלקת אותו על הסכום יצא שנים ותשעה חלקים מאחד עשר וארבע' שתותי החלק מאחד עשר | ||||||
Division of Two Different Fractions by Two Different Fractions |
שער חלוקת שני השברים על שני השברים | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
חלק שלשה רביעים ושמנה תשיעיות על שליש וחומש | ||||||||||
| הורידם על זאת הצורה: | |||||||||||
|
|
| ||||||||||
|
|
אחר כן עשה בכל אחד משתי השטות כמו שקדם מהכאת שני השברים המתחלפים ומה שהתקבץ בשטה התחתונה הכהו בסכום השטה העליונה והוא יהיה הסכום ומה שהתקבץ בשטה העליונ' תכהו בסכום השטה העליונה התחתונה ותחלק מה שהתקבץ על הסכום ומה שיצא הנה הוא מה שרצית והוא שלשה וחמש שמינייות התשיעית ורביעית שמינית התשיעית | ||||||||||
Division of Integer and Fraction by Integer and Fraction |
שער חלוקת השלם והשבר על השלם והשבר | ||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
חלק ששה וחצי על שלשה ושליש | ||||||||
| הורידם על זאת הצורה: | |||||||||
|
|
| ||||||||
|
|
אחר כן עשה בכל אחד משתי השתות כמו שקדם בשער הכאת השלם והשבר אחר כן מה שהתקבץ קבץ מן השטה התחתונה הכהו במעמד השבר מן השטה העליונה יהיה עשרים והוא הסכום אחר כן מה שהתקבץ מן השטה העליונ' תכהו המעמד השבר מן השטה התחתונה יהיה תשעה ושלשי' וחלקם על הסכום יצא אחד ותשע עשיריות וחצי עשירית והוא המבוקש | ||||||||
Division of Integer and Fraction and Fraction of Fraction by Integer and Fraction and Fraction of Fraction |
שער חלוקת השלם והשבר ושבר השבר על השלם והשבר ושבר השבר | ||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
חלק ארבעה ושבע שמיניות ושליש שמינית על אחד וחלק מאחד עשר וחצי חלק מאחד עשר | ||||||||
| והורידם על זאת הצורה: | |||||||||
|
|
| ||||||||
|
|
אחר כן עשה בכל אחד משתי השטות כמו שקדם בהכאת השלם והשבר ושבר השבר ומה שהתקבץ מן השטה התחתונה והוא חמשה ועשרים תכהו במעמד השבר בשטה העליונה יהיו שש מאות והוא הסכום ומה שהתקבץ בשטה העליונה והוא שמנה ועשרים ומאה תכהו במעמדי השבר מן השטה התחתונה יהיה זה ששה ותשעים וחמש מאות ואלפי' חלקם על הסכום יצא ארבעה ושלש עשיריות ושתי עשיריות עשירית וארבעה שתותי עשירית עשירית העשירית | ||||||||
Division of Integer and Two Different Fractions by Integer and Two Different Fractions |
שער חלוקת השלם ושני השברים על השלם ושני השברים | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
חלק חמשה וחמשה שתותים ושש שביעיות על שנים ושלש שמינייות וחמשה חלקים משלשה עשר | ||||||||||||
| והורידם על זאת הצורה: | |||||||||||||
|
|
| ||||||||||||
|
|
אחר כן עשה בכל אחד משני השטות כמו שקדם בהכאת השלם ושני השברים ומה שהתקבץ בשטה התחתונה והוא שבעה ושמנים ומאתים הכהו בסכום השטה העליונה יהיה זה ארבעה וחמשים ושנים עשר אלף והוא הסכום עוד מה שתקבץ בשטה העליונה והוא שלשה ועשרים ושלש מאת תכהו במעמדי השברים בשטה התחתונה יהיה זה שנים ותשעים וחמש מאות ושלשה ושלשים אלף וחלקם על הסכום יצא שנים ושלשים חלק מאחד וארבעים ושביע החלק מאחד וארבעים והוא מה שרצית | ||||||||||||
| וכבר הקדמנו מחלוקת השברים מה שבו די למי שהבינו | |||||||||||||
| ותרגיל בו יקיש על מה שיבוא אחריו בע"ה עוד נמשיך אחר המעשה הזה בקצת חלוקת הזרים ונקצר בו בע"ה | |||||||||||||
|
|
כשיאמ' לך חלק שלשה רביעי חמשה על שני חומשי שלשה | ||||||||||||
| הורידם על זאת הצורה: | |||||||||||||
|
|
| ||||||||||||
|
|
אחר כן התחיל בשטה התחתונה והכה השנים אשר על החמשה בשלשה יהיו ששה והכה בארבעה אשר הם מעמ' השבר בשטה העליונה יהיו ארבעה ועשרים והוא הסכום אחר כן חזור אל השטה העליונה והכה השלשה אשר על הארבעה בחמשה יהיו חמשה עשר והכם בסכום הקו התחתון והם חמשה יהיו חמשה ושבעים וחלקם על הסכום יצא שלשה ושמינית | ||||||||||||
|
|
ואם תרצה קח מן החמשה שלשה רביעהם והוא שלשה ושלש רביעייות אחר כן תקח מן השלש שני חומשהם והוא אחד וחומש | ||||||||||||
|
|
והוא כאילו אמ' חלק שלשה חומשי ששה ורביע על שני שלישי ארבעה וחצי | ||||||||||||
| הורידם על זאת הצורה: | |||||||||||||
|
|
| ||||||||||||
|
|
אחר כן התחיל בשטה התחתונה והכה הארבעה בשנים והשיא מה שעל ראשם יהיו תשעה והכם בשנים אשר על השלשה יהיו שמנה עשר והכם בסכום השטה העליונה יהיו ששים ושלש מאות והוא הסכום אחר כן חזור אל השטה העליונה והכה הששה בארבעה והשיא מה שעל ראשם יהיו חמשה ועשרים והכם בשלשה אשר על החמשה יהיו חמשה ושבעים והכם בסכום השטה התחתונה התחתונה יהיו חמשים וארבע מאות וחלקם על הסכום יצא אחד ורביע | ||||||||||||
|
|
ואם תרצה תקח שלשה חומשי ששה ורביע והוא שלשה ושלשה רביעיים אחר כן תקח שני שלישי ארבעה וחצי והוא שלשה תחלק שלשה ושלשה רביעיים על שלשה יצא אחד ורביע והוא מה שרצית | ||||||||||||
| ודע כי המעשה בכל השאלות שתעשה בכל שטה מהם כמו שקדם לו מן המעשה בשערו ותכה היוצא מן השטה התחתונה בסכום השטה העליונה יהיה מה שהתקבץ הסכום אחר כן הכה היוצא מן השטה העליונ' בסכום השטה התחתונה ותחלק מה שהתקבץ על הסכום יצא מה שרצית | |||||||||||||
| שער אחר ממנו | |||||||||||||
|
|
חלק עשרה על שבע שמיניות חמשה ושליש אלא שליש שנים ורביע | ||||||||||||
| הנה אופן המעשה בזה שתקח משנים ורביע שלישיתם ומן החמשה ושליש שבע שמיניותיהם ותפיל הפחות מן היתר ומה שנשאר תחלק עליו העשרה ומה שיצא הנה הוא המבוקש | |||||||||||||
| שער אחר ממנו | |||||||||||||
|
|
חלק שלשה רביעי שלשה חומשי תשעה על שלוש עשירית ומה שיצא תחלקהו על שני שלישי שבעה אלא חלוקת שנים ושמינית על שבע שמיניות וחצי שמינית | ||||||||||||
|
|
ומעשה בזה שתחלק השנים ושמינית על שבע שמינייות וחצי שמינית יצא שנים וחמש ושליש חומש אחר כן תקח שני שלישי השבעה והוא ארבעה ושני שלישי' ותפיל מהם השנים וחומש ושליש חומש הנשאר שנים ושני חומשים ותכם בשלש עשיריות יהיה זה שבע עשיריות וחמשית עשירית, אחר כן תקח מן התשעה שלשה רביעי שלשה חמשיהם והוא ארבעה וחצי עשירית | ||||||||||||
|
|
והוא כאלו אמר חלק ארבעה וחצי עשירית על שבע עשיריות וחומש עשירית ותעשה כמו שקדם יצא חמשה וחמש שמניות ותבין | ||||||||||||
| שער אחר ממנו | |||||||||||||
|
|
ואם אמר חלק מאה על שנים ומה שיצא על ראשם ומה שיצא על ארבעה ומה שיצא על שליש ומה שיצא על שלשה רביעים ומה שיצא על חמשה ודע כמה ראוי לכל אחד מן החמשה | ||||||||||||
|
|
המעשה בזה שתכה השנים בחצי יהיה אחד והכהו בארבעה יהיו ארבעה והכם בשליש יהיה אחד ושליש והכהו בשלשה רביעים יהיה אחד והכהו בחמשה יהיו חמשה וחלק עליהם המאה יצא עשרים והוא מה שרצית | ||||||||||||
Completion of Fractions |
שער חיתום השברים |
|---|---|
| דע כי השער הזה רב התועלת בכל מעשי החשבון כל שכן מי שרצה מעשה החיתום והנכחות ותשמש בו בכל שאלה ממעשיהם זולת המעט | |
|
|
כשאמר לך בכמה תחתים שליש עד שיהיה האחד |
| הנה זאת השאלה אמנם המבוקש בה באיזה מספר תכה שליש ויהיה היוצא מן ההכאה אחד | |
|
|
הנה המעשה בזאת השאלה שתחלק אחד על שליש יצא שלשה וזה המספר כאשר תכה בו שליש יהיה היוצא אחד |
|
|
וזה המעשה כולל בכל השער הזה מעט ממנו והרב ממנו וכבר ידעת כי אתה כאשר תכה שליש במספר יהיה היוצא שליש אותו המספר הנה האחד אם כן הוא שליש המספר המבוקש והכהו בשלשה יהיו שלשה והוא המספר המבוקש |
|
|
ואם תרצה תשים האחד שלישים יהיו שלשה שלישים וחלקם על הסכום שלשה יצא לך שלשה |
|
|
ואם אמר כמה תחתים שלשה רביעים עד שיהיה אחד |
|
|
חלק אחד על שלשה רביעים ומה שיצא הנה הוא מה שרצית והוא אחד ושליש |
|
|
ואם אמר בכמה תחתים שלשה חלקים מאחד עשר עד שיהיו אחד |
|
|
חלק אחד על שלשה חלקים מאחד עשר יצא שלשה ושני שלישים והוא מה שרצית |
| ואלו אמ' באלו השאלות עד שיהיו שנים או שלשה או חמשה תהיה מחלק אותו המספר כמו שחלקת האחד על השבר הנחתם | |
|
|
והמשל בו אלו אמר: בכמה תחתים שני שלישים עד שיהיו ארבעה |
|
|
חלק ארבעה על שני שלישים יצא ששה |
|
|
וכאשר תכה שני שלישים בששה יהיו ארבעה כמו שאמר |
| ואלו אמ' בכמה תחתים אחד וחצי ושני שלישים וחצי או שלשה ושליש עד שיהיו חמשה או ששה או מה שהוא יותר מן המספר המונח | |
| תחלה תחלק המספר על המספר הראשון המונח ומה שיצא תכהו באותו המספר יחתם המספר הראשון | |
|
|
והמשל בזה אלו אמ': בכמה תחתים שנים וחצי עד שיהיו ששה |
|
|
חלק תחלה הששה על השנים וחצי יצא שנים ושני חומשים ותכם בשנים ושני חומשים תחתים שנים וחצי עד שיהיו ששה |
| והסבה בזה כי כל מספר יחלק אחד משניהם על השני הכה אשר יצא מן החלוקה באשר הוכה במספר הנחלק עליו שב המספר הנחלק | |
| וכבר באר זה אבו כאמל בספר החיתום והנכוחות | |
| פרק | |
| ודע כי החיתום לא יהיה כי אם מן המעט אל הרב | |
| כמו שתחתים שליש עד שיהיה אחד ורביע וחמשה שתותים וששה שביעיות או עשרה חלקים מאחד עשר | |
| ואפשר באלו השאלות שתאמר עד שיהיה אחד או חצי או שנים או מה שהוא יותר מן השבר המונח | |
| וכן אפשר שתחתים שבר אל שבר כשיהיה השבר השני יותר מן הראשון | |
|
|
כמו שתאמר: בכמה תחתים שליש עד שיהיה חצי |
|
|
הנה זה אפשר ותחלק חצי על שליש כמו שקדם יצא אחד וחצי ותכהו באחד וחצי יחותם שליש עד שיהיה חצי |
|
|
וכן שני חומשים עד שיהיו חמש עשיריות |
|
|
הכם בשנים ורביע |
|
|
ואלו אמ': בכמה תחתים שני שלישים עד שיהיה חצי |
|
|
וכן שני חומשים עד שיהיו חמש עשיריות |
| תכם בשנים ורביע | |
|
|
ואלו אמ': בכמה תחתים שני שלישים עד שיהיו חצי |
| לא יחתים מפני כי השני שלישים יותר מן החצי ולא יחתם הדבר הרב וישוב אל מעט מפני כי החיתום הוא התוספת בדבר עד שיגיע אל הגדר אשר נרצה שיגיעהו אליו ואי אפשר שנוסיף בשני השלישים עד שנשיבם אל החצי | |
Degrading |
שער בירידה |
|---|---|
| דע כי הירידה היא הפך החיתום | |
|
|
והמשל בו כשיאמ' לך: בכמה תוריד אחד עד שיחזור חצי |
| וענין זאת השאלה אי זה מספר תכהו באחד ויהיה חצי | |
|
|
וכאשר תרצה שתמצא זה המספר תחלק חצי על אחד ומה שיצא תכהו בו ירד האחד וישוב חציו והוא חצי |
|
|
ואלו אמ': בכמה תוריד שנים וחצי עד שיהיה אחד |
|
|
הנה כאשר תרצה זה תחלק אחד על שנים וחצי ומה שיצא תכהו כן והוא שני חומשים |
|
|
ואלו אמ': בכמה תוריד ששה ורביע עד שיהיה אחד |
|
|
חלק אחד על ששה ורביע יצא ארבעה חומשי החומש ותכהו בארבעה חומשי החומש ירד עד שיהיה אחד |
|
|
ואלו אמ': בכמה תוריד שמנה וחצי עד שיהיו שנים וחצי |
|
|
חלק שנים וחצי על שמנה וחצי יצא חמשה חלקים משבעה עשר ותכם בחמשה חלקים משבעה עשר ירדו עד שיהיו שנים וחצי |
| פרק | |
| ודע כי הירידה לא תהיה אלא מן הרב אל המעט ואי אפשר שתהיה מן המעט אל הרב וזאת השאלה כבר בארתי בשער החיתום | |
Extracting Roots of Integer and Fraction |
שער הוצאת השורש במספר והשבר | ||
|---|---|---|---|
| כבר התבאר בתחילת הספר איך יוצא שורש המספר השלם שיש לו שורש ונרצה לבאר בשער הזה הוצאת שורש השברים שיש להם שורש ואשר אין להם שורש | |||
|
|
כשיאמר לך: כמה שורש רביע | ||
| הוריד הרביע על זאת הצורה: | |||
|
|
| ||
|
|
אחר כן תקח שורש המעמד והוא שנים וקחם סכום אחר כן תקח שורש האחד אשר על הקו והוא אחד ותחלקהו על הסכום יצא לך חצי והוא שורש רביע | ||
|
|
וכאשר הכית חצי בחצי היה רביע | ||
| פרק | |||
| ודע כי כאשר היה השבר סכום אחד קח שורש מה שתחת הקו הוא הסכום ושורש מה שעל הקו נחלק על הסכום ונבאר אותו שנית | |||
|
|
כשיאמר לך: כמה שורש תשיעית | ||
| הוריד התשיעית על זאת הצורה: | |||
|
|
| ||
|
|
אחר כן שורש מה שתחת הקו יהיה הסכום והוא שלשה אחר כן תקח שורש האחד וחלקהו על הסכום יצא שליש והוא שורש תשיעית | ||
|
|
ואם אמר: כמה שורש ארבע תשיעיות | ||
| הוריד הארבע תשיעיות על זאת הצורה: | |||
|
|
| ||
|
|
אחר כן תקח שורש מה שתחת הקו יהיה הסכום והוא שלשה ושרש מה שעל הקו והוא שנים וחלקם על הסכום יצא שני שלישים והוא שורש ארבע תשיעיות | ||
Extracting Roots of Fraction and Fraction of Fraction |
שער אחר ממנו | ||||
|
|
כמה שורש ארבע שמיניות וחצי שמינית | ||||
| הוריד הארבע שמיניות וחצי שמינית בשטה על זאת הצורה: | |||||
|
|
| ||||
|
|
אחר כן הכה השנים אשר הם הסכום בשמנה אשר הם הסכום יהיו ששה עשר ותקח שרשם והם ארבעה והוא הסכום ושמרהו אחר כן חזור והכה הארבעה אשר על השמנה בשנים והשיא מה שעל ראשם יהיו תשעה ותקח שרשם והוא שלשה ותחלקם על הסכום יצא שלשה רביעים והוא מה שרצית | ||||
|
|
ואם אמר כמה שורש שש תשיעיות ורביע תשיעית | ||||
| הורידם על זאת הצורה: | |||||
|
|
| ||||
|
|
אחר כן הכה הסכום בסכום יהיו ששה ושלשים ותקח שרשם והוא יהיה הסכום אשר יחלק עליו אחר כן הכה הששה בארבעה והשיא מה שעל ראשם יהיה חמשה ועשרים ותקח שרשם והם חמשה וחלקם על הסכום יצא חמשה שתותים והוא מה שרצית | ||||
|
|
ואם אמר: כמה שורש שש שמיניות ושמינית השמינית | ||||
| הורידם על זאת הצורה: | |||||
|
|
| ||||
|
|
אחר כן הכה השמנה בשמנה ותקח שורש מה שיצא והוא שמנה והוא יהיה הסכום אחר כן הכה הששה בשמנה והשיא מה שעל ראשם יהיו תשעה וארבעים וקח שרשם והוא שבעה וחלקם על הסכום יצא שבע שמיניות והוא מה שרצית | ||||
| ודע כי המעשה באלו השאלות כמו המעשה בהכאת השבר ושבר השבר | |||||
Extracting Roots of Fraction and Fraction of Fraction and Fraction of Fraction of Fraction |
שער אחר ממנו | ||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
כשיאמר לך: כמה שורש שבע תשיעיות וארבע שמיניות התשיעית וחצי שמינית התשיעית | ||||||||
| הורידם על זאת הצורה: | |||||||||
|
|
| ||||||||
|
|
אחר כן הכה הסכום אשר תחת הקו אחד מהם בשני ומה שהתקבץ בשלישי יהיה זה ארבעה וארבעים ומאה וקח שרשם והוא שנים עשר והוא הסכום אחר כן חזור והכה השבעה אשר על התשעה בשמנה והשיא מה שעל ראשם יהיו ששים והכם בשנים והשיא מה שעל ראשם יהיו אחד ועשרים ומאה ותקח שרשם והוא אחד עשר וחלקם על שורש הסכום אשר הוא שנים עשר יצא חמשה שתותים וחצי שתות והוא מה שרצית | ||||||||
| פרק | |||||||||
| ואם הכית הסכום אשר תחת הקו קצתם בקצת ולא יהיה למקובץ שורש הנה אין לשאלה שורש מדבר | |||||||||
| ועקר המעשה באלו השאלות מדרך המעמד שתבקש פחות מספר שיש לו חצי ושמינית ותשיעית וזה בהכאת אלו המעמדות קצתם בקצת ומה שהיה הנה הוא המעמד אחר כן קח מן מעמד השבר הנז' ומה שיהיה תקח שורשו ותחלקהו על שורש המעמד ומה שיצא הנה הוא המבוקש | |||||||||
| ואם לא יהיה למעמד שורש הנה אין לשאלה שורש | |||||||||
| ואם לא יהיה ג"כ לחלקים הלקוחים ממנו שורש הנה אין לשאלה שורש | |||||||||
| שער אחר ממנו | |||||||||
|
|
כמה שורש תשעה חלקים מאחד עשר וחלק מאחד עשר בחלק מאחד עשר | ||||||||
| הוריד השאלה על זאת הצורה: | |||||||||
|
|
| ||||||||
|
|
אחר כן הכה מה שעל אחד מן האחד עשר בשני והשיא מה שעל ראשם והוא אחד יהיה זה מאה ותקח שרשם שהוא עשרה ותחלקם על הסכום יצא עשרה חלקים מאחד עשר והוא מה שרצית | ||||||||
| פרק | |||||||||
| ודע כי כאשר היה בשאלה שני סכומים מתדמים תקח אחד משניהם ותשימהו הסכום אשר יחלק עליו אחר כן תעשה בשאר השאלה כמו שקדם | |||||||||
|
|
הדמיון בזה כשיאמר לך: כמה שורש חמש שביעיות ושביעית שביעית | ||||||||
| הוריד השאלה על זאת הצורה: | |||||||||
|
|
| ||||||||
|
|
הנה בזאת השאלה שני סכומים מתדמים והם שבעה ושבעה ותקח אחד משניהם ותקחהו סכום יחלק עליו אחר כן תכה החמשה אשר על השבעה הראשונים בשבעה השניים ותשיא מה שעל ראשם יהיו ששה ושלשים ותקח שרשם והוא ששה וחלקהו על השבעה יצא ששה שביעיות והוא מה שרצית | ||||||||
| ואם היו בשאלה שלשה סכומים שנים מהם דומים והשלישי יש לו שורש הנה תקח שורש הסכום ההוא השלישי המתחלף לשנים ומה שהיה תשימהו עם אחד מן הסכומים הדומים סכום יחלק עליו ותעשה בשאר השאלה כמו שקדם | |||||||||
|
|
המשל בו: כמה שורש תשיעית וארבע שמיניות התשיעית וארבע שמיניות שמינית התשיעית | ||||||||
| הורידם על זאת הצורה: | |||||||||
|
|
| ||||||||
|
|
הנה זאת השאלה יש בה שני סכומים דומים והם שמנה ושמנה וסכום אחד והוא תשעה ותקח שורש תשעה והוא שלשה ותקח אחד משני הסכומים הדומים והוא שמנה ויהיה עמך שני סכומים לחלק עליהם והם שלשה ושמנה אחר כך הכה האחד אשר על התשעה בשמנה אשר ילוו התשעה והשיא מה שעל ראשם ומה שהתקבץ תכהו בשמנה השניים ותשיא מה שעל ראשם יהיו מאה וקח שרשם והוא עשרה וחלקם על הסכום יצא שלש שמיניות ושליש שמינית | ||||||||
| ואם היו עמך שני סכומים דומים ושלישי שאין לו שורש הנה אין לשאלה שורש מדבר | |||||||||
| ואם היתה לשאלה ארבעה סכומים שנים דומים ושנים דומים תקח אחד משני הסכומים הראשונים והאחד משני הסכומים השניים ותשים שני אלו הלקוחים סכום תחלק עליו ותמשיך זאת השאלה עד סופה | |||||||||
|
|
דמיון זה: כמה שורש עשרה חלקים מאחד עשר וארבעה חלקים מאחד עשר בחלק מאחד עשר וחמשה שביעיות החלק מאחד עשר בחלק מאחד עשר וארבעה שביעיות משביעית החלק מאחד עשר בחלק מאחד עשר | ||||||||
| הוריד השאלה על זאת הצורה: | |||||||||
|
|
| ||||||||
|
|
הנה זאת השאלה ארבעה סכומים שנים מהם מתדמים והם אחד עשר ואחד עשר ושני הסכומים השניים מתדמים והם שבעה ושבעה ותקח אחד מן השבעה והאחד מן האחד עשר יהיה הסכום אחד עשר ושבעה אחר כן תכה העשרה שעל האחד עשר הראשונים באחד עשר השניים ותשיא מה שעל ראשם יהיה זה חמשה ותכה מה שהתקבץ בשבעה ותשיא מה שעל ראשם ותכה המקובץ בשבעה השניים ותשיא מה שעל ראשם יהיה זה חמשה ועשרים ושש מאות וחמשת אלפים ותקח שרשם והוא חמשה ושבעים וחלקם על הסכום יצא לך עשרה חלקים מאחד עשר וחמשה שביעיות החלק מאחד עשר והוא מה שרצית | ||||||||
| ואם היו בשאלה ארבעה סכומים השנים מהם מתדמים והשנים השניים מתחלפים הכה אחד מן המתחלפי' בשני | |||||||||
| ואם התקבץ מהם מספר יש לו שורש הנה השאלה יש לה שורש ותקח שורש מה שהתקבץ מן ההכאה ותקחהו סכום עם אחד משני הסכומים המתדמים ותעשה בנשאר כמו שקדם | |||||||||
|
|
המשל בו כשיאמר לך: כמה שורש חמש תשיעיות ושבע תשיעיות התשיעית וארבע שמיניות תשיעית התשיעית וחצי שמינית תשיעית תשיעית | ||||||||
| הוריד השאלה על זאת הצורה: | |||||||||
|
|
| ||||||||
|
|
הנה זאת השאלה בה שני סכומים מתדמים ושני סכומים מתחלפים והכה אחד משני המתחלפים והוא שנים בשמנה יהיה ששה עשר ותקח שרשם והוא ארבעה ותקח אחד משני הסכומים המתדמים והוא תשעה ותקח שני מספרים אלו סכום והם ארבעה ותשעה אחר כן תעשה כמו שקדם מהכאת השבר ושבר השבר יצא אחד וארבעים ושמנה מאות וקח שרשם והוא תשעה ועשרים וחלקם על הסכום יצא שבעה תשיעיות ורביעית תשיעית והוא מה שרצית | ||||||||
Extracting Roots of Integer and Fraction |
שער הוצאת שורש המספר והשבר | |||||
|---|---|---|---|---|---|---|
|
|
כשיאמר לך: כמה שורש שנים ורביע | |||||
| הוריד השאלה על זאת הצורה: | ||||||
|
|
| |||||
|
|
אחר כן קח שורש הארבעה אשר הם הסכום והוא שנים ושמרם והוא הסכום אחר כן הכה השנים בארבעה והשיא מה שעל ראשם יהיו תשעה וקח שרשם והוא שלשה וחלקם על הסכום יצא אחד וחצי והוא מה שרצית | |||||
| פרק | ||||||
| דע כי כאשר היה מעמד השבר יש לו שורש הנה אין ספק שיש בשאלה שורש מדבר | ||||||
| שער אחר ממנו | ||||||
|
|
כמה שורש אחד עשר ותשיעית | |||||
| הוריד השאלה על זאת הצורה: | ||||||
|
|
| |||||
|
|
אחר כן תקח שורש התשעה והוא שלשה אחר כן הכה האחד עשר בתשעה והשיא מה שעל ראשם ותקח שורש מה שיצא יהיה זה עשרה וחלקם על הסכום יצא שלשה ושליש והוא מה שרצית | |||||
| ודע כי כל המעשה בשער הזה שתקח מעמד השבר ותקחהו סכום תמיד אחר כן הכה השלם במעמד השבר ותשיא מה שעל ראשו ותקח שורש המקובץ ותחלקהו על הסכום וזה מעשהו כמו שקדם בהכאת המספר והשבר | ||||||
|
|
כשיאמר לך כמה שורש ארבעה וארבע שמיניות ושמינית שמינית | |||||
| הוריד השאלה על זאת הצורה: | ||||||
|
|
| |||||
|
|
אחר כן הבט הסכום ותמצאהו השנים מתדמים ותקח אחד מהם ותקחהו סכום כמו שקדם אחר כן תעשה בשאלה כמו שקדם בהכאת השלם והשבר ושבר השבר ומה שהתקבץ תקח שרשו והוא שבעה עשר וחלקהו על הסכום יצא שנים ושמינית והוא מה שרצית | |||||
| ואלו היה הסכום בלתי מתדמים תכה אחד משניהם בשני ותקח שורש המקובץ ותעשה כמו שקדם | ||||||
| ובמה שזכרנו מן השער הזה יש בו די יוקש עליו מה שיבוא אחריו בע"ה וימשך אחריו בהוצאת שורש המספרים אשר אין להם שורש וזה דבר אי אפשר להגיע אל אמתתו אלא בקירוב והקירוב בו לפי המעשה | ||||||
Approximations |
שער הוצאת השרשים האלמים על דרך קירוב |
|---|---|
Approximations of Integers |
|
|
|
כשיאמר לך כמה שורש חמשה |
|
הנה תקח המספר המרובע היותר קרוב אל החמשה תמצא זה ארבעה ותפילם מן החמשה הנשאר אחד וקרא שם לזה האחד מכפל שורש הארבעה יהיה רביע והשיאהו על שורש הארבעה יהיה שנים ורביע והוא שורש חמשה בקרוב והבין זה |
|
|
וכאשר הכית שנים ורביע בכמותם יהיה זה חמשה וחצי שמינית הנה כבר נפל הקירוב בחצי שמינית נוסף |
|
ואם תרצה שתקריב המעשה יותר מן הקירוב הזה הנה אתה תכפול השנים ורביע עד שיהיו ארבעה וחצי וקרא שם מהם החצי שמינית יהיה זה שמינית תשיעית והפילהו מן הרביע אשר עם השנים ורביע ישארו שנים ושתי תשיעיות ושמינית תשיעית |
|
|
וכאשר תכהו בדומה לו יהיה זה חמשה ושמינית שמינית תשיעית התשיעית והוא יותר קרוב מחמשה וחצי שמינית |
|
ואלו רצית יותר קרוב מזה תהיה כופל השנים ושתי תשיעיות ושמינית תשיעית ותקרא שם מזה שמינית שמינית תשיעית התשיעית ומה שהיה הפיל מן השנים ושתי תשיעיות ושמינית תשיעית ומה שנשאר הנה הוא יותר קרוב מן השורש הראשון |
| שער אחר ממנו | |
|
|
כמה שורש עשרה |
|
|
תביט המספר שיש לו שורש היותר קרוב אל עשרה תמצא תשעה ותפילם מן העשרה הנשאר אחד ותקרא לו שם מכפל שורש התשעה והוא ששה יהיה שתות והשיאהו על השלשה אשר הם שורש התשעה יהיה שלשה ושתות והוא שורש העשרה בקירוב |
| ואם תרצה הכה העשרה באי זה מספר שיש לו שורש | |
|
|
כאלו אתה תכה אותם במאה יהיה המקובץ אלף ותקח שרשם כמו שקדם בקירוב יהיה זה אחד ושלשים וחצי החלק מאחד ושלשים וחלקהו על שורש המאה יהיה זה שלשה וחמשה חלקים מאחד ושלשים וחצי עשירית החלק מאחד ושלשים והוא יותר קרוב משתות |
|
|
ואם אמר כמה שורש חמשה עשר |
|
|
תקח המספר המרובע היותר קרוב אל חמשה עשר והוא ששה עשר והפיל מהם החמשה עשר הנשאר אחד וקרא לו שם מכפל שורש הששה עשר יהיה שמינית ותפילהו משורש הששה עשר הנשאר שלשה ושבע שמיניות והוא שרש חמשה עשר בקרוב |
|
|
ואם אמר כמה שרש עשרים |
| הנה תקח אם תרצה הששה עשר ואם תרצה החמשה ועשרים מפני כי העשרים ממוצעים בין שני אלו המרובעים | |
|
|
וכאלו אתה תקח הששה עשר ותפילם מן העשרים הנשאר ארבעה וקרא להם שם מכפל שרש הששה עשר יהיה חצי וחברהו אל שרש הששה עשר יהיה זה ארבעה וחצי והוא שורש העשרים בקרוב |
|
|
ואם תרצה תקח החמשה ועשרים ותפיל מהם העשרים הנשאר חמשה וקרא להם שם מכפל שורש החמשה ועשרים הנשאר ארבעה וחצי והוא שורש העשרים בקרוב |
Approximations of Integers and Fractions |
שער אחר ממנו |
|---|---|
|
|
כשיאמר לך כמה שורש שנים וחצי |
|
|
הנה מעמד החצי בזאת השאלה אין לו שורש וקחנו סכום אחר כן שים השנים וחצי חציים יהיו חמשה והכם בשנים יהיו עשרה וקח שורש העשרה כמו שקדם יהיה זה שלשה ושתות וחלקהו על השנים יצא אחד ושלשה שתותים וחצי שתות |
| ואם תרצה הכה השנים וחצי באיזה מספר מרובע שתרצה יהיה לו חצי | |
|
|
וכאלו אתה כבר הכית אותם בששה ושלשים יהיו תשעים ותקח שרשם יהיה תשעה וחצי וחלקהו על שרש ששה ושלשים יצא אחד ושלשה שתותים וחצי שתות |
|
|
ואם תרצה כאשר הכית השנים וחצי חציים והכית אותם בשנים יהיו עשרה והכה אלו העשרה בששה ושלשים יהיו ששים ושלש מאות אחר כן הכה השנים מעמד החצי בשרש הששה ושלשים יהיו שנים עשר והוא הסכום אחר כן תקח שרש הששים ושלש מאות והוא תשעה עשר בקרוב וחלקם על השנים עשר והנה מה שיצא הוא המבוקש |
Approximations of Fractions |
שער אחר ממנו |
|---|---|
|
|
כשיאמר לך כמה שרש שליש |
|
|
תבקש מספר שיש לו שרש ויש לו שליש וכאלו אתה תכהו בששה ושלשים יהיו שנים עשר ותקח שרשם והוא שלשה וחצי בקרוב ותחלקם על שרש הששה ושלשים יצא שלשה שתותים וחצי שתות והוא שורש שליש |
|
|
ואם יאמר: כמה שרש שלשה רביעים |
|
|
הנה תכה שלשה רביעים במספר מרובע שיש לו חצי ויש לו רביע כאלו הוא בששה עשר יהיה היוצא שנים עשר וקח שרשם והוא שלשה וחצי בקרוב וחלקם על שרש הששה עשר יצא שבע שמיניות |
|
|
ואם אמר: כמה שורש שלשה שביעיות |
|
|
הכה שלשה שביעיות במספר מרובע יש לו שביעית והוא תשעה וארבעים ותכה בו שלשה שביעיות ויהיה אחד ועשרים ותקח שרש אחד ועשרים והוא ארבעה ושלשה חומשים בקירוב וחלקהו על שורש התשעה וארבעים יצא ארבעה שביעיות ושלשה חומשי השביעית והבין |
| תם ושלם תהלה לאל עולם | |
| אמן | |
Additional Chapters |
|
Multiplication of Fraction by Integer |
שער הכאת השבר במספר השלם |
|---|---|
|
כשיאמר לך כמה ארבעה חומשים בשמנה |
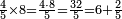
|
העמיד החומש וזה מחמשה וקחם סכום אחר כן קח ארבעה חומשיהם והוא ארבעה והכם בשמנה יהיו שנים ושלשים וחלקם על הסכום ומה שיצא הנה הוא המבוקש וזה ששה וחומש |
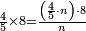
|
ואם תרצה קח אי זה מספר שתרצה סכום אחר כן קח ארבעה חומשיו והכם בשמנה וחלקם על הסכום ומה שיצא הנה הוא המבוקש |
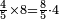
|
ואם תרצה חלק השמנה על החמשה והכה מה שיצא בארבעה ומה שיצא הנה הוא המבוקש |
Multiplication of Fraction and Fraction of Fraction by Fraction and Fraction of Fraction |
שער הכאת השבר ושבר השבר בשבר ושבר השבר |
![\scriptstyle\left[\frac{1}{2}+\left(\frac{1}{2}\sdot\frac{1}{10}\right)\right]\times\left[\frac{1}{3}+\left(\frac{1}{3}\sdot\frac{1}{10}\right)\right]](/mediawiki/images/math/a/1/e/a1e9dab8cb619ed33e62627735ea10b2.png)
|
כשיאמר לך הכה חצי וחצי עשירית בשליש ושליש עשירית |
![\begin{align}\scriptstyle\left[\frac{1}{2}+\left(\frac{1}{2}\sdot\frac{1}{10}\right)\right]\times\left[\frac{1}{3}+\left(\frac{1}{3}\sdot\frac{1}{10}\right)\right]&\scriptstyle=\frac{\left[\left(2\sdot10\right)\sdot\left[\frac{1}{2}+\left(\frac{1}{2}\sdot\frac{1}{10}\right)\right]\right]\sdot\left[\left(3\sdot10\right)\sdot\left[\frac{1}{3}+\left(\frac{1}{3}\sdot\frac{1}{10}\right)\right]\right]}{\left(2\sdot10\right)\sdot\left(3\sdot10\right)}\\&\scriptstyle=\frac{\left[20\sdot\left[\frac{1}{2}+\left(\frac{1}{2}\sdot\frac{1}{10}\right)\right]\right]\sdot\left[30\sdot\left[\frac{1}{3}+\left(\frac{1}{3}\sdot\frac{1}{10}\right)\right]\right]}{20\sdot30}\\&\scriptstyle=\frac{11\sdot11}{20\sdot30}\\&\scriptstyle=\frac{121}{20\sdot30}\\&\scriptstyle=\frac{1}{6}+\left(\frac{1}{5}\sdot\frac{1}{6}\right)+\left(\frac{1}{2}\sdot\frac{1}{10}\sdot\frac{1}{5}\sdot\frac{1}{6}\right)\\\end{align}](/mediawiki/images/math/8/b/4/8b4647cfc89bfd02960993f4d25ee3e0.png)
|
הנה המעשה בזה שתעמיד החצי והעשירית וזה מעשרים והשליש והעשירית וזה משלשים והכה קצתם בקצת יהיה מה שיצא הוא הסכום, אחר כן קח חצי העשרים וחצי עשיריתם יהיו אחד עשר ושליש השלשים ושליש עשיריתם וזה אחד עשר והכה אחד עשר באחד עשר יהיו מאה ועשרים ואחד וקרא להם שם מן הסכום ומה שהיה הנה הוא המבוקש וזה שתות וחומש שתות וחצי עשירית חומש השתות |
| שער מן החלקים | |
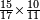
|
כשיאמר לך הכה חמשה עשר חלקים משבעה עשר בעשרה חלקים מאחד עשרה |
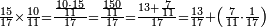
|
הכה עשרה בחמשה עשר יהיו מאה וחמשים וחלקם על אחד עשר יצא שלשה עשר ושבעה חלקים מאחד עשר ותאמר שלשה עשר חלקים משבעה עשר ושבעה חלקים מאחד עשר בחלק משבעה עשר והבין |
| ודע כי אתה כאשר תחלק על אחד מן החלקים הנה יצא השני וזה אמנם יהיה אחר ההכאה | |
Multiplication of Integer and Two Fractions by Integer and Fraction |
שער הכאת המספר ושני השברים במספר והשבר |
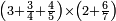
|
כשיאמר לך שלשה ושלשה רביעים וארבעה חומשים בשנים ושש שביעיות |
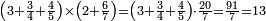
|
ההקש בזה שתשיב השנים ושש שביעיות שביעיות כולם יהיו עשרים והכם בשלשה ושלשה רביעים וארבעה חומשים יהיו אחד ותשעים וחלקם על מעמד השביעית יצא לך שלשה עשר והוא מה שרצית |
![\scriptstyle\left(3+\frac{3}{4}+\frac{4}{5}\right)\times\left(2+\frac{6}{7}\right)=\frac{\left[\left(4\sdot5\right)\sdot\left(3+\frac{3}{4}+\frac{4}{5}\right)\right]\sdot\left(2+\frac{6}{7}\right)}{4\sdot5}=\frac{\left[20\sdot\left(3+\frac{3}{4}+\frac{4}{5}\right)\right]\sdot\left(2+\frac{6}{7}\right)}{20}](/mediawiki/images/math/9/d/d/9dd58266d0822b30998883210c8ed06b.png)
|
ואם תרצה הביט מאיזה מספר יעמוד הרביעית והחמשית וזה מעשרים וקחם סכום אחר כן הכה בהם השלשה והשלשה רביעים וארבעה חומשים ומה שהתקבץ הכהו בשנים ושש שביעיות וחלק מה שהתקבץ על הסכום יצא לך מה שרצית |
Multiplication of Fraction of Integer and Fraction by Fraction of Integer and Fraction |
שער הכאת שבר המספר והשבר בשבר המספר והשבר |
![\scriptstyle\left[\frac{4}{5}\sdot\left(7+\frac{1}{2}\right)\right]\times\left[\frac{2}{3}\sdot\left(3+\frac{3}{4}\right)\right]](/mediawiki/images/math/4/a/7/4a727f221ebcb327b3416722878a8006.png)
|
כשיאמר לך ארבעה חומשי שבעה וחצי בשני שלישי שלשה ושלשה רביעים |
![\begin{align}\scriptstyle\left[\frac{4}{5}\sdot\left(7+\frac{1}{2}\right)\right]\times\left[\frac{2}{3}\sdot\left(3+\frac{3}{4}\right)\right]&\scriptstyle=\frac{\left[\left[\left(5\sdot2\right)\sdot\frac{4}{5}\right]\sdot\left(7+\frac{1}{2}\right)\right]\sdot\left[\left[\left(3\sdot4\right)\sdot\frac{2}{3}\right]\sdot\left(3+\frac{3}{4}\right)\right]}{\left(5\sdot2\right)\sdot\left(3\sdot4\right)}\\&\scriptstyle=\frac{\left[\left(10\sdot\frac{4}{5}\right)\sdot\left(7+\frac{1}{2}\right)\right]\sdot\left[\left(12\sdot\frac{2}{3}\right)\sdot\left(3+\frac{3}{4}\right)\right]}{10\sdot12}\\&\scriptstyle=\frac{\left[8\sdot\left(7+\frac{1}{2}\right)\right]\sdot\left[8\sdot\left(3+\frac{3}{4}\right)\right]}{120}\\&\scriptstyle=\frac{60\sdot30}{120}\\&\scriptstyle=\frac{1800}{120}=15\\\end{align}](/mediawiki/images/math/a/0/d/a0de8e244b25737f2270021ec72debbd.png)
|
הנה המעשה בזה שתעמיד החומש והחצי וזה מעשרה ושמרם והשליש והרביע וזה משנים עשר ושמרם גם כן אחר כן הכה קצתם בקצת יהיו מאה ועשרים וקחם סכום, אחר כן קח ארבעה חומשי העשרה וזה שמנה והכם בשבעה וחצי יהיו ששים ושמרם גם כן אחר כן קח שני שלישי השנים עשר והוא שמנה והכם בשלשה ושלשה רביעים יהיו שלשים והכם בששים אשר שמרת יהיו אלף ושמנה מאות וחלקם על הסכום יצא לך חמשה עשר |
![\scriptstyle\left[\frac{4}{5}\sdot\left(7+\frac{1}{2}\right)\right]\times\left[\frac{2}{3}\sdot\left(3+\frac{3}{4}\right)\right]=6\sdot\left(2+\frac{1}{2}\right)](/mediawiki/images/math/3/7/a/37a42f9ee1deec7ac871dcaa5dab236f.png)
|
ואם תרצה קח ארבעה חומשי שבעה וחצי והוא ששה וקח שני שלישי השלשה ושלשה רביעים והוא שנים וחצי והכם בששה יהיה מה שרצית |
![\scriptstyle\left[\left(\frac{1}{3}\sdot7\right)+\left(\frac{1}{4}\sdot6\right)\right]\times\left[\left(\frac{1}{2}\sdot3\right)+\left(\frac{1}{6}\sdot5\right)\right]](/mediawiki/images/math/4/0/7/407c671e10fc1f475a59f46db1a9fe8c.png)
|
שאלה כשיאמר לך: שליש שבעה ורביע ששה בחצי שלשה ושתות חמשה |
| הנה זאת השאלה שני עניינים: | |
![\scriptstyle\left[\left(\frac{1}{3}\sdot7\right)+\left(\frac{1}{4}\sdot6\right)\right]\times\left[\left(\frac{1}{2}\sdot3\right)+\left(\frac{1}{6}\sdot5\right)\right]](/mediawiki/images/math/4/0/7/407c671e10fc1f475a59f46db1a9fe8c.png)
|
אחד משניהם שתקח שליש שבעה והשיאהו על רביע ששה והכה אותו בחצי שלשה מחובר אליו שתות חמשה |
![\scriptstyle\left[\frac{1}{3}\sdot\left[7+\left(\frac{1}{4}\sdot6\right)\right]\right]\times\left[\frac{1}{2}\sdot\left[3+\left(\frac{1}{6}\sdot5\right)\right]\right]](/mediawiki/images/math/5/a/3/5a3db42e980708f3e6e2327dc4d0f2e6.png)
|
והעניין השני שתקח שליש השבעה ושליש רביע הששה ותכה אותו בחצי השלשה וחצי שתות חמשה ומה שהתקבץ הנה הוא המבוקש |
![\scriptstyle\left[\left(\frac{1}{3}\sdot7\right)+\left(\frac{1}{4}\sdot6\right)\right]\times\left[\left(\frac{1}{2}\sdot3\right)+\left(\frac{1}{6}\sdot5\right)\right]=8+\frac{5}{6}+\left(\frac{2}{3}\sdot\frac{1}{6}\right)](/mediawiki/images/math/3/8/c/38cefe17755c993556e5c3b7d2755bfa.png)
|
ואשר יצא לך מן העניין הראשון שמנה וחמשה שתותים ושליש שתות |
![\scriptstyle\left[\frac{1}{3}\sdot\left[7+\left(\frac{1}{4}\sdot6\right)\right]\right]\times\left[\frac{1}{2}\sdot\left[3+\left(\frac{1}{6}\sdot5\right)\right]\right]=5+\frac{2}{6}+\left(\frac{3}{6}\sdot\frac{1}{6}\right)+\left(\frac{1}{2}\sdot\frac{1}{6}\sdot\frac{1}{6}\right)](/mediawiki/images/math/a/f/1/af1eb5998919287021bdfb435f5e2350.png)
|
ויצא לך מן הענין השני חמשה ושני שתותים ושלשה שתותי שתות וחצי שתות |
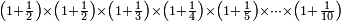
|
שאלה כשיאמר לך: כמה אחד וחצי באחד וחצי באחד ושליש באחד ורביע באחד וחומש כן עד אחד ועשירית |
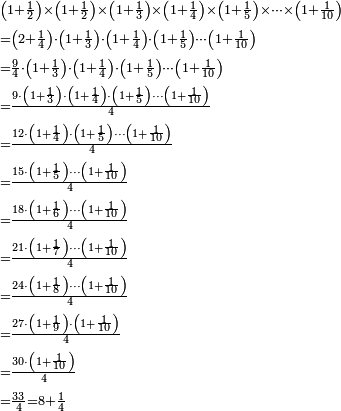
|
הנה ההקש בזה שתכה אחד וחצי באחד וחצי יהיו שנים ורביע והחזירם רביעיים כלם יהיו תשעה והכה אלו התשעה באחד ושליש יהיו שנים עשר והכם באחד ורביע יהיו חמשה עשר והכם באחד וחומש יהיו שמנה עשר והכם באחד ושתות יהיו אחד ועשרים והכם באחד ושביעית יהיו ארבעה ועשרים והכם באחד ושמינית יהיו שבעה ועשרים והכם באחד ותשיעי' יהיו שלשים והכם באחד ועשירית יהיו שלשה ושלשים הנה אלו השלשה ושלשים הם רביעיים כולם וחלקם על ארבעה יצא מה שרצית והוא שמנה ורביע |
Multiplication of Integers |
שער בהכאה מן השלמים על דרך אחרת שלא מן הספר | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| והוא שתשים שני המספרים אשר תרצה להכות האחד באחד בשתי שטות האחת תחת האחרת מדרגת האחדים תחת האחדים ועשרות תחת העשרות וכן כל המדרגות שיהיו בהם | ||||||||||||||||
| ולקצר הלשון אקדים לך כי כל זמן שאומר הכה א' בא' או א' בב' וב' בא' או א' בג' וג' בא' וכן כולם רצוני בו המספר אשר במדרגה פלונית מן השטה העליונה במספר אשר במדריגת פלונית מן השטה התחתונה לעולם אשים בי"ת השימוש על מספר השטה התחתונה וא' רומז על מדרגת האחדים וב' על מדרגת העשרות וג' על מדרגת המאות וד' על מדרגת האלפים וכן בסדר | ||||||||||||||||
| והכונה בדרך הזאת להכות כל אחד ממספרי השטה האחת בכל אחד ממספרי השטה השנית על הדרך אשר אזכיר | ||||||||||||||||
| אם תרצה להכות אחדים ועשרות על אחדים ועשרות כן תעשה: | ||||||||||||||||
| הכה תחילה א' בא' והעולה מן ההכאה הזאת תכתוב בשטה שלישית למעלה כנגד מדרגת האחדים | ||||||||||||||||
| אחר כן תכה א' בב' וב' בא' והמקובץ משתי אלו ההכאות תכתוב בשטה העליונה המתחדשת מן ההכאות כנגד מדרגת העשרות | ||||||||||||||||
| אחר כן תכה ב' בב' והעולה תכתוב בשטה העליונה המתחדשת מן ההכאות במדרגה שלישית עודפת | ||||||||||||||||
| ונשלם המעשה ואשר תמצא בשטה העליונה המתחדשת מן ההכאות הוא המבוקש | ||||||||||||||||
Example: 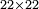
|
והמשל בו אם תרצה להכות שנים ועשרים בשנים ועשרים | |||||||||||||||
| הוריד השאלה בזאת הצורה: | ||||||||||||||||
| ||||||||||||||||
|
תכה השנים הראשונים מן השטה העליונה בשנים הראשונים מן השטה התחתונה ויעלה ארבעה תכתוב ארבעה על השנים הראשונים מן השטה העליונה | |||||||||||||||
| אחר כן תכה השנים הראשונים מן השטה העליונה בשנים השניים מן השטה התחתונה וכן השנים הראשונים מן השטה התחתונה בשנים השניים מן השטה העליונה והעולה משתי הכאות אלו שמנה תכתוב שמנה על השנים השניים מן השטה העליונה | ||||||||||||||||
| אחר כן תכה השנים השניים מן השטה העליונה בשנים השניים מן השטה התחתונה והעולה הוא ארבעה ותכתוב ארבעה במדרגה שלישית עודפת בשטה המתחדשת מן ההכאות הנה העולה ארבע מאות ושמנים וארבעה | ||||||||||||||||
| ודע כי מספר המדרגות אשר יהיו בשטה השלישית המתחדשת מן ההכאות יהיו תמיד כמספר מדרגות שתי השטות המוכות זו בזו פחות שניים זולת העולה מן ההכאה האחרונה כי היא פעמים לא תחדש כי אם מדרגה אחת והוא כשיהיה כלל המקובץ מן ההכאה ההיא פחות מעשרה ואז יהיה מספר המדרגות בשטה השלישית כמדרגות שתי השיטות פחות אחד | ||||||||||||||||
| וכאשר יהיה הכלל המקובץ מן ההכאה האחרונה עשרה או יותר תחדש שתי מדרגות | ||||||||||||||||
| ואם יעלה כלל המקובץ מן ההכאה האחרונה מאה או יותר תחדש שלש מדרגות | ||||||||||||||||
| ודע כי בכל מקום שיהיה המקובץ מן ההכאה פחות מעשרה תכתוב המקובץ בשטה העליונה המתחדשת מן ההכאות כנגד המדרגה אשר אתה בה | ||||||||||||||||
| ואם יהיה המקובץ עשרה או יותר אם ישארו אחדים על העשרה או על העשרות תכתוב האחדים בשטה העליונה המתחדשת מן ההכאות במקום אשר אתה בה | ||||||||||||||||
| ואם לא ישארו אחדים תעשה עגולה בשטה העליונה המתחדשת מן ההכאות לעשות מדרגה ותחזיק במספר העשרות והיו לאחדים בידך כי תחברם עם ההכאה השנית לה שאחד בה עשרה מאשר לפניה | ||||||||||||||||
| ודע כי כאשר נתחדשו בשטה העליונה המתחדשת מן ההכאות כמספר המדרגות היותר גדולה שבשתי השטות המוכות אז נשלמה ההכאה מן המדרגה הראשונה ותעביר עליה קולמוס | ||||||||||||||||
| ותתחיל אחר כן ההכאה מן המדרגה השנית והמקובץ מההכאה ההיא תכתוב בשטה העליונה המתחדשת מן ההכאות במדרגה עודפת ותעביר קולמוס על המדרגה השנית | ||||||||||||||||
| אחר כן התחיל ההכאה מן המדרגה השלישית והמתקבץ מן ההכאה תכתוב במדרגה שנית לעודפת ותעביר קולמוס על המדרגה השלישית | ||||||||||||||||
| ותתחיל אחר כן ההכאה מן המדרגה הבאה אחריה וכן תמיד עד שתגיע להכאה האחרונה | ||||||||||||||||
| ודע כי כאשר יהיה עגול או עגולים בשתי השטות המוכות באיזה מן המדרגות שיהיו ולא יצא חשבון מכלל ההכאה תעשה עגול בשטה העליונה המתחדשת מן ההכאות במדרגה אשר כנגד מדרגת ההכאה | ||||||||||||||||
Example: 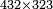
|
והמשל בהיות מדרגות מספרי השטות המוכות שלש הוא שאם תרצה להכות שנים ושלשים וארבע מאות על שלשה ועשרים ושלש מאות | |||||||||||||||
| הוריד השאלה על זאת הצורה: | ||||||||||||||||
| ||||||||||||||||
|
הכה תחלה א' בא' ויעלו ששה ותכתוב ששה בשטה שלישית למעלה כנגד מדרגת האחדים, אחר כן תכה א' בב' וב' בא' ויעלה י"ג תכתוב שלשה כנגד מדרגת העשרות בשטה המתחדשת ותחזיק בידך אחד | |||||||||||||||
|
אחר כן תכה א' בג' וג' בא' וב' בב' ויעלו כ"ד ואחד שהיה בידך יהיו כ"ה תכתוב חמשה בשטה המתחדשת כנגד מדרגת המאות ותחזיק בידך שנים בעבור העשרים ותעביר קולמוס במדרגה הראשונה משתי השטות המוכות | |||||||||||||||
|
ותכה ב' בג' וג' בב' ויעלו י"ז חבר עמהם שנים שהיו בידך יהיו י"ט תכתוב תשעה בשטה המתחדשת במדרגה רביעית עודפת ותחזיק אחד בידך אחר כן תעביר הקולמוס במדרגה השנית משתי השטות המוכות | |||||||||||||||
|
ותכה ד' בג' ויעלו שנים עשר ותחבר עמהם אחד שהיה בידך יהיו שלשה עשר ותכתוב בשטה המתחדשת שלשה במדרגה החמשית ואחד במדרגה הששית ויהיה העולה מאה ושלשים ותשעת אלפים וחמש מאות ושלשים וששה | |||||||||||||||
| ואם יהיו המדרגות ארבע תכה ראשונה א' בא' ותכתוב המקובץ למעלה כנגד מדרגת האחדים | ||||||||||||||||
| אחר כן תכה א' בב' וב' בא' ותכתוב המקובץ כנגד מדרגת העשרות | ||||||||||||||||
| אחר כן תכה א' בג' וג' בא' וב' בב' ותכתוב המקובץ בשטה המתחדשת במדרגת המאות | ||||||||||||||||
| אחר כן תכה א' בד' וד' בא' וג' בב' וב' בג' ותכתוב המקובץ במדרגת האלפים ואז נשלמו ההכאות כמספר מדרגות המספרים המוכים ונשלמה הכאת המדרגה הראשונה ותעביר עליה קולמוס | ||||||||||||||||
| אחר כן תכה ב' בד' וד' בב' וג' בג' ותכתוב המקובץ במדרגה החמשית ונשלמה הכאת המדרגה השנית ותעביר עליה קולמוס | ||||||||||||||||
| אחר כן תכה ג' בד' וד' בג' ותכתוב המקובץ במדרגה ששית ונשלמה הכאת המדרגה השלישית ותעביר עליה קולמוס | ||||||||||||||||
| אחר כן תכה ד' בד' ותכתוב המקובץ במדרגה השביעית ונשלם המעשה | ||||||||||||||||
| וכן אם היו חמש מדרגות או יותר כן תעשה תמיד: | ||||||||||||||||
| הכה תחלה א' בא' אחר כן הכה א' בב' וב' בא' אחר כן א' בג' וג' בא' וב' בב' אחר כן א' בד' וד' בא' וב' בג' וג' בב' אחר כן א' בה' וה' בא' וב' בד' וד' בב' וג' בג' וכן תשלים המעשה על הדרך אשר הזכרתי | ||||||||||||||||
| ואם היו שש מדרגות: | ||||||||||||||||
| תכה תחלה א' בא' אחר כן א' בב' וב' בא' אחר כן א' בג' וג' בא' וב' בב' אחר כן א' בד' וד' בא' וב' בג' וג' בב' אחר כן א' בה' וה' בא' וב' בד' וד' בב' וג' בג' אחר כן א' בו' וו' בא' וב' בה' וה' בב' וג' בד' וד' בג' ונשלמה הכאת המדרגה הראשונה אחר כן תכה ב' בו' וו' בב' וג' בה' וה' בג' וד' בד' ונשלמה הכאת המדרגה השנית | ||||||||||||||||
| אחר כן תכה ג' בו' וו' בג' וד' בה' וה' בד' ונשלמה הכאת המדרגה השלישית | ||||||||||||||||
| אחר כן תכה ד' בו' וו' בד' וה' בה' ונשלמה הכאת המדרגה הרביעית | ||||||||||||||||
| אחר כן תכה ה' בו' וו' בה' ונשלמה הכאת המדרגה החמשית | ||||||||||||||||
| אחר כן תכה ו' בו' ושלם המעשה | ||||||||||||||||
| ועל הדרך הזה יעשה באיזה שעור שיהיה | ||||||||||||||||
| מאזנים לדעת אם טעית בחשבונך בהכאה | ||||||||||||||||
| כאשר ערכת מספר על מספר השלך מה שעלה ט' ט' ודע כמה ישאר | ||||||||||||||||
| אחר כן השליך ט' ט' כל אחד משני המספרים אשר הכית האחד באחר ומה שישאר מן המספר האחד בשטה האחת הכה אותו במה שישאר מן המספר האחר אשר בשטה האחרת | ||||||||||||||||
| אחר כן השליך ט' ט' העולה מהכאת שארית האחד על שארית האחר ואם הוא כמו מה שנשאר מן המספר היוצא מהכאת שני המספרים הגדולים אפשר בו שהוא אמת ואם לא חזור וחשוב שנית כי טעית בחשבונך בלי ספק | ||||||||||||||||
Gelosia (MS Oxford) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
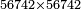
|
נרצה להכות חמשים וששת אלפים ושבע מאות וארבעים ושנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עשה לוח מחמש צדות על חמש על זאת הצורה: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונכה תחלה התחתונה מן הנצבת זו על זו לצד ימין על הראשונה מן השכובות למעלה ונכה תחלה ב' בב' והוא ד', עוד ב' בד' והוא ח', עוד ב' בז' והוא י"ד, עוד ב' בו' והוא י"ב, עוד ב' בה' והוא י', עוד ד' בב' והוא ח', עוד ד' בד' והוא י"ו, עוד ד' בז' והוא כ"ח, עוד ד' בו' והוא כ"ד, עוד ד' בה' והוא כ', עוד נכה ז' בב' והוא י"ד, עוד ז' בד' והוא כ"ח, עוד ז' בז' והוא מ"ט, עוד ז' בו' והוא מ"ב, עוד נכה ו' בב' והוא י"ב, עוד ו' בד' והוא כ"ד, עוד ו' בז' והוא מ"ב, עוד ו' בו' והוא ל"ו, עוד ו' בה' והוא ל', עוד נכה ה' בב' והוא י', עוד ה' בד' והוא כ', עוד ה' בז' והוא ל"ה, עוד ה' בו' והוא ל', עוד ה' בה' והוא כ"ה, ויהיה העולה מן ההכאות כלם: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ד ו ה ו 0 א ב ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ותמצא התחיל קח ראשונה מה שיהיה תחת השטה התחתונה והשטות ההולכות באלכסון מ[......] מימין ממטה או מלמעלה ולשמאל ובתחתונה התחיל ראשונה והם אחדים אם יהיו בהם יותר מתשעה שים מספר העשרת וכתבהו בסוף השטות ההולכות באלכסון וחבר עמו מה שהוספת בה מחבור עשרה מן הקודמת לה וכתוב בם והם עשרות אם יהיו יותר מתשעה קח מספר העשרה שהיו תחת סוף השטה השלישית אחר כן מה שתחת השטה השלישית ההולכת באלכסון והם מאות וחבר עמו מה שהוספת תחת סוף השטה ההולכת באלכסון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שלם הענין בעזרת שדי שדי בברכותיו והתהלה לו על כל ברכה ותהלה אמן | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Degrading the Ranks of Sexagesimal Fractions (MS Guenzburg) |
בהתכת המדרגות והדקים ושאר השברים אל מה שתחתם מן המדרגות השפלות אל מה שלמעלה מהם מן המדרגות והדקים אשר לפניהם לשר הנכבד אבו אל חלפי |
| דע כי הרבה מה שיצטרך בחשבון מעשה הלוחות הכאת השבר והוצאת הגדרים אל פשוט המדרגות והדקים ולהתיחדם אל מה שלמטה מהם ממדרגות השברים והשניים והשלישיים והרביעיים וזולת זה והדרך אשר ראיתי לכל בעלי חשבון הלכו בזה הוא שתשיב המדרגות אשר למעלה מהם אל מדרגות אשר למטה מהם בשובו אותם בשישים אח"כ ותחברום אל מה שיתקבץ המספר אשר במדרגה הרביעית וכן יעשו תמיד עד שיבואו אל המדרגה התחתונה אשר ירצו להתיך המדרגות והדקים אליה | |
| וכך כאשר תהיה כונתם להשיב המדרגה מן המדרגות השפלות אל המדרגה שלמעלה ממנה כשהם יחלקו ג"כ מה שהגיע במדרגה אל שישים כאשר היו יותר מס' ויעלו מה שיצא אל המדרגה אשר לפניה מדרגה אחת וכן היו עושים אחר יחלקו אותם ג"כ בשישים ויעלו מה שיעלה אל המעלה אשר לפניה מדרגה אחת וכן היו עושים עד שהיו מגיעים אל המעלה אשר היו רוצים להשיב השברי' ההם אליה ומבואר שהמעשה היה טורח ועמל וכפל דברים ומבוא לטעיה וטעות והדרך היותר קצר לידיעת זה מה שעשינו באגרת הזאת בארנו וקרבנו מעשהו והקלנו אותו וזה כי אנחנו הנחנו לו כל מה שנרצה בהתכת המעלות והדקים ושאר השברים אשר למטה מהם ולהשיבם אל מה שלמעלה מהם ביותר נקל שיהיה והיותר קרוב וזה תאר המעשה ובאלהים אעזר | |
| כשתרצה להפשיט מה שרצית מן המעשה והדקים והשניים וזולתם מן השברים ולהתיכם אל מה שלמטה מהם מן המדרגות הנה אתה תכתוב מה שעמך מזה אח"כ עיין הלוח אשר לקחנו לזה ובקש המדרגה אשר תרצה שתתיך מה שעמך אליך ותניח בה שתמצא וקח מה שכנגדה ממספרי הציפראות הכתובות וקח ג"כ מה שכנגדה ממספרי ההכאות ומה שיהיה הכה אותו במעלות השלמות אשר עמך והוסיף אותו על מה שהתקבץ מהציפראות מספרם ונהיה תוספת הציפרא לעולם אל מה שנמשך לימינך ומה שהתקבץ מזה הנה הוא מספר מה שבמעלות ההם מחלקי המדרגה אשר תכון להתיך מה שעמד עליה וכתוב אותו ואם היו עם המעלות דקים עיין בלוח מה שכנגד הדקים מספרי הציפרא ומה שכנגד המדרגה אשר ההתכה אליה וקח היתרון אשר בין שני המספרים ומה שיהיה בקש דמיונו במספר הציפראש וכתוב מה שתמצא וקח מה שכנגדו והכה אותו במה שעמך מן הדקים והוסיף על מה שהתקבץ ממה שימשך אל הימין ממספר הציפראש אשר עמך ומה שהתקבץ מזה הנה המספר אותם הדקים מחלק המדרגה אשר חברת אותם אליה אלינו וחבר אותם אל מה שכתבת וכאשר עשית הנה התכת המעלות והדקים אשר עמך אל אותה מדרגה אשר רצית | |
| תם ונשלם | |
| תל"ע אמן ואמן סלה | |
| נשלמו המעשים והוא ספר בחשבון לאבו בכר מחמד בן עבד אללה בן עבאס אלחצאר | |
| והעתיקו ר' משה בר' שמואל בר' יהודה בר' שאול ז"ל אשר מרמון ספרד | |
| נשלמה העתקתו בי"ח יום לחדש אייר שנת אחת ושלשים בעיר מונטפשלייר יע' לטובת עמו ישראל [...] | |
| והנה בזה שלמה העתקתו יום שנים עשר מאדר שני שנת רל"ו מהאלף הששי שהוא אלף וארבע מאות ושמנה שנים מחרבן הבית שתבנה במהרה אמן סלה | |
| [נחרבה הבית ס"ח שנים אחר ההשמה] | |
MS Vatican - Additional Excerpt |
||||||||||||||||||||||||||||||||||||||||||
| אם ישאל אדם להשלים סך אחד לחברו החצי וחבירו לחברו השליש להשלים הסך ההוא בעצמו וכן על הסדר ככה הדרך | ||||||||||||||||||||||||||||||||||||||||||
| אם היו שנים יהיה בו מוצא השנים ומוצא השלשה הכה ב' בג' ויהיו ו' הכה אותו בד' ויהיו כ"ד ובעבו' שהוא נפרד תוסיף אחד ויהיו כ"ה וככה סך הממון וכן על הסדר בסוג תחסר אחד ובנפרד הוסיפהו | ||||||||||||||||||||||||||||||||||||||||||
| ואם תרצה לידע כמה ביד הראשון דע כמה המוצא השני והוא ג' וככה מה שביד הראשון כאשר הם שנים לבד | ||||||||||||||||||||||||||||||||||||||||||
| ואם הם שלשה כבר ידעת כי כשהם שנים יהיה מה שביד הראשון ג' ובעבו' שהוא נפרד תוסף עליה א' ויהיה ד' תכה אותו בד' ויהיה י"ו וככה מה שביד הראשון כאשר הם שלשה | ||||||||||||||||||||||||||||||||||||||||||
| ואם הם ארבעה הנה ידעת כי מה שביד הראשון כשהם שלשה הוא י' י"ו ובעבו' שהוא סוג חסר ממנו אחד ויהיה ט"ו הכה אותו בה' ויהיה ע"ה והוא מה שביד הראשון כאשר הם ד' וכן על הסדר ואחר שתדע סך הממון ותדע מה שביד הראשון תוכל לראות מה שבכל אחד ואחד | ||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||
| נשלם זה הספר תהלה לאל חי והוא ספר בחשבון לאבו מחמד בן עבד אלה בן עבס אלחצר | ||||||||||||||||||||||||||||||||||||||||||
| והשלמתיו אני ברוך הכי"א בר' שלמה אבי ישרו' בר' יואב ישראל | ||||||||||||||||||||||||||||||||||||||||||
| ונשלמה העתקתו יום ה' כ"ה יום לחדש שבט שנת רי"א לפרט קטן והשלמתיו פה הר' הקדש הראלצינו | ||||||||||||||||||||||||||||||||||||||||||
| לטובתיך ולטובת כל עמו ישראל אמן | ||||||||||||||||||||||||||||||||||||||||||
Extracting Cubic Roots of Integer (MS Vatican) |
י' לדעת שרשי המעוקבים ממספר השלם |
|---|---|
| ראה כמה מעלות המספר ההוא אם הם שלשה או פחות חשוב כבראשונה כאשר הם אחדים | |
| לדעת שרשי המעוקבי' יצטרך לדעת תחלה התשעה מעוקבי' מהתשעה אחדים שהם במעלה הראשונה ועל דמיונם תעשה כל שאר המעוקבים בשאר המעלות | |
| אם כן כשהמספר אשר תרצה לדעת שורש מעוקבו הוא עד המעלה השלישית תדע המעוקב אשר הוא יותר קרוב אליו לפניו והמותר תכתוב ותעשה השברים כאשר תדע למטה | |
| ואם המספר הוא יותר מהמעלה השלישית עד השישית תחשוב המעלה הרביעית כאילו הם אחדים והחמישית כאלו הם עשרות והשישית כאלו הם מאות ותדע שרשם כפי הדמיון אשר במעלה הראשונה | |
| וכן תעשה אם המספר יותר מהמעלה השישית עד התשיעית ר"ל כי השביעית תחשוב לאחדים והשמינית לעשרות והתשיעית למאות | |
| וכן עד אין קץ רק של כל ג' מעלות יעלה השורש מעלה אחת הרצון בזה כי אם המספרי' עד ג' מעלות יהיה השורש במעלה הראשונה ואם יעברו המעלה השלישית עד השישית תכתוב השורש במעלה השנית ואם יעבור השישית עד התשיעית תכתוב השורש במעלה השלישית ועל זה הסדר תעשה לאין קץ | |
| ואחר אשר כתבת השורש הראשון במקומו ונשאר לך מהמספרי' הרבה קח מרובע השורש הראשון ותכפול אותו ג' פעמי' ותחלק המספרי' הנשארי' עליו ותעשה באופן תוכל לגרוע מהנשאר מה שאומר והוא שתקח מרובע מה שיעלה בחלוק וכפול אותו על השורש הקודם מוכפל השורש ההוא בג' השורש שעבר הן שיהיה במעלה אחת או שתי אותייות בשתי רק ואם נשאר עדין מהמספרי' תחזור חלילה בזה האופן שתקח לעולם מרובע כאשר עשית בתחלה [.] מעלות עם מ ותכפלהו בג' ותחלק המספר הנשאר עליו ואחר תשלים לעשות כאשר עשית בתחילה והעולה ^ מחובר עם מעוקב מה שיצא בחילוק | |
![\scriptstyle\sqrt[3]{36926037}](/mediawiki/images/math/d/9/8/d981f4270af675c6c80c607d3a90cd2b.png)
|
דמיון רצינו לדעת האותיות שיהיו שורש עקובי אל אלו ח אותיות שהם ל"ו אלפי אלפי' ותתכ"ו אלפי' ול"ז | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומפני שהם שלש מעלות יהיו אותיות השורש העקובי שלשה ולכן הראשון יורשם תחת המאות אמנם בהוצאת האות הראשון די בידיעת השורש העקובי למעוקב הקרוב למספר האותיות מהמעלה האחרונה [ולגרוע המעוקב מאותיות המעלה אחרונה] אבל בהוצאת האחרי' צריך חלוק אחד ושתים כפילות ושלש מגרעות לכל אחד וזה כלל גדול וא"כ האותיות אשר במעלה אחרונה שעולים ל"ו יהיו לאחדי' בידך והמעוקב הקרוב אל ל"ו הוא כ"ז ושורשו ג' ונרשום ג' תחת המאות והוא השורש עקובי ראשון ונגרע כ"ז מן ל"ו וישארו האותיות ט' אלפי אלפי' ותתקכ"ו אלפי' ול"ז | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
רצינו לדעת האות העקובי השני כפלנו מרובע השורש עקובי ראשון שהוא ט' ג' פעמי' ועלה כ"ז והוא המחלק שנחלק עליו האותיות אחרונות אשר מן הנשארו' והם צ"ט כשהיו לאחדים בידך ויצא בחלוק ג' והוא יהיה אות עקובי שני בכפלנו זה הג' על כ"ז המ[..] ויעלו פ"א ונכתבם על האותיות אחרונות שנשארו כדי לגרעם מהם וגם בכפלנו מרובע זה האות [השורש] השני שהוא ט' על ג' כפילות מהשורש הראשון שעולים ג"כ ט' ויעלו פ"א ונכתבם על הפ"א הקודמי' בדרך שאחדיו יעמדו לפני אחדי הפ"א הקודמי' כדי לגרעם ג"כ מן האותיות שנשארו בהוצאת השורש הראשון וגם בכתבנו [כ"ז שהוא] מעוקב זה האות השני על הפ"א שניים בדרך שאחריו יהיו לפני אחדי הפ"א הפא השניים כדי לגרעם ג"כ מהאותיות שנשארו בהוצאת השורש הראשון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכאשר קבצנו אלו הג' מגרעות על הסדר הזה יעלו ח' אלפי' ותתקל"ז וגרענום מהאותיות שנשארו בהוצאת השורש הראשון ידענו כי האות העקובי השני נכון כיון שהיו די למגרעות ועוד נשארו תתקפט אלפי' ול"ז וכתבנוהו לפני הראשון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ורצינו לדעת האות העקובי השלישי כפלנו מרובע הב' אותיות עקוביי' שהם ל"ג ומרובעם אלף ופ"ט ג' פעמי' ועלה ג' אלפי' ורס"ז ועליו חלקנו התתקעט אלפי' ול"ז שנשארו דהיינו האותיות אחרונות שהם תתקע"ט כשהיו לאחדי' ויצא בחלוק ג ויהיה שורש עקובי' שלישי בכפלנו זה הג' על ג' אלפי' אלף ופ"ט שהוא על ג' אלפי' ורס"ז המחלק יעלו ט אלפי' ותת"א ונכתבם למגרעת על מה שנשארו עוד נקח מרובע שורש עקובי שלישי [שהוא ט'] וכפלנוהו על השני שרשי' קודמי' מוכפלי' ג' פעמי' שהם צ"ט כי ג' פעמי' ל"ג עולי' צ"ט וכאשר כפלנו ט' ל על צ"ט עלו תתצ"א נכתבם למגרעת על המגרעת הקודם בהיות אחריו עודפי' לפניו גם נכתוב בזה המעוקב מהשורש שלישי שהוא [..] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ונגרע הג' מגרעות כאשר עשינו באות השני ולא ישאר כלום וא"כ של"ג הוא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Notes
- ↑ אמר: MS V om.
- ↑ בן חצאר: MS V אל חצר
- ↑ ואחר: MS V ואחרי
- ↑ לשם ית': MS O לשי
- ↑ נכבדת: MS O קודם
- ↑ והחשבון: MS O וחשבון
- ↑ להגיע: MS V למגיע
- ↑ שסברתי: MS V שחיברתי
- ↑ והנה: MS V הנה
- ↑ וספרי ... ואספתיו: MS O om.
- ↑ ובהקשים אמתיים: MS V ובהקשיהם האמתיים
- ↑ ומאלהים: MS V ואלהים
- ↑ אזכור: MS V om.
- ↑ השער: MS V והשער
- ↑ אזכור: MS V om.
- ↑ מעשה: MS V מעשי
- ↑ השער: MS O om.
- ↑ במדרגות: MS V במדריגת
- ↑ מדרגות: MS V מדריגת
- ↑ בלקיחת השם: MS V margin
- ↑ והוא אלתסמיה בער': MS V om.
- ↑ השער: MS O om.
- ↑ באלפלג: MS O בפלג; MS V באלפלג הוא אלתמסיאה [אלתסמיאה] נ' בחצות
- ↑ בהגדרה: MS V בהגדרה נ' בלקיחת השורש
- ↑ הם: MS O om.
- ↑ עשרה: MS V עשר
- ↑ אחר: MS V om.
- ↑ איננו: MS V אינו
- ↑ ואלו: MS V ואילו
- ↑ הם: MS V הוא
- ↑ ואחר: MS V אחר
- ↑ הוסף: MS V תוסף
- ↑ השנים: MS O שנים
- ↑ ואחר: MS V אחר
- ↑ הוסף: MS V תוסף
- ↑ הוסף: MS V תוסף
- ↑ הוסף: MS V תוסף
- ↑ הוסף: MS V תוסף
- ↑ הוסף: MS V תוסף
- ↑ שבעה: MS V השבעה
- ↑ הוסף: MS V תוסף
- ↑ שמנה: MS V השמנה
- ↑ ואלו: MS V ואילו
- ↑ הוסף: MS V תוסף
- ↑ התשעה: MS O תשעה
- ↑ ואלו: MS V ואילו
- ↑ הוסף: MS V תוסף
- ↑ הוסף: MS V תוסף
- ↑ העשרים: MS V עשרים
- ↑ הוסף: MS V תוסף
- ↑ השלשים: MS V שלשים
- ↑ תוסף: MS O om.
- ↑ הוסף: MS V תוסף
- ↑ אחר: MS O ואחר
- ↑ הוסף: MS V תוסף
- ↑ הוסף: MS V תוסף
- ↑ הוסף: MS V תוסף
- ↑ מן הדומים: MS O מהדומים
- ↑ כי: MS V להם כלומר
- ↑ כמו: MS V om.
- ↑ הארבעה: MS V ארבעה
- ↑ החמשה: MS V חמשה
- ↑ מדרגת: MS V מדריגות
- ↑ הוסף: MS V תוסף
- ↑ למדרגת: MS V מדריגות
- ↑ האחד: MS V אחד
- ↑ העשרה: MS V עשרה
- ↑ הוסף: MS V תוסף
- ↑ ואלו המאתים: MS O om.
- ↑ אמנם הם: MS O om.
- ↑ האחד: MS V אחד
- ↑ באחדים: MS V om.
- ↑ ואלו: MS V ואילו
- ↑ הן: MS O הם
- ↑ גם כן: MS O ג"כ
- ↑ והיא: MS V והם
- ↑ הוסף: MS V תוסף
- ↑ הזה: MS O
הםזה - ↑ כמו: MS O הוא
- ↑ העשרה: MS V עשרה
- ↑ המאה: MS V מאה
- ↑ אחר כן: MS O illegible
- ↑ הוסף: MS V תוסף
- ↑ אחד: MS V om.
- ↑ ואלו: MS V ואילו
- ↑ וכן שלשת: MS O illegible
- ↑ מדרגת: MS V מדריגות
- ↑ על: MS V om.
- ↑ לעשרות: MS V השמו'
- ↑ עשרה: MS V עשרי
- ↑ מאלה: MS V מאילו
- ↑ האלפים ... האחדים: MS O om.
- ↑ ועשרות: MS O העשרות
- ↑ עוד ... מאות אלף אלפים: MS V om.
- ↑ בו: MS V om.
- ↑ אלף: MS V אל margin נ' אלף
- ↑ והתקצר: MS O והיה צד
- ↑ הענין: MS V עעניין
- ↑ מזכרנו: MS V מזכרונו
- ↑ המדרגות: MS V מדרגות
- ↑ ואחר ... אלף אלפים: MS O twice
- ↑ לו תכלית: MS V תכלית לו
- ↑ שיהיו: MS V שהיו
- ↑ במדרגה: MS V במדריגת
- ↑ שמם: MS V שמה
- ↑ הם: MS O שהיא
- ↑ ארבעה: MS V הארבעה
- ↑ הם: MS O שהם; MS V הארבעה הם
- ↑ במדרגה הרביעית: MS V om.
- ↑ וכן ... שהם: MS V om.
- ↑ וכן: MS O illegible
- ↑ אלפי: MS O אלף
- ↑ האלפים: MS O אלפים
- ↑ ועשרות: MS O והעשרות
- ↑ האלפים: MS V om.
- ↑ אלפים: MS V om.
- ↑ שמם: MS O הם
- ↑ אל: MS O עד
- ↑ והוא: MS O וזה הוא
- ↑ ג"כ: MS V om.
- ↑ והבין זה: MS V ותבין
- ↑ בצורות: MS V בצורת
- ↑ ושמושו ... המספר: MS O om.
- ↑ דע ... האבק: MS O om.
- ↑ אשר: MS V הם אשר
- ↑ MS V: uses usually the Hindu–Arabic numerals throughout the text
- ↑ הנה: MS O om.
- ↑ הם: MS V om.
- ↑ האחדים: MS V האחד
- ↑ ועד: MS V עד
- ↑ הם: MS V om.
- ↑ ועד: MS V עד
- ↑ במדרגה ... שיקדם: MS O om.
- ↑ דבר: MS V דבר צורית נ'
- ↑ דבר יחזיק: MS O כבר יטריד
- ↑ והיא: MS V והוא
- ↑ אשר: MS V אחר
- ↑ לצפר מצד: MS V om.
- ↑ צפר: MS V צורה
- ↑ העשריה: MS V תעשה
- ↑ בו: MS O om.
- ↑ במדרגה: MS V במדרגת
- ↑ בו: MS O בה
- ↑ במדרגה השנית: MS V במדרגת השנים
- ↑ במדרגה: MS V במדרגת
- ↑ וכן: MS V כן
- ↑ ארבעים: MS V הארבעים
- ↑ וחמשים: MS V והחמשים
- ↑ הם: MS V om.
- ↑ וששים: MS V והשישים
- ↑ הם: MS V om.
- ↑ ושבעים: MS V והשבעים
- ↑ הם: MS V om.
- ↑ ושמונים: MS V והשמנים
- ↑ הם: MS V om.
- ↑ ותשעים: MS V והתשעים
- ↑ אתה: MS V אחר
- ↑ גם כן: MS O ג"כ
- ↑ הניח: MS V תניח
- ↑ זאת הצורה: MS V הצורה הזאת
- ↑ וזה כי: MS V והם
- ↑ במדרגה: MS V במדרגת
- ↑ זאת הצורה: MS V הצור' הזאת
- ↑ גם כן: MS O ג"כ
- ↑ ותשעים: MS V ותשעה
- ↑ זאת הצורה: MS V הצורה הזאת
- ↑ ובמדרגה השנית: MS V ובשנית
- ↑ גם כן: MS O ג"כ
- ↑ רצוני לו': MS V ר"ל
- ↑ היו: MS O יהיו
- ↑ תמונת: MS V om.
- ↑ צורת: MS V צורה
- ↑ ואם ... 00ב: MS O om.
- ↑ השלוש: MS O השלשה
- ↑ והתשע: MS O ותשע
- ↑ אילו: MS O אלו
- ↑ במקום: MS V מקום
- ↑ היו: MS V היה
- ↑ היו: MS O היה
- ↑ במדרגה: MS V במדרגת
- ↑ זה: MS V om.
- ↑ אילו: MS O אלו
- ↑ ושמנה: MS O ושלש
- ↑ ואחד ברביעית: MS V כן וברביעית אחד
- ↑ ויהיו: MS V ויהיה
- ↑ היו: MS O יהיו
- ↑ וחמשה: MS V וחמשת
- ↑ ואחרי השנים: MS O ואחר
- ↑ זאת הצורה: MS V הצורה הזאת
- ↑ היו: MS O היה
- ↑ ואחריהם: MS V ואחר השלשה
- ↑ ותשעה: MS V ותשעת
- ↑ היו: MS V היה
- ↑ ואחריו שבעה: MS O twice
- ↑ ואלף: MS O ותאלף
- ↑ צפר: MS V צפרא
- ↑ אילו: MS O אלו
- ↑ היו: MS V היה עמך
- ↑ כאשר תניח: MS O כשתניח
- ↑ ודע ... אשר: MS O om.
- ↑ יתרבה: MS O וזה יתרבה
- ↑ רבות: MS O om.
- ↑ מן המספר: MS O מהמספרים
- ↑ התחיל: MS V תתחיל
- ↑ והניח: MS V ותניח
- ↑ והנח: MS V ותניח
- ↑ המדרגה: MS O om.
- ↑ מדרגות: MS O
אותיותמדרגות - ↑ שלש: MS V שלשה
- ↑ אותות: MS O באותות
- ↑ יוסיף: MS V יתוסף
- ↑ יוסיפו: MS V יתופו
- ↑ אחרי: MS V אחר
- ↑ האותיות: MS V האותות
- ↑ ואם ישארו... לפניהם: MS V om.
- ↑ ואם לא ... לפניהם: MS O om.
- ↑ מספר: MS V המספר
- ↑ המספר: MS V מספר
- ↑ מן: MS V om.
- ↑ אם: MS V ואם
- ↑ הגביהנו: MS V הגביהו
- ↑ אחדים: MS V האחדים
- ↑ אחד: MS V om.
- ↑ התקבץ: MS V תתקבץ
- ↑ והדמיון קבוץ: MS V ודמיון זה קבץ
- ↑ הניח: MS V תניח
- ↑ ואחר: MS V אחר
- ↑ המספר: MS V om.
- ↑ ואחר: MS V אחר
- ↑ ואחד: MS O om.
- ↑ עם ... האחדים: MS V om.
- ↑ והעתיק: MS V ותעתיק
- ↑ ואחד: MS O באחד
- ↑ והרם: MS V ותרים
- ↑ היו: MS O הוא
- ↑ אל האחדים: MS O om.
- ↑ שיתקבץ: MS V שהתקבץ
- ↑ אל: MS V om.
- ↑ וארבעה: MS V וארבע
- ↑ אחת: MS V om.
- ↑ ותחתיהם: MS V ותחתם
- ↑ זאת הצורה: MS V הצורה הזאת
- ↑ ואחר: MS V אחר
- ↑ תקבץ: MS V קבץ
- ↑ אל: MS O על
- ↑ יהיו: MS V יהיה
- ↑ אחר ... על הקו: MS O twice
- ↑ כן: MS O om.
- ↑ המקובץ: MS O מהמקובץ
- ↑ תשים: MS O השיב
- ↑ סוג: MS O מין סוג
- ↑ התחיל: MS V תתחיל
- ↑ על: MS V om.
- ↑ כן: MS O om.
- ↑ יהיה: MS O יהיו
- ↑ המספר האחר: MS V מספר אחר
- ↑ שים: MS V om.
- ↑ במקום האחדים: MS V om.
- ↑ עשרים: MS V העשרים
- ↑ עמידתם: MS V עמידה
- ↑ העליון: MS V om.
- ↑ עשרות על: MS V om.
- ↑ ואחר: MS V אחר
- ↑ השלשה: MS O השלשים
- ↑ האלפים: MS V ראש האלפים
- ↑ מדרגה נוספת קודמת: MS V מדרגת קודמת נוספת
- ↑ שים: MS V תשים
- ↑ ועשרים: MS O ועשים; MS V ושבעים ועשרים
- ↑ עשרות: MS V העשרות
- ↑ יהיו: MS V יהיה
- ↑ יאמר: MS O אמר
- ↑ לך: MS O om.
- ↑ הצפר: MS V צפר
- ↑ יהיה: MS V יהיו
- ↑ אחד: MS V om.
- ↑ ושים: MS O כן קבץ שים
- ↑ כמספר: MS V במדרגת
- ↑ זאת הצורה: MS V הצורה הזאת
- ↑ בהוציא: MS V בהוצאת
- ↑ שיוצא: MS O om.
- ↑ גם כן: MS O ג"כ
- ↑ על: MS O אל
- ↑ מאחת: MS V מאחד מן
- ↑ האלפים: MS V מן האלפים
- ↑ והוצא: MS V ותוציא
- ↑ האלפים: MS V אלפים
- ↑ והנשאר: MS V הנשאר
- ↑ הוצא: MS V תוציא
- ↑ והנשאר: MS V הנשאר
- ↑ הוצא: MS V תוציא
- ↑ הוצא: MS V תוציא
- ↑ שנים: MS V om.
- ↑ הניח: MS V תניח
- ↑ זאת הצורה: MS V הצורה הזאת
- ↑ והשליך: MS V ותשליך
- ↑ ויהיה: MS V om.
- ↑ השלך: MS V תשליך
- ↑ משלשה: MS V מה שלשה
- ↑ ויהיה: MS V om.
- ↑ חבר: MS V צרף נ' חבר
- ↑ אל השלשה: MS O בשלשה
- ↑ והנשאר: MS V הנשאר
- ↑ השלך: MS V תשליך
- ↑ השליך: MS V תשליך
- ↑ נשארו: MS V ישארו
- ↑ שמנה: MS V שמנה מאות
- ↑ המאות: MS V מאות
- ↑ חבר: MS V חבר נ' צרף
- ↑ והנשאר: MS V הנשאר
- ↑ ואחר: MS V אחר
- ↑ השליך: MS V תשליך
- ↑ מן: MS O על
- ↑ ויהיו: MS V יהיו
- ↑ נשאר: MS V הנשאר
- ↑ ואחד: MS V om.
- ↑ אחר: MS V ואחר
- ↑ עשרות: MS V העשרות
- ↑ אחר כן ... בתשעה: MS O twice
- ↑ מדרגת: MS V ראש
- ↑ הפיל: MS V תפיל
- ↑ אחד: MS V האחד
- ↑ והנשאר: MS V הנשאר
- ↑ ותשעים: MS O om.
- ↑ והעמידם: MS V ושימם
- ↑ תשעה: MS O om.
- ↑ מדרגת העשרות ... מדרגת האחדים: MS V על האחדים ותשעה על העשרות
- ↑ וזה: MS O וזהו
- ↑ בקצתם: MS V בקצם
- ↑ שבמספר: MS O ממספר
- ↑ ענינו: MS V ענין כן
- ↑ האחד: MS V אחד
- ↑ גם כן: MS O ג"כ
- ↑ על כל פנים: MS V עכ"פ
- ↑ בקצתם: MS V בקצם
- ↑ האחד: MS V אחד
- ↑ מענינו: MS O ממקומו או מענינו
- ↑ ששה: MS V margin
- ↑ השלשה: MS V שלשה
- ↑ שנים: MS V שתים
- ↑ אחד ועשרים: MS O עשרים ואחד
- ↑ הארבעה: MS V ארבעה
- ↑ ארבעה ועשרים: MS O עשרים וארבע
- ↑ שמנה ועשרים: MS O עשרים ושמנה
- ↑ ששה ושלשים: MS O שלשים וששה
- ↑ החמשה: MS V חמשה
- ↑ הששה: MS V ששה
- ↑ ארבעה וחמישים: MS O חמשים וארבעה
- ↑ השבעה: MS V שבעה
- ↑ ששה וחמשים: MS O חמשים וששה
- ↑ שלשה ושישים: MS O ששים ושלשה
- ↑ שבעים ושנים: MS V שנים וארבעים
- ↑ התשעה: MS V תשעה
- ↑ אחד ושמנים: MS O שמנים ואחד
- ↑ העשרה: MS V עשרה
- ↑ ישמשהו: MS O יש
תמשהו - ↑ המעשה: MS O העשרה margin המעשה
- ↑ וכאשר: MS V כאשר
- ↑ ושבעים: MS V וארבעים
- ↑ תשים: MS V שים
- ↑ השטה: MS O om.
- ↑ תכה: MS V הכה
- ↑ האחרונה: MS V אחרונה
- ↑ השמנה: MS V השמתו
- ↑ אל: MS V om.
- ↑ שמנה: MS V השמנה
- ↑ צפר: MS V הצפ'
- ↑ הקדים: MS V תקדים
- ↑ האחד: MS V אל האחד
- ↑ בשנים: MS V אל השנים
- ↑ במקומם השלשה: MS V השלשה במקומם
- ↑ המספר מן השטה: MS V מספר השטה
- ↑ הששה: MS O השטה
- ↑ והשבעה ... הזאת: MS O om.; על הצורה הזאת MS V om.
- ↑ אחר... השלשה: MS O om.
- ↑ מדרגה: MS V על מדרגה
- ↑ אליהם: MS O עליהם
- ↑ חמשה: MS O
שבעהחמשה - ↑ חמשה: MS V החמשה
- ↑ ואחר: MS V אחר
- ↑ הקדים: MS V תקדים
- ↑ תחלה: MS V תחלק
- ↑ השלשה: MS V אל השלשה
- ↑ במקומו: MS V במקומם
- ↑ החמשה: MS V חמשה
- ↑ מן ההכאה: MS O מההכאה
- ↑ מהכאת: MS O מ
ההכאת - ↑ האחרונה: MS O העליונה
- ↑ אחת: MS V אחד
- ↑ ראשו: MS V ראשה
- ↑ אחר כן... ראשו: MS O om.
- ↑ גם כן: MS O ג"כ
- ↑ השטה: MS V השתה
- ↑ אל: MS V om.
- ↑ תחברהו: MS V om.
- ↑ האחרונ': MS O העליונה
- ↑ ממה: MS V מה
- ↑ שילוה: MS V שילוה אל
- ↑ ותעשה: MS V ותעשה בו
- ↑ תסור: MS V תחדל
- ↑ מה: MS V כמו מה
- ↑ שתכלינה: MS V שתכלה
- ↑ בזה: MS O
באיבזה - ↑ שטות: MS O צורות
- ↑ אחת: MS V אחד
- ↑ ואחר: MS V אחר
- ↑ אשר: MS V המדרגה אשר
- ↑ מן: MS O של
- ↑ העליון ... התחתון: MS O margin
- ↑ אל: MS V om.
- ↑ ותמחה: MS V ותחת
- ↑ שלשה: MS V השלשה
- ↑ ושים: MS O ותן
- ↑ השלשים: MS V השלישית
- ↑ העליון: MS V העליונים
- ↑ במקומו: MS V במקומם
- ↑ ותמחה: MS V ומחה
- ↑ יהיו: MS V יהיה
- ↑ אל: MS V אלו
- ↑ הצפר: MS V צפר
- ↑ השנית: MS O om.
- ↑ בה: MS V בו
- ↑ אליהם: MS O עליהם
- ↑ ותעתיק: MS V והעתק
- ↑ תכה: MS V הכה
- ↑ מחה: MS V ומחה
- ↑ השלשה אשר ילוה: MS O אל מה שילוה
- ↑ אל: MS V om.
- ↑ שם: MS V om.
- ↑ השלשה: MS V בשלשה
- ↑ חמשה: MS V החמשה
- ↑ יהיה: MS O יהיו
- ↑ השלמת: MS V השלמתה
- ↑ וחמשה: MS O twice
- ↑ וזאת: MS V וזה
- ↑ הכאת: MS O
ההכאת - ↑ בשומא: MS V בשומה
- ↑ וידיעת: MS V ביצמת
- ↑ החשבון: MS O וחשבון
- ↑ מאיזו: MS V מאיזה
- ↑ ובו: MS O ובה
- ↑ יודע: MS V יורם
- ↑ ההוא: MS V הוא
- ↑ המספר: MS V מספר
- ↑ ימנהו: MS O ימנה אותו
- ↑ יש: MS V om.
- ↑ לשני: MS V לשנים
- ↑ השלישית: MS V השתות נ' שלישית
- ↑ לו: MS V om.
- ↑ MS V continues in fol. 17r
- ↑ הושלך: MS V יושלך
- ↑ חמשה: MS V om.
- ↑ החומש: MS V המוחש
- ↑ דע: MS V om.
- ↑ כל מספר: MS V המספר
- ↑ וזוגות: MS O וגוזות
- ↑ מאה: MS V מאת
- ↑ מאת: MS V מאה
- ↑ שבעה: MS V שבעה אלף
- ↑ אלף: MS V twice
- ↑ כפלם: MS V יהיה כפלם
- ↑ עשרת: MS V עשרה
- ↑ יהיה: MS V הנה
- ↑ אשר תחלתו: MS O שתחלתו
- ↑ ואין: MS V ולא
- ↑ לו: MS V om.
- ↑ ואין: MS V ולא
- ↑ כ"א וכל ... לו: MS O om.
- ↑ אשר כבר: MS V שכבר
- ↑ כי: MS V om.
- ↑ ממנו חלק: MS V חלק ממנו
- ↑ אחד: MS V om.
- ↑ חלקים: MS V חלקים נ"א הוא ממנו חלק אחד
- ↑ השלשה: MS V שלשה
- ↑ אם כן: MS O א"כ
- ↑ ואחד: MS V והאחד
- ↑ השלשה: MS O
החומשהשלשה - ↑ אם כן: MS O א"כ
- ↑ החומש: MS V חומש
- ↑ גם כן: MS O ג"כ
- ↑ ומן השלשה: MS V ומשלשה
- ↑ ושנים ... רביע: MS O ומן הארבעה רביע ומן השלשה הנה השנים מהם
יהיהשני שלישיים - ↑ ושנים חצי רביע: MS O ומן הארבעה הנה השנים מהם חצי מפני
- ↑ הארבעה: MS V ארבעה
- ↑ השנים: MS V שנים
- ↑ שלשה: MS V שלוש
- ↑ ואם תרצה תאמר שליש ... חמשה שתותים: MS O ושלשה שלשה שתותים ואם תרצה תאמר חצי וארבעה ארבעה שתותים וחמשה חמשה שתותים ואם תרצה תאמר בארבעה שני שלישיים ואם תרצה תאמר בשנים שליש
- ↑ שתי: MS V שני
- ↑ ארבע: MS V ארבעה
- ↑ חמש: MS V חמשה
- ↑ שש: MS V ששה
- ↑ שלש: MS V שלשה
- ↑ ארבע: MS V ארבעה
- ↑ תאמר: MS V om.
- ↑ חמש: MS V חמשה
- ↑ שש: MS V ששה
- ↑ תאמר: MS V om.
- ↑ שלש: MS V שלשה
- ↑ שבע: MS V שבעה
- ↑ ושבעה ... שמיניות: MS O om.
- ↑ שלש: MS V שלשה
- ↑ תאמר: MS V om.
- ↑ שליש: MS O שלישית
- ↑ וארבעה: MS V וארבע א"כ
- ↑ תאמר: MS V om.
- ↑ שבע: MS V שבעה
- ↑ שמנה: MS V מהם שמנה
- ↑ תאמר: MS V om.
- ↑ חמשית: MS V חומש
- ↑ ארבע: MS V ארבעה
- ↑ תאמר: MS V om.
- ↑ תאמר: MS V om.
- ↑ שש: MS V מהם שש
- ↑ תאמר: MS V om.
- ↑ שבע: MS V מהם שבעה
- ↑ תשע: MS V מהם תשע
- ↑ שהקדמנו: MS V שכבר הקדמנו
- ↑ שראוי: MS V
שכברשראוי - ↑ הנה: MS O om.
- ↑ MS V continues in fol. 19r
- ↑ שתקראהו: MS O תקראהו
- ↑ כבר: MS V om.
- ↑ החמשה: MS O חמשה
- ↑ בקצה: MS V בקצת
- ↑ ואשר: MS O ו
כאשר - ↑ מחמשה: MS O חמשה
- ↑ מה: MS O om.
- ↑ תכהו: MS V שהוא תכהו
- ↑ שהוא: MS V om.
- ↑ מן השלש: MS O משלשה
- ↑ שתקרא: MS O שתצא
- ↑ השבעה: MS V תשעה
- ↑ תשימהו ... ואחר: MS V om.
- ↑ ותפיל המקובץ: MS V ותפילהו
- ↑ ויכלה או ישאר: MS V וישאר
- ↑ מה ... השלשה: MS V om.
- ↑ שנים: MS O השנים
- ↑ החמשה: MS O חמשה
- ↑ כן: MS O om.
- ↑ בשלשה: MS O השלשה; MS V om.
- ↑ והפילם: MS V ותפילם
- ↑ השלשה: MS O
השבעההשלשה - ↑ ואחר: MS V אחר
- ↑ ומשוך: MS V ורשום
- ↑ החמשה: MS O חמשה
- ↑ אל: MS V om.
- ↑ והשלשה: MS O ושלשה; MS V והשלש
- ↑ גם כן: MS O ג"כ
- ↑ ושליש: MS V ושלוש
- ↑ רוב: MS V רוב נ' גדול
- ↑ הסכום: MS V הסכום אמאם המורה
- ↑ מה: MS V אל מה
- ↑ הסכום: MS V הסכום כלאימה
- ↑ היוצא: MS V מן היוצה
- ↑ אחד: MS O אל האחד
- ↑ החמשה: MS O חמשה
- ↑ הסכום: MS V הסכום [אלאמם] נ' המורה
- ↑ תשעה: MS O תשעים
- ↑ תפילם: MS O כפלם
- ↑ הנשאר: MS V האפשר
- ↑ שנים: MS O שים שנים
- ↑ והשאירם: MS V והשאירם [וקיים אותם]
- ↑ החמשה: MS O חמשה
- ↑ על כל: MS O הגלגל
- ↑ החמשה: MS O חמשה
- ↑ אחד: MS V אחת
- ↑ תשעה: MS O ותשא
- ↑ להם: MS V om.
- ↑ והששה: MS O וששה
- ↑ ושמנה: MS V בשמנה
- ↑ בששה: MS V בשמנה בששה
- ↑ ותחתיהם: MS V ותחתיו
- ↑ גם גן: MS O om.
- ↑ תכתוב: MS O הכתוב
- ↑ הקו: MS O
הצורההקו - ↑ בצורה: MS V על הצורה
- ↑ המקוימים: MS V הקיומים
- ↑ בו: MS O בה
- ↑ על: MS V אל
- ↑ תכהו: MS O תכה אותו
- ↑ והכה: MS V ותכה
- ↑ יהיו: MS O יהיה
- ↑ והפילם: MS V ותפלם
- ↑ יהיה: MS V om.
- ↑ וקיים: MS V וקיים נ' והוריד
- ↑ על: MS V אל
- ↑ הששה: MS O ששה
- ↑ שלשה: MS O
עשרהשלשה - ↑ כן: MS O om.
- ↑ תמשוך: MS V משוך
- ↑ וכתוב: MS O ותכתוב; MS V
ומשוךוכתוב - ↑ מן הסדר: MS O מהסדר
- ↑ סכום: MS O
הסכום - ↑ שלש: MS V שלשה
- ↑ וזו: MS V וזה
- ↑ MS V continues in fol. 10r; MS V ושמרם נ' ונגביהם
- ↑ הכה: MS V תכה
- ↑ השלשה: MS V שלשה
- ↑ והשיא: MS V ותשיא
- ↑ הפיל: MS V תפיל
- ↑ אחר כן: MS V om.
- ↑ הכהו: MS V תכהו
- ↑ והשיא: MS V ותשיא
- ↑ יהיה: MS O והנה
- ↑ וכבר: MS O כבר
- ↑ חלוקת: MS O חלוק
- ↑ סוגו: MS V זוגו
- ↑ מספר: MS V המספר
- ↑ הוא: MS V והוא
- ↑ סוגו: MS V זוגו
- ↑ והמבוקש: MS O המבוקש
- ↑ הפנים: MS O פנים
- ↑ אתה: MS V אחר
- ↑ במאמר: MS O margin; MS V נ' במאמר
- ↑ אחד: MS O om.
- ↑ שתקרא: MS O תקרא
- ↑ אחד: MS O אחד אחד
- ↑ ותקח: MS V וקח
- ↑ הנה: MS O om.
- ↑ אדם: MS V om.
- ↑ הארבעה: MS V ארבעה
- ↑ משניהם: MS V
מהםמשניהם - ↑ השב: MS V תשיב
- ↑ הנה: MS O om.
- ↑ ישתתפו: MS O
ישתמשישתתפו - ↑ החמשה: MS O הח
ומשה - ↑ החמשה: MS O החמש
- ↑ החמשה: MS O חמשה
- ↑ והמין: MS V ודמיון
- ↑ אם: MS V om.
- ↑ ויסבלהו: MS V ויסבלהו פי' הנחלק יסבול העולה מהכאתו בי"א
- ↑ דמיון: MS V ודמיון
- ↑ חמשים: MS V החמישים
- ↑ ימנהו: MS O ימנה אותו
- ↑ העולה ממנו מן החמשים: MS V
כל זהמן החמישים פי' העולה ממנו - ↑ והכם: MS V ותכם
- ↑ והפילם: MS V ותפילם
- ↑ אם כן היוצא: MS V היוצא אם כן
- ↑ הנחלק: MS V לחלק
- ↑ על: MS O עליו
- ↑ יחלק: MS V החלק
- ↑ אלה: MS V om.
- ↑ הנזכרים: MS V הידועים נ' הנזכרים
- ↑ הנה הוא: MS V twice
- ↑ יצא: MS V ויצא
- ↑ שלש: MS V שלשה
- ↑ MS O adds here a paragraph that does not appear in the original text: שלא מן הספר הנה כבר יצא זה המספר המורכב מן
השלשה בששה ותכהו בשלשה ואחר כן בששה ואם יחלק לי"ב חלקהו בב' ואחר כן בו' או חלקהו בג' ואחר כן בד' ואם יחלק לי"ב חלקם בב"ג ואחר כן בח' או בד' ואחר כן בד' ואם יחלק ל0"ב חלקהובד'בח' ואחר כן בה' ע"כ - ↑ ירבה: MS V ירכב
- ↑ שלשה: MS V השלשה
- ↑ והחמישים: MS V וחמישים
- ↑ זאת: MS V זה
- ↑ השמנה: MS O שמנה
עשר - ↑ אחרית: MS O אחדות
- ↑ המספר: MS V מספר
- ↑ הורידהו: MS O תורידהו
- ↑ השמנה: MS O השמנה [השלשה ותכהו בהם ותפילהו]
- ↑ בשלשה: MS V בשלשה נ' השלשה ותכהו בהם ותפילם
- ↑ הכם: MS V תכם
- ↑ והפילם: MS V ותפלם
- ↑ נשאר: MS V הנשאר
- ↑ במקום: MS O מקום
- ↑ כן: MS O om.
- ↑ תכהו ... שמנה: MS O om.
- ↑ ותכם: MS O והכה
- ↑ והוריד: MS O ותוריד
- ↑ אלו: MS O om.
- ↑ אחד: MS V אחת
- ↑ הם: MS O
אםהם - ↑ אם כן: MS O א"כ
- ↑ עשר: MS O om.
- ↑ הורידם: MS O תורידם
- ↑ יהיו: MS O יהוו
- ↑ אחת: MS O אחד
- ↑ הארבעה: MS V הארבעה
עשר - ↑ הפילם: MS V תפילם
- ↑ השלשה: MS O השנים
- ↑ השלשה: MS O שלשה
- ↑ הכהו: MS V ותכהו
- ↑ יהיו: MS O יהיה
- ↑ והשיא: MS V ותשיא
- ↑ גם כן: MS O ג"כ
- ↑ ארבעה: MS O הארבעה
- ↑ MS V margin וכן יצא מג' וי"ב או מו' וו'
- ↑ המספר: MS V מספר
- ↑ שקדם: MS O שיקדם
- ↑ בשאלה: MS O השאלה
- ↑ גם כן: MS O ג"כ
- ↑ וארבעים: MS V וארבעה
- ↑ ועל: MS O על
- ↑ התשעה: MS O תשעה
- ↑ השמנה: MS O שמנה
- ↑ ועל הארבעה: MS O והארבעה עליהם
- ↑ המספר: MS V מספר
- ↑ והסכום ממה שילוה השמאל: MS O om.
- ↑ ושני: MS O ושנים
- ↑ תשיעיות: MS O התשיעית
- ↑ רביעיות: MS V שביעיות
- ↑ שוב: MS V שוב [נ' חזור]
- ↑ והכם: MS V ותכם
- ↑ והשיא: MS V ותשיא
- ↑ והכם: MS V ותכם
- ↑ אשר: MS O עד אשר
- ↑ והיו: MS V יהיה
- ↑ מהם: MS O עמהם
- ↑ שזכרנו: MS V שאזכרהו
- ↑ תורידהו: MS V הורידהו
- ↑ האחד: MS V האחת
- ↑ אשר הוא: MS O שהוא
- ↑ גם כן: MS O ג"כ
- ↑ הפילם: MS V תפילם
- ↑ הכה: MS V תכה
- ↑ הפילם: MS V תפילם
- ↑ MS O margin האחרון; MS V margin הראשון
- ↑ ותכהו: MS O ונכהו
- ↑ והכהו: MS V ותכהו
- ↑ חמשה תפילם ... אחר כן תכה: MS O om.
- ↑ הראשון: MS O ראשון
- ↑ הפילם: MS V תפילם
- ↑ בחלוקה: MS V בחלוקת
- ↑ וזאת: MS O וזה
- ↑ ושמרם: MS V ושמרה
- ↑ השליך: MS V תשליך
- ↑ החמשה: MS O חמשה
- ↑ והכם: MS V ותכם
- ↑ ויהיו: MS V יהיו
- ↑ שלשה: MS V השלשה
- ↑ והבין: MS V ותבין
- ↑ בעז' האל יתעלה: MS O בע"ה ית'
- ↑ בחצית: MS V בחצות
- ↑ שתרצה: MS V שתרצא
- ↑ השנים: MS O שנים
- ↑ הוריד: MS V הוריד נ' שים
- ↑ מספר: MS V המספר
- ↑ תורידהו: MS V הורידהו
- ↑ ותכהו ... תחת השנים: MS O om.; והורידהו תחת השנים: MS V והורידהו תחת השנים ותכהו בשנים ויכלו בו השמנה
- ↑ השבעה: MS V תשע'
- ↑ אם כן: MS O א"כ
- ↑ תורידהו: MS V הורידהו
- ↑ הששה: MS O ששה
- ↑ כן: MS V om.
- ↑ הארבעה: MS V ארבעה
- ↑ בחלוקה: MS V בחלוקת
- ↑ ושמנים: MS V ושמנה
- ↑ שיהיה: MS V יהיה
- ↑ תחלקהו: MS V תחלקו
- ↑ ארבעה: MS O על ארבעה
- ↑ עד: MS V הוא
- ↑ בהכפיל: MS V בהכפול
- ↑ השער: MS O om.
- ↑ אחד: MS V om.
- ↑ אחד אל מספר: MS O om.
- ↑ כמוהו: MS V כמותו
- ↑ זאת הצורה: MS V הצורה הזאת
- ↑ תוריד: MS V הוריד
- ↑ האחד: MS O אחד
- ↑ האחד: MS O אחד
- ↑ והעשרים: MS O ועשרים
- ↑ זאת הצורה: MS V הצורה הזאת
- ↑ ואחר: MS V אחר
- ↑ כמספר האחדים: MS V על העשרות
- ↑ גם כן: MS O ג"כ
- ↑ מהן: MS O om.
- ↑ נגדרת: MS V נגדרה
- ↑ לו: MS O לה
- ↑ המאה: MS V המאות
- ↑ העשרה: MS O עשרה
- ↑ האלף: MS V אלף
- ↑ לו: MS O לה
- ↑ עשרת: MS V עשרה
- ↑ וגדרו: MS V וגדרם
- ↑ מדרגה: MS V מדרגת
- ↑ לה: MS O om.
- ↑ גדר: MS O om.
- ↑ ההוא: MS O והוא
- ↑ מספר: MS V המספר
- ↑ בו: MS O om.
- ↑ כל: MS O כלל
- ↑ אותו: MS O אותה
- ↑ מדרגה: MS O המדרגה
- ↑ תורידהו: MS V הורידהו
- ↑ אשר חזרת: MS O שחזרת; MS V אשר תחזור
- ↑ בה: MS O בו
- ↑ המוכה: MS V למוכה
- ↑ גם כן: MS O ג"כ
- ↑ המספר: MS V המספר
שנשאר - ↑ ותשאירהו: MS V ותשיאהו
- ↑ אחר כן: MS V om.
- ↑ לה: MS V לו
- ↑ לה גדר: MS V גדר לה
- ↑ תורידהו: MS V הורידהו
- ↑ בו: MS O בם
- ↑ הששה: MS O ששה
- ↑ והכם: MS V ותכם
- ↑ מן הששה: MS O מהששה
- ↑ מספר: MS V המספר
- ↑ תורידהו: MS V הורידהו
- ↑ גם כן: MS O ג"כ
- ↑ הכם: MS V תכם
- ↑ הפילם: MS V תפילם
- ↑ הכה: MS V תכה
- ↑ והפילם: MS V ותפילם
- ↑ אם כן: MS O א"כ
- ↑ ששה: MS O הששה
- ↑ ותשעים: MS O ועשרים
- ↑ זאת הצורה: MS V הצורה הזאת
- ↑ זוג: MS O זוגות
- ↑ ואם: MS O
ואחרואם - ↑ יהיו: MS V היו
- ↑ תורידהו: MS V הורידהו
- ↑ השמנה: MS O שמנה
- ↑ והכם: MS O והכה
- ↑ הפילם: MS V תפילם
- ↑ השמנה: MS V om.
- ↑ כפול: MS V תכפול
- ↑ ותעתיקם: MS O ותעתיק אותה
- ↑ והאחד: MS O ואחד
- ↑ ששה: MS O הששה
- ↑ ותכם: MS O ותכה
ו - ↑ באחד: MS O באחד
האחרון - ↑ ששה: MS V שלשה
- ↑ הכה: MS V תכה
- ↑ והפילם: MS V ותפילם
- ↑ השלשה: MS O הששה margin נ' השלשה
- ↑ והפילם: MS V ותפילם
- ↑ הוריד: MS V והוריד
- ↑ וקדם: MS V והקדים
- ↑ הקודמים: MS O הקדומים
- ↑ שתוריד: MS V שהוריד
- ↑ השנים: MS O om.
- ↑ ואחר: MS V אחר
- ↑ תורידהו: MS V הורידהו
- ↑ ויכלה: MS O יכלה
- ↑ תמצא: MS V תמצא נ' תקח
- ↑ ישאר אחד ... על ראשם: MS O om.
- ↑ תחצה: MS O תחצה margin פי' תשוב לחצי; V תחצה ל"ר תשיב לחצי
- ↑ וזה: MS O twice
- ↑ הם: MS V om.
- ↑ אם כן: MS O א"כ
- ↑ העשרת: MS O עשרת
Appendix: Bibliography
Kitāb al-Bayān / by Abū Bakr al-Haṣṣār (Morocco, 12th century)
– Hebrew translation –
by Moses Ibn Tibbon (Marseille, flourished 1240-1283)
Sefer ha-Tishboret le-Abū Bakr / Sefer ha-Ḥeshbon le al-Ḥaṣṣār
Translated in Montpellier, 1271
Manuscripts:
- 1) Moscow, Russian State Library, Ms. Guenzburg 30/4 (IMHM: f 6711), ff. 124r-189r (1502)
- 2) Oxford, Bodleian Library MS Christ Church 189 (IMHM: f 15581), (cat. Neub. 2457) (1476)
- Liber Arithmetices (ספר החשבון)
- 3) Vatican, Biblioteca Apostolica ebr. 396 (IMHM: f 474), (Montalcino,1451)
Bibliography:
- Aballagh, Mohamed and Ahmed Djebbar. 1987. Découverte d’un écrit mathématique d’al-Hassâr (XIIe siècle): le livre I du Kāmil, Historia Mathematica 14, pp.147–158.
- Kunitzsch, Paul. 2003. A New Manuscript of Abū Bakr al-Hassār's Kitāb al-Bayān, Suhayl (Barcelona), vol. 3, pp. 187-192.
- Suter, Heinrich. 1901. Das Rechenbuch des Abu Zakarija el-Hassar, Bibliotheca Mathematica, vol. 2, pp. 12-40.
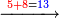
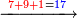
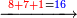
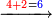
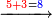
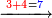



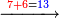
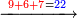


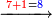
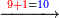
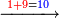
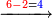
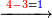
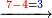
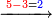
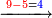
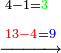
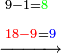
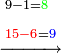




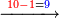
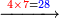
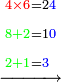
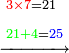
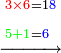
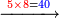
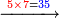
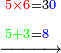
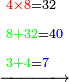
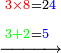
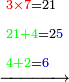
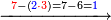
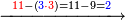
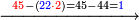
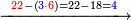
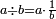
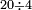
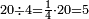
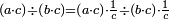
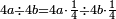
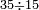
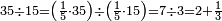
![\scriptstyle\left[a+\left(b\sdot p\right)\right]\div p=b+\frac{a}{p}](/mediawiki/images/math/2/8/0/2801589a692a7665684083b20992e117.png)
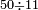
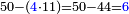
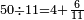
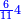
![\scriptstyle\left[\left[a+\left(b\sdot c\right)\right]\sdot d\right]\div\left(c\sdot d\right)=\left[a+\left(b\sdot c\right)\right]\div c=b+\frac{a}{c}](/mediawiki/images/math/7/a/6/7a6804ae701a16b5de85728a97dab776.png)
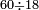
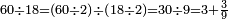
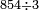
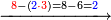
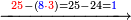
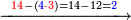
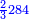
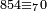
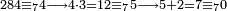
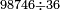
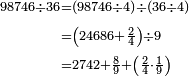
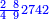
![\begin{align}\scriptstyle2742\equiv_75&\scriptstyle\longrightarrow5\sdot\left(9\equiv_72\right)=10\equiv_73\\&\scriptstyle\longrightarrow\left[3+\left(8\equiv_71\right)\right]\sdot4=4\sdot4=16\equiv_72\\&\scriptstyle\longrightarrow2+2=4\\\end{align}](/mediawiki/images/math/d/c/0/dc0379856089e35c40ac40b6feb5f636.png)
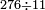
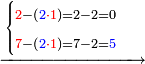

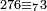
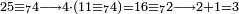
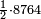
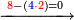
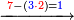
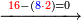
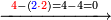
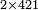
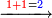
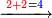
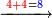
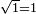
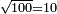
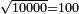
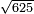
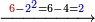
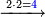
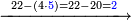
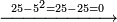
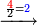
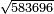
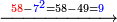
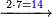
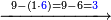
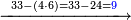

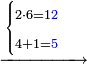
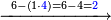
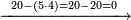
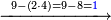
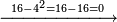
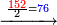
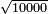

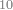
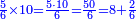
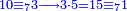
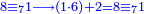
![\scriptstyle\left[\frac{1}{5}+\left(\frac{1}{2}\sdot\frac{1}{5}\right)\right]\times12](/mediawiki/images/math/3/8/d/38d26a85ea2cfc361c9a8a6775ab9e5b.png)
![\scriptstyle{\color{blue}{\left[\frac{1}{5}+\left(\frac{1}{2}\sdot\frac{1}{5}\right)\right]\times12=\frac{\left[\left(1\sdot2\right)+1\right]\sdot12}{2\sdot5}=\frac{3\sdot12}{2\sdot5}=\frac{36}{2\sdot5}=3+\frac{3}{5}}}](/mediawiki/images/math/8/2/b/82b7214d35886f30a758763ed57d4ad0.png)
![\scriptstyle{\color{blue}{12\equiv_75\longrightarrow5\sdot\left[\left(1\sdot2\right)+1\right]=5\sdot3=15\equiv_71}}](/mediawiki/images/math/2/b/9/2b95ff353e77d810fd7e65fdf20efff0.png)
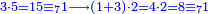
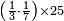
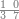
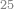
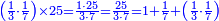
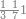

![\scriptstyle{\color{blue}{1\sdot7\equiv_70\longrightarrow\left[\left(0+1\right)\sdot3\right]+1=4}}](/mediawiki/images/math/a/2/9/a29d829f1ef4b74f8244365d33476b81.png)
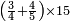
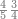
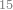
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{3}{4}+\frac{4}{5}\right)\times15&\scriptstyle=\frac{\frac{\left[\left(4\sdot4\right)+\left(3\sdot5\right)\right]\sdot15}{4}}{5}\\&\scriptstyle=\frac{\frac{31\sdot15}{4}}{5}\\&\scriptstyle=\frac{\frac{465}{4}}{5}\\&\scriptstyle=\frac{116+\frac{1}{4}}{5}\\&\scriptstyle=23+\frac{1}{5}+\left(\frac{1}{4}\sdot\frac{1}{5}\right)\\\end{align}}}](/mediawiki/images/math/2/7/3/273466fac6a9559b51a7b7069b60336e.png)
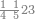
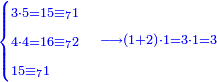
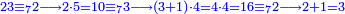
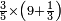

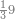
![\scriptstyle{\color{blue}{\frac{3}{5}\times\left(9+\frac{1}{3}\right)=\frac{\left[\left(9\sdot3\right)+1\right]\sdot3}{3\sdot5}=\frac{28\sdot3}{3\sdot5}=\frac{84}{3\sdot5}=5+\frac{3}{5}}}](/mediawiki/images/math/d/a/8/da84c1f0b771c166de26b8c79dad0223.png)
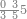
![\scriptstyle{\color{blue}{9\equiv_72\longrightarrow\left[\left(2\sdot3\right)+1\right]=7\sdot3\equiv_70}}](/mediawiki/images/math/3/c/3/3c3121c91013b666a010637f4a3071d2.png)
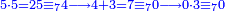
![\scriptstyle\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\times\left(6+\frac{3}{5}\right)](/mediawiki/images/math/7/3/9/739d727bdcdfb4c09f59bba584125807.png)
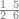
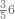
![{\color{blue}{\begin{align}\scriptstyle\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\times\left(6+\frac{3}{5}\right)&\scriptstyle=\frac{\left[\left(5\sdot2\right)+1\right]\sdot\left[\left(6\sdot5\right)+3\right]}{6\sdot2\sdot5}\\&\scriptstyle=\frac{11\sdot33}{6\sdot2\sdot5}\\&\scriptstyle=\frac{363}{6\sdot2\sdot5}\\&\scriptstyle=6+\left(\frac{1}{5}\sdot\frac{1}{6}\right)+\left(\frac{1}{2}\sdot\frac{1}{5}\sdot\frac{1}{6}\right)\\\end{align}}}](/mediawiki/images/math/7/8/3/7832b79c45625e605cefc0e3abe1a5e5.png)
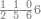
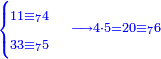
![\scriptstyle{\color{blue}{6\sdot6=36\equiv_71\longrightarrow\left[\left[\left(1\sdot5\right)+1\right]\sdot2\right]+1=\left(6\sdot2\right)+1=13\equiv_76}}](/mediawiki/images/math/9/4/d/94df293f86f42f5d1088566630e401e5.png)
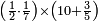
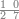
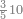
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{1}{2}\sdot\frac{1}{7}\right)\times\left(10+\frac{3}{5}\right)&\scriptstyle=\frac{\left[\left(10\sdot5\right)+3\right]\sdot1}{2\sdot7\sdot5}\\&\scriptstyle=\frac{53\sdot1}{2\sdot7\sdot5}\\&\scriptstyle=\frac{53}{2\sdot7\sdot5}\\&\scriptstyle=\frac{5}{7}+\left(\frac{1}{5}\sdot\frac{1}{7}\right)+\left(\frac{1}{2}\sdot\frac{1}{5}\sdot\frac{1}{7}\right)\\\end{align}}}](/mediawiki/images/math/5/a/1/5a142367a279d416cfee8195c4cf05b8.png)
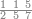
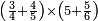
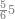
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{3}{4}+\frac{4}{5}\right)\times\left(5+\frac{5}{6}\right)&\scriptstyle=\frac{\left[\left(3\sdot5\right)+\left(4\sdot4\right)\right]\sdot\left[\left(5\sdot6\right)+5\right]}{4\sdot5\sdot6}\\&\scriptstyle=\frac{31\sdot35}{120}\\&\scriptstyle=\frac{1085}{120}\\&\scriptstyle=9+\left(\frac{1}{5}\sdot\frac{1}{6}\right)+\left(\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{6}\right)\\\end{align}}}](/mediawiki/images/math/4/8/8/488a8e0eec7a6a3cb0537e22fc92e489.png)
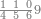
![\scriptstyle\frac{3}{4}\times\left[5+\frac{7}{8}+\left(\frac{1}{6}\sdot\frac{1}{8}\right)\right]](/mediawiki/images/math/f/f/e/ffe897c7d6abf4185f4ffb7c669d3ce1.png)

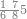
![{\color{blue}{\begin{align}\scriptstyle\frac{3}{4}\times\left[5+\frac{7}{8}+\left(\frac{1}{6}\sdot\frac{1}{8}\right)\right]&\scriptstyle=\frac{\left[\left[\left[\left(5\sdot8\right)+7\right]\sdot6\right]+1\right]\sdot3}{4\sdot8\sdot6}\\&\scriptstyle=\frac{\left[\left(47\sdot6\right)+1\right]\sdot3}{4\sdot8\sdot6}\\&\scriptstyle=\frac{283\sdot3}{4\sdot8\sdot6}\\&\scriptstyle=\frac{849}{4\sdot8\sdot6}\\&\scriptstyle=4+\frac{3}{8}+\left(\frac{\color{red}{2}}{6}\sdot\frac{1}{8}\right)+\color{red}{\left(\frac{1}{4}\sdot\frac{1}{6}\sdot\frac{1}{8}\right)}\\\end{align}}}](/mediawiki/images/math/2/f/4/2f4f3fbe28ac67462e7f4e93d7e349d5.png)
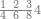
![\scriptstyle\frac{5}{6}\times\left[8+\left(\frac{5}{7}\sdot\frac{1}{9}\right)\right]](/mediawiki/images/math/e/5/f/e5f35b79321220d2b908e6078c54c785.png)
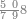
![{\color{blue}{\begin{align}\scriptstyle\frac{5}{6}\times\left[8+\left(\frac{5}{7}\sdot\frac{1}{9}\right)\right]&\scriptstyle=\frac{\left[\left(8\sdot9\sdot7\right)+5\right]\sdot5}{6\sdot7\sdot9}\\&\scriptstyle=\frac{509\sdot5}{6\sdot7\sdot9}\\&\scriptstyle=\frac{2545}{6\sdot7\sdot9}\\&\scriptstyle=6+\frac{6}{9}+\left(\frac{4}{7}\sdot\frac{1}{9}\right)+\left(\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/6/c/d/6cd15d2a875a7396b31e4d132da589e5.png)
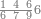
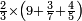

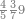
![{\color{blue}{\begin{align}\scriptstyle\frac{2}{3}\times\left(9+\frac{3}{7}+\frac{4}{5}\right)&\scriptstyle=\frac{\left[\left(9\sdot7\sdot5\right)+\left[\left(3\sdot5\right)+\left(4\sdot7\right)\right]\right]\sdot2}{3\sdot7\sdot5}\\&\scriptstyle=\frac{\left(315+43\right)\sdot2}{3\sdot7\sdot5}\\&\scriptstyle=\frac{358\sdot2}{3\sdot7\sdot5}\\&\scriptstyle=\frac{716}{3\sdot7\sdot5}\\&\scriptstyle=6+\frac{5}{7}+\left(\frac{3}{5}\sdot\frac{1}{7}\right)+\left(\frac{2}{3}\sdot\frac{1}{5}\sdot\frac{1}{7}\right)\\\end{align}}}](/mediawiki/images/math/a/d/6/ad6762cd483162f2ab5d29179a128899.png)
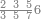
![\scriptstyle\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\times\left[8+\frac{5}{7}+\left(\frac{1}{5}\sdot\frac{1}{7}\right)\right]](/mediawiki/images/math/b/7/f/b7f33a721f2cc7aa748520999089bce0.png)
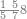
![{\color{blue}{\begin{align}\scriptstyle\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\times\left[8+\frac{5}{7}+\left(\frac{1}{5}\sdot\frac{1}{7}\right)\right]&\scriptstyle=\frac{\left[\left(5\sdot2\right)+1\right]\sdot\left[\left[\left[\left(8\sdot7\right)+5\right]\sdot5\right]+1\right]}{6\sdot2\sdot7\sdot5}\\&\scriptstyle=\frac{11\sdot306}{6\sdot2\sdot7\sdot5}\\&\scriptstyle=\frac{3366}{6\sdot2\sdot7\sdot5}\\&\scriptstyle=8+\left(\frac{3}{5}\sdot\frac{1}{6}\sdot\frac{1}{7}\right)\\\end{align}}}](/mediawiki/images/math/1/d/1/1d121dcd1243323e91e0fffe73d6a1f7.png)
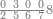
![\scriptstyle\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\times\left[9+\left(\frac{1}{6}\sdot\frac{1}{7}\right)\right]](/mediawiki/images/math/9/6/a/96a8fdd4fab69e58c8a676b813acc28d.png)
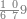
![{\color{blue}{\begin{align}\scriptstyle\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\times\left[9+\left(\frac{1}{6}\sdot\frac{1}{7}\right)\right]&\scriptstyle=\frac{\left[\left(5\sdot2\right)+1\right]\sdot\left[\left(9\sdot6\sdot7\right)+1\right]}{6\sdot2\sdot6\sdot7}\\&\scriptstyle=\frac{11\sdot379}{6\sdot2\sdot6\sdot7}\\&\scriptstyle=\frac{4169}{6\sdot2\sdot6\sdot7}\\&\scriptstyle=8+\frac{1}{7}+\color{red}{\left(\frac{5}{6}\sdot\frac{1}{7}\right)+\left(\frac{2}{6}\sdot\frac{1}{6}\sdot\frac{1}{7}\right)+\left(\frac{1}{2}\sdot\frac{1}{6}\sdot\frac{1}{6}\sdot\frac{1}{7}\right)}\\\end{align}}}](/mediawiki/images/math/9/7/5/9758acd32e2e078b92aaa984cf94abcd.png)
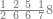
![\scriptstyle\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\times\left(8+\frac{9}{10}+\frac{10}{11}\right)](/mediawiki/images/math/8/c/a/8ca9548a897d46b48ef337cafe7ed47c.png)
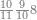
![{\color{blue}{\begin{align}\scriptstyle\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\times\left(8+\frac{9}{10}+\frac{10}{11}\right)&\scriptstyle=\frac{\left[\left(5\sdot2\right)+1\right]\sdot\left[\left(8\sdot10\sdot11\right)+\left[\left(9\sdot11\right)+\left(10\sdot10\right)\right]\right]}{6\sdot2\sdot10\sdot11}\\&\scriptstyle=\frac{11\sdot\left(880+199\right)}{6\sdot2\sdot10\sdot11}\\&\scriptstyle=\frac{11\sdot1079}{6\sdot2\sdot10\sdot11}\\&\scriptstyle=\frac{11869}{6\sdot2\sdot10\sdot11}\\&\scriptstyle=8+\frac{10}{11}+\left(\frac{9}{10}\sdot\frac{1}{11}\right)+\left(\frac{1}{2}\sdot\frac{1}{6}\sdot\frac{1}{10}\sdot\frac{1}{11}\right)\\\end{align}}}](/mediawiki/images/math/2/7/1/27128d31b409e57deaa6858b404c41ff.png)
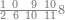
![\scriptstyle\left(\frac{2}{3}\sdot\frac{1}{7}\right)\times\left[6+\frac{9}{10}+\left(\frac{4}{5}\sdot\frac{1}{10}\right)\right]](/mediawiki/images/math/4/c/0/4c07b959f75b107b9a85f4431149a854.png)
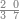
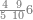
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{2}{3}\sdot\frac{1}{7}\right)\times\left[6+\frac{9}{10}+\left(\frac{4}{5}\sdot\frac{1}{10}\right)\right]&\scriptstyle=\frac{\left[\left[\left[\left(6\sdot10\right)+9\right]\sdot5\right]+4\right]\sdot2}{3\sdot7\sdot10\sdot5}\\&\scriptstyle=\frac{\left[\left(69\sdot5\right)+4\right]\sdot2}{3\sdot7\sdot10\sdot5}\\&\scriptstyle=\frac{349\sdot2}{3\sdot7\sdot10\sdot5}\\&\scriptstyle=\frac{698}{3\sdot7\sdot10\sdot5}\\&\scriptstyle=\frac{6}{10}+\left(\frac{4}{7}\sdot\frac{1}{10}\right)+\left(\frac{2}{5}\sdot\frac{1}{7}\sdot\frac{1}{10}\right)+\left(\frac{2}{3}\sdot\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{10}\right)\\\end{align}}}](/mediawiki/images/math/1/2/8/1288b5815457ec0fc819b79c473f3143.png)
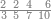
![\scriptstyle\left(\frac{3}{4}\sdot\frac{1}{9}\right)\times\left[8+\left(\frac{5}{6}\sdot\frac{1}{7}\right)\right]](/mediawiki/images/math/d/f/e/dfe926298d98140474daec8e3ef52953.png)
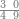
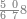
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{3}{4}\sdot\frac{1}{9}\right)\times\left[8+\left(\frac{5}{6}\sdot\frac{1}{7}\right)\right]&\scriptstyle=\frac{\left[\left(8\sdot7\sdot6\right)+5\right]\sdot3}{4\sdot9\sdot6\sdot7}\\&\scriptstyle=\frac{341\sdot3}{4\sdot9\sdot6\sdot7}\\&\scriptstyle=\frac{1023}{4\sdot9\sdot6\sdot7}\\&\scriptstyle=\frac{6}{9}+\left(\frac{3}{6}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)+\left(\frac{3}{4}\sdot\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/5/d/6/5d6f376ea1337d288932ebb9b609f12d.png)
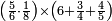
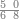
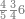
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{5}{6}\sdot\frac{1}{8}\right)\times\left(6+\frac{3}{4}+\frac{4}{5}\right)&\scriptstyle=\frac{\left[\left(6\sdot4\sdot5\right)+\left[\left(3\sdot5\right)+\left(4\sdot4\right)\right]\right]\sdot5}{6\sdot8\sdot4\sdot5}\\&\scriptstyle=\frac{\left(120+31\right)\sdot5}{6\sdot8\sdot4\sdot5}\\&\scriptstyle=\frac{151\sdot5}{6\sdot8\sdot4\sdot5}\\&\scriptstyle=\frac{755}{6\sdot8\sdot4\sdot5}\\&\scriptstyle=\frac{6}{8}+\left(\frac{1}{6}\sdot\frac{1}{8}\right)+\left(\frac{3}{5}\sdot\frac{1}{6}\sdot\frac{1}{8}\right)+\left(\frac{3}{4}\sdot\frac{1}{5}\sdot\frac{1}{6}\sdot\frac{1}{8}\right)\\\end{align}}}](/mediawiki/images/math/5/7/b/57b4cdc1f9970dac71e8e1c6404656d1.png)
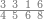
![\scriptstyle\left(\frac{3}{4}+\frac{4}{5}\right)\times\left[6+\frac{7}{8}+\left(\frac{1}{6}\sdot\frac{1}{8}\right)\right]](/mediawiki/images/math/1/d/e/1de58acd88921baf39cf31c2001274d7.png)
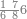
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{3}{4}+\frac{4}{5}\right)\times\left[6+\frac{7}{8}+\left(\frac{1}{6}\sdot\frac{1}{8}\right)\right]&\scriptstyle=\frac{\left[\left(3\sdot5\right)+\left(4\sdot4\right)\right]\sdot\left[\left[\left[\left(6\sdot8\right)+7\right]\sdot6\right]+1\right]}{4\sdot5\sdot8\sdot6}\\&\scriptstyle=\frac{31\sdot331}{4\sdot5\sdot8\sdot6}\\&\scriptstyle=\frac{10261}{4\sdot5\sdot8\sdot6}\\&\scriptstyle=10+\frac{5}{8}+\left(\frac{3}{6}\sdot\frac{1}{8}\right)+\left(\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{6}\sdot\frac{1}{8}\right)\\\end{align}}}](/mediawiki/images/math/b/d/2/bd23cddb8d58bafd363770f3cda8a3b7.png)
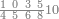
![\scriptstyle\left(\frac{3}{4}+\frac{4}{5}\right)\times\left[6+\left(\frac{1}{7}\sdot\frac{1}{8}\right)\right]](/mediawiki/images/math/a/0/8/a08d4959f373c7157cdca395fae419df.png)
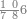
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{3}{4}+\frac{4}{5}\right)\times\left[6+\left(\frac{1}{7}\sdot\frac{1}{8}\right)\right]&\scriptstyle=\frac{\left[\left(3\sdot5\right)+\left(4\sdot4\right)\right]\sdot\left[\left(6\sdot7\sdot8\right)+1\right]}{4\sdot5\sdot7\sdot8}\\&\scriptstyle=\frac{31\sdot337}{4\sdot5\sdot7\sdot8}\\&\scriptstyle=\frac{10447}{4\sdot5\sdot7\sdot8}\\&\scriptstyle=9+\frac{2}{8}+\left(\frac{4}{7}\sdot\frac{1}{8}\right)+\left(\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\right)+\left(\frac{3}{4}\sdot\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\right)\\\end{align}}}](/mediawiki/images/math/c/7/1/c718fac3af216e9191625e10635ee2aa.png)
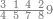
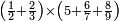
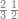
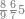
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{1}{2}+\frac{2}{3}\right)\times\left(5+\frac{6}{7}+\frac{8}{9}\right)&\scriptstyle=\frac{\left[\left(1\sdot3\right)+\left(2\sdot2\right)\right]\sdot\left[\left(5\sdot7\sdot9\right)+\left[\left(6\sdot9\right)+\left(8\sdot7\right)\right]\right]}{2\sdot3\sdot7\sdot9}\\&\scriptstyle=\frac{7\sdot425}{6\sdot7\sdot9}\\&\scriptstyle=\frac{2975}{6\sdot7\sdot9}\\&\scriptstyle=7+\frac{7}{9}+\left(\frac{5}{7}\sdot\frac{1}{9}\right)+\left(\frac{5}{6}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/0/7/8/078fee08b98b37284c822e832858d309.png)
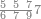
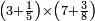
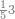
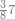
![\scriptstyle{\color{blue}{\left(3+\frac{1}{5}\right)\times\left(7+\frac{3}{8}\right)=\frac{\left[\left(3\sdot5\right)+1\right]\sdot\left[\left(7\sdot8\right)+3\right]}{5\sdot8}=\frac{16\sdot59}{5\sdot8}=\frac{944}{5\sdot8}=23+\frac{4}{8}+\left(\frac{4}{5}\sdot\frac{1}{8}\right)}}](/mediawiki/images/math/f/1/6/f166b8e8f0b9ba3c21ad5a4c29719f0a.png)
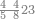
![\scriptstyle\left[2+\frac{3}{5}+\left(\frac{1}{2}\sdot\frac{1}{5}\right)\right]\times\left[4+\frac{7}{9}+\left(\frac{6}{8}\sdot\frac{1}{9}\right)\right]](/mediawiki/images/math/1/9/4/194f683354067debfa65dc8b696fb706.png)
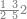
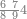
![{\color{blue}{\begin{align}\scriptstyle\left[2+\frac{3}{5}+\left(\frac{1}{2}\sdot\frac{1}{5}\right)\right]\times\left[4+\frac{7}{9}+\left(\frac{6}{8}\sdot\frac{1}{9}\right)\right]&\scriptstyle=\frac{\left[\left[\left[\left(2\sdot5\right)+3\right]\sdot2\right]+1\right]\sdot\left[\left[\left[\left(4\sdot9\right)+7\right]\sdot8\right]+6\right]}{5\sdot2\sdot8\sdot9}\\&\scriptstyle=\frac{27\sdot350}{5\sdot2\sdot8\sdot9}\\&\scriptstyle=\frac{9450}{5\sdot2\sdot8\sdot9}\\&\scriptstyle=13+\frac{1}{9}+\left(\frac{1}{8}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/5/8/c/58c27c47c8ca71ffa101ed22bbd49f0e.png)
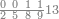
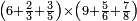
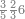
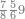
![{\color{blue}{\begin{align}\scriptstyle\left(6+\frac{2}{3}+\frac{3}{5}\right)\times\left(9+\frac{5}{6}+\frac{7}{8}\right)&\scriptstyle=\frac{\left[\left(6\sdot3\sdot5\right)+\left[\left(2\sdot5\right)+\left(3\sdot3\right)\right]\right]\sdot\left[\left(9\sdot6\sdot8\right)+\left[\left(5\sdot8\right)+\left(7\sdot6\right)\right]\right]}{3\sdot5\sdot6\sdot8}\\&\scriptstyle=\frac{\left(90+19\right)\sdot514}{3\sdot5\sdot6\sdot8}\\&\scriptstyle=\frac{109\sdot514}{3\sdot5\sdot6\sdot8}\\&\scriptstyle=\frac{56026}{3\sdot5\sdot6\sdot8}\\&\scriptstyle=77+\frac{6}{8}+\left(\frac{3}{6}\sdot\frac{1}{8}\right)+\left(\frac{1}{3}\sdot\frac{1}{5}\sdot\frac{1}{6}\sdot\frac{1}{8}\right)\\\end{align}}}](/mediawiki/images/math/5/f/4/5f4d416045e2d859c6307d1a74b562a2.png)
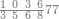
![\scriptstyle\left[2+\frac{3}{4}+\frac{4}{5}+\left(\frac{1}{2}\sdot\frac{1}{5}\right)\right]\times\left[6+\frac{6}{7}+\frac{9}{10}+\left(\frac{3}{8}\sdot\frac{1}{10}\right)\right]](/mediawiki/images/math/c/a/5/ca56729c1329c7234d2a3479bc3a4064.png)
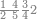
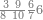
![{\color{blue}{\begin{align}&\scriptstyle\left[2+\frac{3}{4}+\frac{4}{5}+\left(\frac{1}{2}\sdot\frac{1}{5}\right)\right]\times\left[6+\frac{6}{7}+\frac{9}{10}+\left(\frac{3}{8}\sdot\frac{1}{10}\right)\right]\\&\scriptstyle=\frac{\left[\left(2\sdot4\sdot5\sdot2\right)+\left(3\sdot5\sdot2\right)+\left[\left[\left(4\sdot2\right)+1\right]\sdot4\right]\right]\sdot\left[\left(6\sdot7\sdot10\sdot8\right)+\left(6\sdot10\sdot8\right)+\left[\left[\left(9\sdot8\right)+3\right]\sdot7\right]\right]}{4\sdot5\sdot2\sdot7\sdot10\sdot8}\\&\scriptstyle=\frac{\left(80+30+36\right)\sdot\left(3360+480+525\right)}{4\sdot5\sdot2\sdot7\sdot10\sdot8}\\&\scriptstyle=\frac{146\sdot4365}{4\sdot5\sdot2\sdot7\sdot10\sdot8}\\&\scriptstyle=\frac{637290}{4\sdot5\sdot2\sdot7\sdot10\sdot8}\\&\scriptstyle=28+\frac{4}{10}+\left(\frac{4}{8}\sdot\frac{1}{10}\right)+\left(\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{10}\right)+\left(\frac{1}{4}\sdot\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{10}\right)\\\end{align}}}](/mediawiki/images/math/f/5/1/f5121634ed300afa0d6d19d109d3c987.png)
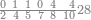
![\scriptstyle\left[2+\frac{1}{3}+\frac{1}{5}+\left(\frac{1}{7}\sdot\frac{1}{8}\right)\right]\times\left[3+\frac{1}{9}+\frac{1}{10}+\left(\frac{1}{6}\sdot\frac{1}{11}\right)\right]](/mediawiki/images/math/2/6/7/2674bbca8a320135a18e2259c80cbc80.png)
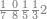
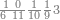
![{\color{blue}{\begin{align}&\scriptstyle\left[2+\frac{1}{3}+\frac{1}{5}+\left(\frac{1}{7}\sdot\frac{1}{8}\right)\right]\scriptstyle\times\left[3+\frac{1}{9}+\frac{1}{10}+\left(\frac{1}{6}\sdot\frac{1}{11}\right)\right]\\&\scriptstyle=\frac{\left[\left(2\sdot3\sdot5\sdot7\sdot8\right)+\left(1\sdot5\sdot7\sdot8\right)+\left(1\sdot3\sdot7\sdot8\right)+\left(1\sdot3\sdot5\right)\right]\sdot\left[\left(3\sdot9\sdot10\sdot6\sdot11\right)+\left(1\sdot10\sdot6\sdot11\right)+\left(1\sdot9\sdot6\sdot11\right)+\left(1\sdot9\sdot10\right)\right]}{3\sdot5\sdot7\sdot8\sdot9\sdot10\sdot6\sdot11}\\&\scriptstyle=\frac{2143\sdot19164}{3\sdot5\sdot7\sdot8\sdot9\sdot10\sdot6\sdot11}\\&\scriptstyle=\frac{41068452}{3\sdot5\sdot7\sdot8\sdot9\sdot10\sdot6\sdot11}\\&\scriptstyle=8+\frac{2}{11}+\left(\frac{5}{10}\sdot\frac{1}{11}\right)+{\color{red}{\left(\frac{3}{9}\sdot\frac{1}{10}\sdot\frac{1}{11}\right)}}+\left(\frac{4}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\sdot\frac{1}{11}\right)+\left(\frac{4}{5}\sdot\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\sdot\frac{1}{11}\right)\\\end{align}}}](/mediawiki/images/math/c/5/d/c5db235b85999e6326b4fb073343ab15.png)
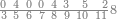
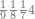
![{\color{blue}{\begin{align}\scriptstyle\left(2+\frac{1}{3}+\frac{1}{5}+\frac{1}{6}\right)&\scriptstyle\times\left(4+\frac{1}{7}+\frac{1}{8}+\frac{1}{9}\right)=\\&\scriptstyle=\frac{\left[\left(2\sdot3\sdot5\sdot6\right)+\left(1\sdot5\sdot6\right)+\left(1\sdot6\sdot3\right)+\left(1\sdot5\sdot3\right)\right]\sdot\left[\left(4\sdot7\sdot8\sdot9\right)+\left(1\sdot8\sdot9\right)+\left(1\sdot9\sdot7\right)+\left(1\sdot8\sdot7\right)\right]}{3\sdot5\sdot6\sdot7\sdot8\sdot9}\\&\scriptstyle=\frac{243\sdot2207}{3\sdot5\sdot6\sdot7\sdot8\sdot9}\\&\scriptstyle=\frac{536301}{3\sdot5\sdot6\sdot7\sdot8\sdot9}\\&\scriptstyle=11+\frac{7}{9}+\left(\frac{3}{8}\sdot\frac{1}{9}\right)+\left(\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{5}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{2}{5}\sdot\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/8/5/d/85de2509a20ed74b97d3babaebb9e031.png)
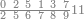
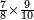

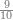
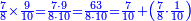
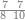

![\scriptstyle{\color{blue}{7\equiv_70\longrightarrow\left[\left(7\sdot8\right)+7\right]\equiv_70}}](/mediawiki/images/math/f/d/8/fd84b5e686ee3e9296cf52634425bc2c.png)
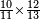
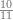
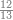

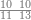
![\scriptstyle\left[\frac{6}{7}+\left(\frac{1}{3}\sdot\frac{1}{7}\right)\right]\times\frac{8}{9}](/mediawiki/images/math/f/9/7/f97a19d668836f661a08889fa51e299c.png)
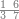

![\scriptstyle{\color{blue}{\left[\frac{6}{7}+\left(\frac{1}{3}\sdot\frac{1}{7}\right)\right]\times\frac{8}{9}=\frac{\left[\left(6\sdot3\right)+1\right]\sdot8}{7\sdot3\sdot9}=\frac{19\sdot8}{7\sdot3\sdot9}=\frac{152}{7\sdot3\sdot9}=\frac{7}{9}+\left(\frac{1}{7}\sdot\frac{1}{9}\right)+\left(\frac{2}{3}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)}}](/mediawiki/images/math/f/2/e/f2e8bf143e298ee677ec736ec72878c5.png)
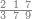
![\scriptstyle\left[\frac{1}{11}+\left(\frac{1}{2}\sdot\frac{1}{11}\right)\right]\times\frac{12}{13}](/mediawiki/images/math/b/3/1/b3108e0fc4b9e093af19900912f9dbb5.png)
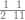
![\scriptstyle{\color{blue}{\left[\frac{1}{11}+\left(\frac{1}{2}\sdot\frac{1}{11}\right)\right]\times\frac{12}{13}=\frac{\left[\left(1\sdot2\right)+1\right]\sdot12}{2\sdot11\sdot13}=\frac{3\sdot12}{2\sdot11\sdot13}=\frac{36}{2\sdot11\sdot13}=\frac{1}{13}+\left(\frac{7}{11}\sdot\frac{1}{13}\right)}}](/mediawiki/images/math/f/1/8/f18858af397e557452eff1ca3042464e.png)
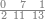
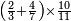
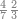
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{2}{3}+\frac{4}{7}\right)\times\frac{10}{11}&\scriptstyle=\frac{\left[\left(2\sdot7\right)+\left(4\sdot3\right)\right]\sdot10}{3\sdot7\sdot11}\\&\scriptstyle=\frac{26\sdot10}{3\sdot7\sdot11}\\&\scriptstyle=\frac{260}{3\sdot7\sdot11}\\&\scriptstyle=1+\frac{1}{11}+\left(\frac{2}{7}\sdot\frac{1}{11}\right)+\left(\frac{2}{3}\sdot\frac{1}{7}\sdot\frac{1}{11}\right)\\\end{align}}}](/mediawiki/images/math/6/4/5/6459e7485ff037e16b64fac321699c82.png)
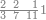
![\scriptstyle\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\times\left[\frac{9}{10}+\left(\frac{7}{8}\sdot\frac{1}{10}\right)\right]](/mediawiki/images/math/5/7/8/5781c5536b7840a71d28f8ec3a3dcbdc.png)
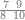
![{\color{blue}{\begin{align}\scriptstyle\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\times\left[\frac{9}{10}+\left(\frac{7}{8}\sdot\frac{1}{10}\right)\right]&\scriptstyle=\frac{\left[\left(5\sdot2\right)+1\right]\times\left[\left(9\sdot8\right)+7\right]}{6\sdot2\sdot10\sdot8}\\&\scriptstyle=\frac{11\sdot79}{6\sdot2\sdot10\sdot8}\\&\scriptstyle=\frac{869}{6\sdot2\sdot10\sdot8}\\&\scriptstyle=\frac{9}{10}+\left(\frac{2}{6}\sdot\frac{1}{8}\sdot\frac{1}{10}\right)+\left(\frac{1}{2}\sdot\frac{1}{6}\sdot\frac{1}{8}\sdot\frac{1}{10}\right)\\\end{align}}}](/mediawiki/images/math/c/9/2/c9226ed09a339b06f56117e6c694d429.png)
![\scriptstyle\left(\frac{3}{4}+\frac{4}{5}\right)\times\left[\frac{10}{11}+\left(\frac{8}{9}\sdot\frac{1}{11}\right)\right]](/mediawiki/images/math/d/d/e/dde0eb7bd402c0e93bfdac59da3033c0.png)
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{3}{4}+\frac{4}{5}\right)\times\left[\frac{10}{11}+\left(\frac{8}{9}\sdot\frac{1}{11}\right)\right]&\scriptstyle=\frac{\left[\left(3\sdot5\right)+\left(4\sdot4\right)\right]\sdot\left[\left(10\sdot9\right)+8\right]}{4\sdot5\sdot11\sdot9}\\&\scriptstyle=\frac{31\sdot98}{4\sdot5\sdot11\sdot9}\\&\scriptstyle=1+\frac{5}{11}+\left(\frac{7}{9}\sdot\frac{1}{11}\right)+\left(\frac{4}{5}\sdot\frac{1}{9}\sdot\frac{1}{11}\right)+\left(\frac{2}{4}\sdot\frac{1}{5}\sdot\frac{1}{9}\sdot\frac{1}{11}\right)\\&\scriptstyle=1+\frac{5}{11}+\left(\frac{7}{9}\sdot\frac{1}{11}\right)+\left(\frac{4}{5}\sdot\frac{1}{9}\sdot\frac{1}{11}\right)+\left(\frac{1}{2}\sdot\frac{1}{5}\sdot\frac{1}{9}\sdot\frac{1}{11}\right)\\\end{align}}}](/mediawiki/images/math/1/a/9/1a9024e8cb48e49fb356f3ee2a2fea6e.png)
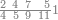
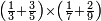
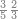
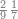
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{1}{3}+\frac{3}{5}\right)\times\left(\frac{1}{7}+\frac{2}{9}\right)&\scriptstyle=\frac{\left[\left(1\sdot5\right)+\left(3\sdot3\right)\right]\sdot\left[\left(1\sdot9\right)+\left(2\sdot7\right)\right]}{3\sdot5\sdot7\sdot9}\\&\scriptstyle=\frac{14\sdot23}{3\sdot5\sdot7\sdot9}\\&\scriptstyle=\frac{3}{9}+\left(\frac{2}{5}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)+\left(\frac{1}{3}\sdot\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/1/3/e/13ea58f02e9ba4a165dc9ee796195bad.png)
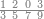
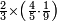
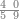
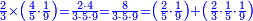
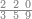
![\scriptstyle\left[\frac{2}{3}+\frac{5}{7}+\left(\frac{1}{6}\sdot\frac{1}{7}\right)\right]\times\left[\frac{4}{5}+\frac{9}{10}+\left(\frac{8}{9}\sdot\frac{1}{10}\right)\right]](/mediawiki/images/math/8/9/c/89c984e9a2e8e2ca9db67ecc3cae4f93.png)
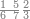
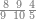
![{\color{blue}{\begin{align}\scriptstyle\left[\frac{2}{3}+\frac{5}{7}+\left(\frac{1}{6}\sdot\frac{1}{7}\right)\right]&\scriptstyle\times\left[\frac{4}{5}+\frac{9}{10}+\left(\frac{8}{9}\sdot\frac{1}{10}\right)\right]=\\&\scriptstyle=\frac{\left[\left(2\sdot7\sdot6\right)+\left[\left[\left(5\sdot6\right)+1\right]\sdot3\right]\right]\sdot\left[\left(4\sdot10\sdot9\right)+\left[\left[\left(9\sdot9\right)+8\right]\sdot5\right]\right]}{3\sdot7\sdot6\sdot5\sdot10\sdot9}\\&\scriptstyle=\frac{\left(84+93\right)\sdot\left(360+445\right)}{3\sdot7\sdot6\sdot5\sdot10\sdot9}\\&\scriptstyle=\frac{177\sdot805}{3\sdot7\sdot6\sdot5\sdot10\sdot9}\\&\scriptstyle=2+\frac{5}{10}+\left(\frac{1}{9}\sdot\frac{1}{10}\right)+\left(\frac{1}{7}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)+\left(\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)\\\end{align}}}](/mediawiki/images/math/0/a/c/0ac80b473de5341b7a109862cac50a39.png)
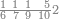
![\scriptstyle\left[\frac{3}{4}+\frac{4}{5}+\left(\frac{1}{2}\sdot\frac{1}{7}\right)\right]\times\left[\frac{7}{8}+\frac{8}{9}+\left(\frac{1}{3}\sdot\frac{1}{10}\right)\right]](/mediawiki/images/math/b/a/6/ba6de07c368359996ed40f8c820d9fd7.png)
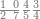
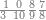
![{\color{blue}{\begin{align}\scriptstyle\left[\frac{3}{4}+\frac{4}{5}+\left(\frac{1}{2}\sdot\frac{1}{7}\right)\right]&\scriptstyle\times\left[\frac{7}{8}+\frac{8}{9}+\left(\frac{1}{3}\sdot\frac{1}{10}\right)\right]=\\&\scriptstyle=\frac{\left[\left(3\sdot5\sdot7\sdot2\right)+\left(4\sdot4\sdot7\sdot2\right)+\left(1\sdot5\sdot4\right)\right]\sdot\left[\left(7\sdot9\sdot10\sdot3\right)+\left(8\sdot8\sdot10\sdot3\right)+\left(1\sdot9\sdot8\right)\right]}{4\sdot5\sdot2\sdot7\sdot8\sdot9\sdot3\sdot10}\\&\scriptstyle=\frac{\left(210+224+20\right)\sdot3882}{4\sdot5\sdot2\sdot7\sdot8\sdot9\sdot3\sdot10}=\frac{454\sdot3882}{4\sdot5\sdot2\sdot7\sdot8\sdot9\sdot3\sdot10}\\&\scriptstyle=2+\frac{9}{10}+\left(\frac{1}{9}\sdot\frac{1}{10}\right)+\left(\frac{2}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)+\left(\frac{1}{8}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)+\left(\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)\\\end{align}}}](/mediawiki/images/math/c/3/0/c307f0aafd415053876451fe9e840f44.png)
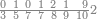
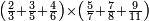
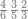
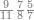
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{2}{3}+\frac{3}{5}+\frac{4}{6}\right)\times\left(\frac{5}{7}+\frac{7}{8}+\frac{9}{11}\right)&\scriptstyle=\frac{\left[\left(2\sdot5\sdot6\right)+\left(3\sdot3\sdot6\right)+\left(4\sdot3\sdot5\right)\right]\sdot\left[\left(5\sdot8\sdot11\right)+\left(7\sdot7\sdot11\right)+\left(9\sdot7\sdot8\right)\right]}{3\sdot5\sdot6\sdot7\sdot8\sdot11}\\&\scriptstyle=\frac{174\sdot1483}{3\sdot5\sdot6\sdot7\sdot8\sdot11}\\&\scriptstyle=4+\frac{7}{11}+\left(\frac{1}{8}\sdot\frac{1}{11}\right)+\left(\frac{4}{7}\sdot\frac{1}{8}\sdot\frac{1}{11}\right)+\left(\frac{4}{5}\sdot\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{11}\right)\\\end{align}}}](/mediawiki/images/math/4/0/1/401e7abc8d1defb14e0e454593c491c7.png)
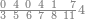
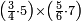
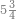
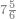
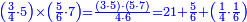
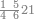
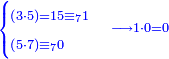
![\scriptstyle{\color{blue}{\begin{cases}\scriptstyle21\equiv_70\longrightarrow0\sdot6=0\\\scriptstyle\left[\left(5\sdot4\right)+1\right]=20+1=21\equiv_70\end{cases}}}](/mediawiki/images/math/0/c/d/0cdc03aab3f4d072107df415047a189e.png)
![\scriptstyle\left[\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\sdot8\right]\times\left[\left[\frac{8}{9}+\left(\frac{1}{5}\sdot\frac{1}{9}\right)\right]\sdot12\right]](/mediawiki/images/math/1/6/0/1600fa727c35dec4f3c4ad5a9afdabb3.png)
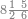
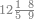
![{\color{blue}{\begin{align}\scriptstyle\left[\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\sdot8\right]&\scriptstyle\times\left[\left[\frac{8}{9}+\left(\frac{1}{5}\sdot\frac{1}{9}\right)\right]\sdot12\right]=\\&\scriptstyle=\frac{\left[\left[\left(5\sdot2\right)+1\right]\sdot8\right]\sdot\left[\left[\left(8\sdot5\right)+1\right]\sdot12\right]}{6\sdot2\sdot9\sdot5}=\frac{\left(11\sdot8\right)\sdot\left(41\sdot12\right)}{6\sdot2\sdot9\sdot5}\\&\scriptstyle=\frac{88\sdot492}{6\sdot2\sdot9\sdot5}\\&\scriptstyle=\frac{43296}{6\sdot2\sdot9\sdot5}\\&\scriptstyle=80+\frac{1}{9}+\left(\frac{3}{6}\sdot\frac{1}{9}\right)+\left(\frac{3}{5}\sdot\frac{1}{6}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/8/7/a/87a796c686c18062d329e860e19096fd.png)
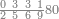
![\scriptstyle\left[\left(\frac{2}{3}+\frac{3}{5}\right)\sdot8\right]\times\left[\left(\frac{6}{7}+\frac{5}{9}\right)\sdot4\right]](/mediawiki/images/math/5/1/a/51a5f2c5f34e3fd50333a6ab3d89872a.png)
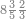
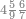
![{\color{blue}{\begin{align}\scriptstyle\left[\left(\frac{2}{3}+\frac{3}{5}\right)\sdot8\right]&\scriptstyle\times\left[\left(\frac{6}{7}+\frac{5}{9}\right)\sdot4\right]=\\&\scriptstyle=\frac{\left[\left[\left(2\sdot5\right)+\left(3\sdot3\right)\right]\sdot8\right]\sdot\left[\left[\left(6\sdot9\right)+\left(5\sdot7\right)\right]\sdot4\right]}{3\sdot5\sdot7\sdot9}\\&\scriptstyle=57+\frac{2}{9}+\left(\frac{2}{7}\sdot\frac{1}{9}\right)+\left(\frac{2}{5}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)+\color{red}{\left(\frac{1}{3}\sdot\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)}\\\end{align}}}](/mediawiki/images/math/3/5/9/359fe81962d6a1156f6fa0c8243052fa.png)
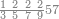
![\scriptstyle\left[\left(\frac{3}{4}\sdot\frac{1}{5}\right)\sdot8\right]\times\left[\left(\frac{5}{6}\sdot\frac{1}{7}\right)\sdot15\right]](/mediawiki/images/math/0/5/f/05f9355bfe0fc140027cb8b0dd02c1ec.png)
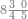
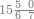
![\scriptstyle{\color{blue}{\left[\left(\frac{3}{4}\sdot\frac{1}{5}\right)\sdot8\right]\times\left[\left(\frac{5}{6}\sdot\frac{1}{7}\right)\sdot15\right]=\frac{\left(3\sdot8\right)\sdot\left(5\sdot15\right)}{4\sdot5\sdot6\sdot7}=2+\frac{1}{7}}}](/mediawiki/images/math/5/4/f/54f19d884fd4f3d92b4474809d32db29.png)
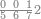
![\scriptstyle\left[\frac{2}{3}\sdot\left(5+\frac{5}{6}\right)\right]\times\left[\frac{5}{7}\sdot\left(8+\frac{4}{9}\right)\right]](/mediawiki/images/math/0/b/f/0bf7045fc49295b61cbc8cb9708697cd.png)
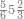
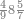
![{\color{blue}{\begin{align}\scriptstyle\left[\frac{2}{3}\sdot\left(5+\frac{5}{6}\right)\right]\times\left[\frac{5}{7}\sdot\left(8+\frac{4}{9}\right)\right]&\scriptstyle=\frac{\left[\left[\left(5\sdot6\right)+5\right]\sdot2\right]\sdot\left[\left[\left(8\sdot9\right)+4\right]\sdot6\right]}{3\sdot6\sdot7\sdot9}\\&\scriptstyle=\frac{\left(35\sdot2\right)\sdot\left(76\sdot6\right)}{3\sdot6\sdot7\sdot9}\\&\scriptstyle=\frac{70\sdot456}{3\sdot6\sdot7\sdot9}\\&\scriptstyle=28+\frac{1}{9}+\left(\frac{2}{7}\sdot\frac{1}{9}\right)+\left(\frac{2}{6}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/3/e/b/3eb1e409939ed2bdd4933855c029fc9f.png)
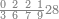
![\scriptstyle\left[\frac{3}{4}\sdot\left[5+\frac{6}{7}+\left(\frac{1}{6}\sdot\frac{1}{7}\right)\right]\right]\times\left[\frac{7}{8}\sdot\left[3+\frac{3}{10}+\left(\frac{1}{9}\sdot\frac{1}{10}\right)\right]\right]](/mediawiki/images/math/e/d/2/ed219e497be7d0951c74faa4e0f2f7d7.png)
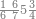
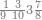
![{\color{blue}{\begin{align}&\scriptstyle\left[\frac{3}{4}\sdot\left[5+\frac{6}{7}+\left(\frac{1}{6}\sdot\frac{1}{7}\right)\right]\right]\times\left[\frac{7}{8}\sdot\left[3+\frac{3}{10}+\left(\frac{1}{9}\sdot\frac{1}{10}\right)\right]\right]=\\&\scriptstyle=\frac{\left[\left[\left[\left[\left(5\sdot7\right)+6\right]\sdot6\right]+1\right]\sdot3\right]\sdot\left[\left[\left[\left[\left(3\sdot10\right)+3\right]\sdot9\right]+1\right]\sdot7\right]}{4\sdot7\sdot6\sdot8\sdot10\sdot9}\\&\scriptstyle=\frac{741\sdot2086}{4\sdot7\sdot6\sdot8\sdot10\sdot9}\\&\scriptstyle=12+\frac{7}{10}+\left(\frac{7}{9}\sdot\frac{1}{10}\right)+\left(\frac{5}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)+\left(\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)+\left(\frac{2}{4}\sdot\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)\\\end{align}}}](/mediawiki/images/math/b/a/6/ba628cb6cc64d2a23a74936c241aacd8.png)
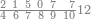
![\scriptstyle\left[\frac{1}{2}\sdot\left(2+\frac{1}{5}+\frac{1}{6}\right)\right]\times\left[\frac{1}{7}\sdot\left(3+\frac{1}{8}+\frac{1}{9}\right)\right]](/mediawiki/images/math/0/0/4/004e700b6414538394bc342a34fa598e.png)
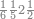
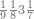
![{\color{blue}{\begin{align}\scriptstyle\left[\frac{1}{2}\sdot\left(2+\frac{1}{5}+\frac{1}{6}\right)\right]\times\left[\frac{1}{7}\sdot\left(3+\frac{1}{8}+\frac{1}{9}\right)\right]&\scriptstyle=\frac{\left[\left[\left(2\sdot5\sdot6\right)+\left(1\sdot6\right)+\left(1\sdot5\right)\right]\sdot1\right]\sdot\left[\left[\left(3\sdot8\sdot9\right)+\left(1\sdot9\right)+\left(1\sdot8\right)\right]\sdot1\right]}{2\sdot5\sdot6\sdot7\sdot8\sdot9}\\&\scriptstyle=\frac{71\sdot233}{2\sdot5\sdot6\sdot7\sdot8\sdot9}\\&\scriptstyle=\frac{4}{9}+\left(\frac{7}{8}\sdot\frac{1}{9}\right)+\left(\frac{2}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{4}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\color{red}{\left(\frac{1}{5}\sdot\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)}\\\end{align}}}](/mediawiki/images/math/1/7/6/1765722a7da0bc617afc2c1d10a08973.png)
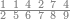
![\scriptstyle\left[\frac{6}{7}\sdot\left[5+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\right]\times\left[\frac{7}{8}\sdot\left[3+\left(\frac{3}{5}\sdot\frac{1}{9}\right)\right]\right]](/mediawiki/images/math/5/f/5/5f53be0be7aff5af1d6d8efd389472f7.png)
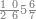
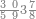
![{\color{blue}{\begin{align}\scriptstyle\left[\frac{6}{7}\sdot\left[5+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\right]&\scriptstyle\times\left[\frac{7}{8}\sdot\left[3+\left(\frac{3}{5}\sdot\frac{1}{9}\right)\right]\right]\\&\scriptstyle=\frac{\left[\left[\left(5\sdot6\sdot2\right)+1\right]\sdot6\right]\sdot\left[\left[\left(3\sdot9\sdot5\right)+3\right]\sdot7\right]}{2\sdot5\sdot6\sdot7\sdot8\sdot9}\\&\scriptstyle=\frac{366\sdot966}{2\sdot5\sdot6\sdot7\sdot8\sdot9}\\&\scriptstyle=11+\frac{6}{9}+\left(\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{5}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{3}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{3}{5}\sdot\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/f/e/0/fe088d6a523834851290f42f0fc5d39b.png)
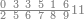
![\scriptstyle\left[\left(\frac{2}{3}\sdot\frac{1}{5}\right)\sdot\left(8+\frac{1}{6}\right)\right]\times\left[\left(\frac{5}{7}\sdot\frac{1}{8}\right)\sdot\left(6+\frac{1}{9}\right)\right]](/mediawiki/images/math/9/a/0/9a08cbb7c870dbf982d1d194761990fe.png)
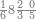
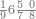
![{\color{blue}{\begin{align}&\scriptstyle\left[\left(\frac{2}{3}\sdot\frac{1}{5}\right)\sdot\left(8+\frac{1}{6}\right)\right]\times\left[\left(\frac{5}{7}\sdot\frac{1}{8}\right)\sdot\left(6+\frac{1}{9}\right)\right]\\&\scriptstyle=\frac{\left[\left[\left(8\sdot6\right)+1\right]\sdot2\right]\sdot\left[\left[\left(6\sdot9\right)+1\right]\sdot5\right]}{3\sdot5\sdot6\sdot7\sdot8\sdot9}\\&\scriptstyle=\frac{98\sdot275}{3\sdot5\sdot6\sdot7\sdot8\sdot9}\\&\scriptstyle=\frac{5}{9}+\left(\frac{2}{8}\sdot\frac{1}{9}\right)+\left(\frac{5}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{2}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{3}{5}\sdot\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{1}{3}\sdot\frac{1}{5}\sdot\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/e/0/a/e0a145b0f36d2ec2e48d31fb61e80e87.png)
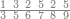
![\scriptstyle\left[\left(\frac{3}{4}\sdot\frac{1}{5}\right)\sdot\left[6+\frac{3}{11}+\left(\frac{5}{6}\sdot\frac{1}{11}\right)\right]\right]\times\left[\left(\frac{5}{7}\sdot\frac{1}{9}\right)\sdot\left[12+\frac{6}{13}+\left(\frac{3}{8}\sdot\frac{1}{13}\right)\right]\right]](/mediawiki/images/math/c/2/2/c22d68f0da0fd67a0798ae11bd0dcc60.png)
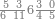
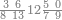
![{\color{blue}{\begin{align}&\scriptstyle\left[\left(\frac{3}{4}\sdot\frac{1}{5}\right)\sdot\left[6+\frac{3}{11}+\left(\frac{5}{6}\sdot\frac{1}{11}\right)\right]\right]\times\left[\left(\frac{5}{7}\sdot\frac{1}{9}\right)\sdot\left[12+\frac{6}{13}+\left(\frac{3}{8}\sdot\frac{1}{13}\right)\right]\right]\\&\scriptstyle=\frac{\left[\left[\left[\left[\left(6\sdot11\right)+3\right]\sdot6\right]+5\right]\sdot3\right]\sdot\left[\left[\left[\left[\left(12\sdot13\right)+6\right]\sdot8\right]+3\right]\sdot5\right]}{4\sdot5\sdot6\sdot7\sdot8\sdot9\sdot11\sdot13}\\&\scriptstyle=\frac{1257\sdot6495}{4\sdot5\sdot6\sdot7\sdot8\sdot9\sdot11\sdot13}\\&\scriptstyle=\frac{12}{13}+\left(\frac{2}{11}\sdot\frac{1}{13}\right)+\left(\frac{8}{9}\sdot\frac{1}{11}\sdot\frac{1}{13}\right)+\left(\frac{7}{8}\sdot\frac{1}{9}\sdot\frac{1}{11}\sdot\frac{1}{13}\right)+\left(\frac{2}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{11}\sdot\frac{1}{13}\right)+\left(\frac{3}{5}\sdot\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{11}\sdot\frac{1}{13}\right)+\left(\frac{3}{4}\sdot\frac{1}{5}\sdot\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{11}\sdot\frac{1}{13}\right)\\\end{align}}}](/mediawiki/images/math/5/c/6/5c611884b977fa2854c2eb5c5f2e6871.png)
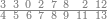
![\scriptstyle\left[\left(\frac{2}{3}\sdot\frac{1}{5}\right)\sdot\left(8+\frac{3}{6}+\frac{4}{7}\right)\right]\times\left[\left(\frac{4}{9}\sdot\frac{1}{10}\right)\sdot\left(18+\frac{6}{11}+\frac{5}{8}\right)\right]](/mediawiki/images/math/9/7/d/97d9dfda0018e2b0241f56adec4bb691.png)
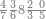
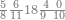
![{\color{blue}{\begin{align}&\scriptstyle\left[\left(\frac{2}{3}\sdot\frac{1}{5}\right)\sdot\left(8+\frac{3}{6}+\frac{4}{7}\right)\right]\times\left[\left(\frac{4}{9}\sdot\frac{1}{10}\right)\sdot\left(18+\frac{6}{11}+\frac{5}{8}\right)\right]\\&\scriptstyle=\frac{\left[\left[\left(8\sdot6\sdot7\right)+\left[\left(3\sdot7\right)+\left(4\sdot6\right)\right]\right]\sdot2\right]\sdot\left[\left[\left(18\sdot11\sdot8\right)+\left[\left(6\sdot8\right)+\left(5\sdot11\right)\right]\right]\sdot4\right]}{3\sdot5\sdot6\sdot7\sdot8\sdot9\sdot10\sdot11}\\&\scriptstyle=\frac{762\sdot6748}{3\sdot5\sdot6\sdot7\sdot8\sdot9\sdot10\sdot11}\\&\scriptstyle=1+\left(\frac{3}{10}\sdot\frac{1}{11}\right)+\left(\frac{3}{9}\sdot\frac{1}{10}\sdot\frac{1}{11}\right)+\left(\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\sdot\frac{1}{11}\right)+\left(\frac{6}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\sdot\frac{1}{11}\right)+\left(\frac{2}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\sdot\frac{1}{11}\right)\\\end{align}}}](/mediawiki/images/math/9/e/2/9e20b1e93f115b1032e4a64662e56870.png)
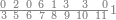
![\scriptstyle\left[\left(\frac{2}{3}+\frac{3}{5}\right)\sdot\left(9+\frac{5}{6}\right)\right]\times\left[\left(\frac{3}{7}+\frac{7}{8}\right)\sdot\left(12+\frac{7}{9}\right)\right]](/mediawiki/images/math/b/b/8/bb89089481d6771d64a646f1b2604e99.png)
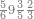
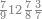
![{\color{blue}{\begin{align}&\scriptstyle\left[\left(\frac{2}{3}+\frac{3}{5}\right)\sdot\left(9+\frac{5}{6}\right)\right]\times\left[\left(\frac{3}{7}+\frac{7}{8}\right)\sdot\left(12+\frac{7}{9}\right)\right]\\&\scriptstyle=\frac{\left[\left[\left(2\sdot5\right)+\left(3\sdot3\right)\right]\sdot\left[\left(9\sdot6\right)+5\right]\right]\sdot\left[\left[\left(3\sdot8\right)+\left(7\sdot7\right)\right]\sdot\left[\left(12\sdot9\right)+7\right]\right]}{3\sdot5\sdot6\sdot7\sdot8\sdot9}\\&\scriptstyle=\frac{\left(19\sdot59\right)\sdot8395}{3\sdot5\sdot6\sdot7\sdot8\sdot9}=\frac{1121\sdot8395}{3\sdot5\sdot6\sdot7\sdot8\sdot9}\\&\scriptstyle=207+\frac{4}{9}+\left(\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{5}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{2}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{1}{3}\sdot\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/e/1/f/e1f881414d66bf16e69504c6eddf39c3.png)
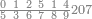
![\scriptstyle\left[\left(\frac{2}{3}+\frac{3}{5}\right)\sdot\left(7+\frac{3}{4}+\frac{3}{5}\right)\right]\times\left[\left(\frac{5}{6}+\frac{5}{8}\right)\sdot\left(4+\frac{5}{6}+\frac{9}{10}\right)\right]](/mediawiki/images/math/b/4/9/b497ed9da24bcbdf311fe9fdd582187b.png)
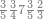
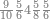
![{\color{blue}{\begin{align}&\scriptstyle\left[\left(\frac{2}{3}+\frac{3}{5}\right)\sdot\left(7+\frac{3}{4}+\frac{3}{5}\right)\right]\times\left[\left(\frac{5}{6}+\frac{5}{8}\right)\sdot\left(4+\frac{5}{6}+\frac{9}{10}\right)\right]\\&\scriptstyle=\frac{\left[\left(2\sdot5\right)+\left(3\sdot3\right)\right]\sdot\left[\left(7\sdot4\sdot5\right)+\left[\left(3\sdot5\right)+\left(3\sdot4\right)\right]\right]\sdot\left[\left(5\sdot8\right)+\left(5\sdot6\right)\right]\sdot\left[\left(4\sdot6\sdot10\right)+\left[\left(5\sdot10\right)+\left(9\sdot6\right)\right]\right]}{3\sdot4\sdot5\sdot5\sdot6\sdot6\sdot8\sdot10}\\&\scriptstyle=\frac{\left(19\sdot167\right)\sdot24080}{2\sdot6\sdot8\sdot9\sdot10\sdot10\sdot10}\\&\scriptstyle=\frac{\frac{\frac{3173\sdot24080}{10}}{8}}{2\sdot6\sdot9\sdot10\sdot10}\\&\scriptstyle=88+\frac{4}{10}+\left(\frac{3}{10}\sdot\frac{1}{10}\right)+\left(\frac{2}{9}\sdot\frac{1}{10}\sdot\frac{1}{10}\right)+\left(\frac{2}{6}\sdot\frac{1}{9}\sdot\frac{1}{10}\sdot\frac{1}{10}\right)+\left(\frac{1}{2}\sdot\frac{1}{6}\sdot\frac{1}{9}\sdot\frac{1}{10}\sdot\frac{1}{10}\right)\\\end{align}}}](/mediawiki/images/math/1/e/1/1e1394cd7adf66817eca7fc89468920a.png)
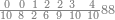
![\scriptstyle\left[\left[\frac{3}{5}+\left(\frac{1}{2}\sdot\frac{1}{5}\right)\right]\sdot\left[4+\frac{1}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\right]\times\left[\left[\frac{6}{7}+\left(\frac{2}{5}\sdot\frac{1}{7}\right)\right]\sdot\left[3+\frac{5}{11}+\left(\frac{5}{8}\sdot\frac{1}{11}\right)\right]\right]](/mediawiki/images/math/7/4/6/746250ab2b55cc29768a628fb82506bc.png)
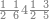
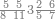
![{\color{blue}{\begin{align}&\scriptstyle\left[\left[\frac{3}{5}+\left(\frac{1}{2}\sdot\frac{1}{5}\right)\right]\sdot\left[4+\frac{1}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\right]\times\left[\left[\frac{6}{7}+\left(\frac{2}{5}\sdot\frac{1}{7}\right)\right]\sdot\left[3+\frac{5}{11}+\left(\frac{5}{8}\sdot\frac{1}{11}\right)\right]\right]\\&\scriptstyle=\frac{\left[\left[\left(3\sdot2\right)+1\right]\sdot\left[\left(4\sdot2\sdot6\right)+\left(1\sdot2\right)+1\right]\right]\sdot\left[\left[\left(6\sdot5\right)+2\right]\sdot\left[\left(3\sdot8\sdot11\right)+\left(5\sdot8\right)+5\right]\right]}{2\sdot2\sdot5\sdot5\sdot6\sdot7\sdot8\sdot11}\\&\scriptstyle=\frac{\left(7\sdot51\right)\sdot9888}{2\sdot2\sdot5\sdot5\sdot6\sdot7\sdot8\sdot11}\\&\scriptstyle=\frac{357\sdot9888}{2\sdot2\sdot5\sdot5\sdot6\sdot7\sdot8\sdot11}\\&\scriptstyle=9+\frac{6}{11}+\left(\frac{6}{10}\sdot\frac{1}{10}\sdot\frac{1}{11}\right)\\\end{align}}}](/mediawiki/images/math/c/f/6/cf69f72c05bf684f58380d95404b90c6.png)
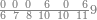
![\scriptstyle\left[\left(\frac{2}{3}\sdot\frac{1}{5}\right)\sdot\left[8+\left(\frac{1}{4}\sdot\frac{1}{6}\right)\right]\right]\times\left[\left(\frac{3}{7}\sdot\frac{1}{8}\right)\sdot\left[12+\left(\frac{1}{2}\sdot\frac{1}{13}\right)\right]\right]](/mediawiki/images/math/b/d/3/bd39d71c41ffa67e9904a9b88747ee73.png)
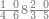
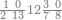
![{\color{blue}{\begin{align}&\scriptstyle\left[\left(\frac{2}{3}\sdot\frac{1}{5}\right)\sdot\left[8+\left(\frac{1}{4}\sdot\frac{1}{6}\right)\right]\right]\times\left[\left(\frac{3}{7}\sdot\frac{1}{8}\right)\sdot\left[12+\left(\frac{1}{2}\sdot\frac{1}{13}\right)\right]\right]\\&\scriptstyle=\frac{\left[\left[\left(8\sdot4\sdot6\right)+1\right]\sdot2\right]\sdot\left[\left[\left(12\sdot2\sdot13\right)+1\right]\sdot3\right]}{2\sdot3\sdot4\sdot5\sdot6\sdot7\sdot8\sdot13}\\&\scriptstyle=\frac{386\sdot939}{2\sdot3\sdot4\sdot5\sdot6\sdot7\sdot8\sdot13}\\&\scriptstyle=\frac{8}{13}+\left(\frac{9}{10}\sdot\frac{1}{13}\right)+\left(\frac{8}{9}\sdot\frac{1}{10}\sdot\frac{1}{13}\right)+\left(\frac{3}{8}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\sdot\frac{1}{13}\right)+\left(\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\sdot\frac{1}{13}\right)\\\end{align}}}](/mediawiki/images/math/4/1/9/419819d1199fd2a93149759f198af2b2.png)
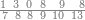
![\scriptstyle\left[\left(\frac{3}{5}\sdot5\right)+\left(\frac{5}{6}\sdot7\right)\right]\times\left[\left(\frac{2}{3}\sdot4\right)+\left(\frac{1}{2}\sdot5\right)\right]](/mediawiki/images/math/9/e/f/9efa063bb7945eb7d7c881b90eeae9c3.png)
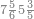
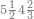
![{\color{blue}{\begin{align}\scriptstyle\left[\left(\frac{3}{5}\sdot5\right)+\left(\frac{5}{6}\sdot7\right)\right]\times\left[\left(\frac{2}{3}\sdot4\right)+\left(\frac{1}{2}\sdot5\right)\right]&\scriptstyle=\frac{\left[\left[\left(3\sdot5\right)\sdot6\right]+\left[\left(5\sdot7\right)\sdot5\right]\right]\sdot\left[\left[\left(2\sdot4\right)\sdot2\right]+\left[\left(1\sdot5\right)\sdot3\right]\right]}{2\sdot3\sdot5\sdot6}\\&\scriptstyle=\frac{\left(90+175\right)\sdot31}{2\sdot3\sdot5\sdot6}=\frac{265\sdot31}{2\sdot3\sdot5\sdot6}\\&\scriptstyle=45+\frac{6}{10}+\left(\frac{2}{6}\sdot\frac{1}{10}\right)+\left(\frac{1}{3}\sdot\frac{1}{6}\sdot\frac{1}{10}\right)\\\end{align}}}](/mediawiki/images/math/d/7/a/d7a550c49a407abb0bd07dda69308da1.png)
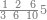
![{\color{blue}{\begin{align}\scriptstyle\left[\left(\frac{3}{5}\sdot5\right)+\left(\frac{5}{6}\sdot7\right)\right]\times\left[\left(\frac{2}{3}\sdot4\right)+\left(\frac{1}{2}\sdot5\right)\right]&\scriptstyle=\left[3+\left(5+\frac{5}{6}\right)\right]\sdot\left[\left(2+\frac{2}{3}\right)+\left(2+\frac{1}{2}\right)\right]\\&\scriptstyle=\left(8+\frac{5}{6}\right)\sdot\left(5+\frac{1}{6}\right)\\\end{align}}}](/mediawiki/images/math/0/c/4/0c43bb54b91614d12040e6bc6015dbbf.png)
![\scriptstyle\left[\left(\frac{3}{5}\sdot3\right)+\left[\frac{3}{4}\sdot\left(2+\frac{2}{3}\right)\right]\right]\times\left[\left(\frac{4}{5}\sdot2\right)+\left[\frac{5}{7}\sdot\left(3+\frac{1}{2}\right)\right]\right]](/mediawiki/images/math/a/c/9/ac90cb543446e9ef209b88692cd48240.png)
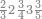
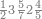
![{\color{blue}{\begin{align}&\scriptstyle\left[\left(\frac{3}{5}\sdot3\right)+\left[\frac{3}{4}\sdot\left(2+\frac{2}{3}\right)\right]\right]\times\left[\left(\frac{4}{5}\sdot2\right)+\left[\frac{5}{7}\sdot\left(3+\frac{1}{2}\right)\right]\right]\\&\scriptstyle=\frac{\left[\left[\left(3\sdot3\right)\sdot4\sdot3\right]+\left[\left[3\sdot\left[\left(2\sdot3\right)+2\right]\right]\sdot5\right]\right]\sdot\left[\left[\left(4\sdot2\right)\sdot7\sdot2\right]+\left[\left[5\sdot\left[\left(3\sdot2\right)+1\right]\right]\sdot5\right]\right]}{2\sdot3\sdot4\sdot5\sdot5\sdot7}\\&\scriptstyle=\frac{\left(108+120\right)\sdot287}{2\sdot3\sdot4\sdot5\sdot5\sdot7}\\&\scriptstyle=\frac{228\sdot287}{2\sdot3\sdot4\sdot5\sdot5\sdot7}\\&\scriptstyle=15+\frac{5}{10}+\left(\frac{8}{10}\sdot\frac{1}{10}\right)\\\end{align}}}](/mediawiki/images/math/a/1/c/a1c642a81a9370d65bc005f53f27a0d4.png)
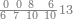
![\scriptstyle\left[\left(3+\frac{1}{2}\right)+\left(5+\frac{1}{3}\right)\right]\times\left[\left(4+\frac{3}{4}\right)+\left(6+\frac{4}{5}\right)\right]](/mediawiki/images/math/d/c/e/dce671800feba457094cdfcc90b5a6f2.png)
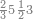
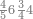
![{\color{blue}{\begin{align}&\scriptstyle\left[\left(3+\frac{1}{2}\right)+\left(5+\frac{1}{3}\right)\right]\times\left[\left(4+\frac{3}{4}\right)+\left(6+\frac{4}{5}\right)\right]\\&\scriptstyle=\frac{\left[\left[\left[\left(3\sdot2\right)+1\right]\sdot3\right]+\left[\left[\left(5\sdot3\right)+1\right]\sdot2\right]\right]\sdot\left[\left[\left[\left(4\sdot4\right)+3\right]\sdot5\right]+\left[\left[\left(6\sdot5\right)+4\right]\sdot4\right]\right]}{2\sdot3\sdot4\sdot5}\\&\scriptstyle=\frac{\left(21+32\right)\sdot231}{2\sdot3\sdot4\sdot5}\\&\scriptstyle=\frac{53\sdot231}{2\sdot3\sdot4\sdot5}\\&\scriptstyle=102+\left(\frac{3}{4}\sdot\frac{1}{5}\sdot\frac{1}{6}\right)\\\end{align}}}](/mediawiki/images/math/0/d/f/0df87612be93f8cdf3d4e4d9d9e15960.png)
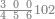
![\scriptstyle{\color{blue}{\left[\left(3+\frac{1}{2}\right)+\left(5+\frac{1}{3}\right)\right]\times\left[\left(4+\frac{3}{4}\right)+\left(6+\frac{4}{5}\right)\right]=\left(8+\frac{5}{6}\right)\sdot\left[11+\frac{2}{5}+\left(\frac{3}{4}\sdot\frac{1}{5}\right)\right]}}](/mediawiki/images/math/0/d/3/0d3c159de6fbc53d0492363dc5639933.png)
![\scriptstyle\left[3+\left[\frac{1}{2}\sdot\left(5+\frac{1}{3}\right)\right]\right]\times\left[4+\left[\frac{3}{4}\sdot\left(6+\frac{4}{5}\right)\right]\right]](/mediawiki/images/math/3/e/2/3e22d62d8b8a2cb5d6852ad408fcd2a3.png)
![{\color{blue}{\begin{align}&\scriptstyle\left[3+\left[\frac{1}{2}\sdot\left(5+\frac{1}{3}\right)\right]\right]\times\left[4+\left[\frac{3}{4}\sdot\left(6+\frac{4}{5}\right)\right]\right]\\&\scriptstyle=\frac{\left[\left(3\sdot2\sdot3\right)+\left[\left[\left(5\sdot3\right)+1\right]\sdot1\right]\right]\sdot\left[\left(4\sdot4\sdot5\right)+\left[\left[\left(6\sdot5\right)+4\right]\sdot3\right]\right]}{2\sdot3\sdot4\sdot5}\\&\scriptstyle=\frac{\left(18+16\right)\sdot182}{2\sdot3\sdot4\sdot5}\\&\scriptstyle=\frac{34\sdot182}{2\sdot3\sdot4\sdot5}\\&\scriptstyle=51+\frac{3}{6}+\left(\frac{2}{5}\sdot\frac{1}{6}\right)\\\end{align}}}](/mediawiki/images/math/0/1/1/0117aa4c164f9729338105293c728d0e.png)
![\scriptstyle\left[2+\left[\left(\frac{2}{3}+\frac{3}{4}\right)\sdot3\right]+\left[\left(\frac{4}{5}+\frac{5}{6}\right)\sdot4\right]\right]\times\left[1+\left[\left(\frac{3}{5}+\frac{1}{2}\right)\sdot2\right]+\left[\left(\frac{3}{11}+\frac{9}{10}\right)\sdot3\right]\right]](/mediawiki/images/math/e/3/8/e381ac62d5a0863c6a7d62fd8b4c2b73.png)
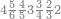
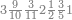
![{\color{blue}{\begin{align}&\scriptstyle\left[2+\left[\left(\frac{2}{3}+\frac{3}{4}\right)\sdot3\right]+\left[\left(\frac{4}{5}+\frac{5}{6}\right)\sdot4\right]\right]\times\left[1+\left[\left(\frac{3}{5}+\frac{1}{2}\right)\sdot2\right]+\left[\left(\frac{3}{11}+\frac{9}{10}\right)\sdot3\right]\right]\\&\scriptstyle=\frac{\left[\left(2\sdot3\sdot4\sdot5\sdot6\right)+\left[\left[\left(2\sdot4\right)+\left(3\sdot3\right)\right]\sdot3\sdot5\sdot6\right]+\left[\left[\left(4\sdot6\right)+\left(5\sdot5\right)\right]\sdot4\sdot3\sdot4\right]\right]}{2\sdot3\sdot4\sdot5\sdot5\sdot6\sdot10\sdot11}\sdot\\&\scriptstyle\sdot\frac{\left[\left(1\sdot5\sdot2\sdot11\sdot10\right)+\left[\left[\left(3\sdot2\right)+\left(1\sdot5\right)\right]\sdot2\sdot11\sdot10\right]+\left[\left[\left(3\sdot10\right)+\left(9\sdot11\right)\right]\sdot3\sdot5\sdot2\right]\right]}{2\sdot3\sdot4\sdot5\sdot5\sdot6\sdot10\sdot11}\\&\scriptstyle=\frac{\left(720+1530+2352\right)\sdot7390}{2\sdot3\sdot4\sdot5\sdot5\sdot6\sdot10\sdot11}\\&\scriptstyle=\frac{4602\sdot7390}{2\sdot3\sdot4\sdot5\sdot5\sdot6\sdot10\sdot11}\\&\scriptstyle=85+\frac{9}{11}+\left(\frac{6}{10}\sdot\frac{1}{11}\right)+\left(\frac{8}{10}\sdot\frac{1}{10}\sdot\frac{1}{11}\right)+\left(\frac{5}{6}\sdot\frac{1}{10}\sdot\frac{1}{10}\sdot\frac{1}{11}\right)\\\end{align}}}](/mediawiki/images/math/5/f/a/5faa637910463a96ec3850e0ef4e2f59.png)
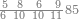
![\scriptstyle\left[\left(2+\frac{2}{3}+\frac{3}{4}\right)+\left(3+\frac{4}{5}+\frac{5}{6}\right)+4\right]\times\left[\left(1+\frac{3}{5}+\frac{1}{2}\right)+\left(2+\frac{3}{11}+\frac{9}{10}\right)+3\right]](/mediawiki/images/math/d/7/7/d77f14b6a5c47d1358f27996043a6568.png)
![{\color{blue}{\begin{align}&\scriptstyle\left[\left(2+\frac{2}{3}+\frac{3}{4}\right)+\left(3+\frac{4}{5}+\frac{5}{6}\right)+4\right]\times\left[\left(1+\frac{3}{5}+\frac{1}{2}\right)+\left(2+\frac{3}{11}+\frac{9}{10}\right)+3\right]\\&\scriptstyle=\frac{\left[\left[\left[\left(2\sdot3\sdot4\right)+\left[\left(2\sdot4\right)+\left(3\sdot3\right)\right]\right]\sdot5\sdot6\right]+\left[\left[\left(3\sdot5\sdot6\right)+\left[\left(4\sdot6\right)+\left(5\sdot5\right)\right]\right]\sdot3\sdot4\right]+\left(4\sdot3\sdot4\sdot5\sdot6\right)\right]}{2\sdot3\sdot4\sdot5\sdot5\sdot6\sdot10\sdot11}\sdot\\&\scriptstyle\sdot\frac{\left[\left[\left[\left(1\sdot5\sdot2\right)+\left[\left(3\sdot2\right)+\left(1\sdot5\right)\right]\right]\sdot11\sdot10\right]+\left[\left[\left(2\sdot11\sdot10\right)+\left[\left(3\sdot10\right)+\left(9\sdot11\right)\right]\right]\sdot5\sdot2\right]+\left(3\sdot5\sdot2\sdot11\sdot10\right)\right]}{2\sdot3\sdot4\sdot5\sdot5\sdot6\sdot10\sdot11}\\&\scriptstyle=\frac{4338\sdot9100}{2\sdot3\sdot4\sdot5\sdot5\sdot6\sdot10\sdot11}\\&\scriptstyle=99+\frac{7}{11}+\left(\frac{5}{10}\sdot\frac{1}{11}\right)+\left(\frac{1}{2}\sdot\frac{1}{10}\sdot\frac{1}{11}\right)\\\end{align}}}](/mediawiki/images/math/8/f/7/8f7894b36588f1639d2e156b3385eaa4.png)
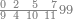
![\scriptstyle\left[2+\left[\left(\frac{1}{2}\sdot\frac{1}{5}\right)\sdot3\right]+\left[\left(\frac{2}{3}\sdot\frac{1}{6}\right)\sdot5\right]\right]\times\left[3+\left[\left(\frac{1}{4}\sdot\frac{1}{7}\right)\sdot4\right]+\left[\left(\frac{5}{6}\sdot\frac{1}{8}\right)\sdot2\right]\right]](/mediawiki/images/math/c/0/b/c0bc2ad5bc456adaef584d86297ba6fa.png)
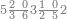
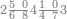
![{\color{blue}{\begin{align}&\scriptstyle\left[2+\left[\left(\frac{1}{2}\sdot\frac{1}{5}\right)\sdot3\right]+\left[\left(\frac{2}{3}\sdot\frac{1}{6}\right)\sdot5\right]\right]\times\left[3+\left[\left(\frac{1}{4}\sdot\frac{1}{7}\right)\sdot4\right]+\left[\left(\frac{5}{6}\sdot\frac{1}{8}\right)\sdot2\right]\right]\\&\scriptstyle=\frac{\left[\left(2\sdot2\sdot5\sdot3\sdot6\right)+\left(1\sdot3\sdot3\sdot6\right)+\left(2\sdot5\sdot2\sdot5\right)\right]\sdot\left[\left(3\sdot4\sdot7\sdot6\sdot8\right)+\left(1\sdot4\sdot6\sdot8\right)+\left(5\sdot2\sdot4\sdot7\right)\right]}{2\sdot3\sdot4\sdot5\sdot6\sdot6\sdot7\sdot8}\\&\scriptstyle=\frac{514\sdot4504}{2\sdot3\sdot4\sdot5\sdot6\sdot6\sdot7\sdot8}\\&\scriptstyle=9+\frac{5}{10}+\left(\frac{6}{9}\sdot\frac{1}{10}\right)+\left(\frac{2}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)+\left(\frac{2}{7}\sdot\frac{1}{8}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)+\left(\frac{4}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)\\\end{align}}}](/mediawiki/images/math/7/a/5/7a5613deb2558b614d861fc254711441.png)
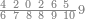
![\scriptstyle\left[\left[2+\left(\frac{1}{2}\sdot\frac{1}{5}\right)\right]+\left[3+\left(\frac{2}{3}\sdot\frac{1}{6}\right)\right]+5\right]\times\left[\left[3+\left(\frac{1}{4}\sdot\frac{1}{7}\right)\right]+\left[4+\left(\frac{5}{6}\sdot\frac{1}{8}\right)\right]+2\right]](/mediawiki/images/math/5/8/d/58d515ef7eab036fb7989bff254d93db.png)
![{\color{blue}{\begin{align}&\scriptstyle\left[\left[2+\left(\frac{1}{2}\sdot\frac{1}{5}\right)\right]+\left[3+\left(\frac{2}{3}\sdot\frac{1}{6}\right)\right]+5\right]\times\left[\left[3+\left(\frac{1}{4}\sdot\frac{1}{7}\right)\right]+\left[4+\left(\frac{5}{6}\sdot\frac{1}{8}\right)\right]+2\right]\\&\scriptstyle=\frac{\left[\left[\left[\left(2\sdot2\sdot5\right)+1\right]\sdot3\sdot6\right]+\left[\left[\left(3\sdot3\sdot6\right)+2\right]\sdot2\sdot5\right]+\left(5\sdot2\sdot5\sdot3\sdot6\right)\right]\sdot\left[\left[\left[\left(3\sdot4\sdot7\right)+1\right]\sdot6\sdot8\right]+\left[\left[\left(4\sdot6\sdot8\right)+5\right]\sdot4\sdot7\right]+\left(2\sdot4\sdot7\sdot6\sdot8\right)\right]}{2\sdot3\sdot4\sdot5\sdot6\sdot6\sdot7\sdot8}\\&\scriptstyle=\frac{1838\sdot12284}{2\sdot3\sdot4\sdot5\sdot6\sdot6\sdot7\sdot8}\\&\scriptstyle=93+\frac{3}{10}+\left(\frac{2}{9}\sdot\frac{1}{10}\right)+\left(\frac{4}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)+\left(\frac{3}{8}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)+\color{red}{\left(\frac{5}{6}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)}\\\end{align}}}](/mediawiki/images/math/0/8/a/08a84fe326c46fb10e5b41567d3d284e.png)
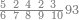
![\scriptstyle\left[\left[\frac{3}{4}\sdot\left(5+\frac{1}{2}\right)\right]+\left[\frac{5}{6}\sdot\left(3+\frac{2}{5}\right)\right]\right]\times\left[\left[\frac{2}{3}\sdot\left(4+\frac{1}{7}\right)\right]+\left[\frac{3}{8}\sdot\left(2+\frac{3}{11}\right)\right]\right]](/mediawiki/images/math/f/4/c/f4cf264503d356d541b3d10d3eb20358.png)
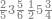
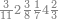
![{\color{blue}{\begin{align}&\scriptstyle\left[\left[\frac{3}{4}\sdot\left(5+\frac{1}{2}\right)\right]+\left[\frac{5}{6}\sdot\left(3+\frac{2}{5}\right)\right]\right]\times\left[\left[\frac{2}{3}\sdot\left(4+\frac{1}{7}\right)\right]+\left[\frac{3}{8}\sdot\left(2+\frac{3}{11}\right)\right]\right]\\&\scriptstyle=\frac{\left[\left[\left[\left[\left(5\sdot2\right)+1\right]\sdot3\right]\sdot6\sdot5\right]+\left[\left[\left[\left(3\sdot5\right)+2\right]\sdot5\right]\sdot4\sdot2\right]\right]\sdot\left[\left[\left[\left[\left(4\sdot7\right)+1\right]\sdot2\right]\sdot8\sdot11\right]+\left[\left[\left[\left(2\sdot11\right)+3\right]\sdot3\right]\sdot3\sdot7\right]\right]}{2\sdot3\sdot4\sdot5\sdot6\sdot7\sdot8\sdot11}\\&\scriptstyle=\frac{1670\sdot6679}{2\sdot3\sdot4\sdot5\sdot6\sdot7\sdot8\sdot11}\\&\scriptstyle=25+\frac{1}{11}+\left(\frac{5}{9}\sdot\frac{1}{11}\right)+\left(\frac{5}{8}\sdot\frac{1}{9}\sdot\frac{1}{11}\right)+\left(\frac{5}{8}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{11}\right)+\left(\frac{6}{7}\sdot\frac{1}{8}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{11}\right)\\\end{align}}}](/mediawiki/images/math/b/4/a/b4af2d9d8a81bddde25a75bb9c41da17.png)
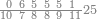
![\scriptstyle\left[\left[\frac{3}{4}\sdot\left(5+\frac{1}{2}+\frac{5}{6}\right)\right]+\left(3+\frac{2}{5}\right)\right]\times\left[\left[\frac{2}{3}\sdot\left(4+\frac{1}{7}+\frac{3}{8}\right)\right]+\left(2+\frac{3}{11}\right)\right]](/mediawiki/images/math/3/4/b/34befb2a8355a40d4b07b397f43dd69e.png)
![\scriptstyle\left[\left(\frac{3}{4}\sdot5\right)+\left[\frac{1}{2}+\left(\frac{5}{6}\sdot3\right)+\frac{2}{5}\right]\right]\times\left[\left(\frac{2}{3}\sdot4\right)+\left[\frac{1}{7}+\left(\frac{3}{8}\sdot2\right)+\frac{3}{11}\right]\right]](/mediawiki/images/math/2/9/0/29093e0012e53f927c9480b5353dc149.png)
![\scriptstyle\left[\frac{3}{4}+\left(5+\frac{1}{2}+\frac{5}{6}\right)+\left(3+\frac{2}{5}\right)\right]\times\left[\frac{2}{3}+\left(4+\frac{1}{7}+\frac{3}{8}\right)+\left(2+\frac{3}{11}\right)\right]](/mediawiki/images/math/6/8/3/683a3a001b63db0b1a13bbd80eeae19b.png)
![\scriptstyle\left[\left(\frac{3}{4}\sdot5\right)+\left[\frac{1}{2}+\left(\frac{5}{6}\sdot3\right)\right]+\frac{2}{5}\right]\times\left[\left(\frac{2}{3}\sdot4\right)+\left[\frac{1}{7}+\left(\frac{3}{8}\sdot2\right)\right]+\frac{3}{11}\right]](/mediawiki/images/math/1/e/7/1e79be1ade90e7e0d8ac84da68b7cd0a.png)
![\scriptstyle\left[\left(\frac{3}{4}\sdot5\right)+\left(\frac{1}{2}+\frac{5}{6}\right)+\left(3+\frac{2}{5}\right)\right]\times\left[\left(\frac{2}{3}\sdot4\right)+\left(\frac{1}{7}+\frac{3}{8}\right)+\left(2+\frac{3}{11}\right)\right]](/mediawiki/images/math/2/e/2/2e2d760b9b1986f571cf28dec3dba804.png)
![\scriptstyle\left[\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\sdot3\right]+\left[\left(\frac{3}{4}+\frac{4}{5}\right)\sdot2\right]+\left[\frac{3}{8}\sdot\left(4+\frac{3}{9}\right)\right]+\left(\frac{2}{3}\sdot\frac{1}{9}\right)](/mediawiki/images/math/6/a/e/6ae04398de7ca6ddeaaac8ce8271944a.png)
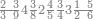
![\scriptstyle\left[\left[\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\sdot3\right]+\left[\left(\frac{3}{4}+\frac{4}{5}\right)\sdot2\right]\right]+\left[\frac{3}{8}\sdot\left[4+\frac{3}{9}+\left(\frac{2}{3}\sdot\frac{1}{9}\right)\right]\right]](/mediawiki/images/math/5/c/7/5c7af9e3236fe968eb5e91d493636d98.png)
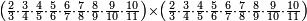
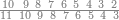
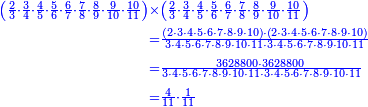
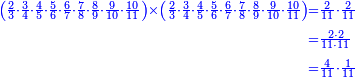
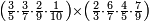
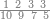
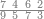
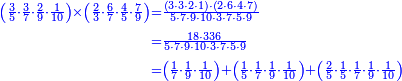
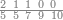
![\scriptstyle\left[\left(\frac{3}{4}\sdot\frac{4}{5}\right)+\left(\frac{5}{6}\sdot\frac{6}{7}\right)+\left(\frac{7}{8}\sdot\frac{8}{9}\right)\right]\times\left[\left(\frac{2}{3}\sdot\frac{3}{4}\right)+\left(\frac{4}{5}\sdot\frac{5}{6}\right)+\left(\frac{6}{7}\sdot\frac{7}{8}\right)\right]](/mediawiki/images/math/9/d/7/9d786b3054d18765a05eec5c1fbeed6c.png)
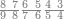
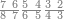
![{\color{blue}{\begin{align}&\scriptstyle\left[\left(\frac{3}{4}\sdot\frac{4}{5}\right)+\left(\frac{5}{6}\sdot\frac{6}{7}\right)+\left(\frac{7}{8}\sdot\frac{8}{9}\right)\right]\times\left[\left(\frac{2}{3}\sdot\frac{3}{4}\right)+\left(\frac{4}{5}\sdot\frac{5}{6}\right)+\left(\frac{6}{7}\sdot\frac{7}{8}\right)\right]\\&\scriptstyle=\frac{\left[\left(3\sdot4\sdot6\sdot7\sdot8\sdot9\right)+\left(5\sdot6\sdot4\sdot5\sdot8\sdot9\right)+\left(7\sdot8\sdot4\sdot5\sdot6\sdot7\right)\right]\sdot\left[\left(2\sdot3\sdot5\sdot6\sdot7\sdot8\right)+\left(4\sdot5\sdot3\sdot4\sdot7\sdot8\right)+\left(6\sdot7\sdot3\sdot4\sdot5\sdot6\right)\right]}{3\sdot4\sdot4\sdot5\sdot5\sdot6\sdot6\sdot7\sdot7\sdot8\sdot8\sdot9}\\&\scriptstyle=\frac{126528\sdot38640}{3\sdot4\sdot4\sdot5\sdot5\sdot6\sdot6\sdot7\sdot7\sdot8\sdot8\sdot9}\\&\scriptstyle=4+\left(\frac{6}{7}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)+\left(\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{9}\sdot\frac{1}{10}\right)\\\end{align}}}](/mediawiki/images/math/5/7/6/576e9f86ccdf738978d95e38dae7b31d.png)
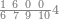
![\scriptstyle{\color{blue}{\left[\left(\frac{3}{4}\sdot\frac{4}{5}\right)+\left(\frac{5}{6}\sdot\frac{6}{7}\right)+\left(\frac{7}{8}\sdot\frac{8}{9}\right)\right]\times\left[\left(\frac{2}{3}\sdot\frac{3}{4}\right)+\left(\frac{4}{5}\sdot\frac{5}{6}\right)+\left(\frac{6}{7}\sdot\frac{7}{8}\right)\right]=\left(\frac{3}{5}+\frac{5}{7}+\frac{7}{9}\right)\sdot\left(\frac{1}{2}+\frac{2}{3}+\frac{3}{4}\right)}}](/mediawiki/images/math/e/9/2/e92972bd46deaef4cdc2328ba839b0ee.png)
![\scriptstyle\left[\left(\frac{2}{3}\sdot\frac{3}{4}\right)\sdot6\right]\times\left[\left(\frac{3}{4}\sdot\frac{4}{7}\right)\sdot8\right]](/mediawiki/images/math/b/b/5/bb5eed5e9b25166de1f36bb9904c0f62.png)
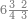
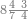
![\scriptstyle{\color{blue}{\left[\left(\frac{2}{3}\sdot\frac{3}{4}\right)\sdot6\right]\times\left[\left(\frac{3}{4}\sdot\frac{4}{7}\right)\sdot8\right]=\frac{\left(2\sdot3\sdot6\right)\sdot\left(3\sdot4\sdot8\right)}{3\sdot4\sdot4\sdot7}=\frac{36\sdot96}{3\sdot4\sdot4\sdot7}=10+\frac{2}{7}}}](/mediawiki/images/math/e/0/d/e0d510f1c13418a27a860d798915e754.png)
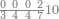
![\scriptstyle\left[\left[\left(\frac{2}{5}\sdot\frac{5}{6}\right)+\frac{1}{2}\right]\sdot3\right]\times\left[\left[\left(\frac{2}{3}\sdot\frac{6}{7}\right)+\frac{3}{5}\right]\sdot10\right]](/mediawiki/images/math/f/5/6/f563fe0da1c5a32c4b4bb95452e54bc5.png)
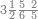
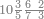
![{\color{blue}{\begin{align}\scriptstyle\left[\left[\left(\frac{2}{5}\sdot\frac{5}{6}\right)+\frac{1}{2}\right]\sdot3\right]\times\left[\left[\left(\frac{2}{3}\sdot\frac{6}{7}\right)+\frac{3}{5}\right]\sdot10\right]&\scriptstyle=\frac{\left[\left[\left(2\sdot5\sdot2\right)+\left(1\sdot5\sdot6\right)\right]\sdot3\right]\sdot\left[\left[\left(2\sdot6\sdot5\right)+\left(3\sdot3\sdot7\right)\right]\sdot10\right]}{2\sdot3\sdot5\sdot5\sdot6\sdot7}\\&\scriptstyle=\frac{150\sdot1230}{2\sdot3\sdot5\sdot5\sdot6\sdot7}\\&\scriptstyle=29+\frac{2}{7}\\\end{align}}}](/mediawiki/images/math/6/f/e/6fe89aa854bd99dd8c9815b52aec94bc.png)
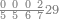
![\scriptstyle\left[\left(\frac{2}{3}\sdot\frac{6}{9}\right)\sdot\left(6+\frac{3}{4}\right)\right]\times\left[\left(\frac{3}{4}\sdot\frac{8}{9}\right)\sdot\left(2+\frac{2}{5}\right)\right]](/mediawiki/images/math/f/a/4/fa4daab5fb3c530e96d4f4be1abe9aec.png)
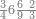
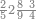
![{\color{blue}{\begin{align}\scriptstyle\left[\left(\frac{2}{3}\sdot\frac{6}{9}\right)\sdot\left(6+\frac{3}{4}\right)\right]\times\left[\left(\frac{3}{4}\sdot\frac{8}{9}\right)\sdot\left(2+\frac{2}{5}\right)\right]&\scriptstyle=\frac{\left[\left(2\sdot6\right)\sdot\left[\left(6\sdot4\right)+3\right]\right]\sdot\left[\left(3\sdot8\right)\sdot\left[\left(2\sdot5\right)+2\right]\right]}{3\sdot4\sdot4\sdot5\sdot9\sdot9}\\&\scriptstyle=\frac{\left(12\sdot27\right)\sdot288}{3\sdot4\sdot4\sdot5\sdot9\sdot9}\\&\scriptstyle=\frac{324\sdot288}{3\sdot4\sdot4\sdot5\sdot9\sdot9}\\&\scriptstyle=4+\frac{4}{5}\\\end{align}}}](/mediawiki/images/math/5/6/6/566930c75890cd2119d9c600444e7d16.png)
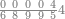
![\scriptstyle\left[\left(\frac{3}{5}\sdot\frac{4}{7}\right)\sdot\left[3+\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\right]\times\left[\left(\frac{2}{3}\sdot\frac{5}{6}\right)\sdot\left[6+\frac{7}{8}+\left(\frac{2}{3}\sdot\frac{1}{8}\right)\right]\right]](/mediawiki/images/math/2/5/5/2550673eb8dc78a12727d2d5dc0b5427.png)
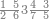
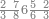
![{\color{blue}{\begin{align}\scriptstyle\left[\left(\frac{3}{5}\sdot\frac{4}{7}\right)\sdot\left[3+\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\right]&\scriptstyle\times\left[\left(\frac{2}{3}\sdot\frac{5}{6}\right)\sdot\left[6+\frac{7}{8}+\left(\frac{2}{3}\sdot\frac{1}{8}\right)\right]\right]\\&\scriptstyle=\frac{\left[\left(3\sdot4\right)\sdot\left[\left(3\sdot6\sdot2\right)+\left[\left(5\sdot2\right)+1\right]\right]\right]\sdot\left[\left(2\sdot5\right)\sdot\left[\left(6\sdot8\sdot3\right)+\left[\left(7\sdot3\right)+2\right]\right]\right]}{5\sdot7\sdot6\sdot2\sdot3\sdot6\sdot8\sdot3}\\&\scriptstyle=\frac{\left(12\sdot47\right)\sdot1670}{5\sdot7\sdot6\sdot2\sdot3\sdot6\sdot8\sdot3}\\&\scriptstyle=\frac{564\sdot1670}{5\sdot7\sdot6\sdot2\sdot3\sdot6\sdot8\sdot3}\\&\scriptstyle=5+\frac{1}{9}+\left(\frac{5}{8}\sdot\frac{1}{9}\right)+\left(\frac{5}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)+\left(\frac{1}{3}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/a/c/b/acb31332e2547744df36b15cb13f9728.png)
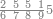
![\scriptstyle\left[3+\left(\frac{3}{5}\sdot\frac{5}{6}\right)\right]\times\left[4+\left(\frac{2}{7}\sdot\frac{3}{8}\right)\right]](/mediawiki/images/math/c/c/6/cc62007c7e8709f4fde684e0c6ff424c.png)
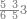
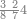
![\scriptstyle{\color{blue}{\left[3+\left(\frac{3}{5}\sdot\frac{5}{6}\right)\right]\times\left[4+\left(\frac{2}{7}\sdot\frac{3}{8}\right)\right]=\frac{\left[\left(3\sdot5\sdot6\right)+\left(3\sdot5\right)\right]\sdot\left[\left(4\sdot7\sdot8\right)+\left(2\sdot3\right)\right]}{5\sdot6\sdot7\sdot8}=\frac{105\sdot230}{5\sdot6\sdot7\sdot8}=14+\frac{3}{8}}}](/mediawiki/images/math/5/6/f/56fd65e0f6f80c7a48fa436664772dee.png)
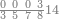
![\scriptstyle\left[2+\left(\frac{3}{7}\sdot\frac{3}{5}\right)+\frac{2}{3}\right]\times\left[3+\left(\frac{3}{4}\sdot\frac{5}{6}\right)+\frac{1}{2}\right]](/mediawiki/images/math/b/a/0/ba08b2bb8f498724f17c160ad860406d.png)
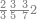
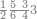
![{\color{blue}{\begin{align}\scriptstyle\left[2+\left(\frac{3}{7}\sdot\frac{3}{5}\right)+\frac{2}{3}\right]\times\left[3+\left(\frac{3}{4}\sdot\frac{5}{6}\right)+\frac{1}{2}\right]&\scriptstyle=\frac{\left[\left(2\sdot7\sdot5\sdot3\right)+\left(3\sdot3\sdot3\right)+\left(2\sdot7\sdot5\right)\right]\sdot\left[\left(3\sdot4\sdot6\sdot2\right)+\left(3\sdot5\sdot2\right)+\left(1\sdot4\sdot6\right)\right]}{2\sdot3\sdot4\sdot5\sdot6\sdot7}\\&\scriptstyle=\frac{307\sdot198}{2\sdot3\sdot4\sdot5\sdot6\sdot7}\\&\scriptstyle=\frac{60786}{2\sdot3\sdot4\sdot5\sdot6\sdot7}\\&\scriptstyle=12+\left(\frac{3}{7}\sdot\frac{1}{8}\right)+\left(\frac{2}{5}\sdot\frac{1}{7}\sdot\frac{1}{8}\right)\\\end{align}}}](/mediawiki/images/math/c/9/a/c9aaf7f1cb867b107db45c5c1f817a03.png)
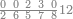
![\scriptstyle\left[\left(\frac{3}{4}\sdot\frac{3}{5}\right)\sdot\left[2+\left(\frac{3}{7}\sdot\frac{5}{6}\right)\right]\right]\times\left[\left(\frac{1}{2}\sdot\frac{3}{4}\right)\sdot\left[3+\left(\frac{2}{5}\sdot\frac{4}{9}\right)\right]\right]](/mediawiki/images/math/0/0/2/002cf582faa984ff0a1368eb7aebc1b0.png)
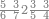
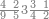
![\scriptstyle\left[\left(\frac{3}{4}\sdot\frac{3}{5}\right)+\left[2+\left(\frac{3}{7}\sdot\frac{5}{6}\right)\right]\right]\times\left[\left(\frac{1}{2}\sdot\frac{3}{4}\right)+\left[3+\left(\frac{2}{5}\sdot\frac{4}{9}\right)\right]\right]](/mediawiki/images/math/b/3/e/b3e06cf82cfbf1b88cd5247af057be96.png)
![\scriptstyle\left[\left[\left(\frac{3}{4}\sdot\frac{3}{5}\right)\sdot2\right]+\left(\frac{3}{7}\sdot\frac{5}{6}\right)\right]\times\left[\left[\left(\frac{1}{2}\sdot\frac{3}{4}\right)\sdot3\right]+\left(\frac{2}{5}\sdot\frac{4}{9}\right)\right]](/mediawiki/images/math/2/c/5/2c55f071b7eb092fc5d75d60bb625023.png)
![{\color{blue}{\begin{align}&\scriptstyle\left[\left(\frac{3}{4}\sdot\frac{3}{5}\right)\sdot\left[2+\left(\frac{3}{7}\sdot\frac{5}{6}\right)\right]\right]\times\left[\left(\frac{1}{2}\sdot\frac{3}{4}\right)\sdot\left[3+\left(\frac{2}{5}\sdot\frac{4}{9}\right)\right]\right]\\&\scriptstyle=\frac{\left[\left(3\sdot3\right)\sdot\left[\left(2\sdot7\sdot6\right)+\left(3\sdot5\right)\right]\right]\sdot\left[\left(1\sdot3\right)\sdot\left[\left(3\sdot5\sdot9\right)+\left(2\sdot4\right)\right]\right]}{2\sdot4\sdot4\sdot5\sdot5\sdot6\sdot7\sdot9}\\&\scriptstyle=\frac{891\sdot429}{2\sdot4\sdot4\sdot5\sdot5\sdot6\sdot7\sdot9}\\&\scriptstyle=1+\frac{2}{10}+\left(\frac{6}{10}\sdot\frac{1}{10}\right)+\left(\frac{3}{8}\sdot\frac{1}{10}\sdot\frac{1}{10}\right)+\left(\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{10}\sdot\frac{1}{10}\right)+\left(\frac{1}{2}\sdot\frac{1}{7}\sdot\frac{1}{8}\sdot\frac{1}{10}\sdot\frac{1}{10}\right)\\\end{align}}}](/mediawiki/images/math/6/8/3/6839097ccb197c5664a20110d5995308.png)
![\scriptstyle\left[\left(\frac{3}{4}+\frac{5}{6}\right)\sdot4\right]+\left[\left(\frac{3}{5}+\frac{6}{7}\right)\sdot3\right]+\left[\left[\frac{5}{6}+\left(\frac{1}{2}+\frac{1}{6}\right)\right]\sdot4\right]+\left[\left(\frac{7}{8}+\frac{8}{9}\right)\sdot\left(3+\frac{1}{2}\right)\right]](/mediawiki/images/math/c/3/1/c3165deb10ccabc5371f0bfe335191b8.png)
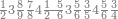
![\scriptstyle\left[\left(\frac{3}{4}+\frac{5}{6}\right)\sdot4\right]+\left[\left(\frac{3}{5}\sdot\frac{6}{7}\right)\sdot3\right]+\left[\left[\frac{5}{6}+\left(\frac{1}{2}+\frac{1}{6}\right)\right]\sdot4\right]+\left[\left(\frac{7}{8}\sdot\frac{8}{9}\right)\sdot\left(3+\frac{1}{2}\right)\right]](/mediawiki/images/math/9/c/e/9ce40373ddb4f78b88a4892a4820e065.png)
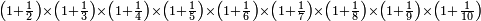
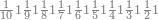
![{\color{blue}{\begin{align}&\scriptstyle\left(1+\frac{1}{2}\right)\times\left(1+\frac{1}{3}\right)\times\left(1+\frac{1}{4}\right)\times\left(1+\frac{1}{5}\right)\times\left(1+\frac{1}{6}\right)\times\left(1+\frac{1}{7}\right)\times\left(1+\frac{1}{8}\right)\times\left(1+\frac{1}{9}\right)\times\left(1+\frac{1}{10}\right)\\&\scriptstyle=\frac{\left[\left(1\sdot2\right)+1\right]\sdot\left[\left(1\sdot3\right)+1\right]\sdot\left[\left(1\sdot4\right)+1\right]\sdot\left[\left(1\sdot5\right)+1\right]\sdot\left[\left(1\sdot6\right)+1\right]\sdot\left[\left(1\sdot7\right)+1\right]\sdot\left[\left(1\sdot8\right)+1\right]\sdot\left[\left(1\sdot9\right)+1\right]\sdot\left[\left(1\sdot10\right)+1\right]}{2\sdot3\sdot4\sdot5\sdot6\sdot7\sdot8\sdot9\sdot10}\\&\scriptstyle=\frac{3\sdot4\sdot5\sdot6\sdot7\sdot8\sdot9\sdot10\sdot11}{2\sdot3\sdot4\sdot5\sdot6\sdot7\sdot8\sdot9\sdot10}\\&\scriptstyle=5+\frac{1}{2}\\\end{align}}}](/mediawiki/images/math/c/4/d/c4d4a5158b5d7f0889a0c66a58f80cb4.png)
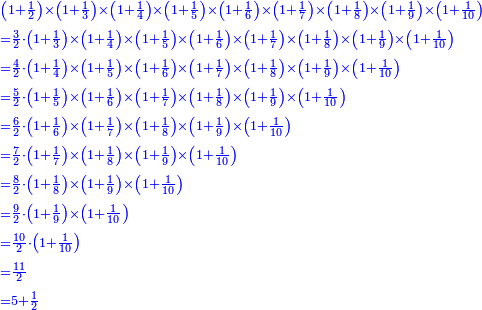
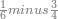
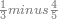
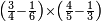
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{3}{4}-\frac{1}{6}\right)\times\left(\frac{4}{5}-\frac{1}{3}\right)&\scriptstyle=\frac{\left[\left(3\sdot6\right)-\left(1\sdot4\right)\right]\sdot\left[\left(4\sdot3\right)-\left(1\sdot5\right)\right]}{3\sdot4\sdot5\sdot6}\\&\scriptstyle=\frac{\left(18-4\right)\sdot\left(12-5\right)}{3\sdot4\sdot5\sdot6}\\&\scriptstyle=\frac{14\sdot7}{3\sdot4\sdot5\sdot6}\\&\scriptstyle=\frac{2}{9}+\left(\frac{3}{8}\sdot\frac{1}{9}\right)+\left(\frac{3}{5}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/e/6/7/e67595574e4a7f85c1ec0f1a1e261903.png)
![\scriptstyle\left[\frac{3}{4}-\left(\frac{1}{6}\sdot\frac{3}{4}\right)\right]\times\left[\frac{4}{5}-\left(\frac{1}{3}\sdot\frac{4}{5}\right)\right]](/mediawiki/images/math/a/e/4/ae4ff6ee9ccb7e44b1386662f2fe7ed1.png)
![{\color{blue}{\begin{align}\scriptstyle\left[\frac{3}{4}-\left(\frac{1}{6}\sdot\frac{3}{4}\right)\right]\times\left[\frac{4}{5}-\left(\frac{1}{3}\sdot\frac{4}{5}\right)\right]&\scriptstyle=\frac{\left[\left(3\sdot6\right)-\left(1\sdot3\right)\right]\sdot\left[\left(4\sdot3\right)-\left(1\sdot4\right)\right]}{3\sdot4\sdot5\sdot6}\\&\scriptstyle=\frac{\left(18-3\right)\sdot8}{3\sdot4\sdot5\sdot6}\\&\scriptstyle=\frac{15\sdot8}{3\sdot4\sdot5\sdot6}=\color{red}{\frac{1}{3}}\\\end{align}}}](/mediawiki/images/math/3/f/7/3f7765a0ac4b3a7d78c5904e6f336a78.png)
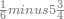
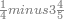
![\scriptstyle\left[\left(\frac{3}{4}\sdot5\right)-\left(\frac{1}{6}\sdot5\right)\right]\times\left[\left(\frac{4}{5}\sdot3\right)-\left(\frac{1}{4}\sdot3\right)\right]](/mediawiki/images/math/4/d/0/4d0df47dc57fcfe2ae9c244e13efc5c6.png)
![{\color{blue}{\begin{align}\scriptstyle\left[\left(\frac{3}{4}\sdot5\right)-\left(\frac{1}{6}\sdot5\right)\right]\times\left[\left(\frac{4}{5}\sdot3\right)-\left(\frac{1}{4}\sdot3\right)\right]&\scriptstyle=\frac{\left[\left(3\sdot5\sdot6\right)-\left(1\sdot5\sdot4\right)\right]\sdot\left[\left(4\sdot3\sdot4\right)-\left(1\sdot3\sdot5\right)\right]}{4\sdot4\sdot5\sdot6}\\&\scriptstyle=\frac{\left(90-20\right)\sdot33}{4\sdot4\sdot5\sdot6}\\&\scriptstyle=\frac{70\sdot33}{4\sdot4\sdot5\sdot6}\\&\scriptstyle=\color{red}{4+\frac{6}{8}+\left(\frac{1}{2}\sdot\frac{1}{8}\right)}\\\end{align}}}](/mediawiki/images/math/9/3/2/9324e292cb84c7138ee9a64ac32cbc94.png)
![\scriptstyle\left[\left(\frac{3}{4}\sdot5\right)-\left[\frac{1}{6}\sdot\left(\frac{3}{4}\sdot5\right)\right]\right]\times\left[\left(\frac{4}{5}\sdot3\right)-\left[\frac{1}{4}\sdot\left(\frac{4}{5}\sdot3\right)\right]\right]](/mediawiki/images/math/d/9/a/d9a6878ee6eb1ba00eb46382912dc1b1.png)
![{\color{blue}{\begin{align}\scriptstyle\left[\left(\frac{3}{4}\sdot5\right)-\left[\frac{1}{6}\sdot\left(\frac{3}{4}\sdot5\right)\right]\right]\times\left[\left(\frac{4}{5}\sdot3\right)-\left[\frac{1}{4}\sdot\left(\frac{4}{5}\sdot3\right)\right]\right]&\scriptstyle=\frac{\left[\left(3\sdot5\sdot6\right)-\left(1\sdot5\sdot3\right)\right]\sdot\left[\left(4\sdot3\sdot4\right)-\left(1\sdot4\sdot3\right)\right]}{4\sdot4\sdot5\sdot6}\\&\scriptstyle=\frac{\left(90-15\right)\sdot36}{4\sdot4\sdot5\sdot6}\\&\scriptstyle=\frac{75\sdot36}{4\sdot4\sdot5\sdot6}\\\end{align}}}](/mediawiki/images/math/9/b/4/9b4b4b3ec449be40db50b07f67efee68.png)
![\scriptstyle\left[\left(\frac{3}{4}\sdot5\right)-\frac{1}{6}\right]\times\left[\left(\frac{4}{5}\sdot3\right)-\frac{1}{4}\right]](/mediawiki/images/math/c/0/e/c0ea2f1eede67f376f403c8953b1890a.png)
![{\color{blue}{\begin{align}\scriptstyle\left[\left(\frac{3}{4}\sdot5\right)-\frac{1}{6}\right]\times\left[\left(\frac{4}{5}\sdot3\right)-\frac{1}{4}\right]&\scriptstyle=\frac{\left[\left(3\sdot5\sdot6\right)-\left(1\sdot4\right)\right]\sdot\left[\left(4\sdot3\sdot4\right)-\left(1\sdot5\right)\right]}{4\sdot4\sdot5\sdot6}\\&\scriptstyle=\frac{\left(90-4\right)\sdot43}{4\sdot4\sdot5\sdot6}\\&\scriptstyle=\frac{86\sdot43}{4\sdot4\sdot5\sdot6}\\\end{align}}}](/mediawiki/images/math/c/9/d/c9d661e2970d60a81899d862a4a21e0c.png)
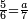
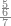
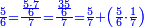
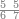
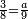
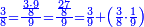
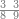
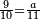
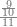
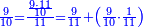
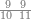
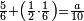
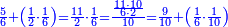
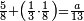
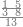
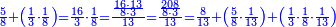
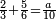
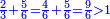
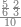
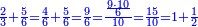
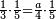
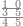
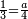
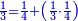
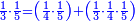
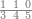
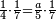
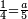
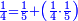
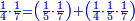
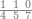
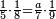
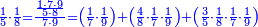
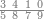
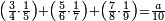
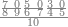
![\scriptstyle{\color{blue}{\left(\frac{3}{4}\sdot\frac{1}{5}\right)+\left(\frac{5}{6}\sdot\frac{1}{7}\right)+\left(\frac{7}{8}\sdot\frac{1}{9}\right)=\frac{\frac{\left[\left(3\sdot6\sdot7\sdot8\sdot9\right)+\left(5\sdot4\sdot5\sdot8\sdot9\right)+\left(7\sdot4\sdot5\sdot6\sdot7\right)\right]\sdot10}{4\sdot5\sdot6\sdot7\sdot8\sdot9}}{10}}}](/mediawiki/images/math/2/b/e/2beb0345b73012dfbd98191c56958b10.png)
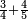

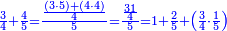
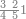
![\scriptstyle{\color{blue}{\frac{3}{4}+\frac{4}{5}=\left[\frac{3}{5}+\left(\frac{3}{4}\sdot\frac{1}{5}\right)\right]+\frac{4}{5}=\frac{7}{5}+\left(\frac{3}{4}\sdot\frac{1}{5}\right)=1+\frac{2}{5}+\left(\frac{3}{4}\sdot\frac{1}{5}\right)}}](/mediawiki/images/math/d/4/b/d4b56f6a049595d4effb8ea40a738abb.png)
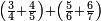
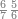
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{3}{4}+\frac{4}{5}\right)+\left(\frac{5}{6}+\frac{6}{7}\right)&\scriptstyle=\frac{\left[\left[\left(3\sdot5\right)+\left(4\sdot4\right)\right]\sdot6\sdot7\right]+\left[\left[\left(5\sdot7\right)+\left(6\sdot6\right)\right]\sdot4\sdot5\right]}{4\sdot5\sdot6\sdot7}\\&\scriptstyle=\frac{1302+1420}{4\sdot5\sdot6\sdot7}\\&\scriptstyle=\frac{2722}{4\sdot5\sdot6\sdot7}\\&\scriptstyle=3+\frac{1}{7}+\left(\frac{4}{6}\sdot\frac{1}{7}\right)+\left(\frac{1}{2}\sdot\frac{1}{5}\sdot\frac{1}{6}\sdot\frac{1}{7}\right)\\\end{align}}}](/mediawiki/images/math/8/d/c/8dc580d8fe5ef86877ef2699bf0d4881.png)
![\scriptstyle\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]+\left(\frac{7}{8}+\frac{8}{9}\right)](/mediawiki/images/math/4/c/4/4c4b65fa69c305cfcc4cb5e5a2e49e9e.png)
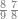
![{\color{blue}{\begin{align}\scriptstyle\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]+\left(\frac{7}{8}+\frac{8}{9}\right)&\scriptstyle=\frac{\left[\left[\left(5\sdot2\right)+1\right]\sdot8\sdot9\right]+\left[\left[\left(7\sdot9\right)+\left(8\sdot8\right)\right]\sdot2\sdot6\right]}{2\sdot6\sdot8\sdot9}\\&\scriptstyle=\frac{792+1524}{2\sdot6\sdot8\sdot9}\\&\scriptstyle=\frac{2316}{2\sdot6\sdot8\sdot9}\\&\scriptstyle=2+\frac{6}{9}+\left(\frac{1}{8}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/d/b/6/db6a560dc18a1b9d1aa86592461eda3d.png)
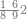
![\scriptstyle\left[\frac{5}{11}+\left(\frac{3}{4}\sdot\frac{1}{11}\right)\right]+\left[\frac{10}{13}+\left(\frac{8}{9}\sdot\frac{1}{13}\right)\right]](/mediawiki/images/math/1/1/1/111cfe95df77cdc573d3d8c3a15e0491.png)
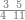
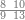
![{\color{blue}{\begin{align}\scriptstyle\left[\frac{5}{11}+\left(\frac{3}{4}\sdot\frac{1}{11}\right)\right]+\left[\frac{10}{13}+\left(\frac{8}{9}\sdot\frac{1}{13}\right)\right]&\scriptstyle=\frac{\left[\left[\left(5\sdot4\right)+3\right]\sdot13\sdot9\right]+\left[\left[\left(10\sdot9\right)+8\right]\sdot11\sdot4\right]}{4\sdot9\sdot11\sdot13}\\&\scriptstyle=1+\frac{4}{13}+\left(\frac{7}{11}\sdot\frac{1}{13}\right)+\left(\frac{4}{9}\sdot\frac{1}{11}\sdot\frac{1}{13}\right)+\left(\frac{3}{4}\sdot\frac{1}{9}\sdot\frac{1}{11}\sdot\frac{1}{13}\right)\\\end{align}}}](/mediawiki/images/math/e/7/4/e747c873d43060966b5a81302034c04b.png)
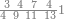
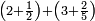
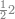
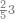
![\scriptstyle{\color{blue}{\left(2+\frac{1}{2}\right)+\left(3+\frac{2}{5}\right)=\frac{\left[\left[\left(2\sdot2\right)+1\right]\sdot5\right]+\left[\left[\left(3\sdot5\right)+2\right]\sdot2\right]}{2\sdot5}=\frac{59}{2\sdot5}=5+\frac{4}{5}+\left(\frac{1}{2}\sdot\frac{1}{5}\right)}}](/mediawiki/images/math/2/9/4/294398e2e2cc3dcbac6fb23f957fbce5.png)
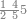
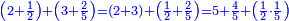
![\scriptstyle\left[8+\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]+\left(6+\frac{5}{7}+\frac{10}{11}\right)](/mediawiki/images/math/5/5/2/5526b3773d4250a1b558ca73bb605f6c.png)
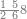
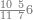
![{\color{blue}{\begin{align}\scriptstyle\left[8+\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]+\left(6+\frac{5}{7}+\frac{10}{11}\right)&\scriptstyle=\frac{\left[\left[\left[\left[\left(8\sdot6\right)+5\right]\sdot2\right]+1\right]\sdot7\sdot11\right]+\left[\left[\left(6\sdot7\sdot11\right)+\left(5\sdot11\right)+\left(10\sdot7\right)\right]\sdot6\sdot2\right]}{2\sdot6\sdot7\sdot11}\\&\scriptstyle=16+\frac{5}{11}+\left(\frac{6}{7}\sdot\frac{1}{11}\right)+\left(\frac{3}{6}\sdot\frac{1}{7}\sdot\frac{1}{11}\right)+\left(\frac{1}{2}\sdot\frac{1}{6}\sdot\frac{1}{7}\sdot\frac{1}{11}\right)\\\end{align}}}](/mediawiki/images/math/5/1/5/515a8c1a15185a11b458c54d79c93225.png)
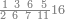
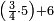

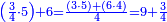
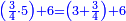
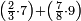
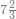
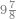
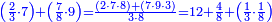
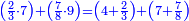
![\scriptstyle\left[\frac{3}{4}\sdot\left(5+\frac{1}{2}\right)\right]+\left[\frac{5}{6}\sdot\left(6+\frac{1}{3}\right)\right]](/mediawiki/images/math/3/8/c/38c6011f1c3aa05525cc220db0b08a58.png)
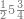
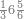
![{\color{blue}{\begin{align}\scriptstyle\left[\frac{3}{4}\sdot\left(5+\frac{1}{2}\right)\right]+\left[\frac{5}{6}\sdot\left(6+\frac{1}{3}\right)\right]&\scriptstyle=\frac{\left[\left[\left[\left(5\sdot2\right)+1\right]\sdot3\right]\sdot6\sdot3\right]+\left[\left[\left[\left(6\sdot3\right)+1\right]\sdot5\right]\sdot4\sdot2\right]}{2\sdot3\sdot4\sdot6}\\&\scriptstyle=9+\frac{3}{8}+\left(\frac{1}{6}\sdot\frac{1}{8}\right)+\left(\frac{1}{3}\sdot\frac{1}{6}\sdot\frac{1}{8}\right)\\\end{align}}}](/mediawiki/images/math/8/c/6/8c644ca7a889c17ffa935c0536595957.png)
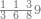
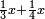
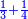
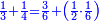
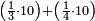
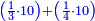
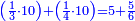
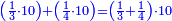
![\scriptstyle\left(\frac{1}{3}\sdot10\right)+\left(\frac{1}{4}\sdot10\right)+\left[\frac{1}{5}\sdot\left[10-\left(\frac{1}{3}\sdot10\right)-\left(\frac{1}{4}\sdot10\right)\right]\right]](/mediawiki/images/math/e/b/f/ebf3b0cdd50dbf66d5b3f14c7e905873.png)
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{1}{3}\sdot10\right)+\left(\frac{1}{4}\sdot10\right)&\scriptstyle+\left[\frac{1}{5}\sdot\left[10-\left(\frac{1}{3}\sdot10\right)-\left(\frac{1}{4}\sdot10\right)\right]\right]\\&\scriptstyle=\frac{\left[\left[\frac{1}{3}\sdot\left(3\sdot4\right)\right]+\left[\frac{1}{4}\sdot\left(3\sdot4\right)\right]+\left[\frac{1}{5}\sdot\left[\left(3\sdot4\right)-\left[\frac{1}{3}\sdot\left(3\sdot4\right)\right]-\left[\frac{1}{4}\sdot\left(3\sdot4\right)\right]\right]\right]\right]\sdot10}{\left(3\sdot4\right)}\\&\scriptstyle=\frac{\left[\left(\frac{1}{3}\sdot12\right)+\left(\frac{1}{4}\sdot12\right)+\left[\frac{1}{5}\sdot\left[12-\left(\frac{1}{3}\sdot12\right)-\left(\frac{1}{4}\sdot12\right)\right]\right]\right]\sdot10}{12}\\&\scriptstyle=\frac{\left[7+\left[\frac{1}{5}\sdot\left(12-7\right)\right]\right]\sdot10}{12}\\&\scriptstyle=\frac{\left[7+\left(\frac{1}{5}\sdot5\right)\right]\sdot10}{12}\\&\scriptstyle=\frac{\left(7+1\right)\sdot10}{12}\\&\scriptstyle=\frac{8\sdot10}{12}\\&\scriptstyle=6+\frac{2}{3}\\\end{align}}}](/mediawiki/images/math/0/9/d/09d0bb0c0f883d141a8035e82ecb2867.png)
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{1}{3}\sdot10\right)+\left(\frac{1}{4}\sdot10\right)+\left[\frac{1}{5}\sdot\left[10-\left(\frac{1}{3}\sdot10\right)-\left(\frac{1}{4}\sdot10\right)\right]\right]&\scriptstyle=\frac{8\sdot10}{12}\\&\scriptstyle=\frac{10}{12}\sdot8\\&\scriptstyle=\frac{8}{12}\sdot10\\\end{align}}}](/mediawiki/images/math/e/f/a/efaafefc165543cc0c9e11348206b5be.png)
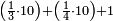
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{1}{3}\sdot10\right)+\left(\frac{1}{4}\sdot10\right)+1&\scriptstyle=\frac{\left[\left[\left(\frac{1}{3}\sdot12\right)+\left(\frac{1}{4}\sdot12\right)\right]\sdot10\right]+\left(1\sdot12\right)}{12}\\&\scriptstyle=\frac{\left(7\sdot10\right)+\left(1\sdot12\right)}{12}\\&\scriptstyle=\frac{70+12}{12}\\&\scriptstyle=\frac{82}{12}\\&\scriptstyle=6+\frac{5}{6}\\\end{align}}}](/mediawiki/images/math/9/d/e/9de4ec09be455f756cd745a865bcee14.png)
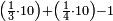
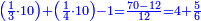
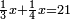
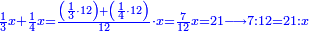
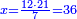
![\scriptstyle{\color{blue}{\frac{1}{3}x+\frac{1}{4}x=\frac{3}{6}x+\left(\frac{1}{2}\sdot\frac{1}{6}\right)x=\left[\frac{3}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\sdot x=21}}](/mediawiki/images/math/a/b/f/abf85e08fa67d4be08fd1afee16d2fbe.png)
![\scriptstyle{\color{blue}{\left[\frac{3}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\sdot a=1\longrightarrow a=1+\frac{5}{7}}}](/mediawiki/images/math/2/9/e/29ee0b3a8e3f9f2d9bc81aa0baf39980.png)
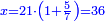
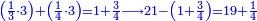
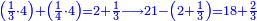
![\scriptstyle{\color{blue}{x=\frac{\left[\left(19+\frac{1}{4}\right)\sdot4\right]-\left[\left(18+\frac{2}{3}\right)\sdot3\right]}{\left(19+\frac{1}{4}\right)-\left(18+\frac{2}{3}\right)}=\frac{77-56}{\frac{3}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)}=\frac{21}{\frac{3}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)}=36}}](/mediawiki/images/math/6/2/8/628b03d73de1aa9586820e6f70b458b2.png)
![\scriptstyle\frac{1}{3}x+\frac{1}{4}x+\left[\frac{1}{2}\sdot\left[x-\left(\frac{1}{3}x+\frac{1}{4}x\right)\right]\right]=10](/mediawiki/images/math/0/9/0/09094cbf4bca71b2ab0b2f4f26a1599b.png)
![{\color{blue}{\begin{align}\scriptstyle x&\scriptstyle=\frac{24\sdot10}{\left(\frac{1}{3}\sdot24\right)+\left(\frac{1}{4}\sdot24\right)+\left[\frac{1}{2}\sdot\left[24-\left[\left(\frac{1}{3}\sdot24\right)+\left(\frac{1}{4}\sdot24\right)\right]\right]\right]}\\&\scriptstyle=\frac{24\sdot10}{14+\left[\frac{1}{2}\sdot\left(24-14\right)\right]}\\&\scriptstyle=\frac{24\sdot10}{14+\left(\frac{1}{2}\sdot10\right)}\\&\scriptstyle=\frac{24\sdot10}{14+5}\\&\scriptstyle=\frac{24\sdot10}{19}\\&\scriptstyle=12+\frac{12}{19}\\\end{align}}}](/mediawiki/images/math/8/e/2/8e214e2346aa94142039ee6e51b84cc9.png)
![\scriptstyle{\color{blue}{\left[\frac{1}{3}\sdot\left(12+\frac{12}{19}\right)\right]+\left[\frac{1}{4}\sdot\left(12+\frac{12}{19}\right)\right]+\left[\frac{1}{2}\sdot\left[\left(12+\frac{12}{19}\right)-\left[\left[\frac{1}{3}\sdot\left(12+\frac{12}{19}\right)\right]+\left[\frac{1}{4}\sdot\left(12+\frac{12}{19}\right)\right]\right]\right]\right]=10}}](/mediawiki/images/math/d/7/e/d7ee7eec4964b01f69ec98180a658e3e.png)
![\scriptstyle{\color{blue}{\frac{1}{3}x+\frac{1}{4}x+\left[\frac{1}{2}\sdot\left[x-\left(\frac{1}{3}x+\frac{1}{4}x\right)\right]\right]=\left[\frac{4}{6}+\left(\frac{3}{4}\sdot\frac{1}{6}\right)\right]x=10}}](/mediawiki/images/math/9/b/8/9b83d19691d0f0a583b6af03da545911.png)
![\scriptstyle{\color{blue}{\left[\frac{4}{6}+\left(\frac{3}{4}\sdot\frac{1}{6}\right)\right]\sdot a=1\longrightarrow a=1+\frac{5}{19}}}](/mediawiki/images/math/9/6/7/967ee9547ff2bd3e6824d92760d04aaa.png)
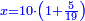
![\scriptstyle{\color{blue}{\left(\frac{1}{3}\sdot6\right)+\left(\frac{1}{4}\sdot6\right)+\left[\frac{1}{2}\sdot\left[6-\left[\left(\frac{1}{3}\sdot6\right)+\left(\frac{1}{4}\sdot6\right)\right]\right]\right]=4+\frac{3}{4}\longrightarrow10-\left(4+\frac{3}{4}\right)=5+\frac{1}{4}}}](/mediawiki/images/math/2/8/7/287ac57f4173c0d09c215d43bf81319f.png)
![\scriptstyle{\color{blue}{\left(\frac{1}{3}\sdot8\right)+\left(\frac{1}{4}\sdot8\right)+\left[\frac{1}{2}\sdot\left[8-\left[\left(\frac{1}{3}\sdot8\right)+\left(\frac{1}{4}\sdot8\right)\right]\right]\right]=6+\frac{1}{3}\longrightarrow10-\left(6+\frac{1}{3}\right)=3+\frac{2}{3}}}](/mediawiki/images/math/b/a/f/bafbe20371801df56381557ff08277fc.png)
![\scriptstyle{\color{blue}{x=\frac{\left[\left(5+\frac{1}{4}\right)\sdot8\right]-\left[\left(3+\frac{2}{3}\right)\sdot6\right]}{\left(5+\frac{1}{4}\right)-\left(3+\frac{2}{3}\right)}=\frac{42-22}{1+\frac{3}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)}=\frac{20}{1+\frac{3}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)}=12+\frac{12}{19}}}](/mediawiki/images/math/b/b/5/bb5ecd813032a74c49bcd9c293e0b4f3.png)
![\scriptstyle{\color{blue}{\left(\frac{1}{3}\sdot1\right)+\left(\frac{1}{4}\sdot1\right)+\left[\frac{1}{2}\sdot\left[1-\left[\left(\frac{1}{3}\sdot1\right)+\left(\frac{1}{4}\sdot1\right)\right]\right]\right]=\frac{4}{6}+\left(\frac{3}{4}\sdot\frac{1}{6}\right)\longrightarrow\left[\frac{4}{6}+\left(\frac{3}{4}\sdot\frac{1}{6}\right)\right]:1=10:x}}](/mediawiki/images/math/4/4/5/445ad22065f2cc72ab3fdb31af4b9c91.png)
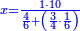
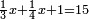
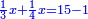
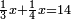
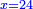
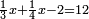
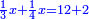
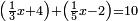
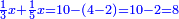
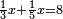
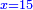
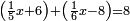

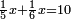
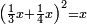
![\scriptstyle{\color{blue}{x=\frac{12^2}{\left[\left(\frac{1}{3}\sdot12\right)+\left(\frac{1}{4}\sdot12\right)\right]^2}=\frac{12^2}{7^2}=\frac{12^2}{49}=2+\frac{6}{7}+\left(\frac{4}{7}\sdot\frac{1}{7}\right)}}](/mediawiki/images/math/a/2/3/a231e7caed858e8722ac84130f9cb4a4.png)
![\scriptstyle{\color{blue}{\left(\frac{1}{3}x+\frac{1}{4}x\right)^2=\left[\left[\frac{3}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]x\right]^2=\left[\frac{3}{9}+\left(\frac{1}{2}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)\right]x^2=x}}](/mediawiki/images/math/0/a/d/0adecca4285cc40c7e3c6d45ff8a4f39.png)
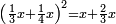
![\scriptstyle{\color{blue}{x=\frac{12^2+\left(\frac{2}{3}\sdot12^2\right)}{\left[\left(\frac{1}{3}\sdot12\right)+\left(\frac{1}{4}\sdot12\right)\right]^2}=\frac{240}{7^2}=\frac{240}{49}=4+\frac{6}{7}+\left(\frac{2}{7}\sdot\frac{1}{7}\right)}}](/mediawiki/images/math/6/0/b/60b09c0d54bbed53bf88bf99dffb9b3f.png)
![\scriptstyle\left[\frac{1}{4}\sdot\left(\frac{1}{3}x+\frac{1}{5}x\right)\right]+\left[\frac{1}{2}\sdot\left[x-\left(\frac{1}{3}x+\frac{1}{5}x\right)\right]\right]=11](/mediawiki/images/math/4/e/4/4e44ec3b676fd08257ac8ed3890d89bb.png)
![{\color{blue}{\begin{align}\scriptstyle x&\scriptstyle =\frac{11\sdot60}{\left[\frac{1}{4}\sdot\left[\left(\frac{1}{3}\sdot60\right)+\left(\frac{1}{5}\sdot60\right)\right]\right]+\left[\frac{1}{2}\sdot\left[60-\left[\left(\frac{1}{3}\sdot60\right)+\left(\frac{1}{5}\sdot60\right)\right]\right]\right]}\\&\scriptstyle =\frac{11\sdot60}{\left(\frac{1}{4}\sdot32\right)+\left[\frac{1}{2}\sdot\left(60-32\right)\right]}\\&\scriptstyle =\frac{11\sdot60}{8+\left(\frac{1}{2}\sdot28\right)}\\&\scriptstyle =\frac{11\sdot60}{8+14}\\&\scriptstyle =\frac{11\sdot60}{22}=30\\\end{align}}}](/mediawiki/images/math/f/d/a/fda285117894cff3f5c3374fb81d536c.png)
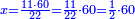
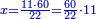
![\scriptstyle\frac{1}{2}x+\left[\frac{1}{3}\sdot\left(x-\frac{1}{2}x\right)\right]+\left[\frac{1}{4}\sdot\left[x-\left[\frac{1}{2}x+\left[\frac{1}{3}\sdot\left(x-\frac{1}{2}x\right)\right]\right]\right]\right]+\left[\frac{1}{5}\sdot\left[x-\left[\frac{1}{2}x+\left[\frac{1}{3}\sdot\left(x-\frac{1}{2}x\right)\right]+\left[\frac{1}{4}\sdot\left[x-\left[\frac{1}{2}x+\left[\frac{1}{3}\sdot\left(x-\frac{1}{2}x\right)\right]\right]\right]\right]\right]\right]\right]=20](/mediawiki/images/math/f/0/8/f084d8fb8895bc719d9d091d4cd15afb.png)
![\scriptstyle{\color{blue}{x\scriptstyle=\frac{20\sdot60}{30+\left[\frac{1}{3}\sdot\left(60-30\right)\right]+\left[\frac{1}{4}\sdot\left[60-\left[30+\left[\frac{1}{3}\sdot\left(60-30\right)\right]\right]\right]\right]+\left[\frac{1}{5}\sdot\left[60-\left[30+\left[\frac{1}{3}\sdot\left(60-30\right)\right]+\left[\frac{1}{4}\sdot\left[60-\left[30+\left[\frac{1}{3}\sdot\left(60-30\right)\right]\right]\right]\right]\right]\right]\right]}}}](/mediawiki/images/math/4/5/a/45a86b2ca30b8abb1a72ed6de2996dfa.png)
![{\color{blue}{\begin{align}&\scriptstyle=\frac{20\sdot60}{30+10+\left(\frac{1}{4}\sdot20\right)+\left[\frac{1}{5}\sdot\left[60-\left[30+10+\left(\frac{1}{4}\sdot20\right)\right]\right]\right]}\\&\scriptstyle=\frac{20\sdot60}{30+10+5+\left[\frac{1}{5}\sdot\left[60-\left(30+10+5\right)\right]\right]}\\&\scriptstyle=\frac{20\sdot60}{30+10+5+\left(\frac{1}{5}\sdot15\right)}\\&\scriptstyle=\frac{20\sdot60}{30+10+5+3}\\&\scriptstyle=\frac{20\sdot60}{48}=25\\\end{align}}}](/mediawiki/images/math/d/6/b/d6bcd8ceafadf1f59a2129a4f8a7691f.png)
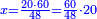
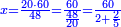
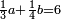
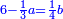
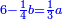
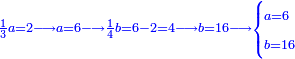
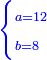
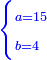
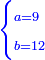
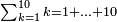
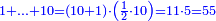
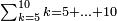
![\scriptstyle{\color{blue}{5+\ldots+10=\left(1+\ldots+10\right)-\left[1+\ldots+\left(5-1\right)\right]=\left(1+\ldots+10\right)-\left(1+\ldots+4\right)=55-10=45}}](/mediawiki/images/math/2/5/c/25c40160eeda3e15cfea8cf849f3d265.png)
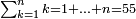
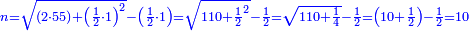
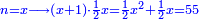
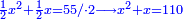
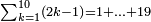
![\scriptstyle{\color{blue}{1+\ldots+19=\left[\frac{1}{2}\sdot\left(19+1\right)\right]^2=\left(\frac{1}{2}\sdot20\right)^2=10^2=100}}](/mediawiki/images/math/5/0/c/50c60912af82352d0e1898f1cacb47ec.png)
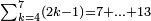
![\scriptstyle{\color{blue}{\sum_{k=4}^7 \left(2k-1\right)=\left[\sum_{k=1}^7 \left(2k-1\right)\right]-\left[\sum_{k=1}^3 \left(2k-1\right)\right]}}](/mediawiki/images/math/d/8/9/d8926021b1c8f71056742a0bc0957c95.png)
![\scriptstyle{\color{blue}{7+\ldots+13=\left(1+\ldots+13\right)-\left[1+\ldots+\left(7-2\right)\right]=\left(1+\ldots+13\right)-\left(1+\ldots+5\right)=49-9=40}}](/mediawiki/images/math/2/4/f/24fa937eba73ddf3dd4d2825358a78c7.png)
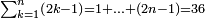
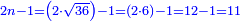
![\scriptstyle{\color{blue}{2n-1=x\longrightarrow\left[\frac{1}{2}\sdot\left(x+1\right)\right]^2=\left(\frac{1}{2}x+\frac{1}{2}\right)^2=\frac{1}{4}x^2+\frac{1}{2}x+\frac{1}{4}=36}}](/mediawiki/images/math/e/4/b/e4b6eaea1b12db82244bd0620f99eec4.png)
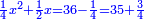
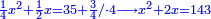
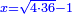
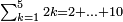
![\scriptstyle{\color{blue}{2+\ldots+10=\left[\frac{1}{2}\sdot\left(10+2\right)\right]\sdot\left(\frac{1}{2}\sdot10\right)=\left(\frac{1}{2}\sdot12\right)\sdot\left(\frac{1}{2}\sdot10\right)=30}}](/mediawiki/images/math/f/5/1/f51017e663db1fbe93036073b3ec2211.png)
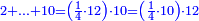
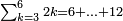
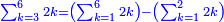
![\scriptstyle{\color{blue}{6+\ldots+12=\left(2+\ldots+12\right)-\left[2+\ldots+\left(6-2\right)\right]=\left(2+\ldots+12\right)-\left(2+\ldots+4\right)=42-6=36}}](/mediawiki/images/math/6/9/4/694f6202ac26b2f6ff5c8632696c15ad.png)
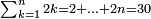
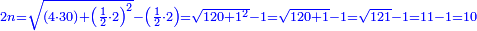
![\scriptstyle{\color{blue}{2n=x\longrightarrow\left[\frac{1}{2}\sdot\left(x+2\right)\right]\sdot\frac{1}{2}x=\left(\frac{1}{2}x+1\right)\sdot\frac{1}{2}x=\frac{1}{4}x^2+{\color{red}{\frac{1}{2}x}}=30}}](/mediawiki/images/math/2/4/5/2451f8705e5c56405c17698fb87145ed.png)
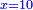
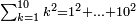
![\scriptstyle{\color{blue}{\sum_{k=1}^{10} k^2=\left(\sum_{k=1}^{10} k\right)\sdot\left[\left(\frac{2}{3}\sdot10\right)+\frac{1}{3}\right]}}](/mediawiki/images/math/c/8/4/c84c0a4d7aaca911422cca587a2083b8.png)
![\scriptstyle{\color{blue}{1^2+\ldots+10^2=\left(1+\ldots+10\right)\sdot\left[\left(\frac{2}{3}\sdot10\right)+\frac{1}{3}\right]=55\sdot7=385}}](/mediawiki/images/math/1/4/c/14c05a4d5f2912d4c244acd5ddec0341.png)
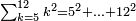
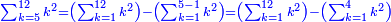
![\scriptstyle{\color{blue}{5^2+\ldots+12^2=\left(1^2+\ldots+12^2\right)-\left[1^2+\ldots+\left(5-1\right)^2\right]=\left(1^2+\ldots+12^2\right)-\left(1^2+\ldots+4^2\right)}}](/mediawiki/images/math/6/e/2/6e28e0321dba374bfb1c4c0834652ebb.png)
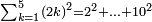
![\scriptstyle{\color{blue}{2^2+\ldots+10^2=\left(2+\ldots+10\right)\sdot\left[\left(\frac{2}{3}\sdot10\right)+\frac{2}{3}\right]=30\sdot\left(7+\frac{1}{3}\right)=220}}](/mediawiki/images/math/b/d/c/bdc2fb35e6fa4d1c08c8a80df3158906.png)
![\scriptstyle{\color{blue}{2^2+\ldots+10^2=\left[\frac{2}{3}\sdot\left(2+\ldots+10\right)\right]\sdot\left(10+1\right)=\left(\frac{2}{3}\sdot30\right)\sdot11=20\sdot11=220}}](/mediawiki/images/math/6/d/6/6d60d79678b2c4e72273b16dc467b0c0.png)
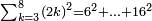
![\scriptstyle{\color{blue}{\sum_{k=3}^{8} \left(2k\right)^2=\left[\sum_{k=1}^{8} \left(2k\right)^2\right]-\left[\sum_{k=1}^{3-1} \left(2k\right)^2\right]=\left[\sum_{k=1}^{8} \left(2k\right)^2\right]-\left[\sum_{k=1}^2 \left(2k\right)^2\right]}}](/mediawiki/images/math/a/2/9/a29327ffceedfd53e0904deac883f127.png)
![\scriptstyle{\color{blue}{6^2+\ldots+16^2=\left(2^2+\ldots+16^2\right)-\left[2^2+\ldots+\left(6-2\right)^2\right]=\left(2^2+\ldots+16^2\right)-\left(2^2+\ldots+4^2\right)}}](/mediawiki/images/math/8/5/9/85903c3a655c1bef04fea8243259bc1d.png)
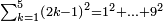
![\scriptstyle{\color{blue}{1^2+\dots+9^2=\left[\frac{1}{2}\sdot\left(9+2\right)\right]\sdot\left[\frac{1}{2}\sdot\left(9+1\right)\right]\sdot\left(\frac{2}{3}\sdot9\right)=\left(\frac{1}{2}\sdot11\right)\sdot\left(\frac{1}{2}\sdot10\right)\sdot\left(\frac{2}{3}\sdot9\right)=165}}](/mediawiki/images/math/7/f/0/7f00cbc70541208fd798b35b74453c11.png)
![{\color{blue}{\begin{align}\scriptstyle1^2+\dots+9^2&\scriptstyle=\left[\left(1+\ldots+9\right)-\left[\left[\frac{1}{3}\sdot\left(1+\ldots+9\right)\right]+\frac{1}{6}\right]\right]\sdot\left(9+1\right)\\&\scriptstyle=\left[25-\left[\left(\frac{1}{3}\sdot25\right)+\frac{1}{6}\right]\right]\sdot10\\&\scriptstyle=\left(16+\frac{1}{2}\right)\sdot10\\\end{align}}}](/mediawiki/images/math/6/e/f/6efbb386b1c0cbca79f602a70aa735af.png)
![\scriptstyle{\color{blue}{1^2+\dots+9^2=\left(9+1\right)\sdot\left(\frac{1}{2}\sdot9\right)\sdot\left[\left(\frac{1}{3}\sdot9\right)+\frac{2}{3}\right]}}](/mediawiki/images/math/5/0/2/5022b8b5b367884f124d8bc23c855d1d.png)
![\scriptstyle{\color{blue}{1^2+\dots+9^2=\left(\frac{1}{2}\sdot9\right)\sdot\left[\left(\frac{1}{3}\sdot9\right)+\frac{2}{3}\right]\sdot\left(9+1\right)=\left(4+\frac{1}{2}\right)\sdot\left(3+\frac{2}{3}\right)\sdot10}}](/mediawiki/images/math/3/2/9/329c377a60c5e1b9e9ba99a6ee2b47d8.png)
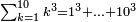
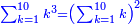
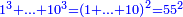
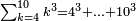
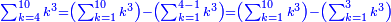
![\scriptstyle{\color{blue}{4^3+\ldots+10^3=\left(1^3+\ldots+10^3\right)-\left[1^3+\ldots+\left(4-1\right)^3\right]=\left(1^3+\ldots+10^3\right)-\left(1^3+\ldots+3^3\right)}}](/mediawiki/images/math/9/c/a/9ca7b7c29df04d1aa0dccbbb8015ee3b.png)
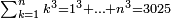
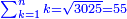
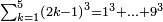
![\scriptstyle{\color{blue}{\sum_{k=1}^{5} \left(2k-1\right)^3=\left[\sum_{k=1}^{5} \left(2k-1\right)\right]\sdot\left[\left[2\sdot\sum_{k=1}^{5} \left(2k-1\right)\right]-1\right]}}](/mediawiki/images/math/8/8/3/8834b23f2fd76c394ed024d9b79b5164.png)
![\scriptstyle{\color{blue}{1^3+\ldots+9^3=\left(1+\ldots+9\right)\sdot\left[\left[2\sdot\left(1+\ldots+9\right)\right]-1\right]=25\sdot\left[\left(2\sdot25\right)-1\right]=1225}}](/mediawiki/images/math/b/e/8/be8bfdb0bd7c9b841c0fab092d364117.png)
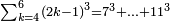
![\scriptstyle{\color{blue}{\sum_{k=4}^{6} \left(2k-1\right)^3=\left[\sum_{k=1}^{6} \left(2k-1\right)^3\right]-\left[\sum_{k=1}^{4-1} \left(2k-1\right)^3\right]=\left[\sum_{k=1}^{6} \left(2k-1\right)^3\right]-\left[\sum_{k=1}^{3} \left(2k-1\right)^3\right]}}](/mediawiki/images/math/6/8/e/68ed7d6fa04eab5decda8d8d4480b4fc.png)
![\scriptstyle{\color{blue}{7^3+\ldots+11^3=\left(1^3+\ldots+11^3\right)-\left[1^3+\ldots+\left(7-2\right)^3\right]=\left(1^3+\ldots+11^3\right)-\left(1^3+\ldots+5^3\right)=2403}}](/mediawiki/images/math/e/5/2/e525fac4c47e39d4215e2c3c5080b11a.png)
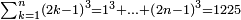
![{\color{blue}{\begin{align}\scriptstyle2n-1&\scriptstyle=\sqrt{4\sdot\left[\sqrt{\left(\frac{1}{2}\sdot1225\right)+\left(\frac{1}{4}\sdot1\right)^2}+\left(\frac{1}{4}\sdot1\right)\right]}-1\\&\scriptstyle=\sqrt{4\sdot\left[\sqrt{\left(612+\frac{1}{2}\right)+\left(\frac{1}{4}\right)^2}+\frac{1}{4}\right]}-1\\&\scriptstyle=\sqrt{4\sdot\left[\sqrt{\left(612+\frac{1}{2}\right)+\left(\frac{1}{2}\sdot\frac{1}{8}\right)}+\frac{1}{4}\right]}-1\\&\scriptstyle=\sqrt{4\sdot\left[\left(24+\frac{3}{4}\right)+\frac{1}{4}\right]}-1\\&\scriptstyle=\sqrt{4\sdot25}-1=9\\\end{align}}}](/mediawiki/images/math/a/2/0/a201101f25ce9a3acd865ee0a1d71ad7.png)
![\scriptstyle{\color{blue}{2n-1=x\longrightarrow\left[\frac{1}{2}\sdot\left(x+1\right)\right]^2\sdot\left[\left[2\sdot\left[\frac{1}{2}\sdot\left(x+1\right)\right]^2\right]-1\right]=1225}}](/mediawiki/images/math/7/e/7/7e76406e4c8986ea4f4c187f9c264c33.png)
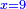
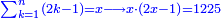
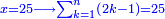
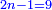
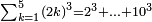
![\scriptstyle{\color{blue}{\sum_{k=1}^{5} \left(2k\right)^3=\left[\sum_{k=1}^{5} \left(2k\right)\right]\sdot\left[2\sdot\sum_{k=1}^{5} \left(2k\right)\right]}}](/mediawiki/images/math/3/4/a/34a235f959489f67963c301d247db10e.png)
![\scriptstyle{\color{blue}{2^3+\ldots+10^3=\left(2+\ldots+10\right)\sdot\left[2\sdot\left(2+\ldots+10\right)\right]=30\sdot\left(2\sdot30\right)=1800}}](/mediawiki/images/math/4/6/4/46426cf626cc98ae66f4116784811d40.png)
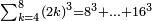
![\scriptstyle{\color{blue}{\sum_{k=4}^{8} \left(2k\right)^3=\left[\sum_{k=1}^{8} \left(2k\right)^3\right]-\left[\sum_{k=1}^{4-1} \left(2k\right)^3\right]=\left[\sum_{k=1}^{8} \left(2k\right)^3\right]-\left[\sum_{k=1}^{3} \left(2k\right)^3\right]}}](/mediawiki/images/math/f/f/7/ff70a904ead24b78c51b51e0a36268ab.png)
![\scriptstyle{\color{blue}{8^3+\ldots+16^3=\left(2^3+\ldots+16^3\right)-\left[2^3+\ldots+\left(8-2\right)^3\right]=\left(2^3+\ldots+16^3\right)-\left(2^3+\ldots+6^3\right)}}](/mediawiki/images/math/8/c/9/8c97aeca0679ed03a4ff6fd63e47434f.png)
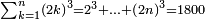

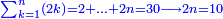

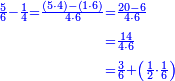
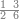
![\scriptstyle\frac{10}{11}-\left[\frac{4}{5}+\left(\frac{1}{2}\sdot\frac{1}{5}\right)\right]](/mediawiki/images/math/a/0/2/a02336007e9bb0f486bfcaadb4e67bca.png)
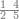
![{\color{blue}{\begin{align}\scriptstyle\frac{10}{11}-\left[\frac{4}{5}+\left(\frac{1}{2}\sdot\frac{1}{5}\right)\right]&\scriptstyle=\frac{\left(10\sdot5\sdot2\right)-\left[\left[\left(4\sdot2\right)+1\right]\sdot11\right]}{2\sdot5\sdot11}\\&\scriptstyle=\frac{100-99}{2\sdot5\sdot11}\\&\scriptstyle=\frac{1}{2\sdot5\sdot11}\\&\scriptstyle=\frac{1}{2}\sdot\frac{1}{5}\sdot\frac{1}{11}\\\end{align}}}](/mediawiki/images/math/2/b/d/2bdda5183fc2db1237ff93b5da247a60.png)
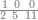
![\scriptstyle\frac{9}{10}+\left(\frac{3}{4}\sdot\frac{1}{10}\right)-\left[\frac{7}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)\right]](/mediawiki/images/math/8/5/1/851b4268ae804ae5e1a8deac3f796057.png)
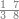
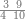
![{\color{blue}{\begin{align}\scriptstyle\frac{9}{10}+\left(\frac{3}{4}\sdot\frac{1}{10}\right)-\left[\frac{7}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)\right]&\scriptstyle=\frac{\left[\left[\left(9\sdot4\right)+3\right]\sdot8\sdot3\right]-\left[\left[\left(7\sdot3\right)+1\right]\sdot10\sdot4\right]}{3\sdot4\sdot8\sdot10}\\&\scriptstyle=\left(\frac{4}{8}\sdot\frac{1}{10}\right)+\left(\frac{4}{6}\sdot\frac{1}{8}\sdot\frac{1}{10}\right)\\\end{align}}}](/mediawiki/images/math/9/b/3/9b39eed76a4c1904307aa89452b54d66.png)
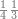
![{\color{blue}{\begin{align}\scriptstyle\frac{9}{10}-\left(\frac{1}{3}+\frac{1}{4}\right)&\scriptstyle=\frac{\left(9\sdot3\sdot4\right)-\left[\left[\left(1\sdot4\right)+\left(1\sdot3\right)\right]\sdot10\right]}{3\sdot4\sdot10}\\&\scriptstyle=\frac{108-70}{3\sdot4\sdot10}\\&\scriptstyle=\frac{38}{3\sdot4\sdot10}\\&\scriptstyle=\frac{3}{10}+\left(\frac{1}{6}\sdot\frac{1}{10}\right)\\\end{align}}}](/mediawiki/images/math/6/d/d/6ddf7a7721c1d6f78386835060a83d7e.png)
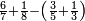
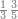
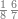
![\scriptstyle{\color{blue}{\frac{6}{7}+\frac{1}{8}-\left(\frac{3}{5}+\frac{1}{3}\right)=\frac{\left[\left[\left(6\sdot8\right)+\left(1\sdot7\right)\right]\sdot5\sdot3\right]-\left[\left[\left(3\sdot3\right)+\left(1\sdot5\right)\right]\sdot7\sdot8\right]}{3\sdot5\sdot7\sdot8}}}](/mediawiki/images/math/c/0/6/c065a9f28cb988c55e2f7d065e4bc388.png)
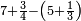
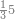
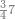
![\scriptstyle{\color{blue}{7+\frac{3}{4}-\left(5+\frac{1}{3}\right)=\frac{\left[\left[\left(7\sdot4\right)+3\right]\sdot3\right]-\left[\left[\left(5\sdot3\right)+1\right]\sdot4\right]}{4\sdot3}=\frac{29}{4\sdot3}=2+\frac{2}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)}}](/mediawiki/images/math/1/b/b/1bb2426dc8d86f50705ecb8c96db54c2.png)
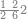
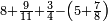
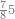
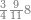
![\scriptstyle{\color{blue}{8+\frac{9}{11}+\frac{3}{4}-\left(5+\frac{7}{8}\right)=\frac{\left[\left[\left(8\sdot11\sdot4\right)+\left(9\sdot4\right)+\left(3\sdot11\right)\right]\sdot8\right]-\left[\left[\left(5\sdot8\right)+7\right]\sdot11\sdot4\right]}{4\sdot8\sdot11}}}](/mediawiki/images/math/c/4/f/c4f990c7bf3eea165aefcda428001adf.png)
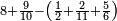
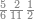
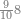
![\scriptstyle{\color{blue}{8+\frac{9}{10}-\left(\frac{1}{2}+\frac{2}{11}+\frac{5}{6}\right)=\frac{\left[\left[\left(8\sdot10\right)+9\right]\sdot2\sdot11\sdot6\right]-\left[\left[\left(1\sdot11\sdot6\right)+\left(2\sdot2\sdot6\right)+\left(5\sdot2\sdot11\right)\right]\sdot10\right]}{2\sdot6\sdot10\sdot11}}}](/mediawiki/images/math/2/7/3/273f5b482370421997a76985c3b4fd63.png)
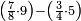
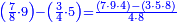
![\scriptstyle\left[\frac{5}{6}\sdot\left(7+\frac{1}{8}\right)\right]-\left[\frac{3}{4}\sdot\left(5+\frac{1}{2}\right)\right]](/mediawiki/images/math/1/a/0/1a043526bbb8467be523a84f4f489d33.png)
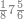
![\scriptstyle{\color{blue}{\left[\frac{5}{6}\sdot\left(7+\frac{1}{8}\right)\right]-\left[\frac{3}{4}\sdot\left(5+\frac{1}{2}\right)\right]=\frac{\left[\left[\left(7\sdot8\right)+1\right]\sdot5\sdot4\sdot2\right]-\left[\left[\left(5\sdot2\right)+1\right]\sdot3\sdot6\sdot8\right]}{2\sdot4\sdot6\sdot8}}}](/mediawiki/images/math/5/4/3/543475fc5f3f09209f9ba5a87fe5dd2a.png)
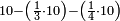
![\scriptstyle{\color{blue}{10-\left(\frac{1}{3}\sdot10\right)-\left(\frac{1}{4}\sdot10\right)=\frac{\left[12-\left(\frac{1}{3}\sdot12\right)-\left(\frac{1}{4}\sdot12\right)\right]\sdot10}{12}=\frac{\left(12-7\right)\sdot10}{12}=\frac{5\sdot10}{12}=4+\frac{1}{6}}}](/mediawiki/images/math/f/4/7/f47d7422f36b9c2a9718d1d1faa7f8a7.png)
![\scriptstyle{\color{blue}{10-\left(\frac{1}{3}\sdot10\right)-\left(\frac{1}{4}\sdot10\right)=\frac{\left[1-\left(\frac{1}{3}+\frac{1}{4}\right)\right]\sdot10}{1}=\frac{\left[1-\left[\frac{3}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\right]\sdot10}{1}=\frac{\left[\frac{2}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\sdot10}{1}}}](/mediawiki/images/math/8/6/b/86bdb9d9142d11c6d15b51afc83a553b.png)
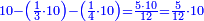
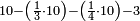
![{\color{blue}{\begin{align}\scriptstyle10-\left(\frac{1}{3}\sdot10\right)-\left(\frac{1}{4}\sdot10\right)-3&\scriptstyle=\frac{\left[\left[12-\left(\frac{1}{3}\sdot12\right)-\left(\frac{1}{4}\sdot12\right)\right]\sdot10\right]-\left(3\sdot12\right)}{12}\\&\scriptstyle=\frac{\left[\left(12-7\right)\sdot10\right]-\left(3\sdot12\right)}{12}\\&\scriptstyle=\frac{\left(5\sdot10\right)-\left(3\sdot12\right)}{12}\\&\scriptstyle=\frac{50-\left(3\sdot12\right)}{12}\\&\scriptstyle=\frac{14}{12}=1+\frac{1}{6}\\\end{align}}}](/mediawiki/images/math/8/e/0/8e03b1f7419fb9eef87f9edc47197809.png)
![\scriptstyle10-\left[\left(\frac{1}{3}\sdot10\right)+\left(\frac{1}{4}\sdot10\right)-2\right]](/mediawiki/images/math/c/5/5/c55fd60a314d17d0af06c011228f7c69.png)
![{\color{blue}{\begin{align}\scriptstyle10-\left[\left(\frac{1}{3}\sdot10\right)+\left(\frac{1}{4}\sdot10\right)-2\right]&\scriptstyle=\frac{\left[\left[12-\left(\frac{1}{3}\sdot12\right)-\left(\frac{1}{4}\sdot12\right)\right]\sdot10\right]+\left(2\sdot12\right)}{12}\\&\scriptstyle=\frac{\left[\left(12-7\right)\sdot10\right]+\left(2\sdot12\right)}{12}\\&\scriptstyle=\frac{\left(5\sdot10\right)+\left(2\sdot12\right)}{12}\\&\scriptstyle=\frac{50+\left(2\sdot12\right)}{12}\\&\scriptstyle=\frac{74}{12}=6+\frac{1}{6}\\\end{align}}}](/mediawiki/images/math/b/e/6/be66b43ed10f47301fde58ef84e53775.png)
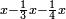
![\scriptstyle{\color{blue}{x-\frac{1}{3}x-\frac{1}{4}x=\left[1-\left(\frac{1}{3}+\frac{1}{4}\right)\right]x=\left[1-\left[\frac{3}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\right]x=\left[\frac{2}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]x}}](/mediawiki/images/math/a/c/9/ac984b4f77457d1f70d9dd3f65c8470b.png)
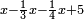
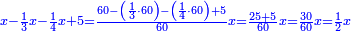
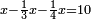
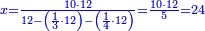
![\scriptstyle{\color{blue}{x-\frac{1}{3}x-\frac{1}{4}x=\left[\frac{2}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]x=10}}](/mediawiki/images/math/d/7/e/d7eced8a372f1155019b2ba68f9cbf3c.png)
![\scriptstyle{\color{blue}{\left[\frac{2}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\sdot a=1\longrightarrow a=2+\frac{2}{5}}}](/mediawiki/images/math/a/1/5/a1510445ab9d35842c983633a69ca022.png)
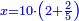
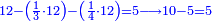
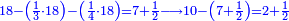
![\scriptstyle{\color{blue}{x=\frac{\left(5\sdot18\right)-\left[\left(2+\frac{1}{2}\right)\sdot12\right]}{5-\left(2+\frac{1}{2}\right)}=\frac{90-30}{2+\frac{1}{2}}=\frac{60}{2+\frac{1}{2}}=24}}](/mediawiki/images/math/1/1/9/11942b410cc814c48c2d53dc5bd80852.png)
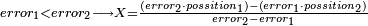
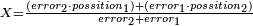
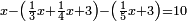
![{\color{blue}{\begin{align}\scriptstyle x&\scriptstyle=\frac{\left[10+\left(3+3\right)\right]\sdot60}{60-\left[\left(\frac{1}{3}\sdot60\right)+\left(\frac{1}{4}\sdot60\right)+\left(\frac{1}{5}\sdot60\right)\right]}\\&\scriptstyle=\frac{\left(10+6\right)\sdot60}{13}\\&\scriptstyle=\frac{16\sdot60}{13}\\&\scriptstyle=73+\frac{11}{13}\\\end{align}}}](/mediawiki/images/math/4/b/e/4be4c71d0785f0f572767d9dc3876625.png)
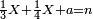 - vice versa:
- vice versa: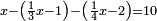
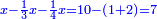
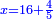
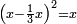
![\scriptstyle{\color{blue}{x=\frac{3^2}{\left[3-\left(\frac{1}{3}\sdot3\right)\right]^2}=\frac{9}{2^2}=\frac{9}{4}=2+\frac{1}{4}}}](/mediawiki/images/math/3/5/4/354ed3bcef77b0793f42e26b1b300c91.png)
![\scriptstyle\left[\left(x-\frac{1}{3}x\right)-\left[\frac{1}{2}\sdot\left(x-\frac{1}{3}x\right)\right]\right]\sdot\left[\frac{1}{3}x+\left[\frac{1}{2}\sdot\left(x-\frac{1}{3}x\right)\right]\right]=x](/mediawiki/images/math/6/3/f/63f6128ef6b1f2fc78645c14988af422.png)
![{\color{blue}{\begin{align}\scriptstyle x&\scriptstyle=\frac{3^2}{\left[\left[3-\left(\frac{1}{3}\sdot3\right)\right]-\left[\frac{1}{2}\sdot\left[3-\left(\frac{1}{3}\sdot3\right)\right]\right]\right]\sdot\left[\left(\frac{1}{3}\sdot3\right)+\left[\frac{1}{2}\sdot\left[3-\left(\frac{1}{3}\sdot3\right)\right]\right]\right]}\\&\scriptstyle=\frac{3^2}{\left[2-\left(\frac{1}{2}\sdot2\right)\right]\sdot\left[1+\left(\frac{1}{2}\sdot2\right)\right]}\\&\scriptstyle=\frac{3^2}{1\sdot2}\\&\scriptstyle=\frac{3^2}{2}=4+\frac{1}{2}\\\end{align}}}](/mediawiki/images/math/8/5/0/85099158bc81eb476954c3d0ee31e206.png)
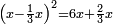
![\scriptstyle{\color{blue}{x=\frac{3^2\sdot\left(6+\frac{2}{3}\right)}{\left[3-\left(\frac{1}{3}\sdot3\right)\right]^2}=\frac{60}{2^2}=\frac{60}{4}=15}}](/mediawiki/images/math/e/4/3/e43a545eabdb35e0c4135f275d231a15.png)
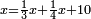
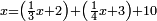
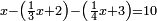
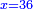
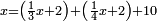
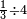


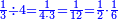
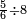

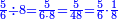

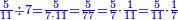
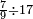


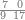
![\scriptstyle\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\div5](/mediawiki/images/math/f/3/5/f35247a33fdf18d5e069da1dd98835fe.png)

![\scriptstyle{\color{blue}{\left[\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]\div5=\frac{\left(5\sdot2\right)+1}{5\sdot6\sdot2}=\frac{11}{60}=\frac{1}{10}+\left(\frac{5}{6}\sdot\frac{1}{10}\right)}}](/mediawiki/images/math/4/9/7/4975680573c957c07c91e1915bc2958c.png)
![\scriptstyle\left[\frac{10}{11}+\left(\frac{3}{5}\sdot\frac{1}{11}\right)\right]\div63](/mediawiki/images/math/9/b/0/9b0959a66fde808099c9dfefd633a000.png)
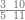
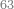
![\scriptstyle{\color{blue}{\left[\frac{10}{11}+\left(\frac{3}{5}\sdot\frac{1}{11}\right)\right]\div63=\frac{\left(10\sdot5\right)+3}{63\sdot11\sdot5}=\frac{53}{3465}=\left(\frac{1}{9}\sdot\frac{1}{11}\right)+\left(\frac{3}{7}\sdot\frac{1}{9}\sdot\frac{1}{11}\right)+\left(\frac{3}{5}\sdot\frac{1}{7}\sdot\frac{1}{9}\sdot\frac{1}{11}\right)}}](/mediawiki/images/math/9/e/c/9ecacee124639362a518f7b68c206004.png)
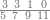
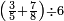
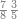
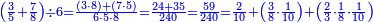
![\scriptstyle{\color{blue}{\left(\frac{3}{5}+\frac{7}{8}\right)\div6=\frac{1+\frac{3}{8}+\left(\frac{4}{5}\sdot\frac{1}{8}\right)}{6}=\left[1+\frac{3}{8}+\left(\frac{4}{5}\sdot\frac{1}{8}\right)\right]\sdot\frac{1}{6}}}](/mediawiki/images/math/6/8/1/68119dba5151950a574d0da08f11f426.png)
![\scriptstyle{\color{blue}{\left(\frac{3}{5}+\frac{7}{8}\right)\div6=\left[\left(\frac{3}{5}+\frac{7}{8}\right)\right]\sdot\frac{1}{6}}}](/mediawiki/images/math/4/5/7/457660597915a0e44233bcf46f94dcf3.png)
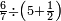
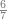
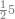
![\scriptstyle{\color{blue}{\frac{6}{7}\div\left(5+\frac{1}{2}\right)=\frac{6\sdot2}{\left[\left(5\sdot2\right)+1\right]\sdot7}=\frac{12}{11\sdot7}=\frac{12}{77}=\frac{1}{11}+\left(\frac{5}{7}\sdot\frac{1}{11}\right)}}](/mediawiki/images/math/5/1/4/514d6c9106ce562aa38b99439fea47f8.png)
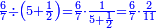
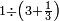
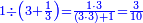
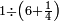
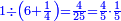
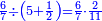
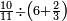
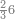
![\scriptstyle{\color{blue}{\frac{10}{11}\div\left(6+\frac{2}{3}\right)=\frac{10\sdot3}{\left[\left(6\sdot3\right)+2\right]\sdot11}=\frac{30}{20\sdot11}=\frac{30}{220}=\frac{1}{11}+\left(\frac{5}{10}\sdot\frac{1}{11}\right)}}](/mediawiki/images/math/6/5/3/653272323c8dcf3d4f551c5f18258e17.png)
![\scriptstyle{\color{blue}{\frac{10}{11}\div\left(6+\frac{2}{3}\right)=\frac{10}{11}\sdot\left[\frac{1}{10}+\left(\frac{1}{2}\sdot\frac{1}{10}\right)\right]=\frac{1}{11}+\left(\frac{5}{10}\sdot\frac{1}{11}\right)}}](/mediawiki/images/math/9/e/3/9e39b6392deca31ed6f06ed7ab1772a3.png)
![\scriptstyle\frac{4}{5}\div\left[3+\frac{6}{7}+\left(\frac{1}{2}\sdot\frac{1}{7}\right)\right]](/mediawiki/images/math/5/7/b/57b7577cb03e6f202ca23aa4cd5ee3c2.png)
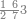
![{\color{blue}{\begin{align}\scriptstyle\frac{4}{5}\div\left[3+\frac{6}{7}+\left(\frac{1}{2}\sdot\frac{1}{7}\right)\right]&\scriptstyle=\frac{4\sdot2\sdot7}{\left[\left[\left[\left(3\sdot7\right)+6\right]\sdot2\right]+1\right]\sdot5}\\&\scriptstyle=\frac{56}{55\sdot5}\\&\scriptstyle=\frac{56}{275}\\&\scriptstyle=\frac{2}{11}+\left(\frac{1}{5}\sdot\frac{1}{11}\right)+\left(\frac{1}{5}\sdot\frac{1}{5}\sdot\frac{1}{11}\right)\\\end{align}}}](/mediawiki/images/math/2/b/f/2bff81cd189abb8c7046c2f6140396f7.png)
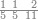
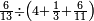
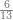
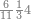
![{\color{blue}{\begin{align}\scriptstyle\frac{6}{13}\div\left(4+\frac{1}{3}+\frac{6}{11}\right)&\scriptstyle=\frac{6\sdot3\sdot11}{\left[\left(4\sdot3\sdot11\right)+\left(1\sdot11\right)+\left(6\sdot3\right)\right]\sdot13}\\&\scriptstyle=\frac{198}{161\sdot13}\\&\scriptstyle=\frac{198}{2093}\\&\scriptstyle=\frac{2}{23}+\left(\frac{2}{13}\sdot\frac{1}{23}\right)+\left(\frac{2}{7}\sdot\frac{1}{13}\sdot\frac{1}{23}\right)\\\end{align}}}](/mediawiki/images/math/2/b/2/2b2eed3f968f12c278902cd48c776b6b.png)
![\scriptstyle\left[\frac{7}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)\right]\div\left(3+\frac{1}{2}\right)](/mediawiki/images/math/a/3/1/a31d77578b5729c94a448c48170007e1.png)
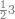
![\scriptstyle{\color{blue}{\left[\frac{7}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)\right]\div\left(3+\frac{1}{2}\right)=\frac{\left[\left(7\sdot3\right)+1\right]\sdot2}{\left[\left(3\sdot2\right)+1\right]\sdot8\sdot3}=\frac{22\sdot2}{7\sdot8\sdot3}=\frac{44}{168}=\frac{2}{8}+\left(\frac{2}{3}\sdot\frac{1}{7}\sdot\frac{1}{8}\right)}}](/mediawiki/images/math/7/a/0/7a05a8d1cd9988fb937c0658d738ffab.png)
![\scriptstyle{\color{blue}{\left[\frac{7}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)\right]\div\left(3+\frac{1}{2}\right)=\left[\frac{7}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)\right]\sdot\frac{2}{7}=\frac{2}{8}+\left(\frac{2}{3}\sdot\frac{1}{7}\sdot\frac{1}{8}\right)}}](/mediawiki/images/math/1/a/3/1a36ed058f5e94d7b4fc60f4788af0d2.png)
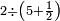

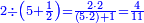
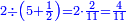
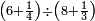
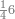
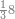
![\scriptstyle{\color{blue}{\left(6+\frac{1}{4}\right)\div\left(8+\frac{1}{3}\right)=\frac{\left[\left(6\sdot4\right)+1\right]\sdot3}{\left[\left(8\sdot3\right)+1\right]\sdot4}=\frac{25\sdot3}{25\sdot4}=\frac{75}{100}=\frac{3}{4}}}](/mediawiki/images/math/c/a/f/caf07083151be12b2c2217d125d96f03.png)
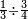
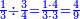
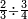
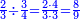
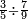
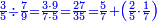
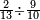
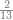
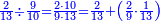
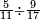
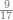
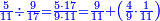
![\scriptstyle\left[\frac{2}{8}+\left(\frac{1}{2}\sdot\frac{1}{8}\right)\right]\div\frac{9}{10}](/mediawiki/images/math/3/b/0/3b05212d5998323229d3e3d7d2023235.png)
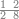
![\scriptstyle{\color{blue}{\left[\frac{2}{8}+\left(\frac{1}{2}\sdot\frac{1}{8}\right)\right]\div\frac{9}{10}=\frac{\left[\left(2\sdot2\right)+1\right]\sdot10}{9\sdot8\sdot2}=\frac{5\sdot10}{144}=\frac{50}{144}=\frac{3}{9}+\left(\frac{1}{8}\sdot\frac{1}{9}\right)}}](/mediawiki/images/math/e/f/0/ef0b69ddf02c2ace081e448bbd7137cb.png)
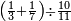
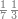
![\scriptstyle{\color{blue}{\left(\frac{1}{3}+\frac{1}{7}\right)\div\frac{10}{11}=\frac{\left[\left(1\sdot7\right)+\left(1\sdot3\right)\right]\sdot11}{10\sdot3\sdot7}=\frac{10\sdot11}{210}=\frac{5}{10}+\left(\frac{1}{7}\sdot\frac{1}{10}\right)+\left(\frac{2}{3}\sdot\frac{1}{7}\sdot\frac{1}{10}\right)=\frac{3}{7}+\left(\frac{2}{3}\sdot\frac{1}{7}\right)}}](/mediawiki/images/math/0/1/b/01ba350cbfbc6c63f89579fae5b980be.png)
![\scriptstyle\frac{2}{3}\div\left[\frac{9}{10}+\left(\frac{5}{8}\sdot\frac{1}{10}\right)\right]](/mediawiki/images/math/d/d/2/dd244e384f4422a279cba9537b8b864b.png)
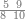
![\scriptstyle{\color{blue}{\frac{2}{3}\div\left[\frac{9}{10}+\left(\frac{5}{8}\sdot\frac{1}{10}\right)\right]=\frac{2\sdot10\sdot8}{\left[\left(9\sdot8\right)+5\right]\sdot3}=\frac{160}{77\sdot3}=\frac{160}{231}=\frac{7}{11}+\left(\frac{4}{7}\sdot\frac{1}{11}\right)+\left(\frac{1}{3}\sdot\frac{1}{7}\sdot\frac{1}{11}\right)}}](/mediawiki/images/math/b/4/1/b41edf85440b28216bac78ab92473c4d.png)
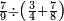
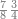
![\scriptstyle{\color{blue}{\frac{7}{9}\div\left(\frac{3}{4}+\frac{7}{8}\right)=\frac{7\sdot4\sdot8}{\left[\left(3\sdot8\right)+\left(7\sdot4\right)\right]\sdot9}=\frac{224}{52\sdot9}=\frac{224}{468}=\frac{6}{13}+\left(\frac{2}{9}\sdot\frac{1}{13}\right)}}](/mediawiki/images/math/7/7/a/77ac664fb41ac9e289545f47dc187fc9.png)
![\scriptstyle\left[\frac{4}{9}+\left(\frac{1}{2}\sdot\frac{1}{9}\right)\right]\div\left[\frac{7}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)\right]](/mediawiki/images/math/8/a/1/8a111107fc608a5ae9f5d99f4f2ec182.png)
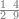
![\scriptstyle{\color{blue}{\left[\frac{4}{9}+\left(\frac{1}{2}\sdot\frac{1}{9}\right)\right]\div\left[\frac{7}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)\right]=\frac{\left[\left(4\sdot2\right)+1\right]\sdot8\sdot3}{\left[\left(7\sdot3\right)+1\right]\sdot9\sdot2}=\frac{216}{396}=\frac{6}{11}}}](/mediawiki/images/math/3/c/c/3ccc74df6aac408d8a4b1919e2a05f57.png)
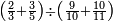
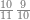
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{2}{3}+\frac{3}{5}\right)\div\left(\frac{9}{10}+\frac{10}{11}\right)&\scriptstyle=\frac{\left[\left(2\sdot5\right)+\left(3\sdot3\right)\right]\sdot10\sdot11}{\left[\left(9\sdot11\right)+\left(10\sdot10\right)\right]\sdot3\sdot5}\\&\scriptstyle=\frac{2090}{199\sdot3\sdot5}\\&\scriptstyle=\frac{2090}{2985}\\&\scriptstyle=\frac{139}{199}+\left(\frac{1}{199}\sdot\frac{1}{5}\right)+\left(\frac{2}{3}\sdot\frac{1}{5}\sdot\frac{1}{199}\right)\\\end{align}}}](/mediawiki/images/math/a/a/8/aa8ba0ced02bc1690dbb9ab54aaef801.png)
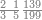
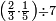
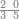
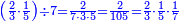
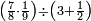
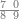
![\scriptstyle{\color{blue}{\left(\frac{7}{8}\sdot\frac{1}{9}\right)\div\left(3+\frac{1}{2}\right)=\frac{7\sdot2}{\left[\left(3\sdot2\right)+1\right]\sdot8\sdot9}=\frac{14}{7\sdot8\sdot9}=\frac{14}{504}=\frac{2}{8}\sdot\frac{1}{9}}}](/mediawiki/images/math/2/7/f/27f699d0cf3873ce5e58be55a0102f6f.png)
![\scriptstyle\left(\frac{9}{10}\sdot\frac{1}{13}\right)\div\left[6+\frac{3}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)\right]](/mediawiki/images/math/4/5/1/451bee3fb541e81d2eb989739ad43640.png)
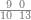
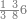
![{\color{blue}{\begin{align}\scriptstyle\left(\frac{9}{10}\sdot\frac{1}{13}\right)\div\left[6+\frac{3}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)\right]&\scriptstyle=\frac{9\sdot8\sdot3}{\left[\left[\left[\left(6\sdot8\right)+3\right]\sdot3\right]+1\right]\sdot10\sdot13}\\&\scriptstyle=\frac{216}{154\sdot10\sdot13}\\&\scriptstyle=\frac{216}{20020}\\&\scriptstyle=\left(\frac{1}{11}\sdot\frac{1}{13}\right)+\left(\frac{5}{10}\sdot\frac{1}{11}\sdot\frac{1}{13}\right)+\left(\frac{3}{7}\sdot\frac{1}{10}\sdot\frac{1}{11}\sdot\frac{1}{13}\right)\\\end{align}}}](/mediawiki/images/math/f/9/2/f92b60fef1e1a7de9996fa691d1cf45a.png)
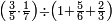
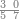
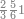
![\scriptstyle{\color{blue}{\left(\frac{3}{5}\sdot\frac{1}{7}\right)\div\left(1+\frac{5}{6}+\frac{2}{3}\right)=\frac{3\sdot6\sdot3}{\left[\left(1\sdot6\sdot3\right)+\left(5\sdot3\right)+\left(2\sdot6\right)\right]\sdot5\sdot7}=\frac{54}{1575}=\left(\frac{2}{7}\sdot\frac{1}{9}\right)+\left(\frac{4}{5}\sdot\frac{1}{5}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)}}](/mediawiki/images/math/a/b/6/ab6bfe5ab16dbf6af13689c50e3ea6d9.png)
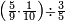
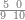
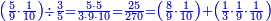
![\scriptstyle\left(\frac{3}{4}\sdot\frac{1}{5}\right)\div\left[\frac{3}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]](/mediawiki/images/math/e/2/6/e2635a129664cacdecfb3781e889b1cc.png)
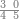
![\scriptstyle{\color{blue}{\left(\frac{3}{4}\sdot\frac{1}{5}\right)\div\left[\frac{3}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\right]=\frac{3\sdot6\sdot2}{\left[\left(3\sdot2\right)+1\right]\sdot4\sdot5}=\frac{36}{140}=\frac{2}{10}+\left(\frac{4}{7}\sdot\frac{1}{10}\right)}}](/mediawiki/images/math/9/b/b/9bbddb7933a55cc8433d45aafffc5091.png)
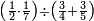
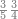
![\scriptstyle{\color{blue}{\left(\frac{1}{2}\sdot\frac{1}{7}\right)\div\left(\frac{3}{4}+\frac{3}{5}\right)=\frac{1\sdot4\sdot5}{\left[\left(3\sdot5\right)+\left(3\sdot4\right)\right]\sdot2\sdot7}=\frac{1\sdot4\sdot5}{27\sdot2\sdot7}=\frac{1\sdot4\sdot5}{378}=\left(\frac{3}{7}\sdot\frac{1}{9}\right)+\left(\frac{2}{6}\sdot\frac{1}{7}\sdot\frac{1}{9}\right)}}](/mediawiki/images/math/0/2/9/029e761b609c867dd36cc1de1303af3f.png)
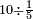

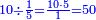
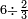
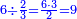
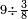


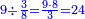
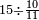
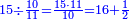
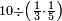
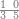
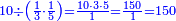
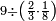
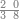
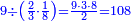
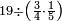
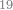
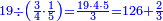
![\scriptstyle4\div\left[\frac{3}{5}+\left(\frac{1}{3}\sdot\frac{1}{5}\right)\right]](/mediawiki/images/math/9/c/8/9c8ab85302d51c8c896d8f72077ae8fd.png)
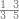
![\scriptstyle{\color{blue}{4\div\left[\frac{3}{5}+\left(\frac{1}{3}\sdot\frac{1}{5}\right)\right]=\frac{4\sdot5\sdot3}{\left(3\sdot3\right)+1}=\frac{60}{10}=6}}](/mediawiki/images/math/f/d/f/fdf853e7cb387a4a045f5680f3209519.png)
![\scriptstyle5\div\left[\frac{10}{11}+\left(\frac{1}{2}\sdot\frac{1}{11}\right)\right]](/mediawiki/images/math/3/2/f/32feea03a00ca4a14965e14d179083f7.png)
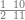
![\scriptstyle{\color{blue}{5\div\left[\frac{10}{11}+\left(\frac{1}{2}\sdot\frac{1}{11}\right)\right]=\frac{5\sdot11\sdot2}{\left(10\sdot2\right)+1}=\frac{5\sdot11\sdot2}{21}=5+\frac{1}{7}+\left(\frac{2}{3}\sdot\frac{1}{7}\right)}}](/mediawiki/images/math/5/d/8/5d8d6cd50418781eae3696c5b7307ac3.png)
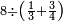
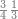
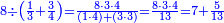
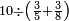
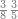

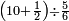
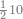
![\scriptstyle{\color{blue}{\left(10+\frac{1}{2}\right)\div\frac{5}{6}=\frac{\left[\left(10\sdot2\right)+1\right]\sdot6}{5\sdot2}=\frac{21\sdot6}{5\sdot2}=\frac{126}{10}=12+\frac{6}{10}}}](/mediawiki/images/math/7/9/2/7925f5ae5d779b34656487249660fe96.png)
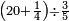
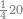
![\scriptstyle{\color{blue}{\left(20+\frac{1}{4}\right)\div\frac{3}{5}=\frac{\left[\left(20\sdot4\right)+1\right]\sdot5}{3\sdot4}=\frac{405}{12}=33+\frac{4}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)}}](/mediawiki/images/math/c/4/d/c4d75fd7abbb83fd4de6801bfb142d79.png)
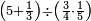
![\scriptstyle{\color{blue}{\left(5+\frac{1}{3}\right)\div\left(\frac{3}{4}\sdot\frac{1}{5}\right)=\frac{\left[\left(5\sdot3\right)+1\right]\sdot4\sdot5}{3\sdot3}=\frac{16\sdot4\sdot5}{9}=\frac{320}{9}=35+\frac{5}{9}}}](/mediawiki/images/math/6/f/1/6f15a7f9658e22d23002357218814539.png)
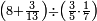
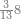
![\scriptstyle{\color{blue}{\left(8+\frac{3}{13}\right)\div\left(\frac{3}{5}\sdot\frac{1}{7}\right)=\frac{\left[\left(8\sdot13\right)+3\right]\sdot5\sdot7}{3\sdot13}=\frac{3745}{39}=96+\frac{1}{39}}}](/mediawiki/images/math/1/5/3/153237cf05244fd68f878cc94f653792.png)
![\scriptstyle\left(6+\frac{1}{2}\right)\div\left[\frac{4}{5}+\left(\frac{1}{2}\sdot\frac{1}{5}\right)\right]](/mediawiki/images/math/a/b/8/ab8d988d4f4fc8d6fd5641aaf3c0ae9f.png)
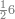
![\scriptstyle{\color{blue}{\left(6+\frac{1}{2}\right)\div\left[\frac{4}{5}+\left(\frac{1}{2}\sdot\frac{1}{5}\right)\right]=\frac{\left[\left(6\sdot2\right)+1\right]\sdot5\sdot2}{\left[\left(4\sdot2\right)+1\right]\sdot2}=\frac{130}{9\sdot2}=\frac{130}{18}=7+\frac{2}{9}}}](/mediawiki/images/math/9/0/4/90401ad811a129498058b68894f94e7c.png)
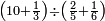
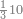
![\scriptstyle{\color{blue}{\left(10+\frac{1}{3}\right)\div\left(\frac{2}{5}+\frac{1}{6}\right)=\frac{\left[\left(10\sdot3\right)+1\right]\sdot5\sdot6}{\left[\left(2\sdot6\right)+\left(1\sdot5\right)\right]\sdot3}=\frac{930}{17\sdot3}=\frac{930}{51}=18+\frac{4}{17}}}](/mediawiki/images/math/d/4/1/d413338a273f068c2ad374f2cca71307.png)
![\scriptstyle\left[4+\frac{3}{8}+\left(\frac{1}{2}\sdot\frac{1}{8}\right)\right]\div\frac{3}{5}](/mediawiki/images/math/3/2/d/32d11722e462ccb9eb7450bb533cbc0c.png)
![\scriptstyle{\color{blue}{\left[4+\frac{3}{8}+\left(\frac{1}{2}\sdot\frac{1}{8}\right)\right]\div\frac{3}{5}=\frac{\left[\left[\left[\left(4\sdot8\right)+3\right]\sdot2\right]+1\right]\sdot5}{3\sdot8\sdot2}=\frac{71\sdot5}{48}=\frac{355}{48}=7+\frac{3}{8}+\left(\frac{1}{6}\sdot\frac{1}{8}\right)}}](/mediawiki/images/math/2/e/1/2e1e893e31a4359aacb7c4ffbb7f8ab4.png)
![\scriptstyle\left[2+\frac{6}{7}+\left(\frac{2}{3}\sdot\frac{1}{7}\right)\right]\div\left(\frac{4}{5}\sdot\frac{1}{6}\right)](/mediawiki/images/math/e/3/b/e3b6d865fd628df8725345bed9550838.png)
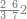
![\scriptstyle{\color{blue}{\left[2+\frac{6}{7}+\left(\frac{2}{3}\sdot\frac{1}{7}\right)\right]\div\left(\frac{4}{5}\sdot\frac{1}{6}\right)=\frac{\left[\left[\left[\left(2\sdot7\right)+6\right]\sdot3\right]+2\right]\sdot5\sdot6}{4\sdot7\sdot3}=\frac{1860}{84}=22+\frac{1}{7}}}](/mediawiki/images/math/2/7/1/271fd8b64cd98eb5af0364510c8109dc.png)
![\scriptstyle\left[9+\frac{5}{6}+\left(\frac{1}{4}\sdot\frac{1}{6}\right)\right]\div\left[\frac{1}{7}+\left(\frac{1}{2}\sdot\frac{1}{7}\right)\right]](/mediawiki/images/math/c/a/c/cac708cd096182197de710a38d627540.png)
![\scriptstyle{\color{blue}{\left[9+\frac{5}{6}+\left(\frac{1}{4}\sdot\frac{1}{6}\right)\right]\div\left[\frac{1}{7}+\left(\frac{1}{2}\sdot\frac{1}{7}\right)\right]=\frac{\left[\left[\left[\left(9\sdot6\right)+5\right]\sdot4\right]+1\right]\sdot7\sdot2}{\left[\left(1\sdot2\right)+1\right]\sdot6\sdot4}=\frac{3318}{72}=46+\left(\frac{6}{8}\sdot\frac{1}{9}\right)}}](/mediawiki/images/math/1/8/8/188ef3818bb11cf20db7a3eb065b8bf6.png)
![\scriptstyle\left[3+\frac{3}{10}+\left(\frac{1}{2}\sdot\frac{1}{10}\right)\right]\div\left(\frac{3}{4}+\frac{3}{11}\right)](/mediawiki/images/math/d/5/0/d50f89556f17cf14018f8175b13f65fe.png)
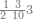
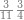
![{\color{blue}{\begin{align}\scriptstyle\left[3+\frac{3}{10}+\left(\frac{1}{2}\sdot\frac{1}{10}\right)\right]\div\left(\frac{3}{4}+\frac{3}{11}\right)&\scriptstyle=\frac{\left[\left[\left[\left(3\sdot10\right)+3\right]\sdot2\right]+1\right]\sdot4\sdot11}{\left[\left(3\sdot11\right)+\left(3\sdot4\right)\right]\sdot10\sdot2}\\&\scriptstyle=\frac{2948}{45\sdot10\sdot2}\\&\scriptstyle=\frac{2948}{900}\\&\scriptstyle=3+\frac{2}{10}+\left(\frac{7}{10}\sdot\frac{1}{10}\right)+\left(\frac{5}{9}\sdot\frac{1}{10}\sdot\frac{1}{10}\right)\\\end{align}}}](/mediawiki/images/math/2/5/f/25f3fbc6899c91ce30eb699b6625f0ed.png)
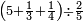
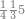

![\scriptstyle{\color{blue}{\left(5+\frac{1}{3}+\frac{1}{4}\right)\div\frac{2}{5}=\frac{\left[\left(5\sdot3\sdot4\right)+\left(1\sdot4\right)+\left(1\sdot3\right)\right]\sdot5}{2\sdot3\sdot4}=\frac{67\sdot5}{24}=\frac{335}{24}=13+\frac{7}{8}+\left(\frac{2}{3}\sdot\frac{1}{8}\right)}}](/mediawiki/images/math/4/0/b/40b94d1ced716f5e67decc3d92050e33.png)
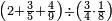
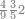
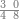
![{\color{blue}{\begin{align}\scriptstyle\left(2+\frac{3}{5}+\frac{4}{9}\right)\div\left(\frac{3}{4}\sdot\frac{1}{8}\right)&\scriptstyle=\frac{\left[\left(2\sdot5\sdot9\right)+\left(3\sdot9\right)+\left(4\sdot5\right)\right]\sdot4\sdot8}{3\sdot5\sdot9}\\&\scriptstyle=\frac{4384}{135}\\&\scriptstyle=32+\frac{4}{9}+\left(\frac{1}{5}\sdot\frac{1}{9}\right)+\left(\frac{1}{3}\sdot\frac{1}{5}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/c/a/f/caf9fd6986650652df3ccb31053b7198.png)
![\scriptstyle\left(8+\frac{3}{11}+\frac{5}{7}\right)\div\left[\frac{5}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)\right]](/mediawiki/images/math/e/5/1/e51880c2c718f84daf210b6c68fb1a69.png)
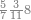
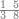
![{\color{blue}{\begin{align}\scriptstyle\left(8+\frac{3}{11}+\frac{5}{7}\right)\div\left[\frac{5}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)\right]&\scriptstyle=\frac{\left[\left(8\sdot11\sdot7\right)+\left(3\sdot7\right)+\left(5\sdot11\right)\right]\sdot8\sdot3}{\left[\left(5\sdot3\right)+1\right]\sdot11\sdot7}\\&\scriptstyle=\frac{16608}{16\sdot11\sdot7}\\&\scriptstyle=\frac{16608}{1232}\\&\scriptstyle=13+\frac{5}{11}+\left(\frac{2}{8}\sdot\frac{1}{11}\right)+\left(\frac{2}{7}\sdot\frac{1}{8}\sdot\frac{1}{11}\right)\\\end{align}}}](/mediawiki/images/math/2/6/3/26345567afe30299608fb53d10404d1a.png)
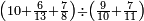
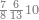
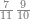
![{\color{blue}{\begin{align}\scriptstyle\left(10+\frac{6}{13}+\frac{7}{8}\right)\div\left(\frac{9}{10}+\frac{7}{11}\right)&\scriptstyle=\frac{\left[\left(10\sdot13\sdot8\right)+\left(6\sdot8\right)+\left(7\sdot13\right)\right]\sdot10\sdot11}{\left[\left(9\sdot11\right)+\left(7\sdot10\right)\right]\sdot13\sdot8}\\&\scriptstyle=\frac{129690}{17576}\\&\scriptstyle=7+\frac{4}{13}+\left(\frac{12}{13}\sdot\frac{1}{13}\right)+\left(\frac{2}{8}\sdot\frac{1}{13}\sdot\frac{1}{13}\sdot\frac{1}{13}\right)\\\end{align}}}](/mediawiki/images/math/c/f/c/cfc98641ae1508c02ddefc70edea0a8e.png)
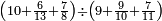
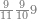
![\scriptstyle{\color{blue}{\left(10+\frac{6}{13}+\frac{7}{8}\right)\div\left(9+\frac{9}{10}+\frac{7}{11}\right)=\frac{\left[\left(10\sdot13\sdot8\right)+\left(6\sdot8\right)+\left(7\sdot13\right)\right]\sdot10\sdot11}{\left[\left(9\sdot10\sdot11\right)+\left(9\sdot11\right)+\left(7\sdot10\right)\right]\sdot13\sdot8}=\frac{129690}{120536}}}](/mediawiki/images/math/5/e/7/5e7c0209fa719072d266c1fd2340aa2e.png)
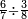
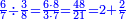
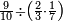
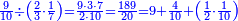
![\scriptstyle\frac{12}{13}\div\left[\frac{1}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)\right]](/mediawiki/images/math/a/8/e/a8e55ff0cbe3a1bbc2b04795da66cd11.png)
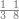
![\scriptstyle{\color{blue}{\frac{12}{13}\div\left[\frac{1}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)\right]=\frac{12\sdot8\sdot3}{\left[\left(1\sdot3\right)+1\right]\sdot13}=\frac{288}{52}=5+\frac{7}{13}}}](/mediawiki/images/math/3/8/3/383b059504fac1676fb11bca94866215.png)
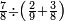
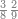
![\scriptstyle{\color{blue}{\frac{7}{8}\div\left(\frac{2}{9}+\frac{3}{8}\right)=\frac{7\sdot9\sdot8}{\left[\left(2\sdot8\right)+\left(3\sdot9\right)\right]\sdot8}=\frac{504}{344}=1+\frac{20}{43}}}](/mediawiki/images/math/6/4/b/64b0d6c35d3ef980ed4ef294e4b97bee.png)
![\scriptstyle\left[\frac{9}{11}+\left(\frac{1}{2}\sdot\frac{1}{11}\right)\right]\div\left[\frac{1}{5}+\left(\frac{1}{2}\sdot\frac{1}{5}\right)\right]](/mediawiki/images/math/f/d/2/fd206d89bd19df846cbc0da8d760d653.png)
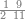
![\scriptstyle{\color{blue}{\left[\frac{9}{11}+\left(\frac{1}{2}\sdot\frac{1}{11}\right)\right]\div\left[\frac{1}{5}+\left(\frac{1}{2}\sdot\frac{1}{5}\right)\right]=\frac{\left[\left(9\sdot2\right)+1\right]\sdot5\sdot2}{\left[\left(1\sdot2\right)+1\right]\sdot11\sdot2}=2+\frac{9}{11}+\left(\frac{4}{6}\sdot\frac{1}{11}\right)}}](/mediawiki/images/math/d/5/b/d5b65f99ebbce183ca4395348f3c468f.png)
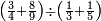
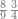
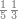
![\scriptstyle{\color{blue}{\left(\frac{3}{4}+\frac{8}{9}\right)\div\left(\frac{1}{3}+\frac{1}{5}\right)=\frac{\left[\left(3\sdot9\right)+\left(8\sdot4\right)\right]\sdot3\sdot5}{\left[\left(1\sdot5\right)+\left(1\sdot3\right)\right]\sdot4\sdot9}=3+\left(\frac{5}{8}\sdot\frac{1}{9}\right)+\left(\frac{1}{4}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)}}](/mediawiki/images/math/b/c/3/bc33799452153a7ae54d804e04f4a4f0.png)
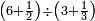
![\scriptstyle{\color{blue}{\left(6+\frac{1}{2}\right)\div\left(3+\frac{1}{3}\right)=\frac{\left[\left(6\sdot2\right)+1\right]\sdot3}{\left[\left(3\sdot3\right)+1\right]\sdot2}=\frac{39}{20}=1+\frac{9}{10}+\left(\frac{1}{2}\sdot\frac{1}{10}\right)}}](/mediawiki/images/math/8/7/6/8768c2ae2ba1d173b5d98708d69e12d9.png)
![\scriptstyle\left[4+\frac{7}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)\right]\div\left[1+\frac{1}{11}+\left(\frac{1}{2}\sdot\frac{1}{11}\right)\right]](/mediawiki/images/math/0/8/e/08e64b5a21bf76029b304cab735acaf4.png)
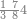
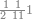
![{\color{blue}{\begin{align}\scriptstyle\left[4+\frac{7}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)\right]\div\left[1+\frac{1}{11}+\left(\frac{1}{2}\sdot\frac{1}{11}\right)\right]&\scriptstyle=\frac{\left[\left[\left[\left(4\sdot8\right)+7\right]\sdot3\right]+1\right]\sdot11\sdot2}{\left[\left[\left[\left(1\sdot11\right)+1\right]\sdot2\right]+1\right]\sdot8\sdot3}\\&\scriptstyle=\frac{118\sdot11\sdot2}{25\sdot8\sdot3}\\&\scriptstyle=\frac{2596}{600}\\&\scriptstyle=4+\frac{3}{10}+\left(\frac{2}{10}\sdot\frac{1}{10}\right)+\left(\frac{4}{6}\sdot\frac{1}{10}\sdot\frac{1}{10}\right)\\\end{align}}}](/mediawiki/images/math/6/6/e/66e2dbe5a5dbc373464eb83672a42ad2.png)
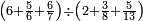
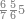
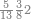
![{\color{blue}{\begin{align}\scriptstyle\left(6+\frac{5}{6}+\frac{6}{7}\right)\div\left(2+\frac{3}{8}+\frac{5}{13}\right)&\scriptstyle=\frac{\left[\left(6\sdot6\sdot7\right)+\left(5\sdot7\right)+\left(6\sdot6\right)\right]\sdot8\sdot13}{\left[\left(2\sdot8\sdot13\right)+\left(3\sdot13\right)+\left(5\sdot8\right)\right]\sdot6\sdot7}\\&\scriptstyle=\frac{323\sdot8\sdot13}{287\sdot6\sdot7}\\&\scriptstyle=\frac{33592}{12054}\\&\scriptstyle=2+\frac{32}{41}+\left(\frac{1}{7}\sdot\frac{1}{41}\right)+\color{red}{\left(\frac{5}{7}\sdot\frac{1}{7}\sdot\frac{1}{41}\right)+\left(\frac{2}{3}\sdot\frac{1}{7}\sdot\frac{1}{7}\sdot\frac{1}{41}\right)}\\\end{align}}}](/mediawiki/images/math/b/d/7/bd747e680dd563a9f83af0fca25d5cff.png)
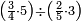
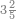
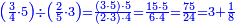
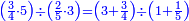
![\scriptstyle\left[\frac{3}{5}\sdot\left(6+\frac{1}{4}\right)\right]\div\left[\frac{2}{3}\sdot\left(4+\frac{1}{2}\right)\right]](/mediawiki/images/math/9/0/f/90f436caad26a7b1c6dd52057663f3a4.png)
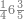
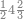
![{\color{blue}{\begin{align}\scriptstyle\left[\frac{3}{5}\sdot\left(6+\frac{1}{4}\right)\right]\div\left[\frac{2}{3}\sdot\left(4+\frac{1}{2}\right)\right]&\scriptstyle=\frac{\left[\left[\left(6\sdot4\right)+1\right]\sdot3\right]\sdot3\sdot2}{\left[\left[\left(4\sdot2\right)+1\right]\sdot2\right]\sdot5\sdot4}\\&\scriptstyle=\frac{\left(25\sdot3\right)\sdot3\sdot2}{\left(9\sdot2\right)\sdot5\sdot4}\\&\scriptstyle=\frac{75\sdot3\sdot2}{18\sdot5\sdot4}\\&\scriptstyle=\frac{450}{360}\\&\scriptstyle=1+\frac{1}{4}\\\end{align}}}](/mediawiki/images/math/0/c/1/0c1e826f3e57c53540f5b3c35c37635b.png)
![\scriptstyle{\color{blue}{\left[\frac{3}{5}\sdot\left(6+\frac{1}{4}\right)\right]\div\left[\frac{2}{3}\sdot\left(4+\frac{1}{2}\right)\right]=\left(3+\frac{3}{4}\right)\div3=1+\frac{1}{4}}}](/mediawiki/images/math/7/d/9/7d94c4cf5abf2b3ca33a98f5bbc1fb84.png)
![\scriptstyle10\div\left[\left[\frac{7}{8}\sdot\left(5+\frac{1}{3}\right)\right]-\left[\frac{1}{3}\sdot\left(2+\frac{1}{4}\right)\right]\right]](/mediawiki/images/math/1/b/7/1b7f16e412d991a2e6ac44c44e98d15a.png)
![\scriptstyle\left[\left[\left(\frac{3}{4}\sdot\frac{3}{5}\right)\sdot9\right]\div\frac{3}{10}\right]\div\left[\left(\frac{2}{3}\sdot7\right)-\left[\left(2+\frac{1}{8}\right)\div\left[\frac{7}{8}+\left(\frac{1}{2}\sdot\frac{1}{8}\right)\right]\right]\right]](/mediawiki/images/math/5/d/0/5d035686f0d758ca5d6e74040f716d33.png)
![{\color{blue}{\begin{align}&\scriptstyle\left[\left[\left(\frac{3}{4}\sdot\frac{3}{5}\right)\sdot9\right]\div\frac{3}{10}\right]\div\left[\left(\frac{2}{3}\sdot7\right)-\left[\left(2+\frac{1}{8}\right)\div\left[\frac{7}{8}+\left(\frac{1}{2}\sdot\frac{1}{8}\right)\right]\right]\right]=\\&\scriptstyle=\left[4+\left(\frac{1}{2}\sdot\frac{1}{10}\right)\right]\div\left[\frac{3}{10}\sdot\left[\left(4+\frac{2}{3}\right)-\left[2+\frac{1}{5}+\left(\frac{1}{3}\sdot\frac{1}{5}\right)\right]\right]\right]\\&\scriptstyle=\left[4+\left(\frac{1}{2}\sdot\frac{1}{10}\right)\right]\div\left[\frac{3}{10}\sdot\left(2+\frac{2}{5}\right)\right]\\&\scriptstyle=\left[4+\left(\frac{1}{2}\sdot\frac{1}{10}\right)\right]\div\left[\frac{7}{10}+\left(\frac{1}{5}\sdot\frac{1}{10}\right)\right]\\\end{align}}}](/mediawiki/images/math/b/9/2/b929f740991d70e5bfb1c8bdea920c15.png)
![\scriptstyle{\color{blue}{\left[4+\left(\frac{1}{2}\sdot\frac{1}{10}\right)\right]\div\left[\frac{7}{10}+\left(\frac{1}{5}\sdot\frac{1}{10}\right)\right]=5+\frac{5}{8}}}](/mediawiki/images/math/b/9/1/b9184232930646867d1c51fe56b117fe.png)
![\scriptstyle\left[\left[\left[\left[\left(100\div2\right)\div\frac{1}{2}\right]\div4\right]\div\frac{1}{3}\right]\div\frac{3}{4}\right]\div5](/mediawiki/images/math/0/c/e/0ce5a89a17928644be23031e62662c90.png)
![{\color{blue}{\begin{align}\scriptstyle\left[\left[\left[\left[\left(100\div2\right)\div\frac{1}{2}\right]\div4\right]\div\frac{1}{3}\right]\div\frac{3}{4}\right]\div5&\scriptstyle=100\div\left[\left[\left[\left[\left(2\sdot\frac{1}{2}\right)\sdot4\right]\sdot\frac{1}{3}\right]\sdot\frac{3}{4}\right]\sdot5\right]\\&\scriptstyle=100\div\left[\left[\left[\left(1\sdot4\right)\sdot\frac{1}{3}\right]\sdot\frac{3}{4}\right]\sdot5\right]\\&\scriptstyle=100\div\left[\left[\left(4\sdot\frac{1}{3}\right)\sdot\frac{3}{4}\right]\sdot5\right]\\&\scriptstyle=100\div\left[\left[\left(1+\frac{1}{3}\right)\sdot\frac{3}{4}\right]\sdot5\right]\\&\scriptstyle=100\div\left(1\sdot5\right)\\&\scriptstyle=100\div5=20\\\end{align}}}](/mediawiki/images/math/8/b/c/8bce1c36060f1ae22620f343fb3d9505.png)
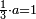
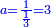
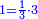
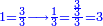
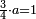
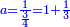
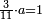
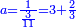
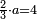
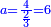
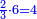
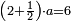
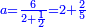
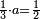
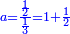
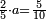
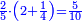
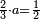
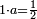
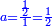
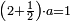
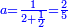
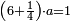
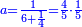
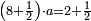
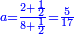
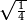
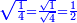
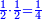
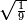

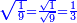
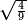

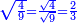
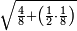
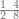
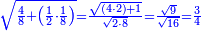
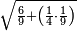
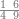
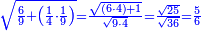
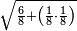
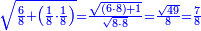
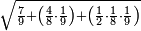
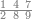
![{\color{blue}{\begin{align}\scriptstyle\sqrt{\frac{7}{9}+\left(\frac{4}{8}\sdot\frac{1}{9}\right)+\left(\frac{1}{2}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)}&\scriptstyle=\frac{\sqrt{\left[\left[\left(7\sdot8\right)+4\right]\sdot2\right]+1}}{\sqrt{9\sdot8\sdot2}}\\&\scriptstyle=\frac{\sqrt{\left(60\sdot2\right)+1}}{\sqrt{144}}\\&\scriptstyle=\frac{\sqrt{121}}{\sqrt{144}}\\&\scriptstyle=\frac{11}{12}\\&\scriptstyle=\frac{5}{6}+\left(\frac{1}{2}\sdot\frac{1}{6}\right)\\\end{align}}}](/mediawiki/images/math/4/6/c/46c73bc6718041a7553c9e291bc85bfd.png)
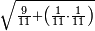
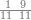
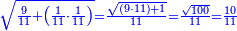
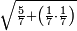
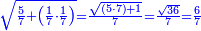
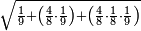
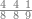
![\scriptstyle{\color{blue}{\sqrt{\frac{1}{9}+\left(\frac{4}{8}\sdot\frac{1}{9}\right)+\left(\frac{4}{8}\sdot\frac{1}{8}\sdot\frac{1}{9}\right)}=\frac{\sqrt{\left[\left[\left(1\sdot8\right)+4\right]\sdot8\right]+4}}{\sqrt{9}\sdot8}=\frac{\sqrt{100}}{3\sdot8}=\frac{10}{3\sdot8}=\frac{3}{8}+\left(\frac{1}{3}\sdot\frac{1}{8}\right)}}](/mediawiki/images/math/6/a/2/6a2c12f460c6aa4c06cf483ec0fcd7db.png)
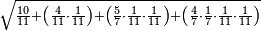
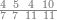
![{\color{blue}{\begin{align}\scriptstyle\sqrt{\frac{10}{11}+\left(\frac{4}{11}\sdot\frac{1}{11}\right)+\left(\frac{5}{7}\sdot\frac{1}{11}\sdot\frac{1}{11}\right)+\left(\frac{4}{7}\sdot\frac{1}{7}\sdot\frac{1}{11}\sdot\frac{1}{11}\right)}&\scriptstyle=\frac{\sqrt{\left[\left[\left[\left[\left(10\sdot11\right)+4\right]\sdot7\right]+5\right]\sdot7\right]+4}}{11\sdot7}\\&\scriptstyle=\frac{\sqrt{5625}}{11\sdot7}\\&\scriptstyle=\frac{75}{11\sdot7}\\&\scriptstyle=\frac{10}{11}+\left(\frac{5}{7}\sdot\frac{1}{11}\right)\\\end{align}}}](/mediawiki/images/math/e/c/3/ec36cc388eabf57d91324061ad202aff.png)
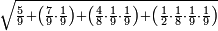
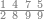
![{\color{blue}{\begin{align}\scriptstyle\sqrt{\frac{5}{9}+\left(\frac{7}{9}\sdot\frac{1}{9}\right)+\left(\frac{4}{8}\sdot\frac{1}{9}\sdot\frac{1}{9}\right)+\left(\frac{1}{2}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{9}\right)}&\scriptstyle=\frac{\sqrt{\left[\left[\left[\left[\left(5\sdot9\right)+7\right]\sdot8\right]+4\right]\sdot2\right]+1}}{\sqrt{2\sdot8}\sdot9}\\&\scriptstyle=\frac{\sqrt{841}}{\sqrt{16}\sdot9}\\&\scriptstyle=\frac{29}{4\sdot9}\\&\scriptstyle=\frac{7}{9}+\left(\frac{1}{4}\sdot\frac{1}{9}\right)\\\end{align}}}](/mediawiki/images/math/b/4/4/b44b47a1912abf5d78c88e57afda21d5.png)
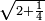
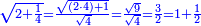
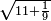
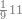
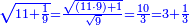
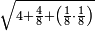
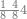
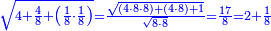
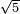
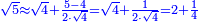
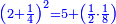
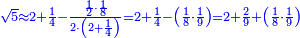
![\scriptstyle{\color{blue}{\left[2+\frac{2}{9}+\left(\frac{1}{8}\sdot\frac{1}{9}\right)\right]^2=5+\left(\frac{1}{8}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{9}\right)}}](/mediawiki/images/math/c/7/e/c7ecbb64983979bd2585829b2ff90688.png)
![\scriptstyle{\color{blue}{\sqrt{5}\approx2+\frac{2}{9}+\left(\frac{1}{8}\sdot\frac{1}{9}\right)-\frac{\frac{1}{8}\sdot\frac{1}{8}\sdot\frac{1}{9}\sdot\frac{1}{9}}{2\sdot\left[2+\frac{2}{9}+\left(\frac{1}{8}\sdot\frac{1}{9}\right)\right]}}}](/mediawiki/images/math/0/2/a/02af5e239bfa7e479b8d4fc3237bda47.png)
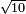
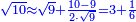
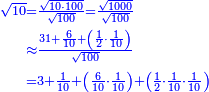
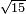
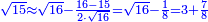
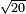
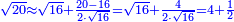
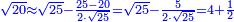
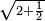
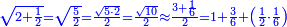
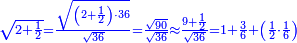
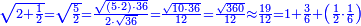
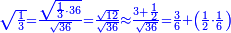
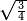
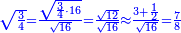
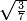
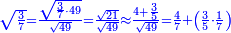


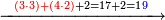
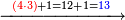
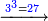
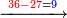
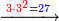
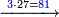
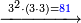
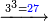

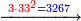
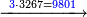
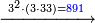

![\scriptstyle\longrightarrow{\color{red}{\sqrt[3]{36926037}}}={\color{blue}{333}}](/mediawiki/images/math/6/5/f/65f700e02a2e957ad7ff516e45bd7f4b.png)