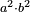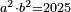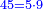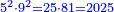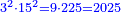Difference between revisions of "לקוטים מספר פראלוקא"
(→Trapezoid) |
(→Trapezoid) |
||
| Line 6,465: | Line 6,465: | ||
|- | |- | ||
| colspan="2"| | | colspan="2"| | ||
| − | ::<math>\scriptstyle{\color{blue}{\frac{\frac{20^2-\left[\left(21-14\right)^2+15^2\right]}{2}}{21-14}+\left(21-14\right)=\frac{\frac{20^2-\left(7^2+15^2\right)}{2}}{7}+7=\frac{\frac{400-\left(49+225\right)}{2}}{7}+7=\frac{\frac{400-274}{2}}{7}+7=\frac{\frac{126}{2}}{7}+7=\frac{63}{7}+7=9+7=16}}</math> | + | ::<math>\scriptstyle{\color{blue}{\begin{align}\scriptstyle\frac{\frac{20^2-\left[\left(21-14\right)^2+15^2\right]}{2}}{21-14}+\left(21-14\right)&\scriptstyle=\frac{\frac{20^2-\left(7^2+15^2\right)}{2}}{7}+7=\frac{\frac{400-\left(49+225\right)}{2}}{7}+7\\&\scriptstyle=\frac{\frac{400-274}{2}}{7}+7=\frac{\frac{126}{2}}{7}+7=\frac{63}{7}+7=9+7=16\\\end{align}}}</math> |
|- | |- | ||
| | | | ||
Revision as of 07:23, 6 June 2023
Contents
| Excerpts Collected from the Book of Fra Luca | [1]לקוטים מספר פראלוקא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Introduction |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 חכמי המספר המשילו האחד אל האל ית' כי כמו שהאל ית' הוא עלת העלות וממנו נאצלו כל הנבראים וכלם צריכין לו והוא אין צריך לאחד מהם כן האחד הוא יסוד כל מספר והוא יסוד כל המספרים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| גם המשילו האחד אל המרכז כי כמו שהמרכז הוא שרש העגול כן האחד שרש ויסוד כל המספרים וממנו נאצלו כל המספרים והוא יסודם ושרשם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנה נרצה לחלק זה המספר לג' חלקים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| החלק האחד ידבר על העיונית מן המספר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והחלק השני ידבר על המעשית מהמספר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [2]והחלק השלישי ידבר על המעשית מההנדסה וזה החלו לעשות בג"ה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Section One - Theoretical Arithmetic |
2 החלק הראשון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אומר כי מספר ה' וו' שומרים את עצמן במרובעם ובמעוקבם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון ה' פעמים ה' הם כ"ה והנה הה' נרגשת ובמעוקבם ה' פעמים ה' הם כ"ה וה' פעמים כ"ה הוא קכ"ה גם היא נרגשת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכך תאמר מהו' כי אם תקח מרובע ו' הם ל"ו והיא נרגשת גם במרובעם כי ו' פעמי' ו' הם ל"ו וו' פעמים ל"ו הם רי"ו גם היא נרגשת במעוקב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן הא' שומרת עצמה במרובע ובמעוקב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ועל כן אמר א"ע בפרשת שמות כי אותיות אהיה שומרות עצמן במרובען ובמעוקבן | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Definition of the superabundant number: The discussion on the superabundant number, such as 12 or 24, for the sum of its parts exceeds over it, i.e. when you sum all the parts generated from 12, the result is 16, so its parts are more than its whole, and this number is called in their language "numero abbondante". | 3 המאמר במספר המוסיף חלק כמו מספר י"ב או כ"ד כי חלקיו מקובצים יעדיפו עליו ר"ל כי כשתקבץ כל החלקים הנעשים מי"ב יעלו י"ו א"כ חלקיו יותר מכלו וזה המספר נקרא בלשונם נומירו אבונדאנטי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Definition of the deficient number: The discussion on the number, which the sum of its parts is less than the number [itself]; as eight, for the sum of its parts, which are the half, quarter and eighth, is only 7; and this number is called in their language "numero povero". | 4 המאמר במספר אשר חלקיו מקובצים מחסירים מהמספר כאלו תאמר מספר שמונה כי חלקיו מקובצים אינם כי אם ז' והוא החצי והרובע והשמינית וזה המספר נקרא בלשונם נומירו פווירו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Definition of the perfect number: The discussion on the perfect number, which is the number, which the sum of its parts is the same as the given number no more and no less; as 6, for when you sum all its parts they are the same as it, since its half is 2, its third is 2, its sixth is 1 and the total is 6, as it is; and this number is called "numero perfetto". | 5 המאמר במספר שלם והוא המספר אשר חלקיו מקובצים הם כמו המספר המונח לא יוסיף ולא יגרע והוא כמו מספר ו' כי כשתקבץ כל חלקיו יעלו כמוהו כי חציו הוא ג' ושלישיתו הוא ב' ושישיתו א' ובין כלם ו' כמו שהיה וזה המספר נקרא נומירו פירפיטו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 המאמר איך נכיר ממספר מה מונח אם הוא שלם או בלתי שלם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ראה אם במדרגת האחדים יש בו ו' או ח' אפשר להיותו מספר שלם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם אין לא ו' ולא ח' הוא נמנע היותו מספר שלם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנועם הוא בזה כי לא תמצא מספר שלם כי אם אחד בכל מדרגה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנה ו' הוא שלם באחדים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכ"ח בעשרות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנה כל המספרים מכל שאר מדרגות נמשכים אחר אלו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המספר השלם במאיות הוא תצ"ו והנך רואה כי הו' נמצאת באחדים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והמספר השלם [3]באלפים תמצא הח' באחדים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תדין בשאר המדרגות אחר קט"ו אלו בא' ו' ובאחר ח' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 המאמר למצא הדרך ואומר כי האל ברא עולמו בששת ימים יען כי מספר ו' הוא מספר שלם וביום ו' נברא אדם להורות כי הוא השלם מכל הנבראים ואומר כי הדרך הוא כך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נמצא הראשון קח אחד וחברהו עם ב' ויהיו ג' ותראה אם מספר ג' הוא מורכב והנך רואה כי הוא פשוט ולכן כפול אותו על ב' ויהיו ו' והוא מספר שלם במדרגה הראשנה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולמצא השני קח א'ב'ד' וקבצם ויהיו ז' ותראה אם הוא מורכב והנך רואה כי הוא בלתי מורכב לכן כפול ז' על המספר האחרון אשר לקחת שהיה ד' ויעלה כ"ח והוא מספר שלם במדרגה שניה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולמצא הג' קח א'ב'ד'ח' וקבצם ויעלו ט"ו והנך רואה כי הוא מורכב מג' וה' ולכן קח מספר האחר שהוא א'ב'ד'ח' י"ו ויעלו ל"א והוא בלתי מורכב כפלם על מספר אחרון שלקחת והוא י"ו ויעלה תצ"ו והוא מספר שלם במדרגת המאיות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולמצא הד' קח א'ב'ד'ח' י"ו ל"ב וקבצם ויהיו ס"ג והוא מספר מורכב מכ"א וג' לכן קח המספר האחר שהוא א'ב'ד'ח' י"ו ל"ב ס"ד וקבצם יעלו קכ"ז וכפלם על המספר האחרון שהוא ס"ד ויעלו ח' אלפים וקכ"ח והוא הרביעי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובזה הדרך תוכל למצא לשאר מדרגות הנמשכות אחר אלו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 המאמר להכיר אם המספר הוא מספר שלם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והדרך הוא כך ראה אם תחלק אותו המספר על חצי שתוכל לחלקו בצימצום והיוצא תשוב לחלקו על חצי והיוצא מן החלוקה עוד תחלק על חצי וכן לעולם עד שתגיע למספר שלא תוכל לחלקו על חצי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואחר שתגיע לאותו המספר בלתי מחולק שוב וחלק כל המספר אשר בקשת לדעת אם הוא מספר (שלם) באותו חלק בלתי מתחלק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד תחלקהו לאותו המספר אשר הוא למעלה ממנו בטור אשר הוא על המספר הבלתי מתחלק וכן לעולם תחלקהו על כל המספרים אשר הם על הטורים העליונים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תוכל לחלק אותו מספר עד שתגיע [4]שלא יצא מן החלוקה כי אם אחד תוכל להכיר כי הוא מספר שלם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם לא תוכל לחלקו אינו מספר שלם וכל אותם החלוקות אשר עשית מאז הגעת באותה חלוקה שלא יכולתה לחלקה על ב' עד שחלקת כל המספר המבוקש עד שהגעת אל הב' הם המספרים אשר ראוי לקחת כדי למצא מספר שלם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל הנה יש לנו מספר תצ"ו ונרצה לדעת אם הוא מספר שלם ומכמה מספרי' הוא מורכב מתחיל מן האחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
חלק תצ"ו על ב' ויצא לך רמ"ח | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
עוד חלק רמ"ח על ב' ויצא לך קכ"ד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
עוד חלק קכ"ד על ב' ויצא לך ס"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
עוד חלק ס"ב על ב' ויצא לך ל"א | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עוד חלק ל"א על ב' ולא תוכל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
על כן חלק המספר המבוקש שהוא תצ"ו על ל"א ויצא י"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
עוד חלק תצ"ו על ס"ב שהוא על ל"א ויצא ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
עוד חלק תצ"ו על רמ"ח שהוא על קכ"ד ויצא ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
עוד חלק תצ"ו על תצ"ו ויצא א' כי מספר תצ"ו הוא על רמ"ח | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| א"כ מספר תצ"ו הוא מספר שלם כי הגעת החלוקה עד א' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והוא מורכב מא' וב' וד' וח' י"ו ול"ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו שידעת הדרך הנזכר למטה וזאת היא הצורה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכל אלו המספרים מקובצים עולים תצ"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| משל אחר הנה ממספר ח' אלפים וקכ"ח נרצה לדעת אם הוא מספר שלם ואם הוא מספר שלם מכמה מספרים הוא מורכב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ראשנה חלק ח' אלפים וקכ"ח על ב' ויצא ד' אלפים וס"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד חלק ד' אלפים וס"ד על ב' ויצא ב' אלפים ול"ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד חלק ב' אלפים ול"ב על ב' ויצא אלף וי"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד חלק אלף וי"ו על ב' ויצא ה' מאות וח' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד חלק ה' מאות וח' על ב' ויצא רנ"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עו' חלקם ויצא קכ"ז | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עו' חלקם ולא תוכל על כן חלק המספר שהוא ח' אלפים וקכ"ח על על קכ"ז ויצא ס"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד חלק קי"ו [5]על רנ"ו שהוא (על) קכ"ז ויצא לך ס"ב ל"ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד חלק ח' אלפים וקכ"ח על ה' מאות (וח') ויצא לך י"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עו' חלק ח' אלפים וקכ"ח על אלף וי"ו ויצא לך ד' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עו' חלק ח' אלפים וקכ"ח על ד' אלפים וס"ד ויצא לך ב' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד חלק ח' אלפים על עצמם ויצא א' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה א"כ תדין כי זה המספר הוא מספר שלם כי אם תקבץ כל החלוקות יצא ח' אלפים וקכ"ח כמו שהוא נרשם פה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 המאמר הוא למצא מספרים כי כשתחלק המספר על חצי וחציו על חצי גם חצי חציו לעולם תוכל לחלקו בלי שום שבר עד שתגיע אל האחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל קח א' וכפלהו ויהיו ב' וכפלהו ויהיו ד' וכפלהו ויהיו ח' כפלהו ויהיו י"ו כפלהו ויהיו ל"ב כפלם והם ס"ד וכן לעולם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ועתה אם תחלק אותו מספר על ב' והיוצא על ב' תוכל לחלקו עד שתגיע אל האחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ומסגלות זה המספר כי אם מאלו המספרים אשר קבצת תקח המספר האמצעי אם הוא נפרד ר"ל אם המספרים אשר יש לך הם נפרדי' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל יש לנו א' ב' ד' ח' י"ו ל"ב ס"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה מספר ח' הוא אמצעי כפלם על עצמם ויהיו ס"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כן אם תכפול הראשון שהוא א' על האחרון שהוא ס"ד יצא ס"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן אם תכפול המספר השני שהוא ב' על הו' שהוא ל"ב יצא ס"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן אם תכפול המספר הג' שהוא ד' על המספר ה' שהוא י"ו יצא ס"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תוכל לעשות ממספרים מתיחסים מיחס אחר כי זה היחס אשר עשינו הוא יחס דופלא שהוא יחס א' אל ב' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כן תוכל לעשות מטריפלא או קואטרופלא או קואינקופלא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנה נעשה מיחס טריפלא שהוא יחס א' אל ג' כמו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי הראשון א' ג' ט' כ"ז פ"א | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אם תכפול האמצעי שהוא ט' על עצמו יעלה פ"א | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כן אם תכפול המספר ראשון שהוא א' על האחרון שהוא פ"א יעלה פ"א | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [6]וכן אם תכפול השני שהוא ג' על הרביעי שהוא כ"ז יעלה פ"א | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן אם תכפול ט' שהוא השלישי על כ"ז עצמו יעלה פ"א | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כן תוכל לעשות מכל היחסים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן אם הם מיחס א' אל ד' הנקרא בלשונם קואטרופלא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון א' ד' י"ו ס"ד רי"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אם תכפול האמצעי על עצמם שהם י"ו יעלה רי"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן אם תכפול ד' שהוא השני על ס"ד שהוא רביעי יעלה רי"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם המספר הם זוגות כגון א' ב' ד' ח' י"ו ל"ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אם תכפול ב' אמצעיים שהם ד"ח יעלו ל"ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כן אם תכפול הראשון על ל"ב שהוא האחרון יעלו ל"ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן אם תכפול השני שהוא ב' על י"ו יהיו ל"[ב] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כן תוכל לעשות אם היחס הוא משלשה או מארבעה או מאיזה יחס אחר שיזדמן ואלו המספרים נקראים בלשונם נומירי אפורפורציאונאטי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 המאמר לקבץ מספרים יחסיים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון לקבץ א ב' וד' וח' וי"ו ול"ב וכן לעולם ראה היחס הבא אחר ל"ב והוא ס"ד הסר ממנו אחד וישארו ס"ג והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11 המאמר לקחת מספרים נפרדים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון לקבץ א ג ה ז ט י"א וכן לעולם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ותכפול כל אחד על ב' יהיה המספר היוצא מספר זוג בלתי מורכב נקרא בלשונם פארי אין פארי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל אם תכפול א' על ב' יהיה המספר היוצא מספר זוג בלתי מורכב מזוג | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן ג' כפול על ב' יעלה ו' והוא מספר מורכב מזוג בלתי זוג | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן ז' וכן ט' וכן י"א כלם כשתכפלם על ב' ותחלקם יהיה המספר היוצא זוג בלתי מורכב מזוג | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12 המאמר על המרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דע כי כשתכפול מספר מרובע על מספר מרובע יהיה העולה מספר מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל אם תכפול ד' שהוא מספר מרובע על ט' יהיה היוצא ל"ו והוא מספר מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן [7]אם תכפול ט' על כ"ה יהיה העולה קרכ"ה והוא מספר מרובע קיז ולא יחטיא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן אם תכפול ד' על כ"ה יעלה ק' והוא מספר מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולדעת השרש תכף כפול שרש זה על שרש זה והיוצא הוא השרש מכפל מרובע על מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל בזה כפול ט' על כ"ה והוא רכ"ה ולדעת שרשם כפול ג' שהוא שרש ט' על ה' שהוא שרש כ"ה ויעלו ט"ו והוא שרש רכ"ה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| גם כשכפלת ד' על ט' ויהיה היוצא ל"ו לדעת שרשם כפול ב' שהם שרש ד' על ג' שהם שרש ט' ויעלה ו' והוא שרש ל"ו ולא יחטיא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תוכל לעשות מכל שני מספרים מרובעים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ודע כי גם זה יצדק במעוקבים כי אם תכפול מעוקב על מעוקב יהיה היוצא מעוקב ושרש זה כפול על שרש זה הוא שרש המספר המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל כפלנו ח' שהוא מעוקב ב' על ס"ד שהוא מעוקב ד' ויעלה תקי"ב ושרשם הם כפל ב' על ד' שהם ח' ולא יחטיא לעולם ודע זה מאד כי הוא סוד במספר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13 המאמר במספרים מתיחסים הנה הראשון יש לו שרש והשני אין לו שרש והשלישי יהיה לו שרש והרביעי יהיה לו שרש מעוקב ושרשו הוא המספר הרביעי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל יש לנו עשרה מספרים מתיחסים מכפל והנה הראשון א ב ד ח י"ו ל"ב ס"ד קכ"ח רי"ו תקי"ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אומר אני כי א' הוא שרש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והד' שהוא השלישי יש לו ג"כ שרש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והרביעי שהוא ח' הוא מעוקב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והה' יש לו שרש שהוא י"ו שרשו ד' שהוא השלישי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והשישי אין לו שרש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והשביעי שהוא ס"ד יש לו שרש מעוקב כי שרשו הוא ד' והוא השלישי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והשמיני אין לו שרש והט' שהוא רנ"ו יש לו שרש והוא י"ו והוא החמישי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והעשירי יש לו שרש מעוקב והוא תקי"ב שהוא המספר הרביעי שהוא ח' כי ח' הוא שרש מעוקב מתקי"ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [8]וכן תוכל לעשות אם המספרים מתיחסים מיחס א אל ג' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל א ג ט כז פא רמ"ג תשכ"ז | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואומר כי א' שהוא הא' יש לו שרש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והשני אין לו שרש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והשלישי שהוא ט' יש לו שרש כי שרשו ג' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והרביעי שהוא כ"ז אין לו שרש כי אם מעוקב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והחמישי שהוא פ"א יש לו שרש מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והשישי אין לו שרש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והשביעי שהוא תשכ"ז יש לו שרש מעוקב כי שרשו ט' שהוא השלישי וכן לעולם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תוכל לעשות אם היחס מא' אל ד' כגון אם האחד א ד' י"ו ס"ד רי"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אומר כי כל אחד יש לו שרש מרובע יען כי הם כפולים על ד' וכבר אמרנו כי כפל מרובע על מרובע לעולם יהיה מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14 המאמר במספרים הנפרדים מתחילים מהאחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אם להוסיף האחד על הנמשך אחריו יהיה מרובע ואותו הסכום תוסיף על הנמשך אחריו יהיה מרובע וכן לעולם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל יש לנו ז' מספרים נפרדים מתחילין מן האחד על משך המספרים כמו הראשון א' ג' ה' ז' ט' י"א י"ג ט"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אומר כי אם תקבץ המספר הראשון שהוא [9]שרש ומרובע עם הנמשך אחריו שהוא ג' יהיה ג"כ מרובע קיח והוא ד' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תוסיף על אלו הד' הנפרד הבא אחריו שהוא ה' עם ד' הם ט' והוא ג"כ מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תוסיף על ט' הנפרד הד' שהוא ז' יהיה מרובע והם י"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תוסיף על י"ו הנפרד הבא שהוא ט' יהיו כ"ה והוא מרובע וכן לעולם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15 הדרך לידע ממרובע מה מונח מכמה נפרדים הוא מורכב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שים שרש אותו מרובע והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל ממרובע כ"ה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קח שרשו שהוא ה' א"כ מספר כ"ה הוא מחובר מה' נפרדים והוא א' ג' ה' ז' ט' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן אם תרצה לדעת ממספר קמ"ד שהוא מרובע מכמה נפרדים הוא מחובר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קח שרש קמ"ד והם י"ב א"כ קמ"ד הוא מחובר מי"ב נפרדים והם א ג ה ז ט יא יג טו יז יט כא כג כן תוכל לדעת מכל מספר מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16 המאמר לדעת ממעוקב אחד איזה אות יש במעלה ראשנה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ראה אם במעוקב במדרגה ראשנה יש בה א' תדין כי בשרש ג"כ יש א' במדרגה ראשנה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תמצא ב' תדין כי בשרש יש ח' בראשנה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם ג' תדין כי יש ז' במדרגה ראשנה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם ד' יש ג"כ בשרשו ד' בראשנה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם ה' יש ג"כ בשרשו ה' בראשנה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם ו' גם בשרשו יש ו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם ז' תדין כי יש ג' בראשנה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם ח' תדין כי בשרשו ב' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם ט' תדין כי בשרשו ג"כ ט' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 17 המאמר למצא מעוקבים על דרך יחסיי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תתחיל מב' וכפלם והם ד' וכפלם והם ח' והוא מעוקב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד כפלם והם י"ו עו' כפלם והם ל"ב עוד כפלם והם ס"ד והוא מעוקב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד כפלם והם קכ"ח עוד כפלם והם רמ"ח עו' כפלם רנ"ו עוד כפלם והם תקי"ב והוא מעוקב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן מג' לג' הכפלות לעולם הוא מעוקב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכמו שהוא היחס מהמספרים אשר הנחת כמו אלו המספרים שהם מיחס א' אל ב' הנקרא בלשונם דופלא כך השרשים הם מיחס דופלא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה כי מעוקב ח' הוא ב' ומעוקב ס"ד ד' ומעוקב תקי"ב ח' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כן תוכל לעשות מיחס א' אל [10]כמו ג' וט' וכ"ז ופ"א ורמ"ג ותשכ"ט | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי מג' לג' המספר הוא מעוקב כי א' הוא מעוקב וכ"ז הוא מעוקב ותשכ"ט הוא מעוקב וכן עד אין סוף | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנך רואה כי אלו הם מיחס טריפלא כן שרשהם הם מיחס טריפלא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי שרש א' הוא א' ושרש כ"ז ג' ושרש תשכ"ט ט' והם מיחס א' אל ג' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תוכל לעשות לשאר מספרים יחסיים והוא דרך נאה ביותר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כן תוכל למצא המרובעים אמנם במרובעים השני הוא המרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובמעוקבים השלישי הוא המעוקב כמו שהוא רשום פה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| זהו יחס דופלא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| זהו מיחס טריפלא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| זהו מהמרובע יחס דופלא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18 המאמר במספרים הנקראים קונגרואיט ומספרים נקראים קונגרי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והדרך בידיעתם הוא זה קח אחד ושנים וחברם ויהיו ג' וכפלם ויהיו ו' ושמרם אח"כ [11]כפול זה על זה ר"ל אחד על שנים ויהיו ב' וכפול ב' על ו' השמורים ויהיו י"ב וכפלם על ב' ויהיו כ"ד וזהו המספר הראשון הקונגרואינט | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ולמצא מרובעו עשה כך תרבע אחד ויהיה אחד אח"כ תרבע ב' ויהיו ד' וחבר בו מרובע א' ויהיו ה' וקח מרובעם ויהיו כ"ה אשר זה המספר הראשון מרובע קונגרו מהמספר הראשון קונגרואינט | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולמצא מספר שני קונגרואינט נעשה ככה קח ב' וג' כמו שעשית מהראשון שחברת הא' והב' כן עתה בעד השני נחבר ב' עם ג' והם ה' וכפלם כמו שעשית מהראשון ויהיו י' אח"כ כפול ב' על ג' כמו שעשית מן הראשון ויהיו ו' וכפלם על י' השמורים ויהיו ס' וכפלם על ב' כמו שעשית מהראשון ויהיו ק"כ והוא מספר שני קונגרואינ' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכדי למצא מספרו קונגרו תרבע ב' ויהיו ד' גם תרבע ג' ויהיו ט' וחברם ויהיו י"ג וקח מרובעם ויהיו קס"ט והוא מספר שני קונגרו כמו שמספר ק"כ הוא מספר קונגרואינט | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולמצא השלישי קח ג' וד' וחברם ויהיו ז' וכפלם ויהיו י"ד אח"כ כפול ג' על ד' ויהיו י"ב וכפלם על י"ד ויהיו קס"ח כפלם על ב' ויהיו ג' מאות ול"ו והוא מספר שלישי קונגרואינט | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ולמצא מרובעו קונגרו תרבע ג' ויהיו ט' גם תרבע ד' ויהיו י"ו חברם ויהיו כ"ה תרבעם ויהיו תרכ"ה וזה המספר הוא מרובע קונגרו השלישי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
חבר מספר קונגרואינט עם מספר קונגרו ויעלה תתקס"א ושרשו ל"א | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ואם מן תרכ"ה תסיר של"ו ישאר עדין רפ"ט והוא מרובע ושרשו י"ז | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולמצא הרביעי קונגרואינט קח ד' וה' וחברם ויהיו ט' כפלם ויהיו י"ח אח"כ כפול ד' על ה' ויהיו עשרים כפול עשרים על י"ח ויעלה ש"ס כפלם על ב' ויהיו ז' מאות ועשרים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ולמצא מספרו הקונגרו תרבע ד' ויהיו י"ו גם תרבע ה' ויהיו כ"ה חברם ויהיו מ"א כפלם ויהיו אלף ושש מאות ופ"א והוא מספרו המרובע קונגרו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנה קונגרו ר"ל כי אם תחבר המספר הראשון קונגרואינ' עם מספר קונגרו מרובעו יהיה מרובע וכן אם תוציא מספר ראשון קונגרואינט ממספר מרובעו קונגרו ישאר ג"כ מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן מכל המספרים אם תחבר הראשון או השני או השלישי [12]או הרביעי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן לעולם תחבר הקונגרו עם הקונגרואינט יהיה מרובע העולה משניהם גם אם תוציא הקונגרואיט מן הקונגרו ישאר מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
המשל למספר קונגרואינט ראשון שהוא כ"ד אם תחברהו עם מספרו קונגרו יעלה מ"ט והוא מרובע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
גם אם תוציא ממספר כ"ה מספר כ"ד ישאר א' והוא מרובע ובזה האופן תוכל להוציא שאלות עמוקות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
19 למצא הדרך איך נמצא מספר אשר יהיה מרובע ואם תוסיף בו ו' ישאר מרובע ואם תוציאנו ממנו ישאר מרובע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הדרך הוא כך תבקש מספר קונגרואינט אחד כי אם תחלקהו על ו' יהיה מספר מספר מרובע והנה הקונגרואינט הראשון הוא כ"ד וחלקהו על ו' ויצא ד' כי הוא מספר מרובע אח"כ חלק הקונגרו הראשון שהוא כ"ה על ד' ויצא ו' ורביע והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי מספר ו' ורביע שרשו ב' ורביע ואם תוסיף בם ו' יהיו י"ב ורביע והוא ג' מרובע כי שרשו ג' וחצי ואם תוציאנו ממנו ישאר רביע והוא ג"כ מרובע כי שרשו חצי אחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
20 דרך למצא מספר מרובע כי כשתוסיף עליו ל' יהיה מרובע ואם תסיר ממנו ל' ישאר ג"כ מרובע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הדרך הוא כך תמצא איזה מספר קונגרואינט כי כשתחלקהו על ל' שהיוצא יהיה מרובע והנה כשתחלק מספר קונגרואינט שני על ל' יצא ד' כי הוא ק"כ והיוצא ד' הוא מספר מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אח"כ חלק מספר קונגרו מרובעו על ל' חלק קס"ט על ל' ויצא לך מ"ב ורביע והוא מרובע כי שרשו ו' וחצי ואם תוסיף בם ל' ויהיו ע"ב ורביע והוא ג"כ מספר מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי שרשו ח' וחצי ואם תחסר ממנו ל' ישאר י"ב ורביע והוא ג"כ מספר מרובע כי שרשו ג' וחצי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
21 דרך למצא מספר מרובע שאם תוסיף עליו ז' יהיה מרובע ואם תחסר ממנו ז' ישאר מרובע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עשה כך תחבר ז' וט' ויהיו י"ו אח"כ תאמר ט' פעמים ט' הם פ"א וי"ו פעמים י"ו הם רנ"ו חברם עם פ"א ויהיו של"ז וכפלם על עצמם ויעלו עוד 113569 כפול ט' על י"ו יעלו קמ"ד אח"כ כפול כ"ה על קמ"ד ויעלה ג' אלפים ות"ר כפול זה על ד' ויעלה י"ד [13]אלפים וד' מאות אח"כ תחלק 113569 על י"ד אלפים וד' מאות ויצא י"א שלמים וי"ב אלפים ותשס"ט חלקים מי"ד אלפים וד' מאות וזהו המספר המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי הוא מספר מרובע ואם תוסיף בם ז' יהיה מרובע ואם תחסר ממנו ז' ישאר ג"כ מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
22 דרך למצא מספר מרובע כי אם תוסיף בו ה' יהיה מרובע ואם תוציאנו ממנו ישאר מרובע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תעשה כנז' ותמצא כי הוא מספר י"א וכ"ז חלקים מקמ"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
23 דרך למצא מספר מרובע כי כשתוסיף בו י"ג יהיה מרובע ואם תוציאנו ממנו ישאר ג"כ מרובע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עשה הדרך כנז' ותמצא כי המספר המרובע המבוקש הוא ל' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
24 דרך למצא מספר כי כשתוציא ממנו ג' שרשיו ישאר מרובע ואם תוסיף עליו ג' שרשיו יהיה מרובע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הדרך הוא כך קח איזה מספר קונגרואינט איזה שתרצה ותחלקהו כפי סכום השרשים שרוצה להוסיף ולגרוע אח"כ חלק מרובעו על אותו מספר קונגרואינטי איזה קח מספרו קונגרו ותחלקהו על אותו הסך שהגיע לך אחר שחלקת אותו על ג' שרשיו והמגיע תכפלהו על עצמו והיוצא הוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל תקח מספר כ"ד שהוא המספר הראשון קונגרואי' וחלקהו על ג' יען כי אמר אם תוסיף או תגרע ג' שרשיו יהיה מרובע ואם תחלק כ"ד על ג' יעלו ח' חלק מספרו קונגרו שהוא מתיחס אל כ"ד שהוא כ"ה ויצא ג' ושמין ותרבעהו על עצמו ויצא ט' ומ"ט חלקים מס"ד והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן אם אמ' כי אם תוציא מן המספר ד' שרשיו או אם תוסיף יהיה מרבע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| היתה מחלק מספר כ"ד על ד' והקונגרו שהוא מתיחס אליו שהוא כ"ה היתה מחלקו על היוצא שהוא ו' ויצא ו' ורביע והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אח"כ תרבעהו ויעלה י"ז וי"ג חלקים מל"ו [14]והוא הדרוש כי אם תוציא ממנו ד' שרשיו ישאר כ"ה חלקים מל"ו והוא מרובע כי שרשו ה' שישיות ואם תוסיף בו ד' שרשיו יעלה ל"ד וחלק א' מל"ו והוא ג"כ מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן ממש כמו שלקחת הדמיון על המספר הראשון קונגרואינטי כן תוכל לקחת המשל אל השני שהוא ק"כ ולחלק היוצא על הקונרגו המתיחס אליו שהוא קס"ט | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תוכל לעשות מכל המספרים אם אמר להוסיף ה' שרשיו על אותו הסכום או אם אמר ו' שרשיו תחלקהו על ו' ואם ז' על ז' אח"כ תחלק הקונגרו המתיחס אליו על היוצא ולכפול אח"כ היוצא והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 25 דרך למצא ג' מספרים מרובעים כי כשתחברם יהיה מרובע ואם תחבר הראשון והשני ג"כ יהיה מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עשה כך תמצא מספר מרובע איזה שיהיה נפרד כגון תשעה כי הוא נפרד והוא מרובע והנה נקח ט' נסיר ממנו א' וישאר ח' וחלקם על ב' ויהיו ד' וכפלם ויהיו י"ו והוא המספר השני | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וט' הוא הראשון ומהג' יש לנו ב' מספרים מרובעים כי כשתחברם יהיו כ"ה והוא מספר מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולמצא השלישי קח כ"ה ותסיר ממנו א' כמו שעשית בראשנה וישאר כ"ד קח חצים כאשר עשית בראשנה ויהיו י"ב ותרבעם ויהיו קמ"ד וזהו המרובע הג' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תחברם יהיו קס"ט והוא מספר מרובע ושרשו י"ג | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| גם הראשון מחובר עם השני הוא כ"ה והוא מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תוכל למצא הרביעי ותעשה כנז' והוא כי עתה שיש לך קס"ט תסיר א' וישארו קס"ח חלקם על ב' ויעלו פ"ד תרבעם יעלו ז' אלפים ונ"ו והוא המספר הרביעי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואתה רואה כי תחבר הראשון היינו ט' עם י"ו הם כ"ה והוא מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תחבר ט' וי"ו וקמ"ד הוא קס"ט והוא מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תחבר ארבעתם יעלה ז' אלפים ומאתים וכ"ה והוא ג"כ מספר מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תוכל לעשות מה' או מו' מרובעים או מזולתם מקובצים שהסך העולה יהיה מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אמנם הזהר שהמרובע ראשון [15]שתקח יהיה נפרד כגון א' או ט' או כ"ה ולא יחטיא לעולם וזה סוד גדול במספר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 26 דרך למצא ב' מספרים אשר מרובעם מקובצים ביחד יהיה מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עשה כך קח ב' מספרים מרובעים אשר שניהם יהיו נפרדים או זוגות כי זולת זה לא תוכל למצא הדרך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונניח כי הב' מספרי' הזוגות יהיו ד' וי"ו שהם מרובעים וזוגות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכפול זה על זה וכבר אמרנו כי כפל מרובע על מרובע הוא מרובע ב' בהכרח כפול ד' על י"ו והם ס"ד קח שרשם והוא ח' וזה אחד מהמספרים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולמצא השני תוסיף ד' על י"ו שהם עשרים וקח מחציתם והם ק' י' ומאלו הי' תסיר המרובע הקטן שהוא ד' הנשאר ו' והוא השני | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי אם תוסיף מרובע ו' על מרובע ח' יהיו ק' והוא מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תניח ב' מספרים נפרדים מרובעים ונניח שהאחד הוא ט' והאחר כ"ה שהם נפרדים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול ה' על כ"ה ויהיו רכ"ה וקח שרשם שהם ט"ו וזה א' מהמספרי' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולמצא השני חבר ט' עם כ"ה ויהיו ל"ד וקח חצים שהם י"ז תסיר ממנו מספר ט' שהנחת שהוא הקטן וישאר ח' והוא השני | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנה הא' מספר ח' והאחר ט"ו ואם תחבר מרובע ט"ו עם מרובע ח' יעלה רפ"ט והוא מספר מרובע ושרשו י"ז | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם לא תרצה לקחת ב' מספרים נפרדים או ב' מספרים זוגיים קח מספרים אחרים מתיחסים אליהם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל מן הב' מספרים מרובעים שהם זוגות שהאחד היה ד' והאחר י"ו קח מספרים אחרים שיהיו מתיחסים אליהם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כאלו תקח האחד עשרה והאחר מ' הנך רואה כי יחס י' אל מ' כיחס ד' אל י"ו ומאלו הב' מספרים תנהוג זה המנהג כאשר ראית | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תרצה שיהיו נפרדים ג"כ תקח ב' מספרים אחרים שיהיו מתיחסים אליהם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל תקח כ"ז וע"ה כי אלו המספרים מתיחסים אל ט' ואל כ"ה כי יחס ט' אל כ"ה כיחס כ"ז אל ע"ה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ותעשה כמו שעשית ממספר ט' וכ"ה ולא יחטיא לעולם והנה תקח י' ומ' שהם זוגות ועשה כמו שעשית מד' וי"ו וכפול י' על מ' והם ד' מאות [16]וקח שרשם שהוא כ' וזהו אחד מהמספרים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולמצא השני תוסיף י' על מ' והם נ' וקח מחציתם והם כ"ה תוציא מהם מ' המספר הקטן שהוא י' ונשאר ט"ו והוא השני | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אח"כ תוסיף מרובע הראשון שהוא ת' על מרובע השני שהוא רכ"ה ויעלו תרכ"ה והוא מרובע ושרשו כ"ה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כן תעשה מב' מספרים נפרדים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| מכ"ז וע"ה והוא שתכפול זה על זה ויעלה ב' אלפים וכ"ה וקח שרשם ויהיו מ"ה והוא הראשון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולמצא השני תוסיף כ"ז על ע"ה ויהיו ק"ב וקח מחציתם והם נ"א הוצא מהם המספר הקטן שהוא כ"ז הנשאר כ"ד והוא השני | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ותוכל לבחון אותו וכן תוכל לעשות כדרך הערכים ותאמר דמ' לראשון שהוא מספר הזוגות שהראשון היה ח' כמה יתן לי וכו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 27 דרך למצא מספר שאם תוסיף עליו עשרה יהיה מרובע ואם תוציא ממנו עשרה ישאר מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עשה כך תרבע המספר שרוצה להוסיף ולגרוע ויהיו מאה תוסיף בם ד' ויהיו ק"ב ותחלקם על ד' ויצא כ"ו והוא הנדרש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי אם תוסיף בם י' יהיו ל"ו והוא מרובע ואם תחסר י' ישארו י"ו והוא מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכדומה לזה אם אמר תמצא לי מספר כי כשתוסיף עליו ו' יהיה מרובע ואם תחסר ממנו ו' ישאר מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תרבע לו' שרוצה להוסיף ולגרוע והם ל"ו תוסיף בם ד' ויהיו מ' חלקם על ד' ויצאו י' והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי אם תוסיף בם ו' יהיו י"ו והוא מרובע ואם תוציא מי' ו' נשאר ד' והוא מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תוכל לעשות מכל מספר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון האומר תמצא לי מספר אשר אם תוסיף עליו ט"ו יהיה מרובע ואם תוציא ממנו ט"ו ישאר מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תרבע ט"ו ויהיו רכ"ה תוסיף בם ד' ויהיו רכ"ט חלקם על ד' ויצא נ"ז ורביע והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תוסיף בם ט"ו ויהיו ע"ב ורביע והוא מרובע ושרשם ח' וחצי תוציא מהם ט"ו וישארו מ"ב ורביע ושרשם ו' וחצי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 28 דרך למצא מספר ולהוסיף עליו עשרה יהיה [17]מרובע ואם תוציא ממנו י"א יהיה מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה תחבר י' עם קכ"ב י"א ויהיו כ"א תסיר ממנו אחד וישארו עשרים וחלקם על ב' ויצאו עשרה ותרבעם ויהיו ק' תוסיף בם י"א שתרצה לחסר ויהיו קי"א והוא הדרוש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי אם תחסר ממנו ממנו י"א ישארו ק' ואם תוסיף בם עשרה יהיו קכ"א והם מרובעים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם אמר תמצא מספר כי כשתוסיף ח' יהיה מרובע ואם תחסר ז' יהיה מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עשה כמו שעשית תחבר ז' עם ח' ויהיו ט"ו תסיר ממנו א' ישאר י"ד וקח חצים והם ז' ותרבעם והם מ"ט תוסיף בם ז' והם נ"ו והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי אם תוסיף בם ח' יהיו ס"ד והוא מרובע ואם תחסר ז' נשארו מ"ט והוא מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אמנם אם מה שתרצה לחסר ולהוסיף יהיה יותר מאחד אין המספר צודק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואתן לך דרך לחסר ולהוסיף יותר מאחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 29 דרך למצא מספר לחסר ממנו עשרה וישאר מרובע וגם להוסיף עליו עשרה ויהיה מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עשה כך קח חצי עשרה והם ה' וכפלם והנם כ"ה תוסיף בם אחד ויהיו כ"ו כי זה המספר אם תוסיף בם עשרה יהיו ל"ו והוא מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תחסר מהם עשרה ישארו י"ו והוא מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן אם אמר מספר תוסיף בם י"ב או תגרעם חסר חצי שהם ו' וכפלם ויהיו ל"ו תוסיף אחד ויהיו ל"ז והוא הדרוש כי אם תוסיף או תחסר יהיה מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תעשה מי"ד קח חצים שהם ז' ותרבעם והם מ"ט תוסיף א' והוא נ' והוא הדרוש כי אם תוסיף או תחסר י"ד יהיה מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 30 דרך למצא ב' מספרים מרובעים אשר א' מוסיף על חברו ז' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עשה מז' ב' חלקי' האחד יהיה ג' והאחר ד' תרבע ד' ויהיו י"ו תרבע ג' ויהיו ט' ואלו הם הב' מספרים אשר האחד מוסיף על חברו ז' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תעשה מי"ג קח החלק הגדול שהוא ז' והחלק הקטן שהוא ו' תרבע ו' ויהיו ל"ו תרבע ז' ויהיו מ"ט ואלו הם המספרים שהאחד מוסיף על חברו י"ג | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולא תוכל לעשות אלו הדרכים כי אם במספרים נפרדים ר"ל שהאחד מוסיף על חברו מספר נפרד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 31 דרך למצא מספר ולהוסיפו על חמשה יהיה מרובע ולחסרו מחמשה יהיה מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קח ב' מספרים שתכפול כל אחד על עצמו והנה נקח ב' וא' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנה מרובע א' הוא א' ומרובע ב' הוא ד' וחברם ויהיו ה' והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי אם תוציא ממספר ה' ד' ישאר א' והוא מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תוסיף [18]תוסיף ד' על חמשה והוא ט' והוא מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אח"כ כפול שרש ט' שהוא אחד מהמספרים הנדרשים על ד' ויהיו י"ב אח"כ כפול ה' ויהיו כ"ה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ותאמ' כי אם תוסיף כ"ד על כ"ה יהיו מ"ט והוא מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| גם אם תחסר כ"ד מכ"ה יהיה מרובע והוא אחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כן תוכל לעשות למצא מספרים והוא שתראה כמה מרובעים מא' עד כ"ד והם א' ד' ט' י"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אח"כ תתחיל מן האחד מהם שתרצה ותקח י"ו וחלק כ"ד על י"ו ויצא א' וחצי וזהו המספר הראוי להוציא ולהוסיף ויהיו מרובעים אח"כ חלק כ"ה על י"ו ויצא א' וט' חלקים מי"ו וזהו המספר המרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי אם תוסיף בו א' וחצי יהיה מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תוציא ממנו א' וחצי ישאר מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תוכל לעשות אם תקח אחד מהמרובעים האחרים כגון א או ד' או ט' כמו שלקחת הדמיון על י"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 32 דרך למצא מספר אשר אם תוציא ממנו ה' יהיה מרובע ואם תוסיף עליו י"ב יהיה מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עשה כך תחבר ה' וי"ב ויהיו י"ז תוסיף בם אחד ויהיו י"ח תחלקם על ב' ויהיו ט' ותרבעם ויהיו פ"א תוציא מהם י"ב כמו שאמר ויצא ס"ט והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי אם תוציא מס"ט ה' ישאר ס"ד והוא מרובע ואם תוסיף בם י"ב יהיו פ"א והוא מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן אם אמר אם תוסיף בם ששה יהיה מרובע ואם תוציא מהם י' ישאר מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תוסיף ו' ויא והיו י"ו תוסיף בם א' ויהיו י"ז ותחלקם על ב' ויהיו ב' וחצי תרבעם ויהיו ע"ב ורביע תסיר מהם ו' וישארו ס"ו ורביע והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תוסיף בם ו' ויהיו ע"ב ורביע והוא מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תסיר ממנו י' ישארו נ"ו ורביע והוא מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 33 דרך למצא מספרים מרובעים מחוברים זה עם זה יהיה מרובע גם אם תחבר בם עשרה יהיו ג"כ מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תעשה ככה תסיר א' מי' וישארו ט' חלקם על ב' ויצא ד' וחצי תרבעם ויהיו עשרים ורביע והוא המספר המרובע שאם תוסיף בם עשרה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עתה תקח ב' מספרים כי כשתקח מרובעם ותחברם יצא עשרים ורביע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תעשה ככה תרבע עשרים ורביע על מאה ויצא ב' אלפים וכ"ה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עתה תמצא ב' מספרים אשר מרובעם מחוברים יהיו [19]ב' אלפים וכ"ה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנה תעשה שתקח שרש ב' אלפים וכ"ה ושרשם קכ"ג מ"ה קח ג' חמישיותיו והוא המספר האחד שהם כ"ז גם קח ד' חמישיותיו והוא המספר השני שהם ל"ו עתה תחלק ל"ו על י' ויצא ג' וג' חמישיות גם תחלק כ"ז על י' ויצא ב' וז' עשיריות אח"כ תרבע ג' וג' חמישיות ויצא י"ב וכ"ד חלקים מכ"ה והוא המספר הראשון גם תרבע ב' וז' עשיריות והיוצא הוא ז' וכ"ט חלקים ממאה והוא השני ותוכל לבחון אותו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 34 דרך למצא מספרים מתילדים בזה הדרך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ג' פעמים ג' הם ט' וד' פעמים ד' הם י"ו ומקובצים הם כ"ה תמצא לי ב' מספרים אחרים מרובעים ומקובצים יעלו כ"ה זולתם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ראה אם הסך יש לו שרש אמיתי ואם יש לו שרש אמיתי הנקרא ראדיצי דיסקריטא כמו מספרינו שיש לו שרש אמיתי ר"ל כ"ה ראה לעולם אם הסך יש לו שרש אמיתי ר"ל כ"ה בקש ב' מספרים אחרים אשר כשהם מחוברי' יחד נעשה מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונניח ב' מספרים אשר האחד ה' והאחר י"ב אשר מרובעהם מחוברים יהיו קס"ט ושרשם י"ג אח"כ קח שרש הב' מספרים הראשנים אשר מרובעם מקובצים יעלו כ"ה ושרשם ה' ותכפול אלו הה' נגד הה' אשר לקחת שהא' ה' והאחר י"ב ויעלה כ"ה גם כפול אותם הה' נגד י"ב ויעלו ס' תחלק כ"ה על שרש המספרים שמצאת שמרובעהם עולה קס"ט ושרשם י"ג חלק י"ג ויצא א' שלם וי"ב חלקים מי"ג גם חלק ס' על י"ג ויצא ד' שלמים וי"א חלקים מי"ג ואלו הם הב' מספרים הנדרשים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי אם תכפול כל אחד מהם על עצמו ותקבץ הכל יעלה כ"ה וכמו שלקחת מספר ה' ומספר י"ב תוכל לקחת מספר ח' ומספר ט"ו אשר מרובע שניהם עלה רפ"ט ושרשם י"ז גם מספרים אחרים וכפול ה' על ט"ו כמו שעשית לעיל על המספרים האחרים ויעלה ע"ה חלקם על י"ז שהוא שרש רפ"ט והיוצא ה' ד' וז' חלקים מי"ז וזהו האחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [20]ולמצא השני כפול ה' על ח' ויצא מ' חלקם על י"ז ויצא ב' וו' חלקי' מי"ז והוא השני כי אם תרבע הראשון על עצמו גם את השני על עצמו ותקבץ העולה יצא כ"ה בצומצום | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 35 דרך למצא מספרים מתחלפים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה ד' פעמים ד' הם י"ו וה' פעמים ה' הם כ"ה ושניהם מחוברים עולה מ"א | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תמצא לי ב' מספרים אחרים אשר מרובעם מקובצים יחד יעלו מ"א | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה תמצא ב' מספרים מקובצים יעלו מ"א ונניח כי האחד ג' והאחר ד' ותרבעם ויעלו כ"ה ו' ושרשם ה' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עתה יש לך ד' מספרים לכל אחד שרש היינו הב' הראשנים והב' שהנחנו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וראוי לכפול הב' מספרים ראשנים נגד הב' שניים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואמור ג' פעמים ד' הם י"ב וד' פעמים ה' הם כ' הסר י"ב מעשרים וישארו ח' והצניעם גם כפול ד' על ד' ויהיו י"ו עוד ג' פעמים ה' ויהיו ט"ו ותחברם והנם ל"א חלק הח' השמורים על שרש הב' מספרים שהנחת אשר עולים כ"ה ושרשם ה' חלק ח' על ה' ויצא א' וג' חמישיות וזהו אחד מהמספרים המבוקשים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| גם חלק ל"א על ה' ויצא ו' וא' חומש וזהו המספר השני | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תרבע א' וג' חמישיות יעלה ב' וי"ד חלקים מכ"ה גם תרבע ו' וחומש ויעלה ל"ח וי"א חלקים מכ"ה ושניהם מקובצים עולה מ"א וזה לא יחטיא לעולם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם נניח כי הב' מספרים השניים הא' ה' והאחר י"ב וכפל ה' בכ"ה וכפל י"ב קמ"ד ומחוברים הם קס"ט ושרשם י"ג וכפול ה' על ד' ויהיו כ' וי"ב על ה' והם ס' תסיר מהם כ' וישארו מ' כפול י"ב פעמי' ד' והם מ"ח וה' על ה' הם כ"ה וחברם והם ע"ג חלק מ' על י"ג היוצא ג' וא' חלק מי"ג גם חלק ע"ג על י"ג ויצא ה' וח' חלקים מי"ג והם המבוקשים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי כפל ג' וא' חלק מי"ג על עצמו הוא ט' וע"ט חלקים מקס"ט וכפל ה' וח' חלקים מי"ג על עצמם הם ל"א וצ' חלקים מקס"ט ושניהם מחוברים הם מ"א שלמים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזהו דרך מולטיפליקרי פירקרוצי כמו שהוא נרשם בספר פראלוקא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [21]ואם המספרים המרובעים המחוברים הם זוג כי אותם אשר עשינו היה חבורם נפרד כמו שראית מכ"ה וממ"א | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אבל אם הסכום הוא זוג כמו האומר ב' פעמים ב' הם ד' וד' פעמים ד' הם י"ו ומקובצים יחד עולה עשרים
תמצא לי ב' מספרים אחרים אשר מרובעהם מקובצים יעלו עשרים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עשה כך נניח מספר ג' וד' כי מרובעהם הם ט' וי"ו ועולה כ"ה ושרשם ה' ועתה כפול ה' על ג' והם ו' וד' על ד' הם י"ו תסיר ו' מי"ו נשארו עשרה אח"כ כפול ד' על ב' והם ח' וג' על ד' והם י"ב ושניהם מחוברי' עולים עשרים אח"כ חלק י' על ה' ויצא ב' וזהו האחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולמצא האחר תחלק עשרים על ה' ויצא ד' והוא השני והם המספרים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [22]ואנו מבקשים מספרים אחרים לכן תחליף הסדר מהקרוצי והוא כי אותו שהיה עומד למעלה תשים למטה ואחד מן המספרים יספיק להחליף ממטה למעלה כמו שהוא רשום למעלה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ועתה כפול ג' על ד' והם י"ב גם כפול ד' על ב' והם ח' תסירם מי"ב וישארו ד' ושמרם אח"כ כפול אינקרוצי ד' פעמי' ד' הם י"ו וג' פעמים ב' הם ו' חברם יחד והם כ"ב אח"כ קח הפארטידור היינו ה' וחלק הד' השמורים על ה' ויצא ד' חמישיו' וזהו אחד מהמספרים
גם חלק כ"ב על ה' ויצא ד' וב' חמישיות וזהו המספר השני | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול ד' וב' חמישיות על עצמם ויהיו י"ו חלקים מכ"ה גם כפול ד' וב' חמישיות על עצמם ויעלו י"ט וט' חלקים מכ"ה ושניהם מחוברים עשרים ותקיש על זה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ע"כ נעתק מהעיון מספר פראלוקא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Section Two - Practical Arithmetic |
השער השני ידבר על המעשית מהמספר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Check |
36 וראשנה נדבר מן המאזנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דע כי רוב האומנים והסוחרי' נוהגים לעשות המאזנים מט' ומז' אע"פ כי תוכל לקחת מאזנים בכל אות ואות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנה המאזנים מז' הם יותר צודקים והם מאזני צדק והטעם הוא זה כי אם יזדמן שתרצה לכתוב מ"ג ותטעה ותכתוב בהפך ר"ל ל"ד כי מוחלפת השטה ותעשה המאזנים מט' לעולם יצא לך ז' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי כן הוא מאזנים ממ"ג כמו מאזנים מל"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אמנם כפי מאזני הז' הנה מאזני מ"ג הם א' ומאזני ל"ד הם ו' ולכן יוכר הטעות במאזני הז' ולא יוכר הטעות במאזני הט' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ועו' טעם אחר כי אם תשכח לשים הציפרא באיזה מספר כל כך יצא המאזנים בלי זירא כמו עם זירא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל אם תרצה לכתוב ארבעים ולא תשים בו כי אם ארבעה ותשכח לשים הזירא הנה מאזנים מד' כמו מאזני ממ' במאזני הט' אמנם במאזני הז' אינו כן כי מאזני ד' הם ד' ומאזני מ' הם ה' ועל כן מצד אלו הב' טעמים מאזני ז' הם יותר צודקים ממאזני הט' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [23]37 דרך לכזב כל המאזנים הם מז' הם מט' או מג' או מד' או מאיזה מספר שיהיה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל הנה יש לנו מספר קכ"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנה המאזנים מט' הוא ז' והמאזנים מז' הוא ה' אם תרצה לכזבם שניהם כפול ז' על ט' ויהיו ס"ג תוסיף ס"ג על קכ"ד ויעלה קפ"ז ועשה המאזנים מט' ומז' יהיו כאשר בתחלה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| או אם תרצה הסר ס"ג מקכ"ד מהנשאר תעשה המאזנים מזה ומזה ויהיו כבתחלה וכן תוכל לעשות מכל המאזנים אחרים כמו מאזני ד' או ה' אם תרצה לכזבם כפול ה' על ד' והם כ' תוסיפם על המספר המונח או תחסרם ויהיו כבראשנה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנה מאזני המגרעת נעשה כך קח המאזנים מהמספר הגדול וקח המאזני' מהמספר הקטן והסר מאזני המספר הגדול מהמספר הקטן וכך יצטרך שיהיו מאזני הנשאר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל חסרנו מט' אלפים ותתע"ו מספר ו' אלפים וה' מאות ומג' הנה הנשאר הוא ג' אלפים וקל"ג הסר התשיעיות מט' אלפים וח' מאות הנשאר ג' גם הסר התשיעיות מו' אלפים וח' מאות הנשאר מאומה הסר מאומה מג' הנשאר ג' כן יצטרך שיהיו מאזנים מג' אלפים והנה הנשאר ג' והוא צודק וכן תוכל לעשות מכל המאזנים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם לא תוכל לקחת מאזני מספר הקטון מהגדול אז תוסיף בו ט' או ז' כפי המאזנים אשר תעשה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עו' תוכל לעשות מא[ז]נים אחרים והוא כי תסור ג' אלפים קל"ג מן המספר הגדול שהוא ט' אלפים ותתע"ו יצטרך שישאר כמו המספר הקטון שהוא ו' אלפים וה' מאות ומ"ג ודוק ותשכח | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Subtraction |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 38 הנה יש כאן דרך נקל ויפה במגרעת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והוא זה המשל נרצה לגרוע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הסר ד' מב' ולא תוכל ראה כמה יחסר מד' ועד עשרה והנה יחסר ו' תוסיף בם ב' שהם למעלה ויהיו ח' תשים ח' למטה עתה יש לך עשירית אחד [24]ותחבר אותו עם הט' מלמטה ויהיו עשרה אח"כ תאמר הסר עשרה מהג' שלמעלה ולא תוכל על כן תוסיף עשרה ועם הג' והם י"ג תסיר מי"ג עשרה הנשאר ג' אח"כ חבר אותם עשרה עם הז' הנמשכים למטה ויהיו ח' תסיר ח' מד' של מעלה ולא תוכל על כן תוסיף בם עשרה ויהיו י"ד תסיר מהם ח' הנשאר ו' וחבר זאת העשרה שהלית עם הב' מלמטה ויהיו ג' הסר ג' מה' שהם למעלה הנשאר ב' הנה הנשאר הוא ב' אלפים ותרל"ח ודוק ותשכח | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Multiplication |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 39 אם תרצה לדעת הכפל נקרא פירקואדרילוטו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נעשה כך קח מרובע אחד כפי המדרגות שתרצה לכפול | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תרצה לכפול ג' מדרגות על ג' מדרגות עשה שיהיה המרובע מד' בתים באורך וג' בתים ברוחב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ועשה שיהיה לעולם בית מיותר באורך על הרוחב ותתחיל לכפול מן האחדים ותשים בכל בית העולה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל נרצה לכפול ג' אלפים ושכ"ה על ג' אלפים ותכ"א | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ותתחיל לכפול א' על א' הנה היוצא א' ושים א' בבית ראשון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד כפול א' על ב' ויעלה ב' ושים ב' בבית שני | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד כפול א' על ד' ויעלה ד' ושים ד' בבית הג' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד כפול א' על ג' ויעלה ג' ושים ג' בבית הרביעי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אח"כ קח האות השניה וכפול ב' על א' ויעלה ב' ושים ב' בשורה האחרת בבית הראשון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד כפול ב' על ב' והם ד' ושים ד' בבית הב' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד כפול ב' על ד' ויהיו ח' ושים ח' בבית הג' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד כפול ב' על ג' ויהיו ו' ושים ו' בבית הד' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אח"כ קח האות השלישית וכפול ד' על א' ויצא ד' ושים ד' בקו השלישי בבית הא' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד כפול ד' על ב' ויהיו ח' ושים ח' בבית שני | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד כפול ד' על ד' ויהיו י"ו ושים ו' בבית השלישי ותחזיק אחד בידך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד כפול ד' על ג' ויהיו י"ב ועם האחד שהחזקת [25]ויהיו י"ג ושים י"ג ושים ג' בבית רביעי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וא' בחמישי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד קח האות הרביעית וכפול אותה עם א' ויהיו ג' ושים ג' בשורה רביעית | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עו' כפול ג' על ב' ויהיו ו' ושים ו' בבית הב' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד כפול ג' על ד' ויהיו י"ב ושים ב' בבית שלישי ותחזיק אחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד כפול ג' על ג' ויהיו ט' תחבר עמם הא' ויהיו עשרה ושים 0 בבית רביעי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וא' בחמישי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עתה תחבר דרך אלכסון ותחבר בראשנה א' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואח"כ תחבר ב' עם ב' שהם בב' בתים באלכסון ויהיו ד' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד תחבר ד' וד' וד' שהם בג' האלכסוניים ויהיו י"ב ושים ב' ותחזיק אחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אח"כ תחבר ג' וח' וח' וג' שהם בד' בתים האלכסוניים ועם האחד שהיה בידך ויהיו כ"ג ושים ג' ותחזיק אחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עתה חבר ו' ו' ו' ועם הב' שיש לך ויהיו עשרים ושים 0 ותחזיק ב' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עתה חבר ג' וב' שהם אלכסוניים ועם הב' שיש לך ויהיו ז' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עתה חבר א' 0 ושים אלף | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עתה תחבר א' שאין לו בית אחר באלכסון ויצא כמו שהוא נרשם בכאן ודוק ותשכח | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 40 דרך כפל אחר נקרא בלשונם ריפליגי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל שהוא מספר אחד מורכב מב' או מג' מספרים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כאלו תאמר מספר ו' שהוא מורכב מג' פעמים ב' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן מספר י"ב יש לו הרבה ריפליגי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי הוא מורכב מג' וד' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| גם הוא מורכב מב' וו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| גם מספר כ"ד יש לו ריפלוגי הרבה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ועל כן כשתרצה לכפול איזה מספר קח א' מהריפליגי וכפול המספר האחד והעולה כפול על החלק האחר והעולה הוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| משל [26]נרצה לכפול כ"ד על י"ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קח הריפליגו מא' מאלו המספרים מאיזה מספר שתרצה וקח ריפליגו אחד מאותם שיש לכ"ד והנה נקח מספר ד' כי הוא מורכב מד' וו' ונכפול ד' על י"ב ויהיו מ"ח אח"כ קח החלק האחר שהוא ו' וכפול ו' על מ"ח ויהיו רפ"ח וכן עולה הכפל מי"ב על כ"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תוכל לעשות מכל המספרים שיש לו ריפליגי לשניהם או לאחד מהם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו י"א פעמים י"ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קח אחד מהריפליגי שיש לו לי"ב והנה נקח ד' כפול ד' על י"א ויהיו מ"ד עוד כפול מ"ד על ג' ויהיו קל"ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 41 דרך אחרת מכפל נקרא אישקאפיצא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נעשה כך קח אחד מהמספרים שתרצה לכפול ותעשה ממנו כ"כ חלקים שתרצה וכפול כל חלק שעשית מא' מהב' מספרים נגד חבירו אח"כ חבר הכל והיוצא הוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון הוא כך נרצה לכפול מ"א על כ"ד על מ' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נעשה מא' מהמספרים אשר תרצה ואח"כ כפול כל החלקים נגד המספר השני והוא נעשה מכ"ד ד' חלקים החלק האחד ד' והחלק האחר ו' והאחר ה' והאחר ט' והנה נכפול ד' על מ' ויהיו ק"ס עו' נכפול ו' על מ' ויהיו ר"מ עו' נכפול ה' על מ' ויהיו ר' עוד נכפול ט' על מ' ויהיו ש"ס אח"כ קבץ כל ההכפלות ויעלה ט' מאות וס' וכך הוא הסך העולה מכפל כ"ד על מ' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| גם אם תרצה לעשות מהב' המספרים הנכפלים חלקים כ"כ שיהיו וכפול כל חלק וחלק מהמספר האחד על כל החלקים מהמספר האחר ואח"כ תקבץ כל ההכפלו' והיוצא הוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל נרצה לכפול י' על י"ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה נעשה מי"ב ג' חלקים ב' וג' וז' ומי' נעשה ג' חלקים ב' וג' וה' והנה נכפול כל חלק מהחלק האחד על כל החלקים מהחלק האחר אח"כ תקבץ כל החלקים והיוצא הוא המבוקש ויעלה ק"כ ודוק ותשכח | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 42 אם תרצה לכפול ב' מספרים ואל הסך היוצא [27]מהכפל יצא בכל מדרגה אאאאאא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תקח כל הא' שתרצה שיצא קכז ב' ותעלם ב' מדרגות ויהיו ב' מאות וקח שלשה עשרות בעד הא' ג"כ ויהיו ל' וחברם עם הב' מאות ויהיו ב' מאות ול' תוסיף בם א' ויהיו רל"א ותכפלם על ד' מאות ופ"א ויצאו ו' מדרגות בכל א' וא' יהיו אאאאאא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תרצה שיצא ב' בכל מדרגה קח ב' פעמים ב' שהם ד' ותעלם אל המאיות ויהיו ד' מאות וקח ג' פעמים ב' שהם ו' ותעלם בעשרים בעשרות ויהיו ס' וחברם עם ד' מאות ויהיו ת"ס וקח הב' ושימנו באחדים ויהיה בין הכל תס"ב וכפלם על תפ"ח ויצאו ו' מדרגות בכל אחת ב' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תרצה שיצאו ו' מדרגות בכל אחת ג' תעשה כפלו שהם ו' ותעלם במאיות ויהיו ו' מאות וקח ג"כ שלשה כפליו בעשרות שהם ט' עשרות וחברם ויהיו תר"צ ותוסיף בם הג' באחדים ויהיו תרצ"ג וכפלם על קפ"א ויצאו ו' מדרגות בכל אחת ג' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תרצה שיצאו ו' מדרגות בכל אחת ד' קח כפלם במאיות ויהיו ו' מאות וקח שלשה כפלם בעשרות ויהיו ק"כ וחברם ויהיו ט' מאות וב' ותוסיפם באחדים הד' ויהיו בין הכל ט' מאות וכ"ד וכפלם על קפ"א ויצאו ו' מדרגות בכל אחת ד' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן אם תרצה שיצאו ו' מדרגות בכל אחת ה' כפלם ותעלם עד המאיות ויהיו אלף כי הם עשר מאיות וקח שלשה כפלם בעשרות והם מאה וחמישים וחברם ויהיו אלף וק"נ ותוסיף ה' באחדים ויעלה אלף וקנ"ה וכפלם על קפ"א ויצאו ו' מדרגות בכל אחת הההההה ואמנם לא יוכל לעבור ו' מדרגות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אם תרצה לכפול שני מספרים אשר בסך העולה יהיה בכל מדרגה אאאאאא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול מאה וארבעים ושלש על ז' מאות וע"ז ויעלה אאאאאא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תרצה שיצא בכל מדרגה בבבבבב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול קמ"ג ב' פעמים ויעלה רפ"ו וזה יכפול על ז'ז'ז' ויצא בבבבבב ו' פעמים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תרצה שיצא גגגגגג בכל מדרגה ומדרגה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול ג' פעמים קמ"ג ויהיו תכ"ט וזה [28]על ז'ז'ז' ויצא גגגגגג | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן אם תרצה שיצא ד' בכל מדרגה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול קמ"ג ד' פעמים והעולה כפול על ז'ז'ז' ויעלה דדדדדד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן בכל מדרגה הההההה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול קמ"ג ה' פעמים והעולה כפול על זזזזזז והיוצא יהיה הההההה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן וווווו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן זזזזזז | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן חחחחחח | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן טטטטטט ולא יחטיא לעולם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 43 אם תרצה לכפול ב' מספרים והיוצא יהיה שוה לעולם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל שהיוצא יהיה באבאבאבאבאבא או גדגדגדגדגדגד או הוהוהוהוהוהו או באופנים אחרים כמו בדבדבדבדבדבד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה אם תרצה כא כפול ב' פעמים כא שהם מ"ב וקח כ"כ עשרות ר"ל מ"ב עשרות ויהיו ת"כ ותחבר עמם כ"א ויהיו תמ"א וכפלם על תפ"א ויצא לך באבאבאבאבאבא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תרצה שיצא לעולם בגבגבג כפול כג ויהיו מאה מ"ו העלה אותם עשרות ויהיו מ"ו עשרות שהם ת"ס תחבר אליהם כ"ג ויהיו תפ"ג וכפלם על תפ"א ויצא באבאבאבאבאבא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אמנם אם תרצה לכפול והיוצא יהיה לעולם ע0ע0ע0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול ע' על(ה) ק"מ קח ק"מ עשרות והם אלף ות"ר תחבר אליהם ע' והם אלף ות"ע והעולה כפול על תפ"א והעולה לעולם יצא ע0ע0ע0 וכן לעולם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 44 אם תרצה לכפול ב' מספרים כל אחד ו' מדרגות והעולה לעולם תהיה ב' אחדים או ב' מדרגות שניים או י"ב שלשה או י"ב ארבעה וכן לעולם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עשה מספר אחד מי"ב אחדים או מי"ב שניים או מי"ב שלשה ותחלקהו על זה המספר 900990 והיוצא המבוקש ר"ל מה שיצא כפול אותו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון זה נרצה לכפול ב' מספרים כל אחד מו' מדרגות ונרצה שהעולה יהיה י"ב מדרגות בכל אחד יהיה אחד 111111111111 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וחלק זה המספר על 900991 וזה כפול על ככה 123321 | 900991 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תעשה משאר המספרים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תרצה שיצאו י"ב מדרגות [29]ככה 121212121212 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חלק זה המספר על זה 900991 והיוצא שהוא כך וזה מבואר בנפשו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תחלק י"ב מדרגות בזה האופן 900991 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| יצא לך 134532 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכפול זה על זה ויצא לך 121212121212 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן כל כיוצא בזה והם שאלות נאותות למבין | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 45 שאלה מי הוא זה ואיזה הוא המספר אשר כשתכפלהו על ל"ב יצאו ו' מדרגות באחת ב' ובאחת ג' כזה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חלק זה המספר על ל"ב ויצא לך תשכ"ו וג' חלקים מל"ב והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תעשה מכל מספר שתרצה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון אחר נמצא ז' מדרגות באחת ד' ובאחרת ו' ונרצה לחלק אותו על מ"ח | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ויצא צ"ו אלפים וח' מאות וא' ושליש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה א"כ אם נאמר לך מי הוא זה ואיזה הוא המספר הכפול במ"ח יצאו ז' מדרגות באחת ד' ובאחת ו' הנה תמצא כי צ"ו אלפים וח' מאות וא' ושליש הוא המבוקש ככה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 46 מי הוא זה המספר אשר כשתחבר בו מאה יהיה רל"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הסר מאה מרל"ד וישאר קל"ד א"כ כשתחבר ק' עם קל"ד יצא רמ"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 47 מי הוא המספר אשר כשתחסר ממנו ע' ישאר קמ"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חבר ע' עם קמ"ד ויעלה רי"ד והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כן תוכל לעשות מהשברים הן מהחבור הן מהמגרעת הן מהכפל הן מהחלוק ודוק ותשכח | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 48 מי הוא זה המספר אשר כשתחלק אותו על כ"ד יצאו ו' מדרגות באחת ד' ובאחת ה' כזה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה כפול כ"ד על אלו המדרגות ויעלה עשרת אלפי אלפים ותשע מאות אלפים וט' אלפים ופ' והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תוכל לעשות מכל מספר ומספר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Progressions |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
49 דרך לדעת כמה יעלה חבור מספרים מתחילין מן האחד מתוך ידיעת חצי מספרו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
קח העולה מחבור חצי מספרו ותכפלהו על ד' ותוציא ממנו חצי מספרו והעולה [30]הוא המבוקש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון נרצה לדעת חבור כל המספרי' מא' עד י"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קח חבור המספרים מא' עד ו' שהוא חצי מספרו והוא כ"א וקח ד' פעמים כ"א והם פ"ד תסיר מהם ו' שהוא חצי מספרו וישארו ע"ח והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
50 דרך לחבר מתחיל מא' על דרך משך המספרים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ראה המספר האחרון עד היכן מגיע תוסיף בו אחד אח"כ קח חצי מספרו שהזכיר וכפול על זה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והוא המבוקש בין זוג בין נפרד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
משל נרצה לחבר מא' עד ו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
הנה מספר ו' חציו שלשה תוסיף על ו' א' ויהיו ז' כפול ז' על ג' ויהיו כ"א והוא המבוקש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תרצה לחבר מא' עד ז' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
קח חצי ז' והם ג' וחצי תוסיף א' על ז' ויהיו ח' כפול ג' וחצי על ח' ויהיו כ"ח והוא המבוקש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תוכל לעשות מכל המספרים ונקרא בלשונם פוגרישיאון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ואם תרצה לחבר מא' עד י"ב על משך הזוגות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ראה כמה מספרים הם והנה הם ו' מספרים תוסיף בם אחד ויהיו ז' קח חצי ו' והם ג' ראה מה יש בם ו' כפלם על ז' ויהיו מ"ב והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ואם המספרים הם נפרדים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
כגון הרוצה לחבר א ג ה ז ט יא יג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והם ז' מספרים כפלם על עצמם והוא הדרוש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
51 אם תרצה לחבר כל הנפרדים מא' עד מספר מה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חבר כל הנפרדי' מחצי מספרו והעולה כפול על ד' והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
דמיון נרצה לדעת חבור כל הנפרדי' מא' עד ט"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וידוע כי מא' עד ט"ו הם ח' נפרדים ועל כן תחבר א וג' וה' וז' שהם חצי ח' ויעלו י"ו כפלם על ד' ויעלו ס"ד וכן עולה כל הנפרדים מא' עד ט"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
52 לחבר כל המספרים המתיחסים מתחילין מאיזה מספר שיהיה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
כגון ג ו' י"ב כ"ד מ"ח צ"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
[31]הסר היחס האחרון שהוא ג' מהראשון שהוא מ"ח וישארו מ"ה קבץ מ"ה עד מ"ח והוא צ"ג והוא המבוקש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
53 לחבר מספרים מתיחסים מא' אל ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
המשל לחבר א' וג' וט' וכ"ז ופ"א | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תסיר היחס הראשון מפ"א שהוא האחרון וישארו פ' וקח חצים והם מ' חברם עם פ"א ויהיו קכ"א והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
54 ולחבר מספרים מתיחסים מא' אל ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
כמו לחבר ב' ח' ל"ב קכ"ח | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הסר הראשון מהאחרון הנשאר קכ"ו ושלישיתם מ"ב וחברם עם קכ"ח ויהיו ק"ע והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכן אם אמר חבר א' ד' י"ו ס"ד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חסר מס"ד א' וישארו ס"ג ושלשיתם כ"א חברם עם ס"ד ויעלו פ"ה והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ובזה האופן תוכל לעשות אם המספרים שתרצה לחבר מיחס א' אל ה' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
כמו א' ה' כ"ה קכ"ה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חסר א' מקכ"ה וישארו קכ"ד ורביעיתם ל"א חברם עם קכ"ה ויעלה קנ"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכן אם הוא מיחס א' אל ו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אחר שתסיר הראשון מהאחרון תחלק הנשאר על ה' והעולה תחבר עם האחרון והעולה הוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן לעולם תחלק על היחס פחות אחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל אם היחס הוא מא' אל ז' תחלק על ו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכל אלו המספרים היחסיים הם צודקים בשלמים ובשברים בין שיתחיל היחס מאחד או מאיזה מספר אחר שיזדמן | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 55 דרך לחבר כל הזוגות מא' דרך המשך כל הזוגות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קח חצי הזוגות וחברם ומהעולה כפלם על ד' ומהסך העולה קח ב' פעמים כמו זוגות חצי מספרו היחס וחסרם והעולה הוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
דמיון נרצה לחבר ח' זוגות מתחילין מן האחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קח חצי ח' והם ד' וקח העולה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
דמיון נרצה לחבר מא' עד י"ו והם ח' זוגות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קח ב' ד' ו' ח' והם עשרים כפלם על ד' שהם חצי הזוגות מהמספר המבוקש והם פ' תסיר ח' ויהיו ע"ב וכך הוא חבר הזוגות מא' עד י"ו וכן תעשה מכל מספר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [32]56 דרך למצא מיחס ב' אל ג' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כאלו תאמר חבר ב' וג' וד' וחצי וו' וג' רביעיות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול ב' שהוא הראשון ויהיו ד' אח"כ כפול ג' פעמים האחרון שהוא ו' וג' רביעיות ויהיו עשרים ורביע תסיר מהם ד' וישארו י"ו ורביע והוא הדרוש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
57 אם תרצה לחבר מספרים מוסיפים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
כאלו תאמר ז' וי' וי"ג י"ט וכ' וכ"ז ר"ל וי"ו וי"ט וכ"ב וכ"ה וכ"ח ול"א | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חבר ז' על ל"א ויהיו ל"ח וקח החצי מהמספרים המבוקשים כי הם ז' וחצים ג' וחצי וכפלם על ל"ח והם קע"א והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכן אם תרצה לחבר מתחיל מד' מוסיף כל אחד ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
כאלו תאמ' ג' וז' וי"א וט"ו וי"ט וכ"ג וכ"ז | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קח חצים והם ד' תוסיף הראשון שהוא ג' על האחרון שהוא ל"א ויהיו ל"ד כפול ל"ד על ד' והם קכ"ו והוא הדרוש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
58 לחבר כל הזוגות על דרך משך המספרים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ראה אותו הסכום שעולה המקובץ וראה כמה המרחק מהמרובע הקרוב לו שעבר והם ה' וכך הם הזוגות המקובצים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנה קבצנו ב' וד' וו' וח' וי' ועולה ל' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן לדעת קבוץ כל הנפרדים על דרך משך המספר מתחיל מן א' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל אם אמר קבצנו כל הנפרדים מתחיל מא' ועלה כ"ה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קח שרש כ"ה והוא ה' וכך הם המספרים נפרדים מתחילי' מא' והם א' ג' ה' ז' ט' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
59 אם תרצה לחבר כל המרובעי' שהם מא' עד עשרה או איזה מספר אחר בין זוג בין נפרד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קח הסכום האחרון שהוא עשרה וחבר בו א' ויהיו י"א חבר י"א וי' והם כ"א אח"כ כפול עשרה על י"א ויהיו ק"י אח"כ כפול זה על כ"א ויעלו ב' אלפים וש"י חלקם על היתרון שהם מי' עד י"א והוא א' ויצא ב' אלפים וש"י וחלקם על ו' ויצא שפ"ז והוא המבוקש והקיש על זה
וכן אם תרצה לחבר כל המרובעים שהם מא' עד י"ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חבר א' עם י"ב ויהיו י"ג אח"כ כפול י"ג על י"ב והם קנ"ו כפלם על [33]כ"ה ויעלו ג' אלפים וט' מאות חלקם על ו' ויצא ו' מאות ונ' והוא המבוקש קל | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
60 ואם תרצה לחבר כל המרובעים הנפרדים שהם מא' עד ט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חבר ט' שהוא הנפרד האחרון על הבא שהוא י"א והם עשרים אח"כ כפלם כנז' והוא שתכפול ט' על י"א ויעלה צ"ט כפול צ"ט על עשרים ויעלה אלף וט' מאות ופ' וחלקם על היתרון שהוא מט' אל י"א שהם ב' ויצא ט' מאות וצ' וחלק זה על ו' ויצא קס"ה והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| גם תוכל לעשות ככה קח שליש ט' שהם ג' וקח רביעית המחובר שהם עשרים והם ה' כפול ג' על ה' והם ט"ו וכפול זה על י"א ויעלה קס"ה והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
61 אם תרצה לחבר כל המרובעים שהם מא' עד י' על דרך הזוגות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חבר י' וי"ב שהוא הזוג הבא והם כ"ב אח"כ כפול ו' על י"ב והם ק"כ גם כפול זה על כ"ב ויעלו ב' אלפים ותר"מ חלקם על היתרון שהם מי' לי"ב שהם ב' ויצא אלף וש"כ וחלק זה על ו' ויצא ב' מאות וכ' והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
62 ואם תרצה לחבר כל המרובעים מכל המספרים שמוסיף על חברו ב' או ג' או ד' או ה' או איזה מספר אחר שתרצה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כאלו נרצה לחבר כל המספרים מד' וח' וי"ב וי"ו וכ' כי כל אחד מוסיף על חברו ד' ומרובעהם הם י"ו ס"ד וקמ"ד רנ"ו ת' תוסיף על כ' המספר הנמשך שמוסיף בו ד' והם כ"ד וחברם עם כ' ויהיו מ"ד ועשה כנז' כפול כ' על כ"ד ויעלה ת"פ וזה כפול על מ"ד ויעלה כ"א אלפים וק"ך וחלקם על יתרון שהוא מכ' אל כ"ד שהם ד' ויצא ה' אלפים ור"פ וזה חלק על ו' ויצא תת"פ והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| או קח שישית כ"ד שהם ד' ורביעית ד' שהוא א' חלק עשרים על א' ויצא כ' כפול כ' על מ"ד ויצא תת"פ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן אם אמר קבץ כל המרובעים שהם ג' ו' ט' י"ב ט"ו כל א' מוסיף על חברו ג' ומרובעם ט' ל"ו פ"א קמ"ד רכ"ה קח המספר הנמשך אחר ט"ו שהוא י"ח וחברם והם ל"ג אח"כ כפול ט"ו על י"ח ויצא ע"ד גם כפול ע"ד על ל"ג ויעלה ח' אלפים וט' מאות וי' וחלקם על ג' שהוא היתרון מט"ו על י"ח והיוצא חלק על ו' ויצא ה' מאות וצ"ה והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 63 שאלה אדם שולח רץ הולך בכל יום עשרים מילין אח"כ שלח אחר הולך ביום ראשון א' ויום ב' ב' ויום ג' ג' וכן בכל יום מוסיף מיל אחד [34]מתי יתחברו זה את זה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול עשרים ויהיו מ' תסיר א' ויהיו ל"ט א"כ בל"ט ימים יתחברו זה את זה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 64 שאלה שנים רצים אחד הולך בכל יום ל' מילין והאחר הולך ביום ראשון ב' וביום (ב') ד' ובג' ו' ובד' ח' מתי ישיגנו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה הסר א' מל' הנשאר כ"ט ובכ"ט ימים ישיגנו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 65 שאלה שנים רצים אחד הולך בכל יום כ"א מילין והאחר הולך בא' ג' ובב' ה' ובג' ז' וכן בכל יום מוסיף ב' מילין מתי ישיגנו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה בכ"א ימים יתחברו ביחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 66 שאלה שנים רצים אחד הולך בכל יום ס' מילין והאחר הולך ביום ראשון ג' וביום ב' ו' וביום ג' ט' וכן לעולם מוסיף ג' מילין ארצה לדעת מתי יתחברו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חלק ס' על ג' והם כ' כפלם והם מ' הוצא מהם א' נשאר ל"ט ובל"ט ימים ישיגו זה את זה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 67 שאלה אם תרצה לדעת מתוך חבור המספרים כמה הם המספרים המחוברים על דרך משך המספרים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון חברנו כל המספרי' עד מספר ידוע מתחיל מן האחד עם ב' ועם ג' ועם ד' וכן עד מספר מה ועלה המחובר נ"א | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה כפול נ"א על ב' והם ק"י וקח שרשם והם י' וכך הם המספרים המחוברים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן אם תרצה לדעת קבוץ כל הנפרדים ועלה המחובר כ"ה כמה הם המספרים המחוברים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קח שרש כ"ה והם ה' וכך הם המספרים הנפרדים מקובצים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולדעת חבור הזוגות מתחילין מן האחד על משך המספר קח השרש שעבר מל' והוא ה' וכך הם חבור הזוגות ב' ד' ו' ח' י' עולה ל' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 68 אמר א"ע והנה מספר חמשה מעוקבו שוה למרובעו ולמרובע כפלו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולמטה ממנו הדבר הפוך [ולמטה ממנו יעדיף המרובע על המעוקב ולמעלה מחמשה הדבר הפוך] ופירוש הדבר כן הוא כי למטה מחמשה קח מרובע שנים הם ד' ומרובע כפלו הם י"ו ועם ד' הם עשרים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנה מעוקב ב' אינו כי אם ח' והנה ערך ח' אל עשרים ב' חמישיותיו וכן מרובע ג' הם ט' ומרובע כפלו הם ל"ו ועם ט' הם מ"ה ומעוקב ג' הם כ"ז וערכם אל ג' [35]חמישיותיו וכן מרובע ד' הם י"ו ומרובע כפלו הם ס"ד וחברם והם פ' ומעוקב ד' הם ס"ד וערכם אל פ' ד' חמישיותיו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אמנם מרובע ה' עם מרובע כפלו הם קכ"ה וכן הוא מעוקב ה' והם שוים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולמעלה מה' הדבר הפוך כי עולה יותר המעוקב מהמרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו מרובע ו' הם ל"ו ומרובע כפלו הם קמ"ד וחברם ויהיו ק"פ ומעוקב ו' הם רי"ו וערך ק"פ אל רי"ו ד' חמישיותיו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן מרובע ז' הם מ"ט ומרובע כפלו הם קצ"ו ושניהם מחוברים הם שמ"ז ר"מ רמ"ז ומעוקב ז' הוא שמ"ג וערך רמ"ז אל שמ"ג ג' חמישיותיו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן מרובע ח' הם ס"ד ומרובע כפלו רנ"ו ושניהם מחוברים ש"ך ומעוקב ח' הם תקי"ב וערך ש"ך אל תקי"ב ב' חמישיותיו ומרובע ט' הם פ"א ומרובע כפלו הם שכ"ד ושניהם מחוברים הם תשמ"ג [ומעוקב ט' הם תשכ"ט] והערך הוא א' חמישית | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן מרובע י' הם ק' ומרובע כפלו הם ת' ושניהם מחוברים הם ת"ק ומעוקב י' הוא אלף וערכם אל ת"ק ב' פעמים כמוהו וכן לעולם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והכלל העולה מזה הוא כי מרובע אחד עם מרובע כפלו הוא ה' פעמים ממעוקבו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Motion Problems |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 69 שאלה איש אחד הולך בכל יום ל"ב מילין ואיש אחר הולך אחריו אחר ו' ימים והשיגו בכ"ה ימים אשאל כמה מילין הלך האחרון בכל יום | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול ו' ימים שהלך הראשון קודם שנסע האחרון על ל"ב ויצא קצ"ב חלקם על כ"ה ויצאו ז' ימים וי"ז חלקים מכ"ה הוסיפם על ל"ב ויהיו ל"ט וי"ז חלקים מכ"ה וכך ילך בכל יום השני ובכ"ה ימים ישיגנו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 70 שאלה איש הולך בכל יום ל' מילין ובסוף ה' ימים אחר רודף אחריו והולך בכל יום ל"ה אשאל בכמה ימים ישיגנו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול ה' שהם הימים שהלך הראשון קודם שנסע השני והם ק"נ וחלקם על היתרון שיש ממהלך המילין שהולך השני על הראשון שהם ה' מילין ויצא ל' א"כ בל' ימים ישיגנו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 71 שאלה אדם הולך ולא ידענו כמה הולך ובסוף ד' ימים איש הולך אחריו והולך [36]בכל יום ל"ה מילין ובסוף עשרים יום השיגו אשאל כמה הולך הראשון בכל יום | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נניח כי הראשון הולך בכל יום א' מיל א"כ בכ"ד ימים עשרים שהלך השני וד' ימים שהלך הוא שנסע קודם חברו הם כ"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אח"כ ראה כמה הלך השני בכ' ימים כפול כ' על ל"ה ויצא ז' מאות חלק ז' מאות על כ"ד ויצא לך כ"ט ושישית מיל כך הולך הראשון בכל יום | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 72 שאלה אדם נוסע מפירושא לרומא בד' ימים ואיש נוסע מרומא ללכת בפירושא בה' ימים ומפירושא לרומא פ' ימים מילין אשאל מתי יפגעו זה את זה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ראה כמה הלך בכל יום אותו שעושה המהלך בד' ימים והנה הולך בכל יום עשרים מילין גם ראה בכמה ימים הלך השני היינו חלק פ' על ה' ויצא י"ו חבר עשרים עם י"ו ויהיו ל"ו א"כ חלק פ' על ל"ו ויצאו ב' שלמים וב' תשיעיות ואז יפגעו זה את זה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 73 שאלה הנה ב' נמלים עומדי' במקום שוה זו עומדת בזוית זו וזו עומדת בזוית זו ומן הקצה אל הקצה ק' אמות והולכות זו לעומת זו הא' הולכת בכל יום שליש אמה וחוזרת רביע אמה והאחרת הולך בכל יום חומש אמה ונוזרת אחור בלילה שישית אמה מתי יפגעו זה את זה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הוצא משליש רביע נשאר חלק אחד מי"ב חבר חלק משלשים עם חלק מי"ב ויצא לך ז' חלקי' משישים וכן הולכים בין שניהם בכל יום חלק ק' עליהם ויצא ז' מאות וס"ב וב' שביעיות ובכך ימים ישיגו זה את זה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 74 שאלה איש יש לו ללכת עשרה מילין ליום הולך ב' ובלילה נזור א' אשאל בכמה ימים ילך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הסר א' מעשרה ונשאר ט' א"כ בט' ימים ילך מהלכו ויען כי אמר כי ביום הולך ג' ובלילה נזור ב' הוצא ב' מעשרה הנשאר שמונה א"כ בח' ימים יעשה מהלכו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 75 שאלה כלב רחוק מארנבת שישים אמה וה' פסיעות מהכלב שוה ז' מהארנבת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [37]אשאל מתי ישיג הכלב הארנבת הנך רואה כי בה' מהכלב עודף הארנבת ב' פסיעות כי בכל ה' מהכלב הולכת הארנבת ז' ולכן תאמר אם ב' שוים ה' ס' כמה שוים ויצא לך ק"נ ובזה הזמן ישיגנו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 76 שאלה לדעת כמה יעלה בתי האשקאקיר לכפול מא' עד ס"ד כפול בזה האופן בא' ב' ובב' ד' ובג' ח' ובד' י"ו וכן לעולם כופל | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה תחבר ד' בתים היינו א'ב'ד'ח' והם ט"ו תוסיף בם אחד והם י"ו וכפלם והם רנ"ו והסר א' והם רנ"ה והוא מה שבבית הח' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אח"כ כפול רנ"ו על עצמם ומה שיעלה הוא מה שבבית הי"ו אחר שחסרת ממנו אחד עוד תשוב ותכפול העולה עם תוספת אחד על עצמם והעולה הוא מה שבבית הל"ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד תשוב ותכפול היוצא על עצמם עם תוספת אחד ומה שיעלה הוא מה שבבית הס"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 77 שאלה אם תרצה לקבץ כל המעוקבים מא' עד י"ב מעוקבי' היינו א' וח' וכ"ז וס"ד וקכ"ה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קח חצי י"ב והם ו' וכפלם על עצמם ויהיו ל"ו אח"כ קח י"ב הוסף בם א' והם י"ג וכפלם על עצמם ויהיו קס"ט כפול קס"ט על עצמם ל"ו והעולה הוא קבוץ כל המעוקבים מא' עד י"ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 78 שאלה אם תרצה לקבץ כל המרובעים מא' עד עשרה כאלו א' ד' ט' י"ו כ"ה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חבר עשרה עם עשרה אחרים והם עשרי' תוסיף בם אחד ויהיו כ"א ושמרם וחלקם על ג' ויצא ז' אח"כ חבר כל המספרים מא' עד עשרה ויהיו נ"ה וכפול נ"ה על ז' ויצא לך שפ"ה והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן אם תרצה לחבר כל המרובעים מא' עד ח' שהם ל"ו כפול ל"ו על ה' וב' שלישיות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 79 שאלה אם תרצה לקבץ כל המספרים והוא שיוסיף השני על הראשון וכן כל אחד מוסיף על חברו אם מעט ואם הרבה הסר המספר הראשון מהאחרון והנשאר הוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כאלו תקבץ ההפרש מג' וח' וי' וי"ג וי"ז וכ"ד ול"ז הנה אתה רואה כי ההפרש מג' אל ח' הוא ה' וכן בכלם יש הפרש מזה לזה וכלם מקובצים הם ל"ד לכן אם תסיר הראשון שהוא ג' מן האחרון שהוא ל"ז הנשאר ל"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שאלה לקחת שרש השברים עם השלמים או משברים [38]בלבד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קח ממה שעל הקו שרשו וממה שתחת הקו שרשו ולחלק שרש שעל הקו על שרש שתחת הקו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון נרצה לקחת שרש ט' חלקים מי"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קח שרש ט' והוא ג' וקח שרש ד' שר' י"ו שהוא ד' ותחלק ג' על ד' והם ג' רביעיות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם הוא מעורב עם שלמים עשה מהשלמים שברים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו אם תרצה לקחת שרש י"ב ורביע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עשה מהי"ב רביעיות ויהיו מ"ט עם הרביעית וקח שרש מ"ט והם ז' וקח שרש ד' והם ב' חלק ז' על ב' ויצא ג' וחצי והוא שרש י"ב וחצי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 80 אם תרצה למצא מספר קונגרו כמו שנז' לעיל קח ב' מספרים איך שיזדמן ונניח כי הראשון ג' והשני ח' ותרבע כל אחד ונניח כי האחד ט' ח' והשני ס"ד ותחברם ויהיו ס"ג ותרבעם והם ה' אלפים ושכ"ט וזהו מספר קונגרו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולמצא הקונגרואינט כך תעשה כפול כל הב' מספרים ג' וח' והם ו' וי"ו וכפול ו' על י"ו והם צ"ו ועתה תחבר הראשון והשני שהם י"א וכפול י"א על צ"ו ויעלה אלף ונ"ו עתה הוצא המספר הראשון שהוא ג' מן המספר השני שהוא ח' הנשאר ה' וכפלם על אלף ונ"ו ויעלה ה' אלפים ור"פ והוא הקונגרואינט | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולבחון אותו חבר המספר הקונגרו עם מספר קונגרואינט ויעלה עשרת אלפים וו' מאות וט' וזה המספר הוא מרובע עתה הוצא ה' אלפים ור"פ מה' אלפים וז' מאות וכ"ט הנשאר מ"ט והוא ג"כ מספר מרובע הנה א"כ אם תוציא או תוסיף יהיה לעולם מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 81 שאלה למצא לי ל"ט מרובעים מתחלפים מקובצי' ביחד והעולה יהיה מספר מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה תקבץ כל המספרי' מאיזה מספרים ונניח כי תקבץ א' וד' וט' וי"ו וכ"ה ו[ל]"ו וכן כלם אשר כלם מקובצים עולה י"ט אלפים וי"ט וזה המספר איננו מרובע ולכן תאמר כי יחסר לך מרובע אחד כי אין לנו כי אם ל"ח ואנו מבקשים ל"ט לכן ראה כי אם תוסיף מספר ל"ט שעולה אלף ותקכ"ה והוא מרובע אם תוסיפהו על המספרים גם איננו מרובע כשהוא מחובר עם ל"ח מספרים מרובעים מחוברים וכן תחפש [39]עד שתמצא איזה מרובע מחובר עם הל"ח מרובעים שיהיה מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואומר לך כי לא תתחיל ממספר א' כי אם ד' וט' וי"ו וכ"ה ול"ו וכן עד ל"ט פחות אחד מהמספר הנדרש ויעלו עשרי' אלף ותתקל"ט ונשאר לך לקבץ מספר ל"ט כך תעשה הסר א' מן המקובץ וישאר עדין עשרים אלף ותתקל"ח וקח חצים והם עשרת אלפים ורס"ט וכפלם על עצמם ויעלה 105452361 וזהו המספר האחרון ר"ל הל"ט והנה המרובע הראשון הוא אחד להתחיל מן האחד וד' וט' וי"ו וכ"ה וכן עד ל"ט אשר כלם מקובצים עולה י"ט אלפים וזה המספר איננו מרובע ולכן תאמר כי יחסר לך מרובע אחד כי אין לנו כי אם ל"ח ואנו מבקשים ל"ט לכן ראה כי אם תוסיף מרובע שהוא הל"ט שעולה אלף ותתכ"ה ותוסיפהו על המספרים גם איננו מרובע על כן תקח המרובע הנמשך שהוא אלף ות"ר ותוסיפהו גם איננו מרובע לכן קח הנמשך שהוא אלף ותרפ"א גם איננו מרובע כשהוא מחובר עם הל"ח מספרים מרובעים מחוברים וכן תחפש עד שתמצא איזה מספר מרובע מחובר עם הל"ח יהיה מרובע והנה תמצא מספר ג' אלפים ותפ"א כי כשתוסיפהו על הל"ח מספרים יעלה אלף ותמ"ז והל"ז הוא אלף ושפ"ט וכן עד שתגיע אל האחד ובזה הדרך תוכל למצא כל המספרים שתבקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Cubic Roots |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
82 שאלה אם תרצה למצא שרש מעוקב מאיזה מספר שיהיה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דע כי ראוי למצא השרש היותר קרוב למספר המונח אח"כ לכפול השרש על עצמו אחר שהוספת בו אחד והעולה כפול ג' פעמים והנשאר תחלק עליו אמנם ראוי שישאר למעלה כ"כ כדי שתוכל לקחת ממנו מעוקב השרש וגם כי תוכל לקחת ממנו מעוקב היוצא כפול על ג' ומהשרש תחסר אחד ותכפול אותו השרש הכפול ג' פעמי' על השרש פחות אחד והעולה כפול על השרש הראשון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון נרצה לקחת שרש י"ו אלפים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה השרש הראשון הוא עשרים ומעוקבו ח' אלפים תוסיף על עשרים [40]א' ויהיו כ"א וכפלם על כ' ויעלו ת"כ כפלם על ג' ויעלו י"ב מאות וס' תן לו ג' ויעלו ג' אלפים וז' מאות ופ' ותוסיף זה על מעוקב [זה הלשון מוטעה] ג' שהם כ"ז ויהיו ג' אלפים וח' מאות וז' כפול אלו הג' שהם השרש השני על ג' ויהיו ט' תסיר מג' א' וישארו ב' כפול ב' על ט' ויהיו י"ח כפול זה על עשרים שהוא השרש הראשון ויהיו ג' אלפים וס' תוסיף ג' מאות וס' על ג' אלפים וח' מאות וז' ויעלה ד' אלפי' ומאה וס"ז ותוסיפם על ח' אלפים שהוא מעוקב הראשון ויעלה י"ב אלפים וקס"ז והוא מעוקב מכ"ג ודוק ותשכח | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון נרצה לקחת שרש י"ו אלפים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה השרש הראשון הוא תוסיף על עשרים א' ויהיו כ"א כפלם על כ' ויעלו ד' מאות וכ' כפלם ג' פעמים ויהיו י"ב מאות וס' תסיר מעוקב עשרים מי"ו אלף הנשאר ח' אלפים תחלק ח' אלפים על י"ב מאות וס' והנה נתן לו ה' כפול ה' ג' פעמים ונתן לו ט"ו תסיר ממנו א' וישארו י"ד כפול ד' על ט"ו ויהיו ס' כפול ס' על עשרי' שהוא השרש הראשון ויהיו י"ב מאות וכפול י"ב מאות וס' על ה' ויעלו ו' אלפים וג' מאות תחבר עמם י"ב מאות ויהיו ז' אלפים וה' מאות תוסיף על זה מעוקב ה' שהם קכ"ה ויהיו ז' אלפים וו' מאות וכ"ה וחברם עם ח' אלפים שהוא השרש הראשון ויעלה ט"ו אלפים וו' מאות וכ"ה והוא מעוקב ט"ו מכ"ה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון אחר נרצה לדעת שרש מעוקב מי"ג אלפים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה השרש הראשון הוא עשרים ומעוקבם ח' אלפים ועד י"ג ישארו ה' אלפים כפול השרש היוצא על עצמם עם תוספת אחד תוסיף בם א' ויהיו כ"א כפלם על כ' ויהיו ת"כ כפלם על ג' ויהיו י"ב מאות וס' ויהיו ג' כפול ג' על י"ב מאות וס' ויעלו ג' אלפים וז' מאות ופ' ותוסיף על זה מעוקב ג' שהם כ"ז ויהיו ג' אלפים וח' מאות וז' כפול אלו הג' שהם השרש השני על ג' ויהיו ט' תסיר מג' א' וישארו ב' כפול ב' על ט' ויהיו י"ח כפול זה על עשרים שהוא השרש הראשון ויהיו ג' מאות וס' תוסיף ג' מאות וס' על ג' אלפים וח' מאות וז' ויעלה ד' אלפים ומאה וס"ז תוסיפם [41]על ח' אלפים שהוא המעוקב הראשון ויעלה י"ב אלפים וקס"ז והוא מעוקב מכ"ג ודוק ותשכח | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נרצה לקחת שרש מזה המספר שהוא 10941048 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קח השרש מהאות הראשנה והם ח' מדרגות והנה ננקד המדרגה הראשנה נעשה בו נקוד אחד גם ננקד המדרגה ד' ועשה ב' בו גם ננקד השביעית ועשה ג' נקודות בו א"כ היוצא הוא מאיות שהוא מג' נקודות והנה תוריד העשרה שהם במדרגה הח' אצל הז' והם י' והמדרגה והשרש מעוקב שעבר הוא בח' הוא ח' א"כ הוא ב' מאות וכפלם על עצמם עם תוספת א' ויעלו מ' אלפי' וב' מאות כפלם על ג' ויעלו ק"כ אלפים וו' מאות חלקם על הנשאר עליהם שהם ט' רבואות וט' מאות אלף ומ"א אלפים ומ"ח ויצא עשרים וכפלם על שלשה ויהיו שישים וכפול זה על עשרים פחות א' שהוא י"ט ויעלו אלף וק"מ כפול זה על מאתים שהוא השרש הראשון ויעלו מאתים אלף וכ"ח אלפים תוסיף זה שרש מעוקב עשרים שהם ח' אלפים ויעלה הכל מאתים ול"ו אלפים תפילם מהנשאר למעלה הנשאר מאתים אלף תצ"ג אלפים ומ"ח אח"כ כפול ר"כ על ר"כ ואחד ויעלה מ"ח אלפים וו' מאות ועשרים כפלם על ג' ויעלה מאה אלף ומ"ה אלפים וח' מאות וס' חלק מאתים אלף וצ"ג ומ"ח עליהם ויצא לך שנים וישאר עדין אלף וג' מאות וכ"ח כפול ב' שהם השרש השלישי על ג' והם ו' וכפלם על ב' פחות א' שהוא א' ויהיו ו' כפול ו' על מאתים ועשרים ויעלו אלף וג' מאות ועשרים תוסיף בם מעוקב ב' שהם ח' ויהיו אלף | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וג' מאות ועשרים וח' תפילם מן האלף וג' מאות וח' הנשאר כלום הנה א"כ השרש היוצא הם רכ"ב ומעוקבם 10941048 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון אחר נרצה לקחת שרש מעוקב מל"ב אלפים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה השרש שעבר הוא ל' ומעוקבם הוא כ"ז אלף ונשאר עדין ה' אלפים אח"כ כפול ל' על ל"א ויעלו [42]כ"ז אלף ותתק"ל חלק ה' אלפים עליהם ונשארו עדין ב' אלפים וב' מאות ועשר ויצא לך אחד כפול זה האחד על ג' ויהיו ג' כפלם על א' פחות א' כי צריך לפחות אחד מן האחד היוצא כפי הדרך הנז' לא ישאר מאומה כפול מאומה על השרש הראשון שהוא ל' ויהיה מאומה הסר מאומה מב' אלפים וב' מאות ועשר וישאר כמו שהוא הסר ממנו שרש אחד שיצא בחלוק וישאר ב' אלפים וב' מאות וט' הסירם מכל המספר שהיה ל"ב אלפים וישאר כ"ט אלפים וז' מאות וצ"ו ושרשם ל"א | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Fractions |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
83 דרך האשקישארי כפי מחבר הספר הנקרא פראלוקא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
נרצה להתיך רמ"ח חלקים מט' אלפים ותרנ"ו שימם ככה 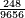
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אח"כ תחלק המספר שתחת הקו על המספר שעל הקו ויצא לך ל"ח ונשאר רל"ב אח"כ תחלק עתה רמ"ח על רל"ב ויצא א' ונשאר י"ו עתה תחלק רל"ב על י"ו ויצא י"ד ונשאר ח' עתה תחלק י"ו על ח' ויצא ב' ולא ישאר מאומה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ובהיות כי החלוקה האחרונה היתה ח' אומר כי זה המספר צריך שכתיבהו על ח' ר"ל כי אם תקח החלק השמיני מרמ"ח יהיו ל"א והחלק השמיני מט' אלפים וו' מאות מנ"ו יהיה אלף וו' מאות וז' ולא תוכל להתיכו עוד כזה 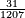
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם לא תוכל להתיכו בזה הדרך תאמ' כי הוא ראשון בלתי מורכב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל נרצה לדעת מהו כ"ג חלקים מל' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תחלק ל' על כ"ג ויצא אחד ונשאר ז' אח"כ תחלק כ"ג על ז' ויצא ג' ונשאר ב' עתה תחלק ז' על ב' ויצא ג' ונשאר א' עתה תחלק ב' על א' ויצא ב' ולא נשאר מאומה והנך רואה כי יען כי לא נשאר מאומה מספרינו לא תוכל להתיכו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
84 אם תרצה לכפול ל' על ה' שישיות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כפול ל' על ה' וחלק על ו' ויצא כ"ה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
85 אם תרצה לגרוע ג' חמישיות מז' שמיניות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
קח מספר שיהיה מורכב מה' וח' והוא מ' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
קח ג' חמישיותיו והם כ"ה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
קח ז' שמיניותיו והם ל"ה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הסר כ"ד מל"ה הנשאר י"א והם י"א חלקים מהמורה שהוא [43]מ' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| You can do so with addition: | וכן תוכל לעשות מהחבור | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כאלו תאמר חבר לי ב' שלישיות עם ג' רביעיות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
קח מספר מורכב מג' וד' והוא י"ב והוא מורה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
קח ב' שלישיותיו והם ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וג' רביעיותיו והם ט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חבר ט' וח' והם י"ז | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חלקם על י"ב שהוא המורה ויצא א' שלם וה' חלקים מי"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Likewise, you can sum integers with fractions, as for every whole unit you take the denominator once. | כן תוכל לחבר שלמים עם שברים כי בעד כל אחד שלם תקח מורה שלם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
86 ואם תרצה לחלק חצי על שליש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
קח המורה והוא ו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וקח שלישיתו והוא ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וחציו והוא ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חלק ג' על ב' והוא א' וחצי והוא המבוקש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Likewise, you can divide integers and fractions, by taking the denominator for every whole unit. | וכן תוכל לחלק שלמים עם שברים שתקח בעד כל שלם מורה שלם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם תרצה לחלק ד' על ב' שלישיות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
שימם כך 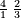
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אח"כ שים אחד תחת הד' כמו שהוא רשום | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אח"כ כפול שתי וערב וכפול ג' על ד' והם י"ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכפול א' על ב' והם ב' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חלק י"ב על ב' ויצא ו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
87 מאיזה מספר חסרת י"ג כי ישארו י"ב ומאי זה מספר חסרת ג' ושליש כי נשאר ד' ושליש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תחבר י"ג עם י"ב ויהיו כ"ה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| גם תחבר ג' וחצי עם ד' ושליש ויהיו ויהיו ז' וה' שישיות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
88 עם איזה מספר חברת כ"ג כדי שיעלה ל"ט | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תסיר מל"ט כ"ג הנשאר י"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
89 עם איזה מספר חברת ו' וחצי כדי שיעלה י"ג וב' חמישיות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תסיר מי"ג וב' חמישיות ו' וחצי הנשאר ו' וי"א חלקים מט"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
90 איזה מספר חלקת על ה' כדי שיצא י"ז | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כפול ה' על י"ז ויצא פ"ה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
91 איזה מספר חלקת על ד' ושביעית כדי שיצא ב' ושמין | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כפול ד' ושביעית עם ב' ושמין ויעלה ח' ומ"ה חלקים מנ"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
92 עם איזה מספר חלקת ל"ו כדי שיצא ט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כך תעשה תחלק ל"ו על ט' ויצא ד' והוא המבוקש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
93 עם איזה מספר חלקת י"ב ורביע כדי שיצא ג' וחצי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חלק י"ב ורביע על ג' וחצי ויצא לך ד' וחצי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואלו הד' שאלות האחת נעשת עם החבור והאחרת עם המגרעת ואחרת עם כפל ואחרת עם חלוק הן מהשלמים הן מהשברים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
94 חבר על ג' חמישיות כדי שיעלה ח' תשיעיות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה ראה איזה מספר ראוי לחבר על ג' חמישיות יעלה ח' תשיעיות הוצא מח' [44]ג' חמישיות הנשאר י"ג חלקים ממ"ה ועם זה ראוי לחבר ג' חמישיות עתה ראה אלו הי"ג חלקים ממ"ה כמה שמיניות יש בו ותמצא כי יש בו ב' שמיניות ונשאר י"ד חלקים ממ"ה וכזה ראוי לחבר על ג' חמישיות ר"ל ב' שמיניות וי"ד חלקים ממ"ה ויעלה הכל ח' תשיעיות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
95 שאלה בה' תשיעיות כמה חלקים מי"ח יש בו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חלק ה' תשיעיות על י"ח ויצא י' חלקים וכך חלקים יש בו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
96 תוציא ג' חמישיות מסכום שביעיות באופן שישאר חצי אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה תחבר ג' חמישיות עם חצי יעלה א' שלם וחלק מי' עתה ראה בא' שלם ועשור כמה שביעיות יש בו ותמצא בו ז' וז' חלקים מי' ומאלו השביעיות צריך להוציא ג' חמישיות וישאר חצי אחד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
97 חלק לי ז' וחצי על מספר מה שהיוצא יהיו ה' שישיות מי"ז וחצי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה קח ה' שישיות מי"ז וחצי והיוצא הוא י"ד וז' חלקים מי"ב וכך ראוי שיבא בחלק עתה חלק ז' וחצי על י"ד וז' חלקים מי"ב ויצא לך י"ח חלקים מל"ה והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
98 הוצא ההפרש שיש מב' חמישיות אל ה' שישיות ממספר כדי שישאר ההפרש אשר הוא מחצי אל ה' תשיעיות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ראשנה ראה ההפרש אשר הוא מב' חמישיות אל ה' שישיות אשר הוא י"ג חלקים מל' גם ראה ההפרש אשר הוא מחצי אל ה' חלקים מט' והוא חלק מי"ח עתה תחבר חלק מי"ח עם י"ג חלקים מל' ויעלה כ"ב חלקים ממ"ה וזהו המספר המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
99 על כמה חמישיות נכפול מספר ג' וב' שלישיות כדי שיעשה ז' וג' רביעיות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חלק ז' וג' רביעיות על ג' וב' שלישיות יצא ב' וה' חלקים ממ"ד עתה ראה בזה כמה חמישיות הם והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
100 חלק ז' וחצי על כל כך תשיעיות שיהיה היוצא ב' ותשיעית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ראשנה חלק ז' וחצי על ב' ורביע ויצא לך ג' ושליש ועל זה המספר צריך לחלק ז' וחצי על ב' ורביע ויצא לך ג' ושליש עתה ראה בג' ושליש כמה תשיעיות יש בו וחלקם על התשיעיות ויצא לך ל' ועל כן [45]תאמר כי על ל' תשיעיות נחלק ז' וחצי ויצא ב' ושלישית | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
101 קח ב' שלישיות מסכום של שמיניות שיהיה היוצא חצי אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ר"ל כמו האומר חצי מאיזה מספר הוא ב' שלישיות או כמו האומר ב' שלישיות מאיזה מספר הוא נכפל כדי שיהיה חצי על כן חלק חצי על ב' שלישיות והיוצא הוא ג' רביעיות וזה החצי הוא ב' שלישיות יען כי כשתקח ב' שלישיות מג' רביעיות יצא רביע עתה ראה ג' רביעיות כמה שמיניות הם ויצא ו' ומזה המספר ר"ל מו' שמיניות תקח ב' שלישיות ויצא חצי היינו מו' שמיניות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
102 תכפול ג' חמישיות נגד ה' שישיות כ"כ פעמים שיצא ה' שמיניות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ראשנה תכפול ג' חמישיות נגד ה' שישיות ויצא חצי ר"ל אח"כ כפול חצי באופן יעשה ג' שמיניות חלק ג' שמיניות על חצי ויצא א' ורביע וכנגד אותו מספר תכפול ר"ל נגד א' ורביע והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
103 תאמר לי ז' תשיעיות מכמה שמיניות שישיות הם ג' חמישיות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ויצא א' וח' חלקים מכ"ז ומזה המספר ז' תשיעיות הם ג' חמישיות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולדעת כמה שישיות הם חלקם על שישית ויצא ז' וז' תשיעיות ו' ומאלו השישיות הם ג' חמישיות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
104 הסר ב' שלישיות מה' שישיות מאיזה מספר שישאר ג' רביעיות מה' שביעיות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קח ב' שלישיות מה' שישיות והם ה' תשיעיות אח"כ קח ג' רביעיות מה' שביעיות והם ט"ו חלקים מכ"ח חברם עם ה' תשיעיות ויצא א' וכ"ג חלקים מרנ"ב ומזה ראוי להסירם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
105 הסר החצי מג' רביעיות מי"ב וחצי מאיזה מספר כדי שישאר ה' שישיות מב' שלישיות מי' ורביע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ראשנה קח ג' רביעיות מי"ב וחצי והם ט' וה' שמיניות ומזה קח החצי שהם ד' וי"א חלקים מי"ו וכך הוא החצי מג' רביעיות מי"ב וחצי עוד ראה מה הם ב' שלישיות מי' ורביע שהם ו' וה' שישיות ומזה קח ה' שישיות ויצא ה' וכ"ה חלקים מל"ו עתה תחבר ד' וי"א חלקים מי"ו מאיזה מספר שישאר ה' [46]וכ"ה חלקים מל"ו וחבר ד' וי"א חלקים מי"ו ויעלה עשרה ונ"ה חלקי' מקמ"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
106 תחבר ההפרש שהוא מב' שלישיות מג' חמישיו' אל ז' שמיניות מח' תשיעיות עם כ"כ חמישיו' שיעשה ההפרש אשר הוא מב' שלישיות מז' תשיעיות אל ז' שמיניות מי"ו חלקים מי"ז | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ראשנה מהו ב' שלישיות מג' חמישיות הם ב' חמישיות עוד ראה מהו ז' שמיניות וח' תשיעיות שהם ז' תשיעיות עתה קח ההפרש שהוא מב' חמישיות אל ז' תשיעיות ר"ל שתסיר זה מזה הנשאר י"ז חלקי' ממ"ה עוד ראה מה הם ב' שלישיות מז' תשיעיות שהם י"ד חלקים מכ"ז אח"כ ראה מה הם ז' שמיניות מי"ו חלקים מי"ז שהם י"ד חלקים מי"ז גם ראה ההפרש אשר הוא מי"ד חלקים מי"ז וי"ד חלקים מכ"ז והוא שתסיר זה מזה הנשאר ב' חלקים מתנ"ט וכך הוא ההפרש ממה ששאל | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
107 שאלה תמצא לי ב' מספרים אשר יהיה חצי ושליש ורביע מזה כמו חומש ושישית ושביעית האחר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
כך תעשה דע תחלה כי כשיש לך לחבר ב' מספרים שברים הנה מה שעומד על המספר האחד הוא כמו מה שעומד על המספר האחר ר"ל כי אם תחבר ב' שלישיות עם ג' רביעיים שימם 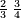
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכפול דרך קרוציטא היינו ג' שהם תחת ב' שלישיות על ג' שהם על הרביעיות ויהיו ט' ושימם על הג' רביעיות וכפול הד' שהם תחת הרביעיות על ב' שהם השלישיות והם ח' ואמור כי כך עולה ב' שלישיות מט' כמו ג' רביעיות מט' ח וכן מכל המספרים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם יש לך שבר ושלם בצד אחד תשברהו ועשה כנז' ויצא לעולם שוה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ועם זאת ההקדמה תוכל לדעת שאלתינו וחבר חצי ושליש ורביע ממספר יעלה א' וא' חלק מי"ב תשבר השלם ועם השבר יהיו י"ג חלקים מי"ב כן תעשה מהמספר האחר חבר חומש ושישית ושביעית ויעלה ק"ז חלקים מר"י עתה כפול א' וחלק מי"ב שהם י"ג חלקים מי"ב על ר"י ויצא אלפים ותש"ל גם כפול הי"ב שהם תחת הי"ג על ק"ז [47]ויצא לך אלף ורפ"ד והשאלה היא נעשת ואומר כי כל כך עולה החומש והשישית והשביעית מאלפים ותש"ל כמו החצי והשליש והרביע מאלף ודוק ותשכח | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ודע כי גם זה שוה בשלמים כמו האומר כפול ד' על ח' עשה מהם כמו שברים בזה האופן 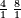 עתה כפול הד' שהם על הא' נגד הא' שהם תחת הח' ויצא ד' ושימם על ד' עתה כפול הח' שהם על הא' נגד הא' שהיא תחת הד' ושימם על הח' ואומר כי כך עולה אם תכפול הד' אשר שמת על הד' נגד הח' כמו אם תכפול הח' נגד הד' כי הכל עולה ל"ב' עתה כפול הד' שהם על הא' נגד הא' שהם תחת הח' ויצא ד' ושימם על ד' עתה כפול הח' שהם על הא' נגד הא' שהיא תחת הד' ושימם על הח' ואומר כי כך עולה אם תכפול הד' אשר שמת על הד' נגד הח' כמו אם תכפול הח' נגד הד' כי הכל עולה ל"ב'
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
משל אחד חבר ב' וחצי עם ג' ושליש עשה מב' וחצי חצאין ויהיו ה' חצאים גם עשה מג' ושליש שלישיות ויהיו י' שלישיות אח"כ חברם דרך שתי וערב וכפול הב' שהם תחת הה' על י' שהם על ג' ויעלו עשרים גם כפול הג' שהם תחת הי' על הה' שהם על הב' ויעלו ט"ו 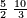 ואומר כי אם תכפול ג' על ט"ו ושליש יעלו חמישים גם אם תכפול עשרים על ב' וחצי יהיו חמישים וזה הדרך מועיל מאד בחכמת האלגיברא ואומר כי אם תכפול ג' על ט"ו ושליש יעלו חמישים גם אם תכפול עשרים על ב' וחצי יהיו חמישים וזה הדרך מועיל מאד בחכמת האלגיברא
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
108 עתה נדבר מענין אחר נקרא בלשונם אינפילצארי והוא זה נרצה לעשות אינפילצא אחת מב' שלישיות כמו שהוא מצוייר פה 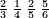
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
הנה נקח הב' שעל הג' ונכפלם על הד' שהם תחת הא' ויהיו ח' וקח הא' מלמעלה ויהיו ט' ושימם על קו אחד כן קח הג' שתחת ב' וכפלם נגד ד' שהם תחת א' ויהיו י"ב ושימם תחת הט' השמורים כך 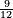 אח"כ כפול הט' נגד הה' שהם תחת הב' והם מ"ה קח הב' שהם לעיל והם מ"ז ושימם על קו אחר כן כפול הי"ב שהם תחת הט' על הה' שתחת ב' ויעלו ס' ושימם תחת מ"ז כך אח"כ כפול הט' נגד הה' שהם תחת הב' והם מ"ה קח הב' שהם לעיל והם מ"ז ושימם על קו אחר כן כפול הי"ב שהם תחת הט' על הה' שתחת ב' ויעלו ס' ושימם תחת מ"ז כך 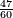 אח"כ כפול מ"ז שעל הס' על הו' שהם תחת הא' ויהיו רפ"ב חבר בם הה' שהם על הו' ויהיו רפ"ז ושימם על קו גם כפול הס' שתחת מ"ז על הו' שתחת הה' ויהיו ש"ס ושימם תחת הקו אח"כ כפול מ"ז שעל הס' על הו' שהם תחת הא' ויהיו רפ"ב חבר בם הה' שהם על הו' ויהיו רפ"ז ושימם על קו גם כפול הס' שתחת מ"ז על הו' שתחת הה' ויהיו ש"ס ושימם תחת הקו 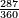 וכך הוא האינפילצא מאלו השברים וכך הוא האינפילצא מאלו השברים
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ודע כי כן תעשה אינפילצי מכל שברים שתרצה לא יצא לך לעולם א' שלם אפי' יהיו השברים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
109 שאלה אם נשאל לך מאינפילצא אחת משברים אשר עלה כך כמה שלישיות וכמה רביעיות וחמישיות ושישיו' היו בה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ואתה תחלק רפ"ז על ו' שהוא השבר האחרון שזכר ויצא לך מ"ז וישאר ה' לחלק על ו' וכך היו השישיות ר"ל ה' שישיות אח"כ כפול מ"ז על ה' שהוא המספר הנזכר אחר האחרון ויצא לך ט' ונשאר ב' וכך חמישיות היו אינפילצאטי ר"ל ב' חמישיות עוד חלק ט' על ד' ויצא לך ב' ויצא א' וכך רביעיות היו ר"ל א' רביע היו באותה א' אינפילצא עוד חלק ב' על ג' ויצא ב' שלישיות ואמור כי ב' שלישיות היו באותה אינפילצא 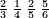
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
110 שאלה ה' חלקים מי"ו מכמה חמישיות ושישיות ושמיניות היה אינפילצאטו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
הנה לא תוכל כמו בדרך הקודם כי לא תוכל לחלק ה' חלקים מי"ו על ח' שהוא השבר אחרון הנז' וזה המספר ר"ל ה' חלקים מי"ו היה יותר גדול אלא שהיה א' אשקישאטו והשפיל סכומו ונעשה כן כפול השברים הנזכרים זה על זה ר"ל החומש על השישית ויהיו שלשים גם זה כפול על ח' ויהיו ר"מ וזהו המבוקש ר"ל המספר האשקישאטו ועתה ראה ר"מ מאיזה מספר הוא אשקישאטו אשר שב י"ו חלק ר"מ על י"ו ויצא ט"ו אח"כ כפול הה' אשר הם על י"ו על ט"ו ויהיו ע"ה א"כ מצאנו מספר קודם שהיה אשקישאטו שהיה נ"ד ע"ה חלקים מר"מ אחר שהיה אשקישטו על ט"ו היו ה' חלקים מי"ו ועתה לדעת ה' חלקים מר"מ מכמה חמישיות ושישיות ושמיניות היה אינפילצאטו חלק ע"ה על ה' ויצא לך ט' ונשאר ג' שמיניות היה האינפילצא עו' חלק ט' על ו' ויצא א' וג' שישיות א"כ ג' שישיות היה באינפילצא עו' חלק א' על חומש ויצא לך א' חומש וככה אינפילצי היה בו ר"ל א' חומש ג' שישיות ג' שמיניות ואחר שהיה אינפילצטו עלה ע"ה חלקים מר"מ ואחר שהיה אשקישאטו שב ה' חלקים מי"ו 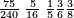
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המאזנים מהריגולא מ' דיטרי אם תהפך השאלה כמו האומר אם מאה שוים כ"ד תתקע"ה [48]כמה שוים מאה ותמצא כי ישוו כ"ד כמו שהנחנו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד משל אחר קלח אם עשרה שוים עשרים שלשים כמה שוים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ותמצא כי שלשים ישוו שישים ותהפך השאלה ותאמר אם שלשים ישוו שישים עשרה כמה שוים ויצא לך עשרים הליט' נרשמת כך ٯ והוא שוה י"ב אונקיו' אלאשוטילי איאלאגרושא שוה י"ח | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
111 שאלה אם דבר מה שוה כ"ה דוקט' ג' מאות כמה שוה ונרצה לנכות ד' על כל מאה לעולם כפול הנקוי הנקרא טארא בלשונם על המאיות שהזכיר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל הנה הזכיר בכאן ג' מאות תסיר י"ב שהוא ד' פעמים ג' ואח"כ תסיר מג' מאות י"ב הנשאר רפ"ח ותעשה אח"כ שאלתך כאלו אמ' אם דבר מה שוה כ"ה רפ"ח כמה שוה ותעשה שאלתך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם הטארא הוא ג' בעד כל מאה תסירם ממאה והעולה תסיר ממה שהזכיר ר"ל מהסכום שהזכיר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ratios |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
112 עתה נדבר על היחסים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואומר כי כל האריכות שמאריך פראלוקא בהקדמת היחסים אינו כי אם להודיע כי כל הענינים שבעולם הם מתיחסים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון כלי הבעלי מלאכות בכל אומנות אפי' איברי הב"ח הם מתיחסים הארך כפי הרוחב וכל החכמות כגון חכמת השיר וחכמת התכונה וכן יתר החכמות הלמוד מהם ביחס ובהדרגה ובזה הוא מאריך הדבור | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואומר כי יחס הדופלא הוא פחות מיחס הטריפלא והטריפלא פחותה מהקואטרופלא והקואטרופלא פחותה מהקואינקופלא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והטעם הוא כי הדופלא הוא מיחס א' אל ב' כי ג' הוא כמו ב' וכמו חציו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
אמנם השישקואיטירציאה מיחס א' אל ה' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והטריפלא מיחס א' אל ג' כי הוא גדול מב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן הקואיאינקופלא הוא גדול מהקואטרופלא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כי הוא מיחס א' אל ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והקואינקופלא מא' אל ה' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אמנם השישקואלטירא היחס גדול מהשישקואיטירציאה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The reason is that the sesquialter ratio is generated from the ratio of 3 to 2, for 3 is as 2 plus its half.
|
והטעם כי השישקואלטירא הוא מיחס ג' אל ב' כי ג' הוא כמו ב' וכמו חציו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The sesquitertian ratio is generated from the ratio of 4 to 3, for 4 is as 3 plus its third.
|
אמנם הששקואיטירציאה הוא מיחס ד' אל ג' כי ד' הוא כמו ג' וכמו שלישיתו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ועל כן הששקואלטירא יען כי הוא מוסיף חציו הוא גדול מהששקאיטירציאה כי אינו מוסיף כי אם שליש [49]והחצי גדול משליש וכן תוכל להכיר איזה יחס גדול מחבירו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
113 שאלה תמצא לי ג' מספרים מתיחסים שיהיו כפולים זה על זה כמו מחוברים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה א'ב'ג' כי הם מתיחסי' כי יתרון על הראשון יש לשני א' וכן יתרון השלישי אל השני א' וכפול א' על ב' והם ב' וכפלם על ג' והם ו' וכן א'ב'ג' מחוברים עולים ו' ובזה האופן תוכל לעשות שאלות רבות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ודע כי אם תקח ג' מספרים אחרים זולת אלו ותכפול המספרים האחרים על ב' כמו המספר הנז' גם תכפול השני הדרוש על המספר השני הנז' ב' פעמים כמוהו וכן תכפול המספר השלישי ב' פעמי' כמו המספר השלישי הנה אלו המספרים כפולים זה על זה יהיו ד' פעמים כמו מחוברים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל הנה מספירינו הראשון היה א' ונכפלהו ויהיו ב' ומספרינו השני היה ב' וכן ח' ד' ומספרינו הג' היה ג' ונכפלנו ויהיו ו' ואומר כי אלו הג' מספרים ר"ל ב' ד' ו' כפולים זה על זה יהיו ד' פעמי' כמו מחוברים כי מחוברים עולים י"ב וכפולים עולים מ"ח | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
114 הנה היחסים הנקראים בלשונם פורפורציאוני הם בלתי ב"ת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה אם היחס הוא מיחס א' אל ב' נקרא דופלא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם הוא מיחס א' אל ג' נקרא טריפלא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם הוא מיחס א' אל ד' נקרא קואטרופלא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תמיד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
שקיאלטירא נקרא יחס ג' אל ב' כי ג' כמו ב' וכמו חציו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ושישקאיטירציאה נקרא מיחס ד' אל ג' כי ד' כמו ג' וכמו שלישיתו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ושישקאיקוארטא נקרא מיחס ה' אל ד' כי ה' הוא מוסיף על ד' רביעיתו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ושישקואיקיאינטא הוא מיחס ו' אל ה' כי ו' כמו ה' וכמו חמישיתו יוסף עליו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם היחס הוא מה' אל ג' נקרא שופירפאריטינש כי ה' כמו ג' ומוסיף עליו ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם המספר מוסיף ג' על האחר נקרא שופירטיפארטיאינש כמו ח' וה' כי ח' כמו ה' ומוסיף עליו ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם מוסיף ד' כמו יחס ט' אל ה' נקרא שופירקואינדרופארטיאינש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואם הוא מוסיף ה' כמו יחס י"א אל ו' נקרא קואינקיפארטיאינש וכן לעולם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [50] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן הנפחי' כאלו תאמר המקבת צריך שיהיה מתיחס הארך אל הרוחב וכן לשאר המלאכות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
115 אם יש לך ג' מספרים מתיחסי' כגון א' ב' ג' ותכפול כל אחד בפני עצמו אח"כ תחבר ההכפלות ואח"כ תחבר אותם המספרים הנה יעלה חבור מרובע שלשתם ב' פעמים ושליש כמו שיעלה חבור שלשתם זה על זה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל א' ב' ג' הנה מרובע א' הוא א' ומרובע ב' ד' ומרובע ג' ט' ומרובע עולים י"ד ואם תחבר א' ב' ג' עולה ו' חלק י"ד על ו' ויצא ב' ושליש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כן אם תכפול ב' וד' וו' כל איש בפני עצמו ותקבץ מרובעם יעלה ד' פעמים וב' שלישיות כמו חבור שלשתם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל כפול ב' והם ד' וכפול ד' והם י"ו וכפול ו' והם ל"ו וחברם ויעלו נ"ו אח"כ חבר ב' וד' וו' והם י"ב והוא ב' פעמים כמו הראשון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן אם תכפול ד' וח' וי"ב כל אחד לעצמו וקבץ הכפלותיהם ויעלה רכ"ד וחלק רכ"ד על חבוריהם היינו ד' וח' וי"ב והם כ"ד ויצא לך ט' ושליש והוא ב' פעמים כמו הראשון כי לא עלה כי אם ד' וב' שלישיות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
116 שאלה אם יש לך משולש או מרובע או עגול ותעשה אורך כל א' מהקוים ב' פעמים כראשון תשברתו יעלה ד' פעמים כמוהו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל מרובע כל צלע ד' אמות הנה תשברתו י"ו אמות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תעשה מרובע כל צלע ח' אמות תשברתו ס"ד והוא ד' פעמים כראשון וכן תדין ממשולש או עגול | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
117 אם יש לך ג' מספרים מתיחסים אם היחס הוא דופלא אם תכפול הראשון על השני יהיה חצי מכפל הראשון על ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל ד' ב' ח' אם תכפול ב' שהוא הראשון על ד' יעלה ח' וכן אם תכפול ב' על ח' יעלה י"ו והוא חציו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן אם היחס הוא טריפלא אם תכפול הא' על הב' יהיה שליש מכפל הא' על הג' כמו ג' ט' כ"ז [51]אומר כי אם תכפול ג' פעמים ט' יעלה כ"ז ואם תכפול ג' פעמים כ"ז יעלה פ"א ופ"א הוא ג' פעמים כ"ז | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כן תוכל לעשות מכל היחסים אם הוא קואטרופלא או קואינקופלא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
118 אם יש לך ג' מספרים מתיחסים ותקבץ שלשתם אח"כ תחלק העולה על כל אחת מהג' מספרים הנה העולה לכל חלק יהיו ג"כ מספרים מתיחסים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל יש לנו ב' ד' ח' והם מתיחסים אומר כי אם תחברם והם י"ד ואם תחלק י"ד על ב' שהוא א' מהחלקים יצא ז' ואם תחלק עו' י"ד על ד' יצא ג' וחצי ואם תחלק י"ד על ח' יצא א' וג' רביעיות ואלו המספרים הם מתיחסים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
119 אם תחבר ג' מספרים מתיחסים הן שיהיו דופלא או טריפלא לעולם המחובר מהם ואותו סך תחלק על כל א' מהמספרים לעולם יהיו שוים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל בדופלא ב'ד'ח' מחוברים הם י"ד ואם תחלקם על ב' יצא ז' ואם על ד' ג' וחצי ואם על ח' א' וג' רביעיו'
כן יעשה מהמספרים אחרים שיהיו דופלא כגון ו' י"ב כ"ד אם תחברם יהיו מ"ב חלקם על ו' יצא ז' כמו בראשנה חלקם על י"ב יצא ג' וחצי חלקם על כ"ד יצא א' וג' רביעיות כבראשנה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל אל הטריפלא ו' י"ח נ"ד מחוברים יהיו ע"ח חלקם על ו' ויצא י"ג חלקם על י"ח ויצא ד' ושליש חלקם על כ"ד ויצא א' וד' תשיעיות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה הדרך בכל היחסים הן דופלא או טריפלא או קואינקופלא בין שיהיו מספרים מתחלפים לעולם העולה יהיה שוה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכמו שתעשה עם ג' מספרים כן תוכל לעשות מד' מספרים ר"ל כי כל אותם הסגולות שיש לג' יש לד' הן דופלא או טריפלא או זולתם מהיחסים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
120 אם יש לך ב' מספרים אם תחברם ומה שיעלה תחלק על אחד מהמספרים ר"ל על הגדול גם אם תחלק העולה על המספר הקטן הנה אלו הב' מספרים יהיה להם אותו היחס כמו שהיה להם קודם שנתחברו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל המספר האחר ו' והאחר י"ב הנך רואה כי זה [52]היחס נקרא דופלא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חברם ויהיו י"ח אח"כ חלק י"ח על י"ב ויצא קמ א' וחצי עוד חלק י"ח על ו' ויצא ג' והנך רואה כי יחס א' וחצי אל ג' הוא דופלא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אם תכפול אלו הב' מספרים ר"ל א' וחצי על ג' ויעלה ד' וחצי וכן ג"כ יעשו אם תחברם הם ג"כ ד' וחצי הנה חבורם כמו הכפל | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| גם אם תחלק ד' וחצי על ג' יצא א' וחצי כמו שהיה אחד מהמספרים גם אם תחלק ד' וחצי על ג' יצא א' וחצי והוא המספר האחר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כן תוכל לעשות מיחס הטריפלא כגון אם היה האחד ג' והאחר ט' אם תחברם יהיו י"ב חלק י"ב על ג' ויצאו ד' חלק י"ב על ט' ויצא א' ושליש הוא ג' פעמים כמוהו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן מכל היחסים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ודע כי לעולם יבא שבר באחד מאלו החלקי' ולא יחטיא יהיה מאיזה יחס שיהיה גם סגולות אלו היחסים ר"ל החלקים מחוברים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אם היחסים הוא דופלא החלקים מחוברי' יהיו שנים יתרים על הדופלא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם היחס טריפלא יהיו מחוברים חמשה זולת השבר הנמצא בכל היחסים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם היחס הוא טריפלא המחובר יהיו ו' זולת השבר הנמצא לעולם בכל היחסים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן מכל היחסים תמצא לעולם בהיותם מחוברים ב' לעולם זולת השבר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל מהנזכר למעלה מו' ומי"ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה היחס הוא דופלא הנך רואה כי החלק הא' הוא א' וחצי והאחר ג' ושניהם ד' וחצי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנך רואה כי יש בו שנים יתרים על הדופלא ודופלא ר"ל כפול כמו שנים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן המשל מהטריפלא האחד היה ד' והאחר א' ושליש ושניהם ה' ושליש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנך רואה כי מוסיף ב' על הטריפלא כי הטריפלא שם נגזר משלשה גם השבר הנמצא בו מורה על היחס | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי אם הוא טריפלא תמצא בשבר שליש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם הוא דופלא תמצא בשבר חצי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם קואטרופלא תמצא בשבר רביע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם קואינקופלא חומש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
121 אם יש לך ב' מספרים מתיחסים כגון ב' וד' אם תרצה למצא השלישי כפול ב' על ד' והם ח' והוא השלישי וכן תוכל לעשות בדרך הערכים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם יש לך הא' והג' ולא תדע הב' כפול הא' על הג' ומהעולה קח השרש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל הא' הוא ב' והג' הוא ח' כפול ב' על ח' והם י"ו וקח שרשם והם ד' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולמצא הא' [53]כפול השני על עצמו ותחלק על השלישי והיוצא הוא הראשון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל השני הוא ד' והג' הוא ח' כפול ד' על עצמם ויהיו י"ו וחלקם על [ח'] ויהיו ב' והוא השני הראשון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם יש לך ג' מספרים ותרצה למצא כפול הב' על הג' והיוצא חלק על הא' והיוצא הוא הד' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל ב'ד'ח' כפול ד' על ח' והם ל"ב חלק על ב' והם י"ו והוא היחס מהמספר הרביעי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולמצא השלישי כפול הא' על הד' וחלק על ב' והיוצא הוא הג' כגון א' בד' י"ו כפול ב' על י"ו והם ל"ב חלק על ד' ויהיו ח' והוא השלישי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תדע הא' והג' והד' ולא תדע הב' כמו ב' ח' י"ו כפול ב' על י"ו והם ל"ב וחלקם על ח' והם ד' והוא השני | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תדע הב' והג' והד' כמו ד' ח' י"ו כפול ד' על ח' ויהיו ל"ב וחלקם על י"ו ויצא ב' והוא הראשון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תדע הא' והב' למצא הג' והד' כפול א' על ב' חלקם על א' והוא הג' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון ב' ד' למצא הג' והד' כפול ד' על עצמם ויהיו י"ו חלקם על ב' ויצא ח' והוא השלישי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולמצא הרביעי תדע מצד השאלות הנזכרות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אם תדע הג' והד' ולא תדע הא' והב' הג' וח' וד' וי"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולמצא השני כפול ח' על עצמם והם ס"ד חלקם על י"ו והם ד' והוא השני | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולמצא הראשון כתוב לעיל | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
122 אם יש לך ד' מספרים מתיחסים הנה הא' והד' הם מחוברים והב' והג' ג"כ הם מחוברים אם תרצה לדעת כל אחד ואחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה כמו שיש לנו ד' מספרים ב' ד' ח' י"ו הנה הא' והד' הם י"ח והב' והג' הם י"ב קח מעוקב י"ב והם אלף ותשכ"ח ושמרם עתה כפול י"ב על שלשה והם ל"ו וחברם עם הי"ח והם נ"ד עתה תחלק אלף ותשכ"ח על נ"ד ויצא ל"ב ושמרם עתה תחלק י"ב על ב' ויצא ו' ושמור ו' גם כפול ו' על עצמם ויהיו ל"ו ומאלו הל"ו תסיר הל"ב השמורים תסיר ב' שהם שרש ד' הנשאר ד' וקח שרשם והם ב' וחברם עם הו' ויהיו ח' וכן היה המספר הג' כי הוא ח' גם מהו' השמורים תסיר ב' שהם שרש ד' וישאר ד' וכן היה השני עתה למצא הראשון כפול ד' על [54]עצמם וחלק על ח' שהוא המספר השלישי ויצא ב' והוא הראשון עתה אחר שאתה יודע הא' והב' והג' תוכל למצא הד' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
123 אם יש לך ג' מספרים מתיחסים ולא תדע כי אם הא' והה' ולא תדע הב' והג' והד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל הראשון (ב') והה' ל"ב כפול ל"ב על ב' ויהיו ס"ד וקח שרשם והם ח' והוא השלישי עתה כפול ב' על ח' ויהיו י"ו וקח שרשם שהם ד' והוא השני עו' כפול הח' על ל"ב והם רנ"ו וקח שרשם והם י"ו והוא הרביעי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
124 אם יש לך ד' מספרים מתיחסים כגון ב' ד' ח' י"ו תחבר הב' והג' והם י"ב עתה תחבר ארבעתם והם ל' הנה י"ב הוא ב' חמישיות מל' עתה תחבר הא' עם הג' ויהיו י' עתה ראה הב' שהוא ד' איזה יחס הוא אצל הי' והם ב' חמישיות ג"כ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
125 אם יש לך ד' מספרים מתיחסים ב' ד' ח' י"ו תחבר הא' עם הב' והם ו' גם תחבר הג' והד' והם כ"ד והנה ו' הוא רביע כ"ד עתה ראה הד' כי הוא רביע מהג' ג"כ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
126 אם יש לך ד' מספרים מתיחסים ב' ד' ח' י"ו הנה הא' והג' הם י' והב' והד' הם עשרים והנה עשרה הוא חצי עשרים עתה ראה יחס הא' אצל הב' והנה הא' הוא ב' והב' הוא ד' והוא ג"כ חציו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
127 אם יש לך ד' מספרים מתיחסים ותקח מספר איזה שתרצה ותחלק אותו מספר על כל אחת מאלו הד' מספרים תמצא כי אותם הד' חלקים יהיו מתיחסים כמו הד' הראשנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| משל ב' ד' ח' י"ו והמספר האחר נניח שיהיה מ"ח חלקהו על י"ו ויצא ג' חלקהו על ח' ויצא ו' חלקהו על ד' ויצא י"ב עוד חלקהו על ב' ויצא כ"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנה אלו הד' הם מספרים מתיחסי' כמו הראשנים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
128 אם יש לך ד' מספרים מתיחסים או בלתי מתיחסים הנה כל כך יעלה כפל הב' עם הג' כמו הא' עם הד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון ב' ד' ח' י"ו הנה ב' על י"ו הם ל"ב וכן ד' על ח' ל"ב וכן אם הא' ב' והב' ד' והג' ה' והד' י' אומר כי הא' שהוא ב' על י' הם עשרים וכן השני ד' על השלישי שהוא ה' הם עשרים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
129 אם יש לך ד' מספרים הא' הוא שרש ב' והב' שרש ארבעי' הנה עשרה פעמים מ' הם ד' מאות ושרשם עשרים והב' יחסים [55]אחרים הא' והב' ד' הנה מרובעם עולה ג"כ עשרים כי מרובע ב' ד' ומרובע ד' י"ו והם עשרים והם שוים אל העשרים ה' השמורים והנה כפל ב' על ח' האחרות מחוברות יהיו ד' מאות כי עשרה ומ' הם חמישים וח' פעמים נ' ד' מאות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנך רואה כי כפל ח' על חמישים הם ד' מאות כמו שהוא הכפל מי' אל מ' ולא יחטיא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
130 ואם יש לך ד' מספרים מתיחסים הנה כל א כפול על חבירו יעלה כפי הכפל שתעשה אחר שחברת הא' עם הד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל ב' ד' ח' י"ו עתה כפול ב' על ד' והם ח' וח' על ח' הם ס"ד וי"ו פעמים ס"ד הם אלף וכ"ד וכן אם תכפול ב' שהוא הא' עם י"ו שהוא ד' יהיו ל"ב וכפלם ויהיו אלף וכ"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
131 ד' מספרים מתיחסים אם תכפול כל אחד לעצמו ועל כל אחד מהאחרים ותחבר הכל יעלה כמו אם תחבר הד' מספרים ואח"כ תקח כפלם בשוה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו ב' ד' ח' י"ו כלם מחוברים עולה ל' כפלם ויהיו ט' מאות עתה כפול הא' עם הב' ועם הג' ועם הד' ושמור העולה עו' כפול הב' על הא' ועם הג' ועם הד' ושמור העולה עו' כפול הג' על הא' ועל הב' ועל הד' ושמור העולה עו' כפול הד' על הא' ועל הב' ועל הג' ושמור העולה אח"כ קבץ הכל ויעלה ט' מאות כמו הט' מאות השמורים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
132 אם יש לך ג' מספרים מתיחסים ותכפול הא' על הב' והעולה כפול על הג' כן יעלה מעוקב שניהם המשל ב' ד' ח' כפול ב' על ד' והם ח' וקח מרובעם יהיו ג"כ ס"ד כן אם תכפול ב' על ד' והם ח' וקח מרובעם יהיו ג"כ ס"ד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
133 אם יש לך ג' מספרים מתיחסים או בלתי מתיחסים ותכפול הב' על הא' והעולה על הג' הנה אם תחלק העולה על א' מהג' מספרים יעלה כמו הב' הנשארים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל הנה הג' מספרים מתיחסים הם ב' ד' ח' כפול ב' על ד' ויהיו א' ח' כפול ח' על ח' ויהיו ס"ד אם תחלק ס"ד על ב' יעלה ל"ב כמו הב' והג' מוכפלים או אם תחלק ס"ד על ד' יצא י"ו כמו הא' והג' כפולים או אם תחלקהו על ח' יצא ח' כמו הא' והב' כפולים וכן [56]ממש תעשה אם המספרים בלתי מתיחסים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
134 אם יש לך ב' מספרים מתיחסים כגון ו' י"ב שהוא דופלא אח"כ קח ג' מספרים מתיחסים מיחס דופלא כמו ב' ד' ח' אומר אם תחבר ד' עם ח' יהיו י"ב כפלם על הקטן מב' מספרים ראשנים שהוא ו' ויהיו ע"ב וכן ממש אם תחבר ד' עם ב' ויהיו ו' וכפלם על המספר הגדול שהוא י"ב ויהיו ע"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
135 אם יש לך ג' מספרים מתיחסים כגון ב' ד' ח' ותכפול הא' עם הג' ויהיו י"ו גם כפול הא' על הב' ויהיו ח' כפול הב' על הג' ויהיו ל"ב וחברם ויהיו נ"ו וכפלם על ב' ויהיו קי"ב ושמרם ואם תכפול עתה כל א' מהג' מספרים על הב' הנשארים יעלו ג"כ קי"ב בזה האופן קח א' וכפלהו על ב' והם ח' ג"כ כפלהו על הג' ויהיו י"ו גם קח השני וכפלהו על הא' ועל הג' גם קח הג' וכפלהו על הא' ועל הב' וחבר הכל ויעלה קי"ב כן תוכל לעשות מג' מספרים בלתי מתיחסים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
136 אם יש לך ג' מספרים מתיחסים כגון ב' ד' ח' אם תכפול כל אחד על הב' הנשארים כמו שעשינו לעיל יעלה קי"ב עתה תחבר אלו הב' מספרים ויעלו י"ד כפלם ויעלו כ"ח חלק קי"ב על ה(כ)"ח ויצא ד' כמו השני עתה תאמר עשה לי מי' ב' חלקים כפולים זה על זה יעלו י"ו שהוא כפל ד' על עצמם שהוא השני הנה תמצא כי האחד ב' והאחר ח' ובזה האופן מצאת כל הג' מספרים מתיחסים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
137 אם יש לך ג' מספרים מתיחסים כגון ב' ד' ח' אשר הא' כפול בעצמו והג' כפול בעצמו כן יעשה הנה יחס הא' כפול שהוא ד' אל הג' כפול שהוא י"ו הוא רביע כך הוא יחס מא' אל ג' כי הא' הוא ב' והג' הוא ח' והוא רביעיתו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
138 איזה המספר הממוצע בין ג' וד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה כפול ד' על ג' והם י"ב וקח שרשם הנה אם כן המספר הממוצע בין ד' וג' הוא שרש י"ב כפי הגיבמיטריקו אמנם כפי הארשמיטיקו הוא ג' וחצי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
139 שאלה איזהו מספר הממוצע בין ג' וד' כך תעשה כפול ד' על ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
140 שאלה לאיש אחד יש לו מרגלית שוקלת [57]טראפישו אחד ושוה מאתים דוקט' ויש לו אחרת שוקלת ב' טראפישי ושוה אלף זהובים גם יש לו אחרת ושוקלת ג' טרפי' כמה תשוה כפי זה היחס | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ראוי למצא אבן אחרת לפי היחס שיש מא' לב' ולומ' אם א' יתן לי ב' כמה יתן לי ב' ויתן לי ד' וזה יהיה משקל האבן הד' ראוי לשקול ד' טראפישי והנך רואה כי ההפרש מא' לב' הוא קואינקופלא והנה ראוי לומ' אם ההפרש מא' טרפישי לב' הוא יחס קואינקופלא כן ראוי שיהיה מב' לג' א"כ השוקלת ג' טראפישי ראוי שישוה ה' אלפים והנה יש לך לכפול אלף על ה' אלפים והעולה הוא ככה 5000000 והנה השרש מזה המספר ראוי שישוה השלישית אשר שוקלת ג' טראפיסי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
141 אם יש לך ג' מספרים מתיחסים וכפלת הא' על הב' ועל הג' וכן כפלת הב' על השנים הנשארים וכפלת הג' על השנים הנשארים עו' כפלת כל אחד על עצמו ועלה הכל שס"א כמה הם הג' מספרים מתיחסים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| זה נזכר לעיל בשאלה השמינית כי אמר כי תקח שרש מהמוכפל והנה שרש שס"א הוא י"ט ועתה תעשה מי"ט ג' חלקים שיהיו מתיחסים והנה תמצא כי האחד יהיה ד' והאחר ו' והאחר ט' והם מתיחסי' משקאלטירא והוא המספר המבוקש כן תוכל לעשות חלקים אחרים אחר החפוש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תוכל לעשות מג' מספרים בלתי מתיחסים כמו האומר עשה לי ג' מספרים ממקובץ קמ"ד קח שרשם והם י"ב עכשו תוכל לעשות מי"ב ג' חלקים מתיחסי' או בלתי מתיחסים ולעולם המקובץ מכל ההכפלות יעלה קמ"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
142 תעשה לי מי"ג ג' מספרים מתיחסים שהחלק הא' כפול בין הב' הנשארים והב' כפול בין הב' הנשארים והג' כפול בין הב' הנשארים יעלה הכל ע"ח | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה זאת השאלה תוכל לתרצה עם השאלה הי"ד האומרת כי ראוי לכפול הסך על ב' ר"ל י"ג ויהיו כ"ו ולחלק ע"ח על כ"ו והוא הג' והנה אם תחלק ע"ח על כ"ו יצא ג' והוא השלישי הסר ג' [58]מי"ג וישאר י' א"כ יצטרך כי בין הא' והב' יהיו י' והנה תאמר עשה לי מי' ב' חלקים כפול הא' על הב' יצא ט' ואולם אמרתי ט' כי ג' כפול על עצמו הוא ט' כי הוא המספר הראשון אשר מצאת ותמצא כי הא' א' והב' ג' והאחר ט' והוא מיחס טריפלא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
143 תעשה לי מי"ט ג' מספרים מתיחסים אשר אם תכפול הא' על הב' והאחר כפול על ג' ויעלה רי"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| זאת השאלה תוכל לעשותה עם סיוע המפתח הט' האומר כי אם תכפול ג' מספרים מתיחסים זה על זה העולה הוא מעוקב השנית על כן קח מעוקב רי"ו והם ו' והוא השנית ונשאר עד י"ט י"ג עתה ראוי לכפול ו' על עצמם ויהיו ל"ו עתה תאמר עשה לי מי"ג ב' חלקים כפול הא' על האחר יעלו ל"ו והנה כי האחד הוא ד' והאחר ט' והאחר ו' והם מתיחסים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
144 תחלק לי עשרה על ג' מספרים מתיחסים שיהיה הא' כפול על ג' כמו ג' פעמים הא' כפול על השני | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה יען כי הזכיר ג' תקח ג' בעד הראשון א' ובעד השני ג' ובעד הג' ג' פעמים כמוהו שהוא ט' וחברם ויהיו י"ג וחלק י' על י"ג ויעלה י' חלקים מי"ג והוא הראשון כפול זה ג' פעמים ויעלה ב' וד' חלקים מי"ג כפול זה על ג' ויעלה ו' וי"ב חלקים מי"ג והוא השלישי והם מתיחסים מיחס טריפלא והנך רואה כי כל אחד ג' פעמים מחבירו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם אמר כי הא' כפול בג' הוא ב' פעמים כמו הא' כפול בב' ותקח בעד הראשון א' ובעד השני ב' ובעד השלישי ד' שהוא ב' פעמים כמו השני וחברם והם א' וב' וד' והם ז' וחלק אותו המספר על ז' והוא הראשון כפלהו על ב' והוא הב' כפלהו והוא הג' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל אם אמ' תעשה לי מי' ג' חלקים שיהיה הראשון כפול על ג' ב' פעמים כמו הראשון כפול על השני חבר א' בעד הא' וב' בעד הב' וד' בעד הג' והם ז' חלק י' עליהם והם א' שלם וג' שביעיות והוא הראשון כפול זה על ב' והם ב' וו' שביעיות והוא השני כפול זה על ב' ויהיו ה' שלמי' וה' שביעיות והוא השלישי והנך רואה כי שלשתם מתיחסי' ושלשתם מקובצים הם י' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
145 שאלה תעשה לי מעשרה [59]ד' חלקים מתיחסים שהחלק הראשון כפול ברביעי יהיה ג' פעמי' כמו החלק הראשון כפול ברביעי בשלישי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה נניח כי הא' א' והב' ג' והג' ט' והד' כ"ז ובין הכל מ' על כן תאמ' אם מ' נתן לי א' עשרה מה יתן לך ומה יוסיף לך והדרך הוא מפורסם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ונמצא כי הא' א' רביע והב' ג' רביעיות והג' ט' רביעיות והד' כ"ז רביעיות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
146 שאלה תשקול לי עם ד' אבנים עד ט"ו קח א' ב' וד' וח' והנם ט"ו ועם אלו הד' תוכל לשקול עד ט"ו ואם חמישיתו יוסף עליו יוכל לשקול עד ל"א | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תרצה לעשות יחס אחר כאלו תאמר תשקול עם ד' אבנים מא' עד מ' קח א' ג' ט' כ"ז והנם מ' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תוסיף אבן אחרת תשקול עד קכ"א וכן לעולם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תרצה לשקול עם ד' אבנים עד ל"ה כבר ידעת כי האחרונה ראוי שתשקול כ"ז תסיר מכ"ז ה' וישארו כ"ב א"כ האבן הראשה א' והאחרת ג' ט' כ"ב לעולם ראה כמה הוא מחסר מאותו מספר שהוא מבקש וכן תחסר מהגדולה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה תוכל למצא יחס טריפלא על זה האופן תתחיל מא' וכפול אותו ויהיו ב' תוסיף בו א' ויהיו ג' והוא השני עוד תחבר השקל הראשון ששוקל א' עם הג' ויהיו ד' כפלם ויהיו ח' תוסיף בם א' ויהיו ט' הנה המספר הג' הוא ט' ולמצא הד' תחבר הג' מספרים היינו א' ג' ט' והם י"ג תוסיף א' ויהיו י"ד כפלם ויהיו כ"ח תחסר אחד ויהיו כ"ז וכן לעולם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
False Positions |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
147 שאלה הנה איש פזר שליש ממונו ונשאר לו י"ח כמה ממונו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
הנה ראוי לקחת המספר הקודם לשלישי שהוא חצי ותוסיף חצי י"ח שהם ט' על י"ח והנם כ"ז וכך היה ממונו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כן תוכל לעשות עם הנחות כוזבות ונניח כי היה ממונו כ"ד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
חסר ממנו שלישיתו ונשארו י"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואנו מבקשים י"ח על כן תאמר אם י"ו נתן לי כ"ד י"ח כמה יתן לי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ויצא כ"ז וכך היה ממונו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
148 שאלה אדם קנה דבר מה ולא ידע כמה אמנם הוא יודע כי הוא מרויח ג' סולדי ושליש בעד כל פיורינו שפזר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה הפיורינו שוה מאה סולדי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כן תעשה נניח [60]כי פזר ל' פיוריני | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה באלו הל' פיוריני הרויח ק' סולדי שהם פרח אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
חברהו עם הל' ויהיו ל"א | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותאמ' אם ל"א שבו ל' כמה ישובו חמישים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
תמצא כי ישובו מ"ח וי"ב חלקים מל"א ובזה האופן קנה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
149 שאלה אם ליט' הכסף מח' אוקיו' מטוב שוה ט' דוקט' עשרים ליט' שיהיה בכל אוקי' עשרה אוקיו' כמה ישוה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותאמר אם ח' שוה ט' י' כמה שוה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תמצא י"א ורביע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפלם על עשרים ויצא רכ"ה וכך הם שוות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
150 שאלה אם ליט' מכסף שיש בכל ליט' י' אוקיו' שוה י"א דוקט' ואיש פרע מכ"ה ליט' מאתים דוקט' מאיזה ליגא הם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תאמ' אם י"א נתן לי י' כמה יתן לי שמונה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| יען כי ח' פעמים כ"ה הם מאתים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ויצא ז' וג' חלקים מי"א ומזאת הליגא הם הליט' ר"ל הכ"ה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
151 שאלה איש אחד רצה לבנות בית ומצא ג' אומנים הא' יעשהו בי' ימים והאחר בח' והאחר בד' אשאל אם שלשתם יעשו המלאכה בכמה ימים יעשוהו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תעשה אותו בדרך הנחות כוזבות ותמצא כי יעשו אותו בב' ימים וב' חלקים מי"ט | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
152 שאלה אדם מצא ממון (החצי) והשליש והרביע עולה חמישים כמה הממון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תקח המורה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וקח חצי ושליש ורביע והם י"ג | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותאמר אם י"ג שבו י"ב כמה ישובו חמישים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנה ישובו מ"ו וב' חלקים מי"ג | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דע כי כשתעשה ב' הנחות וכל אחת מוספת אז ראוי לחסר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן כששתהם מחסרות ג"כ ראוי לחסר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם האחת עודפת והאחרת מחסרת אז ראוי להוסיף | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם האחת מחסרת והאחת עודפת ג"כ ראוי להוסיף | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
153 שאלה ג' אנשים האחד שואל קצבת מה והשני שואל כמו ב' פעמים ממה שיש לראשון עם תוספת ארבעה והשלישי שואל כמו שיש לראשון ולשני עם תוספת ו' ובין שלשתן יש מ'(ד) כמה לכל אחד ואחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נעשה אותו עם הנחות כוזבות ונניח כי היה לראשון ב' א"כ לשני יש לו ח' ולג' יש לו י"ו ובין שלשתן עולה כ"ו ועד מ"ד יחסר י"ח ותאמר עבור ב' שהנחתי חסר י"ח | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נניח הנחה אחרת ונאמר לראשון ג' ולשני עשרה ולשלישי י"ט ובין הכל עולה ל"ב ויחסר עד מ"ד י"ב ותאמ' בעד ג' שהנחתי חסר י"ב ושימם ככה [61]עתה הוצא י"ב מי"ח וישארו ו' והוא הפארטידור | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עתה כפול שתי וערב הב' נגד הי"ב ויהיו כ"ד גם ג' פעמים י"ח ויהיו נ"ד הוצא מהם כ"ד ונשארו ל' חלק ל' על ו' ויצא ה' וחלק השני י"ד וחלק הג' כ"ה והוא המבוקש ותקיש על זה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ודע כי כשהב' הנחות מחסרו' או עודפות ראוי לחסר הקטון מהגדול והנשאר נקרא פארטידור | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם האחת מחסרת והאחת עודפת או האחת עודפת והאחרת מחסרת ראוי להוסיף הגדול על הקטון והוא הפארטידור | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| גם תוכל לעשות זאת השאלה באופן אחר והוא כי תחבר תוספת השני עם הראשון שהוא ד' גם תוספת הג' על הב' שהוא עשרה ויהיו י"ד תחסרם ממ"ד ונשאר ל' חלק ל' על ו' יען כי השני שואל ב' פעמים כראשון ושים בעד הראשון א' ובעד השני ב' כי שואל הכפל ובעד הג' ג' יען כי שואל כמו הראשון והשני ועולה ו' וחלק ל' על ו' ויצא ה' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
154 שאלה תמצא לי מספר א' אשר כשתכפלהו על ד' ותוסיף בו ו' יהיה כמו אם תכפלהו על ו' ותוציא ממנו ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה נניח כי המספר הוא ב' כפלהו על ד' ויהיו ח' תוסיף בו ו' ויהיו י"ד גם כפול ב' על ו' ויהיו י"ב תסיר מהם ד' נשאר ח' ותאמר בעד ב' שהנחתי יחסר ו' שהוא מח' עד י"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד נניח כי הוא ג' כפלם על ד' ויהיו י"ב תוסיף בם ד ו' ויהיו י"ח גם כפול ג' על ו' ויהיו י"ח תוציא ד' וישארו י"ד ויחסר עד י"ח ד' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ותאמר בעד ג' יחסר ד' הוצא ד' ממו' הנשאר ב' והוא הפארטידור אח"כ כפול שתי וערב ב' על ד' והם ח' עו' כפול ג' על ו' והם י"ח תסיר מהם ח' הנשאר י' חלקם על ב' ויצא ה' והוא הדרוש כי אם תכפלם על ד' הם עשרי' תוסיף בם ו' והם כ"ו גם כפול ה' על ו' והם ל' תסיר מהם ד' הנשאר כ"ו ודע כי כל מספר שתוכל לעשות אותו עם הנחה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| גם תוכל לדעת אותו עם ב' הנחות אמנם לא יתהפך כי אותו שצריך ב' הנחות לא תוכל לעשות אותו עם הנחה אחת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
155 שאלה אדם קנה חתיכה מדוק [62]ואם יקנה הקנה ח' זוזים ישארו בידו חמישים זוזים ואם יקנה אותה קמה עשרה זוזים יחסרו לו שמונים זוזים אשאל כמה קנים היתה ארך החתיכה וכמה זוזים הביא בידו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה תחבר נ' עם פ' ויעלו ק"ל חלקם על היתרון שיש מי' לח' שהוא ב' ויצא ס"ה וכך הם הקנים מהחתיכה כי אם תמכור ח' זוזים כל קנה יוסיפו לו חמישים ואם תקנה י' יחסרו שמונים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Euclidean Propositions |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
156 אם יש לך ב' מספרים ותחלק א' מהב' מספרים ותכפול כל חלק על המספר השני הנה הסך העולה הוא כמו מה שיעלה מכפל המספר הראשון על השני | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
המשל הנה ב' מספרים והם י' וי"ב ונחלק י"ב על ב' ועל ג' ועל ה' ועל ב' והנה כלם י"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנה אם תכפול ב' על י' הם עשרים וג' על י' הם ל' וה' פעמים י' הם נ' וקבצם ויעלה ק"כ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וככה יעלה אם תכפול המספר הא' על הב' היינו י' על י"ב כי הם ק"כ גם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו שהוא רשום בתמונה הראשנה מהחלק הב' מאוקלידס | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
157 אם יש לך מספר אחד ותחלק אותו לכ"כ חלקים שתרצה אם תכפול כל חלק על המספר המחולק ותקבץ כל החלקים יהיו שוים אל המספר המחולק כפול על עצמו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
המשל נרצה לעשות מי"ב ג' חלקים ה' ג' ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
אומר אם תכפול ג' על י"ב יעלו ל"ו ואם תכפול ד' יעלו מ"ח ואם על ה' יעלה ס' ותקבצם ויעלו קמ"ד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וככה יעלה י"ב כפול בעצמו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
158 אם תחלק איזה מספר על ב' חלקים ותכפול החלק שיהיה מב' החלקים על המספר המחולק ושמור העולה כך יעלה אם תכפול אותו חלק על עצמו ותוסיף בו העולה מהכפל מהחלק האחד על השני | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
המשל אם יש לנו י"ב ותחלק אותו ח' ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
אומר כי אם תכפול ח' על י"ב יעלה צ"ו ושמרם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכן יעלה אם תכפול ח' על עצמם שהם ס"ד ותכפול ד' על ח' שהוא ל"ב וחברם אל ס"ד ויהיו ג"כ צ"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
159 אם תחלק איזה מספר שיהיה על ב' ותכפול כל חלק על עצמו וג"כ כפול הא' על הב' וכפלם על ב' ותקבץ הכל הנה העולה יהיה שוה אל המספר המחולק כפול על עצמו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
המשל הנה נחלק [63]מספר י"ב על ד' ועל ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנה כפול ח' על עצמם ויהיו ס"ד וד' על עצמם ויהיו י"ו גם כפול ד' על ח' והם ל"ב וכפלם על ב' והם ס"ד קבץ הכל ר"ל ס"ד ול"ב וס"ד יעלה הכל קמ"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והוא שוה אל מרובע י"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
160 אם תחלק מספר אחד לב' חלקים שוים ולב' חלקים בלתי שוים הנה כל כך יעלה כפל החלקים השוים זה על זה כמו כפל החלקים הבלתי שוים זה על זה ותוסיף בם כפל היתרון שיש מהחלק האחד על האחר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
המשל נחלק מספר י"ב לב' חלקים שוים ו'ו' ולב' חלקים בלתי שוים ד' וח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ואומר כי אם תכפול ו' על ו' והם החלקים שוים יעלו ל"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
כך יעלו אם תכפול ד' על ח' שהם ל"ב ותוסיף בם מרובע היתרון שיש מח' אל ו' שהם ב' ומרובעם ד' תוסיפם על ל"ב ויהיו ל"ו גם כן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
161 אם תחלק איזה מספר לב' חלקים שוים ותוסיף בם א' מהחלקי' כפול על עצמו ותוסיף בם התוספת על כל המספר המחולק ותכפול אותו המספר אשר הוספת ותחברם עם כפל אחד מהחלקים אומר כי הוא שוה אל כפל המחצית עם התוספת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
המשל יש לנו מספר י"ב ותחלק אותו על ו"ו ותוסיף על ו' מספר איזה שתרצה ונניח כי נרצה להוסיף על ו' ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והם י' וכפלם על עצמם והם ק' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואומר כי אם תכפול א' מהחלקים השוים על עצמם היינו ו' שהם ל"ו גם תוסיף על כל המספר המחולק שהיה י"ב התוספת שהם ד' ויהיו י"ו ואם תכפול י"ו על ד' שהם התוספת והם ס"ד ותחברם עם ל"ו והם ק' והם שוים אל הק' השמורים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
162 אם יש לך מספר ותחלקהו לב' חלקים בלתי שוים ותכפול החלק הגדול על עצמו גם תכפול המספר המחולק על עצמו ותחבר הב' הכפלות הנה העולה יהיה שוה אל כפל המספר הגדול על המספר המחולק ותכפלהו אח"כ על ב' גם תוסיף על זה כפל החלק הקטן ותחבר הכל יהיה שוה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
המשל נרצה לחלק י"ב על ח' וד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ואומר כי אם תכפול ח' על עצמם יהיה ס"ד גם אם תכפול י"ב על עצמם יהיו קמ"ד ותחברם ויהיו ר"ח ושמרם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
אח"כ כפול ח' שהוא המספר [64]הגדול על י"ב ויהיו צ"ו וכפלם על ב' ויהיו קצ"ב תוסיף בם כפל המספר הקטן שהוא ד' ומרובעם י"ו ויעלה ר"ח והם שוים אל הר"ח השמורי' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
163 אם יש לך מספר ותחלקהו לב' חלקים בלתי שוים אם תוסיף א' מהחלקים על כל המספר ר"ל על המספר המחולק יהיה שוה אל אותו החלק אשר הוספת כפול על כל המספר אח"כ העולה תכפול על ד' ותוסיף על זה מרובע החלק השני | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
המשל נרצה לחלק י"ב על ד' וח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
תוסיף ד' על י"ב ויהיו י"ו ומרובעם רנ"ו ושמרם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
אח"כ כפול ד' שהוספת כפלם על י"ב ויהיו מ"ח כפלם ד' פעמים ויהיו קצ"ב תוסיף על זה מרובע החלק הב' שהוא ח' ומרובעם ס"ד תוסיפם על קצ"ב ויעלו רנ"ו ג"כ והם שוים אל רנ"ו השמורים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וכן ממש יהיה ג"כ אם הוספת החלק הגדול שהוא ח' על י"ב יעלו כ' ומרובעם ד' מאות ושמרם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
אח"כ כפול ח' על י"ב ויעלו צ"ו וכפלם על ד' ויהיו שפ"ד תוסיף בם מרובע החלק האחר שהוא ד' והם י"ו ויהיו ד' מאות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
164 אם תחלק איזה קו לב' חלקים שוים ולב' חלקים בלתי שוים וכפול כל אחד מהחלקים בלתי שוים ותחברם הם כפל מהחלקים השוים נוסף בם יתרון החלק הגדול על הקטן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
המשל נרצה לחלק מספר י"ב לב' חלקי' שוים ו'ו' ולב' חלקים בלתי שוים ח' ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
הנה כפל ח' ס"ד וכפל ד' י"ו וחברם והם פ' ושמרם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אח"כ כפול א' מהחלקים השוים על עצמם ויעלו ל"ו ויתרון החלקים הבלתי שוים האחד על האחר היה ד' כי א' ד' ואחר ח' תוסיף ד' על ל"ו ויהיו מ' והוא חצי פ' השמורים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמבואר בתמונת ל"ו מעשירי מאוקלידס | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
165 אם תחלק איזה מספר על ב' חלקים שוים ואחר תוסיף מספר אחר על המספר המחולק ותרבענו ותוסיף על זה מרובע שהוספת יהיה ב' פעמים כמו כפל ממה שיעלה התוספת הנוסף על החצי עם מרובע החצי נוספים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
המשל יש לנו מספר י"ב ותחלקהו על ו'ו' ותוסיף על י"ב [65]מספר אחר ונניח כי נוסיף בם ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ועם י"ב עשרים ותרבעם ויהיו ד' מאות אח"כ תוסיף בם מרובע ח' שהוא ס"ד ויהיו תס"ד ושמרם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אח"כ קח הח' שהוספת והוסיפם על ו' שהוא החצי ויהיו י"ד ותרבעם ויהיו קצ"ו אח"כ תרבע ו' שהוא ל"ו ותוסיפם על קצ"ו ויעלה רל"ז והנך רואה כי הם חצי תס"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
166 אם תחלק איזה קו על ב' חלקים בלתי שוים ותחלק כל המספר על החלק הקטן יהיה בו תוספת אחד אם תחלק החלק הגדול על הקטן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל נרצה לחלק י"ב על ח'ד' והנה נחלק י"ב על ד' שהוא המספר הקטן והוא ג' ושמרם אחר כן חלק החלק הגדול שהוא ח' על הקטן ויצא ב' והנך רואה כי הוא פחות א' מהג' השמורים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
167 אם תחלק קו לב' חלקים בלתי שוים ותחלק החלק הקטן על הגדול והגדול על הקטן אח"כ חלק החלק היוצא מב' החלקים זה על זה לעולם יצא שוה ר"ל אחד שלם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל מספר י"ב נחלקם על ח'ד' אח"כ נחלק ח' על ד' ויצא ב' גם חלק ד' על ח' ויצא חצי אח"כ כפול חצי על ב' ויצא א' שלם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
168 אם תחלק א' מב' מספרי' ר"ל אם יש לך ב' מספרים בלתי שוים ותחלק הגדול על הקטן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון ח"ד ותחלק ח' על ד' יצא ב' גם תחלק ד' שהוא הקטן על הגדול שהוא ח' ויצא חצי ואומר אם תכפול ב' פעמים חצי יצא אחד שלם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
169 אם יש לך מספר ותחלקהו על ב' חלקים בלתי שוים אומר כי אם תקבץ המספרי' המוכפלים על עצמם ואח"כ תכפול המספר הקטון על הגדול והעולה כפול על ב' ותקבץ זה עם השמור יעלה הכל כמו המספר כפול על עצמו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל יש לנו מספר י"ב וחלקהו על ב' מספרים בלתי שוים על ח' ד' הנה ח' על ח' הם ס"ד וד' על ד' הם י"ו וקבצם והם פ' אח"כ כפול ד' על ח' והם ל"ב וכפלם והם ס"ד ותחברם עם הפ' השמורים יעלו קמ"ד וכן עולה כפל י"ב על עצמם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
170 אם יש לך מספר א' ותחלקהו [66]על ב' [מספרים] בלתי שוים ותכפול כל א' בעצמו ותחברם אח"כ כפול הקטן על הגדול ותכפלהו על ב' והעולה תחסר מב' הכפלו' הנה הנשאר יהיה שוה לכפל המספר הגדול על עצמו אחר שחסרת ממנו הקטן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל הנה המספר הוא י' תחלקהו על ח' ועל ב' הנה כפל אלו הב' מספרים ר"ל ב' על ב' שהם ד' וח' על ח' שהם ס"ד שניהם מקובצים הם ס"ח ושמרם אח"כ כפול ב' על ח' שהוא י"ו וכפלם על ב' והם ל"ב תסירם מס"ח הנשאר ל"ו וכך הוא המספר הגדול עם הקטן כיתרון הגדול על הקטן הוא וו"ו על ו' הם ל"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
171 אם תחלק מספר לב' חלקים בלתי שוים ותחלק הגדול על הקטן ואח"כ תכפול היוצא על הגדול יעלה כמו שיעלה הגדול כפול על עצמו ואח"כ תחלק העולה על הקטן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| משל מספר י' תחלקהו על ח' ועל ב' תחלק ח' על ב' ויצא ד' כפול ד' על ח' ויהיו ל"ב ושמרם אח"כ כפול הגדול על עצמו והעולה שהוא כפל ח' על ח' שהוא ס"ד תחלק על המספר הקטן שהוא ב' יצא ל"ב והם שוים אל ל"ב השמורים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
172 אם יש לך מספר ותחלקהו על ב' חלקי' בלתי שוים הנה אם תחלק כל המספר על הקטן ואח"כ תחלק כל המספר על המספר הגדול ותקבץ הכל יהיה העולה מהמקובץ כמו אם תכפול זה על זה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל יש לנו מספר י' אם תחלקהו על ב' וח' ותחלק י' על ב' יצא ה' גם תחלק י' על ח' יצא א' ורביע וקבצם עם הה' ויהיו ו' ורביע וכן הוא ממש אם תכפול ה' על א' ורביע יצא ו' ורביע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
173 אם תחלק מספר מה לב' חלקים בלתי שוים ואח"כ תחלק הגדול על כל המספר על החלק הקטן גם תחלק כל המספר על החלק הגדול ותקבץ הכל הנה המקובץ יעדיף ב' על קבוץ החלק הקטן על הגדול | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל מספר י' תחלקהו על ח' ב' חלק י' על ב' והם ה' חלק י' על ח' והם א' ורביע וקבצם והם ו' ורביע ושמרם עתה קבץ החלק הגדול שהוא ח' על ב' שהוא הקטן ויצא ד' [67]גם תחלק ב' על ח' והם רביע וקבצם והם [...] השמורי' הם ו' ורביע עודפים עליהם ב' שאינם כי אם ד' ורביע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
174 אם יש לך מספר אחד ותחלקהו על ב' מספרים בלתי שוים ותכפול כל א' מהחלקים על עצמם וקבץ ההכפלות ואח"כ תכפול כל המספר קודם שנתחלק על עצמו ותוציא ממרובעו אותם הב' הכפלות מקובצות והנשאר חלק על ב' ומזה המספר תוציאנו ממרובע חצי כל המספר וקח שרשו אם תוציאנו מהמספר המחוצה יצא החלק הקטון ואם תוסיפנו עליו יצא החלק הגדול | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל המספר הוא י' חלק אותו על ח'ב' ומרובע ח' ס"ד ומרובע ב' י"ו ד' ושניהם מקובצים ס"ח קח מרובע י' שהוא כל המספר שהוא ק' ותוציא מהם ס"ח הנשאר ל"ב וקח חצים והם י"ו תוציאם ממרובע חצי י' שהם ה' ומרובעם כ"ה הנשאר ט' וקח שרשם שהם ג' ואם תוסיפם על ה' שהוא חצי המספר הם ח' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תוציאנו מה' שהוא חצי המספר הנשאר ב' והוא המספר הקטן | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
175 שאלה תמצא לי ב' מספרים מרובעים אשר מרובע כל אחד מהם על עצמו ואח"כ תחברם יהיו נ"ח וכפל האחד על השני יעלה כ"א | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה כפול כ"א על ב' והם מ"ב תוסיפם על נ"ח והם ק' עתה קח שרשם והם י' ועתה עשה מי' שני חלקים כפול הא' על הב' יהיו כ"א הנה האחד ג' והאחר ז' ושניהם י' עתה כפול י' על עצמו והם ט' וכפול ז' על עצמם ויהיו מ"ט ושניהם מחוברים יהיו נ"ח | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
176 שאלה אם תרצה לדעת מב' מספרים אשר כל אחד כפול ואח"כ תחברם אם תרצה למצא אותם המספרים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה נניח כי האחד ח' והאחר ב' כפול ח' על ח' והם ס"ד וב' על ב' והם ס"ד ושניהם ס"ח וכפל המספר הקטן על הגדול עולה י"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אם תרצה למצא כל הב' מספרים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה תחלק ס"ח על ב' ויצא ל"ד וקח מרובעם והם אלף וקנ"ו ומזה תסיר מרובע י"ו שהוא רנ"ו ונשאר ט' מאות וקח שרשם והם ל' תוסיף [68]בם ל"ד והם ס"ד וקח שרשם והם ח' והוא המספר הגדול אח"כ למצא המספר הקטן תסיר ל' מל"ד הנשאר ד' והוא המספר הקטן ר"ל שרשו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
177 שאלה תמצא לי ב' מספרים כפולים זה על זה יעלו י"ו והגדול כפול על עצמו עודף על השני כפול בעצמו ס' כמה הוא הגדול ומה הוא הקטן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה תחלק ס' על ב' ויצא ל' תרבעם ויהיו ט' מאות גם תרבע י"ו על רנ"ו ותחברם עם ט' מאות והם אלף וקנ"ו קח שרשם והם ל"ד תוסיפם על ל' והם ס"ד קח שרשם והם ח' והוא הגדול גם תוציא מל"ד ל' הנשאר ד' וקח שרשם והם ב' והוא הקטן | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
177 השאלה תמצא לי מספר שהאחד יהיה ח' וח' תשיעיות יותר מהאחר וכפול זה על זה לא יעלו כי אם אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כן תעשה קח חצי ח' וח' תשיעיות ויהיו ד' וד' תשיעיות כפלם על עצמם והם י"ט וס"א חלקים מפ"א תוסיף בם אחד ר"ל מה שתרצה שיעלה כפול זה על זה ויעלו עשרים וס"א חלקים מפ"א וקח שרשם והם ד' וה' תשיעיות תחברם עם ד' וד' תשיעיות והם תשעה והוא המספר הגדול והקטון יהיה ד' וה' תשיעיות תחסר מהם ד' וד' תשיעיות הנשאר תשיעית אחד והנך רואה כי הגדול יותר מן הקטן ח' וח' תשיעיות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכפול זה על זה אינו כי אם אחד שלם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
179 אם תחלק מספר אחד לב' חלקים בלתי שוים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו י' תחלק על ב' וח' הנה מרובעים כל אחד על עצמו ומחוברי' עולה ס"ח הנה ההפרש שיש מב' לח' הוא ו' ומרובעו ל"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
180 אם תחלק מספר א' לב' חלקים בלתי שוים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו ח' ב' וכפול כל אחד על עצמו ומחוברים הם ס"ח וההפרש מזה מזה לזה הוא ו' כפלם והם ל"ו תסירם מס"ח הנשאר ל"ב וחצים י"ו כמו שהם הב' מספרים כפולים זה על זה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
181 תמצא לי ב' מספרים אשר שניהם מחוברים יעלו [69]י' ושניהם ג"כ מרובעים כל אחד על עצמו ומחוברים אח"כ יעדיף כ"ח על שני המספרים כפולים זה על זה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה תחלק י' על חצי והם ה' כפלם על עצמם והם כ"ה תסירם מכ"ח נשאר ג' תחלקם על ג' ויצא אחד ושרשו אחד והנה אם תסיר א' מה' נשאר ד' והוא אחד מהב' מספרים ואם תוסיף אחד על ה' ויהיו ו' והוא המספר השני | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנך רואה כי אלו המספרים כפול כל אחד על עצמו ומחוברים עולה נ"ב תסיר מהם כפל הגדול על הקטן שהוא כ"ד נשאר עדין כ"ח כמו שאמרנו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
182 שאלה תעשה לי מי' ב' חלקים שמרובע הגדול יעדיף על מרובע הקטן ס' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה תרבע עשרה והם ק' תסיר מהם ס' הנשאר מ' ואלו המ' חלקם על כפל י' שהם עשרים ויצא ב' וזהו החלק הקטן ועד עשרה יחסרו ח' והוא החלק הגדול | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
183 שאלה תמצא לי ב' מספרים שיהיו מוכפלים על עצמם ותחבר אותם ההכפלות גם תצרף עמהם הכפל ממה שיעלה הקטן על הגדול והעולה יהיה פ"ד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תרבע עשרה והם ק' תסיר מהם פ"ד ונשאר י"ו וזהו הכפל מהקטון על הגדול ואח"כ תאמ' מעשרה תעשה ב' חלקים כפולים זה על זה יעלו י"ו הנה תמצא כי החלק האחד ב' והאחר ח' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
184 אם יש לך לחלק עשרה על ב' חלקי' על ב' ועל ח' ואח"כ תחלק הגדול על הקטן והקטון על הגדול היינו ח' על ב' יצא ד' גם חלק ב' על ח' יצא רביע ושניהם הם ד' ורביע ועל זה המספר תחלק איזה מספר כאלו תאמר י"ז ויצא ד' שלמים ואומר כי אלו תחלק י"ז על אלו הד' יצא ד' ורביע כבראשנה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
185 שאלה תחלק לי עשרה על ב' חלקים בלתי שוים ואח"כ תחלק הגדול על הקטן והקטן על הגדול והיוצא כפול על עשרים יעשה פ"ה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה עשה מי' ב' חלקים ב'ח' חלק ב' על ח' יצא רביע וחלק ח' על ב' יצא ד' ושניהם הם ד' ורביע אח"כ חלק פ"ה על עשרים יצא ג"כ ד' ורביע אח"כ כפול ד' ורביע על עשרים יצא פ"ה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
186 שאלה תעשה מי' ב' חלקים בלתי שוים אשר הגדול מחולק [70]על הקטן והקטן על הגדול ואח"כ תקבץ הכל והעולה כפול על השטח ההוה מכפל המספרים זה על זה יעלה כמו השטח ההוה מב' המספרים כפול כל אחד על עצמו ומקובצים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל ו' ד' חלק ד' על ו' והם ב' שלישיות וו' על ד' והם א' וחצי וקבצם והם ב' ושישית אחד כפול ד' על ו' והם כ"ד כפלם על ב' ושישית והם נ"ב כן ממש יעלה אם תכפול ד' על עצמו הוא י"ו וו' על עצמו ל"ו ושניהם מחוברי' הם נ"ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
187 שאלה חלק לי י' על ב' חלקים בלתי שוים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון ד' ו' ואח"כ חלק י' שהוא כל המספר על ד' יעלה ב' וחצי ואם תחלק החלק הגדול על החלק הקטן יצא א' וחצי היינו ו' על ד' והנך רואה כי הוא אחד פחות מהחלק האחר גם אם תחלק י' על ו' יצא א' וב' שלישיות והוא אחד פחות לעולם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
188 תמצא לי ב' מספרים כי מחוברים יהיו כמו כפולים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כן תעשה שהאחד יעדיף על חבירו אחד או יחסר אחד ונניח כי הא' ג' והאחר ד' כי אם תחלק ד' על ג' יצא א' ושליש ואומר כי זה המספר כפול על ד' יהיה כמו מחובר על ד' כי ד' פעמים א' ושליש הוא ה' ושליש וכן כשהם מחוברים ג"כ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ועל כן תוכל לשאול תעשה לי מי"ג ב' חלקים או מי"ט או מכ"ז או מאיזה מספר שיהיה נפרד ועשה שהאחד יעדיף על חבירו א' ותעשה כנז' כגון אם יאמר תעשה לי מי"ג ב' חלקים שיהיו מוכפלים כמו מחוברים עשה האחד ו' והאחר ז' חלק ז' על ו' ויצא א' ושישית והנה אם תכפול ז' על א' ושישית יעלו ח' ושישית אחד וכן אם תחברם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
189 שאלה אם תחלק י' על ד'ו' ותקבץ הכפלותיהם כל אחת על עצמם יצא נ"ב עתה קח חצי י' שהוא ה' ותרבענו ויהיו כ"ה עתה תקח ההפרש שהוא מד' אל ה' או מו' אל ה' שהוא אחד ותרבענו ויהיה אחד ותוסיפהו על כ"ה ויהיו כ"ו והוא כמו חצי ג"כ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| פירוש מהשאלה של מעלה האומרת תמצא לי ב' מספרים שיהיו [71]כפולים כמו מרובעים ר"ל תעשה מאיזה מספר שיהיה ב' חלקים כי אם תחלק הגדול על הקטן יעשה רבועם כמו קבוצם כמו מספר ז' תחלקהו על ב' חלקים שהאחד יעדיף אחד על חבירו ולא תוכל לעשות זאת השאלה כי אם ממספר ד נפרד כי אם הוא זוג לא תוכל לחלקו שהחלק האחד יעדיף על האחר א' ועל כן מספר ז' חלקהו על ג'ד' אח"כ חלק הגדול שהוא ד' על ג' ויצא א' ושליש ואומר כי זה המספר הוא המבוקש כי כך עולה כפול כמו מרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
190 שאלה איך נוכל למצא ב' מספרים כפולים זה על זה מי"ב שיעלה ל"ו אם תחבר על העולה המספר הקטן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כן תעשה עשה שהאחד יהיה ד' והאחר ח' וכפלם והנם ל"ב חבר בם ד' והם ל"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולמצא אותם אם לא תדעם הסר י"ב מל"ו הנשאר כ"ד אח"כ מי"ב חסר לעולם ב' או מאיזה מספר אחר שיהיה הנשאר י' חלקם על ב' ויצא ה' וכפלם על עצמם והם כ"ה תסיר מהם כ"ד הנשאר א' וקח שרשו והוא אחד ותוציאנו מה' הנשאר ד' והוא המספר הקטן והחלק האחר הוא י"ב מוסף עליו שרש א' והנם י"ג הסר מהם ה' והנם ה' והוא הגדול | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
191) שאלה תעשה מכ"ה ב' חלקים שיהיה יחס האחד בהקש אל י' כיחס י' אל השני | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה קח חצי כ"ה והוא י"ב וחצי ותרבעם והם קנ"ו ורביע ומזה תסיר מרובע י' שהוא ק' הנשאר נ"ו ורביע וקח שרשם והם ז' וחצי תוציאם מי"ב וחצי הנשאר ה' והוא החלק האחד ולמצא השני תוסיף אלו הי"ב וחצי על י"ב וחצי והם עשרים והנך רואה כי הם מתיחסים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כי יחס ה' אל י' כיחס י' אל כ' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
192) שאלה תמצא לי ג' מספרים מתיחסים כמו ב'ד'ח' כי קבוצם י"ד ואם תכפול ב' על ד' והם ח' וח' על ח' הם ס"ד ואם תחלק ס"ד על ב' יצא ל"ב כמו שהוא ד' על ח' ואם תחלק ס"ד על ד' יצא י"ו כמו שהוא ב' על ח' ואם תחלקהו על ח' יצא ח' כמו שהוא ב' על ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
193) שאלה תעשה לי מי"ד ג' חלקים שיהיה הא' כפול על ב' כמו הג' כפול בעצמו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עשה כך תחבר הא' והב' שהם ב'ח' שהם י' וקח חצים ותרבעם והם כ"ה תסיר מזה מרובע הג' שהוא ד' והם י"ו נשאר ט' וקח שרשם והם ג' תוציאם מה' נשאר ב' והוא הא' ותוסיפם על ה' והם ח' והוא הג' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
194) שאלה תעשה לי מי"ב ג' מספרי' שמרובע הראשון יהיה כמו מרובע הב' והג' מחוברים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה הא' הוא ה' והב' ד' והג' ג' הנה מרובע ה' הוא כ"ה כמו מרובע ד' שהוא י"ו וג' שהם ט' כי הם כ"ה לכן כדי למצא אותם קח חצי כ"ה והם י"ב וחצי ומזה תסיר חצי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| מהב' מספרים האחרים שהם מחוברים ג'ד' והם ז' וחצים הוא ג' וחצי ותרבעם והם י"ב ורביע תוציאם מי"ב וחצי נשאר רביע ושרשו חצי וזה תוסיף על ג' וחצי והוא ד' והוא השני גם מג' וחצי תוציא חצי הנשאר ג' והוא הג' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
195) שאלה תעשה מט"ו ג' חלקים האחד ג' והאחר ה' והאחר ז' הנה אם תכפול ג' הם ט' ואם תכפול ה' הם כ"ה ועם הט' הם ל"ד גם כפול ג' על ה' והם ט"ו ותחברם והם מ"ט כמו מרובע ג' שהוא ז' כי עולה ג"כ מ"ט | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולמצא אותם אומר כי תחבר ג' עם ח' והם ט' ומרובעם ס"ד ומזה תוציא מרובע הג' שהוא מ"ט הנשאר ט"ו ואלו הט"ו תוציאם מחצי מרובע הא' והב' מחוברים שהם ח' וחצים ד' ומרובעם י"ו הנשאר א' ומזה תוציא מן החצי ר"ל מד' הנשאר ג' והוא ראשנה ולמצאה שניה תוסיף א' על ד' והם ה' והוא השניה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
196) שאלה אם תחלק איזה מספר על ד' חלקי' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון מספר כ"ב ותחלקם ו'ח' הם ראשנים ז'א' והם אחרונים ואומר כי ו' כפול על עצמו הוא ל"ו וח' כפול על עצמו הוא ס"ד ושניהם מחוברים הם ק' והנה כפל ז' על עצמו הוא מ"ט וכפל א' על א' הוא א' והם חצי ק' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
197) שאלה אם תעשה מי' ב' חלקים בלתי שוים כגון ב'ח' אם תכפול הא' על הב' הם י"ו והקואטרופלא הם ס"ד כי אם תרבעם על ד' הם ס"ד אח"כ תרבע י' והם ק' ומזה תסיר ס"ד ונשאר ל"ו והוא מרובע היתרון כמו שיש מח' אל ב' שהם ו' ומרובעם ל"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
198) שאלה אם תעשה מי"ג ב' חלקים האחד ד' והאחר ט' אשר שרש האחד כפול על שרש האחר עולה ו' ואם תקח חצי י"ג שהם ו' וחצי ותרבעם עולה מ"ב ורביע ומזה תוציא מרובע ו' שהוא ל"ו ונשאר ו' ורביע ומזה תוציא שרש הנשאר ד' הוא המספר הקטן והאחר הוא ו' וחצי נוסיף עליו שרש ו' ורביע ויעלה ט' והוא השני | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
199) שאלה תעשה לי מי"ב ב' חלקים בלתי שוים שהחלק האחד כפול בחבירו יעלה י"ו יותר קח שרש י"ו כלומ' יעשה עשרים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קח מרובע ו' היינו ל"ו תוציא מהם י"ו הנשאר עשרים ומזה תוציא שרש י"ו הנשאר והוצא שרש י"ו מו' הנשאר ב' והוא הקטן גם תוסיף אלו הד' על הו' והם י' והוא החלק הגדול | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
200) שאלה תעשה מכ"ט ב' חלקים אשר אם תוציא חלק הקטן משרש הגדול שישאר ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
כך תעשה עשה שהאחד ד' והאחר כ"ה הנה שרש כ"ה הוא ה' ושרש ד' והוא ב' תוציא ב' מה' נשאר ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנה אם תכפול ג' על ז' שהוא קבוץ ב' שרשים יעלה כ"א והוא כמו היתרון שיש מחלק הגדול על הקטן כי הא' כ"ה והאחר ד' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
201) שאלה תעשה לי מי' ב' חלקים כי אם תוציא שרש הגדול משרש הקטן שישאר ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה תרבע ב' והם ד' תוציאם מי' והם ו' וקח חצים והם ג' ותרבעם והם ט' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
אח"כ קח חצי עשרה שהם ה' כפלם על עצמם והם כ"ה ומזה תוציא הט' נשאר י"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והנה שרש י"ו אם תוציאנו מה' הנשאר א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ואם תוסיפם על ה' ויהיו ט' והם החלקים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
202) שאלה תעשה לי מכ"ט ב' חלקים אשר אם תוציא שרש הגדול משרש הקטן שישאר ג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה קח חצי ג' שהם א' וחצי וכפלם על עצמם והם ב' ורביע וזה תוציא מחצי כ"ט שהם י"ד וחצי הנשאר י"ב ורביע ומזה תקח שרשם שהם ג' וחצי וזה תכפול על הג' ויעלה עשרה וחצי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
וזה תסיר מחצי כ"ט שהם י"ד וחצי הנשאר ד' והוא החלק הקטן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
תוסיף אלו העשרה וחצי על י"ד וחצי והם כ"ה והוא השני | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
203) שאלה תעשה מעשרים ב' חלקים אשר אם תוסיף על החלק הקטן ב' פעמים שרשו הנה מרובע העולה יעלה כמו השטח ההוה מב' מספרים כפולים זה על זה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואומר כי החלק האחד ד' והאחר י"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
קח שרש ד' והם ב' וכפלם על ב' והם ד' ותוסיפם על הד' והם ח' וכפלם ס"ד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
כן אם תכפול הקטן על הגדול ר"ל ד' על י"ו יעלה ס"ד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
204) שאלה תעשה לי מי"ג ב' חלקים אשר שרשהם מקובצים יעלו חמשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תרבע חמשה ויהיו כ"ה תוציא מהם י"ג ונשאר י"ב תרבעם והם קמ"ד תחלקם על ד' ויצא ל"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אח"כ תרבע ו' וחצי שהוא חצי י"ג ויהיו מ"ב ורביע ומזה תוציא ל"ו הנשאר ו' ורביע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
תוציאם מו' וחצי ונשאר ו' וחצי פחות שרש ו' ורביע והאחד יהיה ו' וחצי נוסיף עליו ר"ל כי האחד ד' והאחר ט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
205) שאלה תחלק איזה מספר כאלו תאמר מספר י' לג' חלקים לב' וג' וא' ותכפול הא' על השלישית יעלה י' גם תכפול הראשון על השני יעלה ו' והשני על השלישי יעלה ט"ו ותחבר הכל והם ל"א ותכפלם והם ס"ב ושמרם עו' כפול הראשון על הב' גם כפול השני על הב' הנשארים גם השלישי על הב' הנשארים וקבץ הכל ויעלה ס"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
206) שאלה אם תחלק איזה מספר לג' חלקים כגון י' על ב'ג'ה' אם תכפול כל אחד כנגד הב' הנשארים וקבץ הכל הם ס"ב ומרובעם מקובצים עולה ל"ח ומחוברים עם הס"ב עולים ק' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| על כן אם נשאל לך תמצא מספר מי' חלקהם מוכפלים כל אחד על הב' הנשארות וגם מרובע כל א' מהם על עצמו המקובץ מהכל עולה ק' כמה הם החלקים הראוים לעשות מי' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
207) שאלה תמצא לי ב' מספרים מתיחסים מאיזה יחס שיהיה ואח"כ תמצא ב' מספרים אחרים מתיחסים כפי אותו היחס הראשון שיעלה כ"כ כפול השני מספרים הראשנים זה על זה כמו מה שיעלה מרובעי כל אחד מהם על עצמו מהשנים האחרים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל שיהיה הב' מספרים הראשנים שרש ל' ושרש ר"ע והשניים הם ג' וט' אשר השניים כפול כל אחד על עצמו ומחוברים עולה צ' ורבעם ויעלה ח' אלפים ומאה וכך עולה כפל הראשנים זה על זה ר"ל כ"ז עם ר"ע ואומר כי השטח מהב' שניים כפולים זה על זה שהוא כ"ז אם תכפלהו על ג' מאות אשר הוא העולה מהב' הראשנים עולה ח' אלפים ומאה ושרשם צ' וכן הוא השטח ו' מהראשנים עולה צ' והנך רואה כי יחס הראשנים והשניים הם טריפלא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
208) שאלה תעשה לי מעשרה ב' חלקים שכל חלק וחלק אצל חבירו ומה שיעלה תחבר אח"כ תחלק מרובע אותם הב' מספרים כל אחד כפול על עצמו שיצא י"ו אח"כ תחלק כ"ד על כל חלק מהחלקים והיוצא מקובץ משניהם יעשה ט"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה הנה היחס שיש מי' אל ט"ו כן יש מכ"ד אל י"ו כי כל אחד נקרא שישקאלטירא והנה החלק האחד מי' יהיה ב' והאחר ח' אשר כל חלק כפול על חברו ומחוברים עולה ד' ורביע וכפל מרובעהם עולה ס"ח כי אם תחלקם על ד' ורביע עולה י"ו גם אם תחלק כ"ד על ב' ועל ח' יצא ט"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
209) שאלה אם תחלק מספר ט' לב' חלקים ד' וה' אומר כי אם תכפול ד' על ה' הם עשרים והנך רואה כי כפל ד' על עצמם שהם י"ו על כפל ה' על עצמם ו' שהם כ"ה הם ד' מאות ושרשם עשרים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
210) אם תקח שני מספרי' כגון ד' וי"ב והנה תחלק י"ב על ב' יצא ו' ושמרם אח"כ כפול י"ב על ו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ויצא ע"ב ותכפלם על ב' ויהיו קמ"ד וכך הוא כפל י"ב על עצמם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
211) אם תחלק עשרה על ב' חלקים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כגון על ו' ועל ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
חלק י' על ד' ויצא ב' וחצי גם חלק י' על ו' ויצא א' וב' שלישיות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
אח"כ תחלק ו' על ד' ויצא א' וחצי חלק ד' על ו' ויצא ב' שלישיות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
על כן אמרתי כי הם פחות ב' מהד' ושתות הנשארים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
212) אם תחלק י"ב על ג' ועל ו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
יצא ו' ר"ל ב' מצד זה וד' מצד זה שהם ו' ושמרם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
אח"כ כפול י"ב על ג' ועל ו' ויהיו ע"ב מצד זה ול"ו מצד אחר ושניהם מחוברים הם ק"ח | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
213) אם תכפול מרובע על מרובע העולה יהיה מרובע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
גם אם תכפול מעוקב על מעוקב העולה יהיה מעוקב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
214) שאלה אם תכפול ב' מספרים אשר הסך העולה יש לו שרש הנה אלו הב' מספרים הנכפלים עם השרש ההוה מכפל זה על זה יהיו מספרים יחסיים כי יחס הראשון אל השרש כן יחס השרש אל המספר השני | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל נרצה לכפול מ' על צ' הנה הסך העולה ג' אלפים וו' מאות ושרשם הם ס' אומר כי עתה בכאן ג' מספרים יחסיים והוא כי יחס מ' אל ס' כיחס ס' אל צ' וכן יצא מכל ב' מספרים כפולים זה על זה ולסך יש לו שרש הנה השרש הוא יחס אמצעי בין הא' והג' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| משל אחר נרצה לכפול ג' על י"ב והנם ל"ו ושרשם ו' הנה ו' הוא אמצעי בין ג' וי"ב והנה הראשון ג' והב' ו' והג' י"ב וכלם הם מספרים יחסיים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
215) שאלה יש לנו ג' מספרים מתיחסים והנה העולה מכפל הראשון על השרש השרש הוא אמצעי כמה הוא הא' והג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל יש לנו ב'ח' ל"ב הנה כפל ב' על ל"ב הוא ס"ד ושרשם ח' והוא האמצעי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולדעת הא' והג' תרבע ח' והוא ס"ד ועשה מהם ב' חלקים שיהיה יחס הא' אל הח' כיחס ח' אל השלישי ותמצא כי האחד ב' והאחר ל"ב כי יחס ח' אל ב' כיחס ל"ב אל ח' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
216) שאלה הנה איש יש לו ממון ובסוף ג' שנים עולה תשעה כמה היה בתחלה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה ראוי לחלק ט' על ב' ויצא ד' וחצי וזה היה לו בסוף שנה שניה עתה תחלק ד' וחצי על ב' ויצא ב' ורביע וזה היה לו בסוף שנה ראשנה עתה תחלק ב' ורביע על ב' ויצא לך א' ושמין וזה היה לו בתחלה וזהו כשהיחס מא' אל ב' אמנם כשהיחס הוא מא' אל ג' ראוי לחלק כל השנים על ג' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
217) הנה לפעמים יזדמן כי אם תכפול שרש משרש מספר אחד אע"פ שאין לאותם המספרים שרש אמיתי לפעמים העולה מהכפל יהיה לו שרש משרש אמיתי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון האומר כפול שרש משרש צ"ו על שרש משרש רי"ו הנה אין לשרש צ"ו שרש משרש דישקריטו אמנם לרי"ו יש שרש משרש ד' דישקריטא והוא ד' על כן כפול צ"ו על רי"ו ויעלו עשרים אלף ותשל"ו ושרשם קמ"ד ושרש קמ"ד י"ב והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובזה האופן תוכל למצא אם ישאל אדם תמצא לי ב' מספרים שלא יהיו מרובעים וכפול שרש השרש מזה על שרש השרש מזה והעולה יהיה לו שרש אמיתי והנה תמצא כי המספר הא' יהיה צ"ו והאחר יהיה רי"ו ושרש השרש מזה כפול על שרש השרש מזה יהיה העולה י"ב בצומצום | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
218) אם תכפול שרש מספר מה על שרש מספר מה תכפול המספר האחד על המספר האחר ומהעולה תקח השרש והיוצא הוא המבוקש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון נרצה לכפול שרש ארבעה על שרש תשעה כפול ד' על ט' והם ל"ו וקח שרשם והם ו' והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן אם אין לשום אחד שרש או יש לאחד שרש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו אם תכפול שרש י"ב על שרש י' כי אין לשום אחד שרש כפול י"ב על י' והם ק"כ ושרש ק"כ הוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן אם תכפול שרש ט' שיש לו שרש על שרש י' שאין לו שרש כפול י' על ט' ויצא צ' ושרשו הוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן אם תרצה לכפול שרש משרש מספר אחד על שרש משרש מספר אחר כפול אלו הב' מספרי' זה כנגד זה ומהעולה קח שרש השרש והוא הדרוש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמו האומ' קח שרש משרש ג' וכפול אותו על שרש משרש כ"ז כפול כ"ז על ג' והם פ"א ומפ"א קח שרשם והוא הדרוש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
219) שאלה תמצא לי ב' מספרים בלתי מרובעים אשר שרש השרש מזה כפול על שרש משרש מזה והעולה לא יהיה לו שרש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כאלו תאמר מי' ותכפלם ויהיו ק' אח"כ קח איזה מספר שתרצה כגון מספר ה' ואח"כ קח ק' וחלק על ה' ויצא עשרים והנך כי ה' פעמים עולה ק' כמו שהוא מרובע עשרה ועל כן אם תכפול שרש ה' על שרש עשרים יעלה שרש ק' שהם עשרה
וכבר אמרנו כי אם תכפול שרש השרש מי' על שרש Coza השרש מעשרים יהיה שרש השרש מק' כלומ' עשרה קנג | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
220) שאלה תחלק לי י"ו לג' מספרים מתיחסים מיחס א אל ה' הנקרא קואינקופלא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עשה כך קח בעד הראשון א' ובעד הב' ה' ובעד הג' כ"ה וחברם והנם כ"א וחלק י"ו עליהם ויצא י"ו חלקים מל"א והוא הראשון וכן תעשה מהשני ומהג' וכן תוכל לעשות מכל היחסים בין שיהיה קואינקופלא או קואטרופלא או אי זה מספר אחר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
221) הנה קוסא ר"ל שרש ושינצו ר"ל מרובע [.............] [.....] נומירו ר"ל להביא מספרים מתחלפים במספר אחד כאלו תאמר קרלי' וטורניסי ודוקטי חשבון אחד יקבצם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Quadratic Equations |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכשהוא אומר קובו וצינצו דיצינצו הכל שב אל אלו השלשה כמו שתראה בדמיונות הריגולי מהקוסי הם נכללים בו' דרכים ג' מורכבים וג' פשוטים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| We write the simple [types] and then the compound [types]: | ונכתוב הפשוטים ואח"כ המורכבים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
222) שאלה תמצא לי מספר כי אם תכפול אותו על ד' יעלה כמוהו כפול על עצמו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נניח כי המספר הוא ו' כפול אותו על ד' ויעלה כ"ד וכפלהו על עצמו ויעלו ל"ו ולכן תאמר אם ל"ו יתן לי ו' כ"ד כמה יתנו ויצא לך ד' והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולעשות אותו ריגולא דילאקוסא עשה כך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
קח קושא אחת ו' וכפלהו על ד' והם ד' קוסי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אח"כ תרבע א' קוסא והוא א סינסו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והוא שוה אל ד' קוסי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תחלק מספר הקוסי על מספר הסינסו ויצא לך ד' והוא המבוקש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
223) שאלה תמצא לי מספר כפול על עצמו והעולה כפול על ה' יעלה מ"ה' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נניח כי הוא א' קוסא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כפול אותו על עצמו ויצא א' סינסו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אח"כ כפול אותו על ה' והם ה' סינסי והוא שוה אל מ"ה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
על כן חלק מ"ה אל מספר הסינסו שהם ה' ויצא ט' וקח שרש ט' והוא ג' והוא הדרוש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
224) שאלה תמצא לי מספר כי שלישיתו כפול על ה' יהיה עשרים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נניח כי הוא קוסא אחת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
קח שלישיתו והוא שליש קוסא אחת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכפלהו על ה' והם קוסא אחת וב' שלישיות קוסא הם שוים אל עשרים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
לכן חלק עשרים על א' וב' שלישיות ויצא י"ב והוא הדרוש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| So much for the simple types and these are the compound types: | ע"כ הפשוטים ואלו הג' הם מורכבים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
225) שאלה תמצא מספר כי אם תוסיף אותו על מרובעו יעלה י"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נניח א' קוסא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תרבעהו ויהיה א' סינסו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תוסיף בו א' קוסא ויהיה א' סינסו ועוד א' קוסא והוא שוה אל י"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תחלק הקוסא ויהיה חצי קוסא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כפלהו על עצמו יצא רביעית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תוסיף בו המספר הדרוש והוא י"ב ויהיו י"ב ורביע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה שרש י"ב ורביע פחות חצי הוא שוה הקוסי היינו ג' והוא הדרוש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
226) שאלה תמצא לי מספר כי כשתוסיף בו י"ב יהיה העולה שוה למרובעו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כך תעשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נניח כי הוא א' קוסא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תוסיף בו י"ב והוא א' קוסא יותר י"ב והוא שוה אל א' סינסו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תחלק א' קוסא ויצא חצי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כפלהו על עצמו ויצא רביע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תוסיף בו י"ב ויצא י"ב ורביע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה שרש י"ב ורביע נוסף עליו חצי הוא הדרוש היינו ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
227) שאלה תמצא לי מספר כפול על ה' יעלה כמו מרובעו וכמו אם תוסיף עליו ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כך תעשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נניח שהוא א' קוסא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותרבעהו והוא א' סינסו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תוסיף בו ד' ויהיה א' סינסו ועו' ד' והוא שוה אל ה' קוסי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תחלק הקוסי שהם ה' ויהיו ב' וחצי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כפלם על עצמם ויהיו ו' ורביע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תסיר מהם ד' וישארו ב' ורביע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה שרש ב' ורביע הוא א' ורביע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נוסף על ב' וחצי הוא המספר הדרוש היינו ארבעה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Here end the three compound types. Deduce from this. | ובכאן נשלמו ג' ריגולי מורכבות ותקיש על זה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
228) שאלה תמצא לי מספר אשר אם תוסיף עליו רביע מרובעו יהיה שלשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נניח כי הוא א' קוסא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תרבע אותו והוא א' צינסו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והרובע הוא רביע סינסו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תוסיף בם א' קוסא ויעלה א' קוסא יותר א' רביע סינסו והוא שוה אל שלשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנך רואה כי יש לך פחות מסינסו אחד יען כי אינו כי אם רביע סינסו על כן ראוי שתחשוב כי הוא סינסו אחד היינו כי תחלק הכל על א' רביע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויצא לך א' שלם יותר ד' קוסי והוא שוה אל י"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה לפי זה הדרך תמצא כי הקוסא שוה שרש י"ו פחות שנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| You should do the same also if you have more than one square: | וכן ג"כ ראוי לעשות אם היה לך יותר מסינסו אחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כאלו תאמר ג' צינסו וחצי או א' צינסו ורביע היה ראוי לחלק על ג' וחצי או על א' ורביע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| In conclusion, the fraction should be converted into a whole. | סוף דבר צריך להביא השבר ולעשות ממנו שלם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
229) שאלה תמצא לי מספר אשר אם תכפלהו על עצמו והעולה כפלהו על העולה יהיה שוה כמו מרובע אותו המספר כפול על ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נניח א' קוסא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותכפלהו על עצמו ויהיה א' צינסו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עוד תרבע העולה ויהיה סינסו דיסינסו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה שוה אל ד' פעמים סינסו ר"ל אל ד' סינסי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תחלק ד' אל א' ויצא ד' וקח שרשו והוא ב' והוא המבוקש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
230) שאלה תמצא לי מספר אשר אם תכפלהו על עצמו והעולה כפול פעם אחרת על עצמו יהיה כמו שהוא כפול על ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נניח כי המבוקש הוא א' קוסא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותכפלהו על עצמו ויהיה א' סינסו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה ג"כ כפול על עצמו יעלה סינסו מסינסו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה שוה אל א' קוסא כפול ד' קוסי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תחלק על א' ויצא ח' והנה שרש מעוקב מח' שוה הקוסי והוא המבוקש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
231) שאלה תמצא לי מספר אשר מרובע מרובעו יעלה פ"א | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כך תעשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נניח כי הוא א' קוסא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותרבעהו ויהיה א' סינסו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועוד תרבעהו ויהיה סינסו מסינסו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וזה שוה אל פ"א | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
על כן קח שרש משרש פ"א והוא ג' והוא המבוקש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
232) שאלה תמצא לי מספר אשר על מרובע מרובעו תוסיף מרובעו יעלה עשרים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נניח א' קוסא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וקח מרובעו ויהיה א' סינסו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וקח מרובע מרובעו ויהיה סינסו מסינסו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועו' א' סינסו וזה שוה לעשרים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וקח חצי סינסו ויצא חצי סינסו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותרבעהו על עצמו ויצא רביע סינסו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תוסיף בם עשרים ויצא עשרים ורביע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותסיר מזה חצי הסינסו ויצא עשרי' ורביע פחות חצי והנה שרש הנשאר יהיה שווי הדבר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה השרש הוא ד' וחצי ומזה תסיר חצי הנשאר ד' והוא המבוקש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ר"ל אם תקח שרש ד' שהם ב' הוא המבוקש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
233) שאלה תמצא לי מספר אשר מרובע מרובעו יעלה כמו מרובעו נוסף עליו י"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כך תעשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נניח כי המבוקש היה א' קוסא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותרבעהו והוא א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותרבעהו ויהיה סינסו מסינסו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והוא שוה אל סינסו א' יותר י"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תחלק הסינסו ויצא חצי סינסו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותרבעהו ויהיה רביעית סינסו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והוסיפהו אל י"ב ויהיו י"ב ורביע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועל מרובע י"ב ורביע תוסיף חצי ויעלה שרש י"ב ורביע נוסיף עליו חצי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנה שרש השרש מי"ב ורביע תוסיף עליו חצי היינו כי שרש י"ב ורביע הוא ג' וחצי ויהיו ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וקח מרובעם והם ב' והוא המבוקש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
234) שאלה תמצא לי מספר אשר על מרובע מרובעו תוסיף ד' יעלה כמו מרובעו כפול על ה' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כך תעשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נניח כי המספר היה א' קוסא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותרבעהו ויהיה א' סינסו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותרבעהו ויהיה א' סינסו מסינסו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תוסיף בם ארבעה ויהיו סינסו מסינסו ועו' ד' והוא שוה אל הסינסו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תחלק הסינסי שהם חמשה ויצא ב' וחצי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכפלם על עצמם ויהיו ו' ורביע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תסיר מהם ארבעה וישאר ב' ורביע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועל זה תוסיף ב' וחצי שהוא חצי הסינסו ויעלה ב' וחצי נוסף עליו שרש ב' ורביע והעולה מכל זה הוא שוה אל הקושא היינו שרש ב' וחצי נוסף עליו שרש ב' ורביע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
היינו א' ורביע שהוא שרש מב' ורביע ותוסיף בם ב' וחצי ויעלה ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וקח שרשם והוא המבוקש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Partnership Problems |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
235) שאלה שנים עושים שותפות והנה הראשון שם סכום מה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כך תעשה נניח כי האחד שם א' קוסא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והשני שם ב' קוסי יותר חמשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תחבר הכל ויהיו ג' קוסי יותר חמשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
על כן תאמר אם ג' קוסי יותר חמשה הרויחו ק"כ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
והנה תמצא כי הקושא שוה ה' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה א"כ הראשון שם ה' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והשני ט"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
236) שאלה ג' עושים שותפות הא' שם ד' לחמים וג' חתיכות בשר והאחר ב' לחמים וה' פולייטי מיין והאחר ב' לחמים וד' חתיכות בשר ובעודם אוכלים בא אחר ואכל עמהם ואחרי אכלו ואחרי שתה נתן לשלשתם עשרה טורניסי אשאל כמה יקח כל אחד ואחד מאלו הג' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עשה כך יען כי זה הרביעי נתן עשרה א"כ כל הסעודה שוה מ' אח"כ הסר ג' חתיכות מהראשון וה' פולייטי מהב' קנה וד' חתיכות מהג' שהם י"ב הסירם ממ' נשאר כ"ח והוא שווי הח' לחמים והנה הלחם שוה ג' טורניס וחצי א"כ הד' לחמים מא מהם שוה י"ד וג' חתיכות בשר הם ג' טורניסי והנם י"ז והוא חלק הראשון והוא שאכל משלו י' נשאר ז' וכך יש לו לקבל מהי' טורניסי והשני ב' לחמים שוים ז' וה' פולייטי ה' והם י"ב ואכל משלו י' ויש לו לקבל ב' והג' אכל ב' לחמים הם ז' וד' חתיכות הם ד' והם י"א ואכל משלו י' ויש לו לקבל א' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
237) שאלה ג' הולכים דרך ים לאחד יש לו ברילי ממרוישיאה ומכיל ל' מדות ולאחר יש לו ברילי אחד מגריגו ומכיל מ' מדות ולאחר יש לו בארילי מרומאנילי ומכיל עשרים מדות נזדמן כי נשברו הברילי ואח"כ גבו וחזרו למלאת הברילי אחר שנתקנו אשאל כמה נתערב בכל ברילי וברילי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תחבר כל מה שמכילים והנה האחד מכיל ל' והאחר מ' והאחר כ' וחברם והם צ' ותאמר אם צ' מדות מכילות בג' בארילי כמה יכיל ל' כמה יכיל מ' כמה יכיל כ' ותעשה כנז' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
238) שאלה ב' בני אדם רוצים להוסיף להוליך ספינה בוינישיאה בעד גרושי עשרים בזה האופן כי מה שירויח רב החובל זולתם הם מבקשים חצי הריוח והנה שלשה אנשים רוצים ללכת בוינישיאה ופורעים ל' גרוסי אשאל כמה יגיע לכל אחד ואחד לפרוע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הלא ידעת כי אלו הב' הסכימו לקבל חצי מה שירויח יגיע לחלקם מאלו הל' גרוסי ט"ו כי אלו הג' ראוי שיגיע להם מהריוח כפי דרך הראשנים לכן תאמר אם רב החובל מגיע לו מריוח הראשנים החצי גם לאלו השניים ראוי שיקבלו חצי הריוח בין כלם על כן תחבר ב' בעד הראשנים וג' בעד השניי' ב' בעד רב החובל ועולה ז' ואתה מבקש ל' לכן תאמר אם ל' ישוו ל' כמה ב' ותמצא כי השנים הראשנים ושנים מרב החובל וג' מהג' אחרונים ותמצא כי יצא לך ח' וד' חלקים מז' וכן יגיע לרב החובל וכן יגיע לב' הראשנים כי יגיע לכל א' ד' וב' שביעיות ולשלשה יגיע י"ב וב' שביעיות וכן יגיע לשניים מאלו הל' גרושי ועתה ראוי לראות אם פורעים מכולו זה בזה והנה הראשנים פורעים עשרים גרושי פחות הריוח שיש להם לקבל מהראשני' נמצא שהם פורעים י"א גרושי וג' שביעיות היינו כל אחד יפרע ה' וד' שביעיות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
239) שאלה שנים עושים שותפות האחד שם ג' אלפים ויש לו לקחת מריוח ה' תשיעיות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וראה איזה יחס יש בין ה' תשיעיות לד' תשיעיות והנה הוא ד' חמישיות א"כ השני היה לו לשים ד' חמישיות מאלף שהם ח' מאות וב' ג' אלפים הם ב' אלפים וד' מאות ואתה יודע כי לא שם כי אם ו' מאות ומצד ההתעסקות שהוא מתעסק נחשב לו כאלו שם ב' אלפים וד' מאות והנה אנו יודעים כי הראשון מוסיף ממון כל כך כי ראוי למשוך מריוח ז' תשיעיות א"כ השני לא משך כי אם ב' תשיעיות עתה ראה איזה חלק הוא ב' תשיעיות מז' תשיעיות והם ב' שביעיות א"כ יצטרך שתאמ' (ב') אלפים וד' מאות מאיזה דבר הם ב' שביעיות ותמצא ח' אלפים וח' מאות וכן ראוי שישים הראשון בין הכל | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תרצה לדעת כמה מוסיף הראשון הוצא מח' אלפים וח' מאות ג' אלפים ששם קודם לכן ותמצא ה' אלפים וח' מאות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
240) שאלה שנים עושים שותפות הראשון שם ג' אלפים שיש לו לקבל מהריוח ה' שמיניות והשני שם אלף ויש לו למשוך ג' שמיניות והוא מתעסק עסק השותפות ויקר מקרה כי בא איש אחר והסכים להיות משותף עמהם ושם בשותפות ב' אלפים אשאל כמה ימשוך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ראשנה ראה איזה חלק הוא ג' שמיניות מה שמיניות והם ג' חמישיות מהראשון והנה לו לשים ג' חמישיות מהראשון א"כ ראוי לו לשים ג' חמישיות מהראשון אם לא היה מתעסק בשותפות קנו והנה ג' חמישיות מג' אלפים הם אלף וח' מאות וכבר ידעת כי שם אלף א"כ התעסקו בשותפות שוה ח' מאות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עתה ראה איזה חלק שם השלישי עתה תחבר כל אלו החשבונות היינו אלף גם ח' מאות גם ב' אלפים גם ג' אלפים ועולה הכל ו' אלפי' וח' מאות וזהו הקורפו מהשותפות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עתה לדעת המגיע לכל אחד ואחד ראה איזה יחס יש מה ששם כל אחד ואחד אל כל הסכום וכך ראוי שימשוך כל אחד ואחד עתה תחלק ג' אלפי' על ו' אלפים וח' מאות ויצא ט"ו חלקים מל"ד וכך ימשוך השני ממה שירויחו גם עשה כן מאלף וח' מאות ויצא ט' חלקים מל"ד וכן ימשוך השני וכן מצד השלישי חלק ב' אלפי' על ו' אלפים וח' מאות ויצא י' חלקים מל"ד וכן יגיע לג' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
241) שאלה תעשה לי ממ' ב' חלקים שכ"כ יהיה הא' כפול בג' כמו האחר כפול בד' וכמו האחר כפול בה' וכמו האחר כפול בו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה כפול ג' על ד' וד' על ג' וכל אחד יהיה י"ב א"כ כך יהיה ד' כפול בג' כמו ג' כפול בד' אח"כ חלק י"ב על ה' ויצא ב' וב' חמישיות כפול בה' יעלה י"ב גם חלק י"ב על ו' ויצא ב' א"כ ב' כפול בו' יעשה י"ב וחבר אלו המספרים והם בגד וב' וב' חמישיות והנם י"א וב' חמישיות א"כ תאמר ד' עושים שותפות האחד שם ב' והאחר ג' ואחר ד' ואחר ב' וב' חמישיות והרויחו מ' כמה יקח כל א' וא' והדרך הוא נודע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
242) שאלה שנים עושים שותפות הא' שם ק' ויש לו לקבל מהריוח מה שמגיע לו וח' יותר והשני שם ק"נ ויש לו לקבל הריוח הראוי לו פחות ארבעה והרויחו נ' כמה יגיע לכל אחד ואחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה הוצא מנ' ח' הנשאר מ"ב הוסף בם ד' ויהיו מ"ו ותאמר ב' עושים שותפות הא' שם ק' והאחר ק"נ והרויחו מ"ו כמה יקח כל אחד ואחד והדרך נודע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
243) שאלה ג' עושים שותפות והרויחו מ'ק' מנינים ויש לו למשוך מהריוח כמו חצי הג' הנשארים ולאחר יש לו למשוך כמו שליש מהג' הנשארים ולאחר כמו רביע מהג' הנשארים ולאחר יש לו למשוך עד תשלום הריוח כמה יקח כל אחד ואחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה הנך רואה יען כי אמר כי הראשון מושך חצי הריוח ר"ל כמו הג' הנשארים אם כן ראוי למשוך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולשני יען כי אמר כי יש לו למשוך שליש כמו הג' הנשארים א"כ יש לו למשוך הרביעית ולאחר חומש הריוח עתה קח המורה לאלו החלקים שהם שליש ורביע וחומש והם ס' והשליש והרובע והחומש הוא מז' ויחסר י"ג עד שישים ועתה אמור ד' עושים שותפות הא' שם עשרים ואחר ט"ו ואחר י"ב ואחר י"ג והרויחו ק' כמה יגיע לכל אחד ואחד והדרך הוא נודע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
244) שאלה ב' עושים מסחר עם רב החובל ללכת ברומינא לוינישיאה ויתנו לו ליט' ארבעה ועשו תנאי עם רב החובל כי אם יוליך עוד אנשים כי חצי הריוח יהיה שלהם קרה מקרה כי רב החובל נשא ג' אנשים אחרים כמה ראוי שיפרעו אלו השנים הראשנים נעשה אותו עם הקאטאשינו ונניח כי פרעו עשרים גרושי כל אחד ואחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ודע כי עשרים גרושי שוים ליט' אחת והנה הב' הראשנים יפרעו ארבעים והג' אחרונים יפרעו ס' קח מחציתם שהם ס' ותנם לב' האנשים הראשנים שיפרעו מ' ויעלה ע' ואנו מבקשים פ' לכן יחסר י' עד פ' כי הפ' הם ד' ליט' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד נניח הנחה אחרת ונאמר כי פרע כל אחד כ"ד א"כ הב' ראשנים פרעו מ"ח והג' פרעו מ"ח קח מחציתם שהם ל"ו ותנם לראשנים ועם ממונם יוסיף ד' כי אנו מבקשים פ' ועולה פ"ד ולכן כפול כ' על ד' והם פ' דרך שתי וערב עוד כפול כ"ד על י' ויצא ר"מ וחברם והם ש"כ חבר עשרה עם ד' והם י"ד וחלק ש"כ עליהם והם כ"ב וב' שביעיות וכך פרע כל אחד ואחד מהשנים הראשנים גם הג' אחרונים גם תעשה אותו דרך ריגולא דיטרי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
245) שאלה ארבעה עושים שותפות הראשון משים עשרים דוקטי ויש לו לקבל מהריוח כאלו משים ל' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
כך תעשה תקבץ כל מה שראוי לקבל מהריוח כמו שהתנו והנה הראשון יש לו לקבל ל' ולאחר ע' ולאחר ס' ולאחר ק"נ ואתה רואה כי עולה ג' מאות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תחלק ל' עליהם ויצא ג' חלקים מל"א והוא חלק הראשון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עו' חלק ע' שהוא חלק השני על ג' מאות וי' ויצא ז' חלקים מל"א | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן תעשה מהג' וכן מהד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Grazing Problems |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
246) שאלה שלשה לקחו כר נרחב בעד בהמתם ופורעים ת"ס פרחים והנה הראשון שם בו עזים ד' אלפים וח' מאות מ' יום והשני שם בו ו' אלפים בעד כ"ה ימים והג' שם בו כ' ז אלפים ותר"מ ימים כ"ח | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ראשנה תראה כמה ראוי לפרוע לכל אחד מהם מאלו הת"מ פרחים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ולכן תחבר מנין כל העזים שהם י"ח אלפים ות"מ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותאמר אם י"ח אלפי' ות"מ פורעים ת"ס כמה יפרע ד' אלפים וח' מאות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וכן ו' אלפים וכן ז' אלפים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ותמצא כי הראשון יפרע ק"צ ועשרה חלקים אלפים וח' מאות חלקים מי"ח אלפים ות"מ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והשני יפרע קנ"ט וחלקים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והשלישי יפרע קי"ט וחלקים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עתה כפול העזים מכל אחד וא' כנגד העזים הימים ותחבר כל הסך משלשתם ויעלה תקנ"ה אלפים ותתק"כ וזהו הפארטידור | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אח"כ תאמר אם תתקכ"ה אלפים ותתק"כ פזרו ק' כמה יפזר קל"ב אלפים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ויצא לך ל"ד וקכ"ו חלקי' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תעשה מכל אחד ואחד והדרך הוא נודע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
247) שאלה איש אחד נתן לאריסו ק' שורים יחזיקם ג' שנים ולא החזיקם כי אם י' חדשים עוד נתן לו ק' ועמדו בידו ח' חדשים עו' נתן לו ק' ועמדו בידו ט' חדשים עתה נרצה לחבר אלו הג' מאות רחלים כמה זמן ראוי שיעמדו ביד האריס או ביד הרועה כל מאה ג' שנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה כבר ידעת כי בג' שנים יש ל"ו חדשים הסר מהם י' ונשארו כ"ו עוד הסר מל"ו ח' הנשאר כ"ח עוד הסר מל"ו ז' הנשאר כ"ט וחברם כלם והם פ"ג חלקם על ל"ו ויצא לך ב' כ"ז וב' שלישיות וכן ראוי שיחזיקם הרועה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
248) שאלה איש אחד יש לו חמישים צאן ונתנם לרועה לשמור צאנו בעד ד' שנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כך תעשה קח חצי העזים והם ק' וקח חצים והם נ' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
והנשאר הוא מהבעל הבית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
249) שאלה איש אחד נתן לרועה ג' עזים בעד ה' שנים ואח"כ יש להם לחלק הכל בשוה והנה בסוף ג' שנים וחצי נמצאו העזים נ"ב ורוצים לחלק כמה יגיע לרועה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קח חצי נ"ב והם כ"ו עשה מהג' שנים וחצי מ"ב חדשים והה' שנים ס' חדשים עתה כפול כ"ו על מ"ב ויעלה אלף וצ"ב וחלקם על ס' ויצא לך י"ח וחומש וכך יגיע לרועה והנשאר הוא מהבעל הבית | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
250) שאלה איש אחד נתן לרועה י"א פרים והרועה יש לו ה' משלו וראוי לשמרם [ד]' שנים ואז ראוי לחלק בשוה ובסוף ב' שנים וז' חדשים נמצא בין הכל מ"ב פרים ורוצים לחלק כמה יגיע לכל אחד ואחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תחבר ה' מהרועה עם י"ד מבעל הבית ויהיו י"ט ואתה רואה כי הרועה שם ה' חלקים מי"ט ולכן קח ה' חלקים מי"ט ממ"ב ויצא י"א וא' חלק מי"ט ואח"כ קח חצי מ"ב שהם כ"א עתה קח ההפרש שהוא מי"א וא' חלק מי"ט אל כ"א ויצא ט' וי"ח חלקי' מי"ט עתה עשה חדשים מהה' שנים וז' חדשים שהם ל"א גם מהד' שנים שהם מ"ח ותכפול ט' וי"ח חלקים מי"ט על ל"א ויצא לך ש"ח וז' חלקים מי"ט וחלקם על מ"ח ויצא לך ו' ושפ"ז חלקים מתתקי"ב וחברם עם י"א וא' חלק מי"ט ויעלה י"ז ותל"ה חלקים מתתקי"ב וכך יגיע לרועה והשאר הוא מן הבעל הבית | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
251) שאלה איש אחד נתן לרועה מ' עזים בעד ד' שנים ובסוף ד' שנים יחלקו הריוח לחלקים שוים אח"כ בסוף י"ח חדשים נתן לו ס' עזים כפי קנח אותו היחס אשאל כמה מן הזמן ראוי לחלק | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| זה ראוי לעשות על ריגולי מפוניטורי מזהב על כן כפול מ' על ב' שנים וחצי שיש לו להחזיק עדין כי לא החזיקם מהד' כי אם י"ח חדשי' עתה ראה כמה ראוי להחזיק השישים כפי היחס הראשון והנה ראוי להחזיק אלו הס' עד סוף ד' שנים ולכן כפול ס' על ד' ויהיו ר"מ וחברם עם הק' ויעלה ש"מ עתה תקבץ הצאן שהם מ' וס' והם ק' עתה תחלק ש"מ על ק' ויצא לך ג' וג' חמישיות וכך זמן ראוי שיחזיק אחר הי"ח חדשים שאז נתן לו הס' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
252) שאלה איש נתן לרועה ארבעים צאן ולרועה יש לו עשרה צאן והסכימו כי בסוף ה' שנים יחלקו בשוה והנה בסוף ג' שנים נמצא שהיו ק' צאן ורוצים לחלק כמה יגיע לכל אחד ואחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה תחבר עשרה עם ארבעים ויהיו חמישים ואח"כ תאמר אם נ' שוים ק' כמה ישובו מ' ויצא לך פ' וכמה ישובו עשרה והנה ישובו עשרים וכך יגיעו לרועה ומ' יגיעו לבעל הבית | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עתה ראה כמה היה מגיע לו אם השותפות עמד ג' שנים כפי תנאם הלא ידעת כי היה להם לחלק בשוה א"כ בסוף שנים היה מגיע לו חמישים שהוא חצי ק' ואתה ידעת כי בסוף ג' שנים מגיע לו עשרים א"כ בסוף עשרים היה מרויח ל' יותר ותאמר אם ה' שנים נתן לי ל' ג' שנים כמה יתנו ויצא י"ח וכך יגיע לו בסוף ג' שנים כפי יחס הה' שנים תוסיף י"ח על עשרים ויהיו ל"ח וכך יגיע לרועה וס"ב יגיע לבעל הבית | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
253) שאלה איש שם ביד רועה אחד ל"ו בהמות בא אחר ונתן לו ג"כ י"ח בהמות והשותפות ראוי שימשך ג' שנים וג' חדשים ורביע אז ראוי לחלק בשוה נפל מריבה בין בעל הבית ובין הרועה ב' בסוף א' שנה וה' חדשים ושמין ואז הבהמות הם ע' כמה יקח כל אחד ואחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תעשה מג' שנים וג' חדשים ורביע ימים ויהיו אלף ותע"ז וחצי גם תעשה ימים משנה אחת וה' חדשי' ושמין והם תקי"ג וג' רביעיות קח שלישית ע' והם כ"ג ושליש ויחסר עד ל"ה שהוא חצי ע' י"א וב' שלישיות וזה כפול בעד תקי"ג וג' רביעיות והעולה תחלק על אלף וקע"ז וחצי והעולה תוסיף על כ"ג ושליש והעולה הוא למי ששם י"ח | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
254) שאלה איש נתן לרועה כ"ה עזים ובסוף ד' שנים ראוי לחלק בשוה והנה נמצא כי בסוף ב' שנים וחצי היו ס' כמה יגיע לכל אחד ואחד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה אתה ידעת כי אלו בסוף ד' שנים היו ס' היה מגיע לכל א' וא' ל' ולכן תאמר אם ד' שנים נתנו לי ל' כמה יתנו ב' וחצי ותמצא כי יתנו י"ח וג' רביעיות והשאר עד ס' שהם מ"א ורביע יגיע לבעל הבית | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Rent Problems |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
255) שאלה איש אחד שכר בית בעד עשרים ליט' השנה והנה השוכר נתן למשכיר ר"ל לבעל הבית מ"ח ליט' קודם הזמן וזה נדר לו לחשוב זה שנתן לו לתועלתו ב' בעד כל ליט' בעד חדש ב' מטבעים לא אדע כמה שוים אשאל כמה ידור זה בבית באופן כי בעל הבית יחשוב לו ב' מטבעים בכל חדש ב' כל ליט' לתועלת השוכר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עשה מאלו המטבעים ליט' ר"ל ראה כמה ירויחו אלו המ"ח ליט' לשנה תמימה והנה תמצא כי ירויחו ד' וד' חמישיות ותוסיפם על מ"ח ויהיו נ"ב וד' חמישיות תסיר מהם עשרים הנשאר ל"ב וד' חמישיות עוד ראה כמה ירויחו אלו הל"ב וד' חמישיות לשנה ותמצא כי ירויחו ג' וז' חלקים מכ"ה ותוסיפם על ל"ב וד' חמישיות ויעלה ל"ו וב' חלקים מכ"ה ותסיר מהם עשרים וישארו י"ו וב' חלקים מכ"ה עוד ראה כמה ירויחו אלו הי"ו וב' חלקים מכ"ה בשנה אחת ותמצא כי ירויחו א וע"ח חלקים מקכ"ה בשנה ותוסיפם על י"ו וב' חלקים מכ"ה ויעלה י"ז שלמי' וקפ"ח חלקים מקכ"ה ותוכל לשער זה לימים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
256) שאלה איש אחד שכר בית אחד קליני גינאר בעד דוקטי ס' דוקטי לשנה אח"כ בא איש אחר קליני מאיו ורוצה לעמוד קנט עם זה ואיש אחר בא קליני סיטימ' ורוצה לדור עמם אשאל כמה ראוי שיפרע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה ראה כמה ימים עמד הראשון והנה עמד י"ב חדשים אח"כ ראה כמה חדשים עמד השני והנה עמד ח' חדשים אח"כ ראה כמה חדשים עמד השלישי והנה עמד ד' חדשים עתה תחבר הכל היינו י"ב ח' ד' והם כ"ד וזהו הפרטידור עתה תאמר אם כ"ד נתן לי ס' כמה יתן י"ב וח' וד' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
257) שאלה איש אחד שכר בית בעד ה' שנים לערך י' ליטר' ואמר לבעל הבית אם תתן לי עתה המעות מכל השנה אשכיח אליך ב' בעד כל ליט' לשנה אשאל כמה ראוי שיקבל בעל הבית עתה מכל הה' שנים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עשה כך ראה כמה הרויח זה בכל שנה והנה מרויח ב' אח"כ ראה כמה מרויח בה' שנים והנה מרויח עשרה סולדי דע כי עשרים סולדי הם ליט' והנה הליט' מרוחת בכל הה' שנים עשרה גרוסי תוסיפם על א' ליט' והנם ליט' וחצי כי עשרה גרוסי הם חצי ליט' ועתה תאמר אם ליט' וחצי נתן לי א' כמה יתן לי חמישים ויצא לך ל"ג וו' גרוסי ופיצולי ח' וכן ראוי שיתן לי בעד הה' שנים עתה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
258) שאלה איש שוכר בעד כ"ד לשנה ורוצה שיפרעהו עתה בעד ב' שנים ורוצה שירויח לחשבון עשרים לשנה כמה ראוי שיתן לו עתה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנך רואה כי הה' שנים שוים ו' ולכן תאמר אם שש בין קרן וריוח מכמה יבואו כ"ד כפול ה' על כ"ד וחלק על ו' ויצא לך עשרים וזה בעד שנה ראשנה גם בעד שנה שניה תאמר אם ו' באו מה' ממה יבואו עשרים ותמצא י"ו וב' שלישיות יעלה לו' וב' שלישיות וכך ראוי שיתן לו עתה ויעמוד בבית ב' שנים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
259) שאלה איש שכר לחבירו בית בעד מ' ליט' לשנה ובעל הבית אמר לשוכר תן לי עתה מאה ליטר' וארצה שתרויח עמי י' על כל ככר וככר בכל שנה ושנה אשאל כמה ראוי שיעמוד בבית | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה הנך רואה כי הק' שוים ק"י הסר ממנו שכירות שנה שהם מ' נשאר ע' גם תאמ' אם ק' נתנו ק"י ע' כמה ישובו וישובו ע"ז הסר ממנו מ' ונשארו ל"ז ויש לנו ב' שנים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד תאמר אם ק' שוים ק"י ע"ז כמה ישובו וישובו מ' וי"ד גרוסי הסר מהם מ' ונשארו י"ד גרוסי ויש לנו ג' שנים עוד תאמר אם ק' שוים ק"י כמה ישובו ז' עשיריות כי י"ד גרושי הם ז' עשיריות מליט' ותמצא ט"ו גרושי וד' חמישיו' ותאמר אם בח' מאות גרושי שהם מ' ליט' ראוי לעמוד שס"ה ימים שהם שנה תמימה כמה ראוי לעמוד בעד ט"ו וד' חמישיות ויצאו לך הימים והדרך נודע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
260) שאלה לאיש אחד יש לו שני בתים האחד שוה קל"ז ליט' ושוכר אותו י"ז והאחר יש לו שוה קי"ג ליט' אשאל כמה זמן ירויח י"ז ליט' כמו אותו מקל"ז ובכמה זמן אותו מקל"ז ירויח כמו אותו של קי"ג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה תאמר אם קי"ג היו קל"ז כך ישכור לזו על כן נאמר אם קי"ג היו קל"ז כמה יהיה י"ב יען כי י"ב חדשים לשנה ותמצא כי י"ב ישובו י"ד וס"ב חלקים מקי"ג ובזה הזמן אותו של קי"ג ירויח י"ז כמו אותו של קל"ז | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולדעת אותו של קל"ז ירויח כמו של קי"ג יש לדעת כמה ירויח אותו של קי"ג ותאמר אם קל"ז נתן לי י"ז כמה יתן לי קי"ג אשר זו לזו מרויח לשנה ותמצא כי יתן לי י"ד וג' חלקים מקל"ז ולכן תאמר שירויח אותו של קי"ג לשנה לפי אותו היחס מאותו של קל"ז ולדעת כמה זמן אותו של קל"ז ירויח אותם הי"ד וג' חלקים מקל"ז ר"ל כמה ירויח אותו של קי"ג לשנה תאמ' אם קל"ז היו קי"ג כמה ישובו י"ב ר"ל י"ב חדשי השנה כפול י"ב חדשי השנה כפול י"ב על קי"ג וחלק על קל"ז ויצא ט' ול"ג חלקים מקל"ז ובזה הזמן ירויח אותו של קל"ז י"ד וג' חלקי' מקל"ז | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Barter Problems |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
261) שאלה שנים מחליפים צמר ופשתים יחדו בעל הבגד שוה הקנה במעות ה' ובחלוף משים ו' בחלוף ושואל החצי במעות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עשה כך הסר חצי ו' מו' יען כי שואל החצי בממון וישאר ג' גם תסירם מה' ונשאר ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ולכן תאמר אני מרויח א' עם ב' מה ארויח עם ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותמצא כי ישובו י"ו וכך היה שווי הצמר בראשנה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ובחלוף משים אותו כ"ד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
262) שאלה שנים מחליפים בגד עם צמר הבגד שוה ח' במעות ובחלוף משים אותה ט' ורוצה השליש במעות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עשה כך הסר שליש ט' שהם ג' ונשארו ו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
גם תסירם מח' ונשאר ה' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותאמר [א]ם ה' שוים ו' כמה שוים ל' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותמצא כי שוים ל"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חלק ל"ו על עשרה ותמצא ג' וג' חמישיות וכך שוה הפרח | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
263) שאלה שנים מחליפים בגד עם צמר והנה קנה הבגד שם אותה בחלוף ח' ושואל שליש במעות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
קח שליש ח' שהוא ב' וב' שלישיות הנשאר ה' ושליש ולכן תאמר כי היה שוה במעות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ולבחון אותו תאמ' אם מ' באו מל' מאיזה דבר באו ה' ושליש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותמצא ד' וכך היה שווי הקנה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כדי לנכות השליש שהיה שואל במעות תוסיף ב' וב' שלישיות על ד' והם ו' וב' שלישיות וזהו שווי הקנה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
264) שאלה שנים מחליפים ברזל ועופרת הברזל שוה במעות כ"ח ובחלוף ל"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עשה כן הסר רביעית ל"ו והם ט' הסירם מל"ו נשאר כ"ז | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
גם תסירם מכ"ח ונשאר י"ט | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ולכן אם י"ט שבו כ"ז כמה ישובו כ"א | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ויצא לך כ"ט וי"ו חלקי' מי"ט וכך ראוי לשים העופרת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
265) שאלה שנים מחליפי' צוקרו ובאנבאגיני המאה מהצוקרו שוה במעות תשעה ובחלוף משים אותו י"ב ורוצה השליש במעות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כך תעשה הסר הרביעית שמבקש בעל הבאנבאגיני מהשליש שמבקש בעל הצוקארו וישאר א' חלק מי"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אח"כ תאמר כי בעל הצוקארו מבקש מחבירו חלק א' מי"ב והאחר אינו מבקש כלום | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הסר חלק אחד מי"ב מי"ב שהוא אחד ונשאר י"א | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הנה הקרן יהיה ח' ובחלוף י"א | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ולכן תאמר אם ח' שם י"א כמה ישים ה' וחצי ויצא לך המבוקש | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
266) שאלה שנים מחליפים לאחד יש לו מוך ולאחר זנגביל המוך שוה המאה ט' במעות ובחלוף י"ב ורוצה לתת החצי במעות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דע כי כי כשאיש רוצה לתת חלק מה במעות ראוי להוסיף חלק על החלוף ובקרן ג"כ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן בהפך כשהוא שואל מחבירו חלק מה ראוי לחסר כנז' לעיל | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
על כן קח חצי י"ב והם ו' תוסיפם על י"ב ויהיו י"ח | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
גם תוסיפם על ט' ויהיו ט"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ועל כן תאמר אם ט"ו שבו י"ח כמה ישוה ט"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ויצא י"ח | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ולדעת כמה מוך יקח בעד ז' מאות וס"ח ליט' כפול שתי וערב ק' של מוך נגד י"ח של זנגביל ויצא א' וח' מאות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
עו' כפול ק' של זנגביל נגד י"ח של זנגביל דרך שתי וערב והוא ג"כ אלף וח' מאות ותאמר כי אלף וח' מאות של זנגביל וכך יתן ג"כ המוך כי הדבר יצא שוה כי כך יצא ערך המוך כמו הזנגביל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
267) שאלה שנים מחליפים בגד עם צמר בעל הבגד מוכר הקנה ח' ובחלוף ט' ורוצה השליש במעות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כך תאמר אם ה' במעות שוות ו' בחלוף ק' בממון כמה ישוו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ויצא ק"כ וכך שוה המאה מבעל הבגד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ויען כי אמר כי מרויח ה' בעד ק' הסר ה' מק"כ ונשאר קט"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותאמר אם ק' במנויים שבו קט"ו כמה ישובו ל' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ותמצא כי ישובו ל"ד וחצי וכך הוא שווי מהצמר בחלוף | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
268) שאלה שנים מחליפי' צמר עם בגד בעל הבגד מוכר הקנה במחושבים ז' ובחלוף ח' ושואל השליש בממון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
כך תעשה הסר השליש מח' הנשאר ד' ושליש והוא הקפיטאל ובחלוף ה' ושליש ויען כי הפסיד ה' בעד ק' תאמ' אם ד' ושליש שבו ה' ושליש כמה ישובו ק' ותמצא כי ישובו קכ"ג וחלק א' מי"ג תוסיף בם הה' מהפסד והנם קכ"ח וחלק מי"ג ותאמר אם ק' במנויים שבו קכ"ח וחלק מי"ג כמה ישובו ל' ותמצא ל"ח וי"א חלקים מקכ"ו וזהו שווי הק' מהצמר בחלוף ותבחון אותו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
269) שאלה שנים מחליפים בגד עם צמר בעל הבגד מוכר הקנה ז' ובחלוף משים אותו ח' ושואל רביעית בממון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עשה כך הסר הרובע מז' ומח' וישאר ו'ה' ותאמר אם ה' שבו ו' כמה ישובו ק' ויצא ק"כ וכך שוה בחלוף ויען כי בעל הצמר מרויח י' בעד ק' תוסיף י' על ק"כ ויצא ק"ל ותאמר אם ק' מבגד שבו ק"ל כמה ישובו עשרי' ויצא כ"ו וכך שווי הק' מהצמר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
270) שאלה שנים מחליפי' צמר ופשתים יחדו קנה הבגד שוה ח' במעות מנוים ובחלוף משים אותה ט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עשה כן בעל הבגד שואל השליש במעות הסר השליש ונשאר ו'ה' ותאמר אם ה' ישובו ו' כמה ישובו ק' ויצא לך ק"כ ויען כי בעל הצמר מפסיד י' בעד ק' הסירם מק"כ וישאר ק"י אח"כ תאמ' אם ק' במעות שבו ק"י כמה ישובו ל' ויצא ל"ג וכך שוה הצמר בחלוף | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
271) שאלה שנים מחליפים צמר ופשתים יחדו קנה הבגד שוה ח' ובחלוף משים אותו ט' ורוצה השליש במעות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עשה כך באופן כי בעל הבגד ירויח י' הסר השליש מט' וישאר ו'ה' ותאמ' אם ה' שבו ו' כמה ישובו ק' ונמצא ק"כ ויען כי אמר כי בעל הבגד הרויח י' הסר י' מק"כ וישאר ק"י ותאמר אם ק"י מחלוף שבו ק' מממון כמה יתן ל"ו ויצא ל"ב וח' חלקים מי"א וכך שווי בממון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
272) שאלה איש מחליף עם חבירו צמר ופשתים קנה הבגד שוה ז' ורוצה השליש בממון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ראשנה הסר השליש שהוא ב' ושליש וישאר ד' וב' שלישיות אח"כ כפול ל"ו מהצמר בבגד ק' וחלק על ל' ויצא ק"כ וכך הוא בחלוף ומצד כי בעל הבגד הפסיד י' בעד ק' הסר י' מק"כ וישאר ק"י ותאמר אם ק"י מחלוף שבו ק' בממון מאי זה יבואו ד' וב' שלישיות ותמצא כי יבא מד' וי"ח חלקים מל"ג ואח"כ תוסיף בם ב' ושליש אשר חסרת ויעלה ו' וי"ט חלקי' מל"ג וזהו שווי הבגד בממון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
273) השאלה איש מחליף צמר ופשתים הבגד שוה כ' בממון ובחלוף משים אותו ב' פיוריני וחצי יותר ומבקש השליש בממון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה הסר השליש מב' פרחים וחצי היינו ה' שישיות נשאר א' פרח וב' חמישיות מחלוף א"כ ק' מהצמר כפול כ"ה כנגד ק' והעולה חלק על כ' שהיה שוה בממון ויצא קכ"ה וכך שוה בחלוף | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ויען כי אמר כי בעל הצמר מרויח י' בעד ק' הסר י' מקכ"ה ונשאר הנשאר קט"ו אח"כ תאמר אם קט"ו מחלוף כ"א מק' בממון מאי קסב זה דבר ב' שלישיות ויצא לך א' ול"א חלקים מס"ג פרחים וכך שווי הקנה בממון ותוסיף בם ה' שישיות שהוא שליש ב' וחצי ויעלה ב' וי"ג חלקים ממ"ו ויצא ג' וכ"ג חלקים מק"ה וכך שוה הפרח | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
274) שאלה שנים מחליפים לא' יש לו זינזיברו אשר הק' שוה י"ח דוקטי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קח איזה סכום ונניח כי יש לו מאה מכל א' וא' והנה המאה מהסוקרו שוה כ' ומאה מהמאסיש י"ב ומאה מקנילא י"ו ובין הכל עולה מ"ח מאה מכל א' וא' ומבקש תתפ"ו ולכן תאמר אם מ"ח יהיו תתפ"ו כמה יהיו כ' וכמה יהיו י"ו וכמה יהיו י"ב
והנה הסוקרו יעלה שס"ט ושישית וכך יקח מהסוקרו וכן תעשה מהאחרים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
275) שאלה שנים מחליפים לאחד יש לו צמר ולאחר יש לו אשטמי ופלפל והק' מהצמר שוה ל' בממון אמנם בחלוף לא ידעתי ורוצה השליש בממון והשליש באשטמי והשליש מפלפל והק' מהאשטמי שוה ל' בממון ובחלוף שוה ל"ו והמאה מהפלפל שוה מ' בממון ובחלוף שוה מ"ה אשאל כמה ישוה המאה מהצמר בחלוף למען יצא מספר שוה לכלם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה אם מה ששוה ל' בממון הוא שוה ל"ו בחלוף כמה ישוה מ' בממון ובחלוף ותמצא כי ראוי שישוה מ"ח ותוסיפם על מ"ה ויעלה צ"ג גם תוסיפם על המ' מהאשטמי ויעלה פ' גם על הארבעים מהפלפל ויעלה פ' ויען כי אמר כי בעל הצמר מבקש השליש בממון ושליש באשטמי ושליש בפלפל עשה כך שים כי הק' מהצמר שוה קוסא הסר מהם השליש ויצא ל' פחות שליש דבר ובחלוף ב' שלישיות קוסא עתה כפול ל' פחות שליש נגד צ"ג ויצא לך אלפים וז' מאות וצ' פחות ל"א קוסי אח"כ כפול ב' שלישיות קוסא שהוא החלוף כנגד פ' ויצא לך נ"ג ושליש קוסא וזהו שוה אל אלפים וז' מאות וצ' פחות ל"א קוסא ותמצא כי הקוסא שוה ל"ג וכ"א חלקים מרנ"ג וכך ישוה המאה מהצמר בחלוף | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
276) שאלה שנים מחליפים לא' יש לו צמר אשר בממון שוה כ' ובחלוף כ"א ומבקש הרביע בממון ולאחר יש לו ב' מיני בגד הא' שוה ד' ומשים אותו בחלוף ה' והאחר שוה י"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה ראשנה הסר הרביע מכ' ומכ"ה וישאר י"ג וג' רביעיות וי"ח וג' רביעיות אח"כ קח שווי הב' מיני בגד היינו ה' וי"ב ויעלה י"ז ותעשה חשבון כי אלו הב' מיני בגד אינו כי אם מין אחד ותאמר אם י"ג וג' רביעיות שוה י"ח וג' רביעיות כמה ישובו י"ז ויצא כ"ג וב' חלקים מי"א ואלו הם שווי הב' מיני בגד והנך רואה כי מן אחד שוה ה' לכן הסר ה' מכ"ג וישאר י"ח וב' חלקים מי"א וכך ראוי שישוה הקנה מאותו של י"ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
277) שאלה שנים מחליפים לא' יש לו פלפל בממון שוה הק' ל' ובחלוף משים ל"ה והק' מהננגיברי בשוה בממון כ"ז ובחלוף ל"ג ולאחר יש לו צמר וק' מהצמר שוה עשרה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ראשנה תאמר אם ק' שוים ק"י כמה שוים י' ותמצא י"א ותאמר כי הק' מהצמר שוה י"א ויעקב שואל מזה כמו מזה ר"ל אם יקבל ק' מפלפל כן יקבל ק' מזנגביל לכן חלק י"א על ב' ויצא ה' וחצי ונתחיל עם הפלפל ונאמר אם ל' אתה משים ל"ה כמה אשים ה' וחצי ויצא לך ו' וה' חלקים מי"ב וכן ישוה חצי ק' מצמר מצד הפלפל עוד מצד הזנגביל תאמר אם כ"ז שוה ל"ג כמה ישוה ה' וחצי ויצא לך ו' וה' חלקים מי"ב וכך ישוה חצי הק' מצמר מצד הפלפל קסג עו' מצד הזנגביל תאמר אם כ"ז שוה ל"ג כמה ישוה ה' וחצי ויצא לך ו' מ"ג חלקים מנ"ד וכך ישוה החצי האחר מהצמר מצד הזנגביל ועתה אנו יודעים כמה ישוה חצי ק' מצד הפלפל ומצד הזנגביל עתה תחבר ו' וה' חלקים מי"ב וו' ומ"ג חלקים מנ"ד וישוה י"ג ונ"ג חלקים מק"ה וכן ישוה הק' מהצמר בחלוף עתה תחבר שווי הפלפל ושווי הזנגביל בממון היינו כ"ז ול' ויעלה נ"ז חלקם על ב' ויצא כ"ח וחצי גם תחבר ל"ה עם ל"ג שהוא שווים בחלוף והעולה חלק על ב' ויצא ל"ד ואח"כ תאמר אם כ"ח וחצי שוים ל"ד כמה ישוה י"א שהוא הצמר ויצא לך י"ג וז' חלקים מנ"ז ובזה האופן בעל הצמר ירויח י' בעד ק' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
278) שאלה שנים מחליפים לא' יש לו מג' מיני תבלין היינו פלפל והק' שוה כ"ד ובחלוף משים אותו כ"ח וקאנילא שוה מ"ה ובחלוף משים אותה נ"ג וגארופאנו שוה ל"ד ובחלוף משים אותו מ' והק' מהצמר שוה י"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה תראה שווי הצמר היינו תחלק לחצי ושליש ורביע חציו ו' ושלישיתו ד' ורביעיתו ג' ובין הכל י"ג ועל כן תאמר אם י"ג היה י"ב כמה יהיה ו' וג' וד' והנה החצי יהיה ה' וז' חלקים מי"ג והשליש יהיה ג' וט' חלקים מי"ג והרובע יהיה ב' וי' חלקי' מי"ג ותמצא ו' וי"ט חלקים מל"ט והוא שווי הפלפל וכן תעשה מהקאנילא אתה משים אותה נ"ג כמה אשים אותה ג' וט' חלקים מי"ג ויצא לך ד' וס"ח חלקים מקצ"ה וכן מהגרופלי אם ל"ד שוים מ' כמה ישוה ב' וי' חלקים מי"ג ויצא לך ג' ונ"ז חלקים מרכ"ה וכל זה תחבר ויעלה י"ד וד' אלפים ומ"ג חלקי' ממ"ג אלפים וצ"ה וכן ישוה המאה מהצמר בחלוף | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
279) שאלה שנים מחליפים לא' יש לו בגד ומוכר אותו א' פרח יותר ולאחר יש לו צמר והק' שוה י' בממון ומשים אותו י' בממון ובחלוף משים אותו י"ב ואותו מהבגד נמצא שהרויח פעם וחצי ממון בגד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נניח איזה מספר שתרצה ונניח כי היה לו ד' פרחים א"כ מכרו ה' ונניח כי היה לו לאחד כ"ה קנים ושווים ק' פרחים והוא מבקש כ"כ צמר שישוה קכ"ה פרחים חלק קכ"ה על ערך הצמר בחלוף שהוא י"ב וישוה אלף ומ"א וב' שלישיות וראה כמה שוים אלו האלף ומ"א וב' שלישיות במנוים ויצא לך ק"ד ושישית והקנה שוה ד' והנחנו ה' וראוי להניחה ו' למען ישוב ממונו כמוהו וכמו מחציתו ויחסר לי א' וה' שישיות וזה תניח כמו שעושים ההנחות כוזבות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עו' שוב לעשות הנחה אחרת ונניח כי הקנה שוה ה' ומשים ו' בחלוף גם הק' מהצמר שוים י' בממון י"ב בחלוף ונניח כי היו לו עשרים קנים ושווים בחלוף ק"כ וחלק ק"כ על י"ב שהוא שווי הצמר בחלוף ויצא י' ובממון משים ק' והנך רואה כי אינו מרויח ואינו מפסיד ואני מבקש כי בעל הצמר ירויח ז' וחצי כדי שישוב ממונו כמוהו וכמו חציו ותאמר כי מזאת ההנחה יחסר ז' וחצי ומצד האחרת היה לך פחות א' וה' שישיות ועשה כמו שידעת ותמצא כי הקנה שוה ג' פרחים וכ"ג חלקים מל"ד ושם אותה ד' וכ"ג חלקים מל"ד ושב ממונו כמוהו וכמו חציו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
280) שאלה שנים מחליפים בגד וצמר בעל הבגד הקנה שוה בממון ד' ובחלוף ה' ובעל הצמר הק' שוה י' בממון ובחלוף י"ג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ראשנה תעשה כך אם ד' שבו ה' כמה ישובו י"ב ותמצא כי ישובו י"ב וחצי הנה בעל הצמר מרויח חצי כי מן הדין אינו ראוי למכרה כי אם י"ב וחצי ולראות כמה ראוי לקבל בעל הבגד בממון להיות שוה לחבירו ראה כמה הפרשים מד' לה' והיינו א' עתה תחלק ה' על א' ויצא ה' כן תעשה מהצמר וראה ההפרש שיש מי' לי"ג והוא ג' עתה תחלק י"ג על היתרון שיש מי' לי"ג והוא ד' ושליש ואתה רואה כי חלק הוא ה' ומהצמר הוא ד' ושליש עתה תחלק ד' וחצי על ה' ויצא י"ג קסד חלקים מט"ו וזה החלק הוא בצמר ראוי לקבל בעד הבגד והנשאר עד תשלום א' היינו ב' חלקים מט"ו ראוי לקבל במעות והדבר יצא שוה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
281) שאלה שנים מחליפים צמר ופשתים יחדו קנה הבגד שוה ח' ובחלוף משים אותו י"א ורוצה השליש בממון והק' מהצמר שוה י"ד ובחלוף שוה י"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ראשנה תסיר השליש שהוא ג' וב' שלישיות וישאר א ד' ושליש וז' ושליש ותאמר אם שוה הקנה ד' ושליש ובחלוף ז' ושליש ובאחד יש צמר שוה י"ד ובחלוף י"ו מי ראוי לתת לחבירו נניח כי בעל הבגד שואל קוסא אחת תסיר זה מי"ו וישאר י"ו פחות קוסא אחת גם תסירהו מי"ד וישאר י"ד פחות קוסא אחת ותאמר אם י"ד פחות קושא אחת שוה י"ו פחות דבר כמה ישוה ד' ושליש ותמצא כי ישוה ס"ט ושליש פחות ד' ושליש קוסא חלק על י"ד פחות קוסא אחת ויצא ז' ושליש א"כ הקוסא ישוה י"א ותשיעית תחלק זה על י"ו ששוה הצמר בחלוף ויצא כ"ה חלקים מל"ו וכן יהיה החלק אשר ראוי שישוב לו במעות י"א חלקים מל"ו בבגד ויצא החלוף שוה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
282) שאלה שנים מחליפים בעל הבגד שוה ד' ובחלוף משים ה' ובעל הצמר שוה כ' ובחלוף כ"ד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תאמר ד' פעמים [כ]ד' הם צ"ו וה' פעמים כ' הם ק' הסר מהם צ"ו הנשאר ד' וזה תחלק על יתרון הבגד מהממון בחלוף שהוא א' ויצא ד' וחלקם על כ"ד ויצא שישית אחד כי כן שוה הצמר בחלוף וכן ראוי לו לקבל מבעל הצמר בממון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
283) שאלה שנים מחליפים צמר ופשתים קנה הבגד שוה ה' ובחלוף ח' ורוצה הרביעית בממון וק' הצמר שוה י"ג ומשים בחלוף ט"ו ובעל הצמר הרויח ה' בעד מאה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ראשנה הסר הרביע מח' והנה רביע ח' הם ב' הסירם מה' ומח' ונשאר ו' ג' ויען כי אמר כי בעל הצמר מרויח ה' בעד ק' כפול ו' על ק' ויצא ו' מאות וחלקם על ג' ויצא ב' מאות ותוסיף ה' מריוח ויהיו ר"ה ותאמר כי בעד כל ק' בממון בחלוף משים אותו ר"ה ויען כי אמ' איזה חלק ראוי לתת לו למען יצא המספר שוה נניח כי ראוי לתת לו א' קוסא בממון הסירהו מט"ו נשאר ששוה בחלוף ט"ו פחות קוסא אחת גם גם תסירהו מי"ג ששוה בממון ונשאר י"ג פחות א' קוסא וכפול י"ג פחות א' קוסא כנגד ר"ה ויצא ב' אלפים וו' מאות וס"ה פחות ר"ה קוסי גם כפול ט"ו פחות קוסא א' כנגד ק' ויצא אלף וה' מאות פחות ק' קוסי הסירם מב' אלפים וו' מאות וס"ה ונשאר אלף וקס"ה דבר ותמצא כי הקוסא ישוה י"א וב' חלקים מכ"א וחלק זה על ט"ו ששוה הצמר בחלוף ויצא לך רל"ז חלקים משט"ו וזה החלק ראוי שיתן בעל הצמר לבעל הבגד ויצא החלוף שוה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
284) שאלה שנים מחליפים בגד וצמר קנה הבגד משים אותו בחלוף א' דוקטו יותר ממה ששוה בממון וק' מהצמר בממון שוה כ' ובחלוף משים אותו כ"א והפסיד י' בעד ק' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נניח כי הקנה שוה א' קוסא א"כ בחלוף שוה קוסא יותר ויען כי בעל הצמר הפסיד י' בעד ק' נאמר כי הק' שבו צ' ולכן תאמר אם ק' שבו צ' כמה ישובו עשרים וישובו י"ח וכן תאמר כי שוה הצמר בממון ותאמר אם י"ח שבו כ"א כמה ראוי שנשים א' קוסא תכפול כ"א על א' קוסא ויצא לך כ"א קוסא ותחלקהו על י"ח ויצא לך א' ושישית והוא שוה אל א' קוסא יותר אחד ותעשה בדרך ויצא לך ו' וכך היה הקנה ובחלוף שם אותו ז' והוא נכון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
285) הבן כי אם תאמר איש רוצה רביעית הממון הוא שוה כאלו תאמר איש רוצה שינתן לו רביעית בממון המשל איש מחליף בגד ששוה עשרים ובחלוף משים אותו כ"ג וט' חלקים מי"ז ורוצה רביעית בממון ולאחר יש לו צמר ששוה הק' בממון י"ב אשאל כמה ישימנה בחלוף למען לא יהיה מרומה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ראשנה קח רביעית כ"ג וט' חלקים מי"ז שהם ה' וט"ו חלקים מי"ז ותסיר זה מערכו בממון ומערכו בחלוף וישאר י"ד וב' חלקים מי"ז וי' וי"א חלקי' מי"ז | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ותאמר אם י"ד והחלקים שבו י"ז והחלקים כמה יעלה י"ב ויצא לך ט"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ובדרך אחר נניח כי א' מהם רוצה לתת לחבירו קסה רביעית בממון וכבר ידעת כי כשרוצה לתת איזה דבר ראוי להוסיף וכששואל ראוי לחסר כי אם רוצה לתת חצי ראוי להוסיף כמוהו ואם שואל שליש ראוי להוסיף חצי ממונו ובעד הרביע ראוי להוסיף שליש וכן ראוי לעשות ולכן אם הערך עשרים ושואל שליש ראוי להוסיף חצי שהוא י' ויהיו ל' ולכן תאמ' כי מה ששוה י"ב ראוי שישים אותה ט"ו שהם ה' ותוסיפם לשניהם ר"ל לי"ב ולט"ו ויעלה י"ז וכ' מה יעשה חבירו מעשרים ויצא כ"ג וט' חלקים מי"ז וכמו שראית למעלה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
286) שאלה שנים מחליפים צמר ופשתים יחדו הקנה מהבגד שוה כ"ה ובחלוף שוה ל' ורוצה הרביעית בממון והק' מהצמר שוה ארבעים ורוצה העשור ממה שמשים אותה בחלוף והחלוף יצא שוה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והדרך נודע מצד השאלות שקדמו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
287) שאלה שנים מחליפים צמר ופשתים הבגד שוה ה' ובחלוף משים אותו ח' והק' מצמר במעות שוה חמישים ובחלוף משים אותה בדרך כי בעל הצמר מרויח יותר מבעל הבגד ל"ו וב' שלישיות בעד כל ק' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ראוי לך לדעת הקדמה כי אם תעשה חלוף והרויח י' בעד ק' אתה מרויח העשור וחבירו מפסיד חלק מי"א ר"ל כי מפסיד ט' וחלק מי"א בעד ק' כי המרויח הק' שוים ק"י | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ודע כי המחליף עם חברו לדעת כמה מרויח וכמה מפסיד חבירו קח החלק המבטא שהרויח ותוסיף אותו על החלק שמרויח | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
288) המשל מי שמרויח עם חברו עשרה בעד ק' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| שים עשרה על עשור ק' שהוא חלק מי' ויהיו י"א וזה יהיה החלק שמפסיד המפסיד ושימם ככה א"כ אתה מפסיד י"א ר"ל כי אתה תתן לי מה ששוה ק"י בעד ק' או תאמר כי אתה תתן לי יא בעד י' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והאומר פלוני הפסיד עם חברו עשרים בעד ק' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כבר ידעת כי עשרים חומש ק' תוסיף על חמש א' ויהיו ו' א"כ תאמ' כי הפסיד שישית ממונו בעד ק' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
289) שאלה שנים מחליפים לא' יש לו ברזל ושוה ו' פרחים המאה ובחלוף משים אותו ז' ורוצה לתת לחברו זמן ד' חדשים וחברו יש לו עורות אלים מאדמים ושוה העור במעות ח' גרושי ובחלוף משים אותו ט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה למען יהיה המסחר שוה לזה כמו לזה הלא מן הדין אם בעל הברזל מעלה מו' לז' ראוי לבעל העור שיעלהו מח' לט' ושליש ולכן כפול ז' על ח' ויעלה נ"ו וחלק על ו' ויצא ט' ושליש והנה התוספת מח' עד ט' ושליש הוא א' ושליש וחלק ד' שהם החדשים עליהם ויצא ג' שלמים וכן ראוי שימתין בעל העור לבעל הברזל להיות חלופם שוה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
290) שאלה שנים מחליפים בגד ופשתים קנה הבגד שוה י' ובחלוף י"א וממתין לו שנה תמימה וחברו מוכר ק' מהצמר ל"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה הנך רואה כי בעל הב' מרויח עם י' א' בשנה תמימה והוא עשור ממונו בי"ב חדשים א"כ ירויח בכל חדש חלק מק"כ ותאמר אם י' מרויח חלק מק"כ כמה ירויחו ל"ו ויצא לך ג' עשיריות כפול ג' עשיריות על ח' ויצא לך ב' וב' חמישיות תוסיפם על ל"ו ויהיו ל"ח וב' חמישיות וכן ראוי שישים הצמר בחלוף כדי לעשות לחברו המתנה ח' חדשים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
291) שאלה שנים מחליפים צמר ופשתים הבגד שוה ד' וחצי בממון ובחלוף משים אותו ו' ונותן לחבירו המתנה ח' חדשים והצמר היה שוה בחלוף ט"ו ונתן לחברו המתנה י' חדשים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ראשנה ראה הפרש הזמן מהבגד והצמר והוא ב' חדשים לכן תסיר ההפרש ר"ל הקטן מהגדול הנשאר ב' וראה איזה חלק הוא ב' מח' והוא רביעיתו ושמור עתה קח ממון הבגד בממון שהוא ד' וחצי ואתה רואה כי ההפרש מממון ומחלוף הוא א' וחצי ומזה תקח ומזה תקח רביעיתו ויצא לך ג' רביעיות ותוסיפם על ו' ויצא קסו לך ו' וג' רביעיות וכן ראוי שישוה קנה הבגד בחלוף ותאמר כי ו' וג' רביעיות בא מקנה ששוה בממון ד' וחצי מה יתן לי ט"ו ויצא י' וי' חלקים מי"ז וכך שוה הק' בממון להיות המסחר שוה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
292) שאלה שנים מחליפים בגד עם צמר קנה הבגד שוה ג' ובחלוף ד' ונותן לו זמן י"ב חדשים והצמר שוה ט"ו ונתן לו זמן ו' חדשים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הסר זמן הצמר מזמן הבגד הנשאר ו' וראה איזה חלק הוא ו' מי"ב והנה הוא חציו וכן תסיר החצי מד' הנשאר ג' וחצי וכן תאמר ששוה הבגד בחלוף ותאמר אם ג' וחצי בחלוף יצא מג' בממון מאיזה מספר יצא ט"ו ויצא לך י"ב וב' חלקי' מז' וכך שוה הק' מהצמר בממון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
293) שאלה שנים מחליפי' צמר ופשתים יחדו קנה הבגד שוה י' ובחלוף משים אותו י"ג ונותן זמן י"ב חדש ובעל הצמר הק' שוה בחלוף חמישים ונתן לו זמן ט"ו חדשים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ראשנה ראה כמה מרויח הליט' לחדש מבעל ה' הבגד והנה תמצא פיצולי ו' אח"כ ראה בעל הצמר שהם נ' בט"ו חדשים ויצא לך צ' פיצולי שהם גרושי ז' ופיצולי ו' היינו ג' שמיניות ליט' ולכן תאמ' אם א' ליט' מרויח ג' שמיניות והוא משים אותו בחלוף א וג' שמיניות ולכן תאמ' אם א' וג' שמיניות בא ממה ששוה במחושב א' ליט' מאיזה דבר יצא חמישים ליט' ויצא לך כי הק' מהצמר בממון שוה י"ו וד' חלקים מי"א | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
294) שאלה שנים מחליפי' צמר ופשתים המאה מהצמר שוה בממון כ' ומשים אותו ל' ורוצה החצי בממון ונותן לו זמן י"ו חדשים ולחברו יש לו בגד שוה הקנה ח' ובחלוף י' והיה המסחר שוה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה נניח כי בעל הצמר היו לו ג' מאות ושוה צ' ומזה מבקש חצי הממון שהם מ"ה ומזה נותן זמן י"ו חדשי' והחצי האחר מבקש בגד והנה הבגד בחלוף י' חלק מ"ה על י' ויצא ד' וחצי והנה ד' וחצי בממון שוים ל"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עתה ראה ג' מאות מצמר בממון שוה ס' כך היה ראוי שיתן בעל הבגד לבעל הצמר להיות החלוף שוה אמנם לא נותן לו כי אם ד' קנים וחצי היינו ל"ו ויחסר עד ס' כ"ד וכך היה ראוי שיפרע בעל הבגד להיות החלוף שוה והוא פרע מ"ה א"כ ראוי שנאמ' כי כ"ד מרויחים מ"ה בי"ו חדשים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולדעת כמה עמד הבגד בהמתנה אתה יודע כי כ"ד שוים מ"ה א"כ כ"ד ירויחו כ"א חלק כ"א על כ"ד ויצא ז' שמיניות וכך מרויח הקנה בי"ו חדשים שמגיע לכל חדש ז' חלקים מקכ"ח בעד י"ג קנים ושמין | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
295) שאלה שנים מחליפים הקנה מהבגד שוה ד' ובחלוף ה' והצמר שוה המאה י' ובחלוף י"ג ואמר בעל הצמר לחבירו אני רוצה שתמתין לי שנה וארצה לתת לך חלק מה בממון באופן כי תרויח י' בעד ק' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה תאמר אם ק' שוים ק"י כמה ישוב ד'
ותמצא כי ישוב ד' וב' חמישיות וכך שוה הקנה בממון ובחלוף ה' והצמר שוה י' ובחלוף י"ג עתה ראה ההפרש מי' אל י"ג והוא ג' חלק י"ג בג' ויצא ד' ושליש עתה חלק ד' ושליש על ח' ושליש ויצא לך י"ג חלקים מכ"ה וכן ראוי שיקבל מצמר והנשאר שהוא י"ב חלקים מכ"ה יקבל בממון בסוף השנה והדבר יצא שוה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולבחון תאמר ב' מחליפים צמר ופשתים קנה הבגד שוה ד' ובחלוף ה' ורוצה י"ב חלקים מכ"ה בממון וי"ג חלקים מכ"ה בצמר והצמר שוה י' ובחלוף י"ג אשאל מי מרויח וכמה מרויח בעד כל ק'
כך תעשה נניח כי מחליפים כ"ה קנים ששוים קכ"ה בחלוף ומזה מבקש י"ב חלקים בממון שהם ס' בממון והנשאר שהם ס"ה בחלוף והנה הצמר מקבל לחשבון י"ג המאה בעד ס"ה תקבל ה' מאות וראה כמה שוה בממון ה' מאות מצמר שהם חמישים ועולה ק"י ובעד ק"י נתן כ"ה קנים ששוים בממון ק' א"כ מרויח שלחנות א"כ מרויח י' שהם ק"י | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
296) שאלה הבולונייני שוה בפלורינצא קסז כ"ו פיצולי ובפירושא שוה ל' אשאל אם איש יש לו לקבל ג' מאות בולונייני בפיורינצא כמה שוים בפירושא | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תאמר אם כ"ו שוים ל' ג' מאות כמה שוים ויצא לך שמ"ו וד' חלקים מכ"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
297) שאלה איש אחד יש לו לקבל בפיורינצא ר"נ פרחים וסולדי עשרה ופיצולי ח' והם שוים בפירושא רנ"ט פרחים וט"ו סולדי אשאל אם ארצה לקבל בפירושא ס' פרחים וי"ב סולדי וו' פיצולי כמה ראוי לקבל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה כבר ידעת כי עשרים סולדי הם פרח א' והנה תמצא כי רנ"ו פרחים וי' סולדי וח' פיצולי הם ר"נ פרחים וח' חלקים מט"ו והרנ"ט וט"ו סולדי הם רנ"ט וג' רביעיות פרחים וי"ב סולדי וו' פיצולי הם ס' פרחים וה' שמיניות לכן תאמר אם רנ"ט וג' רביעיות שבו ר"נ וח' חלקים מט"ו כמה ישובו ס' פרחים וה' שמיניות ויצא לך נ"ח פרחים וט' סולדי ואלף ושכ"ז חלקים מג' אלפים וקי"ז | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
298) שאלה איש נדר לתת לאיש אחר ג' מאות מטבעי' פיורינטיני ונתן לו ב' מיני מטבעים היינו בולונייני וגרושוני בולונייני שוה בפיורינצא ה' וחצי ובפירושא שוה ו' ורביע אשאל איזה יותר נכון לו לפרעו בבולונייני או בגרושוני | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| יש לך לדעת כי יש דבר מה שוה בפיורינצא כ"ו ובפירושא שוה ל' כן כל מטבע ששוה בפיורינצא כ"ו שוה בפירושא ל' כי יחס הבולונייני אל הכ"ו הבולונייני כיחס הגרושוני אל הגרושוני וכן מכל מטבע ונניח כי יפרענו במטבע בולונייני ותאמר אם כ"ו מן פיורינצא שוה בפירושא ל' כמה ישוה ג' מאות ויצא לך שמ"ו וחלקים ושמרם וכן תאמר מהגרושוני ותאמר אם ה' וחצי שוה בפירושא ו' ורביע כמה ישוו ג' מאות ויצא לך ש"מ וחלקים א"כ אתה רואה כי יותר טוב לפרעו בגרושוני יותר מבולונייני כי הגרושוני צריך לתת לו ש"מ ומבולונייני צריך לתת לו שמ"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
299) שאלה לאיש יש לו מב' מיני מטבעים מתחלפים כאלו תאמ' ארמיליני מז' טורניסי ומי' טורניסי ובין הכל יש לו מאתים ורוצה להחליפם שיתן לו החלפני מהם קרליני והחליפם ונתן לו צ"ב קרלי' וחצי אשאל כמה ארמיליני מז' וכמה ארמיליני מי' היו בסכום | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה ראה כמה ישוו המאתים אלו היו כלם מז' טורניסי והנה ישוו ע' קרלי' וראה ההפרש שיש מע' אל צ"ב וחצי וההפרש הוא כ"ב וחצי וראה אלו היו כל המאתים מי' טורניסי היו שוות ק' קרלי' וההפרש מצ"ב וחצי עד ק' הוא ז' וחצי חלק כ"ב וחצי על ז' וחצי ויצא ג' קח ג' חלקים ממאתים והם ק"נ וכך יקח מהארמיליני מי' ונ' יקח מאותן ששוות ז' טורניס | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Section Three: Geometry |
החלק השלישי ידבר על ענין המדות ר"ל גיבמאטריאה או ההנדסה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
300 אם יש לך מרובע רבוע י' על י' ויש לך מרובע אחר ב' על ב' לדעת כמה תשבורת הגדול הנקרא רֵיאַה עודף על תשבורת הקטן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כך תעשה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תרבע י' על י' והם ק' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
גם תרבע ב' על ב' והם ד' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חלק ק' על ד' ויצא כ"ה וכך פעמים גדול הגדול על הקטן | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
301 שאלה אם תדע ממרובע אורך הקוים ותרצה לדעת ארך האלכסון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תוכל למצא אורך האלכסון כאלו תאמר הקו האחת מהמרובע ו' והאחר ח' כפול ח' על ו' ויצא מ"ח ו' על ו' ויצאו ל"ו וח' על ח' והם ס"ד ושניהם מחוברים הם ק' ושרשם י' וכך הוא האלכסון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תדע האלכסון עם ארך אחד מהקוים לדעת הקו האחר כמה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כאלו תאמ' שהאלכסון י' והקו הנודע ו' תרבע [י'] על [ו'] והם והם ק' גם תרבע ו' על ו' והם ל"ו תסיר ל"ו מק' הנשאר ס"ד וקח שרשם והם ח' קסח והוא הקו האחר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תדע קו ח' והאלכסון ולא תדע קו ו' למצא אותו תרבע האלכסון והוא ק' גם תרבע ח' על ח' והם ל"ו ס"ד תוציאם מק' ונשאר ל"ו ושרשם ו' והוא הקו האחר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
302 שאלה אם יש לך משולש שוה הצלעו' ותרצה לדעת ארך העמוד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כגון משולש כל צלע עשרה ותרצה לדעת העמוד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול עשרה על עצמם והם ק' הוצא מהם רביעיתם והם כ"ה הנשאר ע"ה וקח שרשם והם ח' וי"א חלקים מי"ו והוא אורך העמוד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
303 שאלה אם יש לך מרובע רבוע כל קו עשרה לדעת האלכסון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול עשרה על עצמם והם ק' וכפלם על ב' ויהיו מאתים וקח שרשם והם י"ד ושביעית אחד והוא האלכסון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
304 שאלה איך נדע מופת כל משולש הן שוה הצלעות או שוה השוקים או מתחלף הצלעות אחר שידעת העמוד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תעשה מרובע אורך הב' קוים הנכוחיים הארוכים יהיו כמו התושבת ואורך הב' קוים הקצרים יהיו כמו העמוד ר"ל חציו וכמו שיעלה תשבורת המרובע כי הוא תשבורת המשולש כמו זה מזה המשולש לא תוכל לדעת העמוד יען כי התושבת מרובעו עולה יותר ממרובע שתי ו' הצלעות מחוברים יחדו כי הצלעות אינם כי אם י"ב כל אחד ושני רבועיהם עולה רפ"ח אמנם מרובע התושבת שהוא כ"ו עולה תרע"ו על כן צריך למדוד העמוד ותכפול העמוד על חצי התושבת או התושבת על חצי העמוד והוא תשברתו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
305 שאלה אם יש לך משולש מתחלף הצלעות כמו אם הצלע האחד ט"ו והא' י"ד והא' י"ג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הנה תשברתו הוא פ"ד יען כי עמודו הנקרא קַאטְיט הוא י"ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תרצה לדעת המופת על זה תעשה מרובע ויהיה התושבת אורך הצלעות הב' הארוכים וחצי העמוד שהוא ו' יהיו ב' צלעות המרובע הקצרים כפול י"ד שהוא התושבת על ו' ויהיו פ"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
306 שאלה אם יש לך משולש שוה השוקים כגון משולש ארך כל קו עשרה והתושבת י"ב | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| לדעת העמוד תרבע הצלע שהוא י' והם ק' וקח חצי התושבת שהוא ו' ותרבעהו והם ל"ו תסירם מק' ונשארו ס"ד ושרשם ח' וכך הוא העמוד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והתשבורת תרבע חצי התושבת שהוא ו' על כל העמוד או חצי העמוד על כל התושבת ויעלו מ"ח וכך הוא התשבורת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והאות המעיד על זה תעשה מרובע על המשולש כזה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנך רואה כי זה המרובע הוא מרובע ארוך אורך הב' קוים הקצרים הם ו' ואורך הב' הארוכי' הם ח' ותשברתו מ"ח ואתה רואה כי כך תשבורת המרובע כמשולש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
307 דרך למדוד משולש בג' מינים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הדרך הראשון הוא ככה כגון משולש מתחלף הצלעות אשר אורך הקו האחד ט"ו והאחר י"ד והאחר י"ג | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול הצלע הקצר והוא י"ג קסט ומרובעו קס"ט גם כפול התושבת שהוא י"ד ומרובעו קצ"ו ותחברם עם קס"ט ויעלה שנ"ב ומזה תסיר כפל הצלע הארוך והוא רכ"ה הנשאר ק"מ חלקם על כפל התושבת שהוא כ"ח ויצא ה' והוא מקום שנפל בו העמוד או חלק ק"מ על ב' והם ע' וחלקם על י"ד ויצא ג"כ ה' הסר ה' מי"ד הנשאר ט' והוא אורך העמוד מהתושבת רחוק מקצה אחד ה' ומהאחר ט' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| או אם תרצה כפול הצלע הארוך והוא רכ"ה על התושבת שהוא קצ"ו וחברם ויעלה תכ"א תסיר מהם הכפל מהצלע הקצור שהוא קס"ט וישאר רנ"ב חלקם על ב' ויהיו קכ"ו חלקם על התושבת ויצא ט' ואתה רואה כי מצאת נפילת העמוד בקצה האחר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דרך שני חבר שני הצלעות שהם י"ג וט"ו והם כ"ח וחלקם על ב' ויצא י"ד וחלקם על ההפרש שיש מי"ג שהוא אחד הצלעות אל י"ד שעלה בחלוק ויצא י"ד או חלק י"ד אל ההפרש יש בין י"ד שעלה בחלוק אל ט"ו שהוא הצלע אחד ויצא י"ד וחלק אלו הי"ד על חצי התושבת שהוא ז' ויהיו ב' תסירם מחצי התושבת שהם ז' וישארו ה' והנה ט' הוא המעמד ארוך וה' הוא המעמד קצור | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דרך שלישי הסר מרובע הצלע הקצור מן מרובע הצלע הארוך היינו מרכ"ה הסר קס"ט הנשאר נ"ו חלקם על י"ד ויצא לך ד' תוסיפם על התושבת ויהיו י"ח חלקם ויהיו ט' ולמצא המעמד קצור הסר ד' מי"ד נשאר י' חלקם על ב' ויצא ה' והוא המעמד הקצור | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אח"כ למצא הקטיטו תרבע הצלע הארוך שהוא רכ"ה הסר ממנו מרובע המעמד הארוך שהוא פ"א ונשאר קמ"ד ושרשם י"ב והוא אורך הקאטיטו או פינדוקולארי או תרבע הצלע י"ג שהוא קס"ט תסיר ממנו מרובע מעמד קצור שהוא כ"ה נשאר ג"כ קמ"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
308) שאלה איך נמדוד משולש בלי עמוד כגון אותו הנזכר חבר הג' צלעות והם מ"ב וחלקם על ב' והם כ"א הסר מהם ט"ו ונשארו ו' הסר מהם י"ד ונשארו ז' כפול ז' על ו' והם מ"ב הסר מכ"א י"ג נשאר ח' כפול ז' על מ"ב ויעלו של"ו כפול של"ו על כ"א ויעלה ז' אלפים ונ"ו וקח שרשם והם פ"ד והוא תשבורת המרובע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
309 שאלה אם יש לך זוית נצב ותרצה לעשות עליו משולש אם תרצה לדעת ארך הצלע המשלים המשולש כמה הוא
כמו אם יש לך זוית נצב כזה ארך כל קו עשרה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול כל קו על עצמו וחברם ויהיו מאתים וקח שרשם והם י"ד ושביעית וכך היא הצלע אשר הוספת על זוית נצב ולמדוד אותו אין צריך עמוד כי הצלע האחד הוא העמוד על כן כפול י' על חצי הצלע האחר שהוא י' וחציו ה' והם נ' וכך הוא תשברתו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
310) שאלה אם תרצה לדעת מתוך ידיעת זה המשולש הקטן אשר א' מהקוים ג' והאחר ד' והאחרת ה' אשר תשברתו הוא ו' מתוך ידיעת זה המשולש הקטן תוכל לדעת תשבורת המשולש הגדול אשר אחד מהקוים הם עשרים והאחרת י"ו והאחר י"ב כי כל צלע מהגדול הוא ד' פעמים צלעי הקטן וידוע כי יחס משולש אל משולש כיחס מרובע אל מרובע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם כל קו הגדול היה ב' פעמי' כצלעי הקטן היה תשברתו ד' פעמים כמוהו ועכשו שהוא ד' יהיה תשברתו י"ו פעמים כמוהו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
311) שאלה איך נוכל למדוד משולש בלי צלעות שהוא שוה קע הצלעות תרבע אחד מהצלעות ומהעולה קח י"ג חלקים מל' וכך יעלה תשברתו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל משולש בכל צלע הוא י' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול י' על י' ויהיו ק' וקח י"ג חלקי' מל' ויעלה מ"ג ושליש וכך הוא תשברתו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
312) שאלה לדעת מרובע הרבוע שחשב אדם בלבו כמה אורך כל קו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תאמר לו שיקח תשבורת המרובע ויוסיף עליו ארך הד' קוים ותאמ' לו כמה עולה ותוסיף על זה ד' וקח שרשם ומזה תסיר ב' והנשאר הוא צלע המרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון אדם חשב מרובע ארך כל צלע ה' והנה תשברתו כ"ה תוסיף בם ד' צלעי המרובע שהם עשרים והם מ"ה תוסיף בם ד' והם מ"ט וקח שרשם והם ז' תסיר ב' והם ה' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
313) שאלה לדעת אורך צלעי המרובע מתוך ידיעת אלכסונו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול האלכסון על עצמו וחלקהו על ב' ומהיוצא קח שרשו והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל האלכסון הוא י"ד ומרובעו קצ"ו חלקהו על ב' ויצא מ"ט ושרשו ז' והוא ארך כל צלע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
314) שאלה אם תדע רבוע האלכסון עם רבוע הצלע כאלו עולה בין שניהם ג' מאות חלקם על ג' והם מאה וקח שרשם והם י' והוא ארך כל צלע ושרש מאתים הוא האלכסון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
315) שאלה אם חברת על תשבורת מרובע רבוע ד' צלעיו ואח"כ תוסיף על אותו הסכום ד' ומהעולה תקח השרש והוא יהיה אורך כל צלע פחות ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
316) שאלה ממרובע לקחתי ארך הד' קוים ונשאר בידי כ"א כמה ארך כל קו מהמרובע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תוסיף על כ"א ד' והנם כ"ה וקח שרשם והם ה' ותוסיף בם ב' והם ז' והוא ארך כל צלע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
317) שאלה אם ידעת צלע המרובע עם האלכסון ועולה מרובע הצלע בעצמו עם מרובע האלכסון בעצמו ושניהם מחוברים כפולים זה על זה עולה ה' אלפים כמה הצלע וכמה האלכסון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חלקם על ב' ויהיו ב' אלפים וה' מאות וקח שרשם והם נ' וקח שרשם והם ז' והוא ארך הצלע וכפול חמישים על ב' והם ק' ושרשם י' והוא ארך האלכסון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
318) שאלה כשחברנו הצלע עם המרובע * עולה האלכסון י"ז כמה ארך הצלע וכמה ארך האלכסון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עשה מי"ז ב' חלקים שהחלק הגדול כפול בעצמו יהיה ב' פעמים מהחלק הקטן כפול בעצמו נניח ונקח משל ונאמ' ב' כפלם ויהיו ד' ואם תחלק הקטן כפול בעצמו יצטרך כי החלק הגדול כפול בעצמו יעלה ח' כי הוא ב' פעמים כמוהו וקח שרשם והם ב' וה' שישיות קבצם עם ב' ויהיו ד' וה' שישיות ותאמר אם ד' וה' שישיות יתן לי ב' כמו החלק הקטן כמה יתן לי י"ז ויצא לך ז' והוא החלק הקטן והחלק האחר י' ושניהם מקובצים הם י"ז | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Rectangle |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
319) שאלה מרובע ארוך ארך השני קוים הנכוחיים הקצרים [ו'] והב' קוים האחרים ח' אשאל כמה האלכסון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כפול ו' על ו' ויהיו ל"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עו' כפול ח' על ח' ויהיו ס"ד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וחברם ויהיו ק' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וקח שרשם ויהיו י' וכך הוא האלכסון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
320) שאלה בכאן מרובע ארוך תשברתו מ"ח והנה חברנו ארך הקו הארוך עם הקו הקצור ויעלה י"ד ארצה לדעת ארך הקו הארוך והקצור | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
קח חצי י"ד והם ז' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומרובעם מ"ט | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הוצא מהם מ"ח ונשאר א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ושרשו א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הוסיפהו על ז' והם ח' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תוציאהו מ[י"ד] ונשאר ו' והוא הקצור | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
321) שאלה בכאן מרובע ארוך אלכסונו י' ומרובעו ק' ותשבורת המרובע מ"ח ארצה לדעת כמה ארך כל צלע מהמרובע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כפול מ"ח על ב' ויעלה צ"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ותוסיפם על ק' ויהיו קצ"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וקח שרשם והם י"ד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ואתה ידעת כי בין השני קוים ארכם י"ד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ולדעת ארך כל צלע חלק י"ד והם ז' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומרובעם מ"ט | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הוצא מהם מ"ח והוא תשבורת המרובע המרובע נשאר א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ושרשו א' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תוסיפהו על ז' והם ח' והוא הארוך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תוציאהו ממנו והוא הקצור | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
322) שאלה בכאן מרובע ארוך אורך אלכסונו י' ובין שני הקוים ארוך וקצר עולה י"ד אשאל כמה כל צלע מהמרובע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תרבע י"ד והם קצ"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
הוצא מהם מרובע האלכסון והוא צ"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חלקם על ב' והוא תשבורת המרובע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ולדעת ארך כל צלע נאמ' הנה תשבורת אלכסון המרובע הוא ק' ועשה כאמור ותמצא האחת ח' והאחר ו' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
323) שאלה בכאן מרובע ארוך ארך הקו הקצור עם האלכסון עולה י"ו והצלע הארוך הוא ח' ארצה לדעת כמה הוא ארך הצלע הקצור והאלכסון: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה כפול י"ו ועלה רנ"ו והוצא מהם מרובע הצלע הידוע שהוא ח' היינו ס"ד ונשאר קצ"ו וחלקם על כפל י"ו שהוא ל"ב ויצא ו' והוא הצלע הקצור ומו' עד י"ו הוא י' והוא ארך האלכסון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
324) שאלה בכאן מרובע ארוך ארך אלכסונו מוסיף על הצלע הקצור ד' והצלע האחר ח' אשאל כמה ארך הצלע הקצור עם האלכסון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה תרבע ח' והם ס"ד תוסיף בם מרובע ד' ויהיו פ' חלקם על כפל ד' שהם ח' ויצא י' והוא האלכסון הוצא מי"ו י' הנשאר ו' והוא הצלע הקצור | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
325) שאלה בכאן מרובע ארוך אשר כפלתי ארך הקו הארוך עם תשבורת המרובע ועלה שפ"ד והצלע הקצור ו' אשאל כמה ארך הצלע הארוך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חלק שפ"ד על ו' ו' ויצא ס"ד ושרשם ח' והוא ארך הצלע הארוך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
326) שאלה מרובע ארוך תשברתו מ"ח חלקנו הצלע הארוך על הצלע הקצור עולה א' ושליש אשאל כמה ארך הצלעות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נניח כי הצלע הארוך היה ד' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| בעבור כי אמ' א' ושליש והקצור ג' ונראה היחס שיש מד' אל ג' והנה כפול ג' על ד' ויצא י"ב חלק עליהם מ"ח ויצא ד' ושרשם ב' וכפול ב' על ג' ועל ד' והנה החלק האחד ו' והאחר ח' א"כ הצלע הארוך ח' והקצור | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| או עשה כך כפול ג' על מ"ח והעולה חלק על ד' והוא ל"ו ושרשם ו' והוא הצלע הקצור | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולדעת הצלע הארוך כפול מ"ח על ד' והעולה חלק על ג' והוא ס"ד ושרשם ח' והוא הצלע הארוך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
327) שאלה ממרובע ארוך מחובר הצלע הקצור עם האלכסו' עולה י"ו והצלע הארוך מוסיף על הצלע הקצור ב' אשאל כמה הצלע הקצור והאלכסון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה תאמר אם תחבר הצלע הארוך עם האלכסון יהיה י"ח כפי מה שאמר כי הארוך מוסיף ב' על הקצור והקצור עם האלכסון הם י"ו על כן כפול י"ו על עצמם וי"ח על עצמם והעולה רנ"ו ושכ"ד וחברם יחד והעולה תק"פ והוצא מהם כפל ב' שהם ד' וישארו תקע"ו ושרשם כ"ד הוצא מהם י"ו ונשאר ח' והוא הצלע הארוך גם הוצא מהם י"ח ונשאר ו' והוא הצלע הקצור ולדעת האלכסון הוצא מי"ו ו' הנשאר י' והוא האלכסון או הוצא מי"ח ח' ונשאר ג"כ י' או מי"ו ו' ונשאר י' והוא האלכסון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
328) שאלה מרובע ארוך אשר תשברתו הנקרא רֵיאַה מחובר עם אורך ב' צלעותיו עולה ס"ב אשאל כמה ארך כל צלע מהמרובע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עשה כך הוצא ב' מס"ב ונשאר ס' אח"כ כפול ב' ויהיו ד' והוסיפם על ס' ויהיו ס"ד ושרשם ח' והוא הצלע הארוך ואם תרצה לדעת הצלע הקצור הוצא ב' מח' ונשאר ו' והוא הצלע הקצור | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
329) שאלה מרובע ארוך כפלתי ארך הצלע הארוך כנגד האלכסון ועלה פ"א והצלע הקצור הוא ו' אשאל כמה הוא הצלע הארוך גם האלכסון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה כפול פ' על עצמם ויעלו ו' אלפים וד' מאות גם כפול ו' ויעלו ל"ו וקח חצי ל"ו והם י"ח ומרובעו הוא שכ"ד ותחברם עם ו' אלפים וד' מאות ויהיו ו' אלפים ותשכ"ד ו' ושרשם פ"ב כי עם חצי ל"ו שהם י"ח הם ק' ושרשם י' והוא אלכסון אח"כ חלק פ' על י' ויצא ח' והוא הצלע הארוך או אם תרצה מפ"ב הוצא י"ח הנשאר ס"ד ושרשם ח' והוא הצלע הארוך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
330) שאלה בכאן מרובע ארוך אשר הוצאתי מתשברתו הצלע הארוך ונשאר מ' והצלע הארוך עודף על הקצור שנים קעב אשאל כמה ארך כל צלע וצלע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תאמר אחר שהוצאתי הצלע הארוך מתשברתו נשאר מ' אם הוצאתי הצלע הקצור מתשברתו הנשאר מ"ב ועל כן עשה כנזכר לעיל בשאלות הקודמות ותמצא כי הצלע הארוך ח' והקצור ו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
331) שאלה בכאן מרובע ארוך כי כשתחבר הב' קוים הארוך והקצור עם האלכסון עולה כ"ד והצלע הארוך עודף על הקצור ב' אשאל כמה ארך כל צלע והאלכסון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה כפול כ"ד והם תקע"ו וכפלם עלה אלף וקנ"ב תוסיף בם כפל היתרון שיש מהצלע הארוך על הקצור והם אלף וקנ"ו ושרשם ל"ד הוצא מהם כ"ד הנשאר י' והוא האלכסון ומכ"ד עד עשרה הנשאר י"ד והוא ארך שתי הצלעות הוצא מהם ב' הנשאר י"ב וחצים ו' והוא הצלע הקצור וח' הוא הצלע הארוך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
332) שאלה בכאן מרובע ארוך אשר ארך אלכסונו הוא עודף ב' על הצלע הקצור אשאל כמה ארך כל צלע | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| לעולם כשהעודף שוה ר"ל כי האלכסון עודף ב' על הצלע הארוך והקו ארוך עודף ב' על הקצור כי הוא שוה כפול היתרון היינו ב' על ה' ויהיו י' וזה יהיה האלכסון עוד כפול ב' עד ד' ויהיו ח' והוא הקו הארוך עוד כפול ב' על ג' והוא הקו הקצור | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Rhombus |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 333) שאלה בכאן מרובע מעויין אשר אם תחבר ב' אלכסוניו עולה ל"ד כמה ארך כל אלכסון והגדול מוסיף על הקטן י"ד כמה ארך כל אלכסון וכמה תשברתו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הוצא י"ד מל"ד הנשאר כ' וחצים עשרה והוא הקצור והארוך כ"ד עתה כפול א' מן אלכסוניו על כל האחר ויעלה ק"כ והוא התשבורת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 334) שאלה בכאן מרובע מעויין אשר ארך אחד מאלכסוניו עם תשברתו עולה קנ"ד כמה ארך כל אלכסון ותשברתו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והגדול מוסיף י"ד על הקטן בהיות כי הב' אלכסונים שוים אל הד' צלעות כנז' לעיל | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 335) שאלה בכאן מרובע מעויין אם תחבר מרובע ב' אלכסוניו עולה תרע"ו ומרובעו כ"ה אשאל כמה כל א' מאלכסוניו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה קח רביע תרע"ו והוא קס"ט וקח שרשם והם י"ג והוא אחד מאלכסוניו ואם תבין כל הדרכי' האמורים לעיל תוכל לשער א"כ האלכסון הארוך עודף על הקטן י"ד והוא כ"ד והאחר י' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Circle |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 336) שאלה אם תרצה לדעת מתוך אלכסון העגלה כמה הקפה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול האלכסון על ג' ושביעית וכך יהיה הקפו כאלו אלכסון העגול י"ד כפול ג' פעמים י"ד ושביעית ויעלה מ"ד וכך ההקף | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| או כפול האלכסון על כ"ב וחלקהו על ז' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם אמר הקף העגולה מ"ד כמה האלכסון חלק מ"ד על ג' ושביעית ויצא י"ד והוא האלכסון או כפול מ"ד על ז' וחלק על כ"ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תרצה לדעת העגול אשר אלכסונו הוא י"ד והקפו מ"ד כמה תשברתו קח חצי האלכסון שהוא ג' וחצי וכפול אותו על חצי הקפו שהוא כ"ב ויעלה קנ"ד וכך הוא תשברתו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| או אם תכפול כל האלכסון שהוא י"ד על חצי הקפו שהוא כ"ב ויעלה ש"ח והעולה חלק על ב' ויצא קנ"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| או תחלק חצי האלכסון שהוא ג' וחצי על כל ההקף שהוא מ"ד ויהיו ש"ח וחלקם על ב' והוא קנ"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| או כפול כל האלכסון על כל ההקף והעולה חלק על י"ד ויצא קנ"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| או כפול כל האלכסון על עצמו ומהעולה קח י"א חלקים מי"ד ויעלה קנ"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| או קח רביעית ההקף שהוא י"א וכפלם על עצמם ויהיו קכ"א וזה כפול על האלכסון שהוא י"ד ויהיו אלף תרס"ד וחלקם על י"א ויהיו קנ"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| או כפול הקפו על עצמו וחלק על י"ב וד' שביעיות כאלו תאמר כפול מ"ד על עצמם ויהיו אלף תתקצ"ו עוד כפול זה על ז' וחלקם על פ"ח היינו על ז' גם על י"א ויצא לך קנ"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 337) שאלה אם תרצה למדוד חצי עגול אשר האלכסון הוא כ"ד אם תרצה לדעת קשת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קח חצי ג' ושביעית שהוא א' וד' קעג שביעיות כפול א' וד' שביעיות על כ"ד ויהיו ל"ז ושביעית וקח חציו שהם י"ח וד' שביעיות וכפלם על י"ב שהוא חצי כ"ד ויצא לך רכ"ו וד' שביעיות וככה תשבורת חצי זה העגול | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 338) שאלה דע כי העגול מוסיף על המרובע שהוא בתוכו ג' חלקים מי"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון עגול אלכסונו ז' הנה תשברתו הוא ל"ח וחצי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והמרובע שהוא בתוך העגול תשברתו הוא כ"ד וחצי הנה ל"ח וחצי מוסיף על כ"ד וחצי ג' חלקים מי"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 339) שאלה עשה עגול תוך מרובע המרובע מוסיף על העגול ד' חלקים מי"א | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון מרובע אשר כל צלעיו ה' הנה תשברתו כ"ה ואם תעשה עגול בתוכו לא יהיה כי אם י"ט ורביע ד' חלקים מי"א | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 340) שאלה בכאן תיבה ארכה ג' אמות וגבהה א' וחצי ורחבו ג' רביעיות אשאל כמה תכיל מחטה באופן כי תכיל כל אמה מרובעת ט' סטארי בתחלה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול ג' על א' וחצי והעולה כפול על ג' רביעיות ויצא לך ג' וג' שמיניות ותאמר אם א' שוה ט' ג' וג' רביעיות כמה ישוה ויצא לך המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 341) שאלה בכאן כרי של חטה עגול אשר סביבו הוא כ"ב וגבהו ג' אשאל כמה חטה תכיל הכרי באופן תכיל כל אמה מרובעת ט' סיטארי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול כ"ב על עצמם וחלק העולה על י"ב ויצא ל"ח וחצי וכך אמות מרובעות יש בכרי כפול זה על ט' ויעלו שמ"ו אשטארי וחצי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 342) שאלה בכאן עגול אשר אלכסונו הוא ז' נרצה לעשות בתוכו מרובע ימשש בכל ד' זויותיו העגול כמו זה כמה כל צלע מהמרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אתה רואה כי אלכסון המרובע הוא כמו אלכסון העגול כי הוא ז' כפול ז' על עצמם ויהיו מ"ט חלקם על ב' ויצא כ"ד וחצי ושרשם שהוא קרוב לה' הוא צלע המרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 343) שאלה בכאן מרובע ארך כל צלע ז' ונרצה לעשות עגול ימשש המרובע כמה הוא אלכסונו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אתה רואה כי ארך אלכסון העגול כמו צלע המרובע ממש היינו ז' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 344) שאלה בכאן משולש שוה הצלעות ארך כל צלע י' ונרצה לעשות בתוכו עגול היותר גדול שאפשר שימשש המשולש כמה ארך אלכסון העגול כזה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אתה רואה כי אלכסון העגול הוא ב' שלישיות מעמוד המשולש והנה עמוד המשולש הוא שרש מע"ה שהוא ח' וי"א חלקים מי"ו קח שתי שלישיות מח' וי"א חלקי' מי"ו והוא ארך אלכסון העגול כזה שהוא ה' וז' תשיעיות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 345) שאלה אם תרצה לדעת מתוך אלכסון העגול שהוא תוך המשולש כמה עמוד המשולש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קח שליש ז' וז' תשיעיות ותוסיף אותו על ה' וז' תשיעיות ויעלה ח' ושליש וכך הוא עמוד המשולש שהוא חוץ לעמוד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולדעת ארך צלע המשולש כפול ח' ושליש על עצמם ויהיו ע"ה תמצא מספר ע"ה יהיו ג' רביעיות ותמצא ק' וקח שרשם והוא י' והוא ארך כל צלע מהמרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 346) שאלה בכאן עגול אשר אלכסונו הוא ח' נרצה לעשו' מרובע על רביעית העגול כמה צלעי המרובע כמו זה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אתה רואה כי אלכסון המרובע כמו חצי אלכסון העגול ואם אלכסון העגול ח' אלכסון המרובע ד' ולדעת הצלע כפול ד' על ד' והם י"ו חלקם על ב' והם ח' וקח שרשם והוא ארך כל צלע המרובע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 347) שאלה בכאן ביבר ארוך ח' רוחבו ו' גבהו ד' והוא מלא מים הושלך תוכו קע"ד אבן ארכה ג' ורחבה ג' וגבהה ג' על כל אמה מרובעת שתשליך תוך הביבר ה' בארילי אשאל אם תשליך זאת האבן כמה יצא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול ג' על ג' והם ט' וזה על ג' והם כ"ז א"כ תשבורת האבן כ"ז כפול כ"ז על ה' ויצא קל"ה וכך ברילי ממים יצאו חוץ אם תשליך שם האבן | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 348) שאלה בכאן ביבר ארכו ח' ורחבו ו' וגבהו ו' והמים גבוהים ד' אמות אם נשליך אבן ארכה ג' וגבהה ג' ורחבה ג' כמה יעלו המים תוך הויוארו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קח תשבורת האבן שהוא כ"ז וקח תשבורת הויוארו ארכו עם רחבו שהם מ"ח חלק כ"ז על מ"ח ויצא לך ט' חלקים מי"ו וכך יגברו המים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 349) שאלה בכאן אבן עגולה אשר אלכסונה הוא ב' אשאל כמה משקלה באופן תשקול כל אמה מרובעת אלף וו' מאות ליט' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה כפול ב' על ב' והם ד' גם זה על ב' והם ח' ומזה תסיר י"א חלקים מכ"א ויצא לך ד' וד' חלקים מכ"א כפלם על אלף וו' מאות ליט' וכך תשקול האבן | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 350) שאלה אם יש לך עגול ותרצה לעשות עגול אחר יהיה ב' פעמים כראשון | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה עשה עגול וחוץ לעגול עשה מרובע ימשש לעגול וחוץ לאותו מרובע עשה עגול אחר ותמצא כי העגול החצון הוא ב' פעמים מהפנימי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 351) שאלה אם תרצה לעשות מרובע יהיה ב' פעמים כמו המרובע האחר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עשה מרובע וחוץ למרובע עשה עגול ימשש וחוץ לעגול עגול ותמצא ותמצא כי המרובע החצון יהיה ב' פעמים מהפנימי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 352) שאלה בכאן מגן אחד עשוי ככה ארך העמוד י"ב והתושבת (ח') ונרצה לדעת כמה תשברתו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תחבר התושבת עם העמוד ויעלה כ' וקח שלישיתם ר"ל ב' שלישיות שהם י"ג ושליש ומהעולה קח י"א חלקים מי"ד ויצא ס"ט וחלקים וככה התשבורת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 353) שאלה אם תרצה למדוד צורה כזאת אשר ארך האלכסון ו' והתושבת ד' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תחבר התושבת עם האלכסון והם י' וקח מחציתם והם ה' ותרבעם והם כ"ה וקח מהם י"א חלקים מי"ד ונשאר י"ט וט' חלקים מי"ד וכך הוא תשברתה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 354) שאלה איש אחד רוצה לעשות סרבל שיהיה ארוך ב' אמות ורוצה לעשות אותו מבגד רחבו אמה וחצי ארצה לדעת כמה אמות יצטרך לעשות אותו הסרבל | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה ידוע הוא כי הסרבל הדיאמטרו הוא ב' פעמים כמו האורך ואם האורך הוא ב' אמות הרוחב הוא ד' על כן תאמר בכאן עגול אשר אלכסונו הוא ד' כמה תשברתו כפול ד' על עצמם ויהיו י"ד וקח מהם י"א חלקים מי"ד הנשאר י"ב וד' חמישיות וכך הוא תשברתו מאמות מרובעות ואנו אמרנו כי הבגד רחב אמה וחצי על כן חלק י"ב וד' שביעיות על א' וחצי ויצא לך ח' וח' חלקים מכ"א וכך בגד יצטרך לעשות הסרבל | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 355) שאלה אדם רוצה לעשות מלבוש מבגד רחב אמה וב' שלישיות ויצטרך מאותו בגד ט' אמות ואח"כ נמלך ורוצה לעשותו מבגד רחב אמה וחצי כמה בגד יצטרך | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול ט' על א' וב' שלישיות חלקם על א' וחצי ויצא י' וכך אמות יצטרך מאותו בגד השני
שאלה בכאן מרובע בלתי מתיחס כזה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חלק ב' קוים נכוחיים היינו ד' וי' וחצי י' הם ה' וחצי ד' הם ב' הסר ב' מה' הנשאר ג' וכפלם והם ט' אח"כ חבר י"ב וי"ו ויהיו כ"ח וחלקם על ב' ויהיו י"ד ומרובעם קצ"ו הסר מהם הט' וישארו קפ"ז הסר מהם שרשם והם י"ג וט' חלקים מי"ג אח"כ חבר ד' עם י' והם י"ד וחלקם על ב' קעה והם ז' כפול ז' על י"ג וט' חלקים מי"ג ויצא לך צ"א וב' שלישיו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תעשה מכל תמונה מתחלפת הצלעות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 356) שאלה אם תרצה למדוד מרובע שהוא מתחלף הצלעות כזה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה כפול ג' על ה' והם ט"ו וכפול ז' על ג' והם כ"א וכפול כ"א על ט"ו והם שט"ו וקח שרשם והם י"ז וכ"ו חלקים מל"ד וכך הוא התשבורת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תוכל לעשות מכל מרובע בין שיהיה ארוך או רבוע או נפתל או מתחלף הצלעות כי כל ד' קוים מתחלפים כשתכפול זה על זה ר"ל ב' מהם איך שיזדמן וכן הב' האחרים זה על זה והסך העולה תכפול זה על זה תמצא תשברתו ולעולם יצא שוה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 357) שאלה אם ד' בראצי מקורדי מספיקות לקשור י' זמורות ק' בראצי כמה זמורות יקשרו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול ד' על ד' והם י"ו גם כפול י' על י' ויהיו ק' ותאמר אם י"ו יקשרו ק' כמה יקשרו ק' ויצא לך תרכ"ה א"כ ק' בראצי יקשרו תרכ"ה זמורות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם אמר ד' בראצי קושרים ק' זמורות עשרה בראצי כמה קורדי יצטרך לקשור תרכ"ה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול תרכ"ה על י"ו והעולה תחלק על ק' ויצא לך שרש ק' שהוא י' והוא הדרוש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 358) שאלה אם פיורינצא מקפת ה' מילין והנה החומה עביה ג' אמות וחצי והפושי אשר היא ברגל החומה עביה י"ד אשאל כמה תקיף פיורינצא חוץ לחומה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ידוע כי החומה עביה ג' אמות וחצי מכל צד וחברם עם י' והם י"ד והם י"ז וחצי וכפלם ויהיו ל"ה כפלם על ג' ושביעית ויצא ק"י א"כ פיורינצא מקפת ה' מילין וק' אמות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 359) שאלה פיורינצא היא עגולה ומקפת ז' מילין ופאדואה היא עגולה ומקפת ב' מילין אשאל כמה פעמי' יותר גדולה פיורינצא מפאדואה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול ב' על ב' והם ד' גם כפול ז' על ז' והם מ"ט חלק מ"ט על ד' ויצא י"ב ורביע וכך פעמים יותר גדולה פיורינצא מפאדואה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 360) שאלה רומא היא עגולה ומקפת ל"ג מילין וקושטאנטינופלי היא בדמות משולש ומקפת מ"ב מילין צלע אחד ט"ו ואחר י"ג ואחר י"ד איזו גדולה מחברתה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קח תשבורת רומא היינו חצי ההקף שהוא י"ו וחצי וכפלהו על חצי האלכסון ויצא פ"ו וה' שמיניות וזה הקף רומא קח תשבורת המשולש מקושטאנטינופולי ויצא פ"ד א"כ רומא יותר גדולה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 361) שאלה איש רוצה לחפור בור ולקבל ד' דוקטי וחפרו באופן כי קבל ד' דוקטי אשאל כמה חפר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תאמר כי בעד י' ראוי לעשות נ"ה יגיעות כמו שהוא מחובר מא' עד י' בעד ד' כמה יגיעות ראוי שיעשה ויצא לך כ"ב יגיעות וכבר ידעת כי מא' עד ו' הם כ"א ואחר ו' הוא ז' ושים אותו העודף מכ"א עד כ"ב ושימהו על ז' ויהיה שביעית אחד א"כ בו' אמות ושביעית אמה ראוי שיקבל ד' דוקטי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 362) שאלה לאיש אחד יש לו ב' שקים אחד מכיל ו' אשטרי ואחד מכיל כ"ד ורוצה לעשות משניהם שק אחד ולחברם אשאל כמה יכיל השק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה חבר ו' עם כ"ד ויהיו ל' אח"כ כפול ו' על כ"ד ויהיו קמ"ד וקח שרשם ויהיו י"ב וכפלם ויהיו כ"ד וחברם ויהיו נ"ד וכך אשטארי יכיל השק | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 363) שאלה בכאן צורה עשויה כדמות כסוי מאלביקו הנקרא פיראמידא גבהה ו' אמות ונרצה לחלקה לשני חלקים שוים במשקל לא במדה באיזה מקום ראוי לחתוך אותה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה כפול ו' על ו' ויהיו ל"ו גם כפול ל"ו על ו' ויהיו רי"ו וחלקם על ב' ויהיו ק"ח וקח ו' שרשו המעוקב וזה יהיה גובה החלק האחד והנשאר עד ו' קעו הוא החלק האחר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 364) שאלה אם יש לפניך צורה כזאת שהיא קטומת הראש אשר שני צלעיו י"ג והראש ח' והתושבת י"ח | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| לדעת מרובעה תחבר הראש עם התושבת ויהיו כ"ו וקח מחציתם והם י"ג וכפול אותם כנגד העמוד שהוא י"ב ויהיו קנ"ו וכך הוא תשברתה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תרצה להשלים הצורה כדמות משולש ותרצה לדעת כמה יצטרך להשלימה עד שיהיה כדמות משולש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול ח' שהוא הראש על י"ג ויעלה ק"ח וחלק ק"ח על היתרון שיש לתושבת אל הראש שהוא י' ויצא י' וב' חמישיות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| גם תוכל לדעתו באופן אחר והוא תדע ערך הראש אצל מה שעודף התושבת והנה העודף הוא י' חלק ח' על י' והם ד' חומשים קח ד' חומשים מי"ג והם י' וד' חומשים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והמופת תאמר אם י"ג שהם הקוים הרחיבו י' שהוא יתרון התושבת אל הראש כמה יתנו י' וד' חומשים ויצא לך ח' א"כ יצטרך שהראש העומד על נקדה עד שירחיב ח' יצטרך י' וד' חומשים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 365) שאלה אם תרצה לחלק משלש שוה הצלעות לב' חלקים שוים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חלק התושבת על חציו ותוציא עמוד מראש המשלש עד חצי התושבת והוא נחלק לב' חלקים שוים כזה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 366) שאלה אם תרצה למדוד איזה דבר מעוקב ר"ל שיש לו ג' רחקים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון אם תרצה לדעת מגדל ארוך י' ורחבו י' וגבהו י' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול י' על י' והם ק' וכפול זה על י' והם אלף וכך הוא התשבורת כל חלק אמה על אמה ברום אמה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם הארך והרוחב אינו שוה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון שיהיה ארכו ו' ורחבו ו' וגבהו עשרה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול ו' על ו' והם ל"ו וכפלם על י' והם ש"ס וכך הוא תשברתו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם הם מתחלפים הארך והרחב והגבה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון אם הארך ו' והרחב ה' והגובה עשרה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול ו' על ה' ויהיו ל' וכפלם על י' והם ש' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 367) שאלה יש לנו משלש ארך הקו האחד ט"ו והשנית י"ד והאחרת לא ידענו אמנם תשבורת המשלש פ"ד אשאל כמה הצלע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כבר ידעת כי כשתכפול חצי העמוד על חצי התושבת הוא תשבורת המשלש ונניח כי הוא י"ד א"כ כשנחלק פ"ד על י"ד יצא חצי העמוד יצא ו' ואם חציו ו' כלו י"ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ועכשו שמצאת העמוד תמצא באיזה מקום רחוק מקו ט"ו נופל העמוד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והנה תעשה כך כפול י"ב על עצמם וט"ו על עצמם ויצא קמ"ד ורכ"ה הוצא מרכ"ה קמ"ד וישאר פ"א וקח שרשם והם ט' א"כ העמוד נופל ט' רחוק מצלע ט"ו א"כ החלק האחר הוא ה' בהכרח כי ט' וה' הם י"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולדעת כמה ארך הצלע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול ה' על עצמם וי"ב על עצמם וחברם ויהיו קס"ט ושרשם י"ג והוא הצלע הנעלם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 368) שאלה בכאן ג' עגולים משעוה הקף הא' ב' והא' ג' והאחר ו' ונרצה להתיכם ולעשות מהם א' עגול כמה יהיה הקפו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול ב' על ב' והם ד' וג' על ג' והם ט' וו' על ו' והם ל"ו וחברם והם מ"ט וקח שרשם והם ז' וכך יהיה הקפו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 369) שאלה כל ח' מספרים או ו' או ד' והוא שיהיו זוגות ומוכפלים ב' מהם איך שיזדמן זה על זה והב' הנשארים ג"כ כפולים זה על זה והעולה מהב' הכפלו' כפול זה על זה וכן מהאחרים הנה באיזה דרך שתכפלם לעולם המספר יצא שוה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל מו' מספרים א'ב'ג'ד'ה'ו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול א' על ב' והם ב' וכפול ג' על ד' והם י"ב כפול י"ב על ב' השמורים והם כ"ד עו' כפול ה' על ו' ויעלה ל' כפלם על כ"ד והם ש"כ ושמרם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד תעשה ההפוך ב' באופן אחר והנה נכפול א' על ג' ד' והם ד' וב' על ג' והם ו' קעז כפלם על ד' והם כ"ד והם ג"כ ש"כ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עוד תהפכם באופן אחר כפול א' על ד' והם ד' וב' על ג' והם ו' כפלם על ד' והם כ"ד וכפול ה' על ו' והם ל' וכפלם על כ"ד והם ש"כ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תעשה מכל ההפוכים איך שתרצה לעולם יצא שוה וכן תוכל לעשות מכל המספרים כשהם זוג | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 370) שאלה כל דבר מרובע וכל להיות בשני מינים או שלם או חצי כדור או פחות מחצי כדור או יותר מחצי כדור | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולדעת כשהוא חצי כשהחץ הוא חצי המתר הוא חצי עגול וכשהחץ יותר מחצי המתר הוא יותר מחצי עגול וכשהחץ פחות מחצי המתר הוא פחות מחצי עגול | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ולמדוד כשהוא חצי עגול כאלו תאמר קשת שמתרו ח' וחצו ד' הוא חצי עגול כפול חצי המתר שהוא ד' על ג' ושביעית והנה יצא י"ב וד' שביעיות והוא ארך הקשת קח חצי י"ב וד' שביעיות וכפול אותם בד' שהוא חצי המתר ויצא לך כ"ה וזהו תשבורת חצי עגול | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ותוכל לדעת תשברתו בדרך אחר והוא שתרבע המתר שהוא ח' והם ס"ד ותקח מזה השביעית ומחצית השביעית שהם י"ג וה' שביעיות הנשאר נ' וב' שביעיות חלקם על ב' והם כ"ה ושביעית והוא התשבורת כמו שאמרנו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| משל לאותו שהוא פחות מחצי עגול כגון קשת אשר מתרו ח' וחצי ב' הוא פחות מחצי עגול | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אם תרצה לדעת קוטר העגולה תרבע חצי המתר והוא שהוא ד' ויהיו י"ו חלק י"ו על החץ שהוא ב' ויצא ח' תוסיף על זה ארך החץ שהוא ב' ויהיו י' והוא קוטר העגולה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 371) שאלה אם יש לך תמונה הולכת ומקצרת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון גוף משולש אשר למטה כל צלע מהמשלש ח' אמות וראשו כל צלע מן המשולש ד' אמות וגבהו ד' אמות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אתה ידעת כי תשבורת התושבת כ"ח אמות פחות שני שביעיות ותשבורת הראש ז' פחות חלק אחד מי"ד וחברם ויהיו ל"ד וט' חלקים מי"ד ואתה ידעת כי גדר תשבורת התושבת מלמטה שהיה כ"ח וב' שביעיות גדרו ה' וב' שביעיות גם שרש או גדר הראש שהיה תשברתו ז' וגדר וחלק אחד מי"ד גדרו ב' וד' שביעיות וחצי שביעית היינו חלק אחד מי"ד כפול ד' וב' שביעיות וחצי שביעית שהוא גדר הראש עם גדר התושבת מלמטה שהיה ה' ושתי שביעיות ועלה י"ד פחות ב' שביעיות ותוסיפם על ל"ד שהיה לך ותשעה חלקים מי"ד ויעלה הכל מ"ח וחצי כפלם על שליש הגובה שהוא ב' ויעלה הכל צ"ז והוא תשבורת גוף המשלש הזה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 372) שאלה תמונה מרובעת אשר ארכה עשרה וארחבה עשרה וגבהה עשרה כמה תשברתה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול י' על י' והם ק' וק' על י' והם אלף וכך תשברתה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם הארך שוה לרוחב והגובה מתחלף | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון אם הארך ו' והרחב ו' והגבה י' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול ו' על ו' והם ל"ו וכפלם על י' והם ש"ס | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם כל רחקיו מתחלפים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון הארך ו' והרוחב ה' והגובה ד' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול ו' על ה' והם ל' וד' על ל' והם ק"כ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם יש לך תמונה משולשת אשר א' מצלעיו ג' והאחר ד' והאחר ו' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| אתה ידעת כי זה המשלש הוא ו' ואם תכפול ו' על הגובה ונניח כי הגובה י' והם ס' וכך הוא תשבורת הצורה הזאת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והרוצה לדעת גובה ממגדל עגול | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון שיהיה קוטרו י' אמות וגבהו י"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה כפול הקוטר על עצמם והם ק' וכפלם על הגובה שהוא י"ד והם אלף וד' מאות קח מהם ג' חלקים מי"ד שהם ג' מאות ונשארו אלף ומאה וכך ממש תעשה קעח אם תוציא מק' שהוא מרובע הקוטר ג' חלקים מי"ד והנשאר כפול על הגובה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם התמונה עולה בשפוע כגון תמונה אשר ארכה ד' ורחבה ד' וגבהה עשרה ועולה ומקצרת כפול ד' על ד' והם י"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכפלם בשלישית הגובה שהוא ג' ושליש ויעלה נ"ג ושליש והוא תשבורת התמונה הזאת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וזה יצדק בכל התמונות מתחלפי הצורות מרובעת או משולשת או מעוגלת כשתדע השטח כפול ב' בשלישית הגובה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם התמונה הולכת ומקצרת אמנם אינה עומדת על נקדה והיא רחבה למעלה ד' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון שהיא למטה ו' בארך וברחב והגובה י' והראש ד' בארך וד' ברוחב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול הראש שהוא ד' עם התושבת ויהיו כ"ד וכפול ו' על ו' והם ל"ו וכפול ד' על ד' והם ע"ו בין הכל וכפלם על ג' ושליש שהוא שליש הגובה ויעלה רנ"ג | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| והוא תשבורתה באיזה דמות שתהיה מרובעת או משלשת אמנם היא עגולה והולכת ומקצרת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון מגדל עגול גבהו י"ב וקוטרה למטה ד' אמות וקוטרה למעלה ב' אמות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קח מרובע ד' והם י"ו ו' ומרובע ב' והם ד' ומרובע ב' בד' הם ח' הוצא ממנו שביעיתו ו' ומחצית שביעיתו הנשאר כ"ב כפלם בד' שהוא שליש הגובה ויעלה פ"ח והוא תשבורת המגדל | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 373) אם תרצה למדוד גוף עגול כמו כדור או דבר אחר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון כדור אשר קוטרו ז' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תרבע הקטר שהוא מ"ט ותכפלם על ג' ושביעית ויעלה קנ"ד והם אמות שטח הכדור כפלם בשתות הקוטר כי שתות ז' הוא א' וא' שתות ויעלה הכל ק"פ פחות שליש והוא תשבורת הכדור | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכפי זה הדרך תוכל לדעת תשבורת שברי הכדור | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כאלו אמ' ספל מלא מים אשר גופו מבפנים מעוגל ופיה עמוק ומעוגל והוא ברחבו ז' אמות והוא עמוק ג' אמות וחצי תוכל לשער כי הוא חצי כדור כפול עמקו ברוחב פיו אשר הוא קוטר הכדור וקבץ הכל וכפלהו ג' ושביעית כמו שעשית בכדור ויעלה בידך ע"ז והוא תשבורת שטח הספל כפלהו על שישית קוטרו שהיה ז' והוא א' ושתות ויעלה הכל צ' פחות שתות והוא תשבורת הספל | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם הספל פחות ממחצית רוחב פיה אם תוציא את קוטרה כמו שהראיתיך למעלה בשטחים מעוגלים תמצא כי הוא ז' לכן כפול ז' אשר הוא פיה בב' אשר הוא העומק ויעלה כפול אותם בג' ושביעית והעולה כפול בשתות הקוטר ויעלה נ"א ושליש והוא תשבורת גוף הספל הזה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם עומק הספל הוא ה' וקוטר שפתו הוא ז' פחות ב' שלישיות ר"ל שרש מ' שהוא ו' ושליש היתה מוצא קוטרה ז' ואם תכפול העומק בקוטר יהיה ל"ה כפלהו על ג' ושביעית ויעלה ק"י והוא תשבורת שטח הספל כפלהו על שישית הקוטר שהוא א' ושישית ויעלה הכל קכ"ח ושליש והוא תשבורת הספל הזה העודף על המחצית | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 374) שאלה אם יש לך רביעית כדור כזה אשר ארך הב' קוים ישרים ד' אמה כמה תשברתה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול ד' על ד' והם י"ו וקח מהם ג' חלקים מי"ד שהם ג' וו' חלקים מי"ד נשארו י"ב וח' חלקים מי"ד וככה תשברתה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 375) שאלה למודוד ק' כדור אשר קוטרו ז' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תרבע ז' על ז' והם מ"ט וכפלם על ג' ושביעית והם קנ"ד כנז' לעיל וכפלם בשתות הקוטר ויעלה ק"פ פחות שליש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| או קח מעוקב ז' שהוא שמ"ג ומזה קח י"א חלקים מכ"א ויעלה ק"פ פחות שליש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הטעם למה לוקחים י"א חלקים מכ"א כי אם תרצה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| לעשות מקוביה שהיא מרובעת לעגלה הוא י"א חלקים מכ"א והפסולת הוא י' חלקים מכ"א כמו שעשה הנסיון פראלוקא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
376 דרך לחבר בשרשים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו אם תרצה לחבר שרש י"ו עם שרש י"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| בהיות כי שני המספרים שוים על כן קח אחד משניהם ו' וכפול אותו על שרש האחר והנה נקח י"ו וכפול אותו על שרש י"ו שהם ד' ויעלה ס"ד וקח שרשם והם ח' וכך עולה כפל חבור שרש י"ו עם חבור שרש י"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם המספרים בלתי שוים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו לחבר שרש י"ו עם שרש ט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חבר ט' עם י"ו והם כ"ה אח"כ כפול ט' על י"ו והם קמ"ד וקח שרשם והם י"ב וכפלם והם כ"ד חבר אותם עם כ"ה והם מ"ט וקח שרשם והם ז' והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| וכן תוכל לעשות מב' מספרים שאין להם שרש אמיתי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כמו לחבר שרש י' עם שרש מ' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| עשה כנז' ויצא לך שרש צ' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| לחבר שרש משרש עשרי' עם שרש משרש עשרים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קח השרש שעבר מעשרים שהם ד' וכפלם והם י"ו וכפול י"ו על עשרים והם ש"כ וקח שרש משרש ש"כ וכך הוא שרש משרש עשרים מחובר עם שרש משרש עשרים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נרצה לחבר שרש משרש פ"א עם שרש משרש פ"א | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קח ד' וכפול אותם והם י"ו וכפלם על פ"א ויעלה אלף ורצ"ו וקח שרשם והם ל"ו ומל"ו קח שרשם והם ו' והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נרצה לחבר שרש משרש ש"כ עם שרש משרש עשרים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חלק ש"כ על עשרים ויצא י"ו וקח שרש משרש י"ו והם ב' תוסיף בם אחד והם ג' וקח מרובע מרובעם והם פ"א ואלו הפ"א כפלם על עשרים והם אלף ותר"כ ושרש משרש זה הוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נרצה לכפול שרשי המעוקבי' כמו לחבר שרש כ"ז עם שרש כ"ז | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קח המעוקב שעבר שהוא ח' וכפול אותם עם כ"ז והם רי"ו וקח שרשם ה' המעוקב והם ו' וכן הוא המחובר משרש כ"ז עם שרש כ"ז | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נרצה לכפול שרש מ' עם שרש מ' שאין להם מעוקב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חלק מ' על ח' ויצא ה' וקח שרש ח' והם ב' חבר בם א' והם ג' וקח מעוקבם והם כ"ז כפול אותם על המספר הקטן שהיה ה' ויעלה קל"ה וקח מעוקבם כן הוא חבור שרש מעוקב מ' עם שרש מעוקב ה' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 377) שאלה אילן גבוה ז' אמות ואדם רוצה לחתכו ובכל הכאה כופף אותו אמה אחת מתי יגיע ראשו בארץ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול ז' על ג' ושביעית והם כ"ב וקח חצים והם י"א א"כ בי"א הכאות יגע ראשו בארץ והטעם הוא כי העץ בהיותו נעוץ הז' אמות מהגובה הם כמו קוטר העגולה שקוטרה ז' והקו הסובב כ"ב ועל כן כשהאילן נופל הוא עושה תנועה סבובית שקוטרה י"א ועל כן בי"א הכאות יפול לארץ ודעהו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 378) אם תרצה לחבר שרש מרובע מי"ו עם שרש מעוקב מח' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול ח' ויהיו ס"ד גם קח מעוקב מי"ו שהם ד' אלפים וצ"ו חלקם על ס"ד ויצא ס"ד וקח שרשם שהם ח' וקח שרשם המעוקב שהם ב' תוסיף בם א' ויהיו ג' וקח מעוקבם והם כ"ז ותרבעם ויהיו תשכ"ט ותכפלם על ס"ד ויעלה מ"ו אלפים ותרנ"ו וקח שרשם | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המרובע שהם רי"ו וקח שרשם המעוקב שהם ו' וכך הוא חבור שרש מרובע מי"ו מחובר עם שרש מעוקב מח' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 379) נרצה לגרוע בשרשים הסר משרש ה' שרש ג' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| יען כי אין שרש לשום אחד מהם תאמר כי הנשאר הוא שרש ה' פחות שרש ג' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נרצה להסיר משרש מ' שרש י' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חבר י' עם מ' והם נ' גם כפול מ' על י' והם ת' וקח שרשם והם עשרים כפלם והם מ' הסירם מנ' הנשאר י' אם נשאר עדין שרש י' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נרצה להסיר שרש משרש עשרים משרש שרש חמשת אלפים וק"נ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חלק ה' אלפים וק"נ על עשרים ויצא רנ"ו והסר שרש השרש שהם ד' הסר מהם א' נשאר ג' וקח מרובע מרובעם שהם פ"א וכפלם על עשרי' ויעלה אלף ותר"כ א"כ הנשאר הוא שרש משרש אלף ותר"פ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נרצה להסיר משרש שרש פ"א שרש משרש י"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חלק פ"א על י"ו ויצא ה' וחלק מי"ו תעשה מהם חלקים מי"ו והם פ"א וקח שרש משרש פ"א שהוא ג' גם קח שרש משרש י"ו שהוא ב' חלק ג' על ב' ויצא א' וחצי הסר אחד מא' וחצי הנשאר חצי וקח מרובע מרובעו ויצא חלק אחד מי"ו וכפלהו על י"ו ויצא אחד שלם וכך הוא הנשאר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נרצה להסיר משרש מעוקב של רי"ו שרש מעוקב שמונה כמה הנשאר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חלק רי"ו על ח' ונשאר כ"ז וקח שרשם המעוקב שהם ג' הסר מהם אחד ונשאר ב' וקח מעוקבם והם ח' וכפלם על ח' שהוא ק"פ א' מב' מספרים והם ס"ד וקח שרשם מעוקב שהם ד' וכן הוא הנשאר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נרצה להסיר משרש ק"ח שרש ד' ר"ל שרשם המעוקב כמה הנשאר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חלק ק"ח על ד' ויצא כ"ז וקח שרשם המעוקב שהם ג' הסר מהם אחד הנשאר ב' וקח מעוקבם והם ח' כפלם על ד' שהוא אחד מהב' מספרים ויעלה ל"ב א"כ הנשאר הוא שרש מעוקב מל"ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נרצה להסיר משרש כ"ז שרש ח' ר"ל שרשם מעוקב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| חלק כ"ז על ח' ויצא לך ג' וג' שמיניות היינו כ"ז חלקים מח' קח שרש כ"ז שהם ג' גם שרש ח' שהם ב' וחלק ג' על ב' ויצא א' וחצי ומזה תסיר א' הנשאר חצי וקח מעוקבו שהוא שמינית ותכפלהו על א' מן המספרים היינו על ח' ויצא (א') שלם והוא הנשאר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נרצה להסיר משרש מרובע מי"ו שרש מעוקב מח' כמה הנשאר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קח מעוקב י"ו והם ד' אלפים וצ"ו וקח מרובע ח' שהוא ס"ד חלק ד' אלפים וצ"ו על ס"ד ויצא ס"ד וקח שרשם המרובע שהם ח' ומהם קח שרשם המעוקב שהם ב' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| הסר מהם אחד הנשאר אחד וקח מעוקבו שהוא אחד וכפלהו על ס"ד ויהיו ס"ד וקח שרשם והם ח' וקח שרשם המעוקב שהוא ב' והוא הנשאר | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 380) נרצה לכפול שרש מ' על שרש י' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול י' על מ' והם ת' וקח שרשם והוא כ' והוא המבוקש כפול שרש מעוקב שמונה על שרש מעוקב ח' כפול ח' על ח' והם ס"ד קח שרשם המעוקב והם ד' והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כמה יעלה כפל שרש מעוקב מח' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול על שרש מעוקב כ"ז כפול ח' על כ"ז ויעלו רי"ו וקח שרשם המעוקב שהם ו' והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נרצה לכפול שרש מעוקב ט' על שרש מעוקב כ"ח | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול ט' על כ"ח ויעלה רנ"ו וקח שרשם המעוקב והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נרצה לכפול שרש מרובע ד' על שרש מעוקב ח' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קח מעוקב ד' והם ס"ד וקח מרובע ח' שהם ס"ד אח"כ כפול זה על זה היינו ס"ד על ס"ד ויעלה ד' אלפים וצ"ו וקח שרשם המרובע שהוא ס"ד ומס"ד קח שרשם המעוקב שהם ד' והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נרצה לדעת כמה יעלה ה' על שרש מרובע ח' קח מ[עו]קב ה' ויהיו קכ"ה וכפלם על ח' ויעלה אלף וקח שרשם המעוקב ויעלה י' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נרצה לדעת מהו שרש משרש י"ו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול על שרש מעוקב מח' כך תעשה קח מעוקב י"ו והם ד' אלפים וצ"ו כן תעשה מח' תרבעם והם ס"ד עוד כפלם על עצמם והם ד' אלפים וצ"ו כפול ד' אלפים וצ"ד על ד' אלפים וצ"ו ויצא 177716 ושרשם ד' אלפים וצ"ו ומזה המספר הוצא שרש משרש המעוקב וקח מס"ד שרשם המעוקב שהם ד' וכך הם הכפל | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נרצה לכפול שרש משרש ג' על שרש מב' שרש המעוקב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קח מעוקב ג' שהם כ"ז וקח מרובע ממרובע ב' שהם י"ו כפול כ"ז על י"ו ויעלו ד' מאות ול"ב ויען כי אין לו שרש אמיתי תאמ' תחלק לי עשרים על שרש חמשה תרבע עשרים והם ד' מאות חלקם על ה' ויצא פ' והנה שרש שמונים הוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 381) נרצה לחלק שרש מאה על עשרים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול שרש מאה על ב' והם מאתים וכפלם והם ד' מאות חלק ק' מאות על ד' מאות ויצא ד' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נרצה לחלק שרש מרובע י"ו על שרש מרובע ד' עשה כך חלק י"ו על ד' ויצא ד' וקח שרשם והם ב' והוא המבוקש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נרצה לחלק שרש מרובע ז' על שרש מרובע ג' חלק ז' על ג' ויצא ב' ושליש ושרש ב' הם א' ושליש והוא היוצא | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 382) נרצה למצא שרשי המרובעי' שאין להם שרש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כגון אם תרצה לדעת שרש מעוקב מז' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כבר ידעת כי א' היה השרש שעבר ומעוקבו א' הסר א' מז' ונשאר ו' גם הסר א' מח' ונשאר ז' ושים ו' על ז' א"כ תאמ' כי שרש מעוקב מז' הוא א' וו' שביעיות | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| נרצה למצא שרש כ"ו הנה השרש שעבר היה ח' הסירם מכ"ו ונשאר קפא י"ח אח"כ הסר ח' מכ"ז הנשאר י"ט תשים י"ח על י"ט א"כ שרשו הקרוב הוא ב' וי"ח חלקים מי"ט | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תרצה למצא שרש המרובעים שאין להם שרש אמיתי או יש להם והם שלמים עם שברים | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כאלו תרצה לדעת שרש י"ב ורביע | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| קח השרש שעבר מט' שהוא ג' וכפלם והם ו' והנה מט' עד י"ב הם ג' ורביע כפול^ ג' על ו' ויצא חצי וקח מרובעו שהוא חלק רביע ותסירהו מהרביע והוא שרשו ג' וחצי | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| תרצה למצא שרש י"ד וחצי קח המרובע שעבר שהוא ט' ושרשו ג' הנשאר ה' כפול ג' והם ו' חלק ה' וחצי על ו' ויצא י"א חלקים מי"ב ושרשם ג' וי"א חלקים מי"ב | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דרך אחר למצא שרש ממספר קטן בקרוב גדול תוסיף בם ב' זירי וקח שרשם ואח"כ חלק היוצא על י' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון נרצה לדעת שרש ב' מ' תוסיף ב' זירי והם ב' מאות וקח שרשם והם י"ד ושביעית חלקם על י' ויצא א' וכ"ט חלקים מע' והוא קרוב מאד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כן תוכל לעשות מהמעוקבים אם תוסיף בם ג' זירי וקח שרשם וחלק היוצא על י' והוא הדרוש | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| דמיון נרצה לדעת שרש ח' שים ג' זירי ויהיו ח' אלפים ושרשם עשרים תסיר מהם א' זירא וישאר ב' והוא שרש ח' | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 383) אם תרצה לדעת תשבורת קטומה כזאת | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כך תעשה תרבע הצלע הקצור אשר הוא י"ג ויעלה קס"ט גם תרבע הצלע האחר שהוא ט"ו ויעלה רכ"ה תסיר מהם קס"ט הנשאר נ"ו תחלקם על ב' וישארו כ"ח חלק כ"ח על מה שעודף התושבת על הראש שהוא י"ד ויצא ב' ואלו הב' תוסיפם על מה שעודף מחצית התושבת על הראש שהוא ז' כי התושבת עודף על הראש י"ד ומחציתם ז' ויצא ט' וכך הוא רחוק העמוד מהצלע ארוך ואם תסיר מז' ב' ישאר ה' והוא מעמד העמוד מהקצור ולדעת תשברתה תחבר התושבת עם הראש והם ל' וחצים ט"ו כפלם על העמוד שהוא י"ב ויצא לך ק"פ והוא תשברתו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 384) ידוע הוא כי אם תעשה מרובע חוץ לעגול ימשש לעגול כי מוסיף על העגול ג' חלקים מי"ד | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| המשל יש לנו עגול אלכסונו ז' הנה הקו הסובב יהיו כ"ב כי ראוי לכפול האלכסון על ג' ושביעית ואם תעשה מרובע חוץ לאותו עגול כל צלע יהיה ז' שוה לאלכסון העגול ותשבורת המרובע יהיה מ"ט שהוא כפל ז' על ז' על כן אם תכפול האלכסון שהוא ז' על ג' ושביעית יעלה כ"ב והוא הקו הסובב וד' צלעות המרובע הם כ"ח כי ד' על ז' הם כ"ח וידוע הוא כי כ"ב הם י"א חלקים מכ"ח ולכן ראוי לכפול האלכסון על ג' ושביעית כי אם תחלק ד' צלעות ותקח י"א חלקים מי"ד יעלה ג' ושביעית וכדי למצא הקו הסובב ראוי לכפול האלכסון על ג' ושביעית כי כך עולה י"א חלקים מי"ד מד' שלמים ר"ל אם תכפול ד' על י"א חלקים מי"ד יצא ג' ושביעית | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Trapezoid |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
385 לדעת תשבורת תמונה כזאת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
[72]והדרך לדעת מרובע זו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כפול מה שעודף התושבת על הראש שהוא ז' והם מ"ט | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כפול ג"כ הצלע הקצור שהוא ט"ו על עצמם ויעלו רכ"ה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תוסיף בם מ"ט ויעלה רע"ד | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תוציאם מת' שהוא כפל הצלע הארוך על עצמו וישאר קכ"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חלקם על ב' והם ס"ג | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
חלקם על מה שמוסיף התושבת על הראש שהוא ז' ויצא מ"ט | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
וחברם עם ז' שהוא מה שעודף התושבת על הראש ויעלה י"ו ובאותה נקודה יפול העמוד ר"ל כי העמוד רחוק מן הצלע הארוך י"ו ואלו הי"ו שיצאו מהחלוקה הוא גבול מעמד העמוד החצוני כי זאת התמונה יש לה ג' עמודים ב' תכונים וא' חצוני כמו שהוא נרשם לעיל | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תרצה לדעת ארך העמוד כפול י"ו על עצמם ויעלו רנ"ו תסירם מכ' שהוא הצלע הארוך ומרובעו ת' הנשאר קמ"ד וגדרו י"ב והוא ארך העמוד וכן העמוד האחר החצוני תדענו בזה הדרך תרבע הצלע הקצור שהוא ט"ו ומרובעו רכ"ה הסר ממנו פ"א שהוא מרובע ט' שהוא המרחק מהעמוד אצל הצלע הקצור הנשאר ג"כ קמ"ד תשרשם י"ב ג"כ ואם תרצה לדעת תשבורת זאת הקטומה נקראת בלשונינו ר"ל חתוכה תחבר י"ד שהוא הראש עם כ"א שהוא התושבת ויעלה ל"ה חלקם על ב' ויעלה י"ז וחצי וכפלם על י"ב שהוא העמוד ויעלה ר"י וכך היא תשברתה | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ואם תרצה לדעת אלכסון העגולה תחבר ט' שהוא גבול מעמד העמוד החצוני עם התושבת שהוא כ"א ויעלה ל' ומרובעו ט' מאות תוסיף בם מרובע העמוד שהוא קמ"ד ויעלה הכל אלף ומ"ד שרשם הוא ארך העמוד כמו שהוא בכאן | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Roots |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
[73]386 אם תרצה לדעת שרש מאיזה מספר שרש מעוקבו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| כפול השרש הראשון על עצמו ואח"כ כפלהו על ג' גם כפול השרש היוצא על ג' ושים בקו אחר ומה שנשאר חלק עליו | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון נרצה לדעת מעוקב י"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
המעוקב שעבר היה ח' תפילם מי"ו הנשאר ח' ושרש מעוקב ח' הוא ב' כפלם על עצמם והם ד' כפלם ג' פעמים והם י"ב ושימם למשמרת | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
עוד כפול ב' שהוא השרש על ג' ויהיו ו' ושימם במקום אחר | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אח"כ חלק הח' שנשארו על י"ב ולא נתן לו כי אם חצי כי אם נתן חלק יותר גדול לא יספיק כפול י"ב על חצי והם ו' ועד ח' נשארו ב' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כפול חצי על עצמו והם רביע אחד כפול רביע אחד על ו' השמורים ויהיו א' וחצי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תגרעם מב' הנשאר חצי תגרע ממנו א' שמינית שהוא מעוקב חצי וישאר ג' שמיניות | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תפילם מכל הסך שהיו י"ו ונשאר ט"ו וה' שמיניות והוא מעוקב מב' וחצי | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ודוק ותשכח | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
387 אם תרצה לדעת משני מספרים כפול כל אחד על עצמו ואח"כ תכפול הכפלת שני המספרים זו על זו ומהסך העולה תרצה למצא אותם המספרים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
כך תעשה קח שרש אותו הסכום וראה מאיזה מספר הוא מורכב והם המספרים המבוקשים | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
דמיון זה כפלנו שני מספרים כל אחד על עצמו ואח"כ כפלנו הב' הכפלותיהם זו על זו ועלה אלפים וכ"ה מי הם המספרים אשר זה המספר מורכב מהם | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
קח שרשם והם מ"ה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ומ"ה מאיזה מספר הוא מורכב מה' וט' | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
על כן כפול ה' על עצמו וט' על עצמו וכפול כ"ה על פ"א ויעלה ב' אלפים וכ"ה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
גם אלפים וכ"ה הוא מורכב מג' וט"ו | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
על כן כפול ג' על עצמם והם ט' וט"ו על עצמם ויעלו רכ"ה וכפול ט' על רכ"ה ויהיו ג"כ ב' אלפים וכ"ה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ודוק ותשכח | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Because My lips shall speak sincerely [Job 33, 3]. | כי שפתי ברור מללו[74] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Appendix: Bibliography
Fra Luca Bartolomeo de Pacioli (Tuscany b. ca.1445 – d. 1514/1517)
– Hebrew translation –
by Gad Astruk? (Venice, ca. 1503)
Manuscripts:
- London, British Library Add. 27039/2 (IMHM: f 5717), ff. 116r-184v (cat. Margo. 1014, 2); (16th century)
Bibliography:
- Steinschneider, Moritz. 1906. Mathematik bei den Juden, Band II: 1551-1840. Monatsschrift für die Geschichte und Wissenschaft des Judenthums 50, p. 336. repr.: ed. Gad Freudenthal, Hildesheim, Zürich, New York: Olms, 2014, p. 140.
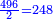
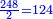
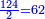
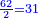
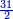 impossible
impossible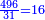
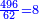
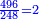
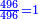
![\scriptstyle{\color{blue}{2\sdot\left[\left[2\sdot\left(1+2\right)\right]\sdot\left(1\sdot2\right)\right]=2\sdot\left[\left(2\sdot3\right)\sdot2\right]=2\sdot\left(6\sdot2\right)=2\sdot12=24}}](/mediawiki/images/math/0/3/f/03fb1c4d938211577965d2fa10b41347.png)
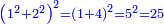
![\scriptstyle{\color{blue}{2\sdot\left[\left[2\sdot\left(2+3\right)\right]\sdot\left(2\sdot3\right)\right]=2\sdot\left[\left(2\sdot5\right)\sdot6\right]=2\sdot\left(10\sdot6\right)=2\sdot60=120}}](/mediawiki/images/math/f/f/c/ffc2b198cef408bd54c50be990d61a5b.png)
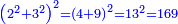
![\scriptstyle{\color{blue}{2\sdot\left[\left[2\sdot\left(3+4\right)\right]\sdot\left(3\sdot4\right)\right]=2\sdot\left[\left(2\sdot7\right)\sdot12\right]=2\sdot\left(14\sdot12\right)=2\sdot168=336}}](/mediawiki/images/math/e/4/1/e411bee01f04a5ce448280abb3408cdd.png)
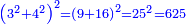
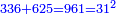
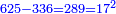
![\scriptstyle{\color{blue}{2\sdot\left[\left[2\sdot\left(4+5\right)\right]\sdot\left(4\sdot5\right)\right]=2\sdot\left[\left(2\sdot9\right)\sdot20\right]=2\sdot\left(18\sdot20\right)=2\sdot360=720}}](/mediawiki/images/math/9/2/9/9293bea2165238f0b59a91ce5200d50c.png)
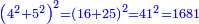
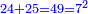
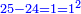
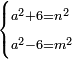
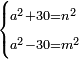
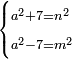
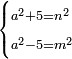
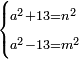
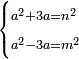
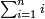
![\scriptstyle\sum_{i=1}^n i=\left[\left[\frac{1}{2}\sdot\left(\sum_{i=1}^n i\right)\right]\sdot4\right]-\left(\frac{1}{2}\sdot n\right)](/mediawiki/images/math/9/b/3/9b30d3071fe9a9feaaa412bf89917f41.png)
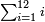
![\scriptstyle{\color{blue}{\sum_{i=1}^{12} i=\left[\left[\frac{1}{2}\sdot\left(\sum_{i=1}^{6} i\right)\right]\sdot4\right]-\left(\frac{1}{2}\sdot12\right)=\left(21\sdot4\right)-6=84-6=78}}](/mediawiki/images/math/3/8/8/388e877cd5177e9ad96a1a1c191a811e.png)
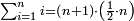
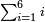
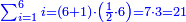
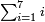
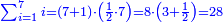
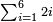
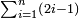
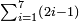
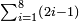
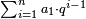
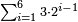
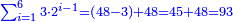
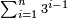
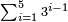
![\scriptstyle{\color{blue}{\sum_{i=1}^{5} 3^{i-1}=\left[\frac{1}{2}\sdot\left(81-1\right)\right]+81=\left(\frac{1}{2}\sdot80\right)+81=40+81=121}}](/mediawiki/images/math/a/a/1/aa1fe8e7a66dbeb11c812b313dca584d.png)
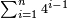
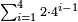
![\scriptstyle{\color{blue}{\sum_{i=1}^{4} 2\sdot4^{i-1}=\left[\frac{1}{3}\sdot\left(128-2\right)\right]+128=\left(\frac{1}{3}\sdot126\right)+128=42+128=170}}](/mediawiki/images/math/b/f/5/bf544ae0a0c5591e1909f66453a286c0.png)
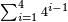
![\scriptstyle{\color{blue}{\sum_{i=1}^{4} 4^{i-1}=\left[\frac{1}{3}\sdot\left(64-1\right)\right]+64=\left(\frac{1}{3}\sdot63\right)+64=21+64=85}}](/mediawiki/images/math/0/6/8/068058cd0b99e7eb28e8b07d9ca99a0c.png)
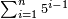
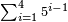
![\scriptstyle{\color{blue}{\sum_{i=1}^{4} 5^{i-1}=\left[\frac{1}{4}\sdot\left(125-1\right)\right]+125=\left(\frac{1}{4}\sdot124\right)+125=31+125=156}}](/mediawiki/images/math/2/a/a/2aae7c53396ae021e03e97e282e33304.png)
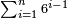
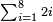
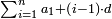
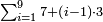
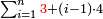
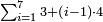
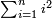
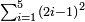
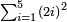
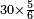
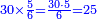
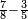
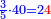
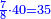
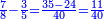
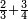
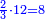
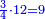

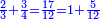
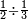
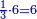
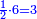
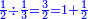
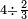
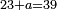
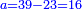
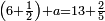
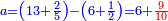
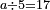
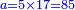
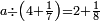
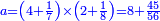
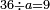
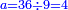
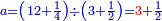
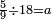
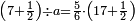
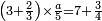
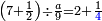
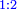
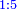
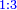
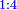

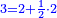

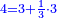
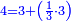

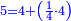

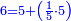

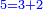

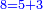
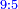
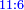 , it is called superquintipartient ratio.
, it is called superquintipartient ratio.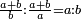
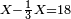


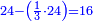
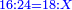
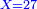
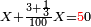
 florin
florin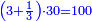 soldi = 1 florin
soldi = 1 florin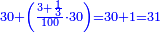
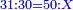
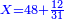
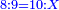
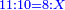
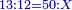
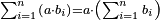
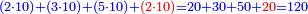

![\scriptstyle\sum_{k=1}^n \left[\left(\sum_{i=1}^n a_i\right)\sdot a_k\right]=\left(\sum_{i=1}^n a_i\right)^2](/mediawiki/images/math/2/a/1/2a190390030d9c138d548197fab10837.png)
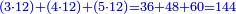
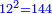
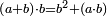
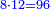
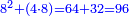
![\scriptstyle a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]=\left(a+b\right)^2](/mediawiki/images/math/8/2/e/82e411d047c5fc9961bdf7306ae1b255.png)
![\scriptstyle{\color{blue}{8^2+4^2+\left[2\sdot\left(8\sdot4\right)\right]=64+16+\left(2\sdot32\right)=64+16+64=144}}](/mediawiki/images/math/7/b/e/7be003be4b5746fc4c5a638e3faa8af3.png)
![\scriptstyle\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2=\left(a\sdot b\right)+\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-a\right]^2=\left(a\sdot b\right)+\left[b-\left[\frac{1}{2}\sdot\left(a+b\right)\right]\right]^2](/mediawiki/images/math/1/8/f/18fb8f53f0d377a271432a7b62a77032.png)

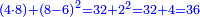
![\scriptstyle\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2](/mediawiki/images/math/a/0/b/a0b403dd8b7c15a5cb1dc47a5f8ca5bb.png)
![\scriptstyle{\color{blue}{\left[\left(\frac{1}{2}\sdot12\right)+4\right]^2=\left(6+4\right)^2=10^2=100}}](/mediawiki/images/math/7/a/6/7a6265fde8ac09f8f11153c42dc8c2bc.png)
![\scriptstyle{\color{blue}{\left(\frac{1}{2}\sdot12\right)^2+\left[\left(12+4\right)\sdot4\right]=6^2+\left(16\sdot4\right)=36+64=100}}](/mediawiki/images/math/4/c/2/4c27ce4db2835f750f86f0d940ed782b.png)
![\scriptstyle\left(a+b\right)^2+a^2=2\sdot\left[\left(a+b\right)\sdot a\right]+b^2](/mediawiki/images/math/5/e/f/5ef738b800e1b84fc257df70a83fb86b.png)
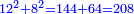
![\scriptstyle{\color{blue}{\left[2\sdot\left(12\sdot8\right)\right]+4^2=\left(2\sdot96\right)+16=192+16=208}}](/mediawiki/images/math/1/2/7/12769f138252fce36451f86efe3c709e.png)
![\scriptstyle\left[\left(a+b\right)+a\right]^2=4\sdot\left[\left(a+b\right)\sdot a\right]+b^2](/mediawiki/images/math/b/3/2/b32320b109ede228563dccc608b448d3.png)
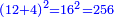
![\scriptstyle{\color{blue}{\left[4\sdot\left(12\sdot4\right)\right]+8^2=\left(4\sdot48\right)+64=192+64=256}}](/mediawiki/images/math/8/a/3/8a3456f080bb1dd5f7c8c7e1bd619968.png)
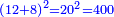
![\scriptstyle{\color{blue}{\left[4\sdot\left(12\sdot8\right)\right]+4^2=\left(4\sdot96\right)+16=384+16=400}}](/mediawiki/images/math/1/3/a/13aaaa27adc9ae7d32e2bdf6079aac7f.png)
![\scriptstyle a^2+b^2=2\sdot\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]^2+\left[a-\left[\frac{1}{2}\sdot\left(a+b\right)\right]\right]^2\right]](/mediawiki/images/math/5/e/8/5e87deb6f6b5cec598e43b4b3374a25c.png)
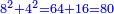
![\scriptstyle{\color{blue}{2\sdot\left[\left(\frac{1}{2}\sdot12\right)^2+\left(8-4\right)\right]=2\sdot\left(6^2+4\right)=2\sdot\left(36+4\right)=2\sdot40=80}}](/mediawiki/images/math/f/6/d/f6d7ba7335b31b7224114ff82784ab7d.png)
![\scriptstyle\left(a+b\right)^2+b^2=2\sdot\left[\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2+\left(\frac{1}{2}\sdot a\right)^2\right]](/mediawiki/images/math/5/e/9/5e9b4c74db157126a2fd01aad4693992.png)
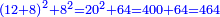
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle2\sdot\left[\left[\left(\frac{1}{2}\sdot12\right)+8\right]^2+\left(\frac{1}{2}\sdot12\right)^2\right]&\scriptstyle=2\sdot\left[\left(6+8\right)^2+6^2\right]=2\sdot\left[14^2+6^2\right]\\&\scriptstyle=2\sdot\left(196+36\right)=2\sdot23{\color{red}{2}}=464\\\end{align}}}](/mediawiki/images/math/d/6/8/d68e6ae4487af0448e21e6cdcb34f698.png)
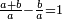
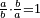
![\scriptstyle\left(a+b\right)^2=a^2+b^2+\left[2\sdot\left(a\sdot b\right)\right]](/mediawiki/images/math/7/2/7/727b0c35fd93a7a347bed8413905049f.png)
![\scriptstyle\left(a-b\right)^2=a^2+b^2-\left[2\sdot\left(a\sdot b\right)\right]](/mediawiki/images/math/e/9/3/e930942bda0e2309464a6f9792c7c011.png)
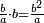
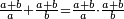
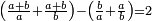
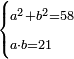
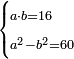
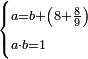
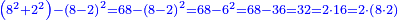
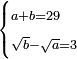
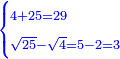
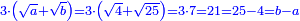
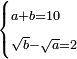
![\scriptstyle{\color{blue}{\left[\frac{1}{2}\sdot\left(10-2^2\right)\right]^2=\left[\frac{1}{2}\sdot\left(10-4\right)\right]^2=\left(\frac{1}{2}\sdot6\right)^2=3^2=9}}](/mediawiki/images/math/6/7/d/67d29d0644442418c5aca4334c1695bb.png)
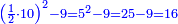


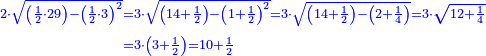
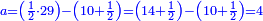
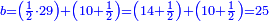
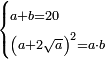
![\scriptstyle{\color{blue}{\left[4+\left(2\sdot\sqrt{4}\right)\right]^2=\left[4+\left(2\sdot2\right)\right]^2=\left(4+4\right)^2=8^2=64}}](/mediawiki/images/math/9/0/3/90383d3bf3a975dd0e8d2dabf4d4aa51.png)
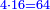
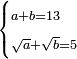
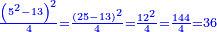
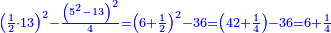
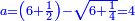
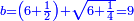
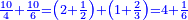
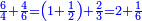
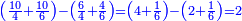
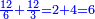
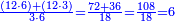
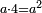
 ] and multiply it by 4; it is 4 roots [
] and multiply it by 4; it is 4 roots [ ] .
] .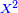 ].
].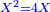
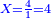
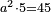
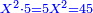
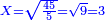
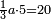
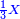 ].
].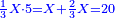
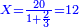
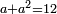
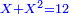
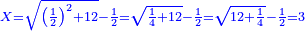
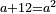
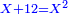
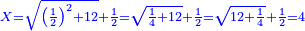
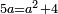
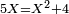
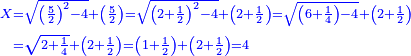
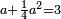
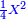 ].
].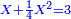
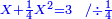

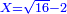
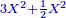 ] or one square and a quarter [
] or one square and a quarter [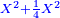 ]: it should be divide by 3 and a half or by 1 and a quarter.
]: it should be divide by 3 and a half or by 1 and a quarter.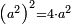
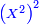 ].
].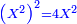
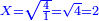
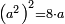
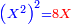
![\scriptstyle{\color{blue}{X=\sqrt[3]{\frac{8}{1}}=\sqrt[3]{8}}}](/mediawiki/images/math/2/4/e/24ec922f41adfd263f4269243a42bf60.png)
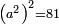
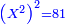
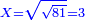
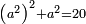
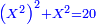
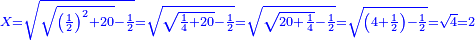
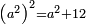
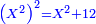
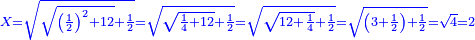
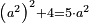
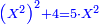
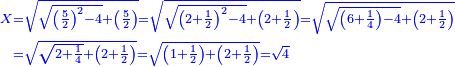


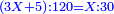
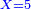
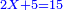
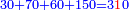
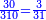
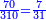
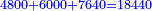
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\left(\frac{1}{2}\sdot200\right)+\frac{\frac{1}{2}\sdot\left(\frac{1}{2}\sdot200\right)\sdot\left[\left(5+\frac{1}{5}\right)-4\right]}{4}&\scriptstyle=100+\frac{\left(\frac{1}{2}\sdot100\right)\sdot\left[\left(5+\frac{1}{5}\right)-4\right]}{4}=100+\frac{50\sdot\left(1+\frac{1}{2}\right)}{4}\\&\scriptstyle=100+\frac{75}{4}=100+\left(18+\frac{3}{4}\right)=118+\frac{3}{4}\\\end{align}}}](/mediawiki/images/math/9/b/d/9bd438b8bd351d53a27a3e547b8ac8bd.png)
![\scriptstyle{\color{blue}{5-\left[6-\left(\frac{1}{2}\sdot6\right)\right]=5-3=2}}](/mediawiki/images/math/7/e/0/7e0822a4f4a936f352f91f9132ecd3bf.png)
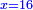
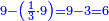
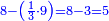

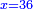
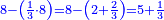
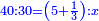
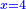
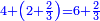
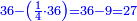
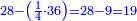
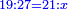
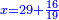
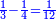
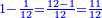
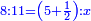
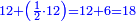
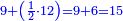
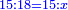
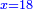

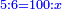
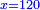
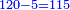
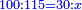
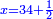
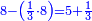
![\scriptstyle{\color{blue}{\left(23+\frac{9}{17}\right)-\left[\frac{1}{4}\sdot\left(23+\frac{9}{17}\right)\right]=\left(23+\frac{9}{17}\right)-\left(5+\frac{15}{17}\right)=1{\color{red}{7}}+\frac{11}{17}}}](/mediawiki/images/math/d/9/e/d9eb261f2f07de35f921e4b990003515.png)
![\scriptstyle{\color{blue}{20-\left[\frac{1}{4}\sdot\left(23+\frac{9}{17}\right)\right]=20-\left(5+\frac{15}{17}\right)=14+\frac{2}{17}}}](/mediawiki/images/math/0/2/b/02b650c4a3b07795b1ff2e0c2300e95c.png)
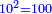
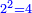
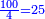
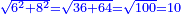
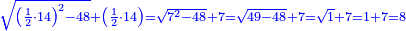

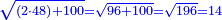
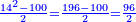
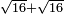
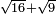
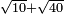
![\scriptstyle{\color{blue}{\begin{align}\scriptstyle\frac{\frac{20^2-\left[\left(21-14\right)^2+15^2\right]}{2}}{21-14}+\left(21-14\right)&\scriptstyle=\frac{\frac{20^2-\left(7^2+15^2\right)}{2}}{7}+7=\frac{\frac{400-\left(49+225\right)}{2}}{7}+7\\&\scriptstyle=\frac{\frac{400-274}{2}}{7}+7=\frac{\frac{126}{2}}{7}+7=\frac{63}{7}+7=9+7=16\\\end{align}}}](/mediawiki/images/math/8/5/3/853a9438477e86615e3065175e324d40.png)
![\scriptstyle{\color{blue}{\left(\sqrt[3]{16-8}\right)^2\sdot3=\left(\sqrt[3]{8}\right)^2\sdot3=2^2\sdot3=4\sdot3=12}}](/mediawiki/images/math/8/6/4/864339c5c49b2bbaf4e979e36cece1fa.png)