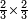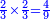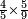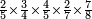Difference between revisions of "Arithmetic Textbook by R. Aharon ben Isaac"
| Line 8,464: | Line 8,464: | ||
|- | |- | ||
| | | | ||
| − | |{|class="wikitable" style="margin-left: auto; margin-right: auto; text-align:center;" | + | | |
| + | {|class="wikitable" style="margin-left: auto; margin-right: auto; text-align:center;" | ||
|- | |- | ||
|0||ת"ף||יב||ר"מ||אם | |0||ת"ף||יב||ר"מ||אם | ||
Revision as of 08:58, 18 April 2020
Contents
Table of Contents
[] [] הראשון [] השני בדרכי [] בדרכי הערכים [] מכפל וחילוק וחיבור [] השאלות שלמים ושברים ומורכבים
הכלל השלשי בערכים משלמים ושברים ומורכבי' וכל כלל מחולק לשערים ולפרקים
|
השני י בכפל המשל מרובע אורכו כרוחבו י"ב ואחר ואחר שלמים ואחרים יא בינין בניין כותלים ומגדלים ובניין ידיעת צירוף האותות יב כותלים [] הקבלה והלוחות יג דרך כפל צורה מרובעת יד ופרק שלישי במגרעת השלמים ומשלים יה פרק בחילוק השלמים ומשלים ושאלה ראובן קנה יו יז יח כ"ד אמות בגד כחק צ"ו פרטים שאל ס סך כל אמה והבחינה ואחר מזמן מעיבור
1[א]
יח יט פרק דף כ משל דף כא מאזני הכפל וה[] דף כא השער פרק ראשון בהקדמה והדבור [] כב השני כג ופיאות האחד וצורה לשלמים ולשברים דף כד לוח לקצר השברים ולערכים ולידיעת המורה כה הכולל ומתחלפי המורים על ד' דרכים כו ועוד ד' דרכים אחרים סדר לכל אחד דף כז ביצור המורה ולוח ומשלים דף כח סדר שלשי בקיצור המורה ומשל וצורה וקיצור השברי כט ואב המורים דף ל מהנעשה מהנשאר בחלוקה והשואת השברים דף לא דרך שני בהשואת השברים ומשלים לב דף לד פרק בכפל השברים דף לה דרך ראשון כולל בכפל השברים ומשלים ודרך שני דף לו פרק עייון ומשל ופרק במגרעת השברים והדרך הראשון דף לז מגרעת מגרעת צורות ומשלים ודרך שני לח לט דף מ פרק חילוק שברים ומשלים מא חילוק דף מב השער ג פרק א חיבור שלמים ושברים ומשלים דף מג לחבר שלמים ושברי שלמים ומשלים דף מד חיבור שלמים ושברים מדברים מתחלפים ליטרין דף מה כיכרים כורין שנים מזלות וחלקים עיבוריין
[1ב]
[] רביעיות [] ג' שלמים וג' רביעיות [] י"ב די' וד' פשי' ב' דרכים [] לסך ה' ליטרין [] פשיטי' [] ח' די וט' פשי' [] עלו ק"כ וג' פשי' על י"ד [דף] מט כפל שלמים ושברי שברים על שלמים ושברים נח שלמים וד' שניות [] חמשיות על מד שלמים וג' חמשיות אחר ז שלמים על ג' רביעיות מד שלמים אחר שלמים ושברי שלמים על שלמים ושברי שלמים כמו יג שלמים וב חמשיות מיב שלמים על כב שלמים וב' שלישיות מט' שלמים דף נ לכפול שלמים ושברי שברי שלמים ע שלמים ושברי שברי שלמים כמו ב שלמים וחצי שלשית יא על עצמו הפרק עוד שלמים על שלמים ושברים כמו ד שלמים הג' על ה שלמים וג רביעיות במגרעת המורכבי' דף נא לגרוע רט"ו שנים וקנ"ג ימים כ"א שעו' וכו' והצורה עוד לגרע שלמים ושברים מ(ש)למים ושברים כמו יד שלמים וח שברים מא מיא בשלם מכד שלמים וט שברים מיג בשלם והצורה ודרך אחרת דף נב לגרוע לגרוע קס"ה ליטרי' ממון ועשרה ד' וט' פשיט דברים מתחלפים ומחצה ורביע מרפ"ז ליטרי' והצורה לגרוע ח' מזלות י"ז מעלו' מ"ב די' וכו' מב' מזלות ואחר והצורות
2[א]
[דף] נג תתקע"ו [] אחר לגרוע שלמים [] כמו קי"א שלמים שלמים [] תשעיות שרצינו לגרוע מקמ"ד תשיעיות עשרית מד' שלמים והצורה דף נד מהעבר דף נה הפרק בחלוק בחילוק שלמים ושברים על שלמים ושברים מורכב רצינו לחלק כ"ב ליטרי' ועשרה די' ושצ"ו פשי' על ששה משל אחר לחלק שלמים על שברים כמו כ"ה שלמים על ג' חמשיות והצורה אחר ג' שלמים וג' רביעיות על ב' שלישים משל אחר רצינו לחלק מ"ט שלמים וה' ששיות על ג' רביעי ששית מ"ב חמשיות והצורה דף נו לחלק שלמים ושברי שלמים על שברי שלמים כמו ק"ח שלמים וד' תשיעיות מי"ח שלמים על ג' שביעיות ח' שלמים והצורה דף נז נז משלים ובחינה ודרך אחרת דף נח פרק במאזני השברים משל במאזני החיבור דף נט משל במאזני הכפל משל במאזני המגרעת משברים משל במאזני החילוק השער הפרק הראשון חלוקתו לד' מינים והקדמה בראשונה המורכב
[2ב]
[] והמשל [] וקכ"ד והצורה [] והצורה [המין] [השני] בהכאת השרשים דף סד שורש מעוקב והצורה דף סה המין השלישי בידיעת שורש מן המספר שאין להם שורש אמתי מחולק זה המין בשני סדרים והסדר הראשון דף סו בשני דרכים משל שורש ה' ומשל מי"א והדרך השני ומשל שורש ח' ומשל שורש ל"ב והסדר השני לדקדק השורש דף סז המין בידיעת שורש השברים ומשלים הרביעי דף סח פרק בידיעת חשבונות נמשכים ובו ג' חלקים הראשון שני מדבר במעלת האחד החלק השני מדבר בשטחים דף סט במספרים נמשכים ובו דרכים ומשלים דף ע ל[] ערכים והדרך הרביעי ומשלים דף עא החלק השלישי מי שלקח ממעוקב חצי צלעו מעוקב הוא לקח שמינית המעוקב משל אחר מי שלקח שלישית הצלע מעוקב לקח חלק מכ"ז עוד לחלק אבן לשקול בו וכו' דף עב הכלל בדרכי השאלות השני שער בשאלות חיבור וחלקתו ל פרקים שער בשאלות כפל חילקתיו ל פרק שער ג' בשאלות גירעון חילקתיו ל פרק שער ד' בשאלות חילוק חלקתיו ל פרק שער ה' בשאלות מעורבות חלקתיו ל פרקין הערה לדרך השלשה וחלוקתה לג' מנהגים ומשלים
3[א]
[דף] עג מנהג
שלישי
ראובן קנה []
[]
[]
ראובן קנה כור חיטה []
בשני פשי' שאלתי []
כמה אוקיות יתן ב[]
עו' אם ד' פשיטי סרגוסה שוים ה' פשיטי ברצילונה []
ולוח השלושה מנהגים מדרך השלישת ודרך שלישי
ודרך בהקדמות הראיות
דף עד משלי ארבעה מספרים מתיחסים
דף עה הדרך
השני המשל מהו המספר אשר חציו ושלישיתו יהיה ששה
מונח
כוזב
דף עה הדרך
השלישי המשל מהו המספר אשר חציו ושלישיתו יהיה ששית
ב' מונחי
כוזבים
דף עו הדרך צורת ב' מונחים כוזבים
הרביעי הדרך הרביעי' שהוא דרך יחידי
משל ג' תלמידים קנו ספר בסך כ"ד די' ולא ידענו מה שפרע על אחד אבל ידענו כי השני פרע כפל הראשון ועוד ג' והשלישי פורע ג' כפלי השני פחות ז'
שאלת כמה פרע כל אחד התשובה והצורה
דף עז צורת השאלה שעברה
משל ג' גרועים אשר סך כולם פ"ה פרחים ומשקלם פ"ה אוקיות ולא ידענו סך הראשונה אבל ידענו כי סך השנית ג' כפלי הראשונה ועוד ה' וסך השלישית ד' כפלי השנית פחות ז' התשובה והצורה ואחר מ[]
[3ב]
[] [] וכו' שאלתי [] הבית אנשים ונשים [] לכל איש כ' פשי ולכל אשה [] כמה אנשים הם וכמה נשים משל אחד חלק [] על אנשים ונשים ונערים לכל איש [] פשיט ולכל אשה פשוט ולכל נער מחצה שאלתי כמה אנשים וכמה נערים דף עט פרק שאלות חיבור שלמים מהו המספר אשר תחבר עליו חציו וחמשיתו ושביעיתו זה על זה לא יהיה אלא שנים מהו המספר אשר תחבר עליו שלשיתו ועל העולה ב' חמשיות מן העולה ועל העולה ג' חמשיות רביעיות מכל העולה ושיהיו י"ג מהו המספר שנחבר עליו חצי שלישית רביעיתו ושלישית רביעית חמשיתו ורבעית חמשית ששיתו ושלא יהיה אלא אחד מהו המספר אשר חיברנו עליו חצי חציו ושלשית ושלישית שלישיתו ורביעית רביעיתו ולא יהיה אלא ז' דף פ חברה ראובן ושמעון עשו חברה ראובן נתן ז' די' ושמעון י"א והרויחו ג' שאלתי כיצד יחלקו והצורה חברה ראובן שמעו לוי עשו חברה ראובן נתן כ"ט ליטרי ושמעון כ"ה ולוי י"א והרויחו י"ג ליטרי כיצד יחלוק והצורה
דף פא חברה ר"ש עשו חברה ראובן נתן ג' די' ביום ראש השנה ושמעון נתן ה' די' ביום ראשון לחודש אדר ושהו בחברה עד ראש השנה הבאה והרויח ד' די שאלתי הראוי לכל אחד והצורה דף פב חברה רש"ל עשו חברה ראובן נתן ג' די' ושהה ד' חדשים ושמעון ד' די' ושהה ה' חדשים ולוי ה' די ושהה ו' חדשים והרויח ששה די' שאלתי כיצד יחלוקו והצורה
4[א]
דף פג ראובן
שמעון
לוי
ושמון נתן []
כלוי ועוד []
העולה ועוד ג' []
ורביעית העולה ועוד ד'
ולוי נתן כראובן ושמעון ושלישית העולה []
ימים ועם זה הממון ושהיתם בחברה הרויחו
ז' ליטרין שאלתי כיצד יחלוקו והצורה
הערה ואם יהיה יכול הערה
דף פד לקצר
השאלות ודרך לקצר ומשל
דף פד פרק הא' שלא נקצר כלל או שלא נוכל לקצר
ששה הב' שנוכל לקצרו פעם או יותר
מני הג' קיצור הממון ולא הזמן
הקיצור הד' קיצור הזמן ולא הממון
הה' קיצור הממון והזמן
הו' קיצור הכפלת הממון והזמן
כל זה בחברות ובדרך השלושה
דף פה משל במין ראשון ראובן נתן ח די'
ושמעון כ"ד והרויחו עשרה והצורה
משל במין השני שנוכל לקצר פעם או יותר
הנה לראובן ח' ולשמעון כ"ד שנוכל
לקצרם ג' פעמים וישובו לראובן
א' ולש(מ)עון ג'
[4ב]
[] הזמן כמו []מון נתן י"ב [] ישארו ד' [] נקצר בחצי יהיו ב' [] וכו' [המין] [משל במין הרביעי] בקיצור הזמן ולא הממון [הרביעי] ראובן ח' ושהה ו' ושמעון י"ב ושהה י"ב יהיה לראובן ח"ג ולשמעון י"ב ב'
|
5[א]
פרק [דף] פז בהשואת הממונות [] הדרך המשל בזה [] ליטר [] שאלה אחרת [] לעליונה אם י"ו מסרגוסה שוה [] מברצלונה ת"ת ליטרי סרגוסה כמה ליטרי ברצלונה יהיו
|
[5ב]
[] [] על י"ז ואם [] ואם מקאשטיללה [] על כ"ו וכן כל הדומה לזה [] מלכים מבאלינסי' [] דיקאדש
|
6[א]
[דף] צ"ז סינשליש [דף] צ"ח סינשלאליש שאלה [] שאלה [] הפרק בשאלות מהו הממון [] חיבור שברים מהו הממון אשר רביעיתו ורביעית
|
[6ב]
[] יהיה ט"ו [] והיוציא יהיה אחד [] והיוציא [] [] והלוחות [] מכל אילן ע"ב כדין ובכל כד [] שאלתי סך התפוחים [] וכו' [] יש לו [] בו ע"ז חורבות בכל חורבה י"א מערות בכל מערה [] קני תרנגולין ובכל קן י"ז בצים אשר מכל ביצה תציא תרנגון אחד וכל תרנגול שוה ג' [] שאלתי מספר כל דבר נפרט
|
7[א]
[דף] קט [] שברים [] שאלה שאלה רצינו [] שאלתי רצינו [] שאלה רצינו כ"ד חלקים [] דף ק"י שאלה רצינו כ"ה חלקים []
|
[7ב]
[] וב' שלישיות [] [] וכפל ממונו והפסיד [] [] נשאר לו כלום [] המספר אשר גרענו ממנו שלישיתו ורביעית הנשאר וששית הנשאר וחמשית הנשאר וחצי הנשאר ושישאר נ'
|
8[א]
דף קכז דף קכח חלק [] הגדול [] שלושה חלק כ"ג פרחים [] דרכים [] ולשלשים []
|
[8ב]
[] ב ראובן לתן [] ד' שנים [] שלא ט"ו ולא [] [] כ"ד ליטרי ולא נתן אלא [] והרויחו שלושים ליטרה שאלתי [] [] ראובן נתן ל' ליטרי ממון ושמעון כ' כורי חיטה [] והרויחו י"ז ליטרה ומזה הריוח ראוי [] ד' ליטרי שאלתי סך כורי החיטה
|
[דף] קל"ט [] [] שאלה הנה [] בכל יום [] [] לכל אחד מן [] בי"ג יום שאלה יעקוב אמר ליוסף בנו אני אתן לך ת"ק די' [] ז' שנים ושתתן לי [] שאלה אחד מברוסה חייב לאחר ברסילונה כו' דף ק"מ שאלה ראובן חייב לשמעון כ"ה [] ורוצה לפורעו בפרחים שאלה ראובן קנה בגד לעשות לבוש אשר רוחבו ז' זרתות ורצה ל[]לו עם בגד אשר רוחבו ג' זרתות כמה יקח מהם שאלה אם ב' פרחים בג' חדשים הרויח ד' די' ג' פרחים בח' חדשי' דף קמא מנהג אם ו' [] בד' חדשי' הרויחו ג' די' ז' אשקוד' ב[] וכו' שלישי אם בגד אחד שוה ט' דוקאדי י"ב אמות [] אם ד' אמות שוה נ"ב די' וס' הם ג' ליטרי שאלתי ה' אמות אחרת [] סוחר קנה בגד בדוקטו די' [] אמות שוה ג' די' וכו' מידה אם כור חיטה בסך י"ח די' ונתן י"ד אוקיות [] עלה הכור כ"ה די' משקל דף קמב אם י"ז פרחים הב' חדשים הרויחו ב' פרחים כ"ד פרחים בכמה וכו' כור חיטה וכו' כור חיטה וכו' משא ענבים כור חיטה דף קמב משא ענבים פרק שני אם ד' פשיטי סרגוסה שוים ה' פשיטי ברצלונה וג' פשיטי שאלות תחבוליות דף קמד בעיר אחד היה מלחמה ויסגרו המבצר בעיר וכולם נ"ה אנשים ח' יהודים י"ג [] גוים כ"א ישמעאל י"ג כושיים וכו' דף קמה הצורה דף קמו הנה היו בידנו עגולות במספר מה ונרשום במ[] לכולם היו שם כוכבים כוכב בכל עגולה והלך כל כוכב בימים מתחלפים שאלתי בכמה מן הזמן ישובו [] להדבק כבראשונה [11ב]
[]קח [] היה אותו [] כולו מעוקב [] מעוקב ה' אורך וה' [] כמה בתים מאלו אשר [] [] אמות ואחר אלכסונו ד' הנה יהיה הגדול [] הקטן ח' פעמים ראובן הלך לבית הרחים מהלך ג' פרסאות עם י"ב שקים מלאים חיטה בעגלה וכל כך היו מלאים שלא יוכל לקשור אותם ומצא בו כלי הטחינה רקים מוכנים ונתן כל החיטה בכלים והניח שם כל השקים רקים וגנבו מהם חמשה או ששה שאלתי כיצד יביא כל הקמח בשקים והערה הנשארים שאלה הנה היה בידינו אבן משקלת מ' ליטרי' ונפל ונעשה ג' חלקים כמה משכל כל חלק שנוכל לשקול מליטרה אחת עד מ' ליטרין
|
10[א]
[דף] קן שאלה אדם קנה [] ה' אמות שאלתי [] אילן חמשיתו בקרקע [] []
|
[10ב]
[] במוגשם [] וכתיבה כקול הא[] [] וכתיבה כרעם והכאת [] [] כקול כינור [] שאין בו הבנה ויש בו כתיבה כקול [] חיים [] כולל ערכים רבים עם כתר לדעת עמו ערכים מת[ח]לפים חלוקת הערכים ערך מן הקטן לגדול ודומה לשברים והם ה' וערך מן הגדול לקטן ודומה לשלמים והם חמשה ערך שלישי הוא ערך שוה וממנו יצאו ערכים מתחלפים צורת הלוח לוח אחר כמו ב' משולשים ובאמצע ד' שורות דף קסו ביאור הה' סוגים אשר הם מן הקטן לגדול ושמותהם בלשון יון
|
9[א]
[דף] קעח [] נאהב [] עשרה [] והנפרד [] ה[] נאהב ה[] [דף] קעט הפרק המין השליש ותולדתו והצורות [] ה[] דף קף ידיעת הרכבת ערכים עם צורה והמין החמשי לוח בידיעת הבודדים והלוח ולדעת הוצאתם והצורות דף קפא ידיעת המורכבים וה[] והלוח דף קפב פרק ד' מדבר בג' מינים עודף ושוה וחסר וצורה ומדבר על המספר המכוון דף קפד מספר מכוונים הם קפה קפז קפח הכל מכוונים והצורות דף קפז דף קפח להוציא המספר הנאהבים גם דף קפ"ט דף קפט דרוש מרובעי ז' כוכבי' לכת ומדבר על זה עד דף קצ"ה והצורות שני דף א' שלושה שכיב מרע וכו' וחברה סדרים דף
[9ב]
[] [] יסוד המספר [] הלמודיות והוא [] שתראה בספרו []קור בזאת החכמה אהרן [] [] בה חכמות רבות אם בן יצחק זצ"ל []
| והיא מבוא והתחלה לחדד השכל ולהשיג בחכמת התכונה וזולתה ממנים אחרים רבים כמו במלאכת העיבור שהיא ענף מן התכונה [כאשר תראה בחיבור לעיבור שקראתיו מקנת כסף] ועוד בענינים רבים בתלמוד ובסחורות ובמטבעות ראתי לחבר חיבור אכלול בו כללי המספר ורוב פרטיו כי הם רבים וזה כדי שלא אשכח מה שלמדתי מהם מרוב קורות הזמן העוברים והעתדים וההוים עלי וללמוד לבני אם יובו בע"ה | |
| I say that the kinds of number are two. | ואומר כי מיני המספר הם שנים |
|
הראשון הוא המספר המשולל מחומר ומדיבור וממחשבה והוא מספר בלא גבול כי הוא מספר בכח לא בפועל והוא בלתי בעל תכלית |
|
המין השני אשר בו המאמר הוא המספר אשר ראשונה המחשבה תגבלהו ויעשה אותו בעל תכלית ואחר יוכל אדם עם הכח הדיבוריי לדברו או לכותבו כפי רצונו ואחר יהיה זה המספר מספר מנוי ומוגבל ויחלק לשנים זוג ונפרד ויסודם האחד כי המספר המנוי הוא קיבוץ |
18[א]
אחדים [] היה מספר[] ואמנם זה המספר [] אל קיבוץ מספרים [] שני מינים אשר המין האחד [] או יותר מונחים ואם תחברם יהיה ה[] גדול בעל תכליס ובעלי המספרים קראו [] חיבור המין השני מן הקיבוץ הוא שיהיו שני מספרי' והאחד מהם כופל את השני בחשבונו והמונה אינו עולה בעניין וקראו לזה המין כפל והרי לך שני מיני הקיבוץ כי החיבור הוא שעשינו מספר גדול ערכים קטנים וכן הכפל שחברנו מספר גדול בסך כפלי הנכפל כמו אם תחבר כ"ב עם כ"ב יהיה היוציא מ"ד וכן אם תכפול כ"ב על ב' יהיה היוציא מ"ד ואם כן שני אילו המינים הם עשית חשבון גדול כולל קטנים והפרוד יחלק גם כן לשני מינים והם הפכים הפך גמור לשנים המינים הנזכרים אשר המין הראשון הוא שיהיה חשבון גדול ונרצה לעשות ממנו שני מספרים או יותר וקראו אותו גרעון כי הוא גורע כל הנרצא וזה [ה]פך החיבור ומזה המין הוצאת השרשים : המין השני מן הפרוד הוא שיהיו שני מספרים אשר האחד מחלק את השני כמספרו והמחלק אינו עולה למניין אלא שהוא מחלק הגדול כמנניו וקראו לזה המין חילוק והוא הפכי לכפל והרי לך שני מיני הפרוד כי גרעון הוא שנעשה ממספר גדול מספרים שנים או יותר וכן החילוק שחלקנו מספר גדול לחלקים כפי המחלק כמו אם
[18ב]
[א1] [] [] ספר והמספר [] הלימודית שהיא כי חלוקת [] מיום שנתתי לבי הלמודיות [] להשיג חוכמות ראבור רבות ד' חלקים [] והתחלה לחדד השכל ולהשיג הא' מספר [] התכונה ומלתה מבנים אחרים רבים כמו במל(א)כת הב' הנדסה העיבור שהוא ענף מן התכונה כאשר תראה בחיבורי לעיבור הג' תכונה שקראתיו מקנת כסף ועוד בענינים רבים בתלמוד ובסחורות הד' מוזיקה ובמטבעות ובזמן ובמשקל ובמידה
| I, the aforementioned Aharon, from the day I began to engage in the craft of weaving gold and silk images, although proficient in it with accuracy and precision, I realized that I lack some of the arithmetical methods required for the subtlety of the craft. | ואני אהרן הנז' מיום שנתתי ואני לבי במלאכת אריגת ציורי הזהב והמשי ואם הוא בידי בחוזק האימות והדקדוק ראיתי שאני חסר כפי דקות המלאכה מקצת דרכי המספר |
| Though I had some knowledge of it, I put my mind and energy to investigate the general practices of number and some of its particular properties, as human knowledge cannot comprehend them all. | ואם קצתו הוא בידי שמתי לבי וכוחי לחקור במספר בדרכים הכוללים וקצת מן הפרטים כי בכולם לא תקיף בהם ידיעה אנושית |
| So I saw fit to write what came within my reach, and put it together into a composition containing the rules of number and most of its many properties, so as not to forget with the passing of events and time what I had learned and to teach them to my sons, God willing. | ובעבור כל זה ראיתי לכתוב מה שבא לידי ולחברו בחיבור אכלול בו כלו כללי המספר ורוב פרטיו כי הם רבים וזה כדי שלא אשכח מה שלמדתי מהם מרוב קורות הזמן העוברים עלי וללמדם לבני אם יזכו בע"ה |
| If a scholar gets hold of this treatise or of Miqnat Kesef (“valuable property”) or ‛Ibbur (“Intercalation”) or […] Tzurat ha-‛Olam (“the shape of the world”), which is Alfarghani in another form, and finds that my language is not that of a learned man, he should not judge me harshly, but give me the benefit of the doubt, because I am a craftsman, as I said, and composed these treatises for my son Joseph. Now I add that, by my sins, he is dead, and this compositions are left as they stood, without order and unedited. Indeed, he was to put them in order and edit them, but now he lies deep, and I am at the end of my days, and I never got to teach him. And so, they are as naught. | ואם יבא זה החיבור או מקנת כסף או עיבור או [] צורת העולם שהוא אלפרגני בצורה אחרת ביד חכם וראה כי הלשון אינו לשון משכיל אל ידיניני לחובה אבל ראוי שידיניני לזכות כי אני בעל מלאכה כמו שאמרתי ועשתי זה לבני ליוסף ועתה הוספתי זה כי בעונותי הוא מת ונשארו כמו שהם בלתי מסודרים ובלתי מתוקנים כי עליו לסדר ולתקן הלשון וזה היותר מסודר אבל הוא עמוק ואני בסוף ימי ולא יכולתי ללמדו ואם כן והיו כלא היו |
19[א]
[א2] ואומר כי מ[] מחומר ומ[] בכח לא בפועל והוא [] בו המאמר הוא המספר אשר [] המחשבה ויעשה אותו בעל תכלית [] לדברו או לכותבו כפי רצונו ואחר יהיה [] ומוגבל ויחלק לשנים זוג ונפרד ויסודם האחד כי המספר המנוי הוא קיבוץ אחדים כסדר אל בעל תכלית והאחד אינו מספר כי גדר המספר הוא קיבוץ אחדים ואומנם המספר יחלק ואמנם חלוקה אחרת אל קיבוץ מספרים ואל פרוד מספרים והקיבוץ הוא שני מינים האחד הוא שיהיו שני מספרים או יותר מונחים ואם תחברם יהיה היוציא מהם חשבון גדול בעל תכלית וקראו לזה חיבור המין השני מן הקיבוץ הוא שיהיו שני מספרים והאחד מהם כופל את השני בחשבונו וקראו לזה המין כפל והפרוד הוא גם כן שני ממינים האחד הוא שיהיה חשבון גדול ונרצה לעשות ממנו שני מספרים או יותר וקראו אותו מגרעת והוא הפך החיבור ומזה המין הוצאת השרשים והמין השני הוא שיהיו שני מספרים אשר האחד מחלק את השני כמספרו והמחלק אינו עולה למנין אלא שהוא מחלק הגדול כמניינו וקראו לזה המין חילוק והוא הפכי לכפל והרי לך שני מיני הפרוד כי גרעון הוא שנעשה ממספר גדול שני מספרים או יותר וכן החילוק שחלקנו מספר גדול לחלקים כפי המחלק כמו אם תגרע
[19ב]
[ב1] [] חלק מ[] [] בכל מין ומין [] ואחר על [] על הגרעון שהוא קל [] ואחלק כל מין ומין [] לחלקים אחרים כמו משלים או [] אבל כפי הראוי כי דרכי המספר הם רבים ומתחלפים וקשים ובעבור זה תשנה או תשלש המשל אם כמו שהוא אם בחומר מתחלף ופעם אומר משל בזולת מקומו הכל כפי סיבה או דבר מה כפי הראוי
| אומנם חלוקת הספר בכללו הוא בשלשה כללים | |
| אשר הכלל הראשון יקיף בדרכי המספר | |
| והכלל השני יקיף בדרכי השאלות | |
| והכלל השלשי יקיף בדרכי הערכים | |
| אומנם חלוקת כל כלל הוא בשלשה שערים | |
| הכלל הראשון אשר יקיף בדרכי המספר חלקתיו בשלושה שערים ושער ד' פרקים מורכב [] | |
| השער הראשון במספר השלמים | |
| השער השני במספר השברים | |
| השער השלישי במספר המורכב משלמים ושברים | |
| הכללהשני אשר יקיף בדרכי השאלות חלקתיו גם כן בשלושה שערים | |
| השער הראשון בשאלות שלמים | |
| השער השני בשאלות שברים | |
| השער השלישי בשאלות מורכבים משלמים ושברים |
20[א]
[ב2] הכלל [השלישי אשר יקיף בדרכי הערכים] [גם כן בשלושה שערים] השער הראשון [] השער השני בערכי [] השער השלשי בערכי ה[] ואחר שבארתי חלוקת כל כלל [] שער לפרקיו השער הראשון מן הכלל [] ולהורות מה שיעדתי בזה הספר הכולל [קראתי שמו מורה] [] אומנם כל שער מג' שערי הכלל יחלק לד' פרקים אשר הפרק האחד יהיה חיבור והשני כפל והשלישי גרעון והרביעי חילוק אמנם בשערי הכלל השני אכתוב כל פרקי חיבור שאלות שלמים זה אחר זה וכן כפל שאלות ראשון ופרק חיבור שאלות שברים אחריו ופרק חיבור שאלות מורכבים אחריו ואחר כפל שאלות שלמים ופרק כפל שאלות שברים ופרק כפל שאלות מורכבים ואחר גרעון שאלות שלמים ופרק שאלות גרעון שברים ופרק גרעון שאלות מורכבים ואחר פרק חילוק שאלות שלמים ופרק חילוק שאלות שברים ופרק חילוק שאלות מורכבים וגם תדע כי הצורך יביאני לכתוב פרקים אחרים אם לצורך ההשואה אם לדברים אחרים כמו שיעדתי* וגם --- בסוף כלל ראשון שער מורכב *ידעתי הערה הכרחית בידיעת האותיות המשמשות במספר ואומר כי באשר המספר המשולל מחומר הוא בלתי בעל תכלית כן הוצרכו חכמי החשבון לקחת צורות או אותיות בלתי בעלות תכלית כי הבעל תכלית לא ימנה את הבלתי בעל תכלית ועל כן הסכמו להניח
The First Part: Numerical Operations
The First Section: Integers
[20ב]
[ג1] [] הם בלתי [] והסיבה שהם [] כי לגודל המספר [] כי ידוע שבכל אומה [] עם אותיותם ו[] [] ואומר כי הת' היא היותר גדולה ואם [] שתכלול יותר מת' לא תוכל למצוא אות אשר תכלול מספר גדול ואם שתכתוב אותיות גדולי המספר יתמו מרוב המספר ואם תכפלם פעמים רבים יהיה [] גדול ובלבול בכתבתם והרי לך כי המספר שאינו מנוי הוא בלתי בעל תכלית והאותיות הם בעלות תכלית ולא יספור הבעל תכלית את הבלתי בעל תכלית או נאמר הקטן את הגדול ובעבור זה הסכמו בעלי המספר להניח ט' צורות אשר הם בלתי בעלות תכלית במעלותיהם כי הט' צורות הם כמו חומר וכאשר הם במעלות הם צורות שונות זו מזו אשר הצורה הראשונה בדרך משל היא אחד ויוכל להיות עשרה או מאה או אלף או מספרים גדולים מאלה לאין תכלית וכן שאר הט' צורות אשר הניחם חכם אחד ואלה הם צורתם א ב ג ד ה ו ז ח ט 0 ועל כל 1 2 3 4 5 6 7 8 9 0 אחד מהם האות הדומה לה מאותיותנו אשר עמהם תנהיג המספר אם תרצה כאשר אני עושה בזה הספר והרי לך כי סיבת המעלות היא גודל המספר וסיבת מעוט האותיות היא המעלות והנה דרך הנחתם היא כי המעלה הראשונה נקראת מעלת האחדים
21[א]
כמנהג הגוים וכן ראוי 0 9 8 7 6 5 4 3 2 1
[ג2] והשנית [מעלת העשרות והשלישית מעלת] המאות [] והמעלה הרביעית [] לאלפים והחמשית ל[עשרות אלפים] [] והששית כשלשית למאות [אלפים] [] ואם כן חילוק ראשון יחלקו המעלות [] ר"ל שילוש הוא אחדים עשרות מאות [] הראשון הוא כמו שהוא והשילוש השני הוא אלפים והשילוש השלשי הוא מספרים כמו שתראה והשילוש הרביעי מספרים אלפים וכל זה תראה בע"ה והרי לך הנחת המעלות וכפי האות שתתן בכל מעלה כך תהיה הוראת המספר כי במעט עיון תראה כי כאשר היו ט' במעלת האחדים שהיא האות היותר גדולה שיכול להיות שאם נוסיף עליה אחד שיהיו עשרה והם אחד במעלה שנית ואם היו ט' במעלה שנית שהם תשעים והוספנו אחד ממינו יהיו עשרה עשרות ויהיו אחד במעלה שלישית שהוא מאה וכן לאין תכלית ומזה תראה גם כן כי כאשר נשיב אחד אחורנית שיהיו עשרה עמו המעלה ההיא ואם תשיב שנים יהיו עשרים ואם שלשה יהיה שלושים וכל זה תראה במעשה בקרוב סדר קריאת שמות למעלות נתנו בזה ב' דרכים הדרך האחד הוא ברור ממה שאמרתי כי כאשר היו לך מעלות כסדר ותכפול שם המעלה עשרה פעמים הנה היוציא יהיה שם השנית לה והמשל מעלת האחדים כפול מה שבמעלה ראשונה עשרה פעמים יהיה היוציא עשרות וזה
[21ב]
[ד1] [] עשרות [] שלשית [] [] המעלה הרביעית [] אחדים [עשרות מאות אלפים]עשרות אלפים מאות אלפים אלף [אלפים עשרות] אלף אלפים מאות אלף אלפים אלף [אלפי אלפים] וכן לעולם והם עשרה מעלות כמו שתראה בזאת הצורה א א א א א א א א א א הדרך השני הוא המנהג היותר טוב והיותר נאות ואם שיהיו מאה מעלות או יותר והוא שתחלק כל המעלות ג' ג' ואחר חלוקתם מג' שמות או תוארים יש להם [] זולת השילוש הראשון שאין לו שם אלא כמו שהוא ושמות [] השילושים הנמשכים אחר השילוש הראשון הם אלפים או מספרים או מורכבים משניהם ודע כי שם מספר הוא אלף פעמים אלף וכל זה תרצה בכ"כ מעלות שהנחתי וב[] מעלה א' שהוא המספר הקטן מן הט' אותיות ואחר נחלק המעלות ג' ג' עם רושם בין כל שילוש א ב ג ד ה ו ז כזה א א א / א א א / א א א / א א א / א א א / א א א / א א א / א וההתחלה מן האחדים ואחר נרשום כל חלק שהוא שלושה מעלות וההתחלה ממעלת האלפים שהוא החלק השני וראשון לשם וזה שנתן א' על א' שהוא ראש השילוש וב' על ראש המעלת השלשית וג' על הרביעית וד' על השלוש החמישית וה' על ראש השילוש השישית וו' על ראש השילוש השביעי וז' על מה שנמצא בשילוש השמיני וטעם שנתן אותיות הרושם על
22[א]
[ד2] המעל[] תחסר [] תשב ותחלק [] א' תורה שכל השילוש [] ובעשרות ובמאות [] הוא מספרים אשר בלעז [] תורה שכל השילוש הוא הוא מורכב [] שעברו שהאחד אלפים והשני מספרים וכן נאמר לזה אלפים מספרים כי בג' נמצא א' וב' ושילוש א' אמרנו אלפים ושילוש ב' מספרים ואם כן שילוש ג' מורכב משניהם ונאמר אלפים מספרים ורושם ד' יורה מספרי המספרים כי הוא כפל רושם ב' ורושם ה' הוא כמו א' [וד'] מורכב הא' אלפים והד' מספרי המספרים וכן כולם שכל מורה נפרד [תאמר] אלפים בעבור הא' וככה מספרים כפי הזוגות אשר בו המשל בזה כפי הצורה המונחת הנה הא' היא מילה נפרדת ואין בה זוג [] על כן [] נאמר אלפים ונאמר בזה השילוש קי"א אלפים ובחלק השלישי יש בו ב' ויורה על מספרים ולא על אלפים ונאמר שהוא קי"א מספרים ובחלק הרביעי יש בו ג' ויש בג' וג' מורכב מא' וב' והנה כאשר אמרנו ברושם א' אלפים וברושם ב' מספרים נאמר בזה השילוש שיש בו א' וב' נאמר בעבור הא' אלפים ובעבור הב' מספרים כי הא' נפרד והב' זוג והוא שם מורכב ויהיו קי"א אלפים
[22ב]
[ה1] [] והוא [] מה שאמרנו [] [] ובזה נאמר מספרי [] המספרים ובחלק השישי [] הא' אלפים ובעבור הד' [] שני פעמים כי שני זוגות בו ונחבר [] ונאמר קי"א אלף [] מספרי המספרים ובחלק השביעי יש בו ו' ובו ג' פעמים ב' ונאמר ג' פעמים מספרי מספרי המספרים [ונאמר] קי"א מספרי מספרי המספרים ובחלק השמיני יש בו ז' ונאמר בעבור הא' אלפים ובעבור ג' פעמים ב' שיש בו מספרים מספרי המספרים ונחבר הכל בדיבור ונאמר קי"א אלף מספרי מספרי המספרים וכסדר הזה תנהיג עד אין קץ שאם תהיה אות הרושם ל' בדרך משל הם ט"ו זוגות וט"ו פעמים תאמר מספרי מספרי וכו' עד ט"ו וא' תהיה אות הרושם לא' תאמר בראשונה אלף אחר מספרים כסך הזוגות משל שני בזאת הצורה שהיא מתחלפת המספרים ובה ה' חלקים וד' שמות וזה צורתם הנה א ב ג ד ג ד ה | ו ז ח | ט ו ז | ג ב א | ב ד החלק הראשון תקמ"ג והשני תתע"ו אלפים והשלישי תשס"ט מספרים והרביעי קכ"ג אלף מספרים והחמשי מ"ב מספרי' המספרים ואם תרצה לחבר הכל בדיבור תאמר תתחיל מן האחרון ותאמר מ"ב מספרי המספרים וקכ"ג אלף מספרים ותשס"ט מספרים ותתע"ו אלפים ותקמ"ג ולשון הלעז מורגל בזה לשם המספרים
23[א]
[ה2]
The First Chapter on Addition |
הפרק [הראשון בחבור] [... ]קצתם בקצתם |
| [...] כפל וגרעון וחילוק וגדר [...] פרט ופרט והשני פרט [וכלל] [...] פרט ופרט מכל מין אחדי [המעלה] [...] בקצת ופרט וכלל הם הנה אחדים על המעלות לאין קץ קצתם בקצת וכלל וכלל [...] כל המעלות חוץ הראשונה קצתם בקצת אלא שבמעשה לא ואמר לא כללים ולא פרטים אלא כמו שיהיו כולם אחדים כי חבור ת' עם ת"ש הוא כמו חבור ז' עם ד' שהם י"א אלא שבמעלותם הם אלף וק' וכן כולם כמו שתראה בע"ה ואומר כי הרוציה לחבר מספרים רבים ולעשות מהם מספר גדול כולל לכולם אם שיהיו דומים או בלתי דומים צריך לכתוב אותם מכוונים כל מין על מינו אחדים על אחדים וכוללים על כוללים ובלבד שיהיו דומים הכוללים הנגדיים כל אחד עם בן גילו וחבר מספרי מעלת האחדים וכל עשרה שתקבץ מהם יהיו אחד במעלת העשרות ואחר חבר מספרי מעלות העשרות וכל עשרה שתקבץ מהם יהיו אחד במעלת המאות והמנהג הזה תנהיג בכל המעלות זה הכלל כל עשרה מאיזו מעלה שיהיה יהיו אחד במעלה הנמשכת לה כי כל מעלה תמשכנה כמו אחדים בערך לנמשכת לה | |
| המשל ראובן חייב ליהודה תפ"ד די' ועוד שפ"ט נסדרם בזאת הצורה | |
| וחבר מה שבמעלת האחדים יעלו י"ג עשה מהעשרה אחד במעלת העשרות ישארו ג' העולה [23ב] [ו1] [...] במעלת [...] מעשרה אחדים [...] מעלת המאות ועם [...] במעלת העשרות ז' והנה [...] וכן אם היו תס"ד ושפ"ט כורי [...] ברזל או משי או דבר מה [...] דרך אחד לכולם ואין צריך משל לכל אחד וכן א[ם] יהיה ג' או ד' טורי החיוב או יותר שתחבר מה שבמעלה ראשונה מכל הטורים ותכתוב חיבור כולם למטה או הנשאר על עשרה או עשרות כי מכל עשרה תכתוב אחד במעלה הנמשכת לה כמו שקדם ואם לא תצטרך לתת מספר באיזו מעלה רשום במעלה ההיא ספרא כזה 0 ודע כי פעמים יהיה באיזה מעלה ספרא ותכתוב תחתיה ספרא ופעמים תהיה ספרא ותכתוב תחתיה מספר ופעמים יהיה מספר ותכתוב תחתיו מספר ופעמים יהיה מספר וכתוב תחתיו ספרא וזאת החלוקה תתאמת בכל המינים כמו שתכף תראה זה בחבור המשל בזה ראובן שמעון לוי השאילו ממון מיהודה הנה ראובן שאל ב' אלפים ושמונים די' ושמעון ג' אלפים ושישים ולוי ד' אלפים ושישים ורצינו לדעת סך כולם נסדרם בזאת הצורה ונחבר מספרי כל מעלה והנה בעבור כי במעלות האחדים לא נמצא דבר נכתוב ספרא תחת [ה]0' ובשני כ' ויהיו ב' בשלישית וספרא תחתיו ובשלישית כולם ספראש אבל נכתוב הב' שעלינו 24 [ו2] מן העשרות [...] ועלה בידינו [...] והרי לך כי המעלה [...] ומעלת העשרות מספר[...] המאות ספראש וכתבנו [...] מספרים וכתבנו מספר תחתיו [...] תמצאינו | |
| משל אחר חיברנו רמ"א כורי חיטה עם תשע"ג יעלו אלף ו[] כורי חיטה ודי בזה כי במקומות אחרים כמו במורכבים או בנמשכים בסדר אעשה חיבור מדברים מתחלפים כמו לטר[] ממון ומשקל ודברים אחרים במקומות הראוים לכל דבר והנה אחר זה ראוי לדבר בחלק השני מן הקיבוץ שהוא הכפל וגם אקצר בו כי יש מקומות להאריך אבל אמנם הראוי ללמוד בראשונה כפל מעלת היסוד שהיא המעלה הראשונה ולוח הרגיל המספר המחוייבת להשיב קנין ועל פה כי זה הלוח שהיא כפל הט' אחדים קצתם בקצת לא תנתן לכתוב ככל הכפל אלא על פה | |
| הישרה להרגיללכפול המעלה ראשונה שלא נתנה להכתב והיא מעלת האחדים וקראתי אותה מעלת היסוד כי כן ראוי שתקרא בעבור דברים רבים ומהם שהיא דומה לאחד כי כאשר תכפול האחד על עצמו אין הכפול יוציא מעצמו כן כשתכפול מעלות על מעלות תגרע מעלה אחת כמו שקדם ועוד כי כמו שהמספר שהאחד אינו נכנס בגדר המספר כן זאת המעלה לא תכנס במספר המעלות |
[24ב]
[ז1] [] נגרע [] במספר [] זולתה יש לה שם [] או מאות או אלפים או מספרים [] שהיא בתוכה אבל יש לה [] מעלת היסוד כי בה תמצא [] המספרים בעצם ובראשונה והמעלות האחר[] הושאלו ממנה כי עשרה [הוא] אחד ומאה הוא אחד וכן אלף ומספר וב' עשרות ומאתים ואלפים הושאלו מב' וכן עד ט' ונוכל לאמר לט' אחדים יסודות ועוד נמצא בה אב"ג שחבורם הוא מספר שוה וכל אחד בפרט הא' הוא יסוד היסודות שאם לא תמצא א' לא תמצא מספר ואם כי המספר תלוי בא' והא' אנינו תלוי במספר לפי שאינו מספר ש[] המספר הוא קיבוץ אחדים והאחד אינו מקובץ מאחדים אם כן אינו מספר ועוד ראה כי המספר הוא שלם או שבר והאחד אינו לא שלם ולא שבר אבל בין שלם ושבר והוא נבדל מהם אבל הפך ב' שלמים הוא חצי והפך ג' שלמים הוא שליש והפך ד' שלמים רביעית וכן לאין תכלית והאחד הוא כמו נקודה או מרכז בין השלם והשבר כזאת הצורה * כי אין חצי אם אין אחד כמו שאין ב' אין והוא סיבת אין אחד ועוד אדבר מסגולות האחד בפרק החילוק ועלה כולם א א א מזה כי כמו שהאחד נבדל ממה ד ג ב א ב ג ד שלפניו וממה שלאחריו כן המעלת האחדים נבדלת מכל המעלות יש לה תואר אחר כי כל המעלות
25[א]
[ז2] תוכל לכפול [] תוכל לכפול [] לדעת כפל כולה [] בלוח הזה [] [] המספר כי [] אינו [] ד' וכפל [] וב' [] הוא [] [] [] [] המעלה [] [ב'] והוא תחילת המספר [] כאשר [] [] [] ורוחב [] [] [] א ב ג [] [ש]לשתם ששה [] []
| כזה | |
The Second Chapter on Multiplication |
הפרק השני בכפל[1] |
| [יד1] [...] יחלק לשני [...] בכל תמונה ותמונה [...] שהוא בכל תמונה [...] מרובע [שוה כלל] צלעותיו [...] צלעותיו [...] [...] ג' מנים אם שוה [...] אם שוה [...] [...] כל ה מביא [...] כתבתי [...] |
ואומר כי המין הראשון מן [] התמונה [] בכפל [] הצלעות הוא [] שתרצה ידעת זאת התמונה הנה ראשונה ראוי [שתראה] ה[] שתרצה בה אם מאמות או מאיזה מספר שתרצה ותכפול אותם על עצמם והיוצא הוא המרובע המבוקש המשל בזה רצינו לדעת מרובע אורכו ג' אמות וכן רוחבו הנה כפלנו ג' על ג' כלומר שנכפול הג' בסך הג' האחרת ג' פעמים יעלה [ט'] והוא שטח התמונה הנרצת כי ג' תמצא [] א א א א א א א א א הצורה ואם תרצה שטח תמונה [] מרובע אשר כל צלע [] האחד על האחר והוא ד' על []
א א א א א א א א א א א א א א א א י"ו והוא שטח התמונה הנרצת [] אמות תמצא בכל צלע בצורה הזאת ואם רצינו מרובע [] אשר צלע האחד יהיה משני מעלות תניח
32[א]
[יד2] זה על זה [] הטור התחתון [] הטור התחתון שהכל [] כאשר קדם שאם תכפול [] נגד מעלת האחדים ואם אחדים [] נגד העשרות ואם אחדים [] ואם מכפל איזו מעלה [] הפרטיים תחת המעלה [] הכללים תחת הנמשכת לה כי כל מעלה היא [] בערך הנמשכת לה כאשר קדם המשל בזה רצינו מרובע אחד שוה הצלעות אשר כל צלע יהיה כ"ו אמה והוא כאומר כ"ו אמות בגד לסך כ"ו די' האמה כמה יעלה או כמו האומר כ"ו משקלי דבר מה לסך כ"ו די' או פרחים או לטרין כמה יעלה הנה נסדרים בשני טורים זה על זה על קו אחד להבדיל הכופל והנכפל מן הכפול ו ב בזאת הצורה הנה כפלנו ו' על ו' ו ב וו' על ב' ואחר ב' על ו' וב' על ו ה א ב' כי כפלנו על מעלה מן הטור ב ה העליון על כל מעלה מן הטור ו ז ו התחתון בצד כפלנו ו' על ו' יעלו ל"ו כתבנו הפרטים שהם ו' תחת האחדים והכללים שהם ל' יהיו ג' בשנית אבל לא נכתבם עד שנעשה כפל אחר לחברם עמו וזה להקל הטורח ונאמר ו' פעמים ב' הם י"ב וג' שהיה לנו הם ט"ו נכתוב הפרטים במעלה שנית והכלל בשלשית והרי לך שכפל הו' כל הטור התחתון ועתה נכפול ב' על כל הטור גם כן ונאמר ב' פעמים ו' הם י"ב נכתוב הפרטים נגד מעלה
[32ב]
[ט1] []רות על אחדים [] נכתוב הפרטים [] שלישית אבל לא נכתבהו [] 0' פעמים ב' שהוא ד' [] במעלה שלישית והיא [] עשרות על עשרות העולה והיה [] והרי שיצאו מכפל [] זה על זה [] קנ"ו ומהשני תק"ד תחברם עם [] והוא שטח התמונה הנרצת המרובעת השוה הצלעות אשר כ"ו אמה בכל צלע והוא הסך מדנרי הכ"ו אמות של [בגד] ואין צריך משל אחר כי הוא כאומר כ"ו אמות בגד לסך כ"ו די' [] עולה תרע"ו די' או כאומר כ"ו משקל נחושת או דבר מה לסך כ"ו די' או פרחים או לטרין וכן תוכל לאמר מכל הדברים שתרצה כי הכפל בפעם אחד הוא וכך לכל המשלים שאביא במרובעות תוכל לשנות חומר השאלה כפי מה שתרצה הערה דע שאם יהיה במספר הנרצה לכפול ספרא שהוא רושם שאין במעלה ההיא דבר [] זה המקום שיהיה השמר מאוד שלא תשכח מעלתה אע"פ שאין בה מספר והמשל בזה בתמונה מרובעת אשר כל צלע מאתים אמות נסדר מאתים על מאתים על קו אחד כ[זא]ת הצורה והוא 0 0 ב גם כן כאומר מאתים ככרי נחושת 0 0 ב לסך מאתים די' כל כיכר הנה נכפול 0 0 0 הספרא הראשונה מן הטור התחתון 0 0 0 0 0 ד 0 0 0 0 ד
26[א]
[ט2] ויהיה ספרא [] השנית ג"פ על ב' וכן [] ותעשה ג' ספרות [] אחד למעלה כי תחת הספרא [] הספרא הראשונה והנמשכות [] התחתון ויהיה הספרא [] וספרא אחרת אחריה במעלת האלפים וד' אחריה במעלת עשרות אלפים ואם כן אחר שתחברם תמצא מ' אלפים והנה יהיה שטח מאתים על מאתים מ' אלפים והוא מרובע שוה הצלעות אשר בכל צלע מאתים אמות באורך וכן ברוחב והוא גם כן סך המאתים כיכרי נחושת או סך החומר שתרצה המין השני מן הכפל הפשוט הוא בכפל בלתי מרובע שוה בצלעות אבל הוא מרובע ארוך ואומר כי כל זמן שתרצה לכפול איזה מספר על אחר בן שיהיה גדול ממנו בן שיהיה קטן הנה השטח היוציא ממנו יהיה מרובע ארוך המשל בזה כפלנו ב' על ג' יעלו ו' והוא שטח ארוך כזה כי הצלע האחד הוא ב' והשני ג' וכן אם א א א תכפול ג' על ד' יעלה י"ב והוא שטח בלתי א א א מרובע כזה א א א א כי הצלע האחד הוא ד' והאחר הוא ג' משל אחר א א א א רצינו לדעת שטח בלתי שוה בצלעותיו א א א א אשר הצלע האחד יהיה ע"ה והשני רמ"ה כזה ה ז נכפול זה על זה כמנהג ה' על רמ"ה יעלו [] ה ד ב [אלף] רכ"ה וז' על רמ"ה יעלו י"ז אלפים תק"ן נחברם יעלו ה ב ב א [י"ז] אלף ק"ן ק"ה אלפים [שע]"ה והוא הדין כאומר רמ"ה לטרין ה א ז א [י"ח] אלף שע"ה ה ז ג ח א פלפל לסך ע"ה שיעלה הסך הנז' מערוך משל אחר אם שאל רמ"ה כורי חיטה לסך י"ט די' כפל י"ט על רמ"ה יעלו ד' אלפים תרנ"ה ויהיה כזאת הצורה
[26ב]
[י1] [] ל"א די' [] וכן נ"ב פרחים לסך [] תשכ"ח וכן כל הדומה [] הכפל בכל דבר אחר הוא []שתראה בע"ה המין הראשון [] החלק השני בכפל המוגשמים [] מעוקב שהוא הגשם אשר ימצאו בו השלושה רחקים שהם אורך ורוחב ועומד והוא ארבעה תמונות סוגיות התמונה הראשונה הוא שתכפול מספר שוה על שוה והיוציא תכפול על שוה התמונה השנית היא שוה על שוה והיוציא על יותר גדול התמונה השלישית היא שוה על שוה והיוציא ביותר קטן התמונה הרביעית כולם מתחלפים ובמשלים תבינם ואומר כי תמונת המעוקב השוה הוא כאשר יהיו שלושה מספרים שוים ותכפול האחד בשני והיוציא בשלישי וזה יהיה שוה בכל צלעותיו והמשל רצינו תמונה מרובעת ומוגשמת אשר כל צלע תהיה שני אמות כפלנו ב' על ב' שהוא האורך על הרוחב יעלו ד' וזה שטח המרובע שרצינו לעשותו מוגשם ואחר כפלנו ד' על ב' יעלו ח' והוא המבוקש אשר היא ב' אמות אורך וב' רוחב וב' עומק משל שני רצינו מעוקב אשר כל צלע יהיה תל"ד כפלנו תל"ד על תל"ד כזאת הצורה יעלה קפ"ח אלפים שנ"ו וזה שטח המרובע ועתה נכפול עוד זה החשבון על תל"ד כזאת הצורה השנית יהיה העולה פ"א תרמ"ו אלפים תק"ד והוא המבוקש אשר כל צלע הוא תל"ד ועיין בזה כי בשאלות אדבר בזה במידות ובבנינים בע"ה התמונה השנית היא שוה על שוה והיוציא על יותר גדול וזה יהיה כמו עמוד המשל בזה רצינו תמונה אשר אורכה ד' אמות ורוחבה ד' והגובה עשרה הנה יהיו כולם ק"ס אמות 27[א] צורה שנית ואם תרצה להחליף צורה ראשונה ד ג ד המרחבים הכל ד ג ד הכופל ו ה ג ח ח א אחד ד ג ד הנכפל ד ב ד ג ה ז ו ג ז א
ח ו 0 ה ו ה ב 0 ג א
ד ב ד ג ה ז ו ג ז א
הכפול ד 0 ה ו ד ו א ח ו ה ג ח ח א
[י2] אלא שיהיה עמה [] על קטן וזאת תהיה [] וגובהו נמוך כמו [] נכפול מספר שוה על שוה [] המשל בזה רצינו תמונת [] אמות והרוחב גם כן [] כ"ה וזה שטח התושבת ואחר כפלנו התושבת שהוא כ"ה על ג' [] יהיו ע"ה והוא המבוקש התמונה הרביעית כולה מתחלפת הצלעות וזה יהיה כאשר יהיה הג' מספרים מתחלפים וזה יהיה כמו כותל המשל רצינו תמונה מוגשמת אשר אורכה י"א אמות ורוחבה ב' וגובהה כ"ז נכפול י"א על ב' יהיו כ"ב וזה תשבת הכותל ואחר כפלנו התושבת על הגובה שהוא כ"ז יהיו תקצ"ד והוא המבוקש והרי לך הד' תמונות המוגשמות אשר תוכל לעשות תמונות מוגשמות לאין תכלית אבל כולם יצאו מאלו דרך אחרת לדעת כל מעוקב כפול השורש על המספר הנמשך והעולה על הקודם לו או בהפך כי הכל שוה ועל העולה תוסיף השורש המשל בזה רצינו מעוקב ג' נכפול ג' על ד' שהוא הנמשך אחריו יהיו י"ב גם נכפול י"ב על ב' שהוא המספר שקודם השורש יהיו כ"ד תוסיף עליהם השורש יהיו כ"ז והוא המבוקש כי הוא כמו ג' על ג' שהוא ט' וג' על ט' הוא כ"ז משל אחר רצינו מעוקב ד' נכפול ד' על ה' יהיו כ' שהוא הנמשך לד' יהיו כ' גם נכפול כ' על ג' שהוא הקודם לד' יהיו ס' נוסיף עליהם השורש שהוא ד' יהיו ס"ד והוא מעוקב ד' דרך הבנינים אם תרצה לדעת כמה לבנים הוצרך עומד או כותל או מגדל תן לבנים שורה אחת כפי אורך ורוחב העמוד או הכותל או המגדל שתרצה וכפול זאת השורה על השורות שתרצה כפי הגובה שתרצה המשל בזה רצינו עמוד שיהיו ג' לבנים על ג' ויהיו ט' לבנים בשטח שהוא השורה הראשונה ורצינו שיהיה גובהו צ"ה
[27ב]
[יא1] [] המבוקש [] אורך ורוחב הכותל [] הגובה שתרצה והוא המבוקש [] כמה שורות יש בו ותכפלם [] בזה הכותל אשר שטחו הוא ח' לפני [] על ט' יעלו ע"ב והוא המבוקש צורת הכותל
ואם תהיה הכותל דק שהוא עובי על עובי שהוא הבנין היותר
דק מכל הבנינים תכפלם גם כן על סך השורות ותדע הלבנים
אשר בכותל או הלבנים שתצטרך לבנות הכותל והמשל בזה הצורה
אשר בה ח' לבנים באורך הכותל זה בגובה כפול ז' על ח' יהיו
צורת הכותל
א ב ג ד ה ו ז ח
10 28[א]
[יא2] נ"ו וכן תמצה כזה [] מזה הבניין כמה שורות [] השיעור כפי הגובה שתרצה [] ולמדוד הגובה תשטח בקרקע [] הגובה שתרצה או תשטח בקרקע [] תשטח מלבנה אחת על אחת הגובה שתרצה [] וכפול מספר שורת האורך על מספר ה[] והם הלבנים שאתה צריך בזה הכותל ואם תרצה מגדל מרובע עם ד' עמודים לד' זויותיו אשר שטח כל עמוד י"ז לבנים ואורך הכותלים בין 0 0 0 | 0 0 0 0 0 | 0 0 0 עמוד לעמוד ה' 0 0 0 | | 0 0 0 לבנים נעיין מספר 0 0 0 | | 0 0 0 הלבנים מד' כותלים 0 0 ומד' עמודים יהיו נ"ו 0 0 לבנים כזאת הצורה 0 0 והם שורה אחת 0 0 ורצינו שיעלה זה 0 0 המגדל שמ"ה שורות 0 0 0 | | 0 0 0 נכפול נ"ו על שמ"ה 0 0 0 | | 0 0 0 שורות יעלו י"ט אלף 0 0 0 | 0 0 0 0 0 | 0 0 0 ש"כ לבניים ואם תאמר רצוני שתהיה זה המגדל כך אמות עיין בכותל אחר כמה שורות יש באמה אחת וכפול השורות שבאמה על נ"ו שהיא השורה הראשונה ומה שיעלה בכפל כפול על מספר האמות שתרצה והוא המבוקש סדר ידעת צירוף האותיות כחכמי דרך אחרת לכפל בצורה מרובעת ויש לה סגולות ראבו רבות וזה שנוכל לכפול קצת בשעה אחת וקצת בשעה אחרת ונוכל לכפול בסדר ושלא כסדר ויהיה הצורה המרובעת כזה סדר
[28ב]
[יב1] [] [] בונות ו' בתים [] בונות ק"ך בתים [בו]נות ה' אלפים ומ' [] אכתוב דרך כללי לדעת [] שורות בשני טורים הטור [] אותיות בסדר [] כי א' אין בו צרוף כלל ויהיו השתי שורות כזה הצורה ואומר כי ב' בונות ב ג ד ה ו ז ח שתי בתים והוא ב ו דב 0בא 0בז 0ד0ה 0בג0ד תחת ב' בטור השנית ועתה לדעת בניין ג נכפול ג על בניין ב שהוא ב' שעבר ויהיו ששה בתים או ששה מחברות והנה ששה מחברות תמצא מג' אותיות כמו שתראה תחת ג' ולדעת בניין ד' נכפול על ו' שהוא הבניין שעבר ויהיו כ"ד תחת ד' ולדעת בניין ה' נכפול ה' על כ"ד שעבר יהיו ק"ך מחברות ולדעת צרוף ו' נכפול ו' על ק"ך שהוא הבניין שעבר יהיו תש"ך מחברות ולדעת צרוף ז' נכפול ז' על תש"ך שהוא הבניין שעבר יהיו ה' אלפים ומ' מחברות ולדעת צרוף ח' נכפול ח' על ה' אלף ומ' שהוא הבניין שעבר יהיו מ' אלפים ש"ך מחברות וכן לאין תכלית כי בצירוף ח' תבות משונות זו מזו תמצא מ' אלף וש"ך תבות משונות זו מזו ובעבור שתראה קצת מהם למין אחבר מהם שלושה בג"ד ואומר כי ב' בונות ב' מחברות א"ב ב"א וג' ששה מחברות וד' כ"ד כמו שאמרתי ואכן משל ומהם תעשה באחדים והמשל ב' בונות ב' כמו א"ב או ב"א או קח האותיות שתרצה אם בסדר כמו א"ב או ב"ג או ד"ג או שלא כסדר כמו א"ד או ב"ת
29[א]
[יב2] או ג"ש [] מג' אותיות [] [] הצורה רמח כי [] ר שיתופן מחר ואם [] חרם מאבג"ד [] מ ח רחם חמר למפרע [יהיו י"ו] עוד [] מרח אחרים בדילוג אחד וד' אחרים בדילוג א אחר למפרע יהיו י"ו גם ד' אחרים בדילוג ב' וד' ד ב אחרים למפרע בדילוג ב' יהיו שמונה וי"ו שלנו יהיו כ"ד ג ואין בם יותר חלוקה וצירוף והמשל והמשל בד' אבנים הנה העיגול יורה לך הדרך כי צרוף ראשון הוא א'ב'ג'ד' והשני ב'ג'ד'א' והשליש ג'ד'א'ב' והרביעי ד'א'ב'ג' והם ד' מחברות עוד ד' למפרע א'ד'ג'ב' שני ד'ג'ב'א' שלשי' ג'ב'א'ד' רביעי ב'א'ד'ג' עוד ד' בדילוג א' ולמפרע ד' אחריה בדילוג א' וכן ד' בדלוג ב' ולמפרע בדילוג ב' ויהיו כולם כ"ד מחברות כזה הצורה
כסדר מפרע כסדר מפרע כסדר מפרע אבגד אדגב אגדב אגבד אדבג אבדג בגדא דגבא בדאג דבאג באגד דאגב גדאב גבאד גאבד גאדב גבדא גדבא דאבג באדג דבגא בדגא דגאב בגאד
דרך לכפול בצורה מרובעת ויש לה סגולות רבות וזה שנוכל לכפול קצת בשעה אחת וקצת בשעה אחרת ונוכל לכפול כסדר ושלא כסדר ויהיה הצורה המרובעת כזה
[29ב]
[יג1]
ה ד ח ו
ה
ג ח
ב ו
ה ב
ד ז
0
א ח
0 ו
א ב
א ב
ה
א ב
א ד
ב ח
א ג
ה א ג ח ג ב ב
ו' אלפים תתמ"ה
על שכ"ז והנה כל מרובע קטן הוא מקום לכל שני המספרים הנוכחיים והקו החולק מזוית לזוית בכל מרובע הוא לתת בחציו העליון הנשאר על עשרות מכל כפל משני נוכחיים ובחצי האחר העשרות ובעבור זה תוכל לקחת כל מספר שתרצה אחרון או ראשון או זה בשעה אחת וזה בשעה אחרת
והמשל תכפול ג' על ה' יהיו ט"ו והם במרובע הנוכחי לשניהם והפרטים שהם ה' תכתוב בחצי העליון וא' שהוא עשרה בתחתון וכן כולם כי כפל ז' על ה' ל"ה תנן ה' בחצי העליון וג' בחצי האחר שהם עשרות וכן כמו שתראה בצורה ז' על ה' [] ועל ד' ועם ח' ועל ו' וכן ב' על כולם וכן ג' על כולם ואחר תחברם ותוציא המספר כפי המשכת קוי האלכסונות כי ה' הוא האחדים וח' וג' שהם י"א הם עשרות קח אחד לק' מן העשרה ונשאר א' שהוא עשרה ובשלשית תמצה ובחא"ה שהם כ"ב ועם א' שעלינו הם כ"ג מאות תניח ג' במקומו ונעלה כ' לב' בטור הרביעי עם בהוב"א שהם י"ו וב' שעלינו יהיו י"ח תניח ח' במקומו ונעלה א' בטור חמשי ועם דבאד"א שהם י"ב יהיו י"ג תניח ג' במקומו ונעלה אחד בטור ששי אשר בו אח"ב יהיו י"ב נניח ב' ונעלה א' בטור שביעי ועם א' שבו יהיו ב' והם ב' מספרים רל"ח אלפים שט"ו ותוכל להפוך הצורה לצד שתרצה
31[א]
[יג2]
וכאן נשלם ה[] שאשמש מ[]
The Third Chapter on Subtraction |
הפרק השלישי במגר[עת] |
| קל ולזה אקצר [...] יכוון המעלות מספר נגד מספר [...] והמספרים וראשונה גרע האחדים מן האחדים והנח זה בכיוון תחת המעלה שגרעתה וכן תעשה לכל המעלות ואם התחתון יהיה יותר גדול מהעליון ולא תוכל לגרוע ממנה קח מהמעלה אשר לפניה אחד ויהיו עשרה במעלה שתרצה ובזה הדרך תנהיג לעולם בכל המעלות ואם תהיה ספרא במעלה אשר לפניה קח אחד מן המעלה השלשית לה ויהיה עשרה בשנית וקח מהם אחד ויהיו עשרה במעלה שתרצה ואם היו ספרות רבות בין מעלתך ובין המעלה אשר בה מספר תשיב אחד אחורנית ויהיו עשרה וקח אחד מהעשרה לאחור ויהיו עשרה וכן עד עולם ובעבור שלא תצטרך לעיין כאשר תשיב אחורנית בכל מעלה ומעלה אומר לך כלל אחד והוא שתקח המספר שתמצה מאיזו מעלה שיהיה ותחזור אותו במעלתך [] ואם יהיו בין שניהם ספרות רבות אלא שתצטרך לחשוב הספרות שבאמצע השתי מעלות ט' כל ספרא והכל יהיה שוה ולהראותך כל זה אמשיל משלים ואומר כי ראובן חייב לשמעון תקע"ג די' ופרע לו שנ"ב והנה רצינו לגרע מה שפרע מן החיוב נתן השני חשבונות |
בסדר מעלותם כזה הצורה נגרע ב' אחדים החיוב ג ז ה מג' ישאר אחד תחת הקו נגרע ה' מז' שהם עשרות הפרעון ב ה ג נשארו ב' עשרות נגרע ג' מה' שהם מאות נשארו ב' השיור א ב ב מאות והנה נשאר מן החיוב רכ"א די' וכן תעשה אם יהיו לטרי' או פרחים או איזה מטבע שיהיה שהכל שוה משל אחר ראובן חיב לשמעון ה' אלפים ומ"ז לטרי ופרע לו תתקנ"ח לטרין נגרע מה שפרע מן החיוב נעשה בסדר שעבר ונשארו ד' אלפים ופ"ט לטרין ז ד 0 ה החיוב ח ה ט הפרעון ט 8 0 ד השיור השיור
[31ב]
[יד1]
[] החיוב [] מין השיור [] [] תת"ק כורי חיטה [] רצינו לדעת הנשאר נגרע [] החשבון בסדר מעלותיו כ [] נגרע ד' מספרא לא נוכל החיוב 0 0 ט נקח אחד מן הט' ונאמר [] הפרעון ד ה ח עשרה במעלת האחדים נגרע הנשאר ו ד מהם ד' ישארו ו' נגרע ה' מט' שחשבנו הספרא לט' בעבור שעברו עליה העשרה למעלת האחדים ישארו ד' נגרע ח' מח' שנשארו מן הט' לא נשאר כלום והנה נשארו מ"ו כורי חיטה ואם תחבר הפרעון והשיור ראוי שתציא החיוב כמו שתראה בבדיקות משל אחר כולו ספרות הנה מספר החיוב הוא מאתים אלפים משקלי צמר ופרע קכ"ג אלפים שמ"ה ויהיה כסדר מעלותיו כצורה הזאת והנה לא נוכל החיוב 0 0 0 0 0 ב לגרוע ה' מספרא נקח הפרעון ה ד ג ג ב א א' מהב' ונעברנו על השיור ה ה ו ו ז כל הספראש עד הראשונה במעלת האחדים ושם יהיה עשרה ונשארו על כל הספראש שבאצמע ט' ט' או תחשב כל ספרא לט' ועל ב' נשאר אחד ועתה נגרע ה' מעשרה שעברנו ישארו ה' וד' מט' ישארו ה' וג' מט'
30[א]
[יד2] ישארו ו' [] וא' מא' לא נשאר [] משקלי הצמר [] משל אחר אם תרצה [] לטרין דנרין []
The Fourth Chapter on Division of Integers |
הפרק הרביעי בחילוק השלמים |
| ואומר כי כאשר החיבור הוא הפך הגרעון כן הכפל הוא הפך החילוק על כן יהיה כל אחד מאזני חברו כאשר אבאר במקומו והנה החילוק הוא מבוקש מן הראוי לכל אחד מן המחלקים הדבר או הממון המונח והנשאר לחלק הם חלקים נשברים הראוים לכל אחד בסך המחלקים באחד ובמקמות אחרים אדבר מזה השיור והנה הדרך שם לחלק הוא שתניח המספר שתרצה לחלק במעלותיו והמספר המחלק למטה מכוון מעלה כנגד מעלה מהמספר המונח כל אחד בור אחד ובלבד שתניח ריוח בין שני הטורים לכתוב היוציא בחלוקה והנה מספר המחלק יהיה או ממעלה ראשונה או ממעלות רבות ואם ממעלה ראשונה תעיין במשל ראשון ואם יהיה המחלק ממעלות רבות אבל אין לו כל כך מעלות כמו שיש[] מספר שתרצה לחלק תן המעלה היותר גדולה מהמספר הקטן שהוא המחלק מצד המעלה הגדולה מן המספר הגדול וימשך אל מה שימשך ואחר תכוין מעלותך ותן לכל אחד הראוי לו מכל מעלה למעלה הנוכחית לה והמספר הראוי תן אותו |
[30ב]
[יה1] [] הראוי לתת [] זה המספר ככל [] הראשונה אשר [] זה החשבון המונח [] מהמחלק ובכל פעם שתחלק [] שאומר תתן מספר אחד בין שני [] הריוח נגד המעלה הראשונה [משל] החילות לחלק ואחר שנתת כל מה שתוכל לתת לכל מעלות המחלק תחזיר אותו אחורנית מעלה אחד ותן לו גם כן כל מה שתוכל לתת לכל מעלה מהמעלות ה[] מהמספר העליון ותן המספר הראוי בין הריוח והוא המספר הראוי לתת לכל אחד מהמחלק אבל כאשר תכתוב זה המספר תחת המעלה אשר החילות לחלק עיין שיספיק לתת [] לכל מעלות המחלק ואם תחזור המחלק אחורנית ואין מספר לקחת ולתת למעלה ראשונה מן המחלק אם לא תתן לו לא באחדים [] תן ספרא במקומו ותחזור המחלק לאחורה והנה תחזור המחלק אחורנית כל כך פעמים עד שיהיו בחלוק אחדי המחלק נגד אחדי המחולק ובכאן תהיה החלוקה האחרונה ואם ישאר [] תחת המחלק או לא ישאר כלום וכל פעם שתחזור המחלק לאחורי תעבור הקולמוס על [] בעבור שלא תתבלבל ואם לא תרצה להעביר עליו הקולמוס תכתוב המחלק על נייר קטן ותעבור הנייר לאחור ועתה הנה אם יהיה המחלק ממעלה ראשנה ממספר אחד כמו מא' עד ט' תוכל לתת אותו למטה נגד מעלת
33[א]
[יה2] האחדים [] אותו אחורנית [] משל ראשון [] רצינו לחלק הצורה נניח [] ד האחדים וניתן מח' ט ז ח לז' אחד ונתן אותו ה ב א תחת א' בריוח כי ממנו חלקנו וישאר א' על ז ח' נשיב הא' לאחור במעלת העשרות ועם ז' אשר היו שם יהיו י"ז נחלקם לז' יבוא לכל אחד ב' נכתוב ב' [] בריוח תחת העשרות כי ממנו חילקנו ישארו ג' על ז' נשיבים לאחור למעלת האחדים על ט' יהיו ל"ט נחלקם לז' יבוא לכל אחד ט' ה' וישארו ד' על ט' לחלק ואם כן המחלק תתע"ט על ג' יבוא לכל אחד קכ"ה די' וד' שביעיות דינר ומזה השיור אדבר במשל רביעי * וגם בפרק מיוחד [] ובאחרים משל שני רצינו לחלק רמ"ו פשיטין לי"ב נסדרם כזה הצורה והנה נתן י"ב המחלק נגד מעלת המאות 0 0 והעשרות למעלה כל מה שנוכל ונמצה ו ד ב בשני המעלות האלה כ"ד נחלוק כ"ד לי"ב 0 ב יעלו שנים לכל אחד כי ב' האחרון נתן ב א לא' וד' נתן לב' שאם ב' לקח א' הנה ב' ב א יקח ד' ונשארו ספרא על ב' ועל ד' להורות שלא נשאר מהם דבר נחזור י"ב לאחור מעלה אחד יבואו אחדים עם אחדים ולא
[33ב]
[יו1] [] כנגד מעלת [] לא לקח א' [] חלק ב' גם כן והנה [] חלקים מי"ב בשלם ועיין [] אם נשארו לחלק אבל אם נחלקם [] ששה ששה חלקים מי"ב בשלם ואם תקצרהו לחציים ישוב לחצי כמו ששה פשיט' לי"ב יהיה מחצה ועיין בו כי בו תראה טעם מה מהנשאר בחלוקה וכן בכל שיור שאם תחלקהו הוא חלק מהמחלק שהוא אחד שלם כי לעולם המחלק הוא אחד משל שלשי רצינו לחלק תצ"ז לטרי ממון על ל"ד
ב בזה הצורה נתן מד' לג' אחד לכל אחד ישאר
ג 0 א' על ד' גם נתן לד' א' לכל אחד כפי מה
א ה א שנקח ג' ישארו ה' על ט' נעבור המחלק ז ט ד לאחור ונעבור הקולמוס עליו ואם לא תרצה ו ד א להעביר הקולמוס עליו תנהו בנייר קטן ד ג ותעבור הנייר לאחור כמו שאמרתי והנה עתה ג' נגד המעלה השנית אשר עליה ה' ועבור הא' אשר במעלה שלישית עם הה' יהיו ט"ו ומט"ו נוכל לתת לג' ה' לכל אחד אבל לא ישאר מז' לתת ה' לכל אחד מהד' ואם כן נתן מהט"ו לג' ד' לכל אחד שהם י"ב וישארו ג' על ה' וספרא על א' ונתן גם כן ד' לכל אחד מהד' יהיו י"ו נקח אחד מג' וו' מז' ונשארו על ג' ב' ועל ז' א' ואם כן עלה בחילק לכל אחד י"ד לטרין וכ"א חלקים מל"ד בלטרה ויהיה כל החשבון מחולק והראוי לכל אחד כי כאשר תחלק אי זה דבר מאי זה מין שיהיה וישארו לחלק מספרים מן המין ההוא הנה אעפי שהם
34[א]
[יו2] שלמים והמ[] מאחד שאם [] ועתה שלא הגיעו ל[] והנה היוציא בחילוק מהשלמים [] אמתי אלא שאינו מדוקדק הראוי [] כצד נקצר זה השבר אם יש בו חלקים נקצר [] תרצה אבל תכף תראה כיצד נחלק זה הנשאר לחלקים ש[] המספר המחולק ואם הם לטרין נעשה מהנשאר דינרי' ופשיטי' ומחצית ורביעי פשוט שהם החלקים היותר קטנים או דרהם במשקל או דקים שניים שלשיי וכ[ן] בזמן וכן כפי חמר כל מין והמשל הבא אחלקיהו עד כלה המשל רביעי רצינו לחלק ב' אלפים תתקפ"ז* על ל"ט *ליט' בזאת הצורה נתן ג' תחת מעלת ב המאות כי לא נוכל לחלק מן האלפים ב' לג' ז 0 אבל נעביר הב' ועם הט' יהיו כ"ט נתן לג' ה ב ז' לכל אחד יהיו כ"א ונשארו ח' על ט' ג ח 0 ועל ב' ספרא ולא נוכל לתת לג' יותר ז ח ט ב מז' לכל אחד בעבור שיספיק לט' גם תן ו ז לט' ממעלת העשרות ז' לכל אחד כמו ט ט ג ג שנתת לג' יהיו 0"ג ישארו ב' על המאות נשיב המחלק לאחור מעלה אחת לצד ימין ויהיו אחדים עם אחדים ונתן לג' מכ"ה אשר שם עם הב' שנחזור לאחור ו' לכל אחד שהם י"ח ישארו במעלת העשרות ז' וספרא על ב' גם נתן לט' ולב' אחד שהם נ"ד מע"ז ישארו כ"ג לחלק כי ה' לקחנו מז' אשר בעשרות ונשארו ב' וד' מז' אשר באחדים ונשארו ג' ואם כן נשארו כ"ג לחלק ואם נרצה שיהיו מחולקים נאמר שעלה מן החילוק ע"ו
[34ב]
[יז1] [] לכל אחד [] הראוי לכל אחד [] מכל אחד וישארו [] שהוא סך הלטרה יעלו ת"ק די' [] י"א די' ונשארו ל"א די' לחלק כופל [] מהם סך הדינר יעלו שע"ב פשיטי נחלקם על [] יעלה לכל אחד י"ו פשיט' ונשארו כ"א פשוט כפלם על ד' שהם סך רביעי הפשוט יעלו פ"ד רביעיות נחלקם על ל"ט יעלו ב' רביעי פשוט שהם מחצה ונשארו ששה לחלק על ל"ט ויהיו ו' חלקים מל"ט ברביע ותוכל לקצרו בשלישית ויהיו ב' חלקים מי"ג ברביע ואם כן הראוי לכל אחד יהיה ע"ו לטרין י"א די' ט' פשיט' ומחצה וב' חלקים מי"ג ברביעית משל חמשי רצינו לחלק ה' אלפים תתנ"ב פרחים לנ"ו כזה הצורה נחלק מ"ה לה' נתן 0 אחד לכל אחד ונשאר ספרא על ה' גם ח ב ב 0 מ"ח לו' אחד לכל אחד כמו שעשינו ב ה ח ה לראשון ישארו ב' על ח' נשיב המחלק ד 0 א מעלה אחת לאחור ואין דבר לתת להם ו ו ו ו אלא ספרא נשיב עוד המחלק לאחור ה ה ונתן מנ"ה לה' ד' לכל אחד ויהיה כ' ישארו נ"ב וספרא על ב' נתן גם לו' ד' לכל אחד שהם כ"ד ישארו כ"ח לחלק שהם כ"ח חלקים מנ"ו בפרח ואם תרצה לעשות מזה השיור די' כפול כ"ח על סך הפרח שהוא עתה י"ד די' יעלה שצ"ב די' חלקם על נ"ו יעלה בחילוק ז' די' ולא נשאר דבר לחלק והנה עלה לכל אחד ק"ד פרחי' וז' די' משל ששי רצינו לחלק קנ"ו לטרי פלפל לי"ד כזה
35[א] יז
[יז2] הצורה []
0 []
ב א 0 י"ו [] ו ה א ונשארו ב' []
א א לכל אחד והב' נשארו []
ד ד א אוקיות הלטרה יעלו פ"ד אוקיות []
א יעלה בחילוק עוד [] אוקיא אחת ונשארו
עשרה אוקיות כופלם על י"ו חלקי האוקיא הנקראים אריאינסוש יעלו ק"ס חלקם על י"ד יעלה בחילוק י"א אריאינס וישארו ח' אריאינסו שהם ב' שלישי ד' שביעיות אריאינס אם תקצר כן משל שביעי רצינו לחלק מאתים ופ"ה אלפים ותתקע"ו כיכרי צמר על שע"ב כזאת הצורה הנה בחלוקה 0 8 2 0 0 0 הראשונה תוכל לתת לכל אחד ז' ו ז ט ה ח ב ונשיב המחלק לאחור ונתן לכל אחד
ח ו ז ששה בחלוקה השנית ונשיב המחלק עוד
ב ז ג לאחור ונתן לכל אחד ח' והנה יעלה
ב ז ג
ב ז ג בחילוק תשס"ח ככרי צמר ונשארו לחלק מאתים ושמונים ככרים כופלם במשקלי הככר שהם ד' יעלו אלף ק"ך משקלים נחלקם לשע"ב יעלו בחלוק ג' משקלים ונשארו ד' משקלים לחלק נכפלם בלטרי המשקל שהם שלושים יעלו ק"ך לטרים ולא נוכל לחלקם על שע"ב נכפלם על י"ב שהם אוקיות הליטרה יעלו אלף ות"מ אוקיות נחלקם על שע"ב יעלה בחילוק ג' אוקיות ונשארו שכ"ד אוקיות לחלק נכפלם על י"ו שהם חלקי האוקיא הנקראים אריאינסוש יעלו ה' אלפים קפ"ד אריאינסו' נחלקם על שע"ב יעלה בחילוק י"ג אריאינס'
[35ב]
[יח1] [] נקצרם ישובו [] אלפים ותתקע"ו [] ממשקל יבוא לכל [] י"ג אוקיות וי"ג אריאינסו [] [] תעיין בבחינה הנה רצינו לחלק ד' אלפים [] שנ"ז דוקאדוש על ל"ב הנה כפל לכל אחד קל"ו דוקאדוש וג' די' וה' פשיטי' ורביע פשוט כמו שתראה בזאת
דוקדוש דינ' פשי' רביעי הצורה והבחינה
ו ג א ג ה א היוצא לכל אחד
המורה בג בג בג בג כפול על המורה שתשיב הכל בב 12 ד מורה כל אחד לחלק מכלל לכלל עד שישוב הכל אל הכלל הראשון וזה שתכפול ראשונה כל חלקי החלוקה על המחלק שהוא ל"ב והוא המורה והוא באמצע הצורה והיוציא בכפל מכל אחד תחלק כל אחד על מורה חלקו כמו הרביעיות שתחלק על ד' ויהיו פשיטי' והפשיט' על י"ב ויהיו די' והדינ' על כ"ב ויהיו דוקאדוש בשאלתנו זאת ובאחרים כמורה כל מטבע שתרצה אם פרחים על י"ו ואם לטרי' על כ' וכן הכל ואחר תחזור הפשי' די' והדי' דוקדוש בשאלתנו כנז' והמשל בזה נכפול הרביע פשוט שהיא אחת במורה שהוא ל"ב יעלו ל"ב רביעיות תנחלקם על ד' שהוא מורה הפשיטין יעלו ח' פשיטי' ונשמור אותם עוד נכפול הה' פשיט' על ל"ב יעלו ק"ס פשיט נחבר עליהם ח' ששמרנו יעלו קס"ח פשיטי' נחלקם על י"ב יהיו י"ד דינ' ונשמרם עוד נכפול הג' די' במורה יעלו צ"ו די' ועם י"ד ששמרנו יהיו ק"י נחלקם על המורה כ"ב יהיו ה' דוקאדוש ונשמרם גם נכפול הדוקאדי' שיצאו בחלוקה שהם קל"ו על המורה יעלו ד' אלפים תנ"ב דוקדוש
36[א]
[יח2] תנ"ב דוקאדוש [] הכל אל הכלל הראשון [] סוחר קנה כ"ד [] כל אמה התשובה נחלק [] וזהו סך כל אמה והבחינה נכפול [] המחלק ותציא סך כל הפרחים סוחר קנה ל' אמות בגד בסך כ"ד פרחים וחלק שאלתי סך האמה התשובה נחלק כ"ד על ל' הנה הוא מחולק שהוא כ"ד חלקים מל' בפרח אחד כז 24/30 נקצרהו אם נרצה יהיו ד' חמשיות פרח או דרך אחרת נעשה מהפרחים די' יהיו שפ"ד אלף תקל"ו נחלקם על ל' יעלה בחילוק נחלקם על ל' אמות יעלה בחילוק י"ב ונשארו כ"ד די' נכפלם בי"ב יהיה תפ"ח פשיט' נחלקם על ל' יעלו יעלו ט' פשי' ונשארו י"ח פשיט נכפלם על ב' יהיו ל"ו מחצות נחלקם על ל' יבוא מחצה ונשארו ו' מחצות והם ששה חלקי מחצה ומקוצרים יהיו חמשית מחצה וכן כל הדומה לזה מאי זה מין שיהיה ממדה ועוד נדבר מזה במקום אחר ועלה מזה כי סך האמה הוא י"ב די' וט' פשיט ומחצה וחמשית מחצה והבחינה נכפול המחצית על ל' יהיו ל' וו' שנשארו יהיו ל"ו מחצית נעשה מהם פשיטין יהיו י"ח פשיט ונשמור אותם גם נכפול ט' פשטי על ל' שהוא המורה יהיו ר"ע ועם י"ח ששמרנו יהיו רפ"ח פשיט חלקם על י"ב יעלו כ"ד די' ונשמרם עו' נכפול הי"ב די' על המורה יהיו ש"ס די' ועם הכ"ד ששמרנו יהיו שפ"ד די' ואם נחלקם על י"ו יעלו כ"ד פרחים [] טובה משל אחר רצי מזמן רצינו לחלק ה' אלפים רל"ז על י"ט שהוא סך המחזור ס' ויהיה כזאת ז ג ב ה הצורה ויהיה היוציא בחילוק רע"ה ונשארו ה ז ב י"ב שנים לחלק כופלם בשס"ה ורביע כמו שתראה ט א
שתראה
[36ב]
[יט1] [] ימים תחלקם [] עשיתי מהם חדשים בעבור [] לכל ולפי זה לא אחלק [] החלוקה נשארו לחלק הג' ימים [] שעות היום יעלו שי"ב תחלקם על [] י"ו שעות ונשארו י"ו לחלק תכפלם על ס' יעלו שהם דקי השעה יעלו ת"נ דקים תחלקם על י"ט יעלו כ"ה דקים ונשארו ה' דקים וכפלם על ס' ונחלק על י"ט יעלו ט"ו שניים ונשארו ט"ו שניים וכן תכפול השיוור על ס' ותחלק על י"ט עד שלא תרצה עוד לדקדק או באיזה שיקרא שלא ישאר כלום ובמקום אחר אעשה אלו החלקים חלקי העיבור בע"ה ודע כי מה שקצרתי באלו המשלים הוא ביאור והאריכות בלבול כי אלו הענינים צריך אדם ללמוד התחלתם ממלמיד כאשר אמר הר"ם במד"ל בעיבור הקטן שעשה ועוד כי במקומות אחרים אשנה ואשליש ועתה אדבר במאזנים שיעדתי לדבור אחר אילו הד' מנים הערה ליחלוק וכיצד נקצר החילוק משל כמו שרצינו לחלק מספר מה על מספר מה והיוציא תהיה מספר מה וזאת החלוקה תציא גם כן אם תחלק חצי המספר על חצי המחלק וכן אם תחלק שלישית המספר על שלשית המחלק שאם תקצר שניהם כשוה על חצי או שלשית או רביעית או כמה שתוכל לקצר שניהם בשוה יציא המספר בחלקה שוה המשל בזה רצינו לחלק ב' אלפים שי"ו על כ"ד יעלה בחילוק צ"ו וחצי גם אם נקח החצי שהוא אלף קנ"ח ונחלק אותו על חצי המחלק שהוא י"ב יעלה בחילוק צ"ו וחצי גם אם ניקח ונחלק הרביעית על []שניהם הרביעית תקע"ט על ו' יעלה בחילוק צ"ו וחצי ואם שלשית הרביעית ר"ל שלשית תתקע"ט שהוא קצ"ו ונחלק אותו על שלישית ו' שהוא ב' יעלה בחילוק צ"ו וחצי וכן כל [] הדומה לזה ועיין בו ואם לא תוכל לקצר שניהם תעיין אם תראה ספרא באחדם תוכל לקצרם בחצי ובחמשית ובעשרית ואם תראה ה' באחדים גם תוכל
37[א]
[יט2] לקצרם [] אם תוכל לקצרם [] והנשאר שלא תמצא הקיצור [] החלוקה עד אחד וזה הקיצור [] בחלוקה והמשל בזה הנה נשאר לנו מחלוקה שס"ח ולא נדע המספר אשר בו נוכל לקצרו נחלק שס"ח המחלק על הנשאר לחלק שהוא קע"ו ישארו י"ו לחלק תחלק קע"ו על י"ו לא [] נשאר דבר וזה יורה כי בי"ו נוכל לקצר שניהם ואז ישובו י"א חלקים מכ"ג כי נחלק קע"ו על י"ו יעלו י"א גם נחלק שס"ח על י"ו יעלו כ"ג ונשארו י"ו וערכם לראשונים שוה ונשברים אדבר לזה בע"ה משל אחר נ"ד חלקים שנשארו לחלק על תתקנ"ו כזה וה נחלק המורה על נ"ד ונשארו ל"ח נחלק נ"ד על ל"ח [] והט נשארו י"ו גם ל"ח על י"ו נשארו ו' גם י"ו על ו' נשארו ד' גם ו' על ד' נשארו ב' גם ד' על ב' לא נשאר כלום ויורה כי על ב' נתקצרו שניהם ובשברים אדבר מז מזה בע"ה וגם אעשה פרק בקיצורי החברות ודרך השלושה בע"ה ית' פרק בסדר מאזני החיבור והכפל והגרעון והחילוק ואומר כי טעם שלא עשיתי מאזנים לכל מין ומין בפני עצמו או לכל משל ומשל הם שתי סיבות האחד שאם כתבתי מאזני בכל דבר תכבד המלאכה ואם עשיתי זה בקצת הספר היה לצורך חילוף השאלות והסיבה השנית בעבור כי החיבור והגרעון כל אחד מאזני חברו וכן הכפל והחילוק ובעבור אלה השתי סיבות עשיתי פרק מיוחד למאזני הארבעה מינים ואומר כי מאזני החיבור הוא שתגרע מן המספר המחובר הטור האחד מן השתי טורים ותשאר השני המשל חיבור תפ"ד עם שפ"ט ד ח ד יעלו תתע"ל כזה הצורה גרע תפ"ד מתתע"ג ט ח ג ישאר שפ"ט אף גרע שפ"ט מתתע"ג ישאר תפ"ד וכן ג ז ח כל הדומה לז' משל אחר משלושה טורים האחד
האחד
[37ב]
[כ1] [] והשלישית [] ומאתים כזה [] בשני טורים הראשונים [] מכל המחובר ישאר הממון [] השלישי שהוא ד' אלפים וס' עוד נזרע חיבור [] השני והשלישי שהוא ז' אלפים וק"ך מהגדול ישאר הממון הראשון שהוא ב' אלפים ופ' או גרע חיבור הראשון והשלישי שהוא ו' אלפים וק"ס מהגדול ישאר הממון השני שהוא ג' אלפים וס' וכן כל הדומה לזה דרך אחרת תחבר חשבון כל הטורים כאחדים בין באורך בין 4 3 2 ברוחב והעולה אחר שתשליכם ט'ט' בכף המאזנים האחד 2 1 3 וגם המקובץ מכל הטורים תשלכים ט'ט' והנשאר פחות מט' תתן 2 2 2 בכף שנייה ואם יהיו שוות מיטב 8 6 7 המשל חיברנו רל"ד עם שי"ב ועם רכ"ב ושלשתם יהיו תשס"ח נחבר הג' שורות כאחדים יהיו כ"א תשלכים ט'ט' נשארו ג _______ ג ג' ונתן ג' בקו המאנים גם שיור המקובץ שהם כ"א הוא ג' וניתן אותו בקו המאנים השנייה השנייה ויורה שהחיבור הוא טוב מאזני הגרעון נחבר המספר הגורע עם הנשאר ותציא הגדול והמשל אחר שגרענו שפ"ט מתפ"ד ישארו צ"ה שהוא הנשאר נחברם עם המספר הגרע שהוא שפ"ט יעלו תפ"ד הגדול או תאמר תפ"ד החיוב ושפ"ט החיוב ד ח ד הפרעון וצ"ה הנשאר לפרוע נחבר הפרעון הפרעון ט ח ג עם מה שנשאר לפרוע ותציא כל החיוב הנשאר ה ט מאזני הכפל נחלק היוציא מן הכפל על אחד משניהם ותצא השני והמשל כפל תפ"ד על שפ"ט הוא קמ"ז אלפים רע"ו והבחינה היא שתחלק זה המספר על הכופל ותציא הנכפל או בהפך מאזני המעוקב נחלק המעוקב על הכופל והיוציא בחילוק תחלק על פעם שנית ותציא הנכפל המשל בזה נכפול כ"ג על כ"ג ותציא
38[א] [כ2] תקכ"ט [] והוא המעוקב [] ותציא תקכ"ט עוד תחלק תק[כ"ט] [] בחלוק ראשון על כ"ג ותציא [] מאזני החילוק כפול המחלק על היוציא [] בכפל תחבר הנשאר ותציא הגדול המחולק המשל במספר הנזכר כפלנו המחלק שהוא שפ"ט על היוציא שהוא א' יעלה שפ"ט חיברנו עמו הנשאר לחלק שהוא צ"ה יעלה תפ"ד הגדול המחולק והרי לך המאזנים האמתיים אבל המנהג לתלמיד המתחיל [] כל עוד שלא הגיע לידיעת הד' מינים הנז' ישמשו עם מאזני ט' או מאזני ז' או שניהם להוציא האמת אם טעה באחד מהם כאשר אפרש עוד ואבאר מאזני ט' ומאזני ז' בקיצור ומהם תדע שאר האחרים ואומר כי מאזני ט' תעשה ראשנה שני קוים האחד נטוי והשני עומד וחותכים זה את זה כמו שתראה בצורה והקו ז הנטוי הוא המשקל שיהיו הימין והשמאל [] 0 + 0 [] והשמאל שוים והדרך הוא שחיברנו תפ"ד עם ב שפ"ט והיוציא יהיה תתע"ג ועתה נספור השטה העליונה כמו אחדים שהיא דח"ד יהיו י"ו תשלך מהם ט' נשארו ז' תתנם על העמוד גם נשאר מהשיטה* השנית ב' תן ב' למטה בעמוד תחבר * השטה ז' עם ב' ישאר ספרא והיא כמו שחיברת תפ"ד שפ"ט וניתן הספרה בקו המשקל גם תראה אם אם נשאר מכל המקובץ ספרא וניתן אותה בקו המשקל גם כן והנה נשאר ספרא והוא טוב מאזני החיבור מטורים רבים ואמר ח ד ה אם יהיו ג' טורים כזאת הצורה תחבר ד ב א תקמ"ח עם קכ"ד ועם שס"ה יעלו אלף ה ו ג ול"ז תשליכם ט'ט' נשארו ב' והם הבחינה ז ג 0 א ב ― ב גם מאלף ול"ז ישארו ב' והוא טוב
מאזני הכפל
[38ב] [כא1] [] ושיור הנכפל [] ושיור כל המספר בכף [] המשקל מוטב []כפל ל"ב על תשס"ה נשליך ה [] ישארו ה' למעלה בעמוד ומן 0 + 0 [] ספרא למטה וכפל ספרא על ה' ספרא בכף 0 המשקל וגם נמצא ספרא בכף הבחינה שהוא שיור היוציא היוציא מכל המספר ויורה שהוא טוב ב ג ה ו ז 0 ח ד ד ב מאזני החילוק תן שיור מה שעלה בחילוק על העמוד ושיור המחלק למטה וכפול שניהם ועל היוציא תחבר הנשאר לחלק אם נשאר והנשאר יהיה השמור בקו המשקל ושיור כל המספר המחולק יהיה בקו הבחינה והמשל חילקנו ה' ג אלפים תי"ב על כ"ב ג + ג הנה יעלה בחילוק ד רמ"ו והנשאר יהיה ג' [] ונתן אותו למעלה בעמוד ושיור המחלק שהוא כ"ב הוא ד' למטה בעמוד וכפלנו שניהם יהיו י"ב תשלך מהם ט' נשארו ג' בקו המשקל וכן נשארו מכל
39[א] [כא2]
וכן נשארו [] כל הדומה לזה [] והנה בדיקת ז' היא [] מהנשאר כמו שעשינו [] הבחינה וזולתה ממספר האחדים [] שלמה בחייוב כמו ט' גם כן שאם [] מקיבוץ ט' לא תמצה הטעות אבל עם שתבדוק עם בדיקת ז' תמצא הטעות בחיוב אבל אם תטעה מחיבור ז' וט' לא תמצא הטעות אבל אם תבדוק בה' או בזולתו מן האחדים ובלבד שלא יהיה עם ג' כי ג' בט' אז תמצא הטעות ואם מחיבור שלושתם או ממספר מורכב משלושתם לא תרגיש הטעות כמו משט"ו שהוא מורכב מט' וז' וה' זה הכלל שמה שלא ירגיש זה יגלה זה אבל אם תטעה מקיבוצם לא תרגיש הטעות כי דרך משל שאם תטעה ממספר שהוא מורכב מכל מספרי האחדים שהוא מדת האפשר לא תרגיש הטעות ודי בזה הערה כי הבדקה השלמה היא חיבור וגרעון כל אחד מאזני חבריו וכן כפל
וחילוק
השער
[39ב] [כב1]
[שער] [] [חל]קתיו לארבעה
[הפרק הראשון בחיבור השברים]
[הפרק השני בכפל] השברים
הפרק השלישי במגרעת השברים
הפרק הרביעי בחילוק השברים
[] פרק הראשון שהוא בחיבור השברים הנה לרוב חילופי הקדמות השברי ראוי הקדמות ודרכים רבים קודם החיבור ואומר ראשונה ההצעות וההקדמות הראויות על זה השער בכלל ומהם בידיעת כיצד נכתוב השברים והמורים וכיצד נקצרם וכיצד נקצר השברים ואב המורים ומה נעשה מהנשאר בחלוקה ואקדים הקדמה ואומר כי גדר המספר הוא ריבוי מקובץ מאחדים ואם כן האחד הוא יסוד המספר כאשר אמרתי במעלת היסוד ואשנה בכאן כי זה מקומו ואומר כי ידוע הוא כי ג' יסודות הם הבורא ית' בברואיו והנקודה בהנדסה והאחד במספר כי כאשר הבורא ית' הוא ראשון ואחרון בברואיו כן הנקודה ראשונה ואחרונה כי תכלית הקו שתי נקודות וכן האחד בכל מספר שהוא ראשון ואחרון כי כל מספר מונח הוא הוא גדול מאחד מן הקודם לו בטבע והרי לך כי כל יסוד תמצאנו בראש ובסוף וגבולו ועוד תדע כי שלושה עולמות הם עולם המלאכים ועולם הגלגלים ועולם השפל והנה העולם המלאכים אינו גוף ולא כוח בגוף כן האל ית' שמו שהוא
40[א] [כב2] יסודם ויסוד [] הענף ואין בו לא [] והנה הושאלה הנקודה [] העליונים ומן התחתונים ואילו [] גשם שאם תחלק הגשם יתחדשו [] קוים ותכלית הקו נקודות [] [] הושאל שם האחד יסוד למספר בעבור רוב סגולותיו שהוא יסוד לעצמו והוא מרובע והוא מעוקב והמספר הבא אחריו הוא *הוא יסוד ונקודה כפלו אשר לא כן בכל המספרים שלא תמצא מספר שיהיה כפל המספר הבא אחריו בעבור כי האחד הוא כמו עילה שאין לו אלא פאה אחת אשר היא עלולה מן האחד וכל מספר יש לו שתי פאות ומה שיעשה האחד בפאה אחת יעשה כל מספר בשתי פיאות קרובות או רחוקות מיחס שוה ולאחד אין לו יחס אלא בפיאה אחת הקרובה אליו [] בעבור שיש [] שם התחלה שהיא תחלת המספר שהיא השנים שהיא כפל האחד והמשל שתקח עשרה ו[] חצי שתי פאותיו שהם ט' וי"א וגם ח' וי"ב וגם ז' וי"ג וכן כל מספר עד סוף הפאה הראשונה הראשונה שהיא אחד * ועוד בעבור כי גשם אחד מספר וכן כל חלקיו לאין תכלית אנו מחלקים את האחד למטה כאשר אנו שתים כופלים אותו למעלה וכאשר שם מספר למעלה בלתי בעל תכלית כן השברים למטה בכל בלתי בעלי תכלית כי כאשר המספר המשולל מחומר ונמשך מן האחד ולמעלה כן אנו כופלים לאין תכלית כן אנחנו מחלקים לאין תכלית ואנו מדמין את האחד כמו גוף אשר אנו מחלקים אותו לאין תכלית ואנו אומרים חצי ושלישית ורביעית וכן חלקים נמשכים לאן תכלית ועוד כי מכל שבר אנו עושין בדמיון שברים לאין תכלית
הנמשכים אחריו שאם תדומה שלא תמצא ימצא אחד לא תדומה מספר כלל ואם תדומה מאין מספר כלל לא תדומה שאין אחד כי אין תלוי זה בזה
[40ב] [כג1] []חלק [] לשלושה [] שבר נקרא בשם [] עוד שכל שבר שהוא [] האחד כי האחד בין השלמים [] הוא יסוד וסיבה להם כמו [] במעלת היסוד והוראת כל שבר הוא המספר השלם שכנגדו שאם השבר תהיה ממעלה ראשונה גם הוראתו תהיה ממעלה האחדים ואם מעשרות יהיה מעשרות כי אני קורא מחצי עד תשיעית מעלה ראשונה והיא כנגד מעלת האחדים ועשרית וחלק מי"א וכן עד חלק מתשעים הוא נגד מעלת העשרות וכן לאין תכלית והאחד במרכז בינהם ואינו הוראה לשום שבר המשל בזה הנה חצי הוא במעלה ראשונה למטה מן האחד והוראתו במעלה ראשונה למעלה מן האחד ובעבור כי חצי הוא השבר היותר גדול הוראתו הם שנים היותר קטן מהמספר והנה השבר והוראתו הם פאות האחד והשבר הבא אחר חצי הוא שליש ממעלה ראשונה למטה מן האחד והוראתו או המורה השלם הוא שלושה * פאות שנייות לאחד [] וכן והם כולם ואם תהיה השבר ממעלה אחת או ממעלות רבות למטה מן האחד נקי תהיה המורה במעלות הדומות להם למעלה מן האחד וביחס וערך שוה לאחד שאם תהיה השבר חלק ממאה ועשר ואחד יהיה הוראתו קי"א ונאמר כי קי"א הוא השלם ועוד כי כאשר נאמר בשלמים זוג ונפרד או זוג הזוג או זוג הזוג והנפרד * כן נוכל או זוג הנפרד
41[א] כג [כג2] נוכל [] כמו שתראה [] שממנה [] הראשונה למ[] חצי עם ב' כי [] [] כי ג' שלישים עושים אחד [] א הנה השברים [] חצי ב הקטנים מן האחד והשניים
שלי ג מן הב' והשלישים מן
רביעי ד הג' כי א' על ב' יורה
חמשי ה חצי וא' על ג' יורה
ששי ו שלישית וא' על
שביעת ז ד' יורה רביעי'
שמינית ח וכן כולם
תשיעית ט עד כי א' על עשרה יורה עשרית וא' על מאה יורה חלק ממאה והנה השניים הם ב' על כל הנמשכים תחתיו והשלישיים ג' על כל הנמשכים תחתיו וכן כולם בהמשכה לאין תכלית ואציר בכאן לוח לוח אחד מא' עד י"א [] ושם תראה בראשו כל השברים אשר תוכל להרכיב מא' עד י"א אבל תעיין ותמצא בו סגולות המורכבים כי כל השברים אשר הם מוכפלים ממיני הנמשכות בסדר כמו שתראה בפרק שני מן השער * אין התפארת לכותבם בלתי המורכב מקוצרנם כמו שתראה דרך הקיצור במקומו והם כזה המקרן ב' רביעיים שישובו לחצי ומב' שלישים שישובו לשלישית וב' ששיים שישובו לשלישית
[41ב] [כד1] [] [] [] לב' [] לחצי וד' עשריות [] לב' חמשיות [] לג' רביעיות []יות ב' שלישות וו' עשיריות לג' חמשיות וכן א' תשיריות ד' חמשיות וכן ערך א' אל ד' כערך י"ב אל מ"ח א
י
יא ט
עשרין ח
תשיעי ז
שמני ו
שביע ה
ששי ד
חמיש ג
רביע ב
שליש חצי
יא י ט ח ז ו ה ד ג ב א כב כ יח יו יד יב 0א ח ו ד ב לג ל כז כד כא יח טו יב ט ו ג מד מ לו לב כח כד כ יו יב ח ד נה נ מה מ לה ל כה כ טו י ה סו ס נד מח מב לו ל כד יח יב ו עז ע סג נו מט מב לה כח כא יד ז פח פ עב סד נו מח מ לב כד יו ח צט צ פא עב סג נד מה לו כז יח ט קי ק צ פ ע ס נ מ ל כ י קכא קי צט פח עז סו נה מד לג כב יא קלב קכ קח צו פד עב ס מח לו כד יב קמג קל קיז קד צא עח סה נב לט כו יג קנד קמ קכו קיב צח פד ע נו מב כח יד וגם נוכל לעשות חלוקות רבות בדילוג או לקצר הנשאר בחלוקה כמו ל"ג שנשארו לחלק על צ"ט ששבו ליסודם שהוא ג' וט' והם ישובו לשליש וגם ישובו לאמצעיים וכל בעל שכל יעיין בו
42[א] [כד2] ומין [] הלוח לטור [] ב' וד' הנה [] בטור שני ששבו [] שלישי לא"ב ערכם [] ושלשית ו' ב' ושבו לא"ב וכן [] ועיין ותראה ובערכים תשכיל עוד ו[] המספר העליון הוא שם השברים והמספר התחתון הוא המורה ר"ל שמורה כמה שברים מן המספר העליון עשו אחד שלם והוא הדין אם יהיו שברים רבים כי העליונים יהיו מספר השברים והמספרים התחתונים יהיו המורים לכל שבר השלם כי לכל שבר מורה אחד אלא שתוכל לעשות מכולם מורה אחד כללי [] או מקצתם כמו שתראה אחר זה בע"ה בד' רדכים ותדע כיצד נקצר המורה ושנמצא בו כל השברים הראוים וענין קיצור המורה הוא רשות לדבר אחד אלא שהוא קל [] המעשה [] וקיצור המורה לדבר אחד הכרחית כאשר תראה במקומו בע"ה דרך בידעת המורה הכולל לשברים רבים מתחלפים ואומר כי מאחר שאמרנו מה הם השברים ומה הוא המורה שהוא הוראת השלם ועתה היה ראוי לנו לכתוב כיצד נוציא המורה הכללי וראשונה אומר דרך הנחת השברים או שברי שברים ואומר שרצינו להניח ג' חמישיות כזה וד' תשיעיות כזה וי"ב חלקים מי"ז כזה וקל"ז חלקים מרמ"א כזה ואם היו רבים הכתיבה היא עם ו' כמו חצי ושלישית להניח ג' חמשיות וד' תשיעיות וי"ב חלקים מי"ז וקל"ז חלקים ורביעית וחמשית ואם שבר השבר ה[] הוא עם מ' או בלי דבר כמו חצי מב' שלשות מג' רביעיות מד' חמשיות או חצי שלישית רביעית ואשוב לסדר השברים שאמרתי שהם ג' חמשיות
[42ב] [כה1] [] והנה [] שברי הראשון [] וד' שלם ואם [] יהיו ט' יהיה [] אחד שלם וגם אם על [] והנה שברי שברים הם כזה [א] – ב – ג והם חצי מב' שלישיות מג' רביעיות שכולם
ב – ג – ד הם רביע שלם ויגרעו ג' רביעיות לתשלום
אחד וכן כל הדומה מזה ובשאלות תראה ותתבונין זה בע"ה ועתה רצינו לדעת מורה כללי לשני טורים או לרבים ושברים מתחלפים שיכללם מורה אחד ואז כאשר יהיו השברים שוים תוכל לעשות מהם כל מה שתרצה אם לחבר או לגרוע או לחלק הכל כפי מה שתרצה וראשונה אומר כי הנחת שברים ממינים רבים יהיו באחד מארבעה דרכים הדרך האחד הוא שיהיו השברים שוים וטורים מתחלפים השני הפך זה שיהיו השברים מתחלפים והטורים שוים השלישי שיהיה השברים מתחלפים והטורים מתחלפים הרביעי הפך זה שיהיה השברים שוים והטורים שוים ופעמים תמצאם מורכבים הדרך הראשון שהוא שוה השברים ומתחלף המורה יחלק לשני חלוקות אם שלא תוכל לקצר המורה הכללי אם שתוכל לקצרו ואפילו הכי תמצא בו כל חלקי השברים ואתן משל לכל אחד ואתחיל בשברים שלא תוכל לקצר המורה הכללי [] א א א א ויהיה כזאת הצורה חצי ושלישית וחמשית [] ב ג ה ז ושביעית ומורהם ב' לחצי ומורה השליש ג' [] 0אב ומרה החמשית ה' ומורה השביעית ז' ועתה
43[א] [כה2] נוציא [] על השליש[] ואם קטון [] כסדר המשל [] יעלה ק"ה עוד [] אשר בו תמצה כל השברים כי [] וחמשיתו מ"ב ושביעיתו ל' [] הדין אם [] שלא כסדר כמו ב' על ז' שהם י"ב וי"ד על ג' שהם מ"ב ומ"ב על ה' שהם ר"י כנזכר משל שני לדרך הראשון בהוצאת המורה הכללי אשר תוכל לקצרו ויהיה כזאת הצורה ואומר א א א א שאם נכפול ונרכיב כל המורים כאשר ב ג ד ו עשינו בעבר יהיו קמ"ד והנה
דדא וו' על ד' הם כ"ד וכ"ד על ו' הם קמ"ד והנה
חצי קמ"ד ע"ב ושלישיתו מ"ח ורבעיתו ל"ו ושישיתו כ"ד ועתה נקצר המורה ונראה אם נמצא בו אלו החלקים והנה נקח חשבון שיהיו בו חצי ושלישית ורביעית ושישית ונמצאו בי"ב כי חציו ו' ושלישתו ד' ורביעיתו ג' ושישיתו ב' ואם כן המורה המקוצר הכללי הוא י"ב אבל אחר זה אדבר בדרכים הראויים לקצר המורה ובכאן אתערך מעט הדרך השני שהוא הפך הראשון שהוא כאשר יהיו השברים מתחלפים והמורים שוים ויהיו כזאת הצורה ואומר ב ג ד כי המורה הכללי הוא בלא קיצור ק"ה ה ה ה ואם תקצרהו יהיה ה' בעבור שלא נצטרך
ה אלא חמשית וגם בה' תמצא ב' חמשיות וג'
חמשיות וד' חמשיות וכן כל הדומה לזה הדרך השלישי שהוא שיהיה השברים והמורים מתחלפים
[43ב] [כו1] [] [] הראשונה [] ושלשה [] הכולל ל' ולא תוכל [] החמשית [] חצי וב' שלשיות וג' [רבעיות] כזה והנה המורה הכללי א ב ג הוא בלי קיצור הוא כ"ד ומקוצר הוא י"ב ב ג ד ובו תמצא גם כן כל החלקים אשר רצית בא הדרך הרביעי שהוא הפך השלישי הוא שהשברים והמורים [] שוים כזה הצורה ב ב ב והנה המורה המורה הכולל בלא קיצור הוא ה ה ה ק"ה והמקוצר ה' ואז תמצא בו כל החלקים
ה ברצית ובעבור שתדע קיצור המורים הכוללים
אכתוב בכאן הסדר וההנהג בידעתם ואם קיצור המורים הוא רשות בשברים שאינו אלא להציל מטורח רב אבל הוא חובה והכרחית בתנועות הגלגלים באיזה זמן ישובו ב' או יותר כוכבים אל המוקים אשר נסעו משם כאשר תראה במקומו בע"ה ודע כי בג' דרכים נוכל לקצר המורה וכל אחד יהיה יותר מקוצר מחברו ואומר כי המורה הכללי יוכל להיות אחד מארבעה דרכים או סדרים האחד שיהיה מורכב מכל המורים בשלמות כמו שאמרתי והשני מקוצר כאשר יהיה מורה מן המורים במורה אחר והשליש מקוצר כפי המספרים הנמשכים מאיזה כפל בסדר והרביעי מקוצר מקיצור המקוצר והנה מאלה הארבעה השלושה מהם []
44[א] [כו2] אבא[ר] [] המורה [] גדולים וקטנים [] הגדולים ותרכיב זה בזה [] א ב ג ד שהיא חצי [] ב ג ד ט וד' תשיעיות [] שלם/ואב הוא רי"ו ועם קיצור הוא [] מקוצר/וג הוא בד' כי חצי נמצאנו בד' וגם ג' נמצא בט' ואם כן נקח ט' וד' ונרכיבם ויהיו ל"ו וזה מורה כללי מקוצר דמיון אחר בזאת הצורה שהוא שלישית וששית וחצי וחלק מי"ד א א א א והנה המורה השלם תל"ב והמקוצר י"ב ג ו ב בא והנה מצאנו כי המורה השלם גדול מהמקוצר בגד\שלם ל"ו פעמים דימיון אחר בזה הצורה בא\מקוצר מעשרה א א א א א א א א א א שברים שהם חצי ושלשית ב ג ד ה ו 0א טו 0ב 0ג 0ו ורביעית וחמשית ושישית
000/000/חווג ועשירית וחלק מט"ו וחלק
0ו מכ' וחלק מל' וחלק מס' כל אלה העשרה שברים נמצאים בס' והמורה השלם הוא ג' אלף מספרים וקס"ח מספרים הסדר השני מקוצר כפי המספרים הנמשכים ומוכפלם על הראשון בסדר מה כמו שתראה כופלם כזה [] כי אם תמצא שני מספרים או יותר מאי זה [] שיהיה הגדול ואז תמצא בו כל חלקי הקטנים והמשל שיהיה המורה חצי שלישיתו []
[44ב] [כז1] [] והם []לא אחד [] כפול ואעפ"י []ספרים שלא [] [] דבר ארוך ולא נמצא [] שאומר באלה הבודדים []בודדים הבאים אחריהם כמו כי הבא אחר י"ט שהוא אחרון בלוח הוא כ"ג ואחריו כ"ט ואחריו ל"א וכן המשכת הבודדים כמו שאבאר סדר מציאותם
א ב ג ה ז יא יג יז יט ב ד ו י יד כב כו לד לח ד ח יב כ כח מד נב סח עו ח יו כד מ נו פח קד קלו קנב יו לב מח פ קיב קעו רח רעב שד לב סד צו קס רכד שנב תיו תקמד תרח סד קכח קצב שך תמח תשד תתלב א פח א ריו
מקומו בע"ה ודע כי מסגולותם הוא שישובו כל פרטי הלוח לראשונים אם תקצרם בחצים ועוד מסגולותם הוא שאם יהיה האחד שבר מאחר שתוכל לקצר שניהם לחציים עד שישובו לראשונים אע"פ שיהיו נמשכי הטור רבים אם שיהיו שניהם במרחק שוה לראשונהם ואם לא יהיו במרחק שוה יתקצרו עד שתשובו השבר לראשון כמו ס"ד שברים מאלף רי"ו שהוא המורה והם אחרונים
45[א] [כז2] מטור [] ישובו [] בעבור שהם [] [] לא ישובו [] י"ו ותכ"ח מהטורים [] ויהיה חלק מל"ח וכן אם תקח [] ואפילו שניהם יתקצרו כמו שאמרתי ואשוב לעניין הסדר [] מטור אחד [] המונה כפי המספרים הנמשכים בסדר ומוכפלים ע"ו ותר"ח מן כמו שאמר[] ואומר שאם תמצה שני מספרים או יותר האחרון ישובו מאיזה המשכה כסדר שיהיה שתקח הגדול ואז תמצא לרי"ו חלקים מקנ"ב בו כל חלקי הקטנים והמשל שיהיה המורה חצי ושלישית ורביעית וחמשית ושמנית ותשיעית וחלק מכ"ה כזאת הצורה א א א א א א א נרכיבם בשלמות ב ג ד ה ח ט הב זה על זה יהיה 00חא המורה השלם רי"ו אלפים והקצר אלף ות"ת כיצד ב' וד' הם בח' שהוא הגדול מן הטור הראשון ונניח ב'ד' ונקח ח' וג' הוא בט' על כן נניח ג' ונקח ט' והנה ה' הוא בכ"ה נניח ה' ונקח כ"ה והנה המורים שהנחנו הם ב' וג' וד' וה' ועשנו מורה מהנשארים שהם ח' ט' כ"ה והוא שכפלנו ח' על ט' יעלו ע"ב וע"ב על כ"ה יעלו אלף ות"ת והוא המוה הכולל משל אחר בזאת הצורה שהוא שמנית וחמשית וחלק מי"ו א א א א א א א א ושישית ושלישית וחלק מל"ו ח ה וא ו ג וג ט הב ותשעית וחלק מכ"ה הנה 00וטבא
[45ב] [כח1] [] והשישית [] ול"ו [] [] [אל]פים ות"ר והם [] בקיצור המורה הכללי [] זה בזה ועם חלקיהם והוא [] כי לא יכולתי לכתוב כל פרטיו [] הם רבים ויחיב בלבול למעיין ולא ארמוז הראוי לחכם ואומר שאם יהיה במורים מורה גדול אשר הוא יבוא מכפל ב' קטנים שנניח הגדול ונקח הקטנים ואם יבוא זה הגדול מכפל ב' מספרים אשר האחד הוא מורה אחר ואין השני מורה בשברים נניח השני בכלל המורים ואם המספר שנניח בכלל המורים הוא חצי ממורה אחר תשליך המורה האחר ובלבד שזה המונח תכפלהו בשנים או במספר זוג וכן אם המונח יהיה שליש או רביעית או חמשית או [] שתשלכהו ובלבד שתכפול המונח בשלושה או בארבעה או בחמשה וכן לנמשכים או במספרים הבאים מהם כמו אם היה שליש וראוי לכופלו בשלושה ויש לך מורה ו' או ט' או י"ב וכן הנמשכים או ח' או י"ב או י"ו והנמשכים לארבעה וכן לכולם ועם [] תבין כל זה בע"ה המשל בזה רצינו לדעת המורה הכללי המקוצר מאילו השברים שהם חמשית ותשעית וחלק מי"ד וחלק מי"ח וחלק מכ"ד וחלק מל"ב וחלק מנ' וחלק מס"ג ויהיה כזאת הצורה נתחיל א א א א א א א א להשליך מן הגדולים ונאמר ה ט דא חא דב בג 0ה גו כי האחרון שהוא ס"ג בא ג ז 0 0 וא 0א 0 מכפל ט' על ז' והנה ט' מורה 00ד0ה ח נמצא אבל ז' אינו נמצא מקוצר ד
46[א] [כח2] כמורים [] לא נכפול [] שהכרח הוא לכפול [] י"ד ונתן ז' תחתיו וספרא [] נמצאים מז' על ט' ועתה נראה [] והוא בא מכפל ה' על עשרה ונניח [] שהנה לנו על עשרה א נמצא חלק או חלקים מנ' [] ה' ונ' ושתתן כ"ה תחת נ' כי בהכפל כ"ה על מספר זוג אז תמצה חלקי ה' ונ' ועתה נראה אם נוכל להשליך ל"ב אם כולו אם קצתו ונניח חלקיו ממנו הנמשכים ממנו אם נוכל להשליך עמהם מורים אחרים והנה חלקיו הם י"ו וח' וד' וב' והנה נוכל להשליך ל"ב כי שהכפל י"ו על מספר זוג ימצא חלק מל"ב ואם חלקי הגדול נמצאים כל שכן הקטנים שהם י"ו ח' ד' ב' ועתה נראה אם נשליך כ"ד ונאמר כי כ"ד ימצא בהכפל ג' על ח' וג' הוא הוא בט' וח' הוא בי"ו ועתה נראה אם נשליך י"ח ואומר כי י"ח ימצא בהכפל ב' על ט' והנה ט' הוא נמצא במורים וב' הוא בי"ו והנה ראינו כי המורים הנשארים להרכיבם הם ה' וט' וז' וי"ו ועשרה והיה המורה השלם ד' אלפים תשנ"ג מספרים תשכ"ח אלפים והמורה המקוצר חמשים אלפים וארבע מאות ואם תרצה לבדקם חלקם לכל אלה השברים ואם תמצאם מוטב ואם לא שוב לעיין ותמצאם סדר בידעת קיצור השברים ואב המורים ואומר כי כאשר יהיה בידך מאיזו חלוקה שיהיה שברים מה מכללים מה ותוכל להשיבם לשבר אחד או לשברים יותר גדולים יהיה יותר טוב מותר ראוי אבל הוא רשות ולא חובה כי גם בלא קיצור תמצא כל השברים או שברי שברים אבל בטורח גדול ולהציל מן הטורח ראוי שתקצרם אם עד תכליתם
[46ב] [כט1] []לא [] תכליתם [] המשל כי האומר [] כל כך נאות [] הכל שוה כי ערך שפ"ד אל [] והוא הדין האמצעיים שהם ז' כי כל [] ואם יהיו השברים תקצר השברים עד קצת או שיהיו מן הנמשכים הבודדים דומים לזוג הזוג והנפרד או לזוג הנפרד שתוכל לחלקם פעמים רבים או פעם אחד ולא ישובו לאחד והמשל קכ"ד חלקים מרפ"ד בשלם כי תוכל לקצרם עד שישובו ללא חלקים מע"א בשלים ועוד יש מין * [] שלישי שלא תוכל עיון לקצר השברים כלל וזה דומה למספר הבודד כמו ע"ג חלקים מצ"ג שלא תוכל לקצרם כלל ועתה אכתוב כללים לדעת באיזה מספר תקצרם כי פעמים יהיו השברים זוג הזוג שתוכל לקצרו עד אחד ואב המורים וזה יהיה בשני עיונים בודד או בהפך ובעבור זה אורך בדרך זו תלך [] העיון הראשון הוא כי המספר אשר עמו תרצק יחד השברים ואב המורים ואומר כי כאשר יהיה בדרך מספר מה משברים ותרצה לקצרם בשלישית או בשישית או בתשעית תעיין ראשונה אם יהיה המספר אשר במעלה ראשונה זוג או נפרד דע שאם יש למספר שלישית יש בו שיש לקצרם עיין במעלת האחדים אם יש בה ספרה תוכלם לקצרם בעשרים ובחמשית ובחצי ואם תוכל להשליכו ט'ט' כמו שתראה במשלים תוכל לקצרו בתשיעית ובששית ובשלישית ואם נשארו באחדים ו' יש לו ששית ושלישית ואין לו תשיעית
47[א] [כט2] ו[] המספר [] ואם [] ב' אין לו אלא [] אלא שביעית כי הוא [] גדול ואולי יהיה בודד [] או עם שתדע הבודדים כמו שתראה בע"ה [] די כי זה הוא ממה שאין הקפה בו אבל שכל המשכיל יקיף בו המשל בזה הרי שהיו לנו קצ"ח שברים מט' אלפים שע"ח בשלם ויהיו בזאת ח ט א הצורה שם השברים למעלה והמורה ח ז ג א למטה וקו מפסיק ביניהם והנה עתה נחבר מעלות השבר[] האחדים מכל מעלה לנמשכת לה כי א' הוא עשרה על ט' ועם ט' היו י"ט נשליך י"ח בט' ישאר א' שהוא עשרה על ח' וח' היו י"ח ונשליכם ולא נשאר כלום ואז נדע כי השברים יתקצרו על תשעית ועל ששית ועל שלישית כי כולם בט' אבל נעיין ונראה אם נוכל לקצר המורה באחד מכל אילו החלוקות נחבר זה על זה כנזר' והנה ט' כפל וג' על ז' הם ל"ז ונשאר א' ועל ח' הוא י"ח ולא נשאר כלום ואם נוכל מצד שניהם לקצרם בשלישית ובשישית ותשעית והרגל המעשה הוא בזה הצורה הנה נתחיל א א בשברים ונאמר כי שלישית קצ"ח הם ס"ו ב ב והם עליו ושלישת המורה הוא ג' אלפים ו ו קכ"ו ונתנם תחת המורה ואז יהיה ערך ח ט א ח ז ג ט ו ב א ג ב ד 0 א א ב ה
[47ב] [ל1] [] אלפים [] נקצרם עוד אם [] ולשמור מן [] הוא כ"ב ושלישית [] נקצרם עוד בחצי יהיו [] הרביעים תקכ"א והנה שניהם [] ולא נוכל לקצרם עוד והנה היה לנו ארבעה מיני שברים וארבעה מני מורים וערך כל אחד עם בן גילו כערך הראשונים וכן כל הדומה לזה והנה זה המשל עצמו הוא בידיעת מה נעשה מהנשאר בחלוקה [] כי זה יועיל בנשאר מן השלמים ובנשאר מן השברים ובשאלות ואומר כי כאשר תחלק איזה מספר מאיזה מן שיהיה ונשארו לחלק מספרים מן המין ההוא די כי ראשונה תוכל לומר כי הנשאר מאיזה מין שיהיה הוא השבר שיהיה ראוי להוסיף על השלמים על אחד כי השלמים היוצאים לכל אחד בחלוקה הוא הראוי לכל אחד מן המספרים המחלקים שהם המורה וזה השבר גם כן שהוא שבר מן המורה באחד שנחשוב המורה לאחד וכבר דברנו מזה בפרק החילוק ואמנם זה החלק הוא מן השלם אבל אינו מן החלקים שיכלל זה האחד כמו בדרך משל אם חלקנו שס"ה יום לשלשים יעלה בחילוק י"ב ונשארו ה' ימים ונוכל לענות כי יבא לכל אחד י"ב ימים וה' חלקים מל' בשלים וזה החשבון מדוקדק בתכלית אבל לא דקדקנו אותו בחשבון החלקים שיכללו הימים שהם שעות ודקים ושניים ושלישים וכן בהמשכה כפי מה שנרצה לדקדוק אם לא בא לשבר מכוון
48[א] [ל2] ומשל [] [] השני הוא המורכבים [] [ש]תחלק המורה ושברי שברים [] על הנשאר ואם אב המורים וזה ל[] נשאר עוד לחלק ואומר כי מאחר כי מיני השברים [] עשה ממנו מורה ושלישית ורביעית וכן כל הנמשכים [] וחלק עליו המורה או לגורעם או לחלקם בעבור חלופם כי חלוק רבי[] שעליו חילקת ואם קשה ומספרים אחרים הם יותר קשים ואם נשוה החמשית נשאר עוד עשה והרביעית למין אחד או נוכל לחלקו בשלמים כמו שתראה ממנו מורה וכן ואומר כי דרך ההשואה נופל אם בשני מני שברים מתחלפים עוד תחזור לחלק אם בשברים רבים [] כי דרך ההשואה היא בכלל זה על זה עד ובפרט כי הפרט הוא בשני מיני שברים כמו ג' רביעיות וד' שיחלק בשלמות חמשיות והנה השואתו היא שתכפול שברי כל אחד על מורה שלא ישאר דבר חברו ואז יהיו שוים ואז תראה השבר הגדול והקטן ותוכל לחבר לחלק ובזה המורה אותם או לעשות מהם מה שתרצה וגם המורים שהיו לכל האחרון תוכל שבר בראשנה לא יהיו נאותים לאילו השברים המחודשים אבל לקצר השני מספרים אם תכפול מורה על מורה יהיה היוציא מורה אחד ואב כללי ואם תתחלק עד אחד לכל השברים השוים המחודשים כאשר קדם באורו והמשל לא תוכל לקצרו בזאת הצורה הא וא נכפול ג' שהוא שברי כי אם באחד הרביעיות על ג ד ה' שהוא מורה החמשיות יעלו ט"ו והמשל בזה ונתנם על ג' ד X ה להורות כי ט"ו שוה לג' וכן נכפול רצינו 20 לקצור אלף רצ"ג ד' שהוא שברי החמשיות על ד' שהוא מורה הרביעיות יעלו י"ו חלקים מאלף שע"ז ונתנם על ד' להורות כי י"ו שוה לד' ואז ידענו כי ג' חמשיות כזה | ג ט ב א וחלק ג' רביעיות קטן מד' חמשיות מאחד כי האחד ט"ו והשני ז ז ג א י"ו אבל לא ידענו זה האחד חלק מכמה בשלם הוא עד השואת שברים שנדע מורה כולל לשני המורים ולדעת זה נכפול השני נחלק המורה על השברים נשארו פ"ד נעשה מפ"ד מורה ונחלק עליו אלף רצ"ג שהיה המורה ונשארו ל"ג ונעשה מהם מורה ונחלק עליו פ"ד שהיה המורה שעבר נשארו י"ח נעשה מהם מורה ונחלק עליהם ל"ג שהיה המורה שעבר נשארו ט"ו נחלק על ט"ו י"ח נשארו ג' נחלק על ג' ט"ו לא נשאר כלום ואם כן בשלישית נוכל לקצור שניהם בצד המורה נחלקהו בשלישית יעלה החילוק [] גם נחלק השברים בשלישית יעלה בחילוק תל"א ואם כן הנשאר מקוצר בשלישית יהיו תל"א חלקים מ[] שלם משל שני קנ"ג חלקים מרל"ד תחלק רל"ד על קנ"ג הנשאר פ"א תחלק קנ"ג על
[48ב] [לא1] [] והוא [] כי ערך ג' אל ד' [] כערך י"ו אל כ' כי [] וד' חמשיות הם כמו [] ג' רביעיות קטן מד' חמשיות מחלק [] זה לזה משני []נים והדרך השני שהוא דרך כוללי לשני מני שברים או לרבים ומזה אדבר והוא שתוציא אב השברים המורים ותחלקהו על השבר המורה הפרטי ותכפלהו על מספר השבריו והוא המבוקש ומשל בג' אב 0ב חמשיות וד' שביעיות כזה תכפול המורים ג ד זה על זה ותציא האב הכולל שהוא ל"ה חלק ה ז ל"ה על ה' בעבור החמשית והיוציא שהוא
הג ז' תכפול על ג' בעבור שאמר ג' חמשיות
ויעלו כ"א תניחם על ג' חמשיות כי ערכם שוה עוד חלק ל"ה על ז' בעבור השביעיות ותציא ה' כפלם בד' בעבור שאמר ד' שביעיות ויעלו כ' תניחם על ד' שביעיות כי ערכם שוה וכן לכל כיוציא בזה הדומה לזה וכן אם היו השברים ממנים רבים שתכפול על המורים זה בזה והיוציא על האחר אם כסדר אם שלא כסדר וכן עד הסוף והיוציא הוא המורה הכולל לכל המורים חלקהו על המורה השבר וכופלהו על מספר השבר ואם אין לו אלא שבר אחר כמו שלשי או חלקהו על השבר והיוציא הוא הראוי כי אין צריך לכפול כי רביעית אין לו מספר שברים משל שני לשברים רבים ממינים מתחלפים כמו שרצינו לשוות חצי ושלישית ורביעית וחמשית שיווי וששית ושביעית ושמנית שאילו המינים הם שוים השברים שברים ומתחלפי המורים כזאת הצורה והמעשה הוא שתכפול המורים מתחלפים
על פ"א נשארו ע"ב תחלק פ"א על ע"ב נשארו ט' תחלק ע"ב על ט' לא נשאר כלום ויורה כי בט' יתקצרו קנ"ג ורל"ד וכל חילוק שיבוא עד אחד תשוהו כי לא יתקצר כי אם באחד והוא משוטף לכל מספר בודד כי דרך משל י"ג חלקים מי"ט תחלק י"ט לי"ג נשארו ו' תחלק י"ג לג' ישאר א' וזה יורה שאין לו חלק זולת א' וכן כל כיוצא בזה ואילו הדרכים תמצה בשלמים ואם כתבתי שם בקיצור
49[א] [לא2] זה על [] קח מזה המורה [] שהוא חצי וקח [] וכרגיל המעשה הוא שנכפול [] 0בד 0חב 0אב חוא 0דא 0בא ה0א []
א א א א א א א [] ב ג ד ה ו ז ח תהיה הרכבת בגדהו []
המורה || 0דח || המקוצר המורה המקוצר ה[] והנה חציו ת"ך ונתנהו על חצי ושלישיתו ר"ף ורביעיתו ר"י על הרביעית וחמשית קס"ח על החמשית ושישיתו ק"מ על השישית ושביעיתו ק"ך על השביעית ושמניתו ק"ה על השמנית והרי לך כל השברים שוים בני אב אחד ותוכל לעשות מהם כמו משלמים ואז ערך א' אל ב' שיורה חציו כערך ת"ך אל תת"ם שיורה השלם* כי כל חצי תת"ם מאלה השברים עושים אחד שלם וכן ערך א' אל ג' כערך ר"ף אל תת"ם וכן ערך א' אל ד' אל ד כערך ר"י אל תת"ם שיורה הרביעית וכן כערך א' אל ה' ואל ו' ואל ז' ואל ח' כן ערך קס"ח וק"מ וק"ך וק"ה אל תת"ם והרי לך הראוי לכולם ויהיו החצי והשליש והרביע וכן כולם חלקים שוים לזה המורה הכולל וכן תנהיג לכל השברים שיהיו חלקהם יותר מאחד אבל אם יהיו חלקהם יותר מאחד כמו ב' שלישיות וג' רביעית ועוד רבים שתקח ב' שלישיות המורה הכולל וג' רביעיותיו וכן כולם כאשר תראה עוד אחר זה בע"ה משל שלישי שיהיו השברים והמורים מתחלפים כמו ג' חמשיות ד' שביעיות וז' עשיריות וה' ששיות כזאת הצורה השואת שברים ובא 0בא זדא הזא נרכיב ה' על ז' והעולה על ז' יעלו
ג ד ז ה ר"י וזה אב המורים ומה שלא
ה ז 0א ו לקחנו עשרה הוא בעבור כי עשרית
0אב
[49ב] [לב1] [] ועתה נקח [] החמשית יהיו [] ג' חמשיות כי כן [] ז' יהיו [] נכפלם על בשלם [] מונח על ד' שביעיות כי כן הוא [] על עשרה יהיו כ"א נכפלם על ז' יעלו [] ז' עשיריות כי כן הוא מרי' וכן נחלק ר"י על ו' היוציא יהיה ל"ה נכפלם על ה' יעלו קע"ה והוא מונח על ה' ששיות כי כן הוא מרי' שהוא המורה הכולל ואז יהיה קכ"ו ג' חמשיות וק"ך ד' שביעיות וקמ"ז ז' עשריות וקמ"ה ה' ששיות ויהיו כל השברים שוים זה אל זה כי ערך השברים המחודשים למורה הכולל כערך השברים הראשונים אל מוריהם וכן כל כדומה לזה משל רביעי בשברי שברים ואומר כי השואת שברי שברים [השוא[ת] שברי אם הוא שבר משבר השבר הוא מן הכלל או הדבר שברים השני ואם הוא שבר השבר נוכל אם נרצה לשוותו עם הכלל הראשון כמו השואל השוואת שבר השבר פחות שברי המספר אשר ממנו נשאל על מורה הראשון השואל והיוציא תניח על האחרון וממנו תקח מה שתרצה כמו שרצינו לשוות ב' שלישיות מג' רביעיות ר"ל לקחת מג' רביע ב שלשיות מג' רבי' כמו שראה בגרעון כפול ג' שברי האחרון על מורה הראשון שהוא ג' יהיו ט' על ג' רביעית נקח מהם מהם ב' שלשיות שהם ו' [] תניחנו על ב' שלשיות ועתה נוציא המורה והוא י"ב תקצר יהיה הנשאל חצי כאשר תקצרהו והנה נעשה זה המשל בדרך השני הכולל והנה הדרך הוא שראשונה תוציא המורה הכולל וממנו תקח החלקים שתרצה ומשל חמשי רצינו
50[א] ל"ב [לב2] ג' [] הוא [] יעלו י"ו [] ג' רביעיותיו שהם י"ב [] ג' שלישיות אחד והוא מה [שרצינו] משל ששי רצינו חצי שלישית א ב ו דב השואת רביעית חמשית כזה הצורה א א א א שברי שברים נוציא המורה הכללי בלא קיצור והוא ב ג ד ה 0בא ק"ך והנה חמשית ק"ך הוא כ"ד מונח על החמשית ורביעית כ"ד הוא ששה והוא על הרביעית ושלישית ששה הוא ב' על השלישי וחצי ב' אחד שזה האחד הוא המבוקש שלמים ושברים משל שביעי רצינו לשוות שלמים ושבר כפול ז ד השלמים במורה השברים וזה כמו ז' שלמים ה ד' חמשיות כפול ז' בה' שהוא המורה יהיו ל"ה חמשיות הג משל שמני רצינו לשוות שלמים ושברים תשוה השברים ה ואחר כפול השלמים על המורה הכללי וזה כמו אחר משלמים שרצינו לשוות שמונה שלמים וה' ששיות וו' שביעיות ושברים וגג | ח | הב וג כזה יהיה המורה מ"ב וחלקי השברים כ"ה בד ה ו ול"ו כפול ח' על מ"ב שהוא המורה יהיו ו ז של"ו חלקי מ"ב והוא הדרוש ותוכל לקצרו בד עד כ"ד חלקי ג' שאם תחלקהו עליו יעלו ח' שלמים משל תשעי שרצינו לשוות שלמים ושברים על שלמים שברים אחר משלמים תשוה כל השברים למורה אחד ואחר כפול השלמים ושברי שברים במורה כמו שרצינו לשוות ד' שלמים וחצי וב' שלישיות וג' רביעיות והחלק השני לבד בזאת הצורה ד' חמשיות ה' ששיות ו' שביעיות בזאת הצורה
[50ב] [לג1] [] נוציא [] [] והוא ת"ך יונח [] על ת"ך יעלו אלף [] השוים למורה ואחר נחלקם [] כמו שתראה במשלים בע"ה משל עשירי שאם יהיו שלמים ושברים על שלמים שלמים ושברים על ושברים תשוה כל השברים למורה כללי כפול שלמים ושברים השלמים במורה והעולה תחברהו עם חלקי שבריו כמו שרצינו לשוות ג' שלמים וד' חמשיות וה' ששיות על ד' שלמים עם חזב | חד 0ה | הבג 0ד הד ב' שלישיות ג | 0חא | ד ה | ד | 0דב ב ג ג' רביעיות 0ו | ה ו | 0ו ג ד הנה המורה 0ו לכולם הוא ס' כפול ג' שלמים על ס' יהיו ק"ף תחבר ק"ף עם חלקי שברו שהם נ' ומ"ח יהיו רע"ח החלק האחד עוד כפול ד' שלמים על ס' יהיו ר"מ תחבר עמו חלקי שבריו שהם מ"ה ומ' יהיו שכ"ה החלק השני וכולם תחת מורה אחד עתה חבר או גרע או חלק זה מזה וכן כל הדומה לזה ובהרגיל המעשה נראה כל זה בע"ה כי בכאן די בזה ודע כי השואת ימים שעות ודקים ושניים ושלישיים ורביעיים והנמשכים הוא שתתן הכל בשבר היותר קטן וזה שתכפול דמים בכ"ד ועל העולה תחבר השעות אשר בידך אם יש שעות ויהיה הכל שעות תכפלם בס' והיוציא יהיו דקים ותחבר עליהם הדקים וכפל הדקים על
51[א] [לג2] כן [] לנמשכים [] הפרק מן [] הראשון ואומר [] אם שיהיו שני מינים או יותר [] שברים עם שברי שברים או שברי [] או מין אחד על ב' מינים או יותר וכן כל מה [] תשוים ראשונה ואחר תחברם והעולה תחלקם על המורים והעולה בחילוק הם השלמים היוציאם מחיבור כל השברים המשל בזה רצינו לחבר ג' חמשיות ג × ד עם ד' שביעיות בזאת ה אב 0ב ה ז הצורה נשוים עם הדרך הראשון כל ג ד חיבור שבר במורה חברו וזה שנכפול ג' על ה ז שבר עם שבר ז' יעלו כ"א מונח על ג' חמשיות גם ד' על הג ה' יעלו ב' מונח על ד' שביעיות גם ה' על ז' יעלו ל"ה שהוא אב המורים למטה ועתה נחבר כ"א עם כ' יעלו מ"א והם שברים מל"ה בשלם שאם תחלקם על ל"ה יציא אחד שלם וששה חלקים מל"ה בשלם כזה א משל שני רצינו לחבר שברים עם שברי שברים הנה חיבור נעשה בזה שתי השואות הראשונה השואת שברים עם שברי שברים השברי שברים והשנית השואת שניהם כי השברי שברים כאשר אקח ממנו הנשאל יהיו כמו שברים עם שברים כמשל שעבר ואחר תחברם וזה כמו שרצינו לחבר ה' תשיעיות עם ד' חמשיות שביעית כזאת הצורה ד ה וראשונה נשוה השברי שברים וזה שנוציא ה ד א ט ה ז הג האג [51ב] [לד1] [] ונתן אותו [] ואנחנו [] והוא [] והוא השואת השברי שברים [] בשלם נשום עם ה' תשיעיות [] שברים עם שברים כמשל הראשון [] זאת הצורה הזא וג והמורה הוא שט"ו וד' תשיעיותיו ה ד הם קע"ה וד' חלקים מל"ה הם ל"ו כי ט הג נחלק שט"ו על ל"ה יעלה ט' [] וט' פעמים האג ד' הם ל"ו כנזכר ואז יהיו שוים כי ערך ה' אל ט' כערך קע"ה קע"ה אל שט"ו וכן ערך ד' אל ל"ה כערך ל"ו אל שט"ו ועוד כי ט' אל ה' פעם אחד וז' חמשיות וכן קע"ה אל שט"ו אל קע"ה פעם וד' חמשיות והנה אחר שהם חלקים שברים שוים ממורה אחד נחברם קע"ה עם ל"ו יהיו רי"א ולא הגיע לשלם כי השלם הוא שט"ו והנה עלה בידינו כי כאשר נחבר ה' תשיעיות עם ד' חומשי שביעית שיהיה העולה רי"א חלקים עשינו כזה אאב משל שלשי רצינו לחבר שברי שברים עם האג חבור שברי שברים תשוים שני פעמים כנזכר ואחר שברי שברים עם נחברם כמו שרצינו לחבר ג' רביעי ד' חומשים עם ב' שברי שברים שלישי ב' חומשים ויהיה כזאת הצורה בא וא ד ו נבקש המורה הכולל לכל שבר השבר ג ד ב ב ויהיה לג' רביעי ד' חמשים כ' ולב' שלישי ד ה ג ה ב' חומשים ט"ו ולקחנו מן הראשון 0ב הא ד' חמשיות והמורה [] וזה השבר ה[] ולקחנו מזה השבר ג' רביעיותיו שהם י"ב וזה המבוקש משברי
52[א]
ל"ד [לד2] השבר [] וזה השבר [] משברי השבר ה[] הוא י"ב חלקים מכ' והשני [] תוכל לקצרו לג' חמשיות להקל [] הד 0ב נשוים יהיו הג' חמשיות מ"ה [] ג ד והד' חלקים מט"ו יהיו כ' חלקים מע"ה [] ה הא שהם שברים שוים אל מורה אחד וחברם יהיו ס"ד
הז
ולא יעלו לאחד שלם ויהיו כזה הו ס"ה חלקים מע"ה בשלם ואם נקצרם בחמשית יהיו הז י"ג חלקים מט"ו ולא נוכל לקצרם עוד כי השברים בודדים ותוכל לעשות אלה ההשואות בדרך אחרת * שתקח המורה ובהשואה אחת הכולל ואם תרצה לקצרו ויהיו כן והנה ד' חמשיות החלק הראשון הם מ"ח וג' רביעיות מ"ח הם [] ל"ו וזה הנשאל משבר השבר הראשון ולשבר השבר השני הנה ב' חמשיות מס' הם כ"ד וב' שלשיות כ"ד הם י"ו והם שבר השבר הנשאל מן השבר השני נחבר ל"ו וי"ו יהיו נ"ב חלקים מס' שאם * בחצי *תקצרם יהיו י"ג חלקים מט"ו בשלם כמו שנזכר ודי בזה כי בחיבור משקל ומידה תלמוד ממה שאמרנו עוד תראה כל זה בחיבור הדברים המתחלפים המורכבים בע"ה
The second Chapter on the Multiplication of Fractions and Fractions of Fractions of all Kinds |
הפרק השני בכפל שברים ושברי שברים למינהם |
| וזה יהיה בשני דרכים אשר הדרך הראשון דרך כולל והשני חלקי | |
| [וראשונה אומר כי כפל השברים הוא] שתכפול שבר על שבר ומורה על מורה והיוצא הוא המבוקש | |
| המשל בזה רצינו לכפול לעולם הכפל לא יעלה לאחד אלא לעולם יהיה שבר כי שבר על |
[52ב] [לה1] [] כי כאשר [] האחד כן [] מן האחד כי [] ט' כן האומר ג' שברים שליש על שליש [] תשעה למ[] כאשר [] זה השער
| הדרך הראשון הכולל בכפל השברים | |
| ואומר כי כפל השברים והשברי שברים הוא שתכפול שבר על שבר ומורה על מורה והיוציא הוא המבוקש | |
| [2]כפל שברים על שברים | |
|
|
המשל בזה רצינו לכפול שברים על שברים כמו ב' שלישיות על הדומה להם |
| כזה | |
| נכפול ב' על ב' יהיו ד' | |
| וג' על ג' יהיו ט' | |
|
|
והנה הם ד' תשיעיות |
| [3]כפל שבר על שבר | |
|
|
משל שני רצינו לכפול ד' חמשיים על ה' תשיעים |
| כזה | |
| נכפול ד' על ה' יהיו כ' ו[] ה' על ט' יהיו מ"ה והם כ' חלקים ממ"ה בשלם שאם תקצרם בחמש יהיו ד' תשיעיות | |
| [4]כפל שברים על שברים | |
|
|
משל שלישי רצינו לכפול שברים על שברים ממנים רבים כמו ב' חמשיות ג' רביעיות ד' חמשיות ב' שביעיות ז' שמניות |
| כזאת הצורה | |
| כפלנו שברים זה על זה יהיו של"ו גם המורים יעלו ה' אלפים ת"ר ויהיו כמו שתראה בסוף הצורה ואם תקצרם יהיו ג' חלקים מחמשים | |
| כפל שברי שברים | |
| משל רביעית בכפל שברי שברים ואומר כי כפל שברי שברים הוא כמנהג שעשינו לשברים כמו שרצינו שרצינו לכפול שברים ושברי שברים כמו ג' שביעיות וד' חמשיו שמנית בצורה |
53[א] ל"ה [לה2] הזאת [] גם במורים [] נקצרם יהיו ג' חלקים [] ממנים רבים כי [] משל אחר שרצינו לכפול [] שברים ושברי שברים כמו חצי ושני שלישי רביעית על | | | [ | ] חצי ושלישית ושלושה רביעי חמשית נכפול שבר על שבר יעלו ששה גם מורה על מורה יעלו ב' מקוצר אלפים תק"פ ויהיו ששה חלקים מב' אלפים תק"פ כז ואם תקצרם יהיו חלק מת"פ הדרך השני הוא שתעשה כמנהג כפל כל שבר שתכפול שבר על שבר ומורה על מורה אלא שתקצרם * אז עם הפוך השברים תוכל והכל שוה המשל בזה רצינו לכפול חצי וב' שלישיות וג' רביעיות וד' חמשיות וה' ששיות ה' תשיעיות על כזה הצורה הנה נרצה איזה שבר ג' עשיריות כזה יהיה דומה לאי זה מורה נפילם ה ג נכפול ונכפול הנשאר שאין להם דומים כי ב' הראשון יהיה מורה הב' ט י שברים השני ונפילם ונשאר שבר א' גם ג' שני יהיה מורה הג' השלישי על שברים ונפילם גם ד' שלשים יהיה מורה ד' רביעי חמשיים ונפילם גם ה' יהיה מורה על מורה מורה ה' חמשי שישיים ונפילם ונשאר ו' שאין לו שבר […] תחת א' ויהיו ט"ו חלקים הראשון ויהיה שישית כזה ואם תרצה לראות אם זה אמת מצ' כזה הא כפול השברים והמורים כמנהג היו השברים ק"ך והמורים 0ט תש"ך תקצרם ישובו לשישית כנזכר ואם לא יהיו דומים מ[] נקצרם צד אלא כב' עם ד' או עם ו' או עם ח' וכן ג' עם ו' או עם יהיו חלק מששה ט' או עם י"ב קח השבר והמורה אשר להם דמיון מה [] כזה א למורה באי זה מקום שתמצאהו ת[]לגהו ותתנהו תחתיו ותחשבהו ו כפי והדרך האחר הוא שנהפוך הה' שברים על העשרה והג' על הט' כזה ג ה ט י תקצרם יהיו הראשון שלישית כזה א והשנית חצי כזה א נכפלם א' על א' יהיו א' וב' על ג' ג יהיו ו' והוא המורה ב [] ששית כנזכ' וכן אם יהיו רבים כמו חצי
[53ב] [לו1] [] [] משל ששי [] מט"ו וה' חלקים [] תשעיים וג' חלקים [] []יחס מה [] השבר הראשון שהוא ב' יחסו אל ד' שהוא השבר המורה השלישי ונקצרהו יהיה חצי זה ראש צורה אחרת והשבר השני הוא ה' יחסו אל המורה הראשון יחס שליש ונקצרהו יהיו שליש והוא שבר שני והשבר השלש והוא ג' יחסו אל ט' יחס שלישית גם כן ונקצרהו והוא שליש והוא שבר שלישי בצורה השנית והשבר הרביעית שהוא ז' יחסו אל כ"ח שהוא המורה השנית יחס רביעית וקצרהו רביעית והוא שבר רביעי בצורה השנית והשבר החמשי הוא ח' יחסו אל י"ב יחס שתי שלשיות נקצרהו יהיה שתי שלשיות והוא שבר חמשי בצורה השנית והשבר השישי שהוא ג' יחסו אל י"ח יחס ששית נקצרהו יהיה ששית והוא שבר ששי בצורה השנית ועתה כפול שבר על שבר יעלו שנים גם כפול המורים יעלו אלף רצ"ו ואם כפלנו כל השברים בשלמות יעלו לאפים ולרבבות ועתה יצא לנו מזה הכפל ב' חלקים מאלף רצ"ו תקצרם בחצי יהיו חלק אחד מתרמ"ח כזה עיון אחר בזה הדרך הוא שכאשר תעשה הצורה השנית ותוכל עוד לקצר תקצר עד שלא תמצא יחס בשבר עם
עד ב' חמשי ותן הא' על הג' במקום ואז יהיה חלק [] בלא קיצור
54[א] [לו2] [] תשיעיות
שהוא ג' יחסו אל ט' יחס ראשון לזה הצורה השנית השני שהוא ד' יחסו אל ח' ואחר הקיצור הוא חצי והוא שבר שני לצורה השנית והשבר השלשי שהם ה' יחסו אל המורה הראשון שהוא ה' יחס שלם ולא נשים לב עליו כי כפל בשלם והשבר הרביעי שהוא ו' יחסו אל עשרה יחס ג'* חמשיות והוא שבר שלישי ס' והשבר החמשי שהוא ז' הוא יחס שלם וחלק לו עם מורה רביעית שהוא ז' וחלק לו והנה עלה מכל זה שליש וחצי וחצי וג' חמשיות וגם עתה ראנו כי שבר ג' השלשי נפל לשלם עם מורה ראשון ונשים א' שעל[יו] על ה' שלקחנו הג' שעליו ואז נשארו לנו חצי וחמשי
כזה כפלנו זה על זה ישאר עשירית כזה 0א מכל הכפל ובאנו עד קיצו ואין צריכי
לקצר עוד ודי בזה בכאן ועיין פלא זה הקיצור הפרק השלישי מן השער השני במגרעת השברי ואומר כי דרך מגרעת השברים הוא הפך החיבור ותצטרך לעיין שיהיה החלק שתרצה לגרוע ממנו או לחלק גדול מן האחר וזה תראה בשני דרכים הדרך הראשון הוא שתעיין בחלוקת השברים ומורהם שאמרתי בזה השער שהם ארבעה מינים אשר הראשון הוא שיהיו השברים שוים והמורים מתחלפים
[54ב] [לז1] [] כאשר [] יותר השבר [] יקטן השבר [] והמורים שוים [] כזה הנה כאשר יתרחק מן [] יגדל השבר מטעם תוספ[ת] [] וזה אינו לאין תכלת כראשון והמין השלישי שיהיו השברים והמורים מתחלפים כזה הנה כל מה שיתרחק מן הראשון יגדל בשני לאין תכלית והמין הרביעי שיהיה השברים והמורים שוים כזה יהיו כולם שוים והגרעון והחילוק בם שוה והכלל כי הראשון כל מה שיתרחק יקטן לאין תכלית והשני והשלישי יגדילו אבל השלישי עם חילוף המורה כי שבריו הם עד סך המורה ותראה ותבין והרביעי שוה ועיין בם אבל ההשואה יהיה על הכל שזה צריך עייון הדרך השני הוא ידוע שהוא דרך ההשואה כמו שקדם ותראה עתה במשלים ואומר כי מאחר שבארתי מני השברים אשוב לכונת הפרק ואומר כי דרך ידיעת גרעון שבר משבר הוא שתשוים ואחר תגרע הקטון מן הגדול המשל בזה רצינו לגרוע ב ג שלישית מחצי בזאת הצורה נשוים כדרך השל הראשון × שנכפול כל שבר על מורה חברו ויהיו על שלישית ב' ו ועל חצי ג' והמורה הכללי ששה גרע ב' מג' ישאר א' שהוא חלק מששה והנה עלה בידינו כי הגורע שלישית
55[א] [לז2] מחצי משל שני [] גרעון ומה' ששיות [] שברים משברים המורה הכללי והוא תת"ם [] ממורה אחד הראשון יהיו של"ו וג' שביעיותו [] רביעיות על השלישי יהיו [] וה' ששיות [] יהיו ת"ש ויהיה בצורה הזאת ואחר נחבר כל שני שברים ואח 0גגא בפני עצמם הב' חשמיות עם וגג 0חד 0גו 00ז הד' שביעיות יהיו תתי"ו ותנם למעלה בין שניהם 0דח גם נחבר השני שברים האחרים אם של אחיו אשר מהם נרצה לגרוע יהיו אלף ש"ל בין [ש]ניהם למעלה ואחר נגרע תתי"ו מאלף ש"ל ישארו תקי"ד חלקים מתת"ם בשלם ואם תקצרם יהיו מ"ג חלקים מע' כזה והנה עלה בידינו כי כאשר גרענו ב' חמשיות וד' שביעיות מג' רביעיות וה' שישיות שישארו מ"ג חלקים מע' בשלם ותוכל לעשות זה בדרך אחרת והוא שתעשה ראשונה שני מורים בזאת הצורה הנזכרת ויהיה מורה המספר הקטן * ב' חמשיות וד' שביעיות ל"ה ומורה המספר שהוא הגדול שהוא ג' רביעיות וה' ששיות הוא כ"ד נקח מן המורה הראשון ב' חמשיות שהוא י"ד ויהיו על ב' גם נקח ד' שביעיות והוא כ' גם מן המורה השנית נקח ג' רביעיותיו שהוא י"ח וה'
דג חג שישיותיו שהוא כ' והרי לך חלקי השברים
דא|0ב חא|0ב מן השני מורים כזה הצורה וגם תוכל להוציאם
בדרך הראשון והוא שתכפול שבר במורה הג דב
[55ב]
[לח1] 51 []ברם [] הכולל שהוא [] גם ד' על ד' יהיו [] ותנחנו על המורה הכולל הנשאר | דאה [] עתה שנים שהם ואח 0גגא [] שרצינו לגרוע מל"ח חלקי' X [] הצורה גם נשוים באחד מן השני 0דח [] הנזכרים יהיה החלק הקטן תתי"ו והגדול אלף ש"ל והשבר הכולל תת"ם ועתה שהכל שוה נגרע תתי"ו מאלף ש"ל ישארו תקי"ד מתת"ם ואם נקצרם יהיו מ"ג [] חלקים מע' בשלם כזה משל שלשי רצינו לגרוע שברים משברי שברים [] כמו שרצינו לגרוע ב' חמשיות מה' ששיות חמשית מד' חמשיות והיה כצורה 0ג 0ב הזאת נמשיך קו מה' לד' להורות כי ה' שבר
מד' וכן קו בין מורה למורה ואחר נשוים 0ג כנזכר ויהיה האב הכולל לשבר השבר ל' והנה
ד' חמשיותיו הם כ"ד על ד' וה' ששיות כ"ד הם כ' וזה השבר המבוקש שהוא כ' חלקים מל' כזה נקצרם ישובו לב' שלישיות או שנגרע השני ספראש שהם במעלת האחדים ישארו ב' וג' במעלת האחדים כזה ואז שבו חלקי השאלה לגרוע ב' חמשיות מב' שלשיות כזאת הצורה
ו 0א נשוים יהיה האב הכולל ט"ו וחלקי הב' חמשיות
ששה וחלקי הב' שלישיות עשרה נגרע ו' מעשרה
הא ישארו ד' והם ד' חלקים מט"ו בשלם כזאת
והנה כאשר גרענו ג' חמשיות מה' ששיות מד' חמשיות ישארו ד' חלקים מט"ו בשלם משל רביעי שרצינו לגרוע
56[א] [לח2] [] רביעיות [] מה' ששיות [] 0ג הז 00א ה0א הזא 0אב
מ'
0דא 0דב שבר שברים
ויהיה האב הכולל לשברי השברים הראשונים ק"מ ולשניים ר"מ והנה השביעיות [] ק"מ הם ק' ונתנם על ה' שביעיו וג' רביעיות ק' הם ע"ה ושני חמשיות ע"ה הם ל' וזה החלק המבוקש לגרוע מן השני שהוא ל' חלקים מק"ם השלם כזה ואם נקצרם יהיו ג' חלקים מי"ד כזה ונוכל לקצרם בדרך קרוב והוא שנפיל הב' ספראש ממעלת האחדים וישארו ג' חלקים מי"ד כנזכר והנה ב' חמשיות מג' רביעיות מה' שביעיות הם ג' שברים מי"ד בשלם ועיין ותראה וזה השבר הראשון אשר רצינו לגרוע מן השני הגדול וכן נעשה לשברי השברים השניים כי מורה השברים הוא ר"ם כנזכר וז' שמניותיו הם ר"י וה' ששיות ר"י הם קע"ה וג' חמשיות קע"ה הם ק"ה וזה המבוקש נקצרם יהיו ז' חלקים מי"ו כזה והם שוים לערך ג' חמשיות מה' ששיות מז' שמיניות ועתה נגרע ג' חלקים מי"ד בשלם מז' חלקים מי"ו בשלם חד חט בזאת הצורה ולא נוכל עד שנשוים
X בעבור שהם שברי מנים מתחלפים
דבב ונוציא האב הכולל והוא רכ"ד נכפול
[56ב] [לט1] [] צ"ח [] ג' חלקי [] והיו מ"ח וז' חלקים []הכל דרך אחד כי זה הדרך [] הדרך השני שעשינו המורה הכולל [] ולקבץ אותו על י"ד וכפלנו היוציא על ג' [] מ"ח וכן עשנו לשבר האחר ונתן מ"ח על השבר הראשון וצ"ח על השני ונגרע מ"ח מצ"ח ישארו נ' והם נ' חלקים מרכ"ד ואם נקצרם לחציים יהיו כ"ה חלקים מקי"ב כזה והרי לך כי י"ב חמשיות מג' רביעיות מד' שביעי' כשתרצה לגורעם מג' חמשיות מה' ששיות מז' שמניות שישארו כ"ה חלקים מקי"ב כנזכר משל חמשי רצינו לגרוע שברים ושברי שברים משברים ושברי שברים כמו ב' שלישיות וחמשית ג' רביעיות חמשית שרצינו לגרוע מג' שביעיות ומה' ששיות מד' חמשיות מח' תשיעיות בזאת הצורה וראשונה נמשיך קו
ג הא 0ב 0וא בטא 0דב משבר
| מ | לשברו
00א 0זב ואחר
נשוה השואה ראשונה השברי שברים ויהיה אב השברי שברים הראשונים ק' וחמשתו כ' וג' רביעיות כ' הם ט"ו
57[א]
עמוד 57ב - חסר [מ1] [] עלה בידנו [] חמשית מג' [] תשעיות שנשארו [] [] בחילוק השברים מאיזה מין [] ויחלק לשני דרכים הפכים אשר האחד [] בחילוק הקטן שבר גדול על קטן והדרך השני בחילוק השבר הקטן על הגדול ובכל משל תראה הדרך השני ואומר כי דרך חלוק השברים מאי זה מן שיהיה תשוים בראשונה השואה אחת או שנים יותר כפי מה שתצטרך ואחר תחלק כמו שיהיו שלמים והיוציא בחלוקה הם שלמים והטעם הוא כי המחלק רביע דבר לרביע דברם יהיה לכולו אחד והנשאר מן החלוקה הוא חלק או חלקים מן המספר שחילקת עליו ואם המספר שתרצה לחלק ואם הוא קטן מן המחלק תדמה הקטן שהם שברים והגדול המחלק שהוא מורה השלם ותאמר כי כסך אילו השברים כפל בחלק כל אחד וזה בדרך השני כי בכל צורה תראה השני דרכים ובזה הסדר תעשה בשלמים כמו במשל שאם תרצה לחלק ב' לג' תן ב' על ג' והוא מחולק שבא לכל אחד ב' שלשיות הדבר המשל בזה רצונו לחלק ב' חמשיות על ג' שמניות בצורה הזאת נשוים ב' על מורה השני וא הא יהיו י"ו וג' על מורה הראשון שהוא ה'
יהיו ט"ו ועשיית המורה הכללי בזה הוא 0ד רשות בדרך ההשואה הראשון אבל בדרך
השני לקחת חלקי כל שבר הוא חובה ועתה הנה נחלק י"ו על
58[א] [מ2] טו יעלו [] השאלה יהיה [] כי ק"ס מחולקים [] ואין להאריך בזה כי [] תדע הכל הטיב בע"ה [] משל שני רצינו לחלק ה' שביעיות וז' [שמיניות על] ב' תשעיות ועשירית וג' שמניות בזאת הצורה וראשונה נשוים 0וחד דאהג ומן האב הכללי 00וג 0ובא על 0באא ד0ה 0טחא שהוא ה' אלפים ומ' נקח ה' 0ד0ה שביעיות שהוא ג' אלפים ות"ר נניחם על ה' שביעיות כמנהג גם ז' שמניותיו עליו שהוא * אלף ק"ך גם * אלף ר"ס העשירית שהוא תק"ד עליו גם ג' שמניות שהוא אלף תת"ץ גם תשיעיותיו ואחר שכולם שוים למורה אחד נחבר הה' שביעיות שהוא עליו שהוא ג' אלפים ות"ר עם חברו שהוא אלף ור"ס יהיו ד' אלפים ותת"ס והם למעלה על שבריהם וכן נחבר השלושה שברים הנשארים אשר הם המחלק ויהיו ג' אלפים תקי"ד [] אשר עליהם השברים כולם לשנים שהם ד' אלפים ותת"ס על לחלק על נחלק ד' אלפים ב' אלפים ותקי"ד ותקי"ד ויעלה בחילוק אחד שלם ונשארו אלף ותתכ"ל ושש"ו ואם נקצרם יהיו אחד כנזכר ותרע"ג חלקים מאלף ותשנ"ז בזאת הצורה א | ואם נהפוך השאלה בדרך השני יהיה כאומר חלק לי ג' אלפים תקי"ד על ד' אלפים תת"ס שיהיה בזאת הצורה נאמר כי המספר הזה הנה הוא מחולק כי לכל אחד
[58ב] [מא1] [] [] על [] וד' חמשיות [] שלישית ב' שלישיות
0טבז 0חדו 00אח 0חד 0דדא 0ואב 0חדו
[] | על [] בעבור 0בזט שיהיה כבר שבר השבר ואחר נוציא האב הכולל והוא ט' אלפים תש"ך וב' שלישיותיו הוא ו' אלפים ת"ף והם עליו ושלישית זה השבר שהוא ו' אלפים ות"ף הוא ב' אלפים וק"ס והוא עליו וב' שלישיות ב' אלפים וק"ס הוא אלף ות"ם ושלשית אלף ות"ם הוא ת"ף והוא על השלישית וזה הת"ף הוא שבר השבר הנרצה לחלק עליו ונשמרהו ואחר נדע הג' רביעיות והד' חמשיות מה' ששיות אשר רצינו לחלק על השבור השמור והנה ה' ששיות האב הכולל הוא ח' אלפים וק' וד' חמשיות ח' אלפים וק' הוא ו' אלפים ות"ף וזה שבר השבר הנרצה נחברהו עם ג' רביעיות האב הכולל ז' אלפים ר"ץ והם אשר רצינו לחלק על השבר יעלו [] אלפים השמור שהוא ת"ף ויעלה בחילוק כ"ח שלמים וש"ל חלקים תשעי' מת"ף כזה 0 | ג ג נקצרם והוא שנטיל הספראש ישארו ל"ג חלקים 0 | ח ד ממ"ח בשלם וזה מה שרצינו ואם תרצה לקצר ובדרך השני אם רצינו לחלק ת"ף על י"ג עוד יהיו י"א מי"ח אלפים ותש"ע נאמר שיבוא לכל אחד ת"ף חלקים מי"ג אלף תש"ע בשלם וזה מה שנרצה בד' מיני השברים והבחינות או מאזנים בסוף ד' מני המורכבים
59[א] [מא2]
The Third Section: Integers and Fractions |
[השער הג'] |
|
הפרק הראשון בחיבור |
|
הפרק השני בכפל שלמים ושברים |
|
הפרק השלשי במגרעת שלמים ושברים |
|
הפרק הרביעי בחילוק שלמים ושברים |
The First Chapter on Addition of Integers and Fractions |
הפרק הראשון בחיבור שלמים ושברים |
| ואומר כי רצינו לחבר השלם והשבר למיניהם הנה נוכל לעשות זה בשני דרכים אשר הראשון האחד הוא שתעשה כל השלמים שברים וחלקם על המורה אחר שתשוים אל מורה אחד והדרך השני הוא שתחבר השלמים ואחר תשויה השברים והעולה מחיבור השברים תחלק על המורה והיוצא בחילוק הם שלמים והנשאר הם חלקי המורה | |
| והמשל מן הדרך הראשון רצינו לחבר ד' שלמים ושני שלשיים עם ה' שלמים וג' רביעיים | |
| בזה הצורה | |
| בשויה השלמים עם מורה שברים יהיו י"ב וב' שברים יהיו י"ד והם שלישיות גם השני עם מורה שברים יהיו כ"ג רביעיות כשוים כזה הצורה [השנית] יהיו שניהם [] |
[59ב] [מב1] [] נחברם [] יהיו [] חלקים מי"ב בשלם []ה המשל בדרך [] וה' יהיו ט' נשויה השברים [] נחלקים על המורה הכללי שהוא י"ב []שהיו לנו יהיו עשרה ונשארו חמשה י"ב[] משל שני רצינו לחבר שלמים ושברים על עם שלמים ושברים כמו י"ג שלמים וחמשה תשיעיות עם כ"ו שלמים ושלשת חמשיות ועם רל"ו שלמים וחצי גא כזאת הצורה נחבר השלמים יהיו רע"ה וב גם נחבר השלמים השברים כמו שעשינו וגב בפרק חיבור שברים יהיו אחד שלם ונ"ט הזב חלקים מצ' כיצד נשויה השברים יהיה האב הכולל צ' והנה ה' תשיעיותיו הם נ' וג' חמשיותיו הם נ"ד וחציו מ"ה ויהיה כזאת הצורה 0ה דה הד נחברם כולם יהיו קמ"ט נגרע מהם צ' לשלם אחד ישארו נ"ט 0ט והם חלקים מצ' כנזכר והנה עלה לנו מחיבור י"ג שלמים וה' תשיעיות עם כ"ו וג' חמשיות ועם רל"ו וחצי רע"ו שלמים ונ"ט חלקים מצ' בשלם והוא הדרוש משל שלשי בחיבור שלמים ושברים משני מנים עם דומיהם כמו כ"ב שלמים ושלשת רביעיות וד' חמשיות עם ל' שלמים ורביעית וב' שלשיות
60[א] [מב2]
כב [] ל השברי' [] נ"ד ס' וג' רביעיות[] ורביעיתו ט"ו וב' שלישיותיו [] נחלקם על המורה יעלו ב' שלמים [] מס' בשלם שאם תקצרם ישובו לז' חלקים מט"ו [בשלם] והנה המחובר מכ"ב שלמים וג' רביעיות וד' חמשיות עם ל' שלמים ורביעית וב' שלישיות יהיה נ"ד שלמים וז' חלקים מט"ו בשלם משל רביעי רצינו לחבר שלמים ושברי שברים על שלמים ושברי שברים כמו רל"ה שלמים ורביעית חמשית עם שכ"ו שלמים וב' שלשיות מג' רביעיות בזאת הצורה הגב עם ובג נחבר השלמים יהיו תקס"א נשוה השברים יהיה אחד הקיצור י"א חלקים מכ' שהם חצי שלם וחלק מכ' בשלם והמעשה אעשה בשני דרכים להרגילך בדרכי המספר הדרך האחד הוא שתקח כל שבר השבר בפני עצמו וקח חלק כל אחד ואחד תשוה את שניהם והעולה משניהם תחבר וחלקם על המורה והם שלמים וכן נעשה נקח הרביעית חמשית מן החלק הראשון שהוא חלק מכ' ושני שלישיות מג' רביעיות מן השבר השני והוא ו' חלקים מי"ב שהוא חצי ואז היה לנו מן השני שברים [] מכ' ומן השני
[60ב] [מג1] [] מורה [] ד' ורביע[י]ת [] כנזכר והוא [] וכן נעשה בשבר השבר [] רביעיותיו הם ט' ושני שלישיות [] השבר השני נקצרהו יהיה [] בצורה המונחת והמורה הכולל מ' ואם נרצה הוא כ' אבל נניח זה והנה חציו הוא כ' מונח על חצי וחלק אחד מכ' הוא ב' והוא עליו נחברם יהיו כ"ב חלקם ממ' בשלם ואן בשבר הזה שלם אבל נקצרם בחצי יהיו י"א חלקים מכ' כנזכר הדרך השני הוא שנשוה המורים אל אב אחד ויהיה ס' ונסדר ג בא 0ג הד השברים בזאת הצורה ונקח ג' רביעיות ס' והם מ"ה וב' 0ו שלישיותיו ל' וזה שבר השבר האחד גם נקח חמשית ס' והוא י"ב ורביעית י"ב הוא ג' וזה שבר השבר האחר נחבר ג' עם ל' יהיו ל"ג וזה המבוקש שהם ל"ג חלקים מ' ס' כזה נקצרם בשלישית ישובו י"א חלקים מכ' כנזכר והנה יצא לנו מחיבור רל"ה שלמים ורביעית חמשית עם שכ"ו שלמים ושני שלישי ג' רביעיות תקס"א שלמים וחצי וחלק מכ' בשלם משל חמשי רצינו לחבר שלמים ושברי שלמים עם שלמים ושברי שלמים כגון ב' שלמים וג' רביעי ד' שלמים עם ה' שלמים ושני
61[א] [מג2] שלישי [] הנה יש בו [] דרך משל אחד [] המשל הוא שתכפול ה[] שבריו וחלק העולה על [] השלמים ואם יש בידך שלמים [] חברם אלהם וכן תעשה בחלק השני [] והמעשה במשלנו שכפלנו ד' בג' יעלו י"ב רביעיות וחלקם על ד' שהוא המורה יעלו ג' שלמים ונשמור אותם או נחברם עם הב' שלמים יהיו ה' בחלק הראשון גם נכפול ו' על ב' שלישיים יעלו י"ב שלישיים מונח על ב' נחלקם על ג' יעלו ד' שלמים וה' שלמים שהיו בחלקו יהיו ט' וה' שהיו לנו היו י"ד והוא המבוקש משל חששי שרצינו לחבר שלמים ושברי שלמים על דומהם בדרך השני והוא שתכפול כל שלם אשר שברו אתה מבקש על שבריו והעולה מהכפל תתן למעלה על שבריו כמו שעשינו בהשואה ואחר תשוים עם מוריהם וחיבורם תחלק על המורה הכולל והעולה הוא המבוקש כמו בזה המשל שרצינו לחבר י"ח שלמים וה' שמניות מי"א יח מי"א שלמים עם כ"ה שלמים וז' כה מח' תשעיות מח' שלימים בזאת הצורה נכפול י"א על ה' יהיו נ"ה שמיניות גם ח' על ז' יהיו נ"ו תשיעיות ויהיו שניהם בזאת הצורה השנית תשוים יהיו האחד תצ"ה והשני
[61ב] [מד1] [] וחלקם [] שלמים וז' [] נ"ה יהיו נ"ו [] והוא המבוקש והנה [] תכפול י"א על ה' יעלו נ"ה [] מורה חברו יעלו שהוא ט' יעלו [] בח' על ז' יעלו נ"ו גם נ"ו על מורה חברו שהוא ח' יעלו תמ"ח תחבר שניהם יהיו תתקמ"ג חלקים על המורה הכולל יעלה בחילוק י"ג וז' ע"בין כנזכר משל שביעי בחיבור שלמים ושברים מדברים מתחלפים מממון ומזמן וממשקל וממדה ואקצר כפי מה שאוכל ואומר שרצינו לחבר רל"ג לטרי ממון וי"ט דנרין וג' פשיט' ומחצה עם תס"ג לטרי ממון י"ב דנרי' עשרה פשי' ומחצה ועם תש"ט לטרי' י"ד די' י"א פשי' ומחצה נקבץ כל מין עם מינו והיוציא יהיה אלף תכ"ז לטרי ממון ז' די' ופשי' ומחצה ויהיה בצורה הזאת וראוי שתדע כי ב' מחצות הרי פשוט וי"ב מחצה פשי' דנרי' לטרי' פשיטי הם דנר א ג טא גהב וכ' דינרין לטרה א 0א בא גוד גרע א אא דא ט0ז מהמחצות המקובץ א א ז זבדא פשוט ישאר מחצה ויהיה הפשיטי כ"ה קח מהם ב' די'
62[א]
[מד2]
קח מ[]
דיני' ופשוט []
משל שמני [ רנ"ב כיכרין] והבחינה עם
וג' שקל[' כ"ח ליט' ט' אוקיות] משל אחר מג'
וי"ב דראהם עם שע"ח כיכרים [ב' שקלי' כ"ד ליט' י"א] טורים גרע
אוקיות ז' דראהם ועם תתקפ"ו כיכרי' [ושקל אחד] מהעולה מכולם
וי"ג לטרין ועשרה אוקיות וי"ד דראהם נקבץ כל מין חיבור הב' טורים
עם מינו והיוציא יהיה אלף תרי"ח כיכרים וישאר הטור
וז' לטרין וח' אוקיות וא' דראהם ויהיה כזאת השלישי או יותר
הצורה דרהם אוקיות ליטר שקלים כיכרים טורים אם יהיו
וראוי בא ט חב ג בהב והמשל בג' טורים
שתדע ז אא דב ב חזג חיברנו
כי י"ו דא 0א גא א וחט ב' ליטרי ממון
דרהם הם א ח ז 0 חאוא וג' די' ז' פשוטי'
אוקיא עם ג' לטרי'
וי"ב אוקיות הם לטרה ושלושים לטרין הם שקל ד' די' ה' פשי'
אחד וד' שקלים הם כיכר ועם ד' לטר ה'
משל תשיעי ממדה רצינו לחבר רנ"ח כורי חיטה די' ג' פשי' ויהיה
וג' ארובש ד' קוארטאליש ג' אלמודיש כזאת הצורה
עם תכ"ג כורים ב' ארוכה ה' קוארטאליש ב' פש די' לט'
אלמודיש ועם קס"ז כורי' ב' ארוביש ב' קוארטאל ז ג ב
א' אלמוד וחבר הכל יהיה תת"ק כורים וז' קוארטרלי ז' ארובלה ב' אלמודיש ה ד ג
ב' אלמודש [] בזאת הצורה וראוי שתדע כי ג ה ד
ד' אלמודש הם קוארטאל וה"ד קוארטאלי [] חיברנו שלושתן
ו' קוארטאליש הב ארובה וד' ארובש הם כאפיז יעלו ט' לטרי'
י"ג די' ב' פשי'
וזה כל הממון
ושמור אותו
והבחינה
חיברנו הב'
טורים
העליונים יהיו ה' ליטרי' ז' די' י"א פשי' גרענום מכל הממון השמור נשאר
הטור השלישי שהוא ד' ליטרי' ה' די' ג' פשי' עוד חיברנו הטור השני והשלישי
שהם ז' לטרי' ט' די' א' פשי' גרענום מכל הממון ישאר הטור הראשון
שהוא ב' ליטרי ג' די' ו' פשי' עוד נחבר שני טורים הראשונה
והשלישית שהם ו' ליטרי ח' די' ט' פשי' גרענום מכל הממון וישאר
האמצעי שהוא ג' לטרי ד' די' ב' פשי' ובזה הדרך תעשה
[] טורים או יותר שתקבץ כולם חוץ מאחד
[] תחזור ה[]
[62ב] [מה1] [] [משל עשירי] מזמן חיברנו תקע"א שנים כ"ו ימים י"ח שעות נ"ה דקים נ' שניים ל"ו שלישיים כ"ט רביעיים עם רנ"ז שנים כ"ט ימים י"ג שעות כ"ט דקים י"א שניים נ' שלישי' מ' רביעיים ועם תקפ"ח שנים י"ו ימים י"ט שעות ל"ח דקים נ"ב שניים מ"א שלשי י"ד רביעיים נחבר הכל ויהיה היוציא אלף תי"ו שנים ע"ג ימים ד' שעות ג' דקים נ"ה שניים ח' שלישים כ"ג רביעיים ויהיה בצורה הזאת _______________________________________ רביעיי' שלישי' שניי' דקי' שעות ימים שנים טב וג 0ה הה חא וב אזה 0ד 0ה אא טב גא טב זהב דא אד בה חג טא וא חחה גב ח הה ג ד גז ואדא
והנה [יד]עת כי ס' רביעיי' הם שלישי וס' שלישיים הם שני רביעי וס' שניים הם דק וס' דקים שעה וכ"ד שעות יום ושס"ה ימים ושש שעות שנה בהסכמה והרשות בידך לעשות השנה עיבורית או כפי מה שתרצה וכן החדשים ובעבור זה הנחתי הימים ולא עשיתי מהם חדשים
63[א] מ[ה]
[מה2] [משל אחד עשר] [] [מזלות כו מעלות נא דקים לב שניים כא שלישים כז] רביעיים [נ חמשיים עם ז מזלות כ"א מעלות ל"ו דקים] מ"ד שניים נ' שלש[ים נח רביעים יו חמשים עם יא מזלות כ"ח מעלות נ"ז [דקים מ"ב שניים ל"א שלישים כ] רביעיים יז חמשים וה[יוציא מזלות יז] מעעלות כ"ה דקים נ"ט שניים מ"ג [שלשים מ"ו רביעים] כ"ג חמשים ויהיה בזה הצורה וכבר ידעת כי המזלות _______________________________________ חמשיים רביעים שלישי' שניי' דקים מעלות מזלות 0ה זב אב בג אה וב 0א וא חה 0ה דד וג אב ז זא 0ב אג בד זה חב אא גב וד גד טה הב זא [] י"ב וכל מזל ל' מעלות וכל מעלה ס' דקים וכל דק ס' שניים וכן לעולם והבחינה תחבר הב' טורים וגרע מן הגדול מן הג' טורים משל שנים עשר רצינו לחבר ד' ימים י"ט שעות שחיברת והנשאר תתקכ"ה חלקים עיבוריים שהוא מותר שבעה תהיה הטור השלישי' מחזורים עם יום אחד י"א שעות תק"ץ חלקים שהוא מותר שהנחת עוד תחבר נ' חדשים יהיה היוציא ו' ימים ז' שעות תל"ה חלקים ב' טורים ותגרעם בצורה הזאת חלקים שעות ימים וזה מותר נ"ז מן הגדול ושאר מחזורים הבט טא ד כי נעשה מאלף הטור שנח[] וכן מאלף ופ' 0טה אא א חלקים שעה לעולם כמו אחת ומכ"ד הגד ז ו שעות יום אחד שאמרתי בפרק ואם יעלה מקיבוץ הימים המאזנים ובלטרי ממון ודי' ופשיט'
[63ב]
[מו1]
[]כאן די בזה אחר דף ה'
[] למיניהם בקונדרס
[] הרוצה לכפול שלמים
[] השלמים על השברים
[] והיוציא בחילוק הוא המבוקש
[] בזה רצינו לכפול י"ג על ג' רביעיות * בזאת הצורה או ג' רביעיות
יג כפול י"ג על ג' שברים יעלו ל"ט רביעיות על י"ג שלמים
כזה וחלקם על המורה שהוא ד' יעלו כי הכל אחד
בחילק ט' שלמים וג' רביעיות והוא המבוקש
משל שני משלמים על שברי שברים כמו שרצינו
לכפול ל"ח שלמים על ב' שלישיות מג'
רביעיות בזאת הצורה נשום והנה חג על
האב הכולל הוא י"ב וג' רביעיותיו
הם ט' וב' שלישיות ט' הם ו' חלקים
מי"ב שהם שבר השבר הנרצה לכפול על ל"ח ולחלק
היוציא על י"ב אבל אם נרצה נוכל לקצרו ויהיה יותר
נקל ויהיה חצי והנה שבה השאלה כאומר כפול []
ל"ח שלמים על חצי כזאת הצורה כפול חג
ל"ח על אחד שהוא השבר יהיו ל"ח חלקים
על המורה שהוא ב' יעלה בחילוק י"ט שלמים והוא המבוקש
משל שלישי משלמים ושברים על שלמים ושברים
כמו ב' שלמים וב' שלשיות על ג' שלמים
וג' רביעיות בזאת הצורה הנה ב על ג
לעשותה בשני פנים הראשונה הוא
שתכפול השלמים על השלמים ואחר תכפול כל שלם
64[א] מו [מו2] בשבר[] שברים [] עליו ויהיו [] ב שלמים על ג' [] הב' שלמים על ג' רביעיות [] השלם האחר על שהוא ג' על ג' שליש[] גם תכפול השברים ג' רביעיות על ב' שלישיות [] השיווי ששה חלקים מי"ב שאם תקצרם יהיו חצי ואחר [] תקבץ הכל ששה שלמים וששה שלישיות שהם ב' שלמים יהיו שמונה ואחד וחצי מששה רביעיות יהיו ט' וחצי וחצי שהיה לנו מהשברים יהיו עשרה והוא המבוקש והפנים השניים אשר בה אעשה כל המשלים הוא שתתן השלמים בשבריהם ואחר כפול שבר על שבר ומורה על מורה והיוצא בחילוק על המורה הם השלמים […] במשל המונח שהוא ב' שלמים ושני שלישיות על ג' שלמים וג' רביעיות כפול ב' שלמים במורה שברו שהוא ג' ויהיו ו' תחברם עם שברו שהוא ב' יהיו ח' שלישיות גם כפול ג' על מורה שברו שהם ד' יהיו י"ב ועם ג' יהיו ט"ו והם רביעיות ויהיו שניהם כזאת 0בא הצורה ואחר כפול שבר על שבר
ומורה על מורה ויהיו ק"ך חלקים בא מי"ב חלקם לי"ב יעלו בחילוק עשרה
והוא המבוקש שאלת סוחר משל ששי רביעי בכפל שלמים ושברי שברים על שלמים ושברים כמו נ"ח
[64ב]
[מט1]
[] [] על מ"ד ג/ה [] [] השברים והוא ל' וקח [] על ד' חמשיות נקח [] כ' וזה השבר המבוקש שהוא כ' ח[] מל' בשלם ו[] [לנו] עסק בד' חמשיות [] עתה יש לנו לכפול נ"ח שלמים וכ' חלקים מל' על מ"ד שלמים וג' חמשיות נסדרם בזה הצורה השנית חה ב0/ג0 על דד ג/ה [] ננהיג בו במשל שלישי שתכפול נ"ח על מורה שבריו שהוא ל' יעלו אלף ותש"ם תוסיף עליהם שבריו שהם כ' יהיו אלף תש"ס נתנם על ל' שהוא מורה שנית שבריו שמור * וכן נעשה למ"ד על ג' חמשיות שנכפול מ"ד על מורה שבריו שהוא ה' יעלו ר"ך נחבר עליו ג' שבריו יהיו רכ"ג חמשיות ויהיו כזאת הצורה השלשי' 0 ו ז א ג ב ב ועתה נכפלם בדרך השברים
0 ג ה שברים על שברים ויהיו
שצ"ב אלפים ות"ף וגם מורה על מורה ויהיו ק"ן חלק השברים שהם שצ"ב על אלפים ות"ף על המורה שהוא ק"ן יעלה בחילוק ב' אלפים ותרי"ו ונשארו פ' חלקים מק"ן ואם תקצרם יהיו ח' חלקים מט"ו והוא המבוקש ואם תרצה להקל מעט בזה הכפל מצד הכ' חלקם מל' תוכל לקצרם ויהיו ב' שלישיות ואחר כפול נ"ח בג'
67[א] [מט2] שהיה [] []מ"א [] השני מ[]
משל חמשי רצינו לכפול [] שלמים כמו ז' שלמים [] ד' שלמים כזה הצורה הנה ראשונה תשויה הד' שלמים בעבור כי ז' על ג/ד מד' מהם נסרו ג' רביעיות והוא שנכפלם במורה השברים שהוא ד' ויעלו י"ו נקח מהם ג' רביעיותם שהם י"ב והם י"ב רביעיות אשר אם תחלקם על ד' יעלו ג' שלמים והנה שבה השאלה לכפול שלמים על שלמים שהם ז' על ג' שיעלו כ"א והוא המבוקש והנה תוכל למצוא הג' רביעי ד' בדרך אחרת והוא שתכפול השלם על שברו כי ד' על ג' הם י"ב רביעיות חלקם על ד' שהוא המורה יעלו ג' שלמים ועתה כפול שלמים על שלימים עלו ג' על ז' כ"א כנזכר משל ששי רצינו לכפול שלמים ושברי שלמים על שלמים ושברי שלמים כמו י"ג שלמים וג' חמשיות מי"ב שלמים על כ"ב שלמים ושני שלישיות מט' שלמים כזאת הצורה גא (וג/ג)/ה מי"ב על בב ב/ג מט' והמעשה הוא שתעשה ראשונה מן השלמים
[67ב] [נ1] [] [] אחד תכפול [] כפל המורים [] שבריו שהוא ה' יעלו [] יהיו ס' נקח מהם ג' חמשיותיו [] שהם ג' על י"ב יעלו ל"ו חמשיות [] חברם עם ס"ה חמשיות יהיו ק"א חמשיתיות כזה א0א והוא החלק הראשון הכופל וכן נעשה לכ"ב שלמים
ה וב' שלישיות מט' שלמים כי כפלנו כ"ב בג' שהוא
מורה שבריו יהיו ס"ו שלישיות גם כפלנו ט' בג' יהיו כ"ז נקח ב' שלישיות כ"ז שהם י"ח שלישיות נחברם על ס"ו יהיו פ"ד והם שלשיות כזה דח והוא הנכפל נכפול ק"א שהיה לנו על פ"ד יהיו ג ח' אלפים תפ"ד נחלקם על ט"ו שהם כפל ה' בג' שהם המורים יעלה בחילוק תקס"ז שלמים וט' חלקים מט"ו שאם תקצרם יהיו ג' חמשיות כזה ג/ה משל שביעי רצינו לכפול שלמים ושברי שברי שלמים על שלמים ושברי שברי שלמים כמו ב' שלמים וחצי שלישית י"א על עצמו כזאת הצורה ב א/ב א/ג אא על ב א/ב א/ג אא הנה ראשונה ו ו נוציא האב הכולל לשברים והוא ששה ונכפול הי"א שלמים על המורה שהוא ששה יהיו ס"ו נקח שלשית ס"ו יהיו כ"ב והם שלישית י"א שלמים וחציו הוא י"א
68[א] [נ2] חלק [] הב' שלמים [] מחצי שלישית [] גב נכפלהו על []
ג על ל"ו שהם כפל []
י"ד שלמים וכ"ה חלקים מל"ו []
משל שמני רצינו לכפול שלמים על שלמים גב כמו ד' שלמים על ה' שלמים וג' רביע[יות] ד' על ה ג/ד כזאת הצורה נתן השלם בשברו ה' [על] ד' יהיו כ' וג' שברים יהיו כ"ג נכפול הד' שלמים על כ"ג יהיו צ"ב רביעיות חלקם על ד' ש[הם] המורה יציא בחילוק כ"ג שלמים והוא המבוקש
הפרק השלשי במגרעת המורכבים משלמ[ים] ושברים דע כי יסוד המגרעת וזולתו מן כפל וחיבור וחילוק בשברים או במורכבים הוא ההשואה ואז יהיו שוים ויהיה נקל לעשות מהם כל מה שתרצה כמו שעשינו במה שעבר בשברים ובמורכבים ועתה במגרעת שלמים ושברים ראשונה תמורת השברים ואחר גרעון אילו מאילו ואז השברים ממורים שוים אין צריך השואה כמו [] וכמו שעשינו בחיבור וכמו שתראה עתה בזה המ[] משל ראשון רצינו לגרוע אלף ורמ"ז וח'
חזור זה הדף ועוד בחיבור [68ב] [נא1] [] ימים כ"א [] שלישי לו רביעיים [] ימים ר"ט שעות [] שלישיים נ"ב רביעיים כ"ח חמשיים [] ראשונה תדע כי כאשר תעבור אחד [לשמאל] חמשי' רביעי שלשים שניים דקים שעות ימים שנים לימין חב בה חג בד 0ג טא בדב דגב הגרוע הוא ששה אה וג אד בה גד אב גהא האב הגורע או שישי זג הא זה וד וד בב חח טא הנשאר ואם מימין לשמאל כל שישים הם אחד כיצד במשל המוטל נגרע נ"א חמשית מכ"ח לא נוכל נעבור רביעי אחד והם ששה עשרות חמישיות ועתה גרע חמשית אחד מח' חמשיות נשארו ז' למטה נ' שהוא ה' מו' שערכנו ומב' שיש בחמשיות נשארו ג' עם ז' ויהיו ל"ז חמשיות עוד נגרע ל"ו רביעיות מנ"ב נשארו ט"ו כי הם נ"א שעברנו אחד עו' נגרע מ"א שלישיות מל"ח ונעבור אחד נשארו נ"ז שלישיים עו' נגרע נ"ב ממ"ב ומאחד שעברנו נשארו מ"ו שניים עוד נגרע מ"ג מל' ומס' שנעבור משעה ישארו מ"ו כי מל' עברנו אחד עוד נגרע כ"א שעות מי"ח שעות נשארו כ"ב שעות עוד נגרע קנ"ג ימים כי עברנו יום אחד מרמ"א כי יום אחד עברנו נשארו פ"ח ימים עוד נגרע רי"ה שנים מרל"ד נשארו י"ט שנים והבחינה נחבר טור [ה]גורע עם טור הנשאר ותציא הטור אשר ממנו גרענו כי נ"א ול"ז חמשים יעלו רביעי וכ"ח
69[א] [נא2] וכן ל"ו [] ל"ח עם השלישי [] שניים ודק אחד [] אחת ועם כ"א יהיו כ"ב [] שעות ויום אחד ועם קנ"ג [] וי"ט יהיו רל"ד שנים והכל בדוק כי שב ה[] ממנו גרענו משל אחר רצינו לגרוע שלמים ושברים משלמים ושברים כמו י"ד שלמים וח' שברים מי"א בשלם מכ"ד שלמים וט' שברים מי"ג בשלם כזאת הצורה נגרע י"ז מכ"ד קד צט ישארו ז' שלמים ואחר תשויה ז"א ח כ"ד ט השברים יהיו ק"ד לגרוע מצ"ט אא גא והמורה קמ"ג והנה בעבור המורה קמג שלא נוכל לגרוע ק"ד מצ"ט ניקח אחד מהז' שלמים ונעשה אותו שברים כסך המורה שהוא קמ"ג נחבר צ"ט עם קמ"ג יהיו רמ"ב וגרע מהם ק"ד נשארו קל"ח והם חלקים מקמ"ג בשלם והנה אחר שגרענו י"ז שלמים וח' חלקים מי"א בשלם מכ"ד שלמים וט' חלקים מי"ג בשלם נשארו ו' שלמים וקל"ח חלקים מקמ"ג בשלם והוא המבוקש דרך אחרת לאלה השאלות והוא שניתן השלמים בשבריהם יהיו בזה המשל הי"ז שלמים עם שבריהם קצ"ה שברים מי"א בשלם והכ"ד עם שברהם שכ"א מי"ג בשלם כזה הצורה הגהב אגהג ואחר נשוים אל מורה אחד
הטא אבג ויהיו הראשון ב' אלפים תקל"ה
אא גא
גדא
[69ב] [נב1] [] [] המורה שהוא [] חלקים מקמ"ג [] [] דברים מתחלפים כמו [] ופשי' וכו' או מזלות מעלות דקים וכו' [או שנים] וחדשים וימים ושעו' וכו' תן המספרים במעלותם ואם לא יספיק תעבור אחד ויהיה כמספר המעלה אשר תעבור אותו כמו שתראה ואם תעבור אותו מעלות יותר מאחד תניח במעלות שבאמצע המספר היותר גדול שיוכל להיות בכל המעלות האמצעיות והמשל בזה רצינו לגרוע קס"ה לטרי ממון ועשרה די' וט' פשיט' ומחצה ורביע מרפ"ז לטרי' הנה ניתן הממון הקטן תחת הגדול במעלותם וניתן ספראש במקום השברים כזאת הצורה ב א אא טא ו רביעי 0 מחצית 0 פשיט 0 דנרי' 0 לטרי' זחב רבע' א מחצית א פשי' ט דנר 0א לטרי' הוא א 0 ב ט אבא ________________________________________________________ ועתה לגרוע רביעית פשיט מספרא לא נוכל [גם] אין מחצה לעבור ולא פשיט ולא די' הנה נקח לטרא אחת מז' ונשארו ו' ונעבור אותה למקום הרביעיות ונאמר שהיא כ' רביעיות ועתה נאמר כי בעבור הלטרה על כל השברים הניח על הדי' י"ט דינרים ועל הפשי' י"א ועל המחצות אחד ועל הרביעיות ב' כי מב' נגרע רביע אחד ונשאר רביע וממחצה נגרע מחצה ונשאר 0' ומי"א נגרע ט' פשיט
70[א] נב[1] [נב2] [] ליטרי' ה' [] נשאר א' והנה [] ורביע פשוט והבחינה תחבר הנשאר עם ה[] משל אחר רצינו לגרוע ח' מזלות י"ז מעל[ות] [מ"ב] דקים ל"א שניים כ"א שלישי י"ב רביעיים מי"ב מזלות נסדרם במעלותם וניתן ספרא במקום שאין מספר ויהיו כזה הצורה נגרע י"ב רביעים מספר לא נוכל 0 טה טה טה טב אא רביעיים 0 שלישיי 0 שניי 0 דקים 0 מעלות 0 מזלות בא רביע בא שליש אב שניים זג דקים בד מעלו זא מזל ח רביע מח שליש חג שניי' בב דקי' זא מעלו בא מזלו ג ___________________________________________________________________ ולא השברים האחרים אבל נעבור מזל אחד על הרביעיים ונאמר שהוא ס' רביעיים ונגרע ממנו י"ב ונשארו מ"ח רביעיי ועתה תכתוב על ספרא שלישיים נ"ט ועל השניים נ"ט ועל השלישיים נ"ט ועל הדקים נ"ט ועל המעלות כ"ט ועל המזלות י"א ועתה גרע כל מין ממינו ישארו בשלישי' ל"ח ובשניים כ"ב ובדקים י"ז ובמעלות י"ב ובמזלות ג' והוא מה שרצינו והבחינה תחבר הנשאר והמספר הקטן ותציא הגדול
משל אחר לגרוע מזלות מעלות עד שלישיות או יותר אם תרצה ממזלות לבד תשטח מזל אחד עד השבר שתרצה ובאחרון תן ס' ובאמצעיים נ"ט בכל אחד ובמעלות כ"ט ויהיה כזה הצורה שנגרע מי"א מזלות שנשארו
מזלות [70ב] [נג1] [] ה' [] ונשארו [] [] וט' מעלות [] מכ"ט נשארו עשרים מעלות [] נשארו י"ח ול"ד שניי מנ"ט נשארו כה [] מכ"ג נשארו כ' שלישיים והבחינה תחבר השני טורים התחתונים שהם הקטנים ותציא י"ב מזלות משל אחר רצינו לגרוע מטבע זהב מאחר ושיהיה דני' ופשיט ואם תרצה מחצות הנה אם קצת מעלות הנשאל לגרוע ממנו הוא קטן הנה הוא קשה מעט אבל קודם שתגרע תעבור סך אחד ממטבע הזהב ותחלקהו על מעלות שבריו ואז תגרע בנקל המשל בזה רצינו לגרוע מאלף רמ"ה דוקאדוש וי"ו די' וט' פשי' כל אלה מתקצ"ה י"ח די' י"א פשי' ויהיה כזאת הצורה בא אב ד הנה בעבור פשי' ט דינ' וא דוקדוש הדבא שלא נוכל לגרוע פשי אא דנרי חא דוקאדש הטה י"א פשי מט' ולא פשי 0א דנרי טא דוקדוש טדו י"ח די' מי"ו נעבור דוקאדו אחד בשבריו ונתן על י"ו די' כ"א ועל ט' פשי' י"ב כי זהו סך הדוקאדו ועתה נגרע י"א פשי' מט' וי"ב שהם כ"א פשי' נשארו עשרה פשי' גם נגרע י"ח די' מי"ו וכ"א שהם ל"ז נשארו י"ט די' גם נגרע תקצ"ה דוקאדי מאלף רמ"ד נשארו תרמ"ט והוא המבוקש ומשלו תראה ממזלות ומלטרי' שהם דומים לזה
71[א] [נג1] [נג2] משל רצינו [] תתקמ"ו [] בזה השואה אל[] ותתנהו על מורה ה[] על ט' וגרע ממנו הח' ישאר א' יהיו [] תשיעית ואחר גרע שלמים משלמים [] לנו אחר שגרענו הנז' תצ"ו ותשיעית כזה א/ט והוא המבוקש והבחינה תחבר הב' הקטנים ותציא הגדול משל אחר שרצינו לגרוע שלמים ושברי שברים משלמים ושברי שברים שלמים כמו קי"א שלמים וששה שביעיות מה' תשיעיות שרצינו לגרוע מקמ"ד שלמים וח' תשיעיות עשרית מד' שלמים כזאת הצורה הנה ראשונה נשויה הג שברי הגורע אאא ו/ז × מ ה/ט דדא ח/ט מ א/א0 מד' ונמצא המורה וה' תשיעיותיו הם ל"ה נקח ו' שביעיות ל"ה והם ל' וזה השבר הנרצה שהוא ל' חלקים מס"ג והנה שב הגורע קי"א ול' חלקים מס"ג כזה קי"א ג0/גו ונשמרם עד שנשויה המספר השני וראשונה נוציא השברים והמורה שהוא צ' ואחר נשויה הד' שלמים והוא שנכפול ד' על צ' שהוא המורה הראשון יעלו ש"ס והוא מורה שני ועשיריתו הוא ל"ו וח' תשיעיותיו הם ל"ב חלקים מש"ס בשלם כי תשעית ל"ו הם ד' וח' פעמים ד' הם ל"ב כנז' והוא השבר השני המבוקש והנה שב המספר ושבריהם לגרוע קי"א שלמים ול' חלקים
[71ב] [נד1] [] בזה הצורה [] בשאלו []רים הם משני מינים [] השואה שלישית וזה [] שנכפול כל שבר על מורה [] חברו ויעלו לעשרת אלפים [] [] ב' אלפים וי"ו [] יהיו השברים שוים אשר [נו]כל לגרוע זה מזה אלא שהשברים הגורעים הם יותר משברי המספר השני ולכן נקח אחד שלם ונעשה ממנו חלקים כפי המורה הכולל מש"ס על ס"ג שהוא כ"ב אלפים תר"ף ונחברם עם שברי המספר שרצינו לגרוע ממנו שהם ב' אלפים וי"ו ואז יהיו כ"ד אלפים תרצ"ו ואחר נסדרם לגרוע זה מזה וגם השלמים ויהיו כזאת הצורה גרענו השברים שברים שלמים מן השברים נשארו י"ג אלפים ו ט ו ד ב ג ד א תתצ"ו מכ"ד אלפים ותר"ף בשלם 0 0 ח 0 א א א א גם נגרע קי"א שלמים מקמ"ג ו ט ח ג א ב ג ישארו ל"ב כמו שתראה בצורה השיור למטה ואם נקצר השברים ישובו לקצ"ג חלקים משט"ו בשלם כזה וזה מה גטא שרצינו ועיין שגם כן תוכל לעשות ההשואה בדרך האג האחד עם מורה אחד וקח חלקיהם וגם כן תוכל לעשות מכל השלמים שברים ותגרע אלו מאלו והנשאר תחלק על המורה והיוציא הם שלמים והכל שוה כי יש בכל מין דרכים רבים אבל די בזה למבין וכן לחכם ויחכם עוד והנה כל המשלים שנתתי בפרק החיבור תוכל ללמוד מהם בגרעון וגם מה שבגרעון בחיבור ואין צריך להאריך
72[א] נ"ד[1]
[נד2] דף ריק [נה1] [] שלמים [] ושברים [] שתתן השלמים [] ותחלקם והיוציא בחלוקה [] נרצה לחלק יהיו שלמים על שברים [] שברים ממין השבר המחלק והעולה [] המשל רצינו לחלק כ"ב לטרין ועשרה דני' וששה פשיט' על ששה ניתן הכל בפשיטי' יהיו ה' אלפים ות"ו כי הכ"ב ליטרי' יהיו ת"מ די' ועוד נכפלם בי"ב יהיו ה' אלפים ר"ף והכל פשי' והעשרה די' עם הששה פשי' יהיו קכ"ו נחברם עם ה' אלפים ור"ף יהיו כולם ה' אלפים ת"ו נחלקם על ששה יעלה בחילוק תתק"א והם פשי' ואם נרצה נעשה אותם די' ויהיו ע"ה די' ופשוט שהם ג' ליטרי' וט"ו די' ופשוט אחד והבחנה כפול מה שיצא בחילוק על ששה ויעלו ג' ליטרי וט"ו די' ופשוט והמשל נכפול הפשוט האחד בששה יעלו ששה פשיט' ונשמרם וששה פעמים ט"ו הם צ' שהם ד' ליטרי' ועשרה די' נשמרם וששה פעמים ג' לטרי' הם י"ח ליטרי' וד' שהיו בידינו יהיו כ"ב ליטרים והנה היו כולם כ"ב ליטרי' ועשרה די' וששה פשיט משל אחר רצינו לחלק שלמים על שברים כמו כ"ה שלמים על ג' חמשיות כזאת הצורה הנה ג/ה | כ"ה נעשה השלמים חמשיות שנכפלם על מורה השברים ויהיו קכ"ה חמשיות נחלקם על ג' יעלה בחילוק מ"א שלם וב' שלישיות ואל תתמה על היוציא בחלוקה שהוא יותר ממה שהיה לנו כי הוא כאומר חלק חצי לחצי
73[א] [נה2] [] כי [] שיהיה יעלה הראוי ל[] חצי דבר אחד לכולו [] [] הוא הראוי לאחד שלם [] ותעיין ותבין שאם תחלק יתחלק ו' על ב' בחלוקה ט' שלמים והנוסף שהם ג' הוא הגורע לתשלום [] שלישיות משל אחר רצינו לחלק ג' שלמים וג' רביעיות על ב' שלישיים תן השלמים בשברו יהיו ד' רביעות ט"ו רביעיו' השוים עם המחלק שהוא ב' שלישי' יהיו כזה הצורה יהיו 45 8 מ"ה חלק על ח' יעלו ה' שלמים וה' שמיניות 15 × 2 משל אחר רצינו לחלק מ"ט שלמים וה' 4 ג ששיות על ג' רביעי ששית מב' חמשיות כזאת הצורה טצב ו 8 48 הנה ראשונה נתן מט ה על ג א ב השלמים בשברהם ו ד ו ה שהם שישיות ונחברם 0בא עם שבריו שהם ה' יהיו רצ"ט ותשמרם לחלק על ג' רביעיות משישית מב' חמשיות תשויה זה השברי שברים ויהיה המורה הכולל ק"ך והנה ב' חמשיותיו הם מ"ח והוא עליו ושישית מ"ח הוא ח' וג' רביעיות ח' [] הם ששה וזה השבר הנרצה אשר עליו נחלק שהוא ו' חלקם מק"ך בשלם והנרצה לחלק הם שישיות ויהיה כזה הצורה 0חחהג וג נשוים כל שבר במורה חברו טטב × ו או בדרך האחרת ויהיו החלקים ו 0בא אשר תרצה לחלק ל"ה אלפים תת"ף והחלקם
[73ב] [נו1] [] הם אלף [] תקצ"ו וכ"ד חלקי' [] תמצאם אם תקצרים [] תתק"ץ ותחלקים על ג' [] ההשואה תוכל לקצר אם תרצה [] זה המשל ורבים ביותר נקל כי תוכל [] עם שתעשה מורה השברים ס' כי ב' חמשיות חמשיות ס' הם כ"ד ושישית כ"ד הוא ד' וג' רביעיות ד' הם ג' וזה שבר השבר הנרצה שהוא ג' חלקים מס' בשלם ואחר תשויה רצ"ט ששיות עם ג' חלקים מס' כזה 0דטזא יהיו על רצ"ט י"ז אלפים תתק"מ והם לחלק על טטב/ו ג/ו0 י"ח שהוא כפל ו' על ג' ויציא בחילוק תתקצ"ו וב' שלישיות מקוצר כנזכ' ואם תרצה תוכל להקל עוד כאשר היו בידך ג' חלקים מס' תקצרם קודם שתשוים יהיו חלק אחד מב' תשויהו על ו' שהוא מורה החלק השני יהיה ו' גם תשויה רצ"ט עם כ' יהיו יעלו ה' אלפים תתק"ף חלקם על ו' יעלה בחילוק תתקצ"ו כנז' והרי לך כי כל זמן שתעיין בהשואה אולי תוכל לקצר מספרך והקל מעליך והכל דרך ישר כי מי יוכל לכתוב הכללים כל שכן הפרטים משל אחר נרצה לחלק שלמים ושברי שלמים על שברי שלמים כמו ק"ח שלמים וד' תשיעיות מי"ח שלמים על ג' שביעיות ח' שלמים כזאת שלמים בז שלמים דב שלמים הצורה וקח מן הח' קח ד יח ג מח שלמים הנשאל והוא ט על ז שנכפול ח' על ז' שהוא מורה שברו יהיו נ"ו נקח מהם ג' שביעיותיו והוא כ"ד
74[א] נו [נו2] ונשמר[] שלא תצטרך [] השברים [] לכפול ח' על [] כי אחר שעש[י]ת כל זה [] פעמים י"ח וכן כדרך זה [] מי"ח שנכפול י"ח בט' יעלו קי"ו [] והם ע"ב כי תשיעית קי"ו הוא י"ח וד' פעמים י"ח הם [ע"ב] ואם תרצה כפול השברים על השלמים אשר תרצה לקחת מהם וה והעולה תתנם עליהם והוא המבוקש ואחר שהיה לנו שברי השלמים שהם ע"ב נחבר אליהם השלמי' שהם ק"ח והוא שנכפלם על מורה אלו השברים שהוא ט' יעלו תתקע"ב והם תשיעיים והשברים אשר נרצה לחלק עליהם שהם כ"ד שביעיים נשויה שניהם כזאת ד0חו ואב הצורה ויהיה המספר הנחלק ו' אלפים
בזט דב תת"ד והמספר אשר עליו נחלק רי"ו ט × ז והיוציא בחילוק ל"א שלמים וק"ח חלקים
מרי"ו בשלם ואם נקצרם יהיו חצי שלם ואם כן המחלק ק"ח שלמים וד' שביעיות מי"ח שלמים על ג' שביעיות מח' שלימים יציא בחילוק לא שלם וחצי וכן כל הדומה לזה משל אחר אם רצינו לחלק מטבעות מתחלפות עם דנר' ופשטי' וכו' או מזלות ודקים ושניי' ו[] או שניי' ח[] וכו' הנה נחלק הגדול ראשונה ומה שיציא בחילוק שמור אותו בשמו כופלהו בסך שהוא אם [] בסך ה[] וכן לטרין או לסך המרובע שיהיה המשל רצינו לחלק רל"ד לטרי ממון וי"ו די'
[74ב] [נז1] [] רל"ד [] לכל אחד [] ונשמרים [] על כ' שהוא סך הלטרה [] י"ו די' שלשו יהיו צ"ו די' נחלקם [] ד' דינ' ונשמור אותם בשמן ונשארו ] נכפלם בי"ב יעלו מ"ח פשיט' ועם ט' של[] יהיו נ"ז נחלקם על כ"ג יעלו ב' פשי' ונשארו י"א פשיט נכפלם על ד' יעלו מ"ד רביעיות נחלקם על כ"ג יעלה בחילוק אחד שהוא רביעית פשוט ונשארו כ"א רביעי' והם כ"א מכ"ג ברביע פשוט כזה אב ועלה מזה כי המחלק רל"ד לטרי' י"ו די' ט' פשיט' גב על כ"ג שעלה לכל אחד עשרה לטרי' י"ד די' וב' פשי' ורביע פשוט וכ"א חלקים מכ"ג ברביע פשוט והבחינה כפול הרביעיות על כ"ג ועם כ"א שנשארו יהיו מ"ד והם י"א פשוט גם כפול ב' פשוט' על כ"ג יהיו מ"ו פשי' וי"א יהיו נ"ז שהם ד' די' וט' פשיט' גם כפול ד' די' על כ"ג יהיו צ"ב ועם ד' יהיו צ"ו די' שהם ד' לטרי' וי"ו די' גם כפול עשרה לטרי' על כ"ג יעלו ר"ל ועם ד' לטר' יהיו רל"ד והנה שב הכל רל"ד לטר' וי"ו די' וט' פשי' ותוכל לעשות זה בדרך אחרת שתעשה הכל מן השבר היותר קטן ואחר תחלוק ואחר החילוק תעלה הכל לכללים כמו במשלנו שנעשה הכל פשיט כי הם השבר הקטן והם נ"ו אלפים שס"א הכל פשי' ועתה תחלקם על כ"ג שהוא המורה יעלה בחילוק ד' אלפים תרצ"ו * ונשארו ט' פשיט ונשמרם בשמן ועתה נחלק די'
75[א] [נז2] אלו הדי' [] רל"ד לטרי' [] לטרי' וי"ו די' [] פרק במ[] מאזני השברים []
[75ב] [נח1]
פרק במאזני השברים ואומר כי
מאזני השברים הם כמאזני השלמים
בעבור כי כאשר תחבר או תגרע או תחלק יהיו
לעולם השברים שוים מאיזה מין שיהיה ועל כן
תנהיג
76[א]
[נח2]
פרק במאזני השברים ואומר כי מאזני השברים הם כמאזני השלמים בעבור כי כאשר תחבר או תגרע או תחלק יהיו לעולם השברים שוים מאי זה מין שיהיו ועל כן תנהיג במאזני השברים כמנהג מאזני השלמים ועם כל הדרכים הנתונים בפרק מאזני השלמים ובעבור שלא תצטרך לעיין ותראה הדרך למין אכתוב כאן משל אחד מכל אחד מבדיקת כל אחד בהפכו חיבור עם גרעון וגרעון עם חיבור כפל עם חילוק וחילוק עם כפל והמשל בחיבור הנה אחר שנחבר שברי המספר נגרע מן המקובץ השבר הקטן וישאר הגדול או נגרע הגדול וישאר הקטן כיצד הרי שחיברנו ק"א חלקים מר"א בשלם עם ל"ג חלקים מר"א גם כן
[76ב] [נט1] [] נג אזא [] א0ג [] ל"ג [] [] הנה אחר שנכפול שברי המספר נחלק [] כאשר תראה כזאת הצורה ויצאו ג ד ה לך שברי המספר כיצד כפלנו ג' רביעיות וד' חמשיות ד ה ו וה' ששיות והנכפל יהיה ס' חלקים מק"ך כזאת הצורה השנית נחלק
0ו כדרך שכפלנו כי כפלנו ג' על ד' והעולה על ה' יהיו ס'
0בא ועתה נחלק ס' על ה' יציא בחילוק י"ב נחלק י"ב על ד' ותציא בחילוק ג' והוא הראשון או נחלק ראשונה ס' על ג' יצא כ' וכ' על ה' יציא ד' או נחלק ס' על ד' ותציא ט"ו גם ט"ו על ג' ותציא ה' והוא השלישי ועשיתי אילו החלוקות להרגילך ובזה הדרך תוכל לבדוק שברים רבים משל אחר במאזני המגרעת אחר שגרענו שברי המספר נחבר השברים הגורעים עם הנשאר מן הגדול ותציא הגדול כיצד נגרע ת"ח מאלף ש"ל יש ישארו תתקכ"ב כזאת הצורה 0 ג ג א הגדול והמאזנים אם זה אמת נחבר השבר הקטן שהוא ח 0 ד הגורע הגורע שהוא ת"ח עם הנשאר מן הגדול שהוא תתקכ"ב ב ב ט הנשאר ותציא הגדול שהוא אלף ש"ל משל במאזני החילוק הנה אחר שחילקנו שברי המספר נכפול היוציא בחילוק על המחלק ועל היוציא בכפל נוסיף הנשאר לחלק ותציא הגדול כמו שחילקנו רנ"ו חלקים מקס"ח שבא אחר ההשואה מב' שלישיות ומששה שביעיות על ס"ג חלקים מקס"ח גם כן שבא אחר ההשואה מג' שמיניות ויהיו כזאת הצורה 0 ואם תרצה לבדוק זה אם הוא אמת כפול היוציא דא והב ד גו
77[א] [נט2] בחילוק שהוא ד' [] עליהם הנשאר שהוא []
Section Four: Roots
השער המורכב [] בעבור רוב [] פרקים הפרק הראשון הראשון בשרשים הפרק השני ב[] מספרים נמשכים הפרק השלישי
| הפרק הראשון חלקתי אותו לד' מינים והקדמה בראשונה ראויה לשרשים המין | |
| המין הראשון בהוצאת בהוצאת השרשים המרובעים השוים והבלתי שוים | |
| המין השני בהוצאת השרשים המעוקבים השוים והבלתי שוים | |
| המין השלישי לדעת שורש איזה מספר מן המספרים שאין להם שורש אמיתי | |
| המין הרביעי בידיעת שורש השברים | |
| הקדמה הראויה לשרשים | |
| ואומר כי המספר המרובע השויה בכל צלעותיו הוא המספר הנכפל על עצמו והוא השורש והנכפל הוא המרובע וטבע הוצאת השורש הוא שאם יהיה מספר מה נכפל משני מספרים מתחלפים והם עושים מספר מרובע ארוך הנה הוצאת השורש חוזיר אותו מרובע שויה מכל צלעיו או לכפל שני מספרים שוים או לכפ וישאר מהשנשאר וזה כגון ב' על ח' |
[77ב] [ס1] [] שורש ד' וזה כי [] אשר תוכל לשנות צלעותהם []חלקיו [] מורכב מב' ולא יותר ואל ב' תחלקנו [] צלע ב' ותהיה כזה א א [] ואם צלעותיו ב' וג' כזה א א א וח' צלעותיו א א ב' וד' וכן עשרה וי"ב יש בו א א א ב' הרכבות ב' על ו'
| וג' על ד' ול' יש בו ג' רכבות ב' על טו וג' על עשרה וה' על ו' : וס' יש לו ה' הרכבות ב' על ל' וג' על כ' וד' על ט"ו וה' על י"ב וו' על עשרה והנה שורש ס' הוא ז' ונשארו י"א ומאלה הערה לכולם והנה גם כפל מרובע על מרובע יהיה מרובע ואם יהיו כמה שיהיו גם תעין כי כל המדריעות הנפרדים יש להם שורש ואן לזוגות שורש ולכן יהיו המדריעות נחלקים במעשה שנים שנים כמו שתראה | המין הראשון בהוצאת השרשים מן המספר המרובע השוה והיוציא יהיה שורש אמתי וזה הדרך עצמו הוא למרובע הבלתי שוה אלא כי מן השוה לא ישאר מספר ומהבלתי שוה ישאר מספר והנה תיקון וסדר המדרגות להוציא השורש כך היא שתחלק ראשונה כל מדרגות מספרך שנים שנים וההתחלה ממעלת האחדים ומן המעלה האחרונה או מן השנים אם יהיו שנים באחרונה תתחיל להוציא השורש או מן האחד אם אין שם שנים וממנה תוציא שורש אחד או מן השנים כי מכל חלק תצטרך להוציא שורש אחד ר"ל חלק מן השורש וקראתי לכל שתי מעלות חלק אחד ותחשוב כל חלק לאחדים ועשרות זולת כאשר תקחינו עם הנשאר מן החלק הקודם לו כי אז יהיה אלפים ומאות כאשר תראה בע"ה ואחר קח החלק האחרון ר"ל בשני מעלות מספרים שבו או מה
78[א] [ס2]
____ ____ ____ ____ הצורה והנה חלקתי מעלות ד ב ו ו 0 ה ט ב המספר שנים שנים ויהיו ד' ב ג ד ה חלקים ועתה ידענו כי המספר הנכפל על עצמו הוא ד' מעלות על ד' מעלות כי לכל חלק ראוי חלק אחד מהשורש והנה נתחיל מן החלק האחרון ונאמר כי המרובע היותר גדול שיש בכ"ט הוא כ"ה ונשארו ד' על ט' והנה שורש כ"ה הוא ה' נתן ה' תחת החלק הרביעי כי ממנו יציא וכבר [78ב] [סא1] [] והנה לדעת שורש [] שורש ונכפול אותו בשנים [] ונאמר שהוא ד' ויהיו אז העשרה [] נכפול ק"ד על הד' ד ד 0 א [] נגרע תי"ו מת"ן כי הד' שנשארו על הט' [] בערך לחלק השלישי ונשארו ל"ד בחלק השלשי והם ג' [] כערך לחלק השני והנה מאחר שהד' הנתון הוא הראוי נכתוב ד' תחת החלק השלישי ואם תאמר כי בעבור שנשאר ל"ד בחלק השלשי שיהיה המספר הנתון ה' הנה יעלה יותר מן הראוי ע"ה ובעבור זה לקחנו ד' כנזכר [] עם מעט עיון תראה המספר הראוי לתת לפני כפל השורש הנמצא והנה לדעת שורש החלק השני עשה כנז' והוא שתכפול השני שרשים הנמצאים שהם ד' וה' שהם נ"ד יהיו ק"ח ח 0 א כזה נתן לפני המספר הזה מספר אחד והראוי הוא ג' ויהיו אז אלף ושמונים ושלושה כזה כפלנו זה המספר על ג המספר הנתון שהוא ג' יהיה העולה ג' אלפים ורמ"ט ג ח 0 א נגרעם מן החלק השני ומהנשאר מן השלישי שהם ג' אלפים ותס"ו ישארו ב' בחלק השלישי וי"ז בשני והם כ"א אלף ות"ש בערך לחלק הראשון והנה מאחר כי ג' הנתון הוא הראוי נכתוב ג' תחת החלק השני ולדעת שום החלק הראשון עשה כאשר עשית וכפול השרשים הנמצאים בשנים שהם עתה תקמ"ג כזה ג ד ה ויהיו אלף ושמונים וששה כזה ויעלה זה המספר מעלה אחד עם המספר שניתן לפניו ו ח 0 א שהראוי הוא ב' ויהיו אז עשרת אלפים ותתס"ב ב כזה ב ו ח 0 א כפלנו זה המספר על המספר הנתון שהוא ב' יעלו כ"א אלפים תשכ"ד נגרעם מן החלק הראשון ומן הנשאר מן השני ומן השלישי שהוא כ"א אלפים תשכ"ד לא נשאר כלום וזה יורה שהמספר המונח שהוא כ"ט מספרים ותק"ו אלפים וקנ"ד שהוא מרובע שוה הצלעות וניתן המספר הנתון שהוא ב' תחת החלק הראשון ויהיה אז השורש שלם כי מה שאמרנו ל[] חלק שורש 79[א] [סא2] הוא בדרך ההשאלה [] תל"ב כזה ב ג ד ה [] [] על עצמו ואם יציא לך [] משל אחר רצינו לדעת שורש [] ותס"ד ואם הוא שוה הצלעות [] __ __ __ __ _ ד ו ד ו ה ד ח ז ה הצורה והנה [] א ה 0 ד ב וראוי להוציא ה' חלקים כאשר [] לזה השורש [] הראשון שהוא החרון אשר בזה ומרובעו הגדול הוא ד' [] ישאר א' על ה' והנה שורש ד' הוא ב' נתן אותו תחת החלק החמשי כי [] ולדעת השורש השני נכפול ב' ה' שהוא השורש הראשון יהיו ד' נתן מספר מה לפניו והנה הראוי הוא ד' ויהיו מ"ד כפלנו מ"ד על ד' הנתון ד כזה יעלו קע"ו נגרעם מקע"ח שיש בחלק הרביעי ד ד ובנשאר בחמשי ישארו ב' ברביעי והוא ק"ק בערך לחלק ו ז א השלישי והנה המספר הנתון שהוא ד' הוא תחת החלק הרביעי ולדעת השורש השלישי נכפול השני שרשים הנמצאים בידינו שהם כ"ד יהיו מ"ח ניתן מספר לפניהם והנה הראוי הוא ספרא לעלות מעלה שאם ניתן א' שהוא המספר היותר קטן יעלה תפ"א לגרוע מרמ"ה ולא נוכל כי רמ"ה קטן מתפ"א ולכן המספר הנתון הוא ספרא ונתן הספרא תחת החלק החמשי השלישי ולא נגרע דבר לא מן החלק השלישי ולא משיור החלק הרביעי ויהיה ב' שהוא החלק החמשי עשרים אלפים כערך החלק השני ולדעת השורש הרביעי נכפול השלשה שרשים הנמצאים שהם יחד רי"ו יהיו ת"ף נתן לפניהם מספר אחד והראוי הוא ה' ויהיו ד' אלפים תת"ה כפלנום על ה' הנתון יהיו כ"ד אלפים וכ"ה כזה ה גרענום ממספרי החלק השני והנשאר מן השלישי ה 0 ח ד ומן הרביעי שהם כ"ד אלפים ותקס"ד ישארו תקל"ט שהם בערך החלק הראשון נ"ג אלפים תתקס"ד והנה המספר הנתון שהוא ה' הוא השורש הרביעי וניתן אותו תחת החלק השני שהוא רביעי [79ב] [סב1] [] הד' שרשים שהם [] אלפים תת"י ניתן לפניהם [] מ"ח אלפים וק"א כפלנום [] הכפול הוא בעצמו כי הכופל [] אינו עולה ולא יורד א [] וק"א מנ"ג אלפים ותתקס"ד א 0 א ח ד ישארו ה אלפים ותתס"ג והנה המספר הנתון שהוא אחד הוא השורש החמש וניתן אותו [] בחלק החמישי שהוא חלק האחדים והעשרות והנה אם ניתן לפני השורש שנים בעבור שלא ישארו ה' אלפים תתס"ג יעלה הכפל יותר ויותר ממה שנצטרך לזה השיור ואם כן הא' הנתון הוא הראוי והנה השיור שנשאר יורה שהמספר המונח שאינו מרובע שוה הצלעות אבל כל חשבון אשר שרשיו [] כל החשבון יורה שהוא מרובע שוה הצלעות הבחינה תכפול השורש [] על עצמו ועל הכפל תוסיף הנשאר ואם יהיה שוה למספר המונח הוא טוב ועוד תעיין שלא יהיה הנשאר אחר הוצאת השורש יותר מכפל השורש שאם הוא יותר מכפל השורש הנה תוכל לתת עוד אחד במספר הנתון שהוא חלק השורש האחרון המשל הנה נניח כי שורש ד' הוא א' ישארו ג' והוא יותר מכפל השורש כי כפל כפל השורש הוא פעם אם כן נוכל לתת ב' בשורש ולא נשאר דבר עוד רצינו שורש ט"ו והוא ג' ישארו ששה שהוא כפל השורש בצימצום ואם כן הוא השורש הראוי וכן כ"ד והשורש ד' ונשארו ח' שהוא כפל השורש בצמצום עוד נניח כי שורש ל"ו הוא ה' ומרובע חמשה הוא כ"ה נגרע כ"ה מל"ו נשארו י"א והוא יותר מכפל השורש כי השורש שהנחנו הוא חמשה וכופלו עשרה והנשאר יותר מעשרה כי הוא י"א אם כן השורש הראוי הוא ששה עוד רצינו שורש מאה נניח 80[א] [סב2] כי הוא ט' [] הוא י"ח והנה י"ט הוא [] בשורש עשרה וכן כולם
הראשון לצד ו ד ו ח 0 א שמאל אשר ממנו ט א ח ב ב נתחיל הוא כ"ט ז ז ד ג והשני נ' והשלישי 0 ה ד ע"ז והרביעי עשרה א ד | 0 א | ז ז | 0 ה | ט ב והחמשי שהוא ה הראשון על דרך א ב ג ד ה ב האמת הוא מ"א ו א ד ועתה רצינו 9 7 ב ג שורש כ"ט ד ב ז א ב א ד ו ח 0 א [80ב] [סג1] [] ישארו ד' על ט' [] חלק שני ויהיו אז החלק [] שנגרע מרובעו מ[] [] שהוא חמשה יהיו עשרה ניתן [] והוא ארבעה ויהיו כזה ק"ד ד [] הנתון כמו שתראה בצורה יהיו תי"ו ד 0 א [] במעלותם בדרך שיהיו האחדים שהם ששה תחת אחדי החלק השני שהם סיפרא והם תחת [] השורש נגרע תי"ו מת"ן נשארו ל"ד על החלק השני וד' התחתון הוא השורש השני ונתנהו בביתו תחת אחדיו חלק שני ועוד רצינו שורש חלק שלישי שהוא ע"ז ועם הנשאר בחלק שני והוא ג' אלפים תע"ז כמו שתראה בצורה נכפול השני שרשים הידועים לנו שהם ד"ה שהם נ"ד על שנים יהיו ק"ח נבקש מספר ראוי לתת לפני ק"ח והוא ג' ויהיו כזה ג הצורה אשר כולם יהיו אלף ופ"ג נכפול כל המספר על ג ח 0 א ג' הנתון והוא השורש יעלו ג' אלפים רמ"ט אשר 9 4 2 ג נגרעם מג' אלפים תמ"ז והוא שניתן אחדי [] הג' אלפים רמ"ט תחת אחדי החלק השלשי אשר בו ע"ז ואחר תגרעם מג' אלפים תע"ז ישארו כ"ב אלפים תת"י וג' הנתון הוא השורש ונתנהו בביתו תחת אחדי החלק השלישי שהם ז' עוד להוציא שורש רביעי אשר בו עשרה נכפול השרשים הידועים שהם הד"ג בשנים יהיו אלף פ"ו נתן לפניהם מספר ראוי והוא ב' ויהיו עשרת אלפים תתס"ב נכפלם על המספר הנתון שהוא ב' יהיו כ"א אלפים תשכ"ז כזה ב הצורה נגרעים מכ"ב אלפים תת"י אחר אשר ב ו ח 0 א ניתן אחדי המספר שהוא ד' תחת אחדי החלק ד ב ז א ב הרביעי אשר בו ספרא ונשארו ק"ח אלפים תרמ"א והנתון שהוא ב' הוא השורש וניתנהו בביתו עוד להוציא שורש החלק החמשי אשר בו מ"א נכפול השברים הידועים שהם הדג"ב בשנים יעלו עשרת אלפים תתס"ד נבקש מספר ראוי לתת לפני 81[א] [סג2] זה המספר [] ק"ח אלפים תרמ"א [] הנתון שהוא אחד יעלה כמו [] ניתן אחדי המספר שהוא אחד תחת [] גם כן ואחר כל הנמשכים לצד שמאל [] שהוא גם כן ק"ח אלף [] לא נשאר דבר ותו[] שוה הצלעות ודי בזה המשל לאיש שהוא משכיל והבחינה כפול האחד השורש על עצמו שהוא נ"ד אלפים שכ"א ותציא כל המספר שהוא [] שני אלפים ותתק"ן מספרים ותשע"א אלפים ומ"א והוא טוב
[81ב] [סד1] [] ותן המספר [] מספרך ותן המספר [] המספר הנתון אחד ותראה אחר [] המעלה הוא גדול לא תכפול דבר [] בחלקו ויהיה מספרי מעלות חלקו כמו שיור [] עשינו [] המרובעות ובעבור כי זה המעשה המעשה קשה לציירו אניח צורות כפי המשכת המעשה בכל הכפלים וראשונה אכתוב לוח מעוקבי כל אחדי המעלה הראשונה בעבור כי לעולם החלק האחרון הנתון אשר ניקח שורש מעוקבו בראשונה [] לא יוסיף שורשו מאחדים ובעבור זה תמצא בטור ראשון מזה הלוח כל אחדי המעלה הראשונה והטור השני מעוקבהם וזה צורת הלוח המשל בזה רצינו לדעת שורש המעוקב הגדול שיוכל להיות בזה המספר שהוא ע"ד אלפים א א ופ"ח או אם הוא מעוקב בלא שיור וראשונה אניח ב ח מעלות המספר ואחלקים ג' ג' ואתן קו תחת כל ג כז חלק ומקום לשרשים ויהיה כזה ואחר נוציא ד סד ח ח 0 / ד ז מעוקב ע"ד והנה המעוקב ה קכה ב ד הגדול שבו הוא ס"ד ו ריו ושורשו ד' כמו שתראה ז שמג בלוח כי ד' על ד' הוא י"ו וי"ו על ד' הוא ס"ד ח תקיב נגרע ס"ד מע"ד ישארו עשרה שהוא עשרת אלפים ט תשכט כערך אחדי החלק הראשון והשורש שהוא ד' נתן אותו תחת החלק השני כי ממנו יציא והרי לנו שורש אחד מן החלק השני ולדעת שורש החלק הראשון לקחנו השורש הנמצא והוא ד' וניתן מספר לפניו והנה הראוי הוא ב' ושניהם יעלו מ"ב כזה ב"ד ועתה נכפול מ"ב על י"ב שהוא ג' כפל השורש ויהיה העולה תק"ד 82[א] [סד2] כזה ד0ה [] שהוא י"ב יהיו אלף וש[] מעוקב ב' שהוא המספר [] השמור [] יהיו ח' אחדים ויעלה כל[] אלפים ושמונים ויהיה כזה נגרע זה המספר [] מן החלק הראשון ומהנשאר בשני והנה הכל שוה כי גם כן [] עשרת אלפים ושמונים משמונה [] ולקחנו המספר הנתון שהוא ב' וניתן אותו תחת החלק הראשון ויהיה אז שורש מעוקב זה המספר המונח מ"ב בשוה והוא שוה בכל צלעותיו ואם תרצה לבדוק אם זה אמת כפול מ"ב על מ"ב שהוא השורש והיוציא על מ"ב ותציא המספר המונח משל שני רצינו לדעת שורש המעוקב היותר גדול שהוא כזה המספר המונח שהוא ח' אלפים ותי"ד מספרים ותתקע"ה אלפים ות"ה כזאת הצורה והוא ד' חלקים נוציא מעוקב החלק ה 0 ד | ה ז ט | ד א ד | ח האחרון שהוא ח' והוא ד ג 0 ב מעוקב ושורשו ב' נגרע ח' מח' לא נשאר כלום וניתן ב' תחת הח' האחרון ולדעת שורש החלק השלישי לקחנו השורש הנמצא שהוא ב' וניתן לפניו מספר אחד והנה אם ניתן א' לפני השורש יעלה יותר מן הראוי תתמ"ז ולכן לא נעשה דבר אלא ניתן ספרא כחלק השלישי ולא נגרע ממנו דבר אלא יהיה שיור לחלק השני וניתן ספרא תחת החלק השלשי ולדעת שורש החלק השני ניקח השני שרשים הנמצאים שהם יחד עשרים וניתן מספר לפניהם והנה הראוי הוא ג' ויעלה המספר ר"ג כזה ג0ב ונכפול זה המספר בשישים שהוא ג' כפלי השורש יעלו י"ב אלפים וק"ף ועוד כפלנו זה המספר על המספר הנתון שהוא ג' יעלו ל"ו אלפים ותק"מ ונשמרים אחר נקח מעוקב המספר הנתון שהוא ג' ויהיה מעוקבו כ"ז ניתן העשרות ניגד אחדי המספר הנתון ויהיה כזה [82ב] [סה1] [] כולם שס"ה [] תכ"ז נגרע זה [] החלק [] בשלישי מ"ט ובשני תקמ"ח [] ותקמ"ח אלפים ואם ניתן מספר [] הגדול הנה יעלה יותר מן הראוי ד' [] ואם כן ג' הוא הראוי כנזכר וניתן ג' שהוא המספר הנתון תחת החלק השני ולדעת השורש הרביעי שהוא תשלום שהוא [] כל השורש ככלל ניתן מספר אחד לפני השרשים הנמצאים שהם ג 0 ב והראוי הוא ד' ויהיה אז מספר השורש עם הנתון ב' אלפים ול"ד כזה ד ג 0 ב נכפול זה המספר בכלל על תר"ט שהוא ג' כפלי השרשים יעלה מספר אחד ורל"ח אלפים ותש"ו כזה ו 0 ז ח ג ב א נכפול זה המספר על המספר הנתון שהוא ד' יעלה ד' מספרים ותתקנ"ד אלפים תתכ"ד ויהיה ד ב ח ד ה ט ד כזה ונשמרם ואחר נקח מעוקב המספר הנתון שהוא ס"ד נחברהו עם המספר השמור וניתן עשרות זה המעוקב עם אחדי המספר השמור ויעלו כל מדרגות המספר השמור מעלה אחד ויהיו מ"ט מספרים ותקמ"ח אלפות וש"ד ד 0 ג ח ד ה ט ד כזה ניגרעם ממספר החלק הראשון ומן הנשאר מן השני והשלישי שיהיה הכל מ"ט מספרים ותקמ"ח אלפים ות"ה ישארו ק"א והרי כי המספר המונח אינו מעוקב אבל המעוקב היותר גדול שבו הוא ח' אלפים תי"ד מספרים ותתקע"ה ות"ד ונשארו ק"א ואם תרצה לבדוק אם זה אמת קח השורש וכפלהו על עצמו והיוציא כפול פעם אחרת על השורש ותציא המונח קיצור המשל אחר שתצייר הכל תחלק מעלות המספר המונח ג'ג' וקח שורש החלק האחרון ותן מספר לפני השורש וכפול המספר הנתון והשורש על ג' כפלי השורש והעולה כפול במספר הנתון ועל הכל תחבר מעוקב הנתון שיהיו עשרות המעוקב ניגד אחדי מספרך 83[א] ס"ה [סה2] המין הש[לישי] [] המספרים [] והוא ב' מזה המין רוב המספר[] סדרים ד' וט' שיש להם שורש אמתי [] ובמעלת העשרות לא תמצא [] האחרים אין להם שורש ואם תרצה לדעת [] תחבר על כל מרובע המספרים הנפרדים הנמשכים בסדר ואז תדעם והנשארים הם המספרים שאין להם שורש אמיתי והמשל בזה האחד הוא מרובע תחבר עליו הנפרד הנמשך לו שהוא ג' יהיו ד' והוא מרובע תחבר על ד' הנפרד הנמשך אחר ג' שהוא ה' יהיו ט' והוא מרובע תחבר על ט' ז' יעלו י"ו והוא מרובע ועל י"ו ט' יהיו כ"ה והוא מרובע וכן לעולם והנה כל הנשארים הם מספרים אשר אין להם שורש אמתי אלא בקירוב ואומנם תמצא קירוב ויותר קירוב כאשר תראה בע"ה ולכן חלקתי זה המין לשני סדרים אשר הסדר הראשון הוא לדעת השורש המוסכם והשני לדעת השורש המדוקדק והיותר מדוקדק אם תרצה הסדר הראשון הוא לדעת השורש המוסכם ויש בו דרכים רבים אבל בראותי הטורח הגדול והתועלת הקטן לא אאריך אלא הראוי להבנת הענין בלבד וכבר ידעת כי כל המספרים אשר אין להם שורש אמתי הם בין שני מרובעים אחד גדול ואחד קטן ואילו המספרים האמצעים הם זוגות לעולם כמו ב"ג בין אל א"ד והוז"ח בין ד"ט בין כל מרובע ומרובע בתוספת שנים ואחר שכל המספרים אשר בין המרובעים הם זוגות נחלקם בשנים חציים קרובים למרובע הקטן וחציים קרובים למרובע הגדול כי ב' קרוב א' וג' קרוב ד' וכן כולם ולזה חילקתי זה הסדר בשני דרכים הדרך הראשון בקרוב הקטנים ואומר כי הדרך הוא שתקח שורש המרובע הקטן ושומרהו
84[א] [סו2] והם השברים [] משל שני רצינו לדעת [] הוא ה' ונשמרהו והנה [] י"ב והנה המרובע הגדול גדול מה[] י"ב ישארו ט' והם והם השברים ו[] יהיו ג' רביעיות והנה עלה בידנו כי שורש ל"ג [] כזה ה ג/ד ואם נכפול השרשים על עצמם יעלו ל"ג וחלק מי"ו בשלם הסדר השני הוא לדעת השורש המדוקדק והיותר מדוקדק אם תרצה ואומר כי הרוציא לדקדק השורש המוסכם קח השורש המוסכם כדרך שאמרנו בסדר ראשון ואחר אם השורש ואחר אם השורש שמצאת הוא גדול גרע מן השברים ואם הוא קטן תוסיף על השברים ואם עם שבר אחד יהיה גדול ואם עם אחר הקרוב לו הוא קטן תכפלהו במספר גדול ואחר תוסיף מאילו החלקים הדקים או תגרע כפי הראוי ואם תרצה לדקדק עוד אחר שעם חלק אחד מן הדקים יוסיף ועם אחר הקרוב לו יגרע כפול עוד במספר גדול ויקטינו השברים ותוכל לעשות זה עם ג' דרכים הא' שתכפול השברים והמורה והשני השברים שתוסיף או תגרע כפי הצורך והשלישי שתוסיף או תגרע מן המורה וכל זה יורה השכל המשל בזה רצינו לדקדק שורש ה' והנה שורשו המוסכם הוא ב' ורביע כזה ב א/ד כאשר אמרנו בסדר ראשון ובעבור שהוא עולה יותר מה' חלק אחד מי"ו נכפול השבר והמורה במאה כי בסדר ראשון כפלנו פ"א חלקים מי"ו נתן ספרא לפני כל אחד יהיו תת"י חלקים מק"ס ובעבור שהוא גדול לא ניקח כולו כי כולו מקוצר ושוב ישוב לרביע אבל ניקח מהמאה שברים צ"ה חלקים ויהיו כזה הט ואז יהיה השורש ב' שלמים וצ"ה חלקם מת' ניתן 00ד הב' שלמים בשברים יהיו תת תחביר עליהם צ"ה יהיה תתצ"ה הטח כזה כופלם על עצמם יהיה תת"א אלפים וכ"ה נחלקם 00ד [84ב] [סז1] [] יהיה מרובעו [] והם חלקים [] השיור הזה נגרע עוד [] דט/ד00 ניתן הב' שלמים בשברם [] יהיו תתצ"ד כזה דטח/ד00 כופלם [] ומורה על מורה יהיו תשצ"ט [] המורה על עצמו שהוא ק"ס אלפים יעלה בחילוק ה' עם גרעון [] וזה יותר קרוב מן הראשון שהוא צ"ה שנשארו אלף וכ"ה ובצד וגרעו תשס"ד ואם תרצה לדקדק עוד כפול כפול השברים והמורה לחשבון יותר ותכפלם כאשר עשיתי ואם הוא גדול גרע עד שאם תגרע יגרעו ואם יגרעו תוסיף או אם יש לך לב כפול המורה ויקטנו השברים או גרע מהמורה ויגדלו השברים או תעיין באילו המשלים [] אם תרצה לקצר הראשון בחמשיות והשני בחצים יהיה יותר נקל וכל זה כפי מה שיורה השכל כי אין להאריך עוד כי די בזה 85[א] [סז2] המין הרביעי ב[] כי השבר ש[] מונח במספר גדול כי ה[] תקצרהו כל מה שתוכל ואחר [] מרובע יחויב שיהיה גם המורה [] לדעת שורש ארבע תשיעיות כזה ד/ט הנה שהוא השבר הוא ב' ושורש המורה הוא ג' ואם כן שורש ד' תשיעיות הוא ב' שלשיות כזה ב/ג ולראות אם זה אמת כופלהו על עצמו ותציא ד' תשיעיות כזה ד/ט משל אחר רצינו שורש י"ב חלקים מכ"ז כזה בא/זב ראה אם תוכל לקצר שניהם והנה תוכל לקצרם בשלישית ויהיה ד' תשיעיות ושורש ב' שלישיות כזה ב/ג וחזור למשל שעבר ואם השברים מתחלפים משל אחר רצינו שורש ק"ף מרמ"ה חלקים כזה חא0/הדב נראה אם נוכל לקצרם והנה יתקצרו בחמשית כי חמשית ק"ף הוא ל"ו וחמשית רמ"ה הוא מ"ט ושניהם מרובעים ורצינו לדעת שורשם ויהיו וג/טד כזה והנה שורש ל"ו הוא ו' ושורש מ"ט הוא ז' ויהיו ו' שביעיו' ו/ז כזה והבחינה ברורה שתכפול ו' שביעיות על עצמו משל אחר רצינו לדעת שורש קמ"ד חלקים מקס"ט כזה דדא/טוא ובעבור כי הוא ג' מעלות נוציא השורש מכל אחד כמנהג השלמים כאשר תראה במין הראשון בארוכה והוא שנקח בראשונה השבר שהוא קמ"ד ונחלק המעלות בב' מצד ימין כזאת ד ד | א הצורה ונוציא שורש החלק האחרון והוא א' ניגרע א' מא' ב א לא נשאר כלום וניתן השורש שהוא א' תחת החלק שיציא ממנו כפול זה השורש בשנים ותן לפניו מספר מה והראוי הוא ב' כפלהו עם [] השורש יהיו כ"ב כפול כ"ב על ב' שהוא הנתון יעלו מ"ד גרע[] מ"ד מן החלק הראשון שהוא מ"ד לא נשאר כלום וניתן ב' תחתיו ואם היו לנו ב' חלקי השורש א"ב שהם י"ב ונאמר כי י"ב הוא שורש קמ"ד שהוא השבר ונעשה כדרך הזה במורה שהוא קס"ט ויעלה בידינו [85ב] [סח1] [] שורש קמד חלקים []ציא בזה ומאלה ממשלים [] שוים ובלתי שוים ומהנשאר מהשרשים [] [] ביד[י]עת חשבונות נמשכים ביחס והם [] ההנדסה ואקדים הקדמה אחת ואומר כי המספר לקו ולשטח ולגשם וכן יהיו שלושה חלקים ואומר כי כמו החלק הא' שהקו בלתי בעל תכלית כן המספר בלתי בעל תכלית וכאשר המספר המנוי הוא בעל תכלית כן הקו המ[] הוא [] בעל תכלית ויאמר כמספר וכאשר יאמר כקו קטון או גדול כן המספר יאמר קטון או גדול וההתחלה מן הב' ובתוספת הבא אחריו שהוא אחד לאין קץ ונתחיל בסגולות המספר הקויי ואומר כי כל מספר הוא שוה לחצי שני מספרים קרובים ממנו או רחוקים מרחק שוה כאשר אמרתי בפרק ראשון בהקדמת חיבור השברים או כפל כל מספר הוא שוה לשתי פאותיו קרובים או רחוקים עד א' החלק השני בשטחים ואומר כי כאשר המספר הוא בלתי בעל תכלית כן תמונות השטחים [] הם בלתי בעלות תכלית כמו משולש שהוא התמונה הראשונה ומרובע ומחומש ומשושה והנמשכים אחריהם לאין תכלית רצוני צלעותהם כמו שרצינו צלעות המשולשים כסדר המספרים הנה כבר ידענו שהקו ימשך מאחד כסדר והמשולש ימשך בתוספת המספר הנמשך כי א' הוא משולש ומרובע ומחומש וכל לכל התמונות בהשאלה כי אם נקח א' וא' ועוד בהמשך א' יציא מספר קויי ואם נרצה משולש יהיה בתוספת ב' הנמשך על א' ויעלו ג' והוא משולש כזה א נוסיף על ג' [] הנמשך אחר ב' שהוא ג' יהיו ו' כזה א ג' בכל צלע א א נוסיף על ו' הנמשך אחר ג' שהוא ד' יהיו יהיו א א עשרה כזה א כל צלע מד' ואם כן יורה כי ג' משולש א א א וו' משולש א א ועשרה משולש וט"ו משולש כולם שוות הצלעות והנה א א א הראשון ג' שהוא בתוספת ב' על א' והשני בתוספת ג' א א א א 86[א] [סח2] ובתוספת ד' ה[] ולדעת הוצאת המרובעים [] בהנחתי אחד בין שניהם והמ[ין] [] שהוא מרובע משאל בהנחה אחד המספר שאחר הא' [] יהיו ד' והוא המרובע השני והנה נניח [] שלקחנו שהוא ד' ונקח ה' ונחברהו עם ד' שהוא המרובע שעבר יהיו ט' והוא המרובע השלישית גם נניח ו' וניקח ז' ונחברהו עם ט' יהיו י"ו והוא מרובע רביעי גם נחבר ט' על י"ו יהיו מרובע חמשי וכן כולם מרובע אחרי מרובע והרי לך צורת האותיות אשר תצטרך לחביר שהם א ג ה ז ט יא יג טו בדילוג האחד אשר הנחנו כי א' וג' הם ד' ומרובע וד' וה' הם ט' והוא מרובע וט' וז' הם י"ו והוא מרובע וי"ו וט' הם כ"ה והוא מרובע וכ"ה וי"א הם ל"ו והוא מרובע וכן לעולם וכל אלו המספרים שלקחנו הם הנפר[ד]ים כסדר ומסגולות אלה הנפרדים כי א' הוא מרובע מושאל ואם נחבר עמו הנפרד השני שהוא ג' יהיו ד' והוא מרובע שני ואם נחבר שניהם עם הנפרד השלישי יהיו א'ג'ה' והם מרובע שלישי שהוא ט' נחבר עמהם הנפרד הרביעי יהיו א'ג'ה'ז' והם י"ו והוא מרובע רביעי נחבר עמהם נפרד החמשה שהוא ט' יהיו אגהז"ט והם כ"ה והוא מרובע רביעי וכן כולם והמחומשים תדעם בשתוסיף על חמשה הנמשך בהנחת שנים והמשושים בהנחת שלושה וכן כולם משולש מרובע מחומש משושה משובע שמינית כמו שתראה בזה הלוח והנה כל המספרים ג ד ה ו ז ח הנמשכים בטבע הם מושטחים גם ו ט יב טו יח כא כן כי א ב ג ד ה שהם נמשכים י יו כב כח לד מ בטבע הם מושטחים כזה הצורה טו כה לה מה נה סה כא לו נא סו פא צו כח מט ע צא קיב קלט [86ב] [סט1] [] אומר כי החלק [] יחלק לד' דרכים במקום [] הראשון הוא במספר אשר [] טבעי ויחלק לשנים [] נפרדות ונמשך בסדר טבעי [] הוא במספר הנמשך בערך הדרך הרביעי הוא משוטף לראשון ולשני הדרך הראשון מן החלק השני הוא במספר נמשך בטבע אשר מקומותיו זוגות יתחיל מן האחד או מאי זה מספר שיהיה ואומר שאם נרצה לחביר מספרים נמשכים בטבע אם הם זוגות כפול חיבור הקצוות על חצי המקומות והיוציא הוא המבוקש או תחבר האמצעיות ותכפלם על חצי המקומות והמשל בזה המספר המונח שהוא מא' עד ו' שהמקומות זוגות כזה א ב ג ד ה ו נחבר הקצוות שהם א' ו' יהיו ז' נכפול [] ז' על חצי המקומות שהם ג' יעלו כ"א והוא המבוקש או תחבר ג"ד מאצע יהיו ז' נכפלם על חצי המקומות יהיו כ"א כנז' משל אחר בזה המספר המונח שהוא ד ה ו ז ח ט שאינו מתחיל מא' אבל הוא נמשך בסדר טבעי והמקומות זוגות נחבר ד' עם ט' יהיו י"ג כפול י"ג על ג' שהוא חצי המקומות יעלו ל"ט והוא המבוקש משל אחר כולל זוג ונפרד עם שיהיו מתחילם מן האחד ובסדר טבעי והוא שתקח האחרון מן הנמשכים עם מרובעו וחציים הוא המבוקש כמו א ב ג ד ה קח האחרון שהוא ה' עם מרובעו שהוא כ"ה יהיו [] ל' וחציים הם ט"ו והוא המבוקש ואם יהיו זוגות כמו א ב ג ד ה ו קח האחרון שהוא ו' עם מרובעו שהוא ל"ו יהיו מ"ב וחציים כ"א והוא המבוקש הדרך * הוא במספר נמשך בטבע אשר מקומותיו נפרדות שני יתחיל מן האחד או מאי זה מספר ואומר שאם תרצה לחבר מספרים נמשכים בטבע עד מקום נפרד מתחילים מן האחד 87[א] [סט2] הוא שתכפול [] והמשל בזה המספר [] כזה | א ב ג ד ה ו ז [] מספר המקומות שהם ז' יעלו כ"ח והוא [] המספר המונח שאינו מתחיל מן האחד [] תכפול האמצעי שהוא ז' על המקומות שהם ז' יעלו [] הדרך השלישי הנמשך בערך אשר מיניו בלתי בעלות תכלית אומנם אזכור מהם קצתם בג' משלים ואומר כי מאחר שהנחתי מספרים נמשכים בדרך טבעי אסדר מספרים נמשכים כערך וראשונה אומר שאם היו מספרים נפרדים מתחילים מן האחד המקובץ מהם שוה למרובע האמצעי כמו במשל א ג ה ז ט אשר חיבורם הוא שוה למרובע האמצעי שהוא ה' יהיו כ"ה משל אחר נניח מספרים נפרדי המקומות גם כן נוציא מהם הנפר[ד]ים וכפל האמצעי מהנפרד יהיה קיבוץ הנפרדים כמו אלה א ב ג ד ה כפול האמצעי האמצעי מן הנפרדים שהוא ג' על עצמו יעלו ט' וכן יעלו אג"ה ואם מה שתוציא מן הנפרדי' שבאמצע הם מקומות זוגות קח המספר שבאמצעם שהוא זוג וכפלו על עצמו הוא מספר הנפרדים כמו שנניח א ב ג ד ה ו ז הנה הזוגות שנשארו הם בד"ו ומרובע האמצעי שהוא ד' הוא י"ו והוא מספר הנפרדים שהם א ג ה ז משל אחר בזה המונח שהוא א ג ה ז ט נפרדי המקומות נוציא מהם הנפרדים שהם ומרובע האמצעי הוא מספר כולם כי האמצעי כ"ה ומספר כולם כ"ה והוא המבוקש משל אחר ואניח מקצת אלה הערכים ועיין ותשכיל [87ב] [ע1] [] אשר יקראו [] בזה בדברים רבים [] רבות כאשר תראם בע"ה והוא [] בכפל ב' ודרך חיבורו הוא שתכפול [] האחרון בחסרון אחד אם יתחיל מאחד [] והמשל בזאת הצורה המונחת [] עד ס"ד יעלו קכ"ה []הוא חשבון כולו והוא המבוקש א ואם לא יתחיל מן האחד אלא שיהיה המספר מזוג ב ו א הזו גם תכפול האחרון בחסרון ד ב ג צורה הראשון והיוציה הוא המבוקש ח ד ו שנית והמשל בזאת הצורה השנית כפול ו א ח ב א האחרון שהוא תקי"ב ותגרע ב ג ו ה ב י"ו הראשון יעלו אלף ושמונה והוא ד ו ב א ה המבוקש הדרך הרביעי המשוטף מן השני דרכים ותמונותיו כפי טבע המספרים שהם לאין תכלית ואזכיר מהם ואומר שאם יהיו שני מספרים נמשכים בסדר טבעי מתחילים מן האחד והאחד נמשך יותר מן האחר מאחד הנה המחובר הנה המחובר משניהם שויה למרובע האחרון הגדול ואם שניהם שוים יהיה המחובר ככפל האחרונים זה על זה ועם חיבור השורש א א והמשל באילו המספרים הנמשכים המונחים הנה האחרון ב ב צורה הגדול הוא ו' ומרובעו ל"ו והנה ל"ו הוא המחובר ג ג ראשונה משניהם ואם יהיו שוים כזה הצורה השנית כפול האחרונים ד ד א א זה על זה יהיו כ"ה תחבר על כ"ה השורש שהוא ה' ה ה צורה ב ב יהיו ל' והוא המבוקש ו שנית ג ג ואם יהיה מספרים רבים נמשכים בסדר מה וההתחלה ד ד א' מן האחד הנ נעיין אם יהיו המקומות זוגות ה ה 88[א] [ע2] או נפרדות [] הנפרדות והמשל בזוגות [] ומעטין כזה הצורה [] א ב ג ד ה ו [] והם כ"[א] ומרובעם [] הם נ"ו וכן יהיה חיבור כל הצורה והוא ה[] א ב ג ד ה ו קח הנפרדים אשר ת[] צורה א ב ג ד ה בסוף המקומות והם א ג ה ז ומרובעם ה[וא] ראשונה א ב ג ד הם א ט כה מט וחיבור כולם הם פ"ד א ב ג והוא המבוקש א ב ג ד ה א ואם היו המספרים המונחים ב ג ד ה א הראשון מתחיל מן הא' והשני ג ד ה צורה א ב מב' והשלישי מג' וכן עד סוף המונח ד ה שלשית צורה א ב ג הגדול יהיו כזה הצורה השלישית הנה ה שנית א ב ג ד המחובר מהם יהיה כמרובע הטור א ב ג ד ה הגדול והמשל הטור הגדול הוא א ב ג ד ה א ב ג ד ה ו ומרבעם הם א' ד' ט' י"ו כ"ה א ב ג ד ה ו ז וחיבור כולם הם נ"ה וכן הוא המסודר מכולם משל אחר מחילק מספר מה כפי הערך שתרצה גרע הנערך מהמספר אשר תרצה לחלק והנשאר תחלק על מקומות הערך שוה בשוה וחברם והוא מה שרצינו לחלק המשל בזה רצינו לחלק ל"ו דינרי' לד' אנשים כפי זה הערך ג ה ז ט וחשבונם כ"ד גרע כ"ד מל"ו ישארו י"ב תחלקם בשוה על כל המקומות יהיו ג' לכל אחד כזה ג ה ז ט חברים יחד ג ג ג ג יהיו לראשון ששה והלשני ולשני שמונה ולשלישי עשרה ולרביעי י"ב והנה ערך העולה לכל אחד כערך המספר המונח הנערך משל אחר רצינו לחלק ס' לד' אנשים כערך ד' ז' י' י"ג וחשבון מספר המקומות הם ל"ד נגרע ל"ד מס' נשארו כ"ו תחלק כ"ו [88ב] [עא1] []ל אחד תחבר [] עשרה וחצי ולשני י"ג וחצי [] וכן כל הדומה לזה והנה מה [] התועלת אלא הם חידוד השכל [] [הגרעון] כי די בזה [המין] השלישי במעוקב ואומר כי הגשם המעוקב הוא ידוע אבל בסגולתו אומר ב' משלים כוללים המשל הראשון הרי שהיה לנו מעוקב אורכו כרוחבו כגובהו ולקח ממנו חצי צלעו [ה]מעוקב ואומר שלקח שמיניתו כי [] ד' הוא ס"ד וצלעו ד' וחצי הצלע הוא ב' וב' על ב' הוא ד' וד' על ב' הוא ח' והוא שמינית כולו ואם לא לקחנו אלא חצי צלעו ואם כן הלוקח חצי צלע המעוקב מעוקב לא לקח אלא שמיניתו משל אחר אם שאל שלשית הצלע הנה לקח חלק מכ"ז והנה נניח צלע שימצא לו שלישית להציל הטורח שלא כמו ו' על ו' והיוציא על ו' יהיו רי"ו המעוקב הגדול נקח שלישית הצלע שהוא ב' ונכפול ב' על ב' יהיו ד' וד' על ב' והיו ח' והנה ח' שהוא מעוקב שלישית הצלע והוא חלק מכ"ה בכלולו ואם כן הלוקח שלישית צלע המעוקב מעוקב לא לקח אלא חלק מכ"ז ככולו וכן אם נקח רביעית * המעוקב מעוקב צלע יהיה חלק מס"ד ואם נקח חמשית יהיה חלק מקכ"ה והנה בשאלות תראה כל זה בע"ה ומסגולותהם משל אחר בחילוק גשם אחד בערך [] ואומר שיהיה בידנו גשם אשר במשקלו י"ג ליטרין ורצינו לחלקו לשלושה חלקים מתחלפים בסדר מה נערך אשר נוכל לשקול עמהם כל הליטרין שנרצה מא' עד י"ג שהוא 89[א] [עא2] שהוא משקל [] אלה נשקול מא' עד י"ג [] ג' וא' לפניו ומשקל ד' הוא ג' [] ו' ט' וג' לפניו ומשקל ז' ו"א ו[] וכן כולם עד י"ג שתתן כל הג' משקלים / ואם [] ליטריין תחלקהו לד' חלקים כזה א' ג' ט' כ"ז ותשקול עמהם בדרך הנזכר עד מ' ליטרין ואם היה המשקל קכ"א תחלקהו לה' חלקים כזה א' ג' ט' כ"ז פ"א ותוכל לשקול עמהם עד קכ"א וכן הנה הדרך ובערך שאתה רואה אשר הוא כל אחד כפול על ג' כי ג' על ג' ט' וט' על ג' כ"ז וכ"ז על ג' פ"א ופ"א על ג' הוא רמ"ג וכן עד מה שתרצה ודי בזה [89ב] הכלל [עב1]
90[א] [עב2] הערה ל[] תמצא ג' [] אשר בו נניח ג' מספרים [] אבל כולם ישובו לשלושה המנהג השני תמצא בו ד' חלקים [] המנהג השלישי תמצא בו ה' חלקים [] והמשל לכולם אשר לדרך הראשון נאמר אם ב' נתן ג' [] ד' וכל זה תראה בתשלום אם נעלם הראשון או השני או שלישי או הרביעי והנה בזה הדרך פעמים יבואו ד' מספר[ים] כמו אם ב' די' בג' ימים הרויחו ד' פשי' ה' די' כמה ירויחו ובזה השאלה תכפול הממון על הזמן ב' על ג' יהיו ו' ואז תשוב השאלה לג' חלקים ואמור אם ו' נתן ד' פשיטי' ה' מה יתן גם פעמים יבואו בזה הדרך ה' מספרים מונחים וישובו לג' גם כן כאומר אם ד' דינ' בג' חדשים הרויחו ה' די' ז' די' בח' חדשים מה ירויחו ועתה כפול כל הממון על זמנו כמו ד' על ב ג' יהיו י"ב וזה חלק ראשון וה' די' חלק שני כמו שהוא וז' על ח' יהיו נ"ו לחלק שלשי וחזר השאלה לג' חלקים ונאמר אם י"ב נתן ז' מה יתן נ"ו כמו שתראה בשאלות בע"ה מזמן ממידה וממשקל אחר שאתן משל או משלים מחמשה דרכים כוללים שיש להוציא כל שאלה כמו שתראה בע"ה המנהג השני ראוי ל[הני]ח בו ד' מספרים הכריחיים כמו אם ג' פרחים בח' ימים הרויחו ה' די' שאלתי ד' פרחים באי זה זמן ירויחם וכמו כן גם כן ראובן קנה בגד בסך ג' פרחים והח' אמות שוה ה' די' שאלתי כמה אמות מזה הבגד יתן ה' די' כאשר סך הבגד הוא ה' פרחים ובמשקל גם כן ראובן קנה כור חיטה בסך ב' די' ונתן ט"ו אוקיות לחם בסך ב' פשיטי' שאלתי כאשר קנה הכור בסך כ"ד כמה אוקיות יתן בשני פשי' המנהג [90ב] [עג1] [] מיניהם ואומנם [] ומורכבים ואומר אם ג' [] שאלתי ד' פרחים באי זה זמן ירויחו [] ח' ימים ה' די' ד' פרחים [] או ראובן [] וסך הג' אמות הוא י"ד די' שאלתי כאשר קנה [זה] בסך [] פרחים כמה בגד יקנו בסך י"ו די' או ראובן קנה כור חיטה בסך י"ב די' ונתן לחם [] אוקיות [] פשי' שאלתי כאשר קנה הכור לסך י"ו די' כמה אוקיות נתן [] פשיטי' או יהיה מג' דברים מתחלפין ומורכבים כמו שנניח ה' וג' שיהיו מתחלפין כמו אם ד' פשיטי סרגוסה שוים לה' פשיטי ברצילונה וג' פשיטי ברצלונה שוים לד' מלשבונה שאלתי ט"ו פשיטין לשבונה כמה מפשיטי סרגוסה יהיו ויהיו המשלים בזה הצורה משלושת מנהגי דרך השלושה אמנם הנהגת דרך השלושה יתחלף בג' דרכים כאשר אמרתי אשר הראשון הוא אם ב ג ד 0 אם ב' שוה ג' ד' אם ב די' בג ימים ד ריוח ה די' 0 מה יהיה שוה כמו אם ד די' בג חדשים ה ירוי' ז דינר' בח חדשים 0 שתראה במנהג אם בא ה וה 0 הראשון _____________________________________ הדרך השני אם אם ג פרחי' ח ימים ה דינר' ד פרחי' 0 ימים ב' לטר' אם ג פרחי' ח אמות ה דינ' ה דינרי' ה פרחי' נחושת שוה ג' דיני' אם 0ב דיני' ב פשיט הא אוקיות ב פשיט דב דינרי ד' לטרי נחושת מה _____________________________________ יהיה שוה הנה ראוי אם ג פרחי' ח ימים ה דינר' ד פרחים ו דינר' שתדע כי כ' ליטרי אם בא פרחי' ג אמות דא דינר חא פרחים וא דינרי נחושת הוא הגבול אם בא דינרי גא אוקיות ב פשיט וא דינר' ב פשיטי' הראשון מן השאלה אם ד פשוט ה פשיט ג פשיט ד פשיט הא פשיטי' וג' השני וד' השלישי והנה תעיין כי הגבול 91[א] [עג2] הראשון הוא הידוע [] ונשאר ג' שהוא הגבול הש[] [] הנשאל הוא כמה לו ואם כן [] השני על הידוע שהוא הראשון [] שהוא השלישי המשל בזה נאמר אם ב' אמות [] אמות מה יהיו שוים נחלק ההפכי שהוא האמצעי שהוא [] על הראשון שהוא ב' יעלו בחילוק ג' נכפול אותו על השלישי שהוא ד' יעלו י"ב והוא הנשאל הנעלם שהוא י"ג פרחים והוא דומה לאמצעי ויהיו כזה אם ב ו ד בא והבחינה מבוארת כי תאמר אם ב שוה ו' שהוא ג' פעמים בו' גם י"ב ג' פעמים בד' או נכפול ד' על ההפכי שהוא ו' יהיו כ"ד נחלקם על ב' שהוא דומה לשלישי יעלו י"ב והוא המבוקש הדרך השלישי וצריך לעיין בזה נרצה לדעת שהוא הגבול השלישי אצל הנודע שהוא הגבול הראשון שהם דומים וניקח כמינו מן ההפכי שהוא הגבול השני והמשל אם ב' ליטרי נחושת שוות ג' פרחים ד' ליטרי נחושת מה יהיה שוה הנה נעיין ערך ד' אצל ב' והוא שתי פעמים וכן ניקח כפל ג' שהוא ו' וד' ליטרי נחוש הם ו' פרחים והבחינה כדרך הראשון נכפול ג' על ד' יהיו י"ב נחלקם על ב' יהיו ו' הפרק בהקדמות הראויות לזה השער ואומר כי הדרכים הפרטיים לדעת כל שאלה ולהוציא ולהוציא לאור כל תעלומה הם רבים אבל על הכלל הם חמשה ואם יש אחת כוללת אחרת אבל לא יתהפך ואומנם חכמי המספר שמו להם שמות מתחלפים כי כל אחד קרא שם כפי רצונו אבל הנרצה אחד ואני אסדרם כאן כל אחד בשמו ואומר כי הראשון הוא דרך השלושה ואומנם מסגולות זה הדרך שהוא מגלה סתרים ומפענח נעלמים והוא מיישר לדרכים הנשארים והוא ראש לכולם והוא משלים מה שנשאל מהם כמו שתראה בע"ה ואומר שמן הראוי שתדע כי כל ארבעה [91ב] [עד1] [] הנה הראשון [] כמו בנים מאחר [] הראשון וכן הרביעי מן [] והשלישי הם אחים וכן השני [] במקומו והנה השני הוא [] בן זוג השלישי ועם זאת זאת [] מספר מה מאלו הד' מספרים [] לידיעת[]אחד נעלם ימצאו בידך ג' מספרים [] השנים מהם הם שוים אם שיהיו אבות אם שיהיה בנים השלישי הוא נפרד שאין לו בן זוג והנה [] לדעת זה הנעלם הנעלם הוא שתקח איזה מן האחים הנמצאים על אשר אין לו בן זוג והיוציא תחלקהו על האח האחד אשר בן זוגו עמו והיוצא בחלוקה הוא בן זוג הנפרד והשמר לך פן תכפול איש על אחיו ולא על בן זוג ולעולם תמצא כי הכפל יהיה אם אמצעי על אמצעי או הקצוות ואתן ארבעה משלים לזה והמשל בזה הנה אלו הארבע בג וט מספרים נערכים ונאמר כי ב' הראשון נעלם ונשאר ג' לבדו וו"ט לבד ויהיו כזאת הצורה 0ג וט הנה ג"ט הם אחים ולא נוכל לכפול ט' על ג' כי הם אחים ולא ט' על ו' כי הוא בן זוגו אבל נכפול ו' על ג' שאין להם קירבה כלל וחלק על האח כי ג' על ו' הם י"ח תחלקם על ט' יעלו ב' והוא הנעלם ובדרך השלושה נאמר מה יתן לנו ג' אם ו' נתן ט' והנה זה הדיבר יורה כי הראשון נעלם כי מלת מה יורה על הנעלם כי הוא ראשון ונכפול האמצעיים והנה כפלנו ג' על ו' יעלו י"ח נחלקם על ט' שהוא אח יעלו ב' וזה הנעלם הראשון משל שני נאמר שהשני נעלם ישאר ב' לבד כזאת הצורה ב0 וט בזאת השאלה ב' מה יתן אם ו' נתן ט' והנה זה הדיבור אם 92[א] [עד2] יורה כי השני נעלם כי [] החיצוניות שהם ב' על ט' [] בד וט הנעלם השני משל שלישי [] כזאת בג 0ט הצורה [] והנה זה הדיבור יורה כי מלת מה היא [שלישית] [ועתה נכפול] החיצוניות שהם ב' על ט' יעלו י"ח וחלקהו על ג' יעלו ו' והוא [] השלישי משל רביעי נאמר כי הרביעי נעלם ישאר ו' לבד [כזאת] בג ו0 הצורה הנה נאמר [] ונאמר אם ב' יתן ג' ו' מה יתן והנה זה ה[דיבור] יורה כי מילת מה היא רביעית ועתה נכפול האמצעים ו' על הבלתי דומה לו שהוא ג' יעלו י"ח נחלקם על אחיו שהוא ב' יעלו ט' והוא המבוקש והנה [בזה] המשל הרביעי נהגתי בכל הספר ואתה תוכל להחליף השאלות בכל אלה המשלים ובלבד שתשמור שלא תכפול דומים כאשר אמרתי כי הדיבור מורה הנעלם כאשר אמרתי ותראהו גם כן בזה הצורה מה אשר בה תלמוד כיצד תניח 0 יתן ג' אם ו נתן ט הג' מספרים מדרך השלושה מה לדעת הרביעי הנעלם ב 0 אם ו נתן ט והנה זה שאמרתי שיהיו אם בא מה בידך שלושה מספרים ב ג 0 יתן ט כאשר אמרת הנה זוגו אם נתן ולהיות בידך שלושה ב ג ו מה 0 מספרים שהם בטור ארבעה כמו [] כי הם כמו בדדח [92ב] [עה1] [] והרי לך [] ובדדח האמצעיות [] וכן אם נכפול [] ח' ואם נחלק על ח' יציא [] שתכפול ח' על ב' ותחלק [] במה שיבא בע"ה תבין כל זה בכאן התוספת [] נקרא מונח כוזב והוא לדעת מספר נעלם תכתוב בו הערה [] שתניח מספר מה איך שיזדמן אליו ובחרו להניח לדרך השלושה מספר שנמצאו בו כל החלקים הנשאלים ל[] הטורח ואם לא בסוף ס"ח נעשה כן אין בכך כלום אלא שיהיו בחשבון שברים והנה עם זה הדרך תמצא מה שלא תמצא עם דרך השלושה אבל עם [] [] דרך השלושה כאשר תראה ואתן בכאן משל אחד ואומר שתניח מספר מה שיהיו בו כל החלקים הנשאלים כמו ששה או י"ב או איזה מספר שנרצה המשל בזה מהו המספר אשר חציו ושלשיתו יהיה ששה נניח ששה כי בו ימציא חצי ושלישי' בשלמות וניקח חצי ושלישית מששה יהיו חמשה ואנחנו שאלנו ששה נלך אל דרך השלושה והוא ישלים לנו שאלתנו ונאמר אם ו' נתן לנו ה' מי יתן לנו ו' ויהיה בצורה הזאת נכפול הקצוות שאין להם אהבה ואחוה יהיו ו ה 0 ו ל"ו חלקים על ה' יעלה בחילוק ז' וחמשית והוא הנעלם ובשאלות תראה שאין צורך לכתבת הספרא במקום הנעלם והנה הבדיקה היא שתתן ז בחמשיות יהיו עם החמשית ל"ו חמשיות וחצי ושלישית ל"ו הם ל' חמשיות חלקם על ה' יעלו ששה שלמים ואם כן ז' וחמשית הוא המספר אשר חציו ושלישית הוא ששה 93[א] עה[1] [עה2] הדרך [] הכוז[ב] [] המונח הכוזב וה[] פעמים שני מספרים אין [] היותר נאותים וראוים הם שתקח [] כל החלקים הנשאלים בשלמות [] כאשר כתבתי במונח הכוזב ומעשה תוקפו וגבורתו בזה הדרך והוא שתקח למונח הראשון מספר מה ואחר תוס[יף] או תגרע החלקים הנשאלים ואם אחר שעשית מלכתך יגר[עו] או יעדיפו תשמור אותו העודף או הגורע משאלתך ואחר תניח מונח שני ותעשה כמו שעשת לראשון ותשמור המספר העודף או הגורע משאלתך ועתה תערוך שאלתך ותערוך שאלתך ותאמר אם מונח כך פחות או יותר כך וכן במונח השני ואחר תדע כי כאשר תציא מן המונחים יותר בשניהם או פחות בשניהם גרע הקטן מן הגדול והנשאר תשמרהו לחלק עליו כי הוא המורה ואם יהיה היוציא האחד עודף והשני גורע תחבר שניהם יחד ושניהם יהיו המחלק וסמנם גרע בשוים ובמתחלף חבר כי פחות ופחות ועודף ועודף בשניהם שוים ופחות באחד ועודיף באחר תגרע הגדול תחבר שניה' ואחר תכפול המונח הראשון על היוציא בשני וכן מן הקטן תכפול המונח השני על היוציא בראשון ותגרע הקטן משניהם מן האחר אם היוציא משניהם יותר מן המבוקש או פחות והנשאר תחלק על השמור הנשאר אשר גרעת זה מזה או תחברם יחד אם היוציא משניהם יהיה אחד עודף ואחד גורע והמחובר חלק על השמור אשר חיברת זה עם זה והיוציא בחילוק הוא המבוקש המשל בזה מה הוא המספר אשר חציו ושלישיתו יהיה ששה נניח מונח אחד ויהיה המונח ששה בעבור שימצאו [93ב] [עו1] [] [] בא [][ו] פחות א [] ה וג [] יב עודף ד [] דב [] ד' ונאמר עם י"ב עוד ד' ונניחם [] והנה בעבור שהיו פחות ועודף נחברם יהיו חמשה והוא המורה לחלק עליו ואחר נכפול המונח הראשון שהוא ששה על העודף בשני שהוא ד' ויהיו כ"ד תתנם תחת ד' גם כפול המונח השני שהוא י"ב על הפחות בראשון שהוא אחד יעלו י"ב תתנם על א' ומאחר כי המונח האחר הוא פחות והשני עודף חברנו שניהם י"ב וכ"ד יהיו ל"ו חלקים על השמור שהוא חמשה יעלה בחילוק ז' וחמשית והוא המבוקש כי חצי ושלישית ז' וחמשית הם ששה עיין במשל דרך השלושה ועוד תראה זה בע"ה ועיין וראה במה שעשינו עם המונח הכוזב ועם דרך השלושה עשינו עם ב' הנחות כוזבות הדרך הרביעי קראתי אותו דרך * יהיה בעבור שעם זה הדרך * יחידי לבד תוכל להוציא רוב השאלות היוצאות עם הדרך השני מונחים הכוזבים וגם שאינו צריך לדרך השלושה ולעולם בזה הדרך תניח לשאלתך אחד [] והוא שתקח אחד לראשון הנעלם ואם אמר כפל או כפלי הראשון בתוספת כך או בפחות כך וכן לאחרים גרע הקטן מן הגדול אם שיהיה העודף מן הפחות או הפחות מן העודף והנשאר אם הוא מן העודף גרעהו מסך מה שקנית והנשאר תחלק על קיבוץ המונחים והיוציא בחילוק הוא 94[א] עו[1] [עו2] הראוי [] על הסך [] בחילוק הוא הראוי [] שנפל בחלקו והנשאר הוא [] כי אין מזה הדרך משל עוד [] תראה ולעולם קיבוץ המונחים הוא [] הוא לראשון הנעלם ואחר שתדע הראשון [] והמשל הראשון שלשה תלמידים קנו ספר אחד בסך [כ"ד די'] [ולא] ידענו מה שפרע כל אחד בספר אבל ידענו כי השני פרע כפל הראשון ועוד ג' די' והשלישי פרע ג' כפלי השני פחות ז' שאלתי כמה פרע כל אחד בספר וערך הזמן שיהיה בידו כפי מה שפרע תשובה תניח אחד לראשון והנה בעבור שאמר כי השני נתן כפל הראשון ועוד ג' תכפול המונח יהיו ב' ותכתוב ג' במקום אחר שיורה ועוד ג' ובעבור שאמר השלישי ג' כפלי השני תכפול כל חלקי השני בג' ויהיו ו' תחת המונח וט' תחת מה שאמר ועוד ג' כי כפלו ט' ותכתוב ז' במקום אחד ותרשום בו פחות ויהיה בזה הצורה [] המונח יהיו ט' והוא המורה לחלק עליו תגרע ז' שהוא הפחות מן העודף שהוא י"ב המונחים ישארו ה' והם מן העודף תגרעם מן פחות א עוד הסך שהוא כ"ד ישארו י"ט תחלקם על ב ג ט' שהוא המורה יעלה בחילוק ב' ותשעית ז ו ט וזה ממון הראשון תכפלם יהיו ד' וב' המורה ט תשיעיות ועוד ג' וזה ממון השני תכפול ממון השני בג' יהיו י"ב וששה תשיעיות ועוד ט' ופחות ז' ותהיה בזאת הצורה השנית ואחר גרע הפחות מן השלשי ישאר [94ב] [עז1] [] ט [] ז ב/ט הזמן שיהיה ביד [] יד ו/ט כל אחד כפי הממון שנתן [] וו' תשיעיות וזה הוא המבוקש ויציא מזה כי ממון הראשון ב' די' ותשיעית דנר והנה ב' שעות ותשעית שעה [] יהיה הספר אצלו בכל יום וממון השני הוא ז' די' וב' תשיעי דנר וז' שעות וב' תשעי שעה יהיה הספר בידו בכל יום והנה ממון השלישי הוא י"ד די' וששה תשיעיות דנר שהם ב' שלישיות דנר שהם ח' פשי' והנה י"ד שעות וב' שלישי שעה שהם מ' דקים יהיה הספר בידו בכל יום כמו שתראה בצורה השלישית המתוקנת והבחינה שתחבר התשיעיות יהיו אחד תחברהו עם כ"ג שלמים יהיו כ"ד והוא המבוקש משל שני ג' גביעים אשר סך כולם פ"ה פרחים וכן משקלם פ"ה אוקיות ולא ידענו סך הראשונה אבל ידענו כי סך השנית הוא ג' כפלי הראשונה ועוד ה' וסך השלישית הוא ד' כפלי השנית פחות ז' תשובה נניח א' לראשונה ואם כן תהיה השנית שהיא ג' כפלי הראשונה ג' ועוד ה' והשלישית שהיא ד' כפלי השנית ופחות ז' יהיה י"ב המונחים ועוד ב' ובמקום אחד פחות ז' פחות א עוד ויהיה כזאת הצורה נחבר המונחים ג ה כולם יהיו י"ו והוא המורה לחלק ז יב ב עליו נגרע הפחות שהוא ז' מן המורה יו מן העודף שהוא כ"ה ישארו י"ח והנשאר יהיו מן העודף נגרעם מסך 95[א] עז[1] [עז2] הכל שהוא [] ד' וג' חלקים [] ד' פרחים וג' חלקים [] מי"ו חלקים באוקיא וסך ה[] חלקים מי"ו ועוד ה' וי"ב יהיו י"ז [] השני הוא י"ז פרחים וט' חלקים מי"ו בפרח [] האוקיא י"ו חלקים וסך השלישי שהוא ד' כפלי השני [] מ"ח ול"ו חלקים מי"ו ועוד כ' ופחות ז' נגרע הפחות מן העודף ישארו י"ג ומ"ח שהיו לנו יהיה ס"א ושנים שיצאו מל"ו יהיו ס"ג וד' חלקים [] מי"ו שהוא רביעית והנה סך הגביע השלישי הוא ס"ג פרחים וד' חלקים אשר הפרח הוא י"ו חלקים והוא רביע פרח ומשקלם הוא י"ז אוקיות וד' חלקים אשר האוקיא הוא י"ו ומקוצר יהיה רביע אוקיא ויהיה כזה הצורה והבחינה חבר שברי הפרח יהיו משל שלישי פרח אחד או אוקיא אחת לראשונה ד ג תחבר הפרחים יהיו פ"ד ועם האחד יו יהיו פ"ה פרחים או אוקיות והוא המבוקש שנית יז ט משל שלישי שלא יעדיף אלא יפחות יו והוא שג' קנו חמור פרדה ללכת שלישית סג ד לרושלים בסך ל' פרחים ולא ידענו מה יו שפרע כל אחד אבל ידענו שהשני נתן ג' כפלי הראשון פחות ד' והשלשי נתן ד' כפלי השני פחות ה' שאלתי סך כל אחד וכמה פרסאות ירכב כל אחד בפרדה נניח כי הראשון נתן א' ואם כן השני נתן ג' שהוא ג' כפלי הראשון ופחות ד' והשלישי ד' כפלי השני ופחות ה' והנה ד' כפלי השני הם יב גם ד' פעמים פחות השני הם י"ו פחות ולעצמו פחות ה' יהיו [כ"א] הפחות כ"ה וקיבוץ המונחים י"ו לחלק עליו ויהיה [95ב] [עח1] [] יהיו כ"ה [] הראוי לראשון וג' [] והשלישי שאמר [] ופחות י"ו שבא מד' כפלי [] תראה בזה הצורה השנית והנה סך [] הוא ג' פרחים וז' חלקים מי"ו [] פחות בפרח וג' פרסאות וז' חלקים [] ט כא/יו ד מי"ו בפרסה ירכב הראשון השלישי נתן לו פד/יו יו בפרדה ה והנה סך השני הוא ט' פרחים שאלה וכ"א חלקי י"ו פחות ד' גרע ד' ראובן שמעון מט' ישארו ה' וא' מן השברים לוי יהודה יוסף יהיו ו' וה' חלקים מי"ו בפרח וסך השלישי הוא ל"ו ופ"ד חלקים מי"ו קנו שור אחד אשר הם ה' שלמים וד' חלקים מי"ו יהיו מ"א וד' חלקים מח' גרע ראובן לקח השלישית הפחות אשר בחלקו שהוא י"ו וה' שהם כ"א ממ"א ישארו כ' פרחים ושמעון הרביעית וד' חלקים מי"ו בפרח שמקוצר הוא רביע ועלה מזה כי סך הראשון ולוי החמישית הוא ג' פרחים וז' חלקים מי"ו בפרח וג' פרסאות וז' חלקי פרסה ויהודה הששית מי"ו בפרסה יהיה הפרדה ביד הראשון וסך השני ו' פרחים ויוסף ה' ליטרין וה' חלקי פרח וו' פרסאות וה' חלקי פרסה יהיה הפרדה ביד שאלתי משקל השני וסך השלשי הוא כ' פרחים וד' חלקים מי"ו בפרח שהוא כל השור רביעית וכ' פרסאות ורביעית יהיה הפרדה ביד השלישי וכן כל נניח מונח הדומה לזה והרי לך צורת שלושתם כוזב כי ליטרי והבחינה חבר חלקי שלושתם ואם יהיו לראשון ג ז/יו השור הם ס' ל' מוטב המשל בזה חלק הראשון ג לשני ו ה/יו הנה שליש ס' שאלה ראובן שלי[] וכו' בשיור לשלישי כ ד/יו הוא כ' ורביעיתו ט"ו וחמשיתו י"ב וששיתו עשרה והנה כולם נ"ז ונשארו ג' ליוסף ואנחנו שאלנו ה' ליוסף עתה נאמר אם ג' בא מס' מאי זה מספר יבא ה' נכפול ה' בס' יעלו ש' נחלקם על ג' יעלו ק' והנה מאה ליטרין משקל השור והבחינה הנה השלישית ל"ג ליטרי' ושליש שהם י"ב אוקיות כי ל"ו אוקיות הליטר' [] בסרקוסה והרביעית כ"ה והחמשית כ' והשישית י"ו ושני שלישיות שהם כ"ד אוקיות נחברם כולם יהיו צ"ה לטרין ועם ה' מיוסף יהיו ק' [] המבוקש שהם לטרי השור 96[א] [עח2] הדרך [החמישי] [] הממון תוסיף על [] הדרך לא אזכרנו אלא [] והמשל בזה שהיו בפתח הבית [כ"ד] [] בעל הבית לעבדו שיחלק לכל איש ב' פשיט' ולכל אשה פשוט שאלתי סך האנשים והתשובה תניח האנשים והנשים שתרצה וחלק להם כמו שאמר ואחר אם נשארו פשיטי' תוסיף על האנשים ותגרע מן הנשים כיצד נאמר כי האנשים ד' והנשים י"ח והנה ב' פשיט' לכל אחד איש יהיו ח' ופשוט לכל אשה יהיו י"ח וח' יהיו כ"ו וגרעו ב' כי אנחנו כ"ד שאלנו גרע מן האנשים ב' יהיו ב' אנשים וכ' נשים והוא יהיה שוה ד' פשי' לב' אנשים וכ' לכ' נשים משל שני חלק ל' לל' אנשים ונשים ונערים אשר תתן לכל איש ב' פשיט' ולכל אשה פשיט' ולכל נער מחצה הנה האנשים הם ז' והנשים ט' והנערים י"ד וכן כל הדומה לזה בחומרים שתרצה ועיין בם [96ב] הפרק הש[ני] [עט1] [פרק] [] [שאלה ראשונה] [] אשר אם תחבר ובו י"ב [] חציו חמשיתו ושביעיתו הא' [] תשובה עם מונח כוזב הב [] מספר שימצאו בו הג [] כי חצי יורה על ב' וחמשית על ה' [ושבעית] על ז' נכפול זה על זה כמנהג ב' על ה' עשרה ועשרה על ז' ע' ונניח כי זהו המספר ונחבר עליו החלקים הנז' שהם חציו שהוא ל"ה וחמשיתו שהוא י"ד ושביעיתו שהוא עשרה נחברם כולם על ע' יהיו קכ"ט והנה המספר שהנחנו הוא ע' והוא כוזב כי אנחנו שאלנו ב' והוא נתן לנו קכ"ט נלך אל דרך השלושה והוא יתן לנו שאלתנו ונאמר אם ע' נתן לנו קכ"ט מי יתן לנו ב' : נכפול הקצוות שהם ב' על ע' יעלו ק"מ נניח השאלה כזאת ה[צורה] חלקם על המספר השני שהוא קכ"ט יעלו החילוק א' ואחר עשר אם ע קכט 0 ב חלקים מקכ"ט בשלם כזה א אא/טבא וזה הוא המספר אשר אם תחבר עליו חציו חמשתו ושבעיתו יהיה עם הכל שנים וזה הוא המבוקש ואם תרצה לבדוק אם זה אמת כי א' וי"א חלקים מקכ"ט הוא המספר אשר אם תחבר עליו החלקים הנזכרי' שלא יעלו אלא שנים הנה מעשה הבחינה כך הוא שתתן השלם בשברו יהיו קכ"ט ועם י"א יהיו ק"מ תחבר על ק"מ חציו שהוא ע' יהיו ר"י חבר על ר"י חמשית ק"מ שהוא כ"ח יהיו רל"ח עוד חבר עליו שביעית ק"מ שהוא כ' יהיו רנ"ח חלקם על קכ"ט שהוא השלם יעלה בחילוק ב' והוא המבוקש שאלה שנית מהו המספר אשר אם תחבר עליו שלישיתו ועל העולה ב' חמשיות מן העולה ועל העולה ג' רביעיות מן 97[א] [עט2] העולה [י"ג] [] כוזב ועם [] האלו השברים בשל[] ס' ונניח כי זה הוא המספר [] נחבר על פ' ב' חמשיותיו שהוא [] רביעיותיו שהם פ"ד יהיו קצ"ו והנה [] כי קצ"ו נתן לנו ואנחנו לא שאלנו כי אם י"ג [] והוא ישלים שאלתנו ונאמר אם ס' נתן לנו קצ"ו מי יתן לנו [י"ג] נניח השאלה בזאת הצורה ותכפול 0ו וטא 0 גא הקצוות שהם י"ג על ס' יעלה תש"ף נחלקם על המספר השני שהוא קצ"ו יעלה בחילוק ג' שלמים וקצ"ב חלקים מקצ"ו בשלם אשר אם תקצרם יהיו מ"ח חלקים ממ"ט בשלם וזהו המספר אשר אם תחבר עליו שלישיתו ועל העולה ב' חמשיות מן העולה ועל העולה ג' רביעיות מן העולה ועם כל זה יעלה י"ג וזה מה שרצינו מעשה הבחינה כך הוא שתתן השלמים בשברם ועל העולה תחבר השברים העודפים על ג' שלמים שהם קצ"ב יהיו תש"ף חלקים מקצ"ו בשלם שהוא המספר המבוקש אשר אם תחבר עליו החלקים הנזכרים יהיו ב' אלפים תקמ"ח שהם י"ג שלמים כיצד המספר הנעלם אשר בקשנו הוא תש"ף חברנו עליו שלישיתו שהוא ר"ס יהיו אלף ומ' חברנו עליו ב' חמשיות אלף ומ' שהם תי"ו יהיו אלף תנ"ו עוד חברנו עליו ג' רביעי אלף תנ"ו שהם אלף וצ"ב עליו יהיו ב' אלפים ותקמ"ח חלקם על המורה שהוא קצ"ו יעלה בחילוק י"ג שלמים ואם כן עלה בידנו כי ג' שלמים וקצ"ב חלקים מקצ"ו הוא המספר הנעלם אשר עם חיבור חלקיו יהיה י"ג כנזכר שאלה שלישית מהו המספר הנעלם אשר אם תחבר עליו שאלה מהו המספר הנעלם אשר חיברנו עליו חצי חציו ושלישית שלישיתו ורביעית רביעיתו ולא יהיה אלא ז' בזה השאלה תצטרך לכפול כל המורים זה על זה ד' על ד' יהיו י"ו וי"ו על ג' [יה]יו מ"ח ומ"ח על ג' פעם שנית יהיו קמ"ד וקמ"ד על ב' והיוצא על [ב' תקע"ו] וזהו המונח נחבר עליו חצי חציו והוא קמ"ד יעלו תש"ך [97ב] [פ1] []תו ורביעית [] תשובה עם [] לאלה []ת וששית יעלו ק"ך ומה שלא [] כי חצי נמצא ברבעית ושלשית [] בפרק קיצור המורים ואם כן נאמר [] המספר הנשאל אשר עם חבור חלקיו יהיה אחד והנה נקח חצי שלשית רביעית ק"ך יהיה ה' כי רביעית ק"ך הוא ל' ושלשית ל' הוא עשרה וחציו ה' נחבר ה' עם * יהיו קכ"ה עוד נחביר ק"ך אליו שלישית רביעית חמשית ק"ך שהוא ב' יהיו קכ"ז כי חמשית ק"ך הוא כ"ד ורביעית כ"ד הוא ו' * הוא ב' כנז' עוד נחבר על קכ"ז רביעית חמשית ששית ק"ך שהוא א' יהיו קכ"ח כי השישית הוא כ' וחמשית כ' ד' ורביעית ד' א' ואם כן כאשר תחבר ה' שיצא מן הראשון וב' מן השני וא' מן השלישי עם ק"ך יהיו קכ"ח ואנחנו לא שאלנו כי אם אחד ויצאו קכ"ז יותר ממה ששאלנו נלך אל דרך השלושה והוא ישלים שאלתנו שהוא כמשל ראשון מדרך השלושה הנה הדרך הוא בזאת הצורה שתכפול 0 א קך קכח האמצעיות שהם א' על ק"ך יהיו ק"ך חלקם על קכ"ח והנה הוא מחולק והוא ק"ך חלקים מקכ"ח בשלם שאם תקצרם יהיו ה' ששיות כי ערך ק"ך אל קכ"ח כערך ה' אל ו' והנה המספר הנעלם הוא ה' ששיות מעשה הבחינה כך הוא שתחזור הה' ששיות אל ק"ך חלקים מקכ"ח בעבור כי בו תמצה החלקים הנזכרים ותקח חצי שלישית רביעית ק"ך והוא ה' ושלישית רביעית חמשיתו והוא ב' ורביעית חמשית שישיתו והוא א' תחבר עם ק"ך שהוא המספר הנעלם ה' וב' וא' יהיה קכ"ח תחלקם על המורה שהוא קכ"ח גם כן יעלה בחילוק אחד שלם 98[א] תש"ך נחבר עליו שלישית שלישיתו שהוא ס"ד יהיו תשפ"ד ונחבר על זה רביעית רביעיתו שהוא ל"ו יהיו תת"ך ואנחנו שאלנו ז' נאמר בדרך השלושה אם תקע"ו נתן לנו תת"ך ז' מי יתן לנו ויהיה כזה הצורה ז 0 תתך תקעו נכפול קצוות יעלו ד' אלפים ול"ב נחלקם על תת"ך יעלה ד' תשנ"ב חלקים מתת"ך וזה המספר אשר אם חיברנו עליו חצי חציו וכו' וכל העולה נחלק על תת"ך יעלו ז' כנשאל [פ2] ואם כן [] הנעלם [] שאלה רביעית []
98[ב] [פא1] []הוא ס"ה [] נכפלם בסך []ת השברים ויעלו [] בחילוק י"ו דנרי' ולא נשאר [] הוא ה' לטרי' וי"ו דינרי' [] נכפול ממונו על הריוח יעלו שכ"ה [] על המורה יעלה בחילוק ה' לטרי' שוים וזה [] [לשמעון] ולדעת הראוי ללוי הנה הנשאר משניהם הוא
99[א] [פא2] בעבור [] חדשים ויהיו י"ב [] ל"ו ונאמר בהשאלה כי הממון [] שמעון בז' חדשיו יהיו ל"ה [] כמו שתראה בצורה ועשה כמנהג [] ע"א שהוא קיבוץ שניהם ויעלו לראובן ג' די' [] ואם תכפלם בי"ב והיוצא תחלק על ע"א יהיו [] ז' וחלק על ע"א ויהיה העולה ג' די' ול"ב חלקי דינר והבחינה תקבץ חלקהם ויהיו דנר וששה יהיו ז' בריוח ודי בזה כי במוקומות אחרים בזה השער תראה שאלות מזה המין יותר קשים ואם תרצה להקל שאלתך תקצר אותה בחצי ואז תהיה לראובן שאלה שביעית ראובן שמעון לוי עשו חברה יחד ראובן ו' ולשמו' עשרה נתן ג' די' ושהה ד' חדשים ושמעון ד' דינר' ולוי ט"ו והמורה ושהה ה' חדשים ולוי ה' די' ושהה ו' חדשים והרויחו ששה די' ל"א וכן תעשה שאלתי כיצד יחלוקו תשובה כפול כפול חדשי כל אחד תעשה בכל שאלה בממונו והיוציא יהיה כמו ממון כל אחד ויהיה לראובן שתקצרנה בחצי י"ב ולשמעון כ' וללוי ל' חברנו כל השלושה סכום יהיו ס"ב או בשליש או והוא המורה בחלקים שתוכל דנר חדשי ממון ריוח דניר פשיט רביעי חלקי רביע לקצרה ראובן ג ד יב א א ג י/סב ואחר זאת שמעון ד ה כ ו א יא 0 נח/סב אחרות [] לוי ה ו ל ב י ג טו/סח המורה סב המורה לחלק עליו ויהיה כל השאלה כזאת הצורה ועתה נראה הראוי לכל אחד כפי ממונו ושהיתו שכפלנו זה על זה ונעשה דף פב ופג ופד תמצה לפנים בין צ"ח וצ"ט [99ב] [פב1] [] אחד על [] יהיה חלק [] תחלקם על המורה [] הנשאר שהוא י"ו על כ' די' [] חלקם על המורה יציא ד' די' [] והנה ג' לטרין ד' די' וע"ד חלקי [] ראובן ובזה הדרך כפול ל"ב על ז' וחלק היוציא על המורה ותציא בחילוק ג' לטרי' ומ' חלקים מע"ד בשלם וזה חלק שמעון עוד כפול ח' על ז' וחלק היוציא על המורה והוא מחולק [] נ"ו חלקים מהמורה שהוא ע"ד בליטרה ותכפול נ"ו על כ' שהוא סך הליטרה יעלו אלף ק"ך תחלקם על המורה יעלו בחילוק ט"ו דינ' ועשרה חלקים מע"ד בדינ' וזה חלק לוי והל"ה עלה בידנו שנפל לראובן מן הריוח שהוא ז' ג' ליטרי' וד' דינר' וכ"ד חלקי דינר שתוכל לקצרו שהם י"ב חלקים מל"ז וחלק שמעון לג' ליטרי ומ' חלקים מע"ד שהם מקוצרים כ' חלקים מל"ז וחלק לוי ט"ו די' ועשרה חלקים מע"ד ומקוצרים ה' חלקים מל"ז וכן כל כיוציא בזה והבחינה הוא שתחבר כל שברי שלשתם והיוציא תחבר עם עם הדי' ומהדי' תעשה ליטרה או ליטרין והיוציא יהיה הריוח והמשל תחבר שברהם יהיו לראובן כ"ד ולשמע' מ' וללוי עשרה תחלקם על המורה יציא אחד ועם הדי' שהם י"ט יהיו עשרים שהוא לטרה וג' לראובן וג' לשמעו[ן] יהיו ז' שהוא הריוח והוא המבוקש וכן היו חלקי' השאלה השמינית שהם שפ"ד לראובן תר"מ לשמעון 100[א] [פב2] וק"ס ללוי [] המורה שהוא [] דינר חברהו עם ה[] הליטרה תחבר אותה [] והוא הריוח דרך אחרת לקציר עוד ועיין בה ותשכיל עם דרכים אחרים שאתן תכף זה ואומר שתקצר הנכפל כל מה שתוכל שוה לכולם המשל בזה בשאלה התשעית [] הנה ממון ראובן המשולח הבא מד' קל"ו הוא תקמ"ד וממון שמעון תקי"ב וממון לוי קכ"ח תקצרים בחציים חמשה פעמים ישובו לראובן יז י"ז ולשמעון י"ו וללוי ד' ולא נוכל יו ז עוד לקצר בעבור ממון ראובן שהוא ד י"ז והנה ש חזרה השאלה כזאת הצורה לז המורה ואתן לזה פרק מיוחד ולדרך השלושה פרק במנהג החברות וגם בדרך השלושה הנה כתבתי בכאן ששה מנים שבאו לידי הא' הוא שלא נקצר כלל או שלא נוכל לקצרו המין השני הוא שנוכל לקצרו פעם או יותר המין השלישי קיצור הממון ולא הזמן המין הרביעי קיצור הזמן ולא הממון המין החמשי קיצור הממון והזמן המין השישי קיצור הכפלת הממון והזמן [100ב] [פג1] [] ראובן נתן [] [] ראובן ח 0א [] שמעון כד [] יעלו לראובן בג המורה [] לשמעון ויבואו לו [] די' וחצי והנה בכל אלו המינים אשמיט עם אלו השכרם מהממון ומהריוח והבחינה כי ז' וחצי וב' וחצי 0בא 0בא הם עשרה שהוא הריוח ח ה עו' בדיקה אחרת תשוי ממונם כד טו בזה הצורה יהיה ה' פעמים כ"ד ק"ך גם ח' פעמים ט"ו הם ק"ך ועשיתי ה' וט"ו כי ה' וט"ו הם חציים בעבור החצים שהריוח משל במין השני שנוכל לקצר פעם או יותר הנה לראובן ח' ולשמון כ"ד שנוכל לקצרם ג' פעמים אשר חציים ד' י"ב ועוד ב' ו' ועוד א' ג' והמורה ד' ראובן ח ד ב א 0א ועיין הקלות כי שמעון כד יב ו ג ד המורה המורה הראשון הוא לב' וזה ד' וכן תעשה אם יהיו בחברה ג' או יותר המין השלישי קיצור הממון ולא הזמן כמו שנתן ראובן ח' ושהה ו' ושמעון י"ב ושהה י"ב נקצר ממונם בחצי ישארו ד' לראובן ו' לשמעון עוד נקצרם בחיצי יהיו ב' לראובן ג' לשמעו' נכפול הממון הנשאר בכל זמנם יהיו ר"ב לראובן ול"ו 101[א] [פג2] ול"ו לשמעון [] המין הרביעי קיצור הז[מן] [] ח' די' ושהה ו' ושמעון [] נקצר הזמן בחצי והיה לראובן [] עוד נקצר בשליש והיה לראובן [] והנה עתה נראה ההפרש נכפול ח' על ו' לראובן יהיו מ"ח וי"ב על י"ב לשמעון יהיו קמ"ד והמורה קצ"ב והריוח עשרה הכל כזה הצורה מח 0א נכפול ונחלק כמנהג יבוא לראובן קמד ב' וחצי ולשמון ז' וחצי ואם נקח קצב המורה המקוצר הראשון בזמן שהוא לראובן ח' ג' שכפלם הם כ"ד ולשמעון י"ב על ו' שכפלם ע"ב כזה והמורה צ"ו הנה נפל לראובן ב' וחצי כד 0א ולשמעון ז' וחצי כנז' והקיצור עב השלישי שב לראובן ח' ולשמעון צו המורה כ"ד כזה ח 0א ונפל לראובן ב' וחצי ולשמון ז' וחצי כד ל"ב המורה המין החמשי הוא בקיצור הממון והזמן כל אחד בפני עצמו כמו שנתן ראובן ח' ושהה ו' ושמעון י"ב ושהה י"ב נקציר ממונם וזמנם יהיו לראובן ד' ג' וכופלם י"ב ולשמעון ו' ו' וכופלם ל"ו והמורה מ"ח והריוח כנז' והמין הששי בקיצור המוכפל מהממון ומהזמן כמו שנתן ראובן ח' ושהה ו' וכפל זה על [101ב] [פד1] [] זה על זה [] לשמון עוד [] עוד נקצרם בחצי [] נקצרם בחצי יהיו ג' [] נקצרם בשליש יהיו א' לראובן ראובן א [] בזה הצורה נכפול א' שהוא ממון שמעון ג [] [] על הריוח שהוא עשרה [] ונחלקם על ד' ד ה תציא ב' וחצי לראובן וז' וחצי לשמעון וראה ועיין ותשכיל כי בלי קצור חלוקת שמעון הוא אלף ת"מ על קצ"ב שהוא המורה ועתה שב החילוק לשמעון ל'[] על ד' ואם עשתי כל השאלות בשלמות בלא קיצור בעבור שלא לבלבל המתחיל והנה בזה הדרך נוכל לפסוק פסקי הקהל או דבר אחר כמו שעשו להשקות הנחלות ושיתין כל אחד כפי נחלתו ואם תעיין תוכל לעשות זה בדרך השלושה כמו שאר דברי תכף מדרך קצור דרך השלושה שהוא עיון יפה והערה גדולה והוא שתקצר לעולם הראשון המשל בזה והשני או הראשון והשלישי שהכל יהיה שוה בין שתקצרם בחצי או בשלשית או ברביעית או באי זה מספר שתוכל לקצרם שאם לא תוכל לקצר הראשון והשני שתקצר הראשון והשלישי ובלבד שתקצר שניהם במספר אחד ואם יש קיצור לשניהם הרשות בידך לקצור מה שתרצה והיותר טוב לקחת הזוג שיותר יתקצר כי זוג אחת דרך משל הראשון והשני יהיה יותר טוב לקציר מראשון ושלישי והוא הדין כאשר תכפול הממון והזמן שחזר השאלה לג' חלקי השלושה שגם תוכל לקצר הראשון והשני או הראשון והשלישי ואתן משלים שתבין מהם המבוקש והמשל 102[א] [פד2] והמשל [] [] יעלו כ"ד וכן [] שאז יהיו א' וג' ונאמר [] [] נכפול ח' על ג' יהיו [] כ"ד כראשון וכן אם נאמר אם [] מה יתן לי הנה נתן ח' [] וי"א חלקים מפ"ח וזה המספר נוכל לקצרם עד יסודם שהם ח' וי"ב וכן אם נקח החלקים אשר בין זה המספר שהוא פ"ח וקמ"ג עד יסודם שהם ח' וי"ג שהם י"א כי י"א פעמים ח' הם פ"ח וגם בהכפל י"ג י"א פעמים נמצא קמ"ג וכל עוד שתקח אמצעי אחד מכלם כמו מ' וס"ה או כל אחד מהאחרים יתן ח' וה' חלקים ממ' שהם שמינית אחר הקיצור וא או תשוים משל אחר אם ג' נתן ו' ט' מה יתן הנה נתן י"ח וכן יתן אם נקצר הראשון והשני או הראשון והשלישי משל אחר אם ג' נתן ג' ג' מה יתן הנה נתן ג' וכן יתן אם נקצר []הראשון מכל אחד יתן ג' משל אחר אם ב' נתן ו' עשרה מה יתן הנה נתן ל' וכן יתן ל' אם נקצר הראשון והשני או הראשון והשלישי משל אחר אם ה' נתן ט"ו כ' מה יתן ס' וכן יתן אם נקצר הראשון והשני או הראשון והשלישית בחמשית כמו שתראה בלוח הקיצורים והוא הדין אם יש בשאלות ממון וזמן שנכפול המומון על הזמן וחזר השאלה לג' חלקי השלושה כמו במשל [102ב] [פה1] [] אם ג ט ח כד [] אם א ג ח כד [] ח' __________________________ [] דרך השלושה אם פח קמג ה ח וא/פח [] אם ח' אם ח יג ה ח א/ח הרויח ג' ל"ב כמה ירויח אם מ ס ה ח הא/מח נכפול ל"ב על ג' שהוא הרויח ___________________________ יהיו צ"ו נחלקם על ח' יציא בחילוק אם ג ו ט י"ח י"ב וכן יציא י"ב אם נקצרם בחצי אם א ב ט י"ח הראשון והשלישי ונאמר כי חצי ח' אם א ו ג י"ח ד' וחצי ל"ב הם י"ו ונאמר אם ___________________________ ד' נתן ג' מה יתן י"ו נכפול י"ו אם ג ג ג ג על ג' יהיו מ"ח נחלקם על ד' אם א א ג ג יעלה בחילוק י"ב כראשון גם אם א ג א ג נקצר ד' וי"ו בחצי יהיו ב' ___________________________ וח' וח' על ג' יהיו כ"ד נחלקם אם ב ו י ל על ב' יעלו י"ב בקיצור ראשון אם א ו ה ל ושני עוד נקצר ב' וח' אם א ג י ל יהיו א' וד' נכפול ד' על ג' ___________________________ יעלו י"ב נחלקם על א' יהיו י"ב אם ה טו כ ס כקיצור שלושתם וכן כל הדומה אם א ג כ ס לזה א טו ד ס הפרק ה _________________________________ בידיעת פרחי' חדשי' ריוח [] חדש השואת הממונות זה אם ד ב ג ח ד אם ח ג לב יב אם ד ג יו יב אם ב ג ח יב אם א ג ד יב 103[א] [פה2] הפרק [] ואומר [] שוה למטבע מדינת [] אשר הדרך הראשון הוא [] השני עם חילוק וכפל הדרך הראשון הוא שתקח מטבע מוסכם [] המדינות מ[] סכום יהיה פרח או [] או אי זה מטבע שיהיה ועמו תסדר שאלתיך ואמור אם זה הסך מזאת המדינה נתן לי זה הסך מהמדינה אשר אני מבקש להשיב זה המטבע למטבע זאת המדינה זה הסך מזאת המדינה כמה יתן לי מהמדינה אשר אני מבקש המשל רצינו להשיב תת"ן לטרי ברצלונה ליטרי סרגוסה נקח פרח אחד שהוא שוה בברצי[ל]ונה י"ז די' ובסרגוסה י"ו ונאמר אם י"ז בברצלונה הוא שוה י"ו בסרגוסה תת"ן לטרי מברצלונה כמה ליטרי יהיו שוים בסרגוסה ברצילונ סרגוס ברצלונ ויהיה השאלה בזאת הצורה אם זא וא 0הח נכפול האמצעיות יעלו י"ג אלפים ת"ר נחלקם על י"ז יעלה ת"ת ליטרי' בשוה ואם כן תת"ן לטרי מברצלונה הם ת"ת ליטרי' מסרגוסה 00וגא 000וגא וא 00ח והבחינה תערוך י"ו על י"ז ות"ת על זא 0הח תת"ן כזא[ת] הצורה ועשינו השואה והנם שוים שאלה אחרת נהפוך השאלה ותהיה בחינה לעליונה ונאמר אם י"ו מס[ר]גוסה שוה י"ז בברצילונה [103ב] [פו1] [] יהיו [] בזאת הצורה כפלנו [] על י"ז יעלו י"ג [] אלפים ות"ר נחלקם [] ואם כן ת"ת לטרי סרגוסה [] והבחינה מבוארת כי אלו [] [] כל אחד בחינה לחברתה משל אחר סוחר חייב לאחר ל"ג אשקודוש ורצה לפורעו בדוקדוש וסך האשקודו * י"ט די' וסך עתה הדוקאדו כ"ב די' נכפול הל"ג אשקודוש על סך האשקודו שהוא י"ט יעלו תרכ"ז נחלקם על סך הדוקאדו שהוא כ"ב יעלה בחילוק כ"ח דוקאדוש וי"א די' משל אחר סוחר חייב לאחר כ"ח דוקאדוש וי"א די' ורצה לפורעו באשקודוש וסך הדוקאדו כ"ב די' וסך האשקודו י"ט די' שאלתי כמה אישקודוש יתן לו התשובה נכפול הכ"ח דוקאדוש על כ"ב יעלו תרי"ז נחבר עליהם י"א די' יהיו תרכ"ז נחלקם על י"ט שהוא סך האשקודו יעלה בחילוק ל"ג אשקודוש והוא המבוקש והנה כ"ח דוקאדוש וי"א די' הם שוים ל"ג אשקודוש וכן כל הדומה לזה משל אחר שרצינו לעשות מפרחים די' או מדי' פרחים כמו קקנ"ב פרחים די' שרצינו לעשותם פרחים תחלקם על סך הפרח אם הפרח שוה די שוים תחלקם על סך הפרח ואם יש בו פשי' כמו בזה המשל שרצינו לעשות מקקנ"ב די' פרחי' והפרח שוה [] די' וב' פשי' י"ד 104[א] [פו2] הנה ב' פשיט' [] אלף תקי"ב נחלקם על [] שהם שישית יעלה בחילוק [] ששיות די' נחלקם על ששה יהיו [] משל אחר רצינו לעשות אלף וקכ"ה די' [] שוה ט"ו די' וד' פשי' נעשה הט"ו די' פשי' [] שנכפלם על י"ב יעלו קפ"ה עם הה' פשיט' והם המחלק וגם נעשה מהפרחים פשיטי' וזה שנכפול אלף קכ"ה על י"ב יעלו י"ג אלפים ות"ק * נחלקם על קפ"ה יעלה בחילוק פשי' ע"ב והם פרחים ונשארו ק"ף פשי' נחלקם על י"ב יעלו ט"ו די' והנה אלף קכ"ה די' יעלו ע"ב פרחים וט"ו די' והבחנה כפול ע"ב על פשיטי' הפרח יעלו י"ג אלף ות"ק תחלקם על י"ב יעלו אלף קכ"ה משל אחר רצינו לעשות מנ' די' פרחים והפרח שוה י"ב די' וד' פשי' נעשה הפרח שלישיות יהיו דינר בעבור הד' פשי' שהם שליש דינר יהיו ל"ז שלישיות עם נחלקם על השליש גם נעשה הנ' די' שלישיות יהיו ק"ך שלישים נחלקם על ל"ז יעלה בחילוק ד' פרחים ונשארו ב' לחלק והם ב' שלישיות שהם ח' פשי' והנה נ' די' הם ד' פרחים וח' פשי' והנה כל אלה תוכל לעשות בדרך השלושה ונאמר אם ל"ז שלישיות דינר שוה פרח אחד ק"ן שלישיות דינ' שהם נ' די' מה יהיה שוה כפול ק"ן על א' יעלו יעלו ק"ן תחלקם על ל"ז יעלו ד' והם פרחים ונשארו ב' שלישיות דינר שהם ח' פשי' והנה ד' פרחי' וח' פשי' יעלו נ' די' וזה בעבור שיש בזה די' ופשי' אבל אם אין פשי' הוא קל לעשות ממטבע אחד מטבע אחר מזהב עשה הכל די' [104ב] [פז1] [] והמשל שרצינו [] הדוקאדוש די' והיוציא [] הוא המורה והיוציא הם פרחי' [] אחד דינ' ופשי' עשה שע המטבעו' [] פשי' מטבע אחת מהנרצה כמו במשל [] קקכ"ג דוקאדוש פרחים והפרח שוה י"ו די' וג' פשי' נעשה מהי"ו די' פשי' יהיו עם הג' קצ"ה והוא המורה לחלק עליו כל פשיטי הדוקאדוש שהם ד' אלפים תתק"ו י"ו אלפים תתי"ב נ"ח אלפים תתע"ב והנה יעלה בחילוק ש"א והם פרחים ונשארו ע"ז פשי' שהם י"ד די' וט' פשי' והנה קקכ"ג דוקדוש הם ש"א פרח' וי"ד די' וט' פשי' ואם יהיה לך אי זה מטבע זהב ותרצה לעשותם מטבע אחר ואם שיהיה מכסף עשה הכל פשי' וחלקם על פשיט' המטבע שתרצה ו' ותרצה מטבע של זהב עשה הכל די' וחולק על י' דינרי המטבע שתרצה והמשל למטבע זהב הרי שהיה ביד סוחר אלף תר"מ אחד ד' אלפים תתק"ך די' הנה עתה אם ירצה לעשותם פרחי' יחלקם על י"ו יעלו ש"ז פרחים וחצי ואם רצה דוקאדוש יחלקם על כ"ב ויעלו רכ"ג דוקאדוש וי"ד די' ואם רצה ליטרין יחלקם על כ' ויעלו רמ"ו לטרין ואם רצה קאשטילאנו יחלקם על כ"ח ויעלו קע"ה קאשטילאנוש ועשרים די' וכן כל הדומה לזה ואם במטבע יהיו פשי' עשה הכל פשי' ואם מה שהיה בידך הם פשיט אי מטבע של כסף ותרצה לעשות מהם מטבע של [] זהב הנה הראוי שתעשה מה שבידך פשי' ותחלק על פשיטי המטבע שתרצה כמו שעשינו למטבע הזהב ואם נרצה להשיב מטבע של כסף מטבע אחר של כסף הנה הוא חלוקת פשיטי הממון הידוע על פשיט מטבע אחד מהנרצה והמשל 105[א] [פז2] והמשל שהיה [] מהם מלכים [] ואם מברצילונה נחלקם על י"ז [] ואם גואניש נחלקם על כ"ו וכן כל [] משל אחר להשיב כ"ט דוקאדוש מלכים [] וסך הדוקאדו כ"ב נכפול כ"ט על כ"ב שהוא סך הדוקאדו יהיו תקל"ח די' עוד נכפלם על י"ב יעלו ז' אלפים תרנ"ו פשיט' ועתה נוכל לעשות מהם כל מטבע מטבע כסף שתרצה ועתה בשאלתנו נחלקם על י"ח פשיט' מלך מואלינסיאה יעלו [] תכ"ה מלכים וששה פשי' והבחינה היא שתעשה מהמלכים דוקאדוש נהפוך השאלה ונאמר רצינו לעשות תכ"ה מלכים מולנסיאה וששה פשי' דוקאדוש הנה סך הדוקאדו כ"ב די' וסך המלך י"ח פשי' נעשה מן הנשאל פשי' וזה שנכפול תכ"ה מלכים על י"ח יעלו עם הששה פשי' ז' אלף תרנ"ו נחלקם על פשיט' הדוקאדו שהם רס"ד יעלה בחילק כ"ט דוקאדוש והנה הבחינה טובה ושבנו מלכים ופשיט דוקאדוש הערה לחילוף המטבעות ידועי הסכום הנה כסך המטבע האחד יהיה המטבע השני והמשל הנה היה בידינו כ"ב פרחים ורצינו לעשותם והמשל נעשה דוקאדוש הנה הכ"ב פרחים שהם כסך הדוקדו הם י"ו דוקאדוש מהפרחים די' וכן כל י"ו דוקאדש הם כ"ב פרחים וכן כל כ"ד פרחים יהיו שנ"ב נעשה שהם כסך הפלומיטה יהיו י"ו פלומיטאש וכל פלומיט' מהם דוקאדוש יהיו כ"ד פרחים וכן כל כ"ח פרחים יהיו י"ו קאשטיללאנוש נחלקם על כ"ב וכל י"ו קאשטילאנוש יהיו כ"ח פרחים וכן כל כ"ח פאלומיטה יעלו י"ו דוקדוש יהיו כ"ד קאשטיללנונוש וכל כ"ד קאשטיללאנוש יהיו כ"ח פלומי' או נעשה בהפך וכן אם המטבעות יעלו או יורידו [105ב] [פח1] []ת שתרצה ואם [] [] י"ו פלומיטאש רנ"א פרחים [] אבל יותר טוב הוא שתקצרם [] הי"ו פאלומיטאש ואמור אם ג' פרחים [] ב' פלומיטש קנ"א פרחים כמה פאלומיטאש יהיו וכן לכל המטבעות הנזכר' תוכל לקצרם משל אחר ת"ק לטרין כמה מלכים מואלינסיא הם הנה בזה שני דרכים הדרך הראשון נעשה מן הלטרין פשיטי' ונחלקם על י"ח שהוא סך המלך בבלינסיאה או נחלקם על סך מטבע אחר שנרצה הדרך השני קח כל כך לטרין שיהיו שוים למלכים שתרצה אם ואלינסאנו או אחר ואמור בדרך השלושה אם כך ליטרין שוים כך מלכים ת"ק לטרי' כמה מלכים יהיו והמשל בזה הנה ג' ליטרה הם שוים מ' מלכים ואמור אם ג' לטר' שוים מ' מלכים ת"ק ליטרה כמה מלכים הם שוים ויהיו לטרי' מלכי' לטרי' כזאת הצורה נכפול ת"ק אם ג מ תק על מ' יעלו כ' אלפים נחלקם על ג' יעלו ששת אלפים תרס"ו והם מלכים וב' שלישיות מלך שהם דנר אחד והראוי שנסדר כל כך ליטרין שיהיו מלכים שוים כמו במשל כי י"ד מלכים הם כ"א די' וי"ג מלכים הם י"ט די' וחצי ועוד י"ג מלכים הם י"ט די' וחצי ושלושתם הם ג' ליטרי' שוים ולכך נאמר אם ג' לטרי' שוים מ' מלכים ת"ק ליטר כמה מלכים יהיו שוים וכן תעשה לכל מטבע שתשוים זה עם זה עם שתגרע או תוסיף עד שיהיו שוים 106[א] [פח2] כי כאשר סך [] נחלקם על י"ו יעלה [] ליטר אחת שוה ט"ו מלכים [] והקש על זה משל אחר רצינו להשיב רמ"ה ק[] ואחר דוקאדוש ואחר אשקודוש הנה סך [] כ"ח די' נכפול רמ"ה על כ"ח יעלו ששה אלף תת"ס נחלקם על י"ו יעלו תכ"ח פרחים וי"ב די' ואם נחלקם על כ"ב יעלו שי"א דוקאדוש ואם נחלקם על כ"א שהוא סך האשקוד יעלו שכ"ו אשקודוש וי"ד די' ואם נחלקם על כ' יעלו שמ"ג לטרין וכן כל הדומה לזה אחרת רצינו להשיב רנ"ב קאשטיללאנוש מזהב גואניש מכ"ו פשיט' גם מלכים מואלינסאה מי"ח פשי' גם מברצלונה מי"ז פשי' גם קפליניש מי"ד פשי' הדרך לכל זה ולדומה לזה שנכפול ראשונה הקאשטיללאנוש על כ"ח ויהיו די' גם נכפול הדינ' על י"ב ויהיו פשיטי' ותשמרם ואחר נחלקם אל מה שנרצה והמשל בזה רצינו לעשות מרנ"ב קאשטיללנוש גואנוש הנה בעבור שנרצה מטבע כסף נעשה מהם פשיטי וראשונה נעשה מהם די' וזה שנכפלם על כ"ח יעלו ז' אלפים ונ"ו די' עוד נכפול אלו הדי' בי"ב יעלו פ"ד אלפים תרע"ב והם פשיטי' ונשמרם ודרך אחרת לעשותם פשיט' ולא די' נכפול רנ"ב על של"ו שהם פשיטי' קאשטיללנו אחד יעלו פ"ד אלפים תרע"ב כנז' נחלקם על כ"ו יעלו [106ב] [פט1] [] י"ו פשיטי' [] ואלינסי' יעלו ד' []לינסו' עוד אם נחלקם [] יעלו ד' אלפים תתק"ף []נה עוד אם נחלקם [] שהוא סך קרלין יעלו ששת אלפים ומ"ח קרליניש וכן תעשה לכל הדומה לזה והבחינה כפול המטבע אשר בידך על סך המטבע עצמו ויעלו כל הפשיטי' אחר תחלק הפשי' על י"ב יעלו הדי' אחר תחלק הדי' על כ"ח יעלו כל הקאשטיללנוש והמשל בקארליניש נכפול ששת אלפים ומ"ח קרליניש על י"ד שהוא סך הקרלין יעלו פ"ד אלף תרע"ב פשיט' נחלקם על י"ב יעלו ז' אלפים ונ"ו די' עוד נחלק הדי' על כ"ח יעלו רנ"ב קאשטיללנוש וכן לכל מין שיהיה 107[א] [107ב] – ריק [צ1] [] הנה זה בשני [] הוא שרצינו להוריד [] במשל אם היה הרבית ק' די' [] שנרצה והקרן קיים [] הוא שלא נרצה להוריד הרבית אלא שיתנו [] בזה הסך הממון הנרצה המשל לדרך הראשון הנה ראובן הלוה אלף די' לסך ק' די' בכל שנה ולאחר זמן רצו להוריד הרבית לסך כאילו היו האלף די' אלף ות"ק לסך ק' שהוא גם כן ט"ו אלפים בעד אלף ואם נאמר בדרך השלושה כנהוג ברוב השאלות לא תציא אמיתי כמו שנאמר אם אלף נתן לנו ק' אלף ות"ק מה יתן לנו הנה נתן לנו ק"ן ואנחנו שאלנו להוריד הרבית לא שיעלה ובעבור זה נקח דרך אחר מדרך השלושה כי הם ג' דרכים כמו שתראה במקומו ונאמר כי באילו השאלות והדומים להם בחומר אחר נכפול הידועים שהם אלף על ק' והיוציא נחלק על הנשאל והמשל בזה הנה זאת השאלה הוא אם אלף נתן ק' די' מרבית אם יהיה אלף ות"ק מה יתן ויהיה כזאת אם 000א 00א 00הא הצורה נכפול אלף על ק' יעלו מאה אלף נחלקם על אלף ות"ק יעלה בחילוק ס"ו די' וב' שלישיות דנר שהם ח' פשיטי' וזה יפרע מן האלף די' אשר בידו במקום [] הק' באלף והבחינה הנה [] נוכל לקצר השאלה להקל תגרע ב' ספראש מכל אחד ונשאר השאלה אם עשרה נתן א' ט"ו מה יתן כזה הצורה אם 0א א הא נכפול עשרה על א' יהיו 108[א] [צ2] עשרה נחלקם על [] וח' פשי' משל אחר אם אלף נתן מאה [] ונאמר אם אלף נתן ק' [] ונאמר אם אלף נתן מאה ב' אלפים מה יתן [] אם 000א 00א 000ב הצורה נכפול הידועים שהם אלף על ק' יהיו מאה אלפים נחלקם על ב' אלפים ותציא בחלוקה חמשים די' והנה חמשים די' יתן בעד האלף אשר בידו וכן תעשה לכל הדומים לאלה כי האלף די' קיימים והרבית יורד והבחינה גרע ב' ספראש להקל מכל אחד ישאר השאלה אם עשרה נתן א' עשרים מה יתן נכפול עשרה על א' יהיו עשרה נחלקם על עשרים והוא מחולק כזה א0/ב0 שהם עשרה חלקים מעשרים גרע הספראש יהיו חצי או תקצרם ישאר חצי והוא חצי ק' שהוא חמשים ממאה שהוא הרבית הראשון הנה זה הסדר תעשה כשתרצה לרדת הרבית אבל כשתרצה שינשאל נערך אל אחר תעשה הדרך השלושה הנהוג והמשל נאמר אם אלף שוה ק' ג' אלפים וק' מה יהיה שוה או אלף שוה פ"ה שכ"א מה יהיה שוה וכן תעשה כאשר תקצר את כולם וזה תראה בדרך השנית והדרך השנית הוא שלא נרצה להוריד הרבית אלא שיתנו מעות לזה הסך אם מעט ואם הרבה ובעבור זה נעשה חשבוננו עם דרך השלשה הנהוג והמשל רצינו לתת תת"ק די' לסך י"ח אלפים באלף ושיהיו בידו ע"ג ימים נאמר ראשונה אם י"ח אלפים נתן אלף תת"ק מה יתן נכפול אלף על תת"ק ותציא ט' מאות [108ב] [צא1] [] או תקצרם ואמור [] [כפול] תת"ק על א' ותחלקם על [] ואחר נאמר אם שס"ה ימי השנה [] מה יתן ויהיה כזה הצורה נכפול [אם הוג] 0ה גז נ' על ע"ג יעלו ג' אלפים תר"ן נחלקם על שס"ה יעלו עשרה די' וזה הראוי לע"ג ימים והבחינה היא שנכפול האמצעיות ויהיו שוות לכפל החיצוניות וגם בערכים תראה זה כי ערך שס"ה אל ע"ג כערך נ' אל עשרה כי ע"ג הוא חמשית שס"ה וכן עשרה הם חמשית נ' וגם אם תשוים יהיו שוים כזה הצורה 0הוג 0הוג משל אחר רצינו לתת תשל"ב הוג × גז לזמן רצ"א ימים לסך 0ה 0א י"ט אלף באלף נאמר ראשונה אם י"ט אלף נתן אלף בשנה תשל"ב מה יתן נסיר הספראש להקל ונאמר אם י"ט נתן א' תשל"ב ויהיה כזא' הצורה כפול תשל"ב על אם טא א בגז א' ויהיו תשל"ב נחלקם על י"ט ותציא בחילוק ל"ח ועשרה חלקי י"ט נכפול אלו העשרה שברים על י"ב יעלו ק"ך נחלקם על י"ט יצא בחילוק ששה פשיטי' וששה חלקים מי"ט בפשוט אבל צריך להשיבם בשברו וישובו תשל"ב חלקים מי"ט ונאמר אם שס"ה נתן לנו תשל"ב רצ"א מי יתן לנו אם הוג בגז אטב ויהיה כזה הצורה נכפול רצ"א על תשל"ב יעלו רי"ג אלפים וי"ב כזה בא0גאב טא 109[א] [צא2] כזה נחלקם על שס"ה [] בא0גאב י"ט יהיו ששת אלפים [] טא וי"ב ותציא בחילוק ל' די' [] נכפלם על י"ב יהיו נ"ט אלפים תק"י [] ותציא ח' פשיט' ונשארו ד' אלפים ס"ד נכפלם על [] אלפים קכ"ח נחלקם על המורה יעלה מחצה ונשארו אלף קצ"ג נכפלם על ב' לעשות פוגישאש יהיו ב' אלפים שפ"ו ולא הגיעו לפוגישה א' והם חלקי פוגישה שהוא זה וחגב והנה עלה מכל זה כי הנותן תשל"ב די' בזמן הגטו רצ"א ימים לסך י"ט אלפים באלף חייב לפרוע מהם ל"ח די' וששה פשי' וששה חלקים מי"ט בפשוט ובעבור שלא היו בידו כל השנה אלא רצ"א ימים חייב לפרוע מהם ל' די' וח' פשי' ומחצה והחלק הנז' מפוגישה והבחינה אמור אם שס"ה נתן ל"ח והחלקים הנז' רצ"א מה יתן והנה נתן ל' די' וחלקים כנז' שאלה אחרת הוא הדרך השני הוא שנעריך מה שלקח כפי הימים אשר בידו ודע כי קוראים סינשל לעשרת אלפים הרבית אלף או לשנים עשר אלף באלף וזה יותר בזול וכן כל מה שיעלה ההלואה יהיה יותר בזול כמו שתראה בזה הלוח כי עשרה אלפים נתן ק' וד' אלפים וי"ב אלפים נתן פ"ג די' וד' פשי' וכו' כמו שתראה במשלים והמשל רצינו לדעת אם עשרת אלפים נתן בסינשאל אלף לזה הסך מה יתן אלף והנה נתן ק' כמו שתראה בטור ראשון מן הלוח ואם הסינשאל יהיה מי"ב אלפים לאלף שהוא יותר בזול גם כפול אלף על [109ב] [צב1] []קם על י"ב אלפים [] [] [] דנרי' דנריו דנרי [] [] 100 1000 1000 10000 [] 4 83 1000 1000 12000 [] לכל שנה 8 66 1000 1000 14000 [] אבל אם שאל ימים 5/9 55 1000 1000 18000 או ימים וחדשים אמור 50 1000 1000 20000 בימים אם שס"ה ימים 8 41 1000 1000 24000 נתן ק' הנשאל מה יתן 4 33 1000 1000 30000 הנה אתן משלים להבין 2/9 27 1000 1000 36000 זה על סך אחד מהסנשאל ולא אכווין לרביע היום 90 900 1000 10000 על שס"ה שלא לבלבל 80 800 1000 10000 למעיין 70 700 1000 10000 שאלה הנה היה 75 900 1000 12000 ביד ראובן 2/7 64 900 1000 14000 אלף די' לסך עשרת 60 900 1000 15000 אלפים אשר בכל שנה 50 900 1000 18000 חייב לתת ק' די' ושהו 45 900 1000 20000 בידו ע"ג ימים 1/2 37 900 1000 24000 שאלתי כמה די' יפרע 30 900 1000 30000 ראובן מן הע"ג 25 900 1000 36000 ימים שהיו בידו אלף די' התשובה אמור אם שס"ה ימים נתן ק' די' ע"ג ימים כמה ראוי שיתן ויהיה כזאת אם הוג 00א גז הצורה הצורה 110[א] [צב2] הצורה נכפול [] יעלה בחילוק עשרים [] שבידו והבחינה נכפול הקצוות וכן הא[] ועוד בחינה אחרת שנזדמן [] זה כי ערך שס"ה אל ע"ג הוא חמשית וכן ב' אל ק' שאלה אחרת הנה ביד ראובן אלף די' לסך עשרת אלפים באלף והסך ק' די' ושהו בידו ז' חדשים וי"ז ימים ממרסו אמור אם שס"ה נתן ק' בשנה ז' חדשים וי"ז ימים מה יתן תן השלם בשברו שתכפול הז' חדשים על ל' יהיו ר"י תחבר על ר"י ד' בעבור ד' מלאים יהיו רי"ד עוד תחבר עליהם י"ז ימים שלנו יהיו רל"א ועתה אמור אם שס"ה נתן ק' רל"א מה יתן כזאת הצורה תכפול רל"א על אם הוג 00א אגב ק' יעלו כ"ג אלפים וק' תחלקם על שס"ה יעל ס"ג וק"ה חלקי שס"ה ואם תרצה לעשות מהם שעות תכפול ק"ה על כ"ד והעולה תחלק על שס"ה והבחנה כנהוג ובעבור שלא [] אעשה בחינה לכל שאלה אכתוב אחר קצת במינו שאלה אחרת הנה ביד ראובן אלף די' לס' עשרת אלפים באלף אשר הסך הוא ק' די' כנז' ושהו בידו ט' חדשים שאילתי הראוי לפרוע לפרוע אמור אם י"ב חדשים נתן ק' די' בט' חדשים מה ראוי לפרוע ויהיה כזאת הצורה תכפול ט' חדש די' חדש' על ק' יעלו תת"ק אם בא 00א ט עה [110ב] [צג1] [] די' וזה הראוי [] [] חיצוניות ויהיה כל אחד תת"ק [] ערך ע"ה אל ק' ג' רביעיות וכן ערך [] ג' רביעיות שאלה אחרת על הסך הנז' ושהו האלף די' ביד ראובן ח' חדשים ממרסו להלן וי"א ימים וט"ו שעות שאלתי הראוי לפרוע הנה נעשה הכל שעות וראשנה נעשה הח' חדשים ימים ויהיו רמ"ה עם ימי המלאים ועוד י"א ימים שהיו לנו יהיו רנ"ו ימים נכפלם על כ"ד שעות כל יום יהיו ו' אלפים קמ"ד הכל שעות וט"ו שעות שהיו לנו יהיו ו' אלפים קנ"ט והם כל השעות הראויות לחלק ועתה נאמר אם שס"ה נתן ק' די' ו' אלפים קנ"ט מה יתן כזאת הצורה נכפול ו' אם הוג 00א טהאו ו' אלפים קנ"ט על ק' יעלו קט"ו אלפים ותת"ק נחלקם על שס"ה אחר שנכפול שס"ה על כ"ה שיהיו ח' אלפים תש"ס והם שעות שס"ה ואיני [] חושב על הרביע יום שלא לבלבל הנה יעלה בחילוק ע' די' וכ"ז חלקים מפ"ז בדינ' אחר הקיצור וזה הע' די' וכ"ז חלק פ"ז הוא הראוי לפרוע באילו החדשים והימים והשעות הערה לבחינות הנה יעדתי לכתוב בחינות לדרך השלושה על דרכים רבים אפע"פ שהם מפוזרים בספר אבל אני אתן בכאן קצת מהם מקובצות על שאלה אחת והיא אם ה' יתן ג' ו' מה יתן הנה נתן ג' וג' חמשיות והבחינה נכפול החיצוניות והאמצעיות והיו שוות וראשונה 111[א] [צג2] תשוים הכל בחמשיות [] ויהיו כזאת הצורה הרא[שונה] [] אם יח ל טו כה [] ט"ו וה[] חמשיות ועם זה אעשה קצת בדיקות הראשונה היא שתכפול האמצעיות והחיצוניות יהיו כל אחד ת"ן והבחינה השנית תהפוך השאלה [] כמו שהיא בחמשיות ואמור אם י"ח נתן ל' ט"ו מה יתן והוא הדין אם תקח הצורה הראשונה אבל לקחתי השנית שלא לטרוח לעשותה חמשיות והבחינה השלשית תן הבנים על האבות בעבור שהם טו יח קטנים יהיו ט"ו על כ"ה וי"ח על ל' כזה הצורה כה ל תקצרם יהיו כל אחד משניהם ג' חמשיות אחר הקיצור והבחינה הרביעית תן האבות על הבנים כ"ה כה ל על ט"ו ול' על י"ח כזה הצורה ויהיו טו יח שוים אחר הקיצור ש ה' שלשיות כל אחד שהם אחד שלם ושתי שלישיות תן תן בחינה חמשית תן כל אב על בנו ותשוים כה ל ויהיו כל אחד ת"ן טו × יח בחינת שברים או שברי שברים הוא שתשוים כמ[ו] שתראה בשאלות ועוד תראה בדיקות אחרות הנה כל אלו הבחינו' ועוד אחרות מפוזרות ואחרות מערכים וזה להרגילך ואשוב ואחרות [111ב] [צד1] []עות לסך סינשאל [] ב' אלפים כנזכ' בלוח [] תאמר אם י"ב אלף נתן [] וגם תוכל לקצר האלפים ותאמר [] מה יתן [המשל] בזה ראובן הלוה לגוי ת"ר די' לסך י"ב אלף לאלף שאלתי הראוי לפרוע לו בכל שנה התשובה הנה תדע זה בדרך השלושה ואמור אם י"ב אלף נתן אלף ת"ק מה יתן כפול ת"ק על אלף והעולה תחלק על י"ב אלפים והיוציא שהוא מ"א די' [] ושתי שלישיות די' שהם ח' פשי' הוא הראוי לפרוע לסך הנשאל וכן אם תקצרם ותאמר אם י"ב נתן א' ת"ק מה יתן כפול ת"ק על א' יעלה ת"ק תחלקם על י"ב ותציא מ"א ושתי שלישיות כנזכר שהם מ"א די' וח' פשי' בכל שנה שאלה אחרת ראובן הלוה לגוי י"ג אלפים לסך י"ב אלף באלף והלך הרבית ר"ג ימים שאלתי הראוי לפרוע לו מאילו הר"ג ימים התשובה תחלק אלף שהוא הראוי לשום לשס"ה ימים ולא נדקדק לרביע יום והיוציא הוא הראוי לכל אחד ואחר אמור אם יום אחד נתן לי כך ר"ג ימים מה יתן לי והמשל נחלק אלף לשס"ה ימים יבוא לכל יום ב' די' ור"ע חלקים משס"ה בשלם דרך אחרת תעשה הכל פשיטי' ואמור אם יום אחד נתן ב' די' ור"ע חלקי שס"ה ר"ג ימים מה יתן לי או תסדר שאלתך בדרך אחרת ואמור אם י"ב אלפים בשס"ה יום נתן לנו אלף די' י"ג אלפים בר"ג ימים מה יתן ויהיה כזה הצורה 112[א] [צד2] ימים דינרי [] ג0ב 000גא [] 000טגוב מספרים תרל"ט אלפים ואחר [] [ד'] מספרים וש"ף אלפים נתנו אלף די' ב' מספרים [תרל"ט מה] יתן נכפול אלף על האחרון הנשאל שהוא שני מספרים תרל"ט יעלו רס"ג מספרים תת"ק אלפים כזה הצורה 000000טגוב אשר נחלקם על הראשון שהוא ד' מספרים ש"ף אלפים ויעלה בחילוק תר"ב די' וקי"ב חלקים מרי"ט בשלם כזה [בא]א מקוצר או דרך יותר נקל אמור אם י"ב אלפים נתן טאב אלף די' י"ג אלפים מה יתן נכפול י"ג אלפים על אלף יעלו י"ג מספרים נחלקם על י"ב אלפים יציא בחילוק אלף פ"ג די' ושליש שהוא ד' פשי' וזה יהיה בשנה אחת [] [] שהיא שס"ה ימים ואנחנו שאלנו ר"ג ימים הנה נאמר אם שס"ה נתן לנו אלף ופ"ג די' ושליש מה יתן לנו ר"ג ימים נעשה שלישיות ר"ג ימים וגם אלף ופ"ג יהיו ט0ו והשני 0הבג נכפול זה על זה שבר על שבר ג ג ומורה על מורה ויהיו מספר אחד ותתקע"ט אלפים ור"ן והם תשיעיות כזה 0הבטזטא נחלקם על שס"ה וראשונה אחר שנכפול ט שס"ה על ט' שיעלו ג' אלפים רפ"ה ויעלה בחילוק תר"ב די' ונשארו קי"ב חלקים מרי"ט בשלם אחד הקיצור בשלישית שתי פעמים ואם כן מי שלקח י"ג אלף די' לסך י"ב אלפים באלף יפרע בר"ג ימים תר"ב די' שאלה [112ב] [צה1] [] תקמ"א דינרי' [] והלך הרבית רכ"ט [] נעשה מן דינרי' פשיטי' [] דינרי' ימים דנרי' [] 000א הוג 000בא [] 00הדאא פשיט בא יהיו קי"ד אלפים ות"ק הכל פשיטי' עם ח' פשיטי' שהיו לנו גם ניתן הימים נשברים שנכפול רכ"ט על קי"ד אלפים ות"ק פשיטי' יעלו כ"ו מספרים ור"ך אלפים ות"ק והמורה י"ב ויהיו כזה הצורה 00ה0בבוב ועתה כפול אלף על זה המספר יהיו בא כ"ו אלפים ור"ך מספרים ות"ק אלפים והמורה י"ב ויהיה כזה הצורה שמור וחלק על ראשון אחר שנשויהו 00000ה0בבוב שנכפול שס"ה ימים על על י"ב בא אלף שיעלו ד' מספרים ש"ף אלפים אשר תכפלם אשר תכפלם על י"ב ויעלה נ"ב מספרים תק"ס אלפים כזה אשר עליו תחלק כי אז [] שוה למספר השמור 0000והבה לחלק ויעלה בחילוק תצ"ד בא וג' אלפים ותתקפ"ו מה' אלפים רנ"ו וחטג כזה וזה מה שראוי לפרוע למי שנתן [] ט' אלפים והבה תקמ"א דניר' וח' פשיט לסך סנשאל שהוא י"ב אלף לאלף שאלה אחרת הלוה לגוי ה' אלף וששה די' וח' פשיטי' לסך סינשאל שהוא י"ב אלפים לאלף כנזכר והלך הרבית ס"ב ימים שאלתי הראוי לפרוע נאמר אם י"ב אלף בשס"ה ימים נתנו אלף ה' אלף ו' די' ח' פשי' בס"ב ימים מה יתנו כזה הצורה ימים פשי' דנרי' ימים דנרי נתן השלם בשברו יהיו 62 8/125006 1000 365 12000 יהיו ס' אלף ופ' והמורה י"ב כי הם פשיטין נכפול ס"ב ימים על הפשיטי' יהיו ג' מספרים תשכ"ד אלפים תתק"ס והמורה י"ב ועתה נכפול זה המספר על אלף יהיו ג' אלפים תשכ"ד מספרים תתק"ס אלפים והמורה י"ב וזה ראוי לחלק על כפל שס"ה {על י"ב אלף שהוא הראשון והעולה תכפול עוד על י"ב ואז יהיה שוה למספר הראוי לחלק ואז יעלה המספר י"ב מספרים תק"ס אלפים כזה 0000והבה וזה יהיה המחלק ויעלה בחילוק ע' די' ותקע"ב חלקים מתרכ"ז מקוצרים והוא הנשאל והנה אם יהיה בשאלתך מספר שתוכל לקצרו כמו באלה השמות שאמר ח' פשיט הנה תוכל [] לאמר ב' שלישיות וכמו שעשית המורה י"ב יהיה ג' ותעשה הכל יותר בקלות וגם במספר המונח ומה שלא עשיתי כן כדי שלא לבלבל למעיין כי הכל דק ועיין} 113[א] [צה2] הפרק [] הממון אשר [] התשובה הנה זאת השאלה [] דרך השלושה ו[] ששה ואנחנו שאלנו שלושה רביעיות [] ונאמר אם ד' נתן לנו ו' מי יתן לנו שלושה רביעיות [] אם ד ו 0 ג/ד כזאת הצורה נכפול הקצוות שהם ג/ד על ד' יעלו י"ב רביעיות נחלקם על ו' שהם כ"ד רביעיות יעלה בחילוק חצי וזה המספר המבוקש שאם נוסיף עליו חציו יהיו ג/ד ג' רביעיות שאלה אחרת מהו המספר אשר חיב[ר]נו עליו חצי שלישיתו ושלישית רביעיתו ורביעית חמשיתו ועם הכל יהיה ב' חמשיות תשובה עם מונח כוזב ודרך השלושה נניח ס' בעבור שימצאו בו כל החלקים בשלמות הנה חצי שלישיתו הוא עשרה כי שליש ס' הוא כ' וחציו עשרה נחברם עם ס' יהיו ע' ועוד נקח שלישית רביעיתו והוא חמשה כי רביעיתו הוא ט"ו ושלשית ט"ו הוא ה' נחבר ה' עם ע' יהיו ע"ה ועוד נקח רביעית חמשיתו והוא ג' כי חמשיתו הוא י"ב ורביעית י"ב הוא ג' נחברם עם ע"ה יהיו ע"ח והנה עלה יותר ממה ששאלנו כי ב' חמישיות שאלנו ונתן לנו המונח ע"ח שלמים נלך אל דרך השלושה והיא יגיד לנו שאלתנו ונסדר דרך השלושה ונאמר אם ס' נתן לנו ע"ח מי יתן לנו ב' חמשיות ויהיה כזאת הצורה נכפול הקצוות ב' על אם ס נתן ע"ח מי יתן לנו ב/ה [113ב] [צו1] [] שהוא [] בחילוק דנר [] ראובן עוד נכפול כ' [] יעלה בחילוק דנר אחד [] שמעון עוד נכפול ל' על ו' יעלו [] יעלו בחלוק ב' דנרי' ונ"ו חלקים מס"ב וזה [] והבחינה כך היא נחבר דנרי כולם יהיו ד' וב' שיצאו מהשברים יהיו ו' והוא הריוח כי השברים הם עשרה ונ"ח ונ"ו וכולם קכ"ד והם ב' כפלי המורה והם שנים וד' שהיו השלמים הם ו' והוא המבוקש ולדעת כמה פשיט' יהיה סך שברי כל אחד כפול שברי כל אחד על י"ב שהם פשיטי הדינר וחלק על המורה והיוציא הם פשיטי כל אחד והנשאר יהיה שברים מס"ב בפשוט כי לעולם ס"ב יהיה מורה לכולם כאשר תראה בזה המשל משל בעשרה שנשארן מראובן תכפלם על י"ב יעלו ק"ך חלקם על ס"ב יעלה בחילוק פשוט אחד ונשארו נ"ח תכפלם על ד' שהם חלוקת הפשוט יעלו רל"ב חלקם על ס"ב יעלו בחילוק ג' רביעיות ונשארו מ"ו חלקים מס"ב ברביע והנה חלק ראובן הוא דנר אחד ופשוט אחד וג' רביעיות ומ"ו חלקים מס"ב ברביע משל בשיור שמעון שהוא נ"ח תכפלם בי"ב יעלו תרצ"ו תחלקם על ס"ב יעלה בחילוק י"א פשיטי' ונשארו י"ד תכפלם בד' יעלו נ"ו והוא מחולק על ס"ב שהוא נ"ו חלקי רביע פשוט מס"ב ברביע והנה חלק שמעון הוא דנר אחד [] וי"א פשי' ונ"ו חלקי רביע אשר ס"ב הוא רביע פשוט משל בשיור לוי שהוא נ"ו חלקים תכפלם על י"ב יעלו תרע"ב תחלקם על ס"ב יעלו עשרה פשיטי' ונשארו נ"ב תכפלם בד' יעלו ר"ח תחלקם על ס"ב יעלה בחלוק ג' רביעיות ונשארו כ"ב חלקים מס"ב ברביע פשוט והנה חלק 114[א] לוי הוא [] כולם בצורה הנ[] יהיו קכ"ד חלקם על [] תחברם עם ו' שהיו לנו יהיו [] פשיט' שהיו לנו יהיו כ"ד שהם [] [] ויהיו ששה ושב הריוח שאלה שמנית ראובן שמעון לוי עשו חבר ראובן נתן בחברה ד' לטרי ממון בי"ט באדם [] משנה פשוטה שסמנה ב[] ושהה כשמעון וחציו ושלשית העולה ורביעית השלשית העולה ושמעון נתן בחברה כראובן וחציו ושלישית העולה ושהה כלוי ועוד י"ב וחצי העולה ועוד ג' ושלישית העולה ועוד ד' ורביעית העולה ועוד ד' ולוי נתן בחברה כראובן ושמעון ושלשית העולה ושהה י"ז ימים ועם זה הממון ושהיתם בחברה הרויחו ז' לטרין שאלתי כיצד יחלוקו תשובה הנה לטרי ממון הנעלמם תדעם עם לטרי ראובן הידועים וזמן שהות הנעלם תדעהו עם זמן שהות לוי הנודע כיצד הנה לטרי ראובן הידועים הם ד' ושהיתו קל"ו יום כיצד הנה שהות לוי הידועים הם ח' ושמע' ושמעון שהה כלוי ח' ועוד י"ב יהיו כ' וחצי העולה שהוא עשרה יהיו ל' ועוד ג' יהיו ל"ג ושלשית העולה שהוא י"א יהיו מ"ד ועוד ד' יהיו מ"ח ורביעית העולה שהוא י"ב יהיו ס' ועוד ד' יהיו ס"ד וזה ימי שהות שמעון ומזה נדע ימי שהות ראובן והנה ימי שהות ראובן הוא כשמעון שהם ס"ד וחציו שהוא ל"ב יהיו צ"ו ושלישית צ"ו הוא ל"ב יהיו קכ"ח ורביעית ל"ב הוא ח' כי ל"ב הוא ^ ויהיו קל"ו כנזכר והנה לטרי שמעון הם ח' בעבור ^ שלישית העולה [114ב] הערה ואם תהיה ממונם ממטבעות מתחלפות כמו שהאחד נתן לטרין והשני די' והשלישי דוקאדוש עשה אותם ממין אחד וכזה תעשה אותם די' ואם תהיה בממון פשיט' בין מכולם בין מקצתם תעשה הכל פשיט' ועשה שאלתך ואחר תחלק חלק כל אחד על י"ב לעשותם די' או על המטבע שתרצה [] הם ד' וחציו [] ס"ד ימים כנז' [] ראובן ושמעון ושלישית [] וכשמעון הם ח' וד' הם י"ב ושלישית [] כנז' וזמן שהיתו ידוע שהוא ח' ימים [] כי ממון ראובן הוא ד' לטרי' ושהיתו קל"ו ימים [] ח' וימי שהיתו ס"ב ולטרי לוי י"ו ושהיתו ח' ימים ויהיה כצורה הזאת ועתה תכפול ממון ראובן בימיו יעלו תקמ"ו לטרי' ימי' הנכפל הריוח לטרי דנר ראובן ד קל"ו תקמד ג ד שמעון ח ס"ד תקיב ז ג לוי יו ח' קכח ט"ו המורה דחאא תקמ"ד כפולי המין תכפלהו על הריוח יעלו ג' אלפים תת"ח תחלקם על המורה שהוא אלף קפ"ד יעלה בחילוק ג' לטרי לחלק ראובן כפול הנשאר שהוא רנ"ו על כ' שהוא סך הלטרא יעלו ה' אלפים ק"ך תחלקם על המורה יעלו בחילוק ד' דנרי' וזה החלק מלטרה דחג מדינר שאם תרצה כפלהו על י"ב שהם פשיט הדנר וחלק דחאא על המורה והיוצא הם פשיטי' כאשר עשתי עוד תכפול ממון שמעון שהוא תקי"ב על ז' יעלה ג' אלפים תקפ"ד חלקם על המורה יעלה בחילוק ג' לטרי' כפול הנשאר על כ' יעלה זה החלק 0דו מדנר עוד כפול ממון לוי שהוא קכ"ח על ז' יעלו דחאא תתצ"ו והם חלקי לטרא מאלף קפ"ד אשר אם תכפלהו על י"ב ותחלק[ה]ו על המורה יצא בחילוק ט"ו די' וק"ס חלקים מאלף וקפ"ד בלטרא בדנר והנה יצא לנו כי חלק ראובן ג' לטרי' וד' דנרי' וחלקי דנר וחלק 115[א] פג שמעון ג' [] והוא מה שרצינו [] הוא על דרך הערבה [] ואם אאריך בזה הפרק אקצר [] שאלה תשיעית זה השאלה היא [] אכתוב לך שתדע לקצר [] אם מספר הממון והזמן תוכל כל אחד לקצרו בחצי [] ברביעית או באי זה חלק שתוכל וזה שתקצר הזמן והממון בדרך אחד שאם תקצר רביעית ממון ראובן שקצר שתקצר ברביעית זמנו גם כן ותקצר ברביעית זמן וממון כל אחד כאשר תראה בזאת השאלה ^ והנשאר ^ובאחרים אחר הקיצור מממון וזמן כל אחד כפול זה על זה והיוציא יהיה כמו בע"ה ממון כל אחד ומקיבוץ כולם יצא המורה ואם לא תהיה כ תוכל לקצר הזמן תקצר הממון וזה מכל אחד בשוה כאשר תראה במשלים מאחר זה ואם תרצה לכפול הממון על הזמן ואחר תקצר הרשות בידך ואחר הקיצור תוציא המורה כמנהג ואומר כי ממון ראובן הוא ד' וזמנו קל"ו ^ וממון שמעון ח' וזמנו ס"ד וממון לוי י"ו ^ וכפל זמנו וממונו וזמנו ח' נקצרם בחצי יהיו לראובן ב' ס"ח ולשמעון הוא תקמ"ד ד' ל"ב וללוי ח' ד' נקצרם עוד בחצי יהיה זמן וממון ראובן א' ל"ד וזמן וממון שמעון ב' י"ו וזמן וממון לוי ד' ב' ולא נוכל עוד לקצר כי ממון ראובן שב לאחד וזה יהיה הנשאר אחר הקיצור מממונם ומזמנם אחר נכפול זמן כל אחד על חלקי דינ לטרי זמן ממון הנכפל ממונו כמנהג א' על ל"ד כה ד ג ראובן לד א לד הרוח יהיו ל"ד וזה ממון עד ראובן וב' על י"ו יהיו מ ג שמעון יו ב לב ז ל"ב וזה ממון שמעון עד וד' על ב' יהיו ח' וזה י טו 0 לוי ב ד ח עד המורה עד [115ב] [] אחד על הריוח [] חלק כל אחד כפול ל"ד [] יצא בחילוק ג' לטרין [] דינרי הלטרה יעלו ש"ב [] ד' דינר וכ"ד חלקי ע"ד בדינר והנה [] והחלק הנזכר מדינר יהיה חלק רבאובן [] כפול ל"ב על ז' וחלק היוציא על המורה ותצא בחילוק ג' לטרין ומ' חלקים מע"ד שהוא השלם וזה חלק שמעון עוד כפול ח' על ז' וחלק היוציא על המורה והוא מחולק שהוא נ"ו חלקים מע"ד בלטרה ותכפול נ"ו על כ' שהוא סך הלטרה יעלו אלף ק"ך תחלקם על המורה יעלו בחילוק ט"ו די' ועשרה חלקים מע"ד בדנר וזה חלק לוי והנה עלה בידנו שנפל לראובן מן הריוח ג' לטרין וד' דינר וחלקי די' שתוכל לקצרו שהם י"ב חלקים מל"ד וחלק שמעון ג' לטרי' וחלקי דנר שתוכל לקצרו ויהיה כ' חלקים מל"ד וחלק לוי ט"ו דינרי וחלקי דינר אשר מקוצר יהיה ה' חלקים מל"ד בדינ' וכן כל כיוציא בזה והבחינה כך הוא שתחבר כל שברי שלושתם והיוצה תחבר עם הדנרי' והדינרים עם הלטרי והיוציא יהיה הריוח כיצד תחבר שברהם יהיו לראובן כ"ד ולשמען מ' ולוי עשרה חלקם על המורה יצא אחד ועם הדנרים שהם י"ט יהיו כ' שהוא לטרה וששה לראובן ושמעון יהיו ז' שהוא הריוח והוא המבוקש וכן היו שברי השאלה השמנית שהם שפ"ד לראובן תר"מ לשמעון וק"ס ללוי יהיו כולם אלף קפ"ד חלקם על המורה שהוא אלף קפ"ד יעלה אחד והוא דנר חברהו על הדינר שהם י"ט יהיו כ' והוא הלטרה תחבר אותה עם הלטראות יהיו ז' שהוא הריוח 116[א] [צח1] עוד אתן דרכים דרך אחרת לקצר עוד ועיין בזה הדרך ותשכיל ואומר שתקצר הנכפל כל מה שתוכל שוה לכולם והנשאר תחלק בריוח הבא מד' קל"ו המשל בשאלה החמשית ^ הנה ממון ראובן המשולח הוא תקמ"ד וממון ^ תשיעית שמעון תקי"ב וממון לוי קכ"ח תקצרם בחציים חמשה פעמים יהיו ישארו יז לראובן י"ז ולשמעון י"ו ולוי ד' ולא נוכל עוד לקצר בעבור ממון יו ז ראובן שהוא י"ז והנה שוה השאלה בצורה ה[] ואתן לזה ד פרק [] ול[] [] כל זה כתוב הפרק [] שאלה ראשונה מ[] חציו ויהיה שלשה [] זאת השאלה תוכל לעשותה עם מונח [] דרך השלושה ונניח ד' וחיברנו עליו חציו [] שאלנו שלושה רביעיות נלך אל דרך השלושה ונאמר אם [ד' נתנו] לנו ו' מי יתן לנו ג' רביעיות נסדרם בזאת הצורה נכפול הקצוות שהם ג' רביעיות אם ד ו 0 ג על ד' יעלו י"ב רביעיות ד נחלקם על ו' שהם כ"ד רביעיות יעלה בחילוק חצי וזה המספר המבוקש שאם תוסף עליו חציו יהיה ג' רביעיות שאלה שנית מה הוא המספר אשר חברנו עליו חצי שלישיתו ושלישית רביעיתו ורביעית חמשיתו ועם הכל יהיה ב' חמשיות תשובה עם מונח כוזיב ודרך השלשה נניח ס' בעבור שימצאו בו כל החלקים בשלמות חצי שלישיתו הוא עשרה כי שלישיתו כ' וחציו עשרה נחברם עם ס' יהיו ע' ועוד נקח שלישית רביעיתו והוא חמשה כי רביעיתו הוא ט"ו ושלישית ט"ו הוא ה' נחבר ה' עם ע' יהיו ע"ה ועוד נקח רביעית חמשיתו והוא ג' כי חמשתו הוא י"ב ורביעית י"ב הוא ג' נחברם עם ע"ה יהיו ע"ח והנה עלה יותר ממה ששאלנו כי ב' חמשיות שאלנו ונתן המונח ע"ח שלמים נלך אל דרך השלושה והוא יגיד לנו שאלתנו ונסדר דרך השלושה ונאמר אם ס' נתן לנו ע"ח מי יתן לנו ב' חמשיות ויהיה כזאת הצורה נכפל הקצוות ב' על [116ב] [] ק"ך והם [] נחלקם על ע"ח [] שנכפול ע"ח ב[] [] על ש"ץ והוא מחולק שהוא ק"ך [] המספר המבוקש שאם חיברנו עליו [] שלישית רביעיתו שהוא שהוא עשרה [] שהוא ששה יעלו קנ"ו והם חלקים מש"ץ [] שתי חמשיות ממנו אם תקצרם ^ וזה מה שרצינו שאלה שלישית ראובן ושמעון עשו חברה יחד ראובן נתן בחברה חצי לטרה ושמעון נתן שלישית לטרה והרויחו רביעית לטרה שאלתי כיצד יחלוקו תשובה תשוה ממונם וקח חלקהם ואחר כפול סך הלטר על הרביעית והיוצא הם דנרי הריוח אשר תחלוק המשל בזה תשוה ממונם יהיה החצי ג' לראובן והשליש ב' לשמעון כי המורה הוא ששה אחר כן כפול סך הלטרה שהוא כ' על א' שהוא הריוח חלקם על מורה הרביע שהוא ד' יעלה בחילוק ה' די' והם הריוח שהם רביעית הלטרה תחבר ממונם יהיו ה' והוא המורה לחלק עליו ויהיה הכל ממון ריוח הראוי כזאת הצורה תכפול ג' על ה' שהוא ראובן ג ג הריוח יעלה ט"ו תחלקם על ה' יעלו שמעו ב ה ב ג' והם דנרי' וזה חלק ראובן גם המורה ה כפלנו ממון שמעון על ה' יעלו עשרה תחלקם על המורה יעלו ב' דנרי' והוא ריוח שמעון והבחינה ברורה והנה חלק ראובן ג' וחלק שמעון ב' והוא המבוקש או דרך אחרת ועיין בה תוציא מורה כללי לחצי ושלישית ורביעית והוא כ"ד או י"ב אם תרצה והנה ^תשוים יהיו כזה הצורה שוים 780 780 156 × 2 390 5 ואם תקצרם בחצי ועוד בשלישו ונשאר כ"ו חלקים מס"ה כזה תשוים עם ב' חמשיות יהיו כל אחד [] 130 130 26 × [] 65 [] 117[א] צ"ט[1] קח חציו [] ממונם ריוח ראובן יב ג [ג] ו ה שמעון ח ב ב [] ה [] המורה כד החמשיות אחד וה' שהיו לנו הם ו' חלקים מ[] כ"ד וששה רביעית כ"ד כנזכר שאלה רביעית ראובן ושמעון משו עשו חברה וראובן נתן ב' שלישיות מד' חומשי ליטרה [כזה] ראובן ב – ד לטרה א – א שנה ושהה חמשית רביעית שנה ושמעון ג – ה ה – ד נתן חמשית מב' שלשיות לטרה כזה שמעון א – ב לטרה א – ב שנה ושהה רביעית מב' חמשיות שנה ה – ג ד – ה והרויחו ג' חמשיות מב' שלשיות פרח שהיה ג ב פרח שאלתי דנרי ריוח כל אחד וימי שהות כל ה ג אחד וכיצד יחולקו הריוח תשובה תשוה ממונם וזמנם והיו חלקהם ואחר תכפול הממון על הזמן בשלמים והיוציא יהיה ממון לכל אחד כאשר עשינו בשלמים ואחר תשוה הריוח וקח חלקו כי הכל שוה ואחר כפול סך הפרח על הריוח וחלק על מורה הריוח והיוציא הם דנרי' המשל בזה הנה שלישית וחמשית ורביעית ימצא בס' והם הראוים והוא יהיה מורה לממון ולזמן ועתה קח ד' חמשי ס' יהיו מ"ד קח ממ"ד ב' שלישיותיו יהיו ל"ב והוא ממון ראובן עוד קח רביעית ס' יהיו ט"ו קח חמשית ט"ו והוא ג' וזה זמן ראובן כפול ג' על ל"ב שהם ממון וזמן ראובן יהיו צ"ו וזהו הנקרא ממון ראובן אחר קח ב' שלישיות מס' יהיו מ' קח חמשית מ' שהוא ח' וזה ממון שמעון עוד קח ב' חמשיות [117ב] [] זמן שמעון [] שמעון ואם כן יהיה [] ישובו לראובן ב' [] סך הפרח שהוא עשרה די על [] ב' חמשים מב' שלשיות הפרח שמורה [] ט"ו יעלה ס' חלקהו על ט"ו שהוא מורה הריוח [] דנרי חביר ממונם ויהיו ג' שהם המורה לחלק עליו ויהיה [] כזאת הצורה כפול ב' על ד' יהיו ח' חלקם על ג' יציא ממון מקצר ריוח ב' די' וב' שלישיות דנר ראובן צ"ו ב שהם ח' פשי' וזה חלק ד ראובן עוד כפול שמעון מח א א' בד' יהיו ד' חלק על המורה ג ג' יציא דנר אחד ושלשית שהוא ד' פשיטי' וזה חלק שמעון והבחינה הוא שתחבר הפשיטי' שהם ד' וח' יהיו דנר אחד וג' דנרים שיצאו בחלוקה יהיו ד' די' והם כל הריוח והוא המבוקש ואם תרצה לעשות כל השאלות שיש בהם שברי שברים כזאת השאלה בלי טורח כלל כפול שברי הממון והזמן יחד והיוציא יהיה הממון המשותף ואחר תקצר אם תוכל גם שברי הריוח כיצד בשאלה הנזכרת כפול שברי ממון ראובן על שברי זמנו יעלה ח' כי ב' על ד' יעלה ח' וח' על א' הם ח' וח' על הא' השנית הם ח' וזה ממון ראובן וכן כפול א' מממון שמעון על ב' יהיו ב' וב' על א' מזמנו יהיו ב' וב' על ב' יהיו ד' וזה ממון שמעון תקצרם יהיו לראובן ב' ולשמעון א' כנזכר ואחר שידענו שאלתנו נכונה ושאלו לנו כמה דינרים הוא ב' שלשיות מד' 118[א] ק[1] חמשיות [] חמשיות מב' שלישי[] ולכל זמן התשובה [] או סך הפרח על השברים וחלק על המורה ואם [] כופלם זה בזה וגם מורהם ועל העולה [] על העולה מהמורים כאשר תראה בזאת השאלה [] בממון ראובן יכפול שבריו זה בזה יעלו ח' וכן יהיה אם תקח ב' שלישיות מד' חמשיות וגם כפול מורהם יהיה ט"ו ויהיה ממון ראובן ח' חלקים מט"ו בלטרה ולדעת כמה דנרים הם תכפול סך הלטרה שהוא כ' על ח' יעלו ק"ס תחלקם על ט"ו שהוא מורה אלו השברים יציא עשרה דנרי' וב' שלישיות דנר שהם ח' פשיט' וזה ממון ראובן ולדעת כמה ימים שהה ראובן כפול שבריו א' על א' יהיו א' והמורה כ' ויהיה זמנו חלק מכ' בשנה תכפול סך השנה שהוא שס"ה על א' יעלו שס"ה ולא נקפיד לרביעית יום בעבור שלא להטריח כאן לעשותם רביעיים או שעות תחלק שס"ה על כ' נוציא בחילוק י"ח ימים וה' חלקים מכ' ביום אשר אם תקצרם יהיו רביעית יום שהוא שש שעות וי"ח ימים ושש שעות זמן ראובן וכן תעשה בממון שמעון וזמנו ותמצאם ב' דינר' וח' פשיטין וזמנו תמצא ל"ו ימים וחצי ואם תרצה לכפול זמן ראובן על ממונו תן הדינרים בפשיטי' ויהיה קכ"ח והימים בשעות ויהיו תל"ח תכפול זה בזה יהיו נ"ו אלפים וס"ד וגם שעות שמעון הם תת"ע וממונו ל"ב פש' תכפול זה בזה יהיו כ"ז אלפים תת"מ ואם תרצה לקצרם הרשות בידך ואם תעיין בזאת השאלה תמצא בה תועלת גדול הפרק הרביעי בשאלות חיבור מורכבים שאלה ראשונה מהו המספר [118ב] [] אחד עשר תשובה [] ונוסיף על ששה י"ב שהם [] הם ד' ויהיו כ"ב ואנחנו [] שלשה ונאמר אם ו' נתן לנו כ"ב מי יתן לנו י"א ויהיה [ו כב 0] יא כזאת הצורה נכפול הקצוות יהיו ס"ו נחלקם על כ"ד יעלו [] והוא המבוקש והבחינה הוא כי הג' וב' פעמים כמוהו וב' שלישיות ממנו יהיו י"א כנשאל שאלה שנית מהו המומן הנעלם אשר חציו ושלישיתו ורביעיתו פחות חמשה יהיו כ"ד והוא כאילו אמר עם אילו החלקים הם כ"ד אבל הוא פחות חמשה ממה שרצינו ואם כן יהיה כ"ט התשובה נניח י"ב והנה חציו ושלישיתו ורביעיתו יהיו י"ג ונאמר אם י"ב נתן י"ג מי יתן כ"ט ויהיה אם יב יג 0 כט כזאת הצורה נכפול הקצוות יעלו שמ"ח וזהו הממון אשר חציו שהוא קע"ד ושלישיתו שהוא קי"ו ורביעיתו שהוא פ"ז הוא ^יהיו כולם שע"ז [] ^ והבחינה ^ חלק שמ"ח על י"ג יעלו כ"ט והוא המבוקש חלקם על י"ג שאלה שלישית מהו המספר הנעלם אשר יעלו כ"ט אשר אם תחבר עליו חצי רביעיתו ושלושת אם נגרע מהם רביעיתו ורביעית רביעיתו ולא יהיה אלא שנים ה' ישארו כ"ד התשובה נניח מ"ח והנה חצי רביעיתו הוא ששה כנשאל ושלשית רביעיתו הוא שבעה ורביעית רביעיתו הוא שלשה נחבר אלו החלקים עם המונח יהיו כולם ס"א ואנחנו לא שאלנו אלא שנים הנה נאמר אם מ"ח נתן ס"א מי יתן לנו ב' ויהיה כזה הצורה נכפול הנשאל שהוא ב' על המונח שהוא מ"ח והעולה אם מ"ח ס"א 0 ב שהוא צ"ו נחלק על ס"א יעלו א' ל"ה חלק מס"א וזהו המספר הנשאל והבחינה תן השלם [] במורה שלו שהוא ס"א ועם ל"ה יהיו צ"ו תחבר לו חצי רביעיתו שהוא י"ב ושלישית רביעיתו שהוא י"ו ורביעית רביעיתו שהוא [] ששה יעלו קכ"ב חלקים מס"א תחלקם לס"א יעלו שנים כנשאל 119[א] [קא1] ^ [] ועשרה חלקי י"ג נשיבם לחלקי י"ג
[קא2] השער [השני בשאלות כפל חילקתיו לפרקים הפרק הראשון בשאלות כפל [שלימים] הפרק השני בשאלות כפל [שברים] הפרק השלשי בשאלות כפל מורכבים הפרק הראשון בשאלות כפל שלימים וראשונה אכתוב [] אחת ואחרת בלי חומר להרגילך שאלה ראשונה אם ד' שוה ג' ה' מה יהיה שוה כזאת הצורה תשובה כפול אם ד ג ה 0 האמצעיות שהם ג' וה' יעלו ט"ו חלקם על ד' יציא בחילוק ג' וג' רביעיות והוא המבוקש והבחינה תשיב השלמים רביעיות יהיו י"ב ועם ג' יהיו ט"ו גם בן זוגו תנהו ברביעיות יהיו כ' והנה ט"ו אל כ' כד' אל ג' כי ג' אצל ד' כמוהו ושלישית וכן ט"ו אצל כ' כמוהו ושלשית או דרך אחרת ועיין תן ג' על ד' יהיו ג' רביעיות וכן תן ט"ו על כ' ותקצרם ויהיו גם כן ג' רביעיות או בדרך אחרת תשוים ג' על ד' וט"ו על כ' יהיו כל אחד ס' כזה 60/(14/20)×60/(ג/ד) שאלה שנית ממון מממון אם ה' פרחים שוה מ' מלכים ל"ט פרחים כמה יהיה שוה כזאת פרחים מלכים פרחי' הצורה תשובה אם ה מ לט 0 כפול האמצעיים מ' על ל"ט יעלו אלף תק"ס תחלקם על ה' יעלה בחילוק שי"ב והוא [119ב] [] אל [] כמ' ח' פעמים [] פעמים אחרת להרגלך [] ותקצרים בחמשית ויהיה [שאלה שלישית] מזמן הנה אומן אחד נשכר עם בעל הבית לעשות מלכתו ונתן לו בד' חדשים ג' פרחים שאלתי אם ישב עמו ט' חדשים כמה יתן לו חדשי' פרחי' חדשי' כמה פרחי ויהיה כזאת הצורה תשובה אם ד ג ט 0 אמור אם ד' חדשים נתן לנו ג' פרחים ט' חדשים כמה פרחים יתן לנו כפול האמצעיות יהיו כ"ז חלקם על ד' יעלה בחילוק ו' פרחים וג' רביעיות פרח וכבר ידעת לעשות מהם דנרים וששה פרחי וג' רביעיות פרח הוא הנעלם המבוקש והבחינה תן הבנים על האבות בעבור שהם קטנים יהיו הראשון ג' רביעיות וכן השניים אחר הקיצור כי כ"ז חלקים מל"ו הם ג' רביעיות אחר הקיצור שאלה רביעית ממשקל אם לטרה מלבונה שוה ז' די' י"ט לטרין כמה די' יהיו שוים ויהיה כזאת הזאת התשובה [] כפול האמצעיות לטרה דנרי לטרין כמה דינר יעלו קל"ג חלקם על א' אם א ז יט 0 והוא העולה ואם כן אם א' נתן ז' י"ט יתן קל"ג והבחינה תן האב על הבן ויהיה שביעית אחר שתקצר השניים או תהפוך השאלה ואמור אם קל"ג נתן י"ט ז' מה יתן כפול האמצעיות שאלה חמשית ממדה אם ערך ד' אמות מבגד הוא י"ז יעלו קל"ג תחלק על קל"ג ות[] א 120[א] [קב1] י"ז [] אם ד יז יג [0] ורבעית דנר שהוא ג' פשי' והוא [] ד' חלקים מי"ז בשליש אחר שתקצר [] 884 884 יהיו דינ' נ"ב והנה ^ [] יהיו רכ"ז [] ד × בה שאלה חמשית מהו המספר אשר כפלנו אותו על ל"ז והיוציא דא אבב מן הכפל יהיה מ"ט הנה כל השאלות האלו הדומות כזה הצורה לזה תמצא דרכים רבים ואתן בכאן ג' בג' משלים ובשברים ובמורכבים ויהיו שוים משל לכל אחד מזה המין אשר הדרך הראשון הוא כאחד מן הדרכים אחר ההשואה הידועים והשני שתתן מה ששאלת על הכופל והשלישי הוא שתחלק הנשאל על הכופל והתשובה לשאלתנו בדרך הראשון ונעשה אותה בדרך השלשה נניח מספר מה והוא ב' כפלנו אותו על ל"ט יעלו ע"ח ואנחנו שאלנו מ"ט ונאמר אם ב' נתן לנו ע"ח מה יתן לנו מ"ט ויהיה כזאת הצורה במשל ה מדרך השלשה נכפול החיצוניות ב' על מ"ט יהיו אם ב עח 0 מט צ"ח תחלקם על ע"ח ויעלה בחילוק אחד וכ' חלקים מע"ח הנה המספר אשר אם תכפול אותו על ל"ט היוציא יהיה מ"ט והבחינה היא שתכפול ל"ט על א' וכ' חלקים מע"ח וראשונה תן האחד במורה שברו שהוא ע"ח ותחבר על העולה כ' חלקים מע"ח יהיו 0ב צ"ח חלקים מע"ח ועתה כפול ל"ט על צ"ח יעלו ג' אלפים תתכ"ב חלקים 78 מע"ח תחלקם על ע"ח שהוא המורה ותציא בחילוק מ"ט כנשאל וגם תוכל לקצר הכ' חלקים ויהיו י' חלקים מל"ט ותן השלם במורה יהיו ל"ט וי' יהיו מ"ט כפול ל"ט על מ"ט שברים מל"ט בשלם יהיו אלף תתקי"א תחלקם על ל"ט ותציא מ"ט כנשאל [120ב] [] יהיה [] זאת השאלה אעשה [] שתתן מה ששאלת על הכופל [] אותו על הכופל [] יהיו ט"ו שביעיות כזה הא/ז חלקם [] ותציא ב' ושביעית וזהו המספר הנעלם [הבחינה] היא שתכפול ב' ושביעית על ז' וראשונה תתן השלמים במורה השבר יהיו י"ד וא' שהיה לנו [] ט"ו שביעיות כפול ט"ו שביעיות על ז' יעלה ק"ה שביעיות חלקם על ז' יעלה בחילוק ט"ו שלמים כנשאל שאלה שביעית מהו המספר שאם כפלנו אותו על ט' והיוציא יהיה אחד תשובה זאת השאלה אעשה עם הדרך השלישי והוא שתחלק הנשאל על הכופל והיוצא הוא הראוי לכפול על הכופל המשל בזה חלקנו א' על ט' ותצא תשיעית וזהו המספר הנעלם והבחינה הוא שתכפול תשיעית על ט' ויעלה ט' תשיעיות תחלקם על ט' ותציא אחד שאלה שמינית מהוא המספר אשר כפלנו אותו על ג' והיוציא על ז' והיוציא על י"ג ושלא יעלה אלא ג' התשובה נניח אחד ונכפליהו על ג' והיוציא על ז' והיוציא על י"ג ויעלה רע"ג ואנחנו שאלנו ג' נאמר בדרך השלושה אם א' נתן רע"ג מי יתן לנו ג' ויהיה כצורה ה[] הזאת אם א רעג 0 ג ועשה כמו שקדם 121[א] [קג1] שאלה [תשיעית] כמספר המשכת הצורה [] מגדלים ובשני ה' ובשלישי ח' [] י"ח כמו שתראה בצורה ראשונה [] צורת א צורת ב צורת ג [] [] מספר מגדלי כל מבצר שומרים שומרי כל מבצר פרחים [] ב' מגדלי' ב מבצר ראשון ג ו ז בד ה' מגדלי' ה מבצר שני ו 0ג ו 0חא ח' מגדלי' ח מבצר שני ט בז ה 0וג י"א מגדלי' אא מבצר רביעי בא בגא ד חבה י"ד מגדלי' דא מבצר חמשי הא 0אב ג 0גו י"ז מגדלי' זא מבצר ששי חא ו0ג ב באו ________________________________________________________ כפי המשכת הצורה השנית והנה שומרי כל מגדל בפרט כמו שתראה בצורה שלישית ושבר כל שומר בכל חדש הם הפרחים שתראה בצורה הרביעית שאלתי מספר כל המגדלים מן הששה מבצרים בכלל וכל השמרים בכלל ובפרט והפרחים בכלל ובפרט הראויים לחדש אחד וגם הראוים לכל שנה בסך י"ד דנרי כל פרח וכולם כמה פרחי דנרים הם התשובה ידוע הוא כי המבצרים הם ששה וגם מגדלי כל מבצר הם לעיין אבל ידעת כולם בכלל כפי הדרך הראשון שנתתי למספרים הנמשכים בסדר שהוא שתחבר הראשון והאחרון יהיו י"ט תכפלם על חצי המקומות שהם ג' יעלו נ"ז והם כל המגדלים ועתה לדעת שומרי כל מבצר הנה שומרי מגדלי המבצר הראשון הם ג' לכל מגדל כמו שתראה בצורה שנית כפול ג' [121ב] [] [] מגדלי המבצר [] יעלו ל' כמו שתראה [] המבצר השלישי שהם ט' על ח' [] ככפל י"ב על י"א והחמשי ר"י [] והששי הם ש"ו שומרים ככפל י"ח על [] בצורת ג' ובכלל הם תשנ"ו ועתה לדעת [] כל אחד וכל הפרחים בכלל אומר כי שומרי מגדלי מבצר [רא]שון הם ששה כמו שיורה הצורה השלשית ולכל אחד ז' פרחים כמו שיורה צורה רביעית תכפול הפרחים בשומרים ז' על ו' יעלו מ"ב והם ראשונים בצורת ה' גם תכפול ל' שומרים מהמבצר השני על פרחי כל אחד שהם ו' יעלו קף פרחים לשומרי המבצר השני עוד תכפול ע"ג שומרי המבצר השלשי על פרחי כל אחד שהם ק' יעלו ש"ס פרחים לשומרי המבצר השלשי גם תכפול קל"ב שומרי המבצר הרביעי על ד' פרחים לכל אחד יעלו תקכ"ח פרחים לשומרי המבצר הרביעי עוד תכפול ר"י שומרי המבצר החמשי על ג' שהם פרחי כל אחד יעלו תר"ל פרחים לשומרי החמשי עוד תכפול ש"ו שומרי המבצר הששי על ב' שהם פרחי כל אחד יעלו תרי"ב פרחים לשומרי המבצר הששי וכולם תרצה בצורת ה' בפרט תחברם כולם יהיו ב' אלפים שנ"ב פרחים והם לכל חדש תכפלם על י"ב יהיו כ"ח אלפים רכ"ד פרחים לשנה ואם תרצה לעשותם דנרי' תכפלם על י"ד יעלו שצ"ה אלפים קל"ו כל זה הדינרים לשומרים לכל שנה וזה מה שרציתי והנה עלה מזה כי השומרים דרך פרט תראם בצורת ג' ובכלל הם תשנ"ו והפרחים דרך פרט תראם בצורת ה' ובכלל הם ב' אלפים שנ"ב לכל חדש תכפלם על י"ב יעלו כ"ח אלפים רכ"ד הראוי לכל שנה כופלם על י"ד היוציא דינרי' והם שצ"ה אלפים קל"ו כל זה כנזכר 122[א] קד[1] [שאלה עשירית] [] [] ובכל בד נ"א תפוחים [] דנרים יעשו כל הפשיט' [] תשובה כפלנו ל"ד [] ב' אלפים תרמ"ח ואם [] יהיה העולה קכ"ד אלפים תתמ"ח והם התפוחים [] פשיטי' יעלו רמ"ח אלפים תרצ"ו והם הפשוטים תחלקם על [] כ' אלף תת"ח והם דנרי ואם תחלקם עוד על כ' יהיו ליטירין ואם על י"ד יהיו פרחים וכן כל הדמה לזה כפי סך הפרח שהוא או שיהיה שאלה יא האומר יש לי גן אחד אשר בו ע"ז חורבות בכל חורבה י"א מערות בכל מערה ח' קני תרנ[גול] ובכל קן י"ז בצים אשר מכל ביצה תצא תרנגולת אחד וכל תרנגול היה שוה ג' די' שאלתי כמה יהיה כל דבר בפרט והרי בכלל תשובה תכפל זה על זה והיוציא על השני והיוציא על השלישי וכן כל מה שיעלו באלה השאלות והמשל נכפל ע"ז על י"א מערות היוציא יהיה תתמ"ז מערות גם כפלנו המערות על ח' קינין יעלו ששה אלף תשע"ו קינין גם כפלנו הקינין על י"ז שהם הבצים או התרנגולים יעלו קט"ו אלפים וקצ"ב והם תרנגולים גם כפלנו התרנגולים על ג' דני' שהם שיווי כל תרנגולת יעלו שמ"ה אלפים תקע"ו דנרי' וכן כל הדומה לזה וכן האומר קניתי תרנגולת בסך מ' פשיטי' ומכרנו הבצים מ' בפשוט ולא ילדה אלא בצה אחד במ' ימים שאלתי בכמה ימים ירויח מ' פשיטי' שהוא סך התרנגולת התשובה תכפול מ' על מ' יעלו אלף ות"ר והנה באלף ות"ר ימים ירויח סך התרנגולת ומכאן ואילך מה שיוליד ירויח וכן רבים לאין מספר שאלה [122ב] [שאלה יב] [] [] [] ובכל מגרש [] נותן ח' [] נותן מס למלך כ' פשיט' [] שאלתי מספר המגרשים ומספר האנשים [] ומספר המשאות ומספר ה[] ומספר ה[] וה[] ומספר [] אם תרצה לעשותם מטבע אחד [] אחר שעשית אותם די' התשובה הנה ראשונה נכפול ה[] על המדינות והם שלושים עוד נכפול שלושים מדינות על מ' כפרים יהיו אלף ומאתים כזה 00בא והוא מספר הכפרים עוד נכפול מספר הכפרים על נ' אנשי כל כפר יעלו ס' אלפים כזה 0000ו והם מספר האנשים עוד נכפול מספר האנשים על ד' כרמים אשר לכל אחד יעלו הכרמים מאתים וארבעים אלף כזה 0000דב עוד נכפול הכרמים על ח' משאות אשר בכל כרם יעלו המשאות מספר אחד ותתק"ך אלפים כזה 00000בטא עוד נכפול המשאות על כ' פשיטי המס ויעלו ג' מספרים תת"מ 000000דחג כזה והם פשיטי המס ועתה רצינו לעשות מפשיטי המס די' נחלקם על י"ב יעלו ש"ך אלפים כזה 0000בג והם די' המס ועתה אם נרצה לעשות מהם קאשטיללנו' נחלקים על כ"ח ואם פרחים על י"ו כי עתה הם מ[] למטבע שנרצה מזהב וכאשר היו פשי' נוכל לעשות מהם המטבע שנרצה מכסף ועתה נעשה מהם 123[א] קה[1] לטרין וזה [] 000וח כזה וזה [] ומתחלפים [] הפרק השני בשאלות כפל שברים שאלתי אם ב' שלישיות שוה ג' חמשיו[ת] שאלתי רביעית מה יהיה שוה אם ב/ג ג/ה א/ד כזאת הצורה תשובה כפול החמציות שבר על שבר ומורה על מורה יהיו ג' חלקים מעשרים כזה ג/כ תחלקם על ב' שלשיות וראשונה תשוים יהיו כזה הג' חלקים מכ' יהיו [] ג' חלקים מכ' [] [] מחולק אדד 0ב [] והוא ג/ב0 × א/זדא [] והנה אם חצי ב' [] מאמה מבגד שוה ג' שביעיות מחצי שני [] פרח חצי שלישית מב' שביעיות אמה מבגד שוה כ' חלקים מקמ"ח בפרח ואם תרצה לדעת כמה זרתות יהיה הבגד כפול סך זרתות האמה שהם ד' על חלקי השבר והעולה תחלק על המורה וכן תעשה בכל שברי אי מין שיהיה כאשר אמרתי והבחינה כך היא שתתן כל שברי השבר בשבר אחד בפני עצמו ותקצרם אם תוכל ואחר תשוה כל אב עם בנו ואחר השיוי תן כל בן על אביו ואם יהיו שברים רבים ולא תוכל להכיר הערך חלק האב על הבן והיוציא בחלוקה יהיה שוה לשניהם המשל בזה תשוה שברי כל אחד בפני עצמו יהיה הראשון אחר הקצור ג' חלקים מכ' ג/ב0 כזה והשנית שביעית כזה א/ז והשלישית חלק מכ"א ג/אב כזה והרביעי שהוא הנעלם כ' חלקים ב0/אאד מתמ"א כזה ב0/אדד ויהיו כולם כזאת הצורה תשוים שנים שנים יהיו ל"ג חלקים אב 0ב אדד 0בד מכ' שהוא הראשון כ"א ולחלק השני ג/ב0 × א/ז א/אב × ב0/אדד כ' חלקים ולחלק השלישי תמ"א חלקים ולחלק השלישי ת"ך חלקים ולחלק הרביעי הנעלם ת"ך והנה ערך כ"א אל כ' כערך תמ"א אל ת"ך שאם תחלק כ"א אל כ' יצא 126[א] קח[1] א' וחלק [] אחר הקיצור [] ואב על אב יעלה מכל [] כי אני מספר מהו המספר אשר יהיו ב' שבי[] שמיניות השני כזאת הצורה [וא דא] יהיו י"ו שביעיות כ"א שמיניות והנה שני ב/ז × ג/ח שביעיות כ"א הם ששה וג' שמיניות י"ו הם ששה גם כן והוא המבוקש אחרת מהו המספר אשר ו' חלקים מי"א יהיו נ"ה שמניות השני כזה הצורה חד הה והנה ששה חלקים מי"א הם שלושים ו/אא × ה/ח כי כשנחלק נ"ה אל י"א יעלה בחילוק ה' וששה פעמים ה' הם ל' וגם ה' שמיניות י"א הם ל' כי חלקנו מ"ח על ח' יעלה בחילוק ו' וה' פעמים ו' הם ל' כשני וכן לכל שני מספרים איך שיהיו כי לכולם דרך אחד אחרת רצינו ג' מספרים אשר ב' חמשיות הראשון יהיו א וה דה כ"ג שביעיות השני וג' שביעיות השני כ"ד תשיעיות השלישי ב/ה ג/ז ד/ט התשובה כפול ה' שהוא מורה הראשון על שברי השנים שהם ג' וד' ועלו ס' על ב' חמשיות גם כפול ז' שהוא המורה השני על שברי האחרים שהם ב' וד' יעלו נ"ו על ג' שביעיות גם כפול ט' שהוא מורה השלישי על שברי האחרים שהם ב' וג' יעלו נ"ד על ד' תשיעיות ועתה ב' חמשיות ס' הוא כ"ד והוא כ"ג שביעיות נ"ו שהוא כ"ד וכן ד' תשיעיות נ"ד הוא כ"ד ואם כן ב' חמשיות הראשון הוא ג' שביעיות השני וג' שביעיות השני הוא ד' תשיעיות השלישי ומש"ל [126ב] בז חטא [] ג ב ד [] ז ג ט [] חד חד חד חד [] וג' שביעיות השני יהיה כ"ב [] וב' שלישיות השלישי יהיה כ"ד תשיעיות רביעי או נוכל לאמר כי ב' חמשיות הראשון כג' שביעיות בג' שביעיות השני וכב' שלישיות השלישי וכד' תשיעיות הרביעי וכן לכל אחד שתקח השבר שתרצה והמשל בזה הצורה הנה נכפול כל מורה על שברי כולם חוץ משבריו ואחר קח מה שיורה כל אחד כמו [] שנקח ה' שהוא מורה הראשון נוכפלהו על שברי האחרים שהם ג'ב'ד' יהיו כ"ד נכפול כ"ד על המורה שהוא ה' יהיו ק"ך ותתנם על ב' חמשיות ואחר נקח ז' שהוא [] מורה ג' שביעיות ונכפלם על בב"ד שהם שברי האחרים יעלו קי"ב תתנם על ג' שביעיות ואחר נכפול ג' על בג"ד יעלו ע"ב נתנם על ב' שלשיות ואחר נכפול ט' על בג"ב יעלו ק"ח נתנם על ד' תשיעיות ועתה נראה כי ב' חמשיות ק"ך הם מ"ח וג' שבעיות קי"ב הם מ"ח וב' שלשיות ע"ב הם מ"ח וד' תשיעיות ק"ח הם מ"ח וכל תנהיג לכל השברים שתרצה שאלות ממינים אחרים אם נרצה חלק או חלקים מאיזה מטבע שנרצה נכפול סך המטבע על השבר ונחלק על המורה והוא המבוקש והמשל רצינו ב' שלשיות לטרה כזה ב/ג נכפול סך הלטרה שהוא כ' על השבר שהוא ב' יעלו מ' נחלק מ' על המורה שהוא ג' יעלה בחילוק 127[א]
[קכ1] [השער השלישי בשאלות גרעון] חלקתיו לשלשה פרקים [הפרק הראשון בשאלות] גרעון שלמים [הפרק השני] בשאלות גרעון שברים הפרק השלישי בשאלות גרעון מורכבים הפרק הראשון בשאלות גרעון שלמים שאלה מהו המספר אשר גרענו ממנו שלישיתו ורביעית הנשאר ושישית הנשאר וחמשית הנשאר וחצי הנשאר ושנשאר ג' תשובה עם מונח כוזב ודרך השלושה נניח ס' בעבור שנמצא בו כל אלו החלקים בלי שבר והנה גרענו מס' שלישיתו ישארו מ' גרענו רביעית מ' ישארו ל' עוד גרענו ששית ל' שהוא ה' נשארו כ"ה עוד גרענו חמשית כ"ה נשארו כ' עוד גרענו חצי כ' נשארו עשרה ואנחנו לא שאלנו אלא ג' נלך אל דרך השלושה ונאמר אם ס' נתן לנו עשרה מי יתן לנו ג' ויהיה כזאת הצורה אם 0ו 0א 0 ג נכפל הקצוות ג' על ס' יעלו ק"ף נחלקם על עשרה ותציא בחילוק י"ח והוא המספר הנעלם אשר אם תגרע ממנו שלישיתו ורביעית הנשאר וששית הנשאר וחמשית הנשאר וחצי הנשא[ר] וישאר אחר כל אלו הגרעונות ג' וכן כל הדומה לזה והבחינה היא שתגרע מי"ח שהוא המספר הנשאל הנעלם שלישיתו וישארו י"ב נגרע רביעית י"ב נשארו ט' נגרע ששית 138[א] [קכו1] [השער הרביעי בשאלו]ת חילוק חלקתיו [לשלשה פרקים] [הפרק הראשון] בשאלות חילוק שלמים הפרק השני בשאלות חילוק שברים הפרק השלישי בשאלות חילוק מורכבים הפרק הראשון בשאלות חילוק שלמים שאלה ראשונה חלק לי י"ז בשני בשני חלקים מתחלפים אשר תחלק הגדול יהיה ד' פעמים בקטן דע כי אלה השאלות תוכל לעשותם באחד משני שלשה דרכים והדרך הראשון יחלק לשני סדרים אשר הסדר האחד הוא לדעת החלק הגדול והנשאר יהיה החלק הקטן שהוא תשלום הסך והסדר השני הוא לדעת החלק הקטן והנשאר הוא תשלום הסך החלק הגדול לתשלום הסך ובאלו השני סדרים לא תוכל לחלק המספר אלא לשני חלקים מתחלפים והדרך השני [] בדרך החברות ואני אתן שאלה לכל אחד מן השלמים וכן [] בשברים ובמורכבים והתשובה לזה השאלה בסדר הראשון מן הדרך הראשון שהוא לדעת החלק הגדול והנשאר לתשלום הסך הוא החלק הקטן וזה יהיה בשתכפול המספר המונח על כפל המספר הגדול הנשאל והעולה תחלק על אחד יותר מכפלי המספר הגדול המשל בשאלתנו נכפול י"ז על כפלי המספר הנשאל שהוא ד' פעמים יעלה ס"ח 144[א] קכו [קכו2] תחלקם על אחד [] יהיו ה' תחלק ס"ח על ה' [] החלק הגדול והנשאר לתשלום י"ז [] הקטן והנה י"ג וג' חמשיות הוא גדול [] ומעשה הבחינה כך הוא בדרכים רבים ואכתוב [] הראשון הוא בכפל והשני בחלוק והשלישי אחר ההשואה ובעבור שלא אאריך אתן לכל משל בחינתו והנה הדרך הראשון בזה המשל הוא בכפל והוא שתתן כל השלמים בשבר[] ויהיו הגדול ס"ח חלקים מד חמשיות והקטן י"ז חמשיות כזה סח יז כפול הקטן על ד' פעמים ויעלה ס"ח והוא ויורה כי הוא ה ה גדול ד' פעמים כקטן והוא המבוקש שאלה שנית חלק לי י"א בשני חלקים מתחלפים שיהיה האחד גדול מן השני י"ח פעמים תשובה בדרך השני והוא הטוב והנקל והוא ידעת החלק הקטן ראשונה ותשלום הסך הוא הגדול וזה הוא שתחלק הסך המונח על אחד יותר מן הכפלים ששאל והיוצא יהיה החלק הקטן המשל בזה תחלק י"א על י"ט שהוא אחד יותר מי"ח ששאל ותציא בחילוק י"א חלקים מי"ט כזה יא/יט וזה החלק הקטן והחלק הגדול יהיה עשרה וח' חלקים מי"ט ח/יט כזה שהם תשלום [] לי"א והבחינה יהיה בחילוק שהוא הדרך השני שיעדי[] והוא שתתן השלמים בשברם כזה הצורה אא/טא חטא/טא יהיה הגדול קצ"ח חלקים מי"ט והקטן ידוע תחלק קצ"ח על י"א ותציא י"ח והנה יש בקצ"ח י"ח פעמים י"א והוא הנשאל שאלה שלישית חלק לי קי"ט די' לד' חלקים מתחלפים לראשון ב' ולשני כראשון וחצי והשלישי ב' פעמים כשני ושלישיתו והרביעי כשלישי וד' שביעיותיו ויהיו המספרים [144ב] [קכז1] [] קי"ט ויהיו כזאת [] הצורה תחבר הד' מספרים [] כ"גין יהיו כ"ג וזה המורה לחלק [] כ"גין עליו ואחר כפול כל אחד [] וג ה כ"גין על הסך המונח וחלק על [] וה אב כ"ג המורה והיוציא הוא הראוי מורה כג לכל אחד וזה הדרך הוא דרך החברות כי לראשון יעלה עשרה די' וח' חלקים מכ"ג ולשני ט"ו די' וי"ב כ"גין ולשלישי ל"ו די' וה' כ"גין ולרביעי נ"ו וכ"א כ"גין הבחינה בבחנת החברות שתחבר השברים ותמצה ב' שלמים ותחברם עם השלמים יהיו קי"ט כנשאל גם בחינה אחרת שתראה אם השני הוא כפל הראשון וחציו והשלישי ב' פעמים כשני ושלשיתו והרביעי כשלישי וד' שביעיותיו ואם יהיה כזה בשאלות הדומות מוטב שאלה רביעית מהו המספר הנחלק על י"א והיוציא יהיה ל"ט {היא מבוארת כי תכפול י"א על ל"ט יהיו תכ"ט תחלקם} תשובה תניח שהמספר הנעלם הוא ב' תחלק ב' על י"א {על י"א אבל} יהיו והוא מחולק ב' חלקים מי"א ועתה אמור {עשתי אותה} אם ב' נתן לנו ב' חלקים מי"א מי יתן לנו ל"ט ויהיה כזאת {בסדר} הזאת כפול החיצוניות שהם ב' אם ב ב 0 לט על ל"ט יעלו ע"ח תחלקם על ב' יא חלקים מא"א וראשונה בשוים ותן ע"ח בי"א יהיו תתנ"ח חלקים מי"א תחלקם על ב' חלקים מי"א כי שניהם שוים ותציא בחילוק תכ"ח וזה הוא המספר הנעלם אשר 145[א] קכז [קכז2] אם תחלקו על י"א [] תחלק תכ"ח הנעלם על [] גם אם תכפול י"א על ל"ט יעלו [] שאלה חמשית מהו המספר הנחלק [] תחלק על ג' והיוציא בחילוק תחלק [] יהיה ז' תשובה תניח המספר שתרצה וחלקהו [] ששאלת ושמור היוציא באחרית ואחר אמור אם זה המונח נתן לי זה המספר אשר בידי מי יתן לי ז' ששאלת המשל בזה נניח כ"ד המספר הנעלם תחלק אותו על ד' ויעלה ו' עוד תחלק ו' על ג' ויעלה ב' תחלק ב' על ב' ויעלה א' ואנחנו שאלנו ז' עתה אמור בדרך השלושה אם א' בא [מכ"ד] ז' מאי זה מספר יבוא ויהיה כזאת הצורה כפול האמצעיות יעלו קס"ח תחלקם על א' ויהיה העולה אם א כד ז 0 קס"ח והוא הנעלם אשר אם תחלקהו על ד' יהיה העולה מ"ב ואם תחלק מ"ב על ג' יעלה בחילוק י"ד ואם תחלק י"ד על ב' יעלה בחילוק ז' והוא המבוקש והבחינה היא אמתת המבוקש או חלוקת כל בן על אביו או בהפך שאלה ששית חלק לי מ"ח פרחים לה' אנשים כזה הצורה לראשון א' ולשני ג' ולשלישי ה' לרביעי ז' לחמשי ט' כזאת הצורה זה הדרך יהיה לכל המספרים הנמשכים בערך א ג ה ז ט מה והדרך לכולם הוא שתגרע מספר המקומות ממספרך והנשאר חלקהו לכל המקומות והיוציא יהיה כערך הנשאל והמשל תגרע מספר הה' מקומות שהוא כ"ה ממ"ח ישארו כ"ג תחלק כ"ג לה' מקומות בשוה יציא לכל אחד ד' וג' חמשיות תחבר ד' וג' חמשיות עם מספר כל מקום [145ב] [קלא1] []נו לחלק שלמים []שלמים ושברים כמו [] ג' שלמים וד' חמשיות כזה [] שלמים כל אחד בשברו יהיה הראשון [] כ"ג רביעיות והשני י"ט חמשיות כי ה' על [] עשרים וג' שבריו יהיו כ"ג רביעיות והוא המחולק והמחלק יהיו י"ט חמשיות כמו שתרצה בצורה הזאת ה0א וז נשום יהיו המחולק ק"ה והמחלק ע"ו גב טא נחלק ק"ה על ע"ו יציא בחילוק אחד ול"ט ד ה חלקים מע"ו בשלם שאלה אחרת לחלק שלמים ושברי שברים על דומהם כמו שרצינו לחלק ששה שלמים וב' שלישיות מג' רביעיות על ד' שלמים וד' חמשיות מב' שלישיות ויהיו ט 0א בזאת הצורה הנה ראשונה ו מ על ד מ נשווה השברי שברים ג' על בא הא ג' יהיו ט' תניחם על ג' רביעיות וב' שלשיות ט' הם ו' כי המורה הוא י"ב וששה מי"ב הם חצי וזה השברי שברים הראשון ותניחם על י"ב כזה ו/בא גם נכפול ה' על ב' יהיו עשרה על ב' שלישיות וניקח מהם ד' חמשיות והנה הם ח' ועתה שבו השברים הראשונים ו' שהם חצי י"ב שהם חצי השלם ולשניים ח' חלקי ט"ו ויהיו כזה הצורה ותן עתה השלמים בשבריהם יהיו ו א/ב ד ח/הא על ב' שהוא מורה שבריו י"ג והמורה ב' עוד ד' שלמים על ט"ו הם ס' וח' משבריו יהיו ס"ח והמורה ט"ו והיו כזאת הצורה ואם צורך למורה הכלל נשום הטא וגא גא חו ב הא 149[א] קל"א[1] [קלא2] יהיה המחולק קצ"ה והמחלק [] בחילוק אחד שלם ונ"ט חלקים מ[] [149ב] [קלב1] [השער החמשי] [בשא]לות מעורבות חילקתיו לארבעה פרקים [הפרק הראש]ון בשאלות מעורבות מקצת הדרכים [הפרק] השני בשאלות תחבוליות [ה]פרק השלישי בשאלות מתחלפות {הפרק הרביעי בתערובת המטבעות ובו ג' סדרים הסדר הראשון בחיבור ובגרעון המשקלים ובידיעת הנקי ממרקוש ושבריו הסדר השני בידיעת התערובת מסכים מתחלפים מכסף הסדר השלישי בידיעת דרכי תערובת הזהב} הקדמה לשני מונחים הנה ראוי שתדע כי בכל שאלה יש חלוקה הכרחית והיא שכל מונח יהיה אם שיגרע האחד מן הסך הנשאל ויעדיף השני או שיגרעו שניהם או שיעדיפו שניהם [] או יגרעו שניהם או יעדיפו שניהם גרע הקטן מן הגדול והנשאר הוא המורה לחלק עליו ואם יהיה האחד עודף והשני גורע [ת]חברם והוא ויהיה המורה לחלק עליו ושמור אותו ואחר תכפול כל מונח בעודף או בגרעון השני וגרע הקטן מן הגדול אם השמור גרעת או תחברם אם השמור חיברתה והנשאר או המחובר תחלק על המורה השמור כי לעולם תחבר או תגרע שני פעמים הראשון לחלק עליו והשני הדבר המחולק אשר ממנו יצא הסך הנשאל שאלה סוחר אחד קנה בגדים נעלמו הפרק הראשון מספרם אבל ידענו כי בכל ד' בגדים פרע בשאלות מעורבות מן פרחים והבגדים והפרחים היו כולם צ"ב שאלתי כמה בגדים קנה תשובה הנה זאת השאלה והפרחים שהוציא תוכל לעשותה עם דרך השלשה וזה ועוד אחרות אעשה עם השני מונחים כדי שתרגילם והנה נניח מונח אחד ונאמר כי ד' בגדים הם בט' פרחים נחביר ד' וט' יהיו י"ג והנה מי"ג עד צ"ב יחסרון ע"ט בזה המונח עוד נניח המונח השני ד' בגדים והם שוים י"ח פרחים נחבר 150[א] קל"ב יח עם ח' בגדים יהיו כ"ו והנה [] צ"ב ונאמר עם ח' בגדים יחסרון ס"ו [] שהם פחות [] בגו ישארו י"ג ושמור [] עם ד פחות עט יג כי הוא המורה [] עם ח פחות סו מונח על הפחות מן [] דוב והעולה משניהם גרע הקטן מן הגדול והנשאר תחלק על השמור והיוציא הוא המבוקש כיצד כפלנו ד' על ס"ו יעלה רס"ד ות[] תחת ס"ו עוד כפול ח' על ע"ט היוציא תרל"ב גרע רס"ד מתר[ל"ב] ישארו רס"ח תחלקים על י"ג השמור יעלה בחילוק כ"ח וד' חלקים מי"ג והנה כ"ח בגדים וד' חלקים מי"ג בבגד קנה ונהשאר מד' צ"ב שהם ס"ג וט' חלקים מי"ג הם הפרחים שהוציא והבחינה היא שתאמר עם דרך השלשה אם ד' בגדים נתן ט' פרחים כ"ח בגדים וד' חלקים מי"ג בבגד כמה והראוי שיתן ס"ג פרחים וט' חלקים מי"ג ויהיה בזאת הצורה נכפול האמצעיות אחר שתתן אם ד ט כח ד 0 כ"ח בי"ג שהם עם הד' שברי' יג שס"ח חלקים מי"ג עתה נכ[פול] על ט' יהיה העולה ג' אלפים שי"ב נחלקם על ד' אחר שתשוים על י"ג שהם נ"ב יעלו בחילוק ס"ג וישארו ל"ו חלקים מנ"ב שאם תקצרם ברביעית יהיו נ"ו חלקים מי"ג והוא המבוקש כנזכר והנה כאשר כאשר לקחתי למונח סך הבגדים כך תוכל לקחת למונח הפרחים כי עם מה שתרצה תוכל לעשות המונח שאלה שנית סוחר אחד קנה ג' סוסים בסך ק"ק פרחים נעלם סך כל אחד בפני עצמו אבל הוא יודע [150ב] [] כפל הראשון ועוד ד' וסך השלשי [] שאלתי סך כל אחד בפני עצמו [] סך הסוס הראשון הוא ה' וכפלו ועוד ד' [] יהיו י"ד והנה לשלשי ג' כפלי השני פחות [] תחברם כולם יהיו נ"ד ואנחנו שאלנו ק"ק והנה [] גרעון קמ"ו במונח הראשון עוד נניח למונח השני [] והנה כפלו לשני ועוד ד' יהיו י"ו וג' כפלי השני פחות ז' [] מ"א לשלשי תחבר שלשתם יהיו ס"ג ואנחנו שאלנו ק"ק []גרעו מזה המונח קל"ז ויהיו שניהם בזאת הצורה ועתה גרע הפחות הקטן מן הפחות תתעו הגדול קל"ז מקמ"ו ישארו עוד ה פחות קמו ט קצא ט' והוא המחלק המורה עוד ו פחות קלז ושמור אותו עוד עשה תרפה גרעון אחר והוא שתכפול כל מונח בפחות המונח השני ו' על קמ"ו ויעלו תתע"ו ותניחם על קמ"ו גם ה' על קל"ז ויעלו תרפ"ה ותניחם על תחת קל"ז ואחר תגרע הקטן שהוא תרפ"ה מן הגדול שהוא תתע"ו ישארו קצ"א והם הראוים לחלק על ט' המורה השמור ותציא בחלוקה כ"א וב' תשיעיות והוא סך הסוס הראשון וממנו תדע האחרים והבחינה היא שאחר שידענו סך הראשון שהוא כ"א פרחים ושני תשיעיות פרח יהיה השני כפל הראשון ועוד ד' יהיו מ"ו פרחים וד' תשיעיות והשלישי שהוא ג' כפלי השני פחות ז' הנה ג' פעמים מ"ו וד' תשיעיות הם קל"ח י"ב תשיעיות גרע ז' ישארו קל"א וי"ב תשיעיות וזה סך השלישי ויהיו שלשה בזאת הצורה תחבר התשיעיות 151[א] קל"ג התשיעיות יהיו ב שלמים ו[] [] הסוס הראשון כא ואם [] הסוס השני מו השלשה הסוס השלשי קלא סך כולם קק שאלה שלישית שאלה סוחר אחד קנה שלושים כורים מחטה ושעורה בס' ת' די' החטה לסך כ"א דינ' והשעורה לסך י"ג דיני' שאלתי כמה כורי חיטה וכמה כורי שעורה קנה תשובה תניח כי כורי החטה הם כ' ואם כן יהיו כורי השעורה עשרה והנה סך כ' כורי חיטה ת"ך ועשרה משעורה קל תחברם יהיו תק"ן ואנחנו שאלנו ת' ונשארו ק"ן ונאמר עם מונח כ' יותר ק"ן עוד נניח מונח שני ונאמר שיהיו כורי החטה י"ח ואם כן יהיו כורי השעורה י"ב והנה י"ב כורי שעורה יעלו קנ"ו וי"ח כורי חטה יעלו שע"ח תחברם יהיו תקל"ד ואנחנו שאלנו ת' והנה זה המונח השני נתן קל"ד יותר מהנשאל ונאמר עם מונח י"ח יותר קל"ד ויהיו שני המונחים בזאת הצורה ועתה גרע היותר 00זב הקטן מן היותר הגדול עם 0ב יותר 0הא וא 0ב שהם קל"ד מק"ן ישארו עם חא יותר דגא י"ו והם המורה לחלק 0חוב עליו ושמור אותו ע"ד תעשה הגרעון השני אחר שתכפול כל מונח ביתרון המונח השני שהם י"ח על ק"ן וכ' על קל"ד והנה י"ח על ק"ן יעלו ב' אלף ות"ש והשני ב' אלף ותר"ף גרע ב' [151ב] [] ות"ש ונשארו כ' והם הראוים [] שהוא י"ו ותציא בחלוק א' ורביע [] כור אחד ורביע כור קנה מחיטה כי [] מונח ונשארו לתשלום שלשים כורים כ"ח כורים [] כור קנה משעורה [והבחי]נה תכפול כור ורביע מחטה לסך כ"א יעלו כ"ו דנרי' וג' פשי' גם תכפול כ"ח וג' רביעיות בי"ג יעלו הכ"ח כורים שס"ד והג' רביעיות ט' דינ' וט' פשי' תחברם יהיו שע"ג די' וט' פשי' וזה סך השעורה תחברם עם סך החטה שהוא כ"ו די' וג' פשי' יעלו כולם ת' כנשאל הערה שאם אמר בגדים או ספרים או סוסים קצתם לס' מה לקצתם לסך אחר או דברים אחרים ומספרים אחרים וסכים מתחלפים הנה הכל דרך אחד אלא חילוף החומרים ומה שאומר מהם אקצר שאלה רביעית סוחר אחד קנה כל כך בגדים נעלמו מספרם אבל הוא קנה אותם ג' בגדים בז' פרחים והוא ידע גם כן כי סך הבגדים והפרחים היו כולם קל"ו * נניח שהבגדים יהיו ג' והסך ז' פרחים תחבר תשובה הבגדים והסך יהיו עשרה והנה שאלנו קל"ו ויגרעו בזה המונח קכ"ו נניח שיהיו הבגדים ו' והסך יהיה י"ד פרחים נחבר הבגדים והסך יהיו כ' והנה בזה המונח יגרעון קי"ו לתשלום קל"ו נגרע קי"ו מקכ"ו ישארו עשרה תשנו לחלק עליו כפול כל מונח עם ג פחות קכו 0א ח0ד על פחות חברו [] עם ו פחות קיו לאחד תשנ"ו ולשני שמ"ח שמח 152[א] קלד נגרע שמ"ח מתשנ"ו ישארו [] בחילוק מ' וד' חמשיות והנה מ' [] היה מה שקנה ותשלומו לקל"ו שהם צ"ה [] והבחינה הנה כל ג' בגדים שוים ז' פרח[ים] אם ג' נתן ז' מה יתן לנו מ' וד' [] יתן צ"ה וחמשית או ת[ה]פוך השאלה ואמור אם ז' נתן [] וחמשית מה יתן והוא יתן מ' וד' חמשיות או תקצר ג' וז' יהיה כל בגד ב' ושליש ואמור אם א' נתן ב' ושליש מ' וד' חמש[] מה יתן בחינה אחרת [] בשברו יהיו ר"ד גם צ"ה בשבר[] יהיו תע"ו תשוים עם ג' וז' כזה ויצאו שוים ח ב ד א ויורה כי כאשר ג' בגדים שוים ז' פרחים ד 0 ב ג מ' וד' חמשיות שוים צ"ה וחמשית X ו ז ד ז ח ב ד א שאלה חמשית ראובן ושמעון עשו חברה ונתחייב ראובן לתן בחרבה ק"ן פרחים ולא נתן אלא ק' ושמעון שנתחייב לתת ק"ק פרחים לא נתן אלה ק"ן והרויח ס' פרחים שאלתי כצד יחלוקו כפי מה שנתנו או שנתחיבו לתת הנה רוב השאל[ות] שיהיו מזה המין הם התשובה נעיין ערך מה שנתחייב כל אחד או מה שנתן והנה על שני דרכים ראובן שנתחייב ק"ן ונתן ק' הנה ערך ק' אל ק"ן הוא הראשון הוא שנעיין ב' שלישיות חמשיות שתקצר ק' על קן וישובו לב' חמשיות כנזכר וערך ק"ק אל ק"ן ערך מה שהתנה משמעון הוא ערך ג' רביעיות והנה נאמר כי ממון הראשון הוא ב שלשי' לתת עם מה שנתן 8 ט וממון לוי ג' רביעיות נשוים בזאת הצורה שאם הוא כמו ב ב ג יהיו לראובן ח' ולשמעון ט' נחבר ממון אצל ג' הוא ב שלישיות ג X ד שניהם יהיו י"ז והוא המורה לחלק עליו וכן כל אחד כמו שתראה מאלו השאלות הדרך השני שאם יהיה מה שהתנו לתת ומה שנתנו מספרים בודדים או אחד מהם שתתן זה על זה ויהיו כמו שברים כמו שתראה בשאלות [152ב] [] החברות תכפול ס' על ח' יעלו [] [ת"ף] תחלקם על י"ז יעלה בחילוק כ"ח פרחים [] וד' חלקים מי"ז בפרח אם תרצה לכפול ד' [] על סך הפרח וחלק על י"ז והיוציא יהיו דנרי כמו שידעת לעשות מהנשאר דנרים [] ולשמעון ל"א פרחים וי"ג יזין והבחינה תקבץ היזין יהיו אחד שלם ול"א לשמעון וכ"ח לראובן יהיו ס' והוא הרויח שאלה ששית הנה ב' או ג' סוחרים או יותר נתפשרו לעשות חברה ונתחיבו כל אחד לתת בחברה סך ידוע ולשהות זמן מוגבל והנה לא נתנו מה שנתחייבו מן הממון ולא שהו כפי מה שנתפשרו מן הזמן והרויחו ממון ידוע שאלתי כצד יחלוקו הנה הדרך הוא שתעיין ותדע כמו שאמרתי ערך כל אחד וזמנו כפי מה שראוי לתת ולשהות או כפי מה שנתנו ושהו ואחר תכפול זמן וממון כל אחד ואחד ואחר תשוה שלשתם וכאשר יהיו שוים תחת מורה כללי תכפול הרוח על הממון כל אחד והעולה תחלק על המורה כמנהג ומשל לשאלתנו ראובן שמעון ולוי נתפשרו לעשות חברה עד ששה שנים ונתחייב ראובן לתת י"ו לטרין ולא נתן אלא י"ב לטרין ולא שהה אלא ה שנים ושמעון היה לו לתת כ' לטרין ולא נתן אלא ט"ו לטרין ולא שהה אלא ד' שנים ולוי היה לו לתת כ"ד לטרין ולא נתן אלא כ' ולא שהה אלא ג' שנים והרויחו שלשים לטרין שאלתי כיצד יחלוקו כפי מה שנתחייבו לתת או מה שנתנו תשובה תערוך ממון ראובן י"ו שחייב וי"ב שנתן תקצרם זה על זה יהיו ג' רביעיות כזה וערך זמנו יהיו ד' וערך זמנו הוא ששיות כי ד' שנים שהה מו' שראוי לו לשהות ומקוצר יהיו ב' שלשיות ה' ששיות כזה כזה תכפול ממונו על זמנו יהיו ו' חלקים מי"ב שהוא חצי מקוצר תכפול ממונו על זמנו יהיו ט"ו טו חלקם מכ"ד ומקוצר יהיו החלקים מח' כזה וזה ממון ראובן וערך ממון שמעון הוא ג' רביעיות כי ט"ו נתן וכ' חייב לתת נתן ט"ו על כ' כזה תקצרם יהיו ג' רביעיות כזה וערך זמנו 153[א] קלה וזה ממון שמעון גם תערוך ממון [] ששיות כזה וערך זמנו חצי כי [] אל ו' חצי נכפול ה' ששיות על חצי יהיו ה' חלקים [] תשוים ראובן טו יב ו כולם טו יב [0א] זג בזאת ה א ה שמעון יב 0ג ט זב הצורה ח ב בא זג ויהיו כז לוי 0א ח ד לראובן ט"ו ולשמעון י"ב וללוי זג זג עשרה ותסדרם בדרך החברות בזה הצורה ותחבר ממונם יהיו ל"ז והוא המורה עתה כפול שלשים על ט"ו ועלו ת"ן תחלקם על ל"ז יעלה לראובן י"ב וששה חלקי ל"ז גם תכפול ל' על י"ב יעלו ש"ס תחלקם על ל"ז יעלה לשמעון ט' וכ"ז חלקי ל"ז גם תכפול ל' על עשרה יעלו ש' תחלקם על ל"ז יעלה ללוי ח' וד' חלקי ל"ז והבחינה תחבר השברים יהיו לטרה אחת והשלמים כ"ט לטרה שיהיו כולם ל' לטרין והוא המבוקש שאלה שבעית ראובן ושמעון עשו חברה ראובן נתן ל' לטרי ממון ושמעון כ' כורי חטה ונעלם סך החטה והרויחו י"א לטרה ומזה הרויח יתכן למי שנתן החטה ד' לטרי שאלתי סך כורי החטה תשובה גרע הד' לטרי' מי"א ישארו ז' למי שנתן ל' לטרה ועתה אמור אמור אם ז' לטרה באו לריוח שלשים לטרה ד' לכמה לטרה יבא נכפול ל' על ד' ונחלק על ז' והביא י"ז ושביעית והנה י"ז ושביעית ליטרה יהיה סך החטה והבחינה נאמר כי ראובן נתן ל' לטרי' ושמעון י"ז לטרין ושביעית ועתה נתן הכל בשביעיות [153ב] [] ק"ך והרויחו י"א ליטרין תסדר [] השאלה בסדר החברות בזה הצורה ותציא [] לראשון ז' לטרין ולשני ד' ליטרין וזה [] יורה כי כ' כורי חיטה יהיו שוים י"ז ליטרין ושביעית ליטרה
והמורה ויהיה בזאת הצורה ראובן הב נכפול ממון כל אחד על הריוח ונחלק שמעו 0ב דא על המורה ותציא לראובן ה' ליטרין לוי הא ולשמעון ד' ליטרין וללוי ג' ליטרין יהודה 0א וליהודה ב' ליטרין והם סך מה שנתן כל אחד המורה 0ז שאלה אחרת הנה רצינו לפסוק פסק לאנשים מה לכל אחד 154[א] קל"ו כפי מה שיש לו מן הממון הנה [] החברות שתתן [] ממון [] לפסוק להם יהיה כמו ריוח ותחבר כל מה [] ואחר כפול הממון על כל אחד והעולה [] והוא הראוי לו לפרוע וכן תעשה לכל אחד ואין ל[] כי כבר ידעת סדר החברות וקיצורם
ויהיו ממונם זמנם ההכפלה בצורה הזאת ראובן ראובן והנה זמן שמעון שמעון ראובן הוא כ"ד לוי לוי חדשים כזה וזמן שהיות [154ב] [] וזמן שהיית לוי י"ב חדשים כזה [] אחד בזמנו יהיה לראובן ק"ך [] קי"ב חלקי קל"ב וללוי קל"ב חלקי קנ"ו ואלה החלקים [] כל אחד תקבצם כולם והוא המורה לחלק עליו [] ואחר תקבצם והדרך שתבקש מורה שיכללם ואם לא [] כפול מורה הראשון על מורה השני והיוציא על מורה השלישי והיוציא הוא המורה כללי כאשר ידעת תחלקיהו על מורה כל אחד והיוציא בחילוק תכפול בשבריו והמשל נכפול מורה ראובן שהוא פ"ד על מורה שמעון שהוא קל"ב והעולה נכפול על קנו שהוא מורה לוי יהיה על העולה מספר אחד תשכ"ט אלפים תשכ"ח ויהיו כזה ח ב ז ט ב ז א והוא המורה הכללי נחלק אותו על מורה ראובן שהוא פ"ד יעלה בחילוק ב' אלפים תקצ"ב כזה ב ט ה 0 ב נכפול זה על שבריו שהם ק"ך יעלו ב' מספרים תע"א אלפים ומ' ויה כזה 0 ד 0 א ז ד ב וזה חלק ראובן גם נחלק המורה הכללי על מורה שמעון והעולה נכפלהו בשבריו ויהיו מספר אחד תס"ז אלפים תרמ"ח כזה ח ד ו ז ו ד א וזה חלק שמעון גם נחלק המורה הכללי על מורה לוי שהוא קנ"ו העולה נכפול בשבריו יעלו מספר אחד תס"ג אלפים תרי"ו כזה ו א ו ג ו ד א ויהיו [] כזה הצורה ועתה נכפול חלק ראובן על הריוח ונחלק ראובן 0 ד 0 ו ז ד ב על המורה הכללי יצא בחילוק שמעון ח ד ו ז ו ד א 0 א ד' שלמים ואלה החלקים שהם לוי ו א ו ג ו ד א ג' מספרים ק"א אלפים קפ"ד המורה ד א ג ב 0 ד ה ויהיו כזה ד ח א א 0 א ג כמו שתראה בצורה השנית ולחלק שמעון ראובן ד שלמים ד ח א א 0 א ג ב' שלמים ואלו החלקים ב ז ח א ז ח ג שמעו ב שלמים ב ז ח א ז ח ג כמו שתראה בצורה שנית לוי ב שלמים ה ה א ג ח ג ולחלק לוי ב' שלמים ואלו השברי ה ה א ג ח ג כמו שתראה בצורה שנית והבחינה 155[א] קל"ז והבחינה תקבץ השברים [] השלמים שהם שמונה יהיו [] אומנם אם נזדמן שתוכל לקצר שאלתך כזאת [] לקצר הזמן והמשל בשאלה זאת שתוכל לקצר זמני [] והנשאר לחציים ויהיו לראובן ששה שלישים כז ול[שמעון ד'] שלשים כזה וללוי ג' שלשי' כזה ועתה נסדר ממונם ראובן כזה הצורה נכפול כל ממון שמעון בזמנו יהיו לראובן ל' חלקים לוי מכ"א ולשמעון כ"ח חלקים מל"ג וללוי ל"ג חלקים מל"ט כמו שתראה בזה הצורה ועתה תשוים וראשונה נכפול לט על ל"ג והעולה על כ"א ותציא זה ז ב 0 ז ב שהוא מורה כללי נחלקהו על מורה כל אחד והיוציא תכפול על שבריו והמשל חילקנו המורה הכללי על כ"א ותציא אלף רפ"ז נכפלם על ל' ותציא ל"ח אלפים תר"י לראובן גם חלקנו המורה הכללי על ל"ג יציא תתי"ט נכפלם על כ"ח ויהיו כ"ב אלפים תתקל"ב לשמעון עוד נחלק המורה הכללי על ל"ט יעלו תרצ"ג ונכפלם על שבריו שהם ל"ג ותציא כ"ב אלפים תתס"ט ויהיו כולם כזאת הצורה נחברם יהיו פ"ד אלפים ת"ד שלמים שברי שלם ראובן 0 א ו ח ג ד' ד ח ד ח ד והוא המורה לחלק שמעון ב ג ט ב ב 0 א ב ב א ה 0 ו עליו ועתה נכפול לוי ב ו ח ב ב ב ב א ח ט ה חלק ראובן על המורה ד 0 ד ד ח הריוח הריוח שהוא עשרה והוא שתתן ספרא לפני כל מספר יהיו לראובן שפ"ו אלפים וק' נחלקם על המורה ותציא החילוק ד' שלמים ומ"ח אלפים תפ"ד וזה הראוי לראובן גם נכפול גם נכפול חלק שמעון בעשרה עם ספרא לפניו יהיו רכ"ט אלפים ש"ך נחלקם על המורה ותציא בחילוק [155ב] [] וזה חלק שמעון גם נכפול [] רכ"ח אלפים תר"ך נחלקם על המורה ותציא [] תתי"ב וזה חלק לוי [] הוא שתמצא ב' שלמים בשברים וח' בשלמים יהיו עשרה שאלה אחרת ראובן עשה צוואה והנח ק"ך פרחים ושלשה בנים ואמר תנו לגדול חצי הממון ולשני שלשיתו ולשלשי [] רביעיתו שאלתי סך כל אחד התשובה נניח י"ב למורה והנה חצי י"ב הם ו' לגדול ושלישית י"ב הוא ד' לשני ורביעית י"ב הוא ג' לשלישי תחבר חלקיהם יהיו יותר מי"ב נלך אל דרך השלושה והוא יתן לנו האמת ואמור אם י"ב נתן [] ו' לגדול ק"ך מה יתן לו וכן תעשה לכל אחד אומנם בדרך החברות הוא יותר נקל ויהיה בזאת הצורה והמורה יהיה י"ג גדול ו והממון יהיה כמו הרויח ועתה שני ד 0 ב א נכפול ק"ך על ו' יעלו תש"ך וחלקם שלישי ג על י"ג ועלה לגדול נ"ה פרחים וה' המורה גא חלקים מי"ג בשלם גם נכפול ק"ך על ד' יעלו ת"ף נחלקם על י"ג יעלו לשני ל"ו פרחים וי"ב חלקי י"ג גם נכפול ק"ך על ג' יעלו ש"ס נחלקים על י"ג יעלו לשלישי כ"ז פרחים ונ"ו חלקים מי"ג וזה הראוי לכל אחד והבחינה היא שתחבר השברים יהיו ב' שלמים תחברם עם השלמים יהיו ק"ך כנשאל והנה בזה הסדר תעשה כאשר תרצה לחלק איזה מספר לחצי ולשלש ולרביעית ולחמשי' וכול כל השברים שתרצה שהוא קשה לחלקם שאלה אחרת שכיב מרע עשה צוואה מרע"ג פרחים ואמר הנה אשתי מעוברת ואני רוציא שתחלקו אלה הרע"ג פרחים בזה הדרך שאם תלד אשתי נקבה שתתנו לאשתי כפל הנקבה ואם תלד זכר שתתנו לזכר כפל אשתי והנה ילדה 156[א] קלח זכר ונקבה שאלתי כיצד יחלוקו [] ולהקל נניח א' לבת וב' לשני שהם שהם כפל האם וכללם הם ז' ועתה נאמר [] [] רע"ג ויהיה בצורה הזאת נכפול החיצ[] אם א ז 0 ג ז ב רע"ג יעלו רע"ג [] ז' יעלו בחילוק ל"ט [] והם חלק הבת נכפול ל"ט יעל ע"ח והם חלק האם שהם כפל הבת ונכפול ע"ח יעלו קנ"ו והם חלק הבן שהם כפל האם והבחינה נקבצם כולם ל"ט וע"ח וקנ"ו ויהיו כולם רע"ג והוא מה שרצינו הנה נרצה לדעת הנשאר בחלוקת דרך השלושה מאי זה מין הוא כאשר יש בה זמן וממון ואומר שהוא מהמין האמצעי שאין לו דומה כי הנעלם שבקשנו אין לו דומה כמו בדרך משל אם ב' דוקאדיש בג' חדשים הרויחו ד' די' שהוא האמצעי ה' דוקאדיש בב' חדשים כמה די' ירויחו ויהיה בצורה הזאת נכפול הזמן הזהב אם ב ג ד ה ב ב' דוקאדוש בג' חדשים יהיו ו' וגם ה' דוקאדיש על ב' חדשים יהיו עשרה ואז חזרה השאלה אם ו' נתן ד' עשרה כמה די' יתן והנה ד' די' הוא האמצעי וממנו וממ תהיה התשובה מן המספר הנעלם שנתן ו' די' ונשארו ד' והם די' נעשה מהם פשיט' יהיו מ"ח נחלקם על ו' יעלו ח' פשיט' ועתה נאמר שאם ו' נתן ד' די' עשרה מה יתן והנה נתן ו' די' וח' פשיט' והנה ערך ו' אל ד' די' כערך עשרה אל ו' די' וח' פשי' ולראות זה לעין נעשה כל הדי' פשיט בעבור הח' פשיט יהיו הד' די' מ"ח פשיט והו' די' ע"ב פשיט נחבר עליהם ח' יהיו פ' פשיט והנה תראה כי ערך ו' אל מ"ח כערך עשרה אל פ' כי עשרה בפ' ח' פעמים וכן ו' אל מ"ח ח' פעמים בחינה אחרת תשוה 0חד 0חד זה עם זה בצורה הזאת יהיה כל אחד [] [156ב] שאלה ה[] [] [] עשרה מזהב [] [וח'] מכסף וז' מנחושת ולקח מזה [] משקלה שאלתי כמה יש בה מכל [] [תשובה] הנה כל אלו השאלות והדומות הם כמו [] כי י' מזהב וח' מכסף וז' מנחושת [] שלושה אנשים וקיבוצם שהוא כ"ה אוקיות הם כמו [] ומה שלקח הוא כמו הריוח ונשוב לשאלתנו ונאמר כי [] אוקיות הוא המורה ועתה לדעת הזהב שבחתיכה נכפול [] שהיא ט' אוקיות על עשרה שהוא הזהב שבכולו יעלו צ' תחלקם על כ"ה יעלו ג' אוקיות זהב וט"ו חלקי כ"ה באוקיא וזה הזהב שבחתיכה עוד לדעת הכסף נכפול ח' על ט' יעלו ע"ב וחלקן על כ"ה יעלו ב' אוקיות כסף וכ"ב חלקים מכ"ה וזה הכסף שבחתיכה עוד לדעת הנחושת נכפול ז' על ט' יעלו ס"ג נחלקם על כ"ה יעלו ב' אוקיות וי"ג חלקי כ"ה מנחושת שבחתיכה וזה מה שרצינו והבחינה תחבר השברים יהיו חמשים תחלקם על כ"ה יעלו שנים תחברם לשלמים יהיו כולם ט' כנשאל שאלה י"ב הנה יש בבית הטוחנים ד' רחים אשר האחד טוחין בכל יום ז' כורי חטה והשנית י"א והשלישית י"ג והרביעית ט"ו ורצה לטחון ש' כורי חטה ולתת לכל אחת מן הרחים די מחסורו שאלתי כמה יטחון בכל יום תשובה כמו החברות שתקבץ ז' י"א י"ג ט"ו יהיו מ"ו והוא המורה והש' כמו הריוח ועתה תכפול ז' על ש' וחלק על מ"ו והיוציא הוא הראוי למי שטוחן ז' כורים גם כפול י"א על ש' וחלק על מ"ו והיוציא הוא הראוי למי שטוחן י"א כורים גם כפול י"ג על ש' והעולה תחלק על מ"ו והיוציא הוא 157[א] קל"ט הראוי למי שטוחן י"ג כורים גם [] תחלק על מ"ו והיוציא הוא הראוי למי ש[] הבחינה כמו החברות
[157ב] [] דרך השלושה ותמצא שאלתך וגם תכון כי כאשר י"ו [] פשיטין מסרקוסטה שוה [] כא כג י"ח מברסילינה כן י"ו לטרין סרגוסאה שוים י"ח לטרין [] ואם תקצרם יענו האמת גם כן כי ח' לטרי סרקוסטה הם לטרי ברסילונה והקש על זה {ולעולם תחילת השאלה תהיה מהע מהעיר אשר והבחינה היא שתעשה כל הלטרין שמיניות ויהיו הכ"א לטרי {הממון או הלטרין קס"ח שמיניות והכ"ג עם שבריו קפ"ט שמיניות ואחר {הידועים ממנו תשוים עם חלקי השאלה ויהיו כזה הצורה {כי בכאן אמר כי ואחר השיווי יהיו שניהם שוים אלף תקי"ב ב א ה א {ליטרי סרגוסה ט ח א ט {כן נסדר שאלה ח ו א ח {ונאמר אם ח' פש'
158[א] ק"מ בגד אשר רוחבו ג' זרתות נצטרך מן הבגד הזה לכפול אורך כל אמה שלנו ד' זרתות והנה הראשון רוחבו ז' זרתות נכפול ז' על האורך [] זרתות מששה אמות יעלו קס"ח זרתות מרובעות [] הראשון אחר כן קח אמה אחת מאשר לו [] מרוחב ותכפול ד' זרתות מאורך על ג' מרוחב יעלו י"ב זרתות מרובעות בזה האמה ואמור אם י"ב זרתות יתן אמה אחת קסח זרתות מה יתן ויהיה כזה הצורה והנה נתן י"ד אמות והנה י"ד אמות אם יב א קסח 0 מזה הבגד תצטרך לכפול הששה אמות והבחינה מבוארת והיא שתכפול י"ד אמות בי"ב זרתות מרובעות שיש בכל אמה ותציא קס"ח שאלה י"ז אם ב' פרחים בג' חדשים הרויחו ארבעה דינרי' ג' פרחים בה' חדשים כמה ירויחו [] תשובה כפול כל ממון בזמנו וישובו החמשה חלקים בדרך ראשון לשלוה ואחר עשה שאלתך והמשל כפלנו ב' פרחים בג' חדשיו יעלו ו' והוא הראשון בשאלה גם כפלנו ג' פרחים בה' חדשיו יעלו ט"ו והוא השלישי בשאלה והריוח נשאר קיים ועתה נאמר אם ו' נתן ג' ט"ו מה יתן בזה הצורה ונכפול ט"ו על ג' יעלו מ"ה תחלקם אם ו ג טו 0 על ו' יעלה בחילוק ז' וחצי והוא מה שהרויח ג' פרחים בה' חדשים והבחינה מבוארת מכמה צדדים כי ו' כפל ג' וכן ט"ו כפל הנעלם שהוא ז' וחצי אותן כל אב על בנו או בהפך או תשוים [158ב] [] שלישי מדרך השלושה []דוש בד' חדשים הרויחו ג' די' ז' אשקודוש [] [ויהיו] ה' די' התשובה כפול ה' שתרצה לדעת [] אשקודוש על ד' חדשים שהם כ"ד ואמור [] כ"ד הם ק"ח תחלקם על כפל ג' על ז' שהם כ"א יהיה יציא ה' שלמים וט"ו חלקים מכ"א שמקוצרות הם ה' שביעיות והנה בה' חדשים וה' שביעיות חדש הרויחו הז' אשקודוש חמשה די' ועיין בצורה והבחינה תהפוך שאלתך ותאמר אם ז' אשקודוש בחמשה חדשים וט"ו חלקים מכ"א נתן לנו ה' די' מי יתן לנו ג' נכפול ד' חדשים על ו' אשקודוש יעלו כ"ד תשוים עם מותרי שברי החודש יעלו תק"ד לחלק על קס"ח הבא מנתנת החדשים בשברו כי ה' על כ"א ובתוספת ט"ו שברים יהיו קס"ח אשר עליו תחלק תק"ד ותציא ג' די' והוא המבוקש אשקודוש חדשים דנרי' אשקודש די' שאלה אחרת ממדה ו ד ג ז ה ממנה ג שלשי דב אב מדרך השלושה אם בגד אחד שויה ט' דוקאדוש וב' אמות שוים י"ב די שאלתי ח0א כאשר עלה הבגד לסך י"ב דוקאדוש כמה בגד יותן בעד ט"ו די' דוקדוש אמות דנרי דוקאדוש דנרי כזא הצורה התשובה כפול ט"ו ט ב יב יב טו על י"ח שבא מכפל ט' דוקאדוש על ב' אמות יעלו ר"ע שתחלקם יח קמד על כפל י"ב די' על י"ב דוקאדוש שהוא קמ"ד יעלה בחילוק א וקכ"ו חלקים מע"ד שהוא ז' שמניות כזה והנה אמה וז' שמניות אמה יותן לנו מזה הבגד בט"ו די' 159[א] קמ"א שאלה ממדה ממנהג שלושה אמות מבגד שוה נ"ב די' וס' [………………] סרגוסה שאלתי ה' אמות מבגד זה כמה ליטרין ממטבע סרגוסה יהיו אמות די' די' ליטרין אמות התשובה כפול ה' אמות ד נב ס ג ה שתרצה על כפל ג' ליטרין על נ"ב שהם קנ"ו רמ קנו ותכפול ה' על ותכפול ה על קנ"ו תשף שיעלה תש"ף תחלקם על ר"מ שהם כפל השני דברים הנשארים שהם ס' על ד' יעלה בחילוק ג' ליטרין ורביעית ליטרה ממטבע סרגוסה שאלה אחרת ממדה סוחר קנה בגד בסך ט"ו די' והג' אמות שוה ז' די' שאלתי אם זה הבגד יוקר וקנה אותו בסך י"ח מה יהיה שוה ה' אמות התשובה הנה תכפול כל ממון על האמות שלו ותשוב ותשוב השאלה לג' חלקים כי ט"ו על ג' יעלו מ"ה וגם י"ח על ה' יעלו צ' עתה אמור אם אם מ"ה נתן ז' צ' מה יתן והנה נתן י"ד כזה הצורה והבחינה ברורה אם הד נתן ז 0ט 0 כי הראשון כפל השלישי וכן השני כפל הרביעי הנעלם שהוא י"ד שאלה אחרת ממשקל ראובן קנה כור חיטה בסך י"ח די' ונתן י"ד אוקיות לחם בשני פש' קרא מקרה וקנה הכור בסך כ"ב די' שאלתי י"ז אוקיות לחם כמה פשיטי' יתן ויהיה כזא הצורה התשובה כפול די' אקיות פשיט די' אוקיות פשיט כל ממון על משקלו יהיה אם חא דא ב בב זא 0 הראשון שכפלנו י"ח על י"ד יעלו רנ"ב והשני כ"ב על י"ז [159ב] [……………] פשיטי נשארו קיימים עתה שחזרו חלקי [……………] אמור אם רנ"ב נתן ב' שע"ד מה יתן ויהיה […………] תכפול שע"ד על ב' יעלו תשמ"ח תחלקהו על רנ"ב יעלה בהב ב דזג 0 בחילוק ב' פשטין ורמ"ד חלקים מרנ"ב בפשוט נקצרם יהיו ס"א מס"ג בשלם והנה כאשר קנה ראובן כור חיטה בכ"ב די' הנה י"ז אוקיות שוים ב' פשי' וס"א חלק מס"ג בפשוט והבחינה תחזור הנעלם בשבריו יהיו תשמ"ח והב' ברנ"ב יהיו תק"ד ואחר תשוים עם רנ"ב ושע"ד כזה הצורה יהיו וטדחחא וטדחחא שוים כמו שתראה עליהם ויורה על אמיתת בהב ד0ה השאלה דזג חדז שאלה אחרת אם י"ח פרחים בה' חדשים הרויחו שני פרחים שאלתי כ"ד פרחים בכמה זמן ירויחם בזאת הצורה כפול פרחי' חדשי' פרחים פרחים חדשים י"ח פרחים עלו ה' חדשים אם יח ה ב כד 0 יעלו צ' תחלקם על כ"ד יעלה בחילוק ג' וג' רביעיות הנה בג' חדשים וג' רביעיות חודש ירויחו כ"ד פרחים ב' פרחים והבחינה הפוך השאלה ואמור אם כ"ד פרחים נתן ט"ו רביעיות חודש י"ח פרחים מה יתן כפול כ"ד פרחים בט"ו רביעיות חודש יעלו ש"ס תחלקם על י"ח אחר שתשוים עם רביעיות החדשים שיפלו ע"ב ותצא בחילוק ה' חדשים והוא המבוקש שאלה אחרת ראובן קנה כור חיטה בסך י"ח די' ונתן ט"ו אוקיות מלחם בשני פשיטי שאלתי כאשר קנה כור חיטה בסך כ"ו די' כמה אוקיות יתן בשני פשיט' ויהיה בצורה די' אוקיות פשי' די' פש הזאת נכפול י"ח שהוא הממון על אם יח טו ב כו ב ט"ו שהוא המשקל יעלו ר"ע תחלקם 160[א] קמ"ב על כ"ו יעלה בחילוק עשרה אוקיות וה' חלקי […………] עשרה אוקיות וה' חלקי י"ג באוקיה יתן מלחם בשני [……] עלה כור החיטה [] לסך כ"ו די' והבחינה הנה ערך י"ח אצל כ"ו שוה לחלקים הנשארים […] תחלק כ"ו על י"ח יעלו א' וד' תשיעיות מקוצר גם ט"ו על עשרה אוקיות ועשרה חלקי כ"ו אשר אחר הקיצור הם ה' חלקים מי"ג כיצד נחלק ט"ו על האוקיות וראשונה תשוים ט"ו עם מורה האוקיות יהיו ש"ץ גם האוקיות בשברו יהיו ר"ע נחלק ש"ץ על ר"ע יעלה בחילוק א' וד' תשיעיות כראשון שאלהאחרת ראובן קנה כור חיטה בסך י"ו די' ונתן י"ז אוקיות לחם בשני פשיט' שאלתי כאשר קנה הכור בסך כ' די' כמה אוקיות יתן בג' פשי' ובזה השאלה תמצא חמשה דברים מונחים והוא מן הסדר השלישי ויהיה כזאת הצורה כור אוקיות פשיט כור פשי התשובה הנה תכפול י"ו די' על די' די' י"ז אוקיות ויעלה רע"ב יו יז ב כ ג וזה חלק ראשון עוד תכפול הב' רעב מ פשיטי שנתנו הי"ז אוקיות על כ' די' תתיו שהוא סך הכור השני יעלו מ' והוא החלק השני ועתה תכפול הג' פשיטי ששאלת על החלק הראשון שהוא רע"ב יעלו תתי"ו תחלקם על החלק השני שהוא מ' יעלה בחילוק כ' אוקות וב' חמשיות מאוקה מקוצר והנה כ' אוקיות וב' חמשיות אוקיה מלחם יתן בג' פשיט והבחינה בשאלה שיבא שאלה ראובן קנה משא ענבים בסך י"ו די' ונתן י"ב אוקיות יין בסך ב' פשי' שאלתי כאשר קנה המשא בסך כ' די' [כמה] אוקיות יין יתן בג' פשי' ויהיה בצורה הזאת בכאן שאלה כפולה [160ב] [] י"ז אל כ"ו שוה לחלקים הנשארים [] תחלק כ"ו על י"ח יעלו א' וד' תשיעיות [] על עשרה חלקים ועשרה חלקי כ"ו אשר אחר הקיצור הם ה' חלקים [] ר"ע גם תן כ"ו בשברי כ"ו יהיו שץ אשר תחלקם מי"ג [] נחלק ט"ו [] יעלה בחילוק א' וד' תשיעיות באחד על האוקיות וראשנה שאלה כ"ב ראובן קנה כור חטה בסך י"ו די ונתן נשוה טו עם מורה י"ז אוקיות לחם בשני פשיט' שאלתי כאשר האוקיות יהיו שץ קנה הכור בסך כ' די' כמה אוקיות יתן בג' פשיטי' ובזה גם האוקיות בש[] השאלה תמצא חמשה דברים מונחים והוא מן הסדר יהיו ר"ע נחלק השלישי ויהיה בזאת הצורה שץ על ר"ע יעל[ה] כור כור תשובה הנה החילוק א וד דני אוקי' פשי' די' פש' אוקיו תכפול תשיעיות יו יז ב כ ג 0 י"ו די' על י"ז אוקיות בראשון רעב מ ויעלה רע"ב וזה חלק ראשון עוד תכפול הב' תתיו פשיטי' שנתנו הי"ז אוקיות על כ' דנר' שהוא סך הכור השני יעלו מ' והוא החלק השני ועתה תכפול ג' פשיטי' ששאלת על החלק הראשון שהוא רע"ב יעלו תתי"ו תחלקם על החלק השני שהוא מ' ועלה בחילוק ב' אוקיות וב' חמשיות מקוצר והנה כ' אוקיות וב' חמשי אוקיה מלחם יתן בג' פשיטי' והבחינה בשאלה שיבוא שאלה כ"ג ראובן קנה משא ענבים בסך י"ו דינרי' ונתן י"ב אוקיות יין בסך ב' פשיט' שאלתי כאשר קנה המשא בסך כ' די' כמה אוקיות יין בג' פשיטי' ויהיה כזאת הצורה תשובה הנה 161[א] קמ"ג זה כמו שאלה [] דני' אוקי' פשי דנרי פש [] יו יב ב כ ג יעלו קצב [] קצב מ על ג' [] תחלקם על כפל [] תקעו דינר שהם מ' יעלה [] י"ד אוקיות וב' חמשיות מקוצר וזה מה שרצינו והבחינה הנה נקח ב' שילשיות י"ד וב' חמשיות אוקיה של יין שהם הראוי לג' פשיטי בעבור שיהיה יותר נקל והיוציא שהוא ט' אוקיות וג' חמשיות הוא הראוי לב' פשיטי' לב' פשיטי' מיין ואחר נשוה דרך שני ט' אוקיות בחלקיו יעלו קל"ז חמשיות וכפלם על דינרי הכור השני יעלו מח 00ו קצ"ב בחלק הראשון כי ט' על כ' יעלו ק"ף וג' חמשיות על [] ה ה כ' יעלו ס' חמשיות נחלקם על ה' ותציא י"ב ועם ק"ף יהיו קצ"ב ואם תקח הג' פשי' אשר בשאלתנו יהיה הראשון קצ"ב והשני רפ"ח והוא קצ"ב וחצי כמו שג' הוא אחד וחצי מב' וכן [] שאלה כ"ד אם ד' פשיטי סרקוסטה שוים ה' פשיט' ברסילונה וג' פשיטי ברסילונה הם שוים ד' פשיטי לדידה לשבונה שאלתי ט"ו פשיטי לישבונה כמה פשיטי סרקוס[טה] סרקוסטה ברסלונה ברסלונה לשבונה לשבונה סרקוסט הם שוים ד ה ג ד טו 0 ויהיו באזת הצורה י"ב כ התשובה ק"ף כפול ט"ו שתרצה לדעת על כפל ד' פשיטי סרקוסטה וג' מברסילונה שהם י"ב יעלו ק"ף תחלקם [161ב] [] לשבונה שהם כ' [] ט"ו פשיטי לשבונה הם ט' מסרקוסט' [] הדומה לזה סרגו' לשבונה לשבונה ברצילו ברצלו' סרגוסטה [] שאלתך בזאת הצורה ט טו ד ג ה ד [] על לו שבא לו מה מכפל ט' קף הפרק השני בשאלות תחבוליות סרגוס' על ד' שאלה ראשונה הרי שרצינו מספרים מה ושנשלך מהם לשבונה יעלו בתחבולה מה שנרצה בחשבון שנרצה וישאר ק"ף אשר תחלקם מה שנרצה כמו במשל מה שהיה בשם ה"ר אברהם בן עזרא מט"ו על מה שבא יהודים וט"ו גוים והשליך הגוים בים במספר ט' והסדר מכפול ט"ו לשבו' היה דם ההגרים וכול' ואעשה משל בסדר עשייתו ואומר על ג' ברצלונה שתכתוב המספר שתרצה מספרות או מדבר שתרצה ותציא ד' פשיטי בעיגול כזה או ארוך אם תרצה ואחר סרגוס או תן רושם במקום מה תחלק ק"ף על והסימן רמוז שתתחיל ממנו כ' שבא מד' דם ההגרים בלט לספור ט'ט' בזאת לשבונה על ה' השאלה ובאחרות ברצלונה ותציא כמו שתרצה ורשום ץ' אשר הוא שאלתי[] על אשר בו נפל וכן כל הדומה לזה סוף המספר וכן סביב העגול עד שתקח החצי בזה השאלה או מה שתרצה באחרות ואחר קח מה שאין עליהם רושם מתחילת 162[א] קמ"ד
[162ב] [] נאמר בדרך הנעלם אם מבצר [] יתן הרשעים אשר בנ"ה אנשים נכפול [] יעלו נ"ה נחלקם על ה' יעלו בחילוק י"א והם [] אמר האדון ניפול גורל ונשליך י"א בחומה [] ואמר אמרו לאי זה מספר נשליכם אמרו הגוים למספר [מ' בעבור] איסור הבשר שהם ימים סגוליים אמרו הישמעלים לחשבון [ל'] בעבור תעניתם שהם ימים סגוליים אמר הכושיים לחשבון ז' [] כמספר ז' כוכבי לכת והיהודים אמרו לחשבון עשרה בעבור [דברים] רבים ענה החכם ואמר מ' ול' וז' ועשרה כולם פ"ז ואין לזה ומספר חצי ולא רביעית ולא חמשית
אבל יש לו שלישית שהם כ"ט [] תרצה ויהיה בלי מחלוקת ויענו כן [] ויאמר החכם ישב האדון תחילה ואחר היהודי [ג'] גוים וד' ישמעלים ג' כושיים ב' יהודים ב' גוים [ה' ישמעלים ד'] כושיים ג' יהודים כושי אחד ג' גויים ד' ישמעלים ב' [כושיים ה' ישמעלים] ב' יהודים גוי אחד ג' ישמעלים ג' גוי ג' כושיים ויהיו [נ"ה] בעיגול ומהאדון נתחיל למנות ונתן א' על הכ"ט וכן תמנה י"א סביב חלילה ואחר שיהיו רשומים כתוב עליו יהודי [] אומה שתרצה ואני סדרתי השני צורות ותוכל להחליפם ל[] שאלה שלישית הנה היה בידינו עגולות במספר מה ונרשום בחלק מה במקום רמוז [] והנה במקום החלק הרמוז היו כוכבים כוכב אחד בכל עגול והולך כל כוכב סיבובו בימים מתחלפים זה מזה שאלתי בכמה מן הזמן ישובו כולם להדבק כבראשונה תשובה ראה המורה היותר מקוצר כמו שהראתך בקיצור המורים ובמספר המורה המקוצר ישובו כולם לחלק הרמוז ואם לא תקח המקוצר האמתי ישובו להדבק כל כך פעמים כפי מה שתוכל לקצרו ואם תרצה לדעת מהלך סיבובי כל עגולה בפני עצמה תחלק המורה שהוא ימי מהלך כולם על כל אחד והיוצא לכל אחד הוא מהלכו המשל בזה הרי שיהיו בידינו ד' עגולות ולכל עגולה כוכב אחד והנה מהלך החיצון בכ"ד ימים ומהלך השני בי"ט ומהלך השלישי בעשרה ומהלך הרביעי בששה ויהיה בזאת הצורה והנה נוציא המורה הכללי מקוצר כמו שאמרתי ויהיה המורה המקוצר ב' אלפים ור"ף כזה ובו תמצא כל החלקים כיצד הנה ו' תמצאם בכ"ד ותשלך 2280 [163ב]
182א קס"ד הפרק הראשון בהקדמות [] ראוי שתדע כי [] לחוכמות כמו לחכמת המספר שאנו בה [] ובשטחים ובגשמים ולחכמת המשיקה בקולות אם אדם אם בקולות הכלים ולחוכמת הרפואה בדפק [] חכמת המספר היא כלי לכולם כי באשר יאמר זה הקו [או זה] הגשם או זה השטח ערכו חצי או שלישית וזולתו כמו [] כי ערך קו ישר אורכו ד' אמות אל קו אחר אשר אורכו כ' א[מות] הנה הוא חמשיתו ונוכל לומר שהערך שיש בין זה לזה הוא [] א' אל ה' בלוחות כפלי הערכים במקום שתמצא א' וה' כי ממ[] ד' וכ' וגם כל שטח אשר הוא מרובע מד' אמות על ד' אמות אצל שטח אשר הוא ח' אמות על ח' שהוא רביעיתו ונאמר כי ערכם כערך א' אל ד' ומשל במוגשם כי ערך מרובע אל כל צלע ד' אמות אצל מרובע אשר כל צלע ח' אמות הוא שמיניתו כי מספר גשם ד' הוא ס"ד וגשם ח' הוא תקי"ב אשר אם תחלקם על ס"ד יעלו בחילוק ח' ואם כן ס"ד הוא שמינית תקי"ב וערכם שהוא כערך א' אל ח' שאם תקצרם ישובו תקי"ב אל ח' וס"ד אל א' וכן נצטרך המספר בחכמת המוסיקה אם בקולות אם בכלים כי נצטרך שיהיה ערך קול אל קול כערך אל ב' או אל ג' או ערכים אחרים כמו שתראה בלוחות עשרה סוגי הערכים שאכתוב בע"ה ופעמים יכווננו בכלי הנגון לעשות הקולות נערכים כקולות האדם כדי שיעשו רצונם ולזה יעשו כלים וכלים מכלים שונים אם שנתנו הערך למתרים זה עב וזה דק כערך מספר אל מספר או שיהיו המתרים שוים והמכה למתרים נערך כי לעולם ההכאה עושה הקול שאין קול בלי הכאה ואין הכאה בלי תנועה והתנועה משותפת לאויר עושה [] ערכי הקולות הם ארבעה האחד קול []כתיבה כקול האדם והפך זה קול שאין בה [] כתיבה כרעם וכרעש וכרוח והכאת גשם [] והשלישי קול שיש לו הבנה ולא כתיבה כקול הכינורות [] הפך השלישי קול שאין בו הבנה ויש בו כתיבה כקול בעלי חיים כמו השה והעורב ודיבוק הנער הנה גם נצטרך המספר וערכו בחכמת הרפואה כערכי משקלי הסמים ובדפק כמו שהרופה מכיר בתנועות דפק החולה אם הוא במהירות או בהמתנה וכפי ערך התנועה מכיר הרופה לחולה וזה הדק מן הערכים כמו שאמר גילינוס מי שירגיל כהרגלי ישיג כהשגתי והנה הערכים בחשבון הם כמאזנים ומי שלא ידע עשרה סוגי הערכים אשר אבארים בע"ה לא יוכל לדעת אמתת השאלות ולא אמתת הדרכים אשר עמהם בחינות השאלות וגם בכאן אכתוב לוח עם כתר משולש והוא מא' עד ט"ו ובו תמצה כל הערכים שתוכל להרכיב מא' עד ט"ו כמו שתורה לך המשולש כי כל זוית עושה ערך כי זוית המשולש הקטן הראשון מורה על א' וב' וערכם ערך כפל והשני ערך פעם וחצי ויש על השנים נזכרים משולש על א' וג' ותורה על ג' כפלים והנה משולש [] שהוא י"ג וי"ד וערכם פעם וחלק מי"ג והנה כל טורי י"ד וי"ג למטה עד אין תכלית יורו כמוהם וישובו אליהם והמשל קצו קפ"ב שהם סוף טורי י"ד וי"ג יצאו מכפל י"ד וי"ג וערכם שוה וגם אם תקח י"ד וכ"ח הנה הם וכל הטורים ישובו לא' ולב' והוא הדין אם תרצה ערכים אחרים שהם בתוך הלוח הנה ערכם כערך העליונים והמשל נקח פ"ד ומ"ח הנה המשולם המורה לי"ד וח' שהוא ערך פעם וששה חלקים מח' שהם ג' רביעיות וכן לכל מספר שתעריך עם אחר כנזכר וזה צורת הלוח 183[א] קס"ה [] שם כולל שהוא ערך והנה [] הראשון ערך מן הגדול לקטן ודומה [] לחלק העליון על התחתון ובו חמשה []כל סוג אכתוב לוח אחד ואם לא יקיפו כל ערכי [] אני אכתוב לוח ^ אשר עליו כתר כחצי כרבע מרובע ^ תכף אחר אילן [] זה כי העליון עם הלוח מב' שורות והרשות בידך השלשה ערכים [] הלוח מכמה שורות כי כולם ישובו לראשונה כי העליון לשברים והתחתון לשלמים ומהם תוכל לעשות לוחות [] תכלית אבל לא יולידו סוגים אחרים זולת העשרה ערך השני הוא ערך מן הקטן לגדול ודומה לשברים ובו גם כן חמשה סוגים ואכתוב להם גם כן ה' לוחות ערך השלישי הוא ערך שוה וממנו יצאו ערכים מתחלפים כמו שתראה במקומו והוא דומה לאחד אשר הוא בין השלמים [וה]שברים וממנו יצאו כל הערכים ואליו ישובו והרי לך צורת עשרה סוגים בשמן מוכפלת פעם וחלק ערך מן הגדול לקטן פעם וחלקים מוכפלת וחלק מוכפלת וחלקים שוה ערך בכלל ערך אמצעי מתחלף מוכפלת פעם וחלק ערך מן הקטן לגדול פעם וחלקים מוכפלת וחלק מככפל וחלקים 184[א] קסה [] הראשון מן החמשה סוגים אשר [] הגדול לקטון שדומה לשלמים לשברים ואומר כי אלה [] יש להם מנים לאין תכלית ואומר כי [הראשון] נקרא תחתיו מוכפלת והוא פשוט [ובלשון י]ון שם זה הסוג הוא שוף מולטיפליקש ומיניו לאין [] המין הראשון תחת מוכפל והשני תחת ג' כפלים [והשל]שי ארבעה כפלים וכן לאין תכלית כמו שתראה בימין [ה]לוח ובשאל ובשמאל הלוח שמות היונים שקוראים לראשון [שו]ף מולטפליקש דובלה ולשני שוף מולטיפלקש טריפלה ולשליש [ק]טרופלה והרביעי קינקופלה וכן בטבע המספר שטופלה []שופלה אוטופלה נוטופלה שהיא סוף הלוח שתחת והנה []פל כל הלוח כתבתי משולש מורה על ערך על שני ^ כמו במשל ^מספרים [] י"ד שבזה הלוח שיורה המשולש שיקיף בהם שערך שניהם [] ערך כפל פעם וג' רביעיות מקוצר וכן כולם כי אין אין להאריך יותר הערה הנה בעבור שלא אעשה פרוש לכל הלוחות אכתוב [] התחלות מן החמשה סוגים ומהם תראה החמשה הנשארים כי [] הפרש מן החמשה לאחרים אלא כי מה שתכתוב למעלה בראשונים []הפוך ותכתוב למטה בחמשה האחרים ומה שתאמר תחתיו לראשונים [] תאמר לאחרונים כמו שתראה והנה תחילת הסוג הראשון הוא בא גא דא ותחילת הסוג השני גב דג הד ותחילת הסוג השלישי דג הד וה ותחילת הסוג הרביעי הב זב טב ותחילת הסוג החמשי חג י"אד י"דה ואלה הם התחלת החמשה סוגים האחרים אלא שהעליון יהיה תחתון כמו שתראה בלוח העשרה סוגים וכאשר תרצה ה[] מכולם תכפול כל טור על הראשונים וכל זה תלמוד מן הלוחות והרי לך הלוחות מן העשרה סוגים 185[א] קס"ו בלשוננו ראשוני שניים שלישי רביעי חמשי ששיים שביעי תחת מוכפלת שני כפלים ב א ד ב ו ג ח ד י ה יב ו יד ז יו ח תחת מוכפלת שלושה הכפלות ג א ו ב ט ג יב ד טו ה יח ו כא ז כד ח תחת ארבעה כפלים ד א ח ב יב ג יו ד כ ה כד ו כח ז לב ח תחת חמשה כפלים ה א י ב טו ג כ ד כה ה ל ו לה ז מ ח תחת ששה כפלים ו א יב ב יח ג כד ד ל ה לו ו מב ז מח ח מולט[] תחת שבעה כפלים ז א יד ב כא ג כח ד לה ה מב ו מט ז נו ח תחת שמונה כפלים ח א יו ב כח ג לב ד מ ה מח ו נו ז סד ח תחת תשעה כפלים ט א יח ב כז ג לו ד מה ה נד ו סג ז עב ח [] והוא פשוט
[] [בלשוננו] ראשוני שניים שלישיי' רביעי' חמשיים ששיים שביעיים ובלשונם [פעם] וחציו ג ב ו ד ט ו יב ח טו י יח יב כא יד שוף שופיר פארטיקולאר שי קואלטירה פעם ושלישיתו ד ג ח ו יב ט יו יב כ טו כד יח כח כא שוף שופר פרטיקולר שי קי טירסיאה פעם ורביעיתו ה ד י ח טו יב כ יו כה כ ל כד לה כח שוף שופיר פארטיקולר שי קי קארטה פעם וחמשתו ו ה יב י יח טו כד כ ל כה לו ל מב לה שוף שופיר פארטקולר שי קי קינטה פעם ושישיתו ז ו יד יב כא יח כח כד לה ל מב לו מט מב שוף שופר פארטיקולאר שי קי שישטה פעם ושביעיתו ח ז יו יד כד כא לב כח מ לה מח מב נו מט שוף שופיר פארטיקולר שי קי שיטימה פעם ושמיניתו ט ח יח יו כו כד לו לב מה מ נד מח סד נו שוף שופיר פארטיקולר שי קי אוטהבה
שוה כאשר תראה בראש צורת א' שוה צורת א' ותן א' תחת הא' הראשונה וחבר א א א שוה הא' עם הא' השנית יהיו ב' והם א ב ד ערך כפול תחת הטור השני עוד תחבר השנים א ג ט ערך משולש שיצאו עם הא' אשר עליהם יהיו א ד יו ערך מרובע ג' חברם עם הא' אשר בטור השלישי א ה כה ערך מחומש יהיו ד' תחת הא' השלישית ואז יהיו א ד יו שב למרובע לך אב"ד שהוא ערך כפול כמו שב א ג ט שב למשולש א ב ד שב לכפול א א א שב לשוה [192ב]
[196ב] [קעז ב] [] הסוג אשר בזה הפרק [] שני מינים אשר הראשון מורכב [] הפרק השלישי ואחר זאת החלוקה [] והיא כי המספר המוגבל יחלק אל [עודף] ושוה וגורע ואילו השלושה מינים יהיו [] פרק והשוה מחולק לשנים [] כולם שמונה מינים וזה צורתם [] וממרובע [] המין ראשון זוג הזוג שוה בכל צלע זוג מין שני זוג הנפרד ובכל טור שלשי זוג הזוג והנפרד מספר מוגבל רביעי מורכב נאהב נפרד מין חמשי בודד מרובע שישי עודף נאהב מספר שמיני שוה שביעי גורע מרובע [] מין הראשון שהוא זוג הזוג הנה הוא כל מספר הנחלק בחצי וכל חלק יהיה זוג עד שיבואו לשנים או לאחד המשל בזה לקחנו ק"ח נחלק אותו לחציים יהיה כל חלק ס"ד גם נחלק ס"ד יהיה כל חלק ל"ב וכן חצי ל"ב יהיו י"ו וחצי יו יהיו ח' וחצי ח' יהיו ד' וחצי ד' יהיו ב' והנה טעם קראו לזה המין זוג הזוג בעבור כי [] הנשאר בחלוקה יהיה זוג והנה תולדת זה המין הוא שתכפול ב' על ב' יהיו ד' וד' על ב' יהיו ח' וח' על ב' יהיו י"ו וי"ו על ב' יהיו ל"ב וכן כולם כמו שתראה בזה הצורה ^ והנה ערך ^ שקראו אותה סולם 197[א] והוא שמן הראוי כי עמו נעלה לידעת דרושים עמוקים ומהם מספר שוה ונאהב ומרובעים שוים כמו שתראה בע"ה קע"ח מל"ב ומכאן [] חלק מרנ"ד ורנ"ה חלק מ[] וק' חלק מאלף וי"ו וד' חלק מ[] וס"ד וא' חלק מכולו וכן תנהיג בידיעת [] כי מספר החלקים יהיו הוראות ומתגלגלים כמו [] עוד דרך אחרת ואם יש עוד בידי דרכים לכוין חלקי המכוון [] []דקת המכוונים בכאן זאת החקירה ואכוין לחקירה יותר עמוקה מן ולמעלה עוד היו שני משיגים לשוה והם שני דרושים עמוקים והוא גם כן דרך הדרוש הראשון הוא שיהיו שני מספרים מסוגלים לאהבה אשר [חלקי] להוציאם הנה האחד יהיה כמספר השני וחלקי השני כמספר הראשון [] הבודד הראשון אלה השני מספרים נאהבים והדרוש השני הוא שיהיו [] הוא א' בדרך מרובע מה שוה מכל הטורים בין באורך בין ברוחב בין הזה ועמו נוציא באלכסון ואמנם יסוגלו שבעה מהם לשבעה כוכבי לכת כל הבודדים ואבאר כל דרוש בפני עצמו אומר כי בזה אחר זה הדרוש הראשון הוא להוציא המספרים הנאהבים המסוגלים להוליד המכוונם לאהבה ואומר כי כל שני מספרים ואחר אשר בידך אשר החלקים השלמים מכל אחד יהיו כמספר חברו הבודד כופלתו והנה תמצא הראשונים בדרך אחד והאחרונים בדרך בשנים ועוד פעם אחרת ויסוד שניהם המספרים הכפולים הנקראים זוג הזוג אחר פעם עד ומהם נוציא הבודידים ומן הבודדים הנאהבים וראשונה שיצא המכוון אומר שנסדר מספרם כפולים שהם זוגי הזוגים מתחילין מן המשל בזה האחד כמה שתרצה ואחר קח א"ב יהיו ג' נגד ב' עוד קח רצינו המכוון שלושה כפולים מא' ועד ד' יהיו ז' נגד הכפול האחרון שלקח[ת] השלישי כי שהוא ד' עוד קח ד' כפולים מא' עד ח' יעלו ט"ו ותתנהו נגד הראשון שהוא האחרון שהוא ח' עוד קח ה' כפולים מא עד י"ו ויעלו ו' והשני שהוא ל"א נגד י"ו וכן ס"ג נגד ל"ב וכן קכ"ז נגד ס"ד וכן כ"ח ידועים ולהם דרך אחרת והנה תחילת [206ב] הבודדים בכאן הוא א' נכפלהו בד' ועל היוציא נוסיף ג' יהיו ל"א והוא בודד ממכוון תצ"ו כי בד' הכפלות שנכפול ל"א תציא תצ"ו וכן יצאו כל המכוונים עם תוספת שתי כפילות על הנמשך אחריו אחריו כי ו' הראשון יציא מכפל ג' ומשתי כפילות ז' יציא כ"ח ומד' כפילות ל"א יצא תצ"ו כי כפל ל"א הוא ס"ב וכפל ס"ב הוא קכ"ד וכפל קכ"ד הוא רמ"ח וכפל רמ"ח הוא תצ"ו והמכוון עוד לבדוק המכוון האחר שהוא ח' אלף קכ"ח נכפול הבודד שעבר שהוא ל"א על ד' יהיו קכ"ד ועם תוספת ג' יהיו קכ"ז נכפלהו ששה פעמים ותציא ח' אלף רכ"ח לבדוק האחר שהוא ק"ל אלף תתי"ו כפול הבודד שעבר שהוא קכ"ז על ד' יעלה תק"ח ועם ג' שהוספנו יהיו תקי"א והוא הבודד נכפלהו שמונה פעמים
207[א] קפח
[207ב] [] ויעלה י"ז [] בן הזוג השלישי כזה ו ט ב ז א [] [] הראשונים בדרך הנזכר נוציא השניים [] זוג הראשונים אמנם יש להם דרך אחרת כנזכר [] ואומר שתקח הכפולים הבאים אחר הכפולים יצאו הראשונים אשר אם הוא בן זוג הראשון שכבר נודע הראשון שיתכן להיות רפ"ד הנה תכפלהו על עצמו בתוספת [] בן זוג שני בתוספת שנים ואם הוא בן זוג שלשי בתוספת [] וכן בתוספת הכפולים וגרע מן העולה בכפל אחד והנשאר [יהיה] בודד כפלהו על הכפול הקודם שלקחת והיוציא יהיה בן זוג שני [ה]משל בזה נרצה להוציא בן זוג הנאהב הראשון אשר בידנו הנה זה הוא הדרך נקח כפול ח' ונכפלהו על עצמו בתוספת א' שהוא ט' יעלו ע"ב גרע מע"ב אחד ישארו עא והוא [בודד] כפול אותו על הכפול הקודם לו בטבע למה שלקחת שהוא ד' עלו קקפ"ד והוא בן זוג הנאהב הראשון והיו שניהם כזה 0 ב ב אמנם החלקים השלמים הם חמשה ד ח ב חצי קמב לא יותר והם חצי ורביעית וחלק מקעא רביעית עא וחלק מקמ"ב וחלק מרפ"ד ויהיה בזה חלק קע"א ד הצורה חלק קמ"ב ב משל שני לתשלום משל שני שעבר חלק רפד א ואומר כי להוציא בן זוג היוציא רפד השני מן הנאהב אשר במשל שני קח כפול י"ו ותכפלהו על עצמו בתוספת שנים שהוא י"ו על י"ח יעלו רפ"ח נגרע מהם אחד ישארו רפ"ז והוא בודד נכפול אותו על הכפול הקודם לו בטבע שהוא י"ח יעלו ב' אלפים 208[א] קפט
רצ"ו והוא בן [הזוג] [] משל שלישי לתשלום [משל שלישי ] ואומר כי להוציא בן זוג [השלישי] קח כפול ל"ב ותכפלהו על עצמו בתוספת [] על ל"ו יהיה העולה אלף קנ"ב נגרע [מהם] אחד [] קנ"א והוא בודד כפול אותו על הכפול הקודם לו [] שהוא י"ו יעלו י"ח אלפים תי"ו הוא בן זוג [] [] במשל שלישי ויהיו שניהם כזה ו ט ב ז [א] ועם זה די לדרוש הראשון והמשכל יבין ו א ד ח [א] הדרוש השני הוא שיהיו מספרי מרובע מה שוה מכל הטורים בין [באורך] בין ברוחב בין באלכסונים ואמנם יסוגלו שבעה מהם לשבעה כוכבי לכת ואומר כי תמונות אלה המספרים הם בלתי בעלי תכלית ומסגולותהם כי השבעה הראשונים הם מסוגלים לשבעה כוכבי לכת וראשונה אומר כי המספר יחלק [אל] זוג ואל נפרד והזוג יחלק אל זוג הזוג ואל זוג הנפ[רד] דף ס"א עד ואל זוג הזוג והנפר[ד] ובמקום אחר תמצא טעם השמות [] ס"ו כי זה האלה ואם יש להם חלוקות אחרות אין זה מקומן מקומו כן זה הפרק יחלק לשלושה סדרים אשר הסדר הראשון ידבר [על] מרובעי הנפרדים והסדר השני ידבר [] במרובעי זוג הזוג והסדר השלישי במרובעי זוג הנפרד וזוג הזוג והנפרד אם ירצה האל ואתחיל מספר דרך תולדות כי לא נמצא אתנו אלא שבעה מרובעים נקראים שבעה מרובעים
[מז1] [] וד' פשיט [] בשני דרכים [] הדרך הראשון הוא [] וג' רביעיות [] דינר נתן הי"ב דינ' [] שלשיות וזה סך כור אחד נכפלם על עשרה יהיו שי"ג נחלקם על ג' שהוא המורה יעלו קכ"ג די' ושליש דנר שהוא ד' פשי' והדרך השנית נתן הי"ב דנ' בפשיטי' ונוסיף עליהם הפשיט' ונכפול אלה הפשי' על הנשאל והעולה אם נרצה דנר' נחלקם על י"ב ויהיו די' והמשל הנה הסוחר קנה עשרה כורי [] חיטה לסך י"ב די' וד' פשיט' נתן הי"ב די' בפשטי' יהיו קמ"ד ועם ד' שהיה לנו יהיו קמ"ח וזה סך כור חיטה אחד נכפול קמ"ח על עשרה יהיו אלף ת"ף פשיט' שהם סך כל החטה ולעשותם דינ' נחלקם על י"ב יהיו קכ"ג די' וד' פשיט' ואם תרצה לעשות מקכ"ג די' פרחים תחלקם על סך הפרח ואם לטרי' על כ' ואם דוקאדש על סך הדוקאדו וכן לכל מטבע שתרצה דרך אחרת כפול שלמים על שלמים והנשברים גם על מה שקנית והכל יהיה שוה והמשל בזה כפול י"ב על עשרה הם ק"ך גם כפול ד' פשי' על עשרה הם מ' פשי' והם ג' די' וד' פשי' ועם ק"כ יהיו קכ"ג די' וד' פשי' כנז' שאלה אחרת ראובן קנה ע"ה משאור ע"ה משאות [] פאשטולי לס' ה' לטרין וז' די' וה' פשיט כל משא שאלתי סך הע"ה משאות תשובה נעשה סך 65[א] מז[1] [מז2] המשא [] ע"ה והוא [] תרצה שיהיו [] תרצה לטרי' חלק [] יהיו ליטרי' והמשל נעשה [] ק"ז די' נכפלם על [] הה' פשוט והם פשטי משא אחת נכפלם על ע"ה יהיו צ"ז אלפים תרע"ה והם פשיטי המכר כולו ונרצה לעשות מהם די' נחלקם על י"ב יהיו ח' אלפים קל"ט די' וי"א פשי' ועתה [] הרשות בידך לעשותם המטבע שתרצה מזהב ועתה נעשה מהם ליטרי' נחלקם על כ' יהיו ת"ו ליטר' י"ט די' ואם כן ע"ה משאות שוים [] ת"ו לטרי' י"ט די' י"א פשיטי' ואם כשהם פשיט' תרצה לעשות מהם לטרי' תחלק הפשי' על ר"ע יעלו [] ת"ו ליטרי' ונשארו רל"ט פשי' לחלק נחלקם על י"ב [] יעלו י"ט די' ונשארו י"א פשיט' וכן אם תרצה לעשות מן הפשי' מטבע אחר אם מכסף או מזהב תחלק הפשיט על פשיטי המטבע שתרצה וכן וכן תעשה בכל השאלות אשר בהם די' ופשי' כי יש בהם שנים דרכים אשר הדרך הראשון הוא שנעשה הכל פשי' ונכפלם על המכר והיוציא הם פשי' נחלקם על י"ב יהיו די' והמשל ראובן קנה ל"ב משאות ענבים לס' ח' די וט' פשי' נעשה הדי' פשיטי' בשנכפלם על י"ב יעלו צ"ו ועם הט' פשי' שהיו לנו יהיו ק"ה פשי' והם [] סך משא אחד נכפלם על ל"ב יעלו ג' אלפים ש"ס פשי' ולעשות מהם די' נחלקם על י"ב ועלו ר"ף די' והם סך הל"ב משאות הדרך השני ראובן קנה ל"ב משאות ענבים לס' ח' די' [65ב] [מח1] [] גם [] על י"ב יעלו [] שהוא סך הל"ב משאות [] שלא להאריך אומר [] והיוציא תחלק על י"ב [] השברים תלמוד זה בע"ה אחרת מן הדרך הראשון שתעשה כל מה שתרצה לכפול פשי' ותחבר עמהם הפשי' ואחר תכפול הפשי' על הנרצה והיוציא הם פשי' ואם תרצה לעשות מהם מטבע כסף תחלקם על סך פשי' המטבע שתרצה ואם תרצה מטבע זהב עשה הפשי' די' שתחלקם על י"ב וחלק היוציא על די' המטבע שתרצה והמשל רצינו לכפול ק"ב די' וג' פשי' על י"ד נעשה הדני' פשיט' בשנכפלם על י"ב יעלו אלף רכ"ב פשי' נחבר עליהם הג' יהיו אלף רכ"ז פשי' נכפלם על י"ד יהיו י"ז אלפים קע"ח וכולם פשי' נחלקם על י"ב * לעשותם די' יעלו אלף תל"א וששה פשי' והם די' ואם תרצה לעשות מהם פרחים תחלקם על סך הפרח ואם לטרי' על כ' וכן לכל מטבע שתרצה והדרך השני הוא שנכפול הדי' על הנרצה ושמרם כי הם די' וגם נכפול הפשי' על הנרצה ויהיו פשיטי' נחלקם על י"ב ויהיו די' אשר תחברם על הדי' השמורים והמשל כפלנו ק"ב די' על י"ד יעלו אלף תכ"ח די' ונשמור אותם גם כפלנו ג' פשי' על י"ד יעלו מ"ב פשי' נחלקם על י"ב יעלו ג' די' וששה נחברם על אלף תכ"ח יעלו אלף פשיטי' תל"א והם די' ועוד ששה פשי' 66[א] [מח2] משל [] [] בחציים יהיו הט' [] נחלק גם נעשה [] חציים כמו המחלק יהיו [] ג' אוקיות וט"ו חלקים מי"ט וזה הראוי לכל [] חלקים על י"ו שהם חלקי האוקיה נקראים אריאינסוש יעל[] נחלקם על י"ט ותציא בחילוק י"ב אריאינסוש ונשארו י"ב והם חלקי י"ט באריאינסו והנה עלה לכל פשוט ג' אוקיות י"ב אריאינסוש י"ב יטין מאריאינסו כזה והבחינה כפול מה שיציא למחצה שהוא אוקייה אחת וי"ד אריאינסוא וששה יטין י"ט פעמים יעלו ל"ו אוקיות שהם ג' ליטרי' כנז' משל אחר סוחר קנה ב' ליטרי סוקרי וחצי בסך ב' די' שאלתי סך כל ליטרה התשובה נחלק ב' די' על ב' וחצי לא תוכל נתן השלמים בשברהם יהיו הסוקרי ה' חציי ליטרה והב' די' כ"ד פשיט חלק כ"ד על ה' יעלה בחילוק ד' פשי' וד' חומשים לחצי הלטרה והבחינה נכפול ד' וד' חמשיות על ה' יעלו כ"ד פשי' אחרת סוחר קנה ד' ליטרין וחצי סוקרי בשני די' וט' פשיט' שאלתי סך הליטרה התשובה תן הכל בשברהם יהיו ט' חציי ליטרה והפשיט ל"ג נחלק ל"ג על ט' יבואו ג' פשיטי' ושני שלישי פשוט וזה ראוי לחצי הליטרה והבחינה כפול ג' ושני שלשים על ט' יעלו כ"ד פשיטי' וכן כל הדומה לזה משל בכפל שלמים ושברי שברים על שלמים ושברים כמו נ"ח [66ב] |