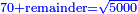Difference between revisions of "משנת המדות"
From mispar
(→Chapter Six) |
(→Chapter Six) |
||
| Line 860: | Line 860: | ||
|style="text-align:right;"|והלא התיכון הזה שהוא אורך ורוחב ועומק היה נראה מבחוץ על גבי הקרשים וצריך שיהיה הבריח הזה בנקובת עוביין של קרשים והרי אין שם עובי כלל אלא חצי אמה בלבד מחציו ולפנים הא כיצד אלא שיהו הנקובות כולן בתוך עובי חצי האמה הנשארה עם חצי הקומה לצד האוהל רביע אמה מיכן ורביע אמה מיכן והבריח מבריחן כדי שיהו ארבעה נאחזים מבחוץ וזה בפנים | |style="text-align:right;"|והלא התיכון הזה שהוא אורך ורוחב ועומק היה נראה מבחוץ על גבי הקרשים וצריך שיהיה הבריח הזה בנקובת עוביין של קרשים והרי אין שם עובי כלל אלא חצי אמה בלבד מחציו ולפנים הא כיצד אלא שיהו הנקובות כולן בתוך עובי חצי האמה הנשארה עם חצי הקומה לצד האוהל רביע אמה מיכן ורביע אמה מיכן והבריח מבריחן כדי שיהו ארבעה נאחזים מבחוץ וזה בפנים | ||
|- | |- | ||
| − | |5) | + | |5) We find the measure of the length of middle bar seventy cubits and a remainder and it is the root of five thousand cubits, which is irrational. |
| − | |style="text-align:right;"|<big>ה'</big> נמצא מקום אורך הבריח התיכון שבעים אמה ושירים והוא עיקר חמשת אלפים אמה ואינו יוצא בחשבון והשירים הזה חציו היה בזוית זה וחציו היה בזוית זה בירכתים ימה הא למדתה מידת העיקר מן התורה סימן לדבר הקודש עיקר כיוצא בו בשולחן שהיה תוכו עיקר צלעותיו שהן שלש [...] [וכן] במזבח הזהב שהיה תוכו עיקר חצי צלעותיו ויצאו להבן בחשבון הוי או' שהעיקר יש בו שהוא יוצא ויש בו שאינו יוצא אבל יוצא הוא בקרוב לו | + | :<math>\scriptstyle{\color{blue}{70+\rm{remainder}=\sqrt{5000}}}</math> |
| + | |style="text-align:right;"|<big>ה'</big> נמצא מקום אורך הבריח התיכון שבעים אמה ושירים והוא עיקר חמשת אלפים אמה ואינו יוצא בחשבון | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|והשירים הזה חציו היה בזוית זה וחציו היה בזוית זה בירכתים ימה הא למדתה מידת העיקר מן התורה סימן לדבר הקודש עיקר כיוצא בו בשולחן שהיה תוכו עיקר צלעותיו שהן שלש [...] [וכן] במזבח הזהב שהיה תוכו עיקר חצי צלעותיו ויצאו להבן בחשבון הוי או' שהעיקר יש בו שהוא יוצא ויש בו שאינו יוצא אבל יוצא הוא בקרוב לו | ||
|- | |- | ||
|6) ''the length of the courtyard shall be one hundred cubits'' [Exodus 27, 18] | |6) ''the length of the courtyard shall be one hundred cubits'' [Exodus 27, 18] | ||
Revision as of 19:05, 18 September 2019
[Chapter One] |
|
| [1)] Geometry is determined by four ways: quadrilateral, triangular, circle, and a segment of a circle. | בארבעה דרכים המדידה נקצבת ואלו הן המרבעת והמשלשת והעגלה והקשותה |
| This is the rule: | זה הכלל |
|
השנייה חצי הראשון |
|
והרביעית חצי השלישית |
|
ושאר האחרות משלבות זו בזו כסינר בבריות |
| 2) The quadrilateral [is recognized] by three ways: by the side, by the diagonal, and by the surface. | ב' המרובעת בג' פנים בצלע בחוט ובגג |
|
אי זו היא הצלע זה המחזיק דופנותיו של גג שנ' רבוע יהיה המזבח[1] |
|
והחוט זה המפסיק מזוית לזוית מן הקצה אל הקצה והוא היותר בארכו של גג |
|
והגג עצמו היא המשיחה |
| 3) The triangle [is recognized] by four ways: by the side, by the base, by the height, and by the surface. | ג' והמשלשת בד' פנים בשני בצלע בקבע בעמוד בגג |
|
אלו הן שני צלע זה השנ' משוכים ימין ויכין שנ' כי ימין ושמאל תפרוצי[2] |
|
והקבע זה ששני צלעים קבועים עליו שני אשר הבית נכון עליהם |
|
והעמוד זה חוט הכולל היורד מבין שני הצלעים לקבע והוא בזוית למקצעות המשכן |
|
והגג עצמו היא המשיחה |
| 4) The circle [is recognized] by three ways: by the perimeter, by the diameter, and by the surface. | ד' העגול בג' פנים בסביבה בחוט ובגג |
|
איזו היא סביבה הוא הקו המקיף את העגול שנ' וקו שלשים באמה יסב אותו סביב [3] |
|
והחוט זה המשוך משפה אל שפה שנ' משפתו אל שפתו[4] |
|
והגג עצמו היא המשיחה |
| 5) The segment of a circle [is recognized] by four ways: by the arc, by the chord, by the sagitta, and by the surface. | ה' והקשותה בד' פנים בקשת וביתר ובחץ ובגג |
|
איזו היא קשת החלק מן העגול שנ' כמראה הקשת אשר יהיה בענן[5] |
|
והיתר זה המחזיק בפי הקשת שנ' קשת דרוכה[6] |
|
והחץ הוא המשוך מאמצע הקשת לאמצע היתר שנ' כוננו חצם על יתר[7] |
|
והגג עצמו היא המשיחה |
| 6) How is the area measured by number? | ו' כיצד מודדין את המשיחה במניין |
|
אתה מחשב אחד על אחד זהו המשיחה והיא אמה על אמה |
|
נמצא הגג השוה בצלעים ובזויותיו הרי אתה מונה אותם מכל צד |
|
והטבלא העומדת שנים מכל צד והזויות שנים והמדידה מחזקת ד' מונים במדת הא' שהיא אמה בתוך אמה |
|
וכשהוא ג' מכל צד הרי היא בו' מינים במדת הא' |
|
וכן ד' על ד' |
|
וה' על ה' |
|
מכאן ואילך צא וחשוב במדה זאת ולמעלה |
| 7) For those that are less than 1 - this is how you divide them: | ז' והפחותין מן הא' כך אתה מחלקן |
|
אמה אחת לשני חוטין והמספיק את זה באמצע מצלע ימין לצלע ימין וכן מרום לתחת |
|
נמצא הגג חלוק בד' פסקאות |
|
ואתה מוצא חצי אמה על חצי אמה ומשיחה עצמה מחלק מ' אמה שהוא רבע מכל צד |
|
וכן שליש על שליש וחומש בתוך חומש בשוים ובחלופים |
|
מכאן ואילך צא וחשוב בשבורים במדה הזאת ולמטה |
| 8) It has already been said: | ח' כבר אמרו |
|
|
מחצה על מחצה הוא מרובע |
|
|
וכן שליש על שליש הוא מתשע |
| For these and for similar, whether they are equal or unequal. | בהן ובדומין להן אלא בשוין ובחלופים |
| How do they know that this is how it is? | מנים להם אב אהוא כך |
|
|
אתה מונה עשרה על עשרה הרי הן עולין ק' |
|
|
וחצי העשר הוא ה' |
|
|
ה' פעמים ה' הם כ"ה והוא רבע ק' |
|
ומעמד הי' בא' ומעמד הק' בי' ואלף בק' |
|
מכאן ואילך צא וחשוב בשבורים במדה האחדים |
| For integers it adds, and for fractions it subtracts. | אבל באחדים הוא מוסיף ובפחותים הוא גורע |
| 9) This is the rule: | ט' זה הכלל |
|
מחצה על מחצה חצי המחצה |
|
ושליש על שליש חצי השליש |
|
וכן מחצה על השליש חצי השליש |
|
וכן רביע על השליש רביע השליש |
| For these and for similar, whether they are equal or unequal. | בהן ובדומין להן בשוים ובחלופים |
Chapter Two |
פרק שני |
| [1)] The one who wants to measure the regular or irregular quadrilateral fields: | הרוצה למוד השדות המרבעות בשוים ובחלופים |
|
מצרף הארך על הרחב והעולה משניהם הוא הרחב המשיחה |
| 2) For the triangle - whether regular or irregular: | ב' ובמשלשת בין בשוים בין בחלופים |
|
מצרף העומד בחצי הקבע והעולה משניהם היא המשיחה |
| והרבה מבואותה בה | |
| 3) The circle how? | ג' העגולה כיצד |
|
מצרף החוט בתוך עצמו ומשליך ממנו שביעו וחצי שביעו והיתר היא המשיחה |
|
כמו חוט שהוא משוך לז' |
|
|
וצרופו מ"ט |
|
|
ושביע וחצי שביע הוא |
|
נמצאת המשיחה ל"ח ומחצה |
| 4) The segment how? | ד' הקשותה כיצד |
|
נותן החץ על היתר שניהם בבת אחת ומצרף אותה בתוך חצי החץ ומעמידן לצד וחוזר ולוקח חצי היתר וצורפו בתוך עצמו ומחלק על י"ד והעולה מוסיפו על העומד והעולה היא המשיחה |
| It has other ways. | ויש בה פנים אחרים |
| 5) The one who wants to measure the quadrilateral [body], whether regular or irregular, which has surface lengthwise, and breadthwise, six faces by number, six wings to each one [Isaiah 6, 2]: | ה' הרוצה למוד את הגג המרובע אפי' שהוא שוה אפי' הוא מחלף שהוא ארך ורחב הגג במניין שש פנים שש כנפים לאחד[8] |
|
מצרף ארך בתוך רחב בתוך העמק והעלה משלשתן היא משיחת הגג והוא הגוף |
| 6) If it were circular, or triangular, or any other shapes, as long as its height is straight and equal: | ו' ואם היה עגול או משולש או לכל מיני צדדין מלבד שיהיה עמקו ישר ושוה |
|
ממה מודד הגג במדד שלו במדה שאמרו ותדע המשיחה והמודע אותה מצרפו בתוך העומק הוא משיחת הגוף |
| 7) The conical, whose apex is sharp and base is planar, whether quadrilateral, or circular, or triangular: | ז' והמשוך ראשו חד וסופו ממוצע ואפי' מרובע או שיהיה עגול או משולש |
|
אתה מודד משיחת הגוף והשלך שני שלישי המשיחה ואחוז השליש אחר ואתה מצרפו בתוך הקומה והעולה הוא משיחת הגוף וראש ועד סוף |
| 8) The one who needs to measure the hill, or a spherical thing, as long as its walls are even from each side, as the hemisphere or its similar: | ח' הצריך למוד התל או דבר מקובה ובלבד שיהיו דופנותיו שוות מכל צד כחצי כדור או כדומה לו |
|
מצרף א' מן החוטין מן הקצה אל הקצה בתוך חצי האחד והעולה משניהם היא המשיחה |
| 9) [The text is unclear] Prism - the prism is either drawn to its upper base, and its upper base is sharp, or drawn to half its truncated base, or any that measures its bottom base and its truncated base, which is the truncated upper base. | ט' עמוד ובעמוד אם היה משוך לראשו וראשו חד או משוך לחציו הקובה או לכל שהוא מכין בסופו ובקטועו שהוא הקטוע הראש |
|
מוחלק זה מזה כשיעור הסוף ומורדו בחשבון האתרוג ומשליך הקטן מן החבל והנשאר הוא משיחת העמוד |
| 10) How it is measured? | י' כיצד משער |
|
כגון עמוד מרבע וסופו ד' אמות בתוך ד' אמות חסר ועולה חסר ועולה וראשו שתי אמות על שתי אמות רבוע וצריך אתה לידע כמה משיחתו וכמה קומתו |
|
וכבר נאמ' באתרוג אלא שזו קטוע |
|
ועדין אי אתה יודע כמה הוא העמוד עד שיכלה אחד מלמעלה |
| 11) In number you measure: as the measure of two from four so is the height of the prism, which is half the height. | י"א במניין אתה משערת מדת שתים מארבעה כן ארך העמוד שהוא חצי המעלה |
|
נמצא כל העמוד עד שיכלה הראש עשרים אמה ועד הקטופה י' אמות |
|
הא למדת שמדת שנים מן הארבעה כמדת הי' מן העשרים |
| 12) The one who needs to measure: takes a third of the sharp upper base and multiplies it by the bottom base, they are 5 and a third, multiplies it by 20, the result is 106 cubits and two thirds of a cubit, and puts them aside.
|
י"ב הצריך למוד אוחז שליש ראשו חד צורף בסוף והם ה' ושליש ומצרפו בתוך כ' אז הם עולים ק"ו אמות ושני שלישי אמה ומעמידן לצד אחד |
| Then, he takes a third of the product of the section, 2 by 2, which is a cubit and a third, and multiplies it by the ten upper cubits, the result is 13 cubits and a third.
|
וחוזר ואוחז שליש צרוף הקטופה ב' על ב' והוא אמה ושליש ומצרפו בתוך עשר אמות עליונות והם עולים י"ג אמה ושליש |
| Subtract them from the 106 and two thirds, [93] and a third remain, which is the [volume] of the truncated body.
|
והשלך מן ר"ו ושלישים נשתיירו שם ע"ט ושליש והוא מ"ב ומשליך אותם מן ק"ו ושלישים נשתיירו שם ש"ט ושליש והוא באת העמוד גוו הקטוע |
| If it were a circle: [multiply the diameter by itself], then subtract from it the seventh and half the seventh, and the remainder is the area. | ואם היה עגול השלך ממנו השביע וחצי השביע זה נשאר בו הוא |
Chapter Three |
פרק ג' |
| [1)] There are five ways of the quadrilaterals, and these are: | חמשה פנים יש במרובעות ואלו הן |
|
ישרה בצלעותיה ובזויותיה |
|
ב' ויש מי שהיא משונה בצלעותיה וישרה בזויותיה |
|
ג' ויש שהיא ישרה בצלעותיה ומשונה בזויותיה |
|
ד' ויש שהיא ישרה משונה בצלעותיה ובזויותיה ושני ארכן שוין לבד ושני רחבן לבד |
|
ה' ויש מי שהיא משונה בצלעותיה ובזויותיה כל עקר |
| 2) [Square] - the equal in sides and angles, which is it? | ב' השוה בצלעות ובזויות איזו היא |
|
כגון עשרה מן צד |
|
מצרף ארך על הרחב והעולה היא המשיחה והם ק' |
|
והצלע האחד הוא עקרה האחד |
|
ושני צלעותיה הם שני עקרה |
|
וכן ג' וכן ד' |
| 3) [Rectangle] - the unequal in sides and equal in angles: | ג' והמשונה בצלעותיה וישרה בזויותיה |
|
כגון ז' בשני צלע וששה בשני צלע |
|
מצרף ארך על רחב שהן מ"ח והיא המשיחה ישרה בצלע וישרה בקו |
| 4) [Rhombus] - the equal in sides and unequal in angles, which is it? | ד' הישרה בצלעותיה ומשונה בזויותיה איזו היא |
|
כגון ה' מכל צד ושני זויות צרים וב' זויות רחבים וב' חוטין מפסיקין זה את זה באמצע הא' משמנה והב' מששה |
|
והרוצה למוד מצרף הא' מן החוטין בתוך חצי חברו והעולה משניהם היא המשיחה כ"ד אמה כזה |
| 5) [Trapezium] - the unequal in sides and angles, the two lengths by themselves, the two breadths by themselves, and the angles are unequal - how it is calculated? | ה' המשונה בצלעות ובזויות ושני ארכן לבד ושני רחבן לבד והזויות עקומות כיצד ממחשבה |
|
אמה פוסקה שנים מזוית לזוית ומעמיד בשניים ומחשב אחד כל בפני עצמה כמדת המשולשת וכן היא המשיחה |
|
וכן אתה מודד חשבון המשנה בכל עקר וכל פסקה לשנים |
|
המרבעות המשונות עשה אותם משלישותיה המשונה בכל עקר כזה פסקה לשנים |
Chapter Four |
פרק ד' |
| [1)] There are three types of triangles: the right-angled, the acute-angled, and the obtuse-angled. | שלש מדות במשלשת ואלו הן הנצבה החדה הפסוחה |
| Which is the right-angled triangle? | איזו היא נצבה |
|
שני צדיה הקצורים מצורפים כל אחד בפני עצמו והוא שוה לראשון |
|
כגון ששה מצד זה ושמנה מצד זה |
|
והעולה מאלו בפני עצמן מאה ומזה בפני עצמן מאה |
|
והצריך למוד מן הקצורים בתוך חצי חברו או ח' בתוך ג' או ו' בתוך ה' והעולה היא המשיחה |
| 2) The angle that stands between the short sides is the right angle. | ב' והזוית שהיא עומדת בין הקצורים היא הנצבה |
| The [right-angled triangle] is half the unequal in sides and equal in angles [= Rectangle] | והיא חצייה של מרובעת שהיא משונה בצלעים וישרה בזויות |
| המבקש לחשבה בעמוד יחשוב כדרכו והוא ששני צלעותיה הקצורים כן הם שני צלעותיה עמודיה והם דומים סמוכים ישרים | |
| 3) | ג' והעמוד המשך מהם אל צד הארוך נופל והוא מקבע |
|
והרוצה למוד |
|
מצרף העמוד בתוך החצי הקבע והעולה מן החשבון היא המשיחה |
| 4) The acute-angled triangle how? | ד' החדה כיצד |
|
שני צלעותיה קצורים או השוים כל אחד ואחד מצורף בפני עצמה קבועים זה עם זה |
|
והצלע השני שהוא הקבוע מצורף בפני עצמו הצרוף הראשון ויותר מן האחרון |
| ויש מן החדה שצלעותיה ישרות | |
|
והרוצה למוד |
| מחשב אותה כנגד הקבע | |
| נמצא הזויות חדות כמדת הראשון כן מדת האחרון מן החדים צלעי | |
| 5) The one who wants to know the measure of the height in an equilateral triangle: | ה' הרוצה לדעת במדת העמוד בצלעות השוות |
|
מצרף את האחד מן הצלעות בתוך עצמו ומשליך המיעוט מן המרובה והנשאר הוא היסוד והנמצא הוא העמוד |
| 6) How it is measured? | ו' כיצד מונים |
|
|
עשרה על עשרה ק' |
|
|
וחצי הצלע השני שהוא ה' מצורף בפני עצמו כ"ה |
|
ומשליך הקטן מן הרב נשאר שם ע"ה והוא היסוד |
|
ועקרו ה' ושירים |
|
והצריך למוד |
|
מצרף העקר בתוך החצי הצלע התחתון והעולה מן המשיחה שהיא מ"ג ושירים |
| ז' שבעה פנים אחרות ממשולשות | |
| equilateral triangle | השוה בצלעותיה כל צלע וצלע |
| ראיה בפני עצמו את האמור של בזה ואת האמור של זה בזה | |
| והמבין בתפוח מצרף אחד מהם בפני עצמו שהם ק' ומשליך את הרבע שהוא כ"ה ונשאר ע"ה | |
| והצריך למוד מצרף ע"ה בתוך כ"ה שהם ג' רבעים ברבע כ"ה אחד והם עולים אלף ות"ת וע"ה ותופש את העיקר והוא המשיחה והוא מ"ג ושירים | |
| מכאן אתה מוצא שהעמוד של חצי הקבע ס"א נופל לעולם | |
| ח' הרי שהוצאת השוה וכן הדומה לו אבל חשבון חלופים אין לך קשת מהם בחשבון המשיחה והמדקדק בהם ישפיל ב' צלעים בין בעמוד עם הקבע | |
| 9) How it is measured? | ט' כיצד משער |
|
כגון משלשת חלופים שהיא חדה בזויות ט"ו מצד ראשון י"ד מצד שני י"ג מצד שלישי |
[Heron's Formula]
|
והצריך למוד מחזיק שלשתן בבת אחת עולים מ"ב |
|
ולוקח את המחצה ורואהו כמה הוא יתר על צד ראשון ומצרף המחצה על היתר שהוא כ"א בתוך ו' והם נעשים קכ"ו ומעמידו לצד |
|
וחוזר שנית ולוקח את המחצה ורואה כמה הוא יתר על צד שני ומצרף את היתר שהוא ז' בתוך קכ"ו הם הראשונים והם עולים ת"ת ופ"ב ומעמידו לצד |
|
וחוזר שלישית ולוקח המחצה ורואה כמה הוא יתר על צד שלישי ומצרף את היתר שהוא ח' בתוך ת"ת וכ"ב האחרים והם עולים ז' אלפים ונ"ו |
|
ועקרם פ"ד והם הם שיעור המשיחה |
| 10) The obtuse-angled triangle how? | י' הפסוחה כיצד |
|
צלעותיה הקצרים כל אחד מהם מצורף בפני עצמו ומוסיפין זה על זה |
|
והצלע הג' שהוא הקבע מצורף בפני עצמו |
|
הצירוף האחרון יתר מן הראשון |
|
כמו ה' מצד ו' מצד זה ט' מצד ז' |
|
נמצאת א' מן הזויות כסוחה ורחבה |
|
נמצא הראשון ס"א |
|
והאחרון פ"א |
| The one who needs to measure: | והצריך למוד |
|
מחשבה ברורה בעמוד עם הקבע |
|
ואם חפץ הוא בחשבון הצלעים והמחצה מחשבה |
|
מדה אחת לעולם |
Chapter Five |
פרק ה' |
| [1)] There are three types of circle: the sphere, the hemisphere, and the circle. | שלש מדות בעגולה ואלו הן התלויה התלולה והשפלה |
| Which is the sphere? | אי זו היא התלויה |
|
זו היא העומדת עקר ד' עגולה מכל צד כדור או שהיתה המשיחה כאבטיח שהיא העגולה לסביבותיה ובלבד עגולתה בשוה ארך ורחב ועמק במדה |
|
כיצד מודד |
|
מצרף את החוטין הא' בתוך חצי עצמו והעולה היא המשיחה והכפל אותה שהן קירותיה |
| 2) Which is the hemisphere? | ב' התלולה אי זו היא |
|
זו שעומדת כחצי התלויה כתל או כמו נקובה ובלבד שתהא שוה |
|
והצריך למוד |
|
מצרף אחד מן החוטין מן הקצה אל הקצה בתוך חצי האחד או בתוך חצי עצמו והעולה היא המשיחה |
| 3) Which is the circle? | ג' השפלה אי זו היא |
|
זו הנתונה על הארץ כשדה עגולה או צורה עגולה |
|
הצריך למוד |
|
מצרף החוט בתוך עצמו ומשליך ממנו שביעו וחצי שביעו והנשאר הוא המשיחה הוא גגה |
| ואם אתה חפץ לידע את הסיבוב חלילה חלילה | |
| הוא מצרף את החוט בתוך ג' ושביע ועולה כ"ב | |
| ואם אתה חפץ לשער את המשיחה | |
| אחוז חצי הסביבה שהיא י"א וצרף אותה בחצי החוט שהוא ג' וחצי ועולין ל'ה' ומחצה כן בראשונה כן באחרונה | |
| [4)] For he says: And he made the molten sea, ten cubits from brim to brim; round all about [Kings I, 7, 23], and its height 30 cubits, as it is said: and a line of thirty cubits did compass it round about. | הרי הוא אומר ויעש את הים מוצק עשר באמה משפתו אל שפתו עגל סביב[9] ושלשים אמה קומתו שנ' וקו שלשים באמה סב אתה סביב[10] |
| מה תלמוד וקו שלשים באמה וגומ' לפי שאמרו בני ארץ בעגולה שהסביבה מחזקת שלש פעמים ושבע כחוט יצא מהם שבוע אחד בעביו של ים לשתי שפתות ונותר ל' שם אמה יסוב אותו סביב ובשעור הזה אחד שוים הימים והמקואות והבורות בארך וברחב ועמק הא למדת מדה העגולה | |
| 5) | ה' ג' דברים נאמרו בקשותה ואלו הן הישרה החסרה והיתרה |
| Which is the semicircle? | איזו היא ישרה |
| כל שהיא עומדת בחצי העגולה לא חסר ולא יתר | |
|
החסרה כל שהיא פחותה מחצי העגולה |
|
והיתרה כל שהיא עודפת על חצי העגולה |
| זה הכלל כל שחצייה עומד פחות מחצי היתר שהיא חסרה | |
| וכל שחצייה יותר מחצי היתר בידוע שהיא יתרה | |
| 6) | ו' הרוצה למוד את היתר הישרה מצרף את היתר בתוך עצמו כולו ומשליך ממנו שביעו והנותר משליך חציו והנמצא הוא המשיחה |
| 7) | ז' והאחרות צריך אתה לידע כמה שיעור עגלתה |
| כיצד מצרף את חצי היתר בתוך עצמו והעולה מחלקו על החץ והנמצא מן החלוק מוסיפו מן החץ והעולה הוא חוט העגולה ואוחז חצי החוט הזה ומצרף אותו בתוך חצי החץ והעולה מעמידו על צד ורואה אם היתה הקשותה חסרה משליך חצה מחצי חוט העגולה ומצרף הנותר בתוך חצי היתר ופוחת אותו מן הצד והנשאר מן המשיחה י"ח ומשליך | |
| ואם היתה הקשותה יתרה משליך העגולה מחצה עצמה ומצרף את הנשאר בתוך חצי היתר ומוסיף אותו על הצד והעולה היא המשיחה כמדת הראשון כן מדת האחרון[11] |
Chapter Six |
פרק ו' |
| [1)]So he says: the length of the courtyard shall be one hundred cubits [Exodus 27, 18] | הרי הוא אומ' אורך החצר מאה באמה[12] |
| אם האורך היה חמשים בחמשים מה תל' לו' ואם הרוחב חמשים בחמשים מאה באמה מה תל' לו' | |
|
וצלעי החצר אינן שוים הא כיצד |
|
חמשים בחמשים לפני אהל מועד לצד מזרחי שבו נתון כיור ומזבח העולה |
|
ושלשה הנותרים חמשים בחמשים שהם דרום ומערב וצפון |
|
עשרים אמה לכל רוח והאוהל באמצע שלשים אורך ועשר רוחב צא מהן אמה אחת לעובין של קרשים |
| נותר שם תשע עשרה אמה לכל רוח נמצא עובין [של קרשים עם הקרקע אמה אחת חסר עוביו] של אדן | |
| 2) Nehemiah says: the sides of the Tent were found from the inside seventy whole cubits; from the outside, with the ground, seventy four cubits, minus the thicknesses of the sockets on each side; on the middle their thicknesses was seventy two cubits minus slightly from each side; mostly their thicknesses was seventy one minus slightly from each side, which is seventy cubits and a remainder; and the top of the planks was just seventy cubits. | ב' נחמיה אומ'[13] נמצאו צידי האוהל מבפנים שבעים אמות שלימות ומבחוץ עם הקרקע שבעים וארבע אמות חסר עובין של אדנים [לכל צד] ובאמצע עובין שבעים ושתי אמות חסר קימאה מכל צד וברוב עובין שבעים ואחת אמה חסר קימאה מכל צד שהוא שבעים אמה ושיריים וראשן של קרשים שבעים אמה בלבד |
|
הא למדתה שהיו עוביין של קרשים מבחוץ כלין ועולין עד הראש |
|
וכנגדן רוחבן של שני קרשים לעומת האורך היו חסירים ועולין לוכסון מיכן ומיכן לשני המקצועות כנגד עוביין של קרשים ובגביהן כלין ועולין כלפי ששה קרשים |
|
והיריעות פרוסות אורכן כנגד רוחבן של אוהל ורוחבן כנגד אורכו |
| 3) It is said: those two planks were smaller than all the planks as the measure of the third of the one | ג' נמצאת אומ' שהיו שני קרשים הללו קטנים מכל הקרשים כשיעור השליש מן האחד |
|
כמה היתה מידתן של קרשים |
|
אמה וחצי רוחב על עשר אמות אורך שהן עולין חמש עשרה אמה |
|
של שני קרשים |
|
אמה וחצי אמה מלמטן וחצי אמה מלמעלן שהן עשר אמות |
|
חצי אמה רוחב על עשר אמות אורך חמש אמות מבפנים וכן לצד השיני קרשים |
|
נשתייר שם אמה אחת מלמטן חסר עולה לוכסון כנגד עוביין של קרשים מבחוץ שבצפון ושבדרום שהן חמש מאות אחרות |
|
כן הוא אומ' והיו תואמים מלמטה[14] |
|
וכת' והיו שמונה קרשים[15] |
|
והיה המשכן אחד[16] לא חסר ולא יותר |
| 4) We find the thicknesses of the planks with half their height, that are against the hangings of the courtyard, their thicknesses there is half a cubit only, no more and no less, which is with half the [hanging?] from the outside 48 planks evenly. | ד' נמצא עוביין של קרשים עם חצי קומתן שהוא לעומת קלעי החצר עוביין שם חצי אמה בלבד לא חסר ולא יתר והוא עם חצי הכלא מבחוץ לארבעים ושמונה קרש בשוה |
| אם כן מה אני מקיים | |
|
והבריח התיכון בתוך הקרשים מבריח מן הקצה אל הקצה[17] |
| והלא התיכון הזה שהוא אורך ורוחב ועומק היה נראה מבחוץ על גבי הקרשים וצריך שיהיה הבריח הזה בנקובת עוביין של קרשים והרי אין שם עובי כלל אלא חצי אמה בלבד מחציו ולפנים הא כיצד אלא שיהו הנקובות כולן בתוך עובי חצי האמה הנשארה עם חצי הקומה לצד האוהל רביע אמה מיכן ורביע אמה מיכן והבריח מבריחן כדי שיהו ארבעה נאחזים מבחוץ וזה בפנים | |
| 5) We find the measure of the length of middle bar seventy cubits and a remainder and it is the root of five thousand cubits, which is irrational.
|
ה' נמצא מקום אורך הבריח התיכון שבעים אמה ושירים והוא עיקר חמשת אלפים אמה ואינו יוצא בחשבון |
| והשירים הזה חציו היה בזוית זה וחציו היה בזוית זה בירכתים ימה הא למדתה מידת העיקר מן התורה סימן לדבר הקודש עיקר כיוצא בו בשולחן שהיה תוכו עיקר צלעותיו שהן שלש [...] [וכן] במזבח הזהב שהיה תוכו עיקר חצי צלעותיו ויצאו להבן בחשבון הוי או' שהעיקר יש בו שהוא יוצא ויש בו שאינו יוצא אבל יוצא הוא בקרוב לו | |
| 6) the length of the courtyard shall be one hundred cubits [Exodus 27, 18] | ו' כמה הוא הקרוב לו כת' ארך החצר מאה באמה[18] וג' |
| מאה אורך על חמשים רוחב חמשת אלפים אמה ועיקרם שבעים ושיריים על שבעים ושיריים וכמה הן שבעים אמה ושבעה עשרונים מן האמה והמצרפן הן עולין ארבעת אלפים אמה ותשע מאות ותשעים ושמונה אמה מחצה חסר קימאה כיצד מצרפן שבעים אמה על שבעים אמה ארבעת אלפים ותשע מאות אמה ושבעים אמה על שבעה עשרנים ארבעים ותשע אמה ושבעה עשרנים על שבעים אמה ארבעים ותשע אמה אחרות ושבעה עשרנים על שבעה עשרנים חצי אמה חסר שלשים וששה חלק מן הסעורה שהאמה כולה ששים סעורה | |
| והסעורה ששים חלק ארבעה פנים לאחד | |
| כבר נצרפו ארבעה פעמים והמדקדק מוסיף במה הוא מוסיף שבעים אמה ושבעה עשרנים וחצי שתות [העשרון] והמצרפן הן עולין ארבעת אלפים ותשע מאות תשעים ותשע אמות ושני שלישי אמה ועשירית הסעורה [ורובע שתות מעשירית] הסעורה והמוסיף הוא עודף על הצירוף [סימן באדם ובה]מה יצאו כנים מן הבהמה |
München, Bayerische Staatsbibliothek, Cod. hebr. 36/11 (IMHM: f 1166), ff. 138v-140r (Istanbul, 1485)
- ↑ שמות כז, א
- ↑ ישעיה נד, ג
- ↑ דברי הימים ב, ד, ב
- ↑ דברי הימים ב, ד, ב
- ↑ יחזקאל א, כח
- ↑ ישעיה כא, טו
- ↑ תהילים יא, ב
- ↑ ישעיהו ו, ב
- ↑ מלכים א, ז, כג
- ↑ שם
- ↑ München: נשלם הפרק ובהשלמתו תמה משנת המדות בעזר יודע חידות
כלל גדול אמ' במדות מרבע ב' קוים כמרבע אלכסונה שורה נתונה נחלקת לב'
ניהוג כל השורה נצבת מחלקיה במרבע הנשאר מתוך המשלש אשר בתוך העגול אתה למד שברי העגול שבסביביו כשתעשה - ↑ שמות כז, יח
- ↑ תלמוד בבלי, שבת, פרק יא, דף צח, ע"ב
- ↑ שמות כו, כד
- ↑ שמות כו, כה
- ↑ שמות כו, ו
- ↑ שמות כו, כח
- ↑ שמות כז, יח
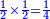
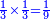
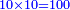
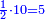
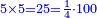
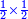 a half of a half
a half of a half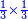 [a third] of a third
[a third] of a third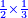 half a third
half a third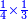 a quarter of a third
a quarter of a third![\scriptstyle\left(2r\right)^2-\left[\frac{1}{7}\sdot\left(2r\right)^2\right]-\left[\left(\frac{1}{2}\sdot\frac{1}{7}\right)\sdot\left(2r\right)^2\right]](/mediawiki/images/math/9/e/5/9e5ab12c81633c66db8fd67cb55a6053.png)

![\scriptstyle{\color{blue}{\left(\frac{1}{7}\sdot49\right)+\left[\left(\frac{1}{2}\sdot\frac{1}{7}\right)\sdot49\right]={\color{red}{10+\frac{1}{2}}}}}](/mediawiki/images/math/7/7/3/77395377a15f4b6e11b4251da8f1a93e.png)
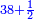
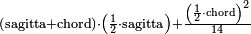
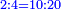
![\scriptstyle{\color{blue}{\left[\left(\frac{1}{3}\sdot4\right)\times4\right]\times20=\left(5+\frac{1}{3}\right)\times20=106+\frac{2}{3}}}](/mediawiki/images/math/a/9/b/a9be8753f9fa17a1625a5623e57df74c.png)
![\scriptstyle{\color{blue}{\left[\frac{1}{3}\sdot\left(2\times2\right)\right]\times10=\left(1+\frac{1}{3}\right)\times10=13+\frac{1}{3}}}](/mediawiki/images/math/5/5/f/55ff0d2c6bb543906be8a352033aaf46.png)
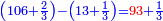

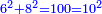
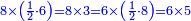
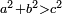
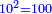
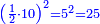
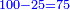 which is the radicand.
which is the radicand.
![\scriptstyle{\color{blue}{\left(\frac{1}{2}\sdot42\right)\times\left[\left(\frac{1}{2}\sdot42\right)-15\right]=21\times6=126}}](/mediawiki/images/math/b/9/0/b90431098477568be7a071d1c3a83bd2.png)
![\scriptstyle{\color{blue}{126\times\left[\left(\frac{1}{2}\sdot42\right)-14\right]=126\times7=882}}](/mediawiki/images/math/1/9/3/193bf55b6a2bfe9cfd4337139d0e88c8.png)
![\scriptstyle{\color{blue}{882\times\left[\left(\frac{1}{2}\sdot42\right)-13\right]=882\times8=7056}}](/mediawiki/images/math/1/8/1/1819119be3ee87c5208756f06980226a.png)

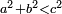
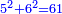
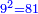
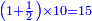
![\scriptstyle{\color{blue}{\frac{\left[\frac{1}{2}+\left(1+\frac{1}{2}\right)\right]\times10}{2}=10}}](/mediawiki/images/math/5/5/1/551a57cefa496076884cb126c301d554.png)