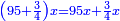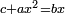Difference between revisions of "ספר האלזיברא"
From mispar
(→First Section: Preliminary Study of the Foundation of Algebra) |
|||
| Line 372: | Line 372: | ||
|style="text-align:right;"|הנה {{#annot:term|275|iHVo}}תאמר כי{{#annotend:iHVo}} מספר ל"א אשר אמרת ושרש מספר ת"ר מחוברים הוא מה שרצית לדעת | |style="text-align:right;"|הנה {{#annot:term|275|iHVo}}תאמר כי{{#annotend:iHVo}} מספר ל"א אשר אמרת ושרש מספר ת"ר מחוברים הוא מה שרצית לדעת | ||
|- | |- | ||
| − | |In order to learn it, a | + | |In order to learn it, a multiplication diagram is described |
|style="text-align:right;"|ולמען תשכיל {{#annot:term|949|mRXe}}אתאר לך{{#annotend:mRXe}} {{#annot:term|303|HN3t}}תמונת הכפל{{#annotend:HN3t}} | |style="text-align:right;"|ולמען תשכיל {{#annot:term|949|mRXe}}אתאר לך{{#annotend:mRXe}} {{#annot:term|303|HN3t}}תמונת הכפל{{#annotend:HN3t}} | ||
|- | |- | ||
| Line 564: | Line 564: | ||
|style="text-align:right;"|על כן יאמ' כי מכפל {{#annot:term|789|RmOb}}חסרון{{#annotend:RmOb}} בחסרון יעלה {{#annot:term|788|ef0g}}תוספת{{#annotend:ef0g}} | |style="text-align:right;"|על כן יאמ' כי מכפל {{#annot:term|789|RmOb}}חסרון{{#annotend:RmOb}} בחסרון יעלה {{#annot:term|788|ef0g}}תוספת{{#annotend:ef0g}} | ||
|- | |- | ||
| − | |In order to bring it closer to perception a | + | |In order to bring it closer to perception a multiplication diagram will be described as drawn in the previous multiplication figure: |
|style="text-align:right;"|ולקרבו אל ציורך אתאר גם לך תמונת הכפל {{#annot:term|545|a3Ly}}באופן אשר{{#annotend:a3Ly}} {{#annot:term|819|uW6o}}צירתי{{#annotend:uW6o}} תמונת הכפל הקודמת | |style="text-align:right;"|ולקרבו אל ציורך אתאר גם לך תמונת הכפל {{#annot:term|545|a3Ly}}באופן אשר{{#annotend:a3Ly}} {{#annot:term|819|uW6o}}צירתי{{#annotend:uW6o}} תמונת הכפל הקודמת | ||
|- | |- | ||
| Line 732: | Line 732: | ||
|style="text-align:right;"|חסר ד' מח' ישאר ד' ומספר ד' {{#annot:term|458|MC5r}}הנשאר{{#annotend:MC5r}} הוא המבוקש | |style="text-align:right;"|חסר ד' מח' ישאר ד' ומספר ד' {{#annot:term|458|MC5r}}הנשאר{{#annotend:MC5r}} הוא המבוקש | ||
|- | |- | ||
| − | |In order to know that it is so, a | + | |In order to know that it is so, a multiplication diagram is described, in which the numbers are multiplied according to the known method: |
|style="text-align:right;"|ולמען תדע כי כן הוא נתאר תמונת הכפל ונכפול המספרי' על הדרך הנודע | |style="text-align:right;"|ולמען תדע כי כן הוא נתאר תמונת הכפל ונכפול המספרי' על הדרך הנודע | ||
|- | |- | ||
| Line 2,338: | Line 2,338: | ||
|- | |- | ||
|figure, geometric illustration | |figure, geometric illustration | ||
| − | |style="text-align:right;"|תמונת, תמונה, תמונתנו | + | |style="text-align:right;"|תמונת, תמונה, תמונתנו |
| + | |- | ||
| + | |multiplication diagram | ||
| + | |style="text-align:right;"|תמונת הכפל | ||
|- | |- | ||
|segment | |segment | ||
Revision as of 15:51, 3 July 2019
ספר האלזיברא
לרבי שמעון מטוט
לרבי שמעון מטוט
Contents
Introduction |
|
| After the praise to God, the name of his praise is Glory | אחרי התהלה לאל אשר שם תהלתו תפארת |
| Illuminating beginning of any discussion and action | ופתח מאיר כל מאמר ומעשה |
| Blessed and exalted be his name a great exaltation | יתב' ויתע' שמו עלוי רב |
Definitions of algebraic terms |
|
| Starting by saying that one should know that the Christians regarded one of the expressions in the equation of the algebraic calculation as having an unknown number, and made it one whole thing in their calculations, which they called cosa | אתחיל ואומר ראוי שתדע כי הנוצרי' בחשבון האלזיברא יקחו חלק אחד מן השאלה בלתי ידוע מספרו ויעשוהו בחשבונם דבר אחד שלם ויקראוהו קוֹסָא |
|
רצונם להורות בזאת התיבה שני עניני' דבר אחד שלם ודבר נעלם לא ידענוהו |
Hence, the author also is doing the same in its translation, and calls it davar [= a "thing"]
|
וכן ולפי כן אעשה גם אני בהעתקתו זאת ובשם אקראנו דבר |
| They called the product of the thing by itself çenso | וכפל הדבר בעצמו יקראוהו צֵינְסו |
|
ושאלתי לחכמי דקדוק לשונם על הוראת זאת התיבה ואמ' לי כי היא מורה מספר קצוב רצונם בזה מספר קצוב לא ידענוהו |
Since the author did not find in his language one word that has this meaning, and he did not want to extend his words by using two words to indicate this meaning, or to invent a new word in the language, he called it by the Hebrew word merubaʼ [= a square] as it is.
|
ובעבור כי לא מצאנו בלשוננו תיבה אחת תורה זאת ההוראה ולא רציתי להאריך בדבורי להורות זאת הָהוראה בשתי תיבות או לחדש תיבה בלשון קראתיהו בשם מרובע כאשר הוא |
They called the square that is multiplied by it self çenso di çenso, and the author named it merubaʼ ha-merubaʼ [= a square of the square]
|
ולכפל המרובע בעצמו יקראוהו צֵינְסו דֵיצֵינְסו ואני אקראנו מרובע המרובע |
They called the cube number cubo.
|
ולמספר המעוקב יקראוהו קוּבוּ |
They called the cube cube cubo di cubo
|
ולמעוקב המעוקב יקראוהו קוּבוּ דֵיקוּבוּ |
The units of the number are called numeri, as their usage in all other places.
|
ולאחדי המספר נוּמְרִי כמנהגם בכל שאר המקומות |
First Section: Preliminary Study of the Foundation of Algebra |
|
| After the introduction, the teaching of its principles will be discussed that should be known and precede the study of algebra | ואחרי הקדמתי זאת אדבר בלמוד שרשיה צריכי' לדעתם ולהקדימם ללימודי חשבון האלזיברא |
| They will be explained as much as possible, starting by that: | ואבארם כפי אשר תשיג ידי וזה החלי |
|
א כאשר רצית לכפול שרש מספר ידוע בשרש מספר |
|
|
כפול המספר האחד על חברו ושרש העולה הוא מה שרצית |
|
ולקרבו אל ציורך אמשול משל |
|
|
כאשר רצית לכפול שרש מספר ה' בשרש מספר י"ב |
|
|
כפול ה' בי"ב יעלה ס' |
|
|
ושרש ס' הוא מה שרצית לדעת |
|
ב ואם רצית לכפול שרש מספר ידוע במספר ידוע |
|
|
עשה מן המספר מרבע בכפול אותו בעצמו אחר תכפול המרבע האחר בחברו |
|
המשל רצית לכפול שרש מספר ז' במספר ג' |
|
|
עשה מג' מרבע והוא ט' |
|
|
ועתה תכפול ז' בט' יעלה ס"ג |
|
|
ושרש ס"ג הוא המבוקש |
This is because the ratio of a square to a square is the same as the ratio of its side to its side multiplied. 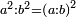
|
וזה מפני כי יחס מרבע אל מרבע כיחס צלעו אל צלעו שנוי ר"ל כפול |
|
ע"כ ראוי לכפול מרבע ז' בכפל ג' בעצמו |
| according to Euclid, Elements, Book VIII, proposition 11 | מתמונת י"א מן המאמ' השמיני לאיקלידיש |
|
ג ואם רצית לכפול שרש מעוקב ידוע בשרש מעוקב ידוע |
|
|
כפול המעוקב האחד בחברו ושרש המעוקב העולה הוא מה שרצית |
|
המשל רצית לכפול שרש מעוקב ה' בשרש מעוקב ו' |
|
|
כפול ה' בו' יעלה ל' |
|
|
ושרש מעוקב ל' הוא המבוקש |
|
ד ואם רצית לכפול שרש מעוקב ידוע במספר ידוע |
|
|
עשה מן המספר מעוקב וכפול המעוקב האחד בחברו ושרש המעוקב העולה הוא מה שרצית |
|
המשל רצית לכפול שרש מעוקב ה' במספר ג' |
|
|
עשה מן ג' מעוקב והוא כ"ז |
|
|
וכפול ה' בכ"ז יעלה קל"ה |
|
|
ושרש מעוקב קל"ה הוא המבוקש |
This is because the ratio of a cube to a cube is the same as the ratio of its side to its side cubed 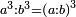
|
וזה מפני כי יחס מעוקב אל מעוקב כיחס צלעו אל צלעו משלש |
| according to Euclid, Elements, Book VIII, proposition 12 | מתמונת י"ב מהמאמ' הח' לאיקלידס |
|
ה ואם רצית לכפול שרש מעוקב ידוע בשרש מרובע ידוע |
|
עשה מן המרבע מעקב |
|
ומן המעקב מרבע |
|
ובזה המעשה השוית השרשים ועשית כל אחד מהם שרש מרבע מן שרש מעקב |
|
|
אח"כ תכפול אחד מהם בחברו ושרש מרבע מן שרש מעוקב העולה הוא מה שרצית |
|
ולמען תשכיל אמשול לך משל במספרי' בעלי שרש ואומ' רצית לכפול שרש מרבע ט' שהוא ג' בשרש מעקב ח' שהוא ב' |
|
|
וידוע כי מכפל ג' בב' יעלה ו' והוא המבוקש |
|
ולפי הדרך אשר זכרנו |
|
|
ראוי לעשות מן ט' מעוקב והוא תשכ"ט |
|
|
ומן ח' מרבע והוא ס"ד |
|
|
כפול ס"ד בתשכ"ט יעלה מ"ו אלפי' תרנ"ו |
|
|
והנה שרש מרבע מן שרש מעוקב מ"ו אלפי' תרנ"ו הוא המבוקש |
| To add a further explanation, the result is reduced to a number, which is possible since the numbers chosen in the example have roots: | ולהוסיף באור נשיב המבוקש אל מספר ונוכל עשוהו מפני כי המספרי' אשר לקחנו במשלנו הם בעלי שרש |
|
|
ונאמר שרש מעקב מ"ו אלפי' תרנ"ו הוא ל"ו ושרש מרבע ל"ו הוא ו' והנה מספר ו' הוא המבוקש כאשר אמרנו בתחלה |
|
מופת זה מובן למבין ממופתי הלמודי' הקודמי' |
|
ו ואם רצית לכפול שרש שרש מרבע ידוע בשרש שרש מרבע ידוע |
|
|
כפול המרבע האחד בחברו ושרש שרש העולה הוא מה שרצית |
|
המשל רצית לכפול שרש שרש מרבע ד' בשרש שרש מרבע ז' |
|
|
כפול ד' בז' יעלה כ"ח |
|
|
ושרש שרש מרבע כ"ח הוא המבוקש |
|
ז ואם רצית לכפול שרש שרש מרבע ידוע במספר ידוע |
|
|
עשה מן המספר מרבע ומן מרובעו מרבע וכפול האחד בחברו ושרש שרש העולה הוא מה שרצית |
|
המשל רצית לכפול שרש שרש מרבע ה' במספר ב' |
|
|
עשה מן ב' מרבע והוא ד' ומן ד' מרבע והוא י"ו |
|
|
כפול ה' בי"ו יעלה פ' |
|
|
ושרש שרש מרבע פ' הוא מה שרצית |
|
ח ואם רצית לכפול שרש מעוקב ידוע בשרש שרש מרבע ידוע |
|
עשה מן המעקב מרבע וממרובעו מרבע |
|
ומן המרבע עשה מעקב |
|
ובזה המעשה השוית השרשי' ועשית כל אחד מהם שרש שרש מרבע מן שרש מעקב |
|
|
אחר תכפול האחד מהם בחברו ושרש שרש מרבע מן שרש מעקב והעולה הוא מה שרצית לדעת |
|
המשל רצית לכפול שרש מעוקב ג' העולה בשרש שרש מעקב ד' |
|
|
עשה מן המעקב שהוא ג' מרבע והוא ט' ומן ט' מרבע והוא פ"א מרבע |
|
|
אח"כ תעשה מן ד' מעקב יהיה ס"ד |
|
|
כפול פ"א בס"ד יעלה ה' אלפים וקפ"ד |
|
|
ושרש שרש מרבע מן שרש מעוקב ה' אלפי' וקפ"ד הוא מה שרצית |
|
ט ואם רצית לכפול מספר ה' ושרש מספר ו' בעצמו |
|
|
עשה על הדרך הזאת כפול ה' בעצמו יעלה כ"ה |
|
|
עוד נכפול שרש ו' בעצמו יעלה ו' |
|
|
הרי ל"א שמרם |
|
|
עוד תכפול מספר ה' בשרש ו' פעמי' על הדרך הזאת |
|
|
ראשונה תכפול מספר ה' בשרש ו' ועשה מן ה' מרבע והוא כ"ה כפלהו בו' יעלה ק"נ והנה שרש ק"נ הוא העולה מכפל מספר ה' בשרש מספר ו' |
|
|
עוד תכפול שרש ק"נ במספר ב' מפני כי אתה רוצה אותו פעמי' ותעשה מן ב' מרבע והוא ד' כפול ד' בק"נ יעלה ת"ר |
|
|
הנה תאמר כי מספר ל"א אשר אמרת ושרש מספר ת"ר מחוברים הוא מה שרצית לדעת |
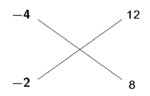
| In order to learn it, a multiplication diagram is described | ולמען תשכיל אתאר לך תמונת הכפל |
|
ואוציא מכל אחד מהמספרים אשר בתמונה קוים נמשכים בה אל המספרי' אשר ראוי לכפלו בהם |
|
|
|
|
י ואם רצית לכפול שרש ל"ב פחות מספר ג' בעצמו |
|
|
עשה ראשונה מן ג' מרבע והוא ט' |
|
|
ועתה תכפול שרש ל"ב בעצמו יעלה ל"ב |
|
|
עוד תכפול שרש ט' פחות בעצמו יעלה ט' יותר |
subtractive × subtractive = additive [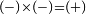 ] ]
|
שראוי לך שתדע שמכפל חסרון בחסרון יעלה יתרון כאשר אבאר |
|
|
על כן תחבר ט' בל"ב יעלה מ"א שמרם |
|
|
עוד תכפול שרש ל"ב בשרש ט' פחות פעמי' על דרך האמור למעלה יעלה שרש אלף קנ"ב פחות |
a number or a measure multiplied by a subtractive = subtractive [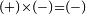 ] ]
|
לעולם מכפל איזה מספר או איזה שעור שיהיה בחסרון יעלה חסרון |
|
|
הנה תאמר כי מספר מ"א אשר שמרת פחות שרש אלף קנ"ב הוא המבוקש |
|
יא ואם רצית לכפול שרש מ"ח ושרש י' בשרש מ"ח פחות שרש י' |
|
|
כפול ראשנה שרש מ"ח בעצמו יעלה מ"ח |
|
|
עוד תכפול שרש י' יותר בשרש י' פחות יעלה י' פחות |
|
|
חסרם ממ"ח ישאר ל"ח |
|
|
עוד תכפול שרש מ"ח בשרש י' יותר יעלה שרש ת"פ יותר |
|
|
הרי בידך ל"ח ושרש ת"פ יותר |
|
|
עוד תכפול שרש מ"ח בשרש י' פחות יעלה שרש ת"פ פחות |
|
|
על כן תחסרנו מל"ח ושרש ת"פ יותר ישאר בידך מספר ל"ח והנה הוא המבוקש |
| Rules of multiplication for expressions of the type (a+b) and (a-b) | ועתה אתן לך כלל |
|---|---|
|
מכפל איזה מספר ביתרון יעלה יתרון |
|
ומכפל איזה מספר בחסרון יעלה חסרון |
|
ומכפל יתרון ביתרון יעלה יתרון |
|
ומכפל יתרון בחסרון יעלה חסרון |
|
ומכפל חסרון בחסרון יעלה יתרון כאשר אמרנו למעלה |
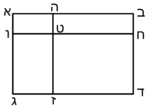
The explanation is accompanied by a geometric illustration for the example: 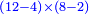
|
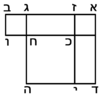
ולהראותך מופת זה נתאר תמונה ונביא דמיון במספר רצינו לכפול מספר י"ב פחות מספר ד' במספר ח' פחות מספר ב' |
| Geometric illustration | ונתאר תמונה כפי המשל הנז' |
|
|
|
|
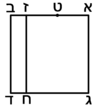
ויהיה שטח אבג"ד |
|
צלע א"ב ממנו י"ב מדות |
|
וצלע א"ג ממנו ח' מדות |
|
ונחסר מצלע א"ב חלק א"ה ממנו ד' מדות |
|
ומצלע א"ג נחסר צלע א"ו ממנו ב' מדות |
|
ונעביר מנקודה ה' קו ה"ז נכוחי לקוי א"ג ב"ד |
|
ומנקודת ו' קו ו"ח נכוחי לקו א"ב ג"ד |
|
ויחתכו שני אלה הקוים בתוך השטח על נקודת ט' |
|
ויחלקוהו לארבעה שטחים |
|
לשטח ט"ג ושטח ט"א ושטח ט"ב שלשתם יחד נקראם רושם התמונה |
|
ושטח ט"ד הרביעי ונקראהו המבוקש כי מספרי שבריו שוה למספר המבוקש העולה מכפל המספרי' הנז' כאשר אתה רואה |
| No need to further elaborate this proof. | אין צורך להאריך במופת זה אליך |
| Now the above mentioned numbers are multiplied by each other, according to the aforementioned method: | ועתה נכפול המספרי' הנז' אחד מהם בחברו כפי הדרך הנז' |
|
ונתחיל לכפול י"ב בח' יעלה צ"ו כמספר שברי שטח א"ד כלו |
|
עוד נכפול י"ב במספר ב' פחות יעלה כ"ד פחות כמספר שברי שטח ט"א ושטח ט"ב |
|
עוד נכפול מספר ח' במספר ד' פחות יעלה ל"ב פחות כמספר שברי שטח ט"א ושטח ט"ג |
|
ואם נחבר כ"ד ול"ב יעלה נ"ו כמספר שברי הרושם ושברי שטח ט"א מחוברי' |
|
ואם נחסרם משברי שטח א"ד כלו שהם צ"ו ישאר שטח ט"ד המבוקש פחות שטח ט"א שמרהו |
|
ותשלים לכפול המספרים הנז' ותכפול ב' פחות בד' פחות יעלה ח' כמספר שברי שטח א"ט |
|
וצריך אתה להוסיפו על השמור להשלים שטח ט"ד המבקש |
The conclusion: subtractive × subtractive = additive: 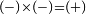
|
על כן יאמ' כי מכפל חסרון בחסרון יעלה תוספת |
| In order to bring it closer to perception a multiplication diagram will be described as drawn in the previous multiplication figure: | ולקרבו אל ציורך אתאר גם לך תמונת הכפל באופן אשר צירתי תמונת הכפל הקודמת |
|
|
|
|
יב ואם רצית לחבר שרש י"ב בשרש מ"ח דרך משל |
|
|
כפול י"ב במ"ח יעלה תקע"ו |
|
|
והנה שרש תקע"ו כ"ד |
|
|
קח שני דמיוניו יעלה מ"ח |
|
|
חבר אליו שני המרבעים שהם י"ב ומ"ח יעלה ק"ח והנה שרש ק"ח הוא המבקש |
Geometric proof (no figure is given): summing the sides of the squares  as two segments of one line as two segments of one line
|
מופת זה נחבר צלע מרבע י"ב וצלע מרבע מ"ח על יושר ויהיו שני חלקי קו אחד ישר |
| It was already clarified in Euclid, Elements, Book II, proposition 4: | וכבר נתבאר בתמונה הרביעית מן המאמר השני לאיקלידס |
When a straight line is cut randomly into two segments, the square on the whole line equals the sum of the two squares that are generated from the two segments plus twice the rectangle encompassed by the two segments. 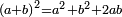
|
כי כאשר נחלק קו ישר לב' חלקים איך שקרה הנה מרבע הקו כלו שוה לשני המרבעים ההוים משני החלקים ולכפל השטח הנצב הזויות אשר יקיפו בו שני החלקים |
|
ועתה הנה כאשר כפלנו שני המרובעים זה בזה הנה שרש העולה שהוא תקע"ו הוא שוה לשטח הנצב הזויות ההוה משני החלקים |
|
וכאשר לקחנו שני דמיוניו עלה בידנו כפל השטח הנצב הזויות אשר יקיפו בו שני החלקים וכאשר חברנו אל זה שני המרובעים עלה בידנו מרבע הקו כלו ושרשו הוא המבקש |
|
יג ואם רצית לחבר שרש ח' בשרש י"ט |
|
כפול ח' בי"ט יעלה קנ"ב והנה אין לו שרש |
|
|
קח שני דמיוני שרש קנ"ב על הדרך הזאת כפול שרש קנ"ב במספר ד' יעלה שרש תר"ח שמרהו |
|
|
חבר שני המרבעים שהם ח' וי"ט יעלה כ"ז |
|
|
הנה תאמר כי שרש העולה מחבור כ"ז עם שרש תר"ח הוא המבקש |
| The proof of this teaching is clear from the preceding one | מופת זה הלמוד מובן מאשר לפניו |
|
יד ואם רצית לחבר שרש מעקב צ"ו עם שרש מעקב שכ"ד |
|
קח המספר היותר גדול שימנה שני אלה המספרי' והוא י"ב |
|
|
חלק אליו צ"ו יגיע בחלוק ח' |
|
|
עוד תחלק אליו שכ"ד יגיע כ"ז |
|
|
הנה צ"ו הוא ח' חלקים מכ"ז ממספר שכ"ד |
|
|
קח שרש מעקב ח' חלקים מכ"ז יהיה ב' שלישים |
|
|
הנה כי שרש מעקב צ"ו הוא ב' חלקי' מג' משרש שכ"ד |
|
|
חבר ב' וג' יעלה ה' |
|
|
הנה חברנו שני שרשי שני המעקבים ועלה ה' |
|
|
אח"כ תעשה מן ה' מעוקב משרש מעקב והוא קכ"ה |
|
|
והנה עלה בידינו מעקב חלקי שני שרשי שני המעקבים כאשר חוברו שמרהו |
|
ועתה לדעת שעור כל אחד מאלו הקכ"ה במדה שבה המעקב האחד צ"ו והמעקב השני שכ"ד נעשה על הדרך הזאת |
|
|
קח החלק האחד מהחמשה חלקי' הנז' והנה הוא חצי שרש מעקב צ"ו |
|
|
עשה מן חצי מעקב ויעלה בידך שמינית אחד |
|
|
הנה מעקב החלק האחד הוא שמינית מספר צ"ו שהוא י"ב |
|
|
כפול י"ב בקכ"ה אשר שמרת יעלה אלף ות"ק |
|
|
והנה שרש מעקב אלף ות"ק הוא המבקש |
| According to the method of leading in paths of uprightness to calculate this calculation in a wise way, the proof was demonstrated. | הנה לפי דרכי בהדריכי אותך במעגלי יושר[1] לחשוב זה החשבון בדרך חכמה הורתיך המופת |
|
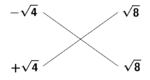
טו ואם רצית לחלק שרש ל על שרש ו' |
|
|
חלק ל' לו' יעלה ה' ושרשו הוא המבוקש |
Relying on [Euclid, Elements, Book VIII, proposition 11]: 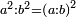
|
וזה מפני כי יחס מרובע אל מרובע כיחס צלעו אל צלעו שנוי |
|
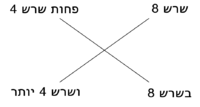
יו ואם רצית לחלק מספר כ' על שרש י' |
|
|
עשה מן כ' מרבע והוא ת' חלק ת' לי' יגיע מ' הוא המבקש |
| The argument of the following case is an explanation also for the two subsequent cases: | הנה אקדים למוד אחד אם תתבונן תבין ממנו מופתי שני הלמודי' הנמשכי' אחריו |
|
יז אם רצית לכפול שרש ח' פחות שרש ד' בשרש ח' ושרש ד' יותר דרך משל |
|
|
חסר ד' מח' ישאר ד' ומספר ד' הנשאר הוא המבוקש |
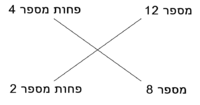
| In order to know that it is so, a multiplication diagram is described, in which the numbers are multiplied according to the known method: | ולמען תדע כי כן הוא נתאר תמונת הכפל ונכפול המספרי' על הדרך הנודע |
|
|
|
|
|
ונתחיל לכפול שרש ח' בשרש ח' יעלה מספר ח' |
|
|
עוד נכפול שרש ח' בשרש ד' יותר יעלה שרש ל"ב יותר |
|
|
הנה בידינו מספר ח' ושרש ל"ב שמרהו |
|
|
ונשלים חשבוננו ונכפול שרש ד' יותר בשרש ד' פחות יעלה מספר ד' פחות |
|
|
עוד נכפול שרש ח' בשרש ד' פחות יעלה שרש ל"ב פחות |
|
|
ועתה נפחות ממספר ח' ושרש ל"ב השמור מספר ד' ושרש ל"ב שראוי לפחות נשאר מספר ד' כאשר אמרנו והוא המבקש או נאמר כי שרש י"ו הוא המבקש |
|
יח ואם רצית לכפול שרש ח' פחות שרש ד' בשני שרשים אחרים יהיה העולה שרש ס"ד לא שרש י"ו |
|
|
חלק ס"ד לי"ו יגיע בחלוק ד' |
|
|
ועתה כפול בח' יעלה ל"ב |
|
|
עוד תכפלהו בד' יעלה י"ו והנה יעלה י"ו |
|
|
והנה בשרש ל"ב ושרש י"ו ראוי לכפלם ויהיה העולה שרש ס"ד וזה מובן בעצמו |
|
יט ואם רצית לחלק שרש ס"ד על שרש ח' פחות שרש ד' |
|
|
חסר ד' מח' ישאר ד' כפול ד' הנשאר בעצמו יעלה י"ו |
|
|
חלק ס"ד לי"ו יגיע ד' |
|
|
ועתה כפול ד' המגיע בחלוק בח' יעלה ל"ב |
|
|
עוד תכפלהו בד' אשר אמרת לפחות שרשו משרש ח' יעלה י"ו |
|
|
והנה שרש ל"ב ושרש י"ו מחוברים הוא המבוקש |
Relying on the rule according to which the dividend is equal to the product of the result of division by the divisor 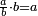
|
זה הלמוד הולך בדרך הקודם כי לעולם המספר המתחלק הוא שוה למספר העולה מכפל המספר העולה בחלוק במספר אשר אליו יתחלק המתחלק |
|
כ וכן אם רצית לחלק שרש ס"ד על שרש ח' ושרש ד' יותר |
|
|
חסר ד' מח' ישאר ד' כפול ד' הנשאר בעצמו יעלה י"ו |
|
|
חלק ס"ד לי"ו יעלה ד' |
|
|
ועתה כפול ד' המגיע בחלוק בח' יעלה ל"ב |
|
|
עוד תכפלהו בד' יעלה י"ו |
|
|
והנה שרש ל"ב פחות שרש י"ו הוא המגיע בחלוק |
| This teaching follows the technique of the previous teaching exactly. | הנך רואה כי זה הלמוד הולך בדרך הלמוד הקודם לא פחות ולא יותר |
Except that in the previous teaching the sought was  , while in the present teaching it was , while in the present teaching it was 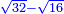
|
רק תחת אמרך בלמוד הקודם שהמבקש הוא שרש ל"ב ושרש י"ו מחברים בזה הלמוד אמרת שהוא שרש ל"ב פחות שרש י"ו |
|
כא ואם רצית לחלק מספר ח' על שרש ח' ומספר ב' יותר או על שרש פחות מספר ב' |
|
|
עשה ממספר ח' מרבע יהיה ס"ד |
|
|
וממספר ב' מרובע יהיה ד' |
| The manipulations lead to the two previous cases | והנה אתה עתה שבת אל שני הלמודים הקודמים לזה והקש על זה |
|
כב ואם רצית לחלק שרש מרבע ו' בשרש מעקב י' |
|
|
עשה מן ו' מעקב יעלה רי"ו |
|
|
ומן י' מרבע יהיה ק' |
|
ובזה המעשה השוית השרשים ועשית כל אחד מהם שרש מרבע מן שרש מעקב |
|
|
ועתה חלק רי"ו על ק' ויגיע ב' וד' חלקי' מכ"ה |
|
|
ושרש מרבע מן שרש מעקב ב' וד' חלקי' מכ"ה הוא המבקש |
|
כג ואם רצית לחלק שרש מעקב ה' בשרש שרש מרבע ח' |
|
|
עשה מן ה' מרבע מרבע ויהיה תרכ"ה |
|
|
גם תעשה מן ח' מעקב יהיה תקי"ג |
|
והנה השוית השרשים |
|
|
חלק תרכ"ה בתקי"ג ויגיע אחד וקי"ג חלקים מתקי"ג |
|
|
והנה שרש שרש מרבע מן שרש מעקב א' וקי"ג חלקים מתקי"ג הוא המבקש |
|
כד ואם רצית לגרוע שרש ח' משרש י"ח דרך משל |
|
|
כפול ח' בי"ח יעלה קמ"ד |
|
|
הוצא שרשו והוא י"ב |
|
|
קח שני דמיוניו ויהיו כ"ד |
|
|
חבר ח' וי"ח יהיו כ"ו |
|
|
חסר כ"ד מכ"ו ישאר ב' ושרש ב' הוא מה שרצית |
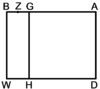
| To show the proof for this it should be taught that: | ולהראותך מופת על זה צריך אני להשכילך |
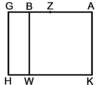
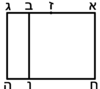
When a straight line is cut randomly into two segments, the sum of the squares on both segments equals twice the rectangle encompassed by both segments plus the square that is generated from the excess of the larger segment over the smaller segment.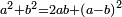 [Euclid, Elements, Book II, proposition 7] [Euclid, Elements, Book II, proposition 7]
|
כי כאשר נחלק קו ישר לשני חלקי' איך שקרה הנה מרבעי שני החלקי' שוים לכפל השטח הנצב הזוית אשר יקיפו בו שני החלקי' ולמרבע ההוה ממותר החלק הגדול על הקטן |
| Geometric illustration
|
|
|
ויהיה קו ישר עליו א"ב ויחולק איך שקרה על נקודה ג' |
|
עוד נחלק מן קו א"ג חלק א"ז ממנו שוה לקו ג"ב שהוא החלק הקטן |
|
וישאר קו ז"ג הוא מותר החלק הגדול על הקטן |
| Supposition: [2·(AG × GB)] + ZG2 = AG2 + GB2 | הנה אומר כי כפל השטח הנצב הזויות אשר יקיפו בו קוי א"ג ג"ב עם המרבע ההוה מן ז"ג מחברים יהיו שוים לשני המרבעים ההוים מן א"ג וג"ב כאשר יחברו |
Proof:
|
ונעשה מן קו א"ג מרבע אגד"ה |
|
ומן קו ג"ב מרבע גבח"ו |
|
ומנקודת ז' נמשיך קו ז"י נכחי לשני קוי א"ד ג"ה |
|
ונמשיך קו ו"ח על יושר עד אשר יפגיש קו ז"י על נקודת כ' |
|
ועתה מפני כי ג"ב שוה לקו א"ז |
|
יהיה קו ז"ב שוה לקו א"ג שהוא החלק הגדול |
|
וקו ב"ו לקו ג"ב שהוא החלק הקטן |
|
א"כ שטח ב"כ שוה לשטח נצב הזויות אשר יקיפו בו שני קוי א"ג ג"ב אשר הם שני חלקי הקו כלו |
|
וגם כן מפני כי קו א"ד שוה לקו א"ג |
|
וקו א"ז שוה לקו ג"ב |
|
יהיה שטח ז"ד גם כן שוה לשטח הנצב הזויות אשר יקיפו בו שני קוי א"ג ג"ב |
|
אם כן שני שטחי כ"ב וז"ד שוים לשטח לכפל השטח הנצב הזויות אשר יקיפו בו שני קוי א"ג ג"ב |
|
ושטח כ"ה הנשאר מן שני מרבעי שני החלקים הוא מרבע שוה למרבע ההוה מן ז"ג שהוא מותר החלק הגדול על הקטן |
|
מפני כי קו כ"ח שוה לקו ז"ג |
|
וקו ה"ח שהוא צלעו השני שוה לקו ז"ג |
|
גם כן מפני כי הוא מותר קו ג"ה שהוא שוה לחלק הגדול על קו ג"ח שהוא שוה לחלק הקטן |
|
הנה שני המרובעים ההוים מן א"ג וג"ב מחברים שוים לשני שטחי ב"כ וז"ד אשר כל אחד מהם שוה לשטח אשר יקיפו בו קוי א"ג ג"ב שהם שני חלקי הקו ולמרבע כ"ה שהוא שוה למרבע ההוה מן ז"ג שהוא מותר החלק הגדול על הקטן כאשר יחברו |
| Q.E.D. | וזה מה שרצינו לבאר |
| Numerical example: | ונעשה דמיון במספר |
|
ויהיה קו א"ג צלע מרבע שבריו י"ח |
|
וחלק א"ג ממנו צלע מרבע שבריו ח' |
|
והוא מרובע א"ה |
|
והנה כאשר כפלנו ח' בי"ח הנה שרש העולה שוה לשטח נצב הזויות אשר יקיפו בו שני החלקי' |
|
וכאשר לקחנו שני דמיוניו עלה בידינו כפל השטח הנצב הזויות אשר יקיפו בו שני החלקים |
|
וכאשר חסרנו מכ"ו שהוא שברי שני המרובעי' נשאר בידנו מרבע מותר החלק הגדול על הקטן |
|
ושרשו הוא המבקש |
Second Section: Algebra |
|
| By his awful name among the nations | ועתה בשם שמו בגוים נורא |
| The study of the algebraic calculation | אחל לדבר בלמודי חשבון האלזיברא |
| Explained briefly | ואבארם ביד שכלי הקצרה |
| Opens with a clarified introduction: | וטרם החילי אציע הצעה מבוארה |
Introduction |
|
|
ואומר ראוי שתשכיל ותדע כי יחס מרבע המרבע אל המעקבי' כיחס המעקב אל המרבע |
|
וכיחס המרבע אל הדבר |
|
וכיחס הדבר אל האחד |
| Explanation: | |
|
וזה מפני כי מספר האחדים אשר בשרש בדבר כמספר הדברי' אשר במרבע |
|
וכמספר המרבעי' אשר במעקב |
|
וכמספר המעקבי' אשר במרבע המרבע |
| This rules should be kept in mind, as they are needed for the proofs of the teachings below | וזאת ההצעה שמרה כי תצטרך אליה במופתי הלמודי' הבאי' אחריה |
| starting by that: | וזה החלי |
The six canonical equations |
|
|
א כאשר הדברים שוים לאחדים |
|
|
חלק האחדים לדברי' והמגיע בחלוק הוא הדבר זה מובן בעצמו |
|
שאלה רציתי לחלק מספר עשרה לשני חלקים כאשר חולק החלק האחד בחברו הגיע בחלוק ה' |
|
עשה על הדרך הזאת |
|
אמור החלק אשר אליו יתחלק הוא דבר שרש אחד |
|
והחלק המתחלק הוא בהכרח חמשה דברים שרשים כמספר אשר הגיע בחלוק |
|
הנה שני החלקי' מחברים הם ששה דברים והם שוים למספר עשרה |
|
וכפי הדרך הנזכר בזה הלמוד |
|
|
ראוי לחלק מספר עשרה לו' ויגיע בחלוק א' וב' שלישי' וככה הדבר |
|
ב כאשר המרבעים צינסי שוים לאחדים מספרי' |
|
|
חלק האחדים למרבעים ושרש המגיע בחלוק הוא הדבר שרש |
|
שאלה רציתי למצא מספר כאשר חסר ממנו שלישיתו מרבע הנשאר הוא מספר כ' |
|
עשה על הדרך הזאת |
|
אמור זה המספר אשר שני שלישיו הם שרש כ' הוא דבר אחד |
|
|
כפול ב' שלישיו בעצמם יהיו ד' תשיעיות מרבע המספר כלו אשר רציתי למצא |
|
ולפי הדרך הנז' בזה הלמוד |
|
|
ראוי לחלק מספר כ' לד' תשיעיות והמגיע בחלוק הוא מ"ה וככה מרבע כל המספר |
|
|
ושרשו הוא מה שרצית |
|
ג כאשר המרבעים שוים לדברים |
|
|
חלק הדברים למרבעים והמגיע בחלוק הוא הדבר |
|
זה הלמוד הולך בדרך הלמוד הראשון מפני כי יחס המרבע אל הדבר כיחס הדבר אל האחד כאשר אמרנו בהצעה |
|
וע"כ אם מרבע אחד ישוה לג' דברים דרך משל |
|
|
דבר אחד ישוה לג' אחדים בהכרח |
|
שאלה רציתי למצא מספר כאשר חסר ממנו שלישית הנשאר הוא שרש המספר כלו |
|
עשה על הדרך הזאת |
|
אמור ב' שלישי זה המספר הוא דבר אחד |
|
|
אם כן המספר אחד כלו הוא דבר אחד וחצי הנה דבר אחד וחצי הוא שוה למרבע אחד |
|
|
וכפי הדרך הנזכ' ראוי לחלק א' וחצי לאחד יגיע א' וחצי וככה הדבר שהוא שני שלישי המספר אשר רצית למצא |
|
|
אם כן המספר כלו הוא ב' ורביע |
|
ד כאשר הדברים והאחדים שוים למרבעים |
|
חלק הדברי' והאחדי' למרבעי' |
|
|
והדברי' המגיעי' בחלוק תחצה וכפול המחצית בעצמו והעולה הוסיפהו על האחדי' המגיעי' בחלוק והעולה קח שרשו והוסיפהו על מחצית הדברי' המגיעי' בחלוק והעולה הוא הדבר |
| Geometric illustration | ולהראותך זה לעין השכל נתאר תמונה ונביא דמיון במספר |
|---|---|
|
|
|
|
ויהיה קו א"ב עשר מדות |
|
וחלק איך שקרה על נקודת ז' |
|
ויהיה חלק א"ז ממנו ח' מדות |
|
ונעשה מן א"ב מרבע אבג"ד |
|
ונעביר בו מנקודת ז' קו ז"ח נכחי לקו א"ג וב"ד |
|
הנה בידינו שטח א"ח שהוא שמנה דברים במספר מדות קו א"ז |
|
כי כל מדה ממדות א"ז מחזקת בשטח א"ח דבר אחד |
|
ושטח ז"ד אשר שבריו כ' מדות |
|
שניהם יחד שוים למרבע א"ד |
|
ועתה הנה לפנינו קו א"ז ארכו ח' מדות כמספר הדברים |
|
ונחלקהו לחצאין על נקודת ט' |
|
והוסף עליו קו ז"ב |
|
וכבר נתבאר בתמונה הששית מן המאמר השני לאיקלידש |
|
כי השטח הנצב הזויות אשר יקיף בו הקו כלו עם התוספת והתוספת אשר הוא שוה לשטח ז"ד אשר תשבורתו מספר ב' במשלנו שניהם יחד שהם ל"ו שוים למרובע הקו המורכב מחצי הקו והתוספת אשר הוא קו ט"ב בתמונתנו |
|
על כן אם תקח שרש ל"ו שהוא ו' יעלה בידך מדת הקו המורכב מחצי הקו והתוספת שהוא קו ט"ב |
|
הוסף עליו מחצית הדברי' שהוא מספר ד' כמספר מדות קו א"ט יעלה י' במדת כל קו א"ב צלע המרבע והוא הדבר |
|
שאלה רצינו למצא מספר כאשר הוספנו עליו כ"ח יהיה שוה לשני דמיוני מרבעו |
|
עשה על הדרך הזאת |
|
אמור זה המספר הוא דבר אחד |
|
|
וכאשר הוספנו עליו כ"ח יהיה דבר אחד וכ"ח אחדים והם שוים לשני מרבעים |
|
והנה כפי הדרך הנזכר בזה הלמוד |
|
ראוי לחלק דבר אחד וכ"ח אחדים לשנים מספר המרבעי' ויגיע בחלוק חצי דבר וי"ד אחדים |
|
|
קח מחצית חצי דבר שהגיע בחלוק יהיה רביע דבר כפלהו בעצמו יהיה חלק אחד מי"ו הוסיפהו על י"ד מספר האחדי' המגיעי' בחלוק יעלה י"ד וחלק אחד מי"ו קח שרשו והוא ג' וג' רביעים הוסיפהו על מחצית הדברים המגיעים בחלוק שהוא רביע דבר יעלה ד' וככה הדבר |
|
ה כאשר המרבעים והאחדים שוים לדברים |
|
חלק הדברי' והאחדי' למרבעי' |
|
|
והיוצא בחלוק הדברי' תחצה ותכפול המחצית בעצמו והעולה תגרע ממנו המספר היוצא בחלוק האחדי' והנשאר זה שרשו והוסיפהו על מחצית היוצא בחלוק הדברי' והעולה הוא הדבר |
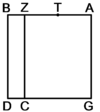
| Geometric illustration | ולהראותך מופת זה נתאר תמונה ונביא דמיון במספר |
|
|
|
|
ויהיה קו א"ג הישר ח' מדות |
|
ונחלקהו לב' חלקי' שוים על נקודת ז' |
|
ויהיה א"כ קו ג"ז ד' מדות |
|
עוד נחלקה לשני חלקי' בלתי שוים על נקודת ב' |
|
ויהיה ג"ב ב' מדות |
|
ונעשה מן קו א"ב מרבע אבה"ו' |
|
ונמשיך קו ה"ו עד ח' |
|
ויהיה קו ח"ה שוה לקו ח"ג |
|
גם נעביר קו ג"ה |
|
ולפי זה יהיה שברי שטח ג"ו י"ב מדות |
|
ועתה הנה לפנינו מרבע אבה"ו ושטח ג"ו שבריו י"ב מדות שניהם יחד שוים לשטח א"ה שבריו שמנה דברים כי כל מדה ממדות קו א"ג מחזקת בשטח א"ה דבר אחד |
|
והנה כפי מה שנתבאר בתמונה החמישית מן המאמר השני לאיקלידש |
|
יהיה המרבע ההוה מן א"ז שהוא ארבע מדות כמספר מחצית הדברים ומרובעו אם כן ידוע שהוא י"ו שוה לשטח ב"ה שהוא שוה לשטח הנצב הזויות אשר יקיפו בו שני החלקים הבלתי שוים ושבריו ידועים שהם י"ב ולמרבע ההוה מן ז"ב אשר הוא מה שבין שני החלקי' |
|
והנה נחסר שטח ב"ה שהוא י"ב מהמרבע ההוה מן א"ז שהוא י"ו ישאר המרבע ההוה מן ז"ב ידוע |
|
קח שרשו והוסיפהו על קו א"ז שהוא מחצית הדברי' יהיה קו א"ב ידוע שהוא צלע המרבע |
| Q.E.D. | וזה מה שרצינו |
|
שאלה סוחר אחד הלך לסחור ובידו קצבת מה והרויח ו' עוד חזר עם הקצבה והרויח כפי הערך שהרויח בפעם הראשונה ונמצא בידו כ"ז רציתי לדעת מספר הקצבה הראשונה |
|
עשה על הדרך הזאת |
|
אמור הקצבה הו' הראשונה היא דבר אחד |
|
|
ומזה הדבר הצליח ועשה דבר אחד וו' וכפי זה הערך מדבר אחד וו' עשה כ"ז |
|
|
הנה יחס דבר אחד עם דבר אחד וו' כיחס דבר אחד וו' עם כ"ז אחדים הנה לפנינו ג' שעורים מתיחסים |
|
וכבר נתבאר מתמונת י"ז מן המאמר הששי לאיקלידש |
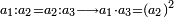
|
כי הכאת הראשון באחרון כמו הכאת האמצעי בדומה לו |
|
|
ועתה כפול דבר אחד שהוא הראשון בכ"ז אחדים שהוא האחרון יעלה כ"ז דברים עוד תכפול דבר אחד וו' שהוא האמצעי בעצמו יעלה מרבע אחד וי"ב דברים ול"ו אחדים |
|
|
ועתה חסר הי"ב דברים משני אלה השעורים השוים ישארו ט"ו שוים למרבע אחד ול"ו אחדים |
|
וכפי הדרך אשר אמרנו בזה הלמוד ראוי לחלק ט"ו מספר הדברי' ול"ו מספר האחדי' לאחד שהוא מספר המרבע ויגיע ט"ו דברי' ול"ו אחדי' |
|
|
אחר תחצה הדברי' יהיו ז' וחצי כפלם בעצמם. עלה נ"ו ורביע תגרע מהם ל"ו אחדי' ישאר כ' ורביע קח שרשו והוא ד' וחצי הוסיפהו על מחצית הדברים שהוא ז' וחצי יעלה י"ב וככה הדבר שהוא הקצבה הראשונה |
|
ו כאשר המרבעים והדברי' שוים לאחדים |
|
תחלק הדברי' והאחדי' למרבעי' |
|
|
והיוצא בחלוק הדברי' תחצה וכפלת את המחצית בעצמו והעולה הוסיפהו על היוצא בחלוק האחדי' ושרש העולה פחות מחצית הדברי' המגיעי' בחלוק הוא הדבר |
| Geometric illustration | ולהראותך מופת זה |
|
|
|
|
נתאר מרבע אגה"ד' |
|
ונחבר אליו שטח בגה"ו שבריו ידועים שוים למספר שני דברים דרך משל |
|
שניהם יחד ר"ל המרבע והשטח שוים למספר מ"ח |
|
וצלע ג"ב משטח גבה"ו שעורו ידוע והוא ב' מדות כמספר הדברי' |
|
ועתה לדעת קו א"ג צלע המרבע |
|
נחלק קו ב"ג לחצאין על נקודת ז' והנה לפנינו קו ג"ב נחלק לחצאין על נקדת ז' |
| ונוסף עליו קו ג"א | |
|
וכבר נתבאר בתמונה הששית מן המאמר השני לאיקלידש |
|
כי השטח הנצב הזויות אשר יקיף בו הקו כלו עם התוספת והתוספת אשר הוא שוה לשטח א"וֹ אשר שבריו ידועים שהם מ"ח ומרבע חצי הקו אשר תשבורתו ידוע שהוא א' שניהם יחד שהם מ"ט שוים למרבע הקו המרכב מחצי הקו והתוספת אשר הוא קו א"ז |
|
על כן אם תקח שרש מ"ט שהוא ז' ככה יהיה קו א"ז |
|
חסר ממנו חצי הקו שהוא ג"ז אשר הוא מדה אחת נשאר קו א"ג ידוע והוא ו' מדות |
| Q.E.D. | וזה מה שרצינו לבאר |
Equations of the higher degrees that can be reduced to the canonical equations of the second degree |
|
|
ז כאשר המעקבים שוים לאחדי' |
|
תחלק האחדים למעקבים וככה מספר אחדי המעקב |
|
|
ושרשו המעקבי' הוא הדבר |
|
זה מובן בעצמו |
|
ח כאשר המעקבי' שוים לדברים |
|
תחלק הדברים למעקבי' |
|
|
והיוצא קח שרשו המרבעי' וככה הדבר |
|
זה הלמוד הולך בדרך הלמוד השני |
|
מפני כי יחס המעקב אל הדבר הוא כיחס המרבע אל האחד |
|
וזה יובן מן ההצעה |
|
ועל כן אם היה מעקב אחד שוה לט' דברים דרך משל |
|
|
יהיה בהכרח מרבע אחד שוה לט' אחדים גם כן |
|
ט כאשר מרבעי המרבעים שוים לאחדים |
|
תחלק האחדים למרבעי המרבעים |
|
|
והיוצא קח שרש שרשו וככה הדבר |
|
גם זה מובן מעצמו |
|
י כאשר מרבעי המרבעים שוים לדברים |
|
תחלק הדברים למרבעי המרבעים |
|
|
והיוצא קח שרשו המעקבים וככה הדבר |
|
זה הלמוד הולך בדרך הלמוד הז' |
|
מפני כי יחס מרבע המרבע אל הדבר כיחס המעקב אל האחד |
|
וזה יובן מן ההצעה |
|
ועל כן אם מרובע מרובע אחד ישוה לכ"ז דברי' |
|
|
מעוקב אחד ישוה לכ"ז אחדי' בהכרח |
|
יא כאשר מרבעי המרבעים שוים למרבעים |
|
תחלק המרבעי' למרבעי המרבעים |
|
|
ושרש היוצא הוא הדבר |
|
זה הלמוד הולך בדרך השני |
|
מפני כי יחס מרבע המרבע אל המרבע הוא כיחס המרבע אל האחד |
|
וזה יובן מן ההצעה |
|
ועל כן אם מרובע מרובע ישוה לט' מרובעי' |
|
|
מרובע א' ישוה לט' אחדי' |
|
יב כאשר מרבעי המרבעים שוים למעקבים |
|
תחלק המעקבים למרבעי המרבעי' |
|
|
והיוצא הוא הדבר |
|
זה הלמוד הולך בדרך הלמוד הראשון |
|
מפני כי יחס מרבע המרבע אל המעקב הוא כיחס הדבר אל האחד |
|
כאשר הקדמנו בהצעה |
|
יג כאשר המעקבים והמרבעי' שוים לדברי' |
|
תחלק המרבעי' והדברי' למעקבי' |
|
|
והמעקבי' המגיעי' בחלוק תחצה וכפלת המחצית בעצמו והוסיפהו על הדברי' המגיעי' בחלוק ושרש העולה פחות מחצית הדברי' המגיעי' בחלוק הוא הדבר |
|
זה הלמוד הולך בדרך הלמוד הששי |
|
מפני כי יחס המעקב והמרבע כל אחד מהם אל הדבר כיחס המרבע והדבר כל אחד מהם אל האחד |
|
כמבואר בהצעה |
|
יד כאשר המעקבי' והדברי' שוים למרבעי' |
|
תחלק הדברי' והמרבעי' למעקבים |
|
|
והיוצא בחלוק המרבעי' תחצה וכפלת את המחצית בעצמו והעולה תחסר ממנו הדברי' המגיעי' בחלוק והנשאר קח שרשו והוסיפהו על מחצית המרבעי' המגיעי' בחלוק וככה הדבר |
|
זה הלמוד הולך בדרך הלמוד הה' |
|
מפני כי יחס המעקב והדבר כל אחד מהם אל המרבע כיחס המרבע והאחד כל אחד מהם אל הדבר |
|
זה יובן מההצעה |
|
טו כאשר המרבעי' והדברי' שוים למעקבי' |
|
תחלק המרבעי' והדברי' למעקבים |
|
|
והיוצא בחלוק המרבעי' תחצה וכפלת את המחצית בעצמו והעולה הוסיפהו על הדברי' המגיעי' בחלוק והעולה קח שרשו והוסיפהו על מחצית המרבעי' המגיעי' בחלוק וככה הדבר |
|
זה הלמוד הולך בדרך הלמוד הרביעי |
|
מפני כי יחס המרבע והדבר כל אחד מהם אל המעקב כיחס הדבר והאחד כל אחד מהם אל המרבע |
Epilogue |
|
| The end. | תם |
| This is the lesson of the algebraic calculations that was sought and found in the Christian books a little here, a little there. | זה הוא שעור מה שבקשתי ומצאתי מחשבונות ספר האלזיברא בספרי הנוצרי' זעיר שם זעיר שם[2] |
| Much of these teachings were made up by Moṭoṭ himself | ורבים מן הלמודים האלה בדיתים מלבי |
| Accusing Mordecai Finzi of writing a book without presenting any proofs | וראוי שתדע אחי הדבק היקר כמ"ר מרדכי יזייא וחפץ ה' ביי"א[3] בכמ"ר אברהם פינצי זלה"ה כי מחבר הספר כל הלמודים האלה בלי ראיות בספרו הביאם ואין אחד מני אלף[4] מן המעינים בו יודע דרך החכם ומאין הוציאם |
| Dedicating the book to Moṭoṭ's brother and his close friend R. Yehudah b. R. Yoseph b. Avigdor | ואני אחיך בראותי אותך ואת היקר מיודעי ורעי ר' יהודה בכמ"ר יוסף יצו"א בכמ"ר אביגדור זלה"ה נכספים לדעתו והיודע בקראנו אליו יודע צריך שיהיה יודע הדבר בדרכי ההיקש המופתי למלאת רצוניכם הוצרכתי להתבונן במופתים ולכתבם אליכם |
| The reasons for the briefness of the work: | אמנם קצרתי בהם לשתי סבות |
|
האחת להשעני ברוחכם הטובה רוח אלקים מרחפת על פני[5] כל חכמה |
|
הסבה השנית לרב טרדת לבי ובשרי בהרפתקי דעדו עלי ובחשבונות רבים בעסקי העולם |
| מכל מקום אם דבר מה יעלם לאחד מכם לקצורי וליאות רוחי בהאריך במופתים אמרתי הנני מוכן להוסיף בו באור | |
| ואין להאריך רק בהעתיר אל ה' ימלא כל משאלותיך[6] יפוצו מעיינותיך[7] מעייני הישועה[8] אמן | |
| כרצונך וכרצון אחיך הדבק הסר אל משמעתך[9] | |
| שמעון בכמה"ר משה יצ"ו בכמה"ר שמעון מטוט זלה"ה | |
| תם ונשלם | |
Notes |
|
Additional excerpt |
|
Additional word problem (appears in a few of the manuscripts containing the work):
|
שאלה אדם אחד החליף כ"ג פרחי' קצתם בליטרי' רומנייולי וקצתם בליט' מרקיאני והפרח שוה מהליט' מרקיאני הכפל ממה ששוה מהליט' רומניולי פחות רביע ליט' ונמצא בידו ל' ליט' רומניולי ול' ליט' מרקיאני רציתי לדעת כמה פרחי' החליף בליט' רומניולי וכמה פרחי' החליף בליט' מרקיאני וכמה שוה הפרח מהליט' רומניולי וכמה מהליט' מרקיאני |
|
עשה על הדרך הזאת |
|
אמור סכום הפרחי' אשר נחלפו בליט' רומניולי הוא דבר אחד |
|
כל אחד מהם נחלף במספר ליט' נעלם |
|
|
והיו ל' ליט' |
|
נשאר הסכום אשר נחלף בליט' מרקיאני הוא כ"ג פחות דבר אחד |
|
נחלפו בשני דמיוני מספר הליט' הנעלם הנזכ' פחות רביע ליט' אחד |
|
|
והיו גם כן ל' ליט' |
|
|
וכן תעשה תכפול כ"ג פחות דבר אחד בב' דמיוני המספר הנעלם פחות רביע אחד וכבר ידעת כי מכפל דבר אחד במספר נעלם אחד יעלה ל' אחדים |
|
ועתה תשלים כל אחד מאלה החלקים ותשוה אותם ותאמ' מ"ו מספרי' נעלמי' ורביע דבר שלימי' בלי חסרון שוים לצ"ה אחדי' וג' רביעי אחד |
|
|
ועתה תכפול מ"ו מספרי' נעלמי' ורביע דבר בדבר יעלה אלף וש"פ אחדים ורביע מרבע |
|
|
וגם כן תכפל צ"ה אחדי' וג' רביעי אחד בדבר יעלה צ"ה דברי' וג' רביעי דבר |
|
|
וכבר ידעת כאשר היו האחדים והמרובעים שוים לדברי' איך תדע מספר הדבר ומידיעת הדבר תדע הכל |
Appendix I: Glossary of Terms
Arithmetic Operations
| addition, additional segment | תוספת |
|
לחבר (ב), תחבר, נחבר, נחבר אליו, חבר אליו, חבר, חברנו אל, חברנו |
|
להוסיפו על, הוסיפהו על (ה), הוסף עליו, הוספנו עליו |
|
נוסף עליו |
|
העולה מחבור |
|
חוברו, יחברו |
|
מחוברים, מחברים |
|
יתרון, יותר |
|
תוספת |
| division | |
|
לחלק, חלק (ה), חלק אליו, תחלק (אליו / ה) |
|
חולק |
|
המתחלק, המספר המתחלק |
|
מספר אשר אליו יתחלק, החלק אשר אליו יתחלק |
|
המספר העולה בחלוק, מספר אשר הגיע בחלוק |
|
יגיע, יגיע בחלוק, המגיע בחלוק, הגיע בחלוק, המגיעים בחלוק, שהגיע בחלוק, היוצא בחלוק (ה), המספר היוצא בחלוק, היוצא |
|
המספר היותר גדול שימנה |
| doubling | |
|
כפלת |
|
קח שני דמיוני, קח שני דמיוניו, לקחנו שני דמיוניו |
|
שני דמיוני, ב' דמיוני ה |
|
פעמי' |
|
הכפל מ |
| to extract a root | קח שרשו, תקח שרש, הוצא שרשו |
|
קח שרשו המרבעי' |
|
to extract a cube root |
קח שרש מעקב, קח שרשו המעקבים |
|
to extract a root of a root, to extract a root of fourth degree |
קח שרש שרשו |
|
שרש (ה), שרש מספר, שרש המספר |
|
שרש מרבע, שרש מרובע |
|
שרש מעוקב, שרש המעוקב, שרש מעקב, שרשו המעקבי' |
| שרש שרש מרבע | |
| שרש שרש מעקב | |
|
שרש שרש מרבע מן שרש מעקב |
|
שרש מרבע מן שרש מעוקב, שרש מרבע מן שרש מעקב |
|
מספרי' בעלי שרש, בעלי שרש |
|
אין לו שרש |
| halving | |
|
תחצה (ה), קח מחצית |
|
מחצית ה, חצי ה |
| multiplication | הכאת (ה), כפל, כפל... בעצמו |
|
לכפלו ב, לכפלם, לכפול, לכפול המספרים, כפלנו, כפול, תכפול, תכפל, כפול ב, נכפול, כפלהו, תכפלהו |
|
שנוי |
|
כפול |
|
מספר העולה מכפל, העולה מכפל |
|
העולה, יעלה |
| בכפול אותו בעצמו, כפול... בעצמם/בעצמו, כפלהו בעצמו, כפלם בעצמם, כפלת את ה... בעצמו, כפלת ה... בעצמו | |
|
דמיוני (ה) |
| subtraction | |
|
לגרוע, תגרע (ממנו ה / מהם) |
|
חסר ממנו, חסרה מ, חסרם מ, תחסרנו מ, נחסר, נחסר מ, נחסרם מ, חסרנו מ, תחסר מ |
|
נפחות מ, לפחות |
|
חסר ממנו |
|
חסרון |
|
פחות |
| minus | פחות |
| plus | יותר |
| to square | עשה מן המספר מרבע |
| a² | מרבע המספר, מרבע |
| a⁴ | מרבע מרבע |
| to cube | עשה מן המספר מעוקב, עשה מעקב |
|
משלש |
Arithmetic Terms
| part | חלק, חלקים |
| parts of, fractions | חלקים מ, חלקי, חלק אחד מ |
| number | מספר |
|
מספר, מספר ה |
| value | מספר ה, מספרו |
| one | האחד |
| units | אחדים |
|
אחדי המספר |
|
מספר האחדים אשר ב, מספר אחדי ה |
| ratio | יחס, יחס ה... אל |
| proportional measures | שעורים מתיחסים |
Calculation Terms
| calculation | חשבונם, חשבוננו, החשבון, חשבונות |
|
לחשוב |
| measure, quantity, value | שעור, שעורים, שעורו |
| the sought | הוא מה שרצית, אשר רציתי למצא, המספר אשר רצית למצא |
| the sought | הוא המבוקש, המבוקש, מספר המבוקש, המבקש, הוא המבקש |
| excess | מותר |
| to result | יהיה, יהיו, ויהיו |
| to result | יעלה, עלה בידנו, יעלה בידך, עלה, יהיה העולה |
| result | העולה |
| procedure | המעשה |
| to use, to make | יעשוהו |
| to do, to operate, to proceed | עשוהו, תעשה, אעשה |
| to transform | לעשות מן, תעשה מן, עשית, עשה (מ / מן) |
| to remain | ישאר, ישארו, נשאר |
| remainder | הנשאר, הנשאר מן |
| to be left with | ישאר בידך, נשאר בידנו |
| to have in one's hand | בידך, הנה בידינו |
| to equalize | השוית ה, תשוה אותם |
| equal to | שוה ל, שוים ל, השוים, ישוה ל, יהיה שוה ל |
| to keep | שמרם, שמרת, שמרהו, שמרה |
| reserved | השמור |
| to give a numerical example | נביא דמיון במספר, נעשה דמיון במספר |
Algebraic Terms
| algebra | חשבון האלזיברא |
| algebraic calculations | חשבונות ספר האלזיברא |
| number, constant | נוּמְרִי, מספר |
| thing, root | דבר, דברים, קוֹסָא |
| square | צֵינְסו, מרובע, מרבע |
| square square x⁴ | צֵינְסו דיצֵינְסו, מרובע המרובע, מרבע המרבע, מרובע מרובע, מרבעי המרבעים |
| cube x³ | מספר המעוקב, מעוקב, המעקבים, קוּבוּ |
| cube cube, x⁶ | מעוקב המעוקב, קוּבוּ דֵיקוּבוּ |
| unknown number | המספר הנעלם, מספר נעלם, מספר ... נעלם, מספרי' נעלמי' |
| unknown | דבר נעלם |
| fixed number | מספר קצוב |
| terms of the equation | החלקים |
| part of an equation, algebraic expression | חלק אחד מן השאלה |
| to restore | תשלים |
Geometric Terms
| figure, geometric illustration | תמונת, תמונה, תמונתנו |
| multiplication diagram | תמונת הכפל |
| segment | חלק, החלקים, חלקי', החלק |
| segment of a line | חלקי קו אחד, חלקי הקו |
| segment… of it | חלק... ממנו |
| point | נקודה, נקודת |
| at point | על נקודת |
| line | קו, קוים |
| the whole line | הקו כלו |
| straight line | קו ישר |
| straight (line) | ישר |
| side | צלעו, צלע, צלע מרבע, צלע המרבע |
| length | ארכו |
| measure | מדה, מדת ה, מדות |
| surface | שטח, שטחים |
| gnomon | רושם התמונה |
| area | שברי, שבריו, מספרי שבריו, מספר שברי, שברי שטח, מספר שברי שטח, שברי הרושם, מספר שברי הרושם, תשבורתו |
| square | מרובע, מרבע, מרבעים, מרובע הקו |
| square on the whole line | מרבע הקו כלו |
| quadrilateral surface, rectangle | שטח הנצב הזויות, השטח הנצב הזויות, השטח הנצב הזוית, שטח נצב הזויות |
| encompassed by the two segments | אשר יקיפו בו שני החלקים |
| אשר יקיף בו הקו כלו עם התוספת והתוספת | |
| encompassed by the (two) lines | אשר יקיפו בו שני קוי, אשר יקיפו בו קוי |
| the difference between the two segments | מה שבין שני החלקי' |
| straight | על יושר |
| parallel to | נכוחי ל, נכחי ל, נכחי לקו |
| to draw | נעביר מ |
| to draw a line | נעביר קו |
| to draw a line from point | נעביר בו מנקודת ... קו |
| to intersect | יחתכו |
| to divide (surface) | יחלקוהו ל |
| to cut from line | נחלק מן קו |
| to construct a square from a line | נעשה מן קו... מרבע, נעשה מן ... מרבע |
| to extend a line | נמשיך קו |
| to meet a line | עד אשר יפגיש קו |
| line is cut into | נחלק קו ישר ל |
| to cut randomly at point | חלק איך שקרה על נקודת |
| to be cut randomly at point | יחולק איך שקרה על נקודה |
| to halve it at point | נחלקהו לחצאין על נקודת, נחלקהו לב' חלקי' שוים על נקודת, נחלק קו ... לחצאין על נקודת |
| to be halved at point | נחלק לחצאין על נקדת |
| to cut into two unequal segments at point | נחלקה לשני חלקי' בלתי שוים על נקודת |
| unequal segments | החלקים הבלתי שוים |
| to draw | צירתי |
Logical Terms
| to say, to state | אומר (כי), אומ', אמור, נאמר, אמרנו (ב), נאמר כי, תאמר כי, אמרת ש, ותאמ', יאמ' כי, אמרתי |
| to say, to tell | ואמ' לי |
| saying | אמרך |
| אשר אמרת ל | |
| to explain, to demonstrate | אבארם, אבאר |
| to be explained, to be clarified | נתבאר (ב / מ ... כי) |
| as clarified | כמבואר ב |
| clear, clarified | מבוארה |
| Q.E.D; this is what we wanted to explain | וזה מה שרצינו לבאר, וזה מה שרצינו |
| להוסיף באור, להוסיף בו באור | |
| to know (that) | לדעתם, לדעת, לדעתו, תדע (כי / ש) |
| knowing | מידיעת ה |
| לא ידענוהו | |
| וכבר ידעת כי, וכבר ידעת | |
| יודע, יהיה יודע ה | |
| the Knower | היודע |
| it is known that | ידוע (כי / ש) |
| to understand | תבין ממנו |
| to be clear from | יובן (מ / מן) |
| clear, understandable | מובן ל |
| מובן מאשר לפניו | |
| clear by itself, understandable by itself | זה מובן בעצמו, זה מובן מעצמו |
| one who understands | מבין |
| to give an example | אמשול |
| example | משל, המשל, דרך משל, משלנו |
| to learn, to become wise | תשכיל |
| to teach | להשכילך כי |
| to deduce, to conclude | הקש על זה |
| by analogy | בדרכי ההיקש |
| way, method, technique | דרך (ה), דרכי |
| to operate according to this way | עשה על הדרך הזאת, נעשה על הדרך הזאת |
| according to the known way | על הדרך הנודע |
| על דרך האמור למעלה, כאשר אמרנו למעלה, כאשר אמרנו, על דרך | |
| according to the abovementioned method | כפי הדרך הנזכר, ולפי הדרך הנז', וכפי הדרך אשר אמרנו |
| teaching | למוד, הלמודים, זה הלמוד, למודי, בזה הלמוד |
| studying | ללימודי |
| proof, argument | מופת, מופת זה, מופתי (ה), במופתים |
| to demonstrate, to show | להראותך זה, להראותך מופת זה, הורתיך המופת, ולהראותך מופת על זה |
| demonstrative | המופתי |
| manner, way | באופן אשר |
| speech, discussion | דבורי |
| to discuss, to speak | לדבר ב, אדבר ב |
| reason | הדבר |
| reason | סבה, סבות |
| meaning, sense | עניני' |
| conception, perception | ציורך |
| evidence, proof | ראיות |
| principles | שרשיה |
| question | שאלה |
| to ask | שאלתי ל |
| rule | כלל |
Philosophical Terms
| wisdom | חכמה |
| path of wisdom | בדרך חכמה |
| wise | החכם |
Economic Terms
| trader | סוחר |
| to trade | לסחור |
| to have, at his disposal | בידו, נמצא בידו |
| amount | הסכום, סכום ה |
| amount | קצבה, קצבת |
| to earn | הרויח |
| value, price | הערך (מ) |
| a man | אדם אחד |
| to exchange | החליף (ב) |
| peraḥim | פרח, פרחי' |
| liṭra | ליטרי', ליט' |
| of Rome | רומנייולי, רומניולי |
| of Marciana | מרקיאני |
| to be worth of | שוה מ, שוה ה... מה... |
| to be exchanged | נחלפו ב, נחלף ב |
Literary Terms
| chapter | מאמר, מאמ' |
| book | ספרי ה, ספרו |
| author | מחבר הספר |
| introduction | הקדמתי |
| translation | בהעתקתו |
Linguistic terms
| grammarians | חכמי דקדוק |
| language | לשונם, לשוננו, בלשון |
| word | תיבה, תיבות |
General Terminology
| .א.ר.כ • | |
|---|---|
| to elaborate, treat at length, lengthen | להאריך (ב), בהאריך ב, להאריך |
| .ב.ו.א • | |
| to bring, to present | הביאם |
| .ב.ק.ש • | |
| to seek | בקשתי |
| .ה.י.ה • | |
| let there be | ויהיה, יהיה |
| generated from | ההוה מ, ההוה מן, ההוים מ, ההוים מן |
| .ה.ל.כ • | |
| to go | הלך ל |
| following, in accordance with | הולך ב |
| .ז.כ.ר • | |
| to note, to mention | זכרנו |
| לפי הדרך אשר זכרנו, על הדרך הזאת, כפי הדרך הנז' | |
| .ח.ד.ש • | |
| to invent | לחדש |
| .ח.ז.ק • | |
| to occupy, tohold | מחזקת ב |
| .ח.ל.ל • | |
| to start, to begin | אחל, החילי, החלי |
| .י.כ.ל • | |
| to be able | נוכל |
| .י.צ.א • | |
| to draw | אוציא מ |
| to derive, to draw | הוציאם |
| .י.צ.ע • | |
| to propose, to offer | אציע |
| explanation, introduction | הצעה |
| .י.ר.ה • | |
| to signify, to mean | להורות |
| meaning | הוראת, ההוראה |
| to indicate | מורה, תורה |
| .ל.ק.ח • | |
| to take | קח, לקחנו, יקחו |
| .מ.צ.א • | |
| to find | למצא, מצאנו ב, מצאתי |
| .צ.ר.כ • | |
| should | צריכי', צריך אתה ל, צריך אני ל, צריך ש |
| to have to | הוצרכתי ל |
| to need it | תצטרך אליה ב |
| no need | אין צורך |
| .ק.ד.מ • | |
| to precede | להקדימם, אקדים, הקדמנו (ב) |
| .ק.ר.א • | |
| to name, to denote | יקראוהו, אקראנו, בשם אקראנו, קראתיהו, נקראם, נקראהו |
| .ר.א.ה • | |
| to see | רואה (כי), בראותי אותך |
| .ר.צ.ה • | |
| meaning | רצונם |
| to wish | רציתי (ל), רצית ל, רצינו ל, רוצה |
| as one wishes | כרצונך, כרצון |
| .ש.ו.ב • | |
| to return | שבת אל |
| to convert, to transform | נשיב |
| .ש.ל.מ • | |
| to finish | תשלים, נשלים |
| to complete | להשלים |
| complete | שלימי' |
| whole | שלם |
| .ת.ח.ל • | |
| to start, to begin | אתחיל, נתחיל |
| should | ראוי ש, ראוי ל |
| Christians | הנוצרי' |
| usage, custom | כמנהגם |
| place | מקומות |
| as much as one can | כפי אשר תשיג ידי |
| to bring closer | לקרבו אל |
| it is, the result is | הרי |
| to describe | נתאר, אתאר לך, אתאר |
| drawn | נמשכים |
| subsequent, following | הנמשכי' אחריו |
| to give | אתן לך |
| intellectual vision | לעין השכל |
| by the measure that | במדה שבה |
| guidance | בהדריכי |
| to observe, to look | להתבונן, תתבונן |
| exactly, no more and no less | לא פחות ולא יותר |
| to return | חזר |
| to succeed, to make profit | הצליח |
| its similar | דומה לו |
| to be finished, to end | תם |
| lesson | שעור |
| a little here, a little there | זעיר שם זעיר שם |
| to devise | בדיתים |
| of one's own heart | מלבי |
| to cleave | הדבק |
| to longed for | נכספים ל |
| precious | היקר |
| reader | מעיינים בו |
| companion, corresponding | חברו |
| brother | אחי, אחיך |
| friend | מיודעי |
| friend | רעי |
| to call upon | בקראנו אליו |
| to write | לכתבם אליכם |
| to abbreviate | קצרתי בהם |
| brevity | קצורי |
| relying on | להשעני ב |
| in any case | מכל מקום |
| unknown, hidden | יעלם |
| prepared, ready | מוכן ל |
| should not | אין ל |
| Euclid | איקלידיש, איקלידס |
| Elements II.4 | תמונה הרביעית מן המאמר השני לאיקלידש |
| Elements II.6 | תמונה הששית מן המאמר השני לאיקלידש |
| Elements VI.17 | תמונת יז מן המאמר הששי לאיקלידש |
| Elements II.5 | תמונה החמישית מן המאמר השני לאיקלידש |
| Mordecai Yaḥya the son of Abraham Finzi | כמ"ר מרדכי יזייא בכמ"ר אברהם פינצי זלה"ה |
| R. Yehudah b. R. Yoseph b. Avigdor | ר' יהודה בכמ"ר יוסף יצו"א בכמ"ר אביגדור זלה"ה |
| Simon b. Moses b. Simon Moṭoṭ | שמעון בכמה"ר משה יצ"ו בכמה"ר שמעון מטוט זלה"ה |
| helplessness of the mind | ביד שכלי הקצרה |
| paths of uprightness | במעגלי יושר |
| one out of a thousand | אחד מני אלף |
| to fulfill desires | למלאת רצוניכם |
| good spirit | רוחכם הטובה |
| worldly affairs | עסקי העולם |
| trouble of the heart and body | טרדת לבי ובשרי |
| the adventures that came upon me | בהרפתקי דעדו עלי |
| spiritual exhaustion | לאות רוחי |
| שם תהלתו תפארת | |
| praising God | התהלה לאל, תהלתו |
| ופתח מאיר כל מאמר ומעשה | |
| יתב' ויתע' שמו עלוי רב | |
| by his awful name among the nations | בשם שמו בגוים נורא |
| spirit of God hovered over the face of | רוח אלקים מרחפת על פני |
| God's purpose shall prosper in his hand | וחפץ ה' בייא |
| entreat the Lord | בהעתיר אל ה' |
| may the Lord fulfill all your requests | ימלא כל משאלותיך |
| Let thy springs be dispersed | יפוצו מעיינותיך |
| the fountains of salvation | מעייני הישועה |
| giveth heed unto thy bidding | הסר אל משמעתך |
| over and done | תם ונשלם |
| Amen | אמן |
Titles - Acronyms
| our honorable teacher Rabbi | כמ"ר |
| the son of our honorable teacher Rabbi | בכמ"ר, בכמה"ר |
| may his memory live in the world to come | זלה"ה |
| rabbi | ר' |
| may God preserve him, and keep him alive | יצ"ו |
Demonstratives
| it | אותו |
| these | אלו (ה), אלה (ה), האלה |
| זה הוא | |
| this | הזאת, זה (ה), זאת (ה) |
| וזה, זה | |
| by this, from this | מזה (ה), בזה |
| in this, for this | בזה ה |
| thereby, in this regard, relating to this | בזה |
| by each other | זה בזה |
| מאלו (ה) |
Pronouns
| a certain, whichever | איזה, איזה... שיהיה |
| I am | אני, הנני |
| you | אתה, הנך, אותך |
| which is | שהוא, אשר הוא |
| it is, which is (result) | והוא (ה), הוא ה, היא |
| which are | שהם |
| something | דבר מה |
| certain | מה |
| what | מה ש |
| by itself | בעצמו |
Adjectives
| one of | אחד מ, אחד מכם |
| each of | כל אחד מהם, אחד מהם, כל אחד מ |
| other | אחר, אחרים |
| last | אחרון |
| middle | האמצעי |
| aforementioned | האמור |
| following, consequent | הבאי' אחריה |
| larger | הגדול |
| known | ידוע, ידועים, נודע |
| unknown | בלתי ידוע |
| whole | כלו, כל (ה) |
| all | כל ה |
| every | כל |
| everything, all | הכל |
| mentioned | הנזכר, הנז', הנזכ' |
| previous | הקודמי', הקודמת, הקודם |
| prior to | הקודמים לזה |
| smaller | הקטן |
| some | קצתם |
| first, firstly | ראשונה, ראשנה |
| first | ראשון, ראשונה |
| much | רב |
| many | רבים |
| many of | רבים מן ה |
| composed of | המורכב מ, המרכב מ |
| other, rest of | שאר ה |
| equal | שוים |
| unequal | בלתי שוים |
Adverbs
| then, afterwards | אח"כ, אחר |
| after | אחרי |
| how | איך |
| randomly | איך שקרה |
| there is no | אין |
| indeed | אמנם |
| without | בלי |
| before | טרם |
| together | יחד, שניהם יחד |
| above | למעלה, למעלה מ |
| already | כבר |
| is so, indeed | כי כן הוא |
| in all | בכל |
| how many | כמה, כמה מה... |
| as, the same as | כמו |
| so is | וככה ה |
| also | וכן |
| and so, thus | וכן |
| according to this, accordingly | לפי זה |
| therefore | לפי כן |
| from where | מאין |
| also | גם, גם כן |
| always | לעולם |
| therefore | על כן, ע"כ |
| now | עתה |
| also, further, likewise | עוד |
| hither | והנה, הנה, הנה כי |
| here | הנה לפנינו, לפנינו |
| necessarily | בהכרח |
| on the first time | בפעם הראשונה |
| namely, i.e. | ר"ל |
| but | רק |
| first, at the beginning | בתחלה |
| instead | תחת |
Conjunction
| or | או |
| then, if so | א"כ, אם כן |
| what, that, which | אשר, ש |
| because (of), since | מפני כי, כי, ל |
| because, since | בעבור כי |
| if | ואם, אם |
| when | כאשר |
| that | כי |
| according to, as, like | כפי, כפי מה ש |
| as, like, the same as | כ, כפי ה |
| in order that | למען |
| until | עד אשר |
Preposition
| as it is | כאשר הוא |
| as | כ, כאשר |
| according | לפי |
| of it | ממנו |
| of | מן (ה) |
| by, according | על |
| on it | עליו |
| with | עם ה |
| inside | בתוך ה |
Appendix II: Bibliography
Simon b. Moses b. Simon Moṭoṭ
Ḥeshbon ha-Alzibra (Calculation of Algebra)
Italy, 1460s
Manuscripts:
- 1) Amsterdam, Portugees Israelitisch Seminarium Ets Haim 47 D 20/42 (IMHM: f 3576), ff. 223r-226r (15th century)
- Ets Haim 47 D 20/42
- 2) Berlin, Staatsbibliothek (Preußischer Kulturbesitz) Or. Oct. 244/14 (IMHM: f 1996), ff. 113r-120r (15th-16th century)
- Or. Oct. 244/14
- 3) Firenze, Biblioteca Medicea Laurenziana Plut.88.46/2 (IMHM: f 17970), ff. 46r-53v (16th century)
- Plut.88.46/2
- 4) Mantova, Comunita Israelitica MS ebr. 10/6 (IMHM: f 790), ff. 122v-133r (15th century)
- ebr. 10/6
- 5) Parma, Biblioteca Palatina Cod. Parm. 2196/3 (IMHM: f 13362), ff. [117r]-[119v] (15th-16th century)
- Parm. 2196/3
Bibliography:
- Lévy, Tony. 2007. L’algèbre arabe dans les textes hébraïques (II). Dans l’Italie des XVe et XVIe siècles, sources arabes et sources vernaculaires, Arabic Sciences and Philosophy 17, pp. 81-107.
- Steinschneider, Moritz. 1893–1901. Mathematik bei den Juden. Berlin-Leipzig-Frankfurt: Kaufmann; repr. Hildesheim: G. Olms, 1964 and 2001. p.193 (h59).
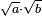
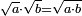

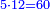
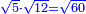
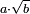
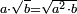
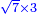
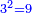
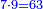
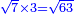
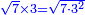
![\scriptstyle\sqrt[3]{a}\sdot\sqrt[3]{b}](/mediawiki/images/math/b/a/c/bacc2f1d5599ecc0f2abfae5338f631c.png)
![\scriptstyle\sqrt[3]{a}\sdot\sqrt[3]{b}=\sqrt[3]{a\sdot b}](/mediawiki/images/math/5/9/8/59816b3801810779536521ea452031dd.png)
![\scriptstyle{\color{blue}{\sqrt[3]{5}\sdot\sqrt[3]{6}}}](/mediawiki/images/math/6/b/c/6bcd61acffa1345e487600bdb7ef40ff.png)
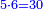
![\scriptstyle{\color{blue}{\sqrt[3]{5}\sdot\sqrt[3]{6}=\sqrt[3]{30}}}](/mediawiki/images/math/0/4/4/04410a255c912fc36d37cc826cc8f8fa.png)
![\scriptstyle a\sdot\sqrt[3]{b}](/mediawiki/images/math/0/2/b/02bad7964ec3b2f880a5b37566afd853.png)
![\scriptstyle a\sdot\sqrt[3]{b}=\sqrt[3]{a^3\sdot b}](/mediawiki/images/math/f/1/c/f1c87b4f7d48f16c0d8284d25da5692b.png)
![\scriptstyle{\color{blue}{3\sdot\sqrt[3]{5}}}](/mediawiki/images/math/a/9/9/a99dd5644ea050837fd5c7b6558148b1.png)
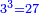
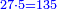
![\scriptstyle{\color{blue}{3\sdot\sqrt[3]{5}=\sqrt[3]{135}}}](/mediawiki/images/math/5/f/f/5ff0f74172d8baecd699fd925848b3af.png)
![\scriptstyle\sqrt[3]{a}\sdot\sqrt{b}](/mediawiki/images/math/9/a/f/9af07a0ad566815bf7c65e737d8dd22f.png)
![\scriptstyle\sqrt[3]{a}\sdot\sqrt{b}=\sqrt{\sqrt[3]{a^2\sdot b^3}}](/mediawiki/images/math/7/8/8/7884d9f29c2b7631d2a0c4340b1d32ea.png)
![\scriptstyle{\color{blue}{\sqrt[3]{8}\sdot\sqrt{9}=2\sdot3}}](/mediawiki/images/math/f/7/8/f78292cfdbe9c405071e1cd7a1fa2151.png)

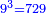
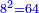
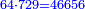
![\scriptstyle{\color{blue}{\sqrt[3]{8}\sdot\sqrt{9}=\sqrt{\sqrt[3]{46656}}}}](/mediawiki/images/math/a/c/7/ac7b3af098b2dcfc5959f48b0c54787d.png)
![\scriptstyle{\color{blue}{\sqrt[3]{8}\sdot\sqrt{9}=\sqrt{\sqrt[3]{46656}}=\sqrt{36}=6}}](/mediawiki/images/math/9/0/6/9060887787a854b576ffece1c5db8438.png)
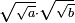
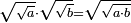
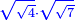
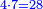

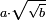
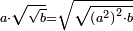
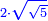
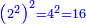

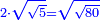
![\scriptstyle \sqrt[3]{a}\sdot\sqrt{\sqrt{b}}](/mediawiki/images/math/b/2/1/b211decc2af8b3186f352d9b02e9a4fb.png)
![\scriptstyle \sqrt[3]{a}\sdot\sqrt{\sqrt{b}}=\sqrt{\sqrt{\sqrt[3]{\left(a^2\right)^2\sdot b^3}}}](/mediawiki/images/math/f/2/6/f266a97adc0e11a6681a85e8134bce86.png)
![\scriptstyle{\color{blue}{\sqrt[3]{3}\sdot\sqrt{\sqrt{4}}}}](/mediawiki/images/math/6/a/2/6a2e44e521ace253aeea448334c43738.png)
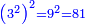
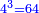
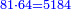
![\scriptstyle{\color{blue}{\sqrt[3]{3}\sdot\sqrt{\sqrt{4}}=\sqrt{\sqrt{\sqrt[3]{5184}}}}}](/mediawiki/images/math/f/4/3/f4308f052f9b1597ed017ab566f338dc.png)
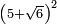
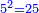
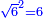
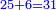
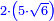
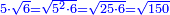
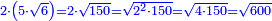
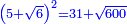
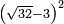
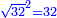
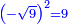

![\scriptstyle{\color{blue}{2\sdot\left[\sqrt{32}\sdot\left(-\sqrt{9}\right)\right]=-\sqrt{1152}}}](/mediawiki/images/math/3/f/9/3f9cb8ab08cf30b52a173a1e4bcb9e9a.png)
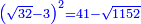
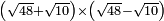
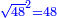

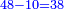
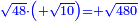

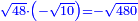
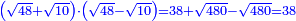
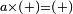
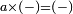
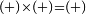


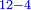
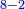

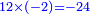
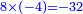

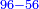
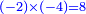
![\scriptstyle{\color{blue}{\left(12-4\right)\times\left(8-2\right)=\left(12\times8\right)-\left[\left(12\times2\right)+\left(8\times4\right)\right]+\left(2\times4\right)}}](/mediawiki/images/math/3/c/6/3c69cb627345100e55a077bfc2be22dc.png) ]
]
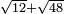

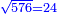
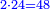
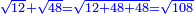
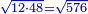
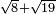
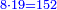 which has no root
which has no root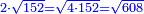
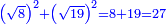
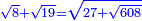
![\scriptstyle\sqrt[3]{96}+\sqrt[3]{324}](/mediawiki/images/math/8/f/5/8f58716ec5d5049f48b1b6af09db62e2.png)
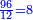
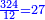

![\scriptstyle{\color{blue}{\sqrt[3]{\frac{8}{27}}=\frac{2}{3}}}](/mediawiki/images/math/1/c/3/1c3949a51077542b74c99c62ecc6027d.png)
![\scriptstyle{\color{blue}{\sqrt[3]{96}=\frac{2}{3}\sdot\sqrt[3]{324}}}](/mediawiki/images/math/3/b/8/3b8e6bdd25a296211c5bf95dbdf86b2e.png)
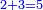
![\scriptstyle{\color{blue}{\sqrt[3]{96}+\sqrt[3]{324}=\frac{2}{3}\sdot\sqrt[3]{324}+\sqrt[3]{324}=\frac{5}{3}\sdot\sqrt[3]{324}}}](/mediawiki/images/math/9/b/8/9b8c6a62940ad76ca98b470851734950.png)
![\scriptstyle{\color{blue}{5=\sqrt[3]{125}}}](/mediawiki/images/math/8/d/1/8d1581c0d1635088ae756979e69cb7e4.png)
![\scriptstyle{\color{blue}{\sqrt[3]{96}+\sqrt[3]{324}=\frac{5}{3}\sdot\sqrt[3]{324}=\frac{\sqrt[3]{125}}{3}\sdot\sqrt[3]{324}}}](/mediawiki/images/math/8/e/8/8e8cdbe91e3aa40ffa6102ddd7618aa7.png)
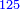 :
:![\scriptstyle{\color{blue}{\frac{1}{3}\sdot\sqrt[3]{324}=\frac{1}{2}\sdot\sqrt[3]{96}}}](/mediawiki/images/math/8/8/1/88121916bb37cd8291a74410a18b54d5.png)
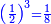
![\scriptstyle{\color{blue}{\frac{1}{3}\sdot\sqrt[3]{324}=\sqrt[3]{\frac{1}{8}\sdot96}=\sqrt[3]{12}}}](/mediawiki/images/math/1/d/0/1d02c68a42f87439a1b82d9abd3bf9df.png)

![\scriptstyle{\color{blue}{\sqrt[3]{96}+\sqrt[3]{324}=\sqrt[3]{125\sdot12}=\sqrt[3]{1500}}}](/mediawiki/images/math/1/5/b/15b298ace9ac68c17bac5a8d1b4403e1.png)
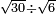
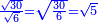
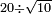
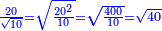
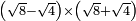
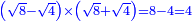
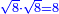
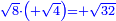

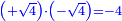
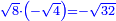

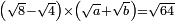
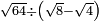
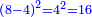
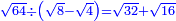
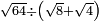
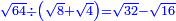

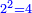
![\scriptstyle\sqrt{6}\div\sqrt[3]{10}](/mediawiki/images/math/9/a/0/9a0da3d2826409356d860ea699ebe6c3.png)

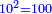
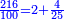
![\scriptstyle{\color{blue}{\sqrt{6}\div\sqrt[3]{10}=\sqrt{\sqrt[3]{2+\frac{4}{25}}}}}](/mediawiki/images/math/9/b/5/9b5e7c1247c52db43d2667d7981f0e8c.png)
![\scriptstyle\sqrt[3]{18}\div\sqrt{\sqrt{8}}](/mediawiki/images/math/7/b/1/7b18ba671efc0ee8603d547c8166247c.png)
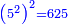
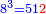
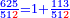
![\scriptstyle{\color{blue}{\sqrt[3]{5}\div\sqrt{\sqrt{8}}=\sqrt{\sqrt{\sqrt[3]{1+\frac{113}{51{\color{red}{2}}}}}}}}](/mediawiki/images/math/7/1/2/71260ba235218e8d6763452cea67114b.png)
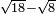




 = (A[B] - AG)2
= (A[B] - AG)2
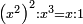
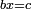
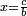
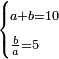


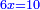
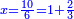
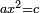
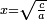
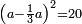
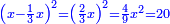
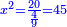

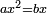
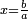
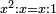
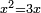
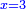
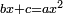
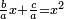
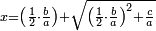
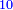


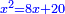 = AC□ + ZD□]
= AC□ + ZD□]![\scriptstyle\left[\left(a+b\right)\sdot b\right]+\left(\frac{1}{2}\sdot a\right)^2=\left[\left(\frac{1}{2}\sdot a\right)+b\right]^2](/mediawiki/images/math/a/0/b/a0b403dd8b7c15a5cb1dc47a5f8ca5bb.png)
![\scriptstyle{\color{blue}{\left[\left(x-8\right)\sdot x\right]+\left(\frac{1}{2}\sdot8\right)^2=20+16=36=\left[x-\left(\frac{1}{2}\sdot8\right)\right]^2}}](/mediawiki/images/math/4/2/5/425c853391f246a97fda2a9f2db8393a.png) = TB2
= TB2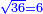
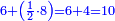
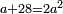
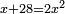
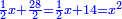
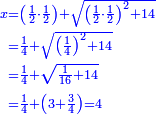
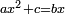
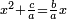
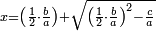


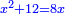
![\scriptstyle\left(a\sdot b\right)+\left[\left[\frac{1}{2}\sdot\left(a+b\right)\right]-b\right]^2=\left[\frac{1}{2}\sdot\left( a+b\right)\right]^2](/mediawiki/images/math/7/b/6/7b6d0c434e8037bd00d19c99fc9fd988.png)
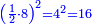
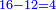
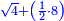
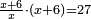
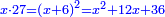
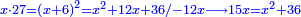
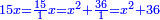
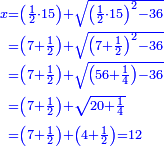
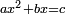
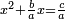
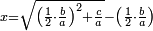
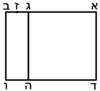


![\scriptstyle{\color{blue}{\left[x+\left(\frac{1}{2}\sdot2\right)\right]^2=48+\left(\frac{1}{2}\sdot2\right)^2=48+1=49}}](/mediawiki/images/math/b/c/6/bc6d151949d2e7705ba1f95484f4197f.png)
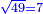
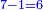
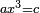
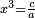
![\scriptstyle x=\sqrt[3]{\frac{c}{a}}](/mediawiki/images/math/5/4/5/545cc36e6c1ddbad6743986c069d36f8.png)
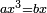
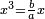
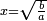
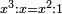
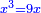
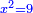
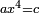
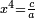
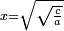
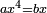
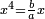
![\scriptstyle x=\sqrt[3]{\frac{b}{a}}](/mediawiki/images/math/6/1/b/61b88ceef15d439699e14ee558e51959.png)
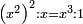
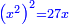
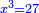
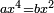
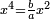
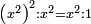
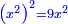
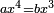
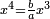
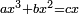
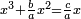
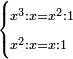
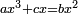
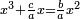
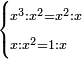
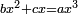
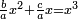
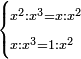
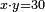
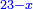
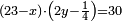
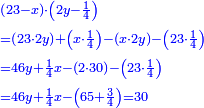
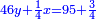
![\scriptstyle{\color{blue}{\left[\left(46\sdot\frac{30}{x}\right)+\frac{1}{4}x\right]\sdot x=1380+\frac{1}{4}x^2}}](/mediawiki/images/math/9/9/5/995117fcefa723cccc081c4fe707c821.png)