Difference between revisions of "מפתח האלגיברה חדשה"
(→Subtraction) |
(→Division) |
||
| (36 intermediate revisions by the same user not shown) | |||
| Line 858: | Line 858: | ||
|style="text-align:right;"|נעשה כך אם האותיות עם האותיות דומות ינוכה מספרם זה מזה והשאירות יושם תחת הקו | |style="text-align:right;"|נעשה כך אם האותיות עם האותיות דומות ינוכה מספרם זה מזה והשאירות יושם תחת הקו | ||
כמו ינוכה ‫3a*a ישאר ‫2a | כמו ינוכה ‫3a*a ישאר ‫2a | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| Line 888: | Line 882: | ||
| | | | ||
|style="text-align:right;"|כי הואיל שינוכו שניהם ‫a וכן וגם ‫b מן ‫x ישאר ‫x-b אז יקחו שניהם סימן הפחיתות וכן תקיש | |style="text-align:right;"|כי הואיל שינוכו שניהם ‫a וכן וגם ‫b מן ‫x ישאר ‫x-b אז יקחו שניהם סימן הפחיתות וכן תקיש | ||
| − | |||
|- | |- | ||
| | | | ||
| Line 894: | Line 887: | ||
== Multiplication == | == Multiplication == | ||
| − | |style="text-align:right;"|בהכפלה | + | |style="text-align:right;"|<big>בהכפלת</big> בהכפלה או בריבוי האותיות מיוחדת מאוחדות זו עם זו בין שתהיו דומות או בלתי דומות |
| − | או בריבוי האותיות מיוחדת מאוחדות זו עם זו בין שתהיו דומות או בלתי דומות אז יכתבו בלי סימן זו אצל זו וזו היא התולדה כמו יכפל נכפיל a עם a יולד aa | + | |- |
| − | אע"פ אף שראוי להיות aba אבל הואיל והמכפיל דומה למוכפל אז יכתוב אצלו | + | | |
| − | + | |style="text-align:right;"|אז יכתבו בלי סימן זו אצל זו וזו היא התולדה | |
| − | וכן אם יש כמות מספרי שיוכפלו כדין והאותיות יכתבו זו אצל זו | + | |- |
| − | ואם יבואו שני אותיות בלי סימן בינתים סמוכות זו לזו אז נדע שהן הולדת ההכפלה | + | | |
| + | |style="text-align:right;"|כמו יכפל נכפיל ‫a עם ‫a יולד ‫aa | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|אע"פ אף שראוי להיות ‫aba אבל הואיל והמכפיל דומה למוכפל אז יכתוב אצלו | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | |ab<br>a||ab<br>c||2a<br>a | ||
| + | |- | ||
| + | |aab||abc||2aa | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|וכן אם יש כמות מספרי שיוכפלו כדין והאותיות יכתבו זו אצל זו | ||
| + | |- | ||
| + | | | ||
| + | |style="text-align:right;"|ואם יבואו שני אותיות בלי סימן בינתים סמוכות זו לזו אז נדע שהן הולדת ההכפלה | ||
|- | |- | ||
| | | | ||
| + | |||
== Division == | == Division == | ||
| − | |style="text-align:right;"|ובחילוק | + | |style="text-align:right;"|<big>ובחילוק</big> האותיות מאוחדות אם האות או האותיות הנחלקות ואות החולקת דומות ובין שתהינה כמות נחלקת וחולקות נרשמות בסימן מספרי או הכמות נחלקת לבד נרשמות נרשמה בסימני המספר |
| − | האותיות מאוחדות אם האות או האותיות הנחלקות ואות החולקת דומות ובין שתהינה כמות נחלקת וחולקות נרשמות בסימן מספרי או הכמות נחלקת לבד נרשמות נרשמה בסימני המספר אז יעשה כדין חילוק המספרי | + | |- |
| − | + | | | |
| − | + | |style="text-align:right;"|אז יעשה כדין חילוק המספרי | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|כמו נחלוק ‫a על ב ‫3a ויהיה הכמות ‫3a הכמות כי האחדות אינו חולק | |
| − | + | |- | |
| − | + | | | |
| − | + | | | |
| − | + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | |
| − | + | |- | |
| − | + | |4b<br>2b||2b | |
| − | + | |} | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|אבל אם האותיות הנחלקות בלתי דומות למחלקת אז נעמוד המחלק תחת הקו ועליו הנחלק כמו בחשבון בציור השברים ויהיה א"כ אות המחלקת מכנה השבר והנחלקת מונה | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|כמו אם נחלק ‫a על ידי ע"י ‫b אז יהיה כזה ‫<math>\scriptstyle\frac{a}{b}</math> | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|וכן ‫a*b ע"י ‫c אז יהיה כך ‫<math>\scriptstyle\frac{a*b}{c}</math> | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|עד כאן ע"כ דברנו מחשבון האותיות בפשוטים או מאוחדי הכמות אבל אם נרצה לידע חשבון המורכבים אשר הם מאותיות רבות ‫<ref>43r</ref>או דומות או מתחלפות עם סימנים או שווים או שונים נצריך שתבחין שיבחן זה באמיתית מה שנבאר בשני כללים כוללים והם | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|‫(א) והאחד אם נחבר העדר או חסרון אל קניין אז יוגרע כמות החסרון (כי לדבר קנין ההעדר הוא שיחסר ממנו מה) | |
| − | + | |- | |
| − | ■( | + | | |
| − | ■( | + | |style="text-align:right;"|‫(ב) וכן אם ינוכה העדר או חסרון מקנין או מהעדר אז נצרך להוסיף החסרון מהכמות בראשונה |
| − | + | |- | |
| − | + | | | |
| − | ■(2 | + | |style="text-align:right;"|ומזה יולד שאם יבואו בחיבור שני סימנים שונים או * למעלה - למטה או להיפיך בהיפוך אז נעשה במקום החיבור ניכוי הקטן מהגדול מן הגדול והנשאר יקבל סימן שהי' ההיה אצל כמות הגדולה ואם הכמות העליון בשווה ולהעדר התחתון אז לא ישאר כלום כמו בחבור זה |
| − | + | |- | |
| − | + | | | |
| − | + | | | |
| − | + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | |
| − | + | |- | |
| − | + | |a*3b-c<br>2a-b*2c | |
| − | + | |- | |
| − | ■( | + | |3a*2b*c |
| − | ■( | + | |} |
| − | + | |- | |
| − | + | | | |
| − | + | | | |
| − | + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | |
| − | + | |- | |
| − | + | |3a*b*2c<br>a-b-1c | |
| − | + | |- | |
| − | + | |4a*c | |
| − | + | |} | |
| − | + | |- | |
| − | + | | | |
| − | + | | | |
| − | + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | |
| − | + | |- | |
| − | + | |4a-2b-3c<br>-2a*3b*c | |
| − | + | |- | |
| − | + | |2a*b-2c | |
| − | + | |} | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|כי בנדון הנזכר הם שני סימנים שונים בתמידית העדר או חסרון אשר קיבוצו ממלא החסרון | |
| − | + | וכדי להקל למתחיל נעשה מהמשלים הקודמים מספרים נודעים כמו | |
| − | + | |} | |
| − | + | ■(A&&pf&&E@1&*&3&-&1@2&-&1&*&2@3&*&2&*&1) | |
| − | + | ■(A&&E&&pf@4&-&2&-&3@-2&*&3&*&1@2&*&1&-&2) | |
| − | + | בניכוי | |
| − | ■(■( | + | בסימנים שונים ו אז נעשה הקיבוץ במקום הניכוי באותה בית כיתה ואותו מספר יקבל סימן העליון הראוי אשר ממנו ינוכה כמו |
| − | + | ■(17x3*18x2-16x*12@9x3*14x2-11x*10@8x3*4x2-5x*2) ■(17x^3+18x^2-16x+12@9x^3+14x^2-11x+10@8x^3+4x^2-5x+2) | |
| − | + | ■(3a*2b*c@a-b*c@2a*3b) | |
| − | + | |- | |
| − | + | | | |
| − | + | |style="text-align:right;"|ולהקל נציג לפניך המשלים במספרים ידועים | |
| − | + | ■(A&b&c) | |
| − | + | ■(א&ב&ג) | |
| − | + | ■(3*2*1&2-x*2@▁(1-1*1)&▁(1*1-1)@2*3&1-2*3) | |
| − | + | ||
| − | + | ואם מספר המנכה גדול ממספר המנוכה (חוץ בכיתה ראשונה) ואצל שניהם סימן היתור * אז נגרע העליון מן התחתון עם סימן הפחיתות כמו | |
| − | + | ■(3a*2b*c&2a*2b*2c@▁(a*3b*3c)&▁(a*4b*3c)@2a-b-2c&a-2b-c) | |
| − | + | ובמספרי הוא כך | |
| − | + | ■(3*2*1&2*2*2@▁(1*3*3)&▁(1*4*3)@2-1-2&2-1-1) | |
| − | + | ואם ננכה מספר העדרי מן העדר הקטון ממנו אז נעשה כמו כן שינוכה העליון מן התחתון והשארית והשאירות יורשם בסימן היתור כמו | |
| − | + | ■(3a-b&2a-3b@a-2b&a-5b@2a*b&a*2b) | |
| − | + | ■(2a-b c@▁(a-3b-a)@a*2b) | |
| − | + | ובמספרי הוא כך | |
| − | + | ■(3-1&2-3@1-2&1-5@2*1&1*2) | |
| − | + | ■(2-1-1@▁(1-3-1)@1*2) | |
| − | + | ויהיה דמיון זה כולל כל הכללים שזכרנו | |
| − | + | ■(9x8-15x6*4x5*5x4-8x3-9x2-4x*9@▁(6x8*10x6-6x5*9x4-12x3-6x2*9x-6)@3x8-25x6*10x5-4x4*4x3-3x2-13x*15) | |
| − | + | בהכפלות האותיות אם יבואו כמות נצמדות ע"י על ידי סימנים ידועים והמכפיל הוא מאות אח' לבדו אז יחובר לכל אחד מאותיות המוכפלות בלי סימן מפסיק ביניהם כנ"ל כאשר ביארנו למעלה כמו | |
| − | + | ■(a*b*c@ d@ad*bd*cd) | |
| − | + | אבל אם הן אותיות רבות המכפילות אשר הם הן כמו כן מחוברות בסימנים אז יחוזר ההכפלה בכל אחד מהאותיות ויעמדו בסדר הראוי כפי כללי ההכפלי ההכפלה המספרית | |
| − | + | והמספרים הנולדים יקובצו כפי כללי החיבור בזאת החכמה אשר זכרנו קדם מאמרינו מהם | |
| − | + | אבל זאת לדעת אם יהיו סימנים המכפילים שווים לסימני המוכפלים בין שיהיו שניהם * או שניהם - שיורשם סימן היתור * להולדת ההכפלה ואם הם בלתי שווים יולידו לעולם הפחיתות כמו | |
| − | + | ■(a*b&a*c@▁(a*c)&▁(a*c)@ *ac*bc& *ac*cc@aa*ab &aa*ac @aa*ab*ac*bc&aa*2ac*cc) | |
| − | + | ■(a*b&a-b@▁(a-b)&▁(a-b)@ -ab*bb& -ab*bb@▁(aa*ab )&▁(aa-ab )@aa-bb&aa-2ab*bb) | |
| − | + | ובמספרי נניח a הוא 2 b הוא 3 c הוא 4 א"כ כזה | |
| − | + | ■(2-3@▁(2-3)@-6*9@▁(4-6 )@4-12*9) | |
| − | + | ||
| − | + | ■(2*3-4@▁(2*3-4)@-8-12*16@*6*9-12 @▁(4*6-8) @4*12*9*16-24*16) | |
| − | + | ואל תתמה באומרינו שנים פחות שלשה כי כן מבואר למשכילים בחשבון האותיות ועל זה נבנה סוד הבריאה יש מן האין כמו שביארנו באריכות בחיבורינו הגדול (חלקות אש"ר) ושם יתנו עידיהן ויצדקו הרבה מופתים טבעים יקרי הערך ולזה כתב החכם השלם כמהר"ר יש"ר מקנדיא במעין חתום תמר ח' וז"ל אודיעך דבר נפלא שתדע להשיב למכחישי אפשרות יש מאין כאשר נאמין אנחנו בני ברית שה' ברא העולם מאין המוחלט והוא שאם תכפול (כפי דרכי האלגיברה) מספרים פחותים מאין יולידו מספרים ואי אפשר להכחיש המלאכה שהיא כבר ברורה ונתאמתה במספרים של ממשות ע"כ והרי לך כמה מספרים אין מולידים יש וכמוהם בלתי בעלת תכלית | |
| − | + | ■(3-7@3-7@ -21*44@4-21 @4-42*44) | |
| − | + | והם 16 | |
| − | + | ועוד נבאר זה כיד ה' הטובה עלינו מסגולות מספרים אלו והכרחם להתר ספיקות רבות | |
| − | + | ■(4-10@8-4@ -36*90@▁(32-80 )@32-116*90) | |
| − | + | והם 86 | |
| − | + | בחילוק חשבון זו נעשה כך אם האות או האותיות של המחלק הם בכיתות הנחלקים אז נסיר את אותיות המחלק עם אותיות הדומות מהנחלקים והנשארים הם כמות המבוקש | |
| − | + | אבל תדע זאת צריך שנדע אם סימני המחלק עם הנחלק הם שווים אז נרשום לכמות היוצא סימן היתור * ואם היו בלתי שווים אז נרשם סימן - וכמו שזכרנו שקדם מאמרינו בכללי ההכפלה כמו | |
| − | + | ├ ■(ab@a )┤|b | |
| − | + | ||
| − | + | ├ ■(abc@b)┤|ac | |
| − | + | ||
| − | + | ├ ■(ab*ac@a a)┤|b*c | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ├ ■(ac*ad*bc*bd@4 * d c * d)┤|a*b | |
| − | + | ||
| − | + | ├ ■(aa-2ab*bb@a-abb=b@a b)┤|a-b | |
| − | + | ובמספרי יהיה a 1 b הוא 2 c הוא 3 d הוא (43v) 4 וא"כ ab דהיינו 2 שנחלק עם 1 יהיה הכמות b דהיינו 2 וכן 3*4*6*8 יחלק על ידי 3*4 דהיינו 21 על ידי 7 יהיה הכמות 1*2 דהיינו 3 וכן תקיש | |
| − | + | אבל אם אותיות המחלקות אינן דומות לאותיות הנחלקות או בכללן או בקצתן אז נמשך קו בין המחלק ובין הנחלק כדמיון שבר ויהיה מכנה שבר המחלק ומונה הנחלק כזה | |
| − | + | ■(ab&bcd&ab*cc&ac-ad@c&ab&d&a*b) | |
| − | + | עד הנה כתבנו ממיני החשבון בשלמי' נשאר לנו לבאר ממיני החשבון בשברים | |
| − | + | בקיבוץ השברים יעשה כמו בקיבוץ השברים מספריים וכמו שהורינוך בכללי קיבוץ בשלמים ואינו מן ההכרח לחדש המלאכה בכללים חדשים כמו נקבץ כזה | |
| − | + | ■(■(4&106)@▁(■(a/2&3a/4))@8) | |
| − | + | ■(▁8@4@▁6@▁01@8)1 1/2 | |
| − | + | בניכוי השברים יעשה כמו בגרעון השברים המספריים רק שתעשה ההכפלה והגרעון ע"ד האלגיברה כאשר הורינוך בשלמים והיו למאורות דמיונות אלו | |
| − | + | אך זאת תדע כי ההכפלת שתי וערב היא היותר נכונה וקלה כמו בקיבוץ כך בגרעון | |
| − | + | ■(2x@▁(■(2x&4x))@■(x/4&x/2)@8) | |
| − | + | ■(14 xx/4-5 2x/3*1 3/4@83xx/4-9x*7 1/4) | |
| − | + | ולפי הכללים שהורינוך יבוא שישאר | |
| − | + | 5 xx/2*3x/3-5 1/2 | |
| − | + | 4/(2x*3) יוגרע (2xx*5)/(2x*3) | |
| − | + | ישאר אחר הקטנת השבר (2xx*1)/(2x*3) | |
| − | + | בהכפלת השברים יעשה כמו במספריים אבל שנעשה ההכפלה ע"ד הכללים שזכרנו בהכפלת השלמים באלגיברה ויהיו להאיר עיני שכלך דמיונות אלו | |
| − | + | ├ ■(▁6x@■(2x/3&3/4)@12)┤| ■(3/4x&2/3x) | |
| − | + | יולד 1/2 xx | |
| − | + | ■(5xx/6&6x/7) | |
| − | + | יולד 30x3/42 | |
| − | + | ובהקטנה 5x3/7 | |
| − | + | בחילוק השברים נעשה כמו בחילוק השברים מספריים דהיינו שההכפלה והאופנים יהיה ע"ד האלגיברה וכמו שהורינוך בחילוק ובהכפלת השלמים ותן עיניך בדמיונות אלו | |
| − | + | ■(3/4&x/2&3/4x&1/2 xx) | |
| − | + | ■(4x@2@3x) יוחלק 6xx ■(6&├ 4/6x┤|&2/3x) | |
| − | + | ■(6x/7&5x3/7) | |
| − | + | |style="text-align:right;"|לוח להוצאת השרשים | |
| − | + | |style="text-align:right;"|והוא מראה דרך ההכפלה בהוצאת השרשים בב"ת | |
| − | + | לוח זה נולד מהכפלת x*1 עם x*1 והנולד יוחזר ויוכפל עם x*1 וכן חלילה עד בלי תכלית : | |
| − | + | שרש | |
| − | + | x מרובע | |
| − | a | + | x2 מעוקב |
| − | + | x3 מרובע | |
| − | + | מרובע | |
| − | + | x4 מרובע | |
| − | + | מעוקב | |
| − | + | x5 מעוקב | |
| − | + | מרובע | |
| − | + | x6 מרובע | |
| − | + | מרובע | |
| − | + | מעוקב | |
| − | + | x7 ג' | |
| − | + | מרובעי' | |
| − | + | x8 מעוקב | |
| − | + | מעוקב | |
| − | + | x9 | |
| − | + | מרובע | |
| − | + | x10 מעוקב | |
| − | + | מרובע | |
| − | + | x2 2 | |
| − | + | x3 3 3 | |
| − | + | x4 4 6 4 | |
| − | + | x5 5 10 10 5 | |
| − | We | + | x6 6 15 20 15 6 |
| − | + | x7 7 2x 35 35 21 7 | |
| − | + | x8 8 28 56 70 56 28 8 | |
| − | + | x9 9 36 84 126 126 84 36 9 | |
| − | + | x10 10 45 120 210 252 210 120 45 10 | |
| − | + | ||
| − | + | מהוצאות השרשים Extraction of Roots | |
| − | + | א מהוצאות שרש מרבע | |
| − | + | להוציא שורש 1) Extraction of Square Roots | |
| − | + | מרובע הוא מספר כפול בעצמותו A square is a number multiplied by itself. | |
| − | + | ולידע שרשו נעשה כך To know its root, we do as follows: | |
| − | + | כמו יש לי מרובע aa*2ab*bb | |
| − | + | ונרצה לידע שרשו As if I have a square a^2+2ab+b^2 and we wish to know its root. | |
| − | + | נראה בראשונה כמה אותיות מתחלפות שיש במרובע וכל כך וכ"כ אותיות פשוטות יבואו בשורש לא פחות ולא יותר First, we see how many different letters there are in the square and that many simple letters will be in the root, no less and no more. | |
| − | + | ובנידון דידן נראה בכל הכתות אינן זולתי אותיות b a וזה אשר יורה כי בשורש לא יבוא זולתי שתי אותיות b a In the matter under discussion, we see in all parts only the letters a b, which indicates that there are only two letters in the root, a and b. | |
| − | + | וכן תקיש אם יבואו ג' אותיות שונות Deduce the same if there are three different letters. | |
| − | + | וא"כ ואם כן נעשה כדין הוצאות מרובה מרובע מספרי רק שנעשה ההכפלה והחלוק כפי מה שהורינו באלב[.] ע"פ Then, we follow the rule of extracting the numerical square [root], but we apply the multiplication and division according to what we instructed. | |
| − | + | וא"כ בנדון דידן מתחיל נתחיל מצד שמאל ונמצא שם aa והוא בעצמו מרובעו כי מרובע a הוא aa In the matter under discussion, we start from the left and we find there a^2, which is a square itself, because the square of a is a^2. | |
| − | + | וא"כ נכתוב במקום השורש a | |
| − | + | וננכה מרובעו ממרובע מן המרבע aa לא ישאר מה So, we write a in the place of the root and subtract its square from the square a^2; nothing remains. | |
| − | + | ואח"כ ואחר כך נכפיל השורש הנמצא יבא 2a | |
| − | + | ונעמידהו תחת כתה שנייה שהיא *2ab Then, we double the found root; the result is 2a. We write it beneath the second part, which is +2ab | |
| − | + | ונחלקהו יבוא *b כדין החילוק שהקדמנו לבארו We divide it by it; the result is +b, according to the rule of division we explained earlier. | |
| − | + | וזה האות השני מן השורש ונעמידהו אצל a This is the second letter of the root. | |
| − | + | We write it next to the a. | |
| − | + | ואח"כ ואחר כך נכפיל השורש החדש שהוא b עם כפל שורש הראשון שהוא 2a ויבוא כדין 2ab Then, we multiply the new root, which is b, by double the first root, which is 2a; the result is 2ab. | |
| − | + | וננכה זה מן 2ab שבמרובע לא ישאר כלום We subtract it from the 2ab in the square; nothing remains. | |
| − | + | ואח"כ נכפיל השורש האחרון הנמצא שהואb בעצמו ויבוא מרובעו bb Then, we multiply the last found root, which is b, by itself; its resulting square is b^2. | |
| − | + | וננכה זה מן הכתה האחרונה ולא ישאר כלום We subtract it from the last part; nothing remains. | |
| − | + | וזה סדרו | |
| − | + | ├ ■(aa*2ab*bb@aa 2a bb@ 2ab)┤|a*b This is its diagram: | |
| − | + | ├ ■(a^2+2ab+b^2@a^2 2a b^2@ 2ab)┤|a+b | |
| − | + | או על דרך היותר קל שתראה כמה אותיות שונות יש במרובע ככה יש שורשי המרובע | |
| − | + | ואח"כ תראה אם מרובע כל אחד נראה ונמצא במספר וגם סימן הכפלתם יחדיו | |
| − | + | ואז תעמיד האותיות פשוטות זה אצל זה עם צורת * או - כפי דינו Or, on the easier way, you can see how many different letters there are in a square, so are the roots in the square. | |
| − | וכן | + | Then, see if the square of each is visible and found in the number, as well as their product by each other. |
| − | + | Then, write the simple letters next to each other with the sign + or - as required. | |
| − | + | כמו נמצא שורש של מרובע זה | |
| − | + | aa*2ab*2ac*bb*2bc*cc As, if we find the root of this square: | |
| − | + | a^2+2ab+2ac+b^2+2bc+c^2 | |
| − | + | הנה נראה כי במרובע זה רק שתי אותיות והן a b c ומרובען נמצא בעצמו כמו aa bb cc וגם סימן הכפלתם 2bc 2ac 2ab ונרשמים כלם בסימן היתור אז נדע כי השורש הוא a*b*c We see that there are only three letters in this square, which are a b c and their squares are found in it, a^2,b^2,c^2, as well as their products 2ab,2ac,2bc, and they are all written with the addition sign; so we know that the root is a+b+c. | |
| − | + | וכן תקיש משאירות המרובע יעשה כמו בחשבון המספרי דהיינו שנכפיל השורש הנמצא ונקבץ להנולד 1 והוא מכנה השבר והנשאר מהמרובע יהיה המונה Apply the same for the remainder of the square, which is carried out as in the numerical calculation: we double the found root and add 1 to the result; this is the denominator of the fraction. The remainder of the square is the numerator. | |
| − | + | ממציאת אמצעי מוערך במרובעים Finding the proportional mean of squares | |
| − | + | אמצעי מוערך בין שני מרובעים נולד אם שני מרובעים יוכפלו זה עם זה ומהנולד נוציא שורש המרובע | |
| − | + | השורש היוצא הוא בשיווי להכפלות השרשים משני המרובעים זה בזה The proportional mean between two squares is generated, if two squares are multiplied by each other, then we extract the square root of the product. | |
| − | + | The resulting root is equal to the product of the roots of the two squares by each other. | |
| − | + | √(a^2∙b^2 )=√(a^2 )∙√(b^2 ) | |
| − | + | מהוצאות שורש המעוקב 2) Extraction of Cube Roots | |
| − | + | מעוקב הוא מרובע כפול בשורשו A cube is a square multiplied by its root. | |
| − | + | ולמצוא שרשו נעשה כך To find its root we do as follows: | |
| − | + | יהיה המספר מעוקב כזה a3*3aab*3abb*b2 Let the cube root be: | |
| − | + | a^3+3a^2 b+3ab^2+b^3 | |
| − | + | וכאן כמו כן נראה אם האותיות דומות או שונות וכמה הן המתחלפות | |
| − | + | ונמצא בכל הכתות לא יותר כי אם a b לבדן וזה יורה שזה השרשים הם a b Here also, we see if the letters are different or similar and how many are those that are different. | |
| − | + | We find that in all the parts there are only a and b and this indicates that the roots are a b. | |
| − | + | ותעשה כן תחילה מצד שמאל ותמצא (44r) a3 שהוא המעוקב בעצמו וא"כ a הוא השורש הראשון Do as follows: first on the left, you find a^3, which is the cube itself, so a is the first root. | |
| − | + | ואח"כ ואחר כך נראה בכתה שניה ונמצא ג' מרובעים a הנכפלים עם b כזה 3aab | |
| − | + | ואז ניקח מרובע שורש הנמצא שהוא aa ונשלשהו ויהיה א"כ 3aa וזה המחלק כת שניה שהיא 3aab ויצא b כדין החלוק | |
| − | + | ונרשום אל השורש a את השורש b הנמצא עם סימן היתור כדין | |
| − | מרובע | + | ואח"כ נעשה כך Then, you look at the second row, we find three squares of a multiplied by b, like this 3a^2 b. |
| − | + | We take the square of the found root, which is a^2, and we triple it; it is 3a^2 and this is the divisor of the second part, which is 3a^2 b; the result is b. | |
| − | א) | + | We write the found root b next to the root a with the addition sign. |
| − | ב) | + | Then, we do as follows: |
| − | + | (א) נכפיל השרש החדש b עם המחלק 3aa ונעמידהו תחת כתה שניה I. We multiply the new root b by the divisor 3a^2 and write it beneath the second part. | |
| − | + | (ב) נכפיל מרובע שרש חדש עם משושל משלש שרש הראשון דהיינו bb עם 3a ונעמידהו תחת כתה שניה II. We multiply the square of the new root by thrice the first root, i.e. b^2 by 3a, and we write it beneath the second part. | |
| − | + | (ג) נעמיד מעוקב שרש החדש שהוא b ומעוקבו 3b 3b b3 b3 תחת III. We write the cube of the new root, which is b and its cube is b^3, beneath b^3 | |
| − | + | ויוגרעו זה מזה ונמצא שעולים זה עם זה וכך סדרם They are subtracted from each other; we find that they coincide; and this is their diagram: | |
| − | + | ■(├ ■(a3@a3@)┤|&├ ■(*3aab@ 3aa@3aab)┤|&├ ■(*3abb@ 3abb@)┤|&├ ■(*b3@ b3@)┤|&a*b) ■(├ ■(a^3@a^3@)┤|&├ ■(*3a^2 b@ 3a^2@3a^2 b)┤|&├ ■(+3ab^2@ 3ab^2@)┤|&├ ■(+b^3@ b^3@)┤|&a+b) | |
| − | + | ואם ישאר מה מהמעוקב שלא יוכל יכול לכנוס בשרש המעוקב נתקנו כך | |
| − | + | שרש מעוקב היוצא נרבע ולהנולד יקובץ השורש והעולה ישולש ולהעולה יקובץ 1 והעולה הוא מכנה השבר | |
| − | + | והנשאר ממנה השבר | |
| − | מרובע | + | וכן תקיש בשאירות שארי שרשים If something is left of the cube that cannot be included in the root of the cube, we correct it this way: |
| − | + | We square the resulting cube root; the root is added to the product; the result is tripled; 1 is added to the product; the result is the denominator of the fraction and the remainder is the [numerator of the] fraction. | |
| − | + | Apply the same for the remainder of the remainder of the root. | |
| − | + | ויתכן יותר מדוקדק בקיבוץ 0 00 000 וכן עד אין תכלית וכל עוד שתרבה יבוא יותר קרוב ויש שכר לעמלך It can be more accurate by adding 0, or 00, or 000 and so on. The more you add, the more accurate it will be, and there will be a reward for your labor. | |
| − | + | ממציאת אמצעי מוערך בין שני מעוקבים Finding the proportional mean between two cubes | |
| − | + | בין שני מעוקבים נמצאים שני אמצעים מוערכים האחד נקרא גדול והשני נקרא קטן | |
| − | + | ואופן מציאתו יעשה כך Between two cubes there are two proportional means, one is called the greater and the other is called the smaller. The way to find them is as follows: | |
| − | + | בראשונה תרבע שורשיהם ותכפיל מרובע הגדול עם שרש הקטן והנולד הוא אמצעי גדול | |
| − | + | ואם תכפיל מרובע הקטן עם שרש הגדול יולד אמצעי הקטן First, square their roots. Then, multiply the greater square by the smaller root; the result is the greater mean. | |
| − | + | If you multiply the smaller square by the greater root, the result is the smaller mean. | |
| − | מהוצאות | + | ויחוסי האמצעיים אלה הם כערך מעוקב הגדול אל אמצעי גדול כך ערך מעוקב קטון אל אמצעי קטון The relation of these means is such that the ratio of the greater cube to the greater mean is the same as the ratio of the smaller cube to the smaller mean. [erroneous] |
| − | + | a^3:(a^2∙b)=b^3:(b^2∙a) | |
| − | + | וכן אם יוגרע השורש הקטן משורש הגדול והנשאר יוכפל במרובע הגדול ולהנולד יקובץ אמצעי גדול אז יעלה מעוקב הגדול Also, if the smaller root is subtracted from the greater root and the remainder is multiplied by the greater square, then the greater mean is added to the product, the result is the greater cube. | |
| − | + | [(a-b)∙a^2 ]+(a^2∙b)=a^3 | |
| − | + | אבל אם השארית השאירות או מרחק השרשים יוכפל במרובע קטון והנולד יוגרע מאמצעי הקטון ישאר מעוקב הקטון But, if the remainder, or the difference between the roots, is multiplied by the smaller square, then the product is subtracted from the smaller mean, the smaller cube remains. | |
| − | + | (b^2∙a)-[(a-b)∙b^2 ]=b^3 | |
| − | + | והוא מבואר להמשכיל This is clear from the thinker. | |
| − | + | ב' מהוצאת שרש מרובע מרובע 3) Extracting the Root of the Square-Square | |
| − | + | מרובע מרובע הוא מרובע כפול במרובעו The square-square is a square multiplied by its square. | |
| − | + | והנה להוצאות שורשו או שאחר שנוציא ממנו שורש המרובע ומהשורש היוצא תחזור ותוציא נחזור ונוציא שורש מרובע והשורש היוצא שנית הוא המבוקש | |
| − | + | או אז אם נרצה להוציאו בפעם אחת נעשה כך | |
| − | + | א) שיבוקש באותיות באותיות בכתה שמאלית המרובע מרובע היותר קרוב ויוגרעו ממנו והשארית יכתב עליו כדין | |
| − | + | ב) שיוכפל השרש אשר יצא וכן מרובעו ומעוקבו כפי מה שהורינו בלוח דהיינו השורש 4 פעמים ומרובעו 6 פעמים ומעוקבו 4 פעמים וישימו ויושמו זה תחת זה דהיינו למעלה המעוקב 4 (44v) פעמים ותחתיו המרובע 6 פעמים ולמטה המינו ממנו השורש ארבע ד' פעמים | |
| − | + | וכן תקיש בהוצאת שארי שרשים שהגדול למעלה והקטן תחתיו | |
| − | + | ג) ואח"כ תחלוק כמו בהוצאות שורש המרובע והמעוקב שהורינוך וכמות החלק הוא שרש השני ואח"כ תעמוד השרש החדש עם מרובעו ועם מעוקבו זה תחת זה באופן שיהיה השרש מקביל נגד המעוקבים והמרובע נגד המרובעים והמעוקב נגד השרשים ותכפילם זה בזה דהיינו השורש עם המעוקבים וכו' ומה שיולד תעמוד תעמיד זה תחת זה כסדר שעמדו ותעמוד ותעמיד תחתיהם מרובע מרובע השרש השני ש בסדר שהקדמנו לבאר ואז יוקבצו יחדיו וקיבוצם יוגרע ממספר שממנו תוציא השרש | |
| − | + | וכן כסדר הזה חוזר חלילה עד בלי שאירות הכתות | |
| − | + | ממציאות אמצעי מעורך מוערך בין שני מרובע מרובעים | |
| − | + | גם בין שני מרובע מרובעים ימצאו שני אמצעים מוערכים האחד גדול והאחד הקטן וימצאו בהכפלת שרש הקטן עם מעוקב הגדול ומזה יולד אמצעי גדול | |
| − | + | ומהכפלת מעוקב הקטון עם שרש הקטן הגדול יולד נולד אמצעי הקטן | |
| − | + | ויחוסו כערך מרובע מרובע הגדול לאמצעי הגדול כך ערך מרובע מרובע הקטן לאמצעי הקטן | |
| − | + | וכך תקיש במציאת האמצעים בשארי הכפלת השרשים ויותר מיחוסי אמצעים אלו בארנו בחבורינו צפנת פענח | |
| − | + | ד' מהוצאת שורש זורזאליד או מרובע מעוקב 4) Extracting the Root of the Square-Cube | |
| − | + | זורזאליד הוא הכפלת המרובע במעוקבו | |
| − | + | וימצא שורשו ע"ד על דרך זה | |
| − | + | א) תבקש שורש מרובע מעוקב מכתה שמאלית ויוגרע כדין | |
| − | + | ב) להכפלת החלקים יורה הלוח דהיינו 5 שרשים 10 מרובעים 10 מעוקבים 5 מרובעי מרובעים ותעמידם זה תחת זה כסדר שהורינוך | |
| − | + | ג) תחלק כדין והכמות הוא השורש השני ואח"כ תעמוד השרש החדש מרובעו מעוקבו ומרובע מרובעו זה תחת זה כסדר שהקדמנו לבארו ויוכפלו זה בזה ותחתיהם יועמד מרובע מעוקב משרש החדש כסדר שהקדמנו ויקובצו וקיבוצם יוגרע מהמספר שממנו יוצא השרש וכן תוכל לשנה ולשלש כפי הצורך | |
| − | + | ה' מהוצאות השורש מעוקב מרובע 5) Extracting the Root of the Squared Cube | |
| − | + | מעוקב מרובע הוא כשנרבע את המעוקב דהיינו שנכפיל המעוקב בעצמו | |
| − | + | והוצאת שורשו תעשה יעשה באופן זה | |
| − | + | א) יבוקש מרובע מעוקב מכתה שמאלית ויוגרע כדין | |
| − | + | ב) להכפלת השורש תעשה כפי מה שהורינוך בלוח הוצאת השרשים ותעמידם כסדר שהקדמנו לבארו ואצלם יעמוד יועמד השורש השני היוצא מחילוק מרובעו מעוקבו מרובע מרובעו מרובעו מעוקבו ויוכפלו זה עם זה ותחתיהם יועמד מעוקבו מרובע כסדר שהקדמנו ויקבצו וקיבוצם יוגרע כנזכר למעלה | |
| − | + | ו' מהוצאת השורש ב' זורזאליד או מרובע מרובע מעוקב 6) Extracting the Root of the Square-Square-Cube | |
| − | + | ב זורזאליד הוא הכפלת המעוקב במרובע מרובעו | |
| − | + | ושורשו ימצא על דרך זה | |
| − | + | יבוקש מרובע מרובע מעוקב בכתה שמאלית ויוגרע כדין | |
| − | + | ב) להכפלת השורש תעשה כפי אשר מראה אותך הלוח ותעמידם כסדר שהקדמנו | |
| − | + | ג) תחלוק כדין ותעמוד אצליהם שורש היוצא מרובעו מעוקבו מרובע מרובע מרובעו מרובעו מעוקבו מעוקבו (45r) מרובע ויוכפלו זה בזה ויעמדו זה תחת זה בגדול החל ובקטן כלה ותחתיהם יועמד מרובע מרובע מעוקבו ויקובצו וקיבוצם יוגרע כנזכר למעלה | |
| − | כמות | + | ז' מהוצאת השרש מרובע מרובע מרובע 7) Extracting the Root of the Square-Square-Square |
| − | + | מרובע מרובע מרובע הוא הכפלת המרובע מרובע במרובעו | |
| − | + | ושורשו ימצא באופן זה | |
| − | + | א) יבוקש מרובע מרובע מרובע מכתה שמאלית ויוגרע כדין | |
| − | + | ב) להכפלת השרש תעשה כפי אשר מראה אותך הלוח ותעמידם בסדר שהקדמנו | |
| − | + | ג) ואצלם יועמד השרש השני היוציא מחילוק כדין מרובעו מעוקבו מרובע מרובעו מרובעו מעוקבו מעוקבו מרובע מרובע מרובעו מעוקבו ויוכפלו זה בזה ותחתיהם יעמוד יועמד מרובע מרובע מרובעו ויקובצו וקיבוצם יוגרע כנ"ל | |
| − | + | ח' מהוצאות שורש מעוקב מעוקב 8) Extracting the Root of the Cubed Cube | |
| − | The question is | + | מעוקב מעוקב הוא כשנעקב המעוקב דהיינו שנכפול אותו בעצמו והנולד יוכפל במעוקב |
| − | תשובה מספר | + | ולהוצאת שרשו נעשה כך |
| − | כמה יתנו | + | א) יבוקש מעוקב מעוקב מכתה שמאלית ויוגרע כדין |
| − | x x | + | ב) להכפלת השורש היוצא ומרובעו וכו' תעשה כפי הוראת כהוראת הלוח ותעמידם כסדר המוזכר |
| − | + | ג) ואצליהם יועמד השרש היוצא מחילוק מרובעו מעוקבו מרובע מרובעו מרובע מעוקבו מעוקבו מרובע מרובע מרובעו מעוקבו מרובע מרובע מרובעו ויוכפלו זה בזה ותחתיהם יועמד מעוקב מעוקבו ויוקבצו וקיבוצם יוגרע כנ"ל | |
| − | + | ט' מהוצאות שורש מרובע מעוקב מרובע 9) Extracting the Root of the Squared-Square-Cube | |
| − | ( | + | מרובע מעוקב מרובע הוא הכפלת הזורזאליד או המרובע מעוקב בעצמו |
| − | + | ושורשו ימצא בדרך זה | |
| − | + | א) יבוקש מרובע מעוקב מרובע מכתה שמאלית ויוגרע כדין | |
| − | + | ב) להכפלת החלקים צא בעקבות הלוח ותעמידם בסדר שהורינוך | |
| − | + | ג) ואצליהם יעמוד יועמד השורש היוצא מהחילוק מרובעו מעוקבו מרובע מרובעו מרובע מעוקבו מעוקבו מרובע מרובע מרובעו מעוקבו מרובע מרובע מרובעו מעוקב מעוקבו ויוכפלו זה בזה ותחתיהם יעמוד יועמד מרובע מעוקבו מרובע ויקובצו וקיבוצם יוגרע כנ"ל | |
| − | + | מהוצאות שורש פרוניק | |
| − | ( | + | פרוניק הוא קיבוץ השורש למרובעו |
| − | + | והנה למציאת שורשו נוציא שורש המרובע והנשאר יורה השורש וא"כ שורש המרובע דומה לשארית | |
| − | + | או בדרך יותר נכון נעשה כך נכפול כולו עם 4 ולהנולד יקובץ עם 1 ונוציא מהעולה שורש המרובע ומהשורש ומן השרש היוציא יגרע נגרע 1 והנשאר יחלק נחלק לשניהם והחצי הוא השורש המבוקש | |
| − | + | וזה מה שיתכן לנו די ביאר מהוצאות השורשים כי תן לחכם ויחכם | |
| − | + | מהוצאות השרשים בשברים עם אם שלימים עם השברים תתיר השלימים לשברים ותוציא השרש ממכנה ואח"כ ממונה והיוציא הוא השורש המבוקש וכן בשברים לבדם | |
| − | השאלה כמה | + | מהוצאות השרשים כשהערך אינו מתמיד וכן משלמים ושברים בשיווי לשלמים ושברים נכתב לקמן באריכות כיד ה' הטובה עלינו אי"ה |
| − | + | מכלל הזהב | |
| − | + | עד הנה עזרנוך במיני המספר נשאר לנו לבאר מערכי המספר והם בכפלים או בהערך או בהעברה | |
| − | + | מספרים מעורכים הם כאילו נאמר כערך מרחק מזה אל זה כך ערך מרחק מזה (45v) לזה אל זה כמו 3÷6:8÷16 | |
| − | + | הנה בכאן ארבע הערכות הערכי' אשר מיוחסהי' מיחוסיהם נבאר לקמן בע"ה מעז"ה | |
| − | + | אבל אם הי' ערך אחד ידוע ונבקש ערך בלתי ידוע אשר יהיה משפטו כערך ראשון אל שני כך ערך השלישי הבלתי לבלתי הידוע הנה חפש זו לגדול תועלתו נקר' כלל הזהב או כלל משלש והוא בכפלים או פשוט או מוכפל. | |
| − | + | הפשוט הוא משלש הערכות לבדן והוא כמו כן ישר או הפוך אשר בזה יבחנו היטב כל מסבב השאלה כי בהרבה דברים נראה כל' הזהב אשר בכל בית נכאת ההגיונים אין כמותו בלתי צודק כשהערך מופסק או בהעסקה בלתי נאותית לכל מסבבי השאלה: | |
| − | + | כלל זהב מוכפל הוא מחמש הערכות אשר מזה יכונה כלל מחומש והוא כמו כן או ישר או הפוך | |
| − | + | והנה מהעסקתם באלגיברה לא ישונה מהעסקה המספרית רק שההכפלה וחילוק נעשה על דרך האלגיברה כמו שהורינוך בכללים הקודמים | |
| − | + | וכשתשים הסימן אשר בחרת במקום הראוי לבוא אז יבוקש כמותו אם נעסוק בו כדין יחוסי אותם מספרים | |
| − | + | כמו 2:3:8:x דהיינו אם ישאל שנים יתנו שלושה כמה כמו יתנו שמנה | |
| − | + | והתשובה ובא התשובה שיתנו x והנה הסימן הזה x הוא המספר אשר שני שלישים ממנו הוא 8 | |
| − | וא"כ | + | והנה לידע כמות x אשר בחרת תעשה השוואת המעורכים שהוא אחד מיחוסיו שאם יוכפלו שתי וערב שישתוו ובנדון דידן כזה |
| − | + | ■(├ ■(2&3@8&x)┤|&├ ■(2x=24@■(2&2))┤|&■(12@)) | |
| − | + | תחלוק שני הכמות עם 2 יצא x=12 והוא הכמות המבוקש כי כערך 2 אל 3 כך ערך 8 אל 12 | |
| − | + | והבחינה כשתכפלם שתי וערב כזה | |
| − | + | משתווים 24=24 ■(2:&3@8:&x 12) | |
| − | + | הי' השאלה אבל בתשובה תעשה כך | |
| − | + | ■(2&03@8&12) | |
| − | + | ותכפלם שתי וערב הם שווים ע"כ הי' הסימן x מראה על 12 וכו' | |
| − | + | כמו שאמרנו והיא באמת הבחינה היותר קלה ונכונה בכל כללי הזהב | |
| − | + | ומזה נולד שתכפיל בכלל משלש ישר האמצעי עם הקצווה ימינית והנולד יוחלק עם השמאלית וההפוך בהיפוכו | |
| − | + | ותוכל לעסוק כפי כל קצורי האחרונים אשר מצאו עד זמננו זה ואשר מצאנו והם כתובים באצבע בחבורינו צפנת פענח | |
| − | + | ויהיו למאורות דמיונות אלו ותן עיניך בהם: | |
| − | + | (א) כת בחורים היו בבית המשתה ושם אכלו ושתו בעד 22 זהו' 49 צ"ל וכל אחד מהם שלם כל כך צ"ל כמספר האישים | |
| − | + | השאלה כמה פרע כל אחד ביחוד וכמה בחורים היו שם. 1) A group of men were in a restaurant. They ate and drank there for 22 zehuvim and 49 z”l. Each of them paid as many z”l as the number of people. | |
| − | + | The question is how much did each pay separately and how many men were there? | |
| − | + | תשובה יראה כי עיקר הנעלם כאן הם מספר הצ"ל שנתן כל אחד מהחברה וממנו יולד מספר הבחורים וכן בהיפוך ונאמר שאחד מהם נתן x וא"כ בהכרח מספר הבחורים היה כמו כן x וא"כ נעמידהו על כלל משלש כזה | |
| − | + | כמה יתנו כלם יתן בחור | |
| − | + | x x : 1 | |
| − | + | ||
| − | וא"כ | + | וא"כ יבוא כדין שיתנו כלם xx כי האחדות אינו חולק ואח"כ נשווה ונאמר xx=1369 שהם הצ"ל עם התר הזהב לצ"ל וא"כ כמו xx הוא מרובע אמיתי בהכרח יהיו ה 1369 כמו כן מרובע אמיתי תוציא משניהם השרש ויבוא x=37 וזה המבוקש כי הבחורים היו במספר 37 וכן נתן כל אחד מהם 37 צ"ל בחון ותראה אמת : |
| − | + | (ב) אחד קנה חתיכה בגד מחזקת ששים אמה אמות בעד סך ידוע ויהיה הסך של זהו' שנתן בעד כלו כלה כמספר האמות שנתן שקנה בעד 6 2/3 זהו' | |
| − | + | השאלה בכמה זהו' פרע כלו אותה וכמה אמות קנה בסך בעד 6 2/3 זהו' 2) One bought a piece of cloth of sixty cubits for a known amount, such that the number of zehuvim that he paid for all of it is the same as the number of cubits he bought for 6 2/3 zehuvim. | |
| − | + | The question is: for how many zehuvim did he buy it and how many cubits did he buy for 6 2/3 zehuvim? | |
| − | + | תשובה הנה עיקר ההעלמה כמה אמות שקנה בעד 6 2/3 זהו' כי הן סיבת ידיעת מספר כלל הזהובי' שפרע ונקח במקום האמות שאינן הבלתי ידועות x ובמקום הממון הבלתי ידוע ב"כ כמו כן x ויעמדהו ונעמידהו על כלל משולש כזה | |
| − | + | בכמה | |
| − | דהיינו | + | כמות האמו' בעד |
| − | + | סך זהו' אמות | |
| − | + | אמות 60 זהו' 6 2/3 x | |
| − | + | ||
| − | + | אז תכפול מספר סך הזהו' עם כמות האמות הידוע ונעסוק בו כדין רעגולי דעטרי יצא 400/x דהיינו סך שהם ת' זהו' שבור אות' על מחולקים ע"י x והם שווים למספר x שהוא סך הששים אמות וא"כ יהיה כך (400-x)/x והנה כדי שנודע המספר שנמצא על צד אחד מספר נודע נעשה כך תכפול הסך 400 נראה שה400 מחולקים ע"י x ואז נכפיל הת' עם x ואז הוא משולל החלוקה דהיינו שנשליך ממנו x וישאר 400 לבדו ואח"כ ואחר כך תכפול נצריך כמו כן לכפול ה xב x כדי שישארו שני שתי כמות שוות באותו שיווי וכמו שכתבנו בכלל השלישי מכללים הכוללים ואז יבוא xx שהוא מרובע אמיתי וא"כ יהיה 400=xx נוציא משניהם שורש מרובע יבוא x-20 ונמצא ששילם בעד 60 אמות 20 זהו' כמספר האמות שהיו לו בעד 6 2/3 זהו' | |
| − | + | (ג) שאלה כמה אנשים אוהבים נאמנים פרעו בסעודה אחת 75 זהו' וכל אחד פרע כל כך כ"כ זהו' כמו 1/3 מספר האנשים | |
| − | וא"כ | + | השאלה כמה היו אנשים וכמה פרע כל אחד מהם ביחוד 3) Loyal friends paid 75 zehuvim at one meal and each one paid as many zehuvim as 1/3 of the number of people. |
| − | + | The question is how many people were there and how much did each of them pay separately? | |
| − | נקבץ | + | תשובה מספר האנשים היו x והואיל אחד נתן כ"כ זהו' כמו 1/3 מספר כלם א"כ החלק הזה יקרא x/3 ואז נעמידהו על כלל משולש כזה |
| − | + | כמה יתנו משלם | |
| − | + | x x/3 1 | |
| − | + | ||
| − | + | נעסוק בו כדין יצא xx/3 וזה שווה למספר 75 כזה xx/3=75 הכפיל נכפל שניהם שניהם עם מספר 3 כדין יצא ההשוואה xx=225 נוציא משניהם שורש המרובע יבוא x=15 שהם מספר האנשים וא"כ הי' כל א' נתן 5 זהו' וכו' ואם כן x/3=5 שהוא מספר הזהב שפרע אחד מהם | |
| − | + | (ד) שאלה אם הי' יש לאחד אנשים על שלחנו שיתן להם מזונות | |
| − | + | ואם יתן אחד מהם 50 ר"ט לשנה בעבור המזונות יזיק הבעל הבית לב"ב 30 ר"ט | |
| − | + | אבל אם יתן אחד מהם 60 ר"ט ירוויח (46r) הבעה"ב הבעל בית 40 ר"ט | |
| − | + | השאלה כמה אנשים היו סועדים על שולחנו | |
| − | + | וכמה המעות לשנה שהוציא הבעה"ב הב"ב | |
| − | + | תשובה מספר האנשים שסעדו היה x וא"כ ואם כן אמור ראשונה אחד נתן 50 ר"ט כמה יתנו x שהוא מספר האנשים יבואו שיתנו כלם 50x ואח"כ ואחר כך נאמר כמו כן אחד יתן 60 ר"ט כמה יתנו x יבוא שיתנו כלם 60x והואיל בכתה ראשונה יזיק לב"ב 30 וא"כ יהיה הסך שהוציא 50x*30 ובשניה הרויח 40 ר"ט וא"כ יהיה הקרן 60x-40 ויהיה א"כ בהשוואה ההשוואה כך 50x*30=60x-40 נגרע משניהם 50x ישאר כזה 30=10x-40 נקבץ לשניהם 40 יהיה כך 70=10x נחלק שניהם עם 10 ויהיה א"כ x=7 שהוא מספר האנשים שסועדים על שולחנו וא"כ מעות המזונות שיוציא הב"ב לשנה הי' הוא 380 והוא מבואר | |
| − | + | (ה) שאלה שלשה פועלים בנו בנין אחד | |
| − | + | שכר הראשון 40 צ"ל ליום | |
| − | + | ושכר השני ליום אחד 50 צ"ל | |
| − | + | ושכר השלישי 60 צ"ל ליום | |
| − | + | והבניין נגמר בק"ך ימים והפועלים קבלו תשלומין בשווה | |
| − | + | השאלה כמה ימים בנה כל אחד מהם | |
| − | + | תשובה אמור מספר ימים של ראשון הם שווים x ושל שני y | |
| − | + | וא"כ מספר הימים של שלישי הם 120-x-y | |
| − | + | וא"כ שכר הראשון 40x | |
| − | + | ושכר השני 50y | |
| − | + | שכר השלישי 7200-60x=60y פי' | |
| − | + | כי תכפיל 60 שכר השלישי עם 120 יהיה 7200 | |
| − | + | אבל קיבל פחות כמספר שכרו שקבלו השנים | |
| − | + | דהיינו -60x-60y | |
| − | + | ולפי נדון השאלה 50y=40x | |
| − | + | נמצא הכמות של 60y 60y בשכר השלישי בכלל משולש כזה | |
| − | + | ├ ■(■(50y-40x&60y) @■(240&0)@■(5&0))┤|48x | |
| − | + | וא"כ כעמוד נעמיד במקום 60y בשכר השלישי 48x כזה 7200-60x-48x=40x | |
| − | + | נקבץ x יחדיו יהיה 108x | |
| − | + | וא"כ השיווי יהיה כזה 7200-108x=40x | |
| − | + | נחבר לשניהם 108x השיווי כזה | |
| − | + | 7200=108x148x | |
| − | + | נחלק שניהם עם 148 יהיה 2/3 4=x [?] או 48 96/148 צ"ל והם הימים של ראשון | |
| + | ואם נכפלם עם 40 יצא 1945 35/37 צ"ל וכן שכר הראשון וככה שכר כלם | ||
| + | ואם נחלקהו עם 50 שכר שני ליום וכן עם 60 שכר שלישי ליום יבואו ימים של שני 38 34/37 וימים של שלישי 32 16/37 | ||
| + | ואם נקבץ השלשה זמנים יחדיו יעלה 120 ימים והוא נכון | ||
| + | (46v) מדמיונות מוערכות | ||
| + | (א) לשני אנשים סך זהו' והם בערך אחד לשני כמו 2 אל 5 ואם מרובע שניהם יוקבצו והיו לאחד יעלה יעלו 11600 זהו' | ||
| + | השאלה כמה היה לאחד מהם זהו' 1) Two men have some zehuvim at a ratio of 2 to 5, such that if the squares of both are summed up to one number, the result is 11600 zehuvim. | ||
| + | The question is how many zehuvim did each one have? | ||
| + | תשובה לכל אחד מהם היה סך x זהו' The answer: | ||
| + | Each has an amount of x zehuvim. | ||
| − | + | והואיל והם כערך 2 אל 5 היה לראשון 2x ולשני 5x Since they are at a ratio of 2 to 5, the first has 2x and the second has 5x. | |
| − | + | מרובע הראשון עולה 4xx ומרובע השני 25xx The square of the first is 4x^2 and the square of the second is 25x^2. | |
| − | + | תחברם יחד יעלה קיבוצם 29xx Sum them together; their sum is 29x^2. | |
| − | + | וא"כ יהיה ההשוואה כזה 29xx=11600 So, the equation is: 29x^2=11600 | |
| − | + | תחלק שניהם עם 29 יצא הכמות כזה xx=400 Divide both by 29; the quotient is x^2=400. | |
| − | + | תוציא משניהם שורש המרובע יהיה x=20 Extract the square roots of both; it is x=20. | |
| − | + | וא"כ מעות הראשון שהוא 2x שווה 40 Hence, the amount of money of the first, which is 2x, is worth 40. | |
| − | + | ומעות השני שהיה 5x היה 100 זהו' And the amount of money of the second, which is 5x, is 100 zehuvim. | |
| − | + | (ב) לאחד נשלחו ג' תיבות ממולאות ספרים ונרשמו במספר 3 2 1 ובכל אחת מהב' מהתיבות כל כך ספרי' כמו ערך המספרים שנרשמו עליהם זו לזו | |
| − | + | דהיינו כמו 1 אל 2 וכמו 2 אל 3 | |
| − | + | ואם נרבע מספר כל אחד מהם ונחברם יחד יעלה קיבוצם 24696 | |
| − | + | השאלה כמה היו ספרים בכל תיבה ותיבה בפרטיות וכמה היו יחדיו בשלש תיבות 2) One was sent 3 boxes filled with books and marked with the numbers 3 2 1, in each of the boxes as many books as the ratio of the numbers written on them (that is, as 1 to 2 and as 2 to 3) | |
| − | + | If we square the number of each of them and add them together, their total sum is 24696 | |
| − | + | The question is how many books were in each box individually and how many were together in the three boxes? | |
| − | + | תשובה בתיבה הראשונה היו x ספרים | |
| − | + | וא"כ הי' בתיבה שניה 2 2x ובתיבה שלישית 3x Answer: in the first box there were x books, so in the second box there were 2x and in the third 3x. | |
| − | + | וא"כ מרובע תיבה ראשונה xx ושני' ומרובע תיבה שניה 4xx ומרובע תיבה שלישית 9xx So, the square of the first box is x^2, the square of the second box is 4x^2, and the square of the third box is 9x^2. | |
| − | + | נקבץ המרובעים יעלה ויעלו 14xx We sum up the squares; the result is 14x^2. | |
| − | + | וא"כ יהי' ויהיה א"כ ההשוואה כזה | |
| − | + | 14xx=24696 Hence, the equation is 14x^2=24696. | |
| − | + | תחלק השני שווים עם 14 יבוא ההשוואה כזה | |
| − | + | xx=1764 Divide the two sides by 14; the resulting equation is: x^2=1764. | |
| − | תשובה | + | תוציא משניהם שורש המרובע ויבוא x=42 Extract the square roots of both; the result is x=42. |
| − | + | וא"כ יהי' זה המספר הספרים שבתיבה ראשונה | |
| − | + | וא"כ הי' בשני' 2x=84 בשניה | |
| − | + | ובשלישית 3x=126 וכו' So, this is the number of books in the first box; in the second 2x=84; and in the third 3x=126. | |
| − | + | (ג) שלשה יש להם מספר זהו' והמספר האחד למספר השני כערך מרובע וכן ערך מספר השני למספר השלישי הוא כערך מרובע | |
| − | + | ואם תקבץ המרובעים יחדיו יהיה 69888 | |
| − | + | השאלה כמה היה לאחד מהם 3) Three had some zehuvim. The number of one is at a square ratio to the number of the second and the ratio of the number of the second to the number of the third is also a square ratio. | |
| − | + | If you sum the squares together, it is 69888. | |
| − | + | The question is how much did each have? | |
| − | + | תשובה לאחד מהם היה x וא"כ היה לשני 4x ולשלישי 16x The answer: one had x, so the second had 4x and the third had 16x. | |
| − | + | אשר מרובע הראשון הוא xx | |
| − | + | מרובע השני 16xx | |
| − | + | מרובע השלישי 256xx So, the square of the first is x^2, the square of the second is 16x^2, and the square of the third is 256x^2. | |
| − | + | נקבצם יחד יעלה 273xx We sum them together; the result is 273x^2. | |
| − | + | וא"כ יהיה 273xx=69888 Hence, it is 273x^2=69888. | |
| − | + | תחלקם עם 237 יהיה הכמות xx=256 Divide them by 237; the quotient is | |
| − | + | x^2=256. | |
| − | + | תוצא משניהם שורש המרובע יצא כך ■(x=16@4x=64@16x=256) Extract the square roots of both; the result is: ■(x=16@4x=64@16x=256) | |
| − | + | (ד) כת בחורים למדו אצל אחד ופרעו לו ונשאל אחד מהם כמה היה הפרעון והשיב אם נחצה 1/6 מ 1/3 יולד מספר ערכיי 1 1/4 שיורה שכל אחד נתן פרע 1 1/4 כמספר כל הבחורים ופרעו יחדיו 45 זהו' 45 | |
| − | The question | + | השאלה כמה היו הבחורים וכמה פרע כל אחד מהם 4) A group of men studied with one and paid him. |
| − | תשובה | + | One of them was asked how much the payment was and he replied: if we halve 1/6 of 1/3 it would give a proportional number of 1 1/4 that indicates that each one paid 1 1/4 of the number of all the men and paid together 45 zehuvim. |
| − | וא"כ | + | The question is how many were the men and how much did each of them pay? |
| − | נקבצם יחד | + | תשובה מספר הבחורים היה x Answer: the number of men is x. |
| − | + | ואחד נתן 5/4 כמספר כלם א"כ נתן אחד מהם 5/4 x Each one paid 5/4 of the number of all of them, so each one paid 5/4 x. | |
| − | + | וא"כ נעמידהו על כלל משולש כזה We arrange it according to the Rule of Three, like this: | |
| − | + | כמה יתנו נתן בחור | |
| − | + | x 5x/4 1 | |
| − | ( | + | How many paid Each paid man |
| − | השאלה כמה | + | x 5/4 x 1 |
| − | The question is how | ||
| − | תשובה | ||
| − | |||
| − | |||
| − | x/ | ||
| − | |||
| − | |||
| − | x/ | ||
| − | + | ונעסוק בו כדין כלל הזהב | |
| − | + | יבוא שכולם יתנו 5/4 xx (47r) והוא שווה למספר 45 We solve it according to the Rule of Three; the result is that they paid a total of 5/4 x^2 and this is equal to the number 45. | |
| − | + | marg.: פי' במספר הזה יש 5 פעמים 9 ואם אתה צריך 4 פעמים 9 הוא 36 הואיל שכל א' נתן 5/4 כמו כל מספר בחורים מזה תוציא שורש מרובע הוא 6 הוא מספר הבחורים | |
| − | + | נתקן כדין יבוא x=6 שהם מספר הבחורים We restore according to the rule; the result is x=6, which is the number of the men. | |
| − | + | וא"כ פרע אחד מהם 7 1/2 זהו' כו' So, each of them paid 7 1/2 zehuvim. | |
| − | + | (ה) תן לי מספר אשר שלישיתו ורביעתו מקובצים יעלה 35 5) Find me a number, such that the sum of its third and its quarter is 35. | |
| − | + | התשובה המספר הוא x Answer: the number is x. | |
| − | + | א"כ יהיו השברים x/4 x/3 והם שווים למספר 35 כזה x | |
| − | + | x/3*x/4=35 So, the fractions are x/4 x/3 and they are equal to the number 35, like this: x/3+x/4=35 | |
| − | + | נמצא נמצי' כינוי כולל דהיינו שנכפול הכינוים יהיה 12 We find a common denominator, i.e. we multiply the denominators; it is 12. | |
| − | + | וא"כ יהיו כזה 3x/12*4x/12 So, they are like this: 3x/12+4x/12 | |
| − | + | וקבוצם אשר קיבוצם עולה 7x/12=35 | |
| + | קבוצם כזה 7x/12 Their sum is: 7x/12=35 | ||
| + | marg.: כפל | ||
| − | + | x=3 1/2 | |
| − | + | תקבצם יחד יעלה קיבוצם 6x*15 | |
| − | + | וא"כ ההשוואה כזה | |
| − | + | ■(6x*15=36@*15-15) | |
| − | + | ├ ■(6x=21@6 6)┤|3 1/2 | |
| − | + | (ה) ד' יחלוקו 112 אמות בגד באופן עליה מספרית שיקבל כל אחד יותר מחבירו הכפל שני אמות יותר | |
| − | + | השאלה כמה קבל אחד מהם | |
| − | + | אמור שהראשון קבל x אמות א"כ יקבלו הנשארים כזה | |
| − | + | ■(14=2x*2@30=4x*6@▁(62=8x*14)@15x*22=112) | |
| − | + | ■(15x*22=112@ -22 22@15x=90@x=6) | |
| − | + | (ו) תן לי העברה נגונית יורדת מששה מספרים אשר קיבוצם עולה 588 | |
| − | + | מה הם המספרים | |
| − | + | אמור x הראשון א"כ הששה מספרים הם כזה | |
| − | + | ■(240=x@120=x/2@180=x/3@60=x/4@04 @48=x/5@▁(x/6)@588) | |
| − | + | נקבצם יעלה כזה 2*9x/20=588 | |
| − | + | נתקן כדין יבוא ההשוואה | |
| − | + | ├ ■(49x=11760@7x=1650@7 7)┤|240 | |
| − | + | (ז) מצוא לי אמצעי מוערך נגוני בין 10 ובין 15 ר"ל תן לי מספר אשר מרחקו מראשון (10) למרחקו משלשה (15) הוא כאותו ערך כמו 10 אל 15 : | |
| − | + | תשובה הואיל וקצווה ראשונה וקצווה שלישית הן 10 : 15 | |
| − | + | האמצעי אשר נבקש נכנה x אשר לפי שיחויב היותו גדול מהראשון ופחות מהשלישי א"כ יהיה מרחק מהראשון x-10 ומהשלישי 15-x | |
| − | + | (כי נגרע בתמידות הקטן מהגדול אשר לא יעשה בחשבון האותיות זולתי בסימן הפחיתות כאשר זכרנו בכללי הניכוי) | |
| − | + | וא"כ נשווה כך כמו 10 אל 15 כך x-10 אל מרחק 15-x אשר ארבע קצוות אלו הם בערכי מדידה נעשה מראשון כאחרון לשיווי שני האמצעיים כי זה אחד מיחוסי הערכיים כאשר זכרנו | |
| − | + | ויהיה א"כ כאן | |
| − | + | 150-10x=15x-150 | |
| − | + | נחבר לשניהם 10x יהיה | |
| − | + | 150=25x-150 | |
| − | + | נחבר לשניהם 150 *150 | |
| − | + | יהיה כזה 300=25x | |
| − | + | נחלוק שניהם עם 25 יהיה 12=x | |
| − | + | והוא האמצעי המבוקש אשר יבחן מהמרחק אשר הוא מ12 אל 10 והוא 2 וכן המרחק מ12 אל 15 הוא 3 והוא מבואר כי ערך 2 אל 3 כערך 10 אל 15 | |
| − | + | וגם יבחן ממה שכתבנו במציאת מספר השלישי בעליה נגונית וכן ימצא עם מה שכתבנו ביחוס השביעי מיחוסי העברה נגונית במציאת אמצעי מוערך יע"ש :[ | |
| − | + | (ח) (47v המשך) לידע השעות השעה אחר צהרים לשעות אשר כבר היו אל השעות אשר עתידין להיות עד חצי הלילה כערך 3 אל 4 | |
| − | + | נאמר שהשעות אשר כבר הלכו להם להן היו x | |
| − | + | וא"כ ואם כן זה הכינוי בתנאי מוחלט שערך x אל 12-x כערך 3 אל 4 וההשוואה כזה | |
| − | + | 3:4=x:12=x | |
| − | + | 3:4=x:12x | |
| − | + | נכפיל שני הקצוות דהיינו שתי וערב כזה ■(3:4 @x:12-x) | |
| − | + | יולד 4x=36-3x | |
| − | + | נקבץ לשניהם 3x יבוא כזה 7x=36 | |
| − | + | נחלק שניהם עם 7 יצא הכמות כזה x=5 1/7 =x 5 1/7 | |
| − | + | והם שעות אשר ע[.]ברו עברו והנשאר מזו הם הן 6 6/7 | |
| − | + | והערך מ 5 1/7 ל6 6/7 או 36/7 אל 48/7 דהיינו 36 אל 48 כערך 3 אל 4 | |
| − | + | והבחינה שאם נחלוק שניהם דהיינו 48 36 עם 12 יצא מהראשון 3 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | וזה מרובע המעות שלוה שמעון This is the square of the money Shimon lent. | |
| − | + | נרבע כמו כן המספר שפרע לוי כזה We also square the amount Levi paid, like this: | |
| − | + | ■(35*x@35*x) | |
| − | + | ■( *35x*xx@175*35x @105 ) | |
| − | + | 270*70x*xx | |
| − | + | ■(35+x@35+x) | |
| − | + | ■( +35x+x^2@175+35x @105 ) | |
| − | + | 270+70x+x^2 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ■(x | ||
| − | ■( | ||
| − | |||
| − | ■(x | ||
| − | ■( | ||
| − | |||
| − | + | מרובע לוי The square of Levi’s [amount] | |
| − | + | יוגרעו שני המרובעים מהדדי והשאירות יורה המרחק כזה The two squares are subtracted from one another; and the remainder indicates the difference, like this: | |
| − | + | ■(270*70x*xx@▁(270-70x*xx)@140x) ■(270+70x+xx@▁(270-70x+xx)@140x) | |
| − | המרחק | + | ולפי זה המרחק בין שניהם הוא 140x According to this the difference between them is 140x. |
| − | + | קח מהמרחק הזה 1/7 והוא 20x | |
| − | + | וזה יעוקב יבוא 8000x3 | |
| − | + | קח ממנו מספר השאול והפרוע דהיינו 70 | |
| − | + | ישאר 8000x3-70 Take 1/7 of this difference; it is 20x. | |
| − | + | It is cubed; the result is 8000x^3. | |
| − | + | Take the loaned and the paid from it, i.e. 70; the remainder is 8000x^3-70. | |
| − | + | ואז יוכפל זה השאירות עם הקיבוץ הנזכר למעלה דהיינו עם 8x3*70 יבוא כזה | |
| − | + | 64000x6*559440x3-4900 This remainder is multiplied by the above-mentioned sum, i.e. by 8x^3+70; the result is: | |
| − | + | 64000x^6+559440x^3-4900 | |
| − | + | וזה שווה למספר 1069925100 כנדון השאלה כזה | |
| − | + | 64000x6*559440x3-4900=1069925100 This is equal to the number 1069925100 as stated in the question, like this: | |
| − | + | 64000x^6+559440x^3-4900=1069925100 | |
| − | + | תקבץ לשניהם 4901 יהיה השיווי כזה | |
| − | + | 64000x6*559440x3=1069930000 Add 4900 to both [sides]; the equation is as follows: | |
| − | + | 64000x^6+559440x^3=1069930000 | |
| − | + | תגרע משני צדדי השיווי סיפרי אחת ישאר כזה | |
| − | + | ■(2 1322 22132 @64000x6*559440x3=1069930000@44 4444 444444 ) Subtract one zero from both sides of the equation; the remainder is like this: | |
| − | + | ■(2 1322 22132 @64000x^6+559440x^3=1069930000@44 4444 444444 ) | |
| − | + | תחלק כלם עם 4 יצא כזה | |
| − | + | 1600x6*13986x3=26748250 Divide all by 4; the result is: | |
| − | + | 1600x^6+13986x^3=26748250 | |
| − | + | (ואף שנוכל להקטין עוד ביות' לא נחוש לזה והכל ברצון החושב) Although we can reduce more, we are in no rush to do so; it is all up to the will of the one who calculates. | |
| − | + | קח חצי מספר המעוקבים 6993 | |
| − | + | ותרבעהו יהיה המרובע כזה 48902049 | |
| − | + | קח מספר המעוקבים מרובעים שהם 1600 | |
| − | We | + | ותכפול אותו עם המספר הפשוט דהיינו עם 26748250 יולד 16048950000 Take half the number of the cubes; it is 6993. |
| − | + | Square it; the square is 48902049. | |
| − | + | Take the number of the squared cubes, which is 1600. | |
| − | + | Multiply it by the simple number, i.e. by 26748250; the result is 42797200000. | |
| − | + | תקבץ אליו מרובע חצי מספר המעוקבי' הנ"ל דהיינו 48902049 יהיה 42846102049 Add to it the square of half the number of the cubes mentioned, i.e. 48902049; it is 42846102049. | |
| − | + | תוציא ממנו שרש המרובע יבוא 206993 | |
| − | + | תגרע משרש המרובע חצי מספר המעוקבים דהיינו 6993 ישאר 200000 | |
| − | + | וזה תחלוק במספר המעוקבים מרובעים דהיינו עם 1600 יבוא 125 | |
| − | + | וממנו תוציא שרש המעוקב יבוא 5 Extract its square root; the result is 206993. | |
| − | + | Subtract half the number of the cubes, i.e. 6993, from this square root; 200000 remains. | |
| − | + | Divide it by the number of the squared cubes, i.e. by 1600; the result is 125. | |
| − | + | Extract its cube root; the result is 5. | |
| − | + | וא"כ x=5 So, x=5. | |
| − | + | ולפי זה 35*x=40 והוא המעות שפרע לוי According to this, 35+x=40, which is the money the Levi paid. | |
| − | + | וא"כ 35-x=30 מעות שלוה שמעון Therefore, 35-x=30 is the money that Shimon lent. | |
| − | + | אמר המחבר אף שלפי הדרך אשר דרכנו בהתר השאלות הקודמות יותר ספק זה כמו כן רצינו להציג לפניך התר השאלה כפי דרך חדש מצוא מאתנו לשתי סיבות The author said: although according to the way we use to solve the previous questions, this doubt is resolved, we also want to present to you the solution of the question according to a new way we found for two reasons: | |
| − | + | הסיבה הראשונה היא כדי שתהינ' לך דרכי ההתר צבורות The first reason: so that you have a collection of solution methods. | |
| − | + | והיה אם לא השיג יד שכלך להתיר עם דרכים הקודמים Even if your mind could not solve it with the previous ways. | |
| − | + | ובפרט עם החלוק אשר סבוך בקרניו [בראשית כ"ב, יג] וצריך עיון רב Especially regarding the division that is “caught in the thicket by its horns” [Genesis 22, 13] and requires much investigation. | |
| − | + | ובסופו לא ימלט אף על פי כן מתיקון ההשוואה בלתי טהורה Eventually, there is no escape but to restore the compound equation. | |
| − | + | לכך תשתה ממקור ולא תצרך למים שאובים For this you will drink from the water source and will not need drawn water. | |
| − | + | ולא נהיה למס מרעהו חסד [איוב ו, יד] We will not be “to him that is ready to faint kindness is due from his friend” [Job 6, 14] | |
| − | + | הסיבה השנית להגדיל חסד בוראינו The second reason is to magnify the grace of our Creator, | |
| − | + | שכמה מעלות טובות למקום עלינו [הגדה של פסח, מגיד, דיינו א] for “How many virtues of goodness did the Place [bestow] upon us!” [Pesach Haggadah, Magid, Dayenu 1], | |
| − | + | כי לא אסף גם מאתנו חסדו בדור האחרון הזה Because He did not withdraw his grace from us in this last generation, | |
| − | + | ולהורות כי הקדמונים כאשר לאו למצוא הפתח [בראשית י"ט, י"א] הזה And to indicate that the ancients, when “they wearied themselves to find the door” [Genesis 19,11], | |
| − | + | והנה הוא סגור אין יוצא ואין בא [יהושע ו, א] And behold it is closed “none went out, and none came in” [Joshua 6, 1] | |
| − | + | והוכו בסנורים [בראשית י"ט, י"א] “They were struck with blinding light” [Genesis 19,11] | |
| − | + | וילכו בחשך ולא ראו אור [יהושע ט, א] “They walked in darkness” and did not “see a light” [Joshua 9, 1] | |
| − | + | חשבו אותו להעדר בלי קנין עלמות They thought it is absent not perpetual acquisition | |
| − | + | וגם החכם השלם הכולל כמהר"ר יש"ר מקנדיאה הודה זה ולא בוש [זבחים קא א, יב] על פי תלמידו נאמן ביתו הכולל כמהר"ר משה ממיץ אשר עמו דבר במראה ולא בחידות [במדבר יב, ח] וז"ל Also, the complete sage our honorable teacher and Rabbi Yashar Mi-Qandia “admitted” this “and was not embarrassed” [Zevachim 101a:12] according to his disciple the faithful of his house our honorable teacher and Rabbi Moshe Mi-Mitz who spoke with him “in sight, not in riddles” [Numbers12, 8] | |
| − | + | אבל לפעמים נבוא אל שיווים שלא נודע אופן הוצאות השרש But, sometimes we get an equation, for which the way to extract the root is unknown. | |
| − | + | כאשר הוא בדרך הנהוג כמשל השלישי שתבוא אל שיווי בין ג 1 ובין א 6 פ ם 57 1/27 As it is in the procedure of the third example, when you get the equation: | |
| − | + | 57 1/27+6x=x^3 | |
| − | + | והקדמונים חתרו למצוא אופן הוצאת השרש כאשר עשו כשהשיווי בין מרובע ובין שרשים עם מספרים ולא יכולו וכלו הזמן היקר עכ"ל The ancients strived to find a way to extract the root, as they did when the equation is between the square and the roots with numbers, but they could not, and they wasted valuable time; end of quote. | |
| − | + | ולמעלה ממנו כתב וז"ל וצריך למצוא זה בחיפוש כאשר אתה מנסה בחלוק לדעת כמה פעמים החולק יכנוס בנחלק כי אין דרך אחר לאלו הדברים היקרים עכ"ד Before it, he wrote: it should be found by investigation, when you try to find out by division how many times the divisor is contained in the dividend, because there is no other way for these precious things; end of quote. | |
| − | + | ומהדמיון שקדם ביאורינו לו והדמיון הסמוך תראה כי לא דברו נכונה However, from the example we explained earlier and the last example, you can see that his statement is not true. | |
| − | + | |- | |
| − | + | | | |
| − | x* | + | :13) One asked his friend to help him in a time of need and wrote him a letter of begging. |
| − | + | :He sent him as many zehuvim as the letters in the letter. | |
| − | + | :If the number of zehuvim is divided into two equal parts, then a hundred is subtracted from one part and a hundred is added to the other part, the added and subtracted are multiplied by each other, the result is squared and the square is divided by 9000, the resulting part is equal to the number resulting when the aforementioned added and subtracted are squared each individually and the squares are summed. | |
| − | + | :The question is: how many zehuvim did he send him? | |
| − | + | |style="text-align:right;"|‫(יג) אחד בקש מאוהבו לעוזרו בשעת דוחקו וכתב לו אגרת תחנונים<br> | |
| − | + | והוא שלח לו כל כך זהו' כפי אותיות שבתוך האגרת<br> | |
| − | + | ואם יחולקו מספר הזהו' בשני חלקי' שווים ויוגרע מחלק האחד מאה ולחלק השני יקובץ מאה ויוכפלו המקובץ והמוגרע בהדדי והנולד ירובע והנולד יוחלק עם ‫9000 שהחלק היוצא הוא בשווה למספר שאם ירובע המקובץ והמוגרע הנ"ל כל אחד ביחוד והמרובעים יקובצו<br> | |
| − | + | השאלה כמה זהו' שלח לו | |
| − | + | |- | |
| − | + | | | |
| − | + | :Answer: say that the number of zehuvim is 2x | |
| − | + | |style="text-align:right;"|תשובה אמור שמספר הזהו' היה ‫2x | |
| − | + | |- | |
| − | + | | | |
| − | + | :So, each part is x. | |
| − | + | |style="text-align:right;"|ואם כן כל אחד מהחלקים היה ‫x | |
| − | + | |- | |
| − | | | + | | |
| − | | | + | :Subtract 100 from one of them; the result is: x-100 |
| + | |style="text-align:right;"|תגרע מאחד ‫100 יבוא ‫x-100 | ||
| + | |- | ||
| + | | | ||
| + | :Add 100 to the other; the result is: x+100 | ||
| + | |style="text-align:right;"|ולהשני תקבץ ‫100 יבוא ‫x*100 | ||
| + | |- | ||
| + | | | ||
| + | :Multiply them by each other; the result is: <math>\scriptstyle x^2-10000</math> | ||
| + | |style="text-align:right;"|תכפילם זה בזה יבוא ‫xx-10000 | ||
| + | |- | ||
| + | | | ||
| + | :Square it; the result is: <math>\scriptstyle x^4-20000x^2+100000000</math> | ||
| + | |style="text-align:right;"|תרבע זה יבוא ‫x4-20000x2*100000000 | ||
| + | |- | ||
| + | |Divide it by 9000; the quotient is as this: <math>\scriptstyle\frac{x^4-20000x^2+100000000}{9000}</math> | ||
| + | |style="text-align:right;"|תחלקם עם ‫9000 יצא כמות החלק כזה <math>\scriptstyle\frac{x4-20000x2*100000000}{9000}</math> | ||
| + | |- | ||
| + | |Then, take the parts and square each by itself, like this: | ||
| + | |style="text-align:right;"|ואח"כ קח כמו כן החלקים ותרבע כל אחד ביחוד כזה | ||
| + | ■(x*100@x*100) ■(x-100@x-100) | ||
| + | ■( *100x*10000@xx*100x ) ■( -100x*10000@xx-100x ) | ||
| + | xx*200xx10000 ■(xx-200x*10000@xx*200x*10000) | ||
| + | ■(x+100@x+100) ■(x-100@x-100) | ||
| + | ■( +100x+10000@x^2+100x ) ■( -100x+10000@x^2-100x ) | ||
| + | x^2+200x+10000 ■(x^2-200x+10000@x^2+200x+10000) | ||
| + | |||
| + | תקבצם יעלו כזה 2xx*20000 Sum them; the result is 2x^2+20000 | ||
| + | וא"כ ההשוואה כזה | ||
| + | (x4_20000x2*100000000)/9000=2xx*20000 So, the equation is: | ||
| + | (x^4-20000x^2+100000000)/9000=2x^2+20000 | ||
| + | תכפיל שניהם עם 9000 Multiply both by 9000 | ||
| + | יצא כזה השיווי The resulting equation is: | ||
| + | x4_20000x2*100000000=18000x2*100000000 x^4-20000x^2+100000000=18000x^2+180000000 | ||
| + | נקבץ לשניהם 20000x2 We add 20000x^2 to both [sides]. | ||
| + | יצא השיווי כזה The resulting equation is: | ||
| + | x4*100000000=38000x2*180000000 x^4+100000000=38000x^2+180000000 | ||
| + | נגרע משניהם 100000000 We subtract 100000000 from both [sides]. | ||
| + | ישאר כזה The remainder is like this: | ||
| + | x4=38000x2*80000000 x^4=38000x^2+80000000 | ||
| + | נקח חצי מספר המרובעים דהיינו 19000 We take half the number of the squares, i.e. 19000 | ||
| + | ונרבעהו יבוא 361000000 We square it; the result is 361000000 | ||
| + | נקבץ אליו מספר הפשוט 80000000 We add the simple number 80000000 to it | ||
| + | יעלה קיבוצם כזה 441000000 Their resulting sum is 441000000 | ||
| + | נוציא מהקבוץ שרש המרובע יבוא 12000 We extract the square root of the sum; the result is 21000 | ||
| + | נקבץ אליו מספר 19000 חצי מספר המרובעים We add 19000 to it, which is half the number of the squares. | ||
| + | יהיה 40000 It is 40000. | ||
| + | נוציא ממנו שרש המרובע יצא 200 We extract its square root; the result is 200. | ||
| + | וא"כ x=200 So, x=200. | ||
| + | ולפי זה 2x=400 המספר המבוקש : According to this, 2x=400 is the required number. | ||
| + | {| | ||
| + | |- | ||
| + | | | ||
| + | :14) One bought two chickens and he was asked how much he gave for one of them. He replied: One is more expensive than the other by a number of zehuvim, such that if their difference is subtracted from the sum of their squares, and the remainder is multiplied by the square of their sum, then the square of their sum is added to the result, the outcome is this number 974213100; but if the numbers are multiplied by each other and half their difference is added to the product, then the result is multiplied by the square of their sum, and the square of their sum is subtracted from the product, the remainder is 485276400. | ||
| + | The question is for how much did he buy one of them and how much did he give for both of them together? | ||
| + | |style="width:45%;text-align:right;"|‫(יד) אחד קנה שני עופות ונשאל כמה נתן בעד אחד מהם<br> | ||
| + | והשיב האחד יקר הערך יותר מהשני מספר זהו' באופן זה<br> | ||
| + | אם מרחקם יוגרע מקיבוץ מרובע שניהם<br> | ||
| + | והמותר יוכפל במרובע קיבוץ שניה‫'<br> | ||
| + | ולהנולד יקובץ מרובע קיבוץ שניהם<br> | ||
| + | אז יבוא המספר הזה ‫974213100<br> | ||
| + | אבל אם המספרים יוכפלו זה בזה<br> | ||
| + | ולהנולד יקובץ חצי מרחקם<br> | ||
| + | והעולה יוכפל במרובע חיבור שניהם<br> | ||
| + | ומהעולה יוגרע המרובע חיבור שניהם<br> | ||
| + | ישאר ‫485276400<br> | ||
| + | השאלה בכמה קנה אחד מהם וכמה נתן בעד שניהם יחדיו | ||
| + | |- | ||
| + | | | ||
| + | :The answer: | ||
| + | :Say that he bought the first for x+a. | ||
| + | |style="text-align:right;"|תשובה אמור שהראשון קנה בעד ‫x*a | ||
| + | |- | ||
| + | | | ||
| + | :So, he bought the other for x-a. | ||
| + | |style="text-align:right;"|א"כ קנה השני בעד ‫x-a | ||
| + | |- | ||
| + | | | ||
| + | :If the acquisition is subtracted from the acquisition, the remainder indicates the difference. | ||
| + | |style="text-align:right;"|אשר אם יוגרעו הקניה מהקניה השאירות יורה המרחק | ||
| + | |- | ||
| + | |When you subtract it, you find that the remainder is 2a and this is the difference, like this: | ||
| + | |style="text-align:right;"|א"כ כשתגרעם תמצא המותר ‫2a והוא המרחק נקבצם כמו כן כזה | ||
| + | |- | ||
| + | | | ||
| + | :{|class="wikitable" style="margin-left: auto; margin-right: 0px;color:blue;" | ||
| + | |- | ||
| + | |The first<br>The second||x+a<br>x-a | ||
| + | |- | ||
| + | |Multiplied by each other||2x<br>2x | ||
| + | |- | ||
| + | |The square of their sum||<math>\scriptstyle{\color{blue}{4x^2}}</math> | ||
| + | |} | ||
| + | | | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | |הראשון<br>השני||x*a<br>x-a | ||
| + | |- | ||
| + | |יוכפלו בהדדי||2x<br>2x | ||
| + | |- | ||
| + | |מרובע קיבוץ שניהם||4xx | ||
| + | |} | ||
| + | |- | ||
| + | |We square each by itself, like this: | ||
| + | |style="text-align:right;"|נרבע כל אחד ביחוד כזה | ||
| + | |- | ||
| + | |colspan=2| | ||
| + | {|class="wikitable" style="margin-left: auto; margin-right: 0px; text-align:center;" | ||
| + | |- | ||
| + | |x*a<br>x*a||x-a<br>x-a | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | | ||*||xa||*||aa | ||
| + | |- | ||
| + | |xx||*||xa|| || | ||
| + | |} | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | | ||-||xa||*||aa | ||
| + | |- | ||
| + | |xx||-||xa|| || | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |xx||*||2xa||*||aa | ||
| + | |- | ||
| + | |xx||*||2xa||*||aa | ||
| + | |} | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |xx||-||2xa||*||aa | ||
| + | |} | ||
| + | יקובצו המרובעים כזה | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | | || ||2xx||*||2aa | ||
| + | |- | ||
| + | | || || || ||2a | ||
| + | |} | ||
| + | |קיבוץ מרובע שניהם<br>המרחק יוגרע מקיבוץ | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |2xx||*||2aa||-||2a | ||
| + | |- | ||
| + | | || || || ||4xx | ||
| + | |} | ||
| + | |מרובע שניהם כזה<br>יוכפלו במרובע קיבוץ שניהם | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |8x4||*||8x2a2||-||8xxa | ||
| + | |- | ||
| + | | || || ||*||4xx | ||
| + | |} | ||
| + | |יולד כזה<br>יקובץ להנולד מרובע | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |8x4||*||8x2a2||-||8xxa||*||4xx | ||
| + | |} | ||
| + | |קיבוץ שניהם כזה | ||
| + | |- | ||
| + | |974213100||וזה שווה למספר כזה | ||
| + | |- | ||
| + | |8x4*8x2a2-8x2a*4xx=974213100||השיווי כזה | ||
| + | |} | ||
| + | |- | ||
| + | |colspan=2| | ||
| + | :{|class="wikitable" style="margin-left: auto; margin-right: 0px; color:blue;" | ||
| + | |- | ||
| + | |x+a<br>x+a||x-a<br>x-a | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | | ||+||xa||+||aa | ||
| + | |- | ||
| + | |xx||+||xa|| || | ||
| + | |} | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | | ||-||xa||+||aa | ||
| + | |- | ||
| + | |xx||-||xa|| || | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |xx||+||2xa||+||aa | ||
| + | |- | ||
| + | |xx||+||2xa||+||aa | ||
| + | |} | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |xx||-||2xa||+||aa | ||
| + | |} | ||
| + | The squares are summed, like this: | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | | || ||<math>\scriptstyle{\color{blue}{2x^2}}</math>||+||<math>\scriptstyle{\color{blue}{2a^2}}</math> | ||
| + | |- | ||
| + | | || || || ||2a | ||
| + | |} | ||
| + | |The sum of their squares<br>The difference is subtracted from the sum of their squares, like this | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |<math>\scriptstyle{\color{blue}{2x^2}}</math>||+||<math>\scriptstyle{\color{blue}{2a^2}}</math>||-||<math>\scriptstyle{\color{blue}{2a}}</math> | ||
| + | |- | ||
| + | | || || || ||<math>\scriptstyle{\color{blue}{4x^2}}</math> | ||
| + | |} | ||
| + | |The sum of their squares<br>Multiplied by the square of their sum, like this | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |- | ||
| + | |<math>\scriptstyle{\color{blue}{8x^4}}</math>||+||<math>\scriptstyle{\color{blue}{8x^2a^2}}</math>||-||<math>\scriptstyle{\color{blue}{8x^2a}}</math> | ||
| + | | | ||
| + | | || || ||+||<math>\scriptstyle{\color{blue}{4x^2}}</math> | ||
| + | |} | ||
| + | |The result<br>The square of the sum of both is added to the result, like this: | ||
| + | |- | ||
| + | |974213100||This is equal to this number | ||
| + | |- | ||
| + | |<math>\scriptstyle{\color{blue}{8x^4+8x^2a^2-8xa^2+4x^2=97423100}}</math>||The equation is as follows | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | :Thus, the equation is obtained in the first way. | ||
| + | |style="text-align:right;"|א"כ ההשוואה עשויה באופן הראשון | ||
| + | |- | ||
| + | | | ||
| + | :In the second way, we do as follows: | ||
| + | |style="text-align:right;"|באופן השני נעשה כך | ||
| + | |- | ||
| + | | | ||
| + | :We multiply the numbers by each other; the result is <math>\scriptstyle x^2-a^2</math> like this: | ||
| + | |style="text-align:right;"|נכפיל המספרים זה בזה יולד ‫xx-aa כזה | ||
| + | |} | ||
| + | ■(x*a@x-a) ■(x+a@x-a) | ||
| + | ■( -xa-aa@xx*xa ) ■( -xa-a^2@x^2+xa ) | ||
| + | יקובץ אליו חצי מרחק שניהם דהיינו a יהיה כזה Half the difference between both, i.e. a, is added to it | ||
| + | ■(xx-aa@ *a) ■(x^2-a^2@ +a) | ||
| + | יוכפל במרובע קיבוץ שניהם כזה It is multiplied by the square of the sum of both, like this: | ||
| + | ■(xx-aa*a@ 4xx) ■(x^2-a^2+a@ 4x^2 ) | ||
| + | ממנו יוגרע מרובע קיבוץ שניהם ישאר כזה | ||
| + | The square of the sum of both is subtracted from it; the remainder is: | ||
| + | ■(4x4-4x2a2*4xxa@ -4xx) ■(4x^4-4x^2 a^2+4x^2 a@ -4x^2 ) | ||
| + | 4x4-4x2a2*4xxa-4xx= 4x^4-4x^2 a^2+4x^2 a-4x^2= | ||
| + | והוא שווה למספר 485276400 | ||
| + | נכפיל שניהם כדי שיהיו שווים להשוואה ראשונה | ||
| + | יולד כזה השיווי This is equal to the number 485276400. | ||
| + | We double both, so they will be equal to the first equation; the result is this equation: | ||
| + | 8x4-8x2a2*8x2a-8x2=970552800 8x^4-8x^2 a^2+8x^2 a-8x^2=970552800 | ||
| + | 8x4*8x2a2-8x2a*4x2=974213109 8x^4+8x^2 a^2-8x^2 a+4x^2=974213109 | ||
| + | קיבוץ שני ההשוואות The sum of the two equations: | ||
| + | 16x4-4x2=1944765900 16x^4-4x^2=1944765900 | ||
| + | נחלק כלם עם 2 יהי' השיווי כזה We divide all by 2; the equation is: | ||
| + | 8x4-2x2=972382950 8x^4-2x^2=972382950 | ||
| + | או בהעתק המספרים כזה Or, by shifting, like this: | ||
| + | 8x4=972382950*2xx 8x^4=972382950+2x^2 | ||
| + | נרבע חצי מספר המרובעים יהיה 1 We square half the number of the squares; it is 1. | ||
| + | נכפיל מספר הפשוט עם מספר המרובע מרובעים דהיינו עם 8 ונקבץ אליו מרובע חצי מספר המרובעים הנ"ל דהיינו 1 יהיה כזה 7779063601 We multiply the simple number by the number of the square-squares, i.e. by 8, then we add to it the square of half the number of the squares, i.e. 1; it is 7779063601. | ||
| + | וממנו תוציא שרש המרבע שהוא 88199 Extract its square root, which is 88199. | ||
| + | תקבץ אל השרש הזה חצי מספר המרובעים דהיינו 1 יהיה | ||
| + | ■(▁(■( 4@88200@88888))@11025) Add half the number of the squares, i.e. 1, to this root ■(▁(■( 4@88200@88888))@11025) | ||
| + | תחלקו עם 8 כאשר לפניך Divide it by 8, as before you: | ||
| + | ומהחלק תוצי' שרש המרובע יהי' | ||
| + | x=105 Extract the square root of the quotient; it is | ||
| + | x=105 | ||
| + | ועכשיו נשאר לנו למצוא כמות a | ||
| + | ויהיה על דרך זה | ||
| + | שני ההשוואות יוגרעו זה מזה כזה | ||
| + | ■(▁(■(8x4*8x2a2-8x2a*4x2=974213100@8x4-8x2a2*8x2a-8x2=970552800))@ 16x2a2-16x2a*12x1=3660300) Now we are left to find the value of a. | ||
| + | It is this way: | ||
| + | The two equations are subtracted from each other, like this: | ||
| + | ■(▁(■(8x^4+8x^2 a^2-8x^2 a+4x^2=974213100@8x^4-8x^2 a^2+8x^2 a-8x^2=970552800))@ 16x^2 a^2-16x^2 a+12x^2=3660300) | ||
| + | השאירות The remainder | ||
| + | תחלק כלם עם x2 והמספר הפשוט יוחלק עם המספר הפשוט השווה ל-x2 Divide all by x^2 and the simple number is divided by the simple number that is equal to x^2. | ||
| + | וכבר מצאת x=105 | ||
| + | וא"כ מרובעו x2=11025 You have already found that x=105. | ||
| + | So, its square is x^2=11025. | ||
| + | יהיה כזה: 16a2_16a*12=332 It is like this: 16a^2-16a+12=332 | ||
| + | תגרע משניהם 12 _12 _12 Subtract 12 from both [sides]. | ||
| + | ישאר כזה 16aa-16a=320 16a^2-16a=320 remains. | ||
| + | תחלק כלם עם 8 יהיה השיווי כזה 2aa_2a=40 Divide all by 8; the equation is: | ||
| + | 2a^2-2a=40 | ||
| + | ובהעתק המספרים כזה 2aa=40*2a By shifting the numbers: | ||
| + | 2a^2=40+2a | ||
| + | תתקן כמו בהשוואה איננה טהורה וא"כ a=5 Restore as a compound equation, so: a=5. | ||
| + | ולפי זה יבא המבוקש כי | ||
| + | x*a=110 : מעות הראשון | ||
| + | x_a=100 : מעות השני According to this the required resulting is: | ||
| + | The cost of the first: x+a=110 | ||
| + | The cost of the second: x-a=100 | ||
| + | {| | ||
| + | |- | ||
| + | |Here ends our purpose thus. | ||
| + | |style="text-align:right;"|ובזה נשלם מגמתינו בזה האופן | ||
| + | |- | ||
| + | |We bow down to our God. | ||
| + | |style="text-align:right;"|ונקוד לאלהינו | ||
| + | |- | ||
| + | |We will sing him a song, | ||
| + | |style="text-align:right;"|ונשורר לו שיר | ||
| + | |- | ||
| + | |With a consonant and two vowels, a consonant and two vowels, a consonant and two vowels, | ||
| + | With opening and closing [of the verse]: | ||
| + | |style="text-align:right;"|ביתד ושתי תנועות יתד ושתי תנועות יתד ושני תנועות בדלת ובסוגר | ||
| + | |- | ||
| + | |Who brings to light all hidden things [Ibn Ezra on Exodus 25, 1,1] | ||
| + | |style="text-align:right;"|אשר הוצא לאור כל תעלומה‫<ref group=note>אבן עזרא על שמות כ"ה א א</ref> | ||
| + | |- | ||
| + | |For the people of God with a wise knowledge | ||
| + | |style="text-align:right;"|לאנשי אל בידיעה מחכימה | ||
| + | |- | ||
| + | |And hints to him the words of all wisdom. | ||
| + | |style="text-align:right;"|ורמז לו דברי כל החכמה | ||
| + | |- | ||
| + | |Until the end of the first part | ||
| + | |style="text-align:right;"|עד כלות חלק הראשון | ||
| + | |- | ||
| + | |He will explain to us the words of an inscribed wisdom [Ibn Ezra on Exodus 25, 1,1] | ||
| + | |style="text-align:right;"|יבינני דבר חכמה רשומה‫<ref group=note>אבן עזרא על שמות כ"ה א א</ref> | ||
| + | |- | ||
| + | |No purpose is withheld from Him [Job 42, 2] | ||
| + | |style="text-align:right;"|ולא יבצר ממנו מזימה‫<ref group=note>איוב מב, ב</ref> | ||
| + | |- | ||
| + | |In the second part and in one word. | ||
| + | |style="text-align:right;"|בחלק שני ובתיבה תמימה | ||
| + | |- | ||
| + | |Praise to the First and the Last. | ||
| + | |style="text-align:right;"|שבח לראשון ואחרון | ||
| + | |- | ||
| + | | | ||
|style="text-align:right;"|סליק | |style="text-align:right;"|סליק | ||
|} | |} | ||
| + | |||
== Notes == | == Notes == | ||
Latest revision as of 17:20, 7 August 2024
Prologue |
|||||||||||
| These are the chronicles and events that introduced to me the algebra my dove, my perfection [Song of Songs 5, 2] | אלה תולדות ומאורעות שקרו לי את האלגיברה יונתי תמתי[note 1] | ||||||||||
| Caught up by cords of [Esther 1, 6] the waste of time and ideas | אחוז בחבלי[note 2] הבלי הזמן ורעיוני | ||||||||||
| Upon my bed [Daniel 2, 29] | על משכבי סליקו[note 3] | ||||||||||
| In thoughts from the visions of the night [Job 4, 13] | מסעיפי' מחזיונות לילה[note 4] | ||||||||||
| The day-star, son of the dawn [Isaiah 14, 12] | והנה היליל בן שחר[note 5] עלה ממסוכתו | ||||||||||
| As a man surprised [Jeremiah 14, 9] | כאיש נדהם[note 6] | ||||||||||
| As a strong man to run his course [Psalms 19, 6] | וכגבור לרוץ ארח[note 7] | ||||||||||
| The gold of the sun was reflected through the window | וזהב השמש נשקף בעד בחלון | ||||||||||
| Through the lattice [Judges 5, 28] | ובעד האשנב[note 8] | ||||||||||
| Peering through the lattice [Song of Songs 2, 9] | מציץ מן החרכים[note 9] | ||||||||||
| My disquieting thoughts have overcome me | ושרעפי הרהיבוני | ||||||||||
| Pushed me out of the bed of laziness | לדחפוני ממשכבי העצלות | ||||||||||
| A sound! My beloved knocks [Song of Songs 5, 2] | והנה קולי דודי דופק[note 10] | ||||||||||
| Get up, let us lodge in the villages [Song of Songs 7, 12] | קום נצא בשדה נלינה בכפרים[note 11] | ||||||||||
| The flowers have appeared in the land; the time of the nightingale has come [Song of Songs 2, 12] | כי הנצנים נראו בארץ ועת הזמיר הגיע[note 12] | ||||||||||
| The rain is over and gone [Song of Songs 2, 11] | הגשם חלף והלך לו[note 13] | ||||||||||
| למה לנצח תקמוט בלא עת | |||||||||||
| לשחוק אמרתי מהולל[note 14] | |||||||||||
| כי מה הוה לאדם[note 15] | |||||||||||
| ברעיון לבו[note 16] | |||||||||||
| שכל ימיו מכאובי'[note 17] | |||||||||||
| וגם בלילה לא שכב לבו [note 18] | |||||||||||
| ואשמע לקולו ויוציאני החוצה מקדם לעיר[note 19] | |||||||||||
| עודנו הלוך ושב | |||||||||||
| והנה השמש יצא על הארץ[note 20] מנרתיקו | |||||||||||
| ואין נסתר מחמתו[note 21] | |||||||||||
| וימן אלהים רוח קדים חרישית ותך השמש על ראשי[note 22] | |||||||||||
| ואתעלף ותקצר נפשי[note 23] | |||||||||||
| לחם הקלוקל[note 24] | |||||||||||
| ותשאל מנוס אנה מחמתה תברח | |||||||||||
| ובקשתי את שאהבה נפשי בקשתיו ולא מצאתיו[note 25] | |||||||||||
| ויצא רוח מלפני אלהים | |||||||||||
| רוח חזק מפרק הרים ושובר סלעי'[note 26] | |||||||||||
| ויאחזני בציצת ראשי[note 27] | |||||||||||
| ויוליכני אל הארץ הטובה[note 28] | |||||||||||
| ארץ אשר ה' דורש אותה[note 29] | |||||||||||
| ועיניו משוטטות בה מראשית השנה עד אחרית השנה[note 30] | |||||||||||
| ארץ נחלי[note 31] ומעינות מים ונהר פלגיו[note 32] ישמח אלהים ואנשים אנשי אל כגנות עלי נהר[note 33] | |||||||||||
| כארזים עלי מים[note 34] רבים לא ישטופהו | |||||||||||
| ומדליו יזלו מור ואהלות וקנמון וכל ראשי בשמים[note 35] | |||||||||||
| ובתוכו אתמלאה ציצים ופרחים וכל עץ מאכל | |||||||||||
| ובאמצעיתו אהלים אשר נטע ה' | |||||||||||
| וסוכה תהיה לצל יומם ומחסה מורם לילה | |||||||||||
| ולפניה עץ קומתו דמתה לתמר וגבהו בחור מארזים | |||||||||||
| עץ שתול על פלגי מים[note 36] | |||||||||||
| ופריו פרי מגדים ממגד תבואות שמש וממגד גרש ירחים[note 37] | |||||||||||
| וריחו כריח התפוח בעצי היער | |||||||||||
| בצלו חמדתי וישבתי ופריו מתוק לחכי | |||||||||||
| אז אחזתי בסנסניו ועליתי על במותיו | |||||||||||
| ויראני משם את כל הככר והנה כלו משקה כגן ה' ואת הים הגדול ורחב ידים שם אניות יהלכון | |||||||||||
| ואשמע אחרי קול רעש גדול קול ענו' מקולו' מים רבי' אדירי' ומשברי ים[note 38] גליו יהמון | |||||||||||
| והים הולך וסוער ויהיה סער גדול בים | |||||||||||
| ויורדי הים באניות עלו השמים ירדו תהומות ונפשם ברעה תתמוגג | |||||||||||
| ורב החובל והמלחים וכל תופשי משוט חתרו להשיב אל היבשה ולא יכלו | |||||||||||
| כי הים סוער ומזעפו מי יקום[note 39] | |||||||||||
| וייראו המלחים לנפשם ויצעקו וידרו נדרים[note 40] | |||||||||||
| וזבח לים בהטלת כליהם להקל מעליהם שיקם סערה לדממ' ושיחשו גליו[note 41] | |||||||||||
| אבל שוא עמלו מנהיגיה בה ויעזבו אותה למקרים | |||||||||||
| ובכל זאת לא נחם אלהים[note 42] למחוז חפצם[note 43] | |||||||||||
| ויחוגו וינועו כשכור[note 44] ולא מיין[note 45] | |||||||||||
| וכל חכמתם תתבלע[note 46] | |||||||||||
| ויהיה כבוא לעת ערב שמשם ובעד כוכבים יחתם[note 47] | |||||||||||
| והנה רוח בסערה סוער בלב ים בקולות ובברקים בעמוד אש וענן[note 48] | |||||||||||
| ויהמם ויסר את מבצרי האניה ותשבר וינערו בים | |||||||||||
| וכל יושביה עמה יבולון | |||||||||||
| צללו כעופרת במים אדירים[note 49] | |||||||||||
| וינתנו מאכל לעם לציים[note 50] | |||||||||||
| וקצתם אחזו בדופני הספינה ובירכותיו ובקרשיו ויעזבו את נפשם לגלי הים לשוט פן תמצאנה פליטה מרדת שחת[note 51] | |||||||||||
| את כל אלה ראו עיני המעשים אשר נעשו תחת השמש[note 52] | |||||||||||
| ויכמרו רחמי ועיני לאו מראות ברעה אשר הגיע לבוטחי' על קורי עכביש ועל משענת קנה רצוץ[note 53] | |||||||||||
| וארד מחודת האילן | |||||||||||
| ואחשוב למצוא תקוה ותוחלת[note 54] להשטים על פני המים | |||||||||||
| ואתן לי מהלכים בין העומדים[note 55] | |||||||||||
| מפה ומפה בדרך לא סלולה[note 56] | |||||||||||
| ובנתיב לא ידע עיט[note 57] | |||||||||||
| עד הגיעי על שפת הים מקום רבים חללים הפילה[note 58] | |||||||||||
| ורבים שכבו בחוצות חבקו אשפתות[note 59] | |||||||||||
| אשר העלה זוטו של ים ורוחם בל אתם | |||||||||||
| ואהי להם למשיב נפש[note 60] | |||||||||||
| Among them there was one girl. | ובחובם נערה אחת | ||||||||||
| Lying on the ground | שטוחה על הארץ | ||||||||||
| Her face buried in the ground | ופניה כבושות בקרקע | ||||||||||
| Virgin of beautiful appearance [Esther 2, 3] | בתולה טובת מראה[note 61] | ||||||||||
| No man had known her [Genesis 24, 15] | ואיש לא ידעה[note 62] | ||||||||||
| Surely the bitterness of death is at hand [Samuel 1 15, 32] appeared at her window | אכן סר מר המות[note 63] עלה בחלונה | ||||||||||
| No breath left in her and her appearance was ruined. | ורוח לא נותרה בה ומראה נשחת | ||||||||||
| She had no form or beauty [Isaiah 53, 2] | לא הוד ולא הדר לה[note 64] | ||||||||||
| The red left ]her face[ and pallor came [Baba Metzia 58, 2, 12] | אזל סומקא ואתי חיורא[note 65] | ||||||||||
| I was astonished at the vision [Daniel 8, 27] | ואשתומם על המראה[note 66] | ||||||||||
| ונפשי נבהלה[note 67] | |||||||||||
| בקרבי והחי יתן אל לבו[note 68] | |||||||||||
| While I kept staring at her, silently to find out [Genesis 24, 21] what would be done to [Exodus 2, 4] her | עודני משתאה מחריש לדעת[note 69] מה יעשה לה[note 70] | ||||||||||
| I looked, and behold, the spirit of life is still in her nostrils [Genesis 7, 22] | ואראה והנה עוד נשמת חיים באפה[note 71] | ||||||||||
| ואמהר לעשות משפט | |||||||||||
| פן אפדה ממות נפשה | |||||||||||
| I took off the linen tunic of the yarn of Egypt [Proverbs 7, 16] over her | ואפשוט את כתנת בד מאטון מצרים[note 72] מעליה | ||||||||||
| לראות היש מצליח דרכי[note 73] | |||||||||||
| וליתן רוח בין הדבקים[note 74] | |||||||||||
| ואריק ממנה המים אשר באו בקרבה | |||||||||||
| ואעריף עליה מים חיים ממקור נוזלים | |||||||||||
| ויהיו כמים קרים על נפש עיפה[note 75] | |||||||||||
| ואשוכה בשמנים הטובים ובאפרסמון נוסף עליהם דברים[note 76] | |||||||||||
| אשר ריחם לא נמר[note 77] | |||||||||||
| ותחי רוחה בקרבה ותפקח עיניה | |||||||||||
| Like doves by the water courses [Song of Songs 5, 12] | כיונים על אפיקי מים[note 78] | ||||||||||
| ואקח אותה על כתיפי ואשא אותה | |||||||||||
| As the nursing-parent carries the sucking child [Numbers, 11, 12] | כאשר ישא האומן את היונק[note 79] | ||||||||||
| Like the eagle on his pinion [Deuteronomy 32, 11] | וכנשר על אברתו[note 80] | ||||||||||
| עד אשר הבאתה אל מקום אויתי למושב לי | |||||||||||
| I put off her raiment of captivity from her [Deuteronomy 21, 13] | ואסור את שמלת שביה מעליה[note 81] | ||||||||||
| I made a bed for her upon a pavement of green, and white [Esther 1,6] | ואציע לה מטות על רצפת בהט ושש[note 82] | ||||||||||
| אשקה אותה יין עסיס ומעשה מרקחים | |||||||||||
| I fed her bread of the mighty [Psalms 78, 25] | והאכלתיה לחם אבירים[note 83] | ||||||||||
| עד שבימים מועטים שבה בריאותה על כנה ועל תלה | |||||||||||
| Then, she opened her mouth with wisdom; and the law of kindness is on her tongue [Proverbs 31, 26] | אז פיה פתחה בחכמה ותורת חסד על לשונה[note 84] | ||||||||||
| Tongue that speaks great things [Psalms 12, 4] | לשון מדברת גדולות[note 85] | ||||||||||
| ואשאל מעמה להודיעני | |||||||||||
| Her ways are ways of pleasantness [Proverbs 3, 17] | דרכיה דרכי נועם[note 86] | ||||||||||
| Why are you like a stranger in the land, like a visitor who stops only for the night? [Jeremiah 14, 8] | ולמה תהיי כגר בארץ וכאורח נטה ללון[note 87] | ||||||||||
| A mockery to all the people, their song the entire day [Lamentations 3, 14] | צחוק לכל העמים נגינתם כל היום[note 88] | ||||||||||
| As one that held his peace [Samuel 1 10, 27] | ותהי כמחריש[note 89] | ||||||||||
| ויהי בדברי אליה יום יום | |||||||||||
| ולא שמעה אלי כפעם בפעם | |||||||||||
| I walked in the garden in the breeze of the day [Genesis 3, 8] | הלכתי לרוח היום בגן[note 90] | ||||||||||
| ומזימותי כל אתי ותפגע בי | |||||||||||
| ולא ראיתיה עד הגיע' אצלי | |||||||||||
| I seemed to her as a deceiver [Genesis 27, 12] | ואהי בעיניה כמתעתע[note 91] | ||||||||||
| ואז בטיתי באפיה | |||||||||||
| ותלהב אהבתה בקרבה | |||||||||||
| Many waters cannot quench love [Song of Songs 8, 7] | ומים רבים לא יוכל לכבות האהבה ההיא[note 92] | ||||||||||
| I held her, and would not let her go, until I had brought her into my mother’s house, And into the chamber of her who conceived me [Song of Songs 3, 4] | אז אחזתיה ולא ארפנה עד שהביאתיה אל בית אמי ואל חדר הורתי[note 93] | ||||||||||
| I bowed before her to the ground seven times [Genesis 33,3] | ואקוד לפניה שבע פעמים ארצה[note 94] | ||||||||||
| ואומר אליה למה לא תחוס על נפש פעליך | |||||||||||
| ולמה אמות לנגד עיניך | |||||||||||
| like water that is poured out on the ground [Samuel 2 14, 14] | כמים הנגרים ארצה[note 95] | ||||||||||
| ותהי כמתחר' על אודותי ועל דברי | |||||||||||
| ותען ותאמר חי ה' וחי נפשי | |||||||||||
| כי לא תמות אתה שעשית לי תשועה גדולה | |||||||||||
| ופורקן ימינך משכה אותי | |||||||||||
| From the slimy clay [Proverbs 40, 3] | מטיט היון[note 96] | ||||||||||
| You brought me out into abundance [Proverbs 66, 12] | ותוציאני לרויה[note 97] | ||||||||||
| אשר זולתך הייתי מיורדי בור ושחת | |||||||||||
| Now I walk in the land of the living [Proverbs 116, 9] | ועתה אתהלך בארצות החיים[note 98] | ||||||||||
| And my soul shall live because of you [Genesis 12, 13] | וחיתה נפשי בגללך[note 99] | ||||||||||
| In this you shall know that [Exodus 7, 17] | ובזאת תדע כי[note 100] | ||||||||||
| בחנתי את מסלול דרכיך | |||||||||||
| והם ישרים בעיני | |||||||||||
| כי מפענח אנכי לך נעלמים | |||||||||||
| ואגיד לך קצת דרכי ישרים הם למוצאי דעת | |||||||||||
| For in a place where he is not known it is permitted for a person to make himself known [Nedarim 62, 1] | כי באתרי' דלא ידעיה שרי אינש לאודועי נפשי[note 101] | ||||||||||
| אני הייתי בת מאחד מיקירי ירושלים | |||||||||||
| They that were brought up in scarlet [Lamentations 4, 5] | האמונים עלי תולע[note 102] | ||||||||||
| Who was exiled with the captives exiled [Esther 2, 6] | אשר הגלתה עם הגולה אשר הגלתה[note 103] | ||||||||||
| Because of the fury of the oppressor’s [Isaiah 51, 13] sword | מפני חמת חרב המציק[note 104] | ||||||||||
| ובמקום שהיו שרים מציקי ואומני מלכי ארץ | |||||||||||
| Slaves ruled over me [Lamentations 5, 8] | עבדי' משלו בי[note 105] | ||||||||||
| My soul was removed from peace [Lamentations 3, 17] | ותזנח משלום נפשי[note 106] | ||||||||||
| I wandered like a stranger in the land [Jeremiah 14, 8] | ואלך כגר בארץ[note 107] | ||||||||||
| וכל רעי בגדו בי | |||||||||||
| I appeared to the Patriarchs [Exodus 6, 3] | וארא אל האבות[note 108] | ||||||||||
| The holy ones that are in the land [Proverbs 16, 3] | הקדושים אשר בארץ המה[note 109] | ||||||||||
| I made myself known to them only by my name [Exodus 6, 3] | ורק בשמי נודעתי להם[note 110] | ||||||||||
| והם כתבו וחתמו ספרי' בשמי | |||||||||||
| כמו הכולל הרופא המפורסם כמהור"ר יוסף שלמה מקנדיאה | |||||||||||
| שיעד להוציא לאור את חיבורו | |||||||||||
| עיר גבורים | |||||||||||
| על האלגיברה | |||||||||||
| ואולי נשבר או נאבד | |||||||||||
| Woe over those who are gone and are not found [Sanhadrin 111, 1] | וחבל על דאבדין ולא משתכחין[note 111] | ||||||||||
| אכן קצת תהילתי אביע לך | |||||||||||
| אני היא המדדת בשעלה מים | |||||||||||
| The entire world [Sanhadrin 97, 1] | וכל חללי דעלמא[note 112] המשימת | ||||||||||
| The rugged shall be made level [Isaiah 40, 3] | עקוב למישור[note 113] | ||||||||||
| For every mountain shall be made low and ever valley shall be lifted up [Isaiah 40, 3] | כי כל הר ישפל וכל גיא ינשא | ||||||||||
| ההרים ירכסון והגבעות הרצדון | |||||||||||
| The pillars of the earth will quake [Job 9, 6] | ועמודי הארץ יתפלצון[note 114] | ||||||||||
| בי יתגאו הגאים | |||||||||||
| ורוזני הארץ נוסדו בי יחד | |||||||||||
| המוציאה כוכבים במספר | |||||||||||
| וכל רז לא אניס לי | |||||||||||
| בידי מאזני משקל ופלס | |||||||||||
| בי יסחרוה הארץ | |||||||||||
| והיתה למס עובד | |||||||||||
| I shall be a pillar of fire for them to lead them on the way [Nehemiah 9, 19] | ואהיה להם לעמוד אש להנחותם בדרך[note 115] | ||||||||||
| In the blackness and the darkness [Proverbs 7, 9] | באישון ואפילה[note 116] | ||||||||||
| Through the valley of the shadow of death [Psalms 23, 4] | בגיא צלמות[note 117] | ||||||||||
| ומיום שיצאת מארצי בשביה | |||||||||||
| נקראתי בלאומים אלגיברה | |||||||||||
| This is my name, and this is my memorial [Exodus 3, 15] | זה שמי וזה זכרי[note 118] | ||||||||||
| Now I will not leave you [Genesis 28, 15] | ועתה לא אעזבך[note 119] | ||||||||||
| For wherever you lodge, I will lodge [Ruth 1, 16] | כי באש' תלין אלין[note 120] | ||||||||||
| From that day on [Samuel 1 18, 9] | ומיום ההוא והלאה[note 121] | ||||||||||
| She did not depart out of the beams of my house. | לא זזה מקורות ביתי | ||||||||||
| I adorned her with frames of gold. | ואשבצה משבצות זהב | ||||||||||
| Dressed with embroideries and scarlet | ולבושה רקמות וארגמן | ||||||||||
| I took her to be my wife. | ואקחה לי לבת | ||||||||||
| I changed her name. | ואשנה את שמה | ||||||||||
| ואכנה אותה סרח בת אשר | |||||||||||
| סרח בגימטריא אלכיברה כשמה האמיתי בלשון הערביים | |||||||||||
| Her light shall shine in darkness [Isaiah 58, 10] | זרח בחושך אורה[note 122] | ||||||||||
| וילכו עמים לאורה | |||||||||||
| Then I said, I come with the scroll of the book which is written [Psalms 40, 8] | אז אמרתי הנה אבוא במגילת ספר כתוב[note 123] | ||||||||||
| Uprightly truthful sayings [Ecclesiastes 12, 10] | יושר דברי אמת[note 124] | ||||||||||
| To show the princes and the peoples her beauty; for she is fair to look on [Esther 1, 11] | להראות לעיני השרים והעמים יפיה כי טובת מראה היא[note 125] | ||||||||||
| I bow the Lord [Genesis 24, 48] | ואקוד לאלהי[note 126] | ||||||||||
| ואהלל לו | |||||||||||
| על כי הרבה חסדו אתי | |||||||||||
| והוא יהי לי לאלהים | |||||||||||
| וינהגני עלמות | |||||||||||
Introduction |
|||||||||||
| מפתח האלגיברה חדשה | |||||||||||
| Algebra is a quantitative philosophy that explores any quantity that can be found and that is not studied by the other rules of arithmetic and geometry. | אלגיברה היא פילוסופיא כמותית חוקרת כל כמות אשר אפשרות למציאותן ואשר לא תחקר בשארי כללי החשבון והמדידה | ||||||||||
| We have no benefit for this in its name, whether its origin is in the land Sheva, or whether it originated from the Greeks. | והנה משמה לא יגיע לנו מזה תועלת אם גזעו בארץ שבא או אם נולד מברכי היונים | ||||||||||
| We will only investigate its essence and say: | רק נחקור אחר הויתה ונאמר | ||||||||||
| The essence of this science is in three general rules: | [1]הוית חכמה זו בשלשה כללים כוללים | ||||||||||
| Perceiving the known and unknown quantity through general rules and the causes of things. By that we apply the known and find the unknown. Therefore, it is called a figurative expression. | בציור הכמות נודעה ובלתי נודע' בכוללות ובמסבבי הדברים ובזה נעשה את הנודע ונמציא הבלתי נודע ולזה יקרא כינוי | ||||||||||
| According to the instructions and the results of the question, we are looking for two equal quantities, one of which is known in whole or in part; this is called an equation. | נחפש לפי הוראות ומסבבי השאלה שתי כמות שוות אשר האחת מהם נודע' בכללה או בחלקה וזה נקרא השוואה | ||||||||||
| Since we learn from a well-known and agreed-upon proposition that if we apply addition, subtraction, multiplication, division, root extraction, to two equal quantities they will always remain in the same equality, we apply manipulations to two given quantities, until we find a known quantity on one side [of the equation] and on the other side remains only the sign of the required quantity. This is called restoration and it indicates the quantity that is still unknown. | הואיל ונלמד מהצעה ידועה ומוסכמת באם נעסוק משתי כמות שוות בשווה ר"ל בקיבוץ בגרעון בהכפלה בחילוק בהוצאת השורש ישארו בתמידית באותו שיווי' כך נעסוק משתי כמות מצואות כל כך עד שנמצא כמות ידוע מצד אחד ומצד השני ישאר רק הסימן של כמות מחופש וזה יקרא הולדה או תיקון וזה המורה כמות הבלתי נודעת עדיין | ||||||||||
| The means needed for the attainment of this science are two: | האמצעיים אשר יוצרכו להשגת חכמה זו הם שנים | ||||||||||
| Signs or letters that differ from the arithmetic numbers, because the arithmetic signs change in the sum of addition, the remainder of subtraction, the product of multiplication and the quotient of division. | סימנים או אותיות אשר הם משונים מחשבון המספרי כי הסימני' המספריים הם משתנים בעלית ההוספה בשאירות הניכוי בהולדת ההכפלה ובכמות החילוק | ||||||||||
| Such as: By adding 5 to 3, the result is the number 8. | כמו בהוספת 5 אל 3 עולה מספר 8 | ||||||||||
| By subtracting 7 from 12, 5 remains. | בניכוי 7 מן 12 ישאר 5 | ||||||||||
| By multiplying 9 by 3, the product is 27. | בהכפלת 9 עם 3 נולד יולד 27 | ||||||||||
| By dividing 32 by 8 the quotient is 4. | בחלוקת בהחליק 8 ב על עם 32 כמות החלק 4 | ||||||||||
| וכן בדומיהם | |||||||||||
| ובזה הם נשארים לעולם בסימנים ויחוברו או יפורדו מסימנים בחיריים | |||||||||||
| בבחינת הוית ובמסבבי השאלה וכמו כן ביחוסי הכמות ובפרטית המספרים אשר הם כבר הם נזכרים ונעשים במיני ובערכי המספר אשר קדם מאמרינו מהם | |||||||||||
| הסימנים אשר יובחרו מהאלגבריים הם אותיות האלפא ביתא או ביותר אַ בֶע צֶע וכו' אשר בעצמותם לא יורו כמות מוגבלת כמו סימני סימני המספרים או אותיות העבריים והיונים ודומיהם מלשונותם המזרחיות לכך מהם עלולים לקבל כמותים כלם נודעים ובלתי נודעים | |||||||||||
| אבל זה יודע כי חכמי האלגיברה שומרים את החילוק הזה כי ירשמו את מספר או כמות ידוע באותיות ראשונות שהם a b c ec ec a b c ואת הכמותים בלתי נודעים ואשר נחקור באותיות אחרונות שלהם שהם z x y z | |||||||||||
| והקדמונים רשמו בכללי קאס שלהם את הפשוטים בלתי נודעים שורשים כזה 3R 2R 1R ודומיהם | |||||||||||
| אבל חדשים מקרוב באו רשמו כזה לפשוטים בלתי נודעים כזה x 2x 3x | |||||||||||
| וכן קראו הקדמונים למרובע בלתי נודעי' צענסוס ורשמו אותו בצורתו z וכן למעוקב בלתי נודע c | |||||||||||
| אבל האחרוני' יסמנו למרובע בלתי נודע בצורת xx ולמעוקב בצורת xxx או כזה x3 x2 | |||||||||||
| תועליות שימשכו מסימנים אלו רבו מלמנות והיושבים ראשונה במלכות הם | |||||||||||
| שנידע בקלות בלי סביכות רעיונינו הסימן שלקחנו והגבול אשר גבלנו להסימן אשר בחרנו כי תמיד ישאר באותו ציור ומזה ימשך | |||||||||||
| שתיכף נראה מאיזה מין ממיני החשבון סימנינו | |||||||||||
| ומי יכול יוכל לבאר הכרחם בהוצאות השרשים עד אין תכלית כאשר נבאר כיד ה' הטובה עלינו לקמן | |||||||||||
| שילוקח במקום שורשי' או מרובעים רבים ודומיהם רק סימן אחד | |||||||||||
| ואין חקר לתועלתו בהשוואה בלתי טהורה כי ומיד יראה לעיני המשכיל ההעדר | |||||||||||
| והנה עד זמנינו זה חשבו להעדר הרבה מקנינים כמותיים להיותם נעדרים מתועליות רבות אשר ימשכו מסימנים בחיריים | |||||||||||
| והנה רבים לו יחכמו הלכו בחשך ולא ראו אור וילכו אחר ההבל ויהבלו ורבים לאו למצוא הפתח בהתיר הרבה מהספיקות וחשבו אותו למעוות שאינו יוכל לתקן | |||||||||||
| והנה הכולל כמהר"ר ישר מקנדיאה כאשר ראה כי לא נעשתה עצתו בתשובו' הרבה מהשאלות כמותיות ע"ד האלגיברה אמר כי בהרבה שאלות קצרה יד האלגיברה מלהושיע | |||||||||||
| אבל כאשר עיניו למרחוק יביטו חשב לתקן העדר הקדמונים בבחרו סימנים חדשי' כאשר כתב תלמידו החכ' כמהר"ר משה ממין בתשובתו לכמהר"ר זרח וז"ל | |||||||||||
| I must inform you the algebra signs that my teacher uses, so that you will easily know everything that comes out of these operations | ואני צריך להודיעך רשומי האלגיברה שישתמש בהם מורי כדי שתדע בקלות כל היוצא מאלו הפעולות | ||||||||||
| The simple number is marked by S | הנה ואני מודיעך המספר הפשוט יורשם עם ס | ||||||||||
| The root by A | והשורש עם א | ||||||||||
| The square by B | והמרובע עם ב | ||||||||||
| The cube by D | והמעוקב עם ג | ||||||||||
| ומרובע של מרובע עם ד | |||||||||||
| ומרובע של מעוקב עם ה | |||||||||||
| וכן לאין תכלית | |||||||||||
| ויש לסימנים אלו תועליות וקלות יותר מרשומי הקדמונים | |||||||||||
| וסימן היתרון ירשום מורי עם אות ת | |||||||||||
| והחסרון עם פ | |||||||||||
| עכ"ד והנה אף שתקן מקצתו לא תקן כלו כי כאשר ברר לו לעצמו אותיות העברים אשר להם כמות מוגבלת לא ימלט משינוים ומהתחלפות אשר מהם ימשכו ביטולים רבים כמבואר | |||||||||||
| [2]מיני החשבון הם ארבעה כי לא ימלט או שנקבץ או שנגרע או שנכפיל או שנחלוק | |||||||||||
| וכל אחד מהן מהם הוא או פשוט או מורכב | |||||||||||
| הפשוט הוא באותיות או סימנים מאוחדים בין מאוחדים עם מאוחדים או מאוחדים עם מורכבים | |||||||||||
| והמורכב הוא בכמות מרובות שיעוסקו שיועסקו במינים אלו | |||||||||||
| לארבע אם אבות החשבון אלו יוצרכו להזכיר או שנים או יותר כמותים והנה גם אלה לא ימלטו מחלוקת ארבע אלו או שיהיה שווים או שאחד יותר מחבירו או האחד פחות מחבירו או שיהיה איש אל אחיו מוערכים | |||||||||||
| ורשמו לסימן השוה השיווי כזה = | |||||||||||
| ולסימן היתור כזה * | |||||||||||
| ולסימן הפחות הפחיתות כזה – | |||||||||||
| ולסימן ההערכה כזה ÷ | |||||||||||
| והנה סימני היתור והגרעון או הם במוניטון מתחלפים | |||||||||||
| כאילו נאמר 2a*2b שהם ב' זהובי' ושני פנים פעמים | |||||||||||
| או c-3d שהם א' צ"ל פחות ג' פשיטים | |||||||||||
| או במספר ובדבר שווה נקרא אצל חכמי החשבון בלתי מסוים | |||||||||||
| כמו 8*2 שהוא 10 או 8-2 8-3 שהוא 6 | |||||||||||
| וסימני ההערכה כזה 2÷3=8÷12 | |||||||||||
| כאילו נאמר כערך 2 אל 3 כך ערך 8 אל 12 | |||||||||||
Addition |
בקיבוץ או בחיבור הסימנים פשוטים | ||||||||||
| נעשה כך | |||||||||||
| אם האותיות דומות אז יסופרו ובעליה ירושמו בסימן מספרי כמו | |||||||||||
| |||||||||||
| אבל אם נחבר אותיות בלתי דומות מאוחדות אז נכתוב אותן בקו אחת עם סימן היתור כזה * כמו נחבר a אל b אז יעלה a*b | |||||||||||
| וכן בחיבור b c d יחדיו יעלה b*c*d וכן תקיש | |||||||||||
Subtraction |
בגרעון הסימנים פשוטים | ||||||||||
| נעשה כך אם האותיות עם האותיות דומות ינוכה מספרם זה מזה והשאירות יושם תחת הקו
כמו ינוכה 3a*a ישאר 2a | |||||||||||
| |||||||||||
| אבל אם האותיות אינן דומות אז נשים את המנכה סמוך למנוכה עם סימן הפחיתות כזה - | |||||||||||
| כמו ינוכה b מן a ואז ישאר a-b | |||||||||||
| וכן ננכה c מן a*b ישאר a*b-c | |||||||||||
| וכן מן x ינוכה a*b אז ישאר x-a-b כזה | |||||||||||
| כי הואיל שינוכו שניהם a וכן וגם b מן x ישאר x-b אז יקחו שניהם סימן הפחיתות וכן תקיש | |||||||||||
Multiplication |
בהכפלת בהכפלה או בריבוי האותיות מיוחדת מאוחדות זו עם זו בין שתהיו דומות או בלתי דומות | ||||||||||
| אז יכתבו בלי סימן זו אצל זו וזו היא התולדה | |||||||||||
| כמו יכפל נכפיל a עם a יולד aa | |||||||||||
| אע"פ אף שראוי להיות aba אבל הואיל והמכפיל דומה למוכפל אז יכתוב אצלו | |||||||||||
| |||||||||||
| וכן אם יש כמות מספרי שיוכפלו כדין והאותיות יכתבו זו אצל זו | |||||||||||
| ואם יבואו שני אותיות בלי סימן בינתים סמוכות זו לזו אז נדע שהן הולדת ההכפלה | |||||||||||
Division |
ובחילוק האותיות מאוחדות אם האות או האותיות הנחלקות ואות החולקת דומות ובין שתהינה כמות נחלקת וחולקות נרשמות בסימן מספרי או הכמות נחלקת לבד נרשמות נרשמה בסימני המספר | ||||||||||
| אז יעשה כדין חילוק המספרי | |||||||||||
| כמו נחלוק a על ב 3a ויהיה הכמות 3a הכמות כי האחדות אינו חולק | |||||||||||
| |||||||||||
| אבל אם האותיות הנחלקות בלתי דומות למחלקת אז נעמוד המחלק תחת הקו ועליו הנחלק כמו בחשבון בציור השברים ויהיה א"כ אות המחלקת מכנה השבר והנחלקת מונה | |||||||||||
כמו אם נחלק a על ידי ע"י b אז יהיה כזה 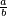
| |||||||||||
וכן a*b ע"י c אז יהיה כך 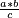
| |||||||||||
| עד כאן ע"כ דברנו מחשבון האותיות בפשוטים או מאוחדי הכמות אבל אם נרצה לידע חשבון המורכבים אשר הם מאותיות רבות [3]או דומות או מתחלפות עם סימנים או שווים או שונים נצריך שתבחין שיבחן זה באמיתית מה שנבאר בשני כללים כוללים והם | |||||||||||
| (א) והאחד אם נחבר העדר או חסרון אל קניין אז יוגרע כמות החסרון (כי לדבר קנין ההעדר הוא שיחסר ממנו מה) | |||||||||||
| (ב) וכן אם ינוכה העדר או חסרון מקנין או מהעדר אז נצרך להוסיף החסרון מהכמות בראשונה | |||||||||||
| ומזה יולד שאם יבואו בחיבור שני סימנים שונים או * למעלה - למטה או להיפיך בהיפוך אז נעשה במקום החיבור ניכוי הקטן מהגדול מן הגדול והנשאר יקבל סימן שהי' ההיה אצל כמות הגדולה ואם הכמות העליון בשווה ולהעדר התחתון אז לא ישאר כלום כמו בחבור זה | |||||||||||
| |||||||||||
| |||||||||||
| |||||||||||
| כי בנדון הנזכר הם שני סימנים שונים בתמידית העדר או חסרון אשר קיבוצו ממלא החסרון
וכדי להקל למתחיל נעשה מהמשלים הקודמים מספרים נודעים כמו |
■(A&&pf&&E@1&*&3&-&1@2&-&1&*&2@3&*&2&*&1) ■(A&&E&&pf@4&-&2&-&3@-2&*&3&*&1@2&*&1&-&2) בניכוי בסימנים שונים ו אז נעשה הקיבוץ במקום הניכוי באותה בית כיתה ואותו מספר יקבל סימן העליון הראוי אשר ממנו ינוכה כמו ■(17x3*18x2-16x*12@9x3*14x2-11x*10@8x3*4x2-5x*2) ■(17x^3+18x^2-16x+12@9x^3+14x^2-11x+10@8x^3+4x^2-5x+2) ■(3a*2b*c@a-b*c@2a*3b) |- | |style="text-align:right;"|ולהקל נציג לפניך המשלים במספרים ידועים
■(A&b&c)
■(א&ב&ג)
■(3*2*1&2-x*2@▁(1-1*1)&▁(1*1-1)@2*3&1-2*3)
ואם מספר המנכה גדול ממספר המנוכה (חוץ בכיתה ראשונה) ואצל שניהם סימן היתור * אז נגרע העליון מן התחתון עם סימן הפחיתות כמו ■(3a*2b*c&2a*2b*2c@▁(a*3b*3c)&▁(a*4b*3c)@2a-b-2c&a-2b-c) ובמספרי הוא כך ■(3*2*1&2*2*2@▁(1*3*3)&▁(1*4*3)@2-1-2&2-1-1) ואם ננכה מספר העדרי מן העדר הקטון ממנו אז נעשה כמו כן שינוכה העליון מן התחתון והשארית והשאירות יורשם בסימן היתור כמו ■(3a-b&2a-3b@a-2b&a-5b@2a*b&a*2b) ■(2a-b c@▁(a-3b-a)@a*2b) ובמספרי הוא כך ■(3-1&2-3@1-2&1-5@2*1&1*2) ■(2-1-1@▁(1-3-1)@1*2) ויהיה דמיון זה כולל כל הכללים שזכרנו ■(9x8-15x6*4x5*5x4-8x3-9x2-4x*9@▁(6x8*10x6-6x5*9x4-12x3-6x2*9x-6)@3x8-25x6*10x5-4x4*4x3-3x2-13x*15) בהכפלות האותיות אם יבואו כמות נצמדות ע"י על ידי סימנים ידועים והמכפיל הוא מאות אח' לבדו אז יחובר לכל אחד מאותיות המוכפלות בלי סימן מפסיק ביניהם כנ"ל כאשר ביארנו למעלה כמו ■(a*b*c@ d@ad*bd*cd) אבל אם הן אותיות רבות המכפילות אשר הם הן כמו כן מחוברות בסימנים אז יחוזר ההכפלה בכל אחד מהאותיות ויעמדו בסדר הראוי כפי כללי ההכפלי ההכפלה המספרית והמספרים הנולדים יקובצו כפי כללי החיבור בזאת החכמה אשר זכרנו קדם מאמרינו מהם אבל זאת לדעת אם יהיו סימנים המכפילים שווים לסימני המוכפלים בין שיהיו שניהם * או שניהם - שיורשם סימן היתור * להולדת ההכפלה ואם הם בלתי שווים יולידו לעולם הפחיתות כמו ■(a*b&a*c@▁(a*c)&▁(a*c)@ *ac*bc& *ac*cc@aa*ab &aa*ac @aa*ab*ac*bc&aa*2ac*cc) ■(a*b&a-b@▁(a-b)&▁(a-b)@ -ab*bb& -ab*bb@▁(aa*ab )&▁(aa-ab )@aa-bb&aa-2ab*bb) ובמספרי נניח a הוא 2 b הוא 3 c הוא 4 א"כ כזה ■(2-3@▁(2-3)@-6*9@▁(4-6 )@4-12*9)
■(2*3-4@▁(2*3-4)@-8-12*16@*6*9-12 @▁(4*6-8) @4*12*9*16-24*16) ואל תתמה באומרינו שנים פחות שלשה כי כן מבואר למשכילים בחשבון האותיות ועל זה נבנה סוד הבריאה יש מן האין כמו שביארנו באריכות בחיבורינו הגדול (חלקות אש"ר) ושם יתנו עידיהן ויצדקו הרבה מופתים טבעים יקרי הערך ולזה כתב החכם השלם כמהר"ר יש"ר מקנדיא במעין חתום תמר ח' וז"ל אודיעך דבר נפלא שתדע להשיב למכחישי אפשרות יש מאין כאשר נאמין אנחנו בני ברית שה' ברא העולם מאין המוחלט והוא שאם תכפול (כפי דרכי האלגיברה) מספרים פחותים מאין יולידו מספרים ואי אפשר להכחיש המלאכה שהיא כבר ברורה ונתאמתה במספרים של ממשות ע"כ והרי לך כמה מספרים אין מולידים יש וכמוהם בלתי בעלת תכלית ■(3-7@3-7@ -21*44@4-21 @4-42*44) והם 16 ועוד נבאר זה כיד ה' הטובה עלינו מסגולות מספרים אלו והכרחם להתר ספיקות רבות ■(4-10@8-4@ -36*90@▁(32-80 )@32-116*90) והם 86 בחילוק חשבון זו נעשה כך אם האות או האותיות של המחלק הם בכיתות הנחלקים אז נסיר את אותיות המחלק עם אותיות הדומות מהנחלקים והנשארים הם כמות המבוקש אבל תדע זאת צריך שנדע אם סימני המחלק עם הנחלק הם שווים אז נרשום לכמות היוצא סימן היתור * ואם היו בלתי שווים אז נרשם סימן - וכמו שזכרנו שקדם מאמרינו בכללי ההכפלה כמו ├ ■(ab@a )┤|b
├ ■(abc@b)┤|ac
├ ■(ab*ac@a a)┤|b*c
├ ■(ac*ad*bc*bd@4 * d c * d)┤|a*b
├ ■(aa-2ab*bb@a-abb=b@a b)┤|a-b ובמספרי יהיה a 1 b הוא 2 c הוא 3 d הוא (43v) 4 וא"כ ab דהיינו 2 שנחלק עם 1 יהיה הכמות b דהיינו 2 וכן 3*4*6*8 יחלק על ידי 3*4 דהיינו 21 על ידי 7 יהיה הכמות 1*2 דהיינו 3 וכן תקיש אבל אם אותיות המחלקות אינן דומות לאותיות הנחלקות או בכללן או בקצתן אז נמשך קו בין המחלק ובין הנחלק כדמיון שבר ויהיה מכנה שבר המחלק ומונה הנחלק כזה ■(ab&bcd&ab*cc&ac-ad@c&ab&d&a*b) עד הנה כתבנו ממיני החשבון בשלמי' נשאר לנו לבאר ממיני החשבון בשברים בקיבוץ השברים יעשה כמו בקיבוץ השברים מספריים וכמו שהורינוך בכללי קיבוץ בשלמים ואינו מן ההכרח לחדש המלאכה בכללים חדשים כמו נקבץ כזה ■(■(4&106)@▁(■(a/2&3a/4))@8) ■(▁8@4@▁6@▁01@8)1 1/2 בניכוי השברים יעשה כמו בגרעון השברים המספריים רק שתעשה ההכפלה והגרעון ע"ד האלגיברה כאשר הורינוך בשלמים והיו למאורות דמיונות אלו אך זאת תדע כי ההכפלת שתי וערב היא היותר נכונה וקלה כמו בקיבוץ כך בגרעון ■(2x@▁(■(2x&4x))@■(x/4&x/2)@8) ■(14 xx/4-5 2x/3*1 3/4@83xx/4-9x*7 1/4) ולפי הכללים שהורינוך יבוא שישאר 5 xx/2*3x/3-5 1/2 4/(2x*3) יוגרע (2xx*5)/(2x*3) ישאר אחר הקטנת השבר (2xx*1)/(2x*3) בהכפלת השברים יעשה כמו במספריים אבל שנעשה ההכפלה ע"ד הכללים שזכרנו בהכפלת השלמים באלגיברה ויהיו להאיר עיני שכלך דמיונות אלו ├ ■(▁6x@■(2x/3&3/4)@12)┤| ■(3/4x&2/3x) יולד 1/2 xx ■(5xx/6&6x/7) יולד 30x3/42
ובהקטנה 5x3/7
בחילוק השברים נעשה כמו בחילוק השברים מספריים דהיינו שההכפלה והאופנים יהיה ע"ד האלגיברה וכמו שהורינוך בחילוק ובהכפלת השלמים ותן עיניך בדמיונות אלו ■(3/4&x/2&3/4x&1/2 xx) ■(4x@2@3x) יוחלק 6xx ■(6&├ 4/6x┤|&2/3x) ■(6x/7&5x3/7) |style="text-align:right;"|לוח להוצאת השרשים |style="text-align:right;"|והוא מראה דרך ההכפלה בהוצאת השרשים בב"ת לוח זה נולד מהכפלת x*1 עם x*1 והנולד יוחזר ויוכפל עם x*1 וכן חלילה עד בלי תכלית : שרש x מרובע x2 מעוקב x3 מרובע מרובע x4 מרובע מעוקב x5 מעוקב מרובע x6 מרובע מרובע מעוקב x7 ג' מרובעי' x8 מעוקב מעוקב x9 מרובע x10 מעוקב מרובע x2 2 x3 3 3 x4 4 6 4 x5 5 10 10 5 x6 6 15 20 15 6 x7 7 2x 35 35 21 7 x8 8 28 56 70 56 28 8 x9 9 36 84 126 126 84 36 9 x10 10 45 120 210 252 210 120 45 10
מהוצאות השרשים Extraction of Roots א מהוצאות שרש מרבע להוציא שורש 1) Extraction of Square Roots מרובע הוא מספר כפול בעצמותו A square is a number multiplied by itself. ולידע שרשו נעשה כך To know its root, we do as follows: כמו יש לי מרובע aa*2ab*bb ונרצה לידע שרשו As if I have a square a^2+2ab+b^2 and we wish to know its root. נראה בראשונה כמה אותיות מתחלפות שיש במרובע וכל כך וכ"כ אותיות פשוטות יבואו בשורש לא פחות ולא יותר First, we see how many different letters there are in the square and that many simple letters will be in the root, no less and no more. ובנידון דידן נראה בכל הכתות אינן זולתי אותיות b a וזה אשר יורה כי בשורש לא יבוא זולתי שתי אותיות b a In the matter under discussion, we see in all parts only the letters a b, which indicates that there are only two letters in the root, a and b. וכן תקיש אם יבואו ג' אותיות שונות Deduce the same if there are three different letters. וא"כ ואם כן נעשה כדין הוצאות מרובה מרובע מספרי רק שנעשה ההכפלה והחלוק כפי מה שהורינו באלב[.] ע"פ Then, we follow the rule of extracting the numerical square [root], but we apply the multiplication and division according to what we instructed. וא"כ בנדון דידן מתחיל נתחיל מצד שמאל ונמצא שם aa והוא בעצמו מרובעו כי מרובע a הוא aa In the matter under discussion, we start from the left and we find there a^2, which is a square itself, because the square of a is a^2. וא"כ נכתוב במקום השורש a וננכה מרובעו ממרובע מן המרבע aa לא ישאר מה So, we write a in the place of the root and subtract its square from the square a^2; nothing remains. ואח"כ ואחר כך נכפיל השורש הנמצא יבא 2a ונעמידהו תחת כתה שנייה שהיא *2ab Then, we double the found root; the result is 2a. We write it beneath the second part, which is +2ab ונחלקהו יבוא *b כדין החילוק שהקדמנו לבארו We divide it by it; the result is +b, according to the rule of division we explained earlier. וזה האות השני מן השורש ונעמידהו אצל a This is the second letter of the root. We write it next to the a. ואח"כ ואחר כך נכפיל השורש החדש שהוא b עם כפל שורש הראשון שהוא 2a ויבוא כדין 2ab Then, we multiply the new root, which is b, by double the first root, which is 2a; the result is 2ab. וננכה זה מן 2ab שבמרובע לא ישאר כלום We subtract it from the 2ab in the square; nothing remains. ואח"כ נכפיל השורש האחרון הנמצא שהואb בעצמו ויבוא מרובעו bb Then, we multiply the last found root, which is b, by itself; its resulting square is b^2. וננכה זה מן הכתה האחרונה ולא ישאר כלום We subtract it from the last part; nothing remains. וזה סדרו ├ ■(aa*2ab*bb@aa 2a bb@ 2ab)┤|a*b This is its diagram: ├ ■(a^2+2ab+b^2@a^2 2a b^2@ 2ab)┤|a+b או על דרך היותר קל שתראה כמה אותיות שונות יש במרובע ככה יש שורשי המרובע ואח"כ תראה אם מרובע כל אחד נראה ונמצא במספר וגם סימן הכפלתם יחדיו ואז תעמיד האותיות פשוטות זה אצל זה עם צורת * או - כפי דינו Or, on the easier way, you can see how many different letters there are in a square, so are the roots in the square. Then, see if the square of each is visible and found in the number, as well as their product by each other. Then, write the simple letters next to each other with the sign + or - as required. כמו נמצא שורש של מרובע זה
aa*2ab*2ac*bb*2bc*cc As, if we find the root of this square:
a^2+2ab+2ac+b^2+2bc+c^2 הנה נראה כי במרובע זה רק שתי אותיות והן a b c ומרובען נמצא בעצמו כמו aa bb cc וגם סימן הכפלתם 2bc 2ac 2ab ונרשמים כלם בסימן היתור אז נדע כי השורש הוא a*b*c We see that there are only three letters in this square, which are a b c and their squares are found in it, a^2,b^2,c^2, as well as their products 2ab,2ac,2bc, and they are all written with the addition sign; so we know that the root is a+b+c. וכן תקיש משאירות המרובע יעשה כמו בחשבון המספרי דהיינו שנכפיל השורש הנמצא ונקבץ להנולד 1 והוא מכנה השבר והנשאר מהמרובע יהיה המונה Apply the same for the remainder of the square, which is carried out as in the numerical calculation: we double the found root and add 1 to the result; this is the denominator of the fraction. The remainder of the square is the numerator. ממציאת אמצעי מוערך במרובעים Finding the proportional mean of squares אמצעי מוערך בין שני מרובעים נולד אם שני מרובעים יוכפלו זה עם זה ומהנולד נוציא שורש המרובע השורש היוצא הוא בשיווי להכפלות השרשים משני המרובעים זה בזה The proportional mean between two squares is generated, if two squares are multiplied by each other, then we extract the square root of the product. The resulting root is equal to the product of the roots of the two squares by each other. √(a^2∙b^2 )=√(a^2 )∙√(b^2 ) מהוצאות שורש המעוקב 2) Extraction of Cube Roots מעוקב הוא מרובע כפול בשורשו A cube is a square multiplied by its root. ולמצוא שרשו נעשה כך To find its root we do as follows: יהיה המספר מעוקב כזה a3*3aab*3abb*b2 Let the cube root be: a^3+3a^2 b+3ab^2+b^3 וכאן כמו כן נראה אם האותיות דומות או שונות וכמה הן המתחלפות ונמצא בכל הכתות לא יותר כי אם a b לבדן וזה יורה שזה השרשים הם a b Here also, we see if the letters are different or similar and how many are those that are different. We find that in all the parts there are only a and b and this indicates that the roots are a b. ותעשה כן תחילה מצד שמאל ותמצא (44r) a3 שהוא המעוקב בעצמו וא"כ a הוא השורש הראשון Do as follows: first on the left, you find a^3, which is the cube itself, so a is the first root. ואח"כ ואחר כך נראה בכתה שניה ונמצא ג' מרובעים a הנכפלים עם b כזה 3aab ואז ניקח מרובע שורש הנמצא שהוא aa ונשלשהו ויהיה א"כ 3aa וזה המחלק כת שניה שהיא 3aab ויצא b כדין החלוק ונרשום אל השורש a את השורש b הנמצא עם סימן היתור כדין ואח"כ נעשה כך Then, you look at the second row, we find three squares of a multiplied by b, like this 3a^2 b. We take the square of the found root, which is a^2, and we triple it; it is 3a^2 and this is the divisor of the second part, which is 3a^2 b; the result is b. We write the found root b next to the root a with the addition sign. Then, we do as follows: (א) נכפיל השרש החדש b עם המחלק 3aa ונעמידהו תחת כתה שניה I. We multiply the new root b by the divisor 3a^2 and write it beneath the second part. (ב) נכפיל מרובע שרש חדש עם משושל משלש שרש הראשון דהיינו bb עם 3a ונעמידהו תחת כתה שניה II. We multiply the square of the new root by thrice the first root, i.e. b^2 by 3a, and we write it beneath the second part. (ג) נעמיד מעוקב שרש החדש שהוא b ומעוקבו 3b 3b b3 b3 תחת III. We write the cube of the new root, which is b and its cube is b^3, beneath b^3 ויוגרעו זה מזה ונמצא שעולים זה עם זה וכך סדרם They are subtracted from each other; we find that they coincide; and this is their diagram: ■(├ ■(a3@a3@)┤|&├ ■(*3aab@ 3aa@3aab)┤|&├ ■(*3abb@ 3abb@)┤|&├ ■(*b3@ b3@)┤|&a*b) ■(├ ■(a^3@a^3@)┤|&├ ■(*3a^2 b@ 3a^2@3a^2 b)┤|&├ ■(+3ab^2@ 3ab^2@)┤|&├ ■(+b^3@ b^3@)┤|&a+b) ואם ישאר מה מהמעוקב שלא יוכל יכול לכנוס בשרש המעוקב נתקנו כך שרש מעוקב היוצא נרבע ולהנולד יקובץ השורש והעולה ישולש ולהעולה יקובץ 1 והעולה הוא מכנה השבר והנשאר ממנה השבר וכן תקיש בשאירות שארי שרשים If something is left of the cube that cannot be included in the root of the cube, we correct it this way: We square the resulting cube root; the root is added to the product; the result is tripled; 1 is added to the product; the result is the denominator of the fraction and the remainder is the [numerator of the] fraction. Apply the same for the remainder of the remainder of the root. ויתכן יותר מדוקדק בקיבוץ 0 00 000 וכן עד אין תכלית וכל עוד שתרבה יבוא יותר קרוב ויש שכר לעמלך It can be more accurate by adding 0, or 00, or 000 and so on. The more you add, the more accurate it will be, and there will be a reward for your labor. ממציאת אמצעי מוערך בין שני מעוקבים Finding the proportional mean between two cubes בין שני מעוקבים נמצאים שני אמצעים מוערכים האחד נקרא גדול והשני נקרא קטן ואופן מציאתו יעשה כך Between two cubes there are two proportional means, one is called the greater and the other is called the smaller. The way to find them is as follows: בראשונה תרבע שורשיהם ותכפיל מרובע הגדול עם שרש הקטן והנולד הוא אמצעי גדול ואם תכפיל מרובע הקטן עם שרש הגדול יולד אמצעי הקטן First, square their roots. Then, multiply the greater square by the smaller root; the result is the greater mean. If you multiply the smaller square by the greater root, the result is the smaller mean. ויחוסי האמצעיים אלה הם כערך מעוקב הגדול אל אמצעי גדול כך ערך מעוקב קטון אל אמצעי קטון The relation of these means is such that the ratio of the greater cube to the greater mean is the same as the ratio of the smaller cube to the smaller mean. [erroneous] a^3:(a^2∙b)=b^3:(b^2∙a) וכן אם יוגרע השורש הקטן משורש הגדול והנשאר יוכפל במרובע הגדול ולהנולד יקובץ אמצעי גדול אז יעלה מעוקב הגדול Also, if the smaller root is subtracted from the greater root and the remainder is multiplied by the greater square, then the greater mean is added to the product, the result is the greater cube. [(a-b)∙a^2 ]+(a^2∙b)=a^3 אבל אם השארית השאירות או מרחק השרשים יוכפל במרובע קטון והנולד יוגרע מאמצעי הקטון ישאר מעוקב הקטון But, if the remainder, or the difference between the roots, is multiplied by the smaller square, then the product is subtracted from the smaller mean, the smaller cube remains. (b^2∙a)-[(a-b)∙b^2 ]=b^3 והוא מבואר להמשכיל This is clear from the thinker. ב' מהוצאת שרש מרובע מרובע 3) Extracting the Root of the Square-Square מרובע מרובע הוא מרובע כפול במרובעו The square-square is a square multiplied by its square. והנה להוצאות שורשו או שאחר שנוציא ממנו שורש המרובע ומהשורש היוצא תחזור ותוציא נחזור ונוציא שורש מרובע והשורש היוצא שנית הוא המבוקש או אז אם נרצה להוציאו בפעם אחת נעשה כך א) שיבוקש באותיות באותיות בכתה שמאלית המרובע מרובע היותר קרוב ויוגרעו ממנו והשארית יכתב עליו כדין ב) שיוכפל השרש אשר יצא וכן מרובעו ומעוקבו כפי מה שהורינו בלוח דהיינו השורש 4 פעמים ומרובעו 6 פעמים ומעוקבו 4 פעמים וישימו ויושמו זה תחת זה דהיינו למעלה המעוקב 4 (44v) פעמים ותחתיו המרובע 6 פעמים ולמטה המינו ממנו השורש ארבע ד' פעמים וכן תקיש בהוצאת שארי שרשים שהגדול למעלה והקטן תחתיו ג) ואח"כ תחלוק כמו בהוצאות שורש המרובע והמעוקב שהורינוך וכמות החלק הוא שרש השני ואח"כ תעמוד השרש החדש עם מרובעו ועם מעוקבו זה תחת זה באופן שיהיה השרש מקביל נגד המעוקבים והמרובע נגד המרובעים והמעוקב נגד השרשים ותכפילם זה בזה דהיינו השורש עם המעוקבים וכו' ומה שיולד תעמוד תעמיד זה תחת זה כסדר שעמדו ותעמוד ותעמיד תחתיהם מרובע מרובע השרש השני ש בסדר שהקדמנו לבאר ואז יוקבצו יחדיו וקיבוצם יוגרע ממספר שממנו תוציא השרש וכן כסדר הזה חוזר חלילה עד בלי שאירות הכתות ממציאות אמצעי מעורך מוערך בין שני מרובע מרובעים גם בין שני מרובע מרובעים ימצאו שני אמצעים מוערכים האחד גדול והאחד הקטן וימצאו בהכפלת שרש הקטן עם מעוקב הגדול ומזה יולד אמצעי גדול ומהכפלת מעוקב הקטון עם שרש הקטן הגדול יולד נולד אמצעי הקטן ויחוסו כערך מרובע מרובע הגדול לאמצעי הגדול כך ערך מרובע מרובע הקטן לאמצעי הקטן וכך תקיש במציאת האמצעים בשארי הכפלת השרשים ויותר מיחוסי אמצעים אלו בארנו בחבורינו צפנת פענח ד' מהוצאת שורש זורזאליד או מרובע מעוקב 4) Extracting the Root of the Square-Cube זורזאליד הוא הכפלת המרובע במעוקבו וימצא שורשו ע"ד על דרך זה א) תבקש שורש מרובע מעוקב מכתה שמאלית ויוגרע כדין ב) להכפלת החלקים יורה הלוח דהיינו 5 שרשים 10 מרובעים 10 מעוקבים 5 מרובעי מרובעים ותעמידם זה תחת זה כסדר שהורינוך ג) תחלק כדין והכמות הוא השורש השני ואח"כ תעמוד השרש החדש מרובעו מעוקבו ומרובע מרובעו זה תחת זה כסדר שהקדמנו לבארו ויוכפלו זה בזה ותחתיהם יועמד מרובע מעוקב משרש החדש כסדר שהקדמנו ויקובצו וקיבוצם יוגרע מהמספר שממנו יוצא השרש וכן תוכל לשנה ולשלש כפי הצורך ה' מהוצאות השורש מעוקב מרובע 5) Extracting the Root of the Squared Cube מעוקב מרובע הוא כשנרבע את המעוקב דהיינו שנכפיל המעוקב בעצמו והוצאת שורשו תעשה יעשה באופן זה א) יבוקש מרובע מעוקב מכתה שמאלית ויוגרע כדין ב) להכפלת השורש תעשה כפי מה שהורינוך בלוח הוצאת השרשים ותעמידם כסדר שהקדמנו לבארו ואצלם יעמוד יועמד השורש השני היוצא מחילוק מרובעו מעוקבו מרובע מרובעו מרובעו מעוקבו ויוכפלו זה עם זה ותחתיהם יועמד מעוקבו מרובע כסדר שהקדמנו ויקבצו וקיבוצם יוגרע כנזכר למעלה ו' מהוצאת השורש ב' זורזאליד או מרובע מרובע מעוקב 6) Extracting the Root of the Square-Square-Cube ב זורזאליד הוא הכפלת המעוקב במרובע מרובעו ושורשו ימצא על דרך זה יבוקש מרובע מרובע מעוקב בכתה שמאלית ויוגרע כדין ב) להכפלת השורש תעשה כפי אשר מראה אותך הלוח ותעמידם כסדר שהקדמנו ג) תחלוק כדין ותעמוד אצליהם שורש היוצא מרובעו מעוקבו מרובע מרובע מרובעו מרובעו מעוקבו מעוקבו (45r) מרובע ויוכפלו זה בזה ויעמדו זה תחת זה בגדול החל ובקטן כלה ותחתיהם יועמד מרובע מרובע מעוקבו ויקובצו וקיבוצם יוגרע כנזכר למעלה ז' מהוצאת השרש מרובע מרובע מרובע 7) Extracting the Root of the Square-Square-Square מרובע מרובע מרובע הוא הכפלת המרובע מרובע במרובעו ושורשו ימצא באופן זה א) יבוקש מרובע מרובע מרובע מכתה שמאלית ויוגרע כדין ב) להכפלת השרש תעשה כפי אשר מראה אותך הלוח ותעמידם בסדר שהקדמנו ג) ואצלם יועמד השרש השני היוציא מחילוק כדין מרובעו מעוקבו מרובע מרובעו מרובעו מעוקבו מעוקבו מרובע מרובע מרובעו מעוקבו ויוכפלו זה בזה ותחתיהם יעמוד יועמד מרובע מרובע מרובעו ויקובצו וקיבוצם יוגרע כנ"ל ח' מהוצאות שורש מעוקב מעוקב 8) Extracting the Root of the Cubed Cube מעוקב מעוקב הוא כשנעקב המעוקב דהיינו שנכפול אותו בעצמו והנולד יוכפל במעוקב ולהוצאת שרשו נעשה כך א) יבוקש מעוקב מעוקב מכתה שמאלית ויוגרע כדין ב) להכפלת השורש היוצא ומרובעו וכו' תעשה כפי הוראת כהוראת הלוח ותעמידם כסדר המוזכר ג) ואצליהם יועמד השרש היוצא מחילוק מרובעו מעוקבו מרובע מרובעו מרובע מעוקבו מעוקבו מרובע מרובע מרובעו מעוקבו מרובע מרובע מרובעו ויוכפלו זה בזה ותחתיהם יועמד מעוקב מעוקבו ויוקבצו וקיבוצם יוגרע כנ"ל ט' מהוצאות שורש מרובע מעוקב מרובע 9) Extracting the Root of the Squared-Square-Cube מרובע מעוקב מרובע הוא הכפלת הזורזאליד או המרובע מעוקב בעצמו ושורשו ימצא בדרך זה א) יבוקש מרובע מעוקב מרובע מכתה שמאלית ויוגרע כדין ב) להכפלת החלקים צא בעקבות הלוח ותעמידם בסדר שהורינוך ג) ואצליהם יעמוד יועמד השורש היוצא מהחילוק מרובעו מעוקבו מרובע מרובעו מרובע מעוקבו מעוקבו מרובע מרובע מרובעו מעוקבו מרובע מרובע מרובעו מעוקב מעוקבו ויוכפלו זה בזה ותחתיהם יעמוד יועמד מרובע מעוקבו מרובע ויקובצו וקיבוצם יוגרע כנ"ל מהוצאות שורש פרוניק פרוניק הוא קיבוץ השורש למרובעו והנה למציאת שורשו נוציא שורש המרובע והנשאר יורה השורש וא"כ שורש המרובע דומה לשארית או בדרך יותר נכון נעשה כך נכפול כולו עם 4 ולהנולד יקובץ עם 1 ונוציא מהעולה שורש המרובע ומהשורש ומן השרש היוציא יגרע נגרע 1 והנשאר יחלק נחלק לשניהם והחצי הוא השורש המבוקש וזה מה שיתכן לנו די ביאר מהוצאות השורשים כי תן לחכם ויחכם מהוצאות השרשים בשברים עם אם שלימים עם השברים תתיר השלימים לשברים ותוציא השרש ממכנה ואח"כ ממונה והיוציא הוא השורש המבוקש וכן בשברים לבדם מהוצאות השרשים כשהערך אינו מתמיד וכן משלמים ושברים בשיווי לשלמים ושברים נכתב לקמן באריכות כיד ה' הטובה עלינו אי"ה מכלל הזהב עד הנה עזרנוך במיני המספר נשאר לנו לבאר מערכי המספר והם בכפלים או בהערך או בהעברה מספרים מעורכים הם כאילו נאמר כערך מרחק מזה אל זה כך ערך מרחק מזה (45v) לזה אל זה כמו 3÷6:8÷16 הנה בכאן ארבע הערכות הערכי' אשר מיוחסהי' מיחוסיהם נבאר לקמן בע"ה מעז"ה אבל אם הי' ערך אחד ידוע ונבקש ערך בלתי ידוע אשר יהיה משפטו כערך ראשון אל שני כך ערך השלישי הבלתי לבלתי הידוע הנה חפש זו לגדול תועלתו נקר' כלל הזהב או כלל משלש והוא בכפלים או פשוט או מוכפל. הפשוט הוא משלש הערכות לבדן והוא כמו כן ישר או הפוך אשר בזה יבחנו היטב כל מסבב השאלה כי בהרבה דברים נראה כל' הזהב אשר בכל בית נכאת ההגיונים אין כמותו בלתי צודק כשהערך מופסק או בהעסקה בלתי נאותית לכל מסבבי השאלה: כלל זהב מוכפל הוא מחמש הערכות אשר מזה יכונה כלל מחומש והוא כמו כן או ישר או הפוך והנה מהעסקתם באלגיברה לא ישונה מהעסקה המספרית רק שההכפלה וחילוק נעשה על דרך האלגיברה כמו שהורינוך בכללים הקודמים וכשתשים הסימן אשר בחרת במקום הראוי לבוא אז יבוקש כמותו אם נעסוק בו כדין יחוסי אותם מספרים כמו 2:3:8:x דהיינו אם ישאל שנים יתנו שלושה כמה כמו יתנו שמנה והתשובה ובא התשובה שיתנו x והנה הסימן הזה x הוא המספר אשר שני שלישים ממנו הוא 8 והנה לידע כמות x אשר בחרת תעשה השוואת המעורכים שהוא אחד מיחוסיו שאם יוכפלו שתי וערב שישתוו ובנדון דידן כזה ■(├ ■(2&3@8&x)┤|&├ ■(2x=24@■(2&2))┤|&■(12@)) תחלוק שני הכמות עם 2 יצא x=12 והוא הכמות המבוקש כי כערך 2 אל 3 כך ערך 8 אל 12 והבחינה כשתכפלם שתי וערב כזה משתווים 24=24 ■(2:&3@8:&x 12) הי' השאלה אבל בתשובה תעשה כך ■(2&03@8&12)
ותכפלם שתי וערב הם שווים ע"כ הי' הסימן x מראה על 12 וכו'
כמו שאמרנו והיא באמת הבחינה היותר קלה ונכונה בכל כללי הזהב ומזה נולד שתכפיל בכלל משלש ישר האמצעי עם הקצווה ימינית והנולד יוחלק עם השמאלית וההפוך בהיפוכו ותוכל לעסוק כפי כל קצורי האחרונים אשר מצאו עד זמננו זה ואשר מצאנו והם כתובים באצבע בחבורינו צפנת פענח ויהיו למאורות דמיונות אלו ותן עיניך בהם: (א) כת בחורים היו בבית המשתה ושם אכלו ושתו בעד 22 זהו' 49 צ"ל וכל אחד מהם שלם כל כך צ"ל כמספר האישים השאלה כמה פרע כל אחד ביחוד וכמה בחורים היו שם. 1) A group of men were in a restaurant. They ate and drank there for 22 zehuvim and 49 z”l. Each of them paid as many z”l as the number of people. The question is how much did each pay separately and how many men were there? תשובה יראה כי עיקר הנעלם כאן הם מספר הצ"ל שנתן כל אחד מהחברה וממנו יולד מספר הבחורים וכן בהיפוך ונאמר שאחד מהם נתן x וא"כ בהכרח מספר הבחורים היה כמו כן x וא"כ נעמידהו על כלל משלש כזה כמה יתנו כלם יתן בחור x x : 1
וא"כ יבוא כדין שיתנו כלם xx כי האחדות אינו חולק ואח"כ נשווה ונאמר xx=1369 שהם הצ"ל עם התר הזהב לצ"ל וא"כ כמו xx הוא מרובע אמיתי בהכרח יהיו ה 1369 כמו כן מרובע אמיתי תוציא משניהם השרש ויבוא x=37 וזה המבוקש כי הבחורים היו במספר 37 וכן נתן כל אחד מהם 37 צ"ל בחון ותראה אמת : (ב) אחד קנה חתיכה בגד מחזקת ששים אמה אמות בעד סך ידוע ויהיה הסך של זהו' שנתן בעד כלו כלה כמספר האמות שנתן שקנה בעד 6 2/3 זהו' השאלה בכמה זהו' פרע כלו אותה וכמה אמות קנה בסך בעד 6 2/3 זהו' 2) One bought a piece of cloth of sixty cubits for a known amount, such that the number of zehuvim that he paid for all of it is the same as the number of cubits he bought for 6 2/3 zehuvim. The question is: for how many zehuvim did he buy it and how many cubits did he buy for 6 2/3 zehuvim? תשובה הנה עיקר ההעלמה כמה אמות שקנה בעד 6 2/3 זהו' כי הן סיבת ידיעת מספר כלל הזהובי' שפרע ונקח במקום האמות שאינן הבלתי ידועות x ובמקום הממון הבלתי ידוע ב"כ כמו כן x ויעמדהו ונעמידהו על כלל משולש כזה בכמה כמות האמו' בעד סך זהו' אמות אמות 60 זהו' 6 2/3 x
אז תכפול מספר סך הזהו' עם כמות האמות הידוע ונעסוק בו כדין רעגולי דעטרי יצא 400/x דהיינו סך שהם ת' זהו' שבור אות' על מחולקים ע"י x והם שווים למספר x שהוא סך הששים אמות וא"כ יהיה כך (400-x)/x והנה כדי שנודע המספר שנמצא על צד אחד מספר נודע נעשה כך תכפול הסך 400 נראה שה400 מחולקים ע"י x ואז נכפיל הת' עם x ואז הוא משולל החלוקה דהיינו שנשליך ממנו x וישאר 400 לבדו ואח"כ ואחר כך תכפול נצריך כמו כן לכפול ה xב x כדי שישארו שני שתי כמות שוות באותו שיווי וכמו שכתבנו בכלל השלישי מכללים הכוללים ואז יבוא xx שהוא מרובע אמיתי וא"כ יהיה 400=xx נוציא משניהם שורש מרובע יבוא x-20 ונמצא ששילם בעד 60 אמות 20 זהו' כמספר האמות שהיו לו בעד 6 2/3 זהו' (ג) שאלה כמה אנשים אוהבים נאמנים פרעו בסעודה אחת 75 זהו' וכל אחד פרע כל כך כ"כ זהו' כמו 1/3 מספר האנשים השאלה כמה היו אנשים וכמה פרע כל אחד מהם ביחוד 3) Loyal friends paid 75 zehuvim at one meal and each one paid as many zehuvim as 1/3 of the number of people. The question is how many people were there and how much did each of them pay separately? תשובה מספר האנשים היו x והואיל אחד נתן כ"כ זהו' כמו 1/3 מספר כלם א"כ החלק הזה יקרא x/3 ואז נעמידהו על כלל משולש כזה כמה יתנו משלם x x/3 1
נעסוק בו כדין יצא xx/3 וזה שווה למספר 75 כזה xx/3=75 הכפיל נכפל שניהם שניהם עם מספר 3 כדין יצא ההשוואה xx=225 נוציא משניהם שורש המרובע יבוא x=15 שהם מספר האנשים וא"כ הי' כל א' נתן 5 זהו' וכו' ואם כן x/3=5 שהוא מספר הזהב שפרע אחד מהם (ד) שאלה אם הי' יש לאחד אנשים על שלחנו שיתן להם מזונות ואם יתן אחד מהם 50 ר"ט לשנה בעבור המזונות יזיק הבעל הבית לב"ב 30 ר"ט אבל אם יתן אחד מהם 60 ר"ט ירוויח (46r) הבעה"ב הבעל בית 40 ר"ט השאלה כמה אנשים היו סועדים על שולחנו וכמה המעות לשנה שהוציא הבעה"ב הב"ב תשובה מספר האנשים שסעדו היה x וא"כ ואם כן אמור ראשונה אחד נתן 50 ר"ט כמה יתנו x שהוא מספר האנשים יבואו שיתנו כלם 50x ואח"כ ואחר כך נאמר כמו כן אחד יתן 60 ר"ט כמה יתנו x יבוא שיתנו כלם 60x והואיל בכתה ראשונה יזיק לב"ב 30 וא"כ יהיה הסך שהוציא 50x*30 ובשניה הרויח 40 ר"ט וא"כ יהיה הקרן 60x-40 ויהיה א"כ בהשוואה ההשוואה כך 50x*30=60x-40 נגרע משניהם 50x ישאר כזה 30=10x-40 נקבץ לשניהם 40 יהיה כך 70=10x נחלק שניהם עם 10 ויהיה א"כ x=7 שהוא מספר האנשים שסועדים על שולחנו וא"כ מעות המזונות שיוציא הב"ב לשנה הי' הוא 380 והוא מבואר (ה) שאלה שלשה פועלים בנו בנין אחד שכר הראשון 40 צ"ל ליום ושכר השני ליום אחד 50 צ"ל ושכר השלישי 60 צ"ל ליום והבניין נגמר בק"ך ימים והפועלים קבלו תשלומין בשווה השאלה כמה ימים בנה כל אחד מהם תשובה אמור מספר ימים של ראשון הם שווים x ושל שני y וא"כ מספר הימים של שלישי הם 120-x-y וא"כ שכר הראשון 40x ושכר השני 50y שכר השלישי 7200-60x=60y פי' כי תכפיל 60 שכר השלישי עם 120 יהיה 7200 אבל קיבל פחות כמספר שכרו שקבלו השנים דהיינו -60x-60y ולפי נדון השאלה 50y=40x נמצא הכמות של 60y 60y בשכר השלישי בכלל משולש כזה ├ ■(■(50y-40x&60y) @■(240&0)@■(5&0))┤|48x וא"כ כעמוד נעמיד במקום 60y בשכר השלישי 48x כזה 7200-60x-48x=40x נקבץ x יחדיו יהיה 108x וא"כ השיווי יהיה כזה 7200-108x=40x נחבר לשניהם 108x השיווי כזה 7200=108x148x נחלק שניהם עם 148 יהיה 2/3 4=x [?] או 48 96/148 צ"ל והם הימים של ראשון ואם נכפלם עם 40 יצא 1945 35/37 צ"ל וכן שכר הראשון וככה שכר כלם ואם נחלקהו עם 50 שכר שני ליום וכן עם 60 שכר שלישי ליום יבואו ימים של שני 38 34/37 וימים של שלישי 32 16/37 ואם נקבץ השלשה זמנים יחדיו יעלה 120 ימים והוא נכון (46v) מדמיונות מוערכות (א) לשני אנשים סך זהו' והם בערך אחד לשני כמו 2 אל 5 ואם מרובע שניהם יוקבצו והיו לאחד יעלה יעלו 11600 זהו' השאלה כמה היה לאחד מהם זהו' 1) Two men have some zehuvim at a ratio of 2 to 5, such that if the squares of both are summed up to one number, the result is 11600 zehuvim. The question is how many zehuvim did each one have? תשובה לכל אחד מהם היה סך x זהו' The answer: Each has an amount of x zehuvim.
והואיל והם כערך 2 אל 5 היה לראשון 2x ולשני 5x Since they are at a ratio of 2 to 5, the first has 2x and the second has 5x. מרובע הראשון עולה 4xx ומרובע השני 25xx The square of the first is 4x^2 and the square of the second is 25x^2. תחברם יחד יעלה קיבוצם 29xx Sum them together; their sum is 29x^2. וא"כ יהיה ההשוואה כזה 29xx=11600 So, the equation is: 29x^2=11600 תחלק שניהם עם 29 יצא הכמות כזה xx=400 Divide both by 29; the quotient is x^2=400. תוציא משניהם שורש המרובע יהיה x=20 Extract the square roots of both; it is x=20. וא"כ מעות הראשון שהוא 2x שווה 40 Hence, the amount of money of the first, which is 2x, is worth 40. ומעות השני שהיה 5x היה 100 זהו' And the amount of money of the second, which is 5x, is 100 zehuvim. (ב) לאחד נשלחו ג' תיבות ממולאות ספרים ונרשמו במספר 3 2 1 ובכל אחת מהב' מהתיבות כל כך ספרי' כמו ערך המספרים שנרשמו עליהם זו לזו דהיינו כמו 1 אל 2 וכמו 2 אל 3 ואם נרבע מספר כל אחד מהם ונחברם יחד יעלה קיבוצם 24696 השאלה כמה היו ספרים בכל תיבה ותיבה בפרטיות וכמה היו יחדיו בשלש תיבות 2) One was sent 3 boxes filled with books and marked with the numbers 3 2 1, in each of the boxes as many books as the ratio of the numbers written on them (that is, as 1 to 2 and as 2 to 3) If we square the number of each of them and add them together, their total sum is 24696 The question is how many books were in each box individually and how many were together in the three boxes? תשובה בתיבה הראשונה היו x ספרים וא"כ הי' בתיבה שניה 2 2x ובתיבה שלישית 3x Answer: in the first box there were x books, so in the second box there were 2x and in the third 3x. וא"כ מרובע תיבה ראשונה xx ושני' ומרובע תיבה שניה 4xx ומרובע תיבה שלישית 9xx So, the square of the first box is x^2, the square of the second box is 4x^2, and the square of the third box is 9x^2. נקבץ המרובעים יעלה ויעלו 14xx We sum up the squares; the result is 14x^2. וא"כ יהי' ויהיה א"כ ההשוואה כזה 14xx=24696 Hence, the equation is 14x^2=24696. תחלק השני שווים עם 14 יבוא ההשוואה כזה xx=1764 Divide the two sides by 14; the resulting equation is: x^2=1764. תוציא משניהם שורש המרובע ויבוא x=42 Extract the square roots of both; the result is x=42. וא"כ יהי' זה המספר הספרים שבתיבה ראשונה וא"כ הי' בשני' 2x=84 בשניה ובשלישית 3x=126 וכו' So, this is the number of books in the first box; in the second 2x=84; and in the third 3x=126. (ג) שלשה יש להם מספר זהו' והמספר האחד למספר השני כערך מרובע וכן ערך מספר השני למספר השלישי הוא כערך מרובע ואם תקבץ המרובעים יחדיו יהיה 69888 השאלה כמה היה לאחד מהם 3) Three had some zehuvim. The number of one is at a square ratio to the number of the second and the ratio of the number of the second to the number of the third is also a square ratio. If you sum the squares together, it is 69888. The question is how much did each have? תשובה לאחד מהם היה x וא"כ היה לשני 4x ולשלישי 16x The answer: one had x, so the second had 4x and the third had 16x. אשר מרובע הראשון הוא xx מרובע השני 16xx מרובע השלישי 256xx So, the square of the first is x^2, the square of the second is 16x^2, and the square of the third is 256x^2. נקבצם יחד יעלה 273xx We sum them together; the result is 273x^2. וא"כ יהיה 273xx=69888 Hence, it is 273x^2=69888. תחלקם עם 237 יהיה הכמות xx=256 Divide them by 237; the quotient is
x^2=256.
תוצא משניהם שורש המרובע יצא כך ■(x=16@4x=64@16x=256) Extract the square roots of both; the result is: ■(x=16@4x=64@16x=256) (ד) כת בחורים למדו אצל אחד ופרעו לו ונשאל אחד מהם כמה היה הפרעון והשיב אם נחצה 1/6 מ 1/3 יולד מספר ערכיי 1 1/4 שיורה שכל אחד נתן פרע 1 1/4 כמספר כל הבחורים ופרעו יחדיו 45 זהו' 45 השאלה כמה היו הבחורים וכמה פרע כל אחד מהם 4) A group of men studied with one and paid him. One of them was asked how much the payment was and he replied: if we halve 1/6 of 1/3 it would give a proportional number of 1 1/4 that indicates that each one paid 1 1/4 of the number of all the men and paid together 45 zehuvim. The question is how many were the men and how much did each of them pay? תשובה מספר הבחורים היה x Answer: the number of men is x. ואחד נתן 5/4 כמספר כלם א"כ נתן אחד מהם 5/4 x Each one paid 5/4 of the number of all of them, so each one paid 5/4 x. וא"כ נעמידהו על כלל משולש כזה We arrange it according to the Rule of Three, like this: כמה יתנו נתן בחור x 5x/4 1 How many paid Each paid man x 5/4 x 1
ונעסוק בו כדין כלל הזהב יבוא שכולם יתנו 5/4 xx (47r) והוא שווה למספר 45 We solve it according to the Rule of Three; the result is that they paid a total of 5/4 x^2 and this is equal to the number 45. marg.: פי' במספר הזה יש 5 פעמים 9 ואם אתה צריך 4 פעמים 9 הוא 36 הואיל שכל א' נתן 5/4 כמו כל מספר בחורים מזה תוציא שורש מרובע הוא 6 הוא מספר הבחורים נתקן כדין יבוא x=6 שהם מספר הבחורים We restore according to the rule; the result is x=6, which is the number of the men. וא"כ פרע אחד מהם 7 1/2 זהו' כו' So, each of them paid 7 1/2 zehuvim. (ה) תן לי מספר אשר שלישיתו ורביעתו מקובצים יעלה 35 5) Find me a number, such that the sum of its third and its quarter is 35. התשובה המספר הוא x Answer: the number is x. א"כ יהיו השברים x/4 x/3 והם שווים למספר 35 כזה x x/3*x/4=35 So, the fractions are x/4 x/3 and they are equal to the number 35, like this: x/3+x/4=35 נמצא נמצי' כינוי כולל דהיינו שנכפול הכינוים יהיה 12 We find a common denominator, i.e. we multiply the denominators; it is 12. וא"כ יהיו כזה 3x/12*4x/12 So, they are like this: 3x/12+4x/12 וקבוצם אשר קיבוצם עולה 7x/12=35 קבוצם כזה 7x/12 Their sum is: 7x/12=35 marg.: כפל 12 [ב] 35 עלה 42[0] שבור 7 עלה 60 נתקן כדין יבוא 60=x x=60 והוא המבוקש We restore according to the rule; the result is x=60 and this is the required. כי שלישיתו 20 עם רביעיתו 15 וקבוצם יעלה מקובצים יעלו למספר 35 Because its third is 20, summed with its quarter, which is 15, is the number 35. (ו) תן לי ג' מספרים שחצי של ראשון ושלישית של שני ורביעית של שלישי הם 3 6) Find me three numbers, such that half the first, plus a third of the second, and a quarter of the third are 3. תשובה ש אמור שכל אחד מהמספרים הם היה x Say that each of the numbers is x. וא"כ בשברים הם כך x/2*x/3*x/4=3 So, the fractions are like this: x/2+x/3+x/4=3 תכפול כל אחד מהשברים עם מספר השלימים הפשוטים שהוא 3 יעלה 6 9 12 Multiply each of the denominators by the simple number; the result is: 6; 9; 12 ואח"כ תחלק כל אחד עם 3 (מספר השרשי') ויבוא שלושה מספרים המבוקשים דהיינו 4 3 2 והוא נכון Then, divide each by 3 (which is the number of the x); the result are the three required numbers: 2; 3; 4 and this is correct. () תן לי מספר אשר שלישיתו יותר מרביעתו 9 תשעה 7) Find me a number whose third exceeds its quarter by nine. תשובה אמור שהמספר הוא x וא"כ שלישיתו הי' x/3 ורביעתו x/4 The answer: say that the number is x, so its third is x/3 and its quarter is x/4. נמצא בהכפלת כינוי כולל והוא 12 By multiplying, we find the common denominator, which is 12. אשר שלישיתו x/4 4x/12 ורביעיתו x/3 3x/21 שלישתו 4x/12 ורביעת' 3x/12 Its third is 4x/12 and its quarter is 3x/12. והוראם והו[..]אל שרש אמור 9 פעמים 12 והואיל שהראשון עודף על חבירו במספר 9 תשעה נוסיף להשלים ההעדר על האחרון 9 תשעה ויהיו שווים כזה 4x/12=3x/12*9 Since the first exceeds the other by nine, we add nine to the latter, to complete the deficit, then they are equal like this: 4x/12=3x/12+9 נגרע משניהם 3x/12 ישאר x/12=9 We subtract 3x/12 from both [sides]; x/12=9 remains. נתקן כדין יצא x=108 הוא המספר המבוקש We restore according to the rule; the result is x=108, which is the required number. שתידע 9 פעמים 12 הוא 108 והוא פשוט שהוא 4/3 פעמים 9 ורביעי' 3 פעמים 9 (ח) תן לי ג' מספרים ש 1/6 של ראשון 1/7 של שני 1/8 של שלישי יעלו 5 8) Find me three numbers, such that 1/6 of the first of 1/7 of the second of 1/8 of the third is 5. תשובה השברים הם כך x/6 x/7 x/8=5 The answer: the fractions are like this: x/6 x/7 x/8=5 תעשה כדין בהכפלה יעלה כזה ■(30@35@04) Apply the rule of multiplication; the result is: ■(30@35@[40]) תחלק כל אחד מהם ביחוד עם 3 יעלו כזה ■(13 1/3&11 2/3&10) והם השלשה מספרים מבוקשים Divide each by 3; the result is ■(13 1/3&11 2/3&10) and these are the three required numbers. כי הששית מעשרה היא 1 2/3 השביעית מי"א ושני שלישים היא 1 2/3 השמינית מי"ג ושלש היא 1 2/3 ■(1 2/3@1 2/3@▁(1 2/3)@5) Because the sixth of ten is 1 2/3; the seventh of 11 and two-thirds is 1 2/3; the eighth of 13 and a third is 1 2/3. (ט) לאחד מעות למזונות שלשה שנים אם יקבץ 1/2 4/5 5/6 מספרו יחדיו יעלה 850 השאלה כמה היה מספר מעותיו וכמה יגיע משנה אחת 9) One has money for food, for three years, such that if he sums up 1/2 4/5 5/6 of the amount, the result is 850. The question: how much is his money and how much is needed for one year? תשובה מספר המעות היה x Answer: the amount of money is x. וא"כ השברים הם 5x/6 4x/5 x/2 So, the fractions are: 5x/6 4x/5 x/2. נקבצם יחד יהיה 128x/60 We sum them together; it is 128x/60. וזה שווה למספר 850 This is equal to 850. או אם נקטין אותו יהיה כזה 32x/15=850 Or, if we reduce it; it is like this: 32x/15=850. תעשה כדין יגיע לשנה אחת 132 111/135 זהו' Apply the rule; the result for one year is 132 117/144 zehuvim. וא"כ מעות כל השלשה שנים 398 7/15 והוא נכון : So, the amount of money for the whole three years is 398 7/16 and this is correct. (י) מאכל היה אצל היונים שנקרא עלה תאנה אשר שלישיתו סולת ושלישיתו בצים ושמיניתו משומן ודבש בשווה וכל החלקים יושמו בעיסה מלושה בחלב מחזקת ט' אונקיאות השאלה כמה משקל כל המאכל וכמה משקל כל אחד מחלקיו ביחוד 10) There is a dish of the Greeks called “a fig leaf”, one third of which is semolina, one third of which is eggs and one eighth of which is fat and honey in equal measure, and all the parts are mixed into a paste kneaded with milk that weighs nine ounces. The question is how much does the whole dish weigh and how much does each part weigh separately? תשובה משקל כל המאכל היה x Answer: the weight of the whole dish is x. וא"כ משקל חלקיו היו כזה סלת ביצים שמן ודבש x/3 x/6 x/8 So, the weights of its parts are: semolina eggs oil and honey x/3 x/6 x/8
ומשקל החלב 9 אונקיות The weight of the milk is 9 ounces. וא"כ ההשוואה כזה אם נקבץ כל החלקים 5x/8*9=8x/8 So, if we sum up all the fractions, the equation is: 5x/8+9=8x/8 נגרע משניהם 5x/8 יהיה 9=3x/8 We subtract 5x/8 from both [sides]; it is: 9=3x/8 תעשה כדין התיקון יבוא x=24 והוא מספר האונקיות ששקל כל המאכל Apply the rule of restoration; the result is x=24 and this is the number of ounces of the whole dish. וא"כ 8=x/3 משקל הסלת 4=x/6 משקל הביצים 3=x/8 משקל השמן והדבש יחדיו : Therefore, the weight of the semolina is 8=x/3; the weight of the eggs is 4=x/6; and the weight of the oil and honey is 3=x/8. (יא) יש ארי נחושת ויש לו שתי עינים ופה וכף רגל אחד ובתוכם קנים חלולים שופכים מים אל כלי והעין ימינית ימלא ממלא הכלי בשני ימים והשמאלית בשלשה ימים וכף בארבעה ימים והפה ממלא אותו בשש שעות אמור לי בכמה זמן ימולא הכלי אם יפתחו כלם יחדיו 11) There is a copper lion; it has two eyes, a mouth and one foot, inside them there are hollow reeds that pour water into a container: the right eye fills the container in two days; the left eye in three days; the foot in four days and the mouth fills it in six hours. Tell me how long it will take the container to be filled, if they are all opened together? תשובה הכלי ימולא בשעות x Answer: the container is filled in x hours. וא"כ החלקים הממלאים ביחוד הם 48 84 שעות So, the parts are filling together 84 hours: מעין ימין ימינית בכמה יהיה x/48 וכן בעין שמאלית בכמה יהיה x/72 וכן x/96 בכף הרגל ועוד x/6 בפה א"כ עמוד על רעגולא 3/x x/48 וכן כלם חשוב ביחוד כ"א בפני עצמו The right eye x/48; the left eye x/72; the foot x/96; and the mouth x/6. נחבר כל החלקים יחדיו יהיו 61x/288 We sum up all the parts; they are 61x/288. והוא שוה לכלי אחד כזה 61x/288=1 It is equal to one container, like this: 61x/288=1 נעשה כדין יבוא 61x=288 We apply the rule; the result is: 61x=288 נחלק שניהם עם 61 יבא יצא 4 44/61=x שעה הזמן המבוקש ודוק We multiply both [parts] by 61; the result is 4 44x/61 hours and this is the required time. (יב) (48v) השאלה א' אחד חלק מספר זהו' לראובן נתן 1/5 לשמעון 1/12 ללוי 1/8 ליהודא 1/20 ליהודה 1/02 ליששכר 1/7 לזבולון 1/4 לגד 30 לדן 105 לנפתלי 360 ונשארי לו 5 השאלה כמה מספר הזהובי' 12) One divides some zehuvim: he gives 1/5 to Reuven; 1/12 to Shimon; 1/8 to Yehudah; 1/20 to Yissakhar; 1/4 to Zevulun; 30 to Gad; 105 to Dan; 360 to Naftali; and he is left with 5. The question is how many are the zehuvim? תשובה מספר הזהו' הי' יהיו x Answer: the number of zehuvim is x. וא"כ השברים כך x/5 x/12 x/8 x/20 x/7 x/4 So, the fractions are like this: x/5 x/12 x/8 x/20 x/7 x/4. נביאם תחת מכנה א' אחד יהיו 143x/168 We convert them into one denominator; they are: 143x/168. נחבר אליהם מספר השלימים יהי' תהיה ההשוואה 143x/168*500=x We add to it the number of integers; the equation is: 143x/168*500=x ואם נתיר x שלם לחלקים יהיה 168x/168 If we dissolve the whole x into fractions, it is: 168x/168. נעסוק כדין יבוא 3360=x שהוא מספר הזהובי' כולם והבן : We apply the rule; the result is 3360=x, which is the number of zehuvim. (יג) התאנה חנטה פגיה [שיר השירים ב, יג] ומספר בתולות הלכו לרעות א"ע את עצמן בשושנים בגן נעול [שיר השירים ד, יב] ונלוה ונלוו אליהם בחורי חמד לשרתם לשרתן ויהי כאשר הטיבו לבם ביין אמרו הבחורים להביא מספר זתים ואשכולות ענבים וכדי שלא להטיל קנאה בסעודה ורצו לדעת את מספר הבתולות והשיבה אחת מהם מהן החלק השלישי והשישי והשנים עשרה ממנו פחות שש מחזיקים בשחוק הקלפים והחלק הרביעי והשמיני יתר עליהם שבע מלקטים פירות הגן ויהי כשמוע א' אחד מהבחורים המענה הזאת השיב המנסה אתן לנו בחידות כבר ידענו החידה כי אם נתן לפי תשובתכן לכל אחת מהבתולות שני זתים ואשכילה א' או ואשכולה אחת אז יתן לנו ההולדה שאם נקח 1/6 1/8 1/24 ממנו ישאר לנו כל כך כ"כ זתים וענבים כמו שהיה מספר הבתולות השאלה כמה הי' מספר הבתולות וכמה מספר הזתים והענבים 13) The fig tree puts forth her green figs [Songs of Songs 2, 13] and a number of girls went to feed themselves among the lilies in an enclosed garden [Songs of Songs 4, 12]. Charming young fellows accompanied them to serve them. When they were merry with wine, the fellows wanted to bring some olives and clusters of grapes. But, in order not to cause jealousy because of the feast, they wanted to know the number of maidens. One of them answered: a third, a sixth and a twelfth of us minus six are playing with cards; a quarter and an eighth plus seven are picking fruits of the garden. When one of the guys heard the answer, he asked: are you testing us with riddles? We already solved the riddle, because, according to your answer, if we give each of the girls two olives and one cluster, then the result is that if we take 1/6 1/8 1/24 of it, we are left with as many olives and grapes as the number of girls. The question is: how many are the girls and how many are the olives and grapes? התשובה מספר הבתולות היו x Answer: the number of girls is x. וא"כ השברים הם כך עם השלמות x/3*x/6*x/12*x/4*x/8*7-6 So, the fractions with the integers are: x/3+x/6+x/12+x/4+x/8+7-6 ואם נביאם תחת המכנה אחד כולל כל השברים במספרים שלימים שהוא 24 וא"כ יהיו השברים כך 8x/24*4x/24*2x/24*6x/24*3x/24*7-6 If we convert them into one common denominator of all the fractions, it is 24, so the fractions are as follows: 8x/24+4x/24+2x/24+6x/24+3x/24+7-6 נקבץ השברים יחד ויהיו 23x/24 3x/24*76 We sum up all the fractions together; they are: 23x/24. יוגרע הפחיתות מן הקנין וישאר 1 The subtractive is subtracted from the additive; 1 remains. וזה דומה למספר הבתולות שהוא x x It is the same as the number of the girls, which is x. ויהיה א"כ 23x/24*1=24x/24 So, it is: 23x/24+1=24x/24. נעשה התיקון כדין יבוא x=24 שהוא מספר הבתולות We restore according to the rule; the result is x=24, which is the number of the girls. [שאלות יד-יח אינן מופיעות בכתב היד] [(יד) כמה עניים בקשו מאיש אחד חונן דלים [משלי כח, ח] לחוננם כמסת ידו והוא עודהו הדל הרי זה בכי יותן [משנה מכשירין ה, א] נתן לראשון 1/6 מהזהו' שהיו לו יתר עליהם 4 ולשני 1/6 מהנשאר יתר עליו 8 ולשלישי 1/6 מהנשאר יתר עליו 12 וכן עשה לשארי עניים שנתן לכל אחד 1/6 מהנשאר בהוספת 4 על השלמים ממי שקדמוהו וכל אחד קבל מעות בשווה השאלה כמה זהו' שחלק וכמה קבל אחד מהעניים וכמה עניים היו 14) Some poor people asked a man “who is generous to the poor” [Proverbs 28, 8] to give to them according to his capacity, but he was still poor, “so it comes under the law of ‘if water be put’” [Mishnah Makhshirin 5, 1]. He gave the first 1/6 of the zehuvim he had plus 4; to the second 1/6 of what remained plus 8; to the third 1/6 of what remained plus 12; and so he gave to the rest of the poor – he gave each 1/6 of the remainder plus 4 integers more than the integers of the one who preceded him. Each received the same amount of money. The question is: how many zehuvim did he distribute, how much did each of the poor receive, and how many were the poor? תשובה נאמר שמספר הזהו' היה x Answer: we say that the number of zehuvim is x. וא"כ קבל העני ראשון x/6*4 So, the first poor man received x/6+4. וא"כ נשאר 5x/6-4 5x/6-4 remained. ואם נכפיל השלם עם מכנה השבר יהיה 5x*24 If we multiply the integer by the denominator of the fraction, it is 5x+24. והששית מהנשאר הוא (5x-24)/36 The sixth of the remainder is (5x-24)/36. אשר קבל עני השני יתר עליו דהיינו 5x*42*8 So, the second poor man received:
(5x-24)/36+8.
והואיל שבנ"ד קבלו כל העניים בשווה אינו מן הצורך למצוא כינויי האחרים רק נשווה כך
(x*4)/6 או (x*24)/6=(5x-24*8)/36 Since all the poor received the same equally, there is no need to find the amounts of the others, we only compare like this:
x/6+4 or (x+24)/6=(5x-24)/36+8 או אם נביא כלם תחת מכנה אחד דהיינו בהכפלה וגם נתיר השלמים אל השברי' יהיה השווי כזה (6x*144)/36=(51-24*288)/36 Or, if we convert all into one denominator, i.e. by multiplication, and we also dissolve the integers into fractions, the equation is as follows: (6x+144)/36=(5x-24+288)/36 ולמלאות ההעדר נקבץ 24/36 אל (*288)/36 יהיה 264 To supplement the subtractive, we add 24/36 to (+288)/36; it is 264. וההשוואה כזה (6x*144)/36=(5x*264)/36 The equation is like this: (6x+144)/36=(5x+264)/36 נכפיל שניהם עם 36 יולד ההשוואה כזו 6x*144=5x*261 We multiply both [sides] by 36; the resulting equation is: 6x+144=5x+264
נגרע משניהם 5x ישאר x*144=264 We subtract 5x from both [sides]: x+144=264 remains. נגרע משניהם 144 ישאר x=120 מספר הזהו' המבוקשים We subtract 144 from both [sides] x=120 remains, which is the required number of zehuvim. וא"כ היו ה' עניים שיחלקו בשווה ויגיע לחלק אחד מהם 24 זהו' : So, there were 5 poor men who shared equally; the share of each of them was 24 zehuvim. (טו) אחד קנה 1200 ליטראות משי כל לטרא בעד ח' זהו' וחזר ומכרן עם רוח 50 למאה בעד כל שנה בזה האופן שיקבל 1/3 לאחר 3 חדשים 1/3 לאחר 6 חדשים והנשאר ישולם אחר 9 חדשים שאלה בכמה חזר ומכרן וכמה הרויח 15) One bought 1,200 liṭra of silk, each liṭra for 8 zehuvim. He sold them with a profit of 50 for every hundred each year, so that he will receive 1/3 after 3 months and 1/3 after 6 months. The rest will be paid after 9 months. The question is: how much did he sell them for and how much did he earn? אמור שהרויח x Say that he earned x. וא"כ כל המעות הראוי לו 9600*x So, all the money he should have is: 9600*x קח ממנו 1/3 והוא כזה 3200*x/3 שיקבל אחר ג' חדשים Take 1/3 of it, which is this 3200*x/3 and this is what he receives after 3 months. כפול החדשים עם המעות יהיה 9600*x Multiply the months by the money; it is: 9600*x חזור וקח פעם השנית והשליש מקרן ורוח השלם וכפול אותו עם 6 החדשים יהיה כזה 19200*2x Take again a third of the fund and the profit and multiply it by 6 months; it is: 19200*2x וא"כ 1/3 הנשאר כפול עם 9 החדשים יהיה 28800*3x Then, multiply 1/3 of the remainder by 9 months; it is: 28800*3x תקבץ אותם יחד יהיו 57600*6x Sum them together; it is 57600*6x. תחלקם עם 9600*x הקרן והריבית כזה Divide it by 57600*6x, which is the fund and the interest, like this: ■(3&&&@576&00&*6x&6@ 96&00&* x&) א"כ על כלל משלש כזה: Then, according to the Rule of Three: כמה רוח קרן מעו' x/96 100 x 9600 amont profit money x/96 100 x 9600
רווח לשנה חדשי' רוח חדשים x/48 12 x/96 6 Profit for a year months profit months x/48 12 x/96 6
וא"כ ההשוואה כך x/48=50 So, the equation is: x/48=50 תכפיל שניהם עם 48 יהיה כזה x=2400 והוא הרווח לכל 1200 ליטראות Multiply both [sides] by 48; it is: x=2400 And this is the profit of all the 1,200 liṭra. א"כ יגיע הרווח על ליטרא אחת 2 זהו' So, the profit of one liṭra is 2 zehuvim. (יו) גרענו משני מספרים ידועים בלתי שווים מספרים שווים ועל הנותרים כעין 3 אל 2 כמה השווים הגרועים : 16) We subtract the same numbers from two known unequal numbers; the remainders are in ratio of 3 to 2. How much are the equal subtracted? התשובה נקל לדעת זה ע"פ האלגיברה Answer: it is easy to find using the method of algebra. ויהיו ד"מ המספרים 16 12 ונניח סך הגרועים x Let the numbers be 16 and 12, for instance and we suppose the subtracted are x. ונציבם כך עם ערכיהם ■(■(16&&x@&3&)&■(12&&x@&2&)) We set them like this with their values: ■(■(16&&x@&3&)&■(12&&x@&2&)) ונכפילם שתי וערב כדרך השברים ויהיו שווים בהכרח כידוע בכפל כל הערכים עם המספרים שישתוו ונמצא שווין השרש 4 והוא המבוקש והא לך סדרו We multiply them crosswise according to the method of the fractions and they are necessarily equal, as known, by multiplying all the values by the numbers, they become equal. We find that x is equal to 4 and this is the required. Here is its diagram: 32-2x=36-3x
*3x *3x
32*x=36 -32 -32 x=4 32-2x=36-3x
+3x +3x
32+x=36 -32 -32 x=4 הבחינה ■(▁(■(12&8@3&2))@24=24) Check: ■(▁(■(12&8@3&2))@24=24) (יח) גרענו משני מספרים שהם 20 18 מספרים שווים וערך הנותרים כעין 5 אל 2 17) We subtract the same numbers from two numbers that are 18 and 20; the ratio of the remainders is 5 to 2. ולפי מה שהורינוך נקל הוא מאוד כי תמצא 50 שווים לשלשה שרשים According to what we taught you, it is very easy, because you find that 50 is equal to three roots. ויהיה א"כ שיעור השרש 16 2/3 המבוקש על סדר זה So, the value of the root is 16 2/3, which is the required. According to this diagram: ■(20-x&18-x@5&2) 40-2x=90-5x
*5x *5x
10*3x=90 -40 -40 ■(&&22@3x&=&50@3 &&33) המבוקש 16 2/3 הבחינה ■(▁(■(1 1/3&3 1/3@2&5))@6 2/3=6 2/3) Check: ■(▁(■(1 1/3&3 1/3@2&5))@6 2/3=6 2/3) (יח) ואולם איך נדע מספר הנגרעים כשהם בלתי שווים הוא על דרך האלגיברה כך נניח ב' שיעורים 36 24 וגרענו חלקים בלתי שווים וערך הנותרים כמו 7 אל 5 נרצה לדעת הנגרעים נניחם כך כאלו הקטן שבנגרעי' x והגדול 2x ונמצא השרש 4 ושני שרשים הם 8 ויהיה המותר הגדול 28 והקטן 20 כזה ■(24-x&36-2x&3x=12@5&7&3 3@&&x=4) ■(168-7x=180-10x@ *10x *10x@168*3x=180@-168 -168@ 12)
ואם תרצה תניח הקטן x והגדול 3x ותמצא הקטן שבנגרעים 1 1/2 ואזי הגדול 4 1/2 והמותר הגדול 31 1/2 והקטן 22 1/2 שערכם כמו 7 אל 5 ושאלות אלו והדומות להן סובלות תשובות רבות כלן נכונות למוצאי דעת] מהעברות אמר המחבר ראינו להקדים לך יחוסי ומציאת ההעברות אשר ידריכו לך הדרך העולה למסילה ישרה ונכונה אשר זולתן תהיה ממשש באפלה בהרבה מהשאלות כמותיות ועתה אכתוב איזה כללים מספר האילגיברא כסדר העברה נקראת מפי ההנדסיים באם מספרים במרחיק או בערך שווים שכל המספרים אשר יבואו אחריהם (49r)בלתי משתנים בערך או במרחק בגדול או בגרעון בעלי' או בירידה היא בכפליים האחת נקראת העברה מספרית אשר ממנה יולד העברה נגונית ודומיהן השנית נקראת העברה הנדסית או מדידי' העברה מספרית היא מלמדות אם מספרים ע"י קיבוץ או גרעון מספר ידוע או מרחק מתגדלים או מתמעטים Arithmetical progression: it indicates if numbers are increasing or decreasing by addition or substruction of a known number or interval שימצא קיבוצם או מרחקם כפי לפי כללי החכמה their sum or increment is found according to the rules of the science יחוסיה הם אלו These are it's relations: אם יוגרעו שני מספרים סמוכים זה מזה הנשאר יורה המרחק If two successive numbers are subtracted from each other the reminder indicates the increment אם יקובץ המרחק למספר הראשון יבוא מספר שני ואם לשני יולד השלישי וכן עד אין סוף If the increment is added to the first number, the result is the second number, if to the second, the result is the third, and so on endlessly ואם בהעברה יורדת יוגרע המרחק מהמספר הראשון יצא השני וכן תקיש If in a decreasing sequence the increment is subtracted from the first number, the result is the second. אם יקובצו שני הקצוות והעולה והעולה יוחצו יוחצה החצי הוא האמצעי מוערך או מספר האמצעי if the two means are summed and the result is divided into half the half is the mean value or the mean number אם מספר השני והשלישי ידועים ותבקש לידע הראשון כך קח בהעברה עולה המרחק שבין שני לשלישי משני ואם בהעברה יורדת יקובץ המרחק לשני המרחק מראשון לשני ושני הוא בשיווי למרחק השני והשלישי וכן עד אין סוף אם האמצעי מוערך יוכפל הוא בשיווי לקבוץ הראשון והאחרון אם המרחק שבין ראשון לשני יוכפל עם המרחק שבין שני לשלישי והעולה יוגרע ממרובע האמצעי הנשאר הוא בשיווי הכמות להכפלת הראשון עם השלישי אם המספר האחרון אינו מוזכר רק מספר המקומות ומספר הראשון והמרחק יוגרע אחד ממספר המקומות והנשאר יוכפל עם המרחק ואם עולה אז יקובץ אל מספר הנולד והעולה הוא מספר האחרון ואם היא יורדת אז ינוכה מספר הראשון if the last number is not mentioned only the number of terms and the first number and the increment is one less than the number of terms by one ואם מספר הראשון אינו נזכר נעשה כך ממספר המקומות יוגרע אחד והנשאר יוכפל עם המרחק ומהנולד אם הוא בעליה ינוכה ממנו מספר האחרון ואם בירידה יקובץ מספר האחרון יוד אם המרחק בלתי ידוע אז יוגרע השתי קצוות זה מזה והנשאר יוחלק במספר המקומות כשיוגרע מהם קודם החילוק אחד וכמות החלק הוא המרחק ואם מספר המקומות אינו ידוע אז יוגרע מספר הראשון והאחרון זה מזה והנשאר יוחלק ממר במרחק ולכמות החלק יקובץ אחד והוא מספר המקומות (49v) קיבוץ שתי הקצוות מוכפל עם חצי מספר המקומות יולד קיבוץ ההערכות כלן : ב מהעברה נגונית העברה נגונית היא העברה אומניות אומנותית אשר בזו המספרים הם סגורים זה בזה בערך והיא מלמדת למלאות ההעדר יחוסיה הם אלו שלש עשרה (א) ערך הראשון לשלישי כערך מרחק הראשון והשני אל מרחק השני והשלישי : (ב) אם יוכפל ערך הראשון לשני עם ערך השני לשלישי יצא בשיווי כחילק הראשון בשלישי (ג) הכפלת ערך שני לראשון עם ערך השלישי לשני בשווה לחילוק השלישי בראשון (ד) קיבוץ מרחק הראשון והשני למרחק שני ושלישי בעליה היא שווה לגרעון ראשון משלישי ובירידה שלישי מראשון (ה) אם יוכפל הערך הראשון לשני עם ערך השני לשלישי והנולד עם מספר השלישי יולד מספר ראשון : (ו) אם יוכפל ערך השני לראשון עם ערך השלישי לשני והנולד עם הראשון יבוא מספר שלישי (ז) אם יוכפל מרחק שתי הקצוות דהיינו מרחק המספר הקטן ממספר הגדול עם קצווה ראשונה דהיינו הקטן והנולד יוחלק עם קצווה אחרונה היא או הגדולה ולהחלק יקובץ קצווה קטנה הכמות היוצא הוא אמצעי מוערך (ח) אם יקובצו שתי הקצות והקיבוץ יוכפל עם אמצעי מוערך אז יבוא בכפלים כהכפלת השתי הקצוות (ט) למצוא עליה נגונית תעשה כך קח כרצונך שני מספרים שהשני גדול מראשון אך לא בכפלים והם שני מספרים העליה ואח"כ ואחר כך קח מרחק הראשון והשני ממספר הראשון ואח"כ תכפיל הראשון עם השני והנולד תחלק עם הנשאר ממספר הראשון כנזכר והחלק היוצא הוא מספר השלישי ואח"כ קח מרחק השני והשלישי ממספר השלישי ותכפיל השני עם השלישי והנולד תחלק עם הנשאר ממספר השני והחלק היוצא הוא מספר הרביעי ותוכל לחזור עד שיבוא מספר גדול מקודם לו או בכפלים או יותר מכפלו כי הכפל סוף העליה : (י) יוד בירידה תעשה כך קח שני מספרים שהראשון גדול משני כאות נפשיך ואח"כ ואחר כך תקבץ מרחק הראשון והשני אל הראשון ואח"כ תכפול הראשון עם השני והנולד תחלק עם הקיבוץ הנ"ל והחלק הוא מספר שלישי וכן תקש : (יא) וגם נול נוכל למצוא העברה נגונית שיוקחו שני שתי הקצוות כאות נפשיך ותבקש לפי יחוס ז' שזכרנו את המספר האמצעי וכמו כן את ממספר הראשון והאמצעי : האמצעי והאחרון ב' תבקש אמצעי מוערך וכן תקיש : (יב) ובקלות תוכל לעשות מהעברה מספרית נגונית כזה תכפיל המספרים זה בזה דהיינו הראשון עם השני והנולד עם השלישי והנולד עם הרביעי וכן עד בלתי תכלית והעולה ממספר כלם תחלוק עם כל אחד מהמספרים של ההעברה נגונית והחלקים הם המספרים של הניגונית : (יג) וכן נוכל לעשות מניגונית מספרית מתחלת מאחדות כזה תחלק מספר הגדול בעצמו יבוא 1 וכן תעשה שתחלוק בגדול כל שארי מספרים והחלקים הם המספרים בהעברה מספרית : ע"כ העתקתי מספר קטון הנקרא מפתח האלגיברה חדשה ג (47v end) העברה הנדסית או מדידית העברה מדידית היא מלמדת אם מספרים ע"י הכפלה או חילוק מרחק ידוע בלתי משתנה מתגדלים או מתמעטים שימצא קיבוצם או שארי דברים שנחפש כפי לפי כללי החכמה יחוסיה והם אלו יחוסי' אם יוחלקו שני מספרים סמוכים זה בזה החלק יורה המרחק (48r) אם בעליה מספר הראשון יוכפל עם המרחק יצא השני וכן תקש ובירידה יוחלק המרחק במספר הראשון יצא השני וכן תקיש (48r המשך) אם יוכפל הראשון והאחרון זה עם זה ונוציא מההולדה שורש המרובע השורש הוא האמצעי מוערך או מספר האמצעי אם השני והשלישי ידועים והראשון אינו נודע אז תחלק עם המרחק את השני ובירידה תכפיל עם המרחק המרחק ערכיים שבין הראשון לשני שווה למרחק שבין שני לראשון לשלישי וכן תמיד אם האמצעי ירובע הוא בשיווי להכפלת שני שתי הקצוות אם המרחק אינו ידוע אז יוחלקו הראשון בשני שני מספרים סמוכים והחלק יורה המרחק אם המספר ראשון אינו ידוע אז תחלק האחרון עם המרחק והיוצא תחלק עם המרחק כל כך כ"כ פעמים כמו מספר המקומות פחות אחד אם מרחק שבין קצווה ראשונה לקצווה אחרונה יוחלק בשם הטעם כשיוגרע מהמרחק קודם החילוק אחדות יורה קיבוץ כל ההערכות לבד מאחרונה לכך אם יקובץ להעולה קצווה אחרונה יעלה קבוץ כלם כלן או אם תרצה תוסיף עוד הערכה אחת ותעשה ותעסוק כדין והעולה הוא קיבוץ המבוקשות : ולבחינת כללים ויחוסים שזכרנו נציג לך איזה בחינות ראשונות לקוחות מהאלגיברה אשר מזה תקש להנשארים : (א) [המשך 47v end] אם תבחין אמיתותו אמיתית הכלל הזה אם בשלשה מספרים מוערכים נחבר שני הקוו הקצוות העולה דומה לכפל האמצעי והוא כמו שזכרנו ביחוס השלישי מיחוסי ההעברה מספרית נעשה כך במקום המספר הראשון יושם a ובמקום כל מרחק x כי a יורה כל המספרים ו x עלול לקבל כל המרחקים ואח"כ נעשה מ a ומ x את הערך השני השלישי כך a∙a*x∙a*2x ואם נקבץ כמות הראשון ושני יעלה יעלו 2a*2x נכפיל האמצעי יהיה כמו כן 2a*2x: (ב) (המשך 48r) בהעברה בהעברה מספרית הסך של מספר ראשון ואחרון שווה לשני מספרים אחרים אשר הם במרחק שווה מן הראשון ומן האחרון שהם מספרים אמצעיים כמו ■(a*2xa*xaa∙a*x∙a*2x∙a*3x∙a*4x@▁(■(a*2x&a*x&a))@2a*4x∙2a*4x2a*4x) [48r חוזר לסעיף ג למעלה] [(ג) ועוד אם נבחן זה שבהעברה הנדסית הולדת מספר הראשון והאחרון שווה למרובע האמצעי כפי מה שזכרנו ביחוס שלישי וששי מיחוסי העברה מדידית יבחן כך יושם במקום קצווה ראשונה a ובמקום שם הטעם התנועות i או e ודומיהן ונעשה ממנו ע"י הריבוי או הכפלה ערכי המדידה כמו eea∙a∙ea ואם נכפיל השני קצוות יולד eeaa ואם נעשה מהאמצעי מרובע יולד כמו כן eeaa: (ד) וכן יבחן בארבע כמות מעורכי מדידיי בין שיהי' ערך מותמד או ערך מופסק תהיה ההולדה ממספר שני הקצוות יחדיו שוים להולדת שני האמצעיים הוא מבואר משני הדמיונות כוללות כזה ■( 2&3&@a ea ea&ea&a ea b eb@ ea&a&b a) ■(2&3&@eaa&eaa&eab eab) (ה) וכן תהיה בחינת הכלל שבהעברה מדידית ההולדה (הכפלת) של שתי הקצוות שווה לשנים אחרים (אם נכפילם יחדיו) אשר הם במרחק שווה מן הקצוות או למרובע האמצעי כמו שנראה מדמיון כולל זה ■(2&3&4&5&6@a ea ea&ea&ea&ea&ea) ■(3&2&&@ea&ea&ea&a) ■(6&6&6&6@eaa&eaa&eaa&eaa) (ו) נוכל לראות מזה בבירור שאם ינוכה הקצווה ראשונה מקצווה אחרונה והנשאר נחלק בשם הטעם 1 שכמות החלוקה יהיה שווה לכל קצוות העברה מקובצות חוץ מקצווה אחרונה כמו בעליה זו אשר לפנינו ■(&2&3&4&5@a ea&ea&ea&ea&ea) ואם תנכה קצווה ראשונה מן אחרונה ישאר ■(5@ea) פחות a כזה ■(5@ea)-a שם הטעם פחות א' הוא e-x ואם נחלק ■(5@ea)-a עם e-1 יהי' כן ■(5@ea) 3 e יצא ■(4@ea) נכפיל e עם ■(4@ea) יולד ■(5@ea) נגרע ■(5@ea) מן ■(5@ea) לא ישאר כלום והואיל בהמוחלק (דהיינו ■(4@ea) נשאר החסרון דהיינו -1 ואותו נכפיל עם הכמות במחשב' ולפי הכלל שזכרנו למעלה לא ינוכה ההולדה מן המוחלק אלא יחובר אליו לכך נאמר א' פעם e^4 a הוא e^4 a נחבר e^4 a ל-1 יתן e^4 a-1 ואם נחלק זה השאירות עם e-1 נעמוד המחלק תחתיו ונעסוק בו כדין ואז יבוא כמות חדש שהוא e^4 a ושאר עוד בהמוחלק e^3 a-a נחלק בו עוד פעם e-1 יצא הכמות e^2 a עם הנשאר e^2 a נחלק בו e-1 יצא הכמות ea עם הנשאר ea-a ואם נחלק בו e-1 יבוא הכמות a בלי שאירות כלל כי כך נאמר ea3e הכמות e:a פעם a הוא ea ננכה מן ea לא ישאר מאומה ואח"כ נאמר א' פעם a הוא a אשר יחובר לפי הכלל שזכרנו אבל לפי שימצא במחולק פחיתות a יעלה זה ההעדר a עם a החיבור ולא ישאר כלום וא"כ יצא לנו מזה החלוקה כמות זו ■(4&&3&&2&&&&@ea&*&ea&*&ea&*&ea&*&a) והם כל קצוות העליה חוץ מהאחרונה כמבואר והמשכיל יבין : וזה מה שיראה לנו די ביאר בבחינת יחוסי ההעברות אשר מזה נלך מחיל אל חיל להאיר עיניך בהתר השאלות העבריות ותן לחכם ויחכם : (א) יש לי שמונה מספרים בעליה מספרית בזה האופן אם יקובצו שני האמצעים יעלו 35 ואם השני קצוות יוכפלו זה בזה נולד 93 מה הם המספרים : תשובה כבר הודעתיך שקיבוץ שני האמצעיים שווה לחיבור שני הקצוות לכך נחלוק 34 שיעלה קיבוץ שני הקצוות כזה הראשון 17-x השני 17*x יוכפלו זה בזה כנדון השאלה ■(■( *17x-xx@289-17x )@289-xx-93) יחובר לשניהם xx תהיה ההשוואה כזה ■(289=xx*93@-93 -93@196=xx) נתקן כדין תוציא משניהם שרש המרובע יהיה כזה 14=x א"כ 17*x:3=17-x שווה 31 והמרחק הוא 4 כי תחלוק מספר המקומות פחות 1 בשאירות גרעון קצווה ראשונה מאחרונה וא"כ המספרים הם 31 27 23 19 15 11 7 3 (ב) תן לי שני מספרים בערך כפל שנים עשרה אשר קיבוצם שווה להכפלתם : אמור x הוא מספר הקטן א"כ 12x הוא הגדול תכנה ותתקן כאשר הורינוך כסדר זה תקבץ x תכפיל x הקטן 12x 12x הגדול 13x 12xx
תגרע משניהם x ■( 1&@12x=13&1=x@12 12&13 12x) (ג) תן לי שני מספרים בערך משלש אשר הכפלתם הוא בשווה לכמות הנשאר אם יוגרעו זה מזה : תשובה אמור x הוא מספר הקטן א"כ 3x הוא מספר הגדול תכנה ותתקן כאשר תראה בסדר הזה תגרע x תכפיל x הקטן 3x 3x הגדול 2x 3xx
■(3x=2/3@3 @3x=3) (ד) חלוק לי 36 בששה חלקים שיהיו בעלייה אחדות אמור שהראשון קבל x א"כ ששה חלקים כזה x הראשון 3 1/2 x*1 השני 4 1/2 x*2 השלישי 5 1/2 x*3 הרביעי 6 1/2 x*4 החמישי 7 1/2 x*5 הששי 8 1/2
x=3 1/2 תקבצם יחד יעלה קיבוצם 6x*15 וא"כ ההשוואה כזה ■(6x*15=36@*15-15) ├ ■(6x=21@6 6)┤|3 1/2 (ה) ד' יחלוקו 112 אמות בגד באופן עליה מספרית שיקבל כל אחד יותר מחבירו הכפל שני אמות יותר השאלה כמה קבל אחד מהם אמור שהראשון קבל x אמות א"כ יקבלו הנשארים כזה ■(14=2x*2@30=4x*6@▁(62=8x*14)@15x*22=112) ■(15x*22=112@ -22 22@15x=90@x=6) (ו) תן לי העברה נגונית יורדת מששה מספרים אשר קיבוצם עולה 588 מה הם המספרים אמור x הראשון א"כ הששה מספרים הם כזה ■(240=x@120=x/2@180=x/3@60=x/4@04 @48=x/5@▁(x/6)@588) נקבצם יעלה כזה 2*9x/20=588 נתקן כדין יבוא ההשוואה ├ ■(49x=11760@7x=1650@7 7)┤|240 (ז) מצוא לי אמצעי מוערך נגוני בין 10 ובין 15 ר"ל תן לי מספר אשר מרחקו מראשון (10) למרחקו משלשה (15) הוא כאותו ערך כמו 10 אל 15 : תשובה הואיל וקצווה ראשונה וקצווה שלישית הן 10 : 15 האמצעי אשר נבקש נכנה x אשר לפי שיחויב היותו גדול מהראשון ופחות מהשלישי א"כ יהיה מרחק מהראשון x-10 ומהשלישי 15-x (כי נגרע בתמידות הקטן מהגדול אשר לא יעשה בחשבון האותיות זולתי בסימן הפחיתות כאשר זכרנו בכללי הניכוי) וא"כ נשווה כך כמו 10 אל 15 כך x-10 אל מרחק 15-x אשר ארבע קצוות אלו הם בערכי מדידה נעשה מראשון כאחרון לשיווי שני האמצעיים כי זה אחד מיחוסי הערכיים כאשר זכרנו ויהיה א"כ כאן 150-10x=15x-150 נחבר לשניהם 10x יהיה 150=25x-150 נחבר לשניהם 150 *150 יהיה כזה 300=25x נחלוק שניהם עם 25 יהיה 12=x והוא האמצעי המבוקש אשר יבחן מהמרחק אשר הוא מ12 אל 10 והוא 2 וכן המרחק מ12 אל 15 הוא 3 והוא מבואר כי ערך 2 אל 3 כערך 10 אל 15 וגם יבחן ממה שכתבנו במציאת מספר השלישי בעליה נגונית וכן ימצא עם מה שכתבנו ביחוס השביעי מיחוסי העברה נגונית במציאת אמצעי מוערך יע"ש :[ (ח) (47v המשך) לידע השעות השעה אחר צהרים לשעות אשר כבר היו אל השעות אשר עתידין להיות עד חצי הלילה כערך 3 אל 4 נאמר שהשעות אשר כבר הלכו להם להן היו x וא"כ ואם כן זה הכינוי בתנאי מוחלט שערך x אל 12-x כערך 3 אל 4 וההשוואה כזה 3:4=x:12=x 3:4=x:12x נכפיל שני הקצוות דהיינו שתי וערב כזה ■(3:4 @x:12-x) יולד 4x=36-3x נקבץ לשניהם 3x יבוא כזה 7x=36 נחלק שניהם עם 7 יצא הכמות כזה x=5 1/7 =x 5 1/7 והם שעות אשר ע[.]ברו עברו והנשאר מזו הם הן 6 6/7 והערך מ 5 1/7 ל6 6/7 או 36/7 אל 48/7 דהיינו 36 אל 48 כערך 3 אל 4 והבחינה שאם נחלוק שניהם דהיינו 48 36 עם 12 יצא מהראשון 3 ומהשני 4 והבין: [47v עובר לשאלה (ב) למטה] ויותר מדמיונות העבריות עיין לקמן ממה שנעסוק בהשוואה בלתי טהורה כיד ה' הטובה עלינו : מדמיונות אשר בהתרן מצא השרשים מעוקב מרובע ומרובע ודומיהם : (end 47r) (א) אחת שואלת לאמה לאמר לה מספר שנותיה ואמה השיבה לה בתי אם תכפילי 1/12 1/6 5/6 1/4 שנותיך ומהעולה תוציא שורש המעוקב יעלו (47v) יעלה שנותיך ל162 השאלה כמה שנים היו לה תשובה מספר שנותיה היו x וא"כ ואם כן השברים הם x/4 x/6 x/12 תכפילם זה בזה יעלה יעלו x3/288 א"כ יהי' ויהיה אם כן x3/288=162 תכפילם יחד עם 288 יהיה x3=46656 ואח"כ תוציא משניהם שורש המעוקב וכי x3 שהוא מעוקב אמיתי יורה שהמספר הדומה לו הוא כמו כן מספר אמיתי מעוקב ויצא x=36 הוא שנות הבת והבן [47v עובר לשאלה (ח) למעלה] (ב) לאחד מעות למזונות שלושה שנים שאם נכפיל 5/6 4/5 1/2 יעלה מספר המעות יחדיו ויולד 576000 זהו' השאלה כמה ממון היה לו תשובה מספר הממון המעות היה x וא"כ יהיו השברים 6x/6 5x/6 4x/5 x/2 תכפילם זה בזה יבוא 20x3/60 והם שווים ל576000 תכפילם עם 60 יולד 20x3=34560000 תחלקם עם 420 יצא הכמות x3=1728000 א"כ תוציא משניהם שורש המעוקב יולד x=120 המעות המבוקש לשלש השנים א"כ יגיע לשנה אחת 40 זהובי' והבן: [עד כאן 47v] ](ג) יש לאחד מספר ר"ט והלך לארץ רחבת ידים לסחור בה והרוויח למאה 1/8 מספר הקרן ואח"כ הרויח עם הרוח 1/4 הרוח למאה וחזר והרויח עם רוח השני 1/2 למאה ממספרו ונמצא שהרויח בפעם שלישית 50 ר"ט השאלה כמה מעות היה לו בראשונה : תשובה מספר הר"ט היה x א"כ עמוד על כלל משלש כזה כמה רוח ר"ט x x/8 100
יצא שירויח x/800 קח ממנו 1/4 וחשוב על כלל משלש כזה כמה רוח ר"ט x/800 xx/3200 100
יצא שירויח בפעם השנית x4/256000000 קח ממנו 1/2 וחשוב על כלל משלש כזה ר"ט x4/256000000 x4/512000000 100
יצא שירויח בפעם השלישית x8/13107200000000000000=50 נתקן כדין יצא כזה x8=655360000000000000000 תוציא משניהם שרש מרובע מרובע כדרך שהורינוך בסי' השביעי מהוצאת השרשים או תוכל להוציאו באופן זה שתוציא מהמספר שרש המרובע ומהיוצ' חזור והיוציא שרש המרובע ומהשרש היוצא תחזור ותוציא שרש המרובע והוא המבוקש כזה 655360000000000000000 25600000000 ├ 160000┤| 400=x (ד) לאחד שני מיני כרכום ונמצא אם ימכור הראשון הליטרא בעד כל כך ר"ט כמו מספר ליטראות מן השני אז יקבל בעדו 72 ר"ט ואם ימכור כל אחד ביחוד הליטרא בעד כ"כ ר"ט כמשקלו ביחוד אז יקבל בעד שניהם יחדיו 180 ר"ט : השאלה כמה היה משקל כל מין ומין : תשובה מן הראשון היה x-y וא"כ היה מין השני x*y תעמוד על כלל משלש כזה ■(1&x-y&x*y) תכפלם זה עם זה כי האחדות אינו חולק כזה תכפיל ■(x-7@▁(x*y)@*xy-yy@xx-xy ) יצא לפי נדון ראשון ההשוואה כזה xx-yy=72 ולפי נדון שני תרבע כ"א ביחוד כזה ■(x*y@▁(x*y)@*xy*yy@▁(xx*xy )@xx*2xy*yy) ■(x-y@▁(x-y)@-xy*yy@▁(xx-xy )@xx-2xy*yy@▁(xx*2xy*yy)) תקבץ שניהם כזה 2xx*2yy=180 ומשני ההשוואות תעשה על ידי קיבוץ וגרעון אחת כזה תחצה השניה ויבוא xx*yy=90 תחבר אליה השוואה ראשונה כזה ■(xx*yy=90@▁(xx-yy=72)@├ 2xx=162┤| 81@ 22) תוציא משניהם שרש מרובע יצא x=y וא"כ נשאר לנו לחקור כמות y נגרע השוואות מהדדי ישאר כזה ■(xx*yy=90@▁(xx*yy=72)@├ 2xx=18┤| 9=yy@2) נוציא משניהם שרש המרובע יהיה y=3 וא"כ ■(├ x-y=9-3┤| 6@├ x*y=9*3┤| 12) והוא נכון וזה מה שיראה לנו מספיק בביאור שאלות אשר היתרן בהשוואה טהורה וראינו לזרזך שתבין היטיב כל אופני ומסבבי השאלה ומהם תעשה הכינוי והשוואה שהם השני חלקים ראשונים בהתר השאלות וכמו שזכרנו בפתיחת דברינו וכמו שהורינוך עד הנה[ (47v המשך) כלל גדול הוא וכשיצא לך השוואה נכונה תתקן שני הכמות בשווה במיני ובערכי המספר וכלל גדול גם אני מועד מודיעך אומר לך שההעדר תמלא בקיבוץ דומה לו והיתרון תחסר בגרעון כמות שווה לו והכפול תחלק והמחולק תכפיל (47v המשך למעלה) (48r המשך) אם ההשוואה מהשוואה בלתי טהורה פי' מכל מה המשלים שזכרנו בא אחר התיקון מצד אחת x או סימן אח' מסימני האלגיברא האלגיברה ומצד השנית מספר ידוע לפיכך נקראת זו תיקון מאומת או השוואה טהורה אבל אם יבוא שנשאר אחר ההשוואה והתיקון לא בלבד x או xx ודומיהן ודומיהם אלא כמו זו (דרך משל)
- x4
- 4x
ואותן 4x לא יוגרעו ממנו כי ישאר כזה xx-4x ויקושר זה למספר הנמצא מפאת אחרת אשר לא נודע כמה הם ה 4x ונקראת זו ההשוואה אשר איננה טהורה וכדי להאיר עיני שכלך ביותר נציג לפניך איזה דמיונות קלות ומהן תעלה במעלות לחקירות יותר נכבדות בעז"ה : שר צבא רוצה לערוך מערכה מחילו אשר הוא 52800 רגלי באופן זו שיהיו בכל הערכה 20 איש יותר מהערכות כלן השאלה כמה יהיו אנשים בכל הערכה והערכה וכמה היו כלן : והנה אם נעסוק בו כדין שארי שאלות נאמר שמספר ההערכות היה x ואם כן מספר הרגליים בכל הערכה והערכה x*20 וא"כ נעמוד כלל משלש כזה כמה מחזקת רגליים הערכה x *20 x 1 יבוא שיחזיקו כלן 52800=xx*20x והנה אף שיוגרע משניהם 20x כדין ישאר כך xx=52800-20x והואיל xx מרובע אמיתי וא"כ יהיה x שווה לשרש מרובע של 52800-20x אבל מספר 20x לא נודע שיוגרע ממספר 52800 שנוציא מהשאירות את שרש המרובע וא"כ יורנו את הדרך אשר נדרוך בהתר השאלה זו והדומות לה תשובה בשאלות אשר יבא בהתרן השוואה בלתי טהורה המציאו ההנדסיים החדשים דרך אחרת בהיתרן מקורו נובע מאשר נבאר כי בשאלה אשר לפנינו לא נאמר בהשוואה כזו xx*20x=52800 רק נאמר כך בהשוואה xx*ax=b ומזה יראה לכל מבין ומשכיל בחשבון האותיות כי הכמות הראשון הוא מרובע בלתי מושלם כי יחסר ממנו 1/4 aa ושורשו האמיתי הוא x*a/2 כי אם נכפיל x*a/2 עם x*a/2 יולד xx*ax*aa/4 כזה ■(x*a/2@▁(x*a/2)@*ax/2*aa/4@▁(xx*ax/2 )@xx*ax*aa/4) וא"כ תהיה ההשוואה כזה xx*ax*aa/4=b*aa/4 כי aa/4 הנחסר נשאל למלאות ההעדר ויקובץ לשניהם וא"כ הם שני מרובעי' אמיתיים נוציא משניהם שרש המרובע יצא x*a שווה לשרש מרובע b*aa/4 יוגרע משניהם 1/2 a ישאר כזה b*aa/4 שרש x= (כי ממספר b יותר aa/4 לא הוציאנו עדיין השרש המרובע כי לא ידענו מה הוא לכך נגרע ממנו a/2 בסי' הפחיתות) וא"כ הכמות המבוקש הוא כזה b*aa/4 a/2 שרש x= נחזור לענינינו כי בנדון דידן a=20=b 52800 וא"כ יהיה חציו של a שווה לעשרה כזה a=10 והמרובע aa=400 וaa/4=100 וא"כ יהיה b*aa/4=52800*100 וא"כ נחבר אליו 100 יעלה 52900 נוציא ממנו שורש המרובע יבוא 230 ננכה ממנו a/2 (שהשאלנו למלאות ההעדר) שהוא 10 ישאר x=220 שהוא מספר ההערכות ואם כן יהיו בכל הערכה 240 אנשים לכך יהיה תשובת השאלה כחשבון זה ■(b=52800@▁(*aa/4=100)@xx*ax*aa/4=b*aa/4=52900) ├ ■(1 @52900@49 )┤|230 b*aa/4=230 שרש x*a/2= -a/2 = -10 x=220:x*20=240 אבל אם נשנה הכינוי בנדון דידן דהיינו שנאמר שמספר האנשים בהערכה אחת היה x ואם כן יהיה מספר ההערכות x-20 וא"כ יהיה על כלל משלש כזה כמה יהיו הערכה מחזקת הערכה x-20 x 1 יבוא xx-20 ויהיה אם כן ההשוואה xx-20=52800 ואם נאמר כדין בהשוואה כזאת ax=b הוא מרובע בלתי מושלם וחסר ממנו aa/4 שאם נחבר לו זה יולד מרובע אמיתי כזה בהכפלה ■(x-a/2@▁(x-a/2)@-xa/2*aa/4@▁(xx*xa/2 )@xx-xa*aa/4) וא"כ נחבר לשניהם ההעדר שהוא aa/4 יהיה השיווי כך 52800*100*aa/4=b*aa/4 xx-ax שהוא 52900 נוציא משניהם שרש המרובע תהיה ההשוואה כך לשרש x-a/2= נחבר לשניהם ab*aa/4=230 שהוא בנ"ד 10 יהיה ההשוואה כך מספר הרגליי' x=240 מספר ההערכה x-20=220 ולפי שa יכול לקבל כל כמות ידוע ו x עלולה לקבל כל מספרים בלתי ידועים לכך נולד מדמיון זה שני כללי' כוללים ע"כ תידע איזה כללים (א) אם בהשוואה בלתי טהורה הכמות הנשארת בנ"ד 20x יורשם בסימן היתור * אז נעשה מחציו שהוא 10 מרובע אמיתי 100 ונחברהו אל כמות ידוע ההשוואה שהוא למשל 52800 ויהיה 52900 נוציא מהקיבוץ שורש המרובע 230 וננכה ממנו חצי כמות הנשארת שהוא 10 והשארית והשאירות 220 הוא המספר המבוקש : (ב) אבל אם לכמות הנשארת 20x סימן הפחיתות - נחבר מרובע החצי חציו 100 הוא מרובע 10 אל המספר הידוע שהוא 52800 ונעשה 52900 ונוציא ממנו השורש המרובע 230 ונחבר להשרש חצי כמות הנשארת שהוא 10 והעולה שהוא 240 הוא מספר המבוקש (48r end) [ועוד נצריך לכלל שלישי שאינו נולד מדמיון זה הוא נולד מדמיון אחר שנבאר אי"ה: והוא (ג) אם כמות הנשארת בסימן היתור והידוע בסימן הפחות (כמו ד"מ xx=20x-36) נעשה כמו כן מחצי כמות הנשארת מרובע אמיתי נגרע ממנו הידוע (דהיינו 36 מן 100) ומהנשאר (64) נוציא שרש המרובע (יהיה 8) נוסיף על השרש (8) חצי כמות בלתי ידוע (10 יהיה 18) והוא כמות x מורכבת כי אם נגרע השרש (8) מחצי כמות נשארת (10) יהיה כמו כן הנשאר (2) אמיתי : אבל זאת נודיעך שאם המרובעים יורשמו במספר שקודם הקיבוץ מרובע חצי כמות השרשים אל מספר הפשוט נכפיל המספר הפשוט עם מספר המרובעי' ולהנולד יקובץ חצי כמות השרשים מרובע כנ"ל ולאחר הקיבוץ או גרעון כנ"ל תחלק מספר העולה או הנשאר עם מספר המרובעים והיוצא הוא המבוקש : והנה עד זמנינו בקשו חשבונות רבות במיני האלגיברה כי חשבו אותה לסוג תכלול תחתיה מינים הרבה עד אין קץ כמו האלגיברה שרשית מרובעת מעוקבת מרובע מרובעת ודומיהן מהשרשים אשר יגדילו תמיד עד בלתי תכלית כן רצו היות האלגיברה מים שאין להם סוף וכאשר כסתה כלימה פניהם להשיב ימינם אחור ולהודות כי בהרבה מהשאלות קצרה יד האלגיברה מלהושיע תלו זה בטבע אותו החשבון כי אופניו יגיעו עד שערי האין סוף ולא מקוצר ידיעתם לכך להראות יקר תפארת גדולת האלגיברה חלקנו אותה לשני חלקים החלק הראשון אשר כבר עסקנו ממנו בשלימות הוא אשר קראינו השוואה טהורה והיא הפשוטית השני נקרא השוואה בלתי טהורה כוללת תחתיה כל המספרים שרשיים עד אין סוף בין שיהיה הערך מתמיד בהוצאת השרשים בין שאינו מתמיד וקודם שנתיר דמיונות רבות בזה החלק נורה לך הדרך בתיקון השוואות מעוקבות מרבע מרבעות ומהם תוליד בשכלך עד מקום שידו מגעת בין המתמיד ובין במופסק ונניח דרך משל x3=6x*40 הנה נקח מספר 40 הפשוט ונחלקהו עם מספרים שונים ואראה המספרים היוצאים ואחבר' עם 6 שהוא מספר השרשים ואם אמצא איזה קיבוץ מהם מספר מרובע אגזור ששרשו הוא שרש המבוקש ד"מ אם אחבר 10 עם 6 יהיה מרובע 16 וא"כ 4 שהוא שרשו הוא השרש המבוקש וכך הוא המעוקב ממנו 64 שוה לששה שרשים שהם 24 ולמספר 40 : דמיון שני יהיה x2=14x-48 הנה נחלוק כמו כן 48 עם מספרים שונים ונגרעם מן 14 ואם אמצא איזה שאירות הוא מעוקב אגזור שהוא שרשו וכן אם אגרע 6 ממספר השרשים שהוא 14 ונשאר 8 מעוקב וזהו השרש כי מרובעו 64 שווה לי"ד שרשים פחות מ"ח כמבואר : דמיון שלישי xxx=12x*65 אוסיף 12 מספר השרשים עם 13 יהיה 25 ושרשו 5 הוא השרש המבוקש דמיון הרביעי הוא x3=200x-672 ■(40&48@2:20&2:24@4:10&4:12@5:8&8:6@1:40&) הנה אם תגרע 56 ממספר השרשים 200 ישאר 144 למרובע ושרשו 12 כזה ■(6-72@2:336@4:198@8:84@10:67 1/5@12:56@14:48@65@5:13@1:65) הודיעני הוצאת השרשים משלמים יחד עם שברים בהשוואה איננה טהורה כשהשיווי בין מרובע יתר שרשים ובין מספרים פשוטים כגון x2*8 x/2=55 11/18 או כזה xx*10x=32 1/2 תשובה בדמיון הראשון נתיר כינוי השבר אל מרובע וזה כשנכפול אותו עם איזה מספר עד שיהיה מרובע במשלנו 55 11/18 נכפול 18 עם 2 ויהיה מרובע 36 וכן נכפיל המכנה 11 עם אותו מספר 2 ויהיה 22/36 ואם השלם כשיותר הכל לשבר יהיה הכל 2002/36 ונקח שרש המרובע והוא 6 ונכפול אותו במספר השרשים שהם 6 1/2 ויהיה 51 ועכשיו אתה צריך להוציא ממספר 2002 השרש מרובע אך תותר ממנו כל כך שתוכל לגרע ממנו המספר ההווה מכפל השרש הנמצא במספר 51 וצריך למצוא זה בחיפוש כאשר אתה מנסה בחלוק לדעת כמה פעמים החולק יכנס בנחלק כי אין דרך אחר לאלו דברים היקרים לכן תבלוש ותשכח שהוא מספר 26 שמרובעו 676 ואם תכפול 26 עם 51 יהיו 1326 ותחברהו עם 676 ויהיה 2002 וזה המספר של 26 הוא שבר לפי כפלת מספר השרשים במספר 6 ולכן תתיר 26 אל שלמים ויהיה 4 1/3 שרש המבוקש : ובדמיון השני נתיר כינוי של שבר המספר הפשוט שהוא 1/2 אל מרובע ר"ל שנכפלהו עם 2 ויהיה 4 והמכונה יהיה 2 ר"ל 2/4 ועם השלם כשיותר יהיה 130 ונקח שרש הכינוי והוא 2 ונכפול בו השרשים והם 10 1/2 ויהיו 21 ועתה צריך להוציא ממספר 130 צלע המרובע אך בזאת שתותיר כל כך שתוכל לגרוע הימנו היוצא מכפל השרש הנמצא עם 21 ועל ידי חיפש לא תמצא אחר כי אם 5 ועם מרובעו 25 הם עולים למספר 130 ותחלקהו עם 2 שבו כפלת השרשים ויצאו 2 1/2 וזה שרש המבוקש : ואולם יש בהתר דמיונות אלו דרך אחר כמו שהורינוך ונבוא בלי חיפוש אל השרש המבוקש בנקלה שיהיה במשלנו זה השני רצונינו למצוא מספר שמרובעו עם כפלו במספ' 21 יעלה למספר 130 ונניח שהוא x ומרובעו הוא xx וכפלו במספר 21 הוא 21x ויהיה א"כ השיווי כזה xx*21x=130 וכפי מה שהורינוך והנה מרובע 10 1/2 חצי מספר השרשים הוא 411/4 ומספר 130 הוא 520/4 שקבוצם 961/4 ושרשם המרובע הוא 31/2 ר"ל 15 1/2 ונגרע מזה חצי השרשים 10 1/2 ויותרו 5 וזה השרש המבוקש ואחר שמצאת זה תחלקהו עם 2 שהרי בתחלה כפלת אותו עם 2 ויהיה 2 1/2 והוא נכון : הודיעו הוצאת השרש משלמים יחד עם שברים כשהשיווי בין מעוקב יתר שרשים ובין מספרים וכן בין מעוקב יתר מרובעים ובין מספרים וכן בין מעוקב יתר מרובעים יתר שרשים ויהיה לדמיון הראשון x3*6x=57 1/27 לדמיון השני x3*6x2=103 19/27 ולדמיון השלישי xxx*3xx*6x=90 10/27 תשובה הקדמונים פתרו למצוא אופן הוצאות השרש בדרך הנהוג וכאשר עשו כשהשיווי בין מרובע ובין שרשי' יתר מספרים ולא יכולו וכלו הזמן היקר עד שנמצא זה הדרך למצוא בפעם אח' השרש שכשיוכה במספר מה יבוא אל סך מספר הנתון והמספר הפשוט יעמוד מצד אחד לבדו ושארי כחות מספריות כלן יחד בפני עצמן : והנה דרך מצאת השרש בדמיון הראשון הוא על זה האופן הנה השיווי הוא כן 57 1/27 שווה ל x3*6x וקודם נתיר השלמים אל השבר שאין צורך להביא השבר אל מעוקב שכנויו 27 הוא מעוקב ושרשו 3 ויהיה א"כ 1540/27 ונקח שרש 27 והוא 3 ונרבעהו והוא 9 ועם זה נכפול מספר השרשים ויהיה 54 ויהיה לפי זה 1540=x3*54x ועתה צריך להוציא שרש מעוקב מספר 1540 אך ורק שיותר ממנו סך כשיוכה השרש במספר 54 יוכל לגרע ממנו וכשתחפש תמצא השרש שהוא 10 שמעוקבו הוא 1000 וכפלו עם 54 עולה 540 וקבוצם 1540 ואתה צריך לחלוק זה השרש עם 3 שהוא שרש 27 ויצא 3 1/3 והוא השרש המבוקש : ואני אביא לך עוד משל ב' לתוספות ביאורו יהיה שיווי בין x3*10x ובין מספר 18 3/8 ובמספרים מדברים תמצא הכינוי מעוקב ודעהו שמספר 8 שרשו 2 ומרובעו 4 ונתיר השלמים אל השברים ויהיו 147/8 ונכפול עם מרובע של 2 שרש הכינוי רצונינו לומר עם 4 מספר השרשים שהם 10 ויהיו 40 ויהיה לפי זה שיווי בין x3*40x ובין מספר 147/8 ונכפול עם מעוקב הוא 147 ועתה צריך למצוא שרש שמעוקבו יחד עם כפלו במספר 40 יעלה למספר 147 ותחפש ותמצא שהוא 3 שמעוקבו 27 וכפלו ב40 הוא 120 ואם נקבצם יעלו למספר 147 וזה המספר 3 נחלק עם שרש המעוקב שכבר הכפלת עם מרובעו דהיינו עם 2 ויצא 1 1/2 והוא שרש המעוקב המבוקש : ובדמיון השני שבו x3*6xx=103 19/27 נתיר המספר כלו אל שברים ויהיו 2800/27 ומספר המרובעים 6 נכפלהו בשרש המעוקב 3 ויהיה לפי זה השיווי כן x3*182=2800/27 ואנו צריכים להוציא שרש זה המספר המעוקב אך יספיק להוציא ממנו ג"כ כפל המרובעי' במספר 18 ותמצא שהוא 10 שמעוקבו הוא 1000 וכפלו עם מספר 18 הוא 1800 ותוציא כמו כן שרש מעוקב ממכנה השבר ויהיה א"כ 10/3 או 3 1/3 השרש המבוקש : ובדמיון השלישי שבו ההשוואה כזה x3*3xx*6x=90 10/27 נתיר כמו כן המספר אל שבריו ויהיה 244/27 וכן נכפול מרובע של שרש מעוקב הכינוי שהוא 9 עם השרשים 6 ויהיו 54 ועם השרש 3 נכפול המרובעי' שהם 3 ויהיו 9 ויהיה השיווי כן 54x*2440=x3*9xx ועתה צריך להוציא שורש מעוקב ממספר 2440 באופן שנותר כפל מרובע שרש הנמצא במספר 9 והכפלת השרש במספר 54 והוא 10 שמעוקבו 1000 וכפל מרובעו במספר 9 הוא 900 והשרש דהיינו עצמו במספר 54 הוא 540 שקיבוצם עולה 2440 תוצי' כמו כן ממכנה השבר מספר המעוקב ויצא 3 דהיינו 10/3 או 3 1/3 וזה הנכסף והנה מציע לפניך סדר הפעולה כלה x3*3xx*6x=90 10/27 ■(3&9&xx@2440&2440&9) 10 מעוקבו 54x 10x3=1000
כפלו עם 54 9xx 54x=540
9xx=900
וקיבוצם הוא x3*9xxx54x=2440 וא"כ לפי תשובה האמתית דהיינו השרש 3 1/3 יהיה 33 3/9=3xx 20=6x וא"כ 37 1/27=x3 שקיבוצם עולה 90 01/27 כנדון ההשוואה וקל למבין : הודיעני נא הוצאת השרש משלמים יחד עם שברים כשהשיווי בין מרובע מרובע יתר מעוקבים יתר מרובעים יתר שרשים ובין מספרים כמו 536/625 x4*250x3*25x2*5x=8568 תשובה סדר התרו הוא כך תוציא מכינוי השבר שרש מרובע מרובע הוא 5 ומרובעו 25 ומעוקבו 125 ויהי' א"כ הכינוי 625 מספר מרובע מרובע מדבר והנה נתיר המספר אל שבריו ויהיה 5355536/625 ואח"כ נכפול מספר השרשים 5 עם 125 המעוקב של שרש מרובע מרובע זה הוא 5 ויעלו 625x וכן נכפול מספר המרובעים שהם 25 במספר המרובע של שרש 5 דהיינו 25 ויעלו כמו כן 625xx וכן נכפיל מספר המעוכבים 250 עם השרש 5 ויעלו 1250x3 ויהיה לפי זה השיווי בזה האופן x4*1250x3*625x2=5355536 ועתה צריך להוציא מזה המספר שרש מרובע מרובע אך שתותיר כל כך ממספר שיוגרע ממנו ההווה מכפל השרש זה הנמצא עם 624x ועם 625x2 ועם 1250x3 וכשתחקור תמצ' המספר שהוא 16 וסדר הפעולה מסודרת לפניך כהלכתה וראה ועשה כתבניתה x4*250x3*25x2*5x=8568 596/625 x4=625x3=125x2=25x=5 ומרובע מרובעו ... 65536 וכפלו במספר 625x ... 10000 וכפל מרובעו 256 במספר 652x2 ... 160000 וכפל מעוקבו 4096 במספר 1250x3 ... 5120000 והקבוץ הוא ... 5355536 וזה השרש 16 צריך שתחלקהו על 5 השרש יצא 1/5 והוא השרש המבוקש : ואחרי הודיעך אלהים את כל זאת לא נצא חפשי מביאור הוצאת השרשים עד שנבאר לך בביאור מספיק ממה שכתבנו לעיל שיש למספר אחד שני שרשים והוא בכלל השלישי הכולל בהשוואה בלתי טהורה יע"ש וגם זכרנו בכללי ההכפלה שמספר' פחותים מאין יולידו יש אשר מזה יתבאר לך שלמספר אחד שני שרשים ויהיה דרך משל המספר 4x4-12x3*9x2 והנה שרשו הוא שלשה שרשים פחות שני מרובעים וג"כ שרשו הוא 2 מרובעים פחות שלשה שרשי' ומי לא ידע שאלו השני שרשים הם מתחלפים שאם השרש שוה 2 יהיה השרש הראשון ששה פחות שמונה והשרש השני שמנה פחות ששה וההבדל ביניהם בבין יש לאין וכאלו רבים בלי תכלית לא יכחישם כי אם גבר עברו יין ומכאן מבואר שלשני מספרים אלו 4x4-12x3*19x2 9x-12x3*4x4 שהם שווים יש להם שרשים מתחלפים והם הנזכרים והדברים מבוארים מאד ויש להם תועלת רב כאשר יבוא במה שאחר זה ואולם יש לנו דרך אחר בהוצאת השרשים בהשוואה בלתי טהורה כמעוקב מרובע מרובע ודומיהם עד אין תכלית דהיינו בחילוק הכמות בשווה עד שנבוא להשוואת המרובעים יתר שרשים ואז נעשה כמו שהורינו והוא הדרך היותר קל ונכון למוצאי ותן עיניך בדמיונות אלו כי משם תראה את אופני התרתן : (א) שני ראשים חלקו למספר ידוע מבעלי מלחמתיהם כל אחד חלק 1200 זהו' והאחד יש לו 40 איש פחות כמו האחד וכל אחד ממספר הפחות קבל 5 זהו' יותר כמו אחד ממספר המרובה השאלה כמה היו אנשים תחת יד כל אחד מהראשים וכמה קבל כל מהאנשים זהו' : תשובה נאמר מספר הפחות היה x וא"כ מספר השני היה x*4x ואם נחלק מספר הזהו' 1200 ב xמספר האנשים יהיה 1200/x וכמו כן נחלק 1200 ב x*4xיהיה מעות השני 1200/(x*4x) ולפי נדון שאלתינו במספר קבל כל אחד יותר 5 כמו אחד מן מספר המרובה וא"כ תהיה ההשוואה כזה 1200/x=1200/(x*4x)*5 כי נכפיל 5 עם x*4x להביאם תחת כינוי שווה וא"כ יהיה כזה (1200=1200*5x*200)/(x*4x) והואיל השני שברים יהיו שווים נעשה מהם שלמים בהכפלת שתי וערב כזה 1200 1400*5x (כי 1/2 3/6 מוכפלים יהיו שניהם 6) תצא ההשוואה כזה 1200xx48000=1400x*5xx נגרע משניהם 1200x יהיה כזה 48000=200x*5xx נחלק כלם עם 5 יבא כזה 9600=40x*xx ולפי כלל ראשון הכולל שזכרנו מרובע חצי כמות בלתי ידוע 400 יחובר אל מספר הפשוט 9600 יהיה 10000 נוצא ממנו שרש מרבע 100 נגרע ממנו חצי בלתי ידוע ישארו 80 וא"כ x=80 והוא מספר הפחות וא"כ מספר המרובה הוא 120=x*40 וכל אחד ממספר הפחות קבל 15 זהו' וממספר היותר קבל כל אחד 10 זהו' : (ב) שני כתות יש להם לחלוק מספר שווה בכתה ראשונה ד' אנשים כמו בשנית ולאחר שנעשה החילוק נמצא שקבל כל אחד מכתה הקטנה 8 זהו' יותר כמו אחד מכתה הגדולה ומספר הזהו' לשתי הכתות יחדיו מחזיק 172 יותר כמספר האנשים בשתי הכתות השאלה מספר כמה מספר הכתות ומספר הזהו' : תשובה נשים במקום מספר האנשים שבכתה שניה הקטנה x וא"כ הגדולה x*4 לכך 2x*176 הוא מספר הזהו' שיש לחלק בשני הכתות ולאחר החלוק קבל אחד מכתה קטנה (2x*176)/x ואחד מהגדולה קבל (21*176)/(x*4) והחלק ראשון דהיינו אחד מהקטנה קבל יותר מהשני 8 א"כ אם נשלים העדר זו דהיינו בקיבוץ אליו 8 יהיו שווים כזה (2x*176)/x=(2x*176)/(x*4)*8 אם נתיר השלם אל הכבד תהיה ההשוואה כזה (2x*176)/x=2x*146*1x*32 אם נקבצם יחד דהיינו 17632 וכן 2x יקובצו אל 8x יהיה כזה (2x*136)/x=(14x*208)/(x*4) ואם נשווה השברים דרך הכפלה שתי וערב יהיה כזה 2xx*184x*704=10xx*208x נגרע משני הפאות 2xx*184x ישאר כזה 704=8xx*24x נחלק שניהם עם 8 תצא ההשוואה כזה 88=xx*3x נגרע מהם 3x ישאר כזה 88-3x=xx ולהוצאות שרש המרובע נעשה כמו שזכרנו בכלל ב' יבוא x=8 וא"כ מספר כתה קטנה 8 והגדולה 12 מקובצם 20 ומספר הזהו' 192 אשר אם נחלקהו עם 8 יצא 24 וכ"כ זהו' קבל איש אחד מכתה קטנה ואם נחלק 192 עם 12 יצא 16 מספר הזהו' שקבל אחד מהגדולה ובזה נכון כל אופני השאלה : וביסוד ההשוואה בלתי טהור' נמשיכו התיר השאלות בחשבוני הזמן התערובות השותפות ובפרטית שאלות מריבית פשוט ומריבית מורכב דהיינו ריבית לריבית חשבוני החילופים ודומיהם מהשאלות כמו (ג) אחד קנה 400 אמות בגד אמה בעד 1 1/2 ר"ט וחזר ומכר אותן עם רווח לאחר באופן זה שיקבל 200 ר"ט לאחר 5 חדשים והנשאר יקח אחר 9 חדשים ונמצא שהרויח 50 למאה לשנה השאלה בכמה חזר ומכר אמה מהבגד וכמה הרוויח בכללו : תשובה אמור שהרויח בכלם x ואם כן ראוי שיקבל בכללו 600*x והנה קבל 200 ר"ט אחר 5 חדשים תכפילה מעות עם הזמן יחדיו כדין הנהוג בחשבוני הזמן יהיה 1000 וא"כ קבל כרחך אחר 9 חדשים הנשאר דהיינו 400*x תכפילם כמו כן יחדיו יבוא 3600*9x תקבצם (דהיינו 1000 מהכפלה ראשונה) יחד יהיה 4600*9x תחלק הקיבוץ הזה עם הקרן והרוח אשר ראוים שיקבלם דהיינו עם 600*x יהיה כדין (600*9x)/(600*x) וא"כ לחקור הריבית למאה תעמוד על כלל משלש כזה רווח ר"ט 100:x:100 ובוא כדין x ולמצוא כמה יגיע הריבית לשנה תעמוד על כלל משלש כזה חדשים רווח לשנה חדשים
- 12 x/6 (4600*9x)/(600*x)
יבוא כדין 50=1200x*2xx כדין ההשוואה וכנדון השאלה תכפלם שניהם עם 9xx*4600x תצא ההשוואה כזה 1200x*2xx=230000*450x נגרע משניהם 450x ישאר כזה 750x*2xx=230000 תרבע חצי מספר השרשים יולד 140625 תכפול מספר הפשוט עם מספר המרובעים בנ"ד עם 2 יהיה 460000 תקבץ אליו מרובע חצי מספר השרשים 140625 יהיה קיבוצם עולה כזה 600625 תוציא ממנו שרש המרובע יהיה השרש תגרע ממנו חצי מספר השרשים 375 ישאר 400 וזה השאירות תחלוק 400 עם מספר המרובעים בנ"ד תחצה אותו יהיה x=200 דהיינו הרויח שהרויח בכל הת' אמות א"כ יגיע לרוח אמה אחת 1/2 ר"ט בחון ותראה כי נכון הוא : (ד) אחד קנה 2160 אמות בגד משי כל אמה בעד 2 1/2 ר"ט וחזר ומכרם באופן זה שיקבל תכף 2160 ר"ט ולאחר ד' חדשים ישולם לו 1620 ר"ט ולאחר 8 חודשים יקבל 2430 ר"ט והנשאר לאחר שנה תמימה ונמצא שהרויח 53 1/3 למאה לשנה השאלה בכמה חזר ומכר אותו וכמה הרויח : תשובה אמור שהרויח בכללו x וא"כ ראוי לו שיקבל 5490*x בעד המכירה כלה וקבל מיד 2160 ר"ט ולאחר 4 חדשים 1620 ר"ט מכפילם ביחד יהיה 19440 וא"כ הנשאר דהיינו x-810 (כי העודף מהמעות שקבל על מספר 5400 ינוכה מן x) קבל במלאת שנה תמימה דהיינו אחר 12 חדשים יוכפלו כמו כן בהדדי ויהיה 12x-9720 יקובצו יהיו 12x-1620 יוחלקו עם 5400*x יהיה כמות החלק כדין ■(▁(12x=1620)@5400*x) יבוא שירויחו x/54 ואם תמצא הריבית למאה עמוד על כלל משלש כזה כמה רוח ר"ט 100 x 5400 100 לשנה עמוד החשבון ולידע כמה ירויח על כלל משלש כזה כמה ירויחו חדשים רווח חדשים 12 x 12x-1620 xx* x*5400 xx*5400*
יבוא כדין 54x*72900=53 1/3 נכפילם שניהם עם 54x*72900 תהיה השוואה כזה xx*5400x=2880x*3888000 נגרע משניהם 2880x ישאר כזה xx*2520x=3888000 תרבע חצי מספר השרשים יהיה 1587600 תקבץ אל מספר הפשוט יהי' 5475600 תוציא ממנו שרש המרובע והוא 2340 תגרע ממנו חצי מספר השרשי' 1200 ישאר x=1088 א"כ הרויח באמה אחת 3 ר"ט ולפ"ז מכר אמה אחת בעד 4 1/2 ר"ט והוא נכון : (ה) אחד לוה לחבירו 100 זהו' על ד' שנים על ריבית וריבית לריבותו ואחר ד' שנים הוסיף הלוה על הקרן 96 זהו' וזהו הנשך ונשך לריבית השאלה כמה יגיע ל100 זהו' על שני שנים : תשובה נאמר שהריבית וריבית לריבית היה x וא"כ נמצא מספר השני שנים כך נעמידהו על כלל משלש כזה
ר"ט
100:x:x יבוא כדין (xx*100x)/100 והנה להמצאות ההשוואה נחבר הריבית משניהם שהוא x שלם או בחלקיו 100x/100 עם (xx*100x)/100 יעלה (xx*200x)/100 והוא שווה למספר 96 כזה (xx*200x)/100=96 נכפיל שניהם עם 100יהיה xx*200x=9600 נחבר אל מספר הפשוט מרובע חצי כמות נשארת (שהוא 200 וחציו 100 ומרובעו 10000) יהיה 19600 וממנו נוצא צלע המרובע יצא 140 נגרע ממנו חצי כמות הנשארת (שהיא 200 וחציו 100) ישאר 40 והוא הריבית וריבית לריבית משני שנים : (ו) אחד לוה לחבירו 100 זהו' על שתי שנים ליתן לו ריבית וריבית לריבותו ולאחר כלות השנים החזיר הלוה למלוה 144 זהו' השאלה כמה הגיע הריבית לשנה אחת : תשובה ריבית שנה ראשונה x שלם או בחלקיו לפי הקרן 100x/100 ריבית שנה היה א"כ כזה (לפי הכלל משלש) xx*100x/100 נחברם יחדיו יהיה 44=(xx*200x)/100 נתקנם בהכפלת שניהם עם 100 יולד כך xx*200x=4400 נחבר למספר הפשוט מרובע חצי כמות הנשארת (שהוא 200 וחציו 500 ומרובעו 10000) יעלה 144000 נוציא ממנו חצי כמות נשארת (שהוא 200 וחציו 100) ישאר 20 וא"כ x=20 והוא ריבית שנה ראשונה : (ו) שלשה יש להם שותפות והניח שמעון יותר מראובן 200 ר"ט ושמעון ולוי יחדיו הניחו 1400 ר"ט ובמלאת שנה תמימה רצו לחלוק ונמצא שהרויחו 120 ר"ט יותר מ1/3 המעות שהניחו יחדיו וראוי לראובן מהרוח 160 ר"ט השאלה כמה הניח כל אחד מהם ביחוד וכמה הרויחו : תשובה נאמר שראובן הניח x ושמעון ולוי יחדיו הניחו 1400 א"כ מעות כלם הוא x*1400 קח ממנו 120*1/3 הרווח יהיה x*586 2/3 הרווח הכולל וא"כ לדעת רווח אשר ראוי ממנו לראובן עמוד על כלל משלש כזה כמה ירויח ירוויחו ר"ט x x/3*586 2/3 x*1400 יבוא שראוי לו (xx/3*586 2x/3)/(x*1400) וזה שווה ל160 רווח הראוי לראובן כנדון השאלה תתקנם כדין בהכפלה יצא כזה xx/3*586 2x/3=160x*224000 תגרה משניהם 160x ישאר כזה xx/3*426 2x/3=224000 תכפול כלם עם 3 יולד כזה xx*1280x=762000 תתקנם כדין ההשוואה בלתי טהורה שהורינוך יצא x=400 וא"כ x*200=600 וא"כ הניח לוי 800 ר"ט : (ח) יש לאחד מעות ונשאל לאמר הכמות והשיב אם נקבץ למספר המעות שיש לו מרובע מרובעו פחות ששה עשרה מעוקבים יותר ארבעים וארבעה מרובעים יותר קנ"ט שרשים יותר 100 יולד מספר מרובע אשר צלעו האחת יורה מספר מעות שאלה כמה היה לו אמור המעות שהיה לו היה x תקבץ אליו x4-16x3*44x2*159x*100 יהיה כזה x4-16x3*44x2*160x*100 נוציא ממנו שורש המרובע בסדר זה שרש המרובע ├ ■(-20 @x4-16x3*44x2*160x*100@x2*2xx-8x-16x-10@*2x )} x2-8x-10 ובהחליף המספרים כזה x2-8x-10=x x2=9x*10 תתקן כדין השוואה בלתי טהורה כזה xx=9x*10 ■(9x(2)@▁(9x(2) )@81(4)@▁(40(4) )@12x(4) )
11(2) ■(4 1/2@▁(5 1/2)@x=10) (ט) יש לאחד שני מיני בשמים ואם ימכור מן הראשון כל ליטרא בעד כל כך ר"ט כמשקל הליטראות השני אז יעלה סך הר"ט כמספר שווה לקיבוץ משקל שניהם ואם ימכור כל אחד ביחוד בעד כל כך ר"ט בליטרא כמשקל כל המין ונקבץ שניהם יחדיו יעלה ר"ט 17 7/4 השאלה כמה משקל כל אחד ביחוד : תשובה אמור שמין הראשון היה x*y וא"כ היה מין השני x-y ולדעת בכמה ימכר מין הראשון עמוד על כלל משלש כזה בכמה ימכר בעד ליטרא x*y x*y 1 יבוא כדין שימכר בעד xx-yy
■(▁(x*y)@*xy-yy@▁(xx-xy )@xx-yy) וזה שווה למשקל שניהם דהיינו 2x וא"כ ההשוואה xx-yy=2x ולפי נדון שני יהיה כך נרבע כל אחד ביחוד כזה ■(■(x*y@▁(x*y)@*xy*yy@▁(xx*xy )@xx*2xy*yy)&■(x-y@▁(x-y)@-xy*yy@▁(xx-xy )@xx-2xy*yy))
xx-2xy*yy
נקבצם יהיה כזה ר"ט 2xx*2yy=17 7/9 נחצה כלם יהיה xx*yy=8 8/9 ולעיל מצאנו כי 2xx-2x=yy א"כ תחבר במקום yy בהשוואה שניה 2xx-2x יהיה 2xx-2x=8 8/9 או בתמורה כזה 2xx=2x*8 8/9 תכפיל כלם עם 9 יצא כזה 18xx=18x*80 (וזה נוכל להקטין בקלות עם נחצה אותו רק אז יהיה בתשבורת ויכבוד ביותר על המחשב) תתקן כדין השוואה בלתי טהורה יבוא x=2 2/3 והנה נשאר לחקור אחר כמות y וזה תעשה כמו שנבאר הנה כבר ידענו שxx-2x=yy וכפי מה שקדם הוא מבואר ש2 2/3=x א"כ מרובעו דהיינו 64/9 |7 1/9=xx┤ ולפי זה 5 1/3=x תגרע זה ממרובע ישאר 1 7/9 תוצא משניהם שרש המרובע דהיינו מ16/9 יצא 4/3 או y=1 1/3 וא"כ x*y=4 מין הראשון x*y=1 1/3
דמיונות מוערכות והעבריות בהשוואה בלתי טהורה
(א) יש לי שבעה מספרים בהעברה מספרית וקצווה אחרונה הגדולה היא 33 ואם יוכפלו שני מספרים קטני' קטנים זה בזה אז יתן 1/3 ההולדה יותר 28 קיבוץ ההערכות כלן השאלה כמה המרחק
תשובה הואיל קצווה אחרונה ידועה והיא בעליה א"כ המספרים הם כזה
מספר 7 ההערכות
קצווה אחרונה
■(33@33-x@33-2x@33-3x@33-4x@33-5x@33-6x)
ולפי זה יוכפלו שני הקטנים כזה
■(▁(■(33-5x@33-6x))@-198x*30xx @99-165x @▁(99 )@▁(1089 )@1089-363x*30xx )
ולדע קבוץ ההערכות כלן תעשה כפי מה שזכרנו ביחסו י"ב מיחוסי ההעברה מספרית כזה
קצווה גדולה 33
קצווה קטנה ▁(33-6x)
תקבץ 66-6x
החצי 33-3x והוא אמצעי מוערך כמספר המקומות תכפול 7 ואז הנולד 231-21x הוא בשווה לקיבוץ כלן והוא שווה 1/3 מהכפלת שני קטנים 28* א"כ נעשה כזה ■(1089-363x*30xx@333 333 3 @363-121x*10xx@*28 ) הנולד מהכפלת הקטנים יוחלק עם 3 השליש מהכפלת הקטנים יקובץ אליו כנדון השאלה יהיה 391-121x*10xx והוא שווה לקיבוץ כלן אם כן השיווי כזה 231-21x=391-121x*10xx לשניהם יחובר 21x יהיה כזה 231=391-100x*10xx או בחילוף הכמותים כזה 10xx*391=231*100x -231 -231 10xx*160=100x xx*16=10x ■(5@5@25@▁(-16)@9) תוציא ממנו שרש המרובע ■(5@3@2=x) המרחק והוא כמות הקטן השרש כפי כלל שלישי הכולל בהשוואה בלתי טהורה כי הגדול בקיבוץ אינו נכון בהתיר שאלתינו זה והבן (ב) תן לי שלשה מספרים בערך משלש באופן זה אם השני קצוות יוכפלו זה עם זה ולהנולד יקובץ כפל האמצעי אז יעלה קיבוצם 168 2) Find me three numbers in a triple ratio, such if the two extremes are multiplied by each other and double the mean is added to the product, the resulting sum is 168. תשובה נאמר שהמספר הקטן היה x ואם כן השלשה מספרים הם ■(x@3x@9x) תכפיל השני קצוות יהיו כזה ■(x@▁9x@9xx) כפל האמצעי תקבץ כזה ▁6x יעלה כזה כנדון השאלה תקטין כלם עם 3 יהיה ■(1 @168=9xx*6x@33 3 3 ) ■(56@*2x) 56=3xx*2x תתקן כדין השוואה בלתי טהורה כאשר לפניך 3 1 תכפיל 168 1 תקבץ 1 1 תוציא שרש המרובע ├ ■(169@ 29)┤| ■(13@ 1) שרש המרובע מספר השרשים ישאר 12 תחלוק במספר המרובעים ■(x=3/4@3x=12@9x=36) (ג) תן לי ארבעה מספרים בהעברה מדידית במרחק ארבעה ביחוס זה שאם נכפול השני קצוות ומהנולד יוגרע קיבוץ השני אמצעיים שישאר 1500 תשובה אמור שקצווה ראשונה היא x והואיל והיא בעליה יהיו המספרים כזה ■(x@4x@16x@64x) קיבוץ שני אמצעים ■(4x@▁16x@20x) השני קצוות יוכפלו יולד כזה ■(x@▁64x@64xx) וממנו יוגרע ■(▁(-20x)@1500=64xx-20x) כנדון השאלה נקטינם עם 4 : ■(3 2 2 @1500=64xx-20x@444 44 4) תתקן כדין השוואה בלתי טהורה כאשר לפניך חצי מספר השרשים ■(55(2)@▁(5(2) )@25(1) ) 375=16xx-5x ■(▁16@6000@▁4@24000@25) שרש המרובע 24025(4){■(155(2)@*▁(5(2) )@160(2)@192)┤ ■(x=5@4x=20@16x=80@64x=320) (ה) תן לי מספר אשר אם יוגרע שרשו ממרובעו שיותר שרשו או שיותרו שנים : תשובה המספר הוא x וא"כ מרובעו xx נגרע ממנו שרשו x יהיה xx-x והוא שווה לשנים ובהעתק המספרים יהיה השיווי כזה 2*x=xx ונקח כדין השוואה בלתי טהורה חצי השרש שהוא 1/2 ונרבעהו יהיה 1/4 ועם מספר 2 כשיקובץ אליו יהיה 2 1/4 דהיינו 9/4 נוציא ממנו שרש המרובע יהיה 3/4 שהוא 1 1/2 ועם חציו של מספר השרש יהיה 2 שלמים ומרובעו 4 ואם תגרע השרש ממרובעו יותר השרש ומכאן פסקו הקדמונים שאי אפשר שתגיע סגולה זו למספר אחר זולת השנים אבל ממה שכתבנו ממספרים פחותים מאין יתבאר שתגיע סגולה זו למספרים אחרי' כמו 4-5 או 3-4 ודומיהם כמבואר : (ו) נשאלנו למצוא מספר כשיוגרע מכפלו כפל מרובעו שישאר המספר בעצמו והדבר הוא מפליא לשומעו : תשובה נקל הוא לבאר זה על פי הכללים שהורינוך בהשוואה אשר איננה טהורה רק שתבחין כל אופני ומסבבו השאלה כאשר כתבנו והזהרנוך בהרבה בהמקומו' לכך בנדון זה אשר לפנינו כשהמרובע פחות משרשו תחשיב שהמספר הוא בשברים (כי בשברים כלם השרש מרוב' ממרובעו כי כן יולד הואיל ובאחד השרש שווה למרובעו כמבואר למשכיל בתשבורת) וא"כ כשתעשה זה בשברים תמצא שהוא 1/2 וא"כ כפלו אחד שלם ומרובעו 1/4 וכפל מרובעו 1/2 אשר אם יוגרע מכפלו ישאר המספר בעצמו דהיינו 1/2 : (ז) הודעני חכם חרשים וחשב מי הוא המספר פחות מאחד שאם תוסיף אותו על מעוקבו שלשה פעמים יהיה שווה אחד ורצוני לדעת זה לא על דרך קרוב אלא האמת המצומצם על דרך המספרים בעלי שמות הרבה : תשובה נניח המספר שהוא x ומעוקבו הוא לפי זה x3 ומשלשו *3x ויהיה א"כ שיוויון בין x3*3x ובין 1 מספר פשוט ונאמר שהשרש הוא שרש כולל של שרש מעוקב *1 1/4 פחות 1/2 שרש כולל של שרש מעוקב 1 1/2 פחות 1/2 רצונינו לומר שתוציא שרש מרובע של מספר 1 1/4 ותוסיף עליו 1/2 ומהקבוץ תוציא השרש מעוקב שאם תגרע מזה השרש הכולל של מעוקב 1 1/4 פחות 1/2 ר"ל שתוציא קודם שרש מרובע ממספר 1 1/4 וממנו תגרע 1/2 ומשאריתו תוציא השרש המעוקב וזה השרש תגרע משרש המעוקב הנזכר המותר יהיה שרש המבוקש תבחן ותראה האמת ונביא משל אחד במספרים מדברים ליתר ביאור ואמיתות הענין יהיה אם כן דרך משל כזה x3*9x שווה למספר 26 והנה נקח חצי 26 והוא 13 ומרובעו 169 ונוסיף עליו חק תמידי מעוקב שלשה שהוא שליש מספר השרשים ר"ל 27 ויהיה 196 ושיוויון השרש יהיה לפי זה שרש כולל מעוקב של שרש 196 יותר 13 פחות שרש כולל מעוקב של שרש 196 פחות 13 ר"ל שתוציא שרש מרובע של מספר 196 שהוא 14 ותוסיף עליו 13 ויהיה 27 ותוציא ממנו שרש המעוקב והוא 3 וכן מהמותר שהוא פחות שרש כולל מעוקב של שרש 196 פחות 13 תוציא שרש המרובע והוא 14 וממנו תגרע 13 וישאר 1 ושרשו המעוקב הוא כמו כן אחד ואם תגרע שרש זה משרש המעוקב הנ"ל שהוא 3 ישאר 2 והוא שוויון השרש המבוקש הנך רואה אם כן שמעוקב אחד יותר תשעה שרשים דהיינו x3*9x כאלו תאמר 26=8*18 ואנכי אבאר לך סדר פעולה זאת במופת אי"ה כי לא ידע אנוש ערכה עד היום : (ח) נשאלנו למצוא בקרוב מספר פחות מאחד שכשיוקח מעוקבו מכפלו שלשה פעמים שישאר אחד : תשובה לפי מה שביארנו למעלה בתיקון ההשוואה בלתי טהורה כשהשיווי בין מעוקבים יתר שרשים ובין מספרים שזה כבד מפני שהערך אינו מתמיד כי חסר המרובע נקל הוא לבאר וסובלת תשובות רבות ואולם מה ששאל השואל שנודיע לו בקירוב השרש כשהשיווי בין x3 ובין 3x-1 הנה כפי הנחתו שרצה שיהיה המספר פחות מהאחדות מצאנו שהוא 347/1000 והוא פחות ובין 348/1000 והוא יותר ותבחנם ותמצאם כמה הם קרובים אל האמת ובהספרים הפחותים מאין יהיה השרש בין 1 879/1000 פחות ובין 879/1000 פחות ואולם אם השרשנו ליקח השרש אפילו שלם יש עוד שרש השייך לשאלה והוא בין 15/10 ובין 16/10 או בדקדוק יותר בין 1 53/100 ובין 1 54/00 או בין 532/1000 ובין 1 533/1000 מדמיונות בהשוואה בלתי טהורה מעוקבות מרובע מרובעות מרובע מעוקבות ודומיהם עד בלי תכלית (ט) תן לי מספר אם נכפיל אותו 27 פעמים ומהנולד נגרע מעוקבו שישאר 54 : תשובה אמור שהמספר הוא x תכפיל אותו 27 פעמים יולד 27x תגרע ממנו מעוקבו שהוא x3 ישאר 272-x3 או x3-27x והוא שווה למספר 54 כזה x3-27x=54 תקבץ לשניהם 27*x27 כזה 27x*27 27x*17 יעלה כזה x3x27=27x*81 תחלק שניהם עם x*3 כזה ├ ■(x3*27=27x*81@x*2 x*3)┤|x2*9=3x+27 או בהעתק המספרים כזה x2-3x*9=27 תגרע משניהם 9 יצא השיווי כזה x2-3x=18 תחבר לשניהם 6x יצא כזה x2+3x=18*6x תחלקם עם x*3 כזה ├ ■(x2*3x=18*6x@x*3 3*x)┤|x=3 השרש המבוקש : (י) תן לי מספר אשר אם נקבץ אותו 12 פעמים ומזה יוגרע מעוקבו שישאר 16 : 10) Find me a number, such that if we sum it 12 times, then its cube is subtracted from it, 16 remains. תשובה אמור שהמספר הוא x וא"כ 12 פעמים הוא 12x יוגרע ממנו x3 מעוקבו ישאר 12x-x3 Answer: say that the number is x. So, 12 times is 12x. Its cube, x^3, is subtracted from it; 12x-x^3 remains או כזה בהעתק המספרים יוגרע משניהם חצי מספר הפשוט כזה Or, by shifting the numbers: Half the simple number is subtracted from both [sides], like this: x3=12x-16 ▁(-8 -8) x3-8=12x-24 x^3=12x-16 ▁(-8 -8) x^3-8=12x-24 וזה יוחלק עם x-2 כזה This is divided by x-2, like this: ├ ■(*2 4@x3-0x2-0x-8@x 2 2 2@x - x)┤|xx*2x*4 ├ ■(+2 4@x^3-0x^2-0x-8@x 2 2 2@x - x)┤| x^2+2x+4 וזה חילק צלע אחת ההשוואה This is the quotient of one side of the equation. וא"כ כמו כן יוחלק הצד השנית כדין שכמות שוות כזה So, the other side is divided also according to the rule, since they are equal: ├ ■(13x-24@ x-12)┤|12 ├ ■(12x-24@ x-12)┤|12 וא"כ ההשוואה כזה x2*2x*4=12
■(▁(-4)@8) So, the equation is:
x^2+2x+4=12
■(▁(-4)@8)
יוגרע משניהם 4 יצא השוואה שנית כזה x2*2x=8 4 is subtracted from both; the result is the second equation: x^2+2x=8 2x יקובץ לשניהם x2*4x=8*2x 2x is added to both: x^2+4x=8+2x זה יוחלק עם x*4 כזה This is divided by x+4 like this: ├ ■(x2*4x=8*2x@ x*4=4*x)┤|2=2 ├ ■(x^2+4x=8+2x@ x+4=4+x)┤|2=2 תתקן כדין ההשוואה בלתי טהור' x2*2x=8 Restore according to the rule of the compound equation: x^2+2x=8 מרובע חצי השרשים ■(1*1@1 ) The square of half [the number of] the roots ■(1*1@1 ) מרובע 9 The square 9 שרש 3 Its root 3 יוגרע חצי מספר השרשים המספר המבוקש ■(▁(-1)@ 2) Half the number of the roots The required number ■(▁(-1)@ 2) ומזה תבין למה שנכנה להשוואה בלתי טהורה מרובעת השוואה בלתי טהורה פשוטית ולמעוקבת מרובע מרובעת ודומיהן עד בלי תכלית השוואה בלתי טהורה מורכבת כי כולן ניתכו ויתוקנו במרובעת כמבואר למשכיל : From this you understand why we call the quadratic equation a simple equation and the cube, the square-square and so on are [called] a compound equation, because they are all dissolve and reduced into a quadratic [equation] as is clear to the scholar. (יב) שמעון ולוי אחים הנה לוה שמעון ללוי מספר זהו' ולוי רצה לגמול החסד שעשה אתו אחיו פרע לו מספר זהו' יותר ממספר הזהו' שקבל מאחיו באופן זה שאם נקבץ מספר שניהם יהיו 70 ואם מרחקם יעוקב ומספר שניהם יקובץ להמעוקב ואז ילקח 1/7 מרחק המרובעים ויעוקב ויוגרע ממנו מספר שניהם והנשאר יוכפל עם הולדת קיבוץ מעוקב המרחק עם מספר שניהם הנזכרים יבוא מספר זה 1069925100 השאלה כמה מספר הזהו' שלוה שמעון ללוי וכמה זהו' חזר ופרע לו לוי 12) Shimon and Levi are brothers. Shimon lent Levi some zehuvim, and Levi wanted to repay the kindness his brother, so he paid him more zehuvim than the zehuvim he received from his brother, such that if we sum the numbers of both, they are 70; if their difference is cubed, and the numbers of both are added to the cube, then 1/7 of the difference of their squares is cubed, the numbers of both are subtracted from it, and the remainder is multiplied by the sum of the cube of the difference with the numbers of both mentioned, the result is this number 1069925100. The question is how much is the number of zehuvim that Shimon lent Levi and how many zehuvim did Levi repay him? תשובה אמור שמספר הזהו' שלוה שמעון היה 35-x Answer: say that the number of zehuvim that Shimon lent is 35-x. (הואיל שניהם מקובצים יהיו 70 ומספריהם בלתי שווים שיוחצו) Since the sum of both is 70 and their numbers are not equal halves. וא"כ מעות שפרע לוי היה 35*x So, the amount of money that Levi paid is 35+x יוקח כמו כן 1/7 מרחק המרובעים כזה 1/7 of the difference between the squares is taken, like this: יעוקב המרחק ■(2x@▁2x@■(4xx@▁2x@8x3)) The difference is cubed: ■(2x@▁2x@■(4x^2@▁2x@8x^3 )) לו יקובץ 70 מספר שניהם 8x3*70 The sum of both, 70, is added to it: 8x^3+70 ירובע מספר כל אחד ביחוד כזה Each number is squared by itself, like this ■(35-x@35-x) ■( -35x*xx@175-35x @105 ) 270-70x*xx ■(35-x@35-x) ■( -35x+x^2@175-35x @105 ) 270-70x+x^2
וזה מרובע המעות שלוה שמעון This is the square of the money Shimon lent. נרבע כמו כן המספר שפרע לוי כזה We also square the amount Levi paid, like this: ■(35*x@35*x) ■( *35x*xx@175*35x @105 ) 270*70x*xx ■(35+x@35+x) ■( +35x+x^2@175+35x @105 ) 270+70x+x^2
מרובע לוי The square of Levi’s [amount] יוגרעו שני המרובעים מהדדי והשאירות יורה המרחק כזה The two squares are subtracted from one another; and the remainder indicates the difference, like this: ■(270*70x*xx@▁(270-70x*xx)@140x) ■(270+70x+xx@▁(270-70x+xx)@140x) ולפי זה המרחק בין שניהם הוא 140x According to this the difference between them is 140x. קח מהמרחק הזה 1/7 והוא 20x וזה יעוקב יבוא 8000x3 קח ממנו מספר השאול והפרוע דהיינו 70 ישאר 8000x3-70 Take 1/7 of this difference; it is 20x. It is cubed; the result is 8000x^3. Take the loaned and the paid from it, i.e. 70; the remainder is 8000x^3-70. ואז יוכפל זה השאירות עם הקיבוץ הנזכר למעלה דהיינו עם 8x3*70 יבוא כזה 64000x6*559440x3-4900 This remainder is multiplied by the above-mentioned sum, i.e. by 8x^3+70; the result is: 64000x^6+559440x^3-4900 וזה שווה למספר 1069925100 כנדון השאלה כזה 64000x6*559440x3-4900=1069925100 This is equal to the number 1069925100 as stated in the question, like this: 64000x^6+559440x^3-4900=1069925100 תקבץ לשניהם 4901 יהיה השיווי כזה 64000x6*559440x3=1069930000 Add 4900 to both [sides]; the equation is as follows: 64000x^6+559440x^3=1069930000 תגרע משני צדדי השיווי סיפרי אחת ישאר כזה ■(2 1322 22132 @64000x6*559440x3=1069930000@44 4444 444444 ) Subtract one zero from both sides of the equation; the remainder is like this: ■(2 1322 22132 @64000x^6+559440x^3=1069930000@44 4444 444444 ) תחלק כלם עם 4 יצא כזה 1600x6*13986x3=26748250 Divide all by 4; the result is: 1600x^6+13986x^3=26748250 (ואף שנוכל להקטין עוד ביות' לא נחוש לזה והכל ברצון החושב) Although we can reduce more, we are in no rush to do so; it is all up to the will of the one who calculates. קח חצי מספר המעוקבים 6993 ותרבעהו יהיה המרובע כזה 48902049 קח מספר המעוקבים מרובעים שהם 1600 ותכפול אותו עם המספר הפשוט דהיינו עם 26748250 יולד 16048950000 Take half the number of the cubes; it is 6993. Square it; the square is 48902049. Take the number of the squared cubes, which is 1600. Multiply it by the simple number, i.e. by 26748250; the result is 42797200000. תקבץ אליו מרובע חצי מספר המעוקבי' הנ"ל דהיינו 48902049 יהיה 42846102049 Add to it the square of half the number of the cubes mentioned, i.e. 48902049; it is 42846102049. תוציא ממנו שרש המרובע יבוא 206993 תגרע משרש המרובע חצי מספר המעוקבים דהיינו 6993 ישאר 200000 וזה תחלוק במספר המעוקבים מרובעים דהיינו עם 1600 יבוא 125 וממנו תוציא שרש המעוקב יבוא 5 Extract its square root; the result is 206993. Subtract half the number of the cubes, i.e. 6993, from this square root; 200000 remains. Divide it by the number of the squared cubes, i.e. by 1600; the result is 125. Extract its cube root; the result is 5. וא"כ x=5 So, x=5. ולפי זה 35*x=40 והוא המעות שפרע לוי According to this, 35+x=40, which is the money the Levi paid. וא"כ 35-x=30 מעות שלוה שמעון Therefore, 35-x=30 is the money that Shimon lent. אמר המחבר אף שלפי הדרך אשר דרכנו בהתר השאלות הקודמות יותר ספק זה כמו כן רצינו להציג לפניך התר השאלה כפי דרך חדש מצוא מאתנו לשתי סיבות The author said: although according to the way we use to solve the previous questions, this doubt is resolved, we also want to present to you the solution of the question according to a new way we found for two reasons: הסיבה הראשונה היא כדי שתהינ' לך דרכי ההתר צבורות The first reason: so that you have a collection of solution methods. והיה אם לא השיג יד שכלך להתיר עם דרכים הקודמים Even if your mind could not solve it with the previous ways. ובפרט עם החלוק אשר סבוך בקרניו [בראשית כ"ב, יג] וצריך עיון רב Especially regarding the division that is “caught in the thicket by its horns” [Genesis 22, 13] and requires much investigation. ובסופו לא ימלט אף על פי כן מתיקון ההשוואה בלתי טהורה Eventually, there is no escape but to restore the compound equation. לכך תשתה ממקור ולא תצרך למים שאובים For this you will drink from the water source and will not need drawn water. ולא נהיה למס מרעהו חסד [איוב ו, יד] We will not be “to him that is ready to faint kindness is due from his friend” [Job 6, 14] הסיבה השנית להגדיל חסד בוראינו The second reason is to magnify the grace of our Creator, שכמה מעלות טובות למקום עלינו [הגדה של פסח, מגיד, דיינו א] for “How many virtues of goodness did the Place [bestow] upon us!” [Pesach Haggadah, Magid, Dayenu 1], כי לא אסף גם מאתנו חסדו בדור האחרון הזה Because He did not withdraw his grace from us in this last generation, ולהורות כי הקדמונים כאשר לאו למצוא הפתח [בראשית י"ט, י"א] הזה And to indicate that the ancients, when “they wearied themselves to find the door” [Genesis 19,11], והנה הוא סגור אין יוצא ואין בא [יהושע ו, א] And behold it is closed “none went out, and none came in” [Joshua 6, 1] והוכו בסנורים [בראשית י"ט, י"א] “They were struck with blinding light” [Genesis 19,11] וילכו בחשך ולא ראו אור [יהושע ט, א] “They walked in darkness” and did not “see a light” [Joshua 9, 1] חשבו אותו להעדר בלי קנין עלמות They thought it is absent not perpetual acquisition וגם החכם השלם הכולל כמהר"ר יש"ר מקנדיאה הודה זה ולא בוש [זבחים קא א, יב] על פי תלמידו נאמן ביתו הכולל כמהר"ר משה ממיץ אשר עמו דבר במראה ולא בחידות [במדבר יב, ח] וז"ל Also, the complete sage our honorable teacher and Rabbi Yashar Mi-Qandia “admitted” this “and was not embarrassed” [Zevachim 101a:12] according to his disciple the faithful of his house our honorable teacher and Rabbi Moshe Mi-Mitz who spoke with him “in sight, not in riddles” [Numbers12, 8] אבל לפעמים נבוא אל שיווים שלא נודע אופן הוצאות השרש But, sometimes we get an equation, for which the way to extract the root is unknown. כאשר הוא בדרך הנהוג כמשל השלישי שתבוא אל שיווי בין ג 1 ובין א 6 פ ם 57 1/27 As it is in the procedure of the third example, when you get the equation: 57 1/27+6x=x^3 והקדמונים חתרו למצוא אופן הוצאת השרש כאשר עשו כשהשיווי בין מרובע ובין שרשים עם מספרים ולא יכולו וכלו הזמן היקר עכ"ל The ancients strived to find a way to extract the root, as they did when the equation is between the square and the roots with numbers, but they could not, and they wasted valuable time; end of quote. ולמעלה ממנו כתב וז"ל וצריך למצוא זה בחיפוש כאשר אתה מנסה בחלוק לדעת כמה פעמים החולק יכנוס בנחלק כי אין דרך אחר לאלו הדברים היקרים עכ"ד Before it, he wrote: it should be found by investigation, when you try to find out by division how many times the divisor is contained in the dividend, because there is no other way for these precious things; end of quote. ומהדמיון שקדם ביאורינו לו והדמיון הסמוך תראה כי לא דברו נכונה However, from the example we explained earlier and the last example, you can see that his statement is not true. |- |
- 13) One asked his friend to help him in a time of need and wrote him a letter of begging.
- He sent him as many zehuvim as the letters in the letter.
- If the number of zehuvim is divided into two equal parts, then a hundred is subtracted from one part and a hundred is added to the other part, the added and subtracted are multiplied by each other, the result is squared and the square is divided by 9000, the resulting part is equal to the number resulting when the aforementioned added and subtracted are squared each individually and the squares are summed.
- The question is: how many zehuvim did he send him?
|style="text-align:right;"|(יג) אחד בקש מאוהבו לעוזרו בשעת דוחקו וכתב לו אגרת תחנונים
והוא שלח לו כל כך זהו' כפי אותיות שבתוך האגרת
ואם יחולקו מספר הזהו' בשני חלקי' שווים ויוגרע מחלק האחד מאה ולחלק השני יקובץ מאה ויוכפלו המקובץ והמוגרע בהדדי והנולד ירובע והנולד יוחלק עם 9000 שהחלק היוצא הוא בשווה למספר שאם ירובע המקובץ והמוגרע הנ"ל כל אחד ביחוד והמרובעים יקובצו
השאלה כמה זהו' שלח לו
|-
|
- Answer: say that the number of zehuvim is 2x
|style="text-align:right;"|תשובה אמור שמספר הזהו' היה 2x |- |
- So, each part is x.
|style="text-align:right;"|ואם כן כל אחד מהחלקים היה x |- |
- Subtract 100 from one of them; the result is: x-100
|style="text-align:right;"|תגרע מאחד 100 יבוא x-100 |- |
- Add 100 to the other; the result is: x+100
|style="text-align:right;"|ולהשני תקבץ 100 יבוא x*100 |- |
- Multiply them by each other; the result is:
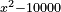
|style="text-align:right;"|תכפילם זה בזה יבוא xx-10000 |- |
- Square it; the result is:
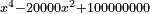
|style="text-align:right;"|תרבע זה יבוא x4-20000x2*100000000
|-
|Divide it by 9000; the quotient is as this:  |style="text-align:right;"|תחלקם עם 9000 יצא כמות החלק כזה
|style="text-align:right;"|תחלקם עם 9000 יצא כמות החלק כזה 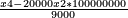 |-
|Then, take the parts and square each by itself, like this:
|style="text-align:right;"|ואח"כ קח כמו כן החלקים ותרבע כל אחד ביחוד כזה
■(x*100@x*100) ■(x-100@x-100)
■( *100x*10000@xx*100x ) ■( -100x*10000@xx-100x )
xx*200xx10000 ■(xx-200x*10000@xx*200x*10000)
■(x+100@x+100) ■(x-100@x-100)
■( +100x+10000@x^2+100x ) ■( -100x+10000@x^2-100x )
x^2+200x+10000 ■(x^2-200x+10000@x^2+200x+10000)
|-
|Then, take the parts and square each by itself, like this:
|style="text-align:right;"|ואח"כ קח כמו כן החלקים ותרבע כל אחד ביחוד כזה
■(x*100@x*100) ■(x-100@x-100)
■( *100x*10000@xx*100x ) ■( -100x*10000@xx-100x )
xx*200xx10000 ■(xx-200x*10000@xx*200x*10000)
■(x+100@x+100) ■(x-100@x-100)
■( +100x+10000@x^2+100x ) ■( -100x+10000@x^2-100x )
x^2+200x+10000 ■(x^2-200x+10000@x^2+200x+10000)
תקבצם יעלו כזה 2xx*20000 Sum them; the result is 2x^2+20000 וא"כ ההשוואה כזה (x4_20000x2*100000000)/9000=2xx*20000 So, the equation is: (x^4-20000x^2+100000000)/9000=2x^2+20000 תכפיל שניהם עם 9000 Multiply both by 9000 יצא כזה השיווי The resulting equation is: x4_20000x2*100000000=18000x2*100000000 x^4-20000x^2+100000000=18000x^2+180000000 נקבץ לשניהם 20000x2 We add 20000x^2 to both [sides]. יצא השיווי כזה The resulting equation is: x4*100000000=38000x2*180000000 x^4+100000000=38000x^2+180000000 נגרע משניהם 100000000 We subtract 100000000 from both [sides]. ישאר כזה The remainder is like this: x4=38000x2*80000000 x^4=38000x^2+80000000 נקח חצי מספר המרובעים דהיינו 19000 We take half the number of the squares, i.e. 19000 ונרבעהו יבוא 361000000 We square it; the result is 361000000 נקבץ אליו מספר הפשוט 80000000 We add the simple number 80000000 to it יעלה קיבוצם כזה 441000000 Their resulting sum is 441000000 נוציא מהקבוץ שרש המרובע יבוא 12000 We extract the square root of the sum; the result is 21000 נקבץ אליו מספר 19000 חצי מספר המרובעים We add 19000 to it, which is half the number of the squares. יהיה 40000 It is 40000. נוציא ממנו שרש המרובע יצא 200 We extract its square root; the result is 200. וא"כ x=200 So, x=200. ולפי זה 2x=400 המספר המבוקש : According to this, 2x=400 is the required number.
The question is for how much did he buy one of them and how much did he give for both of them together? |
(יד) אחד קנה שני עופות ונשאל כמה נתן בעד אחד מהם והשיב האחד יקר הערך יותר מהשני מספר זהו' באופן זה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
תשובה אמור שהראשון קנה בעד x*a | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
א"כ קנה השני בעד x-a | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
אשר אם יוגרעו הקניה מהקניה השאירות יורה המרחק | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| When you subtract it, you find that the remainder is 2a and this is the difference, like this: | א"כ כשתגרעם תמצא המותר 2a והוא המרחק נקבצם כמו כן כזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| We square each by itself, like this: | נרבע כל אחד ביחוד כזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
א"כ ההשוואה עשויה באופן הראשון | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
באופן השני נעשה כך | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
נכפיל המספרים זה בזה יולד xx-aa כזה | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
■(x*a@x-a) ■(x+a@x-a) ■( -xa-aa@xx*xa ) ■( -xa-a^2@x^2+xa ) יקובץ אליו חצי מרחק שניהם דהיינו a יהיה כזה Half the difference between both, i.e. a, is added to it ■(xx-aa@ *a) ■(x^2-a^2@ +a) יוכפל במרובע קיבוץ שניהם כזה It is multiplied by the square of the sum of both, like this: ■(xx-aa*a@ 4xx) ■(x^2-a^2+a@ 4x^2 ) ממנו יוגרע מרובע קיבוץ שניהם ישאר כזה The square of the sum of both is subtracted from it; the remainder is: ■(4x4-4x2a2*4xxa@ -4xx) ■(4x^4-4x^2 a^2+4x^2 a@ -4x^2 ) 4x4-4x2a2*4xxa-4xx= 4x^4-4x^2 a^2+4x^2 a-4x^2= והוא שווה למספר 485276400 נכפיל שניהם כדי שיהיו שווים להשוואה ראשונה יולד כזה השיווי This is equal to the number 485276400. We double both, so they will be equal to the first equation; the result is this equation: 8x4-8x2a2*8x2a-8x2=970552800 8x^4-8x^2 a^2+8x^2 a-8x^2=970552800 8x4*8x2a2-8x2a*4x2=974213109 8x^4+8x^2 a^2-8x^2 a+4x^2=974213109 קיבוץ שני ההשוואות The sum of the two equations: 16x4-4x2=1944765900 16x^4-4x^2=1944765900 נחלק כלם עם 2 יהי' השיווי כזה We divide all by 2; the equation is: 8x4-2x2=972382950 8x^4-2x^2=972382950 או בהעתק המספרים כזה Or, by shifting, like this: 8x4=972382950*2xx 8x^4=972382950+2x^2 נרבע חצי מספר המרובעים יהיה 1 We square half the number of the squares; it is 1. נכפיל מספר הפשוט עם מספר המרובע מרובעים דהיינו עם 8 ונקבץ אליו מרובע חצי מספר המרובעים הנ"ל דהיינו 1 יהיה כזה 7779063601 We multiply the simple number by the number of the square-squares, i.e. by 8, then we add to it the square of half the number of the squares, i.e. 1; it is 7779063601. וממנו תוציא שרש המרבע שהוא 88199 Extract its square root, which is 88199. תקבץ אל השרש הזה חצי מספר המרובעים דהיינו 1 יהיה ■(▁(■( 4@88200@88888))@11025) Add half the number of the squares, i.e. 1, to this root ■(▁(■( 4@88200@88888))@11025) תחלקו עם 8 כאשר לפניך Divide it by 8, as before you: ומהחלק תוצי' שרש המרובע יהי' x=105 Extract the square root of the quotient; it is x=105 ועכשיו נשאר לנו למצוא כמות a ויהיה על דרך זה שני ההשוואות יוגרעו זה מזה כזה ■(▁(■(8x4*8x2a2-8x2a*4x2=974213100@8x4-8x2a2*8x2a-8x2=970552800))@ 16x2a2-16x2a*12x1=3660300) Now we are left to find the value of a. It is this way: The two equations are subtracted from each other, like this: ■(▁(■(8x^4+8x^2 a^2-8x^2 a+4x^2=974213100@8x^4-8x^2 a^2+8x^2 a-8x^2=970552800))@ 16x^2 a^2-16x^2 a+12x^2=3660300) השאירות The remainder תחלק כלם עם x2 והמספר הפשוט יוחלק עם המספר הפשוט השווה ל-x2 Divide all by x^2 and the simple number is divided by the simple number that is equal to x^2. וכבר מצאת x=105 וא"כ מרובעו x2=11025 You have already found that x=105. So, its square is x^2=11025. יהיה כזה: 16a2_16a*12=332 It is like this: 16a^2-16a+12=332 תגרע משניהם 12 _12 _12 Subtract 12 from both [sides]. ישאר כזה 16aa-16a=320 16a^2-16a=320 remains. תחלק כלם עם 8 יהיה השיווי כזה 2aa_2a=40 Divide all by 8; the equation is: 2a^2-2a=40 ובהעתק המספרים כזה 2aa=40*2a By shifting the numbers: 2a^2=40+2a תתקן כמו בהשוואה איננה טהורה וא"כ a=5 Restore as a compound equation, so: a=5. ולפי זה יבא המבוקש כי x*a=110 : מעות הראשון x_a=100 : מעות השני According to this the required resulting is: The cost of the first: x+a=110 The cost of the second: x-a=100
| Here ends our purpose thus. | ובזה נשלם מגמתינו בזה האופן |
| We bow down to our God. | ונקוד לאלהינו |
| We will sing him a song, | ונשורר לו שיר |
| With a consonant and two vowels, a consonant and two vowels, a consonant and two vowels,
With opening and closing [of the verse]: |
ביתד ושתי תנועות יתד ושתי תנועות יתד ושני תנועות בדלת ובסוגר |
| Who brings to light all hidden things [Ibn Ezra on Exodus 25, 1,1] | אשר הוצא לאור כל תעלומה[note 127] |
| For the people of God with a wise knowledge | לאנשי אל בידיעה מחכימה |
| And hints to him the words of all wisdom. | ורמז לו דברי כל החכמה |
| Until the end of the first part | עד כלות חלק הראשון |
| He will explain to us the words of an inscribed wisdom [Ibn Ezra on Exodus 25, 1,1] | יבינני דבר חכמה רשומה[note 128] |
| No purpose is withheld from Him [Job 42, 2] | ולא יבצר ממנו מזימה[note 129] |
| In the second part and in one word. | בחלק שני ובתיבה תמימה |
| Praise to the First and the Last. | שבח לראשון ואחרון |
| סליק |
Notes
- ↑ שיר השירים ה, ב
- ↑ אסתר א, ו
- ↑ דניאל ב, כט
- ↑ איוב ד, יג
- ↑ ישעיה יד, יב
- ↑ ירמיהו יד, ט
- ↑ תהילים יט, ו
- ↑ שופטים ה, כח
- ↑ שיר השירים ב, ט
- ↑ שיר השירים ה, ב
- ↑ שיר השירים ז, יב
- ↑ שיר השירים ב, יב
- ↑ שיר השירים ב, יא
- ↑ קהלת ב, ב
- ↑ קהלת ב, כב
- ↑ קהלת ב, כב
- ↑ קהלת ב, כג
- ↑ קהלת ב, כג
- ↑ יונה ד, ה
- ↑ בראשית יט, כג
- ↑ תהילים יט, ז
- ↑ יונה, ד, ח
- ↑ זכריה יא, ח
- ↑ במדבר כא, ה
- ↑ שיר השירים ג, א
- ↑ מלכים א יט, יא
- ↑ יחזקאל ח, ג
- ↑ דברים ד, כא
- ↑ דברים יא, יב
- ↑ דברים יא, יב
- ↑ דברים ח, ז
- ↑ תהילים מו, ה
- ↑ במדבר כד, ו
- ↑ במדבר כד, ו
- ↑ שיר השירים ד, יד
- ↑ תהילים א, ג
- ↑ דברים לג, יד
- ↑ תהילים צג, ד
- ↑ תהילים צד, טז
- ↑ יונה א, טז
- ↑ תהילים קז, כט
- ↑ שמות יג, יז
- ↑ תהילים קז, ל
- ↑ תהילים קז, כז
- ↑ ישעיהו נא, כא
- ↑ תהילים קז, כז
- ↑ איוב ט, ז
- ↑ שמות יד, כד
- ↑ שמות ו, י
- ↑ תהילים עד, יד
- ↑ איוב לג, כד
- ↑ קהלת א, יד
- ↑ ישעיה לו, ו
- ↑ משלי יא, ז
- ↑ זכריה ג, ז
- ↑ ירמיה יח, טו
- ↑ איוב כח, ז
- ↑ משלי ז, כו
- ↑ איכה ד, ה
- ↑ רות ד, טו
- ↑ אסתר ב, ג
- ↑ בראשית כד, טז
- ↑ שמואל א טו, לב
- ↑ ישעיה נג, ב
- ↑ בבא מציעא נח, ב, יב
- ↑ דניאל ח, כז
- ↑ תהילים ו, ד
- ↑ קהלת ז, ב
- ↑ בראשית כד, כא
- ↑ שמות ב, ד
- ↑ בראשית ז, כב
- ↑ משלי ז, טז
- ↑ בראשית כד, מב
- ↑ מלכים א כב, לד
- ↑ משלי כה, כה
- ↑ ירמיה לו, לב
- ↑ ירמיה מח, יא
- ↑ שיר השירים ה, יב
- ↑ במדבר יא, יב
- ↑ דברים לב, יא
- ↑ דברים כא, יג
- ↑ אסתר א, ו
- ↑ תהילים עח, כה
- ↑ משלי לא, כו
- ↑ תהילים יב, ד
- ↑ משלי ג, יז
- ↑ ירמיה יד, ח
- ↑ איכה ג, יד
- ↑ שמואל א י, כז
- ↑ בראשית ג, ח
- ↑ בראשית כז, יב
- ↑ שיר השירים ח, ז
- ↑ שיר השירים ג, ד
- ↑ בראשית לג, ג
- ↑ שמואל ב יד, יד
- ↑ תהילים מ, ג
- ↑ תהילים סו, יב
- ↑ תהילים קטז, ט
- ↑ בראשית יב, יג
- ↑ שמות ז, יז
- ↑ נדרים ס"ב, א
- ↑ איכה ד, ה
- ↑ אסתר ב, ו
- ↑ ישעיה נא, יג
- ↑ איכה ה, ח
- ↑ איכה ג, יז
- ↑ ירמיה יד, ח
- ↑ שמות ו, ג
- ↑ תהילים טז, ג
- ↑ שמות ו, ג
- ↑ סנהדרין קיא, א
- ↑ סנהדרין צז, א
- ↑ ישעיה מ, ד
- ↑ איוב ט, ו
- ↑ נחמיה ט, יט
- ↑ משלי ז, ט
- ↑ תהילים כג, ד
- ↑ שמות ג, טו
- ↑ בראשית כח, טו
- ↑ רות א, טז
- ↑ שמואל א יח, ט
- ↑ ישעיה נח, י
- ↑ תהילים מ, ח
- ↑ קהלת יב, י
- ↑ אסתר א, יא
- ↑ בראשית כד, מח
- ↑ אבן עזרא על שמות כ"ה א א
- ↑ אבן עזרא על שמות כ"ה א א
- ↑ איוב מב, ב
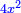

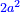


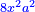

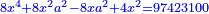
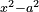 like this:
like this: